С. А. АШМАНОВ, А. В. ТИМОХОВ
ТЕОРИЯ
ОПТИМИЗАЦИИ
i В ЗАДАЧАХ
I И УПРАЖНЕНИЯХ
| КЛАССИЧЕСКИЕ РАЗДЕЛЫ
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
'• ВЫПУКЛЫЕ МНОЖЕСТВА
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ 100 1
ББК 22/18 А98
УДК 519.863(075*8)
Может быть использовано в учебном процессе по специальностям «Математика» и «Прикладная математика»	'
Ашлапов С. Л., Тимохов А. В. Теория оптимнзащш в задачах и упражнениях.— М.: Паука, Гл. род, физ,-мат. лат., 1991.-448 с. ISBN 5-02-014253’0.
tali г «х
Содержит более 90 упражнений и 780 .задач дли самостолтельг пой работы в процессе изучения классических разделов тсорйц оптимизации, линейного ирограммнройапия и теории выпуклых1 множеств. Каждое упражнение представлено 20 вариантами, с три чтобы обеспечить студентов одно» группы индивидуальными зада-пнями. Практически псе задачи снабжены ответами, укомянияип или решениями. Каждый параграф начинается со сводки осповд’ «х фактов, доказательства которых также приведены в книге. 5 то делает ее автономной от других учебных пособий.	I ,
Для студентов, аспирантов и преподавателей, споцналиэпр$ ib-; щихся ио теории оптимизации и выпуклому анализу.	: I 1
Табл. 139. Ия. 106. Бпблпогр. 47 на»в.	11
Рецензенты:
кафедра теории управления и исследования операций МФТИ;
доктор физико-математических паук Л. Л. Петров	।
Ifiayw ля бяо'ккпемЙ
HPJ ччого J
0	 4 ©оПаукао. Фиаматлпт, 1901
vi>Lj(uzj-yi
ISBN 5-02-014253-0
ОГЛАВЛЕНИЕ	в,
решения
Предисловие . ............... 5
Глевл 1. Классические разделы теории оптимизации 9
§ 1.	Сучдсстоовапие ротания. Геометрическая интерпретация задач оптимизации ......	9
Сводка основных фактов ........	9
Упражнения ...................13
Задачи ............. 19	^9
§ 2.	Задача безусловной оптимизации ..... 22 Сводка основных фа1гтов . . ...	V  •***
Упражнения ........... 25 Задачи ............. 28	249
§ 3.	Классическая задача па условный экстремум 35
Сводка основных фактов ........ 35 Упражнения..................  38
Задачи.......................  41	258
Глава 2.~ Линейное программирование ..... 51
§ 4.	Элементы теории линейных неравенств ... 51
Сводка основных фактов ........ 51
Упражнения...............................  .	57
Задачи .....................................  59	288
§ 5, Теория линейного программирования .... 80
Сводка основных фактов ........ 86 Упражнения  ...............................  98
Задачи  ...................................110	314
§ 6.~ Симплекс-метод .ронюннЯ'-задач лилейного программирования .......... 145 Сводка основных фактов..................... .	. 145
Упражнения  ................................154
Задачи.....................................161	370
1*	3
Отлеты, указания, решения
ГлаааЗ, Выпуклые множества......................169
§ 7, Начальные сведения о	выпуклых	множествах	169
Сводка основных фактов....................169
Упражнения .	..........................176
Задачи.......................................181	383
§ 8, Теоремы отделимости н	их	приложения	.	.	.	197
Сводка основных фактов	........	197
Упражнения . . ............................... 203
Задачи .	................. 210	403
Ответы, указания, решения.....................236
Список литературы ...............................441
Список обозначений............................443
Предметный указатель ............................444
ПРЕДИСЛОВИЕ
К настоящему времени теория оптимизации» если и по достигла столь совершенной и законченной формы, как классический математический анализ, то ио крайней мере приближается к такому состоянию. Теория оптимизации находит многочисленные приложения в других разделах прикладной математики, существенно используется при построении численных методов решения экстремальных задач и качественном исследовании математических моделей. Здесь достаточно упомянуть линейное программирование, ставшее мощным инструментом исследования в руках математиков-принладпнков.
Авторы считают, что настало время обучать теории оптимизации столь же основательно, как математическому анализу, линейной алгебре и другим дисциплинам, преподавание которых ведется на первых курсах математических факультетов вузов. В первую очередь это предполагает сопровождение лехщий обязательными упражнениями, позволяющими закрепить теоретический материал и привить минимальные практические навыки. Кроме того, студентам необходимо дать возможность для более глубокого изучения теории путем самостоятельного решения систематически расположенных задач. Последнее особенно актуально в настоящий момент, когда одним: из важнейших направлений совершенствования высшего образования справедливо признана активизация самостоятельной работы студентов. Для этого, одпако, необходимы учебные пособия соответствующего типа. Достаточно вспомнить известные задачники Б. П. Демидовича, И. В. Проскурякова и другие, чтобы попять, какую огромную роль играет подобная методическая литература в обучении студентов, становлении их общей математической культуры. В настоящее время трудно назвать задачник по оптимизации (как, впрочем, и по ряду других
5
разделов прикладной математики), который мог бы сравниться с упомянутыми книгами по методической разработанности, систематичности, широте охвата материала и, наконец, просто ио количеству задач.
Идея написания учебного пособия по теории конечномерной оптимизации, соответствующего современному уровню этой дисциплины н ориентированного на самостоятельную работу студентов, появилась в результате омыта преподавания соответствующего курса на факультете вычислительной математшш и кибернетики МГУ им, М. В. Ломоносова, Согласно новому учебному плану факультета, этот курс является базовым для специализации кафедры исследования операций. На него существенно опираются читаемые затем курсы по численным методам оптимизации, исследованию операций и математическому моделированию, Подобная последовательность курсов отражает современное положение теории оптимизации в ряду прикладных математических дисциплин.
Упомянутый курс по теории конечномерной оптимизации имеет следующую особенность. После каждой лекции студенты получают по три-четыре индивидуальных упражнения, которые они должны выполнить и сдать проверяющим (аспирантам) до следующей лекции. Такая проверка проходит в форме беседы со студентом, в ходе которой выясняется, насколько он усвоил текущий материал. В случае необходимости ему дается консультация. Кроме того, на лекциях формулируется значительное количество задач, решение которых выборочно спрашивается па экзамене. Эти задачи носят относительно элементарный характер и не уходят далеко от лекционного материала. Естественно, если речь идет о пособии, то список задач должен быть существенно расширен, с тем чтобы дать более полное представление о теории и ее приложениях.
В первоначальные планы авторов входило написать учебное пособие, охватывающее и дополняющее материал всего курса. Одпако в процессе работы над рукописью выяснилось, что воплотить этот замысел в пределах отведенного объема не удается. Предлагаемое пособие содержит материал, связанный с программой первого семестра этого годового курса. Сюда входят классические разделы теории оптимизации, линейное программирование и теория выпуклых множеств как часть тесно связанной с теорией оптимизации математической дисциплины — выпуклого анализа. В недалеком будущем авторы 6
надеются подготовить к изданию непосредственное продолжение настоящей книги, в котором будет отращена программа второго семестра — теория выпуклых функций и нелинейное программирование.
Структура книги такова.
В начале каждого параграфа приводится краткая сводка основных понятий п результатов рассматриваемого раздела теории. Следует подчеркнуть, что доказательства практически всех сформулированных здесь теорем приводятся в виде решении соответствующих задач. Такой подход позволяет при сохранении 4 юз дачного £ стиля книги сделать ее полностью автономной от других учебных пособий по теории оптимизации. Вместе с тем отметим, что во всех параграфах, за исключением § 4 и 5. теорет!гческие введения (сводки) в основном следуют работе [39]. По существу, набор введений (вместе с доказательствами) образует конспект первой части читаемого авторами курса.
После введения идет серия упражнений, каждое из которых проставлено 20 вариантами. Это позволяет выдавать студентам одной группы индивидуальные, но равноценные задания. Для выполнения упражнений достаточно лишь твердого знания вводного материала. Опп выражают, по мнению авторов, необходимый для студентов минимум навыков в данной области. Ответы к упражнениям в книге пе приводятся, так как пиане их выполнение было бы существенно облегчено. Вместе с тем в решения упражнений, и ответы к каждому их варианту у авторов имеются, и они готовы предоставить их в личном порядке всем преподавателям, которые пожелают использовать книгу в учебном процессе.
Следом за упражнениями в каждом параграфе идут задачи. Практически все они снабжены ответами, указаниями пли решениями. Характер п назначение задач весьма разнообразны. Некоторые из них служат простыми дополнениями к сводке основных фактов. Имеются задачи, в каком-то смысле аналогичные упражнениям. Это позволяет студенту, испытывающему затруднения при выполнении того или иного упражнения, разобрать решение соответствующей задачи и в результате пайтп подход к.своему индивидуальному заданию. Значительная часть задач посвящена развитию п углублению материала теоретического введения. Изложение доводится здесь до весьма топких результатов, которые можно найти лишь в специальных монографиях. Трудным задачам
7
предшествуют задачи подготовительного характера, так что при известной настойчивости читатель может осилить их и самостоятельно. В форме задач представлены и некоторые новые результаты. Это позволяет надеяться, что далее специалисты найдут здесь нечто для себя полезное.
Таки?! образом, предлагаемая книга позволяет читателю самостоятельно пройти путь от азов до довольно глубоких фактов соответствующих разделов теории оптимизации и выпуклого анализа. Одновременно опа различными способами может использоваться преподавателями при чтении обязательных и специальных курсов, проведении семинарских занятий, зачетов и экзаменов по данным дисциплинам. Некоторые задачи или определенные их подборки могут стать темой доклада на семинаре или курсовой работы. Наконец, книга может служить справочным пособием для всех, интересующихся затронутой здесь тематикой.
В конце кпигп приведен список литературы, использованный авторами при работе. Определенная часть задач взята из этих изданий.
Авторы приносят глубокую благодарность всем, кто в разной форме и степени помог им в работе над книгой. Прежде всего здесь хотелось бы упомянуть сотрудников факультета вычислительной математики и кибернетики МГУ им. М. В. Ломоносова Ф. П. Васильева, А. А. Васина. Э. Г. Давыдова, Д. В. Денисова, С. К. Заврпева. В. Г. Карманова, П. С. Краснощекова, В. В. Морозова. В. С. Панферова, Вик. В. Подииовского, А. Г. Сухарева, В. В. Федорова, а также Н. А. Бобылева, М. А. Красносельского и И. С. Кукушкина. Мы благодарим аспирантов О. Л. Колесова, М. Р. Пахомкину, И. Р. Стропгппу и М. В. Удалкипу, которые осуществляли проверку выполнения упражнений и помогли устранить ряд ошибок.
Большую благодарность авторы приносят В. В. Шестопаловой за ее самоотверженный труд по перепечатке рукописи.
Глава 1
КЛАССИЧЕСКИЕ РАЗДЕЛЫ ТЕОРИИ ОПТИМИЗАЦИИ
Современная теория оптимизации берет свое начало в классическом математическом анализе и имеет тесные связи с линейной алгеброй, аналитической геометрией, другими математическими дисциплинами. Цель данной главы — дать развернутое изложение тех разделов конечномерной теории оптимизации, с которыми студенты знакомятся (норой весьма бегло) йа младших курсах. Таким образом, эта глава может рассматриваться как дополнение к курсу математического анализа и как введение в курс теории оптимизации.
§ 1. Существование решения. Геометрическая интерпретация задач оптимизации
СВОДКА ОСНОВНЫХ ФАКТОВ
1. Исходные понятия. Задачами оптимизации называют задачи отыскания точек минимумов или максимумов функций па заданных множествах. Условимся записывать задачу минимизации функции /(аг) па множестве X в виде
/(я)-* min, я<==Х.	(14)
При этом / будем называть целевой функцией, X—допустимым множеством, любой элемент х^Х— допустимой точкой задачи (14).
Всюду в книге рассматриваются лишь конечномерные задачи оптимизации, т. е. задачи, допустимые множества которых лежат в евклидовом пространстве Rn.
Точка х* е X с= R” называется
1) точкой глобального минимума фушщип / па множестве Х_ или глобальные решением задачи (14), если
/(г*)г^/(г) при всех хеХ;	(1;2)
9
2) точной локал ъного минимума / па X или локальным решением задачи (1.1), если существует такое число е > О, что
/(х*)=^/(х) при всех геХП Ut(x*),	(1.3)
где иг, (я*) ~ (х R".| Их — х*И е) — шар радиуса е с центром в х*.
Если неравенство в (1.2) или (1.3) выполняется как строгое при хч^х*, то говорят, что х*— точка строгого минимума (строгое решение) в глобальном пли локальном смысле соответственно.
Задачу максимизации функции / на X будем записывать в виде
/ (х) -г max, х ® X.	(1.4)
Введенные выше понятия переформулируются применительно к задаче (1.4) очевидным образом. Ясно, что задача (1.4) эквивалентна задаче
—/ (х) ->• min,	я <= X,
в том смысле, что множества глобальных или локальных, строгих или нестрогих решений этих задач соответственно совпадают. Это позволяет без труда переносить утверждения для задачи минимизации на задачу максимизации и наоборот.
Точки минимума л максимума функции / па X объединяются общим названием точки экстремума. При этом сами задачи оптимизации (1.1) и (1.4) называют также экстрема л ъными.
2.	Существование глобального решения. Точная ппж-пяя грань функции / па X, т. о. величина
/* ₽ inf /(х) <== ini / (х), XGX	X
называется значением задачи (1.1). Возможны три случая:
1)	/*>—«□ и /(х‘*)—/* при некотором х*<=Х, т. е. значение задачи конечно и достигается; при этом /♦ *= « min /(х);
х
2)	/* > — со и /(х)> /♦ при всех х<= X, т. е. значение конечно, но не достигается;
3)	/*=—<», т. е. значение бесконечно.
В случае 1) задача (1.1) имеет глобальное решение, в случаях 2) и 3)—не имеет.
Теорема 1.1 (Войерштрасса). Пусть X—компакт (замкнутое и ограниченное множество) в Rn, f—непре-10
рывная. функция на X. Тогда глобальное решение-задачи (1.1) существует.
Функция /, определенная па множестве XcR", называется бесконечно растущей (убывающей) на X, если Нт / (xh) = <х> (lim / (xk)= — оо) для любой такой после-^"‘00	Л-»ОО	__
довательности Uft} <= X, что либо Нтг =х^ Х\Х, либо /i-»w
Пт И = оо.
Л-»оо
Теорема 1.2. Пусть X — произвольное ,множество в R", /— бесконечно растущая непрерывная функция на X. Тогда глобальное решение задачи (1.1) существует.
3.	Квадратичные функции. Функция вида
/И = {Ах, х> + <6, х) -г с = п я	л
= 2 S aliXiXj + s bjZ; + с, (1.5) 1=1
где А = (ау) — симметрическая матрица размера п.Х п, Ъ (аде К", c^R, называется квадратичной.
Теорема 1.3. Квадратичная функция (1.5) либо нс ограничена снизу на R’\ либо имеет на R” точку глобального минимума. Если выполняется второе, то матрица А неотрицательно определена, т. е. <Ля, ж> 5s 0 при всех х R”.
Теорема 1.4. Если, матрица А положительно опре-делена, т. е. (Ах, х>>0 при всех (teR", то квадратичная функция (1.5) является бесконечно растущей на R" и, значит, имеет точку глобального минимума, на. любом замкнутом множестве X <= R*.
При использовании теорем 1.3, 1.4 и ряда других приводимых далее .утверждений оказывается полезным следующий факт линейной алгебры.
Теорема 1.5 (критерий Сильвестра). Пусть Л — симметрическая матрица размера пХп, Тогда
1)	матрица А неотрицательно определена в том и только том случае, если асе ее главные миноры неотрицательны;
2)	матрица Л положительно определена, в том и только том случае, если все ее угловые миноры положи^ тельны.
При этом главным минором матрицы А называется определитель матрицы, получаемой путем удаления из А строк и столбцов с одинаковыми номерами. Если удаля-
11
ются строки и столбцы с номерами от некоторого к до л, то главный мипор называется узловым.
Проекцией точки г’еК” на множество X<=Rn назы
вается точка из X, ближайшая к я0 средн веек точек
Ряс, 1
этого множества. Иными словами, проекция является глобальным решением задачи
/ (я) = Ня — я”!!2 min, х е X, где, заметим, / есть квадратичная функция с единичной матрицей:
/(я) = <я “ я0, я — я°> е= <ж> я> — 2<я°, я> + <я°, я’>.
Теорема 1.6. .Проекция любой точки	на
замкнутое множество X <= Rn существует.
4.	Геометрическая интерпретация задач оптимизации. Геометрические, построения играют важную роль в теории оптимизации. Они, с одной стороны, позволяют наглядно иллюстрировать ряд утверждений данной теоремы, а с другой —могут быть полезными прп отыскании решений простейших конкретных задач оптимизации. Для геометрической интерпретации задачи (1.1), где X<=R2, необходимо изобразить на плоскости множество X и несколько типичных линий уровня функции /, т. е. множеств вида
Ла(/)=’{ж^Кг|/(я) = а}, aeR
(рис. 1, 2). Чтобы отразить характер изменения функции /, у даппой липни уровня полезно ставить знак плюс с той стороны, где / принимает значения, большие а, и знак минус с другой. Поиск глобального решения задачи сводится к нахождению минимального числа а* среди всех таких а, что линия уровня Д/(/) имеет непустое пересечение с X. При этом любая точка я* (= La* (J) f] X 12
является глобальным решением задачи, а число а*^ = /* = /(я*)—о® значением. Решение х* может лежать как внутри (рис. 1), так п на границе (рис. 2) множества X.
За меча пне. Во всех упражнениях и задачах данного параграфа, где требуется найти точки а стрему ма, достаточно дать геометрическое обоснование ответа. Следует, однако, подчеркнуть, что, строго говоря, геометрические соображения являются лишь сродством .выдвижения гипотезы, которая затем должна быть обоснована аналитически. Таков обоснование проводится, как правило, па основе необходимых и достаточных условий экстремума, о которых речь пойдет и следующих параграфах.
УПРАЯШЕПИЯ
1.1.	Найти все значения параметра Л, при которых функция
/(#)==(& — а) х + е<ъ-Е,) <*-e)s
имеет точку глобального минимума на числовой оси R, а также все значения к, при которых величина /* = = inf / (я) конечна, по не достигается:
t к
	а	b	с	а		Ъ	с	а b		G	а		Ь	с
1	1	2	7	6	7	5	9	11	8 G	9	10	8	5	7
2	1	3	5	7	3	5	0	12	4 7-	8	17	8	8'	9
3	9	1	3	8	8	2	7	13	3 1	9	18	7	5	8.
4	5	3	8	9	5	4	8	14	9. 4	7	19	9	0	7’
5	2	3	4	10	7	3	5	15	5 С	7	20	6	2	5,
1.2. Найти все значения параметров Лит, при которых квадратичная функция
/ У) ” кх? + 2аху + bzyz + сх 4- ту
имеет точку глобального минимума на R2:
	а	b	с	а		Ъ	с	а		Ъ	с	а		5	С'
1	2	3	6	о	1	4	—2	11	5	2	15	10	4	3	10'
2	1	8	-1	7	3	2	9	12	1	4	-3.	17	5	8	—io:
3	3	4	0	8	5	3	5	13	4	5	—4 •	18’	3	4-	-15
4	4	5	-8	9	2	5	.—4	14	2	3	8	19	1	3	&
5	5	2	10	10	4	3	—12	15	3	7	0	20	2	5	—2
13
£3. Изобразить на плоскости R2 линии уровня ^М(м)1/М = <Д
где а = 0, 1, 2, следующих функции /(«, у):
a)	az 4- by; д) д |.г| + &|у|;
б)	ах2 4- by1; е) а | х |— b | у |;
в)	az- — by-; яс) az? 4- by3;
г)	az2 4- by;	a) azy — Ьхя-
а b		а b		а Ъ		я b	
1	2 3	6	4 5	11	3 В	1С	1 2
2	3 4	7	5 3	12	G 4	17	8 7
3	5 6	8	3 1	13	7 5	18	5 2
4	7 3	9	4 2	14	1 4	19	В 9
5	9 10	10	8 В	15	8 9	20	5 8
1.4.	Найти проекцию начала координат в R2 на полуплоскость
X = {(.т, у) 1ая 4- by с}:
	а	ь	с	а		Ъ	с	а		Л	с	а		Ь	с
1	•>	1	3	6	1	—5	4	11	1	— 2	1	16	5	-2	5
2	1	-3	1	7	4	1	5	12	2	4	2	17	—3	5	3
3	3	9	4	8	-2	3	1	13	-3	1	5	18	-5	4	9
4	—5	1	3	9	-4	2	2	14	1	4	3	19	5	3	4
5	4	“5	2	10	2	5	3	15	4	3	4	20	-3	4	1
1.5. Найти проекцию точки (a, 6)eR2 на круг
X = {(я, у) + у2 < с2}:
	а	ь	с	а		Ъ	с	а		Ъ	с	а		b	С
1	3	5	3	6	-1	3	2	11	1		4	3	16	-1	5	4
2	4	-1	4	7	6	-1	5	12	1	3	1	17	-2	5	2
3	5	1	5	8	-4	1	4	13	—5	4	5	18	-3	2	1
4	1	2	1	9	2	7	1	14	1	-2	2	19	7	-3	2
5	о	-3	2	10	5	2	3	15	3		3	20	1	4’	4
14
1.6. Найти точки глобального максимума функции /(х, у) = х2 + ау2 на множество
X == {(х, у) | 1x1 + Ыу | С с):
	а	Ъ	С	а		Ъ	с	а		b	с	а		Ь.	с
1	3	2	4	6	5	3	2	11	2	1	3	16	6	ч	9
2	1	2	3	7	10	3	4	12	1/2	1	0	17	1	2	4
3	5	2	9	8	1	4	1	13	4/5	1	1	18	5	2	5
4	2	3	4	9	3	4	9	14	12	3	б	19	20	5	10
5	1	3	3	to	20	4	3	15	8	3	4	20	30	5	20
1.7. Найти точки глобальных экстремумов функции /(х, у) = ах2 — by2 па множество
Аг = {(х, у)| |х+1| + |у — с| ^1):
	а	b	е	а		b с		а		Ъ	С	а		Ъ	С
1	5	2	3/4	0	5	3	1/3	11	6	1	5/2	16	7	3	2/3
2	3	1	1	7	2	1	1/2	12	7	1	3	17	3	9	1/4
3	10	3	7/0	8	7	5	1/5	13	13	5	4/5	18	5	4	1/8
4	5	1	2	9	8	3	5/0	14	9	2	7/4	19	7	9	5/4
5	4	1	3/2	10	11	3	4/3	15	0	7	1/7	20	8	1	7/2
1.8.	Определить все значения параметра 7с, при которых функция
/(х, у) = ах — у
имеет точку глобального минимума на множество
Хг={(х, у)|—х^у ^Ах + Ых|+с},
и найти эту точку:
	а	Ь	с	а		Ь	с	а		b	с	а		Ь	С
1	0	3	5	6	4	0	0	И	8	0	4	16	6	1	3
2	7	0	2	7	7	3	3	12	10	4	1	17	9	2	1
3	8	4	3	8	9	4	5	13	4	1	5	18	5	1	9
4	3	1	1	9	10	3	4	14	6	2	3	19	9	3	5
5	5	2	4	10	2	1	1	15	8	3	2	20	10	2	4
15
ЗАДАЧИ	’	/
1.1.	Пусть X — произвольное множество, /—любая числовая функция на X, <р — возрастающая функция на £7 <= R, причем / (х) е U при любом х е X ♦)/ Доказать, что задача (1.1) эквивалентна задаче
<₽(/(#)).->- min, х^Х
в том смысле, что множества глобальных пли локальных, строгих или нестрогих решений этих задач соответственно совпадают, и, кроме того,
inf ф(/(.т))= ф (inf/(
х •	V X
1.2.	Пусть X — произвольное множество. Для любой функции /, определенной на X, положим /* “ inf/(а:).
х
Доказать, что
а)	(а/ + р) * = а/* + р при всех а, р <= R, а > 0;
б)	(/+g)'*^/* + g*;
в)	если /* > 0, g* 5= 0г то (/  g) * Э* /* - g*;
г)	(min {/, g}) * » min {/*, g*};
д)	(max (/, g})* ^max {/♦, g*);
e)	если /♦>—», g* > —co, to
/ («) g (x) 4- /* • g*	f(x)g*’+ g (x) /♦
при всех x X.
1.3.	Пусть функция /(x,.у) определена па декартовом произведении X X У. Доказать, что
’* a) inf / (х, у) = inf inf / (а:, у) = inf inf / (г, у);
«. ХХУ	X Y	УХ
б) sup inf / (.в, у) < inf sup / (х, у), X Y	У X
1.4. Функция /, определенная па множество Xc=R", называется полунепрерывной снизу (сверху) в точке х^ <=Х, если на условий (я*} с X, lim ж1 =,? следует, что
___	fc-»» г
/(х) <2 Кт / (л:Л) (/(л:) lim / (хк)). Доопределить в пуле
ft-.00	Л-»»
♦) Функция ф называется	(и<ч/бЫ|М10н/сй) па У,
еслп од условий и > v, и, не У следует, что ф(«> > го{у) (соот-ВОТСТВОЕШО ф(и) ф(р)).
16
функцщо числового аргумента
( 1, если я* > О, /(г)=	,	_
*	(— 1, если х<С0|
так, чтобы опа стала полунепрерывной снизу (сверху).
1.5.	Доказать, что функция / непрерывна в точке х в том и только том случае, если опа полунепрерывна снизу к сверху в этой точке.
1.6.	Доказать, что функция / полунепрерывна снизу в том и только том случае, если функция —/ полунепрерывна сверху.
1.7.	Доказать, что сумма двух полунепрерывных снизу функции п произведение полунепрерывной снизу функции на неотрицательное число полунепрерывны
снизу.
1.8*	*). Пусть X<=R" и У «= R"'— произвольные мно-лсества, <р (х, у) — функция на X X У, полунепрерывная снизу на X при каждом фиксированном у *= У и ограни-
ченная сверху па У при каждом фиксированном х^Х. Доказать, что функция / (ж) = sup <р (х, у) полуиеирерыв-Y
па снизу па X.
Указанную функцию f{x) называют поточечным супремумом или верхней огибающей семейства функций {ф(-, у)]уеУ). Важный частный случай этого понятия — поточечный максимум кокйчциго семейства функций: / (х) и шах /{(х).
1.9*	. Доказать следующее обобщение теоремы Вейер-штрасса.
Пусть X — компакт в R", / — полунепрерывная снизу функция па X. Тогда точка глобального минимума / па X существует.
1.10*	. Пусть X — произвольное множество в Rrt, У— компакт в R"1, <р(х, у)— непрерывная (полунепрерывная спизу) функция па XX У. Доказать, что функция /(я) = «niin(p(x, у) непрерывна (соответственно полунепрерыв-
на снизу) па X.
1.11.	Привести примеры, показывающие, что в задаче 1.10 условия компактности У и непрерывности (полуне-прерывпостм снизу) функции ср(х, у] по совокупности аргументов существенны.
•) Звездочкой помочены наиболее пажиыо пз утверждений, Донолпяющнх материал теоретического введения.
2 С, А, Ашманов, А, В. Тимохов
Эйуч^зя (>и6дмотё| ИРКЯС-.ЙГО
17
7
U2*. Пусть X — произвольное множество в Rn, У— компакт в R”, q>(x, у) — непрерывная фушщпя на XX У. Предположим, что при любом фиксированном х X функция ср (ж, у) достигает глобального минимума на У лишь в единственной точке у(х). Доказать, что функция у (л) непрерывна на X.
1.13.	Привести пример, показывающий, что в задаче 1.12 условие компактности У существенно.
1.14.	Пусть числовая последовательность <аА) не убывает, т. о, а* аА+1 при всех /с. Доказать, что lim «л = ft-к»
= sup «й (здесь и ниже допускаются бесконечные зпаче-Л
ппя предела).
1.15*	. Пусть X — произвольное множество в R”, fh (А®1, 2, ...) — такие функции на X, что при любом x<sX последовательность Cfh(x)} не убывает. Доказать, что
a)	lim sup Д (я) = sup lim /А (х); Л'	X
б)	если функция /А (£=>1, 2, ...) полунепрерывны снизу на X и при любом х X последовательность {Д (х)} ограничена сверху, то функция / (®) = lim Д (а) также полунепрерывна снизу на X.
Привести примеры, показывающие, что в утверждениях а) и б) условие неубывания {/*(»)) существенно.
1.16*	. Пусть X—компакт в IV, Д (&=1, 2, ...)—* такие полунепрерывные снизу функции на X, что при любом х<=Х последовательность {Д(я)} не убывает л ограничена сверху. Пусть, далее, х — любая предельная точка последовательности {х*}, где х* —точка глобального минимума функции Д(я) на X. Доказать, что
a)	lim min Д (х) = min lim /л (л?); Л-»«о X	X
б)	х есть точка глобального минимума функции / (х) «= Нт /Л (х) па X.
ft.» ль
Привести примеры, показывающие, что в утвержденл-ях а) л б) условия полу непрерывности снизу функций /Л л неубывания {Д(х}} существенны.
1.17*	. Множествами Лебега функции / на X<=R” называются множества вида
Хц«{я;еХ|/(лг)<р}, ₽«R.
Доказать следующие утверждения:
13
а)	бели X замкнуто л / полунепрерывна снизу на X. то все множества замкнуты*);
б)	если все множества Xt, замкнуты, то / полунепрерывна снизу па X.
Привести пример, показывающий, что в утверждении а) условие замкнутости X существенно.
1.18*	. Доказать обобщение теоремы Вейерштрасса.
Пусть X — замкнутое множество в R", / — полунепрерывная снизу функция па X, причем ее некоторое множество Лебега Х^ непусто п ограничено. Тогда точна глобального минимума функции / на X существует.
1.19,	Доказать, что все множества Лебега бесконечно растущей функции ограничены.
1.20*	. Доказать следующее обобщение теоремы 1.2.
Пусть X—произвольное множество в В”, / — бесконечно растущая полунепрерывная снизу функция на X. Тогда точка глобального минимума функции / па X су
ществует.
1.21.	Доказать теорему 1.3.
1.22.	Доказать теорему 1.4.
1.23.	В связи с утверждением а) теоремы 1.5 привести пример симметрической матрицы, у которой все угловые
ми поры неотрицательны, по которая не является неотрицательно определенной.
1.24.	Пусть X — ограниченное множество в R", функция / непрерывна па замыкании X и дифференцируема на X. Предположим, что для любой точки я Х\Х существует такой вектор h е Rn, что х + ah t= X при всех достаточно малых а>0 и Tim </*(аг 4- ah), h) <10
а-»Щ-
(/' обозначает вектор частных производных). Доказать,что точка глобального минимума функции / на X существует.
1.25.	Пусть /i(a), ...t /„ (а) — функции числового аргумента,. непрерывные при а > 0 и непрерывно дифференцируемые при а>0, причем Ит /Да) « — со ач-о+
(/	= 1, ..., п)'. Доказать, что точка глобального минимума
функции / 0е) == S fi (xj) па множество
Х = keR"
п	1
S xj = 1, Xj~> 0, / = 1, .п j=l
существует.
♦) Пустое множество считается замкнутым ио определению, 2*	19
1.26.	Пусть непрерывная функция / имеет точку глобального минимума на R”. Следует ли отсюда, что f достигает глобального минимума па любом замкнутом множестве X <= Ий?
1.27.	Пусть непрерывные функции / и g имеют точки глобального минимума на замкнутом множестве X<=Rn. Следует ли отсюда, что их сумма / + # также достигает глобального минимума па X?
1.28.	Найти все значения параметра а, при которых функция
/ (я) = (а +1) х 4* а- In х — 2 sin х
имеет точку глобального минимума на множество положительных чисел.
1.29.	Найти все значения параметра я,, при которых функция
№. у) = (а-2)(а- 3)е“ +
Jr -bl
имеет точку глобального минимума па множестве
Х={(я, у)1(о — 4)х2 + у2^1},
а также все значения а, при которых величина /♦ = = inf / (.г, у) конечна, по по достигается.
х
1.30.	Найти все значения параметров а и &, при которых функция у)=*х + ау имеет точку глобального минимума па множестве
X = {(х, у) IЪх2 — 2ху + у2 11.
1.31.	Решить предыдущую задачу при f(xt у) — аху. где <г = ±1.
1.32.	Найти все значения параметра а, при которых функция
/ (Ж1 У)= fa? + — 4)'ля/3
имеет точку глобального минимума ла множестве
Х = {(я, у) 1(<г— 1).т + у2=^1}. ’
1.33.	Найти проекцию точки (1, 3, 8) па .параллелепипед
Х={(г, у, z)|0^z*S2, 4«3у«3 5, 6«Sz^7}.
20
1.34.	Найти проекцию точки (xot yd) на множество Х=((х, у) |аж + by = 1, х^О, у 5s О},
где а > О, 6 > О.
1.35.	Найти все проекции точки (жо, yd) на множество Х = {(х, у) 1^4-у2> 1, у^О).
Найти глобальные решения следующих задач (указанные равенства и неравенства описывают допустимые множества):
1.36.	f(x, у) = ху -> шах, ах + Ьу=^ где н>0, 5>0.
1.37.	/(ж, у) = — In я+ у~+ min, z —у^2, ж + у2^4, л>0.
1.38.	/(г, у)'=* 2х — у	max, я2 + у2*& 1, х — у^О,
£4-у^1.	__
1.39.	/ (аг, у) = х 4- 7 у ->• min, х 4- у > 1, я3 4- у2 = 1.
1.40.	/(л, у)= max {[я — 2|, |у|} -ь min, 2|а:1 —|у|^2.
1.41.	/(я, у)=(х — 1)24-у2-»-min, х~ + у21=2аху, где fisR.
1.42.	/(д?, у)= 4г2 +у2max (min)’, U —314|у —я|=£ < 1. где а^О.
1.43.	Найти локальные решения задачи
ж3 4- у8 max, X2 4- 4у2 < 4.
1.44.	При каких значениях параметра а задача
х + ау~>- max, х3 И- у3 = Зху
имеет глобальное решение, а при каких только локальное?
1.45.	Найти все значения параметра я, при которых задача
2z4,y-»-max, аг — у2=^1,
имеет глобальное решение.
Последние три задачи параграфа посвящены теореме Кукушкина об аксиоматическом определении максимума.
1.46.	Пусть X — компакт в Rn, С (X) — пространство всех непрерывных функций на X, Ф — функционал, ставящий в соответствие каждой функции f<^C(X) число Ф(/). Предположим, что Ф удовлетворяет следующим двум аксиомам:
1) Ф(а/4 р)=аФ(/)Ч-р при всех /<=С(Х), a, peR, а>0*)-,
•) Слева в указанном рапепстяо символ р следует понимать Как функцию на X, принимающую постоянное значение р.
21
2) Ф(шях {/, max (Ф(/), Ф(g)} при всех f,g^ <zC(X).
Доказать, что
а)	Ф(^)=’Р при всех
б)	функционал Ф не убывает, т. е. если f(x)*£g(x) при всех х&Х, то Ф(/)Ф(g);
в)	min/(х)<1Ф(/)max/(я) при всех j^C(X).
1.47	. В предположениях предыдущей задачи поставим в соответствие функционалу Ф следующие множества:
Е} = {s е X | / (х) Ф (/)},	/ <= С (X),
Е = A Ef.
/e<W
Доказать, что
а)	для любого такого зашшутого множества У<=А’’, что YftE — 0, существует функция f^C(X), удовлетворяющая неравенству min / (ж) >- Ф (/);
б)	2?—непустое замкнутое множество;
в)	тах/(ж)^Ф(Д при всех f<^C(X).
1.48	*. Доказать теорему Кукушкина.
В предположениях задачи 1.46 существует такое замкнутое множество Е <= X, что Ф (/) » шах / (,т) при всех /е£(Х).	Б
Заметим, что верно п обратное: любой функционал данного вида удовлотиоряот аксиомам 1) и 2) из 1.46 (см. утверждения а) п г) из 1.2).
§ 2. Задача безусловной оптимизации
СВОДКА ОСНОВНЫХ ФАКТОВ
1.	Условия экстремума. Пусть дана задача безусловной минимизации
/(i*)->min, s^R".	(2.4)
Введем обозначения:
e (dxL Ф’ • ’ ”	<*))
— вектор первых частных производных (градиент) функ 22
ции / в точке
—• матрица вторых частных производных (гессиан) функции / в точке x^Rn. .
Теорема 2.1 (необходимое условно минимума первого порядка). Пусть функция / дифференцируема в точке x*^Rn. Тогда если ж* — локальное решение задачи (2.1), то
/'(**) “0.	(2.2)
Точка z*^Rn, удовлетворяющая (2.2), называется стационарной точкой задачи (2.1) и самой функции /.
Теорема 2.2 (необходимое условие минимума второго порядка). Пусть / дважды дифференцируема в точке z*<=Rn. Тогда если ж* — локальное решение задачи (2.1), то матрица /" (ж*) неотрицательно определена, т. е.
Л>>0 при всех h^R\ (2.3)
Теорема 2.3 (достаточное условие минимума второго порядка). Пусть / дважды дифференцируема в точке x*&Rn, Тогда если /'(я*) = 0 и матрица /" (л*) положительно определена, т. е.
</" (ж*) Л, Л> > 0 при всех h е= R", k =£ 0,	(2.4)
то х* — строгое локальное решение задачи (2.1).
Замечание 2.1. Если в задаче (2.1) вместо min поставить max, то теорема 2.1 остается справедливой в буквальной ее формулировке, а в теоремах 2,2, 2.3 следует поменять на противоположные знаки неравенств в (2.3), (2.4).
Замечание 2.2. Теоремы 2.1—2.3 сохраняют свою силу для задачи минимизации (функции / на множестве Л' R” при условии, что х* ость внутренняя точка этого множества (я* е int X).
Замечание 2.3. Полезно иметь в виду следующее простое правило отбора глобального решения среди стационарных точек задачи (2.1). Если известно, что глобальное решение существует, причем функция / дифференцируема всюду па R”, то этим решением является, очевидно, та стационарная точка, в которой функция / принимает наименьшее значение. В частности, если ста
23
ционарная точка единственна, то она и служит глобаль яым решением. Такны образом, при отыскании глобальных экстремумов фактически нет необходимости использовать теоремы 2.2 п 2.3. Однако при анализе локального доведения функций эти утверждения являются весьма полезными.
2.	Дифференцируемые отображения. Если имеется отображение (вектор-функция) F (/’’<): X Rm, где XcRn, то под F‘(x) будем донимать матрицу частных производных F в точке х е X;
''НМ,.............
где i — индекс строки, / — индекс столбца. Эта матрица называется матрицей Якоби, отображения F в точке х.
Отображение F = (F4): X-+R"* называется дифференцируемым (непрерывно дифференцируемым), если каждая из функций Л (I => 1, ..., ш) дифференцируема (непрерывно дифференцируема) на X. Таким образом, непрерывная дифференцируемость F равносильна тому, что матрица F(x) существует и непрерывна всюду на X.
Для отображения Ft X X У * R*, где X <= Rn, Y g Rm, под Fx(%*, у*) понимается его матрица Якоби по координатам вектора х в точке (я*, у*)е= X X У:
..л-
Следующая фундаментальная теорема математического анализа потребуется для решения некоторых задач из этого и следующего параграфов.
Теорема 2.4 (о неявной функции). Пусть XgR", У — открытые множества, F: X X У Rn — непрерывно дифференцируемое отображение,	у*еУ,
Предположим, что F(x*, у*) = 0, причем матрица Fx ($*, у*) невырождека. Тогда найдутся окрестность U точки х* и окрестность V точки у*, обладающие следующим свойством', для любой точки у <= F существует един ственная точка x(y)<==U, удовлетворяющая условию F(x(y), у) = 0. При отом х(у*) = х*, вектор-функция х(у) непрерывно дифференцируема на V и.
х'(у*)	— [Fx (х*, у*)]"% (я*, у*).
24
Напомним также ценное правило дифференцирования сложных функций: если отображения F: X У и (?: У-»-
IV, где X с R", У <= RCT, дифференцируемы, то отображена е Я: X"”-R\ определенное формулой Я(х) = G(F(x)), , также дифференцируемо и
H'(X)=G'(y)F'(zj, y = F(x),	(2.5)
где, подчеркнем, матрицы Якоби Я'(я), G'(y) и F'(x) ‘ имеют размеры кХп, kXm и тХп соответственно.
; УПРАЖНЕНИЯ к \	2.1. Найти точку глобального минимума функции ?	/(#» У) — ая? Яху "Ь byz — Ях — Зу L J па плоскости R2:													
! ЕГ fi 1			л b			л Ъ		a b		a b			
			1 2 3 4 5	1 2 1 3 1 4 1 5 1 C		6 7 8 9 10	to ГО to to го Ot »s oj to <-*•	H 12 13 14 15	3	1 3	2 3	3 3	4 3	5	16 17 18 19 20	4 1 4 2 4 3 4 4 4 5		
£ и» i; 1	2.2, Найти f(x, y) =				глобальное решение и значение задачи ^т- + г-*тш, г>0, у>0: а;	у								
I » IT jlf'' £	a b c				а		b c	a b c				a b c	
	1 2 3 4 5	2	1	3 3	2	4 1	2	3 3	1	2 2	3	1			6 7 8 10	3	4	1 2	1	4 4	1	2 4	1	3 4	2	3		11 12 13 14 15	-Т« 4- CO M CO 'T »•	M —		16 17 18 10 20	2 3 3 1	1	4 1 1 1 3 1 3 3 1 4	
2.3. Паптп глобальное решение задачи
/(а?, у) = х2 + ху + ау2 — Ъ In х — с In у min, х > 0, у > 0:
25
	а	b	с	а		b	с	а		Ъ	с	а		b	С
1	3/2	2	1	8	7/3	3	2	И	1/8	8	6	16	7/4	4	1
2	1/2	3	2	7	2/3	3	1	12	4	3	4	17	5/2	4	1
3	5/2	2	1	8	2	3	1	13	3/2	4	2	18	1	5	2
4	1/6	8	5	9	3/4	4	2	14	4/5	5	3	10	3/5	5	1
5	7	2	1	10	2/5	5	3	15	1/2	8	4	20	2/3	6	2
2.4. Найти точки экстремумов функции
/(я, //) =	4- by-)
ла плоскости В2*):
	ч	b	а		ь	а		ь	а		b
1	1	2	б	8	3	11	9	1	1’8	4	1
2	7	3	7	2	4	12	3	5	17	G	7
3	1	4	8	2	5	13	3	1	18	4	3
4	8	5	9	7	6	14	7	2	19	1	5
5	1	8	10	ъ *г	7	15	3	6	20	5	6
'2,5. Найти точки экстремумов функции
iw •{- by + с
Vs+f+t
У (ж, у) =
па плоскости R2:
	а	ь	С	а		&	с	а		b	с	а		b	е
1	4	-1	2	6	1	3	—4	И	—2	4	1	16	2	3	3
2	4	2	—•!	7	-1	3	4	12	4	—2	-1	17	3	1	4
3	1	2	4	8	О	5	о	13	6	1	6	18	0	-1	-2
4	3	1	9	9	1	3	-3	14	6	1	-6	19	1	5	4
5	3	-1		10	2	1	3	15	4	6	-1	20	1	—1	—4
2.6. Найти точки экстремумов функции
/ («» у) = «я8 + ал2у + Ьл + ~ у3 + су па плоскости R2:
♦) В подобных заданиях тробуотся исследовать характер каждой экстремальной точки, т. о, вылепить, является ли она точкой глобального или локального, строгого или нестрогого минимума (максимума), 28
	а	b	е	а		Ъ	С
1	—5/4	-5/2	—11/2	11	—2	—2	—17/8
2	—5/4	5/2	1/2	12	_о	2	7/8
3	-5/4	-10	^99 Лжя*	13	-2	—8	-17/2
4	-5/4	10	9	14	-2	8	7/2
5	-5/4	-5	—и	15	-2	-4	-17/4
6	“5/4	5	1	16		4	7/4
7	-5/4	-5/2	—19/3	17	—2	—2	—7/3
8	-5/4	5/2	—4/3	18	-2	2	2/3
9	-5/4	-15/2	-19	19	-2	-6	—7
40	-5/4	15/2	-1	20	-2	6	2
2.7, Найти точки экстремумов фушицш /(х, у)=> х?у~(ах + by + с) па плоскости R~:_________________
	а	b	С	а		b	с	а		b	с	а		ft	С
1	“4' —1		1	0	-2	-1	3	11	—5	-1	5	10	-3	-1	7
0	-3 —1		9	7	-4	1	2	12	-1	1	9	47	—2	-1	9
3	“1	1	3	8	—2	—1	8	13	-1	-1	9	18	-9	1	3
4	—5 -1		4	9	-4	—1	4	14	—3	1	8	19		0	-1	1
5	-1 -I		7	10	— 2	1	6	15	-4	1	5	20	— 9	1	9
2.8. Найти все значения параметра Л, при которых точка (!', 0) является экстремальной для функции
./ (.г, у) «= Ht4?v — /га U (.г у) 4-
+ ((а 4- b — i) к — Ь) х 4- key 4- 2Ъху, и выяснить характер экстремума:
	а	ft	G	а		»	с
1	5/2	1/2	-5/2	и	2		-4
2	3/2	-1/2	-3/2	12	3/2	-3	-—4
3	-1/2	1/2	7/2	13	1	’—4	—4
4	—2	2	8	14	-7/2	5	14
5	—5/2	5/2	19/2	15	-4	6	16
G	—3	3	И	16	7/2	-3/2	-13/2
7	-4	4	14	17	3	-3	—7
8	—5	5	17	18	2	—6	-8
9	—0	6	20	19	5/2	—9/2’	-15/2
10	5/2	-1	-4	20	1	—9	—9
27
ЗАДАЧИ
2,1.	Доказать теоремы 2.1*—2,3.
2.2.	а) Пусть функция / числового аргумента лепре-рывна в точке ж* и дифференцируема при остальных ;С из интервала 77 “(ж* —в, ж* + е), где е>0. Предположим, что f (ж) 0 (<0), если х* — е < х < ж*, и /' (ж) ^=0 (>0), если ж*<ж<ж* + е. Доказать, что ж* —точки минимума (строгого минимума) функции / на U.
б)	Пусть ж* —точка строгого локального минимума дифференцируемой функции / па числовой осп R. Следует ли отсюда, что для всех ж, достаточно близких к ж’’, выполняется	если ж<ж*, и f(x)^0, если
ж >“ ж*?
2.3.	Пусть функция / непрерывна в точке ж*^Ип и дифференцируема при остальных ж и» шара ил(х*), где е>0. Предположим, что </'(ж), ж — ж*>^0 (>0) при всех ж^ 7Л(ж*), ж=/=ж*. Доказать, что ж* — точка минимума (строгого минимума) функции / на Ut(x*)>
2.4.	Пусть функция / числового аргумента имеет производную порядка к—1 в некоторой окрестности U точки ж* и производную порядка /г в самой точке ж*, причем
/' (**) = Г (®*)«... “ /(Д-П (ж*) >= 0, Доказать следующие утверждения:
а)	если ж*— точка локального минимума / (на U) и к = 2т -Ь 1, то (ж*) = 0;
б)	если ж* — точка локального минимума / и к = 2т, то /<Л) (ж*)^= 0;
в)	если к = 2т и ,/(А)(ж*)>0, то ж* —точка строгого локального минимума /.
2.5.	Пусть ж* — точка строгого локального минимума бесконечно дифференцируемой функции / па R. Следует ли отсюда, что /1^(ж*)т£:0 хотя бы при одном 7с?
2.6.	Пусть А = (оц) — симметрическая матрица размера пХп. Предположим, что <Л/г, /г> —0 при всех h^lV". Доказать, что оци0 для любых I, j = l, ..., п, т. р. Л = 0.
2.7.	Пусть А =(п/Л)— кубическая симметрическая матрица размера пХпХп, т. е. индексы i, j, к пробегаю' значения от 1 до п, и для любых i, j, к следует «ил == = где ta» h, kA— произвольная перестановка набора {i, у, к} (таких перестановок шесть, если индексы i, /, к попарно различны, и три, если два лз индекс*"’
28
совпадают). Для любого примем обозначение
п п п
д (Л) = 222	*).
ib>l j=>i fc₽«i
Предположим, что Л [Л] “0 при всех A^R", Доказать, что Д “ 0.
2.8.	Функция /, определенная в некоторой окрестности U точки x*<=Rn, называется трижды непрерывно дифференцируемой в г*, если кубическая матрица
существует в любой точке з<= U л непрерывна в х*. При этом, как известно, матрица fN (х) является симметрической [22, с. 581J.
Пусть функция f трижды непрерывно дифференцируема в точке	являющейся точкой ее локального
минимума. Доказать, что f" (я*) [Л] “ 0 при всех таких h <= Rn, которые удовлетворяют условию /" {х*} [А]= 0; в частности, если /" (ж*) = 0, то /'" (ж*) = 0.
Найтп точки локальных л глобальных экстремумов следующих функций на всей области пх определения:
2.9.	/(ж, у, z) ® х2 4* 2у2 + 5z2 —• 2ху — 4ух — 2z.
2.10.	/ (ж, у) = ае~* + be~v + In (ех+eJ), где а > О, b > 0.
2.11.	f(x, у)= х* + у*~4ху.
2.12.	f(x, у) = (х+у) (х — а)(у~Ь).
2.13.	/(а;, у)>=*х2 — 2ху2 + у* — у\
2.14.	/ (х, у) ™ х -I- у 4- 4 sin х sin у.
2.15.	/(х, у) = хё‘—'(1 4- e“)cos у.
2.16.	j(x, у, z) = х3 + у2 + z2 4~ 12ху + 2z.
2.17.	f(x, у, s) = жу2г3(1 — х — 2у — 3z).
Найти глобальные решения следующих задач:
2.18.	/(я, y,z) = x + т;4-“	*>0,
>0, z>0.
2.19.	/(аг, у) - х2 + у 4- —J-->min, х 4- у > 0. в У
*) По Аналогии с этим для обычной квадратной матрицы 4 = (а{}) можно писать
4 [Л] => <ЛЛ, Л> = 2 2 в«АЛ-
t=l ;=1
Для унификации autiucu мы используем такое обозначение л 2.8.
2D
2.20.	Пусть С — симметрическая матрица размера «X X п, Л — матрица размера т X п. Доказать следующие-утверждения:
а)	если С положительно определена, то обратная матрица С~1 существует и положительно определена;
б)	если С неотрицательно определена, то симметрическая матрица 4С4Т (размера те X т) неотрицательно определена;
в)	если С полоясптельно определена, a rang А = те, то АСАТ положительно определена.
Найти глобальные, решения следующих задач:
2.21.	/(я) = <4х, а:> + <&, min, х <= R”, гдо А — положительно определенная матрица размера пХ ??.. b <= И".
2.22.	}(х)>= 114ж — &Г;2->-тш, x<sRfl, где 4—матрица размера те X л, rang 4 = н, b <= Rm.
Данная задача тесно связана с одним из методов обработки данных. Прежде чем его описать, приводом общую постановку проблемы «ма.шэа 0«nkwx. Рассмотрим некоторый объект, на «вход? которого подается параметр а па «выходе» наблюдается параметр у II Точная зависимость между х и у неизвестна, по есть основания предполагать, что приближенно опа описывается функцией вида р = <р(х, я), где в — некоторый параметр. Предположим, что в результате т опытов (или наблюдений) над объектом получены следующие данные:
х" = (Хр . .	Pj, / i= 1, ,Л1,
т. е, в 1-м опыте значению х* входного параметра соответствовало значение щ выходного. Тогда естественно попытаться так подобрать параметр а, чтобы зависимость указанного вида нанлупллм образом аппроксимировала опытные данные, В качестве моры точности прнблпжеипя обычно берут одну из следующих функций:
/iW- 3	«))а»
i=l
m
/2(«) = 3 К-®)|» тах kt—а)|-jz=l	I4i4nt
Наплучшнм считается такое значение параметра а, при котором выбранная функции принимает папмеиьшес значение. Обработка данных па основе минимизации функции /( называется лсто-дом наименьших квадратов, или методом панлучпюго среднеквадратичного приближении. При минимизации /г и /3 соответственно говорят о «ямлучшел» в корме Ц и яяилучшед равномерном (или чебышевское) лриблмягемни.
Эй
Часто а качестве <р(х, а) фигурирует линейная функция у = <а, х> *= fljxi 4-... 4- в„хв.	(2.8)
Здесь, следовательно, а есть n-мерный вектор. Пусть С есть матрица входныхданкых, т. е. матрица размера пгХ п, строками которой служат векторы х{ (I = 1, .... m), a, d ±= (рь уст) — вектор выходных данных. Тогда метод наименьших квадратов с функцией (2.8) приводит к задаче
/,(«)=	d||’ -+ min, neRn,	(2.7)
которая отличается от 2,22 лишь обозначениями. Отметим, что эта задача всегда имеет глобальное решение в силу теоремы 1,3. Условие rang А ви и 2.22 (соответственно rang С = н в (2.7)) обеспечивает единственность решеппя.
Отметим, что линейные записнмостп возникают чаще, чем ото может показаться на первый взгляд. Пусть, например, постулируется полиноминальная зависимость у от числового параметра I:
У — аа 4- «1* 4- «2<3	4* <М".
Если рассматривать в качестве «входного» вектор х = (1, I, Г), то получаем зависимость вида (2,0).
Рассмотрим другой пример. Многие экономико-математические модели базируются па понятия производственной функции, т. о, зависимости вида у = ср(х, в), где у —объем производства, а х = (х|....хп) — вектор используемых ресурсов. Наиболее
известным примером производственной функции служит функция Кобба — Дугласа
При построении такой функции для конкретного экономического объекта (предприятия, отрасли, сферы производства и целом) параметры ас, «1, ., „ ап оценивают по статистическим данным об у и х = (xt, .хп) за прошлые годы. Для этого обычно переходят к логарифмам:
In у == In о0 + at In х, 4-... 4- ип In хп.
В результате возникает линейная зависимость между «входом» п = (1, Inxi, ..., Inхя) и «выходом» у = 1ну. Затом решается задача тина (2.7).
2.23.	Методом наименьших квадратов найти паплуч-njyto зависимость вида .у «	+ а&ъ для опытных дан-
ных из следующей таблицы:
Нонгр опыта	«1	xi	г/
1	—1	1	—4,5
2	1	1	1,5
3	0,5	2	—2
4	0,5	0	4
31
2.24.	Пусть Л — неотрицательно определенная симметрическая матрица размера п X п, Ъ е R". Доказать, что любая стационарная точка квадратичной функции
/(я) = 4	+ <ь> *>
является точкой ее глобального минимума на R".
2.25.	Найти все значения параметров а, Ъ и с, при которых в точке (1, —4) достигается глобальный минимум функции
/(ж, у) == ая2 4- bxy + у2 4- 6z 4- су,
2.26.	Найти все значения параметров а. и 5, при которых точка (0, 1) является экстремальной для функции
/ fa У) = 2х= + а?ех 4- Ъху 4- 4 №у2 4- ayt
и выяснить характер экстремума.
2.27.	Привести пример дифференцируемой функции / па плоскости R2, сужение которой на любую прямую, проходящую через точку (0, 0), достигает строгого локального минимума в этой точке, но (0, 0) не является точкой локального минимума / па R2.
2.28.	Пусть / — непрерывная функция па R. Доказать, что между любыми двумя ее точками локального минимума лежит по крайней мере одна точка локального максимума.
2.29.	Привести пример дифференцируемой функции / па R2, у которой имеется бесконечно ’ много точек локального минимума и пет ни одной точки локального максимума.
2.30.	Отображение Ft X -* У, где X п У — открытые множества в Rn, называется диффеоморфизмом, если оно взаимно однозначно, причем F и обратное отображение /?-1. у х непрерывно дифференцируемы.
Доказать, что матрица Якоби диффеоморфизма Ft XУ в любой точке яевьтрождепа, причем обратной к пей является матрица Якоби отображения /г-1; у х в точке y = F(x), т. е.
[Г(х)]-1 =(F“,)7i/).
2.31*	. Пусть Ft X -+ У — диффеоморфизм, f(y) — дифференцируемая (числовая) функция на У, у* е У. Рассмотрим функцию ф(.т) = /(7^(.т)) на X и точку я*=* *= F~l(y*). Доказать следующие утверждения:
32
а)	у* — стационарная точка функции / в том и только том случае, если ж* — стационарная точка функции ф;
б)	у* — точка локального (глобального) минимума / в том и только том случае, если я* —точка локального (глобального) минимума <р;
в)	если / дважды дифференцируема в у* и у* — стационарная точка f, то матрица /" (у*) положительно определена в том и только том случае, если матрица ср" (а*) пололснтельпо определена.
2.32	. Пусть ж* — единственная стационарная точка дифференцируемой функции / на R, служащая точкой ее локального минимума. Доказать, что этот минимум является и глобальным.
2.33	*. Построить пример дифференцируемой функции па R2, имеющей ровно одну стационарную точку, которая служит точкой локального, но не глобального минимума.
2.34	*. Построить пример дифференцируемой функции на R2, у которой имеется ровно т стационарных точек и все они служат точками локального минимума.
2.35	. Построить пример дифференцируемой функции на R2, у которой имеется счстпое число стационарных точек и все они служат точками локального минимума.
2.36	*. Пусть / н ср — дважды непрерывно дифференцируемые функции в некоторой окрестности точки ж* е Rn, причем 7'(я*) = 0, матрица f" (я*) положительно определена н, значит, х* является точкой строгого локального минимума /. Рассмотрим функцию ф(я, е)=/(ж)+еср(а:), где 8 е R. Доказать, что существует непрерывно дифференцируемая вектор-функция х(в), переводящая некоторую окрестность V точки 0<=R в окрестность U точки х* и обладающая следующими свойствами: при любом в 7
а)	х(е)" единственная в U стационарная точка функции ф(я, в);
б)	х(в) — точка строгого локального минимума функции ф(х, в);
в)	х(0) = ж*, з/(0) = —	(я*)] “’q>'(х*) и, значит,
х(&) = х* — е [/" (ж*) ] ”!cpz (я*)-Ь о (в).
2.37.	Привести пример, показывающий, что утверждения задачи 2.36 не сохраняются, если х* есть точка строгого локального минимума /, по матрица /" (х*) не является положительно определенной.
2.38.	В дополнение к условиям задачи 2.36 предположим, что х* — точка глобального минимума функции / 3 С. А. Ашманов, А, В. Тимохов	33
яа R’“. Верно ли тогда, что я(е) —точка глобального минимума функции “ф па IV1?
Найти с точностью до о (с) при в -> 0 какие-нибудь точки локального минимума следующих функции:
2.39.	фе(х)= х2 -Ь 86х.
2.40.	i|it (ж, у) = ж3 + у3 — Зху + е (sin пя + 2 sin яу).
2.41*	. Доказать теорему Люстеркика.
Пусть £|, .... gm —непрерывно дифференцируемые функции в некоторой окрестности точки х* е R”, причем
^1(я*)=0,	т,
а градиенты gi (я*). .g™(-г*)линейно независимы. Рассмотрим произвольные векторы	..., йв, дополняю-
щие векторы £1(я*), ;g«(®*) до базиса в R“. Предположим, что вектор Л <s R" удовлетворяет условию
{gi («*). Л) 0, I =* 1. ..т.
Тогда существует такая н-мерпая вектор-функция r(<z) (а R), что для всех достаточно малых по модулю а выполнены равенства
gi(#* + ak + r(a)) = 0, i = 1, ..т,
<д<, г (а) > = 0, i = т + 1, ..п,
и, кроме того,
Иллюстрацией к теореме Люсторппка в случае, m = 1 служит рис. 3. Данная теорема находит ванинао врпмепонпл прп выводе условий экстремума в задачах с ограничениями (см. 3.8, 3.10).
34
§ 3. Классическая задача пл условный экстремум
СВОДКА ОСНОВНЫХ, ФАКТОВ
Классической задачей на условный экстремум приня-то называть задачу минимизации (или максимизации) функции / на множестве Л\ заданном системой из конечного числа уравнений («связей»):
X = {# <= Rn 1 g( (я)« 0, i = 1, ..т).
Запишем эту задачу в виде
/(ж)-^ min, gi(z)=0,	(3.1)
t. Отыскание решения методом исключения переменных. В некоторых случаях возможен следующий подход к отысканию решения задачи (3.1). Допустимое множество задачи представляет собой систему из m уравнений с п пеизиестнымн; при этом, как правило, т<п. Предположим, что х = (и, у)<= Rn X К’1-" п для любого у •= система
g((«, v)^ 0, i® i, m,
из m уравнений с ?п неизвестными имеет единственное решение и = и(и). Тогда задача (3.1) сводится к задаче безусловной минимизации
F(v)=/(u(y), v)-»-niin5 pelV-”’. (3.2)
Если у* — локальное (глобальное) решение данной задачи, то, очевидно, (и(у*), у*)—локальное (глобальное) решение задачи (3.1), и наоборот.
Описанный метод исключения переменных имеет ограниченную область применения, поскольку указанная выпи? однозначная функция и(у) существует далеко не всегда. Кроме того, при выписывании условий экстремума л задаче (3.2) часто возникают довольно громоздкие выражения, Более универсальным является метод Лагранжа, основанный па использовании условий экстремума непосредственно для задач вида (3.1).
2. Условия экстремума. Введем функцию Лагранжа задачи (3.1):
Цху Уо, у) yof(x) -к 2 !№i (*).
fwr I
3*
35
где х ® R*, I/O е 11, У = (01.Пусть
Ь'х(х, ус, у) =* yaf (х) 4- 2yigi (ж)
— градиент функции Лагранжа по ж;
(3.3)
 m
Ь» (ж, уй, у) ₽ y<f (.г) + 3 0igi (*)
— гессиан функции Лагранжа по я.
Следующая теорема, лежащая в основе метода Лагранжа, является центральным фактом классической теории условного экстремума.
Теорема 3.1 (необходимое условие минимума первого порядка, или принцип Лагранжа). Лустъ функция / дифференцируема в точке	функции gi, .... gm
непрерывно дифференцируемы в некоторой окрестности этой точки. Тогда если х* — локальное решение задачи (3.1), то существую?1 число У* и вектор j/*eR', не рае-ные нулю одновременно и такие, что
,	f f	^х(х*, Уо*,^)-О. (3.4)
'	/ \/	/	Условие (3.4) имеет яс-
/ пый геометрический смысл:
--------1	~ Fte?*) ° учетом (3.3) оно означает, ' /I *	? что градиенты }'•(&*) i
i/	\	I	gl(s*), .... gm(x*) являются
’г	\	линейно зависимыми. В ча-
-"'У	Д_ '	'*»	стяости, если 1,то/'(#*)
р? «о	'(зд^сс п должны быть колли-
р|1С 4	псарными. Напомним, что эти
градиенты, если они отличны от нуля, направлены ортогонально к поверхностям (линиям) уровня f(x) = f(x*) и gi (я) = gi (я*) = 0 соответственно, причем их коллинеарность говорит о том, что решение я* должно быть точкой касания данных поверхностей (рис. 4). Фактически это необходимое условие экстремума ужо использовалось при решении некоторых задач из § 1.
Точка ж* X называется стационарной точкой задачи (3.1), если она удовлетворяет (3.4) при некоторых ?/о^О н y*<=R,u> по равных нулю одновременно. При за
этом числа у*. у*, .,ут называются .иножнтслялги Лагранжа, соответствующими я*.
Равенство (3,4) вместе с условном х*^=Х образует систему из ii’Vm уравнений с » + то + 1 неизвестными. При этом всегда можно перейти к п + т неизвестным, рассматривая два случая: уа <=> 0 л у0 => 1.
Любое дополнительное предположение о задаче (3.1), обеспечивающее в теореме 3.1 случай у*=гО, принято называть условием регулярности. При наличии такого условия и саму задачу (3.1) называют регулярной. Для нее достаточно рассматривать лишь регулярную функцию Лагранжа
L (ж, у) = L (ж, 1, у) => / (ж) 4- 2 yigi (*)• i°l
Основными примерами условия регулярности служат условие линейной независимости градиентов gi(x*), ... ..., Ят(.г*)п условие линейности функций gifr), ... ..., gm(.r), т. е. gt(х) = <a\ z> + bit где	&ceR
(г = 1, ..., то).
Теорема 3.2 (необходимое условие минимума второго порядка). Пусть функции f, gi, ..., дважды дифференцируемы в точке х* Пусть, кроме того, функции gi, ..., непрерывно дифференцируемы в некоторой окрестности ж*, а их градиенты gi (ж*). ..., £т(ж*) линейно независимы. Тогда если ж* — локальное решение задачи (3.1), то
<^(*’,у;,У*)Л,Л>>0	(3.5)
при любых у*>0, у*<=Нт5 удовлетворяющих (3.4), и всех таких A es IV1, что
(gi (**). A) « 0, i = 1, ...»то.
(3.6)
Теорема 3.3 (достаточное условие минимума второго порядка). Пусть функции f, gi, ..., gm дважды дифференцируемы в точке ж* s X. Тогда если существуют такие Уо О и у* R"1, что выполняется (3.4) кроме того,
(я*> У*> У*) А, А.)> 0
(3.7)
37
при асах Zi^O, удовлетворяющих (3.6), то .г*— строгое локальное решение задачи (3.1).
Условие (3.6) означает, что вектор k ортогонален к линейному подпространству, натянутому па градиенты £i(^*)« ..мЯт(л*)> Поэтому его называют условием ортогональности.
В отношении теорем ЗЛ—3.3 можно высказать замечания, аналогичные замечаниям 2.1—2.3. В частности, эти утверждения сохраняют свою силу, если в ограничения задачи (3.1) добавлено условие х е Р, по х* е intP.
УПРАЖНЕНИЯ
3.1.	Найти глобальное решение задачи ху3 max, ах + by «а» с
сначала методом исключения переменных, а затем методом Лагранжа:
	л	b	с	а		b	е	а		Л	С	а		b	с
1	2	3	7	G	2	5	(3	11	3	1	10	1ft	ft	О	4
2	1	5	8	7	1	4	8	12	1	5	10	17	ft	2	8
3	3	1	0	8	3	5	7	13	2	7	10	18	8	2	5
4	2	4	9	9	4	3	6	14	4	4	8	11)	В	2	10
5	4	1	8	10	1	0	9	15	4	2	12	20	8	3	11
3.2,	Найти точки экстремумов функции /(.т, у)=ах + Ьу
при условии х2 + у2 == с2 *):
	л	b	с	л		Л	С	а b		с	а		b	с
1	2	-3	5	ft	7	2	4	1!	—2 —5	5	10	5	1	3
9	4	1	3	7	-2	ft	9 м	12	5 —3	1	17	-1	5	1
3	-3	4	2	8	-1	7	5	13	-5 -1	2	18	2	5	2
4	-2	1	1	9	-4	-1	3	14	-7 -1	4	19	-5	3	5
5	2	3	4	Н)	—2	-3	1	15	1 -7	3	20	1	7	4
♦) См. подстрочное примечании к упражнению 2.4.
38
3.3.	Найти точка экстремумов функции /(я, у) = ах2 + 2ху + by2
при условии 4z2 + су2 = 9:
	а	b	с	а	b	с	а	Ь	с	а	Ь с
1	1	1	3	IJ 3	2	2	И 5	8	6	16	7	4 2
>	3	4	5	7 5	4	3	12 5	3	2	17 13	4 1
3	1	1	2	8 3	5	6	13 9	3	1	18	7	И 6
4	1	2	6	9 7	9	5	14 9	7	3	19	9	5 2
5	1	1	1	10 5	2	1	15 3	6	7	20	7	13 7
	3.4. Найти точки экстремумов функции										
				у) =			ах3 + &у3				
при условии дг + у2 =					с2:						
	а	Ь	с	it	&	с	а	b	с	а	b с
1	3	2	2	б 3	1	3	И 1	8	1	16 2	3 4
2	7	3	3	7 4	3	4	12 4	1	5	17 2	7 1
3	1	2	5	8 1	4	5	13 5	3	4	18 8	1 2
4	7	2	1	9 5	2	2	14 2	5	3	19	1	3 5
5	3	4	2	10 3	5	1	15 2	1	2	20 3	7 3
3.5. Найти точки экстремумов функции
/(*, у)=№
при условии аж3 + &у3 — Зеху = d:
	а Ь с	d	а		b с		<1	а		b с	d	а		b с		d
1	9 2 9	—16	(I	12	1	6	-10	11	—1	2 1	—4	16	-7	16	7		2
<>	-30 1 9	8	7	1	0	1	4	12	-4	1 2	-16	17	28	1	7	8
3	—9 2 9-	16	8	4	1	2	16	13	-18	4 9	4	18	1	2	1	12
4	7 2 7	18	у	-7	2	7	—п;	14	У	10 9	. . о	19	1	16	2	12
5	3 2 3	—4	10	36	1	9	-8	15	14	4 7	4	2(1	1	1	1	
3.6.	Найти точки экстремумов функции
/(я, У, з) = <i2^2 -1* b2y2 + cz + 2{аЪху + beyz + acres)
39
лрп условии ах -I- by 4- c2zz =* 3/2:
	а	ъ	с	а		ь	с	а		ъ	с	а		ь	с
1	-5	1	-2	б	6	—1	1	и	5	—4	1	16	6	3	-5
2	1	-4	5	7	1	5	—2	12	-4	2	3	17	-1	7	1
3	-С	5	4	8	-3	2	4	13	1	0	—3	18	5	2	—4
4	1	2	—3	9	—5	2	—5	14	-3	-5	4	19	-3	7	5
5	3	-4	2	10	3	-6	3	15	6	4	-5	20	5	3	—2
Указание: добавить к функции f выражение «я ф- by 4- Л’ и выделить полный квадрат.
3.7.	Найти проекцию начала координат в пространстве R4 на множество
Х = {ж КЧач-Ч- ах% — х< = &, xt + а^з + xt = с):
	а	Ъ	с	а		ъ	с	а		Ъ	с	а		b	е
1	2	9	6	6	2	9	—9	И	1	G	6	16	1	6	—9
2	2	9	-6	7	2	—9	9	12	1	6	—В	17	1	-6	9
3	2	—9	6	8	2	-9	—9	13	1	—6	6	18	1	-6	—9
4	2	—9	—6	9	2	9	18	14	1	—С	—6	19	1	6	12
5	2	9	9	10	, 9	9	—18	15	1	6	9	20	1	6	—12
3.8.	Найти все значения параметра к, при которых точка (0, 1) является экстремальной для функции
/ (я, у) = In (ах ч- 2/с2у) — kbxy Ч- х + су
прп условии +	1, и выяснить характер экстре-
мума:
	а	b	С	а		ъ	е	а		b	с	а		b	<•
1	4	4	3	6	3	3	2	11	2	2	1	16	t	1	0
2	4	-4	3	7	3	-3	2	12	2	-2	1	17	t	—1	0
3	4	-1	3	8	3	—3/4	2	13	о	—1/2	1	18	1	—1/3	0
4	4	1	3	9	3	3/4	2	14	2	1/2	1	19	1	1/3	0
5	4	—2/3	3	10	3	—1/2	2	15	2	-1/3	1	20	1	-1/6 о	
40
ЗАДАЧИ
Найти точки экстремумов следующих функций при указанных ограничениях *):
। 3.1. f(xt у) = у, х2 + у3~Зху = 0.
3.2.	/(я, у) = ^4-у3,	ax + by = i„ где а>0, Ь>0.
3.3.	I (х, у) «во -1 х8 + у, з?- -|- у- = а, где а > 0.
3.4.	/(ж, у) = х sin у,	Зх2 — 4 cos у — 1 = 0.
• 3.5. f(x, у, z)^xyz, йг24-у2+гг = 1, ж4-у4’я = 1.
3.6.	/ (я, у, z) = а?х2 4- Ь2у2 + c2z2 — (а®2 + & у2 "I" cz2)2, х2 4* у2 + я2« 1, где а > b > с > 0.
3.7.	/(ж, у, z)=ix + y4-з24-2(яу4-yz4-за), ж24-у24-4- z = 1.
3.8.	Доказать теорему 3.1.
3.9.	Пусть в условиях теоремы ЗЛ градиенты g^x*), ... ..., gm (#*) линейно зависимы. Следует ли отсюда, что обязательно у$ = О?
3.10.	Доказать теорему 3.2.
3.11.	Привести пример, показывающий существенность условия линейной независимости градиентов gi(.r*), - . • .••»£«(«*) у теореме 3.2.
3.12.	Доказать теорему 3.3.
3.13.	Пусть выполняются условия теоремы 3.3 прп Уо = 0. Доказать, что ж* — изолированная точка допустимого множества задачи (34). ГГрявести пример, когда условия теоремы 3.3 выполнены именно при у9 ® 0.
Найти глобальные решения следующих задач:
3.14.	П ж?7-*-max,	ж,Л>0, /=!,...
J=i	Л=1
,... л, где а;>0, р;>0, а,<>0, Ь>0.
3.15.	2 fj.r;J->“min, =	ж;^0.
где £?;>{), <Ж>>0, Р; > О, Ъ> 0.
346.	2’V~>’niin’ П®?' = *»
J«.l «у J
где с;>0> «./>0, pj>0, &>0. п	fl
3.17.	27>0»
где (Tf>0, <х>0, й;>0, &>0.
•) См, подстрочное примечание к упражнению 2.4
41
3.18.	2	S arTj = Ь- Я;>0, 7=1, ...
...,п, где с;>0, «>>-0, £»>-0, 0<а<1. п	п
3.11)	. 2 Cj.7!j-vinin, 2 ЙЛ" = Ь, где с;>0, а — чет-ji=]	j 1
кое натуральное число, a = («r, ..., дг1) 0 (ср. с задачей 3.2).
3.20.	2	2e^j = i, где С;>О, а>
^>1, а = (flp ..., Лд)5^ 0, b0. п	п
3.21.	2 max (min), 2	ГДС с — fan -«♦
7«1	7=1
.,.. с„)	0,	а.} >0, b > 0, а — четное натуральное
ЧИСЛО, п	я
3.22.	2 max (min), 2 ai I !“=&> W c—(<?n <   ...>Cn)¥=0, «j>0, k>0, a>l.
3.23.	2 I&5 + Cj ]“->- max (min), 2 I -rj Г =* где c = = (c,, ..., en)^0, <x>1, 6>0. n	n
3.24.	у 2 я®-* min, 2 <l}№ =* *= 1» 2’ где a^' juil
bi — заданные числа, причем векторы й«=(ац, ..., а^,... • --1 «in) (' = 1» 2) липейпо независимы.
3.25.	-j <С.т. аг>. 4- <rf, ж} —>- min,	Az = Ь, где С — по-
ложительно определенная матрица размера п X и, Л матрпца размера т X n, rang Л = т, d,^ IV1, Ъ «= R".
3.26.	4-1^' —51®-*-min, Л.л=6, где Л—матрица размера кХп, rang JTen, CeRk, а А и b те же, что и в 3.25.
Напомним, что если Л = Е — одпппчпая матрица размера >г X », то решение дипной задачи ваэыпается проекцией точки 15 на множество X = {z | ?lir = 6}.
3.27.	Пусть А — симметрическая матрица размера «Х?г. Тогда, как известно (см., например, [39, с. 15]), стационарными точками задачи минимизации функции /(г) = <?1д:, х> при ограничении 1Ы1 = 1 являются собственные векторы ж*.....х’1 матрицы А. Если при атом
Хц. — соотвегствующпе им собственные значения п	0' = 2,	7t), то ж’ — глобальное решение за
42
дачи. Вылепить, являются ли остальные собственные векторы локальными решениями этой задачи.
3.28.	Найти все значения параметров а. и б, при которых точка (0, 0) является экстремальной для функции
/(*, у) = (а + 2)ж- 2у
при условии д(аН- е*)+ Ь(у + еу) = 1, и выяснить характер экстремума.
3.29.	Найти все значения параметров а и Ь, при которых точка (0, 1) является экстремальной для функции
/(ж, р) “ х2 + ах *Ь by2
при условии ж2 — ху + у2 = J, и выяснить характер экстремума.
3.30.	Доказать теорему Финслера.
Пусть >! и С’ —матрицы размера »Хв, причем С неотрицательно определена. Предположим, что <Л;г, ж> > 0 для всех таких ;к¥=0, что <<7ж, ж>=0. Тогда матрица Л -НАС положительно определена при любом достаточно большом
3.31.	Пусть Л к В — матрицы размера лХн и ??iX« соответственно. Доказать, что следующие условия эквивалентны г
а)	<Л.ж, ж> > О для всех таких «'/’О, что £х = 0;
б)	матрица Л + КВТВ положительно определена при любом достаточно большом
Пусть, кроме того, rang В = т. Доказать, что из а) или б) следует
в)	матрица
г-[л пГ ь " в (J
размера (п 4- да)Х(« + т) иевырождена.
3.32.	Пусть Л = (а0)—симметрическая матрица размера н X я, В 153 (бу) — матрица размера m X л. .Для любого /с *= 1, ../?. положим
Г\| ч ’	* v • а *«
_бцц ... ^||Л_
А, = (-!)-det nh *
Рассмотрим три условия:
43
a)	</lz, x>> 0 для всех таких x ¥= 0, что Вх •=• 0;
б)	А* >0 для всех fc ® 1, ..., п;
в)	Дк > 0 для всех к ±а 1, ..п.
Доказать, что из а) следует б), а из в) следует а).
3.33.	Пусть А — симметрическая матрица размера вХп, Ь — вектор-строка из R". Для любого А‘=1, ..., п положим
где обозначение взято из 3.32, а б*— вектор из пер* вых к координат вектора 6. Доказать, что следующие условия эквивалентны:
а)	<Дж, я>>0 для всех таких я =# 0, что <Ъ, х> = 0;
б)	либо 6fl < 0, либо бА^0, dotAX) для всех к<=> = 1, ..п.
3.34*	. Рассмотрим задачу (3.1), где функции /, g.
..gm дважды дифференцируемы. Пусть .г* — стационар* пая точка задачи, удовлетворяющая (3.4) вместе с некоторыми 0 и у* е IV’. Пусть, далее, Л = Lx (ж*, у*), В — матрица со строками gi (л:*) (i° 1, ..., м). Предположим, что (в обозначениях из 3.32) ДЛ>0 при всех fc=l, п. Доказать, что ж*— строгое локальное решение задачи (3.1).
3.35.	Рассмотрим задачу минимизации при линейных ограничениях-равенствах
/(х) min, Вх =» d,	(3.8)
где /—дважды дифференцируемая функция, В — матрица размера тХп, rang 5 = от, d<=R‘n. Пусть а:* —стационарная точка задачи (3.8) и Л<=/"(х*). Предположим, что (в обозначениях из 3.32) ДА>0 для всех k= I, - >• ..и. Доказать, что х* — строгое локальное решение задачи (3.8).
3.3G*	. Пусть числовая функция /(.г, с) и от-мернал вектор-фушщня G(x, е) дважды непрерывно дифференцируемы в некоторой окрестности точки (.г*, 0)е IV' X R , причем ранг матрицы Якоби Gx (;>*, 0) (размера /лХн) равен т. Рассмотрим при данном 8 <= IV задачу
f(z, e)-*-niin, G(.r, е)=0	(3-9)
л ее регулярную функцию Лаграплса
L(«, у, е)=/(ж, 8)+<у, G(xt 8)>,
44
где х R'1, у е IV. Предположим, что точка л* вместе с некоторым у* удовлетворяет условиям:
У* 0) = 0, С(х»,0)-0, <д:(х* у*0)Л,Л>>0
при всех таких h ГЯ 0, что G* (.?*, 0) h = 0. Тогда, заметим, я* есть строгое локальное решение задачи (3.9) при е = б (см. теорему 3.3), а у* — соответствующий вектор множителей Лагранжа. Доказать, что существуют непрерывно дифференцируемые функции я(е) и у(е), переводящие некоторую окрестность V точки O^Iv в окрестности U и IF точек х* и i/* соответственно п обладающие следующими свойствами: при любом е <= V
а)	ж (е)—единственная в U стационарная точка задачи (3.9), а р(е)—единственный соответствующий ей вектор множителей Лагранжа;
б)	ж(е)— строгое локальное решение задачи (3.9);
в)	4г(0) = я* у(О)=у*
3.37*	. Пусть в рамках предыдущей задачи /(.г, е) = сз/(.т), (7(ж, е)= (7(ж)“ е (и, значит, к = т). Положим ф(е)==/(я(е)). Доказать, что <p'(s)»= — у(е) при любом ее К
Оставшаяся часть параграфа посвящена разнообразным примерам использования классической теории экстремума. В отличие от предыдущего, где требовалось решать явно сформулированные окстремальпые задачи, здесь всякий раз необходимо сначала формализовать поставленную проблему в впде задачи оптимизации.
3.38.	На плоскости даны точки А и В по одну сторону от прямой I. Пусть С — такая точка на Z, что сумма расстояний от Я до С и от С до В является наименьшей. Доказать, что углы между прямой 1 и отрезками ЯС и ВС равны (задача Герона).
3.39.	Согласно принципу Ферма, свет, исходящий из точки Я и попадающий в точку В, распространяется по той траектории, для прохождения которой требуется минимум врсмОпп. Пусть точки Я и В расположены в различных оптических средах, разделенных плоскостью, причем скорость распространения спета в первой среде равна vi, а,во второй опа составляет yj. Вывести закон преломления света, т. е. охарактеризовать траекторию его движения из Я в В (задача Снеллиуса).
ЗЛО. В данный треугольник АВС вписать параллелограмм ADEF (DZJIMC, ГЯНЯД) наибольшей площадп (задача Евклида).
45
3.41.	Среди всех треугольников, вписанных в данную окружность, найти тот, площадь которого наибольшая,
3.42.	Среди всех треугольников, описанных около данной окружности, найти тог, площадь которого наименьшая.
3.43.	Среди всех треугольников данного периметра 2р найти тот, площадь которого наибольшая.
3.44.	Доказать, что для треугольника со сторонами а, &, с и площадью 6' имеет место соотношение а2 + Ь2 + + с2 5= 4SV3.
ЗЛ5.	Даны угол А и точка Л/ внутри пего. Требуется провести через Л/ прямую, отсекающую от угла треугольник на им спыпей площади.
3.46.	Доказать, что объем V н боковая поверхность S прямого кругового конуса удовлетворяют неравенству
3.47.	Среди всех шаровых сегментов с заданной площадью сферической поверхности лапти тот, объем которого наибольший (задача Архимеда).
3.48.	Среди всех параллелепипедов, вписанных в дивный эллипсоид
а2л? Н- b2y2+ а2&2 = 1,
найти тот. который имеет наибольший объем.
3.49.	На плоскости задай треугольник АВС. Средн всех пирамид с основанием АВС и высотой данной длины найти ту, которая имеет наименьшую боковую поверхность,
3.50.	Непустое множество 5 == {х е К"|^(з:)= 0} называется гладкой поверхностью, если (числовая) функция g непрерывно дифференцируема на R” и ее градиент g'(x) отличен от пуля в любой точке х е S. При этом g'(x) называют нормалью к S в х.
Доказать, что если х— проекция па гладкую поверхность S точки a<£S (см. п. 3 § 1), то вектор х — а ортогонален к S в х, т. е. коллинеарен нормали g'(x).
3.51.	Пусть и S? — две пеиеросекающиеся гладкие поверхности в Rn, Доказать, что если точки x<^S\ и у находятся па ближайшем расстоянии друг от друга среди всех пар точек, одна из которых лежит в Sj, а другая в 5а, то вектор х — у ортогонален к Si в х п к Si в у.
46
3.52.	Пусть 19 *= {z[g(.r)~O} — гладкая поверхность в R”, а и 6 —такие точки из R", что соединяющий их отрезок
(«, й] = telx “Ла + (1 — Л)Ь, 0Л О
не пересекается с 5, х — такая точка из S, что сумма рас-стояппй от а. до ж и от х до b минимальна. Доказать, что нормаль g'(x) является липоппой комбинацией векторов а — х и Ь— х, причем g‘(х) (или —g'(x)) делит угол между этими векторами пополам.
Таням образом, здесь обобщается утиерлщоние задачи 3.38 на случай произвольной гладкой поверхности.
3.53.	В пространстве Rn найти точку х, сумма квадратов расстоянии которой от т данных точек .т’, ..., ас"1 минимальна.
3.54.	На единичной сфере в И'1 пайти точку .г, сумма квадратов расстояний которой от т данных точек ж1, ... .,., ж'“ минимальна.
3.55.	Донное положительное число b разложить па п слагаемых так, чтобы сумма их обратных величин была наименьшей.
3.56.	Данное положительное число b разложить па п слагаемых так, чтобы сумма их квадратов была наименьшей.
3.57.	Найти наименьшее значение суммы «2 + i5, где at b — числа, при которых уравнение
х* + ах? + Ьз? + ах + 1 «= О
имеет хотя бы одни (действительный) корень.
3.58*	. Доказать неравенство между средним геометрическим и средним арифметическим: еслп я:;>0 (/ = 1, ... ..., п), то
Убедиться, что равенство имеет место лишь в случае Xj “... “ хп.
Это и приводимые ппжс классические перадопствя можно до-кпзывап. разлвчпымп способами. Здесь предлагается их вывести путем рассмотрения соответствующих задач на условии» экстремум.
На.йтн глобальные решения следующих задач:
3.59.	/ (х) = xL 4- J + • •  +	+ — -> min,
	, ________ Ж“(й!1, ..., ®n)>0.
47
3.60.	/(ж) еа	max, Яд^ +	+ ж3 4- ^3*4=
= I , Ж = (•'Cj, Z.yi “^"з> ^4)	0.
3.61.	Доказать следующее обобщение неравенства из п	я
3.58: если т} > 0,	0 (/ = 1, ..., п), 2 «,= 1, то ]~[ж/
л
S аЯг Убедиться, что при положительных <Xj равеп-5=1
ство имеет место лишь в случае да =... =» жп.
3.62,	Доказать неравенство между средним арифметик ческам и средним квадратичным:
Убедиться, что равенство имеет место лишь в случае Я71	« • • ®® «Ет1»
3.63.	Пусть я = (Ж|, ..., дг„)>0, e*=>(cit ..., с„)>0, Л
2cj = li р —'Произвольное число из расширенной дей-£**1 — ствлтельпой оси К. Положим
	/ n	у/р 5 crrf 1 » если р е R, р \Jh*1	/
5р(я, с) =	'Y"Lr С- Д я/, если р « 0, >=i max{rM, ,яп), если р = оо, min {дгр ..яп}, если р = — со.
Эта величина при p<^R называется взвешенным средним порядка р чисел Ж1, ..с коэффициентами ci, ... си. Если все cj равны 1/п, то говорят просто о среднем порядка р.
Доказать следующие утверждения:
а)	при любом ненулевом 7 <= R справедливо равенство
8,{х, c) = [Sm^, e>J >'•,
где з? ®	•т’н),
б)	величина 5Р(ж, е) как функция от р непрерывна па R; в частности,
lim Зр (я, с) =	(ж, е),	1 ini Sp (я, c) = S^ (ж, с).
J>-»Q	Р-*±«>
48
3.64*	. Доказать неравенство между взвешенными средними: если я =<(#], .х„)>0, c = (elt ..., сп)>О, п	_
2 CS= 1, /?, tf^R я p<q, то
J4=' 1
5р (iEj	с)»
Убедиться, что равенство имеет место лишь в случае 2»! “• > * •	3?п»
Таким образом, неравенства пз 3,58, 3.61, 3.62 явияются част» пыми проявлениями факта неубывания вэвошоппых средних по их порядку.
3.65*	. Доказать неравенство Коши — Вуняковского п	/”й п *
Зад <1/ 24 24-J=1	г iml >-1
Убедиться, что при у=(уь ..., уп)^0 равенство имеет место лишь в том случае, если 2^«=Л^ (J = 1,	и),
где Х<=11; точнее говоря, левая часть без модуля равна правой, если X О, и правой со знаком минус, если Х^О.
3.66. Найти точную нижнюю п точную верхнюю трапп
функции
/ (я, У)
ах -Ь &у + с /?+7+t
на R2 и выяснить, какая из граней достигается (ср. с упражнением 2.5).
3.67*	. Доказать неравенство Гёлъдера: если р>1, и — -Ь — » 1, то
*	р q
П	/в \1/р / n \l/fl
2|эдК131^|р) (S 1уЛ’) • j-i	/ \j=i /
Убедиться, что при #=(i/i, ..., уп) ч*0 равенство имеет место лишь в том случае, если IxJ₽ = XlyJ’ (/ = 1, ..п), где ?.eR.
3.68*	. Доказать неравенство Минковского: если р > 1,
то
(n	\1/Р	/ п \1/р	/ в \1/р
3 | Xj pj |р 1	<21 2 | |р ]	+ ( 2 | У] |Р)
/ \j=x / \j-i /
Убедиться, что при y=(yi, ..., уп)^0 равенство имеет место лишь в том случае, если a.j = Xyj (j=> 1, ..., п), где К 0.
4 о, а, Ашманов, л, В, Тимохов
49
3.69.	Доказать неравенство Адамара: если А = (бГц)— матрица размера пХп н Д = del Л —со определитель, то
л . п \
Д2 ТТ I	Убедиться, что равенство имеет место
i”l'j=i /
лишь в том случае, если ААГ есть диагональная матрица, П
т. е. 3	— 01ЦШ всех £, к =1, ..и, I =¥= к,
5">
3.70.	Доказать, что при всех а > 1 система
a cos a sin у + хе и = О,
a sin ;т cos у + уех = О
имеет решение, отличное от (0, 0).
3.71.	Доказать, что при всех л >0 система
в.Т	У	II	Л!
имеет решение.
3.72.	Капитан Грант, стоящий на прибрежной скале высотой h м, бросает в море с начальной скоростью и м/с бутылку с письмом о помощи. Под каким углом к плоскости земной поверхности должен быть совершен бросок, чтобы бутылка улетела в море как можно дальше? Сопротивлением воздуха и ростом капитана пренебречь.
3.73.	В колонне-смесителе происходит химическая реакция превращения сырья в ценный продукт. Режимом работы смесителя назовем пару (Т, 0), где Т—общее время реакции, 0 — температура в смесителе, которая поддерживается постоянной п по должна быть меньше заданной величины 0о. Ход реакции при данном режиме (7’, 0) описывается задачей Коши:
К(1)= 4 (0 - 0о) (К -К (I)), #(0) = 0,
где K(t)— концентрация продукта в смесителе в момепт времени t после начала реакции, а ч л К — заданные параметры, 'f > 0, 0 < А’ 1 (А имеет смысл максимально достижимого в данной реакции значения копцситра-цпи). Финансовые расходы при работе смесителя в режиме (7‘, 0) описываются формулой D^pX2^' •Ь Р2(0 — 0о)3, где Д|. дг — известные положительные параметры. Требуется определить режим работы смесителя, обеспечивающий наивысшую концентрацию продукта по окончании реакции при заданном объеме затрат Do.'
Глава 2
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Первой из. «исклаесическпхо задай оптимизации была подробно исследована задача отыскания экстремума линейной функции па множество, заданном линейными неравенствами и равенствами. Раздел теории оптимизации, изучающий такие задачи, получил название линейное п /?оа рамми рован и с,
В данной главе приводятся основные положения линейного программирования, включая теорию двойственности и симплекс-метод. Но начнем мы с теории линейных неравенств, составляющей математический аппарат линейного программирования.
Па протяжении всей главы используются следующие обозначайия.
Под 5'/- (?п, п) понимается совокупность всех матриц размера тХп с вещественными элементами. Если дана матрица Л с°(ли)<= &£(т, п), то ее строки обозначаются через а( (г «= 1, .... т), столбцы — через aJ Если при этом I и / — непустые подмножества множеств т.} и {!, соответственно, то Aj есть матрица со строками щ	А7 —матрица со столбцами а*
(/^ /). Аналогично при данных векторе Ь=(61)^В"' л непустом множестве I с {1, ..., т} под bt понимается вектор с координатами bt (is/). Символ 1/1 обозначает число элементов коночного множества Z.
§ 4. Элементы теории линейных неравенств
СВОДКА ОСНОВНЫХ (ПАКТОВ
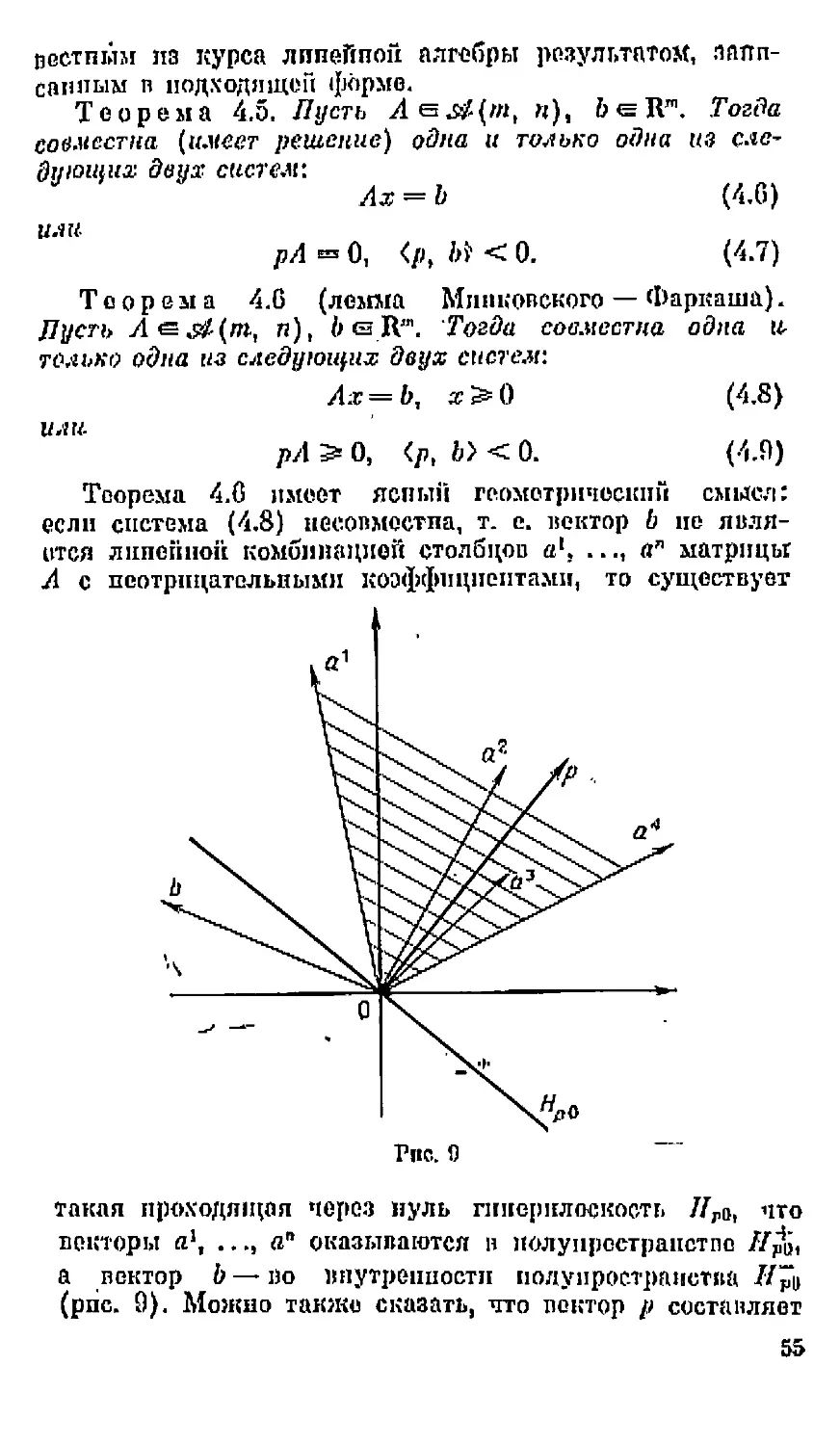
I. Полиэдры и их вершины. Kali известно, множество //а» = {z е R’‘| <а, х> = W,
где a s R", д ’/- 0, & е В, называется гиперплоскостью, а множества
Нм — (х (= Вп ] <а, х) Ь), Н&> = [ге R"| <а, z> £>] 4*	61
— полупространствами, порождаемыми этой гиперплоскостью. Вектор а, называемый нормалью к гиперплоскости НоЬ, к пей ортогонален и направлен в сторону полупространства Мм (рис. 5).
Множество Xс R" называется полиэдром, если его можно представить как множество решений системы из
конечного числа линейных неравенств, пли (что то же самое) как пересеченно конечного числа полупространств, т. е. если
Х = {xeR"|.'k^W ={jsR"|<s(, x>*£b(, j=l, .m}, (4.1)
где Л e^(wt n), b R” (рис. 6).
Для любой точки х^Х обозначим через Цх) множество номеров тех неравенств из (4.1), которые в данной точке выполняются как равенства:
Цх) ~ {i, 1	| <а;, ж> = Ь,}.
(4.2)
Ограничения с номерами из Цх) называются активными в точно х. Так, для точки ж* на рис. 6 активным является только второе ограничение (/(.?*) = (2)).
Точка я* называется вершиной полиэдра X из (4.1), если з*<=Х н среди векторов at (ie/(x*)) имеется и линейно независимых, т. е. rang = п. Другими словами, точка х* <== X является вершиной X, если опа служит единственным решением системы уравнений
Л 2(x'*>Z = &Дх»).
52
Таким образом, для вершины ®* по необходимости |/ (x*) I 5s п. Вершину ir* называют невырожденной, если |/(х*)1=?г (рпс. 7), и вырожденной в противном случае (рис. 8).
Теорема 4.1. Любой полиддр имеет не более конечного числа вершин.
Полиэдр может и не иметь верпшп, как показывает пример полупространства.
Теорема 4.2. Непустой полиэдр X вида (4.1) н.ие-ет1 по крайней мере одну вершину в том и только том случае, если rang А = п. Более точно, при выполнении данного у словил для любой точки х X существует такая вершина я*, что I(x)czl(x*).
Заметим, что равенство <о, х> ~ Ь равносильно неравенствам <п, хУ^Ь, <—а, ж> С — Ь. Поэтому множество
X = {ас <= R" I <аг, хУ bif i = 1, ..k,
<at,x> = bi, i«= JctI, ..., m),	(4.3)
конечно, является полиэдром. Говоря об этом более общем но форме записи полиэдре, под Л и b будем по-прежнему понимать матрицу со строками щ (f»=1, ..., in) и вектор с координатами Ь{ (1 = 1, ... ..., nt), под /(а:*)—множество из (4.2) (в которое уже обязательно входят номера от А"+1 до т). Попятно вершины и теорема 4.2 переносятся па полиэдр (4.3) в буквальной их формулировке, так как присоединение к матрице тех или иных ее строк с обратным знаком не меняет ее ранга.
Чтобы пайтп все вершппы полиэдра X вида (4.3), необходимо для каждого множества /<={1, тУ такого, что 1/1 «=п и квадратная матрица Л1 невырождена, пай-
53
ти решение x системы	Если x^X, to по оп-
ределению x* — вершина. В противном случае следует просто перейти к очередному /.
Выделил! особо полиэдр X вида
X=HRr,|Hx»6i г>0) «
= р s R”
N
}*-•!
a\tj = b, х = (.г,-) О
(V<)
где /I е (ш, п), & «= Rrt.
Для любой точки	IV обозначим через J(x) мно-
жество померон ее положительных координат:
Цх) =* {/, 1 / eg > О).	(4.5)
Теорема 4.3. Непустой полиэдр X вида (4.4) всегда имеет по крайней мере одну вершину. Колее точно, для любой точки, х^ X существует такая вершина х*, что J(z*)<=2 7(х),
Теорема 4.4. Ненулевая точка х*, принадлежащая полиэдру X вида. »(4.4), является его вершиной в том и. только том случае, если векторы a* (j J(x*))t т. столбцы матрицы Л, соответствующие положительным координатам точки #*, линейно независимы^). При этом вершина х* невырождеиа, если |7(х*)| т, и вырождена в противном случае, т. е. если |/(я*) I < ш.
Отметим, что вершины полиэдра (4.4) часто называют его опорными точками.
Чтобы найти все вершины (опорные точки) полиэдра (4.4), необходимо для каждого множества J g с(1,	/л) такого, что столбцы a’ (j J) линейно не-
зависимы, составить систему
У! a’xs = Ь.
jzJ
Если она имеет решение х} (j^J), причем .т>5=0 при всех j s J, то, положив = 0 при всех j <^ (1, ..., u}\J,-получим, что точка a:^(xj)eR"— вершина. В противном случав осуществляется переход к очередному J.
2. Теоремы о разрешимости систем линейных неравенств; Фундаментальную роль в теории линейных неравенств и ее приложениях играют приводимые ниже теоремы 4.6 н 4.7. Теорема 4.5 является фактически из-
*) Если :’ = 0еА' (т. е. Ь = 0), то, очевидно, —вершила X.
54
йостпым из курса лппеГшой алгебры результатом, паттп-санпым в подходящей форме.
Теорема 4.5. Пусть АвЩш, и), b^R”. Тогда совместна (имеет решение) одна и только одна из сле~ днюших двух систем:
Ах = 1>	(4.6)
«лк. рЛ *= 0, <р, М < 0.	(4.7)
Теорема 4.6 (лемма Минковского — Фаркаша). Пусть Ле^(щ., и), doR". Тогда совместна одна к-только одна из следующих двух систем:
Лх=Ь,	(4.8)
или. рЛ 5= 0, <р, Ь> < 0.	(4.9)
Теорема 4.6 имеет ясный геометрический смысл: если система (4.8) нееовместпа, т. е. вектор b ие является линейной комбинацией столбцов а1, ..., ап матрицы Л с неотрицательными коэффициентами, то существует
Рис. 9
такая проходящая через нуль гиперплоскость ПГй, что векторы л1, я" оказываются в полупространстве
а вектор b — во внутренности полупространства Нуц (рпс. 9). Можно также сказать, что вектор р составляет
55
с векторами а1, ..., а" нетупоп угол, а с вектором Ъ тупой. Таким образом, по своей геометрической природе
теорема 4.6 относится к классу теорем отделимости, о которых пойдет детальный разговор в § 8.
Если любое решение системы
Ах b удовлетворяет неравенству <с, х> d, то это неравенство называется следствием данной: системы. Условимся записывать такое соотношение между шши в виде импликации
Ах b - <е, х> d. (4Л0)
Геометрически (4.10) означает, что полиэдр X вида (4.1)
Рис. 10	располагается в полупростран-
стве НТл (рис. 10).
Теорема 4.7 (Минковского — Фаркаша о следствиях). Пусть' А еs£(m, п), freR’*, cell”, d<=R, примем система Ля Ъ совместна. Тогда импликация (4.10) справедлива в том и только гам случае, если совместна
система
рА = с, <р, ЬУ d, р^0.	(4.11)
В одну сторону эта теорема известна еще из школьной программы: если дана система
<а,, я> < bit ie 1, ...» m,
то при любых неотрицательных числах р< (i = 1,..m) неравенство
tn	m
22 Pi (Pi, я>< 2 pd>i 1=1
является ее следствием; причем это тем более верно, если правую часть последнего неравенства увеличить. Нетривиальным является то, что такой способ получения следствий — единственно возможный.
Полезно отметить, что теорему 4.6 можно переформулировать следующим образом: импликация
рА 0 -► <р, Ь> 2s О
справедлива в том и только том случае, если совместна система (4.8). Таким образом, теорема 4.6 это частный случай теоремы 4.7 для однородных неравенств.
5G
УПРАЖНЕНИЯ
4.1.	Изобразит!» на плоскости полиэдр, задаваемый системой неравенств
За?! Ц- ха <1 18,
4^—	—24,
Ъх1 — 12х2	36,
-Ь 3xs^ — 27,
и найти все его вершины:
	а	b	С	а		fe	G	а		Ъ	с	а		b	с
1	2	2	1	6	2	3	2	И	2	4	3	18	2	2	4
2	3	3	1	7	3	4	0	12	3	2	3	17	3	3	4
3	4	4	1	3	4	2	2	13	4	3	3	18	4	4	4
4	6	2	1	0	0	3	2	14	6	4	3	19	б	2	4
5	8	3	1	10	8	4	2	15	8	2	3	20	8	3	4
4.2. Найти все значения параметра к, при которых среди вершин полиэдра в R2, задаваемого системой
Xj -Ь ох» 8,
feXj + Х,<12,
2,r tс.г2 /г,	х2^0,
Имеются вырожденные:	‘
	а	b	с	°		5	с	а		b	с	а		b	с
1	1	б	1	б	2	6	2	И	2	6	3	18	2	4	1
2	4	3	1	7	4	6	3	12	4	6	1	17	4	б	2
3	4	4	1	8	4	2	5	13	I	4	1	18	2	3	3
4	4	2	3	9	4	3	5	14	2	9	2	19	2	4	3
5	4	3	3	10	4	6	5	15	2	3	1	20	4	4	5
4,3. Найти все значения параметра А-, при которых полиэдр в R4, задаваемый системой
(к + «) «1 + *2 + Зжа + 4х(1 < 1,
bxr + кт2 ч- 4ха 4- 5x,t 2»
(к + с) я* — ха 4- 5;г3 -V 6т4 <:3,
х3^0, х(1>0,
57
имеет ио крайней мере одну вершину:
	а	Ь	с	а		Ь	с	а Ъ с			а		b	с
1	1	G	S	6	5	6	7	11	9 -8	7	16	5	24	И
2	11	-18	7	7	3	__9	1	12	И -28	3	17	9	-20	1
3	13	-42	1	8	3	40	13	13	1	12	7	18	13	-22	9
4	7	-10	3	9	1	30 11		14	5 14	9	19	3	4	5
5	9	10	11	10	9	-18	3	15	13 -30	5	20	7	30	13
4.4. Найти вершины полиэдра в R3, задаваемого системой
axt -J-	«« О,
$1 4- Ьх, + ,тя = О,
ai 4' #.! + л‘з — 1) (^ — 1), x3^c(ab— 1):
	а	Ь	с	а		ь	с	а		Ъ	с	а		b	с
1	2	3	—1	0	7	3	-3	11	0	'•>	8	10	2	9	9
2	4	8	•>	7	5	4	5	12	4	2	1/3	17	6	7	4
3	5	7	1/2	8	4	9	<;	13	7	4	7	18	7	9	-3
4	2	4	3	9	3	5	-2	14	5	0	-1	19	9	7	9
5	8	2	1/5	10	6 лл	5	3	15	6	7	1/5	20	5	8	1/4
4.5. Найти все вершины (опорные точки) полиэдра в R4, задаваемого системой
4-	4* т	= !,
Ч-	сх3 Ч-	= 1,
4,
и выяснить, имеются ли среди них {нарожденные:
	а	5	с	И		b	с	л		Ъ с	л		Ъ	с
1	3	G	9	«	2	4	-4	И	3	2	0	16	6	5	-3
2	<>	3	0	7	3	5	-2	12	4	5 -3	17	*>	6	-1
3	5	4	-1	8	3	4	—1	13	5	2 -1	18	4	2	-4
4	6	2	-3	9	2	5	0	14	4	3 -4	19	5	6	0
5	5	3	-4	10	6	3	-3	15	6	4 -2	20	4	0	~2
S8-
4,П. Используя геометрические построения, пайтп все значения параметра Аг, при которых система
(ta-j 4- Ьх2 -h .т3 + (с + 1)	=± к,
(а 4- 3) aj -}-	+ 2)#» + Xj } cjc,j = 2 — к,
«7^0.	7 = 1,..., 4,
совместна:
а b с		п b с		а b с			a h с	
1	5 1 2	13	114	2	И		10 3 3	115	10 4 1
•J	12 4 3	7	0 2 1	12		10 2 5	17	11 3 4
3	8 1 5	Я	13 4 4	13		0 1 3	18	4 1	1
4	9 3 2	9	7 2 2	14		12 3 5	19	14 4 5
5	7 1 4	10	8 3 1	15		9 2 4	20	8 2 3
4.7, Используя геометрические построения,								найти все
значения параметра к, при					которых справедлива им-			
нликацпл								
		Ж1	4- х., <; 12,					
	0 =					-> ст, 4- 5.т« к		•
			0 <2 г.» к					
а b с		a li с		д b с			а b с	
1	8 7 2	6	10 8 1	11		8 10 7	16	10 7 I
2	7 8 7	7	И 7 6	12		9 И 2	17	И 10 8
3	10 11 4	.8	8 9 8	13		7 9 6	18	7 11 3
4	11 0 1	9	7 10 2	14		10 9 8	19	8 11 6
5	9 7 0	10	9 8 7	15		11 7 3	20	9 10 4
ЗАДАЧИ
4.1.	Пусть точки х1, ..., .-г’" принадлежат полиэдру X. Доказать, что их выпуклая комбинация, т. е. точка х вида
тге	тп
х = 2 Xjt1, где	...,/??), Xi = 1,
i-i	i-i
также принадлежит А'.
Ото означает, что полиэдры являются выпуклыми множества-мп, теория которых излагается в гл. 3. Многие результаты этой
59
теории применительно к полиэдрам могут быть доказаны эпачп-только проще, чем и общем случае. Ряд таких результатов с соответствующими ссылками па гл. 3 приподптся ни;ко, Таким образом, данный параграф помимо прочего может рассматриваться как элементарное введений в определенный круг понятий и фактов выпуклого анализа,
4.2.	Пусть X — полиэдр вида (4.3) , где вес векторы at отличны от пуля, и ж* <= X. Доказать, что
а)	ж* является граничной точкой X в том и только том случае, если /(.?*)=/= 0;
б)	ж* является внутренней точкой X в том и только том случае, если 7(.г*)ет 0, т. е. к*=т (ограппчснпя-равеиства отсутствуют), и Лх* < Ъ,
4.3.	Доказать, что следующие множества в R” являются полиэдрами:
Zxo?4 = {х е R” | х *= х° -h ah, «е R|
— прямая, проходящая через точку х° в направлении вектора h 0;
/*ой =	s R” | х = х° -|- ah, а 0)
— луч, выходящий из точки х° в направлении вектора А¥=0;
[ж0, х1] = {х е R"|x = хс + а(х’ — я0), 0 а С 1)
— отрезок, соединяющий точки х° и я1.
4.4.	Пусть X —непустом полиэдр вида (4,3). Доказать, что следующие утверждения эквивалентны:
а)	X — неограниченное множество;
б)	из каждой точки x°sX исходят некоторый луч Zj/и целиком лежащий в X;
в)	система	. i
<flf, h> 0,	к,
<flt, h) = 0, i » Н 1, ..., m,
имеет решение h & 0.
Эквивалентность утверждений а) п б) — общий факт для замкнутых выпуклых множеств (см. теорему 7.20).
4.5.	Пусть X—непустой полиэдр вида (4.3). Доказать, что следующие утверждения эквивалентны:
а)	через каждую точку е X проходит некоторая прямая lxoh, целиком лежащая в X;
60
6)	система
<0f, Л> =0, i = 1, .... w,
т. e. Ah = 0, имеет решоппе Л =0= 0;
в)	rang Л < п.
4.6.	Пусть X — полиэдр вида (4.3) и ж* е X. Доказать, что я* является единственным элементом X в том и только том случае, если система
<at, й>=£0, f.e{l, А*} П/(«♦),
<а<5 Л> = 0, i « k + 1, ..., m,
„мест лишь тривиальное решение h ** 0.
Задачи 4.7 — 4.34 посвшцепы понятию размерности полиэдра. Это понятие вначале формулируется для простейшего класса полиэдров — аффинных множеств.
4.7.	Множество X<=Rrt называется аффинным (иногда говорят — линейным многообразием), если Хж! + .+ (1— Х)г2еХ при всех ж1, геХ, AsR, т. е. если X вместе с любыми своими двумя точками содерясмт проходящую через них прямую*). Доказать, что множество X аффинно в том и только том случае, если для любого г0 еХ множество
L = X — ж0 = {у <= Rn | у = ж — х°, х е X)
является линейным подпространством в R"; при этом L не зависит от выбора ж0 в X.
Указанное подпространство L называется параллельным аффинному множеству X и обозначается через Lin X.
4.8.	Доказать, что множество X <= R" аффинно в том и только том случае, если его можно представить как множество решении системы из конечного числа линейных уравнений, или (что то же самое) как пересечение конечного числа гиперплоскостей, т. с.
X — (жеКЧЛж b} = {x«=Rn|<Oi, ж> = &(, 1=1, ...г т),
(4.12)
где А е M(w, n), b е R".
Таким образом, аффинные множества суть полиэдры, которые можно задать ограппчеппями*равопствами.
*) Одноточечное множество, конечно, является аффинным.
61
4.9.	Доказать, что множество У R" аффинно в том л только том случае, если его можно представить в виде
X = L gs R” | х = + Су = -И 2 с’у}, у = (у£ е R* , I	j“*i
0.13)
где ;r° е R", С «=	(п, s).
4.10.	Размерностью dim Л- аффинного мпожества А* называется размерность параллельного ему линейного подпространства Lin X (см. 4.7)*). Доказать следующие утверждения:
а)	если X—непустое множество вида (4.12), тез dim X *= п — rang /1;
б)	если А'— множество вида (4.13), то diinAr = »= rang С.
4.11.	Доказать, что аффинное множество	яв-
ляется гп.порплоскостыо в том и только том случае, если dim X =* п — 1.
4.12.	Найти размерность аффинных множеств в R4, задаваемых следующими системами:
а)	—.}* .т2	4-	2х4	«а»	—4,
2xt 4- Зя* —Яд •{- хл »	1,
яj 4- 4й!2 “ г3 4- Зх4 =	3;
б)	•?! “2z2 — л- я?4 =±	1,
х, + 4ага 4- Зх3 « — 3, 2^ + 2z2 + 2.т3 + £,j =	2;
в)	.Tj — 2х2 -Ь т3 4- 2,г4 = — 2,
— xt 4- 3;г2	4- •*: =	3,
— .т2 4- -т3 -г 3.?4 =	1.
4.13.	При «сох значениях параметра а найти размерность аффинного множества Л* с R5, задаваемого системой
art 4- 2т2 +	ах3 +	,тл	4-	^гй =	10,
2.Т, — Зя2 +	5з?3 — 2х4	+	хь = — 7,
3.tj .т2 4*	З.т3	4-	4^5 =”	3,
4хг 4- .гг 4*	Н.гв	4*	»»	13.
•) В частности, сели Л' = 0, то в соответствии с аналогичным соглашением для линейных ноднрострииетн полагаем dimA' =s —1.
02
4.14.	Пусть Xri, Х$ — аффинные множества, Х> Х>, но Xi 'AXj. Доказать, что dim Х| < dim Х^.
4.15.	Пусть X—полиэдр вида (4.3), У—аффинное множество, принадлежащее X. Доказать, что dim У С п — rang Л.
4.16.	Пусть X—непустой полиэдр вида (4.3). Ограничение с номером I в системе из (4.3) называется 'жестким, если оно выполняется как равенство всюду на X, и нежестким в противном случае.. Введем обозначение для множества номеров жестких ограничений:
7(Х) = (г, 1 i С m|<a(,	= bt при любом х X).
Подчеркнем, что всегда (А: + 1, ..., т) <=7(Х).
Найти 1(Х) для полиэдров X, задаваемых следующими системами (ограничения считаются пронумерованными в естественном порядке):
а)	оч + #2 < 1,	> О, #2^=0;
б)	+ #2 < 1,	— х2 0, я?!	1/2;
в)	+х2 + х3<1, Ж1 -ЬязЭ* 1,	.т2Х),	5= 0;
г)	Ж1 + 2хэ^1, -Кт2 + Лз < 5,
2zi 'Ь ;г3 = 3.
4.17.	Пусть полиэдр X вида (4.3) непуст. Доказать, что система
рЛ=0, <р, Ь> <0,	& 0, i = Аг,
где р =(р/)е IVя, несовместна.
4.18.	Пусть X — непустой полиэдр вида (4.3), а система
рА => 0, <р, Ь>=0, рл 0, 4=1,...,/с, имеет такое решение р, чтор< >0 при некотором *={1, .А*). Доказать, что fo-o ограничение в (4.3) является жестким, т. о. 1в<=/(Х).
Утверждения из 4.17, 4.18 окажутся полезными при рошоиин нескольких следующих задач. При этом стоит отметить, что ука-iifltHtue в 4.17 необходимое условие пеиустоты X на самом дело является п достаточным, а указанное в 4.18 достаточное условно жесткости — необходимым (см. 4.93, 4.105). Однако пока можно обойтись баз этих более тонких фактов.
4.19.	Показать, что полиэдр X <= R\ задаваемый системой
— 4- 2х4 — 5я3 4- 2а;4 < О,
4^—7^+ ^3“7;г4^ —9,
63
2Х] 4* Зд?2 *“	-J- Жд	1,
“ Ж2 + ^З -I' 2^4 < непуст, и найти ЦХ).
4.20.	Показать, что полиэдр X R4, задаваемый си, стомой
бЖд 4* 2Жд “I” Зд7д 1,
— 2xj 4"	4- 4.т3	.t.j	— 3,
— 3xj — 3#2 + 10xj 4- #4	— 1»
.?! 4- 4ха — Gzg —- 2хл	2,
является аффинным множеством, и пайти его раз-мерность.
4.21.	Найти «се значения параметра а, при которых полиэдр X <=• R\ задаваемый системой
За?> 4- 2.та —	— 5ж4	11,
3#! 4- 5ж2 — 1х3 — ж4 s;C — 4,
Зл^ — 5ж3 — 2з‘3 4- 2ж4 <1	а,
~~ 2.Т| 4- Л'з ”Ь 4* я-д	8»
непуст, и для каждого такого а определить 1(Х).
4.22.	Пусть X — непустой полиэдр вида (4.3), причем множество 7 = И, ...т щ}\/(Х) не пусто. Доказать, что существует точка х s X, в которой все нежесткие ограничения выполняются как строгие неравенства, т. е. Ajx bj.
4.23.	Аффинной оболочкой aff X полиэдра X с: К" (как и любого другого множества в R”; см. § 7) называется пересечение всех аффинных множеств из ТТ, содержащих X. Доказать, что
a)	aff X есть аффинное множество;
б)	еелп X— непустой полиэдр вида (4.3), то aff X =» {ж ® К“|Л1сЛ1ж =
т. е. аффинная оболочка полиэдра порождается системой его жестких ограничений*).
4.24.	Пусть X — непустой полиэдр вида (4.3). Доказать, что X — аффиппос множество в том и только том случае, если
X = {л? о R” [ Л/( х =
♦) Если I е= S3, то формальное равенство	ечктаетч-л
выполненным для всех х <= кроме того, полагаем rang А0 = О (см. 4.25).
G4
4.25*	. Размерностью dim X полиэдра X g R” (как п любого другого выпуклого множества в R”; см. § 7) называется размерность его аффинной оболочки aff X. Доказать. что для непустого полиэдра X вида (4.3) справедлива форзгула dim X == п — rang И f<X1.
4.26.	Пусть X — полиэдр в R”. Доказать, что dim X = «=н в том и только том случае, сслп X имеет внутренние точки, т. е.	(ср. с теоремой 7.19).
4.27.	Доказать, что размерность полиэдра (4.1), гдо b > 0. равна п.
4.28.	Доказать, что размерность полиэдра X ,= (я <= R”(Ля Ь, х 0), где A п), 6 R”, Ъ > 0. равна п.
4.29.	Найти размерность полиэдров из 4.16 (считается. что первые два полиэдра лезкат в R2, остальные — я К3).
4.30,	Папти размерность полиэдра из 4.19.
4.31.	При каждом значении параметра а. пайти размерность полиэдра из 4.21.
4.32.	Найти размерность полпэдров XcR4t задаваемых следующими системами:
л) 2а?! + X., — я3 + .та <	5,
*— 4х2 4- 2х3 — 3#j = — 2, я5>0, я3>0;
б)	2^ — З.г; 4- я3 4- 2г,	3,
— 4#i *|* х3 4* 5я3	— 33,
Zj — 5я3 -Ь .т3 4- ,г4	—10,
Я1 -ь .Tn — Зя3 — Яд =	15,
в)	— 4ял — 2.т3 4- 7я4	7,
— 2xs 4- я3 4- г,=	1,
Х1 — 2$2 4- я3— я4 = —1, — 2я2 4-	4- бх, = 5;
г)	я, 4- я2+ .т3— я.^0,
2ях 4а Зх2 4* 5.т3 4- 6л\ =а 0,
З.тх 4- 4яа 4- 6т3 4- 7яд’^’О, 3.^ + х2 4- я, 4- 4яд = 0.
® И. А. Ашмавов, А, В, Тимохов	65
4.33*	. Пусть X — непустой полиэдр вида (4.4)'. Доказать, что
dim X *= |/| — rang AJ,
где	1 п\х} > 0 при некотором хеХ).
В частности, если существует такая точка ж <= X, что х > 0, то dim X = п — rang А.
4.34.	Найти размерность полиэдров X с R5, задаваемых следующими системами:
а)	2xj *Ь Эх. 4* #3 — Зд?4 -|- 5.т5 «	9,
Xj — 2х2 4- Зх3 +	=	7,
— 4- х3 — х3 4- х4 ~	—5,
— 2хх + З.тг J- 2х3 4- 6.г4 — 8хй <= — 6.
07 > 0» /=!,...,5;
б)	— З.г4 4* 2х3 + ,т3 4- 15х4 — З.г6 => — 3,
2xi + ^2 ~ ®з ~	+ 2г’ь в 2,
Xi — Зх3 4- 2х3 — 5;r,j + хй =	1,
х/^0, /« 1, .5;
в)	Xj — 4х3 4- Зх3 — 2x,i 5хй = 3,
—•* &14" 7й?2 — 4х3 4- х4'— Xj, "= 2,
х/^0,	/ = 1, .... 5.
В задачах 4.35 — 4.76 рассматриваются некоторые вопросы, связанные с понятиями вершины и грани полиэдра. Отметим, что зта тема получит существенное развитие в § 8.
4.35.	Доказать теорему 4.1.
4.36.	Доказать теорему 4.2.
Заметим, что с учетом 4.5 эту теорему можно пороформуяиро-пять следующим образом: полиэдр пмоот по тфайвеп моро одпу порвпшу в том п только том случае, если он во содержит целиком ни одной прямой. В такой форме дапиоо утверждение переносится па пропзлольвые яамкпутао пьшуклыо множества (см. теоремы 8.11, 8,12).
4.37.	Доказать теорему 4,3.
4,38.	Доказать теорему 4.4.
4.39.	Пусть непустой полиэдр X принадлежит полиэдру У, причем Y имеет по крайней мере одну вершину. Доказать, что X также имеет вершину.
GB
Замотпм, что первое уморжденне теоремы 4.3 есть частный случай сформулированного утверждения при У=П+.
4.40й	. Пусть лг, я1, ..., а?*—-точки в R”, ле всо равные пулю. Предположим, что х является неотрпцатель-tn
пой комбинацией точек ж1, ..ж13, т. е. х =	Я.<2Г при
некоторых Xf5=0 (i=l,	т). Доказать, что х мож-
но представить в виде неотрицательной линейной комбинации линейно независимой подсистемы этих точек, т, е. существует такое множество I<= И, .т}, что точки х' (1^1) линейно независимы и яг=2 gt^npn пското-isj
рыхрт^О (i = Z).
4.41.	Используя геометрические построения, найти все вершины полиэдров в R2, задаваемых следующими системами:
а)	2жЛ4-	8,
2^ — 5х2 <2	20,
— Лц 4*	2,
«в Г1
в) — 3#Л 4- 6za 13, 3^-Ь ^2 ’С о,
— ягх-Ь 2гга = 4;
б)	аъ + гп2 о,
я2<9>
4" 2г3 = 4;
г) — 3ix4-2x2< О,
R ‘ л* 4” 2х3	4.
— Зй^ 4*
4.42.	Найти все значения параметра а, при которых среди вершин полиэдра в R2, задаваемого системой
(IX4"	1,
2жЛ 4-	л’з	6,
—— Х^ 4-	2.'д	6,
Х-^ 4”	2я?2	б,
имеются вырожденные.
4.43.	Найти все значения параметра с, при которых полиэдр в R5, задаваемый системой
4* 2з"з ‘ “	Яд 4*	-— д?и	4,
а?! + З.т« 4-	ж3 —	-h 2хй	<	О,
— 4л-2 4-	7.т3 4-	Зх4	— 4жь	1,
2ж4	4- я6	<	3,
Л'|	*Г Лд	1,
имеет хотя бы одну вершину.
§•	67
4.44.	Найти псе вершины полиэдров в R3, задаваемых следующими системами:
а)	— 2z2 + 5т3	4,
4" бйд	9,
— 4я2-ЬЗл31>	1,
д?! + 5ха	3;
б)	+ Зхд 4- 4.т3 <1	8,
2д?^ ““ 2а-3 5«г3	о,
4^1 4- 7х% 4- *^з	^2;
в) 3^4- х’2-Ь й;3<15, 2®i 4- «ь — Зя3 43, о?! 4- 2я2 4- Х3 == 5, 2ж14- бяп 4- Зх3 « 1; г) 4я 2я3 2х3 3^ 2, я-j 4- 4.та 4" 2ж3 4» ^1— ^4- жа<0, — 4- 5я* + *з =* & 4.45. Найти все значения параметра а, при которых полиэдр в R3, задаваемый системой
4-	Зхо 4- 4г3^5, .гг— ^4- я3<2, 5^ -Ь За?2 — Л'3 4, и|“ 4х3 *—1 3, имеет вырожденную вершину.
4.46.	Найти все вершины полиэдров в R4, задаваемых следующими системами:
а)	хх — 2я3 4- 4ж3 —	=» 1,
2&1 4* 3^ 4~ ^з 4- 2x,j о« 3, 7 = 1, ..., 4;
б)	4д?! 4- 5z2 4- х3 — я:4 = 2,
2xj 4-	4 а?з -Ь Зя4 = 5,
ж;^0,	/ “	4;
в)	Xl 4- гса 4- х3 + хл = 3, 2xt — х2 4- х3 — 2г-4 =* 2,
68
Зз\ + х2 — ixs — .т4 = О,
^•>0»	/ =	4.
4Л7. Используя геометрические построения, определить число вершин полиэдра в R5, задаваемого системой — 2^ + 4х* + х3 — ,т4 -ь 3,тй = 2,
2,^ + х., + 4х3 Ч- З.г4 4* 3z6 == 1, У=1,..., 5.
Проанализировать с этих же позиций системы а) л б) из 4.46.
4.48.	Найти все значения параметра kt при которых полпэдр в R’, задаваемый системой
'	X2 — ЗХд 4*Т,| о,
2ял-Ь яа — 2х3 -ь Зя4 «= — 1,
Зя2 4- #э 4- 3#4 =2,
3J;	0, ] = 1, . . . , 4,
имеет вырожденную вершину.
4.49.	Найти размерность и все вершины полиэдра
X
=« <.Т &. R’“
П	’
xj 1, Xj 0> / = 1, ... j л1,
называемого стандартным н-симплексом в R'1.
4,50.	Найти размерность и все вершины полиэдра
Х = k<=R"
П	]
х$ ^=> 1 , х^ 0, / = 1, ..., и?,
Juaj	)
называемого стандартным (n — 1) -симплексом в R".
4.51.	Гранью (непустого) полиэдра X из (4.3) называется его непустое подмножество Г вида
Г =	= bj) = {же=Ип|<«Г1
< b{ii е (1, ..k}\I, <ah х> = bh
ie{/c4-1, ..., mJ UВ, (4.14)
где / — некоторое подмножество мно
жества {1, ..., лг) (рис. И). При этом говорят о собственной грани, если Гч^Х*). Иными словами, грань по-
•) Полиэдр X, конечно, является своей гранью: достаточно ВЗЯТЬ любое 1 GZ {k 4- 1, ,.ffl), U ТОМ ЧИСЛО I е= 0.
69
лпэдра X образуется путем замены некоторых знаков неравенств в системе, задающей X, знаками равенств при условии, что полученная система имеет решение.
Доказать, что любой полиэдр имеет не более коночного числа граней и каждая из них casta является полиэдром.
4.52.	Доказать, что точка х* полиэдра X является его вершиной в том и только том случае, если одноточечное множество Г == (х*) есть грань X.
Таким образом, першииы полиэдра можно определить как ого грани пулевой размерности.
4.53.	Грань полиэдра X, имеющая единичную размерность, т. е. являющаяся отрезком, лучом или прямой, называется ребром этого полиэдра (рис. 11).
Представить в виде (4.14) все ребра полиэдров в R2, задаваемых следующими системами (ограничения считаются пронумерованными в естественном порядке)-;
a)	®i + 2,т2	2,
— 3z2^3, — «1+ *а^1> ж2>0;
в) .?! Ч- ;т2 > О,
Ч + *2 С1 •
б)	+ ге2	4
3.?!	ч- х,	G,
2.тх	— З.г2	3,
4.54.	Пусть X — полиэдр вида (4.3), Г — его. грань вида (4.14). В соответствии с 4.16 под /(Г) будем понимать множество номеров жестких ограничений в системе из (4.14):
/(Г) = {£, 1 =£ i =С тI<(й,	= bi при любом же Г).
Доказать, что в (4.14) всегда можно считать /==>7(Г).
Используя 4.23, данное утнорлгдепно можно высказать в такой форме: сели Г — грань полиэдра X, то Г « X Л aff Г.
4.55.	Грань Г полиэдра X из (4.3) называется невырожденной, если векторы а< (ieZ(F)) линейно независимы, и вырожденной в противном случае.
Доказать, что грань Г размерности d певырождепа, если |/(Г)1=» —в, и вырождена, если |/(Г) I > п —- d.
4.56.	Пусть Г —грань полиэдра X из (4.4). Введем множество
J (Г) = {/, 1 < J	п[.т; > 0 при некотором х е Г).
70
Доказать, что грань Г певырождопа в том п только том случае, еслп среди векторов a* (J е= 7(Г)) имеются т линейно не,зависимых.
4.57.	Пусть Г' — грань полиэдра лпэдра X. Доказать, что Г' — грань при этом грань Г вырождена, то к грань Г' вырождена.
4.58.	Пусть Г — грань полиэдра X, а полиэдр У таков, что Г с У с X. Доказать, что Г — грань полиэдра У (рис. 13).
4.59*	. Вершины я1 и .г2 полиэдра X называются соссд/ш,ии, еслп отрезок {я1, я2] является ребром X (рис, 14).
Доказать теорему <? соседних
Г, а Г — грань Hex’ (рис. 12); еслп
вершинах полиэдра.
Вершины х1 и х~ полиэдра X из (4.3) соседние в том и только том случае, если rangA^n — 1, где / = 2(я1)П ЛI' (ж2).
4.60.	Пусть х1 и ж2 — такие веришны полиэдра X из (4,3), что множества /(я1) и Цх?) различаются лишь одной позицией, т.е.7(д?г)U U), где raffs’), $07(я’). Доказать, что эти вершины соседние.
4.61.	Пусть я1 и х2 — соседние вершины полиэдра X из (4.3), причем эти вершины певырождепьт. Доказать, что /(я1) и I(ж2) различаются лишь одной позицией.
Можно ли в этом утверждении опустить условие невырожденности вершин?
4.62.	Пусть х1 и ж2 —вершины полиэдра X из (4.3), причем х1 певырождеиа. Доказать, что эти лершипы соседние в том я только том случае, если Щя1) Л /(я2) |е«
71
= п —1, т. е. имеется ровно п — 1 общих активных ограничений и точках я1 п я2.
Можно ли в этом утверждения опустить условие невырожденности перпшпы я1?
4.63.	Пусть X — полиэдр в R4, задаваемый системой Я[ + Я 2 < 5, 3^1 — 2x2 5,
—2»! 4- Х2 8, Зя| 4- Х2 —3. Найти (не прибегая к геометрическим построениям) все вершины X, соседние с вершиной я*=(3, 2).
4.64*	. Доказать, что вершины я1 и я2 полиэдра X из (4.4) соседние в том и только том случае, если rang Д' = | )| — 1, где J = /(я’)и 7 (я2), а /(я), папомпим, определено в (4.5).
Здесь уместно отмстить, что условие из теоремы 4.4, онредо-ллкпцоо вершину х данного полиэдра, можно записать в виде rang Д' = |/|, где 7 в /(х).
4.65.	Пусть я1 и я2—такие вершины полиэдра X из (4.4), что множества 7(яг) и 7 (я2) различаются лишь одной позицией (см. 4.60). Доказать, что эти вершины соседние.
4.66.	Пусть я1 и я2 — соседние вершины полиэдра X из (4.4), причем эти вершины певырождеиы. Доказать, что /(я1) и J(я2) различаются лишь одной позицией.
4.67.	Пусть я1 и я2 —вершины полиэдра X из (4.4), причем я1 иевырождепа. Доказать, что эти вершины соседние в том и только том случае, если |7(я1)И 7(я2) | = = т, 4-1.
4.68.	Пусть X— полиэдр в R5, задаваемый системой 4- Зяа 4’ 2я3 + я4 + 8яй «= 4, 2я1— яй 4- Зя3 + З.т4 + 2я6 « 1, *7>0,	/ =	5.
Ыайтп все вершины X, соседние с вершппой (1,1,0,0,0).
4,69.	Пусть Г —грань полиэдра X из (4.3). Доказать, что dim Г >n—rang4.
4.70.	Пусть Г — собственная грань полиэдра X. Доказать, что dim Г < dim X.
4.71*	. Доказать, что непустой полиэдр X пмеет хотя бы одну собственную грань в том и только том случае, если он не является аффинным множеством.
72
4.72.	Грань Г полиэдра X называется минимальной, если сама опа пе имеет собственной грани. Доказать, что любая грань полиэдра содержит его некоторую минимальную грань.
В частности, это означает, что минимальная грань всегда существует.
4.73*	. Доказать теорему о минимальной грани.
Пусть Г —грань полиэдра X вида (4.3). Тогда следующие утверждения эквивалентны:
а)	Г — минимальная грань X;
б)	Г — аффинное множество;
®) dim Г = п~ rang Л, т. е. Г —грань минимально возможной размерности (см. 4.69).
4.74.	Указать минимальные грани полиэдров, задаваемых следующими системами:
-J- 2ха 4" Зх3 2;
б) х/4- х2’4- х34- х4<1,
хх 4- 2хй 4- Зх3 4- 4х4	3,
2хх 4- Зха 4- 4х3 + 5хх	2.
4.75*	. Доказать принцип граничных решений Черника ва.
Пусть Л^^(л?., п), гап&Л = г, 5<=Rm, причем система Лх b совместна. Тогда существует такое множество Zc {1, ..., ш), что rang A г, система Л/х=“Ь: совместна и справедлива импликация
Л/х ** bt -* Лх Ь.
При этом всеода можно считать, что 1/1 = г.
В авторской формулировке данный принцип звучит так. «В каждой совместной ковочной системе липейпых неравенств над полей действительаых чисел, имеющей любой отличный от нуля ранг, можно выделить хотя бы одну такую подсистему того иго рапга и с равным ему числом неравенств, каждое решоиио которой, обращающее все оо неравенства в равенства, удовлетворяет исходной снегомет [43, с. 7] ♦).
Отметим, что теорема о минимальной грани и принцип граничных решений представляют собой различные по форме обобщения основного утверждения теоремы 4.2, В следующей задаче прпио-дится обобщение ее дополлптольиого утверждения.
*) В нашей формулировке тривиальный случай г.= 0 (т. е. /1 =±1 0) допускается; тогда подо просто взять / = 0 (см, подстроч-
ное примечание к 4.23).
73
4.76.	Пусть X — непустой полиэдр вида (4.3). Доказать, что для любой точки х&Х существует такая минимальная грань Г полиэдра X, что /(я)<=/(?).
Задачи 4.77—4.108 посвящены теории существования решений систем линей пых неравенств и уравнении, которая находит многочисленные приложения в теории оптимизации, теории игр, математической экономике и т. д.
4.77.	Доказать теорему 4.5.
4.78.	Доказать теорему 4.6.
4.79.	Доказать теорему 4.7.
4.80.	Используя геометрические построения, найти все значения параметра /с, при которых система
4-	*1“ Зя-., ’ ’ 5^ л* 2,
— Х3 — 2*4 = 21
Х;>0,	/ = 1, ..., 4,
совместна.
4.81.	Используя теорему 4.7 и геометрические построения, показать, что система
Pl— 2Pi— Рз+
— Р1 — ра + 2рз + 2?4	1»
Pi 4- 4ps 4* 2рэ -|- 4р4 3, р{>0, г = 1, ..., 4,
совместна.
4.82.	Обосновать следующее замечание к теореме 4.7.
Пусть в дополнение к сделанным предположениям совместна система
Ах &, <с, хУ dt	(4.15)
т. е. некоторое решение системы Ах «£ Ъ обращает неравенство-следствие в равенство. Тогда для любого решения р системы (4.11) неравенство <р, ЬУ d выполняется как равенство и если существует такое решение х системы (4.15), что <а{, хУ < Ь{ при некотором iе (1, ..., ш), то pi 0.
4.83.	Показать, что решение системы из 4.81 единственно, и найти его.
4.84.	Пусть Л<=^(тп, n), b^R", c<=Rra, <£eR, причем система Ля = Ъ совместна. Доказать, что импликация
Ах *= Ъ -> <с, хУ = d
74
справедлива в том и только том случае, если совместна система
рЛ = с, <р, b> = d.
4.85.	Пусть А<=&Цт, п), b<=Rw, c<=RB, d^R, причем система Л.т -S Ь совместна. Доказать, что импликация
Лз I) -> <с, х) — d
справедлива в том и только том случае, если совместна каждая из систем
рА = с, <р, Ь> = dt р 5= О и
рЛ=—с, <р, &> = — d, р^О.
С геометрической точки зрения здесь сформулировав критерий принадлежности полиэдра X вида (4.1) гиперплоскости II сл.
4.86*	. Доказать теорему Александрова — Фана (Фанъ-Цзн).
Пусть Л^лЯ£(лг, »), b^R,n. Тогда совместна одпа и только одпа из двух систем:
Ъ пли
рЛ « 0, <р, Ь > < О, р 0.	(4.10)
Иными словами, полиэдр X вида (4.1) пепуст в том и только том случае, если система (4.1G) несовместна.
4.87.	Пусть Л<5^(т, п), !>sRrT1, c<=RB, JeR, примем система Л.т<Ь совместна. Доказать, что импликация
Ах b ->- <с, х> <d
справедлива в том и только том случае, если совместна система
рА = с, <р, Ь> < d, р > 0.
4.88*	. Доказать теорему об очистке системы линейных неравенств, влекущей даппое неравенство.
Пусть	n), HR", ceR", deR, прпчем си-
стема И.т b совместна п справедлива импликация
Ах b ->- <с, х>d.
Тогда существует такое множество /<=(!, ..., лг), что гапдЛх=|7| (т. е. строки матрицы А с номерами из
75
I линейно независимы) и справедлива пзшлпкация
AiX С bt “> <с, .т> =С d,
при этом всегда можно считать, что 1/1 «= rang А.
Этот важный результат теории липейпых неравенств проиллюстрировав па рис. 15, где I п= {1, 3}.
4.89.	Показать, что теорема из 4.88 сохранит свою силу, если в указанных двух импликациях неравенство <с, х> =5 (I заменить неравенством <с, я> < d.
4.90.	Пусть Ле^(т, n), IksR*", c<=Rn, fZ^R, причем система Ах < b совместна. Предположим, что неравенство <с, х> А (или <с, х> < d) следует па системы Лл-^, но по следует из любой ее собственной подсистемы, т. е. системы вида Л^^С bJt где 7е {1, ..., тп), [7| < т. Доказать, что rang Л = т.
4.91.	Система неравенств называется неприводимо несовместной, если опа несовместна, а любая ее собственная подсистема совместна.
Пусть Л	/г), ?н>1,	Доказать, что си-
стема Ля^Ь неприводимо несовместна в том и только том случае, если система
рЛ = 0, <р, ЬХО, р>0	(4.17)
совместна и любые m — 1 строк матрицы Л линейно независимы.
4.92.	Пусть Ле«й5(да, n), rang Л = г, 6<=Rra. Доказать, что система Ах Ъ совместна в том л только том блучао, если совместна любая система вида Л;#^ bi, где / с И, ..., л?.), |7| =г+1, гап£Л/ = г.
76
Утверждения задач 4.91, 4.92 открывают возможность для получения разнообразных критериев совместности светом линейных неравивств d терминах определителей. Детальное пиложоппо этого вопроса имеется в [43, 47].
4.93.	Доказать следующее обобщение теорем 4.5, 4.6 и теоремы из 4.86.
Пусть А(} <=	(mt, nj), b* <= if4 (i, / = 1, 2). Тогда
совместна одна и только одна из двух систем:
Лпх1 4- Л1ах“ <2 51,	(4.18)
Лп^1 4- И2йх2 =з й2, х1О, пли
pMu + р*Л21 > о, ргл12 ч- рМ22 = О» <pl,frl>-l-<Pa,b2><0,	р1>0.
В частности, полиэдр X вида (4.3) непуст в том п только том случае, если система па 4.17 песовместяа.
4.94*	. Доказать теорему о дополняющей нежесткосги. Для любого решения (х1, хг) системы (4.18) и любого решения (р, р2) системы
р1Л18 4- рМ52 = 0,	(4.19)
<р\ 51> 4- <Р2» &> = 0, рх>0
выполнены условия дополняющей неэхесткости
pl (Лих1 4- Л18х3 — bl)i =10,	г^1.......mlt (4.20)
4(p^hi + P%x)i =• °1 /- 1.	(4.21)
означающие лишь то, что в каждом из этих произведений по крайней мере один сомножитель должен обращаться в нуль.
Иными словами, если ограничение	в системе (4.19)
является нежестким (см. 4.16), то двойственное ограничение (411х14-Л22®а){<Ь| в системе (4.18) должно быть жестким. Аналогично ио незкесткостп ограничения в системе (4.18) следует жесткость двойственного ограничения (р’Лц4-р*Л21)^ ^0 в системе (4,19), Отметим, что сформулированная теорема обобщает утверждение из 4.18, причем для нее таюко справедливо обратное: жесткость данного ограничения-неравенства одной из
77
спитом (4.18), (4.10) влечет пежосткость двойствоппого ограппче-япя-поравеяства другой (см. 4.1(H).
4.95.	Докапать следующее обобщение теоремы 4.7,
Пусть	nj),	ct=R”J (l, /=1,2)
n rfeR, прилем система (4.18) совместна. Тогда импликация (4.18)-* <с\ я^ + ^с2, справедлива в том и только том случае, если совместна система
рМи +
4-	p^^22 ~
(pU1) + </Л 6sx* ^>0.
Диалогичные обобщения могут быть сформулированы для утверждений задач 4.85, 4.87.
4.96*	. Доказать теорему Вороного — Карвера.
Пусть И<=з^(т, и), freR". Тогда совместна одна и только одна из двух систем:
Ла;<& пли рЛ°0, <р, b>^Of /?>0*).
В то время как теорема Александрова— Фана из 4.86 указывает критерий попустоты полиэдра X вида (4.1), сформулированная теорема указывает критерий пепустоты внутренности этого полиэдра, пли же его л-мориоста (см. 4.26).
4.97.	Доказать обобщение предыдущей теоремы—теорему Моцкина.
Пусть At^^(m, и), ^fR”4 (£ = 1,2,3), причем система Aiz^b1, АгХ^Ь2 совместна. Тогда совместна одна и только одна из двух систем:
Лгя:=*&2, А&<№ или
р14( + р2.4о + р3Аз = О,
<р\ Ь»> + <р*, &а>4- <р»,	<0, ^>0, р«>0.
Предлагаем читателю самостоятельно сформулировать конкретизацию этой теоремы для случая, когда па часть переменных первой системы явно наложено условие неотрицательности (ер. 4.93, 4.95), То же предлагается сделать в отпошеппп теоремы на 4.09.
4.98*	. Доказать теорему Штимке — Фана.
*) Здесь п далее запись для векторов р, q означает, что р 2* «7, «о р Ф ?. Вектор р. удовлетворяющий условию р > О называется полуп&явжителъным.
78
Пусть А е (т, п), й е Rw, причем система Ах Ъ совместна. Тогда совместна одна и только одна из двух систем:
Аж <Ь пли рА = 0, <р, й> <0, р> 0.
4.99.	Доказать следующее обобщение предыдущей теоремы.
Пусть	п), й1 е R'.1 (i = 1, 2, 3), причем
система А1Ж<й’, А2Ж = Ь2, Азж^й3 совместна. Тогда совместна одна и только одпа из двух систем:
Atx й1, Asx * Ь’} Л3х < й3
или	' '
р '/11 + p2As + р3Аз •= 0,
<р», й’> + <р2, й2>4-<р3, й3><0, р’^0, р3>0.
4.100.	Пусть	л). Доказать, что совместна
одна и только одна из двух систем:
а)	Аж«=*0, ж>0 или рА>0 (теорема Г.ордаиа)\
б)	Аж = 0, ж>>0 или рД>0 (теорема II!тимке);
в)	Аж=^0, ж>0 или рА>0, р^О (теорема Билля);
г)	Аж^О, ж>0 пли рА>0, р2>0.
4.101*	. Доказать два варианта теоремы, Танкера о строгой дополняющей нежесткости.
Пусть А ^^(т, п). Тогда
а)	системы Аж = 0, х 5= 0 п рА 0 имеют такие решения жир, что х + рА > 0;
б)	системы Аж 0, ж 5= 0 и рА 0, р 2s 0 имеют такие решения жир, что р — Аж > 0, ж -h рА > 0.
Отметим, что эти утверждения включают в себя теоремы из 4.100. По поводу термина «строгая дополняющая яежесткость» см. замечание после 4.104.
4.102.	Пусть L — линейное подпространство в R", — его ортогональное дополнение. Доказать, что справедливо одио и только одно из двух: либо LflintR”^ т. е. L содерясит положительный вектор, либо L4 П R” ^{0}, т. е. содержит полуполоясительный •вектор. Более того, существуют такие векторы ж<=£ ц у е что ж > 0, у 0, ж + у > 0.
Эгп утверждения имеют ясный геометрический смысл. Если подпространство L на плоскости по пересекается с положительным
79
ортитом, то подпростраистпо .ЕД имеет нетривиальное пересечение с неотрнцатольпым ортитом (рис. 10). Если при этом L совпадет с одной ио координат осей, то в качестио указанных х и у можно взять единичные орты.
4.103*	. Донизать полную теорему Танкера о строгой дополняющей нежесткое™.
Пусть Ле<=^(7«, п) (г, J=*l, 2).
Тогда системы
ЛцХ1 4- /IjoA'^O,
Рис. 1G
0
(4.22)
(4.23)
имеют такие решения (г1, я?) и (р1, р2), что
р1 — (Ица?14*Д12®?)>0, ж1 +(р‘И11 + p2.42i)> 0.
4.104*	. Доказать теорему о строгой дополняющей не-жесткости для неоднородной системы.
Пусть (неоднородная) система (4.18) совместна. Тогда эта система и система (4.19) имеют такие решения (я1, я?) и (р‘, р2), что
Р1 + (& -	- А1йг) > 0,	(4.24)
а;1 4- (рМл-|-рхЛ21)>-0,	(4.25)
т. е. для этих решений в каждом из произведений (4.20), (4.21) а пуль обращается ровно один сомножитель.
Иными словами, если ограничение р| > 0 в систомо (4,19) является жестким, то двойственное ограничение в системе (4.18) должно быть нежестким. Аналогично из жесткости ограничения ж) 0 в сястомо (4.18) следует нежесткость двойственного ограничения d системе (4,19). Таким образом, согласно 4.94, 4.104, в каждой паре взапмодвойственных ограничений-неравенств систем (4.18), (4,19) одно и только одно является жестким. Условия (4.20), (4.21), (4.24), (4.25), взятые вместе, принято называть услоаилми строгой дополняющей нежесткое™.
4Д05. Доказать утверждение, обратное к 4.18.
Пусть X— непустой полиэдр вида (4.3). Тогда еслп foeJ?(X), то система из 4.18 имеет такое решение р, что Р1о>0.
4.106.	Пусть X — непустой полиэдр вида (4.4) и j в s(l, .... п). Доказать, что Zj = 0 прп любом х^Х в том 80
и только том случае, сели система
/»Л>0, <р, й> = 0
имеет такое решение р, что <р, а}>>0.
4.107.	Пусть Л—кососимметрическая матрица, т. е. Лг“— А. Доказать, что
а)	любое решение х системы
Лх>0,	(4.20)
обладает свойством (Ля)/ я/==0	(/=!,...,»);
б)	существует такое решение я системы (4.26), что Ах + х > 0.
4.108.	Пусть 4sj#(m, «)— неотрицательно определенная матрица. Доказать, что система Ля>0, я>0 совместна.
Остальные задачи параграфа посвящены некоторым приложениям теории существования решений систем линейных неравенств. В задачах 4.110—4.118 приводятся разнообразные критерии ограниченности и одпоточечпо-сти полиэдров, дополняющие тригональные результаты из 4.4, 4.6. Наиболее важные критерии основаны па следующем результате.
4.109.	Пусть А	п). Доказать, что система
<сц, А> 0, i = 1, ..., к, к 	(4.27)
< а г, h> = 0,	i к + 1, ..., т,
имеет лишь тривиальное решение /: = 0 в том и только том случае, если rangJ=H и существует такой вектор peR" что
М = 0, Pi > 0, 1=1,..., к, (4.28)
4.110*	. Доказать, что непустой полиэдр X вида (4.3) ограничен в том и только том случае, если гап^Л=;» и существует лектор ре IV", удовлетворяющий условиям (4.28).
4.111.	Доказать, что непустой полиэдр
X ж {х <= R”|Ла: С Ъ, х 5*0),
где Л^^Л(/п, n), &<=RW, ограничен в том и только том случае, если существует такой вектор р е R1", что рА > О, р^0.
4.112.	Доказать, что непустой полиэдр X вида (4.4)' ограничен в том и только том случае, если существует такой вектор р R"’, что рЛ > 0.
G с. А, Лшмапоо, Л, В, Тимохов	81
4.113*	. Пусть X — полиэдр вида (4.3), х*еХ, 7 = =/(х*). Доказать, что х* является единственным элементом X в том и только том случае, если rang Л; = л и существуют такие числа pi (i^2), что
2д^ = 0,	Pt>0, г<={1,
<в/
4.114.	Пусть X— нолпэдр вида (4.4),	7 =>
=^7(х*) (см. (4.5)). Доказать, что х* является едппст-веппым элементом X в том и только том случае, если rang 171 и существует такой -вектор. p<=Rw, что
(p,aS) = 0,	;*е/;
(р, а5) >0, / е {1, ..., n}\J.
4,115.	Доказать, что непустой полиэдр X вида (4.1) ограничен в том и только том случае, если при любом ceR” система
рА == с, р 0	(4.29)
совместна.
4.116.	Доказать, что непустой полиэдр X вида (4.1) целиком лежит в В" в том и только том случао, если существует такая неотрицательная матрица Р размера п X т, что РА = “2?, РЬ 0, где Е — единичная матрица размера п X п.
4.117.	Доказать, что непустой полиэдр X вида (4.1) ограничен в том и только том случае, если существуют такие неотрицательные матрицы Р и Q размера п X mt что РА = —Е, QA — Е, причем отсюда следует, что {P + Q)b >0.
4.118.	Доказать, что непустой полиэдр X вида (4.1) состоит из одной точки в том и только том случае, если существуют такие неотрицательные матрицы Р и Q размера п X т, что РА = —Е, (М (Р 4- Q) Ъ « 0,
Задачи 4.119—4.123 посвящены выводу одного топкого факта теории линейных неравенств — теоремы Хоффмана. Решающим является здесь следующее утверждение, представляющее и самостоятельный интерес.
4.119*	. Пусть X— непустой полиэдр вида (4.1), х* — проекция точки х&Х па X (см. п. 3 § 1). Доказать, что существуют числа (г^7(х*)), при которых
X —	51 PiSt,
82
т. е. вектор я — х* является неотрицательной линейной комбинацией нормалей активных ограничений в точке л* (ркс. 17).
4.120.	Пусть матрица 4s^(w, п) такова, что система рЛ = 0, р>0 несовместна. Доказать, что сущест-
вует число а>0, при котором для любого вектора р 5* 0 справедливо неравенство
max <а<, рАу ^а|р4[], 1 С I <Т71
где, как обычно, at обозначает i-ю строку матрицы Л.
4.121*. Доказать теоре-.му Хоффмана,
Рис. 17
Пусть	X — непустой
полиэдр вида (4Л). Тогда существует такое число а>0, зависящее от матрицы А и не зависящее от вектора Ь, что для любого %<£Х справедливо неравенство
max (<at, д.‘> — /><) ^>ар (яг, X), 1<С1С1Я
(4.30)
где р(.г, X) = inf	расстояние от точки х рр
х'ех
множества X.
Отметим, что теорему Хоффмана можно рассматривать как обобщенно следующего элементарного факта на аналитической геометрии: если даны полупространство Аг = {г П" | <e, x> i} п точка .т X, то рдсстоиипо между ними вычисляется по формуле
Р (х, X) =	((л, ж) Ь).
4.122.	Доказать, что в теореме Хоффмана вместо неравенства (4.30) молено поставить неравенство
m
2 шах (0, <«j,	— i|) ^ар (х, X)
i=i
‘или неравенство
114» - &Н > ар (ж, X).
При этом уже допускается случай » е X.
4.123.	Пусть X — полустой полиэдр вида (4.3). Доказать, что существует такое число а>0 (а="а(4)), при
В*	83
котором для любого справедливо неравенство h	«
У max (0, <я<, .г> — bi) -Ь У | <ej, z> — bt | ар (яг, X). i=*l
В задачах 4.124—4.137 излагаются основные факты теории параметрических систем линейных неравенств. Если выше практически всюду параметры линейной системы считались заданными, то теперь в центре внимания будет вопрос: как меняются свойства этой системы при варьировании ее параметров?
Под Х(Л, Ь) ниже понимается полиэдр вида (4.3) при данных	п) и ftsR1", Для удобства ссылок
напомним вид системы из (4.3):
<alt x>^bi, 1=1, ...,1с,
(4.31)
<Н{, х> = bf, i = k +1, ..., т.
4.124.	Система (4.31) называется устойчивой, если она совместна и остается таковой при малых возмущениях ее параметров. Иными словами, система (4.31) устойчива, если при любых А' и Ь', достаточно близких к А и Ь, полиэдр Х(Л', &') непуст*).
Убедиться, что системы
Ж1 + .т8<1, 2i>0t ж2>0;
я?! -]- ж2 = 1,	0, я>2 ^5* 0;
'	+	2ж1 + 2жг^2
устойчивы, а системы
Ж| + ж2^1, st + s2>l, х, 5= 0, Ж2>0;
1,	+ Ж2 “ 1
неустойчивы.
4.125.	Доказать, что множество всех нар (Л, Ь)<= ^^(т, n)XRm, при которых система (4.31) устойчива, является открытым.
4.120*	. Доказать теорему об устойчивости системы линейных неравенств и уравнений.
Следующие утверждения эквивалентны:
а)	система (4.31) устойчива;
*) В метрпческом смысле матрицы из пг, м) рассматршииот-сл как элементы пространства Rwn.
84
б)	система
рД=О, </>, &>^0, pt 0, i=l, .... к, (4.32) имеет лишь тривиальное решение р = 0;
в)	система
<д(, х> < !>(, г = 1, к,
(4.33)
<дгг, =» b<,	i*=>k + 1, .. „ mt
совместна, а векторы а{ (i = k-|-lt т) линейно ие-з а висим ы.
Полезно отметить, что совместность системы (4.33) равносильна тему, что вес ограничспяя-норапепстна в системе (4.31) являются нежесткими (см. 4.22).
4.127*	. Доказать, что система (4.31) устойчива в том и только том случае, если опа устойчива по правой части ограничений, т. е. при всех Ь", достаточно близких к Ь, полиэдр Х(Д, Ь') пепуст.
4.128.	Пусть система (4.31) имеет такое решение я*, что векторы at (fs/(x*)) линейно независимы. Доказать, что система (4.3!) устойчива. Привести пример, показывающий, что это достаточное условие устойчивости ие является необходимым.
4.129.	Пусть последовательности {Л'), {/>’} и {»') таковы, что Д'->Д, Ь* Ь, х1 <=Х(Д‘, Ъ3) и Доказать, что я^Х(Д, Ъ).
Это простое утверждение означает, что многозначное отображение (Л, £•)-» л (Л, Ь) является замкнутым [29, 32, 39].
4.130*	. Пусть система (4.31) устойчива. Рассмотрим любую точку я°еХ(Д, Ь) и любые такие последовательности {И*}, {&*}, что Л*-*-/!, Ь‘^-Ь, Доказать, что существует такая последовательность (ж*}, что ж’-’-.т0 п ж'<== ®Х(Д’, Ъ3) прп всех достаточно больших $.
Иными словами, утверждается, что многозначное отображение [6’29]"*^^’ полунепрерывно снизу в данной точке (Л, Ь)
4.131.	Привести пример, показывающий, что для неустойчивой системы утверждение из 4.130 может нарушаться, если даже X (4*, Ь3) ¥= 0 при всех д.
4.132*	. Пусть полиэдр if (Л, Ь) непуст л ограничен. Доказать, что при любой матрице Л', достаточно близкой к Д, и любом векторе {/^R'n полиэдр АГ(Д', Ь') ограничен *).
*) Пустое множество считается ограниченным по определению.
85
4.133.	Пусть полиэдр X(Л, Ь) непуст п ограничен. Рассмотрим любые такие последоватольпости {/!'}, (/>’} п te*}, что Л'-“-Л, {&'} ограничена и я* е=Х(Л\ 6*). Доказать, что последовательность U’} ограничена.
В частности, при Ъ’ -> ft это означает, что многозначное отображение (Л, Ь)->-Х(Л, ft) локально огрдннчено в указанной точно (Л, ft) [39].
4.134.	Доказать, что при любой заданной матрице Л«=.й£(т, в) множество всех докторов b^R", для которых полиэдр Х(Л, Ь) непуст, замкнуто.
Полезно отметить, что, в частности, здесь отражен факт замкнутости ыпоготраппого конуса (см. теорему 7.13).
4.135.	Принести пример, показывающий, что в 4.134 матрицу А п вектор Ъ нельзя поменять местами.
4.136*	. Прп заданной матрице	и) введем
обозначения Х(&) = Х(Л, Z>), ]3 = {b|^RB‘lAr(&)^i 0}. Доказать, что существует константа £>0, зависящая только от матрицы Л, при которой для любых Ь, Ъ'&В выполнено неравенство
d(X(&), Х(Ь'))^£И&-Ь'И,
где
d (X, X') = max fsup p (x, X'), sup p (x, X)1 Ixex	k&X' J
есть так называемое xaycdoptjioeo расстояние между множествами X = X(b) и X' = X(&'),
Иными словами, мпогозпачпоо отображение ft->-X(ft) удовлетворяет условию Липшица в метрике Хаусдорфа и, следовательно, непрерывно по Хаусдорфу па В [29].
4.137.	В обозначениях задачи 4.136 доказать, что существует константа Л = £(Л)>0. прп которой для любого Ь^В найдется точка х^Х(Ь), удовлетворяющая неравенству 1Ы1 < Ijlill.
§ 5. Теория линейного программирования
СВОДКА ОСНОВНЫХ ФАКТОВ
1.	Постановка и формы записи задачи ЛП. Задачей линейного программирования (ЛП) называется задача максимизации пли минимизации линейной (функции на полиэдре. Таким образом, задачу ЛП моя«но записать
SG
и впде
<с, а;> -* max. Ля Ъ,	(5.1)’
где Ле^(п», n), &eR"1, c^R". Для дальнейшего полезло выписать отдельна допустимое множество этой задачи:
Xе3 R”]Az b} = {or^WKar, x>^b(, i = l, ...» m).
:(M).
Теорема 5.1. Любое локальное решение задачи ЛП является и глобальным.
Учптып&я это утверждение, в дальнейшем будем говорить просто о решении задачи ЛП.
Полезно отметить, что множество X* решений задачи (5.2) также является полиэдром, поскольку, если опо непусто, это множество представимо в виде
Х* = {хеКЧЛя<&, <с, я>^/*),	(5.3)
где /* —значение задачи (5.1), т. о. /* = sup
Задачу ЛП вида (5.1) называют основной. Ниже указываются другие распространенные формы записи задачи ЛП на максимум, различающиеся способами представления ее допустимого множества. При этом но-преж-нему считаем, что Ле^(т, n),	c^R".
Стандартная задача ЛП:
<с, я> -> шах> Ля <Ь, я^О.	(5.4)
Каноническая задача ЛП:
<с, «>->max, Ах = Ь, х 5^0.	(5.5)
Обадяя задача ЛП:
п
2 суЧ -> шах, iei
га'
(5е) га
2 Дуду => bi, l «в k +1, ..m,
Я;>0,
Аналогичные формы записи используются н для задачи ЛП на минимум, по все неравенства пишутся здесь со знаком
87
Формально говоря, каждая из задач (5.1), (5.4)’, (5.5) является частным случаем общей задачи (5.G): при к = т и s = 0 получаем задачу (5.1), при к~т н s^> = п—задачу (5.4), при /i‘ = 0 п — задачу (5.5). Однако в свою очередь общая задача может быть представлена в форме любой из трех остальных. Так, задача (5.0) принимает основную форму, если заменить в пей систему ограничений-равенств на эквивалентную систему ограпнчений-нерапенств:
п	»
GijXj 5гц	1 и Л И* 1> • •
(5.7)
Еслп к тому же сделать замену переменных
—	vjS?0, / = $ + 1, ..., n, (5.8)
то задача (5.6) примет стандартную форму. Если огра-ниченид-перавепства в (5.6) записать в виде
я
S ai}xi + Н-Ч =	4 = 1, ..., А*,	(5.9)
где ufi (2 = 1,..., к) — дополнительные переменные (формально входящие в целевую функцию с пулевыми коэффициентам]) , и вновь использовать замену переменных (5.8), то задача (5.6) превратится в каноническую.
Вообще любую задачу ЛП па максимум пли минимум с неравенствами, направленными в ту пли иную сторону, можно представить в любой из указанных форм. Для этого наряду с приемами (5.7)—(5.9) необходимо использовать умножение целевой фуйкцпд пли ограппче-вий-неравемсти па — 1, что позволяет переходить от минимизации к максимизации к менять знаки неравенств.
2.	Примеры задач ЛП. Существует большое количество примером задач ЛП в различных сферах практической деятельности. Приведем три примера, ставшие классическими.
Пример 5.1 (задача планирования производства). Пусть некоторое предприятие производит п типов товаров, затрачивая при этом т типов ресурсов. Известны следующие параметры:
«и — количество i-ro ресурса, необходимое для производства единичного количества /-го товара,	(i =
«1,..., щ; / = 1,»);
88
bt — запас i-ro ресурса на предприятии, Z>i>0;
с/—-цена единичного количества /-го товара, с,>0. Предполагается, что технология производства линейна., т. е. затраты ресурсов растут прямо пропорционально объему производства. Пусть число X; показывает планируемый объем производства /-го товара. Тогда допустимым является только такой набор производимых товаров
жп), при котором суммарные Затраты каждого i-ro ресурса не превосходят его запаса:
я
S	i = 1, ,.., m. (5.10)
$«1
Кроме того, имеем следующее естественное ограничение:
х/>0, /^l, п.	(5.11)
Стоимость набора товаров ж ныраясаетсн величиной
п I
3 W	(5.12)
J”!
Задача планирования производства ставится следующим образом: среди всех векторов х, удовлетворяющих ограничениям (5.10), (5.11), найти такой, при котором иедичина (5.12) принимает наибольшее значение. Таким образом, мы получаем задачу ЛП в стандартной форме (5.4) с той лишь спецификой, что матрица А (at)) здесь неотрицательна, а векторы 6 = (6>) и c = (cj) положительны.
Пример 5.2 (задача о рационе). При организации "питания больших коллективов людей, например в армии, больницах и т. п., возникает задача о наиболее экономном рацпопе питания, удовлетворяющем определенным медицинским требованиям. Пусть имеется п продуктов питания (хлеб, мясо, молоко, картофель и т. п.), в которых учитывается m полезных веществ (жиры, белки, углеводы, витамины и т. и.). Известны следующие параметры:
ац — содержание i-ro вещества в единичном количество /-го продукта,	(i*= 1,	щ.; / = 1, ..., н);
bt — минимальное количество i-ro вещества, которое должно потребляться индивидуумом в расчете, скажем, на месяц, bi > 0;
cj—цепа единичного количества j-го продукта, cj>0.
89
Задача о рационе формулируется следующим образом:
Л
S cjXj->minr
5=1
"	(5.13)
2j ОД > Ь{1 i 1, ..т,
zj>0, / =
гдо X] обозначает количество у-го продукта, потребляемого индивидуумом в течение месяца. Иными словами, среди всех рационов питания	..., хл), покрываю-
щих минимальные потребности индивидуума в полезных веществах, необходимо выбрать наиболее дешевый. Отметим, что (5.13)—-это просто стандартная задача ЛП на минимум с неотрицательными параметрами.
Пример 5.3 (транспортная задача). Пусть некоторый однородный продукт (уголь, кирпич, картофель и т. и.) хранится па т складах п потребляется в п пунктах. Известны следующие параметры:
щ — запас продукта на i-м складе, а(>0 (i®=l, ... .... m);
b} — потребность в продукте в у-м пункте, bj > 0 (у = = 1, ..., н),
су—стоимость перевозки единичного количества продукта с Z-го склада в ;-й пункт, сг; > 0.
При этом суммарные запасы равны суммарным потребностям:
T7I	-П
2 <4 = И	(5.14)
i”l	5ml
Транспортная задача ставится как каноническая задача ЛП следующего специального вида:
m п
2 2; Cu<Ti;--»-min5 i=iy=i
n
2 «у = «&	/ = !,..zn,	(5.15)
5=1
m
2 Xlj = bj, J = 1, . .Л, <=i
Z= l, ..., zzi;	n,
где xt) показывает количество продукта, перевозимого с Z-го склада в у'-п пункт. Иными словами, требуется так 50
организовать перевозки продукта со складов в пункты потребления, чтобы при полном удовлетворении потребностей минимизировать суммарные транспортные расходы. Заметим, что4 условие (5.14) является необходимым и достаточным для существования по крайней море одной матрицы перевозок	удовлетворяющей огра-
ничениям задачи (5.15).
3.	Геометрическая интерпретация задачи ЛП. Задачу ЛП с двумя переменны»!!! можно решить геометрически.
Рис, 18
Пусть, nanpimep, дапа основная задача ЛП (5.1) при п = 2. Тогда, следуя общим рекомендациям из н. 4 § 1, необходимо прежде всего изобразить на плоскости допустимое множество этой задачи — полиэдр X впда (5.2). Линин уровня ее целевой функция представляют собой семейство параллельных прямых <с, я>=а (аеВ), прячем пх общая нормаль с «смотрит» в сторону возрастания функции <с, .т>. Поиск решения задачи сводится к нахождению максимального числа а* средн всех а, при которых прямая <с, хУ *= а. имеет непустое пересечение с X. Если такое (конечное) а* существует, то оно является значением задачи. При этом любая точка па прямой <с,	лежащая в X, служит решением за-
дачи, Решение я* может быть как единственным (рис. 18), так п неедпнетвеппым (рис. 19). Если при всех достаточно больших а пересечение прямой <с, хУ « = а с X непусто, то значение задачи бесконечно, и, следовательно. опа нс имеет решения (рис. 20).
Из приведенных рисунков очевиден ряд свойств задач ЛП, которые будут сформулированы в п. 4.
Геометрические соображения могут быть полезными и прп решении некоторых задач ЛП со многими перо-91
меивыми. Пусть, например, дана задача ЛП в канонической форме
п
/	max,
j=i
"	. .	(5.16)
772-*
5*1
О, У tf v  -3 71f
гдо число перемой ных па два больше числа огратшче-пий-ра«еиств, т. е. п - т = 2, причем ранг матрицы
A^=(a<j) ранен т. Тогда две переменные в указанной системе уравнений, скажем и £2, являются свободными, т, е. через них можно выразить все остальные переменные:
xj “ajiXi + aj2,r2 + .3/t /«3.n, (5.17)
где «д, <Zj2, некоторые числа. Подставляя этп выражения в целевую функцию, получаем
/=71Ж1 + 72Г2 + 6,	(5.18)
где Ть 12» 5 ~~ некоторые числа.
Рассмотрим задачу ЛП с двумя переменными:
Tfi^i + "fa^2 -* max, адяИ*йй^з-I-0j>0, / = 3, п, (5.19)
£1	0, Х2 > 0.
Используя геометрические построения, находим ее решение (л-ц ж*). Подставляя эти числа в (5.17), (5.18), получаем решение и значение исходной задачи (5.16). 92
Описанный метод исключения переменных, конечно, применим и в том случае, если в задаче (5.16) число перемениых лишь на единицу больше числа ограничений-равенств, т. ё. №-1й«1 Тогда все сводится к отысканию решения элементарной, задачи ЛП с одной рерс-меипой. Если в задаче (5.16)” нс па все переменные наложено условие неотрицательности, то это приводит лишь к уменьшению числа ограничений в (5.19).
4.	Основные свойства задачи ЛП. Если допустимое множество задачи ЛП непусто и ограничено, то, согласно теореме Вейерштрасса, опа 1гмеет решение. Вместо с тем для задач ЛП справедлива следующая специфическая теорема существования.
Теорема 5.2. Если допустимое множество задачи ЛП непусто, а значение ее конечно, то эта задача имеет решение.
Ипыми словами, для задач ЛП случай 2) из и. 2 § 1 невозможен.
Как и в § 4, под Z(x*) будем понимать множество номеров активных ограничений в точке х*<=Х, где X— полиэдр вида (5.2):
I (я*) = {/, 1 i ml <cr, £*> «» Ъ(}.
Заметим, что па рис. 18 нормаль с целевой функции располагается «между» нормалями щ и а? активных ограничений в точке ,т*. Это означает, что с является линейной комбинацией векторов и at с неотрицательными коэффициентами. Аналогично па рис. 19 вектор с получается умножением на неотрицательное число нормали «1 единственного активного ограничения в я*. Отсюда ясеп геометрический смысл следующего утверждения.
Теорема 5.3 (необходимое и достаточное условие экстремума в основной задаче ЛП). Допустимая точка х* задачи (5.1) является ее решением в том и только том случае, если существуют такие числа у * 0 (г е eZ (а*)), что
с =* 2	(5.20)
Из этого принципиального факта без труда выводится аналогичный результат для задачи ЛП в произвольной форме записи.
Теорема 5.4 (необходимое и достаточное условие экстремума в общей задаче ЛП). Допустимая точка х*
93
задачи (5.6) является ее решением в том и только том случае, если существует такой вектор	е Кт>
что у? 0 при всех i 1, ,.к и
3 U*aij>Cj,	/ = 1, .s,	(5.21)
i-l
m
2 yUij = cj, j = s + 1, ..n, (5.22) f<=l
(I7J	\
2 y*atj — Cj « 0,	/ =	[(5.23)
i«I	/
(П	\
=0’ « = *.•••.*• <5-24)
>1	/
Подчеркнем, что теорема 5.3 есть частный случай теоремы 5.4, поскольку при к^т, 5 = 0 условия (5.21), (5.23) просто отсутствуют, а условие (5.24) равносильно тому, что у* “ 0 при всех £<={!, ...» т}\Цх*).
Из рис. 18, 19 очевиден также следующий важный факт теории ЛП.
Теорема 5.5. Пусть задача ЛП имеет решение, причем ее допустимое множество обладает по крайней мере одной вершиной. Тогда существует такая вершина, которая служит решением задачи. В частности, если решение единственно, то оно обязательно является вершиной.
Таким образом, если задача ЛП па максимум удовлетворяет условиям теоремы 5.5, то для отыскания ее решения достаточно найти все вершины допустимого множества задачи (число которых, согласно теореме 4.1, конечно) и выбрать из них ту, в которой функция принимает максимальное значение.
Описанный метод полного перебора вершин практически применим лишь для малоразмерных задач ЛП, ног скольку при большом числе переменных и ограничений ои требует огромной вычислительной работы. Том не менее именно идея перебора вершин (по не полного, а упорядоченного) лежит в основе эффективного численного метода решения задач ЛП, называемого спмплекс-методом. О нем пойдет речь в § 6.
5.	Понятие двойственной задачи ЛП. Каждой задаче ЛП можно поставить в соответствие другую задачу ЛП, называемую двойственной. Их совместное изучение составляет предмет теории двойственности, являющейся важным разделом линейного программирования. Цент-94
ральныс результаты этой теории —приводимые ниже теоремы 5.9 и 5.10;—по существу, лишь придают иную форму теоремам 5.3 л 5.4. Одпако во многих вопросах пмеипо эта форма оказывается наиболее эффективной.
Для удобства выпишем еще раз обй^ую задачу ЛП:
п
<С, Ж> = 2 ЮХ, i=>l п
У,	I =» 1, .7с,	(5.25)
7*1
п
У я= 5{, 11= к + 1, .т, J«=l
X] 0, у «= 1, ..s.
Двойственной к задаче '(5*25) называется следующая задача: m
<bt у> = 2 bi!/i -* min, i=l
га
2 yi^ij Cjt j = 1, ..., s,	(5.26)
i«»l tn .	•	"
2 У fit) =* Cjt / = $ -M, ..n, i=i
i=^ 1, .7c.
При этом задача (5.25) называется прямой.
Переход к двойственной задаче удобно осуществлять с помощью табл. 1.
Таблица 1
х, 0	. . . xt > 0 х<+1	. . . хп
1гд5?0 • •	«И	. . . alf	в1.»Ь1	• • • а1л		
	4	• * • atu	ал,ж	• • • ahn		bk
»Л+1 • •	йЛ+1.1 • •	• • • «л+м	вм-м+*	 ’ * aA+i.n • •	—	Ьк¥1 9 •
Ут	ЯпИ	• * * агад	вга.«+1	’   дгап		р»
		• а «	£3	• « » ==		
	«1	... С,	с1+1	. . . €п		
85
Сначала в таблицу заносится вся информация о прямой задаче: значения параметров а<}, Ь{ и cJf знаки неравенств или равенств в ограничениях (справа), условия неотрицательности соответствующих переменных (сверху). Затем каждой f-й строке (t-му ограничению прямой задачи) ставится в соответствие двойственная переменная y(t па которую накладывается условно неотрицательности, если справа в отой строке стоит знак неравенства. Внизу проставляются злаки неравенства пли равенства в заяпспмости от того, наложено пли пе наложено условие неотрицательности па соответствующую переменную прямой задачи. После этого двойственная задача «считывается» путем умножения вектора у=(у<) па столбцы матрицы Л = (dtj) и вектор 6s(J().
В табл. 2 указаны прямая и двойственная задачи в наиболее важных частных случаях.
Таблица 2
Формы n.urucn njMINOlt ЗВДЦ’ГИ ЛП	Формы апппси соотви-стпуюикгй nKoftcmeiuiotl йалачи ЛП
OcifGiniRii: <е, .т> max, Ах ъ	Каноническая: <ь,	->• min, У А = с, у > 0
Стандартная: <с, ж> шах, Ллгь,	0	Стапда1>таал: < ь, у> ->- min, уА с, у > 0
Каноническая: <с,	inax, Ах^= ь, х^О	Освоилал: <6, у> -* min, у А > с
6. Основные факты теории двойственности.
Теорема 5.6. Задачи. (5.25) и (5.26) взаимодвойст-венны., т. е. двойственной к задаче (5.26) является задача (5.25).
Ниже под X и У понимаются допустимые множества задач (5.25) и (5.26) соответственно.
Теорема 5,7. Для любых и y^Y выполняется неравенство <с, хУ С <6, уУ.
Теорема 5.8, Пусть х* е X, у* е У. Тогда
1) если
<е, х*У = <Ь, у*У,
(5-27)
то х* есть решение задачи (5.25), а у* — решение задачи (5.26);
2) равенство (5.27) равносильно совокупности условий
«J f S" 0» /в1»	(5.28)
\i=L	/
(П	\
2	) «= О» i «= 1, .&.	(5.29)
?e»i	/
Равенство (5.27) принято называть соотношением двойственности, условия (5.28), (5.29), уже встречавшиеся в теореме 5.4,— условиями дополняющей нежест-кости.
Теорема 5,9 (теорема двойствепиостп). Прямая задача (5.25) г/.иеет решение в том и. только том случае, если двойственная задача (5.2(5) млыег решение; при. этом значения данных задач совпадают, т. е. для любых их решений х* и у* выполнено соотношение двойственности (5,27).
Важно подчеркнуть, что множество решений двойственной задачи совпадает с множеством векторов у* из формулировки теоремы 5.4.
При практическом применении теории двойственности особенно полезным является следующее утверждение, непосредственно вытекающее из теорем 5.8 и 5,9^
Теорема 5.10 (о дополняющей иежесткостп). Точки х* X и у* е У являются решениями езаимодвойст-венных задач (5.25) и (5.26) соответственно в том. и только том случае, если выполняются условия (5.28), (5.29).
Итак, взаимодвойствепные задачи ЛП имеют или пе имеют решения одновременно. Следующая теорема показывает, что уже по их допустимым множествам можно отличить первый случай от второго.
Теорема 5.11. Если, допустимые множества взаи-модвойственных задач (5.25) и (5,26) непусты, то обе они имеют решение. Если же только у одной из них допустимое множество непусто, то ее значение бесконечно, т. е.
если Х=£0, У = 0, то sup (с, х) = то; х
если-Х = &, Y^0tro inf {b, у} = — то.
Y
Отметим некоторые способы использования теория двойственности для отыскания решений простейших за-
7 С, А. Ашманов, А, В. Тимохов	517
дач ЛП. Если из геометрических или иных соображении выдвинута гипотеза о том, что данная точка х*^Х является решением задачи (5.25), то эта гипотеза может быть строго обоснована путем подстановки я* в систему (5.28), (5.29). Критерием истинности гипотезы является разрешимость этой системы относительно у* е У. Отметим, впрочем, что здесь пет необходимости прибегать г: самому понятию двойствен пости: можно использовать непосредственно теорему 5.4 пли, в частности, теорему 5.3.
Более эффективной теория двойственности является в тех случаях, когда двойственная задача решается проще, чем прямая. Если решение у* двойственной задачи (5.26) найдено, то, подставляя у? в (5.28), (5.29), получаем систему на X для определения решения я* прямой задачи (5.25). В некоторых случаях удается решить систему (5.28), (5.29) на декартовом произведении X X У и тем самым одновременно найти решение как прямой, так и двойственной задачи.
УПРАЖНЕНИЯ
5/1. Привести следующую форме:	задачу	ЛП к стандартной
4^1 +	+		шаХл
2^! -г z2 'Н	х3 ~	1,
3% "1“	Z3 ~	2Х
—Ял -г 5.т2 +	2i^y со	4,
х3	0; «3 S	? 0:
/v	W		~ й со		« Й W		~ я; и	
1		6	=. —	11	a	=5	18	^5
2	= < >	7	< >	12	— = г-с	17	> >
3	= 5=3	8	=	13		18	—
4	ЕН	9		14	5s	19	
5	=	10		15	== = >	20	
5.2. Привести следующую задачу ЛГГ к канонической форме:
— жз — mini
98
a?! + Зх2	— ЯЦ	2*
-—Xj[ ~7~	#3	"I” ^4 I
sr2 -1- X3 co 3,
^1	0» ®5 s^ 0*
5.3.	Используя геометрические построения, найти решение следующей задачи ЛП:
Ц- аж2 -> max, а» -г 2хй С 10* За?! 4- 2жй 18* — х2 —5* са?! — a:™ 8с 4- 3 ♦):
	а	&	с	а		b	с
1	5	7	2	11	—5/6	8	1/4
2	1	6	3	12	3	13/2	2
3	-1	6	1/8	13	1	9	1
4	5	9	1	14	-1/3	10	2
5	3/4	7	1	15	7/4	6	3
6	-1/4	10	2	16	-3/4	13/2	1/2
7	4	12	1/2	17	3/2	7	2
8	5/4	9	1/3	18	3	6	1
9	—1	6	1/2	19	4	8	3/4
10	5/6	7	1	20	—1	15/2	1/3
*) В подобных заданиях требуется не только выдвинуть геометрическую гипотезу, что некоторая точка является решением задачи, но и строго обосновать ату гипотезу с немощью изложенной теории.
7*	‘	99
5.4.	Используя геометрические построения, найти решение следующей задачи ЛП:
(IXl 4"		z2 -	-> min
4-	(Ъ	3)#S s	* ъ3
(с — 4)^ 4-		жз 2	сл
3a:i -н			* 11s
	Ох		s 0:
« Ь с		а Ъ е		а Ъ с		а Ъ с	
1	П4 5 0	6	1/2 7 6	11	7/2 5 7	16	1/2 4 9
2	5/4 4 6	7	1/G 8 8	12	9/2 6 9	17	5/3 8 6
3	9/2 7 8	8	5/2 4 7	13	1/5 7 7	18	3/4 5 8
4	7/4 8 7	9	13/3 5 8	14	7/2 4 8	19	1/4 6 8
5	5/2 8 6	10	2/3 0 7	15	1/3 8 9	20	11/2 7 9
5.5.	Используя метод исключения переменных и гео-метричеокпе построения, найти решение следующей задачи ЛП:
axj — Зз3 max.
2xj -f- bxz + #3
2x1 -h 5.t8 — 2#g	0t
CXj. 4" 2x% — >Trj	— 3,
£a > 0s #з > 0:
	а	b	1?	а		Ъ	с	а		b	с	а		b	с
1	10	2	3	6	—2	2	2	И	-1	5	3	16	—2	5	2
2	-1	1	2	7	2	3	4	12	6	6	4	17	4	4	3
3	3	5	4	8	5	5	3	13	10	1	2	18	12	<>	4
4	—3	4	2	9	11	1	4	14	-3	3	3	19	5	3	2
5	12	3	3	10	7	7	о м	15	7	3	4	20	-1	3	4
5.6.	Используя метод исключения переменных ir геометрические построения, найти решение следующей задачи ЛП:
.т, 4" жз -|- с#» 4* шах,
й\ — а* 4-	6я4 — 2®в — с — 15,
1LKJ
rra — я3 —	-|- 6#s = 24,
‘I"	—- Зж4 4- 7я0 = c -f- 24,
fly- Ot / = !,..., 5:
	а	ft	с	л		b	с	л		ft	с	а		ft	с
1	3	5	6	0	1	1	7	11	1	2	8	10	2	2	0
2	5	О А/	7	7	6	3	8	12	8	4	6	17	1	3	7
3	1	5	8	8	2	1	0	13	2	5	7	18	7	4	8
4	3	—1	6	9	3	0	7	14	9	5	8	19	6	О	6
5	4	3	7	10	5	7	8	15	7	—1	б	20	3	3	7
5.7.	Определить, имеется ли решение задачи (4 — 5a)^i 4- 1ОЬя:а -|“ 15сл:3 -> шах, (2а 4* l)a?i — 4Ьлг2 — 6сж3 13, t (5 — 4д)я1 -И 8Ьх^ 4- 12сж3	23,
—(За 4~ 1)31 + 6&х2 4' 9«г3 «С 3
среди точек
«•-(о, 4-, о), «*-(5, «Ч’-тМ
V £tV 1	\	V* t	\	tel/	у
	а	ь	с	а		ft-	С	a ft		с	а		ft	е
1	-1	1	3	G	3	—1	8	11	5 -2	б	10	1	-1	3
2	-1	1	0	7	—3	2	3	12	5 -2	8.	17	1	-1	0
3	'1	1	8	8	-3	2	0	13	-3 1	3	18	1	—1	8
4	3	—1	3	а_	-3	2	8	14	-3 -1	б	19	3	—2	3
5	3	-1	8	10	5	-2	3	15	-3 1	8	20	3	—2	8
5.8.	Принести примеры таких значений параметре р и д, при которых задача
4~ Ьх2 —>- maxj
"Ь РХ2 < 1, — хя > qt > О
а)	имеет пустое допустимое множество;
б)	имеет значение, равное «;
в)	имеет единственное решение;
г) имеет бесконечно много решений:
с ь		a b		а b		a b	
1	3 5	6	2 1	И	7 3	10	2 5
2	3 7	7	6 5	12	7 4	17’	5 2
3	2 3	8	3 7	13	3 2	18	2 7
4	8 3	9	5 8	14	5 3	19	7 2
5	3 4	10	4 7	15	5 «	20	3 1
5.9.	Найти все значения параметра А, при которых точка х* = (6, о) является решением задачи
kxt + (2 — к)ха -> maxj
axt — Ьха Ол
2a?x 4~	Зяа	Ct
Xi 4-	ха	а 4~ b:
	а Ъ	с	а		Ъ	с	a		5	с	а		ъ	с
1	4 -3	7	С	3	1	13	И	3	—1	8	10	5	1	20
2	3 2	14	7	3	-1	0	12	3	—2	7	17	5	2	20
3	2 -1	5	8	4	-1	12	13	4	2	10	18	5	-3	11
4	5 -2	13	9	4	—2	10	14	4	3	19	19	0	-5	10
5	5 4	25	10	4	1	15	15	5	—1	14	20	0	~4	11
5.10.	Найти решение следующей задачи ЛП методом полного перебора вершин:
ЙХ1	4'	+	8й?з ;	н maxj
а?!	+	Ьх2 4-	жз 5	
	4-	я2 4*	сж3	£ 1х
		0х 272	> 0,	Ъ > 0:
	а	Ъ	С	а		b	с	a		Ь	с	a		Ъ	с
1	4/3	Ь	5		4/3	4	0	11	7/3	4	3	16	3/2	9	5
2	3/2	6	4	7J	16/5	3	2‘	12	19/5	6	2	17	7/4	5	4
3	7/3	9	3	8	6/5	2	С	13	3/2	2	4	18	15/4	7	2
4	0/5	3	6	9	9/5	3	4	14	5/3	6	5	19	4/3	5	0
5	5/4	9	7	10	7/2	4	2	15	7/2	5	2	20	7/3	0	3
102
5.11.	Найти решение следующей задачи ЛП методом полного перебора вершин (опорных точек):
й?! 4- Зжг — йг3 — ж4 -> шах,
ахг —	-Ь 1>Хц - 120,
*1 4- х3 — х3 -Ь я4 = 0, .*₽! -1' Ч- ^3 Ч-zi >0,	/ =	4: -
	а	Ь	с	а		Ъ	С	а		Ъ	с	а		Ь	с
1	1	2	2	6	1	5	5	11	1	0	0	16	1	3	3
2	3	5	0	7	2	8	5	12	3	1	0	17	2	5	3
3	5	8	2	8	3	11	5	„13	5	2	0	18	3	7	3
4	7 11		2	9	4	14	5	14	7	3	0“	19	4	9	3
5	9 14		2	10	5	17	5	15	0	4	0	20	5	11	3
5.12. Построить задачу, двойственную к следующей задаче ЛП:
S1 4-	2х2 ->	max.
Зя?х 	4жг ~	h
5zt 4-		2,.
-7^ +	8а?2 со	3r
х3 0:
a# go		<— a: go		a; w		~ pa	
1	<	6	= < =£	11	s?	16	—— 	
2	^2"	7	a» 5s	12	=	5s	17	
3		8	< >	13		18	’C —
4	=	9		14	< = <	19	= =
5	=	10	=	15			^5	2^	20	-c = -
5.13. Даны задача
4“ 2х3 — х3 -> шах,
—#1 4“	— 2х3	а,
.*! + хй 4- 2х3	6,
2.Г1 — .г«	2.т3 <1 с,
0* г'а 0, arg 0,
103
ее допустимые точки
ж1 =
аЧ-4« 2л-f-с >	/4Л“|-с й-Ь2й с —а
7 ,	? , иу, аг -	у-, -^=— > “2“
а таюке допустимые точки
двойственном задачи. Определить, имеются ли среди ;н’пх точек решения соответствующих задач:
	а	b	с	a		b	с	a		b	c	a		b	e
1	5	8	6	6	8	0	7	и	7	10	8	16	8	11	0
2	5	9	7	7	0	10	8	12	7	11	9	17	8	12	10
3	5	10	8	8	CL	12	9	,I<L		-UL	10	18	8	14	11
4	5	12	9	9	6	13	10	14'	7	14	11'	19	8	15	12
5	5	13	10	10	0	14	11	15	7	10	12	20	8	17	13
5,14. Используя теорию двойственности и геометрические построения, найти решение следующей задачи ЛП:
3axj Г1ж3 -Ь 5Ьж3 -h z4 -> min*
—3*i 4-
(2-f-6k3
ж4 > с,
(2+«)жх -J- Зж2. —	5ж3 — Зж4 7Х
zj > О, у = 1у 4:
	л	b	c	a		b	c	a		b	c	a		b	c
1	1	1	4	6	9 in»	1	i	11	3	1	3	16	4-	1	9
*2	1	2	1	7	2	2	3	12	3	2	2	17	4	2	4
*3	1	3	3	8	 о	3	2	13	3	3	4	18	4	3	1
4	1	4	2	9	2	4	4	14	3	4	1	19	4	4	3
5	1	5	4	10	2	5	i	15	3	5	3	20	4	5	2
5.15. Используя теорию двойственности, геометрические построения и метод исключения переменных, найти решение следующе^ задачи ЛП: ,	z
Sa-j-px* — (2-|-12н).г3 -f- (1-гбл.)^,	— ЗЬж6-~>- шах
Ж[ 4~ Зж3 — X}	—- 2х^=1у
104
*2“	2#з+	*4	—1,
Zrb «2—(5Ч-2л—2b>3-h(24-a—(Ь—2)а?5<—6, f 9	Г £>	?
#2“	14^-р	7ж4-Ь	Зл‘6^4х
яцЗ^О, о^Ол	я6^0:
	а.	Ъ	а		Ъ	а		&	а		ъ
1	4	3	0	5	3‘	И	6	3	16	' 7	3
2	5	4	7	6	4	12	7	4	17	8	4
3	6	5	8	7	5	13			18	9	5
4	7	0	0	8	6	14^	9	6	19	10	0
5	8	7	10	9	7	15	10	7	20	И	7'
5?1б. Найти все решения следующей задачи ЛП:
(a—4Ь)ж1 —	Заж2	4*	8z:(	—	4ал4	->-	‘шах,
—(6—1)#! -Ь	(& —3).7„	-!. я3	-Ь (Ь—4).г4	<2	—11
(a—4)#i —	ла-'а	-|-	4я3	—	ах4	—сх
xj > 0,	j =	1,	4.-
Прп этом указать те решения, которые являются вершинами допустимого множества:
	Ct	Ъ	а	а		Ъ	с	а		ь	с	а		b	с
1	3	5	1	6	3	6	1	11	0	6	3	1G	1	6	2
2	3	5	2	7	3	6	2	12	1	5	1	17	1	7	1
3	2	5	1	8	3	6	3	13	1	5	2	18	1	7	2
4	2	5	0	9	9	6	1	14	1	5	3	19	1	7	3
5	2	5	3	10	2	6	2	15	1	G	1	20	1	7	4
S.17.	Прядильная фабрика для производства двух видов прялся использует три тина сырья — чистую шерсть, капрон и акрил. В табл. 3 указаны нормы расхода сырья, его общее количество, которое может быть использовало фабрикой в течение года, и прибыль от реализации тонны пряжи каждого вида.
105
Таблица 3
Тип сырья	Нормы расхода сырья па 1 Т	(т)		Количество сырья (т)
	Вид 1	Вид 2	
Шерсть	0,5	0,2	ООО
Капрон	а	0,6	Ъ
Акрил	0,5 — а	0,2	с
Прибыль от рсалпвацпн 1 т пряжи (р.)	1100	900	
Требуется составить годовой план производства пряжи с целью максимизации суммарной прибыли:
	а	b с	а		Ъ с	а		1> с	а		b с
1	0,1	G20 500	6	0,1	870 510	11	0,2	710 400	10	0,3	690 300
2	0,1	730 500	7	0,1	790 520	12	0,2	880 410	17	0,3	720 300
3	0,1	840 500	8	0,2	920 400	13	0,2	810 410	18	0,3	750 300
4	0,1	650 510	9	0,2	850 400	14	0,2	740 410	19	0,3	780 300
5	0,1	760 510	10	0,2	780 400	15	0,3	660 300	20	0,3	800 300
5.18.	Нефтеперерабатывающий завод может использовать две различные технологии перегонки нефти для производства бспзппа, керосина и солярового масла. В табл. 4
Таблица 4
Папмс110П1НП№ продукция	Выход продушит (т)		Стоимость 1 т готопого продукта (р.)	« С уточнив объем госзаказа (т)
	Технология 1	Технология 2		
Бегезпп	0,6	0,3	100	117
Керосин	0,1	0,3	• 50	54
Соляровое масло	*—	0,3	20	
Отходы	0,3	0,1		
Издержки производства (р.) Загрузка оборудования (мшп.-ч)	а 0,2	b 0,05	1	г
108
приведены данные, показывающие выход продукции, отходы, издержки производства (стоимость нефти, заработная плата, амортизация и т. и.) и загрузку оборудования в расчете на 1 т переработанной нефти. Кроме того, указаны стоимость 1 т готовой продукция п суточный объем государственного заказа, который необходимо удовлетворить.
Ресурс оборудования составляет 75 мапт.-ч в сутки. Все отходы должны пройти через очистные сооруясепия, производительность которых составляет с т/сут. Поставки нефти и спрос на всю продукцию завода деогра-иичены.
Требуется составить суточный план производства с целью максимизации прибыли:
а b с		а Ъ с		а 1) с		а Ъ с	
1	13 37 130	6	21 39 135	11	37 43 140	16	39 45 145
2	15 37 135	1	23 39 140	12	39 45 145	17	31 45 130
3	17 37 140	8	25 39 145	13	37 45 130	18	37 45 135
4	19 37 145	9	29 41 130	14	35 45 135	19	35 45 140
5	2t 37 130	10	31 41 135	15	33 45 140	20	33 45 145
5.19.	Цех выпускает три вида деталей, которые изготовляются па двух станках. На рис. 21 показана техно* логическая схема 'изготовления детали каждого вида с ' X
Станок! ’** станок 2
Деталь 1
Деталь 2
Деталь 3
Рис. 21
указанием времени се обработки на станках. Задан суточный ресурс рабочего времени каждого стайка: b мни для стайка 1, с мпп для станка 2. Стоимость одной детали вида 1, 2 и 3 составляет 3, 1 и 2 р. соответственно. Требуется составить суточный план производства де-
107
талой с целью максимизации стоимости выпущенной продукции:
а Ъ с		а Ъ с		а b е		а Ь с	
1	3 (ЮО 900	0	5 840 450	11	5 870 900	16	4 870 450
О	3 000 (ЮО	7	3 ООО 900	12	5 930 450	17	,5 630 270
3	3 510 750	8	3 У(Ю 510	13	3 720 900	18	3,000 750
4	4 000 450	9	4 (Ю0 900	14	3 000 420	10	4 ,720 900
5	5 060 1)00-	10	4 780 450	15	4 060 000	20	4 750'3G0 1
••— 5.20. Для производства трех видов изделий (Л,1? и С) попользуется сырье типа 1. II и III, причем закупки сырья типа 1 и II ограничены возможностями поставщиков. В табл. 5 приведены нормы затрат сырья, цепы на сырье и на изделия, а также ограничения по закупке сырья.
Таблица 5
'Гии	ПОЛИ 1 пг сыпьн <в.)	Нормы ултрат cu|h<h ил одно изделии (кг)			1J Огрлвпчен n'ii!,'Ho закупки сырт  (ЗГГ) ‘| 1
		л	Н	С	
				,6	1
I	О	1	3	//«	3000 1
II	1	4	1	3	—	1
III	? ь	0	5.	2	3320	(
	Щ'ПЛ ОДНОГО 313-дояил (р.)	Gb -j- 12 -•126	56 -}- 22 / •’/1	с “TV >	1 - 1
Требуется определить план производства продукции с целью максимизации прибыли:
	a	b	c	а		b	c	a		b	c	а		b	c
1	О	1	17	6	3	1	22	11	3	3	26	16	4	2	27
2	9	9	10	7	3	2	23	12	3	4	20	17	4	3	28
3	•3	3	21	8	3	2	24	13	4	1	25	18	4	3	30«
4	9	4	23	9	3	2	25	14	4	1	27	19	4	4	30
5	3	1	21	10	3	3	25	15	4	9	26	20	4	4	32
/ 5.21. Па фабрике производится ткапь двух артикулов. Любая из атпх тканей может изготавливаться па станках одного из двух типов.
108
I
В табл, 6 указаны: произиодптельпость станка каждого тина при изготовлении ткани артикуле» I и 2; суммарные мощности станочного парка фабрики в расчете на одну рабочую педелю; трудовые затраты по обслуживанию станков в минутах рабочего времени на 1 ч работы станка; цена метра ткани каждого артикула.
Таблица б
Tint стапкоо	Мощности (TWC. ’1)	Трудозатраты	ИрО1|Я|1О]иТП!ЛЫ1<№П1 (М/ч)	
			Артикул t	Артикул г
i	30	а	20	15
2	ь 1	"о	12	0
		Поля 1 М ТКП1111 <|Ь)	1$	с
Известно также, что недельный ресурс трудозатрат на обслуживание сташюв ранен 6000 ч.
Требуется составить недельный нлап выпуска тканей с целью максимизации стоимости, изготовленной продукции:
; а b с		а b е		« Ъ с		а Ъ е	
1	10 30 26	G	10 40 28	11	9 30 30	10	8 30 28
2	10 30^8.,	7	10 40 30	12	9 30 32	17	8 31 > 30
3	10 Зб 311	8	10 40 32	13	9 40 28	18	8 30 32
4	10 30 32	9	9 30 20	14	9 40 30	19	8 40 28
5	10 40 26	10	9 30 28	15	9 40 32	20	8 40 30
5:22, Строителям требуются комплекты досок, каждый из которых состоит из а досок длиной 1,5 м и b досок длиной 0,6 м. Kai: следует распилить с четырехметровых досок, чтобы получить наибольшее количество указанных комплектов?
	а	Ъ с	а		ь	с	а		b	с	а		Ъ	с
1	I	3 GGO	6	2	5	770	11	3	7	960	tn	4	9	630
*3	1	3 720	7	9	5	'880	12	3	8	510	17	4	9	(560
3	1	3 780	8	2	5	990	13	3	8	680	18	4	9	690
4	1	3 840	9	3	7	МО	14	3	8	850	Ill	4	9	720
5	2	5 (ИЮ	10	3	7	800	15	4	9	(500,	20	4	9	750
409
ЗАДАЧИ
Задачи 5.1—5.34 посвящены доказательству сформулированных выше основных фактов теории линейного программирования и примерам их использования для отыскания решении задач ЛП небольшой размерности.
5.1.	Доказать теорему 5.1.
5.2.	Преобразовать к основной, стандартной и канонической формам задачу ЛП
2*1	_ 		5*3	->шах.
4;Tt	-1- 3*0 4-		= 4,
-*1	4* бд'з •		> 2,
7Ж1	— *2 4-	2*я	< 5,
	0, х.	& 0.	
5.3.	Преобразовать задачу ЛП к канонической форме так, чтобы число переменных в ионон задаче не превышало трех:
—;Г1 ~г 4*2 -|-	— 3*4 -> шахх
Зя.’! -1-	2*3	а:3	ха	<	5,
-г	За?.»	-1-	4:г3	4~	2x,t	=	6,.
*"-*1 —	-“	д.3	—}—	4*.|	——	—*3Х
0, 2:4
5.4.	Доказать теорему 5.2.
5.5.	Доказать теорему 5.3.
5.6.	Доказать теорему 5.4.
5.7.	Доказать теорему 5.5.
5.8.	Используя геометрические построения, найти решения следующих задач ЛИ *):
а) -р 2х.» —> max б) 2*t -J- *2 — > max, — 2,т3	6,	— .Tj -Н л:,2 < 2,
—a‘j 2л\	4,	xt 4- 2.Т.Э	7,
3*^ -|- 2.т2	12,	4хх — Зл:<>	б,
*1	0;	а;,	0, .г2	0;
в) 7д:х 4- 5л:.,-> min, г) —4” 2л:,. -+ min,
*1 3-	х..	> 3,	2х(	-	Зх4	>	0,
;г,	5х,	> 5.	д:,	—	.га	С	3,
2а’, 4~	а’..	^>4;	2лг,	—	.т2	=	4.
*} См. подстрочное нрвмочаине н унражшшшо 5,3.-
110
5.9.	Используя метод исключения переменных и г метрические построения, найти решения следующих дач Л И:
а)	Зх, — 2ха	— 3Z;|	max,
	— Xj -F 3.1’3	"i~	*3	4,
	7х,	— -*.'Г	16„
	2xi —	—	X;,	2. '
	1-1	0, Хп	0, хя	0;
б)	;Т1	4-	х3 “ 7x.i	4- *г» max,
		4- (5x,i	— 2xs = —7,
	Яс;. —	х:| — 4x,t	4- 6хь = 24,
	xt 4’ ®» —	Х;} — ЗХ4	4- 7х6	32.
Xj 0,	/	1, •	5,
в)	— xi 4- ж2	4-	х4	-Ь	Зх.,	-у	minK
xt 4- 2xa	—	х3	—	5х4	4-	2хй	=	—5,
x’i 4- ж2	4-	я-’я	—	2х4	4"	5х&	=	—2,
— 2ха	4-	х,	4-	3.г’4	—	Зхь	—	6*
xt 0, %	0, х3 0;
г)	-I-	х.	4r	2:e<j	—	О.т,,,	-*•	max,
2xj	—	х>	х,	-	4ж,,	6,
-Ь 2х» — х, -I- 7х4 = 5,
5xt	4'	я*	—	Зх,	—	11,
3xt	4-	2*2	Ч-	*п	—	Зх4	—	7,
0, ] = 1,	4.
5.10. Доказать, что указанные точки х* являются
шеипями соотиетствующпх задач ЛП:
a)	7% — 5.га 4- х,4 -> шах.» 5xi	—	“И 2*а	—	х4	—5*
-|-	*4	Ч-	*з	-г	Зхд	<	14,
xt	—	2хп	—	х3	4-	*.1	3,
®*	=	(1,	2,	-2,	4);
б)	—12^!	—	7х.	4-	4х3	-Н	5ж4	max
---3 Х4	•—	Ха	  Хд	4Хд	10, ------------------------------------- Х^	”|“	ЗХа	"Iе	Хд	  Хд	—“3, 2 #£	-j-	х»	2хд	4-	х4 — 7,
Ха 7> 0, х4 0, ** = (1.0, -1, 3);
и)	.Tj	4"	*з	'г	*з	"I"	->	max,
— .Tt	4-	2х„	4-	Зл3	—	.Гд	<	3,
Х|	—	х.,	4-	хз	4-	2x,i	<;	—1,
3;Г|	-J-	xs	—	x:i	—	Зх4	<;	7,
XJ > О, j = 1, ..., 4,
>
** = (1, 2, 0д 0);
r) jq 4- 2х.	4* xt — zs -> max,
л‘1	4-	х	-|-	х3	4-	2 л:=	5,
Zi	4-	х,	4'	2za	4-	3;гд	4-	-	9,
*:а	-I-	л;»	4-	2z,t	4-	=	6,
xj > 0,	/ = 1...........5,
= (3, 2, 0, 0, 4).
5.11. Определить, имеются ли среди указанных точек решения соответствующих задач ЛЛ:
а)	—2.^! 4~ Зу2 4’ %з -J“ шах, 3®L	4-	4-	2л7з	—	#4	С	3.,
4-	х.,	4-	*3	“ Зх4	<	— 1,
—.5X1	+	2х,	—	а?я	4-	ж *	—3,
z1 =	(lt	3,	0, 3)»
з* (О, -1, 3, 2), х‘ == (5, О, —6, 0);
б)	5жй — Зх3 — 5z,j ->• min,
—2zj —	Ха	4"	4za	4*	a;.j	«С
ж, —	z2	4~	а?3	*Н	2а:,j	3,
3zj 4~	2а.-а	—	х3	—	.г,!	—	5.
х2 9, х$ О, Т1	fo	1	1
•ь	I'-'t	91	21	2}1
х- =	(lt	0,	0t	—2),
х* =	(О,	О,	О,	1);
в)	— xt	4-	Зх3	4-	7z4	шах,
5zj	4-	3z3	—	z3	4-	хл	<	9,
*^^'з	4~	2x}	T*	Zj	9,
—2z,	—	4-	3z3	4-	2z4	=C	—11
,/ ==	1,	...,	4,
- (1, 1, 0, 1). x = (2, 0r 1, 0), X3 = (A, 2, О, H.);
г)	—За?..	-|-	4z3 —	4ar,l	—	->	шахл
За.1!	4"2л*2	—	z3 -1-	2z,t	—	2.т5	=	1,
4" -То ’	—	3z.	—	2z5	О,
4х\	— .г2	4‘	Зягя—	з:,,	—	7.т5	—	2,
,г7	0, j= 1, ..., 5,
х1 = (1, 1, 0, 0, 2),
z- - (1, 0, 2, 1, 1J = (0, 1, 1, 0, 0).
5Л2. Haimt асе значения параметра «, при которых указанные точки х* являются решениями соответствующих задач ЛП:
Н2
а) а^х 4- й:2	->• max.	6) Xi -b	3x2	-> rnax,
2т j	Д'2	с ю. ~	oxj 4-		> 4, -
4- 2т3	С 14, -	2xj —-	Xjj	C 2,
4а\ -И ж2	< Ю. <s	3tt.Tj 4-		8,
** = (2,	6);	.r* =	(0,	4);
и) “Ж14_ Mix* ~г 2«*3 —> —Заг.-р 2то — х3 <		max, ; 0, ~ ц		a2^3
2#!“	x3 4- 2.r3 <	5, <		
2-1 "Г Я* =	X8 4“ xa = Л-n 0, (-1, 0, 3);	2’ =		
г) 4тх -	X2 4- «Xa ->	max,		
	4.t2 4_ x3	1, -		
—	3x2 4- 2*3 <	3, .		
3oi —	2.т2 4~ З.Т3	7,		
,Tj >	0, x,,	0,	> 0,		
	x* =	(0, 1, 3).		
5.13. Найти решения следующих задач			лп	методом
полного персоора вершин:				
a) х, 4"	"H"	max,		
.?! —	-r а’з	4,		
2^ 4-	a% 4- xa	3»		
3*1 4-	t2 -b 2.r3	6,		
—я’х 4’	2xn — xa	—3;		
б) •?! 4“	жа 4- 2*3 4”	3x,t -> min.		
4-	a% 4“ 3x3 4*	4x4 = 12,		
—	a:.» 4“ ®-r —	x.j — 2,		
XJ >	0, / = 1, ...	. 4;		
в)	-f-	2*2 ~ * 3.'С*з	 max,		
—хх 4-	2*2 -H 2*3	1,		
*t 4-	Хд	Xa —	0,		
Xi >	0, ,T2 js^ 0j *3	> 0;		
г) Ti 4-	X2 — 4.T3 +	2x4 -► max,		
“Xi 4-	2xa — 3x3 4-	Хд = —4,		
Зхх —	Л’-s — xa 4“	2*4 < ~3,		
Xi 4-	5*2 4- x3 4-	3x,i < 4,		
	хг > 0, .т3	S: 0.		
5.14.	Используя теорему 5.5 и геометрические ио» строения, найти решения следующих задач ЛИ:
а)	5Ж|	4-	2х2	-J-	a, -> шах,
я,	+	2.т%	—	х	1,
— а,^	-г	*2	-|-	З.т3	6,
—	,т2	-f-	2*я	4,
*1	0, .4'2	0, .Тд О,
8 С, Л, Ашшшои, Л, В, Т1шох01>
ИЗ
б)	7ж± Ч"	8ж2	+	Юж3	->	max,
3^1 —	.То	Ч-	2ж3	2,
2жг 4“	я:2	—	Зж3	<	4,
Жд 4"*	2ж<2	“J“	бЖ3	Of
Жд^О, ж2;>0, ж3	0;
в)	13xj Ч" Зж2 -г 4ж3 —max,	;
5х1 — 2жг Ч’ Зж3 =С 6,	/
—Зжд Ч- 4ж2 -|- ж3 2,	,
4-rj. 4~ ж3 — 7ж3 < —2,
Ж1^0гЯй^>0, ж3 0;	1
г)	4жх 4“ 5ж2 Ч- 6ж3 -> max,	,	i
—жх Ч- 4ж2 — 2ж3	10,
3;q 4* 2ж2 4" Зж3 ^9, 4xj — ж3 4 5xs < 2, Ж?>0, ж2>0, ха >^0.	/
5.15.	Доказать теорему 5.6.	j
5.16.	Доказать теоремы 5.7 и 5.8.	,	,
5.17.	Доказать теорему 5.9.	(	.'
5.18.	Доказать теорему 5.11.	!
5.19.	Построить задачи, двойствоппые	к следующим	I
задачам ЛП:	1
а) 17®! —	5ж2	Ч-	Ч-	ж4 —	8ж5	—>	max.
Зад —			Ж’з -F	4z.t Ч-	7жй		11,
—	5ж3	»—»	5.т3 4-	х.1 ч-	2ж5		—8,
жх ч-	.т2	4-	4-	Зж4 —		— W .	4,
жх >	0,			«4	0;		
б) 4жх —	6ж2		2ж3 4-	З.Тд Ч-	^5	->	min,
жх 4-	2ж3	—-	Зж3 4-	Жд	Зж<		-5,
2жх Ч~	Зж2	1 а	4-	Жд ч-	^Жк “”‘В		1.
—2жх —	жг			Х.1 —			3;
в)	Зх3	—	2ж3 4"	Жд ->-	min	1	
-2Д			ж3 —	Жд =	5i		
2хл 4"	жя	—	2ж3 4~	2ж4 <	7.		
	0,	2	= 1, •	... 4;			
г) 4ад 4'	ж2	1	Жз -|-	2жд 4“			тахл
4жл Ч-	х3		ж3 —	ж,, 4-	^5	2^2*	9»
*1 -Ь	ж3		ж3 Ч'	Жд 4-	6ж5	=	10t
—Жл —	Зж2	ч-	5ж3				1,
%j >0» i = 1.	4.
5.20. Используя теорию двойственности и геометрические построения, найти решения следующих задач ЛП:
а) 7.Т, Ч- ж3 — 4ж4 -> max, я?1 — ж2 Ч’ 2ж3 — ж.,	6,
2жд -[*	ж3	• 1 ]
X] 0,	/ — 1, ...,4,
114
6) Xf	+ х3	+	хъ	-> max,
Xi -J- 2x2 -J- 3x3 —	£,i	—	ж5	6,
— Z2 — 2Xg "j-	£.J	-r	*6	5,
*/	0,	/ = 1, .... 5;
в),	4“ -У 2#3	-j-	x,i	H-	2a:6 —>•	min,
3.Ti 4~	-j_ 4л.*3	2^|	~|~	—	1,
—4tx — Gs2 — x3	-j-	#4	-r	3z. =	—1,
xj 0, / — 1, * < , <),
r) 6x-j -y Зла ~’X1 — 2x,j -> max,
3xL -У 2x2 4- £3 4- 4ж4	0,
2a:^ 4* 2x2 “* я«3	*4 •** 1,
Ж2 0|	0, Ж.,	0.
5.2i.	Используя теорию двойственности, геометрические построения п метод исключения переменных; найти решения следующих задач ЛТ1:
a) 2xj 4- 4*2 — *3 — max,
—2^ -|- 2х> — х3 — a:.j < —2,
Я1	~	#2	4- *з		1.		
З.Г1	-У х2		г *.1 ==	5,		
	>0, жа	> 0,	*4	0;		
~Х1	-У Зг2	у 31 ж3	4“ 25г.,	——	4яг5	max,
Xi	“1	- 4^з	4- 3,-Гд	-L 1		= 2,
	х2 4	ага	4“	*4		Ж5	= 1,
Х1	-У х2 +	10х3	4- 8я!4	4“	*5	< 5,
2а?х	— х2 -У	9я3	4“ 6ж4	t i	5*s	< 0,
	0, Хч	г 0,			2*	> 0;
Зхг -	— 2гй —	 *3 “	max,			
З.г2 + х3 —2, х{ 4~ х2	3,
* хх -У 2х2 4- х3 1, *i>0, я- > 0;
г) 4«j	—	8х2	—	7ж3	—	2ж4	шах,
Зз?2	4.Тд	““	<Z',|	"У	2х&	1S^	1,
4zj	-у	я2	*У	2х3	-У	5ж4	—	Зхй	=	—4,
xi-	4~	%£	4-	хз	4~	2х4	—	хй	=	—1,
£12^0, #2^0, х3 0, х4 0.
5.22.	Найти все решения следующих задач ЛП (при этом указать то решения, которые являются вершинами допустимых множеств):
а)	10^1	4-	17ж2	-У	29х3	->	min,
—2;rt	-|-	5х2	-У	5.тя	—	я(|	—	1,
5a:t	-У	5-та	4-	'Ю^з	—	.т.,	=	2,
0, /  1, ..., 4,
б)	2%i — 4я3 — 4я3 -У 2х4 — «6 -> min, 2х1 —-	~г а?з 4~ За:. ^—2,
8’
।
115
7жх 4"	- - 2ж3 4" й'.| "	—7,
5жх -г Зх5 -1- бж3 — 2ж,| -|- 2х5 =7, Xi>0, ж3 > 0,	> О;
в)	-{-	З.т3	—	4х3	—	ж.,	->	min,
4®i	-j-	ж3	—	Зж5	—	Зж4	—	—2,
—Зхх	-J-	2х3	—	х9	-г	ж.,	— 1,
Жу 0, 7 = 1, »••, 4,
г)	lOxj -г 2,z2 4- &г3 -}- 5ж,, -> min, 2ях 4 2х3 + 2ж3 — ж4 1, 5хх я? -|- Зжа 4-	:> 2,
ж/^ 0, у = 1, ..., 4.
5.23.	Чаеразвесочная фабрика выпускает чай сорта Л п Б, смешивая три ингредиента: индийский, грузинский и краснодарский чай. В табл. 7 приведены нормы расхода ингредиентов, объем запасов каждого ингредиента и прибыль от реализации 1 т чая сорта А и Б.
Таблица 7
Ингредиенты	Нормы расхода (т/т)		0(И-ом запасал (т>
	Л |	в	
Индийский чай	0,5	0,2	600
Грузинский чай	0,2	0,6	870
Краснодарский чай	0,3	0,2	430
Прибыль от реализации 1 т продукции (р.)	320	2Я0	
Требуется составить план производства чая сорта А и Б с целью максимизации суммарной прибыли,
5,24.	Нефтеперерабатывающий завод производит за месяц 1500000 л алкилата, 1200 000 л крокипг-бепаина и 1300000 л изопептона. В результате смешивания этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 90 р. и 120 р.
Определить месячный план производства бензина сорта Л и Б, максимизирующий стоимость выпущенной продукции.
5.25.	Рацион кормления коров иа молочной ферме может состоять из трех продуктов — сена, силоса и концентратов. Эти продукты содержат питательные вещества— белок, кальций л витамины. Чпслеппые данные представлены в табл. 8..- В расчете на одну корову 116
суточные нормы потребления белка и кальция составляют не менее 2000 л 210 г сеответствеппо. Потребление витаминов строго дозировано и долями быть равно 87 мг в сутки.
Таблица 8
Продукты	Питательны» ьешестаа		
	Белов (г/нг)	Кальций (гУнг)	Вптамшм (ме/кг)
Соно	50	10	2
Силос	70	6	3
KoHneiiTjNiTiJ	180	3	1
Составить самый дешевый рацион, еслп стоимость 1 кг села, спяоса и концентрата равна соответственно 1,5, 2 и 6 к.
5.26.	В области имеются два цементных завода п три потребителя их продукции — домостроительных комбината. В табл. 9 указаны суточные объемы производства цемента, суточные потребности в нем комбинатов и стоимость перевозки 1 т цемента от каждого завода к каждому комбинату.
Таблица 9
Заводы	npojmottcnto цемента (т/суг)	Стонмосп» перевозни 1 т цемента (р.)		
		Комбинат 1	Комбинат 2	Комбинат 3
1	"40	10	15	25
2	60	20	30	30
	Потребности в цо-мояте (т/сут)	50	20	30
Требуется составить план суточных перевозок цемента с целью минимизации транспортных расходов.
5.27.	Перед проектировщиками автомобиля поставлена задача сконструировать самый дешевый кузов, используя листовой металл, стекло н пластмассу. Основные характеристики материалов представлены в табл. 10.
Общая поверхность кузова (вместе с дверьми и окнами) должка составить 14 м2; из них пе менее 4 мг и не более 5 м2 следует отвести под стекло. Масса кузова пе должна превышать 150 кг. Сколько металла, стекла и пластмассы должен использовать паилучшпй проект?
117
Таблица 10
Характсргестшсд	Материалы		
	Металл	Стекло ।	Пластэшсса
Стоимость (р./м2)	25	20	40
Масса (кг/м4)	10	15	3
5.28.	В металлургический цех в качестве сырья поступает латунь (сплав меди с цппком) четырех типов с содержанием цинка 10, 20, 25 и 40 % по цепе 10, 30, 40 и 60 к. за 1 кг соответственно. В каких пропорциях следует переплавлять это сырье в цехе, чтобы получить сплав (латунь), содержащий 30 % цинка и прп этом самый дешевый?
5.29.	Цех выпускает три вида деталей, которые изготовляются па трех стайках. На рис. 2'2 показана технологическая схема изготовления детали каждого вида с ука-
занием времени ее обработки иа станках. Суточный ресурс рабочего времени станков 1, 2 и 3 составляет соответственно 890, 920 и 840 мин. Стоимость одной детали вида 1, 2 и 3 равна соответственно 3, 1 и 2 р.
Требуется составить суточный план производства с целью максимизации стоимости выпущенной продукции.
5.30.	Объединение «Комфорт» производит холодильники, газовые плиты, морозильные шкафы и электропечи по цепе 200, 180, 250 и 100 р. соответственно. Постоянным фактором, ограничивающим объемы производства, является фиксированная величина трудовых ресурсов — 12000 человеко-часов в месяц. Выяснилось, однако, что в ближайший месяц дефицитной будет и лц-
118
стовая сталь для корпусов указанных изделий, поскольку поставщики смогут обеспечить лишь 7000 м2 этого материала.
Требуется составить план производства на данный месяц, с тем чтобы максимизировать стоимость выпущенном продукции. Известно, что для изготовления холодильника требуется 2 мй листовой стали и 3 чел.-ч рабочего времени, для газовой плиты — соответственно 1,5 м2 и 3 чел.-ч, для морозильного шкафа—-3 м2 и 4 чел,-ч, для электропечи — 1 м2 и 2 чсл.-ч.
5.31.	Участник экспедиции «Северный полюс» укладывает рюкзак, и ему требуется решить, какие положить продукты. В его распоряжении имеются мясо, мука, сухое молоко и сахар. В рюкзаке для продуктов осталось лишь 45 дм3 объема, и нужно, чтобы суммарная масса продуктов не превосходила 35 кг. Врач экспедиции рекомендовал, чтобы мяса (по массе) было больше муки по край-
ней мере в два раза, муки по меньше молока, а молока по крайней мере в восемь раз больше, чем сахара. Сколько и каких продуктов пужпо положить в рюкзак, с тем чтобы суммарная калорийность продуктов была наибольшей? Характеристики продуктов приведены в табл. 11.
Таблица 11
Характеристики	продукты			
	Мисо	Мука	Мололо	Сахпр
Объем (дм’/кг)	1	1.5	2	1
Калорийность (ккал/кг)	1500	5000	5000	4000
5.32.	На мебельной фабрике требуется раскроить 5000 прямоугольных листов фаперы размером 4X5 м каждый, с тем чтобы получить два'впда прямоугольных деталей: деталь А должна иметь размер 2X2 м, деталь Б — размер 1X3 м. Необходимо, чтобы деталей Л оказалось нс меньше, чем деталей Б. Каким образом следует производить раскрой, чтобы получить минимальное (по площади) количество отходов?
5.33.	Для серийного производства некоторого изделия требуются комплекты заготовок профильного проката. Каждый комплект состоит из двух заготовок длиной 1800 мм и пяти заготовок длиной 700 мм. Как следует раскроить 770 полос проката стандартной длины 6000 мм,
119
чтобы .полупить наибольшее количество указанных комплектов?
5.34.	Колхоз может засеять свои поля пшеницей четырех сортов, урожайность которых зависит от того, будет лк лето дождливым или сухим. Соответствующие данные приведены в табл. 12, Какие сорта пшеницы
Таблица 12
Погода	ypoHiaflitOBTb (п/гп)			
	Сорт 1	Сорт 2	Сорт 3	Сорт 4
Дождливая	25	20	30	15
Сухая	15	20	10	40
и в какой пропорции следует сеять, чтобы максимизировать гарантированный (не зависящий от погоды) урожай?
В задачах 5.35—5.112 мы продолжим изложение теоретических основ линейного програтшрования. Отмстим, что многие пз приводимых ниже утверждений являются следствиями соответствующих фактов о системах линейных, неравенств из § 4. Поэтому для активной работы с последующим материалом необходимо основательно освоить содержанке § 4.
Ради краткости задачу ЛП будем называть допустимой, (разрешимой), если ее допустимое множество' (множество решений) непусто.
5.35.	Рассмотрим допустимую задачу ЛП при наличии только ограничений-равенств:
<е, х> -*• шах, Ах = Ь.
Доказать, что множество ее решений либо пусто, либо совпадает с допустимым множеством, причем последнее имеет место в том и только том случае, если вектор с есть линейная комбинация строк матрицы А, т. с. с = = уА при некотором векторе у.
Таким образом, задача ЛП без ограпнчопий-пераввпств большого иптероса по представляет. В то же время только такая задача ЛП является по своей форме классической задачей па условный экстремум. Отсюда попятно, почему классические методы анализа экстремальных задач оказываются непригодными для задач ЛП, в результате чего здесь приходится использовать иной математический аппарат — теорию лшюйпых неравенств.
,120
5.36.	Рассмотрим основную задачу ЛП (5.1) при Ъ = = 0. Доказать, что множество се решений либо содержит точку я* = 0, либо пусто; соответственно ее значение /* равно либо 0, либо <»,
5.37.	Пусть основная задача ЛП (5.1) допустима. Доказать, что се целевая функция постоянна па допустимом множестве в том и только том случае, если существуют такие векторы у1 0 и У‘^0, что г/’Л = с, у*А = = —с, <у1 + //”, Ь> = 0.
5,38.	Доказать, что стандартная задача ЛП (5.4), где Ъ > 0, разрешима, если выполнено хотя бы одно из следующих условии:
а)	в матрице А имеется по крайней мере одна положительная строка;
б)	матрица Л пеотр|щательна и в ней нет нулевых столбцов.
5.39.	Доказать, что стандартная задача ЛП на минимум
<с, я> -* min, Ах > Ъ, х > 0,
где с 0, разрешима, если выполнено хотя бы одно из следующих условий:
а)	в матрице Я имеется по крайней мере одпп положительный столбец;
б)	матрица А неотрицательна и в пей пет пулевых строк.
5.40.	Пусть при любом векторе csR" основная задача ЛП (5.1) разрешима. Доказать, что ее допустимое множество ограничено.
5.41.	Привести примеры взапмо двойстве иных задач ЛП, у каждой из которых допустимое множество
а)	пусто;
б)	не ограничено.
5,42*	. Пусть X и У — допустимые множества основной задачи ЛП (5.1) и двойственной к ной задачи (см. табл. 2). Доказать, что эти множества не могут быть одновременно непустыми и ограниченными; более того, при любом ненулевом векторе rfsR” справедливы следующие утверждения:
а)	если X непусто и ограничено, то sup(d, = оо;
б)	если У непусто и ограничено, то inf<d, Я#) Е= — ОО,
5.43.	Пусть допустимые множества X и У взаштодвой-стпенпых задач (5.25) п (5.26) непусты и ограничены. Доказать, что тогда
121
а)	ограппчеппя-перавепства в этих задачах отсутствуют, т. е. i = 0, s = 0;
б)	число переменных совпадает с числом неизвестных, т. с. п = т»;
в)	квадратная матрица Л=(а«)’ повырождепа;
г)	множества X п У одноточечны.
5.44*	. Пусть Г — грань полиэдра X пз (5.2) (см. 4.51). Доказать, что Г является множеством решении задачи. (5.1) при некотором с е IV*.
5.45.	Ограничение-неравенство в разрешимой задаче ЛП принято называть закрепленным, еслп оно выполняется как равенство для любого решения задачи, л свободным в противном случае.
Пусть X* — непустое множество решений основной задачи ЛП (5.1), 7* —множество номеров ее закрепленных ограничений:
I* == (г, 1 i т|	ж> = 5,- при всех х е X*}.
Доказать, что существует точка к X*, для которой /(#)=>/*, т. е. активными в х являются только закрепленные ограничения задачи.
Так, па рпс. 19 указанным свойством обладает любая внутренняя точка отрезка-множества решений задачи.
5.46*	. Доказать, что непустое множество X* решений задачи (5.1) является гранью ее допустимого множества X; при этом размерность X* (см. 4.25) вычисляется по формуле dimX* = п— rang Ат»,где Z* взято из 5.45. В частности, X* состоит на одной точки (решение задачи (5.1) единственно) в том и только том случае, еслп rang Л/» *= п.
5.47*	. Доказать принцип граничных решений для задачи ЛП (обобщение теоремы 5.5).
Если множество решеппй основной задачи ЛП (5.1) непусто, то оно содержит грань допустимого множества задачи, имеющую размерность п — rang А п являющуюся аффинным множеством; иными словами, существует такое множество /<={1......?п), что rang Ai<=* rang Л, си-
стема —Z>j совместна и любое ее решение служит решением задачи (5.1).
5.48*	. Доказать теорему об очистке задачи ЛП.
Пусть	основная задача ЛП (5.1) разрешима. Тогда существует такое множество I <= {1,	т.}, что rang Л» =
» |71 п любое решение ж* задачи (5.1) является решением задачи
<с, х> -* max, Aix bj,	(5.30)'
d22
прп этом Ai$*=*bi. Верно п обратное: если л* —решение задач» (5.30) и ж* <^Х, то я* — решение задачи (5.1).
Иллюстрациями к этой тоороме служат рис, 23 и 24, где I {1, 3) н /,=з {1} соответственно.
5.49	. Привести примеры взаимодаойствеппых задач ЛП, у одной из которых решение единственно, а у другой множество решений
123
а) сострит более чем из одпой точки, но ограничено; б) не ограничено.
5.50	. Привести примеры взанмодвойствеппых задач ЛП, у каждой из которых множество решений удовлетворяет условию а) (условию б)) из 5.49.
5.51	. Привести пример взаимодвойственпых задач ЛП, у одпой па которых множество решений удовлетворяет условию а), а у другой — условию б) из 5.49.
5.52	. Пусть множество решений основной задачи ЛП (5.1) непусто. Доказать, что это множество ограничено в том и только том случае, если система <с, х> 3= 0, Ah < 0 имеет лишь тривиальной решение /* = 0.
5.53	. Пусть х* — решение основной задачи ЛП (5.1), / = /(х*). Доказать, что это решение единственно в том и только том случае, если система <е, А> 5* 0, /ПА^О имеет лишь тривиальное решение А = 0.
5.54	*. Пусть основная задача ЛП (5.1) допустима. Доказать, что множество X* ее решений непусто п ограничено в том и только том случае, если rang А = п и существует такой вектор у <= R'", что у А «=» с, у > 0.
5.55	*. Пусть стандартная задача ЛП (5.4) допустима. Доказать, что множество се решений непусто и ограничено в том и только том случае, если существует такой вектор у е Rm, что у А > с, у 5? 0.
5.5G	*. Пусть каноническая задача ЛП (5.5) допустима. Доказать, что множество ее решений непусто п ограничено в том п только том случае, если существует такой вектор у R"1, что у А > с.
5.57	*. Пусть х*—допустимая точка основной задачи ЛП (5.1). Доказать, что х*— единственное решение этой задачи в том и только том случае, если rang = л и существует такое решение у* двойственной задачи, что У *	0 при всех i I (х*).
Парное условие rang — а означает, что г* является воришкой допустимого множества надачп. Второе можно переформулировать так: равенство (5.20) выполнено при некоторых положительных числах у* (i е I (х*)). Так, гга рве. 19 точка я* но удовлетворяет первому условию, а концевые точки множества рошонин — второму.
5.58	*. Пусть х* — допустимая точка канонической задачи ЛП (5.5), J = /(x*) (см. формулу (5.5)). Доказать, что х* — единственное решение этой задачи в том и только том случае, если rang AJ = IЛ (т. е. х* является вершиной допустимого множества задачи) и существует та-124
jtoo решение у* двойственной задачи, что <р*, а!> > при всех jе И, ..n) V.
5.59	*. Доказать теорему о строгой дополняющей пе-усесткистц, для задач ЛП.
Пусть задачи (5.25) и (5.26) разрешимы. Тогда существуют такие их решения х* и у*, что
у* +	2 ацх* ] > 0, i«l, .... к, (5.31)
\ i~i I
х* + ( 31ЖЧ; — ci ] > 0,	; = If...,s,	(5.32)
М=1	/
т. е. для этих решений в каждом из произведении (5.28), '(5.29) в пуль обращается ровно один сомножитель. В частности, если решения задач (5.25) и (5.26) единственны, то они обязательно удовлетворяют условиям (5.31), (5.32).
Отметим, что нрияепителыю к оспоуйой задаче ЛП (5.1) и двойственной к пен последнее утверждение сразу следует из 5.57, 5.5Я, Условия (5.28), (5.29), (5.31), (5.32), взятые вместе, прнплто называть услосиями строгой дололпяюикй ксжеегкости.
5.60.	Рассмотрим взанмодпойствеппые задачи ЛП:
+ х2 шах» *1 + »2 < 1 , 2^4- 2х2 < 2,
0, х2 0,
?А -|-2у3 -> min,
У1 4”	1,
(Л 4- 2г/г > 1, у, >0.
Привести примеры таких их решений, которые а) удовлетворяют; б) не удовлетворяют условиям (5.31), (5.32).
5.61*	. Доказать теорему о закрепленных и свободных ограничениях во взаимодвойствеппых задачах ЛП (см. 5.45):
Пусть задачи (5.25) п (5.26) разрешимы. Тогда в каждой из к + s нар взаимодвойственных ограипчеппй-неравсиств

п
У 3^ ??£,
i = 1, ..., к,
m
xj ^:0, У (Pl} J = 1, . .., S, i=l
одно является закрепленным, а другое —- свободным.
125
5.62.	Найти закрепленные п свободные ограничения в следующих задачах ЛП:
a) 12хх -1- а.-о И- -> ininx
-|- 2г3	1,
Згг — х2	-|- 2%	2Х
0, х3	0;
б)	2‘l.Tj 4- 9х2 — 8г3 -г 12хд ->- min,
—5xj 4- Зх2 + *з + 2л-д < —1,
—*гх ~~~ Зх2 “I- 4г3 ~“ Зж,х 3, ^>0х / = 1,..., 4;
в)	6гг	—	Злтд —	—	13г,t	maxj
2хл	—	z2 — г3	—	4х4	С	2<
Згх	—	г2 — 2г3	—	6г,i	4t
xj >0i i - li —i 4.
5.63*	. Доказать, что решение задачи ЛП единственно в том и только том случае, еслп множество решений двойственной задачи является невырожденной гранью ео допустимого множества (см’. 4.55).
5.64.	Пусть задача ЛП имеет единственное решение. Следует ли отсюда, что у двойственной задачи существует такое решение, которое является невырожденной вершиной ее допустимого множества?
5.65*	. Единственное решение задачи ЛП называется невырожденным (вырожденным)^ еслп оно является невырожденной (вырожденной) вершиной допустимого множества задачи.
Доказать, что задача ЛП имеет невырожденное единственное решение в том и только том случае, если двойственная задача имеет невырожденное единственное решение.
5.66.	Доказать, что если вэаимодвойствепные задачи ЛП имеют по единственному решению, то эти решения невырождены.
По-другому можпо сказать так: еслп задача ЛП имеет вырожденное единственное решение, то двойственная задача имеет более одного решении. Конкретные проявления этого общего факта неоднократно встречались ранее (см. 5.22, 5.33, 5.49).
5.67.	Доказать теорему о доминировании.
Пусть общая задача ЛП (5.25), где s5=1, разрешима. Предположим, что переменная хг (Kr^s) является доминируемой в этой задаче, т. е. существуют такие чпе-12G
ла Xi О, ...Д. 3s О, XJ+i, ..?.и, что
п
fl IГ	fl {J Х,' 3	Ь —— 1 , а ' » f /fl
ja<l
П
flic «= S «ijX;, i = к + 1, ..., m, 5=i
n
Cf <C 2 c;Xj.
5=1
Тогда яу = О для любого решения х* задачи (5.25).
Эта теорема имеет ясный экономический смысл в рамках примера 5.1: если мояшо указать такой набор товаров, производство которого потребуй? пе больше всех ресурсов, чем производство единичною количества r-го товара, а стоимость этого набора будет иышв стоимости одпппцы r-го товара, то r-й товар выпускать но следует.
5,08. Используя теорему о домнппроваппн, панти решения следующих задач ЛП:
a)	a?i + 2я2 -|- Зя3 max, зг, 4z2 4- 2х3 < 8, аг, -Ь , хй 4- < х3 < G,
—'3.Tj	Зя2 2я3	0,
я, — 2яг — 5я3 <С 0, я, 0, х2 0, я3 0;
б)	7я2 —	Зя3	—	4я,[ —>	max,
4~ 7я2 4*	*Гз	”Ь	1’^1
ях	-р 5.т2 —	2аг3	4-	я4	0,
Яд | 2я2 ——	Яд —~ -3,
7 = 1,..., 4;
в)	Xi +	Зх2	4-	#3 4- 7^4	шах,
3#! 4-	2.г2	4*	4* 12я4	8.
—Я, 4-	«2	4-	Зжз 4- 2х4	< 8,
-	2х2	*“- / Яд	2,
2.1?! —	5лг2	—	6.т3 — 1О.т4	=С
аго^О, яг3 0, д;4	0.
5.69*. Доказать теорему Хоффмана для задачи ЛП.
Пусть X* — непустое множество решений основной задачи ЛП (5.1), /* —ее значение. Тогда существует такое число а>0, зависящее от Л и с и пе зависящее от 6, что для любого .г е Ra справедливо неравенство ta! .
У, шах (0, (at, я) — bi) -j- max (0, /♦ — <с, я» ар (я, X*), i-i
127
где р(ж, Х*)= inf Ej; — .r*|]— расстояние от х до X*; ж*(=Х*
в частности, если х—допустимая точка задачи (5.1), то /♦ — <с, х) >ар(ж, X*).
В задачах 5.70—5.108 излагаются основы теории параметрических задач ЛП. При этом в задачах 5.70—5.78, 5.81—5.85 будем использовать следующие обозначения:
Р($)=Р(И, Ъ, с)— основная задача ЛП (5.1) при данном наборе параметров s = (A, &, с) n)XRmXR”;
Х(з)=*Хг(Л, &) — допустимое множество задачи P(s);
Г(х, s) = I(x, Л, Ь)—множество номеров активных ограничении в точке x^X(s);
X*(s)—множество решений задачи P(s);
D(s)— задача, двойственная к P(s);
У(«)=У(Л, с)—допустимое множество задачи D(s)‘, ¥*($)—множество решении задачи D(s);
F(s)— общее значение разрешимых задач P{s) п D(s),
5.70.	Задача P(s) называется устойчивой, если при любом s' из некоторой окрестности s задача P(s') имеет решение. Аналогично вводится понятие устойчивости задачи ЛП в любой другой форме записи. Убедиться, что задачи
X} +^2 -► max, и
хг + за "* шах, Ж1 + жя =* 1,	> 0, х2 >0
устойчивы, а задачи
4-^2 -► max, #i + х%^ 1 и
#1 + Хг max, жг1, aj+ гя 1,	>0, ж2^0
неустойчивы.
Пример второй п четвертой задач показывает, что прп переходе от одной формы записи задачи ЛП к другой свойство устойчивости может быть потеряно.
5.71.	Доказать, что взаимодвонствевные задачи ЛП устойчивы или неустойчивы одновременно.
5.72.	Доказать, что взаимодвойственные задачи ЛП устойчивы в том и только том случае, если устойчивы системы, определяющие их допустимые множества (см. 4.124).
5.73*	. Доказать теорему об устойчивости задач ЛП, Для любого s = (A, bt c)s^(m, »)XR"XR* следующие утверждения эквивалентны:
128
а)	задачи P (s) и D (х)' устойчивы;
6)	rai>gZ=n и существуют такие точки	t/<=
s R"\ что Ax < b, yA у > 0;
в)	множества X*(s) и У*(х) непусты и ограничены.
5.74	*. Доказать теорему об устойчивости задач ЛП по значению и решению.
Пусть задача Р($) устойчива. Тогда
а)	функция F(s) непрерывна в дайной точке 5 (устойчивость по значению);
б)	если последовательности {s'} и {«*} таковы, что •Нт s’1 =i х и	то последовательность U'} ог-
раничепа п любая ее предельная точка принадлежит Х*(х) (устойчивость по решению),
В общих терминах теории ипогозвачпмх отображений утверж-удоико б) можно сформулировать так: отображение x-»-X*(s) ^ло.'.’плыю ограничено « замкнуто в данной тонко з [29, 32, 39].
5.75	. Пусть устойчивая задача Р($) пмеет едппстиоп-'ноо решение. Следует лп отсюда, что прп любом s', до-:'статочпо близком к х, задача Р(з') также имеет единствен пос решение?
5,76	*. Пусть задача Р(з) пмеет невырожденное единственное решение я*(х) (см. 5.65). Доказать, что при ЛЮ1М1М sx, достаточно близком к х. задача Р(з') также имеет единственное невырожденное решение х*(я'); прп этом Иш X* (s') = х* (х) и I(т* (sx), з') = 1 (.т* ($)’, $), л'-*»
т. е. номера активных ограппчелпЙ в точках x*(s') я х* (я) совпадают.
5.77	. Пусть задача P(s) имеет единственное решение г*(х); последовательность ($*} сходится к х, и при любом к задача Р(х*) имеет пепырождеппое едппстпоппое решение ®* (s') .Следует лп отсюда,что Иш .г*(х')=х*(х)?
5.78	*. Пусть множество решений задачи Р (з), где х = e(/lt 5, с), непусто и ограничено. Доказать, что прп лшгшх A', ех, достаточно близких к А, с, п любом Ъ' е ®R° мполссство решении задачи Р(з'), где хх=(Лх, 6х, с'), также непусто п ограничено, если только ята задача допустима.
5.79	*. Доказать, что следующие утверждения эквпва-лоптпы:
а)	стлпдартпал задача ЛП (5.4) и двойственная к пой устойчивы;
б)	существуют такие точкп ,r^Rn и r/eR1" иго Ах < &, х > 0, уА > с, у 0;
& С. А. Лигманов, Л, в, Томохов	[129
в)	множества решений задачи (5.4) и двойственной к ной непусты и ограничены.
JDtMotjsm, что формулировать аналогичный факт для лаиоппчг-ской задачи ЛП (5.5) пот необходимое•», поскольку с точпостын до перемены местами прямой и двойственной задач on vji;o отри-я:ен л 5.73.
5.80	*. Положим и "=(1, .... 1)esR“, i\«=*(l, J)eR". Прп данном числе а^О обозначим через Х*(а) множество решений стандартной задачи ЛП
<с — ан, х> -*• шах,
Ах Ъ 4- ар, х > 0,	(5.33)
а через Z’(a) ее значение.
Доказать теорему о регуляризации задачи ЛП.
Пусть задача (5.33) прп а&0 (т. ё. задача (5.4)) разрешима. Тогда
а)	прп любом а>0 задача (5.33) устойчива;
б)	lim F (а) ₽з Z'(0); a-o-f-
в)	множества Х'*(а)	(а>.0) ограничены в совокуи
кости;
г)	если последовательности {«Д и te1} таковы, что ссл-*О, ац>0, Х*(аА) п ж'-ьа:, то геХ*(0).
Отметим, что сформулированная тоорема легко перопоептен по задачу ЛП й лю-бой форме записи. Папримор, если дана оспоиплн задача ЛП (5.1), то поело приведения ее к стандартной форме получается следующее сомейстгю задач вида (5.33):
<с — а«, я’> — <е + aw, xs> max,
Лх’ — Ax'1Ь -|- aw, ж5 5? О, х1^ 0,
Полезло заметить, что в силу 5.79 рта задача при а = О неустойчива. если даже задача (5.1) была устойчивой.
5.81	*. Пусть задача Р(.ч) устойчива и. значит, функция F(£) определена в некоторой окрестности данной точки s, Прп заданном элементе h<^srf-(ni, м)ХК,яХ’Кл величину
F' (st Л) «» b‘m a->a+	a
т. e. производную функции F по направлению h в точке $, принято называть маргинальным значением задачи Р(з) по наира влеплю h.
Доказать теорему о маргинальных - значениях задачи ЛП.
130
Если задача Р($), где b, с), устойчива, то ее маргинальное значение ио любому направлению *=(Л. 5, с) существует и вычисляется по формуле F'(stty = max min L(x, у, h) >=> ябх*(») уеу»о)
<=» min шах L(x,yth), (5.34) jrt=Y*(e) ХЕХ*О)
где L (%, у, x> + <yt 5 — ЛяХ В частности, а) еслп А = (Л, 0, 0), то
F'(s, Л) = — min max <у, Лх} =—. max min <у, Лт>; ХбА’*(>) ЬЧ=У*{«)	t43Y*(») хеЛ'*(4)
б) сели h = (0, Ъ, 0), то
F'(s,h) = min <J>, у};	(5.35)
V<=Y*O)
в) если /г=(0, 0, с), то
F’(s, Л) = max <<\ я>.	(5.36)
xeX«(j)
5.82.	Пусть задача P(s), где s = (.4, &, с), Л’ = (аи)’, & = (&(), с = (с>), устойчива. Доказать, что все право- и левосторонние частные производные функции P(s) в данной точке $ существуют в вычисляются по формулам
9F+ mm yi, дЬ1 i»eY*O)
0F~
($) = max yh iier*W
эр* dci
(«) = max .г,-, xGX«(4)
c№~
(a) = min Xjt
	($}	(s'! если
V)=|	dbi	dej ™ ССЛЛ dcj I ", <»)",«• “Л11 ", (’)<»> см“
где i = 1,..., m; /=1, ..u.
5.83.	Пусть задачи Р($) и D(s) имеют но единственному решению я*(«) и #*($) соответственно. Доказать, что функция F(s) непрерывно дифференцируема в дан-»•	131
ной точке $, причем частные производные F в $ вычисляются по формулам
- ($')=> yi {s) Xj (s),	(s) «=» yi (s),	(s) « %j (s)>
(5.37)
гдо i=l, m; / = 1, ..., n, а величины a^, bi, Cj имеют тот же смысл, что и в 5.82.
5.84.	Привести пример таких s = (A, b, с) п h = = (А, Ъ, с), что задача P{s + cth) разрешима прп любом а>0, но величина f (s, Л) не существует.
5.85.	Привести пример таких $ = (Л, Ь, с) п Л = в(Л 6, с), что величина f{s, h), а также макепмнн и минимакс в (5.34) существуют, но первое равенство в (5.34) не выполнено.
В задачах 5.86—5.92 матрица Л считается постоянной. Соответственно будем использовать обозначения Р(Ь, с), Х{Ь), Х*{Ъ, с) я т. п. Кроме того, введем множества
В = | b s Rm | Ах b при некотором х е В”), С *= [с е= Rn| у А = с при некотором у е R™). Ясно, что В и С непусты.
5.86.	Доказать, что множества Д и С замкнуты.
5.87.	Доказать, что для любых bf ^В, с‘е С, %г О (i= 1, 2) следует Xjb1 + Шг^В, Xtc1 С.
Это означает, что В и С являются выпуклыми конусами (СМ. § 7).
5.88.	Доказать, что задача Р{Ь, с) имеет решение в том и только том случае, если b е= В, с ® С\ иными словами, областью определения функции Е{Ь, с\ является декартово произведение В X С.
5.89.	Пусть задачи Р{Ь, с) и Р{Ь', </) разрешимы. Доказать, что задачи
<b'-b, р>min,	реу*(ь, с),	(5.38)
<cz — с, .т> -+• шах,	я <= X* (6, с)	(5.39)
также разрешимы.
5.90*	. Доказать теорему об устойчивости задачи ЛП по значению и решению при постоянной матрице коэффициентов.
а)	Функция Р{Ь, с) непрерывна всюду на В У. С {устойчивость по значению}',
132
б)	если последоватсльпостп {Б’1}, {<?} и {л^) таковы, что bh^Bt Б* ->- b, с^<=С, ch-»-c и а?<™Х*{1Л, <?), то X*(b, c)c/J0 и Jim р(Д А’*(Б, с)) = 0, т. е. прп доста-А-»«>
точно больших к вес решения задач Р (Б\ <г) близки к множеству решений задачи Р{Ъ, с) {устойчивость по решению) .
Подчеркнем, что в отлпчпо от теоремы из 5.74 последовательность {zA} здесь может быть и псограпичоппой. Согласно терминологии теории многозначных отображений, свойство б) означает иолунопрерывпость сверху отображения (&, с) -с) [32, 33).
5.91	*. Задача Р{Ъ, с) называется устойчивой по направлению h == (б, с) R”1 X XRn, если эта задача, а так-,с .ас ясе задача Р(БЧ-ссБ, с + ас) прп любом достаточно малом а > 0 разрешимы.
Доказать теорему об устойчивости задачи ЛИ относительно изменения целевой функции и правой части ограничений по направлению.
Задача Р(Б, с) устойчива по направлению 7г (Б, с) в
Х*(Ь,с)
Рис. 25
еелп разрешимы следующие
y^Y*{b, с),	(5.40)
z^X*{b, с).	(5.41)
том и только том случае, задачи ЛИ:
<Б, у> min,
<с, г> ’->• шах,
Иллюстрацией этого •утверждения при Б“0 служит рис. 25.
5.92	й. Доказать теорему о маргинальных значениях задачи ЛИ относительно изменения целевой функции и правых частей ограничений.
Если задача Р (Б, с) устойчива по направлению h = = (Б, с), то маргинальное значение
Р'{Ь, с, k) = Jim +	H-«g)-^(&, с)
a-»o+	a
существует и вычисляется по формуле
F'{b, с, h) = шах <с, я> -Ь min <Б, у). (5.42) хеХ*(Ь,с)	1ЛёУ»(Ь,е)
Отмстим, что формула (5,42) совпадает с формулой (5.34) для h = (0, 5, с). Суть приведенной теоремы состоит в том, что здесь
133
предельно ослабляются условия, при которых сохраняется утверждение теоремы ни 5.81 для направлений h укола иного пода, Ilcno.ii,-пуп 5.92, Можин соответствующим оГцнкюм ослабить услоннн, при которых справедливы формулы (5,35), (5.36) и первые четыре формулы в 5.82,
В задачах 5.93—5.99 считаются постоянными матрица .4 и лектор Ь. Соответственно используем обозначения P(c)f X, /(,?*), Х*(с) и т. д.
5.93	. Пусть задачи Р(е’) и Р(с2) разрешимы. Доказать, что
F (Х,е‘ + Л2сЛ) AtF (с1) 4-	(с2)
при любых Xi 3s 0,	0.
В частности, ото означает, что функция F(c) является выпуклой (см., шшрнмер, [39]).
5.94	. Пусть задача Р(с) разрешима. Доказать, что /г(ле) = V(<‘) при любом Х>0, т. е. функция F(c) по-ложптелыю однородна первой степени.
5.95	*. Доказать теорему об устойчивости задачи. ЛП относительно изменения целевой функции (ср. с 5.73).
Следующие утверждения эквивалентны:
а)	задача Р(с) устойчива, т. е. при любом с' из некоторой окрестности точки с задача jPCe”) разрешима;
б)	множество X* (с) непусто и ограничено;
и) rang .4 =п и существуют такие точки	уе=
s IV', что Ля Ь, у А — с, у> 0.
5.96*. Доказать теорему об инвариантности решения задачи ЛП при малом возмущении целевой функции.
Пусть задача Р(с\ разрешима. Тогда при любом с, достаточно близком к с, все решения задачи Р(с'), если они существуют, являются решениями задачи Р(с), т. о. Х*(с')<=Х*(с) (рис. 26). Более того, для любого ЛеЙ" обозначим через X (А) множество решении задачи
<А, .т> max,	х е X* (с).
Тогда существует число а > О, при котором X* (с -Ь аД)1=1 X (А) для всех таких а и А, что 0 < а a, ПАП = 1.
Таким образом, множества X*\c + ah) и Х(Л) пусты или непусты одновременно, что согласуется с 5.91 при Ь = и.
134
5.97*	. Пусть задача Р(с) пмеет едппствеппое решение я*. Доказать, что прп любом с\ достаточно близком к о, та же точка .г* служит единственным решением задачи Р(с') (рис. 27) п, следонатольпо, F(c)=<x*1 с'>, т. е. функция Г (с) является линейной в некоторой окрестности данной точки с.
Отсюда, в частности, следует, что для справедливости третьей формулы в (5.37) при / = 1 .... п лет необходимости требовать сдипствоппости решения двойственной задач и.
5.98.	Пусть функция F(fi) определена в некоторой окрестности точки с и дифференцируема в этой точ
ке. Доказать, что тогда решение задачи Р(с) единственно.
5.99.	Пусть вершина х* допустимого множества задачи Р(с) является се решением (возможно, пеедппствен-пым). Доказать, что та же точка а:* служит единственным решением задачи Р(с4), где с'— любой вектор вида с' а с т ’2J Wb М > 0 (г <= Z (-я**))-
Таким образом, пеодвпстиеппость решен ня можно устранить сколь угодно малым возмущенном нелепой функция. Иллюстрацией служит здесь тот :ко рис. 2С.
В задачах 5.100—5.108 считаются постоянными матрица А и вектор с. Соответственно используем обозначения Р(Ь), Хг(&), Х*(Ь) и т. и. Кроме того, ппже встретится множество /?, определенное перед текстом задачи 5.86.
5.100.	Пусть задача Р(Ь) разрешима. Доказать, что прп любом Ъ' В задача Р(Ь') также разрешима (ср. с 5.78).
5.101.	Пусть задачп P(6J) и Р(&2) разрешимы. Доказать, что
F (Х1&14- Ы>2) > UF{bl) 4- UF (Ь2)
при любых Xi 5*0, U 5s 0.
Отсюда следует, что функция F(b) является яогпутой (см., например, [39]).
5.102.	Пусть задача Р(Ь) разрешима. Доказать, что F(kb} = XF(b) прп любом Х5*0, т. с. функция 7?(&) положительно однородна первой степепп.
5.103.	Пусть задача Р(Ь) разрешима в b' 5= Ъ, Доказать, что F(b')?*F(b), т. е. функция ?’(б) по убывает.
135
<5.104. Пусть задача P(b) разрешима. Через е' обозначим f-й единичный орт в R"1 (I 1, ..т). Доказать следующие утверждения:
а)	если yi = 0 для некоторого */*еУ*(&), то F(b -I- aef) = F(b) прп всех a> 0;
б)	если ?/f L> 0 для любого у* «н У*(&)’, то П(Ь + а,е*у> >/'"(&) прп всех а>0.
5.	105*. Доказать теорему об устойчивости задачи ЛП относительно изменения правой части ограничений (ср. с 5.73 л 5.95).
Следующие утверждения эквивалентны:
а)	задача Р(5) устойчива, т. е. при любом Ъ' из некоторой окрестности точки Ъ задача Р(&') разрешима;
б)	множество У* (5) непусто и ограничено;
в)	существуют такие точки #<sR" и y^Rm, что
<Ь, уА = с, у 5= 0*).
5.106*	. Пусть задача Л(Ь) имеет единственное решение у*. Доказать, что F(b')=<y*l &'> врп любом достаточно близком к Ь.
Такам образом, для справедливости второй формулы в (5.37) при 1 = 1...w пот необходимости требовать едппствеппостп ро-
той ня задачи Р(Ь).
5.107.	Пусть функция F(b) определена в некоторой окрестности точки Ъ и дифференцируема в этой точке. Доказать, что решение задачи D(b) единственно.
5.108*	. Доказать теорему о полной устойчивости задачи ЛП 7Ю решению относительно изменения правой части ограничений.
Пусть задача Р(&) разрешима, а последовательность {/?} такова, что ЪК^В и Ък^Ъ. Тогда
ft-.ro
№*(&)) = 0, где символ d обозначает хаусдорфово расстояние между множествами (см. 4.136).
Ипымп словами, отображение Ъ-+Х*(Ь} является ио только полунепрерывным сверху, что следует из 5.90, по и полунепрерывным снизу.
5.109.	Показать, что задача кусочпо-лпнейпого программирования
/($)= шах «Д х) -J- од)-»-min, х<=Х, (5.43) ft=i........«
•) Условие существования такой точки у, т. о, допустимости двойственной задачи Й(Ъ), можно заменить требованием разрешимости прямой задачи Р(&).
13в
где cn^Rrt, rf*<=R (Ze5=51, ...» «)’, a X — полиэдр в R”, может быть сведена к задаче ЛП *).
5.110.	Показать, что задач п
/ (я) = max | (<?, х) + | ->• min, х s X, (5.44)
/(я) = S К«А х) + <?а1—»-min,	х<=Х,	(5.45)
Л=1
где c’,ERm! <4<=R (Л«1, ...» л), а X—полиэдр в R”, могут быть сведены к задачам ЛП, причем опп разрешимы, еслп X 0.
Отмстим, что задачи типа (5.44), (5.45) возникают при липой-пой аппроксимации зависимостей с соответствующими критериями точности (см. замечание после задачи 2.22),
5.111.	Свести к задаче ЛП задачу дробно-линейного программирования
/ в min’ *е х* (57iG>
где с, р<= Ия; d; q е R; X — непустой ограниченный полиэдр в R“, причем <р, х> + q^Q для любого х*=Х.
5.112*	. Доказать (путем построения соответствующей пары взапмодвопственных задач) теорему о линейном минимаксе.
Для любой матрицы А 3$ (т, п) и непустых поли-эдров Х cz Rn, Y <— R,n введем величины
R = 4sup inf <у, Лх>, S «и inf sup <у, Лх>, яех yer	ver х&х
Тогда. R = 5; при этом
а)	еслп R < », то R = inf (у, Лх*) для некоторого ITGY
х* е X, т. е. супремум R достигается;
б)	еслп £>—'», та «$'»==• sup <у*, Лх) для некоторого Х<аХ
у* У, т. е. ппфпмум S достигается.
Частвым случаем этого утаорждения является основная тво-рема теории матричных игр [5, 34], получаемая при

!г <=
Y = ‘ у s R”
2^=4 i“l J
•) Иными словами, требуется построить такую задачу ЛП, по решениям которой легко восстанавливаются решоиня исходной задачи.
137
Заключительная часть параграфа посвящена в основном примерам аналитического решения задач ЛП. с произвольным числом переменных.
5.113.	Рассмотрим задачу ЛП с одним связующим ограничением
<с, х> шах, <л, х> == Ь, х > 0,	(5.47)
где	fteR,	Найти все решения
этой задачи при условии» что а>0, 5>0. Указать те решения, которые являются вершинами допустимого мпо-гкества.
5.114.	Рассмотрим задачу (5.47) при условии, что первые к координат вектора а положительны (l<fc<n), а остальные отрицательны и 5>0. Выяснить, когда данная задача разрешима; указать прп этом все ее решения.
5.115.	Найти все значения параметра 7с, при которых задача
— 4хо — 5х3 Зх4 -> шах,
2xt 4- ж2 — 7% —	= 2,
4,
разрешима, и указать ее решение.
5.116.	Найти решение задачи
2гх “Ь х2	4-	Зт3	4* 2^4 4-	я6	4- 25с -> шах,
”1”	*”	Д?з	“ 12Хд	4” *0 1,
5х, -|- 6х2	4*	7а:3	4~ 4а:,। —	хъ	— Зх0 = —7,
2xs 4* 5.г3 -Ь 10ж1 4~ 2^6 4-	« 52,
J == 1,	4.
5.117.	Считая, что а>0, найти решения следующих задач ЛП:
а)	<с, а;>->• шах, <а, х>*=Ъ, x^d, где <а, d><&;
б)	<с, £> -+ шах, <а,	= Ь, 0 < х d, где 0 < b <
< <а, d>;
в)	<с, я> -> max, <а, х> = Ь, d° < х С d, где <g, d°> .< < b< <«, d>.
5.118.	Найти решения следующих задач ЛП:
а)	10х[ 4- 4^2 4- 9я3 + 2x4шах,
2.К| 4- xs 4- Зхз 4* #4 = 21,
O^xjd, О С Х2 =£ 4,	О^Хз-^6,	0 < Xi С 3;
б)	— 2x2 + Зхз -► max,
ад 4~ ха 4- Хз535 Ь,
О iti о, 0	4, 0 яз 1,
где 0 < b < 10;
138
и) ’X| — 2^2 + Зх» -* max,
*i+ #2+ хз'-^Ь,
ОХ| 5, О С хо4, 0<х3=^ 1, где b > О;
г) (5xi + 3x2 + 2хз -Ь Яац -< max-, 3j?i -h яа -I- 2х3 -г 2х.; =* 23,
— 1 =Sx(^4, 2-^хо^З, 5*£хз^7, —4^X4 <2;
д) 3xi + 7.?2 — Южз + 3;г4 -»- max,
Xj -Ь Х2 7 2.тз -Ь 4x4 < 33,
1 ад 4, —3 =С #2 4, —1 яз С 2, 6 ям 7.
5.119.	Колхоз собирается засеять четыре ноля птпс-ппцей и кукурузой. В табл. 13 указаны площадь каждого поля, урожайность па нем обеих культур, а также Таблица 13
Поле	Площадь (га)	УрошаПлость (п/гл)	
		Пшеница	Кукуруаа
1	400	20	35
2	300	35	50
3	200	25	40
4	100	80	45
	Цена 1 ц (р.)	7	5
закупочные цены. Согласно госзаказу- колхоз обязан произвести пе менее 12 000 ц пшеницы; спрос как па пшеницу, так и на кукурузу неограничен.
Требуется определять такое сочетание посевов пшеницы и: кукурузы па полях, прп котором валовый доход от реализации урожая будет наибольшим.
5.120.	Какой должна быть цепа па пшеницу в предыдущей задаче, чтобы выполнение госзаказа не противоречило экономическим интересам колхоза?
5.121.	Пусть полиэдр ArcR,; ограничен и имеет внутренние точки. Требуется поместить в X сферу наибольшего радиуса. Сформулировать эту задачу кик задачу ЛП.
5.122.	Найти окружность наибольшего радиуса, лежащую в полиэдре A'cR2, который задается системой:
3#! Ч- 4х2 <1 50,
—5.TJ Ч-12х3	60,
15^ — 8х2	120,
яр :> 2,	о.
130
5.123.	Найти сферу наибольшего радиуса, лежащую в полиэдре
Х = (г е RB | Ах ^Ъ,	0),
где матрица И=^(лг, к) и вектор b е R"‘ положнтель’ пы. Конкретизировать ответ для следующих данных:
А =
4
1
1 1 Г
2 5 2
7 7 1.
'15
&= 40
Leo
5.124.	Построить задачу, двойственную к транспортной задаче ЛП (см. (5.15)).
5.125.	Построить задачу, двойственную к блочной задаче ЛП:
к
3 <cft, zft)->-inax, й=1
fp=l
^>0, fc=l..........к,
где заданы А е .$£ (???*, и*),	nft), bh ^lCh,
?(=Rn* (/r=l.......K)iidf=Rm.
5.126.	Построить задачу, двойственную к Яншышче-кой линейной задаче планирования производства:
т
2(сг, 2?)->тах, r=i
Л^Са:*-1, f = l, .... Т,
?>0,	Т,
где заданы Л»ел?(п, п), c’^R” (£=1, Т) и Х° е R".
Исследование этой задачи с помощью теории двойственности приводит к так называемой теореме о магистрали. Подробное изложите магистральной теорпп — одного из важнейших разделов математической экономики — мом.ио найти о [6]. Том же читатель встретит большое количество других примеров использования тео-рпи двойственности при изучении экономико-математических моделей.
140
5.127.	Найти решение задачи п
S^j^bt, ^₽ii • ••, л, 1И1
®j>0,	7 = 1, ...»n,
где b15= 0, ..., bn > 0, ci > c2 >... > c„ > О.
5.128.	Найти решение предыдущей задачи при указанных ниже п и Ь = (Ь[, Ьв) (коэффициенты ci > > 02 >..  > с„ > О любые):
a)	n = 6, Ь=*(2, 1, 6, 5, 3, 4);
б)	п=7, Ь = (1, 5, 2, 4, 2, 7, 6);
в)	п = 5, Ь = (2, 4, G, 7, 9);
Г) ^5, Ь = (8, 6, 5, 3, 2).
5.129.	Найти значение и все решения задачи п
+	n — 1,
4" *П bm
где bi, ..Ьп-г произвольные ч^сла.
5.130.	В следующем месяце предприятие планирует выпускать определенный продукт, для производства которого требуются п видов сырья. Известны следующие параметры:
<ij > 0 — количество /-го сырья, необходимое для производства единичного количества продукта (/ = 1, ..., п);
bj > 0 — остатки j-то сырья па предприятии па конец текущего месяца;
Pt > 0 — цепа одной единицы /-го сырья;
d > 0 — количество денежных средств, которое предприятие может затратить па закупку дополнительных объемов сырья в текущем месяце.
Какие виды сырья и в каком количестве следует закупить предприятию, чтобы обеспечить максимальный объем производства в следующем месяце?
5.131.	В табл. 14 указаны конкретные значения параметров предыдущей задачи при п = 3. Построить для этого случая зависимость максимального объема производства от величины денежных средств d и вычислить оптимальные объемы закупки сырья при d = 3, 12, 36.
141
Таблиц а 14
i	ai	Ъ’	
i	0,2	4	3
2	0,0	18	1
3	0,3	12	2
5.132, На овощную базу и рибы	желе з недороде л ы и
состав, доставивший А топи овощей. Имеется п бригад грузчиков, предложивших своп услуги пл следующих условиях: бригада j берется разгружать по а} тонн в день по расцепке р) рублей за топну (/=li	») За каж-
дый день простоя состава бала платит штраф с рублей!.
Какпе договоры па разгрузку состава следует заключить базе, чтобы минимизировать суммарные расходы, и сколько диен при этом будет продолжаться разгрузка?
5,133. Найти решение предыдущей задачи прп следу-
ющих данных;
/1 -300, п = 4, с = 250,
«1 — 10, да = 20, йз — 30, <24 = 40, pi = 10, р2 — 15, ps — 20, р4 — 25.
5.134*	. Линейной задачей оптимального управления в дискретом времени называется задача ЛП следующего вида:
2} ((?, -г1) -I- {Ь*, н')) -> max,
z* = Лг-У”1 4- Biu*,	t = 1, ..7',	(5.48)
Dtu	t = 1, Г, -
где заданы J.-i^.яЦл, п),	т),	лг),
d1 е R\ <? е R", Ь‘ eRh1 (/ = 1..Г), аР е R".
Прп этом трактуется как состояние некоторой системы, а и' —как управление системой в момепт времени t. Введем множества допустимых управлений
U< = (и еИ‘”|Ящ-Srf’l.	/-1, ...» Т,
Последовательность управлений ul^Ut (t = 1, .... Т) называется оптимальной, если вместе с соответствующей (однозначно определяемой из (5,48)) последовательностью состоянии лт| (/ = 1, .... У) опа образует решение задачи (5.48).
Рассмотрим векторы p£<xRn (fral, ..7) , определяемые следующими рекуррентными формулами:
рТваст, д'=p(+I.4f + с\ f = y—1, ,.1. (5.49)
142
Введем семейство функций Гамильтона:
, . ^(п) = <//2?е-Ьг>\ и>, Д = :!....2Г.
Доказав, что для задачи (5.48) справедлив дискретный принцип максимума.
Пусть задача (5.48) разрешима. Тогда последовательность управлений я‘e-tZ. (/== 1, .Т) оптимальна в том и только тим случае, если
i$t (^) = шах^&'^и), I = 1, .Т.
Отсюда, d частности, следует, что оптимальная воследоиатрлв-поегь управлений но зависит от начального состояния я9.
5.135.	Пусть понтеры	(4!=1, ..1'р) опреде-
ляются по рекуррентным формулам (5.49), где у!» =у1, с‘ = с, причем матрица А имеет п непарно различных собственных чисел Z,>, ..Лп, отличных от единицы. Обо значим через Q матрицу размера пХл, у которой рн столбец является собственным вектором матрицы Л, соответствующим собственному числу "Kj (/ = 1, ..., л). 1 •'Л'/Чким

где Е{ — матрица размера п X л, у которой элемент на пересечении /-го столбца и /-и строки расой единице, а остальные элементы — нуля. Доказать, что
'=*.....г-
5.136.	Па территории охотничьего хозяйства обитают популяция волков и популяция косуль. Динамика роет этих популяций определяется следующплих статистическими закономерностями. Численность волков составляет долю а от количества косуль в предыдущем год}' (роль основного регулятора здесь играет миграция волков). Естественный темп роста поголовья косуль за год равен р, однако каждый полк- уничтожает в год в среднем у косуль.
Содержаний охотничьего хозяйства предполагает расходы в размере с рублей в год в расчете на одну косулю.
Хозяйство имеет право продавать по более <1 охотничьих лицензий за год, причем лицензия па отстрел волка стоит Z»i рублен, а для охоты па косулю — рублей.
143
Как следует организовать продажу лицензий'с целью максимизации суммарной прибыли за Т лет? Параметр d считается столь малым ц сраниешш с начальной численностью животных, что при любой организации продажи лицензии в точение Т лет пн одпа из популяций не может быть уничтожена подлостью.
Предложить общий способ решения задачи и получить численный ответ для случая, когда
а = 4-'- 'Р V = 6, ё = 2, Ъг = 100, Ьа = 50, Т = W.
5.137.	Распространение вирусной эпидемии описывается следующим образом. Различают два понятия: больные и вирусоносители. В течение месяца доля а больных умирает, доля р вирусоносителей заболевает, а число вирусоносителей в 7 раз больше суммарного количества всех больных л вирусоносителей в прошлом месяце.
Только что изобретена вакцина против этой болезни. Через год будет построен завод для се производства п все население можно будет вакцинировать. Однако до этого момента изготовление вакцины ведется в лабепо-торных условиях, и ее не хватает даже для больных к вирусоносителей. Известно, что за месяц доля Л вакцинированных больных условно выздоравливает (переходит в разряд вирусоносителей), доля ц вакцинированных вирусоносителей выздоравливает полностью.
Как следует ежемесячно распределять имеющееся количество доз вакцины между больными п вирусоносителями, чтобы за год умерло как можно меньше больных?
Предложить общий способ решения задачи и полу--чить численный ответ для случая, когда
а = —	В = —	V = 11	}	~	ц = 1.
к 5'	Р li*	Y 10*	Л	з’	"	3
5.138.	Кооператив, располагающий некоторой суммой денег, собирается ваять в аренду па несколько лет по- 1 мещенне нронзводствсивото назначения, купить оборудо- , ванне и организовать выпуск товаров широкого потребления с целью накопить к концу аренды максимальный объем денежных средств.
Условия аренды и характеристики оборудования таковы, что каждый рубль основных фондов (стоимости оборудования) приносит за год чистую прибыль а рублей. В то же время основные фонды амортизируют (изнашиваются в процессе эксплуатации) с темпом щ т. е. стон-
144
мостъ обррудовання к концу года составляет (1 — |х)-ю часть его стоимости на качало года. Показателя ап и. удовлетворяют соотношению О <- р < а < 1. Неравенство р < а означает, что прибыль, приносимая основными фондами, превышает потери от их амортизации. Условие сс< I говорит’ о том, что каждый рубль, вложенный в основные фонды, окупается ио за одни год, а за больший период службы оборудоиаипя,
Кооператив планирует закупать дополнительное оборудование в начале каждого года, используя прп этом только накопленные средства.
Требуется выяснить, при какой продолжительности аренды задуманное предприятие имеет смысл, определить оптимальную политику капиталовложений (закупки оборудования) и вычислить величину накопленных денежных средств за Т лет аренды.
§ 6. Симплекс-метод решения задач
л инейного программирования
СВОДКА ОСНОВНЫХ ФАКТОВ
1. Введение. Спмп.текс-мотод является основным численным методом решения задач ЛП. В этом параграфе будут отражены лишь его принципиальные положения. Болес детальное изложение (в частности, подробное обсуждение вычислительных аспектов метода) имеется, например, в книгах [5, 11, 15, 26, 30, 46]. Там же приводятся и другие численные методы линейного программирования.
Симплекс-метод описывается применительно к канонической задаче ЛП
<с, хУ -+ шах,
. ,	. л	(6.1)
Ля о, х > 0,	' 1
где Д Е^(т, л), Ъ & It”, с® R*. Это не ограничивает общность метода, так как любая задача ЛП может быть представлена в форме (6.1) (см. п. 1 § 5). Естественно считать, что 6^0, так как иначе задача (6.1) тривиальна (см. задачу 5.36). Кроме того, предположим, что rang А = т, т. е. все строки матрицы Л линейно независимы. К этому можно прийти, исключив из системы Ая=Ь линейно зависимые уравнения, что обычно и делается в рамках специальной процедуры, предшествующей симплекс-методу (см. я. 4).
10 G. Л. Лшмаиоп, Л, В, Тдиохов	145
Обозначим через X допустимое множество* задачи (6.1), т. О.
Х = {х^1{'1|Лх = Ь1 ж^О).
Напомним, что, согласно теореме 4.4, точка х множества X является его вершиной (опорной точкой) в том и только том случае, если векторы as (/еДя)), т,- о. столбцы матрицы А, соответствующие положительным координатам точки я, линейно независимы. Прп этом вершина х невырождепа, если Щя) I = mt и вырождена в протпвпом случае, т. е. если |У(ж) | <т.
Базисом вершины х множества X называется произвольная система пз т линейно независимых столбцов матрицы ?1, включающая в себя все столбцы, соответствующие положительным координатам точки х. Другими словами, система (а'|/<= J), где J<= И.zi), есть базис вер-
шины если это базис в R™ (в обычном слгысле) и J(x)<^J. Переменные х} (/<=/), соответствующие данному базису J), называются базисными.
Ясно, что невырожденная вершина х пмеет единственный базис {«'|/ <= J (я)}. У вырожденной вершины базисов может быть несколько, причем условие rang Л =т обеспечивает существование по крайпей мере одного базиса.
Симплекс-метод представляет собой вычислительную процедуру, которая генерирует последовательность вершин х°, а;1, вместе с некоторыми их базисами. Ыа очередной Z-й итерации в зависимости от текущего значения параметров лпбо делается один из двух выводов:
1) я/— решение задачи (6.1);
2) задача (6.1) но имеет решения,
либо строится следующая вершина я!+|. Если прп этом вершина х1 невырождепа, то в повой вершине целевая функция принимает заведомо большее значение:
<с, л,+1> > <с, я‘>. '	(6.2)'
Если же вершина х1 вырождена, то лпбо выполняется условие (6.2), либо я‘+1 т. е. перехода к повой вершине по происходит, а итогом итерации является лишь замена одного базиса вершины х* другим. Перебор базисов может продолжаться несколько итераций, по рано пли поздно находится такой базис, при котором осуществляется переход в новую вершину с большим значением целевой функции.
Подобная процедура за конечное число итераций приводит к выводу 1) пли 2), поскольку число вершин ноли-146
ядра X конечно и средн них обязательно имеется решение задачи (6.1), еслп ома вообще разрешима (см. теоремы 4.1, 4.3 и 5.5).
Приступим к более детальному описанию.
2. Итерация симплекс-метода. Пусть па начало t-й итерации ужо получены вершина .г' и ее базис {а>1;<“71). Для краткости положим х =- я‘, J = J*.
Поскольку {«'1/ ® 7) есть базис в R"1, то все столбцы матрицы И можно представить как лппойпыо комбинации столбцов из базиса, т. е.
&к = 2	и, (6.3)
J<sJ
где Xja (/ s 7) — некоторые числа. Вычислим величины
Дл = 2 efiih — <>л, к «1, ..п, (6.4) J£j
Параметры XJ(t принято называть коэффициентами замещения, а параметры Д4— оценками замещения. Для любого к& 7, очевидно, имеем
И, еслп / =я к, ?-^=л	 г г>> Дл = О. (О.о)
(0, еслп ; е	' 1
В зависимости от знаков параметров Хд, Д* при j с= 7, k&J (т. е. /с<=?{!, ..., л)\7) выполняется хотя бы одно из трех условии:
I. Для любого помора k^J справедливо неравенство
Д* fl-
'll. Существует такой помер з<^7, что Д, <0 и Хл 0 при всех j е= 7.
III. Существует такой номер s&J, что Д,<0 п %;1>0 при некотором J s J.
Каждому из этих условий соответствует одно па следующих трех правил симплекс-метода.
Теорема 6.1 (правило оптимальности). Если выполняется условие I, то х—решение задачи (6.1).
При этом решение у двойственной задачи может быть найдено как решение невырожденной квадратном системы линейных уравнений
<у, а}> = с<, у «= J.
Теорема 6.2 (правило отсутствия решения). Если выполняется условие II, то задача (6.1) не имеет решения.
10*
147
Пусть теперь выполняется условие’ III. Для указанного там номера $ положим
а ей min	(6.6)
л‘е/Л;а>о
Пусть минимум в (6.6) достигается на номере г, т. е.
а™—,	г&7, Ата>0.	(6.7)
Лгв
Введем множество номеров
Г=(ЛИ)Ш	(6.8)
в точку с координатами
	если	j<s /\{г),
а,	если	7 = 5,	(6.9)
А	если	7^'.
Теорема 6.3 (правило перехода к новой вершине). Точка х' является вершиной множества X, а {<?| j J'} — ее базисом; при этом
<с, х'> = <е, х> - аД,.	(6.10)
Указанные вершина п ее базис берутся для расчетов па следующей, :(14-1)-й, итерации: д/*1 =*x\ Прп этом говорят, что столбец аг выводится из базиса, а столбец а* вводится в баапс. Элемент называется ведущим.
Теперь мы мошем конкретизировать возможные ситуации при переходе от к х**1, упоминавшиеся в п. 1. Если число а из (6.6) положительно, то на (6.10) и условия Д1<0 следует (6.2). Неравенство а>0 заведомо выполнено, если вершина х невырождепа, так как в этом случае J = J (ж), т. е. х} > 0 прп всех 7 /. Если же вершина х вырождена, то по исключено, что найдется такой помер г <= J, для которого > 0 п хг = 0. Тогда окажется, что а «= 0 л х' = х, т. о. итогом вычислений по формулам (6.6) —(6.9) будет лишь замена базиса (a'l/sj) вершины х се же базисом {аЯ/е J') *).
Заметим теперь, что процедура, описанная перед теоремой 6.3, содержит некоторую неопределенность: там не уточняется, как следует выбирать номер s нз условия Ш и номер г из условий (6.6), (6.7), если таких $ пли г пе-
•) По этой причине теорему 6.3 более точно следовало бы называть правилом перехода к новому бавису.
148
сколько. Существуют примеры, показывающие, что при определенном выборе этих поморов описанная. процедура может привести к циклическому перебору базисов одной и тон ;ке вырожденной вершины [30, с. 125]. В таком случав говорят, что произошло зацикливание симплекс-метода. Однако возможность этого неблагоприятного явления полностью исключается, если применять особые правила выбора г и $. Простейшее правило такого сорта состоит в следующем.
Теорема 6.4 (правило Блэнда для устранения зацикливания). Пусть при выполнении условия III выбирается «первое подходящее з, а затем первое подходящее га, г. в.
s =s'min {k J [ Дл < 0),
{х, ]
У е J |	0,	а1»
л/а J
где а определено в (6.6). Тогда зацикливание симплекс-метода невозможно.
Итак, на следующей, (£+1)-й итерации необходимо выразить через базис	=/'} вершины а<+1 == х'
все столбцы матрицы Л:
cJ1 = 2	51	k =* 1, ..п,
JGJ'	J<3J\{r>
а затем вычислить параметры
Дл =« 2 «Ал — «л. * “ 1....«•
Вообще говоря, определение коэффициентов ?-jh требует решения соответствующих систем линейных уравнений, что является довольно трудоемкой операцией. Однако оказывается, что параметры	можно легко рассчи-
тать па базе уже известных велпчнп Дл.
Теорема '6.5 (связь между параметрами последовательных итераций). При любом ^==1, ..., п выполняются соотношения
Т^гл, если /е/\(4 лг«
-т22',	если
Лгл	д
Д^, «= Дд —г	Х/д»
лг*
(6.11)
(6.12)
149
3. Симплекс-таблица. При органкзацип вычислений пп симплекс* методу основной конструкцией является так называемая симплекс-таблица Т, соответствующая даю ной вершине х и се базису {«;1; е 7). Эта таблица представляет собой матрицу размера (?п 4* 1)Х(п+1)
Таблица 15
«1	«п Ъ
«	в	*	в	*	*
а	В	А	V	*	в
		
а*	?.д	...	?.^л	...	?.;{	. . .	Tj
t	» • “ •	•
а	а	*	в		•
	♦	В	в	V	
ат	^>1	♦ ♦ • ^rJt	• • •	*г
*	В*	•	А	В	в
«	•	•	*	в	В
	В	*	*	*	•
л	л, ... Ад . . . Д4 ... А,,	<С, *>
(табл. 15). Над столбцами таблицы записываются буквенные обозначения а1, .. ч а’1, Ъ столбцов матрицы Л и вектора правых частей ограничений задачи (6.1), а с левой стороны таблицы — обозначения я/ (j'e J) столбцов, образующих базис, п обозначение А. На указанные места таблицы заносятся численные значения параметров АЛ, xj, Л‘в1, .... п), <с, я>*). В дальнейшем под строкой а! таблицы Т будем понимать (и + 1)-мерпый вектор (Л/..... A*,, х>), под строкой А — вектор (Aj..Ап,
<с, «>).
После заполнения таблицы Т проводится ее анализ на основе правил симплекс-метода. Еслп выполняется условие I пли II, то расчеты закапчиваются. Еслп же выполнено условие III, то осуществляется переход к симплекс-таблицс Т\ соответствующей новой вершине х' и ее базису {д'|/ е J'} (табл. 16). Для этого выбираются номера з п г, удовлетворяющие условиям III и (6.7) (в случав
*) Отмстим, что подобно тому, как в первых п столицах стоят коэффициенты разложения воюгоров о’,.... а” во базису {«*[/е/}, в последнем столбце располагаются коэффициенты рцалозконнл вектора b по тому же базису: Ь = Ах = у «^.. Этим объяс-j<=J
няотся использование ооозпачоиая Ь.
150
неопределенности выбора используется правило Блэнда). Ведущий элемент к„ в таблице Т помечается для наглядного указания па то, что столбец аг должен быть выведен из базиса, а столбец а‘ -введен в пего. В таблице Т‘ слева вместо ат ставится а’, а остальные буквенные обозначения остаются неизменными. Из сопоставления формул ($.7) —
Таблица 16

&
а*
а*
а*
,ап
'jfc
*/!»
г.

О
г а*
'th
х,

1
Кп
Д
Д!
Дп
<Л У>
А
О
(6.12)	ясно, что вычисление параметров таблицы Т' сводится к следующим л.4елеигир«ыл( операциям со строками таблицы У:
1)	для получения строки а} таблицы Т' при /е еД(г} из строки а1 таблицы Т вычитается ее строка аг, умноженная на коэффициент
2)	для получения строки а* таблицы Т* строка аг таблицы Т делится па коэффициент
3)	для получения строки Д таблицы Т' из строка Д таблицы Т вычитается ее строка аг, умноженная па коэффициент Д,/Хг,.
При этом (в соответствии с (6.5)) элемент столбца а* таблицы 2’', стоящий на пересечении со строкой а’, оказывается равным единице, а все остальные его, элементы равны нулю.
Затем проводится анализ таблицы Т'» Если выполняется условие III, то осуществляется переход к следующей симплекс-таблпце л т. д.
4.	Поиск начальной вершины и ее базиса. При описании спмплекс-метода мы предполагали, что уже известны какая-то вершина к0 множества X и ее некоторый базис.
151
В некоторых частных случаях проблема нх отыскания ре шается совсем просто.
Пусть, например, дана стандартная задача ЛП
<с, х> -> max,
Ax^b, х О,
где А е J/' (т, п.), b е R"', с <= R*», причем 6^0. Чтобы применить к этой задаче симплекс-метод, ее необходимо привести к канонической форме:
<с, х> -* max, Лз + и = &, х ** 0, н>0.
(6.13)
Обозначим через Z допустимое множество задачи (6.13);
Z я
з «о (х, и) В+хВ?
71	»П	)
2 a^xj -J- 2} & i=i	i=i	J
где <?' есть i-й единичный орт в R" (1 = 1,	т). Ясно,
что точка z = (0, Ъ) является вершиной множества Z, а система {е1, е’а)— ее базисом. Их и можно принять за начальные при решении задачи (6.13) спмплекс-ме-тодом. Соответствующая спмплекс-таблпца составляется без труда, поскольку коэффициенты разложения векторов я1, ..., ап по указанному базису совпадают с пх координатами.
Рассмотрим теперь один из общих способов построения начальной вершины — метод искусственного базиса.
Пусть дана задача (6.1). Без ограничения общности будем считать, что b > 0. Рассмотрим задачу
2н|->н11н,	(6.14)
i=i
Ля 4- и = Ь,	х 0, и 0,
имеющую решение но теореме 5.2. Допустимые множества задач (6.13) и (6.14) совпадают. Применим к задаче (6.14) симплекс-метод, начав с той же вершины z = (0, Ъ) множества Z. В результате будут найдены:
а)	решение s°=*(x0, н°) задача (6.14), являющееся вершиной Z;
б)	базнс M/е/} U	всршнпы js°; согласно
определению, это означает, что векторы а1 (/’е^), е1 линейно независимы, |/| + l/|=m, J(xQ)<=Jt Z(u°)c;/;
152
в)	коэффициенты разложения по этому базису всех столбцов матрицы Л и единичных ортов в R'"; пае будет интересовать лишь разложение столбцов:
aft = 3 а* ‘I- 2®Vth, /с(6.15) д=т <gi
Возможны следующие случаи.
А.	к0 =# 0. Тогда легко доказывается от противного» что допустимое множество X задачи (6.1) пусто.
Б. н° = 0. Тогда, очевидно» xQ является вершиной X. Чтобы построить ее базис, рассмотрим три подслучая.
Б.1. 1 = 0. Тогда {а*!/®/) —базис я*1. При атом формула (6.15) переходит в (6.3) и, чтобы начать процедуру симплекс-метода для решения исходной задачи (6.1), достаточно вычислить соответствующие оценки замещения по формуле (6.4).
Б.2. 1^0 и Цг.’^0 при некоторых re7, s®п) (точнее, s<£J). Тогда система WI/ Е 74 U	где
I' = 7 U (а), Г = 7\(г), также образует базис вершппы зР = (х°, 0). Коэффициенты разложения по этому базису столбцов матрицы Л вычисляются по формулам, аналогичным (6.11). Если для нового базиса также выполняется условие Б.2, то описанную процедуру следует повторить. В результате за конечное число шагов мы придем к Б.1 плн Б.З.
Б.З. 7¥=0 и Hih = O при всех i®7, 7с = 1, ..., п. В этом случае формула (6.15) также предстанет в виде (6.3), т.е.
ah = 3 a%h, к = 1, .п. (6.1,6)
Однако система {аЧ/ е 7) пе является базисом в Rm, поскольку |7| < т. Положив I = {1, ..., т}\1, введем следующие обозначения: А — матрица со строками а< (ieZ), а’— j-н столбец матрицы А (/“1,	п), Ъ —
вектор с координатами bt (г ® 7). Тогда
1)	rang А « 171, т. е. строки матрицы А линейно независимы;
2)	система Ах = Ъ равносильна системе Ал •= 5, т. е. в исходной задаче (6.1) ограничения г> = bt, где 1<=1, являются «лишними»;
3)	<aJlf е 7} есть базис вершины хР множества X, записан кого в виде
X = {х <=Rh|Ах » 5, х S* 0).
153
Рассматривая в векторных равенствах (G.16) лишь ко ординаты с номерами z «= 7, получаем раз^южеппо по ука-данному базису всех столбцов матрицы А.
Таким образом, метод искусственного базиса позволяет помимо прочего выявить и исключить из системы Ах == b линейно зависимые уравнения, т. е. перейти к эквивалентной задаче ЛП, у которой матрица ограничений пмеет полный строчный ранг.
УПРАЖНЕНИЯ
s/ 6.1, Пусть полиэдр в Rc задается системой
axi — 5х2 -Ь «з- 2,т4 —	4;	= — 1,
bxi -Ь bxs —	4- -г Ьхь л’о = “Ь
—2а?| — 5х2 -{' З.т3 — ,т4 сх& — г,- — 2, ^>0, / —	..,6.
Найти все базисы ого вершины ж0 — (0, 0, 1,- {, 0, 0).
	а	b	с	а		b	с	л		ъ	с	а		ъ	с
1	1	2	-3	6	1	5	-8	11	1	1	-2	10	С	0	2
2	1	1	2	7	—4	2	2	12	—4	0	-3	17	—4	О	-3
3	11	-1	2	8	-19	5	-3	13	1	1	-4/3	18	26	—4	7
4	6	.0	1/3	fl	—14	4	I	14	3	-1	2	19	3	2	-3(
5	2	4	—19/3	10	—9	3	2	15	9 и	4	1	20	1	-4	71 i
v 6.2. Сформулируем три утверждения относительно задачи ЛП и вершины я0 ее допустимого множества:
А. х° — решение задачи.
Б. Задача не пмеет решения.
В.	Существует вершина, в которой целевая функция принимает большее значение, чем в зР.
Используя правила симплекс-метода, выяснить, какое из этих утверждений пмеет место, в следующих случаях:
а)	—2х4	5х2 — 7x3 4- вл-.t 4- Зхс max,
3xj 4- г2 4- 2х3 4- Ь.гл 4- 4х5 — 15, —хг 4- сх2 — х3 4’ 2x.j_— х6 = —4,
Xj 0,	/ — 1, ..,, 5,
x®=(l, 0, 0, О, 3) :
154
	я	b	С	а b		€	а b		с	а b		с
1	I	—I	1	6	1 —7'	0	11	LO 1		16	3 -1	—1
•)	0	-7	1	7	2 -1	-1	12	-1 -0	-3	17	-2 -8	1
3	2	—1	1	8	1 2	1	13	1 —5	9	18	-1 -Й	3
4	1	-1	-1	9	5 -6	1	14	6 —7	3	19	3 -5	—2
5	1	—5		2	10	3 -1	1	15	2 -5	0 лл	20	7 -6	2
б)	«1	2's	+	а-з —	Зяц	"I”	x6	->	max,
-{-	«x2	-f-	at;, —	3x*.t	-I-	4z6	=	3,
at4	—“	Лд -F	СЛ. ।	1,
XJ	о >	/	’ 1 f	•• •»	")I
*°~(2, 0,1, 0, 0):
	<2	Ъ	с	а		Ъ	с	а		1)	с	а		ь	с
1	-1	»J	2	6	0	О	3	И	2	1	-3	16	—*>	1	2
2	О	1	2	7		0	—1	1	12	-3	—2	1	17	2	3	1
3	-1	0	-3	8	-0	2	3	13	0	2	-3	18	-1	3	-"5
4	0	1		2	9	0	-1	3	14	-1	2	1	19	О	1	5
5	4	2	3	10	-4	1	—4	15	-5	3	-3	20	3	-4	1
в)	.?(	—	3za	-|-	a:;t	-j-	at,।	-F	at5 ->- max,
2x,	-F	3x2	-|-	<rar3	-F	7,r4	-F	9z6 = &,.
a’i	—	a'a	-F	tr4	-j-	&r0 = 21
Zj 0, j ~ 1, o;
a:°-(0, 0, (Ь-1Л)/а, 2, 0):
	а	ь	С	а		b	с	а		Ъ	с	а		b	с
	-1	5	О	6	—"7	12	6	11		9	8	2	16	-6	«8	2
<2	-6	12	3	7	-G	10	3	12	—8	12	3	17	4	19	1
3	9	18	3	8	о	15	2	13	-3	10	6	18	-1	12	3
4	—4	10	5	9	3	19.	1	14	—7	8	2	19	-2	5	о
5	^3	8	4	10	1	19	3	15	3	15	4	20	5	16	9 •W
б.З. Используя теорию спмилекс-мстода, вапти все зпа“ ^ппя параметра /г, при которых точка х* ~ (1, 2, 0, 1, 0)
155
является решенном задачи
Зх4 -Ь	ахй	4“	кгя	—	5,г4	—	2Ах5	maXj
—я*! *|-	Хц	4-	Зх3	—	х4	4*	2ха	=	О,
3X1	—	*3	4*	2х4	—	х6	=	5,
bxi "Ь	сх%	4~	#3	4“	ха	=	Ъ 4~ 2с,
X] О, J = 1, ..., 5:
	а	ь	е	а		Ъ	с	а		Ъ	с	а		b	1 с
1	12	-1	-3	б	3	0	-1	11	8	-1 -3		16	10	1	1
2	7	1	1	7	17	2	3	12	7	ю 1 г		17	1	—*>	—5
3	15	2	3	8	8	1	1	13	9	1	1	18	9	0	—1
4	5	0	-1	9	0	—1	-3	14	15	-3 —7		19	19	2	3
5	3	—2	—5	10	21	о лл	3	15	~1	0 -1		20	-5	—1	-3
"V 6.4. Решить спмплекс-методом следующие задачи ЛП. начав с указанных першип допустимых мпо?кеств*):
а)	сл'1 4- х2 4-	*я	4-	4-	Хь ->	шах,
2.Г1 4" Зх2 4“	5хя	4-	7х4	-|-	9ха =	Ь,
Xi — х2	-}-	х4	4-	2ха =	с4
*1>0, 7 = 1, ...15;
х° = (0, 0, (&-7с)/5, с, 0):
	а	Ъ	с	а		1)	е	а		Ъ	с	а		Ь	с
1	2	8	1	6	3	32	4	11	4	15	2	16	5	22	3
2	1	9	1	7	2	33	4	12	2	16	2	17	1	23	3
3	5	10	1	8	1	34	4	13	3	17	2	18	4	24	3,
4	4	И	1	9	5	35	4	14	5	18	2	19	3	25	3
5	3	12	1	10	4	ЗВ	4	15	1	19	2	20	2	26	3 ' 1
б)	а?! 4“ а^л — 2*а -I- х4 4- 2х& — xe -> шах, —*i 4- *2 4- *з 4- (Ь—0)х4 4- (с4-1)*с 4- *в = 3,, 2xi 4- х3 4- 2х3—2(Ь4-3)х44-(2с4-1)х5 + 5х0 *= 6t 3xt 4-	4“ 2ха—3(Ь4-2)х44-(2с4-1)х5 4- 6х9 —.6,
х;>0,	/=4,...,6;
х°=(0, 0, 3, О, 0, 0), начальный базис — {а1, а\ а3}:
♦) В этой н следующих упражнениях в случае неопределенности выбора он од иного н выводимого столбцов использовать правило Блайда,
15В
а Ъ с I а Ь с a b с I а Ъ с
i	-1	4	5	3	-5	4	1	И	-2	3	2	16.	-4	4	4
2	—3	3	4	7	—4	3	2	12	-3	4	3	17	-3	3	3
3	-4	2	3	8	-1	2	3		-4	5	4	18	-2	2	2
4	—5	1	2	9	-2	1	4	14	-1	2	5	19	-I	1	1
5	-2	5	1	10	-3	5	5	15	-5	1	1	20	—С	5	5
в)	я#!	+	+	5&а + 6яй-нтах,
2^1 +	4- ж3 -НЬ_М);г44- (с—3)ж5 — 2х6 = 1,
3xr -h Зх2 Н- х3 4- Ья4 +(с—12)х5 — 11а:в = 3,
—i£j -h 2.Гд — — (&Н-3)л4 — (с-И1)я6 — 12жв = 2, 2j>0,	; =	6;
л”«(О, 1, О, О, 0, 0), начальный базис — {а1, а2, а3}:
	а	b	с	«		ь	с	а		b	с	а		Ь	с
1	—4	2	0	0		3	3	11	-7	6	4	16	-6	4	2
2	-G	3	2	7	—7	5	3	12	—5	3	2	17	-7	2	2
8	-3	0	1	8	-8	6	2	13	-с	5	5	18	-5	4	3
4	—7	4	2	9	-5	4	1	14	—4	3	1	10	-8	5	1
5	—9	3	1	10	-8	7	5	15	-9	6	3	20	-7	3	1
G.5. Решить сммплекс-мвтодом задачу
xt —	«а —	+	аж4 -> шах,
4-	2га —	z3	4-	2,
bxt 4-	га 4-	—	2^4 ^2,
-}-	а;а 4- 4жа	4*	2х4 <2 6,
xj 0,	/ — 1, •) 4,
предварительно приведя ее к каноническому виду:
	а	Ъ	е	а		b	е	а		ъ	с	а		Ъ	С
1	2	3	—1	6	5	9	3	11	2	1	2	16	3	3	1
2	3	1	1	7	4	3	6	12	3	3	4	17	4	1	2
3	4	2	-1	8	6	1	5	13	5	2	•^1	18	3	1	0
4	7	2	3	1)	2	2	2	14	7	1	5	19	4	1	3
5	8	3	4	10	5	3	7	15	0	3	3	20	5	2	6
157
.	6.G. Найти методом искусственного базиса вершину
V полиэдра Аг’в IV, задаваемого системой
4'	= 5,
4- бх2 “ £3 — z,t — с,
— 4^ 4- -Ь 2г4 = 8, £/>-0, / =	4:
а Ь с		а Ъ с		а b с		а b с	
1	2 1 2	6	7 1 3	И	5 1 4	16	3 1 5
2	3 2 3	7	8 2 4	12	6 2 5	17	4 2 6
3	4 3 4	8	2 3 5	.13	7 3 .0.	18	5 3 7
4	5 4 5	9	3 4 0	14	8 4 7	19	6 4 8
5	С 5 G	10	4 5 7	15	2 5 8	20	7 5 9
>/ 6.7. Решить спмплекс-методом следующую задачу ЛП, начальную вершину методом
—	3.тй-->- шах,
= а, й ______I
предварительно определив искусственного базиса:
— 2;Сд + х» -Ь
2?! — Я’2 ч- X, —
ч 1 •‘•2	"3 I f.Lf’4
/ = 1, ..„5:
	а	5	с	а		Ъ	с	а		ь	е	а		ь	С
1	1	1	9	6	6	2	2	11	2	2	3	1G	3	ъ	4
2	О	1	2	7	7	2	2	12	4	2	3	17	6	2	4
3	3	1	2	8	9	1	3	13	6	2	3	18	3	3	4
4	4	1	2	Q	4	1	3	14	3	1	4	19	6	3	4
5	5	2	2	10	6	1	3	15	0	1	4	20	3	4	4
G.8. Найти решение задачи
Sxj 4*	6% 4-	13х3->- min,
5»1 + (5 — а)х2 4* (12 — а)х3 2,
—Ч 4- «а	< 2,
ха 4- х3 > 3,
2я\-I-	Зл72 4-	Сх3>1,
bxt — (b 4- с)т2 — c£z	—15
158
-путем применения снмплокс-метода к двойственной задаче, начиная с вершины у° —(0, 1, 1, 2, 0):
	а	Ь	с	а		6	с	а		Ь	с	а		b	С
1	1	1	4	в	1	1	3	И	9	1	2	10	1	5	1
2	3	1	4	7	3	2	3	12	7	2	<>	17	1	4	1
3	5	1	4	8	5	2	3	13	5	3	2	18	1	3	1
4	7	1	4	9	7	1	3	14	3	4	2	19	1	2	1
5	9	1	4	10	9	2	3	15	1	1	2	20	1	1	1
6.9. Металлургический цех в качестве сырья закупает латунь типов I, II и III — различные по процентному составу сплавы меди п цинка (с некоторыми добавками)—и переплавляет ото сырье в отношении 1:1:3, с тем чтобы получить сплав, содержащий 57 % меди и 34 % цинка.
Появилась возможность покупать сырье новых типов ,IVf V и VI. Характеристика сырья каждого типа приведена в табл. 17. Какое сырье следует покупать теперь цеху и в каких пропорциях его переплавлять, с тем
Таблица 17
Тип сирья-	Содержаний люди (%)	CORl'fiMUHHO HtllUtll (%)	Стойкость (р./НГ)
I	75	20	5
11	(Ю	30	3
III	50	40	2
IV	а	95 — а	с
V	b	90 — 5	2'
VI	45	40 -	1
чтобы выпускать тот же.сплав, расходуя па сырье как можно меньше денег?
а Ь с		а		Ь	с	с		Ь	с	а		Ъ	С
1	72 5$ 4,2	6	72	70	4,2	И	68	65	3,4	16	74	60	4,4
2	72 (10 4	7	68	58	3,4	12	08	70	3,4	17	74	62	4,6
3	72 62 4,2	8	68	60	3,2	» л	72	по	4,2	18	74	G4	4,4
4	72 64 4	’0	68	02	3,4	14	68	58	3,2	19	74	65	4,6
5	72 65 4,2	10	68	01	3,2	15	74	58	4,6	20	74	70	4,6
159
0J В покарпс для вынечкп четырех видов хлеба используются мука двух сортов, маргарин и яйца. Имеющееся оборудование, производственные площади и поставки продуктов таковы, что в сутки можно переработать пе более а кг муки сорта 1, Ь кг муки сорта II, с кг маргарина, d штук яиц. В табл. 48 приведены нормы расхода продуктов, а также прибыль от продажи 1 кг хлеба каждого вида.
Таблица 1
Han«Ciionaiino продукта	Норми расхода па 1 кг хлеба (но апдал)			
	1	2	3	4
Мука I (кг)	0.5	0,5	(1	0
Мука II (кг)	0	0	0,5	0,5
Маргарин (кг)	0,125	0	0 '	0,125
Яйцо (шт.)	2	1	1	1
Прибыль (к./кг)	14	12	5	°
Требуется определить суточный план выпечки хлеба, максимизирующий прибыль:
abed	abed
1	250	200	(И)	1380	11	210	180	50	1180
2	290	200	70	1540	12	2<Ю	190	90	1380
3	350	200	80	1740	13	300	200	70	15(Ю
4	380	200	90	1880	14	330	210	80	1720
5	290	150	50	1280	15	370	220	90	11100
6	300	150	ОО	1330	16	220	160	50	И СО
>4	ЗЮ	150	70	1480	17	270	2!0	6.0	1440
8	330	150	80	1800	18	310	190	70	1580
9	400	150	90	1820	19	340	200	80	1720
10	240	100	50	1080	20	390	180	90	I860
6.11. Для рытья котлована объемом а м3 строители получили три экскаватора, Мощный экскаватор производительностью 22,5 м3/ч расходует л час 10 л бензина; Аналогичные характеристики среднего экскаватора — 10 м3/ч п Ъ л/ч, малого — 5 м3/ч и 2 л/ч. Эскаваторы могут работать все одновременно, не мешая друг другу. Запас бензина у строителей ограничен п равен с литров. Если рыть котловап только малым экскаватором, 'то бен-зипа заведомо хватит, по это будет очепь долго. Каким 160
образом следует использовать имеющуюся технику, чтобы выполнить работу как можно скорее?
	а	ь	с 1	а		Ъ	с
1	1350	10/3	548	11	1890	11/3	777
2	1080	4	460	12	1200	4	510
3	1080	11/3	444	13	1800	10/3	728
4	1440	10/3	580	14	1380	4	580
5	1140	4	480	15	1620	11/3	666
6	1350	11/3	552	10	1500	4	630
7	1620	10/3	656	17	1980	10/3	800
8	2160	11/3	888	18	1890	11/3	780
9	1200	4	500	10	I860	4	780
10	1320	4	550	20	1140	4	470
ЗАДАЧИ
6.1. Пусть полиэдр в R8 задается системой
4zi 4- 7я?а 4- 2г3 — Заг4 4*	4' 4жв = 4,
—Zi — 2х34- зг3 4- «4	“ ®e =
, — Зх3 —	— хъ 4- 2х0 ~ О,
Xj.Z^- О, J = 1,	6.
Найти все базисы его верш'лпы я°=(0, 1, 0, lt 0, 0).
6.2. Пусть полиэдр в	R5 задается системой
+ .Tg 4- Зхэ	4*	5я4 4- 6я5 =	3,
я3 4- Ss	4- (&	—	S)®4 + 2se =	1,
Зях 4* 2ii 4-	+	5я4 4* 2®s —	1,
а?/	0, / = 1,	5.
Найти все базисы его вершины х° =(0, 0, 1, 0, 0) в зависимости от параметра к,
,6.3. Сформулируем три утверждения относительно задачи ЛП и вершины .г0 ее допустимого множества:
/ГА. ж0 — решение задачи.
Г, К Задача не имеет решения.
ч\В. Существует вершина, в которой целевая функция принимает большее значение, чем в я°.
’ Используя правила симплекс-метода, вылепить, какое чз этих утверждений имеет место в следующих случаях: а) 2х£ — 4ха 4- гз ~ я* 4- Зхб-> шах,
—5zl 4* 6я3 — 7я3 +, ®4'4' 14я6 — —7,
— 5х2 — 10г3 — 4х/4- 20х5 — —10, я-j. 0, J = 1,5;
а* = (2,0, 0,3,0);
^1 С- А. Апшппор, А. В, Тимохап	161
б)	— хх	+	бх2	Н-	х3 -И 4х(1	4-	2х5	max,
5хх	-j-	х2	—	х3 — 4х4	= —1,
—4хх	-|-	х»	-Ь	2х3 -|- бх4	+	Зх5	= 5,
•2*/	0» 7 =	»••» о;
а? = (О, 1, 2, Ot О);
в)	Зх2 — 7х3 -|- х4 — хь ->- max, 2хх 4“ х3 “I- 2х,х -j- х3 — 1, Юхх 4- 4х2 — 9х3 4- 2хл — х6 — 3,
zj:>0, /«I, ..,,5;
х* = (O,i, 0,0,4);
г) хх — Зх2 ”Xj 4- Й-2 2хх
х/ О,
-|- 4х3 — 2х4 — Зх5 ->- min,
®3 ~Ь #4	1>
— 2х3 — 6x,t 4- 2х5 = 4, у = 1,	5;
х° = (2, 1, О, О, 0).
6.4.	Используя теорию симплекс-метода, пайтп все значения параметра к, прп которых точка х* является решением соответствующей задачи:
а)	хх 4“ к“х.£ — 2х3 4- 2frx,t 4" 5х5 — 10х3 ->- шах,
—2хх — Хд 4- Лч 4- 2х0 = 2, 2хд •]- х2 “г х3	= 2,
—2хх	— х3 4- ^4 4- 2х6	=2,
sj > 0,	6,
х* = (0, 1, 1, 3, 0, 0);
б)	хх	4“	3frx2 -|-	2х3	4*	15х« —	А,2х5	4_ бхс —> max,
2хх	4-	х2 4~	2х3	4-	x,t -h	xs	4- х„ = 5,
хх	4-	х8 4*	х3	4“	2хд	4" Хд — 4,
+ х2 4- 2х;1	4* х5 = 4,
^;>0, / = 1, ...,6;
х* = (0, 3, 0, 0, 4, 1);
в)	— Зхх 4" А*х2 4" 2х3 4* Хд — 2Л*х5 -р 5х,5	max,
5хх — Зх2 — х3 4* 2х4	4- хв — 4,
2®1	4_ жз "Ь 4' #5 4* х* = 4,
-7хЛ -|- 4х2 4- 2х3 - Зх, - 4 = 2.5, ^>0, 7 — 1, з*=(0, 0,1,2, 0,1).
162
6.5.	Решить симплекс-мстодом следующие задачи ЛИ, чан с указанных вершин допустимых множеств:
a)	5xj + а*а -j- 2т3 4~ *4 —> шах,
*1 ” *а 4- *з — 41
2*i -Ь *3	*4 — о,
xj 3^ 0, у —• 1, ..., 4, я0 == (0, 0, 1, 5);
б)	.тг 4- Эха 4- х3 — я., -> шах, а?! 4* 2^2	4**.i = 3,
—-Ь *2 + *3=1,
*у 0, j = 1, .»•, 4,
*° = (О, О, 1,3);
в) 3xt -}- 7,т3 4"	4%	— 3s,।	4- 2zfi	4“	2яв	->	max,
—xL -г 3tfs -j-	2т3	+ *.t	+	*о	4"	Зт0	=
4xj — 2яя —	Зт3	— 4*(1	4_	Хц	—	7ха	=	—2,
*у > 0, /	=	1, ..., 6;
*в = (О, О, 1, О, 1, 0);
г) *х + 3*8 4- 2*з 4- 4x,i — 2хй -+ min,
—*i 4- *з -"‘	~	2,
*2 *з 4~ *4 —“ 2,Tj ±= О,
4' *2 .	4- Зх.1 -|- *и = 7,
.Ту 0,	/ = 1, ..., 5;
*° = (3, 1, 1, О, 0);
д) Зад — 2z2 4~	*з	4"	3*д	4' Зж5	->• шах,
2*1 — *2 -Г	*3	4-	*4	+ *5	= 2,
—4#! 4' 3.Tj —	—	ж4	— Зя5	= —-4,
З.гх -Ь Заъ 4'	Зт3	-Ь	5яд	= 3,
*j >0, у ’— 1, ..., 5;
= (1, О, О, О, 0);
е) 4- Зяа — 2.т3 — а?д -Ь ,т5 4’ З.?й -> max,
*з 4- *з 4-*.1 — *б 4“ *о=4,
*i “ *а — *з + *,1 4- 4жа — Зхй = —1,
*i 4- *2	-|- x,i 4- *5	= 1,
*i 4- *й 4' *3 4- *4	4- *о = 1,
*/>0, / = 1,...,6;
afi = (О, 1, О, О, О, 0).
6.6.	Решить симплекс-методом следующие задачи ЛП в стандартней форме, предварительно преобразовав их к ll*	163
каноническому виду:
а)	— Xj. 4- хл — 2х3 + Зх4 4- хъ -> max,
я, 4- 2х» — *« — 2х. 4- xs <1 3,
—*1 — *3+ ^3 + 2х4 4-я6 < 1,
2ях 4- х3 4" Я’з	1»
zj > 0> / =	. 5‘»
б)	xL -Ь 2яа —- 4z3	—>- max,
Xt “	— Я3 4-^4<l>
2хг — *г 4- я3 < 3,
—*х -|- Зя2 “ 2яа —	2,
xj 0, у — 1, ..., 4;
в)	xL 4* ^2 4“ *8 — 2*4 -> min,
2x1 “ «а ‘Ь =С 3, + *3 +	— ^4 < 1,
Xi 4-2^3 — х3 <21, xt 4*3яз — 2я3 4- *4 <21, xj 7 =	—» 4.
6.7.	Для каждой нз указанных ниже систем обозначим через X множество ее решений. Используя метод искусственного базиса, определить, является ли полиэдр X непустым множеством. В этом случае найти его вершину х°, исключить линейно зависимые уравнения системы и указать соответствующий базис я°: *
а)	а?! 4- ха 4- 2х3 4- 2*4 = 1, + 2я4 = 1, х;>0,	7=1, ...,4;
б)	xt 4- ль 4* 2я3 4*	= 4,
ях — 2xt 4- Зх3 = 5, 3xj + 7х3 4“ 2х4 = 13, я/> 0, у = 1,	4;
в)—я?! 4" 2?а 4- 2х3 — 2х4 = 3,
“* Жд 4- <т3 ——* х4 " О,
2^1 —	4- 2х3 4- Зх4 = 6,
7 = 1>—, 4;
г) 2хх 4- 2-2 4'	+	Ж5	~	5»
—4xt — 2ха 4~ #3 4* 4- Зх5 = 9,
2&Х 4- 2хй 4- 2х3 — х4 4- Зхб = 12,
0, j = 1,	5;
Д)	—	2?а	4- 2*з 4~	=	3,
—2xj 4*	2*3	— 3*з 4*	=	5,
*1 4“	®а	4-	=	2,
У = 1,...,4;
16-4
о) fol 4	4 7л?з 4	— 6,
4- я3 — 2x,t = 3,
«1	4- 2«3 4“	— 1,
> О, 7	*> •••» 4.
6.8. Решить симплекс-методом следующие задачи ЛП,
определи!* начальные вершины методе^ искусственного базиса:
a)	—2xt 4* 2«г 4* хз 4- 2я4 — Зд:6 -+ max,
—2Xj 4“ Х2	«4	~~ 1,
a?i — «2 4- 2жа 4- х4 4* «в = 4, —ajj 4 ж2	— «6 = 4,	>
«7>0, 7 = 1, ..., 5;
б)	5хх — 2хй 4"	4- ®5	4-	2ха	шах,
2л?£	-j-	«3	2«4 4*	4*	«в	“	11
i3«i 4-	«з	4	«4 ““	4“	«о	—	2,
—5^! 4	«а —	2«3	4	^4	~	я0	=	3,
®7>0,	/ = 1.....6;
d) 5»! 4 4«2 4 З«3 4	— Зхь -»• max,
2^i 4	4* #з 4 ®4 — «6 = 3,
«1 — яа 4 «4 4- «6 = 1, 4—"2«j “	— «3 4“ «4	,
я;>0, / = 1, ..., 5;
г) 2хг 4	«г	—	«3	4	3«4	—	2«й	->	min,
84 4	2«з	4	З«3	4	9«4	4	=	30,
5«i 4	я2	4	2«з	4	5«4	4-	бхБ	sw	19,
Ж1 4"	4	4	=	3,
Xj 0, J — 1, ,,,, 5.
6.9. Решить следующие «адачп ЛП в осповпой форме, приме и и ti симплекс-метод к соответствующей двойственной 'задаче:
3«j 4 2х2 4 %	max,
2rj —	-|- х3	1,
“*«1 4	«з	«3	1
«j —	2«3	4" З«3	—6,
«1 4	4 «з	2,
2г, 4-	«з	— Зх3	12;
19^! 4 .та 4 16«3-->- max,
а)
б)
в)
2хх —	«2 4-	3«а	<-2,
3Xj —	5«2 4*	7«3	< -10,
4xt 4	3«2 4*	«з	сз,
«! 4	*2«2		з,
3«!		2«д	<-1;
-	|- бх, —	Зх3	max,
—3«i -	~ «2 ‘1*	«з	>2,
-“23^ -	- 4«3 “И	«з	>5,
105
-—2я. *1* 2я:п 4-
—,Т1
6.1,	0. Вычислить радиус наибольшего шара, вписанного в полиэдр X gz R3, который задается следующей системой неравенств:
2-i “1“ Xg “|“	1,
— «а “ Ъ < 1.
£г — Х2 -f- Яд 1 ,
4* лг —	1
—2-1 "Ь .Тй + я3 1
—.?! + Х2 — Хз ?С О
(см. 5.121).
6.11.	Па звероферме могут выращиваться песцы, черно-бурые лпсы, пут.рии н порки. Для их питания используются три вида кормов. В табл. 19 приведены нормы расхода кормов, их ресурс и расчете на день, а также прибыль от реализации одной шкурки каждого зверя.
Таблица Hi
Вод норма	Нормы расхода нормой (кг/декь)				Ресурс вор-МО>1.(ПГ)
	Песец	Ласа	Путрип	Парка	
I	1	2	1	2	300
И	1	4	9	О	400
III	1	1	3	2	ООН
Прибыль ришкурка	6	42	8	10	
Определить, сколько и каких зверьков следует выращивать на ферме, чтобы прибыль от реализации шкурок была наибольшей,
6.12.	Завод изготовляет корпуса для холодильников в комплектует их оборудованием, поставляемым без ограничений другими предприятиями. В табл, 20 указаны нормы трудозатрат, затрат материалов для изготовления корпусов, ограничения по этим расурсам в расчете па месяц и прибыль от реализации холодильника каждой из пяти марок.
Найти месячный план выпуска холодильников, максимизирующий прибыль.
6.13.	Для серийного изготовления детали механический цех может использовать пять различных технологий 166
Таблица 20
Haip№i!Oii;ii»sic рссудоа	Марка холоди.'1Ы|И<л					Объем ресурса
		2.	3	4	5	
'Трудозатраты (<к>л.-ч)	0	3	5	4	4	» 9000
Металл (м:)	<>	2	4	5	0	рзоо
Пластик (№)	1	3	9	0	4	4000
Краска (кг)	1	2	3	3	2		5000
Прибыль (р.)	40	70	120	12(1	50	
ев обработки на токарном, фрезерном, строгальном и пь’пь ф'бвальном станках. В табл. 21 указало время (в минутах) обработки детали на каждом станке в зависимости от технологического способа, а также общий ресурс рабочего временя станков каждого вида за одну смену.
Табл и ц а 21
Станин	Т<1Хнологпчсенп<| сшхобы					Ресурс лрекелп станков (мни)
	»	2	3	4	5	
Токарный	2	1	3	0	1	4 100
<1>1>езер11ы11	1	0	О	а	1	2 000
.Строгальный	1	О	0	3	2	5 800
Шлифовальный	3	4	2	1	1	10 800
Требуется указать, как следует использовать имеющиеся технологии, с тем чтобы добиться максимального выпуска продукции.
Задачи 6.14—6.28 посвящены обоснованию сформулированных ранее основных положений симплекс-мето да и некоторым дополнительным фактам. Решающую роль играют здесь утверждения следующих трех задач.
6.14.	Пусть я—вершина допустимого множества X задачи (6.1), {а'|/ е /} — базис этой вершины, Хд, ДА (/Я=/, Jc —' J. .... л.)—соответствующие коэффициенты и °ЩЩки замещения (см. (6.3), (6.4)). Рассмотрим любую т»йую. точку х' R”t что Лх' = Ь. Доказать, что
п
2	3'7» j J,
к" |
»
У1 AftX/t «= (с, х> — (с, х').
(6.17)
(6.18)
167
6.15.	В обозначениях предыдущей задачи рассмотрим любой номер любое число а и точку 2?<=Rn с координатами
	‘ Xj’— aX;s, если	у'е/,
х} = -	а,	если	у $,	(6.19)
	, 0,	если	/ 9= «Л у =7^= $.
Доказать, что Ах' = b и <с, х'> = <с, х> — аД,.
6.16.	В обозначениях задачи 6.14 рассмотрим любые такие г е / й s что Ф 0 (случай Х„ < 0 по исключается). Доказать, что система («4у е J'}, где J' определено в (6.8), является базисом в Rm, причем коэффициенты разложения по нему векторов а’, ..., а” вычисляются но формуле (6.11).
6.17.	Доказать теорему 6.1.
6.18.	Доказать теорему 6.2.
6.19.	Доказать теоремы 6.3 и 6.5.
6.20.	Доказать теорему 6.4.
6.21.	Обосновать . утверждения, сформулированные при разборе случаев Б.2 и Б.З из п. 4.
6.22*	. Доказать, что для невырожденной вершины х справедливо утверждение, обратное к теореме 6.1: если .г—решение задачи (6.1), то выполнено условие I.
6.23.	Привести пример, когда вырожденная вершина х является решением задачи (6.1), но условно I нс выполняется.
6.24*	. Доказать, что если вырожденная вершина а1 является решением задачи (6.1), то существует такой базис этой вершины, прп котором условие I выполнено.
6.25*	. Пусть условие I выполняется в следующей усн-.чеппой форме: Дл > 0 прп всех к & J. Доказать, что х — единственное решение задачи (6.1).
6.26*	. Доказать, что для невырожденной вершины х справедливо утверждение, обратное к предыдущему: если х — единственное решение задачи (6.1), то ДА>0 прп всех k<AJ = J (.г).
6.27.	Пусть вершина х является решением задачи (6.1), прячем для некоторого ее базиса выполнено следующее условие: существует такой помер s £ J, что Д, =: = 0 и Хр С 0 при всех у <= J (ср. с условием II). Доказать, что множество решений задачи (6.1) неограпичено, 6.28*. Доказать, что если па даппой птерацпп симплекс-метода происходит переход от вершины х к отличной от пео воршппе x't то они соседние (см. 4.59, 4.64).
Глава 3
ВЫПУКЛЫЕ МНОЖЕСТВА
В этой главе излагается теория выпуклых множеств, которая вместе с теорией выпуклых функций образует важный раздел современной математики — выпуклый диализ. Понятия м факты выпуклого анализа играют фундаментальную роль в теории оптимизации и особенно пелинейиом программировании*), Они находят широкое применение и в других областях прикладной математики: теории игр, исследовании операций, математической акокомике и др. Как справедливо отмечается в предисловии -книги [38J, «выпуклый анализ — это раздел, изучить который целесообразно математикам самых различных направлений, и классических, и прикладных, и обязательно тем, чьи исследования связаны с экстремальными задач ами^.
§ 7.	Начальные сведения о выпуклых множествах
СВОДКА ОСНОВНЫХ ФАКТОВ
1.	Аффинные множества. Множество X <= R" называется аффинным, если ?.зг1 +(1 — X)xz^X при всех я1, Z^R, т. е. если X вместе с любыми своими двумя точками содержит проходящую через них прямую**).
Теорема 7.1. Множество .Y<=R’4 аффинно в том и только том случае, если для любого е X множество
L — X — xl3 = {ij^ R”|y “z — х°, же X)
•) Как уже отмечалось в предисловии, выпуклые функции и нелинейное программпровапио должны составить предмет другой кошм аналогичного характера, которую авторы надеются нависать “ водалоком будущем.
♦♦) Считается, что пустое лгаоясество прппадложнт всем вв'о-Длмым в пп. 1, 2 классам множеств. Вместе с тем в дальнейшем ~вдрааумовшэтся, если по оговорено иротивпое, что участвующие а Рассмотрениях множества непусты.
169
является линейным подпространством в R"; при этом 1. не зависит от выбора я0 в X*).
Указанное подпространство L называется параллельным аффинному множеству X и обозначается через Lin X.
Теорема 7.2. Множество Л'<=К" аффинно в том и только том случае, если его можно представить как множество решений системы из конечного числа линейны.!
Рис. 28	Рис- 2J)
уравнений, или (что то же самое) как пересечение конечного числа гиперплоскостей, т. е.
X = (х & RnMa; = &} = {£<= Rn| <л(, #> == bh i « 1, ..m.}r где A &{т, n), Rw.
Следствие 7.1. Любое аффинное множество Xе <= R" замкнуто, причем, если X & R", то X принадлежит некоторой гиперплоскости и, значит, X не имеет внутренних точек, т. е. hitX = 0.
2.	Выпуклые множества и выпуклые конусы. Множество называется выпуклым, если Ля* Ъ(1 —
*) Отметим, что это теорема, а также теоремы 7.2, 7.10 уже ирпводилксь рлпоа в связи с изученном простевших представителей выпуклых множеств — полиэдров (см. задачи 4.7, 4.8, 4.40). 170
s x прп всех xl, rel, Х^[0, 1], т. е. если X вместе с любыми своими двумя точками .т1 и а2 содержит соединяющий их стрелок.
Так, па рис. 28 изображено выпуклое множество, а на рис, 29 — певыпуклое.
Множество X <= R” называется
1) конусом, если Хя е X при всех я <= X, % О, т. е. осли X вместе с любой своей точкой х содержит проходя-щнй через нес луч с началом в нуле (рис. 30);
'2) выпуклым конусом, если ?чж‘ + fax2 X прп всех я1, х2 <= X, 0, fa S5 0, т. е, если X одновременно является выпуклым множеством и конусом (рис. 31).
Теорема 7.3. Пусть X, —выпуклые множества в R”. Тогда их пересечение X =* (] Xi также выпук-ло. Здесь I — любое (конечное или бесконечное) множество индексов.
Теорема 7.4. Пусть Х>, ..., Хы—выпуклые множества в R", оц, ..а1П— любые числа. Тогда множество
X = S cqXj = b:<=Rn | ж= «{.г1, х* s Xi, i = 1, ..mJ, i—1	I	i=l	J
называемое линейной комбинацией множеств Xj, .... Х„„ выпукло. В частности, выпуклы сумма и разность выпуклых' множеств Х[ и Хг, т. е. множества
Х{. ± Хг = {# е R’'U = .т1 ± я2, х1 е Х|, ж2 е Хг).
. Теорема 7.5. Пусть X — выпуклое множество в R". Тогда его замыкание X также выпукло.
• Аналогичные утверждения справедливы для конусов w выпуклых конусов»
-В связи с понятием суммы множеств отмстим следующее полезное утверждение.
. Лемма 7.1. Сумма двух замкнутых множеств, хотя выгодно из которых ограничено, замкнута.
3.	Комбинация точек и оболочки множеств. Пусть «j ..хм — точки из R". Их лппейпая комбинация Hl
S ^{Сказывается
<=*i
m
1)	выпуклой, если 0, i «> 1, ..., in, М « 1;
2)	неотрицательной, еелп i = l, ..., nt;
m
3)	аффинной, если =
171
Теорема 7.6. Выпуклое множество (выпуклый ко* нус, аффинное множество) содержит всевозможные вы. пуклые (неотрицательные, аффинные) комбинации св'з-их точек.
Рпс. 32
Рис. 33
Рпс. 34
Пусть X •— произвольное множество в R”. Пересечение всех выпуклых множеств (выпуклых конусов, аффинных множеств) нз R", содержащих X, называется егн выпуклой (конической, аффинной) оболочкой и обозначается через convX (coneX, affX) (рис. 32—34).
Ясно, что conv X — выпуклое множество, и если X выпукло, то conv X = X. Аналогичные замечания можно высказать относительно cone X и aff X. Отметим также, что множество aff X всегда замкнуто в силу следствия 7.1. Отсюда легко выводится, что для любого X <= R” справедлива формула aff X aff X.
Теорема 7.7. Выпуклая (коническая, аффинная) оболочка произвольного множества X совпадает с множеством всевозможных выпуклых (неотрицательных, аффинных) комбинаций точек из X.
172
; Теорема 7.8. Пусть Хь .»., Хт — произвольные множества в R". Тогда
COHV [ 2 Х| | “= 3 conv Xi.
\i-l /	<»1
Пусть я’, .. ,, ж” — точки из R”. Множество
X = conv (ж1, ..of*} называется выпуклым многогранником (рис. 35)’, множество
X = cone {ж1, ..., ж"1} г- многогранным конусом (рпс. 36), множество
X = conv {ж1...ж*)	+ cone {ж**1, ..., ж”1}
— многогранным множеством :(рис. 37).
Иными словами, многогранное множество — это сумма выпуклого многогранника и многогранного конуса.
Теорема 7.9. Сулмеа конечного числа многогранных множеств (выпуклых многогранников, многогранных конусов) также является многогранным множеством (выпуклым многогранником, многогранным конусом).
Теорема 7.10. Если точка х является неотрицательной комбинацией точек ж1, ..., ж”, не равных нулю одновременно, то х можно представить в виде неотрицательной комбинации линейно независимой подсистемы этих точек.
Следствие 7.2, Пусть X — произвольное множество в Rn. Тогда любую точку из cono X можно представить в виде неотрицательной комбинации не более п точек из X.
173
Теорема 7.11 (Каратеодори). Пусть X—произвольное множество в R”. Тогда любую точку из convX можно представить в виде выпуклой комбинации не более п-Ы точек из X.
х = р*к
Р  сопи {х1,	.г5}
Рис. 37
Теорема 7.12. Если X — компакт в R°, то conv X также является компактом.
Теорема 7.13. Выпуклый многогранник есть компакт. Многогранный конус и многогранное множество замкнуты.
k. Относительная внутренность выпуклого множества. Точка х множества X<=R” называется его относительно внутренней точкой, если	(я) Л aff X <= X при некото-
ром е>0 (см. рпс. 34), т. е. если из условий {ж*) <= aff X, -> х следует, что хп е X при всех достаточно больших к.
Совокупность всех относительно внутренних точек множества называется его отрицательной внутренностью и обозначается через ri X. Множество X называется относительно открытым, если X = ri X.
Ясно, что если iritX & 0, то riX = intX. В самом деле, если	то том более inl(aff Х)=# 0; тогда
affX^R" в силу следствия 7.1, по в таком случае определения int X и ri Х’ просто совпадают.
Теорема 7.14. Пусть X — непустое выпуклое множество в Re. Тогда ri X 0.
174
{Теорема 7.15. Пусть X — выпуклое множество в R”, jtsriA", у <= aff X. Тогда х можно представить в виде х = 't.y +,(I — X) з. где К ^(0, 1), z <= X (рпс. 38).
Т е о р е м а 7.16. Пусть X — выпуклое множество в R”, х е ri X, у X и А ^(0, I ]. Тогда точка 4*.(1 — А) у принадлежит ri X (рпс. 39).
Рис. 38
Следствие 7.3. Пусть X — выпуклое множество в R". Тогда его относительная внутренность ri X также выпукла.
Т е о р е ма 7.17. Пусть X — выпуклое множество в R". Тогда X « ri X, ri X = ri X, int X = int X.
Подчеркнем, что последняя формула справедлива и в том случае^еслп int X =*0, т. е. пз этого условия следует, что int АС = 0.
Напомним, что множество 5X = 5'\inlX называется Драницей, а любая его точка — граничной точкой множества X <= R".	_
Множество T&X₽X\riX пазовом относительной границей, а его точки — относительно граничными точками множества X <= R".
Из теоремы 7.17 непосредственно получаем следующее .утверждение.
’ Теорема 7.18. Пусть X — выпуклое множество в Rn. Тогда дХ = дХ, rd X *= vd X.
5. Размерность выпуклого множества. Размерностью ..dim X выпуклого множества X <= Rn называется размерность линейного подпространства, параллельного его аффинной оболочке, т, с. dim X = dim [Lin(aff X) ],
Так, размерность точки (одноточечного множества) равпа нулю, размерность отрезка, луча, прямой — единице независимо от размерности пространства, в котором оип лежат. Если X = 0, то полагаем dim X = —1.
175
Теорема 7.19. Пусть X — выпуклое множество в R”, Тогда. dimX = n в том и только том случае, если intX^0.
6. Неограниченные выпуклые множества. Напомним, что лучом, исходящим из точки xQ <н Rft в направлении ненулевого вектора h R'*, называется множество
а^0|.
Теорема 7.20. Пусть X — неограниченное замкнутое выпуклое множество в R'1. Тогда
1) для любой точки х°^Х существует ненулевой вектор h е R” такой, что l*oh cz X; иными словами, us каждой точки множества X исходит некоторый луч, целиком лежащий в X (рис, 40);
2) если 1*оЛс:Х при некотором х°^Х, то ithdX при любом х^Х] иными словами, если некоторый луч содержится в X, то луч в том же направлении, но с началом в любой другой точке множества X также содержится в X (рис. 40).
(непустого) множества X с R’1
Рис, 40
Рецессивным конусом называется множество
Я (X) = |/i е Rfl | l*oh cz X при некотором sc0 (= %}.
Здесь считается, что = {л^}. Поэтому всегда 0 <= К(Х). С учетом теоремы 7.20 следующая теорема очевидна. Теорема 7.21. Пусть X — замкнутое выпуклое мно-
жество в Rn. Тогда
1) X неограничвно в том и только том случае, если К{Х)^ {0);
2) К{Х)— замкнутый выпуклый конус, причем Х(Х) = {/jeR^^czX},
где х° — произвольная точка из X.
УПРАЖНЕНИЯ
7.1. Найти минимальное средн всех значений параметра 7с, при которых множество
X «= (ж е R2 |,(оя1 Ч-1) я2 Ъ, х2 А*)
176
выпукло:
а &		а b		а b		а b	
1	2 1	6	1 2	11	2 2	16	4 4
2	1 5	7	5 3	12	1 3	17	5 4
3	4 2	8	3 1	13	3 2	18	1 1
4	5 1	9	4 5	14	5 2	19	2 4
5	3 4	10	2 3	15	4 3	20	3 3
7.2. Доказать, что множество
X = [ж s IF | tUi +	4- сх! 0, х2 0}
является выпуклым конусом, и изобразить его на плоскости:
а b с		а Ъ с		a b с		а b с	
1	2-7 6	0	4 -5 -6	11	2 1-3	16	6 —1 —5
2	3	4 -4	7	5 -13 6	12	3 1 -4	17	2 7 3
3	2—5 2	8	5 —17 6	13	3 -1 -2	18	2 -3 —5
4	2 —5 -3	0	3 -1 -4	14	5 -8 -4	19	6 1—5
5	4 —15 9	10	•o’ со со	15	5 —2 -3	20	4 -5 —6
7.3. Изобразить па плоскости сумму двух							выпуоых
множеств: отрезка X “и1, х‘					Ъ где х1	= 4, а ,	=	
=(4, 3), и							
	1) круга		€= Rz| — &)2 +i(X2 —			с)2 11;	
2) -квадрата Ха = (я <= IV				!Н«	1 — &| ^ 1,		. —cl 1);
3) треугольника Х& = conv {(					-2, -1), (1, Ь)		. (3, -С)):
а Ъ с		а Ь с		а b с		а Ь с	
1	1 2 1	6	-2 4 3	11	0 2 1	16	2 4 2
0	0 3 2	7	1 3 1	12	-2 3 2	17	12 3
3	-14 3	8	0 2 2	13	14 3	18	0 3 1
4	2 2 1	9	-13 3	14	0 2 3	19	-14 2
5	0 3 2	10	2 4 1	15	-13 1	20	2 2 3*
12 с, Л, Ашманов, А, В, Тимохов
177
7.4.	Изобразить па плоскости сумму треугольников X^convtfO, 0), (2, 0), (1, 2)} и
-Y2 = eonv{.(2, а), (5, Ь), (3, с)}:
	я	ь	е			ъ	С	а		Ь	е	а		&	С
1	2	О	1	6	3	3	2	И	4	4	3	10	1	1	0
2	2	3	1.	7	3	4	2	12	4	5	3	17	1	2	0
3	2	4	1	8	3	5	2	<3	4	6	3	18	1	3	0
4	9	5	1	9	3	6	2	14	4	7	3	19	1	4	0
5	О м	6	1	10	3	7	2	15	4	8	3	20	1	5	0
7.5.	Изобразить на плоскости многогранное, множество Лг = conv {(—1, —I), (1,а), (b, —2)} + соне {(2, 1), (с, 1)}:
	а	Ъ	е	а		Ъ	с	а		li	и	а		b	с
1	1	2	3	0	1	2	4	И	1	3	4	16	1	3	5
2	2	2	3	7	2	2	4	12	2	3	4	17	2	3	5
3	3	2	3	8	3	2	4	13	3	3	4	18	3	3	5
4	4	2	3	9	4	2	4	14	4	3	4	19	4	3	5
&	5	2	3	10	5	2	4	15	5	3	4	20	5	3	5
7.6.	На плоскости К2 заданы пять точек: х' =(-«, 0), .г2 =1(0, 2), х*=(Ь, 2), z4=(Z>, 0), ^=1(0,-3),
а также точка ж® ^(с, —3/2), прнпадлеясащая conv {я1, ..,, я6). Указать все такие наборы номеров {£, /, к} <= {1, ..5), что о conv {ж1, а?, «“):
	<i Ъ	с	л		Ь	е	а		b	С	а		b	е
1	3 10	1	6	О	12	1	11	3	12	5	16	3	15	1
2	4 10	-1	7	3	12	4	12	6	15	5	17	2	12	2
3	5 10	4	8	4	15	7	13	0	15	3	18	2	12	4
4	5 8	—1	9	2	10	2	14	6	3	-1	19	5	12	3
5	5 0	-2	10	6	5	-2	15	8	4	—3	20	2	10	4
178
7.7.	В пространстве R3 заданы пять точек: ж* = (—2, 3, 1), х2 = (а, Ъ, 1), .^=(24, 0, 2), я<^(0, -12, 2), *5=(-3, -12,4),
а также точка ж°=(с, 0, 1), принадлежащая cone <ж’..z5). Указать все такие наборы померев
;{i, /, k} <= И, ..5)t что я0 е cone Uf, зЛ аЛ:
	а	Ъ	С	а		b	С	а		b	с	а		b	с
1	3	4	3	0	4	4	4	11	5	3	1	16	6	4	3
2	4	4	0	7	4	4	1	12	5	3	G	17	3	4	1
3	(5	4	4	8	8	5	3	13	0	5	4	18	3	4	4
4	В	5	9	9	0	5	0	14	0	5	-1	19	4	4	-1
Й	5	3	—1	10	5	3	0	15	5	3	2	20	6	4	5
7.8. В пространстве R3 заданы шесть точек: ^(-2, 1, «), х2-(7, -3, 6), ^=(с + 2, -1, -а), х* = (1, -1, -1 -а), ^=(1,0, 1), ле=(-9-с, 4, а — Ь),
о
а также точка .г° »2 Представить я? в виде выпук-5=1
лоб комбинации пе более четырех из точек ж1, ..,, .т°:
а Ь с			а b		с	a be			а Ъ		С
1	4 —10	4	G	1 —1	5	И	1 -1	2	16	2 —4	3
2	3 -7	4	7	2 -4	1	12	1 — 1	1	17	2 -4	4
3	3 -7	3	8	3 —7	2	13	3 —7	1	18	2 -4	5
4	1 -1	4	9	4 -10	3	14	4 -10	5	19	3 —7	5
5	1 -1	3	10	2 -4	2	15	4 -10	2	20	4 -10	1
7.9.	В пространстве R3 заданы шесть точек:
** =(4, -3, 2), ,г2='(щ 6, 3), я3 = (—4, О, Ь), ^=,(^442, 0, 7 — 6), .т5 =(а — 16, 9, 36 -1-1),
^=(2а- 16, 21, 6),
а также точка х°==(е, —3, d), принадлежащая cone {«’, гс2, я3}. Представить в виде неотрицательной
12»	179
комбинации точек я’, .4., так, чтобы сумма коэффи циептов была минимальной:
abed		abed		abed		abed	
1	4 1 20 18	0	1 5 14 28	11	1 4 14 24	16	2 5 16 2Г>
2	1 2 14 20	7	3 2 18 20	12	5 1 22 18	17	3 4 18 24
3	2 3 10 22	8	2 1 16 18	13	4 3 20 22	18	5 3 22 22'
4	3 1 18 18	9	2 4 16 24	14	6 5 24 26	19	5 6 22 28
5	4 2 20 20	10	1 3 14 22	15	5 2 22 20	20	3 5 18 26
7Л0. Для каждой us точек .т1^(д, 1), я2 = (™2, 0), аг3 =!,(& 1) определить, при каких значениях параметра к опа принадлежит относительной внутренности полиэдра X с: R2, задаваемого системой
—3®, + (Ь + 2>а < 6,
5хх +
2г, > —10,
2®i —
cz& 5с,
tej. —
х3	— 2k,
6zx — (6 — е)ха 3(6 -j- с):
	а	b	с	a		Ъ	с	а		ъ	с	а		г»	с
1	—1/3	3	5	6	—2/3	2	5	И	-1	1	2	16	-1/3	3	7
2	0	4	6	7	—4/3	3	4	12	”-1	1	3	17	0	4	6
3	-2/3	2	4	8	0	4	5	13	'-2/3	2	3	18	0	4	7
4	1	7	8	9	1/3	5	8	14	—2/3	2	6	19	1/3	5	6
5	1	7	9	10	2/3	6	8	15	-1/3	3	6	20	1/3	5	7
7.11.	При каждом значении параметра к пайти размерность множества X R®, задаваемого системой
аа?! — Ъха 4- сх3 —1,
а®х 4- te, — сх3 1,
За#! 4- bx2 — сх3 > 1,
180
a
а b c
a
а Ъ c
2
3
5
2
1
5
4
3
8
4
2
8
8
3 2
5 7
4
8
7
8
9
10
3
5
1
2
4
4 6
C 2
2
9
2
5
7
6
11
12
13
14
15
5
1
3
2
4
8
4
8
2
4
7
5
5
4
8
16
17
18
19
20
1
5
2
4
3
6
6
2
2
4
4 6
3 9
3
7.12.	Вычислить и изобразить па плоскости рецессивный конус К(Х) множества
X =i (ае R21 ал* + + Ьхх 4-	с):
	а	Ъ	с	а		Ъ	с	а		Ъ	с	а		Ъ	с
1	3	5	1	в	8	4	2	11	6	4	4	16	4	4	1
2	5	7	3	7	1	5	5	12	1	3	5	17	5	3	3
3	2	4	5	8	3	3	3	13	5	5	3	18	7	5	4
4	3	7	4	9	9	7	1	14	7	3	1	19	2	2	5
5	1	9	2	10	9	5	4	15	9	9	2	20	7	7	2
ЗАДАЧИ
7Л. Доказать, что множество X выпукло в том и только том случае, еслп %iX + КгХ =(Xi + Хг)Х при всех Xi >
О, ?-2	0.
7.2.	Пусть X — замкнутое множество, причем для любых точек ж’, х*^Х существует такое число Хе(0, 1), что Хж’ -Ь(1 — %)ж2е X. Доказать, что X выпукло. Привести пример, показывающий, что условие замкнутости X здесь существенно.
Доказать выпуклость следующих множеств в R2.
7.3.	X =
7.4.	X = {arlaii^o 1, х\ > 0).
7.5.	Х=* {xlsin^i ^х$, 0 <31^ л).
7.6.	X (х| Z1
7.7.	Используя геометрические построения, найти минимальное среди всех значений параметра к, при которых множество
X = [жеR2|Xi + Z8<1,	>ft)
выпукло.
181
7.8.	Доказать, что шар в R" является выпуклым множеством.
7.9*.	Пусть Л — неотрицательно определенная матрица размера п X п. Доказать, что множество
X = (я <= Rn| <Л.т, х> а)
выпукло прп любом а>0, причем если а = 0, то X — линейное подпространство.
7.10.	Доказать) что множество
Х = [.теК3|.^-2зд + ^С0, *i>0] является выпукл f-гм конусом. Изобразить этот конус.
7.11.	Пусть X)... ХП1 выпуклые множества в
К1, ..., R 7Л соответственно. Доказать, что их декартово произведение X = Х[ X.., X Х,„ также выпукло.
7.12.	Пусть Л: R"-*• R“ — линейное отображение, X с R" и У R” — выпуклые множества. Доказать, что множества
Л (X) <= {у е R"11 г/ — Лх прп некотором я:<= X}, Л-‘(У)= {.re R"|^e П,
т. е. образ X и прообраз У, также выпуклы.
7.13.	Убедиться, что теорема 7.4 является частным случаем утверждении из 7.11, 7.12.
7.14.	Доказать теорему 7.5.
7.15.	Изобразить на плоскости сумму множеств Хг~U‘<=R2|i = 1, 2}, Ха = Ue R2K +
7.16.	Доказать, что сумма открытого и произвольного множеств открыта.
7.17,	Доказать лемму 7.1.
7.18.	Привести пример двух замкнутых выпуклых множеств, сумма которых незамкнута,
7.19.	Привести пример двух замкнутых выпуклых конусов, сумма которых незамкнута.
7.20.	Проекцией множества X cR" X Rm (на пространство первых п координат) называется множество
Р(Х)= {у е R"| (у, г)еХ при некотором з Rtt}. Доказать, что проекция выпуклого множества выпукла.
7.21.	Доказать, что проекция компакта ость компакт.
7.22.	Привести пример замкнутого выпуклого множества, проекция которого незамкнута.
7.23.	Привести пример эамквутого выпуклого конуса, проекция которого незамкнута.
182
7.24.	Пусть Xb Ха — выпуклые множества в IV X R"'. Доказать, что множество
Х = ((У, s)^R“Xirb(yt ?)eXt( (у, z2)ex2,
s = z1 4- z2 нрн некоторых s’, z2 s R,n), называемое частичной суммой множеств Xi ц Х2, выпукло.
Заметим, что в продельных случаях » =0, га == 0 это множество имеет соответствен по вид X = Xj 4- X’2s Л* = X*i fl Х}.
7.25.	Пусть Х>, Хг — выпуклые множества в R”. Доказать, что множество
Х= U (XX.П (1 “
о<?. <1
называемое инверсной суммой множеств Х| я Xs, выпукло.
7.26.	Пусть Xi, Ха — выпуклые множества в IV, Доказать, что множества
Х« П U (ХХ, + (1-Х)4
XciXjj XJs’l
У= и и (XX, 4-(1—К)я),
хеЛ'а
называемые полной тенью и полутенью множества Х\ относительно множества («источника света») Хг, выпуклы.
7.27*	. Пусть Х|, ..., Хм — выпуклые множества n R”, Л—выпуклое множество в R"', причем АсВ?. Доказать, что множество
(ш	\
2 к & (х„ ..хт), i-1	/
выпукло. Привести пример, показывающий, что условие Лс К здесь существенно.
7.28.	Доказать теорему ПоЛтеровича — Спивака.
Пусть X — конус в R", причем X <= R", и для любых х. у в X векторы
miuU, у} ^(minU;i уР), max k, p}=(maxUj, уД) принадлежат X. Тогда X — выпуклый конус.
Привести примеры, показывающие существенность здесь того, что X — конус л X сг И*.
В задачах 7.29—7.80 рассматриваются разнообразные вопросы, связанные с понятиями комбинации точек и оболочек множеств.
183
7.29.	Доказать теорему 7.6.
7.30.	Доказать теорему 7.7.
7.31.	Доказать теорему 7.8.
7.32,	Доказать теорему 7.9.
Еще раз напомним, что теорема 7.10 уже была приведена о упдо задачи 4.40. Следствие 7,2 с учетом теоремы 7.7 очевидно.
7.33.	Доказать теорему 7.11.
7.34.	Доказать теорему 7.12.
7.35.	Доказать теорему 7.13.
7.36.	Пусть X “ замкнутое выпуклое множество,
(А = 1, 2, ...), 2 ?-л = 1,причем точка
Л*"1 со
х = 2	существует (т. е. ряд сходится). Доказать, что
х^Х. Существенно лп здесь условие замкнутости X?
7.37*	. а) Пусть Xj — произвольное множество, Хг — выпуклое множество, Я — ограниченное множество в R", причем Xi + Л с AX> + Л. Доказать, что Xi с Хъ.
б) Пусть X), X?—замкнутые выпуклые множества, А — ограниченное множество в Ra, причем Х| + А « = Xs + А. Доказать, что Xi = Xz.
Найти выпуклые и конические оболочки следующих множеств в R2.
7.38.	Х = |s]«i=x»l.
7.39.	X = (л? |’я?хв .Tjl^sOJ.
7.40.	X = {.rktXa =’ I).
7.41.	X =» {ж| sin #5 = xzt 0 xi =£ я).
7.42.	Х={*|Л = ^}.
7.43.	Доказать, что выпуклая оболочка открытого множества открыта.
7.44.	Верно ли, что выпуклая оболочка замкнутого множества п коническая оболочка выпуклого компакта замкнуты?
7.45.	Пусть X — произвольное множество в R”. Доказать, что
cone X = U (% conv X).
В частности, еслп X — выпуклое множество, то cone X = = U (АХ); еслп X — конус, то cone X = conv А',
184
7.46.	Пусть X — выпуклый компакт в R” л 0 & X. Доказать, что cone Хг — замкнутое множество. Существенно ли здесь условие выпуклости X?
7.47.	Пусть X “ произвольное множество в R№. Доказать
cono(conv X) = conv(cone Х)= cone Xt
aff (conv X) =» conv (aff X) «= aff X,
.л если 0 <= X, то
aff(cone X)^ cone (aff X)» aff X,
причем в атом случае affX является линейным подпространством. Верпа ли последняя формула для произвольного X?
7.48.	Пусть X — произвольное множество в R". Доказать, что
aff (cone X) = cone X — cone X.
Изобразить суммы следующих пар множеств в R2.
7.49.	Xi = conv {(1, 2), (1, -3)),
X2 = conv{(2, -3), (4, -1), (0, 1), (3. 2)}.
7.50.	X! =* conv {<4. 1), (-3, i), (2, -4)}, X2 = conv{(-1, 0), (1, 3), (—2, 2)).
7.51.	Пусть Xt, ..., X» — произвольные множества в R *, Rnfn соответственно. Доказать, что
conv(Xi X ... X Xm) = conv X) X ... X conv Xra,
aH(Xt X ... X X„) = aff Xt X... X aff Xm,
и если OeXt, OsXn, то
cone (Xi X ... X Xrm) = cone X) X ... X cone Xrffl.
Верна ли последняя формула для произвольных множеств?
7.52.	Пусть A; R" Rm — линейное отображение, X — произвольное множество в R”. Доказать, что
conv Л-(X) = A (conv X), cone Л*(X) = Л'(cone X), aff А (Х) = Л (aff X).
7.53.	Доказать, что образ многогранного множества (выпуклого многогранника, многогранного конуса) прп линейном отображении также является многогранным
185
множеством (выпуклым многогранником, многогранным конусом).
7,54.	Доказать, что прообраз полиэдра при лппейлом отображении является полиэдром.
Верно также то, что при линейном отображении образ полиэдра является полиэдром, н прообраз многогранного множества — многогранным множеством. Непосредственное доказательство этих утверждений затруднительно. Однако о учетом 7.53, 7.54 они немедленно следуют из теоремы 8.14.
7.55.	Убедиться, что теоремы 7.8, 7.9 являются частными случаями утвержден»’» из 7.51—7.53 (ср, с 7.13).
7.56.	'Пусть А'|, Аг„, — произвольные множества » IV’. Доказать, что
(nt V м
2 АГ1 = 3 affXlt
(tn	\	frl
У Xi) = 2 «one Xj. i=l	/	i=l
Верпа лп последняя формула для произвольных, множеств?
7.57.	Пусть Ari, ..., Хы— произвольные множества в IV’. Доказать, что
/ гл	\	к
cone I U А'} = 2 conc А\, \i“l f	1—1
(ni	\	™
U A^j I = 2 aff X,-. i-1 /	1-1
Верпа лп последняя формула для произвольных множеств?
7.58.	Пусть А"г, Хт — выпуклые множества в Rn. Доказать, что
conv ( (J A'i j = U г R" | х = 2 А1Ж1, ж1 s Аг{,
Xi;>о, f = i,..., т, 2M = i i-1 cone ( (J Ad a LeR’1|x = У. Apr1, x1 e Xi, \i—i /	1	i—i
Aj^O. i i® 1, ..., mi.
186
7.59.	Если Аг].Хю — выпуклые конусы в R”, то пз
7.45, 7.57 или из 7.58 легко выводится, что
/ m	\	™
cons’ и A'j = У, X,-. \i«-l /	i=l
Доказать следующий более тонкий факт.
Пусть Art, ..., Х,„_1 — выпуклые конусы, Хт — выпуклое множество в R", причем 0 <= Х,п. Тогда
/ III \	11*
conv I (J А\ I « У A'j.
Привести пример, когда в данной формуле выпуклая оболочка незамкнута, в то время как сумма замкнута.
7.60.	Пусть Х{ = conv У,, где. У< — произвольное множество п R” (»‘я|,	т). Доказать, что
(гд	\	/ m	\
U Ад = conv I и УИ.
i»’l /	\iaI /
7.61.	Пусть Xi, ...t Xw —выпуклые мпогограпппкп в (tn \
U X,-1 также яв-f~i /
ляотся выпуклым многогранником. Справедливо ли аналогичное утверждение для многогранных множеств?
7.62.	Пусть А\ = conv У< + cone Zh где У<, Zt — произвол ьиы и множества в R" (i = l, ...t т). Доказать, что
/ ?л	\	j тл	\	/ m	\
conv | U Xi =conv I U У,- + cone U X L
V-’l	/	\f=l	/	\<“1	/
7.63.	Пусть A], ..Xa — многогранные множества I m \
в Rn. Доказать, что множество X conv I U Xi I также \i"»L	/
является многогранным.
7.64.	Пусть П (IV)—множество всех подмножеств пространства R”. Отображение //: ЩИ")-* П(Ип) называется операцией взятия  оболочки, если оно удовлетворяет трем аксиомам:
1)	X «= Н (X) для любого X с R-’;
2)	Я(Я(Х))«Я(Х) для любого XС Ил;
3)	из условия XУ<= R” следует Я-(Х) <= Н(У).
Убедиться, что операции conv, cone, aff являются операциями взятия оболочки.
187
7.65.	Пусть X — произвольное множество в R”. Пересеченно всех замкнутых выпуклых множеств (замкнутых выпуклых конусов)! содержащих X, называется его з«.я-кнутой выпуклой (замкнутой комической) оболочкой в обозначается через conv X (cone X). Доказать, что
а)	операции conv н cone, а также просто операции замыкания множества являются операциями взятпя оболочки; _____________________________
б)	convX convX, cone X == cone X.
7.66.	Пусть H: П (И") П (И*1) — операция взятпя оболочки. Множество X <= К" назовем Н-въгпуклым, если X >= = Я(У) при некотором I'cR™, Доказать, что
а)	множество X R” является //-выпуклым в том и только том случае, если X = Н (X);
б)	для любого X <= R” множество Н(Х) есть пересечение всех //-выпуклых множеств пз IV, содержащих X.
7.67.	На плоскости R2 заданы пять точек: я1 = (—2,2), з2 = (4, i)t ®3 = (1, 4), я4=*(—1, 3), а?^(3, 3), а также точка я°=(2, 1), принадлежащая соне {г1, ..л5}. В качестве иллюстрации теоремы 7.10 и следствия 7.2 указать все такие наборы номеров {$, /) >= {1, ,..t 5), что
cone (ж', V}.
7.68.	На плоскости R* заданы шесть точек: V = «=(-3, 1), ^ = (-3, 3), ^=(2, 5), «4=(4, 4), Z5 = «==(5, —2), .т3 = (0, —1), а также точка х° « (3, 1), принадлежащая conv{я1, ..., ле1. В качество иллюстрации теоремы 7.11 (Каратеодори) указать все такие наборы номеров {:, /, к} <= {].61, чт0 x°^conv(.V, xJ, д:Л1.
7.69.	В пространстве R3 заданы пять точек: гс1=(2, 8Г 2), яй~(6, 2, 2), х3 = (0, -8, 4), ^=(9, -6, 3), я® = «=(—6, 9, 3), а также точка ж°=(1, 1, 1), принадлежащая cone {ж1....ж5}. Указать все такие наборы померон
{i, j, к> <= (1, ..51, что <= cone aJ, а?1}.
7.70.	В пространстве R3 заданы шесть точек: .г1 «=>(1, 1, -1), *2-(lt -1, 0), ^-(0, -1, -1), ^=(-1, 1,1), хй=>(—3, 1, —1), .ге=(2, —5, 1). Выяснить, принадлежит ли точка ж° = 0 множеству convU1, .... я6}, н в случае положительного ответа представить в виде оыпуь’’ лой комбинации не более четырех из точек z1,	я°.
7.71.	В пространство R3 заданы шесть точек: я1 =* =(1, -1, 1), я2=(-5, 12, 7), х3=(3, 1, 0), 3, 3), ^=(2, 4, 9), я6 =(2, 3, 4), а также точка я0=г = (—-1, 9, 16), принадлежащая cone{xJ, я3, ж4). Представить в виде неотрицательной комбинации точек х1, .
188
я* так, чтобы сумма коэффициентов была минимальной-
• 7.72й. Точки ж’, ж’п из Rrt называются аффинно за-вцсимыми, если существуют числа %ь ..., Хт, не равные Нулю одновременно и такие, что
m	m
2м = о.
i«“L	i«”l
в противном случае точки s’, ..., жт называются аффипг йо независимыми. Доказать, что следующие утверждения довиналентпы:
7, а) точки ж‘, хы аффинно независимы;
б)	точки х2 — х1....хт — ж1 линейно независимы;
в)	точки (ж1, 1), ..., (ж", 1) линейно независимы.
' Отсюда следует, что максимальное число аффпппо пезышен-feix точек в Rn равно n + 1.
Г
J- 7.73. Выпуклая оболочка т + 1 аффинно независимых точек называется т-мерным симплексом. Доказать, что к а) размерность го-мерного симплекса равна го;
н б) размерность выпуклого мпоясества X совпадает с 'Максимальной размерностью симплексов, лежащих в X. * 7.74*. Доказать следующий аналог теоремы 7.10.
Еслп точка х является выпуклой (аффинной) комбинацией точек ж1, ..., жст, то х молено представить в виде йыпуклоп (аффинной) комбинации аффинно независимой подсистемы этих точек.
, 7.75. Пусть ж1, .... ж™ — линейно независимые точки
ГЛ
® х — их линейная комбинация, т. е. х = 2 причем
^#=0. Доказать, что точки ж1, ..., жт-1, х линейно не-зависимы.
j- 7.76. Пусть ж*....Xм — аффинно независимые точки
?ж- их аффинная комбинация, т. е.ж = 2 М*1» 2^< “
-	1—1	<“i
1, причем Л„,ГАО. Доказать, что точки ж*....я"1-1, ж
аффинно независимы.
7.77*	. Доказать следующее уточнение теоремы Кара-теодори.
. Пусть X — мноясество в R*1, имеющее не более п связных компонент. Тогда любую точку ив convX можно Представить в виде выпуклой комбинации пе более п *O'IQK из X.
•189
Множество А с X называется связкой колгноямгой мпожсст ва А', если оно является объединением псех связных нодмш.-жести А‘, содеряинцих некоторую точку е X.
7.78*	. Доказать теорему Радона.
Пусть х’, ..., хл — точки из R", причем пъ > п + 1. Тогда множество номеров I Ml, ..zn} можно так разбить па два непересекающихся подмножества 1\ н /2, что
conv {л’Ь‘ 7|) П conv {ж'|I /j} т6 0.
7.79*	. Доказать теорему Хелли для конечного числа множеств.
Пусть X'i, ..., Агт — выпуклые множества в R”, причем /п>п + 1. Предположим, что каждые п +1 из этих множеств имеют общую точку. Тогда все они имеют общую точку.'
7.80*	. Доказать теорему Хелли для бесконечного числа множеств.
Пусть Xt (г е 7)—выпуклые комитеты в R", каждые п + 1 из которых имеют общую точку. Тогда все они имеют общую точку.
Теоремы Хелли, Радона и Каратеодорп относятся к числу важнейших фактов конечномерного выпуклого анализа, Их раипообраз-иые применения ложно найти в [ 14, 25, 25].
Задачи 7.81—7.104 посвящены понятию относительной внутренности, играющему весьма важную роль в выпуклом анализе. Читателю, стремящемуся овладеть техникой выпуклого анализа, мы рекомендуем отнестись к отим задачам с повышенным вниманием.
7.81.	Доказать теорему 7.14.
7.82.	Доказать теорему 7.15.
7.83.	Доказать теорему 7.1G.
7.84.	Доказать теорему 7.17.
7.85.	Доказать теорему 7.19.
7.86.	Пусть X произвольное множество в R" и х EriX. Доказать, что t/X.rJH aff Аг<= ri X при некотором е > 0.
Поскольку aff (ri X) с: aff X, то ато означает, что ri (ri X) s= euriX, т. е. riA' есть относительно открытое множество. Отсюда слодуот, что вторую формулу в теореме 7.18 можно’ продолжить;
А’ = vd X «и rd (ri Ar).
7.87.	Доказать, что любое аффинное множество относительно открыто.
В частности, ri {•*} 1= (z} для любого х<=К".
190
7.88.	Пусть X — выпуклое множество в R". Доказать, что aff(riX)e aff X.
7.89.	Пусть XIf Xs — выпуклые множества в R". Доказать, что любое мз соотношений
Xj ®= Xs, riXj8=11*1X2, riXa^XicXa
влечет остальные два.
7.90.	Пусть выпуклые множества Х[ и Xs таковы, что Х> <=%2. Следует ли отсюда, что riXi<=ri^?
7.91*	. Пусть_Xs, Xs — выпуклые множества в R", причем Л*1 <= Xi и Х| Л ri Xz =& 0. Доказать, что ri Xt ri Xs«
7.92.	Пусть Xt, Хг—выпуклые множества в R", причем Xi «= aff Хг и Xt Л ri Xi =5^ 0, Доказать, что пХ|П Л ri Х2 0,
В частности, если П 0, то ri A'i П iaUY;^ 0.
7.93.	Пусть A’), ...j Хст — выпуклые множества в R *» .Rm соответственно. Доказать, что
ri (X, X ... X Xm) = ri X, X ... X ri X«.
7.94*	. Пусть 4:Rn-‘“Rnl — линейное отображение, X — выпуклое множество в R", Доказать, что ri Л (X)« = Л (i*i X).
7.95.	Пусть X), ..., Х,„ — выпуклые множества в R”, а>, ., .t otm — любые числа. Доказать, что
<	/ m \ m
ri I 2 <*iXi = 2J af ri Xj.
1 i—1	/ fol
7.96	*. Пусть A*. R" R"1 — линейное отображение, У — выпуклое множество в R"', причем Л“‘ (ri У)ч* 0. Доказать, что
ri Л~‘ (У) - Л"» (ri У), А’1 (У)« А-‘ (У).
Привести пример, показывающий, что условие Л”1 (У) & ¥-• 0 не обеспечивает этих соотношений. 
7.97	*. Пусть X), ..., Хт — выпуклые множества в R’1, Л1	1ft
причем П i'iXi^0. Положим П Хр Доказать, что 1-1
affX= П affXi, Х^ПХь nX^firiXt. i=l	i=l	i«l
Привести пример, показывающий, что условно Х=£ 0 не обеспечивает этих соотношений.
7.98	*. Пусть X — непустой полиэдр вида (4.3), 1 »= = I (X) — множество номеров жестких ограничений в си-
191
стеме, задающей X (см. 4.16), и /“{I, ...» т}\1. Доказать, что
riХ = {хеRft|4f®“&/, Л/£<&Д
где к случае 1 = 0 или J = 0 соответствующее из двух условии считается тривиально выполненным.
7.99	й. Пусть X — множество на 7.27. Доказать, что
(ГЛ	\
SMriXi ,
<=1	/
7.100.	Пусть Xh ..., Хт —выпуклые множества в Rn.
Положим X = conv | U Xj, У = сопе| U ХИ (ср. с, \i«i /	\i=>i	/
7.58). Доказать, что
ГЛ
ж i= 2 ж< п о»
<Di
m	1
i =» 1, . .., Hl, 2 S=n llj
I	J
Hm	1
a?«s 2	X,>0, i = l, . ..,w|.
i=i	J
7.101*	. Пусть X^convU1, .... ж”) — выпуклый многогранник, Y = cone {«’, ...,	— многогранный конус.
Доказать, что
ri X = {х
Г1У я {ж
m	tn	>
X = 2	0, i «Э 1| . Hl, 2	~ 1 Г >
1=1	i-1	J
m	j
X = 2	> о, 4 = 1,..., Ш.
i-1	)
7.102*	. Пусть X — ограниченное выпуклое множество в R™. Доказать, что любой луч, выходящий из точки х о ri X и лежащий в aff X, пересекает относительную границу гдХ в единственной точке.
7.103.	Пусть множество X<=R" таково, что 6X^0 и любой луч, выходящий из произвольной точки xs-riX, пересекает г5Х_пе более чем в одной точке. Доказать, что замыкание X выпукло.
7.104*	. Доказать, что множество X с R" аффинно в том и только том случае, еслп тдХ = 0, т. е. X==X = riX. 192
Приведем теперь несколько задач па тему размерности выпуклого множества ♦)'.
7.105.	Пусть X — выпуклое множество в R". Доказать, что dim (ri X) = dim X = dim X.
7.106.	Пусть X — выпуклое множество в R". Доказать, что dim(X 4- х°)‘= dim X прп любом «= R".
7.107*	. Пусть Xi, Ха —выпуклые множества в R", причем riXt Л riXa^J#. Доказать, что
dim (Х[ П Х2) ™ dim X] + dim Хг — dim (Х( 4- Xj).
Это утиерящеппо является .обобщением известной теоремы о размерности поросочоппл двух лппешплх подпространств [21, с. 59].
7.108.	Привести пример, показывающий, что условие Лг| П Х2 0 по обеспечивает формулы из 7.107.
7.109.	Пусть Х[, Хг —выпуклые множества в R", причем Xi Л inlXs7/5 0. Доказать, что dim(Xt П XsJ^dim Хь
7.110.	Найти размерность выпуклых множеств XcR3, задаваемых следующими системами:
a) xl 4-«а 4-^<1,
•&L + Х% Ху ^^1» б) xt 4- ж2 4- =а 1,
, ®х 4-	4-«8 С
«14-«9 4-лг|<1, «1 4- «я 4- «3<1» «1	0» «з 0» «з 0}
в)	ях4- «а 4* «зС!, 11
’—г "Ез
«14- «2 4- «з<1;
г)	а?! 4- х2 4- ^3<3, «1«а«з^1’	«2^0, .Г3^0.
В заключение параграфа остановимся на свойствах неограниченных выпуклых множеств и их рецессивных Конусов.
♦) Напомним, что ряд задач, посвящепных раэморпостп полиэдров, был приведен в § 4 (см. также 7.73, 7.85).
(•, а, Ашманов, Л, В. Тимохов
193
7.111.	Доказать теорему 7.20.
7.112.	Описать рецессивные конусы К(Х) множеств А' из 7.3—7.6.
7.113.	Найти все с <= R", при которых множество
X с={я <==Rn|H.rll+<c1 хХ 1)
неограпичепо.
7.114.	Привести пример, показывающий, что условие замкнутости X в теореме 7.20 существенно.
7.115.	Пусть АС — выпуклое множество в R”. Предположим, что с: X при некоторых х е ri X и h s R". До-казать, что er ri X.
7.116*	. Доказать следующее уточнение теоремы 7.20 для незамкнутых множеств.
Пусть X — неограниченное выпуклое множество, в R". Тогда
1)	для любой точки гс°«=пХ существует такой ненулевой вектор h е R", что l*ofl с: ri X;
2)	если X прп некотором х° X, то /Ja с ri X прп любом х & ri X.
7.117*	. Пусть X — выпуклое множество в R". Доказать, что К (АГ)— замкнутый выпуклый конус, причем X(riX)^X(X) = X(X), riAf + K(X)<=riX, X +
7.118.	Пусть X — выпуклый копус в R". Доказать, что Я(Х) = Х.
7.119*	. Пусть X — выпуклое множество в RA, h <= R”. Доказать, что h.<sK(X) в том и только том случае, если Л.*= Ип1Аах*г где х'^Х,	(/с = 1, 2, ...) nlimA/,t=Cl,
Л-»“»	й-»то
7.120.	Пусть Х[, ..., Хт — произвольные множества в R \ ..., R Л соответственно. Доказать, что
K(Xi х... х хи) =* к (Xt) х... х к (х«);.
7.121,	Пусть Х( —выпуклые множества в R". пересечение которых непусто. Доказать, что
Х('П П К {Xi). \iei / lex
7.122.	Пусть Ari, ..., Xm—выпуклые множества, а 	 Ут	— ограниченные выпуклые множества bR".
Доказать, что
К (conv ( (j (Xi -Ь Yi))1) = X (conv ( (J \	\ fi=L	/ / l\ \i«»l	/ /
В частности, K(Xt У>) =
194
7.123.	Пусть X|. .. .,Xrra — выпуклые множества в Rn. Доказать, что
К (conv ( U хЛ ] = К ( 2 ХИ. \	\<=1	//	\<“1	/
В частпостп, Л'(conv (Х\ Ц {0})) = A'(Xi).
7.124.	Рецессивным подпространством (непустого) выпуклого множества X Rs называется множество
L (X) = |/г, R" [ ^0/i с X при некотором аР е X
где 1хок = [ж <= R”[г == ж” -}- ah, а<= RJ—прямая, проходящая через точку ж0 в направлении вектора h (здесь допускается случаи к —О, когда прямая вырождается в точку). Доказать, что ЦХ)—линейное подпространство в R", причем L(X) = Х(Х) 0 (-Х(Х)).
Описать рецессивные подпространства следующих множеству
7.125.	X ={ж <= R3|.ri + х2 + ж3 > 1).
7.126.	X = {ж g= R314 + £ С1] •
7.127.	Пусть X — непустой полиэдр вида (4.3). Доказать, что
Х(Х) - Ui RNK«o ЛХ 0, i = 1, ..Л,
<щ, Л>= 0, I ® к +1, ..т),
L(X)^Ui^Rn\<at, Л> = 0, i-1, ..., те)
(ср. с 4.4, !4.5).
7.128.	Пусть X — замкнутое выпуклое множество в Rn, L — линейное подпространство в R”,	— ортогональное
дополнение к нему. Доказать следующие утверждения:
а)	если L с: L(X), то X « X П L3- + L\
б)	если £(Х)<=Л, то множество XflZA не содержит пи одной прямой.
Таким образом, взяв L А(Х'), получаем, что любое замкнутое выпуклое множество можно рлзлояпггь на сумму лппенного под-прогтраистпа и зпмкнутого выпуклого множества, по содержащего пн одной прямой.
7.129й	. Пусть A: R” *> R"1—линейное отображение, X — выпуклое множество в R”, причем множество L =
: 13»	195
I
= Я(Х)Л UsR"|A& = 0} является лилейным подпространством. Доказать, что
ЛХХ)« А(Х), К(Л (X)) - Л (К (X));
в частности, осин X замкнуто, то Д(Х) также замкнуто.
Указанное условно па L можно записать в сладу ищем виде: если h^K(X) a Ah<=aQ, то -ЛеОД, С учетом 7.124 ясно, что ото условие равносильно также включению LczL(X). Аналогичные замечания можно высказать в отношении задач 7.131, 7.132.
7.130.	Привести примеры, показывающие существенность условия на L в 7.129.
7.131.	Пусть Xi, ...» Х« —выпуклые множества в R”, причем множество
£=.р>е1Г’*|Л-(/?), 7?<=Х(Х{),
2fc*-o
является линейным подпространством. Доказать, что
m	m _	/ m \ tn
2 х,» 2 хъ х 2 х, - 2 х:(х,);
i=»l i«“l ~ \l“l / I ““I
в частности, если множества Xh ..., Хя замкнуты, то их сумма также замкнута.
7.132.	Пусть Xi, Хг — выпуклые множества в R", причем множество Х = К(Х|)П(“К{Хг)) является линейным подпространством. Доказать, что
ХГ+Т2 = Xi 4- Х2, К{Хх 4- Х2)- ОД)+ К(Хг\\
в частности, если множества Ал и Х2 замкнуты, то их сумма также замкнута.
Это утверждение является обобгцевпем для выпуклых множеств леммы 7.1: если, например, множество Xj ограничено, то К(Х\)« {0} п, значит, L=^ {0}.
7.133*	. Пусть A: Rn -* Rm — линейное отображение, У — выпуклое множество в Rn‘, причем дополнительно выполняется хотя бы одно из следующих условий:
1) А-ЧйУ)»/’#;
2) У замкнуто и A^iY)1/10.
Доказать, что Я(А”\(У))«4~1.(Л(Г) )\
10В
Полезно отметить, что формула для прообразов, аналогичная формуле а 7.129, была указана в 7.06, прячем там такжо потребовалось условие 1). При условии 2) эта формула выполняется тривиально, так как прообраз замкнутого множества при непрерывном отображении замкнут.
7.134. Привести пример существенности условий 1) пли 2) в 7.133.
7.135. Убедиться, что первая (формула в 7.127 есть частный случай формулы из 7.133.
§ 8. Теоремы отделимости и их приложения
СВОДКА ОСНОВНЫХ ФАКТОВ
1. Сильная отделимость точки от замкнутого выпуклого множества.
Теорема 8.1. Пусть X—замкнутое выпуклое множество в R", я* (а)— проекция точки	на X (см.п. 3
§ 1). Тогда
<а — я* («), х — Лх
при всех х е X,
Геометрически это означает, что векторы а —ях (а) и я — -”Пх(а) образуют неострый
угол (рис. 41). Простой пере-	Рпс
формулировкой теоремы 8.1 получаем утверждение, являющееся исходным пунктом теории отделимости.
Теорема 8.2 (Минковского об отделимости точки от множества). Пусть X —замкнутое выпуклое множество в Rn, а — точка в R", не принадлежащая X. Тогда существуют такие р R" u {J <= R, что
<р, х> р < <р, а> при всех х^Х.
Более точно, этому условию удовлетворяют р=за —лх(а) и р=<р, ял(й)>.
Иными словами, утверждается существование такой гиперплоскости Мр9, что множество X оказывается в одном из полупространств, порождаемых //рРг а точка а — внутри другого: ХсНрр aeint/fjp (рис. 42). Кроме
187
того, прп указанных конкретных р и р гиперплоскость Ягр содержит хотя бы одну точку из X: лх(а)® Лр0. Еслй «зять любое число |3', удовлетворяющее условию р < р' < < <р, аУ, то получим
sup <р, ж> < р' < <р, а>. х
В током случае говорят, что гиперплоскость сильно отделяет точку а от множества X (рис. 42).
2.	Опорные гиперплоскости. Гиперплоскость IIназывается	_
1)	опорной к множеству ArcR" в точке а^Х. если X содержится в одном из полупространств, порождаемых
этой гиперплоскостью, а сама опа содержит точку а, т,. е.
<р, х-Хр=<р, аУ при всех ж«=Х;	i(8.1)
2)	собственно опорной к X в а, если опа служит опорной к X в «, но пе содержит целиком X, т. е.
</;, хУ < fJ прп некотором, ж е X. (8.2)
198
На рпс, 43, 44 изображены собственно опорные гиперплоскости, па рпс. 45 — просто опорная гиперплоскость.
Полупространство, порождаемое гиперплоскостью, опорной (собственно опорной) к X и й, и содержащее Аг, также называют опорным (собственно опорным) кХпа.
Теорема 8.3. В любой граничной точке а выпуклого множества X <= R™ существует опорная гиперплоскость.
Теорема 8.4. В любой относительно граничной точке а выпуклого множества. X с IV существует собствен'-пая опорная гиперплоскость.
3.	Отделимость двух множеств. Множества Х| л Х% пз Rn называются
1)	отделимыми, если существуют такие peRr', и р s R, что
<р, .г1) р <р, лг> прп всех я1 <= Xi, х* *= XV, (8.3)
2)	собственно отделимыми, если существуют такие р и р, что выполняется (8.3) л, кроме того,
<р, ж1) < <р, .72> прп некоторых •= Xi, я2 «= Х2; (8.4)
3)	сильно отделимыми, если существуют такие р и р_. что
sup <р, л*> < р < inf <р, я*>.	(8,5)
Л’1	ха
Геометрически отделимость множеств Xt и Хг означает, что их можно поместить в разные полупространства, порождаемые некоторой гиперплоскостью Вг,0: Xr сг 7/рр, Хй <z Ярр. При этом говорят, что гиперплоскость Яр# разделяет Х| л Хг; саму гиперплоскость ЯлП называют разделяющей. При собственной отделимости исключается вырожденный случай, когда оба множества лежат в разделяющей их гиперплоскости. Сильная отделимость говорит о том, что множества находятся па положительном расстоянии от разделяющей их гиперплоскости, а значит, и друг от друга (см. теорему 8.7). Множества на рис, 4G сильно отделимы, па рпс. 47—49 собственно отделимы, на рис. 50 просто отделимы.
Теорема 8.5. Если выпуклые множества Х| <= Rn и Xz с R" не пересекаются, то они отделимы.
Это утверждение является упрощенным вариантом следующей фундаментальной теоремы выпуклого аиа7 лнаа.
199
Тс о ре я a 8.6 (Фепхоял о собственной отделимости). Выпуклые множества X'i R* и Х% <= R” собственно от-делимы в том и только том случае, если их относительные внутренности riX| и п.Х% не пересекаются.
Рис. 50
Отметим также следующий результат.
Теорема 8.7. Выпуклые множества Xi^R" и ,¥2 <= R11 сильно отделимы в том и только том случае, если расстояние между ними положительно^ т. е.
р(Х,,Ха)« inf h1 —a2j|>0. x'eA-!
Следствие 8.1. Если замкнутые выпуклые множества Х\ и X? не пересекаются и хотя бы одно из них ограничено, то они сильно отделимы, 300
4.	Сопряженные множества. Сопряженным к данному множеству X = R" называется множество
X*=i {реR"|<р, л> < 1 при всех хеX}.
Ясно, что X* всегда замкнуто, выпукло и содержит нуль. При этом,
1)	если X — конус в R”, то
X* = {р е Rn| <р, х> 0 прп всех х X),	(8.G)
т. е. X* также является конусом я состоит пз векторов, составляющих неострый угол с- любым вектором из X (рис. 51);
Рис. 51
2)	если X — линейное подпространство в R", то
X* а {ре R"| <р, ж> = 0 прп всех х «= X),	'(8.7)
т. е. X* ость линейное подпространство, ортогональное к X: Х* = ХХ (рис. 52).
Теорема 8.8. Пусть ж1, ..., .т” — точки, из R”. Сопряженным к многогранному множеству
X = conv {«', ..., я*) + cone (я**1, ..., ж”) является полиэдр
X* =, {ре R"! <р, ж‘> «5 4, i = 4, ..., fc, <р, г‘> О, i = k + 1.................................яг). (8.8)
Теорема 8.9. Пусть	n), 6^Rm. Если по-
лиэдр Х = {а;еК,‘|Л®^ Ы непустл то сопряжённым к
201
нему является множество
X* = (р с= R"lp = цЛ пун некотором q 0, <щ, &>	1).
(8.9)
Множество
X** = (Х*)* = (ж <= R"| <ж, р> 1} при всех р X*}
называется вторым сопряженным к множеству X <= IV. Теорема 8.10. Для произвольного множества- Xс
R" справедлива формула
X**«conv(XU W)).	(8,10)
В частности, если X — замкнутое выпуклое множество, содержащее куль, то X** => X.
5.	Крайние точки выпуклого множества. Точка х выпуклого множества X <= IV' называется крайней, если ее нельзя представить в виде
ж = ?.ж' + (1 - X)ж2, ж», ж2 s X, ж1 =# ж2, 0 < X < 1. (8.11)' Совокупность всех крайних точек множества X обозначим через Я.(Х).
Таким образом, точка ж является крайней в X, если её нельзя поместить внутрь отрезка, концы которого ле-жат в X. Например, у треугольника крайними точками слулсат его верпшны, у луча — начало, у круга — все точки окружности.
Теорема 8.41. Множество крайних точек полиэдра совпадает с множеством его вершин (ель п. 1 § 4).
Приведем лемму, которая яв-/	-	ляотся полезным инструментом
' /	\ для доказательства следующих ос-
’	— X ] повпых теорем теории крайних
Д ------- j точек (см, 8.112, 8.113). Сама
' формулировка леммы опирается на теорему 8.4.
Лемма 8.1. Пусть X—вы-
Рве, 53	пуклое множество в R™, Я « Яр>—
гиперплоскость, собственная опорная к X в точке а^тдХ, т. е, выполнены условия (8.1), (8.2), Положим Г а X П Я (рпс. 53). Тогда
202
1) любая крайняя точка в Г является крайней и в X, г. е. £1(Г)<=£(%);
2) dim Г < dim X.
Теорема 8.12 (критерий существования крайней точки). Пусть X — замкнутое выпуклое множество в R'1. Тогда X имеет хотя бы одну крайнюю точку в том и только том случав, если X пе содержит прямых, т. е. множеств вида
lxQh =* (sc е Rn | я ®= -Ь аЛ, а <= R),
где х° <= R", fa «== R”, h «/= 0.
Теорема 8.13 (Минковского о представлении выпуклого компакта), Пусть X—выпуклый компакт в R”. Тогда X = conv Е(Х), г, е. X совпадает с выпуклой оболочкой множества своих крайних точек.
6. Эквивалентность понятий полиэдра и многогранного множества. Полиэдр, являющийся ограниченным множеством, называется ограниченным] полиэдр вида X = = {я е= R" |Ля 0) — однородным.
Теорема 8.14 (Минковского — Вейля). Пусть Хс <=Rn. Тогда
1)	X является ограниченным полиэдром в том и только том случае, если X — выпуклый многогранник]
2)	X является однородным полиэдром в том и только том. случае, если X — многогранный конус]
3)	X является полиэдром в том и только том случае, если X — многогранное множество.
И® данной теоремы с учетом теорем 7.9, 8.8, а также того простого факта, что пересечение конечного числа полиэдров есть полиэдр, получаем следующие выводы (см. также замечание после задачи 7.54).
Теорема 8.15. 1) Пересечение конечного числа многогранных множеств является многогранным множеством.
2) Сумма конечного числа полиэдров является полиэдром.
3) Множество, сопряженное к полиэдру (многогранно^ му множеству), является полиэдром (многогранным множеством).
УПРАЖНЕНИЯ
8.1.	Вывести уравнение гиперплоскости, сильно отделяющей точку х? =*(3, 2, 1, 1) от множества X с R4, ко-
203
торов задается системой
Злгг +	ага	4-	ог3 —	9х4	<1 7,
—хх —	z3	н-	Зж3 4-	bzt	<: 1,
4"	4ха	—	5^з 4*	2^4	9,
2а?4	Зз?5	4-	2х3 4~	5:
	а	Ъ с	а		Ъ	с	а		b	с	а		Ъ	с
1	6	—1 —1	6	-3	0	4	11	2	5	0	18	4	0	5
2	3	6 1	7	3	2	4	12	2	1	3	17	9	1	0
3	-1	—1 2	8	-1	4	0	13	-3	6	-1	18	4	7	—1
4	1	4 — 1	9	7	1	—1	14	-2	—2	3	19	-2	5	1
5	6	0 -1	10	8	0	1	15	7	-2	1	20	8	2	1
8.2.	Вывертя уравнение гиперплоскости, опорной к множеству
keR3
в точке аР=>(а, Ъ, с):
	а	b	с	а		5	с
1	-6/5	12/5	0	11	0	9/5	_4
2	-8/5	0	3	12	6/5	0	—4
3	0	9/5	4	13	8/5	-9/5	0
4	6/5	0	4	14	0	12/5	-3
5	0	12/5	3	15	8/5	0	3
6	8/5	9/5	0	16	6/5	12/5	0
7	0	-9/5	4	17	0	—12/5	3
8	6/5	—12/5	0	18	—6/5	0	4
9	8/5	0	—3	19	-8/5	-9/5	0
10	0	-9/5	-4	20	0	—12/5	—3
8,3.	Вывести уравнение гиперплоскости, опорной к множеству
X « [ж t= R31 Хц > 4 + «5) 204
и отделяющей его от точки я0 ^(а, &, с):
	а	5	с	а		b	с
1	5/4	5/16	15/16	11	9/8	27/32	3/2
' 2	4/3	2/3	13/12	12	5/4	5/4	15/8
3	5/3	5/9	7/9	13	9/8	9/32	1
4	5/4	15/16	• 23/16	14	4/3	4/9	17/18
5	5/3	10/9	10/9	15	5/3	5/6	11/12
6	3/2	3/2	7/4	18	11/9	22/27	4/3
7	3/2	3/8	13/16	17	7/5	14/25	24/25
8	5/4	5/8	9/8	18	3/2	3/4	1
9	10/9	10/27	19/18	19	4/3	8/9	23/18
10	13/9	26/27	11/9	20	11/9	11/27	1
8.4.	Выяснять, при каких значениях параметра к гиперплоскость //цп, где р ^(2к, к, 1), ₽> = 3, является опорной в точке —2, 3) к полиэдру Х<= R3, задаваемому системой
axt 4- Зха 4-	< а,
4* ®а + а?3 < 4,
2®! + Ъхл 4- аг»	5 — 2&,
—— 2я3 — cz3	3 — Зс
(имеется в виду включение X cz /?7р):
а Ь с			а		5 с		а		b	с	а		Ъ	с
1	5 -1	1	6	2	1	3	11	3	-2	1	16	2	1	4
2	3 -1	1	7	5	-1	3	12	5	—1	2	17	2	-2	4
3	2 -1	2	8	3	-1	3	13	2	—2	3	18	3	-2	2
4	3 0	3	9	5	1	2	14	3	—2	3	19	2	-1	3
5	5 1	1	10	2	-2	2	15	5	1	0	20	3	0	1
8.5.	Вывести уравнение гиперплоскости, разделяющей множества
Хг = {х е R21>1, xt> 0}, св	с, Xl<b
205
a b с	a b c
1	1/9	2/3	8/3	11	1/4	1/2	9/2
2	4	1	9	12	25	2	18
3	1/4	1	9/4	13	9/4	5	5/4
4	25	12	3	14	9	8	9
5	1/9	16/3	1/3	15	25	3	12
6	25	18	2	16	1/4	9/4	1
7	25	9	4	17	1/9	1/3	16/3
8	1/4	9/2	1/2	18	25	4	9
9	1/9	8/3	2/3	19	9/4	5/4	5
10	9	2	8	20	1	4	1,
8.6.	Пусть конус Ari <= R4 задастся системой
A*j 4 2&2 —	—- 2x^	0,
—2zx — Зха 4-	4- 5».t iC 0»
— 2x3 4 3xj — 5x.! <2 0,
а конус Xs <= R4 — системой
3%i 4 «•?<! 4 «я — l&B.t =C 0,
—bxt — 2x2 — Зхя 4 2x.t 0,
—xt 4 a* 4 cx3 4 2x,j =C 0-
Обозначим черед P множество, состоящее из нуля в R4 и всех таких векторов р е= R4. что гиперплоскость //го разделяет Х| и Л\ т. е. Л\ сг Я^>, Х3 <г Пр0.
Показать, что Р — двумерный копус в R4, и найти его образующие, т. е. такие векторы р1 и р2, что Р = ==» cone Ср1, р5}:
а Ъ с		а		ь	с	а		ь	с	а		ь	с
1	1 1Л [ те	6	1	1	3	11	3	—G	-"1	16	3	—2	-1
2	1	1	2	7	1	2	4	12	1	2	5	17	1	1	5
3	12 2	8	1	9	7	•13	3	—1	0	18	1	2	3
4	со 1 со	9	3	-4	-1	14	1	1	8	19	1	1	4
5	3 -1 —1	10	1	1	6	15	1	О м	6	20	1	1	7
20В
8,7.	Найти и изобразить па плоскости множество, со-фяжеипоо к конусу
X = {'г s IV]a,n Xi Xi 0}:
	а	&	а		Ъ	л		b	а		1)
1	— 1	•>	6	0	2	11	-2	0	16	-3	0
2	1	2	7	1	3	12	-1	4	17	0	4
3	~1	1	8	-1	3	13	1	4	18	3	4
4	2	3	fl	-3	3	14	2	4	19	-4	0
5	-1	9 **	10	—2	3	15	0	3	20	1	5
8;8. Найти и изобразить па плоскости множество, сопряженное к многогранному конусу
Х*=сопе((«, Ь), (4. 1), (2, 2)}:
	а	Ъ	а		ь	а		b	а		b
1	9	3	6	1	2	11	-1	1	10	-2	1
2	2	4	7	1	3	12	—1	2	17	-2	2
3	2	5	8	1	4	13	-1	3	18	—2	3
4	9	6	0	1	5	М	—1	4	(9	-2	4
5	2	7	10	1	б	15	-1	5	20		2	5
8.9.	Найти и изобразить па плоскости множество, сопряженное к выпуклому многограннику
X = conv{(e, й), (1, -1), (2, 5)J:
	а	b	а		Ь	а		Ь	а		b
1	3	9	6	3	3	11	4	—1	10	4	—0
9	4	3	7	5	3	12	5	-1	17	4	0
3	5	4	8	4	4	13	3	1	18	5	1
4	4	9	9	5	5	14	3	9	19	5	0
5	5	2	10	3	-1	15	4	1	20	3	4
8.10. Найти и изобразить на плоскости множество, сопряженное к многогранному множеству
х ₽= convex, ь), ^4’ 4)’ (4* -4)]+
4- cone {(с, с — 1), (1, 0)}:
207
	а	ь	с	а		b	с
1	—1	0	2	И	-1	-1/4	2
2	-3/4	0	3	12	-3/4	-1/4	3
3	—2/3	0	4	13	—2/3	—1/4	4
4	-1/2	0	5	14	-1/2	-1/4	5
5	—1/3	0	0	15	-1/3	-1/4	8
0	—1	1/4	2	1(3	—1/2	1/3	2
7	-3/4	1/4	3	17	—2/3	1/3	3
8	-2/3	1/4	4	18	—2/3	1/3	4
8	—1/2	1/4	5	10	-1/2	1/3	5
10	-1/3	1/4	6	20	-1	-1/3	6
8.11.	Найти и изобразить на плоскости множества, сопряженные к полуплоскостям
Х1 =={£<= R2|&T1 + Ъх$ < с),	%2 — {я е R2|O1 + ЪХ2^ с},
Хз = Гл е R2|fi£i + bxi —с):
	а	Ь	с	а		b	с	а		Ъ	С	а		Ъ	с
1	2	3	5	в	2	4	7	11	1	3	4	16	2	3	6
9	1	4	5	7	4	2	7	12	3	1	4	17	3	0	6
3	2	5	7	8	5	1	б	13	1	2	3	18	5	0	6
4	3	2	5	9	1	5	0	14	2	1	3	19	2	5	6
5	4	1	5	10	2	Б	7	15	5	2	7	20	1	3	5
8.12.	Найти и изобразить па плоскости множество, сопряженное к полиэдру
X = {х <= R2|aXj + Ь%2 < с, 2гi 'г Зхг 6, —3xi -г 5x2 15}:
	а b	с	а b		с	а		b	С	« Ъ		с
1	-2 -4	2	6	—1 —15	6	и	-2	—15	10	16	1 -15	3
2	-1 -0	2	7	-2 -9	2	12	0	- 1	1	17	2 -5	10
3	—2 -21	6	8	-4 -24	8	13	0	— 1	2	18	1 -3	6
4	-1 -12	4	9	-1 -6	3	14	0	-1	3	19	1 -2	6
5	—2 —20	10	10	-4 -21	16	15	0	—1	4	20	2 —9	
208
8.13.	Нантн всо значения параметра Л, при которых выпуклое множество X в R4, определяемое неравенствами
(Я| — GA's)2 +|(Х2 — £з)2 4* (&-®з + 5х4)2	10,
cart + кхг — 2яз 4~ Зкх\ ’С 0,
обладает крайними точками:
	а	b с	а		b с	а		b	с	а		b	с
1	4	1 1	в	1	-1 -1	11	4	2	1	16	2	2	—1
2	1	2 —1	7	2	1  1	12	3	1	1	17	4	1	—1
3	2	-1 —1	8	3	2 -1	13	2	1	—1	18	4	2	—1
4	3	1 -1	9	1	1 -1	14	1	2	1	19	1	1	1
5	9 лл	2 1	10	3	-1 -1	15	4	~1	-1	20	3	2	1
8.14.	Определить все значения параметра /с, при которых точка х(к) является крайней в многограннике
X — conv {ж1, я2, я?, я4, я (/с)} с R3, *да
я‘—(—2, а, 1), 3^(5, 1,-4), я3=(Э,-1, Ь),
-(1,1,2)\ я(1’)Ч(1, с, Л):
	а	Ъ	с	а		Ь	е	а Ъ		с	а		ъ	с
1	8	3	2	6	10	-1	3	И	9 —1	2	16	11	-3	3
2	9	1	2	7	9	—3	2	12	11 3	3	17	8	—1	2
3	10	-3	3	8	И	2	3	13	8 —2	2	18	11	1	3
4	11	—1	3	9	8	1	2	14	10 —2	3	19	9	2	2
5	8	-3	2	10	10	3	3	15	9 —2	2	20	10	1	3
8.15.	Рассмотрим выпуклый многогранник
X -conv<(i, а), (-2, 1), (-1, 3), (5, 0), (0, -2), (с, 1)}, содержащий нуль. В качестве иллюстрации к доказательству теоремы 8.14 (см. 8.114) проделать следующие операции:
1)	вычислить X* по теореме 8.8;
2)	представить X* как выпуклый многогранник;
3)	вычислить X** по теореме 8.8;
14 С, А, Ашмйпои, А, В. Тимохов	209
4)	представить X как полиэдр, убедившись, что X в» X**:
	а	b	с	а		b	с	а		Ь	С	а		b	с
1	3	6	4	0	3	7	3	И	4	7	3	1G	3	7	2
2	4	4	3	7	3	4	2	12	3	3	2	17	4	.5	2
3	4	7	4	8	4	3	2	13	3	6	3	18	3	5	2
4	3	5	3	9	4	5	4	14	4	4	2	19	4	С	4
«5	3	7	5	10	3	4	3	15	4	В	3	20	4	5	3
8.16. Представить как полиэдр многогранное множество X из упражнения 8.10.
8.17. Представить как многогранное множество полиэдр
X = {ле	+ bx3 =£ с, Л|4-л2^2, 2xt —Зла^б):
	а	b	С	а		b	с	а		b	с	а		ь	С
1	2	4	4	С	1	2	5	11	2	4	5	16	1	2	3
2	2	3	5	7	1	3	4	12	2	5	В	17	9	5	8
3	1	3	3	•8	2	5	15	13	1	3	4	18	1	3	5
4	1	4	4	9	1	4	10	14	1	4	5	19	1	4	6
5	1	5	5	10	1	5	10	15	1	б	0	20	1	5	8
ЗАДАЧИ
8.1*	. Доказать, что проекция любой точки а <= Rn на замкнутое выпуклое множество X <= R" единственна.
^^Золоо топкое обратное утооряаденно будет приведено в задаче
8.2.	Доказать утверждение, обратное к теореме 8.1.
Пусть X — произвольное множество в Rft, а <= R”. Тогда если точка л* s X удовлетворяет условию
<а — я*, ж — я*>	0 прп всех х&Х,
то л* — проекция точки а па X.
8.3.	Пусть X — замкнутое выпуклое множество в Rrt. Доказать, что оператор проектирования ях(я) обладает свойством нерастяжепия расстояний, т. с.
Ия^(я*) — Лх(а2) И Яа’ — д2И при всех а1, а2 <= R".
210
Задачи 8.4—8.46 посвящены теории отделимости двух множеств л некоторым ее следствиям.
8.4.	Доказать теорему 8.1.
8.5.	Доказать теорему 8.3.
8.6.	Доказать теорему 8.4.
8.7.	Доказать теорему 8.6.
8.8,	Доказать теорему 8.7 и следствие 8.1.
8.9.	Вывести уравнение гиперплоскости, отделяющей точку #°=(—1, 2, 1, —3) от множества	которое
задается системой
5Xj Ц- — 5я3 — Зж,, 1,
Зд?£ 2&а	4"	2,
Зя3 4- я3 4- 2хл < О, 4- л, 4* 3% — Яд 9.
8.10.	Вывести уравнение гиперплоскости, опорной к множеству
X = {я <= R31 — 2^2 4- 10л;2 4- С^з 4-	25}
в точке .т° = (4, 1, 1).
8.11.	Вывести уравнение гиперплоскости, опорной к множеству
[.rell3|^^4 4- я3}
»и отделяющей его от точки Л e I “‘р ?5» Jgb
8.12.	Выяснить, при каких значениях параметра к гиперплоскость Ярц, где р “=!(—3fr. 12, 2к), £ = 12, является опорной в точке .т° == (2, 1, 3) к полиэдру X <= R3, задаваемому системой
4- 8яа -f- я3 < 13, —2^ 4- 3#а 4- я3 < 2,
— 2^2 — я8	2,
—'5х^ +	+ 2я?3	—*3.
(Здесь и в 8.13 имеется в виду включение X с: Ярд.)
8.13.	Найти все значения параметра к, при которых гиперплоскость //₽*, где р =i(/c, 1, —2, — А2 — 4А* + 4, -1), Ps2/c4-l, является опорной в точке я° =»(2, 1, 0, 0, 0) 14*	2И
к полиэдру X <= Rs, определяемому системой
~ «я +	— Зх4 = 1>
4- Зх3 — 5®4 + яг5 — 3,
> О, 1 = 1, ‘..1 5.
8.14.	Найти лее значения параметра к, при которых полиэдр X R3, задаваемый системой
Йг( 4* агЯ	1»
®i 4* ®з 2»
~" 2?j 4* 2Jg ^гг
2а^ аг3 <2 О,
— 2ra 1,
®з — За?з 2,
лежит в полупространстве Н^, где р=(—3, 3 — к, Л), 0 = 8.
8.15.	Вывести уравнение гиперплоскости, разделяющей выпуклые множества
= К21зй(я1 — 1)^3, a?t < 1),
Xi = fc es R2| (z2 4 4)'(вч + 2) > 3,	> - 2).
8.16.	Вывести уравнение гиперплоскости, разделяю-щей выпуклые множества
Хй = [ге Ra|za>-, 2?i>0 I	* Ж-
8.17.	Пусть конус Xi <= R4 задается системой
~4*	4” 2^3 О,
2®! — Зх3 4- «з + < О, 3^ — ха — 8ха 4- < О,
а конус Xi <= R* — системой
”4“ 2j?a 4“ 2»4 О, —2®! + 4^а — 5л:3 — Зх4 О, —Saijt 4- 2?а 4" 17#з 4"	0.
Обозначим через Р множество, состоящее из пуля в R4 п всех таких векторов р е R4, что гиперплоскость Я,^ разделяет Xi и Xi, т. е. Х1 с Я^|, Ха с Яр0.
2U
Показать, что Р — двумерный конус в R4, п найти ого образующие, т. о. такие векторы р* и р\ что Р = =» соне {р1. р4}.
8,18.	Пусть полиэдр Xi <= R4 задается системой
3-1			^1,
	— *з ‘		С-2,
	h х2 — х3		£1,
-Х1	4- #3 ~		
а долнэдр Хз с R4 — системой
— Bsj— za + 2x3—	1,
— J&i —7яа 4-4:г3—	1,
— 7х3 + Зх, — 2а?4 — 3, — Зя?2 2.гй ““ 2&4	1»
Найти гиперплоскость, разделяющую и Хг.
8.19.	Пусть гиперплоскость Яр? является опорной к множеству X в точке а е X, причем а есть выпуклая положительная комбинация точек я1, .... ят из X, т. е.
а=>ЗМД ?н>0, 1 = 1, ...,т, 3^1 = 1*
Доказать, что эти точки лежат в 1/рц.
8.20.	Доказать, что любая гиперплоскость, опорная к конусу, проходит через пуль.
8.21.	Доказать, что любая гиперплоскость, опорная к аффинному множеству, его содержит.
8.22.	Доказать, что гиперплоскость Я₽з, опорная к шару Uj(ar) в его граничной точке д, единственна и определяется параметрами р = а — ж®, £ = <р, а>.
8.23.	Пусть X — ограниченное множество в R". Доказать, что при любом р g Rn существует такое число [J, что гиперплоскость /1% является опорной к X.
8.24.	Пусть полиэдр X лежит в полупространстве Доказать, что существует такое число а Р, что гиперплоскость НРь является опорной к X.
8.25.	Привести пример замкнутого выпуклого множества X, для которого утверждение задачи 8.24 неверно.
8.26.	Пусть X — выпуклое множество в R",	— ги-
перплоскость, собственно опорная к X, т. е. выполняются условия (8.1), (8.2). Доказать, что <р, х> < 0 при всех х^пХ, т. е. riXсintЯрр.
213
8.27.	Пусть выпуклые множества Х\ и Хг собственно отделимы с помощью гиперплоскости //Р?, т. е. выполняются условия (8.3), (8.4). Доказать, что <р, я*> <<р,я2> прп всех я* ri X't, х2 е НХг, т. е. выполнено по крайней море одно из двух: riX^ с: int 27^ пли ri Х2 cz
8.28*	. Пусть X — замкнутое выпуклое множество в R”, причем X & IV. Доказать, что X ость пересечение всех полупространств, опорных к X.
Даппоо утиерзкдоино получит существенное усиленно в 8.168.
8.29.	Замкнутое множество X с Rn называется строго выпуклым, если W Ч-.(1 — А)х2 е int X прп всех .т1, х2^ ^Х, я1 =#ж2, л<=(0, 1). Показать, .что шар Щ(х°) является строго выпуклым множеством, а куб
XB(x°) = |®gR’'||^—	]=*!,
пе является.
8.30*	. Пусть X — замкнутое выпуклое множеств в R™. Доказать, что X строго выпукло в том п только том случае, если любая гиперплоскость //₽₽, опорная к X в произвольной точке а е дХ, пересекается с X только по этой точке: ЯрП П X = {«).
8.31*	. Доказать следующее уточнение теоремы Кара-теодорп.
Пусть X — произвольное множество в R". Тогда любую точку из conv X, лежащую па границе conv X, можно нредставпть в виде выпуклой комбинации не более л точек из X.
8.32.	Показать, что в задаче 7.36 условие замкнутости X лишнее.
8.33*	. Доказать, что выпуклые множества 2X1 п Хо из R” отделимы в том п только том случае, если выполняется по крайней мере одно из двух условий:
1)	riXi П пХ2 = 0;
2)	att(XlUX2)¥=R*.
Если при этом 0 X], 0 Хг, то условие 2) можно заменить следующим:
2') aff X, -I- aff Х3 IV.
8.34*	. Пусть X — выпуклое множество в R”, причем Xf]intR4- = 0. Доказать, что существует ненулевой вектор р 0, для которого </?, х> 0 при всех х е X.
8.35.	Пусть X — замкнутое выпуклое множество в R”, причем X Л {0}. Следует ли отсюда, что существует 2(4
вектор р > О, для которого <р, я> 0 при всех х •= X (ср. с 8.82)?
8.36.	Пусть X — замкнутое выпуклое множество в R'1, отличное от RN, причем его дополнение Rft\X также выпукло. Доказать, что X — полупространство.
8.37.	Пусть Х|, Аг2 — выпуклые множества в R", причем ri Х| П ri А% «= 0. Предположим, что дополнительно выполняется хотя бы одно из следующих условии:
а)	Х| ограничено;
б)	Xi — конус;
в)	Xi — полиэдр.
Доказать, что Xi и Х$ можно собственно отделить с помощью гиперплоскости, опорной к Хь
8.38*	. Доказать теорему Хана — Банаха (в геометрическом форме).
Пусть Х| — аффинное, Ха — выпуклое множества в Rrt, причем Х1 П ri Xjj « 0. Тогда Xi и Ха можно собственно отделить с помощью гиперплоскости, содержащей Х|.
8.39.	Пусть Х|, Хз — замкнутые выпуклые множества в R", причем Х| П Х2 = 0, а множество L •= K-(Xt) П Х(Х2) является линейным подпространством. Доказать, что Xt и Хз сильно отделимы.
Напомним, что Л’(X)—рецессивный конус множества X (см. п. 6 § 7).
8.40*	. Доказать, что нопересекающяеся полиэдры Xj и Хз из R” сильно отделимы,
8.41*	. Доказать модификацию теоремы Хана — Банаха для полиэдров.
Пусть Xt —аффинное множество, Хз —полиэдр в R1", причем Х| П Хз «и 0. Тогда X) и Х’з можно отделить с помощью гиперплоскости, содержащей Х| п не пересекающейся с Хз.
8.42.	Можно ли в теореме из 8.41 предполагать, что Ха — просто замкнутое выпуклое множество (ср. [28, с. 30, упр. 5])?
8.43.	Пусть Xi, Хз — замкнутые выпуклые множества в R", причем Xj П Хз = 0. Следует ли отсюда, что существует такой вектор р. для которого <р, я1) < <р, ж2> прп всех ж1 е Xi, х2 е= Х2?
8.44.	Пусть Xi и Х« — полиэдры в R’1, причем Х| Л Х2 0. Предположим, что существуют вектор р и ЧИСЛО Р, ДЛЯ которых
<р, л:> р при всех zsA'i Л X*.
215
Доказать, что существуют векторы р1, р2 и числа pi, £2, для которых
<р‘, х> Pi при всех х е Х|,
<рг, х> рг при всех х е Ха, р1 + р2 = р, р, + Рг р.
Это утперждонио допускает естественное обобщовне ва случай коночного числа полиэдров (см. 8.56). Здесь оно фигурирует в качество леммы к решению следующей задачи, где приводится однп на наиболее тонких фактов теории отдолимостп,
8.45*	. Доказать теорему Рокафеллара.
Пусть Xi — полиэдр, Ха — выпуклое множество в К”, причем Х| П ri Х2 = 0. Тогда Х( п Хг можно собственно отделить с помощью гиперплоскости, не содержащей Хг.
8.46.	Можно ли в теореме Рокафеллара предполагать, что Xi — просто выпуклое множество?
В задачах 8.47—8.59 излагаются основы теории отделимости конечного числа множеств.
8.47.	Множества Xi, ..., Хщ из R" называются
1)	от^елллсыли, еслп существуют векторы р1, рт из R”, не равные нулю одновременно, и числа pi, ..., p„ такие, что
<р{, а^> р< прп всех х{ е ХС| I — 1, ..., т, (8.12) тл	m
S	2 01<О;	(8.13)
<“1	<*«*1
2)	собственно отделимыми, если существуют векторы р1, ..., рт и числа Pt, ..., рст такие, что_выподпяются условия (8.12), (8.13) л, кроме того, <рг, х'У < р< прп некоторых i п я* es Х<;
3)	сильно отделимыми, если существуют р’, ..., рт и Pi, такие, что выполняются условия (8.12), (8.13)
ш
и, более того, X Р< < 0.
Показать, что
а)	попятил отделимости, собственной и сильной отделимости двух множеств являются частными случаями данных определений;
б)	если 0еХ( (1 = 1,	т), то из (8.12), (8.13)
следует, что Ps ^... = Рм *= 0.
Таким образом, если Xt,..., Xm — конусы, а X*, ...,	— со-
нряжоппые к ввм конусы (см. (8.6)), то условно (8.12) можно за-ипсать в виде pl s X* (/ = 1,...,»»), оставлял л (8.13) лишь первую сумму,
21G
8.48*	. Пусть Xs, Xm — выпуклые множества в R", тп
причем П Xi =» 0. Доказать, что эти множества отделимы.
8.49*	. Доказать, что выпуклые множества Хь ..., Хт из R” собственно отделимы в том и только том случае,
если П ЙХ< = 0.
8.50.	Доказать, что выпуклые множества Xi, Хщ из R" сильно отделимы в том и только том случае, если
inf max р (z, Xf) > 0.
8.51.	Пусть X[, ..., Xm — замкнутые выпуклые множества в R", причем хотя бы одно из них ограничено и
П Х{ «= 0. Доказать, что опп сильно отделимы.
<’и1
8.52.	Доказать, что полиэдры Х>, Хп из R", не имеющие общей точки, сильно отделимы.
8.53.	Пусть Х(, ..., Хт — выпуклые конусы в Rn, т
причем П Xi = {0}. Доказать, что существуют векторы {«•г
р1 е X* (i«l, ..., m)> не ранные пулю одновременно тп
и такие, что 3 Р = 0-
1-1
8.54*	. Пусть Xi, ..., Xm —выпуклые конусы в Rn. ш
Доказать, что Л й Xi = 0 в том и только том случае, <=>1 *
если существуют векторы/? f=Xj (i = 1, т) такие, m
что 2 Р* = 0 и <р\ х‘> < 0 прп некоторых i и х'е Х(, 1-1
8.55*	. Доказать теорему Дубовицкого — Милютина.
Пусть Х|, Х,п — выпуклые конусы в Rn, причем (га—14	\
П int Х< I П 1<—г	/
Л Хт = 0 в том и только том случае, если существуют векторы р*&Х* (f«l, ..., тп), не равные пулю одно-m
временно и такие, что 2 Р1 =“ 0* i«»i
8.56.	Пусть Xi, Хт —выпуклые множества в Rtt, причем выполняется хотя бы одно пз следующих
217
условий:
1)	f] й 5^ 0;
t*3!
»i
2)	Ар . Xm — полиэдры и П X\ =5^ 0-
Предположим, что существуют вектор p п число p, для которых
тп
<p, #><:p при всех яе П Aq.
i=»l
Доказать, что существуют векторы р1, ..рт и числа &i, .. рп1} для которых
<р‘, #т> р( при всех х*
Т71	Trt
%р1 = р, 3fr=CP-i“I	i—1
8.57.	Привести пример, показывающий, что утверждение 8.56 становится неверным, если вместо условий 1) к»
или 2) потребовать лишь условие П Аг^0.
8.58.	Доказать, что выпуклые множества Xi, ..., Хт из IV отделимы в том и только том случае, если при некотором is{l...... ???} либо множество F« = П Х$ пу-
сто, либо множества Х< и Fi 0 отделимы.
8.59*	. Доказать, что выпуклые множества Ari, ..Х,л из IV отделимы в том к только том случае, если выпол* няется по крайнем: мере одно из двух условий:
тп
1)	П нХх~0; toil
2)	aff (АлU ( П	прп некотором i<= И, ..., тл}.
\ W'/i })
7)f
Если при этом Ое П А\, то условно 2) можно за-(гя1
менять следующим:
2г) affX'j+ Г1 aff X; XV при некотором ?.
j'/j
В задачах 8.60—8.109 излагаются элементы теории сопряженных множеств, играющей важную роль в выпуклом анализе и его приложениях.
8.60.	Доказать теорему 8.8.
218
8.61.	Доказать теорему 8.9.
8.62.	Доказать теорему 8.10.
8.63.	Найти si изобразить на плоскости множество, сопряженное к многогранному конусу
Х = cone {(—3, 1), (2,3), (4t 5)}.
8.64.	Найти и изобразить па плоскости множество, сопряженное к выпуклому .многограннику
X = conv{‘(“3, -2), (-1, 4), (1, 1)}.
8.65.	Найти п изобразить па плоскости множество, сопряженное к многогранному множеству
X = conv((—4, -1), (—2, -1), (—2, 1))4-
4- cone {(2, 1), (1, 0)).
8.66.	Найти и изобразить па плоскости множества, сопряженные к полуплоскостям
а)	Лг| = (х <^R21 — 4- 2хй 3);
б)	Х2 = {ж е R21 -лп 4- 2х2 > 3);
в)	Х3 = {xeRH—xi 4-2x2^— 3).
8.67.	Найти и изобразить па плоскости множество, сопряженное к полиэдру
X = (х <= R2! — Зж| 4- 2хг 7, .ri 4- 5хг =С 9, .	— Л;2	3, “Х2	1).
8.68.	Доказать, что для произвольных множеств Xi и
Х2 из условия X] <= Х2 следует Xs g Х1о
8.69.	Г1 усть Х(, Аг3 — замкнутые выпуклые множества в R", содержащие пуль. Доказать, что
а)	еслп ХхсХа, toX2c,Y,;
б)	если X* = Х*г ToXi^Xj.,
8.70.	Пусть X — произвольное множество в R". Доказать, что
X* =(£)♦ ~(conv X)* =(conv(X U (0)))« =‘Х***.
8.71.	Пусть X—выпуклое множество в R”. Доказать, пто Х* = {0) в том и только том случае, если X = RU.
8.72.	Пусть X — выпуклый конус в IV. Доказать, что X 4- X* = R", X Л X* = (0).
_ Зто утверждение является обобщением известной теоремы лилейной алгебры о разложении пространства R" в прямую сумму ортогапальпых подпространстн.
219
8.73.	Доказать, что тары Z7e(0) п 17|/f(0) (е > 0) являются взаимно сопряженными множествами, т. с. [f7t(0)l*-£/I/c(0).
8.74.	Доказать, что шар 47f(O) является единственным множеством в R", которое совпадает со своим сопряженным.
8.75.	Найти множество, сопряженное к эллипсоиду
X ₽= L е Rn I 2 «Я < И.
I	I j=i	J
8.76.	Найти множество, сопряженное к шару Ui(x°). Прп каких я? это множество ограничено?
8.77*	. Пусть X — произвольное множество в R°. Доказать, что
а)	X ограничено в том п только том случае, еелп OeintX*;
б)	X* ограничено в том и только том случае, если О oint (conv X).
8.78*	. Конус Xc=Rn называется заостренным^ если из условия ±л:®Х следует я = 0, т. е. X не содержит прямую, проходящую через пуль. Доказать следующие утверждения:
а)	если X — заостренный замкнутый выпуклый ко-пус, то intX*=#0;
б)	если X—конус п inlX**/’#, то X заострен, причем для любого р е int X* следует
<р, х> < 0 при всех х еХ, х& 0.
8.79.	Привести пример, показывающий, что в утверждении а) задачи 8.78 условно, замкнутости X существенно (ср. с 8.85).
8.80*	. Пусть Xi, Хг —замкнутые выпуклые конусы в R", причем Xl заострен, X, (0), Xt(lX2 = {0). Доказать, что существует ненулевой вектор р, для которого
<р, г’> <0sS <р, ж2> прп всех xl eXh
я1 =/= 0, х? е Х$.
8.81.	Привести примеры, показывающие, что в 8.80 условие замкнутости обоих конусов существенно.
8.82*	. Пусть X —замкнутый выпуклый конус в R", причем X П R-i- {0}. Доказать, что существует вектор р > 0, для которого <р, х> «С 0 при всех х X (ср. с 8.34, 8.35).
220
Ниже под Х(Х) и L(X) понимаются рецессивный конус и рецессивное подпространство множества X (см. и. 6 § 7 и 7.124).
8.83.	Пусть X — выпуклое множество в Rn. Доказать следующие формулы для второго сопряженного к X:
Х**« U (ЬХ), Х** = U (ХХ)ЦХ(Х).
8.84*	. Пусть X — выпуклое множество в R". Доказать, что
Х(Х**)-Х(Х), L(X**)«L(X).
8.85*	. Пусть X—выпуклое множество в R1*. Доказать, что X не содержит прямых в том и только том случае, если intX* & 0.
Отметим, что в сралпенпи о 8.78, а) здесь замкнутость X но требуется, ао зато и пе требуется, чтобы прямая проходпла через какую-то особую точку множеств» X.
8.86.	Пусть X — произвольное множество в R". Доказать, что
Х(Х*)<=’(соноХ)* = (р sR”Kp, 0 при всех
8.87.	Пусть X — произвольное множество в R”. Доказать, что
L(X*)>= (psRa|<p, ж> =0 прп всех х <= X), причем это множество совпадает с (affX)*, если 0<=Х. Привести пример, показывающий, что условие 0 <= X здесь существенно.
8.88.	Пусть X — выпуклое множество в R". Доказать, что
[X (X) ] * = сопеХ», [L (X) ] * = af£ X* причем
cone X* = е R” | SUJ) <р, я> < соj, aff X* = cone X* — cone X*.
8.89*	. а) Пусть X —выпуклое множество в R”. Доказать, что
dim X* ₽= п — dim L(X).
221
б)	Пусть X — замкнутый выпуклый крпус в R". Доказать, что
dimХ* = п — dint[XЛ (-Х) j.
Эти утверждения обобщают известную теорему линейной алгебры о размерности подпространстве, ортогонального к линейному подпространству A'cR", согласно которой <limA'-L = = /г — dim л\
8.90.	Пусть X—выпуклое множество в R”, а^Х. Множество
Р = Р(а, Аг)= {p«=RnKp, я> =£ <р, а> при всех ж<^Х)
называется опорным конусом к X н а (ненулевые элементы множества Р суть нормали опорных гиперплоскостей к X в а). Множество
F = У (а, X) = {h «= R“|a + ah X при некотором а > 0) называется конусом возможных направлений относительно X в а. Доказать, что
а)	Р — замкнутый выпуклым конус, 7—выпуклый конус;
б)	P* = Vt 7*=Р;
в)	dim Р = п — dim[7 П (—К)].
dim V = к - dim [Р Л (—Р) ].
Привести пример, показывающий, что конус V может быть незамкнутым.
8.91.	Пусть Агь ..., Аг«-, — конусы, X,.,—произвольное множество в R”. Доказать, что
/ ™	\*	Л1
2х, = п хЬ \i°’l /	i=L
Привести пример, показывающий, что прп произвольных Х|,..., Х™ эта формула неверна.
8.92.	Пусть Хь ..., Хи,..! — замкнутые выпуклые конусы, Хл> — замкнутое выпуклое множество в R", причем О е Х|П. Доказать, что
♦
Привести пример, показывающий, что условие замкнутости множеств здесь существенно.
8.93.	Пусть Х1( ..., X,,, — выпуклые множества в R", удовлетворяющие хотя бы одному из следующих условий:
909
ишм
1)	0 <= int Xf при всех i— 1. ..m — 1; Ш
2)	nriXt^0; i-i
3)	Xi,.... XTO —полиэдры.
Ill
Доказать, что множество 3 Х< заляшуто.
8.94*. Пусть Xt, .... Xm-t — выпуклые конусы, Xm — выпуклое множество в R”, причем 0<^Хт. Предположим, что дополнительно выполняется хотя бы одно из следующих условии:
1)	ПпХ^0;
2)	Xt....Xm — полиэдры;
3)	прп некотором /<=(!, nil множества Xi (i«=Z) суть полиэдры и
(Л ХАП(Л г1ХЛ=£0.
4<=/ ) \igl }
Доказать, что
/та	\*	™	*
I Л 1 =»	х<.
\i=l /	i—'1
Данной утверждение является одним из центральных фактов теории сопряженных множеств.
8.95.	Вычислить множество, сопряженное
a)	iK полушару X = {.т е R" 11Ы1 j,	0);
б)	к шаровому сегменту X ® {д; R" 1 ILrll < 1, х 0).
8.96.	Пусть Х{ (/<=/)—произвольные множества в Rn. Доказать, что
[conv (U Хг\Г = f U Х<Г= Л X?.
L 4G/ Л 4е/ J ter
8.97.	Пусть Xf (i^J) — замкнутые выпуклые множества в R’1, причем tl<= Л Доказать, что
i<s/
( Л ХА* = conv ( (J X*V
4<5/ J	\iG/ )
8.98.	Пусть Хь ..., Хя —выпуклые множества в R". tin ________ тл
причем 0 е Л ц Л	Доказать, что
(m	/ m TV
П Х| ] = conv и Xi |.
f=i /	\<=i	/
223
Отметим, что своего рода логической связкой между формула* ми утапиымя п задачах 8.92, 8.94, с одной стороны, и задачах 8.97, 8.98 — с другой, служит задача 7.59,
8.99.	Пусть Х[, .... Хт-1 — конусы, Хт — произвольное» множество в пространствах R \ R m-1, R m соответственно. Доказать, что
(X, х... X хт)* = X* х... X Х«.
8.100*	. Доказать, что в условиях задачи 7.129 справедливо равенство
Л(Х**) = [Л(Х)]**.
8.101*	. Доказать, что в условиях задачи 7.133 справедливо равенство
Л->(У**) = [Л“1(У)]**
В задачах 8.102—8.104, 8.108 под Л*: Rm -* R'1 понимается отображение, сопряженное к линейному отображению A: IV'-‘-R"’. Напомним, что опо определяется условном
<Л*у, ж> = <у, Лж> для всех х ® Rn, у <= И1п.
Если при этом отображение Л порождается матрицей Л (что мы имеем в виду далее), то отображение Л* порождается транспонированной матрицей Лт, т. е. А*у=* =*Ату=уА.
8.102.	Пусть Л: R" -> R” — линейное отображение и L = {(.г, у) es И” X R”|у « Ля) — его график. Доказать, что
Zr* = {(р, q) <= Rre X Rm|р = — qA},
т. е, L* является графиком отображения —Л*.
8.103.	Пусть Л:_ R" R" — линейпое отображение, X — произвольное множество в R", Доказать, что
[Л (X)]* = (Л*)"1^*)«{у s Rw | уЛ <= X*).
8.104*	. Пусть Л: RnRm — линейное отображение, У — выпуклое множество в R”. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
1) Л"‘(пУ)*0;
2) У —полиэдр и Л“,(У)ч£= 0.
Доказать, что
[Л-1 (У)]’ = Л» (У*) ® [р а R" | р ~ qA, д = у*1.
224
8.105.	Пусть выполняются условия задачи 8.104. Доказать, что для любого вектора р <= R'1 совместна одна и только одна из следующих двух систем:
Ла: «= У, <д, х> > 1 иля $Л == р, q& У*.
Вынести отсюда теорему 4.6.
8.106.	Пусть Л®^(т, л), p^R”. Доказать, что совместна одна н только одна из следующих двух систем:
11ЛхИ<1, <р, х> > 1 или дЛ = р, llgll^l.
8.107.	Показать, что теорема 8.9 (представляющая собой-простую переформулировку теоремы 4.7; см. 8.61) ость частный случай утверждения задачи 8.104.
8.108.	Пусть A: R" Rm — линейное отображение, XcR“ и У <=Rm —выпуклые множества, одно из которых является конусом, а замыкание второго содержит нуль. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
1)	пХПЛ-'(пУ)^0;
2)	X и У — полиэдры;
3)	X — полиэдр и X Л Л-1 (ri У)¥= 0\
4)	У— полиэдр и ri X Л Л-1 (У)=# 0.
Доказать, что [X Л Л (У) ] ♦ « X* + А ♦ (У*).
8.109.	Пусть выполняются условия задачи 8.108. Доказать, что для любого вектора p<=R" совместна одна и только одна из следующих двух систем:
Ля У, х X, <р, х> > 1 или
$ + qА =» р, s <= X*, q е к*.
Вывести отсюда теорему из 4.86.
В задачах 8.110—8.159 приводятся некоторые факты теории крайних точек и крайних подмножеств выпукло* го множества.
8.110.	Доказать теорему 8.11.
8.111.	Доказать лемму 8.1.
8.112.	Доказать теорему 8.12.
8.113.	Доказать теорему 8.13.
8.114.	Доказать теорему 8.14.
8.115.	Ыайти все значения параметра /«, прп которых выпуклое множество X в R\ определяемое системой
(Ж1 - 2z2)2 + («2 -1- ^)2 + (.г3 Н- 2.г4)?	8,
kxi — 2x2 + 5кхь + 10x4 = 0, обладает крайними точками.
15	G. Л- Лшжшоп, Л. В. Тамохоы	225
8.11G. Определить все значения параметра k, прп которых точка or(fc) является крайней в многограннике
X =1 conv {ж1, ж2, л3, ж1*, ж (7с)} с R3, где
ж1=(—1,2,3), ж2=(5,1,4), ж3 = (1,-6,-1), ж<-(1,-2,4),
8.117.	Рассмотрим выпуклый многогранник
Х = conv {(-2,1), (—1,2), (1,3), (3,3), (4,-1), (3,-3)}, содержащий пуль. В качестве иллюстрации к доказательству теоремы 8.14 (см. 8.114) проделать следующие операции:
1)	вычислить X* но теореме 8.8;
2)	представить X* как выпуклый многогранник;
3)	вычислить X** но теореме 8.8;
4)	представить X как полиэдр, убедившись, что
8.118.	Представить как полиэдр мпогограниое множество из 8.65.
8.119.	Представить выпуклый многогранник conv {(-1,3,1), (2,-1,1), (0,1,1),
(—1,—3, —3), (0,0,0)} в виде полиэдра.
8.120.	Доказать, что точка х выпуклого множества X является крайней в том и только том случае, если-из условий
тга
Xj^O, £т=1,...,лг,
trt
3 X, = I
следует, что для любого 1=*1, ..., т либо х{^х, либо Х< = 0.
Иными слонами, крайнюю точку х множества X пельзи представить в виде выпуклой комбинации по только двух, по в большого числа точек из X, отличных от х.
8.121.	Пусть X и У — выпуклые множества, причем У с: у. Доказать, что любая крайняя точка в X, принадлежащая У, является крайней в У, т. е. £(Х)П Y^E(Y). 22U
8.122.	Пусть X'— выпуклое множество, У—такое его подмножество, что Х=сопуУ. Доказать, что E(X)<^Y.
Данное утверждение) с учетом теоремы 8.13 означает, что множество крайних точен выпуклого компакта Л' является минимальным среди исех подмножеств X, выпуклая оболочка которых сояпадпвт g Л*,
8.123.	Пусть X — выпуклый компакт в R” и dim Х = т. Доказать, что X имеет не менее т +1 крайних точек.
В частности, если	то X имеет во мовоо «4-1 край-
fl их точек.
8.124.	Пусть Х = сопу(я*, я”*’} — m-мерный симплекс в R™ (см. 7.73). Доказать, что каждая из точек я1, ..., ят,н является крайней в X
,8.125. Доказать, что единственной крайней, точкой заостренного конуса (см. 8.78) является пуль, а пезаост-репный копус крайних точек по пмеет.
8.126.	Пусть X — выпуклый компакт, Ха — замкнутый выпуклый копус и X = X 4- Х%. Доказать, что Е(Х)=£
0 в том и только том случае, если конус X заострен; при этом из условий я = я’ 4-я2, зеЕ(Х), .г1 еА\ я2^Хг следует, что яг = 0, х ej?(X) и, таким образом, Е(Х)<= С^(АГ>).
8.127*	. Рассмотрим многогранное множество
X ® conv {«*, ..я*14- соне (я41, ..., я”1},
где точки ж1, ,я* попарно различны, а копус cone {я'1+’> ят) заострен. Доказать, что
а)	£(Х)с{Ж'......я”);
б)	точка х* (1 < i < ???.) является крайней в X в том и только том случае, если
я1’ & conv (я1,	а/-1, яг+|,	я*) 4" cone (я’"**1, .... я”1}.
8.128.	Привести пример выпуклого компакта, множество крайних точек которого незамкнуто.
8.129.	Выпуклое подмножество Г выпуклого лшоже-ства XcR’ называется крайним в X, если из условий
я^Ля1 +i(l — Л)яае=Г, я|,я2<=Х’,
следует, что я1, г^Г. Описать все крайние подмножества квадрата, круга, конуса па плоскости. Убедиться, что крайние точки множества X суть ого крайние подмножества пулевой размерности.
15*	227
8.130.	Доказать, что выпуклое подмножество Г выпуклого множества X является крайним в X в том н только том случае, если из условий
tn
хаЗМб!1! ««ex, Xt>0, 11=1,..., т, i««i
Xi =» 1 »=i
следует, что для любого i«=i, ..., т. либо д^<=Г, либо Xf = 0.
8.131.	Доказать, что любое крайнее подмножество Г выпуклого конуса X является конусом.
8.132.	Доказать, что выпуклое подмножество Г выпуклого конуса X является крайним в X в том и только том случае, если из условий
х и= 2 Г> х£еХ,	i«=l, ..., m,
i«i
следует, что для любого I5®!, ..., т либо .т'<= Г, либо Х( = 0.
8.133.	Доказать, что множество Г из леммы 8.1 является крайним подмножеством в X.
8.134й	. Доказать, что для полиздра X и его собственного подмножества Г следующие утверждения эквивалентны:
а)	Г — крайнее подмножество X;
б)	Г —грань X (см. 4.51);
в)	Г = X Л 7/рр, где II ¥(, — гиперплоскость, опорная к X.
Отмотпм, что для пронзяольиого выпуклого множества X из а) по следует в) (см. 8.1G0),
8.135.	Пусть Г' —крайнее подмножество Г, а Г — крайнее подмножество выпуклого множества X. Доказать, что Г? —крайнее подмножество X (ср. с 4.57).
8.136.	Пусть Г — крайнее подмножество выпуклого множества X, а выпуклое множество Y таково, что с: У с X. Доказать, что Г — крайнее подмножество У (ср. с 4.58, 8.121).
8.137.	Доказать, что пересечение любого числа крайних подмножеств выпуклого множества X является крайним (возможно, пустым) подмножеством X.
8.138.	Пусть X — выпуклое множество, Г — крайнее подмножество X, У—выпуклое подмножество X, причем Г П ri У Доказать, что У с: Г.
228
8.139.	Пусть Г — собственное крайнее подмпожостоо выпуклого множества X. Доказать, что Гс=г#Х.
8.140*	. Пусть X— замкнутое выпуклое множество. Доказать, что X имеет хотя бы одно собственное край псе подмножество в том и только том случае, если X пе является аффинным множеством (ср. с 4.71).
8.141.	Пусть /V —замкнутое выпуклое множество. Доказать, что любое ого кранное подмножество Г замкнуто.
8.142.	Пусть Г|,	— крайние подмножества выпук-
лого множества X, причем ri Pj П ri Га & Доказать, что Г1 = г2.
8.143.	Пусть X и У — выпуклые множества, причем У<=ХПг<7Х. Доказать, что существует крайнее подмножество Г множества X, удовлетворяющее условиям У^ с Г е r<? X.
8.144.	Пусть X и У — выпуклые множества, причем У <= X. Пересечение всех крайних подмножеств множества X, содержащих У, называется крайним носителем У в X к обозначается через Г* (У). Доказать, что Г = =1Гл’(У) является единственным • крайним подмножеством X, которое удовлетворяет условиям У <= Г и У П г! Г 0.
8.145*	. Пусть А*|, Х*2—выпуклые множества и Аг = = Х| ПХгч^^. Доказать, что множество Г является крайним подмножеством X п том и только том случае, если Г = Г|ПГ2, где Г| и Гг — некоторые крайние подмножества Х| и Аг2 соответственно.
8.146*	. Пусть А'], Хг — выпуклые множества п Х = = Х|+Хз. Доказать, что если Г—-крайнее подмножество X, то Г = Г] + Гг, где Г[ п Гг —некоторые крайние подмножества множеств Аг| п Агг соответственно.
Привести пример, показывающий, что обратное неверно; сумма крайних подмножеств и Хг не обязана быть крайним подмножеством X.
8.147.	Учитывая 8.134 и теорему 8,14, будем называть крайние подмножества многогранных множеств гранями.
Доказать, что гранями выпуклого многогранника X = = convСт’, ..., х'“) могут быть лишь множества вида Г convP, где Р с= {о;1, ..д"}.
8.148*	. Рассмотрим выпуклый многогранник X = = conv (.с1,	ж"1) и множество Г = сопуР, где Р<=
с= fa1, я’11}. Обозначим через Q совокупность всех тех точек множества 1х', .,,, .г"1}, которые не принадлежат Г. Доказать, что Г является гранью X в том н только том случае, если aff Г П conv Q = 0 (рис. 54).
229
8.149.	Доказать, что гранями многограппого конуса Х«=*сопе{я!, ас1"} могут быть лишь множества вида Г = cone Р, где Р <= (ж1, ...r”, 0).
8.150*	. Рассмотрим многогранный конус X = = cone.(z1, хт} и мпожестно Г = сопеР, где Р<= {s’, .... z"1). Обозначим через Q объединение пуля и
р •{ дЛ<г5}.
Рис. Г>4
совокупности всех тех точек множества {ж\ ..z"1}, которые пе принадлежат Г. Доказать, что Г является гранью X в том и только том случае, если aff Г П cone Q = = {0) и конус сопо£ заострен (см. 8.78).
Привести пример, показывающий, что условно заостренности конуса cone Q здесь существенно.
8.151*	. Доказать, что гранями многогранного множества
X = conv (z1, ..л?} + cone {а?4'1, ...г"*)
могут быть лишь множества вида Г = conv Р + cone Qt где Р с= к1, ..л/1), Q с= {z',+1, ..z'", 0).
8.152.	Выпуклый многогранник Х<= IV называется двуясмежностным, если любые его две вершины (крайние точки) ж1 и х* являются соседними, т. е. отрезок [ж1, я2] служит гранью X (см. 4.59). Убедиться, что двухсмежностпьимм многогранниками в R3 являются отрезки, треугольники, треугольные пирамиды и только они-.
8.153.	Рассмотрим в IV выпуклый многогранник X, натянутый па m точек вида
*(0 = (Ms. Л *4), i = l.....w-
Доказать, что все эти точки являются вершинами А’’, причем X — двухсмежносткый многогранник.
Таким образом, если при л = 1, 2, 3 число вершин двухсмож-постиого многогранника в Rn но превышает и й то уже при п = \ такой многогранник может плоть любое число поршни. Большое количество других интересных фактов комбинаторной теории многогранников можно пайти п [18], 230
Задачи 8.154—8.159 посвящены важным результатам о представлении выпуклых замкнутых множеств, выступающим как обобщение н развитие теоремы 8.13. При атам выяснится, что среди всех крайних подмножеств особую роль наряду с крайними точками играют крайние лучи. Введем следующие обозначения:
(г(Х)—объединение всех крайних толок и крайних лучей в X;
II (X)—конус крайних направляющих в X, т. е. множество, состоящее из пуля и всех таких векторов /ггА0, что при некотором х^Х луч 1хь является крайним в X.
8.154.	Пусть X — замкнутое выпуклое множество в IV, пе содержащее прямых, причем dimX>1. Доказать, что X = conv(r#X) и, более точно, любая точка х&Х принадлежит некоторому отрезку с концами в гдХ.
8.155*	. Доказать теорему К ли.
Пусть X — замкнутое выпуклое множество в R", не содержащее прямых. Тогда
X = conv G (X) = conv Е (X) + cone II (X).
8.156.	Пусть X — заостренный замкнутый выпуклый копус в R”. Доказать, что Х = сопе//(Х), причем здесь (в случае X =5^(0)) множество Ii{X) представляет собой объединение крайних лучен в X.
8.157.	Пусть X — замкнутое выпуклое .множество в Rn. Доказать, что
Х = conv G(X П Lx) + L =
= conv Е (X Л ZA) -I- cone //(X П М) + L, где L = £(Х) —рецессивное подпространство множествах (см, 7.124), причем множество XTIZA пе содержит прямых.
8.158.	Пусть Хг — замкнутый выпуклый конус в R". Доказать, что X ^cono II(X П М) + L, где- L X П (—X), причем конус X Л Lx заострен.
8.159*	. Пусть X—-замкнутое выпуклое множество в R". Доказать, что X является многогранным множеством (полиэдром) в том и только том случае, еслп число крайних подмножеств X конечно.
В задачах 8.160—8.173 излагаются основы теории выступающих точек и выступающих подмножеств выпуклого множества.
8.160.	Подмножество Г выпуклого множества XgR™ называется выступающим, если оно представимо в виде
231
Г я» X П где — гиперплоскость, опорная к X, Иными слонами, выступающее подмножество является множеством решений задачи максимизации (или минимизации) некоторой линейной функции /(.т)=<р, х> (рт^О) на X. Точка а^Х называется выступающей, если {«) — выступающее подмножество X, Совокупность всех выступающих точек множества X обозначим через 5(Х).
Согласно 8.30, любая граничная точка замкнутого строго выпуклого множества является выступающей. В силу 8.133 любое выступающее подмножество выпуклого множества X является крайним, Если X — полиэдр, то верно и обратное: любая его собственная грань является выступающим подмножеством (см. 8.13*5).
Привести примеры, показывающие, что как одноточечное, так и неодпоточечное крайнее подмножество выпуклого множества может ле быть выступающим.
8.161*	. Пусть X — выпуклый компакт в R"t «eR", Доказать, что точка из X, наиболее удаленная от а, является выступающей в X.
8.162.	Пусть X — 'выпуклый компакт в R", а<£Х. J\p-казать, что существует точка	которая находится
па большем расстояшш от а, чем от любой точки из X, т. е.
На — уII > Нт — f/ll прп всех х *= X.
8.163*	. Доказать теорему Страшсвича.
Пусть X — выпуклый компакт в R’*. Тогда
X = conv S (X) = conv 5 (X).
8.164.	Пусть X —выпуклый компакт в R". Доказать, что любая крайняя точка в X является пределом некоторой последовательности выступающих точек, т. о. £(Х)«=5(Х).
Это включение, вообще говоря, нелмл адмоннть иа ршюистио (см. 8.128).
8.165*	. Пусть X — замкнутое выпуклое множество в Rn. Доказать, что X имеет по крайней мере одну выступающую точку в том и только том случае, если X по содержит прямых; при атом 1И(Х)<= 6’(Х).
8.166.	Гиперплоскость //гц называется касательной к множеству X «= R” в точке а & X, если опа является единственной опорной к X в а. Полупространство, порождаемое этой гиперплоскостью и содержащее X, также называют каеагслъиы.и к X в а, Указать все касательные гп-232
перплоекостп к отрезку, квадрату, кругу па плоскости.
8.167.	Пусть X— замкнутое выпуклое множество в R", причем 0«=intX. Доказать, что полупространство Hpl = U S R” I <Р» лг> 11 является касательным к X в том и только том случае, еслп р — выступающая точка сопряженного множества X*. т.’ е.	и р^О.
8.168*	. Доказать теорему о касательных полупространствах.
Пусть X — замкнутое выпуклое множество в IV, прячем intX-^# д А1/-IV. Тогда X есть пересечение всех полупространств, касательных к X.
8.169.	Пусть X — замкнутый выпуклый копус в R". Доказать, что полупространство 77^0=-=	е R"|<p,
является касательным к X в том и только том случае, если /оР—- выступающий луч сопряженного конуса X*.
8.170.	Доказать теорему Страшевича —• /Гли для конусов.
Пусть X' —заостренный замкнутый выпуклый конус в IV, причем ЛЛ=#(0}. Тогда X «соне где Т(Х) — объединение всех выступающих лучей в X.
Данное утверждение является частным случаем теоремы из 8.173, Оно приводится отдельно, поскольку может Сыть доказано проще л поучительной. Утверждения следующих двух задач окажутся полезными при доказательстве общей теоремы Страшван-ча — Кли.
8.171.	Пусть гиперплоскости 7/^,, 77г1, Ягт таковы, что пересечение /7РП Л 77^ непусто и принадлежит 7/гт, причем Н^^Нп, Доказать, что 7/Р., П//qa *= #j.n П //гТ.
8.172.	Пусть выпуклое множество X и гиперплоскость 7/Рл таковы, что X 0 7/рП = {я:0}, по г0 не является крайней точкой в X. Доказать, что dimX^ 1.
8.173*	. Доказать теорему Страшевича. — Кли.
Пусть X — замкнутое выпуклое множество в IV, пе содержащее прямых. Тогда X =iconv7’(X), где Т(Х) — объединение всех выступающих точек и выступающих лучей в X.
В заключение параграфа приведем три топких факта выпуклого анализа — теоремы Моцкппа, Бурбаки и Красносельского. В задачах 8.174—8.177 проводится подготовка к доказательству первой из этих теорем.
8.174.	Пусть х — выпуклая комбинация точек
(1=1, .... m), пе лежащих в шаре Обозначим
233
через У множество всех пар (у, r)<^R”XR, удовлетворяющих условиям (рис. 55)
^(x)c£7r(y), x<^Ur(y),	М,..„Л1
Доказать, что У ограничено.
8.175.	Пусть X — замкнутое множество, У — выпуклый компакт п R", причем X и У пересекаются в единственной точке а, лежащей на границе У: ХЛУ = {«),
Рис. 56
a^OY (рпс. 56). Известно, что точка Ъ принадлежит внутренности любого полупространства, опорного к У в а. Доказать, что любой малый сдвиг множества У в направлении вектора h b — а устраняет касание с X, т. е.
ХП(У+а(5-а))=0
прп всех достаточно малых а > 0.
Рис. 57
8.177. Пусть
Убедиться, что точка Ъ удовлетворяет указанному условию, если b<sY, ЪФа. и У строго выпукло (см. 8.29).
8.176.	Пусть замкнутое множество X пересекается с шаром в единственной точке а, лежащей па его граппце (сфере). Пусть 5е[7г(у), Ъ^а. Доказать, что
ХП(7г(тИ-а(5-а)) = 0
прп всех достаточно малых а>0. шар Ut{x) лежит в отличном от него
шаре £7г(у), причем границы этих шаров (сферы) имеют общую точку b (рпс. 57). Пусть a&Ur(y), a^=b. Доказать, что шар, получаемы!! любым малым сдвигом
234
шара Ur(y) в направлении вектора h = b — a, также содержит С\(ж), т. с.
(х)с Ur {у + а(Ь - а))
при всех достаточно малых а>0.
8.178*	. Доказать теорему Моцкина.
Пусть X — замкнутое множество в Ru, причем любая точка из R" имеет единственную проекцию на X. Тогда X — выпуклое множество.
8.179.	Подчеркнем, что в теореме Моцкшщ имеется в виду проекция относительно евклидовой нормы 11x11 ’= = У<я, «:>, которая порождает шары, являющиеся строго выпуклыми множествами. Привести пример, показывающий, что утверждение теоремы становится неверным, если взять за основу, например, норму ||z|] = max |a;j|, не обладающую указанным свойством (см. 8.29).
8.180.	Пусть X — замкнутое множество в R", обладающее следующим свойством: для любой точки xeR" существует такое 8 > 0, что пересечение X с шаром С7г(дг) непусто и выпукло. Доказать, что X выпукло.
8.181.	Множество Х<=Й" называется локально вы-пуллшг, если у любой точки х<^Х существует такая окрестность U, что множество X fl U выпукло.
Пусть X—замкнутое, локально выпуклое множество и отрезки (а, 6], [6, с] лежат в X. Доказать, что отрезок [а, с] также целиком принадлежит X.
8.182*	. Доказать теорему Бурбаки.
Если X —- связное, замкнутое и локально выпуклое множество, то X выпукло (ср. с 8.180).
8.183.	Множество Х^Й™ называется звездным относительно своей точки а?, если для любой точки х^Х отрезок (ж°, я] целиком лежит в X. Доказать, что множество X звездно относительно любой своей точки в том и только том случае, если опо выпукло.
8.184*	. Доказать теорему Красносельского.
Пусть X —- компакт в R”, обладающий следующим свойством: для любых n+l точек я1, ..., я"+1 из X существует такая точка что [ж0, а/|«='Х мри всех 1 = = 1, ..., п +1. Тогда X — звсздпое множество относительно некоторой своей точки.
ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
ГЛАВА 1
•§ ।
1,2, л) Следует lift 1,1 прп ip(u) «о + [к
б) Дли любого л <= X имеем /(а) -{• g(x) /* -! S*. Поэтому (/-I-.?)’ = inf (/(;г) -|- g (,т))	/• •]. g*.
п) Домааываетсп пшигегнчпо,
г) Пусть х gh А'. Тогда
{min {/,	(Дх), g{.x))
Поэтому
{min {/, g))* inf / (j-) = /•.
Аналогично донааывиетсп,
чти выражение слепа но превосходит g*. Следовательно,
{min {/, g})* =£ mio {/*, g‘}.
В то ;но время ш!и {/(-с), ff(jc)} min {/♦. g“) и, значит, (miu (/, g})‘ min (/*, <?•}.
д) Дли любого хе А' имеем mnx{/{x), g{x)} тех {/*, g*}. Поэтому
{тих {/, g}}* > шах {/♦, g*)-
с) Раскрыть неравенство (f(x) — /*)(g(x) — g*) 5=0.
1.3.	По сути дело требуется привести те же рассуждения, что и и дощ|:»11тсл1лтво утверждений г) и д) лидачн 1.2.
1Л./(0)=—1 (/(0) = 1). __
1.0.	Использовать формулу Нш (— f^)) — — Um /(х,4)> Й-то
1.7.	Исполыинтть формулу
lim («1/1 (?) -j- а.,/., (^)) lioi /j (x,i) -|- а„ lim /г(.т?1).
Л-.00	11 -<Ю	II —
где а> > 0, а2 0-
1,8.	Пусть {г11) <= X, lim х''‘-.ге X. Дли любого у <= Y чмо-ом <р(А	Отсюда с учетом нолупепреривностп спину
Ф(х, у) но х получаем
ф (*. У} < lim <р (х\ у) < lim / (х1^).
Й—оо	Л-«со
236
Следовательно,
/ (х) = sup Ф (х, у)< lim / (xJl), У	ft-*CO
т. о, [ полунепрерывна снизу па X.
1.9.	Пусть нослодоватслыюсть {х,!} с X такопа, ’ что lim /(«*) = inf/(я) = /*. Поскольку X — ном пикт, то {zft} имеет  .v
придельные точки в X. Пусть без огрпппчошгя обгцпоотн пел отд последовательность сходится к некоторой точке я* се X. Тогда I1MO0M
/ {**) =с lim / (^9 = /*
и, значит, /(л*) == /♦. Таким образом, х* —точка глобального минимума / па X.
1.10;	Сначала рассмотрим случай, когда ср{т, у) полунепрерывна снизу по XX К Пусть {ж*)с=Х, lim^stsy. Отметим, fc-.oo
что определенно функции /(х) как минимума корректно в силу 1.9. Поэтому /(®*) =^чр'(х\ при некотором yh се У. Пусть нодносле-донатольиостн (хlm] и Ь ”*) токовы, что
lim / (^m) — lim / (j?) , lim
Л*-*1ЛЬ	ТП^оо
Тогда о учетом нолуиеирерыппостп снизу ф(х, г/) на XX У нмосм lim f{xh)= lim / (x,t<n) a Km ф(хЛм, уЛ™)>ф(х,
m—«	m-'M
t, e. / полунепрерывна снизу па X.
Если <р(т, у) ноирерыапа па X X У, то непрерывность /(х) па X следует из только что доказаниого, а также па 1.8.
1*11. Рассмотрим функцию ip(z, у) = max {0, 1—х;/) н мпо-жсстпа X = У = [0, <»). Здесь
(1, если z = 0,
1 Х ‘ [0, если я> 0,
т, <*. / полунепрерывна сверху, ио не снизу.
Рассмот^тм функцию
,	.	[ху/(х2-Нг),	если .т2-|-у2ч60,
Й> [X, у)	J=	'
4	1	(0,	если х = у = 0,
п множества X =	У	=	[—1,	1].	Функция <р непрерывна но каждой
переменной и отдельности, но разрывна в нуле но совокупности церемонных. При этом
, . fO, если т=0, f tg\ = |	'
'	1/2, если х-/'О,
т. о. / нолуиоирерывпа сверху, но но сивву,
237
1.12.	Пусть {х*} <= X, Нт xfi = х X. Обозначим у* = у(х*). k—oo
Требуотся показать, что предел последовательности {у*} существует п равен у(х). Поскольку У — компакт, то {у*1} пмщ< предельные точки. Пусть t/ —любая из ппх н подпоследовательность 1р т1 сходится к у. По определению у* пмеом
ф («Ат» уАта) С ф С**”1! у) при всех у <= У.
'Переходя здесь к пределу с учетом непрерывности <р па XX У, получаем
ф(х, у) ^ф(х, У) ирп всех у<=У.
Слодователыю, у = у(х). Таким образом, последовательность {уА} имеет единственную предельную точку у(х).
1.13.	Для фушщпп /(х. у) = (ху — O’fy'-'-l- 1) на К ХИ имеем
, . fl/x, если х^О, у (Х) IS J [О, еелп х = 0,
1.15.	а) С учетом 1.14 имеем
lim fh (х) = «юр (х), х «а X,
Il-»OO	ft
lim sup fh (x) sup sup fh (x).
k-rOO X	h' X
I/
Нужное рапепстно следует теперь па 1,3. а).
б) Поскольку/(х) «= sup f{{ (х).то можно использовать 1.8.
Требуемые примеры:
. , . . [1, х = 0.
б) А(х) = max{0, 1—-А-х}, X = [0, !] (ср. с ответом к 1.11).
1.16. Прежде всего отметим, что точка х* существует в силу
1.9,	а точки ж — и силу компактности X, причем х <= X, Без ограничении общности будем считать, что последовательность {х*1} сходится к х. Требуется показать, что
Нш /А(х*) = шш / (х)	/ (х).
ft-»CO	Д
Но
х я х
Поэтому остается доказать лишь следующее: дли любого е. > О существует такое X, что
f(x) — MX*) < е при всех
(I)
Так как по определению /(х) = Ига/А(х), то найдется
Л-»ОО такое т, что
+8/2.
233
Поскольку функция /т полунепрерывна снизу И аг* а-, то существует такое Ка, что
/т(л’)	/,„(хА) + е/2 при всех Л 3= Я*.
Из условии поточечного неубывания функции следует, что
/«(**)	при всех k^sm.
Складывая пыпнеаппые неравенства, приходим к (1), гдо К «= = max (za, /Г©}.
Примерами существенности условия полупепрорывпости функций /* служат
.	. .	(О, 0<z< i/k,
а)	и, х = о, 1Д<х<1;
6)/ft(*)«{^ я = о’ **=!/*.
Примерами существенности условия неубывания {/*(*)} являются примеры ив ответа к 1.15, гдо в б) следует паять = l/k, L17. а) Пусть {**} <= Х$, ПгпяА « .т. Поскольку {х*} с X u X Л-»о»
замкнуто, то х <= X. Так как /(гА) р п / полунепрерывна снизу, то /(«X Нт/(«*)<₽, т. о. Следовательно, А'о замкнуто.
б)	Пусть {а:А}с=Х, НтхЛ = я(оХ. Допустим, что а = Л->ОО
g= lim /(xft)< / (j). Выберем такое 0, что а<0</(х). Тогда Лт+w
г^Л'цппто асе время существует подпоследовательность [г/”1}, ложащая в Хр- При атом lim = х, Мы пришли к протпворе-тткоо
япто с замкнутостью Хр, Следовательно, /(х)^а, т. о. / полунепрерывна снизу.
Требуемый пример: f(x) = In х, X — множество положительных чисел.
1Л8. С учетом 1.17 множество А'п есть (непустой) компакт. Тогда, согласно 1.9, функция / пмоот точку глобального минимума па X». Яспо, что она жо- является точкой глобального минимума
1.20.	Пусть последовательность {zA} с X такова, что lim / (r^) = inf / («) «= /*. Поскольку /—бесконечно растущая а-*» х
функция иа X и /• < со, то, рассуждая от противного, получаем, что (яЛ) ограничена н любая ее предельная точка лежит n X. Остается повторить копцовку решения зодачн 1.9.
1.21.	Предположим, что /* = inf/ (*) > — ос. Как известно пп
из курса лнпеипой алгебры, для симметрической матрицы Л существует такая невырожденная матрица С размера «Хм, что С^ЛС ость диагональная матрица. Пусть ее диагональными элементами служат числа М, .... Ап. Положим а = Тогда для
239
любого yeR” пмеом
.я
/ (Cj?) = 2} (м? + <№) -Н > /♦. i=l
Отсюда СЛОДУОТ, ЧТО При любом i — I, . ,п функция	(Уj) =
= ?,j0i -J- djj/j ограничена снизу; па числовой осп К Тогда либо At > О, либо At = О, <?[ = 0, и во полком случае ф< пмеот пп 11 точку глобального минимума у*. Ясно, что х* = Су*, где у» есть точка глобального минимума функции / на R" (ср. 2.31).
Далее пусть /♦ > —оо, по Л по является псотрпцательпо определенной, т. е. существует такой х е R", что <Лх, х) < О, Тогда, очевидно, lim / (Ах) » — «>, что противоречит условию /• > —со.
1.22.	Допустим, что f но является бесконечно растущей па R”, т. е. существует_____такая последовательность (1А)сПг’| что
lim 1x4 = w, по lim / (zh) < <». Полознпм hk =± xh/||x*||. Боз or-7<-»оо	Л-»сч
равпчоннн общности можно считать, что {А*} сходится к некоторому h ф 0. Тогда
Г- /У)
= <ЛЛ, А>.
Но ото противоречит положительной определенности Л. 0 Г
1.23. 4= о — 1 0 •
-1
0
0 OJ
1.24.	Пусть х* — точка глобального минимума / па X, существующая но теореме Вейеригграсса. Предположим, что х* е Х\Х. Рассмотрим соответствующий вектор л из условия задачи. Положим ф(а) = /(х*+аА). По теоромо Лагранжа о конечных прн-ращопилх для любого достаточно малого а > 0 пайдетсн такое е е= t= (0, а), что
ф(а) — ф(0) =з гр'(а)а = </'(х* + ей), А>а < 0,
По ото противоречит выбору х*. Таким образом, х’сХ _	п
1.25.	Пусть хеХ\Х, т. о, 2*je1,	всех / =
/=1
== 1, .... п и х/ = 0 хотя бы прп одном /. Беа ограничения общности предположим, «по Х| =	= х* = 0, ih+t >0, ..., х„ > 0. Рас-
смотрим вектор k <= № с координатами
{1,	если / =1.....ft,
— k/(n—к), если / = й-|-1, ..., я.
Тогда, очевидно, х 4- ah = X прп псах достаточно малых а > 0 и 240
lim </'(* + e
a-»o+
2 >5 S’~r^)V-w-T \j>«l	J=fc+1,	'	'/
Остается использовать 1.24,
1.2f	t. Нот, по следует. Рассмотрен, функцию /(ж, у) = ж5 и мпо-jkogtko X = {(ж, у) <= Н![жу I},
1.27,	Нет, пе следует. Рассмотреть фупкцпп /(х) »= |х|/(1 + г1), g(x) =s [ж — 1|/(1 4- х1) п мшмксство А' = R.
1.28.	Если я > 0, то lim / (ж) = — со. Если а —1, то X -+0-I-
lim / (ж) =± — о». Если “1 < л < 0, то / является бесконочпо рас-ЗЙ-.И5
тущей па указанном множество. Еслп, наконец, а <= О, то /'(0) < 0 (ср. с 1.24) и lim / (ж) ст оо, Слсдоиательпо, точка глобального х-»«
минимума существует в случае —4<д^0 и отсутствует в остальных случаях.
1.29.	Точка глобального минимума существует прп а ==> 2, а в 3 п а > 4; величина /* конечна, во по достигается ирн в < 2 и 3 < a tg: 4.
1.30.	Неравенство, определяющее X, можно записать в виде (6 — I)*3 4- (ж — у)2	1. Следовательно, если b > 1, то X ограни-
чено и, значит, / при любом а имеет па X точку глобального минимума. Если Ь = 1, то лишь при а =□ —1 величина /• = inf / (ж, у) конечна и достигается. Если b.< 1, то прп любом а точка минимума отсутствует.
1.31.	Требует рассмотрения лишь случай b 1. Еслп прп атом а « —1, то точка минимума / па X отсутствует, так как (ж, ж) е X для всех ж и lim / (ж, х) = — <х>.
Х-*оо
Пусть а = 1. Если Ъ > 0, то точка минимума существует, поскольку для любой точки (х, у) еХ справедливо
f (*, у) = *У > Ьх ~ *
£
н, значит, / является бесконечно растущей па X. Еслп t = 0, то, как нетрудно показать, /♦ =± inf / = —1/2, но эта величина
не достигается. Еслп 6 < О, то /* — —оо, так как (ж, 1) е X прп dcox х 2/6 и lim f (х, 1) ~—со.
'	X-» — as
1.32.	Дли любой точки (х, у). удовлетворяющей условию у* « = 1 — (а — 1)х, имеем (ж, ц) еХ и
/(ж, У) == 4х®4- (й-4)х(1 — (а — 1)х) =
= (4 — (а- 1)(а —4))х24* (а —4)X. Следовательно, если (« — 1) (в — 4)	4, то для последовательно-
сти ((жъ у,)} такой, что (я —1)х,->-—со при з-уоь и у, = = 1 —(a —l)xg, получаам (в — 4)ж4->-—<» и lim f(xt у \ = — оо, »-»оо '	1	7
18 с. А, Ашмапар, А. В. Тимохоа
241
Таким обрлвом, псобходпммм условном с.угцоствонаппя точки глобального минимума является неравенство
(а — 1)(л — 4) <4.	(I)
Покажем, что это усло'ние и достаточно. Пусть ((х4, у*))сА', Нт(Ы+1М) — со. Тогда обязательно |х4| то, я без огра-Г.-*,"К» ' 1 1 ' ' f
ннчеиил общности можно считать, ЧТО либо Xt <», либо I, -* —СО.
Если (а — 4)х« -*• + «>, то очевидно, что
Ни» / (.гг У Л *= <».	(И)
Пусть (и — 4)х4 ->— то. Тогда
/ (х«« И») >4srs + (« - 4) гд.(1 - (« ~ 1) ®,) =
= (4 — (а — 1) (fl — 4)) ж; -Ь (а — 4) хл.
Прп этом из (I) вновь получаем (II). Следовательно, / япляотся бесконечно растущей па X. Таким образом, точка глобального минимума / на X существует в том я только том случае, если « удовлетворяет (I), т. е. О < а < 5.
1.33.	(1, 4, 7).
1.34,	Из рпс. 58 лспо, что проекции (ж, у) точки (ж* Уи) па прямую ях + by = I должна удовлетворять системе
ах - • Ъу = 1, -2-- = -2——.
« Ь
Решай ее, находим, что
ж-жй.Ь(1-ижо-Ьг/())^— b у = у9 -Ь (I - «0 - Ч)^Р*
Проекция точки (ж0| рц) на X определяется теперь по формула (.г, у), если ж 5= 0, у>0, (7, у) = (О, 1/Ь), если ж<0, .l/й, 0), если у <0.
242
1.35.	Если (*о, Wo) е X, то проекцией служит сими точка (лч» JA>)- Если л-j + < 1, jro>0, то из .рпс. 59 ясно, что проекция (х, у) ДОЛЖНО удовлетворить система
«2 4* № = 1» Xfao = у/у» > о.
решал ее, находим, что
Пусть теперь Уо < 0. Тогда если ].т<,| > 1, то проекцией служит точка (х0, 0); если —1<х0<0, то —точка (—I, 0); если 0<х0г^
1, то — точка (1. 0). Наконец, если х0 = 0, у<, s= 0, то проекциями являются псе точки (.г, у) такие, что xs 4- у* = 1, у 5= 0, п если х0 “ 0, у0 < 0, то — точки (—I, 0) и (•-!, 0).
1.36.	Геометрическая интерпретация задачи приведена на рис. 60. Отсюда видно, что решенном является такая точка (х*, у*), в которой ироходшцая через нос липин уронил функции / (гипербола) касается прямой йг-г^=1. Условном касания служит
Л?/ df\
Koiiiiniioupiiocrb градиелта I и кекторп (а, Ь), Следовательно, (х*, у*) есть рошоино системы
ax -|- by «= |, у[а = х/Ь.
Отсюда х* = 1/(2п), у* я 1/(21?).
1-37, Геометрическая интерпретация задачи приведена па рис. 61 (здесь к itn следующих рисунках X обозначает допустимое мпоигоство). Отсюда видно, что решенном служит такай точка (**, У*), » которой ироходящан через нес линия уровня функции / касаотсл прямой х — у — 2, Из этого условии находим, что х* = «ад 1, у* t= —1.
1.38,	Из рпс. 02 ясно, что решением (х*, р*) служит точка пересечения прямых X — у =Я 0 и х + У в 1, т. е. х* = у* <= 1/2.
1-39. Решениями служат точки (1, 0) и (0, 1) (рпс. 63).
1.40,	Решениями служат две точки (х*, ±р*) такие, что <«*» &1*) удовлетворяет системе 2х—w = 2. 2 — х ==< у (рис, 04). Отсюда х* = 4/3, / «= 2/3.
16*	^43
1,41.	Если ]а| < 1, ю X состоит па одпнствепкой точки (О, 0), которал и служит рошенном. Если |а| 3= 1, то X ость обтдгдппопио прямых у =1 А*|Х и у = ktx, гдо Й! е= а — |'а2 — 1, Д-2 = а -J- )'аа — 1.
Puq. GO
Еслп а 1 (рис, 05), то рошопнем («•, у*} является проекции точки (1, 0) ни ирямую у = ftix, т. е.
Еслп же a*g — 1, то решенном является проекция точки (!, 0) на прямую у «= к&.
244
24$
1.42.	Рассмотрим сначала задачу максимизации. Из геометрических соображений ясно, что се глобальное рошоние находится среди точек (3, а 4-1) и (4, л) (рпс. Об). Неравенство /(3, «4-1) < < /(4, «) равносильно неравенству а < 27/2, Следовательно, решением является: точка (4, «), ес-
если а > 27/2; любая нз этих точек', если в = 27/2.
Обратимся к задаче мииимп-зицин. Понятно, что ее глобальное решение находятся на отрезке, соединяющем точки (2, п) и (3, я — 1) (рис. ОС). Этот отрезок описывается условиями х 4- у ~ = « 4- 2, 2 < х 3. Выражая отсюда у и подставляя н формулу для f{xt у), приходим к задаче минимизации функции tp(x) = = 5х2 — 2 (а -|- 2)х на числовом отрезке [2, 3J. Отсюда несложно
нолучаем, что решенном исходной задачи мннимпзвцнц служит: точка (2, и), еслп 0^«^8;
/1	4	\
точки I ^-(в "1_ 2)» "д' (в + I» если 8 < а < 13; точка (3, а — 1), если и 5= 13.
1.43.	Локальными решениями служат точки (2, 0) и (0, 1) (рис. С7).
Рнс. 06
1.44.	Допустимое множество задачи представляет собой кривую! называемую декартовым листом (рис. 68), Очовпдп0| что лишь ирн а~1 глобальное рошоние существует и равно (3/2, 3/2)» Прп
246
wex остальных A имеется локальное рошеппо, по яплягощсося ГЛрблЛ1|Н Ы'Ь
1,45.	— 2	а < 1.
1.46.	л) Из аксиомы 1) имеем Ф(Ц Р) = Ф(Р) + Р к Ф(2р)
п= 2Ф(Р)- Слодовптельио, Ф(р) = р.
б)	Использовать аксиому 2),
в)	. Положим р.= min f (ж), Р„ = max / (.г). Имеем р( /<х) А х - х
Рз при всех xgX, Нужные цораиепства следуют теперь из в) и б).
247
1Л7. в) Для любого г е Y имеем х & Е и, следовательно, су-щоствует токая функция /еС(Х), что х^Е^ т. о. /(г) ><!>(/). Это означает, что открытые множества
Uf «= {z е У |/(х) > Ф(/)},	/ s С{Х),
образуют покрытие множества У. Пользуясь компактностью У, выделим из этого покрытия копочиое подпокрытие £/у , ...,Ч/у . Рассмотрим функцию
/(*) = шах {A(z) - Ф(/,),..Jn(z) - Ф(/т)}, х <= X.
Используя аксиомы 1) и 2) пэ 1.46, получаем, что Ф(/) =а 0. В то же время для любого х<=У существуют такой кодекс 1б(1, ... ..., ю}, что xst/yp и, значит,
/(*) ^А(х) - Ф(/<) > 0 <!»(/).
Таким образом, / — искомая фушщпя.
б) Если предположить, что Е «= 0, то в п) можпо взять У = «= X. Но это приводит к противоречию с первым перппепством из 1.46, в), Замкнутость Е следует из непрерывности функций /.
в) Указанное неравенство равносильно определению Е,
1.48.	Докажем, что искомым является множество Е из 1,47. Если Е = X, то нужная формула есть следствие неравенств 1.46, в) и 1.47, в).
Пусть Е ¥= X. В силу 1.47, в) достаточно показать, что max / (х) Ф (/) при всех /еС(А'). Предположим, что это по
так*, т. е. существует функция geC(X), для которой
шох g (х) < Ф {§).
Е
Тогда найдется множество U, открытое в Хи такое, что
Е g U, sup g (х) < Ф (g).	(I)
Положим У s=« Х\ U. Из 1.47, а) следует, что существует функция /еС(Х), для которой
шт /(х)>Ф(/),	(И)
Рассмотрим функция
/ (х) = max (/ (х) — Ф (/), 0}, х е X, g(x) = g(x) — sup#(z), z<=X.
Из (II) следует, что fix) >0 прп всех х е У. Тогда, поскольку У — компакт, а функции /ng непрерывны, найдется столь большею число а > 0, что
а/(х)>^(х) при всех хе У.-	’ (III)
Для любого is U по оиредсленнто Jug имеем 7(х) ^0, j?(x) 248
«<0. Следиватеяьпо, перовенстно из (III) справедливо при всех хеУи^ = Л< Тогда из 1.46, б) заключаем, что Ф(а/)^Ф(^). Но, согласно йксиомил I), 2) из 1.46 и формуле (I), должно лмдол-пяться обратное иораиенство:
Ф(<х7) = аФ(П «0<Ф(«.
§ 2
2.1.	Пусть х* — локлльиое решение задачи (2.1). Зафиксируем любой вектор h cs R*. Тогда если функция / дифференцируема II х*, то
0</(х’ + аЛ) -/(х*) = </'(**), аЬ>+о(а)
прп всех достаточно малых а. Разделив обо части иоравенства па «>1)н перейдя I? пределу при а-►О, получаем, что </'(х*), Л>
0, Отсюда при А « —/'(х*) следует (2.2).
Если же f дважды дифференцируема н х*. то с учетом (2,2) имеем
О < / (х* + аЛ) - / (х*) = у <у (**) (аЛ), аЛ> -|- о(а=) при всех достаточно малых а. Разделив обо части неравенства па а1 и перейдя к пределу при а-»-0, получаем (2.3).
Пусть теперь выполнены условия (2.2), (2.4) п но-прожпему / дважды дифференцируема в х*. Предположим, что х* ио является строгим локальным решенном задачи (2.1), т, е. существует такая иослсдовительноеть {х*}, что
х* Ф х*, х*->-х*,	/(**) =£/(х*).
Представим х* в виде
т^х’ + ад/?1, где 0^=4а1* —х* И, ~ (z7‘— х*).
&
Поскольку ||/?|| = I, то без ограничения общности М01КП0 считать, что W-b-h =/= 0. Учитывая (2.2), имеем
0> У(^) - У(х‘) = 4 </’ («•) (аАЛЛ), аАЬ*> + о (оф.
Разделив обо части поравспстиа па а£ и перейди к проделу, получаем противоречие с (2.4).
2.2.	а) По теореме Лагранжа о коночных приращениях для любого х е {/, х ejb х*, найдется такое а е (0, I), что
/(-«=•)-У(л) =/'(х + а(х*^-х))(х*-х)^0 (<0).
б) Нет, по слодувт. Рассмотреть функцию
. /(«) =
ч
« (п . , 1 \ х’ 12 Ч- г h
<	*6 j
х^О, х== 0.
249
2.3.	При данном я е Ut. (х*). х=/=х*> положим ф(а)=/(х4-4-а(х* —х)). По теореме Лагранжа найдется таков ае(0, 1),
/ (**) - /	(1) - ф (0) = <р' (а) = </' (х -|- а («•-*)), *•-*> =
-=	</' Iх -г а (х* — х)), х» — (х 4- а (х* — х))> СО « 0)
2.4.	Применяя формулу Тейлора с остаточным членом в форме Пенно, получаем пр» всех достаточно близких к нулю k
/ (х* -I» Л) - f (х*) = j-, /f<) (х*) hk -J- о (АЛ) =
Отсюда легко выводятся требуемые утверждения.
2.5.	Пет, пе следует. Рассмотреть функцию
/(х) = |е 1/Х ’	*46 0,
|0, х = 0;
2.7.	Пусть е( обозначает f-й единичный орт пространства И*’. Тогда при k cf получаем б = А [Л] «= ащ. Возьмем Л =и е1 ф гдо i }. Тогда
О :=« Л [Л] = аш + ajjj 4- 3(auj + <Ьл) = 3(a,-r> 4~ «л0-
Если же h == 2е‘ 4- eJ, где £ «^ /, то
0 = Д[/<] =8аш 4- «л/ 4~ 3(4<t|ij 4- ojjt) = 3{4kiij + «jjf).
Следовательно, atti “ «яг =“ 0. Пусть теперь h = e* -Ь e? e\ гдо i Ф /, / ч6 A', k Ф i. Имеем
0 = Я [Л] = aui 4" aiii + Яш + 3(flru 4- о/я 4- aif>> +
4* a.W 4-	4*	4’ Caijh = Ga<jh-
2.8.	Рассмотрим при данном Л е IV1 функцию <р(а) = /(х* 4-4-аЛ). Выпишем для псе формулу Тейлора третьего порядка с остаточным членом в форме Пеано:
Ф («) - ф (0) = ф' (0) а 4- of ф" (°)	«р* (0) а3 4- о (“3)-
Прп этом <р'(0) = </'(*♦),&> =0, ф"(<0 =Г(х*)Р'1. Ф"'Ю) = = /'"(*•)[А]. Слодоявтольно, если /"(ж*)!./*] ==0, то при всех достаточно малых по модулю а имеем
0 < f (х* 4- ah) - / (х*) = Г (х») [Л j а3 4- '> («’)•
Еслп поделить это соотношение на а1 > 0 (<0) и норептп к пределу прп а-*-0, то получим, что /'"(х*)[Ч 5=0 «0). Таким образом, /"'(х*)[А] =0. Частное утверждение следует из 2.7.
250
2.9.	Согласно теореме 2.1, точки экстремума функции / обязаны удовлетворять системе
df
дх 2ж —2№0,
Of
— 2х — 4s =0,
^= 10s —4у —2 = 0,
Эта система имеет единственное регпепно х* = 2, у* = 2, г* = 1. Заметим, что функция / является квадратичной. При этом
’ 2 -2 О*
Г -2	4 -4 .
. 0—4	10.
Угловые миноры матрицы /" положительны: г 2 — 2'1
2>0, del I 2	4 =4>0,	<1о1/я=8>0.
Тогда ио критерию Сильвестра матрица /* положительно определена, н, апачи г, в силу теоремы 1.4 функции / имеет точку глобального минимума на R\ Согласно замечанию 2,3, таковой и является точка (2, 2, I).
2.10.	Выпишем необходимые условия акстремума порвого порядка:
г?/
-т—~ — ле flr.
<7 _
в* 4-в» “р*
“°-
Эта система имеет единственное решение:
х* = In (о 4- }г«6), у* — In (& + рП»).
Заметим, что функция f является бесконечно растущей па R2, Тогда но теореме 1.2 опа имеет точку глобального минимума. Таковой, слодо1шт1?лы!о, п служит точка (х*, у*).
2.11.	Выпишем необходимые условия экстремума:
|^ = 4хя —4у —О, ^=4/-4т = О.
Эта система имеет три решении: (0, 0), (1, 1), (-“1, —1). Вычислим гессиан функции /:
— 4
Имеем
12х2
— 4 12/ '
/* (0, 0) =
О — 4"
4 О ’
Г (1,о= Г (-<.-!) «ГЛ 12}
251
Матрица /"(О, 0) анаконеопредолепа. Тогда по теореме 2,2 точка (U, О) ио является экстремальной. Матрица /"(i, !) положительно определена. Тогда из теоремы 2.3 следует, что (1, 1) п (—1, —1) суть точки (строгого) локального минимума. Заметим далее, что функция / является бесконечно растущей на К1. Поэтому f достигает глобального минимума. Значения / в точках (!, 1) п (— 1, —1) совпадают. Слодонатольпо, каждая ns mix яялнстся точкой не только локального, но п глобального минимума. (После этого ясно, что исследование матриц /"(±1, ±1) было фактически липшим.)
2.12.	Выпишем необходимые условия экстремума:
~ (2х л. у - а} (у -Ь)=0,
т= (2у х — ft) (ж — я) =-: 0.
Эта система имеет четыре рошеплл: (a, —я), (ft, —ft), (я, Ь) и (ж* у»), гдо ж* (2а — ft)/3, y*=(2ft — а)/3. Вычислим гессиан /:
,.v	[2 (у —ft)	2(жу)—a—ft]
' 3 [2 (ж-|- у) — а — ft 2(я—а) ]•
Имеем
/Jr{a м_Г~2<а'Н>) '’в-‘й1
/* (Л, — &) = [_д „ ь _ 2 (а + Л)]’
Г (а>!j)» [a ц. I, а о &]» ГЧ**» tf*)== —+	г]’
Предположим, что в -) Ь #= 0, Тогда, попользуй теоремы 2.2 и 2.3, получаем, что первые три точки по являются экстремальными; в точно (ж*, у*) достигается локальный минимум, если а. 4- ft < О, и локальный максимум, если a 4- ft > 0. Яспо, что глобальным этот экстремум но является. Пусть теперь а ft =» 0. Тогда лее четыре точки «сливаются» в одну точку (я, —я). При этом /"(я, —а) = О, п, значит, теорвмы 2.2, 2.3 неприменимы, Заметим, однако, что /(яЦ-а, —а 4-е) = 2е’. Отсюда следует, что точка («, —я) не является экстремальной прп л 4- ft =» 0. Тот же вывод получим, ис-д’1/
ходи из 2.8, поскольку, например, aTfly zjy"= я, значит, 0.
2.13.	Функция / имеет едипстпениуго стационарную точку (0, 0).
Теоремы 2.2, 2.3 здесь «по работают». Поэтому требуется специальное нселедспншне поведения / л (0, 0). Положим х р2, у = е. Тогда /(х, у) = —8s. Отсюда следует, что точка (0, 0) по яилнется экстремальной.
2.14.	Функция / имеет бесконечное число стационарных точек вида
х = (— 1)Л+1 iy = <_	?L|
252
где к, т — О, ±1, ±2, ... С помощью теорем 2.2, 2,2 получаем, что д (х, У) достигается локальный минимум, если А четно, и» нечетно, л локальный максимум, если Л почетно, m четко; если жо А + nt четпо, то точка (х, у) пе является экстремальной.
2.15.	Стационарными точками функции / являются точки вида (О, 2Ая) п (—2, (2А + 1)я), где к = 0, =Ы, ±2, ... Из теорем 2.2, 2.3 следует, что в точках (I), 2Ая) достигается локальный минимум, й точки (—2, (2Аф 1)я) «из являются .ткстромпльньгми.
2.1G.	Функция / имеет дно стационарные точки: (0, 0, —1) п (24, —144, —1). При этом /(е, 0, —1) —/(0, 0, —1) = е’. Отсюда ясно,’ что первая точка по является экстремальной. Применяя теорему 2.3, убеждаемся, что во второй точке достигается локальный (но по глобальный) минимум.
2.17.	Функция / имеет следующие стационарные точки:
1)	X = у = Z « 1/7;
1 — Зз
2)	х = 0, У — —2—• =
3)	У = 0, х и з любые;
4)	; ез 0, х и у любые.
С помощью теоремы 2.3 получаем, что в точке па 1) достигается строгий локальный максимум. Глобальным этот максимум по является, поскольку lira /(1,у, 1) = а>. Путем нопосродст-
У-+—ОФ
венного анализа локального поведення функции / выводим, что в точке (х, 0, :) из 3) достигается нестрогий локальный минимум, если xz(l — х — З2) > 0, и нестрогий локальный макепмум, если хз(1 —х —3;) <0. Все остальные стационарные точки из 2)—4) не яешнются экстремальными,
2.18.	«Пункция / является бесконечно растущей в области х > >0, у > 0,’ ; > 0 н, следовательно, имеет том точку глобального минимума. Единственной стационарной точкой функции и указанной области служит (1/2, 1, 1). Значит, эта точка п является глобальным решением задачи (см. замечания 2.2 н 2.3).
2.19,	Функция / является бесконечно растущий в области ® + р>0. В самом деле, если х-ноо, у-*-<х> или х + у->-0 при условии х-|-у>0( то /”><». Пусть у-»-—оо п х-|-у>0. Тогда x-t-oo п /(х, у) ^!=xs — х, т. е, /-»-с0. Едннствеппой стационарной точкой функции / в области х-|-у>0 и, следошпельпо, глобальным рошенном задачи служит точка (1/2, 1/2).
2.20.	а) Допустим, что С~’ на существует. Тогда система С.т <= О плюет решение х ф 0. Прп этом (б’х, х> «я 0, что противоречит положительной определенности С.
б)	Для любого yeR” положим х =» уЛ = Лту. Тогда с учетом неотрицательной определенности С имеем
<у, ЛСЛту> = <х, (7х) ^0,
в)	Пусть у #= 0. Тогда х = уЛ — ненулевой вектор, так как обратное означало бы, что строки матрицы Л линейно зависимы, *• в, rang А < т. Следовательно, <х, <7х> > 0 и силу подшкнтоль-чой определенности С.
2,21.	Используя теорему 1.4, формулу /'(х) =Лх-{-5 к 2.20, получаем, что единственной стационарной точкой и, следовательно, глобальным решенном задачи является х* = — Л_,А.
(Отметим, что этот результат отнюдь по решает проблему численного отыскания минимума указанной квадратнчпой фуяк-
253
дни, поскольку обращение матрицы является довольно трудоемкой вычнслнтёльной процедурой. По этой причине разраоотипы более экономные численные методы минимизации кввдраткчпых функций, позволяющие избегать я иного вычисления обратной матрицы, например метод сопряженных градиентов [ЗЯ, с. 2U1). Аналогичное замечание можно сделать в отношении задач 2.22. 3.25, 3.26.)
2.22.	Функции / является квядратичкой:
/(х) =i (Лх — Ь, Лх — by == <ЛтЛх, х> — 2<ЛТ5, z> Ц- <6, £>,
При этом матрица ЛТЛ положительно определена (см.. 2.20). Тогда из 2.21 следует, что глобальным решением служит точка х* е= = (ЛЪ1)“’ЛТА.
2.23.	Матрица входных данных и вектор выходных данных имеют здесь нид
0.5 2 ’
0.5 0_
“—4,5“
1,5
— 2 _ 4 _
В соответствии со сказанным перед формулировкой этой задачи н ответом к задаче 2.22 паилучшая зависимость получается при
(Л|. «2) = (CrC)“,CTri.
Последовательно проводя вычислении), имеем
5/2 1
. 1 б]’
/Г7М-» = Г Ж -1/И1
V	1/14	5/28J’
СТ в = (7, -7),	(«., в2) = (7/2, -7/4).
2.24.	Пусть /?(х*) «=Лх* + й = 0. Для любого xcR” в силу неотрицательной определенности А имеем
<Л(х —X*), х —х*>^0.
Последовательно преобразуя это неравенство с учетом того, что Лх* — —Ь, получаем
{Ах, х) — 2<Лх*, х) -)- <Лх*, я*>	0,
<Лх, х> + 2{Ь, х> >-<Лх*. х’> = </1х*, х*> 4- 2<fc, х*>,
/(х)5=/(х*).
Следовательно, ж* — точка глобального минимума / па Rn.
2.25.	Выпшиом, учитывал теоремы 2.1, 2.2, критерий Сильвестра, а также 2.24, необходимые и достаточные условия глобального минимума и точке (1. —4):
^7 (1, — 4) — 2а — 41> 4- 6 = 0.--^(1,-4)-/г-84-с = 0,
4и Ь2.
254
Отсюда получкой искомые a, b it с:
а = 13-2с,	& = 8-с,

2.26.	Выпишем необходимые условии экстремума в топке (О, I):
(О, 1) = (4х -}- а3ех 4- &у) |(0 1) = ?-]-U О,
(0, 1) - (bx Ь*у 4- и) |(1)1 |} Ь3 4- а = О.
Этим условиям удоллвтпоряют три пары параметрон: а = b = 0; a == 1, Ь = —I; а = —!, b = 1. Ясно, что при а = Ь = 0 и точка (О, 1) достпгаотси нестрогий глобальный минимум. Далее вычислим гессиан / в точке (0, 1):
Г (0, 1) ==
4 4~ fl3 ь ь ь3
.Если д «= 1, b — —1, то эта матрица внпкоясопределони, и, значит, по теореме 2.2 точка (0, 1) но является экстремальной. Если а = = —1, 6 >= 1, то /^(0, 1) положительно определена н, следовательно, но теореме 2.3 н точке (0, 1) достигается строгий локальный минимум. Этот минимум глобальным не является, поскольку lim /(х, 0) = — ©о.
2.27.	Примером служит функция / из 2.13.
2,29.	Примером служит функция / из 2,15.
2.30.	По определению обратного отображения имеем F~l{F(tx)} » х. Применял цогшее правило (2.5), получаем
=Я, у = Г(х),
где Е — единичная матрица.
2,31.	в) Имеем фЧ**) ==/Чу*)^Ч®*)» где матрица F'fx*) иовы-рождепа (см. 2.30). Поэтому условия фЧ**) ж 0 н /'(у*) = 0 эквивалентны.
б)	Пусть у*— точка локального минимума /, в х* не является точкой локального минимума ®. Тогда найдется такая но-слодоватолыюегь {хл} <= А', что lim х“ — х* и
k—<x>
ф(^) == /№л)) <ф(*Ч = /(/Ч**))-
Положнм y* = F(xA). Имеем lim y!l = у* = F (х*) и /(yh) <
Но это противоречит тому, что у*—-точка минимума /. Обратное утверждение доказывается аналогично. Доказательство Для точек глобального минимума еще проще.
в)	Ноиосредстиепные вычисления матрицы ф"(**) с учетом равенства /Чу*) = 0 приводит к формуле
ф'Ч**) =
Нужное утверждение следует теперь из 2.20, 2.30,
2.33,	Рассмотрим функцию /(х, w) =x’-hy’ — Зху. Опа имеет Две стационарный точки: (1, 1) н (0, 0), причем в (1, 1) достнга-
255
стоя локальный, по по глобальный минимум. Виодом множеств У«е{(1, y)|jf>0), содопжащео (1, i) и по содержащее (0, 0), п диффеоморфизм F: №-»-У лида F(x, у) (ж, с*). Построим функцию
ср (ас, у) s= f(F(x, у)) i= л3 + е3” — Зхе*.
Из 2.31 следует, что (I, 0) = F~I(1, 1) — ее однпстоелпая стадно-парная точка, д которой достигается локальный, по пе глобальный минимум. Впрочем, в атом нетрудно убедиться к псносредствепио.
Другим примером, получаемым из несколько иных соображений, служит функция
К I
ф (х, у) ю (Зл2 — 2л3) ev I --tH,
Л 14- г о
2.34.	Рассмотрим чнелопой мпогочлеп
ф(х) = (х- 1)(х —2)... (х-(2m -1))
в функцию
X
f id = J Ф (0 di + ?
о
на Д’. Ясно, что у / имеется — 1 стационарных точек вида (к, 0), гдо к » 1,..., 2гя — I. При этом > <Х если к нечетно, п ф'(£) < 0, если к четно. Следовательно, матрица
Г(А,',О)=[^ <>1 L ”
явлпстсл положительно определенной при почетных к и знак»* пеопрсделоплой при четных к. Итак, / имеет роано пг точек ло-
Рис. 69
нальпого минимума вида (t, 0), гдо к*= 1; 3, ..м 2m— i. Рассмотрим теперь миожестио
У == {(л, у) |созях < у}
(рпс. 69). Опо содержит все тонкп минимума / п по содержит ос*
266
-ильных стацпопарпых точек. Виодом диффеоморфизм F: К’->-У рпдл у)=(х, cos лх + еу). Тогда, согласно 2.31, (функция
в
Ф (®< У) = / (F (*> У)) ~ f (С М -Ь (cos лх + ev)2 о
вмоет ровно т стационарных тонок па R2, п псе они являются точками локального минимума. Таковыми служат всо то жо тонки (Я, 0), гдо к = 1, 3, ..., 2?л — 1, поскольку прп диффеоморфизме F они остаются «на мосте».
2.35,	Если в предыдущей схеме рассуищеппй взять функцию /(*, у) = cos лх 4- уг,
то получим функцию <у(х, у) = СО5 XX + (СОЗ ял 4- в’)’, удоплет-норяющут путному требованию.
(Отметим, что функция из 2.15, являющаяся ответом it 2.29, здесь ио подходит, так как наряду с бесконечным числом точек мпппмумп опа имеет бесконечное число других стационарных точек.)
2.30.	Рассмотрим в окростностп точки (х* 0) <= R* X R непрерывно дифференцируемое отображение F вида
F(x, 8) = ^'(х, в) =i /'(х) + е<р'(х).
Имеем F(x*. 0) *= /'(х*) = 0, прячем матрица F'x (х*, 0) = ]" (х*), будучи положительно определенной, перырождопа (см. 2.20). Тогда по теореме 2.4 о неявной функции существует единственная вектор-функция х(в), переводящая некоторую окрестность V точки ОеН в окрестность U точки х* и такая, что F(x(e),e) = = ф/(х(в), е)"Ез 0 для всех тек'; прп этом х(0) =х’>, функция х(в) непрерывно дифференцируема па 7 н
(0) = - [Z< (х*. О)]"1 F* (х*, 0) = -ХГ (х*)Г1Ф'
Таких! образом, имеют место свойства а) и в). Кроме того, нз положительной определенности матрицы /"(х*) и непрерывности х(е), /г'(х), ф"(х) легко следует, что при достаточно малых по модулю в Матрица ty* {* (e)t к) = /*(® (в)) + еФ'7 (* (®)) татке по-лоиептелыю определена, т. о. справедливо б),
2.37.	Функция /(х) = х1 имеет точку строгого минимума х*= 0, но /л’(0) =0, Функция ^(х, с) х4 —ex’ при в>0 имеет три стационарные точки: xi (в) « 0, х2(е) = Уе/2, х3(е) = —}’в/2. В первой достигается строгий локальный максимум, в двух остальных _ строгий локальный минимум. При этом limx{ (в) == 0 для с-»о
любого Г = I, 2, 3, п функции xj(e), xi(e) в пуле педпффороп-Нируемы.
2.36.	Нет, по верно. Рассмотреть функцию (х, в) =txa-f-cx8.
2.39.	х (в) = —	-J- о (в). Использовать 2.3G.
х	К
2.40.	х (в) = f -f- тр ел о (е>; у (в) = 1 -|- ел -|- о (в).
17
С- А. Ашманов. А, В. Тямохоа	257

2.41.	Рассмотрим отображение F(r, a) (г&П™, аеВ) со еле. дующими координатами:
(х* + аЛ -И г),	1=1,	ni,
<ар r>,	1 =л»*|-1,
Из условий теоремы следует, что Е яопрерыино дифферепцпру-?. мо в некоторой окрестности точки (0, 0)е R™ X Л, причем /''(О, 0)’= <= 0. п матрица ^(0,0), строками которой служат яокторм £{(**),	«ky+i’*"» fln, новыроящепа. Таким образом,
F удовлотворкот поем ‘условиям теоремы 2.4 о неявной функции. Поэтому существует такая л-мерная вектор-фупкция г(а) |«еП), что для всех достаточно малых по модулю а выполнено раиепсткп /‘(г(а)« а) => 0, т. е.
£<(х* 4-а/г }- г(а)) s= 0,	1=1,..,, гл,
<о£, г(а)> = 0,	£ = ж Ц-1, п,
п, кроме того,
г (0) = 0, г' (0) = -	(Q, 0)]"> F'a (0, 0).
Заметим, что
< (0. 0) = «/1 (**). *>.....<4 («♦) *)- 0.   I 0) « 0.
Следовательно,
0 = г- (0) = lim r(«kzr(°l = lim JM й-»о л а-» о w
§ 3
3.1.	Составим функцию Лагранжа
. Д= Хор + ?.(х’ + 1Р —Згу).
Выпишем в соответствии с принципом Лагранжа необходимые условия экстремума:
-^- = зЦх5-»)=о, ^ = х0+зхй=-»)=о, (/«и	V *f	V
г3 т Ji’“ 3xji =± о, (Хь 1) ф 0.
Яспо, что здесь ?. «/= 0, Поэтому можно считать, что ?. = —1. В током случае выписанная система имеет два решения:
1)	Э|/2, у = ’М,	= 3(“/4-3/з) >0;
2) х = у = 0, Хо.= 0.
Вычислим госсиап функции L по х, у:
258
При значениях из I) (и 7. « —1) эта матрица отрицательно определена. Тогда из теоремы 3.3 следует, что (i^S, j/^) — точка локального (»о во глоиалыюго) максимума. При значениях на 2) матрица //' является знаксшеонределешюм. Однако здесь нельзя воспользоваться теоромоп 3.2, так как градиент функции g(x, у) = с= Xs -|- у3 — Згу в топко (0, 0) обращается в нуль (см. ЗЛЯ). Чтобы исследовать характер этой стационарной точки, нолоя;пм х = «= fry. Тогда условие g(x, у) = 0 равносильно тому, что
3/г	3ft
х~ ^ + Г у~ Лэ-|-Г
Отсюда с учетом вида функции / ясно, что точка (0, 0) по является экстремальной.
3.2.	Учитывая, что ограничение линейно, моясно рассмотреть функцию Лагранжа вида:
L = -у х3 -{- “ у3 -|- ?. (1 — ах — бу).
Вышинам необходимые условия экстремума:
” = г- — 7л = 0,	— /,b — Q, лх-|-бу=1.
Бев труда проверяется, что я случае а Ф Ь эта снстома имоот два решения;
Zj = «1/2(йЗ/2 _j. b3^-t| р( „ ftiyj(rt3/2+ Ь3/2)-|,	_ (ЛЪ1 + ^2)-2;
хг = «’«- б3'2)-*, у2 = б'/’(б»'г - a3/2)-’, ?,г = (а™ -
Если жо а = Ъ. то решением служит только (х>,	7.,). Выпишем
гессиан функции Л по х, у и условие ортогональности (3.f):
ahl + bh^ = 0.
2А?
Прп данном условии имеем
<ZZ6, Л> = 2хб* -|- 2уЛ* = -р- (Ьх -Ь ау).
Величина бх4-ау положительна в точке (xt, yt) и отрицательна в точке (xj, у-}). Тогда из теорему 3.3 следует, что (xt, yj—точка строгого локального минимума, а (хй уг) (прп й =/= б) — точка стро-forp локального максимума. Если <г «= б, то в точке (xi, yi) Достигается глобальный’ минимум. Если же «#= б, то ии одни из двух указанных точек но доставляет глобального зкетвемуми.
ЗЛ Ясно, что можно рассматривать регулярную фушгцию Лаг-Рашка:
L = у г3 -J- у -г Ч- У2 ~ я).
Вы1лцщ!М необходимые условия экстремума:
= х2 + Ах = 0, -^7 = 1 +	= °. х~ 4- У® = “•	(I)
Я*	259
Если х t= 0, то у = ±)'в, X —ifу. Если же х '/- О, то х —д, у == —-X*-1 н № + Х~2 = л. При а <2 это уравнсппе корней но iniv-от, Если а 2, то корнями служат X i д, ) — ±6“*, гдо 6 =
1=8	4- V®2 — Таким образом, если 0 < « < 2j то система
(I)	имеет дна решении:
^=0.	4=-^;
/- 1
га =*' 0, </2 —	|/а, Лл — -р=".
Если «	2, то к ним добавляются еще четыре:
*3=“ь>	^з’3’ —Ь-1,
«4 = Ь,	л(1 = — Ь\
*(, = - ь“\ У5 = - &>	Х5 Ь-15
ХО = Ь~\	УС = Ь,	х0 = -ь_Ч
Вычислим гессиап фупкцни L ио х, у:
1’2* -KJTo’l “1 о .'11'
Эта матрица отрицательно определена при (дц, р(, XJ и положительно определена при (хг, у2, Х2). Следовательно, (х1( у() и (®й у?)—точки локального максимума и минимума соотвотстпдн-ло. Для анализа остальных стационарных точек выпишем условии ортогональности:
2х/ц 2jr?i2 = 0.
При данном условии н условиях х ₽ — X, у == —X”1 пмоем
<Ь"Л, х> = (2х Л) Л® -L Ml = X (Х4 - 1) л=.
Положим <р(Х) =Х(Х‘— 1). Пусть я >2 и, значит, &>1. Тогда <р(Х3) >0, <р(Х<) <0, ф(Х5) <0, <р(Х«) >0. Отсюда и силу» теоремы 3;3 заключаем, что (х;, Pi) и (я®, у&)— точки локальиогй минимума, a (xt, у4) и (xj, yj)—точки локального максимума,
Пусть теперь а = 2 п, значит, b os 1. Тогда указанные четыре решения осливпются» п два:
= !/j = —I, с= 1» s IM — Х4 = —1.
При атом Ч'(Х3) ая ср(Х4) = 0 н, значит, теоремы 3,2, 3,3 аоиршш-пимы. Для дальнейшего анализа данных стационарных точек цероидом к иолирпым координатам:
z s= Д/2 соз 4'( У V2 sin i}>,
F (ф) ±а / (X, У) = У 2 I -g- COS3 Ф -h sin l|»j.
Тонко (—1, -I) соотпотствуот угол ф = 5л/4, точке (1, 1) — yi";1 ±а л/4. Непосредственные вычисления показывают, что при эти*
260
ф рыло.чпоио F'OIO	= О, ПО «/> 0. Тогда п силу 2.4
«кэзвииые $ н0 sioryt быть точками локального экстремума функ-ддн ?’(Ф) Иа Р’ “"Ч- Н° 1)70 означает, что (—1, —1) и (I, I) но „иляюгся точками локального экстремума функции /(х, у) ирп VCJE0HI14 X14- у5 — 2.
Обратимся теперь к вопросу о глобальных экстремумах (которые существуют но теореме Вонсрштрасса). Если «=С 2, то, как доказано, (хь yj — единственной точка локального, а значит, и глобального максимума. Пусть « > 2. Вычислим значения / в точках локальных максимумов:
/(*r	/(*4. ь-а - 4 *з+4 • f(жб> tfs) < °-
Отсгоди следует, что максимальным значением / является
/* = max р/«, 4 4’ 4}*
- t 1
Оно дос типе г гя при (хь yi), если V«> з*&34-у, н при (х<( у<) п противном случае. Отметим, что оба этих случая возможны. Например, если взять а близким к 2, то точкой глобального максимума окажется (xi, у>); если жо а. достаточно велико, то ею будет (х<, у<). Рассуждения для глобальных минимумов аналогичны.
3.	4. Без труда проверяется, что градиент функции у(х, у) = = 3х1— 4 cos у — 1 но может обращаться п нуль для точек (г, у), удовлетворяющих условию g(x, у) =0. Поэтому moikho сразу рассматривать регулярную функцию Лагранжа:
L = х siu у •{* Л(Зхг — 4 cos у — 1).
Выпишем необходимые условия экстремума:
QL	дБ
= sin у -{- 6Хх i= 0,	= х cos у 4- 4Л sin у 0,
Зх3 — 4 cos у — 1 = 0.
Отсюда находим, что х3 !, cos у = !/2. Следовательно, имеются четыре группы стационарных точек:
1} х = 1, у = л/3 -|- 2A-n:
2)	х ев —I, у >=£ я/34- 2 Ал;
3)^=1, у = -л/3 4- 2 А-л;
4)	х =г — (, у l= — л/3 4- 2 Ал,
где к = 0, ±1, ±2,	Заметим, что функции f пмеот точки гло-
бальпгло максимума и минимума па множестве g(x, у) иО (поскольку это множество ограничено при дополнительном условии Q У 2л, по илпг)к>л(ем_на ,чпачоння / н g). По / =а 7'3/2 в любой точке1 no 1), 4) п / = —)'3/2 в любой точке it:i 2), 3). Следоаатель-4) суть точки глобального .максимума, а 2), 3) — глобэльпо-г° минимума.
э Градиенты функций из ограппчоннп задачи равны (2х, *У< 2:) ц j( j)b эг(1 декторы лппеппо зависимы лишь в случае j- ”=> у = Но точки вида (х, х, х) по лежат в допустимом чвежестоо. Следовательно, можно рассматривать регулярную
201
функцию Лагранжа:
L «= хух 4- Цх3 + л= 4- s’ - I) 4- и(х 4- у 4- s -1). Выпишем необходимые условия экстремума:
дБ дх	= yi 4- 2л« 4' 11 — 0>	0)
дБ ду	= xs 4* 2ху 4~ И =	(И)
дБ di	— ху -|~ 2XS 4- И — °,	(1П)
	** 4- У3 4- а2 = 1, х: 4" У + ’	!	(IV) (V)
Из (I)—(III) имеем
(х-р)(2Х-х) «=0, (у-:)(2Х-х) =0, (;-г)(2Х-у) =0.
Как отмочено выше, случай х =* у = s здесь невозможен. Поэтому случай х у, уф:,:^=х также недопустим. Таким образом, могут представиться лишь следующие три случая: х = у =/= г, у =-> = з<й=ж, - = х =/= у. Пусть х «= у gfc г. Тогда х = у = 2Х и, значит, ;= 1 —4?. и силу (V). Теперь из (IV) следует, что 8/Л-|-4- (1 — 4Х)3 = 1. Отсюда 7. = 0 или ?. =я 1/3. В результате находим две стационарные точки:
zj |= У1 ея 0, 2|	1; хг = yj = 2/3, гг = —1/3.
Рассматривая остальные два случая, находим еще четыре стационарные точки:
х3 =1, уз = =3	0; х< = —1/3, уч =э ;< = 2/3;
ха = se = 0,	у<, ея 1; хо = so = 2/3, 	уо =* —1/3.
При этом
fix и, х\ = 1 0*	1=1, 3,5,
>) 1 — 4/27,	1 = 2, 4, С.
Поскольку глобальные экстремумы существуют, то (ж<, у<, i<) при 1= 1, 3, 5 (1о2, 4, 6)—точки глобального максимума (минимума).
3.G. Составим регулярную функцию Лагранжа:
L = /(х, у, s) 4- М*а 4- У2 4- s’ - 1).
Выпишем необходимые условия экстремума:
^ = 2х (еГ — 2я (ох2 4- by* 4- с?) 4- ?,) = О,
= 2у (Ь2 — 2Ь (ах2 4- by2 -Ь “') 4- X) = 0,
= 2г (с2 — 2с (ах2 4- by- 4- cs2) + X) = 0,
4- у! 4- =’ = 1.
Укажем находимые отсюда стационарпыо точки и значения в Ш’* функции /:
262
I)	X = У га 0, sra±f, / &= О;
2)	X = 2 = 0, у = ±1, f = 0;
3)	«=• ±1, №Z = O, / = 0;
4)	х — 0, у = £ = Ч;	(б с)” >
5)	х = 3-± —, у —О, /=у(а —с)2;
6)	* = У ~ ± р-р г = 0, / = “ (« — Ь)2.
Отметим, что точки глобального экстремума существуют, Соло-ставили приведенные значения функции /, приходим к выводу, что. и точках из 1)—3) достигается глобальный минимум, в точках ив 5) — глобальный максимум. Остается проанализировать точки из 4) к 6). Возьмем, например, точку (0, i/V'2, 1/)'2). Ен соответствует д,= Ьс. Вычислим при данных значениях гесснвп функции L по ’ 2:
Условии ортогональности приводит здесь к соотношению Лг4-Лз = в 0. С учетом этой связи имеем
’ 4 <£*А, Л> = (а - b) (а - с) h* - 2А3Л= - 2<?2А* - UchJ^ =
=(а - Ь) (а - с)Л* - 2 (Ь - с)2Л|,
гдо, заметим, (а — А) (д — с) > 0, Следовательно, форма <£"А, Л> мснкот_при1П1мать разные злаки. Тогда по теореме 3.2 точка (О, l/J'2, 1/]г2) не является экстремальной. Аналогично показывается, что пе являются экстремальными другие точки из 4) и 6).
3.7.	Для точек (х, у, г), удовлетворяющих указанному равен-Стлу, имеем
/(х, у, с) = (х у -J- г)« -И х + у + z — 1.
Положим u = x4-y-f-z. Тогда задача сводится к отысканию то-ЧОК Экстремума функции tp(x, у, и) =к34*и прп ограничении
-г У2 + и — х — у = 1, котороо мо;кпо записать также в впде
(х-1/2)г+	=3/2,.	(I)
Ясно, что (х, р, к.) е= (1/2, 1/2, 3/2)—точка строгого локального иаисцяума, а любая точка (х, у, —1/2), удовлетворяющая условию
(x-l/2)2+(y-W = 2,	(II)
есть точка нестрогого глобального мпппмума функции ф прп огра-юпепкц (j). Следовательно, (х, у, г) е= (1Д 1/2, 1/2) —точка стро-.°ро локального (но по глобального) максимума, а любая точка 1?, г), удовлетворяющая условию (II) и равенству х-Р У + = ==
203
= —1/2,—точка нестрогого глобального минимума исходной: функции У при ограничении х2 -Ь р2 + = 131 1-
3.8.	Приведем три одинаково поучительных доказательства.
Доказательство, осколки нов на исключении переменных (классическое). Пусть градиенты ffj (**), ..., g^(x*) линейно зависимы, т. с. существуют числа у±, ..., не рапные нулю одновременно и такие, что
ГЛ
У u's'i (z*) = 0.
i=i
Тогда число Уд = 0 и иоктор у* = (у*....у* ) удовлетворяют ус-
ловию (ЗЛ).
Тоиорь рассмотрим нетривиальный случай, когда указанный градиенты линейно независимы. Положим (1(х) = (g-.(x), ... .,,, £т(я:)). Тогда rangG'(x*) = m, и бон ограничения общности можно считать, что первые m столбцов матрицы G'(x*) лппейио независимы. Разобьем вектор j: на две части: х = (и, г), гдо и= (хь .... хт), к = (хпнь .*п). Отображение <?(«. и) удовлетворяет всем условиям теоремы 2.4 о неявной функции: оно ио-ирврывпо дифференцируемо в окрестности точки («•, в*), где «• = (а£,\х*™), р- =	**), причем G« к*) = О,
а матрица G't («*, а*) пепырождена. Поэтому существует такая т-морпая пскторфункцпн u(p) (pg TV1”’”), что для всех к, достаточно близких к t>e, иыиолвспо
G(u(v), ») =0	(I)
и, кроме ТОГО.
H(p*)=u\ и' (а*) ^-[g„(«*,	(«», а*). (II)
Вводом функцию /г(г.‘) =t/(к(к), у). По условию точка х* == = («•, v*) является локальным решенном исходной задачи (3.1). Отсюда с учетом (I). (II) легко выводится, что г* ость точка локального минимума функции F(k)- Используя цепное правило дифференцирования (2.5), а ташке (II), получаем
О =т F’ (₽•) = < («•, а*) «' (о*) + /' («*, ₽*) ==
- - /,; («*, »•) [g; (W, о’)]-1 ^(н*, а*) у' («•, а*). (Ш) Вводом т-мерный вектор
.'/♦ = - У,', («’, »*) [<?ц (“% ₽*)]“’•	<IV)
Тогда (III) можно иерипислть в нпде
у; (к*, о*) -|-у*< («*, й*)=о.
При :>том само равенство (IV) рапкосплг.но следующему:
Уи (»*,«•) d-У*<?и (»‘,?*) = 0-
264
Последние два рлиопстяа, взятые вместо, означают, что {'(**) -f- r/*G'(x’) =» О,
т. е.
/4 (**. 1, »•) = г (*•) н- 3 y*s\ (-«♦) ~ о.
(рз!
Доказатсдъсгво, осноояпнос на теореме Лгосгернпка. Пусть грд-диоиты gL (ж*), ...,	(»♦) линейно независимы (в противном слу-
чае, как отмечено выше, теорема тривиальна). Рассмотрим систему линейных уравнения относительно А Rn:
</'(«♦), A>e-1,	(D
<ffj («♦)»*> = 0,	.....m.	. (II)
Предположим, что она имеет решение Л. Тогда но теореме Люс-терпикв (см. 2.41) найдется такая п-мерная поктор функция г(а) (йеИ), что для всех достаточно малых но модулю а выполнено
( tft(z* + aA + r(a))«0,	1=1,(III)
и, кроме того,
/t.nn~^ = o.	(IV)
й-»о
Равенства (III) означают, что точка х(«) = х* + alt-|-г(а) й»лл-отся допустимой и задаче (3.1). При этом с уютом дифференцируем ости / в ж* имеем
/ (* (а)) ~ / (**) = </' (**), «А + г («)> -|- о (а) =
I\ I /и 7 *1 Г(а)\ , °(ИЛ - “ ^</ (х*), А> -|- ^/' (х*), -Ь
Отсгодэ н из (I), (IV) следует, что }{х{<х}} </(«•) при всех достаточно малых а > 0. Мы нр>ннлп к противоречию с том, что х* — локальное решение задачи (3.1). Таким образом, система (I), (II) по имеет решояня. Но это возможно лишь н том случае, если ринг матрицы данной системы меиьше гл -I- 1, т. е. иокторы /'(ж*), #'(af»), ...,	(ас*) линейно зависимы.
Деказатсл^тео, основанное па штрафных функциях (прп дополнительном нредно.южепшг, что функция / испрорывпо дифференцируема в точке х*). Поскольку х* — локальное решение задачи (3.1), то существует столь малое число я > 0, что ж* есть точка глобального минимума / па У «= A' fl 1/е(х*), где, напомним, X обозначает допустимое множостло задачи (3.1), а 1/г(х*) — шар радиуса & с центром и ж*. Для любого А = 1, 2, ... введем функцию
m
4 = f 4- * S 4 (*) 4- И * - Г-. f=i
Пусть ж* —точка глобального минимума /д(х) па Ut(x*), существующая ио теореме Вейорштрасса. Без ограничения общности бу-
205
дом считать, что последовательность {**} сходится к некоторой точке S <= Ut(x*).
Для любого Л- == 1, 2,... имеем А(хк) АС**), т. о.
тэт
/(xfe)4-fc 2	—Х*[р< Дя»).	(I)
1=1
Отсюда слодует, что
ff{ (я) = Iimg{ (xft) =0, issl, ..., m. ft->50
Таким образом,’X eX f| Ut(x*) = Y n, значит, ^/(x). Отсюда и из (I) получаем
/(x*) 4- Их* — х*||г</(х).
Переходя здесь к пределу, убеждаемся, что х = х*. Итак, Вт хк = х*. Тогда при всех достаточно больших Л имеем г* s Л->оо ешК/Дя*) и, значит, /£(х*) = 0, т. о.
ш
/' (а*) Н- 2k 2 g{ (?') gj (хл) -j- 2 (xh - я*) = 0. (II) I=>1
Введем числа
у}»(i-н*4 2	(**)]
\ i=l /
(m	\ —i/a
1 4“ 4fc2 2 *1 (x&) I I«1	/
i = 1, m.
Тогда (II) можно переписать в виде
4/' <xft)+2 У& И + М (** ~ **) = 0-	(Ш)
i=i
Поскольку вектор (у£, I/J, •••>1^) легкнт па единичной сфере в R’n+I, то без ограничен и л общности можно считать, что при любом (t=0, 1, т последовательность (у*] сходится к некоторому числу у*, При атом (у*, у*,	у*) =?ь,о7 Переходя к пре-
делу и (III), получаом (3.4).
3.9.	Нет, пе следует. Простейшим примером служит задача z2 -»* min, х3 = 0.
Можно указать и мепео трпопальпый пример:
/ (ж) = min, gj (х) = х| 4-я®— 1 =О, ^<1)=я1^з:2 + *з’"1 = 0’ х = (х1* хг’ *з)-
260
Точно s* = (0, 1, 0) является глобальным решением этой задачи. При этом градпепты = (О, 2, 0) п g^ (.г*) = (О, 3, 0) липой и о зависимы. Составим функцию Лагранжа:
L = WW +	+ У1£«(*)-
Вышпием необходимые условия экстремума:
= 2уЛ + 2уЛ + Зу„.т| = О,
9L
Их~ = 2^^ Зул2 = О, а
Ц“ = Зуах® — 0.
Прп z в х* здесь моиспо взять любое уо, а также любые yi и у3, удовлетворяющие уело лито 2у> -Ь Зг^ е= 0.
3.10.	Пусть У* = 1, у* я ft удовлетворяют условиям (3.4), (3.6) (случай у>0 легко сводятся к данному). По теореме Люсгор-шлю существует такая п-моряая воктор-фупкцпя г(а) («ей), что для’ всех достаточно малых по модулю а выполнено
£{(ж(<х)) = О, i со 1, .... лч,	(I)
где х(а) «= я* + aft 4- г(а), и, кроме того,
" lim-““=0.	(II)
а->0 а
Ия (I) следуот, что
L (х (а), у*) 2= / (х (а)) j} yfa-tx (а)) = / (х (а)).
fra}
Аналогия «о £(х*, у*) = /(**). При этом /(«•)	/(х(а)) для всех
достаточно малых по модулю а. Положим Л (а) «= я (а)—х* = «я аЛ -|- г(а). Тогда, используя (3.4), имеем
0С / (х (а)) - / (х*) - L (х (а), р*) ~ L (х% у*) =
<**, У*)> Л («))+ 4 QJx(1*' h А “Ь ° “
“ 4	(х*’ h (аьь +° (®2)’
Отсюда
'‘+^)+-WU-
Переходя здесь к проделу с учетом (И), получаем (3.5) (при 1).
267
3.11.	Подходит любая из двух задач, приведенных в ответе к
3.9.	Покажем ото для Полоо сложной второй задачи. Имеем
Поставим в соответствие решению х* » (0, 1, 0) множители у*=1, у* = — 3, у* = 2, удовлетворяющие условию 2у* -{- Зу* = 0. При этих значениях получаем
0 О’ в 0 0 0.
Условно ортогопальпостп сводится здесь к равенству h2 = 0. Но при А = (Ai, 0, А3), й| Ф 0, иелнчипа ty = ~/,!1 отрицательна.
3.12.	Пусть х* по является строгим локальным решением зада* чн (3.1). Тогда пайдется последовательность {х*}, удовлетворяющая услоппям
x*e.Y, х* х*. х*->х*г /(х*)	/(х*).
Представим х* в виде
xh х* 4- где а& — [| xft — х* 3,	= ~-(xft — а-.*).
Поскольку ||А*|| = 1, то без ограничения общности можно считать, что Afc->- h & 0, Имоом
0 = gj (агА) ~ £г 1>*) =	(г*), аА/?') 4’ о (ah), I = 1, ..., п>.
Поделив эти соотношения па а* к перейдя к пределу, получаем (3.6). В то ясе время с учетом условия (3.4) можем записать 0 > У*/ (xh) — y*f (х«) = L (х\ у*, у») — L (х*, у*, у») =
=* 4 {L* (**’ & **)	«лА*> + ° («*)•
Отсюда
Ah
Пороходя здесь к пределу, получаем противоречие с (3.7).
3.13.	Это следует пз самой теоремы -3.3. Если в ее рамках у* = 0, то х* является строгим локальным решением по только задачи (3.1), по п задачи мапепмпзицвп топ жо функция па том же мпоячсетво. Это возможно лишь в тривиальном случао, когда х* — изолированная допустимая точка. Примером служит задача
z1-+min, xj-h4 = lt *i + *3 = 1
и ее иэолиропашшя допустимая точка (0, 1).
268
З.И. Задача имеет решение я** *(ж*) в силу теоремы ВоГгер-штрлссй *). При этом из лида целевой функция ясно, что ж* > 0. Следовательно, принцип Лагранжа здесь применим. Перейдем к эквивалентной задаче максимизации логарифма целевой функции. Поскольку задача регулярна, ое функцию Лаграгпка можно записать в виде
L=“ ;=1	\i=i	/
Выпишем необходимые услевпя экстремума:
st	в—i
^=-'4 + ^7 -°, /=1.......................  (D
2}в^ = Ь, Х;>0, / = !......п.	(II)
i<“i
Из (I) выражаем xj через у:
/ cs> \VA>"
' }°1.......”• (Ш>
Подставляя эти выражения и (II), пэходнм множитель Лагранжа
It " ji	, ССа
у*=“ трр А= V-дД- Подстаияяя у = у* в (III), получаем b	& PJ
стацноиорпую точку задачи:
# / <Xjl> \1/fV xs = J
Таи как эта точно единственна, то опа я является решением задачи.
3.15. Целевая функция задачи является бескопочпо растущей па допустимом множество. Тогда но теореме 1,2 решение задачи существует. Из вида ограничения-равенства ясно, что г* > 0. Применяя принцип Лагранжа, убеждаемся, что единственной стацпо-яарной точкой, а значит, я решенном задачи янллотсн востер
**=(ж*)> гдо
р yw/ ib V/gJ
U/	1
n
ЛаЙ
Г=1
Oj/a;
*-2
J=1
*) Здесь и всюду далее в указаниях к § 3, если пе оговорено противное, под решением экстремальной задачи понимается глобальное рёшопио.
269
3.1G. Здесь, кик п выше, целевая функция нвляется бесконечно растущей па допустимом множестве. Поэтому решение задачи существует. Им является едппствеипая стационарная точка х* =
а..?, х«=0), *;=4(-£	,
3.18.	(Пункция /(/) = /а удовлетворяет условию lim /' (Z) = оо.
Поэтому' из 1.25 следует, что решение х* данной задачи существу’ от. Проводя стандартные рассуждения на оспою принципа Лагранжа, получаем, что
3.19.	Поскольку а четно, то целевая функция является бесконечно растущой. Следовательно, решеаие задачи существует. Составим (регулярную) функцию Лагранжа:
п	/ п
ь — 2 cj^j + у * — У, J—1	\	Л=>1
Выпишем необходимые условия экстремума:
“ =	- уа; = О, / ~ 1...п,	(I)
п
3«rt = i..	(П)
J=I
Учитывая, что а — 1 нечетно, из (I) однозначно выражаем xt через у; ,
/ул, xi = ас> J
/ = I.........
(Ш)
Подставляя эти выражения в (ll)t находим множитель Лагранжа:
/ ь
где
п /а«\хЛа-1}
^2	>о.
J=1 '
270
Подставляя у — у* в (Ш), получаем стационарную точку задачи:
Так как эта то’пга одннстнениа, то опа и является решением задачи.
3,20.	Решение задачи существует, так как со целевая функция является бесконечно растущей. Составим (регулярную) функцию Лагранжа:
L = 2 ejI *j Г 4- * - 2 е/;) j=i	\ j=i /
Отметим, что функция ср(О = |/|в, где а> 1, является всюду дифференцируемой, прпчом !/(/) = ар|а-* sign t. Поэтому принцип Лагранжа здесь применим. Выипшем необходимые условия экстремума:
= acj | ж,- |а-‘ sign — уа} = 0,	/ = !........  (I)
j
ri
2 =ь-	<“>
j=i
Заметим, что здесь у ф 0, так как Ъ #= 0. Рассмотрим два случая: I) у > 0. Тогда из (1) следует, что signxs i= sign к/, n поскольку aj = | a; | sign gj, to
acj|xj|’1"1 = p|aj|, / == 1, n.
Отсюда
/ у I л. I
= ( ‘ ctej") sign*>,	<ш)
Подставляя t)nr шаражепня в (II), получаем н 2l»H j=l
Решей нем этого уравнения служит
Подставляя у = у* н (Ш), получаем стационарную точку задачи: .	/ I д,|
г* = (х?),	Signe.. (IV)
271
2) у < 0. Тогда sign Xf =» —sign д/. В этом случае приходил к уравнению
JI
-у|а?-|\1/(а'”П ас. I

которое пе пмоот решения, так как Ъ > 0.
Таким образом, единственной стацпопарпоп точкой п, значит, решением задачи л винетен (IV).
,21.21. Обо экстремальные задачи имеют решении по теореме Войорштрасса. Боз труда показывается, что их стационарными точками служат л* = (xj j ц —х*, где
•=‘'1	, л = у„, (_i	>о.
'•Л> \“J	‘ я’Ь,/
(При проверке этого следует учесть, что уравпоппе вида ^«“Чга = « > 0, где а —четкое число, имеет два корпя: у <= ± а^1^.) л:
Заметим, что У, CjX* >м0. Следовательно, х» и — х* — решения i
задач макевмнзацип и минимизации.соответственно.
3.22.	Решоипями задач максимизации и мниимизпцип явлпют-сл соответственно точки х* (х*) п — х*, гдо
в
♦ I b\^af\ С:| УЛ®^)
:*= 4 V sign^’
«/<«—!>
х ai /
,=--1	\ J /
3,23.	Обе экстремальные вадачн имеют решения по теореме ВсГгерштрэсса. Составим (регулярную) функцию Лагранжа:
п	/ п \
j=i	\	5=1
Выпишем необходимые условия экстремума: дГ. dxi
(II)
|“ 1 sign (х; -|- с.) — уа | л, р-*1 sign х. — 0, (I)
/ - 1...".
11 2Ы“=^
Из (1) следует, что %} = ?.cj (/ = 1, ..., л) при некотором ?.. В самом деле, если х/ = 0, то в (I) ио необходимости tj = 0, Поэтому указанное ривенство справедливо при любом Пусть xj */*
=~= 0. Тогда (I) можно переписать и виде
a-i sign
9
^-1=1/.
272
Отсюда очепндко, что cj/xj — 14 где |i = |f/||/(e-,>sign у — 1. Если ц к= 0, то у = I. Но тогда система (I) аляедомо нс имеет решении, так как с = (ci, ..п е„) & 0, Таким образом, р #= О, и остается колотить 7. •= 1/ц.
Подставляя теперь х, = Xcj u (II), находим
Х = ±(4)Х/“. ГЛ° '1 = 2Ы“
Таким образом, стационарными точками обоих задач являются х* = (**) и —х*, где
*	( Ь W"
А} *
Подставляя эти точки в целевую функцию, убеждаемся, что х* и —х"—решения задач максимизации п минимизации соответствен ио.
3.24.	Решении задачи существует в силу теоремы 1.2. Составим (регулярную) функцию Лагранжа;
п	7 n \ f «1^
L=4 2 -I- К - 2 ядЛ и- ы \ - Жл-
r-1	\ iaL /	\	7=1
npiipiumiiiiafi к пулю ее частные производимо по х}, получаем
= Wil -I- IMij, J = 1, ..., п.	(I)
Подстпилпл гни выражения в ограшг'мпшя задачи, приходим к системе относительно yi и
РУ1 + fill = &i, гу> 'I' № m Ьг,
где у = <«!. Я1>, г <«i, да), q <aj, я3). Поскольку щ и «2 линейно независимы, то /и/ > г2 в силу цорвионстиа Коши — Бупн-ковского {саг. 3.65). Следовательно, система имеет одинствсиноо решвпяц:
Подставлял эти иыражошгя в (I), получаем решение задачи.
3.25.	Решение видами существует в силу теоремы 1А. Составим (регулярную) функцию Лнгрпшка':
1
7. (х, у) == у <Сх, х> -5- « х> -|- <у, b — Лх>.
•Прпра вином к нулю ос. град поит no х: Сх -|- d — у А = 0. Отсюда с учетом 2.2U имеем х = С“г{уЛ — d) = С~'Ату — C~'d. Подстап-ллл ;>то nijpiisKcirirc в систему ограничений к ипопь учитывая 2.20, получаем у =; [ЛС"[Лг)-'г(б-f-Лб'-^/). Следовательно,
х* = <7-1Лт[/1С'-1Лт]-1(Ь 4- ЛС“^) - c-'d
единственна)! стационарная точна задачи. Ока н явлнотся ее рошин нем.
18 С, л. Ашманов. А. в. Тимохов	273
3.26.	Petnonuo д:*._вычисляотся по полученной выше формуле при С ЯТЯ, d 1= В частности, если Л = Е, то
z* = 5 — Лг [Z/P'J “1 (45 — Ь).
3.27.	Нот, не являются. Применить теорему 3.2 с учетом того, что собственные лекторы симметрической матрицы, соответствующие различным собственным зпачопням, ортогональны.
3.28.	Составим (регулярную) функцию Лагранжа:
X(z, у, X) =s (« 2)s — 2у Х(«(х + сх) 4- Ь(у -г «у) — 1)
и выпитом необходимые условия экстремума и точке (О, 0):
(0, 0, X) = а 2 4- U (1 + «х) |(0,0Д) = л 4- 2 + 2Аа = О,
(О, О, X) - - 2 4- ХА (1 4- *v) |(О>о,у = “ 2 4- 2X5 = О,
(а (х 4’ с*) 4- й (У 4-У)) |(о,о) = а + b ~ *•
Эта система имоот два рошепия:
1)	а = -1, Ь = 2, X = 1/2;
2)	а = 2, 5 «= —1, X = —1.
Вычислим гессиан функции L по х, у в точно (О, О, X):
Для вектора А = (1ц, Аа), удовлетворяющего условию ортогональности ahi 4- bhs = 0, имеем
<ZZA, Л> = X (яй[ 4- W*“) = ХА 4- i)
Если Аг>#0, то величина <£"А, А> отрицательна яря значениях из 1) и положительна прп значениях нв 2). Тогда но теореме 3.3 в точке (0, 0) достигается строгий локальный максимум, если а ~ = —1, 5 ±= 2, ц строгий локальный минимум, если а = 2, b = —1. Более того, в каждом нз двух случаев точка (0, 0) является точкой глобального экстремума. Докажем это, паирнмор, для случая а = —I, А = 2. Пусть (х, у) удовлетворяет условию
—(г 4- с’) 4-2(1/ 4~ е’) = 1.
Требуется показать, что х — 2у 0. Допустим обратное: х > 2у. Тогда
2(у *f* es) — 1 = х 4- eY > 2у -b c4u.
Отсюда приходим к противоречивому неравенству 2 > сУ 4- е“и.
3.29.	Составим функцию Лагранжа:
L(ii у, X) «= ж14~ а2 4* by14“ X(s* — жу 4" у’— О*
274
Hbtirnirrc.M пеобходнмып условия экстремума в точке (0, 1):
OL
(0, 1. X) = 2х а 4- X {2х—у) |((мМ = а - к О,
— (0,1, X) = 2Ау -|’ X (- * -I- 2'/) l(o,IД) ^2(Н«= 0.
Таким образом, точка (0, 1) является стационарной при любых таких а к б, что « + Ь = 0, причем X = а — соответствующий мио-житель Лагралзка, Выпишем гессиан L но х, у и. точно (0, 1, ?.) при указанных а, Ь и X:
.,_р + 2Х -X 1_Г2(1 + <0 -*1 ь “[ -к 2&4-2aJ“[ -a 0J’
условие ортогональности в точке (0, f) имеет лид Л> = 2AIf Еслп вектор h = {hi. А») удовлетворяет этому услояшо, то
<МА, А> = 2(14- а) А- - 2q/4jAa = (2 я) Ар
Слодовательпо, (О, I) является точкой строгого глобального минимума (максимума) прп любых таких «г и б, что а > —2 (соответственно я < —2) к ft = —«.
Остается рассмотреть случай а = —2, А = 2. ypaanenne кривой хг — .ту -|- у* = 1 можно записать в следующем параметрическом виде:
. 1 .
X = cos ф 4" 47? s,n Ф» г **
1 .
у = СОЗ ф — S1n ф.
Прп этом точка (0, i) соответствует значение параметра Фо = —п/3. Подставляя указанные выражений в формулу для /(х, у}, получаем функцию
F (ф) = 2 4- у= е os ^2ф 4- -у) — с оз |ф - -jj-J.
Ее, очевидно, можно разложить в ряд Тейлора в толке ср*. Тогда, Поскольку эта функция но является постоянной, хотя бы при одном А должно выиолият’я Г(П) (фо) В. Заметим, однако, что (ф) == cos ^2ф 4-	4- соз (ф —
рю а*, рл — некоторые числа, и, значит, ^“Чфо) =0 при всех А. Следовательно, ?’<»+>) (ф0) г/, о хотя 6e,i при одном А. Поэтому точка фо но является экстремал!,поп для F(cp) (см. 2.4). Таким образом, и случае д яа — 2, Ь — 2 точка (О, 1) не является экстремальной для функции /(х, у) при указанием огракпчопип.
3.30,	Рассмотрим задачу
/ (®) =	-> mitl> <Cx> > О, II «1 - 1-
18*
275
Ясно, mo функция / является бесконечно растущей па допустимом многкествб задачи, Следовательно, задача имеет глобальное решение ж*. Возьмем любое число X > —/{»*). Тогда для любого ж. удовлетворлющего условию <Сх, г> >0, имеем /(ж) ^/(х*) >—X. Отсюда путем простых преобразований получаем, что
<(A + XC)x,x>>0.	(I)
Для остальных ненулевых ieR" (и силу неотрицательной определенности С) выполняется (б>, х> = 0. Поэтому дли них по* равенство (1) следует из условий задачи.
3.31.	Условно Вх = 0 равносильно тому, что
0 = ||2?х||3 еэ Вх) = <ВтВх, х).
При атом матрица ВТВ неотрицательно определена (см. 2.20). Тогда ц» а) следует б) в силу теоремы Фипслера (см. 3.30). Обратное очевидно.
Пусть rang В = гл я выполнено а). Допустим, что матрица С вырождена, т. о. существует такой вектор (х, у) 5* о, что
Ах 4- JFy » 0, Вх = 0.
Если х = 0, то Вту ез уВ = 0, и, значит, у = 0, так как rang В еэ = Л1. По это невозможно, Следовательно, х Ф 0. Имеем
<-4г, ж> = — <.Вту, з> =* — <у. Вх) ±=s 0.
что противоречит п). Таким образом, в) справедливо.
3.32,	Из 3.31 с учетом критерии Сильвестра выводим, что условно а) равносильно следующему: дли всех к = 1, ..., л к всех достаточно больших ?.
dol(.4ft-{-XB^Z?;()>0.	(I)
Заметим, что
А мТл о
о
Е,п
4


где J-ui и Л'ь— единичные матрицы размори m X г» п X-X Л codt вотствснно. lf:i известных cnoiicTii определителей имеем


det

0 1
Поскольку определитель произведения двух матриц равен произведению их определителей, то
del (Лй- |-M>fo) =
A irT П	ГД
7 «(-l)mXmdol
Sb ” £m J
I* ®Г
IA
= (-“ l)m det
(И)
276
Отсюда и нз (I) легко выводятся требуемые утверждения. Прп атом следует учесть, что определитель является непрерывной функцией слоях элементов,
3,33.	Пусть ужо проведены при m “ 1 рассуждения из решения предыдущей задачи вплоть до первого равенства в (II). Далее очевидно, что
4
— dot
= dot Ah — ?Лд.
— 1
Таким образом, условие а) равносильно тому, что dot Ль — Х6* > О для всех Л = 1, л и всех достаточно больших X, Ясно, что в свою очередь это эквивалентно условию б).
3.34.	Эго немедленно следует из 3.32 п теоромы 3.3.
3.35.	Поскольку rang S « га, то в (3.4) заведомо у* 7'-’ 0, н можно считать У* = 1. При этом (х*, I, у*) =/’(х*). Остается псполь:1 опить 3,31.
3.3G.	Рассмотрим п окрестности точки (х*, у*, 0) eR"XK”X X К* непрерывно дифференцируемое отображение в R1* вида
Л’ (х, у, а) =	(.г, у, а).
Цо условию Fix'*, у*, 0) =0, G(x**, 0) =0. Матрица Якобн отображения (/’’, б'): R” X йя X R*-»-К'1 X Hrrx по координатам вектора (ж, у) в точке (х*, у*, 0) имеет вид
Вг
or
гдо И = Lx (ж*, у*. 0), В = Gx (ж*, 0). Поскольку rang В = т и (ЛА, А) > 0 прп всех таких h Ф 0, что Bh = 0, то матрица-С не-пырождоиа и силу 3.31. Таким образом, для отображоппи (F, G) п точки (ж*, у*, 0) выполнены все условия теоремы 2.4 о неявной функции. Поэтому существуют единственные функции х(&) н у(е), всцЮЕюдлщно но которую окрестность V точки 0^R* в окрестности U n IV точек ж* н у* соответственно, и такие, что
ЭДе), у(е), е) ₽ 0, G(x(e),e)=0;
прп атом функции х(е), у(е) нопрорывпо дифференцируемы па V и ж(0) = х*, у(0) = р*. Таким образом, они обладают свойствами я) и в). Чтобы получить б), достаточно с учотом теоремы 3.3 попадать, что для любого близкого к пулю 8 справедливо
(L* (е)« У (е)< е) А> Л) > 0
пр» всех таких А '/ 0, что G'x (ж (в), е) h = 0.
Допусти, что ото не так. Тогда найдутся такие последовательности {е*1} и {Л'1}, что 11m еЛ иж 0, G* (х(еЛ), с*)	=0, ?АЛЦ =
1, lim Ал = Л=;&0 н
(LJ (.(?), Д.‘),е‘)	0.
277
Переходя к продолу, получаем у*, 0)7/, Л)<о,
£>*, 0)Л=0.
Применяя к <р(а) —
Ио ото протппоречнт условиям задачи.
3.37. Конкретизируя приведенные выше построения, получаем /'И)) + И8)6,(хИ) = 01	(I)
G(x(e))=8.	(П)
цепное правило дифференцирования (2.5) и учитывая (I), имеем <р'(е) = /'(г(е))х'(е) =
*±= —у(е)С?'(;Е(еЗ)®'(е>, где, подчеркнем,	п а/(е)
суть матрицы размера т X п п л X m соответственно. Дифференцируя (II), приходим к формуле
Gz(i(e))sz(e) = Е,
гдо Е — единичная матрица размера от X иг. Таким образом, Ф'(е) => •—у(е),
3.38, В обозначениях, указанных на рпс. 70, соответствующая экстремальная задача формулируется следующим образом:
а b sin а sin р mia*
я etg а -{- l> cig р = MN, 0 < а < гс, 0 < р < я, гдо а, Ъ и MN заданы. Еслп (а, р) — ее рошоппе, то, согласно принципу Лагранжа, существует такое число X, что
асоза . . а
. 2 "f* Аг . 2 —' О, sin а sin а i^i+x » =0. Sin2 р * sin2 Р
Отсюда получаем, что cos а и cosP, и, значит, а = р.
3.3&. Согласно принципу Ферма, и однородной оптической среде свот распространяется прямолинейно. Следоватольпо, траектория движения спота из Л л В есть ломаная АСЕ, где С лежит на границе сред. В обозначениях, указанных на рис. 71, соответствующая экстрвмальпая задача формулируется так:
а Ь
г»! sin а t>2 sin р m,n’
a cig а -г i> etg р = ,1 ГЛ',	0 < а < я, 0 < Р < я.
Отсюда аналогично ренюяшо предыдущей задачи получаем, что cos а
т. е. отпошепно косинусов углов падения и нроломле-005 Р	•
пня равно отношению скоростей света в данных средах.
278
3.40.	Вводом следующие обозначения: Л<7<= i>, АВ = с, AF х, АВ = EF = ц (рис. 72). Тогда площадь параллелограмма ADEF рампа l> = 10 sin Л. Из подобии треугольников АВС п FEC получаем, что cz -{- by = be. В результате приходим к задаче
xtj-r tnnx, ex 4- by t= be,
ним образом, у искомого параллелограмма ADEF ворпшшл D, В, F являются серединами соответствующих сторон треугольника АВС.
3.41.	Искомый треугольник АВС но может быть тупоугольным, так как площадь такового заведомо мошило площади некоторого прямоугольного треугольника, вписанного в ту же окружность (рис. 73). Следовательно, центр окружности 0 но выходит за треугольник АВС, Обозначим через се, р, f углы АОВ, ВОС, СОВ соответственно (рис. 74). Тогда площадь треугольника вычисляется
1 п
по формуле iS = тг Bz (sin а -}- sin р 4" ain'y), где R — радиус описанной окружности. Таким образом, приходим к задаче
sin а + sin р -|- sin •> шах,
а 4* р 4- f «= 2л, а5s0, р>0, 7	0.
279
Ее решение: а = р = у =^* я. Слодовятольио, искомый треугольник ЛИС является риппостороппнм.
3.42.	Дли площади треугольника справедлива следующая формуле:
„	1 2 / а, р у \
5=2"r Ic1»'2’H'c,S”H-c,E“Ii
где а, р, f — углы треугольники, г—радиус вписанной окружности. Полому задача сводится к следующей:
а р , V
ctg ~2 4* clS "2" 4* C1S Т “* тш’
а4-Р4-7 = я, а > О, р>0, 7 > 0.
Ес решеппо: а = р s= 7 =± п/3, Таким образом, искомый треугольник является равносторонним.
ЗЛЗ. G учотом формулы Гер опа задача формализуется следующим образом:
S = (р — а) (р — b) (р — с) -+ max, а 4- b + с = 2р, р > а, р > Ъ, р > с,
где а, Ь, с — длины сторон треугольника. Если обозначить ,т с= = Р — в, У = р ~”Ъ, с в р — с, то приходим к задаче
xyz max, я 4* у -j- z = Р> х > 0, у > 0, z >0.
Ее решение: х = у *= z » р/3. Таким образом, искомый треугольник является равносторонним.
3.44.	Рассмотрим задачу
a34-£i34-c3->-min,	р (у — п.) (у — Ъ) (р — с) = 5»,
а 4- 6 4-с — 2р =0, р>а, р > Ь, р > с,
где поромеппыми являются а, Ь, с и р, a 3 фиксировано. Для равностороннего треугольника доказываемое неравенство выполппот-сл как равенство. Поэтому достаточно полазать, что решение задачи (I) образуют а, Ь в с, ранные друг другу. Положим х «= = Р — «> У = р — Ь, - >= р — с. Тогда задачу (I) можно переписать в виде
(у 4-z)24- («4-з)24- («4- у)2-»-min,
(х-у у 4- z}xy: i= S2, х > 0, y>0, z>0.
Из теоремы 1,2 следует, что решение (ж, у, z) дайной задачи существует. При этом градиент функции (х -|- у 4" 2)^ps н точке (ж, у, :) отличен от нуля, Тогда, согласно принципу Лагранжа, существует такой число А, что
2(ж 4- =) + 2(ж + у) 4- X(2zyz 4’ (У 4- г)рг) = 0,
2(У 4- 2) 4- 2(х 4- у) 4- А(2ху= 4- (*4- s)^) = 0,
2(р 4- =) 4- 2(ж 4- ’) 4- А(2ху= 4- (х 4- и)^и) ст 0.
Вычитая из первого равенства второе, получаем
(ж - у) (2 - Аг (х 4-у 4-*)) = 0.
280
Если ж =5^ у, то ?. > 0. По и этом случае выписанная система по имеет решении в облистн * > 0, у > 0, ; > 0. Таким образом, я = у. Аналогично иокаиыпастся, что у = z и z = х.
3.45.	В обозначениях, указанных па рис. 75, имеем
^лвс = Т s‘n 0*1 ?в)*ЛЯ’ ИС, АВ = Sjn »
________rsin fr	_ rsiPY, _ sin Уд АС ~ sin (0 + v8) ►	= sin (а + yj ’ МС ~ sin (р -J- уг) •
Задача формализуется тонорь следующим образом:
sin a sin Р	.	. о .
-5iR(a+T,pn(f—^)^т11'' «-!-»“«. « + ?,<•>. 0 + ?,<* где иорсмоипым» являются к н ?, a Yi и к» даны. Применяя принцип Лагранжа, волучаем. что ВМ = МС. Следонатоиыю, прямую подо пронести так, чтобы ос отрезок меисду сторонами угля	$/
долился данной точкой Л1 по-полам.	/ X.
3.46.	Пусть I — образую- / X. щня конуса, а—угол между / образующей и основанном. /	,
.Тогда	/	Р X.
1 • .	X'
V = тг я/3 cos2 a sin а,	&tt_fZ--------------------X—
•>	А
6’ а rtl5 сод а.	р|1Сг 75
.Следовательно, j	<11	я
cos а sin5 а = 7^ cos а (1 — cos2a).
Ocnicieii заметить, что глобальный максимум функции гр(0 а = /(! —1-) достигается в точке i = 1/|'3 и равен 2/(3)'3).
3.47.	Если /? — радиус сегмента, h — его высота, то, как известно, обт.ем сегмента равен зт/г5(Я —* Л/3), а ого сферическая поверх-носи» —2я/М. Таким образом, имеем задачу
^'j-FiBin, ЛЛ=^а, 0</^2Л,
где» п — копстпитл. Если (й, й)—ее решение, то h=^B. Следовательно, искомый шаровой сегмент является пояушаром.
ЗЛЯ. Пусть х, у, z — координаты вершины параллелепипеда, лежащей в нервом координатном трохграпном угло. Тогда приходим к задаче
Йхг/1-к jiiox, (Ar2-j-б’у5 + с2;2 — 1» «>0| У 0, = 0.
е»р«|„™№ («,. 3.14):»	» =	==*-7^.
281
3.49.	Пусть О— основание высоты пирамиды, js — расстояние от О до прямой АВ, палтое со знаком пятое, осин О лежит ио ту жо сторону от АВ, что и треугольник АВС, ц со знаком минус в обратном случае. Аналогично определим у и г (рис. 76). Тогда приходим к задано
4“ (а Ухй h’ -|- Ь У у1 Л2 *г с У-2 -|- Л‘) -*• min,
4 («х-Ну-г “) =*5’> W
гдо а, Ь, с “Стороны треугольника ЛВС, S — ого площадь, Л —длина иысоты пирамиды. Решение задачи удовлЬтиоряет услоппго х кв
га у л. Следовательно, О есть центр окружности, вписанной п треугольник АВС.
3.50.	По определению проекции х ячллотся решением задачи
g(x) ±= 0.
Применяя пршщпп Лагранжа, немедленно получаем нужный факт (ср, с геометрической интерпретацией этого принципа, л„. „	данной после теоремы 3.1).
З.эД Точка х является ршпением задачи
||х — all Ч- ||х — 1<|| min, у(х) = 0.
Тогда, согласно принципу Лагранжа, существует таков число X, что
х “ а _ х— b
оXа и ‘Ь Их — i’ll 'I'	= °'
или
. , ,	« — х Ъ — х
}'S W J«—х[] +р“Х| '	W
Отметим, что X */= 0, так как ооратпоо означало бы, что точка х <= е$ лежит на отрезке (а, Ь]. Из (I) вытокаот, что иектор Xg'(x) является диагональю ромба со сторонами единичной длины, а следовательно, и его биссектрисой, m
3.53.	х=±У х’. т ЛаЛ
/=»1
WI
3.54.	Еслп х0 — 2	0, то х =х°/||х°||; если х° = 0, то х —
5=1
любая точка сферы.
3.55.	Всо слагаемые равны bjn (см. задачу 3.17 прп cj = а/ в= ==1, а=1).
232
3.50.	Все слагаемые равны Ь/и (см. задачу 3.19 прп fj = oj в =± 1, а = 2).
3.57.	Сделаем замену переменных t = х Ч- 1/х. Тогда указанное урапиеапо можно переписать в виде *24’«*4*6 —2 = 0. При атом i обязано удовлетворять условию р| ^2. Получаем аидачу
й-' ь* mtn, *г 4- at b — 2 = 0,	11 [	2,
Пусть (а, Ь, 0 — ее решение (существующее по теореме 1.2). Предположим, что |t| >2. Градиент функции $(я, Ь, /) = /24-е/4-4-6 — 2 не обращается в нуль. Тогда, согласно принципу Лагранжи, должно существовать такое число у, что
2а4- yt □ 0, 26 4- у = 0, у(2/ 4- а) = О, tJ4-a/4-fe — 2 = 0, |*| >2.
Одиико лта система „есоимостпа. Таким образом, возможен лишь случаи |*| =2. Если t = 2, то приходим к задаче
а1 -|- 62 -* mid, 2а-|~ 6 = •—2.
Ее решение: а —4/5, Ь = —2/5. Аналогично при I = —2 получаем а = 4/5, 6 = —2/5. Следовательно, наименьшее значение cyst-мы лг4-62 равно 4/5 и достигается на двух указанных нарах (я, 6).
3.58.	Рассмотрим задачу 3.14 при aj = £tj «= aj = 1:
п	и
2Ii = bl /=!,...,«• 1	j=i
Опа имеет единственное решение х* = (6/л,6/п). Возьмем лю-п
бые числи ху 0 (/=!,.,«) п положим .6=2 х>‘ Тогда /=1
П	31	/ L \(1
4)	.
J=1	j=l	\" /
причем равенство имеет место лишь в случае xI = ,,. = zn.
3.59.	Применяя неривспство между средним арифметическим и средним геометрическим, получаем
/ х г	х о
/ И Э (« 4- О V Т"Т"  ’  ’	I)2[/(n +1\
\ 1 **1	*2	— 1	/
причем рипепстно достигшим лишь в том случае, если
* =А_А_	*»	2
Ж1 хд - xs “ • ’  Хя_д - х„ 
Отсюди находим единственное решение задачи:
> 1 /(U+1) ..	-2 - _ .3	, _п
=	а:2 = хг =	гп^х1.
283
• 3,60. Для любого допустимого х имеем
1
/ (х) -	<
! /Ц4-1^ + га-Ь¥Л'
2 \	4
1 1 L
2*4» “ 512’
причем равенство достигается лишь и случае 2xi =я xizj cs х} «= <= x3XiXt) т, е. прп *1 = 1/8, х2 = 2, аг3 ел 1/4, х, = 1/2.
и
3.61.	Рассмотреть задачу З.И при aj » ctj, У1, ctj = 1, fly = 1.
3.62.	Рассмотреть задачу 3.21 (па максимум) при с} = aj = = 1, а «= 2.
3.63.	Положим 5р±=5;,(х, с). Имеем х?=с,>1ПЯ-7'=1-|-4’РInzy-f-о(р), где о (р)—бесконечно малая при р->0. Следовательно,
Поэтому lim $_ = .£ . Далее, пусть без ограничения общно-,/НЮ	”
стп 5<.> i= лг. Тогда
Отсюда заключаем, что limi’ =Л'ес, Точно так }ко доказывл-Р~»4Й	'
отся, что lim St)=S_6Cl, Остальные утверждении очевидны,
3.64.	Если р = —со пли 7 — <», то неравенство•очевидно. Докажем его для конечных р и q путем последонотсльного анализа различных случаев. Положим £г(х)	<$п(.г. с).
1)	0 < р < q = 1. Рассмотрим задачу 3.18 прп nj = сд а = р: п	п
2 <у£-*11М1Х, у, С-x. = ъ, x-j>0, 5=1	5“J
Ее единственным рошопием служит ноктор я* (&, ..., Ь). Отсюда легко выводится, что для любого х = (х>) > 0 справедливо
'^г(я'}	(I)
причем равенство имеет место лишь в том случае, если xf = ... ... — х„.
2)	0 < р < q. Используя (1) и утверждение а) задачи 3.63. получаем
5р(х) =	РМ^)]’/* = 8ч{х). (II)
284
3)	р = 0 < г/. Норавонство So (г) S4(x) можно получить продольным переходом в (И) с учетом утверждения б) задачи 3,63 или путем рлссмотреппп задачи 3.14 при ctj = aj = cj, р; = а.
4)	р < q 0. Вновь используя утворжденпо а) задачи 3.63, имеем
Sp(x) =	= bq(x).
5)	p < 0 < q. Согласно узко доказанному, справедливо


3.65.	Если у = 0, то неравенство очевидно. В противном слу-:чве рассмотреть задачу 3.21 при cj => у/, af *=г 1, а = 2.
3.(16	, Согласпо перааепстпу Koinit — Пупякояского,
I / (*. У) К

Пусть с > 0. Тогда /(х, у) = АГ в том случае, если (а, Ъ, с) = *= ?.(х, у, 1) прп некотором ?<5=0. Отсюда X = с, и, значит, я «= = д/с, у = b/с. В то же время по существует таких (х, у), что 7(х, у) = —«V, поезюльку условия (а, Ь, с) = Х(х, у, 1), Xs^O несовместны, Однако
7(*. 0>
ля 4- Ьу
>_y> + i,’S£S_m.
/ а	>. \
При этом lim / р— — t == — m« Такны образом, если с > 0, то (-*—оо \ С	С /
inf f (х, у) = — ж, sup / (я, у} = М,
R2	R2
причем лишь верхняя грань достигается. Если с < 0, то аналогично показывается, что
inf / (х, у) = — Л/, sup / (х, у) = а»,
к-	II2
причем лишь нижняя грань достигается. Если с = 0, то грани —т и т достигаются лишь и тривиальном случае « = b = 0.
3.67,	Ясно, что неравенство достаточно доказать для xj^O, У) > 0(/ — 1,п), у <= (р|,	у„) #= 0. Рассмотрим задачу 3.22
при о = у), aj = 1, а => р:
п	я
У «lax, X | xi |Р = Ь' j=i
Ее единственным решенном служит точка х*= (®*)r ГД° / к \i/p	”	”
4=(4) os1"-"’ '1=2^(р“1>=2‘'’-
285
Возьмем любые числа	(/ = !,...,«) и положим Ь =-
-1] *?♦ Тогда
А-
”	2L	/ /. \i/p
2 < 2	= (~A )	Л b,/P^>
>1	/rai
причем равенство имеет место лишь в том случае, если = л’ </=1г ..., н), т. о. если х? =;	= ZyJ (/ = 1, ..., п)
при некотором X 0.
3,68.	Если к =а 0, то неравенство очевидно. В противном случае рассмотреть задачу 3.23 нрн с} = у/, й = р,
3.69.	Прежде всего отметим, что если ЛЛТ “ диагональная матрица, то
Д2 ез Jet Я det "Лг = det (ЛЛТ) = JJ f 2 ftij ) • f«l \J=1	/
Рассмотрим теперь задачу максимизации Д2 па множестве всех матриц Л ш= («о) размера п X », удовлетворяющих ограничениям
....... (’)
прп заданных > 0 (случай, когда 1ц <= 0 хотя бы при одном I, тривиален, так как тогда Д = 0). Заметим, что эта задача имеет глобальное решение по теореме Вейерштрасса, причем ее значение положительно. Выпишем функцию Лагранжа
п	? п	\
i=*l \j“l	/
Напомним, что по теореме Лапласа для любого i = 1, ...» п справедливо равенство
я
2Vy м
где Д(/ — алгебраическое дополнение элемента ац (/, / = 1,..я). Таким образом, если Я = (ац)—глобальное решение задачи, то
0L
+ 2yiaU = °'	i,  -1 п.
гдо Уо, У< (I = 1. .. ,,л) — некоторые числа, по равные пулю одновременно. G учетом (1) ясно, что Ф 0. Случай t/t « О также невозможен, так как тогда Д</ <== 0 (/ = 1, .,,, п) и, значит, Д — ±= 0. Следовательно, для любого i => 1, ..., и имеем
Дц =	/ =j 1, ., „ я,	(П)
286
при некоторых At =£ 0. Вспомним тоиорь, что но свойствам определителей
я
^iyaAj & 0» А = 1, ..., п, / =/= А. j^i
Отсюда п из (П) звключаом, что
2иЯЬ‘йЛ?~®' Ц = 1,
,т. о, Л/1Г есть диагональная матрица.
3,70.	Рассмотрим функцию
/ (z, у) — 2а sin л sin у ех"+ь’*.
1 Оип является бесконечно растущей на R2 и, следовательно, имеет А точку глобального минимума, Заметим теперь, что указанная сн-7<отома равносильна следующей:
 д//дх = 0, д//ду = 0, Точка (О, 0) удеплетвпряот данной системе, по
А матрица
rW'") = [2« ’”]
^пакопеопродолапа. Поэтому (0,0) -t'Ha может быть точкой миипму-Ама /. Таким образом, система за-<водомо имеет ощо одно решение, 3.71. Рассмотреть задачу
ах’ + У2-** min, хе? 4- ув* = 1.
3,72. Выберем систему координат так, как указано на рис. 77, ..Пусть (х(0. {/(/))—траектория полета камня, выпущенного под 'углом а. к плоскости земной поверхности. Тогда
2(0) = 0, р(0) = Jt, х(0) = reoset, у(О) = г sin а.
Согласно второму закону Ньютона, 3(Т) = 0, у(1) е= —g, где g — ускоренно свободного падения. Отсюда получаем, что
х (t) = vl cos a, у (0 = —~т rt sin a -}’ л-
Дальность полета определяется моментом времени /•, для которого у (4*) =0, п равна i’/*co5a. Следовательно, искомый угол а* п соответствующий момент t* образуют решение задачи
i4 cos a max, — у’ 4- sin a 4- h = 0, t > 0, — n/2	a n/2.
Отсюда находим, что ct*=aresin	-— .
У 2(i>s4-ftg)
287
3.73. Решенном указанной задачи Копит является
K(t) = K (t —	0<Т>£Т.
Поэтому искомый режим (Г*, 0*) служит решением задачи (О— Оф) Г-»-max, PiT2 + Дг(О — О»)3 = Д»» ^->0, 0 Оо
(ср, с 3.14}. Отсюда находим, что
ч D \1/2	/о D \1/;!
А.Г1) о* с-о -|_ М
5 pJ ’	° bV> р» / *
т* =
§ 4
4.1.	Пусть X имеет впд (4.1). Тогда
Лх = У, XjAx* < Ъ 2 = &• («1	i=l
Следовательно, х (= X.
4.2.	Пусть 7(а*)'У=0, т. е. существует такой помер I, что <й1, i*> = Ь{. Рассмотрим точку х‘ — х* + еаь Для любого О О имеем
<Л<, х*> = <а<, «♦> -Ь в||а<||а > Ь<,
т. о, х* X. Прп атом lim х' а я*. Следовательно, х* — границ-с-.е
пая точка X. Пусть тенор!, /(х*) = 0, т. о. /U* < Ь. Тогда, очевидно, при всех х, достаточно близких к х’, вынолпопо Лх < bt т. о. х’ — внутренняя точка X. Этим доказаны оба утверждения.
4.3.	Пусть а1, .... а""1 — базис ei лпнойпом подпространство L-, ортогональном к прямой L /«л. Тогда, как известно, Л = (/<-L)J-, т. е.
/сл = (г е К" | (йх> = 0, I = 1г ..п — 1}.
Следовательно,
= (хе R"I <л^ *> = <fll, = I. — 1}.
При этом луч и отрезок можно представить, например, следующим образом:
П е К” 1 <Л’ *> <Л’
[х°, х1] {xeRn | <Л, х> < <4, х1»,
где h=xl — xfl.
4.4.	Яспо, что из в) следует б), а из б) следует а). Пусть сира-водлшю а), т. е. существует такая послодовател1»ность {«*} сХ, что 288
lim J .г41| = oo. Положим A’ = т—yr. Тогда
f-ют	И * J
fi{ jjЦ »	1 = 1,
bj
(al> A1) = -pjj, I = A -h 1» ♦m.
Так как ЙЛ’11 = 1, то боз ограничения общности можно считать, что последовательность {А*} сходятся к некоторому вектору Л 0. Переходя к продолу в (I), получаем, что А —решение системы из в). Таким образом, а) влечет в).
4.6.	Пусть указанная система имеет рошоппе h 0, Тогда, очевидно, «♦ + «АеХ при достаточно малых а>0, т, о, Х"/»{х*}. Пусть, напротив, существует точка х е X', отличная от х*. Тогда вектор Л=ж — х* является решенном данной системы.
4.7.	Ясно, что L — аффиппоо множество и 0 <= Л. Тогда для любых i1. i’e6 и ?, ей имеем
Ххх е= 1яг -}- (1 — X) *0 е L,	х1 -|- х" = 2 х14- -ту х’^ е L,
т. с. по опродолопшо L — лппойпоо подпрострапство.
Пусть AjcaX —х1, гдо I'eA'. Возьмем любую точку х (= С. Поскольку х!—х°еб. то х + (ж* — ха) L. Следовательно, is L + х° — I1 = Х' —х' t=s Zi, т. о, £>с;£|. Включение L\<=.L доказывается аналогично. Таким образом, Ai = L.
4.8.	Пусть Л' — аффинное множество и х* s X. Тогда множество Zz ся X — х°, как в любое другое лпнойиов подпространство в R", можно представить в вндо
Ii = (я е Дп|Лг = 0}t
гдо .4	«$£(/?!, п). Ясно, что прп &:= Ах° получаем (4.12). В обрат-
ную сторону утверждение очевидно.
4,9.	Использовать 4.7 н тот факт, что любое линейное подпространство LcR" можно представить в виде
Ь = {*(=Rn|x = Су, yeR'},
где С1ЕЛ?(», а).
4.10,	В случаях а) и б) соответственно имеем:
Lin Х=з {х <= RB|Jx = 0), LinX = {xeR"|x = Су, |/eR’}.
Остается использовать известные факты линейной алгебры [21, с. 57, 78].
4.12.	а) (—1); б) 2; в) 1. Привести системы к треугольному виду.
4.13.	Вычитая из третьего уравнения сумму первых двух, а из четвертого сумму второго п удвоенного первого, приводим систему к следующему эквивалентному виду*:
Xl ‘I' Ч + «В +	+ ЗХ5 =* 10»
2*i“4+	б’а-2*!* хь=-7«
(3 —с)ха	=0,
2 (3 — а) х3	= 0.
с. Л. Ашмопоп, А. В. Тимохов	289
Ясно, что эта система имеет рошенне, причем ранг ее матрицы ранен 2 при а =13 и район 3 прп а’=/=3. Поэтому dim X — 3 прп и = 3 п dim X — 2 при а /« 3.
4.14,	Линейные подпространства, параллельные Xi п Xit связаны теми же соотношениями: Lm Xj 'ст Lin Х& Lin Xt =/= Lin Xs. Поэтому утверждение следует из соответствующего факта лилейной алгебры (21, с, 57].
4.15.	Случай У =з 0 тривналоп. Пусть
У = {х е R1* I Сх в t?} f=jh 0,
гдо Cs-яф, и), tieR'. Предположим, что при некотором I{1, . m] вектор <Т( пе является лкнойпой комбинацией строк ci, ..ct матрицы С, т. о. система уС — д< несовместна. Тогда, согласно теореме 4.5, система
Ch = 0, («(, hy Z> О
имеет решение Л. Рассмотрим любую точку х <= У. Тогда, очевидно, х -г ah <5 У для любого а <= R и х 4- «Л $= X для достаточно больших <х > 0. Ио ото противоречит условию У с X. Такпм образом, каждый из Deicropoa аи ..яст линейно зависит от ci, .. п сг. Отсюда н из теоремы о размерности линейной оболочки [21, с. 57] легко выводится, что rang Л rang С. Следовательно, с учетом 4.10 имеем
dim У = л — rang С <: п — rang А.
4.10.	а) 7(Х) ^0- б) Z(X> =. (1, 2, 3}; в) I(X) = (1, 2, 4}; г) ЦХ} = {1, 3, 4}.
4.17.	Еслп предположить, что указанная система ныеот решение р, то, взяв х е X, приходим к противоречию:
0 = <рЛ, i> = <р, АхУ <р, Ъу С 0.
4.18.	Пусть Го /(X), т. о, < Ь{(| прп некотором х е X, Тогда получаем противоречие:
0 = <рА, х> = <р, АхУ < <р, ЪУ = 0.
4.19. Пусть А — матрица указанной системы, Ъ— вектор ее правых частей. Рассмотрим систему рЛ =0, </>, Ъу = 0, т. о.
	г—1	2	-5	2	0ч	
	4	— 7	1	-7	— 9	
(Pr Лн р3> рд	— 2	3	— 1	1	1	= 0.
	. 1	-1	1	2	3.	
Приводя эту спетому к треугольному виду, убеждаемся, что ев общее решение выражается формулами
о	1	3
Л=°> ^ = -2^- Рз=2Р<-
Поскольку здесь можно взять р* > 0, то, согласно 4.18, имеем (2, 3, 4}с=/(Х), если только Хф0. Общей решение системы уравнений, получаемой путем замены знаков неравапств во втором, третьим и четвертом условиях эпиками равопстя, можно записать так:
г, == 10—2х3 — 7*4, «а i= 7 — х3 — 5т«.
290
Подставлял эти выражения в первой неравенство исходной системы, получаем
—5*з — х< -Р 4	0.
Плирпмор, при х3 = ж< = 1 это неравенство лыпилняется как строгое. Следовательно, Х^0 ц ЦХ) {2, 3. 4k
4.20.	Повторяя схему решении задачи 4.19, рассмотрим систему типа рЛ твз 0, <р, f?> и 0. Ее общее решение записывается в индо pt = Pi = Pi, рл=гО. Следовательно, {1, 2, 4}с/(Х), если только А' ¥= 0. Общее решение соответствующей системы из трех уравнении имеет влд
14	22	2	1	8	5
9 +	9	*з“ 9 ‘V	ж2= 9	+ 9	жз+ 9	ХГ
Подставляя эти выражения в третье неравенство исходной системы, убеждаемся, что оно всегда выполняется, и поэтому ого можно просто отбросить, по изменив А'. Таким образом, полиэдр X с: R* задается системой из трех уравнений ранга 2. Иными словами, X — аффинное множество размерности 2 (см. 4.10).
4,21.	Пусть, км: обычно, Л —матрица указанной системы, Ь — вектор оо правых частей. Рассмотрим систему рЛ = 0, р 0. С точностью до скалярного множителя ее решоиие единственно: р к* (1, 0, 1, 3). При этом <д, ЬУ =«-|-35. Следовательно, если а < —35, то X == 0в силу 4.17.
Пусть а —35. Тогда из 4.18 заключаем, что {1, 3, 4} с Z(A'), Повторяя прием, изложенный выше, приходим к выводу, что Заведомо существует S е X и I(А') =» {1, 3, 4}.
Пусть теперь « > —35. Тогда при достаточно малом е > 0 и указанном 5 =s (xi, £») вектор я» (5|, х2 —е, х$, £4) обращает все неравенства исходной системы в строгие. Следовательно, А'¥=0п /(X) = 0.
4.22.	По определению нежесткого огрепичелия для любого is/ существует такая точка х{ sX, что <щ, х(> <Ь{, В качество х можно взять любую выпуклую комбинацию точек (ii=7) с поконептельиыми коэффициентами (см. 4.1).
4.23.	б) Обозначим правую часть доказываемой формулы через У. По определению I» 7(АГ) имеем ХсУ. При этом У —аффинное множество. Тогда aff X с У в силу определения off X. Остается доказать обратное включение. Пусть х<=У. Если 7=?{1, ...» от}, то сразу очевидно, что х е X с= пП X, Поэтому будем считать, что J = {1	«0W	непусто. Возьмем точку £ на 4,22. Поскольку
Jj* = Ьг, Лг* со bi, Л/* < bJf то заведомо найдется достаточно малое а > 0, при котором точка у = х + а(х — х) принадлежит X.
1 а — 1 —
1	а к ri м ооразом, точку х можно представить в виде х=~£У 4- —— *» где А'с aff X. Тогда х <= aff X, так как aff X — аффинное множество. Следовательно, У с; aff X,
4,24	Ясно, что множество X является аффнпвым в том и только том случае, если X н= aff X. Остается использовать 4.23.
4.25	. утверждение непосредственно следует па 4.10, 4.23.
4.26	. Пусть X — полиэдр вида (4.3), где можно считать, что всо векторы й< отличны от пуля. Тогда, согласно 4.25, 4.22, 4.2, каждое из двух утверждений задачи равносильно тому, что в системе, алдающой X, пет жестких ограничений, т. о, 7(Х) «= 0.
4.29	, a) dimX±=2; ojdimX'aO; в) dim А’= 1; г) dimX=l.
19*	291
4.30	» dim’X=2,
1—1, a C —>15,
2, a = -^35;
4, a> —35.
4.32. a) dimX = 3. Точна x — (0, 1, 1, 0) eX обращает neo неравепствв спстомы в строгие.
6)	dim X « 2. Повторяя схему решения задач 4.19, 4.20, получаем, что ЦХ) =л {1, 2, 4). При этом rang Лцд) = 2.
в)	dim X >== 2. Найти общее решение системы уравнений .и подставить его в неравенство.
г)	dim X = 1.
4J	33. Положим Г={1, ..., п}\Л Пусть в* обозначает 1-й единичный орт в R", El —- матрицу со строками е4 ({<=/). Согласно 4.25, имеем
dim X — n — rang I
(D
Заметим, что столбцы матрицы Es с номерами из Z, будучи единичными ортами, линейно независимы, а остальные ее столбцы (с поморами из J) равны нулю. Отсюда очевидно, что
rang
Л 1
а!
— I 11 4- гапВ А3 га
(л — | J |) + гап£ Л"7.
(И)
Из (I), (II) следует нужная формула,
(Дли дальнейшего полезно отмстить, что формула (II) справедлива для любых I и Д удовлетворяющих услоашо Z = H, ,п)\Л)
4.34. а) Общее решение системы уравнений можно записать в индо
х1 = 2х4 — 3^4-4,	ха=0, ®в = -*4 + »в4-1.
Это решение неотрицательно, например при х< = х6 = 1, т. о. лектор (3, 0, 1, 1, 1) принадлежит X. Следовательно, X Ф 0 п J с= >(Х) = {1, 3, 4, 5} (в обозначениях задачи 4.33). Поскольку rang AJ =з 2, то dim X = 2,
б) dimX<=2.
в) dim X i= 3.
4.35. Пусть полиэдр X имеет вид (4.1). Согласно определению, любая ого вершипа х* является единстненпым решенном системы вида Aix-sbi, гдо Z — некоторое нодмяожество множества {1,.... ш} (как отмечалось, достаточно взять 1 = /(х*)). Ио число таких систем конечно. Поэтому число вершин X но более чем конечно.
4Ж Пусть х е X. Положим 1 =2I(x), J <=* (1, ..,, т) \ /. Если rangг=з nt то по определению точка х есть ворпшпа. Пусть rang/h < л. Это означает, что столбцы матрицы Лх лмнойио зависимы, Следовательно, найдется такой ненулевой вектор й е R", что Aik ₽= 0. При этом заведомо Азк =т^ 0, поскольку Ah. 0 в силу условия rang л = л. Без ограничения общности будем считать, что среди координат вектора Ajh имеются положительные, т. е. <«1» й> > 0 прп некотором I е Д Рассмотрим точку х' <=а х + ай,
292
гдо Иё R. При любом а имеем Л/х' = fa. Выберем максимальное а такое, что Ajx’ fat т. е. х' е X (рнс. 78). Ясно, что
а = min	—-т-—тг—.
f&r > л> <aj,h)>0
Пусть этот минимум достигается па индексе А-, т. о. Ае7, <ал, А> > 0 и <ял, х'> = ^Положим Z'= Z(x'). Тогда I U {£} с I'
(рис. 78). При атом од по является линейной комбинацией векторов at (l s /), так как иначе из условия Л/Л = 0 следовало бы, что <«л( А> «= 0. Таким образом,rang 4JZ>-raiig Лу. Если rang Af, =ал, то х' — вершина X. В противном случае следует повторить описанную процедуру применительно к х'. Ясно, что за конечное число шагов ата процедура приведет к вершине ж*, причем такой, что 1(х) с / (ж*).
В обратную сторону теорема очевидна.
4.37.	Перепишем (4.4) в впде
X =э (х <= Нп|Лж = b, —Ех 0),
где Е — единичная матрица размера и X п- Ясно, что rang ^,J= == л. Понтону сущестноваппе вершины данного полиэдра непосрод-ствеипо следует’ из теоремы 4,2, Пусть теперь хе А', В силу той шв теоремы 4.2 найдется такая воршнна ж*, что /(ж) cz /(х*), В дайной случао ото означает только следующее: если х; = 0, то г* =0;другпми словами, еслиху >0, то xj >• 0. Таким образом, 7(х*) с Цх},
4.38.	Полошим 7 = 7(х*), I = {1, .л) \7(х*). Пусть с1 обозначив? r-м единичный орт и ft”, /<г —матрицу со строками е* {i I). Согласно определению, точка х‘е.\' нвляотся вершиной X и том и только том случае, если
гл 1
rang I =5 л.
293
Прпмопля формулу (II) из рошоппп задачи 4.33, закапчпваем доказательство первого утверждения теоремы. Второв непосредственно следует из того, что для рцссматрпиаомого полиэдра множества /(х) (из (4.2)) и Цх) связаны соотношением
|/(х)|с=>о + (л-|7(х)|).
4-39. Можпо, например, воспользоваться замечанием после .чадачн 4.36.
4.40.	Еслп х = 0, то утверждение тривиально: достаточно взять с пулепым’ коэффициентом любую точку х* Ф 0. Пусть х 0. Рассмотрим по условию непустой полиэдр
{т	»
XeRm| = Х = (Х,)>0 . i=i	J
В силу теоремы 4.3 этот полиэдр нмоет по крайней море одну воршппу ?.*. Согласно тоо|юмо 4.4, точки xl (ее±7(Х*)) липейпо независимы, Следовательно, эти точки образуют искомую подсистему.
Прнмоо доказательство данного утверждения можно iiiiftui в [5, с, 68; 39, с. 60].
4.41.	а) Полиэдр п ого четыре иеркппттд изображены на рис. "9 •).
б)	Полиэдр представляет собой отрезок с концамн-верпшиами (-2, 3) и (8, —2).
в)	Полиэдр представляет собой луч с пачалом*ворпн!иой (2, 3).
г)	Полиэдр состоит из одной точки-верпшпы (2, 3).
4.42.	а сз —1/2, а =1 3/2. Соответствующие положения прямой ах, + х2= 1 показаны на рпс. 80 штриховыми линиями. Заштрихован полиэдр, задаваемый последними тремя перавепствамн.
*) Здесь п далоо на рисунках, где изображены полиэдры, цифры в скобках возле прямых соответствуют порядковым номера1’ ограничений.
294
4.43,	Прежде всего отметим, что полиэдр непуст, так как содержит пулевую точку. Ясно, что ранг матрицы системы меньше 5. т. о. ее столбцы линейно аивпеимы в том и толыюм том случае, если
л 2
1	3
О -4
— 1
1
7
= 0,
Единстненпым решением этого ураввоппя служит а = 2/5. Следовательно, по тооремо 4,2 полиэдр пме&т ворпшпу при всех а </= 2/5 п но имеет прп д = 2/5.
4.44,	а) Используем общую схему поиска перши», описанную в п. i. Последовательно рассмотрим все множества /с{1, ...( 4}, состоящие на трех элементов.
1)	1 си {1, 2, 3}. Система Л г* » bt имеет здесь вид х1-2хй4-5х3 = 4,
4х1“* ^з + ^З139’
Ес единственное решение—точка (1, 1, 1)—удовлетворяет четвертому ограничению системы. Следовательно, эта точка —вершина полиэдра.
2)	/ —(1, 2. 4}. Решая соответствующую систему, находим вершину (2. —1, 0),
3)	/ = (1,3, 4}. Находим ворпшпу (—1,0,1).
4)	/ = {2, 3, 4}. Решеппо соответствующей системы—точка (—2, 1, 3) — по удовлетворяет первому ограничению системы п поэтому но является старшиной полиэдра.
Таким пбралня, всего вершин три.
б)	(1, I, 1); в) (34,  10, 1), (20, -G,-3); г) (-2, I, 1), (2, 2, 0).
295
4.45.	В данном случае вырожденной вершиной может был» только решение спстемы из четырех урапноппй, получаемой путем замены всех знаков неравенств в исходной системе знаками ра-венете. Единственным решением системы пл последних трох уравнений служит точка (I, 0, 1). Опа удовлетворяет норному уравнению, т. о. является вырожденной верпшпой, при л = 1.
4.40.	а) Воспользуомсл оппсапной в конце п. I схемой етыска-Ш1Л вершин полиэдров вида (4.4). Ясно, что для указанной системы требуется перебрать лишь такие множества Z'c {1,4), которые состоят ровно из двух элементов, Последовательно рассмотрим эти шесть множеств.
1)	J {1, 2}. В данном случао система 5J <^х< = Ь &
имеет вид
I] “ 2x1 = 1>
2xi + 3i2 = 3.
Ее решение: zj = 11/7, ха = Ф. Поскольку оба этих числа пеотри-цательны, то точка (‘1/7, 1/7, 0, 0) — вершина полиэдра.
2)	/ = {1, 3}. Решение соответствующей системы: xi = il/7r х3 is -—1/7. Так как г» < 0, то этот случай не даот вершины,
3)	] в= {1, 4}, Находим вершину (5/4, 0, 0, 1/4).
4)	У = <2, 31. Находим вершину (0, 11/14, 9/14, 0).
5)	! = (2, 4). Решение соответствующей системы лмоот отри-цатольные координаты: хг =л —5, х4 = 9.
8) J = {3, 4). Находим вершину (0, 0, 5/9, 11/9).
Таким образом, всего вершин четыре.
б)	(11/4, О, О, 8П). (О, 11/19. 0. 23/16), (0, 0, 11/4, 3/4).
в)	(1. 1, 1, 0), (11/8,0, 5/6, 19/24),
4.47.	На рнс. 81 изображены иектор-столбцы я1, ..., «s матрицы указанной системы уравнений и вектор 5 ео правых чистой. Отсюда видно, что вектор Ь может быть иеотрицатолыюй комбинацией двух из этих столбцов в том п только том случае, если ОДНИМ 1Н1 пих является д4. Таким образом, всего вершил четыро.
296
4/<8. Пусть, как обычно, л4 —столбцы рлсоматрпиаомоП системы, b — вектор ее правых частей. Заметны, что система лРлч <?х3 -I- u’x< = Ь заведомо по имеет неотрицательного решения, так как в оо цервой строке слове стоят отрицательные элементы, a справа— положительный. Таким образом, задача сводится к следующей: при каком зпачепян параметра А вектор Ь является неотрицательной линейной комбинацией вектора а1 с одним из векторов а*, а* мда а*? Чтобы сократить вычисления, изобразим ид
рис, 82 векторы й1, а\ 5, получаемые па векторов а1, .«4, Ь отбрасыванием их первых координат. Отсюда видно, что вектор 5 является неотрицательной комбинацией вектора а‘ только с вектором if*. Решая систолу Д’ж1 + «*жз = 5, находим яц es 3/4, хз == 5/4. Следовательно, искомый параметр А может быть только таким, нри котором указанные числа удовлетворяют системе e1^ -f- а^з «= Ь, Отсюда А = 35/3.
4.49.	dim X = п. Вершинами служат я единичных ортов в R», а также точка 0.
4.59.	dim X = л — I. Вершины то жо, что и в 4.49. кроме О, 4.52. Пусть ж” —вершина полиэдра X вида (4.3), т. о. rang-Л; п, где / = /<ж’). Тогда х* является единственным решением уравнении Лыг = Ъь Следовательно, множество
Г = Х|Л;г = А/},
будучи гранью X, состоит только по точки г*. Пусть, напротив,
{ж») = {* <= Х|Л/х = 6j)	(I)
при некотором 1 <= (1,ж). Тогда /с/(г*) и, значит, соотношение (I) сохранит свою силу, если считать I /(ж*). Допустим, что ж* не является вершиной А', т. о. rang И; < я. Тогда Ajh =» О прп некотором А =£ 0. Ясно, что s*4-aA-sX для числа а, достаточно близкого к нулю, и в то же время Л^(г* Н-аЛ) = 5,. Ио это противоречит (I).
4.53.	а) Полиэдр (будучи треугольником) пмоот три рвбра-от-рвзка. представимых в виде (4.14) при I = {•!}, (3), {4}.
б)	Имеются ребро-отрезок (/ =r {1}) н два ребра-луча
в)	Имеются два робра-ярлмых (7 = {1), (2)).
207
4.54.	Ясно, что множество I из (4,14) принадлежит /(Г). По-от ом у
{х <= Х|Лцrjx = &/<(•>} g Г.
В то же время справедливо и обратное включение), поскольку из условия ig Г мо определению /(Г) следует, что Лцг|Х =
4.55.	Согласно определению, грань Г иевырождена, если |7(Г) | =raHg4/iD, и вырождена, оелп |/(Г)| > rang Лг(Г>. В то жо время размерность грани Г, как и любого другого полиэдра, пычисляется но формуле den<]imr = n— гапя-Лцп (см. 4,25).
4.56.	Положим 11=’{1  н)\/(Г). Пусть с* обозначает t-ii единичный орг в RR, Ei — матрицу со строками с*	Со-
гласно определению, грань Г указанного полиэдра пенырозкдапа в том и только том случао, если
m 4-1 / ] = rang
Л ‘ л.1*
Остается использовать формулу (II) из решения задачи 4,33. 4.57и Пусть X, Г имеют вид (4.3), (4.14), а
Г = {х <= Г | Л;,х =г 4»г},
гдо Г с {1...т). Тогда
1 {х X | Л^х ——	Л^/Х ==?	,
т. е. Г' — грань X, Пополнительное утверждение очевидно, поскольку/(Г) с/(Г).
4.58. Пусть X, Г имеют вид (4.3), (4.14), а
Y = {х eRR|Cx d),
где Сс±лф, n), (i5R’, Поскольку YcX, то У представим в виде У is {xeX|Cx^d}, т. о, в систему, задающую У, всегда можно включить вес ограничения, издающие X. При этом
Г i= {у<= У|Л|Х г= Ь/}, т. о, но опредолеппго Г есть грань У.
439. Пусть [х1, xs] — ребро X, т, о.
(х\ Xs] = {х е X | Лрх
где в силу 4.54 можно считать Г => /([х‘, Xs]). При этом, согласно 4.25, имоом
1 = dim [х1, х2] = л — rang Ар.
Заметим далее, что неравенство <яц х> обращается в равенство всюду па отрезке [х’, хй] тогда и только’ тогда, когда оно обращается в равенство па его концах. Следовательно,
Z([x\ хй))=/(х')П/(**),
т. е. Г “ /. В одну сторону утверждение доказано.
Пусть теперь rang Л/ = п — 1. Тогда прежде всего х1 ч* х’, так как иначе / = 7(х‘) н гаинЛг = п. Рассмотрим грань Г «= {х Х|Л22 = Z>j} полвадра X, Поскольку х’, х2еГ, то 298
[x1, z1] сГ, Тогда из 4.58 следует, что я1, s’ — вершины Г. Кроме того, имеем
dim Г dim [х1, л3] = I.
В то ;ко время 7с/(Г) п, значит, rang Ai	rang Лдгь Поэтому
dim Г = » — rang Л1£г>	л — rang At = 1,
т, о. dim Г = 1. Таким образом, Г — одномерный полиэдр, имеющий г1 и ж’ своими вершинами. Но этим свойством обладает только Г=[ж\^].
4.80. Нз условии задачи следует, что г1 ф я? и
I = /(s’) R 7(х3) « 7(х‘) \ {4 « Z(x’) \ {$}.
При ЭТОМ	~ &д(х<) G==4«2) по определению 1(х)
и, значит, Л/ж' es2 bi (i ss= 1, 2). Таким образом, система Atx = Ь, имеет два различных рошопия. Тогда rang42^?t— 1. В то зко время rang Л; л — 1, так как rang 4^*^ = я и |/| ±= ы |/(х!) | — 1 •). Слодовательно, raug4/Qn—I. Остается при* моимть 4.59.
4.61.	Согласно определению повырождоппой вершины, имеем [/(ж1) | = |/(х2) | = л. Поэтому еслп указанное условно пе выполнено, т, е. 7(х2) имеет по крайней мере два элемента, ве лежащие в /(ж1), то множество / «/(ж1) Q/fx2) содержит по более п — 2 элементов. Но это противоречит условию rang Л; = н — 1 из 4.59.
Опустить условие невырожденности вершин нельзя. Чтобы миоясество /(х1) в /(xJ) различались лишь одной позицией, опп должны, как минимум, иметь одинаковое число элементов. Однако ото заведомо пе так, еслп лишь одна нз соседних вершин певы-розкдена.
4.62.	Применить 4.59 с учетом того, что |/(х')| =» л.
Опустить условие невырожденности вершины х1 пельзл. Рассмотреть полиэдр
X *= {х еRJ|xi + х21, 2х1 Ч- 2ж2	2, хР> 0, х2 0}.
4.63,	Вершина х* невырозкдена н 7(х*) = {1, 2}. Поэтому, согласно 4.62, достаточно найти решения систем вида 4jx е= iit где 7 = {1, 3), {1, 4}, (2, 3}, {2, 4}, и выбрать среди них то, которые принадлежат X. Ответ: х1 = (—1, б), х3= (—1/9, —8/3).
4.64.	Положим h =» {1, .... п}\ J(x’) 0-1.2) и I = 7( Л It = «=> {1, ..., n) V, Согласно 4.59, вершины х1 'и х2 соседние в том п только том случае, если
гл 1 rangl I = п — 1.
Остается попользовать формулу (II) пз решения задачи 4.33.
4.65.	Если множества /(х1) (I = 1,2) различаются лишь одной позицией, то их дополнения h =={!,..п} \ J(s’) р =а 1,2) обладают том же свойством. Поэтому можно применить 4.60.
4,66.	Применить 4.61.
4.67.	Применить 4.62 плп непосредственно вывести из 4.64.
4.68.	(О, 10/11, 7/11, О, 0), (О, 11/10, 0, 7/10, 0), (О, О, О, 0, 1/2),
*) Если у матрицы исключить одну строку, то со ранг либо пе изменится, либо уменьшится на единицу.
299
4.69.	Поскольку заведомо rang Л д Г)	rang Л, то <1>тГш
=з л — rang/l/irj^n— rang Л.
4.70.	Поскольку Г gX, то aff Г caffX. Допустим, кто аИГ = = aff X. Тогда X <= aff X m off Г. Поэтому с учетом замечания посла 4.54 имеем X с X aff Г = Г, т. о. Г =± X, что противоречит условию задачи. Таким образам, aff Г Ф aff X, л, значит, в силу 4.14, 4.25 получаем dim Г = dim aff Г < dim aff X = dim X
4.71. Пусть X — полиэдр вида (4.3), а Г —- его собственная грань вода (4,14). Рассмотрим любое точки х°е <= Х\Г п z1 s Г, Тогда <а<, х®> < Ь{ при некотором £ <= I п в то же время <а/, х1> = Ьс Для точки хшп = х1 4- а(х° — а1), где и < 0, ямсом <а«, хУ > й(, т. о, X но содержит прямую, проходящую через х° и х’ (рпс. S3), Следовательно, X пв является аффинным множествам.
Пусть, напротив, X—пеаффкпноа множество вида (4.3). Тогда 1(Х) чЧ1,..«О п в силу 4.22 существует та-<«j, z°> < Ь{ нри всех I 7(Х). Кроме того.
пая точка t’eA', что (щ,	< Ь{ при всех 1<£ЦХ), Кроме того,
X^affX, и, зпачпт, существует точка х<~аИХ\Х. С учетом 4.23 ясно, что па отрезке [х°, х] найдется такая точка х1 <= X, что <а(,	= bt при некотором f & /(X) (рис. S3). Тогда
Г = {x'<=X|<rt/, х'> = М
ость собственная грань полиэдра X (х°е*Г, х( еГ),
4.72.	Еслп Г — минимальная грань X, то все доказано, В противном случае Г имеет собственную грань Г'. При этом Г' — грань X в силу 4.57. Далее рассуждений повторяется для Г'. Эта процедура за коночное число шагов приведет к минимальной грани полпэдра X, так как любая новая грань собственно вкладывается в предыдущую, а число граней конечно (см, 4.51),
4.73.	Из а) следует б) в силу 4.57, 4.71. Исиольауя 4.15, 4.60, из б) выводим в). Паконоц, в) влечет а) благодаря 4.69, 4.70.
4.74.	Минимальные грани задаются следующими системами:
a)	si + хл + z3 = 1,
Xt + 2xj Зхэ = 2;
б)	X) Ч* Xj -f* Xj	1, и Z| 2xj 4- Зхз -f- 4x< » 3,
2xi -J- 3x4 + 4®j 4- 5x4 = 2 2xt -j- 3xs -j- 4z3 + 5z, = 2.
4.75.	Пусть X —множество решений системы	Г —ми-
нимальная' грань X, существующая согласно 4.72. Положим I = /(Г). Учитывая 4.24 и замечание после 4.69, утверждения б) и в) из 4.73 можно переформулировать так:
Г =з{х eRr’[4jx t=s &j), rang 4/«и г.
Отсюда ясно, что I удовлетворяет основному утворладеиню сформулированного нрппцпна. Если |/| > г, то существует тлкоо V gi, что rang-42, — г и | f'| и г. Прп этом системы Altx = bJf и Лгх ез 6/ равносильны.
4.76.	Для любой точки xsX рассмотрим грань полиэдра X вида
Г* *=» {х's X|4j(B)X' ™ 5г(к>}.
300
Согласно 4.72, существует такая минимальная грань Г этого полиэдра. что Г с: Г'. Имеем 1(х) с 1(Г') сг 7(Г).
4.77.	Если предположить, что одновременно существует роше-ико z системы (4.6) и решение р системы (4.7), то приходим к противоречию:
О > <Р, &> => <А Лх> = <рЛ, х> = 0.	(I)
Предположим теперь, что система (4,6) несовместна. Это означает, что вектор Ъ по принадлежит линейному подпространству Л, натянутому на столбцы матрицы Л. Пусть ZA — подпространство, ортогональное к Z., Тогда, как известно, Lea (М)\ т. о.
L t= (z е R" | <р, х>	0 при всех р е /А).
Поскольку b ф L, то найдется такой вектор р е /А (т, о. рА = 0), что <р, i»> =5^ 0. При этом боз ограничения общности можно считать, что <р, Ь> <0. Таким образом, р — ношение системы (4,7), 4.78. Тот факт, что системы (4,8) и (4.9) но могут иметь решение одновременно, доказывается с помощью цепочки, аналогичной (I) из решения предыдущей задачи.
Основное утвепждоппо теоремы о совместности хотя бы одной из спетом (4,8), (4.9) докажем индукцией по числу « столбцов (/=(,.,,, и) матрицы Л. Случай п = 1 оставляем разобрать читателю.
Пусть « > 1 п при число столбцов матрицы Л, меньшем н, утверждение узко доказано. Предположим, что система (4.9) несовместна. Тогда это том более верно для системы (4.7). По в таком случае совместна система (4.6). Требуется показан., что среди ее решений существует неотрицательное. Для этого достаточно указать процедуру, позволяющую по даппому решению, если око имеет отрицательные компоненты, яостропть новое, у которого отрицательных компонент по крайней мере па одну меньше.
Итак, пусть числа xj (/ = !,..., п) таковы, что
у, «Ч=ь-/«“»!
п без ограничения общности 0 при j±= 1, .к и X) < 0 при / = А 4-1,..., п (случай к = 0, когда все Xj < 0, не исключается).
Рассмотрим вектор
Л .	п-1
с = 2	-|-апхл= Ь — 2 ^xi'	(!)
i=i
Допустим, что существует вектор р, удовлетворяющий системе
<д, аЗ>^0, /=1........л-1, <р, с><0. (II)
Тогда из (1) получаем, что <р, а"> > 0, <р, А> < 0. Следовательно, р — решение системы (4,9). Но это противоречит исходному предположению. Таким образом, система (II) по имеет решения. Тогда по предположению индукции существуют такие числа (/ ±= 1, .... п — 1), НТО
п-1
2 а7у/= с.
/-1
301
Отсюда я ив (I) следует
П-1	п-1
= 2 «Ч
5=1
Т. 0.
Л „	п-1
2Л^+ 2 «*(®j+y;)-Hn*o=*a.
5=1	5=Л+1
Нуяшля процедура построена.
(Мы привели одно из нлгабрапчеышх (финптиых) доказательств теоремы 4.6, относящейся к важнейшим фактам теории линейных неравенств. Другие ее алгебраические доказательства имеются в [43, 47), Традиционное дшшзателг.ство, основанное пп теории отделимости, можно найти в (3!)]. Хоти one выглядит наиболее простым, однако g учетом подготовительной работы, пожалуй, проигрывает приведенному выше.)
4.79. Пусть импликация (4.10) справедлива, по система (4.11) насовмостпа, Тогда по будет совместной система
рЛ	= С	р у -j i \	1 <
<р,ь>4-х = л ~И ’ fU ; , Р>0, х^о.
р>о, ?.>о	I* W
Следовательно, по теореме 4.8 существует такой вектор (л, ?) е « R" X К, что
[jT лТ
Ъ 1]>0
Ах -р yi> О, у>0,
<с, х> -J- yd < 0.
Возможны два случая.
1)	х> 0. Тогда для точки х = — xft имеем Лх	bt <с, sy > d.
Ио зто противоречит (4.10).
2)	7 = 0. Тогда 4x^0. <с, х> <0. По условию существует такая точка х*, что Лх* Ь. Положим ха = х* — ах. Для любого а.>0 имеем Лх’ Ь. В то же время <с,	при «->-«>. По
ото также противоречит (4.10).
В одну сторону теорема доказана. Пусть теперь система (4.11) имеет решение р, а точка х такова, что Лх Ь. Тогда
х> (рЛ, ху '=г (pt ЛхУ ^р, ЬУ <7,
т. о. импликации (4.10) справедлива,
4.80.	Из рпс. 84 (гдо, нак обычно, а*, ..., а* — вонтор-столбды матрицы системы, i> — вектор ее правых частой) ясно, что система имеет репгонпо в том и только том случае, еслп вектор с! находится в Заштрихояаппоп области, исключав его левое крайнее положение. Осюда легко получается ответ: —3 < к sc (.
4.81.	Рассмотрим ату систему как систему типа (4.11). Тогда согласно теореме 4.7 опа имеет решение в том н только том слу-302
чао, если справедлива импликация
— 2^— x„<4 ~ Ж1 4" 2х2 2
"*•	+ ж2	3,
причем система, стоящая здесь слева, должна быть совместной. Но оба этих факта очевидны из рпс, 85, где заштриховано множество решений левой системы.
4.82.	Пусть х п р —решения систем (4.15), (4.11). Тогда {р> by ^р, /1х^ == (р^1, %У =х хУ = d.
Следовательно, <р, Ь> = d. Если предположить, что р< > О, <oj, х> < i>( прп некотором I, то в вынпсаппой цепочно неравенство будет строгим, что невозможно.
303
4.83.	11л рпс, 85 впдио, что то’пгд (2, 1) является решением системы типа (4,15), причем второе в третье неравенства в этой точке выполняются как строгие. Тогда, согласно 4.82, любой решение исходной системы имеет вид (/»i, 0, 0, />♦), После этого уже одпозпа’шо находятся р} = 1/3 н /»г =з 2/3,
4.84.	Это ^мистически известной пз курса линейкой алгебры утверждение можно доказать на основе теоремы 4,5 точно так же, как из теоремы 4.0 была выведена теорема 4,7 (см. 4.79).
4.85.	Применить теорему 4.7 к каждой пз импликаций Лх^Ь-г <с, ху d, Ах b	<—с, г> — d
п учесть 4.82.
4,86,	Пусть система Ах^.Ь несовместна. Тогда, очевидно, справедлива импликация	
Ах — kb 0 Л 0.
В силу теоремы 4.7 существует такой вектор j?, что
дЛ = 0, (д, — Ь> = 1, р 0.
4.87.	Рассматриваемая импликация равносильна тому, что система
Лх Ъ, <—с, х>	—d
по имеет решения. Тогда в силу 4.80 существует такой вектор (р, к) eRMX R, что
рЛ — ке = 0, <д,	— kd < 0, р 0, к& 0.
Cjryuaft к и 0 невозможен, так как о„ противоречит совместности системы Ах b (см. 4.86). Поэтому к > 0. Тогда р = у р— решение указанной системы.
В обратную сторону утверждение очевидно.
4.88.	Из теоремы 4.7 и условий задачи следует, что совместна система (4.11), т. е.
2Piei = ff.	Pi>°. / = |......»’•
i=»l	<=1
С учетом той же теоремы 4,7 требуется показать, что существует множество I с {1,я»), прп котором векторы nj (fc=7) линейно независимы и совместна система
д£>0, ts/, (I) 1ет	1^1
В свою очередь, для этого достаточно убедиться в следующем: осла прп данном множество / система (I) совместна, по векторы а( (/ е /) линейно зависимы, то существует такое его собственное подмножество У, что система (I) прп замена I па У также совместна.
Итак, пусть р = (pt) — решение системы (I). Если вметоры at (ie 1) линейно зависимы, то найдутся числа ?.< (/е/), по раи-304
t?^ie нулю одновременно tt такие, что
SMi-o,	(ID
tel
Случай 2	= 0 лишь упрощает дальнейшие рассуждения,
tel
Пусть 2 О* Тогда без ограниченна общности можно счп-tei
т&ть, что
2М1<0-	(«О
tej
Из условия задачи следует, что система <щ, х> b[ (I е /) имеет решение. Тогда ц силу соотношения (II), (Ш) несовместимы с тем, что kt 0 при всех t <= I. Поэтому kt < 0 хотя бы для одно* го i s /. Из (II), (Ш) заключаем, что
2 (Pi + «а,) а{ = с при всех а е R, iei
2 (Pj + aXj) С при всех а 0. lei
Выберем максимальное а 5=0 такое, что	(ге/).
Mono, что а С «> ц /л, 4- ак\ = 0 при некотором Ле/. Следователь-no, множество V = I \ {Л} удовлетворяет нужному требованию. Основное утверждение теоремы доказано. Дополнительное утверждение очевидно, поскольку если векторы д( (re/) линейно независимы. то всегда можно найти такое множество 1' с (1,..., га), что /с/', |/'|*=аглп£Л п векторы «( (/<=/') линейно незавненмы. При этом выполняется тривиальная импликация
yij/X bjf —>• AjX	bj.
4.89.	Проходит та ясе схема доказательства. Необходимо лишь вместо теоремы 4.7 попользовать 4.87.
4.90,	При этих условиях в 4.88 возможен только случай /=!,..../я).
4.91.	Пусть система & неприводимо песовмсстпа. Поскольку оиа просто песовмсстпа, то, согласно 4.86, существует ponioifito р системы (4.16), Если предположить, что pt =я 0 при некотором i е {1, .... т), то опять же в силу 4.86 получим, что несовместна система А:х Ьг, гдо / = {1, ..,, т) \ {0. Но это противоречит определению неприводимо несовместной системы. Таким образом, р > 0, т. о. система (4.17) совместна. Далее, условие неприводимой посовместпостн системы Лх Ь можно выразить также в следующей форме: при любом I «=« 1, ..., т поравопство <fif, z> > b{ следует пз системы Atz Ьг, где / = {1, ,.,, пг}\{1), и не следует пз любой ее собственной подсистемы. Тогда rang At = t=m— 1 в силу 4.90. В одну сторону теорема доказана. Простое доказательство обратного утверждения оставляем читателю.
4.92.	Пусть система Ах о несовместна. В частности, это означает, что несовместна система Ах >±з Следовательно, по теореме Кропекера —• Капеллп rang (И, b) ^=> r-f-1. Пркмеплл 4.88 к импликации из решения задачи 4.86, находим такое множество 20 С. А. Ашмаиол. А. В. Тимохов	305
Z<= (1...rn}, ЧТО |/1 вп г 4- 1, rang (Л/, bf) = г4- 1 д снравидЛл-
ва импликация
А{х — ),5j	0 Л О,
т. о, систола Л/х С h несовместна. Поскольку система Агх =г Ь, тем болей несовместна, то rnngzlj = rang(?i|, 5») — ! =; г.
В другую сторону утверждение тривиально.
4.93,	Переписать систему (4.18) в виде
Ли»14-
И21х1 + Л22*"< &2,
~ Я81*Х~
— Ex1 =^0
и применить 4.8G.
4.94.	Имеем
0 <p'Xii 4- р’Лгн х*> + <р1Л1»4-,раДя» х®> i=
= <Р*> А1 [X14- 4(sx2> 4' <р’, Л21х’ 4* Яих2> йС
< </Л й’> + <РВ 9, &’> « о.
Это возможно лишь в том случае, еслп два фигурирующих здесь пераиепства выполняются как равенства, т. е.
0=<рЧ1 -I- ,'Чг г1> “ И (₽Ч1+'43)j -ъ- .
Л“1
0 я (pl> лх/+2 4 Gv1+- ь% <==1
В первой на этих сумм все слагаемые неотрицательны, по второй неположительны. Отсюда приходим к (4.20), (4.21).
4.95. Применить теорему 4.7, переписав систему (4,18), как в указании к 4.93.
4.9В. Допустим, что первая система несовместна. Тогда прв любом фиксированном с > О справедлива импликация
Ах 4- Хе b -+ Л 0,
Система, стоящая здесь слава, имеет решение; дм является пара (х, X,), где х —любой вектор, а —достаточно большое до модулю отрицательное число. Применяя теорему 4.7, получаем, что оущесг*. вует вектор р, для хготорого
рА = 0,	</>, с> «= 1, <р, Ь> 0, р & 0,
т. е. р — решение второй нз указанных систем.
Тот факт, что системы по имеют рмнеипн одпопромвппо, легко доказывается от противного.
306
4.97. При любом с > О применить 4.95 к импликации
AjX Ь\
Af = Ь2,
Л..*+Хс<Ь3 «J
->-Х>0.
4.9& Порошиной вторую па указанных спотом в индо
—Атр = 0, <&, р> О, —Ер < О.
Допустим, что эта система несовместна. Тогда, согласно 4.97, су-
ществует такой вектор (х, X, к) еП'1ХЙи, что
Х>0, «>0-
Зпвншом эти соотношения несколько иначе:
Лд< ХА, X 3? 0.
Возможны два случая.
1) X > 0. Тогда Л(х/Х) <А.
2) X = 0. Пусть #* —любое решение системы Их^Ь. Тогда Л (х + «♦) < Ь.
Итак, во всяком случае система Ах < b совместна.
4.99.	Соответствующим образом дополнить схему решения задачи 4.98.
4.100.	Все утверждения являются частными случаями предыдущих результатов. Например, а) следует из 4.96 при b = О и замене Л на —Лт.
4.101.	а) Пусть утверждение неверно, т, о, система
Ах	=0,
— х	<0,
— Лгр<0,
— г — Лтр < О
но имеет решения. Тогда, согласно 4.97, найдется такой вектор (ч, г, з, е) е= х R1* X пп X R", что
qA — г — I =0,
— sAT ~ 1АТ = О,
г>0,	f > 0.
Отсюда I < <р1, A (s + 0 = 0. Поэтому
<(, О О, s + t>< <<М, * + О = <Ъ Л(*-Н)>=0,
т, о. t s= 0. Но это противоречит условию i > 0.
б)	Применить утворждопис а) к матрице (Л, JJ), где Е — единичная матрица размера т X л>.
4.102.	Первое утворзкдоппс — ппаче сформулированная теорема Гордапа из 4.100. В самом доле, пусть А	и)—матрица,
строки которой образуют базис в L. Тогда
Ь=з {у ейа|у=>рЛ, РбПи), IA- = {®е Д,’|Лх=5 0}.
20»
307
Прп атом порвал из альтернатив равпосплг.па сопместностп спето-мы рА > 0, а вторая — системы Лх = 0, i>0. Второе утверждение ость следствие утверждения а) из 4.101.
4.103.	Применить утверждений б) задачи 4.101, приводя указанные системы к соответствующему виду.
4.104.	Рассмотрим следующую систом5’ типа (4.22):
+ Л12л2 — дУ < О,
+	(I)
^>0,	?.>0.
Соответствующая система типа (4.23) пмоот вид Р^а + P24j| > 0.
AiJ2 + p42^°.	<п>
<А ь1) -j- <Л ь2> о> р1 > о.
Поскольку система (4.18) совместил, то, согласно 4.93, любое решение системы (И) обращает норавеистио <р‘, &•> + <д2, i>2> О в равенство. Тогда в силу 4.103 системы (I) u (II) имеют такие решения (х1, х2, ?.) п (д’, р2), что ?. > 0 н
р'-Ь (М1 — Ли*1 — /1|»г3) > О,
®* + (РХЛп 4*	> О*
Следовательно, X-’(я1, х2) и д’)—решения систем (4.18), (4.19). удовлетворяющие условиям (4.24), (4.25).
4.105.	Данное утверждение — частный случай предыдущего, 4.100. Конкретизировать 4.94, 4.104.
4.107.	а) При любом х <= R" имеем
—<Лх, х> =я <Лтх, г> = (г, Лх>.
Слодоветояыю, <Лх, х> = 0.
б)	Применяя утверждение б) задачи 4.101 к матрице —Л, получаем, что существуют векторы qup, для которых
И^,>0, 4^0, —рА =зАр^Ъ, р^0, р -f- Aq > 0, (? -f- Лр > 0.
Положим г =э р 4- q. Тогда Ах 0, х О 0 п Ах + х > 0.
4.108.	Применить теорему Билля из 4.100,
4.109.	Указанное условие относительно системы (4.27) равносильно совокупности следующих двух:
1)	система Ah = 0 пмоот лишь репюние k = 0,
2)	система Aih<0,Ajh = 0, где 7	А), 7={А + 1,...
..., ?п) не имеет решения.
По I) — это ипая запись условия rang Л =». В то же время, согласно 4.99, условно 2) эквивалентно совместности системы (4.28),
4.110.	Утверждение непосредственно следует из 4.4, 4.109.
4.111,	4.112. Применить 4.J 10, учитывая, что для данных полиэдров ранг матрицы системы равен п.
4.113.	Утверждение непосредственно следует нз 4.G, 4.109.
308
4.114.	Положим 7 «= {1, ...» гг)\Л Пусть с( обозначает /-й единичный орт в R1*, йг —матрицу со строками ж	Согласно
4.113, точка х* является единственным элементом X в том п только том случае, если
(I)
/А1 rang
и существуют такие иоктор peR151 я числа дч > 0 (!<=!), что
М—S 7^ —°>	(Н>
tel
Но, как ужо было показано (см. решения задач 4.33, 4.38), формула (I) равносильна формуле raDgA/le=! PI- В 10 жо время (II) мозкпо переписать в виде
t .	(О, /sJ,
(Ч	/ «= -4 .
4.115.	Пусть Л' ограничен. Тогда при любом ceRa величина <7 = зи_р <с( х> конечна. Применял теорему 4.7, получаем, что система (4.20) совместна,
Пусть теперь X неограничен. Тогда, согласно 4-4, существует такой вектор h 0, что АЛ 0. Ясно, что прп с =* h система (4,29) несовместна.
4.116.	Пусть с> есть /-й единичный орт в IV. Тогда условие X <= R^_ равносильно тому, что для любого / s» 1,..., и справедлива импликация
0.
Согласно тсорсмо 4.7, последнее имеет место в том и только том случае, если для любого у ₽= 1, ..., п существует такой вектор pj е IV”, что
2S9	<р*,ь>^о. д^О.
Таким образом, в качество Р можно взять матрицу со строками Р* (/=я 1,.... л).
.4.117. Ограниченность X равносильна следующему: для любого / = 1, ..п существуют такие числа «; и Р/ (<zj Pj) , что справедливы импликации
Ах	Ъ	<—«Л ХУ
Ах	Ь	<eJ,	Рь
Применяя тоорему 4.7, получаем сформулированный критерий огранпчеапостн X. Далее, если матрицы Р и Q обладают указанными свойствами, то при любом х^Х имеем
(Р-J- <?)Ь.>. (Р + <2)Лх₽=-»-Ь®«0.
4.118.	Рпссмотроть выше случай aj » pj (/ = !,..п).
ЗОН
4.119.	Допустим, что утверждение иеиорио. Тогда, согласно теореме 4,6, пмеет решение Л е!г система
<а(,Л><0,	(I)
<х —х*, Л>>0.	(П)
Из (I) очовпдпо, что х*Ц-аЛ<=Х при всех достаточно малых а > 0, Используя (II), для достаточно малого а > 0 получаем Ik’ + alt — x||J => Их* — х||2 + 2а<л* — ж, Л> -|- а2||й||2 =
« Их* - х||» 4- а(—2<х - х*, Л> + cdlftlF) < |[х* - х112, т. о. точка х* + аЛеХ находится па более близком расстоянии от х, чем х*. Но ото противоречит предположению, что х* — проекция х па X.
4.120,	Пусть утверждение неверпо. Тогда для любого к = 1, 2,.... найдется такой Boicrop />* =	>0, что
(«i,	i= l,	(I)
m
При этом всегда можно добиться того, что 2 $ — 1 • Боз огра-пичепнп общности будем считать, что/'/‘-►р >0. Умножая /-о неравенство в (I) па р% (I — 1,..., т) и складывая, получаем
<т	к
У fat, phA>=II /л 9s < 4-1 /л J.
1=1	/
Следовательно, ||р*И11 < 1/А. Отсюда продельным переходом выводим, что ИМ || =± 0. Но это противоречит условию задачи.
4.121.	Рассмотрим любое такое множество номеров /<=(!, ... ..., т}, что векторы я<	ливеппо независимы. Матрица Л,
заведомо удовлетворяет условию еадачп 4.120. Поэтому найдется такое число а, > 0, что
“е“	,S ₽А>>Кг|,2'Л|
при всех	(/<=/). Покажем, что нужным свойством обла-
дает число ai=ininaj>0, (Где минимум берется по всем указанный J.
Рассмотрим любую точку ie X. Пусть х* — ее проекция па X, т. е. р(х, X) «= ||х —х*||. Согласно 4.110, существуют такие числа Pi О 0<=/(х*)), что
х —х* = У! р{а,.
С учетом 4.40 выбором такое множество fc/(x*), что векторы <ч (I I) лпнойпо независимы и
г —	I11)
iel
310
прп некоторых (Jef). Tow, используя (I) и (II), получаем
шах (<«{,*>-^)> max (<а0 *>-&<) = J, <£	*С— а
= max Zev ж — i*\ — max /а{| У, > i<si	j’ei у"
>«|S	— а:*|1 = ар(г, X).
Остается заметить что а зависит только от матрицы А.
4.122.	Для любого зе^Д” очевидно, что m
У шах (0, («{, X) ~ ъг) > max «а(, ®> — Ь,), i=«l	1«<т
|Дх — ЬЦ> max (<alsx> — i{).
Ki<ra
4.123.	Представить каждое равенство в (4.3) как два неравенства и применить 4.122.
4.126.	Пусть утверждение а) справедливо, а б) пет, т. е. существует йену левое .решение р системы (4.32). Для любого сколь угодно малого в > 0 рассмотрим вектор Ъ* = b — ер. Если допустить, что существует zeA'H, ^‘), то приходим к противоречию:
О = (рА, д:> = <р, Лх> <р, г»е> — ellpIP < 0.
Таким образом, Х(4, Ь1} «= 0. Но ото противоречит а). Итак, из а) следует б).
Пусть, напротив, б) справедливо. Если а) неверно, то найдутся такие" последовательности {Л*} п {&*}, что А*-»-Л, Ь*->Ъ и Л'(Л*, б’) — 0 при любом s. Тогда) согласно 4,93, существует такой вектор р*, что
р’Л* = 0, <р’,Ь’><0, j4>0, /-1..........к. (I)
Прп »том можно считать, что lip’ll » 1. Боз ограничения общности предположим, что р*->р ч&О. Переходя к пределу в (I), получаем, что р — решение системы (4.32). Противоречие. Поэтому не б) следует а).
Пусть по-прежнему б) справедливо. Отсюда, в частности, следует, что Х(Л, Ь) (см, 4.93). Тогда система (4.33) совместна, так как в противном случае, согласно 4.97, система (4.32) имеет такое решение р, что р{ > 0 при некотором i е {1,,. „ к}. Предположим, что векторы a< (1 =i к -Ь1, .. щ) линейно зависимы, т, е. ГЛ
У р{й| = 0 при некоторых числах р« (<=Л4-1,	т),
не равных пулю одновременно. Тогда для любого x^Xpl, 4>) имеем
Я1	 тп	/ тп	\
3 ^Ь<= S /’l<ai»a:>=\ 3 Р1вР 1) = 0‘
<=Л-р1	1««Л+1	\{=fc+l	/
Следовательно, вектор р =я (0, ..О, px+i, ..pw) является нетривиальным решением системы (4,32), что невозможно. Итак, из б) следует в). Обратное доказывается еще проще.
311
4.127.	Бели система (4.31) неустойчива, то система (4.32) имеет нетривиальное решение. Тогда, как нока:шно нише, система (4.31) неустойчива ио праной части играннчоинн.
4.128.	Пусть р — некоторое решение системы (4.32). Требуется показать, что р = 0. Предположим, что р< > 0 вря каком-либо i е {1, ,,к} \ /(**). Тогда приходим к противоречию:
О = <М, **> = <Р, Лж*> < <р, by 0.
Следовательно, /ч = 0 прп всех f^7(z*). Но тогда
О = рЛ = У, Pjflj.
Отсюда в силу линейной пезавнеимосгп векторов я< (^е7(х*)) получаем, что р< =0 при всех ie 7(х*),
Примером служит третья система пз 4.124.
4.130.	При любом фиксированном г = 1, 2, ... присоединим к устойчивой системе (4.31) поравепстпа
—1/гС*3<*“-Н/г,	/ = 1, ..., п,	(I)
В точке х° все они выполняются как строгпе; Тогда пз 4.126 следует. что система (4.31), (IJ также устойчива. Значит, пайдотся такой помер sr, что для любого s > s> существует точка Xs, удовлетворяющая условиям
^<=Х(Л\Ь4), |х?- x®[ci/r, /-1..............>. (II)
Прп атом можно считать, что sf < и (г» 1, 2,.), Теперь для любого выберем ха из (II), где помор г таков, что зт
s < sr+!. Ясно, что z’-»-®0.
4.131.	См. ряс. 86, где
Х = [zeR2|a:2<0,
Xe = ^E<=R2|—~ 4-С0, x2>C>j,	« = 1,2, ...
4.132.	В силу 4.110 ограниченность полиэдра Х(Л, Ь) равносильна тому, что система
рЛ = О, pt >- 0, i = 1,.,., к,
совместна и rang 4= л. Тогда, согласно 4.125, 4.126, при любой матрице Л', достаточно близкой к Л, система
рЛ' е= 0, р< >0, 1 = 1,..., к,
также совместна u rang Л' = я. Следовательно, если прп такой матрице А' и произвольно взятом Ъ' полиэдр Х(А', Ь') непуст, то он ограничен.
4.133.	Пусть {**} псограпнчопа. Положим к*	Боз
ограничения общности будем считать, что к * -* к ф 0. Условие х* е Х(Л*, $•) можно церспислть в виде к* <= Х(А‘, 1|х‘Ц''Ь'). Переходя здесь к продолу (см. 4.120), получаем, что ksX(A, 0), Но это противоречит 4.4.
4.134.	Пусть носледоиательпость {is)t такова, что Х(Л, Ь*}	0
п Предположим, что Х(Л, Ь) = 0. Тогда, согласно 4.93, 312
nsraai решение p система
M в= О, <р, Ь> <0, pt 0, 1 = 1........Л. (I)
Дли достаточно большого л следует <д, йл> <0, т. о. р лвляотсп также решопиом системы (I) прп звмепе Ь па Ь’. Но тогда, вновь пснольаул 4.93, получаем, что л(4, Ь*) « 0, Противоречие,
4.135.	См. рис. 87, где
=	— ^i+^CO, s2>lj, ««=1,2,...
4.I3G.	Согласно теореме Хоффмана в форме 4.123, существует тикоо число а = а(Л) > 0, что при любом х е Х(Ь')
ар (х, X (Ь))С 3 mttX (°’ <ЙР г> ~ М + 3 I <?f» «> - ь< | <
i=I	i=M-l
с 21max(°- bi-M-* 3 lb<-hl< i-l	i=fc-rl	£=1
_	/ in
с *И« у 3 Сч ь<)313 Ум
где послодпео неравенство следует не неравенства Кошп — Будя-конского. Таким образом,
зир р(х, Х(Ь)хУ™|Ь' — И. яех<ь')	а
313
Аналопмпо получаем, что
sup
хеад	СС
Следовательно, можно положить £ &= imfa.
4.137. Рассмотреть в 4.1315 случай- Ь* ±ап О,
§ 5
5.1.	Пусть х* — локальное, по по глобальное решение задачи (5.1). Тогда найдется такая точка х, что	<с, х> >
> <е, х’>. Вводом точку хх = \х + (1 — Для любого К е е (0, 1] имеем
Лхк =* ЬАх + (1 - Х)Лх* < ).Ь + (1 — Л) 5 = Ь,
<с, оЛ> %<с, х> (1 — Л) <с, х*> > <с, х’>.
При этом 11тпа?' = х*. Следовательно, х* по является локальным х-*о
решением задачи. Противоречие.
5.2.	Основной форма:
2х1~	—5х3->шах,
4ll + 35f3“l"
— 4х, — Зх„ —	—4,
А	А	«3
е1'-ц>+ Vs* ~2«
7*х — ^в + ^з^5’
— *!	<0,
““	О»
стандартная форма:
2х — х — би., -Ь 5уч -+ жах, А	Л	<1	о
^4-3X3+ U3- 1>3<4,
-4^ — 3^— и34- п3^-4,	(I)
«1-^4- «3— Ра<~2,
Ч~ ха-|-2иа-2о3<5,
^>0, xfi>0, и3>0, на>0;
капоиичискал форма:
2х. ~ хл — 5и. -|- 5р„ 0>и>„ -|- 0«к» -* шах, 1	4*	J	Ч»	М	М
4^4-3^-Ь «а- »а	=4,
— «i’l-GXjj-- н3.-Ъ »3— и.».,	=2,	(И)
7xi“ ,т2 + 21'з~~ 2ь'э 4" 1рз = 5'
*!>0, х2>0, ка>0, t»3>0, ^„>0, к’3>0.
314
В (I), (И) сделана замена переменной z3e=u3 — щ, uj^O, uj^sO, а в (И), кроме того, введены переменные юг^0, wj^O для нппведеипя пераисистн к равенствам.
5.3.	Вводя дополнительную переменную жа > О, запишем норное ограничен не в виде равенства
3zj 4* "Ь х3 -|-4- sj 5.
Выразим из итого и второго ограничения переменные xt п ж-, ио связанные условном неотрицательности:
Ж| = 5хз + ц — ЗхН-’З, я2 = —8х3 — 2х4 4- 4xs — 2.
Подставлял данные выражения в целевую функцию п в третье ограниченно, приходим к задаче
— ЗВж_ — 12х. 4- 19ж. max, 3	4’5	’
4х34- бг4— *6 = —2,
5.4.	С учетом сказанного.» и, 1 теорему достаточно доказать, например, для канонической задачи ЛП (5.5), Итак, пусть ее допустимое множество X непусто и /* = sup(c, IXW- Предположим, что утверждение теоремы неверно, т, о. система
Лх = Ь,
<с,
пе имеет решения. Тогда по леммо Минковского — Фаркаша (теорема 4.С) найдется такой вектор (р, X.) е !Vn X R, что
рЛ + Хс^О, <Р, 5> + ?./•< 0.
Отсюда для любого х е X получаем
<лс, х> 5: <—рЛ, х> из —<р, Лх> => —-<р, Ь> > X/*.
Следовательно,	f
inf <Хс, х> > Kf* X sup <с, аг>«
Очевидно, однако, что пи один из случаев k «= 0, ?. > 0, X. < 0 здесь невозможен.
5.5.	Пусть «♦ — решение задачи (5.1), по пе существует чисел iq^-0 (ie У(х’)), удовлетворяющих снстомо (5.20). Тогда по лемме Минковского — Фаркаша найдется такой вектор fteRa, что
<fll, Л>С.0, fe /(«*),
<с,Л>>0.
Отсюда для любого I е I(г*) и всех а 5= 0 следует
<щ, лг* 4-	= h 4- а<й<, й> < bi.
315
Для любого iе{1,	и всех достаточно малых а>0
имеем
<а(, х* + ай> = <а<, х*> -Ь а<й<, й> < Ь{, поскольку <а<, «•><&<. Таким образом, для всех достаточно малых а>0 точка х*-|-«Л допустима и задаче (5.1). В то жо время
<с, х* 4- аЛ> = <с, х*> 4* «<с, й> > <с, ®*>.
по это противоречит тому, что х*— решение задачи (5.1). В одну сторону теорема доказана.
Пусть, напротив, существуют неотрицательные числа Р* (1е/(«•)), удовлетворяющие системе (5.20). Тогда для любой допустимой точки х задачи (5.1) имеем
<«, х> - 2 р* <я1< *> 'С 2! ш
“ 2 Ъ <ai’ х*> =* <с, *•>,
т. о. х* — решение задачи (5.1).
5.G. Отметим, что указанное в теореме 5.3 условие экстремума можно переформулировать следующим образом: существуют числа Р*>0 (1 = 1, ♦..,!») такие, что
m 2ffifl« = cl» 7 = 1.....п»
i=l
р* (2вц**—М =0> fi=i.............т-
\j=i !
Продета они теперь общую задачу ЛП (5.6) как основную:
2^-ыпах, i=i
я
2 aijXj 1 Й, ДОИ1
П	П
—2 aijxj “ ^0	1 = й 4~ 1, ..., Щ,
1=1	1=1
—	0,	/ = 1, з.
Согласно сказанному выше, условие экстремума в этой задано звучит так: существуют неотрицательные числа у* (i = 1, .... й), Uf, t»( (/= й4-1, ..., и), zj (/ = 1, ...,«) такие, что
k	tn
21 (ui-vi)aij-si = ej’ i = i.......*.
i=l	<=Л+1
Л	rn
2 (ui“yi)flij —c5<	/ =
<=1	l»*h+i
316
1/*	aiJXS ~ bi j	°'	1 = 1' • k>
-y>0,	...S.
Система (5.21)—(534) получается из выписанной, если положить y* i=ut — v* (f=s&+l, .... л») и исключить за счет перехода к поравеистеам норомопные zj (/ «а 1, ..., $).
5.7.	Достаточно доказать теорему, например, для основной задачи ЛП (5.1). Пусть х — ее некоторое решение. Тогда по теореме 5.3 существуют такие числа У*^0 (ie / (я)), что
с= S &W	С1)
isJ(x)
В силу теоремы 4.2 имеется такая вершина х* допустимого мно-жостпа задачи (5.1), что Цх) а/(х*). Положим I/*—0 для мех
Рис. 88
£<= Т(х*)\Цх). Тогда (I) можно переписать в виде (5.20). Следовательно, х* — решение задачи (5.1).
5.8.	а) Геометрическая интерпретация задачи приведена ял рис. 88, Отсюда видно, что решенном служит точка пересечения прямых —х, 4- 2*2 = 4 » Зх[ 2х2 = 12, т. е. х* = (2, 3).
Приведем аналитическое обоснованно ответа. В точке х* по самому ее оироделопню активными являются второе и третьо or-реничвпня. Поэтому, согласно теореме 5.3, точка х* является ро-пюннсм задачи в том н только том случае, если существуют числи ^2 5= 0,	5= 0. удоллотиорягащно системе
,	<-1,2)уа+(312)рз=а(1, 2),
т. о,
—’Л + Зй = 1, 2рг 2рз = 2.
317
Ио ее рошоппо существует л положительно: у* у* = 1/2. Сло-дователыю, указанная геометрическая гипотеза верна.
(В качестве обсуждения приведенного метода проверки ответе предположим, что на основании неверного геометрического чор-тоип1 плп по иным причинам была выдвинута гипотеза, что реже* ином задачи служит точка поресечепня прямых 3xt — 2хг = G и 3*! 4- 2х; = 12. Тогда мы пришли бы к системе
3yt -I- Зу3 = 1,
— 2yt 4- 2уэ = 2,
О,
которая пс имеет решения. В результате доппая гипотеза была бы отвергнута.)
б) «• в (3, 2); в) х* = (1, 2); г) «• = (1, -2).
5.9. а) Из третьего ограничения имеем
хз = 2xi — то—2.	(I)
Подставляя ото выражоппе в деловую функцию п первые дна ограничения, а также учитывая, что zj^u, приходим к задаче
2х14~ х,,->-тох,
3^4-2^12,
2х! — *2^2, х, 0, х 5= 0.
Из гсомотрпчоскпх соображений обнаруживаем и проверяем по теореме 5.3, чтох* =4, х*=0 — решение данной задачи. Подстав? ляя зги числа в (I), получаем г* = G. Следовательно, х* = *= (4, О, G) — решение исходной задачи.
б) Выразим из системы уравнений перемеппые xi, xj, Xj.‘
Хд i^»	8	*
xa=s 154-5^ — 3z&,	(II)
х3±п— 9-1- *44-&г6.
Подставляя данные выражения и целевую функцию и учитывая условии неотрицательности, приходим к задаче
— 7х44-3х6-ч-шах,
®44* *ь^8,
— 5*4 + 3*5'С
х4 4- Зх6 > 9.
*4 2= °1 *6^ °«
318
Ес рошоиче:** = 0, я* = 5. Подставляя отн числа в (II), получаем х* = 3, х* = 0, х* =6, Следовательно, х* = (3, 0, 0, 0, 5) — решение исходной задачи.
1 п) х* = (7/2, О, О, 3/2, -1/2).
г) Из системы уравнений получает
Х| = Х4 -]- 2, х2 — —2X4 +1, ха га 4xi — 1.
Отсюда приходим к одномерной задаче ЛП
— 2хд + 1-> шах,
4х4 + 2<6,
х;ч-2>о,
-2^ + i^O,
4x4 — 1^0,
’Т. О;
Х4 -> into,	1/4 <; х< <; 1/2.
Следовательно, х* — (9/4, 1/2, 0, 1/4) — решение исходной задачи, 5,10, а) Точка х* допустима, причем активными в пой являются мерное и третье ограничения (/(х*)	{1, 3}), Согласно тео-
реме 5.3, следует убедиться в совместности системы
I/i«t + Уд«з “ с, У1> 0, рз О,
где «г = (5, -1, 2, -1), в3 = (1, -2, -1, 1), с = (7, -5, 0, 1). Поскольку опа имеет решение у* = 1, у* = 2, то х*— решение денной задачи ЛП. ***
и) Точка х* допустима, причем активными в ней являются первое п третье (х2 5= 0) ограпичолпл-перавепстиа. Согласно теореме 5.4, следует убедиться в совместности системы тина (5.21) — (5.24). В данном случае опа сводится к следующей (уа = О):
-Зух + 2у3 = -12,
-^“2^ = 4,
4ух + У3==5,
У^О.
Поскольку I/*— 2, Уз и — Зудовлеиюряют данным соотношениям, то х* — решвпво.
5.11. а) Непосредственной проверкой убеждаемся, что точка недопустима, а х2 н «’ — допустимые точки задачи. Значения целевой функции в точках х2 и ха ранптл 0 и —10 соответственно. Таким образом, сроди указанных точок решением молют быть только х2. С помощью тооромы 5.3 нокааываотсл, что х2 дойстиятельпо лаллотсн решением.
319
В остальных задзппях решениями являются: б) ж3; в) г’ п rJ; г) х\
5.12. а) Точка х* = (2, G) допустила, причем активными в ион являются первое н второе ограничения. Тогда, согласно теореме 5.3, эта точка является рошеппом задачи в том и только том случае, если совместна система
(2, 1)^1+(1,2)^=» (а, 1),
1/1 О, К2 Э? О, т. о,
2ух4"	=
j/j 0, у„ 5= 0.
Указанная система уравнений имеет единственное рошоипо: у*=(2а — 1)/3, '/* = (2 — а)/3. Отсюда получаом ответ: 1/2 а 2.
б) 0<а^2/9.
в) Согласно теорсмо 5.4, параметр а удовлетворяет нужному условию в том н только том случае, если система
-3^-1-РдЯ — 1,
2^4-^35=70,
— У± + У3 “ 2л,
У 2 5= О
имеет решение. Отсюда получаом отлет: —1/2 а ’С 3/4.
г) Аналогично в) составляем спетому
4у34-Зау3>4,
— Зу2— 2j/3== — 1.
2у„ 4~ Зу3 « «,
Уа5=^|
Отсюда вытекают условия па о: 2/3 а 3/2, 9а9 — 14л — 8	0.
Поскольку яти условия противоречивы, то х* по является р-ептевп-ем задачи пп прп каких значениях а.
5.13.	а) В табл. 22 отражен процесс поиска вершин допустимого множества по общей схеме из и. 1 § 4 п указаны зпачопвя в них целевой функции. Из сопоставления этих значений слодуот, что среди поршни решенном может быть только г* = (—5, 1, 10). С помощью тооремы 5.3 убеждаемся, что х* действительно является решенном •).
•) Отмстим, что для использования и подобных ситуациях теоремы 5.5 необходимо сначала доказать, что решение задачи существует. В данном случае доказательство этого не проще, чем прямая проворна оптимальности х* на основе теоремы 5.3.
320
б)	В табл. 23 отражен процесс поиска вершин (опорных тонок) допустимого мпояшетва по специальной схеме пз п. 1 § 4 л зчеазапы значения в них целевой функции. Наименьшее зпичо-п«0 достигается в точно х* = (0, 0, 20/7, 6/7). Решеппо задачи существует, нос кольну оо допустимое множество ограничено. Тогда рашоппо в силу теоремы 5.5.
Таблица 22
Множостпо 1	Вершила	Зяачоапо целовал функции
{I. 2, 3)	(1. -1, 2)	2 .
{1. 2, 4)		
{1/3,4}	(-5, 1, Ю)	6
{2, 3, 4}	(0, 0, 3)	3
		— 1*
Таблица 23
Множество J	Вершина	Зпачеппо целевой фушщил
{1.2}	(7. 5, 0, 0)	12
(1.3)	—”	-
{13}	(4, 0. 0. 2)	10
{2,3}	(0, 3/2, 7/2, 0)	17/2
{2, 4}		—
(3, 4)	(0, 0, 20/7, 6/7)	58/7
в)	Воришками служат точки х1 = (0, 0, 0), z1 •= (1, 0, i), х3 = (0, 1/4, 1/4); при ©том z1 — решение задачи.
г)	Вершинами служат точки х1 = (—1, 0, 2, 1), х2 = (5, <4, О, —7k х’=а (1, 0, 0, —3); при этом х2- п х^ — решеппя задачи.
5.14.	а) Складывая, первые три ограничения, убеждаемся, что допустимое множество задачи ограничено, Следовательно, задача разрешима, и по теореме 5.5 существует такое ее решение, которое является вершиной допустимого множества. Примепонпо здесь метода полпого Перебора вершпп потребовало бы рассмотрения С| = 20 случаев. Замётом, однако, что по опредолеппто любая вершина должна обращать в равенства но крайиой мере три из имеющихся шести ограничений. Сладоватольпо, верншпа-рошеппо либо обращает в равенства нерпы© трп ограппчопия, либо пмеет но крайней мере одну нулевую координату, в то время как остальные дно образуют решение получающейся задачи ЛП с двумя переменными. Таким образом, достаточно рассмотреть всего четыре случал, в одпом из которых требуется решить систему из трех уравнений, а в каждом на трех остальных (ri = 0, xj = 0 или хц = 0) — по задаче ЛП с двумя переменными. В результате находим точки (1, 1, 2), (0, 9/7, 11/7), (2, 0, 1) к (1, 0, 0), среди которых пмоетсл решение исходной задачи. Значение целевой фупк-
21 С. А, Ашыоиоо, А, В, Тиммов	321
цпи в этих точках райпо 9, 29/7, 11 и 5 соответственно. Слодова-телыто, решопием служит точка «• = (2, 0, 1).
б) х* = (1, 2, 0); в) х* = (1, !, 1); г) х* = (0, 3, 1),
5.15.	Перепишем. задачу (5.29) в лпдо эквивалентной задачи типа (5.25):
mH
2 ("^)^->-тах, 1=1
ТЛ
2 (— fl;i) «Ч < ~ <>	/> 1.....s>
7=1
Wl
2 (-«>{hi = -cp / = «+!,.... П, 1=1
yi>0,	7=1, ...,7г,
гдо ад.|= rtjj. По определению задача, дпонствошшя к этой зада-че, имеет лид
П
2(-С;)х;-^т1п, 7=1
2 xi (— «Ji) > — &J,	7=1,..., k,
7=1
11
2 xj (- %-i) = — &ls 7 = It + 1, ..., m, 5=1
«y>0,	/ = 1.....s.
Но это лишь иная форма записи задачи (5.25).
5.16.	Дли любых х <= _Y и у е У имеем п	п / т \ т / п \ т
2 cfi < 2 ( 2	) xj = 2 (2 eifi < 2	с1)
7=1	7=>i \!=i У	\j=i / 7s=i
что доказывает теорему 5.7,
Далее, если при некоторых .? еХ п I/* е У выполняется (5.27), то для любого геХ с учетом теоремы 5,7 пмеом <с, х> =£ <&, уУ “ <с, **>, т. о. х* —решение задачи (5.25). Аналогично нокпэыллотся, что р*—* решение задачи (5.26).
Наконец, условно (5.27) равносильно тому, что в цепочке (I) прп х га х*, у = у* оба неравенства обращаются в равенства. А это и свою очередь эквивалентно условиям (5.28), (5.29).
5.17.	В силу теоремы 5.6 достаточно доказать теорему 5.9 лишь в одну сторону. Пусть задача (5.25) имеет решение х*. Тогда по теореме 5,4 существует такой повтор у* е У, что выполнены условия (5,28). (5.29), Из теоремы 5.8 заключаем, что у*— решение задачи (5.26) и <с, я*> =э <&, р*>.
5.18.	Если Хг =/= 0, У 0, то с учетом теоремы 5.8 каждая из задач (5.25) н (5.26) удоплетверяотусловиям творомы 5,2 и поэтому имеет решение. Если же X =/= 0, У = 0, по sup <с, х> < оо,
322
то в силу той же теоремы 5.2 задача (5,25) пмоот решение. Тогда но теореме 5,9 должна иметь решение я задача (5.26), что противоречит условию У = 0.
5,19.	а) Составим таблицу перехода к двойственной задаче, как она описана ип. 5 (табл. 24).
Отсюда получаем ответ;
Таблица 24
о
Уз
11
8 4
11^4-3^2 4- 4y3->min, 3^ — Уа4“ У3>17, — ух + 5у34- У3 = —5, — ^+5^+ ^з^1’ 4^1— уа4-3уа^1, 7У1~ 2у2— у3 = —8, ^>0, уг>0.
5.2р.	а) Перейдем к двойственной задано:
0ух —
4~ ЗУл г? ?s
— уг4- у2>о, 2^— у2>1, — Ух > — 4, ^>0, у,,>0.
С помощью геометрических построений находим ее решоппе у* ==> я* (9/5, 13/5). В этой точно ангнпнымп являются первое п третье ограничении, причем обе ее координаты иолоиштольпы. Тогда, согласно теорема 5.10, точка х* является решением исходной задачи ii том и только том случае, если	а х* п х* удов-
летворяют системе
xi -;-2х3 = б, 2хд— я3 - — 1,
*з^0.
(D
21*
323
Отсюда х* = 4/5, х*—13/5. Следовательно, х* = (4/5, 0, 13/5, 0) — решение исходной задачи.
(Отмстим, что одновременно с втим строго обосновано, что указанной точка у* является решением двойственной задачи. Если бы была допутцона геометрическая ошибка в определении рошоипя двойственной задачи, то система типа (I) по имела бы решении па основании тон жо теоремы 5.10.)
б)	х* = (0, 0, 11, 0, 27); в) х* » (0, 3/19, 1/19, 0, 0); г) «• = = (-1, 3/2, 0, 0).
5.	21. а) Исключал переменную х< = 5 —	— хг, приходим к
задаче
бх2 5*2 “ *3 “*тах>
Хх ~Ь	3,
*х— ^з + ^з^1'	(П
Зх^-J- Xj 'Сб,
х^^О,
Построим к данной задаче двойственную:
3yx + if#-|- 5y3-)-min,
У1 + Уа4-Зу3>5,
3yt —уа+ у3 5s 5,	(II)
— УХЧ’У2 « — 1,
У1>0, Уа>0, У3>0.
Исключая yt = У1+1, получаем задачу
4у2 -h 5у3 ->mln,
2уа 4~ Зу3 4,
2у2+ У3^2,
У2 о, У3>О.
С помощью геометрических построений находим ее решоппе. у* а 1/2, у* = 1. Тогда у* => (3/2, 1/2, 1) — решений задачи (II), Поскольку всо координаты вектора у* иолозкнтельпы, то, согласно теоремо 5.10, решение (х*, х*,х*) задачи (1) должно удовлетворять система
^Ч-Зхд — гэ = 3, а!~ Ii + 23 = 1.
3*х +	5-
Отсюда г* =3/2, х* е= 1/2, х* =0. Следовательно, рошенном исходной задачи является х’ = (3/2, 1/2, 0, 0).
324
б) « (2, 0 —7, О, I); D) х* = (2, 1, -5); г) я* = г= (О, 1/3, 1/3, О, 5/3),
5.22. а) Перейдем к двойственной задаче
у1-|- 2h _^П1ах>
-2у,4- 5уа< 10.
5ух4‘ 5у2<17,
^ + 10^^29,
— Уд- Уа<0.
С помощью геометрических построений паходнм ео решение р* = (1, 12/5). В этой точке активными являются первые три ограничения, Тогда, согласно теореме 5.10, точка х = (xj, xj, хз, ц) Служит рошокпем прямой задачи в том п только том случае, еслп «<  =3 0 Я ;	— 2х14’.5х2+ 5*3 = 1,
5хх4-5г2-|-10х3:=2,	(Г)
*1^0,	0, о.
Общао решопно данной системы можно записать в виде
*! = 7 (1 5*э),
9
*з^35 0-5*3)’	<П)
О Хз 1/5.
Эти соотношения омоете с равенством х, = О описывают множество всех решений исходной задачи. Сюда входят две вершины .ее допустимого множества: х1 ев (1/7, 9/35, 6, 0) п я2 = (0, 0, 1/5, 0). Порвыо три координаты этих точек могут быть получены из (1) как вершины соотиетствующого полиэдра в IV или из (II) при Хз — 0 и х3 = 1/5,
б)	Выражая хз п» уравнения, приходим к задано
9Zj — 5х„— 2хд -|’
— Ия — 11хл 1&г 4- 6х.	— 25,
1-34	/j,
5х24- 2г3	^-7.
*1^ 0, *2 0*	^"0*
Рассмотрим двойственЕсую задачу
25ух 4- 7у3 -ь шах,
НУ^ЬО^О,
ИУд — ЭУп^ — З,
16ух”- 2у3 =з *— 2,
325
-%	<2,
у1о, ys>0.
Нетрудно убедиться, что допустимое множество двойственной задачи состоит из единственной точки >jt « 0, у2 = 1, Тогда точка (xIf х21 хд, х<) является решением задачи (1) в том п только том случае, если xt = 0 и
Н^ + Шз-Нбх^б, 9Xj 5г.,	2х3 = 7,
хэ>0.
Эту систему можно переписать п виде
xg = Y (0^, — 5*2 ~ 7), &3х1 —29хг>81, хх>0, х2>о.
Эти соотношения вместе с равенствами
«4 = 0. *6	(7 “ Ч “ ЗХ2 ~ Ч)
описывают множество всех решений исходной задачи. Сюда вхо-' дит одна вершина со допустимого множества: х == (81/83, 0, 74/83, О, —134/83).
в)	Множество решеппй описывается соотношениями
21=13Z2^13’ г2^°> хз={3а:2'^13’ Яд = 0*
При этом только один решение х = (1/13, 0, 10/13. 0) является вершиной допустимого множества.
г)	Множество решений описывается соотношениями х2 = 2 — 5xt — Зх3, х, =а О, 8»х + 4х3>8, 5*J- 3x^2, xg^0.
Вершинами являются следующие решения:
х’ = (1/4, 0, 1/4, 0), х2 « (3/8, 1/8, 0, 0), х’ = (2/5, 0, 0, 0).
5.23.	Пусть аи н х2 — объемы производства (в тоннах) чая сорта Л и Б соответственно. Тогда задача формализуется следующим образом:
320х, -f- 290хЛ ->- max, X	А
0,5^ + 0,2x^600,
326
0,2^ 4* 0,вж2 < 870,
O.SXjH- 0, 2х2<-530,
О, 2g О,
С помощью геометрических построений находим ее решение: г* = 600, х* = 1250*
5.24.	Пуси. х} и x-j — месячный объем производства (в тысячах литрон) бензина сорта Л и Б соотвотствеппо. Тогда приходим к задаче
90х, 4- 120г. -► max, д •
"s’ 'Ь *2* Ж2 1500,
4 Ж1 + 4 < I200»
4" "з*г2	1300,
х1>°, 12>0*
Ее решение: х* = 2700, я* = 1200.
5.25.	Пусть хг, xs, х3 — количество (в кг) сена, силоса и концентратов соотиетстионно, входящею в рацион одной коровы. Тогда приходим к задаче типа 5.9, а):
1,5хх-1- 2х„ 4- &г3-> min, 50Xj *b 70.r2 -f- 180хэ > 2000, 10.^4- 4+ Ч^210’ 2ХД 4- Зх24-	*3 = 87,
я, 0, х^ 2^- 0, «г	0.
Ес penreniro: х* = 6, х* ™ 25, я* = 0.
5.26.	Пусть x/j (« аа 1, 2; / =t 1, 2, 3) —объем перевозок цо-лгонта с /-го заводи на /-й комбинат. Тогда приходил к транспортной задано ЛП следующего вида:
10-х 4-	4- 25.г 4- 30*Л, 4- 50г -|- ЗОх ->-min,
11	л;	J4	««Л	"V
*n4- *J2H- *i3	=<
+	*22 +	*23 =* 60’
хп	.гй1	=50,	(I)
XJ2	"1“ *23	~ 20’
*13	”1“ *”з = 30’
»v>0, / = 1,2; / = 1,2,3.
327
В системе ограничений любое уравнение является лппоГшой ком-бпяацвой остальных. Поэтому из мео можно удалить, например, второе ураопоппе. Из оставшихся уравнений легко получаем
х13=	40-^-^,
*21 S	^11’
г23=	~'Г12’
*а3 = — 1° + *п-|- xi2.
В результате приходим к задаче 1 zn 4-2*i2-►max,
*11 "I" *12
О 50, 0 Xjg 20,
(И)
С помощью геометрических построений находим ое рошепне: г*! = 20, х*2 = 20, Из (II) получаем остпльпыо компоненты решения задачи (I): **3 а 0, х*х = 30, х*2 — 0, х*2 = 30.
5.27.	Пусть ль хз, хз —- используемое количество (н м2) металла, стекла и пластмассы соответственно, Тогда получаем следующую задачу ЛП:
25х1 -J- 20х2 40х3 -> min,
10xx4-15«s4* Зх3<150,
*1 ’Ь ®г *1' жз а х^О, 4 С «2 С 5, х3^-0.
Ее решение: х* ~ 00/7, х* = 4, х* = 10/7.
5.28,	Обозначим через xj массу (в кг) /-го типа сырья, которое пснользуотся для получения 1 кг требуемого сплава. Тогда поставленную задачу можно формализовать следующим образом:
Юх^ 4- 30х„ -|- 40х3 G0xfl min,
Юх1 20х2 4- 2эх3 4- 40*,t « 30,
VI- га+	I4el'
«у>0,	/ =
Ее решение х* = (1/3, 0, 0, 2/3) может быть пандспо, например, методом полного иеробора вершин (см. 5.13); Таким образом, l-iimi.im дешевым является сплав норного и четвертого типов сырья в отношении 1:2.
5.29.	Обозначим через х} объем выпуска /-й детали. Тогда получаем задачу тина 5.14:
Зх, -j- хл 4- 2х.. max,
+	я;3<890,
328
4	+2zs<020,
x. -|- 4i„	< 840,
z2^0,
Ев решение; г* = 0, x*= 210, x* 4G0.
5.30.	Обозначим через jci, xt, x3, r< нлаплруомоо к выпуску количеств холодилкипноя, газовых плит, морозильных шкафов и еяектропечеи соответственно. Тогда получаем следующую задачу ЛИ:
10 (20 4- 1&л, -[- 25г3 -|-10* J max, гх^-1,5^4- З.г34- С 7000, Зхг 4- Зх2 4- 4х3 4- 2х4 < 12 000, ^.^0,	4.
ч
Применял теорию двойствепностп и геометрические построении (см. 5.20), находим решение »той задачи; г* = аг * =2000, х*= > i=a*= 0.
5.31.	Обозначим через xh х3, х3, х< массу (в кг) мяса, муки, молока п сахара соответстаенно. Тогда задачу можно записать в следующем виде:
500 (Зх2 4- 10^2 4- Юх3 4- 8^) max, г14~ г2 4- х3 "I"	35,
_	х, 4-1,&?2 4- 2х34- х4 <45,
-®х4- 2х»	(П
“ *2 4- *3 о>
— ^з'Ь8^
®4 ^0-
Мы наложили условно неотрицательности только на .гц, поскольку неотрицательность остальных переменных следует нз четырех последних ограничений.
Построим двойственную задачу:
35ух 4- 45у2	min,
4- У3— 1/3	“3,
-Ь 1,5у2 4- 2у3 — у4	= 10,
уг4- 2у2	4-у4— Уа = Ю,
^4*	+8*6> 8»
у{>о, ; = i....5.
(И)
329
Выразим из параш: трех уравнений воромонпыо уз, yt, Уз через У1 и
i^-i- У2 — 3, У^З^-ЬЗ.5^-16, У4 = Й, •{* 5,5^2 — 26.
Подставляя эти выражения в (II), приходим к падано
7^-1- 9гл,-*~тт,
НухН- 15у„> 72,
Р1“|* У2> 3, 3yx4-3,5ys> 16, + 5,5у2 26^
Ух>0, У4>0.
Решоппом этой задачи является точка у* - О, у* = 4,8, л которой второе, третье и четвертое ограничения выполняются как
2
Способ
Слосюб 1
Способ 4	Способ 5
Рпс. 89
строгиа неравенства. Это означает, что для решения у* ладами (II) кмоют место соотношения у* =0, у2 >0, у* > 0, у’ >0, у* > 0. Тогда, согласно теореме 5.10, решение х* задачи (I) должно удовлетворять системе
jti + 1 ,5tj -|- 2za + Х{ 45,
xi = 2хз, я-j х3, Хз 8x4.
Отсюда г* = 10, ж* =г* =8,2*0 1,
330
5.32. На рис. 89 указаны пять способов раскроя листа, кеяц-цпстею получаемых деталей обоих ипдов п площадь отходов. Существуют ощо песколысо способов раскроя, по они либо эквпв'а-лоитны перечисленным, либо заведомо хуже.
Пусть-xj—число листов фанеры, которые будут кроиться по •,у-му способу. Тогда получаем следующую задачу ЛИ:
х> + 2хг 4" хч ’г 2х$ “> min,
4xj + Зх2 -|- 2х3 + z^^ -J- 2х2 Н-4х3 + 5xd + 6xfi,
«14’ «2 + х3 + х.:4-хь ==5000,
х.>0,	7=1,
... Ес решение: х* = 2000,	= 0, х* етЗООЮ, т* = г* = 0.
х 5,33. В табл. 25 перечислены возможные способы раскроя 4*-стаидартпой полосы, причем заведомо пвоптнмальиыо способы (на-4 пример, пуль заготовок по 1800 мм л семь заготовок по 700 мм) t отброшены.
Таблица 25
Способы раскрои	Количество получ,ч«и« оаготосои	
	ifleo мм	700 мм
1	0	8
2	1	G
3	2	3
4	3	0
Пусть xj — количество стандартных полос, раскраиваемых по /•му способу, а — число комплектов. Тогда заготовок длнпои 1800 и 700 мм будет получено x2 + 2x3-J-3x< и 8xj + Gx2 + 3x3 штук со-отиотствопно. Требуется найти решение следующей задачи ЛП:
а -> тоах, *«4-2*3 4‘2*.
8х± -] бх2- Ц- Зх3 5= 5а, ж14- я24- Vh ж4 = 770> х?.^0, /=!,.. .,4.
Рассмотрим двойственную задачу: 770yj-»-min, “8У34-У3^=О.
— у1“6у24-у3>0, “2уг —Зуг4-у3>0, “%!	4~у3^о,
(И)
331
20р|-5у2	=1,
Выражал из носледвого уращмшня у?, приходим к задаче 770уз м- min, 16^4-5^ >8, 7^-1- 5у3>6, — 4у1 + 5у3>31 — Зу,4- У3>о, 2у х Ch >!>0.
Решенном этол задачи служит точка у* = 3/11, у3е=9/11. Тогда у? s= (3/11, 1/11, 9/11)—решение задачи (II). В точке у* норное ограничение задачи (II) иынолпяотся как строгое неравопстко, а следующий три обращаются в равенства. Тогда, согласно теоремам 5.0 и 5.10,набор (г*,	**, а)ш)ллотол решением задачи (I)
в том и только том случае, селил-* =± 0, ft* = 770у* = (Ш), а остальные ого компоненты удовлетворяют системе ^4-2^-1-3^ = 12450, 0хг -|-Зхэ	=3150,
*2 4- *34-	770,
s2>0, о, ®. >0. л	«9	"ж
Эта система имеют бесконечно много решении, которые можно описать так:
хг = 280 -[• Т4, Х3 => 490 — 2х«, 0	245.
По смыслу задачи величины	должны быть целыми чис-
лами. Поэтому следует наложит!, донолннтсльноо предположение, что о?4 — «слое число. Каждая получаемая отсюда схема раскроя я* = (О, **, «*, с*) обеспечивает получение максимального числа комплектен, равного а* = 030.
534. Пусть zj —доля всей колхозной лапши, засеянной пшеницей /-го сорта, а — гараптпроваипып урожай. Тогда приходим к задаче ЛП, аналогичной предыдущей:
a-»-max,
25хх 4- 20х2 4* 30хэ 4- 15х4 а, 4- 20z2 4- 10Xg 4- 40хд а, ^-1- ^4- za4- х4 = 1, «1^0, /«=1, .,,,4.
832
Применяя тот же метод, находим рсшояне: я* = х* = 0, х* = 5/9, х*= 4/9. Таким образом, следует сеять цшеппцу только сортов 3 п 4 в отношении 5:4.
5.35. Можпо применить, папрпмер, теорему 5.4, учитывая, что в данном случао к s <= 0 и, значит, условия (5.21), (5.23), (5.24) просто отсутствуют.
5.37.	Применить 4.85.
5,38.	В обоих случаях допустимое множество задачи непусто (так как содержит ио крайней мере х «=» 0) и ограничено. Поэтому утвержден но следует из теоремы Войерштрасса.
5.39.	В обоих случаях допустимое мпожеспю задачи непусто. При этом значение задачи ограничено снизу пулом. Остается применит г. теорему 5,2,
(Здесь можно также применить 5.38 к двойственной задаче, й-затсм использовать теорему 5,9.)
5.40.	Пусть X пеограппчопо. Тогда, согласно 4.4, существует такой вектор h ф 0, что Ah 0 и, значит, Л (г* -j- ah) b прп любых ? еХ и ajs 0. Отсюда следует, что задача (5,1) прп с == А во пмо-от решения, поскольку lim <с, х* 4- dh) = °°.
5.41.	Укажем лишь прямые задачи:
a) Xj + хй max, б) г14-гп->тах|
— -I- «8 < 1;	— хг — х2 с о.
5.42.	Если X п У одновременно непусты н ограничены, то, согласно 4.4, системы Л« 0 и уЛ = 0, у 0 имеют лишь пулевые решения. Но это противоречит теореме Танкера (см. 4.101).
Докажем дополнительные более сильные утверждения. (При атом воспользуемся языком теории диойствовпости ЛП, хотя можно было бы опираться только па теорему’ 4.7 о следствиях.)
а)	Из конустоты и ограниченности X следует, что задача (5.1) имеет решение. Тогда по теореме 5.9 нмеот решеиие и двойственная к пой задача. Поэтому заведомо оо допустимое множество непусто. Предположим, что доказываемой утверждение неверно, т. о. при некотором d > 0 значение задачи
<c?i у>-*тах, уе=У
конечно. Тогда пз теорем 5.2, 5.9 следует, что двойственная задача
<с, Л> -»-min, ЛЛ^й
разрешима. Пусть Л — допустимый вектор этой задачи. Поскольку <1^10, то A <j4= 0. При этом для любых х е X и а 5= 0, очевидно, имеем z-«/iеX, т. о, множество X поограиичеио, Противоречив.
б)	Из нопустоты п ограниченности У следует, что при любом <} е Н” задача
<g, y>-»-miD, у<=У
имеет решение. Тогда имеет решение п двойственная задача
<с, х> max, Лх д.
833
Пусть х* — допустимый воктор этой задачи при q «= —а«, гдо с е= = (1, ..., 1) eRlrt, а>0. Ясно, что для «сох достаточно больших а. Если d>0, то <d, /lza> <d, г> = —а<й, с>, п, значит, lim (d,	= — со.
а-»<м
5.43.	Для доказательства (от кротивного) утверждения а) принести задачу (5,25) к основной форме и использовать утверждение а) задачи 5.42, подбирая воктор d соответствующим образом. Остальные утверждения легко выводятся из общих фактов о системах линейных урпппеппй.
5.44.	По опроделонито грипп Г = (ze ХрЪх « 5/} прп кеко-тором / = {1,	ж). Если ( = 0, тоГ*=Хн подходит c=tO.
Пусть 7 =/= 0. Положим
Для любых х е Х\Г и х* s Г имеем
<с, г> е= 2 <<Ч. *> < 2 bi w S <ЛЬ х*> = <с« х*>» <е/	fsl (е/
т. е. рошопнямп задачи (5,1) являются точки из Г п только окп.
5.45.	Если I* = (1, ..., т), то подходит .любая точка xgX*.
В противном случае положим /== {I, ..., т)\1* */= 0. По определению I* для любого_itsJ существует такая точка г'еР, что <*Ч, xf> < !ц. Пусть х — пронзаольпял выпуклая комбинация точек х*	с положительными коэффициентами (см. 4.1).
Тогда х е А’* я <<if, £> < bi прп всех I <= J. Иными словами, Г(.г) с 7*. Включение /*сг /(х) очевидно. Таким образом, 7(х) *= 7*.
(Отмстим, что основное рассуждепно повторяет решение лвда-чн 4.22 учетом того, что множество X* решений задачи ЛП является полиэдром.)
5Л6. Покажем, что X* совпадает с гранью X вида г={2е х । лиг'’- ь;;}.
По опрсделоянго 7* имеем X* cz Г. Пусть х е Г и, значит, I* czJ(х). Применяя теорему 5.3 к точке х из 5,45, получаем, что существуют числа у( 5? О (/<= Г»), прп которых
с= 2 ^iai-	М
iGl*
Положим >fi =0 для всех i 7(х)\1*. Тогда равенство (I) можно переписать в^видо
««“ 2 W1-
Отсюда н силу тон и?о теоремы 5.3 следует, что х е X*. Таким образом, Г с X*, т. о. X4 = Г. При этом dim Г е= п — rang Лдп « силу 4.25, По в данном случае /(Г) = /* но определению /•.
5.47. Утверждение пспосредствеино следует из 4.72, 4.73 и 5.46.
5.48. Применяя 4.40 к формуле (I) из решения задачи 5.46, получвем, что существует такое множество 1 с !*, для которого rang Л; 1= |/| и
е » 2	0)
1GT
834
прп пскотормх у* 5= О (Ге Л. Для любого репгеппя х* задачи (I) имеем / с /• g /(х*), т. е. 4/х* = bt, Тогда из (I) л теоремы 5.3 следует, что х* — решение задачи (5;30). Ойратиое утверждение очевидно, поскольку допустимое множество задачи (5.30) шире допустимого множества задачи (5.1).
(Отметим, что порван часть ирпмого утверждения теоремы непосредственно следует из 4.8$, если рассмотреть импликацию
/U й->- <С, Х> /*,
где Г — значение задачи (5.1), По доказательство равенства Л^х* => bt потребовало бы дополнительных соображении,)
5,49,	Укажем лишь прямые задачи:.
а) х1 -|- *2->max, б) х -|- х„ max,
-j- 2х2 С 1> *х 4- хи С 1.
“Р 1 >
0, Хд 0;
Ранее встречались п 5.59. Прямые задачи: а) хх+ -►max,
Ч_ 1 >
-(• 2х2 2, о, 0;
более сложные примеры
б) х14-х3~*чпах,
(см. 5.22, 5.33).
5.51,	Прямая задача:
^-т х,.-> max,
М^1’
Х^	1,
> 0, х„ 0.
5.52,	5.53, Применить 4.4 н 4.6 к множеству решений задачи (5.1), жшпеанцому в виде (5.3).
5.54.	Пусть X* непусто п ограничено. Тогда яз 4. НО с учетом (5.3) следует, что rang = п и рЛ — Хс = 0 при некоторых р > О, Х>0. Положим у = Х_,р. Тогда уЛ = с, у>0. При (Л \
_ J = П;
Пусть, пнпротпн, rang Л = н и уА с прп некотором у > 0. Последнее означает, что задачи, двойственная к (5.1), допустима. Тогда X* ф 0 в силу теоремы 5.11. Остается гпювь использовать 4.110.
5.55.	Представить задачу (5.4) н основной форме и применить 5.54.
5.56.	Представить задачу (5.5) в стандартной форме и применить 5.55,
335
5.57.	Применить 4.113 по типу решения задачи 5.54.
5.58.	Представить задачу (5.5) в основной форме и применить 5-57; затем учость формулу (II) из рошонпя задачи 4.33.
5.59.	Пусть /* —значешю задачи (5.25). Тогда множество ее решений определяется следующей системой;
п
1	= 1, .... ft,
J=1
11
2	aifj = bi, i ^ * + 1, ..., m,	(I)
2*л>/*> *,>о»	....®-
5=1
Если рассматривать ее как систему тпиа (4.18), то соответствующая система тина (4.19) имеет вид
гл
2 Piau~Ч’^0' 7 = 1> —» s* {«i
гз
2	=	/ “ * “1_ • • •» Щ	(II)
i«=l
ш
2 Pibi — № т	1«=1, ..,ft, л>0.
1«1
Заметим, что любое решение х системы (I) обращает неравенство. <с, х> 5= /• в равенство. Тогда, согласно 4.104, системы (I) ц (II) имеют такие решения а* и (р, к), что Л > 0 и
р<+р{— 2%-®*) > °» i=zi............*»
\	5°»1 г
г* + ( 2 PiaiJ "	) > °»	/ = 1...5-
Ясно, что х* и у* >= К”1р удовлетворяют нужным требованиям, (Другое доказательство этой теоремы, основанное непосредственно па теории двойственности в ЛП, можно пайти в [39, с. 177].)
5.60. а) ж* = (1/2, 1/2), у* = (1/3, 1/3); б) «♦ = (1, 0),	=
= (1. 0).
5.61. Утпорлщенне нопосредстпеппо слодуот из 5.59 и теоремы 5.10.
5,02, а) Рассмотрим двойственную задачу:
ух+2у2-*- таХ«
4^ + 3^ <12,
Ух- 1,
2^ + 2^^ 8,
Ух^0> уа^о.
336
Используя геометрпчсскио построения, паходпм, что единственным рошенном данной задачи служит точка р* = (0, 4), в которой вк-: типны первой, третыз и четвертое (г/i э= 0) ограничения. В силу единственное! и решения отп же ограничения и только онн являются закрепленными. Следовательно, соответствующие ограничения в неходкой задаче (ад >0, х3 0, 4xt + х2 + хз 1) свободнее, а остальные закрепленные.
б) Ограничении х> 0, х2 0, x«£sO свободные, остальные закрепленные.
в) Ограничения	— х2 — 2х} — бх< 4,	х2^0 свобод-
ные, остальные закреп ионпыо.
' 5.63. Ограничимся доказательством утверждения для основной Задачи ЛП (5.1). Пусть X* и У* —непустые миожоства решений аадачл (5.1) п двойственной к ней, /* —множество закрепленных ограничении задачи (5.1), J* — множество свободных ограничений двойственной задачи:
/*=={!, t	f	m| <д<, х> а Ь{ при всех х.^ X*),
/♦ = {£, 1	i С > 0 при некотором у е У*}.
В силу 5.46 множество X* состоит из одного элемента в том я только том случае, еелп
rang = в.	(1)
•В то же время, согласно 4.36, грань У* допустимого множества двойственной задачи является певырозкдвпной в том и только том случае, если средн векторов at (ie/*) имеется п линейно по-зайкенмых, т. с.
rang = п.	(П)
Но из 5.01 следует, что /* = J*. Таким образом, условия (I) и (II) совпадают.
5.64.	Пет, ие следует. Пвнрнмср, задача х3->-тах,
’’j ~Ь ^2	^"3	1,
Xi ~Ь “Ь хз	•
Xi “ х2	Х3	1
— X — Х„ + X =С1 JL «а	ы
имеет единственное решспно х* = (0, 0, I). При- атом множество, решении двойстве и ной задачи совпадает с ее допустимым множеством, имеющим только две вершины: у1 = (1/2, 0, 0, 1/2) и у2 = “= (0, 1/2, 1/2, 0), причем каждая из них является вырожденной.
(Предлагаем читателю самостоятельно разобраться, возможен лн подобный пример в классе задач ЛП с двумя переменными.)
5.65.	Если решение прямой задачи ЛП единственно, то, согласно утверждению из 5.63, множество решений двойственной задачи является невырожденной гранью ее допустимого множества. Если к тому же решение прямой задачи певырождено, то в силу того же утверждения, примененного в другую сторону, решение двойственной задачи единственно.
с, Л. Ашманов, А. В, Тимохов	537
5.G6. Предположив обратное,. приходим к противоречию с 5.63, 5.67. Пусть у — произвольней допустимая точка (в частности, решение) диойстлеппой задачи (5.26). Тогда
tn	rn Э / п \	| n	/ m	\	п"
2	2 I 2 fl<Aj 1	=> 2	( 2	I	2 cA? >л»
1=1	1=1 V=1 /	\ik*l	/	j*»l
Остается использовать теорему 5.10.
5M Ниже под я1, йй, .'понимаются столбцы матрицы огра-inricuirii, под С], ci( ... — коэффициенты целевой функции, под **= (я*, х*, ...)*- решеппс рассматриваемой задачи.
а)	Поскольку а* а3 и Сг < сз( то х* = 0. В результате приходим к задало ЛП с двумя переменными, решая которую находим г* — 2 и х* = 3.
б)	Заметим, что а4 5= 2<? 4- ая, причем в последней координате этого вокториого неравенства стоит знак равенства. Кроме того, с< < 2с 1 -I- cj. Тогда я* = 0, п получаем задачу типа 5.9. Ее реше-пно: х* — 0, х£ = 4/3, х* == 17/3.
в)	В данном случае а’^а1—а1, с$<с2 — с(, а4 > 2а1 4- За5, щ < 2ci -)• 3cj, Тогда г* = х* = 0. После этого легко находятся х* = — 2, г* = 6.
5.69,	Применить 4.121, 4.122 к множеству X*, заданному в виде (5,3).
5.71.	Утверждение непосредственно следует из теоремы 5.9.
5.72.	В одну сторону утверждение очевидно, в другую непосредственно следует ив теоремы 5.11.
5.73.	Согласно 4.126, утверждение б) равносильно устойчивости систем
Л« 5 н уЛ = с, у 0,	f
определяющих Х(у) и Y(s). Значит, о учетом 5.72 утверждения а) и б) эквивалентны, Эквивалентность б) и в) непосредственно следует из 5.54, 5.56.
5.74.	Пусть s 5= (Л, Ь, с). Согласно теоремам 5.8 и 5,9, условия х е Х*($), у (= У*(«) равносильны соотношениям
Лх < Ь, уЛ = с, у 0, <с, х> = <5, у>;	(I)
Рассмотрим любыо такие последовательности {$*}, {**}> (у*), nt0 sft = (Л*,	с*),	х*<= X*(s*), у*® F*(s*), Тогда
It-» «г
Л*х* Ъ\ уМ* = с\ у* 5? 0, <с\ хк> = <5*, уА>. (П)
Из 5.73 следует, что множество решений системы (I) непусто и ограничено. Йезтому последовательности {х*} и {у*} ограничены в силу 4.133. Пусть х и у — их произвольные предельные точки. Боз потери общности можно считать, что х*-*-х, уА->-у.. Переходя к пределу в (II), получаем (I). Следовательно, xeX*(sj. Утверждение б) доказано. Для докозательства а) остается заметить, что
lim Г (?‘) = lim <с\	= <с, х> = Р (л).
/(->«>	Л-»ей
ззз
5.75,	Нет, пе следует. Рассмотреть задачу
х3-*-тах,
^•"1 4"
—Х1Ч*«8'С1.
А
5.76.	Пусть s 5= (Л, Ь, с). Примем обозначения 1 «я 7(x*(s), $), j=s= (1, .... m)V. Согласно 5.57, 5.G5, условно задачи равносильно тому, что Л г —невырожденная матрица размера пдп, ai*(s)— еднпствоипое решение системы
Л:х =s bi, Ajx < bj
и существует единственное решение У* («) е R” системы
Ыг = с, уг>0.
Ясно, что прп любом s' = (Л', Ь', с'), достаточно близком к з, матрица Л-i также пввырождепа, а системы
Луг ет bj, ,/lj х < b’j
п
y2dj = c\ y2>0
имеют единственные решения z*(s') и у* («'), непрерывно завя-ешцио от s'.
5.77.	Нот, но следует. Рассмотрим задачу
х3“* max,
(1 Ц-а)^ —х2<0,
— (1 — a)z1 + ®2<0,
*2^1,
где «j* о, Эта задача имеет вырожденное единственное решение (J, I) при « = 0 и невырожденное единственное решение (0, 0) при любом достаточно малом a > 0.
5.78.	Рассмотрим семейство множеств вида
Р') = {хе R"|A'« =£ У, <с', х> у),
где з'= (4', 5', с'). По условию при зет (Л, Ь, с) множество %(s> F(s))=X*(s) поиусто и ограничено. Тогда согласно 4.132 для любых Л', с', достаточно близких к Л, с, н любых b' <s Km, ? еП множество Z($', р') ограничено. Пусть при атом существует 5'), Положим {И = <с', х>. Тогда Z(s', {!') #=0, Ясно, что множества решении задачи P(s') п задачи
<с', х> “> шах, х е Z(s't ^')
совпадают. Следовательно, X*(s') непусто и ограничено. 22»
339
5.79.	Согласий 4.120, утверждение б) равносильно устойчиво стп светом, определяющих допустимые множества задачи (5.4) и двойственной к ион. Остается использовать 5.72 и 5.55.
5.80.	Ниже под ж* и у* понимаются рошоння соотаотствепип задачи (5.4) п диойствеппой к иен.
а)	Еслп а > 0, то
Лх* Ъ < b 4- ап, у*Л 5г с > с — агт,	(I)
п, значит, задача (5.33) устойчива в силу 5.79.
б)	Согласно (I), точки г* и у* допустимы н задаче (5.33) и двойственной к пей прп любом а > 0. Поэтому
F(a) <с — аи, х*> =; Г(0) —а<и, х*>,
(И) Г(а) <5 + ап, у*> = F(0) 4- а<о, у*>.
Слодователъпо, Пт F(a) = F (0).
в)	Рассмотрим любые a>0« jeX‘(a). С учетом (II) имеем
<с. *> <У*Д х> = <у*. Лх> <у*, Ъ 4-ап> =
= F(0) 4-а<1/\ v> ^/?(a)4-a<u, **> 4-а<У*. v>.
Тогда
a<w, х> = <—c4~au, х> 4- <<?, х> — F(a) 4- <с, ж> 5=
^а<н, ж*> 4-»<у*, у>.
Слодовательпо,
<«> х> < <л, х*у 4- <у*, у>,
где и > 0, х 3= 0. Это и означает, что множества А'*(а) (а> 0) or* раничвны и совокупности.	1
г)	При указанных а* п имеем
<с — ajtw, х*> = F(a»i), ЛхА Ъ т «ау, хл 0.
Пороходя здесь к продолу с учетом б), получаем
<с, x>=F(0), Ах Ь, х^О,
г. о. ж <= Х*(0).
5.81.	Согласно 5.73, множества Х*($) и Т*(у) пспусты п ограничены. Тогда с учетом 1.10 мокенмпп п минимакс в формуле (5.34) существуют. Йромо того, и силу 1.3 имеем
max min Lix. y,h)^ min max L(xt у, Л).
xex*(j) уеУ*{«)	keY»(«) x£.v*(4}
Поэтому достаточно доказать перво© и последнее неравенства в следующей цепочно:
inju max Л (г, у, А) )im <р (а) С уеу*{«) ж<=Л’*(«)	я^оТ
< lim ф (а) < max min L (х, у, Л), (I) а-,о+ хеХ*О)
где
т(а)=..лс+«ц-?А
МО
Пусть последовательность {а*} такова, что ccjt>0, а*-»-0 п
Нтф(ад)= Нт <р(а).	(II)
Д-»сч ' ’ а *♦04*
Рассмотрим любую токую последовательность (х*}, что х* <= еЛ*(5 + в^‘) ИР» исох достаточно больших А, Учитывал 5,74, можно считать, что	Для любой точки у<еГ*(«)
имеем
-г otjfc/j) = <с -и а^, х*>
=£ <с 4- акс, «*> -ь <у, Ь + алК — (Л -г а»11)г’,> ==
= <&, У> 4* <с — М, **> 4-ahL(x\ у, Л) =
= <ь, р> 4-«^(Л у, Л) == Р(4 + а*Ь(х\ у, А).
Следопэтольпо,
Ф(а*)^£(Д у, Л).
Отсюда с учетом (II) получаем
Шл ф (a) L (х, у. Л). a**Ot-
Поскольку это пераоопство выполняется для любой точки у е ePW, то
Кт ф (а) < mia L (ж, у, Л). а-»о+	уеУ*(«)
Здесь * —некоторая точка на Поэтому последнее поравопст-во в (1) справедливо. Точно так же с использованием двойствоп-вых соображений доказывается первое неравенство. Частные утверждения нояосродстввнно следуют из (5.34).
5,82.	Последовательно рассмотреть в 5.81 случаи
А = (0,	01 гдо в( — f-й единичный орт в К”;
h = (0, 0, е^), где cs — J-й единичный орт в К”;
Л = (Д 0, 0), где Л—матрица из «), у которой алс> монт па нороссчоиви i-й строки и /*го столбца ранен единице, а остальные элементы равны пулю. При этом учесть, что, например,
dF~
гдо А = (0, с*, 0). При выводе последних двух формул полезно помнить, что векторы из У*($) неотрицательны, тогда как координаты векторов из X* (з) могут иметь разные знаки,
5.83.	С-утцестновапис частных производных функции F в некоторой окрестности точки s п пх непрерывность в самой этой точке легко яыподятся из 5.66, 6.76 н 5.82.
5.84.	Пусть
841
Тогда задача Р($ -|- ай), т, о.
х -хтах,
— <%г2 < О,

X
1
разрешима для любого «Ss 0 (и даже aeR). При этом
F (в -|- аЛ) = (О’ U,
если к = О, если а > 0.
Следовательно, F'(s, А) не существует. 5^85. Пусть
Тогда при любом а О задача Р($ + аА), т. е. axj	->- max,
xl — ах£ О, *i	<1
разрешима и F(s-|-aA) — а. Слодоватодыю, ^'(з, k) = 1. В данном случае
£(*. U, Л) = *14- 1/1X2, Х*(з) = {х <= Hs|xf 0} и, как нетрудно проверить, У*(з) = {0}, При этом Макепмпп и минимакс в (5.34) равны нулю,
5.86. Утиорнщонко непосредственно следует па 4.134.	.
5.88. Зто утверждение— простое следстнио тоором 5.9 и 5.11. 5,89. Запишем задачу (5.38) в виде
<l»' —&, y>->min, уЛ = с, <у, A> *zF(b, с), р > 0. По условию опа допустима. В то же время допустима и двойственная задача
<с, х> —<xF(b, с) -►•max, Ли — аА	— А, а^О,
поскольку ее ограничениям удовлетворяет любая точка х<=Х(Ь') вместо с « 1=1. Таким образом, обе эти задачи разрешимы по тоо-ремо 5.11. Аналогично докалывается разрешимость задачи (5.39).
5.90. а) Пусть (А, с)(=/?Х£, (А\ ^^Ву^С и (Ал, ch) -> -*(&, с). Рассмотрим любую точку х<=Х*(Ь, с). Поскольку х<= еЛ'(А), то, согласно 4.136, существует такая последовательность {я*}, что х*-*-* и	Тогда с*) >	х*>. Переходя
п этом неравенстве к пределу, получаем
Игл F (t* ch) > <<?, х> = F (А, с), k-Kn
т. с. F полунепрерывна снизу в точно (А, с). Из аналогичных рас-суждений для двойственной’задачи следует, что F полунепрерывна сверху, а зпачпт, и непрерывка в тонко (А, с).
б) То, что в условиях утверждения б) задача Р(А, с) разрешима (Х*(А, с),^0), сразу вытекает из 5.86, 5.88, Далее, в силу 342
5.G9 существует такое 'тело а>0, «ио прп любом It справедливо перлийлство
lit
а|| ?1 —21 nut!C (0» (fli« x>‘)ь<) ‘Ь шах (°’l' c) ~ ^c‘ *^) ।
где J* — проекция тонки xh на X*(b, с). При этом
F(b, c) — <c, £h> = F(b, c) — <c*, xA> -J-	— e, x* — ;fh> 4-
-h — c, xA> F(bt c) ~~ I’’(b\ c*) + Hcft ~~ ell -fix* — 2*11 + q>(c*), где ф(сА) — впвчепие задачи
<сА — с, х> ->- mux, х е X*(Ь, с), имеющей решении в силу 5.89, Применял тс этой задаче утверждение я), иолучаом, что Птп <р(<Л) = ф(с) t= 0. Таким образом, Л-»оэ
П1
d| г*1 — г1* У, max (О, 1^- — max (б, (&, с) —	<?1) +
4>“1
+ Р1-₽||’11®Л- хА|-|-ф(с&)). (I)
Пусть боз ограничения общности lim	— Л, где 0^
Л-м»
Л Й«, Если допустить, что Л = со, то, поделив обе части неравенства (I) пп Цх* —хА|| п перейдя к пределу, получаем проти-.воречие: «-z;0. Таким образом, А < со. Тогда о помощью продельного перехода непосредственно u (1) выводим, что аЛ^О, т. о. •Л = 0.
5.91.	Если задача Р{Ь, е} устойчива по направлйЕппо h, то разрешимость' вадач (5.40) и (5.41) непосредственно следует из 5.89. Пусть, напротив, задачи (5.40) и (5.41) разрешимы. Зашипел задачу (5.40) в виде
<5, !/>->* min, уЛ = с, <b, у> F(b, с), у 5» 0. Двойственная к пей задача выглядит следующим образом:
<с, х> — *fF(b, с) шах, Лх — fb S, ’(0.
Ограничение <b, у> Г(Ь, с) в задаче (I) является закреплоп-пым, Тогдв, согласно 5.G1, существует такое рошоиво (х*, *(*) аада-Ч1| (II), что к* > 0, и, _слеДовательио, Лх а&, где x=x*/Y*i а = l/'f*. Итак, Ь-}-аГе2? при некотором а>0. Аналогично из разрешимости задачи (5,41) выводится, что cH-[Jc <=C прп некотором р > 0. Отсюда и по 5.87, 5.88 легко получить, что ^задача Р(Ь*}-а5, сН-^п) разрешима при всех а<=[0, a], |J<=[0, ЭД. Рпс-емптрмиап здесь случай а = р, приходим к выводу, что задача ^(Ь, с) устойчива но направлению h.
5.92.	Приводимое низко доказательство в основном повторяет схему решения задачи 5.81. Но только вместо 5.74 мы используем 5,90.
(I)
(П)
343
Прежде всего отметки, что величины, стоящие в праной части формулы (5.42), определены в силу 5.91. Положим
F (i> -J- ai, с -} ас) — F (&, с)
Ф (а)	.
Пусть последовательность {а*} такова, что а&>0, а*->-0 п lim q> (ак\ = lim ср (а). Рассмотрим любую такую послецова-h-xo ' тельпость {л*}, что	с-Ьа^с) при всех достаточно
больших к. Согласно 5.90, существует последовательность {!’*}, удовлетворяющая условиям хк^Х*(Ь, с) и lim [| я?1 —	|] = 0.
л->«>
Для любой точки у<= /*((», с) имеем
F(b 4- а*5, с 4* а»/) = <с 4* алс, я*> <с 4- аде, zh> 4-+ <У, Ь+аЛ — Лх*> «= <1>, у> + <с — уЛ, лЛ> 4-
4- Ок«г. **> 4- <5, У» = ?(Ъ, с) 4- «>(<«, *К> 4- <5. У».
Следовательно,
ф (“л) < < **> + у) = <с, ift> 4- <с, zh — sfe> 4' <5, у> С
< шах <с, г> 4-ЦсЦ • Ilfe —+ хеЛ’*(Ь,с)
Переходя здесь к пределу с учетом выбора {ад}, получаем Кт ф (а) С max <с, л> 4- <6, у>, а-»о+	?с&Х*(4»,с)
п, значит,
Пт ф(а)< max <с,	4- m'n	У>-	(I)
«-♦&-F	хех*(ь,с)	yey*(ti,c)
Точно так же с использованием двойственных соображений показывайся, что ппжпий предел lim Ф (а), напротив, по меньше <х-»о+ „
полнчипы, стоящей в (I) справа, Таким образом, величина с, Л) существует к вычисляется по формуле (5.42).
5.93.	Учитывая 1.2, имеем
F № + */) = s“| <Xicl +	«> <
< вир <?,	4- Xfl sup <CS, х> =	(?) 4- F (?).
л Х(=х	XGX
5.95. Используя 5.40, 5.91, легко получаем, что а) влечет б). В силу 5.78 из б) следует а) (и даже несколько большее). Эквивалентность б) и в) отмочена в 5.54.
5.9В. Пусть x-g А'*(с-Ь а/i). а>0. Для любого jeX*(c) имеем <с, х> > <с, х>, п в то жо время If+ «/*1	<с4*зЛ, л>.
Тогда <Ь,	*>, т. е. zeX«Z(l»). Следовательно,
Х*(с 4* сей) g X.	_
Далее, согласно 5.69, существует такое число а > 0, что
®> 5® ар(х, Х*(с))
344
прп всех х&Х. Пусть х^Х. Поскольку ХсХ*(с), то F(c) = =₽ <с, х>. Рассмотрим любую точку х^Х и со проекцию х* па Х*(с), т. е. р(х, АГ*(с)) = ||z —2*11. Тогда для любого а>0 по-лучасм
<с4-а^ *> ^^(с) — ар(х, Х*(с}) Ч-а<Л, х> =»
= <с, х> — а|(х — х*|] + а<А, х*> 4* а<Л, ® — »•>
<с, х> — «Их —х*|| 4-а<Л, х> + а||Л||.|1ж —ж*0 >=
= <с + аЛ, х> 4- (а||АЦ —а)||х —х*||.
Следовательно, если Ozga<ca я |]Л|| =* 1, то х_еХ*(с4-ай), т. о, X о X* (с + аА). Таким образом, Х*(с 4- аА) = X.
5.97.	Утверждение непосредственно следует из 5.99. Приоодем, однако, независимое доказательство. Обозначим через / = /(z*) множество активных ограничений в точке х*. Согласно 5.57, система
2 Vс, Vi > 0, i е /, iei
совместна к rang/h = n. Тогда из 4,125, 4.126 следует, что при любом с', достаточно близком к с, система
У У1«{ = с',
У1 > о,.
is Л
также совместна. Вновь используя 5.57, получаем, что х* — единственное рошопке задачи Р(сЛ).
5.98.	Рассматривая в 5.92 направления h = (0, ±с*), гдо d— J-n единичный орт в П" (/ = I, ..., к), получаем
птах
Х6Л*(С)
Х.= J
др*
dcs
(с) = 1г(0=
(с) = min z dcj хеЖ) -
Отсюда ясно, что множество Х*(с) состоит пз одной точки,
5.09.	Положим I = /(*♦). Согласно теореме 5.3, существуют числа у*>0 ({<=/), удовлетворяющие равенству (5.20). Введем чпеяа => у* + Xj > 0 (i s 7). Тогда
fe/	1«!/
При атом rnngyij g= н, так как х* — вершина. Остается использовать 5.57.
5.R10. Использовать 5.88.
5.101,	5.102, 5.105—5.107. Эти утверждения легко выводятся путем применения соответствующих результатов из 5.93—5,95, 5,97, 5.98 к двойствонпон задаче D(f>). Нетрудно доказать их я непосредственно.
5.104.	а) Поскольку указанная точка у* допустима в задаче D(b Ч-ае1'), то
F(b -|- aef) (6 -( at!1, у*> = F{b) 4- а.<с*, ji*> == F(b).
Отсюда л пз 5.103 слодуот нужное утверждение.
345
б)	Согласно 5.92, пелпчппа
F' (l>, с’) = lim + сх->о-|- ci
существует п иычнсляотск по формуле
F' (b, е*) = min у,.
wsY*(W
По условию веллчлла, стоящая здесь справа, положительно, Следовательно, F{b -(- а<?-) > /’(/;) при всех достаточно милых «>0, и значит, вообще при всех а > 0, так кик F пе убывает.
5.108.	Применяя 4.136 к множеству
Х*(Ь) ® (хеП’Мх-^ Ь, <с, x>
получаем, что существует константа L = L(A, с) >0, для >готороп
<*(Х*(бк), х*(ьу) //(||4»л — г»|| + р’(&*) -/<’(&) I)-
Отстода и из 5.90 следует нужное утверждение,
5.109.	Рассмотрим задачу ЛП
а->' min,
"п th ctj к ==	(I)
«si
Ясно, что еслп х* — решение зодонн (5,43) и а*е=/(а:<‘), то (г*, а*)—решение задачи (1). Напротив, если (х*, а*)—решение задачи (1), то х*— решоппо задачи (5,43) и /(л*) «= а*.
(Отметим, что этот прием мы уже фактически использовали в ретеппп задач 5.33, 5.34.)
5.110.	Указанные задачи сводятся соответственно к следующим задачам ЛП:
а-> min,
^с\ х) CS,	/» — 1, •.«, S,
—<с\ х> — tin й а.	А == 1, ..#,	(I)
х (= X
и
«
У ал->пц‘1>, ft=x
<с\ х> -f-ф, sga.i:,	s,	(II)
— <?>, х> — d/л, а*, к = 1, ..я, х X.
Ясно, что при X г/з 0 задачи (I) п (II) допустимы, а их зпачопнн ограничоим снизу нулем. Тогда, согласно теореме 5,2, эти задачи, а значит, и задачи (5.44), (5.45) раарсчиимы.
5.111.	Из условии следует,- что величина <р, х> -h 7 либо положительна, либо отрицательна всюду на X. Пусть без ограннчо-346
пня общности <р, г> -}• <j > 0 для любого геЛ' п X={x«=lV'| Лх &}•
Рассмотрим следующую задачу ЛИ:
<с, s) ad min,
Л=-аЬ<0,	(I)
<р, s>-(-а? = 1,
а>0.
Пусть х*—решение задачи (5X6). Покажем, что
л*	1
—=	' Л£* ~~т ****	-"' 1
<Р, х»> 4- q '	<р, х*> 4- q
осп, рвшецне задачи (1). Прежде исого заметим, что точка (£*, а*) допустима в задаче (1). Пусть (;, а)—любая друган ее допустимая точка. Тогда а>0, так как при а = 0 получаем, что Л;^0 и -	0, а это противоречит условию ограппчеппостл X (см. 4.4).
Следогютельно, z = s/a —допустимая точка задачи (5.46). Поэтому
<с,х*>-М	<е,*>-М
<Р, «*•> +5	<Р.	+ 9 ’
что можно перекисать в виде
<с, =♦> 4-a’d	(с, r> -bad,
Тпкнм образом, (s’, a*) — решение задачи (I), Аналогично показывается, что если (с*, а*) — решение задачи (I), то х* = z*ja* —-решение задачи (5.4G).
5.112, Пусть
X = {я € IV1 |	d>}, Y = {у е R« | уС2 ds},
где <71 <= /•/•(A‘i. «),	A‘2),dl G= iV'1.	Тогда, со-
гласно теоремам 5.9. 5.11, для любого х<=Х имеем
Й|(<у,Лх>— inf <у, Лх> — аир <d2, и) Саи=гД«.
U>0
(супремум по пустому множеству считается рапным — °°), Следовательно,
Л=7 sup	sup
*	u^O
r e. R ость значение задачи ЛП
<d?, н) -ктпх, — Лх 4- С^и — о, < л1, 11^=0.
(I)
347
Аналогично получаем, что 5 есть шшчонне задачи
(d1, н> -ь min,
— уЛ 4“ vC'i <= О,
УС2 >	(II)
v >0.
По задачи (I) и (II) вэаимодвойствоппы. Поэтому R га S. Пусть —<»</{< оо, т, о. допустимое множество задали (I) непусто, а значение се конечно. Тогда ио теореме 5.2 эта задача имеет решение (х*, и”), Ясно, что х* удовдетворнет равенству из а). Если жо R i=s —оо, то данное равенство справедливо для любого ж* е X. Утверждение б) доказывается аналогично.
5.113.	Рассмотрим двойственную задачу
iiy-t-min, ye 5= с.
Ее решением является число у* = max (в»fa А. Обозначим че-к?<л' " 33
рез 1 множество номеров, па которых достигается указанный максимум. Тогда
(= с.,	/ е J,
По теореме 5.10,решением прямой задачи служит любая такая допустимой точка х = (xj), что xj == 0 при всех При атом решения
Ь .
где е1 обозначает J-й единичный орг в R", являются вершинами допустимого множества. Естественно, решение единственно, сслн / состоит из одного элемента.
5.114.	Согласно теореме 5.11, данная задача разрешима в том и только том случав, если двойственная задоча допустима, т. о. если
с,-
шах min	(I)
L4j*k’aj A+i<J4a“j
Пусть /]С{1, ..ч к} и 7гс{Л-М, ..., м)—множества поморов, на которых достигаются указанные максимум и минимум соответственно. Тогда вели соотношение (I) выполняется как строгое неравенство (как равенство), то решением исходной задачи служит любая такая допустимая точка х (xj), что xj = 0 при всех / (соответственно ; 9* (J, (J А)).
5.115.	Согласно сказанному выше, задача разрешима в том и только том случае, когда
. Г* “41	. (-5 _3_1_ ч
шах| 2> 1 |min|________7’—1| —
348
т. о. если к С *-6; при этом ее решение я* описывается формулой _.f(0, 2, О, 0), если —В;
[(1, 0,0,0), если —	—6.
5.116.	х* = (8, О, 0, 17, 10). Выразив переменные x<j п ха черви остальные, приходим к задаче типа (5.47).
5.117.	Во всех трех задачах без ограничения общности предположим, что
cl “1
с,
а)	Замена переменных х' = х — d приводит к задаче типа (5.47). Решенном служит точка х* с координатами

7=1,
б)	Выбором максимальный номер is {0, 1, ..., n — 1), для которого
У, «/j < ь
j«=i
(при к = 0 эта сумма считается ровной пулю). Покажем, что решением задачи служит точка х* с координатами
tfj, 7=1.....................*,
7
/ Л \ / Р“2вЛ) \ ieil / /
о. 7 = Л + 2 п.
:Ясно, что эта точка допустима. В частности, условно х^+1	^л+1
обеспечиваотсл выбором к, Рассмотрим двойственную задачу
уb -|- <*, d>->-niin, ра + ? S' с, z S= О
и ее допустимую точку (у*, =♦), гдо
= si = nwx (°* et“ ЯЛ 7=1,
Точки s’ н (у*, :*) удовлетворяют условиям донолияющой но-Жосткости:
~j (х> — dj) е= 0, j = 1, ..., н,
(y*fii + zi ~ е;)=0'	7 =® 1,  •., п.
Тогда по теореме 5.10 эти точки — рошоппя прямой н двойственной задач соответственно.
349
и) Данная задача сводится к предыдущей заменой переменных х' = х—<1\ Выберем максимааьпын номер Ле {О, 1, ..., я —1), для которого
ft	п
2«Л+ 2 М<ь-
j=i	j=ft+i
Тогда решением служит точка х* с коордппатамп
/-1...k.
Л	n \ I
b— ai^i— 2 аА] К+1> / =
4 / = Л + 2.........n.
5.118.	a) я* « (1, 4, 5, 0).
0<ft<l, 1 ft < 6, O^ftCiO.
Перейти к переменным yi = x3, уг = *s, Уз = x2.
(0, 0. ft),
в) x»=	0, 1),
(5, 0, 1).
0 < ft <1, i^b<6, Ь< oo.
Привести задачу к виду
*i “ 2*2 + 3ia + °'х4 - юах’
x1-h x34- x4=ft,
0^115^5, 0^12^4, O^xj^l, 0^x<^<?, где d — любое число, большее ft.
1*) х* s= (2, 3, 5, 2).	,
д) x* г= (3, 4, —I, 6). Сделать замену поромеппой х3 = — х3.
5.119.	Пусть xf и у/ —площади, отподимые иод посевы шпоии-цы н кукурузы соответственно ла /-м поле. Тогда приходим к следующей задаче:
7 (20X1 т 35х2 + 25х3 + 30г<) + 5 (35yi + 50у2 + 40у3 + 45у<) шах, 20xi + 35х2 + 25xj 4- 30х< 5= 12 000,
Х1 + У1 = 400, xt -|- у* i= 300, xj -(* Si 13 200, х< -Ь у< = 100, x/SsO, У1 0, / =	4.
После преобразований получаем задачу типа 5.117, б):
7^-г У2 + 5у3 Н- Зу4 -> max, 4yt 4* 7yfi + 5у3 -Ь 6у4 = 2900, О < pi 400, 0 у2 300, 0 уэ 200, 0 у< 100,
350
Таблица 26
Поли	Пшеница	Кукуруаз
1	——	400
2	300	—
3		200
4	50	50
Оптимвльноо сочетание носовой указано и табл. 26.
5.120.	Вопрос сводится к следующему: при каких  зпачопинх -аарпмстра р задача без ограничения, связанного с госзаказом:
р (2Gxt 4- ^5ха 4* 25хз 4- ЭОдц) +
Ь 5(35t/i 4- 50у2 + 40j/j 4’ 45yt) -»-max,	(I)
24 4* f/i = 400, х2 -{- yi = 300, Хз 4' Уз в 200,	4* 1/< = 100,
xj 0, у/ 0, j 13 1, ,.,, 4, •имеет такое решение ((xj), (у/)), что
20х, 4- 35xs 4- 25zj 4- 30z, 12 000?
.^Задачу (I) можно привести к виду
(4р — 35)хг4- (7р — 50)х2 4- (5р — 40)Хз 4- (6р — 45)х4 -► шах, 0-5*^400, О^ха^ЗОО, О <х3^ 200, 0^х<^100. /Отсюда легко получаем, что искомыми являются
Р 45/6 = 7,5,
.	5.121. Если X имеет вид (5.2), то задачу мо:кпо записать так:
г -> шах,
<а{, х) 4- rgtffll 1>(, I = 1,..,, гл,
ТДе 1-е ограниченно прп г > 0 означает, что сфера радиуса г с центром в £ принадлежит полупространству Я^. (проверьте с помощью неравенства Коши — Буияконского).
5.122. Согласно сказанному выше, требуется решить следующую задачу ЛП (ха = г):
x3-*-max,
3Xj+ 4®а4- 5*3< .50,
4-13x^60,	(1)
15Хд — 8xfi -|' 17*з 120, 	4“ *3	“ ">
— «а 4-	*з«?0.
351
Перейдем к двойственной задаче:
50уг -|- 60у2 4* 120у3 — 2jrit -* min, 3^1“ 5у2+ 15уа — y,t =0, 8у$	— Уь-0,
5^ + 13»^+ 17р34- У,j 4'^5 =1> J/j О, I — 1, ..., 5.
Выразим переменные Уъ у«, уа через yi п у2: Л ~ 24	2	6
5	9	35
^4 = 8	2	2	^г*
1 , о ,59
• h = ~ ‘з+Ч+'З’^-
(И)
(Ш)
Отсюда приходим к задаче
— Рх —5ya-»-min, 15	1
"2 у1 + ‘о у2^24’
9	,	35	5
2/1 + 2	8’
л , 56	1
8^ 4- 3 и2 > у-
Используя геометрические построения, находим ее решение: у* = = 0, у* = 1/28. Учитывая (III), получаем решение задачи (II):
У1~ °> у* = 28' у* = 84’ Уд=0> ^*=У*
При атом ео впачеиие равпо 25/7. Тогда, согласно теоремам 5.9 п 5.10, рошовпо (-т*, х*, х*) задачи (I) обращает и равепстпд оо второе, третье и пятое ограничения, причем х* = 25/7. Отсюда без труда находим xj = 41/7, х* = 25/7. Таким образом, (х*, х£)— центр искомой окружности, а г = х* — ее радиус. Эта окружность каеаотси граней полиэдра, порождаемых прямыми—5xt 4-12х2 = = GO, 15zt — 8rj ед 120, ха = 0 и находится на столь близком расстоянии от двух других pro граной, что получить ответ с помощью геометрических построений практически невозможно.
5.123. Требуется решить задачу
г -+ шах,
Дх4-гй^5,	(I)
— X -|- гс с о,
гдо « = (ifaiO, .... Iltfmll), « = (1, .... 1)еКш. ’Ясно, что со рашс-352
пне существует. Запишем двойственную задачу:
<*, У> -► rain,
уЛ — 2 = 0,	(II)
<У> а>-!-<*.«> =1, у 0, г>0.
Для любого допустимого вектора (у, s) задачи (П), очевидно, п5'с<!м s е> уЛ > 0. Следовательно, сслп (х*, г*) — рошеппо задачи (I), то х* = г*е. Иными словами, искомая сфера касаотсл ко-ордииатиых гнпорилоскостой = {х g R” I х.» о). (В двумерном случае это означает, что оо цоптр всегда лежит на биссектрисе координатного угла.) Прп этом г* находится кик микенмальппе среди чисел г, удовлетворяющих условию г(Лв 4-a) sg b, т, е.
Ь1	-	6»
г* = min v / ‘ " V" Ш1П	•
l<Um(^ + eh l<Um "
2а<ЖМ
Jal
При указанных данных имеем
.	. ( 15	40	60 ) \
г	13^7.	—2«
(2, 2, 2/2).
5.124. Составим таблицу перехода к двойственной задаче, например, при m 5= 2, п «=± 3 (таол. 27). Отсюда ясно, что прп произвольных л» п п двойственная задача имеет вид
2 в^ + 2 bjff/^им», i=l J“1
pt + 7j с«ь 1=1,..., гл; / = 1,
n.
(I)
Отмотпм, что при исследовании транспортной задачи двойственную
Таблица 27
хп>0			^13 > 0		0 *яз>0	xsi^	0
Pi	1	1	1	0	0	0	=
Ра	0	0	0	1	1	1	
<11	1	0	0	t	0	0	
7»	0	1	0	0	1	0	7=
ffa	0	0	1	0	0	1	1=
	’С		=с				
	сп	(? j н	е13	Сч) |	С-»>		
С. Л. Ашманов, Л. В. Тимохов
&2 Л
«1
«з
353
задачу чаще записывают в виде п	та
У,	2 «i/’i-’'П^.
5=1	4=1
<ц — P^ctj I =>-1,.... m;
т. е. о Ш переменные р< заменяются на —р<. 5.125. Составим таблицу перехода к двойственной задача, па-пример, при &	3 (табл. 2В). Подчсркном, что здесь уясе в клет-
Т а б л п ц а; 28
с1 с:	с1
нах стоят целые матрицы и ве^ггоры. Иа таблицы ясно, что двойственная задача пмеет впд
к
2	+ <9. d> -* min,
h=i
p\ix 4-qBj, > с\	К,
р* > О, к =1 1, ..К' q > 0.
5.126.	Из табл. 29, где Т *= 4, ясно, что двойственная задача имеет вид
<р\ г°> -> min,
4 = 1,..., Т-1, ртДг>ст, р'^0,	4 = 1,.;., Т.
5.127.	Ясно, что допустимое множество задачи непусто и ограничено. Слодовлтольно, опа имеет решение x*=(21*i •-•«**) Пусть р* = (р*,	у*) —решение двоГютпенноп задачи
п
2 Mi * min> i=i
354
л
I «у
>0,
/“i, -о л, i = 1, .,., n.
(Л
Согласно теореме 5.10, точки x* и у* должны, удоплотворлтъ условиям дополняющей пежесткости	*
х*(	/=1......	(П)
\<=7	/
/ *	\
vi 2**-й«Н°. 1=1........п* <1П>
w«*i	/
Таблица 29
	X1 > 0	ж4 0		х*>0
р'	я.	0	0	0 <
	—Е	Ла	0	0 <о
р3	0		иа	0	0
р*	0	0	—Е	л4	0
			>	
	с1	с3	с4	с<
Пусть к— минимальный помер, па котором достигается min Hicn
т. О. bh<bit	1-1......ft-14.	(IV)
&fc=C&i	....л.	(V)
Покажем, что -т* = н «; = 0,	/ = 2, ,.„Л.	(VI)
Допустим, что ж* > 0 при некотором / е {2, .	А-}, Тогда,
п согласно (II), имеем У, у* = <к. Поэтому 1=7 П	П
V*— 1=	V* — 2 V* > cj-i ~~ cj > °*
{=j-l	i=J
•) Естественно, еслп к = 1, то даппоо условно, а также условно (VI) отсутствуют,
355
Отсюда п силу (И!) следует У х* = l»j_v Теперь с учетом (IV) получаем	. .
Л	J-I
2 Л* > 2} **,в= ^-1 > i=l	i=l
По это противоречит допустимости точки ж* « исходной задаче.
Итак, условие (V!) справедливо.
Предположим, чтог*<Ьй. Тогда у* -О в силу (III), (VI). Поэтому
3	2 »?>%>««.„
i=A+l	1“Л
что, согласно (II), влечет х*+,1 = 0.Учитывая (V), (VI), имеем Д+1
\S = Ж1 < < fyt+i-
Следовательно,	=0. Повторяя ото рассуждение, прнходпи к
выводу, что у* = 0. Но это противоречит допустимости р* в задаче (I), где сп >0.
Таким образом, мы определили пориыо к координату точки л*. Остальные ев координаты образуют решение задачи
п
У Inax, <
2 Ь| £>д,} I e k -{- f ,’•••> n> y=a-f-i
Xj>0,	/ =	....n.
Применяя теперь уже it этой задаче оинсаппую процедуру, находим следующие насколько координат точки ж*. Ясно, что за конечное число таких шагов будут найдены все координаты этой точки.
5.128. а) В соответствии со сказанным выше решение х* =» = (ж*.....ж*)	находится за три шага:
1-й шаг. х* =< 1, х* =0.Псроходпм it задано
+ е4®*+ съхь + свгв шах»
ху	<5,
гз+ г4
*34- х4+	<2,
^з'Ь ггЛ
350
2’fi mar. x* =2, x* =0, x* = 0. Пореходпм к задаче
ctxs шах,
1'.
3-й ш а г. л) х* ±= 1.
б)	х* = (I, I, 0, 0. О, 4, 0).
в)	х* = (2, 2, 2, 1, 2).
г)	х* » (2, О, О, О, 0).
5.129. Задача, двойствоппал к походной, имеет вид
я
2 b.>f) -+ шах,
yj + y^i^1’ / = t	(I)
УJ "I” Ifn	•
^•>0.
Выражая из первых n — 1 уравнений все перемеппыо чороз уп, находим, что
1 — Уnt сели/ и л разной четности,
(II) уп, если j п п одннакшюн четности.
Рассмотрим дна случал.
1) п почетно. Тогда у, = уп, п, пспол«>зул последнее уравнение в (I), получаем, что единственной допустимой точкой и. следовательно, решенном задачи (I) служит вектор р* = (1/2, ... ..., 1/2). По теореме 5.9 зпияенпе /• исходной задачи совпадает се значением задачи (I), т, о.

Согласно теореме 5Л0, лектор х* — (х*, ..., х*) является решением исходной задачи в том п только том случае, если оп обращает все ограничения в равенства.
Отсюда находим, что
(при k = 1 первая сумма отсутствует). Например, еелп п =5, тс
4	*3+*4-М«
357
— 2 (" Ь1 + Ь2 + ?J3 ~	+ %)'
<=4(&1“Ь2 + Ь3 + Ь4-Ь6)>
2) п четно. В этом случае общее решоппе системы уравнений из (I) оипсыпаетсл соотпошсчгиямн (II) (т. о. последнее уравнение липшее). Тогда задача (I) сиодится к следующей:
п
упВ ->тах, 0 < уп < 1, где В = 2 (” 1)4“
(Ш)
Решением задачи (III) слушнт число

1, если В>0,
О, если В<0, любое число из (0,1], если 2? = 0.
Рассмотрим трп эти возможности.
а)	В>0, Тогда решение	...,у*) задачи (I) имеет
впд
(О, если / почетно, (1, если / четно.
Прп этом /♦ = &г Ч- (и +... •(* Ьп. По теореме 5.10 лектор г ±= (zi,..., zn) является решенном исходной задачи в том п только том случае, если оп допустим и обращает и раненствл псе ограничения с четными номерами, т. о.
Z|t=&n —хя,	(IV)
Яа&+1 ” b2k~“r<ih> ft—1, ...» g—ii	(V)
xsfc+i J~xsfc+2=^S ^гМ‘1« Л —0, 1,	2	1- (VI)
Подставляя в (VI) пыраясения для переменных с нечетными по-мерами из (IV) и (V), получаем
— lia»	(VII)
—	Wl"^'	(VIII)
Перепишем иорввепства (VIII) в виде
Гг* = ZjA4-2 + bfk —	— Uja, b — 1, • • •» "2 Ъ (^)
358
гдо	(ft = 1,	n/2 — 1) — дополнительные переменные.
Из (IX) можно все переменные с четными номерами выразить через я*:	..._____।
n-l	n/a—1
»«,=.»,+ 2(-<>**,- 2	1=1......f->- <X|
3=aTi	5=fc
Из (VII) и (X) при 1;<= ! получаем условно на числа н^ (/с «= = 1...«/2 — 1):
П/2-1	П
2 «3>-^ 2(-i)S=5-	(»)
Г 4=1	4=1
Примем обозначении
п—1
ВЛ=5(-1)% Л = 1, .... п-1,
П/2—1
Vk==‘ 2 U‘^'	&= 1,	1.
1=Л
Тогда пз (IV), (V), (X) и (XI) следует, что множество решений исходной задач» описывается формулами
Zi=-xn-u bn,
га41 ~ хп + ^2h~ УЛ* fc= 1, ..., "g*—1,
л
— хп ~ ^2Л-Ь1~Ь 1,Л’	*—1» •••!
гдо хя произвольно, а числа у* удовлотлоряют соотпотеппям О on/i-i "2 fi В = — bi 4- Ь8 —.,. 4- Ья.
Нанрнмор, ослн n = G, то — гц4-Ьв1 ж2 = же-Ь\-й3-Ь^-\“уг ®3 = “®fl + i3-b4 + ^-byr ^ = ^4- ь4“^-у2-
Ха = -Х<1 + Ьб-Ь
где х6 пропзнольно и 0	£ i1, Bi
б)	В < О, В этом случае аналогично предыдущему получаем, что множество ромюииц исходной задачи описывается* формулами
ж2Л-15=1 ~" xn	1 vk’ Ji — lt ‘"t 2*
X2fc + В21Я- Vh •	== 1....i~ 1 •
^n-i ~ — xa ’b ^n-i*
359
где хп произвольно, а числа а* удовлетворяют соотношениям
О С Уял-1 Hi Щ —В.
Прп атом /♦ = fti -J- 5s +... + Ья_|.
в)	В =з 0. В даппом случае множество решений описывается формулами
л « 1, ,..,0 — 1,
где хп произвольно,
5.130.	Обозначим чарез X планируемый объем производства продукта, через У) объом закупки /-го сырья. Тогда ноставлеппый вопрос приводит к’следующей задаче ЛП;
X -> шах,
+	/ = 1, ,.пп,
(D
п
2 Pj^i yj > °« / = 1...........”•
5=1
Пусть (х*, у*, .... у*) -ее решоппе. Покажем, что
У* = шах {0, «;Х* —	/ = 1.....л,	(II)
Допустим противное, т. о.
yJ>0, «;Х*<5?-+У*	(III)
прп некотором /, Рассмотрим задачу, двойственную к (I):
n
2	= d,
7»*i
Q^Xj^p}t, /=!,...,«.
Если (x*, .... x*, t*) — ее решение, то, согласно теореме 5.10, на (HI) следует, что xj к х* в 0. Поэтому <* = 0 в, впачпт, xj = ... = я* = 0, что невозможно. Таким образом, формула (II) справедлива. По тогда X* является корнем уравнения п
f (X) = 2 О ших {°« ЯЛ “ Ы = d‘	(*v>
5=1
Чтобы’панти X*, положим е; = bj/aj (/ = 1, л) п боз ограничения общности будем считать, что С| са ^... сп. Функция /(X) непрерывна к строго возрастает от 0 до <» па полуинтервале [с,, со). Поэтому корень X* уравнения (IV) существует п едппст-вон. Определим помер к из условия
Л- са шах {/|/(с>) < </, 1 < /	л).
300
Поскольку /(cA4-i) то, очевидно, с* < ?.♦ ^ cft.H ♦). Ия полуип-ТОрПЭЛО (ед, <*ан] фулКЦНЯ /(?,) 11МООТ ППД
k
/(» =
УИ1
Следовательно, максимальный объем производства вычисляется по формуле
/ к \-i / л
^2 Pjai I И н- S /’Л
\j“i /	\ j=i
Подставлял ?.♦ в (II), находим оптимальные объемы закупки сырья:
• ( /=1,
1 I 0,	/ = А?+ 1, ..., П.
5.131.	В данном случае ci — 20, с2 «30, cj = 40, /(ей = О, /(с2) в 6, /(с3) *= 18,
Ь* («О =
—pg—, если 0<d<8 d-f-30
“тго—, если б < d< 18
(14-54
—j-g—•, если d> 18
(*=М),
(А = 2),
(А = 3).
График этой функции иэобраясоп па рпс. 90.
рис. 90
Оптимальные объемы закупки сырья при указанных значениях d приведены н таил. 30.
5.132.	Обозначим через xj количество тонн овощей, которое поручено разгрузить /-и бригаде, черев 1 — количество дней, ва которые весь состав будет разгружен. Тогда задача минимизации
•) Если ft = п, то формально полагаем cP+i — <».
34)1
расходов может быть записана в следующем ппде:
2 /7^- + ci^min, JI=X
n Sxjes^i j"l
0 xj	лjit	f == 1, > > >) n<
Рассмотрим двойственную задачу
ЛХ-i-max,
Ь— Ui^Pi, i
л
2 ej^j1=3 с*	go
j*»i
yj 3* О, I « 1..n.
Заметим, что с точностью до обозначений (II) совпадает с (I) из решения задачи 5,130. Повторял приведенную там схему рассуис-допни. предположим без ограничения общности, что pi
Вводом функцию
л
/ (х) — 2 ajП1ах {°«ь ~ Pj} j<=i
и помер
k =г гоах {/1|(pj) < с, 1 < J в).	(III)
Тогда решение (^*, у*, .... у*) задачи (И) удовлетворяет условиям /(>.•) ® с, рь < X* =£рк+1 и
4=т«{0А--Р,}=(’‘’_7>°' %*’+;’*’ „ civ)
(Можно легко вывести япттуго формулу для X*; по здесь’ это несущественно.) Согласно теореме 5.10, наборах*, .... я*, яв-ляется решением задачи (I) в том и	только	том	случае,	когда
xJCojf, У*(^~«/*)=0.	/=1.п,	(V)
*;>о,	(х* -1$ - р}) - о,	/=i.л,	(vi)
24~л.	(VH)
7=1 Из (IV) следует, что условия (V) u (VI) выполнены, еслп I* > О 362
11
о.
/al, .... ft, Л=*-р1..«•
Отсюда п пз (VII) легко получаем, что
/л
2»;-j=I
Таким образом, базе следует привлечь ft самых дешевых (по цене за топку) бригад п распределить работу между ивмп про-норционвльно их производительности. При атом время разгрузки
Таблица 31
ЛохР
tP
IF
dl
определяется, естественно, как отношение всего объема работы к суммарной произяоднтельпости привлекаемых бригад. Число ft, вычисляемое по формуле (ill), тем больше, чем больше штраф за простой состава. Если штраф очень нелик (с > /(рге)), то надо привлекать все « бригад. Полезно обратить внимание па то, что самая дешевая бригада всегда нолушт работу независимо от ее производительности.
5.133,	В данном случае /(pi)=0, /(pa)>=50. /(р3) =а 200, /(р<) = 500. Следоватольпо, ft = 3. При этом Р и 5,t*- 50, х* = 100, х* = 150, х* =а 0.
5.134.	Составим таблицу перехода к двойственной задаче дли случал 7 = 4 (табл, 31; в незаиолпвпных местах стоят нули).
363
Отсюда ясно, что при произвольном Т задача, двойственная к (5/8), имеет вид
(Д 4,*°) н- 3 dV> *”‘‘п’
pT = cr pt = ptwAt + сг, ( = Г„1.......... 1(	ф
qlDt рфг qt 0, t = 1...............Т,	(II)
где (1) совиадает с (5.49). Пусть векторы q* (I = I, ..., Г) образуют решение дноцственяой задачи. Тогда, согласно теореме 5,10, носледоватольпость управлений u‘(=Ut (1=1, .... Т} оптимальна it том п только том случае, если
<9«,	d‘> = 0,	/ = 1, .... Г,	(III)
ио н силу той же теоремы 5.10 (или 5.3) условия (II), (III) равносильны тому, что при каждом фиксированном Ы1, лектор и' яилнется решением задачи
^г(и) = (p‘Dt	Ь1, «> max,
'	Dm	d‘.
5.135.	ЯспоГ1 что
р‘ =±с(Е + Л + дт + ..,. + л^),	1=1.......Т,
гдо £ — единичная матрица размера пХк. В то же время из известных фактов линейной алгебры [21, с, ;125] слодуот, что при любом т = !, 2, ...
0
Отсюда
° 2 bjQEjQ"1 ° 2 j^i	j=i
Таким образом,
р* - < 2 о+* >+м+• • •+’J-) «,=' 2	
i=l	J=1
(Ясно, что если одпо пз собственных чисел равно 1, то множитель при соответствующей матрице окажется равным просто T-t-M.)	f
5.130.	Обозначим через rj, численность волков а косуль соответственно в конце года /, через wj, число лицензий, выдап-364
пых дли охоты на колко» н косуль соответствепио п году t. Положим
.*-(44 “'“(“Ь"})’
л = [_° р]’
Тогда формальная запись рассматриваемой задачи такова:
т	т
2 <С, г1) 4- 2 <&, t?> -илах, i=i	<«-1
х* ю Лх,_| — и*, t = 1,..., Г,
о'3*0,	Т,
гдо е == (I, 1), (xj, —заданный вектор, описывающий начальную численность популяций. Требуемое по смыслу условие х‘ О считается выполненным в силу предположения о малости параметра d. Отметим также, что вместо неравенства <е. u'> d сразу поставлено равенство, поскольку, очевидно, хозяйству всегда выгодно выдавать псе d лицензий (этот факт нетрудно вывести п формально).
Согласно дискретному принципу максимума, последовательность допустимых управлений и* (<=!,..., Т) оптимальна и том и только том случае, если для любого < = 1, .... 7* вектор и1 является решенном следующей задачи ЛП:
<//, K>-*-niax,
<е, н> = d, и О,
гдо Л* « Ъ — pf, ргс=р'+,И4-с (£ == 1, ..., Т — 1), рт = с. Следовательно,
и
(d, 0), если
(О, d), еслп ’Л|’<йа’
любой допустимый вектор) если — Ла.
Для удобства вычислений вводом н рассмотрение вектор с = = (1, —I). Тогда неравенство А1Х > Ад равпоспльпо условию <А‘, е> > 0. Из 5,135 следует, что
,	1-Х*	4-Х*
Р - 4_х c^-l- сЛа, t 1, Г,
X	ш
где т =1 Т — 14-1. Поэтому
t _	1 - АУ	I - XI
<Д, <с/?1>в>_т— сЛз, tf>.
355
Используя обозначения из 5.135, для имеющихся числовых данных получаем:
, _£ . _1
Л1 ~ 5 ’ "2 = 5
= ( 0 1/25\ ^-6 7/5 Г
» aJL/-5	1\ я_*/30 -1\
1	25 iso зо/ 2	^3\150 -5/
<^=(12,-—), сЛ2 = (- 12,
. ~	72	„ ~	02
<сЛг «> — 5 I	«>---5 .
oY 31 ( iV 5) “TVs) •
G помощью калькулятора убеждаемся, что поравонство <Ле, ё> >0 выполнено только при т == I, 2, 3, т.. о. при I — 10, 9, 8. Тикни образом, it первые сонь дет слодуот продавать только лицензии для охоты на косуль, в последующие три года —только на отстрел полков.
5.137, Обозначим через ж*, ж* число больных п вирусоносителей соответственно в концо месяца 1, через wj, «о — количество вакцинированных больных н вирусоносителей соотвотстисппо о месяце t, Положим** =± (**, *1), «* = (“[, “»),
4гпр_а ₽\ /?=(“?•	°\ с = (-1,0).
X Y ?/ X % -14
Пусть п месяце t производится dt индивидуальных доз накцппы. Тогда сформулированная задача мозкот быть записана в виде
т
a S <с’ + тах»
4=1
х1 и Ах1”1 Виг,
Г (7 = 12),
<е, u'> = dlf tt'S? 0, f «=« 1, ..., Г,
где в » (1, 1),х° ±= (я®, ж®) — заданный вектор, описывающий численность больных и вирусоносителей перед началом вакцинации.
Согласно дискретному принципу максимума, последовательность допустимых управлений и* = Т} оптимальна в том п только том случае, если для любого t = 1, .... Г вектор «( является рошенном следующей задачи ЛП:
<Л*, и> шах,
<е, u> = dt, «>0,
366
где h1 р*В, рг = р'+’4 4-с (<•₽=!, ..п У— 1), рт =» с. Следовательно,
’ (<М). если (h1, "сУ > 0,
u* =	(0, dfl, если </?,	< 0,
• любой допустимый вектор, если <Л', с )> « 0,
где с = (1, —1). Из 5,135 получаем, что	„__
1-хУ ~	1-?Л
<Л , е> га J __е> + 1 — Х2 (cRiB> е>’
где х=зТ — t+i. Проведем вычисления для имеющихся числовых данных:
/ 4/5	4/11 \ .8	л-3
дн/ю 11/10Г 1 Т »“ То'
0 = ( 5 — 8 \	М 8\
Q \il ИГ к ~ 143 U11 5/
„ _ 1 ( 55 40^ п _ 1 (	88 —40^
1	143 \121 88/	2	143	121	55/
^i = -jh<*“55’“40>‘ ^ = —^(-88,40), „Г-2/3	0\
\ 2/3 -1/3/
сЛ1В в <30’ 40)1 eIi2B ° 4^9 <256’ “ 40>’
п п ~	10	, „ „ -	298
(сП^В, е> =1 — 42д , <cR2B, f)= 429 ’
io /	/ я V / з V*\
</?, е> = qqqq ^82335— 888("10J J*
С помощью калькулятора паходпм, что иоравепство <Л', е> > >0 выполнено только при т = 1, 2,	6, т, е. прп t е= 12, 11, ...
..., 7. Таким образом, в первые полгода следует вакцинировать только вирусоносителей, а и оставшиеся полгода — только больных.
5,138. Введем следующие обомгачепия:
н« — стоимость оборудования, апкуилоппого и начало года t (текущие капиталовложения);
Kt — величина основных фондов па начало года i с учетом текущих каппталовлоасеппй;
St—сумма долог па начало года t за вычетом затрат па текущие канлталовложенни.
Положим ’(=± 1 — д. Тогда проблему онроделеппя оптимальной политики капиталовложений можно формализовать в виде
367
следующей задачи ЛП:
ST 4* ceffr max,
’I' wn
5< = 5t_1+aA',_x-ufl
5j Of
« = 1,	T.
....Л
.....r,
(i)
где Яо = 0, So > 0 — заданна» сумма начальных денежных средств. Целевая функции ныражпот объом накопленных денег к копцу года Т — началу года Т -f- 1. Заметим, что (I) ие относится к классу задач тина (5.48), поскольку содержит условие St 0, Поэтому дискретный принцип максимума здесь неприменим,
Составим таблицу перехода к двойственной задаче для случая Г=а 4 (табл, 32). Отсюда ясно, что при произвольном Т двой-
ственная задача имеет вид Sept min,	* ‘
г«вПй + в%1’	....Л
t = l...T,	(If)
Pi>ri>	t = i...T,
•де полагаем гтц = 0, дт+i = 1, Очевидно, что задачи (I) п (II) (оиустимы, а поэтому, согласно тоореме 5Л1, обе имеют решение.
Из структуры ограничений задачи (II) ясно, что для минимизации целевой функции слодуот стремиться к уменьшению каж-дон из переменных рт, pi. Поэтому для решения (rt, pt; I — = 1,..., Г) задачи (II) имеют место соотношения
р{ =шах {г6 р^,}, f = l.....Т.
Положим
X = Шах {/|п >р(н,
Если множество и фигурных скобках пусто, считаем х = 0. Поскольку гт =i а, рт+i = 1 н а < 1, то т < Т, По определению т имеем
n^Pr+t, I —-c+i, .... Т.
В таком случае	’
Pt = max {n, pt+i} — рж = 1, f = х -J-1,..Т.
Тогда
rt = '(п+i + a,	t— х, ..Т,
где, на помним, гт+1 = 0. Из этих соотношений получаем
I _ уТ-^1
rt — а' 1___у •	1 — t, Т.
Слодовательпо, fl 1 _	|
х = тахй а —у---------> 1, 1 sg t< Tj.
Отсюда нетрудно вывести явную формулу для т. Обозначим
(1—4^
1 ~ —а~~ J > !•
Тогда, очевидно, т = max {0, Г —Г}, где ?* = !_(? J—целая часть числа Q.
Предположим для простоты, что Q пе являатся целым числом. В таком случае неравенство Гт-н 1 выполняется как строгое. При этом г-г < гт-1 < ... < rt+i. Таким образом,
1— pt>rt, I = тф-1,.... Т.
Отсюда в силу теоремы 5.10 следует! что решение (Kt, Si, щ; I = 1, ..Т) задачи (I) должно удовлетворять условию
«: = 0,	(«т + 1, ...,Т.	(Ill)
Пусть х » 0. Тогда «г = 0, Kt = 0, St = So> I = 1, ..T, т. о. при Т 7 аренда не имеет смысла.
Предположим теперь, что т 3= 1. Поскольку
рт я= max (гу, 1} в г<,
то н случае т > I можем записать
гт_| тгт -ф агт« (•( 4- а) Гт > г„
24 с, Л. Лшмаиов, Л, □, Тимохов	309
так как ‘f а = 1 — р 4-а > 1. Продолжая вычисления, нетрудно уосднпсл, что
Pi = rt>	l = i.....т,
/,е = 0Ч-а)1“%	£ =	т.
Следовательно, pt > Pt+i, t еа 1,.т.
Ясно, что это неравенство справедливо и при т = 1. Отсюда, применяя теорему 5.10, павлокдем следующую информацию отпо-сптольпо решения задачи (I):
St = 0, t = i, .. „ т.	(IV)
Из (III), (IV) следует, что остальпыо компоненты решения должны удовлетворять условиям:
Kf =	+ uf	т,
"1 = 5о* ut = aKt-i’ l-2........*;
Kf = ji	=	•if,
= Sf—i ’I'i.i i = T-|-l, T.
Отсюда непосредственно находим, что решеппе задачи (I) вычисляется по формулам
Kt - (« + ?)'"15(|,	(я1, .... т,
3^ — 0,	т,
«<=«(« + ?) ,-2Я(р	« = 2...т;
= T«-t (а + А’о>	t = т 4- 1.Г,
1 —*
St = а (а + Y)T—1 .	*90, т + 1........Т,
* I
и{ ™0,	£ =±т-]- 1, ..., т,
а значение задача — ио формуле
1 —ут-х+1
8Т -Ь <хКт » а (а + у)т“ *-5rt.	(V)
Таким образом, оптимальная политика кнпнталопложспий (прп Т > Т) состоит в следующем: первые т лот всю прибыль следует затрачивать па ириобрвтопне нового оборудовании, после чего, иа-oGdpdt, кэшп’плоняожепнп следует прекратить. При этом к концу года Т обтаем накопленных денежных средств составит величину (V).
§ R
С>.1. Необходимо выяснить, какие из спетом столбцов {а-*, о’. о«) (/ = 1, з, 5к 6) линопко независимы*). С этой целью вычпе-
♦) Здесь н далее под а’, лг, ... понимаются столбцы матрицы рассматриваемой системы урдвнеппн.
370
лим четыре опро’ штеля:
	Мк-	<4/7	-3		2	7	-3
К	!	|*^Ч( ! J 1 4	Г 1 1Ф	1	= 0,	1		2	1
t 4	0 / 1	— 1		со 1	1	-1
* F f **						
I-*	i	1/ 7	— 3		4	7	-3
/	[	1	11 о	— 1	— 2	1
j’'	- 1	— 1		2	1	— 1
= 2.
^3
Отсюда J ключаем, что базисами вершины слуакат системы {л3, л’, а4/II {л®, а’, о4}.
tUJ, Ёся> к 4, к *#= 15, то базисами служат систолы {д’, а’, в3}, {/, а‘, с1} и {д’, «4, <?}; если к = 15, то базисами будут только пернря п третья на указанных систем. При к = 4 базисы отсутствуют (в атом случае ранг матрицы равен 2),
О. а) Е.’птствепкым базисом вершины хй яиляетси систола векторов (о*, а4};. Выразил через этот Саэнс столбцы в’, «* cis. Составллсл систему
г ii^.12 4- «*Ап => а’,
*. е,
—5Х|э 4* Х« = (J, А|;— 4?ч;	—5.
Находил 1и₽-1, ?,(;= I.
Аналогично из систол
alXis + а*/.|з	= <r\	alAi$ 4-	~	«5
находим Хи и 2, Au = 3,	Ajs =	—4, A«	=—в.	Вычислил	одеп-
ки гамещоннл:
Дг = 2Aij — ?,{2 4-4» 1»
Aj = 2Xj5 — An — 1 = 0, As *s 2?4i$ — 2,(j — 3 = —5.
Поскольку Дб < 0, Xis < О, А» < 0, то, согласно теореме G.2, имеет место утверждение Б.
'б) Проводи вычисления, аналогичные предыдущим, получаем «И “ ~у‘.<А Mi s 3> 0. Тогда по теореме G.3 имеет место ут-порждонис В,	.	' »\
в) В данном случае Д1 = 8, Aj =а А, = 0. Поэтому в силу тсо-рсмыб.1 справеддипо утверждений А.
г) Утверждений Б и В одновременно,
6;4,.ц) Нетрудно видеть, что ^ — невырожденная вершина. Решая системы
а’Х» 4- в’Хд, 4- а4А<ь к = 1, 5, G,
находим
^’25	^8S
A2fl~ —1,

371
Вычислим оценки замощения:	\
Д1 Я Л® - 2k - 3, As « А2 4- 2А - 3, До u=\ /? + 2А + 8.
Иа теоремы GJ—0.3 следует (см, 6J22), что ныпАщдонпая вершина х* является решением задачи при данном к н\ом и только том случае, оелп Д> > 0, Дз 0, Дй 0, Решая эту сиАсму неравенств, получаем ответ: 3 к ^4.	\
б) к ^2,	\
н) Таких к не существует.	|
СЛ). а) Столбцы «3 и а* образуют естествспш-цабазцс в R2, и, значит, коэффициенты рааложаиил по нему столбцов а1 и «2 совпадают с их координатами, С учетом этого легко строЛгя начальная симплекс-таблица (табл. 33). Для удобства вы’шсасняп оценок Таблица 33*) в1	а*	е? а*	b
f.i= 1
в3
а4
Д
Хм — 1	Х31	!	Х»-1	Хм “0	хэ= 1
Х41 = 2	Xjs == 1	А[3— 0	Хи = 1	
А| — —1	Да=-2	Д3= о	Д< = 0 |	(с, х) = 7
с, =з 5 . f; = 1 с3 = 2 щ = 1
замещении слева от таблицы записал столбец из коэффициентов цел спой функции, соответствующих базису {«3, а4), а снизу—строка всех со коэффициентов. Тогда вычисление оценки Дл сводится к умножению указанного столбца по столбец коэффициентов (?.?*, Х<*) и вычитанию из результата коэффициента сл, стоящего снизу.
Для построенной енлгплекс-таблицы' выполнено условие Ш, причем в качостве столбца, вводимого в базис, можно взять а* или
Таблица 34
л1 а2 а3 а4 Ъ
л1	1 а»	0 Д	0	-1	1	0 3	-2	1 —3	1	0	1 3 8
в®. Следуя правилу Блэнда, выберем а1 ($=1). Поскольку хз/Хл = 1, xJXlt = 5/2, то из базиса следует вывести а5 (г = 3). Тикни обрезом, ведущий! является элемент Ал- Проделав ггрообра-зоввнпп, указанные в п. 3, получаем новую симплекс-таблицу
•) В данной таблице для большей ваглндпостп выписаны обозначения числовых параметров. В дальнейшем они опускаются.
372
(табл 34). Здесь выполнено условно III, причем ведущим являет-си элемент Л«. Переходим к следующей сияалекс-таблицс (табл 35). Теперь ведущим служит элемент ?.1г. Строим очередную симплекс-таблицу (табл. 36). Здесь выполнено условно I. Следовательно, г* =» (О, 5i в, 0) — решение задачи, <с, г*> •= 17 — ос зпа-чопно.
Таблица 35
а1 аг а3 а4 I»
о1	1	0	11 /а4		1/3	2
						
О’	0	1	-2/3		1/3	1
Д	0	0	—1		1	И
Таблица ЗВ
а1 а3 а3 а4 b
б) х« = (3. 0, 4, 0).
п) Начальниц и дно последующие спмплокс-таблицы сведены воедино и табл. 37. Отсюда заключаем, что решением служит точка х* (3, 0, 0, 0, 0, 2).
	а1			а3	а4	Таблица 37			
						а6	а»	ь	
а3		—1	1	1	1	0	2	1	
«»		II	1 1	0	-1	1	-1	1	
А		—<)	—1	0	5	0	4	6	
й»		0	2	1	0	1	III	о W	
а1		1	1	0	-1	1	-1	1	
Д		0	4	0	0	5	“1	11	
а*		0	2	1	0	1	1	2	
а»		1	3	1	-1	2	0	3	
Д		0	6	1	0	6	0	13	
г| *	(0> 1, 0, 1, 1). Перобтп к элдлче макепмнавцип. Д) Выберем в качестве базиса вершппы 2° систему (а1, а’, <?}. процесс вычислений показан в табл. 38. В того находим решение: 1	(0, 0, 1, О, 1).									
373
о) Процедура симплекс-метода (с пропилом Блэнда) приводит к перебору базисов вернпшы z’:
{в1, а2, в8 в4} -> {и5, а2, а3, а4}	{л5, д2, а®, а4},
Прн этом для третьего базиса оказывается выполненным условие I. Следовательно, х® — решение задачи.
Таблица 38 •)
а1 д4 л3 Л* a4 Ъ
а1
а4
О3 А
аг
а» д’ А
а® а1 а3 А
10	0	1	11
0	10	р~|	о о
0	0	1	~	— 1	о
О 0	0—2—13
1—10 О 11
0	10 I Г о
0	0	1	0-10
О 2	0	0	—1	3
1 о
1
1	1	0	0	0	4
6.6. а) Впадем дополнительные неотрицательные переменные xa, xj, хя, приводящие ограничения-неравенства к равенствам. Поскольку правые части ограничений положительны, то переменные ze, z?,.zs можпо взять за базисные. Соответствующие нм столбцы а®, ге?, 'а8 являются единичными ортами в R3, и, значит, коэффициенты разложения по этому базису вшеторов а1, .... а5 соппадвют с их координатами. Три итерации симплекс-мотода указаны и табл, 30. Отсюда aaitnionaoM, что решением исходной задачи служит точка х* = (0, 3, 0, 2, 0), в которой первое ограниченно является пеактпппым.
б) z* = (9/4, 3/2, 0, 1/4).
в) ±•=(1,0,0, 0).
6.7. а) Согласно методу искусственного базиса, требуется решить симплекс-мот едем задачу
— х. — х„	шах,
5 б	1
®х + «2 + 2*8 + Ч + ла	«1,
Я1	+*6 = !-
Xj^-0, /=1, «.., 0,
♦) Здесь я далее ненужные элементы в последней епмплокс-табляцо опущены,
374
с иоршнпы z = (О. О, О, О, J, 1). Процесс вычислений иока-“ „ Лпч 40 В результате приходим к случаю Ь и, белое точно, ™ ” “оЬ.2 ш ». 4 (Кедпм^о. X ;А Й и = (1. О 0. 0) -йлпппша X- яря атом в базис вместо л4 можно ввести aJ пли а\ Чтобы 1ЩОСТК «2> произведем соответствующие аломонтарнме опо-
Т а б л » ц а 39
	а1	л3	(Iя	л«	а®	ап	в’	(I®	&
а*	1	2	—1 -	-2	1	1	0	0	3
ад	-1 -1		1	2	1	0	i	0	i
д8	2	1	1	-4		0	0	0	i	1
Д	1	-1	2 — 3		— I	0	0	0	0
я«	—3	0	—3	0	1	1	0		2	1
а?	1	0	2	1	1	0	1	1	2
а3	2	1	i —1		0	0	0	1	1
Д	3	0	3 -4		—1	0	0	1	1 '
д«-									1
а*									2
в3									3
Д	7	0	Н	0	3	0	4	5	9
Таблица 40
	вг	С4 О	rt a	а1	а»	а«	b
в4	п	1	2	2	i	0	i
& о	1	0	—1	2	0	1	1
А	• I ь>	-1		0	0	0	1 to
"в	1	1	2	CM	1	0	t
а®	0	—1	-3	0	—1	1	0
А	0	i	1	4	2	0	0
рации с интересующей пас частью последней симллекс-твблнцы (табл. 41). В итого получаем ио только базис {«’, л2} вершины х°, по и коэффициенты разложения по этому базису столбцов д5 и а4.
б)	Вычисления, аналогичные предыдущим, прняодйт к случаю Б,3 (таил. 42). Отсюда заключаем, что х° » (2, 0, 1, 0) — ьориш-па X; при этом третье ураппешю в системе, определяющей X, «в-ляотси липшим. Исключая его, получаем эконвалоптпую систему, при которой вектор-столбцы «' = (1, I) и «3 = (2, 3) образуют базис вершины хЧ
в)	я° = (5, 0, 1, 0). Применение метода искусственного базиса приводит здесь цспосродствотю к случаю БД.
375
	г) а° =» (0, 0, 7, о, 0), {а1, л8, л4)—базис з? (случай Б.2), Д) Полиэдр X пуст (случай Л).		
	0) Xй = (1,	3, О,	6); одпо нз уравнений является липшим
(случаи b.d).			
	6.8. а) Ход вычислений отражен в табл. 43. За первые четыре		
итерации находится			вершина допустимого множества псходпой
			Таблица 41
			л1	а2 л3 н4
		л1	1	12	2
		а»	0	—1—3	0
		а1	1	0—12
		аа	0	13	0
			Таблица 42
	л1	а2	ла	л4 л® л® а>	ь
а8	□	1	2	110	0	4
а4	1	-2	300105	
а?	3	0	7	2	0	0	1	13
Д	—5	1	-12	-3	0	0	0	-22
а1	1	1	2	1'10	0	4
а«	0	-3	1-1-110	1
а?	0	—3	1-1-301	1
Д	0	6	—2	2	5	0	0	—2
а1	1	7	0	3	2
а3	0	-3	1-1 1
а?	[0	0	0	0	0
А	0	0	0	0	3	2	0	0
задачи — (0, 5, 4, О, 1)- Одновременно с зтпя получены коэффициенты разложения столбцов л* и я4 по базису {я2, л3, о3}. Затем вычисляются оценки замещения для псходпой явдачи и за одну итерацию находится ее решение х* = (О, 9, 0, 8, 5), б) х* => (0, 9/2, 0, 0, 4, 3/2).
в) х* = (0, 1,0, 2,0).
г)	х* i= (0, 3, 8, 0, 0).	*•
6.9. а) Двойственную задачу можно записать в впде
- - У.г 4- (% “ 2tf4 - 12уь -> max,
2^ —у2 4-У3 -Н/4 -Ь2у6=3,
376
-^Ч-Уз-З^ + З^ -Ьу6 = 2,	(J)
+	+₽4-Зу6-1.
У7>0.	/=!,..., 5;
ттпнмппяя метод кскусотвоппого .базиса (с правилом Блэядо), наедимАршину V = (8, 16, 3, о, 0) задача (1). После этого за
Таблица >53
	. а1	а’	Is		а4	а4	а’	а7	а”	&
а4	-2	и -	-1		-1	0	1	0	0	1
аТ	1	-1	2		1	1	0	1	0	4
(fl	—1	1	0		0	—1	0	0	1	4
А	2	—1 -	-1		0	0	0	0	0	—9
а9	-2	1 -	-1		-1	0	1	0	0	1
а’	-1	0	1		0	1	1	1	0	5
а»	1	0	1		1	-1	—1	0	1	3
Д	0	0	-	-2		-1	0	1	0	0	-8
afl	—1	1	0		0	"-1	0	0	1	4
а3	-2	0	0		-1	|~|	2	1	—1	2
а9	1	0	1		1	-1	—1	0	1	3
Д	2	0	0		1	-2	—1	0	2	-2
в»	—2	1	0		-1/2	0				5
afl	—1	0	0		-1/2	1				1
а3	0	0	1		1/2	0				4
Д	0	0	0		0	0	1	1	1	0
Д	1	0	0		-1	0				11
а3 а4 в4										о us а>
Д	1	0	9 м		0	0				19
одпу нторацию получаем решение
V* = (2, 7/4, 0, 3/4, 0)
задачи (1).*тОгда согласно сказанному поело теоремы 6.1 решение х*— \xi« хз» ^з) примой задачи может быть найдено пз поиырож-
377
денной скотомы
Ч -®24-*3 = t -xi +х2-лгз = 1«
Х1 + Ч.+ жз = 2*
Отсюда получаем, что х* = (2, 3/4, —9/4).
б) у* = (О, 2, 3. 1, 0) — решение! диойстнеплоп задачи; х* е= = (1/5, 1, —4/5) — решение прямой задачи.
и) у* = (0s 1, о, 2, 0) — решение- двойственной задачи; множество решений прямой задачи ояисываетсн формулами
_	7_ 3	__L±	_7	8
xl —	2	'I' 2	z3’ Х2 — 2 ” 2 лз’	3	ха 3	‘
0.10. Требуется папти значение г* задач» г -> max, + +
Х1 ®<} 4" r 1.
г1-'жз+1з + г1/3< 1,
+ х2 — х3 4- г Уз , “ г1 + ®2 + *3 + г Уз 1, —	— г3 4- п/з С 0.
Решая двойственную задачу енмплокс-методом, а затем используя теорему 5.9, получаем ответ: г* = }'3/2.
6.11.	Па звероферм© следует держать 100 песцов, 150 нутрий it 25 норок.
6.12.	Нужно выпускать 2000 холодильников маркп 1 к 1000 холодильников мирки 3.
6.13.	Следует пзготонлять 1200 деталей по технологии 1,1700 — но технологии 2 к 400 — по технологии 4.
6.14.	Имеем
» = S «Ч = 2 (2	4 - 2 (2 W1Y
ft=i ft=i \ jej / jeJ \л^1	/
В то же время п ь= 2иЧ-= 3 °Ч-j=l
Отсюда с учетом единственности разложения ио базису получаем формулу (6.17). Формула (0.18) доказывается цепочкой равенств: u	ri ,	.
Лх-ч	Л—1 XjGJ	1
(п \ п
2	" S сл = S w- <с- х'>
л=1	/	/EJ
- <с,	— <С, х'>.
378
6.15.	Имеем
~ 2а1 (ч -	’ .2,+ “ (“'~ 3 "М =
J£J	?«=“'	X	t
±±г 2 a^j =" &•
>е/
Вторая фер»Ула с учетом (6.5) ость частный случай форму-лы бЛО^ Любой вектор peR" можно выраяпть через базис {«J|/*=7). ff±3X£rtJ^= a^4-«rp,.
jgJ JeJ\{r}
В свою очередь, используя формулу (6.3) прп к = я, вектор ат мояс-по выразить через систему {а^/е= Г}:
J— у а1-^~ <ч
Таким образом, любой воктор yeR"’ лпнебпо выражается через векторы ai	т. о. эти m воктороп образуют базис и IV*.
Далее, подставлял выражение (I) п (6.3), получаем
»‘= 2 А*+Рг~ 2
rh
jk
\ _|_ at ^rh _ лга /
Это и доказывает формулу (0.11).
6.17.	Теорема нопосрсдстпешю следует пз формулы (6.18): если Дл 0 при всех к «= 1, ..,, п п х' е X, т. о. Ах' = Ь, х' 0, ТО <С, Х> <<!, а'>.
(Другое стандартное доказательство теоремы 6.1, осповаппое па теории двойственности, можно найти, например, в [39].)
6.18.	Рассмотреть точку х' вида (6.19), гдо а —сколь угодно большое, положительное число.
6.19.	В силу выбора а по формуле (6.6) имеем х' 5= 0 я J(z') с: oJ. С учетом этого теорема 6.3 и формула (G.11) непосредственно следуют из 6.15, 6.16. Остается доказать формулу (6.12). Используя (6.11), получаем
. S
3GJ \ р>
370
6.20,	Предположим, что утверждение теоремы меверпо, т. о, существует вырожденная вершина х допустимого множества задачи (6,1). на которой алгоритм симплекс-метода с правилам Блэнда порождает цикл длиной в Т итераций. Более точно, пусть {а*[/ е7() —базис вершины х па I-й итерации (f == 1, .... Г), ^!(il Дд	&=1,	соответствующие коэффициенты п
оценки замещения; прп атом
Л+1 = (Л\{п}) U {^}, t >= 1, ..., Т, /т+1« /|,	(I)
где
$f -min Л|Ал<°]>	ПО
rt =*min р s Jt | Xj,:>0, ±y=iOj.	(Ill)
Обозначим через q панбольший средн всех поморов столбцов матрицы Л, вводимых в бизнс во время цикла, и пусть л’ вводится на итерации т, т. е.
q == s- = max st.
х ь=1...т ‘
(IV)
Иа (I) следует, что существует такая итерация, па которой столбец я’ будет выведен из базиса, т. о. ? => п прп некотором t <= е{1, ...» Г}. Рассмотрим при данном I точку x'(=R" с координатами
еслн/е/р
I,	если/ = *,.
О,	еелп/^/р / Xf4
(V)
Тогда Ах' = Ъ в енлу 6.15, Применяя формулу (6.18) к базису {оф е 7г) воршипы х п точке х', получаем
п
2 Ajrj = <с, х - хг> га 2	j <0- (VI)
5=1	j’eJ i
Покажем, одпако, что каждое из проиэводопий Ajxj (/ = 1, является неотрицательным. Рассмотрим четыре случая.
1)	/<=7Г. Тогда Д) = 0 (см. (6.5)1.
2)	/ = q. Тогда Aj< 0, так как q = sT. В то же время q =» п и, зпачнт, > 0, ху = 0 (см. (III)). Поэтому из (V) следует, что х'. == —	< 0. Таким образом, Д]ху > 0.
3)	/$ё/г, / < q. Тогда из условия q = fx н формулы (И) выводим, что Aj ^О. Рассмотрим три случая.
За) j<=Jt. Поскольку /ЙА, то х> = 0. Тогда из условия j < q =s rt и формулы (III) заключаем, что XjSt^O. Поэтому в силу (V).
36) / га st. Тогда xj = I.
380
Зй) / £ Jt, i Ф Тогда == 0.
Ktnif, для »сОХ иолслУ'^я ДИ > °-
4) /£А. />?• Предположим, что / е 71. Тогда с учетом условия получаем, что существует итерация I', на которой столбец <и вводится в Савис, т, о. / = Ss> > q, Но это противоречит формуле (IV). Слодоватсльио, / Jt. Из (IV) вытекает также, что у 4 st. Поэтому*} = 0« силу (V),
Таким образом, мы пришли к противоречию с (VI).
6J21. Утверждения из Б.2 очевидны в силу 0.16.
Докажем утверждения 1)—3) пз Б.З. Пусть для определенности /=={!>..ч 0, 1 ='(^ -г 1, .-т}, гдо 1 1С л». Тогда I = /. По-условию векторы в’, ...,	ен'1, с™ образуют базис верши*
вы. я? п, значит, базис в R"’. Тогда определитель матрицы, составленной из координат этих векторов, отличеп от пуля:
aU	aLl	0	... 0
		»
		»
	•	♦
all	all	0	... 0
ai+i.i •••	1	... 0
		»
 •		
а	•		
atnj	••• °ml	0	... 1
Ф 0.
(I)
Рассмотрим векторы а< (ап, «п) ({<=!,	и»), Из
(I) следует, что векторы fft (i = 1,..., I) лнпойпо независимы. Тогда векторы at j= (а<[.«ц, а<,	..., аа) (1 = 1,,,., 1) там более
лнпойпо независимы, т. о. rang Л = I, Утверждение 1) доказало.
Далее, поскольку векторы r7< (1 s= 1, . .м I) образуют базис в W, то
I ~
«гвЗ“Мг« Г = * + 1, .... Л1,	(П)
i=l
при некоторых i(r; иными словами,
I г = Ь|-1................т;	I. (Ill)
i=i
Перепишем формулу (6.16) в шжоордппвтиом виде:
I
агЛ=2агА-г1> г—1, ...,ж; fc = i,	(IV)
J“>1
И,j (III), (IV) для любых г = I -J-1, ..., w, k вя 1т п получаем
4, / '	\	X I
• i \	J	SIS aU^jk ) Vjr “ S aUiVfr«
J=1 \i=»L	/	{«1 \J=1	/	i=1
KH0»r°BTpinveT/|,,t0 Ф°₽мУла 00 Рас,,рострапяотся па полные стро-
I
er“2rtiViH reJ-^-i, ..., ж.
£=1 ”
331
При этом, поскольку Х° (з X, то
ь? <йп ~ 2 <а<. г<*> Vir ° 2 М<г i»l	i=l
ДЛЯ ItCOX Г = /-1-1, . .„ >П. СЛОДОПЛТОЛЬПО, ОСИН ЙХ1=Т, Т. о. <аъ x> = ii< (/ = 1,,,,, /), то
I	I
<°n	= 2 <ai. *> ?<г = 2 Mir=ъг
i=l	i«l
для всех г и / + 1,.... m, Утпернгдеппо 2) доказано.
Из (1) заключаем, что вектор-столбцы 51 = (щд, ..., щ,<) О линейно яезанпсимы, т. о. они образуют базис в IV. С учетом этого утверждений 3) очевидно.
6.22.	Если условие I пе выполняется, то в силу разрешимости задачи (0.1) может выполняться лишь условно III. Поскольку вершина х иевырождеиа, то, согласно теореме 6.3. существует такая вергпипа х', что <с, х') > (с, х>. Но это противоречит тому, что х — решение задачи (0.1).
6,23.	Рассмотрим задачу
хг	-ь max,
«>-Ь	2г.,+	«=={,
*	о*	«9
ri"l*	ж» = 1,
^Л^б,
Пело, что пырождеппая верптппа я* = (1, 0,0) является решением задачи. Возьмем в качество бпзпеа х* систему {о1, о1}. Имеем
Дз = сД1з + С2?>и — сз= 1  (—1) -1-0-1 — 0 = —I,
т. о. условие I по выполнено. Более сложным примером служит задача 6.5, о).
6.24.	Соответствующим образом донолпить схему решения задачи 6.22.
6.25.	Испо.икювать формул!’ (6.18).
6.26.	Пусть утверждение неверно. С учетом 6.22 эта означает, что Д, = 0 при некотором s J =/(я), Рассмотрим точку х' вида (0.19), где число а > I) столь мало, что х'5?0, т. о, х'^Х, Имеем <с, х> ™ <с, «'> •= ссД, « 0, т. о. точка х' х также является региеппем задачи (6,1). Противоречие.
6.27.	В решении предыдущей зодачн можно шгять любое а > 0.
6,28.	Согласно 4.64, требуется показать, что одпп пз воктороп а* (/е J(x) U/(х')) линейно выражается черев остальные, ужо линейно пвзавпеимые векторы. Воспользуемся обозначениями (6.0)—(6.9). Условие х'=& х рашюенльпо тому, что а>0. Тогда, очевидно,
J(x) U /(*') = /(х) U7(x) UM, гдо
7(х) = {/ (= J\J(x) 1?.,. < 0} = {/ <== /[xj = 0, ?,/, <0).
382
«слонин a> о слодуот также, что для любого /<= ДУ (х) ныиол-1оио яоравеаст»» Xj. 0. Поэтому, используя (G.3), имеем
«•=3«Ч= 3 «'>*+ 3 «V
jl=J	jGJ(x)
В то ;ко время векторы «J (/е/(х) ОЛ*)) линейно независимы как часть базиса верпшпы х,
(Отмстим, что если вершина х невырождепа, то доказанное утисрзидоиис можно нолос£едст1ишно вывести из 4,67, так как в этом случае =йу/(х)=' 0.)
§ 7
7,2.	Пусть ж1, г’еХ и х(Х) = Хх* 4* (1 — Х)х2. Допустим, что х(Хр) мри некотором ?.ае= (0, 1). Положим
7.] ® зир{X |х(X) е .X, 0	X Xq},
Xi = inf{Х|х(X) sX, X«<u 1).
В силу вамкиутости X имеем x(Xt) еХ, «(Xj) еА', При этом Xi < <Х0<Хг, Ясно, что точки х(Х|) и х(Хг) по удовлетворяют условию’задачи. Противоречие. Следовательно, х(Х) e.Y ври «сох Хе е (0, 1), т. о. X выпукло.
Примером служит множество рациональных чисел.
7.3.	Пусть х, у sX, т. e.^i<22, У1<02. Для любого X е (0. 1), используя неравенство между сродним арифметическим и средним геометрическим, имеем
[Ххг+ (1 - X) у,]* = Х2^ 4- (1 - X)3 ir2 + 2Х (1 - X) <
< Х\ 4- (1 — ХГ у3 4- 2Х (1 - X) /	<
Х\ 4- (i - X)2 у.2 4- X (1 - X) (ха 4- Р2) - Х*3 4- (1 - X) у2.
Следовательно, Хл 4- (1 — X).у е X, т. о. X выпукло.
7.5.	Пусть х, у е X. Учитывая 7.2, достаточно показать, что норас е %' В СЯОК> опоРвдь’ Д,1Я этого достаточао проворить
sin х -|- sin у х* 4- у ------2------- < sin —2~.
Применяя тригониметричоскшз формулы, приходим к зкиквалепт-пому перанонстну
( , xi . vAf х у \ ^sin -у — sin I cos -j- — соэ ~^1 < 0,
которое, очевидно, выполнено, так как 0	*£ л, 0	i/i л,
7.7,	k = 1 (рЦС> gi).
383
7.9.	Пусть х, у е X. Тогда
/ l\ 1 \ 1	1 \	1	1
yjJ, 7* + у Уу~ 4-<Лх,х>+4-<Лу, у> +
111!
-|- g- У> — -jj- <Ar, х> 4- V <ЛУ> У> — 4- <Л (* — У). х — У><
1	1
< *2 <Л1> х> н_ ” <ЯУ»	< “•
С уютом 7.2 ото означает, что X выпукло. Пусть теперь а = 0. Тогда X является такаю конусом, причем <Их, х> = 0 для любого
х е X. Поэтому если х, у ts X; X <= К, то х 4- у <= X, Хх е А’, т. о. X — лппейноо подпространство.
7.10,	Яспо, что X — конус. Для любых х, уеХ, используя неравенство Коши — Пуликовского и неравенство между сродпнм арифметическим и сродним геомотрпчоскнм, имеем
(’1 -F у,)2 - 2 (х2 4- У1) (х3 + р3) -ь (х2Ч- у/ =
= № - 4*3 + 4) + И Ч2Ул + yf) +
+ 2 (V1 + хара - г/.Х, - x^3) С
2 (/*?	К*1 + hx3 - Vs) <
<2 (з. / vm -	~
384
, । е х. Следовательно, X — выпуклый конус. Оп пзобра-т- с* * рпС. £12. Сечением конуса плоскостью хл е=> const > 0 яплл-1К0П П - (х — х -I- < г?, сечением плоскостью .т2 = 0 — ко-ется круг Vi 2 9'	2 3
пу° 71Ъ Х'Рассмотреть отображение Л (х\ .. „ хта) = «iх1 -?-.., 4-’а„*х|’\ w х1 е R^_ G = 1,..., «»)•
* 7 14, Пусть х, у cz ¥, Хе? [0, 1], .=₽?х4-(1 —МУ- По определению ммд'дая существуют такно последовательности {гЧсХ, {у]|с л, JTd у*^кольну А выпукло, то точка г — Хх* *: (t X) р прспадложпт X для всех ft. Прп этом s*-»- г. Следовательно, z <= X, т. о.
X— выпуклое множество.
7.15.	См. рпс. 93.
7.16.	Воспольловатьск очевидной формулой 4- Х2 sa U (Xj-J-X) ’ “	“	Х&Л а
и том фантом, что объединен не любого числа открытых множеств открыто.
7.17.	Рассмотрим множество Х= ”4-2, гдо У —компакт, а Z — зашшутоо мпожостпо. Пусть {х^} с X к х* -> х. Имеем
дД — yh J. Д ук G у( -к е 2.	(I)
Поскольку последовательность {;/} ограничено, то из (1) следует, что {;*} также ограничена. Пусть без ноторп общности
•+ 2, Тогда
х = у 4- х, у <= У, : е Z,
г, о. ге Л". Таким образом, X — замкнутое множество,
7.18,	Примером служат множество X из 7,4 и множество
Рпс. 93
Их сумма .¥ 4- У = {х е Rj|x2 > 0}— нозвмкнутоо мпожестио.
7.19.	Примером служат конус X пз 7.10 п конус
У = (хе R*|x| =	= 0).
nXvC^nrn £ 4- У = {х <= RJ|x] > 0} U и У — незамкнутое множество, 7.20. Это следует пз 7.12, поскольку Р(Х) ес711 образ X прп ото-брФКОипп Р(х, {/) = х, гдо х g R”. y^Rm. Разумеется, данями фанг легко доказать н пепосродстиеппо. 7 Примером служит конус пз и ого проекция на плоскость nQPB>-’J дпух К0°РД1’п«т-
7.26. Ограничился доказательством выпуклости множества (Для х риссуждокнл лить упрощаются, причем яынуклоечь лдось по требуется). Пусть х1 <z Y (f = 1, 2), <х«= (0, I) п х ® С, А, Ашмпноп, Л, В, Тимохов	385
Aj
= ox1 4 (I — а)*9 Тогда =• ?.<у1 4 )h*f прп некоторых y{ e= Xi.
?u 1 и JU = 1 — ?.i fl ™ i, 2). Положим p = aX( 4 4 (1 — a)?.j3= 1 n •( = 1 — p. Если p> 1, то можем записать
(1-a)X2 \	(1 -a)|i
>J ft / т Ц ? s”l' V
Отсюда очевидно, что * t= У. Если ясо 0 ш 1, то Xt =	= 1. Тогда
х па ar/1 4 (1 — a) р2 <= X, cz У.
727. Пусть х, уеХ п as (0, !). Тогда
m	гл
»=2м‘
4=1	4=1
при некоторых Л, |iеЛ и xf, i=X( (I = 1,	m). Впедем иск*
тор ц = a?. 4 (1 —а)ц ^Л, Для каждого помора 1=1, ..^ т в случае 1Ц > 0 положим
aX{ (l-a)h ‘ " *14 Х ‘
Если жв ip вя 0 и, значит, = ц< =0, то выберем и* произвольно в Х{, Тогда, очевидно,
m
аг 4 (I — а) у =□ У, i)^1 s X.
i=l
Пример сущестнонностн условия ЛсВ”: m = l, X1 = Rlp1 Л t=i R; тогда X =^4. U (— R^.) — повыпуклее множество.
7.28. Доказательство проведем ипдукцпой по размерности в пространства R”. Прп n = 1 утверждение очевидно. Пусть оно ужо доказано для пространства Rn-‘, где и 3= 2. Рассмотрим любые г, у X. Требуется показать, что х 4- у <= X. Вводом векторы п = га min {х, у), г га max {х, р). Ясно, что х 4 у = в 4 о, и у. Следовательно, достаточно убедиться в том, что к -|-1> <z X. Если и «= 0, то в 4* и — 11 X, Пусть в ч^'О. Положим
1 j 1 -
Хгп mil) -А>1>0.
jiuj>o !^-7г??5«3
Будем считать, что минимум здесь достигается на померо 4 в п. Тогда ?.а о п Хвге = уя. Поэтому
(Н-1) «; С «у 4	1 •!- 4) v>'
(1 4-Х) «п = «п + в„ = (l 4- у) ₽П’
(I)
(П)
Обозначим через У проекцию конуса X на пространство первых л“1 координат (см. 7.2Л). Ясно, что У —конус и И”-\ замкнутый относительно операций min и max. Поэтому, согласно предположению ИНДУКЦИИ, У —НЫПуКЛЫЙ КОПУС. ВеКТОрЫ («1,	«п-|)<
(ri,	принадлежат У. Тогда их сумма татке припадао-
386
Я;Пт У. Иными словами, существует такой вектор w е X, что u>j =
2, its 4- Для всех / = 1,...,в — 1. При этол из (1), (И) следует: если «п + %, то и 4- v a max {w, (1 -р К)«} <= X;
еслп и»п> ип4- уп, то « + » = пНп"Ь s
Теорема доказана. Требуемыми примерами служат множества X, = {z Е R2[0	zt < 1, 0 < zj < 1 или zi га хЛ > 1},
х,-1Ч.и(-пу.
7.2ft. Пусть X — выпуклое множество. Требуется показать, что для-любого m s= 1, 2, из условий
i’eX, Xi>0, i-	(I)
i*nl	i=“L
следует, что x e X. Проведем индукцию по m. Если m = 1, то высказывание тривиально. Иреднодож.пм, что оно ужо доказано для w ц пусть условия (I) выполнены прп ж = А4-1. Еслп Хл+t = 1, то Х[ = ... = Хл = 0 и, значит, х = хт е X. Если же Xx.|.f <. 1, то можем записать
к >.
гдо 5 *=21—г—*1’ (11)
1 ~ ЛА+1
Ясно, что х — выпуклая комбинация точек я1, ,.Тогда по предположению иидукцин z еХ. Поэтому из (II) с учетом выпуклости X следует, что х X.
Утверждения для выпуклого конуса п аффинного множества доказываются еще проще.
7.30. Обозначим через Z множество всевозможных выпуклых комбинаций точек из X. Нетрудно показать, что % выпукло. Прп этом X с Z. Тогда conv X с 2 ио определению выпуклой оболочки. В то SKO время, если У — выпуклое множество и Xс У, то 2е У в-силу теоремы 7.6. Но тогда 2 сconvX опять жо ио определению выпуклой оболочки. Таким образом, conv X = Я.
Рассузкдення для конической и аффинной оболочек аналогичны.
7Л$1. Ограничимся рассуждениями для m и 2. Поскольку Х< cz с соду Х( (/ = 1,2), то Xi -|- Хг о: conv Xi 4- conv Хг. Следовательно,	(	...	-Л1М/
conv (Xj 4- Хг) с conv Xt 4" conv Xj.
Докажем обратное включение, гласно тооремо 7.7,
Пусть х е conv Xi 4- conv Хг. Со-
25*
л	I
~ ~ь i=»l
a	i
i=i
387
х
при некоторых у4 е A’i, zt е A\ Xt О, ц< > О (I е 1,Jt; / « = 4,..., I). Положим t = Xigj. Тогда, очевидно,
A I	kt
«2 2%-(?+»'), 2 2ч«-«,
Г.
т. е. хе conv (Л’| ~Ь Х2).
7.32. Если даны два выпуклых многогранника
А’> ® conv{x’, .. ., г*}, Х4 = conv{y', ,.., у1}»
то, согласие теореме 7.8, имеем
X] + Х2 = conv{x4 + уф = 1,.. п Л; /=!,..., !}♦
Если даны два многогранных копуса
Xi = соие{х\ ..., х*}, Х2.= сопе{у‘,..у1},
то, очевидно, Х| 4- A's = сопе(х‘,Д у4}.
7.33. Рассмотрим в пространство Hll+I множество А = А'Х{1). т. о. совокупность точек вида {х, I), гдо х ts X. В силу теоремы 7.7 условия х conv X и (х, 1) е cone Л эквивалентны. Остается применить к А следствие 7.2,
734. Рассмотрим любую последовательность (лА) с conv X. Согласно теореме 7.11, дли любого к имеем
п-и	н+1
**“2^ ^1®^. ^>0. 1=^1, .... п-Н, 2	=
1=>1	i=l
Последовательности {у*}, 1^1} 0®®	•••» и + ограничены.
Следовательно, {х4*} также ограничена. Пусть х*->х. Без потери общности можно считать, что	Тогда
>1+1	П + 1
х = У, У,	0» i — 1, ..., n-J-1, 2 ^j= 1>
i«=i	»-“i
t. e. x i= conv А'. Таким образом, множество conv X ограничено и вамкпуто, т. о. является компактом.
735. Первое утверждение непосредственно следует па теоремы 7.12. Рассмотрим многогранный конус А' =* conetx1, ..., хм) с: cR1*. Пусть {у*} с X u jA-+-y. Допустим, что у^Х, т. е. система
m
2 = у> = •••»	w
(“1
песовмсстпа. Тогда по теореме 4.0 существует такой вектор р <= е К”, что
<Р, я‘>^о, 1 = 1,...,™, <Р, JJ.X0.
Для достаточно большого к имеем <р, у*> < 0. Вновь применяя теорему 4.6, получаем, что система (1) ирп замене у иа р* также несовмсстпа, т. о. у* ф. X. Противоречие. Таким образом, у <н Аг, т. е. А' — замкнутое множество.
Отметим, что, по существу, мы повторили схему рассуждений из решеппя задача 4.134.
388
Доказательство замкнутости многогранного конуса, оспоаап-яоо на теорема 7.10, можно найти в [5, с. 60; 39, с, 63],
С учетом лолмы 7,1 замкнутость многогранного множества очевидна.
7.36, Положим Р4 - 2 h.' Нз 1G0DCMU 7-с слодуот, что у' Л«1
А
— _L 2 ^feaA х (s=l,2, Поскольку у’-* у, то уе fe=i
<= X == X.
Утверждение справедливо и без условии замкнутости X По в таком случае для его доказательства требуется приплочь теорию отделимости (см. $.32),
7.37.	а) Зафиксируем любую точку геХь Построим последовательности {«*) п {у*} по следующему правилу, В качестве д’ возьмем любую точку нз Л, Если топка ah ужо ностроепа, то, нс-иользуя условно задачи, выберем точки у^еХг и аН1еЛ таким образом, что
х -{- ак = у*14* о*+\ fc= I, 2, ...
Просуммировав порвыо s из этих равенств п поделив результат pa s, иол уч им
х-|-£ = х*-|-1-!2., где х9 = £ V у\	(I)
s	*	s£i
Поскольку X? выпукло, то *’<” А’г в силу теоремы 7.6. Переходи к пределу в (I) с учетом ограшгчениости Л, получаем, что z'-i-z, т, е, х <= Хя. Следовательно, X <=. Хз.
7.38.	conv X — [х (x'j солю X =	>0] U {0}.
7.39.	conv X = [х 1 х® <1^. Х1 ^.21 UJ0)i
cono X = int U {0}.
7.40.	conv А' = соле X = IP,
7.41.	conv X = fzlsin Xi х2^ 0, 0 ^Х]	я},
cone X = {х|х, > ar3u> 0} U {0}.
7.42.	conv Ar =t (х | exi xj, cone X = {* j eXj < x2, x2 > 0} Ц {0} JJ
. 7ЛЗ. Пусть X—’Открытое множество.' Тогда X = intXc сInt (conv X), причем множество inl(convX) выпукло в силу следствия 7.3. Поэтому convXcint(convX). Отсюда int(convX) =
conv А', т. с. множество conv X открыто.
7Л4. Нот, наверно. Примерами служат замкнутые множества 7.38, 7.39 и выпуклый компакт
X =ф <= R2 [ з* 4- (х4 —'.1)2< 1).
7.45.	Применить теорому 7.7.
7.46.	Применить 7.45. Условие выпуклости X существенно. При-МОром служит МИОгКОСТВО
Х *= (’ ® К5 | х* 4- (х2 - l)n- < 1, х8 = 1) U {(0, 0, - 1)}.
389
7.47.	Прп произвольном X последняя формула неверна. Примером служиг Л’ = ((1, 0), (0. 1)}.
7.49.	Согласно теорию 7.3, сумма Xi -f- Л’2 является выпуклой оболочкой восьми точек:
(3, -I), (5, 1). (1, 3), (4, 4), (I, 0), (3, 2), (-1, 4), (2, 5).
Нанеся эти точки па чертеж; убеждаемся, что Xi -V Лг2 представляет собой шестиугольник с порншиимн и указанных точках, кроме (1, 3) и (3, 2). Эти точки оказываются выпуклыми комбинациями остальных.
7.59.	Сумма Л'| + Л2 ость шестиугольник с вершинами (—5, 3), (-2, 4), (2, 4), (3,-1). (1, -4), (-4, 1).
7.51.	Ограничимся риссуждоннямп для гл & 2 (ср. с решением задачи 7.31). Включение conv (Ar( X Х2) с conv A\ X conv д2 очевидно. Пусть х s ennv X| X conv А'з, т. е, л =» (у, г), гдо
h	I	k	I
= 1
i==l	j=l <~1	J~l
при некоторых yf e Xi, z} e .V2, ?<	0, p.j 0 (i = 1, ..k, / =
1)	. Положим ijtj = Xiiv, *lj’ (j/1, z*) sXiXAj. Тогда, очевидно,
Л I . ft I
x=2 2V- 2iho = 1«
1=1 j-c-1	i=l j«i
т. e. ж e conv(X't X Xs). Первая формула доказана. Вторая доказывается также (следует лишь убрать условия At 3=0, |b>0). Для доказательства третьей формулы в рассуждениях, аналогичных приведенным, вместо точек вида (у1, sJ) следует рассмотреть точки вида (;/>, 0) и (0, г'). Для произвольных множеств эта формула неверна. Примером служат множества Х| = t= {!}.
7.52.	Докажем лишь первую формулу. Включение conv А (X) с .с/(conv X) очевидно с учетом 7.12. Пусть ye4(convX), т о. у =* Лх, где
ТП	П|
я	^<=х, As^=0, 1 = 1,...,m, У, А{ = 1.
1=1	1=1
rn
Тогда, поскольку у = У A^lxf, то у «= conv А (.¥).
1=1
7.53.	Применить 7.52;
7^4. Пусть даны линейное отображение Л: Rn->-R'n, порождаемое матрицей Лел1(и, и), я полиэдр У «= {у е R'n|Z?y tl), гдо /?<= J/(A‘, m), <i е 11* Тогда, очевидно,
Л-'(У) = {ж е= IV] (ВА)х d}..
7.5G. Для произвольных мпожести последняя фюрмула непер „а. Примером служат множестпл A'i = {(1, 0}}, Х?= {(0, 1)}.
300
7,57.	Первая формула очевидна, Вторую потрудпо^донаэать ио-посредственно, но мы выведем се из первой и пз 7.47, 7.56:
/ ш \	m \\
aff U х, =аИ cone U Х4 =
\i=l */	\	//
= aff J 5} соне Х{| = У, aff (соне Х}) ^aff Xf. \i=>l	/ h-t	i=*l
Дли произвольных множеств эта формула неверна. Примером служат все те же множества Xj = {(I, 0)} и Хг {(0. Ш-
7.58.	Докажем первую формулу прп гл = 2. Положим X
2= conv(X| и Х3) п
У = (х е R"l* = >.х* -К (1 — ?.)х8, ж* е Хь х5 е Х2, 0	1}.
Йсно, что Ус: X. Пусть хеX, т. о.
h	I	h	I
« » 2 'W* + 2	3 *£ + S j‘j = 1
i=l У«"1	1=1	?=1
прп некоторых г/1 е Xlt :J е Хг, 5= 0, pj 0 (I = 1, .ft; / *= h	I
к 1, ...I). Положим ?.= ^ /.j, u = 2 Пу Случаи 7. = 0 н p. =± t=->l	j»'=I
= 0 тривиальны. Поэтому будем счптпть, что X > 0, р > 0. Тогда
До теореме 7,6
При атом	/.+ р = 1, т. е. х <= Y. Следовательно,
X ея у. Вторая формула легко выводите» нв 7.45, 7.57.
/ m	X	я*
7.59.	Примем обозначения Л = couv ( (J XJ, Й = X ХР По-
Ч-'1 /	p.t
скольку 0 е Л„, то очевидно, что 7,ж (= ХП1 при всех х е Хп, п ?. <= e fO, t J, С учетохг этого из 7.58 легко выводится, что Л с; 13. Следовательно, Л <= В. Пусть х В, т. с.
m
Х= 2^’ Хр i = l. ...,m.
1=1
При любом к «= 1, 2,... положим
jffciio, что Л п т\_е. хсееЛ. Таким образом, йсЛ п, пачит, В d Л. Формула Л = В доказана. Требуемый пример:
х( e= {z е RS|Х1 = о), х4 =•{*.= IF|X! = 0, О с- л-J I}.
391
7.G0	. Достаточно заметить, что
Yt с Xj =i conv F{ с conv
I = 1, ..., nt,
7.61.	Применить 7.60. Для многогранных множеств аналогичное» утнерждепно несправедливо. См, пример к 7.59.
7.62.	Обозначим мпожестоа, стоящие под анонами замыкании и левой п правой части доказываемой формулы, через А п Л соответственно. Поскольку Хг< с IJ, то н А с В. Следовательно, Л с В. Пусть х <= В, т. о.
tn	m Ц	m /
221Й
i=I»=I	ir-ljal '
при некоторых уЧ e У(, s<* e %<, juj > 0, T] r« > 0 (1=1,..., m; / = 1, ..., s i= 1,..., 1{). Положим
*1
Xj — 2 i*ijt i — i,..., i?i.
Если X{> 0 прп всех 1,..., m, то можем записать
Вырая?еппв в скобках представляет собой точку, принадлежащую Xi. Тогда, очевидно, х е Л. Если же ?.( = 0 при некоторой 1, то заведомо « <= Л. Это следует из того, что коэффициенты p<j (1 = I,..., m; / = 1,..., fc<) можно мтошо вопить* так, что нов они станут положительными, а их сумма будет по-прежнему равна единице (детали рассуждений оставляем читателю). Таким обра
зом, В <г Л и, значит, В с Л, т. о. Л = В.
7.G3	. Применить 7.62 п теорему 7.13,
7.67.	{1, 2}, (2, 3), {2, 4}. {2, б). См. 4Л7 и рис, 81.
7.68,	Л, 3, 5), (1, 4, 5}. (2, 3. 5), {2, 4, 5), (3, 5, 6}, {4, 5, 6).
7.69.	(1, 2, 3}, {1, 3, 4}. (1, 4, 5), {1, 3, 5), (2, 4, 5}. Рассмотреть векторы, коллинеарные ж1, ,,,, ж5, у которых третья координата равна I, л воспользоваться геометрпчеекиип построениями на плос-
кости первых двух координат, имея в виду эквивалентность, указанную в доказательство теоремы 7.11 (см. 7.33).
7.70.	Необходимо либо показать, что система
в j =ж°,
Г«"1
3
j=i
о, /= 1, .... 6,
носовместпа, либо пайти некоторую вершину множества со решений. Применяя метод искусственного базиса из § 6 (с прввп-392
лом Блзпда), находим вершину с координатами 1	„	1	,	1	, _	3
^-g'	^2 — 4»	^з-	4’	*4“*б~и‘
Следовательно, точка z° = О представима в виде выпуклой комбинации точек г1, ..., х4 с коэффициентами Ль ..., Л« соответствен по.
7.71.	Требуется решить следующую задачу ЛП:
в
— У Лл- ->- шах,
в
2-^; = я°>	Л/^З, /=1, ..., 0.
Применяя симплекс-метод с начальным базисом {г1, s’ х4}, находим решение с координатами
А[ = 1, Xj га 0, Zj = 0, 2ц = 2, Xj = 1,	== 0.
Следовательно, я? = я1 -|- 2х4 -}- х"' —- искомое представлепно.
7.73.	а) Пусть А ®’, .... х“ — аффнппо независимые точки и X = conv{x°, г1,..., я”1}. Тогда aff X — aff{z°, г1,..Xя} (см. 7.47). Отсюда ясно, что L Lin(afEX) =affX—х* ость лнионпоа подпространство, натянутое па векторы х1 — х°, .... zm — х°, В силу 7.72 эти векторы лппойпо независимы. Следовательно, dim А' = га dim L = т,
б)	Пусть Р га conv{z°, я1, ,.я"1} — максимальный по размор-иёств симплекс, лежащий н А’, т. о. z°, х1, ..., х“—максимальная по числу влемедтол система аффинно независимых точек в X. Тогда, очевидно, X а aff Р и, значит, aff X <а aff Р. В то жо время Рс^Х, и поэтому aff Pcz aff А', Таким образом, aff X га aEfP. Отсюда, dim X = dimP,
7.74.	Утверждение для выпуклой комбинации представляет собой- уточнение теоремы Каратоодори, которое доказывается том же методом (см. 7.33,-а ташке 7.72). Доказательство утверждения для аффинной комбинация лспользуот вместо теоремы 7.10 аналогичный известный факт для произвольных линейных комбинаций.
7.75.	По существу, этот фа1ст отражен в 6.16. Дадпм ого прл-ш—1
мое доказательство. Предположим, что У,	—0- Тогда
<«=1
°= У, а(х14-сс У AjZ1 га У (a1H-a>.1)zi4-aXmz,n. i*=l	i«=l 1«=1
Поскольку точки х’, ..., хт линейно независимы, то а< + aXf е= о 4=1 > - у» т — 1) и аАт >= 0. Но 2.т	0. Тогда а = 0 и, значит,
“°	и 5=1 1, ..., иг—I). Таким образом, точки х1, ..., хт-‘ х л«ие«щ0 пезанпенмы.
М. Применить 7.72, 7.75,
ено fcLEca“ zsconv^r ’о 0econv(AF—х). Поэтому утвержде-достаточно доказать для точки 0 в предположении, что
ЭОЗ
О е conv X. Согласно теореме Каратеодерн,
пЧ-1	М’1
О=2м1, W**®*', Лг>0, !-i..................«4-1,	2?’i=1-
1=1
U) Допустим, что точку 0 нельзя продета вить и индо выпуклой ком-бииацки но более п точек пз X. Тогда л с > 0 прп всех 1= I, ... ,п -f-1 и, как следует из 7.74, точки г1,,.zn+1 аффинно независимы. Используя 7.72 и 7.76, заключаем, что прп любом I « 1,... ..., п 4-1 точки 0, я’, . • л1-', zl+l, . <хп+1 аффпнко независимы п, значит, точки ®‘, .... ж'~‘, ян'1,	я"*1 линейно независимы,
т. е. образуют базис в И". Рассмотрим многогранные конусы
Ki = —’Conefx1,i?"1, z**1,.... z”4'1},	i«l,..4n + l. (II)
Ниже будет показано, что
1)	X Л Kt 0 при всех I ® I,nf i; a+i
2)	U Я, = НП; {=i
3)	A't 0 Ki Q X = 0 при всех /, I 1, ..п 4-1; 1^1.
Из этих утверждений следует, что в каждом конусе Kt (1 =» as 1, .... п -г 1) содержится по'крайней море одна связная компонента множества л. В самом деле, при любом i	л 4-1, со-
гласно 1), существует точка я<=ЛгПЛ'<. Пусть Я — объединение всех связных подмножеств X', содержащих а. Тогда, как легко показать, А — снйзнае множество. Обозначим через L объединение конусов X], ..ATf-i, /Gfr, ..A'nH. Тогда Kt U Л => Rn, A'< Л A f| П Л = 0 в силу 2) и 3). Отмстим, что по теореме 7.13 конусы К< и L замкнуты в R”. Тогда множества В = Kt 0 А и £*= L П Л замкнуты в Я. При атом В {j С и= А и В П С sn 0. Но А связно. Поэтому либо В «= Я, С =я 0, либо В =* 0, С = А. Второй случай невозможен, так как о П 4 = В. Следовательно, В = Я, т. е. Л с с К,.
Итак, на утверждений 1)—3) следует, что X имеет но крайней море п +1 связных компонент, а это противоречит условию задачи. Остается доказать 1)~3).
Утверждение 1) лепосредетшшно вытекает пз (I), (II): для любого 1= 1,вф I имеем xl t= X и
(Ш)
Докажем 2), Пусть ieRn, Поскольку векторы х1, ,.ч zn об-Л
разуют базис в Rn, то х= У, р.х{ при некоторых Ц[, ,.ч цл. Ес-1и»1
лк |ii 0, ..., Дп^О, то х<=Л^н- Пусть |ч > 0 при некотором I.
Примем обозначение а =* щах ~ Тогда а > 0 ъ =>
А;	1 и
в |1< — a?.i 0 (i с= (,..и) п yj = 0. При атом
’I	м-1	п
г= 2 н*	2	2	Y/-«^+1*n+I.
i=l	i-X	1=1
Слодопатольпо, zeif/, что доказывает 2).
394
Предположим, что утверждение 3) неверно. Тогда найдутся точки re-V к индексы i, I (i ¥= 0 такие, что xsXi П-о-ь Следовательно,
— I = 2 «/’• ” х = 2	v)
i</< I
при некоторых <х2^0 и flj 5= 0. Подставим во вторую формулу выражение для х1 из (III):
>/1Л	i&i
Даппая формуле п первая на формул (IV) укапывают разложении вектора ~х по одному к тому же базису х1, .... х'”’, х,+\ •	х”+1.
Следовательно, соответствующие коэффициенты вотнх разложениях должны совпадать. В частности, а» ~ — pAt/Xi. Это возможно якни» в том случае, если ai =	= 0. Таким образом,
-*= 2
j&i,l
Положим а = 1 4- 2 aj' Тогда
J/U
0--^-т4-£~ V
jyfiiJ
т, о. точка 0 оказалась представленной в виде isiimyiG’ioii комбинации п точек’ из Л', и это противоречит предположению,
7.78.	Согласно 7.72. точки х*, ..., х,п аффпппо зависимы. Рассмотрим указанные н 7.72 числа Xi, ,.., ХП1. Положим
Л = р<=7|>.< ^0), /а={<е71Хг<0).
хс= 2 м* = — 2 ?-1х£- ? = 2 = - S ?ч>°-Hsi/l	is/»	tsrt <е/а
Тогда точка уух является одновременно выпуклой комбинацией точек х( ОеЛ) их1
7.79.	Докажем теорему индукцией ио т. При /п г=> л 4- 1 утверждение тривиально. Пусть «г > п 4- 1 я дли любых nt — 1 множеств теорема уже доказала. Тогда для каждого i s= 1, .... гл существует точки х’ е П A\- По теорвмо Радона (см. 7.78) fe'/f
мпожчч’тво I = {I, ..„ ;м) можно так разбить па пепоресекшощпе-ся множества /1 п что найдется точка х s conv У> f| conv где 1'l = {х'П <= 7|), У2 = {x1 [/&/2). При этом, очевидно, 1'1=.л х<- у„ cz П Следовптелыю, х е f) А\, ie/2	(e/j-	<=i
7.80.	Предположим, что П Xi = 0. Зафиксируем индекс JGZ
'об/. Тогда для любого хеА^ найдется такой шадскс
395
I e I, что x X{ и, зпаппт, xi e Y{, гдо У{ = Rh\AY Таким образом, X, C U У,-, причем множества Y{ открыты. Ио, как известно ’о jei
из любого покрытия компакта открытыми множествами молим выделить конечное подпокрытие. Следовательно, существует такое копочпоо подмножество что X, с U Ур т. е. Xi
° {еГо	0
П( П ХЛ = 0, а ото противоречит 7.79.
ve^o /
7.81.	Сначала предположим, что ОеХ; Пусть х’, .... в”1 —мпк. епмальная (по чпелу nt) лппаГшо независимая система элементов множества л и L — липоппоо подпространство, натянутое на ат» элементы, т. е.
Х{<=И, 1 = 1,
m
(I)
Покажем, что L = aff X. Согласно выбору х1, ...» хт, пмеом XcL. Тогда affXcZr по определению аффиппой оболочки. В то же время любую точку пз L можно рассматривать как аффпппую комбинацию точек х1, ..., ж”*, 0 из X:
тл	m	/	гл	\
X	-I- 1 - 3 Ч ’°-	(П)
<=i	i«a	\	i=i /
Поэтому I aff X п силу теоремы 7.7.
Для любой точки х <= L указанное л (I) представление одппст-воппо. Иными словами, па L определены однозначные функции %t(x) (i *= 1, ,.п л») такие, что
m
х = 2 М®)'1, !«=•!
Ясно, что эти функции лппенпы п, значит, непрерывны па I. Рассмотрим теперь любую точку х вида
х =	।	, ?.j 0, i — 1, ..>, m,	1.
<«»1	i=i
Из теоремы 7.С с учетом (11) следует, что х е X. Кроме того, ?.[ =* = M(S). Тогда в силу неирсрьишости фупкцпй Л<(ж) существует такое с > 0, что для любого х е L f| Ut{x} справедливы иораленстиа
тп
i = l, ш, У, (х) <.1»
(=1
Следовательно, х^Х. Таким образом, aff X Л Ut(x) <=Х, т. е-х е= ri X.
Пусть топорь 0§^Х. Положим У гаХ — х°, гдо х°еХ. Тогда ОеУ и по доказанному лышо существует точка у е ri У. Ясно, чК' х i=i p4-x°eriX.
7.82. Для любого <хеП положим х(й) = «х -J- (! — а)у. Тогда :(а) е aff X п Вт х(а) = х. Поскольку xeriX, то найдется тй-
Qt-*1
896
_ число сс> 1, что точка	прпнадлезкпт X. Прп этом
*°°	+ (1 _ К)г, гдо 1- 1/а.
Пусть {с*} craffX, z*->-z. Требуется показать, что :кеХ при всех достаточно _больтпих к.
Поскольку у<=Х, то существует такал последовательность G X, ЧТО У* -> у. Положим И* = У* — у, t»* >== S* — £. Тогда
sk₽s+P»^Xx+ (1-Х)	+^=Хх*4’(1-Х)у*,
ГДО
-д , X — 1 д , 1 д яг wх-р —д-— и 4" v .
Ясно, что точка 5* является аффинной комбипациой точек х, у*, w. Д с, каждая пз которых заведомо лезкнт и aff X *=> aff X, Поэтому J* е aff X в силу теоремы 7А В то же время так как iX-ъО, о*-*-0,.Тогда из условии jetIA' следует, что прп всех достаточно больших к. Но о таком случае п .*h е X, поскольку X выпукло. _______ _	_
7.84.	Ясно, что ri X с X, Пусть у t= X. По теореме 7.14 существует x«=riX. Для любого Х<=(0;1] положим	+
4* (1 — ?.)у. Тогда :(к) eriX й силу теоремы 7.16 nlims(l) = у.
____	_ ______ _	?.-о
Поэтому у е ri X. Следопптельпо, X с ri X т. с. X ri Х^_
Поскольку aff X = aff X, то rt X с: ri X. Пусть х е= ri X. Возьмем yeriX. Тогда, согласие теореме 7Д5, имеем х = Ху 4- (1 — Х)з, гдо X е (0, 1), s Вновь используя теорему 7.10, получаем, что л <= ri X. Итак, ri X е ri X, т. о. ri X ==» ri X, __
Если int X 0, то формула hit X «= int X совпадает сколько что доказанной. Пусть int X «= 0. Предположим, что int X 0. Тогда том более inlfaff X) = intfaff X) ч6 0. Поэтому affX = R4 в силу следствия 7.1. В талом случае riXoalntX. Но riX=jb0. Прети верен ио. Следовательно, itilX = £f,
7.85.	Если dim X = п, то aff X « R". Тогда intX =« ri X 4* 0. Напротив, если int X ч6 0, то aff X = TV", значит. dim X ил п.
7.8$.	Поскольку xeriX, то ^77в (х) Г) aff^X сс X прп ноко-”>рвмв°>0. Рассмотрим любое se (0, г?). Пусть уе(7в(х)Г1 naftX, Ясно, что существует S > 0, пря котором Ut(y) с Ue(x). ьледоаатедьпо, ^(у) П flff Хс X, т, е. у <= ri X.	____
7.88.	С учетом тооромы 7.17 пмоом aff(rtX) «= aff(riX) = «'OffXmaffX.
т'ол ГСРПМС>ПП71* теорему 7.17.
Н°т» по следует. Примером слуткпт отрезок и одпп пз С‘О концов.
7.91.	Пусть xeriXi и yeXjflriXj. Согласпо теореме 7.15, Тог^я1 х + С1 — * при некоторых А е (0, 1) и з е Xt с Х}.
® е Г1 Х2 в сяду теоремы 7.18, т. е. ri Х< е Н Х2.
4- (115 ЛУ^ть ж ® г| X»с nff Xt' у X? л ri x2 п Z(X) = Kx + Ma 7ед Toi‘«a =(^) e ri Xi при любом К <- (0, 1) (теорема 7.16). статорлгко 0Ьга°Д1,7ся, что z(X) <= г1Х2 прп любом X е (0, 1), до-•«точно близком к пулю.
387
7.93.	Утверждение очевидно о учетом второй формулы из 7.51.
7.9*5	. Пусть у гЬЛ (X), х°еепХ. Положим у° = Лх° s Л (X). Из теоремы 7.15 следует, что у = ?.у°Ч- (1 — А)р' при некоторых ?. <=з (0, 1) п y’ie/ifX), т. е. 1? = Лг\ где х'еХ. Тогда г/ «= «вз И(?,х°4- (l-l)x’j, причем Ах°+(1 — А)х] eri X в сплу тео-ремы 7.16, Таким образом, pc=H(riX), т. е. riH(X) tzM(riX).
Пусть у <= A (ri X), у5 е ri Л (X). Тогда у = Их, у* = Лх° прп некоторых х е ri X. х^ е А'. Вновь используя теорему 7.15, можем пшикать х = Ах° -Ь (1 —• А)х’ при некоторых А ее (0, 1), х’ е= X. Отсюда получаем у = Ах = Аг? 4- (1,— А)Лх‘. Тогда у е ИЛ (Д’) в силу теоремы 7.16. Итак, 4(ri X) o;ri Л(Х).
7.95.	Применить 7.93, 7.94 (ср, с 7.13).
7.96.	Пусть хе ИЛ”1 (У), х° е Л“’(п У). Тогда Их^У, Лх’е епУ. Из теоремы 7.15 следует, что х = Ах04-(1— А)х* прп не-которых А е (0. 1) и х* (=Л”,(У). Поэтому Лх = АЛх6-|-4* (1 — А)Их] п У я силу теоремы 7.16, т, о. ге Л~*(г1 У).
Пусть хеЛ-^НУ). Требуется показать, что ®епЛ“ЧУ). Дли этого достаточно убедиться в следующем: если {>*} cz сг а(Г(Л-1(У)) и хА-*х, то хАеИ"’(У) прп всех достаточно больших А’. Ясно, что
aff(Л"1 (У)) с: Л"1 (aff У).
Таким образом, Лх* е aff У, Лх^-нЛхег! У. Тогда Их* е У при всех достаточно больших А. Первая формула доказана. Докажем вторую. _____________ _
Включение Л”((У) е: Л“’ (У) очевидно. Пусть х <= Л-ЦУ), х’ е: (нЛ“’(г1У) и х(А) « Ах° 4- (1 — А)х. Из теоремы 7.18 следует, что при любом А«=(0, 1) точка Их(А) = АЛх’ -f- (1 — А)/1х нри-иадлеяспт НУ, т. о. х(А) sH~'(ri У) сД-*[(У). Прп этом Нтх(А)=зх. Тогда х е Л"1 (У), ?.-*о
Требуемый пример: п я» та t=± 2, И(х(| х2) = (xj, 0), У = = jnlRl U {(0, 0)}.
гл	_ т _ т
7.97.	Включения aff ХС П aff X,, X cz f) X,, П ri Х< с ri X I”!	i=l <"*1
Очевидны (опи справедливы для любых множеств). Зафиксируем гл
точку уе= П riX£.
<=ч
тп
Пусть хе П aff X,. Тогда точка г (А) =а Ах4-(1 — А)р npip надлежит множествам Xt (1 =j 1, ..., п?) прп любом А, достаточно близком к 0. Иными словами, точка х ость аффинная комбинация точек у, г(А) еХ (?.=/> 0). Следовательно, х е aff X.
гл
Пусть хе П А'{ п по по-прежнему -(А) = Ах-[ (1— 1=1
ТП
С учетом теоремы 7.18 имеем s (А) е f] rl X, С X при любом А <=: ее (0, 1). Поскольку lim z (А) = г, то х <= X.
398
Пусть । 0 — X)? Я» .v G П rlX<
x s ri X, Из теоремы 7.15 следует, что 2i=Xy4* прп некоторых А е (0, 1) м :е X. По тогда х <=
в силу теоремы 7.10.
^Требуемый пример: Xi — объединение внутренности треугольна ц одной из ого верпшп, Х2 —сторона треугольника, содержа’ щвя эту вершину.
7.9В.	Будем считан»! что /	0, J =/= 0 (иначе рассуждения
лишь упрощаются). Ясно, что Х = Y ПИ, где
У = {ze В"|Л/® = 6j}, Z = {ze Rn]Ajz i;}.
Поскольку Y — аффинное множество (точиео, Y =>a(IX; см. 4.23k w  ji у г® У. Легко проверяется, что int И = {л е К”|Л/а: < t>j). Him этом У П intZ уь 0 я силу 4.22. Тогда на 7.97 следует, чти xi*V =я ri У П ri Z = У Л int 'Z.
7.99.	Сначала предположим, что А Л int R™ =?ь 0 и, значит, rlAcxinlR™ (см, 7.91), Обозначим правую часть доказываемой формулы через У. Пусть же riX', pe-riA, у{ GiriX{ (4 = 1, ... ..., л*) п у => S <= X. Из теоремы 7.15 следует, что х = ау -|-
m
4- (1 —a)s при некоторых ке(0, 1) и геХ, т. о. s— 2
4=1
где t]eA, :(еХ< (1 = 1, ..., nr). С учетом теоремы 7.16 пмоам
?. = ар -Ь (1 — а)т] епА, X>Q,	(I)
• z1 =	-|-ц — ajTifb^^sriXp 4=1, ...» m, (II)
При этом 1=2 т, а, х е У. Итак, ri X g У.
4=1
m	ст
Пусть г<= У, уе= riX. Тогда 1=^?.^*,	ПРЦ
4=1 t	f=i
некоторых a <=riA, xl EiiXt, p<=A, j/'eA’i (i =» 1, ..., m). Поскольку AferiA, з'егЩ to (ср. с решением задачи 7,82) Найдется такое число р > 1, что
П = р?.4-(1-р)И<=Л,	П>0,	(III)
il - PXpif1 (1 р) ЩЧГ1? Х„ 1 = 1...........т, (IV)
тп
и» nua’JiiT, z = 2 X. Положим a = 1 — 1/р. Тогда равон-
стиа из (III), (IV) можно нероппейть в виде равенств нз (I), (II).
UfHi этад х Ку	(1 ~ а) г е к х. Следовательно, У с ri X, т. о.
Пусть теперь Л П intK(£ = 0. Введем множество /<={1, ...
’ • » ^}» состоящее из таких индексов 1, что ?.< > 0 хотя бы при одном А (= Л. Положим
R^={beRTn|Xi^0, 1е/; 1{ = 0, /£/}.
399
Заметим, что ri R*. ~ [X е= Rw | Х{ >0, I е Г, Х, = 0, 1^2).
Прп этом, очевидно,Л с R^, X f| ri tt£gb 0 и, значит, ri Л g ri R (см. 7,91). Таким образом, множества Л\ (i /) можно просто и> ялючить из рассмотрения, а для оставшихся множеств Х( (1 е /) повторить приведенные пыню рассуждении.
7.100.	Применить 7.99 при
Л = U е R”11/.|>0,	1=1,.„,и, У, —• 1
I	i«l
И Л.= R? соотвотстпенно.
7.101.	Рассмотреть и 7.100 случай. Х< sa {х() (1 = 1, ..., гл).
7.102.	Пусть	X (h^O), Поскольку xeriX,
х + alt е X црн достаточно малом a > 0. Положим а* = = sup(a > 0|z 4- ait <з X}. Так как X ограничено, то а* < <». При атом х 4- a*h е X\ri X = rd X. Если a <= (0, а*), то. z 4- ah е ri X и силу теоремы 7.10. Если же а> а9, то х + ah ^Х в силу выбеь pa a*. TaiutM образом, луч 1^, нероссшаот т0Х в одпиствопион точке х + a*h,	___ _	___ __
7.103.	Сначала покажем, что riX = X. Включений ri X g X о'и> видно. Пусть обратное включение неверно, т. е. существует такал точка х е X, что z <j& ri X. Тогда х е rd X. Рассмотрим любую точку хйейХ. Введем обозначение х(Х) = Хх4- (1 — >.)Л Положим
X* =а вир {XIz(X) е ri X, 0 X < 1), х* «= х(Х*),
Ясно, что х* ri X п в то жо время х* е ri X с X, т. е. х* е rd X. При этом х” х, так как ж £ ri X. Таким образом, на луче, выходящем из точки х* и проходящем через точку х, лежат но крайней море две точки из rd X, а это противоречит условию задачи. Формула ri X = X доказана. Остается доказать следующее: если х\ х2 <= ri X, X е (0, 1), то точка х = Хл' -Ь (1 — X)*1 принадлежит X. Пусть это поперло. Тогда, очевидно, па каждом из интервалов (z\ 5-) к (z, х2) лежит ио кранной мере одпа точка из rd X, По это означает, что на луче, выходящем из точки z1 и проходящем через топку z-, лежат но крайней мере две точки из тдХ. При-тиворечко.
7.105. Поскольку dim X = dim(aff X), то утверждение следует из равепста aff (riX) = «ИХ = affX (см. 7.88).
7.107. Учитывая 7.100, можно считать, что OeXiQXs. Тогда множества Lf = aff X, и «= affX2 являются лпнойпымн подиро^ странствами. Используя 7.56, 7.97 и отмочоппую теорему линейной алгебры, получаем
dirnfXj п Хт) «я dim(a!f(Xi П Х2)) =±
= dim(i| п Lj} es dim Zt 4- dim Z2 — dim(Zi 4- Zj) =
«= dimXj 4- dim X3 — dim(aff(X, 4- Xa)) ₽=
= dimXi 4- dimXj — dim(X| 4.X2).
400
MOSuXx- [-1, OJ,X2= ГО, 1].
7,i00. Применить 7.92, 7.107 u теорему 7.19.
7Л10.'Э) dim X = 3.-Множество X имеет внутреннюю точку /д,.о, 9), где 1/2 < а < 1'2/2,
' б) Обозначим через Л> к Аг множества, задеваемые огранпчо-„„йм.павоиством и огрвничониями-веравеяствами соответственно, ягпо что (V3, 1Д 1/3) e.Y; р iulX3. Тогда, используя 7.109, полу-что dim X = dim 2.
в) dim X = 1. Учесть, что сумма левых частой первых двух и{5рВ1Мшств равна левой части третьего неравенства,
е г) dim X в= 0.
7.1И	. 1) По условию существует такая последовательность ню llx^gсо. Для любых х°еХ, <х^=0 и Л = 1, 2, ... доложим
?	+ аЛ\ гдо ??.
Дли всех достаточно больших к имеем а ВяА — ха|| и, значит, J*.eX в силу выпуклости X. Поскольку L|/laU >= 1, то без ограиичо-шш общности можно считать, что ЛЛ—►* h =#= 0. Тогда £*-t-x°4-ak. Таким образом, х° 4- ah $= X X. Иными словами, 1хоЛ с: X.
2} ПустьЛ^дСХ. Для любых жеХ, а^0 и к = 1, 2, ... положим
. ? = х -h ah (х° — х) = у (х° 4- ahh) -f- (1 — у) z.
Поскольку х° 4- akh & X, то п х* <= X. Прп атом я* ->-® 4‘ «Г*. Следовательно, х 4' аЛ е X = X, т. о. с X.
7.112.	Иаврпмер, для X па 7.3 л 7.4 соответственно пмоом Х(Х) = {Л G R11 Л1 = 0, Ла 0} и К (X) = 1^,.
7.113.	Депо, что X —замкнутое выпуклое множество и ОеХ. Тогда, согласно теоромо 7.21, ото множество воограннчопо в том и только том случае, если существует такой вектор Лей”, что Л =£ 0 п ah X при всех а 0, т. о. (]Л|| 4* <с, Л> 0. Отсюда о учетом неравенства Коша — Буля невского легко выводится, что искомыми являются всо векторы с, удовлетворяющие условию 11«11 1.
7.114.	Дли открытой полосы с добавленной граничной точкой оба утверждения теоремы по выполняются.
7.115.	По условию х ah е X при любом а 0. Но
1	U
* + ^ = ТГПг“1"а4Л (« + (а+ *)Л)>
гдо х е riX, х 4- (« 4- 1)Л о X. Тогда из теоремы 7.10 следует, что * + аЛ е н х, т. о f+h с ri X.
эопот^71|г^ИМСВКТЬ те°Р6МУ й мно,к®стпУ « затем псполь-7»117. Применять 7.UG и теорему 7.21,
2^
Q. A, AmM4inoD< Л, В, Тимохов	401
7.119. Пусть h^K(X), т. о. g X при некотором seX; иными слонами, точка х* га х 4- Mr принадлежит X при любом к га 1, 2, ... Положим Ла га 1/fr. Тогда, очевидно, Лд«Л —
Пусть, напротив, Л = Нт ?,Лх\ где х* «= X, Ла > О и Л-^от
lim — 0. Рассмотрим любые! х&Х и а^О. При всех доста-Л-»®>
точно больших Л имеем аЛч < 1, и поэтому точка xft = (I — аЛл)х -|-
аХкхк лежит в X, Ио хЛ->-х 4- ай. Следовательно, х + аЛ <= X, Та. кии образом, йеШ) = К(Х) (см. 7.117).
7.122.	Применить 7.58, 7.119.
7.123.	Обозначим через Л и В выпуклую оболочку и сумму со. ответственно. Сначала предположим, что OeA'i (1 = 1, .... or). Тогда Лх еХ{ ирн всех х &Х<, Л ,= [0, 1]. В таком случае пз 7,58 следует, что А <= В. Кроме того, ясно, что В a: mA. Таким образом,
Х(Л) еВДс£(|«Л) = Х(А),
т. о. Х(А) = К(В). Обратимся к общему случаю. Рассмотрим любые точки z1 е Xt (i i«= 1,	ж). Тогда с учетом 7.122 получаем
К (4) = К (conv ( U (Х( - г1))) = К (	(Х{ - х1) ) = К (В).
7.125.	£(Х) = (х R’lx, 4" + хз = 0}.
7.126,	Л(Х) га {х е IVjxi = х2 — 0).
7.128.	а) Как известно, М-|- В га Rn. Пусть zeX. Тогда х = = у + й, где у <= £Л, /< eic ЦХ). При атом у = х — к еX в силу 7.124 и теоремы 7,21. Таким образом, X с X f] Д Обратное включение совсем очевидно; X f|	с= X + Ь с X.
б)	Пусть Uc А'П ЛА. Тогда к <= Л(Х) сL. и поскольку L f) /А га (0), ТО к = 0.
7.129.	Включения
A (X) <= 4(Х), А (Х(Х)) с Х(4 (X))
справедливы при любом X. Первое легко следует из непрерывности отображения А, второе —из ого линейности в определения рецсс-еввпого конуса. В самом деле, пусть g ^А(Х(Х)), т. е. g = Ab, гдо к Х(Х). Тогда х -|- аЛ е X лрн некотором хеХ'и всех а > 0. Отсюда Лх 4- «Ай е А (X), т. е. е= X(A (X)).
Далее, поскольку L с. А(Х), то согласно 7,128 имеем X g У П Отсюда с учотом вида L получаем
Л(Х)сА(ХЛ7Л).	(I)
Докажем теперь следующее вспомогательное утверждение:
если у* «« Ла*-, х* е X П 4х (й == 1, 2, ...) и
посдадонательпость {у*} ограничена, то	(П)
{г*} также ограпнчоиа.
402
допустим противное, т. е, при указанных условиях ||х*||->•«>. дЛ
Положим ==	$ =* 1, 2, . ..). Вез ограничения общности мож-
0 6ПЦгап>. что А*->-Л ’"АО. Тогда Л <= А'(Х) = А'(А') в силу 7.117, ? 119. Кроме того, Ah «= 0 и Л <= J,-, Слодовательио, А с= L П /А т* 0, Полученное противоречие доказывает утверждение (II). Отсюда легко ныподптсп, что множество Л(У(]/.А) замкнуто. Тогда с уютом (D получаем
Л(Х) сЛ(ХП/-х) сЛ(Х).
Первая формула доказала. Для доказательства второй напомним, что. рецессивный конус пе меняется при сдвигах множества, т. е. Х(Х + ^°) = А(Х) (см. 7.122), Поэтому можно считать, что 0^ gtiAr, Пусть ?еК(Л(Х)). Тогда из 7.110 (или 7.117) следует, что А?еЛ(Х) прп всех к = 1, 2, ... С учетом (I) имеем kg => ж Лх*, где х* е X П L2-. Положим ft?i = рА Поскольку 0 <= ri X с7 и А > 1, то Л* i= X П /А При этом g = Ah*. Тогда в силу (II) последовательность (Л*} ограничена. Пусть боа потери общности Л*.-»-Л. Тогда д = ЛЛ м Л <=Х(Х) = Х(Х) (см. 7,117, 7.119). Таким обрпэом, g ёА(К(Х)).
7.130.	Рассмотрим оператор проектирования Лх Х|, где х = (xs, xj) е R2. Тогда для мпожостла X па 7.4 по выполняется первая формула и 7.129, а длн X из 7.3 — вторая формула. В обоих случаях множество L = {х s R2|xj = 0, XiSsO) но явллотся лп-пойным подпространством.
7.131.	Применить 7.120. 7.129 (ср. с 7.13, 7.95).
7.132.	Конкретизировать 7.131.
7.133,	Пусть h е л(Л~*(У)), т. о. х4-ай еЛ^*(У) прп некотором хеХ и всех а^0. Отсюда следует, что Л*4-аЛЛ s У, т. е.
А'(У), и, значит, h <= Л~’(Л'О’)).
Пусть, напротив, Л еА",(л(У)). т. е. Ah ^K(Y). Если выполняется условие 1), то выбором х Л_,(г1 У). Тогда Ах s ri Y п из 7.116
следует, что Лх + аЛй<=У прп всех а^0. Ипымп словами, я4-aft еЛ”1 (У), т. е. Л <=А(Л_|(У)). Еслп жо выполняется условно 2), то с уютом теоремы 7.20 в приведенном рассуждении можно ваять любую точку хеЛ"*(У).
7.13f.	Подходит пример, указанный в рошопип задачи 7Ж ^.135. Рассмотрим для простоты полиэдр X вида (4,1). Если трактовать Л как лкпеПпоо отображен по, то X = Л-1 (& — ^+)* При этом К (b — R* ) = — R",.
§ 8
Пусть х1 и х2—две проекции точки a na X, т. с. 8х1 — = — В® --aj= inf Цг —cj. Тогда треугольник с поршлпамн «, х1 П я x<sX ornfi^ Явля£1ТСл равнобедренным, .Любая внутренняя точка х его ПЬ10Кпиил [А з2] лежит пя более близком расстоянии от вершн-зто п ЧОМ ж* и х1; и то же время х е X в силу выпуклости X. Но противоречит определению проекции. .26»
403
8.2,	Добавляя ±д во второй член указанного скалярного про. пзводвнпя, а затем используя неравенство Коши—-Бупяковсжиг,. получаем
Их* — в||г^ <2* — а, х — й> 5^ lb* — efj • III —йП.
Следовательно, ||х* —д|| ^гЦх — «Ц пр» всех гсА', т. о. s* —про. опция а на X.
82.	Положим Ъ ® лх(л’) — rtx(oJ). Из таоремы 8,1 слодуег, что
<й’—nx(«!), —J»> ^0, <«2 —Лх(а2), ЬУ 0.
Складывая эти неравенства, получаем
Ш2^ <«•-«’ &>^||«’-а2Ц.|1Ж
8.4.	Прежде всего отмстим, что проекция пх(а) сущоствугг в силу теоремы 1.6. Для краткости положил х* = лх(д). Для любых геХ в Хе (0, 1], используя выпуклость X в определенно проекции, имеем
Их* - afF < ИА* + (1 - Х)х* - а||»	U (а* - а) + X (х - х*) ||г =
=» Их’ — я||а-1-2Х(х* — a, х-х*> + ?Л’* — х*|?.
Следовательно, 2<х* — и, х — #♦> + ХЦх—г’Ц2^ 0, Переходя здесь к пределу прп Х->-0( получаем пузкпоо неравенстло.
8.5.	По условию веОХ. По дХ ОХ в силу теоремы 7.1 Я. Следовательно, найдотся такая последовательность {а*}, что а*^Х (Л 1, 2, .,и о* “► и. Тогда по теореме 8.2 существуют такпа векторы рк (к = 1, 2, что'
<РА, х> < <р\ в'|> при всех х е X.	(I)
Поскольку 0, то можно считать, что ftp* II е± 1. Пусть без ограничения общпостп	Переходя в (I) к пределу и по-
лагая Р = <р, аУ, получаем (8.1)
8.6.	Поскольку а^гдХ = гЭХ (теорема 7.18Ь_то найдется такая последовательность {л*}, что а* & aff X, akq£X (А и !, 2, ..,) п Вводом лекторы
Согласно теореме 8.2, для птпх векторов выполнено соотношение (1) мз решения предыдущей задачи. Поскольку Пр*К 1> то боа ограничения общности можно считать, что р*-»-р ¥= 0. Тогда, пак и выше, приходим к (8.1), Покажем теперь, что соотношение (82) выполнено для любой точки xj= ri X. По определению ri X существует в > 0, ври котором 1Л(х) ПаИХсХ. Введем точим ^«тт + eph (А = I, 2, ...). Тогда, очевидно, х*<= £/в(х).
Кроме того, х* ость аффинная комбинация точек х, а* п Яу,(«АХ принадлежащих aff X = aff X. Тогда п х' aff X в силу теоремы 7,6. Итак, хЛ <= Уе(х) П «ff X g; X, Но x*-f-x ер. Поэтому х 4* + ер & X. Тоиорь из (8.1) получаем
₽ 5= <р, S 4- ерУ = <р, х> + е|?Я! > <Р> х>.
404
S.7.	Пусть ri Х( П ri Xi = 0. Рассмотрим множество X =* riXi-" r’^‘ 1»ыиукло_в силу слодствия 7,3, Прп атом 0*^ X, ядзмоншы дпа случая: О^Х и 0еХ\Х<хг5Х. Применяя в пер-jt случае теорему 8.2, а во втором — теорому 8.4, получаем, что ££десгрует вектор /j, д;пп-готорого
<р, ХУ <Р, 0> =а 0 при всех х <= X,
<р, х><0 при некотором 5<еХ.
С учетом определении X это означает, что справедливо соотношение
<Р>	<Р, *2> иР“ «СОХ 2* <= г! X], Xs Е П Х5,	(I)
а.также соотношение (8.4). Поскольку Xf с Х< = n Х< (i *= 1, 2) в силу теоремы 7.17, то в (I) вместо riX< можно поставить Х<. Следовательно,
sup <р, ж1) < inf <р, аГ>.
Xi	А2
При любом лежащем между этими двумя числами, получаем (8.3).
Пусть теперь выполняются соотношения (8,3), (8Л) и в то же время существует х е ri Х| П ri Ха. Рассмотрим столь молоо по модулю а<0, что х1 =z-|-a(xi — я) еХ< (i = 1, 2), где точки я1 .и xs взяты на (8Л), Тогда
<Р, я’> = <р, я> 4- а«р, х‘> — <р, х» > _	________
> <Р, х> + а(<Р, х®> — <р, я» =5 <р, х2>, что противоречит (8.3).
8,8.	Пусть р(Xi, Х-) > 0. Это равносильно тому, что множество X га Х, — Х2 пс содержит нуль. Поскольку X замкнуто и выпукло, то по теорема 8.2 существует такой вектор р, что sup <р, я> < 0. Отсюда легко приходим к (8.5).
Пусть, напротив, выполняется (8.5). Тогда число
в= Inf <Р, х2> — SUp<p, X1) inf <р,х2 —Х1> A's	Ai	«’e-Xj
x2t=Xs
Положительно. Для любых я* еХ>, x3eXj, используя норапспство Коши — Бупяковского, получаем, что е =£</», х~— я1> <iljpllllx'-’ — xll|.	Следовательно, Их* — x2ll elipfl-1. Отсюда
Р(Х|, Хг) > 0. Теорема 8.7 доказана. Для вывода следствия 8.1 достаточно проверить, что при указанных там условиях p(Xi, X») > 0. Это утвержден но можно доказать также путем непосредственного upi»U)nouiifl теоремы 8.2 к множеству X = Xi — Xj с учетом лем-
8-9. Достаточно сродп неравенств, задающих X, найти то, кото-Р°в не выполняется для точки я0. В данном случае это— третье неравенстпо, В качество искомой можно взять гиперплоскость
Зяа 4* Zj -f- 2^4 = 0.
8,10.	Матрица квадратичной функции /, стоящей в ловой ча-СТп указанного неравенства, неотрицательно определена. Тогда
405
множество X выпукло в силу 7.9. Поскольку прп этом / дп^'Ф»-репцпруема, то, очевидно, искомой опорной гиперплоскостью ннлн. ется касательная плоскость к границе дХ = {х!/(л) = 25} в тп-ь ко х9. Уравнение этой плоскости имеет ппд jt —=» и, Конкретпзпруя ого, получаем отлет: 3xj 4-	4’	= 25.
8.11.	Согласно теореме 8,2, нужным свойством обладает гиперплоскость лида <р, л) = ₽, где р ж0 — jf, р «= <д, J>, а х есть проекция точки zn па X. Поскольку x°^X, то точка х дожит ца границе А' и, значит, является решенном задачи
/ , 5V । { 5V /	15\=	.	„ . 2
+	+(*а-Гб/	~>П11П’ 3‘з=эгх’ + 4
Отсюда находим х >= (—1, 1/4, 17/16). Искомое уравнение имеет вид: —32xt 4- 8zj — l(kr} = 17,
8.12.	Число It обладает нужным cbdhcihom п том и только том случае, если точка является рошенном задачи ЛП
(р, г>->шах, х^Х.
Мы пришли к задаче типа 5.12. Применяя теорему 5.3, получаем, что 36/23^ к ^84/37.
8.13,	Искомые значения к идентифицируются так лю, как п выше. По в данном случае для их нахождении удобнее использовать теорию снмилекс*метода (см. 0.4), Отсюда находим, что А- I.
8.14.	Согласно теореме; 4.7, параметр к удовлетворяй! условию задачи в том и только том случае, когда существует такой вектор q<5 R?H ЧТО
— ?! +	— 74	= — 3,
- 73 - 2г71 - 2^	70 = з - Л,	(1}
73-Н3-7.1	-4 = *;
?! +2<72	+(?5 + 4<S-	(П)
Общее решение системы уравнений (I) имеет вид
7j — ?4 4“ ?6 -Ь 70 -г 3.
72=2г/4’Ь vf-fy’
^ = -7.1-^+ 4 + *’
Условие неотрицательности переменных имеете с (П) приводит к системе
О < < — '7Ь п- 2'/e ’I- Л»
5 —4<л. — 5?Л
О =С 7Л ’С j	’>	0,	0.
Таким образом, система (I), (П) имеет неотрицательное решение в том ц только том случаи, если разрешима система
0^7s<2ge4-A",
О <-^(.^-57^4-5,	7в>0.
406
диалогично данная система имеет решение, если только —fr/2 =£ 1, 5б З5 0.
Окончательно получаем, что условию задачи удовлетворяют все к & п только они.
8,15.	Нетрудно убедиться, что мпожостна Xi и Х2 пересекаются /касаются) и единственной точке х =± (хь х2), гдо xi =и —1/2, | ₽= —2. В качестве разделяющей гиперплоскости можно взять касательную прямую к графику функции
3
(х1) х* — 1
В точке X1, т. о. прямую Jill •]- Зх3 =а —8.
8.16.	3xt + 2^1	6}'2.
8,17.	Обозначим через Л и В матрицы систем, задающих конусы Xi и Хг соответственно.
По определению мпожестяа Р включеппо р еР имеет место тогда и только тогда, когда выполнены одновременно импликации
Лх < 0<р, г> 0, Вх О-i- <—-р, x>'sC0.
Согласно теоромо 4.6, получаем, что р е Р в том н только том случае, когда имеют решения q t= R3, ге IV следующие системы:
gA = р, q 0; гВ ~ —р, г > 0.
Заметим, что векторы q и г удовлетворяют системе
qA 4- гВ = 0, g 0, г 0.	(I)
Наоборот, еслп (г/, г)—решение (I), то р =а qA == — гВ е Р.
Таким образом, для описания множества Р достаточно найтп все решения системы (1).
Применял метод Гаусса исключения неизвестных, из (I) находим
'/х = —Зг2-|-бг3, ^2га-г3,
7з = “гг + 3гЗ’ Г1 = 2гЯ~ Ч*
Учитывал условие неотрицательности на нее переменные, получаем, что г2 и гз должны удовлетворять соотнонюниям
3	5
2 гз га < 3 гз’ гз °’
При атом, р ~ —гВ « Г2« + гД где а == (4, —8, 7, 1), Ь = *= (J, 5, —20, 2).
Полошив г; = 3, гз = 2 и г2 5, г3 3, получаем образующие конуса Р;
Р1 = (16, -14, -19, 7), р* = (26, -25, -25, 7).
8.18.	Пусть A ix 51 и А^х Ь4 — системы, задающие соответ-стйелно А'| п Х5, <р, х) = р — гиперплоскость, разделяющая эти «Но’,костил, т, о.
<Р. «> < Р Для нсох а Xt,
<—р, z> г£ =1 р для всех х е Xs,
407
Согласно теореме <1.7, вектор р п число 0 задают разделяющую гиперплоскость в том и только том случае, когда найдутся такие векторы	и reRl, что
( = Р, гЛ3 = — р,
Достаточно, следовательно, найти решение (q, г) системы
0/Д 4- гЛ3 =» 0, q 0, г О,	(I)
<'/, Ь'> + <г, *2>^0.	(II)
Общее решение системы уравнений (I) имеет вид
ffl^“ri + 2r2'b3r3“ Г4>
Г1~ гз“ rs + 2V
*«*= 2^4-5^+^+ r4.
Г1	+ Г4-
Условия неотрицательности переменных и вместо с неравенством (II) дают систему
П 2г3 4- Згз — г»,
П rt 4- г3 — 2г«,
и > Юга 4“ 0гэ — <1г<.
Эта система неравенств имеет решение в той и только том случае, если
г2 4- г* — 2г< < 2г3 4- Зг3 — г<,
Югя 4" 8г3 — 4г<	2г3 4- 3rs — г<,
т. о. если
—г3 — 2г3 — г«<0, 8г3 4* Зг3 — Зг< 0.
Таким образом, можно, например, положить и = 2, га = 0, г3-е= = 1, г< = 1, Тогда р = — гЛ2 =s (9, 9, —9, 6), 0 = —<г, Ь5) = 0. Уравнение разделяющей гиперплоскости имеет вид
3®i 4- 3ss — 3z3 4- 2г< = 0.
8.19.	Пусть выполняется условие (8.1), гдо, очевидно, X мощно заменить па X. Если предположить, что <р, <т*> < 0 прп некотором /, то приходим к противоречию:
<р, «> == 2	< ₽ 2 Х{=Р «= <р. «>.
(=1	i=l
8.20.	Можно применить 8.19, представив точку в, через которую проходит опорная гппорнлоскость, как полусумму точек 0 и 2а, &23. Взять “Р = sup <р, г>.
X
8.24	Даппов утверждение — иная форма теоремы 5Д2.
408
9,25. X = [х с= 11’1x1*2	1, Х| > 0).
8Д6. Применить 7-61. Отметим, что в доказательство теоремы 8,4 (см. 8.6) этот факт был обоснован лишь для некоторой гиперплоскости, собственно опорной it X в двипоп точке.
8.28.	Это непосредственно следует из теоремы 8,2.
8.30,	Пусть X строго выпукло. Предположим, что существуют гиперплоскость м различные точки д’, «’<= X такие, что X с сЛрр.	Тогда, с одпой стороны, а = 0,5о' -|- 0,5о5 <=
е//рр, а с другой стороны, а е (nt Хс lnL7/^jv Противоречие.
Пусть теперь X по является строго выпуклым, т. о, существуют в\ о2 е X, а1 ч* а2, А (0. 1) такие, что а = Ла1 Ц- (1 — А)«’ ф int X, т. е. а «= дХ. Тогда по теорем© 8.3 существует гиперплоскость Йт& опорная .к X в я. Прп этом й1, а3е /7г.р в силу 8.19. Таким образом, пересеченно .V П Ярг, содержит болео одной точки.
8.31.	Пусть х е convX П ?(convX). Тогда но теореме Карлтоо-дорп тошеу х МОЗК1Ю представить в виде п	п
1гаХ^1г1' х*ееХ, >о, 1 = 0, 1, ...,п, 2^1=1’ <=0	<*0
где будем считать, что Ас > 0 прп всех 1 = 0, 1, ,.п и (иначе утверждение донизано). Вместо с том но теореме 8,3 существует гп-нерплоскасть 77р$, оперная к convX и точке х. Тогда пз 8,19 следует, что х1 <= Йрц прп всех 1 = 0, !,..,, л. Отсюда зпхлючаом, что и тэчвк ж1 — х”, .... ж” — ж° лежат в линейном подпространство 7/«0 и поэтому они линейно зависимы. Но тогда точки Д ж1, ..., х" аф-фпппо зависимы (см. 7.72). Следоиатольпо, точку ж можно представить в виде выпуклой комбинации по более п пл этих точек (см. 7.74).	_
8.32.	Положим Р = conv{®’, ..., а* ...}. Ясно, что хеР. Допустим, что х & ri Р, т. е. х <= г<Э Р. Тогда по теореме 8.4 существует гиперплоскость 7/рр, собственная опорная к Р о точке х. Легко показывается (как в решении задачи 8.19), что **^/7^» прп всех й « 1, 2, ... Следовательно, Р с П^, Но зто противоречит тому, что гппернлоскость //^ — собственная опорная к Р. Таким образом, х е ri Р g; Р cz X.
8.33.	Пусть множества Xt п Xj отделимы п Ягп — разделяющая их гиперплоскость. Допустим, что ri Xt fi ri Xj =/= 0. Тогда по теореме 8.6 эти множества по могут быть собственно отделимы, т. а. X, <= //Jlfl. Хг с: Я;1Р. Поэтому aff(X, и Х?) с //гр. Следовательно, afffXtUXj) ¥= Rn. Обратное утверждение очевидно в силу следствии 7.1 п теоремы 8.G.
Если OeXi, 0e.Y2) то эквивалентность условий 2) п 2') пс-посредстлеппо следует пз 7.57.
&34.	Применить теорому 8.5 к множествам X п int R".
8.35.	Нет, нс следует. Рассмотреть множество
Х={жеПг1ха1 + (х2 + 1)г^||.
8.3Й	. Обозпачпм У = Ra\X. Согласно теореме 8.5, существует такая гиперплоскость ЯРр, что Хс//”р, У с 7/^. Но У —открытое множество. Поэтому У = ini У с int /7^. Тогда 7/JJp =
Rn\int Я+3 с КП\У i=X, т. о. X = 7/"р.
409
8.37,	Согласно теореме 8,0, существуют такие р п р, что ньпю.-ь полы условия (8.3), (8.4). Если Xt ограничено, то нужными свонст, вами обладает гиперплоскость //па, гдо а= sup <р, z).
x^A'j-
ТТусть Xi —конус. Тогда О^р, так как 0 (= Xf, В то же про. мя для любого х s Xi имеем <р, Аг> р при «сох к > 0 п, апач и г, <р, х> 0. Отсюда яспо, что гиперплоскость Я^5 искомая.
Наконец, если Х> — полиэдр, то следует использовать 8.24.
8.38.	Утверждение попосредстиепно следует из 8.21 и 8.37 с условием и), поскольку пффиппое множество Х| являотся нолнндр’оц и riX| — Xt (см. 7.87). Можно также применить 8.37 с условном П) (ото более простои факт) к линейному пространству У, = Xi — и множеству Кг = Х2 — z, гдо х е Х|.
8.39.	Положим X = Х| — Хг. Тогда 0 §4 X, причем X замкнуто п силу 7J32. Остаотся применить теорему 8.2 it Аг и « = 0.
8Л0. Пусть Х< = (хе Д"|Л,-х^ t>f) ’ (i а= 1, 2). Тогда условие Xt П Х2 = 0 равносильно тому, что система
А 1X2^6’,	Ь2
несовместна. В атом случае, согласно 4.86, существуют такпе векторы г/ 5s 0,	5= 0, что
+ g2.42 = 0,	Ь’> 4- <«’, Ь?> < 0.
Положим р = г/Я| = —tf24j, р1 еа <д|, Ь1), р: = — (<Д Jl2>. ТОГДЙ при всех х е Xt имеем
<Р, *> « <?‘Лг, х> = <5l, ?ltx> <//’, &> = Pt.
Аналогично показывается, что </>, х) 5^ Pi мри всех х & Х3. Следе-лательпо,
sup<p, *>=£0 <р <1пГ <Р, *>, А\	1	3	А'3
т. о. X) н Х2 сильно отделимы,
8.41.	Последовательно применить 8.40, 8.37 и 8.21.
8Л2. Пет, нельзя. Рассмотрим прямую X» = {# sK’|x] = 0. xj = 1} и замкнутый выпуклый конус X пз 7.10. .Легко провернется, .что единственная гиперплоскость, проходящая через Xt и остая-лнющая X в одном ив своих полупространств, задается уравненном xi =s 0. Опд пересекается с X но лучу Х| = 0, х2 пп 0, xs 5= °.
8.43.	Пет, не следует. Подходит указанный выше пример.
8.44,	Пусть Xi = (г е IV’ptfX iif) (/ = 1, 2). По условию задачи справедлива импликация
Л1« fri, /Ijx Ь2-»’ х)
причем система слови совместна. Тогда, соглнспо теореме 4.7, существуют такие неотрицательные ниггеры г/, что
4- 52Л2 = р, <<?', ft’> + <72, Ь2>	₽.
Яспо, что векторы р1 « <?’Лi, р2 = 92А;г и числа Щ = <г/, Ьв>, {Ь --= <72, Ь!) облвдают нужным свойством.
8.45. Докажем утверждений ппдукциоГг но ft = dimXi. Ес.чл к 0, т. е, X] —одноточечное мпежостяо, то утверждение следуй пз теором 8.2. 8.4. Пусть опо ужо доказано нрн к < гл, и пусть dim Xi = ль Согласно теореме 8.6, существует гиперплоскость Ярп-410
разделяющая Xi и Хй т. е. Х± с //j^, Х„ с= //+р и лн-S	либо Х;<£/7,ф. Если Х^Ирь то утверждение дока-
7>аио. Поэтому будем считать, что Хйс^Нм и, значит, Х^Н^. J Далее, если Х| П 7Лф = 0. то полиэдры Х( п II сильно отделимы с помощью некоторой пшорнло-скостп (см, S.40). Эта пшер-плоскость обладает нужным свойством, поскольку Х2 С= Н;,fi.
 Остается рассмотреть случаи, косна множество Г = X, П Hv(i непусто, "• о. гиперплоскость Ящ> является, соист-TMjjHioii опорной к Xi (рис. 94). Ясно, что Г —нолиздр. Пр» этом ГПг1Х5 = sspj, так как ко условию X, f| ri Х2 = =s 0. Кроме того, ditn Г < t?i (ем. лемму 8.1). Тогда, согласно индуктивному предположению, существуют вектор г; я число а такие, что (q, х>^а	прп
<?, *> 5= а	крн
(д,х>>а при некотором геА\
всех x >= Г, всех х (= X , 1
(I)
(II)
(III)
(ряс, 94). Из (1) и 8.44 следует, что существуют лекторы р1, р® и числа Pi, р? такие, что
<р1, х) при всех xg4	(IV)
при всех z <= I/j.p,	(V)
Р1 + р’ = 7,	+
(VI)
Используя (И), (V), (VI), для любого х<=Хгс=/7рр получаем
СЛ х> = </Л *> — <Р2> *>	—
Прп атом <р’, х> > |3| для х на (111). Отсюда и на (IV) заключаем, что гиперплоскость II до искомая (рис. 94).
Р Pi
8.46.	Ист, нельзя. Рассмотреть множества
Х1=!: [хе R21-|-х;< 11, Х„ = [re R“ | хА = 1, 0=^хлС1Ь
8.48.	Рассмотрим в RBm множество X = Х| X •  • X Xm и множество У всех точек вида у е= (z, ..., =), где :eR". Из условий Задачи следует, что эти множества выпуклы и не пересекаются. Тогда по теере.мо 8.5 существует ноиулавой вектор р <=> (/>’, ...
Pm) ^Rrthl такой, что для любых х = (я1, ..., хт) еА, у = *= (2, ...,:) е Y справедливы соотношения
тл	rn	/ m \
</\ *> = У, <Д **> < </>, у> = 2	2> = \ У Д ” /•
i=l	\l=l /
Поскольку с здесь может мевнтт.сп произвольно в Rn, то но псоб-т	m
ХоДимостн 2 Р1 0 ”i <Щ«'игг, 2 (р*<	‘С® при всех X1 1=Х{
1=1	1=1
411
(I = 1, ..., тп). Отсюда следует, что прп любам i = 1, . л» пне-m
ло Pj = sup </>*, конечно и ^jjPi < 0-Таким образом, множест-Х{	|.~1
ва X....Х„> отделимы,
8.49.	Применить теорему 8.6 для множеств X п У пз решении задачи 8.48. Прп атом учесть 7.93.
8.50.	Легко показывается, что указанное перавепство равносильно условию р(Х, У) > 0, гдо X п’У —мпожестна из решения задачи 8.48. После этого остается применять теорему 8.7.
8.51.	Проверить, что здось выполнено неравенство пз 8.50.
852.	Повторить схему рассуждений пи пепюипя задачи 8.40.
8.53.	Применить 8,48 к множествам X‘l\{0}, X?,..., Х^ и учесть сказанное после задачи 8.47.
8.54.	Утверждение неносродсгвешю следует из 8.49.
/’ц-i -	\
8.55.	Заметим, что условно П ml XI Л Хт 0 равпосиль-\ *=1 г
/ttj-i \
но условию | Л int X'j I Л пАгт= 0 (см. 7.92). Поэтому с учетом
8.54 достаточно доказать следующее: если вшегоры // е X* (I m
т) пе равны нулю одновременно и = 0, т0 О’*» х{У<
< 0 ври некоторых ! и J'e X*. Пусть это неверно, т. о. для любого 1=1, ..., w следует, что <pJ, х> = 0 при всех ж<=Х<. Тогда для I с= i, ж — 1 имеем р1 «= 0, так как intX* ь/= 0. Но в этом случае и рт => 0. Противоречие.
8.56.	Если выполняется условие 2), то утверждение доказывается но схеме, нсполмовэппоп при решении задачи 8Л4.
Пусть выполнено условие 1). Если р = 0, то утверждению тривиально: подходят р1 к= ... = р” = 0 и Pi = ... =	= 0. Поэтому
будем считать, что р т= 0. Тогда пз условий задачи следуот, что множества int/Z^j, Х|,...,Х„ но пересекаются. Применяя 8.49, получаем, что существуют векторы j, ...» и числа к, ••• >.п *fm ДЛЯ КОТОРЫХ
<7, Ж> у ирп всех X е Я+р,	(I)
<$*,	прп всех ж1 <=Xt,	/ — 1, m, (II)
тп	m
?+2«i=0* jjVi+v<0’	<ш>
i=l	<•»!
причем либо прп некотором ж<=я+р,	(IV)
либо <<f, х{> < прп некоторых I и J'gA'i.	(V)
Условно (I) означает, что имеет место импликация
<-/>. *> *5-₽-►<?, «>«
412
Тогда из теоремы 4.7 следует, что q — — ?.р, —f при некого-сом Л > Допустим, что А = 0 п, значит, g = О, у 0. Если прп {йом выполняется условно (IV), то *f>0, п из (II), (Ш) заклю-чаем, что множества А'(1 ..., лп сильно, а поэтому п собственно отделимы. Но ото противоречит 8.49. Если выполняется условие /у), то также получаем, что множества Х|, Агт собственно от-палимы. Таким образом, возможен лишь случаи X > 0. Тогда из III), (1П) слодуот, что нужным свойством обладают />* = А"1'/1, L=₽VYc (f =* I, ..н m).
8,57.	Пусть m —2, Х1>2 = {х е R31 (^ ± 1)а-)-zf < 1), р=> ₽(0,1), Р^О. Тогда первому п третьему нз соотношений в 8.56 удовлетворяют лишь р’ = (—Л, 0), дэ = (ц, 0), где Х> 0, р>0, и в, = [Ji = 0. При атом р14- ps Р-
8.58.	Пусть -Vi, ..., Arm отделимы, т. о. существуют векторы р1,..., Ргп, не равные пулю одновременно, п числи_В|, ...» |5Я, удовлетворяющие условиям (8.12), (8.13), Если Yi = 0 при некотором Ц то утверждение в одну сторону доказано. В противном случае длн любого i очевидно, что
<р{, ®>	< <pS У> прп всех х<~Х(, уеУь (I)
Для любого такого i, что р1 0, это означает отделимость множеств Х( п У<-
Докажем обратное утверждение. Еслп У< = 0 при некотором I, то множества Xj (j =/= 1) отделимы в силу 8.48. Тогда множества X1t ..., А'п, также отделимы (достаточно дополнить соответствующую систему векторов н чисел элементами р{ = М< = 0). Пусть теперь прп некотором i множества Х{ и У< 0 отделимы, т. о. существуют ^0 и {Ji, удовлетворяющие условию (I). Если i П т! Х< = 0, то, согласно 8.49, множества Xj (j ¥= I), а значит, к множества А'], ..Арш даже собственно отделимы. В противном случае, применяя 8.56 ко второму неравенству лз (I), получаем, что существуют векторы pi (/1) н числа {Jj (/ /= 0, для которых
t <р\ **> Р; при всех z> s Xj, J /, 2)^ = “?*, 2 Рр
Вместо с первым неравенством лз (I) это означает, что множества А1, ..Л'п, отделимы, ш
8.59.	Пусть Xi, ..., Аг„ отделимы, по П ri	Тогда для
любого I из 1,, т множество	непусто и, болоо того,
Tl’X’i П ri У< Ф 0 в силу 7.97. Согласно 8.58, множества Х{ и У< отделимы при некотором' L Тогда из 8.33 следует, что aff (А’< U Ут) т,”п. Обратное утверждение очевидно с учетом 8.33, 8.49 н 8.58. тп
Если 0 е f| Xit то возможность замены условия 2) па 2') Подуют из 7Л7, 7.97.
8.69,	Обозначим правую часть формулы (8.8) через У. Пусть ? е А'*, Для любого i => С .. н А' имеем <р, г{> I, так как х< е X.
аналогичных соображении для любых { = &+!,..., m и Х>0 ^одует, что <д, х* -|- лх4> 1. Поделив это соотношение на А и перейдя к пределу прп а->-<», получаем, что <р, i4>^0. Таким
413
образом, р е У. Пусть, напротив, р е У. Любую точку х <= X моигц0 представить в виде
х =	। Aj О» I = 1, .м, Xj = 1.
1=1	i=i
Следовательно,
т	k	k
<Р, *> «= 2 *1	< S **> < 2 'ч = *.
1«>1	I=i	f=i
т. с, р е X*. Таким образом, X* => У.
8.61.	Заметим, что множество X'* состоит из таких векторов ? для которых справедлива импликация	*
Лх <: Ь <р, х> 1.
Поэтому формула (8.9) непосредственно следует из теоремы 4.7.
8.62.	Обозначим правую часть формулы (8.10) через У. Если х е X, то но определению X* имеем <р, х> 1 при всех р <= X» По ото же означает, что х е X1”. Таким образом, X с X**. Тогда поскольку множество Х*# замкнуто, выпукло и содержит пуль, то УсХ**
Допустим, что обраткой включение нс выполняется, т. о. су* щестпует «еХ**\У. Тогда по теореме 8.2 найдутся такие р и j), что
<д, я> < {J < <р, «> прп всех л е У.
Поскольку 0 е У, то |3 > 0. Положим р = fHp. Тогда
<д, я> < 1 < </“, «> при всех х е У.	(I)
Паноминм, что X cz У. Тогда из норного неравенства в (1) следует, что р^Х*. В таком случае <д, «>	1, так как ue-V*. Но эго
противоречит второму нс’равснству в (I). Таким образом, X*’ с. У п, значит, X** еа У.
8.63.	Согласно теореме 8.8, имеем
X* ~ {р € К’| - Зр, + дг 0, 2/ч + Зра.сО, 4д, + 5рг =£ 0}.
Отсюда
{oil	5	)
Р 6=1 К” I "у" 1*2 Рд	Рл ’
ИЛИ
Х*= cone{(-3, -1), (5, -4)}.
8.G6.	Применить теорез^ 8Д 5	11
8.67.	X* cs conv ~ ~1 ”sF^*
Применить теорему 8.9 пли теоремы 8.8, 8,10 с учетом того, что указанная выпуклая оболочка содержит нуль.
8,69. Применить теорему 8.10 и 8Ж
8.70. Последнее равенство следует из теоремы 8.10. Остальпио
очевидны.
8.71. Пусть X#’R", т, о. существует точка cn=IV, по лсЖ®* щая в X. Тогда по теореме 8.5 найдется такой ненулевой вепЮР
414
ди цто <р, г> <р, «> прп всех xt=X. Если <р, а> =£0, то Д ®	"	1
еХ*. Если <р, я> > О, то ? = fl) Р Е Таким образом, С» п& (0). В обратную сторону утверждение очевидно.
X 8.72. С учетом (8.6) формула А П X* еа {0} очевидна, причем runv'iUiocTb X здесь по требуется. Допустим, что Х4-Х*^ПИ. Yorjiu, согласи» 8.71, лайд&тся такой вектор <7 =£ 0, что
<г/, х +' р> 0 при всех х <= X, р <= X*.
Полагая здесь р = 0, получаем, что ?е X*. Аналогично при х <=г 0 {ояводпм, ’ПО q е= Х‘\ Но ото противоречит формуле X* Л X** = ^73. Положим X=Ut(0), У — У|/г(0). Пусть реХ*, р=#=0. Вязьмой х=ы ер/НрН. Тогда z<=X п, значит, <р, х> = ellpH =£ 1. .ТЙпм образом, р«=У, т, о. Х*сУ. Пусть, напротив, p<=Y. Для любого х е х имеем <р, *>< (] РН®1<Т’е = L СлсДовательпо, п е Xе, т. е. У с X*. Итак, X* = У.
1	8.74. Пусть некоторой множество X удовлетворяат условию
X»«= X. Тогда для любого теX = X* «гмеем <*, х> = ]|zF1, Слодолатольно, X <= ЕЛ(О). Отсюда с учетом 8.68, 8.73 получаем
У((0) = [^(0)]*сХ*«Х
П „2
Развить схему решения
Таким образом, X = С7|((У
8.75.	X*^|peR” задачи 8.73.
8.76.	♦ == {р|11р|| 4- <р, х°>	1}. Это множество огра-
ничено и том и только том случае, если ||«°|| < 1 (см. 7.113 пли 8.77).
* 8.77. а) Пусть X ограничено, т, о. X с UT{0) при достаточно большом г > 0. Тогда с учетом 8.68, 8.73 имеем
Уе(0) с X», где е из 1/г,
(О
т. е. О е iniX*. Напротив, если выполняется (I), то Хф*с17г(0). Но X cz X**, Следовательно, X ограничено.
б) Согласно утверждению а), множество X* ограничено п том оД0ль’,° ™м случае, если OetntX**. Но в силу теорем 7.17 н o.W имеем
int X** = jnt (conv (X (J {0})) = int (conv (X"(j {0})).
О?сюда без труда выводится, что условия OeinlX** и (cwv X) эквивалентны.
8.78. а) Допустим, что _ int X* = 0. Тогда aff X* ч* Rn (в про-ивиои случае int X* = ri X*, и нолучаом противоречие с теоремой ™О:)ГОЯУ X* содержатся в некотором гиперплоскости, т. с. УЩествуст такой вектор z f/л 0, что
<х, р> = 0 при всох р е X*.
8&S	±*(=Х***. По X** cs X в силу теоремы 8,10.
а7йт, конус X не является заостренным. Противоречие.
415
б) Пусть ze.Y, г=рО. По опроделеппго X* писем
<г, />Х О при всех р <= X*,
т. с. X* с. Н~о. Следовательно, int Xr* с int/f“0. Ипымн словами, для любого peinlX* справедливо <х, р><0. Таким образом, сели int X* 0, то из условии х е X, я </-• 0 следует —х ф. X, т. о, конус X заосгрсп.
8.79.	Конус X» {zeR3|xt > 0} U {0} заостроп. Прп этом X* Zjjjp где h = (—1, 0), и, значит, ini X* « 0.
8.80.	С учетом 8.78 ясно, что нужным свойством обладает любой вектор peint Х’1*Л(—Хд). Требуется лишь показать, что ото пересеченно непусто. Допустим противное. Тогда, согласии теореме 8,5, найдется такой вектор х^О, что <х, р‘>^0с
<*> —Р2У при всех /АеХ*, рг<= X*. Отсюда л из теоремы 8.10 следует, что хе X** = Хх, »eXj* = X2. По ото противоречит условию X! П Хг = {0}.
8.81.	Рассмотреть конусы
Аг, =d* е R31 х, > 0 или х, = 0, х* > 01,
Х2 — е R |	«= 0, Хд 0j,
а также конусы
X, ~ R”, Х3 [х <= R2|х±<О| U{0}.
8.82.	Применить 8.80 к конусам Хх = — R£ п Ха = “X.
8.83.	Первая формула легко выводится из 7.58 и теоремы 8,10, Обратимся ко второй формуле. Пусть геХ**, Тогда, согласно первой формуле, х= lim лйЛ, где Ал е [0, Ц, у* е X {It ез 1, 2, ...).
л->»
Без ограничения общности можно считать, что Ал-»-?.е [0, 1]. Возможны два случая:
1)	А > 0, Тогда последовательность {р*} ограничена, и можно считать, что у*-»-у еХ При этом х = Ау.
2)	A ess 0. Тогда х е Х(Х) в силу 7.119.
Таким образом, включение cz доказано. Обратное включонно доказывается столь же просто.
8.84.	Первая формула сразу следует из 7.117, 7.123 и тооромы 8.10. Ее можно вывести также из 8.83. Вторая формула с учетом 7.124 очевидна.
8.85.	Пусть X содержит прямую 1*^ (Л=/.О). Тогда <р, х° + ай> 1 при всех р е X* и аеП. Отсюда следует, что <р, А> = 0. Таким образом, X* с Яла н, значит, int X* = 0.
Пусть теперь ini X* s= 0. Тогда X* с Я^ при некотором А 0. Следовательно, foA = Я*о е: X**, т. е. A gh £(Х4*) =t ЩХ) (см-8.84). Иными словами, I с X при некотором х° е. X,
8.86.	Поскольку cone X — конус, то
(cone X) ♦ е= {р е R " | <₽, хУ	0 нрц всех х g cone X}.
Ш
«я теоремы 7.7 следует, что здесь спрапа символ сове можно ону-стить. т. о. «праводлвдо второе из указлнпых равенств.
Далее, пусть />еХ(Х»), т. е. существует такой вектор ? <= X*, что 7 +apis Xе прп всех а 0,-Тогда во определении) X* для любого хеХ имеем <fl + ap, х> 1 при всех aisO. По ото возможно лишь в том случае, если <р, х> 0, Таким образом, р € (сопеХ)*. Остается повторить эти рассуясдепня в обратном порядке.
8.87.	Если ОеХ, то affX есть лнпсйпоо подпространство. С учвтом этого доказательство аналогично решению задачи 8.86, Требу оный пример: X = (z е R!|*i = 1}. Здесь
(affX)*“{p^K2l/h^l, Р2^О}Г L(X*)=(0}.
8.88,	Применял 8.86 к множеству Xе, получаем, что К(Х*Л) = (соло X*-)*. При этом Х(Х**) =г= Х(Х) (см. 8.84), Тогда с учетом Теоремы 8.10 имеем
[Л'(Х)Р = (сопоХ*)** «сопоХ*,
Аналогично с помощью 8.87 доказывается фопму’ла для ЩХ)|*. Необходимо лишь учесть, что nff X* замкнуто.
Докажем формулу для соло X*. Пусть р е cone X*, т. о. р = X? при некоторых ?. ^0u q^X* (см. 7.45), Требуется показать, что 6up<p,z><co. Если 7.1=0, то вто очовпдпо, Пусть К > 0. хе л
Тогда р/>. = q е X* п, значит, <р/?„ х> 1 при всех х е А. Таким образом, sup </), х> Х<оо. Остается повторять эти рассуяс-ЯЕ.Х
доппя в обратном порядке.
.Формула длн аПХ* следует из 7.47, 7.48.
8.89,	а) Исполхдуя 8.88, имеем
dim X* = dim (aff X*) = dim [£(X)|* = я — dim £(X),
поскольку	есть подпространство, ортогональное к L(X)
(см. (8.7)').
б) В данном случае L{X) = X П (—X) в силу’ 7.118, 7.124.
8.90.	б) Докажем сначала вторую формулу. Пусть р s V*. Рассмотрим любую точку хеХ. Из выпуклости л следует, что Л=х-аеУ. Тогда <д, й> s^O. Таким образом, р <= Р. Пусть, iiaiipcrriiEi, р <= Р. Рассмотрим любой вектор й <= У, Тогда найдется такое а > 0, что л = а + ай е X. Прп этом <р, sS. <р, а>,Отсюда' <р, й> 0. Следовательно, р V*. Итак, V* == Р. Тогда У = Р* в силу тоорэмы 8.10,
в) Использовать б) и 8.89.
Требуемый пример: X = [я е R21 ,т| -f- < 1), а = (1, 0).
8,91.	Ограничимся рассуждениями для п» = 2. Пусть Ре (Xi Х3)*, т, о.
<р, z> + х2>	1 при всех х1 Е Xh х2 <= Хг,
Полотен здосе, г’ = 0е Х>, получаем, что р е X*. Возьмем любые ?’ е Х|, х2 е Ху, Поскольку Х| — конус, то прп любом 7.	0 имеем
\Р, 7.x14- д!>>	1, Это возможно лишь в том случае, если
Об х‘> г^0, т, о. peX’J. Таким образом, реХ*ПХ^. Пусть,
с. Л, Ашманов, Л. В. TiLMoxiM)	417
напротив, /'е А'’ПА'*, т. е.
<р, х'> О, <р, хг> 1 прп «сох x’<=A'i, x2t^Xt.
Складывая эти перавепстпя, получаем, что р t= (Xi + Х2)*.
Требуемый пример: №2, Xt = Х2±=± 6^(0). Здесь (X, Ф Хг)* = П1/2(0), по Xjnxj = С/, (0) (см. 8.73).
8.92.	Используя теорему 8.10 и 8.91 ирнмопитольно к mhojkoct-вам X*, .... Xj^, имеем
m	тл А
л х{= л XJ
Я1	1=1
Переходи и сопряженным множествам, получаем нужную формулу.
Тробуомын пример: ш = 2, X^-inlR2, U {0), Хг <=а {х <= К3| « 0}. Здесь (X, П Х9)* = R1, ио X* + X* = {z е= R21 х., <о}.
8.93.	Ограичнмся рассуждениями для т = 2.
Если 0 е ini Х1( то множество X* ограничено (см. 8.77) и.-знп-чпт, множество Х*4-Х* замкнуто (см. лемму 7.1).
Пусть ri X, П ri Х2 ф 0, Учитывал 7.132, достаточно показать, что множество L = Х(Х*)л(—-K’(Xj)) является линейным подпространством, т. о. но условия h <= 1> следует —h е L. Согласно 8.86, условие Л е L равносильно соотношениям
<Л, х'> ^0	(А, х2> прп всех х1 <= Xh «*ёЛф (I)
По в силу теоремы 8.6 множества Х( п Х9 но могут бытьсобствешш отделимыми. Поэтому неравенства в (I) обязаны выполняться кап равенства. Иными словами, вектор Л там можно заменить на —А( т. о, —Л е Л.
Если Х| и Х2 — полиэдры, то по теореме 8.15 множество X* 4- X* также является полиэдром и, значит, замкнуто.
8.9f	i. Если пыполннется условно 1), то
где последовательпо использованы утверждения задач 8.70, 7.97, 8.92 н 8.93.
Если выполняется условие 2), то нужная формула сразу следует из 8.92, 8.93,
Пусть выполняется условно 3). Положим
Х= А Х„ У = П ХЙ
1-2/
Согласно предположениям, X есть полиэдр, 0 i= X, Г — выпуклее множество, ОеУ я ХПпУч^ф (см, 7.97); кроме того, если ж <= /, то V —выпуклый конус; если же ni <£/, то X — выпуклый конус. Сначала допустим, что те /.
418
С учетом узко доказанного достаточно убедиться в том, что
(ХЛК)* = Л’* + У*.	(I)
Положим У = X Л aff К. Тогда, во-первых, ЛГПУ = ИПУ.	(И)
Вр.рторых, У есть выпуклой мнеяшство, ОеУ, У — выпуклый ко-яус; при атом У Л ri г У- 0, У с aff У п, значит, ri У Л ri У ф 0 (см. 7.92). Тогда в. силу утверждения данной задачи с условном 1) пмеом
(У Л У)* = У* 4-У*.	(Ш)
В-третьих, X п aff У являются иолнадрамв, причем aff У-ко-Ыус, Тогда пз утверждения задачи с условием 2) следует
У* в Xе + (aff У)*.	(IV)
В-четвертых, У и nff У трнпиалвво удовлетворяют условию типа 1); поэтому
У* + (aff У)* = (У Л аП У)* = У*.	(V)
.Соединял формулы (П)—(V), приходны е (I).
Точно та же схема рассуждении проходит и в случае, когда pi^/. Стоит лишь подчеркнуть, что формула (111) здесь будет по-прежнему справедлива, поскольку теперь уже V является выиу|мым конусом,
8.95.	а) X- =	(0) - /&, где h = (1, 0, .0);
£) Х^У3(0)-К".
8.90.	Утверждение следует из определения сопрлжеппогл множества.
8,97.	Используя теорему 8.10 H.8.9G применительно к множествам А'* (1 е /), имеем
Л Х,=1 Л X?'m fcoiiv / U X?U*. ter ‘	‘	\ V'sJ )}
Переходя к сопряженным множествам, получаем нужную формулу.
8.98.	Имеем
(nt	/ m	\*	/ nt	_	/ те
Л X,) =з П XJ = 1 П Х-] = conv ( j X* ,
<~1	7	\<-1	J	М=1 7 \i=i	7
Где использованы утверждения задач 8,70, 7.97 и 8.97.
8.99.	Провести" рассуждения, близкие к решению задачи 8.91.
8.100.	Образ обтюдппопня любого числа множеств прп произвол!,поя отображении совпадает с объодняоппеы образов от их множеств. Тогда, используя 7.129, 8.83, получаем
л(х**)=,л( и (хх)их(Х)^ =
= и (U(X))IM(A'(X>) =
= и (Ы^)иХ(Л(Х))МЛ(Х))**.
27»
419
8.101.	Прообраз объединения любого числа множеств при про-напольном отображения сооиадает с объедиЕЮпием прообрипип этих множеств, Поэтому, оелн выполняется условие 1), то, всио.н.. зул 7.SK5, 7,133, 3.83, получаем.
А-1 (У*») = U (М"1 (Г)) U А-1 (К (У)) =
= и (ха-1 (У)} и К (И-1 (У)) = М"1 (У)!**. KU1
Если нее выполняется условие 2), то множество Л“‘(У) является замкнутым в силу непрпрывпости отобраяюппп А. В этом случш.-достаточно использовать лишь 7.133 п 8.83.
8.102,	Пусть (д, q) (gL*. Тогда длн любого jeII’1 имеем
0 = <Р. *> + <7, Ах> = <р, х> 4- <rpl, х>.	(1)
Это возможно лишь в том случае, соли р = —qA. Напротив, если р = — <М, то (1) всегда выполнено и, значит, (д, q) eL*.
8.103.	Пусть q g[A(A')]’i т. е, <7, jr>s£ 1 при всех У е Л(А).
Тогда для любого хеX имеем
<7, АхУ = <qA, хУ < 1,
т. о. ?А i= X*. Таким образом, [А(АГ)]* с: (Л*)“’(Х?). Обратное включений доказывается столь же просто.
8.104.	Используя 8,101, а затем 8.103 применительно к отображению А* н множеству У*, получаем
(А-^У)]»* ±=г А~|(У**) = (А*(У*)]*,
гдо, подчеркнем, 0еЛ*(У*), так как ОеУЛ Переходя с учетом 8.70 к сопряженным множествам, выводим
[А_,(У)]*.= А* (У’).
Остается показать, что множество Л* (У*) замкнуто.
Пусть выполвопо условие 1). Учитывая 7.129, достаточно проверить, что из условий деЯ(У*), А*д = 0 следует — /)еЛ'(Р), Согласно 8.86, условно р еЛ'(Р) равносильно тому, что
<Р,У>^0 при всех у<=У.	(1)
Допусти,хг, что <д, у> < 0 при некотором уеК Тогда <р, у> < 0 при всех у е ri У (см, 8.26). Но по условию A~l(ri У) 0. т. е. Az е ri У прп некотором х е R", Тогда <д, Лх> = <А*р, х> п= 0. Противоречие. Такпм образом, в (I) стоит равенство для всех р^У, Поэтому вектор д там можно заменить на —д, т, е. ~р (= Л'(У*), Следовательно, множество Л*(У*) замкнуто.
Если выполнено условно 2), то в силу 7.53 и теорем 8.14, 8.С’ множество А*(У*,) является полиэдром и, значит, замкнуто.
8.105,	Если допустить, что одновременно существуют рои»’-пне х норной системы и решение q второй, то приходим к противоречию:
1 < <р, х> = <г/Л, х> с» <7, Ля> =£ 1.
Пусть первая система пе имеет решеппп, т. о, из условии Лж<е 5 следует <р, хУ 1. Это означает, что д gz [Л-1 (У)]*, Прнмоня» 8.104, получаем, чти существует решение второй системы.
420
С точностью до обозпачеппи теорема 4.6 получается отсюда при У = —KJ,.
8.1015. Утверждение сразу следует нз 8.105 при V=;17i(0). (Отметим, впрочем, что данный конкретный фант нетрудно выверти и непосредственно пл теоремы 8.2.)
8,107. Полиэдр X нй теоремы 8,0 можно представить в виде А~1 (У), где У = Ь —- К™. Прп атом с учетом 8.91 имеем
Гу = [i}*n(-R,p* = //{;jnKT4! - Ье1Г|<?, &>ci, 7>о}.
S.198. Исиользопать 7,Г>4, 7.96; 8.94 и 8.164,
8.109. Указанная теорема получается прп А’ = — R", •у« {0}.
8.110. Проводом рассуждения для полиэдра А' вида (4.1), .Пспользуя введенные в § 4 обозначения. Пусть х* — крайняя точ-tKa и А', Положим / = /(,«♦), J =и (|t ,,,, ш}\/. Тогда Л;х® <= Ьц  Aj-* < I>j. Допустим, что существует точка х^=х* удовлетвори ю-.щая услоиню ?1 ,£ = Ь/, Выберем столь милое а>> 6, что для точек х’ х® -f- а(х — х*) п х1 = х* — «(£—х*) выполняются неравенства Л^х1 < bj, Ajx3 < 5/, При этом, очевидно, Atx1 = bi, Art3 = bt. Следовательно, Лх’ ==; b, Лх2^Ь, т. e. x1, x1 e X. Ho x* =. 0,5x‘ -Ь 0,5x2 п х‘=?=хл Это противоречит предположению, «по х* — крайняя точка и X, Токим образом, х* — единственное ро-шеопе слстомы Atx = bi. Тогда по определению х* — вершина X.
. Пусть, напротив. х* — ларншпа X. Предположим, что х* можно представить в виде
х« = Xxi 4- (1 — A)xs, х', х« <= X, 0 < А < 1.
Тогда для I = /(х«) имеем
Ьг = Л>х* = КЛ,Х1 + (1 - А)Л,х2 A/;, -j- (1 — A) 1ц = bt.
’Отсюда Л|х‘ = bh Alx2 = bl. По это возможно лишь в том случае, /если х1 вз х1 = х®, т, е. х® — крайняя точка в X.
 8.111. 1) Пусть х<=Х(Г), но х<£ E(X)t т. о. ± можно нрсдста-' япть н виде (8.11). Тогда, используя (8.1), получаем
'  Р = <Р, *> = А<д, х‘> -J- (I -Х)<д_. х’> < Ар + (1 - МР = ₽.
.Отсюда <д, х‘> =i <р,' ха> = р, т. о. х1, х2<~ХГ)// = Г, Вместо  О‘ (8Д1) это озпачаот, что хб££(Г), Противоречие. Следовательно, .;«еЛ’(Х),
1 - 2) Ясно, что aff Г с aff А’, Допустим, что абГ- аГГХ. Тогда .« cz all X = аИ Г с Я. По это противоречит (8.2). Таким образом, ' aff Г ть aff X. Отсюда следует (см. 4,14), что
dim Г = dim (aff Г) С dim (aff X) = dim X.
8.112.	Пусть существует zs fi(X) п в то же время с;Х Ори некоторых *° и h =/= 0, Тогда из теоремы 7,20, примененной по •^Дельности к лучам и	следует, что /хл<=Х, В частио-
Ст11. х1 = х 4- h е X и z'' = z —A s X. Прп этом х и 0,5xl + 0,5х2 н х' =а= xJ, т. с. х Ь'СХ). Полученное противоречие доказывает ™ОроМу Ц Од1(у сторону.
421
Предположим теперь, что X по содержит прямых. Покажем, чт<» Е(Х)=^0 нпдукциой по размерности X. Если dim X = 0, т. <-X — одиоточечние множество, ю утверждение тривиально. Пусть оно уже доказало при dim X’ < л», и рассмотрим случай dim А' = гл. Выберем какую-нибудь точку легН. (Ясно, что гдХ^=0, тан как любая прямая, проходящая через две различные точки мп<>-
Рис. 95
«костил А, пересекает rd А; иначе бы эта прямая лежали в А’,) Рассмотрим множество Г пз ломмы 8.1, Ойо замкнуто, выпукло к шп, подмножество X не содержит прямых, При этом dim Г < ж. Тогда по ппдуктнвпому предположен tno £(Г)^0. По /;(Г) с=Ь’(А'). По. атому £(Х)
8.113.	Включение conv Е(X) с G X очевидно, так как Л’(А') а А я X’ выпукло. Включение А' с. a conv R(«¥) докажем индукдиеи по dim А’, Если dlmX = 0, то утверждение очевидно, Пусть оно ужо доказано при dim X < ж, и пусть dim X т. Для произволь
ной точки а о rd X рассмотри»: множество Г пз леммы 8.1. Поскольку Г —выпуклый компакт и dim Г < w, то, согласно индуктивному иредпологкопню, Г с conv Е(Г). Таким образом, л еГс conv Е(Г) g conv £(Х), Мы показали, что rtf А'с= convE(A').
Рассмотрим теперь любую точку x^riX. Поскольку А' —ком-
пакт, то, очопидио, эта точка принадлежит некоторому отрезку с концами х1, хг, лежащими в rd X. Следовательно,
х е conv (ж1, ж2!} ед conv (rd X) er conv (conv Е(А')) i== conv Е(Х).
Таким образом, ri А'с convZ:(A'} и окончательно имеем X = rd X у ri А' с conv Д'(Х).
8.114.	Пусть X— ограниченный полиэдр. Из теорем 4,1 и 8,11 следуют, что X имеет коночное число крайних точек, тогда А' •— выпуклы» многогранник в силу теоремы 8.13.
Пусть X —однородный полиэдр, Рассмотрим мпожостш» У ея {х & R"| |xj| 1, / = 1, .... «} it Р = X П Г (рпс. 95). Лен», что р — ограниченный полиэдр. Тогда, согласно доказанному шлнг, /’ есть выпуклый многогранник, т. о. /> = conv{xl, ,, „ хм), где х‘, хт— некоторые точки „о R”. Боа труда нокпэыпаотсн, что п таком случае X = сопе {х1, ..., л"}, т. о, А’ — многогранный конус.
Пусть дан полиэдр X r= {х е RB|/ix б), где Л g з/-(л, »). bcR'. Рассмотрим в 1Р14! однородный полиэдр
Л' = {(хЛ) sR" xRpIx-pi-^O, р^О).	(I)
В силу доказанного выше К есть многогранный конус, т. о.
Х₽сопе{(*', р(), .... (*то> Pm)}.	(”>
где (я1,	.,,, (xw, pln) — некоторые тонки из R"+‘. Заметим, что
положительные числа в (II) всегда можно заменить одпйпцпми-Это позволяет без ограничения общности считать, что
422
. =s Рл = !, Ра.м = ... = рП| == 0. Тогда (II) приобретает вид Л'=.еоно{(Л 1),..,, (x\ 1), (хН‘,0),..„ (дЛО)}. (Ill)
Покажем, что в таком случае
X = conv {х1,,..,, дЛ) 4- сопо {х*+1, 1,Xм). (IV)
Обозначим правую часть агой формулы чиров Y. Пусть х еЛ', т. 0. (х, 1) s К в силу (1), Тогда из (III) следует
>п	Л
*=*......(V)
i=l	Ь-1
Цо это в точности означает, что У, Итак, X с: У, Пусть хе У, т. о. справедливо представление (V). Из соиоставления (I) н (III) имеем
Лх1 Ъ,., г, Дх* A, Лх**15$ 0,..., Лхт 0.
Поэтому тп	h	k
Лх = >1 /чЛх’ < у, ^Лх1 < а У = ь, i=l	i=l	i=X
т. о. xglX. Формула (IV) доказана. Следаватольио, X —многсгран-.ное множество.
Таким образом, мы доказали в одну сторону каждое из трех утверждений теоремы 8.14.
Пусть теперь X — многогранное мможостио. Поскольку при сдвигах многограннее множество остается многогранным, а ио-лйэдр — полиэдром, то можно считать, что 0 <= X. В силу теоремы 8.8 сопряженное множество X* является полиэдром. Тогда ни доказанному выше X* есть многогранное множество. Вновь iijin-монян теорему 8.8, получаем, что X** есть полиэдр. Но X ей X** в силу теорем 7.13 и 8.10. Слодоватольио, X — полиэдр. В частности, если X —выпуклый многогранник и, значит, л — компакт (см. теорему 7,13), то X — ограниченный полиэдр. Еслп X —многогранный конус и, значит, X* — однородный полиэдр (см. теорему 8,8), то X — однородный полиэдр.
8.115.	Согласно теореме 8,12, множество X ие имеет крайних точек и том и только том случае, если оно содержит целиком какую-либо прямую. Пусть ’1д- токаи прямая. Поскольку Ot=X, то из теоремы 7.20 следует, что прямая 1<л также целиком ложи г it X. В таком случае для вектора А = (/rIr ..., /;<) должно яынолпвться неравенство
(А! - 2А})3 + (й2 + А,)« 4- (А3 + 2А<)3 8/а3
при любом а =# 0. Это возможно, лишь если
А| = 4/, й2 ез 2/, Aj =- “2f, /ц = 1
иРи некотором 1^0, Подставлял эти числа ио второе ограниченно, *Маю1цоо X, получаем, что к eh 1.
Таким обрезом, множество X содержит прямую лишь в том олуше, когда А-= 1. Следовательно, при всех к 1 множество X пмевг крайний точки.
423
8.11G.	Воспользуемся следующим очевидным сообраисониом (см. 8.127): точка х(Л) является крайней к X и том и только том случае, если ее можно сильно отделить от миогограшпщ, conv {х1,..,, х‘), т. е. если существует такой лектор /»= (pIr р2| pj), что
<р, х(Л)> < <р, гО. /=1.....4.
В данном случае эта система имеет вид
2р2 — Зр2 -Ь (Л — 3) дз < О,
— 4р* - 2р2 -|- (А — 4) р3 <0,	(1)
5р2 Ч’(аЧ" !)Р3<0,
К -|- (Л - 4) Р3<0.
Из (I) получаем раппосильпую систему неравенств
—2рэ Ц- (Л — 4)ps < 4ps < (Jp2 — 2(А — З)р3,
5/>s+ (Л + 1)р3 < О, p}4-(*~z«)ps<0.
Следовательно, система (1) совместна тогда и только тогда, когда совместна система
“2ps + (Л - 4)р3 < 6р3 - 2(Л - 3)ps,
Г>Р2 < — (А Ч- l)pJr
р2<—(А —4)р3
или система
(23Л - 42) р3 < О,
(И) (1 1А —.42)р; <0.
Нетрудно видеть, что система (II), а значит, и система (I) совместим, если только А < 42/22 или k > 42/11.
&! 17.. Согласно теореме 8,8, мьэ.кество А'* задается системой перинеиств
— 2/\ Ч-P2 <1, “Р, )• 2Л.< 1.	Pi Ч- Зр2 < 1,
3/>j Ч- Зр2 1,	4р( - р2 <1, Зрх — Зра < 1.
С помощью геометрических плстроений походим крайние точки нолиэдра X* и представляем его и виде выпуклого многогранники: ™	17 *	51 / 1 1\ Л 1\ /4 1\ /2 Ml
X =conv^~ 3’ “ 3/Ц“ J’ 3/ (°r 3 J’ \15’ isj' \U' ~ l-> Я*
По теореме 8.8 находим X** i .ik иолладр,. задаваемый системой неравенств
— 4хх — 5х2 <3,	— Ч-** С 3> xs<3i
4«j4-	15, 2хх — С 9.
Поскольку О Е А", то X «= X** по теореме 8,10; поэтому полу-чопнан система неравенств н определяет X как* полиэдр.
424
8.118.	Xs= {xe R’|—Xix£ 1, — xt .j. хг^3, — x, + 2хг rS 4},
8.119.	Согласно теореме 8.8, множество X* задается системой перлаенств
“/\-|-Зр2 +л,<1,
2/^— Р* -гР3^1,
А»
-/>1-Зл.-Зр3<1.
Можно показать. что соотВатствующая однородная система имеет -только тривиальное poincKlio. Это означает, что X* — ограниченный иолиздр (см. 4.4). Используя теоремы 8,11, 8.13, получаем
X* = conv {(0, 0. 1). (8, 8, —9), (—4, -2, 3), (—4, -4, 5)),.
Поскольку О^Л’, то на теорем 8.8, 8.10 выводим, что Л* == Л"** можно задать следующем системой неравенств:
*3С1.
,	8Xj -{- 6*2 — 9z3< 1,
—	2г24-Зг3^1,
— 4^ — 4хйН- 5т3 < I.
8,120.	Допустим, что в указпппом представления, например, г1 </•» х н >,! > 0, Тогда ?»1 < 1 п
х X
тп
i=2	1
При этом X пл^г1 (если .г е± х1, то х =» х\ что противоречит предположению). Следовательно, точка х нс является крайней в X, В обратную сторону утверждение очевидно.
8.122.	Использовать 8.120.
8.123.	Если X имеет бесконечное число крайних точек, то . утверждеппе доказано. Пусть s’, х* — все крайние точкп X. Ио теоремы 8.13 следует X = conv {х1, .. „ х*}. Поскольку dim Л' е— = ;л, то. согласно 7.73. п X существуют т -р I аффинно пеззвпеп-. мых точек у1, ..., ym+1, Так кик все они являются выпуклыми : комбинациями точек х1, ..., х*, то точки (у1, 1), .... (t/m+’, 1) у представляют собой (неотрицательные) линейные комбинации то-V. 4QK (х1, 1),(х*, 1). При атом точки (у!, 1),..., (pm+l, 1) лииой-,1; по независимы (см. 7.72), Тогда	I в силу известного факта
лииойпоГг алгебры (см., панрпмор, Г12, с. 131).
8.124.	Использовать 8.122, 8.123.
. . 8.126. Для доказательства основного утверждения использовать лемму 7.1 и теорему 8.12.
Пусть х =х'-Ь х2,‘где хе£(Х), х‘ <^ХЬ zseX}, Предположим, что хг£/=0. Поскольку 0e-V?1 то XiaX и. зпачпт, х1 <= X, Положим = х14 2z2 е X. Тогда х = 0,5х° + Й.5х’ н х° х5. Но <Вто противоречит условию хей(А’). Таким образом, х2 = 0, т. о, 1 <= х1 s Xi. Тогда х е Ь’(А\) в силу 8.121.
8.127.	а) Использовать 8.122, 8.124»,
425
б)	Для ттределвнпостп Судом считать, что I = 1. Пуст» х!^£(Х),т. е.
х* = Ау + (I —А)с, гдо Здесь
1-1
s *1£ж<» П1^0, 1=1
У»:еА’, у^ ', 0 < А < 1. (|) h
' “ 1| . .,, 171 ,	— I,
£-1
а
< =	5j’li=L
1=1
Тогда	1
m	ft
*’ = S VlA Yi = X|lJ + (l-Х)П1>0. 1 = 1.............
1=1	1=1
(11}
Допустим, что 71 ев L Тогда f< = 0 п, значит, Ц[ = д4 «= 0 для п»
любого 1 = 2, А; кроме того, 2 Y^raO. Отсюда с уче-
1=!Н-1
том заостреипсстп конуса еошфб**1, ..., хи) логко выводится, что
дли любого f=l'+l, ..., ж либо xf = 0, либо Y< *= (I и шитому = 0. Таким образом, у = 2 ±в х1, по ото противорочит (I).
Сяодоиатольпо, < 1. Тогда (II) можно Еюрсппслть н впдо
l-V V* £ х ~2t i-т/ •
i=i
Vi Yi
г«° 2г=7 = ‘-
$=а	1
Иными слоплмп,.
х1 ecoriv {хг,,аЛ} -}- сопо {х4*-*,..,, xm}. (III)
Пусть теперь ? ^ВД, по формула (III) спраиедлшщ. Тогда пз 8.126 слодуот, что ж1 — крайняя точка множества conv{x!,.. „хЧ. и в то ясс кремп х* <= conv{x7, х*}. А это протлиорочнт 8.I2P.
8.128.	Примером служит нынуклая оболочка X окружности X &а [х е Rs | *1+ с= 1, х3 = 0} н отрезка X} ® {ie R3|*i => I, я? = 0, —1	I). Точка x = (I, 0, 0) нрпппдложпт злимпанню
мпожестна крипппх точек X, но сами крайней по яв.чпотсл.
8.КД).	Доказательство аналогично решению зидачн 8.120.
8.131.	Рассмотрим лтооЕле хеГи^ 0- Если X > 1, то из представления
х = у().х).|’(1-{)•<).
гдо е X, 0 е X, следует, что Ах <= Г, 0 е Г. Если же 0 < t ю Ах = Az -(• (I — А). - U е Г в силу выпуклсгстн Г. Таким образам, Г — конус.
8.133.	Применить 8.19.
Ш
8.134.	Пусть Г— крайнее подмкожестпо полиэдра X ппдв (4.1).
Полежим
/ = {>'» 1 i xg ж | <о<, х) = &г при всех х е Г},
;={1......И}\/
£ докажем, что Г совпадает с гранью X вида У «=± (хеХ|Л,х = &,}.
Включение ГсУ очевидно. Пусть хе У. Используя выпуклость Г, нетрудно покопать (ср. 4.22), что существует точка .г Г, для которой Лj.т < bj (если J = 0, то это неравенство счптаетсн тривиально выполненным при любом .?)• Выберем столь малое: а>0, что . %/!)< bj* W1 У = х + а(х—®). При этом,_ очевидно. А1у = Ь1 н, айвчнт, j/e-V. Выразим х чоре-л х и у: х <з» Хх 4- (1 — к)у, где Х = а/(1-|-а). Отсюда, поскольку Г—крайнее подмножество X, “заключаем, что х<= I'. Таким образом, Ус Г, т, о. Г <=s У. Мы по-илзвлп, что и» а) следует б). Импликация б) о в), по существу, совпадает с утвержденном аадачп 5.44. Импликации в) => а) носит общий характер (см. 8,133).
8.138.	Пусть 1еУ- Рассмотрим любую точку геГЦйК. Па теоремы ".15 следует, что х = Хд+(1 —Х)л при покоторых де е {(>. 1), ’c^YcX, Тогда уе Г, так как Г — крайнее подмножеств» X.
8.13!)	. Применить 8.138 к множеству У => X.
8.14(1	. Пусть Г — собственное крайнее подмножество X. Тогда Г ст rrf X в силу 8.139. Поэтому заведомо r& X 0. Отсюда, согласно 7.104, множество X ни является аффинным. Пусть, напротив, X — иоаффшшоо множество и, значит, гдХ=£0. Рассмотрим гиперплоскость ЯРу, собственную опорную к X и точке а е гй X. Тогда Г = X П Ям —- собственное крайнее подмножество X (см. 8.133).
8.141.	Применить 8.138 к множеству У = Г.
8.142.	Применить 8,138 сначала к множествам Г = Г|, У = Г2, а затем к множествам Г = Г2, У = Гт.
8.143.	П;а 8.133, 8.138, 8.139 следует, что указанным условиям удовлетворяет множество Г = X Л Я^. где //^—гиперплоскость, 'собствониая опорная 1с X в произвольной точке а е ri У.
8.144.	Ясно, что Р = 1\(У) — Крайнев подмножество X (см.
8.137) и У с Г. Допустим, что У Л ri Г = 0. т. е. Ус Г Л гй Г. Тогда, согласно 8.143. найдется такое крайнее подмножество Г' мио-•япьстви Г, что У cz Г'cz rti Г. При этом Г' — крайнее лодмпожест-ло X (см. 8.135). Отсюда, поскольку Г —краГтпй носитель У и X, следует, что Г с; Г', Но это противоречит условию Г' с; гй Г. Таким образом, У Л ri Г 0. Единственность легко выводится из 8.138.
8.145.	Пусть Г—(непустое) крайнее подмножество X. Покажем, что Г = Г| Л Г2, где Г1 н Гу — крайние носители Г в X» п Х2 соответственно, т. е. такие их крапине подмножества, что
Г с Г,, ГЛпГ|чЛ0э Гс|\ Г Л г! Г;-т^0
(см. 8.144). Имеем Г с= Гт Л Г? и. кроме того, ri Г<= ri Гт, ri Гс ri Га (см. 7.91). Поэтому с учетом 7.97 нолучаом
Г Л li (Г, Л Г2) = Г Л ri Г| Л П Г2 =/= 0.
.Следовательно, Г1ЛГ2сГ п силу 8.138. Таким образом, Г = Г, Л Г2.
427
В обратную сторону утперждонно очевидно.
8.146.	Положим
Г] =а {х е Х| |х -Ь у е Г при некотором у (= Х2), Гг «= {х е X2|ai 4- х е Г мри некотором и е Xi).
Яспо, что Г с l*i -Ь Г* Пусть я <= Г» -I- Г21 т. о. х = х1 4- х», где <“ Гь х" е Го и, аиачпт, i1 ye Г, ; -{- х2 <= Г ирн некоторых у <= е Хг, s <= Х|, С учетом выпуклости Г имеем
у х -Ь v (I/ -Ь =) = 7 <** Н- у) -I- 4 (г ’I"x!l) Г*
Отсюда, поскольку Г — крайнее подмножество X, ввключаом, что х i= Г. Таким образом, Pi 4- Г? с Г, т. о. Г = Г| 4“ Гз.
Покажем тонера, что Г[ — крайнею подмножество Х|. Пусть
х = Ху 4- (I хе Гь у.геХь 0<Х<1,
По определению Ti прп некотором и @ Х2 справедливо
хт«еГ, т. е. Цр 4-и) 4-(I — Х)(з-НО Г.
Отсюда у4-н<=Г, = 4-пеГ к, значит, у, :еГ|. Это н требонл-лось показать. Аналогично доказывается, что Г2—крайнее подмножество Х2.
Требуемым пример: Xi = Х2 = [О, I], Fi = {0}, Г2 = {1).
8.147.	Пусть Г — грань X и Р — совокупность всех тех точик Множества {х1, ,г"'}, которые принадлежат Г. Тогда conv Р с Г, так как Г — выпуклое множество. В то же время на 8.130 очеинд-ио, что Г с; conv Р. Таким образом, Г = conv Р.
8.148.	Положим У = conv Qс X. Пусть Г —грань X, по существует точка х t= aff Г П Г. Рассмотрим любую точку у е ri Г. Тнк Kate x^affr, то найдется столь малоо число Ае (0, 1], что точка : = Ах 4- (1 — А) у лежит в грани Г. Тогда но определения» грипп х^ Г. В то же время условие jeF говорит о том. что т ость выпуклая комбинация точек на Q, Тогда в силу 8.130 по крайней мере одна из ятлх точек принадлежит Г, т. о. Г П Q #= 0. Мы пришли к противоречию с определением ().
Пусть теперь aff Г n К — 0. Тогда н силу 8.41 существует тикая гиперплоскостт, Ярц, что
аНГс/7р|>, yaiiit/Z“p.	(I)
Поскольку (х1,	х"1} с Г (J Q G Г U У, то очевидно, что X =
всопу(ГиУ)- Отсюда и из (I) легко выводится, что X g П~р п Г = X fl Таким образом. Г — грань X (см. 8.133).
8.149.	Использ1М1лт|, 8.131, 8.132 в схеме рассуждений, ationoi яч-пон решению задачи 8.147. Можно также представить X в виде
ТП
X» У /+{
1=Л °*f
и применить утверждение задачи 8.146 (точнее, ого очевидное огюч-' щепне па ш множеств). При атом учесть, что гранями луча являются лишь начало координат л сам луч.
428
8.159.	Подожни У “ cone С* Пусть Г — грань Л', Тогда, используя 8,132, нетрудно ноназать (но схеме из решения задачи 8,148), что
аПГПУ={0}.	(I)
Предположим, что конус У по заострен, т, о. ± уе У при покото-ром у ч* 0. Для любой точки хеГ можем записать i =	у*(-
.|_ (-^у). Отсюда, пповь используя 8.132, получаем, что уеГ. По это противоречит (I).
Пусть, напротив, выполняется условие (1) и конус У ааостреп. Тогда ‘ из 8.21, 8.80 следует, что существует гиперплоскость !!&, дли которой
ШГ<=Яр0, У<=/Г-, Yfi//p(| = {0).
Отсюда н пз о’ювидпой формулы X <=а сопе(Г (J У) заключаем, что X <= 77“ и Г «а» X Л //ро, т. е- Г — грань X.
Требуемый пример: Х = сопе{(1, 0), (0, 1), (0, —1)), Р = = {(1.0)}.	'
8.151.	Это непосредственно следует пз 8.I4G, 8.147 и 8.140.
8.153.	Зафиксируем произвольные индексы /,	гл)
и рассмотрим полипом
/(О sa («— /)*(/ — к)5 = оз + а,1 + ъР 4- ajp -|- а,!'.
Имеем
/(/)e/(ft)=0, /(J) > 0 прп всех 1'^}, к. (I) Введем гиперплоскость П#, гдо р = (а>, а?, «э, а<), р = —ад. Из (!) следует, что -х (?) <= 7/jhi. я(А') //Ffl, x(i) s int Я*р при всех 1 к. Отсюда легко выводится, что [*(/), х(£)} =ХПЯУл—• грош, многогранника X, а х(/) и х(к) — его вершины (см. 8,133. 8,135).
8.154.	Поскольку множество X по содержит прямых, то его рвцвг.гппиый копус К(Х} заострен. Тогда, согласно 7.117, 8,78, су* щеегнует вектор р int[X(X)j*; прп атом для гиперплоскости U = //Р0 выполняется условие
ад п я = {0}	(О
(рис. 9В). Пусть L 1= Lin(aff X)—линейное подпространство, па-ралами,лоо atfX В силу извосткои теоремы линейной алгебры имеем
dim(& П П} = dim L + dim Я — dim(L U Н}.
Здесь dim L = dim X > 1, dim// e л — 1, dim(L (J H) n, Следовательно, dim (L f| 11} > 0. Иными словами, существует 'ненулевой вектор Л е L П Н.
Рассмотрим теперь произвольную точку х X и прямую (рис, 96). Поскольку Ь <= L = off л — х, то (хлспИХ. Так как Л е 7/, то пз (1) следует, что h(£K(X} н — h<£.K(X). Сказанное означает, что пересеченно прямой Л/, с множеством X представляет собой отрезок, концы которого лежат п rtfX,’ Поскольку х нрп-падло;ннт этому отрезку, то утверждение доказано.
429
8.155.	Ясно, что convG(A’) cz А'. Вшгючеппо XazcnnvG(X) до. коисом индукцией по dim X. Если dim X I, то X является точкой, отрезком пин лучом, для которых ото включений очевидно. Пусть оно уже доказано при dim X < и, где т > 1, и пусть dim X t^= рц С учетом 8.154 достаточно показать, что rt) X g; convG(X), Для про-
извольной точки aetdX рассмотрим миожиство Г пл лиммы 8.1, По индуктивному предположению ГссопуЩГ). В частности, л <= conv С?(Г). Заметим теперь. что Г —крайней подмножество X и, значит, &'(Г) <= (7(Х) {см. 8.133, 8.135). Таким образом, я <= <=convG(X). Формула X оз convG(X) доказана.
Далео, осин крайний луч н X, то его начало х япляотсв крайней точкой в X (см. 8.135). Следовательно,
G(X) с Е(Х) + //(X) с conv £(Х) + cone//(X)
п, значит,
X = conv G(X) с conv Е(Х) -f- cone //(X).
В то же время //(X) — ото, прежде всего, подмножество роцосснп-кого конуса Х(Х). Поэтому с учетом 7,117 имеем
conv Е{Х) + соне II(X) с X + К(Х) сд X.
8.156.	Использовать 8.125, 8,155.
8.157.	Использовать 7.128, 8.155.
8.158.	Использовать 7.118, 7.124, 8.125, 8.157,
8.151L Пусть X имеет копенное число крайних подмножеств. Используя 8.157, продета ним X в виде
X = conv Е(У) -J- cent; //(У)
где L ±= L(X), У = X П С учетом 8.145 ясно, что множеспю У вслед за X имеет конечное число крайних подмножеств п, в 430
частности, крайних точек и крайних лучей. Таким образом,
К(¥) = (ж1,..., х*), сопоЯ(У) = conn {/Р, ,/1’},
В то же прими нодпрострииетио L можно продстоннть в индо cone(±7?, .... гЬ&г}, гдо 61, ..., 6Г —базис п Л. Следовательно,
Л’ = convfx1,..х*} + сопе(Л',.,h‘, ±Л\ .. ., ±6Г},
т/ с. X — мпогограппое множество,
Обратпоо утверждение очевидно (см, 4.51, а ташке 8.151).
8,100. Рассмотрим выпуклой множество X = conv(X| U Хэ), гдо Xt .= [хе Ila (xt х t)s 1]. Четыре ого нрайпно точки с координатами (±1, ±1) по яиляютсп выступающими. Рассмотрим выпуклый конус
Л' = сопе{(х1( х2, 1) <= R’l (*!, х?) IS X),
гдо X — указанное выше множество. Четыре луча вида IjJ,, где Л = (±1г±1, 1), япяяются крайними, но по выступающими подмножествами /С
8.161. Пусть х° —точка па X, наиболее удаленная от й, т. о.
Ц ж0 — a j i= jnaxjjx — а В = р, .тех
Это означает, что шар J7|i(«), будучи строго выпуклым множест-иои, содержит X, причем ,tIJ лежит па его границе (рис,. 97). Тпгда «° яплпетея выступающей точкой шара, а значит, п множества X.
8.162. Поскольку X—компакт, то число М ~ апр ||.г— а[|
конечно. Пусть I) = Пд(й) —‘Проекция точки а на X (рис. 98). Рассмотрим точку у= я |-а(& — а), гдо
м-
а> 2U —«Г
Рассмотрим любую точку z X. Добавляя ±я по второй члеп скалярного произведения из теоремы 8.1, получаем
<1» — а, х — а> J: ||6 — аЦ2.
431
Поэтому
III — ylF 2= II (x — «) — а(Л — a) |p t=
~ lix-a|P-2c4<x-e, b - «> +a2||ft - flj|2
AP - 2a||fr - all2 4- На - pH2 < ll« ~ y|p.
Рме, 99
8.164.
8.165.
%
Применить 8.122, Пусть X но соле
КЛ63. Положим У = conv 5(A). Ясно, что УсА', Допустим, что обратное включение пенерно, т. е. существует точка в(=А‘\У. Посколыгу У —выпуклый компакт, то, согласно 8.1G2, найдется та*
кая точка у (= R", что
На — yD > Их — у|| при всох х е У, (I)
Пусть х? — точка во X, панболео удл-лониая от у. Тогда z'-'e: ,$(Х) <= У в силу 8.161. Подставляя 1° в (I), получаем
Ila — у|| > ||ж’ —иII.
Ио это противоречит выбору л°. Таким образом, X = У. Далее, множество convS(X) замкнуто в силу теоремы 7,12. Поэтому
X = Y = conv S(X) с: convS(X) с: X
п, значит, X = convS(X).
63.
нт прямых. Тогда Е(Х) ч6 0 в силу
теоремы 8.12. Рассмотрим произвольную точку xQ <=Е(Х). Требуется показать, что при любом в > 0 шар содержит хотя бы одну точку из £(Х). Рассмотрим выпуклый комнат Y X П П.Ур(х°), гдо р > е. Ясно, что х^-ЕСУ) (см. 8.136). Поэтому, согласно 8.164, существует точка zf=S(Y) Q £7е(ж0) (рпс. 90). Включение	означает, что существует гиперплоскость Нгь для
которой У cz Zfpp, Y П НТф га {х). Отсюда п на условия х е Ut(:P)cz g ini Uptx*) легко выводится, что X g /7^, X Q II= {х}, т. о. ге>!(А'). Таким образом, £(Х) cS(X),
Обратное утверждение цепосредствоиио следует из теоремы 8,12, поскольку любая выступающая точка является краппей.
8.167. Пусть полупространство является касательным к X в некоторой точке а е X, т. е.
<Р, х>	1 = <р, а> при всох хеХ	(I)
п пз условия
<5, х>	1 = <7, а> ирп всех teX	(II)
следует, что д = р (поскольку 0 <= int X, то при рассмотрении гиперплоскости Ядя, опорной к X, всегда можно полагать а= 1). Рассмотрим гиперплоскость nat. Поскольку л е X, то X* с 7/^j по определению X*. При этом из (I) следует, что р <= X* Л 7/о1, т. с. гиперплоскость 7/<ц является опорной К X* в топко р. Пусть q е 432
•-Х*|)//л. Тогда справедливо (11), и, значит, q ~ р. Таким об-IjiaiiM, X* П = {/О, т. с. р — выступающая точка множеств» X*. ’ Пусть, напротив, р ф 0 — выступающая точка А'*. Тогда, иреж-до всего,' pe.V, и, значит,Xе: Ii~v При этом но определению •jjbKiушпощей точки существует такой вектор b е R"i что
<Ь, $><<&, Р> яри всех qeX*, q «5* Р- (Ш)
Заметим, что </►, р> >0, так как 0 & X*. Положим « = Ь/(Ь, р>. '.Тогда <р, д> = I, я (HI) можно переписать в индо
<7, «> < 1 при всех qt=X*, q ф р. (IV)
^Отсюда заключаем, что а <= Х“ = Аг. Таким образом, полуирост-ipfiHCTBo H~t является опорным к X в точке а. Допустим, что су-Щсстяуст еще одио полупространство JI~V опорное к X в точке а, г, с.
/'	<17, х> 1 = <7, «> 'фи псех х е X.
^Отсюда следует, что 7бХ\ Тогда g = p п силу (IV). Таким об-.разом, полупространство является касательных! к X в указаЕЕ-ной точке а.
8Л6& Вез ограничения ойщпостее можно считать, что OelntX. Тогда X* ость выпуклый компа!» (см. 8.77), Поэтому, согласно 8,103, имеем	_________
X* ^convS’(X’).
Отсюда с учетом 8.70 получаем, что
X = X" = [convS(X*)]« =± [S(X*)P.
Прп этом $(Х*) #= {0}, так как X 9й;R". Слодовательпо,
Х= fl
1Х=8(Х»), 1*5*0
^PV
.где в силу 8.167 полупространства (р е S (X*), р=/=0) яв-ляются касательпымЕ! к X.
8.109. Доказательство проводится по схеме, близкой к решению .задачи 84G7. Поэтому изложим ого лини» вкратце.
Пусть полупространств /7“0 является касательным к копу-су X в некоторой точке в <= Аг, т. е.
<Р, г) .<0 = (р, я> при всех ieX	(I)
п на условии
(7, z> 0 = <7, «> прп всех хеХ	(И)
следует, что
q и Ар при некотором А>0,	(III)
Ясно, что здесь можно считать а^О (каслтольпая гиперплоскость к конусу не можот пересекаться с ним только в пуле). При этом нз яынпспешых условий легко выводится, что
Ге//;. х*пяав = й.	(IV)
т‘ е' го1>~ выступающий луч в X*.
2В С. А, Ашманов, А, В. Тимохов	433
Пусть, иппротин, выступающий луч и А’*, т. е, при но. Котором пенулвиом п <z К” выполнено (IV). Отсюда ал кл килем, ч7и спраледлпво (1) п на условия (II) следует (HI); при атом ilG-. eA'” = ,V. Tjikiixi образом, полупространство является t;.i-ептельным к X в я.
8.170.	С. учетом теоремы 8.10 достойно доказать, что Л'* -= = [7’(А')|*. Поскольку Т(Х)с.Х, то А4 <= [7’(А’) ] •. Пусть теперь р & А’’, 11п условий задачи следует, что ini А* =И= 0 (см, 8.78) и Л'ф ф R". Тогда, согласно 8.20 и 8.1(18, найдется нолупрострвпстио Jl^t касательное к А'” и по содорлсдщсс р, т. о. <х, р> >0. Применил 8,169, получаем, что Q — иыстунающпй луч конуса А'*“ ь= ®= А’ н, следовательно, хе^.сТ(Х). По тогда норавепстнп <р, х> > 0 означает, что р [Т(А')]*. Тикнм образом, (Г(А)]* <= А’*.
8.171.	По условию имеет место импликации
<g, х> = а)
причем система слеза совместна. Тогда, согласно 4.84, существуют такио числа Ai и /.j, что
г = Aip 4- Хяг/, к = Atp 4- Aja.	(1)
Прп этом Х2ч^О, так как Ягт ч6 77рр. Пусть х е 77j.fi Л /7гт, т. о. <р, х> =	(г, х> = у. Тогда из (I) следует, что <7, х> = а, т. с.
х е Z/qs, Таким образом, II-ф П Ни <= Htr, Л 11<га< Обратное включении очевидно.
8.172.	По условию х” допускает представление
х° в= Zz1 4- (1 —А)х2, где х’, х” <= X, х1 х1, 0 < ?. < I.
Прп этом х1, х2<£ Ит,& Боз ограничении общности предположим, что <р, ж’> < £. Тогда, очевидно, <р, х2> > р. Обозначим через I прямую, проходящую через точки х1 лх" (7 = xs_xi). Покажем, что X с. I. Пусть существует точка х е Х\/ и без огра ничей пи общности <д, х> < ^. Тогда иойдетсл таксе число |х.е (0, 1), что точка у == дх 4- (1 ~ Ц)х2 удовлетворяет условию (р, р> = ji, т. е. и <= е А' П ffpfi. (рис. 1OD). Поскольку у Xй <= I. то у #= х°, по это противоречит условию задач и. Следовательно, А'сг/, п так как A' =/t{x,)). то dim А' — 1, 8.173. Пр!1 dim X ^1 ут-норигдеппо тршитльно. Поэтому будем считать, что dim Х^>
2. Примем обозначение У
г- conv Г (Д'). Ясно, что У <= сс А'. Предположим, что обратное нключопно новерпо. Тогда, применяя теорему 8.2 к множеству У и любой точке из гиперплоскость 11{.?„ для которой
(1>
(И)
Рис. 100
А'\У, подучаем, что существует
z = X Л 77f.fi 0.
у Л = 0.
434
Миоямттао Z замкнуто, выпукло и как лодмпожеетно .V по со,портит прямых. Тогда, согласно 8.105, это множество имеет выстунаю-utyjo точку г’, т. е. существует такая гиперплоскость что znz/4K = {/'}.	(Ill)
Из 8.IG5 следует также, что Е(Х} с$(Х) с У. В то зко время
•£ Z <= Тогда х* £(Х) в силу (II).
Допустим, что z° «л ri л\ Тогда, используя 7.07, получаем, что е ri X Л Я«я ri (X Л Нр(|) = ri Z.
С учетом (III) ото возможно лишь и том случае, ослп Zdll^ (см. ;8.2<>). Тогда пз (I), (III) выводим
X Л =и Z = Z Л U,,«! = (х0).
Следовательно, dimX = I и силу 8.172, по это противоречит предположению.
Итан, х° ф ri X. Введем аффинное множество М = Hltp П
Из (I), (III) имеем X Л М *=> {х’1}, и, значит, riX П М = Тогда, применяя 8.38, получаем, что существует гиперплоскость //гт, УДоо-летвирдкнцая условиям
X с= //“, М с= ПгГ	(IV)
Эта гиперплоскость яилнетсп опорной к X и точке х°. Тогда по определению Г = X Л ЯгТ есть отступающее подмножество Аг. При атом х°^Л‘(Г), так как Л'(Г) с^Е(Х) (см. 8.135) и ж”ф*Х(Х). Допустим, что //,т =//)Ц1. Возьмем любую точку те #(!’), сущест-пупнну io в силу теоремы 8.12, Тогда, с одном сто|Юнм, х <н Г с; с //,/ =я а и другой стороны, х еА’(Х) с: У. По ото противоречит (II), Таким образом, Нп Ф 11^ Тогда из 8.171 ц формул (1), (Hl),- (IV) получаем
Г Л Я;ч) = X Л Ип Q Н„р X Л lfVA Л Я,Ф = И П = №}•
Следом г ел ьпо, dim Г = I (см. 8.172). Поскольку X не содержит прямых, то Г может быть лини» лучом или отрезком. Если Г — луч, а зппчвт, и выступающий луч множества X, то Г <=. У но определению У, Если г хо (х1, х2]—отрезок, то х1, х2 е £(Г) е: сА‘(Х) <z У, и поэтому также Ге У. По это включение заведомо ни выполняется, так кик х°еГ\У, Таким образом, нроднолонпт, что Х-<£У, мы пришли к прогпиоречню. Следоиагол||НО. X <= У, т. о. X <= У.
тп
8.174.	По условию х= У, Xjz*, где ?и > 0 (1 = 1, ..., гл), тл
2}Х,= 1’ Включение (7е(х) с= £/г(р) равносильно тому, что
—* yll	г—е, Таким образом, мпожоспю У состоит из таких
U»P (аг, г), что
!1х‘ — И > г, 1 = 1.....................гл.
281
435
Пусть (у, г) У. Примем обозначения.с* == xf— у, = ||xf— (I, j г= !,,.,, wt). Используя (II), получаем
dt) и ||af — aJ|l} =3 |faf|i2 -f- rJaJ,||J — 2<«\ aJ> >•- 2г5 — 2(al, ttJ>.
Поэтому
<«f, sJ> r2 — dt где d =: у шах _-. fj
Тогда
m 12 m tn	mm
2 ь/ =22	<«'. »’>> P - rf)2 2 W,=^ -
1“>1 I i=lj»*l	1^4 2=1
Таким образом, о учотом (I) нмоем (г— e)s^r!*- d. Отсюда г=_< (eJ 4- d)/(2s) = r0, и, значит, ||х —у||г£г0— в. Следовательно, У оттичояо.
8,175.	Пусть утверждение псверпо, т. е. существует послсдови-тольность чисел а* > О (Z; = 1, 2, сходящаяся к пулю и такая, что
А'П (У-|-ot*(& —л)) &0, т. о.
= ЛА + ал(Ь —д)	(1)
при некоторых я* е А', у* е У (А- е= 1, 2. ...). Поскольку X П У = кя {«.), то либо х* 9^ У, либо аЛ = a е <?У. В любом случае согллс-ио теоремам 8.2 и 8.3 существует такой вектор р*, что Вр*|1 = 1 и
<р\ у> < <р\ х*> при всех у <= У.	(II)
Без- огрпннчеппя общности можно считать, что р* р =£ о п р* -► у <= У, так как У—компакт. Тогда нз (1) следует, что к лЛ-t-y, причем уеА' и силу замкнутости А'. Поэтому ’ у = д. Переходя теиерь л (II) к пределу, получаем
<Р, У> <Р< «> == 6 при всех у е У,
т. е. полупространство является опорным к У в л, В то же время, если в (II) подставить точку у = у\ то с учетом (I) получим, что <р\ а> <р*, 5>, л, значит, <р, а> <р, &>, Таким образом, Ъ<£ inLZZ”p. ио это противоречит условию па 6.
8Л76, Применить 8.175, учитывая, что UT (у) — строго выпуклый комиокт.
8,177.	Примем обозначения
А' = RR\n,(y), Y = U<(z), Z = Ur(y).
Имеем Х’Г|У= {5}, Ье^У. При этом полупространство, опорное к шару У п точке 1>, одинствепно и одпоиромопио является опорным к шару Z в тол ясе точка. Поскольку ttt=Zt а^= b и Z — строго выпуклое множество, то а прииадлежлт внутренности указанного полупространства. Тогда, согласно 8.175, при всех достаточно малых a > 0 имеем
А'П (У+ «(« — &)) = 0.
Отсюда У-|- а(л — b) a: Z. и, значит. Ус Z -J- a.(h — л).
8.178.	Предположим, что множество А’ пепынукло, т. о. существуют такие точки ®‘,	А’, х.<= [«i, х3], что х&Х. Поскольку А
436
зпмкпуто, то X П ГЛ(я) *== 0 при некотором е> 0. Обозначим через X множество всех пар (=, р), удовлетворяющих условиям
UL(x) с 4/р(2), X П = 0-	(О
Заметим, что Z 4= 0, так кик (х, е) eZ. Из (I) слодуот, что х‘ & Uf,{z^ (< =з 1, 2). Тогда в силу 8.174 множество Z ограничено.
Пусть r-ss sup р. Рассмотрим такие пары (г\ рл) 6 Z (к (*,р)е2
а₽ 1, 2, .,.), что р*•>/' Беа ограничоппя общности можно считать, что ;Л -ь у. Ila выбора г и замкнутости X следует, что
U'(x)cUr(tj), XftlW) 4=0.
Несть иеХ’Пи,(у), Для любой точки *еХ в силу (I) имеем ||л — з''11 > рл (* = 1, 2, ...), и, значит, 1|х — у|| г 5s ll« ~ ylJ. Следовательно, точна а есть проекция точки у па X, причем
||и — рй ж г. По по условию Таким образом, ХПУг(у) = = {«}, причем а лежит па границе шора ГЛ (у). Возможны дал случая.
1)	Границы шаров Ut(x) п 1Л(р) имеют общую точку b (рнс. 101). Заметим, что и 41 6, так как а<=Х, Г'<вГЛ(*) н ХП П ГЛ (*} = 0. Тогда, согласно 8.176 н 8.177, существует такое а > 0, что для точки - = у т- ар — я) справедливы соотношения
Ut(x}cUr{:}t
(II)
задачи ата проекции единственна.
X П Ur(t) = 0.
2)	Шир ГЛ(т) лежит во ппутропностп шара ГЛ (у). Тогда мы приходим к (11), применяя ужо только 8.176 при произвольной точегс Ь i= Uг{>/), к •/« а.
Из (II) следует, что (:, г) е7, и, более того, найдется число Р " Л^длп которого (з, р) <= Z. По ото противоречит выбору г. Таким обризпм, X выпукло.
8.1711.	Проекция любой точки нз К2 на мпожество X =э •= {т е R'-'|x(jr7 л= 1, х, > 0} отпоентельяо нормы IM = = max{|xi|, |х2|) единственна, по X певшнукло (рис. 102).
8.180.	Пусть хе Rn и Ус = X П 4* 0, Яспо, что проекции точки х на мпонюства X и Уе совпвдвют. Следопательпо, если множество Уе выпукло, то проекция х на X едиистпонна (см. 8.1). Тогда X выпукло и силу 8.178.
8.181.	Вудом считан., что точки я, Г» и с не лежат па одной прямой, так как иначе утверждение тривиально. Введем множество
Г={».|*е[МЪ 1«> сХ).
Это множество непусто и замкнуто, так как Ъ е У и X замкнуто. С.телонателЕ.ио, в Y существует точка у, ближайшая к с. Если у <=* •= е, то утверждение'доказано. Предположим, что у с (рнс. 103).
437
Рассмотрим треугольник Т =и conv{«, у, с). В силу выбора д дли любого х <= (у, cj множество [о, z] П (J'VY) непусто. Тогда мно-
жество 2 = [а, у] П (TVY) также непусто, Кроме того, Z замкнуто, Поэтому a Z существует тонка блпжнпшая it у. По условию существует такая' окрестность U точки	у] g X, что
Рис. 103
Рпс. 102
-мпожестио X f|.t7 иьшущчо. При этом можно считать, что сама окрестность U тикжо iiiiiiiyiuui (и противном случае достаточно неревтп it inapy 1/к(=) G <7), Рассмотрим дна случаи,
1)	;= у (рпс. 104). Пусть [а, у] П U = Г«, Й. к, У1 Г U = = [у, у|, Отметим, что «Ер, у] е X и ре^, с | <= X. Таким оПрппом, точки у, и, р. лежат f.i выпуклом мпожестпо (X f| (/) П Поэтому натянутый иа них треугольник также лежит и этом множестве, а значит, н и множество X П 'Л По тогда, очевидно, точка с = у ио может быть продельной для множества Г\Х.
Рис, 104
2)	г 5й у (рис. 105). Пусть [а, у] П U « [н, и), причем г/е <5	{/] Тогда vq=Z и силу выбора Иными словами, существу-
ет такай окрестность И точки у, что РрГсХ. Ясно, что пайдо'г-си точка 1еУпК лежащая внутри треугольника Г, При этом х е U П И fl с: (X Г) V) П Л Тогда, как и выше, заключаем, чти треугольник, натянутый па точки х, и, у, лежит в X f| Тг Отсюда понятие, что : Z.
Таким образом, в обоих случаях мы пришли к противоречию. Слодонательпо, у «= с, т. о. [«> с] er X.
438
8.182.	Для любой точки аеХ рпсемотрпм множество
S = {z| (а, .т] g Л'}.
Это множество непусто я замкнуто п Л', так как « е$ и X аамкиу-то n IV1, Покажем, что 5 открьпо в Аг. Пусть 6 е5, т. о. |«. i] с .V. jlo условию существует такая окрестность U точки (>, что множество A' f| U выпукло. Тогда для любой точки ceA'fl U следует, что [Л, rj G.V Л l> cz А", а поэтому рт, с] сА' в силу 8.181, Таким пбрн-»пм, c<^S. Мы показали, что A (\UczS. Это и’означает. что 5 открыто ci X. Ihatf, непустое множество 5 с А' одновременно замкнуто н открыто и X. По определению спинного множества А' такое возможно лишь к том случае, если 5 = X. Следовательно, X выпукло.
8.184.	Сопоставим каждой точке х <=Х множества
<S(x) = {fl | [л, я] G X},	7(х.) в» conv 5 (х).
Поскольку Л' — компакт, то 8(х) также является компактом; поэтому F(x) —выпуклый компакт в силу теоремы 7.12. По условию задачи любые » + I из множеств Д'(х) (^e.V) пмегот общую точку. Тогда множества К(х) (г <= X) тем более обладают этим свойством. Следовптельпо, в силу 7.80 все множества V(x) (х е А')
Рпс. 106 ‘
имеют общую точку. Пусть а с= f] V (х). Покажем, что а х<^Л
е f| £ (х), т. е. А' зооздпо относительно а (отметим, что сразу по хеХ
очевидно даже включение а е А’). Предположим, что а 0 Л (х), «G-V
т. о. существуют такие точки ,т (= А’ л ц е [а, х], что у X. Поскольку X замкнуто, то А'Л Пг(д) =0 при некотором г>0. Примем обиапптенни :(?.) я= у -(• А(х — у) и
Т = snp(A. 0 | X* Л ПгСф/)) = 0 прп всех А'с= [0, А]}.
Ясно, что А < 1 < «о. Положим : = :(?,), Тогда, очоапдпо, X f| П8УР(:)^0 и
X fl ПГ(:(А)) == 0 прп всех A s [0, А).	(I)
Пусть Пгр — гиперплоскость, опорная к шару Уг(г) в некоторой
430
точно (О е= X п ^т(з), т. о.	Ur (z) с: 7/"р (рис. IM). До-
пустим, что у;ко доказаны следующие утверждении:
1) а е int Hpfri
2) Л’(ю)сл+.
Отсюда следует, что V (ip) а 1Г^ п, значит, в V(w), Но это противоречит выбору а.
Итак, остаотсд доказать I) п 2). Гиперплоскость 11^ определяется параметрами р ю — s, jj = <р, ш) (см. 8,22), Следовательно, утверждение 1) равносильно тому, что <ю —г, л — ш><0. Прод-пояожнм, что это неравенство иоверно. Тогда
0^ <ю — г, а—ш> «= <к>— г, (а — з) (з —ty)>< <w — z, a — s>. Ио a — з = p(y — x) при ^некотором ц > 0. Поэтому <«' — г, z--p><0. Заметим, что з(Л —в) = з — с(х — у). Тогда при достаточно малом е> 0 имеем
Qw —г(Х — с)||21= ||(w —s) 4-E(z — y)|F »
= ||w “ з|[2 + 2e<it> — s, х — у> + е2|[х — p|J* «я
s= г2-|-£(2<и1 —3, z — у>4-е|]х— Jill’) <А (II) Таким образом,
ХП^(Г-8))^0.	(Ш)
Ио это противоречит (I), Утверзкденпо 1) доказано.
Предположим, что утверждение 2) пеаорпо, т, е. существует точка b е ini //~р, при которой (fc, ri>] с А'. Используя выкладки, аналогичные (II), получаем, что ||w-ra(f> —ю) — =||а < г2 прп достаточно малом а>0. Это неравенство сохранится, если залепить с па :(А — е) при достаточно малой е > 0. Отсюда вновь приходим к (III).
СПИСОК ЛИТЕРАТУРЫ
i.	Акулич И. Л. Математическое п^юграммировшше и примерах и задачах,— М.: Высш. hik„ 1986.
2,	Л л о к с е о и В. М., Голое» О. М., Тихомиров В. М, Сборник задач но оптимизации: Теория. Примеры. Задачи.—Мл Паука,- 1984.
3.	Алексее в В. М., Тихомиров В. М., Ф ом и ц С. В, Оптимальное управление.— Мл Наука, 1979.
4.	Астафьев И. II. Линейные неравенства и выпуклость.—Мл Лаука, 1982.
5.	А ш манов С. А. Липепное программирование.—- M.t Наука, 1981,
0. A in маной С. А, Введение в математическую зкономнку.— M.t Наука, 1984,
7.	Базара М,, Шетти К. Нелкпейноо программирование. Теория и алгоритмы.— Мл Мир, 1932.
8.	Белоусов Е. Г. Введение в выпуклый анализ и целочисленное программирование.— М.: Изд-во МГУ, 1977,
9.	Бурбаки И. Топологические векторные пространства.— Мл ИЛ, 1959.
10.	- Вагнер Г, Основы исследования операций. Т. 1, 2.—Мл Мир, 1972-1973.
11.	Васильев Ф. П. Чпслепвые методы решения экстремальных вадвч,— Мл Паука, 1988;
12.	Гельфанд И. М. Лекции ио линейной алгебре —Мл Наука, I960.
13,	Гольштейн Е. Г., Юдин Д. Б, Новые поправления в лннеГшом программировании.—Мл Con. радио, 1960.
14.	Данце р Л., ГрюнбаумБ,, К л к В; Теорема Хеллп — Мл Мир, 1968.
15.	Данциг Дж. Линейное программирование, его обобщения п применения.— М,: Прогресс, 1983.
16.	Демидович Б. П. Соорппк задач и упражнений по математическому анализу,— Мл Наука, 1977.
17.	Демьянов В, Ф., Васильев Л. В. Недиффереицнруомаи оптимизации.— Мл Наука, 1981.
18.	Е м е л и ч ев В, А., Копа л о в М. М., Кравцов М. К, Многогранники, графы, оптимизации (комбинаторная теория многогранников).— Мл Наука, 1981.
19,	Еремин И. И., Астафьев Н. И. Введение в теорию лилейного я выпуклого программирования.— Мл Наука, 1976.
20.	Заславский Ю. Л. Сборник задач ио липенному программированию.— Мл Наука, 1969.
21.	Ильин В. А., Позпяк Э, Г. Линейная алгебра,—Мл Наука, 1978.
441
22,	Ильи» В. Л„ Свдовпичпй В. А., Се идоп Ел. X, Математический иивлпэ.— М.: Ilayrai, 1979.
23.	Иоффе Л. -Д„ Тихомиров В, М. Теории экстремальных вндач,— М.: Наука, 1374,
24.	Калихмап И. Л. Сборник задач но математическому программированию.— М.: Высш, пи;,, 1975.
25.	Карлин С. Мотематпческие методы п теории игр, программировании к экономике.— М.: Мир, 196’4.
2G.	К а р м в и о в В. Г. Математическое программирование.— М.1 Паука, 1986,
27,	Кузнецов 10. П„ Ку в у бон В, И.( Волошин ко Л. В. Математическое программирование.— М.: Высш, шк., 1989.
28; Л о их т ве й с К. Выпуклые множество.— М.: Паука, 1935.
39.	М а к а р о в В. Л,, Р у б и и о а Л. М. Математнчоскан теория экономической динамики п равновесия.— Мл Паука, 1973.
30.	Моисеев Н. II., Папп пион ICE П., Стол я роли Е, И, Методы оптимизации.— М.: Наука, 1078.
31.	Морозец В, В2 Сухарев Л. Г., Федорой В. В. Исслсь допапно операций в задачах и упражнениях.— М.; Высш, шк., 1980.
32.	Пн к ай до X. Выпуклые структуры и математическая экономика.—М.: Мир, 1972.
33.	Обе и 7K.-II., Эйланд И. Прикладной пелппонный анализ.— М.: Мир, 1988.
34.	Оуэн Г. Теория игр.— М.; Мир, 1971.
3;>, П а п а д и м и т р и у X., Ста иглиц К. Комбинаторная оптимизация. Алгоритмы н сложность.— М.: Мир, 1985.
30.	Пелиц Б. Т. Введение и оптимизацию.— М.: Пауки. 1983,
37.	Пшеничный Б. II. Выпуклый анализ н экстремальные задачи.— М.: Паука. 1989.
38.	Рокафоялар Р. Выпуклый опилив,— М.: Мир, 1973,
39.	Сухарев Л. Г., Тимохов Л. В.. Федореи В, В. Курс методов оитпмпяацни.— М.: Паука, 1980.
40.	Тихомиров В. М. Рассказы о максимумах п минимумах.— М.: Наука, 1980.
41,	Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления.'Г. I.— М,: Пауки. 11109.
42.	Хедли Дж. Пелинспноо п динамическое программирование.— М.: Мир, 1907.
43.	,4 ер н н кон С. П. Линейные неравенства.— М.: Паука, 1968.
44.	Ш п-к и и Е. В. Лннойныо пространстнн и отображении.— М.: Изд-во МГУ. 1987.
45.	Эльстер К,-Х., Ройпгардт Р„ Шойбло М., Донат Г. Введение и нелинейное программирование.— М.: Паука, 1985.
40. Юдин Д, Б., Гольштейн В, Г. Линейное программирование.— М,: Паука, 1909,
47. Лпионпыо неравенства и смежные вонросы/Под род. Г. У, Куин и Л. У. Танкера,— М.: ПЛ, 1959.
СПИСОК ОБОЗНАЧЕНИИ
R — mhojkcctimj действительных чисел, числопал прямая.
R" — я-мсрпой вещественное евклидово прострянстпо, х = (xi, ..., тп), х° = (дг®.	— стандартные обозначения
элементов (точек, векторов} из R” при произвольном н; дли обо-;ин»чсч11111 координат данного племонтя используется тот зко символ с индексом tunuiy. дли обозначения ралличпых влементов чаще всего пркмоиистея верхний индекс.
(х, у}. (J, У, -) —иногда используемые оиоапнчеппя элементов ля IV м П’ соответственно.
т|
<-г, иУ =	скалярное произведение элементов гну
j=i пл К",	_______
=тУ(х, хУ — норм» элемента х е Rn.
1/е(х*) — шар радиуса е>0 с центром в точке
Дли повторов х н ц пз R" шипом;
х 3s у, если Xj прп нсех / = л;
х > [I, если Xf > itj нрн псех	«;
х > у, если х&= у, но х- у.
Вектор х называется лгог/шчит-ельныл, лоаежигсльным, полу-положнтсльны.ч, если x3sl\ х>0 и х>0 соответственно.
R” ~ {ж elU*| »!><)) — неотрицательный ортапт в R”.
Лг— матрица, трапепоннроваппал к матрице Л.
Л ~1 — матрица, обратная к квадратной матрице Л.
del Л, |Я | — определитель квадратной матрицы Л.
rang Л — рпнг матрицы Л.
/1 —одинпчн1и1 квадрат пин матрица (на дипгопали стоят единицы', остальные элементы — пули).
Если даны матрица Л = (о^) размера л»Х« н векторы х s R”, ye Rm, то:
п
Ля — вектор u:t Rw с координатами (Лт),- — У,
r’l я
уЛ — вектор из R” с координатами (уЛ);~ УрЧр т. о. у Л = Лту.
{х*} е А' — иослсдоватолз.пость точек аЛ (It = 1, 2, ..принадлежащих множеству А', символы верхнего н ппзкиего пределов числовой последовательности или функции.
Нт / (х), lim ./ (,т) — пряно- и левосторонние пределы фу«к-X—14 — цпи / числового аргумента и точке «.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Анализ данных 30
Аффинно зависимые точки 189
Базис вершины 140	и>-
Базиспви переменная 140
Ведущий элемент 15.1
Вектор долуноложитолы1ыГ| 78
Воргпниа полиэдра 52
------ невырожденная 52
Вавошепвоо среднее 48
Госспап функции 23
Гиперплоскость 51
— касотельняя 232
—	опорная 198
---собственной 4П8
—	разделяющая 198
Градиент 22
Граница множества 175
---относительная 175
Грань множества 229
—	полиэдра 69
--минимальная 73
---чюиырождеппзя 70
---соистпсппая 69
Двойственная воромонпвя 90
Двойственности соотношение 97
Диффеоморфизм 32
Доминируемая переменная 126
Задача Архимеда 40
—	безусловной оптимизации 22
—	Горопа 45
— дипамичоская л л ли пропан в л йронэебдетил 140
—	дробпо-липейпого программирования 137
—	Евклида 45
—	коиочиоморнан 9
—	кусочно-линейного програм-
мирования 136
Задача линейного программирования (ЛП) 8(1
-----блочная 140
•------ диопг.тиоипал 95
----—Допустимая 120
-----каноническая 87
------общая 87
------ основная 87
— ----прямая 95 '
------разрешимая 120
------стандартная 87
------устойчивая 128
•-------по значению и по ре-
шению 129, 132
—  -----по направлению 133
— па условный экстремум клас-сн’гескаы 35
— о рационе 89
— оптимального управления в дискретном времени 142
—	онтнмнзацнн 9
— планирования производства 88
—	регулярная 37
—	Спеллнуса 45
— транспортная 90
—	экстремальная 10
Зацвклтшиио симилонс-мотода 149
Значение задачи 10
Конус 171
—	возможных направлений 222
—	выпуклый 171
—	заостренный 220
—	крайних направляющих 231
—	многогранный 173
—	опорный 222
—	рецессивный 176
Коэффициенты замещения 147
Крайний носитель множества 229
Критерий Сильвестра 11
444
JIitiioihiAji комбинация аффнп-кал 171
-—• выпуклая 171
2 -—множеств 171
— —неотрицательная 171
- ЛпнеГшоо многообразие 61
* Линейное программирован не 51
Линия уровня функции 12
, Луч 17С)
— крайний 231
\ Маргинальное видчевне авдачп
Ji ЛП 130
Матрица входных данных 31
?? — кубическим симметрическая "i_	28
— нмлояштелшю определенная
L 11
 — Якоби 24
; Метод исключении цоремеппых 35
— искусственного базиса 152
— наименьших квадратов 30
— полного перебора вершин 94
Минор матрицы главный И
—-----угловой 12
Многогранник даухсможност-иый 230 выпуклый 173
Множеств» отделимые 199, 216
— собственно отделимые 199, 216
— сильно отделимые 199, 216
Множество аффинное 61, 169
— второе сопряженное 202
— выпуклое 170
. — — локально 235
— допустимое 9
— звездное 235
— Лебега 18
— многогранное 173
— относительно открытое 174
— сопряженное 201
— /Авыпуклое 188
Мпо:кптол11 Лагранжа 37
Паилучшсс приближение в норме It 30
----равномерное (чебышея-скоо) 30
Нерппепство Адамара 50
— Гельдера 49
— Коши — Буилковского 49
— между tianeiiiOHtiiiiMH средними 49
Неравенство между средним арифметическим и средним геометрическим 47
-------------квадратичным 48
— Минковского 49
Нормаль к глнерилоскости 52
—	к поверхности 46
Оболочка аффинная 64, 172
—	выпуклая 172
-	— ««минутая 188
Ограничение активное 52
—	двойственное 77
— жесткое (нежесткое) 63
— закрепленное (свободное) 122
Ограничения изанмодпойстиеи-пые 125
Операция взятия оболочки 187
Относительная внутренность множества 174
— граница множества 267
Отображение дифференцируемое 24
Оценки замощения 147
Поверхность гладкая 46
Подмножество выступающее 231
— крайнее 227
Подпространство, параллельной аффинному множеству 61, 170
— рецессивное 195
Полиэдр 52
— ограниченный 203
— однородным 203
Полная топь множества 183
Полупространство 52
— касательное 232
— опорное 198
Полутень множества 183
Поточечный супремум 17
Правила симплекс-метода 147, 148
Правило Бланда 149
— цепное 25
Принцип граничных решении Черникова 73
-----— для задач ЛП 122
— Лагранжа 37
— максимума дискретный 143
Проекция множества 182
—	точки па множество 12
Размерность аффинного множества 62
—	выпуклого множества 175
—	полиэдра 65
445
Разность множеств 171
Ребро полиэдра 70
Решение задачи глобальное О
•-----строгое 10
----ловвлыюо 10
— — ЛИ невырожденное 12G
Связная компонента множества ИЮ
'-Снмплскс-метод 145
Снмилокс-тпблпцн 150
Симплекс Ш'МОряып 189
— стандартный 09
Система неравенств пепрпподн* мо носовмоятппя 70
----г п уравнений устойчивая 84
— ---------по праной чисти
ограпичалин 85
Следствие системы неравенств э(5
Спотпошение двойстиошгостн 97
Соседние вершины полиэдра 71
Состояние управляемой системы 142
Среднее порядка р 48
Сумм и множеств 171
------ инверсная 183
----частичная 183
Теорема Александрова — Фана 75
— Бурбпки 235
— Войерш трасса 10, 17
— Вилли 79
— Вороного — Кярворп 78
— Гордина 71)
— Дпонстпспнрстн 97
— Дубовнцкяг’о — Милютина 217
— Каритеодорн 174, 189
- Кап 231
— Красносельского 235
— Кукушкина 22
— Люсторпика 34
— MiiuitLincKoro о продетаh.to-hhii выну и л riiTi компакта 2U3
— — об отделпмиетп 197
— Минковского — Вейлц 29-3
— (лемма) Минковского — Фор-наша 55
— — о следствиях 5G
— Моцкпии о выпуклых множествах 235
----о неравенствах 78
— о домпинрованни 120
Теорема о достаточном уеаопнп
минимума
23. 37
второго порядки
---допояпякнце и пожесткост и для системы линейных неравенств 77
---------вадачн ЛП 97
---аппренлоллых н свободных ограничениях 125
— — кпеателвиых полупрострлп-стах 233
----линейном мппнмаксо 137
— — маргинальных шнпнлшях задачи ЛП 130, 133
— — матричных играх основная 137
--- минимальной грипп полиэдра 73
---необходимом условии минимума второго порядка 23, 37
-----------первого порядка 23, 38
---— и достаточном условиях окстромума в задаче ЛП 93
---нсяиной функции 24
---регулприяацнн вадач ЛП КЮ
— — соседних вершинах поли □дрв 71 _
---строгой дополняющей ио-1КОСТКОСТИ для системы линейных неравенств 80
-------------ввдачп ЛП 125
— оо ппварлаптпостп решения впдачп ЛП 134
---очистке систем лилейных неравенств 75
— — — эпдичп ЛП 122
--устойчивости системы ли-
нейных неравенств 84
—-----ладами ЛП 128, 129, 132,
133, 134, 130
— Полтероппча — Спивака 183
— Рпдгша 199
— Рокафеллпрл 213
—	Страпмишчп 232
—	С.тршпевпча — Клп 233
—	Танкера 79, 80
—	Фенхеля 200
—	Фипслерл 43
—	Хана —Банаха 215
--для полиэдров 215
—	Хелли 190
—	Хиффмзпп83
•--для задачи ЛП 127
446
Теорема Штпмкс 79
' -7 Штпмке — Финн 78
Текрнп JUKHLcriieiiiiijCTH 94
Точка шлетуняющая 232
1 — граничная 175 «^допустимой 9
. — крпйняя 202
1 —.минимума!)
—	опориди 54
' ‘ —оти>'|С.ител11Иг1 ипутрошшн 174
—	тропнчпвн 17.5
—	стационарная 23, 36
’ ’ — экстремума 10
i;
i * Упраплонпо системой 142
•' Условие ортогональности 38
•	регул яриисти 37
I I’’ У слепня донолпяющей поягест-, ’,t	кисти для систем	.’шлейных
\	псраврнстп 77
। ’* -— -----задач ЛИ 07
Условия строгой дополняющей пожветкпети для гнетем ли-пейнюх неравенств 86
---------— задач ЛП 125
Функции бесконечно растущая (убыпиницаи) 11
— возрастающая (ноубывоиз-щал) 16
— Гамильтона 143
— квадратичная 11
— Кобба — Лугласа 31
— Лйгрнщкп 35
— — регулярная 37
— нолупенрерыпцал спину (сверху) 16
—	nphimoACTEieiiijaii 31
—	целевая 9
Хаусдорфово расстояние 86
Элементарные операции и евм-цяекс-методе 151
I ] ।
Пиучиоо пэдаппо
АШМАНОВ Станислас Александрович
ТИМОХОВ Александр Васильевич
ТЕОРИЯ ОПТИМИЗАЦИИ В ЗАДАЧАХ II УПРАЖНЕНИЯХ
Лим'дуниццй род.-игцнсй К, Ю. Ходен
Редактор II. if, Воронина
Художественный редпютр Т. II, Кояъчеико Техкп чсский редактор Е. U, Морозова Корректор М, Л. Слнгркоа
. 1ГБ Лт 32877
Сдано и iiiiflop 2O.P3.nt), Подиислно к печати d5.02.DI. формат $4x108732. Бумага тиногрдфеи-ал Л* 2. Гарнитура обыкноосшнш. Печать высопан, Уел. лоч. л. 23.52. Уел. ир.-отт. 23,52. Уч.-нпд, л. 2<5,4?. Тирши II 000 о)гл. Закин ХЗ 12U. Дона 2 р. 10 к.
Пздител1.ск-о-»(101ипрдстве|[пое н i<Hiironi]im)>i; объединение vllliyttil» r.'iniiitiiii редакция 4>ил|||1О*мате^1цткчее):ой литердтури 117071 Мрскпл Б-71, ЛсиннскиЛ нрисиеят, 15
Четпертпп типография пэдптельетап «Пауки» 030077 г. lioBocnoiipci! 77, Ст.ишслпиского. 35