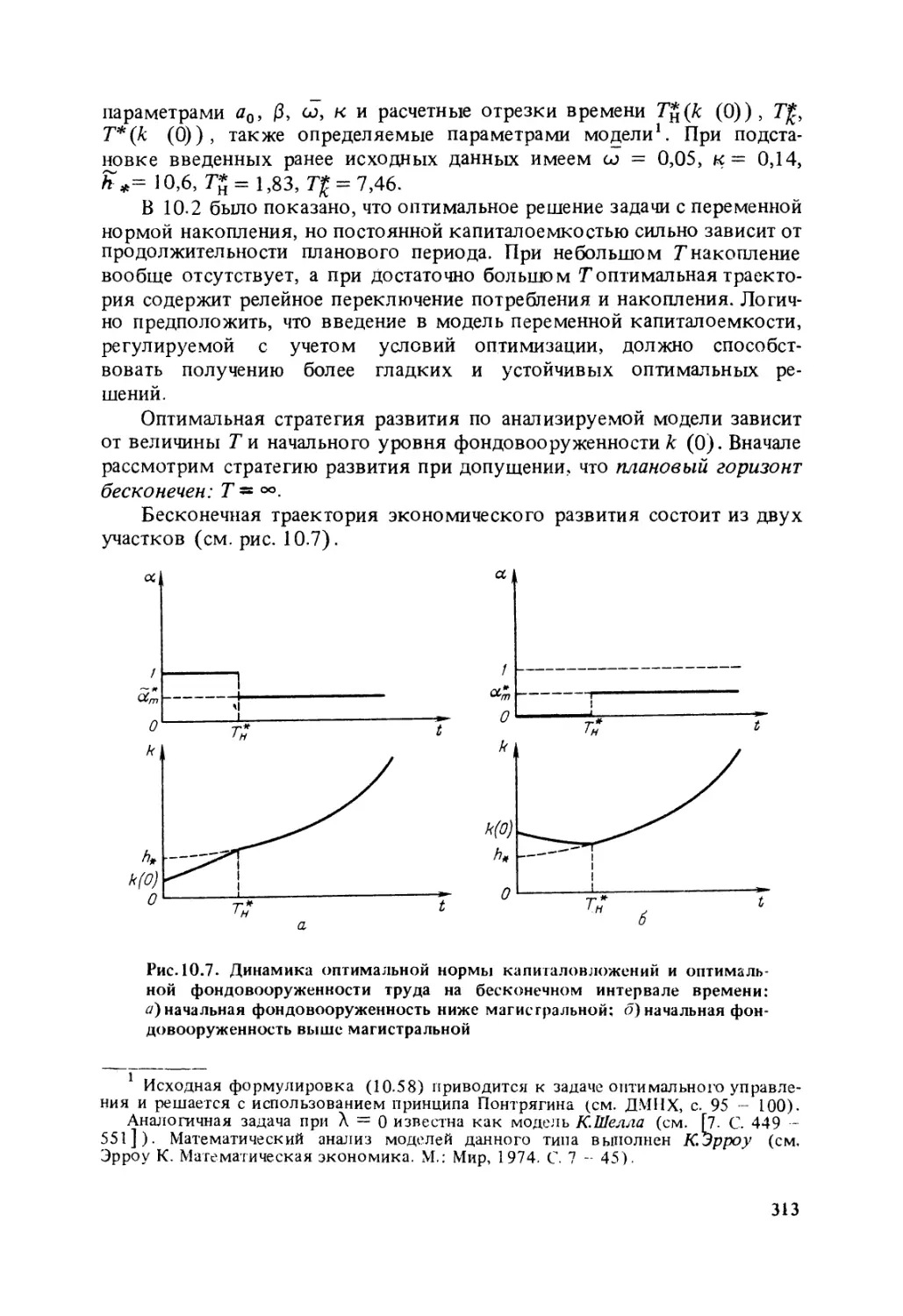
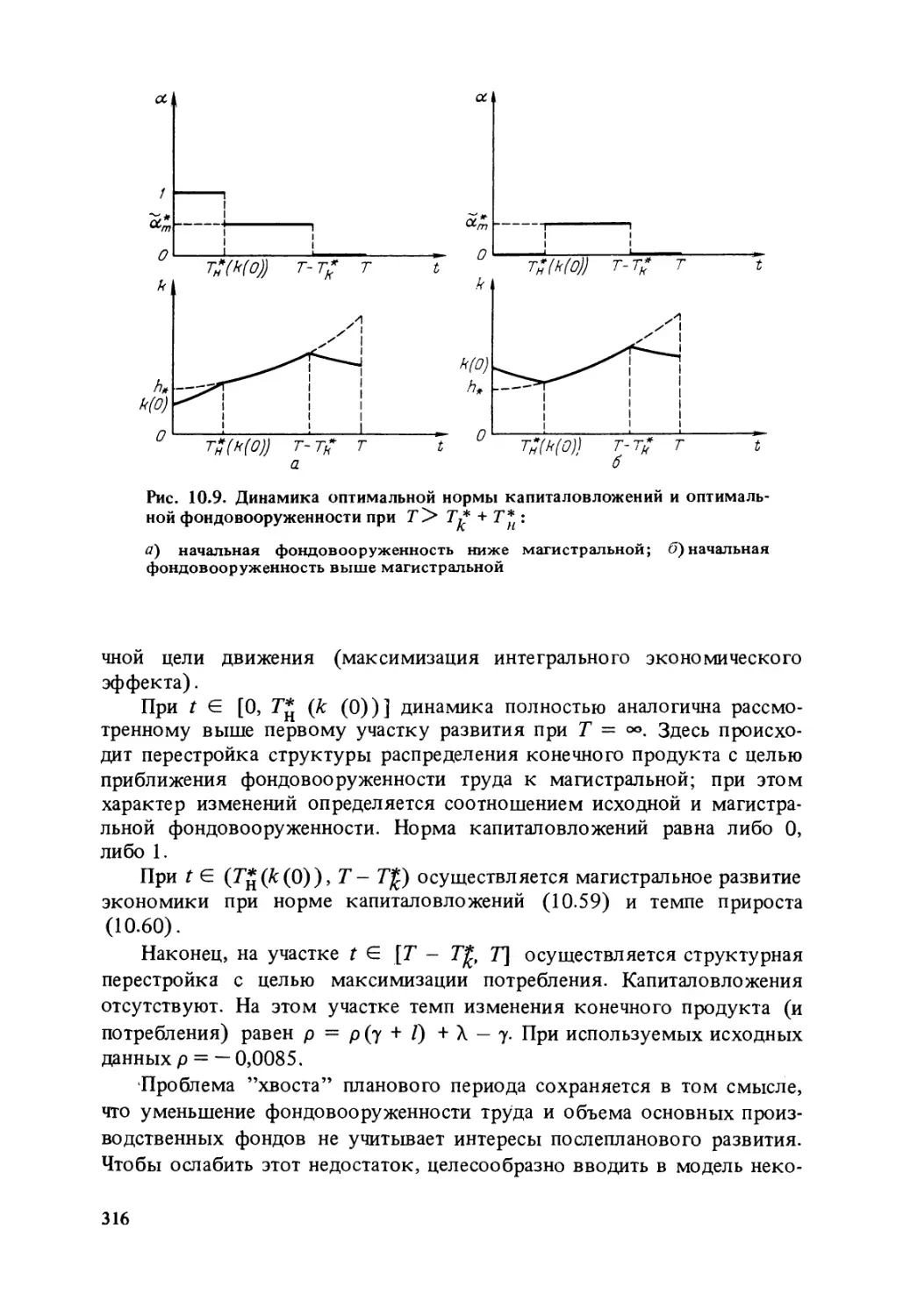
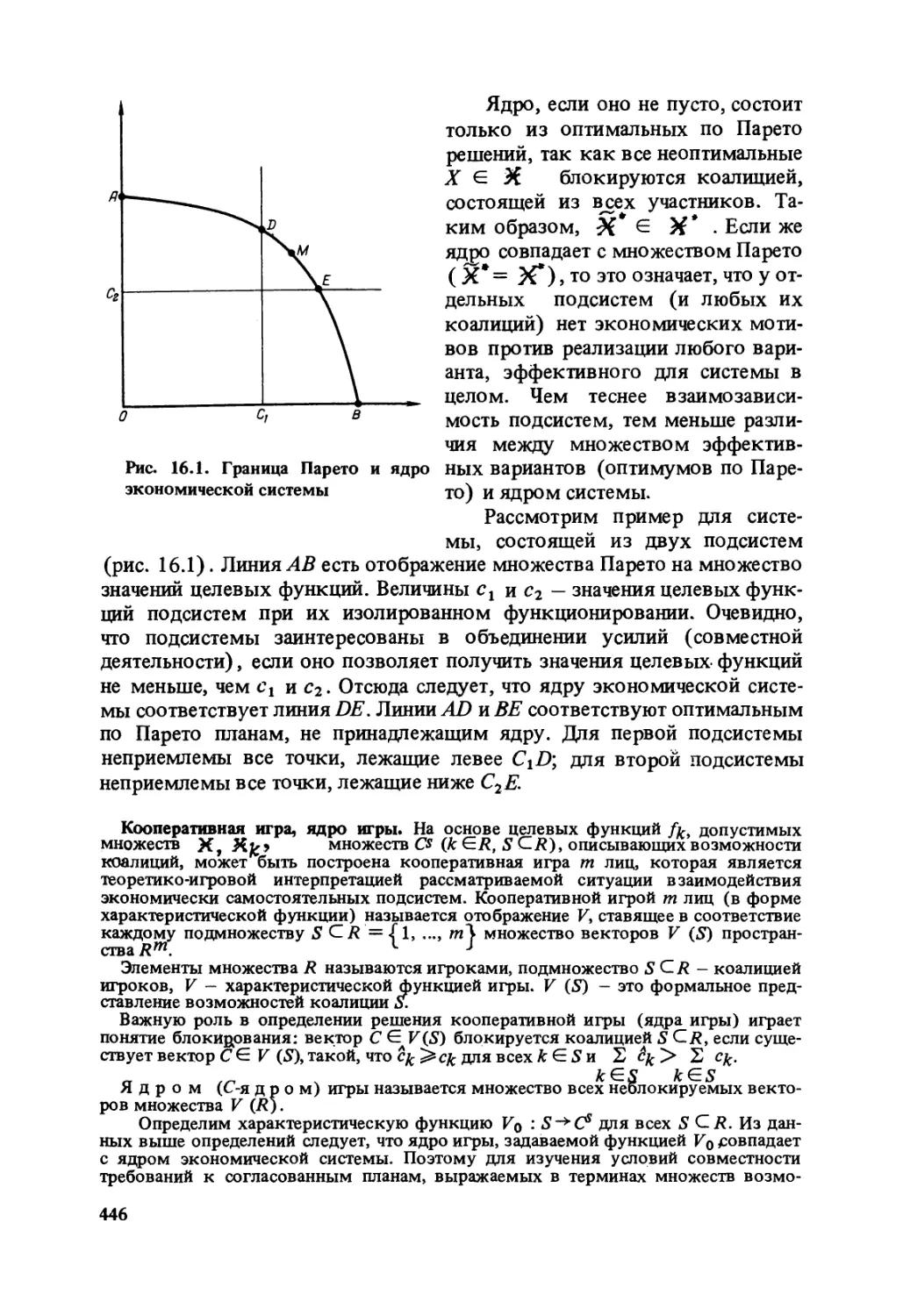
Author: Гранберг А.Г.
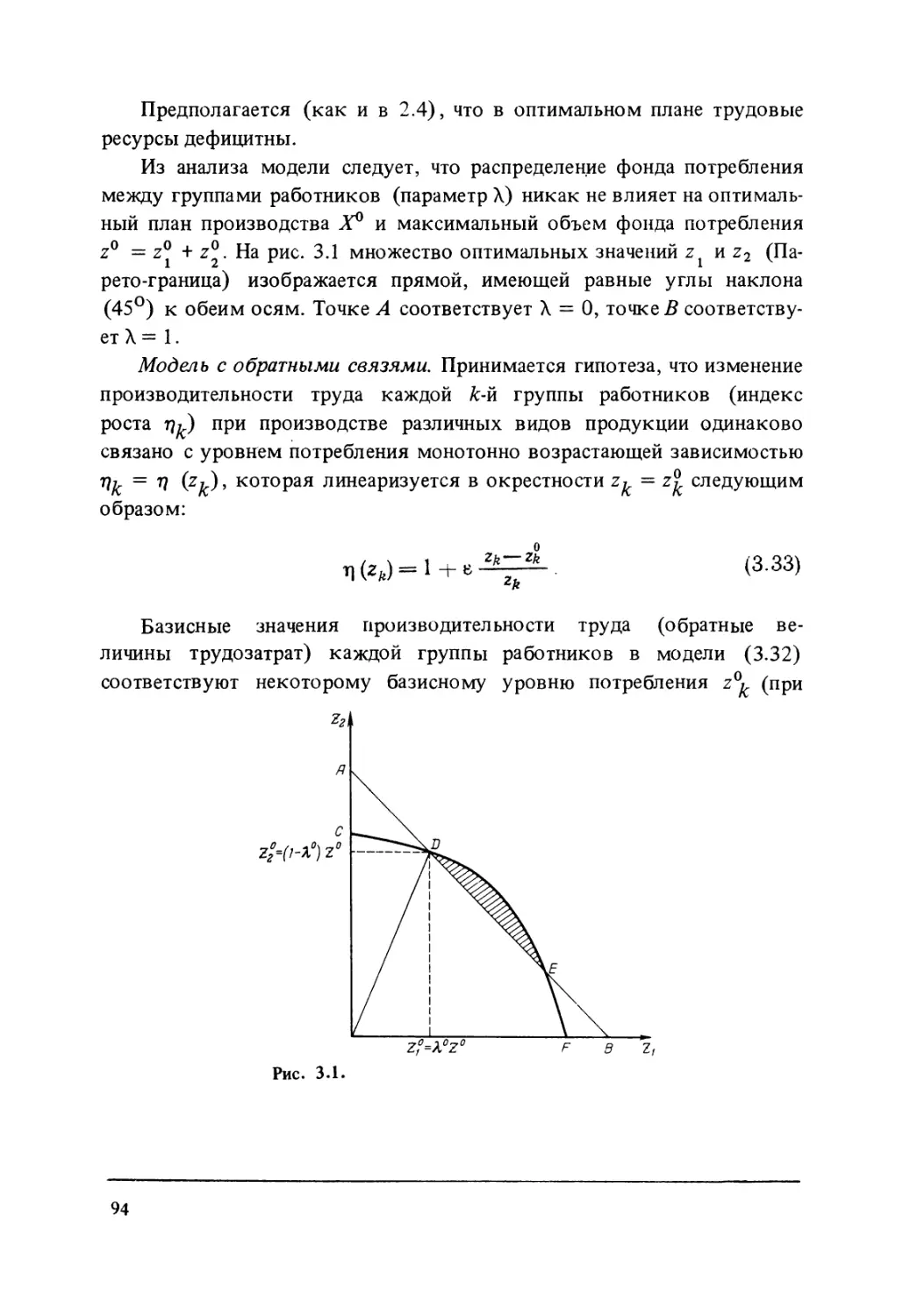
Tags: управление экономикой экономика политическая экономика математическое моделирование
ISBN: 5-282-00659- 6
Year: 1988
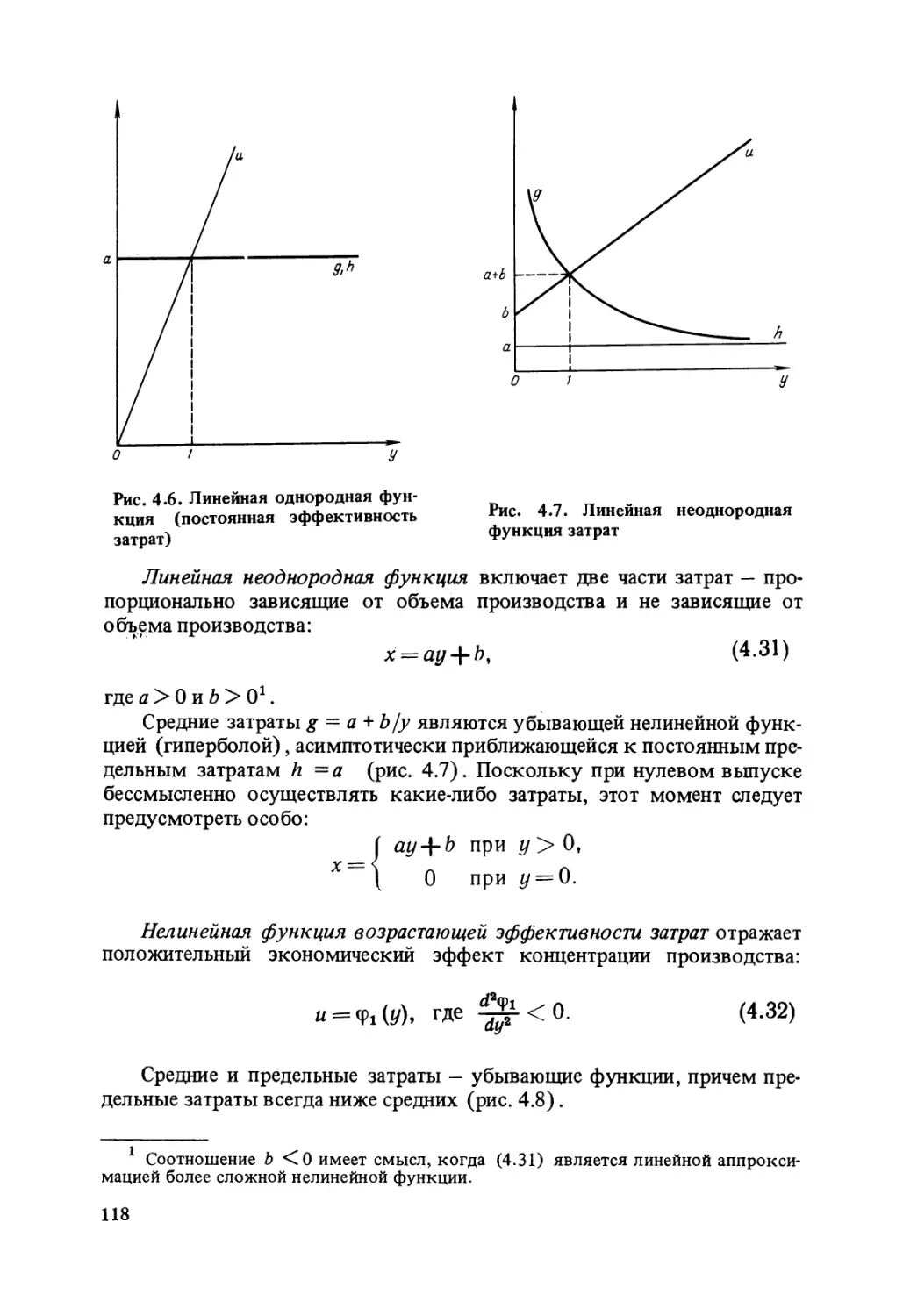
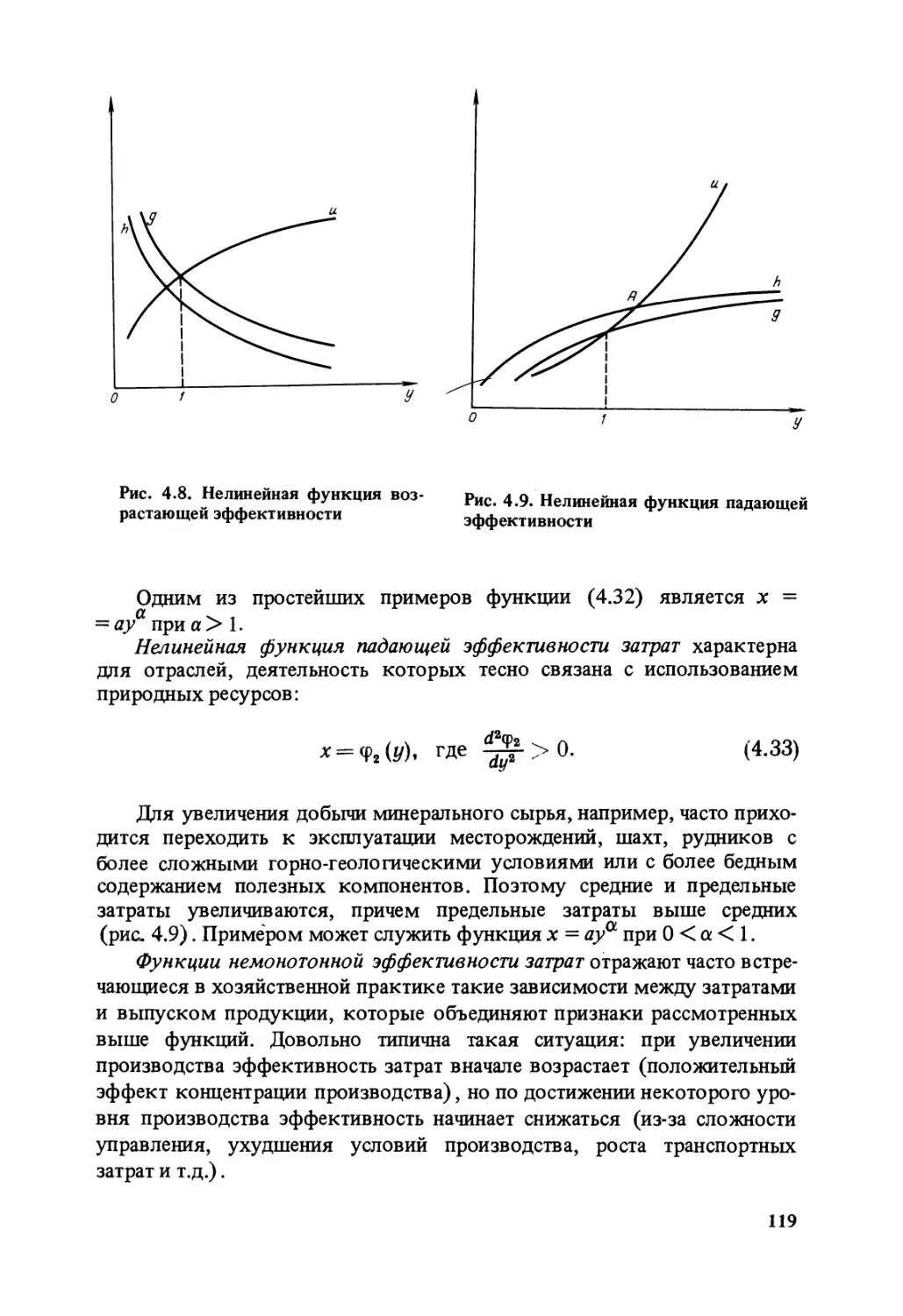
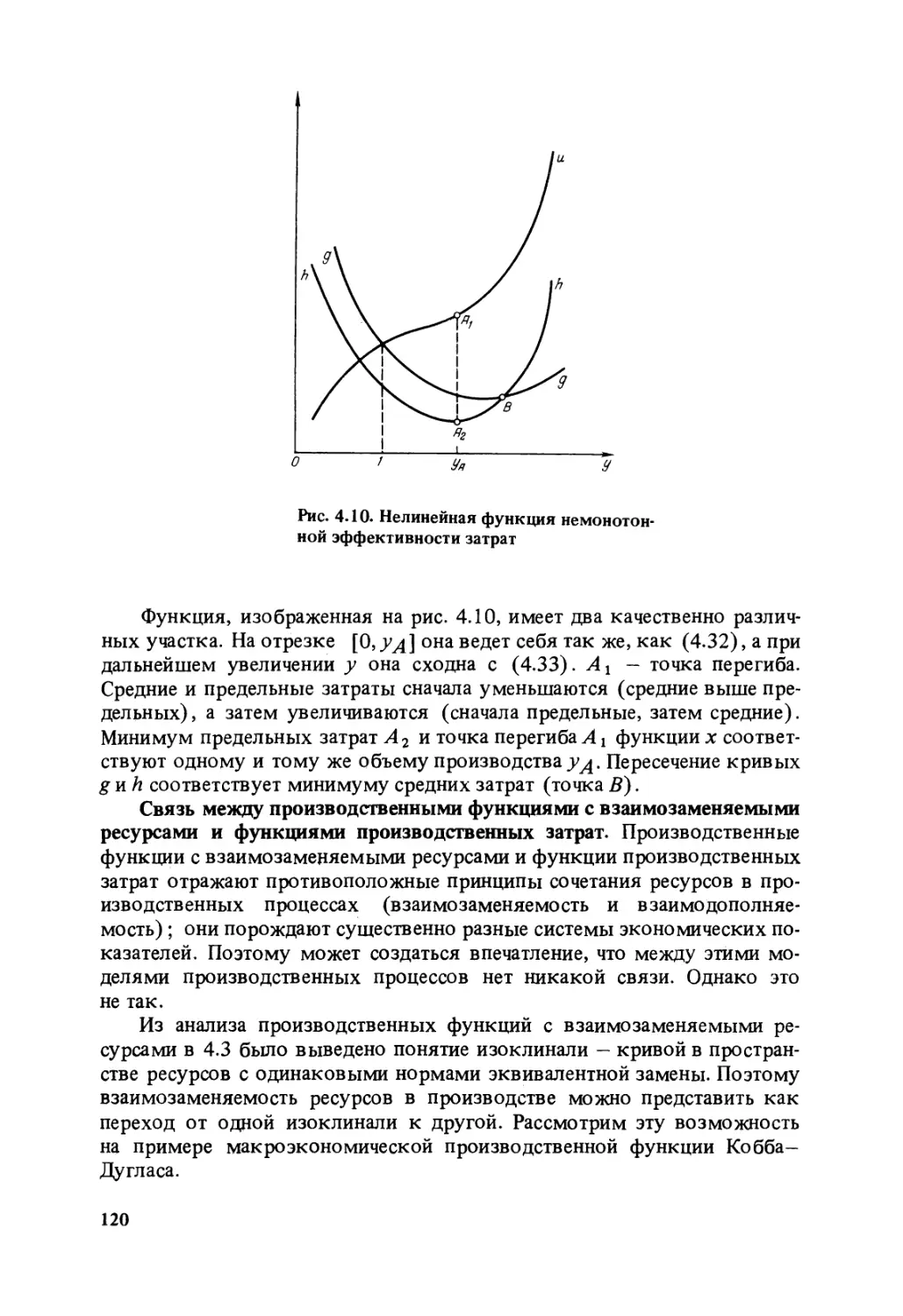
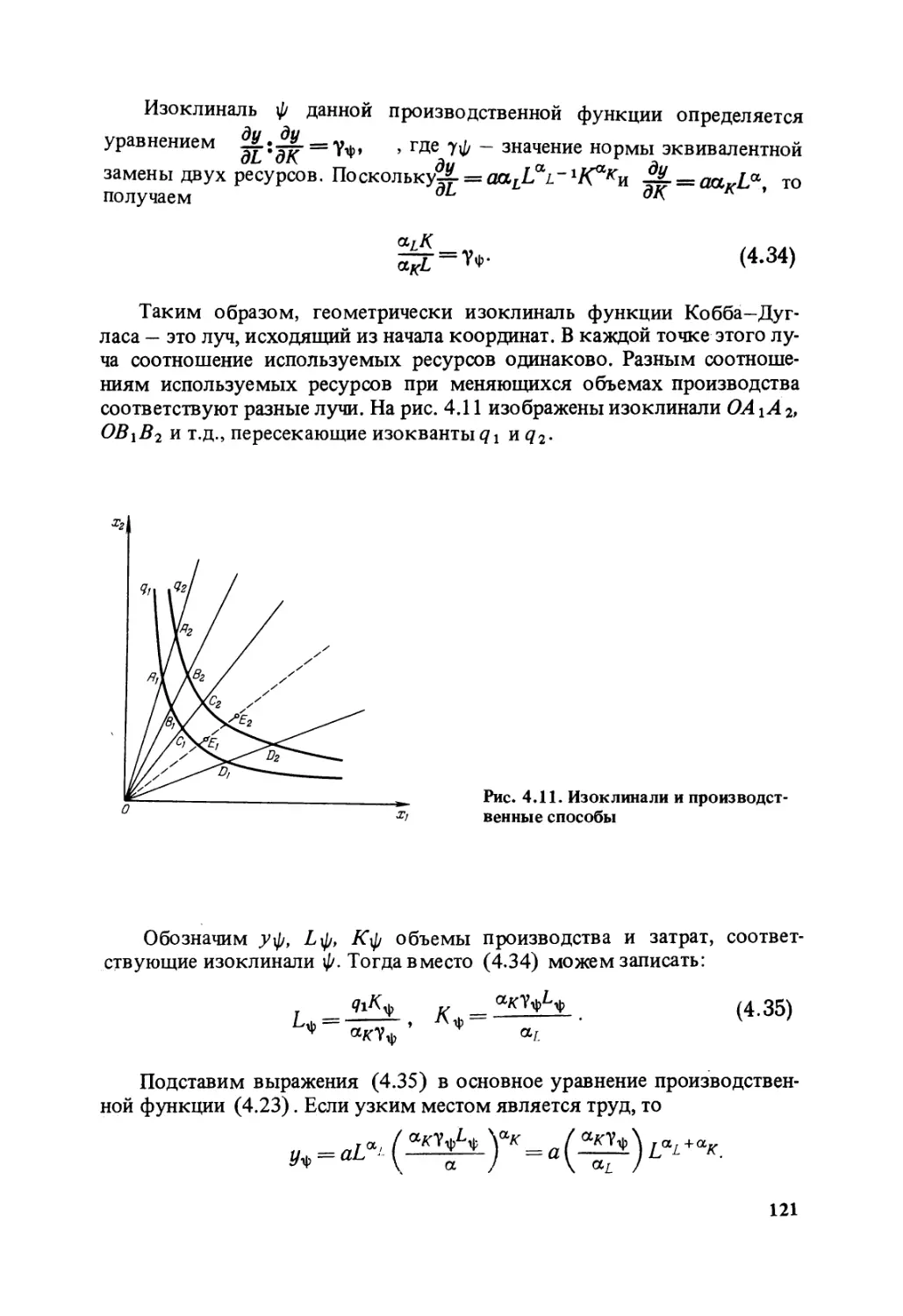
Text
А. Г. Гранберг
МОДЕЛИРОВАНИЕ
СОЦИАЛИСТИЧЕСКОЙ
экономики
Допущено Государственным комитетом СССР
по народному образованию в качестве учебника
для студенте высших учебных заведений,
обучающихся по специальности
’’Экономическая кибернетика”
Москва-Экономика 1988
ББК 65.050.9(2)
Til
Редактор Ф.П. Дорохов
Рецензенты:
кафедра математических методов анализа экономики
экономического факультета МГУ, член-корреспондент
АН СССР B.JI. Макаров
0604020102 - 232
Г 63 - 88 ©Издательство „Экономика”, 1988
011(01) - 88
ISBN 5 - 282 - 00659- 6
ПРЕДИСЛОВИЕ
Моделирование экономических процессов, тесно связанное с компьюте¬
ризацией, в последние десятилетия является наиболее быстро развиваю¬
щимся направлением экономической науки и ее важнейших приложений.
Поэтому учебный курс ’’Моделирование социалистической экономи¬
ки” - один из основополагающих в процессе формирования современ¬
ного экономиста.
Главными задачами курса являются: 1) расширение и углубление
теоретических знаний о качественных свойствах экономической систе¬
мы, количественных взаимосвязях и закономерностях экономического
развития, механизмах управления народным хозяйством; 2) овладение
методологией и методикой построения, анализа и применения математи¬
ческих моделей экономических процессов; 3) изучение наиболее харак¬
терных моделей и получение навыков практической работы с моделями,
используемыми в практике или подготовленными к внедрению. Таким
образом, курс ’’Моделирование социалистической экономики” имеет
одновременно теоретическое, методологическое, методическое и кон¬
кретно-прикладное назначение.
Содержание и структура данной книги отражают позицию автора
в отношении роли математического моделирования в экономической на¬
уке и хозяйственной практике, возможности синтеза экономических и
математических знаний. Основная направленность данной книги —
анализ теоретических и прикладных проблем социалистической экономи¬
ки средствами математического моделирования, а не изучение собствен¬
но математических методов, применяющихся в экономике. Иначе гово¬
ря, первична экономическая проблематика, а математический аппарат
(как инструмент познания) — вторичен. Поэтому значительное‘место в
книге уделяется логическому анализу социалистической экономики и
ее альтернативным модельно-теоретическим представлениям, структури¬
зации проблем планирования и управления народным хозяйством.
Автор стремится показать, что математическое моделирование сущест¬
венно расширяет возможности экономического анализа, позволяет сфор¬
мулировать новые постановки экономических задач, приводит к новым
теоретическим результатам, интенсифицирует планово-управленческую
деятельность, повышает качество принимаемых экономических решений.
Чтение книги требует математической подготовки, в первую очередь
по линейной алгебре, дифференциальному исчислению и дифференциаль¬
ным уравнениям, математическому программированию и в меньшей
степени по теории вероятностей, математической статистике, теории игр,
теории оптимального управления. Из-за ограниченного объема книги
математические доказательства часто опускаются; такие случаи сопро¬
вождаются ссылками на источники с доказательствами.
Более подробное изложение многих рассмотренных в книге вопро¬
сов дано в предшествующих работах автора, на которые даются регуляр¬
ные постраничные ссылки1. Для параллельного и подготовительного чте¬
ния рекомендуется учебное пособие А.В.Лотова ’’Введение в экономи-
ко-математическое моделирование” (М.: Наука, 1984), для получения
дополнительных сведений — ’’Экономико-математический словарь”
Л.И.Лопатникова (М.: Наука, 1987). Структура нашей книги позволяет
’’подстраивать” к ней специальные учебные пособия по отдельным
направлениям экономико-математического моделирования.
Рассматриваемая автономно, книга имеет легко обнаруживаемый
педагогический пробел: в ряде глав не хватает примеров, задач, упраж¬
нений. Это - сознательная жертва. Планируется отдельное издание
практикума по моделированию социалистической экономики, в точности
соответствующего структуре данного учебника, а также тиражирование
компьютерных разработок (информационных массивов, машинных
программ, инструкций для пользования в диалоговом режиме) по всем
темам учебного курса.
Ряд глав написан с участием В.П.Бусыгина, Б.Н.Киселева, Л.И.По¬
лищука, А.Г.Рубинштейна, В.И.Суслова (точные указания авторства да¬
ются в ДМНХ и ВСМ). Большую работу по подготовке рукописи вы¬
полнили Т.П.Захарова, В.А.Сарафанова, Сон Ден Сун.
Автор признателен рецензентам книги и коллегам, вносившем
многочисленные критические замечания и конструктивные предложе¬
ния при обсуждении рукописи и предшествующих публикаций, и особен¬
но студентам Новосибирского университета и других вузов, невольно
участвовавшим в многолетних экспериментах по отладке учебного курса.
Отзывы читателей помогут автору точнее определиться в дальнейшей
научной и педагогической работе.
1 Гранберг А.Г. Математические модели социалистической экономики. М.:
Экономика, 1978 (в дальнейшем - сокращенно ММСЭ); Гранберг А.Г. Динамичес¬
кие модели народного хозяйства. М.Г Экономика, 1985 (сокращенно — ДМНХ),
Гранберг А.Г., Суспицин С.А. Введение в системное моделирование народного
хозяйства. Новосибирск: Наука, 1988 (сокращенно - ВСМ).
ВВЕДЕНИЕ
В хозяйственной практике человека математика используется с момента
своего зарождения. На протяжении тысячелетий арифметика и геометрия
применялись для разнообразных измерений и вычислений. Однако даль¬
нейшее развитие математики долгое время определялось в основном
потребностями естественных и технических наук и внутренней логикой
самой математики. Именно математике во многом обязаны своими до¬
стижениями астрономия, физика, химия, биология.
Когда мы говорим о применении математики в экономике, то имеем
в виду не просто проведение различного рода экономических расчетов,
а использование математики для изучения экономических закономерно¬
стей, получения новых теоретических выводов, нахождения наилучших
экономических решений. Главные преимущества математики как сред¬
ства научного познания раскрываются при построении математических
моделей, заменяющих в определенных отношениях исследуемые объек¬
ты. Математические модели экономики, отражающие с помощью мате¬
матических соотношений основные свойства экономических процессов и
явлений, представляют собой эффективный инструмент исследования
сложных экономических проблем.
Довольно распространено мнение, что применение математики и
математического моделирования в экономике — новая страница в разви¬
тии экономической науки, связанная с появлением электронной вычис¬
лительной техники. Такое мнение является глубоким заблуждением.
Применение математических методов в экономике имеет богатое прош¬
лое; забвение этого прошлого серьезно обедняет и искажает историю
экономической мысли.
Изучение предшествующего опыта экономико-математических
исследований дает ответы на важные методологические и содержатель¬
ные вопросы экономической науки, позволяет избежать многочисленных
ошибок в применении математических методов, помогает оценить воз¬
можности и перспективы использования математического моделирова¬
ния в экономике, выбрать наиболее эффективные направления дальней¬
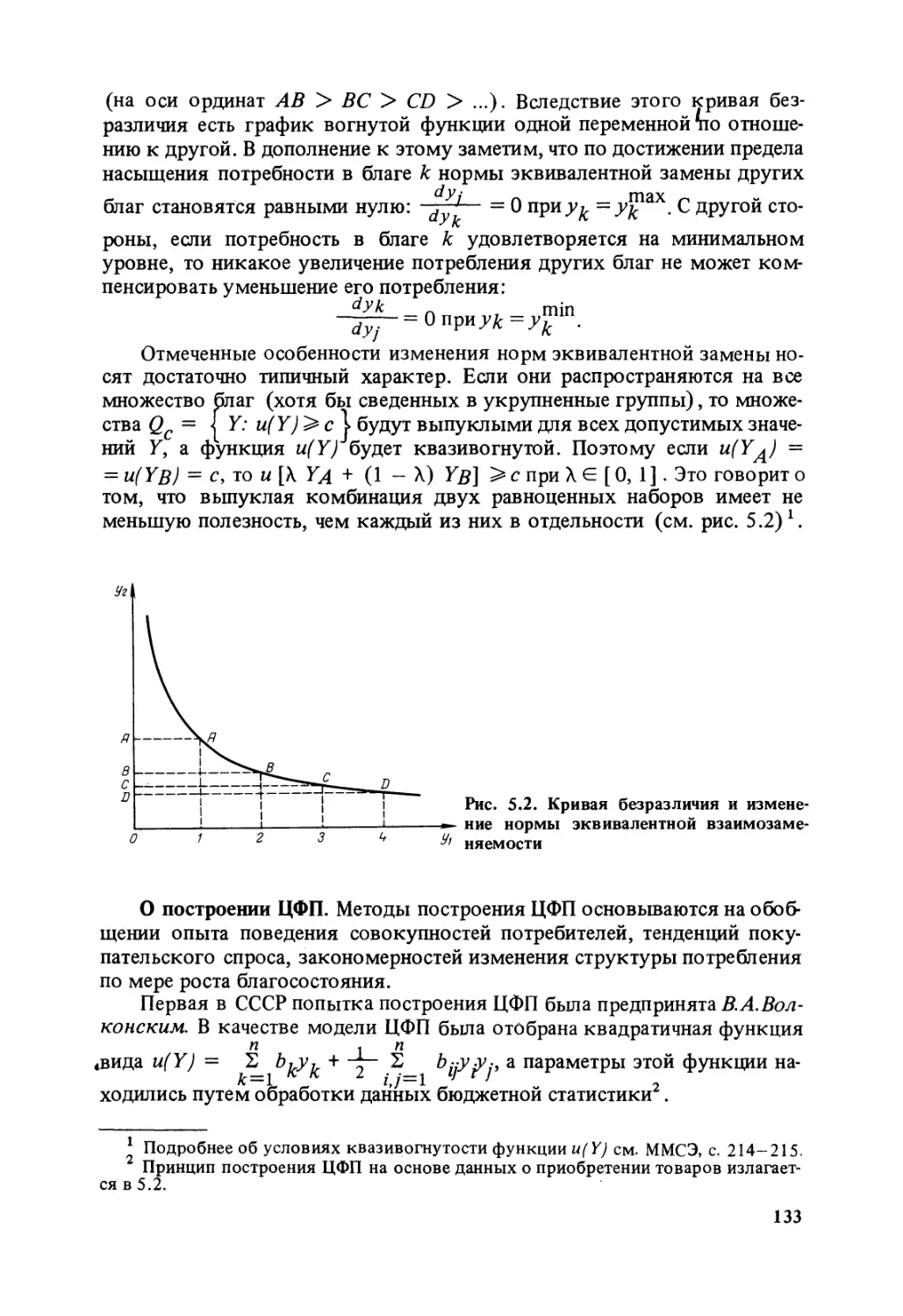
шего развития экономических исследований. Многие научные результа¬
ты использования метода математического моделирования в экономике,
полученные десятки и даже более ста лет назад, не потеряли своей акту¬
альности.
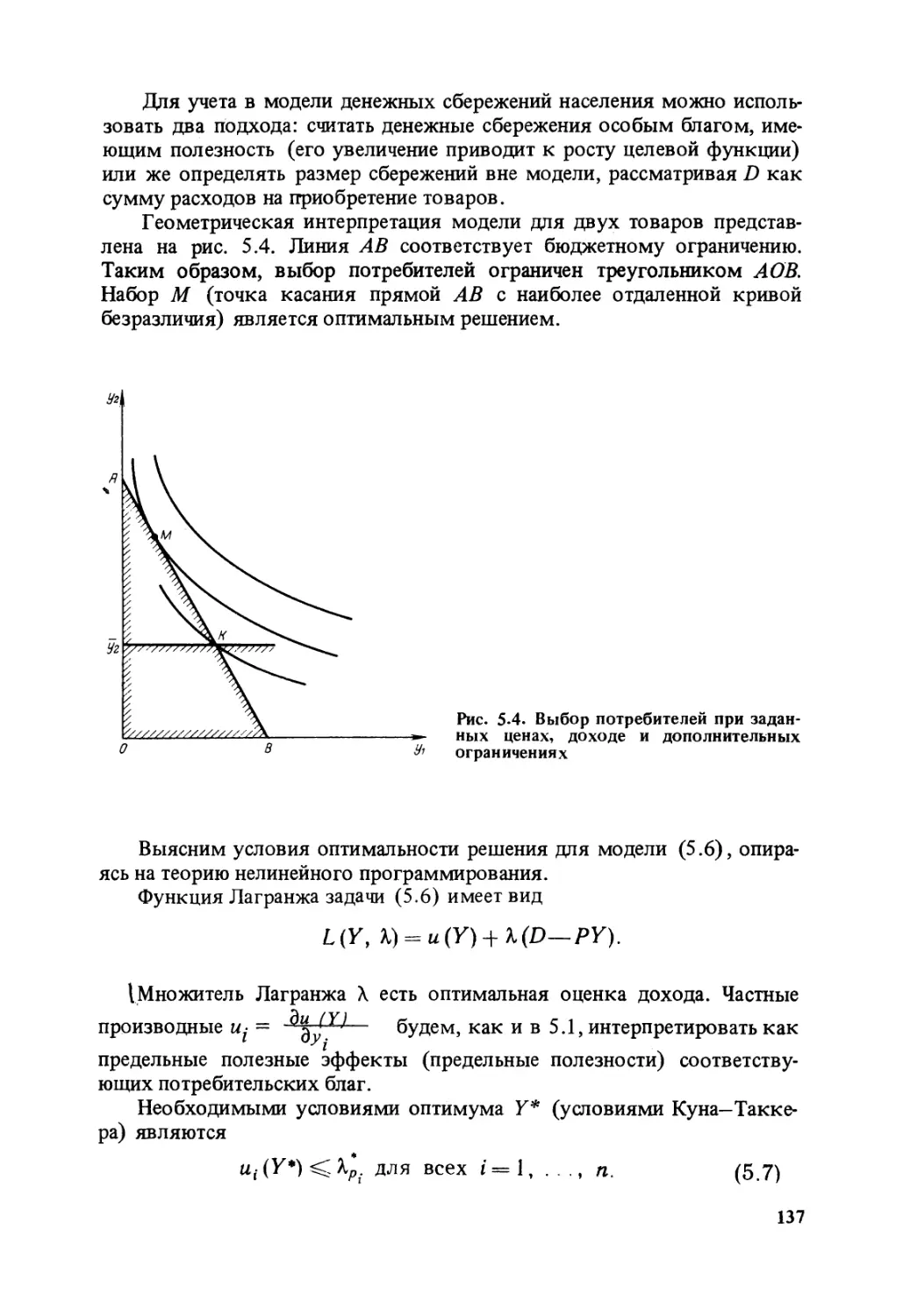
Стремление использовать математику в качестве инструмента иссле¬
дования отличало еще родоначальников экономической науки. Так,
У.Петти (1623—1687), основатель классической политической экономии,
писал в предисловии к своей „Политической арифметике”: вместо
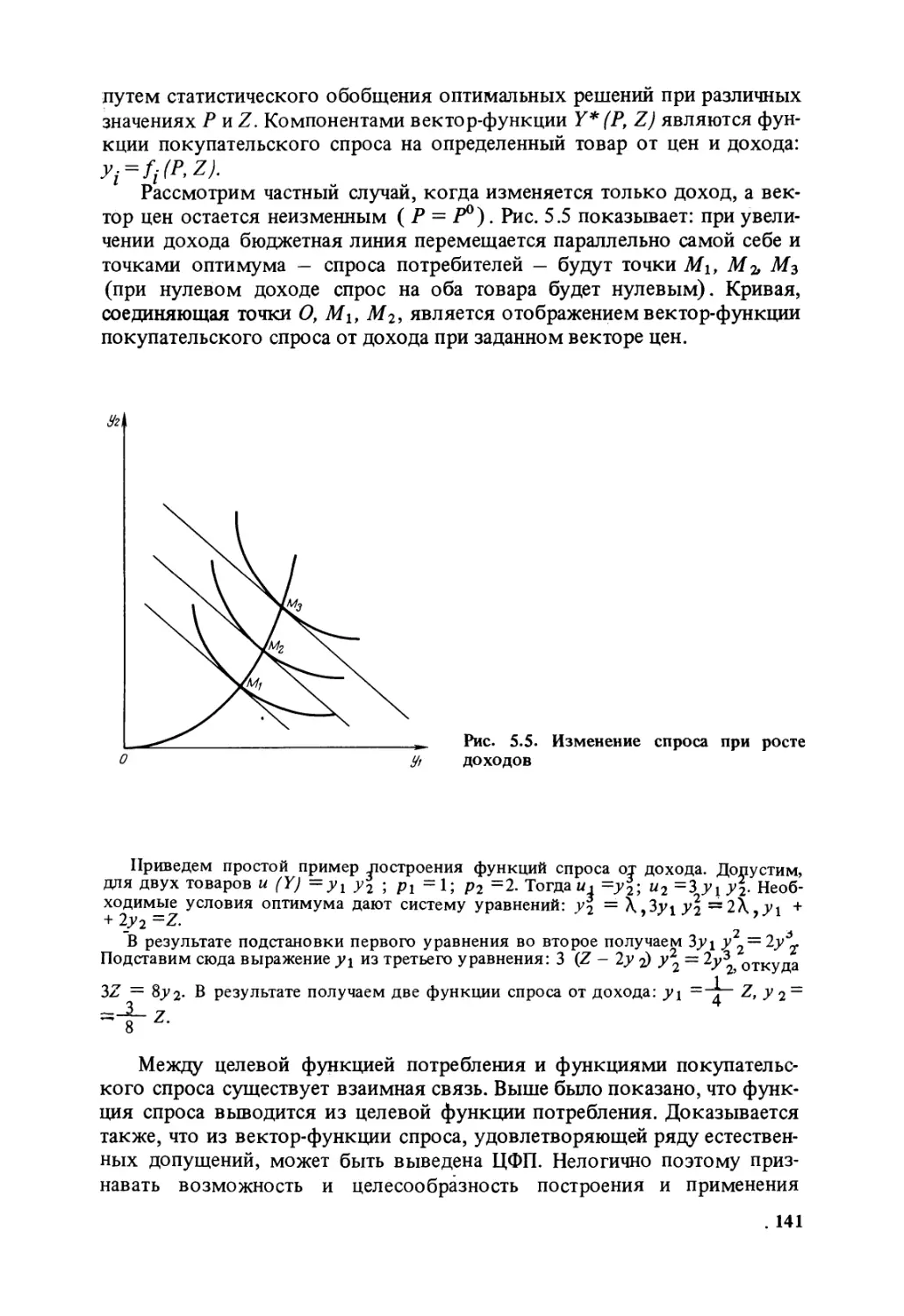
того, чтобы употреблять слова только в сравнительной и превосходной
степени и прибегать к умозрительным аргументам, я вступил на путь
выражения своих мнений на языке чисел, весов и мер...”. Однако упот¬
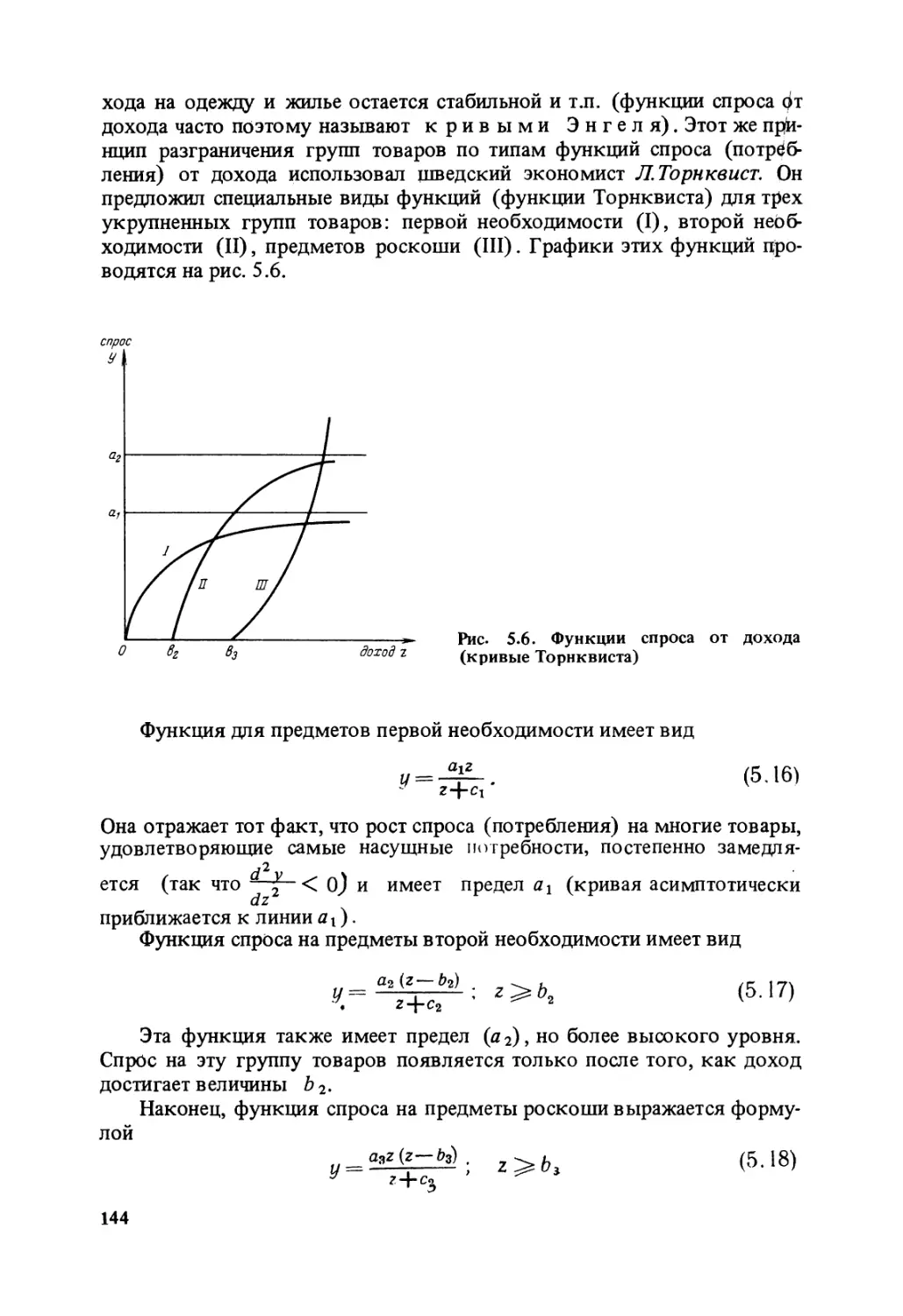
ребление „чисел, весов и мер” характеризует только начальную стадию
использования математики.
Первая в мире модель народного хозяйства была создана француз¬
ским ученым Ф. Кенэ (1694—1774). В 1758 г. он опубликовал первый
вариант своей знаменитой „Экономической таблицы”, получивший наз¬
вание „зигзаг”; второй вариант — „арифметическая формула” — был
опубликован в 1766 г. „Эта попытка, — писал КМаркс о таблице
Ф.Кенэ, — сделанная во второй трети XVIII века, в период детства поли¬
тической экономии, была в высшей степени гениальной идеей, бесспорно
самой гениальной из всех, какие только выдвинула до сего времени
политическая экономия”1. КМаркс неоднократно обращался к анализу
„Экономической таблицы”. Уже в наше время „Экономическая табли¬
ца” Ф.Кенэ послужила основой для построения и развития многочислен¬
ных математических моделей общественного воспроизводства.
Значительное влияние на развитие методологии экономико-матема-
тических исследований оказали труды К Маркса. Опираясь на опыт
Ф.Кенэ, КМаркс разработал значительно более содержательные схемы
воспроизводства, вывел условия простого и расширенного воспроизвод¬
ства в виде алгебраических уравнений и неравенств, исследовал сложные
количественные взаимосвязи процесса общественного воспроизводства.
Основной экономический труд К.Маркса „Капитал” содержит немало
примеров плодотворного использования математического метода. Так,
при изучении закона тенденции нормы прибыли к понижению К.Марксом
дается обстоятельный параметрический анализ формулы средней нормы
прибыли (при этом К.Маркс пишет, что исследование сначала движется
в чисто математической области). В отделе о земельной ренте приводят¬
ся уравнения, связывающие абсолютную, дифференциальную и
суммарную ренту. Скрупулезно анализируются взаимозависимости
прибавочной стоимости, цены рабочей силы, производительности труда,
интенсивности труда и длины рабочего дня. Ряд важнейших политэконо-
мических положений формулируется К.Марксом математически: соот¬
ношение стоимости и производительной силы труда, законы изменения
массы прибавочной стоимости и денежного обращения, условия форми¬
рования цены производства и т.д.
К.Маркс высоко ценил математику как орудие научного познания.
П.Лафарг в воспоминаниях о К.Марксе писал: „В высшей математике он
находил диалектическое движение в его наиболее логичной и в то же
1 Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 26. Ч. 1. С. 345.
время простейшей форме. Он считал также, что наука только тогда
достигает совершенства, когда ей удается пользоваться математикой”1.
Многие зрелые годы К.Маркс посвятил самостоятельному изучению ма¬
тематики. Его наследие содержит обширные математические рукописи, в
том числе его собственные работы по дифференциальному исчислению2.
С какой целью К.Маркс занимался математикой? Имеются истори¬
ческие свидетельства, что он вел подготовительную работу, стремясь в
полной мере использовать математические знания в политэкономических
исследованиях3. Эти планы КМаркс не успел осуществить.
Однако несмотря на многочисленные примеры плодотворного ис¬
пользования математического метода, последний все же не играл веду¬
щей роли в экономических исследованиях К.Маркса. В немалой степени
это было обусловлено теми задачами качественного изучения природы
капиталистического способа производства, которые были главными и в
„Капитале”, и в других экономических трудах К.Маркса.
Сказанное отнюдь не умаляет заслуг КМаркса в развитии экономи-
ко-математических исследований. Но значение его трудов прежде всего
нужно видеть не в конкретных результатах использования математики, а
в создании теоретического фундамента для плодотворного развития эко¬
номической науки на основе применения всех эффективных методов
исследования, включая и метод математического моделирования.
Система теоретико-экономических положений К.Маркса служит
отправным пунктом для создания многих математических моделей
капиталистической и социалистической экономики. Пожалуй, особенно
ярко значение трудов К.Маркса проявляется при моделировании про¬
цесса общественного воспроизводства.
Схемы расширенного воспроизводства К.Маркса были развиты
В.И.Лениным, который модифицировал их с учетом условия роста ор¬
ганического строения капитала и задач развития социалистического
общества. Позднее учеными-марксистами были созданы многочисленные
обобщения и математические интерпретации схем воспроизводства.
Непосредственное влияние схем К.Маркса прослеживается во мно¬
гих мак ро моделях, построенных экономистами различных науч¬
2 Воспоминания о Марксе и Энгельсе. М.: Госполитиздат, 1956. С. 66.
„Математические рукописи” К.Маркса впервые полностью опубликованы
(одновременно на русском и немецком языках) в 1968 г. издательством ,,Наука”.
Кроме оригинальных работ К.Маркса они содержат конспекты и выписки из книг,
которыми он пользовался.
Об одном конкретном своем намерении К.Маркс писал Ф.Энгельсу 31 мая
1873 г.: „... Ты знаешь таблицы, в которых цены, учетный процент и т.д. и т.д.
представлены в их движении в течение года и т.д., в виде восходящих и нисходя¬
щих зигзагообразных линий. Я неоднократно пытался - для анализа кризисов -
вычислить эти up and downs как неправильные кривые и думал (да и теперь еще
думаю, что с достаточно проверенным материалом это возможно) математически
вывести из этого главные законы кризисов” (Маркс К., Энгельс Ф. Соч. 2-е изд.
Т. 33. С. 72).
ных школ. Дальнейшим развитием двухсекторных схем расширенного
воспроизводства стали модели межотраслевого баланса.
Использование теоретического наследия К.Маркса в экономико¬
математических исследованиях не ограничивается только построением
макроэкономических и межотраслевых моделей воспроизводства. Раз¬
работанные К.Марксом положения теории трудовой стоимости,
прибавочной стоимости, средней прибыли и цены производства, земель¬
ной ренты и др. находят применение в моделях общественно необходи¬
мых затрат, ценообразования, формирования и распределения доходов
и т.д. Большое влияние экономической теории К.Маркса на развитие эко-
номико-математических исследований признается и современными уче¬
ными Запада.
Важную роль в развитии экономической науки XIX века сыграла
математическая школа в политической экономии. Ее виднейшие пред¬
ставители О.Курно, Г.Госсен, J1. Вальрас, У.Джевонс, Ф.Эджворт, В.Па¬
рето внесли большой вклад в разработку проблем потребления, механиз¬
ма спроса и предложения, формирования издержек производства,
сбалансированности (равновесия) экономики. Широко используются
понятия кривых безразличия и ядра экономической
системы Ф.Эджворта, многоцелевого оптимума
В.Парето, общего экономического равновесия JI.Валь¬
раса и др.
В конце XIX — начале XX в. в экономической науке Запада получи¬
ло развитие статистическое направление, ставившее своей главной зада¬
чей изучение экономических циклов и прогнозирование хозяйственной
конъюнктуры на основе методов математической статистики. Заслугой
этого научного направления является разработка методических вопро¬
сов обработки экономических данных, статистических обобщений и по¬
строения математико-статистических моделей.
В дореволюционной России возможности и проблемы применения
математики в экономике привлекали внимание многих ученых. В рус¬
ских изданиях критически обсуждались работы западных экономистов-
математиков, а с конца XIX в. появляются оригинальные экономико¬
математические исследования В. К Дмитриева, В.И.Борткевича, В.С.Вой-
тинского, P.M. Оржнецкого, В.В.Самсонова, Н.А.Столярова, Н.Н.Шапош-
никова и др.
Наиболее крупным экономистом-математиком дореволюционной
России был В.К.Дмитриев (1868-1913). Его первая известная работа
„Теория ценности ДРикардо. Опыт органического синтеза трудовой
ценности и теории предельной полезности” была опубликована в 1898 г.
Главный научный труд В.К.Дмитриева „Экономические очерки” вышел
в 1904 г. Основной конструктивный научный вклад В.К.Дмитриева
состоит в построении модели полных народнохозяйственных затрат
труда и сбалансированных цен в виде системы линейных уравнений с
технологическими коэффициентами. „Формула В.КДмитриева” спустя
8
несколько десятков лет нашла применение в моделировании межотра¬
слевых связей и в СССР, и за рубежом.
В истории экономико-математических исследований особое место
принадлежит Е.ЕСлуцкому (1880—1948), широко известному своими
работами по теории вероятностей и математической статистике. В 1915 г.
он опубликовал в итальянском журнале статью „К теории сбалансиро¬
ванности бюджета потребителя”1. Спустя двадцать лет эта статья получи¬
ла мировое признание. Лауреат Нобелевской премии Д.Хикс в книге
„Стоимость и капитал” (1939) писал, что Е.Е. Слуцкий был первым эко¬
номистом, сделавшим серьезный шаг вперед по сравнению с классика¬
ми математической школы.J
Значительное развитие в русской экономической науке конца XIX —
начала XX в. получили исследования по применению методов математи¬
ческой статистики. Ведущую роль здесь играл АЛ. Чупров (1874-1926),
под руководством которого выполнялись интересные работы по кор¬
реляционному анализу экономических явлений2.
Создание первого в мире социалистического государства выдвину¬
ло перед экономической наукой принципиально новые задачи. Уже
в годы гражданской войны и восстановления народного хозяйства
закладывались основы новой методологии и организации экономиче¬
ских исследований. Огромное значение в восстановлении экономической
науки, создании общегосударственной системы учета, планирования и
управления имели научные труды и деятельность В.И.Ленина.
Экономико-математические исследования в СССР в 20-е годы прово¬
дились в основном по двум направлениям: применение математических
методов в изучении хозяйственной конъюнктуры и экономическом регу¬
лировании; моделирование процесса расширенного воспроизводства.
Задачи первого направления диктовались условиями нэпа. Выполня¬
лись многочисленные работы по анализу временных рядов и сезонных
колебаний, краткосрочным прогнозам, изучению влияния различных
экономических регуляторов. В 1922 г. был создан Конъюнктурный ин¬
ститут при Наркомфине, который возглавил талантливый ученый
Н.ДКондратьев (1892-1938).
В историю мировой науки Н.Д.Кондратьев вошел как автор кон¬
цепции больших циклов конъюнктуры (или „длинных
волн”) периодичностью 40—60 лет3. Особую популярность эта кон¬
1 В 1963 г. статья была издана на русском языке в сборнике „Экономико¬
математические методы”. М.: Изд-во АН СССР, 1963. Вып. 1. Статья сопровождает¬
ся комментарием советских экономистов-математиков ВЛ.Цолконского и
АЛ.Коиюса.
2 См. Чупров А.А. Основные проблемы теории корреляции. О статистическом
исследовании связи между явлениями (1926) .М.: Госстатиздат, 1960.
3 Кондратьев Н.Д. Большие циклы конъюнктуры // Вопросы конъюнктуры.
1925. № 1. Вып. 1.
цепция завоевала в 80-е годы в связи с изучением долговременных тен¬
денций научно-технического прогресса. Только под эгидой Международ¬
ного института прикладного системного анализа по этой теме было
проведено уже три конференции.
В математико-статистических исследованиях экономических явле¬
ний получили развитие традиции русской школы статистиков. Были
начаты работы по демографическому анализу, изучению спроса и пред¬
ложения, моделированию сферы личного потребления. Здесь можно
отметить ряд теоретических работ С.С.Бюшгенса и Л.А.Конюса1, иссле¬
дования ЛН.Юровского по теории цены2.
На развитие в СССР синтетических статистических работ по анализу
процесса социалистического воспроизводства и построение балансовых
моделей народного хозяйства большое влияние оказывали ленинские
указания о необходимости систематизированного учета массовых
данных в масштабе всей страны, собираемых по одной определенной
программе и сводимых вместе специалистами-статистиками, о принци¬
пах построения сбалансированного народнохозяйственного плана. Уже
в первом советском хозяйственном плане — плане ГОЭЛРО, разработан¬
ном при участии и под руководством В.И .Ленина, — содержались важные
предпосылки для построения народнохозяйственных моделей (формули¬
ровка целей и ограничений, использование балансового метода, единство
материально-вещественного и стоимостного аспектов плана и т.д.).
Выдающимся достижением советской статистики явилась разработка
первого в мире баланса народного хозяйства СССР за 1923/24 хозяй¬
ственный год. Этот баланс включал наряду со сводными показателями
воспроизводства также и таблицы межотраслевых потоков предметов
труда и средств труда. Работа ЦСУ СССР на много лет опередила зару¬
бежные статистические исследования как по сводным балансовым
таблицам (национальным счетам), так и по межотраслевым балансам
(методу input - output)3.
Во второй половине 20-х годов проводились работы по совершенст¬
вованию статистических основ межотраслевого баланса и по математи¬
Бюшгенс С.С., Конюс А.А. К проблеме покупательной силы денег // Во¬
просы конъюнктуры. 1926. Т. II; А.А.Конюс (р. 1895) - старейшина советской
экономико-математической школы - и до настоящего времени активно продолжа¬
ет исследования в области моделирования покупательского спроса и потребле¬
ния, теории стоимости, по динамическим моделям экономики.
2
Юровский JI.H. Очерки по теории цены. Саратов, 1919.
В.В.Леонтьев, лауреат Нобелевской премии, признанный лидер в теории и
методологии построения межотраслевых моделей, родился в России (1906 г.). Он
был хорошо знаком с балансом народного хозяйства СССР за 1923-1924 гг. и даже
опубликовал на эту работу рецензию в журнале „Плановое хозяйство” (1925.
№ 12). Свои собственные крупные работы по анализу межотраслевых связей
В.Леонтьев начал в США в 1931 г., а первые его публикации межотраслевых ба¬
лансов США за 1919 и 1929 гг. относятся к 1936 г. Известны его большие заслуги
в развитии, математическом оформлении и популяризации идей межотраслевого
баланса и организации работ по межотраслевым балансам во многих странах мира.
10
ческому моделированию межотраслевых связей. В 1926 г. Я.Шатунов-
ский прочитал в Коммунистической Академии доклад „Математиче¬
ский опыт учета элементов народного хозяйства посредством системы
линейных уравнений” (ранее система уравнений межотраслевых связей
рассматривалась В.К.Дмитриевым). Интересные попытки применить
математические методы для изучения структуры и образования народ¬
нохозяйственных затрат предпринял Л.Лубны-Герцык. Таким образом,
к концу 20-х годов в СССР уже были разработаны многие экономиче¬
ские и математические проблемы межотраслевых моделей народного
хозяйства.
Большое внимание уделялось советскими экономистами развитию
схем воспроизводства К.Маркса и В.И.Ленина, их усложнению и мате¬
матической формализации. Л.Крицман обобщил анализ схем воспроиз¬
водства на случай трех, четырех и, наконец, п подразделений обществен¬
ного воспроизводства. В работах В.Позднякова, В. Староеского, А.Ор¬
леанского и др. проводились математические преобразования схем и
параметрический анализ важнейших соотношений.
Большое значение имела разработка Г.А.Фельдманом (1884—
1958) математических моделей экономического роста. Г.А.Фельдман
был одним из авторов плана ГОЭЛРО, работником первого состава
Госплана СССР. Свои основные идеи по моделированию социалистиче¬
ской экономики он базировал на марксовых схемах расширенного вос¬
производства, предложив свой оригинальный вариант схемы расширен¬
ного воспроизводства, причем не только в алгебраической, но и в графи¬
ческой форме1.
Основная модель роста Г.А.Фельдмана выражала взаимосвязи тем¬
па роста национального дохода, изменения фондоотдачи и производи¬
тельности труда, структуры использования национального дохода. Эта
модель имела не только теоретическое значение: она использовалась
в разработке первого генерального плана развития народного хозяйства
СССР на 15—20 лет, которая проводилась в конце 20-х — начале 30-х
годов. Статьи Г.А.Фельдмана намного опередили работы Д.Кейнса,
Р.Харрода, Е.Домара и других западных экономистов по макроэкономи¬
ческим динамическим моделями в еще большей степени — исследования
по двухсекторным моделям экономического роста (с выделением двух
подразделений)2. Но за рубежом научные результаты Г.А.Фельдмана
долгое время оставались незамеченными. Они были „открыты” там толь¬
ко после Великой Отечественной войны и вызвали огромный интерес.
Фельдман Г.А. К теории темпов народного дохода (Под углом зрения народ¬
ного хозяйства СССР) // Плановое хозяйство. 1928. № 11, 12; Аналитический
метод построения перспективных планов // Плановое хозяйство. 1929. № 12.
Первая модель роста Е.Домара, близкая односекторной модели Г.А.Фельд¬
мана, была опубликована только в 1938 г. В современной'литературе она более
известна как модель Харрода - Домара (см. гл. 10).
11
Обе статьи были полностью опубликованы в США в 1964 г. и детально
проанализированы.
Работы Г. А.Фельдмана имеют и обще методологическое значение для
моделирования социалистической экономики. В них содержится четкая
(и удивительно современная) аргументация необходимости использо¬
вания математических методов в народнохозяйственном планировании:
„Нельзя представить несложного метода проектирования такого сложно¬
го аппарата, каким является народное хозяйство. С другой стороны,
мы не знаем более совершенной формы анализа, чем математика... Мы
убеждены, что более или менее совершенное планирование народного
хозяйства может быть осуществлено лишь на основе четкой, математи¬
чески сформулированной теории; только тогда споры по планам могут
быть сведены к принципиальным установкам и целевым заданиям при
полной уверенности в безошибочности расчетов”1.
Научные поиски Н.Д. Кондратьева также привели его к макроэконо¬
мическому моделированию. В 1930-1934 гг., находясь в политизолято-
ре, он разрабатывал динамическую макромодель в виде дифференциаль¬
ных уравнений. О замысле и содержании этого направления научной дея¬
тельности Н.Д. Кондратьева стало известно совсем недавно2.
Исследования по моделированию социалистической экономики,
успешно начатые советскими учеными, к сожалению, не получили разви¬
тия в 30-е годы. Насаждавшийся упрощенческий подход к экономиче¬
ской теории, огромные кадровые потери экономической науки в резуль¬
тате политических репрессий сказались на состоянии и престижности
экономико-математических исследований. Лишь в конце 30-х годов
произошли события, оказавшие впоследствии большое влияние на эко¬
номическую науку и хозяйственную практику3.
В 1938 -1939 гг. ленинградский математик JI.B.Канторович (1912—
1986) в результате анализа ряда проблем организации и планирования
производства сформулировал новый класс условно-экстремальных за¬
дач с ограничениями в виде неравенств и предложил методы их решения.
Эта новая область прикладной математики позже получила название
„линейное программирование”. В США линейное программирование
было переоткрыто ДжДанцигом в конце 40-х годов. Ныне приоритет
J1.В.Канторовича признан во всем мире. В 1975 г. JI.В.Канторовичу
совместно с американским ученым Т.Купмансом за исследования по
оптимальному распределению ресурсов была присуждена Нобелевская
премия.
В книге „Математические методы организации и планирования про-
Плановое хозяйство. 1928. № 12. С. 177-178.
См. Экономика и математические методы. Т. XXIV. Вып. 2. 1988.
Более подробное изложение отдельных этапов развития экономико-мате¬
матических исследований за рубежом, в дореволюционной России и в СССР (до
30-х годов) см. в ММСЭ, с.’ 11-23.
12
изводства” (1939) JI.В .Канторович изложил опыт применения линейного
программирования для решения разнообразных экономических задач:
распределение работ между видами оборудования, комплексное исполь¬
зование сырья, раскрой материалов, распределение посевных площадей
между культурами, составление плана перевозок и т.д. В этой же книге
он ввел понятие разрешающих множителей (впоследствии
названных им объективно обусловленными оценка¬
ми) и установил их связь с оптимальным планом. В более поздних
работах Л.В. Канторович расширил сферу применения линейного прог¬
раммирования в социалистической экономике, сформулировав задачи
отраслевого и народнохозяйственного оптимального планирования.
Спустя два десятилетия после своего возникновения линейное програм¬
мирование стало важным инструментом выбора планово-экономических
решений на всех уровнях социалистического хозяйства.
В 1939 г. почти одновременно с Л.В .Канторовичем ленинградский
экономист В.В.Новожилов (1892-1970) опубликовал свою работу „Ме¬
тоды соизмерения народнохозяйственной эффективности плановых и
проектных вариантов”. В ней содержались важные теоретические поло¬
жения, ставшие потом органической частью теории оптимального плани¬
рования социалистической экономики. В.В.Новожилов сформулировал
задачу оптимального народнохозяйственного плана (на минимум трудо¬
вых затрат), принципы соизмерения затрат и результатов при оптималь¬
ном планировании.
Экономико-математические исследования в 30 — 40-е годы не ограни¬
чивались только работами Л.В.Канторовича (и его учеников) и
В.В.Новожилова по оптимальному планированию. В этот же период вы¬
полнялись исследования по рационализации транспортных перевозок
(А.Л.Лурье, В.Н.Толстой), разработке методов отбора вариантов капи¬
таловложений (особенно в энергетике и транспортном строительстве),
применению математико-статистических методов в анализе производст¬
венных процессов. Однако достижения в области экономико-математи¬
ческих методов были мало известны экономистам и слабо использова¬
лись в хозяйственной практике.
Новый этап в развитии экономико-математических исследований в
СССР начался во второй половине 50-х годов, что было вызвано поиска¬
ми новых подходов к плановому руководству социалистической эконо¬
микой, а также принципиально новыми возможностями проведения
экономических расчетов и обработки экономической информации, воз¬
никшими благодаря появлению ЭВМ.
В 1957—1958 гг. создаются первые специализированные экономико¬
математические подразделения: Лаборатория по применению математи¬
ческих и статистических методов в составе Академии наук СССР, лабо¬
ратория в Институте электронных управляющих машин, Вычислитель¬
ный центр при Госплане СССР, отдельные группы в ряде научно-исследо-
вательских институтов. Разрабатываются учебные курсы, предназначен¬
13
ные для повышения математической подготовки экономистов. В вузах
открываются первые отделения для подготовки специалистов по приме¬
нению в экономике математических методов и электронной вычисли¬
тельной техники. Для разработки новых проблем, возникших на стыке
экономики, математики, кибернетики, были привлечены крупные твор¬
ческие силы.
Выдающуюся роль в организации и пропаганде экономико-матема¬
тических исследований, в создании советской экономико-математиче¬
ской школы сыграл академик B.C.Немчинов (1894-1964).
В апреле 1960 г. состоялось Научное совещание о применении мате¬
матических методов в экономических исследованиях и планировании,
созванное Президиумом АН СССР. Оно подвело первые итоги нового
этапа экономико-математических исследований, определило наиболее
важные направления их дальнейшего развития. Большое значение для
создания единой методологической основы экономико-математических
исследований имели фундаментальные работы Л.В.Канторовича „Эконо¬
мический расчет наилучшего использования ресурсов” (1959), В.В.Но¬
вожилова „Измерение затрат и их результатов в социалистическом
хозяйстве” (1959), В.С.Немчинова „Экономико-математические методы
и модели” (1962). За этот цикл работ их авторам в 1964 г. была присуж¬
дена Ленинская премия.
В 70-х годах начался переход от использования математических
моделей для решения отдельных задач к их системному применению в
автоматизированных системах планирования и управления. Этот переход
требовал решения двух основных проблем: во-первых, объединения
отдельных моделей экономических процессов и явлений в системы
(комплексы) моделей; во-вторых, непосредственного включения
моделей в процесс планирования (или управления), создания новых пла¬
ново-управленческих технологий, базирующихся на системном исполь¬
зовании математических методов и ЭВМ. Важным шагом в решении ука¬
занных проблем стала разработка автоматизированной системы
плановых расчетов (АСПР) в Госплане СССР и Госпланах союзных
республик1.
Было бы неверно представлять развитие экономико-математических
исследований в СССР как путь непрерывных побед, тем более что
суровая (и далеко не всегда справедливая) критика не позволяла эконо-
мистам-математикам почивать на лаврах. В начале 60-х годов энтузи¬
асты надеялись буквально за считанные годы математизировать весь
процесс планирования и управления народным хозяйством. В действи¬
тельности все оказалось намного сложнее. Проникновение математиче¬
ских моделей в действующую систему управления требовало больших
Наиболее полное изложение итогов экономико-математических исследо¬
ваний на начало 80-х годов дается в десятитомной серии монографий под общим
названием „Вопросы оптимального планирования и управления народным хозяй¬
ством”, опубликованных в 1982-1985 гг. издательством „Наука”.
14
организационных усилий и часто не приносило ожидаемых эффектов;
но одновременно глубже осознавались реальные возможности моделиро¬
вания и условия реализации этих возможностей1.
Каковы же главные причины, тормозившие внедрение экономико¬
математических моделей в практику планирования и управления? Во-
первых, действовавший хозяйственный механизм затратного типа оттор¬
гал многие попытки использования моделей для выявления резервов,
более эффективного использования ресурсов, улучшения структуры
производимой продукции в интересах потребителей и т.д. Во-вторых,
разработанные экономико-математические модели зачастую не обеспе¬
чивались необходимой информацией и средствами технической реализа¬
ции. В-третьих, предлагавшиеся модели не учитывали подготовленности
практиков, специфики их работы. Сыграло свою роль ц несовершенство
многих моделей.
Трезвая оценка современного состояния и путей развития экономи-
ко-математического моделирования — необходимое условие для успеш¬
ного решения новых задач, возникающих в ходе перестройки советской
экономики.
. Эти вопросы широко обсуждались на страницах журнала „Экономика и
математические методы” в 1987 г. (см. выпуски 4,5).
Ра здел I
ТЕОРЕТИКО-МЕТОДОЛОГИЧЕСКИЕ ПРОБЛЕМЫ МОДЕЛИРОВАНИЯ
ГЛАВА 1
МЕТОД МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ В ЭКОНОМИКЕ
1.1. Моделирование как метод научного познания
Моделирование в научных исследованиях стало применяться еще в глу¬
бокой древности и постепенно захватывало все новые области научных
знаний: техническое конструирование, строительство и архитектуру,
астрономию, физику, химию, биологию и, наконец, общественные науки.
Большие успехи и признание практически во всех отраслях современной
науки принес методу моделирования XX в. Однако методология моде¬
лирования долгое время развивалась независимо отдельными науками.
Отсутствовала единая система понятий, единая терминология. Лишь
постепенно стала осознаваться роль моделирования как универсального
метода научного познания, как важной гносеологической категории.
Понятия „модель” и „моделирование”. Сущность процесса модели¬
рования. Термин „модель” широко используется в различных сферах
человеческой деятельности и имеет множество смысловых значений. Мы
будем рассматривать только такие „модели”, которые являются инстру¬
ментами получения знаний.
Модель — это такой материальный или мысленно представляемый
объект, который в процессе исследования замещает объект-оригинал
так, что его непосредственное изучение дает новые знания об объекте-
оригинале.
Под моделированием понимается процесс построения, изучения и
применения моделей. Оно тесно связано с такими гносеологическими
категориями, как абстракция, аналогия, гипотеза и др. Процесс модели¬
рования обязательно включает и построение абстракций, и умозаключе¬
ния по аналогии, и конструирование научных гипотез. Поэтому естест¬
венно задать вопрос: является ли моделирование особым методом науч¬
ного познания, не является ли оно синонимом процесса теоретического
исследования или процесса познавательной деятельности вообще?
16
Главная особенность моделирования в том, что это метод опосредо¬
ванного познания с помощью объектов-заместителей. Модель выступает
как своеобразный инструмент познания, который исследователь ставит
между собой и объектом и с помощью которого изучает интересующий
его объект. Именно эта особенность метода моделирования определяет
специфические формы использования абстракций, аналогий, гипотез,
других категорий и методов познания.
Необходимость использования метода моделирования определяется
тем, что многие объекты (или проблемы, относящиеся к этим объектам)
непосредственно исследовать или вовсе невозможно (когда объект
недосягаем, как, например, ядро Земли и глубины Вселенной, либо еще
реально не существует: будущее состояние экономики, будущие потреб¬
ности общества и т.п.), или же это исследование требует много времени
и средств.
Процесс моделирования включает три элемента: 1) субъект (иссле¬
дователь), 2) объект исследования, 3) модель, опосредствующую отно¬
шения познающего субъекта и познаваемого объекта. Сущность процесса
моделирования схематически отображена на рис. 1.1.
Пусть имеется или необходимо создать некоторый объект А. Мы
конструируем (материально или мысленно) или находим в реальном ми¬
ре другой объект В — модель объекта А. Этап построения модели предпо¬
лагает наличие некоторых знаний об объекте-оригинале. Познаватель¬
ные возможности модели обусловливаются тем, что модель отображает
(воспроизводит, имитирует) какие-либо существенные черты объекта-
оригинала. Вопрос о необходимой и достаточной мере сходства оригина¬
ла и модели требует конкретного анализа. Очевидно, модель утрачивает
17
свой смысл как в случае тождества с оригиналом (тогда она перестает
быть моделью), так и в случае чрезмерного во всех существенных отноЛ
шениях отличия от оригинала.
Таким образом, изучение одних сторон моделируемого объекта осу¬
ществляется ценой отказа от отражения других сторон. Поэтому любая
модель замещает оригинал лишь в строго ограниченном смысле. Из этого
следует, что для одного объекта может быть построено несколько „спе¬
циализированных” моделей, концентрирующих внимание на определен¬
ных сторонах исследуемого объекта или же характеризующих объект с
разной степенью детализации.
На втором этапе процесса моделирования модель выступает как
самостоятельный объект исследования. Одной из форм такого исследо¬
вания является проведение „модельных” экспериментов, при которых
сознательно изменяются условия функционирования модели и система¬
тизируются данные о ее „поведении”. Конечным результатом этого этапа
является множество (совокупность) знаний о модели R.
На третьем этапе осуществляется перенос знаний с модели на
оригинал — формирование множества знаний S об объекте. Этот процесс
переноса знаний проводится по определенным правилам. Знания о
модели должны быть скорректированы с учетом тех свойств объекта-
оригинала, которые не нашли отражения или были изменены при постро¬
ении модели. Мы можем с достаточным основанием переносить какой-
либо результат с модели на оригинал, если этот результат необходимо
связан с признаками сходства оригинала и модели. Если же определен¬
ный результат модельного исследования связан с отличием модели от
оригинала (неадекватностью), то этот результат переносить неправо¬
мерно.
Четвертый этап — практическая проверка получаемых с помощью
моделей знаний и их использование для построения обобщающей теории
объекта, его преобразования или управления им. В итоге мы снова
возвращаемся к проблематике реального объекта.
Для понимания сущности моделирования важно не упускать из
виду, что моделирование — не единственный источник знаний об объекте.
Процесс Моделирования „погружен” в более общий процесс познания.
Это обстоятельство учитывается не только на этапе построения модели,
но и на завершающей стадии, когда происходит объединение и обобще¬
ние результатов исследования, получаемых на основе многообразных
средств познания.
Моделирование — циклический процесс. Это означает, что
за первым четырехэтапным циклом может последовать второй, третий
и т.д. При этом знания об исследуемом объекте расширяются и уточня¬
ются, а исходная модель постепенно совершенствуется. Недостатки, об¬
наруженные после первого цикла моделирования, обусловленные малым
знанием объекта и ошибками в построении модели, можно исправить
в последующих циклах. В методологии моделирования, таким образом,
заложены большие возможности саморазвития.
О формах моделирования. Метод моделирования может применять¬
ся для исследования объектов любой природы, и в свою очередь любой
объект в принципе может стать средством моделирования. При этом
18
природа выбранного объекта-модели оказывает большое влияние на
методику познавательного процесса.
Все множество моделей принято делить на два больших класса:
модели материальные (предметные) и модели идеальные
(мысленные) . Первые воплощены в каких-либо материальных объектах,
имеющих естественное или искусственное происхождение (отобранные
в природе или созданные человеком для целей исследования); вторые
являются продуктом человеческого мышления; операции с такими
моделями осуществляются в сознаний человека.
В классе материальных (предметных) моделей наиболее характерны
физические модели. Они представляют собой материальные
объекты той же природы, что и объект-оригинал. Подобие оригинала и
модели в данном случае заключается в подчинении одним и тем же
законам соответствующей области явлений. Физическое моделирование
особенно распространено в технических науках. В экономике физиче¬
скому моделированию близко соответствует понятие реального (полево¬
го) экономического эксперимента, хотя здесь аналогия
далеко не полная. Например, результаты экспериментирования на одном
предприятии (системы учета, планирования, оплаты труда, хозрасчета)
переносятся на всю отрасль, т.е. совокупность объектов близкой эконо¬
мической природы. Но в экономике возможности физического модели¬
рования (экспериментирования на реальных объектах) принципиально
ограничены. Это объясняется целым рядом причин: изучение отдельных
частей народного хозяйства не может дать полного и правильного пред¬
ставления об экономической системе в целом, трудно элиминировать
внешние воздействия на экономический объект. Наконец, проведение
крупных реальных экспериментов требует больших затрат (ресурсов и
времени) и связано с существенным риском.
Класс идеальных (мысленных) моделей объединяет довольно разно¬
образные модели, различающиеся прежде всего по степени формализа¬
ции действительности. В научном познании основным видом идеальных
моделей являются знаковые модели, использующие определен¬
ный формализованный язык. В свою очередь важнейшим видом знако¬
вых моделей являются логико-математические модели,
которые выражаются на языке математики и логики.
Математическое моделирование в широком смысле — метод иссле¬
дования, основанный на аналогии процессов и явлений, различных по
своей природе, но описываемых одинаковыми математическими зависи¬
мостями. В современной научно-технической творческой деятельности
математическое моделирование является, безусловно, важнейшей
формой моделирования, а в экономических исследованиях и практике
планирования и управления — доминирующей формой1. Математиче¬
ское моделирование есть выражение универсального процесса математи¬
зации научного знания. На новом этапе своего развития математическое
моделирование тесно связано с компьютеризацией.
1 В группе математических моделей можно выделять предметно-ма¬
тематические модели, являющиеся вычислительными устройствами
(специализированными или универсальными), реализующими логико-математи¬
ческие модели (см. ММСЭ, с. 35-37).
19
Математическое моделирование полностью укладывается в рассмот¬
ренную выше общую схему процесса моделирования. С развитием
математики, электронной вычислительной техники, общеметодологи¬
ческих и предметных наук разнообразие математических моделей не¬
прерывно возрастает, рождаются все новые формы математического
моделирования.
Математическая модель объекта (процесса, явления) как опреде¬
ленная математическая задача („модель-задача”) включает как минимум
две группы элементов: 1) характеристики объекта, которые нужно оп¬
ределить (неизвестные величины), - компоненты вектора У = (у[)\
2) характеристики внешних (по отношению к моделируемому объекту)
изменяющихся условий — компоненты вектораХ =(xjj. „Модель-задача”
может включать также совокупность внутренних параметров объекта
А. Условия и параметры, описываемые X и А, рассматриваются как
экзогенные (т.е. определяемые вне модели) , а величины, состав¬
ляющие вектор У, — как эндогенные (т.е. определяемые с по¬
мощью модели).
Математическую модель можно интерпретировать как особый пре¬
образователь внешних условий объекта („входа”) X в искомые характе¬
ристики объекта („выхода”) У. По способам выражения соотношений
между внешними условиями, внутренними параметрами и искомыми
характеристиками математические модели делятся на два основных
типа: функциональные и структурные.
Основная идея функциональных (или кибернетических) моделей —
познание сущности объекта через важнейшие проявления этой сущности:
деятельность, функционирование, поведение. Внутренняя структура при
этом не изучается, а информация о структуре не используется. Образом
объекта, изучаемого посредством функциональной модели, является
„черный ящик” — объект, внутренняя структура которого совершенно не
видна. Функциональная модель имитирует поведение объекта так, что,
задавая значения „входа” X, можно получать значения „выхода” У (без
участия информации об А). Построить функциональную модель — это
отыскать оператор Z), связывающий. X и У:
У = D (X). (1.1)
Структурные модели отражают внутреннюю организацию объекта:
его составные части, внутренние параметры, их связи с „входом” и
„выходом” и т.д. Наиболее распространены два вида структурной
модели :
а) все неизвестные выражаются в^виде функций от внешних условий
и внутренних параметров ^
yj=ff(A, X), / GJ; (1.2)
б) неизвестные определяются совместно на основе системы соотно¬
шений /-го вида (уравнений, неравенств и т.д.) :
4>i(A,X, Y) = 0,iel. 0-3)
20
Очевидно, что получить решение в виде соотношения (1.2) заманчи¬
во и с практической точки зрения (простота расчетов по формулам),
и главным образом для создания наглядной теории соответствующей
области явлений. Однако для многих математических задач решения не
могут быть выражены в формульном, аналитическом виде1. Для реше¬
ния задачи (1.3), не сводящейся к задаче (1.2), требуется найти
алгоритм2. Однако анализ такой задачи может не только давать
алгоритм для нахождения частных решений (для заданной совокупности
внешних и внутренних параметров), но и обнаруживать общие (качест¬
венные) свойства решений, не зависящие от конкретных значений пара¬
метров.
Функциональные и структурные модели дополняют друг друга. С
одной стороны, при изучении функциональных моделей возникают ги¬
потезы о внутренней структуре объекта, объясняющей его функциони¬
рование, и тем самым открывается путь для структурного моделиро¬
вания. С другой стороны, анализ структурных моделей дает ценную
информацию о том, как объект реагирует на изменение внешних
условий.
Появление ЭВМ третьего—четвертого поколений с широко развитыми
возможностями человеко-машинного диалога внесло новое качество в
методологию математического моделирования. ЭВМ перестала быть
только средством выполнения расчетов по уже построенным моделям и
алгоритмам („большим арифмометром”). Новое направление исследо¬
ваний, в которых ЭВМ играет важную роль в самом процессе построения
модели и проведении модельных экспериментов, получило название
имитационного моделирования, а соответствующие
модели — наименование имитационных.
Общепринятой трактовки термина „имитационное моделирование” и соответ¬
ствующего ему английского термина „simulation” пока не существует. Трудно
также провести четкую границу между имитационными моделями и моделями,
которые неправомерно трактовать как имитационные независимо от режима их
использования.
Большинство определений имитационных моделей сходятся в том, что под¬
черкивают такие признаки, как постоянное взаимодействие человека и ЭВМ,
достаточно точное воспроизведение механизма функционирования объекта, первич¬
ность моделирующего алгоритма по отношению к модели, проведение модельных
экспериментов.
Более широкое понятие „имитационная система” обычно объединяет использо¬
вание разнообразных типов моделей, но обязательно в режиме активного человеко-
машинного диалога с соответствующим программным обеспечением. Близким по
смыслу является понятие „модельно-программный комплекс”.
1 Например, решения алгебраических уравнений пятой и более высоких степе¬
ней не могут быть выражены формулой; многие дифференциальные уравнения
не имеют решений, которые можно было бы выразить в „конечном” виде через
аналитические функции, алгебраические операции и операции интегрирования.
Вычисление по формуле представляет собой частный случай алгоритма
(формульный алгоритм). Но не каждый алгоритм можно выразить в виде
формулы.
21
1.2. Особенности применения метода
математического моделирования в экономике
Проникновение математики в экономическую науку связано с преодо¬
лением значительных трудностей. В этом отчасти была „повинна” мате¬
матика, развивающаяся на протяжении нескольких веков в основном в
связи с потребностями физики и техники. Но главные причины лежат
все же в природе экономических процессов, в специфике экономической
науки.
Сложность экономических процессов и явлений. Большинство объ¬
ектов, изучаемых экономической наукой, может быть охарактеризовано
кибернетическим понятием сложная система.
Наиболее распространено понимание системы как совокупности
элементов, находящихся во взаимодействии и образующих некоторую
целостность, единство. Важным качеством любой системы является
эмерджентность - наличие таких свойств, которые не присущи
ни одному из элементов, входящих в систему. Поэтому при изучении
систем недостаточно (а иногда и невозможно) пользоваться методом их
расчленения на элементы с последующим изучением этих элементов в
отдельности. Одна из трудностей экономических исследований — в том,
что почти не существует экономических объектов, которые можно было
бы рассматривать как отдельные (внесистемные) элементы.
Сложность системы определяется количеством входящих в нее
элементов, связями между этими элементами, а также взаимоотношени¬
ями между системой и средой. Экономика страны обладает всеми приз¬
наками очень сложных систем. Она объединяет огромное число элемен¬
тов, отличается многообразием внутренних связей и связей с другими
системами (природная среда, экономика других стран и т.д.). В народ¬
ном хозяйстве взаимодействуют природные, технологические, соци¬
альные процессы, объективные и субъективные факторы.
Задачей экономической науки в социалистическом обществе явля¬
ется не только познание (объяснение) объективных экономических
законов, но и разработка методов преобразования экономики посред¬
ством сознательного управления ее развитием. Поэтому экономическая
теория (включающая методологию планирования и управления) явля¬
ется, с одной стороны, отображением объективных свойств реальной
экономической системы социализма, а с другой стороны — орудием
ее сознательного преобразования. Экономическое развитие целенаправ¬
ленно, однако цели этого развития непрерывно конкретизируются и мо¬
дифицируются под влиянием изменений объективных социально-эконо¬
мических условий.
Сложность экономики иногда рассматривалась как обоснование
невозможности ее моделирования, изучения средствами математики.
Но такая точка зрения в принципе неверна. Моделировать можно объект
любой природы и любой сложности (тезис о принципиальной невозмож¬
22
ности моделирования объекта равносилен утверждению о его принципи¬
альной непознаваемости). И как раз сложные объекты представляют
наибольший интерес для моделирования; именно здесь моделирование
может дать результаты, которые нельзя получить другими способами
исследования.
Потенциальная возможность математического моделирования
любых экономических объектов и процессов не означает, разумеется,
ее успешной осуществимости при данном уровне экономических и мате¬
матических знаний, имеющейся конкретной информации и вычислитель¬
ной технике. И хотя нельзя указать абсолютные границы математиче¬
ской формализуемости экономических проблем, всегда будут
существовать еще неформализованные проблемы, а также ситуации, где
математическое моделирование недостаточно эффективно.
Особенности экономических наблюдений м измерений. Уже длитель¬
ное время главным тормозом практического применения математиче¬
ского моделирования в экономике является наполнение разработанных
моделей конкретной и качественной информацией. Точность и полнота
первичной информации, реальные возможности ее сбора и обработки во
многом определяют выбор типов прикладных моделей. С другой
стороны, исследования по моделированию социалистической экономики
выдвигают новые требования к системе информации.
В зависимости от моделируемых объектов и назначения моделей
используемая в них исходная информация имеет существенно различный
характер и происхождение. Она может быть разделена на две категории:
о прошлом развитии и современном состоянии объектов (экономичес¬
кие наблюдения и их обработка) и о будущем развитии объектов,
включающую данные об ожидаемых изменениях их внутренних пара¬
метров и внешних условий (прогнозы). Вторая категория информации
является результатом самостоятельных исследований, которые также
могут выполняться посредством моделирования.
Методы экономических наблюдений и использования результатов
этих наблюдений разрабатываются экономической статисти¬
кой. Поэтому отметим только специфические проблемы экономиче¬
ских наблюдений, связанные с моделированием экономических процес¬
сов.
В экономике многие процессы являются массовыми; они
характеризуются закономерностями, которые не обнаруживаются на
основании лишь одного или нескольких наблюдений. Поэтому модели¬
рование в экономике должно опираться на массовые наблюдения.
Другая проблема порождается динамичностью экономиче¬
ских процессов, изменчивостью их параметров и структурных отноше¬
ний. Вследствие этого экономические процессы приходится постоянно
держать под наблюдением, необходимо иметь устойчивый поток новых
данных. Поскольку наблюдения за экономическими процессами и об¬
работка эмпирических данных обычно занимают довольно много време¬
23
ни, то при построении математических моделей экономики требуется
корректировать исходную информацию с учетом ее запаздывания.
Познание количественных отношений экономических процессов и
явлений опирается на экономические измерения. Точность
измерений в значительной степени предопределяет и точность конечных
результатов количественного анализа посредством моделирования.
Поэтому необходимым условием эффективного использования матема¬
тического моделирования является совершенствование экономических
измерителей. Применение математического моделирования заострило
проблему измерений и количественных сопоставлений различных ас¬
пектов и явлений социально-экономического развития, достоверности
и полноты получаемых данных, их защиты от намеренных и технических
искажений.
В.И .Ленин отмечал, что для успешного применения математики
наука должна дойти до такой ступени, на которой ей удается выделить
достаточно однородные и простые элементы, могущие быть сделанными
объектом счета. В экономике эта задача существенно затруднена. Здесь
практически нет полностью однородных элементов (одинаковых пред¬
приятий, одинаковых по своим потребностям и вкусам потребителей
и т.д.), и установление относительной однородности (по некоторым
признакам) требует серьезного исследования.
В процессе моделирования, особенно на народнохозяйственном
уровне, возникает взаимодействие „первичных” и „вторичных” эконо¬
мических измерителей. Любая модель народного хозяйства опирается
на определенную систему экономических измерителей (продукции,
ресурсов, элементов и т.д.) . В то же время одним из важных результатов
народнохозяйственного моделирования является получение новых
(вторичных) экономических измерителей — экономически обоснован¬
ных цен на продукцию различных отраслей, оценок эффективности
разнокачестренных природных ресурсов, измерителей общественной
полезности продукции. Однако эти измерители могут испытывать влия¬
ние недостаточно обоснованных первичных измерителей, что вынуждает
разрабатывать особую методику корректировки первичных измерителей
для народнохозяйственных моделей.
С точки зрения „интересов” моделирования экономики в настоящее
время наиболее актуальными проблемами совершенствования экономи¬
ческих измерителей являются: оценка результатов интеллектуальной
деятельности (особенно в сфере научно-технических разработок, инду^
стрии информатики), построение обобщающих показателей социально-
экономического развития (используемых в макромоделях), измерение
эффектов обратных связей (влияния хозяйственных и социальных ме¬
ханизмов на эффективность производства).
Случайность и неопределенность в экономическом развитии. Диа¬
лектический детерминизм утверждает объективный характер причини
ности экономического развития, но не отождествляет полностью при¬
24
чинность с необходимостью и не отрицает роли случайности. В плановом
социалистическом хозяйстве важнейшие экономические процессы пере¬
стают быть стихийными, но сохраняют характер массовых процессов,
обязательно включающих случайные (стохастические) компоненты.
Непредвидимые случайности могут быть вызваны природными явления¬
ми, изменениями в международной обстановке, научно-техническими
открытиями, различными субъективными факторами. Таким образом,
экономические закономерности имеют стохастический характер
Такое понимание детерминизма противостоит как индетерминизму,
отрицающему объективный характер причинности и абсолютизирующе¬
му действие случайности, так и механистическому детерминизму, в соот¬
ветствии с которым реальные экономические связи должны рассматри¬
ваться как строго однозначные, а будущее развитие — как полностью
предопределенное.
Для методологии планирования социалистической экономики важ¬
ное значение имеет понятие неопределенности экономиче¬
ского развития. В исследованиях по экономическому прогнозированию
и планированию различают два типа неопределенности: „истинную”,
обусловленную свойствами экономических процессов, и информа¬
ционную”, связанную с неполнотой и неточностью имеющейся информа¬
ции об этих процессах. Истинную неопределенность нельзя смешивать
с объективным существованием различных вариантов экономического
развития и возможностью сознательного выбора среди них эффективных
вариантов. Речь идет о принципиальной невозможности точного выбора
единственного (оптимального) варианта.
В развитии социалистического хозяйства неопределенность вызыва¬
ется двумя основными причинами. Во-первых, ход планируемых и
управляемых процессов, а также внешние воздействия на эти процессы
не могут быть точно предсказуемы из-за действия случайных факторов и
ограниченности человеческого познания в каждый данный момент.
Особенно характерно это для прогнозирования научно-технического
прогресса, потребностей общества, экономического поведения. Во-
вторых, общегосударственное планирование и управление не только не
всеобъемлющи, но и не всесильны, а наличие множества относительно
самостоятельных экономических субъектов с особыми интересами не
позволяет точно предвидеть результаты их взаимодействий. Неполнота
и неточность информации об объективных процессах и экономическом
поведении усиливают^тинную неопределенность.
На первых этапах исследований по моделированию социалистичес¬
кой экономики применялись в основном модели жестко детерминистс¬
кого типа. В этих моделях все параметры (например, коэффициенты и
свободные члены уравнений) предполагаются точно известными. Однако
детерминистские модели неправильно понимать в механистическом духе
и отождествлять их с моделями, которые лишены всех „степеней
свободы” (возможностей выбора) и имеют единственное допустимое
25
решение. Классическим представителем жестко детерминистских
моделей является оптимизационная модель народного хозяйства, приме¬
няемая для определения наилучшего варианта экономического развития
среди множества допустимых вариантов.
В результате накопления опыта использования жестко детерминист¬
ских моделей были созданы реальные возможности успешного при¬
менения более совершенной методологии моделирования экономиче¬
ских процессов, учитывающей стохастику и неопределенность. Здесь
можно выделить два основных направления исследований. Во-первых,
усовершенствуется методика использования моделей жестко детермини¬
стского типа: проведение многовариантных расчетов и модельных эк¬
спериментов с вариацией конструкции модели и ее исходных данных;
изучение устойчивости и надежности получаемых решений, выделение
зоны неопределенности; включение в модель резервов, применение
приемов, повышающих приспособляемость (адаптивность) экономичен
ских решений к вероятным и непредвидимым ситуациям. Во-вторых,
получают распространение модели, непосредственно отражающие сто¬
хастику и неопределенность экономических процессов и использующие
соответствующий математический аппарат: теорию вероятностей и мате¬
матическую статистику, теорию игр и статистических решений, теорию
массового обслуживания, стохастическое программирование, теорию |
случайных процессов.
Проверка адекватности моделей. Сложность экономических процес¬
сов и явлений и другие отмеченные выше особенности экономических
систем затрудняют не только построение математических моделей, но и
проверку их адекватности, истинности получаемых результатов. (В
теории моделирования часто используется понятие „верификация”.)
Марксистско-ленинская философия учит, что критерием истинно¬
сти познания в конечном счете является практика. Однако само понятие
„практика” может трактоваться неоднозначно. Его содержание сущест¬
венно обогащается при переходе от анализа естественных явлений (не
зависящих от воли людей) к общественным явлениям, протекающим
под влиянием сознательной деятельности.
В естественных науках достаточным (но не всегда необходимым)
условием истинности результатов моделирования и любых других
форм познания является совпадение результатов исследования с наблю¬
даемыми фактами1. Категория „практика” совпадает здесь с категорией
„действительность”. В экономике и других общественных науках
понимаемый таким образом принцип „практика - критерий истины”
в большей степени применим к простым дескриптивным моде¬
лям, используемым для пассивного описания и объяснения действи¬
тельности (анализа прошлого развития, краткосрочного прогнозирова¬
ния неуправляемых экономических процессов и т.п.) .
1 Трудности проверки законов существуют и в естественных науках. Это отно¬
сится, например, к первому закону Ньютона (см. комментарий в [3. С. 31-32]).
26
Однако в социалистическом обществе главная задача экономиче¬
ской науки конструктивна: разработка научных методов планирования
и управления экономикой. Поэтому распространенный тип математи¬
ческих моделей социалистической экономики — это модели управля¬
емых и регулируемых экономических процессов, используемые для
преобразования экономической действительности. Такие модели назы¬
ваются нормативными. Если ориентировать нормативные
модели только на подтверждение действительности, то они не смогут
служить инструментом решения качественно новых социально-экономи¬
ческих задач.
Специфика верификации нормативных моделей экономики состоит
в том, что они, как правило, „конкурируют” с другими, уже нашед¬
шими практическое применение методами планирования и управления.
При этом далеко не всегда можно поставить чистый эксперимент по
верификации модели, устранив влияние других управляющих воздей¬
ствий на моделируемый объект.
Допустим, предложена новая модель для расчета годового народнохозяйст¬
венного плана. Для проверки ее правильности можно было бы поставить такой
эксперимент: составить план по модели и через год сравнить итоги развития народ¬
ного хозяйства с прогнозом по нашей модели и с утвержденным государственным
планом. Что может дать такой эксперимент? Даже если наша модель очень совер¬
шенна, а план был составлен далеко не лучшим образом, итоги экономического
развития страны будут, по-видимому, ближе к утвержденному народнохозяйствен¬
ному плану, чем к прогнозу по модели. Это объясняется тем, что государственный
план включает директивные задания и их ресурсное обеспечение, опирается на сис¬
тему контроля за выполнением плановых заданий и экономический механизм,
стимулирующий выполнение плана и регулирующий явления, непосредственно
не охватываемые планированием.
Ситуация еще более усложняется, когда ставится вопрос о верифи¬
кации моделей долгосрочного прогнозирования и планирования (как
дескриптивных, так и нормативных). Ведь нельзя же 10—15 лет и более
пассивно ожидать наступления событий, чтобы проверить правильность
предпосылок модели.
Несмотря на отмеченные усложняющие обстоятельства, соответствие
модели фактам и тенденциям реальной экономической жизни остается
важнейшим критерием, определяющим направления совершенствова¬
ния моделей. Всесторонний анализ выявляемых расхождений между
действительностью и моделью, сопоставление результатов по модели с
результатами, полученными иными методами, помогают выработать пути
коррекции моделей.
Значительная роль в проверке моделей принадлежит логическо¬
му анализу, в том числе средствам самого математического моде¬
лирования. Такие формализованные приемы верификации моделей,
как доказательство существования решения в модели, проверка истин¬
ности статистических гипотез о связях между параметрами и переменны¬
ми модели, сопоставления размерностей величин и т.д., позволяют сузить
класс потенциально „правильных” моделей.
27
Внутренняя непротиворечивость предпосылок модели проверяется
также путем сравнения друг с другом получаемых с ее помощью след¬
ствий, а также со следствиями „конкурирующих” моделей.
Оценивая современное состояние проблемы адекватности матема¬
тических моделей социалистической экономике, следует признать, что
создание конструктивной комплексной методики верификации моделей,
учитывающей как объективные особенности моделируемых объектов,
так и особенности их познания, по-прежнему является одной из наиболее
актуальных задач экономико-математических исследований.
1.3. Классификация экономико-математических моделей
Математические модели экономических процессов и явлений более крат¬
ко можно назвать экономико-математическими моделями. Для класси¬
фикации этих моделей используются разные основания.
По целевому назначению экономико-математические модели делят¬
ся на теоретико-аналитические, используемые в исследова¬
ниях общих свойств и закономерностей экономических процессов, и
прикладные, применяемые в решении конкретных экономических
задач (модели экономического анализа, прогнозирования, управления) .
Экономико-математические модели могут предназначаться для ис¬
следования разных сторон народного хозяйства (в частности, его произ¬
водственно-технологической, социальной, территориальной структур)
и его отдельных частей. При классификации моделей по исследуемым
экономическим процессам и содержательной проблематике можно выде¬
лить модели народного хозяйства в целом и его отдельных подсистем —
отраслей, регионов и т.д., комплексы моделей производства, потребле¬
ния, формирования и распределения доходов, трудовых ресурсов, цено¬
образования, финансовых связей и т.д.
Остановимся более подробно на характеристике таких классов
экономико-математических моделей, с которыми связаны наибольшие
особенности методологии и техники моделирования.
В соответствии с общей классификацией математических моделей
(см. 1.1) они подразделяются на функциональные и струк¬
турные, а также включают промежуточные формы (структурно¬
функциональные) . В исследованиях на народнохозяйственном уровне
чаще применяются структурные (и структурно-функциональные) моде¬
ли, поскольку для планирования и управления большое значение имеют
взаимосвязи подсистем (однако и здесь есть немало исключений, напри¬
мер, макроэкономическая производственная функция). Типичными
структурными моделями являются модели межотраслевых связей (см.
гл. 7—9, 11, 13) . Функциональные модели широко применяются в эконо¬
мическом регулировании, когда на поведение объекта („выход”) воз¬
действуют путем изменения „входа”. Примером может служить модель
28
поведения потребителей в условиях товарно-денежных отношений.
Один и тот же объект может описываться одновременно и структурной,
и функциональной моделью. Так, например, для планирования отдельной
отраслевой системы используется структурная модель, а на народнохо¬
зяйственном уровне каждая отрасль может быть представлена функ¬
циональной моделью, например „функцией отклика”.
В 1.2 уже показывались различия между моделями дескриптивными
и нормативными. Дескриптивные модели отвечают на вопрос: как это
происходит? или как это вероятнее всего может дальше развиваться?,
т.е. они только объясняют наблюдаемые факты или дают вероятностный
прогноз. Нормативные модели отвечают на вопрос: как это должно
быть?, т.е. предполагают целенаправленную деятельность. Социалистиче¬
ская система хозяйства объективно требует активного вмешательства
в течение экономических процессов - это и определяет ведущую роль
нормативных моделей. Типичным примером нормативных моделей
являются модели оптимального планирования, формализующие тем или
иным способом цели экономического развития, возможности и средства
их достижения (см. гл. 2, 8, 10,11, 13).
Применение дескриптивного подхода в моделировании социалисти¬
ческой экономики объясняется необходимостью эмпирического выявле¬
ния различных зависимостей в экономике, установления статистических
закономерностей экономического поведения социальных групп,
изучения вероятных путей развития каких-либо процессов при неизменя-
ющихся условиях или протекающих без внешних воздействий, Примера¬
ми дескриптивных моделей являются производственные функции и
функции покупательского спроса, построенные на основе обработки ста¬
тистических данных (см. гл. 4, 5, 9, 10).
Является ли экономико-математическая модель дескриптивной или
нормативной, зависит не только от ее математической структуры, но и от
характера использования этой модели. Например, модель межотраслево¬
го баланса дескриптивна, если она используется для анализа пропорций
прошлого периода или же для экстраполяционного прогноза. Но эта же
математическая модель становится нормативной, когда она применяется
для расчетов сбалансированных вариантов развития народного хозяй¬
ства, удовлетворяющих конечные потребности общества при плановых
нормативах (коэффициентах) производственных затрат.
Многие экономико-математические модели (особенно на народно¬
хозяйственном уровне) сочетают признаки дескриптивных и норматив¬
ных моделей. Типична ситуация, когда нормативная модель сложной
структуры объединяет отдельные блоки, которые являются частными
дескриптивными моделями. Например, межотраслевая модель (балан¬
совая или оптимизационная) может включать функции покупатель¬
ского спроса, описывающие поведение потребителей при изменении
доходов. Подобные примеры характеризуют тенденцию эффективного
сочетания дескриптивного и нормативного подходов к моделированию
29
экономических процессов. Дескриптивный подход широко применяется
в имитационном моделировании.
По характеру отражения причинно-следственных связей различают
модели жестко детерминистские и модели, учитывающие
случайность и неопределенность1. Необходимо разли¬
чать неопределенность, описываемую вероятностными законами, и не¬
определенность, для описания которой законы теории вероятностей
неприменимы. Второй тип неопределенности гораздо более сложен
для моделирования (см. гл. 2) .
По способам отражения фактора времени экономико-математичес¬
кие модели делятся на статические и динамические. В
статических моделях все зависимости относятся к одному моменту или
периоду времени (например, году). Динамические модели характеризу¬
ют изменения экономических процессов во времени. По длительности
рассматриваемого периода времени различаются модели краткосрочного
(до года), среднесрочного (до 5 лет), долгосрочного (10—15 и более
лет) прогнозирования и планирования. Само время в экономико-мате¬
матических моделях может изменяться либо непрерывно, либо дискрет¬
но (например, с шагом в один год) .
Модели экономических процессов чрезвычайно разнообразны по
форме математических зависимостей. Особенно важно выделить класс
линейных моделей, наиболее удобных для анализа и вычислений и
получивших вследствие этого большое распространение. Различия между
линейными и нелинейными моделями существенны не только с матема¬
тической точки зрения, но и в теоретико-экономическом отношении,
поскольку многие зависимости в экономике носят принципиально нели¬
нейный характер: эффективность использования ресурсов при увеличе¬
нии производства, изменение спроса и потребления населения при росте
доходов и т.п. Теория „линейной экономики” существенно отличается от
теории „нелинейной экономики”. От того, предполагаются ли множества
производственных возможностей подсистем (отраслей, предприятий)
выпуклыми или же невыпуклыми, существенно зависят выводы о воз¬
можности сочетания централизованного планирования и хозяйственной
самостоятельности экономических подсистем.
По соотношению экзогенных и эндогенных переменных, включае¬
мых в модели, они могут разделяться на открытые и закры¬
тые. Полностью открытых моделей не существует; модель должна
содержать хотя бы одну эндогенную переменную. Полностью закрытые
1 Применяемое часто деление экономико-математических моделей на детер¬
министские и вероятностные не совсем точно, оно расходится с терминологией,
принятой в марксистско-ленинской философии: во-первых, не следует противо¬
поставлять детерминистский и вероятностный подходы, ибо последний находится
в рамках детерминизма, во-вторых, неверно отождествлять вероятностность со
всеми проявлениями случайности и неопределенности. Более строго под вероят¬
ностными следует понимать модели, базирующиеся на теории вероятностей.
30
экономико-математические модели, т.е. не включающие экзогенных пе¬
ременных, исключительно редки; их построение требует полного абстра¬
гирования от „среды”, т.е. серьезного огрубления реальных экономиче¬
ских систем, всегда имеющих внешние связи. Подавляющее большинст¬
во экономико-математических моделей занимает промежуточное положе¬
ние и различаются по степени открытости (закрытости).
Для моделей народнохозяйственного уровня важно деление на
агрегированные и детализированные. В дальнейшем
для народнохозяйственных моделей с очень высокой степенью детализа¬
ции моделируемых процессов используется краткий термин „микро¬
модель”, а для агрегированных народнохозяйственных моделей —
термин „макромодель”1.
В зависимости от того, включают ли народнохозяйственные модели
пространственные (территориальные) факторы и условия или не включа¬
ют, различают модели пространственные и точечные.
Таким образом, общая классификация экономико-математических
моделей включает более десяти основных признаков. С развитием
экономико-математических исследований проблема классификации при¬
меняемых моделей усложняется. Наряду с появлением новых типов
моделей (особенно смешанных типов) и новых признаков их классифи¬
кации осуществляется процесс интеграции моделей разных типов в более
сложные модельные конструкции.
н.
.4. Этапы экономико-математического моделирования
Основные этапы процесса моделирования рассматривались в 1,1. В раз¬
личных отраслях знаний, в том числе и в экономике, они приобретают
свои специфические черты. Проанализируем последовательность и
содержание этапов одного цикла экономико-математического модели¬
рования.
1. Постановка экономической проблемы и ее качественный анализ.
Главное здесь — четко сформулировать сущность проблемы, принимае¬
мые допущения и те вопросы, на которые требуется получить ответы.
Этот этап включает выделение важнейших черт и свойств моделируемого
объекта и абстрагирование от второстепенных; изучение структуры объ¬
екта и основных зависимостей, связывающих его элементы; формулиро¬
вание гипотез (хотя бы предварительных), объясняющих поведение и
развитие объекта.
2. Построение математической модели. Это — этап формализации
экономической проблемы (ситуации) , выражения ее в виде конкретных
математических зависимостей и отношений (функций, уравнений, нера¬
1 Следует указать на довольно распространенное отождествление народнохо¬
зяйственных и макроэкономических моделей.
31
венств и т.п.). Обычно сначала определяется основная конструкция
(тип) математической модели, а затем уточняются детали этой кон¬
струкции (конкретный перечень переменных и параметров, форма
связей): Таким образом, построение модели подразделяется в свою
очередь на несколько стадий.
Неправильно полагать, что чем больше факторов учитывает модель,
тем она лучше „работает” и дает лучшие результаты. То же самое можно
сказать о таких характеристиках сложности модели, как используемые
формы математических зависимостей (линейные и нелинейные) , учет
факторов случайности и неопределенности и т.д. Излишняя сложность
и громоздкость модели затрудняют процесс исследования. Нужно учиты¬
вать не только реальные возможности информационного и математи¬
ческого обеспечения, но и сопоставлять затраты на моделирование с
получаемым эффектом (при возрастании сложности модели прирост
затрат может превысить прирост эффекта).
Одна из важных особенностей математических моделей ■'$- потенци¬
альная возможность их использования для решения разнокачест¬
венных проблем. Поэтому, даже сталкиваясь с новой экономиче¬
ской задачей, не нужно стремиться „изобретать” модель; вначале необ¬
ходимо попытаться применить для решения этой задачи уже известные
модели.
В процессе построения модели осуществляется взаимоприспособ-
ление двух систем научных знаний — экономических и математических.
Естественно стремиться к тому, чтобы получить модель, принадлежащую
хорошо изученному классу математических задач. Часто это удается
сделать путем некоторого упрощения исходных предпосылок модели, не
искажающего существенных черт моделируемого объекта. Однако воз¬
можна и такая ситуация, когда формализация экономической проблемы
приводит к неизвестной ранее математической структуре. Потребности
экономической науки и практики в середине XX в. способствовали раз¬
витию математического программирования, теории игр, функциональ¬
ного анализа, вычислительной математики. Вполне вероятно, что в
будущем развитие экономической науки станет важным стимулом для
создания новых разделов математики.
3. Математический анализ модели. Целью этого этапа является вы¬
яснение общих свойств модели. Здесь применяются чисто математические
приемы исследования. Наиболее важный момент — доказательство су¬
ществования решений в сформулированной модели (теорема существо¬
вания). Если удастся доказать, что математическая задача не имеет
решения, то необходимость в последующей работе по первоначальному
варианту модели отпадает; следует скорректировать либо постановку
экономической задачи, либо способы ее математической формализации.
При аналитическом исследовании модели выясняются такие вопросы,
как, например, единственно ли решение, какие переменные (неизвест¬
ные) могут входить в решение, каковы будут соотношения между ними,
32
в каких пределах и в зависимости от каких исходных условий они
изменяются, каковы тенденции их изменения (асимптотические свой¬
ства) и т.д. Аналитическое исследование модели по сравнению с эмпири¬
ческим (численным) имеет то преимущество, что получаемые выводы
сохраняют свою силу при различных конкретных значениях внешних
и внутренних параметров модели.
Знание общих (качественных) свойств модели имеет столь важное
значение, что часто ради доказательства подобных свойств исследова¬
тели сознательно идут на идеализацию первоначальной модели. И все же
модели сложных экономических объектов с большим трудом поддают¬
ся аналитическому исследованию. В тех случаях, когда аналитическими
методами не удается выяснить общих свойств модели, а упрощения
модели приводят к недопустимым результатам, переходят к численным
методам исследования.
4. Подготовка исходной информации. Моделирование предъявляет
жесткие требования к системе информации. В то же время реальные воз¬
можности получения информации ограничивают выбор моделей, пред¬
назначаемых для практического использования. При этом принимается
во внимание не только принципиальная возможность подготовки инфор¬
мации (за определенный срок), но и затраты на подготовку соответст¬
вующих информационных массивов. Эти затраты не должны превышать
эффект от использования дополнительной информации.
В процессе подготовки информации широко используются методы
теории вероятностей, теоретической и математической статистики (ор¬
ганизация выборочных обследований, оценка достоверности данных,
определение вероятных значений параметров и т.п.). При системном
экономико-математическом моделировании исходная информация, ис¬
пользуемая в одних моделях, является результатом функционирования
других моделей.
5. Численное решение. Этот этап включает разработку алгоритмов
для численного решения задачи, составление программ на ЭВМ и непо¬
средственное проведение расчетов. Трудности этого этапа обусловлены
прежде всего большой размерностью экономических задач, необходи¬
мостью обработки значительных массивов информации.
Обычно расчеты по экономико-математической модели носят мно¬
говариантный характер. Благодаря высокому быстродействию современ¬
ных ЭВМ удается проводить многочисленные „модельные” эксперимен¬
ты, изучая „поведение” модели при различных изменениях некоторых
условий. Исследование, проводимое численными методами, может су¬
щественно дополнить результаты аналитического исследования, а для
многих моделей оно является единственно осуществимым. Класс эконо¬
мических задач, которые можно решать численными методами, значи¬
тельно шире, чем класс задач, доступных аналитическому исследованию.
6. Анализ численных результатов и их применение. На этом заключи¬
тельном этапе цикла встает вопрос о правильности и полноте резуль¬
Зак. 2414 33
Условные обозначения-.
Последовательные связи этапов
* Возвратные связи этапов (корректировка)
Рис. 1.2. Связи этапов экономико-математического моделирова¬
ния
татов моделирования, о степени практической применимости по¬
следних.
Математические методы проверки могут выявлять некорректные
построения моделей (доказывается неразрешимость модели или не под¬
тверждаются принятые статистические гипотезы) и тем самым сужать
класс потенциально правильных моделей. Неформальный анализ теоре¬
тических выводов и численных результатов, получаемых посредством
модели, сопоставление их с имеющимися знаниями и фактами дейст¬
вительности также позволяют обнаруживать недостатки постановки
экономической задачи, сконструированной математической модели,
использовавшейся информации. На основе этих результатов определя¬
ются направления совершенствования модели, ее информационного и
математического обеспечения.
Взаимосвязи этапов. На рис. 1.2 изображены связи между этапами
одного цикла экономико-математического моделирования. Первые пять
этапов более дифференцированно характеризуют процесс экономико¬
математического моделирования, чем общая схема моделирования (см.
рис. 1.1) : этапы 1 и 2 соответствуют этапу I общей схемы, а этапы 3, 4,
5 — этапу 11 общей схемы. Наоборот, заключительный этап 6 включает
этапы III и IV общей схемы (перенос знаний о модели на объект-ориги-
нал, проверку и применение этих знаний) .
Обратим внимание на возвратные связи этапов, возникающие вслед¬
ствие хрго, что в процессе исследования обнаруживаются недостатки
предшествующих этапов моделирования.
Уже на этапе построения модели может выясниться, что постановка
задачи противоречива или приводит к слишком сложной математической
модели. В соответствии с этим исходная постановка задачи корректиру¬
34
ется. Далее математический анализ модели (этап 3) может показать, что
небольшая модификация постановки задачи или ее формализации дает
интересный аналитический результат.
Наиболее часто необходимость возврата к предшествующим этапам
моделирования возникает при подготовке исходной информации (этап
4). Может обнаружиться, что необходимая информация отсутствует
или же затраты на ее подготовку слишком велики. Тогда приходится
возвращаться к постановке задачи и ее формализации, изменяя их так,
чтобы приспособиться к имеющейся информации.
Поскольку экономико-математические задачи могут быть сложны
по своей структуре, иметь большую размерность, то часто случается, что
известные алгоритмы и программы для ЭВМ не позволяют решить задачу
в первоначальном виде. Если невозможно в короткий срок разработать
новые алгоритмы и программы, исходную постановку задачи и модель
упрощают: снимают и объединяют условия, уменьшают число факторов,
нелинейные соотношения заменяют линейными, усиливают детерминизм
модели и т.д.
Недостатки, которые не удается исправить на промежуточных этапах
моделирования, устраняются в последующих циклах. Но результаты
каждого цикла имеют и вполне самостоятельное значение. Начав иссле¬
дование с построения простой модели, можно быстро получить полезные
результаты, а затем перейти к созданию более совершенной модели,
дополняемой новыми условиями, включающей уточненные математиче¬
ские зависимости.
По мере развития и усложнения экономико-математического
моделирования его отдельные этапы обособляются в специализирован¬
ные области исследований, усиливаются различия между теоретико-ана-
литическими и прикладными моделями, происходит дифференциация
моделей по уровням абстракции и идеализации.
Теория математического анализа моделей экономики развилась в
особую ветвь современной математики — математическую
экономику. Модели, изучаемые в рамках математической эконо¬
мики, теряют непосредственную связь с экономической реальностью;
они имеют дело с исключительно идеализированными экономическими
объектами и ситуациями. При построении таких моделей главным прин¬
ципом является не столько приближение к реальности, сколько получе¬
ние возможно большего числа аналитических результатов посредством
математических доказательств. Ценность этих моделей для экономиче¬
ской теории и практики сострит в том, что они служат теоретической
базой для моделей прикладного типа (других уровней абстракции и
идеализации).
Довольно самостоятельными областями исследований становятся
подготовка и обработка экономической информации и разработка мате¬
матического обеспечения экономических задач (создание баз данных
и банков информации, программ автоматизированного построения
2* 35
моделей и программного сервиса для экономистов-пользователей).
На этапе практического использования моделей ведущую роль должны
играть специалисты в соответствующей области экономического анализа,
планирования, управления. Главным участком работы экономистов-
математиков (специалистов по экономической кибернетике) остается
постановка и формализация экономических задач и синтез процесса
экономико-математического моделирования.
1.5. Место математического моделирования
в экономической науке и экономической практике
Исследования по моделированию социалистической экономики под¬
разделяются на три основные группы: 1) теоретические (раз¬
работка проблем политэкономии социализма и теоретико-методологи¬
ческих проблем планирования и управления социалистической экономи¬
кой) ; 2) прикладные (решение практических задач планирования
и управления); 3) инструментальные (создание новых инстру¬
ментов для научной и практической деятельности экономистов, плано¬
виков, управленцев).
Математическое моделирование и развитие экономической теории.
Вопрос о роли математики и математического моделирования в раз¬
витии экономической теории в течение многих десятилетий являлся
предметом острых дискуссий, не прекращающихся и в настоящее время.
Можно выделить две крайние позиции по этому вопросу. С одной
стороны, это трактовка экономико-математического моделирования
как единственно возможного способа создания и углубления строгой
экономической теории. С другой стороны, отрицание каких-либо воз¬
можностей математического моделирования в достижении новых теоре¬
тических результатов.
Переоценка роли математики в теоретико-экономических исследо¬
ваниях была свойственна некоторым представителям математической
школы и политической экономии в XIX в. и идеологам эконометрики в
конце 20-х годов нынешнего столетия. Л.Валърас и У.Джевонс, напри¬
мер, утверждали, что политическая экономия есть наука математиче¬
ская, а ряд более современных экономистов-математиков характери¬
зовали экономическую теорию как систему выводов, сделанных из
математических моделей, или же настолько широко трактовали понятие
„модель”, что оно по существу отождествлялось с понятием „теория”.
Противоположная оценка возможностей математики в развитии
экономической теории, как правило, связана с превратными представле¬
ниями о самой сущности математики и математических методов иссле¬
дования. Так, довольно распространено мнение, что математика якобы
не может изучать качественную сторону явлений природы и общества.
На самом же деле предметом математики является как количествен¬
36
ный анализ отношений качества, так и качественный анализ количествен¬
ных отношений1. Эти черты современной математики находят отражение
в построении и использовании экономико-математических моделей.
Правильной оценке роли математики в теоретических исследованиях
мешают широко распространенные сравнения ее с жерновами, мясоруб¬
кой и другими чисто механическими системами. Отождествлять матема¬
тическое исследование с механической обработкой — это значит сущест¬
венно обеднять эвристические способности современной математики2.
Влияние математики и математического моделирования на экономи¬
ческую теорию носит многосторонний характер.
Внешне математизация экономической науки проявляется в измене¬
нии и обогащении языка последней. При этом дело отнюдь не сводит¬
ся к использованию математических символов и формул. Более важно,
что применение математического языка способствует уточнению многих
экономических категорий (понятий), лучшей систематизации теорети¬
ческих знаний.
Однако математика — это не только особый язык, который легко
переводится на другие языки. Сердцевину математики составляет сово¬
купность приемов математических доказательств — особая форма логи¬
ческих рассуждений. Математические доказательства, как правило, не¬
возможно выразить нематематическим языком, „переводу” поддаются
лишь исходные предположения и получаемые выводы. Очевидно, более
глубокая математизация любой науки (и в том числе экономической)
заключается в использовании самого математического мышления и
математической техники, а не только языка математики3 .
1 Современная математика содержит такие области, которые занимаются в
основном проблемами качественных отношений (теория множеств, алгебра,
топология, математическая логика, теория алгоритмов и др.) . Кроме того, проб¬
лемы качественного анализа присутствуют во всех традиционных „количествен¬
ных” областях математики (проблемы разрешимости, поведения семейства реше¬
ний, единственности, устойчивости и т.п.) .
2 Английскому философу, логику, экономисту Дж.СтМиллю (1806-1873)
и английскому естествоиспытателю Т.Г.Гексли (1825-1895) принадлежит аналогия
между математикой и мельничными жерновами. Так, Т.Г.Гексли говорил: „Матема¬
тика, подобно жернову, перемалывает то, что под него засыпают, и как, засыпав
лебеду, вы не получите муки, так, исписав целые страницы формулами, вы не
получите истины из ложных предпосылок” (цит. по кн.: Крылов А.Н. Мои воспо¬
минания. М.: Изд-во АН СССР, 1945. С. 111). Данная аналогия подчеркивает важ¬
ность правильных предпосылок для математического исследования. Однако она
упрощенно характеризует отличие математического результата от исходного науч¬
ного материала. Математическое доказательство более уместно сравнить, например,
с действием атомного реактора, изменяющего одновременно физико-химические
свойства, молекулярную и атомную структуру исходного вещества.
3 Математический язык в теоретико-экономическом исследовании может при¬
меняться как своего рода „строительные леса”. Когда сооружение научного „зда¬
ния” заканчивается, эти леса можно убрать. Но без предварительного возведения
лесов построить здание зачастую невозможно.
37
Известно, что основным методом математического исследования
является аксиоматический метод. Суть его состоит в сле¬
дующем. На первой стадии исследования формулируется система ак¬
сиом — исходных положений, принимаемых без доказательства. Далее на
основе аксиом проводится математическое рассуждение, в результате
которого получаются некоторые выводы (например, в виде теорем),
заключающие в себе новые знания. Ценность математического исследова¬
ния заключается как раз в том, чтобы из небольшого числа аксиом полу¬
чить возможно больше следствий. Этим аксиоматический метод привле¬
кателен для всех естественных и общественных наук, активно воздей¬
ствуя на формирование и обновление важнейших научных парадигм.
Некоторое представление о методологии получения новых теорети¬
ческих знаний на основе математического моделирования было дано в
1.4 (этапы 3 и 5). При этом выделялись два возможных методологиче¬
ских подхода: а) аналитическое исследование модели и б) обобщение
численных „модельных” экспериментов. Получаемые теоретические
результаты выражаются в виде общих (качественных) свойств решений
соответствующих моделей. Естественно, степень общности этих теорети¬
ческих результатов зависит от назначения и особенностей изучаемых
моделей. Многочисленные примеры получения теоретико-экономиче¬
ских результатов на основе анализа экономико-математических моде¬
лей обсуждаются в последующих главах книги.
Без теоретических знаний, полученных на основе экономико-матема¬
тического моделирования, невозможно себе представить современные
концепции народнохозяйственного оптимума, соизмерения затрат и ре¬
зультатов, экономического роста, согласования экономических инте¬
ресов, социально-экономической сбалансированности и т.д.
Вне математики сейчас нельзя даже сформулировать многие важные
экономические понятия и тем более исследовать закономерные связи
между этими понятиями. Ряд важных экономических показателей яв¬
ляется результатом экономической интерпретации абстрактных матема¬
тических понятий. Например, показатели эффективности производствен¬
ных ресурсов и полезных эффектов потребительских благ опираются на
понятия частных производных и множителей Лагранжа, коэффициенты
полных затрат продукции соответствуют элементам обратной матрицы,
определение траекторий максимального экономического роста связано с
понятиями собственных значений и собственных векторов и т.д. Матема¬
тический анализ моделей заставляет искать содержательные экономиче¬
ские аналогии тем или иным абстрактным математическим величинам и
отношениям, привлекает внимание исследователя к таким особенностям
реальных экономических процессов, которые приоткрываются благо¬
даря математической формализации.
Математическое моделирование интенсифицирует процесс теорети¬
ко-математического исследования. Расширяются границы мысленного
эксперимента, появляется возможность „проигрывать” на ЭВМ различ¬
38
ные теоретические гипотезы, изучая последствия их реализации (напри¬
мер, разные принципы ценообразования, финансирования, распределе¬
ния доходов). Математика настолько глубоко проникает в ткань эконо¬
мической науки, что нередко бывает сложно отделить экономические
знания от математических. Поэтому более правильно говорить даже не
просто о применении математики в экономической науке, а о процессе
взаимодействия экономической и математической наук, поднимающем
экономическую теорию на качественно новый уровень.
Однако при всех своих преимуществах и далеко не исчерпанных воз¬
можностях метод математического моделирования не вытесняет другие
методы развития экономической теории.
Критерии полноты и истинности теорий и характер применения мате¬
матических доказательств в чистой математике и в экономической науке
существенно различаются. В математике нет проблемы истинности акси¬
ом и результатов в смысле соответствия их объективной реальности.
Для достижения математических результатов достаточно, чтобы система
аксиом была полной и внутренне непротиворечивой. Поэтому для
математики могут быть одинаково приемлемы разные системы аксиом,
ведущие к разным выводам (например, геометрия Евклида и геометрия
Лобачевского - Римана); подтверждение же каких-либо выводов фак¬
тами не является доказательством в математическом смысле. Иное дело
в экономической науке. Аксиоматически построенная экономическая
теория обязательно должна найти подтверждение в экономической прак¬
тике. Если какие-либо исходные предпосылки экономико-математиче¬
ской модели неверны, то безупречное математическое доказательство
все равно даст ложные результаты. Не менее важно правильно интер¬
претировать результаты, полученные посредством математических до¬
казательств. Большую опасность представляют попытки использовать
строгие результаты за рамками тех предпосылок, при которых резуль¬
таты доказательны1.
Таким образом, начальный и конечный пункты экономико-матема¬
тического моделирования лежат вне математики. Поэтому безусловно
Еще одна особенность применения аксиоматического метода в экономике
связана с цикличностью процесса экономико-математического моделирования.
Как уже отмечалось, при моделировании не ограничиваются формулированием
единственной системы предпосылок для последующего математического анализа.
В рамках циклического процесса моделирования используется гипотетико-
дедуктивный метод, при котором первоначальные предпосылки высту¬
пают не как аксиомы (по определению не требующие доказательства), а как гипо¬
тезы, полезность которых проверяется на каждом цикле моделирования. При
этом математика не остается нейтральной к проверке предпосылок: с ее помощью
обнаруживается противоречивость предпосылок или их неполнота, что стимулирует
создание более совершенной системы предпосылок. Тождество между исходными
предпосылками модели и аксиомами сохраняется только в пределах одного цикла
моделирования. В этом смысле аксиоматический метод является частным случаем
гипотетико-дедуктивного.
39
необходимы другие средства познания, обеспечивающие выбор правиль¬
ных предпосылок и правильную экономическую интерпретацию форма¬
льных результатов. Чисто математическими средствами можно постро¬
ить формально-логическое ядро экономической теории, но не теорию в
целом.
Математическое моделирование экономических процессов — ком¬
плексный метод исследования, не ограничивающийся только примене¬
нием математики. Но и он не может претендовать на роль единственного
научного метода развития экономической теории, так как, во-первых, не
все стороны экономической жизни полностью формализуемы, а во-
вторых, в некоторых ситуациях математическое моделирование не явля¬
ется лучшим из доступных методов исследования. По-видимому, невоз¬
можно установить какие-либо жесткие границы эффективного исполь¬
зования математического моделирования в экономической теории.
Эти границы неизбежно изменяются по мере расширения и уточнения
экономических знаний, прогресса в области математики, кибернетики,
информатики. И поэтому правомерен вывод о том, что применение
математического моделирования является необходимым, но недоста¬
точным условием развития экономической теории. Отсюда вытекает
требование рационального сочетания различных методов теоретико¬
экономических исследований.
Роль прикладных экономико-математических исследований. Можно
выделить по крайней мере четыре аспекта применения математических
методов в решении практических экономических проблем.
1. Совершенствование системы экономической информации. Мате¬
матические методы позволяют упорядочить систему экономической ин¬
формации, выявлять недостатки в имеющейся информации и выраба¬
тывать требования для подготовки новой информации или ее коррек¬
тировки. Как уже отмечалось в 1.2,1.4, разработка и применение эконо¬
мико-математических моделей указывают пути совершенствования
экономической информации, ориентированной на решение определен¬
ной системы задач планирования и управления. Прогресс в информаци¬
онном обеспечении планирования и управления опирается на бурно
развивающиеся технические и программные средства информа¬
тики.
2. Интенсификация и повышение точности экономических расчетов.
Формализация экономических задач и применение /ЭВМ многократно
ускоряют типовые, массовые расчеты, повышают точность и сокращают
трудоемкость, позволяют проводить многовариантные экономические
обоснования сложных мероприятий, недоступные при господстве „руч¬
ной” технологии.
3. Углубление количественного анализа экономических проблем.
Благодаря применению метода моделирования значительно усиливаются
возможности конкретного количественного анализа: изучение взаимо¬
действия многих факторов, оказывающих влияние на экономические
40
процессы, количественная оценка последствий изменения условий
развития экономических объектов и т.п.
А. Решение принципиально новых экономических задач. Посредством
математического моделирования удается решать такие экономические
задачи, которые иными средствами решить практически невозможно,
например: нахождение оптимального варианта народнохозяйственного
плана (использование математического программирования), имитация
крупных народнохозяйственных мероприятий (модельные экспери¬
менты на ЭВМ), автоматизация контроля за функционированием слож¬
ных экономических объектов.
Сфера практического применения метода моделирования ограничи¬
вается возможностями и эффективностью формализации экономиче¬
ских проблем и ситуаций, а также состоянием информационного, мате¬
матического, технического обеспечения используемых моделей. Стрем¬
ление во что бы то ни стало применить математическую модель может
не дать хороших результатов из-за отсутствия хотя бы некоторых
необходимых условий.
В соответствии с современными научными представлениями системы
разработки и принятия хозяйственных решений должны сочетать
формальные и неформальные методы, взаимоусиливающие и взаимодо¬
полняющие друг друга. Формальные методы являются прежде всего
средством научно обоснованной подготовки материала для действий
человека в процессах управления. Это позволяет продуктивно исполь¬
зовать опыт и интуицию человека, его способности решать плохо фор¬
мализуемые задачи,
В последние десятилетия интенсивно разрабатываются и распро¬
страняются комплексные научные подходы, включающие применение
математического моделирования: системный анализ, тео¬
рия решений, программно-целевые методы и др,
В системном анализе принято делить все множество проблем на четыре группы:
1) стандартные; 2) хорошо структуризированные; 3) плохо структуризирован-
ные; 4) неструктуризированные. Проблемы первой группы, отличающиеся наи¬
большей ясностью, решаются при помощи стандартных приемов и алгоритмов
(примером могут служить задачи „прямого счета”). Вторая группа проблем в на¬
стоящее время является основным объектом применения экономико-математи-
ческого моделирования. Решение третьей группы проблем возможно путем сочета¬
ния формализованных и неформализованных методов и процедур. Наконец, четвер¬
тая группа проблем непосредственно не поддается строгому научному анализу;
это - область применения эмпирических и эвристических приемов. Развитие знаний
изменяет распределение проблем между указанными группами. Неструктуризиро¬
ванные проблемы могут превращаться в слабоструктуризированные, а те - в
хорошо структуризированные. По мере развития этого процесса возможности
применения математического моделирования расширяются.
Для перевода планового управления народным хозяйством на ка¬
чественно более высокий уровень недостаточно создания „хороших”
моделей экономических объектов и даже более универсальных методик
поиска планово-управленческих решений, включающих использование
41
экономико-математических моделей. Необходима глубокая перестройка
всей системы управления, включая ее методические, информационные,
технические, кадровые, организационно-правовые аспекты. Без такой
перестройки модели часто становятся чужеродными элементами,
вызывая реакцию отторжения.
Главный путь практического применения экономико-математичес¬
ких моделей — „встраивание” их в целостные автоматизированные тех¬
нологии управления. В сфере народнохозяйственного планирования
такой принципиально новой технологией является по замыслу автома¬
тизированная система плановых расчетов (АСПР) Госплана СССР и
Госпланов союзных республик.
Литература
1. Введение в теорию и методологию системы оптимального функционирования
социалистической экономики. М.: Паука, 1983.
2. Кобринский Н.Г., Майминас К.З., Смирнов А.Д. Экономическая кибернетика.
М.: Экономика, 1982. Гл. 1, 2.
3. Моисеев II.Н. Математика ставит эксперимент. М.: Наука, 1979.
4. Немчинов B.C. Избранные произведения. Г. 3- М.: Наука, 1968-
5- Раяцкас Р.Л.. Плакунов М.К. Количественный анализ в экономике. М.- Наука,
1987.
ГЛАВА 2
МАТЕРИАЛЬНЫЙ АСПЕКТ ЭКОНОМИКИ
Ввиду чрезвычайной сложности экономической системы попытки ее
моделирования сразу в целом оказываются безуспешными. Более
продуктивными являются методологические подходы, при которых
вначале анализируются средствами моделирования отдельные аспек¬
ты и уровни экономики, а затем осуществляется ее систем¬
ное моделирование. Именно такая последовательность приняв
та в настоящей книге.
Первый шаг исследования — моделирование материального
аспекта одноуровневой экономики.
2.1. Материальный аспект экономики
как объект моделирования
Материальный аспект экономики — это взаимодействие различных
элементов производительных сил, рассматриваемое вне определенных
общественных форм (экономических и социальных). Важнейшими час¬
тями „материальной” экономики являются сфера производ¬
ства и сфера потребления1. Люди в „материальной” эконо¬
мике выступают в двоякой роли: 1) как потребители, определяющие
цели производства; 2) как трудовой ресурс - необходимый элемент
производства2.
1 В литературе по системному анализу и экономической кибернетике часто
выделяют про и з в одственно-техно логический аспект экономи-’
ки (см., например, [3. Гл. 3]). Материальный ;i ! кг - более широкое понятие.
Наряду с производственно-технологическими пр< . ами он охватывает и матери¬
альную сторону процессов потребления и жп > но деятельности (развития че¬
ловека).
Уточним также, что изучение материального аспекта экономики не тре¬
бует полного абстрагирования от общественных форм; достаточно зафик¬
сировать влияние некоторого организационно-экономического и социально-
экономического механизма (существующего или ожидаемого).
2 Итак, человек - это одновременно и главная цель, и важнейшее средство
экономического развития. В гл. 3 обосновывается необходимость более широкого
подхода к человеческому фактору при моделировании социально-экономической
системы.
43
Математическое описание материального аспекта экономики содер¬
жит множество уравнений и неравенств/характеризующих возможности
производства и использования разнообразных видов продукции й ресур¬
сов, осуществления видов трудовой деятельности, технологические
условия, соотношения экологического равновесия и т.п. Основная задача
моделирования — поиск лучших решений среди множества допустимых.
Каждое „решение” — это некоторый вектор X, элементами которого
являются показатели развития экономики.
Формально задача выбора и принятия решения может быть пред¬
ставлена парой < X, >->, где X — множество допустимых (осуществи¬
мых) решений, — правила выбора (порядок предпочтения) вариантов
решений на множестве X1.
В соответствии с принятыми предположениями множество X харак¬
теризует ресурсно-технологические возможности народного хозяйства
на основе первичной (микро) информации о всем разнообразии продук¬
тов, ресурсов, технологий, потребностей. При этом не учитываются
ограничения, связанные с организационно-хозяйственными структурами,
отношениями собственности, экономическими интересами, социальными
особенностями и т.п.
Различные модели выбора экономических решений, в том числе
модели прогнозирования и планирования, можно рассматривать как
особые конкретизации сформулированной общей задачи. Главными раз¬
новидностями общей модели являются балансовые и оптими¬
зационные модели.
Балансовая модель позволяет находить допустимые варианты реше¬
ний X Е X. Но модель не содержит какого-либо механизма сравнения
вариантов по их предпочтительности, т.е. проблема поиска лучших
решений остается за рамками модели2.
Теоретически балансовая модель может отражать материальное вос¬
1 Общая задача выбора и принятия решений является динамической.
Это означает, что: 1) любое допустимое решение ХЕ:^представляет собой вектор
показателей, различающихся по моментам времени (например, объемы производ¬
ства одноименной продукции в разные моменты рассматриваются как разные
компоненты вектора X); 2) множество Охарактеризует возможности развития/
народного хозяйства в различные моменты времени и изменяется в самом процессе
планирования; 3) совокупность правил отбора вариантов решений ^ включает
также правила сопоставления вариантов, различающихся динамическими характе¬
ристиками, и эти правила в процессе функционирования экономики могут изме¬
няться.
2 Возможность нахождения определенного (единственного) решения посред¬
ством модели достигается за счет включения большого числа экзогенных перемен¬
ных. Это означает, что данная модель обязательно предполагает использование
других инструментов поиска решений (в том числе других моделей), сужающих
область X. В этом смысле балансовая модель не является полной (законченной)
моделью. Но многие элементы балансовой модели (описание множества X)
включаются в более общие модели народного хозяйства.
44
производство с любой степенью детализации. Однако практическое при¬
менение имеют только агрегированные балансовые модели. Примером
моделей данного типа являются межотраслевые балансы
народного хозяйства, оперирующие с такими экономически¬
ми агрегатами, как отрасли производственной и непроизводственной
сферы, агрегированные виды продукции, ресурсов и потребностей.
Оптимизационные модели являются инструментами выбора лучших
решений (с точки зрения принятых критериев выбора) из допустимых.
По сравнению с балансовыми моделями они являются не только более
развитыми, но и в большей мере соответствуют логике планово-управ¬
ленческой деятельности.
2.2. Оптимизационная микромодель
народного хозяйства
При социалистическом способе производства создаются объективные
предпосылки для оптимизации экономических решений в масштабе
всего народного хозяйства. Поэтому оптимизационная модель народно¬
го хозяйства может рассматриваться как одно из основных модельно¬
теоретических представлений социалистической экономики1.
В основе анализируемой модели лежат три предположения: 1) су¬
ществование критерия оптимальности для народного хозяйства в целом
и возможность его математической формализации; 2) существование
нескольких допустимых вариантов развития народного хозяйства; 3) ог¬
раниченность области производственных возможностей народного хо¬
зяйства в каждый момент и любой промежуток времени.
Задача математического программирования и оптимальное планиро¬
вание. В современной математике использование принципов оптималь¬
ности занимает важное место: математический анализ, вариационное
исчисление, математическое программирование, теория оптимального
управления, теория игр и т.д. Эти принципы нашли широкое применение
в различных науках, в том числе и в экономике. Наибольшее воздей¬
ствие на развитие современных теоретико-экономических представлений
оказало математическое программирование — сложив¬
шаяся в последние полвека область математики, разрабатывающая
теорию и численные методы решения многомерных экстремальных задач
с ограничениями.
Рассмотрим структуру задачи математического программирования
Принципы выделения основных модельно-теоретических представлений
(основных типов теоретических моделей) социалистической экономики излагают¬
ся в ММСЭ, с. 67-73.
В данной книге вслед за оптимизационной микромоделью другие типы теоре¬
тических моделей социалистической экономики кратко характеризуются в гл. 3,
а более подробно - в разделе III.
45
с точки зрения соответствия ее проблеме поиска оптимальных решений в
масштабе народного хозяйства.
Всякая задача математического программирования включает две
группы условий: 1) критерий оптимальности в виде аналитической
функции (максимизируемой или минимизируемой); 2) условия, опре¬
деляющие множество допустимых решений. При этом задача поиска
экстремума имеет смысл, если множество допустимых решений непу¬
сто, не сводится к одной точке, а целевая функция на этом множестве
ограничена („сверху” — при максимизации, „снизу” — при минимиза¬
ции) . Важно также отметить, что множество допустимых решений и кри¬
терий оптимальности формулируются независимо друг от друга.
Проблема оптимизации народного хозяйства имеет общие черты с
задачей математического программирования.
Во-первых, социалистическое общество характеризуется единством
цели, выраженной в основном экономическом законе формации: обес¬
печение полного благосостояния и свободного всестороннего развития
всех членов общества В процессе планирования и функционирования
народного хозяйства необходимо находить такие решения, которые
в наибольшей (максимальной) степени отвечают сформулированной
общей цели.
Во-вторых, в народном хозяйстве существует большая свобода вы¬
бора вариантов развития. Это объективное свойство экономики имеет
принципиальное значение для планирования как осознанной целенап¬
равленной деятельности; ведь отсутствие возможности выбора означало
бы бессмысленность каких-либо усилий по планированию. Основными
факторами, порождающими многовариантность экономического раз¬
вития, являются: 1) взаимозаменяемость производственных ресурсов,
технологических процессов, потребностей общества, способов их удов¬
летворения; 2) научно-технический прогресс, создающий новые возмож¬
ности развития общественного производства и порождающий новые
потребности; 3) объективная возможность разнообразного распределения
и использования ресурсов общества во времени и пространстве.
В-третьих, потребности общества в каждый данный момент и в
любой промежуток времени превышают возможности их полного удов¬
летворения вследствие ограниченности ресурсов народного хозяйства и
ограниченности роста эффективности их использования. Целесообразно
различать два рода ограниченности ресурсов: абсолютную ограниченность
невоспроизводимых ресурсов (некоторые виды природных
ресурсов, трудовые ресурсы в пределах примерно 15-летнего планового
периода) и относительную ограниченность воспроизводимых
ресурсов, обусловленную тем, что в исходном состоянии экономики
46
имеются строго определенные количества этих ресурсов и темпы их рас¬
ширенного воспроизводства ограничены1.
Многовариантность плановых решений и ограниченность возможнос¬
тей удовлетворения потребностей общества в любом промежутке време¬
ни формально выражаются в там, что множество допустимых вариантов
развития народного хозяйства X непусто, не сводится к одной точке и
ограничено сверху.
Как уже пояснялось, множество X задается системой многих урав¬
нений и неравенств, характеризующих материальный аспект экономики.
В общем виде каждое условие, входящее в X, можно записать как
gs(X)<b„
где s — номер условия; X - «-мерный вектор, характеризующий значе¬
ния показателей развития народного хозяйства; gs (X) — функция от
вектораХ; bs — параметр, ограничивающий значение 5-й функции.
Допустим, что общее число условий (ограничений) составляет
т, т.е, s Е М, гдеМ = ( 1, ..., гп^. Кроме того, будем полагать, что все
компоненты векторов л должны быть неотрицательными величинами.
Тогда вместо абстрактного выражения X Е X можем дать более конкрет¬
ное описание условий выбора допустимых вариантов развития народного
хозяйства (g,(X)<6„ S€M,
U>0. (2|)
ИЛИ
( g(X)^b,
{хУо. (22>
где g (X) = [#s (X)] — m-мерная векторная функция от X; Ъ = (bs) -
m-мерный вектор-столбец.
Условия (2.1) или (2.2) , являющиеся формальной записью множест¬
ва допустимых вариантов развития народного хозяйства, полностью
соответствуют описанию множества допустимых решений в общей
задаче математического программирования.
Сложнее обстоит дело с идентификацией общей цели развития
При анализе предпосылок оптимального планирования обычно обращается
внимание только на ограниченность невоспроизводимых ресурсов. Однако этого
недостаточно для доказательства ограниченности возможностей максимального
удовлетворения потребностей общества в любом промежутке времени.
Неограниченный рост эффективности народного хозяйства (с точки зрения
цели) был бы возможен и при ограниченности невоспроизводимых ресурсов,
если бы неограниченными могли быть темпы роста производительности труда
и уменьшения удельных затрат природных ресурсов. Поэтому для доказательства
ограниченных возможностей удовлетворения непрерывно растущих потребностей
общества необходимо обосновать ограниченность (в рамках каждого периода) воз¬
можностей роста объема воспроизводимых ресурсов и повышения эффективности
использования всех видов ресурсов.
47
социалистической экономики и критерия оптимальности (целевой фун¬
кции) задачи математического программирования. Из единства цели
социалистического общества еще не следует, что эту цель можно выра¬
зить некоторой максимизируемой (или минимизируемой) функцией.
Наиболее развитыми (но не единственно возможными) математи¬
ческими моделями глобального критерия оптимальности являются ска¬
лярная целевая функция/(X) и векторная целевая функцияF(X). Фун¬
кция f (X) интегрирует все многообразие целеустремлений общества.
Функция F (X) = [f (X)] представляет собой набор частичных целевых
функций f (X), выражающих более однородные, непосредственно несво¬
димые цели. Подключение целевых функций f (X) и F (X) к условиям
(2.1) или (2.2) дает соответственно модель скалярной оп¬
тимизации и модель векторной оптимизации.
Вопросы существования и построения функций обсуждаются в
2.3—2.5. Пока же примем гипотезу: общая цель развития социалистиче¬
ской экономики может быть выражена (хотя бы приближенно) в виде
функции / (X) таким образом, что максимизация этой функции будет
соответствовать максимизации уровня удовлетворения потребностей
общества.
Теперь задача нахождения наилучшего варианта развития народного
хозяйства полностью совпадает со структурой общей задачи математи¬
ческого программирования: max
g(X)<b, (2.3)
Х^О
Вектор X* называется оптимальным, если
f{X*)^f{X) при Х^О}
Не исключается, что модель (2.3) дает несколько оптимальных век¬
торов, которым соответствует одно и то же максимальное значение
т
Поскольку возможных вариантов развития народного хозяйства бес¬
конечно много и каждый вариант должен удовлетворять очень многим
условиям, то нереально пытаться найти оптимальный вариант путем
конструирования каждого варианта в отдельности и последующего их
сравнения. Нахождение оптимального варианта развития народного
хозяйства в принципе возможно только при помощи математического
программирования.
Однако реализовать эту принципиальную возможность далеко не
просто. Прежде всего следует учитывать поистине фантастическую раз¬
мерность единой задачи построения народнохозяйственного плана (аст¬
рономическое число всех переменных и ограничений). Необходимо при¬
нять во внимание и сложный характер взаимосвязей, которые приводят
к труднорешаемым типам оптимизационных задач (нелинейным, стоха¬
48
стическим). Принципиальные сложности возникают и при формализации
критерия народнохозяйственного оптимума.
Представление проблемы выбора оптимальных народнохозяйствен¬
ных решений в виде единой задачи математического программирования
имеет прежде всего теоретико-методологическое значение. Разработка
принципов построения оптимизационных моделей народного хозяйства,
выявляющих общие признаки и свойства оптимальных планов и эконо¬
мических механизмов их осуществления, явилась крупнейшим достиже¬
нием экономико-математической школы. Оптимизационный подход
к экономике — это прежде всего способ современного экономического
мышления, форма организации экономических знаний и истолкования
экономических факте.
Данное направление моделирования имеет и важное прикладное зна¬
чение. Оптимизационная микромодель как теоретическая конструк¬
ция является основой для построения оптимизационных моделей народ¬
нохозяйственного уровня, рассматриваемых в гл. 8, 10,11,13.
Недостатки задачи математического программирования как логиче¬
ской основы оптимального планирования. Структура задачи математиче¬
ского программирования отражает существенные черты проблемы опти¬
мизации народнохозяйственных решений, но все же не дает адекватного
математического описания этой проблемы. Наиболее серьезный недоста¬
ток задачи математического программирования как логико-математи-
ческой основы модели народнохозяйственного оптимума заключается в
отсутствии связей между целями экономической системы и ее допусти¬
мыми состояниями, в том, что критерий оптимальности формулируется
априорно по отношению к области допустимых решений.
В реальной социально-экономической системе имеет место взаимо¬
действие общественных потребностей (целей) и общественного произ¬
водства — материальной основы удовлетворения этих потребностей.
С одной стороны, общественное производство служит удовлетворению
сложившихся общественных потребностей. Но, с другой стороны, раз¬
вивающееся производство непрерывно порождает новые потребности,
создавая материальные носители этих потребностей — новые виды про¬
дукции, изменяя условия жизни и труда. Кроме того, от степени удов¬
летворения потребностей и развития способностей членов общества за¬
висит общественная производительность труда, т.е. сама область допу¬
стимых вариантов развития народного хозяйства.
Таким образом, цели, которые ставятся обществом, не могут быть
априорными по отношению к возможностям развития народного хо¬
зяйства, и наоборот, возможности развития народного хозяйства зависят
от уровня реализации общей цели — удовлетворения потребностей об¬
щества. Поэтому для адекватного математического описания процесса
выбора оптимальных народнохозяйственных решений требуется более
сложная математическая структура, нежели математическое программи¬
рование.
49
Но из сказанного вовсе не следует, что для решения проблем народ¬
нохозяйственного оптимума использовать математическое программиро¬
вание нельзя или нецелесообразно. Такой вывод был бы поспешным,
тем более что другого столь разработанного математического аппарата
пока не существует. Математическое программирование обладает многи¬
ми достоинствами и еще не исчерпанными возможностями. В частности,
поиск народнохозяйственного оптимума может быть представлен как
итерационный процесс взаимного уточнения целей народного хозяйства
и возможностей их осуществления; на каждом шаге этого процесса ис¬
пользуется модель математического программирования.
2.3. Народнохозяйственные критерии оптимальности
В .И.Ленин сформулировал общую цель социалистического общества
как обеспечение полного благосостояния и свободного всесто¬
роннего развития всех членов общества. Математическая форма¬
лизация общей цели социалистического общества является одной из важ¬
нейших проблем моделирования.
Главное требование к любой модели, формализующей цели развития
социалистической экономики, - это ее применимость для сравнения и
упорядочения (ранжирования) различных вариантов планово-эк оно ми-
ческих решений. Никакое разумное хозяйствование не было бы возмож¬
но, если бы плановый орган не обладал умением сопоставлять возмож¬
ные варианты плановых решений и выбирать лучшие из них.
Между двумя вариантами Л и В возможны три типа отношений пред¬
почтения: либо вариант А лучше варианта В (А В), либо вариант В луч¬
ше варианта А (В>*А), либо варианты А и В равноценны (А ~ В). Одна¬
ко, если проводить попарные сравнения вариантов для выбора наилуч¬
шего, то процесс перебора может стать практически бесконечным.
Поэтому целесообразно разработать формализованные процедуры срав¬
нения и выбора на всем множестве допустимых вариантов.
Данная задача в принципе может быть формализована различными
способами, в том числе и в виде задачи нахождения экстремума функ¬
ции, упорядочивающей множество вариантов по их предпочтительности.
Такой способ формализации критерия выбора обладает многими удоб¬
ствами, позволяя использовать хорошо разработанные математические
методы оптимизации. При этом необходимо подчеркнуть, что постановка
вопроса о принципиальной осуществимости построения критерия выбора
в виде целевой функции вытекает из умения общества (или его предста¬
вительного органа) сопоставлять различные альтернативы. Противопо¬
ложная точка зрения, объясняющая способность (или неспособность)
выбора лучших альтернатив знанием (или незнанием) соответствующей
математической функции, является неверной, идеалистической.
В теории оптимального планирования наиболее разработаны две
50
основные постановки народнохозяйственных задач: максимизация це¬
левой функции общественного благосостояния и минимизация срока
достижения определенных целей. Критерии оптимальности, используе¬
мые в этих задачах, могут рассматриваться как первичные глобальные
критерии, из которых выводятся вторичные (производные) и упрощен¬
ные критерии оптимальности.
Целевая функция общественного благосостояния. Понятие „целевая
функция общественного благосостояния” (ЦФБ) является кратким
обозначением наиболее общего критерия оптимальности в виде аналити¬
ческой функции и (X). Эта функция в принципе должна определяться на
всем множестве количественных показателей, характеризующих в дина¬
мике разнообразные условия жизни общества: удовлетворение матери¬
альных и духовных потребностей, условия труда и возможности выбора
сферы трудовой деятельности, экологические условия, сохранение
здоровья и т.д. и т.п. Для экономических исследований область опреде¬
ления и (X) может быть ограничена множеством „экономических” благ
(потребляемые продукты и услуги, возможности использования свобод¬
ного времени и т.д.).
ЦФБ и (X) прежде всего отражает факт сопоставимости различных
вариантов развития народного хозяйства с точки зрения удовлетворения
общественных потребностей. Ее величина возрастает при переходе от ме¬
нее предпочтительных вариантов к более предпочтительным.
Пусть, например, вариант А (вектор^) лучше варианта В (вектора
Xg), т.е. ХД г=^ Xg. Тогда значения функции и (X) в точках Xд и Xj$
должны удовлетворять условию: и (Хд) > и (Xq). И наоборот, если
Xg S— ХД, то u(Xg) > и(Хд). При равноценности вариантов А и В долж¬
но выполняться равенство и (Хд) = и (Xg). Определенное значение функ¬
ции и (X) = с соответствует некоторому множеству равноценных (или
безразличных) вариантов.
Существование функции и (X), обладающей указанными общими
свойствами, может быть формально выведено из системы аксиом.
Аксиоматика ЦФБ отражает закономерности роста благосостояния и
выбора альтернатив прежде всего в сфере потребления, а также необ¬
ходимые условия измерения.
Среди этих аксиом отметим две, имеющие наиболее очевидную интерпретацию.
Аксиома сравнимости. Для любых Хд и Xg имеет место одно из соотношений:
либо Хд ^Xg либо Xg 'р—Хд, либо Хд ~ Xg (эта аксиома уже формулировалась
выше).
Аксиома транзитивности. Если Хд ^Xg и Xg с— Х& то Хдс-Xq Если бы
не выполнялось условие Хд Xq то функцию и (X) нельзя было бы построить,
так как не могут одновременно выполняться условия и (Хд) >w (Xg), и (Xg) >
>и (Хс), и (Хд) <и (Хс).
Если к ЦФБ предъявляется только одно требование — упорядочение
различных вариантов по их предпочтительности, то отсюда следует
вывод: любые функции, одинаковым образом упорядочивающие
51
варианты, являются равноправными ЦФБ. Иными словами, ЦФБ опре¬
деляется неоднозначно.
Если и (X) — ЦФБ, то и (X) = у [и (X)] (суперпозиция функций
tp и и), также является ЦФБ, когда у (и) — монотонно возрастающая
функция (т.е. у (и) > 0). Одинаковая применимость многих целевых
функций объясняется тем, что имеет смысл не численное значение функ¬
ции и (X), зависящее от выбранной шкалы измерений, а способ упорядо¬
чения различных вариантов X по их предпочтительности.
Однако если к ЦФБ предъявлять более жесткие требования, нежели
простое упорядочение вариантов (сопоставление в терминах „лучше”,
„хуже”, „равноценно”), например умение отвечать на вопрос, н а -
сколько лучше или хуже какой-либо вариант по сравнению с другим,
то класс допустимых ЦФБ резко сужается.
Построение ЦФБ предполагает решение многих фундаментальных
проблем науки о человеке и обществе (физиологии, медицины, психо¬
логии, социологии, эстетики и др.), систематизацию обширной и разно¬
образной информации. Теоретически возможны два полярных подхода
к построению ЦФБ: нормативный и дескриптивный.
Нормативный подход предполагает возможным построение целевой
функции исключительно по данным науки о наиболее рациональных
условиях человеческой жизни („как надо жить”). Дескриптивный под¬
ход основан на обобщении фактически наблюдаемого поведения об¬
щества (посредством обработки статистических данных о массовом по¬
ведении, материалов социологических обследований и т.п.). Научная
методика построения ЦФБ должна сочетать нормативный и дескриптив¬
ный подходы.
Построение ЦФБ не является единственным полезным выходом ис¬
следований по ЦФБ. Не меньшее значение имеют теоретические выводы,
полученные из анализа свойств целевой функции. Эти выводы использу¬
ются в практической работе по оптимальному планированию, в том числе
при построении упрощенных критериев оптимальности, моделировании
процессов потребления (см. гл. 5, 8).
Минимизация срока достижения заданных целей. Такая постановка
задачи оптимизации развития народного хозяйства предполагает, что
известно некоторое „идеальное” состояние Х^, к достижению которого
следует стремиться. „Идеальным” состоянием можно считать набор
(вектор) благ, полностью удовлетворяющих потребности общества по
современным научным представлениям. Это, разумеется, не исключает
того, что по мере продвижения к намеченному „идеальному” состоянию
последнее будет корректироваться.
Если период планирования достаточно продолжителен, то необхо¬
димо определить такую траекторию развития народного хозяйства, при
которой вектор X достигается за минимальное время (задача оп¬
тимального быстродействия). Если же состояние X недо¬
стижимо в течение планового периода, то ставится задача макси¬
52
мального приближения к уровню удовлетворения общест¬
венных потребностей, заданному вектором X ^ ,
При использовании рассматриваемого критерия главным является
обоснование системы рациональных нормативов, ха¬
рактеризующих отдаленную цель развития народного хозяйства. Но
открытым остается вопрос об удовлетворении общественных потреб¬
ностей на этапах продвижения к данной цели. И поэтому вполне возмож¬
но, что подчинение развития народного хозяйства только одной конечной
цели может давать такие траектории, при которых неудовлетворительно
решаются проблемы повышения благосостояния на отдельных этапах
планового периода.
Целесообразно дополнить рассматриваемый критерий оптимальности
условиями, гарантирующими более или менее равномерный рост благо¬
состояния. Например, минимизировать потери благосостояния общества
при движении к идеальному состоянию:
СВ
W = \ \uv- u(t)] dt.
о
Данный критерий совмещает теоретические представления о ЦФБ
и основную идею критерия минимизации срока достижения заданной
цели: и (t) — значение ЦФБ в момент t, и = и (X^) — значение ЦФБ
при полном удовлетворении рациональных потребностей; при этом
предполагается, что и (t) < и В отличие от обобщенной (динамиче¬
ской) ЦФБ, в которой вектор X включает использование благ в разные
моменты времени, функция и (t) = и [X(t)] определяется для каждого
момента времени в зависимости от количеств используемых в этот же
момент благ.
Дерево целей. В планировании и управлении сложными системами
широко используется методика программно-целевого планирования
(ПЦП), сочетающая формализованные (математические) и неформали¬
зованные (экспертные) приемы анализа и принятия решений. Важной
составной частью этой методики является построение дерева целей.
Дерево целей систематизирует иерархию целей развития сложной
системы. Каждая цель верхнего уровня представляется в виде подцелей
следующего уровня таким образом, что объединение подцелей пол¬
ностью определяет исходную цель. Все цели доводятся до конкретных
целевых нормативов. Так, например, цель „питание” в конечном счете
конкретизируется в виде научно обоснованных норм потребления про¬
дуктов питания на душу населения, цель „одежда” — в виде норм пот¬
ребления товаров, рассчитанных исходя из условий жизни и на основе
изучения спроса групп населения с высшим доходом, и т.п. Посредством
целевых нормативов можно установить связь дерева целей с рассмотрен¬
ным выше критерием минимизации срока достижения заданных целей.
Взаимосвязь и соподчиненность различных целей оцениваются с
помощью специальных коэффициентов. Здесь используются два подхода:
53
порядковый (ранжирование) и количественный (нормирование) .Ран¬
жирование целей состоит в том, что каждой цели приписыва¬
ется порядковый номер, устанавливающий ее относительную важность
для достижения цели более высокого уровня. При нормировании
целей для каждой из них устанавливаются коэффициенты значимос¬
ти. Ранжирование или нормирование целей осуществляется на основе спе¬
циальных методик экспертных оценок, среди которых наибольшую из¬
вестность получил дельфийский метод.
Составной частью методики ПЦП является разработка сценари¬
ев будущего. Они позволяют дать общую оценку возможностей
удовлетворения потребностей общества в исследуемом периоде и
уточнить систему целей. В целом методика ПЦП дополняет методы по¬
строения критериев оптимальности, особенно в отношении таких трудно-
формализуемых аспектов целенаправленной деятельности общества, как
наука, образование, здравоохранение, охрана окружающей среды,
оборона.
Проблема критерия оптимальности с позиций общей методологии
моделирования. В проблеме построения народнохозяйственных крите¬
риев оптимальности фокусируются все основные трудности моделирова¬
ния социально-экономических процессов: переплетение многих факто¬
ров различной природы, сложности наблюдений и измерений, сочетание
самоорганизуемости и управляемости, взаимодействие субъекта и объ¬
екта моделирования, стохастичность и неопределенность и т.д.
Иногда высказывается соображение, что применение оптимизаци¬
онных моделей в планировании народного хозяйства невозможно, так
как еще не построен „правильный” критерий оптимальности. Это сооб¬
ражение основано на иллюзиях, что формула „правильного” критерия
может быть определена вне практической деятельности по оптимизации
социально-экономических решений, что эта формула „объективно суще¬
ствует” вне активной общественной практики и вне общественного
сознания и наука должна только отыскать эту формулу.
Известно, что в процессах планирования и управления цели уточня¬
ются и модифицируются; в окончательном виде они формируются в
процессе реального функционирования объектов. Абсурдно было бы
отказываться от оптимизации планирования народного хозяйства только
по той причине, что какие-то принимаемые в данный момент цели в по¬
следующем могут изменяться. Плановое развитие всегда осуществля¬
ется на основе определенных целевых установок; в то же время оно
обязательно включает механизм корректировки первоначальных целей и
генерирования новых целей по мере достижения более высокого уровня
экономического развития и удовлетворения материальных и духовных
потребностей. При этом учитывается положительное воздействие более
полного удовлетворения потребностей и развития способностей трудя¬
щихся на эффективность общественного производства.
В 2.2 уже отмечалась принципиальная условность народнохозяй¬
54
ственных моделей, в которых критерии оптимальности (целевая функ¬
ция) задаются априорно. Напрашивается вывод, что процесс нахождения
реального (а не только формального математического) оптимума с по¬
мощью математических моделей должен включать процедуры уточнения
и корректировки критериев оптимальности.
Вопрос о возможностях построения и применения критерия опти¬
мальности следует рассматривать с позиций общей методологии приме¬
нения математического моделирования в научных исследованиях и прак¬
тике. Ведь народнохозяйственный критерий оптимальности есть особая
математическая модель общественных целеустремлений. И когда ставит¬
ся вопрос о практическом построении такой модели, то на первых порах
речь может идти лишь об упрощенном, схематизированном представле¬
нии системы общественных целеустремлений. Если же руководствовать¬
ся чересчур строгими требованиями к начальной формулировке
критерия оптимальности, то практические разработки в области опти¬
мального планирования никогда не смогут выйти из начальной стадии и
поэтому не смогут быть реализованы даже те возможности оптимиза¬
ционных моделей, которые не зависят от конкретного вида критерия
оптимальности.
Реалистический подход состоит в такой организации оптимального
планирования, когда наряду с приближенной оптимизацией народного
хозяйства с помощью упрощенных моделей расширяется фронт фунда¬
ментальных исследований по моделированию целей развития социалисти¬
ческого общества.
2.4, Взаимные задачи оптимизации народного хозяйства
Вернемся к рассмотрению оптимизационной модели народного хозяй¬
ства (2.3). Среди условий, образующих множество допустимых вари¬
антов X, важную роль играют ограничения по ресурсам. Если s - индекс
ресурса, то gs (X) — функция общих затрат этого ресурса, bs — общее
количество (запас) ресурса в народном хозяйстве.
Из всех видов ресурсов можно выделить дефицитные ресурсы
(один или несколько). Ресурс называется дефицитным, если
любое уменьшение его количества приводит к уменьшению оптимально¬
го значения целевой функции. Всякий дефицитный ресурсу в оптималь¬
ном плане X* используется полностью, т.е. вектор X* обращает нера¬
венство gSQ (X) < bSo равенство. Но понятие „дефицитность ресурса”
более жесткое, нежели цонятие „полное использование ресурса”, так как
последнее не означает, что увеличение ресурса обязательно изменит оп¬
тимальный план.
Выделим из всех ограничивающих условий для специального рас¬
смотрения ограничение по некоторому дефицитному ресурсу q (X) < Q,
где q (X) - функция общих затрат этого ресурса, Q - общее его коли¬
55
чество. Все варианты X Е X должны удовлетворять этому ограничению,
и хотя бы для одного варианта оно будет выполняться строго как равен¬
ство. Множество допустимых вариантов, образованное в результате
исключения из условий, описывающих множество X, условия
q (X) < Q, обозначим X.
Количество ресурса Q можно рассматривать как параметр, опреде¬
ляющий множество допустимых вариантов X (Q). При 3iomX(Q) есть
общая часть (пересечение) множества X и множества таких вариантов,
для которых выполняется условие q (X) < Q, а именно:
Теперь сформулируем другую задачу.
Пусть G — параметр, характеризующий определенный уровень
(значение) максимизируемой целевой функции / (X). Обозначим через
X (G) множество допустимых вариантов, которое является пересече¬
нием множества X и множества таких вариантов, для которых выпол¬
няется условие f (X) > G:
3L(G) = Ir)\X:f(X)>G].
На множестве X (G) будем минимизировать функцию затрат выде¬
ленного ресурса q (X).
Таким образом, имеем пару оптимизационных задач:
A) f(X) -шах, (2.4)
B) q{X) . min. X£X(G) (2.5)
Задачи А и В называются в з аимными. Как было показано,
эти задачи имеют общую часть множества допустимых решений X, а
различия между ними сводятся к следующему: функция f (X), максими¬
зируемая в задаче А, образует ограничивающее условие в задаче В, и
наоборот, функция # (X), ограниченная в задаче А, является минимизи¬
руемой в задаче В.
Вариант X задачи А является оптимальным, если
f(X) max f(X).
. xeiz(Q)
Вариант X задачи В является оптимальным, если
q(X) — min а (XV ^
X €*(<?)
Принципиально важным является вопрос: при каких условиях ре¬
шения задач А и В могут совпадать. Ответ дает обитая теорема взаим¬
ности1 : если для каждого оптимального варианта X задачи А выполня-
1 Теорема сформулирована и доказана А.Г.Аганбегяном и К.А.Багриновским.
Доказательство см. в ММСЭ, с. 113.
56
л л
ется условие q (X) = Q, а в задаче В задано G = / (X), то решения задач
А и В (т.е. множества их оптимальных вариантов) совпадают.
Понятие взаимных оптимизационных задач и теорема взаимности
имеют важное теоретическое значение. Они устанавливают „равнопра¬
вие” и условия эквивалентности двух основных модификаций оптими¬
зационных моделей народного хозяйства.
При решении задачи на максимухм целевой функции общественного
благосостояния получаем и (X*) = С*. Общая теорема взаимности указы¬
вает, что в качестве народнохозяйственного критерия оптимальности
может быть выбрана также функция затрат любого дефицитно¬
го ресурса. Использование этого критерия будет давать то же реше¬
ние (те же оптимальные планы), если соблюдается условие и (X) > С*.
Для применения теории взаимных задач нужно из всего множества
ресурсов выделить хотя бы один ресурс, который благодаря своим
специфическим свойствам мог бы рассматриваться как устойчиво дефи¬
цитный ресурс.
Таким особым ресурсом является труд. Его исключительное
положение среди всех других видов ресурсов (с интересующей нас точ¬
ки зрения) объясняется рядом причин. Во-первых, количество трудовых
ресурсов в каждый данный момент ограничено, и их увеличение сравни¬
тельно мало зависит от развития экономики (почти не зависит в преде¬
лах 15-летнего планового периода). Во-вторых, трудовые ресурсы явля¬
ются наиболее универсальным ресурсом; относительный избыток тру¬
довых ресурсов в одной какой-нибудь сфере деятельности может быть
направлен в другие сферы деятельности (материального производства,
отраслей услуг, образования и культуры и т.д.). В-третьих, в социалисти¬
ческом обществе одним из важнейших факторов повышения благососто¬
яния и всестороннего развития членов общества является увеличение
свободного времени трудящихся за счет сокращения рабочего
времени (свободное время является компонентой вектора, на котором
определяется ЦФБ). Поэтому экономия труда (в отличие от экономии
других производственных ресурсов) не только создает предпосылки для
ускорения развития народного хозяйства за счет расширения сферы
труда, но и может непосредственно увеличивать уровень благосостояния:
абсолютное сокращение затрат труда в народном хозяйстве создает
возможности допшшительного сокращения рабочего дня, увеличения
свободного времени и создания более благоприятных условий для все¬
стороннего развития личности.
Таким образом, можно сделать вывод, что в корректно поставлен¬
ной задаче на максимум ЦФБ трудовые ресурсы общества будут дефи¬
цитны. Отсюда следует, что во взаимной задаче можно минимизировать
функцию общих затрат труда.
57
Необходимо уточнить, что речь идет о минимизации именно общих затрат
труда без какого-либо приведения различных видов труда к одинаковому уровню
сложности, квалификации и т.п. Как известно, ресурсы и затраты труда дифферен¬
цируются по профессионально-квалификационному и половозрастному составу.
Но абсолютной ограниченностью характеризуются только трудовые ресурсы в
целом. Отдельные же виды трудовых ресурсов воспроизводимы в широких грани¬
цах и поддаются трансформации. Условия трансформации трудовых ресурсов (пе¬
ремещение из одной группы в другую) и затраты на трансформацию (образование,
переквалификацию) должны включаться в общую модель народного хозяйства
как особые ограничения и переменные. Следует также заметить, что при динамиче¬
ской постановке задачи для каждого отрезка времени (например, года) вводится
особое ограничение по трудовым ресурсам и поэтому в соответствии со смыслом
теоремы взаимности минимизироваться могут трудовые затраты любого отрезка
планового периода.
Конкретизируем положения теории взаимных задач применительно
к народнохозяйственным оптимизационным моделям.
Пусть t (X) — функция общих затрат труда за какой-либо период
времени, L — общее количество трудовых ресурсов в среднем за тот же
период (в соответствующих единицах измерения) .
Тогда задача А будет иметь вид
и(Х) -max, X€#(L), (2.6)
где
X(L)= ХП[Х: t(X)<L J.
Обозначим максимальное значение целевой функции — С*.
Задача В (взаимная) имеет вид
t{X) min, X€3E(C), (2.7)
где
Х(С)= ХП[Х:и(Х)>С\.
Таким образом, критерий минимизации затрат труда не противо¬
речит главной цели развития социалистического народного хозяйства
и при определенных условиях выступает эквивалентом критерия мак¬
симизации удовлетворения потребностей общества. Преимущества кри¬
терия минимизации трудовых затрат состоят в ясности экономического
смысла и простоте количественного выражения. Очевидно, измерение
затрат на производство различных продуктов и услуг является гораздо
более легкой задачей, чем систематизация наборов благ по их общест¬
венному полезному эффекту. Решение народнохозяйственных задач с
рассматриваемым критерием позволяет оценивать эффективность тех
или иных хозяйственных мероприятий величиной сэкономленных трудо¬
вых затрат (подробнее см. в ММСЭ, с. 113—119).
58
Однако оптимизация по критерию трудовых затрат не избавляет от
необходимости сопоставлять различные допустимые варианты по степени
удовлетворения общественных потребностей, поскольку общая форму¬
лировка взаимной оптимизационной задачи предполагает знание не
только ЦФБ, но и ее максимально достижимого уровня. Вместе с тем
теория взаимных задач открывает дорогу различным приближен¬
ным методам поиска оптимального варианта развития народного
хозяйства, обеспечивающего максимально возможное удовлетворение
потребностей общества. Критерий минимизации трудовых затрат следует
рассматривать в первую очередь как инструмент итеративного процесса
нахождения оптимального варианта развития народного хозяйства1.
Взаимные оптимизационные задачи замечательны не только тем,
что их конкретные решения при определенных условиях совпадают.
Общими являются и многие качественные свойства взаимных задач.
Это обстоятельство используется при математическом анализе народ¬
нохозяйственных моделей (см., например, гл. 8). Теорема взаимности
используется также и для построения эффективных вычислительных
методов.
Л
2.5. Многоцелевая (векторная) оптимизация
Построение глобального критерия оптимальности (или скалярной целе¬
вой функции) не является необходимым условием поиска оптимальных
народнохозяйственных решений. Более общей моделью народного хо¬
зяйства является модель векторной оптимизации, или оптимизационная
модель с векторной целевой функцией.
Векторная целевая функция F(X) = [f (X)] включает такие частич¬
ные целевые функции fl (X), которые не сводятся (по крайней мере на
первом этапе моделирования) в единую целевую функцию и выражают
степени удовлетворения различных потребностей общества: повышение
материального благосостояния, удовлетворение социальных запросов
членов общества, упрочение и развитие систем общественных отношений,
обеспечение безопасности развития и т.п. Благодаря этому обходятся
трудности непосредственного сопоставления наиболее разнокачествен¬
ных целей.
Будем исходить иэ<гого, что рост каждой частичной целевой функ¬
ции соответствует увеличению степени удовлетворения определенных
групп потребностей. Очевидно, общий уровень удовлетворения потреб¬
ностей безусловно возрастает, когда значение хотя бы одной целевой
функции возрастает, а значения остальных не убывают.
1 Такая трактовка критерия минимума трудовых затрат в социалистическом
хозяйстве была впервые обоснована В.В.Новожиловым.
Подробнее о применении критерия минимизации затрат труда в итеративных
оптимизационных расчетах см. в ММСЭ, с. 118.
59
Решение, оптимальное по одной из частичных целевых функций, на-
зывается субоптимальным, В общем случае субоптимальные
решения для разных частичных целевых функций не совпадают. Отсюда
вытекает необходимость выбора таких решений, которые являются
наилучшими с точки зрения совокупности частичных целевых функций.
Эффективные решения (оптимум по Парето). Вариант X будем на¬
зывать эффективным, если не существует какого-либо другого
варианта X, для которого значения всех функций fl (X) не меньше
fl(X), а значение хотя бы одной функции строго больше1. Иначе говоря,
не существует такого X, что F (X) ^ F(X).
Множество эффективных вариантов обозначим#*. Такое множество
называют множеством Парето, а элемент этого множества
оптимумом по Парето (по имени известного итальян¬
ского экономиста-математика конца XIX — начала XX вв.) .
Любое из решений X Е X* СХ не может быть улучшено ни по одной
частичной целевой функции fl (X) без ухудшения по какой-либо другой
из них. Например, если из множества X* возьмем два таких варианта
Хд и Xg, что fl 1 (Ха)>/1} (ХВ), то обязательно найдется какая-нибудь
г2-я функция, по которой f 2 (Хд) </*2'(Хд).
Первый логический этап векторной оптимизации — нахождение мно¬
жества X*. При этом основное внимание можно сосредоточить на иссле¬
довании множества эффективных значений функции F = (fl).
Решить указанную задачу в полном виде, как правило, трудно.
Ситуация облегчается, если множество # замкнуто и выпукло, а макси¬
мизируемые функции fl (X) — вогнутые (т.е. задачи субоптимизации
есть задачи выпуклого программирования).
При выполнении указанных условий справедливы следующие утверждения:
1) для любого X Е #* существует такой полулоложительный вектор А =
= (КА с компонентами, удовлетворяющими равенству v \= 1, что шах
/=1 X 6#
[ AF (X)] достигается для X =Х; ^
2) если задан вектор А= (^)-> 0, где Z А 1, то задача max [aF(X)\да¬
ет эффективные варианты (один или несколько ^ X е X * X^dk
Иначе говоря, любое решение задачи векторной оптимизации является реше¬
нием задачи скалярной оптимизации с целевой функцией 9которая представляет
собой взвешенную (или средневзвешенную) сумму частичных целевых функций.
Второе утверждение указывает конструктивный метод определения эффективных
вариантов: необходимо решать задачу скалярной оптимизации с целевой функцией
Ys(X)-> рассматривая как меняющиеся параметры, на которые наложены условия
1 В дальнейшем следует различать знаки > и > . Знак ^ допускает, что все
нестрогие неравенства могут выполняться как равенства. Знак ^ показывает, что
хотя бы одно неравенство обязательно выполняется как строгое неравенство. В
частности, соотношение X 0 означает, что все компоненты вектора X неотри¬
цательны (X ^ 0) и хотя бы одна компонента строго положительна.
60
к
\ > 0 и 2 \* = 1. В случаях когда Л- орт (имеет только одну положительную
1 = 1
компоненту, равную единице), получаем субоптимальные решения.
Если множество X невыпукло и не все fl (X) вогнутые, то нахожде¬
ние эффективных вариантов усложняется. Применяются разнообразные
приемы зондирования Парето-границы и нахождения ее характерных
точек (в частности, вершин многогранника).
Определение множества эффективных решений сужает область вы¬
бора наилучших решений. Следующий этап выбора решений представля¬
ет собой поиск компромисса между несовпадающими и противо¬
речивыми целями. Требуется определить принципиальную схему разум¬
ного компромисса, которая позволила бы выделить в некотором смысле
наилучшее решение или минимальное множество, внутри которого ре¬
шения неразличимы по своей предпочтительности. Наиболее распростра¬
нены две схемы компромисса между частичными целевыми функциями:
условная субоптимизация и скаляризация векторного критерия оптими¬
зации.
Условная субоптимизация. Пронумеруем частичные целевые функ¬
ции так, что „главная” (непосредственно максимизируемая) целевая
функция получает первый номер. Векторную функцию без первой час¬
тичной функции обозначим F (X), а вектор фиксированных значений
функций — Q. Имеем задачу:
fl(X) -max, X££f][X:F(X)^Q\. (2.8)
По существу прикладные оптимизационные модели являются, как
правило, моделями условной субоптимизации. Например, непосредствен¬
но максимизируется величина национального дохода или фонда потреб¬
ления, а уровни достижения других целей народного хозяйства (удовлет¬
ворение духовных потребностей, улучшение условий труда, повышение
обороноспособности и т.п.) фиксируются в ограничениях модели.
В качестве максимизируемой в принципе может быть выбрана любая
из частичных целевых функций и любая из них может быть ограничива¬
емой функцией. Таким образом, можно сформулировать и решить к
задач условной субоптимизации. Первоначально заданные уровни частич¬
ных целевых функций могут корректироваться в результате анализа
субоптимальных решений.
Выбор компромиссного решения на основе условной субоптимиза¬
ции может быть формализован. Пусть Q*= (Q*) — вектор субоптималь¬
ных значений целевых функций, А = (Д-) — вектор отклонений от Q*;
Д = (А*} ) — максимально^допустимые отклонения от Q* . Можно
сформулировать такие задачюскалярной оптимизации:
fx{X) -max, X^Xf][X:F(X)^Q*~ Д«] (2.9)
61
- максимизация одной частичной целевой функции при максимально
допустимых отклонениях от оптимальных значений других целевых
функций;
t = 2
max, X g ЗЕ (2.10)
— максимизация разности одной частичной целевой функции и штрафной
функции отклрнений от субоптимальных значений других целевых
функций, где у1 — монотонно возрастающая функция.
Легко видеть, что полная формализация выбора компромиссного
решения требует принятия дополнительных допущений (о значениях
Д9и вида функций <рг (Д/) ).
Методика условной субоптимизации хорошо отражает специфику
многоэтапного процесса построения народнохозяйственного плана, в
котором трудно проводить грани между критериями оптимальности и
ограничениями, а параметры всех условий последовательно уточняются
по мере накопления необходимой информации и сужения области
выбора оптимальных решений.
Скаляризация (свертка) векторного критерия оптимальности.
Основными вопросами, возникающими при реализации данного подхода,
являются учет приоритета (различной степени важности) частичных
критериев оптимальности, нахождение разумных компромиссов между
ними, сопоставление масштабов измерений различных критериев.
Рассмотрим некоторые приемы построения скалярной целевой
функции на основе частичных целевых функций.
Выше отмечалась возможность использования функций ^ (X) =
к А
= Е X-у (X) при выборе эффективных вариантов. Преимуществом
/ =1
такой скалярной функции является наглядная имитация влияния коэф¬
фициентов приоритета X/ на выбор оптимальных решений. Недостатком
данной функции является то, что она допускает резкую дифференциацию
значений частичных целевых функций; например, возможно, что только
одна функция fl (X) будет положительной. Поэтому модель оптимиза¬
ции со скалярной функцией
Гг(Х)= 2 Ktf‘(X)
t=l
должна дополняться условиями, ограничивающими дифференциацию
уровней частичных функций. При обосновании коэффициентов Xz- необ¬
ходимо также учитывать масштабы изменений частичных функций.
Принцип „справедливого” компромисса при объединении
нескольких критериев можно математически выразить в более сильной
форме. Мы можем, в частности, считать справедливым такой компро¬
мисс, когда при сравнении вариантов решений относительное снижение
62
по одним критериям не превосходит относительного повышения по
другим. Такому условию отвечает функция
Г2(Х)=П f‘(X). (2.11)
1=1
Например, варианты Хд и!п являются эквивалентными с точки зрения
двух критериев f1 (X) и/1 (л), если
П(ХА) /2(*л)
F(XB) f*(XA) *
При использовании функции (2.11) допускается, что все частичные кри¬
терии одинаково важны. Различную степень важности частичных критери¬
ев можно учитывать в функции вида
Гз(Х)= п [№)]V (2.12)
С= 1
В более развитом виде принцип справедливого компромисса учиты¬
вается посредством уравнивания уступок от субоптимальных значений-
частичных целевых функций.
В практике моделирования довольно распространен принцип
равномерной оптимизации. Идея его заключается в стрем¬
лении более или менее равномерно увеличивать степень достижения всех
разнокачественных целей. При этом общей целью оптимизации является
максимальное приближение к „идеальному” состоянию, задаваемому
вектором F* = (f^) = [fi (X*7)] .
Степень достижения „идеального” состояния по каждой частичной
f (X)
целевой функции определяется как Qj = — . Общая скаляризо-
ванная целевая функция имеет вид
<Г4(Х) = 011116,.. (2.13)
i
Определение max min 0/ можно интерпретировать как „подтягива¬
ние” наиболее „отстающего” из критериев (степени удовлетворения
какой-то группы потребностей) до уровня других критериев (степени
удовлетворения других групп потребностей). Поскольку в функции
(2.13) сопоставляются только относительные величины, трудности
соизмерения различных целевых функ!щй обходятся. Этим во многом
объясняется широкое использование принципа максимина
в прикладных оптимизационных моделях (см. гл. 8,11—13)
Обозначим min 0/ = 0. Отсюда следует, что 0 < или же
/ (X) > 0, i = 1, к. Поэтому задача нахождения max min ©г* может
i
63
быть представлена в виде максимизации числа в с дополнительными
ограничениями по частичным целевым функциям:
0 —* max,
Х€£П [X:F(X)>Fv0]- (2.14)
Рассмотренные приемы скаляризации векторного критерия опти¬
мальности показывают, что между моделями скалярной и векторной
оптимизации нет жестких границ. Векторная оптимизация не есть только
отрицание оптимального планирования с глобальным (скалярным)
критерием оптимальности. Использование методов скаляризации век¬
торного критерия снова приводит нас к оптимизационной модели с
единым критерием (т.е. здесь происходит „отрицание отрицания”).
Но возвращение к модели с единым критерием оптимальности осущест¬
вляется на качественно новой основе.
Если в ранее анализировавшихся моделях народного хозяйства
принципы сочетания разнокачественных целей постулировались и гло¬
бальный критерий вводился априорно, то в моделях векторной опти¬
мизации единый критерий в определенном смысле генерируется.
Выбору единого критерия оптимальности предшествует исследование
множества эффективных вариантов и обсуждение возможных схем
компромисса между частичными критериями.
В то же время необходимо подчеркнуть, что модель векторной
оптимизации предоставляет больше возможностей для участия исследо¬
вателя в процессе поиска лучших решений.
Квазиоптимизация. Суть задачи квазиоптимизации состоит в том, что
находится не оптимальное решение, а некоторое множество решений,
близких к оптимальному. Такое множество X С ^ называется к в а з и-
оптимальным множеством.
Рассмотрим типичную постановку квазиоптимизационной задачи.
Необходимо найти множество вариантов из X Е X, для которых значение
максимизируемой целевой функции ffX) уступает максимальному
значению этой функции не более заданной величины Af:
1 = ЭЕ П [X: f (X) > max f (X) — АЛ. (2.15)
хеш
Большой интерес представляет соединение принципов квазиоптими¬
зации и векторной оптимизации.
Задачу квазиоптимизации можно трактовать как определение мно¬
жества решений, вполне удовлетворительных с точки зрения главного
критерия оптимальности. Тогда на множестве X можно выбирать реше¬
ния, удовлетворяющие требованиям других, менее важных критериев
оптимальности, например max ffX). Действительно, если скалярный
критерий fl(X) не учитывает всего многообразия целей развития народ¬
ного хозяйства, то, вероятно, можно ценой некоторого отступления от
максимума/1/^ попытаться учесть требования других критериев.
64
Учет всей совокупности критериев оптимальности, упорядоченных
по степени важности (приоритету), возможен при использовании метода
прследовательной квазиоптимизации.
Пусть все критерии оптимальности (частичные целевые функции)
пронумерованы в соответствии со своей важностью: fl(X), f1 (X), f (X)...
Последовательная квазиоптимизация представляет собой многоэтапный
процесс решения квазиоптимизационных задач на последовательно
сужающемся множестве допустимых вариантов. На первом этапе оп¬
ределяется квазиоптимальное множество
Хх -X П [X: f1 (X) >mzxf1(X)~ ДГ1].
хе х
На втором этапе — квазиоптимальное множество
Хг =#i П [X:f(X)> та х/ (X) - hf\.
хе Хх
и т.д.1 На этапах последовательной квазиоптимизации можно применять
все рассматривавшиеся выше методы векторной оптимизации.
2.6. Оптимизация народного хозяйства
в условиях неопределенности
Проблемы оптимизации планово-экономических решений анализирова¬
лись выше при допущении о возможностях точного задания всей инфор¬
мации о целях и условиях развития народного хозяйства. На самом деле
исходная информация, которую необходимо принимать во внимание при
выработке хозяйственных решений, может быть трех типов: опреде¬
ленная — когда соответствующие условия и параметры известны точ¬
но; вероятностная — когда условия и параметры выражаются
случайными величинами (случайными функциями) с известными зако¬
нами распределения их вероятностей; неопределенная — когда
исчерпывающая характеристика условий и параметров отсутствует и
законы распределения случайных величин неизвестны. Неопределенность
в свою очередь имеет широкий диапазон: от полного неведения до
такого положения, когда относительно точно можно указать верхние и
нижние пределы значений случайных величин и даже определить интер¬
валы наиболее вероятных их значений.
Первому типу исходной информации адекватны жестко детермини¬
стские модели. Второй тип информации позволяет применять соответ¬
ствующий математический аппарат: теорию вероятностей и математиче¬
скую статистику, стохастическое программирование, теорию статисти¬
ческих решений, теорию массового обслуживания и т,д. Трудности
1 Подробнее см. в ММСЭ, с. 143-144. *
3 Зак. 2414 65
математической формализации проблемы нахождения наилучших реше¬
ний в масштабе народного хозяйства в значительной мере обусловлены
именно тем, что существенная часть информации о народнохозяйствен¬
ных процессах сводится к третьему типу. Расширение знаний уменьшает
степень неопределенности будущего, но не может полностью ее уст¬
ранить.
Теория и методология оптимального планирования в условиях не¬
определенности развиваются двумя путями: 1) усовершенствование
моделей жестко детерминистского типа и создание гибкой методики их
использования; 2) разработка математических методов и моделей,
учитывающих в явном виде стохастичность и неопределенность экономи¬
ческих процессов.
Подход к оптимизации в условиях неопределенности с использова¬
нием моделей детерминистского типа. Рассмотрим методические основы
комплексного подхода к оптимизации экономических систем, сочетаю¬
щего гибкое использование моделей жестко детерминистского типа со
специальными методами учета случайных факторов и неформальными
приемами поиска лучших решений1.
В этом подходе можно выделить четыре основных этапа: 1) форми¬
рование множества сочетаний условий, характеризующих изучаемый объ¬
ект; 2) решение оптимизационных задач для каждого сочетания условий
и определение зоны неопределенности оптимальных решений; 3) изуче¬
ние приспособляемости (адаптации) каждого варианта из зоны неопре¬
деленности к различным сочетаниям исходных данных; 4) выбор реше¬
ний в зоне неопределенности.
Этап 1. Целью первого этапа является формирование достаточно
представительного множества сочетания условий (исходных данных)
развития народного хозяйства. Для этого прежде всего систематизиру¬
ются основные ситуации, осуществление которых в определенные сроки
и в определенных масштабах нельзя точно предвидеть (например, от¬
крытие новых месторождений полезных ископаемых с определенными
запасами, освоение теормоядерной энергии, создание принципиально
новых машин и технологических процессов, изменения международной
обстановки). Данный этап, следовательно, тесно связан с методами ситу¬
ационного анализа и сценариев. Для формирования сочетаний возмож¬
ных условий используется также метод статистических испытаний (ме¬
тод Монте-Карло).
Рассматривается как можно более широкий диапазон возможных
значений неопределенных условий и параметров. Далее устанавливаются
приближенные вероятностные характеристики соответствующих данных:
экспертные оценки крайних значений интервала изменения случайной
величины, распределение внутри этого интервала и т.д.
1 Этот подход развит в Сибирском энергетическом институте СО АН СССР
под руководством JI.A. Мелентьева и А.А.Макарова.
66
Этап 2. Для практических целей достаточно рассматривать обобщен¬
ные (генерализованные) сочетания условий. Каждому такому 5-му
сочетанию условий соответствует своя оптимизационная задача. Если
имеется N сочетаний условий, то решается N оптимизационных задач и
находятся соответствующие множества оптимальных вариантов X*. Для
облегчения вычислений используются параметрическое прог¬
раммирование (с помощью которого определяются семейства
оптимальных решений, зависящих от изменения одного или нескольких
параметров) и методы ускоренного пересчета оптимизационных задач
(корректировки оптимальных вариантов) при изменении некоторых
исходных данных.
Объединение множеств всех оптимальных вариантов X* определяет
зону неопределенности - множество вариантов X = X* U
U X* U . . „ U Xjy, каждый из которых является оптимальным хотя бы
при одном реально возможном сочетании исходных данных (т.е. X— это
множество потенциально оптимальных вариантов, а „обычный” опти¬
мальный вариант X* является одним из многих вариантов этого мно¬
жества: X* £ Х*СХ С X).
При анализе зоны неопределенности обнаруживается, что многие
допустимые варианты не входят в Хи многие ограничивающие условия
также не влияют на формирование X. Эти варианты и условия исключа¬
ются из дальнейшего рассмотрения.
Этап 3. На данном этапе осуществляется имитация процесса приспо¬
собления (адаптации) экономической системы к меняющимся услови¬
ям. Исследуется приспособляемость каждого варианта из зоны неопре¬
деленности к различным сочетаниям исходных данных.
Прежде всего разрабатываются специальные мероприятия, которые
обеспечивают осуществление основных вариантов при разных сочетаниях
условий (такие мероприятия называют подстроечными). После
этого дополнительно решается (S-l) N оптимизационных задач (S -
число основных вариантов), в результате чего определяется матрица
оптимальных значений целевой функции f(X), имеющая S строк и N
столбцов. Элемент матрицы fsn показывает оптимальное значение целе¬
вой функции для s-ro варианта, реализуемого при л-м сочетании условий
(в теории игр такая матрица называется платежной).
Исследования данного этапк эффективны при использовании специ¬
альной адаптивной модели, включающей набор „подстроечных” меро¬
приятий и определяющей результаты оптимизации народного хозяйства
при возможных сочетаниях исходных данных.
Этап 4. При отборе лучших вариантов решений, входящих в зону
неопределенности, предпочтение отдается решениям, устойчивым по
отношению к широкому диапазону изменения исходных условий, т.е.
реализуемым при возможно большем числе сочетаний исходных данных.
В условиях неопределенности различные варианты плановых реше¬
ний должны оцениваться также с точки зрения приспособляемости к
3* 67
изменениям условий, возможности заблаговременной подготовки к
новым условиям и скорости осуществления такой подготовки. Эти
дополнительные требования к потенциально оптимальным вариантам
характеризуются следующими взаимосвязанными понятиями: манев¬
ренность — возможная скорость перестройки планов в зависимости
от изменения условий; эластичность — способность плана к пере¬
стройке внутренней структуры без существенных потерь в уровнях до¬
стижения конечных целей; надежность — потенциальная вероят¬
ность осуществления планового варианта; адаптивность —
способность плана приспосабливаться к возникающим новым (ранее не
предусмотренным) условиям.
Важное значение для выбора плановых решений имеет сопоставление
затрат или потерь эффекта, связанных с реализацией определенного ва¬
рианта в иных условиях по сравнению с теми, при которых он является
оптимальным (эти затраты или потери эффекта называются экономи¬
ческим риском). Величины экономического риска rsn > О,
показывающие потерю эффективности (уменьшение значения целевой
функции) при реализации 5-го варианта в ситуации п, вычисляются
по формуле
rsn = fn fsn*
где f% — максимальное значение / (X) по п-му сочетанию исходных дан¬
ных.
Для выбора лучших вариантов, входящих в зону неопределенности
и реализуемых при разных сочетаниях исходных данных, используется
ряд формальных критериев из теории игр и статистических решений.
В основе этих критериев — сопоставление величин fsn и гт.
Отметим сначала простейший случай, когда по какому-либо вари¬
анту s0 ПРИ любых сочетаниях исходных данных выполняются соотно¬
шения fsQn**fsnwllirSon^rsn, S=1 ,—>S;s =£s0;n = 1,...,7V. Очевидно,
что вариант s0 безусловно предпочтительнее других. Но такой случай
является чрезвычайно редким. Типичной является задача сопоставления
вариантов, имеющих как лучшие, так и худшие характеристики по
сравнению с другими вариантами. Это и вынуждает использовать спе¬
циальные критерии.
Критерий Вальда рекомендует выбирать такой вариант, при котором
в худших условиях достигается наибольший эффект:
Фг — max min fsn.
s n
Критерий Сэвиджа рекомендует выбирать вариант, при котором ве¬
личина риска минимальна в самой неблагоприятной ситуации (т.е. мини¬
мальны отрицательные последствия, если выбор окажется ошибочным) :
68
0„ = min шах г
SIX'
s n
Эти исходные критерии выражают предельную осторожность (край¬
ний пессимизм) в оценке возможных последствий изменения условий
развития народного хозяйства.
Критерий Гурвица представляет собой компромиссное правило вы¬
бора и занимает промежуточное положение между позициями крайнего
пессимизма и крайнего оптимизма. При сравнении величин эффектов
он имеет вид
Ф, = шах
S
a min fsn + (1 —a) max /*„1, 0 < а < 1.
При а = 1 критерий Гурвица превращается в пессимистический кри¬
терий Вальда, а при а = 0 — в критерий крайнего оптимизма, рекоменду¬
ющий выбирать тот вариант, при котором значение целевой функции
максимально в наилучших условиях.
При сравнении величин экономического риска критерий Гурвица
приобретает форму
Ф4 — min £Р max rsn + (1 — (3) min rsn^, 0 < Р < 1.
При /3 = 1 этот критерий превращается в пессимистический крите¬
рий Сэвиджа, а при /3 = 0 — в крайне оптимистический критерий, реко¬
мендующий выбирать тот вариант, для которого в наихудших условий
отрицательные последствия минимальны.
При установлении коэффициентов а или (5 используется следующее
соображение: чем опаснее ошибочный выбор, тем выше должна быть
мера . ’’страховки” и поэтому тем ближе к единице должен быть
коэффициент а (или /3). Понятно, что жизненно важно застраховаться от
наиболее неблагоприятных ситуаций и очень больших потерь на приспо¬
собление экономической системы к критическим условиям (неурожай,
крупные катастрофы и т.п.).
Формальные критерии не гарантируют однозначного выбора плано¬
вых решений в условиях неопределенности, но они позволяют сузить
множество потенциально оптимальных вариантов (зону неопределенно¬
сти). Варианты, не отвергнутые^) формальным критериям оптималь¬
ности, называют равноэффекгивными (равноэкономичными).
Обозначим множество равноэффективных вариантов тогда в соот¬
ветствии с принятыми ранее обозначениями С К* С Окончатель¬
ный выбор планового решения на множестве ЗР* осуществляется уже
неформальным образом путем сопоставления сильных и слабых сторон
вариантов X Е X* в разных ситуациях и учета дополнительных факто¬
ров, не нашедших отражения в оптимизационной модели.
69
Рассмотренные вопросы оптимизации народного хозяйства приводят
к выводу, что фактор неопределенности должен приниматься во внима¬
ние не только при использовании детерминистских экономико-математи¬
ческих моделей в плановых расчетах, но и в процессе построения моде¬
лей. Экономико-математические модели должны включать резервы и
запасы, специальные виды деятельности, повышающие маневренность,
эластичность, надежность, адаптивность развивающегося народного хо¬
зяйства, информацию о корректирующих вариантах (’’подстроечных”
мероприятиях) и затратах на адаптацию в неопределенных ситуациях.
Применение специальных математических методов. В современной
математике разрабатываются разнообразные подходы к решению задач
поиска и принятия решений с учетом стохастики и неопределенности.
Для исследования проблем оптимизации народного хозяйства боль¬
шой интерес представляет стохастическое программирование — совокуп¬
ность методов решения оптимизационных задач вероятностного харак¬
тера.
Существуют различные постановки задач стохастического програм¬
мирования, отличающиеся определениями понятий плана задачи и реше¬
ния задачи. При так называемой жесткой (или одноэтапной)
постановке задачи стохастического программирования план — это детер¬
минированный вектор X, а целевая функция и множество допустимых
решений включают случайные компоненты. Например, часто использу¬
ется жесткая постановка задачи на максимум математического ожида¬
ния целевой функции:
м [/ (X, V)] —щах,
g(X, т)<6(т),
Х^О,
Т€Г,
где М — символ математического ожидания; у — набор случайных пара¬
метров; Г — множество значений у, проявляющихся с положительной
вероятностью.
При так называемой н е ж е с т к о й постановке (или двухэтап¬
ной задаче) на первом этапе выбирается некоторый вектор X >0, а
на втором этапе находится вектор £, корректирующий решение первого
этапа. Вычислительные методы стохастического программирования раз¬
работаны пока в основном только для линейных задач. Это создает серь¬
езные препятствия для широкого использования стохастического про¬
граммирования в моделировании народного хозяйства.
Для совершенствования методологии моделирования экономичес¬
ких процессов, включающих элементы неопределенности, весьма пер¬
70
спективной является разработка математических методов анализа
нечетких (или размытых) множеств. Кроме того, получают распростра¬
нение адаптивные математические модели. Примером использования
адаптивного подхода в моделировании являются модели с переменными
структурными коэффициентами, значения которых последовательно
уточняются в процессе функционирования модели.
Можно предвидеть, что специальные математические методы и мо¬
дели будут находить все большее применение для оптимизации экономи¬
ческих решений в ситуациях с элементами неопределенности. Однако
необходимо подчеркнуть, что процесс выработки плановых решений в
условиях неопределенности в принципе не может и не должен быть пол¬
ностью формализован. Окончательное принятие решения остается за
человеком.
Литература
1. Введение в теорию и методологию системы оптимального функционирования
социалистической экономики. М.: Наука, 1983. Раздел II. Гл. 1 - 3.
2. Интрилигатор М. Математические методы оптимизации и экономическая тео¬
рия. М.: Прогресс, 1975.
3. Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Экономическая кибернетика.
М.: Экономика, 1982. Гл. 3.
4. Петраков Н.Я., Ротарь В.И. Фактор неопределенности и управление экономи¬
ческими системами. М.: Наука, 1985.
5. Полищук Л.И. Анализ многокритериальных экономико-математических мо¬
делей. Новосибирск: Наука, 1988.
6. Раяцкас Р.Л., Плакунов М.К. Количественный анализ в экономике. М.: Наука,
1987. Гл. 5.
7. Цели и ресурсы в перспективном планировании. М.: Наука, 1 985-
8. Шаталин С.С. Функционирование экономики развитого социализма. М.: Изд-
во МГУ, 1982. Гл. 1.
ГЛАВА 3
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ МЕХАНИЗМ
Понятие ’’социально-экономический механизм” выражает взаимодейст¬
вие организационно-хозяйственных и социальных структур и регулято¬
ров, обеспечивающих функционирование экономической системы. Это
понятие охватывает организационно-хозяйственный и социальный аспек¬
ты экономики.
Моделирование социально-экономического механизма не достигло
еще такой степени полноты и универсальности, как моделирование ма¬
териального аспекта экономики. Это объясняется как большей сложно¬
стью объекта моделирования, так и приниженной ролью экономических
и социальных регуляторов в действовавших в течение ряда десятилетий
системах управления социалистическим народным хозяйством. Пока
можно говорить о существовании ряда альтернативных и дополняющих
подходов к моделированию социально-экономического механизма в
целом, его подсистем и важнейших элементов.
Данная глава может рассматриваться как введение в проблематику
моделирования социально-экономического механизма.
Анализ принципов соизмерения затрат и результатов (3.1) выполня¬
ет роль связующего звена между исследованиями материального аспекта
экономики с позиций народнохозяйственного оптимума и теорией эко¬
номических регуляторов (категорий товарно-денежных отношений),
содействующих достижению народнохозяйственного оптимума. Далее
(3.2) формулируются основные ’’собственные” проблемы моделирова¬
ния социально-экономического механизма. И в заключение (3.3) харак¬
теризуется новый тип моделей (с ’’обратными связями”), объединяю¬
щий материальный, организационно-хозяйственный и социально-эконо¬
мический аспекты экономической системы.
Рассматриваемые в данной главе общие подходы к моделированию
социально-экономического механизма конкретизируются в разделе II
применительно к верхнему уровню экономической системы (товарно-
денежные отношения в сфере распределения и потребления, единство
материально-вещественных и стоимостных пропорций воспроизводства,
денежный оборот в народном хозяйстве и т.д.) и в разделе III, где народ¬
ное хозяйство моделируется как многоуровневая система.
72
3.1. Принципы соизмерения затрат
и результатов в оптимальном планировании
В социалистической экономике локальные решения должны быть
ориентированы на достижение общей цели — максимально возможное
удовлетворение потребностей общества. Но этот главный принцип социа¬
листического хозяйствования может быть реализован только в том слу¬
чае, когда применяемые органами управления д отдельными хозяйст¬
венными ячейками измерители затрат и результатов деятельности при¬
водят в соответствие понятия глобальной и локальной экономической
эффективности так, что решения, эффективные с народнохозяйственных
позиций, оказываются эффективными для каждой хозяйственной ячей¬
ки, и наоборот.
Один из важнейших выводов теории оптимального планирования со¬
стоит в том, что принципы измерения затрат и результатов тесно связаны
с задачей построения и реализации оптимального народнохозяйственно¬
го плана: проблемы построения плановых цен, ставок заработной платы,
нормативов эффективности капиталовложений, нормативов рентных
платежей, платежей за природные ресурсы и т.п. не являются автоном¬
ными проблемами, а представляют собой определенные аспекты общей
теории оптимального планирования народного хозяйства.
Анализ оптимизационных моделей народного хозяйства позволяет
наметить некоторые подходы к проблеме соизмерения затрат и результа¬
тов. Рассмотрим сначала, какого рода измерения можно выполнять с
помощью народнохозяйственных критериев оптимальности. Опираясь
на теорию взаимных оптимизационных задач, будем в дальнейшем испо¬
льзовать два народнохозяйственных критерия: ЦФБ и(Х) и функцию
общих трудовых затрат t(X).
До сих пор функции и(Х) и t(X) записывались так, как будто они
определяются на одинаковых множествах переменных. В действитель¬
ности же функция и(Х) определяется на множестве показателей, непо¬
средственно характеризующих уровень общественного благосостояния;
будем далее называть эти показатели ’’благами”. Функция же t(X) опре¬
деляется на множестве показателей, характеризующих интенсивности
различных видов деятельности.
Пусть xi — объем использования г-го блага, xj — интенсивность /-го
вида деятельности.
Будем предполагать, что функции и(Х) и t(X) непрерывно дифферен¬
цируемы, т.е. имеют непрерывные частные производные1.
Одним из условий непрерывной дифференцируемости функций и(Х) и t(X)
является то, что аргументы и могут принимать непрерывные значения. Хотя
количества некоторых благ не могут дробиться до бесконечности (количество
автомобилей, телевизоров и т.п.), но в масштабах народного хозяйства недели¬
мость такого рода несущественна. Это верно и в отношении измерения интенсив¬
ностей видов деятельности, производящих различные виды продукции и услуг.
73
ТТЛТ1 Ъи(Х)
Частная производная ЦФБ и^ — характеризует предель¬
ный полезный эффект от использования блага i,
т.е. прирост ЦФБ при увеличении использования блага i на ’’малую еди¬
ницу”.
Ъг(Х)
Частная производная трудовых затрат Гу = — характеризует
предельные трудовые затраты вида деятельно с-
т и /, т.е. прирост затрат труда в народном хозяйстве при увеличении
интенсивности вида деятельности / на ’’малую единицу”.
Частные производные щ и ту несут важную информацию о соотно¬
шениях народнохозяйственных результатов и затрат при использовании
разнообразных видов общественных благ и деятельности. Однако рас¬
сматриваемые сами по себе они не могут служить универсальными изме¬
рителями народнохозяйственных затрат и результатов.
Во-первых, щ и rj — переменные величины, численные значения
которых определяются выбранным вариантом развития народного хо¬
зяйства (вектором X). Поэтому вне определенного варианта X значения
щ и Tj невозможно определить и невозможно применять.
Во-вторых, показатели и^ и ту, рассматриваемые независимо от дру¬
гих условий развития народного хозяйства, не соизмеряют затраты с
результатами. Величины щ характеризуют только зависимость непо¬
средственного полезного эффекта от использования б. цц без учета того,
какие затраты должно нести общество для удовлетворения потребнос¬
тей в этих благах. Наоборот, величины т/ показывают только зависимо¬
сти трудовых затрат в народном хозяйстве от увеличения интенсивностей
соответствующих видов деятельности вне связи с тем, каков полезный
эффект от этих видов деятельности.
В-третьих, поскольку продукция многих видов деятельности непо¬
средственно не используется в качестве благ (например, ’’чистые” сред¬
ства производства: руда, чугун, нефть, технологическое оборудование),
то эта продукция не получает оценок полезного эффекта типа щ. Наобо¬
рот, так называемые ’’даровые блага природы”, оказывающие сущест¬
венное влияние на уровень общественного благосостояния, не находят
отражения в показателях Tj.
Из сказанного можно сделать вывод, что необходимо сконструиро¬
вать систему таких экономических показателей, которые, сохраняя
свойства показателей предельных полезных эффектов и предельных тру¬
довых затрат, были бы способны соизмерять все частные виды затрат и
результатов с позиций народнохозяйственного оптимума. Для этого не¬
обходимо выяснить более глубокие свойства оптимальных народнохо¬
зяйственных решений.
Оптимизационная модель народного хозяйства и оптимальные оцен¬
ки. Для анализа принципов и методов соизмерения затрат и результатов
будем рассматривать достаточно общую модель народного хозяйства,
которая является задачей нелинейного программирования.
74
Пусть народное хозяйство есть объединение двух сфер: сферы
производства (материального и нематериального), включающей
различные виды деятельности / G TV* , и сферы потребления,
включающей использование различных видов благ i Е N2 непосредствен¬
но для удовлетворения потребностей общества. В число видов деятельно¬
сти включаются процессы производства разнообразной продукции и
услуг и процессы доведения производимой продукции до конечного ис¬
пользования (т.е. сфера обращения, обмена). Интенсивности видов
деятельности характеризуются вектором Хг = (лу), а объемы использо¬
вания благ — вектором Х2 = (хг). Общий же вектор переменных модели
имеет вид
Xt
X.
, NtUNt = N.
Все ограничивающие условия модели разделяются на две группы:
балансы производства и использования видов продукции (средства
производства и блага, в том числе нематериальные) и ограничения по
невоспроизводимым ресурсам. Общий индекс продукции — sx Е Mi,
причем N2 CMi. Общий индекс ресурсов — s2 СМ2. При этом Mi UМ2 =
= М. Из принятых предположений следует, что функции производства и
затрат определяются на векторе Xх, а ЦФБ — на векторе Х2.
Введем новые обозначения:
g\(Х\) = [gsx(X 1)] - вектор-функция конечной продукции сферы
производства (т.е. разностей между произведенной и использованной
продукцией в сфере производства);
'iifXi) = \gsJX 1)] - вектор-функция затрат ресурсов;
Q = (Я5 ) — вектор фиксированных объемов использования продук¬
ции в сфере Потребления (допускается 2 = 0);
R = (rs2J — вектор объемов имеющихся ресурсов.
Балансы производствами использования продукции представляют
собой неравенства g\(Xx) %Х2 + Q, т.е, конечной продукции должно
быть достаточно для удовлетворения потребностей (фиксированных и
переменных) сферы потребления. Вектор-функция gif-Xl) должна удов¬
летворять условию: существуют такие векторы Хх > 0, что g\(Xx) 0.
Это условие может быть названо условием продуктивно¬
сти экономической системы. Если данное условие не
выполняется, то в замкнутой экономической системе не может осуще¬
ствляться даже простое воспроизводство1.
Модель в целом имеет вид:
u (Х2) - - max,
gi (Xi)—Х2 > Q, ф ^
1 Понятие продуктивности экономической системы подробнее рассматривается
в гл. 6 и 7 на примере линейных межотраслевых моделей.
75
(з j-j
X,>0, x2>0.
Модель (3.1) в общем случае должна трактоваться как динамичес¬
кая. Допустимость и необходимость такой трактовки следует подчер¬
кнуть, чтобы исключить возможность противопоставление статического
и динамического оптимумов. Множество невоспроизводимых ресурсов
М2 включает главным образом невоспроизводимые природные ресурсы,
число видов которых с увеличением длительности планового периода
сокращается; они становятся воспроизводимыми и переходят в множе¬
ство Mi (например, трудовые ресурсы, ресурсы чистой воды, биологи¬
ческие ресурсы океана).
Из теории нелинейного программирования следует, что каждому
ограничению модели соответствует свой множитель Лагранжа1. Обозна¬
чим векторы-строки множителей Лагранжа для первой группы нера¬
венств V = (vSl) и для второй группы неравенств W = (wS2).
В соответствии со смыслом множителей Лагранжа имеем:
= .?“(*«) >-0 или ^>0; (3.2)
—dQ — '■ —dqSl
и (Хг) v. г. » ди(.
■ ,р > 0 или ws -
oR — dr
цул=ди{х1) >0 или = ди (х1) 0_ (3>3)
S2
Соотношения (3.2) означают, что при увеличении задания по конеч¬
ному использованию продукции sx на ’’малую единицу” оптимальное
значение ЦФБ уменьшается на величину v£ . Если же в систему поступит
(как внешний ресурс) ’’малая единица” этой продукции, то оптимальное
значение ЦФБ увеличится на v* . Соотношения (3.3) означают, что при
увеличении ресурса $2 на ’’мал^ю единицу” оптимальное значение ЦФБ
увеличивается на vvf2.
Величины vи wf имеют разнообразные названия: двойственные
переменные, оценки оптимального плана, объективно обусловленные
оценки, теневые цены, цены оптимального плана и т.д. Мы будем ис¬
пользовать название ’’оптимальные оценк и”.
Оптимальные оценки обладают важными свойствами соизмерителей
затрат и результатов в оптимизируемой социалистической экономике.
Во-первых, оптимальные оценки являются характеристиками дефи¬
цитности продукции и ресурсов в народном хозяйстве. Степени дефицит¬
ности определяются формулами (3.2), (3.3), Положительные оценки
1 Изложение основных выводов из теории нелинейного программирования
см. в ММСЭ, с. 158 - 163.
76
означают, что любое увеличение расхода соответствующей продукции
или уменьшение соответствующего ресурса уменьшает оптимальное
значение ЦФБ. Если же оценки продукции или ресурса равны нулю,
это означает, что они не являются дефицитными: увеличение расхода
продукции или уменьшение ресурса не влияет на значение ЦФБ.
Из (3.2), (3.3) следует, что полный дифференциал ЦФБ в окрест¬
ности максимума равен
du — 2 vltdqS'+ 2 w\tdrSi.
SjgMi Sj,€M2
Поэтому оптимальное значение ЦФБ остается неизменным, если
S v'tldqs= 2 wltdr,t. (3.4)
Si в Af i s2 € M 2
Формула (3.4) определяет соотношения эквивалентной вза¬
имозаменяемости.продукции и ресурсовв оптима¬
льном плане. Например, требуется найти соотношения эквивалентной вза-
dfLк .. = .УУ^ > 0
имозамены продукта к и ресурса h.Из (3.4) получаем drfr v%
Рассматриваемые ниже свойства оптимальных оценок являются
следствием необходимых условий оптимума задачи нелинейного про¬
граммирования (условий Куна - Таккера) 1. В частности, из так называ¬
емых условий дополняющей нежесткости вытекают соот¬
ношения между оптимальными оценками и балансами продукции и
ресурсов в оптимальном плане X*:
а) *s = <7s,. если oj, > 0, (3.5)
т.е. если оптимальная оценка продукции положительна, то излишков
продукции не производится
б) 1^ = 0, если gSi{Xl)—x*Sx> qSx> (3.6)
т.е. оптимальная оценка продукции нулевая, если производятся излиш¬
ки продукции;
в) gs, (*!*) = r*S если wst > °- (3-7)
т.е. если оптимальная оценка ресурса положительна, то ресурс использу¬
ется полностью;
г) ш*5 = 0, если gs,(X{)<rSt, (3.8)
1 Подробнее см. в ММСЭ, с. 124 - 129.
77
т.е. оптимальная оценка ресурса нулевая, если ресурс недоиспользуется.
Итак, соотношения (3.2) - (3.8) характеризуют оптимальные оцен¬
ки как показатели сбалансированности продукции и ресурсов в народ-
ном хозяйстве и универсальные измерители экономической эффектив¬
ности всех внешних по отношению к моделируемой системе источников
и потребителей продукции и ресурсов.
Рассмотрим теперь свойства оптимальных оценок как измерителей
затрат и результатов производственной деятельности. Из условий Куна -
Таккера следует:
dsi (*П - w• dga (*D
dXi dXi
или в развернутом виде
dgsxW) dgsAxl)
2 2 <3-9>
steMt OXf s2€ M 2 ox/
rbgs,(Xd ,
Матрица частных производных —— = [—], sx GMb
/ E TVi объединяет показатели предельной производительности и предель¬
ных затрат видов деятельности.
Каждый элемент этой матрицы показывает, насколько изменится объем коне¬
чной продукции Si при увеличении интенсивности /-го вида деятельности на ’’малую
единицу”. Этот элемент может быть любого знака, так как любой вид деятельно¬
сти одни виды продукции производит (и тогда частная производная имеет знак
’’плюс”), а некоторые другие — затрачивает (и тогда частная производная имеет
знак ’’минус”). Но должен быть положительным хотя бы один элемент для каждо¬
го вида деятельности (столбца матрицы) и для каждого вида продукции (строки
матрицы). Если бы эти условия не соблюдались, то это означало бы, что имеются
такие виды деятельности, которые не выпускают, а только затрачивают продук¬
цию (их использование абсурдно), и имеются такие виды используемой в народ¬
ном хозяйстве продукции, которые не производятся ни одним видом деятельности
(это невозможно в замкнутой экономической системе).
Матрица ~ [ ^ ] ,s2 &М2, / Е Ni, характеризует
предельные затраты ресурсов видами деятельности. Каждая из величин
0^. >0 показывает, насколько увеличатся народнохозяйственные
затраты ресурса s2 при увеличении интенсивности /-го вида деятельности
на ’’малую единицу”.
Обозначим символом <pj суммарную оценку предельного выпуска
всех видов конечной продукции /-м видом деятельности и \pj — суммар¬
ную оценку предельных затрат всех ресурсов этим же видом деятельности:
ф/= 2 дх- ; 2 дх/ •
s.eM, ах1 s,eM, axJ
78
Теперь вместо (3.9) можем более кратко записать:
/€ЛГ,. (3.10)
Экономический смысл условий (3.10) состоите следующем: в опти¬
мальном плане по каждому виду деятельности суммарная оценка преде¬
льного выпуска продукции не превышает суммарной оценки предельных
затрат.
Из условий дополняющей нежесткости вытекает, что если /-й вид
деятельности включается в оптимальный план (х*> 0), то по этому
виду деятельности имеет место строгое равенство суммарных оптималь¬
ных оценок предельного выпуска и предельных затрат:
ф/ = Т|)* для ЛГ/ > 0. (3.11)
Если же по какому-либо виду деятельности суммарная оценка
предельных затрат выше суммарной оценки предельного выпуска про¬
дукции, то этот вид деятельности не включается в оптимальный план:
лг* = 0, если Ф/<г|)/. (3.12)
Таким образом, оптимальные оценки продукции и ресурсов в опре¬
деленном смысле приводят в соответствие народнохозяйственную и
локальную эффективность различных видов деятельности.
Допустим, что построен оптимальный план X* и определены оптима¬
льные оценки V* и W*. Возникает вопрос, выгодно ли отдельным хозяй¬
ственным ячейкам, представляющим определенные виды деятельности,
уклоняться от выполнения плана при заданных оценках затрат и резуль¬
татов? Из (3.11), (3.12) следует, что это нецелесообразно, так как при
соблюдении плана гарантируется безубыточность производства, а боль¬
шего достичь невозможно. С дцугой стороны, неэффективные с на¬
роднохозяйственных позиций ввды деятельности (или их интенсивное
ти) являются, как правило, убыточными для хозяйственных единиц
Следовательно, система оптимальных оценок является средством реа
лизации оптимального народнохозяйственного плана: те, кто не выпол
няет план, оказываются в худшем положении по сравнению с теми, кто
его выполняет.
Оптимальные оценки являются также важным ориентиром при по¬
строении народнохозяйственного плана ’’снизу”. Поскольку соотноше¬
ния (3.10) — (3.12) являются признаками народнохозяйственного оп¬
тимума, то, зная оптимальные оценки, можно так выбирать интенсивно¬
сти различных видов производственной деятельности, чтобы по крайней
79
мере приблизиться к выполнению условий (3.10) — (3.12).Пусть, например,
по какому-нибудь к-му виду деятельности имеем $k(V*, X) > \pk(W*, X).
Это означает, что целесообразно увеличить так как этот вид деятель¬
ности приносит доход. Если же, наоборот, оказывается, что $k(V*> X) <
X), то fc-й вид деятельности либо вообще неэффективен, либо
применяется в неэффективных масштабах.
Чтобы более ясно показать зависимость оптимальных оценок про¬
дукции от производственных затрат в оптимальном плане f сделаем до¬
полнительное предположение. Известно, что существует много видов
деятельности, выпускающих по одному виду продукции (добыча руды,
нефти, оказание транспортных услуг, производство кинофильмов и т.п.)*
Поэтому правомерно допустить, что в каком-либо виде деятельности
/о изготавливается только один вид продукции s0. Естественно принять
за единицу интенсивности /0 выпуск единицы продукции s0 (за вычетом
внутрипроизводственных затрат этой же продукции). Тогда формула
(3.11) имеет вид
dgSl(Xi)
= ~Ьхи + Уh ПРИ Х1 > 0- (3.13)
s, € Af,
причем
, dgt,(X$
Sj 6 М, 3 дх /о
Эта формула по своей структуре аналогична формуле цены или
полной калькуляции производственных затрат. Оценка равна сумме
всех материальных затрат, соизмеренных также по оптимальным оцен¬
кам продукции, и всех затрат ресурсов, соизмеренных по оптимальным
оценкам ресурсов. Связь с оптимальным планом выражается в том, что
элементы материальных затрат и затрат ресурсов определяются как при¬
росты общественно необходимых затрат в народном хозяйстве, обуслов¬
ленные дополнительным включением в оптимальный план рассматрива¬
емого вида деятельности с единичной интенсивностью.
Таким образом, оптимальные оценки продукции являются измери¬
телями общественно необходимых затрат на производство продукции1.
В этом отношении оценки продукции (т.е. экономически воспроизводимых
ресурсов) принципиально отличаются от оценок невоспроизводимых или естест¬
венно воспроизводимых ресурсов. Но, как известно, многие виды ресурсов, рань¬
ше представлявшие собой исключительно ’’дары природы”, становятся результата¬
ми деятельности человека (искусственное разведение лесов, культивирование
диких растений, искусственное воспроизводство рыбных запасов, производство
чистой воды и т.п.). И если такие виды деятельности включаются в оптимальный
план, то оптимальные оценки соответствующих ресурсов начинают регулироваться
затратами воспроизводства.
80
Рассмотрим теперь, какое отношение имеют оптимальные оценки
продукции к измерению полезных эффектов благ. Из условий Куна —
Таккера следует
t*Nt. (3.14)
du[X2J
Частные производные щ — — , как уже отмечалось, характери¬
зуют величины предельного полезного эффекта благ, измеряемого при¬
ростом ЦФБ. Условия (3.14) показывают, что в оптимальном плане пре¬
дельные полезные эффекты благ не превышают значения оптимальных
оценок продукции. Для благ, используемых в оптимальном плане, пре¬
дельные полезные эффекты равны оптимальным оценкам продукции:
и\ при х\ > 0. (3.15)
Равенство оптимальных оценок продукции и предельных полезных
эффектов является важным признаком оптимального плана сферы
потребления. Построение этого плана можно представить как процесс
выбора такой структуры потребления (использования благ), при ко¬
торой значения предельных полезных эффектов и оптимальных оценок
продукции уравновешиваются.
Оценки продукции, используемой для увеличения благосостояния,
должны одновременно удовлетворять формулам (3,2), (3.5), (3.6),
(3.11), (3.13). Это означает, что оптимальные оценки продукции явля¬
ются одновременно измерителями дефицитности (сбалансированности)
продукции, общественно необходимых затрат на ее производство и об¬
щественной полезности ее использования.
Очевидно, что выводы, полученные из анализа общей модели народ¬
ного хозяйства, сохраняют свою силу и для моделей с более простой
математической структурой, в частности для линейно-программных
народнохозяйственных моделей, анализируемых в гл. 8,11, 13.
Соизмерение затрат и результатов при максимизации общественного
благосостояния и минимизации затрат'труда. Вернемся к рассмотрению
пары взаимных оптимизационных задач (2.6) и (2.7). Каждой задаче
соответствует система оптимальных оценок. Обозначим оценки (как
двойственные переменные) одинаковых ограничений задач Л. и В соотве¬
тственно вектором Y = (у5) и вектором Y = (у5). Пусть со — оценка
трудовых ресурсов задачи Лид— оценка ограничения по уровню благо¬
состояния в задаче В.
Доказьюается следующее утверждение1.
1 Аганбегян А.Г., Багриновский К.А., Гранберг А.Г. Система моделей народно¬
хозяйственного планирования. М.: Мысль, 1972. С. 131 - 134.
81
Если Y* и со* есть оптимальные оценки задачи А и со* > 0, то для
оптимальных оценок задачи В выполняются соотношения:
F* = -V F* > (Зл6)
(О*
: (О*
Как уже отмечалось в 2.4, выполнение услстия со* > 0 является
следствием рационального ведения народного хозяйства. Таким обра¬
зом, оптимальные оценки одинаковых ограничений взаимных задач
А и В соответственно пропорциональны, причем коэффициентом пропор¬
циональности является обратная величина оптимальной оценки трудовых
ресурсов.
Оптимальные оценки трудовых ресурсов со* и уровни благососто¬
яния IX* являются обратными величинами. Если оценка со* =' *\f^~^~no-
oL
казывает, насколько увеличится оптимальное значение ЦФБ при увели¬
чении трудовых ресурсов на ’’малую единицу” (или, иначе, характери¬
зует предельный полезный эффект труда),то оценка д* = , на¬
оборот, показывает, насколько возрастут затраты труда при увеличении
уровня благосостояния на ’’малую единицу”.
Анализ взаимных оптимизационных задач позволяет выявить неко¬
торые новые аспекты соизмерения затрат и результатов, имеющие теоре¬
тическое и практическое значение.
Рассмотрим вначале пару упрощенных взаимных задач, в которых
отсутствуют общие ограничения. Такое упрощение формально соответ¬
ствует гипотезе, что труд является единственным дефицитным ресурсом
и условия его использования полностью определяют область допустимых
планов.
Задача А0: и(Х) -> max, t(X)<L, Х>0.
Задача В°: t(X) -► min, и(Х) > С*, X > 0.
Будем пользоваться ранее введенными обозначениями w*- = ^ . —
Э t(X*)
(предельный полезный эффект) и т*= — (предельные трудовые
затраты). При этом допускается, что функции и(Х) и t(X) имеют общую
область определения, iEN°.
Для оптимальных планов выполняется ряд условий (они являют¬
ся частными случаями условий Куна — Таккера и дополняющей не же ст-
кости) :
для задачи А0 л 4 , 1Tft /о i о\
<оЧ?, АГ°; (3.18)
и} = (й*т,\ если х\ > 0; (3.19)
х} = 0, если а\ <со*т,-; (3.20)
82
для задачи В0
Ц*ы?<т,\ (• € ЛГ°; (3-21)
= если х?>0; (3-22)
х* = 0, если [д*«г<т<’. (3.23)
Эквивалентные равенства (3.19) и (3.22) говорят о том, что для
всех включенных в оптимальный план видов продукции предельные
полезные эффекты пропорциональны предельным трудовым затратам:
-^г = оо* или = |л* для всех х) >0. (3.24)
V щ
Условия (3.19), (3.22), (3.24) также можно выразить как равенства
отношения предельных полезных эффектов и предельных трудовых
затрат для любых производимых и используемых в оптимальном плане
7 7 ик тк
видов продукции к и I: = .
и* rf
Соотношения предельных полезных эффектов и предельных трудо¬
вых затрат в точке оптимума характеризуются угловыми коэффициен¬
тами касательной.
К.Маркс писал в ’’Нищете философии”: ”В будущем обществе... количество
времени, которое будут посвящать производству того или иного предмета, будет
определяться степенью общественной полезности этого предмета” . ф. Энгельс
в ’’Анти-Дюринге” прямо указывал, что при социализме ”план будет определяться
в конечном счете взвешиванием и сопоставлением полезных эффектов различных
предметов потребления друг с другом и с необходимыми для их производства
количествами труда”2. Рассмотренные выше условия оптимального плана явля¬
ются математически выраженной конкретизацией теоретических положений клас¬
сиков марксизма.
Перейдем теперь к анализу взаимных задач на основе общей модели
народного хозяйства. Для этого из^множества видов ресурсов М2 выде¬
лим общие трудовые ресурсы. Очевидно, что при этом сохранят свою
силу все соотношения оптимального плана, оптимальных оценок, затрат
и результатов. Формальные отличия будут состоять лишь в том, что,
помимо выделения особого баланса трудовых ресурсов, в качестве осо¬
бого элемента затрат всюду выделяются трудовые затраты. Все внимание
можно сосредоточить на анализе задачи на минимум трудовых затрат:
t (Xi) -►min, (3.25)
* Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 4. С. 97.
83
2 Там же. Т. 20. С. 321.
*,(**>< Я, (3-25)
Ы(Х2)>СГ
x,>0. x,>0.
Этой задаче соответствуют оптимальные_оценки трех типов: оценки
продукции V* = (v^), оценки ресурсов W* = (w$2), оценка уровня
благосостояния д*. Все эти оценки могут интерпретироваться как изме¬
рители влияния ограничений задачи на минимальную величину трудовых
затрат в народном хозяйстве:
p. a(Xj) ■ dtjxl) . dt(xl)
K ^~dQ— • W - -dR ' U “ dC*
Особый интерес представляет экономическая интерпретация опти¬
мальных оценок ресурсов. В рамках динамической модели невоспроиз¬
водимые ресурсы не являются результатами труда (ни живого, ни ове¬
ществленного). В чем же экономический смысл трудовой меры этих
ресурсов?
Увеличение различных ресурсов есть фактор повышения народно¬
хозяйственной производительности труда. Оно может давать такой же
эффект, как и непосредственное сокращение затрат труда. В системе
общественного производства различные ресурсы частично заменяют
труд и выступают как средство экономии труда. Это и объясняет право¬
мерность измерения в трудовых единицах даже тех ресурсов, которые
не содержат никакой трудовой субстанции.
По каждому виду деятельности выполняется соотношение
z f *j£0<f!gSL+ z
s,€M, OXJ OXJ s{€ Mj /
причем для х*> 0 оно выполняется как равенство.
Правая часть соотношения (3.26) характеризует сумму предельных
Э tfXf)
затрат всех ресурсов в их трудовом измерении. При этом ~ ~^xj есть
прямые (непосредственные) предельные затраты труда /-го вида дея¬
тельности, а ^ w* — косвенные предельные трудовые
S2 е м2 si dxi
84
затраты /-го вида деятельности1. Последние представляют собой прирост
трудовых затрат во всем народном хозяйстве, вызванный увеличением
интенсивности /-го вида деятельности. Поскольку использование какого-
либо дефицитного ресурса h дает экономию труда (в размере wjj единиц
труда на каждую ’’малую единицу” ресурса), то привлечение этого ре¬
сурса для /-го вида деятельности уменьшает возможности его эффектив¬
ного применения в других видах деятельности и тем самым увеличива¬
ет непосредственные затраты труда во всем народном хозяйстве на ве-
личину wfj =—щ—
Косвенные трудовые затраты, овеществленные в материальных
затратах (затратах продукции других видов деятельности), содержатся
в отрицательных элементах левой части соотношения (3.26). Эту часть
затрат удается выделять по тем видам деятельности (/0), результатом
которых является только один вид продукции (5о) :
2 + 2 wl (3.27)
Si€Mi 0Xh 0Xh s,€M2 OXh
(s0( M,)
Правая часть неравенства (3.27) представляет собой весь прирост
затрат труда в народном хозяйстве при выпуске единицы продукции
s0 видом деятельности /0. Сюда включаются непосредственные трудовые
затраты, трудовые затраты, овеществленные в потребляемых видах
продукции, и трудовые затраты, обусловленные использованием нево¬
спроизводимых ресурсов. При х*> 0 оптимальная оценка продукции
равна общественно необходимым затратам, труда на прирост производ¬
ства этой продукции.
Для тех видов продукции, которые используются непосредственно
для удовлетворения потребностей общества, по аналогии с формулами
(3.14), (3.15) получаем
li*Ui*<vj*ieN2(3.28)
li*uf =vj* для Xj* > 0. (3.29)
На основе (3.29) можем записать также
—* *
= ju* или = w* для всех x*j > 0. (3.30)
щ Vi
Полученные соотношения имеют более общий характер по сравнению
с формулами(3.19),(3.22),(3.24). Существенное отличие между этими
В.В.Новожилов для обозначения общей суммы предельных затрат в оптималь¬
ных оценках ввел понятие ’’дифференциальные затраты”, а для обозначения кос¬
венных предельных затрат - понятие ’’затраты обратной связи”.
85
соотношениями заключается в степени охвата трудовых затрат. В упро¬
щенных формулах учитывались только непосредственные предельные
трудовые затраты на производство продукции, а формулы (3.28) —
(3.30) учитывают предельные общественно необходимые затраты труда,
включающие приросты затрат на всех участках народного хозяйства.
Таким образом, для производимых и используемых для удовлетво¬
рения потребностей общества видов продукции предельные общественно
необходимые затраты труда пропорциональны предельным полезным
эффектам. Это соотношение выражает одно из важнейших свойств
оптимальных оценок как соизмерителей затрат и результатов при опти¬
мальном планировании народного хозяйства.
Оптимальные оценки и ценностные показатели. Оптимальные оценки
имеют много сходных черт с ценами, нормативами эффективности ре¬
сурсов, различными видами рент и другими ценностными показателями.
Выше было продемонстрировано, что оптимальные оценки измеряют
общественно необходимые затраты на производство и общественную
полезность продукции, характеризуют народнохозяйственную эффектив¬
ность используемых ресурсов, учитывают спрос и предложение, обеспе¬
чивают безубыточность всех производств, эффективных с позиций
всего народного хозяйства, ориентируют на выбор таких локальных ре¬
шений, которые оптймальны в народнохозяйственном масштабе. Поэто¬
му теория оптимальных оценок и практическое исчисление оптимальных
оценок имеют важное значение для решения многих проблем хозяй¬
ственного расчета.
Характерно, что большинство изменений, происходивших за послед¬
ние три десятилетия в практике образования экономических нормати¬
вов, отражали принципиальные свойства оптимальных оценок продукции
и ресурсов, хотя это редко признавалось. Среди основных изменений
можно назвать введение платы за производственные фонды, введение
платы за природные ресурсы и учет дифференциальной ренты в некото¬
рых отраслях добывающей промышленности, в лесной промышленности
и сельском хозяйстве (в форме рентных платежей, попенной платы,
дифференциации зональных цен, учитывающей естественные различия
условий производства), ликвидацию большинства планово-убыточных
производств (продукция которых необходима народному хозяйству),
учет в ценах качества продукции и полезного эффекта у потребителей
для взаимозаменяемых видов продукции, частичный учет спроса и пред¬
ложения в ценах на товары народного потребления.
Однако отождествление оптимальных оценок и категорий товарно-
денежных отношений неправомерно. Оптимальные оценки выступают
соизмерителями затрат и результатов, строго говоря, только внутри
модели оптимального одноуровневого планирования. Но эта модель,
как известно, не отражает организационно-хозяйственную и социальную
структуру, различные коллективные и индивидуальные интересы, эконо¬
мические формы взаимодействия звеньев народного хозяйства. Трак¬
86
товка оптимальных оценок как цен, нормативов эффективности ресур¬
сов, рент и т.д. означает их экономическую интерпретацию за рамками
предпосылок оптимизационной одноуровневой модели народного хозяй¬
ства.
Исследование ценностных показателей как элементов реального
хозяйственного расчета в принципе должно осуществляться в рамках
более сложных моделей народного хозяйства, объединяющих ресурсно¬
технологические, организационно-хозяйственные, социальные аспекты
функционирования и развития экономической системы.
3.2. Подходы к моделированию элементов
социально-экономического механизма
Важнейшей чертой коренной перестройки управления народным хозяй¬
ством СССР являются переход от преимущественно административных
к преимущественно экономическим методам руководства, к управле¬
нию интересами и через интересы, к широкой демократизации управле¬
ния, всемерной активизации человеческого фактора.
Происходящие перемены в принципах и формах управления предъя¬
вляют значительные требования к экономико-математическому модели¬
рованию, Очевидно, что моделирование экономики как единого оптими¬
зируемого объекта с полной централизацией плановых решений являет¬
ся недостаточным. Необходимо разрабатывать модели социалистическо¬
го народного хозяйства, включающие процессы функционирования
экономически самостоятельных объектов и групп населения, экономиче¬
ские и социальные механизмы их взаимодействия, сочетания интересов.
Применяемые модели должны давать ответы не только о желаемых
конечных состояниях экономики, но и характеризовать ’’поведение”
основных хозяйственных субъектов, приводящее к тем или иным состо¬
яниям в социально-экономическом развитии; они должны описывать
не только материальные потоки процесса общественного воспроизвод¬
ства, но и движение денежных средств, планово-управленческой инфор¬
мации.
Речь идет, однако, не об отрицании рассмотренного в гл. 2 подхода
к моделированию народного хозяйства, ограниченного материальным
аспектом экономики и акцентирующего возможности централизованно¬
го планирования, а о его качественном дополнении и усилении,
Основными проблемами разработки и применения экономико-ма¬
тематических моделей, интегрирующих материальный, организационно¬
хозяйственный и социально-экономический аспекты, являются:
1) моделирование отдельных хозяйственных звеньев, функциони¬
рующих в условиях перестраивающегося социально-экономического
механизма;
2) моделирование подсистем социально-экономического механизма;
87
3) построение синтезирующих моделей народного хозяйства (сис¬
тем моделей), обеспечивающих сбалансированное и оптимальное разви¬
тие экономики при сочетании централизованного руководства и само¬
стоятельности хозяйственных звеньев.
Модели хозяйственных звеньев. В сфере производства основным
хозяйственным звеном является предприятие (объединение). Цели и ус¬
ловия его функционирования определяются Законом СССР о государ¬
ственном предприятии (объединении), вступившем в действие с 1 янва¬
ря 1988 г.
Построение детализированной и полной модели предприятия пред¬
ставляет сложную проблему, требующую специальных знаний. Для хара¬
ктеристики основных подходов к моделированию достаточно схемати¬
ческого описания деятельности предприятия в условиях нового хозяй¬
ственного механизма. Введем ряд обозначений для каждого А>го пред¬
приятия:
Хк — план предприятия (реализация продукции — со знаком ’’плюс”,
получение материально-технических средств, использование трудовых
и природных ресурсов — со знаком ’’минус”); термин ’’план” является
условным и применяется для краткости; по существу Хк — это вектор,
характеризующий значения ингредиентов ’’входа” и ’’выхода”;
Як — множество технологически возможных вариантов функциони¬
рования предприятия;
Xfc - часть плана предприятия, связанная с выполнением госзаказа
(объемы реализации продукции и получения ресурсов — с разными зна¬
ками) ;
X^ — часть плана предприятия, осуществляемого по хозяйственным
договорам и посредством свободного товарообмена (объемы реализа¬
ции продукции и приобретение ресурсов - с разными знаками) ;
р1, р2 — векторы соответствующих цен на продукцию и нормативов
платежей за ресурсы (включая платежи за производственные фонды*
трудовые и природные ресурсы);
а — нормативы отчисления дохода предприятия в бюджет и выше¬
стоящие организации;
dk — размер сальдо прочих денежных поступлений и платежей (дота¬
ции, сальдо кредитов, фиксированные платежи и т.д.) ;
zk — хозрасчетный доход предприятия.
Необходимость выделения двух частей ’’плана” и двух векторов
ценностных показателей объясняется условиями переходного периода,
когда госзаказ сохраняет черты директивных заданий, а значительная
доля средств производства поступает по линии государственного мате¬
риально-технического снабжения (по лимитам и фондам). Векторы
р1 и р2 различаются прежде всего по номенклатуре реализуемой и при¬
обретаемой продукции; кроме того, одни и те же виды продукции
могут иметь различные цены в зависимости от канала реализации и по¬
ступления.
88
Поскольку предприятие функционирует на принципах хозрасчета,
его модель должна включать не только ресурсно-технологические усло¬
вия, но и балансы доходов и расходов. Величина дохода, полученного
после возмещения производственных затрат, составляет р1Х^+ р2Х\.
Предприятие может выбирать одну из двух ’’моделей” полною хоз¬
расчета и самофинансирования. Первая модель основана на нормативном
распределении прибыли. Вторая модель (модель коллективною подря¬
да) базируется на нормативном распределении дохода, соответствующе¬
го сумме pl Xfc + р2Xfc. Выберем для нашего анализа вторую модель,
важнейшим элементом которой является норматив а. Предприятие в
этом случае заинтересовано в максимизации хозрасчетного дохода
zk — О — а) (р1 Х}с + р2Х]с) + dk, используемого на образование фондов
развития производства, науки и техники, социального развития, опреде¬
ляемых по нормативам, и фонда оплаты труда, образуемого как остаток
хозрасчетного дохода. При этом определяющее долговременное значение
имеет рост доходов от производственной деятельности (р1 Х^. + р2Х^)\
прочие источники финансовых ресурсов (входящие в dfc) решают теку¬
щие, конъюнктурные задачи.
Схематически модель предприятия выглядит следующим образом:
Xk
Xk = X\ + Xl
(1—a) (plX\ + р2Х\) + dk - max. (3.31)
Итак, предприятие самостоятельно решает вопросы своего произ¬
водственно-технического и социального развития в интересах кол¬
лектива трудящихся, осуществляет прямые хозяйственные связи с дру¬
гими предприятиями и организациями на договорной основе (в том
числе и соглашения о ценах р2). Отношения с вышестоящими органами
управления включают: 1) выполнение госзаказа и получение обеспечи¬
вающих его ресурсов (вектор Х^); 2)/применение установленных эко¬
номических регуляторов: утвержденных цен, нормативов платежей
за производственные фонды, трудовые и природные ресурсы, процентов
за кредит, нормативов распределения дохода; 3) в виде исключения —
получение дополнительного финансирования.
Основным звеном социальной сферы является семья. Здесь
происходит удовлетворение основных физиологических, материальных
и духовных потребностей, осуществляется воспроизводство рабочей
силы. Соответственно группировка населения (семей) проводится по
ряду признаков: уровню и структуре, доходов и потребления, профес¬
сионально-квалификационной структуре, половозрастной структуре. В
гл. 5 анализируются модели поведения потребителей, осуществляющих
выбор продуктов и услуг для удовлетворения своих потребностей при
меняющихся доходах, потребительских цепах и насыщенности рынка.
89
Моделирование подсистем социально-экономического механизма.
Для основных функциональных подсистем социально-экономического
механизма необходимо разрабатывать особые модели (комплексы мо¬
делей): ценообразования, финансово-кредитного планирования и регу¬
лирования, формирования доходов населения, распределения средств
производства и предметов потребления и др. С помощью этих моделей
изучается влияние различных регуляторов (цен, рент, налогов, банков¬
ских ставок и т.д.) на функционирование экономических объектов и
всего народного хозяйства, экономическую эффективность производ¬
ства, экономическое положение различных социальных групп. При по¬
строении ценностных показателей используются свойства оптимальных
оценок.
Совместное действие регуляторов должно быть направлено на сти¬
мулирование хозяйственной активности и повышение эффективности
производства, приведение различных хозяйственных звеньев к равным
условиям с точки зрения результативности трудовой деятельности
(элиминирование влияния природно-географических факторов, неоди¬
накового исходного экономического состояния, других внешних об¬
стоятельств посредством рентных платежей, дифференцированного нало¬
гообложения и т.д.), совмещение общегосударственных, коллективных,
индивидуальных интересов, достижение материально-финансовой сбалан¬
сированности в народном хозяйстве. Вместе с тем посредством социаль¬
но ориентированной дифференциации некоторых ценностных регуля¬
торов и соответствующего распределения общественных фондов потреб¬
ления должно осуществляться выравнивание возможностей удовлетво¬
рения потребностей групп населения в тех областях, где распределение
по результатам труда может создавать чрезмерные социальные разли¬
чия (воспитание подрастающего поколения, охрана здоровья, доступ к
культурным ценностям).
Большая сложность построения моделей социально-экономического
механизма по сравнению с моделями ресурсно-технологического типа
объясняется необходимостью описывать экономическое пове¬
дение как реакции коллективов и индивидуумов на изменение внеш¬
них (по отношению к ним) экономических условий. На основе изучения
закономерностей экономического поведения строятся функции
отклика различных объектов. Например, функция отклика пред¬
приятия (объединения) характеризует изменение плана (вектора X)
в зависимости от изменения оптовых цен, нормативов отчислений в
бюджет, процентов за кредит. Функции отклика потребителей, называе¬
мые функциями покупательского спроса, описы¬
вают изменение спроса на различные товары при изменении потребитель¬
ских цен и доходов.
Построив функции отклика (как особые экономико-математичес¬
кие модели), можно решать задачи управления производством и потреб¬
лением путем изменения значений экономических регуляторов.
90
/ Модели экономического взаимодействия подсистем (звеньев) на¬
родного хозяйства. Планы отдельных хозяйственных (производственных
и потребительских) подсистем (звеньев) , получаемые на основе автоном¬
но используемых моделей, в общем случае несовместимы. Это выражает¬
ся в несовпадении ’’входов” и ’’выходов” взаимосвязанных моделей,
невыполнении общих народнохозяйственных условий (балансов продук¬
ции и ресурсов и др.)* Необходимы поэтому обобщающие модели (или
системы моделей), которые позволяли бы согласовьюать локальные
плановые решения и находить их оптимальные композиции.
Синтез моделей подсистем народного хозяйства (производственных
звеньев, групп населения, органов управления), условий их экономичес¬
ких взаимоотношений, общих ресурсно-технологических условий и це¬
лей развития приводит к построению народнохозяйственных моделей,
называемых моделями экономических (или с о ц и а л ь-
н о-э кономических) взаимодействий.
Модель экономического взаимодействия подсистем народного хо¬
зяйства имеет более сложную конструкцию по сравнению с оптимизаци¬
онной одноуровневой народнохозяйственной моделью и предназначается
для изучения более широкого круга проблем. К ним относятся: нахожде¬
ние вариантов (планов) сбалансированного развития и соответствую¬
щих параметров социально-экономического развития, при которых
локально оптимальные решения совместимы друг с другом; конструи¬
рование условий (элементов социально-экономического механизма),
создающих заинтересованность в сотрудничестве различных хозяйствен¬
ных звеньев и возможности согласования их интересов.
Моделирование народного хозяйства как многоуровневой поли-
структурной системы (производственно-технологической, организацион¬
но-хозяйственной, социальной) требует обобщения основных понятий,
сформулированных и анализировавшихся в гл. 2.
В рамках модели экономического взаимодействия понятие ’’сбалан¬
сированность” охватывает не только материальную, но и финансовую
сбалансированность (как соответствие доходср и расходов), и материа¬
льно-финансовую сбалансированность (как соответствие денежных пото¬
ков и их материального покрытия) в функционировании каждого хо¬
зяйственного звена и народного хозяйства в целом. Понятие ’’оптималь¬
ность” означает не просто достижение максимума некоторого обобщаю¬
щего целевого показателя социально-экономической системы (напри¬
мер, ЦФБ), а наилучшее сочетание оптимумов подсистемы, отражающих
общегосударственные, коллективные, индивидуальные интересы1.
В рамках оптимизационного социально-экономического подхода рассматри¬
вавшаяся в 2.3 целевая функция и(Х) может быть признана в качестве целевой
функции общества, если вся совокупность членов общества в процессе принятия
индивидуальных и коллективных решений действительно стремится к максимуму
этой функцйи. ЦФБ и(Х) можно рассматривать как некоторое объединение целе¬
вых функций для однородных социальных групп и целевой функции центрального
91
Подробный анализ моделей социально-экономического взаимодей¬
ствия и связанных с ними фундаментальных понятий дается в гл. 16.
Перспективным подходом к исследованию сформулированных проб¬
лем является имитационное моделирование. Имитаци¬
онные системы, включающие средства человеко-машинного диалога,
позволяют испытывать множество вариантов усовершенствования и
синтеза элементов социально-экономического механизма. Примеры
экспериментального изучения социально-экономического механизма
с помощью имитационных систем см. в [4. С. 25 - 37] . Частным случаем
имитационных систем данной проблемной ориентации являются деловые
игры.
3.3. Модели с обратными связями производства,
распределения и благосостояния
При моделировании материального аспекта экономики (гл. 2) применя¬
лась следующая схема взаимодействия ’’экономического” и ’’социаль¬
ного”: в социальной сфере вырабатываются требования (социальный
заказ) к Производству ’’ради человека”; сфера производства в меру
объективных возможностей (ресурсно-технологических, включая и по¬
тенциал трудовых ресурсов) выполняет эти требования; далее происхо¬
дит распределение произведенных потребительских благ. В этой схеме
на первый взгляд все гармонично связано и, разумеется, не случайно,
что теоретический анализ и практическое применение оптимизацион¬
ных экономико-математических моделей, отражающих логику данной
схемы, стали крупным достижением экономической науки.
Однако приведенная теоретическая схема односторонне отражает
роль человеческого фактора. Она не учитывает обратной связи — воз¬
действия мотивационных механизмов, распределительных отношений,
повышения благосостояния (включая развитие способностей) на эффек¬
тивность производства, ресурсно-технологический потенциал. Челове¬
ческий фактор распадается на два несвязанных элемента: ’’ресурсный”
и ’’потребительский”.
Включение недостающей обратной связи в модели взаимодействия
производственной и социальной сфер принципиально меняет условия
и свойства оптимальных социально-экономических решений. Множество
производственных возможностей становится зависимым не только от
наличия производственных ресурсов и имеющихся технологий, но и от
форм активизации человеческого фактора.
органа, выражающей интересы государства и общества в целом. Один из возмож¬
ных способов такого объединения - суммирование этих целевых функций с опре¬
деленными весами: и(Х) = где коэффициенты выражают участие
(или долю) каждой группы в гтовышении общественного благосостояния.
92
Обратим внимание на один важный момент. Если принимать произ¬
водственные возможности как технологически предопределенные, то
при условии их оптимального использования выделение дополнительных
благ для какой-то группы работников неизбежно ущемляет интересы
других групп. Но если принимать во внимание, что стимулирование ра¬
ботников с высшей производительностью труда расширяет производ¬
ственные возможности, то получаем иной вывод; частичное перераспре¬
деление благ между группами работников в соответствии с эффектив¬
ностью их труда может улучшить благосостояние всех групп.
Рассмотрим простую модель производства и распределения потре¬
бительских благ в двух модификациях: ’’ортодоксальную” и с обратной
связью ’’потребление — производительность труда”.
В производстве участвуют две группы работников, производящих одни и те
же виды продукции. Определенная доля продукции направляется на формирование
фонда потребления с фиксированной материально-вещественной структурой.
Максимизируется общий фонд потребления при некоторых условиях его распреде¬
ления между двумя группами работников.
Пусть X — вектор объемов производства;
*1, t2 — векторы затрат труда работников первой и второй групп на
производство единицы продукции;
Li, Ь2 — лимиты трудовых ресурсов первой и второй групп (макси¬
мальные объемы затрат труда);
X — множество допустимых вариантов производства (не включает
ограничений по трудовым ресурсам);
2 — общий объем фонда потребления;
с — вектор, переводящий объемы производства в общий фонд по¬
требления;
2i, z2 — объемы фонда потребления групп работников.
Модель без обратных связей. Производительность труда (и соответ¬
ственно трудоемкость продукции как обратная величина) не зависит от
распределения фонда потребления. Принимается, что фонд потребления
распределяется между группами работников в пропорции, задаваемой
параметром X Е [ 0,1 ] — долей первой группы в обще^л фонде потребле¬
ния. Соответственно доля второй группы равна 1 — X.
Модель выглядит следующим образом:
t3XKL2;
<3-32>
г2 = (1— Я) г;
z —► шах.
93
Предполагается (как и в 2.4), что в оптимальном плане трудовые
ресурсы дефицитны.
Из анализа модели следует, что распределение фонда потребления
между группами работников (параметр X) никак не влияет на оптималь¬
ный план производства Х° и максимальный объем фонда потребления
z° = z° + z°. На рис. 3.1 множество оптимальных значений и z2 (Па-
рето-граница) изображается прямой, имеющей равные углы наклона
(45°) к обеим осям. Точке А соответствует X = 0, точке В соответству¬
ет X = 1.
Модель с обратными связями. Принимается гипотеза, что изменение
производительности труда каждой к-й группы работников (индекс
роста Tfy) при производстве различных видов продукции одинаково
связано с уровнем потребления монотонно возрастающей зависимостью
Tfy. = т? (^), которая линеаризуется в окрестности z^ = zj? следующим
образом:
Л (2/г) = 1 -h е
(3.33)
Базисные значения производительности труда (обратные ве¬
личины трудозатрат) каждой группы работников в модели (3.32)
соответствуют некоторому базисному уровню потребления z0^ (при
94
z/c = z\ имеем nk(zk) = !)• При
увеличении zfc производительность
труда растет. Параметр е характе¬
ризует интенсивность обратной свя¬
зи (влияния уровня потребления
на производительность труда).
Изменение производительности
труда в зависимости от уровня
потребления можно учесть в пра¬
вых частях балансов трудовых
ресурсов, поскольку одинаковый
рост производительности труда при
производстве различных видов
продукции равнозначен увеличению
трудового ресурса: L (zfc) = Пк (1 + ■
zk ~ zk
+ е
zk
Таким образом, в исходной модели (3.31) заменяются только
ограничения по трудовым ресурсам:
1 + е^=£);
Включение этих условий в модель в общем случае приводит к изме¬
нению Парето-границы множества значений вектора (zl9 z2). При этом
максимальная величина общего фонда потребления z зависит от пропор¬
ций распределения между группами. Особый интерес представляет
анализ случаев, когда от включения обратных связей Въшгрывают все
группы работников. X
Характер воздействия обратных связей существенно зависит от параметра интен¬
сивности 6.
При умеренной интенсивности (см. рис. 3.1) базисный вариант D сохраняет
свойство Парето-оптимальности. Вместе с тем Парето-граница (кривая CF) содер¬
жит участок DE с возросшими (при неизменных распределительных пропорциях)
уровнями потребления каждой группы работников. Этому участку соответствует
более высокая, нежели в базисном варианте, доля в общем фонде потребления
группы работников, имеющей более высокую оценку трудовых ресурсов (на
рисунке - группа 1).
Сильные обратные связи (большее значение 6) создают возможности для пре¬
вышения каждой из групп уровня потребления, достигаемого в базисном варианте
(точка D). Сам этот вариант, оставаясь допустимым, утрачивает Парето-оптималь-
ность (рис. 3.2). Данный эффект объясняется тем, что приоритет в распределении
фонда потребления, данный работникам с повышенной эффективностью труда,
позволяет настолько увеличить производство потребительских благ, что при их рас¬
пределении могут выигрывать и другие группы работников.
95
Первоочередной задачей разработки моделей с обратными связями
является систематизация количественных зависимостей, характеризую¬
щих влияние различных механизмов распределения и альтернатив повы¬
шения благосостояния на параметры эффективности производства. По¬
строение таких моделей требует разработки системы показателей бла¬
госостояния, формализации содержательных взаимосвязей между произ¬
водством и потреблением, соответствующего информационного обес¬
печения с помощью переписей населения, отчетных межотраслевых ба¬
лансов, единовременных выборочных обследований доходов, расчетов по
демографическим моделям и т.д. По-видимому, будет целесообразно
создание системы таких моделей.
Литература
1. Основные положения коренной перестройки управления экономикой. Материа¬
лы Пленума ЦК КПСС 25 - 26 июня 1 987 г. М.: Политиздат, 1987.
2. Введение в теорию и методологию системы оптимального функционирования
экономики. М.: Наука, 1983. Раздел III.
3. Казакевич Д.М. Экономические методы в плановом управлении. Новосибирск:
Наука, 1985.
4. Моделирование в процессах управления народным хозяйством. М.: Наука,
1984.
5. Хозяйственный механизм в системе оптимального функционирования социалис¬
тической экономики. М.: Наука, 1985. Раздел I.
6. Шаталин СО. Функционирование экономики развитого социализма. М.: Изд-во
МГУ. 1 982. Гл. 3.
РАЗДЕЛ II
МОДЕЛИРОВАНИЕ НА НАРОДНОХОЗЯЙСТВЕННОМ УРОВНЕ
ЧАСТЬ А.
ЭКОНОМИЧЕСКАЯ СТАТИКА
Экономическая статика и экономическая
динамика - это связанные друг с другом стадии исследова¬
ния экономических систем, отличающихся характерными проб¬
лемами и методологическими подходами.
Предмет экономической статики — анализ состояний народ¬
ного хозяйства и его частей за отдельные моменты или краткие
промежутки времени. Главный постулат статического анализа
заключается в том, что в течение рассматриваемого временного
интервала ресурсно-технологические возможности и потребности
общества не изменяются. В соответствии с этим основными за¬
дачами экономической статики являются оптимальное распре¬
деление разнообразных ресурсов между возможными направ¬
лениями их использования, анализ структуры и взаимосвязей на¬
родного хозяйства, достижение общей пропорциональности и
сбалансированности экономики. Эти задачи, решаемые с помо¬
щью статических моделей, занимают важное место в науке и
практике, но они далеко не исчерпывают проблем анализа, пла¬
нирования, управления народным хозяйством как развиваю¬
щейся, динамической системы. В рамках статического модели¬
рования не могут изучаться такие проблемы, как воспроизвод¬
ство населения и основных фондов, научно-технический прог¬
ресс, развитие системы общественных потребностей и т.п. Одна¬
ко изучение статических моделей — необходимая часть пути к
более сложным дина мическим моделям экономики,
включающим статические модели как конструктивные элемен¬
ты. Не следует только забывать, что выводы, полученные на ос¬
нове статических моделей, нельзя переносить на ситуации, не
укладывающиеся в рамки предпосылок статического анализа.
4 Зак. 2414 97
Рис.Д.1. Основные связи между главами раздела II
Часть А раздела о моделировании на народнохозяйственном
уровне включает пять глав. Сначала рассматриваются узловые
проблемы моделирования отдельно сферы производства и отде¬
льно сферы потребления (гл. 4 и 5). Полученные выводы затем
используются для построения и анализа комплексных народно¬
хозяйственных моделей (гл. 6, 7, 8), получивших применение
в экономических исследованиях и планировании.
98
ГЛАВА 4
МОДЕЛИРОВАНИЕ СФЕРЫ ПРОИЗВОДСТВА
4.1. Технология и производственные возможности
Производственные возможности народного хозяйства в любой момент
времени определяются двумя группами факторов: а) технологическими
условиями производства, которые выражаются зависимостями между
затратами различных ресурсов (воспроизводимых и невоспроизводи¬
мых) и выпуском продукции; б) объемами и качеством наличных ресу¬
рсов. В гл. 2 и 3 уже вводились понятия и общие математические описания
видов деятельности, ограниченности ресурсов, множества допустимых
вариантов развития. Рассмотрим более подробно элементы и свойства
ресурсно-технологических возможностей народ¬
ного хозяйства. г
Пусть X = (д^*) обозначает вектор затрат ресурсов, i Е М, М = { 1,
..., т} ; Y = (yj) — вектор объемов производства, ; Е N, N = | 1, ...,
п | . Воспроизводимые средства производства одновременно являются
и продуктами, и ресурсами. Поэтому все виды ресурсов можно разбить
на два подмножества: М\ — воспроизводимые ресурсы (они же продук¬
ты), I*! Е Mi, MtCN; М2 — невоспроизводимые ресурсы, i2 Е М2. При
этом объемы невоспроизводимых ресурсов в каждый данный момент
ограничены: Х2 < R. Кроме того, необходимо учитывать различия в рас¬
ходовании предметов труда и.основных фондов. Первые полностью
расходуются в одном производственном цикле (затраты имеют размер¬
ность потока); вторые используются многократно (объемы использо¬
вания в каждом производственном цикле имеют размерность запаса).
При исследовании народнохозяйственного процесса производства затра¬
ты и выпуски так называемых промежуточных продуктов (полностью
потребляемых в сфере производства) иногда исключаются из непосред¬
ственного рассмотрения.
Среди различных пар векторов (.X, Y) рассматриваются технологи¬
чески допустимые пары, которые называются техноло гиями
(или технологическими процессами). Технологическая
допустимость означает возможность получить из затрачиваемых (исполь¬
зуемых) ингредиентов вектора X вектор продукции Y. Совокупность
4* 99
всевозможных допустимых технологий (X, Y) образует технологи¬
ческое множество народного хозяйства Z1 „
Нас, естественно, интересуют наиболее экономные преобразования
ресурсов в продукты. Пусть (1Ь Yi), (Х2, Y2) — две допустимые тех¬
нологии и (Xi, Y1) Ф (Х2, Y2). Технология (Xi, Yi) называется более
эффективной, чем (Х2, Y2), если выполняется соотношение: Хх < Х2,
У! > Y2, т.е. по первой технологии затраты не больше, а выпуски не ме¬
ньше, причем хотя бы по одному ингредиенту затрат или выпуска имеет
место строгое неравенство. Технология (X* V*) называется эффек¬
тивной (оптимальной по Парето), если не существует другой до¬
пустимой технологии, более эффективной, чем (X*, Y*). Множество
всех эффективных технологий обозначим Z*.
Множество производственных возможностей народного хозяйства
может быть представлено в виде:
I (X, У) €2.
<4'!>
При ограниченных невоспроизводимых ресурсах за определенный
промежуток времени может быть произведено ограниченное количество
продукции. Очевидно, что выбор эффективных вариантов производства
продукции и использования ресурсов будет осуществляться на множест¬
ве Z*.
Социалистическое общество заинтересовано в получении наибольших
количеств конечной продукции, однако проблема выбора лучшей струк¬
туры конечной продукции (оптимального вектора Y) не может решаться
только с позиций производства; здесь прежде всего необходимо учиты¬
вать социальные потребности. Поэтому общая модель производственного
планирования формулируется как задача нахождения множества эффек¬
тивных вариантов {X, Y) путем максимизации векторной функции Y на
множестве (4.1):
(*, П€2,
(4.2)
Y max.
В отличие от чисто технологической эффективности допустимых па¬
раметров (X, Y) G Z*, эффективные варианты задачи (4.2) учитывают
также и ограниченность ресурсов, направления использования которых
определяются стремлением получить больше конечной продукции.
1 Обычные предположения о свойствах технологий гаранти^ют, что множество
Z является замкнутым выпуклым конусом в пространстве Rm п.
100
4.2. Производственные функции
и функции производственных затрат.
Основные понятия
Технологическое множество Z и его подмножество Z* можно описать
в виде системы соотношений.
F(X, Y, А) = 0, (4.3)
где А — вектор параметров. Такая обобщенная форма выражения зависи¬
мостей между используемыми ресурсами и выпусками продукции по¬
лучила название производственной функции, Производствен¬
ная функция (4.3) — это функциональная (кибернетическая) модель
сферы производства, определяющая ’’выход” Y по данным о ’’входе”
X (зависимость между X и Y в общем случае многозначна). Народное
хозяйство представляется здесь как ’’единая фабрика”, у проходной ко¬
торой регистрируется все, что на нее поступает (X), и все, что из нее вы¬
пускается (F).
Теоретическому смыслу производственной функции народного хо¬
зяйства отвечают такие методы потребления, когда принимаются во вни¬
мание только эффективные технологии или эффективные варианты мо¬
дели (4.2) .\Определяемые объемы производства конечной продукции
являются максимальными в том смысле, что при заданных затратах ре¬
сурсов нельзя увеличить производство ни одного продукта, не уменьшив
при этом производство хотя бы одного другого продукта.[в отличие от
структурных оптимизационных моделей народного хозяйства, напри¬
мер (4.2), общая производственная функция является функциональной
моделью объекта с непосредственно не наблюдаемыми оптимизационнык-
ми способностями. Это - своего рода ’’оптимизирующий черный ящик”.
Построение и анализ общей производственной функции народного
хозяйства представляют исключительно трудную задачу. Поэтому в прик¬
ладных исследованиях основное внимание уделяется частным видам
общей производственной функции.
Производственная функция
У) = // (-*/). Х/ = (* 1/. • хт,) (4.4)
характеризует максимально возможный объем выпуска продукта в зави¬
симости от использования разнообразных ресурсов. Каждой точке Xjсо¬
ответствует единственный максимальный выпуску® 1.
Очевидно, что функция (4.4) может описывать однопродук¬
товые технологии, но не применима для характеристики комплекс¬
ных технологических процессов, выпускающих одновременно несколько
видов продукции.
1 Точнее: yfl <// (X/)t max y/l =f; (Xj).
101
Различаются два основных типа производственных функций: произ¬
водственные функции с взаимозаменяемыми ресурсами (см. 4.3) и прои¬
зводственные функции с взаимодополняемыми ресурсами (см. 4.4).
Наряду с производственными функциями в исследованиях производ¬
ственных возможностей народного хозяйства широко применяются
функции производственных затрат. Функция
*/ = Ф<(у) (4-5)
называется функцией производственных затрат ресурса i от объемов
выпуска разнообразных продуктов. Такие функции уже использовались
в теоретическом анализе моделей народного хозяйства (см. гл. 2, 3).
В экономическом анализе часто применяются функции затрат на про¬
изводство одного продукта:
*|/“Ф ц(У/)- (4-6)
Если ресурс i не используется в комплексных технологических про¬
цессах, то функция (4.6) аддитивнаГ
**—2 хи = 2 ф(4.7)
jeN j*N
Ниже будет показано, что функции производственных затрат могут
интерпретироваться как функции, обратные производственным функци¬
ям с взаимодополняемыми ресурсами (см. 4.4).
Производственные функции и функции производственных затрат
применяются в анализе производственных процессов на различных
уровнях народного хозяйства. Хотя при этом могут использоваться
однотипные математические описания, содержательный смысл и спо¬
собы построения производственных функций (функций производствен¬
ных затрат) в этих случаях существенно различаются.
На микроэкономическом уровне рассматриваемые математические
модели являются описаниями конкретных (элементарных) технологий
и выводятся из соответствующих технологических (инженерных) дан¬
ных. Производственные же функции (функции производственных зат¬
рат) сложных объектов (предприятий, отраслей, регионов, народного
хозяйства в целом) являются математическими моделями, характеризу¬
ющими абстрактные технологии, т.е. обобщенные зависимости
между затратами ресурсов и выпусками продукции.
Прямой переход от моделей конкретных технологий к модели абс¬
трактной технологии трудно осуществим из-за различий ’’языков”
моделирования простых и сложных производственных объектов. В тех
сравнительно редких случаях, когда объекты микро- и макроуровней
описываются сходными математическими моделями, производственные
функции (функции производственных затрат) сложных объектов могут
102
строиться путем агрегирования соответствующих функций
более простых объектов. Так, например, если объекты разного уровня
описываются линейными балансовыми моделями с производственными
функциями в виде производственных способов (см. 4.5), то параметры
производственных способов объектов более высокого уровня рассчи¬
тываются путем агрегирования производственных способов объектов
нижнего уровня (см. 6.5).
Как правило, построение обобщенной производственной функции
(функции производственных затрат) представляет собой довольно
сложную задачу моделирования абстрактной технологии. Здесь исполь¬
зуются два основных подхода: оптимизационный и статис¬
тический. Эти подходы соответствуют двум основным типам
моделей экономических объектов - структурным и функциональным.
Суть оптимизационного подхода состоит в том, что производствен¬
ная функция (или функция производственных затрат) получается пу¬
тем обобщения решений оптимизационной модели при меняющихся
условиях. Например, производственная функция народного хозяйства
может быть выведена из анализа решений модели (4.2) при меняющем¬
ся векторе R1. Очевидно, что свойства построенной таким способом
производственной функции определяются исходной оптимизационной
моделью.
Статистический подход к построению обобщенных функций осно¬
ван на обработке наблюдений о различных соотношениях затрат ре¬
сурсов и выпусков продукции. В математическом отношении он опи¬
рается на теорию корреляционного и регрессионного анализа. Процесс
построения функции включает отбор существенных факторов, выбор
вида функции (математической модели), статистическую оценку ее
параметров, проверку статистической надежности2. Найденная зависи^
мость между затратами (’’входами”) и выпусками (’’выходами”)
является функциональной моделью (’’черным ящиком”) соответству¬
ющего производственного объекта.
При моделировании (на народнохозяйственном уровне) произ¬
водственные функции и функции затрат применяются двояким обра¬
зом: как самостоятельные математические модели производственных
объектов (см. гл. 4, 9, 10) и как элементы более сложных моделей на¬
родного хозяйства (гл. 6—8, 10—13). В системном моделировании
народного хозяйства (см. раздел III) производственные функции и
функции производственных затрат часто применяются как функции
отклика экономических подсистем, характеризующие реакции (от¬
клик) соответствующей подсистемы на поведение (принимаемые реше-
! ния) других подсистем.
Для этого используются различные методы: параметрическое программиро¬
вание, теория планирования эксперимента и т.д. Общей чертой этих методов явля¬
ется многократная реализация исходной модели, в результате чего ’’набирается”
информация о зависимости выходных параметров от входных.
2
Предполагается, что читатель знаком с основами корреляционно-регрессион¬
ного анализа.
103
4.3. Производственные функции I \
с взаимозаменяемыми ресурсами. v
Показатели использования ресурсов
Общие свойства функций. Предположение о взаимозаменяемости ресур¬
сов в производственной функции yj = fj(Xj) означает, что один и тот же
объем выпуска продукции может быть получен при разных комбинациях
ресурсов, отличающихся тем, что затраты одних ресурсов больше, а дру¬
гих — меньше. Ниже мы будем опускать индекс /, если речь идет о функ¬
циях производства одного продукта.
Сформулируем некоторые свойства производственных функций
с взаимозаменяемыми ресурсами:
а) если X = 0, то у = 0;
б) если Х^ > Х^, то f (X^) >f(X^)9 причем если Х^ > Х&, то f (Х^ )>
>f(X^)\ из этого, в частности, следует, что у > 0 при Х> 0. Если у = Опри
положительных затратах некоторых ресурсов, но при xs = 0, то это
означает, что ресурс s абсолютно необходим для производства хотя бы в
малых количествах (например, труд, электроэнергия и т.п.)1.
Отмеченные свойства отражают ряд реальных условий производства
и правил разумного хозяйствования.
Производственные функции могут задаваться не только в аналити¬
ческой форме, но и в виде таблиц. В качестве примера приведем таблицу
выпуска продукции в зависимости от затрат двух видов ресурсов: рабо¬
чей силы и средств производства (см. табл. 4.1) 2.
Таблица 4.1
Пример табличной производственной
функции с двумя взаимозаменяемыми ресурсами
-Затраты средств t
Затра- производства
ты труда
10
20
30
40
50
60
50
44
55
63
69
75
80
60
69
88
100
110
119
126
70
91
115
132
145
156
166
80
110
139
159
174
188
200
90
128
162
185
203
218
232
100
145
183
209
230
247
263
110
160
202
231
254
273
291
120
175
221
253
277
299
318
130
189
239
273
300
323
344
140
203
256
293
322
347
369
150
216
273
313
343
370
393
160
229
290
332
364
392
417
В том случае, когда увеличение производственных затрат какого-либо ресурса
s сверх величины x's приводит к уменьшению объема производства, надо непосредст¬
венно использовать x's, а излишек *„• - х'■ >0 оставить в резерве.
2 Пример заимствован из деловой игры ’’Экономическая система” (авторы
Д.Колеман и Т.Харрис, США).
104
Множество точек, удовлетворяющих уравнению постоянного вы¬
пуска f(X) = q, называется изоквантой. На рис. 4.1 изображено
семейство изоквант — кривых в пространстве двух ресурсов; эти изо¬
кванты соответствуют объемам выпуска продукции qXt q2, 4з* В об¬
щем случае изокванты — это поверхности в га-мерном пространстве
ресурсов. Поскольку X > 0, то все изокванты находятся в неотрицате¬
льном ортанте.
ции и изоклинали
В табл. 4.1 можно указать комбинации ресурсов, принадлежащие изоквантам,
например: комбинации (60, 10) и (50, 40) дают q =69; комбинации (80, 10) и
(60,40) дают q =110; (100,10) и (70,40) дают q = 145 и т.д.
И з общих свойств производственных функций вытекает ряд свойств
изоквант: они никогда не пересекаются друг с другом; большему вы¬
пуску продукции соответствует более удаленная от начала координат
изокванта; если все ресурсы абсолютно необходимы для производства,
то изокванты не имеют общих точек с осями координат. Далее будут
обсуждаться свойства изоквант, соответствующих определенным клас¬
сам производственных функций.
Средняя и предельная эффективность использования ресурсов.
Для характеристики эффективности производственных ресурсов при¬
меняются два основных показателя:
средняя эффективность ресурса
7(*)
Xг
(4.8)
105
предельная эффективность ресурса
дх{
(4.9)
Величина v/X) показывает предельный прирост выпуска продукта
при увеличении затрат ресурса i на ’’малую единицу”. Из свойства (б)
производственных функций с взаимозаменяемыми ресурсами следует,
что vi > 0. Как правило же, vi > 0. При этом особенно важен характер
изменения эффективности дополнительных количеств используемого
ресурса.
_ d*f (X)
Если v/i ^2 * это означает, что предельная эффективность
ресурса падает. Такая ситуация вполне объяснима. Например, если
в производстве какого-либо продукта увеличивать затраты труда, сохра¬
няя неизменными объемы других ресурсов, то предельная производи¬
тельность труда будет снижаться из-за уменьшения вооруженности еди¬
ницы труда средствами производства. Важно понимать, что уменьшение
предельной эффективности ресурсов типично только в условиях эко¬
номической статики, т.е. при неизменном научно-техническом уровне
^ и неизменном качестве используемых ресурсов.
Условие = <0 в западной литературе часто называют ”за-
dxi
коном убывающей предельной эффективности ресурсов”. Уменьшение предельной
эффективности перестает быть ’’законом”, как только мы начинаем учитывать на¬
учно-технический прогресс. Сущность данного ’’закона” проанализирована В.И.Ле¬
ниным в статье ’’Аграрный вопрос и критики Маркса” (Полн. собр. соч. Т. 5. С.
100-10.3).
На рис. 4.2 приведены три типичных графика, характеризующих вли¬
яние увеличения затрат ресурса / при неизменных объемах других ре¬
сурсов: 1 — изменение выпуска продукции у; 2 — изменение средней
эффективности ресурса -щ; 3 — изменение предельной эффективности
ресурса vi. Как видим, функция 1 растет, но ее рост замедляется. Функ¬
ции 2 и 3 убывают, причем предельная эффективность ниже средней эф¬
фективности.
Иначе изменяется средняя и предельная эффективность определенно¬
го (z-го) ресурса при увеличении затрат других ресурсов. Как правило,
выполняются соотношения:
1Фк, (4.Ю)
dxk Х{ дхк
|^ = WI>0j (4.11)
tk дхк дх, дхк
106
Рис. 4.2. Функции абсолютной (1), средней
(2) и предельной (3) эффективности ресурса
Это объясняется тем, что увеличение затрат труда к улучшает усло¬
вия применения ресурса z. Например, производительность труда зависит
не только от качества самого труда, но и от условий приложения труда.
В частности, производительность труда увеличивается при росте фондо¬
вооруженности.
Эквивалентная заменяемость ресурсов. Изменение выпуска продук¬
ции при небольших изменениях затрат нескольких ресурсов выражается
полным дифференциалом dy — 2. v. dx.. Условия эквивалентной вза-
/€ГЛ/ 1 1
имозаменяемости ресурсов в точке Х° = (х? ) выводятся из формулы
2 v,(X*)dxt = 0. (4.12)
i€M
В частности, предельная норма эквивалентной заменяемости каких-либо
двух ресурсов Ни I определяется формулой
VI (х°)
vk(X°
<0.
(4.13)
Процессу эквивалентного замещения одних ресурсов другими
соответствует движение вдоль изокванты. Поэтому изокванту называют
также кривой замещения.
Если затраты ресурса к увеличиваются, то для сохранения объема
производства на прежнем уровне затраты ресурса /, как правило, можно
107
уменьшить. Отсюда следует такое свойство изоквант: это убывающие
функции по отношению к каждой оси (т.е. они имеют отрицательный
наклон). В пространстве двух ресурсов норма эквивалентной заменя¬
емости — это тангенс угла между касательной к изокванте и соответст¬
вующей осью координат. На рис. 4.1 нормы эквивалентной заменяемос¬
ти второго ресурса по отношению к первому в точках A lf Вх, С\ равны
тангенсам углов уА, ув, ус. Комбинации ресурсов, для которых преде¬
льные нормы эквивалентной замены одинаковы, образуют в пространс¬
тве ресурсов кривые, называемые изо клиналями. На рис. 4.1
изоклиналь I соединяет точки 2?ь В2, В3, а изоклиналь II — точки Сь
С2, Сз.
Анализ закономерностей изменения предельных норм эквивалент¬
ной замены позволяет еще более конкретизировать форму изоквант.
При увеличении использования ресурса I его предельная эффективность
падает, и поэтому дополнительные затраты этого ресурса высвобождают
все меньшее количество ресурса к. Таким образом, предельная норма
эквивалентной взаимозаменяемости двух ресурсов постоянно умень¬
шается.
Рассмотрим, к примеру, комбинации затрат из табл. 4.1, принадлежащие одной
изокванте q = 273: А = (110, 50), В = (130, 30), С= (150, 20). Первое увеличение
затрат труда на 20 ед. высвобождает 20 ед. средств производства, второе увеличе¬
ние затрат труда на 20 ед. высвобождает уже только 10 ед. средств производства
и т.д.
Это означает, что в пространстве двух ресурсов изокванты являют¬
ся графиками вогнутых функций (одной переменной относительно
другой). Если эта особенность предельных норм эквивалентной заменя¬
емости распространяется на множество всех т ресурсов, то изокванты
обладают двумя дополнительными свойствами: множества {X: f(X)>
> Q J выпуклы и изокванты имеют асимптоты, совпадающие с осями
координат или параллельные им (подробнее см. М.К.Плакунов, Р.Л.Раяц-
кас. С. 40- 54; ММСЭ. С. 175).
Эластичности производства и взаимозаменяемости ресурсов. Для
характеристики влияния каждого ресурса на рост производства, помимо
показателей средней и предельной эффективности, используется также
понятие эластичности выпуска от затрат различ¬
ных ресурсов. Коэффициент эластичности 5/ показывает предель¬
ное отношение относительного прироста производства к относительному
приросту затрат /-го ресурса:
Ау
6,= Пт (4.14)
' &Х1-+0**1 dxi У
Xi
108
На рис. 4.3 изображены изокванты трех производственных функций, проходя¬
щие через одну точку (с координатами х? =х%) и отличающиеся коэффициентами
эластичности в этой точке. Изокванта 11 с равными коэффициентами эластичности
симметрична относительно биссектрисы положительного ортанта. Изокванта I
(5д <£2) имеет относительно меньший наклон к оси х1} а изокванта III (5j >
2), наоборот, больший наклон к оси хх.
Рис. 4,3. Изокванты и коэффициенты эластич¬
ности
В общем случае коэффициент эластичности — это непрерывная функ¬
ция от*0. В экономических расчетах часто используются средние коэф¬
фициенты эластичности, определяемые не для каждой точки Х°, а для не¬
которых интервалов изменения компонент вектора А"0. Такие коэффи¬
циенты соответствуют формуле
б Д£ _Дх,- (4 15)
1 у Xi
В теории производственных функций применяется также понятие
эластичности взаимозаменяемости ресурсов. Коэффици¬
ент эластичности замены ресурсов характеризует отношение относитель¬
ного изменения соотношения затрат ресурсов к и / к относительному
изменению предельной нормы эквивалентной заменяемости этих ресур¬
сов:
ah __iL;^L=iiL.YfcziL. (4.16)
Ы Ч_ УМ дУЫ 1*к
XI
109
Чем выше эластичность замены ресурсов, тем в более широких
пределах они могут заменять друг друга. При бесконечной эластичности
(ок1 = + °°) не существует никаких границ для взаимозаменяемости
ресурсов. Наоборот, при нулевой эластичности (oki = 0) возможность
замены отсутствует. В этом случае ресурсы взаимодополняют друг дру¬
га и обязательно должны использоваться в определенном комплекте
(см. 4.4).
На рис. 4.4 изображены изокванты с различными коэффициентами эластичнос¬
ти замены двух ресурсов в интервале 0 ^ О ^ °°. Прямоугольная ломаная ЛВС
является изоквантой при О = 0. Сокращение одного ресурса нельзя компенсиро¬
вать сколько угодно большим увеличением другого ресурса. Три изокванты имеют
положительные эластичности 0\, О2, СТд. При этом более выпуклые к началу коор¬
динат изокванты соответствуют меньшим коэффициентам эластичности: 0\ <(*2 ^
< (73. Наконец, прямая АС представляет собой изокванту с бесконечной эластично¬
стью замены ресурсов. Она имеет формулу а\Х\ ■+■ <*2*2 гДе а\ ла2 ~ положи¬
тельные числа. Предельная норма замены ресурсов на этой изокванте не меняется:
У12
__ ар_
*1
Рассмотренные эластичности выпуска по ресурсам и эластичности
взаимозамены ресурсов наряду с показателями общей эффективнос¬
ти ресурсов (’’отдачи на масштаб”) являются основными характеристи¬
ками абстрактной технологии.
Анализ типовых производственных функций. При статистическом
подходе к построению производственных функций важным этапом яв¬
ляется выбор математической зависимости от количества параметров,
110
включаемых в аппроксимирующую функцию1. На первый взгляд при
заданном составе ресурсов производственная функция тем ’’лучше”,
чем больше она включает параметров. Однако на самом деле это не так.
С увеличением числа оцениваемых параметров сильно возрастает
число необходимых наблюдений, обеспечивающих точность и надежность
статистических оценок (число наблюдений должно быть как минимум
в 5—6 раз больше числа параметров). Усложняется и экономическая
интерпретация свойств функции. Здесь мы сталкиваемся с типичным
противоречием метода моделирования, когда стремление к возможно
более полному и точному воспроизведению объекта-оригинала препят¬
ствует использованию главных преимуществ этого метода познания.
Поэтому в теоретических и прикладных исследованиях (особенно на
макроуровне) отдают, как правило, предпочтение производственным
функциям с небольшим числом параметров, удобным для вычислений
и интерпретации (подробнее о статистических методах построения
производственных функций см. Г.Б.Клейнер, гл. 2; М.К.Плакунов,
Р.ЛРаяцкас, гл. 6).
Однородные производственные функции* Функция у = f(X) назы¬
вается однородной п-й степени, если выполняется следующее
соотношение:
f(KX) = Xnf(X). (4.17)
Это означает, что при увеличении затрат всех ресурсов в X раз объем
производства возрастает в \п раз. Показатель степени однородности
п характеризует изменение эффективности производства с увеличением
производственных затрат (’’отдача на масштаб”).
Теоретически возможны три случая: 1) эффективность остается по¬
стоянной (п = 1); 2) эффективность снижается (п < 1); 3) эффектив¬
ность возрастает (п > 1). В условиях неизменного научно-технического
уровня указанные ситуации имеют место в различных отраслях народ¬
ного хозяйства.
Снижение эффективности производства при увеличении его объема есть след¬
ствие рационального ведения хозяйства. Это объясняется тем* что для производства
в первую очередь используются наиболее благоприятные возможности. По мере же
увеличения производства приходится использовать все менее эффективные ресур¬
сы и технологические процессы (бедные месторождения, старое оборудование и
т.п.). Однако в некоторых отраслях, особенно в обрабатывающей промышлен¬
ности, увеличение производства (точнее, его концентрация на определенных пред¬
приятиях) позволяет увеличить эффективность использования ресурсов за счет эко¬
номии на общих расходах, мало зависящих от объема производства, более полного
использования основных фондов и т.п. В целом по народному хозяйству положи¬
1 Согласно теореме Вейерштрарса всякая непрерывная функция (хо¬
тя бы в некоторой ограниченной области своих аргументов) может быть сколь
угодно точно аппроксимирована полиномом ^ = Д() _j_ aiX\ -f- а2х2 + Яц*1 +
+ й12*1*2 + ^22*2+ • • •
111
тельные и отрицательные влияния роста производства на эффективность использо¬
вания ресурсов при неизменном научно-техническом уровне в значительной мере
погашают друг друга. Поэтому в пределах краткого времени величина п для народ¬
ного хозяйства в целом близка единице.
Для однородной функции справедлива формула Эйлера
2 =
i€M 0Xi
(4.18)
Разделив обе части этого уравнения на у, получим
(4.19)
ду Xi
Выражение ^7 *~jj~ есть коэффициент эластичности 6/. Поэтому п
равно сумме коэффициентов эластичности выпуска по затрачиваемым
ресурсам.
Проанализируем подробнее экономический смысл формул (4.18)
и (4.19) при п = 1:
у ду_.х .
дх- ‘
ieM ах‘
■у\
(4.20)
(4.21)
ду
Поскольку qp — это предельная эффективность единицы ресурса
ду
z, то дх;'** было бы заманчиво интерпретировать как общий объ¬
ем продукции, произведенной за счет ресурса /. Весь объем производства
у (или единица произведенной продукции) как бы складывается из час¬
тей (или разлагается на части), произведенных за счет использования
каждого ресурса в отдельности. Выражение (4.21) показывает также, что
сумма коэффициентов эластичности однородной производственной
функции первой степени равна единице. Из этого в свою очередь
следует, что если все коэффициенты эластичности неотрицательны
(6/>0), то ни один из них не может быть больше единицы (б/<
<1).
112
Изложенные экономические интерпретации выражений (4.20)
и (4.21) имеют сугубо условный характер, не вытекающий из техноло¬
гической природы производственных функций. Нельзя забывать, что на
самом деле продукция может создаваться только путем взаимодействия
ресурсов. И если какой-либо ресурс s абсолютно необходим для произ¬
водства (из х$ = 0 следует у = 0), то никакие затраты других ресурсов
не могут привести к созданию продукции. Конструктивное значение
показателей предельной эффективности заключается не в том, что они
определяют роль (вклад) каждого ресурса, а в том, что они позволяют
изучать влияние изменения затрат различных ресурсов на изменение
объемов производства.
Однако в западной экономической науке интерпретациям формул (4.20) и
(4.21) придается исключительно большое значение. Эти формулы используются
в теории ’’трех факторов производства” и теории ’’вменения” для объяснения
процесса создания стоимости (вменение капиталу, труду, земле соответствующих
частей стоимости) и теоретического обоснования принципа распределения создава¬
емой стоимости на заработную плату, прибыль, ренту (в соответствии с предельны¬
ми продуктами труда, капитала, земли, как основными факторами производства).
Необходимо строго отделять анализ производственных функций как инстру¬
мента изучения технико-экономических условий производства от попыток исполь-/
зования производственных функций в теориях образования стоимости и распреде¬
ления доходов.
Степенная (мультипликативная) производственная функция. Широ¬
кое распространение в экономических исследованиях имеет функция вида
у=>а П tfi. (4,22)
(ЩМ
Она обладает рядом достоинств: включает небольшое число имею¬
щих явный экономический смысл параметров, имеет производные выс¬
ших порядков, в большинстве случаев удовлетворительно выравнивает
эмпирические данные, весьма удобна для оценки параметров (в частнос¬
ти, благодаря тому, что является линейной относительно логарифмов:
log у = log a *f- 2 pi log х{). Эта функция включает только безусловно не¬
обходимые ресурсы: если какой-либо xs - 0, то у = 0. Параметр а ин¬
терпретируется как показатель общей эффективности ресурсов (он при¬
водит также в соответствие размерности затрачиваемых ресурсов и произ¬
водимой продукции).
В соответствии с (4.14), (4.15), (4.16) предельная норма эквивален-
—aiXk
тнои замены ресурсов Ум — » коэффициент эластичности выпуска
по /-му ресурсу 6/ = аи коэффициент эластичности замены ресурсов okl —
= 1. Из уравнения нормы эквивалентной замены следует, что изоклиналь
степенной производственной функции — луч, исходящий из нача¬
ла координат:
ИЗ
^lxk __ q %k g &k
при 7^ ~ ~ ckl~ const имеем akxi kl или xi k at
В макроэкономических исследованиях чаще всего применяется фу-,
нкция (4.23), характеризующая зависимость производства национально¬
го дохода (конечного общественного продукта) от объемов использо¬
вания двух основных производственных факторов — рабочей силы (L)
и производственных фондов (К):
y = aLaiKa«. (4-23)
Функцию (4.23) впервые построили и применили в экономическом
анализе американские исследователи [СКобб и П.Дугласi Впоследствии
она стала называться функцией Кобб а — Д у глас а.
Характеристики использования ресурсов, выводимые из функции
Кобба—Дугласа, имеют сравнительно простую аналитическую форму.
Средние эффективности ресурсов: ^ = aLaL ~ 1 К0,дд* =
= aLaL Как ~ предельные эффективности ресурсов: уг =
= aaLLat ~ 'К**, Ж = a*KLaL К?* ~ 1.
Коэффициенты эластичности характеризуют влияние увеличения
затрат (использования) труда и производственных фондов на рост
производства. Принято называть производственный процесс трудо¬
интенсивным, если aL > ак, и фондоинтенсивным, если
aK^>aL'
Частным случаем (4.23) является функция первой степени, для
которой aL + ак = 1. Ее можно записать в виде
y^aL^K1-** (4-24)
Заметим, что данные в соотношениях между выпуском и затратами труда и
средств производства, приведенные и табл. 4.1, удовлетвоояют формуле, очень
близкой (4.23) и (4.24): у = 4,595 /.0,330 . ^ _ 40)0,660 _ о,075. При этом
слагаемое 0,075 объясняется ошибками округления.
В СССР наиболее известные работы по построению и анализу функ¬
ции Кобба—Дугласа выполнены Б.Н.Михалевским, А.И.Анчишкиным,
ДА. Черниковым.
Приведем расчеты функции Кобба-Дугласа по данным о динамике националь¬
ного дохода, численности занятых в материальном производстве и основных произ¬
водственных фондов, опубликованным в статистических ежегодниках ”Народ¬
ное хозяйство СССР” за 1970-1980 гг. Следует оговорить, что специальной работы
по очистке динамических рядов и спецификации производственных факторов не
проводилось. Поэтому результаты имеют главным образом иллюстративное
значение. а \ - а
Для функции вида у =а0 L К получены следующие значения параметров
(национальный доход 1970 г. принят за 1): а0 = 1,01, (X = 0,41 8. Статистические
характеристики: коэффициент детерминации R = 0,9933, остаточная дисперсия
Оост = 0,0003, значение критерия Дарбина-Уотсона равно 1,18 (подробнее см.
ДМНХ, с. 83-85).
114
Функцию Кобба — Дугласа удобно использовать для анализа зависи¬
мости производительности труда iyjL) от его фондовооруженности
(K/L). При условии oll + aj( = 1 из (4.24) следует
-»=а(£ )1-<\ (4-25)
Поскольку по смыслу а/, > 0, то производительность труда растет
медленнее фондовооруженности. Однако этот вьюод, строго говоря,
справедлив только для экономической статики, т.е. в рамках существую¬
щих технических условий и качественных характеристик ресурсов.
\ Функииц г ппгтпяннпц эластичностью замены ресурсов. Рассмат¬
риваемая производственная функция (функция ПЭЗ) имеет общий вид
п
У — а0( 2 р. /426)
\ i € М '
Она является однородной функцией степени п и получается реше¬
нием дифференциального уравнения при о = const, где о определяется
формулой (4.16). В функции ПЭЗ все эластичности замены ресурсов
^ „ 1 1-0
okl равны между собой: okl = о, при этом а = у + у или р =—~— .
Если р > 0, то 0 < а < 1; если же -1 < р < 0, то а > 1. Функция ПЭЗ
в общем случае имеет неединичную эластичность замены. При о = 1 (или
р-> 0) функция ПЭЗ преобразуется в степенную производственную
функцию (4.22). Это означает, что рассматривавшиеся выше степенные
производственные функции (в том числе макроэкономическая функция
Кобба—Дугласа) являются предельным случаем функции ПЭЗ.
При р —1 (а-*+°°) эластичность замещения стремится к бесконеч¬
ной и форма изоквант приближается к линейной. При р +°° (а 0)
эластичность замещения стремится к нулевой и форма изоквант приб¬
лижается к прямоугольной.
В макроэкономическом анализе чаще всего применяется двухфак¬
торная функция ПЭЗ (ее называют также функцией Соло у):
п
у — aa(aLL~p-\-акК~р)р (4.27)
Для функции национального дохода СССР (4.27) при п = 1 и ак = 1 - ai путем
обработки динамических рядов за 1970-1980 гг. по справочникам ’’Народное хо¬
зяйство СССР” (по той же методике, что и для функции Кобба-Дугласа) полу¬
чены следующие параметры и статистические характеристики: я0 =0,99, ai =
= 0,257, р = 1,994, ЯГ = 0,9966, оьст = 0,0002, DW = 2,16.
Подробнее о функциях ПЭЗ см. С.А.Ашманов, С. 220-225; А.В.Ло-
тов, С. 86-92. Однородные производственные функции с переменной эла¬
стичностью замены рассматриваются в: М.К.Плакунов, Р.Л.Раяцкас,
С. 154- 162.
115
4.4. Производственные функции с взаимодополняемыми
ресурсами и функции производственных затрат
Наблюдаемые изменения в структуре используемых ресурсов часто
объясняются не столько замещением ресурсов в рамках одной и той же
технологии производства, сколько изменением самих технологий или со¬
четанием различных жестких технологий. В предельном случае (при ну¬
левой эластичности замены ресурсов) мы получаем производственную
функцию с взаимодополняемыми ресурсами.
Основные понятия. Производственная функция с взаимодополня¬
емыми ресурсами может быть выражена следующим образом:
У = min fs (xs),
seM
(4.28)
где fs (xs) - объем производства, который может быть получен при ис¬
пользовании s-ro ресурса в количестве xs при условии, что другие ресур¬
сы имеются в достаточном количестве. Максимальный объем производ¬
ства^ определяется узким местом, т.е.' количествомТакого ресурса, ко¬
торый обеспёчивает наи!^ бъем производства.
Изокванты функции (4.28) в пространстве двух ресурсов представ¬
ляют собой прямые углы (рис. 4.5). Их расположение определяется тем,
при каких минимальных затратах ресурсов достигаются определенные
объемы производства. Кривые ОА]А2А3 характеризуют минимальные
затраты ресурсов, обеспечивающие различные объемы производства. Все
точки изокванг, не лежащие на этих кривых, являются неэффективными
комбинациями затрачиваемых ресурсов при любых разумных критери-
Рис. 4.5. Изокванты взаимодополняемых ресурсов:
а — постоянные соотношения затрат; б — изменяющиеся соотношения
затрат
116
От функций (4.29) можем перейти к семейству обратных функций,
характеризующих зависимости-затрат от объемов производства, т.е. к
функциям производственных затрат: f
- ^ ‘
xs = Vs(y)’ (S€M). CJ ‘ (4-29)
ifis(y) - это минимальное количество ресурса s, которое нужно затратить
дня выпуска продукта в количестве у.
Для анализа функций производственных затрат (4.29) введем но¬
вые понятия: qs — средние затраты s-ro ресурса; hs — п р е д е-
льные затраты s-ro ресурса. Средние затраты рассчитываются по
формуле qs = х$/у. Предельные затраты hs характеризуют прирост затрат
ресурса s при увеличении выпуска продукции на ’’малую единицу”:
hs = dxs/dy. В дальнейшем изложении индекс ресурса опускается; это
позволяет интерпретировать получаемые результаты как относящиеся
не только к определенному ресурсу, но и к совокупным производствен¬
ным затратам (например, в ценностном выражении)1.
При у = 1 общие затраты всегда равны средним: х(1) =g(l). Общие
затраты являются суммой всех предельных затрат: х(у) = £h(g)dy.
Соотношения между средними и предельными затратами зависят от
свойств функции х = у (у).
Функцию х можно представить в виде х = gy. Тогда h = —=
dfz ds ^
= S + У dy~ • При этом знак производной - - характеризует изменение
средних затрат. Если ^ > 0, то средние затраты возрастают; если
^ < 0, то они снижаются; если ■ ^ = 0, то средние затраты остают¬
ся постоянными. Отсюда вытекают следующие соотношения:
а) средние затраты возрастают, когда предельные затраты выше сре¬
дних: ^ ^ >0; б) средние затраты снижаются, когда предельные
затраты ниже средних: ~~г~~ — < 0; в) средние затраты остаются
У У dg h—g *
постоянными, если они равны предельным затратам: ~ ^ ~ — ~"у = 0-
Анализ типовых функций производственных затрат. Наиболее прос¬
той функцией затрат является линейная однородная, харак¬
теризующая производственные процессы с постоянной эффективностью
затрат:
х = ау; а> 0. - (4.30)
Средние и предельные затраты функции (4.30) постоянны и равны
между собой: g = h= a (рис. 4.6).
В явном виде ценностные соотношения затрат и выпуска продукции (в том
числе общие, средние, предельные издержки, валовой доход, прибыль) анализиру¬
ются в ММСЭ, с. 190-196.
117
Рис. 4.6. Линейная однородная фун¬
кция (постоянная эффективность
затрат)
Рис. 4.7. Линейная неоднородная
функция затрат
Линейная неоднородная функция включает две части затрат — про¬
порционально зависящие от объема производства и не зависящие от
объема производства:
х = ау + Ь, (4.31)
где а > 0 и b > О1.
Средние затраты g = а + Ь/у являются убывающей нелинейной функ¬
цией (гиперболой), асимптотически приближающейся к постоянным пре¬
дельным затратам h =а (рис. 4.7). Поскольку при нулевом выпуске
бессмысленно осуществлять какие-либо затраты, этот момент следует
предусмотреть особо:
ау + b при у > О,
* — ^ 0 при у = 0.
Нелинейная функция возрастающей эффективности затрат отражает
положительный экономический эффект концентрации производства:
и = Ч>Ау), где ^г<0.
(4.32)
Средние и предельные затраты — убывающие функции, причем пре¬
дельные затраты всегда ниже средних (рис. 4.8).
1 Соотношение Ъ <0 имеет смысл, когда (4.31) является линейной аппрокси¬
мацией более сложной нелинейной функции.
118
Рис. 4.8. Нелинейная функция воз¬
растающей эффективности
Рис. 4.9. Нелинейная функция падающей
эффективности
Одним из простейших примеров функции (4.32) является х =
= ауа при а> 1.
Нелинейная функция падающей эффективности затрат характерна
для отраслей, деятельность которых тесно связана с использованием
природных ресурсов:
/ \ ^2ф2
*=Фг (У)’ гДе
0.
(4.33)
Для увеличения добычи минерального сырья, например, часто прихо¬
дится переходить к эксплуатации месторождений, шахт, рудников с
более сложными горно-геологическими условиями или с более бедным
содержанием полезных компонентов. Поэтому средние и предельные
затраты увеличиваются, причем предельные затраты выше средних
(рис. 4.9). Примером может служить функция х — ауа при 0 < а < 1.
Функции немонотонной эффективности затрат отражают часто встре¬
чающиеся в хозяйственной практике такие зависимости между затратами
и выпуском продукции, которые объединяют признаки рассмотренных
выше функций. Довольно типична такая ситуация: при увеличении
производства эффективность затрат вначале возрастает (положительный
эффект концентрации производства), но по достижении некоторого уро¬
вня производства эффективность начинает снижаться (из-за сложности
управления, ухудшения условий производства, роста транспортных
затрат и т.д.).
119
Рис. 4.10. Нелинейная функция немонотон¬
ной эффективности затрат
Функция, изображенная на рис. 4.10, имеет два качественно различ¬
ных участка. На отрезке [0, уд\ она ведет себя так же, как (4.32), а при
дальнейшем увеличении у она сходна с (4.33). Ах — точка перегиба.
Средние и предельные затраты сначала уменьшаются (средние выше пре¬
дельных), а затем увеличиваются (сначала предельные, затем средние).
Минимум предельных затрат А 2 и точка перегиба A i функции х соответ¬
ствуют одному и тому же объему производства^. Пересечение кривых
g и h соответствует минимуму средних затрат (точка В).
Связь между производственными функциями с взаимозаменяемыми
ресурсами и функциями производственных затрат. Производственные
функции с взаимозаменяемыми ресурсами и функции производственных
затрат отражают противоположные принципы сочетания ресурсов в про¬
изводственных процессах (взаимозаменяемость и взаимодополняе¬
мость) ; они порождают существенно разные системы экономических по¬
казателей. Поэтому может создаться впечатление, что между этими мо¬
делями производственных процессов нет никакой связи. Однако это
не так.
Из анализа производственных функций с взаимозаменяемыми ре¬
сурсами в 4.3 было выведено понятие изоклинали — кривой в простран¬
стве ресурсов с одинаковыми нормами эквивалентной замены. Поэтому
взаимозаменяемость ресурсов в производстве можно представить как
переход от одной изоклинали к другой. Рассмотрим эту возможность
на примере макроэкономической производственной функции Кобба-
Дугласа.
120
Изоклиналь ф данной производственной функции определяется
уравнением 9 Где уф — значение нормы эквивалентной
замены двух ресурсов. Поскольку^- = aaLLaL~ 1/С°6а"и -^- = oa^La то
получаем dL дК к ’
получаем
alK
aKL
Таким образом, геометрически изоклиналь функции Кобба—Дуг¬
ласа — это луч, исходящий из начала координат. В каждой точке этого лу¬
ча соотношение используемых ресурсов одинаково. Разным соотноше¬
ниям используемых ресурсов при меняющихся объемах производства
соответствуют разные лучи. На рис. 4.11 изображены изоклинали ОА \А 2,
ОВхВ2 и т.д., пересекающие изокванты и q2.
Рис* 4.11. Изоклинали и производст¬
венные способы
Обозначим уф, Ьф, Кф объемы производства и затрат, соответ¬
ствующие изоклинали ф. Тогда вместо (4.34) можем записать:
L Л «УТ+Ц, (4 35)
* а/.
Подставим выражения (4.35) в основное уравнение производствен¬
ной функции (4.23). Если узким местом является труд, то
JK = a L^k.
121
Если же объем производства лимитируется только основными фондами,
то
При сбалансированности ресурсов оба эти равенства должны выполнять¬
ся одновременно.
Пусть
i 1
и / ai V*,
L a/ Vх*
Ч^г) \aW
Будем исходить из того, что + ак = 11. Тогда получаем произ-
водственную функцию с взаимодополняемыми ресурсами, соответст¬
вующую ф-му соотношению ресурсов:
у^ = min(4-36^
\ aL* ам> /
От (4 .36) можем теперь перейти к функциям производственных
затрат:
= (4.37)
\К^ = ак^у^.
Если некоторые количества продукции у^ производятся при раз¬
ных соотношениях^затрат 7^, то общий объем производства составит,
очевидно, у = y^. Меняя 7^, получим различные соотношения
затрачиваемых ресурсов. Общие затраты ресурсов при различных 7^ рав¬
ны суммам:
N
N
К== А йК*У*-
1 т
1 Общий случай, когда (X^ ^1» анализируется в ММСЭ, с. 197-198.
122
При этом чем больше число N, тем точнее получается результат. Пояс¬
ним это с помощью рис. 4.11. Точки Bl9 С\, Dx характеризуют коли¬
чества ресурсов, необходимые для получения одного и того же объема
производства. Соединив эти точки прямыми, получаем ломаную
А\В\ C\D\. Эта ломаная аппроксимирует соответствующую изокванту
функции Кобба—Дугласа. Чем больше проведено изоклиналей (базовых
соотношений затрачиваемых ресурсов), тем лучше ломаная аппроксими¬
рует изокванту. При N—* 00 ломаная сливается с изоквантой.
Результаты анализа макроэкономической (двухресурсной) произ¬
водственной функции справедливы и для однородных производственных
функций первой степени со многими ресурсами:
где — затраты ресурса s на производство единицы продукции при ф-й
комбинации ресурсов.
Таким образом, взаимозаменяемость ресурсов в процессе произ¬
водства можно учитывать посредством сочетания фиксированных ком¬
бинаций взаимодополняемых ресурсов. Необходимым условием пере¬
хода от производственных функций с взаимозаменяемыми ресурсами к
функциям с взаимозаменяемыми ресурсами и функциями производст¬
венных затрат является линейность уравнений изоклиналей.
4.5. Анализ производственных способов
Производственные способы и их сочетания. Понятие ’’производственный
способ” является, с одной стороны, конкретизацией понятия ’’вид дея¬
тельности”, введенного в гл. 3 при анализе общей модели народного хо¬
зяйства; с другой — это обобщение линейных однородных функций
затрат.
Интенсивность применения способа ф будем обозначать как jcj,;
эта интенсивность может измеряться объемом какого-либо выпускаемо¬
го продукта, какого-либо затрачиваемого ресурса и т.п. Каждому спосо¬
бу ф соответствует вектор А ф = (а$ф), компонентами которого являют¬
ся коэффициенты выпуска продукции (со знаком ’’плюс”) и затраты
различных видов продукции и ресурсов (со знаком ’’минус”). Очевид¬
но, невозможно произвести какой-либо продукт, не затратив других
ресурсов или продуктов. С другой стороны, способы, в которых продук¬
ция вообще не выпускается, не могут найти применения. Поэтому в каж¬
дом векторе — используемом в народном хозяйстве производственном
способе — обязательно содержатся как положительные, так и отрицатель¬
ные компоненты.Выбор единицы изменения интенсивности влияет на абсо¬
лютные значения коэффициентов asно не влияет на их соотношения.
123
Совокупность производственных способов образует матрицу А =
= (as\p); s G Му ф С N. Как правило, в производстве могут одновременно
применяться несколько способов (свойство аддитивности). При этом
обычно предполагается, что характеристики одного способа не зависят
от применения других способов (свойство автономности). Из этих двух
свойств следует, что линейные комбинации базовых способов образу¬
ют н^овые способы. Например, если А2у...у Afc — базовые способы,
то 2 Аф Хф; Хф > 0; 2 Хф = 1 дает новый способ. Однако способы,
ф= 1
являющиеся линейными комбинациями базовых способов, не имеет
смысла непосредственно включать в условия оптимизационной модели,
так как они формируются автоматически в процессе решения.
Общие результаты функционирования всех способов по каэдому
ингредиенту s выражаются суммой 2 а5ф хф. Разобьем множество
\pGN
всех ингредиентов на два подмножества: продукты и воспроизводимые
ресурсы Si Е Mi и невоспроизводимые ресурсы s2 £М2. Тогда
2 аз{ф хф означает выпуск конечной продукции вида sx (т.е. раз-
ность произведенной и использованной продукции в сфере производст¬
ва), а 2 а$2ф хф — общие затраты невоспроизводимого ресурса s2
l// G7V
(при этом поменяем знаки коэффициентов так, чтобы а$2 ф>0).
Обозначив ySl объем конечной продукции вида sl5 rjs2 - наличные
ресурсы вида s2i получаем основные ограничения линейной модели
производства:
( 2 as,^ = ysr s,
ГГ ^ л„ <4‘39>
2 Ом>Хф s*€Mr
V Я1)€Л/
Система уравнений и неравенств (4.39) является конкретизацией
соответствующих условий общей модели оптимального планирования.
Они включаются во всякую линейную статическую модель народного
хозяйства.
Анализ однопродуктовых способов. Рассмотрим особенности про¬
изводственных способов, в каждом из которых изготавливается только
один продукт. Интенсивности применения таких способов естественно
измерять объемом выпуска продукта. Вектор Аф в этом случае вклю¬
чает только одну положительную компоненту (единицу выпускаемого
продукта); все остальные компоненты — отрицательные и нулевые.
Поскольку способы производства аккумулируют самые разнооб¬
разные признаки дифференциации производственных условий (по тех¬
нологии, организации, взаимозаменяемости ресурсов и т.п.), то число
способов (даже для одного продукта) может быть очень велико. Поэ¬
тому актуальна задача отбора только эффективных способов.
124
нологии, организации, взаимозаменяемости ресурсов и т.п.), то число
способов (даже для одного продукта) может быть очень велико. Поэ¬
тому актуальна задача отбора только эффективных способов.
Введем понятие абсолютно неэффективного спо¬
соба. Пусть в сравниваемых способах производится продукт s0. Коэф¬
фициенты затрат а$ф будем рассматривать по абсолютной величине
(со знаком ’’плюс”). Способ у производства продукта s0 абсолютно не¬
эффективен, если существует какой-либо другой способ или выпуклая
комбинация других способов, при которых равный выпуск продукта
осуществляется при меньшем потреблении хотя бы одного ресурса и не
большем потреблении других ресурсов.
Задача выявления абсолютно неэффективных способов в общем слу¬
чае сводится к доказательству совместности системы из т неравенств и
уравнений. Однако существуют и более простые правила. В частности,
абсолютно неэффективным является всякий способ <р, в котором все
коэффициенты затрат не меньше, чем соответствующие коэффициенты
какого-либо другого способа со, и хотя бы один коэффициент больше,
т.е. а > asco, s £ Му s ф s0 (одно из неравенств выполняется как стро¬
гое).
Сравнительно легко проверять способ на абсолютную неэффектив¬
ность путем сопоставления его с выпуклой комбинацией двух других
базовых способов. Так, способ </? является абсолютно неэффективным
в том случае, если найдутся хотя бы два других способа coi и со2, комби¬
нация которых дает более эффективный способ:
flsqp > flscoAl S -ф S0t ^2>0Т X1-(-X2=l
(одно из неравенств выполняется как строгое). Обратимся к рис. 4.11.
В пространстве затрат двух ресурсов изображены способы производства
А, Ву С, D, Е и две выпуклые изокванты, соответствующие равным объ¬
емам производства. Как видим, изокванты не проходят через точки
Ei и Е2. Это означает, что комбинации способов С и D позволяют произ¬
вести то же количество продукции с меньшими затратами обоих ресур¬
сов. Следовательно, способ Е абсолютно неэффективен1.
Оптимальное сочетание производственных способов. Пусть один про¬
дукт производится несколькими способами. Каждый вид затрачива¬
емых ресурсов ограничен. Требуется максимизировать общий выпуск
продукта.
Имеем задачу линейного программирования:
N
^>0; (4-40^
1 Подробнее о выявлении неэффективных производственных способов см.
ММСЭ, с. 201-202.
125
2 X* шах.
yp€N
Попытаемся выявить свойства решений этой задачи, опираясь на тео¬
рию линейного программирования и теоретические положения о соизме¬
рении затрат и'результатов в оптимальном планировании (см. гл. 3).
Очевидно, что решение задачи (4.40) всегда существует (благодаря
тому, что а3ф > 0, Ъ$ > 0). При этом оптимальный план может быть
единственным или же число оптимальных планов бесконечно. В случае
единственности оптимального плана число используемых произ¬
водственных способов (имеющих > 0) не может превосходить числа
ресурсов (т). Поэтому чем больше ресурсов учитывается в задаче, тем
больше способов может войти в оптимальный план.
Следует уточнить, что максимальное число положительных величин
Хф > 0 не может превышать числа полностью используемых ресур¬
сов. Это уточнение важно, пс‘скольку в оптимальном плане задачи (4.40)
не все ресурсы могут использоваться полностью. Экономически это объ¬
ясняется тем, что в имеющихся способах производства взаимозаменя¬
емость ресурсов недостаточна. Поэтому чем разнообразнее способы по
соотношениям коэффициентов а$ф, тем больше число полностью исполь¬
зуемых ресурсов. Таким образом, существует определенная зависимость
между числом входящих в оптимальный план способов, числом учитыва¬
емых в задаче ресурсов, числом и дифференциацией способов.
Пусть X* — оптимальный план, включающий определенный набор
производственных способов. При увеличении всех ресурсов в
X раз набор производственных способов не изменится, а интенсивность
применения каждого способа и всего объема производства
х* = S х! увеличится в X раз. Таким образом, модель (4.40) можно
Ф
интерпретировать как особую форму однородной про¬
изводственной функции первой степени. Эта форма
записи производственной функции наглядно демонстрирует ее экстре¬
мальную природу.
Запишем задачу, двойственную к (4.40) :
2 as^(os > 1, f € N,
s € M
a>s>0, s€M, (4.41)
2 bjas —* min.
seM
Решение задачи (4.41) всегда существует: W* = (w*). Как было по¬
казано в гл. 3, w*- оптимальная оценка s-го ресурса, характеризующая
предельную эффективность 5-го ресурса. Из теории линейного програм¬
мирования следует, что по мере увеличения bs величина w* снижается
(кусочно-постоянным образом), т.е. предельная эффективность ресурса
126
уменьшается. Таким образом, решение задачи (4.40) при меняющемся
параметре bSo (и фиксированных значениях всех других bs) дает непре¬
рывную кусочно-линейную функцию выпуска продукта
от величины затрачиваемого ресурса s0.
Нормы эквивалентной взаимозаменяемости ресурсов в оптимальном
плане равны обратным соотношениям оптимальных оценок этих ресур-
hbk wi
сов: —ЛДГ = ' ^ля ИСП0ЛЬЗУемых в оптимальном плане спосо¬
бов выполняется равенство 2 а8ф w*= 1. Если же способ не входит
в оптимальный план, то 2 а5ф wf> 1. Разность Ал, = 2 ds\b nf — 1
s^M s&M
показывает, насколько уменьшится объем выпуска, если в оптимальный
план принудительно ввести единицу продукта, производимого ф спосо¬
бом.
Литература
1. Ашманов С.А. Введение в математическую экономику. М.: Наука, 1984. Ч. III.
2. Клейнер Г.Б. Производственные функции. М.: Финансы и статистика, 1986.
3. Маленво Э. Лекции по макроэкономическому анализу. М.: Наука, 1985.
4. Павлов В.Н. Технологический прогресс и полезность средств производства.
Новосибирск: Наука, 1987.
5. Плакунов М.К., Раяцкас Р.Л. Производственные функции в экономическом
анализе. Вильнюс: Минтис, 1984.
ГЛАВА 5
МОДЕЛИРОВАНИЕ СФЕРЫ ПОТРЕБЛЕНИЯ
В разделе I был сформулирован ряд важнейших проблем моделирования
народного благосостояния в общей концепции планирования и управле¬
ния народным хозяйством: обоснование и построение критериев, обес¬
печивающих выбор наилучших вариантов удовлетворения потребностей
общества, соизмерение общественной полезности потребительских благ
и общественных затрат на производство продукции, создание экономи¬
ческого механизма распределения потребительских благ. В вданной
главе эти проблемы рассматриваются более подробно, но в основном
с точки зрения целей, задач и возможностей моделирования на народно¬
хозяйственном уровне.
Более полное и дифференцированное исследование сферы потребле¬
ния осуществляется посредством особых функциональных подсистем
моделей (см. [3], [5]). Эти подсистемы включаются в многоаспект¬
ные и многофункциональные системы моделей народного хозяйства,
логика построения которых рассматривается в разделе III.
5.1. Целевая функция потребления.
Соизмеримость и взаимозаменяемость потребительских благ
Целевая функция потребления (ЦФП) и — u(Y) — одна из наиболее
общих математических моделей целеустремлений в сфере потребления.
Она определяется на более узком множестве благ по сравнению с целе¬
вой функцией общественного благосостояния. Вектор переменных
Y > 0 включает разнообразные виды продукции и услуг, используемых
в сфере потребления, но в этот перечень не входит ряд социальных,
экологических и других условий жизни общества. Такое ограничение
области определения целевой функции позволяет, однако, более тща¬
тельно исследовать проблемы роста материального благосостояния. ^
Общие свойства ЦФП. Являясь частным случаем ЦФБ, функция
u(Y) сохраняет ее общие свойства как инструмента упорядочения различ¬
ных наборов (вариантов) потребительских благ с точки зрения удов¬
летворения потребностей общества (см. 2.2). Ряд свойств ЦФП удобно
изучать, используя геометрическую интерпретацию уравнений и (Y) — с,
128
где с — меняющийся параметр, характеризующий значение (уровень)
ЦФП.
/ В пространстве п потребительских благ уравнению u(Y) = с соответ¬
ствует определенная поверхность равноценных (или безразличных)
наборов благ. В теории потребления такие поверхности получили назва-
, ние поверхностей безразличия-1. На множестве допустимых
значений Y можно построить семейство (карту) поверхностей безраз¬
личия. При этом важно отметить, что, хотя ЦФП определяется неодно¬
значно, семейство поверхностей безразличия единственно, т.е. не зави¬
сит от выбора монотонно возрастающего преобразования.
Рассмотрим пространство двух благ (см. рис. 5.1). Такая геометри¬
ческая интерпретация возможна, если разнообразные блага агрегировать
в две группы (например, продукты питания и непродовольственные то¬
вары, включая услуги) либо рассматривать различные комбинации двух
благ (потребительских комплексов) при фиксированных значениях
всех других благ. Уровни ЦФП изображаются на плоскости в виде кри¬
вых безразличия. На рис. 5.1 приведены три кривые безразли¬
чия, соответствующие значениям ЦФП сь с ъ с3.
Уг
Рис. 5.1. Кривые безразличия в пот¬
реблении
Разумно для начала допустить, что функция u(Y) является строго
возрастающей по всем своим аргументам, т.е. увеличение потреб¬
ления любого блага при сохранении уровней потребления всех
других благ увеличивает значение ЦФП. Если Ya > Yb, то u(Ya) >
> u(Yjb)- Поэтому более удаленная от начала координат по¬
верхность безразличия соответствует большему значению ЦФП,
а сам процесс максимизации ЦФП на некотором ограничен-
Впервые понятие поверхностей безразличия использовал английский эконо¬
мист-математик Ф.Эджворт в 80-х годах XIX в.
5 Зак. 2414
129
ном множестве можно интерпретировать как нахождение допустимых
точек, принадлежащих кривой (поверхности) безразличия, максималь¬
но удаленной от начала координат.
Поверхности безразличия не могут пересекаться. В противном слу¬
чае получалось бы, что один и тот же набор благ одновременно соответ¬
ствует нескольким разным уровням материального благосостояния.
Поверхности безразличия имеют отрицательный наклон к каждой оси
координат. Поскольку u(Y) — функция, возрастающая по всем аргумен¬
там, то наборы Ya и Yb не могут быть равноценны, если Yu4 > Yb (и тем
более если Ya > У/?). При движении по поверхности безразличия в лю¬
бом направлении какие-то значения у\ будут возрастать, но какие-то
другие должны обязательно уменьшаться1.
Возьмем произвольную точку А (см. рис. 5.1) и проведем через нее прямоу¬
гольную систему координат. Следствием принятого предположения является то,
что в построенной системе координат в квадранте 1 располагаются комбинации, бе¬
зусловно, более предпочтительные, чем Л; в квадранте 3 - варианты, безусловно,
худшие по сравнению с А; в квадрантах 2 и 4 находятся комбинации благ с раз¬
личными отношениями предпочтения к набору А, в том числе и равноценные
(кривая безразличия, содержащая набор А, обязательно проходит через квадранты
2 и 4). Очевидно, кривые (поверхности) безразличия должны удовлетворять ус¬
ловию: если Yb >- Ya и Yd >- Yb, то на отрезке AD всегда найдется точка (£>),
лежащая на одной кривой безразличия с точкой В. Более подробный анализ воз¬
можных (типичных) и невозможных форм кривых безразличия см. в ММСЭ,
с. 208-209.
Для более адекватного отражения закономерностей изменения пот¬
ребления и облегчения практического построения ЦФП могут вводиться
дополнительные условия, ограничивающие область определения ЦФП
реально допустимыми и достижимыми структурами потребления.
Следует учитывать, в частности, что потребление ряда благ безусловно
необходимо или не может существенно снижаться по сравнению с ранее
достигнутым уровнем. Верхние же границы потребления отражают
полное удовлетворение (насыщение) соответствующих потребностей,
превышение которых не увеличивает благосостояния. При построении
ЦФП для ее включения в сводную модель народного хозяйства необхо¬
димо также проводить агрегирование конкретных потребительских
благ в укрупненные группы, например в ’’потребительские комплексы”,
удовлетворяющие определенные потребности.
Обозначим минимальные и максимальные значения объемов потреб¬
ления соответственно yf^n и ^аХ. При этом $111 > 0, yf^X < + °°. Тог¬
да множество допустимых наборов потребительских благ, на котором
определяется ЦФП, есть
Y = {Yl KmIn У <С углахj
1 Легко видеть аналогию между свойствами поверхностей безразличия и изо¬
квант производственных функций.
130
Введение верхних границ сближает задачи максимизации ЦФП и
минимизации срока достижения заданных целей. ’’Идеальное” состояние
У v , на достижение которого направляется развитие народного хозяй-
. ства, может быть выбрано в качестве вектора yrmax.
Соизмеримость и взаимозаменяемость потребительских благ. Общие
принципы соизмерения различных потребительских благ по их общест¬
венной полезности рассматривались в гл. 2, 3. Возможность такого рода
соизмерений вытекает из сопоставимости различных вариантов (набо¬
ров) потребительских благ с точки зрения удовлетворения потребнос¬
тей общества. Именно общественное благосостояние является при со¬
циализме той общественной мерой ’’для количественной стороны полез¬
ных вещей”, о которой писал К.Маркс1.
Разнообразные по своему назначению потребительские блага непо¬
средственно количественно несравнимы между собой в силу качествен¬
ных различий и количественной несопоставимости их естественных
свойств (непосредственные сравнения по естественным свойствам
возможны только в рамках узких групп потребительских благ, напри¬
мер сравнение продуктов питания по их калорийности). Однако самые
разнообразные потребительские блага сопоставимы в том смысле, что
их потребление увеличивает общественное благосостояние2.
Показатели прироста общественной полезности благ выводятся из
ЦФП как частные производные щ = —> 0. Они характеризуют при¬
рост общего уровня потребления в результате увеличения потребления
блага i на ’’малую единицу”, т.е. предельный полезный эффект (или пре¬
дельную полезность) /-го блага. Таким образом, количественные оценки
полезности отдельных благ являются результатом^ построения ЦФП. В
конечном счете соизмеримость отдельных благ по общественной полез¬
ности есть следствие сопоставимости различных наборов потребитель¬
ских благ их по предпочтительности с точки зрения удовлетворения
общественных потребностей.
Неоднозначность определения ЦФП имеет своим следствием неоднозначность
частных производных. Однако соотношения между частными производными
остаются неизменными для любой ЦФП, определенной с точностью до монотонно
возрастающего преобразования. Если и (У) = ф [и(У)], то по правилу дифферен¬
цирования сложных функций
диУ , ди (Y)
ду,[ — ф ду.
Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 23. С. 44.
Принцип соизмерения полезных эффектов потребительских благ в определен¬
ном смысле аналогичен соизмерению продуктов по трудовым затратам. Различные
продукты едины между собой в том, что на их производство затрачивается труд. Но
это лишь одна сторона единства различных продуктов. Вторая сторона единства про¬
дуктов состоит в том, что в результате их использования в сфере потребления
возрастает общественное благосостояние.
5* 131
ы- = ф'ы,\
Видно, что </? '(и) > 0 является общим множителем для всех частных производных,
Изменение значения ЦФП при малом изменении ее аргументов при
п
ближенно выражается полным дифференциалом du(Y) = X u^dy^
Если же уровень благосостояния не изменяется, то 2 и^У\ = О
Из последней формулы выводятся соотношения эквивалент¬
ной взаимозаменяемости благ. Допустим, что количества
всех благ, кроме благ к и /, не изменяются. Тогда u^dy^ + Ujdy. = О,
откуда
= f1Jl (К \\
dyk и,ш
Таким образом, коэффициент (норма) эквивалентной заменяемости
благ обратно пропорционален соотношению предельных полезностей
этих благ, взятому с обратным знаком. Поскольку все и^ > 0, то обя¬
зательным свойством является < 0 (причем хотя бы для некото-
dyk
рых к и / эти отношения строго отрицательны).
Изучение закономерностей поведения потребителей показывает,
что если потребность в определенном благе удовлетворяется в незначи¬
тельной степени, то коэффициенты заменяемости (вытеснения) другими
благами для сохранения определенного уровня потребления высоки. Но
при увеличении потребления этого блага коэффициенты эквивалентной
заменяемости другими благами неуклонно уменьшаются. Это явление
объясняется тем, что при возрастании использования блага удовлетво¬
ряются все менее насущные потребности, а на определенном этапе может
наступить и полное насыщение.
В изменении коэффициентов эквивалентной заменяемости прояв¬
ляется определенная очередность удовлетворения отдельных потребнос¬
тей. На низких уровнях благосостояния удовлетворяются прежде всего
самые насущные, естественные потребности (например, потребности в
пище). Даже очень большой прирост благ, обеспечивающий удовлетворе¬
ние потребностей более высокого порядка (например, музыкальное
образование), не может компенсировать отказ от благ, удовлетворяющих
эти, более насущные в данных условиях потребности. Но по мере насы¬
щения первоочередных потребностей блага, удовлетворяющие потребно¬
сти более высокого ранга, получают все более высокую общественную
оценку.
Вернемся к анализу формы поверхностей (кривых) безразличия.
На рис. 5.2 изображена кривая безразличия, которой соответствуют
непрерывно уменьшающиеся нормы эквивалентной замены. При после¬
довательном увеличении потребления первого блага на единицу потреб¬
ление второго блага сокращается, но величина этого сокращения убывает
132
(на оси ординат АВ > ВС > CD > ...)• Вследствие этого кривая без¬
различия есть график вогнутой функции одной переменной тго отноше¬
нию к другой. В дополнение к этому заметим, что по достижении предела
насыщения потребности в благе к нормы эквивалентной замены других
dy j max
благ становятся равными нулю: ~^у^— = ® ПРи?к ~?к ^ другой сто¬
роны, если потребность в благе к удовлетворяется на минимальном
уровне, то никакое увеличение потребления других благ не может ком¬
пенсировать уменьшение его потребления:
-^=0при/*=^1П
Отмеченные особенности изменения норм эквивалентной замены но¬
сят достаточно типичный характер. Если они распространяются на все
множество благ (хотя бы сведенных в укрупненные группы), то множе¬
ства Qc = j У: и(У) > с | будут выпуклыми для всех допустимых значе¬
ний У, а функция и(У) будет квазивогнутой. Поэтому если u(Yд) =
= u(YB) = с, то u [\ Ya + (1 - X) Yb] > с при X £ [ 0, 1 ]. Это говорит о
том, что выпуклая комбинация двух равноценных наборов имеет не
меньшую полезность, чем каждый из них в отдельности (см. рис. 5.2) 1.
О построении ЦФП. Методы построения ЦФП основываются на обоб¬
щении опыта поведения совокупностей потребителей, тенденций поку¬
пательского спроса, закономерностей изменения структуры потребления
по мере роста благосостояния.
Первая в СССР попытка построения ЦФП была предпринята В.А.Вол¬
конским. В качестве модели ЦФП была отобрана квадратичная функция
п , п
«вида u(Y) = 2 b^y^. + 2 а параметры этой функции на¬
ходились путем обработки данных бюджетной статистики2.
1 Подробнее об условиях квазивогнутости функции u(Y) см. ММСЭ, с. 214-215.
Принцип построения ЦФП на основе данных о приобретении товаров излагает¬
ся в 5.2.
133
ЦФП была построена для трех агрегированных групп товаров:
и (К) = (1 — 1,841а) у, + (1-2,054а) уг+(\-2,116а) у3 +
+0,668-10-41/? +1,230-10-4f/,i/2+1,243-10-4!/1‘/з +
-4 0,506- 10~4уг4-1.104- 10_4Уг.1/з+0,492- 10_4(Д.
Все параметры и переменные данной ЦФП относятся к средней семье; параметр
а означает число детей в семье, у\ - потребление продуктов питания, у 2 - потреб¬
ление промышленных товаров, у3 - потребление платных услуг (все - в ценност¬
ном выражении).
Методология моделирования потребления на народнохозяйственном
уровне исходит из представлений о системе (’’дереве”) потребностей.
Потребностям первого ранга соответствуют потребительские комплек¬
сы, такие, как ’’Продовольствие”, ’’Одежда и обувь”, ’’Жилище”, ’’Пред¬
меты и услуги для домашнего хозяйства” и т.д. Потребности нижестоя¬
щих рангов реализуются в группах благ определенного назначения и т.п.
вплоть до конкретных предметов потребления и услуг. Уровни развития
потребительских комплексов (или объемы потребления по группам
благ) являются переменными ЦФП, включаемой в модель народного
хозяйства, например межотраслевую.
Теоретический анализ, построение и практическое использование
ЦФП выполнены под руководством К.К.Вальтуха. В основе предложен¬
ной им ЦФП лежат две гипотезы: 1) существование минимальных и мак¬
симальных уровней различных потребностей; 2) монотонное снижение
норм эквивалентного замещения уровней удовлетворения потребностей.
Область существования рассматриваемой ЦФП — это множество У =
={y:Ym*n < У < УТnax } . На рис. 5.3 изображено семейство кривых
безразличия, удовлетворяющих указанным выше гипотезам.
У2
Рис. 5.3. Кривые безразличия в ограни¬
ченной области
134
Вводится показатель степени удовлетворения определенной потреб-
е - yj-y?in
ности по сравнению с минимальным уровнем: i и?8*—ыт,Г1 ^че“
ddj ’ /
видно, что ву G [0,1]. Тогда будет показывать изменение сте¬
пени удовлетворения потребности в группе благ (потребностей) / отно¬
сительно изменения степени удовлетворения потребности в группе благ к.
Поскольку dOt = — и dQb = — то —
dy, уГх—уТ * уГ*~уРп ' dBj
пропорционально' . Следовательно, характер изменения
при увеличении соответствует поведению нормы эквивалентной заме-
dyj
няемости при увеличении yfc.
Принятым исходным гипотезам удовлетворяет, в частности, такая
формула ^ • -
dbj 0/(1 -ад
dQk- ~ (1—ву) •
(5.2)
Из (5.2) выводятся:
‘-0''лй '-*** •
0/ d0J - 0ft d0ft’
i-ey fi-e*
0/
Л/—
откуда
/л 0/—0у = — Iti 0^ + -f- с09
8/6*
Выражение (5.3) есть формула семейства кривых безразличйя для
двух групп благ. Семейство кривых безразличия для всего множества
благ (потребностей) выражается формулой
п
п - 2 Ь,
П 0j# 1=1 = (5.4)
f=i
Таким образом, получаем ЦФП, выраженную в величинах степеней
удовлетворения потребностей:
п
а[0(К)] = П 0,/=Л (5.5)
i = 1
135
ЦФП (5.5) определена в «-мерном единичном кубе и является
строго возрастающей функцией всех своих аргументов (|^“ > 0) для
всех значений 0/, кроме 0/ = 1. При этом и = 0, если хотя бы одно
0/ = 0. Отметим также, что вариантам Y с одинаковой степенью удовлет¬
ворения потребностей во всех группах благ соответствует прямая, со¬
единяющая точки Ymm и Ymax (диагональ многогранника допустимых
значений F).
/
5.2. Моделирование поведения потребителей j]
в условиях товарно-денежных отношений ^
Основная часть потребительских благ распределяется между членами
общества платным образом через торговлю и общественное питание.
Поэтому для планового управления сферой потребления первостепен¬
ное значение имеет исследование закономерностей поведения потребите¬
лей на рынке. В основе построения моделей поведений потребителей ле¬
жит гипотеза, что потребители, осуществляя выбор товаров при установ¬
ленных, ценах, имеющихся доходах и с учетом других обстоятельств,
стремятся максимизировать уровень удовлетворения своих потребнос¬
тей.
Анализ простой модели поведения потребителей. Пусть имеется п
видов товаров. Исследуется поведение какой-либо группы или всей со¬
вокупности потребителей1. Спрос потребителей — это вектор Y = (у.).
При известных ценах на различные товары Р = (pi) и величине дохода D
потребители могут выбирать только такие комбинации товаров, которые
п
удовлетворяют условию 2 Piyi (бюджетному ограничению). Пред¬
полагается, что предпочтения потребителей на множестве товаров выра¬
жаются целевой функцией u(Y).
Простая модель поведения потребителей имеет вид
u(Y) -*max,
?Y<D, (5.6)
Y> 0.
Постулированный принцип оптимального поведения потребителей, разумеется,
не следует понимать так, что потребитель перед тем, как купить какие-либо товары,
проводит скрупулезные вычисления с помощью своей целевой функции на основе
информации о полезных свойствах и ценах для всего множества товаров. Этот
принцип отражает только генеральную тенденцию многочисленных актов потреби¬
тельского выбора, а модель (5.6) - одно из возможных математических описаний
такой тенденции.
Укрупнение однородных групп потребителей и тем более их объединение в од¬
ну группу снижают практическую ценность модели. Однако анализ модели поведе¬
ния ’’совокупного” потребителя важен для понимания логики экономического ре¬
гулирования в области производства и распределения потребительских благ.
136
Для учета в модели денежных сбережений населения можно исполь¬
зовать два подхода: считать денежные сбережения особым благом, име¬
ющим полезность (его увеличение приводит к росту целевой функции)
или же определять размер сбережений вне модели, рассматривая D как
сумму расходов на приобретение товаров.
Геометрическая интерпретация модели для двух товаров представ¬
лена на рис. 5.4. Линия АВ соответствует бюджетному ограничению.
Таким образом, выбор потребителей ограничен треугольником АОВ.
Набор М (точка касания прямой АВ с наиболее отдаленной кривой
безразличия) является оптимальным решением.
Рис. 5.4. Выбор потребителей при задан¬
ных ценах, доходе и дополнительных
ограничениях
Выясним условия оптимальности решения для модели (5.6), опира¬
ясь на теорию нелинейного программирования.
Функция Лагранжа задачи (5.6) имеет вид
L(Y, K) = u(Y)+k(D—PY).
[Множитель Лагранжа X есть оптимальная оценка дохода. Частные
производные — будем, как и в 5.1, интерпретировать как
предельные полезные эффекты (предельные полезности) соответству¬
ющих потребительских благ.
Необходимыми условиями оптимума Y* (условиями Куна—Такке-
ра) являются
и((У*)^Лр{ для всех / = 1, . .., п. (5.7)
137
При этом
U;(Y*) = kp. при у\ > 0. (5.8)
Если же u/Y*) < X* , то соответствующий товар i не приобретается
(y*i= 0). Pi
Очевидно, X* > 0, что соответствует полному использованию дохода
(PY* = D).
Равенство (5.8) можно записать так:
и' (УJ = X* для у\ > 0 (5.9)
Р:
или же
L
и^р} = f- для у\ > 0 и у) > 0. (5.10)
Это означает, что потребители должны выбирать товары таким об¬
разом, чтобы отношение предельной полезности к цене товара было оди¬
наковым для всех товаров. Или, что равносильно, предельные полезнос¬
ти выбираемых товаров должны быть пропорциональны ценам.
Направления использования модели. Основными направлениями
использования модели являются: изучение зависимостей покупательс¬
кого спроса от цен и доходов, построение ЦФП, регулирование цен и
доходов для достижения сбалансированности спроса и товарного предло¬
жения.
Целевая функция потребления не может наблюдаться непосредствен¬
но. Но она может быть выявлена при анализе поведения потребителей,
если это поведение достаточно хорошо описывается моделью (5.6).
Методика ’’восстановления” целевой функции потребления включа¬
ет несколько этапов.
Сначала выбирается одна или несколько математических моделей
(формул) целевой функции, удовлетворяющих некоторым теоретичес¬
ким гипотезам (например, квадратичная или логарифмическая функ¬
ция).
Из анализа модели (5.6) известно, что для разнообразных товаров,
приобретаемых при различных ценах и доходах, теоретически должны
выполняться условия (5.8). Поэтому каждому сочетанию s наблюдаемых
величин покупок и цен соответствует п уравнений uf(Ys) - Xs = ef, где
^— погрешность. Далее ставится стандартная задача математической ста¬
тистики: оценка параметров системы регрессионных уравнений. При этом
требуется, чтобы число уравнений существенно превышало число неиз¬
вестных параметров. В заключение проводится сравнение первоначаль¬
но выбранных математических моделей и в конечном счете принимается
138
та из них, которая наилучшим образом аппроксимирует статистические
наблюдения.
Пусть^в качестве модели целевой функции избрана квадратичная функция
и(У) — 2 bhy, 2 b..y-y-. Она удобна тем, что ее первые частные пронз¬
ав “ /,/= 1 11 1 1
водные — линейные функции. Поэтому мы получаем для каждого наблюдения
систему уравнений линейной регрессии: b. + S b..ys. — Xs ps. Требуется опре-
п (п + I) 1 /=1 11 1 1 „
делить п + ^ параметров и by (матрица коэффициентов В — (Ьц) - сим¬
метрична). Каждое статистическое наблюдение прибавляет п уравнений и одну
неизвестную Xs. Поэтому необходимо провести столько наблюдений N, чтобы число
nN стало существенно больше, чем п + п(п^ ^ + yv. Например, если п =50, то
N должно быть существенно больше 25. Это показывает, что задача построения
целевой функции предъявляет большие требования к регулярности статистических
наблюдений о приобретении товаров.
Прямое использование модели (5.6) определяет вектор покупатель¬
ского спроса Y при фиксированных ценах и доходах. При этом предпола¬
гается, что сфера производства должна обеспечить выпуск потребитель¬
ских товаров в соответствии с предъявляемым спросом. Однако воз¬
можна и другая постановка задачи: известен вектор Y0 товаров, которые
могут быть реализованы, и требуется установить такие цены и общий до¬
ход, чтобы спрос потребителей соответствовал товарному предложению.
Опираясь на выведенные выше условия оптимального выбора, сформу¬
лируем задачу нахождения значений цен и доходов, балансирующих
спрос и предложение:
и,(У) = ьР,;
2Piy!=D, (5-П>
где «1 — число реализуемых товаров.
Имеем («! + 1) уравнений и (п1 +2) неизвестныхръ D, X. Зафикси¬
руем значение одной неизвестной, например, дохода или цены какого-
либо товара. В результате приходим к системе, имеющей одинаковое
число неизвестных и уравнений. При соблюдении некоторых формаль¬
ных требований система имеет решение (оно может быть не единствен¬
ным), которое дает значения цен и доходов, балансирующих спрос и
предложение по всем видам реализуемых товаров.
Обобщения модели поведения потребителей. В модели (5.6) допус¬
кается, что выбор потребителей ограничен только величиной дохода.
В реальности же покупательский спрос сдерживается недостаточным
предложением (дефицитом) ряда товаров; это обстоятельство может
существенно деформировать оптимальную структуру потребления1.
1 По этой причине описанная выше методика ’’восстановления” ЦФП по данным
о фактических покупках может давать систематические ошибки.
139
Обратимся к рис. 5.4. Если предложение второго товара равно у2) то
оптимальным решением становится точка К, которой соответствует
меньшее, чем в точке М, значение целевой функции и(у i, у2).
В модели для всей совокупности потребителей ограниченное предло¬
жение некоторых товаров (/ £ 1\) легко учесть, введя дополнительные
условия
i€/i(sr,> 0). (5.12)
Очевидно, что вследствие этого необходимые условия оптимума
усложняются. Условия пропорциональности предельных полезностей и
цен (5.8) сохраняются только для реализуемых недефицитных ховаров
(/ ^ /i). Что касается реализуемых дефицитных товаров (у *• > 0, / Е1Х),
то для них должны выполняться условия
Ui(Y*) = x;. + v}, (5.13)
где vj— оптимальная оценка дефицитности z-го вида товаров.
Анализ и расчеты по расширенной модели (5.6), (5.12) могут осу¬
ществляться в два этапа. Если заранее известен круг дефицитных товаров
(по которым выполняются соотношения yi = yi , то их потребление
можно зафиксировать, рассчитать ’’остаточный” доход D = D —
- 2 Pi yi , а для недефицитных товаров использовать исходную мо-
/Е/
дель (5.6).
Представляет интерес моделирование ситуации, когда часть дефи¬
цитной продукции распределяется по фиксированным ценам, а другая —
по ’’свободным” ценам, обеспечивающим сбалансированность спроса и
предложения (имитация свободного рынка и многоканального распреде¬
ления продукции).
Следует отметить, что учет дефицита в моделях поведения отде¬
льных групп населения имеет значительно более серьезные последст¬
вия. Возникает необходимость отражения нереализованного спроса
(избыточных, или вынужденных, сбережений) ; требуется устанавливать
особые правила распределения дефицитных товаров между группами
потребителей (при фиксированных ценах) либо вводить дифферен¬
цированные и свободные-цены.
5.3. Функции покупательского спроса I
Связь модели поведения потребителей и функции спроса. Пусть в модели
(5.6) цены и доход рассматриваются как меняющиеся параметры (для
удобства переменную дохода будем обозначать в дальнейшем Z). Тогда
решением параметрической оптимизационной задачи (5.6) будет вектор-
функция Y* = Y* (Р, Z). Она может быть выведена аналитически либо
140
путем статистического обобщения оптимальных решений при различных
значениях Р и Z. Компонентами вектор-функции Y* (Р, Z) являются фун¬
кции покупательского спроса на определенный товар от цен и дохода:
y^tyP.Z).
Рассмотрим частный случай, когда изменяется только доход, а век¬
тор цен остается неизменным ( Р = Р°). Рис. 5.5 показывает: при увели¬
чении дохода бюджетная линия перемещается параллельно самой себе и
точками оптимума - спроса потребителей — будут точки М\, Мъ Мъ
(при нулевом доходе спрос на оба товара будет нулевым). Кривая,
соединяющая точки О, Mi, М2) является отображением вектор-функции
покупательского спроса от дохода при заданном векторе цен.
Рис. 5.5. Изменение спроса при росте
доходов
Приведем простой пример лостроения функций спроса от дохода. Допустим,
для двух товаров и (У) = уг у2 ; рх =1; р2 =2. Тогда^ -y\; и2 =3yi у\. Необ¬
ходимые условия оптимума дают систему уравнений: у\ = \,3yi у\ =2\ у л +
+ 2у2 -Z. 7
В результате подстановки первого уравнения во второе получаем 3yi у22=2у^
Подставим сюда выражение уi из третьего уравнения: 3 (Z - 2у 2) У\ = 2уъ охкуда
2 “У ъ откуда
3Z — Ъу2. В результате получаем две функции спроса от дохода: yi =-J— Z, у 2 —
Z
8
Между целевой функцией потребления и функциями покупательс¬
кого спроса существует взаимная связь. Выше было показано, что функ¬
ция спроса выводится из целевой функции потребления. Доказывается
также, что из вектор-функции спроса, удовлетворяющей ряду естествен¬
ных допущений, может быть выведена ЦФП. Нелогично поэтому приз¬
навать возможность и целесообразность построения и применения
. 141
функций спроса и одновременно отрицать понятие ’’целевая функций
потребления”, а также все теоретические выводы, вытекающие из ее су¬
ществования1 .
Анализ влияния на покупательский спрос изменения цен и доходов
удобно проводить на основе необходимых условий оптимума модели
(5.6).
Если дифференцировать равенства (5.8) и равенство PY* = D по до¬
ходу и ценам, то будем получать системы из (п + 1) уравнений для част-
о У1 д X* Э у* Э X* и it
ных производных 0-zf и и . Например, дифферен¬
цирование бюджетного равенства по доходу и цене р^ дает уравнения:
v tyi 1 * v dyi
2 pt -р- =1 и 1/J = — 2 /?, -jp- .
дг у* t.= 1 дрк
ду* Эу*
Знаки частных производных и характеризуют важные
свойства товацюв^как объектор покупательского спроса. Для большин¬
ства товаров -g У21 > 0 и —< 0. Исключение составляют ’’малоцен¬
ные” товары, спрос на которые при увеличении дохода снижается (среди
продуктов питания это — хлеб, картофель, низкокачественные жиры и
т.п., среди промышленных товаров — обувь и одежда устаревших моде¬
лей и фасонов и т.п.). В свою очередь среди товаров с — < 0 могут
Э у*
встречаться и такие товары2, которые имеют -g ^—> 0.
Функции спроса являются однородными нулевой степени относитель¬
но всех цен и дохода: у\ (а Р, a Z) = у\ (Р, Z) при а > 0. Действительно,
пропорциональное изменение цен и дохода не влияет ни на положение бюд¬
жетного ограничения (определяющего область выбора потребителей),
ни на целевую функцию. Покупательская способность (реальный доход)
и соотношения цен остаются неизменными, меняется только масштаб
цен.
1 Функции покупательского спроса характеризуют зависимости, которые легко
обнаруживаются и проверяются эмпирически (в отличие от целевой функции пот¬
ребления) . Поэтому функции спроса могут помочь в выборе модели (формулы)
целевой функции и ее параметров. Например, из того, что спрос на многие товары
с увеличением дохода изменяется нелинейно, следует вывод, что те модели целевой
функции, которые индуцируют линейные функции спроса, являются неадекватны¬
ми (кстати, в эту группу попадают квадратичные и логарифмические функции).
1 Парадоксальное увеличение спроса на товар при увеличении цены на этот же то¬
вар впервые было обнаружено в конце XIX в. в Ирландии. Таким товаром оказал¬
ся картофель, составляющий основную часть рациона питания бедных слоев населе-
Ъу*
ния. Товары, имеющие > 0, в теории потребления принято называть т о-
варами Гиффина.К ним могут относиться только товары, расходы на кото¬
рые занимают значительный удельный вес в бюджете потребителей.
142
\ В соответствии с формулой Эйлера для однородных функций имеем
I п д у i д у; -
X — Vi + 3—i—2 = 0: i= 1,..., n. Разделив почленно обе части ра-
О Pj о z ’ ’ r
венства шур получим
2 ^L.EL + ?£-. —, » = 1, ..... п. (5.14)
/= 1 др/ У/ ' dz у{ ' v ;
Выражение £? = 1 есть коэффициент эластич¬
ности спроса на товар / от дохода, характеризующий
относительное изменение спроса по отношению к относительному изме-
0 у . р .
нению дохода. Выражение Щ = ч ■* • —^ есть коэффициент
IJ о Р j у j
эластичности спроса на товар i от цены на то¬
вар /, характеризующий относительное изменение спроса по отноше¬
нию к относительному изменению цены.
Из (5.14) следует
£? = — 2 Epih (5.15)
/= 1
Если , то Е? > 0, откуда Б Щ < 0 (т.е. хотя бы один коэф¬
фициент эластичности от цены дол&сеЬ быть отрицательным). Если же
< о (малоценный товар), то Ef < 0 и | Е? > 0 (т.е. хотя бы
один коэффициент эластичности от цены7 должен быть положи¬
тельным) .
Построение общих функций спроса у\ =f(P,z) для всей совокупнос¬
ти товаров требует очень значительных объемов информации и по трудо¬
емкости сопоставимо с построением ЦФП по эмпирическим данным.
Поэтому в экономическом анализе и прогнозировании чаще использу¬
ются частные функции покупательского спроса для отдельных групп
товаров, которые характеризуют изменение спроса либо только от до¬
хода, либо только от цен, либо от дохода и цен на те же выделенные
товары.
Функции и коэффициенты эластичности спроса от дохода. На прак¬
тике функции покупательского спроса строятся и применяются глав¬
ным образом для отдельных групп товаров. При этом выбираются та¬
кие типы функций, которые отражают устойчивые тенденции (эмпири¬
ческие закономерности) изменения спроса и потребления при увеличе¬
нии дохода.
В конце XIX в. немецкий статистик Э.Энгелъ сформулировал эмпи¬
рические законы потребления и построил кривые, в соответствии с кото¬
рыми с ростом дохода доля расхода на питание уменьшается, доля рас¬
143
хода на одежду и жилье остается стабильной и т.п. (функции спроса с^т
дохода часто поэтому называют кривыми Энгеля). Этот же при¬
нцип разграничения групп товаров по типам функций спроса (потреб¬
ления) от дохода использовал шведский экономист Л.Торнквист. Он
предложил специальные виды функций (функции Торнквиста) для трех
укрупненных групп товаров: первой необходимости (I), второй необ¬
ходимости (II), предметов роскоши (III). Графики этих функций про¬
водятся на рис. 5.6.
спрос
Рис. 5.6. Функции спроса от дохода
(кривые Торнквиста)
Функция для предметов первой необходимости имеет вид
V = (5.16)
y Z+CX
Она отражает тот факт, что рост спроса (потребления) на многие товары,
удовлетворяющие самые насущные потребности, постепенно замедля¬
ется (так что < 0) и имеет предел ах (кривая асимптотически
dz
приближается к линии а х).
Функция спроса на предметы второй необходимости имеет вид
у г ' г>ь* (517)
Эта функция также имеет предел (02), но более высокого уровня.
Спрос на эту группу товаров появляется только после того, как доход
достигает в ел ичины b 2.
Наконец, функция спроса на предметы роскоши выражается форму¬
лой
аяг(г-Ь3) & (5.18)
144
Эта функция не имеет предела. Спрос возникает только после того,
как доход превысит величину Ьъ и далее быстро возрастает (так, что
1 Функции (5.16)-(5.18), однако, не дают полной характеристики
закономерностей изменения спроса при увеличении доходов и недостаточ¬
на отражают специфику различных групп товаров. В частности, они опи¬
сывают только монотонное изменение спроса, хотя для некоторых групп
товаров существуют точки максимума (для малоценных товаров, спрос
на которые сначала возрастает, а затем снижается) и точки перегиба
d2y
(когда с возрастанием дохода —j— сначала положительна, а затем
dz
становится отрицательной, что улавливается логистической кривой).
Исследования по данным бюджетной статистики и статистики роз¬
ничного товарооборота СССР показывают, что зависимости расходов
населения на большинство товарных групп достаточно хорошо аппрок¬
симируются степенной функцией у — aza (являющейся линейной отно¬
сительно логарифмов: log у = log а + a log z), дробной квадратичной
функцией, функциями вида (5.16)-(5.18) и некоторыми другими.
Приведем в качестве примера функции спроса от расходной части доходов по
некоторым товарным группам, полученные по данным розничного товарооборота :
мука, хлеб, хлебобулочные изделия: Igy =3,838 + 0,453 Igz ;
мясо и мясопродукты: Igy = 2,642 + 1,007 Igz;
одежда и белье: Igy = - 2,762 + 1,028 Igz ;
ювелирные изделия: Igy = - 39,510 + 3,828 Igz.
Широкое применение в анализе изменения спроса при небольших
изменениях дохода находят коэффициенты эластичности Е2. . В зависи¬
мости от величины Е2 все товары делятся на четыре группы: малоцен¬
ные товары (Е( < 0); товары с малой эластичностью (0 < Е( < 1);
товары со средней эластичностью (значения Ej близки единице) ; товары
с высокой эластичностью {Ef 1).
Для большинства видов функций спроса у = f(z) коэффициенты
эластичности EZf также являются функциями, зависящими от z. Поэтому
в общем случае ими можно пользоваться как числами только в окрест¬
ности определенной величины дохода. С этой точки зрения большим
удобством обладает степенная функция, имеющая постоянный коэффи¬
циент Е2 = а.
Расход потребителей на определенную группу товаров (у) зависит от
количества приобретаемых товаров (q) и от среднегрупповой цены (р).
Поэтому общий коэффициент эластичности расхода Е? можно предста-
1 Расчеты функций спроса и коэффициентов эластичности, приводимых в 5.3,
выполнены Л.М.Рувинской.
145
вить в виде суммы двух коэффициентов (от количества и средней цены^:
е-'-|Ч-(*-7) + (*-7)- И’
Заметим, что по многим товарным группам увеличение расхода (на
приобретение происходит главным образом за счет роста средней це^ы.
По данным о динамике розничного оборота за 1961 -1985 гг. получены следую¬
щие значения коэффициентов эластичности спроса от дохода: мясо и мясопродук¬
ты: 1,218; молоко и молочные продукты: 1,132; мука, хлеб, хлебобулочные
изделия: 0,479; другие продовольственные товары: 0,658; одежда и белье: 1,Q04;
радиотовары: 1,912. Необходимо иметь в виду, что существенное влияние
на рассчитываемые коэффициенты эластичности оказывает дефицитность ряда
товаров.
Функции спроса и коэффициенты эластичности от цен. Спрос на каж¬
дый товар в общем случае зависит от цен на все товары. Однако получить
достаточную информацию для построения функций общего вида уz- =
= ф (Р) очень сложно, тем более что в СССР розничные цены в течение
длительного периода менялись довольно редко. Поэтому в прикладных
исследованиях ограничиваются, как правило, построением и анализом
функций спроса для отдельных товаров в зависимости от изменения це¬
ны на этот же товар или на группу взаимозаменяемых товаров.
В настоящее время в СССР товары, имеющие —< 0, не занимают
значительной доли в бюджетах населения, и поэтому товары Гиффина
(имеющие ^ > 0) отсутствуют, т.е. все товары имеют отрицатель¬
ные коэффициенты эластичности Ец.
Однако по абсолютным значениям коэффициентов Е& товары раз¬
личаются существенно. Их можно разделить на три категории: товары с не¬
эластичным спросом в отношении цены (Ец > —1); товары со средней
эластичностью спроса в отношении цен (ЕР по модулю близки едини¬
це); товары с высокой эластичностью (Е& < — 1). С ростом цены рас¬
ход на приобретение товаров этих трех категорий соответственно уве¬
личивается, сохраняется на прежнем уровне, уменьшается.
Например, по данным статистики ВНР получены следующие значения коэффици¬
ентов по товарам для мужчин (отрицательный знак опущен): рубашки - 0,20,
пальто зимние - 0,37, обувь - 0,52, верхний трикотаж - 1,39.
Коэффициенты Ец (i Ф /) называются коэффициентами пе¬
рекрестной эластичности. По знаку этих коэффициентов
товары можно разделить на взаимозаменяемые и взаимодополняемые.
Если для товаров i и / имеем Е.. > 0, это означает, что товар i заменяет
в потреблении товар у (на това]р i переключается спрос при увеличении
цены на товар /). Примером могут служить многие продукты питания
(мясо и рыба, сливочное масло и маргарин, овощи и фрукты). Если же
146
p
Efj < 0, это служит признаком того, что товар i дополняет товар / в про¬
цессе потребления (увел^ение цены на товар / приводит к уменьшению
срроса не только на этот товар, но и на товар /, например автомобили
и бензин).
5.4. Нормативный подход к прогнозированию
и планированию потребления
Дескриптивный подход к моделированию потребления, основанный на
изучении поведения потребителей в условиях товарно-денежных отно¬
шений, в принципе не способен решать ряд проблем планирования сферы
потребления, особенно для долгосрочного периода. Во-первых, многие
виды благ имеют нетоварную форму распределения (жилье, обществен¬
ные фонды потребления, частично нормированное распределение ряда
предметов потребления и т.д.). Во-вторых, вследствие ряда причин
(изменение ценностных представлений в обществе, появление новых ви¬
дов потребительских благ и т.д.) возможности экстраполяции выявлен¬
ных закономерностей фактического поведения потребителей уменьша¬
ются по мере расширения горизонта планирования. Принципиальную не¬
достаточность анализйровавшихся в 5.2, 5.3 типов моделей должен
компенсировать нормативный подход.
В основе нормативного подхода к планированию структуры и дина¬
мики потребления лежит концепция удовлетворения рациональных, ра¬
зумных потребностей, измеряемых соответствующими целевыми норма¬
тивами. В гл. 2 обосновывалось, что минимизация срока достижения уров¬
ня рациональных нормативов (условно — ’’идеального” состояния) явля¬
ется одним из общих критериев оптимизации развития экономики. Там
же рассматривалось понятие дерева целей — инструмента программно¬
целевого планирования, использующего иерархическую систему функ¬
циональных и предметных целевых нормативов.
Рациональные нормативы характеризуют современные научные
представления об уровнях разумных потребностей по основным группам
предметов потребления и потребительских услуг (см., например, табл.
5.1). Они учитывают комплекс физиологических, психологических,
экологических, социальных факторов, определяющих ’’качество” жизни
Разработка рациональных нормативов не ставит задачу строгой регла¬
ментации потребления по всему ассортименту продуктов и услуг, а оп¬
ределяет только ориентацию для развития потребления и производства1
Безусловно, что под влиянием изменения социальной среды и новых зна-
Предпринимавшиеся в 50-60-х годах попытки оптимизации структуры потре¬
бления только по физиологическим параметрам (’’задача диеты”), а также норми¬
рования ассортимента непродовольственных товаров на основе только физичес¬
ких характеристик (’’задача о рациональном гардеробе” и т.п.) себя не оправда¬
ли.
147
ний о человеке и обществе рациональные нормативы должны кор¬
ректироваться.
Как инструменты планирования рациональные нормативы применя¬
ются не по отдельности, а системно. Например, из табл. 5.1 видно, что по
некоторым продуктам питания (хлебу, картофелю, сахару) фактичес¬
кое потребление в настоящее время превышает рациональное. Но из
этого, разумеется, не следует целесообразность немедленного снижения
фактического потребления, поскольку это неизбежно отразится на
общем уровне потребления. Такое снижение допустимо только при
одновременном продвижении к рациональным нормам объемов пот¬
ребления других (взаимозаменяемых) продуктов1. '
Таблица 5.1
Рациональные нормативы потребностей и степени их насыщения
Виды потребительских благ
Рациональ¬
ный норматив
Объем потреб¬
ления (нали¬
чия) в 198S г.
Степень насы¬
щения, %
А. На душу населения в год
Хлеб и хлебопродукты, кг
110
133
121
Картофель, кг
97
104
107
Овощи и бахчевые, кг
146
102
70
Фрукты свежие, кг
113
46
41
Сахар, кг
40
42
105
Мясо и мясопродукты, кг
82
61
75
Молоко и молочные продукты, кг
405
323
80
Ткани - всего, кв. м
50
37
74
Трикотаж верхний, шт.
4,0
2,1
53
Обувь кожаная, пар
3,6
3,2
89
Б.
На 100 семей, шт.
Радиоприемники и радиолы
250
96
38
Телевизоры
135
97
72
Холодильники
110
91
83
Швейные машины
98
65
66
Стиральные машины
72
70
97
Нормативы рационального потребления, сведенные в систему и рас¬
считанные для определенного типа семей (включая и средний), образуют
рациональный потребительский бюджет. Исходя из современных пред¬
ставлений такому бюджету соответствует месячный среднедушевой
доход в 220—235 руб., что примерно в 2 раза превышает уровень сред¬
него фактического бюджета. При этом рациональный потребительский
бюджет охватывает не только потребление платных материальных благ
и услуг, но и нормативы жилищной обеспеченности, бесплатных и льгот-
Вопрос о выборе траекторий движения от фактического потребления к рацио¬
нальному рассматривается в 8.2.
148
ных услуг за счет общественных фондов потребления. Потребительские
бюджеты (как фактические, так и рациональные) дифференцируются
по социально-демографическим группам. Одна из важных задач соци¬
альной политики заключается в том, чтобы для наименее зажиточных
слоев населения гарантировалось достижение минимального потребитель¬
ского бюджета (или прожиточного минимума)1.
Построение рационального потребительского бюджета и входящих
в него рациональных нормативов в существенной мере опирается на
современную структуру потребления ’’опережающих” групп населения
(не только по доходам, но и по культурно-образовательному уровню
и другим характеристикам социального статуса). Таким образом, норма¬
тивный подход использует результаты дескриптивного подхода к изуче¬
нию потребления, в частности модели поведения потребителей и функции
покупательского спроса. С другой стороны, представления о рациональ¬
ном потреблении должны активно применяться для регулирования
покупательского спроса и нетоварного потребления посредством науч¬
ной пропаганды, цен (стимулирующих или препятствующих), рекламы
и антирекламы.
Литература
1. Вальтух К.К. Целевая функция потребления: анализ и практическое использова¬
ние. Новосибирск: Наука, 1980.
2. Введение в теорию и методологию системы оптимального функционирования
социалистической экономики. М.: Наука, 1983. Раздел 2.
3. Константинов В.М. Моделирование роста народного благосостояния в народно¬
хозяйственных планах и прогнозах. М.: Наука, 1986.
4. Маленво Э. Лекции по микроэкономическому анализу. М.: Наука, 1985. Гл. II.
5. Райцин В.Я. Модели планирования уровня жизни. М.: Экономика, 1987.
6. Система экономико-математических моделей для анализа и прогноза уровня
жизни. М.: Наука, 1986.
7. Шевяков А.Ю., Кирута А.Я. Моделирование сбалансированности и согласования
плановых решений в сфере народного благосостояния. М.: Наука, 1986.
Расчеты показывают, что для достижения показателей среднего рационального
потребительского бюджета к 2000 г. необходимо поддерживать среднегодовые
темпы увеличения ресурсов для потребления на уровне 4,5%. При таком темпе
показатели рационального бюджета для всех групп населения могут быть достиг
нуты примерно в 2010 - 2015 гг.
ГЛАВА 6
МОДЕЛИ МЕЖОТРАСЛЕВОГО БАЛАНСА
6.1. Межотраслевой баланс общественного продукта.
Система показателей
Межотраслевой материальный баланс. Для отражения системы матери¬
ально-вещественных связей процесса воспроизводства общественного
продукта разрабатывается межотраслевой материальный
б а л а н с. Он объединяет показатели производства и использования
разнообразных видов продукции и услуг. Сводная таблица межотрас¬
левого материального баланса строится из двух схем:
а) ’’поступление ресурсов — использование ресурсов”^
xt +s{= X +kj, i^.1; (6.1)
/s/
б) ’’производство продукции — распределение продукции”:
xi— 2 Xjj + yj, i£I. (6.2)
/€/
В системах равенств (6.1) и (6.2) используются следующие обозна¬
чения: xi — объем производства продукции /; si — прочие ресу¬
рсы продукции i (импорт, запасы и резервы на начало периода и
т.д.) ; x.j — затраты продукции / на производство продукции /; к• — ко¬
нечное использование продукции i (непроизводственное потребление,
возмещение выбытия и расширение основных фондов, экспорт, возме¬
щение потерь, запасы и резервы на конец периода); у^ — объем конечной
продукции /.
При этом уI = кi - s. (конечное использование продукции за выче¬
том поступления прочих ресурсов).
Межотраслевой материальный баланс может разрабатываться в
различных единицах измерения. Баланс, в котором используются
пр лредмуществу физические (натуральные) измерители, называ¬
ют м е жлГт р а л~^в ы м баланс о м в натуральном вы*
р а ж е н иц.
150
Специфика межотраслевых балансов в натуральном выражении состоит в том,
что они охватывают не весь валовой общественный продукт, а только важнейшие
виды продукции (например, отчетный межотраслевой баланс СССР в натураль¬
ном выражении за 1959 г., включал 157 видов продукции, а за 1972 г. - 247 ви¬
дов). Поэтому они не могут полностью (и конкретно) расшифровать расход про¬
дукции на производственные нужды. Особой статьей в этих балансах является
’’прочее производственное потребление”, включаемое в к. или у.. В последние го¬
ды стал разрабатываться межотраслевой баланс смешанного типа (’’натурально¬
стоимостный”) , охватывающий весь общественный продукт (см. 7.1) .
Межотраслевые материальные балансы строятся также в единых
измерителях для всех видов продукции (ценностных, трудовых). Такие
балансы целесообразно рассматривать как составную часть более общих
балансовых построений, охватывающих одновременно и материально¬
вещественные взаимосвязи, и взаимосвязи по образованию обществен¬
ных затрат. Как правило, схема 6.1 используется при построении межот¬
раслевых балансов в натуральном выражении, а схема 6.2 — при постро¬
ении балансов в ценностном (трудовом) выражении, в которых конк¬
ретные виды продукции объединяются в отрасли.
Межотраслевой баланс общественного продукта. Построение меж¬
отраслевого баланса общественного продукта основано на принципах
деления валового общественного продукта по материально-вещественно¬
му и стоимостному составу. Сводная таблица межотраслевого баланса
общественного продукта состоит из четырех основных разделов-квад-
рантов (см. табл. 6.1).
Таблица 6.1
Схема межотраслевого баланса общественного продукта
’v - ■ ■ -
Распределение
\продук-
Текущее производственное потребление в
отраслях
Конеч¬
ная про¬
Валовой
продукт
Затра- ции
ты на про-4^
изводство X.
1
2
п
итого
дукция
(по эле¬
ментам)
Материальные
затраты отрас¬
лей
п
1
*11
*12
Х1„
*1/
/=1
п
У\
*1
2
*21
*22
Квад¬
рант!
* 2П
Д '*
п
У г
Квад¬
рант II
*2
п
ХП 1
*П 2
хпп
X х .
/=1 п>
хп
151
Продолжение
V
Распределение
продую
Зат¬
раты на
производстве
Текущее производственное потребление в
отраслях
Конеч¬
ная про¬
дукция
(по эле¬
ментам)
Валовой
продукт
Итого
п
2 хц
/=1
П
2 Xf 2
/•=1
п
S JC.
/=1 1П
п п
2 Ь.
/=1/=1 9
п
А"
П
2*.
i=l г
Условно-чистая
продукция (по
элементам)
zi
Квад¬
рант
III
п
&
Квад¬
рант
IV
Валовой про¬
дукт
*2
П
V ¥
^ X.
/=1/
Jr квадрант — межотраслевые взаимосвязи по использованию продук¬
ции на текущее производственное потребление (возмещение потреблен¬
ных в производстве предметов труда и производственных услуг);
II квадрант — материально-вещественный состав конечной продук¬
ции народного хозяйства (используемый национальный доход и затраты
на возмещение основных фондов);
Ш^квадрант — стоимостной состав конечной продукции народного
хозяйства (созданный национальный доход и амортизация основных
фондов);
IV квадрант — перераспределение конечной продукции.
Главную связующую роль в системе показателей межотраслевого
баланса общественного продукта играет I квадрант. Он содержит основ¬
ной массив информации, используемой для анализа межотраслевых
связей.
В I квадрант не включаются показатели простого воспроизводства основных
фондов. Это объясняется, во-первых, требованиями основной модели, в соответ¬
ствии с которыми необходимо строго выделить затраты, непосредственно завися-
^щие от объемов производства (затраты на простое воспроизводство фондов к
этой категории затрат не относятся); во-вторых, трудностями статистического
учета взаимного соответствия возмещения основных фондов в натуре (возмеще¬
ние выбытия фондов и затраты на капитальный ремонт) и по стоимости (аморти¬
зационные отчисления).
В общей таблице межотраслевого баланса общественного продукта
ортогонально совмещаются два частных межотраслевых баланса —
материальный (квадранты I—II) и баланс затрат (квад¬
ранты I—III)1.
1 О методах учета и измерения продукции в межотраслевом балансе обществен¬
ного продукта см. ММСЭ, с. 248-250.
152
В I и II квадрантах отражаются важнейшие материально-веществен-
ные взаимосвязи и пропорции народного хозяйства, выраженные в сто¬
имостных измерителях: отраслевая и материально-вещественная струк¬
тура фонда текущего производственного потребления; отраслевая и
материально-вещественная структура использования фонда конечной
продукции народного хозяйства и национального дохода; взаимосвя¬
зи между валовым общественным продуктом, фондом текущего произ¬
водственного потребления и используемой конечной продукцией народ¬
ного хозяйства. По каждой отрасли соотношения показателей выража¬
ются уравнением (6.2), а в целом по народному хозяйству выполняется
равенство
2 #£= 2 2 Хи 4" 2 yit (6.3)
1 € J i € / / € / i € /
В I и III квадрантах отражение находят важнейшие стоимостные
соотношения и пропорции общественных затрат: стоимостной состав
продукции каждой отрасли; отраслевая и материально-вещественная
структура фонда возмещения (текущего производственного потребле¬
ния и амортизации); отраслевая структура созданного национального
дохода и его первичное распределение на оплату труда и чистый доход;
стоимостная структура валового общественного продукта. По каждой
отрасли объем произведенной продукции равен суммарным затра¬
там:
i € I
где Zj — условно-чистая продукция отрасли /, включающая амортизацию,
оплату труда и прибавочный продукт. В целом же по народному хозяй¬
ству выполняется равенство
2 *,= 2 2 хи+ 2 z}: (6.5)
/ € / /€/*€/ / € /
Единство материально-вещественного и стоимостного состава вало¬
вого общественного продукта, конечного продукта и национального
дохода проявляется в сбалансированности итогов межотраслевого
баланса по строкам и столбцам:
итоги одноименных строк и столбцов (по одним и тем же отраслям)
равны, а поэтому равны объемы распределяемой продукции и объемы
производственных затрат:
2 хи ~г — 2 xki + z,, i£l;
jef *€/
153
объем валового общественного продукта как сумма распределенной
продукции отраслей равен объему валового общественного продукта
как сумме всех производственных затрат:
2 х{ = 2 Xj\
<е1 /в/ (6.6)
2 2 X[j — 2 уj — 2 2 Xjj 4- 2 Zj.
i€ I /6/ t € / j6/i€ / /€/
Поскольку 22 X- = 22 x - (это равенство выполняется автомати-
/ / J j i lJ
чески), то из (6.6) непосредственно следует, что объемы конечного об¬
щественного продукта по материально-вещественному и стоимостному
составу всегда равны:
2 !/,•= 2 г/. (6.7)
i € / / € I
В IV квадранте межотраслевого баланса общественного продукта
дается подробная характеристика процессов перераспределения наци¬
онального дохода. Здесь показывается, как полученные в сфере матери¬
ального производства первичные доходы населения (заработная плата
рабочих и служащих, личные доходы колхозников и членов кооперати¬
вов и т.д.), государства (прибыль, налог с оборота, лесной доход и т.д.)
и колхозно-кооперативных предприятий перераспределяются через раз¬
личные каналы (финансово-кредитную систему, сферу обслуживания,
общественно-политические организации).
Система показателей квадрантов III и IV является основой для пос¬
троения финансовых балансов (или балансов доходов и рас¬
ходов). Объединение же показателей квадрантов III—IV (по горизон¬
тали) и квадрантов II—IV (по вертикали) позволяет строить матери-
а л ь н о-ф инансовые балансы, характеризующие соответствие
денежных доходов населения, государства, организаций и их материаль¬
ного покрытия (фондов потребления, капитальных вложений и т.д. в
их материально-вещественной структуре).
Условием взаимно однозначного соответствия межотраслевых
балансов, использующих различные измерители, является неизменность
соотношений масштабов измерителей по каждому виду продукции.
Например, если в одном межотраслевом балансе (в натуральном выра¬
жении) электроэнергия измеряется в киловатт-часах, а в другом балансе
(в ценностном выражении) — в рублях, то каждому рублю электро¬
энергии, используемой в самых различных направлениях, всегда должно
соответствовать одинаковое количество киловатт-часов. Такое взаимно
однозначное соответствие предполагает не только единственность цены
(тарифа), но и единство методов учета продукции.
154
Показатели межотраслевого материального баланса в ценностном
выражении, удовлетворяющие указанным условиям, обозначим х^ , yj ,
Ху, а для межотраслевого баланса в натуральном выражении оставим
прежние обозначения xif у-, хн. Тогда х> = Е + у . , а вместо (6.4)
iiij i j ij i
имеем
Z{=2itj+zj, /€/• (6-8)
i€ /
Если — единая цена z-го вида продукции, то = р • х. ; jT. =
• = Pi Ху . В последующем анализе межотраслевых моделей
предполагается, что применяемые методы учета и измерения продук¬
ции в ценностном выражении удовлетворяют сформулированным выше
требованиям отражения материально-вещественных связей.
-р,
4
^6.2. Основная модель межотраслевого баланса
Одним из важнейших теоретических принципов моделирования народ¬
ного хозяйства является совместный анализ материально-вещественных
и стоимостных взаимосвязей (принцип двойственности).
Общие выводы, вытекающие из такого подхода к процессу обществен¬
ного воспроизводства, рассматривались в гл. 3. Основные соотношения
межотраслевого баланса общественного продукта (6.2) и (6.4) позво¬
ляют более конкретно анализировать совместно два аспекта межотрас¬
левых связей: а) по производству и распределению продукции; б) по
формированию общественных издержек производства и цен.
Модель межотраслевых материально-вещественных связей. Соотно¬
шения I и II квадрантов межотраслевого баланса общественного продук¬
та (6.2) характеризуют зависимости между (2п + п2) величинами х^
Ур Хц. Но они носят слишком общий характер. Для построения матема¬
тической модели решающее значение имеет предположение о том, что
X- есть функция от объема производства этой продукции: хн = фц(х-),
” ч ч 1
/, /' 6 I. Подставим значения х^ в (6.2), получим систему из п уравнений:
*,.= 2 <р,7(*/)+£„ *'€/. (6-9)
/€/
В простейшей модели используется предположение о пропорциональ¬
ной зависимости между затратами и объемами производства, т.е. вводят¬
ся линейные однородные функции производственных затрат:
xu = auxj. (6.10)
155
Коэффициент пропорциональности а - > 0 называют коэффици¬
ентом прямых затрат продукции i на производство единицы
продукции /. Эти коэффициенты в совокупности образуют квадратную
матрицу
Л=(«,7), »,/€/.
В табл. 6.2 приводятся коэффициенты прямых материальных затрат,
полученные в результате обработки ряда межотраслевых балансов
СССР1.
Таблица 6.2
Коэфффициенты прямых материальных затрат межотраслевого баланса СССР
Тяже-
Легкая
Стро¬
Сельс¬
Транс¬
Торгов¬
Прочие
лая
промы¬
итель¬
кое и
порт и
ля, заго¬
отрасли
промы¬
шлен¬
ство
лесное
связь
товки и
матери¬
шлен¬
ность
хозяй¬
матери¬
ального
ность
ство
ал ьно-
техни-
ческое
снабже¬
ние
произ¬
водст¬
ва
Тяжелая промышлен¬
0,4644
0,0452
0,4593
0,1682
0,2409
0,0648
0,1694
ность*
Легкая промышлен¬
ность**
0,0176
0,3520 0,0069 0,0351
0,0072
0,0196
0,0092
Строительство
-
-
-
-
-
-
-
Сельское и лесное хо¬
0,0141
0,2922
0,0006 0,1924
-
0,0108
-
зяйство
Транспорт и связь
0,0787
0,0178
0,0019
0,0144
0,0015
0,0082
0,1404
Торговля, заготовки и
0,0185
0,0735
-
0,0322
-
-
0,1636
материально-техни¬
ческое снабжение
Прочие отрасли матери-
0,0026
0,0008
0,0005
0,0008
0,0009
0,0060
0,0037
ального производства
Итого
0,5959 0,7815 0,4692 0,4431 0,2505 0,1094 0,4863
* Включает все отрасли промышленности, кроме легкой и пищевой.
** Включает собственно легкую промышленность, а также пищевую.
Подставив значения а^ из (6.10) и (6.9), получаем систему из п\
линейных алгебраических уравнений с 2п переменными х^ и у-:
Х(= 2 ciijXj
jel
(6.11)
Для построения этой таблицы, а также табл. 6.3-6.7 используются усреднен¬
ные данные межотраслевых балансов общественного продукта СССР за первую по¬
ловину 80-х годов. Они могут анализироваться в сопоставлении с данными межот¬
раслевого баланса СССР за 1972 г., приведенными в ММСЭ, гл. 7.
156
или
2 (fi,y—'at/)xj = yit (6.12)
/€/
где — элемент единичной матрицы:
. 1 при i = /
в, '
iJ { 0 при
В векторно-матричной форме имеем
X = AX+Y или (Е—А)Х=У, (6.13)
где X = (х-) — вектор-столбец объемов производства; Y = (у.) — вектор-
столбец конечной продукции; Е — единичная матрица порядка п.
Данная система может иметь единственное решение, если из общего
количества переменных величин х- и у. число неизвестных не превышает
числа уравнений (это условие является необходимым, но недостаточ¬
ным) . Принятие одних величин за известные, а других — за не¬
известные определяется постановкой конкретной экономической за¬
дачи (см. 6.6).
Систему уравнений (6.13) можно представить в виде
*=(£ — ДГ1Г, (6.14)
где (Е - А)л — матрица, обратная к (Е - А). Вопрос о существовании
и свойствах такой матрицы рассматривается в 6.3.
Запись модели межотраслевых связей в виде (6.14) создает опре¬
деленные преимущества^гяаналйза межотраслевых пропорций и много¬
вариантных плановых расчетов. Если известны варианты конечной про¬
дукции — векторы У, то варианты объемов производства (векторы X)
определяются как вектор-функция от Y. Экономический смысл коэффи¬
циентов Ъф образующих квадратную матрицу В = (Е - А)'1 = (&//),
i, / Е /, состоит в том, что они характеризуют объемы производства про¬
дукции /, необходимые для получения единицы конечной продукции
вида /. Коэффициенты матрицы В = (Е - А) ~1 межотраслевого баланса
СССР приводятся в табл. 6.3.
Соотношение переменных и параметров модели при разных системах
измерения. Выше было показано, что при использовании единой цены на
каждый вид продукции и одинаковых методах учета достигается взаим¬
но однозначное соответствие между показателями межотраслевых ба¬
лансов в натуральном и ценностном выражении. В частности: х'- =
= Pi у] = Pi yt xtj = p. xir Но так как x•• = afj Xj и x(j = a j;- x-,\o
157
Таблица 6.3
Коэффициенты матрицы (Е - А) 1 межотраслевого баланса СССР
Тяжелая
промыш¬
ленность
Легкая
промыш¬
ленность
Строитель¬
ство
Сельское
и лесное хо¬
зяйство
Транспорт
и связь
Торговля,
заготовки
и материа¬
льно-техни¬
ческое сна¬
бжение
Прочие
отрасли
материа¬
льного про¬
изводства
Тяжелая промышленность
1,9681
0,3661
0,9079
0,4406
0,4779
0,1460
0,4294
Легкая промышленность
0,0596
1,5898
0,0385
0,0834
0,0259
0,0363
0,0345
Строительство
-
-
1,0000
-
-
-
-
Сельское и лесное хозяйство
0,0566
0,5835
0,0308
1,2769
0,0179
0,0292
0,0223
Транспорт и связь
0,1581
0,0673
0,0752
0,0554
1,0402
0,0217
0,1777
Торговля, заготовки и материально-
техническое снабжение
0,0436
0,1430
0,0212
0,0559
0,0117
1,0074
0,1758
Прочие отрасли материального произ-
0,0057
0,0037
0,0031
0,0027
0,0023
0,0065
1,0061
водства
Итого
2,2917 2,7534
2,0768
1,9149
1,5759
1,2471
1,8458
Xij PiXij PidijXj Pi
n . , —- = (Ъ. 15)
,J Xj PJXJ P/XJ Pi
В векторно-матричной форме имеем
Х = РХ, Y— PY, A = PAP-\ (6Л6)
где Р - | р- | — диагональная матрица цен; Р"1 =|^—|— диагональная
матрица величин, обратных ценам. В линейной алгебре матрицы А и Я',
связанные соотношением (6.16),называются подобными.
Полученные формулы могут иметь более широкую интерпретацию.
В частности, они характеризуют соотношения между величинами меж¬
отраслевой модели в ценностном выражении при изменении цен (пере¬
оценке продукции); в этом случае Р — 1Р/ } — матрица индексов из¬
менения прежних цен. Система уравнений материального баланса в
’’новых” единицах измерения, отличающихся от базовых, может быть за¬
писана так:
Х = (Е—Л)"1 К. (6-17)
Используя (6.14) и (6.16), получаем Р(Е - А) ~х Y = (Е- А)ЛР¥,
откуда
(£—Л)-1 = Р(£—Л)"1/»-1. (6.18)
Таким образом, матрицы В = (Е - А) 4 и В = (Е- А)~1 также яв-
ляют% подобными.
Дополнение модели ограничениями по производственным ресурсам.
Возможности роста производства ограничены имеющимися ресурсами,
невоспроизводимыми в каждом выбранном промежутке времени. В
условиях экономической статики к невоспроизводимым относятся
природные и трудовые ресурсы, а также элементы основных фондов.
Распространив предположение о пропорциональности затрат и объемов
производства на множество ограниченных ресурсов, получим дополни¬
тельную систему линейных неравенств
2 fs/Xj^Rs, s<tMv (6.19)
/€/
где / • — прямые затраты ресурса s на производство единицы продук¬
ции/.
Частным видом ресурсов (узкого назначения) являются наличные
производственные мощности по каждому виду продукции N., характе-
159
ризующие максимально возможные выпуски продукции в единицу
времени (например, год):
Xj<Nj, /€/■ (6-2°)
К производственным ресурсам формально могут быть отнесены
элементы чистой и условно - чистой продукции (амортизация, оплата
труда, прибавочный продукт). Это объединение имеет смысл лишь по¬
стольку, поскольку изменения условно-чистой продукции в зависимости
от изменения объемов производства могут рассчитываться по левой час¬
ти формулы (6.19).
Модель межотраслевых зависимостей цен. Уравнения цен могут быть
выведены из соотношений I и III квадрантов межотраслевого баланса
общественного продукта. Примем, что z. = г- xj, где ту — коэффициент
условно-чистой продукции на единицу объема производства продукции
/. Тогда из (6.8) следует
pjXf— 2 pftijXj + rjxj*
i € /
pj— ^ ai/Pi + rj, i
i € I
(6.21)
В векторно-матричной форме имеем
Р = РА+ г (6-22)
Ф
ИЛИ
Р(£_Л) = Г, (6-23)
откуда
р = г(Е — А)~1, (6-24)
где Р = (pj) — вектор-строка цен; г = (гр — вектор-строка коэффициен¬
тов условно-чистой продукции.
В том случае, если коэффициенты а^ и ту рассчитаны на единицу про¬
дукции в ценностном выражении (на 1 руб.), то Pj — индексы изменения
(корректировки) исходных цен.
Модель межотраслевых зависимостей цен (6.21) является двой¬
ственной по отношению к модели межотраслевых матери¬
ально-вещественных связей (6.12). Действительно, соотношения ура¬
внений этих моделей аналогичны соотношениям условий двойствен¬
ных задач линейного программирования. Кроме того, обязательно вы-
160
полняется равенство 2 гт- х^ = £ р.- у-9 т.е. объем созданной в народном
w /^1 1 1^1 Ч
хозяйстве конечной продукции (по стоимостному составу) равен сум¬
марной оценке используемой конечной продукции. Данное соотношение
эквивалентно условию равенства функционалов прямой и двойственной
задач линейного программирования.
Рассматриваемая модель является инструментом экономической
политики в области ценообразования. С ее помощью можно изучать
(и предвидеть) влияние изменения цен в одних отраслях на уровни цен
и рентабельности в других отраслях, влияние увеличения оплаты труда
в некоторых отраслях, выравнивания рентабельности, налога с оборота,
изменения платы за фонды и т.п. на всю систему цен. Главное преиму¬
щество модели — в возможности взаимной балансировки цен на про¬
дукцию всех отраслей.
Системы уравнений (6.21) —(6.24) выражают межотраслевые зави¬
симости цен в наиболее общем виде. Более конкретные формулы исчис¬
ления сбалансированной системы цен различаются способами определе¬
ния коэффициентов условно-чистой продукции: /у = Sj + Vy + га-, где sy —
амортизация, Vj — оплата труда, rrij — прибавочный продукт. В 6.5 анали¬
зируются наиболее характерные модификации уравнений цен при конк¬
ретизации способов исчисления условно-чистой продукции.
Анализ основных допущений модели. Модель межотраслевого
баланса (в двух своих формах) связана с принятием ряда упрощающих
предположений, которые зачастую выходят за рамки применяемых
в практике народнохозяйственного планирования допущений. Это об¬
стоятельство само по себе не может служить доводом против исполь¬
зования данной модели, но оно требует разработки практичных и гибких
приШЬв согласования формальных свойств модехйис реальной действи¬
тельностью. Переход к более совершенным и сложным моделям осуще¬
ствляется либо путем отказа от некоторых предположений исходной мо¬
дели, либо путем ее дополнения новыми зависимостями.
Область существования решений. Модель материально-веществен-
ных связей (6.11) или (6.12) имеет неограниченную область решений.
Задавая произвольные значения используемой конечной продукции
Ур можно получить сколь угодно большие значения объемов производ¬
ства х^ Точно так же, если в модели межотраслевых зависимостей цен
будем произвольно устанавливать коэффициенты условно-чистой про¬
дукции ту, то можем получать неограниченно большие, но тем не менее
удовлетворяющие условиям модели значения цен Pj. Единственное ус¬
ловие, которое накладывается на эндогенные переменные моделей, —
их неотрицательность (х;- > 0, pj > 0).
Дополнение модели материально-вещественных связей условия¬
ми ресурсов (6.19) и (6.20) ограничивает область допустимых значе¬
ний величин Xj и у..
Пропорциональность затрат и объемов производства. В основе коэф¬
фициентов а- планового межотраслевого баланса лежат нормативы
6 Зак. 2414 161
расхода материальных ресурсов на единицу продукции или объема ра¬
бот, широко применяемые в практике народнохозяйственного планиро- «
вания. Однако в целом ряде отраслей производства (особенно в сельс¬
ком хозяйстве, добывающей промышленности, на транспорте), а также
и для некоторых видов потребляемых ресурсов (топлива, вспомогатель¬
ных материалов и т.д.) предположение о пропорциональности затрат
и выпуска продукции является слишком грубым; к нему приходится
прибегать только ввиду недостатка более точных знаний. Включение в
модель ограничений по ресурсам, а также применение модели цен распро¬
страняют исходную гипотезу прямой пропорциональности также на
функции затрат труда, фондов, условно-чистой продукции..
В гл. 7 рассматриваются возможности включения в модель более
точных зависимостей между затратами и выпуском продукции.
Производство продукции только одним способом. Формально все
расчеты на основе модели исходят из допущения, что каждый вид про¬
дукции может производиться не более чем одним способом. Реальный
смысл вводимого в модель единственного производственного способа
для каждого вида продукции состоит в том, что этот способ является
комбинацией разных способов, т.е. усредненным производственным
способом. Это ’’усреднение” различных способов (расчет средневзве¬
шенных отраслевых коэффициентов прямых затрат) осуществляется
на стадии формирования исходных данных для модели межотраслевого
баланса на основе изучения и прогнозирования прогрессивных технико¬
экономических тенденций и перспектив развития отраслей.
Более общие межотраслевые модели, допускающие использование
нескольких способов в производстве определенных видов продукции,
анализируются в гл. 8. С
Производство только одного вида продукции каждым способом.
В модели межотраслевого баланса предполагается, что в каждом про¬
изводственном процессе получается лишь один вид продукции. Посколь¬
ку же каждый вид продукции производится только одним способом,
то общее число способов всегда равно числу видов продукции (отрас¬
лей) . В ряде отраслей промышленности (особенно в химии, цветной ме¬
таллургии) и в сельском хозяйстве часто встречаются процессы произ¬
водства сопряженной (комплексной) продукции: извлечение несколь¬
ких металлов при переработке одной руды, совместное получение нес¬
кольких химических продуктов, получение нескольких продуктов
при убое скота и т.д. В межотраслевой модели отражение этих процес¬
сов осуществляется путем применения различных приемов распределе¬
ния затрат между отдельными видами продукции. Производство сопря¬
женной продукции рассматривается как несколько самостоятельных
производств, в которых получается только по одному виду продукции.
Из данного свойства модели непосредственно следует неотрицатель¬
ность всех элементов затрат х> 0, а,7 > 0, /_• > 0.
ч V У
162
Модель межотраслевого баланса, включающего отрасли, производя¬
щие несколько видов (групп) продукции, рассматривается в гл. 7.
Открытость модели. Возможность и эффективность использования
народнохозяйственных моделей во многом определяются соотношения¬
ми эндогенных и экзогенных величин. С этой точки зрения модель меж¬
отраслевого баланса может быть отнесена к классу ’’широко откры¬
тых” моделей. При решении основных задач по модели межотраслевого
баланса (нахождение эндогенных величин хz- и pj) допускается, что эле¬
менты используемой конечной продукции (yj) и условно-чистой проду¬
кции (Tj) не связаны между собой и могут определяться независимо от
объемов производства и цен. В действительности это не так. Напри¬
мер, такая часть конечной продукции, как производственное накопле¬
ние, не может быть задана независимо от объемов производства, пос¬
кольку является условием роста последнего. Потребление предметов
потребления и услуг во многом зависит от оплаты труда в сфере произ¬
водства, т.е. от объемов производства. Потребности в экспорте и импор¬
те продукции связаны с производственными возможностями народного
хозяйства (обеспеченностью ресурсами) и т.д. Введение ’’известных”
величин в плановые расчеты по межотраслевой модели означает лишь
то, что эти величины рассчитываются за рамками модели и вследствие
этого не могут быть точно сбалансированы между собой. Чем больший
’’вес” имеют экзогенные величины, тем меньше самостоятельное значе¬
ние расчетов на основе модели. Поэтому закономерно, что совершенст¬
вование моделей межотраслевых связей идет в направлении уменьшения
их ’’открытости” (см. гл. 7, 8).
6.3. Математический анализ модели
межотраслевого баланса
Свойства матрицы А. Матрица коэффициентов прямых материальных
затрат А относится к хорошо изученному в математике классу неот¬
рицательных матриц (подробнее см. [2. Ч. I. Гл. 1 ] ). Но ко¬
эффициенты матрицы А не могут принимать произвольные положитель¬
ные значения. Очевидно, что все диагональные элементы матрицы А дол¬
жны быть меньше единицы., В противном случае производство лишается
всякого смысла (если а- > 1, то х^ > xj). Существуют и другие менее
очевидные ограничения значений коэффициентов выражающие требо¬
вания общественного производственного процесса.
В частности, произведения коэффициентов, симметричных относительно глав¬
ной диагонали, должны быть по крайней мере меньше единицы: а% ащ < 1. Для
того чтобы пояснить необходимость этого условия, рассмотрим следующий при¬
мер. Пусть производственная система изготовляет два продукта: уголь и металл.
При этом на производство 1 т металла расходуется 2 т угля, на 1 т угля - 1 т ме¬
талла {а 12 <*2 1 =2). При таких коэффициентах затрат производство превращается
в особый способ уничтожения ресурсов, так как для изготовления металла в
6* 163
конечном счете требуется еще большее количество металла, а для добычи угля —
еще большее количество угля. ’’Производство” не только не может дать конечной
продукции, а непрерывно должно субсидироваться извне ресурсами угля и метал-
-1 -2
тиворечит соотношениям ’’нормальной” экономики.*
ла. Коэффициенты матрицы (Е - А) =
отрицательны, что также про-
Особенности матриц в ценностном и натуральном выражении. Указан--
ные выше ограничения на значения отдельных коэффициентов не зависят
от применяемых единиц измерения, так как в соответствии с (6.15) а'ц =
= aii; ^Ik ^kl ~ alk ак1 Однако в общем случае выбрр единиц измерения
существенно влияет на анализ свойств матриц межотраслевого балан¬
са. Для матриц межотраслевого баланса в ценностном выражении обыч¬
но выполняются условия 2 д.* < 1, / Е I (см., например, последнюю
/ЕI '
строку табл. 6.2). Если же для некоторой к-й отрасли 2 а^ > 1, то эко¬
номически это означает, что данная отрасль настолько убыточна, что ее
убытки перекрывают расходы на амортизацию и оплату труда. Очевид¬
но, что в условиях хозрасчета такое состояние отрасли совершенно не¬
приемлемо.
Из линейной алгебры известно, что одна из норм матрицы А опреде¬
ляется как \\А|| = max 2 д,7. Следовательно, \\А\\ < 1, когда 2 аИ< 1,
/ г€1 11 г<EI »
/ Е /. Например, для приведенной выше матрицы межотраслевого балан¬
са СССР \\А || =0,7815.
Из того, что 1И11 < 1, вытекает ряд следствий, важных для экономи¬
ческого анализа:
1) lim Am — 0; ?
m оо
2) £ + Л-Мг+ ..+/4*4- ■ •=(£ — А)-1; (6.25)
3) (Е-АГ1^ 0:
4) все собственные значения Хг- матрицы А по модулю меньше еди-
ницы, а наибольшее собственное значение положительно (теорема Фробе-
ниуса—Перрона) 1;
5) все главные миноры матрицы (Е - А) положительны и меньше
единицы.
В матрицах межотраслевого баланса в натуральном выражении
условия 2 а - < 1, j Е / практически никогда не выполняются. Более то¬
го, многие коэффициенты этих матриц больше единицы. Однако можно
попытаться подобрать такие новые измерители (матрицу Р), что для
подобной матрицы А =РАР~1 будет выполняться условие ||JT || < 1
и следствия (6.25). Из линейной алгебры известно, что подобные матри-
1 Матрица межотраслевого баланса СССР (см. табл. 6.2) имеет max Ay = 0,5400
(корень Фробениуса-Перрона). i
164
*
цы имеют равные по величине собственные значения и главные миноры
(матрицы (Е - А) и (Е — А ) также являются подобными, так как
Р(Е-А)РГ~1 -Е- РАР~1 =Е-А.
Понятие о разложимых и неразложимых матрицах. В теории матриц
ра зложимыми называются такие матрицы^, которые одновре¬
менной перестановкой строк и столбцов приводятся к виду
А =
О
(6.26)
где Ац, А22 — квадратные блоки, включающие ненулевые элементы;
О — блок, состоящий только из нулей; * — блок, элементы которого
могут принимать любые значения.
Матрица А неразложима, если для нее не существует таких од¬
новременных перестановок строк и столбцов, которые приводили бы ее к
разложимой форме (даже несмотря на наличие большого числа
нулевых элементов). Если матрица А неразложима, то каждая отрасль
непосредственно или косвенно использует продукцию всех других
отраслей, а ее продукция непосредственно или косвенно расходуется при
производстве продукции всех других отраслей, т.е. все пары отраслей
находятся в двусторонней связи (подробнее о свойствах неразложимых
матриц и об использовании этих свойств в экономическом анализе и
плановых расчетах см. [ 1. С. 194 — 214] ).
Продуктивность матрицы А. Введенное в гл. 2 общее понятие про¬
дуктивности экономической системы в модели межотраслевого баланса
связывается исключительно со свойствами матрицы А. Продуктивной
экономической системе соответствует такая матрица коэффициентов
А, которая обеспечивает возможность получения конечной продукции
(вектора Y) при соответствующих пропорциях развития производства
(векторе X).
Матрица А называется продуктивной, если существует неот¬
рицательный вектор X > 0, позволяющий получить положительный
вектор конечной продукции: (Е - А)Х = Y > 0. Для неразложимых
матриц определение продуктивности имеет более общий вид. Неразло¬
жимая матрица А продуктивна, если существует такой вектор X > 0,
что (E-A)X=Y> 0.
Для отчетного межотраслевого баланса (в котором всегда ^.>0) свойство про¬
дуктивности проверяется очень просто. Если Y> 0, то система продуктивна. Одна¬
ко если некоторые у( о, то из этого еще нельзя сделать вывод о непродуктивно¬
сти матрицы А. Можно, взяв вместо неположительных компонент вектора У поло¬
жительные значения, рассчитать новые значения X. И если при этом окажется, что
X ^ 0, то матрица А продуктивна.
Продуктивность матрицы А можно определить и по отношению к
модели межотраслевых зависимостей цен. Матрица А продуктивна,
165
если существует такой вектор Р > 0, что Р(Е -А) = г > 0. Неразложимая
матрица А продуктивна, если существует такой вектор Р > 0, что Р(Е -
-А) =г> 0.
Это означает, что можно подобрать цены, обеспечивающие получение неотрица¬
тельной чистой продукции во всех отраслях и хотя бы в некоторых отраслях
положительной чистой продукции. Для отчетных межотраслевых балансов в цен¬
ностном выражении убедиться в том, что матрица А продуктивна, как правило,
очень просто: достаточно, чтобы zj ^ 0, / Е / и хотя бы для одного / было zj > 0.
Однако если эти условия не выполняются, то нельзя утверждать, что матрица Л
непродуктивна.
Для продуктивности матрицы А необходимо и достато¬
чно, чтобы выполнялось одно из нижеследующих условий.
1. Все главные миноры матрицы (Е - А) положительный меньше
единицы.
Например, главный минор первого порядка 1 — ау > 0. Условия
выполняются, если ац < 1. Главный минор второго порядка
>0,
еслиагЛг< ^~arr> O-^sX1-
Матрицы, соответствующие главным минорам, также являются
продуктивными. Поэтому все основные свойства матрицы А распростра¬
няются на матрицы блоков отраслей и комплексов отраслей. Главный
минор п-го порядка D, г.е. определитель матрицы (Е — А), также заклю¬
чен в пределах 0 < D < 1. Отсюда, в частности, вытекает существование
матрицы (Е - А) 4 .
2. Все собственные значения матрицы А по модулю меньше единицы.
3. Матрица (Е - А) _1 полуположительна.
В свою очередь условие (Е - А) _1 ^ 0 является одним из важней¬
ших следствий продуктивности матрицы А. Если матрица А неразложи¬
ма, то матрица (Е — А) _1 строго положительна.
Для продуктивности матрицы А достаточно, чтобы 2 а« < 1,
z Е /
j Е /. Вытекающие отсюда следствия рассматривались выше.
Если матрица А продуктивна, но достаточное условие продуктивности не выпол¬
няется, то всегда можно подобрать такие новые измерители продукции (вектор Р),
что это условие будет выполняться. Но если матрица Л непродуктивна, то никакая
система измерителей не исправит дефекта. Например, в рассмотренной выше
производственной системе ’’уголь - металл” не существует таких положительных
-w Pl ^
цен pi и р2, чтобы одновременно удовлетворялись неравенства а ^ 1
Р2
^ р2
(или 2Pi <; р2) и а 21 — — 1 (или Р2 < Pl).
Коэффициенты косвенных и полных народнохозяйственных затрат.
Взаимозависимости отраслей в процессе общественного производства
166
количественно могут быть выражены системой коэффициентов прямых,
косвенных и полных затрат продукции и ресурсов. Каждый коэффици¬
ент полных затрат представляет сумму прямых и косвенных затрат,
обусловленных выпуском единицы определенного вида продукции.
Принципиальное их отличие от коэффициентов прямых затрат состоит в
том, что они являются не отраслевыми или внутрипроизводственными,
а народнохозяйственными показателями.
Полные затраты на производство определенной продукции. Поста¬
вим перед собой такую задачу: определить сумму каждого вида затрат,
прямо и косвенно необходимых для производства единицы продукции.
Образование полных затрат наглядно демонстрируется с помощью
схемы процесса последовательного наслоения прямых и косвенных
затрат, имеющей вид бесконечно ветвящегося ’’дерева”. В образовании
коэффициентов полных затрат участвуют все коэффициенты прямых
затрат1, а сам процесс бесконечен. Схема отражает особенности образо¬
вания полных затрат невоспроизводимых (’’внешних”) ресурсов: цепо¬
чки прямых и косвенных затрат обрываются в ячейках затрат ресурсов,
так как эти затраты не участвуют в процессе образования других косвен¬
ных затрат (см. ММСЭ, с. 267).
Введем дополнительные обозначения: ~ косвенные затра¬
ты цикла m соответственно продукции / и ресурса s\ - сум¬
мы прямых и косвенных затрат до цикла m включительно соответствен¬
но продукции i и ресурса s; c\jy Fsj — полные затраты соответственно
продукции / и ресурса s.
Количественное выражение коэффициентов косвенных и полных
затрат может быть получено из анализа схемы.
Косвенные затраты первого цикла - это прямые затраты на производство того
количества средств производства, которое потребляется при изготовлении единицы
продукции. Они определяются следующим образом:
ац — 2 а-ра^г, f*si — 2 fskabi-
kei *€/
Косвенные затраты второго цикла выражаются уже более сложным образом.
Суммируются элементы косвенных затрат второго цикла по первым индексам,
и каждый элемент является произведением трех коэффициентов прямых затрат.
Например, дСУ = a\\^naii + ••• +amania^i + ••• +апа1пап] + — + а\паппащ. Если
продолжим цепи взаимосвязей, то получим косвенные затраты третьего, четвертого
цикла и т.д. Последовательно учитывая косвенные затраты все более высокого
цикла, т.е. дальше отстоящего от данного процесса производства, в пределе
должны получить коэффициенты полных затрат. Однако поэлементные вычисле¬
ния становятся все более громоздкими. И осуществлять их становится практиче¬
ски невозможно, если не прибегнуть к обобщению расчетов в виде математичес¬
ких формул.
Коэффициенты косвенных затрат первого цикла имеют наиболее простую стру¬
ктуру: они слагаются из произведений коэффициентов прямых затрат. При опре¬
делении косвенных затрат второго цикла соответствующие коэффициенты прямых
затрат умножаются на отдельные слагаемые косвенных затрат первого цикла.
Если предварительно суммировать слагаемые косвенных затрат первого цикла,
то получим компактные формулы косвенных затрат второго цикла:
1 Это строго справедливо для неразложимых матриц.
167
aif — 2 a!ka(k'>, i£I; $> = 2 jskaif, s£M.
*€1 ke I
Используя метод индукции, можно показать, что общие формулы
косвенных затрат для любого цикла имеют вид
а\Т = ^ а/йа^-1); (6.27)
Л6/
/<*?>= 2 МГ>. (6-28>
7 £€/
где га — любое целое положительное число (при этом а ^ =akj)-
Практические расчеты показывают, что с учетом косвенных затрат
до третьего — пятого циклов для большинства видов продукции и ресур¬
сов получается хорошее приближение к полным затратам.
Например (см. табл. 6.2 и 6.3), прямые затраты продукции тяжелой промышлен¬
ности на 1000 руб. продукции легкой промышленности составляют 45,2 руб., а
полные - 366,1 руб. (в 8,1 раза больше). Косвенные затраты первого цикла равны
95,2 руб., второго цикла - 83,4, третьего цикла - 57,8 ... пятого цикла - 21,2 руб.
Сумма прямых и косвенных затрат до пятого цикла включительно составляет
92,6 % полных затрат.
Выведем общие формулы коэффициентов полных затрат.
По определению полных материальных затрат как суммы прямых
и всех косвенных затрат (при га -><») имеем
CU = аи + а?> + a\f + . . . + <> + - . . (6.29)
Подставив в (6.29) выражения (6.27) для различных циклов, полу¬
чим
Сц = а,у + 2 aitlakj -f 2
1 * € /
2 ■ ■ ■ =a,7+ 2 ailt(ak; + a$+ .. . +- . . .).
k€ I btl
Очевидно, что при aty + a ^ + ... + a^j ~ 1 * + ... = ckj>
В итоге получаем
c// = fl// + ^ aikckj• (6.30)
*€/
Для определения коэффициентов полных материальных затрат на
производство единицы продукции / требуется решить систему из п урав¬
нений (6.30) с фиксированными / и / = 1, ..., п. Для определения всей
матрицы коэффициентов полных затрат сц необходимо решить п таких
систем уравнений.
168
Формула коэффициентов полных затрат ресурсов выводится анало¬
гично:
Fs; = fsj+ 2 nr = f,j+ I 2 !,:АГ " fs; + 2 и 2 air1'-
т— I т—\ k€ I k £ I m=I
Таким образом,
F.,=f.j+ 2 /,Л/. (6.31)
kei
По формуле (6.31) исчисляются полные затраты труда, основных
фондов и других производственных ресурсов, а также коэффициенты
полных затрат элементов условно-чистой продукции. После того как
определены коэффициенты c]q, вычисление коэффициентов Fsj не пред¬
ставляет какой-либо трудности.
Экономическая сущность коэффициентов полных затрат может ис¬
следоваться также с иных позиций. Для этого можно рассмотреть про¬
цесс образования полных затрат определенного вида продукции (или
ресурса) на производство всех видов продукции (см. [1. С. 146 —
150]). Такой подход приводит к следующим формулам коэффици¬
ентов полных затрат:
Ct/ = au+ 2 cikak/; (6.32)
*6/
Fsj-fss+2 Fs^r (6.33)
kei
Соотношения матриц коэффициенте прямых, косвенных и полных
затрат. Пусть - матрица коэффициентов косвенных материальных
затрат цикла т\ /т^ — матрица косвенных затрат ресурсов цикла т;
С - матрица коэффициентов полных материальных затрат; F — матри¬
ца коэффициентов полных затрат ресурсов. Тогда формулы (6.27),
(6.28), (6.30), (6.31) в матричном виде записываются так:
Aim)=A А{т~х)\ (6.34)
fm)=f.A'm-»; (6.35)
С^А + АС; (6.36)
F=f+fC. (6.37)
В соответствии с (6.34) А1 = А • А = А2, А^ = А * А^ = А3 и
т.д. В общем же случае матрица косвенных материальных затрат цикла
(т) равна (т + 1)-й степени матрицы А :
Л(т) = А{т + 1) (б 38)
169
Из определения полных материальных затрат следует
оо оо
С = А + 2 А(т) = 2 Л("” (6.39)
т=1 т=1
В линейной алгебре известно аналогичное разложение в степенной
ряд: (Е - A)~l = Е + А + Л2 + ... +А^т^ + ••• (если -> 0 при т
°°). Очевидно, что если существует (£ — А) 4 и Ат -> 0 (при m -> <»)
то1
С = (£-Л)-1~£. (6.40)
Пользуясь матричными обозначениями, легко показать, что форму¬
лы (6.30) и (6.32), (6.31) и (6.33) тождественны (см. ММСЭ,
с. 267).
Таким образом, между коэффициентами матриц С = (су) и В =
= (Е - A)~l = (bij) имеется качественное и количественное соответ¬
ствие. При выводе формул для су суммировались все материальные
затраты, прямо и косвенно связанные с выпуском единицы продукции
/. При этом получение единицы продукции / рассматривалось как конеч¬
ная цель всего общественного производства, но эта единица продукции
не включалась в затраты. Коэффициент же(^/)позволяет ответить на
вопрос: каковы полные потребности в продукции /, необходимые
для получения" продукции вида /. Он _вкдючает' полные производст-
,•бШкые'~затрать1|^) и, „саму,, единицу конечной продукции (если i = /),
которую также нужно произвести, но которая не является затратами
производства в узком смысле:"## = сц + 6j/: Экономическое различие'
между коэффициентами {ffinЪц заключается в том, что первые'отражают
структурные взаимосвязи" промежуточного и ,конечного^ продуктаГ~а“
вторые — структурные взаимосвязи валового и конечного ^продукта.
Коэффициенты ШтрёгбН^стёй в ресурсах для получения единицы*
конечной продукции в точности совпадают с коэффициентами полных
затрат ресурсов на производство единицы продукции. При этом коэф-
1 Формула (6.40) получается также из (6.36): .
/
\ /
С=А(Е+С),
С + Е =А(Е + CJ + Е,
(Е - AJfC+AJ =Е,
(Е -А)~'(Е -А)(С + Е) =(Е-А)~\
С + Е = (Е-Ар1.
170
фициенты прямых и полных затрат ресурсов обладают важным свойст¬
вом: сумма прямых затрат на производство валового общественного
продукта равна сумме полных затрат, отнесенных на конечную продук¬
цию:
2 /,/*•■= 2 ^ • S$M <б-41)
/ € / / 6 I
Существование решений модели межотраслевого баланса. Сфор¬
мулируем две основные теоремы для модели межотраслевых материа-
льно-вещественных связей и модели межотраслевых зависимостей
цен.
1. Если матрица А продуктивна, то для любого полуположительного
вектора Y > 0 система (Е - А)Х = Y имеет единственное полуположи-
тельное решение X > 0. Иными словами, каждому вектору конечной
продукции (Т > 0) соответствует только один вектор объемов произ¬
водства (X > 0). Для неразложимой матрицы А любому Y > 0 соответ¬
ствует единственный строго положительный X > 0.
2. Если матрица А продуктивна, то для любого полуположительного
вектора чистой (условно чистой) продукции г > 0 существует единст¬
венный полу положительный вектор цен Р > 0. Иначе говоря, если взять
любой вектор чистой (условно чистой) продукции (г > 0), то ему соот¬
ветствует только одна система цен (Р> 0). При условии неразложимо¬
сти А любому г > 0 соответствует единственный строго положительный
Р > 0 (геометрическое истолкование условий существования решений
уравнений межотраслевых связей см. в ММСЭ, с. 275 — 276).
Покажем, что для существования единственного X > 0 при любом
Y > 0 необходимо и достаточно, чтобы В = (Е - А)~1 > 0 (заметим,
что в этой матрице строго положительными являются хотя бы диагональ¬
ные элементы).
Достаточность принятого условия очевидна. При bfj > 0 и yj > 0,
/, / е 7 (и хотя бы один из элементов у\ и один из элементов b[j положи¬
тельны), все произведения bijyj неотрицательны и хотя бы одно произ¬
ведение строго положительно, например: Ь^кУк. при у у. > 0. Поэтому
xi = D bijyj > о, / £7 и хотя бы одна xi > 0.
/Е7
Необходимость принятого условия обнаруживается при следующем
рассуждении. Если хотя бы один элемент £/& < 0, то найдется такой
вектор Y > 0, в котором только к-я компонента положительна, а осталь¬
ные — нулевые. Тогда получится х/ = Ьцук < 0.
Обычно свойства модели межотраслевого баланса анализируются в предполо¬
жении, что У > 0. Известно, однако, что отдельные компоненты вектора конечной
продукции могут принимать отрицательные значения, например, по импортируе¬
мой продукции. Это ни в коей мере не является признаком непродуктивности си¬
стемы межотраслевых связей. Свойства, доказанные в предположении У7> 0, ну¬
жно понимать так, что в продуктивной системе всегда могут быть получены
наборы конечной продукции, не имеющие отрицательных компонент (например,
если народное хозяйство откажется от импорта).
171
Вместе с тем отрицательные значения отдельных элементов конечной продукции
не могут быть чрезмерно большими по абсолютной величине. Если, например,
величины одной группы конечной продукции (г) неотрицательны, а величины
другой группы конечной продукции (s) отрицательны, то должны выполняться
условия
ZftftVr ^ ^bfsys, i СУ.
Г S
Аналогично доказательство существования решений уравнений цен
Р (Е- А) =г, опирающееся на условие (Е - А) -1 > 0.
6.4. Применение межотраслевого баланса в анализе
материально-вещественных и трудовых пропорций
Межотраслевой баланс является ценным инструментом исследования си¬
стемы взаимосвязей и пропорций народного хозяйства. В применении
межотраслевого баланса для экономического анализа можно различить
два методических подхода: 1) анализ информации, непосредственно
содержащейся в таблицах межотраслевого баланса (аналитическая об¬
работка таблиц); 2) анализ на основе моделей межотраслевых связей.
При первом подходе используются в основном традиционные приемы
экономико-статистического анализа. Мы будем рассматривать такие на¬
правления анализа, которые базируются на применении математических
моделей.
Анализ взаимосвязей валового и конечного общественного проду¬
кта. Коэффициенты матрицы В = {Е - А)~1 выражают соотношения
между отраслевой структурой конечного продукта и отраслевой струк¬
турой валового продукта. При использовании стоимостных измерителей
коэффициент bj = 2 by определяет потребность в валовом обществен¬
ном продукте для получения единицы конечной продукции из отрасли
/. Как видно из последней строки табл. 6.3, значения коэффициентов
bj различаются почти в 2 раза даже при укрупненной классификации
отраслей народного хозяйства (максимальный коэффициент (2,7534) —
по легкой промышленности, минимальный (1,2471) - по торговле,
заготовкам, материально-техническому снабжению).
Поэтому изменения отраслевой структуры конечного продукта
(при сохранении его общего объема) могут ощутимо сказываться на
объеме валового общественного продукта. Это обстоятельство должно
приниматься во внимание при обосновании таких макроэкономических
пропорций, как соотношения валового продукта, конечного продукта
и национального дохода.
Например, если бы в объеме конечного продукта доля строительства повыси¬
лась на 5 процентных пунктов (пп.), а доля легкой промышленности уменьшилась
также на 5 пп. (что может означать маневр в пользу ускоренного развертывания
инвестиционных программ, в том числе жилищного строительства), то за счет этого
172
отношение валового общественного продукта к конечному продукту уменьшилось
бы на (2,7534 - 2,0768) • 0,05 = 0,0338. При неизменном общем объеме конечно¬
го продукта это означало бы уменьшение потребности в валовом общественном
продукте примерно на 20 млрд. руб. в год.
Представляет также интерес анализ зависимостей объемов производ¬
ства отраслей от общего объема конечного продукта при неизменной его
отраслевой структуре. Пусть у — общий объем конечного продукта,
а = (а/) — вектор-столбец отраслевой структуры конечного продукта,
2 Щ = 1.
/е 7
Тогда
Х = (Е-АУ'ау = £у, (6.42)
где Р = (Е - А)~1а — вектор коэффициентов потребностей в продукции
разных отраслей для получения единицы общего объема конечного про¬
дукта фиксированной структуры.
По усредненным данным межотраслевых балансов СССР на каждые
1000 руб. конечного продукта требуется производить: продукции тяже¬
лой промышленности — на 1033 руб., продукции легкой промышлен¬
ности — на 583, продукции сельского и лесного хозяйства — на 351
руб. и т.д. При стабильной структуре конечного продукта отраслевая
структура валового общественного продукта определяется коэффици¬
ентами
Ус
Р/
2 В;
i € I
t € Г
^^одель межохрашевош баланса позволяет изучать не только струк¬
турные, но и дйнамические соотношения между валовым и
конечным общественным продуктом.
Отношение валового продукта к конечному продукту ф) есть
средний по народному хозяйству коэффициент потребностей в валовом
продукте на единицу конечного продукта; соизмерителями различных
видов продукции служат цены (вектор Р). В соответствии с принятой
методикой для динамических сопоставлений ’’физических” объемов
валового и конечного продукта текущего (или планового) года (индекс
1) и базисного года (индекс 0) применяются цены базисного года:
роХо ро (£—л0)-1 Y0
Ро роуо роуо ’
_ро*1 po(E^A1)-1Y1
Pi роу1 Р°УХ
173
Динамика соотношения физических объемов валового и конечного
продукта характеризуется индексом
Р, Р° (E-A')-iY'P*Y*
_ Р° (£— Л0)"1 Y°P°Y1 ‘
Если f > 1, это значит, что валовой продукт растет быстрее конечно¬
го в
го продукта. Если же ■ ■ < 1, то рост конечного продукта обгоняет
Ро
рост валового продукта.
Допустим, что конечный продукт увеличивается в неизменной
отраслевой структуре темпом о. Тогда
R Р° (Е—А1)~1аУ° Р° (E—A1)-1Y°t
Pi — P°aY° P°Y° ’
Pi Р° (E^A1)~1Y°
Ро Р°(£— A^-'Y0
В этом случае изменение пропорции между валовым и конечным
продуктом целиком определяется динамикой коэффициентов матрицы
(Е - А)_1. Если, например, сумма коэффициентов хотя бы по одной
отрасли уменьшилась, а по другим — не увеличилась, то конечный про¬
дукт увеличивается быстрее валового продукта.
Допустим теперь, что конечный продукт изменяется в любых соотно¬
шениях, но матрица (Е — А)'1 остается неизменной. В данном случае
Pi
индекс —-— зависит исключительно от структурных сдвигов в конеч¬
но
ном продукте. Если в составе конечного продукта увеличивается удель¬
ный вес отраслей, имеющих высокие коэффициенты bj (металлургии,
химической промышленности, легкой и пищевой промышленности),
то это способствует опережающему росту валового продукта; если же
увеличивается удельный вес конечной продукции электроэнергетики,
сельского хозяйства и т.п., это создает возможности для опережающего
роста конечного продукта.
174
Таким образом, соотношение физических объемов валового и коне¬
чного продукта изменяется только в результате взаимодействия динами¬
ки материалоемкости производства и динамики отраслевой структуры
конечного продукта.
Данные о динамике используемого конечного продукта не публикуются Госком¬
статом СССР. Поэтому воспользуемся данными о динамике национального дохо¬
да, используемого на потребление и накопление, имея в виду, что различия темпов
роста конечного продукта и используемого национального дохода не очень велики.
За 25-летний период (1985 г. к 1960 г.) валовой продукт увеличился в 3,87 раза,
а национальный доход, используемый на потребление и накопление, - в 3,36 раза.
Но произведенный национальный доход вырос точно так же, как и валовой про¬
дукт (в 3,87 раза). Это означает, что опережающий рост валового продукта объя¬
сняется главным образом изменением структуры используемого национального
дохода (в том числе за счет нарастающего отклонения от объема произведенного
национального дохода за счет потерь и внешнеторговых отношений), а не изме¬
нением материалоемкости производства.
Рассмотрим особенности динамики валового и конечного продукта
в текущих ценах. При этом
PiXi pi(£—Л1)"1*'1.
Pi piyl — piyi
Р1 (Е — Лг) “1 Y1 Р°К°
7Г--ро(£_до)-1у°р1К1 '
При сравнительном анализе индексов и —>г~ интересно вы-
Ро йр
явить возможности противоположных изменений и /3 i.
Предположим, что отраслевая структура конечного продукта не¬
изменна, а матрица (Е - А)~* изменяется так, что М- <bj для всех/Е I.
в и
Тогда “jg" < 1- Однако вполне возможно, что > 1. Это может
происходить при увеличении цен на продукцию с большими коэффициен¬
тами bj. В другом крайнем случае, когда матрица (Е — А) 4 неизменна,
а изменяется только структура конечной продукции, также возможны
противоположные изменения (31 и р'1. Например, удельный вес конеч¬
ной продукции отраслей с меньшими значениями bj увеличивается
(и в результате этого < 1), но это влияние перекрывается ростом
цен на продукцию отраслей с большими коэффициентами bj . В реаль¬
ной действительности, когда одновременно изменяются и коэффици¬
енты материальных затрат (одни повышаются, другие понижаются),
и структура конечной продукции, неравномерное изменение цен может
приводить к значительным расхождениям индексов -С— и .
Ро Ро
175
По данным межотраслевых балансов СССР коэффициент @ изменяется следую¬
щим образом: 1959 г. - 2,076, 1966 г. - 2,203, 1972 г. - 2,183, первая половина
80-х годов (усредненный коэффициент) - 2,367. Этой тенденции увеличивающих-
А
ся коэффициентов и, следовательно, роста индекса -^-^соответствует и динамика
Ро
отношения валового продукта к национальному доходу, используемому на потре¬
бление и накопление (в текущих ценах): 1960 г. - 2,10, 1970 г. - 2,254, 1980 г. -
2,375, 1985 г. - 2,434.
Определение полных народнохозяйственных затрат на фонды конеч¬
ного продукта. С народнохозяйственных позиций производство разли¬
чных видов продукции осуществляется для обеспечения различных фон¬
дов конечного общественного продукта.
Пусть q — номер фонда конечного продукта. Тогда
Х = (Е—=2 (E-A)-IY*.
Q V
Здесь ХЯ = (Е- АУ'уЧ — вектор объемов производства, обеспечиваю¬
щих q-й фонд конечного продукта.
Основную часть конечного общественного продукта образуют фонды
потребления и накопления. Непосредственно на них расходуется пример¬
но 40 % валового общественного продукта. Полные же потребности
этих фондов составляют около 90 % валового общественного продукта.
При этом легкая промышленность и сельское хозяйство в основном
обслуживают фонд потребления; продукции тяжелой промышлен¬
ности на единицу фонда накопления расходуется примерно в 1,4 раза
больше, чем на единицу фонда потребления; продукция строительства
на фонд потребления вообще не расходуется (см. табл. 6.4).
Еще большие различия в структуре конечного использования продукции об¬
наруживаются при детализации классификации отраслей. Например, продукция
металлургии, электроэнергетики, топливной, химической промышленности и
промышленности строительных материалов непосредственно на фонды потребле¬
ния и накопления почти не используется. Значение этих отраслей для обеспечения
фондов потребления и накопления проявляется косвенно - через систему меж¬
отраслевых взаимосвязей по производственному потреблению. При этом продук¬
ция металлургии и промышленности строительных материалов используется в
конечном счете преимущественно для фонда накопления; продукция же топливной,
электроэнергетической, химической, лесной промышленности в большей части ис¬
пользуется для фонда потребления, однако на каждую единицу фонда накопления
этой продукции расходуется существенно больше, чем на единицу фонда потреб¬
ления.
В целом на 1000 руб. фонда потребления в первой половине 80-х
годов требовалось 2511,7 руб. валового общественного продукта, а
на 1000 руб. фонда накопления — 2164,1 руб., т.е. на 13,8 % меньше1.
1 По расчетам на основе межотраслевого баланса за 1972 г. эта относительная
разница была вдвое меньше (6,9%) (см. ММСЭ, с. 280).
176
Таблица 6-4
Потребности в продукции отраслей
для обеспечения фондов потребления и накопления
Отрасли
Производство продук¬
ции на 1000 руб.
фонда пот¬
ребления,
РУб
фонда на¬
копления,
руб.
Во сколько раз полный
расход продукции боль¬
ше прямого
на фонд по¬
требления
на фонд на¬
копления
745,7
1044,3
3,2
4,7
998,8
181,5
1,6
2,1
-
576,5
-
г,о
548,2
223,0
3,9
2,0
93,4
91,1
*
*
107,8
41,0
*
*
17,7
6,7
1,3
2,2
Тяжелая промышленность
Легкая промышленность
Строительство
Сельское и лесное хозяйство
Транспорт и связь
Торговля, заготовки и матери¬
ально-техническое снабжение
Прочие отрасли материального
производства
Итого валовой общественный 2511,7 2164,1
продукт
2,51
2,16
* Прямой расход отсутствует.
При изменении в используемом национальном доходе соотношения
между потреблением и накоплением изменяются объемы валового
общественного продукта и продукции большинства отраслей. Напри¬
мер, при увеличении доли накопления (и сохранении прежнего объема
национального дохода) сокращается объем необходимого валового
общественного продукта и должно уменьшиться производство в отрас¬
лях промышленности группы Б и сельском хозяйстве, но зато должно
увеличиться производство в отраслях промышленности группы А и
строительства.
Общие потребности народного хозяйства в производственных ресур¬
сах также могут быть распределены между фондами конечного продук¬
та (по формуле RУ = В табл. 6.5 приводятся расчеты потребно¬
стей в основных производственных фондах и трудовых ресурсах на со¬
здание фондов потребления и накопления.
Таблица 65
Потребности в основных производственных фондах
и трудовых ресурсах на 1000 руб. фондов потребления и накопления
На фонд потребле¬
На фонд накопле¬
ния
ния
Основные производственные фонды, руб.
2231,5
2106,3
Трудовые затраты, годовых работников
0,1705
0,1706
177
Для характеристики возможностей роста народного хозяйства
принципиально важное значение имеет тот факт, что на 1000 руб. прирос¬
та фонда накопления потребность в дополнительных основных фондах
существенно превышает 1000 руб. Это означает, что абсолютное увели¬
чение накопления основных фондов с позиций данного года неэффектив¬
но, а абсолютные масштабы накопления ограничиваются ранее созданны¬
ми основными фондами1. Своеобразие современных пропорций годово¬
го цикла воспроизводства заключается в том, что полная фондоемкость
накопления несколько ниже полной фондоемкости потребления (на
5,6%). Поэтому увеличение доли накопления в используемом наци¬
ональном доходе (при неизменном его общем объеме) несколько умень¬
шает потребности в основных производственных фондах для данного
года. Раньше полная фондоемкость накопления заметно превышала
полную фондоемкость потребления2. Происшедшие изменения объяс¬
няются в первую очередь особенно быстрым ростом фондоемкости
сельскохозяйственного производства, обеспечивающего своей продук¬
цией фонд потребления.
Анализ структуры и динамики полных трудовых затрат. При об¬
щественном разделении труда любой продукт является совокупным
результатом деятельности множества отраслей производства. Коэффи¬
циенты полных затрат на производство продукции охватывают как
непосредственные затраты живого труда на заключительной стадии из¬
готовления продукции, так и все затраты труда на предшествующих ста¬
диях производства данной продукции, овеществленные в потребленных
средствах производства. Величина Tjxj означает полную трудоемкость
всей произведенной продукции / как выражение ее общей стоимо¬
сти, Z Tjxj означает совокупные затраты труда, овеществленные во
всем Общественном продукте, как выражение стоимости валового об¬
щественного продукта.
В структуре полных трудовых затрат выделяются прежде всего
затраты живого труда (прямые трудовые затраты) и затраты
прошлого, или овеществленного, труда (косвенные
трудовые затраты). Широко распространено мнение, что доля затрат
живого труда в совокупных трудовых затратах должна уменьшаться
Если бы фондоемкость накопления была меньше 1000 руб., а срок создания
основных фондов - меньше одного года, то расширенное воспроизводство основ¬
ных фондов осуществлялось бы за счет основных фондов, создаваемых в этом же
году; это был бы принципиально иной тип расширенного воспроизводства. Под¬
робно данная проблема анализируется в гл. 10.
Отметим, что полная фондоемкость накопления непрерывно увеличивается уже
в течение длительного периода. По данным межотраслевых балансов СССР она
составила (в расчете на 1000 руб.): в 1959 г. - 1226,6 руб., в 1966 г. - 1310,6 руб.
(см. ММСЭ, с. 281).
В 1959 г. полная фондоемкость 1000 руб. потребления равнялась 1057,8 руб.,
в 1966 г. - 1178,6 руб. (см. ММСЭ, с. 281).
178
вследствие того, что затраты живого труда на производство единицы
продукции снижаются быстрее, чем могут уменьшаться удельные матери¬
альные затраты (тем более что последние могут и увеличиваться). Такое
рассуждение некорректно. В соответствии с марксистской теорией об¬
разования стоимости экономия живого труда ’’обесценивает” труд,
овеществленный в потребляемых средствах производства. Поэтому
экономия живого труда сама по себе не влияет на долю затрат живого
труда в полных трудовых затратах.
Пусть a, t, Т — соответственно коэффициенты материалоемкости,
прямой трудоемкости и полной трудоемкости валового общественного
продукта, д — доля затрат живого труда в полных трудовых затратах.
Очевидно, Т= t ' , причем -у \ -- есть скалярный аналог матрицы
(Е - А) 1, /I = 1 — а. Таким образом, если макроэкономические пара¬
метры а, t, Т уже рассчитаны для определенной отраслевой структуры
валового общественного продукта, то доля затрат живого труда зависит
только от материалоемкости. Она равна доле произведенного националь¬
ного дохода в валовом общественном продукте. Например, в 1985 г.
было: а = 0,582, ц = 0,418 (в текущих ценах). Если материалоемкость
снижается, то доля затрат живого труда (и национального дохода также)
растет, и наоборот.
Перейдем к анализу динамики затрат живого и овеществленного
труда в многоотраслевой экономике.
Затраты живого труда на производство валового продукта равны
tX, полные трудовые затраты на производство валового продукта рав¬
ны t(E - А)~1Х, доля затрат живого труда в полных трудовых затратах:
/X
t (Е—А)-1 X ‘
Изменение доли затрат живого труда характеризуется индексом
fXi РХЧор — А0)-*- Х°
ц0 ~ toXWiE—А1)-1 X1 '
Если ~r~ > 1, то доля затрат живого труда возрастает, если ^ < 1,
М о До
эта доля уменьшается. Заметим, что измерители объемов производимой
продукции остаются неизменными (это могут быть натуральные изме¬
рители или сопоставимые цены).
Предположим, что коэффициенты затрат живого труда во всех отра¬
слях уменьшаются одинаково в / раз (/ — любое положительное число), а
отраслевая структура валового продукта остается неизменной, т.е. tll =
= t°,Xl =кХ°,к> 0.
Тогда
179
(Li!
,х0"" *
Полученный результат подтверждает сделанный выше вывод, что до¬
ля затрат живого труда в полных трудовых затратах остается неизмен¬
ной при любом пропорциональном снижении коэффициентов затрат
живого труда. Это происходит потому, что пропорциональное уменьше¬
ние затрат живого труда во столько же раз обесценивает затраты овеще¬
ствленного труда и во столько же раз снижает полные трудовые затраты.
п Mi
При сделанных допущениях динамика индекса определяется
Мо
исключительно изменением коэффициентов матрицы (Е - -4) . Если
уменьшается хотя бы один коэффициент этой матрицы (а другие оста¬
ются неизменными), то доля затрат живого труда увеличивается: >
, Мо
> 1. Таким образом, увеличение доли затрат живого труда является
следствием роста эффективности использования материальных ресурсов.
В реальной экономике динамика соотношения затрат живого и ове¬
ществленного труда складывается под влиянием различных изменений
коэффициентов материальных затрат, структуры валового продукта
и неравномерного снижения затрат живого труда в разных отраслях.
Если в народном хозяйстве материалоемкость производства в целом
снижается, это создает устойчивую тенденцию увеличения доли живого
труда. Если же материалоемкость в целом возрастает, то преобладающей
становится тенденция уменьшения доли затрат живого труда в полных
трудовых затратах на производство валового общественного продукта.
6.5. Применение межотраслевого баланса
в анализе стоимостных пропорций
Сравнительный анализ систем цен. Как отмечалось в 6 2, модель меж¬
отраслевых зависимостей цен (6.21) - (6.24) используется для расчетов
и сравнительного анализа систем цен при разных способах начисления
условно-чистой продукции (ry = Sj + Vj + mj). Рассмотрим некоторые
характерные модификации общей модели ценообразования.
Формула ’’стоимости” (распределение прибавочного продукта
пропорционально оплате труда). Пусть п1 — единая по народному хо¬
зяйству норма прибавочного продукта (mj = ттг vj). Тогда
Pi = 2 aijPi - S(. -I- (1 -i- Я,) Vj, j (6.43)
180
или в век то рно-матричном виде
P = A4 + s + (H- njv, (6.44)
где s, v — матрицы-строки коэффициентов амортизации и оплаты труда.
Выражения (6.43), (6.44) могут быть упрощены, если амортизацию
распределить по материально-вещественному составу (как затраты
продукции машиностроения, строительства, животноводства) и добавить
к соответствующим коэффициентам матрицы А. Получим матрицу А
Вместо (6.43), (6.44) теперь имеем
Pi = 2 + 0 * лОи,, / 6 (6.45)
i €J
Р = РА + {\ + njv (6.46)
или
Р=(1 + Я1)я(£—А)-\ (6.47)
Выражение V = v(E - А)~1 в (6.47) есть вектор коэффициентов
полных затрат оплаты труда (народнохозяйственной зарплатоемкости
продукции). Таким образом, цены прямо пропорциональны коэффици¬
ентам полных затрат оплаты труда (заработной платы). Коэффициент
7Г1 является общим множителем для всех цен и влияет только на аб¬
солютный уровень цен, но не ка их соотношения.
При использовании формул (6.43), (6.44) получаемые векторы
цен ввиду малых значений коэффициентов sj (в большинстве отраслей)
почти пропорциональны полным затратам оплаты труда и мало зависят
от значения тт1.
Цены по формулам (6.43) - (6.47) тесно связаны с трудоемкостью продукции.
Если бы оплата туда была одинаковой во всех отраслях, то было бы vj = kt, где
к - оплата единицы затрат труда, и
Pi — . £ /Pi-Ьs/ 4(1 +л,) kt, ,§3; (6.48)
р) 'а‘/Р: ■+ (• + Jtl) ki, /<£ 5Г; (6.49)
или
Р~РА-¥ |1 -t-Jtj) kt,
откуда Р=(1+лг)Ы(Е— А)-*, (6.50)
P~(l+„i)kT,
181
т.е. цены прямо пропорциональны полным трудовым затратам (с коэффициентом
пропорциональности (1 + Я\к)> а коэффициенты полных трудовых затрат на 1 руб,
продукции отраслей равны. Поэтому дифференциация коэффициентов полных
трудовых затрат, рассчитанных по данным межотраслевых балансов в ценностном
выражении, свидетельствует об отклонениях фактических цен от цен, построенных
по формулам (6.48) - (6.50). Например, по расчетам на основе усредненного
межотраслевого баланса СССР коэффициенты полных трудовых затрат даже в раз¬
резе 7 отраслей различаются в 1,9 раза.
Формула "усредненной стоимости” (прибавочный продукт пропор¬
ционален себестоимости продукции). Пусть Я2 — единый по народному
хозяйству норматив прибавочного продукта на единицу себестоимости.
Тогда
Р/
= (.^ aupi + sf + x/j (I + /е/ (6.51)
или
p = (l4-n2)(A4 + s + i;); (6.52)
P = (l + n2)(s + v) [E—( 1 + ji2) A]-\ (6.53)
Отсюда следует, что соотношение цен зависит от норматива прибавочного
продукта тг2 (через коэффициенты матрицы ( [Е - (1 + тт2 М ] 4 ) •
Формула цены производства (прибавочный продукт пропорционален
сумме используемых производственных фондов). Отличительная особен¬
ность ценообразования по этой формуле состоит в том, что одновремен¬
но с исчислением цен требуется переоценивать производственные фонды
и амортизационные отчисления.
Пусть d^j — величина производственных фондов z-го вида (продук¬
ция машиностроения и строительства, скот), используемых в производ¬
стве единицы продукции /; эта величина есть сумма основных и оборот¬
ных фондов (dy = d(®) + d(®fy ), w-j — норма амортизации /-го вида
основных фондов, используемых в производстве единицы продукции /
(доля годового износа); 7Г3 — единый по народному хозяйству норматив
прибавочного продукта на единицу используемых производственных фо¬
ндов. Общая сумма производственных фондов (в ценностном выраже¬
нии) , используемых в производстве единицы продукции /, равна 2 d^pj9
( \ / £ / У
а общая сумма амортизации — соответственно 2 w-jd
Система уравнений цен принимает вид * е ^
Pi = 2 auPi + 2 ( 2 di/pA+v, (6.54)
i € I i € / \ i € 1 J
182
или
Р = РА + PwD<OC) + л 3PD + v; (6.55)
P = v(E—A—wD'0C,—n3D)-1, (6.56)
где D^oc\ D — соответственно матрицы коэффициентов основных про¬
изводственных фондов и всех производственных фондов; w — матрица
коэффициентов годового износа основных производственных фондов.
Во всех рассмотренных модификациях модели ценообразования
присутствует свой норматив прибавочного продукта (я1? п2, я3). Этот
норматив нельзя устанавливать произвольно, поскольку с ним связаны
важные макроэкономические пропорции. Чтобы однозначно определить
систему цен, следует ввести нормирующее условие. Это может быть,
например, условие неизменности общей суммы расходов на приобрете¬
ние населением товаров и платных услуг:
= (6.57)
i в/
где заданными являются у?— объем приобретения /-го товара (услуги);
/ — общая сумма покупок населения. Смысл условия (6.57) состоит в
том, чтобы при изменении цен не уменьшить общую покупательную спо¬
собность населения.
В табл. 6.6 приводятся индексы изменения цен по отраслям, рас¬
считанные по трем формулам ценообразования по данным усредненного
межотраслевого баланса СССР. При этом в системы уравнений вводилось
нормирующее условие (6.57). Системы уравнений для определения цен
по формулам ’’усредненной стоимости” и цены производства решались
итеративным методом.
Вследствие укрупненности отраслей и принятия ряда чрезмерно упрощающих
гипотез (единство оптовых и розничных цен, свободное перераспределение налога
с оборота и т.п.) полученные результаты имеют главным образом иллюстратив¬
ное значение. Все же они позволяют судить о наиболее существенных деформациях
сложившейся системы цен. В частности, высокие индексы цен по отрасли ”сель-
ское и лесное хозяйство” подтверждает мнение Госкомстата СССР:’’Уровень цен не
всегда отражает общественно необходимые затраты труда на производство продук¬
ции. Часть национального дохода, созданного в сельском хозяйстве, реализуется
в форме налога с оборота и прибыли в пищевой промышленности... а также в лег¬
кой промышленности” .
.— Взаимосвязи стоимостной, материально-вещественной и функциона¬
льной структур конечного продукта. Метод, который применяется при
исчислении коэффициентов полных затрат продукции и ресурсов (см.
6.3), состоит в том, что непосредственные затрат до бесконечности
разлагаются на свои первичные элементы. Такой метод может применя¬
ться и в анализе стоимостной структуры производства.
1 Народное хозяйство СССР за 70 лет: Юбилейный стат. ежегодник/ Госкомстат
СССР. М.: Финансы и статистика, 1987. С. 122 - 123.
183
Таблица 6.6
Индексы изменения цен при использовании
различных моделей ценообразования
Отрасли
Ценообразование по формулам
’’стоимости”
(TTj =0,847)
’’усредненной
стоимости”
(7Г2 =0,187)
цены производ¬
ства* (7Т3 =
= 0,171)
Тяжелая промышленность
0,863
0,880
1,032
Легкая промышленность
0,974
1,026
0,934
Строительство
1,130
0,993
1,001
Сельское и лесное хозяйство
1,321
1,100
1,225
Транспорт и связь
1,001
0,897
1,437
* Без переоценки амортизации.
Величина совокупного общественного продукта и стоимость (цена)
любого вида продукции непосредственно распадается на три основных
элемента: Р = с + v + т. Величина с в свою очередь может рассматривать¬
ся как стоимость определенной массы продукции, которая также распа¬
дается на свои основные элементы. Продолжая этот процесс разложения
перенесенной стоимости, получим в пределе, что стоимость (цена)
продукции целиком разлагается в конечном счете на оплату труда V и
прибавочный продукт М, но таким образом, что К+ М = с + v + т.
При существующей методике построения межотраслевого баланса
амортизация отделена от материальных затрат. Поэтому общая система
уравнений цен имеет вид
Р = РА 4- s -f v + т,
откуда
Р = s (Е— А) 1 ■+ v(E — A)"1 -f т (Е—А)“
к/
(6.58)
где S = (S-) = $(Е — А)А — вектор-строка коэффициентов полных
затрат амортизации; V = (Vj) = v(E - A)~l — вектор-строка коэффи¬
циентов полных затрат оплаты труда; М = (МЛ =т(Е- А)'1 - вектор-
строка коэффициентов полных затрат прибавочного продукта.
Таким образом, цена единицы продукции равна сумме коэффициен¬
тов полных затрат амортизации, оплаты труда и прибавочного продукта.
Если же анализируются соотношения межотраслевого баланса в ценно¬
стном выражении, то цена единицы ’’продукции” равна, естественно,
единице: Sj + Vj+Mj=l,j G7 (см. табл. 6.7).
184
Таблица 6-7
Коэффициенты полных затрат амортизации,
оплаты труда и прибавочного продукта
по данным усредненного межотраслевог о баланса СССР
Тяжелая
промыш¬
ленность
Легкая
промыш¬
ленность
Строитель¬
ство
Сельское и
лесное хозя¬
йство
Амортизация
0,2038
0,1365
0,1625
0,1634
Оплата труда
0,3569
0,4553
0,5238
0,6267
Прибавочный продукт
0,4393
0,4082
0,3137
0,2099
Коэффициенты Sj, Vj, Mj характеризуют влияние, которое оказы¬
вает изменение объемов и структуры используемой конечной продукции
на формирование фондов амортизации, оплаты труда, прибавочного про¬
дукта. Например, коэффициент полных затрат оплаты труда в тяжелой
промышленности (0,3569) показывает, что при увеличении продукции
тяжелой промышленности на 1000 руб. прирост фонда оплаты труда в
народном хозяйстве должен составить 356,9 руб.; коэффициент полных
затрат прибавочного продукта в легкой промышленности говорит о том,
что при увеличении на 1000 руб. конечного использования продукции
этой отрасли фонд прибавочного продукта в народном хозяйстве возра¬
стет на 408,2 руб. и т.д. Очевидно, что если в составе используемого ко¬
нечного общественного продукта увеличивается удельный вес продукции
сельского хозяйства и строительства, то в народном хозяйстве быстрее
должен расти фонд оплаты труда. Если же возрастает удельный вес про¬
дукции тяжелой промышленности, то быстрее должен увеличиваться
объем прибавочного продукта.
Существенное влияние на стоимостную структуру производимого
конечного продукта (условно-чистой продукции) оказывают также
изменения в функциональной структуре используемого конечного про¬
дукта, прежде всего изменение пропорции между потреблением и накоп¬
лением.
Очевидно, что увеличению фонда потребления должен соответство¬
вать увеличивающийся фонд оплаты труда, а росту фонда накопления —
увеличивающиеся финансовые ресурсы за счет прибавочного продукта.
Однако при сложившейся в народном хозяйстве СССР системе цен,
рентабельности, оплаты труда рост накопления в большей степени увели¬
чивает фонд оплаты труда в производственной сфере, а рост потребления
в большей степени увеличивает объем прибавочного продукта (см.
табл. 6.8). Такое соотношение коэффициентов полных затрат оплаты
труда и прибавочного продукта на единицу фондов потребления и нако¬
пления создает некоторую напряженность в поддержании материально¬
вещественной и финансовой сбалансированности народного хозяйства.
Это еще не означает неизбежности диспропорций, поскольку спрос и
предложение потребительских и инвестиционных товаров можно регу-
185
Таблица 6-8
Потребность в элементах условно-чистой продукции на 1000 руб.,
фондов потребления и накопления по данным
усредненного межотраслевого баланса СССР
(в руб.)
пировать за счет перераспределения прибавочного продукта в непроиз¬
водственной сфере, изменения пропорции между личным и обществен¬
ным потреблением, регулирования материально-вещественной (отрас¬
левой) структуры фондов потребления и накопления. Тем не менее це¬
лесообразно содействовать изменению выявленного соотношения вели¬
чин оплаты труда и прибавочного продукта, необходимых для формиро¬
вания и использования фондов потребления и накопления.
Следует отметить, что проводимые в СССР мероприятия по совершенствованию
системы оптовых и розничных цен, увеличению и упорядочению заработной платы
в различных отраслях нашли отражение в существенном сглаживании различий
между коэффициентами оплаты труда и прибавочного продукта на потребление и
накопление. Так, оплата труда на единицу фонда накопления была выше, чем на
единицу фонда потребления: в 1959 г. - на 69 %, в 1966 г. - на 40, в 1972 г. - на
43, в первой половине 80-х годов - на 8 %. Величина прибавочного продукта на еди¬
ницу фонда потребления была выше, чем на единицу фонда накопления: в 1959 г. -
на 52 %, в 1966 г. - на 35, в 1972 г. - на 44, в первой половине 80-х годов - на
14 % (см. ММСЭ, с. 282). Это, несомненно, облегчает решение проблемы согласо¬
вания материально-вещественных и стоимостных пропорций в народном хозяйстве
СССР.
6.6. Плановые расчеты на основе
модели межотраслевого баланса
\
Расчеты сбалансированных уровней производства исходя из вариантов
конечной продукции. Модель межотраслевого баланса позволяет прово¬
дить в кратчайшие сроки расчеты многих вариантов производственной
программы отраслей, обеспечивающих задания по удовлетворению конеч¬
ных потребностей народного хозяйства. Для этого решается система урав¬
нений X — АХ + Y при различных векторах Y. На основе сравнительного
анализа рассчитанных вариантов плана производства из них отбираются на¬
иболее приемлемые для последующего уточнения и более глубокого
обоснования. Такой порядок плановых расчетов ориентирует на достиже¬
ние определенных конечных результатов (повышение уровня жизни на¬
селения, расширение производственных мощностей, увеличение экспорта
и т.п.). Аналогичные задачи взаимоувязки объемов производства и коне¬
чного использования продукции решаются при корректировке планов.
186
Проведение расчетов значительно упрощается, если предварительно
находится матрица (Е - А)~1. Тогда при корректировке заданий по
конечной продукции легко определять необходимые изменения в планах
производства: kX = (Е- А)~1 ДУ.
Главная проблема плановых расчетов по модели межотраслевого
баланса — подготовка исходной информации, т.е.
плановых коэффициентов затрат и вариантов конечной продукции.
Коэффициенты затрат на производство продукции изменяются во
времени. Поэтому в плановых расчетах нельзя ограничиваться только ис¬
пользованием коэффициентов, полученных из отчетных межотраслевых
балансов и любых других статистических источников. Наиболее распро¬
страненные методы определения плановых коэффициентов материаль¬
ных затрат рассматриваются в гл. 12.
Поскольку конечная продукция разнородна по своему экономичес¬
кому назначению, то ее планирование осуществляется отдельно по ка¬
ждому фонду (личное и общественное потребление, производственное и
непроизводственное накопление, экспорт и импорт и т.п.). При подготов¬
ке вариантов конечной продукции широко используются предплановые
обоснования и информационные материалы ко многим разделам госу¬
дарственных планов развития народного хозяйства (’’Уровень жизни”,
’’Торговля”, ’’Внешнеэкономические связи”, ’’Образование, культура и
здравоохранение” и др.).
Для планирования конечной продукции применяются также специ¬
альные экономико-математические модели. Здесь можно выделить два
основных подхода: использование макроэкономических моделей для
определения общих объемов конечного продукта, фондов потребления,
накопления и т.д. с последующей детализацией их отраслевой структу¬
ры; построение структурных моделей отдельных функциональных эле¬
ментов (фондов) конечного продукта. Второй подход наиболее широко
применяется при обосновании вариантов непроизводственного потребле¬
ния (см. гл. 5).
Для определения объемов продукции для накопления оборотных
фондов, экспорта, возмещения потерь и т.д. часто принимаются извест¬
ными не абсолютные величины, а коэффициенты, характеризующие долю
расхода продукции на эти нужды от объема производства; эти коэффици¬
енты добавляются к диагональным коэффициентам материальных зат¬
рат. Более совершенным способом отражения взаимосвязей между про¬
изводством и конечным использованием продукции является построение
расширенных моделей межотраслевого баланса, в которых неко¬
торые элементы конечного продукта становятся эндогенными перемен¬
ными. Примером может служить модель, рассматриваемая в гл. 7.
В рамках статической моделй наибольшие трудности возникают при
определении плановых объемов капитальных вложений, поскольку по¬
требности в капиталовложениях мало связаны с условиями развития
народного хозяйства только в одном рассматриваемом году. Эти труд¬
ности усугубляются, когда модель используется в расчетах не на бли¬
187
жайший год, а на последний год перспективного периода (конец пятилет¬
ки) . Введение в статическую модель капиталовложений как экзогенных
величин позволяет решить только одну задачу: определить вли¬
яние того или иного вектора капиталовложений на изменение объемов
производства и потребностей в ресурсах. Для решения более широкого
круга задач балансовой увязки объемов производства, капиталовложе¬
ний и конечного использования продукции требуется дополнять стати¬
ческую модель некоторыми динамическими соотношениями (см. 13).
Обоснование производственной программы со стороны производ¬
ственных ресурсов. Модель межотраслевого баланса для плановых
расчетов включает ограничения по общим ресурсам и производствен¬
ным мощностям. При краткосрочном планировании производственные
возможности ограничены в основном сложившимся распределением
трудовых ресурсов и основных фондов. Однако в течение одного года
лишь в малой степени можно перераспределить рабочую силу и основ¬
ные фонды между различными отраслями и поэтому главными ограни¬
ченными ресурсами являются производственные мощности, понимае¬
мые как максимально возможные объемы производства соответствую¬
щих ВИДОВ ПРОДУКЦИИ .
На основе данных о производственных мощностях проводятся
расчеты сбалансированных вариантов производства и конечной продук¬
ции. Например, можно рассчитать размеры конечной продукции при
максимально возможном использовании производственных мощностей
по всем отраслям (т.е. когда Xj = Мр j £7) :
У1 = 2 {btJ-a„)Nh *€/.
i 6/
Анализ соотношений мощностей и объемов производства в народ¬
ном хозяйстве СССР показывает, что полное использование всех произ¬
водственных мощностей не всегда целесообразно по двум причинам:
во-первых, вследствие несбалансированности мощностей по отдельным
отраслям, а во-вторых, из-за чрезмерно высоких издержек на некоторых
предприятиях. Поэтому существует проблема оптимального использо¬
вания (или оптимального недоиспользования) производственных мощ¬
ностей с целью получения желаемых объемов конечной продукции. Для
этого необходимо сравнивать множество плановых вариантов. Решение
данной проблемы значительно упрощается при переходе к оптимизаци¬
онным межотраслевым моделям (см. гл. 8).
Составлением плана процесс планирования не заканчивается. В ходе
выполнения плана, как правило, обнаруживаются несоответствия в раз¬
витии отдельных отраслей производства. При этом те величины, которые
при составлении плана принимались заданными и неизменными (коэф¬
фициенты затрат, структура агрегированной продукции, ввод новых мо¬
щностей и выбытие изношенного и морально устаревшего оборудования,
экспорт и импорт продукции и т.п.), могут принимать другие значения.
188
Возможные отклонения в ходе осуществления народнохозяйственного
плана могут быть учтены заранее путем разработки нескольких плано¬
вых вариантов, рассчитанных на различный уровень трудно поддающих¬
ся точному предвидению факторов (урожайность сельскохозяйственной
продукции, импорт и т.д.) или на различный уровень достижения качест¬
венных показателей (снижение норм расхода, рост производительности
труда и т.п.).
При использовании модели межотраслевого баланса в перспектив¬
ном (среднесрочном и долгосрочном) планировании методика обосно¬
вания производственных возможностей народного хозяйства услож¬
няется. Основные производственные фонды и производственные мощно¬
сти, необходимые в последнем году планового периода, в значительной
мере создаются в течение планового периода. Поэтому статическая
модель может использоваться только как составная часть динамической
модели (иметь ’’входы” и ’’выходы”, соединяющие ее со статическими
моделями для других лет планового периода) либо дополняться дина¬
мическими соотношениями (см. гл. 13).
Плановые расчеты со смешанным составом неизвестных. В реальной
плановой работе нет резкой грани между двумя стадиями обоснования
народнохозяйственного плана: со стороны общественных потребностей и
со стороны производственных возможностей. Как правило, бывает
известно, что по некоторым видам продукции имеющиеся производст¬
венные возможности должны использоваться максимально (они лими¬
тируют удовлетворение потребностей), а по другим — объемы производ¬
ства должны быть рассчитаны в зависимости от потребностей в конечной
продукции. Поэтому при расчетах плана производства по ряду лимити¬
рующих средств производства (например, по электроэнергии, прокату
черных металлов, синтетическим материалам) вначале могут устанавли¬
ваться задания по объемам производства и находиться объемы конечной
продукции, а по остальным видам продукции - задаваться объемы конеч¬
ной продукции и вычисляться объемы производства.
Целесообразность фиксации некоторых объемов производства в плановых расче¬
тах по модели межотраслевого баланса вытекает также из технологических и
социально-экономических особенностей отраслей, например из предопределенно¬
сти выпуска продукции затратами прошлых лет (сельское хозяйство, строитель¬
ство, некоторые машиностроительные отрасли). К задаче со смешанным составом
неизвестных сводятся также корректировочные расчеты в процессе выполнения
плана, когда требуется выйти на плановые задания по некоторым объемам произ¬
водства и некоторым видам конечной продукции. При этом, в частности, учитыва¬
ется, что к диспропорциям в народном хозяйстве может приводить не только недо¬
выполнение, но и перевыполнение планов по отдельным отраслям и видам продук¬
ции, особенно при напряженном положении с ресурсами.
Сформулируем задачу плановых расчетов по модели межотраслево¬
го баланса со смешанным составом неизвестных.
Пусть все виды продукции (отрасли) разбиваются на две группы:
1) продукты (т видов), по которым искомыми являются объемыпро-
189
изводства, — вектор Хх, а задаются объемы конечной продукции — век¬
тор Y1 = Ci (оба вектора размерности т) ; 2) продукты (п - твидов),
по которым задаются объемы производства (например, в соответствии с
максимальным использованием мощностей или в соответствии с зада¬
ниями перспективных планов) - вектор Х2 = Q2 > а искомыми являются
показатели конечной продукции — вектор У2 (оба вектора размернос¬
ти п - т).
Тогда решение системы относительно Хх и У2 возможно следующим
образом. Вначале решается подсистема порядка т
(Е-АХ1)ХЛ = С, + A12Q,
и находится вектор Хх. Затем вектор Хх подставляется в подсистему
порядка п - т:
Yt = (E-AjQt-AtlXt,
каждое уравнение которой содержит по одному неизвестному и реша¬
ется независимо.
Аналогично решается задача корректировки плана, когда требуется
учесть влияние отклонений от плана выпуска продукции второй группы
продуктов (АХ2 = AQ2) на валовые выпуски первой группы продуктов
(ДЛ^ ) и конечную продукцию второй группы (А^) ПРИ условии выпол¬
нения заданий по конечной продукции первой группы (ДУ^ = 0).
Литература
1. Аганбегян А.Г., Гранберг А.Г. Экономико-математический анализ межотрасле¬
вого баланса СССР. М.: Мысль, 1968.
2. Ашманов С.А. Введение в математическую экономику. Ч. I.
3. Коссов В.В. Межотраслевые модели (теория и практика использования). М.:
Экономика, 1973.
ГЛАВА 7
РАЗВИТИЕ МОДЕЛИ МЕЖОТРАСЛЕВОГО БАЛАНСА
Важнейшими направлениями развития основной модели межотраслево¬
го баланса являются: 1) расширение модели за счет включения в систему
межотраслевых связей новых аспектов, факторов и условий; 2) пере¬
смотр специфических допущений исходной модели и построение уточ¬
ненных моделей. В данной главе рассматриваются наиболее характерные
модификации межотраслевых балансовых статических моделей, по¬
лучившие применение в экономических исследованиях и планирова¬
нии народного хозяйства. Первое направление представлено моделями,
анализируемыми в 7.1 — 7.6; второе направление — моделями с уточ¬
ненными и обобщенными межотраслевыми производственными свя¬
зями (7.7).
7.1. Межотраслевой натурально-стоимостный баланс
(модель, учитывающая организационную
структуру народного хозяйства)
В основной модели межотраслевого баланса исполь'зуется принцип
’’чистой” отрасли. Это означает, что отрасль рассматривается как объе¬
динение производств, выпускающих однородную продукцию. Методика
учета продукции и затрат по ’’чистым” отраслям имеет ряд преиму¬
ществ с точки зрения отражения производственно-технических (матери¬
ально-вещественных) связей в народном хозяйстве, но при этом теряется
адресность аналитических и плановых расчетов, ибо реальное планирова¬
ние и управление осуществляются не по ’’чистым”, а по ’’хозяйствен¬
ным” отраслям, представляющим собой совокупность предприятий и
объединений, подчиненных различным ведомствам (министерствам
и т.п.).
С различиями между ’’чистыми” и ’’хозяйственными” отраслями
тесно связана проблема согласования плановых показателей в натураль¬
ном и стоимостном выражении. В то время как планирование производ¬
ства в натуральном выражении ведется по всему народному хозяйству
и основным профилирующим ведрмствам, планирование в стоимостном
191
выражении (валовая и товарная продукция) осуществляется только в
разрезе ведомств.
С целью более активного применения модели межотраслевого балан¬
са в практике планирования и управления в модель включаются показа¬
тели организационной структуры народного хозяйства и взаимосвязи
между ’’чистыми” и ’’хозяйственными” отраслями. Модель такого
типа, получившая название ’’развернутый натурально-стоимостный
баланс”, разработана в Научно-исследовательском экономическом
институте при Госплане СССР под руководством Ф.Н.Клоцвога.
В этой модели наряду с множеством видов продукции /, / Е.1Д =
= jl, ..., п ] рассматривается также как множество отраслей и ведомств.
В дальнейшем математическом описании принимается, что каждой отра-
k соответствует одно ведомство (министерство и т.п.): k Е Q, Q =
ели К СООТВ(
= {1
' Модель натурально-стоимостного баланса включает три группы
условий.
Главную часть модели образует система уравнений производства и
распределения продукции в натуральном выражении:
х, = 2 auXj + 2 aik 4 анХ; + у{, i £ 3, (7.1)
/ € 9 k€Q
где xi, xj — объемы производства продукции видов i и j по полному на¬
роднохозяйственному ассортименту в натуральном выражении; хк —
объем валовой (или товарной) продукции отрасли к\ ау — коэффициент
прямых затрат /-й продукции на производство единицы /-й продукции
(как и в основной модели межотраслевого баланса в натуральном выра¬
жении) ; aik — коэффициент прямых затрат г-й продукции на производст¬
во единицы продукции отрасли к; — удельный вес прочего производс¬
твенного потребления /-й продукции в общем объеме производства этой
же продукции; у^ - объем конечного использования /-й продукции (как
и в основной модели).
В уравнениях (7.1) используются два типа коэффициентов затрат:
’’продукт на продукт” (ау) и ’’продукт на отрасль” (aik)- Необходи¬
мость использования двух типов коэффициентов определяется специ¬
фикой существующей нормативной информации. Коэффициенты ау
разрабатываются, как правило, для основных потребителей продукции;
коэффициенты aik представляют собой расход продукции, не расшифро¬
ванной по отдельным продуктам — потребителям, на 1 млн. руб. валовой
(товарной) продукции отрасли (соответствующего ведомства).
Вторая группа условий модели характеризует организационную
структуру производства продукции в натуральном выражении:
А = Р/Я/» / € У* k € Q» (7-2)
192
к к
где Xj — объем производства /-й продукции в к-й отрасли; /3• — удельный
вес отрасли (ведомства) к в общем объеме производства /-и продукции;
при этом ]3у> 0, 2 0^= 1.
1 kEQ I
Каждой отрасли (ведомству) к соответствует вектор коэффициен¬
тов / £X характеризующих ее специализацию, соотношение профиль¬
ных непрофильных видов продукции и т.п.
Третья группа условий — уравнения валовой (товарной) продукции
отраслей (ведомств):
у k к k
1 V,Pj X,
** = ' 1-Ук • (7.3)
где доля товарного выпуска /-й продукции (т.е. учитываемой и вало¬
вой L товарной продукции) от общего объема производства этой проду¬
кции в А:-й отрасли; р^— средняя оптовая цена единицы /-й продукции,
вырабатываемой на предприятиях к-й отрасли; у^ — удельный вес про¬
чей продукции отрасли, не выделенной в качестве самостоятельных
позиций натурально-стоимостного баланса, в общем объеме валовой
(товарной) продукции к-й отрасли.
Совокупность условий натурально-стоимостного баланса (7.1) —
(7.3) содержит п + ns + s уравнений и столько же переменных xj, Xj, х^
(при заданных у{). В результате расчетов по модели определяются
сбалансированные и увязанные с общеэкономическими показателями
объемы производства в натуральном выражении (по важнейшим видам
продукции) и в стоимостном выражении (по отраслями ведомствам),
потребности народного хозяйства в важнейших видах материальных
ресурсов по направлениям их использования.
В дополнение к (7.1) — (7.3) модель может включать ограничения
по внешним ресурсам (трудовым ресурсам, основным производствен¬
ным фондам, производственным мощностям), а также дополняться
уравнениями элементов условно-чистой продукции.
Число уравнений и переменных в модели можно сократить путем подстановок.
Подставив (7.2) в (7.3), получаем:
д W$xi
1—V* /«7
где = — — общий коэффициент, характеризующий выход валовой (то-
/ 1 ~ 7к
варной) продукции к-й отрасли с единицы /-й прздукции.
’’Сжатая” модель включает условия (7.1), (7.4), а расчеты по формуле (7.2)
проводятся после определения значений дсу.
Условия (7.4) можно также исключить из основной системы уравнений, подста¬
вив их в (7.1) и сделав соответствующие преобразования:
2 aikxk= 2 aik 2 = 2 <7,7х/,
ksQ keQ /6J 1 /«7
7 Зак. 2414 ^93
где 0^ — Е ajfcwkозначает косвенные затраты /-й продукции на производство еди-
к £ О
ницы /-й продукции, обусловленные производством ’’нерасшифрованной” продук¬
ции.
Вместо (7.1) получаем
Х{ = 2 {d[j + о[/) Xj-^cci iXi -{- yi, (7.5)
/eJ
или
2 (б/у—а,-,•—a,-j — а//)*/ = <//, i£9 , (7.6)
/€?
а в векторно-матричной форме
ЛГ=ЛЛГ+К. (7-7)
Г=(£— А)Х. (7.8)
где Л = (% + дгу + of/) - квадратная матрица «-го порядка.
В результате всех преобразований приходим к системе уравнений межотрасле¬
вого баланса производства в натуральном выражении. Однако это
не возврат к исходной модели межотраслевого баланса (6.11) - (6.14). Сущест¬
венное преимущество полученной системы уравнений (в любой форме из (7.4) —
(7.7) заключается в том, что она сопровождается информацией об организацион¬
но-хозяйственной структуре производства (коэффициенты аац, fyj; vj; pj, %
и полученные на их основе qjy). Это позволяет после определения объемов про¬
изводства в натуральном выражении рассчитывать по формулам (7.2) — (7.4)
объемы производства в разрезе хозяйственных отраслей и балансировать объемы
производства в натуральном и стоимостном выражении.
Модель натурально-стоимостного межотраслевого баланса непосред¬
ственно применяется при разработке годовых и пятилетних народнохо¬
зяйственных планов начиная с девятой пятилетки. В 80-х годах плановые
натурально-стоимостные балансы охватывали 30 отраслей народного
хозяйства и промышленности, 27 промышленных министерств, около
200 продуктов в натуральном выражении.
На начальных этапах плановой работы результаты расче¬
тов по натурально-стоимостному балансу используются в качестве исход¬
ных данных для формирования показателей отраслевых и функциональ¬
ных разделов плана и составления материальных балансов. На зак¬
лючительном этапе разработки плана натурально-стоимостный
баланс используется для проверки взаимной сбалансированности основ¬
ных показателей развития народного хозяйства. В условиях происходя¬
щей перестройки народнохозяйственного планирования натурально-сто-
имостному балансу отводится важная роль в обосновании системы госу¬
дарственных заказов и их увязке с общеэкономическими пропорциями.
7.2. Моделирование материально-финансовых связей.
Межотраслевой баланс денежного оборота
Процесс общественного воспроизводства сопровождается движением
денежных средств (в наличной и безналичной форме) между его участ¬
никами. Многочисленные экономические субъекты выступают платель¬
щиками и получателями денег, кредиторами и заемщиками и т.д. Важ¬
194
нейшие данные для совместного анализа народнохозяйственного оборота
в его материальной и денежной формах содержатся в межотраслевом
балансе общественного продукта с развернутыми квадрантами И, III,
IV (см. 6.1). Для более глубокого и подробного изучения движения
денежных средств во взаимосвязи с материальными потоками разра¬
батывается сводный материальн о-ф инансовый ба¬
ланс (СМФБ).
В своей развитой форме СМФБ представляет собой систему таб¬
лиц, ориентированных на исследование различных аспектов материаль¬
но-финансовых отношений в народном хозяйстве (см. [8. Раздел III.
Гл. З])1. СМФБ является одной из форм интегрированной системы
национальных счетов, получившей распространение во многих
странах. В частности, упрощенная стандартная система национальных
счетов, разработанная ООН, применяется более чем в 100 странах. Опре¬
деленной модификацией СМФБ является система моделей ’’доход —
товары”, разработанная под руководством В.Д.Белкина [в].
Рассмотрим одну из моделей материально-финансовых взаимосвя¬
зей в народном хозяйстве — межотраслевой баланс денеж¬
ного оборота (МБ ДО). Методика построения и анализа такого
баланса разработана Ш.Б. Свердликом [7].
По принципам и методике построения, а также информационному
обеспечению МБ ДО тесно связан с межотраслевым балансом общест¬
венного продукта. Система показателей МБДО образует шахматную
таблицу, в которой по подлежащему (получатели денег) и сказуемому
(плательщики) показываются одни и те же экономические субъекты:
отрасли, население, финансов о-кредитные органы. Таблица МБДО имеет
ту же структуру, что и табл. 6.1, т.е. ортогонально совмещает показатели
четырех квадрантов (см. табл. 7.1).
В квадранте I отражаются денежные потоки между хозрасчетными
субъектами, квадранты II и III содержат денежные потоки (доходы и ра¬
сходы) между финансово-кредитной системой и хозрасчетными субъе¬
ктами. В квадранте IV отражаются потоки между отдельными звеньями
финансово-кредитной системы.
Для описания соотношений между показателями МБДО будем ис¬
пользовать те же символы, что ив 6.1. Однако их экономическое содер¬
жание иное.
Величина — общий доход /-го субъекта; хц — доход /-го субъекта,
получаемый от /-го субъекта; у\ — доход /-го субъекта, получаемый от
финансово-кредитной системы; zj — доход/-го субъекта, передаваемый в
финансово-кредитную систему.
Каждая строка квадрантов I — II — это уравнение получаемых дохо¬
дов: х( = 2 хц + yt\ каждый столбец квадрантов I - III — это уравнение
/
1 Большой вклад в разработку СМФБ народного хозяйства СССР и союзных
республик внес Б.Л.Исаев (1921 - 1982).
7* 195
Таблица 7.1
Укрупненная схема межотраслевого баланса денежного оборота
Плательщики
Получатели денег^^^^^^
1
2
3
Итого
Финансово¬
кредитная
система
Всего
1. Отрасли материального
производства
*11
*1 2
*13
2*i /
/
У1
*1
2. Хозрасчетные отрасли
непроизводственной
сферы
*21
Квадрант I
*22 * 23 2x2/
/
Квадрант II
У 2 *2
3. Население
*31
*32
*33
2*3/
Уз
*3
Итого расходов
2*ii
i
2*/2
i
2*13 Ъщ
i i i
ЛУ1
i
Еде/
7
финансово-кредитная
система
Квадрант III
Zi z2 z3
Xzj
Всего
*1
*2
*3
bxj
]
Квадрант IV
расходов: xj = 2 ху + zj. Каждая пара одноименных строк и столбцов ха¬
рактеризует баланс доходов и расходов соответствующего экономичес¬
кого субъекта. Итоги одноименных строк и столбцов совпадают: х^ =
= лу, / —j • 2л = 'Ezj. Денежные расходы финансово-кредитной системы
(величины^) — это расходы ’’бюджетных” отраслей, платежи за продук¬
цию, направленную на централизованные государственные нужды, выпла¬
ты населению, не связанные с оплатой труда, и т.д. Денежные доходы фи¬
нансово-кредитной системы (величины zj) — это взносы в бюджет, пла¬
тежи за продукцию, поступившую по импорту, и т.д.
По данным МБ ДО СССР за 1972 г. совокупный денежный оборот равнялся
1184 млрд. руб., что в 1,65 раза превышало объем валового общественного про¬
дукта. Из этого объема 546,7 млрд. руб. составили доходы промышленности,
77,4 млрд. руб. - доходы строительства, 117,7 млрд. руб. - доходы сельского
хозяйства, 231,8 млрд. руб. - доходы населения, 123,1 млрд. руб. - оборот финан-
сово-кредитной системы. Убыточными (т.е. требовавшими чистых дотаций от фи¬
нансов о-к ре дитной системы) были сельское хозяйство и хозрасчетные отрасли
услуг [7. С. 104 - 105].
При построении математической модели МБДО принимается допу¬
щение о пропорциональности денежных потоков общим доходам пла¬
тельщиков: x.j = a-jx.9 где а- - доход /-го субъекта, получаемый от
/-го субъекта в расчете на общий доход /-го субъекта (или доля общего
дохода /-го субъекта, выплачиваемого /-му субъекту). По аналогии с
основной моделью межотраслевого баланса будем называть параметры
ау коэффициентами прямых денежных затрат.
196
При указанном допущении модель МБДО имеет тот же вид, что и
основная модель межотраслевого баланса:
X/ = 2 аих, + у(, i£l (7.9)
/е/
ИЛИ
X = AX+Yf (7.10)
где А = (я#), X = (х/), Y = (у/), /, / Е /; / — множество получателей доходов
и плательщиков.
Каждый поток х^ по строкам отраслей производственной и непроиз-,-
водственной сфер является денежным выражением расхода продукции
или услуг на возмещение материальных затрат, капитальных вложений, из¬
менение материальных запасов. За редчайшим исключением потоки
ху неотрицательны1, поэтому можно исходить из того, что все коэффи¬
циенты aij неотрицательны, А > 0. Вследствие этого условия существо¬
вания и полуположительности (положительности) решения систем
(7.9) или (7.10) аналогичны условиям для основной модели межотра¬
слевого баланса.
Однако анализируемая система межотраслевых связей более замкну¬
та по сравнению с системой материально-вещественных связей, так как
охватывает не только текущие материальные затраты, но и часть капи¬
тальных затрат, а также связи, обусловленные доходами и расходами
населения. Поэтому достаточные условия продуктивности (2 ay < 1,
i Е/
/ Е Г) выполняются далеко не всегда (см. табл. 7.2). В рассматриваемом
примере общие расходы превышают доходы в сельском хозяйстве и
хозрасчетных отраслях услуг (вместе с ’’наукой”).
Вместо (7.10) можем записать
Х=(Е—А)-1 У, (7.11)
где элементы матрицы В = (Е- А) ~1 характеризуют отношения между
доходами экономических субъектов и расходами финансово-кредитной
системы. Элемент bij матрицы (Е — А) 4 показывает, насколько увели¬
чивается общий доход /-го субъекта при увеличении на единицу выплат
/-му субъекту из финансово-кредитной системы. Для краткости коэф¬
фициенты bij будем называть коэффициентами полных де¬
нежных затрат.
Они могут быть отрицательными в тех случаях, когда сокращение материаль¬
ных запасов превышает сумму всех других затрат отрасли i на производство в отра¬
сли /.
197
Таблица 7.2
Коэффициенты прямых и полных денежных затрат за 1972 г.
(первое число в клетке - прямые затраты, второе число - полные затраты)
-^^Плательщики
Получатели денег'
1
2
3 ,
4
5
6
1. Промышленность
0,445
4,562
0,527
3,988
0,231
4,474
0,311
3,824
0,487
7,062
0,687
4,179
2. Строительство
0,043
0,464
0,032
1,475
0,101
0,657
0,112
0,572
0,711
1,523
0,014
0,512
3. Сельское хозяйство
0,113
0,874
0,827
0,223
2,263
0,017
0,840
1,486
0,123
0,983
4. Остальные отрасли матери¬
ального производства
0,091
0,489
0,004
0,441
0,052
0,566
0,022
1,446
0,779
0,013
0,474
5. Хозрасчетные отрасли услуг
и наука
0,009
0,130
0,007
0,144
0,002
0,174
0,028
0,169
0,004
1,258
0,055
0,184
6. Население
0,106
1,266
0,333
1,510
0,433
1,972
0,383
1,593
0,473
2,793
2,308
Итого расходов
0,808
7,786
0,903
8,387
1,043
10,110
0,872
8,445
1,674
14,901
0,891
8,640
Как видно из табл. 7.2, коэффициенты полных затрат, как правило,
во много раз превышают соответствующие коэффициенты прямых за¬
трат. С помощью модели МБДО и коэффициентов полных денежных
затрат можно анализировать и прогнозировать (по аналогии с методами,
рассмотренными в 6.4 — 6.6) разнообразные зависимости между расхо¬
дами (доходами) финансово-кредитной системы и доходами (расхода¬
ми) экономических субъектов и общим объемом денежного оборота.
7.3. Моделирование межотраслевых взаимосвязей
производства, личного потребления и доходов населения
В основной модели межотраслевого баланса связи производства, потреб¬
ления и доходов населения отражаются односторонне. Модель позволяет
анализировать, как потребление населения воздействует на производство
(Yn -> X), а объемы производства влияют на формирование доходов
населения (X Z), но при этом допускается возможность независимых
изменений объемов и структуры потребления и условий оплаты труда.
Естественно стремление замкнуть контур связей производства, потребле¬
ния и доходов, построить более общую модель для комплексного иссле¬
дования межотраслевых зависимостей.
Рассматриваемая расширенная модель межотраслевого баланса имеет
следующие особенности:
198
в составе продукции, направляемой для конечного использованияу(,
выделяется часть, реализуемая за счет доходов населения yi (z)f и ’’про¬
чая” конечная продукция j)/:
у,- = У г (2) + t/i, (7.12)
где z равен той части совокупного дохода населения, которая расходует¬
ся на приобретение товаров и услуг;
в модель включается баланс доходов населения, в котором выделя¬
ются доходы, получаемые в сфере производства zj, и ’’прочие” доходы z:
%*A*i)+ (713>
где 7 — доля потребительских расходов в совокупном доходе населения;
вводится условие баланса расходов населения:
2 Р1У((г) = г (7.14)
iei
Отметим, что соотношения (7.12), (7.13) по своему экономическо¬
му содержанию соответствуют строке и столбцу ’’население” межотрас¬
левого баланса денежного оборота.
Общая модель включает условия (7.12), (7.13) и систему уравнений
производства и использования продукции:
xi = ^ xij + Hi (z) + Уй t I € I (715)
/ ei
Основная задача плановых расчетов по модели (7.12) — (7.14) — оп¬
ределение объемов производства xf и доходов населения z при заданных
объемах ’’прочей” конечной продукции и ’’прочих” доходов населения.
Типовые функции покупательского спроса y/z) рассматривались в
5.3. Некоторые из них носят ярко выраженный нелинейный характер.
Однако кусочно-линейная аппроксимация функций потребления позво¬
ляет сохранить линейность общей модели межотраслевых связей и прие¬
мы ее структурного анализа. Линейная аппроксимация функций потреб¬
ления дает тем лучшие результаты, чем в меньших интервалах изменяет¬
ся доход. Именно такая ситуация имеет место при использовании расши¬
ренной модели в краткосрочном прогнозировании и планировании.
Это дает возможность с успехом применять линейные функции у\ (z) =
= aizz + bi при ожидаемых интервалах изменения дохода z < р.
Линейные функции потребления обладают еще тем преимуществом,
что избавляют от необходимости включать в общую межотраслевую
модель условие (7.13). Если все показатели межотраслевого баланса
даются в ценностном выражении, то равенство Б ajzz + bf = z выполня-
/е/
199
ется автоматически при построении линейных уравнений регрессии спо¬
собом наименьших квадратов (в этом случае tS afz = 1; 2 Ъ\ = 0).
i £ / / Е /
В условиях действующей системы оплаты труда величина дохода,
получаемого в каждой отрасли производства, также может быть пред¬
ставлена в виде линейной функции zj = azjxj + zj, где azj - коэффициент
пропорциональности оплаты труда и объема производства, zj — величина
дохода, не зависящая от объема производства.
Введем векторно-матричные обозначения в расширенной модели:
^ ^ ~ (Ifi “t- Z = 2 2 Zj.
/€/
Получаем следующую систему уравнений межотраслевых зависимостей
производства, потребления и доходов:
X = AX + a,z f К,
— z=azX -+ z.
(7.16)
Система (7.15) обладает свойствами, во многом аналогичными
свойствам основной модели межотраслевого баланса. Матрицу этой си¬
стемы
“Л
1
можно называть п родуктивной, если существует такой неотрица¬
тельный вектор [ X Z]' > 0, что
ге-А -а/]
тХ‘
-а; 1
L V J
Z
>0
Будем исходить из того, что в системе (7.16) продукция измерена в
ценах и матрица А удовлетворяет достаточным условиям продуктивно¬
сти неразложимых матриц модели межотраслевого баланса (т.е. 2 ау <
< 1 для всех/*Е/ и 2 ay < 1 хотя бы для одного /). 1
i GUI л
Для того чтобы матрица А была продуктивна, должны выполняться
условия, более жесткие по сравнению с условиями продуктивности
матрицы А, так как система межотраслевых связей получает дополни¬
тельную нагрузку в виде затрат на личное потребление и ’’затрат” до¬
хода1 .
*В соответствии с правилами построения линеаризованных функций потребле¬
ния 2 = 1. Для продуктивности матрицы Л достаточно, чтобы 2<7я +
+ yazj < 1,/ €=/.
200
'Е—А
— аг]
1 ,
ГРп
V -
=
~аг
1 1
Lp«
pj
Необходимым и достаточным условием продуктивности является
полуположительность матрицы
Основное свойство анализируемой расширенной модели межотрасле¬
вого баланса состоит в том,дчто при продуктивности матрицы А любому
положительному вектору [Yz]' соответствует единственный полуполо-
жительный вектор [X z]
Рассмотрим особенности элементов матрицы В, являющихся коэф¬
фициентами полных затрат в межотраслевой системе, охватывающей
взаимосвязи производственного потребления, оплаты труда, структуры
личного потребления. В соответствии с формулами обращения блочных
матриц имеем:
Рп = (Е—A)~l + (Е—A)~lazc£ (Е—Л)"1 R,
$и = (Е—Л)-1а2#,
Р21 = Яа;(£-Л)-‘,
Р22 '
1 -(ь(Е-А)-*аяу
R.
В образовании всех коэффициентов полных затрат принимает участие
множитель
R
1 —a2(E—A)-1azy
Он определяет знаки всех элементов обратной матрицы и их порядковые
соотношения с коэффициентами полных затрат основной модели межот¬
раслевого баланса.
Коэффициент /З22 характеризует прирост расходной части доходов
0Z
населения на единицу прироста фиксированного дохода R = —;— . Оче-
OZ л
видно, что для полуиоложительности всех элементов матрицы В необ¬
ходимо и достаточно, чтобы R > 0. Если же R > 1, то все ненулевые
коэффициенты матрицы ^ превышают соответствующие коэффициенты
полных затрат основной модели межотраслевого баланса,
201
Величина R зависит от двух коэффициентов: a z (Е - A) mlaz и у.
Покажем, что в нормальных экономических условиях a z (Е - А) ~х az ^
<1.
Исходим из того, что
X ajj+ azj < 1, /е/,
/е/
т.е. сумма материальных затрат и оплаты труда не выше цены в каждой отрасли.
В векторно-матричной форме это выражается как е (Е - А) > aZi где е = (1, 1,...,
1). Умножим обе части неравенства на (Е - A)~laz. Получим е (Е - А) • (Е —
- A)'1 az > a'z (Е - A)~laz, откуда eaz > az (Е - A)~l • az. Но так как eaz = 1,
то az (Е - Aj'1 az < 1, что и требовалось доказать.
Обозначим
а’г(Е—А)"1аг — с.
Тогда
\—су
По данным усредненного межотраслевого баланса СССР за первую по¬
ловину 80-х гг., с = 0,465. Значения у в экономике с относительно сбала¬
нсированным спросом и предложением колеблются вокруг единицы.
Поскольку же с существенно меньше единицы, то R > 1. Действительно,
при указанном с условие R > 1 выполняется при у > 0,683, т.е. при рас¬
ходовании населением ежегодно более 68,3 % получаемых доходов. В
частности, при 7=1 получаем R = 1,869, при у = 0,8 имеем R = 1,274.
Перейдем к анализу других блоков матрицы В.
Коэффициенты блока рп характеризуют полные потребности в про¬
дукции отраслей для получения ’’прочей” конечной продукции. Эти
коэффициенты в дополнение к коэффициентам матрицы (Е - А)~1
включают затраты, возникающие вследствие взаимодействия производ¬
ства, потребления., доходов. Сопоставления элементов матриц А, В,
Рп показывают, что многие коэффициенты затрат расширенной модели
превышают в десятки раз соответствующие коэффициенты полных и
прямых затрат основной модели межотраслевого баланса. При этом в
наибольшей степени возрастают затраты отраслей, формирующих основ¬
ную часть фонда личного потребления.
Коэффициенты блока @12 показывают полные затраты отраслей на
прирост доходов, не зависящих от объемов производства. Вектор 012
может быть представлен в виде трех векторов: прямых затрат продук¬
ции на единицу дохода az\ затрат, обусловленных взаимосвязями по
производственному потреблению [(Е — А)~1 - Е] az, и затрат, обуслов¬
ленных взаимосвязями с доходами населения [ (Е - A) ~1az (R — 1)].
202
Коэффициенты вектора @12 обычно в несколько раз превышают соответ¬
ствующие коэффициенты вектора az.
Коэффициенты блока @21 показывают полные затраты дохода на
’’прочую” конечную продукцию. Они включают: прямые доходы az,
доходы, обусловленные производственными связями аz [(# - Л)~1 -
- Е] (т.е. косвенные затраты оплаты труда основной модели межотрас¬
левого баланса), и ’’вторичный эффект дохода” (R — 1 )а z (Е - А)~1.
Коэффициенты полных затрат дохода (оплаты труда) расширенной
модели больше соответствующих коэффициентов полных затрат основ¬
ной модели в R раз. Эти коэффициенты позволяют проследить влияние
изменения объемов и структуры ’’прочей” конечной продукциина изме¬
нение доходов населения (примеры коэффициентов матрицы В в сопо¬
ставлении с коэффициентами основной модели межотраслевого баланса
приводятся в ММСЭ. С. 304 - 306).
Таким образом, включение в общую модель функций потребления и
доходов населения значительно усиливает возможности анализа и плани¬
рования межотраслевых связей. Дальнейшим шагом в развитии модели
межотраслевого баланса может стать введение функций потребления
и доходов по группам населения, дифференцированных по уровню до¬
хода и структуре потребительских расходов.
Ж 7.4. Межотраслевая модель
^ взаимодействия экономики
и окружающей среды
На современном этапе развития общества огромное значение имеет
охрана окружающей среды (воздушного и водного бассейнов, почвен¬
ного покрова, животного мира и т.д.) от отрицательных антропогенных
воздействий. Борьба с загрязнением среды требует все возрастающих
затрат, приводит к созданию новых производств по переработке и уни¬
чтожению вредных отходов. В результате расширяется сама сфера обще¬
ственного производства: она включает не только создание материальных
благ, но и разнообразные виды деятельности по уменьшению загрязнения
окружающей среды, восстановлению природных ресурсов.
О масштабах этой деятельности в СССР говорят следующие данные. В 1986 г.
объем нормативно-очищенных вод достиг 23 куб. км; количество вредных ве¬
ществ, уловленных (обезвреженных) газопылеулавливающими установками и
сооружениями, составило почти 208 млн. т; общая сумма затрат на охрану приро¬
ды и рациональное использование природных ресурсов равнялась около 10 млрд.
руб.
^ Первая межотраслевая модель, охватывающая взаимосвязи эконо-
мики и окружающей среды, была предложена В.Леонтьевым и Д.Фор-
дом. Она включает две группы отраслей (производств) : отрасли матери¬
ального производства и отрасли, уничтожающие вредные отходы. Основ¬
ные условия модели выражаются системой уравнений:
203
Г*,'
Ап
АгЛ
||
г ул
х,\
_ А н
II
kJ
г!
[~у.\
(7.17)
В системе (7.16) векторы Хх, Yx и матрицами соответствуют вели¬
чинам основной модели межотраслевого баланса, Х2 — вектор объемов
уничтоженных загрязнителей, Y2 — вектор объемов неуничтоженных за¬
грязнителей, А12 — матрица затрат продукции на единицу уничтожае¬
мых загрязнителей, А21 — матрица выпуска загрязнителей на единицу
производимой продукции, А22 — матрица выпуска загрязнителей на еди¬
ницу уничтожения загрязнителей.
* Если на все виды деятельности по уничтожению загрязнителей среды
распространить предположения основной модели межотраслевого балан¬
са (число способов равно числу видов продукции и в каждом способе
производится только один вид продукции), то матрицы А12 иА22 будут
содержать только неотрицательные элементы, причем А 22 будет квадрат¬
ной матрицей. Очевидно также, что А21 > 0.
В прикладных моделях перечень уничтожаемых загрязнителей мень¬
ше перечня существующих загрязнителей. Расширение первого перечня
происходит по мере того, как концентрация определенных загрязнителей
становится существенной с точки зрения условий жизнедеятельнсти или
производства и по мере создания технических и экономических возмож¬
ностей для борьбы с загрязнителями среды.
Рассмотрим второе матричное уравнение из (7.17) Х2 — А2\Х\ +
+ А22Х2 — Y2. Сумма А2\Х\ + А22Х2 показывает объемы загрязнения от
всех видов производственной деятельности. Вектор Х2 зависит не только
от этой суммы, но и от допускаемых размеров неуничтожаемых загряз¬
нителей Y2. В принципе максимально допустимые значения компонент
вектора Y2 определяются условиями экологического равновесия или
принятыми стандартами качества окружающей среды, однако они могут
устанавливаться также и исходя из реальных технико-экономических
возможностей. Деятельность по уничтожению загрязнителей имеет
смысл (т.е. соответствующие xj > 0), если Y2 <А21Хх + А22Х2. Поэто¬
му для общности вместо матричного равенства можно записать Х2 >
>a21x1+a22x2-y2.
Матрица
В=-
Е1 А п А12
/4 21 Е А 22
'■ -1
вп
В»\
J
вп
^22 J
является обобщением матрицы коэффициентов полных затрат продук¬
ции. Элементы, входящие в_блоки этой матрицы, имеют следующее
экономическое содержание: Вп — коэффициенты полных затрат произ¬
водимой продукции на единицу конечной продукции, В12 - коэффициен¬
ты полных затрат продукции на единицу уменьшения неуничтоженных
204
^згрязнителей, B2l — коэффициенты необходимого уничтожения загряз¬
нителей на единицу конечной продукции; В22 — коэффициенты необхо¬
димого уничтожения загрязнителей на единицу уменьшения неуничто-
жеиных загрязнителей.
Соотношение £ > О является необходимым условием функциони¬
рования расширенной системы межотраслевых связей. Его выполни¬
мость во многом зависит от эффективности (технологичности) вклю¬
чаемых в систему видов деятельности по уничтожению загрязнителей.
Имеющиеся способы уничтожения некоторых загрязнителей требуют
столь высоких материальных затрат, что добавление к матрице А со¬
ответствующих строк и столбцов может приводить к тому, что в матри¬
це В будут появляться отрицательные коэффициенты.
Пусть условие В > 0 выполняется, вектор Yx фиксирован, а вектор
Y2 показщвает допустимые размеры неуничтожаемых загрязнителей
(например, на уровне прошлого года). Тогда
X? - XI = B^Y.-B^Yl
Повышение требований к качеству окружающей среды выражается в
том, что новый вектор Y2 будет иметь меньшие значения компонент,
чем вектор Y2, т.е. Y2 = Y2 — AY2, ДУ2 > 0. При ДУ = Y2 достигается
полная очистка.
Более строгие требования к очистке ведут к увеличению объемов
производства (по сравнению с Х°х и Х%): АХг = B\2AY2 > 0, ДХ2 =
= B22AY2 > 0. Максимальные приросты производства АХ% и ДА"* полу¬
чаются при полной очистке: ДЯ? = В\2 Y$, АХ* = В22 Y2•
Система (7.16) может быть использована также для решения задачи
со смешанным составом неизвестных. Например, надо найти Хг и Y2
при заданных Yx и Х2. Для этого вначале решается система Хх = (Е\ -
- Ац) 1 (А 12Х2 + Yi), а затем находится вектор неуничтоженных
загрязнителей: Y2 =A2iXi - (Е2 - А22 )Х2.
Главные трудности в использовании рассматриваемой модели состо¬
ят в подготовке надежной информации для блоков Ап, А21у А22. В по¬
следние годы здесь наметились позитивные изменения, связанные с об¬
щим расширением информационного обеспечения эколого-экономичес-
ких исследований и практической деятельности по охране окружающей
среды. Относительно проще определить коэффициенты блока А 21. Это
позволяет использовать исходную модель в следующем сокращенном
варианте:
I х,-л
\ <7Л8>
В этой системе выпуск и уничтожение загрязнителей не оказывают
205
влияния на производство традиционных видов продукции и их конечное
использование. В то же время система (7.17) позволяет учитывать влия¬
ние материального производства и конечного использования продукции
на уровни загрязнения. Увеличение загрязнения вследствие роста конеч¬
ной продукции характеризуется матрицей А21 (Е\ - А ц)~1.
На основе модели (7.16) могут быть построены более общие модели
взаимодействия экономики и окружающей среды. В частности, можно
учитывать загрязнение среды в сфере потребления (загрязнение атмосфе¬
ры выхлопными газами автомобилей, водных бассейнов бытовыми
стоками и т.п.). В модели могут также найти отражение процессы утили¬
зации отходов производства и продуктов очистной деятельности. Для
этого в матрицы А12 и А22 наряду с коэффициентами затрат продукции
на уничтожение загрязнителей включаются коэффициенты выхода по¬
бочной продукции (например, утилизация сернистого ангидрида, лету¬
чих углеводородов и угольной пыли, отходов атомных электростанций
и т.д.) на основе метода ’’отрицательных коэффициентов”, рассматрива¬
емого в 7.7.
Дополнением модели (7.16) служат ограничения по ресурсам/^! +
+ f2X2 < R. Эти же ограничения выражаются через коэффициенты пол¬
ных затрат ресурсов как
FiYi—F,Y,<R, (719)
где Fx = f\Bn +/2^21 — матрица коэффициентов полных затрат ресур¬
сов на единицу конечной продукции, F2 = fiBn +/2^22 — матрица коэф¬
фициентов полных затрат ресурсов на единицу уменьшения неуничтожен¬
ных загрязнителей. Всякое уменьшение компонент вектора Y2 увеличи¬
вает потребности народного хозяйства в ресурсах (которые направляют¬
ся на борьбу с загрязнением среды). Поэтому анализ условий (7.18) поз¬
воляет определить варианты максимально возможного (с точки зрения
народнохозяйственных ресурсов) улучшения состояния окружающей
среды.
7.5. Межотраслевые модели с внешними связями
В основной модели межотраслевого баланса общественного продукта
страны внешнеэкономические связи непосредственно не рассматрива¬
ются, а учитываются в векторе конечной продукции: экспорт — со зна¬
ком плюс, импорт — со знаком минус. Для того чтобы исследовать воз¬
можности и эффективность развития внешнеэкономических связей и их
влияние на систему народнохозяйственных пропорций, необходимо
экспорт (вектор V) и импорт (вектор W) отделить от конечного исполь¬
зования продукции на потребление, накопление и прочие внутренние
нужды (вектор Y):
Y=Y+V-W. С7-20)
206
Аналогичное уточнение необходимо сделать и для модели межот¬
раслевого баланса отдельного региона. В этом случае V и
W будут обозначать соответственно векторы вывоза продукции за преде¬
лы региона (включая экспорт) и ввоза продукции из всех других реги¬
онов (включая импорт).
Межотраслевые связи по производству и распределению продукции
как для страны в целом, так и для отдельных регионов формально опи¬
сываются одной моделью
Х = АХ+?4 V—W. (7.21)
Однако экономические роли внешних связей страны и региона
существенно различны. Во-первых, экономика страны гораздо более зам¬
кнута, чем экономика регионов. Так, доля внешнеторгового оборота
СССР в валовом общественном продукте составляет примерно 9 %;
доля же суммарных объемов вывоза и ввоза в валовом продукте союз¬
ных республик и экономических районов существенно превышает 50 %
(за исключением только крупнейших республик — РСФСР, Украины,
Казахстана). Во-вторых, международные и межрегиональные (внутри
страны) экономические связи имеют принципиально иные финансовые
условия и последствия (требования к сбалансированности торговых и
платежных балансов, денежные операции, кредитные отношения и т.п.).
В-третьих, имеются серьезные различия в методике учета и оценки
связей между странами и регионами (в пределах одной страны) . Напри¬
мер, специфическими методическими вопросами являются перевод
экспортируемой продукции во внешнеторговые цены и, наоборот, им¬
портируемой продукции — во внутренние цены, использование для учета
межрегиональных поставок статистики транспорта и материально-техни¬
ческого снабжения1.
Анализ влияния внешних связей на экономику страны и региона. Ме¬
тодические приемы экономического анализа и плановых расчетов на ос¬
нове модели (7.19) во многом схожи с теми, которые рассматривались в
6.4, 6.6. Важно отметить, что осуществляемая в СССР регулярная разра-
Межотраслевые балансы СССР строятся, как правило, в ценах конечного по¬
требления, т.е. с включением налога с оборота, торгово-транспортной накидки,
внешнеторговой наценки и т.п. Данные же о внешнеторговом обмене (в частности,
публикуемые в статистических справочниках ’’Народное хозяйство СССР”, ’’Вне¬
шняя торговля СССР”) даются в валютных рублях (с пересчетом иностранной ва¬
люты по курсу Госбанка СССР). По межотраслевым балансам импорт значитель¬
но превышает экспорт, а по указанным статистическим справочникам экспорт
превосходит имиорт (на несколько млрд. руб. в год).
Для сопоставимости величин экспорта и импорта с показателями производства
и использования продукции внутри страны применяются переводные коэффици¬
енты.
207
ботка межотраслевых балансов не только в целом по стране, но и по
всем союзным республикам и некоторым экономическим районам поз¬
воляет анализировать систему межотраслевых, внешнеторговых и
межрегиональных связей, включая сопоставления региональных и народ¬
нохозяйственных структур, изучение влияния внешней торговли и меж¬
регионального обмена на народнохозяйственные и региональные пропор¬
ции.
Данные об экспорте (вывозе) и импорте (ввозе) в сопоставлении с
объемами производства и потребления продукции по отраслям произ¬
водства характеризуют только непосредственное влияние внешних свя¬
зей на формирование и распределение ресурсов определенных видов
продукции и соответственно лишь прямое участие соответствующих от¬
раслей в международном и общесоюзном разделении труда. Ограничен¬
ность анализа только этих данных — в недоучете межотраслевых взаимо¬
связей, возникающих вследствие обмена продукцией различных от¬
раслей. Поэтому важное значение имеет анализ полных потреб¬
ностей (затрат), обусловленных экспортом и импортом продук¬
ции.
Полные потребности в продукции отраслей для обеспечения экспор¬
та определяются по формуле
Xv = (E—A)"1V. (7.22)
По каждому виду продукции ’’полный экспорт” учитывает
не только прямой экспорт этой продукции, но и объемы ее про¬
изводства, необходимые для экспорта (вывоза) всех других видов
продукции.
Полное уменьшение объемов производства различных видов продук¬
ции в результате импорта, или ’’полный и м п о р т”, определяется по
формуле
XW = (E—A)-*W. (7.23)
При этом учитывается не только прямой импорт соответствующей
продукции, но и все косвенные межотраслевые влияния импорта проду¬
кции всех отраслей на, объемы производства.
Показатели полного экспорта и полного импорта удобно использо¬
вать для регулирования структуры внешней торговли с целью достиже¬
ния лучшей сбалансированно ста и повышения эффективности народно¬
го хозяйства. Например, для уменьшения дефицита металла в стране
можно не только увеличивать импорт металла, но и сокращать экспорт
или увеличивать импорт металлоемкой продукции. Для более эффектив¬
ного использования отечественных ресурсов нефти и природного газа
может быть целесообразнее экспортировать не первичные ресурсы, а
продукты их глубокой переработки и т.п.
208
Расчеты, выполненные по данным региональных межотраслевых балансов, по¬
казывают, что, как правило, полный вывоз и полный ввоз продукции намного
превышают соответствующие величины прямого вывоза и ввоза. Например, пол¬
ный вывоз топлива из Латвии в 23 раза превышает прямой, лесопродукции из
Армении — в 25, продукции сельского хозяйства из Литвы - в 40 раз.
Результирующими показателями внешнеторгового и межрегиональ¬
ного обмена являются величины полного сальдо, определяе¬
мые как разности между полным экспортом и полным импортом. Они
характеризуют изменения объемов производства соответствующих от¬
раслей в результате обмена продукцией всех отраслей. При сопостав¬
лении прямого и полного сальдо обмена могут иметь место три случая:
1) полное сальдо по абсолютной величине больше прямого и имеет тот
же знак (это свидетельствует о том, что косвенные связи усиливают на¬
правленность непосредственного обмена); 2) полное сальдо по абсолют¬
ной величине меньше прямого, но сохраняет тот же знак (это показыва¬
ет, что влияние косвенных связей противоположно видимому направле¬
нию непосредственного обмена, но не ’’перевешивает” результат непо¬
средственного обмена); 3) полное и прямое сальдо имеют противопо¬
ложные знаки (это говорит о противоположных результатах прямых и
косвенных связей по обмену продукцией).
Проводившееся исследование по всей системе республиканских межотрасле¬
вых балансов СССР в укрупненной классификации дало следующее распределение
соотношений прямого и полного сальдо: первый тип - 77,5 % всех случаев, второй
тип - 14,5, третий тип - 8%. При этом соотношение третьего типа чаще всего наблю¬
дается при обмене электроэнергией и продукцией сельского хозяйства (см. [ 2.
С. 231 - 232]).
Величины экспорта и импорта в модели межотраслевого баланса
нельзя рассматривать как полностью свободные (экзогенные) пере¬
менные. Возможности варьирования этими величинами ограничиваются
условиями внешнеторгового баланса. Если А — минимально допустимое
сальдо внешнеторгового обмена в ценностном выражении (оно может
быть любого знака), Pv — вектор средних экспортных цен, Р^ — вектор
средних импортных цен, то должно выполняться условие
pvV—PwW^ Д. (7.24)
В региональных моделях условие (7.22) необязательно, поскольку
в современном экономическом механизме отношения между регионами
не являются хозрасчетными в полном смысле. Однако расчеты и сопоста¬
вления сальдо межрегионального обмена могут использоваться для ана¬
литических целей.
Внешнеторговый и межрегиональный обмен оказывают влияние не
только на структуру производства, но и на потребности во ’’внешних”
ресурсах. Полные потребности в ресурсах на экспорт и полная их эконо¬
мия от импорта рассчитываются по формулам
Rv = FV, Rw = FW. (7.25)
209
Путем изменения структуры обмена продукцией можно регулиро¬
вать потребности в ресурсах, учитывая их наличие и эффективность.
Например, если в определенном периоде дефицитность капиталовло¬
жений более существенна, чем потребность в дополнительных трудовых
ресурсах, то целесообразно стремиться к менее капиталоемкому экспор¬
ту и более капиталоемкому импорту, компенсируя эти изменения стру¬
ктуры внешней торговли увеличением экспорта более трудоемкой
продукции1.
Аналогичный анализ проводится и на основе региональных моделей.
В ^астности, установлено, что в результате межреспубликанского товаро¬
обмена из РСФСР ежегодно, с одной стороны, косвенно ’’вывозится”
на несколько миллиардов рублей основных фондов, а с другой сторо¬
ны — косвенно привлекается около миллиона годовых работников.
На этом примере видно, что структурная перестройка межрегионального
товарообмена может существенно сглаживать диспропорции в террито¬
риальном распределении трудовых ресурсов и производственного аппа¬
рата.
Модификации модели с внешними связями. Существует и использу¬
ется довольно значительное число модификаций народнохозяйственных
и региональных межотраслевых моделей, отличающихся способами отра¬
жения внешних связей и транспорта как отрасли, обеспечивающей внеш¬
ние связи.
Модель с выделением недополняющего импорта. В основном вариан¬
те модели межотраслевого баланса допускается возможность развития
в стране и каждом регионе любой отрасли производства. Такое допуще¬
ние реалистично только при очень значительном уровне агрегации отрас¬
лей. Невозможность организации некоторых производств объясняется
прежде всего природными факторами (запасы полезных ископаемых,
флора и фауна, почвенно-климатические условия). Ограниченный набор
производства может быть также следствием социально-исторических
условий, или низкой экономической эффективности, или отставания в
научно-техническом прогрессе.
Отмеченные обстоятельства позволяют разделить все множество
отраслей /, / Е / на подмножество отраслей производства, имеющихся в
стране (регионе): iltjx Е /х, и подмножество отраслей производства,
отсутствующих в стране (регионе): /2, /2 Е /2. Экспорт продукции
осуществляют только отрасли первой группы, а импортируемая продук¬
ция этих отраслей дополняет ресурсы собственного производства, т.е.
является ’’дополняющим” (’’конкурирующим”) импортом, или ввозом.
Расчеты такого рода, проведенные В.Леонтьевым, неожиданно обнаружили
(в противовес сложившемуся мнению), что в результате внешнеторгового обмена
США ’’экспортируют” труд и ’’импортируют” капитал. Этот факт вошел в мировую
литературу как парадокс Леонтьева.
210
Потребности в продукции отраслей второй группы полностью удовлет¬
воряются за счет импорта, который получил название ”недополняющего”
(’’неконкурирующего”).
С учетом указанных предположений модель межотраслевого баланса
производства и распределения продукции объединяет две подсистемы
уравнений:
21
Yt = Wt.
(7.26)
(7.27)
Для определения вектора Х± достаточно решить первую систему
уравнений (при заданном Yx = Yx + Vx - Wi)9 а затем, подставив Xx
во вторую систему, найти Г2 (при заданном W2) либо W2 (при задан¬
ном Y2 )•
Применительно к экономике СССР модели (7.24) , (7.25) актуальны
прежде всего для регионального звена. Поэтому в дальнейшем будем их
анализировать в терминах региональной экономики.
Разбиение отраслей на два подмножества и выделение затрат недо¬
полняющего ввоза существенно изменяют экономическое содержание и
численные значения региональных коэффициентов полных затрат. Из
(7.26), (7.27) следует
'Ег- -Аи 0
.WY.
— Ап Е„
Уг
У*
(7.28)
Матрица
В =
ГЕг—Аи 0 '
-1
В12
[~Аи
^21
^22.
— это матрица коэффициентов полных затрат, характеризующих потреб¬
ности в продукции, производимой в регионе (первая группа отраслей) и
ввозимой из других регионов (вторая группа отраслей) , для обеспечения
конечных потребностей данного региона. Эти коэффициенты имеют бо¬
лее ограниченную сферу применения по сравнению с коэффициентами
полных затрат основного варианта модели. Они правильно определяют
полные потребности в продукции собственного производства и внешних
ресурсах, но охватывают лишь часть всех затрат народного хозяйства.
Так же как и коэффициенты полных затрат основного варианта
модели, коэффициенты матрицы В могут использоваться для определе¬
ния полных потребностей в продукции для обеспечения различных фон¬
дов конечного продукта. Особый интерес представляют расчету необхо-
211
димых объемов л недополняющего ввоза для обеспечения вывоза про¬
дукции W[v> = В21 Vi и экономии недополняющего ввоза в результате
дополняющего ввоза продукции B2l .
По правилам обращения блочных матриц
Вц = (Е1 -АцТ1; ^i2=0;£2i =A2i (Е-АцГ1; 622 = Е2. (7-29)
Особенность коэффициентов'полных затрат рассматриваемой моди¬
фикации межотраслевой модели состоит в том, что они совершенно не
учитывают затраты на производство продукции второй группы отраслей
(в образовании коэффициентов полных материальных затрат не прини¬
мают участия блоки А12 и А22). Формулы для 312 и В22 говорят о том,
что изменение конечного потребления продукции второй группы отрас¬
лей не оказывает влияния на объемы производства продукции первой
группы, а только приводит к равному изменению ввоза и объемов про¬
дукции второй группы отраслей.
Модель с коэффициентами вывоза и ввоза. Определение значений
вывоза и ввоза для отдельного региона встречает значительные трудно¬
сти, поскольку требует межрегиональных согласований. Для облегчения
этой задачи используются гипотезы о пропорциональной зависимости
вывоза и ввоза от объемов производства и потребления продукции в ре¬
гионе:
V,. = #*,-. (7.30)
wi--yf>(xi + wi-vi}. (7.31)
Из (7.31) следует
w
' = -ТЗ^г = ( 7-vP = (7 32)
где oi = -у—1 ^ 0 (так как п0 смыслу 1, у^< 1).
Соответственно сальдо вывоза-ввоза определяется как
Vj—Wi = xt = 0^.. (7.33)
Очевидно, что эти функции имеют смысл только для продукции,
производимой в регионе (i Е3\), так как для i G72 вывоз отсутствует,
а ввоз определяется уравнениями (7.29).
С введением (7.33) в систему балансов продукции отраслей подмно¬
жества получаем
+ + (7.34)
212
или
*, = (£1-0,-^)-^. (7.35)
где 6г = 0,-j — диагональная матрица коэффициентов сальдо вывоза-
ввоза, а матрица (Ег - вг - Ап)~1 характеризует полные потребности
регионов в выпуске продукции для конечного использования с учетом
фиксированных соотношений между производством и межрегиональным
обменом.
Рассматриваемая модификация довольно распространена в исследо¬
ваниях по региональным межотраслевым балансам. Изложенный метод
коэффициентов применяется также при отражении экспорта и импорта в
народнохозяйственных балансах. Однако адекватность и возможности
данной модели не следует преувеличивать. Если гипотеза о прямой
пропорциональной зависимости между вывозом и производством одно¬
именной продукции (7.28) более или менее разумна, то гипотеза о том,
что с увеличением производства продукции в регионе должен пропорци¬
онально возрастать ввоз этой же продукции (7.31), является гораздо
менее убедительной. Недостаток изложенной модели состоит не только
в отмеченном парадоксе, но и в отсутствии достаточно конструктивных
подходов к прогнозированию коэффициентов вывоза-ввоза (подроб¬
нее о моделях с различными способами отражения вывоза и ввоза см.
[2. С. 29-42]).
Модификация уравнений по транспорту. В основной модели меж¬
отраслевого баланса транспорт рассматривается как обычная отрасль
производства, на которую распространяется допущение о пропорцио¬
нальности затрат ее продукции и объемов производства отраслей, исполь¬
зующих транспорт*
х = S Ох/Ху, (7.36)
Т /€/
где т — индекс транспортной отрасли1.
В действительности объем транспортной работы региона складыва¬
ется из четырех составляющих: а) перевозок, обеспечивающих внутри¬
региональное потребление; б) перевозок, обеспечивающих вывоз про¬
дукции, производимой в регионе; в) перевозок, обеспечивающих ввоз
продукции для внутрирегионального потребления; г) транзитных пе¬
ревозок.
Введем дополнительные обозначения:
В соответствии с действующей классификацией к отраслям материального
производства относится только грузовой транспорт, продукция которого полно¬
стью потребляется в сфере производства и не попадает в сферу конечного исполь¬
зования (ут = 0) • Отсутствие в балансах транспорта данных вывоза и ввоза (vT =
= 0, Wj = 0) вытекает из принятой методики построения таблицы межотраслевого
баланса и оценки продукции.
213
или
ajj — затраты транспорта на внутрирегиональные перевозки единицы
продукцииу-й отрасли;
aft затраты транспорта на вывоз единицы продукции /-й отрасли;
a'jjt— затраты транспорта на ввоз единицы продукции у-й отрасли;
qjj — затраты транспорта на транзитные перевозки продукции у-й от¬
расли.
Затраты транспорта по обслуживанию у-й отрасли составляют:
*т/ = a(x/—v/ + wj) + a^Vj + a£f'wf + qxj
XV = OjjXj + atyvj + a^wj + qTh (7.37)
где
=* Ат/}—«г/» ау'8=5—
Для / Ej2, естественно, aTjxj = 0.
Общий объем транспортной работы региона равен
хт= 2 ’axfxf + 2 2 <7^4-^. (7.38)
/ € J, / € У / € У
Объем транспортной работы во многом определяется географией
межрегиональных связей как данного региона, так и других регионов,
осуществляющих транзит через территорию данного региона (от этого за¬
висят коэффициенты и величины qT). Эта проблема со всей
остротой встает при объединении региональных моделей в межрегиона¬
льную систему (подробнее о построении уравнений по транспорту и их
информационном обеспечении см. [2. С. 42 - 47] ).
7.6. Межрегиональные межотраслевые балансы
Межрегиональные межотраслевые модели являются эффективным ин¬
струментом анализа и планирования территориальных пропорций народ¬
ного хозяйства. С одной стороны, они синтезируют региональные межот¬
раслевые модели, с другой — представляют собой пространственную
развертку сводных (’’точечных”) межотраслевых моделей народного
хозяйства. В дальнейшем будем исходить из того, что территория страны
разделена на т регионов и будем обозначать г — регион-производитель (по¬
ставщик), s - регион-потребитель (получатель) ; ry s Е R, R = |1,..., .
Схемы объединения региональных моделей. Возможны три основные
схемы объединения региональных межотраслевых моделей, допускаю¬
щие множество модификаций.
214
Первая схема сводит все региональные модели в ’’точечную” модель
народного хозяйства, совпадающую с основным вариантом модели меж¬
отраслевого баланса. При этом региональные величины производства,
конечного использования продукции и наличных ресурсов складывают¬
ся, а коэффициенты прямых затрат сводной модели рассчитываются как
средневзвешенные величины из региональных.
Вторая схема сохраняет часть элементов региональных моделей
(объем производства, коэффициенты затрат), другую часть суммирует
(внутрирегиональное конечное использование продукции, региональные
ресурсы), третью часть исключает из рассмотрения (межрегиональные
поставки продукции). Соотношения объединенного межотраслевого
баланса производства и распределения продукции принимают вид
2 Хг = 2 ArXr+Y + D, (7.39)
г€ R reR
где/) — вектор сальдо экспорта-импорта.
Необходимо пояснить, что условия (7.37) не являются законченной
моделью, а только характеризуют принцип объединения региональной
информации. При заданных векторах Y, D число переменных объемов
производства (пт) превышает число уравнений (п). Поэтому для нахо¬
ждения решений требуется вводить дополнительные условия.
Третья схема приводит к построению межрегиональных моде¬
лей. Она сохраняет все условия и информацию региональных моде¬
лей и, кроме того, включает условия согласования межрегиональных
связей:
Xr= ArXr+ Yr + Vr—W\ r£R,
2 Vr— 2 Wr = D. (7.40)
r*R r*R
При отражении географии межрегиональных связей в региональных
моделях система (7.38) модифицируется следующим образом:
ХГ=АГХГ+ 2 Xrs— 2 X9r+Yr, г€Я, (7.41)
SGR s£R
s Ф г s Ф г
где — вектор вывоза продукции из r-го региона в 5-й, XrSr — вектор
ввоза продукции из s-ro региона в г-й.
Очевидно, что в (7.39) автоматически выполняется условие
2 2 = 2 2 X”.
Г€Я S€R r$R s*R
Сальдо экспорта-импорта должно заранее распределяться между регио¬
нами и учитываться в векторах Yrm
215
Третья схема объединения региональных моделей также не дает за¬
конченной межрегиональной модели; получаемая система соотноше¬
ний сохраняет много степеней свободы, в частности по выбору межреги¬
ональных связей. Общее назначение второй и третьей схем заключается
в том, что они создают информационно-структурную основу для постро¬
ения различных типов многорегиональных и межрегиональных моделей.
Любая модель этого класса ’’собирается” по заданной схеме из региона¬
льных блоков (анализ модификаций схем объединения региональных
межотраслевых моделей см. в [2. С. 55 — 56] ).
Принцип построения межрегионального межотраслевого баланса.
Межрегиональный межотраслевой баланс как форма представления
экономической информации имеет вид шахматной таблицы. В подлежа¬
щем показываются регионы-производители, в сказуемом — регионы-по¬
требители. Каждый блок этой таблицы, или ’’большая шахматная клет¬
ка” (rs), содержит межотраслевые потоки текущего производственного
потребления и конечного использования продукции.
Соотношения показателей межрегионального межотраслевого ба¬
ланса производства и распределения продукции по горизонтали выража¬
ются следующей системой равенств:
х? = Б 2 хГЦ + 2 ~yY, i£l, r£R, (7.42)
s € R i € / a € R
где x[ — объем производства продукции z-й отрасли в регионе г;
хобъем продукции /-й отрасли, поставляемой из региона г в регион
s для производства продукции /-й отрасли; y\s— объем продукции /-й
отрасли, поставляемой из региона г в регион s для конечного исполь¬
зования.
Условия (7.42) можно также записать иначе:
*?= 2 х?\ i£l, геЯ, (7.43)
$ € R
где
2 (7.44)
/6/
Как уже указывалось, при объединении условий региональных
межотраслевых балансов по третьей схеме возникает избыточное число
переменных. Это же свойственно и системе соотношений (7.40). Модель
межрегионального межотраслевого баланса является результатом таких
преобразований схемы объединения региональных моделей, в результате
которых устраняется множественность выбора межотраслевых и меж¬
региональных связей. Математическая модель межрегионального балан¬
са — это система алгебраических уравнений, имеющая единственное ре¬
шение. Устранение всех степеней свободы достигается посредством вве¬
216
дения дополнительных параметров, фиксирующих структуру некоторых
территориальных пропорций1.
Ниже рассматривается модель межрегионального межотраслевого
баланса, предложенная американскими исследователями ЛМозесом ^
X Ченери в середине 50-х гг. (другие модификации модели межрегиона¬
льного межотраслевого баланса анализируются в [3. Гл. 1 — 3] ).
Модель межрегионального межотраслевого баланса с торговыми
коэффициентами. Главной спецификой рассматриваемой модели явля¬
ется гипотеза устойчивости структуры снабжения каждого региона
продукцией всех отраслей.
Обозначим через £f долю r-го региона в общем потреблении (про¬
изводственном и непроизводственном) продукции z-й отрасли в реги¬
оне 5. Коэффициенты#^ получили название ’’торговых*’:
^ SY — 1 > i € J
r€R
Тогда
+ (7.45)
Подставляя (7.45) в (7.43), получаем
4= 2 gW 2 OifX^yl) 2 2 f 2 i£l, r£R.
seR ч/б/ /sefl/б/ mR (7 46)
Два вида коэффициентов (g^ и c^) можно объединить в один:
ft = g'Mr (7.47)
Коэффициент q}y характеризует затраты продукции i-й отрасли в
регионе г, необходимые для выпуска единицы /-й продукции в регионе
5. При этом
2 (fij = asif.
reR
Подстановка (7.47) в (7.46) дает
^=2 2 cffiXj 4 2 grisys{, i£ly r£R. (7.48)
seR I € / s€ R
В векторно-матричной записи системы уравнений (7.46) и (7.48)
имеют вид
Х^ОАХ+ОУ, (7.49)
X=QX + GY, (7.50)
Иные принципы преобразования и дополнения схем объединения региональ¬
ных моделей приводят к построению оптимизационных межотраслевых моделей
(см. гл. 8) и моделей экономического взаимодействия регионов (см. гл. 16).
217
где G = (Grs), г, 5 ЕЛ, а каждый блок Grs — диагональная матрица из
коэффициентов gfs9 А — блочно-диагональная матрица из матриц Аг;
векторы Ху Y — композиции региональных векторов Xr, Ys.
Системы уравнений (7.49) и (7.50) можно выразить через обратные
матрицы:
X = (G~1—A)~1 У (7.51)
или
X = (E—Q)1OY (7.52)
По своему экономическому содержанию Г = (G~1 — А) ~1 = (Е —
— Q)~lG — это межрегиональная матрица коэффициентов полных затрат
продукции. Каждый элемент этой матрицы характеризует объем про¬
изводства продукции /-й отрасли в r-м регионе, необходимый для конеч¬
ного использования единицы продукции /-й отрасли в s-м регионе.
Уравнения межрегионального баланса производства и распределения
продукции дополняются региональными ограничениями по использо¬
ванию невоспроизводимых (и нетранспортабельных) ресурсов — такими
же, как в основной модели регионального межотраслевого баланса. Это
позволяет рассчитывать матрицу межрегиональных коэффициентов
полных затрат ресурсов.
С помощью модели межрегионального баланса осуществляются
разнообразные аналитические расчеты. Типовыми задачами являются:
1) определение объемов производства в разных регионах и региональ¬
ных потребностей в трудовых ресурсах, основных фондах и других ви¬
дах затрат в зависимости от территориальных пропорций конечного ис¬
пользования продукции; 2) определение конечной продукции и потреб¬
ностей в трудовых ресурсах, основных фондах и других видах затрат для
разных регионов в зависимости от территориальных пропорций произ¬
водства. Используются также аналитические приемы, рассматривавши¬
еся в разд. 6.4 — 6.6, 7.5. В рамках межрегиональных моделей реализу¬
ются также все изучавшиеся выше направления развития основной
модели народнохозяйственного межотраслевого баланса.
Принципиально важно, что с помощью этих расчетов комплексно
учитываются влияния изменений условий производства и потребления в
одних регионах на экономические показатели других регионов.
В СССР построено довольно значительное число межрегиональных межотрасле¬
вых балансов, в том числе в разрезе двух экономических зон страны (РСФСР и
остальной части СССР), по Средней Азии, Закавказью, восточным районам РСФСР
(см. [3. Гл. 4 - 6] ). Анализ этих балансов выявил ряд интересных результатов.
Например, расчеты по двухзональному балансу показали, что 12,2 % валового
218
общественного продукта РСФСР используется для конечного потребления в других
союзных республиках, туда косвенно передается 11 % трудовых ресурсов произ¬
водственной сферы и 13,1 % основных производственных фондов. Каждая единица
продукции РСФСР, направляемая на нужды остальных союзных республик, на 8 %
более фондоемка и на 4 % менее трудоемка, чем продукция, идущая в РСФСР.
При этом РСФСР в относительно большей степени осуществляет затраты на фонд
накопления второй зоны страны, чем на ее фонд потребления, тогда как в затратах
остальных союзных республик преобладают затраты на фонд потребления РСФСР.
7.7. Уточнение и обобщение
межотраслевых производственных связей
Уточнение функций производственных затрат и условия взаимозаменяе¬
мости ресурсов. Наиболее простой способ уточнения зависимостей меж¬
ду затратами и выпуском продукции — переход от линейных однород¬
ных функций (6.10) и (6.19) к линейным неоднородным функциям
материальных затрат и затрат внешних ресурсов:
хц = aijxj "Ь ^i7» (7.53)
xs/ = f s/Х/ + dsj. (7.54)
Возможны два подхода к построению функций (7.53) и (7.54):
разделение производственных затрат на переменные и постоянные и ли¬
нейная аппроксимация теоретических или эмпирических зависимостей
между затратами и выпуском продукции.
При_ первом подходе параметры функций получают следующий
смысл: ау и fsf — затраты /*-й продукции (s-ro ресурса) на единицу при¬
роста производства /-й продукции, dij и dsj — постоянные затраты
на все производство /-й продукции. Свойства таких функций были
рассмотрены в 4.4. Коэффициенты ау и fsj, не учитывающие в явном виде
разделение затрат на переменные и постоянные, зависят от того, нас¬
колько правильно спрогнозированы объемы производства. Поэтому
переход к непосредственному использованию предельных коэффициен¬
тов затрат повышает точность расчетов.
Определение постоянных затрат возможно по данным статистического учета.
Доля условно-постоянных затрат в таких отраслях, как электроэнергетика, маши¬
ностроение, промышленность строительных материалов, составляет до 25 - 30 %.
Следует отметить, что выделение постоянных затрат труда и основных фондов
имеет более существенное значение, чем выделение постоянных материальных
затрат. Это объясняется тем, что на действующих предприятиях имеется довольно
значительная часть персонала и основных фондов, потребность в которых не меня¬
ется даже при существенных изменениях выпуска продукции. Проблема выделения
постоянных затрат получила практическое решение при разработке межотрасле¬
вых балансов по некоторым республикам и экономическим районам СССР.
Второй подход к построению функций (7.51) и (7.52) состоит в
линеаризации более сложных зависимостей между затратами и выпуском
219
продукции. В этом случае параметры dц и dSJ- уже не всегда можно трак¬
товать как постоянные затраты, ибо допускается dy < 0, dsj < 0 (соответ¬
ственно ау > ay, fsj >fSj).
Модель межотраслевого материального баланса с функциями затрат
общего вида (линейными или нелинейными)
*.•= 2 Ч>ц(Х/)^У1, i£3 (7.55)
/ €9
обладает иными свойствами, нежели линейная. Существование решений в
такой модели (при заданныху{) зависит от вида функций (ху). Типична
неединственность решений при заданныхyf. Значительно усложняются ме¬
тоды нахождения решений. Однако главным препятствием в построении
нелинейных моделей являются трудности в информационном обеспече¬
нии.
Надо иметь в виду, что межотраслевая модель, оперирующая с агрегированны¬
ми группами продукции (отраслями) и объединяющая показатели по всем произ¬
водственным способам, непосредственно не улавливает основные технико-эконо¬
мические факторы, обусловливающие нелинейность затрат от выпуска продук¬
ции: падение предельных затрат с ростом концентрации производства в обрабатыва¬
ющей промышленности, возрастание предельных затрат с переходом к более бед¬
ным месторождениям полезных ископаемых и т.п. Для построения нелинейных
функций материальных затрат и затрат ресурсов требуется обобщение информации
об изменении эффективности развития отдельных отраслей при изменении объе¬
мов производства. Теоретически наиболее правильно получать такую информацию
в результате решения задач оптимального отраслевого планирования (вычисления
функций отклика).
Модель межотраслевого баланса в принципе может включать усло¬
вия взаимозаменяемости ресурсов в виде производственных функций
(см. 4.3). Тогда число уравнений в модели увеличивается на п (произ¬
водственные функции) и появляются новые неизвестные — затраты
продукции и ресурсов (xjj, хsj):
xi = fj (хф xsi) * - /' € з, s 6 м,
xi~ 2 xij\yi' ^€3,
/«* (7.56)
2 s £M.
/€#
Более доступно применять межотраслевую модель смешанного типа:
балансы продукции оставить без изменений (с линейными функциями
затрат), а взаимозаменяемость учитывать только для внешних ресурсов:
x/ = f/(xs/)’ i€3’
xi = 2 ‘€3.
je9 (i-д')
2 xsj ^ rs> s € M
i€9
220
Как показано в 4.4, однородная производственная функция первой
степени может заменяться набором производственных способов с разны¬
ми соотношениями затрат взаимозаменяемых ресурсов. Поэтому, если
производственные функции, входящие в (7.57), удовлетворяют этим
условиям, можно перейти к эквивалентным линейным межотраслевым
моделям с избыточным числом переменных х/ф, характеризующим
объемы производства продукции при определенных сочетаниях взаи¬
мозаменяемых ресурсов:
{ 2 = 2 ciijtyXjty ~\~ у 1У i £
*6 м. Р-58>
/. ч?
Для получения единственного решения модель (7.58) должна быть
дополнена критерием выбора наиболее эффективных комбинаций про¬
изводственных способов; в результате этого модель межотраслевых
связей переводится в класс оптимизационных моделей (см. гл. 8).
Модели межотраслевых взаимодействий. Такое название получили
модели, разрабатывавшиеся с начала 70-х годов в ЦЭМИ АН СССР, а
затем в Институте экономики и прогнозирования научно-технического
прогресса (ИЭиПНТП) АН СССР под руководством Ю.В.Яременко.
Модели межотраслевых взаимодействий объединяют основные соот¬
ношения межотраслевого баланса и эконометрические модели элемен¬
тов производственных затрат и конечной продукции.
В отличие от основной модели межотраслевого баланса система
уравнений производства и распределения продукции не позволяет найти
решение, она лишь устанавливает необходимые балансовые соотно¬
шения:
xi= 2 xij 2 yih, i£3, (7.59)
iea htH
где h — функциональный элемент конечной продукции, Н — множество
этих функциональных элементов.
Главную особенность модели составляют уравнения потоков распре¬
деления продукции, учитывающие такие факторы, как ограниченность
ресурсов, интенсивность спроса, замещение одних видов ресурсов други¬
ми, взаимозависимость отраслей при распределении ресурсов. Уравнения
потоков хц имеют следующий общий вид:
xij = <' + aljXi 4 aljXj + afix,t + Щхф (7.60)
где qj, — параметры, характеризующие влияние на величину потока
соответственно объема ресурсов /-й продукции и размеров спроса со
стороны производства /-й продукции; параметр, характеризующий
влияние объема поставок /-й продукции смежному потребителю (произ¬
221
водству к-й продукции), участвующему в распределении этой продук¬
ции; аУ — параметр, характеризующий влияние параллельного потока
затрат е-й продукции, также входящего в состав материальных затрат,
на производство /-й продукции (он может быть замещающим или допол¬
няющим). Коэффициенты а,у в уравнениях (7.60) оцениваются с помо¬
щью эконометрических методов.
Приведем несколько примеров уравнений межотраслевых потоков, параметры
которых оценивались на основе данных за 1960 - 1980 гг. (см. [5. С. 25, 28]):
*010? = 0,268 4- 0,465 (х01 — х0101) + 0,007*07.
= -5,584+0,972х10+(- 1,239+Н^) (*7и+*««).
^isii = 2,378-f-0,014*i! -|-0,026x16 -f-0,167/.
Индексами обозначены отрасли: 01 - черная металлургия, 07 — машиностро¬
ение и металлообработка, 10 - промышленность строительных материалов; 11 -
легкая промышленность, 14 - строительство, 15 - сельское хозяйство.
Очевидно, что уравнения потоков должны периодически пересматри¬
ваться на базе обновляемой информации. В практических расчетах урав¬
нения (7.60) строятся только для важнейших потоков1, а второстепен¬
ные потоки определяются ”в целом” с помощью так называемых урав¬
нений до счета.
Производство сопряженной продукции и использование комплекс¬
ного сырья. В основной модели межотраслевого баланса используется
допущение, что в каждом производственном процессе создается только
по одному виду продукции. Но поскольку в ряде отраслей промышлен¬
ности и сельского хозяйства распространены процессы производства со¬
пряженной (комплексной) продукции, это вынуждает условно распре¬
делять технологически неразделимые затраты между отдельными видами
сопряженной продукции. В результате возникают ошибки в расчетах
объемов производства и потребностей в ресурсах.
Отмеченных недостатков позволяет избежать метод отрица¬
тельных коэффициентов. Модель межотраслевого баланса
строится в разрезе ’’основных” продуктов, выделяемых в каждом ком¬
плексном производстве. На каждый основной вид продукции рассчиты¬
ваются коэффициенты затрат (со знаком плюс) и коэффициенты вы¬
пуска ’’побочной” продукции (со знаком минус), т.е. на ’’основной”
продукт относятся все затраты, связанные с выпуском всей сопряженной
продукции, но зато выход ’’побочной” продукции рассматривается как
результат производства ’’основного” продукта.
Например, в черной металлургии три моделируемых потока дают около
82 % валовой продукции отрасли, в электроэнергетике один моделируемый по¬
ток - 60, в сельском хозяйстве два потока -11 % (см. [5. С. 17]).
222
Пусть Xj — объем производства ’’основной” продукции вида /, ац —
коэффициент затрат выпуска продукции i на единицу ’’основной” про¬
дукции Тогда
При этом
*,= 2 aiiXj + yt, i£3 (7.61)
/€*
Xt = x{ 2 aikxk,
ks K,
где Kj - множество видов ’’основной” продукции, при производстве
которой получается (как ’’побочная”) продукция /.
В векторно-матричной форме имеем
X = AX+Y или X=(E-A)-'Y.
Матрица (Е - А)~1 может содержать отрицательные элементы.
Если коэффициент матрицы Ьц < 0 (чаще всего ему соответствует
% < 0), это означает, что при увеличении конечного использования про¬
дукции / объем производства ’’основной” продукции i должен умень¬
шаться, поскольку возрастает производство этой же продукции в качес¬
тве ’’побочной”.
Рассматриваемый метод учета сопряженной продукции и комплекс¬
ных затрат может быть применен и для решения проблемы получения и
использования в народном хозяйстве ценных отходов производства.
Особенно важное значение это имеет для правильного учета потребностей
и ресурсов металлолома (известно, что за счет лома черных металлов
выплавляется примерно половина всей стали). При введении в модель
межотраслевого баланса уравнения производства и распределения ме¬
таллолома в соответствующем столбце матрицы показываются все виды
затрат на заготовку тонны лома, а в строке — коэффициенты выхода
лома при производстве единицы различных ’’побочных” продуктов
(со знаком минус) и коэффициенты затрат лома на изготовление еди¬
ницы различных видов ’’основных” продуктов (со знаком плюс).
Литература
1. Комплекс моделей перспективного планирования. М.: Наука, 1986. Гл. 5.
2. Межотраслевые балансы в анализе территориальных пропорций СССР. Ново¬
сибирск: Наука, 1975.
3. Межрегиональные межотраслевые балансы. Новосибирск: Наука, 1983.
4. Методические указания к разработке государственных планов экономическо¬
го и социального развития СССР. М.: Экономика, 1980. Разд. 7.
5. Моделирование межотраслевых взаимодействий. М.: Наука, 1984.
6. Модель ’’доход - товары” и баланс народного хозяйства. М.: Наука, 1978.
7. Свердлик Ш.Б. Общественный продукт и денежный оборот. Новосибирск:
Наука, 1981.
8. Система моделей народнохозяйственного планирования. М.: Наука, 1982. Разд.
2, 3.
ГЛАВА 8
ОПТИМИЗАЦИОННЫЕ МЕЖОТРАСЛЕВЫЕ МОДЕЛИ
8.1. Общая линейная оптимизационная модель
Линейная оптимизационная модель общего вида была сформулирована
и исследована Л. В. Канторовичем. Она получила название о сновной
задачи производственного планирования. Данная
модель является частным случаем общей модели оптимального плани¬
рования народного хозяйства. Составные элементы модели уже изуча¬
лись выше: это производственные способы, балансы производства и
использования продукции и ресурсов.
Построение модели. Воспользуемся понятиями и обозначениями,
введенными в 4.5. Имеется множество производственных способов
ф Е N; — интенсивность применения способа ф; А^ = (а3ф)— век
тор производственного способа ф\ все множество ингредиентов разби¬
вается на два подмножества: продукты и воспроизводимые ресурсы
(продукты для промежуточного и конечного использования) Si Eilfj;
невоспроизводимые ресурсы s2 ^М2. Основные ограничения линейной мо¬
дели производства (4.39) необходимо конкретизировать лишь в отно¬
шении структуры конечной продукции.
В составе конечной продукции выделим постоянную и переменную
части ySl = qSl + ySl. Постоянная часть включает минимально необхо¬
димые объемы продукции для непроизводственного потребления (это
могут быть объемы, достигнутые в прошедшем периоде), накопления,
возмещения выбытия основных фондов, внешнеторгового обмена и т.д.
Переменная часть конечной продукции максимизируется в заданном ас¬
сортименте :
F—* шах, у8л > a5iz, Si € Л4»
где z — число комплектов переменной части конечной продукции, —
количество продукции sx в одном комплекте.
Общая модель имеет следующий вид:
224
(1) 2 ciSt^x^ ^tfsj' si€Mj4
y\>GN
(2) 2 aS2^ < л s2 6 M2,
\И w
(3) ^>0, (8.1)
(4) 2>0,
(5) z —- max.
Для того чтобы задача (8.1) имела решение, необходимо, чтобы,
во-первых, матрица выпуска и материальных затрат производственных
способов А = а5гф обладала свойством, аналогичным свойству продук¬
тивности матрицы (Е - А) межотраслевого баланса (т.е. обеспечивала
бы возможность получения положительной конечной продукции), и,
во-вторых, чтобы значения qs- не были чересчур большими, т.е. такими,
чтобы при z = О выполнялись ограничения (2).
Важной качественной характеристикой оптимального плана модели
(8.1) является число применяемых производственных способов (пере¬
менных > 0).
Из теории линейного программирования известно, что оптимальный
план задачи в случае его единственности и невырожденности содержит
столько положительных основных и дополнительных (приводящих не¬
равенства к равенствам) переменных, сколько имеется ограничений.
При этом число положительных основных переменных равно числу ог¬
раничений, которые в оптимальном плане обращаются в равенство.
Единственность и невырожденность оптимального плана можно рас¬
сматривать как типичное свойство модели (8.1). Допустимо также при¬
нять, что в оптимальный план включается переменная z* > 0. Отсюда
следует, что если п — число видов продукции и т — число невоспроизво¬
димых ресурсов, то максимальное число применяемых производствен¬
ных способов равно п + т — 1 (из общего числа N). В действительности
же число применяемых способов будет равно пх + тх — 1, где игпх —
число видов продукции и ресурсов, по которым в оптимальном плане
неравенства превращаются в равенства (пг тг <га).
Оптимальные оценки и анализ оптимального плана. Модели (8.1)
соответствуют оптимальные оценки всех видов продукции (v£ ) и не¬
воспроизводимых ресурсов (w^2). Оценка
д1*
v^--dqs,
характеризует уменьшение максимального числа комплектов конечной
продукции при увеличении постоянной части конечной продукции вида
st на ’’малую единицу”. Оценка
д~г*
8 Зак. 2414 225
показывает прирост максимального числа комплектов при увеличении
ресурса s2 ”на малую единицу”. Соотношения, определяющие значения
оптимальных оценок, выводятся из условий двойственной задачи линей¬
ного программирования.
Все оценки неотрицательны. При этом оценки хотя бы одного вида
продукции и хотя бы одного вида ресурсов должны быть положительны
(в противном случае план, относительно которого рассчитаны оценки,
может быть улучшен).
Для каждого производственного способа выполняются соот¬
ношения
2 aStivlt— 2 as,iDM'sJ<0, i|(8.2)
s,€M, 52€Mj
означающие, что суммарная оценка выпускаемой продукции не превы¬
шает суммарной оценки всех затрачиваемых ресурсов.
При z* > 0 выполняется равенство
2 I.
s,€M,
И если ассортиментные коэффициенты пронормированы так, что
2 a5j = 1, то значения оценок продукции колеблются вокруг едини-
s 1 ЕЛ/1
цы (если оценки некоторых видов продукции меньше единицы, то оцен¬
ки каких-нибудь других видов продукции больше единицы). Остальные
общие соотношения между величинами х*,, v* , и условиями (8.1),
(8.2) определяются условиями дополняющей не жесткости:
•^ф 0=^> 2 ^si^s, = ^
Si € М t s2 € Af 2
Sj 6 M l sg € Ai 2
2 as,^— asz* > qs =» v’s = 0,
N
v's, > 0=> 2 as,^—asz* = qs
y\>eN
^ aSt^ <C гws ^ — 0,
При использовании оптимизационных моделей в планировании обы¬
чно не ограничиваются расчетом только одного оптимального варианта.
Необходимо анализировать, какие изменения произойдут в оптимальном
плане, если будут изменяться исходные данные. Рассмотрим некоторые
направления анализа оптимального плана.
226
Влияние изменения ограничений. Зависимости максимального зна¬
чения целевой функции от изменения параметров ограничений непосред¬
ственно характеризуются значениями оптимальных оценок продукции
и ресурсов. Пропорциональное изменение (увеличение или уменьшение)
всех параметров ограничений не меняет значений оценок. При увеличе¬
нии qst оценки растут (до тех пор, пока существует решение задачи).
При увеличении г$2 оценки снижаются (до нуля).
Возможности эквивалентной взаимозаменяемости конечной продук¬
ции и ресурсов в ограничениях модели определяются уравнением
(8.3)
Следует заметить, что количественные соотношения эквивалент¬
ной взаимозаменяемости, вытекающие из уравнения (8.3), справедли¬
вы только при таких значениях AqSl и ArS2, которые не изменяют значе¬
ний оптимальных оценок.
Для того чтобы проанализировать влияние изменения ограничений на
интенсивность применения различных производственных способов,
упорядочим условия задачи. Пусть для оптимального плана первые
(пi + mi) ограничений выполняются как равенства, а остальные (п —
- пх) + (т - тх) ограничений выполняются как строгие неравенства.
Изменим также нумерацию переменных так, что положительными в
оптимальном плане будут первые (пх + тг — I) переменных производ¬
ственных способов и переменная z.
Тогда матрица модели может быть представлена в виде следующей
блочной матрицы:
\ (п, 4 mt)
(п—п,) +- (/71—т,)
^11* а1
А “1
12
^21» а2
^22
(я, -1- ту)
N—(П\+тЛ—1)_
Введем новое обозначение для вектора ограничений, перенумеровав
компоненты этого вектора в соответствии с новой нумерацией ограни¬
чений: b = [bx b 2 ] \
Для оптимального плана справедливо уравнение
Ни -а,)
?
= bt.
откуда
хх
2*
(8.4)
8*
227
Обозначим первые (пг + т1 — 1) строк матрицы (Ап, — 1
через Вп, а последнюю строку — через (Зп . Тогда
х\ = Вг1Ьи (8.5)
z* = Mi- (8-6)
Формулы (8.5) и (8.6) характеризуют зависимости оптимальных
интенсивностей производственных способов и максимального числа
комплектов от ’’жестких” ограничений задачи. Коэффициенты матрицы
Вп являются аналогом коэффициентов полных потребностей в продук¬
ции модели межотраслевого баланса; однако они могут иметь различные
знаки, так же как и коэффициенты вектора (Зп.
Очевидно, что для корректировки интенсивностей применяемых спо¬
собов и числа комплектов продукции могут использоваться формулы:
Д*; = ВПДЬ„ (8.7)
Д2* = Р11ДЬ1. (8.8)
Однако они верны только при сохранении базиса оптимального плана
задачи (набора векторов, соответствующих положительным перемен¬
ным). Базис оптимального плана не изменяется, пока переменные, во¬
шедшие в оптимальный план, будут неотрицательны. Это означает, что в
анализируемой модели условиями сохранения базиса оптимального пла¬
на являются Лч
+ 0, (8.9)
Р„ (<? + ДЬ) > 0. (810)
Из этих условий находятся границы допустимых изменений каждой
компоненты вектора Ъ и области допустимых изменений одновременно
нескольких компонент вектора Ъ. Сохранение базиса оптимального пла¬
на является также условием неизменности оптимальных оценок.
Включение в оптимальный план дополнительных производственных
способов. Может оказаться, что в оптимальном плане большая часть
имеющихся производственных способов не будет использоваться и пре¬
обладающая часть продукции будет производиться небольшим числом
способов. Такая ситуация нежелательна с точки зрения маневренности,
надежности, адаптивности плана. В связи с этим интересно изучить, к
каким последствиям приводит включение в оптимальный план дополни¬
тельных способов.
Эффективность производственных способов ф измеряется оценками
производственных способов:
Дч,= I asys— 2 0.
St е Mi s26M2
228
Для способов, вошедших в оптимальный план, Д^ = 0, а для спосо¬
бов, не вошедших в оптимальный план, Аф <0 (в случае единственности
оптимального плана Аф < 0). Оценки Аф показывают, насколько умень¬
шится значение целевой функции при включении в оптимальный план
ранее не входившего в него способа с единичной интенсивностью. Если
же интенсивность вводимого способа равна хф}то значение целевой фун¬
кции уменьшится на Афхф.
Рассмотрим, как повлияет включение дополнительных способов
(вектора Х2) на интенсивности применения оптимальных (базисных)
способов (вектор Х\). Добавив к вектору Ьх произведение — А\2Х2,
получим на основе (8.5)
х; = ви(ьг-Апхг).
откуда
д Х\ = — ЬпА1шХг (8.И)
Кроме того, изменение максимального числа комплектов конечной
продукции при включении вектора Х2 составит
Д?=-р1ИгЛ- <8Л2)
Формулы (8.11) и (8.12) справедливы при сохранении базиса опти¬
мального плана, т.е. при условиях
B„(6i—'41гХ2)>0,
'hAbi-AltXt)>0.
С помощью оценок способов можно изучать целесообразность
включения в условия народнохозяйственной задачи новых способов.
Новый способ у может войти в оптимальный план, если А^ > 0. Это
условие может быть использовано для проектирования новых эффектив¬
ных производственных способов.
Рассмотренные направления и методы анализа оптимального плана
являются универсальными для всех линейных оптимизационных моде¬
лей. Однако в более частных моделях экономико-математический анализ
выявляет специфические и даже неожиданные свойства оптимальных
решений.
229
\j 8.2. Критерии оптимальности в прикладных моделях
В практике народнохозяйственного моделирования находят применение,
как правило, относительно простые критерии оптимальности. Использо¬
вание упрощенных критериев не противоречит теоретическим принци¬
пам оптимального планирования, поскольку процесс оптимизации на¬
родного хозяйства включает процедуры уточнения критериев. Однако
упрощенные критерии оптимальности должны обосновываться с по¬
зиций более общих моделей общественных целеустремлений, анализиро¬
вавшихся в гл. 2 и 5.
Рассмотрим несколько критериев оптимальности, выражающих
стремление к достижению максимально возможного уровня удовлетво¬
рения материальных потребностей населения (уровня потребления)
при выборе вариантов развития народного хозяйства. Так же, как и
в гл. 5, будем обозначать: Y — вектор благ, используемых на потребле¬
ние; и (Y) — функция, характеризующая уровень потребления.
Максимизация фонда потребления в фиксированных ценах. Наибо¬
лее общим показателем социальной результативности годового цикла
воспроизводства, применяемым в статистике и планировании, является
физический объем фонда потребления1. Однако приемлемость этого по¬
казателя как критерия оптимальности вариантов народнохозяйственно¬
го плана во многом зависит от методики соизмерения различных видов
потребительских благ, образующих фонд потребления.
По принятой методике отдельные блага, входящие в материально¬
вещественный состав фонда потребления, соизмеряются посредством
неизменных цен прошлого периода р? Поэтому максимизация общего
фонда потребления означает, строго говоря, не максимизацию потреби¬
тельского эффекта, а максимизацию некоего суррогата стоимости про¬
изведенных предметов потребления при условиях воспроизводства
прошлого периода. По-видимому, цены прошлых лет малопригодны для
соизмерения полезных эффектов благ в вариантах развития хозяйства.
Недостатки таких цен как экономических измерителей особенно прояв¬
ляются при появлении новых видов товаров и услуг, значительных
изменениях материально-вещественной структуры фонда потребления.
Другого рода возражение против применения рассматриваемого
показателя в качестве критерия оптимальности обусловлено линейно¬
стью соответствующей ему функции
и 00 = 2 pii/j. (8.13)
Совместно с фондом потребления следует учитывать и потребительское иму¬
щество (основные непроизводственные фонды, предметы потребления длительно¬
го и многократного пользования). Но этот вопрос выходит за рамки экономичес¬
кой статики; к нему мы вернемся в гл. 12.
230
Из линейности функции (8.13) следует, что нормы эквивалентной
заменяемости благ определяются соотношениями фиксированных цен
и поэтому являются постоянными:
Ау< _ _ р1_
*у/ рЧ'
Но это противоречит закономерностям роста потребления (изменения
норм эквивалентной заменяемости) и основным тенденциям изменения
покупательского спроса. Включение линейной функции (8.13) в народ¬
нохозяйственную модель приводит, как правило, к чрезвычайно ’’бедно¬
му” решению, т.е. в оптимальный план входит лишь незначительное
число наиболее ’’выгодных” потребительских благ, для которых отно¬
шение установленных в прошлом цен к затратам ресурсов оптимизиру¬
емого периода является наибольшим. Такого рода ’’оптимизация”, по-
видимому, имеет мало смысла.
Недостатки линейного критерия можно смягчить, вводя в условие модели до¬
полнительные ограничения на значения отдельных продуктов или их групп. Реше¬
ние в этих случаях будет получаться более ’’богатым”. Однако это улучшение
решения (в смысле приближения к реальности) будет достигаться не за счет крите¬
рия оптимальности, а, наоборот, в результате недоверия к нему.
Напрашивается отрицательный вывод о целесообразности непосред¬
ственного применения традиционного показателя физического объема
фонда потребления в качестве критерия оптимальности. Однако совер¬
шенствование методики оценки продукций может расширить допусти¬
мость применения данного показателя. Из анализа свойств ЦФП (см.
разд. 5.1) следует, что в окрестности оптимума Y* нелинейная функция
и (Y) может быть заменена линейной функцией 2 щ(У*)у1, где соизме¬
ряющими ’’ценами” являются частные производные Применение
такой линейной функции предполагает уточнение значений коэффици¬
ентов щ (Y*) в процессе итеративных оптимизационных расчетов. Улу¬
чшение методики исчисления физического объема фонда потребления
возможно и на базе реальных цен. Новые цены лучше учитывают об¬
щественную полезность продуктов, чем цены прошлых лет. Общеприз-
нана необходимость более полного учета этого фактора при реформе
потребительских цен. Поэтому целесообразно перейти к исчислению
динамики физического объема фонда на базе цен настоящего периода.
Максимизация потребления в заданном ассортименте. Данный
подход к оптимизации потребления уже применялся в 8.1. Здесь мы
дадим этому подходу более широкую экономическую интерпретацию
и проанализируем ряд его модификаций.
Пусть z — количество комплектов (наборов) потребительских
благ, ау — коэффициент, характеризующий количество /-й продукции
в комплекте (ассортиментный коэффициент).
231
Структура потребления продукции выражается условием z =
У i
= min{-7—), которое соответствует системе линейных неравенству
/е t*i
i E I. Допускается, что при решении задачи на максимум комплектов
некоторые виды продукции могут получаться в излишке (сверх комп¬
лектов) . Такие случаи в оптимизационных задачах возможны при нали¬
чии комплексных производств.
Таким образом, задача максимизации потребления в заданном ас¬
сортименте включает условия:
2 - тзх.
а,г, i €1.
Коэффициенты щ удобно нормировать так, чтобы 2 щ = 1. Если
/ Е /
z — общий объем фонда потребления и 2 а/ = 1, то коэффициенты
/’ Е/
щ означают удельный вес /-й продукции в фонде потребления.
Остановимся на вопросе экономического обоснования ассортимент¬
ных коэффициентов.
Широкое применение имеет подход к определению структуры потре¬
бления, базирующийся на системе норм рационального потребления
продуктов питания, промышленных товаров, жилья, различных услуг.
Принимается, что коэффициенты щ пропорциональны соответствующим
нормам рационального потребления. Тогда максимизация потребления
в заданном ассортименте будет обозначать равномерное приближение к
рациональным нормам. Возникающую задачу можно интерпретировать
как максимизацию степени равного удовлетворе¬
ния рациональных потребностей. Действительно, если
Fv= yi^- вектор рациональных потребностей, в — степень удовлетворе¬
ния рациональных потребностей, в Е [0, 1 ], то имеем
0 — шах; g 15)
Ч; >
Очевидно, что если щ = ку{?где к — коэффициент пропорциональ¬
ности, к > 0, то условия (8.14) и (8.15) эквивалентны. На рис. 8.1 а
точка А соответствует рациональным потребностям. Все наборы благ,
удовлетворяющие заданному ассортименту, находятся на луче ОА. Точ¬
ка В — пересечение луча с границей множества производственных
возможностей — является оптимальным решением.
Существенный недостаток условий оптимизации (8.14), (8.15)
заключается в том, что допускаются неоправданно резкие изменения
сложившейся структуры потребления. Известно, что различные рацио-
232
Рис. 8.1
нальные потребности удовлетворяются в настоящее время не в одина¬
ковой степени (см. табл. 5.1). В этой ситуации мгновенная перестройка
фактической структуры потребления на ’’рациональную” неизбежно дол¬
жна привести к уменьшению потребления ряда видов благ (например,
хлеба, картофеля, сахара), которое не может быть сразу же компенсиро¬
вано ростом потребления других видов благ (например, мяса, фруктов).
Поэтому целесообразно изменить условия оптимизации таким образом,
чтобы обеспечить плавность изменения структуры потребления. Для
этого следует перейти к задаче максимизации прироста потребления
в заданном ассортименте.
Обозначим: yt — потребление z-й продукции в базисном году; A yi -
прирост потребления продукции i по сравнению с базисным; щ — ассор¬
тиментный коэффициент прироста потребления продукции i (удобно,
чтобы 2 а/ = 1); z — число комплектов прироста потребления. Тогда
условия максимизации формулируются следующим образом:
г —+ шах,
Oi>yi+aiz,
(8.16)
Соответственно меняется и постановка задачи максимизации степени
удовлетворения рациональных потребностей:
9
max,
1/(>у? + (у7-у?)0. *€Л
(8.17)
233
где в — степень удовлетворения потребностей по сравнению с достигну¬
тым уровнем, 0 Е [0, 1] •
На рис. 8.1 а показано, что потребление благ увеличивается от исход¬
ной точки Y0 прямолинейно в направлении к точке А. При этом структу¬
ра потребления постепенно приближается к рациональной. Оптимальным
решением будет точка D.
Другой подход к определению структуры потребления тесно связан
с понятием и свойствами ЦФП (см. 5.1).
Выбранному ассортиментному вектору соответствует, как это видно
на рис. 8.1, эффективный (оптимальный по Парето) вариант
потребления. Но вовсе не обязательно, что он будет оптимальным с
позиций ЦФП. Поиск лучших вариантов может быть продолжен путем из¬
менения ассортиментных коэффициентов.
Вместе с решением задачи на максимум потребления в заданном
ассортименте получаются оптимальные оценки продукции V = (v().
Соотношения этих оценок характеризуют возможности заменяемости
продукции в окрестности найденного оптимального решения при сохра¬
нении числа комплектов. Допустим, при сопоставлении оценок продук-
V f
тов / и / обнаруживается, что ~ = 3. Это означает, что при существую¬
щих производственных возможностях увеличение потребления единицы
продукта i вынуждает сократить потребление продукта / на три единицы.
Но с точки зрения полезного эффекта потребления такая замена нецеле¬
сообразна: за единицу продукта i можно ’’пожертвовать” максимум две
единицы продукта /. Таким образом, продукт / имеет большую относи¬
тельную потребительскую ценность, чем это следует из первоначальных
условий задачи. Поэтому необходимо увеличить ассортиментный коэф¬
фициент по продукту /. Подобные изменения ассортиментных коэффи¬
циентов могут производиться неоднократно. Целью этих изменений
является достижение равенства отношений оптимальных оценок про¬
дуктов и коэффициентов эквивалентной заменяемости продуктов в
потреблении, т.е. выполнение необходимых условий максимума ЦФП
на множестве производственных возможностей.
На рис. 8.1 б показано, что изменения положения ассортиментных
лучей (i0КУ OL и др.) в принципе должны привести в точку М —
точку максимума ЦФП. Структура потребления, соответствующая лучу
ОМ, будет оптимальной с позиций ЦФП.
Теоретически, разумеется, проще применить ЦФП, которая избавит от необ¬
ходимости многократных пересчетов оптимизационной задачи. Но построение
ЦФП требует предварительного упорядочения множества допустимых вариантов
потребления. В то же время известно, что значительно проще ’’узнать”, какой из
двух - трех конкретных вариантов лучше, чем умозрительно проранжировать все
допустимые варианты по их предпочтительности.
Максимизация уровня потребления при заданных функциях потреб¬
ления. Функция потребления у( = 7Г/ (z) характеризует изменение потреб¬
234
ления определенного блага в зависимости от изменения общего уровня
потребления z. При этом величина z может характеризовать уровень
ЦФП, объем фонда потребления, степень удовлетворения рациональных
потребностей, величину доходов населения и т.п. Рассматривавшиеся вы¬
ше условия оптимизации (8.14) — (8.17) представляют собой линейные
функции потребления. Однако законам роста потребления, как это по¬
казано в гл. 5, в большей степени соответствуют нелинейные функции.
Рассмотрим более общую по сравнению с (8.17) формулировку
условий максимизации степени удовлетворения рациональных потреб¬
ностей:
0 —* max,
yi > tfi -+■ Ф,- (0), t 6 /, (8-18)
Й€[0, П-
Для различных благ необходимо построить функции потребления
У] = Уf + 4>i (Р)> У которых $j(6) = 0 при в = 0 и ф(6) = уJ- >>°при
в = 1. Основное отличие данных условий оптимизации потребления от
ЦФП заключается в том, что заранее выбирается (хотя бы предваритель¬
но) траектория перехода от одного уровня удовлетворения потребно¬
стей к другим, более высоким уровням.
_Очевидно, для всех благ, по которым yf < yjf необходимо, чтобы
<#(0) > 0 и y'i(6) > 0. Скорость увеличения потребления различных
благ должна зависеть от достигнутой степени удовлетворения соответ¬
ствующей потребности и насущности этой потребности. Для тех благ,
по которым фактическое потребление значительно уступает рациональ¬
но^ форме, следует выбирать функции ускоренного роста, имеющие
ф(в) > 0. Наоборот, если фактическое потребление близко к рациональ¬
ным нормам, то дальнейший рост потребления может быть замедляю¬
щимся: $(6) < 0. В расчетах по оптимизационной межотраслевой моде¬
ли в ГВЦ Госплана СССР используются функции потребления вида
Уг = У° + fyO0*, где ki = yf - yf и с\ > 0. При с\ = 1 имеем линейные функ¬
ции, при с\ > 1 — функции с возрастающей скоростью роста, при с\ < 1 —
функции с замедляющейся скоростью роста потребления.
В качестве особых функций потребления можно использовать функ¬
ции покупательского спроса от дохода у\ = ft(z) и максимизировать
величину дохода. Как было показано в 5.3, максимизация дохода насе¬
ления при фиксированных розничных ценах строго связана с задачей
максимизации ЦФП. Однако при произвольных ценах маловероятно,
что вариант потребления, наилучший по критерию дохода, будет наилу¬
чшим и по значению ЦФП. Теоретически необходимо применять такие
цены, при которых функции спроса потребителей приводят в точку
максимума ЦФП (в точку М). Пересчет цен может осуществляться на
235
основе информации об оптимальных оценках продукции и целесообраз¬
ной заменяемости продукции в окрестности оптимума так же, как и
при уточнении ассортиментных коэффициентов (подробнее см. ММСЭ,
с. 241).
8.3. Оптимизационные модели
на основе матрицы межотраслевого баланса
Общая линейная оптимизационная модель построена на основе матрицы
таких производственных способов, что каждый из них может выпускать
несколько видов продукции, каждый вид продукции может выпускаться
несколькими способами.
Далее будем рассматривать оптимизационные модели, сохраняющие
некоторые специфические допущения модели межотраслевого баланса:
сначала — 8.3 — модели, в которых каждый способ выпускает только
один продукт и каждый продукт выпускается только одним способом,
а затем — 8.4 — модели, в которых сохраняется только первое из указан¬
ных допущений. Такая последовательность анализа моделей выбрана для
того, чтобы ’’перекинуть мост” между моделями межотраслевого балан¬
са и оптимизационными моделями народного хозяйства и проследить
изменение свойств решений при изменении предпосылок и включении в
модель новых условий.
Модель межотраслевого баланса как частный случай оптимизацион¬
ных моделей. Оптимизационные межотраслевые модели неправомерно
противопоставлять моделям балансового типа. Во-первых, основные
условия балансовых моделей обязательно включаются в оптимизацион¬
ные модели. Во-вторых, балансовые модели могут интерпретироваться
и исследоваться как частный случай оптимизационных моделей.
Рассмотрим систему уравнений межотраслевого баланса производ¬
ства и распределения продукции совместно с ограничением по трудовым
ресурсам производственной сферы:
,2 (б,7—а,7)Xj = i/}, i$I,
'l, t^^L. (8 ,9)
/€/
Основная задача плановых расчетов (см. 6.6) состоит в том, чтобы
при заданном векторе Y° = (yf) и имеющихся трудовых ресурсах L
найти вектор необходимых объемов производства X = (xj). Эту задачу
можно представить в виде задачи линейного программирования:
2 (б//—*€Л (8.20)
/в/
236
*/>0, /€/, (8.20)
2 //X/ min.
/€/
Очевидно, что реальным экономическим условиям отвечают только
такие решения X* = (хр, при которых 2 tjx*<:L.
Задаче (8.20) соответствует двойственная задача, с помощью кото¬
рой находятся оптимальные оценки продукции v*
isi—аif^Vi^
i£l, (8.21)
2 max.
iei
Оптимальный план Х* задачи (8.20) характеризуется следующими
свойствами:
он единственный;
если У0 > 0 (или У0 > 0 и А — неразложимая матрица), то Х*> 0;
балансы производства и распределения продукции выполняются
строго как равенства, т.е. излишки конечной продукции не произво¬
дятся;
оптимальный план X* не зависит от коэффициентов целевой функ¬
ции tj > 0.
На рис. 8.2 видно, что оптимальный план является вершиной
’’клюва” при любых допустимых наклонах целевой функции. Обе зада¬
чи (и прямая, и двойственная) всегда имеют единственное решение,
если матрица А продуктивна и У0 > 0. Прр этом решение прямой опти¬
мизационной задачи сводится к решению системы уравнений 2 ^5/ -
- aij) xj = yf, z Е/, и поэтому оно не зависит от значений коэффициентов
tj минимизируемой функции. Решение двойственной задачи находится из
системы уравнений
и поэтому оно не зависит от коэффициентов ^максимизируемой функ¬
ции. Оптимальные оценки продукции равны коэффициентам полных
трудовых затрат. Равенство функционалов прямой и двойственной задачи
2 tjx,= 2 ifivf
/ € / i € /
237
Рис. 8.2
имеет место при любых поло¬
жительных значениях tj и у^
Оно означает, что суммарная
оценка всей конечной продукции
равна сумме трудовых затрат в
народном хозяйстве.
Оптимизационная модель
межотраслевого баланса продук¬
ции и производственных мощ¬
ностей. В 6.6 отмечалось, что
при краткосрочном планирова¬
нии наиболее существенными ог¬
раничениями роста производства
являются наличные производст¬
венные мощности. Решение дол¬
жно удовлетворять условиям
Xj < Mj, где Mj — максимально
возможный выход продукции / с производственных мощностей планиру¬
емого года. Включим в модель условия максимизации прироста конеч¬
ной продукции в заданном ассортименте, обозначив Q = (Qj) — вектор
заданных объемов конечной продукции.
В векторно-матричных обозначениях модель имеет вид:
(Е — А)Х— az>Q,
г>0,
z -+ шах.
Решение существует, если значения компонент вектора Q заданы не
слишком большими. Оптимальный план обращает первую группу усло¬
вий в равенства, поскольку невыгодно производить сверхкомплект¬
ные излишки конечной продукции. Поэтому в дальнейшем анализе ис¬
ходим из того, что
(Е— А)Х—az = Q,
откуда
Х = (£ — А)~1ая + (Е — Л)'1*?.
(8.23)
Поскольку (Е— А) 1 >0,a>0,б>0,топригХ)условиеЛГ>0всег-
да выполняется. Вследствие этого исходная задача (8.22) сокращается:
(Е — A^'az^N — (Е— Л)’1*?,
шах.
238
Вектор Р = (Е - А)'1 а представляет собой коэффициенты полных
потребностей в продукции для получения одного компонента конечной
продукции; М = М - (Е - A)~lQ есть вектор максимально возможных
объемов продукции для получения переменной части конечной продук¬
ции. Очевидно, что
z* = max z = min . (8.24)
Определив z*, находим
Х* = Рг*-Ь(£—A)~lQ.
Таким образом, z* определяется ’’узким” местом в системе производ¬
ственных мощностей. Как правило, мощность только одного вида про¬
дукции будет использоваться полностью. Оптимальная оценка мощно¬
сти по этому виду продукции (к) равна wj! = . Выявление дефицит¬
ной мощности служит сигналом для ее максимального расширения за
счет концентрации строительства на пусковых объектах, дополнительных
поставках оборудования, изменения специализации существующих
предприятий, режима их работы (сменности) и т.д.
Для подготовки программы первоочередных мероприятий по расши¬
рению производственных мощностей целесообразно упорядочить мощ-
_ Mj
ности по их дефицитности. С этой целью рассчитаем показатели Zj = ,
характеризующие максимальное число комплектов конечной продук¬
ции, которое можно получить с мощности вида / при условии неограни¬
ченности других мощностей. Теперь упорядочим ряд чисел zj, начиная с
z* = minzy. При новой нумерации разности (z^+i - показывают
прирост числа комплектов конечной продукции после ’’расшивки”
очередного А;-го ’’узкого” места в системе производственных мощностей.
Модели с ограничениями по общим ресурсам. Рассмотрим модель,
в которой балансы производства и распределения продукции дополня¬
ются ограничениями по общим невоспроизводимым ресурсам:
(Е—А)Х—az>Q,
X > О, (8.25)
z ^ О,
z —шах.
239
или
Подставляя (8.23) в ограничения по общим ресурсам, получаем
f(E—Л)"1аг<Л
Ф (8-26)
где $ = № = f(E — Л)~1а — вектор полных затрат ресурсов на один
комплект прироста конечной продукции, R = R - f(E - А)~lQ = 7$ —
вектор ресурсов, которые могут использоваться для получения перемен¬
ной части конечной продукции.
Из (8.26) следует:
г* = max z = min
(8.27)
этого ресурса будет положительна: = -1— , а оптимальные оценки
Максимальное число комплектов достигается, как правило, при
полном использовании только одного ресурса (к). Тогда только оценка
Vk
всех видов продукции будут пропорциональны коэффициентам полных
затрат дефицитного ресурса: vf= w^Fkj- Если же в оптимальном плане
используются полностью несколько ресурсов, то система оптимальных
оценок ресурсов и продуктов будет не единственной.
Полное использование только одного вида ресурсов как типичное свойство
оптимального решения не обязательно связано с ’’ассортиментным” критерием
оптимальности. Для сравнения рассмотрим модель, в которой условия максимиза¬
ции переменной части конечной продукции заданы в виде ЦФП, а остальные усло¬
вия модели (8.25) сохраняются.
Выразив К через У, приходим к сокращенной модели:
FY R,
К^гО. (8.28)
и (У) —- шах.
где F = f(E_ - Л) 1 - матрица коэффициентов полных затрат ресурсов, R =R -
-f(E-AflQ-
Оптимальное решение всегда существует и является единственным. Оптималь¬
ный план У* есть точка касания наиболее удаленной от начала координат поверх-
240
ности безразличия и выпуклого многогранника, образованного условиями FY <
Если эта поверхность безразличия касается вершины многогранника, то это
означает полное использование нескольких ресурсов. Однако вполне возможней,
что максимум и (Y) достигается на одной из граней многогранника, т.е. при полном
использовании только одного ресурса.
Таким образом, общим свойством рассмотренных в данном разделе
моделей является то, что оптимальный план чаще всего достигается при
полном использовании только одного ресурса. А это означает, что только
один вид ресурсов влияет на формирование оптимального решения.
Данное свойство не адекватно экономической реальности; оно обуслов¬
лено недостатком моделей.
В рассмотренных моделях почти отсутствуют возможности манев¬
рирования ресурсами, имеющими различную дефицитность. По каждому
виду продукции задается только один производственный способ, а поэ¬
тому технология производства слабо реагирует на выявляющиеся в про¬
цессе оптимизации соотношения наличия ресурсов и потребностей в них.
Напрашивается вьюод о том, что оптимизационные модели должны
включать условия выбора между различными способами производства
одноименной продукции.
8.4. Оптимизационные межотраслевые модели
с производственными способами
Модель с минимизацией затрат труда. Построим модель, представляю¬
щую собой обобщение модели межотраслевого баланса, записанной в
форме (8.20). Пусть каждый вид продукции производится несколькими
способами ipj Е Tj, Tj — [ 1, ..., sy j , но каждым способом выпускается
только один продукт. Введем новые обозначения: х/^. — объем произ¬
водства продукции / способом \pj; — коэффициент прямых затрат
продукции i на производство единицы продукции / способом \pj; tjф. —
затраты труда на единицу продукции /, производимой способом \pj.
Тогда
/«/.*,€ Т. (б‘7 >У‘' 1 € 1'
/ 6 Л 'Фу 6 7/,
^ min.
/6/, J J
(8.29)
Межотраслевая, а точнее — межтехнологическая модель (8.29)
всегда имеет решение, если выполняются условия, аналогичные ус¬
ловию продуктивности матрицы А модели межотраслевого баланса.
241
Например, допустимое решение может быть получено, если включить
в план по одному способу для каждого вида продукции. Так может быть
п
составлено П Sj систем уравнений межотраслевого баланса производства
и распределения продукции, каждая из которых имеет решение, если
матрица А продуктивна.
Анализ модели позволяет выявить ряд специфических свойств.
Теорема 1. При положительном век юре Y0 > 0 производятся все
продукты и каждый продукт производится только одним способом.
Доказательств о. По-прежнему будем исходить из предположения, что
оптимальный план - единственный. Введем в условия дополнительные переменные
Ду/ (излишки конечной продукции сверх минимально необходимых объемов ур,
превращающие неравенства в равенства.
В каждом i-м уравнении
2 (6/ ,• — а..,ф /ф . &У{ = y°j
j€T, УФ/ /ч7
положительными являются только коэффициенты при переменных xi^j. Но по¬
скольку все у9 > 0, j и все
^•€ Т{ ^ ^ >
т.е. в оптимальном плане должны производиться все виды продуктов.
Максимальное число положительных переменных в оптимальном плане равно
п (числу уравнений). Следовательно, в каждой сумме переменных £ х; . по-
ложительной может быть только одна переменная. Иначе говоря, в оптималь¬
ном плане каждый продукт производится только одним
способом.
Следствие. Из теоремы следует, что поскольку число возможных
положительных переменных исчерпывается переменными способов про¬
изводства, то все Ду/ в оптимальном плане равны нулю. Иными словами,
оптимальный план обращает исходные неравенства в равенства.
Пусть X* — оптимальный план модели (каждая его компонента
есть интенсивность применения какого-то ’’лучшего” способа произ¬
водства); А* — матрица коэффициентов материальных затрат, состав¬
ленная из способов, которые вошли в оптимальный план. Матрица А*
аналогична матрице А межотраслевого баланса с той лишь разницей,
что вместо средневзвешенных коэффициентов из разных способов в
ней представлены коэффициенты только ’’лучших” способов. Матрицы
А* и (Е - А*) обладают теми же экономико-математическими свой¬
ствами, что и матрицы межотраслевого баланса. Отметим, в частности,
существование матрицы (Е - А*)~1 > 0. Элементы матрицы (Е -
- А*)”1 являются коэффициентами полных потребностей в выпуске
продукции для получения единицы конечной продукции в оптимальном
плане. Оптимальный план удовлетворяет следующей системе урав¬
нений:
(£— A*)X* = Y* или X* =^(Е- A*)~1Y\
242
Теорема 2. Базис оптимального плана, а следовательно, и выбор
’’лучших” способов остаются постоянными при любых изменениях
положительного вектора Y°.
Доказательство. Для того чтобы базис оптимального плана оставался
неизменным при переменном векторе Y°, достаточно в соответствии с (8.9), чтобы
выполнялось условие (Е - A*)~l Y0 > 0. Поскольку матрица (Е - А*)-1 > 0,
условие (Е - A*)~l Y0 > 0 выполняется всегда при любом Y0 > 0 и тем более при
ГО > 0.
Пусть для некоторого Y0 > 0 получено решение X*. Базис полученного решения
(Е - А*) остается неизменным и тогда, когда вектор будет изменяться любым
образом в положительной области (0 < Y0 < + °°). Если базис оптимального пла¬
на - неразложимая матрица, то теорема распространяется на случай Y0 > 0. Это
означает, что вычислив матрицу (Е - А*)~1 для одного варианта конечной про¬
дукции, можно неоднократно использовать ее для расчета производственной про¬
граммы при других вариантах конечной продукции.
Из задачи, двойственной (8.29), следует, что для способов, вошед¬
ших в оптимальный план (*Д. > 0) » выполняются условия
Поэтому вектор оптимальных оценок продукции V* = (vf) определя¬
ется решением системы уравнений V* = V*A* + t* или V* = t (Е -А*Г1.
Видим, что оптимальные оценки продукции в рассматриваемой
модели равны коэффициентам полных трудовых затрат, исчисленным по
лучшим производственным способам для каждого вида продукции.
Следствие. Оптимальные оценки v*ne изменяются при любых
изменениях положительного вектора У0. Поскольку в соответствии с
теоремой 2 базис оптимального плана остается постоянным при любых
изменениях вектора Y0 в положительной области, то, следовательно, не
изменяются и оптимальные оценки (задача исчисления оптимальных
оценок в рамках рассматриваемой модели относится к тому редкому
классу экстремальных задач, оптимальный план которых не зависит от
коэффициентов целевой функции).
Модели с условиями максимизации конечной продукции. Рассмо¬
трим другую формулировку модели с производственными способами:
произвести максимальное число комплектов конечной продукции при
ограниченных трудовых ресурсах:
2 (б,7—ацъ,)*л|>а,г>0, f
/е /, 1|>уб тj >' 1
jeJ.tyjtTj J J
*/*у>0, Ь € г/> (8.30)
z>0,
z —* max
243
Нетрудно установить, что модели (8.29) и (8.30) являются взаим¬
ными. В первой модели фиксируютсяу°= щ z° и минимизируются затра¬
ты труда, а во второй модели максимизируются z при фиксированном
ресурсе труда. И если в первой модели z° = max z, то в соответствии с
теоремой взаимности оптимальные планы двух моделей совпадают,
трудовые ресурсы используются полностью, а оптимальные оценки
продукции пропорциональны.
Модель (8.30) сохраняет основные свойства оптимального плана
и оптимальных оценок модели (8.29): 1) производятся все продукты
и каждый продукт производится только одним способом (для этого
должно выполняться одно из условий: либо матрица способов неразло¬
жима, либо все щ > 0) ; 2) выбор лучших способов и оптимальные
оценки не зависят от заданий по конечной продукции (ассортиментных
коэффициентов); 3) не производится ’’излишков” конечной продук¬
ции.
Отметим важное новое свойство: набор производственных способов
в оптимальном плане и значения оптимальных оценок не зависят от
величины имеющегося ресурса. Действительно, поскольку L есть един¬
ственная отличная от нуля компонента вектора ограничений задачи, то
изменение L означает растяжение или сжатие вектора ограничений. Но
такое преобразование не влияет на базис оптимального плана.
Вектор объемов производства и затраты трудовых ресурсов выража¬
ются через матрицы коэффициентов полных затрат, сформированных
из ’’лучших” способов:
Х* = (Е -/l»r1a2 = p*z, (8.31)
t* = (£ — Л *) -1 a z = t*z. (8.32)
где j3* = (E - A*)'1 a — вектор потребностей в выпуске продукции для
получения одного комплекта конечной продукции, т* = t(E - А*)~1 а —
полные трудовые затраты для получения одного комплекта конечной
продукции.
Максимальное число комплектов составляет
(8.33)
Подстановка (8.33) в (8.31) дает
244
т.е. максимальное число комплектов и объемы производства прямо про¬
порциональны количеству имеющихся трудовых ресурсов. Оптимальная
* 1 ~
оценка трудовых ресурсов w* = —является постоянной величинои.
Вывод о том, что изменение объемов и структуры конечной продук¬
ции (при Y > 0) не оказывает никакого влияния на выбор лучших про¬
изводственных способов, позволяет расчленить процесс оптимизацион¬
ных расчетов и анализа оптимальных решений на три стадии: 1) нахож¬
дение лучших производственных способов и минимальных затрат труда
при заданном векторе конечной продукции на основе модели(8.29);
2) определение объемов и структуры переменной части конечной про¬
дукции (можно использовать различные критерии и условия макси¬
мизации) ; 3) расчет сбалансированного плана производства, обеспе¬
чивающего выпуск конечной продукции при ограниченных трудовых
ресурсах.
В качестве примера рассмотрим модель, включающую условия максимизации
ЦФП.
Решив задачу (8.29) с У0 = 0, определим матрицу А*, вектор оптимальных
оценок продукции, равных коэффициентам полных затрат, исчисленным по луч¬
шим производственным способам V* = Г* потребности в трудовых ресурсах для
обеспечения постоянной части конечной продукции T*Q и остаток трудовых ресур¬
сов для выпуска переменной части конечной продукции L = L - T*Q > 0.
На второй стадии решается задача максимизации ЦФП при ограниченных трудо¬
вых ресурсах:
и (У) —► max,
(8.35)
F > о.
Решение задачи (8.35) дает вектор Y*. В соответствии с условиями Куна -
Таккера
ui(Y*Xw*Tu tg/,
и,(К*)ад*7\*, у] >0,
~P-=w\ ус > 0. (8.36)
t
Таким образом, в оптимальном плане рассматриваемой модели предельные
полезные эффекты используемой конечной продукции пропорциональны полным
трудовым затратам, исчисленным по лучшим производственным способам. Опти¬
мальная структура конечной продукции ’’подбирается” так, чтобы отношения
(8.36) выравнялись по всем используемым видам конечной продукции. Но выбор
структуры конечной продукции не оказывает никакого влияния на значения
оптимальных оценок продукции. /
На третьей стадии расчетов по модели находим вектор объемов производства
X* = А *Х* + Q + Y*; он будет сбалансирован с имеющимися трудовыми ресурса¬
ми. Аналогичным образом проводятся расчеты по модели, включающей другие
возможные критерии и условия максимизации конечной продукции.
245
Расширенные оптимизационные модели. Анализировавшиеся в
данном разделе оптимизационные межотраслевые модели характеризу¬
ются специфическими свойствами, создающими значительные удоб¬
ства при проведении оптимизационных расчетов и анализе оптимальных
решений. Однако эти свойства не являются адекватным отражением оп¬
тимизируемой реальной экономики, а обусловлены тем, что выбор про¬
изводственных способов осуществляется с позиций наиболее эффек¬
тивного использования только одного ограниченного ресурса — труда.
Решения, получаемые с помощью рассматриваемых моделей, должны
интерпретироваться как условно оптимальные, получаемые
в предположении, что трудовые ресурсы являются единственным дефи¬
цитным ресурсом в народном хозяйстве. Эти условно оптимальные
решения должны затем корректироваться с учетом использования дру¬
гих ограниченных ресурсов.
Проведенный анализ упрощенных моделей (включая рассмотренные
в 8.3) позволяет вывести ряд правил построения оптимизационных
моделей народного хозяйства. Очевидно, что одностороннее развитие
модели (только увеличение числа учитываемых ресурсов или только
увеличение числа включаемых в модель производственных способов)
оказывается малорезультативным, так как значительная часть вводимой
в модель информации не оказывает влияния на оптимальное решение.
Конструкция модели должна быть ’’сбалансирована” по составу вклю¬
чаемых элементов.
Условия оптимизационных моделей с производственными спо¬
собами следует дополнять ограничениями по ряду невоспроизводимых
ресурсов (как в 8.3), а также другими условиями и факторами, изучав¬
шимися в гл. 7. В результате такого расширения моделей свойства
оптимальных решений существенно усложняются. Однако поэтапный
анализ условно оптимальных решений (при временном отключении
некоторых условий) позволяет прослеживать связь со свойствами
простых оптимизационных моделей (подробнее об этом см. в ММСЭ,
с. 332 - 334).
Основное прикладное назначение оптимизационных статических
межотраслевых моделей — расчеты и анализ вариантов краткосрочных
(годовых) планов развития народного хозяйства. Но значение исследо¬
ваний статических моделей этим не ограничивается. Статические модели
для отдельных временных отрезков являются составными частями
моделей, объединяющих условия развития народного хозяйства за ряд
лет. Поэтому построение и анализ статических моделей — это неизбеж¬
ный этап разработки и освоения более сложных динамических моделей
народного хозяйства.
246
8.5. Оптимизационные модели с блоком
внешнеэкономических связей
Включение в оптимизационную межотраслевую модель условий внешне¬
экономических отношений расширяет возможности оптимизации народ¬
нохозяйственных решений.
В наиболее простом виде внешнеэкономические связи учитываются
в оптимизационной модели как свободные переменные экспорта vj и им¬
порта W(, вводимые в балансы производства и распределения продукции,
а также одного ограничения на минимально допустимое сальдо внешне¬
торгового обмена (7.22).
Дополнение моделей, рассмотренных в 8.3 и 8.4, этими условиями
изменяет свойства оптимальных решений. Собственное производство
некоторой продукции может замещаться импортом, в оптимальный
план может включаться дополнительный способ производства, оптималь¬
ные оценки продукции становятся зависимыми от экспортных и импорт¬
ных цен и т.д.
Однако получаемое при этих условиях оптимальное решение оказы¬
вается ’’бедным” с точки зрения материально-вещественной структуры
внешнеторгового оборота. В оптимальные планы попадают экспорт и
импорт ограниченного числа видов продукции, а оптимальные планы
простейших моделей, например (8.29), (8.30), включают, как правило,
не более одного экспортируемого и не более одного импортируемого
вида продукции.
Для получения более содержательных решений с точки зрения
структуры внешнеэкономических связей и их влияния на народнохо¬
зяйственные пропорции необходимо включать в оптимизационные
модели более дифференцированное описание блока внешнеэкономиче¬
ских связей. Отметим некоторые возможные подходы.
1. Отражение условий торговли на отдельных рынках. Торговые
отношения с различными партнерами осуществляются, как известно,
при разных условиях (используемые валюты, соотношения экспорт¬
ных и импортных цен, условия кредитования и т.д.). Поэтому условия
сбалансированности внешней торговли должны выполняться не только
в целом, но и по видам рынков и даже двусторонним связям. Пусть
к — индекс внешнего рынка (например, это рынок СЭВ, или рынок со
свободно конвертируемой валютой, или рынок с клиринговыми расче¬
тами), к Е S. Тогда в оптимизационную модель включаются условия:
р(У„-рГ^к^Ак, k$S, (8.37)
При этом для обеспечения общей финансовой сбалансирован¬
ности могут устанавливаться ограничения на вектор величин Д£,
kes.
247
2. Включение ограничений спроса и предложения по группам това¬
ров. Учитывая предельные емкости отдельных рынков по экспорту и
импорту, долгосрочные торговые соглашения, а также внешнеполитичес¬
кие условия, на отдельные внешнеторговые переменные v^ и W/# могут
накладываться односторонние и двусторонние ограничения:
cT<Vik<c?r, (8.38)
dT < Щ* < dT\
при этом все параметры — неотрицательны.
3. Учет зависимостей внешнеторговых цен от объемов торговли.
Масштабы внешнеэкономической активности СССР оказывают сущест¬
венное влияние на цены мировых рынков и двусторонних сделок. При
значительном увеличении экспорта цена на соответствующий товар,
как правило, снижается, при увеличении же импорта цена может и повы¬
шаться. Зависимости валютной выручки (затрат) от объемов экспорта
(импорта) можно выразить в виде кусочно-линейных функций. В част¬
ности, общая выручка от экспорта /-й продукции на рынок к составит
2 Piku vikn> где vikiX - объем экспорта на отрезке [сгЛ:м_1, с/£м], кото¬
рому соответствует неизменная цена
Расчеты по оптимизационной народнохозяйственной модели с внеш¬
неэкономическими связями не принимают во внимание, что определя¬
емые варианты внешней торговли могут противоречить интересам дру¬
гих стран или нарушают сбалансированность мировой экономической
системы. Это абстрагирование приемлемо только на стадии выявления
направлений развития внешнеэкономических связей, эффективных с по¬
зиций народного хозяйства. Мировая экономика не только воздействует
на экономику СССР, но и испытывает заметное влияние внешнеэкономи¬
ческой деятельности СССР. Поэтому более адекватным подходом к мо¬
делированию участия СССР в международном разделении труда является
включение модели СССР в глобальную экономическую модель1.
8.6. Оптимизационные
межрегиональные модели
Оптимизационные межрегиональные межотраслевые модели (ОМММ)
представляют собой такие конкретизации третьей схемы объединения
См., например: Будущее мировой экономики. Доклад группы экспертов
ООН во главе с В.Леонтьевым. М.: Международные отношения, 1979; Межреги¬
ональные межотраслевые модели мировой экономики. Новосибирск: Наука, 19,83i.
Применяемые в указанных работах модели по своей структуре близки межреги¬
ональным межотраслевым моделям, рассматриваемым в 7.6 и 8.6.
248
региональных моделей (см. 7.6), в которых сохраняется свобо¬
да выбора межотраслевых и межрегиональных связей.
Основные элементы ОМММ уже изучались выше. Это народнохозяй¬
ственные критерии оптимальности — 8.2, условия региональных межот¬
раслевых блоков, включая особенности транспорта, — 7.5, условия меж¬
региональных связей — 7.6.
Рассмотрим одну из модификаций статической ОМММ со следую¬
щими обозначениями:
х[ — объем производства й продукции в регионе г\
хгт — объем продукции транспорта в регионе г;
х^— объем поставки z-й продукции из региона г в регион s (непо¬
средственно учитываются связи только между смежными регионами);
z — фонд потребления в целом по стране;
q[ — фиксированная часть конечной продукции /-го вида в регионе г\
Nf — объем z-й продукции, который может быть получен с имеющих¬
ся производственных мощностей в регионе г\
Lr — лимит трудовых ресурсов для производственной сферы в ре¬
гионе г;
а?- — затраты /-й продукции на производство единицы /-й продукции
в регионе г \
a^j — затраты z-й продукции на единицу транспортной работы в ре¬
гионе г\
arTrj— затраты транспортной работы на внутрирегиональные перевоз¬
ки единицы /-й продукции в регионе г\
а™— затраты транспортной работы на перевозку единицы/-й продук¬
ции из региона г в регион s\
t- — затраты труда на производство единицы /-й продукции в регионе
г;\
trT — затраты труда на единицу транспортной работы в регионе г;
аГ — доля фонда потребления, приходящаяся на использование z-й
продукции в регионе г(2а[= 1).
г, i
Модель включает следующие условия:
1. Балансы производства и распределения продукции
x?i ^ 2 o!ijXrj “Ь ^ xris— 2 хъ{ I* 6 Л (8.39)
/ € / S Ф Г S Ф Г
2. Балансы работы транспорта
А. > 2 arxri(xrj+ 2 х8/— 2 хгЛ + 2 агх)х]\ r£R\
/ € / \ s ’Ф- г $ф г ) бф г, jel
этом предполагается, что затраты на межрегиональные перевозки
йёсет регион-отправитель (до смежного региона-получателя).
249
После преобразования условий получаем:
Ху= 2 а^х) + 2 Щ—а%)хГ,*+ 2 a"tfs, r£R. (8.40)
/ 6 У s ФТГ S ф г
/ 6 I
3. Балансы трудовых ресурсов
2 trjxrj + trxxrx^Lr, r£R. (8.41)
/€/
Хотя трудовые ресурсы распределены между регионами (так, чтобы
D Lr = L), но после получения оптимального решения можно скор-
r G R г
ректировать величины L , ориентируясь на соотношения оптимальных
оценок труда (перераспределяя часть трудовых ресурсов из регионов с
низкими оценками в регионы с высокими оценками).
4. Ограничения на производственные мощности
/€/, r£R (8.42)
5. Критерий оптимальности
zmах (8.43)
Ассортиментные коэффициенты а[ одновременно характеризуют и
материально-вещественную, и территориальную структуру фонда потреб¬
ления. Доля региона г в народнохозяйственном фонде потребления со¬
ставляет
kr= 1 а[,
i € /
Решение задачи (8.39) — (8.43) при фиксированном векторе X = (\г),
\г > 0, XXr = 1 дает вариант развития регионов и страны, который яв¬
ляется эффективным (оптимальным по Парето) в том смысле,
что его нельзя улучшить в интересах какого-либо региона, не ухудшая
положения хотя бы одного другого региона.
На примере ОМММ можно продемонстрировать существенные
различия ’’точечных” и ’’пространственных” моделей народного хо¬
зяйства.
В 8.3 анализировалась точечная оптимизационная модель (8.22)
с ограничениями на производственные мощности и показывалось, что
в оптимальном плане модели полностью используется мощность, как
правило, только одного вида продукции (единственное ’’узкое” место).
Если из рассматриваемой ОМММ исключить ограничения по трудовым
250
ресурсам (8.41), то получим полностью сопоставимое пространственное
обобщение модели (8.22). Однако благодаря возможностям простран¬
ственного перемещения продукции, производимой в разных регионах
на ограниченных мощностях, в оптимальном плане межрегиональной
модели обеспечивается более полное использование мощностей раз¬
личных отраслей. Допустима и такая ситуация, когда мощности во всех
регионах полностью используются. Этой ситуации соответствуют наибо¬
лее интенсивные межрегиональные связи (по числу положительных
переменных х™).
ОМММ применяются для исследования влияния территориальных
факторов на тенденции развития народного хозяйства, выработки
концепции развития и размещения производительных сил, обоснова¬
ния важнейших территориальных пропорций, оценки возможностей и
последствий сближения региональных уровней экономического разви¬
тия и благосостояния. Для исследования проблем долгосрочного харак¬
тера и связанных с распределением и использованием значительных капи¬
тальных вложений применяются динамические постановки ОМММ (см.
[3. С. 87 -99]).
Литература
Канторович Л.В. Экономический расчет наилучшего использования ресурсов.
М.: Изд-во АН СССР, 1959.
Моделирование народнохозяйственных процессов. М.: Экономика, 1973.
Гл. XII.
Система моделей народнохозяйственного планирования. М.: Наука, 1982.
Разд. 1, гл. 4; Разд. 3, гл. 4.
ЧАСТЬ Б.
ЭКОНОМИЧЕСКАЯ ДИНАМИКА
Предмет экономической, динамики - исследование важнейших аспек¬
тов развития экономической системы, качественных и количественных изменений
производительных сил, производственных отношений, хозяйственного механизма.
Если экономическая статика изучает допустимые и рациональные состояния
экономики, то экономическая динамика исследует процессы (последователь¬
ности состояний и переходы от одних состояний к другим), определяет возможные
и лучшие траектории развития.
По своей проблематике экономическая динамика является не только обобще¬
нием экономической статики; она охватывает и качественно новую область проб¬
лем. Эти проблемы вытекают из воспроизводственного подхода
к экономическому развитию. В соответствии с теорией общественного воспроизвод¬
ства функционирование экономики рассматривается как непрерывно возобновля¬
ющийся процесс, как последовательность повторяющихся и взаимосвязанных
воспроизводственных циклов.
При статическом подходе в системе общественного производства выделяются
три последовательно связанные макроэлемента: 1) производственные ресурсы
как ’’вход” экономической системы, 2) процесс производства как трансформация
ресурсов в продукцию, 3) продукция, направляемая на различные цели. Отличите¬
льная особенность статической схемы — отсутствие обратных связей ’’продукция —
ресурсы”.
Цикл общественного производства, рассматриваемый в рамках экономической
динамики (процесса общественного воспроизводства), имеет более сложную
структуру (см. рис. Д.2). Принципиальной особенностью приводимой схемы
является включение источников пополнения производственных ресурсов и об¬
ратных связей, характеризующих воздействие конечной продукции данного цикла
производства на последующий ход воспроизводства.
Согласно схеме только продукция, используемая на оборонные нужды, пол¬
ностью выбывает из дальнейшего воспроизводственного процесса. Обратные свя¬
зи от процесса потребления отражают влияние повышения уровня удовлетворе¬
ния материальных и духовных потребностей населения, а также механизмов рас¬
пределения потребительских благ на демографические процессы и эффективность
использования производственных ресурсов. Эти связи, имеющие не производст-
венно-техно логический, а социальный характер, обозначаются пунктиром.
Таким образом, воспроизводственный подход к экономическому развитию
порождает целый ряд проблем, не возникающих в рамках статического анализа:
воспроизводство населения и природной среды; распределение производимой
конечной продукции на текущие нужды и будущее развитие; определение режимов
воспроизводства производственных ресурсов (в особенности основных произ¬
водственных фондов); взаимосвязь и согласование циклов воспроизводства
населения, трудовых ресурсов, производственных фондов, общественного про¬
дукта, потребительских благ и т.д. Особо важное значение на современном этапе
развития социалистической экономики приобрела проблема интенсифика¬
ции общественного производства — обеспечение дальнейшего экономического
развития не за счет увеличения массы вовлекаемых ресурсов, а главным образом
за счет повышения эффективности их использования и качества выпускаемой
продукции.
Часть Б объединяет пять глав. В гл. 9 рассматриваются основные категории эко¬
номической динамики, используемые в исследованиях тенденций и закономерно¬
стей экономического развития, а также некоторые простейшие динамические мо-
252
Население
Производ¬
ственные
-►
Процесс
производст¬
—►
Продукция
Процесс
потребле-
ресурсы
ва
ния
Природная
среда
Рис. Д.2. Цикл общественного производства
дели (трендовые, факторные, лаговые). Гл. 10 посвящена анализу и применению
макроэкономических (крупноагрегированных) моделей в исследованиях проблем
расширенного воспроизводства. В гл. 11 изучаются теоретические структурные
(детализированные) модели как инструмент анализа количественных взаимоза¬
висимостей между технологией производства, структурой производства и темпа¬
ми роста. Вместе гл. 10 и 11 образуют единый проблемно-методологический блок.
Гл. 12 и 13 носят более прикладной характер. Вначале рассматриваются основные
конструктивные элементы межотраслевых динамических моделей, а в заключи¬
тельной главе дается анализ основных типов межотраслевых моделей и решаемых
с их помощью задач прогнозирования и планирования.
Изучение взаимосвязанных разноаспектных и взаимодополняемых динамичес¬
ких моделей базируется на знании моделей экономической статики. Наиболее ва¬
жные связи между главами второго раздела показываются на рис. Д.1.
ГЛАВА 9
ОСНОВНЫЕ ПОНЯТИЯ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ
9.1. Характеристики экономического развития
Траектории и динамические рады. В основе динамического анализа ле¬
жит понятие траектории. Траектория описывает состояние изучае¬
мого объекта (или значения изучаемого показателя) как функцию от
времени:
Q = Q(t), /€[0, Г], (9.1)
где [О, Т] — конечный отрезок, на котором определена траектория1.
При этом время t может учитываться как по моментам (или интер¬
валам), так и непрерывно2. В первом случае (9.1) называют также ди¬
намическим (временным) рядом. По временному призна¬
ку экономические показатели делятся на моментные (например, числен¬
ность населения и объем основных фондов на начало года) и интерваль¬
ные (объем производства за год и т. п.).
В табл. 9.1 приводятся несколько динамических рядов интервальных
показателей. Они будут использоваться в дальнейшем для расчетов ха¬
рактеристик экономического развития, трендов, производственных
функций.
Динамические модели прогнозирования и планирования, оперирую¬
щие с дискретным временем, так или иначе связаны с определением ве¬
личин (скаляров или векторов), образующих динамический ряд. Напри¬
мер, если период планирования равен Т лет и разбит на годовые отрезки,
то, зная х (0), необходимо определить * (1), х (2), ..., х (7). В средне¬
срочных и долгосрочных прогнозах и планах все задания и ориентиры
также выражаются в тех или иных показателях динамического ряда.
Применение динамических рядов в анализе, прогнозировании и пла¬
нировании требует введения системы показателей, характеризующих их
свойства и тенденции изменения.
1 В теоретических моделях экономической динамики исследуются также беско¬
нечные траектории: t Е [0, °°].
2 Этим формам регистрации времени соответствуют два типа уравнений динами¬
ческих моделей: конечно-разностные и дифференциальные.
254
Таблица 9.1
Динамические ряды некоторых показателей экономического
и социального развития СССР за 1975-1985 гг.*
Год
Произведенный
национальный
доход (в сопо¬
ставимых ценах),
млрд. руб.
Капитальные
вложения в на¬
родное хозяйство
(в сопоставимых
ценах), млрд. руб.
Валовой
сбор
зерна,
млн. т
Число
родивших¬
ся, тыс. чел.
1975
397,5
128,5
140,1
4611
1976
418,6
134,3
223,8
4720
1977
439,7
139,2
195,7
4693
1978
460,8
147,6
237,4
4763
1979
472,8
148,7
179,2
4807
1980
490,9
150,9
189,1
4851
1981
505,9
156,5
158,2
4961
1982
527,0
161,9
186,8
5100
1983
548,1
171,0
192,2
5392
1984
563,2
174,3
172,6
5387
1985
584,2
179,5
191,7
5374
* Рассчитано по справочникам ” Народное хозяйство СССР
Характеристики скорости и интенсивности изменения динамического
ряда. Основными показателями развития являются абсолютный
прирост, темп роста, темп прироста. В динамическом ана¬
лизе эти показатели важно использовать совместно.
Вначале рассмотрим основные показатели изменения динамического
ряда двух последовательных моментов (интервалов) времени — 0 и 1:
абсолютный прирост:
(9.2)
темп роста:
тепм прироста:
^i/o — Qi Qo»
Qi
Pl/0 “ Qo
(9.3)
(9.4)
Абсолютный прирост за единицу времени характеризует скорость
изменения уровня, темп роста характеризует интенсивность из¬
менения, темп прироста — относительную скорость изме¬
нения.
Показатели изменения динамического ряда могут вычисляться при
постоянной и переменной базе. За постоянную базу принима¬
ется один уровень динамического ряда, как правило, начальный. Пере-
255
Таблица 9.2
Показатель
База показателя
постоянная (базисный
показатель)
переменная (цепной показатель)
Абсолютный
прирост
Темп роста
Темп прироста
Sf/o -Qt~ Qo
Qt
Vo Q0
Qt - Qo
P'/o~ Qo
$t/(t - lj -Qt ~ Qt - l
_ . Qt
vt/ft - ij =^—i
Qt-Qt-l
Ptl(t-X) - - Qt l
менной базой служит предшествующий уровень. Показатели на постоян¬
ной базе называются базисными, а на переменной базе — цепны¬
ми (см. табл. 9.2).
Между базисными и цепными абсолютными приростами и темпами
роста существуют формулы взаимоперехода (см. ДМНХ, с. 11-12).
В качестве количественной иллюстрации введенных понятий рас¬
смотрим данные о росте национального дохода СССР, рассчитанные по
табл. 9.1 (см. табл. 9.3).
Предельные (непрерывные) абсолютные и относительные приросты.
В теоретическом анализе экономической динамики удобно рассматри¬
вать время и показатели динамического ряда как непрерывные величи¬
ны, обладающие в ряде случаев дополнительными свойствами (диффе¬
ренцируемость и т.д.). Это позволяет применять для характеристики
Таблица 9.3
Характеристики динамики произведенного
национального дохода СССР за 1976-1985 гг.
Год
Абсолютный прирост,
млрд. руб.
Темп прироста, %
Абсолютное
ускорение,
млрд. руб.
базисный
цепной
базисный
цепной
1976
21,1
21,1
5,3
5,3
3,1
1977
42,2
21,1
10,6
5,0
0,0
1978
63,3
21,1
15,9
4,8
0,0
1979
75,3
12,0
18,9
2,6
-9,1
1980
93,4
18,1
23,5
3,8
6,1
1981
108,4
15,0
27,3
3,1
-3,1
1982
129,5
21,1
32,6
4,2
6,1
1983
150,6
21,1
37,9
4,0
0,0
1984
165,7
15,1
41,7
2,8
-6,0
1985
186,7
21,0
47,0
3,7
5,9
256
’’поведения” траектории аппарат дифференциального исчисления. Соот¬
ветствующие характеристики скорости и интенсивности будем называть
непрерывными.
Непрерывный абсолютный прирост является производной абсолют¬
ной величины по времени:
J(fl_ tun (9.5)
д/ -► о ьг at
Непрерывный темп прироста является производной по времени ло¬
гарифмической функции абсолютного показателя:
dQ (t)
dt dlnQ(t) м
pW="W - = sr— (9-6)
Дополнительной характеристикой скорости развития является
абсолютное ускорение
Ф# = б»+о/г—<9-7)
Оно измеряется как разность между последующим и предшествующим
абсолютными приростами. Для непрерывного случая — это вторая произ¬
водная абсолютной величины по времени:
~ _ тп = d*Q(t) 9 8)
~ dt dt2 ' ' ;
Средние характеристики развития. Для обобщающей оценки скорос¬
ти и интенсивности изменения динамического ряда используются средние
характеристики. В свою очередь, для исчисления средней каждого пока¬
зателя применяется множество способов. Эти способы, как правило, ори¬
ентированы на решение различных содержательных экономических за¬
дач. Наибольшее значение имеют два принципа исчисления средней:
1) исходя из общего абсолютного прироста за период; 2) исходя из сум¬
мы абсолютных уровней за период.
Средний абсолютный прирост. Определяющим условием первого,
наиболее распространенного способа исчисления данного показателя
является величина абсолютного прироста за весь период:
т
X 14 J )
= = QL~qo , (9.9)
Второй способ ориентирован на сумму абсолютных уровней за
период: ^
Т t-1 _ 2 (ZQt — TQ0) /q i л\
2 T (Т 4- П Т(Т+\) '
9 3ак. 2414 257
Таблица 9.4
Средние абсолютные приросты и средние темпы прироста
капитальных вложений в народное хозяйство СССР
(в сопоставимых ценах)
Период
Абсолютные при¬
росты, млрд. руб.
Темпы прироста,
%
*1
*2
Р1
Р2
Седьмая пятилетка (1961-1965 гг.)
3,32
2,83
6,17
5,56
Восьмая пятилетка (1966-1970 гг.)
5,60
5,13
7,51
7,28
Девятая пятилетка (1971-1975 гг.)
7,26
6,83
6,87
6,82
Десятая пятилетка (1976-1980 гг.)
4,48
5,21
3,27
3,86
Одиннадцатая пятилетка (1981-1985 гг.)
8,48
5,91
3,53
3,72
Величина 02 есть средняя арифметическая из последовательных цеп¬
ных абсолютных приростов, взвешенная по их порядковым номерам,
взятым в обратной последовательности1. Зная (или задав) значение <$2,
можно определить сумму значений интересующего показателя за Тлет:
т
2
г= 1
(9.11)
Показатели 61 и <$2 равны между собой, если последовательные абсо¬
лютные приросты постоянны (рост по линейному закону) . При последо¬
вательном увеличении цепных абсолютных приростов > 62 и наоборот.
Второй показатель среднего абсолютного прироста имеет особое
значение для характеристики динамики капитальных вложений, посколь¬
ку пятилетний план включает задание по объему капитальных вложений
за пять лет. Сравнение показателей средних абсолютных и относительных
приростов дается в табл. 9.4.
Средний темп роста. Задачам обобщенной оценки интенсивности эко¬
номического развития в наибольшей степени отвечают две модификации
среднего темпа роста: средний геометрический и сред¬
ний параболический (полиномиальный).
Первый показатель ориентирован на общий темп роста за период и
представляет собой среднюю геометрическую из последовательных цеп¬
ных темпов роста:
£ ГГ! Гр Q ГГ!
17! = у/Щ(( - 1) = V ЧТо = V-Q—
(9.12)
Второй показатель ориентирован на сумму динамического ряда.
Задача ставится следующим образом: определить темп роста, при кото¬
ром исходя из начального уровня можно получить заданную сумму уров-
1 Вывод формулы см. в [2. С. 29-30].
258
т
ней за период (т.е. известны <2о и Б Qt). Тогда т?2 определяется решени-
t=1 1
ем уравнения
Величина т?2 — это положительный корень данного уравнения (пара¬
болы Г-го порядка). При Т> 2 уравнение не имеет аналитического реше¬
ния. Поэтому вычисления т?2 осуществляются приближенными методами»
(в частности, методом Ньютона) или же по специальной таблице1. _
Средний темп r?i зависит только от крайних значений ряда, темп т?2—
от всех значений._Если цепные темпы роста постоянны в течение всего
периода, то 771 = Т72. Если цепные темпы уменьшаются, то т?х < г\г и на¬
оборот.
9.2. Типы экономического развития. Трендовые модели
Сглаживание динамических рядов и трендовые модели. В составе дина¬
мического ряда в принципе можно выделить четыре компоненты: 1) гла¬
вную (’’вековую”) тенденцию, или тренд; 2) регулярные колебания
относительно тренда (типа циклов); 3) сезонные колебания; 4) оста¬
ток, или случайную компоненту, отражающую влияние разнообразных
факторов стохастического характера. Не обязательно, чтобы конкретный
динамический ряд включал все указанные компоненты; это зависит от
сущности процесса, выражаемого динамическим рядом. Для рядов,
характеризующих динамику мак ро процессов социалистической эконо¬
мики, типично присутствие по крайней мере первой и четвертой ком¬
понент.
Одной из важнейших задач исследования динамических рядов явля¬
ется установление общих закономерностей или тенденций развития. Для
решения этой задачи используются разнообразные приемы уменьшения
колеблемости динамического ряда (сглаживающие фильтры), среди
которых можно выделить два основных метода: сглаживание ряда с
помощью скользящей средней и аналитическое выравнивание.
Метод скользящей средней состоит в том, что средние показатели
рассчитываются последовательно по периодам (1, /), (2, 7 + 1), (3,7+ 2)
и т.д. Если период равен пяти годам (7 = 5), то среднегодовые величины
условно приписываются к третьему году соответствующего пятилетия.
Метод скользящей средней используется при определении базы контракт¬
фрагмент из таблицы для определения средних параболических (полиномиаль¬
ных) темпов роста приводится в ДМНХ, с. 16. Ои. также: Казинец JI. С Темпы рос¬
та и абсолютные приросты. М.: Статистика, 1975. С. 183-187; Четыркин Е. М. Ста¬
тистические методы прогнозирования. 2-е изд. М.: Статистика, 1977. С. 191.
9* 259
ных цен на основе усреднения предшествующего пятилетнего ряда цен
мирового рынка, а также в других областях планово-экономических рас¬
четов, требующих сглаживания сильных колебаний. Ограниченность
метода скользящей средней в том, что он слабо учитывает специфику
заключающихся в динамических рядах трендов и колебаний.
Аналитическое выравнивание динамического ряда — это метод выра¬
жения тенденций развития в виде функции изучаемого показателя от
времени, называемой моделью тренда. Возможность построения
и сравнения различных моделей тренда облегчает задачу отражения спе¬
цифических черт инерционности (эволюционности) развития разнообраз¬
ных экономических процессов.
Типы экономического развития и их трендовые модели. Различные
экономические процессы и один и тот же процесс, но в разные промежут¬
ки времени могут существенно различаться по характеристикам разви¬
тия. За основу типизации экономического развития удобно взять дина¬
мику абсолютных приростов. В этом случае можно выделить как мини¬
мум четыре типа экономического роста:
I — постоянный рост (характеризуемый постоянным или близким к
нему абсолютным приростом);
II — увеличивающийся рост (характеризуемый увеличивающимся
абсолютным приростом);
III — уменьшающийся рост (характеризуемый уменьшающимся абсо¬
лютным приростом);
IV — рост с качественным изменением характеристик на протяжении
рассматриваемого периода1.
Рассмотрим трендовые модели, отражающие основные особенности
типов экономического роста. Поскольку важным свойством тренда
является гладкость, при выборе трендовых моделей предпочтение отдает¬
ся непрерывным и дифференцируемым функциям. В отличие от показа¬
теля фактического динамического ряда Q значения трендов будем обоз-
начать .
Тип роста I. Экономический рост с постоянным абсолютным прирос¬
том описывается линейной функцией
xt=a + bt, (9.14)
где а — теоретический уровень базисного года; Ъ — постоянный ежегод¬
ный абсолютный прирост (Ъ =~jj~ = <5) •
Темп прироста pt = монотонно убывает и асимптотически
приближается к нулю. Заметим, что если аппроксимируется динамика
прошлого развития, то параметры а и Ъ могут не совпадать с фактичес¬
ким уровнем базисного года £>0 и средним абсолютным приростом 5 х.
1 Аналогичную классификацию можно построить для динамики с систематичес¬
ким снижением абсолютного прироста.
260
Тип роста II. Характерный случай развития с увеличивающимся абсо¬
лютным приростом описывается показательной или экспоненциальной
функциями:
Xf = a(l-{-ЬУ; (9.15)
xt = aebt, (9-16)
где а — теоретический начальный уровень (а > 0) ; b — постоянный темп
прироста.
В (9.15) b — дискретный темп ежегодного прироста (Ь = р), в
(9.16) — непрерывный темп прироста (b = р). Абсолютные приросты
рассматриваемых функций непрерывно возрастают.
Из сравнения двух эквивалентных представлений (9.15) и (9.16)
одной и той же траектории xt следует:
(1+р)=ер. (9-17)
В соответствии с формулой разложения экспоненты в степенной ряд
ef> = 1 + р + 2
*=2
откуда следует, что 1 + р> 1 + рир>р. Только при достаточно малых
р и р и ограниченном t можно считать (1 + Ь)г я&еЪг
Например, & =0,05иГ=5; тогда
(1+&)‘= 1,276, (Р* = 1.284 ,
т.е. разность меньше одного процентного пункта. Но, например, если Ъ = 0,10 и
t — 20, то
(l+ft)< = 6,724, ew = 7,389,
а разность превышает 56 процентных пунктов.
Другой характерный случай в рамках типа II — рост с постоян¬
ным абсолютным ускорением Этот случай описывается
параболой второго порядка с положительными параметрами:
xt = a + bt + ctat (9.18)
для которой
8t = b + 2ct, ф = 2с.
Темп прироста функции (9.18) — переменная величина:
b+2ct
" a+bt+ct2 *
Она может изменяться двояким образом: 1) либо монотонно убыва¬
ет; 2) либо на начальном интервале времени возрастает, а затем убывает
(подробнее см. ДМНХ, с. 21).
261
Функция (9.18) хорошо отражает тенденции развития многих эконо¬
мических процессов, когда абсолютные приросты продолжают увеличи¬
ваться, а темпы прироста снижаются. Более широкими аппроксимацион-
ными возможностями обладают параболы высших порядков. Но их
общим недостатком является необходимость оценивания большего
числа параметров.
Для анализа динамики типа II удобна также обобщенная
экспоненциальная функция, исходящая из предположения
переменных темпов прироста:
dxdt
р*=—•
Проинтегрировав это выражение в интервале от 0 до г, получаем
Г Р tdt
Xi = XJ (9-19)
В качестве функций pf могут использоваться анализировавшиеся
выше линейная, экспоненциальная, параболическая и другие функции.
Тип роста III. В рамках данного типа целесообразно различать: IIIа —
уменьшающийся рост, не имеющий предела; Шб — уменьшающийся
рост, имеющий предел (насыщение).
Моделями тренда, отражающими тип экономического роста Ша,
могут служить, например, следующие функции с положительными пара¬
метрами: линейно-логарифмическая
xt = a + b In 5 = (9.20)
степенная
xt = atby fi = abtb~l, b< 1. (9.21)
Функции, служащие моделями роста типа шб, имеют предел. Это, напри¬
мер, гипербола первого порядка (при а, Ь> 0):
*, = а — limxt = a- (9.22)
1 1 t-+ 00
Тип роста IV. Характерным свойством трендовых моделей, описыва¬
ющих данный тип развития, является наличие точки перегиба t*, в кото¬
рой абсолютное ускорение равно нулю и меняет свой знак:
ф(П = $ = о.
Этим свойством обладает ряд функций, рассматривавшихся выше, но
имеющих параметры разного знака. Ограничимся ситуацией, когда уве¬
личивающийся рост сменяется уменьшающимся ростом. Для этой ситуа¬
ции применимы следующие функции: линейно-логарифмическая второго
262
порядка при с < 0 (t* = е 2с ); парабола третьего порядка при
d<0(t* = - ъТУ
К этому классу трендовых моделей относится также логистическая
функция
*■--!+==*■ (9'23)
имеющая
6f = abce~ct (b + e-ct)-*, <* = lnil, limxt = a
b t -*■ 00
(предел роста).
Более общие задачи анализа динамики с меняющимися тенденциями
развития решаются с помощью квазиполиномов и сплайн-
функций.
Построение трендовых моделей. Методика построения трендовых
моделей экономического развития представляет собой сочетание качест¬
венного экономического анализа и формальных математико-статистичес¬
ких процедур. Построение трендовой модели включает ряд этапов.
1. Выбор класса функций тренда F(t), yjjt) G F(t), k = 1,..., К j .
Разработанные пакеты программ построения и анализа трендовых моде¬
лей включают много десятков временных функций. Для построения
модели определенного экономического показателя целесообразно огра¬
ничить множество испытываемых функций, отобрав те, которые отража¬
ют главные особенности динамики исследуемого показателя.
2. Оценивание параметров функций f^(t) Е F(t). Оценка параметров
трендовых моделей проводится методами регрессионного анализа. Для
линейных и линеаризуемых моделей широко используются модифика¬
ции метода наименьших квадратов. Разработаны также более сложные
методы нелинейного оценивания.
3. Расчет значений формальных критериев аппроксимации. Для
характеристики близости тренда к аппроксимируемому динамическому
ряду применяется несколько формальных критериев: сумма квадратов
отклонений значений тренда от фактических значений, значение коэффи¬
циента детерминации и т.д. Предпочтительны те функции тренда, кото¬
рые имеют лучшие значения критериев.
4. Анализ остаточной компоненты динамического ряда. Остаточная
компонента динамического ряда е (t) должна удовлетворять ряду фор¬
мальных требований (независимость, постоянство дисперсии, подчинение
нормальному закону распределения).
5. Выбор функции тренда. Результатом предшествующих этапов
является построение, как правило, нескольких функций тренда для
одного показателя. Выбор ’’лучшей” функции проводится путем сопо¬
ставления значений формальных критериев аппроксимации, процедур
263
оценивания параметров по их сложности, свойств остаточной компонен¬
ты, а также возможностей экономической интерпретации и использова¬
ния той или иной функции в ретроспективном анализе и прогнозирова¬
нии. Таким образом, данная задача является по своей сути компромис¬
сной, полностью неформализуемой.
При выборе функции тренда важно учитьюать, будет ли она исполь¬
зоваться только для ретроспективного анализа или также для прогнози¬
рования (т.е. за границей периода, для которого оценены параметры
функции). В первом случае требуется, чтобы функция хорошо сглажива¬
ла весь исходный динамический ряд. Если же функция тренда предназна¬
чается для проведения прогнозов, то предпочтение отдается функции,
имеющей лучшие характеристики аппроксимации для последней части
динамического ряда. Это объясняется тем, что тенденции развития, скла¬
дывающиеся в конце ретроспективного периода, оказывают, как прави¬
ло, наибольшее воздействие на будущее развитие.
Пример построения и анализа трендовых моделей. Рассмотрим задачу по¬
строения и выбора трендов произведенного национального дохода СССР за 1975 —
1985 гг., имея в виду их использование не только для анализа прошлых тенденций,
но и для прогнозирования.
В табл. 9.5 даются характеристики шести моделей, имеющих достаточно хоро¬
шие значения стандартной ошибки сглаживания (аосх) и коэффициента детермина¬
ции (R2). Заметно хуже они только у экспоненциальной функции, имеющей посто¬
янный темп прироста (р = 0,037). Линейная, линейно-гиперболическая, параболи¬
ческая и обобщенная экспоненциальная функции отражают примерно постоянный
абсолютный прирост и плавное снижение темпов прироста (например, обобщенная
экспонента - примерно на 0,1 процентных пункта в год). Логистическая кривая
имеет предел роста (а = 978,65). Из функций с четырьмя параметрами выделим
параболу третьего порядка с параметрами: а = 374,30, Ъ = 24,78, с = -1,29, d —
= 0,07 (аост= 4,19, Я2 =0,9989).
Таблица 9.5
Параметры и основные статистические характеристики функций
тренда произведенного национального дохода СССР за 1975—1985 гг..
(в сопоставимых ценах, млрд. руб., Г0 = I960 г.)
Функция
а
Ъ
с
аост
R2
Линейная
382,47
18,21
_
7,29
0,9980
Линейно-гиперболическая
387,03
17,76
-6,879
7,52
0,9979
Экспоненциальная
391,51
0,037
-
18,15
0,9950
Парабола
381,99
18,422
-0,0182
7,26
0,9980
Обобщенная экспоненциальная при
р = Ъ + ct
383,75
0,047
-0,0008
8,21
0,9978
Логистическая
978,65
1,551
0,0750
10,07
0,9972
Прогнозирование на основе трендовых моделей. Сущность методики
экономического прогнозирования с помощью трендов заключается в их
временной экстраполяции. При этом исходят из предположения, что
выявленная для прошлого периода тенденция сохранится и в будущем,
хотя бы ближайшем. Более конкретные условия допустимости и право¬
264
мерности экстраполяции трендов могут быть сформулированы следую¬
щим образом: а) период, для которого построен тренд, достаточен для
выявления тенденции развития; б) анализируемый процесс устойчиво
динамический (а не скачкообразный) и обладает инерционностью;
в) не ожидается сильных внешних воздействий на изучаемый про¬
цесс, которые могут серьезно повлиять на тенденцию развития.
Важное значение имеет нахождение доверительного ин¬
тервала прогноза. Расчет доверительного интервала позволяет опре¬
делить область (интервальный прогноз), в которой с определенной веро¬
ятностью следует ожидать прогнозируемую величину.
В 70-х и первой половине 80-х гг., когда в экономическом развитии
СССР преобладали инерционные тенденции, кратко- и среднесрочные
прогнозы на основе трендовых моделей имели вполне приемлемую точ¬
ность. Ускорение экономического развития в 1985—1986 гг. сделало
невозможным механическое применение трендовых моделей с парамет¬
рами, рассчитанными по прошлому динамическому ряду.
Результаты прогноза произведенного национального дохода на 1981-1983 гг. по
четырем трендовым моделям, построенным по статистике 1970-1980 гг., приво¬
дятся в ДМНХ, с. 29. Фактические значения объема национального дохода находят¬
ся внутри доверительных интервалов прогнозов (при доверительной вероятности
95%): 1981 г. - по всем четырем моделям, 1982 г. - по двум моделям (параболе
второго порядка и линейно-логарифмической функции второго порядка). Ошибки
прогноза за три года находятся в интервале 1,5-3,2%.
Прогноз объема национального дохода на 1986 г. по трендам, приведенным в
табл. 9.5, дает следующие результаты: по линейной функции - 600,9 млрд. руб.
(в тех же неизменных ценах), по параболе второго порядка - 600,5 млрд., по обоб¬
щенной экспоненте с линейной функцией темпа - 598,8 млрд. руб. Фактический же
объем национального дохода в 1986 г. составил 608,3 млрд. руб. Эта величина не
’’попала” даже ни в один доверительный интервал (с вероятностью 95%) прогноза
по всем шести функциям.
Прогнозирование с помощью трендов — один из простейших методов
статистического прогнозирования. Его использование, безусловно,
оправданно при недостаточности знаний о природе изучаемого процесса
или отсутствии статистических данных, необходимых для применения
более совершенных (и, как правило, более сложных) методов прогнози¬
рования. Экстраполяция по трендам может применяться также как на¬
чальный, отправной этап комплексной методики прогнозирования, отве¬
чающий на вопрос о последствиях продолжения прежних тенденций раз¬
вития. В этом случае экстраполяционный прогноз интерпретируется как
один из гипотетических вариантов, с которым сопоставляются другие
варианты прогноза, полученные с помощью более совершенных методов.
Сплайн-функции. Одно из важных требований к функции тренда —
это ее гладкость. Однако не всегда удается подобрать гладкую функцию
с небольшим числом параметров и приемлемой точностью аппроксима¬
ции динамического ряда для всего анализируемого временного интерва¬
ла. В такой ситуации задачу сглаживания динамического ряда можно
решить с помощью интерполяционной, или сглаживающей, сплайн-функ¬
265
ции, представляющей собой кусочно-гладкую функцию, отдельные кус¬
ки которой склеены гладким образом.
В качестве кусков сплайн-функции обычно выбираются многочлены
(полиномы). Полиномиальным сплайном степени п называ¬
ется составленная из кусков полиномов степени не выше п непрерывная
кусочно-полиномиальная функция, все производные которой до порядка
п — 1 включительно непрерывны.
Методику построения и применения сплайн-функций проиллюстри¬
руем на примере кубического сплайна.
Если ось времени t Е (—°°, °°) разделяется на k частей: (tj, tj+i), j =
= О, 1,..., k—\, где t0 = —°°, tk = 00, то на каждом из интервалов (tj, tj+ \),
j = 1, 2,..., k—1 сплайн является кубической параболой
з (t—tfY
S/(*> ~й~'
а на интервале (—°°, tx) — кубической параболой
So (ч — ^ Д/о »
t=Q 11
где ajj — коэффициенты разложения сплайна.
Значения соответствующих коэффициентов параболы третьего по¬
рядка показьюают: д0/ — сглаженное значение динамического ряда в точ¬
ке tj ( j Ф О); aXj — абсолютный прирост в точке tj (; ¥=0)у a2j — абсолют¬
ное ускорение в точке tj (; =£О); a3j — прирост абсолютного ускорения на
интервале (tj, tj+i).
Применение сплайнов вместо обычных функций тренда эффективно,
когда внутри анализируемого периода меняется характер развития. При
этом сплайн помогает выделить подпериоды, внутри которых динамика
показателя не претерпевает сильных изменений.
Сглаживающий кубический сплайн произведенного национального дохода СССР
за 1960-1985 гг. при условии сглаживания |s (tj) - Qtj\ < / G [0,26] имеет
пять подпер йодов: 1960-1961, 1961-1963, 1963-1968; 1968-1973, 1973-1985 гг
(см. табл. 9.6).
До 1968 г. динамика национального дохода СССР характеризовалась положи¬
тельным и увеличивающимся абсолютным приростом. В подпериоде 1968-1973 гг.
Таблица 9.6
Параметры сглаживающего кубического сплайна
произведенного национального дохода СССР за 1960—1985 гг.
(в млрд. руб.)
к
tk
<*0к
а\к
а2 к
аък
0
1961
158,76
10,37
-0,00
0,85
1
. 1963
180,64
12,08
1,71
-0,20
2
1968
258,13
18,06
0,69
-0,14
3
1973
354,17
19,78
0,00
0,00
266
преобладала тенденция к уменьшению абсолютного ускорения (за эти годы абсо¬
лютный прирост увеличился всего на 1,7 млрд. руб.). Наконец, самый длинный под-
период (с 1973 г.) - когда абсолютный прирост национального дохода в среднем
стабилизировался.
Сплайн может соединять как куски одинаковых функций, различаю¬
щихся только значениями параметров, так и разные виды функций. С
помощью сплайнов удобно ’’восстанавливать” отсутствующие (из-за про¬
белов в статистике) элементы динамического ряда. Для прогнозирова¬
ния проще всего использовать последний кусок сплайн-функции. И в
этом случае использование сплайна предпочтительнее простой экстрапо¬
ляции по трендовой модели, построенной по информации последней час¬
ти ретроспективного периода, поскольку при оценке последнего куска
сплайна улавливается переход от более раннего этапа развития к ’’совре¬
менному” этапу.
9.3. Экстенсивные и интенсивные факторы развития.
Факторные модели
Экономическое развитие есть результат взаимодействия многих факто¬
ров, среди которых важно различать экстенсивные и интен¬
сивные. Сочетания этих двух групп факторов определяют типы эко¬
номического роста (расширенного воспроизводства). Экстенсив¬
ный рост — это увеличение производства исключительно за счет
количественного увеличения вовлекаемых ресурсов прежнего качества.
Интенсивный рост — это рост производства исключительно за
счет его совершенствования (в том числе повышения качества использу¬
емых ресурсов) при неизменных физических объемах вовлекаемых
ресурсов. В реальной экономике, как правило, сочетаются признаки и
экстенсивного, и интенсивного роста. В зависимости от преобладания
экстенсивных или интенсивных источников роста можно говорить о
преимущественно экстенсивном и преимущест¬
венно интенсивном типах экономического развития. Так, если
за счет повышения эффективности производства достигается свыше 50%
прироста продукции, то имеем преимущественно интенсивный тип.
Экстенсивный или преимущественно экстенсивный путь развития
народного хозяйства может использоваться только на ограниченных
временных интервалах, поскольку приводит к неизбежному исчерпанию
источников роста. Необходимым условием сохранения высоких темпов
развития при увеличении роли интенсивных факторов является повыше¬
ние эффективности использования производственных ресурсов — выхода
продукции на единицу затрат. Поэтому к числу важных задач экономи¬
ческой динамики относятся измерение и прогнозирование
эффективности производства.
Основными частными показателями экономической эффектив¬
ности являются производительность труда, фондоотдача, выпуск продук¬
267
ции на единицу затрачиваемых сырья и материалов, урожайность и т.п.
Общее свойство этих показателей в том, что они характеризуют действие
каждого производственного фактора в отдельности (’’однофакторный”
подход). Методология определения совокупной (интеграль¬
ной) эффективности используемых факторов производства основыва¬
ется на изучении процесса их взаимодействия (’’многофакторный”
подход). Показатели эффективности производственных факторов
(ресурсов) делятся также на средние и приростные (пре¬
дельные)1.
Однофакторные модели экономического роста. Однофакторная
модель экономического роста выражает зависимость динамики объема
производства (yt) от динамики одного из производственных факторов
(xit):
yt = fi(xit)- (9.24)
Функция (9.24) является динамическим вариантом производ¬
ственной функции, основанной на предположении взаимо¬
дополняемости производственных факторов. Эта функция условно
’’приписывает” результат производства какому-то одному производст¬
венному фактору (в зависимости от его количества, качества, эффектив¬
ности использования). Все однофакторные модели экономического рос¬
та объединяются условием
yt = min f, (Xlt) (9.25)
— (
С функцией (9.24) связаны частные показатели эффективности ис¬
пользования ресурсов: а) поинтервальные (годовые)
.. — у* *
б) средние за период (если х\ — интервальная величина)
__ т I т
M'ffi, rj= 2 yJ 2 хп;
i=i * t=i
в) приростные
Уи —У и
V{^==^=^:-
Из приведенных формул следует, что средние и приростные эффек¬
тивности ресурсов в общем случае — переменные величины; они изменя¬
ются и во времени, и в зависимости от величины используемого ресурса.
При анализе экономической динамики часто ставится вопрос о долях
прироста продукции, получаемых за счет экстенсивных и интенсивных
1 Анализ средних и предельных показателей эффективности для экономической
статики проводился в 4.3.
268
факторов. Попытаемся ответить на этот вопрос, представив объем произ¬
водства как произведение количества используемого ресурса (однород¬
ного состава) на эффективность его использования.
Для простоты опустим соответствующие индексы: у =хц. Прираще¬
ние этой функции за произвольный промежуток времени составит
Ау = (х + Ал:) (ц = fiA* + х&\л + АлгАц
Таким образом, прирост производства разлагается на три слагаемых,
экономический смысл которых можно интерпретировать следующим
образом: fiAx — прирост, полученный за счет прироста затрат ресурса,
хАц — прирост, полученный за счет прироста эффективности использова¬
ния ресурса, AxAfi — прирост, полученный в результате взаимодействия
приростов количества и эффективности ресурсов. Формально последнее
слагаемое неразложимо; всякие ’’эвристические” способы его разложе¬
ния условны.
Только в предельном случае приращение функции полностью разла¬
гается на две части: dy = fidx + xdfi.
Непрерывный темп прироста производства также разлагается на две
части — темп прироста ресурса и темп прироста его эффективности:
_ dy _ pdx xdy, _ fi* , n i n
у Х]Х Х\Х X Ц
В практике экономического анализа применяются различные услов¬
ные приемы разложения члена АлгА/i.
По методике Госкомстата СССР, при расчете долей прироста производства, полу¬
чаемого за счет численности работников (\х) и за счет производительности труда
Од), весь ’’совместный эффект” относится к фактору роста производительности
труда:
^ цДл; л t л JtAfi-!-ДхДц
Л*=“57в Ту
Если расчет ведется с использованием темпов роста (прироста), то применяют¬
ся формулы:
Ру Р»
За 1971-1985 гг. в СССР производство национального дохода выросло на 94%,
производительность общественного труда - на 70%. Следовательно, затраты труда
1,94
увеличились на 14% ( t 7Q = 1,14). ’’Чистая” доля прироста за счет затрат труда
, , 0,14
составляет 15% (' ' ), ’’чистая” доля прироста за счет производительности труда -
74,5% ( o^l") и формально неразложимая часть прироста - 10,5% ("*0*94^° ^
По методике Госкомстата СССР, доля прироста за счет производительности труда
равна 86% (1 - 0,14 = 0,745 +0,105).
В некоторых ситуациях принятая методика разложения общего прироста между
двумя факторами дает особо странные результаты. Например, в Казахской ССР
промышленное производство за 1941-1965 гг. выросло в 12 раз; при этом числен¬
ность работников увеличилась в 3,76 раза, а производительность труда - в 3,19 ра¬
за. Поскольку численность увеличилась в большей степени, чем производитель¬
ность, то, казалось бы, за счет этого фактора получена большая доля прироста произ¬
269
водства. Однако применяемая методика дает обратное соотношение: за счет при¬
роста численности - 25%, за счет прироста производительности труда — 75%.
Суть задачи распределения между двумя факторами ’’спорной” части прироста
производства демонстрируется на рис. 9.1. Общий прирост производства равен
заштрихованной площади. ’’Чистый” прирост за счет увеличения количества ресур¬
сов равен площади ABGD, ’’чистый” прирост за счет увеличения эффективности
равен площади BFHC. Площадь ’’спорного” участка равна Дх:Л/z..Наиболее распро¬
страненная методика целиком присоединяет ее к площади BFHC. В литературе
обсуждаются и другие предложения: разделение ’’спорной” части пополам, разделе¬
ние пропорционально Дх и /Sfi и т. п.
Рис. 9.1. Разложение общего прироста
производства на части
Повышение эффективности использования производственных фак¬
торов и интенсификация производства — взаимосвязанные, но не тож¬
дественные понятия. Рост эффективности — необходимое условие интен¬
сификации растущего производства. Однако не всякий рост эффектив¬
ности означает, что осуществляется интенсификация. Например, в деся¬
той пятилетке производительность общественного труда (т.е. эффектив¬
ность трудовых ресурсов в производственной сфере) возросла на 17%.
Но за счет этого фактора было получено 75% прироста национального
дохода (по методике Госкомстата СССР), в то время как в девятой
пятилетке — 82,5%, следовательно, уровень интенсификации материаль
но го производства за счет трудового фактора несколько снизился. Приз
наком интенсификации является повышающаяся доля прироста, получае
мого за счет увеличения эффективности производственных факторов
Многофакторные модели экономического роста. Многофакторная
модель в отличие от одно факторной отражает взаимодействие ряда про
изводственных факторов с учетом изменения их качества, эффективное
ти использования, а также общих последствий научно-технического про
гресса и совершенствования организации общественного производства
Многофакторная модель экономического роста является динамическим
вариантом производственной функции с взаимозаменяемыми ресурсами
Ее удобно представить в следующем виде:
i/t—f(xt> Аи t), (9.26)
270
где xt - вектор физических объемов производственных ресурсов; At -
вектор параметров, характеризующих качество и эффективность исполь¬
зования ресурсов.
Функция (9.26), как правило, строится на основе динамических
рядов объемов производства и используемых производственных ресур¬
сов, т. е. как уравнение многофакторной регрессии. Анализ
таких функций как элементов динамических моделей народного хозяй¬
ства и самостоятельных макроэкономических моделей дается в гл. 10.
Здесь мы ограничимся кратким рассмотрением возможностей динами¬
ческих производственных функций в анализе эффективности использо¬
вания ресурсов и роли экстенсивных и интенсивных факторов.
На основе функции (9.26) определяются средние и предельные
Pit показатели эффективности использования ресурсов:
4i __ /(**, At, t) t _df(Xt, Аь t)
l Xit — e
X;f UXlt
С помощью показателей mt и vit анализируются сочетания производ¬
ственных факторов, приводящие, например, к наибольшему росту произ¬
водительности труда или к наибольшей экономии некоторых природных
ресурсов и т.п. Вследствие того что параметры функции (9.26) изменя¬
ются во времени, результаты такого анализа могут существенно отли¬
чаться от выводов, получаемых из анализа статических производствен¬
ных функций.
Признаком повышения эффективности использования производст¬
венных факторов в динамике является положительность производных
по времени:
>о- ^ > 0
dt ^ ' dt ^
Если средняя эффективность z-ro ресурса повышается, то темп прироста
производства будет выше темпа прироста соответствующего ресурса.
В основе многофакторного анализа роли экстенсивных и интенсив¬
ных факторов экономического роста лежат разложение полного прира¬
щения функции многих переменных и экономическая интерпретация
элементов такого разложения. Формально полное приращение функции
п переменных нельзя представить в виде суммы п слагаемых, соответст¬
вующих приращениям аргументов (если они не стремятся к нулю).
Поэтому нельзя получить и точных однозначных оценок ’’вклада” каж¬
дого фактора в прирост функции. Экономический смысл этого вывода
очевиден: эффект взаимодействия факторов нельзя приписать
действию каждого фактора в отдельности. В принципе возможно только
условное разложение на части, соответствующее какой-либо принятой
упрощающей гипотезе:
Aj(X, A, t)^SAf(Xi) + Af(A) + Af(t), (9.27)
i <ЕМ
271
где Affxj) — условный прирост, полученный за счет увеличения физичес¬
кого объема z-ro ресурса; AffAJ — условный прирост, полученный за
счет изменения эффективности использования ресурсов (он делится
между отдельными факторами в зависимости от структуры вектора А) ;
— условный прирост, полученный за счет ’’нейтрального” прогресса
(т.е. не относящегося к какому-либо конкретному фактору).
При переходе к предельным значениям справедливо
Эf(X, А, О
dy= 2
i El М
Э.л
dxf +
Эf(X, A, t)
ЪА
-ФА +
эга, л, п
dt, (9.28)
т.е. полный дифференциал ’’точно” разлагается на части, соответствую¬
щие всем производственным факторам. Однако эта формула имеет толь¬
ко теоретическое значение, ибо в реальных задачах экономической дина¬
мики изменения значений производственных факторов нельзя восприни¬
мать как бесконечно малые.
На основе многофакторных моделей роста (макроэкономических производст¬
венных функций) выполнен ряд исследований роли различных факторов экономи¬
ческого развития СССР. Они показывают, что до начала 80-х гг. экономика СССР
развивалась преимущественно экстенсивным путем. По различным методикам
доля интенсивных факторов в приросте национального дохода (конечного продук¬
та) оценивалась, как правило, в интервале от 1/3 до 1/2 (см.,например,[ 1. С. 253],
[6. С 77]).
Рис. 9.2. Динамика производства национального дохода, со¬
вокупных затрат и их эффективности в седьмой-одиннад¬
цатой пятилетках (в процентных пунктах прироста)
272
Альтернативный подход к оценке роли экстенсивных и интенсивных
факторов базируется на соизмерении и суммировании затрат основных
производственных факторов (в частности, по народнохозяйственной
трудоемкости). После расчета динамики общих затрат используется та
или иная модификация разложения прироста производства между при¬
ростом затрат и изменением эффективности затрат.
По расчетам акад. А. Г.Аганбегяна, прирост совокупных производственных зат¬
рат составлял: седьмая пятилетка - 22%, восьмая пятилетка — 20, девятая пятилет¬
ка — 21, десятая пятилетка - 13, одиннадцатая пятилетка - 9%. На рис. 9.2 изобра¬
жены построенные им графики относительных пятилетних приростов национально¬
го дохода (верхний график) и производственных затрат (нижний график).
Если разность индексов прироста национального дохода и производственных
затрат относить целиком к действию фактора повышения эффективности произ¬
водственных затрат, то доля интенсивных факторов в приросте национального
дохода составит: седьмая пятилетка - 31%, восьмая пятилетка - 51, девятая пяти¬
летка - 25, десятая пятилетка - 38, одиннадцатая пятилетка - 47%.
9.4. Воспроизводственные циклы и временные лаги
Типы воспроизводственных циклов и их продолжительность. Процесс
общественного воспроизводства представляет собой взаимопереплетение
многих частных воспроизводственных (циклических) процессов, суще¬
ственно различающихся по своей продолжительности.
В большинстве отраслей промышленности, создающих предметы тру¬
да и предметы потребления, продолжительность производственных про¬
цессов измеряется минутами, часами, сутками, но в судостроении она
может превышать год. В земледелии производственный цикл чаще всего
занимает один год, в выращивании крупного рогатого скота — несколь¬
ко лет. Производственный цикл в строительстве крупных объектов
может превышать десять лет (гидроэлектростанции), в лесном хозяйст¬
ве — несколько десятилетий.
Другие воспроизводственные циклы, входящие в систему общест¬
венного воспроизводства, — воспроизводство населения, основных фон¬
дов, природной среды — имеют продолжительность, многократно превы¬
шающую длительность процессов материального производства. Важной
характеристикой воспроизводства населения, основных фондов, элемен¬
тов биосферы является срок жизни. Это понятие, относимое к
большим неоднородным совокупностям, имеет довольно сложную ста¬
тистическую природу (например, средняя продолжительность жизни
населения).
Изменения в одном частном воспроизводственном процессе, как
правило, вызывают существенные изменения в динамике других процес¬
сов. Поэтому в исследованиях общественного воспроизводства важное
место занимают задачи синхронизации частных воспроизводст¬
венных циклов.
273
Временные лаги и лаговые модели. Взаимосвязи между элементами
социально-экономического процесса, как правило, не мгновенны. Между
причинами и следствиями, стимулирующим воздействием и его эффек¬
том, вложением ресурсов и получением продукции имеется промежуток
времени, называемый временным лагом (или лагом за¬
паздывания, просто лагом).
Простейшая лаговая модель имеет вид
yt=f (xt_T). (9.27')
Величина yt в момент t определяется значением xt в момент t - т,
где т — временной лаг. Модели такого типа широко используются в рет¬
роспективном динамическом анализе и в прогнозировании (например,
модели ’’экономического барометра”).
Если лаговое соотношение связывает значения одного и того же показателя в
разные моменты времени, то имеем авторегрессионную модель
yt ~f(yt-r)- Авторегрессионная модель общего вида выражает зависимость значе¬
ния показателя в определенный момент времени от значений этого же показателя
в предшествующие моменты: 0
yt— 2 axyt-x+zt> (9.28')
т= 1
где ат - коэффициент линейной регрессии; Q - максимальная величина авторегрес¬
сионного лага; et — остаточная составляющая.
В моделировании экономической динамики особо важное значение
имеют следующие виды лагов: инвестиционные — охватываю¬
щие период от начала проектирования объекта до его ввода в действие на
полную мощность; главной составной частью инвестиционного лага
является строительный (от начала строительства до ввода объек¬
та); демографические — от рождения до вступления в трудо¬
способный возраст (16 лет) и начала трудовой деятельности после полу¬
чения общего образования и профессиональной подготовки (наиболее
вероятный интервал — 17—23 года). Общая черта указанных лагов в том,
что они характеризуют продолжительность ’’созревания” элементов про¬
изводительных сил.
В большинстве экономических и социальных процессов лаг не явля¬
ется строго определенной величиной, а как бы размыт (распределен) во
времени. Первый тип лага называют со с р е до точенным (как в
модели (9.270 > второй — распределенным. Линейная модель
распределенного лага имеет вид
г/t = S (oTXf_x 4 е*, (9.29)
т= 1
где сот — неотрицательные параметры, совокупность которых называют
структурой лага; et — остаточная компонента.
274
В целом ряде задач экономической динамики временной лаг пред¬
ставляет собой характеристику не запаздывания событий, а их упрежде¬
ния. Например, объем капитальных вложений в прирост основных произ¬
водственных фондов (х), осуществляемых в году t, определяется тем,
какие производственные мощности (новые основные производственные
фонды) нужно ввести в последующие годы, т.е. в интервале [t + rmjn ,
t + Tmax] • Поэтому взаимосвязь капитальных вложений и ввода новых
основных фондов описывается следующей моделью с распределенным
лагом:
2/*(*„). (9.30)
/ Т = 1
^ Для интервала (ттах - ттт) могут определяться различные статис¬
тические характеристики (средняя величина лага, лаговая структура или
закон распределения лагов); в рассматриваемом конкретном случае —
это доли ввода фондов в каждом году.
Периодические колебания. Динамический ряд может включать
регулярные (или периодические) колебания относительно тренда. Ха-
>рактерным примером периодических колебаний являются циклы ка¬
питалистического хозяйства. Периодические колебания существуют и в
социалистической экономике, однако они имеют иную природу.
Рассмотрим колебания внутри демографического процесса и порож¬
даемые ими колебательные тенденции в других социально-экономичес¬
ких процессах.
Демографический процесс обладает большой инерционностью. Нару¬
шения его монотонности ощущаются в течение многих десятилетий. Так,
огромные человеческие жертвы, понесенные советским народом во вре¬
мя Великой Отечественной войны (20 млн. человек), и значительное сни¬
жение рождаемости в этом же периоде вызывают периодические колеба¬
ния показателей рождаемости, смертности, вступления в трудоспособ¬
ный возраст и т.д. Они усиливаются также демографическим эхом пер¬
вой мировой и гражданской войн (из-за уменьшающейся численности
населения детородного возраста, родившегося в период 1915—1920 гг.).
Все это повлекло за собой снижение рождаемости в 60-е гг. (min в 1968—
1969 гг.). Следующий циклический спад числа новорожденных ожидает¬
ся в ближайшее время. Динамика родившихся приближенно описывается
авторегрессионной моделью (9.28), в которой параметр aT=at, t—т озна¬
чает коэффициент рождаемости в году г населения, родившегося в году
t — т. Наибольший коэффициент рождаемости имеют женщины в возрас¬
те 20—25 лет.
Анализ длинных динамических рядов рождаемости в СССР выявляет
довольно плавные колебания, которые накладываются на понижающий¬
ся тренд. Хорошая аппроксимация такого рода динамических рядов
достигается посредством кв азиполиномов, сочетающих полино¬
миальные, экспоненциальные и тригонометрические функции. Например:
275
*(/)= S ai.f2iea3i t
i'=l 1
sin
(a * it)
(9.31)
Динамический ряд рождаемости за 1950—1985 гг. с максимальной
относительной погрешностью менее 1% описывается частным видом ква¬
зиполинома (9.31), включающим экспоненту и две циклические компо¬
ненты:
X (0 = 2,4e0,02t + l,3e~0’1Ifcos(0,460-0,74e-°’1IfX
X sin (0,460 - 0,Ole0’05 cos (1,570; o\CT = 0,02; R1 = 0,9212.
Достаточно хорошую аппроксимацию дает также парабола четвертого
порядка (см. рис. 9.3):
X (0 = 4,26 + 0,34? - 0,039/2 + 0.00145?3 — 0,0000166г4;
а20ст = 0,031; R2 =0,8166.
1>ис- 9-3- Динамика родившихся в СССР в 1950 - 1985 гг.: 1 - основ-
ная компонента квазиполинома; 2 — парабола четвертого порядка*
3 — линеиныи тренд у *
276
Динамические и структурные характеристики демографического процесса ока¬
зывают влияние не только на современное состояние экономики (потенциальное
количество и половозрастная структура трудовых ресурсов, распределение населе¬
ния по группам потребителей, потребности в детских учреждениях, потенциальные
контингенты общеобразовательных школ, ПТУ, вузов, численность выходящих на
пенсию и т.д.)» но и на будущее ее развитие. Так, резкое сокращение рождаемости
в первой половине 40-х гг. уже имело своим следствием два циклических уменьше¬
ния притока трудовых ресурсов - в 60-х и 80-х гг. Современная ситуация с трудо¬
выми ресурсами усугубляется тем, что в 1,5—2 раза возрастает численность выходя¬
щих из трудоспособного возраста. Поэтому практически весь прирост общественно¬
го производства в СССР в 80-е гг. должен обеспечиваться за счет повышения произ¬
водительности труда.
На современном этапе экономического развития СССР действует ряд
других факторов, вызывающих периодические колебания. Так, наличие
большой доли физически и морально устаревшего оборудования в про¬
мышленности СССР требует резкого увеличения доли продукции маши¬
ностроения, направляемой на замену выбывающего оборудования, что в
свою очередь вызывает изменения многих других воспроизводственных
пропорций (между потреблением и накоплением, старыми и новыми
рабочими местами и т.д.). Эти изменения повторятся (хотя бы в ослаб¬
ленной форме) по истечении срока службы вводимого оборудования.
1
Литература
Анчишкин А.И. Прогнозирование роста социалистической экономики. М.: Эко¬
номика, 1973.
2. Казинец Л.С. Темпы роста и структурные сдвиги в экономике. М.:
Экономика, 1981.
3. Кобрин с к ий Н. Е., Майминас Е. 3., Смирнов А. Д. Экономическая кибернетика.
М.: Экономика, 1982. Гл. 3, 7.
4. Сплайн-функции в экономико-статистических исследованиях. Новосибирск*
Наука, 1987.
5. Статистические методы анализа экономической динамики. М.: Наука, 1983.
6. Черников Д.А. Темпы и пропорции экономического роста. М.: Экономика,
1982. Гл. 1, 2.
7. Четыркин Е.М. Статистические методы прогнозирования. 2-е изд. М.: Статисти¬
ка, 1977.
ГЛАВА 10
МАКРОЭКОНОМИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Макроэкономическими моделями принято называть модели народнохо¬
зяйственного уровня, оперирующие крупноагретированными (макро¬
экономическими) показателями. В рамках макроэкономического моде¬
лирования исследуется функциональная структура экономических агре¬
гатов, например деление общественного производства на два подразделе¬
ния (производство средств производства и производство предметов по¬
требления), национального дохода — на фонды потребления и накопле¬
ния, основных фондов и трудовых ресурсов — на используемые в произ¬
водственной и непроизводственной сферах.
Существенными достоинствами макроэкономических моделей явля¬
ются их малая размерность, доступность для глубокого математического
анализа, возможность исследования народного хозяйства при небольшом
количестве исходных данных, быстрота проведения многовариантных
расчетов.
Макроэкономические модели являются эффективным инструментом
теоретических исследований процесса расширенного воспроизводства
на базе использования категорий политической экономии. В то же время
модели данного класса имеют и важное прикладное значение. Они испо¬
льзуются для выработки концепции экономического и социального раз¬
вития, при изучении возможных альтернатив экономической политики
и их долговременных последствий, для прогнозирования и планирования
системы обобщающих показателей народного хозяйства. К настоящему
времени разработаны многие сотни модификаций макромоделей, систе¬
матизация которых и выбор среди них наиболее характерных представи¬
телей данного класса моделей становятся все более сложной научной
задачей.
В данной главе анализируется последовательность логически свя¬
занных между собой макроэкономических моделей. Критериями от¬
бора моделей являются важность исследуемых с их помощью проблем
экономической динамики, типичность моделей с точки зрения прин¬
ципов и методов экономического и математического анализа, возмож¬
ность ’’сборки” из простейших моделей более сложных модельных
конструкций.
278
В 10.1, 10.2 расширенное воспроизводство общественного продукта и
национального дохода рассматривается как замкнутый процесс с прису¬
щими ему потенциальными возможностями. Здесь изучается серия
моделей, различающихся условиями регулирования динамики, исходя
из общественных потребностей и целевых установок. В 10.3 рассматри¬
ваются факторные модели экономического развития в виде макроэко¬
номических производственных функций. Далее осуществляется переход
к более сложным макромоделям, синтезирующим линейные модели
воспроизводства общественного продукта и макроэкономические
производственные функции. В 10.5 излагаются основные выводы, выте¬
кающие из схем расширенного воспроизводства классиков марксизма-
ленинизма, и результаты экономико-математического анализа динами¬
ки двух подразделений общественного производства. В заключительной
части главы обсуждается вопрос о применении макроэкономических
моделей в практике народнохозяйственного прогнозирования и плани¬
рования.
10.1. Модели динамики общественного продукта
и национального дохода
Введем обозначения, применяемые для всех рассматриваемых ниже мо¬
дификаций моделей воспроизводства общественного продукта и наци¬
онального дохода: х — валовой общественный продукт; у — националь¬
ный доход; а — материалоемкость валового общественного продукта
(0<л<1).
Допускается, что экспорт и импорт равны друг другу (внешнеторго¬
вое сальдо равно нулю), потери включаются в используемый националь¬
ный доход. При этих условиях объемы произведенного и используемого
национального дохода равны.
Баланс производства и распределения валового общественного
продукта для каждого момента (промежутка) времени имеет вид
х = ах+уу (10.1)
откуда
х =
Т&'У (10.2)
Коэффициент А = у — характеризует соотношение валового обще¬
ственного продукта и национального дохода (или мультиплика¬
тор валового общественного продукта). Это — скалярный аналог
279
матрицы коэффициентов полных затрат статической модели межотрас¬
левого баланса (см. гл. 6) 1.
Динамика коэффициентов а и А может выражаться функциями
времени а = a(t), А = A(t). С учетом динамики материалоемкости про¬
изводства соотношение между валовым общественным продуктом и
используемым национальным доходом принимает вид
x(t) = A(f)y(f). (10.3)
По данным о динамике валового общественного продукта и национального до¬
хода СССР за 1960 - 1986 гг., значение коэффициента а колеблется в интервале
0,51 - 0,59, а коэффициента А - в интервале 2,03 - 2,43 (в текущих ценах).
В частности, в 1986 г. а = 0,588, А — 2,427. Материалоемкость валового общест¬
венного продукта в сопоставимых ценах в последние 10-15 лет уменьшается еже¬
годно в среднем на 0,4 — 0,5 процентных пункта.
В динамических народнохозяйственных моделях используемый на¬
циональный доход разделяется как минимум на две части, выполняющие
разные функции в процессе расширенного воспроизводства:
накопление основных производственных фондов (и); в дальнейшем
эту часть для краткости будем называть ’’накоплением”;
остальная часть используемого национального дохода (непроизвод¬
ственное потребление, непроизводственное накопление, прирост матери¬
альных оборотных средств, государственных материальных резервов,
потери) ; в дальнейшем для краткости будем называть эту часть ’’потре¬
блением” (с). В случае необходимости состав этой части используемого
национального дохода может изучаться дифференцированно.
Зная формулу перехода от национального дохода к валовому про¬
дукту (10.3), сосредоточимся на анализе динамики национального
дохода:
y(t)= u{t) + c(t). (10.4)
Ниже анализируется ряд модификаций модели воспроизводства на¬
ционального дохода, построенных на основе (10.4).
Простейшая модель. Наиболее простая модель воспроизводства на¬
ционального дохода формулируется при использовании двух допуще¬
ний: а) пропорциональности производственного накопления прироста
национального дохода в тот же момент времени; б) независимости
(экзогенности) динамики потребления:
уЦ)=вШ + сЦ). (10.5)
В отличие от коэффициентов ау статического межотраслевого баланса (затра¬
ты /-й продукции на производство единицы/-й продукции) коэффициент а включа¬
ет не только текущие производственные затраты, но и затраты на возмещение
выбытия и капитальный ремонт основных производственных фондов.
280
Таким образом, простейшая модель воспроизводства национального
дохода выражается линейным неоднородным дифференциальным урав¬
нением первого порядка.
Коэффициент В - капиталоемкость национального дохода (отноше¬
ние производственного накопления к приросту национального дохода);
этот коэффициент называют также а к селератором1.5=М,
где Ъ — капиталоемкость валового общественного продукта2. В последу¬
ющих числовых иллюстрациях принимается а = 0,6, b = 1,4, откуда В =
= 3,5.
В соответствии с (10.5) при заданном параметре В динамика нацио¬
нального дохода определяется траекторией c(t). Проанализируем поведе¬
ние решения при разных гипотезах о динамике потребления.
1. с (t) = 0. Гипотеза, что весь национальный доход направляется на
расширение производства и потребление отсутствует, разумеется, нере¬
алистична. Но она позволяет оценить максимально возможный темп
увеличения национального дохода, ограниченный только материалоем¬
костью и капиталоемкостью производства. При с (t) = 0 в соответствии
с теорией дифференциальных уравнений имеем
y(t) = y( 0)ё*‘. (10.6)
Величину р = будем называть технологическим тем-
а
пом прироста.
Приняв В = 3,5, получаем р = 0,286; это соответствует постоянному ежегодному
приросту на 33,1 %. При таком темпе удвоение национального дохода достигается
за 2,4 года, утроение - за 3,8 года.
В общем случае акселератор - это коэффициент пропорциональности между
выходной величиной и скоростью изменения входной величины.
Исходное соотношение имеет вид:
Но поскольку
dx — А аУ
dt л dt '
то
281
Рассматривая значение коэффициента капиталоемкости националь¬
ного дохода как функцию времени В = B(t), получаем
у«У=у(0)<Ш,
где
J ( ds
f>«) “J B(sV
О
С возрастанием B(t) технологический темп убывает, а с уменьшением
B(t) — увеличивается1.
2. c(t) = с(0) = const. Общее решение уравнения (10.5) представим в
виде
y(t) — ye в ’, + <?(0).
При Г = 0 имеем у(0) = у + с (0) или р = j(0) - с(0).
Отсюда
у«) = 1уф)-с(0)]ев 1 + с(0). (10.7)
Очевидно, y(t) > 0, если j(0) > с (0), т.е. в начальный момент по¬
требляется не весь национальный доход. Тогда в соответствии с (10.7)
национальный доход растет возрастающим темпом, поскольку в объеме
y(t) непрерывно увеличивается ’’вес” слагаемого
Ы0)-С(0)]Д
В начале периода (при t «5 0) темп прироста ру составляет
В
1 СЖ
— у (0)
1 kt
В частности, при В (f) = В (0) е имеем
1 _ 1 Г _ 1—е~М
р(<) В (0) J ов кВ (0) '
При этом, если к >0, то рост национального дохода затухает и имеет предел
тщ'
Подробнее о влиянии динамики коэффициента В на технологический прирост
см. в ДМНХ, с. 49.
282
В пределе (при t -юо) он увеличивается до 1/В.
Например, если ДО) = 600 млрд. руб., с(0) = 480 млрд. руб., В = 3,5, то за пер¬
вый год прирост составит 6,62%, за пятый - 14,57, за десятый - 25,37%. За 10 лет
при таких темпах национальный доход увеличился бы в 4,92 раза, а доля потребле¬
ния уменьшилась бы с 0,8 до 0,186.
3. c(t) = с (0)е . Это означает, что потребление увеличивается с не¬
прерывным темпом прироста г. Общее решение имеет вид
y(t) = ye 3 ‘+с (°)е
Из него при t = 0 находим
/г\\ с(°)
У = У(°)-Т=в?-
Таким образом,
у (0 =
0(0)-
с(0)
1 — Вг
1
1 +Вг
с(0)ег
(10.8)
Экономически приемлемые траектории изменения национального
дохода получаются только в том случае, когда заданный темп прироста
потребления меньше технологического темпа прироста национального
дохода: г < —— . В противном случае (при г > ) доля накоплений
в ts
быстро падает, а вместе с ней уменьшается и темп прироста националь¬
ного дохода. Далее, в некоторой точке tx темп становится равным нулю,
а в точке *t2 объем национального дохода становится равным нулю
(подробнее см. в ДМНХ, с. 50 — 51). Поэтому принимаем г < , отку-
даЯг<1.
Траектория изменения национального дохода в этом случае зави¬
сит от знака коэффициента первого слагаемого в (10.8). Преобразуем
этот коэффициент следующим образом:
У(0У
с (0) By (0)
Вг 1 —Вг
1 —
g(0)
»( 0)
— г
Обозначим
1-
cJ9l
0(0).
в
:Ро.
283
Величина
1 с п /п\
1 “FW - “ t°>
есть норма производственного накопления в начальный момент времени.
Отсюда р0 равен произведению этой нормы на технологический темп
прироста, или отношению нормы производственного накопления в на¬
чальный момент времени к капиталоемкости прироста национального
дохода:
Ро — в '
Подставив р0 в (10.8), получим
y(t) = By( 0)f^re*i+T-±Trc(0)e«. (10.9)
Из (10.9) следует, что поведение решения во многом зависит от со¬
отношений между г и ро •
Рост с постоянной и монотонно изменяющейся нормой накопления.
Проанализируем три типа экономического развития, различающиеся
темпами прироста потребления и динамикой нормы накопления: 1) г =
= р0; 2) г>р0; 3) г<р0.
Постоянная норма накопления. При г = р0 первое слагаемое в
(10.9) обращается в нуль. Темп прироста национального дохода равен
темпу прироста потребления:
У<*) = ПГв?с( 0)*"- (|0Ю>
Экономическое развитие осуществляется с постоянной нормой на-
1 а0
копления а0 = а(0). Поскольку ■ —~г с(0) =^(0) и г = р0 = — ,
то эквивалентным является решение в более простом виде:
y(t) = y( 0)ев 1. (10.11)
В соответствии с (10.11) при постоянной норме производственного
накопления темп прироста национального дохода пропорционален норме
накопления и обратно пропорционален капиталоемкости прироста на¬
ционального дохода. При а0 = 0,20 имеем р = 0,057.
В современной экономико-математической литературе модель (10.11) более
известна как модель Харрода-Домара. Однако впервые она была сформулирована
советским экономистом Г. А.Фельдманом в конце 20-х гг. (что признается запад¬
ными экономистами-математиками) и использовалась при разработке первого ге¬
нерального плана развития народного хозяйства СССР (см. ДМНХ, с. 52).
284
Следует подчеркнуть, что в модели (10.11) норма производственного накопле¬
ния не может интерпретироваться как регулируемый параметр (экзогенная пере¬
менная) . Если принимается а ^=Оо> то динамика национального дохода описывается
более сложным образом, чем по формуле (10.11). Этот случай анализируется
в 10.2.
Уменьшающаяся норма накопления. При г > р0 первое слагаемое
решения (10.9) отрицательно, второе положительно. При этом первое
слагаемое по абсолютной величине растет быстрее второго. Вследствие
этого темп прироста национального дохода падает, норма накопления
уменьшается до нуля, а затем становится отрицательной. Поведение ре¬
шения качественно аналогично рассматривавшемуся выше случаю
г > . Здесь также можно установить моменты достижения нулевого
темпа (fi) и нулевого объема национального дохода (f2)* Например,
при г = 0,08 имеем t\ = 4,98, t2 = 11,16.
Увеличивающаяся норма накопления. При г < р0 оба слагаемых
в решении (10.9) положительны, при этом первое слагаемое растет бы¬
стрее второго. Поэтому темп прироста национального дохода непрерыв¬
но увеличивается от р0 в начальный момент до -jp в пределе. Норма на¬
копления также непрерывно увеличивается.
Рассмотренные три варианта динамики и структуры национального
дохода, различающиеся соотношениями темпов г и р0, изображены на
рис. 10.1. Заметим, что варианту 2 качественно соответствует поведение
решения (10.8) при г > , а варианту 3 — поведение решений (10.6),
(10.7).
На неограниченном интервале времени при постоянной капитало¬
емкости ’’интересы” потребления и накопления уравновешиваются при
Рис. 10.1. Динамика национального дохода (а) и производственного на¬
копления (б) при экспоненциальном росте потребления: 1) г = Ро <>
2)г> р0, 3) г< ро
285
г = р0. Если г > р0, то реальный выигрыш в объеме потребления достига¬
ется только на отрезке [0, tx]. Если же г < р0, то темп национального
дохода возрастает только за счет опережающего роста накопления. Оче¬
видно, что и такой тип экономического развития (’’накопление ради на¬
копления”) может быть целесообразным только на ограниченном интер¬
вале времени. Таким образом, анализ модели обнаруживает существен¬
ные недостатки траекторий развития при условии монотонно понижаю¬
щейся или монотонно повышающейся нормы накопления в течение
длительного времени.
Модели с лагами капитальных вложений. Во всех анализировавших¬
ся выше моделях допускалось отсутствие лага между производственным
накоплением и приростом национального дохода. Это — серьезное упро¬
щение реальности. Как отмечалось, инвестиционные лаги являются
важными характеристиками процесса воспроизводства.
Модель с сосредоточенным лагом. Обозначим величину сосредото¬
ченного лага т. Тогда u(t) = В (t + г), а общая модель воспроиз¬
водства национального дохода приобретает вид
y(t) = B^t(t + T) + c{t). (10.12)
При постоянной норме производственного накопления а0 получаем
следующее обобщение модели
о013»
Модель (10.13) представляет собой дифференциальное уравнение с
запаздывающим аргументом (или дифференциально-разностное уравне¬
ние). Исследование этого уравнения (см. ДМНХ, с. 56) дает формулу
для определения темпа прироста национального дохода ру9 равного
темпу прироста потребления:
р/«Л=^. (10.14)
Из анализа (10.14) следует, что ру монотонно убывает при увеличе¬
нии т. Уменьшение темпа национального дохода при постоянном, а тем
более увеличивающемся лаге объясняется тем, что все возрастающая
величина накопления ’’замораживается” и не может использоваться для
расширения производства. Увеличение доли накопления а0 Е [0, 1] хотя
и поднимает темп национального дохода, но уже медленнее_пропорци-
онального увеличения. В табл. 10.1 приводятся значения ру(г) при В =
= 3,5 и трех значениях а0 •
Анализ модели (10.12) с заданной траекторией потребления с (t) =
= с (Q)ert выявляет свойства, аналогичные свойствам модели без лага,
286
Таблица 10-1
т
Ру СО
Оо = 1
а0= о,2
а0 =0,1
0
0,286
0,057
0,029
1
0,226
0,054
0,028
2
0,194
0,052
0,027
3
0,171
0,049
0,026
4
0,154
0,047
0,025
но при болеее низких темпах национального дохода (см. ДМНХ,
с. 57).
Модель с распределенным лагом. Производственное накопление с
распределенным лагом определяется по формуле
u(t) = £ B(t, Т)^(т),
1-t U
где B(t, т) — затраты капитальных вложений в момент t, необходимые
дня получения единицы прироста национального дохода в момент г. При
этом затраты капитальных вложений ’’распределяются” внутри периода
протяженностью в лет. Общая капиталоемкость в момент t составляет
2 B(s, t).
S — t — т
Континуальный аналог формулы и (t) имеет вид
оо
и (0 - s В (t, г) -4f~dT, где J В (t, т) dt =В (t).
t ' ■ dt t
Будем предполагать, что В (t, г) — убывающая функция от т. Этому
предположению соответствует, в частности, функция
В —
B(t, *) = — е° ,
в которой параметр о характеризует степень распределенности лага
(чем больше а, тем более растянут лаг). Например, при о = 2 имеем
^ В (tx) dt = 0,92В,
при 0 = 4 *
t+x
J B(t, T)dt = 0,71 В.
t
При постоянной норме накопления и (г) = а0у (t), и поэтому
аоУ(0 = -£-§е о ^(т)dx.
t
287
Преобразования этого уравнения приводят в конечном счете к реше¬
нию:
У У)~У (0)ев + а° *. (10.15)
Таким образом, учет распределенного лага при развитии с постоян¬
ной нормой накопления приводит к уменьшению постоянного темпа
«о «о
прироста национального дохода от — до •
10.2. Оптимизация динамики национального дохода
Критерии и условия оптимизации. Конечные цели развития социалисти¬
ческой экономики в наибольшей степени отражает динамика потребле¬
ния с (Г). Поэтому для оптимизации динамики национального дохода за
фиксируемый плановый период [0, Т\ в качестве максимизируемой
целевой функции естественно взять
т
с(Г)—\с (t) dt, (10.16)
о
т.е. максимизировать суммарный фонд потребления за плановый
период1.
Более общий подход к максимизации потребления за период учиты¬
вает, что эффект от единицы потребления (потребительский эффект)
в разные моменты времени неравнозначен и может быть измерен посред¬
ством некоторой функции q = q(t).
Функция q (t) называется в звешивающей. Она сопоставляет,
или ’’взвешивает”, потребление в разные моменты времени. Общеприз¬
нанной является гипотеза о существовании потребительских предпочте¬
ний во времени: полезный эффект благ настоящего выше полезного
эффекта §лаг будущего. В соответствии с этой гипотезой взвешивающая
функция q(t) должна обладать следующими свойствами: 1) q(t) > 0,
т.е. потребление в любой момент времени увеличивает интегральный
уровень потребления; 2) q{t) — монотонно убывающая функция (с
убывающими ’’весами”); 3) lim q (г) = 0, т.е, ’’вес” потребления отда¬
ленного будущего стремится к нулю.
Удобно в качестве взвешивающей функции взять убывающую
экспоненту q (t) = ё~ ^ при со > 0. В начальный момент времени потреб-
Далее предполагается, что функция с (t) либо ’’очищена” от элементов, не име¬
ющих отношения к потреблению (накопление оборотных производственных фон¬
дов, прирост резервов, потери и т.д.), либо доля этих ’’прочих” элементов зафикси¬
рована.
288
ление имеет вес <7(0) = 1, а затем вес убывает с непрерывным темпом
Ф; lim e~u>t = 0. Например, при со = 0,05 имеем q (5) = 0,779, <7(10) =
t -+ оо
= 0,607, 4 (20) = 0,368 (о научных подходах к объяснению и количест¬
венной оценке предпочтений потребления во времени см. в ДМНХ,
с. 60-61).
Итак, более общая целевая функция диско нтированного
потребления, частным случаем которой (при со = 0) является (10.16),
имеет вид
C(T)^4e-atc(t)dt. (10.17)
Возможности оптимизации динамики национального дохода, задан¬
ной уравнением
у (t) = вЩЦг-с (t),
заключаются в регулировании соотношения между потреблением и на¬
коплением/Рассмотрим несколько возможных подходов.
Оптимизация с нерегулируемой нормой накопления. Анализируемые
ниже оптимизационные динамические модели национального дохода
включает в качестве ограничивающего условия уравнение распределе¬
ния национального дохода на накопление и потребление, фигурировав¬
шее в 10.1 как самостоятельная модель. Особенность данного условия
в рамках оптимизационной модели в том, что c(t) становится эндоген¬
ной переменной.
Максимизация суммарного потребления без учета инвестиционного
лага. Совмещение простейшей модели динамики национального дохода
(10.5) и целевой функции (10.16) дает оптимизационную модель
у(/) = В^ + с(0, <10Л8>
г
С{Т)== \c{t) dt—* max.
Представим (10.18) в виде задачи оптимального уравнения с крите¬
рием
I [У (0—и (0] dt-—> max.
Применение принципа максимума Понтрягина позво¬
ляет получить аналитические решения. Они существенно различаются
дня краткосрочного и долгосрочного периодов планирования (при этом
10 Зак. 2414 289
граница, разделяющая краткосрочный и долгосрочный периоды, опре¬
деляется величиной капиталоемкости национального дохода)1.
1. При Тимеем следующую оптимальную траекторию:
и* (0 = 0. У* (0 = ^(0 = 0(0),
а* (0 = 0, С*(Т)=у(0)Т.
Таким образом, когда длительность планового периода не превосхо¬
дит коэффициента капиталоемкости национального дохода, накопление
и экономический рост вообще неэффективны. В данном случае динами¬
ческий оптимум — это простое воспроизводство национального дохода
и его полное использование на потребление. Величина В характеризует
минимальный срок, в рамках которого накопление может быть эффек¬
тивным с точки зрения "интересов” потребления (см. замечания по
этому поводу в 6.4). В этом смысле динамическая модель при Т < В
сходна со статической.
Очевидно, что по крайней мере в рамках краткосрочного и средне¬
срочного планирования производственное накопление не может рас¬
сматриваться как полностью эндогенная переменная. Необходимо обес¬
печивать определенный уровень накопления исходя из интересов раз¬
вития в послеплановом периоде.
2. При Т > В оптимальная траектория качественно изменяется в
точке t = Т - В. 1
Для t Е [0, Т - В] имеем^*(г) =у(0)е в \ w*(f) *=y*(t),c*(t) =
= 0, a* (f) = 1, т.е. на первом этапе планового периода весь националь¬
ный доход используется на накопление и увеличивается максимально
возможным (технологическим) темпом.
Для t Е [Т — В, 7] оптимальная траектория имеет вид
т__
у* (0 =Р(Т-В) = у(0)ев~\ и* (t) = 0,
С* (0 = ^(0, «•(/) = (>.
Объем национального дохода стабилизируется и весь используется на
потребление:
С(Г) = В</(0)ехр(|—1
Таким образом, в точке t = Т — В происходит так называемое р е-
лейное переключение режима воспроизводства национального
дохода, что является необходимым условием достижения максимума
Прямое сопоставление величин В и Т правомерно, ибо в динамической систе¬
ме они имеют одинаковую размерность (время). Коэффициент В характеризует
инерционность экономики (запаздывание реакции системы на внешний импульс).
Подробнее об этом см. в [5. С. 174 - 175].
290
Рис. 10.2. Траектории развития в задачах оптимального управления (у -
национальный доход; с — потребление; и — производственное накопле¬
ние:
а) без дисконтирования потребления; б) с дисконтированием потреб¬
ления
С(Т). Заметим, что первое релейное переключение происходит в точке
t = 0: скачок накопления с и (0) до у (0) и падение потребления от с(0)
до нуля.
Оптимальные траектории развития при Т > В изображены на рис.
10.2а. Национальный доход — кривая KLM, накопление — KLNP, потреб¬
ление — ONLM. Площадь заштрихованного прямоугольника NLMP
равна С*(Т).
При В = 3,5 и Т = 10 максимальный уровень национального дохода (3846)
достигается в t = 6,5; С*(10) =13452. При Т — 20 точка переключения сдвигается
на 10 лет (Г = 16,5), благодаря чему достигается фантастический рост националь¬
ного дохода и суммарного потребления. Для сравнения укажем, что при росте
с постоянной нормой накопления а = 0,20 и тех же прочих исходных данных
суммарный фонд потребления за 10 лет составляет 6474, а за 20 лет - 17 940.
Каков же реальный смысл оптимума задачи (10.18)? По-видимому,
получаемое решение можно трактовать как те хнологически
достижимый оптимум (с точки зрения максимума интеграль¬
ного потребления), который не может быть превзойден при заданном
параметре В. И с этой точки зрения задача (10.18) близка модели (10.5)
при с (t) = 0, в которой определяется технологический темп прироста
национального дохода. Безусловно, такой оптимум не удовлетворяет
многим требованиям социально-экономического характера, т.е. априори
не является социально-экономическим оптимумом.
Но надо отдавать отчет в том, что включение в модель дополнительных
10*
291
условий (в частности, сглаживание релейного режима) неизбежно умень¬
шает величину технологически достижимого интегрального фонда потре¬
бления.
Главными недостатками решения задачи (10.18) являются его
сильная зависимость от величины Т и релейное изменение структуры на¬
ционального дохода. Очевидно, что экономически недопустимы участки
развития как с полным отсутствием потребления, так и простого воспро¬
изводства с отсутствием накопления. Неприемлемым является также
резкое изменение траектории развития в зависимости от величины Т:
при ее уменьшении (так, что Т < В) становится неэффективным
накопление, при значительном же увеличении (или использовании
принципа скользящего планирования) момент потребления вооб¬
ще не наступает. Важный теоретический результат анализа моде¬
ли — выявление особой роли коэффициента В в процессе воспро¬
изводства.
Максимизация дисконтированного потребления без учета инвести¬
ционного лага. Можно предположить, что релейный характер динамики
национального дохода в оптимизационной модели обусловливается
недостатком применяемой целевой функции, в которой равные объемы
потребления в разные моменты времени учитываются как равноценные.
Поэтому целесообразно проанализировать модель с целевой функци¬
ей (10.17) вместо (10.16):
уЦ) = вЩР- + с(*),
at (10.19)
С (Г) = Г e~atс (t)dt.
о
Важную роль в анализе модели (10.19) играет величина ’’скорректи¬
рованной капиталоемкости”
В = —(0^)*
Функция В (со) — возрастающая при со = (0, ~£~)*
При малом СО коэффициент В мало отличается от В: lim В (со) —В. Например,
~ со~* 0
В (0,05) =3,85у В (0,10) =4,31. Поведение решения (10.19) существенно зависит
также от того, соблюдается ли условие соВ < 1. Поскольку общепринятые оценки
параметра со находятся в интервале 0,05 - 0,10, данное неравенство выполняется
с большим запасом; это обстоятельство используется в последующем ана¬
лизе.
Анализ модели (10.19) с использованием принципа Понтрягина
приводит к выводу, что качественный характер ее оптимальной траекто¬
рии не изменяется по сравнению с решением модели (10.18).
1. При Т < В национальный доход не растет и весь используется
на потребление. Поскольку В > В, то длительность периода, в рамках
292
которого накопление неэффективно, увеличивается по сравнению с зада¬
чей на максимум недисконтированного суммарного потребления.
2. При Т> В оптимальная траектория имеет релейное переключение
в точке t = Т — В . Рост с максимальным темпом р = -Jp заканчивается
раньше, чем в модели (10.18). Максимальный уровень национального
дохода
у* (Т - В)= /(0) exp ~ (1 - соВ) иВ
меньше, чем в точке переключения модели (10.18). Хотя ’’этап потребле¬
ния” становится более продолжительным, суммарный фонд потребления
С* = By* (Т — В) оказывается меньше из-за более низкого постоянного
уровня потребления.
На рис. 10.26 изображены траектории развития, соответствующие максимуму
дисконтированного потребления, и их смещения по сравнению с рис. 10.2а. Пло¬
щадь Vl л/Р меньше площади NLMP.
При со = 0,05 и Т = 10 максимальный уровень национального дохода (3480)
достигается в t =6,15; С* (10) = 13398. При со = 0,10 максимум национального
дохода достигается раньше (в t = 5,69), но его объем уменьшается (3051). Снижа¬
ется и суммарный объем потребления (13 150).
Итак, надежда на то, что благодаря дисконтированию можно устра¬
нить релейный характер динамики национального дохода и сильную за¬
висимость оптимальной траектории от величины Г, не оправдалась.
Необходимы более радикальные способы регулирования динамики и
структуры национального дохода.
Оптимизация с учетом инвестиционного лага. Отметим основные
особенности оптимальною решения задачи, включающей сосредоточен¬
ный инвестиционный лаг г ( в соответствии с (10.12)).
Первая особенность выражается в том, что при t Е [0, т\ динамика национально¬
го дохода предопределяется динамикой накопления в предплановом периоде:
У (О = У о (О* На этом участке можно управлять только распределением националь¬
ного дохода. Оптимальное решение имеет вид и* (t) =0, с* (г) =yo(t). Принцип
максимума применяется при Г >7.
Если т < Т < г + В, то по-прежнему накопление неэффективно и весь националь¬
ный доход должен направляться на потребление. Максимальное значение у (f) до¬
стигается в точке г.
Инвестиционный лаг увеличивает длительность планового периода,
в рамках которого накопление неэффективно с точки зрения интересов
потребления.
Развитие с релейным переключением осуществляется при Т >т + В. Здесь в отли¬
чие от оптимальных решений (10.18) - (10.19) выделяются четыре (а не два)
участка развития:
а) при t [0, f] динамика объема национального дохода предопределена:
у* (Г) ==.Уо (О* весь национальный доход направляется на накопление;
б) при Г £ \т, Т — Т — В] национальный доход растет максимально возмож¬
293
ным темпом и по-прежнему весь используется на накопление;
в) при t Е [Т — Т — В, Т — В] национальный доход продолжает расти, но уже
весь направляется на потребление;
г) при t Е [Т - В, Т] объем национального дохода остается неизменным и
весь используется на потребление .
Таким образом, при Т> т + В основные качественные характеристи¬
ки оптимальных траекторий сохраняются и с учетом инвестиционного
лага. Но при этом момент релейного переключения смещается к началу
планового периода и появляются два участка инерционного роста дохода
t Е [0, г] и t Е [Т — т — В, Т - В], равных по продолжительности вели¬
чине лага (см. рис. 10.3).
Оптимизация с динамическими и структурными ограничениями.
Рассмотрим два подхода к улучшению свойств оптимальных траекторий.
Оба они связаны с включением дополнительных условий, огра¬
ничивающих резкие скачки темпов и структуры национального
дохода.
Включение условия непрерывного роста потребления. Простейший
способ получения гладкой траектории потребления - замена интеграль¬
ной целевой функции С(Т) условием максимизации параметра непреры¬
вного роста потребления:
£?(0 = *(0)ехр(г<), (10.20)
г —► max.
Анализ решения данной задачи обнаруживает качественное сход¬
ство с решением уравнения (10.9) при г > р 0. Накопление не¬
прерывно уменьшается и в точке tx становится равным нулю. Одно¬
временно нулевым становится и темп прироста национального до¬
хода. Следовательно, максимизация потребления осуществляется в
ущерб будущему экономическому развитию (подробнее см. ДМНХ,
с. 68).
Рассмотрим более гибкое условие непрерьюного роста потребления.
Для этого разделим объем потребления на две части: экзогенную
(растущую с минимально необходимым темпом г < р0) и эндоген¬
ную (оптимизируемую):
с (t) = ct (/) + с2 (t),
Ci(f) = c(0)exp(r/), (10.21)
т
С2(Т) = 5 С2 (t) dt — max .
о
294
Рис. 10.3. Рост национального дохода в задаче опти¬
мального управления с инвестиционным лагом
Применение принципа максимума Понтрягина дает следующие ре¬
зультаты:
1. При Т<:В получаем такое же решение, как и для задачи (10.18).
Это вполне объяснимо, поскольку условие роста сх (г) перекрывается
ростом с2 (t). По-прежнему накопление в рамках периода продолжите¬
льностью Т <2? неэффективно.
2. При Т> В оптимальная траектория, как и для моделей (10.18) —
(10.19), имеет ряд характерных участков с границей t = Т- В.
На первом участке темп прироста национального дохода непрерывно
увеличивается, на накопление выделяется максимально допустимая
часть национального дохода, потребление растет минимально необходи¬
мым темпом г. На втором участке объем национального дохода остается
неизменным и весь используется на потребление (см. рис. 10.4).
Таким образом, совмещение условий оптимизационной мо¬
дели (10.18) с требованиями гарантированного роста потребления по¬
зволяет получать сглаженные траектории развития. Путем регулирова¬
ния величины г находим решения с разным сочетанием близких и долго¬
срочных целей экономического развития. Так, увеличивая/*, мы ускоря¬
ем рост потребления на первом этапе развития (до t = Т - В), но зато
295
уменьшаются уровень годового по¬
требления на втором этапе и сум¬
марное потребление за плановый
период. Уменьшая г, мы проигры¬
ваем в потреблении на первом
этапе, но зато выигрываем на
втором и в сумме.
Недостатком получаемых тра¬
екторий является отсутствие нако¬
пления на отрезке t Е [Г - В, Т\,
вследствие чего исключается рост
потребления в послеплановом пери¬
оде. Этот ’’эффект хвоста”
планового периода фиксированной
продолжительности присутствовал
и в ранее анализировавшихся опти-
Рис. 10.4. Траектория развития в задаче маЛьных решениях. Чтобы избежать
оптимального управления с минималь- - постановке задачИ)
ным ростом потребления обо- ^
знамена динамика национального дохода поступим так же, как И С TpaeKTO-
на рис. 10.2а) рией потребления на первом этапе.
Введем для t > Т - В условие
«(/) = « (Т—В) exp [s (/ — Т ■+ 5)],
где s — минимально необходимый темп прироста накопления, обеспечи¬
вающий увеличение национального дохода в интересах потребления в
послеплановом периоде.
Введение в модель дополнительных ограничений на минимальное и максималь¬
ное значения нормы производственного накопления, а также целевой функции
с дисконтируемым потреблением
(Т) = J ехр (—сot) с2 (t) dt
позволяет получить еще более сглаженные траектории развития и в большей степе¬
ни совмещать интересы текущего и будущего потребления (анализ соответствую¬
щих формулировок оптимизационной модели см. в ДМНХ, с. 70 - 71).
Оптимизация с постоянной нормой накопления. Пусть норма нако¬
пления а Е [0,1] поддерживается постоянной на протяжении планового
периода [0, Т\. Требуется определить величину а*, при которой макси¬
мизируется суммарный фонд потребления
г
C(T) = lc(t)dt.
о
Вместе с этим находится оптимальный постоянный темп прироста на-
ционального дохода р* = -g—.
296
В соответствии с (10.11)
с (t) = у (0) (1 —a) exp (-J- t у,
откуда
т
С(Г)У(0)0-«)$ехр (т*)Ш-
0
Таким образом, необходимо найти а* при следующих условиях:
г
(1 —а) [ exp f t J dt max, (10.22)
о
а€[0, 1].
Заметим, что если принять а = 0, то в начальный момент времени
потребление будет максимальным (с(0) =^(0)), но зато в дальнейшем
оно не будет расти и его суммарный объем за период составит С = у0Т.
Если же выбрать а > 0, то в начальный момент времени потребление
будет меньше максимально возможного, но затем будет возрастать.
Поэтому при некоторой продолжительности планового периода поло¬
жительная норма накопления будет обеспечивать больший суммарный
фонд потребления, чем нулевая норма накопления1.
Доказываются следующие свойства оптимальной нормы накопления
как функции продолжительности планового периода:
1. При Т Е [0, 2В] имеем а* (Т) = 0. Это означает, что националь¬
ный доход не растет: у*(t) —у (0);
1 В отношении величины Of' (Т) справедливо асимптотическое условие
«•(Г)^1 -±
и двусторонняя оценка
1
Для оптимального темпа р* существует асимптотическое условие
1 1
В Т
и двусторонняя оценка
^ 1 1
в ' т
297
2, При Т > 2В величина а* (7) положительна и монотонно возрастает
с увеличением Г;
3. lim а* (Т) = 1.
J1 -> оо
Оптимальный темп прироста национального дохода (и равные ему
темпы потребления и накопления) при постоянной норме накопления
является возрастающей функцией от продолжительности планового пе¬
риода:
Анализ поставленной задачи подтверждает полученные ранее выводы
о важной роли коэффициента металлоемкости и продолжительности
планового периода для определения оптимума потребления и накопле¬
ния. Графики функций а* (Т) и р* (Т) изображены на рис. 10.5.
Переход к задаче с максимизацией дисконтированного потребления
мало изменяет свойства оптимальных траекторий (см. ДМНХ, с. 74 —
75).
Таким образом, при оптимизации постоянной нормы накопления
обнаруживается сильная зависимость решения от выбора продолжитель¬
ности планового периода. Это свойство отражает возрастающий приори¬
тет накопления в интересах повышения жизненного уровня при расшире¬
нии горизонта предвидения. Однако при этом в точке t = 0 приходится
резко изменять соотношение между потреблением и накоплением. В
силу структурных ограничений, не учитываемых в макромодели (раз¬
личный материально-вещественный состав фондов потребления и накоп¬
ления^ подобный резкий маневр трудно осуществим. Поэтому следует
рассмотреть возможность более плавного изменения соотношения
между потреблением и накоплением.
Выход на режим роста с постоянной нормой накопления. Каждая
из рассмотренных выше задач оптимизации динамики национального
дохода ”в чистом виде” обладает определенными недостатками. Оче¬
видно, что с помощью только формальных методов оптимизации
соотношения потребления и накопления вряд ли можно добиться прием¬
лемых результатов. Проведенный анализ позволяет сформулировать ряд
требований к динамике национального дохода и его структуры:
1) норма накопления не должна неограниченно приближаться к 0 и 1;
2) должны быть сглажены релейные переключения и накопления; 3) полу¬
чаемое решение (в том числе с постоянной оптимальной нормой накоп¬
ления) в начале периода не должно сильно зависеть от выбираемой его
длительности.
Эти требования можно выполнить, сочетая рассмотренные выше по¬
становки задач (как с заданием траекторий c(t), так и с максимизацией
потребления) на различных интервалах долгосрочного планового перио¬
да в соответствии с поставленными целями.
298
Рассмотрим задачу
постепенного выхода на
режим роста с постоян¬
ной нормой накопления.
Начальная норма на¬
копления составляет
а(0). В течение плано¬
вого периода [0, 7]
необходимо выйти на
более высокую норму а
и в дальнейшем под¬
держивать ее постоян¬
ной.
Переходный режим
развития определяется
на отрезке [0, ?] , так
что а(?) = а (? < Т).
Постепенное увеличение
a(t) может быть обеспе¬
чено, в частности, при
постоянном темпе при¬
роста потребления г <
Д(0)
В
Рис. 10.5. Зависимость оптимальной
нормы накопления а* и оптимального
темпа прироста национального дохода
р* от продолжительности планового
периода
<
. Тогда в соответствии с (10.9) при t G [0, t] норма накопления
будет монотонно увеличиваться от а0 до а.
Момент t достижения заданной нормы накопления определяется из
уравнения a(f) = а, которое имеет единственное решение (см. рис.
10.6а). Это — точка пересечения возрастающей кривой a (t) и ординаты
a(t) = а. Увеличивая г, можно увеличивать t и наоборот. Например,
требуется перейти от исходной нормы накопления а(0^ = 0,17 к а = 0,20.
При г = 0,03 получаем t = 1,64, при г = 0,04 получаем t = 2,96.
Постоянная норма накопления может не задаваться, а определяться
одновременно с переходом на режим развития с оптимальной нормой
накопления в зависимости от продолжительности оставшегося планового
периода. Тогда й и ? определяются из уравнения а (?) = а* ( Т - t),
которое также имеет единственное решение (см. рис. 10.65). Это точка
пересечения возрастающей кривой a(t) и убывающей кривой а* (Т - t),
рассчитанной путем оптимизации постоянной нормы накопления. Пусть,
к примеру, г = 0,03, Т = 20. В этом случае пересечение двух кривых
происходит в t = 0,9 и a(t) = а* (Т-t) =0,5.
Изложенный подход применим и в том случае, когда начальную
норму накопления целесообразно уменьшить: а < а(0). Тогда следует
выбрать г > . Это обеспечивает постепенное снижение a{t) до а за про¬
межуток [0, ?], где t < Т.
299
Рис. 10.6. Динамика нормы накопления: постепенное увеличение до фик¬
сированной постоянной 0а) и постоянной оптимальной (б)
Рассмотренные макромодели выявляют качественные свойства оп¬
тимальных траекторий национального дохода при различных способах
экономического регулирования. Каждая модель в отдельности обладает
определенными недостатками, которые, как правило, являются гипер¬
трофированными достоинствами (предельное использование гой или
иной возможности получения лучшего решения с точки зрения формаль¬
ного критерия). Теоретическая и практическая ценность моделей данно¬
го типа существенно возрастает при их комплексном применении.
10 3. Факторные модели экономического развития
Общие представления о факторных моделях экономического роста и
связанных с ними показателях эффективности и интенсификации были
даны в 9.3. Модели данного типа (о дно факторные и многофакторные)
представляют собой динамические варианты производственных функ¬
ций.
Макроэкономические динамические производственные функции.
На макроэкономическом уровне важнейшими факторами производства
выступают живой труд (рабочая сила) и производственные фонды, а
результатом производства — конечный общественный продукт (или на¬
циональный доход). Поэтому целесообразно сосредоточить внимание на
двухфакторной производственной функции общего вида
(10.23)
где y{t) — объем конечного продукта (или национального дохода);
L (t) — используемая рабочая сила (или затраты труда); К (Г) — испо¬
льзуемые основные производственные фонды.
300
Применение макроэкономической производственной функции
(МПФ) как самостоятельной модели экономического роста предполага¬
ет, что y(t) определяется исходя из заданных траекторий L и К; воз¬
можно также задавать траектории у и какого-либо одного фактора и
определять в соответствии с (10.23) траекторию другого фактора.
МПФ может также включаться в состав более сложных макроэкономи¬
ческих моделей, в которых/, и А*являются эндогенными переменными
(см. 10.4).
Анализ динамики производительности труда —\— (г) и фондоотда-
У
чи д- (t) с помощью МПФ (а не по фактическим динамическим рядам)
позволяет, во-первых, элиминировать влияние случайностей, во-вторых,
учитывать эффект взаимодействия с другим производственным факто¬
ром. Применение МПФ для выявления динамики общей эффективности
основано на элиминировании влияния увеличения объемов используе¬
мых ресурсов.
Главной проблемой спецификации динамической МПФ является
отражение научно-технического прогресса (НТП). В теории производст¬
венных функций различаются две основные формы НТП: 1) нейтра¬
льный, т.е. не относящийся к каким-либо производственным факторам
в отдельности и не изменяющий их относительную эффективность;
2) материализованный в определенных произ¬
водственных факторах (ненейтральный), что отражается в
повышении их эффективности. Обычно предполагается, что во времени
аналитическая форма МПФ не меняется, а изменяются только ее параме¬
тры под влиянием НТП.
При указанных предположениях МПФ с нейтральным НТП имеет вид
y(t) = A(t)f[L(t), K(t)], (10.24)
где А (t) — функция, отражающая влияние всех непосредственно не учи¬
тываемых факторов; условно это совокупное влияние можно принять за
’’нейтральный НТП”. В частности, А (Г) = а0еы, где а0 - параметр мас¬
штабирования и начальной эффективности производства (в момент t = 0
.он переводит объемы используемых ресурсов в объем производства);
X — непрерывный темп прироста за счет нейтрального НТП.
Материализованный в производственных факторах НТП выражается
динамикой их эффективности aL (t) и ag (t). Если удается построить
временные функции эффективности производственных факторов, то
МПФ приводится к виду
y(t) = A (t) f [aL (t) L it), aK (t) К (0]- (Ю-25)
С помощью aL (f) и a% (t) объемы затрачиваемых ресурсов в различ¬
ные моменты времени приводятся к одинаковому качеству (по их эф-
301
фективности). При этом удобно за эталон качества принять ресурсы,
использовавшиеся в момент t = 0. Выражение (10.25) можно упро¬
стить, приняв
a, (t)L(t) = L*(t) и aK(t)K(t) = K*{t),
где L* и К* — редуцированные объемы используемых ресурсов. Тогда
y(t) = A(t)f[L*(t), K(t)]. (10.26)
Таким образом, отражение двух форм НТП позволяет исследовать
динамику конечного продукта (национального дохода) за счет трех
групп факторов: 1) увеличение объемов используемых ресурсов
(L (t) и К (t))\ 2) изменения общей эффективности производства, или
нейтрального НТП {A(t))\ 3) изменения эффективности отдельных
ресурсов (aL (t) и (Г)). Для двухфакторных МПФ общий прирост
производства может быть условно разложен на пять составляющих,
обусловленных приращениями АЛ, Дя^, Д£, Дя#, ДК.
Принято различать три типа НТП по экономической результативно¬
сти : трудосберегающий (фондоемкий), фондосберега¬
ющий (трудоемкий) и симметричный (или нейтральный)1,
Реальный НТП совмещает элементы этих идеальных типов. Для экономи¬
ки СССР последних десятилетий характерен преимущественно трудосбере- .
гающий (фондоемкий) тип НТП с растущей фондовооруженностью,
снижающейся фондоотдачей, опережающим ростом производственных
фондов по сравнению с ростом занятости и производимого национально¬
го дохода.
Типовые МПФ. Наибольшее применение в теоретическом и прик¬
ладном макроэкономическом анализе имеют два вида МПФ: мульти¬
пликативная (чаще именуемая функцией Кобба — Дуг¬
лас а) и функция с постоянной эластичностью заме¬
няемости ресурсов (ПЭЗ). Эти функции обладают преимуще¬
ствами с нескольких точек зрения: 1) они хорошо экономически интер¬
претируются; 2) имеют небольшое число параметров, что облегчает
их статистическую оценку; 3) соответствующие им показатели экономи¬
ческого роста, эффективности, интенсификации имеют удобную аналити¬
ческую форму.
Общими свойствами функций Кобба — Дугласа и ПЭЗ являются од¬
нородность и постоянная эластичность заменяемости ресурсов (см.
4.3).
Динамическая функция Кобба - Дугласа
y{t) = A (t) Lai (t) Ka4t) (10.27)
1 Классификации НТП, связанные со свойствами МПФ, предложены Д.Хиксом,
Р.Харродом, Р.Солоу (см. ДМНХ, с. 79 - 80; [7. С 433 -- 442] ; [8. С 77 - 109] ).
302
отличается от ее статического варианта (4.23) множителем A{t).
Чаще всего принимается А (Г) = а0еЛГ; с учетом этого
у (t) = a/tLar. (t) К’-к(/). (10.28)
Степень однородности функции Кобба — Дугласа определяется
суммой aL + aj(. Для статической модели обычно принимается aL +
+ = 1. Но для динамической функции такое условие слишком жестко.
Типично соотношение aL + ag > 1, отражающее рост общей эффективно¬
сти производственных факторов в динамике. Если сумма aL + /= 1, то
можно осуществить нормировку коэффициентов эластичностей:
а*
“Р. —=1—э-
1 aL~\~aK
Тогда вместо (10.28) получаем
y(t) = а0е^' [L (t)P К (/)i-3]a;. + aA-. (10.29)
Логарифмируя, а затем дифференцируя по t функцию (10.28),
получаем соотношение между темпами прироста конечного про¬
дукта (национального дохода) и производственных факторов:
In y(t) = In а0 4- М + af In L (t) -f aK In К (t),
Py = h 4- ОС/Р/ -г &kPk- (10.30)
Таким образом, темп прироста конечного продукта (национального
дохода) есть сумма автономного темпа и взвешенной суммы темпов
прироста производственных факторов. Если ру > pL и ру > p/с, то это
означает увеличение эффективности обоих производственных факторов
(рост как производительности труда, так и фондоотдачи). Для эконо¬
мики СССР в течение продолжительного периода фондоотдача несколько
снижается, вследствие чего рк > ру > pL. Из (10.28) следует, что при
рк > ру> pi > 0 положительный темп X имеет место только при % < 1.
Если же ак > 1, то X < 0.
Функции (10.28), (10.29) имеют только один ’’динамический” па¬
раметр X. Учет динамики НТП, материализованного в производственных
факторах, осуществляется в форме (10.25), (10.26). Дальнейшая дина¬
мизация МПФ может проводиться путем включения в нее переменных
коэффициентов эластичности.
Динамическая функция с постоянной эластичностью заменяемости
ресурсов имеет вид ^
у (t) = A (t) [aLL (t)-« акк (t) -“] « . (Ю.31)
303
Она отличается от статического варианта (4.27) множителем A (t).
Напомним, что ai, а% — параметры степени трудоемкости и фондоемко¬
сти макротехнологии; со — параметр, связанный с эластичностью заме¬
щения ресурсов; у — коэффициент ’’отдачи на масштаб” (степень одно¬
родности функции), характеризующий интенсификацию производства.
Если о — эластичность замещения ресурсов, то
1 — о 1
® = —• ^F+70-
В простейшем случае
А (/) = а0ек‘, ак = 1 —а,, у = 1 •
Таким образом, в функции ПЭЗ мак ро технологи я характеризуется
как минимум четырьмя параметрами (<а0, \ aL, со). Нейтральный НТП
измеряется параметрами а0, Л, 7, ненейтральный — параметрами ак,
0/,, со.
Макроэкономическая функция ПЭЗ по сравнению с функцией
Кобба — Дугласа обладает двумя преимуществами: 1) позволяет более
явно разделить влияние НТП между двумя производственными фактора¬
ми; 2) эластичность заменяемости ресурсов не задается априорно равной
единице, а ’’оценивается”.
Обобщение функции (10.31) возможно путем динамизации параме¬
тров ai, ак, со, у, в частности с помощью трендовых моделей. Более
сложным является переход к функции с переменной эластичностью
заменяемости ресурсов. Простейшим ее случаем является функция, в
которой эластичность со является функцией времени.
Однофакторные макроэкономические функции. Наиболее простые
МПФ выражают зависимости конечного продукта (национального до¬
хода) от затрат живого труда и производственных фондов:
у (0 = Ф/. [L (0* *] 1 у (0 = [к (0. *]•
Построение и анализ таких функций могут предшествовать применению
двухфакторных МПФ. Принципиальный недостаток данного подхода
состоит в том, что динамика y(t) рассматривается в зависимости от ди¬
намики производственных факторов, взятых в отдельности.
Более содержательным является выведение одно факторных функ¬
ций показателей эффективности производства из двухфакторных МПФ.
С этой точки зрения наиболее удобна функция Кобба — Д/гласа первой
степени. Из нее выводится функция производительности груда v =
304
в зависимости от фондовооруженности к = —■-— :
v(t)=a^tkl-fi(t), (10.32)
где (1 — Р) — коэффициент эластичности по фондам, @ — коэффициент
эластичности по труду.
Поскольку 1 - /3 < 1, производительность труда растет медленнее фон¬
довооруженности при условии, что X невелико. При этом по аналогии с
(10.30)
р,-А. + (1—Р)р*. (Ю.ЗЗ)
Зависимость производительности труда от фондовооруженности
может вводиться как самостоятельная МПФ. Например:
v(t) = a0e*‘k»(f), (10.34)
где параметры а0, ф} ц оцениваются самостоятельно и отличаются от
параметров я0 Д, (1 -/3), входящих в (10.32).
Построение и анализ макроэкономических производственных функ¬
ций в СССР. Построение МПФ осуществляется, как правило, на основе
динамических рядов затрат ресурсов и результатов производства1.
Корректное построение производственной функции требует ’’очист¬
ки” эмпирических динамических рядов. Здесь решается ряд задач: а) выя¬
вление и исключение аномальных элементов динамических рядов; б) сгла¬
живание резких колебаний (в частности, из-за колебаний объемов сельско¬
хозяйственного производства); в) обнаружение и элиминирование авто¬
корреляции исходных данных и остаточных членов уравнения производ¬
ственной функции; г) проверка факторов на коллинеарность и др.
При измерении динамики конечного продукта (национального дохо¬
да) необходимо последовательно применять принцип сопоставимости цен
с учетом ассортимента и качества производимой продукции. Специфика¬
ция затрат живого труда включает измерение качественных характеристик
рабочей силы (профессионально-квалификационного состава, трудового
стажа, образовательного уровня, отраслевой структуры трудовых ресур¬
сов и т.д.) и их влияния на производительность труда. Спецификация про¬
изводственных фондов наряду с измерением динамики физического объе¬
ма производственных фондов должна отразить воздействие функциональ¬
ной, возрастной, отраслевой структуры фондов на их народнохозяйствен¬
ную эффективность.
Примеры построения функций Кобба — Дугласа и ПЭЗ для конечно¬
го продукта (национального дохода) СССР с соблюдением указанных
выше требований приводятся в ДМНХ, с. 84 — 86.
Возможно построение МПФ путем обобщения решений динамических оптими¬
зационных моделей, включающих воспроизводство и использование конечного про¬
дукта (национального дохода) и основных производственных факторов.
305
Оценка параметров МПФ непосредственно по данным о динамике национального
дохода, численности занятых в материальном производстве и объемах основных
производственных фондов за 1960 - 1985 гг., опубликованным в статистических
ежегодниках ’’Народное хозяйство СССР”, дает следующие результаты.
Для функции вида
у = а»/-1' К'1 -Р
получено: а0 = 1,022, 0 = 0,4618- При этом коэффициент детерминации R2 =
= 0,9969, остаточная дисперсия 0^^ = 0,0003, значение коэффициента Дарбина -
Уотсона DW =0,81. Соотношение темпов прироста таково: Ру = 0,462р£ + 0,5 38p/f.
Точность прогноза по данной функции невелика. При подстановке фактических
значений L и К* за 1986 г. ошибка прогноза на 1986 г. составляет 3,0 %.
Для функции
у = а$е L А
получены значения: а0 = 1,038, Х = - 0,0294, di =0,2399, %• = 0,9749. Статистичес¬
кие характеристики: R2 = 0,9982, Оост = 0,1)0016, DW = 1,63. Темпы прироста
связаны уравнением ру = - 0,0294 + 0,2399pi + 0,9749p/f- Поскольку в перспе¬
ктиве не будет прироста занятости в производственной сфере, можем допустить,
что pi = 0. Тогда для компенсации отрицательного X необходимо, чтобы pg = 0,03.
Для обеспечения ежегодного прироста национального дохода на 4% необходимо,
чтобы рк = 0,071.
Для функции 1
у = а0 [а/ L_0) (I —а/.) К~^] (0
имеем: а0 = 1,002, ai = 0,3588, со = 0,8088, Яг = 0,9984, а* =0,00014, DW =
= 1,58.
Наконец, для функции ПЭЗ с экспоненциальным множителем получено: а0 =
= 0,966, X = 0,025 2, aL = 0,5926, со = 3,0294, R2 = 0,9982, Оост = 0,00016, DW =
= 1,76.
Необходимо подчеркнуть важность всех этапов построения МПФ.
Некритическое использование эмпирических данных, недостаточная
спецификация производственных факторов, применение упрощенных
методов оценивания параметров являются причинами получения нена¬
дежных, противоречивых и ней нтерп ре тируемых результатов. Попытки
использования таких результатов серьезно компрометируют не только
конкретные приложения производственных функций, но и аппарат
МПФ вообще.
10.4. Расширенные модели экономического роста
Модели экономического роста, анализировавшиеся в 10.1, 10.2, отобра¬
жают воспроизводство общественного продукта и национального дохода
вне зависимости от других элементов общественного воспроизводства.
В них не учитывается влияние трудовых ресурсов и уже созданных про¬
изводственных фондов на динамику и структуру национального дохода;
производственное накопление не связывается с необходимостью повы¬
шения производительности труда. Факторные же модели экономическо¬
го роста, рассматривавшиеся в 10.3, исходят из экзогенной динамики
306
производственных факторов, т.е. являются чрезмерно ’’открытыми”.
Объединение условий простых макроэкономических моделей позволя¬
ет преодолевать их односторонность.
Синтез производственной функции и балансов производственных ре¬
сурсов. Макроэкономические производственные функции логично до¬
полнить балансами трудовых ресурсов и основных производственных фо¬
ндов, характеризующими процессы формирования величин L(t) и К(t).
Предварительно уточним ряд понятий, использовавшихся ранее. В
данном разделе величина у означает конечный продукт (национальный до¬
ход плюс возмещение выбытия основных производственных фондов), и —
валовые производственные капитальные вложения (накопление и возме¬
щение выбытия основных производственных фондов). Принимается, что
возмещение выбытия составляет yK(t), где у — фиксируемый параметр.
Таким образом,
= (10.35)
Динамика трудовых ресурсов достаточно хорошо описывается
трендовыми моделями. Для последующего анализа удобнее всего выб¬
рать экспоненту. Тогда в момент t величина трудовых ресурсов произ¬
водственной сферы составит L{0)е^9 где Z,(0) — ресурсы в момент
t = 0; I — темп прироста трудовых ресурсов. Потребность же в трудовых
ресурсах в момент t составляет ^ у (г), где v (t) — функция произ¬
водительности труда (например, (10.32) или (10.33)).
С учетом принятых допущений получаем баланс трудовых ресурсов
производственной сферы:
y(i) = L(0)e“, (10.36)
v(t)
откуда определяется максимально возможный объем конечного продук¬
та с точки зрения обеспеченности трудовыми ресурсами:
y(t) = L(0)e**v(t). (10.37)
Очевидно, что при неизменной производительности труда конечный
продукт может расти темпом, не превышающим /. Если же экзогенный
(или гарантированный) темп прироста производительности труда равен
5, то
y(t) = L(0) к (0)е<'+«>' = i/(0) <?<'+«>'. (10.38)
307
Результаты 10.1 — 10.2 необходимо дополнить следующим утвержде¬
нием: траектории национального дохода (конечного продукта) с темпом
ру достижимы, если ру < / + 5. При подстановке (10.32) в (10.37) полу¬
чаем
у (0 a0ektkv~^ (t) L (0) elt = a0L (0) ‘К1** (t). (10.39)
Подставляя (10.34) в (10.37), получаем
у (t) = a,L (0) tf(» (/) (Ю.40)
Введем в функцию Кобба — Дугласа (10.28) временную функцию
трудовых ресурсов:
у (0 = а0е« [L (0) eltfi Ках (/).
Проведя преобразования, получаем
у (t) = a0Lai (0) е^+ 1ак) ‘Ka«(t). (10.41)
Уравнения (10.39) — (10.41) увязывают двухфакторные производ¬
ственные функции и баланс труда с ростом фондовооруженности труда
или объема основных производственных фондов. Поэтому они могут
использоваться как однофакторные производственные функции. Однако
основное их назначение — включение в более общие макроэкономичес¬
кие модели, в которых А:(г) и K(t) являются эндогенными переменны¬
ми.
Отметим, что соотношение между k(t) и K(t) непосредственно выте¬
кает из определения фондовооруженности труда
K(t) = k(t)L(o)elt. (10.42)
Объединим теперь производственную функцию с балансом конечно¬
го продукта. С учетом (10.35)
уЦ) = *Шл-уК(Ц + с.(*). (10.43)
dt
Заменив y(t) двухфакторной производственной функцией общего
вида, получаем
dK (О
dt
■ f[L(t), К (t))~yK (t)—c{t). (10.44)
308
Попытаемся далее совместить выведенные соотношения с принципа¬
ми регулирования норм накопления, рассматривавшимися в 10.1 — 10.2.
Модель с фиксированной нормой капитальных вложений. Обозна¬
чим через а долю капитальных вложений в конечном продукте. Тогда
u(t) = ay (t) = af[L(t), A*(0] • Подставляя это выражение в (10.35),
получаем
*ML=af[L(t), K[t)-yK(t)]. (10.45)
В последующем анализе будем использовать вначале функцию
Кобба — Дугласа первой степени, а затем — ее общую форму.
Подставив (10.39) и (10.42) в (10.45), получаем
aa9L (0) h ‘k1 - f> (t)--yL (0) Pk (t). (10.46)
Другое выражение можно получить, дифференцируя (10.42):
L(0)e“^+/M0)e«*(0- (10.47)
Приравнивая правые части (10.46) и (10.47) и проведя преобразо¬
вания, приходим к
= aa0ek,k1- f> (t) — (I — у) k(t). (10.48)
(it
Решением данного дифференциального уравнения является
а,
k[t) = h(t)e* ,
(10.49)
где И (г) — временная функция, определяемая параметрами к (0), а0, X,
а, 0, т,/ (см. ДМНХ,с.89).
При этом 4 х
lim h (t) = ( аа0 V = Л.,
где к = 1 + Y+
Итак, темп прироста фондовооруженности труда асимптотически
приближается к величине —^ , асимптотой фондовооруженности явля-
ется k. (t) = h.eT‘.
309
Пусть, к примеру, а0 = 2,5, X = 0,02, / = 0,01, /3 = 0,65, у = 0,1, &(0) = 13,68
тыс. руб. Тогда = 0,0308, к (5) = 12,92, Лг*(5) = 8,20, к (10) =12,94,
£*(10) = 9,56, к{20) = 14,79, £*(20) = 13,00. Фактическая и асимптотическая
фондовооруженность сближаются.
В соответствии с (10.39) и (10.42) получаем
/ 1+±\ .
*/(<)= 0,1(0) Л*-Р(0«^ +р/ , (10.50)
(i+—N t
K(t) = L (0) h (t) e' e ) . (10.51)
Этим траекториям соответствуют асимптотические траектории
y*(t) и K*(t) при h(i) = h*. При этом траектория^ (Г) может находи¬
ться как ниже, так и выше траектории у*(г), в зависимости от £(0) и
устанавливаемого а.
Принимая во внимание, что u(t) — ay(t) и с (f) = (1 - a)y(t), при¬
ходим к выводу, что динамика основных производственных фондов,
конечного продукта и его функциональных элементов стремится к раз¬
витию с постоянным темпом прироста рт> являющимся суммой темпа
прироста трудовых ресурсов в производственной сфере и асимптоти¬
ческого темпа фондовооруженности труда:
р.-1 + f <10-52>
Существенным отличием полученного результата от решения модели
с постоянной нормой накопления (10.11) является то, что темп рт не
зависит от нормы производственных капиталь¬
ных вложений. Однако эта норма положительно влияет нашст
фактического конечного продукта y(t) через множитель h\ ~ P(t).
При использованных выше исходных данных рт = 0,0408. В диапазоне
нормы производственных капиталовложений а Е [0, Т] имеем у (t) >
>у* (г).
Проанализированная ситуация экономического роста с фиксированной нор¬
мой производственных капиталовложений известна в литературе как модель
Солоу, или Солоу - Свена (см. комментарий в ДМНХ, с. 91 - 92).
Для большей сопоставимости полученных выводов с моделью, излагавшейся в
10.1, перейдем к формулам национального дохода, используя (10.50) - (10.52):
(*+-)'
у(0—?*(/) = L(0)[e0Ai-f»(O —(01 13 ' • <10'53)
yt(t)-yKm(t) = L(0)[a0hl^-yht]e^ Э / (Ю.54)
Полученные траектории качественно не отличаются от траекторий конечного
продукта.
Отметим особые свойства модели, включающей функцию Кобба —
310
Дугласа при ai + ак f=\. Используя аналогичные приемы математичес¬
кого анализа, что и для функций первой степени, получаем решение в
виде
»«)= (0)*“Ч')ехр (£Sl't) (Ю.55)
При 0 < а% < 1 динамика .у (г) аналогична динамике в (10.50).
Темп прироста конечного продукта стремится к темпу
pm 1—‘
Другие свойства фактической и асимптотической траекторий развития
при 0 < < 1 качественно также не отличаются от результатов анализа
при aL = /3, а/с = 1 — Р, 0 < /3 < 1. Однако при ак > 1 модель приобретает
качественно иные свойства (см. ДМНХ, с. 92).
Оптимизация с постоянной нормой капитальных вложений. Логичес¬
ким развитием рассмотренной выше модели является оптимизация
постоянной нормы производственных капитальных вложений. При этом,
как и в 10.2, максимизируется суммарное потребление за любой проме¬
жуток времени (в том числе и дисконтированное потребление).
Ввиду того, что анализ модели требует довольно длинных ма¬
тематических выкладок, ограничимся экономической интерпретацией
конечных результатов (более подробное изложение см. в ДМНХ,
с. 93 - 94).
Постоянной норме капиталовложений ат = 1 — Р соответствуют
траектории конечного продукта, потребления, капиталовложений и осно¬
вных производственных фондов, имеющие одинаковый постоянный
темп прироста рщ = / + ~р~ . Экономическое развитие с неизменной
структурой и наивысшим темпом роста принято называть магистра¬
льным, а соответствующую траекторию — магистралью.
Итак, оптимальная норма ат при магистральном развитии равна
эластичности конечного продукта по основным производственным
фондам1. Такое определение известно как ’’золотое правило
накопления” (впервые этот результат получил Е.Фелпс).
Для немагистральной траектории роста потребления норма = 1 — р
в общем случае не является оптимальной. Оптимальная норма а* должна
обеспечивать максимум суммарного или дисконтированного потребле¬
ния за плановый период [0, Т] :
т
а) С (а, Г) = $(1— a)y{t)dt-^ max, а£[0, !], (10.56)
о
Этот вывод имеет экономический смысл только при 0 </3 <1.
311
б) С, (а , Г) = /(1 — 'a)e~03ty(t)dt -+ max,a£ [О, 1], (10.57)
О
где у (г) определяется из (10.50).
Отметим два свойства оптимальных норм капиталовложений а* и
а*, являющихся решением (10.54), (10.55).
1. Чем продолжительнее плановый период [0, Т], тем больше опти¬
мальная норма а* для данного периода соответствует магистральной
am — 1 ~ Р:
lim a* (Т) — 1 —р.
7* -► ос
2. Чем выше дисконт потребления со > 0, тем меньше а *.
В соответствии с приведенными выше исходными данными магистральная
норма ат = 0,35. Приведем расчеты оптимальных норм а* (Г) и а*(Т) при раз¬
ной продолжительности планового периода и дисконте потребления со =
= 0,08:
а* (5) = 0, а* (10) = 0,02, а* (20) = 0,21,
а® (5) = 0, а*(10) = 0. а* (20) = 0,16.
Решения проанализированной модели обладают существенными пре¬
имуществами по сравнению с решениями моделей из 10.2, в которых
оптимальная норма накопления гораздо сильнее зависит от продолжи¬
тельности планового периода и не стремится к какому-либо устойчивому
уровню внутри отрезка [0, 1 ] .
Оптимизация с переменной нормой капитальных вложений.
Рассмотрим задачу максимизации дисконтированного потребления
на одного работника производственной сферы за период [0, Т) :
Г _£i£L е-ы dt —шах. (10.58)
J ^ (О
о
Эта целевая функция дает почти те же результаты, что и мак¬
симизация дисконтированного потребления на
душу населения, но при этом упрощает формулы расче¬
тов.
Функция c(t) выражается через y{t) по формуле (10.50), которая
включает экспоненциальный множитель с темпом (/ + _^~)- После преоб¬
разований (10.56^ входящий в нее экспоненциальный множитель получа¬
ет темп (— со + -р—); в дальнейшем принимается обозначение: со = со —
— . В анализе решения важную роль играет число h *, определяемое
312
параметрами а0, |3, oj, к и расчетные отрезки времени Т£(к (0)),
Т*(к (0)), также определяемые параметрами модели1. При подста¬
новке введенных ранее исходных данных имеем со = 0,05, к= 0,14,
£*= 10,6, Т* = 1,83, Ц = 7,46.
В 10.2 было показано, что оптимальное решение задачи с переменной
нормой накопления, но постоянной капиталоемкостью сильно зависит от
продолжительности планового периода. При небольшом ^накопление
вообще отсутствует, а при достаточно большом Топтимальная траекто¬
рия содержит релейное переключение потребления и накопления. Логич¬
но предположить, что введение в модель переменной капиталоемкости,
регулируемой с учетом условий оптимизации, должно способст¬
вовать получению более гладких и устойчивых оптимальных ре¬
шений.
Оптимальная стратегия развития по анализируемой модели зависит
от величины Т и начального уровня фондовооруженности к (0). Вначале
рассмотрим стратегию развития при допущении, что плановый горизонт
бесконечен: Т » 00.
Бесконечная траектория экономического развития состоит из двух
участков (см. рис. 10.7).
' н
1
<*т
О
т*
> н
Рис. 10.7. Динамика оптимальной нормы капиталовложений и оптималь¬
ной фондовооруженности труда на бесконечном интервале времени:
ci) начальная фондовооруженность ниже магистральной; б) начальная фон¬
довооруженность выше магистральной
Исходная формулировка (10.58) приводится к задаче оптимального управле¬
ния и решается с использованием принципа Понтрягина (см. ДМНХ, с. 95 - L00).
Аналогичная задача при X = 0 известна как модель К.Шелла (см. [7. С. 449 -
551]). Математический анализ моделей данного типа выполнен КЭрроу (см,
Эрроу К. Математическая экономика. М.: Мир, 1974. С. 7 - 45).
313
При t £ [О, Г£] оптимальная норма капиталовложений принимает
только одно из двух значений: 0 или 1. Если &(0) < /Г*, то требуется
максимально быстро поднять фондовооруженность, поэтому a* (t) =
= 1 (рис. 10.7). Если же fc(0) > h *, то, наоборот, в интересах максими¬
зации потребления не следует затрачивать капиталовложения, поэтому
a*(t) = 0, а фондовооруженность снижается (рис. 10.7). В этом случае
объем основных производственных фондов уменьшается (поскольку
отсутствует возмещение выбытия фондов), а объем конечного продукта
изменяется темпом р = X + Щ + у(3 — у. При используемых исходных
данных это дает Ру = — 0,0085.
При t > Г* должна поддерживаться постоянная норма ка¬
питаловложений
“т = =“— (1 Р)> (10.59)
СО —X
представляющая собой модификацию ’’золотого правила накопления”.
При использовании прежних исходных данных получим ат = 0,247.
В точке t = 7* траектория выходит на магис¬
траль с постоянным темпом прироста конечного продукта, потребле¬
ния, капиталовложений и основных производственных фондов:
(10.60)
При используемых исходных данных р'*1 = 0,0408. Фондовооружен¬
ность, так же как и производительность труда, растет темпом -4- =
= 0,0308. Р
Перейдем к анализу динамики экономического развития при огра¬
ниченной продолжительности планового периода Т< «>. Здесь принципи¬
ально важны два случая.
1. т <П + Тн(к$).
Оптимальная норма• капиталовложений можт принимать только
два значения: 0 или 1.
При к (0) > h* исходный уровень фондовооруженности достато¬
чно высок и поэтому при небольшом плановом горизонте капитало¬
вложения нецелесообразны: а* (t) = 0 для всех t Е [0, Т]. Траектория
аналогична первому участку развития при бесконечном периоде, когда
к (0)>h* (см. рис. 10.7).
314
Рис. 10.8. Динамика оптимальной нормы капиталовложений и оптималь¬
ной фондовооруженности при продолжительности планового периода
Т*<Т<Т*к- Тц и начальной фондовооруженности ниже магистральной
Если же А;(0) < h*, то поведение решений качественно различается
для т<Т* (к(0)) и Т*(к (0)) <Т<Т£+Т*.
Когда плановый период короток, а именно Т <Т* (к{0)), тогда не¬
эффективно затрачивать капиталовложения и а*(/) = 0. Решение полу¬
чается аналогичным рассмотренному выше случаю.
Но если Т > Г*(&(0)), то капиталовложения в начале периода це¬
лесообразны, оптимальная норма капиталовложений равна единице.
Однако недостаточная длительность планового периода не позволяет
довести фондовооруженность до магистрального уровня. По достижении
некоторого Т <Т£(к (0)) норма капиталовложений становится равной
нулю и все ресурсы конечного продукта переключаются на потребление.
Итак, в этом случае
*•«)={ u!
\ о, т
<t<f,
f <t<T
(см. рис. 10.8).
2. Т>Т%+Т*(к(0)).
Оптимальная траектория состоит из трех участков: стартового, ма¬
гистрального, финишного (см. рис. 10.9). Использование ’’автодорож¬
ной” терминологии имеет веские основания. Начальный участок — это
продвижение к магистрали, на которой можно развить максимальную
постоянную скорость. Попав на магистраль, целесообразно проехать по
ней возможно большую часть пути (длительности планового периода).
Завершающая часть пути — съезд с магистрали для достижения коне-
315
Рис. 10.9. Динамика оптимальной нормы капиталовложений и оптималь¬
ной фондовооруженности при Т > Tj* + Т * :
я) начальная фондовооруженность ниже магистральной; &)начальная
фондовооруженность выше магистральной
чной цели движения (максимизация интегрального экономического
эффекта).
При t G [0, Г* (к (0))] динамика полностью аналогична рассмо¬
тренному выше первому участку развития при Т = Здесь происхо¬
дит перестройка структуры распределения конечного продукта с целью
приближения фондовооруженности труда к магистральной; при этом
характер изменений определяется соотношением исходной и магистра¬
льной фондовооруженности. Норма капиталовложений равна либо 0,
либо 1.
При t Е (Г*(А;(0)), Т - Т£) осуществляется магистральное развитие
экономики при норме капиталовложений (10.59) и темпе прироста
(10.60).
Наконец, на участке t Е [Г - 7^, 7] осуществляется структурная
перестройка с целью максимизации потребления. Капиталовложения
отсутствуют. На этом участке темп изменения конечного продукта (и
потребления) равен р = р (т + /) + X — 7- При используемых исходных
данных р = — 0,0085.
Проблема ’’хвоста” планового периода сохраняется в том смысле,
что уменьшение фондовооруженности труда и объема основных произ¬
водственных фондов не учитывает интересы послепланового развития.
Чтобы ослабить этот недостаток, целесообразно вводить в модель неко¬
316
торые ограничения на конечные состояния, например к (Т) >к,а (Т) >
> а и т.п.
Важно отметить, что при Т > 7-£ + Г* (£(0)) продолжительность
стартового и финишного участков не зависит от Т. С увеличением Т
все большая часть траектории проходит по магистрали. Поэтому анали¬
зируемая модель особенно привлекательна для долгосрочного прогно¬
зирования и планирования. Главной особенностью оптимальной траекто¬
рии является магистральный участок развития, на котором поддержи¬
ваются постоянными максимально возможный темп и основные мак¬
роэкономические пропорции. Исключаются релейные переключения
потребления и накопления, а также чрезмерная зависимость поведения
решения от Т. При достаточной длительности планового периода
’’переходные” этапы с резкими структурными сдвигами занима¬
ют относительно небольшую часть траектории. Кроме того, для
финишного участка легко применяются сглаживающие регулято¬
ры.
10.5. Моделирование динамики двух подразделений
общественного производства
Схемы воспроизводства К.Маркса — В.И.Ленина и макромоделирова¬
ние. Схемы простого и расширенного воспроизводства, разработанные
К.Марксом применительно к капиталистическому хозяйству и развитые
впоследствии В.И.Лениным, играют исключительно важную роль в эко¬
номической теории социализма и методологии макро моделирования.
Подробный анализ схем воспроизводства классиков марксизма-лениниз¬
ма содержится в литературе по политической экономии и общеэкономи¬
ческим проблемам. Поэтому ограничимся кратким рассмотрением схем
воспроизводства с точки зрения возможностей конструирования на их
основе моделей экономической динамики.
Будем использовать следующие обозначения: х — объем произве¬
денной и реализуемой продукции, с — фонд возмещения используемых
средств производства, v — необходимый продукт, m - прибавочный
продукт. Элементы продукции и затрат первого и второго подразделений
отмечаются индексами I и II. Из анализа схем воспроизводства следует,
что без поддержания определенных материально-вещественных и стои¬
мостных пропорций невозможно ни простое, ни расширенное воспроиз¬
водство.
Балансы продукции I и II подразделений по стоимостному составу
имеют вид
Xi=Ci + Ui + m
Яи^н + он + тн. (10.61)
317
Основное условие расширенного воспроизводства выражается
неравенством
(10.62)
Прибавочный продукт в каждом подразделении распределяется на
накопление (в средствах производства Ас и в предметах потребления
Ду) и потребление (тп) : т\ = Ас\ + Av\ + т\п, т\\ = Аси + +
+ т\\п. При этом необходимо, чтобы величина Avj + т\п в форме средств
производства была обменена на эквивалентную величину предметов по¬
требления, а величина Ас\\ — в форме предметов потребления — на эк¬
вивалентную величину средств производства.
При расширенном воспроизводстве (с учетом накопления) в каж¬
дом годовом цикле необходимо осуществить обмен между двумя подра¬
зделениями и внутри них в следующих пропорциях (см, рис. 10.10).
*17 =
Рис.10.10
Результатом обмена продукции в соответствии с рис 10.10 являются
балансы распределения продукции двух подразделений:
*1 = (С1 + си) +
возмещение потребленных
средств производства
*11 = + иП + т\п + "*111.) +
непроизводственное потребление
(Д^! + Лсп)
ение (
одства
(Ду, 4- Аи„)
накопление средств
производства
(10.63)
накопление предметов
потребления
Совмещение (10.61) и (10.63) дает систему уравнений межотрасле¬
вого баланса общественного продукта в разрезе двух подразделений.
Соотношения расширенного воспроизводства (10.61), (10.63)
содержат избыточное число переменных. Поэтому для построения опера¬
ционной модели (числовой или формализованной) необходимо вводить
ряд дополнительных допущений о зависимостях между переменными,
как правило, в виде структурных параметров.
Возможность включения в схемы воспроизводства различного рода
структурных параметров и их комбинаций приводит к большому раз¬
318
нообразию макроэкономических моделей, конструируемых на базе
схем воспроизводства. Характерным признаком этих моделей яв¬
ляется то, что включаемые в них структурные параметры отно¬
сятся как к материально-вещественным пропорциям (например,
коэффициенты
£1 £ll Aci
*\ ' ’ Aci + Дсц
и т.п.), так и к пропорциям стоимостным (нормы прибавочного продук¬
та в подразделениях, доли распределения прибавочного продукта подра¬
зделений на потребление, накопление средств производства, накопление
предметов потребления и т.п.)1.
Динамика двух подразделений в моделях воспроизводства общест¬
венного продукта. Проанализируем рассматривавшиеся в 10.1, 10.2, 10.4
модели воспроизводства общественного продукта и национального до¬
хода с точки зрения динамики I и И подразделений. Возможность такого
анализа облегчается тем, что в указанных моделях нами выделялись
такие элементы валового общественного продукта, как фонд возмеще¬
ния потребленных средств производства, фонд производственного на¬
копления, фонд непроизводственного потребления и накопления, форми¬
руемые за счет производства либо средств производства, либо предметов
потребления.
Линейные модели с экзогенной динамикой потребления. Объемы
производства продукции I подразделения и II подразделения в соответ¬
ствии с обозначениями, принятыми в 10.1, удовлетворяют равенствам:
хг = Ау—с, х2^с. (10.64)
Пусть Pi и р2 — темпы прироста продукции I и II подразделений;
7i и 72 — доли I и II подразделений в валовом общественном продукте
(7i +72 =0- Тогда
*4rj- (Ю-65)
Систематизируем основные выводы, вытекающие из анализа трех
типов экономического развития, различающихся темпами прироста
потребления и динамикой нормы производственного накопления. Вна¬
чале будем исходить из того, что параметры макротехнологии — коэффи¬
циенты А и В — не изменяются во времени.
1. Постоянная норма накопления: a (t) = а0, г = —g~ = Ро-
1 Анализ разнообразных модификаций схем расширенного воспроизводства
и моделей, сконструированных на их основе, см. в Гз1, Г4, гл. II, [7, гл.
II, III, X].
319
Поскольку рс= Ру = Ро и у- “ (1 “ ао)> 10 Pi — Р2 ~ Ро> 71
= 1 -х^1 = х<1 _а°^
Итак, темпы двух подразделений постоянны и одинаковы; доли под¬
разделений в валовом продукте не изменяются. Вводя прежние исходные
данные (А = 2,5, В = 3,5, а0 = 0,20), получаем р0 = 0,057, ух = 0,68,
72 = 0,32.
2. Уменьшающаяся норма накопления как следствие г >р0.
Доля II подразделения растет за счет уменьшения нормы производ¬
ственного накопления: р2 >Pi. Однако темпы прироста валового проду¬
кта и национального дохода падают. В точке tx эти темпы становятся
нулевыми; еще раньше — при t = tx <t2 достигает максимума и начи¬
нает уменьшаться продукция I подразделения. В точке t2 нулевым ста¬
новится объем продукции Д подразделения. Например, при г = 0,08 на-
ходим?! = 3,24, t\ =4,98,72 = 9,8.
3. Увеличивающаяся норма накопления как следствие г <р0.
Доля I подразделения и темп I подразделения растут за счет увели¬
чения нормы накопления. Пределами их роста являются: lim pj (0 =
1 ч t~^°°
— -^г = 0,286, lim 7i (0 =1. Например, при г = 0,04 имеем pt (5) =
= 0,11, р! (10)Г=°0,185, рх (20) = 0,275, ух (5) = 0,73, 7i (Ю) = 0,82,
7i (20) = 0,97.
Общий вывод состоит в том, что при сделанных допущениях (в ча¬
стности, неизменности коэффициентов А и В) монотонно снижающаяся
или монотонно повышающаяся доля I подразделения может быть оправ¬
дана только на ограниченных интервалах времени, когда ставятся задачи
резкого ускорения роста уровня жизни или резкого увеличения произ¬
водственного потенциала.
Рассмотрим теперь, какое влияние на динамику соотношения двух подразделе¬
ний оказывает изменение во времени коэффициентов А и В.
Допустим, B{t) = b(t)A = bifyAekt и к > 0 (т.е. увеличивается только прямая
капиталоемкость при неизменной материалоемкости). Тогда в условиях постоян¬
ной нормы накопления соотношение объемов продукции I и II подразделений
согласно (10-63) остается неизменным, а темпы 1и И подразделений уменьшаются
одинаково. Если же при росте капиталоемкости поддерживается постоянный
темп роста потребления, то доля продукции I подразделения падает и динамика
качественно аналогична траектории, соответствующей постоянной капиталоемко¬
сти и условию г >р0. При снижении капиталоемкости (£<0) и постоянном темпе
потребления имеем противоположные изменения динамики соотношения двух под¬
разделений. И в этом случае картина качественно не меняется по сравнению с раз¬
витием при постоянном коэффициенте В и условии 1 <р0.
Изменение коэффициента А во времени оказывает более сложное влияние на
динамику двух подразделений, поскольку вызывает изменение и коэффициента
В (так как В = ЬА). В частности, если А (t) —A (0)emt, то при постоянном Ъ (Г) =
= Ь имеем В (f) =B(0)emt, а вместе с этим и рассмотренные выше последствия
для соотношения двух подразделений, обусловленных изменениями темпа и струк¬
туры национального дохода. С этими последствиями сочетается влияние А (t) на
пропорцию между валовым продуктом и национальным доходом.
Проанализируем динамику двух подразделений при постоянной норме произ¬
водственного накопления Од и A(t) = А (0)emt, где т > 0. Темп прироста II под-
320
разделения и производственного накопления монотонно уменьшается до нуля,
тогда как темп роста I подразделения имеет пределом величину т. Доля II подра-
1 CIq YYlt
зделения уменьшается: 72 (О = ^ ^ в ; доля I подразделения соответствен¬
но увеличивается. При снижении материалоемкости (т<0) изменения имеют про¬
тивоположное направление.
Линейные оптимизационные модели. В 10.2 анализировались макро¬
экономические модели, в которых оптимизация осуществлялась путем
выбора политики распределения национального дохода на потребление
и накопление. Проинтерпретируем полученные результаты с точки зре¬
ния динамики двух подразделений общественного производства.
1. При Т < В рост производства неэффективен, весь национальный
доход используется на потребление. Отсюда xf (t) = (А — 1)у(0),
*2(0 = У (0)- Соотношение между подразделениями не меняется:
А — 1 1
71 =-х~'^ = Х-
2. При Т > В динамика двух подразделений качественно изменяется
в точке t = Т - В. Здесь происходит релейное переключение потребления
и накопления.
Для t Е [0, Т - В] весь национальный доход направляется на накоп-
ление. Поэтому ** (г) =х (0)е в \ xf (?) = 0, yf (t) = 1.
Для f Е [Т - В, Г\ объем национального дохода стабилизируется
и весь направляется на потребление. Поэтому xf (t) = (А - 1 )у(Т- В),
х* (0 = У (Т - В). Соотношение двух подразделений на этом отрезке
не меняется.
Получаемые решения неудовлетворительны прежде всего в социаль¬
но-экономическом смысле. Этим обусловлены попытки сглаживания
скачкообразной траектории с помощью дисконта потребления и ряда до¬
полнительных условий (непрерывный рост потребления, минимальный
уровень накопления в конце периода, ограничения на интервал измене¬
ния нормы накопления и т.д.). Подходы, рассмотренные в 10.2, приво¬
дят также к сглаживанию динамики двух подразделений.
Решения задачи оптимизации постоянной нормы производственного
накопления также сильно зависят от продолжительности планового
периода.
При Т < 2В рост производства отсутствует, соотношения двух под¬
разделений не меняются: *f(r) = (А - 1)^(0), xf(t) = у (0), ух =
= — , у2 = . При Т>2В норма накопления монотонно возрастает
с увеличением Т и вследствие этого увеличиваются темпы прироста
обоих подразделений, равные друг другу. Общим свойством оптималь¬
ных траекторий при любом Т является то, что при неизменных А и В
соотношения объемов двух подразделений остаются постоянными.
Расширенные модели с взаимозаменяемыми ресурсами. Общим свой¬
ством моделей, объединенных в 10.4, является изменение соотношения
используемых производственных факторов. Указанное свойство имеет
11 Зак. 2414 321
прямое отношение к динамике двух подразделений, поскольку повыше¬
ние фондовооруженности труда требует при прочих равных условиях
ускорения роста I подразделения, а понижение фондовооруженности от¬
носительно уменьшает потребности в средствах производства.
Анализ моделей 10.4 с точки зрения динамики двух подразделений несколько за¬
трудняется тем, что деление конечного продукта на две части - производственные
капиталовложения (и) и остальной конечный продукт (с) - не совпадает с делени¬
ем его на средства производства и предметы потребления. Но поскольку доля
средств производства, включаемых в состав с (накопление производственных
оборотных фондов), относительно невелика, отождествление темпов величин
с it) и х2 (t) несет незначительные погрешности. Предполагается также, что коэф¬
фициент А не меняется.
Главным результатом анализа указанного класса моделей является
выявление асимптотических траекторий и магистралей экономического
развития. Помимо свойств, рассматривавшихся в 10.4, асимптотические
траектории и магистрали характеризуются равными темпами и неизмен¬
ными соотношениями объемов I и II подразделений.
На участках выхода на магистраль соотношение темпов I и II подраз¬
делений устанавливается в зависимости от соотношения начальной и
магистральной фондовооруженности труда (fc(0)) и h*. Если &(0) <
< h*, то необходимость увеличения фондовооруженности приводит к
ускорению капиталовложений и соответственно к опережающему росту
I подразделения. Если же fc(0) >/**,, то целесообразность снижения фо¬
ндовооруженности в интересах увеличения фонда потребления приводит
к опережающему росту II подразделения.
На финишном участке оптимальной траектории, где форсируется
рост потребления, преимущественным темпом увеличивается II подраз¬
деление.
В заключение заметим, что деление общественного производства
на два подразделения и моделирование динамики этих подразделений
есть первый шаг перехода от макроэкономических к структурным (ме¬
жотраслевым) моделям народного хозяйства, которым посвящены гл.
11-13.
10.6. Макроэкономические модели
в системе прогнозирования и планирования
Проанализированные в данной главе модели дают представление о
проблемной организации макроэкономического моделирования: возмо¬
жные темпы экономического развития, оптимальное соотношение потре¬
бления и накопления, взаимодействие основных факторов в процессах
воспроизводства, влияние научно-технического прогресса на динамику,
эффективность и интенсификацию производства, динамика и взаимосвя¬
зи двух подразделений общественного производства и т.д. Именно важ¬
ность и разнообразие содержательной проблематики определяют в пер¬
322 г
вую очередь широкую сферу применения макроэкономических моде¬
лей.
В практике прогнозирования и планирования макроэкономические
модели используются преимущественно на начальной и заверша¬
ющей стадиях подготовки народнохозяйственных прогнозов и пла¬
нов.
При разработке концепции предстоящего развития страны с помо¬
щью макроэкономических моделей проводится сравнительный анализ
возможных альтернатив достижения экономических и социальных
целей. На этой стадии важна не столько точность конкретных проекти¬
ровок, сколько выделение и всестороннее исследование узловых проб¬
лем, системный анализ динамики народного хозяйства в целом. Здесь
в наибольшей степени проявляются познавательные возможности макро¬
моделей, выявляющих сложные связи между исходными предположе¬
ниями (условиями, гипотезами) и их далеко не очевидными следстви¬
ями. С этой точки зрения даже модели, дающие неудовлетворительные
решения (например, с релейными переключениями потребления и нако¬
пления), весьма полезны, ибо предостерегают от ошибок в экономичес¬
кой политике, стимулируют целенаправленный поиск более эф¬
фективных плановых решений и разработку более совершенных
моделей.
На начальных этапах прогнозирования и планирования особенно
важно изучить возможно более широкое множество альтернатив разви¬
тия народного хозяйства. Для этого по макромоделям проводятся
многовариантные прогнозные расчеты. Варианты прогнозов, различа¬
ющиеся качественными альтернативами решения социально-экономичес¬
ких задач и количественными оценками экзогенных переменных и па¬
раметров моделей, обычно объединяются в следующие группы: инер¬
ционные, пессимистические, наиболее вероят¬
ные, оптимистические.
На конечной стадии прогнозирования и планирования макроэконо¬
мические модели используются как инструмент проверки сбалансиро¬
ванности частных прогнозов и плановых проектировок (межотрасле¬
вых, отраслевых, территориальных и т.п.). Здесь могут выявляться не¬
соответствия значений обобщающих показателей развития народного
хозяйства, получаемых по макро моделям и при своде частных прогно¬
зов (проектов). В результате анализа причин этих расхождений вносят¬
ся необходимые корректировки в частные прогнозы или исходные
условия макро мо дел ей.
Однако возможности макроэкономического моделирования не сле¬
дует переоценивать. Во-первых, макро моделирование в принципе не
охватывает существенную часть задач планирования (планирование
по межотраслевым комплексам, отраслям, регионам различного ран¬
га, производственным объединениям и предприятиями т.д.). Во-вторых,
макромодели неизбежно упрощенно учитывают влияние структурных
11* 323
факторов на значения макропоказателей, вследствие чего возникают
так называемые ошибки агрегирования1.
Например, такой макроэкономический параметр, как материалоем¬
кость валового общественного продукта, представляет собой суммар¬
ную и средневзвешенную величину из большего числа коэффициентов
материальных затрат:
а = ^ Pkaks^s'
k, s € /
где (ifa — затраты ft-го продукта на производство единицы 5-го продукта;
Рк — цена &-го продукта; \s — доля 5-го продукта в валовом обществен¬
ном продукте; / — множество всех видов продукции, входящих в вало¬
вой общественный продукт. Изменения структуры производства и соот¬
ношений цен существенно влияют на общую материалоемкость, но эти
факторы могут учитываться только экзогенно.
Разработка детализированных народнохозяйственных моделей и мо¬
делей подсистем народного хозяйства в принципе позволяет прогнозиро¬
вать все макроэкономические показатели. Кроме того, детализирован¬
ные модели необходимо использовать для уменьшения ошибок агреги¬
рования, содержащихся в макромоделях. Поэтому может возникнуть
вопрос, а нужны ли вообще макромодели и не проще ли полностью за¬
менить их детализированными моделями?
Вывод о ненужности макромоделей столь же односторонен, как и
представление о доминирующей роли макромоделей в системе модели¬
рования народного хозяйства. Макроэкономические и детализированные
народнохозяйственные модели не исключают, а дополняют друг
друга.
Исследования, предварительно проведенные на основе макроэконо¬
мических моделей, облегчают и ускоряют построение и использование
более сложных детализированных народнохозяйственных моделей
(анализ взаимосвязей между факторами, отбор основных альтернатив
развития, определение области наиболее вероятных значений ключевых
показателей и т.п.). С другой стороны, на основе расчетов по детализи¬
рованным моделям уточняются значения макроэкономических парамет¬
ров. Таким образом, между макроэкономическими и детализированны¬
ми моделями осуществляются взаимный обмен информацией и взаим¬
ное согласование результатов, включающее операции дезагрегирования
и агрегирования. Важно, чтобы разработка и применение макроэкономи-
Ошибкой агрегирования называется разность Дк* между результатом агреги¬
рования детализированных показателей (вектора X), рассчитанных по детализиро¬
ванной модели (или ряду детализированных моделей), и значением агрегированно¬
го показателя хф , определяемого по макромодели Дс* = GX - хф, где G - опера¬
тор агрегирования (см., например, об ошибке агрегирования в межотраслевых
балансах в ММСЭ, с. 254 - 255).
324
ческих и детализированных моделей осуществлялись на основе единого
информационного обеспечения.
Главной особенностью современного этапа разработки макроэконо¬
мических моделей и их применения в прогнозировании и планировании
является переход от эпизодического использования отдельных относи¬
тельно простых моделей к созданию интегрированных моделей и комп¬
лексов макроэкономических моделей, включаемых в действующую
технологию планирования в виде подсистем АСПР. При этом, как пра¬
вило, совмещаются нормативный и дескриптивный подходы. В частности,
следует отметить ускорение работ по эконометрическому
моделированию.
В Научно-исследовательском экономическом институте при Госпла¬
не СССР разработана модель прогнозирования темпов и пропорций
развития народного хозяйства в разрезе двух подразделений.
Модель включает: производственные функции, балансы продукции и основных
фондов, эконометрические зависимости отдельных структурных элементов конеч¬
ного продукта и потоков продукции, функции ввода и выбытия основных произ¬
водственных фондов и т.д. Модель используется при подготовке средне- и долго¬
срочных прогнозов ( [9] ).
В Центральном экономико-матемагическом институте АН СССР
совместно с Главным вычислительным центром при Госплане СССР
создан комплекс макромоделей планирования (КМП), представляющий
собой многоцелевую человеко-машинную систему взаимосвязанных
моделей перспективного народнохозяйственного планирования.
КМП включает четыре основных компонента: банк моделей, банк данных,
систему манипулирования данными, систему конструирования моделей (диало¬
говый пакет эконометрического моделирования). В состав банка моделей входит
пакет однопродуктовых эконометрических моделей, определяющих динамику
важнейших макроэкономических показателей. Во всех моделях присутствует
основной набор уравнений, дополняемый в различных моделях специфическими
для них уравнениями. Диалоговый пакет эконометрического моделирования пред¬
назначен для построения регрессионных уравнений макропоказателей на основе
банка данных. С помощью средств этого пакета осуществляются ’’сборка” урав¬
нений и балансовых тождеств в различные макроэконометрические модели, нахож¬
дение решений моделей, перестройка моделей в режиме диалога [6].
Модель системы макроэкономических показателей, созданная в
Институте экономики и организации промышленного производства
Сибирского отделения АН СССР, предназначается для анализа вариантов
темпов роста макропоказателей с учетом взаимодействующих факторов,
изучения целесообразных сочетаний интенсивных и экстенсивных факто¬
ров роста, определения эффективности различных программ осущест¬
вления капитальных вложений, оценки влияния нормы производствен¬
ного накопления на темпы и пропорции экономического роста и т.д.
[4]
325
Разработки макроэкономических моделей активно осуществляются
и в ряде союзных республик. Республиканские макро модели и компле¬
ксы моделей эконометрического типа, разработанные в научно-исследо¬
вательских центрах РСФСР, УССР, Казахской, Латвийской, Литовской
и других союзных республик, по своим предпосылкам, структуре,
методике построения и применения довольно близки к моделям на¬
роднохозяйственного уровня.
Литература
1. Анчишкин А.И. Прогнозирование роста социалистической экономики. Раздел III.
2. Ашманов С.А. Введение в математическую экономику. Часть III.
3. Дадаян B.C. Макроэкономические модели. М.: Наука, 1983.
4. Казанцев С.В. Макромоделирование расширенного воспроизводства. Новоси¬
бирск: Наука, 1980.
5. Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Экономическая кибернетика.
М.: Экономика, 1982. Гл. 7.
6. Комплекс моделей перспективного планирования. Гл. 1, 2.
7. Моделирование народнохозяйственных процессов. Гл. I - III, X, XIII.
8. Плакунов М.К., Раяцкас Р.Л. Производственные функции в экономическом
анализе.
9. Черников ДА. Темпы и пропорции экономического роста. М.: Экономика,
1982. Гл. 2, 4,5.
ГЛАВА 11
ТЕОРЕТИЧЕСКИЕ СТРУКТУРНЫЕ МОДЕЛИ
Структурные модели экономической динамики в отличие от макроэко¬
номических включают описание материально-вещественной структуры
народного хозяйства и взаимосвязей между отдельными видами произ¬
водства. Атрибут ’’теоретические” подчеркивает главное назначение
моделей и отделяет их от класса прикладных структурных моделей
народного хозяйства.
Большинство рассматриваемых в данной главе моделей является
традиционным предметом математической экономики,
специализирующейся на математическом исследовании формализованных
теоретико-экономических конструкций. В этих исследованиях первосте¬
пенное внимание уделяется таким проблемам, как определение множества
технологически допустимых траекторий, качественные свойства траекто¬
рий, методы нахонодения эффективных и оптимальных траекторий. Для
анализа свойств теоретических моделей характерным является установ¬
ление соотношений между математическими и экономическими понятия¬
ми (например, собственные числа матрицы и темпы роста, собственный
вектор и структура производства, динамические двойственные оценки и
принципы соизмерения затрат и результатов во времени).
Выводы математической теории экономической динамики достига¬
ются ценой сильных упрощений реальных процессов и вследствие этого,
как правило, непосредственно не приложимы к практическим задачам.
Однако многие результаты исследования теоретических моделей прояв¬
ляются в прикладных (более реалистичных) моделях в ослабленном и
трансформированном виде. Поэтому теоретические модели служат
методологическим эталоном при сооружении много элементных прик¬
ладных моделей экономической динамики, позволяя существенно со¬
кращать эмпирическую работу по их построению и анализу.
11.1. Динамические межотраслевые модели
Отличительный признак теоретических межотраслевых динамических
моделей — описание соотношений ’’затраты — выпуск” в форме матриц
межотраслевого баланса, где каждый вид продукции пред-
327
ставлен только одним производственным способом, а в каждом способе
выпускается только один продукт. Место динамических межотрасле¬
вых моделей среди моделей экономической динамики определяется
тремя моментами* Во-первых, они являются детализированными (дезаг¬
регированными) аналогами моделей воспроизводства общественного
продукта и национального дохода (см. 10.1, 10.2). Во-вторых, они пред¬
ставляют собой обобщения статических (балансовых и оптимизацион¬
ных) межотраслевых моделей (см. гл. 6, 8). В-третьих, они служат те-
оретико-методологической основой прикладных динамических моделей
с матрицами межотраслевого баланса (см. гл. 13).
Динамическая модель В.Леонтьева. Предложенная В.Леонтьевым в
начале 50-х гг. динамическая межотраслевая модель является классичес¬
ким примером использования систем дифференциальных уравнений в
исследовании проблем экономического роста. Построение этой модели
удобно представить как дезагрегирование элементов простейшей дина¬
мической модели воспроизводства общественного продукта (см. 10.1),
при котором эндогенные и экзогенные макро переменные заменяются
векторами, а технологические макропараметры — матрицами. Модель
имеет вид
X(t) = AX(t) + B*£& + C(t), (11.1)
гдеХ(/) = [х; (t) ] — вектор-столбец объемов производства; d^L(lL—
' ■ dt
= — вектор-столбец абсолютных приростов производства; c(t) —
dt
вектор-столбец потребления (включая непроизводственное накопле¬
ние) ; А = (аф — матрица коэффициентов прямых материальных затрат
(в отличие от коэффициентов статического межотраслевого баланса
коэффициенты в динамической модели включают также затраты на
возмещение выбытия и капитальный ремонт основных производствен¬
ных фондов); В = фф — матрица коэффициентов капиталоемкости
приростов производства (затраты производственного накопления на
единицу прироста соответствующих видов продукции; смысл этих
коэффициентов будет уточнен ниже); /, / Е/, / = jl,п Поскольку
dXV)_(F Ал-г dY(t)
dt ^ dt ’
то вместо (11.1) может исследоваться система дифференциальных урав¬
нений
К(0 = В(£-Л)-1^ + С(0, (11.2)
328
тле В (E - A)~1 — матрица коэффициентов полной
приростной капиталоемкости, т.е, полных затрат произ¬
водственного накопления на единичные приросты элементов используе¬
мого национального дохода1.
Предполагается, что матрица А продуктивна, В дальнейшем анализе
удобно считать матрицу А неразложимой, а матрицу В — невырожденной
(см. разъяснения в ДМНХ, с. 124). Тогда (Е - A)~l > Е + А, В (Е -
-А)'1 >В.
Очевидно, что экономический смысл имеют только решения^ (0 >
> 0. Как будет показано далее, экономическим предпосылкам модели
(11,1) соответствуют только неубывающие траектории X(t), т.е.
d-§P->o.
Решение системы (11.2) при > 0 в силу неотрицательности
матриц (Е-А)-1 и В(Е - А)'1 гарантирует, что
У(0>0, *(*)>о,
В соответствии с теорией дифференциальных уравнений решение
систем (11.1) и (11.2) проводится в три этапа: а) определяется общее
решение однородной системы уравнений при с(?) = 0; б) находится
частное решение неоднородной системы; в) из начальных условий
рассчитываются неопределенные постоянные общего решения.
Динамика замкнутой производственной системы. Проанализируем
систему однородных уравнений:
V(t) = B(E—А)~г-^Р- (11.3)
dt
Решение этой системы характеризует предельные технологические
возможности развития производства при заданных матрицах А и В,
когда все ресурсы национального дохода направляются на расширенное
воспроизводство. Такая же ситуация на примере макромодели исследо¬
валась в 10.1.
Естественно, возникает вопрос: существует ли траектория системы
(11.3) У(0 = У(о)^ с постоянным темпом прироста д, одинаковым
для всех компонент Y(t), аналогичная траектории (10.6) национального
дохода в макроэкономической модели (рост с технологическим темпом
р)? Ответ на поставленный вопрос предполагает исследование (11,3)
при различных матрицах А, В.
Далее будет рассматриваться также случай, когда матрицы В к В (Е - А)~*
включают не все производственное накопление, а только накопление основных
производственных фондов.
329
Общее решение системы (11.3) может быть представлено в виде
^(0=2 (11.4)
где X/ — корни характеристического уравнения п-то порядка
det [Е—ХВ (Е—А)-1] = 0;
Kj — соответствующие X/ собственные векторы матрицы В(Е —
- А) ~1, — постоянные, определяемые из системы уравнений
2 = К (0). (11.5)
i=i
В общем случае решение (11.5) содержит несколько отличных от
нуля компонент dj. Поэтому в типичной ситуации единственная траек¬
тория системы (11.3), выходящая из начальной точки Y(0), представля¬
ет собой комбинацию экспонент, растущих с различными темпа¬
ми. То есть развитие точно по закону Y(t) = Y(0)е№ невозможно, что
существенно отличает межотраслевую модель от ее макроэкономическо¬
го прототипа.
Однако определенное сходство решений замкнутых макроэкономи¬
ческой и межотраслевой систем все же сохраняется. Это сходство опре¬
деляется влиянием на решение (11.4) слагаемого dKe^.
В соответствии с принятыми допущениями матрица В (Е - А) _1 положительна.
Согласно теореме Перрона она имеет положительное собственное число s (к о-
рень Фробениуса - Перрона), превосходящее по модулю все прочие
собственные числа это# матрицы, и соответствующий ему строго положительный
собственный вектор К. При этом собственные векторы, соответствующие отлич¬
ным от s собственным значениям, обязательно имеют компоненты различных
знаков.
Величина s заключена между максимальной и минимальной суммами элементов
— 1 ^ _ -
столбцов матрицы В (Е - А) . Обозначим через В4 2 р.. сумму элементов
/ / £/ '
/■го столбца этой матрицы. Тогда min5". ^ ^ тах
1 1 /
i 1
Соответственно величина /к~~ л заключена в промежутке
s
min ^ К шах ■1
• ^5 'V ^ 11ШЛ » •
/ в/ / в/
Таким образом, показатель экспоненты X является обратной величи¬
ной к некоторой средней из коэффициентов полных отраслевых капи¬
талоемкостей. В случае же равенства этих коэффициентов (Bj = В0,
Л 1 *
/ £ /) имеем X = ——, что аналогично формуле технологического темпа
330
прироста (см. с. 281). Это дает основание назьюать величину X техно*
логическим темпом прироста в межотраслевой
динамической модели.
Траектория Yx (t) является суммой экспонент. Очевидно, что при
t -* оо в ней начинает преобладать слагаемое с максимальной (среди
номеров I с dj ф 0) вещественной частью X/. Возможны две взаимоис¬
ключающие ситуации: 1) доминирующей является экспонента е ,
2) доминирует экспонента с темпом X/ Ф X.
В первом случае темпы прироста продукции каждой отрасли при
t -> оо стремятся к технологическому темпу роста X, а отраслевая струк¬
тура национального дохода в пределе определяется пропорциями ком¬
понент собственного вектора К. Во втором случае динамика Yx(t) во
все большей степени определяется собственным вектором АГ/, имеющим
компоненты различных знаков. Поэтому при достаточно больших t
в решении Yt(t) непременно появляются отрицательные компоненты
(подробнее см. в ДМНХ, с. 124 - 127).
Таким образом, решение (11.4), в котором доминирует слагаемое
с темпом, отличающимся от X, экономически неприемлемо.
Отмеченные особенности решений принципиально отличают межот¬
раслевую модель от ее макроэкономического аналога (10.5), где реше¬
ние теряет допустимость только в результате непомерных требований к
росту потребления.
Пример 11.1
Рассмотрим народное хозяйство в разрезе двух отраслей. Пусть
А =
0,2
0,3
0,3'
0,4.
Я =
0,5
1,0
0,5
0,8
Х(0) =
50 "1
.50 J *
У( 0) =
Заметим, что агрегирование матриц А и В при базисной структуре производства
дает те же значения макроэкономических параметров, что использовались в гл.
10: а =0,6, Ъ = 1,4. _
Вычисляем матрицы (Е - А) и В =В (Е - А)
(Е — А)~1 =
1,54
0,77
0,77'
2,05
В =
1,16
.2,16
1.41
2.41
Полная капиталоемкость национального дохода равна 3,5, как и в иллюстрациях
к гл. 10.
Находим все элементы решения (11.4):
Кх (/) = 40,4
0,35
0,61
£0,276* 9 6
1,15
—1,00
г-14,2*
(1°).
Технологический темп прироста равен 0,275; он соответствует корню Фробе-
ниуса — Перрона s = 3,64. Ему соответствует также собственный вектор
к Г 0,351
L—0,61 J-
331
Второе слагаемое в выражении (1°) очень быстро стремится к нулю. Поэтому темп
прироста национального доходу и его отраслевая структура очень быстро прибли¬
жаются соответственно к Л и К. Отраслевая структура валового продукта также
быстро приближается к структуре, определяемой соотношением компонент вектора
(Е — А)'1 К. Уже при t = 30 различия фактических и асимптотических темпов и
структур становятся меньше 0,001.
Семейство траекторий системы (11.3) с числовыми данными приме¬
ра изображено на рис. 11.1. Траектория с постоянным темпом X есть
луч ОА. Конус ВОС есть множество состояний, в которых —— > 0.
Траектория, выходящая из исходного состояния F(0), быстро прибли¬
жается к лучу ОА. Однако начальная часть траектории не соответствует
предположению о неотрицательности • Отметим, что все прочие
траектории (исходящие из любой начальной точки) также стремятся
к лучу ОА. Войдя в конус допустимых решений, траектория уже оста¬
ется в нем. В теории дифференциальных уравнений семейство траекто¬
рий такого типа называют седлом (пример с неприемлемыми
результатами и соответствующая геометрическая иллюстрация рассма¬
триваются в ДМНХ, с. 128 — 129).
Экономический рост при различных траекториях потребления.
Представим общее решение системы (11.2) в виде суммы общего реше¬
ния однородной системы Yi(t) и частного решения неоднородной систе¬
мы Y2{t):
Y(t) = Y,(t)+Yt(t). (U.6)
По аналогии с 10.1 будем рассматривать траекторию потребления в
виде C(t) = С(Q)ert, т.е. принимая, что компоненты вектора потребления
растут одинаковым постоянным темпом г ^0, причем С(0) >0.
Частное решение Y2(t) определяется следующим образом:
К2 (t) = [Е—rB (Е-А)~1]~ХС (0)**. (11.7)
Объединяя (11.4) и (11.7), получаем общее решение системы в
виде:
К(0= 2 qtK/^ +[Е — гВ{Е—А)-Ч~1Сф)е«. (11.8)
1=1
При известных (однозначно определенных) значениях Щ, X/ кон¬
кретные решения (11.8) находятся путем задания темпа прироста потре¬
бления г и расчета соответствующих заданному г значению qf .
1 Неопределенные постоянные <7, общего решения (входящие в Y\ (t)) находят¬
ся из решения системы уравнений
2 qiKi = Y (0)-[Е-гВ (Е-А)-1]-^ (0).
/= 1
332
Анализ допустимых значений г
можно проводить по аналогии с ана¬
лизом макромодели (10.8). Доказы¬
вается, что экономически приемлемые
траектории национального дохода по¬
лучаются при г < X (см. ДМНХ, с. 130).
Исследование качественно различ¬
ных ситуаций в рамках условия
0 < г < X обнаруживает значительное
сходство решений макроэкономичес¬
кой и межотраслевой моделей. Раз¬
личия поведения решений в значитель¬
ной мере объясняются влиянием отра¬
слевой структуры начальных условий,
т.е. векторов Y (0) и С0 (подробнее
см. в ДМНХ, с. 131).
Пример 11.2.
Воспользовавшись данными примера 11.1, определим решения относительно г в
двухотраслевой системе:
Рис. 11.1. Траектории замкнутой
производственной системы (прием¬
лемая альтернатива)
У m = _£i.e®.276t_|_f8_e-n.2<_|—L (21—35,1 г) ert\
аг а, ах
уг (t) = 1,26 -52- 0i87 .£*_ _|_ J_ (11 +32,5r)
cti аг аг
ai = —0,256r2 - 3,564r +1;
a2 = —3,582r2-50,577r +2,844;
a3 = —2,828r2 — 3,423r + 1,156.
Найдем решения (11.8) при трех значениях темпа прироста потребления: гу = 0*
г2 —0,056; г3 =0,10. Получаем:
1) ух (/) = 2,844е0’275*-Ы,156е-14'18* + 21;
у2 (t) = 5,003е0’275*— 1,003e-i4’18* + 11;
2) У1 (0 = М95е~14’18* 4-23,805е°’05в*;
у2 (t) =■■ 1,036е~14’18*+ 16,03е°’0бв*+11;
3) у\ (/)=—3,509е°’275*+ 1,275е-14’18* + 27,284е0’1*;
у2 (t) = —6,173е0'276*— иОбЗе-^^ + гг^Збе0»1^
Отображения типичных траекторий в пространстве Y (t) показываются на рис. 11.2.
При постоянном уровне потребления (г = 0) темпы прироста ух (г) и у2 (О быстро
приближаются к технологическому темпу прироста Л = 0,275; при этом устанавлива¬
ется пропорция ух ; у2 =2,84 : 5,00.
Траектория, отвечающая г = 0,056, ближе всех соответствует типу пропорциональ¬
ного роста с постоянной нормой накопления, анализировавшемуся в 10.1 (напомним,
что по условиям примера был рассчитан Ро = 0,057). В этом случае начиная с некото¬
333
Рис. 11.2. Траектории продукции, ис¬
пользуемой на потребление и накопле¬
ние, при постоянных темпах роста
потребления:
1) магистраль; 2) 0<гО0; 3) асим¬
птотическая траектория роста с постоян¬
ной нормой накопления; 4) г=г$\
5) г >г0
выполняющие особые
рого момента времени все функциона¬
льные и отраслевые компоненты ва¬
лового продукта и национального до¬
хода растут темпом, практически рав¬
ным Ро = 0,056, а структура произ¬
водства и использования продукции
стабилизируется (в частности, У\ :
:у2 =23,8: 16,0).
Наконец, при г =0,10 рост У\ тл у 2
происходит только на начальном отрез¬
ке траектории, после чего начинает
уменьшаться объем у2, а затем и уг.
Одновременное уменьшение У\ и у£
означает, что накопление и приросты
производства становятся отрицатель¬
ными, т.е. решение теряет допусти¬
мость. Далее и траектория Y (г) быст¬
ро уходит в отрицательную область.
Связь результатов межотрас¬
левой динамической модели и ма¬
кромодели расширенного воспро¬
изводства может быть усилена
посредством классификации и аг¬
регирования отраслей по функци¬
ональному назначению производи¬
мой ими продукции. Вместо
’’обезличенных” отраслей, пред¬
ставленных только порядковыми
номерами, целесообразно выде-
функции в процессе воспроиз-
лять отрасли,
водства.
Первый шаг в этом направлении был сделан в 10.5, когда в матери¬
альном производстве были выделены I и II подразделения. Теперь целе¬
сообразно I подразделение разделить на производство орудий труда
(отрасль 1) и производство предметов труда (отрасль 2). В результате
получаем трехотраслевую систему (предметы потребления — отрасль
3), которую можно исследовать с помощью межотраслевой динамичес¬
кой модели.
В указанной трехотраслевой системе капитальные вложения осуще¬
ствляет только отрасль 1, отрасль 2 обеспечивает только промежуточное
потребление (накопление оборотных фондов для простоты учитывается
в виде ’’добавки” к текущему производственному потреблению), а весь
фонд потребления обеспечивается отраслью 3 (подробный анализ см.
в ДМНХ, с. 133- 136). J
Обобщения модели В. Леонтьева.* i5 модели (111) используется
ряд упрощающих допущений, облегчающих решение системы дифферен¬
циальных уравнений и соответствующий теоретический анализ. Наряду
с критической оценкой допущений рассматриваемой модели важно
определить пути ее совершенствования.
334
Включение условий ”необратимости” капитальных вложений и пе¬
реход к системе неравенств. В исходной модели вектор производствен¬
ных накоплений (чистых капитальных вложений) связан с приростами
производства соотношением U(Г) = В без ограничений на знаки
приростов. В этом случае
dx/(t) ^ _ dxj(t)
если —jrt < 0, то и ufj = bij < 0.
Формально это означает возвращение ресурсов в балансы продукции
по полным нормам капиталоемкости (полное деинвестирование), что
совершенно нереалистично.
Поэтому решения систем (11.1) и (11.2) можно использовать толь¬
ко в том случае, если они удовлетворяют дополнительному условию:
£><>■
(11.9)
Строго говоря, добавочное условие (119) не является необходи¬
мым. Важно не запретить отрицательные приросты, а исключить фено¬
мен ’’обратимости” капитальных вложений. Поэтому более обоснован¬
ным является непосредственное включение в модель условий ’’необра¬
тимости” капиталовложений:
dxj (t)
' dt
(11.10)
где
dxj (t)
dt
dxj (t)
dt
0,
если
если
dxj (t)
dt
dxj (t)
dt
<o;
С учетом (11.10) модель принимает вид
X (t) АХ (t) ■+■ В
dX
dt
- С (t).
Однако система уравнений (11.11) может не иметь допустимых
траекторий, проходящих через заданную начальную точку ^(0) > 0.
Именно так обстоит дело, если, например, C(t) = 0, а вектор А'(О) не
принадлежит ’’конусу допустимости”, образ которого на плоскости
(Уь Уг) показан пунктиром на рис. 11.1. В связи с этим целесообра¬
зно заменить систему уравнений (11.11) системой неравенств:
X{t)^AX(t) f В
dX
dt
C(t).
(11.12)
335
Благодаря этому удается йзбежать многих возникавших в пред¬
шествующем анализе проблем. Доказывается, что в замкнутой про¬
изводственной системе (при С (f) = 0) максимально возможный пос¬
тоянный темп прироста X существует при любом начальном состоя¬
нии Х(0) > 0. Для модели (11.12) доказывается существование
траектории, на которой объемы производства и потребления продукции
всех отраслей растут с постоянным темпом прироста г0 (см. ДМНХ, с.
138 - 139).
Учет резервов производственных мощностей. В модели В.Леонтье-
ва, так же как и в простейшей макромодели вопроизводства общест¬
венного продукта и национального дохода, предполагается, что прирост
производства может осуществляться только за счет производственного
dxj(t)
накопления: из u^(t) = 0 следует —— = 0. В действительности рас¬
ширение производства может осуществляться и в результате более
полного использования имеющихся производственных мощностей
(основных производственных фондов).
Обозначив через Mj(t) максимально возможный объем производст¬
ва продукции /-й отрасли на действующих основных фондах в году Г,
можем ввести условия: x{(t) <M/(f). И поэтому, если *,(0 < MAt),
' dx: (г) ' '
то становится допустимым и-At) = 0 при — > 0.
Ч ctt
Построение межотраслевых моделей с инвестиционными лагами.
В модели В.Леонтьева, так же как и в простейшей макромодели воспро¬
изводства, предполагается мгновенность превращения производствен¬
ного накопления (капитальных вложений) в приросты производства.
Естественное усовершенствование модели — включение инвестиционных
лагов (сосредоточенных и распределенных). Так, если определять
инвестиционный лаг в каждой /-й отрасли как сосредоточенный и рав¬
ный ту, то система уравнений производства и распределения продукции
приобретает вид
X, (t) = 2 ai(x, (t) + 2 bisr Tj) + ct (t), id I (11.13)
/€/ /€7
Инвестиционные лаги могут дифференцироваться не только по от¬
раслям — ’’потребителям” капитальных вложений, но и по материально¬
вещественным элементам капитальных вложений (продукция машино¬
строения, строительства и т.д.). В динамическую межотраслевую модель
могут быть включены также и распределенные лаги; при этом изменяет¬
ся смысл матрицы В.
Методы решения систем дифференциальных уравнений с лагами
(запаздывающими аргументами) разработаны достаточно хорошо,
однако качественный анализ решений существенно усложняется.
336
Учет динамики коэффициенте материалоемкости и капиталоемко¬
сти производства. Одним из наиболее сильных допущений анализируе¬
мой модели является неизменность во времени матриц материальных
и капитальных затрат А и В. При этом вне модели остается важнейший
фактор экономической динамики — научно-технический прогресс. /
Включение в модель матриц A(t) и B(t), зависящих от времени,
повышает ее прикладное значение. Теоретический анализ обобщенной
модели остается доступным при достаточно простых законах изменения
A (t) и В (/■)> например при равномерном изменении всех коэффициен¬
тов матрицы или коэффициентов отдельных строк матрицы.
Оптимизационные модели с матрицами межотраслевого баланса.
В 10.2 изучались возможности перехода от макроэкономической моде¬
ли с экзогенной траекторией потребления к оптимизационным моделям,
в которых максимизируется суммарное потребление (или дисконти¬
рованное суммарное потребление) за плановый период. Изучавшиеся
подходы можно распространить на межотраслевую динамику.
Пусть максимизируется суммарный фонд потребления за плановый
период т
\ GC(t) dt<
о
где соизмерение различных потребительских благ осуществляется посре¬
дством вектора постоянных коэффициентов G = (gy-) > 0 (т.е. приме¬
няется та же методика, что и при исчислении ’’физических” объемов
экономических агрегатов с помощью неизменных цен). Максимизация
этой функции осуществляется при условиях:
X (<) = АХ (t) 4 В — 4 С (t);
^^>0; (11.14)
Х(0)=Х0.
Включение условия S* 0 гарантирует ”необратамость” кали-
таловложений.
Оптимизация при условиях (11.14) позволяет находить такие траек¬
тории, которые дают большую (точнее, не меньшую) величину суммар¬
ного потребления / GC (t)dt по сравнению с любой экзогенной траекто¬
рией потребления.
При анализе макроэкономической модели было установлено, что
максимизация суммарного потребления достигается путем сосредото¬
чения всех ресурсов национального дохода в разные моменты времени
либо целиком на потреблении, либо на производственном накоплении
337
при мгновенном (релейном) изменении режима воспроизводства.
Исследование модели (11.14) с использованием принципа максиму¬
ма Понтрягина выявляет во многом аналогичные свойства оптимальных
траекторий.
Доказывается существование величины Т0 > 0, такой, что:
а) если Т < Т0, то производство не увеличивается и весь националь¬
ный доход потребляется:
(*) = <$ (0 “*«(0). “? = 0; *€/;
б) если Т > Т0, то аналогичная ситуация имеет место в конце плано¬
вого периода на отрезке [Т — Т0, 7] , где весь национальный доход так¬
же целиком расходуется на потребление:
ЯУ) = сЩ) = у;(Т — Т0); u?(t) = 0; i£l.
Производственное накопление осуществляется на отрезке [0, Т —
- Г0], однако не гарантируется, что uf(t) > 0 для всех отраслей.
Особенность оптимальной траектории межотраслевой модели состо¬
ит также в том, что в один и тот же момент времени различные отрасли
’’ведут” себя по-разному.
Таким образом, поведение оптимального решения существенно за¬
висит от продолжительности планового периода. При достаточно боль¬
шой величине Т оптимальная траектория обязательно содержит скачко¬
образные изменения потребления и накопления, хотя бы по продукции
некоторых отраслей. Моменты этих структурных перестроек определя¬
ются более сложными зависимостями, чем в макроэкономической мо¬
дели (подробный анализ см. в ДМНХ, с. 141 - 142).
Пример 11.3.
Возьмем матрицы Л, В и вектор Y (0) из примера 11.1. Пусть G = (1,1).
В результате расчетов находим, что точкой переключения режима является Tq =
= 3.
При Т^З имеем:
У\ (0 = с[ (Я = ух (0) = 25,2; у\ (/) = с*2 (t) =у2 (0) = 15,0;
«1 (0 = «2 (0 = 0.
При Т^>3 траектория состоит из двух участков:
1. t Е [О, Т — 3] . На этом участке траектории:
У\ (0 = 65,2 —40е-®*#. yz (0= «а (0= 15*-0f3*,
и*1 (f) = 7,5e-°-3t, cUt)=- б^.г—47,5е-°'», &{t) = 0.
2. t Е [Т- 3, Г] . На этом участке:
338
»i (О =Ъ (*) =у! (Т—3) = 65,2—98,4е-®’«;
yl (<) = са (0 =у'г (Г—3) = 36,9e-°l3t;
Ml (0= «2 (0—0.
Для смягчения резких изменений оптимальной траектории можно
использовать ряд приемов, рассматривавшихся в 10.2, в том числе:
а) разделение потребления на экзогенно и эндогенно определяемые
части и условия непрерывного роста потребления; б) введение нижних
и верхних пределов нормы производственного накопления.
Однако в оптимизационных межотраслевых моделях число резких
изменений траектории во много раз больше, чем в макроэкономических
моделях, и поэтому для сглаживания оптимальных траекторий могут
требоваться более дифференцированные регуляторы (см. ДМНХ, с,
144).
Подключение регулирующих условий к (11.14) уменьшает значение
целевой функции потребления, но зато обеспечивается гладкость дина¬
мики потребления, накопления и производства. Параллельно уменьша¬
ется сильная зависимость оптимальных решений от продолжительности
планового периода и снижается острота проблемы ’’хвоста” планового
периода (деформации структуры производства и распределения продук¬
ции в конце периода).
11.2. Модели расширяющейся экономики
и магистральное развитие
Основные понятия. В рамках экономической статики изучались понятия
допустимых и эффективных технологий, технологических множеств,
а также важнейшие их свойства (см. гл. 4). Здесь мы будем рассматри¬
вать обобщения этих понятий для дискретного времени t = 0, 1, ..., Т
(Т < °°). Отрезок времени между соседними моментами [f, t + 1]
называется элементарным отрезком времени.
Пусть X(t) - «-мерный вектор затрат в момент t, Y(t + 1) — п-мер¬
ный вектор выпуска продукции в момент t + 1. Технологическая до¬
пустимость пары (X, Y) означает возможность, используя технологию
периода t, получить в момент Г + 1 из затрачиваемых в момент t ингре¬
диентов вектора X вектор продукции Y. Совокупность всевозможных
допустимых технологий (X, Y) в момент t образует технологическое
множество Zf. В теоретических моделях экономической динамики
используется ряд предположений о структуре технологического мно¬
жества, на основе которых доказываются основные теоремы о свойствах
эффективных технологий и технологического множества (см, ДМНХ,
с. 145 - 148).
Технологически возможная траектория представляет собой после¬
довательность | (Xf, Yt + l) GZt, t = 0, 1,..., T — 1j. Такая траектория
339
допустима, если вектор Х0 совпадает с заданным начальным состояни¬
ем Х0. Укажем на два типа таких траекторий.
Первый тип траекторий характеризуется тем, что Yt + \ = Xt + 1,
т.е. продукты воспроизводятся в замкнутой производственной системе
без каких-либо ’’входов” и ’’выходов”. Тогда технологически допусти-
:ехнологически д<
Xt J , t = о,т,
такую,
мая траектория составляет последовательность ,
что (Xt, Xt + l) е Zt.
Траектория I Xf j называется эффективной (по конечному
состоянию), если для всякой допустимой траектории j Xf j из соотноше¬
ния Xj>Xj следует, что Xj = X^ .
Рассматриваемый тип траекторий используется при изучении предель¬
ных возможностей роста. Непроизводственное потребление в этом
случае можно учитывать в векторах Xt как дополнительные норматив¬
ные затраты.
Второй тип траекторий учитывает потребление в явном виде. Произ¬
водимая продукция разделяется на две части — производственное и не-
производственное потребление: Yt = Xt + Q. Для такого типа траекто¬
рий понятие эффективности трансформируется. Выделение эффектив¬
ных траекторий из допустимых осуществляется только путем сравнения
векторов потребления.
Траектория | Xf, Xf + j + С* + j1 EZt, t = 0,..., Т - 1 назьюается
эффективной, если для всякой траектории J Xt, Xt + 1 + Ct + 11 £
G Zt, t = 0, ..., T- 1 из соотношений Q > Cf следует, что Ct = Cf,t =
= 1
Важной характеристикой существующего множества Z является
технологический темп роста, определяемый следующим
образом.
С каждым технологическим процессом (X, Y) G Z связйвают число
yi
77 (X, Y) = min_ — , являющееся темпом роста данного процесса.
/=1, л хг
Технологическим темпом роста называется число
т,в = тах{т1,(Х, У)|(Х, Y)^Z).
При естественных предположениях относительно Z технологическо¬
му темпу роста щ соответствует траектория
{Xf|X, = T,$X0}, t=\, т.
Она назьюается траекторией максимального сбалан¬
сированного роста, или магистралью.
Впервые существование магистрали в структурных моделях экономической
динамики обнаружил Дж. фон Нейман. Поэтому магистраль (траектория макси¬
мального сбалансированного роста) именуется неймановской траекто¬
рией или неймановским лучом.
340
Посредством теоретических моделей рассматриваемого типа изуча¬
ется не только технологический, но и ценностный аспект экономики.
Вводится понятие цен, устанавливающих взаимное соответствие между
эффективными (оптимальными) технологиями и рентабельностью (в
том числе максимумом прибыли; см. ДМНХ, с. 146 — 148).
Модель Неймана. Первой и наиболее известной абстрактной моде¬
лью расширяющейся экономики является модель Дж. фон Неймана,
сформулированная еще в начале 30-х годов.
Модель Неймана задается парой матриц А и В. Матрица А = (ajj)
характеризует затраты продуктов / = 1, ..., т при использовании различ¬
ных технологических способов / =1, ..., п с единичной интенсивностью.
Матрица В = (by) объединяет коэффициенты выпуска соответствую¬
щих продуктов при использовании различных технологических способов
с единичной интенсивностью. Обе матрицы имеют одинаковую размер¬
ность тхп. Предполагается, что числа ау и ^удовлетворяют следующим
ограничениям:
(1) 2 af/>0 (/ = 1, .... п)>
(2) Ьц > 0 (i — 1, .., ( т).
Условие (1) означает, что в каждом способе используется хотя бы
один продукт. Условие (2) означает, что каждый продукт может быть
произведен хотя бы одним технологическим способом.
Обозначим через Z = (Zj) вектор интенсивностей использования
технологических способов. Тогда технологическое множество модели
Неймана можно представить в следующем виде:
{(X, Y)\X = AZ, Y = BZ, Z > 0}.
Наиболее характерное допущение модели Неймана состоит в том,
что вся произведенная в момент t продукция затрачивается на производ¬
ство продукции в момент t + 1:
1). ,/ (11.15)
В окончательном виде модель представляет задачу максимизации
числа т? — темпа роста замкнутой производственной системы:
г) —> шах,
BZ^tr\AZ. J (11.16)
341
Максимальное число т?, при котором выполняется условие (11.16),
называется технологическим темпом роста и обозна¬
чается г}. Вектор Z, при котором достигается т}, назьюается о птима-
л ь н ы м. Как уже отмечалось, этот вектор (неймановский луч) явля¬
ется магистралью.
По аналогии с моделью межотраслевого баланса (см. разд. 6.3)
вводится понятие п родуктивности. Технологическое множест¬
во модели Неймана продуктивно, если существует Z > О, такой, что
(В — A)Z > 0. Это означает возможность превышения выпуска над за¬
тратами одновременно по всем видам продукции. Если технологическое
множество продуктивно, то 77 > 1, следовательно, имеем расширенное
воспроизводство.
Производственно-технологическим соотношениям (11.15), (11.16)
можно поставить в соответствие систему ценностных соотношений. Для
этого введем в рассмотрение вектор цен Р = (рф.
Общая оценка продукции, произведенной /-м способом при его ис¬
пользовании с единичной интенсивностью, равна 2 рф//, а общие за-
т i = 1 у
траты в ценностном выражении — 2 рщ\ Тогда величина
i = 1
tn т
^ J1 PiblJ^ PiUU
есть показатель ’’рентабельности”/-го технологического способа.
Задача определения ценностных соотношений формулируется сле¬
дующим образом. Определить неотрицательный вектор Р и число /3,
для которых
Р —* min,
(11.17)
л
Величину /3 принято называть экономическим темпом рос¬
та модели, а соответствующий этой величине вектор цен.Р — о п-
тимальным. Величина 0 означает минимальный уровень рентабель¬
ности, при котором суммарная оценка произведенной продукции не пре¬
вышает суммарной оценки затрат по всем производственным способам.
Задачи (3.29) и (3.31), определяющие оптимальные структуры
производства и цен, технологический и экономический темпы роста, на¬
зываются двойственными. Во многом эта пара сходна с двой¬
ственными задачами математического программирования.
Отметим, что задачи (11.16) и (Ц.17^ являются однородными,
и, следовательно, оптимальные векторы Z и Р определяются лишь с точ¬
ностью до положительного множителя. Это свойство связано с замкну¬
тостью модели и отличает (11.16) и (11.17) от двойственных задач
342
математического программирования. Доказывается, что для рассмотрен¬
ных задач всегда j3 < т}. Если матрицы А и В неразложимы (точнее,
модель ’’неприводима”), то j3 = г).
Взаимообусловленность материальных и ценностных свойств модели определя¬
ется системой неравенств
(В—i]i4)Z^0, ZSaO; (11.18)
Р(В— РЛ)<0, Р^О, (11.19)
Р(В—r(i4)Z = 0, (11.20)
P(B—$A)Z=0. (11.21)
Решение (Z, Р, ГЬ Р) системы (11.18) - (11.21), удовлетворяющее условию
PBZ > 0, существует, причем р\ = 0 тогда и только тогда, когда
п п
Л 2 aijZj < 2 bijZj.
/«=1 У — l J J
zj = 0 тогда и тодько тогда, когда
п rt
Р 2 dijpi > 2 bijpi.
i= 1 i = l
Приведенные соотношения схожи с условиями двойственной задачи линейного
программирования, и им может быть дана аналогичная экономическая интерпре¬
тация: 1) для оптимальных технологических способов суммарная оценка выпуска
равна суммарной оценке затрат; 2) если в технологическом способе суммарная
оценка затрат превышает суммарную оценку выпуска, то такой способ неоптима¬
лен; 3) если оптимальная цена продукта положительна, то по такому продукту
балансовое соотношение производства и распределения продукции реализуется
как равенство; 4) если баланс производства и распределения продукции выполня¬
ется как строгое неравенство, то цена данного вида продукции равна нулю.
Частный случай модели Неймана. Пусть в каждом технлогическом
способе выпускается только один продукт и каждый продукт произво¬
дится только одним способом. Это означает, что число продуктов равно
числу способов (/, / = 1,..., и), матрица В — единичная, матрица А — мат¬
рица межотраслевого баланса, Z — X и означает вектор объемов
производства.
Задача максимизации темпа роста производства в этом случае прини¬
мает вид
г\ —► шах,
]АХ. (11.22)
Важным свойством данной задачи является то, что ее решение удов¬
летворяет условию
Х = т\АХ. (11.23)
343
Выпуск всех продуктов растет одинаковым темпом, и отсутствует
перепроизводство каких-либо продуктов. Соотношение (11.23) можно
записать в виде
= (11.24)
Легко видеть, что — положительное собственное значение матри¬
цы А (корень Фробениуса — Перрона), X — соответствующий этому
собственному значению собственный вектор. Тем самым устанавливает¬
ся соответствие между математическим понятием собственного значения
матрицы и экономическим понятием максимального* темпа роста произ¬
водства. Необходимым и достаточным условием расширенного воспро¬
изводства (существования т? > 1) является продуктивность матрицы А,
Задача определения темпа экономического роста и сбалансирован¬
ных цен в рассматриваемом случае имеет вид
Р —► min,
Р<РРЛ. <11Л*>
А А
А При неразложимой матрице А имеем (3 = т?, а оптимальные векторы
X и Р строго положительны и единственны (с точностью до положитель¬
ного множителя).
Пример 11.4*
Применим частный случай модели Неймана для анализа двухотраслевой систе¬
мы. Возьмем матрицы материальных затрат (А) и капитальных затрат (В) из при¬
мера 3.1. Предположим, что основные производственные фонды служат 8 лет;
тогда при равномерном росте производства и фондов ежегодно должна возмеща¬
ться 1/8 капитальных затрат. Добавив 1/8 коэффициентов капиталоемкости к ма¬
трице А, получим
-Г0*
U
0,2625 0,3625
425 0,5 J-
М^ссимальное собственное число матрицы Л равно 0,79, откуда rf= 1,266. Пола¬
гая atj = 1, получаем = 1,459. Видим, что оптимальное соотношение объемов
производства довольно близко к соотношению на магистральной траектории зам¬
кнутой системы В. Леонтьева (примерЗ.1). *
При переходе к формуле экспоненциального роста {ег —1,266) получаем непре¬
рывный темп прироста Р = 0,236. Эта величина достаточно близка к технологичес¬
ким темпам прироста, рассчитанным в 10.1 и 11.1 по макроэкономической и меж¬
отраслевой моделям воспроизводства.
Использование результатов теоретического анализа. Важнейший
результат анализа моделей расширяющейся экономики состоит в дока¬
зательстве существования магистрали — траектории максимального про¬
порционального роста (т.е. с постоянным во времени максимально
возможным темпом роста и неизменной структурой производства).
344
В частности, в модели Неймана траектория (t^Z)^_q является магистра¬
лью в пространстве интенсивностей технологических способов, а траек¬
тория 0bz)7= q — магистралью в пространстве выпусков продукции.
Магистраль не зависит от длительности планового периода и является
эффективной траекторией для любого конечного интервала времени.
Применительно к широкому классу моделей экономической дина¬
мики доказываются теоремы о магистрали, утверждающие, что при до¬
статочной продолжительности планового периода оптимальная траекто¬
рия динамической модели независимо от начального состояния и целевой
функции (или заданного конечного состояния) близка в том или ином
смысле к магистрали. Модель, для которой справедлива теорема о маги¬
страли, называют магистральной моделью.
Теоремы о магистрали существуют в слабой, сильной и
сильнейшей формах (см. ДМНХ, с. 153 — 154). В частности, из
теорем о магистрали в сильной и сильнейшей форме следует, что при
любом начальном состоянии Х0 и конечном состоянии Xj (определяемых
нормативно или с помощью целевой функции за период [О, Т], так,
что Xj > Х0) оптимальная траектория состоит из трех участков: 1) дви¬
жение от Х0 в направлении магистрали; 2) движение по магистрали
или в непосредственной близости (параллельно) к ней; 3) движение
от магистрали к Xj (см. рис. 11.3).
Теоремы о магистрали утверждают, что продолжительность старто¬
вого и финишного участков траектории не зависит от длительности
планового периода. Поэтому по мере увеличения планового периода
все большая часть траектории будет проходить по магистрали или в непо¬
средственной близости от нее. Таким образом, поведение оптимальной
траектории при продолжительном плановом периоде зависит главным
образом от структурных параметров модели и в меньшей степени от це¬
левых функций, начальных и конечных условий1.
Главным направлением обобщения и развития теоретических моде¬
лей расширяющейся экономики является расширение исходных допуще¬
ний и условий с целью более полного отражения факторов экономичес¬
кого развития. В первую очередь следует отметить необходимость:
1) учета непроизводственного потребления, 2) включения ограниченных
(невоспроизводимых или ограниченно воспроизводимых) ресурсов,
3) учета изменений во времени технологических матриц, отражающих
научно-технический прогресс (о развиваемых в настоящее время подхо¬
дах см. ДМНХ, с. 155 - 156; [4. Гл. 2, 3] ).
Напомним, что в разд. 10.4 анализировались магистральные мак¬
роэкономические модели, в которых магистраль определяла макси¬
мальный темп роста и постоянные пропорции для таких показателей, как национа¬
льный доход, капитальные вложения, основные фонды потребления. Оптимальные
траектории этих моделей с конечным интервалом времени также состоят из трех
Участков.
345
Рис. 11.3. Оптимальная траектория
и магистраль (для случая двух
Построение обобщенных теоре¬
тических моделей расширяющейся
экономики существенно облегчает
анализ прикладных динамических
моделей, придавая ему необходимую
целеустремленность.
11.3. Динамическая модель
Л.В.Канторовича
Оптимизационная динамическая мо¬
дель Л.В.Канторовича занимает важ¬
ное место в распространении и
развитии принципов оптимального
народнохозяйственного планирова-
II mat ItVA|/UVftU ж—.ж* л т.
технологических способов или двух ния. Она является обобщением изве-
видов продукции) стной ’’основной задачи производст¬
венного планирования” (см. 8.1) и
формулируется как задача линейного программирования. На ее основе
можно оптимизировать развитие различных экономических объектов
(предприятия, отрасли, региона, народного хозяйства в целом). Но эта
общность модели затрудняет отражение специфических особенностей
моделируемых объектов (например, для народного хозяйства в целом —
это взаимозависимости между производством, капитальными вложе¬
ниями, основными фондами). Поэтому модель Л.В.Канторовича право¬
мерно относить к классу теоретических моделей.
Динамические производственные способы. В рассматриваемой мо¬
дели народное хозяйство представлено как объединение двух сфер:
сферы производства, включающей разные виды деятельности, и сферы
потребления, включающей использование различных видов благ.
Время учитывается в модели дискретно. Временной такт модели
может быть различным (год, пятилетка и т.п.). Мы остановимся на мо¬
дельной постановке с годовым тактом, имеющей наибольшее практичес¬
кое применение.
Описание производственной сферы (ее технологического множест¬
ва) строится на основе ’’сквозных” динамических производственных
способов. Компонентами (ингредиентами) производственных способов,
как и в статической модели (см. 4.5), являются коэффициенты выпус¬
ка продукции (со знаком ’’плюс”) и коэффициенты затрат различных
видов продукции и ресурсов (со знаком ’’минус”). Вектор Аф, харак¬
теризующий производственный способ, включает столько частей, сколь¬
ко выделяется временных отрезков. При этом один и тот же продукт
или ресурс s, рассматриваемый в разные отрезки времени, выступает как
особый ингредиент:
346
Ay =
АЛ
где t—\y . . ., Т.
LAvt^
Динамические способы отражают характеристики как уже действу¬
ющего производства (на момент 1), так и процесс создания и функцио¬
нирования новых мощностей. Если в — срок создания новой мощности
и t0 — год начала ее создания, то соответствующий производственный
способ имеет на отрезке [Г0, t0 + в] только неположительные компонен¬
ты; положительные компоненты в данном способе (т.е. коэффициенты
выпуска) появляются только начиная с (t0 + в + 1)-го года, Научно-
технический прогресс проявляется в тенденции снижения коэффициен¬
тов затрат и увеличения коэффициентов выпуска одноименных ингре¬
диентов по мере увеличения t.
Как и в 4.5, будем обозначать N — множество производственных
способов (i/z Е N), Мх — множество воспроизводимых продуктов и ре¬
сурсов (sj G Mi), М2 - множество невоспроизводимых ресурсов (s2 £
ЕМ2). Допускается, что множества Мх и М2 изменяются во времени.
Основные соотношения модели. Для каждого года t модель
включает две группы балансов: 1) производства и распределения
продукции:
о, s^Mt, t = TTT, (11.26)
2) невоспроизводимых ресурсов:
2 cis^tXty ^fs2ty s2 £ t=ly Т. (11 27)
В составе продукции, используемой на потребление и другие нужды,
не связанные с развитием производства, выделяются переменная (мак¬
симизируемая) и фиксируемая (экзогенная) части:
ySlt = ySlt + qs<t- (11.28)
Общая структура оптимизационной динамической модели допускает
возможность различной формализации выбора структуры потребления и
целевых функций потребления (подробнее об этом см. 12.3). Ограничимся
здесь наиболее простыми способами формализации, исходящими из
идей Л.В.Канторовича.
Пусть для каждого года t уровень максимизируемой части потребле¬
ния характеризуется величиной Zf (например, это число комплектов
потребительских благ), структура максимизируемой части потребления
задается коэффициентами as^ t > 0. Тогда
ys,t><*sitzu Si€Mu 1=ТГТ. (11.29)
347
Целевая функция модели Uопределяется на векторе (z1,zj), т.е.
U = q>(zlt гт). (11.30)
В частности, можно использовать такие варианты целевой функции:
г т
гт—^шах, 2 zt-^ max, 2 qtzt-+ шах,
/=i /=i
где ^ — дисконтирующий множитель.
Динамическая модель, объединяющая условия (11.26) — (11.30),
приобретает вид:
2 CLSlypt^ si€ Ml9 t—1, T\
j€N
2 CLs2tytXty ^ Ts ti ^2 € ^2» ^ 1 /ii qi \
/ € N (11.01)
^>0;
Ф (*!• .. •, *r) — max-
Анализ модели (11.31) для линейных и сводящихся к ним функций
ip базируется на теории линейного программирования. Модель имеет
решение, если:
1) матрица производственных способов Ах = (а81ф{), включающая
только коэффициенты выпуска и затрат ингредиентов Sj Е Мi, обладает
следующим свойством, аналогичным свойству продуктивности матрицы
(Е — А) статического межотраслевого баланса: существует неотрицатель¬
ный вектор X = (хф), обеспечивающий получение положительной конеч¬
ной продукции ? + Q = (ySi t + qSi t) > 0;
2) значения экзогенных величин qSit не слишком велики; необхо¬
димо, чтобы при zt = 0,t = 1 ,Т выполнялись условия (11.27).
При анализе статического варианта линейной оптимизационной моде¬
ли отмечалась важность таких характеристик оптимального плана,
как число вошедших в него производственных способов (т.е. число
положительных переменных х^) и число полностью используемых ре¬
сурсов. ’’Рациональная геометрия” оптимизационной модели определя¬
ется соотношением числа ингредиентов, продолжительности расчетного
периода, числа производственных способов.
При малом числе включаемых в модель ингредиентов и небольшой
длине планового периода информация о производственных способах
может полезно использоваться только в небольшой степени. Наоборот,
если число вводимых в модель производственных способов будет мало
348
по сравнению с числом ингредиентов, то в оптимальном плане значитель¬
ная часть ресурсов будет недоиспользоваться, а ряд видов продукции —
производиться в избытке (см. ДМНХ, с. 161). Эти следствия из теории
линейного программирования используются при конструировании при¬
кладных оптимизационных моделей.
Динамические оптимальные оценки. Обозначим вектор-строку
оптимальных оценок продукции
,/ = Kt). t=\,T
(он соответствует условиям (11.26)) и вектор-строку оптимальных
оценок невоспроизводимых ресурсов
s2eMi t=l9T
(он соответствует условиям (11.27) ).
Анализ оптимальных оценок статической модели Л.В.Кан-
торовича дан в 8.1. Специфика оптимальных оценок динамичес¬
кой модели в том, что они соизмеряют общественно необходимые
затраты, дефицитность продукции и ресурсов и общественную полез¬
ность производимой и используемой продукции во времени.
Типичной является ситуация, когда оценки воспроизводимой про¬
дукции падают во времени, что является в первую очередь следствием
внедрения более эффективных технологий. Динамика оценок природ¬
ных ресурсов складывается под влиянием взаимодействия двух тенден¬
ций: уменьшения удельных затрат ресурсов вследствие научно-техничес¬
кого прогресса и абсолютного сокращения (вплоть до полного исчерпа¬
ния) доступных к использованию ресурсов. Поэтому возможным явля¬
ется чередование роста и снижения этйх оценок во времени.
На основе динамических оптимальных оценок определяются соотно¬
шения эквивалентной замены разновременных выпусков и затрат.
Условием эквивалентной замены является равенство
2 2 vSit&qSit= 2 2 wSatArSit. (11.32)
t= 1 S! € М ^ t=l s2€
Соотношение (11.32) позволяет определять условия эквивалентного
изменения динамики вовлечения ресурсов в хозяйственный оборот
(в пределах устойчивости базиса), например соотношения эквивалентной
замены ресурсов 1икв годы V и Г'.
Оптимальные оценки разных лет можно нормировать. Наиболее
простой способ нормирования состоит в переходе к векторам оценок,
имеющих одинаковые покомпонентные суммы для каждого года:
349
где
Р* =
/ 2 Us,t + 2 W,A х-
\sl€M\ /
Коэффициенты характеризуют относительную общую эффективность
использования продукции и ресурсов в разные годы планового периода.
С их помощью можно приводить оптимальные оценки к какому-то
одному году.
Оптимальные оценки являются важным инструментарием соизмере¬
ния разновременных затрат и результатов производственной деятель¬
ности.
Из условий задачи, двойственной к (11.31), имеем
ф е N (изз)
или в относительных оценках:
2 0*(2 as^tvSit—< 0, (П34)
r ~ 1 st
Экономический смысл условий (11.33) состоит в том, что в оптималь¬
ном плане по каждому виду деятельности суммарная за плановый период
оценка общего предельного выпуска продукции не превышает суммарной
оценки общих предельных затрат. При этом для способов, не вошедших в
оптимальный план, неравенства (11.33) выполняются как равенства1.
С помощью оптимальных динамических оценок можно оценить эф¬
фективность новых производственных способов, не включавшихся в рас¬
чет оптимального плана. Использование нового способа убудет эффектив¬
но, если для него выполняется условие (11.33). Благодаря этому свойству
оценок удобно целенаправленно готовить для народнохозяйственной мо¬
дели информацию, улучшающую первоначальные оптимальные решения.
Литература
1. Ашманов С А. Введение в математическую экономику. Ч. I, гл. 2, 3.
2. Канторович JI.B. Экономический расчет наилучшего использования ресурсов.
М.: Изд-во АН СССР, 195 9. Приложение I.
3. Макаров В.Л., Рубинов А.М. Математическая теория экономической динамики
и равновесия. М.: Наука, 1973. Гл. II - IV, VI.
4. Черемных Ю.Н. Математические модели развития народного хозяйства. М.: Изд-
во МГУ, 1986.
1 Не обязательно, чтобы во все годы расчетного периода ’’прибыль” вошедших
в оптимальный план производственных способов была неотрицательна. Возможно
наличие убытка, например, в первые годы периода. Однако образовавшийся убы¬
ток должен быть компенсирован получением в другие годы положительной ’’при¬
были” с учетом изменения общей эффективности использования продукции и ре¬
сурсов.
ГЛАВА 12
ЭЛЕМЕНТЫ ПРИКЛАДНЫХ ДИНАМИЧЕСКИХ
МЕЖОТРАСЛЕВЫХ МОДЕЛЕЙ
В отличие от теоретических моделей, предназначенных для анализа об¬
щих динамических и структурных закономерностей экономического
развития, прикладные межотраслевые модели ориентированы на реше¬
ние конкретных практических задач, возникающих на разных стадиях
предплановых исследований и разработки народнохозяйственных пла¬
нов.
Практическая направленность динамических межотраслевых моде¬
лей требует учета большего числа факторов и условий, а также более
конкретного их математического описания, чем в теоретических моде¬
лях. Прикладные динамические межотраслевые модели должны опира¬
ться на реально доступную экономическую информацию.
В настоящее время разработано и используется довольно большое
число различных динамических межотраслевых моделей. Однако при
внешнем разнообразии этих моделей подавляющее большинство из
них включает ограниченное число сходных элементов, описывающих
отдельные блоки экономической системы и отдельные связи между
ними. Совокупность таких элементов образует элементную б а-
з у динамических межотраслевых моделей. Каждая модель данного
класса — это сборная конструкция из некоторого числа типовых элемен¬
тов. Поэтому создание новых моделей данного класса охватывает два
уровня проблем: 1) развитие элементной базы, 2) совершенствование
принципов синтеза типовых элементов. При конструировании динами¬
ческой модели народного хозяйства необходимо, во-первых, описать
условия развития экономики для каждого выделенного интервала
времени, во-вторых, установить взаимосвязи между состояниями эконо¬
мики в различные интервалы времени.
В пределах каждого временного интервала условия динамической
модели являются более или менее полным отображением структуры
цикла общественного производства (см. рис. Д2). Динамическая модель
народного хозяйства включает ряд связанных между собой блоков
(подмоделей), которые характеризуют основные экономические про¬
цессы (частные процессы воспроизводства): а) процесс производства,
его развитие и обеспечение ресурсами, распределение произведенной
351
продукции, б) воспроизводство основных фондов и его взаимосвязи
с процессом производства, в) процесс потребления (удовлетворение
материальных и духовных потребностей населения) и его воздействие
на процесс производства. Вопрос моделирования этих трех важнейших
экономических процессов рассматривается в 12.1—12.3.
Важную роль в динамике народного хозяйства играют также вос¬
производство населения и трудовых ресурсов, воспроизводство и вос¬
становление различных природных ресурсов. ’’Выходы” этих процессов
обязательно учитываются в динамических народнохозяйственных моде¬
лях (численность населения, и особенно в трудоспособном возрасте,
количество природных ресурсов, доступных к эксплуатации, и их ка¬
чественные характеристики и т.д.).
Показатели прикладных динамических моделей делятся на две ос¬
новные группы: 1) эндогенные (регулируемые, или управляе¬
мые) переменные, 2) экзогенные (регулирующие, или управ¬
ляющие) переменные. Разделение всех переменных на экзогенные и эн¬
догенные определяется не только типом модели, но и целями проводимого
с ее помощью исследования, характером (режимом) ее использования.
При расширении модели (дополнении ее новыми зависимостями), из¬
менении целей исследования, удлинении расчетного периода часть экзо¬
генных переменных переходит в эндогенные.
Совокупность экзогенных переменных и параметров образует
массив исходной числовой информации. Дпя расчета (прогнозирования)
параметров широко используются разнообразные вспомогательные
модели, в частности трендовые, авторегрессионные, факторные.
12.1. Межотраслевые
производственные связи
Необходимыми элементами любой модели народного хозяйства являют¬
ся зависимости между затратами различных ресурсов (воспроизводимых
и невоспрризводимых) и выпуском продукции. Эти зависимости выра¬
жаются производственными функциями, функци-
я ми ftp оизводственных затрат, набором альтернативных
производственных способов. Применительно к экономи¬
ческой статике указанные понятия анализировались в гл. 4. Динамичес¬
кий подход к моделированию производственных процессов требует
отражения изменения зависимостей между затратами и результатами
производства под влиянием факторов социально-экономического разви¬
тия, и в первую очередь научно-технического прогресса. Большинство
прикладных межотраслевых моделей оперирует линейными за¬
висимостями между производственными затратами и выпуском продук¬
ции. С этой точки зрения прикладные модели ’’повторяют” теоретичес¬
кие модели, анализировавшиеся в гл. 11. Принципиальные же отличия
352
прикладных моделей от теоретических в отражении зависимостей ”за-
траты — выпуск” состоят в следующем: 1) для прикладных моделей
неприемлемы упрощающие допущения о неизменности во времени
матриц производственных способов (как в моделях Леонтьева и Ней¬
мана) ; каждому моменту (отрезку) времени соответствует своя матрица
производственных затрат, вследствие чего теряются некоторые ’’заме¬
чательные” свойства теоретических моделей; 2) в прикладных моделях
ингредиенты производственных затрат группируются по функционально¬
экономическому признаку (коэффициенты материалоемкости, фондо¬
емкости, трудоемкости и т.п.) и для каждой группы применяются
специализированные методики расчета и прогнозирования; тем самым
конкретизируется структура абстрактных технологических способов
моделей Неймана и Канторовича.
В прикладных динамических моделях используются два представле¬
ния производственных способов: а) для каждого отрезка времени
вводится особый производственный способ (как в моделях Леонтьева,
Неймана); б) для всего расчетного периода вводится единый (’’сквоз¬
ной”) способ (как в модели Канторовича). В большинстве типовых
моделей для описания действующего производства используется первое
представление производственных способов, т.е. компоненты способа
ф ENменяются во времени:Аф^= (аф(),Т= 1, Т.
Множества таких производственных способов для t = 1, Тобразуют
динамический ряд матриц ’’затраты — выпуск”. Динамические модели
с изменяющимися во времени матрицами производственных способов
разделяются на две группы: 1) модели с матрицами классического
межотраслевого баланса (в которых каждая отрасль представлена
только одним способом, выпускающим только один вид продукции);
2) модели, в которых одной отрасли может соответствовать несколько
производственных способов.
Рассмотрим вначале вопросы формирования динамических матриц
межотраслевого баланса. Основную информационную нагрузку несут
три матрицы производственных затрат:
а) матрица материалоемкости (коэффициентов прямых материаль¬
ных затрат) A (t) = (afj), г, / = 1, п;
б) матрица фондоемкости (коэффициентов потребностей в средне¬
годовые основных фондах на производство единицы продукции) D(t) =
= (cjjy), i = 1, rii,j = 1, п (где пх — число фондосоздающих отраслей);
в) матрица трудоемкости (коэффициентов прямых затрат труда)
l(t) = (f),i = T7n.
Наибольшее практическое применение пока получили укрупненные
межотраслевые динамические модели в стоимостном выражении в ра¬
зрезе 16 — 25 отраслей. Так, например, комплекс межотраслевых моде¬
лей, разработанный ГВЦ Госплана СССР и ЦЭМИ АН СССР (см. гл. 13),
включает 18 отраслей материального производства, в том числе две
фондосоздающие отрасли (машиностроение и строительство), и трудо¬
12 Зак. 2414 353
вые ресурсы в целом. При такой классификации отраслей матрица A (t)
имеет размерность 18 х 18, матрица D (t) —2x18, матрица / (t) —
1 х 18. Гораздо большую детализацию имеют динамические модели
натурально-стоимостного межотраслевого баланса. Они включают 150 —
250 важнейших видов продукции в натуральном выражении и, кроме
того, укрупненные отрасли материального производства.
Методика формирования коэффициентов матриц производствен¬
ных затрат объединяет различные подходы: а) статистическое прогнози¬
рование (применение трендовых, авторегрессионных, факторных моде¬
лей) ; б) методы технико-экономического нормирования и проектиро¬
вания; в) агрегирование параметров оптимизационных отраслевых
моделей; г) формализованные аналитические методы; д) экспертные
оценки.
Теоретически наиболее обоснованными являются вторая и третья
группы методов. Их регулярное применение требует создания обще¬
союзной автоматизированной системы плановой информации и функци¬
онирования системы моделей оптимального планирования.
Для укрупненных и автономно используемых динамических моде¬
лей наиболее характерно использование методов статистического прогно¬
зирования, экспертных оценок, выборочного обоснования отдельных
важнейших коэффициентов, простых аналитических методов, в которых
используется обобщенная информация о динамике производственных
затрат по строкам и столбцам матрицы1.
Одним из наиболее известных аналитических методов прогнозирования коэффи¬
циентов материальных затрат является метод RAS, предложенный Р.Стоуном.
Название данного метода связано с формулой расчета коэффициентов на плановый
период: А1 = RA°S, где А0 - матрица базисного года, А1 - матрица планового
года, R - диагональная матрица из коэффициентов г^ характеризующих среднее
изменение коэффициентов затрат продукции i (по строке), S - диагональная ма¬
трица коэффициентов sp характеризующих общее изменение материалоемкости
продукции/ (по столбцу). Таким образом, коэффициенты матрицR hS (их число
равно 2п) выражают общие гипотезы об изменении материалоемкости, на основе
которых определяются все коэффициенты матрицы А1.
При разработке детализированных межотраслевых моделей, в част¬
ности моделей натурально-стоимостного баланса и баланса производст¬
венных мощностей, в большей степени используются технико-экономи¬
ческие нормативы материалоемкости, фондоемкости, трудоемкости
производства и методы пофакторной корректировки важнейших коэф¬
фициентов затрат.
В рамках укрупненных моделей трудно улавливаются различия
между конкретными технологиями производства, формами органи¬
зации производства, комбинациями взаимозаменяемых материальных
Сущность технико-экономического проектирования коэффициентов затрат и
метода агрегирования норм расхода материальных ресурсов излагается в [2.
С* 91 93, 96 — 981.
354
ресурсов и т.п. Этим объясняется тот факт, что большинство исполь¬
зуемых динамических межотраслевых моделей, рассматриваемых в гл.
13, включает по каждой отрасли либо единственный усредненный способ,
либо два способа производства: 1) на мощностях, создаваемых до начала
планового периода (’’старых” мощностях) и 2) мощностях, создаваемых
в течение планового периода (’’новых” мощностях)1.
Обозначим производство на ’’старых” мощностях знаком <0>, а про¬
изводство на ’’новых” мощностяхо— знаком <—>. Тогда вектору объемов
производства первым способом X соответствуют матрицы Д а век¬
тору объемов производства вторым способом X — матрицы A, D,L
Актуальность и возможности введения в межотраслевую модель
информации о различных производственных способах по отраслям
усиливаются при детализации отраслевой классификации и переходе к
номенклатуре натурально стоимостного баланса. Целесообразно в пер¬
вую очередь включать в оптимизационные межотраслевые модели спосо¬
бы экономии материальных ресурсов, варианты крупных проектов,
информацию о принципиально новых технологических системах.
Соотношения ’’затраты — выпуск” в межотраслевых динамических
моделях могут выражаться также производственными функциями с
взаимозаменяемыми ресурсами и многофакторными функциями произ¬
водственных затрат. Методы формализации этих соотношений в принци¬
пе мало отличаются от тех, которые применяются для статических меж¬
отраслевых моделей (см. 7.7, а также ДМНХ, с. 173 - 174).
12.2. Взаимосвязи капитальных вложений,
основных производственных фондов и динамики производства
Одно из важнейших требований к динамическим народнохозяйственным
моделям — отражение экономического кругооборота ’’производство —
капитальные вложения — основные фонды — производство”. Модельное
описание этого кругооборота допускает ряд модификаций, отличающих¬
ся полнотой, используемыми показателями и связями между ними.
Взаимосвязи капитальных вложений, основных фондов и производст¬
ва выражаются в двух типовых условиях динамических моделей: 1) балан¬
сах производства и распределения продукции; 2) балансах основных
производственных фондов (или производственных мощностей).
Связи капитальных вложений с основными фондами, производствен¬
ными мощностями, динамикой производства. В межотраслевых моделях
производственные капитальные вложения выражаются вектором пере¬
менных U = (U}), / Е /х, где множество I^ включает п! видов продукции,
используемых в качестве элементов капиталовложений; это же множе¬
ство индексов характеризует вещественный состав производственных
фондов (виды оборудования, зданий, сооружений и т.п.).
1 Эти способы называются также ’’базисным” и ’’приростным”.
12* 355
Распределение производственных капиталовложений на простое
воспроизводство (iип) и расширенное воспроизводство (иР) основных
фондов (производственных мощностей) характеризует их воспро¬
изводственную структуру. Динамика производственных
капиталовложений непосредственно связана с воспроизводством основ¬
ных фондов (производственных мощностей) и косвенно — с будущей
динамикой производства.
Введем необходимые обозначения: Ф/+(Г) - объем основных произ¬
водственных фондов z-го вида на начало года t\ Ф+ у (Г) — общий объем
основных производственных фондов /-й отрасли на начало года Г;
Фу(0 — объем основных фондов вида /, занятых в /-й отрасли на начало
года t\ Д<P(t) — прирост основных производственных фондов в году
t (с соответствующими индексами); ЛГу — производственная мощность
(максимально возможный выпуск) по /-й продукции (J ЕI); ДМу — при¬
рост производственной мощности по /-й продукции.
Использование понятия ’’производственная мощность” целесообразно только в
детализированных моделях, включающих достаточно однородные виды продукции.
Поэтому в агрегированных моделях, как правило, используется понятие основ¬
ных фондов, а не мощностей. В порядке упрощения иногда прирост мощности за¬
меняется приростом объема производства Дху.
Капиталовложения для простого воспроизводства основных фондов
(и^) зависят от объемов и степени физического и морального износа
функционирующих основных производственных фондов. Приближенно
И?(0= 2 у\,ФиЦ), i£lb (12.1)
/€/ ' 7
где уц — доля затрат на возмещение выбытия основных фондов в объеме
действующих фондов.
Дня уточнения зависимости (12.1) необходимо использовать модели
распределенного лага. Коэффициент ^у определяется прежде всего возра¬
стной структурой основных фондов (см., например, ДМНХ, с. 176).
Капиталовложения для расширенного воспроизводства основных
фондов (и?) зависят от будущих приростов основных фондов (произ¬
водственных мощностей), удельных капиталовложений и инвестицион¬
ных лагов. При анализе этих зависимостей можем использовать предпо¬
ложения 11.1.
Вначале рассмотрим упрощенный случай с сосредоточенными лага¬
ми. Пусть инвестиционный лаг в /-й отрасли равен 7у. Тогда
u?(t)= 2 b\^0+j(t + xj), i€/i, (12.2)
/€/
где by — затраты капиталовложений /-го вида для прироста единицы ос¬
новных фондов в /-й отрасли (этот параметр часто называют коэффици¬
ентом приростной фондоемкости).
356
При использовании понятия производственной мощности получаем
и?(О btfiMjV + y), i£li. (12.3)
/€/
Соотношение, аналогичное (12.3), имеет место и при определении
капиталовложений, необходимых для приростов производства Дху.
В дальнейшем мы не будем отдельно записывать условия, содержащие
Дху, поскольку они полностью совпадают с соотношениями для Mfy.
Как уже пояснялось в 11.1, соотношения (12.2) и (12.3) имеют
смысл только при неотрицательных значениях ДФ+у, ДМу, ДXj. При отри¬
цательных значениях этих величин соответствующие капиталовло¬
жения равны нулю. Возможность ’’инверсии” капитальных вло¬
жений обычно не принимается во внимание в народнохозяйствен¬
ных моделях.
Коэффициенты bjp включенные в (12.2), (12.3), отличаются по
своему смыслу, величине и методике исчисления. В (12.2) эти коэф¬
фициенты характеризуют материально-вещественную структуру капи¬
таловложений, расходуемых на создание новых фондов #^1)-
В (12.3) коэффициенты bjj соответствуют удельным капиталовложениям
на прирост единицы мощности или продукции.
Более реалистичные зависимости капиталовложений от прироста
основных фондов (производственных мощностей) или будущих при¬
ростов производства должны учитывать распределенный ин¬
вестиционный лаг. При этом сохраняются общие принципы
увязки капиталовложений с приростами основных производственных
фондов или производственных мощностей, в том числе условия необ¬
ратимости капиталовложений.
Введем дополнительные обозначения: в — максимальный срок ове¬
ществления капитальных вложений в прирост основных фондов (произ¬
водственных мощностей) или прирост продукции; Ь-?— капиталовло¬
жения /-го вида, затрачиваемые в году t, для прироста в году г единицы
основных фондов (или единицы производственной мощности, или
получения прироста единицы продукции) в /-й отрасли. Тогда
ИЛИ
t+ef
„{-(<)= S sVjAMy(T). (12.5)
/'€/ T =*
357
Соотношения (12.4), (12.5) характеризуют’’спрос” на капиталовло¬
жения соответствующих лет; они включаются в балансы производства и
распределения продукции.
В свою очередь величины ввода основных фондов (производствен¬
ных мощностей) в году г зависят от предшествующих капиталовложе¬
ний в отрезке [т — в, т] . В дальнейшем АФ и будут обозначать объе¬
мы ввода фондов (мощностей), и (Гт) — капиталовложения, сделанные
в году t для года т. Предполагая полную сопоставимость измерителей
объемов капиталовложений и фондов, получаем:
t = Т-0
где
дф (Т) = 2ЛФ+У (г), и (tx) =J«i (tr).
Длительность инвестиционного лага не позволяет описать в рамках
любого фиксированного расчетного (планового) периода взаимосвязь
между капиталовложениями, вводом фондов и развитием производства
как замкнутый процесс. Общая сумма капитальных вложений за период
всегда состоит из трех частей: ил — вложений для завершения создания
фондов, начатого в предшествующем периоде; иг — вложений, связан¬
ных с процессом создания фондов, начинающимся и заканчивающимся
в течение планового периода; ьР — вложений, создающих задел для
ввода фондов в послеплановом периоде. Таким образом, в полной мере
эндо генными являются только капиталовложения и^, поскольку
вложения в значительной мере предопределены плановыми решения¬
ми предшествующего периода, а эффект вложений иг не может быть
обоснован с точки зрения целей планового периода.
Пусть, например, максимальный лаг капиталовложений — 3 года, длительность
планового периода - 5 лет. Тогда капиталовложения 1-го планового года: и (1) =
= и (1,1) +и (1,2) +и (1,3) +м (1,4); ввод фондов в 1-м году планового периода:
Дф( 1) =и(- 2,1) + и (-1,1) + и (0,1) + к (1,1). Сумма капитальных вложений за
плановый (пятилетний) период равна 2 и (t), в том числе iA =и (1,1) +и (1,2) +
t == 1 г
+ и (1,3) +и (2,2) +м (2,3) +и (3,3); и =и (1,4) +м(2,4) +и (2,5) +и (3,4) +
+ и (3,5) +и (4,4) +и (4,5) +и (5,5); ив=и(3,6) +и (4,6) +и (4,7) +и (5,6) +
+ и (5,7) +и (5,8).
В приводимых выше условиях величина лага относится к капиталь¬
ным вложениям в целом. Однако в межотраслевых моделях необходимо
принимать во внимание дифференциацию лага по материально-вещест-
венным элементам вложений. Так, для транспортных средств этот лаг
составляет несущественную величину, для большинства видов монтиру¬
емого оборудования — несколько месяцев, и только строительный лаг,
358
как правило, превышает один год. В общем случае максимальный срок
овеществления капитальных вложений d(j имеет два признака: вид
фондов (/) и отрасль назначения (j).
Основными способами увеличения производственных мощностей и
повышения эффективности фондов являются реконструкция, расшире¬
ние действующих объектов, новое строительство. Они существенно раз¬
личаются параметрами затрат и инвестиционных лагов. Введение этих
способов в динамическую модель расширяет возможности выбора ин¬
вестиционных решений и, как правило, повышает точность результатов.
Балансы основных производственных фондов и производственных
мощностей. Необходимые для народного хозяйства объемы ввода
основных производственных фондов (производственных мощностей),
определяющие в свою очередь динамику капиталовложений, устанавли¬
ваются посредством балансов фондов (мощностей). Принципы постро¬
ения балансов фондов и мощностей в основном совпадают. Поэтому
чтобы избежать повторов, сосредоточимся на рассмотрении элементов
балансов основных фондов, отметив в конце характерные особенности
построения балансов производственных мощностей.
Ресурсы основных фондов в году t Е [0, 7^ склады¬
ваются из основных фондов на начало года Ф (f) и прироста фондов в
течение года, образующегося из ввода фондов ДФ(?) за вычетом выбы¬
тия фондов W(t). Объем среднегодовых фондов <P(f) является главной
характеристикой физического объема данного производственного
фактора:
ФЦ) = Ф (0 + Р*ЛФ (t) — W (t), (12.7)
где (3Г - коэффициент среднегодового ввода фондов в году t (отношение
среднегодового ввода к абсолютному); W (t) — среднегодовое выбытие
фондов.
Соотношение (12.7) справедливо для общего объема основных фон¬
дов по всему народному хозяйству, для каждого вида фондов i Е/1э
для каждой отрасли — потребителя фондов / Е /, наконец, для каждого
сочетания индексов i и/.
При равномерном вводе фондов в течение года 0^ = 0,5; если же
ввод смещен на вторую половину года (что типично для растущей эконо¬
мики), тб < 0,5.
Величина выбытия фондов зависит от их объема и структуры. Дан¬
ная зависимость определяется многими факторами, в том числе норма¬
тивными сроками службы фондов, возрастной структурой фондов,
предшествующей динамикой ввода и выбытия. В прикладных динамичес¬
ких моделях обычно принимаются упрощенные зависимости, например:
w (<)=?{,*(<). (12-8>
359
где 7^ — доля выбытия фондов в году t по отношению к фондам на на¬
чало года.
При гипотезе единовременного выбытия всех фондов, достигающих
критического возраста, имеем W(t) = ДФ(Г — £). В нижеследующем
анализе предполагается, что фонды служат максимум £ лет и в течение
этого срока ежегодно частично выбывают.
Объем фондов на начало года представляет собой сумму вводов
фондов в предшествующие % лет с учетом их частичного выбытия:
Ф(/)= *2 АФ(т,0= s' у$АФ(т), (12.9)
Гx-t-l
где у'$— коэффициент ’’дожития” фондов, введенных в году г, до года t.
Например, фонды на начало года 2 образуются из фондов, вводимых начиная с
1
года - 6 с учетом их ’’дожития”: ф(2) — 2 АФ (7, 2) ; к ним добавляется вели-
т=-6
чина £Ф(2). С другой стороны, введенные в году 2 фонды входят в балансы после¬
дующих лет вплоть до года 9.
Величина выбытия фондов W(t) в соответствии с принятыми пред¬
положениями составляет
w (*) = [Ф(*) + ДФ(0]—_ 2 аф(т, г+1),
%=t+1 -£
откуда путем подстановок (12.9) получаем:
W(t)= *2 (y‘w — ?irllT) АФ (x)-t-(l — х) (12.Ю)
Переход к среднегодовому выбытию фондов осуществляется с
помощью коэффициента среднегодового выбытия 0^, который, как и
коэффициент j(3^, уменьшается при смещении выбытия на вторую поло¬
вину года:
W(t) = pwW{t). (12.11)
Наконец, величину среднегодовых фондов <P(t) через первичные
переменные АФ(т) можно^вывести двояким образом: 1) подставляя
в (12.7) значения Ф(г) и W (t) из (12.9) - (12.11), 2) как взвешенную
сумму \*0(t) + (1 — \)*Ф(Т + 1) с соответствующей расшифровкой
слагаемых но (12.9). В обоих случаях выражение объема среднегодовых
фондов включает переменные АФ (г) при rE [t — £, t] .
Потребности в основных производственных
фондах в году t определяются производственной программой данно¬
360
го года и достигнутой эффективностью использования основных фондов.
Вектор потребностей в основных фондах составляет D(t)X(t). Поэтому
в целом по народному хозяйству должно выполняться соотноше¬
ние
где
ф(*) = [Ф,.+ («1-
Следует иметь в виду, что рассмотрение Ф/+ (г) как суммарных ре¬
сурсов фондов предполагает возможность перераспределения имеющих¬
ся основных фондов между отраслями. В действительности же перерас¬
пределение фондов, закрепленных за определенными отраслями, может
требовать значительных затрат различных ресурсов и времени (демон¬
таж оборудования, перестройка зданий) или же вообще неосуществимо
(например, по специализированному технологическому оборудо¬
ванию) .
Если исключить возможность межотраслевого перераспределения
фондов, имеющихся на начало года, то должны выполняться соотноше¬
ния
dijWxjW^uit). *€Л, /’€/. (12.13)
При использовании информации о производственных мощностях
вместо (12.13) должно выполняться условие
xf(t)^Mf(t)% /€/ (12.14)
При этом
Мf (t) = Mj (f) + (Г)— Mw (0* (12.15)
где мощность на начало года Mj (t) определяется_по формуле, аналогич¬
ной (12.9), среднегодовое выбытие мощности Myyit) — по формулам,
аналогичным (12.10), (12.11). Существенное отличие описания динами¬
ки мощностей сострит в том, что введенные ранее мощности могут уве¬
личиваться (за счет так называемых организационно-технических меро¬
приятий). Это означает, что коэффициенты входящие в формулы
для мощностей, могут возрастать и превышать единицу.
Рассмотренные зависимости используются для ’’сборки” таких бло¬
ков динамических межотраслевых моделей, как ’’капитальные вложе¬
ния”, ’’основные фонды”, ’’производственные мощности”.
361
12.3. Динамизация моделей
сферы потребления
Динамический подход к моделированию сферы потребления по срав¬
нению со статическим подходом (см. гл. 5) требует изучения ряда
новых проблем: отражение процесса изменения потребностей и потреби¬
тельских предпочтений, соизмерение важности удовлетворения потреб¬
ностей в настоящем и будущем, учет особенностей использования благ
многократного и длительного пользования, определение допустимых
и эффективных траекторий динамики потребления и отложенного
покупательского спроса.
Динамизация целевой функции потребления. Как было показано
в 5.1, статическая целевая функция потребления (ЦФП) определяется
на множестве значений вектора Y, компонентами которого являются
объемы потребления различных видов продукции и услуг за фикси¬
руемый промежуток времени (например, год). Динамическая ЦФП
должна определяться на множестве значений траекторий Y (t).
При динамизации ЦФП необходимо дополнительно учесть следующие
обстоятельства: 1) различия между благами однократного (единовре¬
менного) и многократного (длительного) пользования; 2) неравно¬
ценность потребительского эффекта от использования благ в разные мо¬
менты времени; 3) изменение ЦФП во времени. Указанные требования
отражаются в динамической ЦФП вида
v= 2 q(t)v[Y (г), t], (12.16)
t = 1
а при непрерывном времени
OD
К = $</(<МУ(*), t]dt
О
(анализ динамических ЦФП такого вида в советской литературе впервые
выполнил В.Ф.Пугачев).
Интегральная ЦФП для всего интервала планирования образуется
из ЦФП, соответствующих отдельным моментам (интервалам) времени.
Это позволяет разделить две проблемы: соизмерение различных наборов
благ (и отдельных благ) друг с другом и соизмерение эффектов потреб¬
ления во времени.
Функция q(t), называемая взвешивающей, анализировалась в
10.2. Она сопоставляет ЦФП для разных отрезков времени. Выраже¬
ние v [Y(t)y t] означает, что ЦФП изменяется во времени. Причинами это¬
го могут быть изменения состава качеств потребительских благ, сдвиги
в структуре потребностей (не только вследствие динамики потребнос¬
тей однородных социальных групп, но и в результате изменений соци¬
альной структуры населения). Среди компонент векторов Y(t) следует
362
различать блага кратковременного (однократного) пользования (под¬
множество и.) и блага многократного и длительного пользования
(подмножество tt2)- Величина у[ (t), / Е Ц2 означает объем используемо¬
го блага в году t с учетом его накопления в предшествующем периоде
(а не только объем приобретения или поступления в году t).
Соизмерение полезных эффектов различных потребительских благ,
используемых в разные моменты времени, осуществляется с помощью
частных производных функций (12.16). Vft= — характеризует при-
оу it
рост интегрального уровня потребления (или интегральный предельный
полезный эффект) в результате увеличения использования /-го блага на
’’малую единицу” в момент t. При этом
к„=»(0
где — неириведенный предельный полезный эффект от использования
/-го блага в момент t. Соотношения эквивалентной взаимозаменяемо¬
сти потребления различных благ в динамике выводятся из формулы
полного дифференциала ЦФП (см. 5.1).
Особенности воспроизводства и использования благ многократного
и длительного пользования. Рассматриваемая группа потребительских
благ включает основные непроизводственные фонды (жилье, объекты
коммунально-бытового обслуживания, образования, здравоохранения
и культуры, средства пассажирского транспорта и т.п.) и предметы
домашнего имущества (одежда, обувь, мебель, культурно-бытовые
предметы и т.п.). В соответствии с закономерностями роста жизненного
уровня роль этой группы потребительских благ, и особенно основных
непроизводственных фондов, непрерывно возрастает.
Участие благ многократного и длительного пользования в процессе
потребления во многом аналогично роли основных производственных
фондов в процессе общественного производства. Потребительские,блага
данной группы участвуют в процессе потребления всей своей накоплен¬
ной массой, многократно превышающей объем их годового приобрете¬
ния (поступления). С другой стороны, текущее приобретение (поступле¬
ние) предметов многократного и длительного пользования оказывает
большое влияние на степень удовлетворения потребностей в последу¬
ющие годы (вследствие значительных сроков эксплуатации).
Производство, накопление и использование благ многократного
и длительного пользования отражается в двух типовых условиях дина¬
мических народнохозяйственных моделей: 1) балансах производства и
363
распределения продукции (направление капитальных вложений на при¬
рост и возмещение основных непроизводственных фондов); 2) балансах
основных непроизводственных фондов и потребительского имущества
(формирование ресурсов и их использование).
Формализация этих условий аналогична рассматривавшимся в 12.2
уравнениям производственных капитальных вложений и балансов основ¬
ных производственных фондов. Различия способов формализации опре¬
деляются в первую очередь гипотезами о сроках службы и выбытия
элементов основных непроизводственных фондов и потребительского
имущества.
Рассмотрим балансы фондов и имущества. Пусть g\ (г) - объем ис¬
пользуемого /-го блага на конец года t, gf(t) — среднегодовой объем
используемого блага, >7(т) — объем его поступления в году т, 0 —
максимальный срок службы блага. При гипотезе единовременного выбы¬
тия фондов (элементов имущества) имеем
£.(*)= 2 УЛ*)- <1217)
t=*-0
Если же принять более реалистичную гипотезу о ’’распределенном” вы¬
бытии фондов (имущества), при котором yTt — коэффициент дожития
фондов (имущества), поступивших в году г и используемых в году
Л то
gi(t)= 2 (12.18)
X — t — "
Объем используемых благ длительного пользования более точно
измерять в среднегодовом исчислении. Для этого можно использовать
соответствующие формулы среднегодовых основных производственных
фондов.
Таким образом, ЦФП, характеризующая уровень удовлетворения
материальных потребностей в году t, должна включать вектор Уi (t) =
= L>’/(0L / е U, по группе предметов однократного (единовремен¬
ного) пользования и вектор G2 (t) = [gy(0] , ^ U2 — по группе пред¬
метов многократного (длительного) пользования:
v{t) = v\Yl{t), G2(01 (12.17а)
Векторы Y1 и G2 можно объединить в один: Y = (Y6’2) = О'/).
ГДе Г У г, i€U,
yt~\gi, 1 €Иг
364
Тогда можно записать: v(t) = v[Y(t)] и уточнить формулу динамичес¬
кой ЦФП (12.16)
т __
2 q(t)v[Y(t)y t]. (12.186)
Критерии и условия оптимизации потребления в прикладных дина¬
мических моделях. Прикладные динамические модели включают, как
правило, упрощенные критерии оптимальности. Важно, однако, чтобы
упрощенные критерии соответствовали теоретическим принципам выбо¬
ра оптимальных решений с учетом их долговременных последствий,
а схема оптимизационных расчетов предусматривала возможность
уточнения критериев по мере получения дополнительной инфор¬
мации.
Помимо критерия оптимальности динамические межотраслевые
модели могут включать специальные условия, регулирующие динамику
и структуру потребления, а также соотношения между потреблением и
накоплением.
Динамическую ЦФП и ее упрощенные варианты необходимо приме¬
нять в моделях, в которых условия для различных моментов времени
взаимосвязаны. В упрощенных же динамических моделях (с прямой и
обратной рекурсией, квазидинамических) допустимо применять крите
рии максимизации потребления для отдельных отрезков времени, рас¬
сматривавшиеся в 8.2. Однако применение статических критериев в рам¬
ках динамических моделей обладает спецификой. Во-первых, необходи
мо учитывать весь объем накопленных благ многократного и длительно
го пользования и сроки их службы; во-вторых, необходимо пересматри
вать значения параметров (в частности, минимальных и максимальных
уровней удовлетворения потребностей) в зависимости от достигаемых
состояний удовлетворения потребностей в предшествующих отрезках
времени.
Максимизация фонда использования потребительских благ. В 8.2
анализировались достоинства и недостатки статической постановки за¬
дачи на максимизацию фонда потребления в фиксированных ценах
(8.13), а также возможности улучшения методики оценки продукции,
расширяющие допустимость применения данного показателя в качестве
критерия оптимальности.
В динамических моделях одним из наиболее простых критериев оп¬
тимальности, отражающим некоторые теоретические свойства динамичес¬
кой ЦФП, является максимизация взвешенной суммы фонда использо¬
вания потребительских благ:
# = L(/)2 (12.19)
t— 1 £ € /
365
где р° — сопоставимые цены (подробнее см. ДМНХ, с. 189).
Максимизация потребления при заданных траекториях. Статические
народнохозяйственные модели часто включают следующую формулиров¬
ку условий оптимизации потребления: максимизировать общий уровень
(или прирост уровня) потребления при заданном ассортименте потребля¬
емых благ или заданных функциях потребления (см. 8.2). Аналогичные
формулировки применяются и в динамических моделях, но они до¬
полняются условиями регулирования динамики потребления.
Рассмотрим задачу максимизации прироста общего уровня потребле¬
ния (удовлетворения потребностей) при постоянных структурных
коэффициентах прироста.
Пусть у? — объем использования г-го потребительского блага в ба¬
зисном году, AZ (f) — прирост уровня потребления в году t по сравне¬
нию с базисным годом (прирост физического объема фонда потребитель¬
ских благ, или числа комплектов потребительских наборов, или степени
удовлетворения рациональных потребностей), щ — ассортиментный ко¬
эффициент _прироста уровня потребления.
Тогда yi (г) > у^ + aj/SZ (t). Для того чтобы получить траектории с
непрерывным ростом уровня потребления, следует включить в модель
условия минимально необходимого роста (по аналогии с моделями в
10.2 и 11.1),в частности: Z (г) > (1 + r)fZ(0) или AZ (г) = [(1 + г)т -
— 1]Z (0), где г — минимально необходимый темп прироста уровня
потребления (могут применяться и другие трендовые модели, рассмо¬
тренные в 9.2).
Условия оптимизации потребления в ’’полностью” динамической
модели (см. определение в 13.1) запишутся следующим образом:
г max
0f(*)>0f(O)+ «([(!+'■)* — 1]Z° *€Л <=1. т- (12.20)
Модели с прямой рекурсией для года t включают условия:
AZ (t) — max;
7t(0>^(°) + a.AZW- *€/• (12.21)
Другой подход к оптимизации динамики потребления основан на
идее достижения целевых нормативов (норм рационального потребле¬
ния). Этому подходу соответствует статическая постановка (8.18).
В дополнение к (8.18) вводятся условия монотонного роста степени
удовлетворения рациональных потребностей, которые можно выразить
различными трендовыми моделями, например в (t) > t6, где 5 — мини¬
мальный годовой прирост степени удовлетворения потребностей (если
рациональные нормативы предполагается достичь за Т лет, то 5 ^
366
~ jTv . Тогда динамическая межотраслевая модель будет включать
условия:
б —«■ шах;
Й(9>Й + Ф<1?(*)]. i£U,t=\,T (12.22)
ё€[0, 1].
Оптимизационная задача с условиями (12.22) ориентирована на бы¬
стрейшее и одновременное достижение нормативов рационального по¬
требления. При этом движение к более высокому уровню удовлетворе¬
ния потребностей осуществляется по заранее выбранным (хотя бы
предварительно) траекториям.
Литература
1. Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Экономическая кибернетика.
Гл. 5.
2. Методические указания к разработке государственных планов экономического
и социального развития СССР. М.: Экономика, 1980. Гл. 7.
3. Моделирование народнохозяйственных процессов / Под ред. В.С.Дадаяна. М.:
Экономика, 1983. Гл. VIII.
4. Озеров В.К. Анализ динамики социалистического расширенного воспроизвод¬
ства. Новосибирск: Наука, 1984.
5. Черников Д.А. Темпы и пропорции экономического роста. М.: Экономика,
1982. Гл. 3.
ГЛАВА 13
ПОСТРОЕНИЕ И ПРИМЕНЕНИЕ ДИНАМИЧЕСКИХ
МЕЖОТРАСЛЕВЫХ МОДЕЛЕЙ
13.1. Типы прикладных динамических
межотраслевых моделей
и характер их использования
Общие требования к прикладным моделям. Прикладные межотраслевые
модели синтезируются из типовых элементов. Состав этих элементов и
схема синтеза определяются прежде всего конкретным назначением
модели, возможностями ее информационного, математического, техни¬
ческого обеспечения.
С точки зрения участия в процессе народнохозяйственного планиро¬
вания выделяются вспомогательные (или аналитичес¬
кие) и. основные (или плановые) модели.
Расчеты по вспомогательным моделям проводятся, как правило,
научно-исследовательскими институтами. Получаемые результаты слу¬
жат для подготовки аналитических и прогнозных материалов для плано¬
вых органов. При этом выходные показатели модели могут не совпадать
с принятыми и утверждаемыми показателями. Более строгие требования
предъявляются к плановым моделям, предназначенным для использо¬
вания в реальном процессе планирования. Отметим главные из них.
1. Ориентация на решение конкретных планово-экономических
задач и действующую систему плановых показателей.
2. Информационная обеспеченность. В тех случаях, когда модель
требует разработки новой или перестройки имеющейся информации,
необходимо обоснование целесообразности проведения такой работы с
точки зрения повышения качества плана. Методика перестройки инфор¬
мации должна создаваться вместе с математической моделью.
3. Технологичность модели. Это понятие означает, что модель должна
опираться на реальные возможности вычислительной техники и про¬
граммно-математического обеспечения; учитываются также квалифика¬
ция пользователей и временные ограничения, накладываемые порядком
и сроками разработки плана.
368
4. Возможность использования модели в интерактивном режиме с
участием плановиков-практиков. При этом должны предусматриваться
условия изменения конфигурации модели, оперативного просмотра по¬
лучаемых результатов, корректировки исходной информации.
Плановые модели не могут создаваться независимо от действую¬
щей технологии планирования. Но из этого не следует, что модели долж¬
ны только пассивно к ней приспособляться. Разработка и эксперимен¬
тальное использование моделей (вначале как ’’вспомогательных”) стиму¬
лируют появление задач, не решавшихся ранее в практике планирования,
и формируют ’’социальный заказ” системе статистической и плановой
информации.
Одним из общих требований к динамическим межотраслевым
моделям является их приспособленность к проведению многовари¬
антных расчетов. Это относится не только к балансовым моде¬
лям, определяющим допустимые траектории экономического развития,
но и к оптимизационным моделям, дающим лучшее решение с точки
зрения выбранного критерия оптимальности. Необходимость проведения
многовариантных расчетов обусловливается целым рядом причин.
Во-первых, конкретные цели экономического и социального разви¬
тия, выдвигаемые на тот или иной плановый период, относительно про¬
тиворечивы (конкурентны). Всегда сохраняется необходимость вы¬
явления и сопоставления альтернатив развития, обеспечивающих разную
степень достижения тех или иных целей.
Во-вторых, поскольку динамические межотраслевые модели вклю¬
чают разнообразные факторы и условия, важно изучать влияние отдель¬
ных факторов (условий) и их сочетаний на экономическую динамику.
С этой целью проводятся вариантные расчеты с изменяющейся конфигу¬
рацией модели.
В-третьих, исходная информация для динамических моделей имеет в
принципе ограниченную точность. Поэтому важно учитывать влияние на
модельное решение погрешностей в информации, а также различного ро¬
да неопределенностей, выявлять устойчивые и неустойчивые результаты.
При использовании динамической модели детерминистского типа множе¬
ство вариантных решений получается как результат сочетания гипотез
о численных значениях экзогенных переменных (параметров).
Основные типы динамических межотраслевых моделей. Главны¬
ми признаками классификации рассматриваемых моделей являются:
а) длительность периода, охватываемого моделью; б) способ связи
между моментами (интервалами) времени.
Прикладные динамические модели делятся на среднесрочные
(до 5 — 10 лет) и долгосрочные (10и более лет), что соот¬
ветствует существующим стадиям планирования народного хозяйст¬
ва: пятилетний план (с разбивкой по годам), Основные направления
экономического и социального развития на 15 лет, Комплексная
программа научно-технического прогресса на 20 лет. Расчетный
369
период долгосрочной динамической модели может выходить за границы
разрабатываемых общегосударственных прогнозов и планов. Он может
определяться исходя из продолжительности связанных между собой
моделируемых воспроизводственных циклов (прежде всего инвес¬
тиционного, научно-технического, демографического), т.е. превышать
20 — 25 лет.
Отметим основные изменения в содержании и методологии плани¬
рования (и соответственно моделирования) по мере расширения гори¬
зонта планирования.
1. Постепенно снижаются требования к детальности плановых пока¬
зателей; описание условий динамических моделей становится более
агрегированным. Важнейшее требование к отражению условий отдален¬
ного будущего состоит в том, чтобы они позволяли правильно оценивать
долговременные последствия текущих планово-управленческих реше¬
ний.
2. Уменьшается предопределенность экономического развития
сложившимися условиями, расширяется область выбора траекторий раз¬
вития. Соответственно сужаются возможности применения различного
рода экстраполяций прошлых тенденций (пассивных прогнозов) и
вообще моделей дескриптивного типа (включая эконометрические).
Возрастает роль моделей нормативного типа, ориентированных на поиск
лучших альтернатив развития.
3. Усиливается значение учета факторов стохастической и динамичес¬
кой неопределенности. Поскольку точное предвидение будущего в
принципе невозможно, динамические модели должны предусматривать
возможности многовариантных расчетов типа ’’если..., то...”, давать
интервальные прогнозы (например, с выделением пессимистического,
оптимистического, наиболее вероятного вариантов), предусматривать
процедуры выбора решений в зоне неопределенности. Таким образом,
по мере увеличения длительности расчетного периода задачи применения
динамических моделей смещаются от попыток дать возможно более
точный однозначный прогноз к поиску устойчивых динамических зако¬
номерностей при широком спектре гипотез об условиях будущего
развития.
4. Усиливается необходимость и создаются более благоприятные
возможности учета обратных социально-экономических связей процесса
общественного воспроизводства. Такие обратные связи, как влияние
уровня удовлетворения материальных и духовных благ на демографи¬
ческий процесс и эффективность производства, проявляются весьма
медленно и формализуются значительно труднее материально-вещест¬
венных связей. Реальные возможности исследования указанных обрат¬
ных связей создаются в рамках долгосрочных динамических моделей
с элементами неопределенности.
Пока типична ситуация, когда и для среднесрочных, и для долгосроч¬
ных прогнозно-плановых расчетов применяются модели с одинаковой
370
логической структурой. Адаптация моделей к решению задач с разными
временными горизонтами выражается главным образом в учете особен¬
ностей подготовки исходной информации, разной степени детализации
(агрегирования) показателей, изменении интервалов прогнозируемых
параметров.
По способу взаимоувяжи условий экономического развития между
отрезками времени динамические межотраслевые модели делятся на
три типа: 1) модели с прямой рекурсией (рекуррентные); 2) модели с
обратной рекурсией и квазидинамические; 3) ’’полностью динамичес¬
кие” модели (модели с двусторонней связью отрезков времени)1.
В дискретных моделях с прямой рекурсией расчеты ве¬
дутся последовательно от начала к концу периода: сначала находится ре¬
шение для t = 1, затем для t = 2 и т.д. Таким образом, решение для мо¬
мента (интервала) t оказывает влияние на решение для последующих
моментов (интервалов), но обратное влияние формально отсутствует.
Основной недостаток моделей данного типа — в том, что решение, полу¬
чаемое на каждом временном шаге, непосредственно не учитывает
долговременные цели развития и объективные условия, складываю¬
щиеся за пределами одного временного шага. Для смягчения указанного
недостатка должны проводиться корректировочные расчеты.
Второй тип упрощенных динамических моделей объединяет две
разновидности. В моделях с обратной рекурсией сначала
решается задача на последний год расчетного периода, а затем расчеты
ведутся в последовательности от конца к началу периода. Таким обра¬
зом, решение для года t оказывает влияние на решение для года t — 1,
но опять в одностороннем порядке2.
Такой порядок расчетов (начиная с последнего года) подчиняет
планирование достижению конечных целей, и в этом важное преимуще¬
ство моделей с обратной рекурсией. Однако при такой методике не
всегда получаются удовлетворительные решения для промежуточных и
особенно для начальных лет, поскольку недостаточно учитывается их
специфика, в частности значительная предопределенность условиями
предпланового периода. Например, может оказаться, что первоначальный
темп роста капиталовложений является слишком напряженным для4
промежуточных лет или погодовая динамика производства скачко-
Данная классификация динамических моделей близка к делению методов
экономического прогнозирования на:1) инерционные (из прошлого в на¬
стоящее и будущее) ; 2) инверсионные (от желаемого будущего к насто¬
ящему) ; 3) смешанные, или гибридные (с элементами инерцион¬
ности и инверсии во времени).
2 Одновременно с определением переменных последнего года (объемов про¬
изводства и использования продукции, распределения ресурсов и т.д.) обычно
рассчитываются также объемы капитальных вложений или ввода основных фондов
за весь расчетный период и их распределение по годам периода (например, путем
фиксации закона роста капиталовложений или основных фондов), что позволяет
затем рассчитывать другие показатели по годам периода.
371
образна. В этом случае необходимо корректировать исходные гипотезы о
динамике капиталовложений (основных фондов) и другие условия,
связывающие отрезки расчетного периода.
Более простая разновидность упрощенных динамических моделей
предназначается для определения показателей только последнего года
расчетного периода. Связь с базисным годом и динамикой развития
внутри расчетного периода осуществляется посредством балансов капи¬
таловложений или основных фондов за весь период. Такую разновид¬
ность модели будем называть квазидинамической.
Модели с прямой и обратной рекурсией объединяет общее свойство:
они распадаются на ряд статических задач, связываемых условиями пере¬
хода от одного года к другому (в прямой или обратной последователь¬
ности) .
Модели третьего типа — полностью динамические — яв¬
ляются наиболее адекватным инструментом исследования экономической
динамики. В этих моделях условия разных отрезков расчетного периода
по их влиянию на решения взаимосвязаны двусторонне. Дискретные по¬
лностью динамические модели не разбиваются на последовательно решае¬
мые задачи, относящиеся к отдельным временным отрезкам, а решаются
целиком. Однако большая размерность полностью динамических моделей
создает определенные трудности при их практической реализации.
Примеры указанных трех типов динамических моделей рассматрива¬
ются в 13.2 — 13.5. Приводятся только такие модели, по которым накоп¬
лен большой опыт использования в предплановых исследованиях и
непосредственно в планировании. Эти модели разработаны в ГВЦ и
НИЭИ Госплана СССР, ЦЭМИ АН СССР, ИЭиОПП СО АН СССР. Всюду
используются единые обозначения, введенные в гл. 12. Условия моделей
в некоторых случаях стандартизируются и несущественно упрощаются в
соответствии с рассмотренными в гл. 12 типовыми элементами.
13.2. Рекурсивные модели
Наиболее известные и близкие друг другу динамические межотрасле¬
вые модели рекурсивного типа были разработаны в середине 60-х гг. в
ИЭиОПП СО АН СССР (Н.Ф.Шатиловым) и НИЭИ при Госплане СССР
(Ф.Н.Клоцвогом).
В настоящее время модель НИЭИ включена в систему расчетов на¬
роднохозяйственного плана под названием ’’укрупненная динамическая
модель межотраслевого баланса в стоимостном выражении” (см. [5.
с. 88-95]).
Данная модель разрабатывается в стоимостном выражении в разрезе
18 — 25 отраслей производства. Она включает три типа балансовых урав¬
нений: балансы производства и распределения продукции, балансы ос¬
новных фондов и баланс трудовых ресурсов.
372
1. Балансы производства и распределения продукции:
x,(t)= 2 ai,Xj(t)+ 2 VtiUj[t) + yi(t) + gt(t), i£l. (13.1)
/ € / / € /
При этом
У{ (*) = $ + (0. <7/ (?) -
прочая конечная продукция.
Таким образом, (13.1) образуется путем сочетания соотношений
статической межотраслевой модели и упрощенного соотношения
(12.2). Коэффициенты Ьц характеризуют материально-вещественную
структуру капитальных вложений (расход продукции машиностроения
и строительства на 1 млн. руб. капитальных вложений в /-ю отрасль).
2. Балансы основных производственных фондов по отраслям-потре¬
бителям:
d'jXj (0 =<P+j{t-\) + b<P+i(t)-W+J(t). (13.2)
При этом
w+,(*) = №+/(*-!)•
Таким образом, равенства (13.2) объединяют в несколько измененном
виде условия (12.7), (12.8), (12.13). Здесь следует отметить две особен¬
ности.
Объемы основных фондов непосредственно балансируются только
по отраслям-потребителям. Предполагается, что материально-веществен¬
ный состав фондов (по элементам / G U ) балансируется коэффициента¬
ми by и Tj-j/. Основные фонды не приводятся к среднегодовым. Потреб¬
ности и ресурсы фондов рассчитываются на конец года; т.е. по сравне¬
нию с обозначениями <P+/(f) в 12.2 здесь имеется сдвиг на один год.
Из (13.2) получаем, что необходимый ввод в действие основных
производственных фондов в году t составляет
A <P+J{t) = d‘jx/(t)—(l — yWj)<P+J(t— 1) (13-3)
Связь производственных капитальных вложений и ввода основных
производственных фондов, представленная в гл. 12 соотношением
(12.2), в рассматриваемой модели имеет вид
dtjXj(t)-(\-ytw)0+J(t-\)
U/(t) — -r^—t . (13-4)
• — fy-ф/
373
где \jjf — норма прироста задела незавершенного строительства; ^ —
доля прочих капитальных вложений (не связанных с вводом фондов)
в общем объеме производственных капитальных вложений.
3. Баланс трудовых ресурсов:
2 ljX/{t) = L(t). (13.5)
/€/
Ставится условие обязательного использования трудовых ресурсов.
Общее число условий (13.1), (13.3) - (13.5) равно Ъп + 1. При
этом равенства (13.3) выполняют роль уравнений-определений. Они
используются для расчета ввода фондов ДФ+/(0 после нахождения
объемов производства. При подстановке (13.4) в (13.1) получаем для
года t систему из п + 1 уравнений, содержащую п + 1 неизвестных xj(t),
A z (Г).
Модель может дополняться условием, регулирующим долю произ¬
водственных капитальных вложений в конечном общественном продук¬
те:
2 и;{1)--=агу({) (13.6)
/€/
Оно связьюает результаты межотраслевой модели с расчетами по
макроэкономическим моделям и балансу народного хозяйства.
Расчеты по модели организуются в следующем порядке. На начало
года t = 1 известны объемы фондов Ф+у (0). Решается система уравнений
для t — 1 и находятся величины Ф+/(1) = Ф+/ (0) + ДФ+/ (1) - W+j (1).
Затем переходим к задаче для года (t + 1) и т.д.
Рассматриваемая модель используется на разных стадиях разработки
перспективного плана. На предварительной стадии при помощи модели
уточняются общеэкономические показатели, полученные на основе
макроэкономических моделей и расчетов балансов народного хозяйства.
В процессе вариантных расчетов исследуется влияние различных направ¬
лений структурной политики и динамики эффективности производствен¬
ных ресурсов на темпы и пропорции развития. На стадии разработки
основных направлений экономического и социального развития страны
с помощью модели уточняются и балансируются проектировки развития
отдельных отраслей производства.
Модель динамического межотраслевого баланса Н.Ф.Шатилова и
ее многочисленные обобщения используются в предплановых исследо¬
ваниях1 . Отличия основного варианта модели от рассмотренной выше
рекурсивной динамической модели заключаются в следующем: 1) балан-
Н.Ф.Шатилов (1931 - 1977) - автор ряда крупных работ по теории расширен¬
ного социалистического воспроизводства. Созданная им прикладная модель дина¬
мического межотраслевого баланса оказала заметное влияние на развитие и приме¬
нение динамических моделей народного хозяйства.
374
сы производства и распределения продукции строятся отдельно по про¬
дукции I и II подразделений; 2) балансы основных производственных
фондов даются как по отраслевой принадлежности, так и по вещест¬
венному составу, то есть по элементам Фу, i G /х, / Е /; 3) выбор объе¬
мов и структуры потребления осуществляется с помощью ’’шкалы
потребления”, позволяющей выбирать лучший вариант потребления при
совместности всех других условий (подробный анализ основной модели
и ее модификаций см. в ДМНХ, с. 200 - 205, [8], [11]).
13.3. Модели с обратной рекурсией
Характерной особенностью структуры динамических моделей с обратной
рекурсией является выделение двух блоков условий: а) блока расчетов
на последний год планового периода; б) блока развертки решения по
годам планового периода. Ниже приводятся три модели такого типа,
разработанные в ГВЦ Госплана СССР, ИЭиОПП СО АН СССР и НИЭИ
при Госплане СССР.
Балансовая модель с обратной рекурсией. Рассматриваемая модель
предложена БМ.Смеховым и ЯМ.Уринсоном. Она входит в состав
подсистемы АСПР ’’Сводный народнохозяйственный план”. Модель
включает 18 отраслей производства, в том числе две фондосоздающие
(машиностроение и строительство)1.
Условия для последнего года планового периода. В рассматривае¬
мой модели условия для года Т имеют две специфические особенности:
1) баланс основных фондов дается одним уравнением, т.е. без разбивки
фондов по видам и назначению; 2) максимизируется степень достижения
нормативов рациональных потребностей.
1. Балансы производства и распределения продукции:
X (Г) = АТХ (T) + bTu(T) + (Yv — У0) в + q (Т), (13.7)
где и(Т) — объем чистых производственных капитальных вложений;
в — степень достижения рациональных норм удовлетворения потребно¬
стей; Ьт — вектор материально-вещественной структуры капитальных
вложений; Y0 — вектор непроизводственного потребления базисного
года; Yv — вектор рациональных норм потребления; q(T) — вектор
’’прочей” конечной продукции (включая и У0).
В целях упрощения расчетов функции потребления, зависящие от в,
приняты линейными (в отличие от общего случая, рассмотренного в 12.3).
В запись модели внесены незначительные унифицирующие изменения (на
основе элементов гл. 12) ; используются введенные ранее обозначения, преиму¬
щественно в векторно-матричной форме.
375
2. Баланс основных фондов:
<1гХ(Т)+(Ф*-Ф°н)в + Ф°н=Ф(0)т&°+ s 7&‘и(/) + Рг*и(Л.
t=i
(13.8)
Уравнение (13.8) объединяет движение и производственных, и не¬
производственных основных фондов. Потребности в основных произ¬
водственных фондах определяются как dTX(T), где dT — вектор коэф¬
фициентов среднегодовой фондоемкости. Потребности в непроизводст¬
венных фондах (индекс ”н”) определяются как сумма (Фц — Ф«)0 +
+ Ф°н. Правая часть уравнения включает элементы, близкие к (12.11), в
том числе дожитие фондов, вводившихся до года Г, среднегодовой
ввод фондов в году Т.
3. Баланс трудовых ресурсов:
lTX (Т) = L (Г). (13.9)
Уравнение (13.8) включает неизвестные величины u(t) не толь¬
ко для года Г, но и для предшествующих лет планового пери¬
ода. Поэтому в модель необходимо ввести специальные условия,
связывающие соответствующие эндогенные переменные для раз¬
ных лет.
В рассматриваемой модели принимается
и(*) = и(0)[1+Д(*)ог], (13.10)
где
u{t) — u(0)
Д(*) =
«(1)— «(0)
— фиксируемый коэффициент, характеризующий отношение при-
роста капитальных вложений за t лет к их приросту в первом году
периода;
„ ц(1)—и(0)
«(0)
— эндогенная переменная, означающая темп прироста капитальных вло¬
жений в первом году периода.
Таким образом, условие (13.10) предопределяет закон роста капита¬
льных вложений, но параметр этого роста не задается, а является эндо¬
генной переменной. Если, например, принимается линейный закон роста
капитальных вложений, то u(t) = и(0) + ot. В этом случае Д(0 =з= t.
Типу экономического роста с увеличивающимися абсолютными прирйЬс-
376
тами соответствует ряд чисел Д(0> растущих быстрее натурального
ряда1.
Подстановка (13.10) в (13.8) приводит к задаче для года Т, вклю¬
чающей п + 2 уравнений (13.7) — (13.9) и п + 2 неизвестных Х(Т), 0, а.
Решение для года Т позволяет выполнить расчеты по восстановлению
всей траектории для t = 1,..., Т— 1.
Действительно, если определена величина а, то по (13.10) вычисля¬
ется траектория u(t). Затем для каждого года t в отдельности можно
находить решения системы уравнений (13.7), (13.9) с неизвестными
Х(г),в .
Рассмотренная балансовая модель используется на начальных эта¬
пах разработки перспективного плана, когда еще отсутствуют деталь¬
ные проектировки по отраслям. Основной функцией модели является
определение сбалансированной системы показателей на последний год
планового периода и оценка достижимости целевых социально-эконо¬
мических показателей. Простота и компактность модели обеспечивают
возможности оперативного расчета и сравнительного анализа большого
числа вариантов в режиме диалога. В комплексе моделей сводного на¬
роднохозяйственного планирования результаты расчетов по данной мо¬
дели используются при подготовке исходной информации и начального
приближения для полностью динамической модели.
Оптимизационная модель с обратной рекурсией. Примером модели
данного типа является разработанная в ИЭиОПП СО АН СССР оптими¬
зационная межрегиональная межотраслевая модель (ОМММ). Она испо¬
льзуется в предплановых исследованиях территориальных пропорций
народного хозяйства, в частности при подготовке региональных разде¬
лов Комплексной программы научно-технического прогресса СССР.
Статическая ОМММ рассматривается в 8.6. Ее динамизация зак¬
лючается в следующем. Во-первых, капитальные вложения модели¬
руются как воспроизводимый ресурс с оптимизируемыми параметрами
роста (различными по регионам); при этом капиталовложения отража¬
ются в балансах продукции последнего года планового периода (допол¬
нение условий (8.39)) и в виде особых балансов капиталовложений
за весь плановый период. Во-вторых, производство продукции харак¬
теризуется двумя способами: производство на мощностях, созданных
до начала планового периода, и производство на мощностях, созданных
в течение планового периода.
Будем рассматривать непосредственно не всю динамическую ОМММ,
а ее ’’точечный” аналог, совпадающий также с типовым региональным
Задача определения параметра о> соответствующего другим законам роста
капитальных вложений, существенно усложняется в рамках балансовой модели.
При анализе оптимизационной модели с обратной рекурсией будет рассмотрен
более универсальный спосрб нахождения неизвестных параметров роста капиталь¬
ных, вложений.
377
блоком ОМММ (полное описание динамизированной ОМММ см. в [9,
с. 267]).
1. Балансы производства и распределения продукции года Т:
X+X^Ak + AX + U + oA+q. (13.11)
Капитальные вложения учитываются по своему материально-вещест¬
венному составу U = (щ) ,/G/p Структура потребления задается векто¬
ром а = (а/),/е/.
2. Ограничения по невоспроизводимым производственным ресурсам
(природным, трудовым) на год Т:
SX + SX^R, (13.12)
где S — матрицы коэффициентов затрат ресурсов; R — вектор налич¬
ных ресурсов.
3. Балансы производственных капитальных вложений навесь плано¬
вый период:
НХ + НХ^ 2 U{t)y (13.13)
где А н — матрицы удельных капитальных затрат соответственно на
поддержание производства на ’’старых” мощностях и для получения
прироста продукции на ’’новых” мощностях.
4. Ограничения на объемы производства на ’’старых” мощностях:
(13.14)
где $ — вектор максимально возможных объемов производства, кото¬
рые можно получить в последнем году планового периода на производ¬
ственных мощностях, действовавших на начало планового периода.
5. Условия неотрицательности переменных:
X, X, £/(<), z>0. (13.15)
6. Критерий оптимальности:
z—*т ах. (13.16)
Для завершения построения модели необходимо связать друг с дру¬
гом величины U (Т) и 2 U (t). Если исходить из определенного закона
t = 1
роста капиталовложении в течение планового периода, то капиталовло¬
жения последнего (Г-го) года и их сумма за все годы могут быть пред¬
378
ставлены в виде функций известных капиталовложений базисного года
щ(0) и неизвестных параметров ежегодного роста капиталовложений о.
При линейном законе роста капиталовложений
м,(Г) = и((0) + Га„ (13.17)
I щ (г) = Гц,(0) + Г(-У-Ц, «€/»• (13.18)
/ = 1
Подстановка этих выражений в (13.11) и (13.13) не нарушает
линейности модели. Однако для развивающейся экономики более есте¬
ственным является рост капиталовложений с изменяющимися абсолют¬
ными приростами.
Динамике с постоянными темпами прироста соответствуют
U,.(7’)=(l+^)r«,(0), (13.19)
2 и,- (0 -(1 + q,) [(1 -Ц ц (0), £ е /i (13.20)
/= 1 °1
Включение (13.19) и (13.20) в (13.11) и (13.13) дает задачу сепа¬
рабельного программирования, для которой, так же как и для задачи
линейного программирования, разработаны стандартные программы
численной реализации на ЭВМ, включенные в пакеты прикладных про¬
грамм. Кусочно-линейная аппроксимация функций (13.19) и (13.20)
приводит к задаче линейного программирования с дополнительными
ограничениями. Однократное решение задачи линейного программиро¬
вания дает решение исходной задачи с любой требуемой точностью
(подробнее см. ДМНХ, с. 210).
Расчеты оптимальных вариантов по модели проводятся на период
10 — 20 лет. При этом наряду с определением показателей на последний
год планового периода (например, 20-й) целесообразно по упрощенной
модели рассчитывать (при уже известных значениях о/) показатели
последних лет пятилеток (т.е. 10-го, 15-го). Минимальная продолжитель¬
ность расчетного периода должна быть достаточной для создания и ос¬
воения крупных мощностей.
Оптимизационная модель межотраслевого натурально-стоимостного
баланса. Динамическая модель натурально-стоимостного межотраслевого
баланса разработана в НИЭИ при Госплане СССР под руководством
Ф.Н.Клоцвога. Модель предназначается для среднесрочного планирова¬
ния. Отметим характерные особенности этой модели: 1) объемы капита¬
льных вложений в целом за плановый период и в последнем году плано¬
вого периода являются эндогенными переменными; 2) модель включа¬
379
ет балансы основных производственных фондов по отраслям-потреби-
телям; 3) критерий оптимальности — максимум объема используемого
национального дохода в последнем году планового периода; 4) модель
включает развернутый блок внешней торговли с эндогенными перемен¬
ными объемов экспорта и импорта важнейших видов продукции; 5)
учитываются условия выбора оптимальной структуры использования
взаимозаменяемых материальных ресурсов (видов топлива, конструк¬
ционных материалов, сырья для легкой промышленности) в виде осо¬
бых производственных способов; 6) учитываются взаимосвязи между
розничным товарооборотом и всем фондом потребления; 7) вводятся
ограничения на объемы производства ряда сырьевых продуктов
и двусторонние ограничения по основным элементам конечного
продукта.
Модель, по которой проводились расчеты к плану на одиннадцатую пятилетку,
содержала около 200 основных видов промышленной и сельскохозяйственной
продукции, 33 министерства и 26 отраслей народного хозяйства и промышлен¬
ности. Число ограничений общего вида (не считая ограничений на отдельные пере¬
менные) - 289, число переменных - 607, что говорит о довольно широких воз¬
можностях оптимизации решений.
Поскольку большинство соотношений моделей аналогичны тем,
которые включены в статическую модель натурально-стоимостного
баланса и укрупненные динамические модели, рассматривавшиеся
выше, ограничимся анализом двух специфических условий: а) балан¬
сов основных производственных фондов; б) условий взаимозаменяе¬
мости материальных ресурсов.
Взаимосвязи между объемами производства, капиталовложениями
и основными производственными фондами во многом аналогичны
(13.2) — (13.4). Специфика заключается в увязке объемов производства
и капиталовложений последнего (пятого) года планового периода с
капитальными вложениями и приростами основных производственных
фондов за весь период (пять лет). Допускается, что капитальные вло¬
жения в течение пяти лет увеличиваются с постоянным абсолютным
приростом 5 (формально он может быть и отрицательным). Тогда
5
2 u(t) = bu{Q)+ 156=2^(0) + Зы(5).
t= 1
Отсюда
5
2 u(t) — 2а (0)
= з . (13.21)
На основании (13.21) и следуя предположениям, используемым
в (13.2) — (13.4), получаем по каждой отрасли:
380
*f*J (5)-(‘ -Y. .) ФЧ (0) 2uy (0)
«/(5) = з(П^4) ~ <1322>
где коэффициенты 7vvy, </?* в отличие от (13.4) относятся к пятилетне¬
му периоду.
Условия взаимозаменяемости материальных ресурсов учитываются
в модели следующим образом. В баланс взаимозаменяющей продукции
z-го вида входит алгебраическая сумма расхода и экономии z-й продук¬
ции (г/) в связи с взаимозаменяемостью (в дополнение к ’’традицион¬
ным” способам производства с коэффициентами расхода a\f) :
0 = ^аихи, (13.23)
Ь 1
где хДс — объем замены продукта к продуктом z; xjf — объем замены
продукта z продуктом /; bjj — коэффициент замены продукта z продук¬
том U отражающий технологические возможности взаимозаменяемости.
Значения переменных xji определяются в результате расчетов по мо¬
дели. В частности, экспериментальные расчеты показали высокую эффек¬
тивность дополнительного производства пластмасс для замены черных
металлов в машиностроении и строительстве, повышении удельного
веса угля в топливно-энергетическом балансе (главным образом из-за
его меньшей полной металлоемкости), замены химическим волокном
шерсти и хлопка. Вариантные расчеты развития народного хозяйства
СССР, проведенные на основе модели, продемонстрировали ее возмож¬
ности для обоснования темпов, пропорций и отраслевой структуры
экономики, оценки влияния отдельных плановых решений на общеэко¬
номические показатели, анализа воздействия различных факторов и их
сочетаний на конечные народнохозяйственные результаты.
13.4. Квазидинамические модели
межотраслевого баланса продукции
и производственных мощностей
При моделировании материально-вещественного аспекта процесса обще¬
ственного воспроизводства в разрезе конкретных видов продукции
целесообразно использовать понятие производственной мо¬
щности. Основные зависимости между капитальными вложениями,
объемами производства и характеристиками воспроизводства произ¬
водственных мощностей выведены в 12.2. Они являются специфически¬
ми элементами моделей межотраслевых балансов производственных
мощностей, которые сочетаются с типовыми условиями, характеризую¬
щими производство и распределение продукции, использование других
видов ресурсов.
381
Статическая модель межотраслевого баланса продукции и производ¬
ственных мощностей анализировалась в 8.3.
Для перспективных предплановых расчетов применяются к в а з и-
динамические модели межотраслевого баланса продукции и
производственных мощностей в детерминистской и вероятностной по¬
становках. Квазидинамическая модель включает наряду с условиями
для последнего года планового периода (балансы производства и распре¬
деления продукции, ограничения по производственным мощностям, тру¬
довым ресурсам и т.п.) также ограничение по объему капитальных вло¬
жений, расходуемых на создание производственных мощностей за весь
плановый период. Она отличается от рассматривавшихся выше моделей с
обратной рекурсией тем, что не содержит в явном виде ’’связки” между
капитальными затратами последнего года и суммой капитальных вложе¬
ний за плановый период.
Рассмотрим модели, разработанные в ИЭиОПП СО АН СССР. Основ¬
ная модель в детерминистской постановке по своей структуре наиболее
близка к оптимизационной модели с обратной рекурсией, а по инфор¬
мационному обеспечению — к межотраслевым натурально-стоимостным
балансам. Особенностями модели являются ограничения на объемы про¬
изводства в последнем году планового периода:
А<М° + ДЛ4, (13.24)
а также одно ограничение на объем капитальных вложений за весь плано¬
вый период:
(13.25)
где ДЛ/ = (Mf/) — вектор-столбец приростов производственных мощно¬
стей за счет капитальных вложений; h = (hj) — вектор-строка коэффици¬
ентов капитальных вложений на прирост единицы мощностей; G —
объем капитальных вложений за весь плановый период, обеспечивающий
прирост производственных мощностей.
Кроме этих условий, модель включает балансы производства и рас¬
пределения продукции (в упрощенной форме по сравнению с (13,7) и
(13.11)) и ограничение по трудовым ресурсам в виде неравенства.
Максимизируется конечная продукция в заданном ассортименте.
С использованием ранее введенных обозначений модель в целом
имеет вид
X = АХ -}-&Z *4"
ЛДМ<6; (13.26)
382
X >0; дм>0; (13.26)
z—> max.
Для анализа свойств оптимальных решений, получаемых по данной
модели, целесообразно провести ряд преобразований. Прежде всего
систему уравнений балансов производства и распределения продукции
и ограничения по трудовым ресурсам можно выразить относительно
максимизируемой величины z:
X = pz + Q; *|3-27)
„г«Т, (|3-28>
где
р = (Р/) = (£-Л)“1а,
Q = {Q{) = (E-A)-'q.
л = 1(Е—Л)”1 а;
T=L—l(E — A)-xq.
Естественным требованием является L > 0. Поскольку X > 0 при z >
> 0, то уравнения балансов производства и распределения продукции
могут быть исключены из оптимизационной задачи путем подстановки
(13.27) в (13.24). Получаем сокращенную запись модели относительно
неизвестных z и бМ:
Р z—ДМ<М°—Q;
ЛАМ < G;
nz<L; (13.29)
ДМ >0;
г —+ шах.
В данной модели максимум z при сколь угодно больших капиталь¬
ных вложениях ограничен сверху имеющимися трудовыми ресур¬
сами:
maxz<2 = ~,
л *
383
где L — трудовые ресурсы, которые остаются после удовлетворения по¬
требностей в фиксируемой конечной продукции; 7г — полные тру¬
довые затраты на один комплект максимизируемой конечной про¬
дукции.
Представляет интерес взаимная по отношению к (13.29)
задача определения минимальной величины капитальных вложе¬
ний для обеспечения максимального уровня конечной проду¬
кции z:
t
AM>|3z — М°А- Q;
ДМ>0; (13.30)
hAM—- min.
J*
Очевидно, что минимум суммы капитальных вложений достигается
при
AM; = max (J3-z — 0)=^AM%,
Тогда
min G -=G* = hAM*.
Вьщеление капитальных вложений, превышающих величину G*, не мо¬
жет привести к дополнительному увеличению z из-за дефицитности тру¬
довых ресурсов. Заметим, что это свойство оптимального плана обусло¬
влено тем, что в рассматриваемой модели не отражается связь между
производительностью и фондовооруженностью труда. Решение задачи
(13.29) целесообразно только при G <G*. Но тогда maxz <z, ограниче¬
ние по труду выполняется как неравенство, и поэтому его можно исклю¬
чить из задачи (13.29).
Модель (13.29) без ограничения по трудовым ресурсам целесооб¬
разно анализировать как задачу параметрического программирования
относительно экзогенной переменной G G [0, G*] . Очевидно, что z =
= z(G) — монотонно возрастающая по G функция при 0 < G < G*,
а ограничение по объему капитальных вложений выполняется как равен¬
ство (при положительной оценке капитальных вложений).
При G= 0 ввод новых мощностей отсутствует. Имеем статическую
модель, в которой величина z ограничивается сверху, как правило,
единственным ’’узким” местом - одним видом производственной мо¬
щности: о
max z (G) = min —-g-—. (13.31)
G= 0 i€l P'
384
При увеличении G в оптимальный план начинают входить перемен¬
ные ДМ/. Последовательность их вовлечения в оптимальный план можно
интерпретировать как процесс последовательного расширения ’’узких”
мест в системе производственных мощностей.
При этом Ш?> 0 только в том случае, когда j3z - Ш. = Af?- Q.. Величина
т* — шах
M\-Qi
характеризует тот минимальный уровень конечной продукции, при котором исчер¬
пываются все резервы производственных мощностей, созданных до начала плано¬
вого периода. Для обеспечения уровня конечной продукции z° требуется величина
капитальных вложений G° = h (pz° - М° + Q). Имеющиеся в народном хозяйстве
свободные резервы производственных мощностей (кроме нормативных) относи¬
тельно невелики по сравнению с потребностями увеличения производства в долго¬
срочном периоде. Поэтому весьма вероятно, что G° < G*. При G° ^G имеем
AM = MG)-<W° + Q ^0, (13.32)
а максимум z определяется по формуле
г (О) = 0-h(M«-Q) (13 33)
На отрезке [G°, G*] максимум конечной продукции и величины
приростов мощностей являются монотонно возрастающими линейными
функциями от объема капитальных вложений.
Определив z (G) при заданной G по (13.33), находим ДЛ/ по (13.32).
Наконец, по (13.27) находим вектор объемов производства X. Таким
образом, оптимальный план исходной модели (13.26) и его важные стру¬
ктурные и динамические характеристики могут определяться без непо¬
средственного решения задачи большой размерности.
Экспериментальные исследования по квазидинамической модели
межотраслевого баланса производственных мощностей проводятся на
основе информации межотраслевых натурально-стоимостных балансов,
информации сводных балансов производственных мощностей, разраба¬
тываемых примерно по 300 видам продукции, нормативов удельных
капитальных вложений на приросты мощностей. Целесообразно распро¬
странить на модель межотраслевого баланса производственных мощ¬
ностей рассматривавшиеся выше направления развития модели натураль-
но-стоимостного баланса: введение условий взаимозаменяемости матери¬
альных ресурсов (а также способов экономии материальных ресурсов
путем введения мощностей с прогрессивными технологиями) и условий
13 3ак. 2414 385
выбора структуры внешней торговли, розничного товарооборота и фон¬
да потребления. На базе моделей межотраслевого баланса производствен¬
ных мощностей проводятся теоретические и экспериментальные иссле¬
дования возможностей вероятностного подхода к решению проблем
сбалансированности и оптимизации плановых решений. В разработанных
моделях параметры исходных матриц и векторов рассматриваются как
случайные величины, заданные на конечных отрезках с некоторым за¬
коном распределения вероятностей. Имитация неопределенности осуще¬
ствляется с помощью метода статистического моделирования (см. ДМНХ,
с. 218 — 219, а также [3]).
Решения, наилучшие в вероятностной постановке, качественно и
количественно отличаются от оптимальных решений задач в детерминист¬
ской постановке. Одно из наиболее существенных отличий — появление
резервных мощностей. Назначение резервных мощностей в
рассматриваемых постановках — удовлетворение дополнительных по¬
требностей в материальных ресурсах, которые возникают из-за того,
что конкретная реализация матрицы А может оказаться менее благопри¬
ятной, чем заложенная в детерминированную оптимизационную модель.
Вследствие выделение части капитальных вложений на создание резер¬
вных мощностей оптимальные объемы производства и конечной продук¬
ции, определяемые в вероятностных моделях межотраслевых балансов
производственных мощностей, оказываются меньшими, чем в детерми¬
нистских моделях. Экспериментальные исследования приводят к выво¬
ду, что коэффициент использования производственных мощностей в
промышленности СССР должен составлять в среднем 92 — 94 %. Расшире¬
ние состава случайных параметров и увеличение интервала распределения
ведут к уменьшению объемов производства, конечной продукции и
уровня оптимального использования мощностей.
13.5. Динамические модели с двусторонними
связями отрезков планового периода
В данном разделе анализируются прикладные межотраслевые модели,
которые в соответствии с классификацией в 13.1 могут быть отнесены к
типу ’’полностью динамических”. Принципиальным преимуществом
моделей этого типа по сравнению с рекурсивными и квазидинамически¬
ми является более адекватное отражение причинно-следственных зави¬
симостей между прошлым, настоящим и будущим развитием народного
хозяйства. Особенность ’’полностью динамических” моделей с вычисли¬
тельной точки зрения заключается в том, что показатели, относящиеся
к различным временным отрезкам (годам, подпериодам) планового
периода, определяются посредством решения единой ’’межвременной”
задачи. Соответственно возрастают требования к математическому и
техническому обеспечению проводимых расчетов.
386
Среди моделей, отвечающих формальным признакам ’’полностью
динамических”, целесообразно различать модели со ’’слабой” и ’’силь¬
ной” экономической взаимосвязанностью временных отрезков. Приме¬
рами моделей со ’’слабой” экономической взаимосвязанностью явля¬
ются обобщения оптимизационных рекурсивных моделей, в которых
взаимосвязанность временных отрезков достигается благодаря включе¬
нию интегральной целевой функции. ’’Сильная” экономическая взаимо¬
связанность временных отрезков достигается благодаря достаточно
полному отражению в модели долговременных инвестиционных процес¬
сов с помощью сквозных динамических производственных способов,
лаговых соотношений распределения капитальных вложений, воспроиз¬
водства основных фондов, производственных мощностей и потребитель¬
ского имущества.
Ниже рассматриваются две модели с временными взаимозависимо¬
стями. Первая (с распределенными лагами) в полной мере относится
к динамическим моделям с ’’сильной” взаимосвязанностью. Вторая
занимает в этом смысле промежуточное положение, обладая важными
свойствами полностью динамических моделей и сохраняя преимущест¬
ва моделей рекурсивного типа.
Модель с распределенными лагами. Межотраслевая балансовая мо¬
дель с распределенными инвестиционными лагами.предложена Э.Ф.Ба-
рановым ([6, С. 273 — 284]). Она включает уравнения балансов про¬
изводства и распределения продукции и балансы основных фондов и
представляет собой систему из 2пТ линейных уравнений (где п — число
отраслей). Позднее балансовая модель была преобразована ИС.Матли-
ным в оптимизационную путем замены равенств неравенствами (по
балансам фондов), введения ограничений по трудовым ресурсам, усло¬
вий формирования фонда потребления и критерия оптимальности ([2.
С. 60- 65]; [9. С. 168 - 184]).
Ключевыми элементами модели являются зависимости между капи¬
тальными вложениями, вводом и выбытием основных производствен¬
ных фондов и объемами производства. Ниже приводится модификация
модели, включенная в комплекс укрупненных межотраслевых моде¬
лей, разработанный ГВЦ Госплана СССР и ЦЭМИ АН СССР. В запись
модели внесены изменения унифицирующего характера.
1, Балансы производства и распределения продукции:
t + Qf
х; (t) = 2 а‘цХ/ (0+2 2 Щ ДФ+/ (т) + sit [С(0] + Ч( (*).
/€/ Т=Г/€/
i£5y t=\7T. (13.34)
Зависимость, определяющая потребности в капитальных вложениях
на расширенное воспроизводство для i Е 1г, в точности соответствует
(12.4); Sff — функция, преобразующая вектор целевых показателей в
конечную продукцию /-й отрасли.
13* 387
2. Балансы основных производственных фондов по отраслям-потре-
бителям: t _ х
^,.(0<Ф°+/(0+ 2 АФ+j(т)4-Р/ЛФ+у(t), /67, *=777. (13.35)
X- 1
Здесь используются упрощенные по сравнению с (12.7), (12.9),
(12.13) зависимости. Отметим, что вплоть до года t + в объемы дей¬
ствующих производственных фондов предопределены капитальными
вложениями допланового периода.
3. Балансы трудовых ресурсов:
2 ljX/(t)^L(t)-slt[C(t)j, (13.36)
/€/
где — функция, характеризующая потребности в трудовых ресурсах
для непроизводственной сферы в зависимости от вектора достигаемых
целевых показателей.
4. Критерий оптимальности. Максимизируется функция, определя¬
емая на векторе целевых показателей за весь плановый период, в част¬
ности:
2 (С#) —► max. (13.37)
t-1
Кроме обязательных условий (13.34) — (13.37) (их число равно
1пТ, что при стандартной 18-отраслевой классификации и плановом го¬
ризонте в 15 лет дает 540 уравнений и неравенств), модель включает ог¬
раничения для отдельных лет планового периода (по объемам производ¬
ства некоторых отраслей, фонду капитальных вложений, использованию
отдельных ресурсов) и для пятилеток (по фонду капитальных вложе¬
ний), а также условия неотрицательности переменных xj (t) и ДФ+/ (f).
Рассматриваемая модель имеет относительно узкие возможности опти¬
мизации. С точки зрения методологии оптимизационного подхода наибо¬
лее искусственным является априорное жесткое установление распреде¬
ленных инвестиционных лагов по всем отраслям.
Оптимизационная многопериодная модель. Многопериодные модели
совмещают ряд преимуществ рекурсивных и полностью динамических
моделей. В них расчеты ведутся на последние годы пятилетий, связы¬
ваемых в рамках долгосрочного периода. Рассматриваемая ниже модель
разработана в НИЭИ при Госплане СССР, предназначена для обоснований
темпов, пропорций, отраслевой структуры экономики на долгосрочный
период.
Модель построена в разрезе укрупненных отраслей промышленности
и народного хозяйства. Ее принципиальной особенностью является учет
взаимозаменяемости основных производственных фондов и трудовых
ресурсов. Распределение капитальных вложений между отраслями осу¬
ществляется не только для увеличения производства, но и с целью
388
регулирования роста производительности труда через рост его фондо¬
вооруженности.
Ниже дается описание модели без блока внешней торговли и с не¬
значительными'упрощениями.
1. Балансы производства и распределения продукции:
*,.(/)= 2 0^,(0+ 2 fyu,. (<)+<*( А* (0+ 7.(0.
/в/ /€/
;е/, t = 5, 10, 15, Т. (13.38)
Капитальные вложения и конечная продукция (в том числе для при¬
роста уровня потребления) входит в (13.38) так же, как в (13.1). При
этом kz (Г) представляет собой кумулятивный прирост от нача¬
ла планового периода, т.е. для t = 10, 15, ... величина Дг(г) вклю¬
чает Az (Г-1).
2. Уравнения потребностей отраслей в основных производственных
фондах:
+ j£l, t = 5, 10, 15, .... Т. (13.39)
Уравнение (13.39) существенно отличается от формулировавшихся
ранее соотношений по основным производственным фондам. Здесь:
Ф+j (t) — основные производственные фонды в ;-й отрасли на конец
года tf dj — ’’гипотетический” коэффициент фондоемкости (соответству¬
ющий гипотезе, что не будет корректирующей его взаимозаменяемости
между основными фондами и трудовыми ресурсами), sj (f) и rj (г) —
объемы основных фондов, направляемых на изменение фондовооружен¬
ности труда.
3. Уравнения потребностей отраслей в капитальных вложениях за
пятилетний период:
«/ (I) = Ф} [ф+/ (t)-vp>+/ (t—5)] + Nj (t)-Nj (*-5),
/€/; / = 5, 10, ..., T; 1=1, 2, ...,
lk (т. e. t = 5l, T = blk), (13.40)
где ipj— коэффициент пересчета ввода основных фондов в объем капи¬
тальных вложений; т* — коэффициент дожития фондов, действовав¬
ших на начало пятилетки; Nj (t) — незавершенное строительство на
конец года t. Предполагается, Что незавершенное строительство состав¬
ляет определенную долю от производственных капитальных вложений:
Nj (t) =vrM;-(0-
4. Уравнения капитальных вложений в последнем году пяти-
летия:
uj{t) = \[uj(l)-2uf(t-b)\, /€Л < = 5, 10, ..., Г,
/= 1, 2, ..., /*. (13.41)
389
Посредством уравнений (13.41) связываются объемы капитальных
вложений за пятилетие и в последнем году пятилетия. Используется
гипотеза о линейном росте капиталовложений по годам пятилетия.
5. Балансы трудовых ресурсов по отраслям:
l,(<)*=/;*,(о—-*»&(<)+"МО. /==5, 10, •••’ т’ (1342)
где Lj (t) — численность занятых в /-й отрасли в году t; j — ’’гипотети-
ческий” коэффициент трудоемкости продукции; ij — коэффициент
взаимозаменяемости трудовых ресурсов и основных производственных
фондов в /-й отрасли за пятилетие I (экономия живого труда за счет уве¬
личения основных фондов).
6. Критерий и условия роста уровня потребления по пятилетиям:
Az(t)—*max; Az(tf)^к1 Az(Г), / = 5, 10, 7\
/= 1, 2 (13.43)
Максимизируется общий прирост уровня потребления за плановый
период (Г лет) при условиях, регулирующих динамику роста потребле¬
ния по пятилетиям. Для обеспечения более равномерного развития по
пятилетиям модель включает ряд дополнительных ограничений: условия
неубывания капитальных вложений по пятилетиям, минимальные доли
капитальных вложений в конечном продукте по пятилетиям и т.п.
Экспериментальные расчеты по модели проводятся на 10-летний
период (два пятилетия). В решении оптимизационной модели уровень
всех основных экономических показателей оказывается выше, чем в
вариантах развития народного хозяйства, рассчитываемых с помощью
балансовой модели при использовании той же базы данных. Выше оказы¬
вается и уровень фондовооруженности труда. Расчеты показывают эф¬
фективность развития по трудосберегающему направлению (с положи¬
тельным sj) таких отраслей, как угольная промышленность, машино¬
строение, лесная промышленность, сельское хозяйство, строительство;
а по фондосберегающему направлению — черной металлургии, электро¬
энергетики, химической промышленности и некоторых других.
13.6. Совершенствование
динамических межотраслевых моделей
и их использование в народнохозяйственном планировании
На современном этапе выделяются два направления разработки и внед¬
рения динамических межотраслевых моделей:
1) создание моделей, более полно и адекватно отражающих взаимо¬
действие факторов экономического и социального развития;
2) активное включение моделей в технологию разработки народно¬
хозяйственных планов.
390
Совершенствование конструкций прикладных динамических меж¬
отраслевых моделей соответствует общим тенденциям развития эконо-
мико-математического моделирования. В первую очередь следует отме¬
тить тенденцию к построению интегрированных моделей, охватываю¬
щих разнообразные факторы и типы связей народнохозяйственных
процессов.
В интегрированных моделях, как правило, совмещаются норматив¬
ный и дескриптивный подходы к моделируемым процессам. Наряду с
традиционными для межотраслевых моделей нормативными соотноше¬
ниями затрат и выпуска, ресурсов и потребностей они включают также
зависимости эконометрического типа (например, ’’модели межотрасле¬
вых взаимодействий”, разрабатываемые под руководством Ю.В.Яремен-
ко [6]).
Значительным продвижением в методологии народнохозяйственного
моделирования является построение моделей, охватывающих воздей-^
ствие элементов хозяйственного механизма на материально-веществен¬
ный аспект воспроизводства (моделей с обратными связями). Так, в
ЦЭМИ АН СССР выполняются экспериментальные исследования по
моделям, учитывающим влияние материального стимулирования и
уровня удовлетворения платежеспособного спроса (товарно-денежной
сбалансированности) на эффективность производства (в частности, на
производительность труда), различные формы эндогенного научно-тех¬
нического прогресса.
Встраивание межотраслевых моделей в реальную технологию народ¬
нохозяйственного планирования осуществляется в рамках развивающейся
подсистемы АСПР Госплана СССР ’’Сводный народнохозяйственный
план”, С этой целью в ГВЦ Госплана СССР и ЦЭМИ АН СССР разработан
комплекс укрупненных межотраслевых моде¬
лей, в НИЭИ при Госплане СССР создан центральный ком¬
плекс задач АСПР, включающий группу взаимосвязанных межот¬
раслевых моделей. Основные черты ’’технологического” подхода харак¬
терны и для процесса использования динамических межотраслевых
моделей при подготовке Комплексной программы научно-технического
прогресса СССР и в других предплановых исследованиях.
Рассмотрим в качестве типового примера комплекс укрупненных
межотраслевых моделей (КММ). Комплекс создавался на основе обоб¬
щения предшествующего опыта использования отдельных межотрасле¬
вых моделей в практике плановых расчетов. Состав и особенности по¬
строения комплекса определяются сферой его применения, и прежде
всего характером и последовательностью решения конкретных задач в
процессе разработки сводного раздела плана экономического и социаль¬
ного развития СССР [2].
Комплекс позволяет: 1) проводить расчеты по укрупненным меж¬
отраслевым моделям в автономном и совместном режимах; 2) форми¬
ровать показатели объема и структуры конечного продукта исходя из
391
заданных социально-экономических целей; 3) осуществлять работу
в диалоговом режиме (формирование, просмотр, корректировку, не¬
которые виды преобразования информации); 4) проводить расчеты
сводных и аналитических показателей на основе решений межотрасле¬
вых моделей; 5) осуществлять справочно-информационные функции.
Для эффективного выполнения перечисленных выше функций в
составе комплекса имеются соответствующие информационные, про¬
граммно-математические, инструктивные и технические средства. Основ¬
ными частями комплекса являются:
а) банк межотраслевых моделей;
б) база данных комплекса;
в) целевой блок комплекса;
г) блок расчета сводно-аналитических показателей;
д) программы, обеспечивающие диалоговый режим;
е) справочный блок комплекса.
Банк межотраслевых моделей обеспечивает решение основных
планово-экономических задач, которые стоят перед подсистемой ’’Свод¬
ный народнохозяйственный план”. Он включает универсальную статичес¬
кую модель (см. гл. 6), пол у динамическую модель с обратной рекур¬
сией (см. 13.3), целевую динамическую модель с распределенными
лагами (см. 13.5), динамическую модель с изменяющейся конфигурацией.
Использование различных моделей в составе единого комплекса созда¬
ет значительные преимущества, поскольку результаты одной из моделей
могут быть исходными для другой. При этом расчеты, проводимые
по моделям, чередуются с анализом полученных результатов и коррек¬
тировкой исходной информации.
Можно выделить следующие основные задачи, решаемые отдельны¬
ми моделями при их совместном функционировании в рамках комплек¬
са:
1) с помощью статической модели проверяется сбалансированность
показателей в базовом году и устраняются выявленные дисбалансы,
тем самым обеспечивается нормальный ’’стартовый” уровень показате¬
лей динамических моделей;
2) с помощью полудинамической модели на предварительной ста¬
дии разработки перспективного плана определяется область, в которой
должны находиться основные ресурсы и результирующие показатели
(объемы капитальных вложений, непроизводственное потребление и
др.); полученные значения используются в качестве начального прибли¬
жения и ограничений динамической модели;
3) полудинамическая и динамическая модели при работе с целевым
блоком комплекса позволяют проверить достижимость заданных целе¬
вых показателей с точки зрения обеспеченности основными видами
ресурсов (материальными, трудовыми, капитальными), а так¬
же определить оптимальную траекторию достижения заданных це¬
лей;
392
4) целевая динамическая модель, используя результаты расчетов по
динамической модели с изменяющейся конфигурацией, позволяет уточ¬
нить основные показатели первой пятилетки планируемого периода с
учетом капитальных вложений допланового периода и лагов их осво¬
ения.
Таким образом, при совместном режиме функционирования от¬
дельные модели дополняют друг друга; при этом облегчается и
ускоряется поиск приемлемого решения, повышается его надеж¬
ность.
База данных обеспечивает хранение разнообразной информации
и эффективную работу с ней пользователей комплекса. Она вы¬
полняет важные интегрирующие функции, позволяя связать отдель¬
ные части комплекса в единое целое (подробнее об этом см. гл.
17).
Целевой блок комплекса является инструментом проработки кон¬
кретных целевых социально-экономических проблем развития народ¬
ного хозяйства. С его помощью исходя из задаваемых социально-эконо¬
мических целевых показателей (уровень доходов на душу населения,
обеспеченность жилой площадью и т.д.) определяются необходимые
объем и структура конечного общественного продукта. Тем самым
’’внешние” социально-экономические установки связьюаются с ’’внут¬
ренними” показателями межотраслевых моделей, и с помощью послед¬
них проверяется возможность реализации заданных целей с точки зрения
обеспечения их необходимыми ресурсами.
Блок расчета сводно-аналитических показателей предназначен для
определения производных (обобщающих и синтетических) характери¬
стик развития экономики. Входными для него являются результаты ре¬
шения динамических моделей комплекса, а в качестве выходных фор¬
мируются различные аналитические таблицы, которые выдаются на
экран видеотерминала (печать). Здесь рассчитываются такие показа¬
тели, как национальный доход и его распределение на фонды потребле¬
ния и накопления, совокупный общественный продукт, динамика и стру¬
ктура капитальных вложений и основных фондов, изменение показате¬
лей эффективности общественного производства и т.д.
Сервисным элементом комплекса межотраслевых моделей являет¬
ся справочный блок. Его назначение — помочь пользователю ориенти¬
роваться в структуре комплекса, выполняемых им функциях и правилах
работы с ним.
Рассматриваемый комплекс межотраслевых моделей в свою очередь
является составной частью комплекса моделей сводного перспективного
планирования (КМП), разработанного в ЦЭМИ АН СССР. Этот комплекс
дополнительно включает подсистему эконометрических народнохозяй¬
ственных моделей, модели финансового и территориального пла¬
нирования, а также модели нижестоящих уровней иерархии (см.
гл. 17).
393
ЛИТЕРАТУРА
1. Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Экономическая кибернетика.
Гл. 8, 9.
2. Комплекс моделей перспективного планирования. Гл. 3, 11.
3. Лавровский Б.Л. Анализ сбалансированности производственных мощностей
промышленности СССР. Новосибирск: Наука, 1983. Гл. 8, 9.
4. Маевский В.И. Межотраслевые пропорции общественного производства (проб¬
лемы формирования). М.: Экономика, 1986.
5. Методические указания к разработке государственных планов экономического
и социального развития СССР. М.: Экономика, 1980. Гл. 7.
6. Моделирование межотраслевых взаимодействий. М.: Наука, 1984.
7. Моделирование народнохозяйственных процессов. Гл. VIII.
8. Озеров В.К. Анализ динамики социалистического расширенного воспроизвод¬
ства.
9. Система моделей народнохозяйственного планирования. Раздел II, гл. 2, 3.
10. Смехов Б.М., Уринсон Я.М. Методы оптимизации народнохозяйственного плана.
М.: Экономика, 1976.
11. Шатилов Н.Ф. Анализ зависимостей социалистического расширенного воспро¬
изводства и опыт его моделирования. Новосибирск: Наука, 1974.
РАЗДЕЛ Ш
МОДЕЛИРОВАНИЕ НАРОДНОГО ХОЗЯЙСТВА
КАК МНОГОУРОВНЕВОЙ СИСТЕМЫ
ГЛАВА 14
ОБЩИЕ ПРИНЦИПЫ И ПРОБЛЕМЫ СИСТЕМНОГО МОДЕЛИРОВАНИЯ
НАРОДНОГО ХОЗЯЙСТВА
14.1. Необходимость системного моделирования
Вопрос о концепции моделирования социалистической экономики стал
актуальным в начале 60-х годов. К этому моменту эконо мико-мате мати-
ческие исследования в СССР получили уже довольно широкое распро¬
странение и имели высокие темпы развития; накапливался опыт постро¬
ения и использования моделей разнообразных экономических объек¬
тов. Становилось все более очевидным, что в социалистической эконо¬
мике математическое моделирование может реализовать свои потенци¬
альные возможности только в том случае, если охватит народное хозяй¬
ство в целом. Но каким образом, с помощью каких модельных кон¬
струкций можно эффективно изучать все народное хозяйство?
Определенные надежды некоторое время связывались с развитием
методологии оптимизации планово-экономических решений. На основа¬
нии успешного опыта построения межотраслевых балансов и простейших
оптимизационных народнохозяйственных моделей допускалась возмо¬
жность создания единой оптимизационной модели народного хозяйства
(супермодели), которая в деталях описывала бы все социально-
экономические процессы и решение которой давало бы оптимальный
народнохозяйственный план. Насколько обоснована эта идея с теорети¬
ческой и практической точек зрения?
Для экономической теории представление задачи разработки и реа¬
лизации народнохозяйственного плана в виде единой оптимизационной
модели имеет определенные преимущества, в особенности для изучения
общих свойств оптимизируемой экономической системы, принципов
соизмерения затрат и результатов (см. гл. 2; 3.1). Однако построение и
применение такой модели представляются практически неосуществимы¬
ми; уязвима идея и в теоретическом отношении. В чем основные причины?
395
Первая группа причин связана с возможностями информационного
и технического обеспечения моделирования, с методологией математи¬
ческого описания социально-экономических процессов.
Во-первых, супермодель экономики требует полной централизации
всей информации, создания такой системы сбора и передачи первичных
данных ”с мест” в ’’центр” (без какого-либо агрегирования и отсева),
которая гарантировала бы полноту, оперативность, безошибочность
ввода в супермодель огромного информационного массива; столь же
надежной и быстродействующей должна быть система передачи решений
’’центра” каждому исполнителю. Современные средства технической ин¬
форматики, не говоря уже об организационных факторах, пока не поз¬
воляют реализовать эту идею.
Во-вторых, построение супермодели в соответствии с ее полным
замыслом приводит к оптимизационной задаче фантастической размер¬
ности (по числу переменных и параметров) и чрезвычайно сложного типа
(сочетающего нелинейность, многоэкстремальность, стохастичность и
т.д.). Требуемые для ее решения (в приемлемые сроки) вычислительные
мощности на много порядков превышают возможности всего существу¬
ющего парка компьютеров.
В-третьих, построение адекватной супермодели трудноосуществимо
и нерационально с позиций методологии моделирования сложных си¬
стем. Опыт моделирования технических и отчасти биологических сис¬
тем убедительно показывает, что попытки одноуровневого математиче¬
ского описания сложных объектов во всех деталях неизбежно порожда¬
ют много погрешностей, усиливают нестабильность решений, отражаю¬
щих поведение объектов (из-за невозможности локализовать отдельные
’’возмущения”, стохастичность, неопределенность). К тому же концеп¬
ция супермодели не принимает во внимание наличие в социально-эконо¬
мической системе многих неформализуемых и трудно формализуемых
факторов.
В будущем, по-видимому, указанные затруднения, стоящие на пути
создания и реализации супермодели экономики, станут в принципе
преодолимыми. Хотя сложность народного хозяйства и соответственно
трудности централизованного управления экономикой будут возрастать,
опережающий прогресс информатики и математического моделирования,
безусловно, расширяет технические и математические возможности
централизованной обработки информации и централизованного управле¬
ния. Но надо ли стремиться только к такому использованию расширяю¬
щихся возможностей науки и техники?
Наиболее глубокие причины, вынуждающие к принципиальному
отказу от идеи супермодели, имеют социально-экономическую при¬
роду. Действительно, супермодель — это математический образ централи¬
зованно управляемой экономики, в которой отношения между участ¬
никами экономического воспроизводства построены исключительно
на командах ’’центра” и точном их исполнении на ’’местах”. В такой
396
предельно регламентированной системе не принимаются во внимание
интересы социальных групп, трудовых коллективов, индивидуумов,
в ней нет места инициативе и творчеству, активизации ’’человеческого
фактора”. К этому можно добавить, что попытки централизации обра¬
ботки информации и принятия хозяйственных решений оказываются
безумно дорогой затеей, не говоря уже о разрушающей силе бюрократи¬
зма. Таким образом, концепция централизованно управляемого хозяй¬
ства и отражающая ее основные положения математическая супермодель
экономики несовместимы с основными принципами социализма и де¬
мократии.
Процесс планового управления социалистической экономикой
всегда, т.е. при всех модификациях организации управления в различных
социалистических странах и на разных этапах их развития, разделяется
между подсистемами (звеньями) различных уровней. В этом процессе
централизованное управление сочетается с хозяйственной самостоятель¬
ностью и инициативой; каждое управленческое звено обеспечивает не
только передачу сигналов ’’сверху вниз” и ’’снизу вверх” (команды и
их выполнение), но и осуществляет поиск наилучших способов выполне¬
ния получаемых заданий (рекомендаций, заказов) и удовлетворения
интересов соответствующей хозяйственной подсистемы. Соответственно
и концепция моделирования народного хозяйства должна ориентировать¬
ся на создание не супермодели, а системы моделей, описывающей функ¬
ционирование и взаимодействие подсистем народного хозяйства.
14.2. Демократический централизм
в управлении и требования
к системному моделированию экономики
Основным принципом организации управления социалистическим народ¬
ным хозяйством является демократический централизм. В соответствии
с этим принципом деятельность центральных управленческих органов
сочетается с самостоятельностью различных хозяйственных звеньев,
в процессе управления участвуют широкие массы трудящихся. Поиск
лучших методов и форм управления, идущий на протяжении уже дли¬
тельного периода в СССР и других социалистических странах, заключает¬
ся в развитии, углублении, более полной реализации возможностей демо¬
кратического централизма. ’’Суть коренной перестройки управления
экономикой страны — переход от преимущественно административных к
преимущественно экономическим методам руководства на всех уровнях
и управлению интересами и через интересы, к широкой демократизации
управления, всемерной активизации человеческого фактора”1.
1 Материалы Пленума Центрального Комитета КПСС, 25 - 26 июня 1987 г
М.: Политиздат, 1987. С. 84.
397
Обращаясь к эволюции взглядов советских экономистов на прин¬
ципы управления социалистическим народным хозяйством, необходимо
подчеркнуть вклад основоположников и виднейших представителей
экономико-математической школы.
В докладе на июньском (1987 г.) Пленуме ЦК КПСС М.С.Горбачев
привел выдержку из статьи академика B.C.Немчинова, опубликованной
в журнале ’’Коммунист” еще в 1964 г., о порочности механистического
подхода к управлению экономикой1. B.C.Немчинов обосновал идею
’’хозрасчетной системы планирования”, включающей понятия плана-
заказа, контрольных цифр, систему хоздоговорных отношений, коллек¬
тивные формы оплаты труда. Перспективы совершенствования плани¬
рования он непосредственно связывал с системным моделированием,
использующим принципы экономической кибернетики2. Работам В.С.Не-
мчинова, а также близким к ним в теоретическом отношении работам
Л.В.Канторовича, В.В .Новожилова, А.Л.Лурье и др. были принципиально
чужды как технократические представления о централизованно управля¬
емой экономике, так и анархо-синдикалистские тенденции децентрали¬
зации. Основная теоретико-методологическая линия, связывающая уг¬
лубление демократического централизма в управлении с системным
моделированием социально-экономических процессов, продолжалась
и в 70-е — 80-е годы. Благодаря этому многие идеи проводимой ради¬
кальной реформы управления получили экономико-математическое
обоснование.
Системы моделей народного хозяйства, ориентированные на практи¬
ческое применение, должны обладать существенными преимуществами
по сравнению с действующим инструментарием подготовки и реализации
плановых и управленческих решений. Этим определяется характер тре¬
бований к конкретным разрабатываемым системам моделей. Всю сово¬
купность требований можно разделить на две группы. Первая группа —
это требования к планированию и управлению вообще, выдвигаемые
’’Примитивное понимание взаимоотношений между большими и малыми
экономическими системами может создать лишь такую окостенелую механичес¬
кую систему, в которой все параметры управления заданы заранее, а вся система
зал имитирована сверху донизу на каждый данный момент и в каждом данном
пункте... Такая залимитированная сверху донизу экономическая система будет
тормозить социальный и технический прогресс и под напором реального процесса
хозяйственной жизни рано или поздно будет сломана” (Коммунист. 1987. № 11.
С. 25).
2 ”... Социалистическое общество может рассматриваться как единая экономи¬
ческая система, распадающаяся на различные отраслевые и территориальные под¬
системы той или иной сложности... а также на первичные хозяйственные единицы.
Проблема управления такой сложной совокупностью экономических систем требу¬
ет особого кибернетического подхода к изучению их поведения и процессов их
взаимодействия, включая процессы самоорганизации и самонастройки... Для опи¬
сания и изучения такого взаимодействия приходится строить особую систему эко¬
номических моделей, положив в ее основу модели отдельных предприятий и строек
и завершив ее многоразмерными и малоразмерными макроэкономическими мо-
делями” [13. С. 75 - 76, 83 - 84].
398
независимо от того, используется или нет аппарат системного моделиро¬
вания (целевая направленность, охзат всех существенных аспектов,
проблем и факторов социально-экономического развития и ускорения
НТП, материально-вещественная и финансовая сбалансированность, сов¬
мещение народнохозяйственных и локальных интересов, дифференци¬
рованный подход к социальным группам и др.). Вторая группа — это
специфические требования к системе моделей как части управленческой
технологии: быстродействие и надежность, информационная и техничес¬
кая обеспеченность, возможности работы в диалоговом режиме, сходи¬
мость итеративных согласований решений подсистем и т.д.1.
Для построения и использования системы моделей народного хозяй¬
ства требуется решить три основные проблемы: структуризовать народ¬
ное хозяйство, т.е. выделить хозяйственные звенья разных уровней
(подсистемы народного хозяйства), которые должны стать объектами
моделирования, и описать связи между ними; разработать модели для
хозяйственных звеньев; разработать методы согласования решений
различных хозяйственных звеньев и синтеза общего народнохозяйст¬
венного плана.
Структуризация народного хозяйства. В практике социалистическо¬
го планирования и управления народное хозяйство всегда рассматрива¬
ется как многоуровневая система. Отличительной особенностью народ¬
ного хозяйства СССР является сочетание и взаимопереплетение несколь¬
ких организационных иерархий, среди которых важнейшими являются
иерархии отраслевого и территориального планиро¬
вания и управления.
Многоуровневая система народного хозяйства включает как верти¬
кальные, так и горизонтальные связи внутри каждой иерархии плани¬
рования и управления, а также связи между различными иерархическими
структурами. Например, производственные объединения и предприятия
связаны не только с вышестоящими органами отраслевого управления,
но и вступают в хозяйственные отношения друг с другом; кроме того,
они подчиняются (хотя бы в некоторых аспектах своей деятельности)
территориальным органам. Народное хозяйство является системой
полицентрической: одно хозяйственное звено может одно¬
временно координироваться несколькими центрами.
Значение структуризации народного хозяйства для разработки
системы моделей определяется тем, что выделение хозяйственных подси¬
стем и самостоятельных звеньев означает необходимость построения
соответствующих экономико-математических моделей и установления
зависимостей между ними. Наиболее общим критерием для определения
В работе [16. С. 25 - 30] формулируются 12 требований, которые с некоторы¬
ми дополнениями и оговорками можно рассматривать как ’’программу-максимум”
практической реализации систем моделей народнохозяйственного планирования
на ближайшее время.
399
границ каждой подсистемы (звена) служит теснота связей составляю¬
щих ее элементов внутри данной подсистемы и с элементами других
подсистем. Обособление подсистемы как самостоятельного экономи¬
ческого объекта (и объекта моделирования) оправдано тем более, чем
сильнее ее внутренние связи и чем слабее связи внешние.
Прикладные разработки системы моделей оптимального планирова¬
ния опираются в основном на существующую организационную структу¬
ру народного хозяйства. Вместе с тем из анализа народного хозяйства
с позиций системного моделирования могут следовать предложения
по совершенствованию существующей организационной структуры.
Такие предложения преследуют цели более полной оптимизации отдель¬
ных подсистем, более эффективного согласования локальных оптиму-
мов с глобальным оптимумом народного хозяйства и т.п. Так, например,
экономико-математические исследования по оптимальному отрасле¬
вому планированию и анализу структуры межотраслевых связей сти¬
мулировали образование новых объектов планирования и управле¬
ния — межотраслевых программн о-ц елевых ком¬
плексов, обеспечивающих выполнение крупных народнохозяйст¬
венных задач (топливно-энергетический, агропромышленный, машино¬
строительный и другие комплексы) и соответствующих органов управ¬
ления (государственных комитетов, бюро Совета Министров СССР).
Разработка моделей подсистем и отдельных звеньев. После разби¬
ения народного хозяйства на подсистемы для каждой из них необхо¬
димо разработать экономико-математическую модель или группу связан¬
ных моделей. Модель подсистемы включает описание внутренних усло¬
вий ее развития (собственные ограничения, определяющие область до¬
пустимых планов), внешних связей (’’вход” и ’’выход”) и, как правило,
критерий оптимальности. При конструировании локальных оптимиза¬
ционных задач вопросы определения ограничений и критерия оптималь¬
ности следует решать совместно. Нельзя корректно сформулировать
ограничения, пригодные для любых критериев, так же как нельзя кор¬
ректно сформулировать критерий, одинаково приемлемый при различ¬
ных ограничениях.
При разработке отдельных моделей в рамках общей системы моде¬
лей необходимо определить круг тех вопросов, которые должны реша¬
ться с помощью той или иной модели. Например, при оптимизации
производственной программы народного хозяйства требуется устано¬
вить, по какой номенклатуре продукции объемы производства должны
рассчитываться в модели верхнего уровня (укрупненной модели народ¬
ного хозяйства), по какой — в моделях межотраслевых комплексов,
в моделях отдельных отраслей и т.д.; необходимо также устано¬
вить, какие плановые производственные задания должны передаваться
нижестоящим звеньям и поступать от вышестоящих звеньев. Аналогич¬
ная проблема ’’разделения труда” между разными моделями возникает
при оптимизации пространственной структуры народного хозяйства:
400
распределение круга плановых задач между моделями сводного терри¬
ториального планирования, моделями крупных регионов, моделями тер¬
риториально-производственных комплексов, промышленных узлов и
т.п.
Согласование решений в системе моделей. Решения^ получаемые
изолированно для отдельных подсистем, как правило, несовместимы
Это выражается в несоответствии ’’входов” и ’’выходов” взаимосвязан
ных моделей, в невыполнении общесистемных ограничений при объе
динении решений подсистем. Но даже если решения подсистем в сово
купности образуют допустимый план, то крайне маловероятно, что полу
ченный таким путем народнохозяйственный план будет оптимальным
Сущность проблемы согласования моделей состоит в том, чтобы путем
изменения их ’’входов” и ’’выходов” получить сочетание (композицию)
решений подсистем, дающее по крайней мере сбалансированное решение
для всей системы. В реальном процессе функционирования социалисти¬
ческой экономики согласование ее отдельных частей осуществляется
двумя способами: непосредственным планированием хозяйственной
деятельности (установление плановых заданий по объемам производ¬
ства, объемам выделяемых ресурсов, объемам сбыта продукции и
т.д.) и экономическим регулированием на основе планомерного исполь¬
зования ценностных регуляторов и механизмов договорных отношений.
Схемы согласования решений в системе моделей, как правило, имитиру¬
ют важнейшие черты реальных механизмов управления экономической
системой.
Система моделей народного хозяйства включает, как минимум,
четыре основных блока: А - блок моделей верхнего уровня (народно¬
хозяйственные модели и модели отдельных функциональных подсистем
народного хозяйства), В — блок моделей отраслевых систем (многоотра¬
слевых комплексов, отраслей, подотраслей), С - блок региональных
моделей (союзных республик и экономических районов, административ¬
ных территориальных единиц, территориально-производственных комп¬
лексов и т.п.), D — блок моделей предприятий и объединений. Общая
структура системы моделей с основными информационными связями
(’’входами” и’’выходами”) представлена на рис. 14.1.
Каждый блок системы может включать не только модели разных
объектов (например, конкретной отраслевой системы или определенно¬
го района), но и разные модели для одного и того же объекта. Особо
сложную структуру имеет блок А, объединяющий разноаспектные народ¬
нохозяйственные модели (точечные и пространственные, агрегированные
и детализированные, для различных сроков планирования и т.д.) и спе¬
циальные модели функциональных подсистем народнохозяйственного
планирования и прогнозирования (научно-технического прогресса, вос¬
производства населения и трудовых ресурсов, уровня жизни и т.п.).
Блоки и отдельные элементы системы моделей связаны двусторон¬
ними информационными потоками. Здесь можно выделить 6 типов
401
связей: 1) вертикальные производственные связи ABD (народное хозяй¬
ство — многоуровневые отраслевые системы — предприятия и объедине¬
ния) ; 2) вертикальные территориальные связи ACD (народное хозяйст¬
во — многоуровневые региональные системы — предприятия и объеди¬
нения) ; 3) вертикально-горизонтальные связи между отраслевыми
системами (внутри блока В); 4) вертикально-горизонтальные связи
между региональными системами (внутри блока С) ; 5) горизонталь¬
ные связи между отраслевыми и региональными системами ВС (сочета¬
ние отраслевых и территориальных решений); 6) горизонтальные связи
между предприятиями и объединениями (внутри блока Z>).
Практически реализуемая система моделей является ’’открытой”:
она не исчерпывает всех задач планирования (особенно на первых этайах
реализации) и требует внешнего информационного дополнения. Поэтому
каждое ее звено не только связано с другими звеньями системы, но и
имеет дополнительные ’’входы”. В то же время каждое звено системы
может (хотя бы частично) функционировать в автономном режиме, т.е.
иметь самостоятельные ’’выходы”.
Обмен информацией между моделями, входящими в систему, ор¬
ганизуется таким образом, чтобы в результате итеративных пересчетов
найти вариант плана народного хозяйства в укрупненных показателях,
увязанный с проектировками хозяйственных подсистем разного уро¬
вня. Идеалом является построение оптимального сводного плана, пол¬
ностью согласованного с локально-оптимальными планами. Однако этот
идеал может достигаться только приближенно; практически реализуе¬
мая система моделей всегда будет отличаться от теоретических схем
согласования оптимальных решений. Она неизбежно будет включать
не полностью формализованные связи между отдельными моделями,
приближенные алгоритмы согласования. И чем сложнее практически
реализуемая система моделей, тем меньше возможностей для строго¬
го математического согласования решений отдельных моделей, тем
402
существеннее роль неформальных процедур, применяемых в процессе
практического использования системы моделей.
Осуществляемая радикальная реформа управления народным хозяй¬
ством СССР серьезно изменяет требования к моделированию экономиче¬
ских объектов (подсистем) и связей между ними.
Во-первых, изменяются содержание, формы и методы централизо¬
ванного руководства, в том числе планирования на народнохозяйствен¬
ном уровне. Усиление стратегической роли и разнообразие функций
сводного планирования, осуществляемого Госпланом СССР, требуют
создания развитого комплекса моделей народнохозяйственного уровня,
обеспечивающего выработку научно обоснованных рекомендаций по
стратегии социально-экономического развития, повышению сбалансиро¬
ванности экономики, планированию и распределению государственных
заказов, обоснованию контрольных цифр, расчетам важнейших экономи¬
ческих нормативов.
Во-вторых, хозяйственные звенья переводятся на преимущественно
экономические методы управления. Введение в действие Закона СССР
о государственном предприятии (объединении) меняет не только харак¬
тер функционирования основного производственного звена, но и перево¬
дит в основном на хозрасчетные принципы деятельность других звеньев
народного хозяйства (например, административно-территориальных еди¬
ниц). Модернизация созданных и разработка новых моделей подси¬
стем народного хозяйства должны идти по двум главным направле¬
ниям: придание им свойств хозрасчетных объектов и усиление соци¬
альной ориентации (в интересах соответствующих групп населе¬
ния).
В-третьих, перестраиваются формы связей между хозяйственными
звеньями. Сужение сферы административных методов управления
(связей типа ’’приказ — исполнение”), расширение договорных хозяй¬
ственных отношений, переход на оптовую торговлю средствами матери¬
ально-технического назначения, расширение сферы финансово-кредитных
отношений, безусловно, должны быть отражены в построении связей
между элементами системы моделей. Очевидно, что меняется и порядок
предпочтений в отношении типов систем моделей. Усиливается
значение таких версий системного моделирования, в которых согла¬
сование решений и интересов достигается посредством экономических
механизмов.
Разработку и внедрение систем моделей планового управления на¬
родным хозяйством правомерно рассматривать как один из важных
инструментов проводимой реформы. Поэтому сроки создания ча¬
стей и вариантов таких систем необходимо синхронизировать со всем
комплексом мероприятий по отладке хозяйственного механиз¬
ма, разработке прогнозов и планов развития народного хозяй¬
ства.
403
14.3. Основные подходы к построению
систем моделей народного хозяйства
Развитие экономико-математических исследований пока не привело к
созданию теории и методологии планового управления социалисти¬
ческой экономикой на базе какого-либо единого, общепризнанного мо-
дельно-теоретического представления. Продолжаются поиск и апроба¬
ция различных научных подходов и их возможных сочетаний.
Декомпозиционный и композиционный подходы. В теоретических
и экспериментальных работах по системному моделированию народного
хозяйства выделяются два принципиальных подхода, получивших назва¬
ния декомпозиционного и композиционного. Они существенно различа¬
ются по формализации целей развития народного хозяйства и его под¬
систем, отражению роли централизованного управления и хозяйствен¬
ной самостоятельности, описанию механизма взаимодействия подсистем,
применяемому математическому аппарату.
В основе декомпозиционного подхода, как правило,
лежит представление, что народное хозяйство может быть описано
(хотя бы теоретически) в виде глобальной оптимизационной микромо¬
дели, которую можно разбить на ряд моделей подсистем и получить
оптимальный вариант развития народного хозяйства в процессе итератив¬
ного согласования локальных решений.
Выделение подсистем и построение их моделей (множества допусти¬
мых вариантов развития и локальных критериев оптимальности) осуще¬
ствляются одновременно с выбором схемы (алгоритма) согласования
решений моделей подсистем., При этом локальные критерии специаль¬
ным образом выводятся (редуцируются) из глобального критерия опти¬
мальности. Согласование решений моделей подсистем одного уровня ие¬
рархической структуры народного хозяйства осуществляется через
модели подсистем более высокого уровня (в частности, модели ”цент-
ра” в двухуровневой системе), которым придаются координирующие
функции (вертикальное согласование). На верхнем уровне системы
моделей выделяется модель центральной подсистемы, а в качестве целевой
функции используется народнохозяйственный критерий оптимальности.
Математическую основу декомпозиционного подхода составляет
математическое программирование. Согласование решений осуществля¬
ется в итеративном процессе обмена информацией между моделями
низовых и координирующих подсистем. Информация может преобразо¬
вываться при передаче ее между уровнями иерархии: сжиматься при дви¬
жении на верхние уровни и детализироваться при ее движении в обрат¬
ном направлении. Координирующие воздействия состоят в уточнении па¬
раметров критериев оптимальности и условий, формирующих множе¬
ство допустимых планов подсистем.
В процессе согласования решений выделяются два типа информаци¬
онных потоков: 1) натуральные показатели, характеризующие непосред¬
404
ственно материально-вещественные взаимосвязи и ресурсно-технологи¬
ческие возможности подсистем (задания и объемы производства про¬
дукции и услуг, лимиты и потребности в ресурсах общесистемного на¬
значения и т.д.); 2) ценностные показатели (цены, ставки заработной
платы, процент за кредит, оценки дефицитности и эффективности про¬
дукции и ресурсов и т.д.).
Централизованное планирование при декомпозиционном подходе
сохраняет решающую роль. Децентрализуются главным образом обра¬
ботка информации и проведение плановых расчетов. Экономические под¬
системы рассматриваются как обособляемые локальные звенья, но
критерии их развития строятся таким образом, чтобы выбираемые реше¬
ния в наибольшей мере отвечали народнохозяйственному критерию.
По существу здесь нет проблемы согласования глобальных и локальных
интересов, поскольку вменяемые подсистемам критерии не обязательно
отражают их собственные (внутренние) интересы. Итеративные процеду¬
ры, присущие декомпозиционным методам, реализуют не процесс согла¬
сования локальных и народнохозяйственных интересов, а осуществляют
настройку параметров вменяемых локальных критериев на достижение
народнохозяйственных целей.
Система моделей композиционного типа ’’собирается”
из моделей подсистем народного хозяйства. Ее главные отличия от си¬
стемы моделей, построенной на принципе декомпозиции, состоят в сле¬
дующем. Во-первых, локальные критерии оптимальности отражают
внутренние (имманентные) интересы подсистем, а не выводятся из
глобального критерия; во-вторых, эти локальные критерии заранее не
сводятся в глобальный критерий оптимальности. Таким образом, эконо¬
мические подсистемы рассматриваются как объекты, ориентирующиеся
в своей деятельности на собственные интересы, а одной из важнейших
функций централизованного управления является согласование интере¬
сов подсистем, включая интересы центральной подсистемы. Критерий,
выражающий в конечном счете народнохозяйственный оптимум, при
таком подходе может быть получен синтезом локальных критериев
оптимальности при некоторых условиях сочетания интересов подсистем.
Система моделей, построенная в соответствии с композиционным
подходом, состоит из двух основных частей: условий, описывающих
функционирование отдельных подсистем, и координирующих условий,
связывающих эти подсистемы. При этом координирующие условия,
как правило, имитируют существенные аспекты реального экономичес¬
кого механизма (экономические рычаги и методы функционирования).
Следует отметить, что путем изменения правил, регулирующих взаимо¬
отношения между подсистемами (элементов экономического механиз¬
ма), можно влиять на процесс расчетов вариантов развития народного
хозяйства и его подсистем.
Важным классом моделей композиционного типа являются модели
экономического взаимодействия подсистем с локальными критериями
405
оптимальности (модели социально-экономического
взаимодействия). В них народное хозяйство рассматривается
как социально-экономическая система, в которой оптимум достигается
в результате согласования интересов социалистического государства
(выражающего интересы общества как единой системы) и отдельных
хозяйственных подсистем (в том числе и социальных групп) посредством
экономического механизма.
Возможности применения моделей экономического взаимодействия
в настоящее время усиливаются благодаря расширению экономической
самостоятельности объектов, переходу на преимущественно экономичес¬
кие методы управления, в том числе в процессе согласования планов
подсистем, и достижению сбалансированности народного хозяйства.
В рамках композиционного подхода для исследования экономических
механизмов согласования решений все шире используются методы
имитационного моделирования и деловые игры.
Подходы, различающиеся по степени детализации внутренних и
внешних связей. Важной проблемой построения системы моделей являе¬
тся выбор разумной детализации математического опи¬
сания подсистем народного хозяйства и связей между ними. Эта пробле¬
ма присутствует как при декомпозиционном, так и при композиционном
принципах построения системы.
Будем рассматривать условно два крайних случая описания связей:
А — агрегированное, D — детализированное. Одна из
центральных идей многоуровневого планирования и управления народ¬
ным хозяйством состоит в осуществлении взаимоперехода: АА DD,
то есть между макроописанием экономики АА и ее макроописанием
DD (здесь первая компонента описывает степень детализации внутренних
связей подсистем, вторая — внешних связей).
Тип АА.. Модели этого типа описывают народное хозяйство в агреги¬
рованных показателях. Наиболее характерными примерами являются
макроэкономические и межотраслевые модели (см. гл. 6 — 8, 10 — 13),
являющиеся важными инструментами сводного народнохозяйственного
планирования. Однако применяемое в них агрегированное описание
недостаточно для планирования подсистем народного хозяйства (отрас¬
лей, регионов и т.п.) и тем более — его первичных элементов.
Тип DD. Этот тип моделей объединяет два принципиально различаю¬
щихся подхода: построение микромодели народного хозяйства или
’’равномерно детализированной” системы моделей. Как отмечалось
в 14.1, построение микромодели народного хозяйства (’’супермодели”)
практически недостижимо, однако движение в направлении АА DD
имеет определенные причины и, как известно, находило отражение в ис¬
тории планирования социалистической экономики (стремление к более
конкретному и адресному планированию).
Первоначальные проекты системного моделирования также шли по
пути выделения все более мелких экономических единиц, прямой дета-
406
Таблица 14.1
Типы моделей (систем моделей) народного хозяйства
по степени детализации взаимосвязей
— Внешние связи
Внутренние связи''' —
А
D
А
АА
AD
D
DA
DD
лизации взаимосвязей, соотношений и условий протекания экономичес¬
ких процессов, то есть ориентировались на идеал DD. Но их практическая
реализация столкнулась с рядом серьезных проблем методологического,
организационного, информационного характера и потребовала новых
идей1. Возможные подходы к разрешению противоречий между агреги¬
рованными и детализированными описаниями экономических объектов
и связей между ними иллюстрируются в табл. 14.1.
В таблице демонстрируется возможность построения модельных
конструкций народного хозяйства AD и DA, занимающих промежуточ¬
ное положение между макромоделями экономики АА и микромоделями
(детализированными системами моделей) DD.
Основной специализацией системы моделей типа AD является изуче¬
ние межподсистемных взаимосвязей, механизмов их регулирования,
условий согласования локальных и глобальных оптимумов, методов
нахождения согласованных решений. Внутренние условия развития
любой подсистемы учитываются при этом лишь в той мере, в которой
они определяют связь ее ’’входов” и ’’выходов”. Таким образом, систе¬
мы типа AD реализуют кибернетический подход, когда
основным назначением модели объекта (подсистемы) является много¬
кратное преобразование входных параметров в выходные. Другими
словами, модель объекта выступает прежде всего как функция
отклика данного объекта на решения, принимаемые на других уро¬
внях и другими объектами планирования.
В системе моделей, построенной по типу DA, главное внимание
уделяется внутренним условиям развития подсистемы. Но их анализ
осуществляется с учетом внешних взаимосвязей на ’’фоне” развития
народного хозяйства в целом. Такой подход получил наименование
рефлекторного. При его применении в системном моделировании
обычно выделяется некоторая подсистема, которая описывается с необ¬
ходимой степенью детализации внутренних условий ее функционирова¬
ния, а другие подсистемы и их взаимосвязи между собой и с изучаемой
подсистемой представляются агрегированно. Развитие рефлекторного
подхода обусловлено необходимостью изучения отдельных подсистем
1 Подробнее эволюция концепций системного моделирования народного хозяй¬
ства рассматривается в гл. 17.
407
в составе единого народнохозяйственного комплекса (подробнее см.
гл. 17).
Разработка специализированных систем моделей народного хозяйст¬
ва по типам AD и DA не только позволяет решать многие практические
задачи многоуровневого моделирования, но и открывает конструктив¬
ный путь постепенного создания более развитых и детализированных
систем моделей народного хозяйства:
А А -> AD DD; А А ^ DADD.
Схемы согласования решений в системах моделей. Принципы и ме¬
тоды согласования решений между отдельными связываемыми друг с
другом моделями являются важнейшими признаками того или иного
методологического подхода к системному моделированию народного
хозяйства.
В декомпозиционных схемах прямые и обратные связи между под¬
системами различных уровней иерархии диктуются соответствующими
алгоритмами блочного математического программирования. Согласова¬
ние решений подсистем одного уровня происходит не непосредственно
(путем горизонтальных взаимодействий), а через подсистему более вы¬
сокого уровня. Типичный недостаток декомпозиционных систем — не¬
обходимость проведения, как правило, большого числа итераций для
достижения приемлемой степени согласованности решений (см. гл. 15).
Частным случаем декомпозиционного подхода является а п п р о-
ксимационная схема согласования решений различных уров¬
ней. Ее главная особенность состоит в том, что модели нижнего уровня
используются для генерирования достаточно представительного множе¬
ства вариантов развития путем сжатия или аппроксимации решений,
поступающих в модели более высокого уровня.
При композиционном подходе (в частности, в моделях экономичес¬
кого взаимодействия) согласование решений имитирует действие экономи¬
ческих механизмов (например, балансирование спроса и предложения
путем изменения цен); при этом могут сочетаться как вертикальная,
так и горизонтальная координация подсистем. Анализ моделей позволя¬
ет выделять множества сбалансированных вариантов развития народно¬
го хозяйства, улучшающих положение всех подсистем, а также множе¬
ства вариантов решений, где интересы различных подсистем вступают в
противоречия и требуется находить компромиссы.
Главно# особенностью рефлекторного подхода, как было показано
выше, является детализированное описание интересующего объекта и аг¬
регированное — остального народного хозяйства. При нахождении реше¬
ния рефлекторной модели для одного объекта (или одной группы объе¬
ктов) не требуется итеративных согласований; необходимо только
установить сопряжения между ’’входами” и ’’выходами” детализирован¬
ной и агрегированной подсистем народного хозяйства. Гораздо более
408
сложной и мало исследованной проблемой является совмещение
условий и решений нескольких рефлекторных моделей, в
которых детально описываются разные объекты (многоотраслевые
комплексы, регионы и т.п.).
Особым случаем является согласование моделей с одно¬
сторонними связями. Целесообразность использования таких
схем обусловлена тем, что не для всех планово-экономических проблем
необходимо проведение расчетов по полному контуру системы моделей
народного хозяйства. Нередко можно ограничиваться расчетами, учиты¬
вающими только односторонние связи моделей подсистем и объектов.
Это существенно облегчает задачу согласования решений, но вместе
с тем требует тщательного обоснования правомерности такого под¬
хода.
В модельных комплексах типа ’’верх—низ” вначале определяются
значения переменных моделей более высокого уровня иерархии. Затем
решаются задачи нижестоящих уровней при ограничениях на локальные
переменные, определяемые в моделях предыдущего уровня. Например,
в многорегиональных моделях расчет региональных параметров ведется
вслед за переменными национального уровня таким образом, чтобы
их сумма совпадала с соответствующими национальными переметы-
ми. По схеме ’’верх — низ” организован комплекс моделей планирования
(КМП), разработанный в ЦЭМИ АН СССР. В нем все модели распределе¬
ны по пяти иерархическим уровням. Схема расчетов предусматривает
последовательное решение соответствующих задач разных уровней с
активным участием экспертов (плановых работников) в уточнении
первоначальных гипотез о поведении параметров, анализе промежуточ¬
ных результатов, выделении целевых и экзогенных переменных для
следующего этапа расчетов, определении области изменения управля¬
емых параметров в вариантных расчетах и тд.
Другим типичным примером комплекса моделей, организованного
по типу ’’верх — низ”, является взаимосвязанное функционирование
моделей планирования и моделей выполнения плана. Дня разработки
реалистичных вариантов развития экономического объекта недостато¬
чно научиться строить модели планирования. Применяется особый
класс моделей — модели реализации плана, которые опи¬
сывают собственно функционирование планируемого объекта, например
последовательность актов производства, распределения и потребления
продукции, этапы движения населения и формирования трудовых ре¬
сурсов и т.д. Модели реализации плана имеют, как правило, дескриптив¬
ный характер и принадлежат к классу имитационных моделей. Хорошо
учитывая прошлые тенденции и описывая внутренние условия развития
объекта, эти модели требуют внешнего определения целевых установок:
плановых показателей развития, экономических нормативов и т.д.
Такого рода информацию обеспечивают нормативные модели планиро¬
вания.
409
Комплексы моделей, организованные по типу ’’низ — верх”, менее
распространены, хотя существует целый ряд задач планирования, для
которых проведение расчетов по этой схеме оказывается эффективнее
других схем согласования решений. Например, модели нижнего уровня
приспосабливаются для генерирования множества вариантов развития
соответствующих подсистем (идея аппроксимационного подхода), а
на втором этапе эти варианты включаются в модель верхнего уровня.
Примером использования схемы ”низ — верх” является методика оцен¬
ки крупных региональных проектов с использованием модельного ком¬
плекса СИРЕНА (см. гл . 17).
Можно отметить основные методические трудности организации
прикладных расчетов по схеме ”низ — верх”. Первая из них (как и в
случае применения схемы ”верх — низ”) — это установление предельных
масштабов оцениваемых подсистем, которые еще допускают односто¬
ронний тип связей. Вторая трудность состоит в том, что на выбор аль¬
тернативных вариантов развития выделенных подсистем может влиять
регулярная ошибка, обусловленная различием методик прогнозиро¬
вания экзогенных параметров модели верхнего уровня и расчета свод¬
ных вариантов развития подсистемы, полученных из моделей нижнего
уровня.
Особым случаем проблемы согласования решений является совме¬
стное использование разнотипных моделей одного объекта — норматив¬
ных, эконометрических, имитационных и т.п. Эти модели могут разли¬
чаться также акцентами в изучении объекта, привлекаемой информаци¬
ей. Согласование таких моделей не является ’’классическим”; точнее
говорить о необходимости их совместимости, взаимодополняемости,
непротиворечивости. Это достигается взаимным контролем и коррек¬
цией исходных предпосылок, условий моделей, управляющих парамет¬
ров, промежуточных решений.
14.4. Аспекты исследований
по системному моделированию
Системное моделирование народного хозяйства включает все аспекты
экономических исследований и форм их обеспечения.
Теоретические исследования. Постановка проблемы моделирования
народного хозяйства как многоуровневой системы выдвигает ряд сло¬
жных теоретических задач: принципы выделения экономических под¬
систем и механизмы их взаимодействия (в том числе соотношение
централизованного управления и экономической самостоятельности),
согласование народнохозяйственных и локальных интересов и их выраже¬
ние в формализованных критериях оптимальности, методы построения
экономических и социальных регуляторов и т.д. При многоуровневом
моделировании народного хозяйства многие классические результаты
410
математико-экономического анализа оказьюаются недостаточными,
требуют переосмысливания, обобщения, корректировок.
В рамках декомпозиционного подхода главное внимание в теоре¬
тических исследованиях уделяется доказательствам условий, при кото¬
рых сочетание локальных оптимумов дает глобальный оптимум (теоре¬
мы локализации), нахождение регуляторов, помогающих такому выбо¬
ру локально-оптимальных решений, композиция которых давала бы
глобальный оптимальный план (см. гл. 15).
Композиционный подход в системном моделировании, как было
показано выше, открывает более широкие возможности для изучения
роли экономических механизмов и ’’человеческого фактора” в оптима¬
льном функционировании народного хозяйства. Основные теоретичес¬
кие результаты получены при анализе моделей многоцелевой оптимиза¬
ции (с разными участниками) и моделей экономического взаимодей¬
ствия. Среди них можно отметить: определение и характеристика
свойств эффективных решений (оптимум по Парето), которые нельзя
улучшить в интересах какого-либо участника (экономической подсисте¬
мы), не ухудшая положение хотя бы одного другого участника; нахо¬
ждение и анализ состояний (траекторий) экономического равновесия,
в которых при заданных условиях экономических взаимоотношений
уравновешиваются интересы различных участников при соблюдении об¬
щей сбалансированности народного хозяйства; выявление условий эко¬
номической заинтересованности в создании объединений (коалиций)
и особых состояний (ядра, квазиядра и т.п.), когда подсистемам эконо¬
мически невыгодны обособления из общей экономической системы
(см. гл. 16).
В настоящее время эти направления теоретических математико¬
экономических исследований усиливаются благодаря возможностям
машинной имитации концепций хозяйственного механизма. Созданный
экономико-математический инструментарий (различного типа модели,
программное обеспечение, компьютерная техника) позволяют ’’проиг¬
рывать” последствия тех или иных изменений в хозяйственном механиз¬
ме, интенсифицировать поиск более совершенных его модификаций.
Особенно важны модельные исследования ’’смешанных” хозяйствен¬
ных механизмов, не укладывающихся в классические схемы многоуро¬
вневой оптимизации и экономического равновесия, более адекватно
отражающих сочетания централизованного управления и хозяйственной
самостоятельности, административных и экономических рычагов уп¬
равления, организационные структуры и правовые условия.
В теоретических исследованиях на основе моделей прослеживается
стремление к более полному охвату социально-экономических процес¬
сов (а не только производственно-технологических), изучению мотива¬
ционных механизмов воздействия распределительных процессов на
экономическую эффективность производства, взаимоотношений соци¬
альных групп, подходов к решению проблем социальной справедливости.
411
Осуществляется переход к социально-экономическим моделям с обрат¬
ными связями.
Прикладные исследования. Общим свойством прикладных работ
по системному моделированию является проведение расчетов с целью
получения согласованных вариантов развития народного хозяйства и
его подсистем. Выделяются три основные формы (и назначения)
таких исследований: экспериментальные разработки, прогнозы и
предплановые обоснования, расчеты к народнохозяйственному
плану.
Системы (комплексы) моделей являются инструментом интенсив¬
ного изучения тенденций, гипотез, закономерностей экономического
и социального развития. На стадии вычислительных экспериментов
обычно варьируются структура модельного комплекса, условия и пара¬
метры отдельных моделей. Работа с модельным комплексом в инте¬
рактивном режиме позволяет целенаправленно генерировать
информацию о ’’поведении” экономических объектов. Такой режим
работы выдвигает особые требования к оперативной доступности и
’’децентрализованной” реализуемости модельных комплексов. В этом
отношении существенным преимуществом обладает рефлекторный
подход, позволяющий различным научным коллективам параллельно
работать с информацией о ’’всем” народном хозяйстве, но с акцентом
на определенные проблемы.
Прогнозные и предплановые разработки с помощью комплексов
моделей предъявляют более жесткие требования к достоверности ис¬
пользуемой информации и определенности получаемых результатов.
Вместе с тем сохраняется целесообразность построения альтернативных
сценариев развития, проведения многовариантных расчетов, изучения
влияния изменений условий, управляющих переменных и параметров
моделей. На этой стадии прогнозно-плановой деятельности важнейшая
роль отводится Комплексной программе научно-технического прогрес¬
са на 20-летний период. Системное использование экономико-матема¬
тических моделей непосредственно в технологии разработки народно¬
хозяйственных планов осуществляется в рамках создания автоматизи¬
рованной системы плановых расчетов (АСПР) Госплана СССР и Госпла¬
нов союзных республик (см. гл. 17) .
Инструментальные исследования обеспечивают развитие самого эко¬
номико-математического аппарата как для теоретических, так и для
прикладных разработок. Отметим, что речь идет о специальном инстру¬
ментарии для системного моделирования народного хозяйства. Важны¬
ми направлениями этих исследований являются:
развитие сложившихся подходов к построению систем моделей и
поиск новых форм и методов системного описания и решения народно¬
хозяйственных проблем (например, сочетание имитационного и класси¬
ческого математического моделирования, построение экспертных систем
и т.д.);
412
разработка более эффективных алгоритмов согласования решений в
системе моделей;
создание развитого математического обеспечения систем моделей
с учетом прогресса вычислительной техники; главная тенденция заклю¬
чается в формировании ’’дружественного” пользователю сервиса для ра¬
боты с информацией, моделями, результатами расчетов.
В гибко организуемых системах моделей для исследования опреде¬
ленных проблем можно выбирать наиболее эффективные экономико¬
математические средства. Общая методическая схема определяет, какие
модели и в какой последовательности участвуют в расчетах, какие
параметры этих моделей и каким образом корректируются на различных
этапах, как обрабатываются и используются получаемые результаты.
Отдельные компоненты методического, информационного, математи¬
ческого обеспечения системы моделей обрабатываются в эксперимен¬
тальных расчетах.
ГЛАВА 15
МНОГОУРОВНЕВАЯ ОПТИМИЗАЦИЯ
НА ОСНОВЕ ДЕКОМПОЗИЦИОННОГО ПОДХОДА
15. 1. Основные черты
декомпозиционного подхода
Как отмечалось в 14.3, основная предпосылка декомпозиционного
подхода заключается в том, что составление оптимального народно¬
хозяйственного плана может быть описано как процесс итеративного ре¬
шения глобальной оптимизационной задачи (или метамодели),
разбитой на ряд оптимизационных задач подсистем народного хо¬
зяйства.
Метамодель и модели подсистем. В качестве метамодели процесса
оптимизации народного хозяйства будем использовать анализировав¬
шуюся в 2.2 оптимизационную микромодель со скалярной целевой фун¬
кцией, записываемую в форме
f(X)-^> max. (15.1)
Она позволяет определить такой вариант развития народного хозяй¬
ства X* Е Х , называемый оптимальным, при котором
/(А*) = шах/(Л:).
хеж
Рассмотрение народного хозяйства как совокупности его взаимодей¬
ствующих подсистем позволяет конкретизировать структуру множества
X • Допустимые варианты развития народного хозяйства должны удов¬
летворять ограничениям двух типов: глобальным (общим хотя
бы для нескольких подсистем) и локальным (относящимся
только к каждой подсистеме в отдельности). Пусть в народном хозяй¬
стве выделено т подсистем и х^ — многокомпонентный вектор состояния
к-й подсистемы. Тогда допустимое состояние всей системы описывает¬
ся композицией локальных векторов X = (х\, ..., хт). Метамодель
народного хозяйства может быть записана в виде
414
/(*j. •• •. *«,)—► max; (15.2)
g (Xi, xm) < 0; (15.3)
**€£*• (15.4)
Она имеет блочную структуру. Ограничения (15.3) являются гло¬
бальными, (15.4) — локальными.
Представления о метамодели (15.1) и ее конкретизации (15.2) —
(15.4) позволяют сформулировать модель выбора реше¬
ний отдельных подсистем. В общем случае такая модель
строится с учетом внешних связей рассматриваемой подсистемы:
fk(xki ck) ^max> (15.5)
Xk€%k(Qk)'
Здесь (qjc ) — множество допустимых планов к-й подсистемы, зави¬
сящее от внешних связей. Для производственных подсистем множество
допустимых планов определяется в основном ресурсно-технологическими
условиями, а вектор qк представляет собой производственные задания
(заказы), объемы выделенных ресурсов и т.д. Локальный критерий
оптимальности fk (jc&, ск) для производственной подсистемы выражает
результаты хозяйственной деятельности в деньгах. Вектор ск может оз¬
начать меняющиеся экономические нормативы (цены, ставки кредита,
нормативы фиксированных платежей и т.д.). Локальный критерий оп¬
ределенным образом выводится из глобального критерия оптималь¬
ности.
Вектор называется оптимальным планом к-и подсис¬
темы, если
fk (4* сп)= шах fk (xk, ck)
хкеЧ(Ч)
при заданных qк и с£. Композиция локально-оптимальных планов под¬
систем при произвольных параметрах внешних связей может не только
не дать оптимального плана системы в целом, но и не быть допустимой
по общесистемным условиям. Согласование планов подсистем и постро¬
ение оптимального народнохозяйственного плана осуществляется по¬
средством корректировки условий модели (15.5): ограничений (вели¬
чин qfc) и локальных критериев (величин ск). При этом используются
три основных метода координации решений: лимитный, ценностный,
лимитно-ценностный.
При использовании лимитных методов согласование
решений происходит посредством корректировок величин q^. В подси¬
стемах вырабатываются показатели эффективности использования
415
общесистемных ресурсов. Их сравнение происходит в координирующей
задаче. В результате анализа ресурсы могут быть перераспреде¬
лены в пользу подсистемы с большей эффективностью их испо¬
льзования.
При использовании ценностных методов согласование
решений подсистем достигается регулированием ценностных показателей
.cfc, через которое учитывается меняющаяся дефицитность общесистем¬
ных ресурсов. По сравнению с лимитным методом направления инфор¬
мационных потоков противоположны. Из локальных задач в координи¬
рующую задачу поступают обобщенные натурально-технологические
характеристики оптимальных планов подсистем. В координирующей
задаче композиции локально-оптимальных планов оцениваются с то¬
чки зрения нагрузки на общесистемные ресурсы и вырабатываются
показатели дефицитности ресурсов общего назначения, которые затем
используются при уточнении параметров локальных задач.
В смешанных методах (лимитно-ценностных) для коор¬
динации решений используются принципы натурального (уточнение
qk) и ценностного (уточнение cfc) регулирования.
Условия согласования народнохозяйственного и локального опти-
мумов. В общем случае проблема согласования решений в системе
моделей понимается как проблема согласования локальных оптиму-
мов, получаемых при решении отдельных задач подсистем, и глобаль¬
ного народнохозяйственного оптимума. Тип моделей подсистем опреде¬
ляет процедуру согласования их решений, и, наоборот, выбранная схе¬
ма согласования локальных решений влияет на структуру моделей
подсистем, получаемых декомпозицией исходной модели.
При использовании лимитных методов декомпозиции для каждой
подсистемы строится задача вида
!Лч) — тах=
£*(**)<?*• <15-6)
Xh €
Здесь — множество допустимых планов к-и подсистемы, определен¬
ных внутренними условиями развития подсистемы (не зависящих от
параметров внешних связей) ; условия gfc (xfc) описывают в явном
виде зависимость планов подсистем от внешних условий. Очевидно, что
Kk (Sk) = {xk^Xlc -gk (хк) <Як}■
В схемах вертикальной координации (с использованием задачи
’’центра”) согласование решений локальных задач (15.6) осуществляет¬
ся путем корректировки параметров qjc. Целью процесса координации
является определение таких значений qfc, которые позволяли бы получить
оптимальные планы подсистем, допустимые по общесистемным услови¬
ям и максимизирующие целевую функцию / (X).
416
Народнохозяйственная модель, декомпозицией которой получены
модели подсистем (15.6), имеет следующий вид:
2 fk(xk) max;
т
2
Л= 1
m
V / (15-7)
^ gk(xk)^Qy
k= 1
Легко видеть, что модель (15.7) является частным случаем метамоде¬
ли (15.2) в предположении сепарабельности функций/ (х)
и#(*)-
Пусть Xfc Vfc — решение локальной задачи (15.6) для к-и подсистемы
и двойственной к ней; X* = (xf, •••,*^2) — решение народнохозяйствен¬
ной задачи (15.7), v* — вектор оптимальных оценок общесистемных
ограничений.
Основные утверждения о соотношении решений задач (15.6) и
(15.7) состоят в следующем.
1. Если в локальных задачах (15.6) определить вектор внешних
связей = qk (xj£), то композиция их локально-оптимальных планов
Х° = (#i, ..., х^) является одним из оптимальных решений метамо¬
дели (15.7).
2. Предположим, что решения локальных задач (15.6) с параметра¬
ми
виям:
а) при всех к = 1, ..., т векторы оптимальных оценок совпадают,
т.е. Vfc = v* = (vf, ..., v*), где п — число общесистемных ограничений
задачи (3.7);
б) при выполнении условия (а), если какая-либо оценка vf> О,
т 1
ТОИД !«# = «*•
Тогда композиция локально-оптимальных планов Х° = (*?, ...,
х^) составляет оптимальный план метамодели (15.7).
Доказательство утверждений достаточно простое и основывается на
сопоставлении свойств функций Лагранжа локальных и глобальных
задач (см., например, [2. С. 167 — 180] ).
При использовании ценностных методов декомпозиции задача
для каждой подсистемы принимает вид
(168)
1/2 14 Зак. 2414 417
fit
внешних связей qfc такие, что 2 qj£ < q удовлетворяют двум у СЛО-
им- к в1
Она включает только локальные ограничения, а критерий оптимальности
выводится определенным способом из глобального критерия. Функция
fk(xk, ск) аккумулирует информацию об общесистемных ограничениях
(в частности, учитывает затраты общих ресурсов). Локальным критерием
производственных систем может быть максимизация прибыли или дру¬
гого показателя хозяйственной деятельности подсистемы в денежном
выражении (разности между суммарным хозяйственным результатом
и суммарными затратами). Вектор содержит ценностные показатели,
устанавливаемые ’’центром”.
При использовании народнохозяйственной модели типа (15.7)
локальный критерий (xfa cfc) в модели к-й подсистемы, обеспечива¬
ющей согласование локальных и глобального оптимумов, имеет вид
fk(xk> ck) = fk(xk) ck£k(xk)• (15.9)
Действительно, при выполнении условий теоремы Куна — Таккера
можно построить задачу ’’почти безусловного” экстремума
т т
F(x)= 2 max,
k= i k=i (15.10)
Xfr £k=\, • • •»
которая распадается на ряд подзадач
/*(**)—•bgk(*k)-~ max,
Если в локальной задаче подсистемы (15.8) с критерием (15.9)
определить параметры ск равными оптимальному значению вектора
оценок задачи (15.10), то, во-первых, к-я компонента оптимального
народнохозяйственного плана X* = (*f, х%, ...,**,) является оптима¬
льным решением локальной задачи; во-вторых, композиция локально¬
оптимальных планов Х° = (*?, ..., Хт) составляет оптимальный план
метамодели (15.7).
Основной вьюод состоит в том, что теоретически возможно постро¬
ить такие локальные критерии, которые содержат необходимую и доста¬
точную информацию для того, чтобы каждая подсистема, максимизируя
этот критерий и учитывая только собственные ограничения, могла бы
получить план являющийся частью народнохозяйственного оптима¬
льного плана. Это означает, что оптимальный народнохозяйственный
план можно построить, указывая подсистемам только показатели типа
цен, а в остальном предоставляя им полную свободу в выборе плановых
решений. Однако из математического анализа данного вопроса следует,
418
что такая возможность осуществима, когда модели подсистемы (15.8)
являются только такими задачами выпуклого программирования, в
которых либо множества допустимых планов подсистем строго вы¬
пуклы, либо целевые функции подсистем строго вогнуты. Уже для слу¬
чая линейных задач такая возможность неосуществима, т.е. централи¬
зованное установление только показателей типа цен (с&) недостаточно
для согласования локальных оптимумов с глобальным; требуется
более сильное вмешательство ’’центра” в процесс построения локаль¬
ных планов (см. [2. Гл. IV] ).
Примеры декомпозиционного подхода в экономическом анализе.
Пример 1. При анализе общей модели оптимального планирования
В.В.Новожилов ввел понятие дифференциальных затрат,
включающих наряду с прямыми затратами по определенному направле¬
нию также затраты обратной связи, учитывающие дополнительные за¬
траты в народном хозяйстве в связи с отвлечением ряда дефицитных
народнохозяйственных ресурсов по оцениваемому направлению1.
Рассмотрим задачу распределения ограниченных капиталовложений
между заданными направлениями их использования i = 1, ..., т (напри¬
мер, объектами строительства). По каждому направлению существует
зависимость уровня текущих затрат от величины выделяемых вложе¬
ний С/ = fi (К{). Обычно предполагается, что // (Kj) < 0, // (К{) > 0.
Задача состоит в распределении капиталовложений между направлени¬
ями их использования, обеспечивающими минимум суммарных теку¬
щих затрат
т т
С— 2 I min,
i= I i= 1
(15.11)
m
2 Kt = K.
i=i
Легко видеть, что оптимальное распределение К* = (Кf, ..., К^)
может быть получено как композиция изолированных локально-опти-
мальных решений К* осуществляемых на основе локальных критериев
£, + £„•/Ci-^min, (15.12)
где величина норматива Ен задается оптимальной оценкой X* ограниче¬
ния по капитальным вложениям в задаче (15.12) (Ен = — X*) и харак¬
теризует предельную экономию суммарных текущих затрат при испо¬
льзовании капиталовложений.
1 Новожилов В.В. Проблемы измерения затрат и результатов. М.: Экономика,
1967. Гл. 5.
1/2 14* 419
Если исходная задача (15.11) охватывает все направления капитало¬
вложений и К означает общую величину капиталовложений по народ¬
ному хозяйству, то Ен интерпретируется как народнохозяйственный
норматив эффективности капиталовложений, а локальные критерии
(15.12) — как приведенные затраты на создание и функционирование
объектов капиталовложений. Задание норматива эффективности Ен
на оптимальном уровне - X* и использование показателя приведен¬
ных затрат позволяют децентрализовать процесс составления оптималь¬
ного плана распределения капиталовложений и обеспечить совмести¬
мость локальных и народнохозяйственных оптимумов.
Пример 2. Анализируя задачу оптимального распределения посев¬
ных площадей между различными культурами, JI.В.Канторович по¬
казал возможность применения рентных оценок для нахождения оп¬
тимального решения1.
Для случая монокультурного хозяйства такие оценки должны удо¬
влетворять условию
Ui = wQ{—с{ (Q,) — шах, (15.13)
где с\ (Qf) — зависимость затрат на z-м участке от объема производства
Qi (предполагается возрастающей с падающей эффективностью затрат) ;
со — норматив предельных затрат на заданный объем сельскохозяйст¬
венной продукции по всем земельным участкам.
Оптимизационная задача, порождающая локальные критерии
(15.13), имеет вид 1
т
с = 2 с{ (Q{) —► min;
{= 1
I Q; = Q. (15.14)
1 = 1
Ъс
Норматив со* задается оптимальной оценкой X* = чл ограничения
по производству сельскохозяйственной продукции.
Линейный аналог задачи (15.14) еще яснее выявляет смысл локаль¬
ного критерия (15.13) как рентной оценки земельного участка.
m
*=1
(15.15)
S qfii^Q",
i= i
0<xf<S,., t= 1- .... я»-
1 Канторович Л.В. Экономический расчет наилучшего использования ресурсов.
М.: Изд-во АН СССР, 1959. С. 115 - 129.
420
Здесь х(, Sj — размеры, используемые и возможные для использования
участков земель /-го качества; Cjt qj — затраты и урожайность в расчете на
1 га.
Пусть земельные участки занумерованы в порядке возрастания
удельных затрат —— . В оптимальном плане задачи (15.15) в обработку
включаются участки, первые в ряду восходящих удельных затрат
qi 42 q/o
причем все участки, кроме ’’замыкающего”, используются полностью,
а посевные площади замыкающего участка (с номером /0) выбираются
лишь в размере, обеспечивающем сбор урожая с него в объеме, дополня¬
ющим объемы производства на предшествующих участках до потреб¬
ности (0. Индивидуальные затраты худшего участка определяют норма-
тив замыкающих затрат со* = —г- , а рентные оценки используемых в
41 о
оптимальном плане участков задаются разницей замыкающих и инди-
. CiQ Ci ч л
видуальных затрат щ = u>*qi — ci = (— “7 qi, i = 1, —, го-
HIq hi
15.2. Итеративные методы построения
детализированного оптимального плана
Суть итеративных методов согласования решений в системе моделей
состоит в проведении однотипных повторяемых этапов расчетов (итера¬
ций) , на каждом из которых изменяется лишь часть информации, необ¬
ходимой для построения оптимального народнохозяйственного плана.
В типовой модели подсистемы (15.5) такими показателями являются
входные параметры zfc = (ск, q^), в совокупности задающие вектор ин¬
формации на очередной (/-й) итерации z = (4,2^).
Вектор параметров согласования решений на следующей итерации
z вычисляется по результатам решений моделей подсистем к =
= 1, ..., т, которые, в свою очередь, определяются значениями входных
показателей z . Следовательно, между z и z существует зависимость
zl+1 = P(zt),
в соответствии с которой может быть определена последовательность
промежуточных входных показателей z . Предельный вектор этой по¬
следовательности z*, если он существует, принадлежит множеству непо¬
движных точек отображения Р (z* = Р (z*)) и определяет стационарное
решение задачи согласования. Действительно, очередное уточнение пара¬
14 Зак. 2414 421
метров согласования z* P(z*) снова возвращает к z*f что, в свою
очередь, обусловливает повторение решений задач подсистем.
В условиях устойчивых задач подсистем (т.е. когда малым измене¬
ниям входных данных соответствуют малые изменения их решений)
используются приближенные оценки окончания процесса согласования
IIz — z 11 < 6. Процесс заканчивается, если на очередной итерации
изменения параметров согласования не превосходят заданной точности
расчетов е.
Для того чтобы построить итеративный метод согласования решений,
необходимо: 1) определить оператор Р, т.е. алгоритм итеративного пере¬
счета параметров согласования; 2) доказать сходимость последователь¬
ности промежуточных решений, в частности последовательности 1 z j;
3) доказать оптимальность стационарной точки процесса. Наиболее
трудной частью построения метода обычно является доказательство его
сходимости.
Типичные утверждения формулируются следующим образом: если итеративный
процесс сходится, то он сходится к согласованному решению. В случае когда
выбранный алгоритм согласования, не обеспечивает сходимости последователь¬
ности параметров согласования | zl } , обычно переходят к модифицируемой по¬
следовательности {z1)с членами, определяемыми соотношениями zl + 1 = (1 +
+ apl + 1, где компоненты вектора z* + 1 задают очередное приближение для вход¬
ных параметров задач подсистем. Сходимость последовательности z1 обеспечивает¬
ся надлежащим выбором значений параметра управления процессом согласования
Of
Основные математические результаты системного моделирования
на основе принципа декомпозиции получены для задач блочного
программирования, к которым относятся модели (15.2) —
(15.4) и (15.7). В 15.1 уже рассматривались свойства лимитных и ценно¬
стных методов блочного программирования. Более подробное их изло¬
жение дается в ВСМ, с. 69 — 76.
Достоинствами лимитных методов являются естественная структу¬
ризация координирующей и локальных задач, экономическая интерпре¬
тируемость процесса согласования решений. Вместе с тем эти методы
имеют серьезные недостатки. Задачи подсистем сохраняют размерность
(по ограничениям) исходной метамодели. Акцент делается на прямое
регулирование взаимоотношений между подсистемами, что предполага
ет директивный характер управления.
Для линейных моделей алгоритм оптимального распределения лими
тов впервые был предложен Я.Корнай и Т.Липтаком (см. ВСМ, с. 70 — 71)
Вследствие линейности затрудняется проверка оптимальности распреде
ления общих ресурсов между подсистемами, поскольку стационарная
точка процесса согласования решений подсистем характеризуется неедин
ственностью двойственных оценок хотя бы для одной подсистемы
Последнее затрудняет и содержательную интерпретацию этих оценок как
показателей эффективности использования общесистемных ресурсов.
422
Среди ценностных методов согласования решений наиболее изве¬
стен алгоритм Данцига — Вульфа для линейных моделей
(см. ВСМ, с. 73 — 75). Основные особенности этого алгоритма состоят
в следующем.
Оптимальный план подсистемы, соответствующий глобальному
оптимуму, получается как композиция локально-оптимальных планов,
рассчитанных при разных векторах ценностных показателей. По этой
причине данный алгоритм не является примером ценностного подхода
к согласованию в чистом виде. Последнее возможно при более сильных
требованиях к структуре исходной задачи (строгая выпуклость мно¬
жества производственных возможностей или строгая вогнутость це¬
левых функций подсистем). Итеративный процесс является конечным,
что объясняется конечным числом выделенных подсистем и структурой
допустимых множеств локальных задач.
В стационарной точке процесса поиска глобального оптимума наблю¬
дается неединственность оптимального плана функционирования хотя
бы у одной подсистемы. Это означает, что окончательный выбор планов
функционирования подсистем требует дополнения механизма исполь¬
зования ценностных показателей другими соображениями, позволяющи¬
ми совместить локальные оптимумы с глобальными.
Рассмотренные примеры декомпозиционных алгоритмов относятся к методам
вертикальной координации решений моделей подсистем. В алгоритмах
гори зонтальной координации модель ’’центра” необязательна. Увязка
решений локальных подсистем может осуществляться прямым обменом корректи¬
рующей информацией между подсистемами одного уровня. Каждая подсистема
предъявляет смежной подсистеме заявку на ее продукцию вместе с оценкой эффе¬
ктивности использования этой продукции и в свою очередь получает от нее объе¬
мы предполагаемых поставок и затраты на их производство.
Общая схема разложения задачи математического программирования на отдель¬
ные блоки и смешанный тип согласования локальных задач предложены Е.Г.Голъ-
штейном. На каждом шаге локальной задачи уточняются параметры целевой функ¬
ции и векторы ограничений и используются прогнозные значения переменных блоков
и расчетных оценок. Функции ’’центра” состоят в последовательном уточнении
управляющих параметров локальных задач на основе простых рекуррентных соотно¬
шений. Для всякой разрешимой исходной задачи метод гарантированно сходится.
15.3. Построение агрегированного
народнохозяйственного плана,
согласованного с детализированными
локально-оптимальными планами
В рассмотренных выше постановках задачи согласования плановых
решений для верхнего и нижнего уровней планирования степень детали¬
зации плановых показателей остается неизменной, т.е. количество основ¬
ных переменных сохраняется. Для практической реализации гораздо
более доступен другой подход, когда при переходе с нижних на верхние
уровни системы осуществляется последовательное Сжатие информации
14* 423
(уменьшается и число ограничений, и число переменных). При этом свод¬
ный народнохозяйственный план разрабатывается только в агрегирован¬
ных (укрупненных) показателях, а балансировка детализированных
показателей должна достигаться в процессе горизонтального взаимодей¬
ствия подсистем (например, путем хозяйственных договоров между
производственными, снабженческими, сбытовыми, торговыми организа¬
циями). Современная перестройка системы планирования народного
хозяйства в СССР реализует именно такой принципиальный подход.
Пусть X — агрегированный вариант развития народного хозяйства,
Ш — множество всех допустимых агрегированных вариантов (X £
еХ), / (X) — агрегированный народнохозяйственный критерий опти¬
мальности.
Множество получается в результате агрегирования детализирован¬
ных условий развития народного хозяйства. Например, агрегированные
нормативы расхода ресурсов являются средневзвешенными величинами
и зависят от структуры выпуска продукции (’’весов” ее отдельных ви¬
дов), объединяемой в один агрегат; агрегированные производственные
мощности есть взвешенные суммы мощностей по конкретным видам
продукции, т^. также зависят от структуры выпуска и т.п. Поэтому
множество К определенным образом зависит от детализированных
пропорций народного хозяйства X— —*Хт) •
Общая модель оптимизации народнохозяйственного плана в агреги¬
рованных показателях (оптимизационная модель верхнего уровня)
может быть записана в следующем виде:
f(X) max;
XeX(xlt ..., хт).
(15.16)
Построение сводного (агрегированного) народнохозяйственного
плана не исчерпывает, однако, всей проблематики народнохозяйственно¬
го планирования. Для каждой подсистемы должен разрабатываться
более детализированный план. Разработка планов подсистем может
осуществляться на основе локально-оптимизационной модели (15.5).
Запишем эту модель в несколько ином виде:
fk(xk» ck)—*mах;
(15.17)
Як)'
Выражение (X ,qk) означает, что множество допустимых планов к-й
подсистемы зависит от заданий по сводному народнохозяйственному
плану (вектор X) и горизонтальных связей между подсистемами (век¬
тор qk).
Имея варианты развития всех подсистем (векторы xi, хт),
можно путем агрегирования получить сводный вариант по народному
424
хозяйству (вектор jf). Оператор агрегирования планов подсистем,
сводящих детализированные показатели в показатели сводного народ¬
нохозяйственного плана (например, объемы выпуска различных видов
станков сводятся в общий объем валовой продукции станкостроитель¬
ной промышленности и т.п.), обозначим G (хх,..., хщ) •
Сформулируем теперь понятие согласованных решений
(планов). Сводный народнохозяйственный план, полученный на основе
модели (15.16), будем называть согласованным с планом подсистем,
рассчитанным по моделям (15.17), если выполняются два условия.
Первое условие заключается в том, что ’’входы” и ’’выходы” сво¬
дного и локального планов должны совпадать: множество допустимых
сводных планов X (Х\,...9хт) учитывает локально-одтимальные планы
хк ~ х%\ множества допустимых планов подсистем^/? (X , qfc) учитыва¬
ют показатели сводного оптимального плана (X = Х°). Второе условие
согласования выражается в том, что при агрегировании локально-опти¬
мальных планов (jc 1, ..., x%i) должен получаться вариант,^совпадающий
с оптимальным сводным планом X 0, т.е. G (х?,..., х%д = X 0.
Сформулированные требования к согласованию сводных и локаль¬
ных планов являются довольно жесткими; добиться их точного выполне¬
ния — задача трудная. Поэтому при реализации изложенных принципов
в практической плановой работе необходимые условия согласования
могут выступать в более ослабленном виде (например, согласование
в заданных интервалах точности или только по важнейшим показате¬
лям и т.д.).
Математические схемы согласования агрегированных и детализи¬
рованных планов рассматриваются в 15.4, 15.5.
15.4. Итеративное агрегирование
Принципиальным отличием методов итеративного агрегирования от
других декомпозиционных подходов является наличие операто¬
ров агрегирования и дезагрегирования ин¬
формационных потоков между задачами разных уровней. Каждый
конкретный метод агрегирования характеризуется определенными
правилами перехода от исходных показателей к агрегированным и нао¬
борот. Простейшим правилом агрегирования является суммирование от¬
дельных групп исходных (детализированных) показателей. Часто ис¬
пользуются также взвешенные суммы (например, при переходе от нату¬
ральных к стоимостным показателям при фиксированных ценах) или
средние величины.
Координирующая задача, получаемая посредством агрегирования,
содержит меньшее число переменных, чем исходная. После нахождения
решения координирующей задачи и его дезагрегации по заданным прави¬
лам строится решение (точное или приближенное) исходной задачи
(метамодели).
425
Рассмотрим типичную постановку задачи согласования решений
подсистем с использованием методов итеративного агрегирования.
Пусть исходная задача имеет вид:
т
k-1
2 i= 1 я; (15Л8)
Л=1
xk^0, k = 1, . . ., m.
Здесь cfc, xfc — векторы размерности тк\ bi — вектор размерности
щ\ Aik — матрица размерности щ х тк.
Символами Mfc и обозначим множества индексов компонент
соответствующих векторов. Обозначим через Л правый оператор аг¬
регирования (агрегирование по столбцам), Г - левый оператор агреги¬
рования (агрегирование по строкам) задачи (15.18).
Операторы Л и Г являются в данном случае матрицами размерности
Б тк • К иЬ- 2 щ, где параметры К и L задают размерность агреги-
к — 1 / = 1
рованнои задачи.
Внутренняя структура операторов Л и Г зависит от типа объединения
детализированных способов и условий в агрегированную номенклатуру.
Для упрощения последующих рассуждений будем предполагать, что
матрицы Aik задачи (15.18) агрегируются в число (матрицы размерно¬
сти 1 х 1). В этом случае агрегированная задача имеет размерность
п х т, каждая к-я группа способов представима в ней одним обобщен¬
ным способом, каждая i-я группа условий агрегируется в одно ограни¬
чение.
С использованием операторов агрегирования Л и Г исходная задача
(15.18) ’’свертывается” в задачу меньшей размерности следующего
вида:
т _
2 ckyk шах;
к=\
2 Амь^Ь,, i=\,...,n; (15.19)
6= 1
У„ > о, Л = 1т.
Параметры с = (?i, ....с^), b = фх> ..., Ьп), А= {Aik), i =М, 2,
к = 1, ..., т рассчитываются следующим образом: с = с А, Ь= ГЬ, А —
= ГА А, где с, Ъу А — векторы коэффициентов целевой функции, ограни¬
чений и матрица задачи (15.18).
Между решениями задачи (15.18) и ее агрегированной версией
(15.19) существует тесная взаимосвязь.
426
1. Пусть параметры операторов агрегирования Л = (\$к) и Г =
= (тп) определяются решением задачи (15.18) — х£ и двойственной
к ней - uf. \sk = xsk, S е Mfc; к = 1, m, yrj = re Nj; i = 1,n.
Тогда оптимальные решения агрегированных прямой и двойственной к
ней задач v*}) могут принимать значения 1 или 0. При этом, если
векторы Xfc и® имеют хотя бы па одной ненулевой компоненте, то
соответствующие^ = 1, 1.
2. Если операторы агрегирования определяются через нормирован¬
ные решения исходной задачи (15.18) и двойственной к ней
^sk — Xskj 2 k=l, ..., tn9
ls€Mk
yri = u°r([ I u%; r^Nf, i= 1, .... n,
I re Ni
то справедливы следующие утверждения:
а) векторы у° = (у?9 • • */m)> = с компонентами
у% = Б Xsk>vi= 2 игь к= 1,т, /= 1,..., и являются решениями
агрегированной задачи (Г5.19) и двойственной к ней;
б) если у* = (у{, у*тл Uj, ип) - прямое и двойственное
решения агрегированной задачи (15.19), то векторы х%= (xfk, ...,
u*=z(ufi, ..., w^7), A: = 1, ..., m, i = 1, ..., и с компонентами, полу¬
ченными дезагрегацией решения у*, v* х*= Ау*, и* = v*r или
x*sk = Wk 5 G%' *=!,■••, m; u*n = vf%, r G7VZ, i = 1,. . ., n
являются решениями исходной задачи (15.18) и двойственной к ней.
Рассмотрим в качестве примера исходную задачу (15.16) размерности 2x2:
*1^0, х2^0;
anXl+aliX2<bu (15-20)
а21х1^~а22х2 ^
С\Х\^‘С2Х2—* шах.
С помощью операторов агрегирования по столбцам Л= (Хь Х2) и по строкам
Г= (71, У2) легко построить агрегированную задачу размерности 1x1:
0;
ау<Ь\ (15.21)
су —^ шах,
ГДе b = “Ь У2^2* С == ^1^1 + ^2^2»
а — YiOnXi + 71^12^2 Н” Y2fl2i^i + 72^22^2 •
427
Пусть л:0 — (X?, х2),и° “ ки1>ли2) ~ оптимальные решения задачи (15.20) к
^ойственной к ней и Л = (xv х2), Г° = (и®, и\). Тогда из оптимальности х°,
и и определения параметров агрегированной задачи (15.21) следует, что
с = сЛ° = сх° = и°Ь = Г°Ь = Ь\
(15.22)
Ъ = Г°6 = и*Ъ = и°Ах° = г° • Л -Л° * а.
Из соотношений (15.22) следует, что оптимальные решения агрегированной за¬
дачи и двойственной к ней равны 1. о тЧ)
Пусть компоненты операторов агрегирования Л , определяются нормиро¬
ванными оптимальными двойственными планами:
= Л=1, 2;
у? = + i = 1, 2.
Тогда векторы у*=х\+xl и = ul + ul оптимальны в агрегированной задаче
(15.22) и двойственной к ней.
Действительно, допустимость очевидна:
- и°-Ах°-у° __ u°b _nQ<>_r.
^ («* + «!) «1 + «4
Л- v°u*Ax° _ сх° ао__~
vа~(u!+ul)(xl+xl)-4+х2~с ~с
“ о _ О О» 0L
и су —сх =и Ъ = v Ъ.
Если решение агрегированной задачи существует, то оно равно у* = b/а. С другой
стороны, согласно утверждению 2а, у0 = х? + х2 - также решение (15.21). Сле-
^15^0) ЬН°5 У —у*= Ъ[а и х* = А у* = А у0 = х° допустимы в исходной задаче
Отмеченные соотношения между решениями исходной задачи и ее
агрегированного аналога дают возможность построить процесс согла¬
сования решений. Как и в других декомпозиционных схемах, исходная
задача (15.18) разбивается на локальные задачи подсистем и координи¬
рующую задачу. Последняя обычно представляет агрегированный аналог
(уменьшенную копию) исходной задачи. Композиция локально-опти¬
мальных планов подсистем, полученных на очередной итерации, задает
очередное приближенное решение задачи (15.18). По соотношению
между решениями агрегированной задачи yfa ^ и локальных задач х^9
ifl точнее, по разнице
шах
\Ук— 2 4k
, maxi
I 2 Ufi I
к
I
* 1
I T*Ni 1
можно судить о степени близости промежуточных решений к глобально¬
му оптимуму.
Если точность приближения не достигнута, то дезагрегацией реше¬
ния координирующей задачи (15.19) можно получить рекомендуемые
верхним уровнем планы х^ и ценностные показатели и = Jrv в
428
детализированной номенклатуре, которые используются для уточнения
параметров локальных задач для следующего этапа расчетов. По реше¬
нию задач подсистем на каждой итерации уточняются компоненты опе¬
раторов агрегирования Л и Г.
Таким образом, операторы агрегирования Л и Г не только преобра¬
зуют информационные потоки (сжимая или развертывая состав входной
информации), но и определяют направления итеративных расчетов.
Приближение промежуточных решений к глобальному оптимуму (реше¬
нию исходной задачи (15.18))эквивалентно приближению промежуточ¬
ных операторов агрегирования Л^, к операторам ’’оптимальной струк¬
туры” А°, Г . Дезагрегацией решения соответствующей сводной задачи
(15.19) можно получить детализированное решение исходной задачи
(15.18).
Для дальнейших рассуждений удобнее рассматривать операторы
преобразования информации Л и Г в виде векторов X = (Xi, Х^и
У = (Ть Уп)> гДе ит/ — параметры сжатия fc-й группы технологи¬
ческих способов и /-й группы условий задачи (15.18) в агрегированные
к-й способ и z-e ограничение.
Пусть Xfc = (Xifc, Xmkk)> li = (Уцу ущг) — нормированные
веса агрегирования:
h>°>V(>0, 2 kti=l, 2 yr,= 1, /г= 1, ..m; t= 1, ..я.
sqMk reN.
Тогда агрегированные показатели строятся следующим образом:
= 6,. = vА. = *'= 1, ft. (15.23)
Агрегированная задача имеет вид:
т
2 --max;
k~\
2а1Ф<ьл (и-ЭД
yk ^О, k— К .. т-
Пусть Л — множество весов агрегирования, при которых задача
(15.24) разрешима, у = (ух, ..., ут), v = (vx,..., vm) — решение агреги¬
рованной задачи и двойственной к ней, F (X, 7) - значение целевой
функции задачи (15.23), (15.24) в оптимальном решении у. Справедли¬
во следующее утверждение.
Пусть х° = (хг, *772), и° = (w?> ип) - решение исходной пря¬
мой задачи (15.18) и двойственной к ней, Х°, у0 - отвечающие им веса
агрегирования
429
Kk=x?ski 2 •***’ k= 1 m-
I seMu
v%=u°ri j 2 r==]’ ■ • •’n-
Тогда векторы X°, 70 задают седловую точку функции F (X, 7) на мно¬
жестве А, т.е. для всех (X, 7) G Д
F(K y°)<F(l\ y°)<:F(X\ у). (15.25)
Свойство оптимальных весов агрегирования позволяет охарак¬
теризовать направление итеративных расчетов. Переход от (/ - 1)-й
итерации к итерации / должен сопровождаться уменьшением функци¬
онала по переменным у и увеличением его по переменным X. Оптималь¬
ные планы двойственных агрегированных задач на итерации (7 — 1),
т.е. * и ^выбираются таким образом, чтобы способы двойствен¬
ных задач, оцененные в этих показателях, были в лучшем случае ”безу-
быточны”:
i = 1
m
tfr1 2 Mk1^1^ 0.
k=i
Опираясь на свойства симплекс-метода решения задач линейного
программирования, можно утверждать, что на итерации I функционал
F (XZ, -/) увеличится, если веса агрегирования у^ будут выбраны
так, что ’’новый” к-й агрегированный способ >
рассчитанный по формулам (15.23), будет эффективным в оценках
(/ — 1)-й итерации:
п
(15.26)
Аналогично, для того чтобы уменьшить функционал F (X, у) по
переменным у, необходимо на шаге I выбрать такие веса (Х^, т), чтобы
по некоторым агрегированным ограничениям план шага (/ — 1) был
невыполним (’’сверхрентабельность” в двойственной задаче, рассматри¬
ваемой в качестве прямой):
_ m _
k-\
430
Большинство известных декомпозиционных методов воспро¬
изводят в той или иной форме выражение (15.26) в качестве
критерия подсистемы,, оптимизирующей свое состояние в детали¬
зированных показателях. При использовании методов итератив¬
ного агрегирования такой критерий может быть представлен в
виде:
(, Г
\ <= 1
ik
max.
Здесь 1 yt 1— вектор дезагрегированных оценок /-й группы ус¬
ловий, получаемых из оценки /-го агрегированного ограничения на шаге
(/— 1). Аналогично, вектор 1 у^~ ^можно рассматривать как реко¬
мендуемый верхним уровнем детализированный план функционирования
к-й локальной подсистемы. На основе этих рекомендаций могут быть
уточнены задания подсистемам по выпуску продукции в детализирован¬
ной номенклатуре, скорректированы объемы выделяемых общесистем¬
ных ресурсов и т.д. В этом смысле методы итеративного агрегирования
включают в себя черты лимитных и ценностных схем согласования
плановых решений.
Задачи подсистем выступают в методах итеративного агрегирования
не столько ’’поставщиками” детализированных планов (последние можно
получить дезагрегацией сводных планов координирующей задачи), ско¬
лько генераторами операторов агрегирования и дезагрегирования инфо¬
рмационных потоков.
В качестве примера рассмотрим процесс решения задачи (15.20) методом итера¬
тивного агрегирования. Простейшая схема состоит в следующем:
а) для очередного значения весов агрегирования Х^ = (Х^, Х^2), У = (У19 У^2) по
решениям задачи (15.21) и двойственной к ней - У и - рассчитываются детализи¬
рованные двойственные планы = Xjк = 1,2; ul = l/yjT/ = l, 2;
б) планы лиI проверяются на эффективность используемых способов и сба¬
лансированность по ресурсам:
= — — vlylci2k ^ О* 2;
Э1т = b{—anXiy1 — сц 2^2 У1 *0, i = lt2;
в) рассчитываются векторы P\, Ру — направления изменения X^, У; в агрегиро¬
ванных способах решения прямой и двойственной задач вес эффективных детали¬
зированных способов должен быть увеличен, неэффективных — уменьшен. Это
можно учесть следующим образом:
; f 1, если 3ifc = max3irs»
Pkk =
\ 0
I о
s
для остальных k\
если 3lUi = min 3lurt
г
для остальных i;
431
л/ + 1 7 + 1
г) новые значения параметров агрегирования Л , у рассчитываются обыч¬
ным образом: 1
Х<+1=(1 —аг)Хг + а
y + i==(l_pl)Yi + PIPV
Здесь 0 <а/ < 1, О </3/ < 1 - параметры процесса;
д) переход к (а).
15.5. Методы аппроксимации
производственных возможностей
Другой подход к согласованию решений в системе моделей, основан¬
ный на агрегировании информации при ее движении с нижних уровней
системы и детализации в обратном направлении, связан с аппроксима¬
цией множества производственных возможностей. Центральной идеей
этого подхода является передача вышестоящему уровню информации о
возможностях подсистем в относительно узкой области — окрестности
предполагаемого оптимума. Комбинирование различных способов
аппроксимации производственных возможностей объектов разного
уровня позволяет построить систему моделей многоступенчатой опти¬
мизации, последовательно реализующую принцип обратимого сжатия
экономической информации [ 16J 1.
Производственные возможности любого хозяйственного объе¬
кта (предприятия, отрасли, народного хозяйства в целом) могут
приближенно описываться двумя способами: построением выпук¬
лого многогранника и заданием аппроксимирующей гиперплоско¬
сти.
Прй аппроксимации с помощью выпуклого многогран¬
ника объект может быть представлен в виде:
z = 2 а1У, 25'=1 (15.27)
I 1
Здесь z — вектор продукции (положительные компоненты) и затрат
(отрицательные компоненты); аг — опорные планы развития и функ¬
ционирования объекта, выбранные некоторым способом в аппроксими¬
руемой области; ^ — интенсивность использования /-го опорного пла¬
на.
Эквивалентная матричная запись условий (15.27) имеет вид:
z = At el=\, (15.28)
где А — матрица опорных планов, % — вектор интенсивностей их исполь¬
зования (внутренних переменных хозяйственного объекта), е — вектор,
все компоненты которого равны единице.
1 Этот подход разрабатывался в ЦЭМИ АН-СССР под руководством В.Ф.Пугачева.
432
Совместное функционирование объектов описывается вектором
z — 2z , где каждый z задается условием (15.27) или (15.28).
к
Варианты функционирования объекта определяются критерием
оптимальности / (z) и внешними условиями, задающими его взаимосвя¬
зи с другими объектами экономической системы (ресурсные ограниче¬
ния и т.д.). В общем виде эти условия можно записать как z>b. Поло¬
жительные компоненты вектора z отражают задания объекту по выпус¬
ку конечной продукции, отрицательные — выделенные ему ресурсы;
нулевые компоненты относятся к условиям, описывающим производст¬
во и использование промежуточной продукции.
Сделанные предположения позволяют сформулировать модель
объекта, включающую аппроксимацию его производственных возмож¬
ностей:
f(z) — шах;
г^Ъ, (15-29)
z*=/4|, е\= 1.
Варьируя параметры модели (15.29), можно получить совокупность
локально-оптимальных планов zs и на их основе уточнить аппроксима¬
цию производственных возможностей (15.27) в окрестности предпола¬
гаемого оптимума
z = 2zs?s. 2?s=l> (15.30)
S .S
заменяя условиями (15.30) соотношения (15.26). Будем далее предпо¬
лагать, что аппроксимация (15.27) описывает производственные возмо¬
жности в окрестности оптимального варианта его развития.
Второй способ аппроксимации — построение в окрестности ожида¬
емого оптимума одного уравнения (аппроксимирующей ги¬
перплоскости) с точным равенством для оптимального плана
задачи (15.29).
Основные этапы построения такой гиперплоскости состоят в следу¬
ющем. Пусть z° — оптимальный план объекта (задачи (15.29)), v° —
оптимальные оценки внешних условий (z >b). Если вектор z = z® +
+ Az (при малых Az) допустим в задаче (15.29), то очевидно А/=/(z) —
- f (z°) < 0. Рассматривая же Az как параметр задачи (15.29), изменение
ее критерия можно оценить как А/ = v°Az, откуда v° (z - z°) < 0, и,
переходя к нормированным оценкам /г/ = i^/v°z0, имеем в окрестности
n L
hz^ 1. (15.31)
z° уравнение гиперплоскости
433
Очевидно, что для оптимального плана z° условие (15.31) выполняется
как равенство.
Аппроксимация (15.31) показывает, что в окрестности оптималь¬
ного плана допустимы изменения структуры выпускаемой продукции
(или ресурсов), но только такие, при которых сохраняется неравенство
hz < 1, т.е. при которых замена одних видов продукции другими произ¬
водится в соответствии с коэффициентами производственной взаимоза¬
меняемости h.
Использование аппроксимации (15.31) позволяет перейти к агреги¬
рованному описанию объекта введением обобщенного продукта Z =
= hz и одним линейным ограничением z < 1.
Распространяя процедуру агрегирования на параметры внешних
условий Ъу В — hb, можно сформулировать исходную задачу развития
объекта в агрегированных показателях:
J (Z) —► max;
I. (15.32)
Здесь / (Z) — критерий оптимальности модели объекта (15.29), перефо¬
рмулированный в агрегированных показателях. В задаче (15.32) отсут¬
ствует информация о возможных изменениях структуры агрегирован¬
ных показателей. Поэтому операторы дезагрегирования двойственных
оптимальных решений Z, V задачи (15.32) определяются в пред¬
положении сохранения прежней структуры выпуска и оптимальных
цен:
z = v= Vh. (15.33)
Основное свойство введенных процедур дезагрегирования состоит
в том, что детализированные планы (z, v), определенные в соответствии
с (15.33), сохраняют уровень стоимостной оценки агрегированного ре¬
шения Z:
и, 2 = Vhz*Z = V (hz°) Z = Vz~
Наиболее последовательно методы аппроксимации производствен¬
ных возможностей используются в системе моделей много¬
ступенчатой оптимизации, отражающей основные черты
оптимального планирования производственно-технологической структу¬
ры экономики. Построенная на этих идеях экспериментальная много¬
ступенчатая народнохозяйственная модель объединяет три уровня произ¬
водственной иерархии: предприятие — отрасль — народное хозяйство.
Модель имеет следующий вид:
434
u(x)—■+ max;
x = 2^ ^ b;
k
xk = ^ixkl\
I
x!*1 = Akl\kl\
^^<1; (15.34)
tkl>0.
Здесь и (jc) — народнохозяйственный критерий оптимальности; А^ -
матрица опорных планов /-го предприятия к-й отрасли; х — допусти¬
мый план предприятия, рассматриваемый как комбинация опорных пла¬
нов; хк = £х;^план£-й отрасли, составленный в детализированной
I ^ к ~
* номенклатуре: х = Ъх — народнохозяйственный план в детализирован¬
ной номенклатуре. ^
Вектор х распадается на вектор конечного продукта (с неотрица¬
тельными компонентами) и вектор суммарных затрат лимитирован¬
ных ресурсов (с неположительными компонентами), включающий в
данной постановке как народнохозяйственные, так и отраслевые ре¬
сурсы. Вектор b включает ограничения по лимитированным ресурсам,
фиксированным элементам конечного продукта (запасы, сальдо экспор¬
та-импорта) .
Использование этой модели как основы трехступенчатой оптимиза¬
ции народного хозяйства рассматривается в ВСМ, с. 90 — 93.
15.6. Согласование решений
с использованием функций отклика
Модели подсистем, входящие в многоуровневые системы моделей,
как правило, достаточно громоздки. Они представляют собой большое
число функциональных зависимостей, связывающих входные (х) и вы¬
ходные (у) параметры:
Ф(*, г/) = 0. (15.35)
Разработка алгоритмов согласования решений таких моделей, их
теоретический анализ, проведение экспериментальных расчетов — ве¬
сьма трудоемкие операции. Однако основное назначение модели под¬
системы в системе моделей заключается не в получении тщательного и
хорошо обоснованного плана ее функционирования, а в многократ¬
435
ном преобразовании входных параметров в выходные. Другими слова¬
ми, модель подсистемы в системе моделей интересна прежде всего как
функция отклика на решения, принимаемые на других уровнях иерархии
планирования. Поэтому естественно стремление заменить сложную и гро¬
моздкую исходную модель подсистемы функцией отклика, показываю¬
щей явную зависимость выходных параметров модели объекта от вход¬
ных: у=ф(х).
В общем случае процесс построения функций отклика достаточно
сложный. Однако существует метод, описывающий зависимость между
параметрами ’’входа” и ’’выхода” с заданной точностью для любой
сколь угодно сложной исходной модели — планирование эк¬
сперимента.
В теории планирования эксперимента разрабатываются процедуры выбора
числа и условий проведения опытов (в данном случае - реализации исходной
модели с конкретным выбором входных параметров), необходимых и достаточ¬
ных для решения поставленной задачи (для построения функций отклика, аппрок¬
симирующей интересующую нас зависимость с заданной точностью). Исходная
модель реализуется несколько раз при различных входных параметрах, в результа¬
те чего ’’набирается” информация для построения зависимости выходных парамет¬
ров модели от входных, т.е. функции отклика. Этот метод позволяет построить
функции отклика, замещающие любые модели, даже сложные имитационные,
не поддающиеся непосредственно математическому анализу.
Замена исходных моделей в системе моделей упрощенными функ¬
циями отклика позволяет резко сократить время на числовые экспери¬
менты, существенно разнообразить их, перенести внимание исследовате¬
ля с решения отдельных задач на сами процессы согласования и цирку¬
лирования информации.
Функции отклика весьма компактно описывают исходные объекты.
В связи с этим их параметры несут, как правило, значительную смысло¬
вую нагрузку, более ’’прозрачной” становится содержательная сторона
процессов преобразования информации в ходе согласования решений.
Рассмотрим возможности использования функций отклика для со¬
гласования решений в двухуровневых системах.
При известных технологических возможностях отраслевой системы
плановые задания xj по выпуску продукции отрасли определяют ее потре¬
бности в продукции других отраслей и в общесистемных ресурсах ftj (xj).
Задача согласования состоит в нахождении вариантов развития отраслей,
балансирующих спрос и предложение производимой продукции с учетом
конечного потребления, и сводится к решению нелинейной модели меж¬
отраслевого баланса:
х(— 2 fii (xj) = */,-, t = 1, .... /г. (15.36)
/=1
Существование решения (15.36) обеспечивается достаточно есте¬
ственными требованиями к оператору промежуточного продукта —
436
n
It fij (xj), /=1, n (монотонность, непрерывность, в некоторых
случаях выпуклость).
Возможны два подхода к построению функций отраслевых издер¬
жек: параметрический анализ оптимизационных отраслевых задач и ме¬
тод обработки статистических данных.
В первом случае для относительно простых отраслевых моделей
удается построить аналитические зависимости потребностей отрасли в
продукции других отраслей. Построение и анализ функций затрат ста¬
тистическими методами осуществляются в два этапа. Сначала с использо¬
ванием статистических данных исчисляются величины совокупных
затрат в отраслях народного хозяйства. Затем полученные данные обра¬
батываются при помощи процедур многофакторного корреляционно-
регрессионного анализа.
Согласование решений в системе ’’народное хозяйство — регионы”
включает несколько этапов моделирования. На первом этапе стро¬
ится двухуровневая система моделей с региональными моделями на
нижнем уровне. На втором этапе региональные модели замещаются
функциями отклика. На третьем этапе проводится собственно согласо¬
вание. Модель каждого региона включает балансы производства и рас¬
пределения продукции, балансы наличия и использования капитальных
вложений и трудовых ресурсов, критерием оптимальности принят фонд
непроизводственного потребления в заданной отраслевой структуре (см.
7.5, 8.3). Плановые задачи, решаемые на региональном уровне, заключа¬
ются в определении для каждого региона плана производства, обеспечи¬
вающего максимум непроизводственного потребления, исходя из задан¬
ных лимитов капитальных вложений и сальдо вывоза-ввоза продукции.
Задача верхнего уровня состоит в определении для каждого региона
лимитов капитальных вложений и заданий по ввозу-вьюозу продукции.
Параметрами функций отклика регионов выбираются объемы про¬
изводства и фонд непроизводственного потребления; факторами — вы¬
деляемые регионам капитальные вложения и сальдо вьюоза-ввоза по тра¬
нспортабельным видам продукции.
Замещение региональных моделей функциями отклика регионов
приводит к межрайонной нелинейной модели с критерием максими¬
зации фонда непроизводственного потребления в заданной территори¬
альной структуре и ограничениями на суммарные капитальные вло¬
жения и сальдо вывоза-ввоза транспортабельной продукции по стране в
целом (близкая модель обсуждалась в 8.5).
Таким образом, в двухуровневой системе моделей согласование реше¬
ний с использованием функций отклика подсистем разбивается на два
этапа. Сначала одновременно во всех подсистемах проводятся вариантные
расчеты по локальным моделям и строятся функции отклика подсистем.
Затем на верхнем уровне осуществляется замена в координирующей
модели локальных блоков построенными функциями отклика и рас¬
437
считывается оптимальный народнохозяйственный план. Данная схема
согласования решений предполагает однократный обмен информаци¬
ей: снизу в координирующую модель поступают функции отклика
подсистем; сверху в локальные модели — оптимальные параметры
внешних связей.
15.7. Согласование решений
в системе моделей методами рефлекторного моделирования
Важным классом задач планирования, изучаемых методами системного
моделирования, являются задачи исследования развития отдельной под¬
системы (или нескольких подсистем) в составе народного хозяйства.
Организация взаимосвязанных расчетов по народнохозяйственным
и локальным моделям проводится с использованием рефлекторного
подхода1.
По существу рефлекторные схемы согласования решений (см. гл.
14) реализуются построением так называемых гибридных моделей,
объединяющих условия взаимодействующих моделей. Можно выде¬
лить два типа гибридных моделей, описывающих взаимосвязь ’’под¬
система — народное хозяйство”: народнохозяйственные модели с де¬
тализированным описанием условий функционирования выделенной
подсистемы и модель подсистемы с агрегированным описанием оста¬
льной части народного хозяйства. В прикладных исследованиях гибрид¬
ные модели конструируются обычно не слиянием взаимодействующих
моделей в единую модель, а постепенным развитием одной из моделей
в направлении учета условий другой.
На примере блока межотраслевых связей рассмотрим фрагмент
гибридной модели, объединяющей свойства народнохозяйственной
межотраслевой межрегиональной модели и региональной модели, опи¬
сывающей развитие локальных объектов.
Детализация межотраслевых связей в народнохозяйственной моде¬
ли проводится путем выделения в классификации чистых отраслей,
с одной стороны, отдельных продуктов в натуральном выражении, с
другой — конкретных объектов (крупных предприятий, промышленных
узлов или их групп) и комплексных региональных или межрегиональных
программ (фактически таких же объектов, но и в стадии их становления
или переорганизации).
Общий вид детализированного регионального блока межотрасле¬
вых связей представлен в табл. 15.1, где А — символ матрицы прямых
Рефлекторное моделирование (программирование) как подход к моделиро¬
ванию больших систем предложено венгерским экономистом Г.Шимоном. Сходный
принцип используется в ИЭиОПП СО АН СССР при разработке специализированных
модельных комплексов народного хозяйства (см. гл. 17).
438
Таблица 15.1
Детализированный региональный блок межотраслевых связей
Конкретные объекты
Прочее хозяйство региона
Отдельные
продукты
В ю - А ю
Е-Лц
-А 12
Прочая продукция
#20 - -420
-А 21
Е-Аъ
материальных затрат, В — символ матриц выпусков отдельных продук¬
тов или прочей продукции. Это — один из вариантов матрицы модели
натурально-стоимостного баланса, в котором, во-первых, оставлены
балансы по прочей продукции, во-вторых, описываются не хозяйствен¬
ные отрасли в полном объеме, а некоторые конкретные хозяйствен¬
ные объекты.
Возможны самые разнообразные ’’усеченные” варианты данного
блока; обязательны в нем подблоки: либо Вю — Аю (балансы по
отдельным продуктам между локальными объектами), либо Е - А п
(межпродуктовых связей), либо Е - А22 (межотраслевых связей).
Если модель включает только блоки последнего типа, то это обычная
межотраслевая модель без выделения конкретных продуктов и объе¬
ктов, Если в модели только блоки Е — Ац, то речь идет о межпродук-
товом балансе, при этом прочая продукция представлена агрегированно:
ее затраты в функционале, затраты на нее (а также по конкретным объе¬
ктам, если они выделены) — в правой части условий. Если модель
включает только блок Bl0 — A\0i то имеем одну из форм обычной
модели группы конкретных объектов (многоотраслевых или терри¬
ториально-производственных комплексов), при этом затраты прочей
продукции должны быть агрегированно отражены в функционале, а
затраты на прочее хозяйство — в правой части условий.
Основные методические проблемы в применении рефлекторного
подхода связаны с корректным сочетанием в гибридных моделях раз¬
ных типов описания экономических подсистем (агрегированного и дета¬
лизированного) .
ГЛАВА 16
СОГЛАСОВАНИЕ РЕШЕНИЙ НА ОСНОВЕ
ЭКОНОМИЧЕСКИХ МЕТОДОВ
16.1. Моделирование экономических
взаимодействий: общая характеристика
Подход к разработке и согласованию плановых решений, рассматрива¬
емый в этой главе, базируется на определенной совокупности теорети¬
ческих представлений: народное хозяйство рассматривается как слож¬
ная система, имеющая ряд подсистем; каждая подсистема обладает
собственным критерием оптимальности, отражающим ее внутренние
(имманентные) интересы; функционирование народного хозяйства
(в том числе планирование) есть процесс взаимодействия различных
подсистем; наконец, взаимодействие подсистем осуществляется посред¬
ством экономического механизма, т.е. является экономическим взаимо¬
действием, цель которого — наилучшее сочетание интересов отдельных
подсистем и системы в целом.
Эти теоретические представления являются основой для построения
довольно широкого класса народнохозяйственных моделей, называе¬
мых моделями экономического взаимодействия.
Предварительное понятие о моделях этого типа давалось в 3.2.
Общая модель экономического взаимодействия подсистем представ¬
ляет собой более сложную конструкцию по сравнению с оптимизацион¬
ной моделью народного хозяйства. Это — модель не только планирова¬
ния, но и функционирования экономической системы, сочетающей
централизованное управление с хозяйственной самостоятельностью и
широким использованием товарно-денежных отношений. Она отражает
не только производственно-технологическую, но и организационную,
и социальную структуру экономики.
Часто модели такого типа называют моделями экономи¬
ческого равновесия. Это название суживает содержание и
признаки рассматриваемого класса моделей экономики. Термин ’’равно¬
весие” имеет статический оттенок и, как правило, используется для
характеристики состояний. При описании процессов обычно применяет¬
ся расширенное понятие — ’’динамическое равновесие”, но и оно характе¬
ризует не столько сам процесс, сколько его конечный результат или
440
тенденцию. Понятие ’’экономическое взаимодействие” является более
общим; оно включает определение равновесия (статического и динами¬
ческого) как особого состояния экономического процесса, но не огра¬
ничивается этим.
Принципиально важно, чтобы модель экономического взаимодей¬
ствия позволяла изучать не только отдельные состояния равновесия,
но и сам процесс функционирования экономической системы, основной
тенденцией которого должно быть стремление к достижению устойчи¬
вой траектории сбалансированного развития. Поэтому общая модель
экономического взаимодействия подсистем народного хозяйства должна
быть динамической и включать описание механизмов перехода от нерав¬
новесных состояний к равновесным и выхода из равновесных состояний
при структурных перестройках народного хозяйства1. Однако созданные
в работах по математической теории экономического равновесия поня¬
тийный аппарат и инструментарий исследования имеют более универсаль¬
ное значение и могут с успехом использоваться при анализе и решении
более общих типов моделей экономического взаимодействия.
Любая народнохозяйственная модель экономического взаимодей¬
ствия объединяет модели отдельных подсистем (включая модель ’’цен¬
тральной” подсистемы) и общие для всех подсистем условия развития
народного хозяйства. При этом модель каждой подсистемы содержит
локальный критерий оптимальности (целевую функцию), описание
множества допустимых решений, определяемого внутренними условия¬
ми развития подсистемы, и баланс экономических взаимоотношений с
другими подсистемами. Вторая же часть модели (общие ресурсно-техно¬
логические ограничения) необходима для координации (согласования)
хозяйственных решений подсистем.
Согласование оптимальных решений подсистем осуществляется,
как правило, путем выбора системы экономических нормативов (цен,
тарифов, ставок заработной платы, нормативов распределения прибыли
и т.п.)2. Значения (параметры) этих нормативов, которыми должны
руководствоваться хозрасчетные звенья, могут быть получены двумя
способами: либо эти параметры устанавливаются централизованно,
либо они вырабатываются в процессе функционирования народного хо¬
зяйства и являются результатом соглашения между подсистемами
На этом основании некоторые частные случаи моделей экономического
взаимодействия называют неравнрвесными.
2 Имеются и другие типы моделей взаимодействия подсистем, в которых эконо¬
мические нормативы (прежде всего цены) предполагаются заданными, могут быть
’’неравновесными” или вообще не участвовать в процессе согласования решений.
Координация решений подсистем в этом случае осуществляется центральным
планирующим органом путем распределения лимитов на общие для разных под¬
систем ресурсы или установления заданий по выпуску продукции. Модели такого
типа предполагают более высокую централизацию плановых решений. Они ближе
к моделям многоуровневой оптимизации народного хозяйства.
441
(’’договорные” цены и т.п.). В первом случае предполагается существо¬
вание некоторой народнохозяйственной модели (или центрального ком¬
плекса моделей), посредством которой находятся балансирующие
экономические нормативы. Во втором случае модель экономического
взаимодействия должна описывать построение народнохозяйственного
плана не как единичный акт (соответствующий однократному решению
математической задачи и однократному обмену информацией между
подсистемами), а как итеративный процесс принятия и согласования
плановых решений подсистем разного уровня.
В динамической модели экономического взаимодействия отражается
изменение всех условий во времени, в том числе эволюция критериев
оптимальности подсистем и условий экономических взаимоотношений.
Наряду с ценами, ставками доходов и т.п. в модель включаются такие
динамические регуляторы, как банковский процент, норматив эффекти¬
вности капитальных вложений, соизмерители полезного эффекта от
потребления в разные моменты времени. Решения модели экономическо¬
го взаимодействия получают динамическую трактовку как определение
множества эффективных траекторий развития экономической системы.
Анализ моделей экономического взаимодействия показывает, что
общие свойства их решений не противоречат свойствам народнохозяй¬
ственного оптимума. Более того, на основе моделей экономического
взаимодействия можно получать теоретические результаты, существенно
дополняющие анализ оптимизационных моделей народного хозяйства.
В частности, доказывается принципиальная возможность максимизации
глобальной целевой функции посредством децентрализованных дей¬
ствий отдельных подсистем в рамках определенного экономического
механизма.
Балансирующие экономические нормативы в модели экономическо¬
го взаимодействия обладают свойствами, во многом аналогичными свой¬
ствам оптимальных оценок продукции и ресурсов, получаемых в резуль¬
тате решения оптимизационной модели с глобальным критерием опти¬
мальности. Они также характеризуют сбалансированность пропорций
между производством и потреблением, потребностями и возможностя¬
ми их удовлетворения, являются измерителями общественно необхо¬
димых затрат и общественной полезности продукции. Но анализ моделей
экономического взаимодействия требует более сложного математическо¬
го аппарата, нежели классические оптимизационные модели.
Разработкой принципов коллективной рациональности, играющих
важную роль в формировании требований к совокупности принимае¬
мых решений в различных ситуациях ’’конфликта и сотрудничества”
взаимосвязанных объектов, занимается особая математическая дис¬
циплина — теория игр. Логический анализ и сопоставление после¬
дствий принятия тех или иных концепций ’’решения” игр является
методом исследования ситуаций взаимодействия.
442
Модели народного хозяйства, описывающие взаимодействие подси¬
стем и отдельных участников с особыми интересами, впервые исследо¬
вались представителями математической школы политической эконо¬
мии. Первая модель такого типа, получившая название ’’модель общего
экономического равновесия”, была предложена Л.Валърасом в 70-х
годах XIX в. Однако доказательство существования равновесия для
упрощенного варианта модели Вальраса было получено А.Вальдом
только в 1935 — 1937 гг. Важным этапом в развитии экономической
теории моделей экономического равновесия следует считать работы
КЭрроу, Г.Дебре, Л.Мак-Кензи, выполненные в 50-х годах нынешнего
столетия. Наибольшую известность получила модель конкурентного эко¬
номического равновесия Эрроу -Дебре. Эта модель стала объектом
многочисленных исследований и обобщений.
Модели равновесия, разрабатываемые учеными Запада, относятся,
как правило, к моделям дескриптивного типа, т.е. представляют собой
попытки объяснения процесса функционирования рыночного хозяйства,
но не управления им. Ряд предпосылок, используемых в моделях
равновесия капиталистической экономики, далек от реальности (нап¬
ример, предположение о совершенной конкуренции). Нередко мо¬
дели равновесия использовались в идеологических целях — как
доказательство эффективности и социальной справедливости свобод¬
ного предпринимательства (рыночной экономики) по сравнению с плано¬
вой социалистической экономикой. При этом равновесие интерпретиро¬
валось как состояние гармонии классовых интересов и справедливого
распределения благ. На самом же деле ’’гармония” и ’’справедливость”
в моделях конкурентного равновесия капиталистического хозяйства
(в частности, в модели Эрроу — Дебре) зависит от начального распреде¬
ления собственности и априорных коэффициентов распределения чисто¬
го дохода на прибыль, заработную плату и т.п. Таким образом, решение
важнейших классовых конфликтов вынесено за рамки модели как нечто
заданное.
Для исследования социалистической экономики интерес представля¬
ет прежде всего математическая теория моделей равновесия, имеющая
более универсальное применение. Неправомерно отождествлять конк¬
ретные признаки теоретических моделей равновесия, изучавшихся
учеными Запада, с общими принципами построения моделей экономиче¬
ского взаимодействия для планирования и управления социалистической
экономикой.
В советских экономико-математических исследованиях модели
рассматриваемого типа длительное время воспринимались в лучшем
случае как теоретический инструмент без особых надежд на его практи¬
ческое применение. С конца 60-х годов предпринимались отдельные
попытки приспособления теоретических моделей экономического вза¬
имодействия (в частности, модели Эрроу — Дебре) для анализа ряда
аспектов функционирования реальной социалистической экономики.
443
Интерес к моделям экономического взаимодействия значительно по¬
вышается благодаря переходу от преимущественно административных
к преимущественно экономическим методам управления социалисти¬
ческим народным хозяйством.
16.2. Основные понятия
экономических взаимодействий
Экономический оптимум по Парето. Пусть в народном хозяйстве выде¬
ляется т подсистем. Введем следующие обозначения:
Xfc — план к-й подсистемы;
ск ~fk V^k) ~ Долевая функция к-й подсистемы;
X = (X1, •••> Хт) план системы как композиция планов подси¬
стем;
С = (сх, ..., ст) — вектор значений целевых функций подсистем;
Xjt — множество допустимых планов к-й подсистемы;
— множество допустимых планов системы в целом, состоящих
из композиции допустимых планов подсистем и удовлетворяющих
дополнительным общесистемным ограничениям.
Из совокупности моделей подсистем можно составить задачу
векторной оптимизации на множестве допустимых вариан¬
тов развития подсистем и системы в целом с целевой функцией F (А') =
= (Л (X гfm (Хт)):
F (X) -*тах;
Х=(х19...,хт)ех .
Решение этой задачи позволяет находить эффективные вари¬
анты (оптимальные по Парето).
Допустимое решение X* = (Xf, ..., X* ) (ему соответствует вектор
С* = (с*, ..., Cm)) является эффективным, если не существует
другого допустимого решения X = (АГ1} ..., Хт), которому отвечает
вектор С* = (с*, с*^), такой, что сд- > с? доя всех к = 1, ..., т и
т т
S ск> S с*1.
к = 1 к = 1 К
Эффективное решение X* совокупности подсистем — это такое
допустимое решение всей системы, при котором ни одна из подсистем
Часто понятие оптимальности по Парето, как и дальнейшие его обобщения,
определяется непосредственно для векторов С. Однако для наших целей удобно
говорить об эффективности решений подсистем. Эти трактовки определения эф¬
фективности эквивалентны, если иметь в виду соответствие допустимых решений
х и векторов распределения эффекта С.
444
не может улучшить свое положение (увеличить значение своей локальной
целевой функции), не ухудшая положения хотя бы одной из остальных
подсистем. Можно сказать, что понятие оптимальности по Парето выра¬
жает такой принцип коллективной рациональности (такое экономичес¬
кое поведение), согласно которому ’’хорошо делать так, чтобы кому-
нибудь стало лучше, если при этом никому другому не становится
хуже”.
Ядро экономической системы. Принадлежность к множеству эффек¬
тивных решений является разумным требованием к выбору согласован¬
ного планового решения в системе из нескольких экономически само¬
стоятельных участников. В стремлении получить решение, оптимальное
по Парето, выражается единство интересов различных подсистем. Но
разные оптимальные по Парето решения неодинаково выгодны для
разных подсистем. Поэтому введенное понятие оптимальности является
довольно слабым, оно не исключает того, что какая-либо подсистема
(или группа подсистем, коалиция), действуя самостоятельно, не сможет
(не смогут) достигнуть более предпочтительных для них вариантов
развития.
В подобных ситуациях какая-либо подсистема или группа подсистем
может быть заинтересована и имеет возможности воспрепятствовать
реализации некоторых оптимальных по Парето планов. Это означает,
что требование оптимальности по Парето не учитывает возможности
участников и коалиций влиять на выбор совместных планов подсистем.
Эти возможности и их влияние на потенциальные исходы процессов со¬
гласования решений изучаются в рамках кооперативной тео¬
рии игр многих лиц.
Формализованное описание возможностей коалиции S С R} R — jl, ..., т } мо¬
жет быть осуществлено путем спецификации множества Cs векторов, составленных
из значений целевых функций. При этом С £ С* в том и только в том случае, если
существует допустимый план X = ..., Хт), Xд. ^3^, который данная коалиция
может обеспечить ’’собственными” силами и такой, что С% (Xfc) ДЛЯ всех
к Е S.
Очевидно, что при свободном выборе решений вектор X £ X не будет реали¬
зован, если существует коалиция S и вектор С €= С? такие, чтоД^ (Х^) и
2 fk(xk) < 2 ск- В этом случае говорят, что коалиция S блокирует вектор X.
kGS kGS
Введенные понятия возможностей коалиций и блокирования позво¬
ляют сформулировать второе требование к выбору согласованного реше¬
ния в системе, состоящей из нескольких подсистем. Это требование
принадлежностей такого решения ’’ядру экономической системы”.
Допустимое решение X* €Е X принадлежит ядру экономической
системы, если не существует ни одной блокирующей его коалиции.
Множество оптимальных по Парето решений будем обозначать
через X*» а множество решений, принадлежащих ядру, — через X*
445
Ядро, если оно не пусто, состоит
только из оптимальных по Парето
решений, так как все неоптимальные
X £ ЭС блокируются коалицией,
состоящей из всех участников. Та¬
ким образом, X £ X* • Если же
ядро совпадает с множеством Парето
(Я*= уС) , то это означает, что у от¬
дельных подсистем (и любых их
коалиций) нет экономических моти¬
вов против реализации любого вари¬
анта, эффективного для системы в
целом. Чем теснее взаимозависи¬
мость подсистем, тем меньше разли¬
чия между множеством эффектив-
Рис. 16.1. Граница Парето и ядро ных вариантов (оптимумов по Паре-
экономической системы то) и ядром системы.
Рассмотрим пример для систе¬
мы, состоящей из двух подсистем
(рис. 16.1). ЛинияАВ есть отображение множества Парето на множество
значений целевых функций. Величины сх и с2 — значения целевых функ¬
ций подсистем при их изолированном функционировании. Очевидно,
что подсистемы заинтересованы в объединении усилий (совместной
деятельности), если оно позволяет получить значения целевых функций
не меньше, чем сх и с2. Отсюда следует, что ядру экономической систе¬
мы соответствует линия DE. Линии AD и BE соответствуют оптимальным
по Парето планам, не принадлежащим ядру. Для первой подсистемы
неприемлемы все точки, лежащие левее C±D\ для второй подсистемы
неприемлемы все точки, лежащие ниже С2Е.
Кооперативная игра, ядро игры. На основе целевых функций /^, допустимых
множеств X, множеств CS {к £/?, S С/?), описывающих возможности
коалиций, может быть построена кооперативная игра т лиц, которая является
теоретико-игровой интерпретацией рассматриваемой ситуации взаимодействия
экономически самостоятельных подсистем. Кооперативной игрой т лиц (в форме
характеристической функции) называется отображение К, ставящее в соответствие
каждому подмножеству S C. R = /1, тЛ множество векторов V (S) простран¬
ства Rm. 1 ■*
Элементы множества R называются игроками, подмножество SC.R - коалицией
игроков, V — характеристической функцией игры. V (S) — это формальное пред¬
ставление возможностей коалиции S.
Важную роль в определении решения кооперативной игры (ядра игры) играет
понятие блокирования: вектор С £ К(£) блокируется коалицией S Сд, если суще¬
ствует вектор СЕ V (5), такой, что для всех к £ S и 2 $к > Ё
kes
Ядром (С-я дром) игры называется множество всех неолокируемых векто¬
ров множества V (R).
Определим характеристическую функцию Vq : 0s для всех S C.R. Из дан¬
ных выше определений следует, что ядро игры, задаваемой функцией Vq совпадает
с ядром экономической системы. Поэтому для изучения условий совместности
требований к согласованным планам, выражаемых в терминах множеств возмо¬
446
жностей коалиций подсистем С5, можно использовать теоремы о непустоте ядра
кооперативной игры т лиц.
Равновесные решения в экономической системе. Дополнение модели
векторной оптимизации народного хозяйства определенным экономичес¬
ким механизмом позволяет перейти к задаче выбора на множестве эф¬
фективных планов (ядре экономической системы). ’’Устройство” эконо¬
мического механизма зависит от конкретных особенностей моделируе¬
мых процессов экономического взаимодействия. Но общей чертой
всякого экономического механизма является использование цен (как
измерителей затрат и результатов деятельности каждой подсистемы) и
других экономических нормативов.
При заданном векторе экономических нормативов р допустимыми
являются решения, составляющие подмножество Xfc (р) множества % ^
всех вариантов функционирования к-й подсистемы. Оптимальные с пози¬
ций к-й подсистемы планы X £(/0 представляют собой решения задачи
fk{Xk)—-max; (16.1)
Хк€Як(р). (16.2)
Через Q обозначим множество возможных значений векторов р.
Для^ произвольного вектора р Е Q получаемые локальные решения
SCk (р) могут не удовлетворять условиям допустимости (их компози¬
ция может не принадлежать X ) •
Вектор управляющих параметров р* Е Q называется баланси¬
рующим (или равновесным), если среди оптимальных
планов подсистем, рассчитанных при данном векторе параметров, найду¬
тся такие, которые образуют допустимый план системы в целом, т.е.
план, удовлетворяющий общим для всех систем условиям.
Иными словами, существуют X*k € SC\ (р) такие, что X* Е X » где
Х* = (Х\, Х'т).
Пара (р*у X*) называется состоянием (траекторией)
равновесия, если вектор р* является балансирующим:
XktXkijr) и х*=(х;, *;)€•*■.
Описанный принцип выбора согласованных решений следует приз¬
нать удовлетворительным только в том случае, если порождаемые
им планы принадлежат ядру экономической системы.
Полученное состояние (траекторию) равновесия не следует трак¬
товать как абсолютно наилучшее решение проблемы согласования
интересов всех подсистем. Равновесие (р* X*) достигается в рамках
установленных принципов экономических отношений,
в том числе принципов распределения благ и доходов. При изменении
447
этих принципов могут получаться иные состояния (траектории) равно¬
весия.
Некооперативная игра и равновесие по Нэшу. В ряде практически
интересных случаев можно построить некооперативную игру (т + 1)
лиц, решения которой соответствуют равновесным состояниям.
Задать некооперативную игру (т + 1) лиц в нормальной форме с
зависимыми множествами стратегий — это указать для каждого уча¬
стника к: а) множество его возможных стратегий Zfc; б) для каждого
набора стратегий zx EZXizk- \ EZk - &к + 1 Е Zk + 1,zm + 1 £
e Zm + 1 других участников — множество его допустимых стратегий
%к (z 1, ..., zk — 1, zk+ 1, zn ¥ l); в) функцию вьшгрыша, определен¬
ную на множестве всех возможных композиций решений участников
Uk (z\,zm + l) • Число Uk (zi,zm + l) дает оценку к-м участником
’’ситуации”, описываемой стратегиями z/ Е Z/ игроков i = 1, ..., т + 1.
Набор стратегий (zt, zm, zm + l), zk E Zk назьшается решением
по Нэшу рассматриваемой игры, если выполняется следующее соот¬
ношение :
Uк (^1* • • •» Zfa Zfi+l* • • •» ^от+l) =
= max (/fe (zlf . . ., , 2Л+1);
2* € (^1» ■ • •» Zfc-i» + Z„+1), £ = lt . . /71.
Стратегия z^ называется при этом оптимальной. Определение, таким об¬
разом, указывает, что оптимальная стратегия игрока к является допусти¬
мой и среди других допустимых стратегий характеризуется наибольшим
выигрышем.
Построение некооперативной игры для рассматриваемой ситуации
производится следующим образом.
Множество Zm + \ стратегий участника с номером т + 1 центральной
подсистемы описывает все возможные управляющие воздействия. Будем
обозначать его через М. Оно не зависит от стратегий, выбираемых други¬
ми участниками, т.е. при всех возможных наборах стратегии других
участников (zb zm), zi Е Zf, i = 1, ..., m множество допустимых
стратегий участника т + 1 Zm + \(zlf ..., zm) совпадает cAf. Целевая
функция Um + 1 (zi, ..., zm + l) выбирается таким образом, чтобы зада¬
ча подсистемы
Vm+i(Zi, ■ ■zm+l)~^max; гт+1£ М
’’порождала” ее функцию отклика — правила разработки центральной
системой управляющих параметров (экономических нормативов).
Участник за номером к (к = 1,..., т) при данном векторе управляю¬
щих воздействий zm + \ = р Е М решает задачу (16.1) — (16.2). Таким
образом, Zk = XjjiZk (zi,...,zfc_ i ,zfc+ l,...,zm + l) = Zk (zm+ l) =
448
= Хд; (р), т.е. в формировании допустимых стратегий подсистемы с номе¬
ром к принимают участие лишь стратегии центральной подсистемы.
Далее, Uk (zi, zk -Г, zk, zk + 1, zm + l) =fk (zk}9 т.е. оценка
каждой подсистемой ситуаций (zl9 ..., zk _ l, zk, zk + 1, zm + l)
зависит только от ее собственной стратегии — вектора Е X к-
Ниже основные понятия и результаты теории кооперативных и не¬
кооперативных игр применяются к моделям экономического взаимо¬
действия.
16.3. Общая модель экономического
взаимодействия подсистем
Модель и ее основные свойства. Пусть в народном хозяйстве выделяются
т подсистем нижнего уровня (к = 1, ..., т) и одна подсистема верхнего
уровня с номером т + 1 — центральная подсистема. Будем предполагать,
что подсистемы могут обмениваться результатами своей деятельности.
Интенсивность акого обмена для подсистемы к будем характеризовать
вектором Д& — сальдо обмена. Тогда каждый план Хк подсистемы к
естественно представлять в виде
Хк = (хк, А*)€**, (16-3)
где вектор Хк описывает интенсивность различных видов внутренней
деятельности подсистемы; }(к~ множество допустимых планов к-й под¬
системы. Цели развития каждой подсистемы выражаются в виде функ¬
ции /д., зависящей лишь от выбранных вариантов интенсивности внутрен¬
ней деятельности — векторов хд-. Будем предполагать также, что условие
X Е X допустимости общего решения всей системы можно представлять
как условие сбалансированности обмена результатами деятельности
21 Aft = 0. (16.4)
k=l Х
С рассматриваемой системой может быть сопоставлена кооператив¬
ная игра с характеристической функцией следующего типа: пусть X —
композиция возможных планов подсистем X = (Х2, Хт), таких, что
выполняется условие 2 Afr = 0- Тогда С Е (У в том и только в том
£ £ £ j. *
случае, когда (х^.),kES (здесь, как и выше, S СR = |1,..., m > —
произвольная коалиция подсистем, а О — множество значений целевых
функций участников).
Следующее утверждение дает условия непустоты ядра для рассмат¬
риваемого класса моделей взаимодействия1.
Утверждение 1. Предположим, что множества X к непустые, выпук¬
лые, замкнутые, ограниченные, а функции вогнутые, непрерыв¬
1 Подробное обсуждение нижеследующих утверждений см. в BCM, с. 117 - 119.
449
ные (к = 1, ..., т). Пусть также каждое множество Х^содержит вектор
(хк> 0)1 Тогда ядро рассматриваемой игры непусто.
Перейдем теперь к описанию некооперативной игры, соответствую¬
щей рассматриваемой системе, и условий существования равновесных
решений. Будем предполагать, что управляющим параметром централь¬
ной подсистемы является вектор цен р. В качестве множества возмож¬
ных векторов цен Q рассмотрим совокупность всех неотрицательных
векторов соответствующей размерности, все компоненты которых в
сумме равны 1. Будем считать, что множество (р) ,pEQ состоит из
подмножеств всех возможных векторов, удовлетворяющих (приданном
р) условию финансовых балансов внешних связей следующего типа:
(р, Л*)>0. (16.5)
Для спецификации некооперативной игры (т + 1) лиц с зависимыми
множествами стратегий остается определить задачу подсистемы верхнего
уровня — (т + 1)-го участника. Предположим, что он решает следующую
задачу: для каждого набора ((хь Дх), (хщ, Ага)) планов подсистем
найти вектор цен р Е Q, минимизирующий в стоимостном выражении
общее сальдо обмена, т.е.
p€Q;
ГП1П.
Исследуем теперь связь между равновесными состояниями данной
модели взкимодействия и решениями по Нэшу соответствующей игры
(т + 1) лиц.
Утверждение 2. Пусть (р* X*) — состояние равновесия. Тогда пара
(р*, X*) является точкой Нэша соответствующей игры.
Действительно, векторы Xfc = (xfc, Z^J) являются решениями задачи
к-и подсистемы (к = 1, т) при векторе цен р*. Далее, вектор р*
т
является решением задачи подсистемы т + 1, так как Б Д£ = 0.
к = 1
Обратное утверждение, вообще говоря, неверно, однако имеет место.
Утверждение 3. Пусть (р*, X*) — точка Нэша. Тогда определяемые
m
ею решения подсистем нижнего уровня непротиворечивы, т.е. 2
> 0, где Д£ - планы по обмену продукцией, соответствующие равновес¬
ным решениям, составляющим вектор X*.
Утверждение 4. Пусть (р*, X*) — точка Нэша и выполнены следую¬
щие предположения:
Это означает возможность изолированного (без обмена) функционирования
каждой подсистемы. В теории кооперативных игр такое состояние (изолированное
функционирование) называется точкой ’’статус-кво’*.
450
1) для данного р* и каждого к (к = 1, т) ограничение (16.3)
выполняется как равенство для соответствующих вектору X* планов по
обмену продукцией Д£ к = 1,т, т.е. (р*, Др = 0;
2) продукты желательны в том смысле, что, если цена продукта
равна нулю, сальдо обмена по этому продукту, вычисленное в соответ¬
ствии с "юбыми оптимальными при данном векторе цен решениями
подсистем, является отрицательным, т.е. если X*k = {x*k%
р{ = 0, то 2 А* < 0, где д/ обозначает компоненту с номером i вектора
k= 1 К
Д&. Тогда (р*, X*) — состояние равновесия.
Данное утверждение позволяет установить теорему существования
состояния (траектории) равновесия в рассматриваемой системе на ос¬
нове следующего утверждения о существовании решения по Нэшу
соответствующей ей игры (т + 1) лиц.
Утверждение 5. Предположим, что, как и в условиях утверждения 1,
множества X/fcявляются выпуклыми, замкнутыми, а функции /д. —вог¬
нутыми, непрерывными (к = 1, ..., т). Предположим также, что для
всякого к = 1, т множество Xyfc содержит вектор (х^у Д^), такой,
что Дд. > 0 (т.е. каждая подсистема может произвести положительное
количество каждого из обмениваемых продуктов). Тогда описанная
выше игра имеет состояние равновесия.
Указанные условия обеспечивают выполнение условий теоремы
о существовании точки Нэша игры (га + 1) лиц.
Соотношение ядра и равновесия. Связь двух подходов к исследова¬
нию рассматриваемой системы (кооперативного и некооперативного),
а также эффективность равновесных решений подсистемы описывают
следующее.
Утверждение 6. Предположим, что (р*, X*) — равновесное решение,
а ограничение (16.5) во всех задачах подсистем при векторе цен р* —
существенно в том смысле, что (р*, Др = 0 для всех планов по обмену
продукцией, соответствующих векторам X Е К , полученным компози¬
цией множества оптимальных решений X*k € (Р*) задач подсистем.
Тогда X* принадлежит ядру рассматриваемой системы (см. ВСМ,
с. 120).
Обратное утверждение, вообще говоря, неверно, так что ядро (когда
не пусто) содержит кроме равновесных согласованных планов (когда
таковые существуют) и другие согласованные планы.
Математическое исследование связи между ядром и равновесием
приводит к выводу, что ’’различия” между ними проистекают в основ¬
ном из-за малого числа взаимодействующих подсистем и что при увели¬
чении числа подсистем эти различия имеют тенденцию убывать1.
Наиболее простой случай - реплицирование (дублирование, повторение)
подсистем. Идея такого реплицирования и первый результат о ’’стягивании” ядра
к равновесию принадлежат У.Эджворту. Геометрической иллюстрацией этого
служит так называемый ’’ящик Эджворта” (см. ВСМ, с. 121-123; а также [18],
[21] )-
451
Нечеткие коалиции и нечеткое ядро. Формально нечеткой коалицией
называется любой набор а = (а1? ат) неотрицательных чисел — ’’до¬
лей” участия подсистем в данной коалиции. При этом говорят, что такая
коалиция блокирует X = (Хг, ... Х^ = (*£, Д^), если сущест¬
вуют возможные варианты функционирования подсистем (х^, Дд.) Е
Е Xyfc, такие, что
2аА=0;
v-kfk (х) > a-kfk
т т
к = ^kfk (%к) ^ ^ ^akfk (*&)•
В частности, если = О для всех к tfzS и = 1 для к Е S, то приходим
к старому понятию блокирования по коалиции S.
Нечетким ядром называется множество векторов X Е X,
не блокируемых никакими нечеткими коалициями.
При естественных предположениях устанавливается эквивален¬
тность нечеткого ядра и множества равновесных решений и тем
самым — двух теоретических подходов: кооперативного и некооператив¬
ного. Таким образом, равновесные решения в определенном смысле
удовлетворяют наиболее жестким требованиям к оптимальности в мно¬
гоцелевой системе и никакие другие решения этим требованиям не
удовлетворяют.
Утверждение 7. Предположим, что для каждого к = 1,m функция
fk (Xfc) является вогнутой, непрерывной, а множества Xfc — выпук¬
лым компактом. Пусть X* Е — точка нечеткого ядра. Пред¬
положим также, что для всякого к = 1, m существуют А (xfa Д^) е
G (•% 4fc) € Щ . такие, что fk (х к) > fk (х*к) и £% > 0. Тогда
найдется вектор р*, такой, что состояние (р*, X*) является равновеси¬
ем (схему доказательства см. в ВСМ, с. 124 -- 125).
Свойства модели взаимодействия с ф 0. Выше предполагалось,
что для каждой подсистемы выполняется условие (р, Д^) = 0.
Утверждение S. Будем считать, что выполнены все предположения
утверждения 7, за исключением условия, что X* принадлежит нечеткому
ядру. Пусть вместо этого X* — эффективная точка множества X • Тогда
существуют числа стакие, что
тп
2 ю* “ о (16.6)
*= I
и (р* X*) является равновесием в модифицированной модели экономи¬
ческого взаимодействия, полученной заменой условия (16.3) финансо¬
вых балансов внешних связей каждой подсистемы на соотношения:
0&, Д*)>а>*. (16.7)
452
Далее, при априорно заданных величинах сальдо внешних связей срав¬
новесное решение в указанной модифицированной модели экономичес¬
кого взаимодействия определяет оптимум по Парето в условиях, анало¬
гичных предположениям утверждения 6, т.е. имеет место следующее ут¬
верждение.
Утверждение 9. Предположим, что (р*t X*) является равновесным
решением модифицированной модели экономического взаимодействия
с априорно заданными величинами сальдо внешних связей Предполо¬
жим также, что ограничения (16.7) в соответствующих задачах подсис¬
тем (при векторе цен р*) являются существенными. Тогда А"* является
оптимальной по Парето точкой множества X .
Следует отметить, что равновесие в модифицированной модели
экономического взаимодействия существует не при любых априорно
заданных величинах сальдо обмена cofc, к = 1,..., m.
Исследование условий, обеспечивающих существование равновесия в модифици¬
рованных моделях экономического взаимодействия, можно провести в соответст¬
вии с той же схемой, что и для частного случая этих моделей, соответствующих
ситуации 6^. = 0 (утверждения 2 - 5).
Соотношение равновесия и глобального оптимума. Решение модели
экономического взаимодействия можно определить на основе решения
оптимизационных задач со скалярным критерием оптимальности, задав
определенные соотношения между локальными критериями оптимально¬
сти отдельных подсистем. Пусть эти соотношения характеризуются набо¬
ром неотрицательных величин Xfc, D Х& = 1, показьюающих доли
к е R
отдельных подсистем к Е R в общем значении функционала / (X), где
X = (Xi, ..., Хт)- Тогда скалярный критерий оптимальности можно
записать в виде
f*(Xk)>WX); (16.8)
f(X)—>max. (16.9)
Таким образом, общая оптимизационная задача определяется усло¬
виями (16.3), (16.4), (16.8), (16.9).
Между решениями оптимизационной модели со скалярным критери¬
ем оптимальности и модели экономического взаимодействия существует
тесная взаимосвязь. На основе решения модели экономического взаимо¬
действия можно определить такие соотношения между целевыми функ¬
циями подсистем при которых одно из решений соответствующей
оптимизационной задачи совпадает с рассматриваемым решением модели
взаимодействия. Наоборот, на основе решения оптимизационной модели
со скалярным критерием оптимальности можно определить сальдо
при которых одно из решений соответствующей модели взаимодей¬
ствия совпадает с рассматриваемым решением оптимизационной модели.
453
При этом оптимальному решению оптимизационной задачи, где все
ограничения (16.8) существенны, соответствует равновесное решение
модели экономического взаимодействия, а оптимальному решению
оптимизационной задачи, в котором имеются несущественные ограни¬
чения (16.8), соответствуют так называемые квазиравновес-
ные решения модели экономического взаимодействия.
Эта связь используется в алгоритме поиска равновесных или ква-
зиравновесных решений в модели экономического взаимодействия.
Поиск осуществляется путем последовательных расчетов оптимизацион¬
ной задачи, в которой от шага к шагу корректируются соотношения
целевых показателей отдельных подсистем (величины Х^).
Основное отличие оптимизационной модели со скалярным критери¬
ем оптимальности от модели экономического взаимодействия состоит в
следующем. В оптимизационной модели априорным является распреде¬
ление благ (эффекта) между подсистемами (значения величин Xfc), а
в модели взаимодействия априорно задаются экономические взаимоот¬
ношения между подсистемами (величины со&) •
Рассмотренные типы моделей неправомерно противопоставлять,
во-первых, из-за их формальной связи, во-вторых, эти модели базируют¬
ся на общем информационном обеспечении и вопросы совершенствова¬
ния описания условий производства и потребления для отдельных под¬
систем (множеств ) в них могут решаться одинаково; в-третьих,
предлагаемые алгоритмы решения модели взаимодействия базируют¬
ся на решении последовательности оптимизационных задач с глобальным
критерием оптимальности. Таким образом, эти два типа моделей следу¬
ет рассматривать как взаимодополняемые инструменты исследований.
Подробный пример расчетов по модели экономического взаимодей¬
ствия рассматривается в ВСМ, с. 128 — 134.
16.4. Опыт построения и анализа
моделей экономического взаимодействия
Прикладные исследования по моделям экономического взаимодействия
долгое время сдерживались отсутствием эффективных алгоритмов их
решения. Только в последние десятилетия разработки в этой области
экономико-математического моделирования отличаются не только
стремлением объяснить важные характеристики социально-экономичес¬
ких процессов, но и ориентацией на получение численных результатов.
Одна из первых прикладных моделей взаимодействия, основанная
на поиске равновесных решений, была разработана норвежским ученым
ЛЙохансеном в конце 50-х годов. В ней объемы производства и распре¬
деления ресурсов определяются взаимодействием на так называемых
’’конкурентных рынках” производителей, максимизирующих прибыль,
и потребителей, максимизирующих полезность. Наряду с объемными
454
(физическими) характеристиками определяются цены, выравнивающие
спрос и предложение, и стоимостные оценки факторов (норма прибыли
на капитал, зарплата). Модель была ориентирована на доступную в то
время норвежскую статистику и вычислительные средства. J1.Йохансе¬
ном был предложен эффективный метод нахождения решений в модели,
состоящий в ее линеаризации на каждом шаге итерационных расчетов
и последующем решении соответствующей системы линейных уравне¬
ний.
Появление эффективных алгоритмов поиска равновесных решений
в начале 70-х годов значительно активизировало прикладные исследо¬
вания по моделям экономического взаимодействия. Эти модели в на¬
стоящее время достаточно активно используются в количественном
экономическом анализе и оказывают влияние на формирование эконо¬
мической политики, оценку альтернативных мероприятий этой полити¬
ки. Только в последние несколько лет разработаны различные модели
для более чем 25 стран мира. В значительной мере они представляют
собой обобщение и развитие модели J1.Йохансена. При надлежащем
переосмыслении, критическом анализе и адаптации накопленный здесь
опыт моделирования может быть использован и в социалистических
странах. Об этом, в частности, свидетельствует венгерский опыт постро¬
ения и применения прикладных моделей экономического взаимодейст¬
вия (Э.Залаи, П.Киш).
Хотя разработанные к настоящему времени прикладные модели
базируются в основном на предположениях неоклассической теории,
западные исследователи все больше отказываются от многих из них
(предположений о совершенной конкуренции, гибкости цен, совершен¬
ной мобильности продуктов и факторов и т.д.). Вместо них в модели
вводятся поведенческие закономерности и особенности хозяйственного
механизма, характерные для изучаемых стран. Такое направление иссле¬
дований получило название ’’неоклассического структурализма”.
Исследования по построению и использованию современных прикладных моде¬
лей взаимодействия основываются на теоретических разработках по различным
механизмам экономического регулирования и в свою очередь стимулируют раз¬
витие таких разработок. Это работы в области теории ожиданий, несовершен¬
ных рынков, неопределенности, динамического равновесия. В последнее десятиле¬
тие существенно сократился разрыв между разработкой теоретических положений
и их включением в прикладные модели экономического взаимодействия.
В моделях этого типа теперь довольно часто используется концепция Барро -
Гроссмана о взаимосвязи между рынками потребительских товаров и труда,
базирующаяся на принципе ’’рациональных ожиданий” . Развитый английским уче¬
ным Р.Портесом и его коллегами подход, базирующийся на использовании неравно¬
весных решений, открывает широкие возможности эмпирических исследований
различных проблем и феноменов в экономике, в частности проблем ’’экономики
дефицита”, изучавшихся венгерским экономистом Я.Корнай.
Различные подходы к использованию моделей равновесия с середи¬
ны 60-х гг. выдвигаются советскими экономистами-математиками.
1 В ее рамках формально показывается, в частности, что дефицит потребитель¬
ских товаров оказывает дестимулирующее воздействие на трудовую активность.
455
Так, ВЛ.Волконским было, в частности, показано, что математический
аппарат равновесных моделей вовсе не привязан к изучению статических
систем и может эффективно использоваться для описания процессов
экономического развития; обращалось внимание на возможность на
основе таких моделей анализировать роль налога с оборота и системы
двух прейскурантов цен: розничных и оптовых.
Заслуживает внимания использование принципа экономического
равновесия в исследованиях коллектива под руководством В.Д.Беякина
(комплекс моделей типа ’’доход — товары” для исследования взаимо¬
связанных процессов производства, распределения и потребления с уче¬
том внешнеэкономических связей).
В последующие годы получили распространение исследования по
моделям, где согласование решений различных хозяйственных звеньев
осуществляется с активным использованием неценностных регуляторов.
Эти модели связаны с отказом от предположения об абсолютной гиб¬
кости цен, явным отражением наличия дефицитных и неходовых ресур¬
сов и товаров. Решения таких моделей взаимодействия получаются, как
правило, при неравновесных ценах.
ВМЛолтерович разработал подход к согласованию решений на ос¬
нове схем рационирования дефицитов и избыточных благ. Этот под¬
ход предусматривает включение в задачи подсистем физических
ограничений и бюджетных неравенств в фиксированных ценах. Решения
модели определяются выбором разбиения благ на дефицитные и избы¬
точные, а также параметров ограничений по ним исходя из равенства
совокупного спроса и предложения. Такие модели позволяют исследо¬
вать проблемы преодоления дефицита, соответствия потребительских
и производственных (розничных и оптовых) цен, бюджетного регули¬
рования через налог с оборота.
В книге Э.М.Бравермана и М.И.Левина [1] разработаны инструмен¬
тарий и понятийный аппарат использования квот по дефицитным ресур¬
сам в качестве одного из основных механизмов управления экономи¬
кой. Проведено исследование типовых моделей функционирования
экономики при неценностном регулировании.
В.ЛМакаровым [5] предложен подход к исследованию взаимодейст¬
вия экономических подсистем, основанный на системе договоров. Им
получены условия существования системы договоров, отклоняться от ко¬
торых невыгодно ни одной из подсистем, а также проведен нормативный
анализ таких решений (связь с ядром и равновесием). Значительный
вклад в разработку динамических конструкций моделей равновесия
внесли В J1 .Макаров и АМ.Рубинов [4] .
Поставленная задача перехода от преимущественно административ¬
ных к экономическим методам руководства на всех уровнях народного
хозяйства СССР радикально изменяет отношение к разработке и приме¬
нению моделей экономического взаимодействия. Эти модели должны
стать важным инструментом научного обоснования, с одной стороны,
456
централизованного планирования с активным использованием экономи¬
ческих рычагов и стимулов, с другой — взаимоотношений самостоятель¬
ных экономических объектов.
Представляется актуальной и вполне реальной разработка моделей
экономического взаимодействия, включающих предприятия, регионы и
центральные органы управления. Такие модели могут помочь в конкре¬
тизации принципов установления и количественной оценке основных
параметров платы за трудовые и природные ресурсы, нормативов распре¬
деления доходов; они могут использоваться также для изучения правил
распределения государственных заказов и заказов отраслевых и терри¬
ториальных органов управления, включая их размещение на конкурент¬
ной основе, способствовать решению вопросов перехода от централизо¬
ванного фондирования к оптовой торговле средствами производства.
Первоочередной является направленность разрабатываемых моде¬
лей на изучение социально-экономических проблем, таких, как реализа¬
ция принципов распределения по труду и социальной справедливости,
сбалансированность спроса и предложения потребительских товаров
и платных услуг.
Ниже на примере двух моделей экономического взаимодействия
рассматриваются достаточно типовые приемы конструирования и анали¬
за моделей данного класса.
16.5. Модель экономического взаимодействия
государства и населения в сфере труда и потребления
Рассмотрим идеализированную экономическую систему, в которой
реализуются следующие принципы функционирования. Планирование и
управление производством централизованы. Привлечение членов общест¬
ва в сферу производства осуществляется через материальное стимули¬
рование. Распределение благ производится в соответствии с количеством
и качеством используемого труда. У членов общества имеется свобода
выбора при удовлетворении потребностей в рамках получаемых дохо¬
дов.
В народном хозяйстве выделяются т + 1 подсистем: центральная
подсистема (государство) и т групп населения (по социальному поло¬
жению, профессионально-квалификационному составу, типу семей и
т.п.).
Экономические отношения заключаются в следующем: государство
выплачивает заработную плату трудящимся за использованную рабочую
силу, взимает налоги, предоставляет пособия и распределяет общест¬
венные фонды потребления. Население приобретает на денежные доходы
потребительские товары — продукты сферы производства.
Каждая подсистема стремится максимизировать свою целевую
функцию. При этом целевая функция государства отражает общие
15 Зак. 2414 457
интересы развития социалистического народного хозяйства (укрепление
общественного строя и обороноспособности, научно-технический про¬
гресс, охрана природной среды, решение коренных проблем повышения
уровня жизни, обеспечение условий будущего развития и т.д.), а целевые
функции групп населения — стремление к повышению уровня благосо¬
стояния соответствующей группы.
Введем обозначения:
X — вектор-столбец объемов производства конечной продукции
(производственный план народного хозяйства);
Z — вектор-столбец объемов продукции, используемой для обще¬
государственных нужд;
Yk — вектор-столбец продукции, потребляемой к-й группой населе¬
ния;
Ijc — затраты труда к-й группы населения;
lk — использование труда к-й группы населения в сфере производ¬
ства;
Р — вектор-строка цен на продукцию;
Uk — оплата единицы труда к-й группы населения;
U(Zf X) — целевая функция центральной подсистемы (в упрощенном
варианте U = U(Z);
Uk(Yk) — целевая функция k-й группы населения;
Lk — ресурс труда k-й группы населения, Lk >0;
Qk ~ сальдо финансовых отношений государства с к-й группой
населения (налоги — со знаком ’’минус”, денежные пособия и другие
выплаты — со знаком ’’плюс”).
Общая модель состоит из трех частей: модели центральной подсис¬
темы, моделей групп населения и общих условий для всех подсистем.
Модель центральной подсистемы:
U (Z, X)—>-шах;
(16.10)
*€*(/х U;
(16.11)
т т
Р (■X—Z) ^ 2 2
(16.12)
*=i k=i
Z> 0;
(16.13)
>0, k= 1, т.
(16.14)
Условие (16.21) означает, что возможности производства зависят
не только от имеющихся у государства средств производства и природ¬
ных ресурсов, но и от величин используемых трудовых ресурсов. При
этом К включает только неотрицательные векторы X. Условие (16.21)
выражает баланс доходов и расходов государства.
458
Модель к-й группы населения:
МЫ—*тах; (16.15)
lH<Lk; (16.16)
v^ + q.^PY.i (16.17)
/*> Oj (16.18)
0. (1619)
Условие (16.17) отражает баланс доходов и расходов А:-й группы
населения. В качестве одного из благ может быть выделено свободное
время.
Общие условия согласования решений для всех подсистем:
x>z+2rft; (16-2°)
fe+l
lk=lh, k=\, . . т. (16.21)
Условие (16.20) представляет собой систему балансов производства
и распределения продукции. План производства X определяется исходя
из производственных возможностей и потребностей общества, выражен¬
ных в целевых функциях государства и населения. Распределение произ¬
веденной продукции происходит на основе сочетания общегосударствен¬
ных интересов и интересов групп населения, с использованием социали¬
стического принципа распределения по труду и товарно-денежных отно¬
шений в сфере потребления. Условие (16.21) выражает требование
равенства затрачиваемого и используемого труда.
Роль цен и ставок заработной платы состоит в том, чтобы выравни¬
вать спрос и предложение по различным видам товаров и категориям
трудовых ресурсов. Система балансирующих (равновесных) цен и ста¬
вок заработной платы (Р*9 v*i,v*m j гарантирует (при некоторых пред¬
положениях), что балансы доходов и расходов (16.12), (16.17) будут
выполняться как равенства.
Условия существования равновесия д, модеди (16.10) - (16.21) формулируются
в виде требований к множеству (/1} 1т) и целевым функциям U(Z, XJ и
ик(Ук,Л Для существования равновесия достаточно, чтобы выполнялись следующие
условия: ^ ^
1) К (I ь 1т/ ^ 0, где 0 - нулевой вектор (X = 0);
2) множество выпукло, ограниченно и замкнуто;
3) не существует видов деятельности, в которых продукция получается без
каких-либо затрат;
15* 459
4) технологические процессы производства необратимы;
5) функции U(Z, X) и Uj^JYfc) вогнуты;
6) существует XЕ Xтакой, что к = 1,m и ^>0.
Важным требованием к организации общественного производства
при социализме является обеспечение полной занятости трудоспособного
населения. Исходя из этого можем принять = /ф к = 1, т. Тогда
условия (16.26) и (16.28) исключаются, вместо (16.27) следует запи¬
сать tfcLfc + qfc >PYjCi а вместо (16.31) — /д- =Lк = 1,т.
Особенностью рассмотренной модели и ее упрощенной модификации
(с полным использованием трудовых ресурсов) является то, что ставки
заработной платы v£ определяются эндогенно, в зависимости от эффек¬
тивности труда и соотношений спроса на рабочую силу соответствующей
категории и ее предложения. В действительности же при формировании
заработной платы учитываются и другие факторы. Регулируя ее, госу¬
дарство активно влияет на формирование денежных доходов и покупа¬
тельского спроса различных групп населения.
Пусть Dfc — централизованно планируемая величина доходов к-й
группы населения (включая заработную плату и другие денежные посту¬
пления) . Учитывая заданное использование рабочей силы, получаем сле¬
дующий вариант модели экономического взаимодействия.
Модель центральной подсистемы:
Щг, &)—+гпах; (16.22)
(16.23)
т
P(X-Z)>£Dh; (16 24)
0. (16.25)
Модель к-й группы населения:
и* (К*)-* max; (16.26)
PYk^Dk; (16.27)
Yk>0' (16.28)
Общие условия для всех подсистем:
т
к- 1
460
(16.29)
Второй вариант модели (16.32) — (16.39) в еще большей степени
акцентирует внимание на проблеме распределения потребительских
благ с использованием товарно-денежных отношений (см. числовой при¬
мер в ВСМ, с. 144- 146).
Основные направления развития рассмотренных вариантов модели
экономического взаимодействия — конкретизация множества допусти¬
мых планов производства, выделение производственных подсистем и
включение механизма экономических взаимоотношений в сфере произ¬
водства.
16.6. Модель экономического взаимодействия регионов
Основной вариант модели. Пусть территория страны разделена на т
регионов, которые могут обмениваться п видами продукции. Множество
ресурсно-технологических возможностей каждого региона s Е R =
= ^1,..., ^конкретизируется следующим образом:
0, Vs ^ О, (16.30)
AsXs + Gsus -j- Hsvs >bs+ (16.31)
где векторы Xs = (xf, ..., J&,), и* = (щ, ..., i£), vs = (vf, $ on-
ределяют соответственно объемы производства, вьюоза и ввоза транспор¬
табельных продуктов, а величины Xs характеризуют степень достижения
намеченных целей регионального развития. Заданные т5-мерные векто¬
ры-столбцы bs характеризуют фиксированные правые части, а сР — вклю¬
ченные в целевые установки ресурсы и потребности; As — матрица спо¬
собов производства, Gs и — матрицы способов вывоза и ввоза.
Совокупность наборов
*, = (**, us, Vs, Xs), (16.32)
удовлетворяющих условиям (16.40) и (16.41), обозначим через
рассмотрим прямое произведение этих множеств Ус = X,../5£т >
характеризующее всевозможные варианты экономического развития
народного хозяйства
* = {**}»<=* = {(■**» us, vs,Xs)}seR. (16.33)
При аэтом, естественно, реализуемы лишь сбалансированные решения
X Е , при которых
2 щ > 21 vh / =1 > • • •»(16.34)
seR seR
461
т.е. суммарный вывоз по каждому транспортабельному виду продукции
не меньше его суммарного ввоза. Выделяемое этим условием подмно¬
жество глобальных планов X обозначим через X.
Основной характеристикой сбалансированного глобального плана
X Е X служит отвечающий ему га-мерный вектор X с компонентами
\s(X) = ls(Xs) = Xs, s£R, (16.35)
указывающими достигаемые значения региональных целей (критериев
оптимальности).
Предположим, что заданы региональные сальдо обмена
со = (со1, со2, . . o>m),s2p = 0, (16.36)
а также положительный нормирующий вектор I = (7Ь 1п)> выделяю
щий множество Р(со) расчетных цен на обмениваемую продукцию
p = (pi, ■ •, рп); Pj>°'f&fPj =1 > (ie.31)
согласованных с принятым масштабом региональных сальдо обмена.
Тогда при фиксированных ценах pGP(oj) каждый регион решает следу¬
ющую экстремальную задачу.
Локааъная задача s-го региона. В множестве Xs всех допустимых
планов (16.43), выделяемых условиями (13.40) и (16.31), определить
такой, при котором
pus — pvs ^ со5; (16.38)
ks—►max. (16.39)
Пусть Xs (<4s, р) — множество оптимальных решений этой задачи.
Цены р Е Р (oj) являются равновесными, если в соответствующих
локальных задачах имеются оптимальные решения (16.32), порождаю¬
щие сбалансированное решение (16.33) (т.е. удовлетворяющее (16.44)).
Отсутствие равновесных цен в модели может быть связано с тем,
что отдельные регионы не могут достичь требуемых сальдо торговых
балансов со. Эти регионы мы условно называем ’’неблагополучными”,
а остальные — ’’благополучными”. Для ’’неблагополучных” регионов
условия (16.38) — (16.39) заменяются следующими: pus - pvs -> max.
Расчетные цены р, при которых в указанным образом модифициро¬
ванных региональных задачах имеются оптимальные решения, порожда¬
ющие сбалансированный вариант народнохозяйственного развития,
будем называть кв ази равновесными. В зависимости от спо¬
462
соба изменения исходных сальдо могут быть получены различные ква-
зиравновесные решения.
Рассмотрим некоторое v — параметрическое семейство оптимизаци¬
онных задач со скалярным критерием оптимальности, отвечающее
га-мерным положительным векторам v.
v-задача. При фиксированном положительном векторе v — (ух, ...,
vm) определить величину р и сбалансированный план (16.33), удовлет¬
воряющий ограничениям (16.30), (16.31) и (16.34), исходя из условий:
4>Pvs. (16.40)
р—►max. (16.41)
Можно показать, что оптимальному решению ^-задачи, где все огра¬
ничения (16.40) существенны, соответствует равновесное решение мо¬
дели экономического взаимодействия, а оптимальному решению оптими¬
зационной задачи, в котором имеются несущественные ограничения
(16.40), соответствует квазиравновесное решение модели экономичес¬
кого взаимодействия. В этом решении регионы, которые могут обеспе¬
чивать свои сальдо обмена, максимизируют целевые функции, а регионы,
которые этого сделать не могут, максимизируют свои платежи.
Равновесные решения определяют оптимальные по Парето распреде¬
ления эффекта.
Рассмотренные ранее классические понятия ядра и нечеткого ядра
непосредственно применимы к изучаемой модели при нулевых региона¬
льных сальдо.
При фиксированном векторе региональных сальдо (16.36) под не¬
четким cj-ядром исследуемой экономической системы понимается мно¬
жество всех эффективных решений оптимизационной ^-задачи, которые
не блокируются никакими так называемыми со-допустимыми коалици¬
ями R ' С R, удовлетворяющими условию 2 со_ < 0.
s Е R 9
Аналогично при фиксированном векторе региональных сальдо
под нечетким со-ядром исследуемой системы условимся понимать мно¬
жество всех эффективных решений оптимизационной модели, которые
не блокируются никакими так называемыми оьдопустимыми нечеткими
коалициями с долями участников hs Е [0; 1], удовлетворяющими сле¬
дующему однородному условию: X км. < 0. Доказывается что
sER 1
распределения эффекта, отвечающие любым эффективным равновесным
ценам р ЕР(со), совпадают с нечетким co-ядром рассматриваемой эконо¬
мической системы.
До сих пор предполагалось, что все межрегиональные перевозки про¬
дукции осуществляются через один центр. Выделение нескольких таких
центров, не меняя существа модели, позволяет задавать любые способы
описания межрегиональных связей, в том числе межрегиональные поста¬
463
вки, как в оптимизационной межрегиональной межотраслевой модели
(см. 8.6). Можно также считать, что величины us и v5 отражают только
часть межрегиональных поставок, осуществляемую по линии горизон¬
тальных взаимодействий, а централизованные поставки фиксированы
и включены в векторы bs.
Другие возможные обобщения модели, а также методы решения
обсуждаются в ВСМ, с. 150 — 156.
Приложения моделей экономического взаимодействия регионов.
Одна из первых попыток использования моделей такого типа для меж¬
региональных исследований была предпринята в 1965 г. американскими
учеными УЛйзардом и П.Айзардом. Построенная модель представляла
собой весьма пространное описание экономических и неэкономических
условий равновесия, однако в принципе не ориентировалась на практи¬
ческое использование. С математической точки зрения она укладывается
в рамки известной модели Эрроу — Дебре.
В советской литературе первые попытки формулировки моделей
конкурентного равновесия (типа Эрроу — Дебре) для анализа межрайон¬
ной экономики были предприняты В.А.Волконским и М.Г.Завельским.
Состояние равновесия В. А.Вол конский интерпретировал как систе¬
му договоров с указанием цен на весь период действия договора, причем
никому невыгодно уклоняться от предложенного ему договора. В.А.Вол-
конский не противопоставлял модели равновесия и оптимизационные
модели с глобальным критерием. Он отмечал, что возможно использо¬
вание товарно-денежного или рыночного механизма для организации
процесса децентрализованной выработки оптимального плана, но такой
процесс нуждается в регулировании. М.Г.Завельский предлагал исполь¬
зовать принцип равновесия для описания взаимодействия экономичес¬
ких районов и отраслей народного хозяйства, которые рассматривались
им как ’’производители” и ’’потребители”. Районы как ’’производи¬
тели” за определенную плату предлагают отраслям свою территорию.
При этом они максимизируют уровень жизни своего населения. Отрасли
предъявляют спрос на территорию отдельных регионов для размещения
своего производства. При этом они максимизируют прибыли.
Приведенная выше модель экономического взаимодействия реги¬
онов (МЭВР) и опыт ее практического использования подробно пред¬
ставлены в [15]. Первые прикладные расчеты взаимодействия крупных
экономических районов в экономике СССР были выполнены в ИЭиОПП
СО АН СССР в 1972 - 1975 гг.
В период с 1976 по 1983 г. МЭВР в составе модельного комплекса,
включающего также оптимизационную модель с глобальным критерием
оптимальности, использовалась в совместных исследованиях ИЭиОПП
СО АН СССР и исследовательского центра Секретариата ООН по моде¬
лированию долгосрочных перспектив развития мировой экономики.
ГЛАВА 17
ОПЫТ РАЗРАБОТКИ И ПРИМЕНЕНИЯ СИСТЕМ МОДЕЛЕЙ
НАРОДНОГО ХОЗЯЙСТВА
17.1. Экспериментальные разработки систем моделей
Обзор проектов системного моделирования. Проекты построения систем
моделей для планирования народного хозяйства СССР выдвигались в
ряде научных коллективов с начала 60-х г. Эти проекты основывались на
идеях декомпозиционного и композиционного подходов, анализировав¬
шихся в гл. 15 и 16. Однако в большинстве случаев содержание проектов
ограничивалось формализованным описанием народного хозяйства как
многоуровневой системы и интерпретацией возможностей теоретических
схем и алгоритмов согласования решений.
Ниже характеризуются только такие проекты, которые прошли эта¬
пы экспериментальной отладки информационного и математического
обеспечения и проведения экспериментальных расчетов. Рассматривае¬
мые экспериментальные системы моделей отличаются своей ’’специализа¬
цией”, составом отдельных звеньев и внешними связями, методами
получения согласованных решений.
Система моделей многоступенчатой оптимизации. Она разработана в
ЦЭМИ АН СССР (под руководством В. Ф.Пугачева) и предназначена для
использования при подготовке долгосрочных и пятилетних планов разви¬
тая народного хозяйства. Система охватывает три уровня: отрасль, мно¬
гоотраслевой комплекс, народное хозяйство в целом, акцентируя внима¬
ние в основном на структурном и технологическом аспектах развития
(см. [16]).
Общая схема расчетов включает несколько этапов. На первом этапе
на основе демографических моделей, макроэкономических моделей,
моделей потребительского спроса рассчитываются варианты конечного
продукта, достижимые при принятых гипотезах экономического и соци¬
ального развития. На втором этапе осуществляются вариантные расчеты
по межотраслевой модели и определяются интервалы допустимых изме¬
нений объемов производства отраслей. Следующий этап состоит в прове¬
дении оптимизационных расчетов по отраслям и многоотраслевым ком¬
плексам.
465
Состояние народнохозяйственного оптимума достигается в итератив¬
ном процессе увязки решений иерархически связанных подсистем, осно¬
ванном на последовательном применении методов многоступенчатой
аппроксимации производственных возможностей (см. 15.5). Их главная
особенность состоит в том, что на каждом вышестоящем уровне рассмат¬
ривается лишь часть множеств допустимых планов объектов нижестоя¬
щего уровня, находящихся в окрестности их оптимальных планов. На
уровне предприятия эта окрестность задается выпуклой комбинацией
локально-оптимальных планов (аппроксимирующим многогранником) ;
на уровне отрасли — аппроксимирующей гиперплоскостью.
В рамках исследований по данному проекту получены важные ре¬
зультаты по проблемам построения народнохозяйственного и локальных
критериев оптимальности. На основе системы моделей в ГВЦ при Гос¬
плане СССР проводились оптимизационные расчеты по многим отраслям
и ряду межотраслевых комплексов, использовавшиеся при подготовке
проектов пятилетних планов.
Система моделей оптимального народнохозяйственного планирова¬
ния в отраслевом и территориальном разрезах. Она разработана в ЦЭМИ
АН СССР в рамках общей концепции оптимального функционирования
социалистической экономики. Вариант такой системы, созданный под
руководством Э.Ф. Баранова и И.С.Матлина, опробован в эксперимен¬
тальных расчетах в середине 70-х годов.
Система включает модели регионов, межотраслевых комплексов,
сводную и функциональные модели верхнего уровня. Горизонтальные
связи между моделями регионов и межотраслевых комплексов описыва¬
ются моделью миграционных процессов и подсистемой моделей транс¬
портного комплекса. Проверка отраслевых и региональных планов на
согласованность осуществляется в координирующей модели верхнего
уровня. Если необходимой степени согласованности этих планов не до¬
стигнуто, осуществляется новый цикл расчетов с уточнением планов раз¬
вития многоотраслевых комплексов и возможностей их реализации по
региональным условиям.
Опыт эксплуатации экспериментального варианта позволил присту¬
пить к разработке и реализации уточненного варианта системы моделей
перспективного планирования, получившего название СМОТР (Согласо¬
вание Моделей Отраслевых и Территориальных Решений) (см. [16]*
разд. П , гл. 6 ). Эта система моделей предназначена для предваритель¬
ных стадий перспективного планирования и имеет трехуровневую орга¬
низацию: блок укрупненных расчетов экономического и социального
развития народного хозяйства в агрегированной номенклатуре (18 от¬
раслей материального производства) ; блок расчетов народнохозяйствен¬
ных пропорций и проверки их согласованности с отраслевыми и регио¬
нальными решениями в детализированной номенклатуре (около 260
важнейших видов продукции); блок расчетов показателей развития
отраслей (многоотраслевых комплексов) и регионов и обеспечение их
466
согласования в детализированной номенклатуре. Наиболее продвинулись
в прикладном отношении работы по первым двум уровням, составившие
самостоятельный комплекс моделей планирования (см. 17.3) .
Система моделей оптимального территориально-производственного
планирования. Первоначальный ее вариант был предложен А.Г.Аганбегя-
ном в 1962 г. и в течение продолжительного периода разрабатывался в
ИЭиОПП СО АН СССР.
Основные принципы конструирования и реализации данной системы
моделей состоят в следующем.
1. Цель функционирования системы — построение оптимальных
вариантов народнохозяйственных планов в укрупненных показателях,
согласованных с более детализированными оптимальными планами
подсистем разного уровня.
2. В системе охватываются и сочетаются главным образом два аспек¬
та народнохозяйственного планирования: производственный и террито¬
риальный.
3. Система строится ’’открытой”, т.е. предусматривается использова¬
ние внешней информации о прогнозах по научно-техническому прогрес¬
су, социальному развитию и т.д., получаемых посредством других моде¬
лей (систем моделей) или иными способами.
4. Система должна включать такие модели, которые методически
достаточно отработаны и испытаны при решении практических задач;
при этом каждая модель может использоваться в автономном режиме
или в рамках локализованной подсистемы моделей.
5. Согласование решений по моделям, входящим в систему, осущест¬
вляется с использованием как строго формализованных методов, так и
эвристических приемов, прошедших экспериментальную проверку при
решении практических задач.
Система моделей включает пять основных блоков: А — группу моде¬
лей сводного народнохозяйственного планирования (’’точечные” модели
народного хозяйства); В — группу моделей территориального народно¬
хозяйственного планирования (’’пространственные” модели народного
хозяйства); С — подсистему моделей планирования многоотраслевых
комплексов и отдельных отраслей; D — подсистему моделей региональ¬
ного планирования (модели республик и регионов, областей, территори¬
ально-производственных комплексов, промышленных узлов и т.д.);
Е — модели производственных объединений и предприятий (главным
образом как генераторы информации для моделей более высокого уров¬
ня). При этом допускается, что для одного экономического объекта
может строиться несколько моделей, прежде всего разноаспектных.
Главной структурной особенностью данной системы является раз¬
деление моделей народнохозяйственного уровня на два типа: ’’точеч¬
ные” и ’’пространственные”. Пространственные (многорегиональные)
модели занимают центральное положение в архитектуре системы по раз¬
нообразию обрабатываемой информации и рассчитываемых показателей,
467
числу прямых и обратных связей с другими блоками системы, синтези¬
рующим (системообразующим) функциям. Это обстоятельство оказало
значительное влияние на последующую эволюцию системы (см. 17.3).
Наиболее полное изложение первого этапа проведенных в ИЭиОПП
СО АН СССР исследований по системе моделей дано в [2]. Были получе¬
ны теоретические результаты по проблемам построения критериев опти¬
мальности и согласования глобального и локальных оптимумов в рам¬
ках декомпозиционного подхода. Разработано и доведено до практичес¬
кой реализации значительное число народнохозяйственных, отраслевых,
региональных моделей.
Система моделей оптимального размещения производства. Эта систе¬
ма разрабатывалась в СОПСе при Госплане СССР под руководством
М.М.Албегова как инструмент обоснования Генеральной схемы раз¬
вития и размещения производительных сил СССР (см. [16]). Она по¬
зволяет решать задачу выбора вариантов размещения и развития пред¬
приятий различных отраслей по территории страны с учетом локализации
ряда производственных ресурсов (природных, трудовых). Система
объединяет модели развития и размещения отдельных производств и
комплексов; распределения и использования локализованных ресурсов;
развития и размещения производства в отдельных регионах.
Для согласования отраслевых и региональных решений используют¬
ся зависимости выпусков продукции и затрат на их производство от
величин выделяемых региональных ресурсов. Построение этих зависи¬
мостей основано на параметрическом решении отдельных отраслевых
задач развития и размещения производства. Другой вид зависимостей,
используемых для согласования решений, составляют затраты региональ¬
ных ресурсов как функции масштабов производства на предприятиях
региона. Уточнение внутрирегиональных пропорций происходит с исполь¬
зованием внутрирайонной пространственной модели, учитывающей тер¬
риториальную дифференциацию факторов размещения внутри района,
агломерационный эффект (возникающий при совместном размещении
предприятий разных отраслей), нелинейность затрат на локальные ре¬
сурсы.
Эволюция концепций системного моделирования. К середине 70-х го¬
дов определилось главное направление прикладных разработок по си¬
стемному моделированию экономики — подготовка к включению от¬
дельных моделей и комплексов моделей в автоматизированную систему
плановых расчетов (АСПР) Госплана СССР и Госпланов союзных респуб¬
лик. В эскизный проект АСПР Госплана СССР, утвержденный в 1977 г.,
было включено четыре альтернативных проекта системного моделирова¬
ния. Предполагалось, что после научной доработки и опытной эксплуата¬
ции один-два варианта (или их модифицированная комбинация) будут
включены во вторую очередь АСПР. Однако этого не произошло. Ни
одну из предлагавшихся экспериментальных систем моделей народнохо¬
зяйственного планирования в полной мере реализовать не удалось. Уси-
468
лившаяся работа по включению моделей в реальный процесс планирова¬
ния дала новое понимание требований, предъявляемых к отдельным
моделям и комплексам моделей, выявила ряд неприемлемых методичес¬
ких, организационных и других предпосылок и свойств первоначальных
проектов системного моделирования. Отметим типичные их недостатки.
Во-первых, это итеративный процесс получения согласованных реше¬
ний для всего народного хозяйства и каждой его подсистемы в отдель¬
ности.
Во-вторых, это слишком ’’глобальный” характер разрабатывающих¬
ся систем моделей планирования, неприспособленность их для исследова¬
ния отдельных важных проблем, в том числе различными пользова¬
телями.
В-третьих, это трудности поэтапного ввода в действие предлагавших¬
ся систем моделей. Дело в том, что в соответствии с их архитектурой
готовность системы к работе лимитировалась готовностью последнего
конструктивного элемента, например модели какой-либо отрасли или
какого-либо региона; система моделей могла начать функционировать,
как правило, только при полном наборе всех ее элементов, включая
соответствующее информационное, программное и математическое обес¬
печение. Но, как известно, положение с разработкой различных экономи¬
ко-математических моделей далеко не одинаково и поэтому ориентация
на ’’замыкающих” разработчиков сильно сдерживает возможности комп-
лексирования полностью готовых элементов, затягивает апробацию
завершенных связок (комплексов) моделей.
В-четвертых, внедрение сложных многоуровневых и многоаспект¬
ных модельных комплексов сдерживалось слабой заинтересованностью
планово-управленческих органов и их функциональных подразделений.
Даже в Госплане СССР не находилось такого отдела, который мог бы
эксплуатировать какую-либо систему моделей в целом.
Со второй половины 70-х годов в ЦЭМИ АН СССР, НИЭИ и ГВЦ при
Госплане СССР, ИЭиОПП СО АН СССР постепенно вырабатывались но¬
вые представления о ближайших задачах системного моделирования
народного хозяйства. Наиболее существенные продвижения были связа¬
ны с разработкой специализированных модельных комплексов, учиты¬
вающих технологию планирования и предплановых исследований, воз¬
можности информационного, математического, технического обеспече¬
ния и профессиональную подготовленность пользователей.
Создание ряда модельных комплексов позволяет наметить новые
задачи системного моделирования народного хозяйства. Отдельные
модельные комплексы могут функционировать в автономном режиме,
учитывая важнейшие системные взаимосвязи. Вопросы согласования в
системе моделей разделяются на согласование решений внутри модель¬
ных комплексов и между ними. Быстро расширяющийся арсенал техни¬
ческих и программных средств позволяет по-новому подходить ко всем
стадиям экономико-математического моделирования: подготовке ин¬
469
формации, построению моделей, организации расчетов, анализу результа¬
тов решения. Вопросы регулярного использования моделей для подго¬
товки и принятия плановых решений рассматриваются теперь как часть
общей проблемы развития технологии народнохозяйственного планиро¬
вания1.
Современный этап прикладных экономико-математических исследо¬
ваний характеризуется прежде всего рядом технологических особен¬
ностей: прогрессом в способах получения, обработки и передачи инфор¬
мации; накоплением фонда моделей и автоматизацией сборки модель¬
ных конструкций; изменениями в режимах использования экономико¬
математических моделей.
Информация. Изолированные массивы исходных данных, используе¬
мые для решения однотипных задач, интегрируются в банки данных,
которые служат информационным фондом для широкого класса задач.
Создаются информационно-поисковые системы, банки данных ретро¬
спективного анализа, прогнозирования социально-экономического раз¬
вития отдельных хозяйственных звеньев и народного хозяйства в целом
и т.д. Организация проблемных банков информации осуществляется
на основе универсальных и специализированных систем управления база¬
ми данных (СУБД), позволяющих осуществлять процедуры накопления,
обновления, поиска и преобразования информации.
Модели. Создание типовых элементов и блоков моделей разнообраз¬
ных объектов народного хозяйства позволяет осуществлять конструиро¬
вание моделей на базе современных технических и программных средств
и возможностей организации и ведения информации, синтезируя модели
с заданными свойствами2.
Использование моделей. Основным методом работь1 с модельными
комплексами становится сценарный анализ, позволяющий проводить
целенаправленные прогнозы по моделям с изменяющимися условиями и
параметрами. На языке модельных конструкций это означает, что анали¬
зу подлежат не только эндогенные переменные модели (интенсивности
технологических способов, объемы использования ресурсов и т.д.), но и
фиксированные параметры (структура технологических способов, сво¬
бодные части ограничений, коэффициенты целевой функции и т.д.), рас¬
сматриваемые как экзогенные переменные. В необходимых случаях
1 Подробнее о новой технологии планирования, базирующейся на системном
использовании экономико-математических методов и вычислительной техники,
см. [9], [17].
2 Эти принципы конструирования моделей близки принципам, используемым
при создании гибких автоматизированных производств (ГАП) в промышленности,
систем автоматизированного проектирования (САПР) при организации проектных
работ, автоматизированных рабочих мест (АРМ) в научных исследованиях. Основу
указанных автоматизированных систем составляют совокупность типовых (’’эле¬
ментарных”) модулей и методика их сопряжения в определенные комплексы.
Выбор конкретной сети, коммутирующей первичные модули в комплексы с задан¬
ными свойствами, определяется конкретными целями и предоставляется пользова¬
телю системы.
470
могут меняться условия моделей и взаимосвязи между моделями.
Для прикладных экономико-математических моделей все более
характерной становится тенденция отделения функций разработчика от
функций пользователя. Это ведет к необходимости разработки специаль¬
ных языков пользователя, созданию развитого программного сервиса
для сопровождения процесса решения и анализа задач. Не менее важным
в развитии диалоговых режимов использования моделей является соче¬
тание формализуемых и неформализуемых процедур анализа и принятия
решений на всех этапах проведения расчетов.
17.2. Применение моделей
в автоматизированных системах планирования
Современное понимание требований к моделям и модельным комп¬
лексам сформировалось в существенной мере под влиянием проекти¬
рования и развития автоматизированной системы плановых расчетов
(АСПР).
АСПР представляет собой систему разработки государственных пла¬
нов экономического и социального развития на основе системного при¬
менения экономико-математических методов и вычислительной техники.
Как информационная система АСПР предназначена для автоматизации
сбора, накопления, хранения и обновления информации в процессе разра¬
ботки планов и контроля за их выполнением. Как вычислительная систе¬
ма АСПР предназначена для автоматизированной обработки данных и
решения различных плановых задач с использованием ЭВМ. Как органи¬
зационно-технологическая система АСПР обеспечивает структуризацию
процесса планирования и организацию всех видов работ по составлению
государственных планов.
В соответствии с организационной структурой планирования народ¬
ного хозяйства общая структура АСПР объединяет АСПР Госплана СССР,
АСПР Госпланов союзных республик, АСПР местных плановых органов1.
Во внутренней структуре каждой АСПР выделяются иерархически свя¬
занные компоненты: подсистема, блок, задача.
Подсистемы подразделяются на два вида: функциональные, осущест¬
вляющие подготовку разделов планов экономического и социального
развития, и обеспечивающие, создающие методы и средства для функ¬
циональных подсистем. Функциональные подсистемы подразделяются
на четыре уровня: I — подсистема ’’Сводный народнохозяйственный
план”; II — сводные подсистемы (сводные ресурсно-балансовые и свод¬
но-функциональные) ; III — комплексные отраслевые подсистемы;
IV — отраслевые подсистемы.
1 Планирование отраслей как особых подсистем, а также предприятий (объеди¬
нений) осуществляется в рамках ОАСУ и АСУП.
471
Блок — это часть подсистемы. Блоки функциональных подсистем
выделяются по принципу целевого объединения планово-экономических
задач и соответствуют, как правило, разделам и подразделам планов.
Блоки обеспечивающих подсистем объединяют однородные обеспечиваю¬
щие средства и методы.
Под планово-экономической задачей (ПЭЗ) в АСПР понимается
последовательность процедур получения, преобразования, анализа, офор¬
мления информации, на основе которой осуществляется подготовка пла¬
новых документов и происходит принятие планового решения. АСПР
определяет последовательность и методы решения отдельных планово¬
экономических задач, их соответствие объектам и органам планирова¬
ния, регламентирует состав и потоки информации. В результате процесс
планирования все больше приобретает характер производственной дея¬
тельности со своей технологией и инструментарием.
Технология планирования в СССР имеет содержательную и формаль¬
ную части. Содержательная часть определяется целями и задачами плани¬
рования, особенностями действующего организационно-хозяйственного
механизма. Она отображается в АСПР логическими моделями планового
процесса трех уровней.
Первый уровень представлен принципиальной логической схемой пла¬
нирования, определяющей связь между различными режимами функцио¬
нирования АСПР (долгосрочное, пятилетнее, годовое планирование) и
стадиями планового процесса (концепция, основные направления, про¬
ект плана). Модели второго уровня, получившие название сводно-задаю-
щих схем, разрабатываются для каждого режима функционирования
АСПР и определяют взаимосвязь функциональных подсистем по стадиям
планирования. Модели третьего уровня — функционально-структурные
схемы — отражают процесс разработки плана на уровне каждой подсисте¬
мы. При построении функционально-структурных схем используется
сочетание графического и описательного способов отображения: на мат¬
ричную сетку, отражающую организационную структуру АСПР и стадии
разработки плана, наносятся последовательно и параллельно осуществля¬
емые планово-экономические задачи. В результате получается графомат¬
ричная модель планового процесса, увязывающая организационную и
логическую его структуры. Логическая последовательность выполнения
планово-экономических задач отображается ориентированным графом.
Формальная часть технологии планирования определяется методами
планово-экономических задач, определенных логическими моделями
планового процесса. Эта часть технологии планирования описывается в
конкретных методиках и способах расчетов, обоснования и принятия
плановых решений. Развитие методов моделирования, вычислительной
техники, программного обеспечения позволяет расширить круг ПЭЗ,
допускающих формализованные описания, облегчить их анализ и расши¬
рить возможности человеко-машинного диалога в процессе выработки
плановых решений.
472
Формализуемые задачи в АСПР подразделяются на два класса. Пер¬
вый составляют задачи прямой обработки данных — прямые плановые
расчеты, информационно-справочные задачи, задачи обработки текстовой
информации. Второй класс ПЭЗ составляют задачи, решаемые с исполь¬
зованием экономико-математических моделей и их комплексов.
Место каждой экономико-математической модели в процессе разра¬
ботки плана, источники входной и направления выходной информации,
последовательность и порядок расчетов определяются на основе анализа
функционально-структурных схем. ’’Встраивание” экономико-математи¬
ческих моделей в реальную технологию планирования требует взаимной
адаптации как моделей, так и планового процесса.
Технология планирования, реализуемая в АСПР, формировалась под
воздействием ЭММ и вычислительной техники: возникают планово-эко¬
номические задачи, ранее не решавшиеся в плановой практике, изменяет¬
ся система статистической и плановой информации. С другой стороны,
новая технология планирования предъявляет к экономико-математичес¬
ким моделям ряд специальных требований. Они формулировались выше
применительно к межотраслевым динамическим моделям (см. 13.1,
13.6). Эти требования распространяются и на системы моделей.
Современный этап прикладных исследований по системному модели¬
рованию народного хозяйства — это создание интегрированных модель¬
но-программных комплексов, включаемых в автоматизированные систе¬
мы предплановых исследований и АСПР.
17.3. Комплексы моделей в перспективном планировании
и предплановых исследованиях
Современные тенденции в системном моделировании народного хозяйст¬
ва демонстрируются ниже на трех характерных проектах.
В ГВЦ и НИИЭИ при Госплане СССР создан и развивается централь¬
ный комплекс задач (ЦКЗ) АСПР, используемый в процессе подготовки
перспективных планов. В ЦЭМИ АН СССР в контакте с ГВЦ и НИЭИ при
Госплане СССР разработан комплекс моделей планирования (КМП). В
ИЭиОПП СО АН СССР осуществляются два проекта по созданию и при¬
менению модельных комплексов для предплановых обоснований разви¬
тия народного хозяйства и его основных подсистем.
Рассматриваемые комплексы моделей имеют различную ’’специали¬
зацию”, но реализуют в основном одинаковые методические, техничес¬
кие, организационные идеи. Общими их чертами являются: проблемно-
ориентированный характер комплексов моделей (при этом сужение
предмета и объекта моделирования по сравнению с первоначальными
проектами систем моделей компенсируется большей конкретностью);
интегрирование моделей и их комплексов, их типовых модулей (созда¬
ние ’’банков моделей”); информационное, программное, техническое
473
’’обустройство” модельных комплексов (создание банков данных,
информационно-поисковых систем на базе универсальных и специализи¬
рованных СУБД, программных средств решения задач, анализа результа¬
тов расчетов и т.д.) ; методы работы с модельными комплексами (орга¬
низация доступа пользователей, создание диалоговых средств общения,
применение сценарного анализа и т.п.).
Центральный комплекс задач АСПР Госплана СССР. Данный ком¬
плекс моделей (задач) ориентирован на проведение многовариантных
расчетов основных показателей экономического и социального развития
страны, достижение общеэкономической и межотраслевой сбалансиро¬
ванности. По состоянию на 1986 г. ЦКЗ включает 254 взаимосвязанные
планово-экономические задачи, 25 отраслевых и 11 сводных подсистем
АСПР. Основу автоматизированной технологии функционирования ком¬
плекса составляют три компонента: 1) единая для всех планово-эконо-
мических задач номенклатура отраслей и продуктов; 2) специальные
разработочные формы, с помощью которых регламентируется обмен
информацией между подразделениями Госплана; 3) сеть ЭВМ, объединя¬
ющая вычислительные средства ГВЦ Госплана СССР и мини-ЭВМ, уста¬
новленные непосредственно в отделах Госплана СССР. Информационные
потоки в ЦКЗ обеспечивают взаимосвязи между планово-экономически-
ми задачами, решаемыми внутри отделов Госплана, в разных отделах,
между его подразделениями и соответствующими министерствами и
ведомствами СССР и Советами Министров союзных республик.
В ЦКЗ включены наряду с методами прямых плановых расчетов и
целый ряд экономико-математических моделей. Процесс разработки
основных показателей пятилетнего плана в ЦКЗ содержит несколько
этапов.
1. Разработка предварительной (укрупненной) гипотезы развития
народного хозяйства. Гипотеза характеризуется комплексом сводных
и отраслевых (в разрезе 18 отраслей) показателей. Входной информаци¬
ей на этом этапе являются целевые установки концепции социально-эко¬
номического развития страны, демографические прогнозы, рациональ¬
ные нормы потребления, данные Комплексной программы научно-техни¬
ческого прогресса и т.д.
Основную роль на этом этапе играет подсистема ’’Сводный народно¬
хозяйственный план”. Все планово-экономические задачи выполняются в
ней с применением экономико-математических моделей. Используются
макромодели экономического роста, укрупненные межотраслевые
модели, модели демографических расчетов, модель рационального потре¬
бительского бюджета.
2. Конкретизация предварительной гипотезы развития народного
хозяйства в системе натуральных и стоимостных показателей. На этом
этапе в сводных подсистемах проводятся более детальные расчеты. Наи¬
более важная роль отводится модели натурально-стоимостного межот¬
раслевого баланса. По этой модели с использованием результатов реше¬
474
ния задач всех сводных подсистем в подсистеме ’’Сводный народнохо¬
зяйственный план” проводятся вариантные расчеты. Получаемые резуль¬
таты являются исходными для предложений к Основным направлениям
пятилетнего плана. Они передаются во все сводные и отраслевые под¬
системы.
3. Формирование предложений отраслей. Расчеты осуществляются в
25 отраслевых подсистемах, в том числе подсистемах ’’Топлив но-энерге-
тический комплекс”, ’’Сельское хозяйство”, ’’Транспорт”, ’’Торговля” и
подсистемах отраслей промышленности.
В подсистемах отраслей промышленности на основе предложений
министерств и исходных показателей к Основным направлениям эконо¬
мического и социального развития страны определяется потребность в
продукции отраслей промышленности. При этом в различных подсисте¬
мах используются как прямые плановые расчеты, так и различные эконо-
мико-математические модели (статистические, оптимизационные). Пот¬
ребность в продукции отрасли является основой для расчета показателей
оптимального развития и размещения отрасли. Результаты решения опти¬
мизационных задач являются основой для подготовки проектов планов
в отраслевом разрезе.
4. Корректировка отраслевых предложений и расчетов материаль¬
ных, трудовых и финансовых балансов. На этом этапе отраслевые подси¬
стемы передают результаты решения своих задач в соответствующие
сводные подсистемы. Во всех сводных подсистемах проводятся расчеты
соответствующих балансов, проверяется согласованность предложений
отраслевых подсистем. Этот процесс, как правило, итеративный, т.е. из
сводных подсистем скорректированные данные по лимитам ресурсов
' поступают вновь в отраслевые подсистемы.
5. Формирование сбалансированной системы показателей — предло¬
жений к Основным направлениям экономического и социального разви¬
тия страны на пятилетие. На этом этапе проводится заключительная про¬
верка согласованности разработанных в отраслевых и сводных подсисте¬
мах предложений. Это — итеративный процесс. Особую роль в нем игра¬
ют экономико-математические модели развернутого натурально-стои-
мостного и укрупненного стоимостного межотраслевых балансов.
Важнейшим направлением развития ЦКЗ является создание интегри¬
рованных межподсистемных комплексов задач. Первоочередными из
них рассматриваются: комплекс расчетов показателей планов социально¬
го развития и повышения уровня жизни народа; интегрированный ком¬
плекс территориального народнохозяйственного планирования; расчеты
по межотраслевым комплексам (топливно-энергетическому, агропро¬
мышленному, машиностроительному, транспортному и т.д.). В работах
по развитию АСПР особо выделяется создание информационно-вычисли¬
тельного комплекса и межподсистемного комплекса задач сквозного
планирования научно-технического прогресса.
Задачи создания межподсистемных комплексов (и в том числе раз¬
вития ЦКЗ) предъявляют новые требования к используемому экономи-
475
ко-математическому инструментарию: развитие методов увязки системы
межотраслевых и финансовых балансов; формирование структуры ко¬
нечного продукта, отвечающей социально-экономическим целям плано¬
вого периода; отражение в коэффициентах плановых межотраслевых
моделей достижений НТП и т.д. В связи с проводимой реформой управ¬
ления экономикой весьма актуальным является моделирование хозяйст¬
венного механизма. В рамках ЦКЗ это прежде всего увязка натурально¬
вещественных и финансовых пропорций, система расчетов важнейших
экономических нормативов, моделирование сферы распределительных
отношений.
Комплекс моделей перспективного планирования. Данный комплекс
моделей (КМП), разработанный в ЦЭМИ АН СССР, предназначен для
оперативного ведения аналитических и плановых вариантных расчетов
показателей развития народного хозяйства в режиме долгосрочного пла¬
нирования [8]. Комплекс создавался на основе обобщения предшеству¬
ющего опыта использования отдельных моделей в практике плановых
расчетов и разработки совместно с ГВЦ Госплана СССР комплекса ук¬
рупненных межотраслевых моделей (см. 13.6).
В КМП все модели распределены по пяти иерархическим уровням.
На первом уровне используются однопродуктовые эконометрические
модели (определяющие величины общественного продукта, националь¬
ного дохода, долю накопления в национальном доходе и другие макро¬
показатели) . На втором уровне используются много секторные эконо¬
метрические модели, в которых макропоказатели, полученные на верх¬
нем уровне, детализируются по отраслям народного хозяйства. На осно¬
ве решений эконометрических моделей формируются целевые показате¬
ли, ограничения и параметры моделей третьего уровня — межотраслевых
моделей и моделей финансового планирования. На четвертом уровне
рассматривается трехзональная территориальная модель. Пятый уровень
представлен отраслевыми и региональными моделями планирования и
блоком моделей межрайонного транспорта.
Технологическая схема расчетов предусматривает последовательное
решение соответствующих задач разных уровней с активным участием
экспертов (плановых работников) в уточнении первоначальных гипотез
о поведении параметров, анализе промежуточных результатов, выделе¬
нии определяющих целевых и экзогенных переменных для следующего
этапа расчетов, определении области изменения управляющих парамет¬
ров в вариантных расчетах и т.д.
Организационно-методическая схема расчетов обеспечивается разви¬
тыми информационными, программно-математическими, инструктивны¬
ми и техническими средствами. Основные компоненты КМП — банк
моделей, целевой блок, база данных, система манипулирования данны¬
ми, система разработки моделей.
База данных обеспечивает хранение разнообразной информации и
эффективную работу с ней пользователей модельного комплекса и
476
выполняет важные интегрирующие функции, позволяя связывать отдель¬
ные части комплекса в единое целое. Через базу данных результаты рас¬
четов из одной модели передаются на вход другой, связываются целевой
блок и межотраслевые модели, программы расчета сводно-аналитичес¬
ких показателей и модели и т.д. Кроме того, через базу данных осущест¬
вляется связь комплекса с ’’внешним миром”. Наряду с информацион¬
ными массивами база данных включает соответствующие программные
средства, обеспечивающие доступ к ней со стороны пользователей и раз¬
личных прикладных программ. Эти средства дают возможность просмот¬
ра, корректировки, считывания и записи информации, удаления и дубли¬
рования отдельных модулей и т.п. Основные программы базы данных
реализованы в диалоговой постановке.
Хранимыми элементами в базе данных являются также отдельные
уравнения, тождества, типовые блоки соотношений между основными
экономическими показателями, используемые системой разработки
моделей при их сборке.
Система манипулирования данными (СМД) предназначена для обра¬
ботки и представления в удобной для пользователя форме исходной
информации и результатов решения задач. Быстрой обработке получае¬
мых результатов, их анализу, сравнению между собой служит специально
разработанный диалоговый язык. СМД включает средства изменения
текстовых и числовых модулей, а также набор математических действий
над таблицами. Использование СМД в режиме взаимосвязанных расчетов
позволяет накапливать их результаты, формировать на специализирован¬
ном языке последовательность выполнения расчетов по комплексу моде¬
лей. Совместно с базой данных СМД составляют системообразующую
сферу для комплекса моделей планирования.
Система разработки моделей объединяет программные средства фор¬
мирования новых моделей или модификации имеющихся на основе хра¬
нящихся в базе данных уравнений, тождеств, типовых блоков отдельных
условий, а также генерации новых уравнений. СМД обеспечивает откры¬
тость комплекса, возможность адаптивной подстройки используемых
моделей для решения конкретных планово-экономических задач.
Функционирование КМП обеспечивается развитыми программными
средствами. Основными принципами, принятыми при их разработке,
являются: обеспечение полной автоматизации расчетов по взаимосвязан¬
ным моделям и организация программного обеспечения на модульной
основе.
Специализированные комплексы моделей в предплановых исследо¬
ваниях. Разрабатываемые в ИЭиОПП СО АН СССР проекты СИРЕНА
(СИнтез РЕгиональных и НАроднохозяйственных Решений) и СОНАР
(Согласование Отраслевых и НАроднохозяйственных Решений) имеют
общую методологическую и информационно-техническую основу, но раз¬
личную проблемную ориентацию. Они используются при разработке мно¬
говариантных прогнозов, разделов Комплексной программы научно-те х-
477
нического прогресса, оценке народнохозяйственных последствий осуще¬
ствления крупных производственных, социальных, научно-технических
программ.
Модельные комплексы, составляющие методическую основу проек¬
тов СИРЕНА и СОНАР, имеют общие базовые модели народнохозяйст¬
венного уровня. Более детальное исследование проблем крупных регио¬
нов и многоотраслевых комплексов осуществляется с помощью специа¬
лизированных оптимизационных межрегиональных межотраслевых
моделей (ОМММ), в которых особо интересующий объект описывается
более подробно, т.е. реализуется рефлекторный подход (упрощенная
исходная ОМММ рассматривалась в 8.6).
Например, специализированная ОМММ-Украина включает более дета¬
лизированный блок по Украинской ССР, специализированная ОМММ-хи-
мия — детализированный блок по химическому комплексу и т. д. В свою
очередь к специализированным ОМММ подключаются особые модели
(или группы моделей) отдельных регионов и отраслей, модели целевых
программ, крупных объектов. Такая конструкция модельных комплек¬
сов обеспечивает получение оптимальных и сбалансированных решений
на верхнем уровне, согласованных с более детальным обоснованием
вариантов развития конкретных региональных и отраслевых подсистем и
объектов. Оба проекта предполагают расширение круга пользователей,
заинтересованных в оценке возможностей и эффективности развития
’’своих” объектов с позиций народного хозяйства. Благодаря тому, что
пользователи подключаются к модельному комплексу со своими инфор¬
мационными массивами, обновляется общий информационный банк.
Характерной формой использования модельных комплексов
СИРЕНА и СОНАР является проведение сценарных расчетов. Под сцена¬
рием понимается исследование какой-либо важной проблемы или сово¬
купности гипотетических проблемных ситуаций путем проведения целе¬
направленных вариантных расчетов по моделям с изменяющимися усло¬
виями, управляющими переменными и параметрами. В отличие от обыч¬
ных вариантных расчетов каждый сценарий объединяет группу вариан¬
тов, описывающих определенную стратегию или проблему и различаю¬
щихся обычно лишь значениями параметров.
На основе ’’народнохозяйственных” сценариев проводится исследо¬
вание влияния на процессы долгосрочного социально-экономического
развития и на развитие отдельных регионов и межотраслевых комплек¬
сов крупных изменений, которые могут происходить в народном хозяй¬
стве СССР в обозримой перспективе. Группа ’’региональных” сценариев
ориентирована на изучение влияния возможных изменений в социально-
экономическом и техническом развитии конкретного региона на обще¬
союзные темпы и пропорции, межрегиональные связи и тенденции разви¬
тия данного региона и остальных районов страны. Группа ’’отраслевых”
сценариев используется при изучении влияния меняющихся условий раз¬
вития отдельного межотраслевого комплекса (отрасли на конечные
478
народнохозяйственные результаты и пропорции общественного произ¬
водства, исследовании взаимодействия сопряженных отраслей при согла¬
совании стратегий их развития. Наибольший интерес представляют ’’ком¬
плексные” сценарии, в которых совмещаются гипотезы об изменении
различных народнохозяйственных, отраслевых и региональных факторов
и условий социально-экономического развития.
Общий прогресс в развитии рассмотренных комплексов моделей в
значительной мере будет определяться взаимным обогащением ос¬
новных принципов их построения и использования, совмещением эле¬
ментов и блоков методического, информационного, математического
обеспечения.
Литература к разделу III
1. Автоматизированная система плановых расчетов. М.: Экономика, 1980.
2. Аганбегян А. Г., Багриновский К. А., Гранберг А. Г. Система моделей народно¬
хозяйственного планирования. М.: Мысль, 1972.
3. Браверман Э. М., Левин М. И. Неравновесные модели экономических систем.
М.: Наука, 1981.
4. Введение в теорию и методологию системы оптимального функционирования
социалистической экономики. М.: Наука, 1983.
5. Волконский В. А. Проблемы совершенствования хозяйственного механизма
М.: Наука, 1981.
6. Казакевич Д. М. Экономические методы в плановом управлении. Новоси
бирск: Наука, 1985.
7. Канторович JLB. Экономический расчет наилучшего использования ресурсов
М.: Изд-во АН СССР, 1960.
8. Комплекс моделей перспективного планирования. М.: Наука, 1986.
9. Кулешов В. В. Модельное обеспечение технологии плановых расчетов. Новоси¬
бирск: Наука, 1980.
10. Макаров В. Л., Рубинов А. М. Математическая теория экономической динами¬
ки и равновесия. М.: Наука, 1973.
11. Макаров В.Л. Экономическое равновесие: Существование и экстремальные
свойства. Итоги науки и техники (современные проблемы математики) .Т. 19
М.: ВИНИТИ, 1982.
12. Маленво Э. Лекции по микроэкономическому анализу. М.: Наука, 1985
13. Новожилов В.В. Проблемы измерения затрат и результатов. М.: Экономика.
14. Пурков В.И. Декомпозиция в задачах большой размерности. М.: Наука, 1981
15. Рубинштейн А. Г. Моделирование экономических взаимодействий в территори
альных системах. Новосибирск: Наука, 1983.
16. Система моделей народнохозяйственного планирования. М.: Наука, 1982
17. Уринсон Я. М. Совершенствование технологии народнохозяйственного плани
рования. М.: Экономика, 1986.
18. Хильденбрант В. Ядро и равновесие в больших экономиках. М.: Мир, 1986.
19. Хозяйственный механизм в системе оптимального функционирования социа¬
листической экономики. М.: Наука, 1985.
20. Шаталин С.С. Функционирование экономики развитого социализма. М.: Изд-во
МГУ, Г982.
21. Экланд И. Элементы математической экономики. М.: Мир, 1983.
ОГЛАВЛЕНИЕ
Предисловие 3
Введение . . 5
Раздел I
Теоретико-методологические проблемы моделирования 16
Глава 1
Метод математического моделирования в экономике . . 16
1.1. Моделирование как метод научного познания 16
Понятия ’’модель” и ’’моделирование”. Сущность процесса модели¬
рования (16). О формах моделирования (18)
1.2. Особенности применения метода математического моделирования
в экономике 22
Сложность экономических процессов и явлений (22). Особеннос¬
ти экономических наблюдений и измерений (23). Случайность и
неопределенность в экономическом развитии (24). Проверка аде¬
кватности моделей (26)
1.3. Классификация экономико-математических моделей 28
1.4. Этапы экономико-математического моделирования 31
1.5. Место математического моделирования в экономической науке и
экономической практике 36
Математическое моделирование и развитие экономической теории
(36). Роль прикладных экономико-математических исследований
(40)
Литература 42
Глава 2
Материальный аспект экономики 43
2.1. Материальный аспект экономики как объект моделирования .... 43
2.2. Оптимизационная микромодель народного хозяйства 45
Задача математического программирования и оптимальное плани¬
рование (45). Недостатки задачи математического программиро¬
вания как логической основы оптимального планирований (49)
2.3. Народнохозяйственные критерии оптимальности 50
Целевая функция общественного благосостояния (51). Миними¬
зация срока достижения заданных целей (52). Дерево целей (53).
Проблема критерия оптимальности с позиций общей методологии
моделирования (54)
2.4. Взаимные задачи оптимизации народного хозяйства 55
2.5. Многоцелевая (векторная) оптимизация 59
Эффективные решения (оптимум по Парето) (60). Условная суб-
480
оптимизация (61). Скаляризация (свертка) векторного критерия
оптимальности (62). Квазиоптимизация (64)
2.6. Оптимизация народного хозяйства в условиях неопределенности 65
Подход к оптимизации в условиях неопределенности с использова¬
нием моделей детерминистского типа (66). Применение специаль¬
ных математических методов (70) *
Литература I 71
Глава 3
Социально-экономический механизм 72
3.1. Принципы соизмерения затрат и результатов в оптимальном плани
ровании 73
Оптимизационная модель народного хозяйства и оптимальные оцен
ки (74). Соизмерение затрат и результатов при максимизации об
щественного благосостояния и минимизации затрат труда (81)
Оптимальные оценки и ценностные показатели (86)
3.2. Подходы к моделированию элементов социально-экономического
механизма . 87
Модели хозяйственных звеньев (88). Моделирование подсистем
социально-экономического механизма (90). Модели экономичес¬
кого взаимодействия подсистем <звеньев) народного хозяйства
(91)
3.3. Модели с обратными связями производства, распределения и бла¬
госостояния . . 1 92
Литература 96
Раздел II.
Моделирование на народнохозяйственном уровне 97
Часть А. Экономическая статика 97
Глава 4
Моделирование сферы производства 99
4.1. Технология и производственные возможности 99
4.2. Производственные функции и функции производственных затрат.
Основные понятия 101
4.3. Производственные функции с взаимозаменяемыми ресурсами. По¬
казатели использования ресурсов .1/. 104
Общие свойства функций (104). Средняя и предельная эффектив¬
ность использования ресурсов (105). Эквивалентная заменяемость
ресурсов (107). Эластичности производства и взаимозаменяемости
ресурсов (108). Анализ типовых производственных функций
(НО)
4.4. Производственные функции с взаимодополняемыми ресурсами и
функции производственных затрат 116
Основные понятия (116). Анализ типовых функций производст¬
венных затрат (117). Связь между производственными функция¬
ми с взаимозаменяемыми ресурсами и функциями производствен¬
ных затрат (120)
4.5. Анализ производственных способов 123
Производственные способы и их сочетания (123). Анализ однопро-
481
дуктовых способов (124). Оптимальное сочетание производствен¬
ных способов (125)
Литература 127
Глава 5.
Моделирование сферы потребления 128
5.1. Целевая функция потребления: Соизмеримость и взаимозаменяе¬
мость потребительских благ 128
Общие свойства ЦФП (128). Соизмеримость и взаимозаменяемость
потребительских благ (131). О построении ЦФП (133)
5.2. Моделирование поведения потребителей в условиях товарно-денеж¬
ных отношений 136
Анализ простой модели поведения потребителей (136). Направле¬
ния использования модели (138). Обобщения модели поведения
потребителей (139)
5.3. Функции покупательского спроса 140
Связь модели поведения потребителей и функций спроса (140).
Функции и коэффициенты эластичности спроса от дохода (143).
Функции спроса и коэффициенты эластичности от цен (146)
5.4. Нормативный подход к прогнозированию и планированию потреб¬
ления 147
Литература 149
/
у
Глава 6
Модели межотраслевого баланса 150
6.1. Межотраслевой баланс общественного продукта. Система показа¬
телей 150
Межотраслевой материальный баланс (150). Межотраслевой баланс
общественного продукта (151)
6.2. Основная модель межотраслевого баланса 155
Модель межотраслевых материально-вещественных связей (155).
Модель межотраслевых зависимостей цен (160). Анализ основных
допущений модели (161)
6.3. Математический анализ модели межотраслевого баланса . 163
Свойства матрицы А (163). Коэффициенты косвенных и полных ^
народнохозяйственных затрат (166). Существование решений мо¬
дели межотраслевого баланса (171)
6.4. Применение межотраслевого баланса в анализе материально-веще-
ственных и трудовых пропорций 172
Анализ взаимосвязей валового и конечного общественного про-
дукта (172). Определение полных народнохозяйственных затрат
на фонды конечного продукта (176). Анализ структуры и динами¬
ки полных трудовых затрат (178)
6.5. Применение межотраслевого баланса в анализе стоимостных про¬
порций 180
Сравнительный анализ систем цен (180). Взаимосвязи стОимост- Г"-"’4
ной, материально-вещественной и функциональной структур конеч¬
ного продукта (183)
6.6. Плановые расчеты на основе модели межотраслевого баланса .... 186
Расчеты сбалансированных уровней производства исходя из вари¬
антов конечной продукции (186). Обоснование производственной
482
программы со стороны производственных ресурсов (188). Плано¬
вые расчеты со смешанным составом неизвестных (189)
Литература 190
Глава 7
Развитие модели межотраслевого баланса 191
7.1. Межотраслевой натурально-стоимостный баланс (модель, учитыва-
юшдя организационную структуру народного хозяйства) 191
7.2. Моделирование материально-финансовых связей. Межотраслевой
баланс денежного оборота 194
7.3. Моделирование межотраслевых взаимосвязей производства, лич¬
ного потребления и доходов населения 198,
7.4. Межотраслевая модель взаимодействия экономики и окружающей
среды . . Г ^20
7.5. Межотраслевые модели с внешними связями
Анализ влияния внешних связей на экономику страны и региона
(207). Модификации модели с внешними связями (210)
7.6. Межрегиональные межотраслевые балансы 214
Схемы объединения региональных моделей (214). Принцип пост¬
роения межрегионального межотраслевого баланса (216). Модель
межрегионального межотраслевого баланса с торговыми коэффи¬
циентами (217)
7.7. Уточнение и обобщение межотраслевых производственных связей 219
Уточнение функций производственных затрат и условия взаимоза¬
меняемости ресурсов (219). Модели межотраслевых взаимодей¬
ствий (221). Производство сопряженной продукции и использова¬
ние комплексного сырья (222)
Литература 223
Глава 8
Оптимизационные межотраслевые модели 224
8.1. Общая линейная оптимизационная модель 224
Построение модели (224). Оптимальные оценки и анализ опти¬
мального плана (225)
8.2. Критерии оптимальности в прикладных моделях 230
Максимизация фонда потребления в фиксированных ценах (230).
Максимизация потребления в заданном ассортименте (231). Мак¬
симизация уровня потребления при заданных функциях потребле¬
ния (234)
8.3. Оптимизационные модели на основе матрицы межотраслевого ба¬
ланса 236
Модель межотраслевого баланса как частный случай оптимизаци¬
онных моделей (236). Оптимизационная модель межотраслевого
баланса продукции и производственных м9ЩНостей (238). Модели
с ограничениями по общим ресурсам (239) "
8.4. Оптимизационные межотраслевые модели с производственными
способами 241
Модель с минимизацией затрат труда (241). Модели с условиями
максимизации конечной продукции (243). Расширенные оптими¬
зационные модели (246)
8.5. Оптимизационные модели с блоком внешнеэкономических связей 247
8.6. Оптимизационные межрегиональные модели 248
Литература 251
483
Часть Б. Экономическая динамика 252
Глава 9
Основные понятия экономической динамики 254
9.1. Характеристики экономического развития 254
Траектории и динамические ряды (254). Характеристики скорости
и интенсивности изменения динамического ряда (255). Средние
характеристики развития (257)
9.2. Типы экономического развития. Трендовые модели 259
Сглаживание динамических рядов и трендовые модели (259). Ти¬
пы экономического развития и их трендовые модели (260). Пост¬
роение трендовых моделей (263). Прогнозирование на основе
трендовых моделей (264). Сплайн-функции (265)
9.3. Экстенсивные и интенсивные факторы развития. Факторные модели 267
Однофакторные модели экономического роста (268). Многофак¬
торные модели экономического роста (270)
9.4. Воспроизводственные циклы и временные лаги 273
Типы воспроизводственных циклов и их продолжительность (273).
Временные лаги и лаговые модели (274). Периодические колебания
(275)
Литература 277
Глава 10
Макроэкономическое моделирование 278
10.1. Модели динамики общественного продукта и национального дохода 279
Простейшая модель (280). Рост с постоянной и монотонно изме¬
няющейся нормой накопления (284). Модели с лагами капиталь¬
ных вложений (286)
10.2. Оптимизация динамики национального дохода 288
Критерии и условия оптимизации (288). Оптимизация с нерегули¬
руемой нормой накопления (289). Оптимизация с динамическими
и структурными ограничениями (294). Оптимизация с постоянной
нормой накопления (296). Выход на режим роста с постоянной
нормой накопления (298) f ^
10.3. Факторные модели экономического развития С^ОО у
Макроэкономические динамические производственные функции 4 ^
(300). Типовые МПФ (302). Построение и анализ макроэкономи¬
ческих производственных функций в СССР (305)
10.4. Расширенные модели экономического роста 306
Синтез производственной функции и балансов производственных ре- ?—*
сурсов (307). Модель с фиксированной нормой капитальных вложе¬
ний (309). Оптимизация с постоянной нормой капитальных вложе¬
ний (311). Оптимизация с переменной нормой капитальных вложе¬
ний (312)
10.5. Моделирование динамики двух подразделений общественного про¬
изводства 317
Схемы воспроизводства К. Маркса - В. И.Ленина и макромодели¬
рование (317). Динамика двух подразделений в моделях воспро¬
изводства общественного продукта (319)
10.6. Макроэкономические модели в системе прогнозирования и плани¬
рования 322
Литература 326
484
Глава 11
Теоретические структурные модели . 327
11.1. Динамические межотраслевые модели 327
Динамическая модель В. Леонтьева (328). Динамика замкнутой
производственной системы (329). Экономический рост при раз¬
личных траекториях потребления (332). Обобщения модели В. Ле¬
онтьева (334). Оптимизационные модели с матрицами межотрасле¬
вого баланса (337)
11.2. Модели расширяющейся экономики и магистральное развитие ... 339
Основные понятия (339). Модель Неймана (341). Использование
результатов теоретического анализа (344)
11.3. Динамическая модель Л.В. Канторовича 346
Динамические производственные способы (346). Основные соот¬
ношения модели (347). Динамические оптимальные оценки (349)
Литература 350
Глава 12
Элементы прикладных динамических межотраслевых моделей ... 351
12.1. Межотраслевые производственные связи 352
12.2. Взаимосвязи капитальных вложений, основных производственных
фондов и динамики производства 355
Связи капитальных вложений с основными фондами, производст¬
венными мощностями, динамикой производства (355). Балансы
основных производственных фондов и производственных мощнос¬
тей (359)
12.3. Динамизация моделей сферы потребления 362
Динамизация целевой функции потребления (362). Особенности
воспроизводства и использования благ многократного и длительно¬
го пользования (363). Критерии и условия оптимизации потребле¬
ния в прикладных динамических моделях (365)
Литература 367
Глава 13
Построение и применение динамических межотраслевых моделей 368
13.1. Типы прикладных динамических межотраслевых моделей и харак¬
тер их использования 368
Общие требования к прикладным моделям (368). Основные типы
динамических межотраслевых моделей (369)
13.2. Рекурсивные модели 372
13.3. Модели с обратной рекурсией 375
Балансовая модель с обратной рекурсией (375). Оптимизационная
модель с обратной рекурсией (377). Оптимизационная модель
межотраслевого натурально-стоимостного баланса (379)
13.4. Квазидинамические модели межотраслевого баланса продукции и
производственных мощностей 381
13.5. Динамичесьсие модели с двусторонними связями отрезков плано¬
вого периода 386
Модель с распределенными лагами (387). Оптимизационная мно¬
гопериодная модель (388)
485
13.6. Совершенствование динамических межотраслевых моделей и их
использование в народнохозяйственном планировании 390
Литература 394
Раздел III
Моделирование народного хозяйства как многоуровневой системы 395
Глава 14
Общие принципы и проблемы системного моделирования народно¬
го хозяйства 395
14.1. Необходимость системного моделирования
14.2. Демократический централизм в управлении и требования к систем
ному моделированию экономики
Структуризация народного хозяйства (399). Разработка моделей
подсистем и отдельных звеньев (400). Согласование решений в си
стеме моделей (401). £
14.3. Основные подходы к построению систем моделей народного хозяй
ства
Декомпозиционный и композиционный подходы (404). Подходьг
различающиеся по степени детализации внутренних и внешних свя
зей (406). Схемы согласования решений в системах моделей (408)
14.4. Аспекты исследований по системному моделированию
Теоретические исследования (410). Прикладные исследования
(412).
395
397
404
410
Г л а в а 15
Многоуровневая оптимизация на основе декомпозиционного под¬
хода 414
15.1. Основные черты декомпозиционного подхода 414
Метамодель и модели подсистем (414). Условия согласования на¬
роднохозяйственного и локального оптимумов (416). Примеры
декомпозиционного подхода в экономическом анализе (419).
15.2. Итеративные методы построения детализированного оптимального
плана 421
15.3. Построение агрегированного народнохозяйственного плана, согла¬
сованного с детализированными локально-оптимальными планами 423
15.4. Итеративное агрегирование 425
15.5. Методы аппроксимации производственных возможностей 432
15.6. Согласование решений с использованием функций отклика 435
15.7. Согласование решений в системе моделей методами рефлекторного
моделирования 438
Глава 16
Согласование решений на основе экономических методов 440
16.1. Моделирование экономических взаимодействий: общая характе¬
ристика 440
16.2. Основные понятия экономических взаимодействий 444
Экономический оптимум по Парето (444). Ядро экономической
486
системы (445). Кооперативная игра, ядро.игры (446). Равновес¬
ные решения в экономической системе (447). Некооперативная
игра и равновесие по Нэшу (448).
16.3. Общая модель экономического взаимодействия подсистем 449
Модель и ее основные свойства (449). Соотношение ядра и равно¬
весия (451). Нечеткие коалиции и нечеткое ядро (452). Свойства
модели взаимодействия с Ф 0 (452). Соотношение равновесия
и глобального оптимума (453).
16.4. Опыт построения и анализа моделей экономического взаимодейст¬
вия 454
16.5. Модель экономического взаимодействия государства и населения
в сфере труда и потребления 457
16.6. Модель экономического взаимодействия регионов 461
Основной вариант модели (461). Приложения моделей экономи¬
ческого взаимодействия регионов (464).
Глава 17
Опыт разработки и применения систем моделей народного хозяй¬
ства^ 465
17.1. Экспериментальные разработки систем моделей 465
Обзор проектов системного моделирования (465). Эволюция кон¬
цепций системного моделирования (468).
17.2. Применение моделей в автоматизированных системах планирования 471
17.3. Комплексы моделей в перспективном планировании и предплано¬
вых исследованиях 473
Центральный комплекс задач АСПР (474). Комплекс моделей пер¬
спективного планирования (476). Специализированные комплек¬
сы моделей в предплановых исследованиях (477).
Литература к разделу III 479
Гранберг А. Г.
Г77 Моделирование социалистической экономики: Учеб.
для студ. экон. вузов. - М:: Экономика, 1988. - 487 с. -
ISBN 5-282-00659-6
Учебник написан известным советским специалистом, чле-
ном-корреспондентом АН СССР. В нем рассмотрены современ¬
ные теоретические подходы и практические методы моделирова¬
ния экономичеЪких процессов и особенности использования
математического аппарата при их изучении. Учебник отличается
доходчивостью изложения, достигаемой с помощью хорошо
подобранных примеров и графиков.
Для студентов экономических вузов, обучающихся по специ¬
альности ’’Экономическая кибернетика”. Может быть использо¬
ван в системе повышения квалификации работников экономи¬
ческих и плановых органов.
0604020102-232
г " ■ ■ ■■ 63-88 ББК 65.050.9 (2)
011 (01)-88
Учебная
Гранберг Александр Григорьевич
МОДЕЛИРОВАНИЕ СОЦИАЛИСТИЧЕСКОЙ ЭКОНОМИКИ
Зав. редакцией А. С. Воронин
Мл. редактор Е. Е. А ндреева
Худож. редактор Е. А. Ильин
Техн. редактор А. В. Кузюткина
Корректоры Е. А. Киселева, J1’ М. Филькова
Оформление художника А. Р. Косолапова
ИБ № 3175
Сдано в набор 03.06.88. Подписано в печать 03.10.88. А08340.
Формат 60 х 88 1/16. Бумага офсетная № 2. Гарнитура пресс-
роман. Печать офсетная. Уел. печ. л. 29,89/29,89 усл.кр.-отт.
Уч.-изд.л. 31,68. Тираж 16000 экз. Заказ 2414. Цена 1 р. 40 к.
Изд. № 6614.
Издательство ’’Экономика”, 121864, Москва,
Бережковская наб-, 6.
Ленинградская типография № 4 ордена Трудового Красного Зна¬
мени Ленинградского объединения ’’Техническая книга” им.
Евгении Соколовой Союзполиграфпрома при Государственном
комитете СССР по делам издательств, полиграфии и книжной
торговли. 191126, Ленинград, Социалистическая ул., 14.