А.  Киселев
 СИСТЕМАТИЧЕСКИЙ
 КУРС  АРИФМЕТИКИ

А. КИСЕЛЕВ
СИСТЕМАТИЧЕСКИЙ
КУРС АРИФМЕТИКИ
К 150-летию
со дня рождения
А. П. Киселева
Орел
Орловский государственный университет
2002

УДК 511.1
К 44
Печатается по решению оргкомитета Всероссийской
научно-практической конференции
«Актуальные проблемы обучения математике
(к 150-летию со дня рождения А. П. Киселева)»
Киселев А. П.
Систематический курс арифметики. Реп¬
ринтное издание к 150-летию со дня рожде¬
ния А. П. Киселева / Предисловие Ф. С. Авдее-
К 44 ва. — Орел: Изд-во Орловского государственно¬
го университета, 2002. С. 264.
Настоящая книга является репринтным изда¬
нием учебника 1912 года «Систематический курс
арифметики» А. П. Киселева, который представ¬
ляет единое систематизированное изложение кур¬
са арифметики для старших классов.
Книга предназначена для широкого круга чита¬
телей: учителей, студентов, научных работников.
УДК 511.11
К 44
© Орловский государственный
университет, 2002
Подписано в печать 30,09.2002 г. Формат 84х108’/32.
Печать офсетная. Бумага офсетная. Уел. п. л. 13,86.
Тираж 400 экз. Заказ № 5456
Отпечатано в ОГУП «Орловская областная типография «Труд
302028, г. Орел, ул. Ленина, 1.

ПРЕДИСЛОВИЕ
Орловщина — родина многих талантливых людей,
ставших по праву нашим культурным достоянием, веч¬
ным капиталом России. Выдающийся русский педагог-
математик Андрей Петрович Киселев — один из них.
«Систематический курс арифметики» — первый
из многих учебников, принесших всеобщее призна¬
ние уроженцу города Мценска Орловской области.
Только его «Геометрия» выдержала 42 (!) издания,
более 30 раз издавалась «Алгебра», до 1938 года было
36 изданий учебника, который держит в руках чита¬
тель. С 1938 года, когда «Систематический курс ариф¬
метики» был утвержден в качестве стабильного, его
общий тираж составил 3 миллиона экземпляров.
Жизнь не стоит на месте. Современная математика,
как и школьное образование в целом далеко ушли впе¬
ред. Однако и в наше время учебники А. П. Киселева
остаются актуальными. По словам академика А. Н. Ти¬
хонова, они не потеряли своей значимости «благодаря
высокому педагогическому мастерству, простоте, до¬
ходчивости и логичности изложения».
Представляется, что это именно то, чего порой так
недостает современным школьным учебникам. Педа¬
гогическая общественность России, представители на¬
уки, психологи, врачи, все, кому не безразличны про¬
блемы школьного образования, не безразлично буду¬
щее страны, — давно бьют тревогу: чересчур акаде¬

— 4 —
мичные, не учитывающие возрастных и психологичес¬
ких особенностей детей учебники наносят непоправи¬
мый ущсро здоровью юных россиян. Не случайно эта
проблема вынесена на уровень Правительства и Прези¬
дента России.
Вот почему издание «Систематического курса ариф¬
метики» — это не только дань уважения и призна¬
тельности выдающемуся педагогу-математику в год его
150-летия, Ь-О еще и назидание современным авторам
школьных учебников. Школе нужны такие учебники,
в которых не упущено главное, нет лишнего, где дос¬
тупность, простота и ясность в изложении сочетаются
с высокой точностью и научностью определений, где
строго соблюдается мера между наукой, логикой учеб¬
ного предмета и психологией школьника... Словом,
такие учебники, как «Систематический курс арифме¬
тики» А. П. Киселева, хорошо знакомый не одному
поколению наших сограждан.
Талант, трудолюбие, богатый 25-летний педагоги¬
ческий опыт А. П. Киселева должны быть востребова¬
ны и сегодня, в век информационных технологий. Уве¬
рен в том, что каждый обратившийся к этой книге
получит не только начальные математические знания,
но и прочную основу, хороший задел для дальнейше¬
го совершенствования, приобретения знаний, отвеча¬
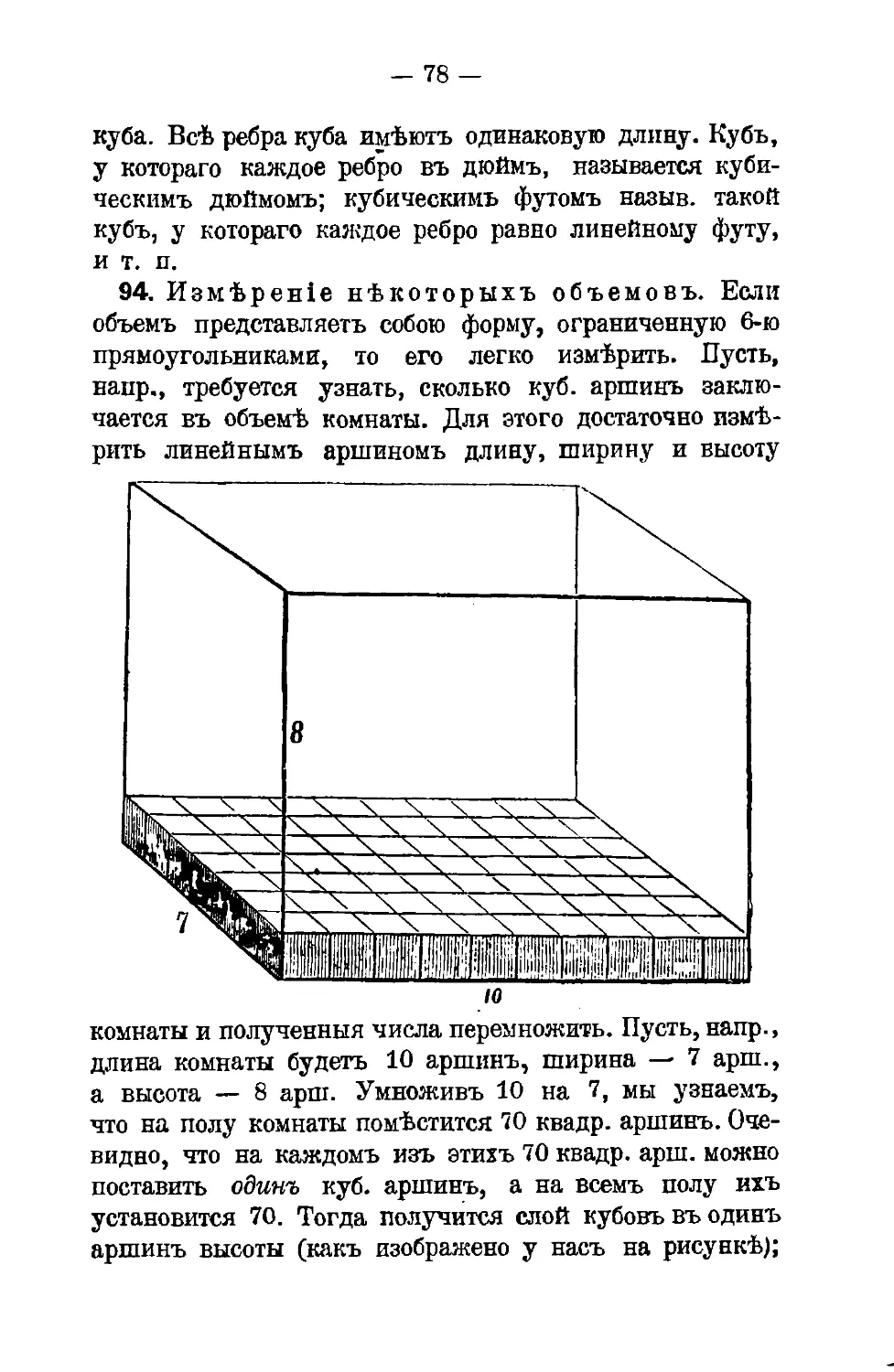
ющих основным требованиям времени, пополнения
нашего главного богатства — интеллектуального по¬
тенциала нации.
Ф. С. Авдеев,
доктор педагогических наук, профессор.

А. КИСЕЛЕВЪ.
СИСТЕМАТИЧЕСКИ
КУРСЪ АРИ0МЕТИКИ.
Допущенъ Уч. Ком. М. Н. Пр. въ качествЬ руководства для среднихъ
учебныхъ заведетй, мужскихъ и женскихъ (Журн. М. Н. Пр. 1910,
май), рекомендована Уч. Ком. при Св. СинодЬ для употреблешя
въ духовныхъ училищахъ въ качеств^ руководства (Церк. В'Ьд. 1892,
J6 37), одобренъ Учебн. Ком., состоявшимъ при собственной Его
Императорскаго Величества Канцелярш по учрвждешямъ Императрицы
Мар1и въ качества руководства для всЬхъ средннхъ учебныхъ ваве-
дешй етого ведомства (иавЪщеше отъ 11 января 1901 г., J6 822),
одобренъ Деп. Торговли и Ман., какъ пособ1е для коммерческихъ
училшцъ (ивв'Ьщеше отъ 30 мая 1898 г., № 14228), допущенъ къ
употреблетго въ старшихъ классахъ городскихъ и уЬздныхъ учи¬
лшцъ, внлюченъ въ каталогъ квигь для учительскихъ библ1отекъ.
Для кадетскихъ корпусовъ рекомендованъ, какъ руководство.
Издан1е двгдцать четвертое.
к
о
X
ю
tr-
rt
К
S
И»данУ> хнижваго магавина
а. в. думнова.
вож» формою
.НасгЬдн. 6р. С&даввыхъ*.
MOCRBA.
Тов&ркцемае .Печатня С. П. Яковлев**. Петровка» Салтыкове*!! вер.» д. Т-ства, •»
19 12.

/
w . I' ’	11 .

— 7 —
ПРЕДИСЛ0В1Е.
Къ четвертому издажю. Хотя успехъ первыхъ трехъ из-
данШ „Систематическаго курса ариеметики" даетъ объек¬
тивное основан1е думать, что этотъ учебникъ достаточно
нриспособленъ къ потребностямъ нашихъ среднихъ учебныхъ
заведетй, тЬмъ не менее, приступая къ 4-му издатю, мы
сочли нужнымъ подвергнуть тщательному пересмотру содер¬
жите прежнихъ издашй, съ целью, во-первыхъ, более согла¬
совать его съ последними программами и учебными планами,
а, во-вторыхъ, достигнуть возможно большей простоты въ
изложенш.
Главнейпйя особенности 4-го издашя заключаются въ
следующемъ:
1. Согласно замечашямъ Учен. Ком. Мин. Нар. Пр. сде¬
ланы изменетя въ определенга первыхъ четырехъ действШ,
причемъ въ основу определенШ поставлено понятае о суммгъ.
2. Во всемъ курсе строго проведено различ!е между ве¬
личиною и ея значениями.
3. Въ курсе дробей проведена большая систематичность.
4. Дано более научное определете пропорциональности
величинъ и указаны признаки прямой и обратной пропорщо¬
нальности для руководства въ чаетныхъ случаяхъ.
5. Согласно последнимъ программамъ. помещены въ самомъ
тексте нумеращи славянская и римская, а также—въ сокра-
щенномъ изложенш—метрическая система меръ.
6. Добавлена статья о приближенныхъ вычисленгяхъ,
проходимая въ 6-мъ классе реальныхъ училищъ.
Въ седьмомъ издажи, помимо редакщонныхъ улучшенШ,
сделаны еще следунящя изменетя:
1 Указанъ (мелкимъ шрифтомъ) способъ еокращеннаго де¬
ления. принятый ныне во многихъ французскихъ учебникахъ
ариеметики.

— 8 —
2. Улучшено определение процента съ целью придать ему
большую общность.
3. Изм’Ьненъ способъ рЪшешя задачъ на цепное правило
съ целью его упрощения.
4. Въ статьё „Приближенныя вычисления" сделаны н*ко-
торыя добавления и приведены примеры съ целью придать
большую полноту и практичность изложение этого важнаго
вопроса.
Въ десятомъ изданж существенно дополнена статья подъ
назватемъ ИЗадачи на вычисленге времениВо-первыхъ,
для такихъ задачъ указанъ другой npieMb решетя, чаще
всего практикуемый въ действительности; во-вторыгъ, уяснено
(мелкимъ шрифтомъ) различ!е между календарнымъ счетомъ.
по которому промежутокъ времени выражается въ невподн*
постоянныхъ единицахъ, каковы месяцы и годы, и точнымъ
счетомъ, по которому промежутокъ времени измеряется по¬
стоянными единицами: неделями, сутками и подразделениями
сутокъ. Делая эти добавления, мы имели въ виду поставить
эту статью и въ практическомъ, и въ теоретическомъ отно-
шенш въ уровень со всеми остальными статьями „Система¬
тическаго курса ариеметики". Впрочемъ, добавления такъ рас¬
положены, что если бы преподаватель, по недостатку времени
или по другимъ причинамъ, пожелалъ ограничиться сообще-
шемъ ученикамь сведенш въ объеме прежнихъ издашй, онъ
вполн* имеегь возможность это сделать, только выключивъ
изъ текста некоторый строки.
Въ томъ же издании добавлены общгя формулы для р*-
шеюя вадачъ на проценты и на учетъ векселей; эти добав¬
ления могуть быть полезны при повторены ариеметики, а
также для всехъ т*хъ лицъ, который ищутъ въ учебникахъ
практическихъ указашй для быстрейшаго производства вычи-
слеюй.
Въ некоторыхъ местахъ улучшено изложеше и приданъ
внешности более удобный видъ.
Четырнадцатое издаже тщательно просмотрено съ целью,
где только возможно, сделать иэложеше более яснымъ и про-
стымъ, а также и съ целью сокращетя учебнаго матер1ала
безъ нарушешя стройности курса. Изъ более важныхъ изме¬
нений, сдЬланныхъ въ этомъ изданш. ук&жемъ следующая:

— 9 —
1. Объяснеше умножетя и д'Ьлетя десятичныхъ дробей
(§§ 192 и 196) изложено на основанш правилъ умножетя
н делетя обыкновенныхъ дробей, а не на основанш изме¬
няемости произведетя и частнаго дробныхъ чиселъ при
изменены данныхъ чиселъ, какъ это делалось въ предыду-
щихь издае!яхъ; вследмтае этого § 176, въ которомъ раз-
сматривается эта изменяемость, напечатанъ теперь мелкимъ
шрифтомъ, какъ необязательный при прохождены.
2. Ариеметическое отношеше и ариеметическая пропорщя,
какъ не представляющая теоретическаго интереса и не имею-
шдя практическихъ применений, выпущены совсемъ съ целью
уменьшить количество учебнаго матер1ала.
3. Кратному отношены» дано более научное определение
(§ 212), сближающее его съ темь, которое разсматривается
въ геометры.
4. При объяснены решетя задачъ на простое и сложное
тройное правило на первое место выдвинуть споеобъ при-
веден5я къ единице, вследсттае чего является возможность
сократить изложение главы о пропорцш (такъ §§ 220, 221
и 222, въ которыхъ говорится объ изменены членовъ про¬
порцш безъ нарушения ея, о сокращены пропорцш и объ
уничтожены дробныхъ членовъ пропорцш, могутъ быть- опу¬
щены безъ ущерба для курса).
5. Изложеше сложнаго тройного правила значительно упро¬
щено и сокращено.
Въ пятнадцатомъ изданы несколько улучшено изложетв
статьи: „ Обращен» е перюдпческихъ дробей въ обыкновенная".
Двадцатое издаже содержать много добавлений и нзме-
нешй. Укажемъ главнейшая (въ порядке следоватя парагра-
фовъ):
§ 29. Добавлено о случаяхъ Нычитан1я, когда уменьшаемое
меньше вычитаемаго или равно ему.
§ 45. Добавлепо разъяснение случаевъ умножетя, когда ка¬
кое-либо изъ данныхъ чиселъ равно 1 или 0.
§ 96. Добавлена выноска о соотношении аптекарскаго веса
съ метрическими мерами
§§ 102 и 103. Упрощены определешя раздробления и пре-
вращешя.

— 10 —
§ 116. Упрошено изложете признака делимости наб.
§ 133. Помещавшееся въ предыдущихъ издатяхъ въ конце
этого § следств1е: „частныя, получаемыя отъ делешя двухъ
чиселъ па ихъ обшаго наиб, делителя, суть числа взаимно про-
стыя“ выброшено изъ этого параграфа, такъ какъ въ этомъ
месте курса ариеметики истина эта остается безъ приме-
нешя. Она помещена теперь въ § 155, где, при объяснены
сокращешя дробей, въ ней является надобность.
Вследъ за § 142, озаглавленеымъ: „Происхождение дроб¬
ныхъ чиселъ отъ измерены'1 добавленъ новый § (143-й по
нумерацш 20-го издашя): „Происхождение дробныхъ чиселъ
отъ делешя целаго числа на равныя части"; этимъ, конечно,
достигается более полное уяснен] е значешя дробнаго числа.
§§ 183 и 184. Упрощено определете десятичной дроби и
изменено объяснеше изображен 1я ея.
§ 192. Два отдельныя правила умножетя десятичной дроби
на целое число и десятичной дроби на десятичную дробь заме¬
нены однимъ правиломъ.
§ 240. Упрощено решеше задачъ на проценты.
§§ 243 и 244. Значительно упрощено решеше задачъ на
учетъ векселей сведешемъ ихъ на соответствующая задачи
на проценты (мы руководились при этомъ замёчашемъ, вы-
сказаннымъ въ отзыве Учебнаго Комитета М. Н. Пр. о 12-мъ
изданш нашего учебника „Краткая ариеметика для Городскихъ
училшцъ").
Изъ немпогихъ изменений, введенныхъ въ21-е и 22-е из¬
дашя, укажемъ следующая:
Соотношен1е между обыкновеннымъ аптекарскимъ весомъ
и метрически.мъ, которое прежде помещалось въ выноске къ
§ 96. теперь отнесено нами ниже, после изложения десятич¬
ныхъ дробей, а именно къ § 209, въ которомъ говорится о
метрическихъ мерахъ.
Въ § 110 мы теперь ограничиваемся изложешемъ только
двухъ -есновныхъ истинъ о делимости, опуская третью („если
сумма двухъ слагаемыхъ и одно изъ этихъ слагаемыхъ де¬
лятся на какое-нибудь число, то и другое слагаемое разде¬
лится на пего:£); сообразно этому теперь несколько изменено
изложете § 116.

—11 —
Правило § 130 (о нахожденш дЬлителей составного числа)
выражено теперь бо.т£е ясно и подробно, равно какъ и пра¬
вило § 157 (о приведенш дробей къ наименьшему общему
знаменателю)
Въ § 166 добавлено (мелкимъ шрифтомъ) разъяснеше, что
данное въ этомъ параграфа опредЪлеше умножетя на дробь
не противоречив опредЬлетю умножетя на целое число.
Въ § 170 упрощено разъяснеше второго свойства произ-
ведетя (чтобы умножить какое-нибудь число на произведете,
достаточно....)
Въ § 212 подробнее разъяснено вначете отношетя, когда
опо есть целое число и когда оно есть дробь.

I

— 13 —
ОТДЪЛЪ ПЕРВЫЙ.
Отвлеченныя цЬлыя числа.
I. Счислен1е.
1.	Попятiе о числ£. Одинъ предметъ да одинъ
предметъ составляютъ два предмета: два предмета да
одинъ предметъ составляютъ три предмета; три да одинъ
составдяютъ четыре... Одинъ, два, три, четыре... и т. д.
называются целыми числами.
Число одинъ называется иначе единица.
Всякое ц'Ьлое число, кром! единицы, предстабляетъ
собою собраше единицъ.
Число наз. предметнымъ (или конкретнымъ), если оно
сопровождается назвашемъ т'Ьхъ предметовъ, изъ кото-
рыхъ составлено; напр., пять карандашей.
Число наз. отвлеченными, если неизвестно, собраше
какихъ предметовъ оно представляетъ; напр., пять.
Въ начал! курса мы будемъ говорить только о чис-
лахъ ц'Ьлыхъ.
2 Естественный рядъ чиселъ. Если къ еди¬
ниц! присоединимъ еше единицу, къ полученному чи¬
слу снова присоединимъ единицу, къ этому числу опять
присоединимъ единицу и т. д., то получимъ естествен¬
ный или натуральный рядъ чиселъ:
одинъ, два, три, четыре, пять, шесть, семь и т. д.
Наименьшее число въ этомъ ряду единица; наибать-
шаго числа н!тъ, потому что ко всякому числу, какъ
бы валико оно ни было, можно прибавить еще единицу;
значить, естественный рядъ чиселъ можетъ быть про-
должаемъ безъ конца.

— 14 —
3. Счетъ. Чтобы им^ть ясное понятге о собранш цред-
метовъ, мы должны сосчитать ихъ. Счетъ состоитъ въ
томъ, что, отдЬляя одинъ предметъ за другимъ (на самомъ
д’Ьл'Ь или только мысленно), мы называемъ каждый разъ
число, составившееся изъ отд-Ьленныхъ предметовъ. Такъ,
считая столы въ класс'Ь, мы отд’Ьляемъ мысленно одинъ
столъ за другимъ и говоримъ: одинъ, два, три, четыре и т. д.
Чтобы ум^ть считать до какого угодно большого чи¬
сла, надо научиться называть всякое число.
Способъ составлять назватя для всякихъ чиселъ назы¬
вается словеснымъ счислемемъ или словесною нумеращею.
Способъ выражать всякое число особыми письменными
знаками называется письменными счислежемъ пли пись¬
менною нумеращею.
Ознакомимся сначала со счислешемъ чиселъ до ты¬
сячи, а загЬмъ и со счисдешемъ другпхъ чиселъ.
4. Словесное счислен1е до тысячи. Первый
десять чиселъ носятъ слЪдуюшдя названья: одинъ, два,
три, четыре, пять, шесть, семь, восемь, девять, десять
(или десятокъ). Съ помощью этихъ назвашй и еще
н'Ькоторыхъ другихъ можно выражать и друпя числа.
Положимъ, наир., мы желаемъ назвать число поставлен-
ныхъ зд’Ьсь черточекъ:
Для этого отсчитываемъ десять черточекъ и отд’Ьля-
емъ ихъ отъ остальныхъ; потомъ отсчитываемъ еще де¬
сять черточекъ и отдЬляемъ ихъ отъ остальныхъ. Про-
должаемъ такъ отсчитывать по десятку до гЬхъ поръ,
пока либо совеЬмъ не останется черточекъ, либо ихъ
останется мен’Ье десяти. Теперь сосчитаемъ десятки и
оставшаяся черточки (или единицы); такъ какъ десят-
ковъ оказалось четыре, а оставшихся черточекъ три, то
мы можемъ число веЬхъ черточекъ назвать такъ: четыре
десятка, три единицы.

— 15 —
Когда въ чпсле окажется более десяти десятковъ, то
лоступаюгь такъ же, какъ если бы эти десятки были
отдельный единицы, т.-е. отсчитываютъ десять десят¬
ковъ, потомъ еще десять десятковъ, снова десять десят¬
ковъ ит. д. до гЪхъ поръ, пока можно. Каждые десять
десятковъ называютъ однимъ словомъ: сто или сотня.
Положиыъ, что въ какомъ-нибудь числе оказывается:
сотенъ—три, десятковъ—пять и оставшихся единицъ—
семь; такое число можно назвать такъ: три сотни, пять
десятковъ, семь единицъ.
Если сотенъ въ числе окажется более десяти, то счи-
таютъ ихъ тоже десятками. Каждыя десять сотенъ на¬
зываютъ однимъ словомъ тысяча.
5.	Сокращетпе нйкоторыхъ назван1й. Въ
нашемъ языке употребительны некоторый сокращенныя
назван!я чиселъ. Такъ, десять да одинъ назыв. одинна¬
дцать (т.-е. одинъ-на-десять); десять да два наз. двена¬
дцать (т.-е. две-на-десять) и т. п. Два десятка наз. два¬
дцать (т.-е. два-десять); три десятка наз. тридцать (т.-е.
три-десять) п т. д. (четыре десятка наз. сорокъ). Две
сотни наз. двести; три сотни наз. триста и т. д.
6 Письменное счислен1е до тысячи. Пер-
выя девять чиселъ обозначаются особыми письменными
знаками или цыфрами: 1, 2, 3, 4, 5, 6, 7, 8, 9. Съ по¬
мощью этихъ девяти цыфръ и десятой О (нуль), озна¬
чающей отсутств1е числа, можно изобразить всякое число.
Для этого условились: простыя единицы ставить на
первомъ месте справа, десятки—на второмъ месте, сот¬
ни—на третьемъ месте; напр.: триста сорокъ пять изо¬
бразится такъ: 345) триста сорокъ: 340, _ триста: 300,
триста пять: 305.
Съ левой стороны изображешя числа не принято писать
нулей; такъ, вместо -024 пишутъ короче: 24, потому
что п въ первомъ, и во второмъ изображенш цыфра 2
стоить на второмъ месте, а цыфра 4—на первомъ, и,
следовательно, 2 означаетъ десятки, а 4—единицы.

— 16 —
Все цыфры, кроме нуля, называются значащими цыф
рами.
Число, изображаемое одною цифрой, называется одно-
значнымъ, двумя цифрами—двузначнымъ, многими циф¬
рами—многозначнымъ .
7 Словесное счислеше чиселъ, большихъ
тысячи. Когда считаемыхъ иредметовъ более тысячи,
то составляютъ изъ нихъ столько тысячъ, сколько можно;
затемъ считаютъ тысячи К остаишяся единицы я назы-
ваютъ число техъ и другихъ; напр.: двести сорокъ ты¬
сячъ пятьсотъ шестьдесятъ две единицы.
Тысяча тысячъ составляешь миллюнъ; тысяча миллю-
новъ—билл1онъ (или миллиарде); тысяча биллюновъ—
триллюнъ и т. п. Такимъ образомъ можешь получиться,
наир., следующее назвагае числа:
Сто восемьдесятъ миллюповъ триста сорокъ девять
тысячъ пятьсотъ шестнадцать единицъ.
8 Составныя и главныя единицы. Десятки,
сотни, тысячи, десятки тысячъ, сотни тысячъ, миллюны,
десятки миллюповъ, сотпи миллюповъ, биллюны и т. д.
называются составными единицами. Изъ нихъ тысячи,
мшшоны, биллюны, триллионы и т. д. называются глав¬
ными единицами; къ нимъ прнчисляютъ также и про-
стыя единицы. Все остальныя составныя единицы прея-
ставляютъ собою либо десятки, либо сотни этихъ глав-
нихъ единицъ.
9 Письменное счислен1е чиселъ, боль¬
шихъ тысячи. Пусть требуется написать число: три¬
дцать пять биллюновъ восемьсотъ шесть миллюповъ семь
тысячъ шестьдесятъ три единицы. Его можно было бы
написать при помощи цыфръ и словъ такъ:
35 биллюновъ 806 миллюновъ 7 тысячъ 63 един,
или короче такъ:
35’806’7’63
если условимся, что первая справа запятая заменяешь

— 17 —
собою слово тысячъ, вторая—слово миллюновъ, третья—
слово биллюновъ, четвертая—слово тршшоновъ и т. д.
Подобно этому:
15’36’801 означало бы: 15 милл. 36 тысячъ 801 ед.
3’3’205’1	„	3 билл. 3 милл. 205 тысячъ 1 ед.
Но такой способъ писан] я иы'Ьетъ много неудобствъ.
Положимъ, напр., что въ выраженш: 4’57’8 запятыя
стерлись, а остались только одн'Ь цыфры: 4578. Тогда
нельзя было бы прочесть число, такъ какъ неизвестно,
каюя цыфры означаютъ миллюны, каюя—тысячи и
кагая—единицы. Для изб-Ьжатя этого и другихъ не¬
удобствъ числа пипхутъ такъ, чтобы между двумя сосед¬
ними запятыми всегда стояли три цыфры. Напр., вместо
такого изображен1я: 4’57’8, пишутъ:
4’057’008
При этомъ запятыя становятся безполезпыми, потому
что и безъ нихъ мы будемъ знать, что первыя справа
три цыфры означаютъ число единицъ, следуюиця три
цыфры означаютъ число тысячъ, следующая за этими три
цыфры—число миллюновъ и т. д. Напр.
567 002 301 означаетъ 567 милл. 2 тыс. 301 ед,
2 008 001 020	„	2 билл. 8 милл. 1 тыс. 20 ед.
15 ООО 026	„ 15 милл. 26 ед. и т. п.
10.	Какъ прочесть число, написанное циф¬
рами. Чтобы легче прочесть число, изображенное длин-
нымъ рядомъ цыфръ, напр., такое 5183000567000, отде-
ляюгь въ немъ справа по три цыфры до техъ поръ,
пока можно:
5’183’000’567’000.
Первая справа запятая заменяетъ слово „тысячъ",
вторая — „миллюновъ", третья—„биллюновъ", четвер¬
тая— „триллюновъ". Значить, наше число должно быть
прочтено такъ: 5 трилл. 183 билл. 567 тысячъ.
2 Заказ № 5456

— 18 —
11.	Знач сшемфстъ, занимаемыхъцыфрами.
При такомъ способ^ писашя чиселъ каждое М’Ьсто, зани¬
маемое цыфрой, им'Ьетъ свое особое значеше, а именно:
на 1-мъ М’ЬсгЬ справа ставятся простая единицы
2-мъ
„ „ десятки
„ 3-мъ
ГУ
„ сотни
4-мъ
УУ
„ „ единицы тысячъ
5-мъ
п
„ „ десятки тысячъ
„ 6-мъ
п
,, ,, сотни тысячъ
7-мъ
ГУ
„ „ ед. миллюновъ
„ 8-мъ
п
„ „ дес. миллюновъ
я 9-мъ
ТУ
„ „ сотни миллюновъ
, 10-мъ
УУ
„ „ ед. биллюновъ
т. д.
12. Двоякое
з н а ч е н i е цыфръ. Такимъ обра-
зомъ, наше письменное счислеше основано на употре-
бленш 10 цыфръ, им’Ьющихъ двоякое значеше: одно въ
зависимости отъ начерташя цыфры, другое въ зависи¬
мости отъ мЪста, занимаемаго цыфрой, а именно: изъ
двухъ налисанныхъ рядомъ цыфръ лЪвая означаетъ еди¬
ницы въ 10 разъ болбиля, чЪмъ правая.
13.	Разряды единпцъ. Различный единицы, ко¬
торыми пользуются при счисленш, разд’Ьляютъ на раз¬
ряды: простая единицы называются единицами 1-го раз¬
ряда, десятки—единицами 2-го разряда, сотни—едини¬
цами 3-го разряда и т. п. Составная единица, по срав-
иенш съ другою, меньшею ея, называется единицею
высшего разряда, а по сравнент съ единицею, большею
ея, называется единицею низшего разряда; такъ, сотня
есть единица высшаго разряда сравнительно съ десят-
комъ и единица низшаго разряда сравнительно сътысячею.
Всякая составная единица содержитъ въ себФ 10 еди-
шщъ сл’Ьдующаго низшаго разряда; напр., сотня тысячъ
содержитъ въ себЪ 10 десятковъ тысячъ; десятокъ ты¬
сячъ—10 тысячъ и т. д.

— 19 —
Разряды единицъ группируютъ въ классы, къ 1-му классу
относятъ первые три разряда: сотни, десятки и единицы;
ко 2-му классу относятъ слЬдунище три разряда: тысячи,
десятки тысячъ и сотни тысячъ и т. д. 1-й классъ есть
классъ единицъ (содержитъ сотни, десятки и единицы еди¬
ницъ); 2-й классъ—нлассъ тысячъ (содержитъ сотни, десятки
и единицы тысячъ) и т. д.
14.	Сколько въ числЬ заключается всЬхъ
единицъ даннаго разряда. Пусть требуется
узнать, сколько въ числЬ 56284 заключается всЬхъ со¬
тенъ, т.-е. сколько сотенъ заключается въ десяткахъ ты¬
сячъ, въ тысячахъ и въ сотняхъ даннаго числа вмЬстЬ. Для
этого разсуждаемъ такъ: на третьемъ мЬстЬ въ данномъ
числЬ стоитъ цыфра 2; значить, въ числЬ есть 2 про¬
стыл сотни; следующая влЬво цыфра 6 означаетъ ты¬
сячи, т.-е. десятки сотенъ; следующая цыфра 5 озна¬
чаетъ десятки тысячъ, т.-е. сотни сотенъ; значить, всего
сотенъ будетъ: 5 сот. 6 дес. и 2, т.-е. 562. Такъ же
узнаемъ, что въ данномъ числ'Ь всЬхъ десятковъ 5628.
Правило. Чтобъ узнать, сколько въ числЬ заключается
всЬхъ единицъ данкаго разряда, надо отбросить цыфры,
означавший кизиле разряды, и прочесть оставшееся число.
Различныя системы счислен!я.
15.	Описанная выше система счислешя называется десятич¬
ной, потому что по этой систем!) 10 ед. одного разряда соста¬
вляютъ составную единицу слЬдуклцаго высшаго разряда. Чис¬
ло 10 называютъ поэтому основажемъ десятичной системы
счислешя. Всякое число N по этой систем!) представляется
разложеннымъ на простыя единицы, десятки, сотни, тысячи
ит. д., при чемъ число единицъ каждаго разряда меньше
10. Если положимъ, что въ числ'Ь N содержится простыхъ
единицъ а, десятковъ Ь, сотенъ с, тысячъ d и т. д., то по
десятичной систем* это число представляетъ собою сумму:
дг— а+ъ. ю-fc. юн-& 104-е. lO'-j-...
2*

I
— 20 —
Можно вообразить себе друпя системы, въ которыхъ зг
основаше принято какое-нибудь иное число. Если, напр.,
за ос-новаше веять число 5, то получится пятиричная сис¬
тема счислешя, по которой 5 ед. одного разряда должны
составить единицу следующего высшаго разряда. Такимъ
образомъ, по пятиричной системе единица 2-го разряда
должна быть пятерка, ед. 3-го разряда—пять пятерокъ,
или 5*, ед. 4-го разряда—пять разъ по пяти гаггерокъ или
53 и т. д. По этой системе число N представлялось бы такъ:
N=a+b. 5-fc. 5*-j-d. 53-fe. o4-j-...
где каждое изъ чиселъ: а, Ь, с, й, е... было бы меньше
5-ти. Для выговаривашя чиселъ по этой системе достаточно
было бы дать особыя назвашя первымъ пяти числамъ и не-
которымъ составнымъ единицамъ (которьш въ этомъ случае
считались бы главными).
16. Для письменнаго изображешя чиселъ по десятичной
системе употребляются 10 различныхъ энаковъ. Для другой
системы счислешя потребовалось бы иное число цыфръ.
Напр., для пятиричной системы достаточно было бы сле-
дующихъ пяти цыфръ: 1, 2, 3, 4, 0. Действительно, число
5 представляло бы по этой системе одну единицу 2-го раз¬
ряда и, след., выразилось бы такъ: 10. Число 6 предста¬
вляло бы одну ед. 2-го разряда (пятерку) и одну ед. 1-го
разряда и, слёд., выразилось бы такъ: 11, и т. п. Для изобра-
жешя чиселъ по системе, у которой основаше превосходить
10, было бы недостаточно нашихъ цыфръ. Напр., для две¬
надцатиричной системы пришлось бы придумать особые
знаки для чиселъ десять и одиннадцать, потому что наши
обозначения этихъ чиселъ выражали бы тогда друпя числа,
именно: 10 означало бы одну единицу второго разряда, т.-е.
дюжину, а 11 означало бы одну ед. 2-го разряда и одну
ед. 1-го разряда, т.-е. тринадцать.
17. Покажемъ, какъ можно число, написанное по десятич¬
ной системе счислешя, изобразить по какой-либо другой
системе. Для примера положимъ, что требуется число 1766
выразить по пятиричной системе при помощи пяти 8наковъ:
О, 1, 2, 3, 4. Для этого уэнаемъ сна-	1766	|5
чала, сколько въ 1766 заключается	26	353	15
единицъ 2-го разряда, т.-е. пятерокъ.	—j	.jQ|3
Ихъ оказывается 353, при чемъ остает- —^ ой iTr
ся одна ед. 1-го разряда. Теперь узнаг- 1
емъ, сколько въ 353 пятеркахъ заклю-	0	4 2

— 21 —
чается единицъ 3-го разряда. Такъ какъ единица 3-го раз¬
ряда содержитъ 5 ед. 2-го разряда, то надо 353 разделить
на 5. Разделивъ, узнаемъ, что въ 353 пятеркахъ заклю¬
чается 70 ед. 3-го разряда и 3 ед. 2-го разряда. 70 ед. 3-го
разряда превращаемъ въ единицы 4-го разряда; эти послед-
тя—въ единицы 5-го разряда и т. д. Такимъ образомъ
находимъ, что 1766 содержитъ: 2 ед. 5-го разр., 4 ед. 4-го
разряда, 3 ед. 2-го разр. и 1 ед. 1-го разр.; след. 1766 изоб¬
разится по пятиричной системе такъ: 24031.
Пусть еще требуется изобразить 121380 | 12
121380 по 12-ричной системе. 13	101151	12
Обозначая 10 черезъ а, 11 черезъ “jg lil 8421 12
b, найдемъ, что данное число изоб-	—ot- о тл1 -t o
разится такъ: 5 а 2 И.	__	_	—
О 11	10	5
18. Решишь теперь обратный вопросъ: изобразить по де¬
сятичной системе счислешя число, выраженное по другой
системе. Пусть, напр., требуется число 5623, написанное
по 8-ричной системе, перевести на десятичную систему. Э.то
можно было бы выполнить, вычисливъ формулу:
^==3+2.84-6.8*4-5.88=2963.
Но проще поступить такъ:
5623 Раздробимъ 5 ед. 4-го разр. въ единицы 3
Х8	разр., для чего умножимъ 5 на 8 (потому что
40 “	единица 4-го разряда содержитъ по восьмиричной
_|_5	системе 8 ед. 3-го разр); къ полученному числу
~4^~	приложимъ 6 ед., находящаяся въ данномъ числе,
уо	Раздробимъ единицы 3-го разряда въ единицы 2-го
фгсг	разр.; къ полученпому числу приложимъ 2 ед.,
находящаяся въ данномъ числе. Раздробимъ еди-
~т	ницы 2-го разр. въ ед. 1-го разр.; къ получен-
370	ному числу приложимъ 3 ед., находяпцяся въ дан-
Х8	номъ числе. Получимъ 2963.
2Q60	Если число, написанное по системе не-десятй-
4-3	ричпой, требуется изобразить по другой системе,
2у03~	тоже не-десятиричной, то предварительно перево-
дятъ первое число на десятиричную систему, а
затемъ уже это число на новую систему.
19. Система десятичнаго счислешя распространена почти
повсеместно (даже среди большинства дикихъ народовъ).
Мнопе видятъ причину такой распространенности въ томъ,
что каждый человекъ еъ дбтства привыкаетъ считать при

помощи 10 палъцевъ об-fcnxe руке. Однако, десятичное счи-
слеше не принадлежите ке самыме удобныме. Напр, удобнее
была бы 12-ричная система, которая, не требуя для изобра-
жешя чиселъ большого числа цыфръ, обладаете важнымъ
свойствомъ, что основаше ея д-Ьлится безъ остатка на 2, на
3, на 4 и на 6, тогда какъ основаше нашей системы дЬлится
только на 2 и на б. Въ теоретическомъ отношеши предста¬
вляете некоторый удобства система двуричная, которая,
впрочеме, для практическим, ц-Ьлей совеЬме неудобна, таке
каке по этой систем-Ь даже небольшое число выражается длин-
ныме рядоме цыфръ (напр., "число 70 выражается таке:
1000110). Но каковы бы ни были недостатки десятичной
системы, она настолько укоренилась своею давностью и по-
всем’Ьстныме распространешеме, что было бы безполезно
поднимать вопросе о зам-Ьн-Ь ея другою системою. Ке тому
же новая система счислешя потребовала бы переработки
всфхе книге и таблице, составленныхе по десятичной систем!*,
что представляло бц почти невыполнимый труде.
Употребляемый нами цыфры и самая система письменнаго
счислешя заимствованы европейцами у арабове (ве начал!*
XIII стол-Ьчтя). Воте почему эти цыфры называюте арабскими.
Но есть основаше думать, что арабы, ве свою очередь, заим¬
ствовали эту систему оте индайцеве.
П. Сложен!е.
Задача. Ве коробочку положили 5 спичеке, готоме 7
спичеке, эатбме еще 2 спички. Сколько вс-Ьхе спичеке ока-
залось вч» коробочк!*?
Ве коробочка оказалось 14 спичеке, число, которое полу¬
чается оте сОединешя трехе чиселе: 5, 7 и 2 ве одно со¬
брате.
20.	О и р е д -6 л е н i я. Два, три и бол-fee числа могутъ
быть соединены нъ одно число, которое называется ихъ
суммой. Такъ, 5 спичеке да 7 спичеке да 2 спички мо¬
гутъ быть соединены въ одно число: 14 спичекъ. Число
14 есть сумма трехъ чиселъ: 5, 7 и 2.
Нахождение по н-Ьсколькимъ даннымъ числамъ одного
новаго числа называется ариеметическимъ дЬйств1емъ (или
просто д-Ьйств!емъ).

— 23 —
Ариеметичесное дййствю, посредствомъ нотораго нахо¬
дится сумма нйснольнихъ даккыхъ чисель, наз. сложежемъ.
Данныя для сложетя числа наз. слагаемыми.
Слагаемыхъ можетъ быть два, три и болйе.
Сумма содержитъ въ себй вей единицы слагаемыхъ.
3 а м й ч а н iе. Выражешя: „къ 7 прибавить 3“, „къ 7
приложить 3“ и т. п. означаютъ то же самое, что „найти
сумму 7-ми и 3-хъ“.
21. Основное свойство суммы. Сумма не зави-
ситъ отъ того порядка, въ какомъ мы соединяемъ еди¬
ницы слагаемыхъ. Такъ, если требуется найти сумму б,
7 и 2, то мы можемъ къ б присоединить 7, потомъ 2;
или къ 5 присоединить сначала 2, потомъ 7; или къ 7
присоединить 2, потомъ 5. Можемъ поступить и такъ:
взять какую-нибудь часть 7-и, присоединить къ ней
какую-нибудь часть 5-и, потомъ присоединить оставппяся
единицы по одной, по двй или какъ-нибудь иначе.
Всегда получимъ одну и ту же сумму 14.
22. Сложеше двухъ однозначныхъ чиселъ.
Чтобы узнать сумму двухъ однозначныхъ чиселъ, доста¬
точно къ одному изъ нихъ присчитать вей единицы дру¬
гого. Такъ, присчитывая къ 7 вей единицы числа 5,
иаходимъ сумму 12.
Чтобы умйть быстро складывать всяшя числа, слй-
дуетъ запомнить вей суммы, которыя получаются отъ
сложешя двухъ однозначныхъ чиселъ.
23. Сложен1е многозначнаго числа съ
однозначнымъ. Пусть требуется сложить 37 и 8. Для
этого отъ 37 отдйлимъ 7 ед. и сложимъ ихъ съ 8; полу¬
чимъ 15. Эти 15 ед. приложимъ къ 30; но 15 все равно,
что 10 да 5. Приложивъ къ 30-ти 10, получимъ 40;
приложивъ къ 40 еще 5, получимъ 45.
Можно поступить и такъ. Отдйлимъ 3 ед. отъ 8 ед.
и приложимъ ихъ къ 37, чтобы дополнить 37 до 40;
тогда получимъ 40 и еще б ед., оставппяся отъ 8-ми;
т.-е. получимъ 45.

— 24 —
Слйдуетъ привыкнуть выполнять эти дййсгая въ умй
и притомъ быстро.
24.	Сложеше многозначныхъ чиселъ. Пусть
требуется найти сумму чиселъ: 13653, 22409, 1608 и
346. Для этого сложимъ сначала простая единицы всйхъ
слагаемыхъ, потомъ ихъ десятки, затбмъ сотни и т. д.
Чтобы при этомъ не смйшать между собою единицъ раз-
личныхъ разрядовъ, напишемъ данный числа одно подъ
другимъ такъ, чтобы единицы стояли подъ единицами,
десятки подъ десятками, сотни подъ сотнями и т. д.,
подъ послйднимъ слагаемымъ проведемъ черту:
13653 Сложивъ единицы, получимъ 26, т.-е. 2 де-
22409 сятка и 6 единицъ; 2 десятка запомнимъ, что-
1608 бы ихъ сложить съ десятками данныхъ чп-
346 селъ, а 6 единицъ запишемъ подъ чертою,
38016 подъ единицами слагаемыхъ. Сложивъ де¬
сятки (вмйсгЬ съ тйми 2 десятками, кото¬
рые получились отъ сложетя единицъ *), получимъ
11 дес., т.-е. 1 сотню и 1 десятокъ. 1 сотню мы запом¬
нимъ, чтобы ее сложить съ сотнями, а 1 десятокъ напи¬
шемъ подъ чертою, на м'Ьстй десятковъ. Отъ сложешя
сотенъ получимъ 20 сотенъ, т.-е. ровно 2 тысячи; эти
2 тысячи запомнимъ, чтобы ихъ прибавить къ тысячамъ,
а подъ чертою напишемъ 0 на мйсгЬ сотенъ. Продол-
жаемъ такъ дййсттае далйе.
Замйчаше. Если слагаемый числа таковы, что
сумма единицъ каждаго разряда ихъ не превосходить
9-ти, то безразлично, въ какомъ порядкЪ производить
сложеше: отъ низшихъ разрядовъ къ высшимъ, или
наоборотъ. Въ другихъ случаяхъ начинать сложеше съ
высшихъ разрядовъ неудобно, потому что отъ сложетя
единицъ низшаго разряда могуть получиться одна или
*) При этомъ полезно всегда начинать сложеше съ того числа, ко¬
торое только что запомнили, чтобы не держать его долго въ умЬ.
Такъ, складывая десятки, надо говорить: 2 да 5... 7 да 4... 11.

— 25 —
несколько единицъ следующаго высшаго разряда, п
тогда придется изменять ранее написанную цыфру.
25. Пра вило с л о ж е н i я. Пишутъ слагаемыя одно
подъ другимъ. такъ, чтобы единицы стояли подъ едини¬
цами, десятки подъ десятками, сотни подъ сотнями и
т. д.; подъ последнимъ слагаемымъ проводить черту.
Сначала складываютъ простыя единицы, потомъ де¬
сятки, за десятками—сотни, за сотнями—тысячи и т. д.
Если отъ сложешя единицъ какого-либо разряда по¬
лучается однозначное число, то пишутъ его подъ чер¬
тою на томъ месте, которое приходится подъ склады¬
ваемыми единицами; если же получается двузначное чи¬
сло*), то единицы его пишутъ подъ чертою, а десятки
запоминаютъ, чтобы сложить ихъ вместе съ единицами
следующаго высшаго разряда.
26. Сложен1е большого числа слагаемыхъ.
Если требуется сложить много слагаемыхъ, то обыкно¬
венно разбивають ихъ на несколько группъ, производятъ
сложеше въ каждой группе отдельно и затЬмъ полу-
ченныя суммы соединяютъвъодну. Такъ, пусть требуется
сложить 10 слагаемыхъ: 286, 35, 76,108, 93, 16, 426, 576,
45, 72. Разобьемъ эти слагаемыяна группы, напр., такъ:
1-я группа.
2S6
108
426
576
1396
Сложивъ три суммы въ одну, найдемъ 1783.
27. Поверка сложен!я. Чтобы убедиться, что
A'McTBie сдёлано верно, надо его поверить. Для
2-я группа.	3-я	группа.
Общая
сумма.
35	16	1396
93	45	204
76	72	133
204	13Г	~	1733
*) Трехзначное число могло бы получиться только тогда, когда
число слагаемыхъ болЪе 11; но въ такомъ случаЬ удобнее произво¬
дить сложеше по группамъ, какъ указано въ § 26-мъ.

— 26 —
поверки сложетя обыкновенно складываютъ слагаемый
во второй разъ въ иномъ порядк-Ь, ч-Ьмъ въ первый,
напр., производя сложеше снизу вверхъ. Если при вто-
ромъ сложенш получается та же сумма, то весьма в-Ь-
роятно, что сложеше произведено в-Ьрно *).
28.	Увеличен1е числа на другое число.
Увеличить число на нисколько единице значите прило¬
жить къ числу эти нисколько единице. Если, напр.,
требуется увеличить 80 на 25, то надо къ 80 приложить
25, т.-е., другими словами, найти сумму 80-н и 25-и.
ILL Вычитан1е.
Задача. Въ коробочк-Ь было 17 еничекъ; изъ нея вынули У
спичеке; сколько спичеке осталось въ коробочк-Ь?
Для р'Ьшешя задачи надо найти такое число, которое, сло¬
женное се 9-ю, составляете 17.
29.	0предЪлен1е. Вычиташемъ наз. ариеметическое
дЬйств1е, посредствомъ котораго по данной сумм% и одному
слагаемому находится другое слагаемое.
Такъ, вычесть изъ 17-ти 9 значить: по данной сумм!*
17 и данному слагаемому 9 найти другое слагаемое (8):
другими словами, узнать, какое число надо сложить съ
9-ю, чтобы получить въ сумм-Ь 17.
Такое д-Ьйете принято называть вычиташемъ потому,
что посредствомъ него узнается также, какое число оста¬
нется отъ большего дакнаго числа, если отъ него отдЬ-
лимъ (отнимемъ, вычтемъ) меньшее данное число. Такъ,
когда мы по сумм-Ь 17 и слагаемому 9 нашли, что
другое слагаемое должно быть 8, то мы узнали вм-Ьст-Ь
съ т-Ьмъ, что если отъ 17 отд-Ьлимъ 9 ед., то останется 8 ед.
При вычиташи данная сумма наз. умекьшаемымъ, дан¬
ное слагаемое — вычитаемыми, а искомое слагаемое—
*) B-Ъроятно, а не наверное, потому что и при второмъ сложе¬
нш можетъ быть сделана ошибка, подобная той, какая была при
первомъ сложенш.

— 27 —
остаткомъ. Такъ, если изъ 17 вычитается 9, то 17 есть
уменьшаемое, 9 вычитаемое; искомое число 8 есть оста-
токъ. Остатокъ ваз. иначе разностью, такъ какъ онъ
означаетъ также, на сколько данная сумма (уменьшае¬
мое) разнится отъ даннаго слагаемаго (вычитаемаго).
Замйчашя. 1) Уменьшаемое не можетъбыть мень¬
ше вычитаемаго, такъ какъ сумма не можегь быть
меньше слагаемаго; наир., нельзя изъ 17 вычесть 20.
2) Если уменьшаемое равно вычитаемому, наир., если
изъ 17 вычитается 17, то не остается никакого числа; при¬
нято говорить, что въ этомъ случай остатокъ равенъ О*).
3) Выражешя: „отнять 9 изъ 17“, или „найти, сколько
будетъ 17 безъ 9", означаютъ то же, что и „вычесть
9 изъ 17“.
Вычиташе однозначнаго числа.
30. Чтобы безъ затруднешя вычитать всякое число,
надо сначала научиться вычитать въ умй и притомъ
быстро однозначное число изъ однозначнаго и двузнач-
наго. Искомая разность легко находится посредствомъ
сложетя. Напр., чтобы узнать, сколько будетъ 15 безъ
8, пробуемъ прибавлять къ 8 различныя числа, пока
не получимъ 15; 8 да 7 составляютъ 15; слйд., 15
безъ 8 будетъ 7.
Вычитан1е многозначнаго числа.
31. Примйръ: изъ 60072 вычесть 7345.
Будемъ держаться того же порядка, какъ и при сло-
женш, т.-е. станемъ вычитать единицы изъ единицъ, де¬
сятки изъ десятковъ и т. д.
*) Такъ какъ уменьшаемое равно вычитаемому, сложенному съ
остаткомъ, то, принимая, что при равенств* уменьшаемаго и вычн-
таемаго остатокъ есть 0, мы должны также принять, что прибавить
къ числу О значить оставить это число базъ изм*нен1я. Равнымъобра-
зомъ принимаютъ, что вычесть изъ числа 0 значить оставить это чи¬
сло безъ измЪнешя.

т
— 28 —
5 ед. изъ 2 ед. нельзя вычесть; беремъ отъ 7 део
одинъ десятокъ, разлагаемъ его на единицы и прикла-
дываемъ къ 2; получимъ въ умепьшаемомъ единицъ 12,
52727... . остатокъ или разность,
а десятковъ 6. Чтобы запомнить, что десятковъ въ
уменыпаемомъ не 7, а 6, поставимъ точку надъ цифрою 7.
5 ед. изъ 12 ед. .. 7 ед. Пишемъ 7 ед. подъ чертою
на м-ЬстЬ единицъ.
4 дес. изъ 6 дес  2 дес.; пишемъ 2 подъ чертою
на м'Ьс'гЬ десятковъ.
3 сотни изъ 0 сотенъ вычесть нельзя. Обращаемся къ
тысячамъ уменыпаемаго, чтобы взять отъ нихъ одну
для раздроблешя въ сотни. Но тысячъ въ уменыиаемомъ
нЬтъ. Тогда обращаемся къ следующему высшему раз¬
ряду, т.-е. къ десяткамъ тысячъ; если бы и ихъ не
оказалось, мы взяли бы сотни тысячъ и т. д. Въ на-
шемъ пример* въ уменыпаемомъ есть 6 десятковъ
тысячъ; беремъ отъ нихъ одинъ (въ знакъ чего ставимъ
точку надъ цифрою 6) и раздробляемъ его въ простыя
тысячи; получимъ 10 тысячъ. Отъ этихъ 10 тысячъ
беремъ одну и раздробляемъ ее въ сотни: тогда получимъ
сотенъ 10, тысячъ 9, а десятковъ тысячъ 5. Поставимъ
точку надъ цифрою 0 тысячъ и условимся, что 0 съ
точкой будетъ означать число 9. Теперь продолжаемъ
вычиташе: 3 сотни изъ 10 сотенъ.... 7 сотенъ; 7 тысячъ
изъ 9 тысячъ.... 2 тысячи; наконецъ, 5 десятковъ
тысячъ уменыпаемаго перейдутъ въ остатокъ безъ вся-
каго изменешя, такъ какъ изъ нихъ ничего не вычитается.
Вотъ еще примеры на вычиташе:
60072
7345
уменьшаемое
вычитаемое
6000227
4320423
1679804
500000
17236
4S2764

— 29 —
Замйчан1е, Вычиташе удобн-Ье производить отъ
низшихъ разрядовъ къ высшимъ потому, что при такомъ
порядка мы, въ случай надобности, всегда можемъ взять
одну единицу изъ высшихъ разрядовъ уменыиаемаго
для раздроблешя ея въ единицы низшаго разряда.
31.а. Правило вычитан1я. Пишутъ вычитаемое
подъ уменьшаемымъ такъ, чтобы единицы стояли подъ
единицами, десятки подъ десятками и т. д.; подъ вычи-
таемымъ проводятъ черту.
Сначала вычитаютъ единицы изъ единицъ, потомъ
десятки изъ десятковъ, зат-Ьмъ сотни изъ сотенъ и т. д.
Получаемый отъ вычиташя числа ставятъ подъ чер¬
тою на м'Ьст'Ь единицъ, когда вычитались единицы, на
мгЬстгЬ десятковъ, когда вычитались десятки, и т. д.
Если число единицъ какого-нибудь разряда въ умень-
шаемомъ окажется меньше числа единицъ того же раз¬
ряда въ вычитаемомъ, то въ уменыпаемомъ ставятъ точку
надъ первой слЪва отъ этого разряда значащей цыфрой,
а также и надъ каждымъ изъ нулей, которые могутъ на¬
ходиться между этимъ разрядомъ и первой сл’Ьва зна¬
чащей цыфрой; тогда при дальшЬйшемъ вычитати при-
нимаютъ, что точка, стоящая надъ значащей цыфрой,
уменыпаетъ ея значеше на единицу; точка, стоящая
надъ нулемъ, обращаетъ его въ девять; цыфра же,
стоящая направо отъ цыфры съ 'точкой, увеличивается
въ своемъ значеши на 10.
32. Поверка вычитан!я. Такъ какъ уменьшаемое
есть сумма, а вычитаемое и остатокъ суть слагаемый, то,
чтобы повфрить вычиташе, достаточно сложить вычитае¬
мое съ остаткомъ; если получится-число, равное умень¬
шаемому, то весьма вероятно, что д’Ьйсте сд’Ьлано В’Ьрно.
33. Уменыпеше числа на другое число.
Уменьшить какое-нибудь число на нисколько единицъ
значить вычесть изъ него эти нисколько единицъ. По¬

— 30 —
этому, если, напр., требуется 100 уменьшить на 30, то
надо изъ 100 вычесть 30 (получится 70).
34. Сравнен1е двухъ ч и с е л ъ. Часто приходится
узнавать, на сколько единицъ одно число больше или
меньше другого. Чтобы узнать это, надо отъ болынпго
изъ двухъ чиселъ вычесть меньшее. Напр., чтобы узнать,
на сколько 20 меньше 35 (или на сколько 35 больше 20)
надо изъ 35 вычесть 20; тогда найдемъ, что 20 меньше
35 (или 35 больше 20) на 15 единицъ.
35. Обрат ныя д,Ьйств1я. Два .д’Ьйсттая называются
обратными, если искомое число перваго дёйствш служить
даннымъ для второго, а одно изъ данныхъ чиселъ перваго
действия служить искомымъ для второго.
Сложеше и вычиташе суть д'ЬйствЕя обратный. Действи¬
тельно, при еложенш даются слагаемыя, а отыскивается ихъ
сумма; при вычитанш, наоборотъ, дается сумма и одно сла¬
гаемое, а отыскивается другое слагаемое.
IV.	Славянская и римская яумерац1и.
36.	Славянская н у м е р а ц i я. Въ церковныхъ
книгахъ и въ памятникахъ славянской письменности
употребляются для изображения чиселъ буквы славян-
скаго алфавита. Когда буква означаетъ число, то ста-
вятъ надъ ней особый знакъ, называемый титломъ ("),
чтобы сразу было видно, что эта буква означаетъ не
звукъ, а число. Сл’Ьдуюнця 27 буквъ служатъ для вы-
ражешя первыхъ 9 чиселъ, 9 десятковъ и 9 сотенъ:
3 (1), в (2), “ (3), а (4), . (5), s (6.) 3 (7), п (8),
* (9), 7 (Ю), к (20), л (30), м (40), й (50), 8(60),
о* (70), п (80), ч (90), f (100), 1 (200), 7 (300),
V (400), f (500), х (600), $ (700), ш (800), ц (900).
Нисколько буквъ подъ титломъ, написанныхъ рядомъ,
означаютъ число, равное сумме чиселъ, выражаемыхъ
каждою буквою. Для обозначешя тысячъ передъ чнс-

— 31 —
ломъ ихъ ставится знакъ *. Напр., обозначеше *«опд выра-
жаетъ число 1884. Буквы ставятся въ томъ порядкй, въ
какомъ слйдуютъ числа въ славянскомъ произношенш.
Напр., число 15, произносимое „пять-на-десять“, пишется
такъ: еТ, т.-е. вначалй ставится буква, означающая 5,
а за нею буква, означающая 10.
37.	Р имская ну мера шя. Такъ какъ римстя
цыфры и въ настоящее время употребляются иногда для
выражешя чиселъ, то полезно ознакомиться и съ ними.
Римляне употребляли для выражешя чиселъ только слй-
дуюнце семь знаковъ:
1=1, V=5, Х=10, L=50, С—100, D=500, М=1000.
Ихъ способъ выражать числа существенно отличался
отъ нашего. У насъ цыфры измйняютъ свое значеше
съ перемйною мйста, а въ римской нумерацш цыфры
на всякомъ мйсгЬ сохраняютъ свое значеше. Когда на¬
писаны нисколько римскихъ-цыфръ рядомъ, то число,
выражаемое ими, равно суммй чиселъ, выражаемыхъ
каждой цыфрой; напр., ХХУ означаетъ сумму 10-и,
10-и и 5-и, т.-е. 25; CLXV означаетъ 165 и т. п.
Исключеше изъ этого правила составляюгь только слй-
дуклщя числа:
4 = IV, 9 = IX, 40 = XL, 90 = ХС, 400=CD, 900=СМ.
Въ этихъ изображешяхъ значен!е лйвой цыфры вы¬
читается изъ значешя правой.
Послй этого понятны будутъ слйдуюнця изображен!я
чиселъ:
1 = 1, 11 = 2, 111 = 3, IV = 4, V = 5, VI = 6, VII = 7,
VIII = 8, IX = 9, Х = 10, XI = 11, XII = 12, XIV=14,
XVIII = 18, XIX = 19, XX = 20, XXIX = 29, XLII = 42,
LXXXIV = 84, XCV = 95, ССС = 300, DC = 600,
DCC = 700, MDCCCLXXXIV = 1884.

1
32 —
Число тысячъ изображается такъ же, какъ число еди¬
ницъ, только съ правой стороны, внизу, ставятъ букву
т (mille—тысяча); напр.:
CLXXXmCCCLXIY = 180304.
V.	Изм’Ьнете суммы и остатка.
38. Такъ какъ сумма содержить въ себ'Ь все еди¬
ницы слагаемыхъ, то очевидно, что:
Если къ какому-либо слагаемому прибавимъ несколько
единицъ, то сумма увеличится на столько же единицъ;
Если отъ какого-либо слагаемаго отнимемъ несколько
единицъ, то сумма уменьшится на столько же единицъ.
Примеры 73	73	73
18	20	(ув. на	2)	18
40	40	30	(ум.	на	10)
131	133	(ув. на	2)	121	(ум.	на	10)
Этими свойствами суммы иногда пользуются при уст-
номъ сложенш. Пусть, напр., требуется къ 427 при¬
ложить 68. Искомую сумму мы найдемъ быстро, если къ
427 приложимъ не 68, а 70 (получимъ 497), а загЬмъ
уменынимъ найденное число на 2 (получимъ 495).
39. Если изм'Ьнимъ нисколько слагаемыхъ, то сумма
иногда увеличится, иногда уменьшится, или же можетъ
остаться безъ перемены. Чтобы предугадать заранее,
что произойдеть съ суммою, надо предположить, что
сначала изменено только одно слагаемое, потомъ дру¬
гое, затЬмъ третье... и каждый разъ определять, какъ
будетъ изменяться сумма. Напр.:
30	Увеличимъ 1-е	слаг.	на	10	. .	40
25	Увеличимъ 2-е	слаг.	на	5	. .	30
75	Уменынимъ 3-е	слаг.	на	8	...	67
130	?

— 33 —
Отъ увеличетя перваго слагаемаго на 10 сумма уве¬
личится на 10. Отъ увеличетя второго слагаемаго
на 5 сумма еще увеличится на 5; значить, противъ преж-
няго она увеличится на 10 и на 5, т.-е. на 15. Отъ
уменыиешя третьяго слагаемаго на 8 сумма уменьшится
на 8; значить, противъ прежней она увеличится на
15 безъ 8, т.-е. на 7 и, игЬд., будетъ 137.
Подобными соображешями полезно иногда руково¬
диться при устномъ сложенж. Пусть, напр., требуется
сложить 31, 28 и 31 (числа дней въ январе, феврале
и марте). Вместо этого сложимъ 30, 30 и 30 (полу¬
чимъ 90). Найденная сумма будетъ надлежащая, такъ
какъ мы уменьшили первое и третье слагаемый каждое
на 1, зато второе слагаемое увеличили на 2 единицы.
40. Такъ какъ уменьшаемое есть сумма, а вычитае¬
мое и остатокъ слагаемый, то легко понять, что:
Если къ уменьшаемому прибавимъ н-Ьсколько единицъ,
то остатокъ увеличится на столько же единицъ-,
Если отъ уменьшаемаго отнимемъ несколько единицъ,
то остатокъ уменьшится на столько же единицъ;
Если къ вычитаемому прибавимъ нисколько единицъ, то
остатокъ уменьшится на столько же единицъ;
Если отъ вычитаемаго отнимемъ нисколько единицъ, то
остатокъ увеличится на столько же единицъ.
Указанныя свойства полезно иметь въ виду при уст¬
номъ вычитанж. Чтобы вычесть, напр., 28 изъ 75, мы
можемъ вычесть изъ 75 не 28, а 30 (получимъ 45), но
зато полученное число мы должны увеличить на 2 (по¬
лучимъ 47).
41. Если станемъ изменять одновременно и вычи¬
таемое, и уменьшаемое, то остатокъ иногда увеличится,
иногда уменьшится, или же можетъ остаться безъ пе¬
ремены. Напр.:
50 Увеличимъ на 10 ... 60
15 Увеличимъ'на 15 ... 30
35	У
3 Заказ X? 5456

— 34 —
Отъ увеличены уменынаемаго на 10 остатокъ уве¬
личивается на 10; отъ увеличешя вычитаемаго па 15
остатокъ уменьшается на 15. Значить, къ остатку при¬
бавляется 10 и отнимается 15; отъ этого остатокъ
уменьшается на б; значить, онъ будетъ 30.
Сл'Ьдуетъ обратить особое внимаше на случаи, когда,
несмотря на измене Hie данныхъ чиселъ, остатокъ не
изменяется:
Если уменьшаемое и вычитаемое увеличимъ на одно
и то же число, то остатокъ не изменится;
Если уменьшаемое и вычитаемое уменьшимъ на одно
и то же число, то остатокъ не изменится. Напр.:
50 увел, на 10 . .60 умен, на 10 . .40
15 увел, на 10 . . 25 умен, на 10 . . 5
35	35	35
VI.	Знаки д’вйетвШ, скобки, Формулы.
42 Зн аки действ!й. При письменномъ решети
задачъ часто приходится писать рядомъ другъ съ дру-
гомъ данныя числа для различныхъ действШ. Въ та-
кихъ случаяхъ полезно отличать одно дейстае отъ дру¬
гого посредствомъ какихъ-нибудь знаковъ. Услови¬
лись обозначать сложеше знакомь плюсъ-]-, авычиташе
знакомь минусъ —. Напр.:
446	446
+235	235
681	211
Иногда бываетъ нужно, не производя действШ на
самомъ деле, только указать знаками, кагая дейштая
надо выполнить надъ данными числами. Положимъ, наир.,
надо указать, что числа 10, 15 и 20 требуется сло¬
жить. Тогда пишутъ данныя слагаемыя въ одну строчку
и ставятъ между ними знакъ сложетя: lO-j-15—J—20.

— 35 —
Такъ какъ сумма не зависитъ отъ порядка, въ какомъ
соединяемъ единицы слагаемыхъ, то безразлично, въ ка¬
комъ порядк'Ь писать слагаемня.
Если надо указать, что изъ одного числа требуется
вычесть другое, то пишутъ уменьшаемое и вычитаемое
въ одну строчку^ и ставятъ между ними знакъ—. Такъ,
выражеше 10—8 означаетъ, что надо изъ 10 вычесть 8.
Выражеше 104-15+20 читается такъ: 10 плюсъ 15
плюсъ 20, или же сумма 10-ти, 15-ти и 20-ти. Выра¬
жеше 10—8 читается такъ: 10 минусъ 8, или же раз¬
ность 10-ти и 8-ми.
Если надъ данными числами надо произвести рядъ
посл'Ьдовательныхъ сложешй и вычиташй, то пишутъ
числа въ строку въ томъ порядкЪ, въ какомъ надо про¬
извести надъ ними д^йстя. Такъ, выражеше 10+15—2
означаетъ, что къ 10-ти надо сначала приложить 15 и за-
тЬмъ отъ полученной суммы отнять 2.
43. Знаки равенства и неравенства. Въ
ариеметик'Ь употребительны еще знаки: =, > и <\ Пер¬
вый наз. знакомъ равенства и зам'Ьняетъ собою слово
„равно" или „равняется"; два друше наз. знаками не¬
равенства и означають: знакъ > „больше", а знакъ <
„меньше"; напр., выражешя 7 -J- 8 = 15, 7+ 8 >10 и
7 —|- 8	20 читаются такъ: 7 плюсъ 8 равно 15; 7-)-8
больше 10; 7 + 8 меньше 20 Сл'Ьдуетъ помнить, что
знаки >и< должны быть обращены остреемъ угла къ
меньшему числу.
44 Скобки и формула. При р’Ьшенш задачъ
весьма полезно раньше совершешя дЬйствШ указать, ка-
шя дЬ>йств1я и въ какомъ порядк'Ь надо выполнить надъ
данными числами, чтобы дойти до ответа на предло¬
женный вопросъ. Положимъ, напр., что для рЬшешя
какой-нибудь задачи надо сначала сложить 35 и 20,
нотомъ эту сумму вычесть изъ 200. Чтобы указать это,
пишутъ такъ:
200—(35+201
3*

— 36 —
Здесь сумма 35-f 20 заключена въ скобки, передъ ко¬
торыми поставленъ знакъ—; тогда этотъ знакъ означаетъ,
что изъ 200 надо вычесть не 35, а сумму 35-J—20, т. е. 55.
Иногда выражеше, содержащее скобки, -приходится
заключить въ новыя скобки; въ такомъ случае употре-
бляютъ скобки различной формы, чтобы отличить ихъ
одне отъ другихъ; напр., такое выражеше:
100 + { 160—[60-)-(7-|-8)]}
означаетъ: сложить 7 и 8 (получимъ 15); найденную
сумму (15) сложить съ 60 (получимъ 75); вычесть най¬
денное число (75) изъ 160 (получимъ 83): сложить
полученное число съ 100 (получимъ 185)*).
Выражеше, показывающее, кажя действ1я и въ какой
последовательности надо выполнить надъ данными числами,
чтобы получить искомое число, наз.“ формулой.
Вычислить формулу значить найти число, которое по¬
лучится после выполнешя всехъ действШ, указанныхъ
въ формуле.
VII.	Умножен1е.
Задача. Одна тетрадка стоить 7 коп.; сколько стоять 4
таыя тетрадки?
Для решетя задачи надо найти сумму 7-j—7-4-7—]-7, т.-е.
повторить число 7 слагаемымъ 4 раза.
45.	Определен!е. Умножежемъ называется ариеме-
тическое действ1е, посредствомъ. нотораго одно данное
число повторяется слагаемымъ столько разъ, сколько въ
другомъ данномъ числе находится единицъ.
Такъ, умножить 7 на 4 значить повторить число 7
слагаемымъ 4 раза, т.-е. найти сумму 7-j-7-j-7-j-7.
Такимъ образомъ, умножеше представляетъ собою сло-
жеже одинаковыхъ слагаемыхъ и, след., оно всегда мо-
жетъ быть выполнено посредствомъ обыкновеннаго сло-
жешя. Но такое сложеше очень утомительно въ томъ
*) Скобки такой формы: ( ) обыкновенно наз. простыми, такой фор¬
мы: [ J прямыми и такой: ( } фигурными.

— 37 —
случай, когда число слагаемыхъ велико. Ариеметика
указываетъ болйе удобный способъ нахождешя суммы
одинаковыхъ слагаемыхъ посредствомъ особаго дййств1я,
называемаго умножешемъ.
Число, которое должно повторить слагаемымъ, назы¬
вается множимымъ, а число, которое ноказываетъ, сколько
разъ надо множимое повторить слагаемымъ, называется
множителемъ. Число, полученное послй умножешя, на¬
зывается произведешемъ. Напр., когда 7 умножается на
4, то 7 есть множимое, 4 множитель, а получившееся
послй умножешя число 28 — произведете.
. Множимое и множитель безразлично наз. сомножителями.
Принято обозначать умножеше посредствомъ особаго
знака. Если, напр., 7 надо умножить на 4, то пишутъ
такъ: 7X4, или 7.4, т.-е. пишутъ множимое, справа
отъ него знакъ умножешя (косой крестъ или точка),
а справа отъ знака ставятъ множителя; такое обозначе-
Hie замйняетъ собою сумму 7-(—7—(-7 -|—7.
45,2. Замйчан1я. 1) Множитель всегда число отвле¬
ченное, такъ какъ онъ означаетъ, сколько разъ множимое
должно быть повторено слагаемымъ; множимое мо-
жетъ означать единицы какого-угодно на¬
зван! я, наир., аршины, рубли, карандаши и т. п.;
произведете означаетъ единицы того же
назван!я, какъ и множимо-e; такъ, если7 рублей
умножаются на 4, то получается 28 рублей.
2) Если множимое равно 1, то произведете равно множи¬
телю; такъ, IX5 —5, потому что сумма 1—|—1-J-1 —J— 1-J-1
составляетъ 5.
8) Если множимое равно 0, то и произведете равно 0;
напр.,0Х^ = 0, потому что сумма O-fO-J-0-j-O равна 0.
4)	Если множитель есть 1, то произведете принимается
равнымъ множимому; напр., произведете 5 X1 прини¬
мается за 5, потому что выражеше 5X1 означаетъ, что
5 надо повторить слагаемымъ одинъ разъ, а это пони-
маютъ въ томъ смыслй, что 5 надо взять одинъ разъ.

— 38 —
5)	Если множитель есть нуль, то произведете принимается
равнымъ 0; напр., 5Х° = °-
46.	Увеличен1е числа въ нисколько разъ.
Увеличить число въ 2 раза, въ 3 раза, въ 4 раза и
т. д.—значить повторить это число слагаемымъ 2 раза,
3 раза, 4 раза и т. д. Напр., увеличить 10 въ 5 разъ—
значить повторить 10 слагаемымъ 5 разъ, или умножить
10 на 5. Такимъ образомъ увеличеше числа въ нисколько
разъ выполняется умножежемъ, тогда какъ увеличен ie
числа на какое-нибудь число выполняется сло-
жешемъ.
47 ПеремЬстительное свойство ироизве-
ден1я. Возьмемъ кагая-нибудь два числа, напр., 50 и
36, и составимъ произведете 50X36. Это произведете
представляетъ собою сумму:
50-}-50-|-50	(36	разъ).
Такъ какъ сумма не зависигь отъ того порядка, въ
какомъ мы соединяемъ единицы слагаемыхъ, то мы мо-
жемъ найти эту сумму, между прочимъ, такъ: возьмемъ
отъ каждаго слагаемаго по одной единицЬ, тогда полу¬
чимъ 36 единицъ; возьмемъ еще по одной единиц’Ь,
опять получимъ 36 ед.; возьмемъ въ третий разъ по од¬
ной единицЬ, получимъ въ третШ разъ 36 ед. Такъ
какъ отъ каждаго слагаемаго нашей суммы можно брать
по одной единицЬ 50 разъ, то, выбравъ'веЬ единицы,
мы получимъ 36 единицъ, повторенныя 50 разъ; значить:
36 разъ	50	разъ
ВО—J—60—J—50—{— .... =36—(—36—{-36-{- ....
т.-е. 50X36=36X50.
Итакъ, произведете не измЬняется отъ перемЬны мЬстъ
сомножителей.
i

— 39 —
Умножеше однозначнаго числа на однозначное.
48.	Таб лица у м н о ж е н i я. Пусть требуется умно¬
жить 7 на 3. Для этого достаточно повторить 7 сла¬
гаемыхъ 3 раза:
7X3=7-1-7+7=21.
(семь да семь—четырнадцать, да еще семь—двадцать
одинъ).
Чтобы умгЬть быстро производить умножеше всякихъ
чиселъ, надо запомнить всЬ произведешя однозначныхъ
чиселъ. Для этого составляютъ, при помощи сложешя,
таблицу умножешя и заучиваютъ ее.
Таблица умножетя.
2X2= 4
2X3= 6
2X4= 8
2X5=10
3X2= 6
3X3= 9
3X4=12
3X5=15
4X2=8
4X3=12
4X4=16
4X5=20
5X2=10
5X3=15
5X4=20
5X5=25
6X2=12
6X3=18
6X4=24
6X5=30
7X2=14
7X3=21
7X4=28
7X5=35
8X2=16
8X3=24
8X4=32
8X5=40
9X2=18
9X3=27
9X4=36
9X5=45
2X6=12
2X7=14
2X8=16
2X9=18
3X6=18
3X7=21
3X8=24
3X9=27
4X6=24
00
сч
II
¥
4X8=32
4X9=36
5X6=30
5X7=35
5X8=40
5X9=45
6X6=36
6X7=42
6X8=48
6X9=54
7X6=42
7X7=49
7X8=56
7X9=63
8X6=48
8X7=56
8X8=64
8X9=72
9X6=54
9X7=63
9X8=72
9X9=81
Обыкновенно эту таблицу заучиваютъ такъ:
2V2= 4	 дважды	два—четыре
3>(2= 6	 дважды	три—шесть
   ..•••••
5X3=15 трижды пять—пятнадцать и т. п.
L

— 40 —
При этомъ достаточно заучить только тй произведе¬
ния, которыя напечатаны крупно: остальныя отличаются
отъ этихъ только порядкомъ сомножителей.
Умножеше многозначнаго числа на однозначное.
49. Примйръ. 846X5-
Принято располагать дййсттае такъ:
846 т.-е. пишутъ множимое, подъ нимъ множителя;
X5 подъ множителемъ проводятъ черту; сбоку ставять
4230 знакъ умножеШя. Подъ чертою пишутъ цыфры
произведешя по мйрй toi’o, какъ ихъ получаютъ.
Умножить 846 на 5 значить повторить 846 слагаемымъ
5 разъ. Повторимъ 5 разъ сначала единицы множимаго,
потомъ его десятки, затймъ сотни. Произведете найдемъ
по таблицй умножешя.
Пятью 6... 30 ед., т.-е. 3 десятка; ставимъ 0 подъ
чертою на мйсгЬ единицъ, а 3 десятка запоминаемы.
Пятью 4 десятка—20 десятковъ; да 3 дес... 23 дес..
т.-е. 2 сотни и 3 дес.; ставимъ 3 десятка подъ чертою
на мйсгЬ десятковъ, а 2 сотни запоминаемы.
Пятью 8 сотенъ... 40 сотенъ; да 2 сотни... 42 сотни;
ставимъ подъ чертою 42 сотни, т.-е. 4 тысячи и 2 сотни.
Произведете 846 на 5 оказывается 4230.
50. Правило умножешя многозначна г-о
числа па однозначное. Пишутъ множимое, подъ
нимъ множителя, подъ множителемъ проводятъ черту.
Умножають (по таблицй умножешя) единицы множи¬
маго на множителя. Если отъ этого умножешя полу¬
чится однозначное число, то его пишутъ подъ чертою
на мйстй единицъ; если же получится двузначное число,
то' десятки его запоминаютъ, а единицы пишутъ подъ
чертою.

Умножаютъ затЬмъ (по таблицЬ умножешя) десятки
ыножимаго на множителя и къ полученному числу при-
кладываютъ въ умЬ то число десятковъ, которое могло
получиться отъ умножешя единицъ. Если послЬ этого
получится число однозначное, то его пишутъ подъ чер¬
тою на мЬстЬ десятковъ; если же получится число дву¬
значное, то десятки цго запоминаютъ, а единицы пишутъ
подъ чертою.
Такъ же умножаютъ на множителя сотни множимаго,
за сотнями—тысячи множимаго и т. д.
Умноживши последнюю цыфру множимаго, пишутъ по¬
лученное отъ этого число, хотя бы оно было и'двузнач-
ное, подъ чертою, влЬво отъ ранЬе написанныхъ цыфръ.
Умножеше на 10, на 100, на 1000 и вообще на 1
съ нулями.
51.	ПримЬръ. 1.	358X10.
Умножить 358 на 10 значить повторить 358 слага¬
емымъ 10 разъ. Чтобы легче узнать, сколько получится,
повторимъ 10 разъ каждую изъ 358 единицъ. Одна еди¬
ница, повторенная 10 разъ, даетъ десятокъ; значить,
если каждую изъ 358 ед. повторимъ 10 разъ, то по¬
лучимъ 358 десятковъ, что составляетъ 3580 единицъ.
ПримЬръ 2.	296ХЮ00
Одна единица, повторенная 1000 разъ, составляетъ
одну тысячу; сдЬд., 296 единицъ, повторенный 1000
разъ, составляютъ 296 тысячъ, что пишется такъ: 296000.
Правило. Чтобы умножить число на единицу съ нулями,
достаточно приписать ко множимому справа столько нулей,
сколько ихъ есть во множитель *)•
*) Въ этомъ можно также убедиться, принявъ во внимаше, что
произведете не изменяется отъ перестановки сомножителей; на осно-
ванш этого свойства произведете 296X1000 равносильно нроизведе-
Е1Ю 1000X296: а повторивъ 1000 стагаемымъ296разъ, получимъ 296000.

— 42 —
Умножен1е на какую угодно значащую цыфру
съ нулями.
52.	ПримЬръ 1.	248X30.
Умножить 248 на 30 значить повторить 248 слага¬
емымъ 30 разъ. Но 30 слагаемыхъ можно соединить
въ 10 одинаковыхъ группъ, по 3 слагаемыхъ въ каж¬
дой группЬ:
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
248
744
744
744
~74Л
744
744
744
744
744
744
ВмЬсто
того,
чтобы
248
повторять
3 раза, мы
мо-
жемъ
умножить
248 на 3,
и вмЬсто
того,
чтобы
744'
повторять 10 разъ, мы можемъ умножить 744 на 10.
Значить, для умножетя какого-нибудь числа на 30
достаточно умножить его' на 3 и полученное произведе¬
те—на 10 (для чего надо приписать справа одинъ нуль).
Прим'Ьръ 2.	895X400.
Въ этомъ примЬрЬ требуется повторить 895 слага¬
емымъ 400 разъ. Но 400 слагаемыхъ можно соединить
въ 100 группъ, по 4 слагаемыхъ въ каждой группЬ.
Чтобы узнать, сколько единицъ въ одной группЬ, надо
895 умножить на 4 (получимъ 3580); чтобы затЬмъ
узнать, сколько единицъ во всЬхъ группахъ, надо 3580
умножить на 100 (для чего достаточно приписать 2
нуля).
ДЬйсхв1е располагають такъ:
248
ХЗО
7440
895
Х400
358000

— 43 —
т.-е. пишутъ множителя такъ, чтобы нули его стояли
направо отъ множимаго.
Правило. Чтобы умножить число на значащую цыфру
съ нулями, достаточно умножить множимое на эту знача¬
щую цыфру и къ произведена приписать справа стольно
нулей, снольно ихъ есть во множителЪ.
Замйчаше. Правило этого (и предыдущаго) пара¬
графа выражено не совсЪмъ точно: умножать на цыфру
нельзя, такъ какъ цыфра—не число, а письменный знакъ
числа; когда мы умножаемы на 7, мы умножаемы не на
цыфру 7, а на число, изображаемое этой цыфрою. Точно
такъ же: не къ произведение приписываются нули, а
къ цыферному изображенш произведешя, и не столько
нулей, сколько ихъ есть во множителй, а столько нулей,
сколько ихъ есть въ цыферномъ изображенш множителя.
Однако, ради краткости рйчи, мы будемъ и далйе
уйотреблять ташя неправильныя выражешя, условив¬
шись понимать ихъ указаннымъ образомъ.
Умножеше на многозначное число.
53.	Примйръ. 3826X472.
Умножить 3826 на 472 значить повторить 3826 сла¬
гаемымъ 472 раза. Для этого достаточно повторить 3826
слагаемымъ 2 раза, потомъ 70 разъ, потомъ 400 разъ
и полученныя суммы соединить въ одну; другими сло¬
вами, достаточно 3826 умножить на 2, потомъ на 70,
затймъ на 400 и полученныя произведешя сложить.
3826	3826
X 472	Х472
7652	7652
267820	26782
1530400	15304
1805872	1805872

1
— 44 —
ДЬйств1е расположимъ такъ: пишемъ множимое, подъ
нимъ множителя, подъ ыножителемъ проводимъ черту.
Умножаемъ множимое на 2 и полученное произведете
пишемъ подъ чертою; это будетъ первое частное произ¬
ведете. Умножаемъ множимое на 70; для этого доста¬
точно умножить множимое на 7 и къ произведенш при¬
писать справа одинъ нуль; поэтому мы ставимъ 0 подъ
цифрою единицъ перваго частнаго произведешя, а цыф¬
ры, получаемыя отъ умножешя множимаго на 7, пишемъ,
по порядку ихъ получешя, подъ десятками, сотнями и
прочими разрядами перваго частнаго произведешя Это
будетъ второе частное произведете. Умножаемъ множи¬
мое на 400. Для этого достаточно умножить 3826 на 4
и къ произведению приписать справа два нуля. Пишемъ
два нуля подъ единицами и десятками второго частнаго
произведешя, а цыфры,получаемыя отъ умножешя мно¬
жимаго на 4, пишемъ, по порядку ихъ получешя, подъ
сотнями, тысячами и прочими разрядами второго част¬
наго произведешя. Тогда получимъ третье частное произ¬
ведете. Подъ последними частнымъ произведешемъ про¬
водимъ черту и складываемъ в с$ ихъ.
Для сокрагцешя письма обыкновенно не пишутъ ну¬
лей, указанныхъ нами жирнымъ шрифтомъ (см. на
предыдущей странице прим’Ьръ умножешя, помещен¬
ный направо); при этомъ надо только помнить, что,
умножая множимое на цифру десятковъ множителя,
мы должны писать первую полученную цыфру подъ
десятками перваго частнаго произведешя; умножая на
цыфру сотенъ множителя, пишемъ первую полученную
цыфру подъ сотнями предыдушихъ частныхъ произве-
дешй и т. д.
Зам1зчан1е. Если въ числе цыфръ множителя есть
1, то, умножая множимое на эту цыфру, надо иметь въ
виду, что, когда множитель есть 1, произведете при¬
нимается равнымъ множимому.

— 45 —
ПримЬръ:	470827
X 0Q013
1412481
470827:
2S24962j;:1
28255740751
54.	Правило умножения на многозначное
число. Подписываютъ подъ множимымъ множителя и
подъ множителемъ проводить черту.
Умножаютъ множимое на значапця цыфры множите¬
ля: сначала на цыфру его единицъ, потомъ на цыфру
его десятковъ, затЬмъ на цыфру сотенъ и т. д.
Получаемый отъ этихъ умножетй частныя произве-
дешя пишутъ подъ чертою одно подъ другимъ, наблю¬
дая, чтобы первая справа цыфра каждаго частнаго про-
изведешя стояла на одной вертикальной лиши съ тою
цыфрою множителя, на которую умножаютъ.
ВсЬ частныя произведетя складываютъ между собою.
Умножеше чиселъ, оканчивающихся нулями.
55.	ПримЬръ 1.	2800X15-
Умножить 2800 на 15 значить повторить 2800 сла¬
гаемымъ 15 разъ. Если станемъ находить эту сумму
обыкновеннымъ сложешемъ:
2800	то нули слагаемыхъ, очевидно, пе-
2800	рейдутъ и въ сумму, а 28 сотенъ
повторятся слагаемымъ 16 разъ. От-
15 разъ сюда заключаемъ, что для умножетя
-j-	 2800 на 15 достаточно умножить
28 на 15 и къ произведешю при¬
писать 2 нуля.
...00

— 46 —
ДЬйств!е располагаютъ такъ:
2800 т.-е. пишутъ множителя такъ, чтобы нули
X 15 множимаго стояли направо отъ множителя, про-
140 изводятъ умножете, не обращая внимашя на
28 вули множимаго, а къ произведен!ю ихъ ири-
42000 писываютъ справа.
Примйръ 2.	358X23000.
358	Чтобы повторить 358 слагаемымъ 23000 разъ,
X 23000 можно повторить 358 слагаемымъ 23 раза
1074	(т.-е. умножить 358 на 23) и полученное число
716 повторить слагаемымъ 1000 разъ (т.-е. умно-
8234000 жить на 1000, для чего достаточно приписать
справа три нуля). ДЬйств!е располагаютъ такъ
какъ указано на примйрй*).
Примйръ 3.	57000X3200.
57000	Для умножешя 57000 на какое-нибудь чис-
X 3200	ло, надо умножить на это число 57 и къ про-
114	изведент приписать три нуля. Но чтобы
171	умножить 57 на 3200, надо умножить 57
"182400000	на 32 и къ произведешю приписать два нуля.
Поэтому, когда множимое и множитель окан¬
чивается нулями, производить умножеше, не обращая
внимашя на нули, и къ произведешю приписываютъ
столько нулей, сколько ихъ есть во множимомъ и ео
множителй вмйстй.
56.	Умножен1е въ обратномъ порядкй. Во
всйхъ нредыдугцихъ примйрахъ множимое умножалось
сначала на единицы множителя, потомъ на его десятки,
загЬмъ на его сотни и т. д. Но можно производить умно¬
жеше въ обратномъ порядкй. Напр.:
*) Примере 2-й можно свести къ примеру 1-му, основываясь на
неизменяемости произведешя отъ перемены местъ сомножителей.

— 47 —
2834	2834
Х568	X568
22672	14170
17004	17004
14170	22672
1609712	1609712
Единственная разница между этими пргемами умноже-
шя—та, что, подписывая частныя произведешя одно подъ
другимъ, приходится отступать влево, если дЬйсттйе ве¬
дется по первому npieMy, и вправо, если оно совершается
по второму приему. Первый пр1емъ более употребите-
ленъ.
57.	Поверка умножен1я. Такъ какъ произведете
не изменяется отъ перемены местъ сомножителей, то
для поверки умножешя достаточно совершить его во
второй разъ, умножая множителя на множимое. Напр.:
532 Поверка:	145
X 145	X	532
2660	290
2128	435
532	725
77140	77140
Оба произведешя оказались одинаковы; след., весьма
вероятно, что дейстше сделано jrfipHO.
Произведете нЪснолькихъ сомножителей.
58.	Определен! е. Пусть имеемъ несколько чиселъ
напр., 7, 5, 3 и 4. Составимъ изъ нихъ произведете
такимъ образомъ: умноживъ первое число на второе,
получимъ 35; умноживъ 35 на третье число, получимъ
105; умноживъ 105 на четвертое число, получимъ 420.
Число 420 называется произведешемъ четырехъ сомно¬
жителей 7, 5, 3 и 4. Для обозначешя такихъ после-
довательныхъ умножешй пишутъ данныя числа въ одну
строчку въ томъ порядке, въ какомъ требуется произ¬

водить надъ ними умножеше, и ставятъ между ними
знакъ умножетя. Такимъ образомъ выражетя:
3.	4. 2. 7 или ЗХ4Х2Х7
равносильны такому:	[(3.4).2].7
т.-е. означаютъ, что 3 умножается на 4, полученное
произведете—на 2 и это последнее произведете—на 7.
59.	ПеремЪстительное свойство лреизведе-
н i я. Произведете не изменяется отъ перемены местъ со¬
множителей.
Мы уже убедились въ этомъ для произведешя двухъ
сомножителей (§ 47). Но это же свойство принадлежитъ
и произведешю сколькихъ угодно сомножителей. Напр.,
вычисливъ каждое изъ произведешй:
2.	б 3. 4. 7 2. 3. 4. 5. 7 4. 7. 3. 2. 5 7. 2. 3. 4. 5
отличающихся порядкомъ сомножителей, мы получимъ
одно и то же число 840.
Чтобы доказать это свойство, будемь вести разсуждеше въ
такой последовательности.
Во 1) докажемъ, что можно переставить, не изменяя
произведешя, двухъ рядомъ стояшихъ сомножителей; напр.,
докажемъ, что если въ произведенш 2. 5. 3. 4. 7, переста-
в мъ сомножителей 3 и 4. то произведете не изменится.
Отбросимъ пока поелфдняго сомножителя; тогда получимъ
такое произведете: 2. 5. 3. 4 или 10. 3. 4. Чтобы вычи¬
слить это произведете, надо 10 повторить слагаемымъ 3 раза
и полученное число повторить слагаемымъ 4 раза; значить:
10.3.4=(10+10+10)-|-(10-)-10-fl0)4-
+(10-fl0-j-l0)-f(10-f-10-fl0)
Возьмемъ отъ каждаго слагаемаго этой суммы по 10; тогда
получимъ 10 —|—10 —|—10 —|—10, т.-е. 10. 4. Взявъ отъ каждаго
слагаемаго еще 10, снова получимъ 10.4. Наконедъ, взявъ
въ третШ разъ по 10, получимъ еще 10. 4. Всего мы такимъ
образомъ получимъ: 10.4-)-lt).4-)-Ю.4, т.-е. 10.4.3.
Значить, 10.3.4=10.4.3. Умноживъ каждое изъ этихъ про¬
изведений на отброшеннаго раньше сомножителя 7, мы не
нарушимъ равенства между ними; тогда будемъ им4ть:
10.3.4.7=10.4.3.7

— 49 —
Во 2) докажемъ, что можно переставить, не измйнйя
проивведемя, двухъ нанихъ угодно сомножителей; напр., до¬
кажемъ, что въ произведенш 2.5.3.4.7 можно переставить
сомножителей б и 7.
Сомножителя 5 можно переставить съ 3, потому что эти
сомйожители стоять рядомъ. ЗатЬмь, по той же причин^,
5 можно переставить съ 4 и, накойецЪ, съ 7. Такимъ обра-
зомъ сомножитель 5 будетъ переведенъ на то мйсто, которое
эанимвлъ прежде сомножитель 7, и мы будемъ имёть про¬
изведете 2 . 3 . 4 . 7 . Б. Переставляя теперь сомножителя
7 съ 4, а потомъ съ 3, мы переведемъ его на то м'бсто,
которое прежде занималъ сомножитель 5. Такимъ образомъ:
2.5.3.4.7=2.7.3.4.5
Наконецъ, въ 3) докажемъ, что произведете не изменится,
если переставимъ его сомножителей накъ угодно; напр., до¬
кажемъ, что въ произведенш 2 . 5 . 3 . 4 . 7 сомножителей
можно переставить такъ: 3.7.5.4.2
Сравнивая последнее произведете съ данпымъ, нидимъ,
что сомножитель 3 долженъ стоять на 1-мъ мйстй. Для этого
мы пом'Ъняемъ его местами съ 2, что можно сделать по
доказанному равьше. . Тогда получимъ повое произведете
3 . 5 . 2 . 4 . 7. Теперь сомножителя 7 приведемъ на второе
м'Ьсто; для этого переставимъ его съ 5; получимъ 3.7.2.4. б.
Въ этомъ произведенш переставимъ б съ 2; тогда получимъ:
3 . 7 . 5 . 4 . 2. Теперь всЬ сомножители приведены въ тре¬
буемый порядокъ, при чемъ произведете ни разу не измени¬
лось.
Такъ какъ каждый изъ сомножителей можетъ быть
поставленъ на конце, т.-е. можетъ быть принять за мно¬
жителя, то вей они часто называются множителями.
60.	Какъ умножить на произведете. Мы
вйдйди (§ 52), что если требуется умножить какое ни¬
будь число на 30 (т.-е. на произведете 3 . 10), то дос¬
таточно умножить множимое на 3 й полученное число
на 10; также для умножешя какого-нибудь числа на
400 (т.-е. на произведете 4 . 100) можно умножить это
число на 4 и полученное число на 100. Подобнымъ об¬
разомъ можно поступать всегда, если множитель пред-
стайляетъ собою произведете. Пусть, напр., требуется
умножить 10 на число 12, которое равно произведешю 3.4.
4 Заказ Кп 5456

— 50 —
Объяснишь, что для этого достаточно 10 умножить
на 3 и полученное произведете умножить еще на 4.
Действительно, умножить 10 на 12 значить найти сумму:
10+10+10+10+10-|-10+10+10-fl0+10-l-10-|-10
Но сумму эту мы можемъ вычислить, между прочимъ,
такъ: соединишь слагаемый въ 4 одинаковыхъ группы
по 3 слагаемыхъ въ каждой группе:
(ю + ю -f ю) + (ю -f ю -}- ю) -f (Ю + ю + lo) 4-
(10 4- 10 4- 10);
тогда въ каждой группе единицъ будетъ 10.3, а во
всехъ группахъ ихъ окажется:
(10.3)4410.3)4-(10.3)4-(10.3), что равно 10.3.4
Подобно этому можно убедиться, что
7.24=7. (2.3.4)=7.2.3.4=14.3.4=42.4=168
Такимъ образомъ, чтобы умножить на произведете нЪ-
сколькихъ чиселъ, достаточно умножить множимое на пер¬
ваго сомножителя, полученное произведете — на второго,
последнее произведете—на третьяго и т. д.
Этимъ пользуются иногда при устномъ умноженж;
напр., чтобъ умножить 36 на 8, т.-е. на 2.2.2, можно
36 удвоить (получимъ 72), еще удвоить (получимъ 144)
и еще разъ удвоить (получимъ 288).
61.	Какъ вычислить произведете не-
сколькихъ сомножителей. Пусть требуется вы¬
числить произведеше7.2.4.5.Вм,Ьстотого,чтобы совершать
умножешя въ томъ порядке, въ какомъ написаны со¬
множители, мы можемъ соединить ихъ въ кашя-нибудь
группы, напр., такъ: (7.4).(2.5), сделать умножеше въ
каждой группе отдельно и полученным числа пере¬
множить:
7.4=28; 2.5=10; 28.10=280.
Действительно, чтобы умножить число 7.4, т.-е. 28,
на произведете 2.5, достаточно умножить 28 на 2 и
полученное число еще- на 5; тогда получимъ 28.2.5,
а это все равно, что 7.4.2.5; это же произведете оди¬
наково съ даннымъ произведешемъ 7.2.4.5 (такъ какъ

— 51 —
произведете не изм-Ьняется отъ перемЪны ыЪстъ сомно¬
жителей). Итакъ,
чтобы вычислить произведете нЪсколькихъ сомножите¬
лей, можно соединить ихъ въ катя угодно группы, сде¬
лать умножеше въ каждой группЬ отдельно и полученный
числа перемножить.
Конечно, всего лучше соединять сомножителей въ
татя группы, при которыхъ умножеше произвести
всего удобнее. Напр., чтобы вычислить произведете
25.7. 4 . 8, всего удобнее поступить такъ: 25 . 4=100;
7 8 = 56; 56.100 = 5600.
62.	Степень. Произведете нЪсколькихъ одинаковыхъ
сомножителей называется степенью, при чемъ произведе¬
те двухъ одинаковыхъ сомножителей называется второй
степенью, произведете трехъ одинаковыхъ сомножите¬
лей называется третьей степенью, и т. д.
Такъ, произведете 5.5, т.-е. 25, есть вторая степень
5-и, произведете 3.3.3, т.-е. 27, есть третья степень
3-хъ, произведете 2.2.2.2, т.-е. 16, есть четвертая
степень 2-хъ.
Степени выражають сокращенно такъ:
2 . 2 . 2 = 23 (2 въ 3-й степени),
3.3.3. 3 = 3* (3 въ 4-й степени) и т. п.
т.-е. пишутъ число, которое беретвя сомножителемъ, и
надписываютъ надъ нимъ съ правой стороны другое
число, показывающее, сколько въ степени одинаковыхъ
сомножителей; это второе число называется показателемъ
степени.
VIII.	Д'Ьлет^е.
Предварительное замЪчаже. Если какое-нибудь число раз¬
ложено на равный части, то каждая часть получаеть назва-
Hie, указывающее, сколько такихъ частей во всемъ числ’Ь.
Такъ, если число разложено на 5 равныхъ частей, то каждая
часть наз. пятою частью числа, которое разложено, если на
20 равныхъ частей, то каждая часть наз. двадцатою частью
I*

— 52 —
и т. п. Вторая часть наз. иначе половина, третья часть—
треть и четвертая часть—четверть.
Задача 1. Роздано 24 листа бумаги поровну 6-ти учени-
камъ. Сколько листовъ получилъ каждый ученикъ?
Для решетя задачи достаточно найти шестую часть 24-хъ
листовъ. Предположимъ, что шестая часть будетъ 2 листа;
тогда всЬ 6 частей составили бы 2X6, т.-е. 12 листовъ, что
меньше 24-хъ; предположимъ, что шестая часть будетъ 3 ли¬
ста; тогда число, которое разлагается на части, было бы
3X6, т.-е. 18, что все-таки меньше 24-хъ. Допустимъ, что
шестая часть окажется 4 листа; тогда въ 6-ти частяхъ бу¬
детъ 4X6, т.-е. ровно 24 листа. Значить, каждый ученикъ
получить по 4 листа.
Мы видимъ, что въ этой задача требовалось найти такое
число, которое, умноженное на 6, составило бы 24; значить,
въ задача по данному произведенш 24 и множителю 6 требуется
отыскать множимое 4.
Задача 2. Роздано ученикамъ 24 листа бумаги по 6 ли¬
стовъ каждому. Сколько учениковъ получили бумагу?
Для р,Ьшен1я задачи надо узнать, сколько разъ отъ 24 ли¬
стовъ можно отнимать по 6 листовъ, или, другими словами,
сколько разъ въ 24 (листахъ) содержится 6 (листовъ). Пред¬
положимъ, что только 2 раза; тогда все число листовъ было
бы 6X2, т.-е. 12, что меньше 24-хъ. Предположимъ, что
6 листовъ содержатся 3 раза; тогда всЬхъ листовъ было бы
6X3, т.-е. 18, что все-таки меньше 24. Допустимъ, что
6 листовъ содержатся 4 раза; тогда вс!зхъ листовъ было бы
6X4, т.-е. ровно 24. Значить, по 6 листовъ получили 4 уче¬
ника.
Въ этой задач!; требовалось найти число, на которое надо
умножить 6, чтобы получить 24; зд'Ьсь по данному произве¬
дены) 24 и данному множимому 6 требовалось найти множи¬
теля 4.
63.	ОпредЪлен1е. ДЪлешемъ наз. ариеметическое
AtfiCTBie, посредствомъ котораго по данному произведешю и
одному изъ сомножителей отыскивается другой сомножитель.
Такъ, разделить 24 на 6 значить узнать: какое число
сл’Ьдуетъ умножить на 6, чтобы получить въ произве¬
денш 24 (другими словами: найти шестую часть 24-хъ);
или на какое число сл’Ьдуетъ умножить 6, чтобы по¬

— 53 —
лучить въ произведенш 24 (другими словами: сколько
разъ 6 содержится въ 24-хъ).
При д-Ьленш данное произведете наз. дЪлимымъ,
данный сомножитель — дЬлителемъ, а искомый сомно¬
житель—частными. Такъ, въ приведенномъ примере 24
есть делимое, 6 делитель, а искомое число, т.-е. 4 —
частное.
Д Ьлете обозначается знакомь :, который ставятъ между
делимыми и делителемъ, при чемъ делимое пишется на¬
лево, а делитель направо отъ этого знака; напр., 24 : 6.
Какъ знакъ делешя иногда употребляется черта, напр.-^
Изъ определения следуетъ, что делете есть дЬйстне, об¬
ратное умиожежю, потому что- при делети дается то, что
отыскивается при умножешя (т.-е. произведете), и отыски¬
вается то, что при умяоженш дается (т.-е. сомножитель).
64. Свойство частнаго. Величина частнаго не зави-
ситъ отъ того, означаетъ ли оно множимое или множителя.
Пусть, напр., делимое будетъ 24, а делитель 6. Иско¬
мое частное можегь означать или множимое, или мно¬
жителя. Въ первомъ случае оно есть такое число, ко¬
торое надо умножить на 6, чтобы получить 24. Во вто-
ромъ случае оно есть такое число, на которое надо умно¬
жить 6, чтобы получить 24. Такъ-какъ произведете не
изменяется, когда мы множимое и множителя поменяемъ
местами, то въ обоихъ случаяхъ искомое число должно
быть одно и то же, именно 4, такъ какъ
если 4X6 = 24, то и 6X4=24.
Такимъ образомъ, узнаемъ ли мы шестую часть 24-хъ,
или узнаемъ, сколько разъ 6 содержится въ 24, въ
обоихъ случаяхъ получаемъ одно и то же число 4.
65. Делен!е съ остаткомъ. Пусть требуется
разделить 27 на 6. Пробуя умножать чисто 6 на 1, 2, 3,
4, 5	,	мы замечаешь, что ни одно изъ произведений
не равно 27. Значить, предложенное делете нельзя
выполнить. Подобна этому нельзя выполнить делете

— 54 —
12 на 5, 50 на 7 и т. п. Однако, мы условимся го¬
ворить: „разделить 27 на 6“, „разделить 12 на 5“ и
т. п., разумея при этомъ, чтобы была разделена наи¬
большая часть д'Ьлиыаго, какая только можетъ разде¬
литься на делителя. Такъ, наибольшая часть 27-и, де¬
лящаяся на 6, есть 24; это число и требуется разде¬
лить, когда говорятъ: „разделить 27 на 6“.
При такомъ деленш получается остатокъ, т.-е. избы-
токъ делимаго надъ тою его частью, которая делится.
Такъ, деля 27 на 6, мы получаемъ въ остатке число 3.
Остатокъ всегда меньше целителя, если только мы це-
лимъ действительно наибольшую часть делимаго, какая
только можетъ разделиться на делителя.
Когда делеше происходить съ остаткомъ, то полу¬
чившееся при этомъ частное наз. приближенными част¬
ными. Такъ, деля 27 на 6, мы получаемъ приближенное
частное 4. ДЬйств1е можно обозначить такъ:
27 : 6 = 4 (ост. 3),
номещая въ скобкахъ остатокъ отъ делешя.
Конечно, приближенное частное тоже имеетъ двоякое
значете, смотря по тому, означаетъ ли оно множимое,
или множителя. Такъ, делете 27 : 6 = 4 (ост. 3), озна¬
чаетъ: или, что разделивъ 27 на 6 равныхъ частей, мы
получимъ въ каждой части по 4 единицы, причемъ
3 ед. останутся не разделенными, или, что въ 27 число
6 содержится 4 раза, причемъ еще остается 3 единицы.
Для сокращетя речи неточное частное мы бу-
демъ просто называть частными.
При рЬшеши весьма ыногихъ вадачъ приходится находить
неточное частное. Пусть, напр., намъ предложена такая
Задача. 27 листовъ бумаги раздавали 6-ти учениками, всемъ
поровну; по скольку листовъ получили каждый ученики?
Въ задаче не сказано, все ли листы бумаги розданы
учениками, или несколько листовъ осталось; подразумевается
только, что роздали столько бумаги, сколько было можно.
Значить, чтобы увнать, сколько получили каждый ученики,

— 55 —
мы должны раздЬлить на 6 или 27, если это возможно, или
же наибольшую часть 27-и, какую только возможно разде¬
лить на 6.
Когда делеше совершается съ остаткомъ, то делимое
равно произведена делителя на частное плюсъ остатокъ.
Такъ, если 84 . 10 = 8 (ост. 4), то 84 = 10 Х8 + 4-
Действительно, когда мы умножимъ неточное частное
на делителя, то получимъ ту часть делимаго, которая
была разделена; если же приложимъ къ этому произве-
детю остатокъ, то получимъ все делимое.-
. Когда делете совершается безъ остатка, то делимое
равно произведешю делителя на частное.
66.	Когда употребляется делен!е. При ре-
шеши задачъ делете употребляется въ следующихъ
4-хъ случаягь:
1) Когда надо узнать, сколько разъ меньшее данное
число содержится въ большемъ данномъ числе. Такъ,
чтобы, определить, сколько разъ 8 руб. содержатся въ
48 руб., достаточно найти, на какое число следуетъ
умножить 8 руб., чтобы получить 48 руб.; здесь по про-
изведенш 48 и множимому 8 требуется отыскать множи¬
теля; а это узнается делетемъ (8 руб. въ 48 руб. со¬
держатся 6 разъ).
2) Когда надо узнать, во сколько разъ одно данное число
больше или меньше другого данкаго числа, потому что
узнать это—значить определить, сколько разъ большее
данное числоч содержитъ въ себе меньшее. Такъ, "узнать,
во сколько разъ 63 больше 9, значить определить,
сколько разъ 63 содержитъ въ себе 9.
3) Когда требуется одно данное число разложить на не¬
сколько равныхъ частей. Пусть, напр., требуется разло¬
жить 60 на 12 равныхъ частей (другими словами:
требуется найти двенадцатую часть 60-ти). Для этого
достаточно определить, какое число надо умножить на
12, чтобы получить 60; здесь по произведенш 60 д

— 56 —
множителю 12 требуется отыскать множимое; а это
узнается делешемъ (искомая часть равна 5).
4)	Когда надо данное число уменьшить въ нисколько
разъ, потому что уменьшить, напр., 60 въ 12 разъ зна¬
чить вместо 60-ти взять одну его двенадцатую часть.
67. Наименован1е единицъ делимаго, де¬
лителя и частнаго. Когда дЬлешемъ узнается,
сколько разъ одно число содержится въ другомъ, то
делимое и делитель (а также и остатокъ, если онъ есть)
могутъ означать кагая угодно единицы, но только одного
и того же наименоватя; при этомъ частное показываетъ,
сколько разъ делитель содержится въ делимомъ, и по¬
тому его можно разсматривать, какъ число отвлечен¬
ное; напр., въ 50 рубляхъ (делимое) содержатся 8 руб¬
лей (делитель) 6 разъ (частное), при чемъ 2 рубля по¬
лучаются въ остатке.
Когда же делешемъ узнается часть делимаго, то де¬
литель разсматривается, какъ число отвлеченное, показы¬
вающее, на сколько равныхъ частей разлагается дели¬
мое; делимое же и частное (а также и остатокъ, если
онъ есть) могутъ выражать кашя угодно единицы, но
только одного и того же наименовашя; напр., разде-
ливъ 62 пера на 12 (равныхъ частей), получимъ 5 перь-
евъ и остатокъ 2 пера.
Обыкновенно при обозначены действ1я назвашй еди¬
ницъ не пишутъ, а только подразумеваютъ.
68. Дележе можно выполнять посредствомъ сложежя,
вычиташя и умножешя. Пусть, напр., требуется разде¬
лить 212 на 53. Искомое частное мы можемъ иайти:
1)	Сложетемъ:	53 -|- 53 = 106;	106 -(- 53 = 159;
159 + 53 = 212.
Оказывается, что 53 надо повторить слагаемымъ 4
раза, чтобы получить 212; значить, искомое частное
есть 4.

— 57 —
2) Вычитатемъ:
 212	 159	106	 53
53	53	53	53
159	106	53	0
Оказывается, что 53 отъ 212 можно отнимать 4 раза;
значить, искомое частное есть 4.
3) Умножетемъ: 53X2 = 106; 53X3 = 159;
53X4=212. Искомый сомножитель, т.-е. частное, есть 4.
Однако, эти способы неудобны, если частное выра¬
жается болыпимъ числомъ; ариеметика указываетъ болЬе
простой npieMb, который мы теперь и разсмотримъ.
69. Какъ узнать, будетъ ли частное одно¬
значное или многозначное. Легко узнать, бу¬
детъ ли частное менЬе или болЬе 10-и. Для этого стоить
только умножить (въ умЬ) делителя на 10 и сравнить
полученное произведете съ д^лимымь.
ПрнмЪръ 1.	534 : 37=?
Если 37 умножимъ на 10, то получимъ 370, что мень¬
ше 534; значить, дЬлимое больше делителя, повторен-
наго 10 разъ, т.-е. частное должно быть 10 или больше 10.
ПримЪръ 2.	534 :’68=?
Если 68 умножимъ на 10, то получимъ 680, что боль¬
ше 534; значить, частное должно быть менЬе 10.
Когда частное меггЬе 10, то оно выражается одного
цыфрою (есть число однозначное), а когда частное равно
10 или бол’Ье 10, то оно выражается нисколькими циф¬
рами (число многозвенное).
Покажемъ сначала, какъ находится частное однознач¬
ное, а загЬмъ и многозначное.
I. Нахождение однозначнаго частного.
70. Разсмотримъ два случая: когда д'Ьлитель тоже
однозначный и когда Д'Ьлитель многозначный.

— 58 —
1) Когда делитель и частное состоять изъ одной
цыфры, то частное легко находится по таблице умножежя.
Напр., частное 56:8 равно 7, потому что, перебирая по
таблице умножешя различный произведешя числа 8,
находимъ, что семью 8 какъ разъ 56; отъ д^лешя 42:9
получается неточное частное 4, такъ какъ четырежды 9
36, что меньше 42, а пятью 9 составляетъ 45, что боль¬
ше 42; значить, въ частномъ надо взять 4, причемъ
въ остатке получится 6.
2) Когда делитель состоитъ изъ нЪсколькихъ цыфръ,
а частное изъ одной цыфры, то это частное находится
посредствомъ испытангя одной или нЪсколькихъ цыфръ.
Прим'Ьръ.	43530 : 6837.
Такъ какъ въ этомъ примере делимое меньше дели¬
теля, умноженнаго на 10, то искомое частное выражается
одною цыфрою. Чтобы найти эту цыфру, поступаемътакъ:
Отбросимъ въ делителе все цыфры, кроме первой
слева, т.-е. возьмемъ изъ делителя только 6 тысячъ.
Въ делимомъ отбросимъ справа столько же цыфръ,
сколько ихъ отбросили въ делителе, т.-е. возьмемъ изъ
дел имаго только 43 тысячи. Теперь зададимся вопросомъ,
на какое число надо умножить 6 (тысячъ), чтобы по¬
лучить 43 (тысячи) или число, близкое къ 43 (тыся-
чамъ)? Изъ таблицы умножешя находимъ, что если 6
(тысячъ) умножимъ на 7, то получимъ 42 (тысячи), а
если умножимъ на 8, то окажется 48 (тысячъ). Изъ
этого заключаемъ, что искомое частное не можетъ
быть больше 7; но оно можетъ быть 7 или меньше 7;
меньше 7-ми оно окажется тогда, когда отброшенныя
нами въ делителе 837 ед., будучи умножены на 7, со¬
ставить такое число, которое превзойдетъ 1 тысячу,
оставшуюся отъ 43 тысячъ делимаго, вместе съ 530
единицами. Начнемъ исцыташе съ цыфры. Для этого

— 59 —
умвожимъ делителя на 7:
6837 Получилось больше делимаго; значить, цыфра
X 7	7 не годится. Испытаемъ следующую меньшую
47859	цыфру 6. Для этого умножимъ	делителя	на 6:
6837	Получилось меньше 43530;	значить,	част-
X 6	ное должно быть 6, при чемъ	получится	оста-
41022	токъ *). Чтобы узнать этотъ	остатокъ,	надо
изъ 43530 вычесть 41022:	43530
41022
2508
71.	Первую цыфру для испытаюя можно найти иначе.
Возьмемъ тотъ же примерь:
43530 : 6S37
Заметивъ, что делитель очень мало отличается отъ 7
тысячъ, узнаемъ, на сколько надо умножить 7 (тысячъ),
чтобы получить 43 (тысячи)? По таблице умножешя на-
ходимъ, что шестью 7 будеть 42, а семью 7... 49. Изъ
этого заключаемъ, что частное не можетъ быть меньше
6-ти. Начнемъ испытание съ цыфры 6. Умножимъ де¬
лителя на 6 и вычтемъ произведете изъ делимаго;
если останется больше 6837, то цыфра 6 мала, и тогда
надо испытать цыфру 7; а если останется меньше 6837,
то цыфра 6 годится. Остатокъ оказался 2508; значить,
цыфра 6 годится.
*• ГГ,
Такъ полезно поступать всегда, когда вторая цыфра
делителя больше 5. Напр., делитель 6837, благодаря
тому, что у него вторая цифра больше 5, ближе под¬
ходить къ 7000, чемъ къ 6000.
*) Для сокращешя работы, прежде чЪмъ писать въ частномъ
испытуемую цыфру и умножать на нее всего дЪлителя, умножаютъ
на нее въ умю только первыя 2 пыфры дЬлителя и сраввиваютъ
полученное произведете съ соотвЪтствующими разрядами делимаго.

— 60 -
П. Нахожден1е многозначнаго чаетнаго.
72.	ПримЬръ 64508 : 23
Въ этомъ примЬрЬ дЬлимое больше д'Ьлителя, повто-
реннаго 10 разъ; поэтому частное должно содержать
болЬе одной цыфры.
При объясненш способа нахождешя этихъ цыфръ
мы будемъ предполагать, что д’Ьлитель означаетъ мно¬
жимое, а искомое частное означаетъ множителя, т.-е. что
нашнмъ дЬлешемъ мы узнаемъ, сколько разъ 23 содер¬
жатся въ 64508 (напр., сколько разъ 23 рубля содер¬
жатся въ 64508 руб.).
ОтдЬлимъ делителя отъ дЬлимаго вертикальною чер¬
тою; подъ дЬлителемъ проведемъ горизонтальную чер¬
ту; подъ этою чертою будемъ писать цыфры чаетнаго по
мЬрЬ. ихъ нахождешя.
64508J23	ОпредЬлимъ сначала, наной высшж раз-
46; М 2804 рядъ будетъ въ часткомъ.
185;;	Въ дЬлимомъ высший разряда—десятки
184;;	тысячъ, а потому прежде всего узнаемъ
108	не будутъ ли и въ частномъ десятки ты-
92	сячъ? Десятковъ тысячъ въ частномъ ие
16	будетъ, потому что число 23, умноженное
на 10000, составить 23 десятка тысячъ,
а въ дЬлимомъ только 6 десятковъ тысячъ. Будутъ ли
въ частномъ тысячи? 23, умноженный на 1000, соста¬
вить 23 тысячи; въ нашемъ дЬлимомъ тысячъ болЬе
23; значить, въ частномъ будутъ тысячи.
Сколько тысячъ въ частномъ? 23 содержится 1000
разъ въ 23 тысячахъ; 23 тысячи въ 64 тысячахъ повто¬
ряются 2 раза; слЬд., 23 въ 64 тысячахъ содержится
1000Д-1000 разъ, т.-е. 2 тысячи разъ. Ставимъ въ частномъ
цыфру 2 и будемъ помнить, что эта цыфра означаетъ
тысячи.

— 61 —
Умножимъ 23 на 2 тысячи и вычтемъ полученное
число изъ дЬлимаго. Чтобы умножить 23 на 2 тысячи,
достаточно умножить 23 на 2 л полу¬
ченное число на тысячу. Получимъ 46
тысячъ. Подпишемъ 46 подъ тысячами
д'Ьлимаго я вычтемъ.
Отъ 64 тысячъ осталось 18 тысячъ, а
отъ всего д'Ьлимаго должны остаться эти
18 тыс., да еще 508 един., т.-е. 18508.
Въ этомъ числЬ 23 не можетъ содержаться
тысячи разъ, потому что оно менЬе 23 тысячъ.
Чтобы узнать, снольно сотенъ въ частномъ, возьмемъ
въ остаткЬ только 185 сотенъ (для чего снесемъ къ
остатку отъ тысячъ следующую цыфру Д'Ьлимаго 5) и
разсуждаемъ такъ: 23 содержится 100 разъ въ 23
сотняхъ; 23 сотни въ 185 сотняхъ повторяются 8 разъ;
сл'Ьд., 23 въ 185 сотняхъ содержится 8 сотенъ разъ.
Пишемъ въ частномъ цыфру 8 направо отъ ранЬе на¬
писанной цыфры 2, такъ какъ сотни ставятся направо
отъ тысячъ. Умножимъ 23 на 8 сотенъ и вычтемъ 184
сотни изъ 185 сотенъ. Отъ сотенъ останется одна сотня,
а отъ всего дЬлимаго останется еще 08 ед.; значить,
полный остатокъ будетъ 108. Въ этомъ остаткЬ 23 не
можетъ содержаться ни одной сотый разъ, потому что 108
менЬе 23 сотенъ.
Чтобы узнать, снольно десятновъ въ частномъ, возьмемъ
въ остатк’Ь только одни десятки (для чего снесемъ къ
остатку отъ сотенъ слЬдующую цыфру дЬлимаго 0) и
разсуждаемъ такъ: 23 содержатся 10 разъ въ 23 десяткахъ;
23 десятка въ 10 десяткахъ не содержатся ни разу; слЬд.,
десятковъ въ частномъ не будетъ вовсе. Пишемъ въ част¬
номъ цыфру 0 направо отъ прежде написанныхъ (потому
что десятки пишутся направо отъ сотенъ) и сносимъ слЬ¬
дующую цыфрудЬлимаго 8, чтобы имЬть полный остатокъ.
Остается- еще узнать, сколько единицъ въ частномъ?
23 въ 108 содержатся 4 раза. Пишемъ въ частномъ
46
185
184
2804
108
92
16

— 62 —
цыфру 4 направо отъ прежде написанныхъ цыфръ, умно¬
жаемъ на нее 23 и вычитаемъ произведете изъ 108,
чтобы узнать последшй остатокъ.
Такъ какъ въ частномъ мы писали цыфры въ поряд¬
ке, принятомъ нумеращей, то остается только прочесть
число, написанное подъ чертою: 2804.
Вотъ еще 2 примера деления:
1470035	7
3480000! 15
14!j111 '210005
301 j|]
7!! 11
48 1} 1
7||;|
45 !|!
0035
30: j
35
30; L
232000
0
ООО
72, а. Другое объясяен1е д е л е н i я. Въ предыду-
щемъ параграфе мы объяснили нахождете частнаго, разсмат-
ривая делете, какъ дейеттае, которымъ находится множи¬
тель, т.-е. какъ дейетше, которымъ узнается, сколько разъ
делитель содержится въ делимомъ. Но можно вести все объ-
яснете иначе, разсматривая делете, какъ нахождете множи¬
маго, т.-е. какъ разложете даннаго числа на равныя части.
Объяснимъ это на томъ же примере:
64508 : 23
Это значить: разложить 64508 ед. на 23 равныя части
(напр., разделить 64508 рублей поровну между 23 человека¬
ми). Но десятку тысячъ въ каждой части, очевидно, не по¬
лучается, но получится по нескольку тысячъ. Чтобы узнать,
по скольку именно, возьмемъ въ делимомъ 64 тысячи и раз-
делимъ ихъ на 23 равныя части. Въ каждой части получится
2 тысячи. Пишемъ въ частномъ цыфру 2. Если въ каждой части
2 тысячи, то въ 23 частяхъ ихъ будетъ 46. Вычитаемъ 46 тыс.
изъ 64 тысячъ; остается 18 тысячъ, котОрыя предстоитъ
разделить на 23 равныя части. Очевидно, тысячи не полу¬
чится. РаДдробимъ 18 тысячъ въ сотни и приложимъ 5 сотенъ
делимаго. Получимъ 185 сотенъ. Раэделивъ ихъ на 23, полу¬
чимъ въ каждой части по 8 сотенъ. Пишемъ въ частномъ
цыфру 8 на месте сотенъ. Умноживъ 8 на 23, узнаемъ, что
во всехъ частяхъ сотенъ будетъ 184; вычитаемъ ихъ изъ 185.
Остается 1 сотня, которую предстоитъ разделить на 23 рав-

— 63 —
кыя частя. Раздробимъ ее въ десятки; получимъ 10 десят¬
ковъ. Отъ дЬлешг ихъ на 23 въ частномъ не получимъ десят¬
ковъ; ставимъ въ частномъ цыфру 0 на мЬстЬ десятковъ.
Раздробимъ 10 десятковъ въ единицы и приложимъ 8 ед.
делимаго; получимъ 108 ед. РаздЬливъ ихъ на 23, наидемъ
4 ед. Пишемъ цыфру 4 въ частномъ на мбстЬ единицъ.
73. Правило цЬлегпя. Пипгутъ делимое и дели¬
теля въ одной горизонтальной строке, отделивъ ихъ
другъ отъ друга вертикальною чертою. Подъ делите-
лемъ проводить горизонтальную черту, подъ которою
пишутъ цыфры чаетнаго, по мере ихъ получешя.
Отделяютъ въ делимомъ отъ левой руки къ правой
столько цыфръ, чтобы изображаемое ими число содер¬
жало делителя, но менее 10 разъ.
Делять отделенную часть делимаго на делителя.
Полученную цыфру пишутъ въ частномъ.
Умножаютъ делителя на найденную цыфру чаетнаго
и произведете вычитаюгь изъ отделенной части делимаго.
Къ остатку сносятъ следующую вправо цыфру де¬
лимаго и полученное после снесешя число делятъ на
делителя: цыфру отъ этого делешя пишутъ въ частномъ
направо отъ ранее написанной цыфры.
Умножаютъ делителя на вторую цыфру чаетнаго и
произведете вычитаюгь изъ того числа, которое было
разделено для получешя второй цыфры чаетнаго.
Къ остатку сносятъ следующую цыфру делимаго и
полученное после снесешя число делятъ на делителя.
Продолжаютъ такъ дейетше до техъ поръ, пока въ
делимомъ не окажется цыфръ для снесешя.
Если въ остатке, после снесешя къ нему надлежа¬
щей цыфры делимаго, получитец число, меньшее дели¬
теля, то пишутъ въ частномъ 0, а къ остатку сносятъ
следующую цыфру делимаго.
74. Сокращенное де лен1е. Когда делитель одно¬
значный, то для сокращешя письма полезно привык¬

— 64 —
нуть производить въ умЬ всЬ вычиташя, выписывая
только остатки. Напр., такъ:
563087 j_6	 или	еще	короче:
563087
23
50
28
47
5
93847
6
5 93847
гдЬ цыфра 5 подъ чертою означаетъ
послЬдшй остатокъ.
Можно не писать вычитаемыхъ и при всякомъ дЬленш;
при этомъ лучше всего вычитате производить такъ, какъ
будетъ объяснено на слЬдующемъ примЬрЬ:
4830278
31187
29478
1238
5648
855
Умножаемъ 5648 на 8 и производимъ
вычитате изъ 48302 такъ: восьмью
8... 64;64изъ 2 вычесть нельзя; при-
бавляемъ кь 2 число 70;64 изъ 72,
остается 8; пишемъ 8 подъ цыфрою
2. ЗамЬтивъ теперь, что мы увеличили уменьшаемое на 70 со¬
тенъ, т.-е. на 7 тысячъ, запомнимъ цыфру 7 съ тЬмъ, чтобы
настолько же увеличить потомъ и вычитаемое; восемью 4...
32 да 7 (въ умЬ)... 39; 39 изъ 40... 1 (мы увеличили
уменьшаемое на 40 тысячъ, т.-е. на 4 дес. тысячъ;) пи¬
шемъ 1 подъ цыфрою 0, а 4 запоминаемъ. Восемью 6... 48
да 4 (въ умЬ) 52; 52 изъ 53... 1; пшпемъ 1 подъ цыфрою
3, а 5 запоминаемъ. Восемью 5... 40, да 5... 45; 45 изъ
48... 3; пишемъ 3 подъ цыфрою 8. 1-й остатокъ есть 3118;
сносимъ къ нему следующую цыфру дЬлимаго 7. Продол-
жаемъ дЬлете такъ далЬе.
Подобное вычитате, очевидно, основывается на томъ, чтс
остатокъ не изменяется, если уменьшаемое и вычитаемое
увеличимъ на одно и то же число. Каждый разъ къ умень¬
шаемому прибавляютъ столько единицъ слЬдующаго высшаго
разряда, сколько нужно для того, чтобы можно было вычесть
произведете цыфры дЬлителя на цыфру частнаго.
Упрощеше дЪлешя въ томъ случай, когда дели¬
тель оканчивается нулями.
75.	Случай 1, когда дЬлитель есть едини¬
ца съ нулями. РаздЬливъ какое-нибудь число на

— 65 —
10, на 100, на 1000 и т. д., мы узнаемъ, сколько въ
этомъ числе заключается десятковъ, сотенъ, тысячъ и
г. д. Но это же можно узнать и по правилу нумерацш,
указанному нами ранЬе (§ 14). Напр.:
54634 : 10 = 5463 (ост. 4)
54634 : 1000 = 54 (ост. 634)
Такимъ образомъ, чтобы разделить число на 1 съ ну¬
лями, отдЪляютъ въ делимомъ справа столько цыфръ,
снольно есть нулей въ делителе; тогда оставиляся цыфры
делимаго представляютъ собою частное, а отделенный—
остатокъ.
76.	С лучай 2, когда делитель есть какое-
нибудь число, оканчивающееся нулями.
Примеръ:	389224	:	7300
3892SS | 7368 Делитель представляетъ собою 73 сотни.
365!	53	Чтобы	узнать, сколько разъ содержатся 73
сотни въ делимомъ, разобьемъ его на две
части: на сотни и единицы. Въ делимомъ
всегь сотенъ 3892 и еще 24 единицы. 73
сотни делителя могутъ содержаться только
въ одной изъ этихъ частей, именно въ сотняхъ. Чтобъ
узнать, сколько разъ 73 сотни содержатся въ 3892
сотняхъ, надо 3892 разделить на 73. Разделивъ, на-
ходимъ, что 73 сотни въ 3892 сотняхъ содержатся 53
раза, при чемъ 23 сотни остаются. Приложивъ къ 23
сотнямъ 24 единицы делимаго, получимъ 2324; въ этомъ
числе 73 сотни не содержатся ни разу; след., 2324
единицы будутъ въ остатке.
Вотъ еще примеръ, въ которомъ и делимое, и де¬
литель оканчиваются нулями.
35086 | 7366
292:
242
219
2324
5800
Итакъ, когда делитель оканчивается нулями, зачерки-
ваютъ въ немъ эти нули и въ делимомъ зачерниваютъ
5 Заказ № 5456

— 66 —
справа столько же цыфръ; оставиляся числа делятъ и къ
остатку сносятъ зачерннутыя цыфры делимаго.
77.	Поверка д,Ьлен1я. Д’Ьлете можно поверять
умножешемъ, основываясь на томъ, что делимое равно
дЬлителю, умноженному на частное (плюсъ остатокъ,
если онъ есть).
ПримЪръ:	8375 | 42	199
42;
417
378
199 X 42
398
796
395	8358
378	_|_	!7
17	8375
Мы умножили частное 199 на делителя 42 и къ по¬
лученному произведешю приложили остатокъ 17. Такъ
какъ после этого получилось число, равное делимому,
то весьма вероятно, что д'Ьйств1е сделано верно.
78.	Какъ разделить на произвелeHie. Пусть
требуется разделить 60 на произведете 5 . 3, т.-е. на
15. Разъяснимъ, что для этого достаточно разделить 60
на 5 и полученное частное разделить еще на 3:
60 : 5 = 12;	12	: 3 = 4.
Действительно, первымъ делешемъ мы, можно сказать,
разлагаемъ 60 на 5 равныхъ частей, при чемъ въ
каждой части получается 12; вторымъ делешемъ мы разла¬
гаемъ 12 на три равныя части, при чемъ въ каждой части
получается по 4. Это можно наглядно изобразить такъ:
60
12 + 12 + 12 + 12 + 12
4—|—4—)—4 4+4+4 4+4+4 4+4+4 4+4+4
Отсюда видно, что если 60 разложимъ на 15 рав¬
ныхъ частей, то получимъ то же самое число 4, какое
мы получили после нашего второго делешя.
Подобнымъ образомъ можемъ разъяснить, что для
делешя, положимъ, числа 300 на произведете трехъ мно-

г
— 67 —
жителей, вапр., на такое 3.5.4, можно разделить 300
сначала на 3 (получимъ 100), это частное разделить на
5 (получимъ 20) и последнее частное разделить на 4
(получимъ 5).
Вообще, чтобы разделить наное-нибудь число на произве¬
дете, достаточно разделить это число на перваго сомно¬
жителя, полученное частное на второго сомножителя, это
частное на третьяго и т. д. (предполагается при этомъ,
что каждое д'Ьлеше выполняется безъ остатка).
Этимъ можно иногда пользоваться при устномъ де¬
лежи; напр., чтобы разделить 1840 на 20, мы прини-
маемъ во внимаше, что 20 = 10.2 и дЪлимъ 1840 на
10 (получимъ 184) и найденное число на 2 (получимъ 92);
подобно этому, чтобы разделить какое-нибудь число на
8, равное 2.2.2, можно делимое разделить на 2, по¬
томъ еще на 2 п еще на 2.
IX. Изм-Ьнен1е произведен!я и частнаго.
ИзмЪнеме произведен!».
79.	Если увеличимъ множителя въ неснольно разъ, то
произведете увеличится во столько же разъ.
Если, напр., при умножеши 15Х$ мы увеличимъ
множителя въ 2 раза:
15X3	15X6
то и само произведете увеличится въ 2 раза, такъ
какъ умножеше 15 на 3 представйяетъ собою нахожде-
nie суммы трехъ слагаемыхъ: 15 -J—15 —|-15, тогда какъ
умножеше 15-и на 6 есть нахождете суммы 6 такшсъ же
слагаемыхъ: 15—J—15 —(—15 —(—15 —(—15 —|—15, а последняя
сумма больше первой въ два раза.
Если увеличимъ множимое въ неснольно разъ, то про¬
изведете увеличится во столько же разъ. Такъ, если
въ примере 15X3 мы увеличимъ множимое въ Зраза,
т. е. возьмемъ 45 X3, то и произведете увеличится
въ 3 раза; действительно, первое произведете пред-
ставляетъ собою сумму трехъ слагаемыхъ: 15-j-15-j-15,
5*

— 68 —
и второе произведете представляегь собою также сумму
трехъ слагаемыхъ: 45 + 45 + 45, но каждое слагаемое
второй суммы въ три раза болЪе каждаго слагаемаго
первой суммы; значить, вторая сумма въ три раза боль¬
ше первой суммы.
Если умеиьшимъ множителя или множимое въ несколь¬
ко разъ, то произведете уменьшится во столько же разъ.
Напр.: 20 X 2 = 40; 10X2 = 20; 5Х2 = Ю и т. п.
80. Зная эти изм1шетя произведешя, мы можемъ иногда
упростить умножеше. Пусть, напр., надо умножить 438
на 5. Умноживъ 438 на 10, получимъ 4380; такъ какъ
5 меньше 10 въ 2 раза, то произведете 438X5 должно
быть вдвое меньше 4380, т.-е. оно равно 2190.
Подобно этому, если требуется умножить какое-нибудь
число, напр. 32, на 25, мы можемъ умножить это число
на 100 (получимъ 3200) и полученное произведете умень¬
шить въ 4 раза (получимъ 800).
81. Если оба сомножителя изменяются одновременна
то произведете иногда увеличится, иногда уменьшится,
или же останется безъ перемены. Чтобы определить
заранее, что сделается съ произведетемъ отъ одновре-
меннаго изменетя обоихъ сомножителей, следуетъ пред¬
положить, что сначала изменено только одно множимое,
а потомъ и множитель. Увеличимъ, напр., въ произве¬
дены: 15 Xе = 90 множимое въ 3 раза, а множителя въ
2 раза:
15X6 = 90; 45X12=?
Чтобы узнать, что сделается съ произведетемъ, раз-
суждаемъ такъ: отъ увеличетя одного множимаго въ 3
раза произведете увеличится въ 3 раза, т.-е. будетъ
не 90, а 90+90+90. Отъ увеличешя затемъ множителя
въ 2 раза произведете, еще увеличится въ 2 раза; зна¬
чить, оно теперь будетъ:
(90+90+90)+{90+90+90)
т.-е. сравнительно съ начальнымъ произведетемъ оно
увеличится въ дважды три раза (въ 6 разъ). >•

— 69 —
Такъ же можно объяснить, что если множимое увели¬
чится въ 5 разъ, а множитель—въ 7 разъ, то произведе-
Hie увеличится въ пятью семь разъ, т.-е. въ 35 разъ.
Въ томъ же примере уменыпимъ множимое въ 3 ра¬
за, а множителя въ 2 раза:
15X0=90; 5X3=?
Отъ уменыпетя одного множимаго въ 3 раза про¬
изведете уменьшится въ 3 раза, т.-е. вместо 90 сде¬
лается 30; отъ уменыпетя загЬмъ множителя въ 2 раза
произведете еще уменьшится въ 2 раза, т.-е. сделается
вместо 30-и 15. Значить, отъ этихъ двухъ изменешй
произведете уменьшится въ дважды три раза, т.-е. въ
6 разъ.
Въ томъ же примере увеличимъ множимое въ 6 разъ,
а множителя уменыпимъ въ 2 раза:
15X6=90; 90X3=?
Отъ увеличен1я одного множимаго въ 6 разъ про¬
изведете увеличится въ 6 разъ, а огь уменынешя за-
темъ множителя въ 2 раза это увеличенное въ 6 разъ
произведете уменьшится въ 2 раза. Значить, после
двухъ этихъ изменешй произведете увеличится только
въ 3 раза (въ 6 : 2 раза).
Если одинъ сомножитель увеличится, а другой умень¬
шится въ одинаковое число разъ, то произведете не
изменится, потому что отъ увеличил одного сомножи¬
теля произведете увеличится, а огь уменыпетя другого
сомножителя оно уменьшится во столько же разъ. Напр.,
15X6=90; 30X3=90; 5=18=90.
82.	Если одинъ изъ сомножителей увеличится на каное-
нибудь число, то произведение увеличится на это число,
умноженное на другого сомножителя.
Такъ, если въ примере 8X3=24 увеличимъ множи¬
теля на 2, т.-е. 8 будемъ умножать не на 3, а на 5,
то тогда 8 Повторится слагаемымъ не 3 раза, а 5 разъ;
значить, произведете будетъ больше прежняго на 8+8,
т.-е. на 8.2.

— 70 -
• Такъ же можно разъяснять, что если од инь изъ со¬
множителей уменьшится на какое-нибудь число, то про¬
изведете уменьшится на то же число, умноженное на
другого сомножителя.
82а. Основываясь на этомъ свойстве произведешя, мы
можемъ иногда упростить умножеше. Пусть, напр., тре¬
буется умножить 523 на 999. Дополнимъ множителя до
1000, т.-е. увеличимъ его на 1. Тогда получимъ произ¬
ведете 523 , 1000, которое находится сразу: 523000.
Это число более искомаго на 523; значить, искомое
произведете получится, если изъ 523000 вычтемъ 523
(получимъ 522477).
ИзмЪнеше частнаго.
83.	Когда дЬлеше совершается безъ остатка, то при
изменены делимаго и делителя частное изменяется слЪ-
дующимъ образомъ:
Если увеличимъ делимое въ несколько разъ, то частное
увеличится во столько же разъ, потому что, увеличивая
делимое и оставляя делителя безъ перемены, мы, зна¬
чить, увеличиваемъ произведете и оставляемъ одного
сомножителя безъ перемены; а это возможно только
тогда, когда другой сомножитель (т.-е. частное) увели¬
чится во столько же разъ. Напр.;
10 : 2=5; 20 : 2=10; 30 : 2=15 и т. п.
Если увеличимъ делителя въ несколько разъ, то част¬
ное уменьшится во стольно же разъ, потому что, когда
увеличенъ одинъ сомножитель (делитель), произведете
(делимое) останется безъ перемены только тогда, когда
другой сомножитель (частное) уменьшится: во столько
же разъ. Напр.:
48 : 2=24; 48 : 4=12; 48 : 6=8 и т. п.
Обратно: если уменьшимъ делимое въ несколько разъ,
то частное уменьшится во столько же разъ;.
если уменьшимъ делителя въ неснольно разъ, то част¬
ное увеличится во столько же разъ.

— 71 —
Зам'Ьтимъ, что когда при д^ленш получается остатокъ,
то эти выводы не всегда бываютъ верны. Напр.:
29 : 6=4 (ост. б) 29 : 3=9 (ост. 2).
84.	Когда делимое и делитель изменяются одновре¬
менно, то частное иногда увеличится, иногда умень¬
шится, или же останется безъ изменения. Чтобы узнать
заранее, какъ изменится частное, надо предположить,
что сначала изменено только делимое, а потомъ и де¬
литель.
Следуетъ обратить особенное внимаше на те случаи,
когда частное остается безъ изменешя.
1) Если делимое и делителя увеличимъ въ одинаковое
число разъ, то частное не изменится, потому чтоотъуве-
личешя делимаго частное увеличится, а отъ увеличешя
делителя оно уменьшится въ одинаковое число разъ.
Такъ, если въ примере 60:15 = 4 увеличимъ дели¬
мое и делителя въ 5 разъ, то получимъ 300:75 = 4.
2) Если делимое и делителя уменьшимъ въ одинановое
число разъ, то частное не изменится, потому что отъ
уменьшетя делимаго частное уменьшится, а отъ умень-
шешя делителя оно увеличится Въ одинаковое число
разъ.
Такъ, если въ томъ же примере уменьшимъ делимое
и делителя въ 5 разъ, то получимъ 12:3 = 4.

ОТДТ.ЛЪ ВТОРОЙ
Именованныя цЬлыя чнсла.
I. Изм'ЬреМе величинъ.
85.	Понятiе о величине. Все то въ предметахъ
или явлетяхъ, что можетъ быть равно, больше или
меньше, наз. величиною. Такъ, весъ предметовъ есть
величина, потому что весъ одного предмета можетъ быть
равенъ весу другого предмета и можетъ быть больше
или меньше веса другого предмета.
Вотъ величины, наиболее знакомыя каждому изъ насъ:
Длина (называемая иногда шириною, иногда высотою,
толщиною...);
Поверхность, т.-е. то, что ограничиваем предметъ
съ разныхъ сторонъ;
Объемъ, т.-е. часть пространства, занимаемая пред-
метомъ;
Весь, т.-е. давлеше, производимое предметомъ на гори¬
зонтальную подпору,
Время, въ течете котораго совершается какое-либо
явлете или дейсше;
Цена и многгя друпя величины.
Заметимъ, что плоская поверхность предмета (напр.,
поверхность стола, пола и т. п.) называется площадью;
внутреншй объемъ какого-либо сосуда или ящика наз.
вместимостью или емкостью.

— 73 —
66.	3 наче Hie величины. Каждая величина мо¬
жетъ иметь безчисленное множество значешй, отличаю¬
щихся одно отъ другого только тЬмъ, что одно значеше
больше, другое меньше. Напр., величина, называемая
длиной, въ разныхъ предметахъ вообще им'Ъетъ различ¬
ный значешя; такъ, у листа бумаги длина иная, чемъ
у комнаты, у линейки и пр. Иногда можетъ случиться,
что у двухъ предметовъ длина окажется совершенно
одинаковой; тогда говорить, что у этихъ предметовъ длина
им'Ьегь одно и то же значеше.
87.	И змЪрен1е значен1я величины. Поло-
жимъ, что мы хотимъ составить себе ясное поняые о
длине какой-нибудь комнаты; тогда мы изм’Ьряемъ ее
при помощи другой длины, которая намъ хорошо из¬
вестна, напр., при помощи аршина. Для этого откла-
дываемъ аршинъ по длине нашей комнаты сколько разъ,
сколько можно. Если аршинъ уложится по длине комнаты
ровно 10 разъ, то говоримъ, что длина ея равна 10
аршинамъ. Подобно этому, чтобы измерить весь какого-
либо предмета, мы беремъ другой весь, который намъ
хорошо иэвестенъ, напр., фунтъ, и узнаемъ (помощью
весовъ), сколько разъ фунтъ содержится въ измеря-
емомъ значенш веса. Пусть онъ додержится ровно 5
разъ; тогда говоримъ, что весь предмета равенъ 5
фунтамъ.
Известное намъ значеше величины, употребляемое для
измерешя другихъ значешй той же величины, наз. еди¬
ницею этой величины. Такъ, аршинъ есть единица длины,
фунтъ—единица веса и т. п.
Для каждой величины выбираютъ несколько единицъ,
одне более крупныя, друпя более мелмя. Такъ, для
измерешя различныхъ значешй длины, кроме аршина,
употребляюгъ еще: сажень, версту, вершокъ, фууъ и
друпя. Если, напр., въ длине комнаты аршинъ содержится
не ровно 10 разъ, а съ некоторыми остаткомъ, который
меньше аршина, то этоть остатокъ измеряютъ при по-

— 74 —
моща более мелкой единицы, напр., вершкомъ. Если
случится, что въ остатке вершокъ уложится 7 разъ, то
говорять, что длина комнаты равна 10 аршинамъ 7
вершкамъ.
Измерить накое-либо значеню величины значить выразить
его при помощи одной или несколькихъ единицъ этой
величины.
88.	Въ каждомъ государстве правительство установило
определенный единицы для главнейшихъ величинъ.
Сделаны разъ навсегда образцовая единицы: образцовый
аршинъ, образцовый фунть и т. п., по которымъ при-
готовляютъ единицы для обиходнаго употребления. Еди¬
ницы, вошедлдя въ употреблете, называются мерами.
Разсмотримъ главнейппя меры, употребляемая у насъ
въ Россш.
89- Меры разстоян1й:
миля =	7	верстамъ	сажень	= 7	футамъ
верста =500 саженямъ	футъ	=12	дюймамъ
сажень =	3	аршинамъ	дюймъ	=10	лишямъ
аршинъ =	16 вершкамъ
Такъ какъ аршинъ втрое меньше сажени, а сажень
содержигь 84 дюйма (12X7), то 1 арш.=28 .дюймамъ.
Прилагаемъ здесь для нагляднаго сравнения две меры:
Замечан1я. 1) Меры разстояшй называются линей¬
ными, потому что онЬ служатъ для измерешя длины
различныхъ литй.
2)	По сравнешю одна съ другой однородный меры,
т. е. меры одной и той же величины, бываюгъ высшаго
Меры, употребляемыя въ Россш.
вершокъ
дюймъ

— 75 —
и низшаго разряда. Такъ, сажень есть мЪра высшаго
разряда по сравненш съ аршиномъ и низшаго разряда
по сравнетю съ верстой.
3)	Единичными отношешемъ двухъ однородныхъ м'Ьръ
называется число, показывающее, сколько разъ меньшая
Mipa содержится въ большей. Такъ, единичное отноше-
Hie между саженью и аршиномъ есть 3.
90.	Miры поверхностей. Для измЪрешя поверх¬
ностей употребляются мЪры, называемыя квадратными,
такъ какъ онЬ имЗпотъ форму квадрата. Квадратомъ
называется такой четыреугольникъ, у котораго всЬ 4
стофоны равны и всЬ 4 угла одинаковы. Квадратный
дюймъ есть квадратъ, у котораго каждая сторона равна
линейному дюйму; квадратный вершокъ есть квадратъ,
у котораго каждая сторона равна линейному вершку
и т. д.
Квадр. дюймъ	Квадр.	вершокъ
91.	Изм^реше н'Ькоторыхъ площадей. Если
площадь имЪетъ форму четыреуголъника съ одинако¬
выми углами (форму прямоугольника), то ее лег¬
ко измерить. Пусть, напр., требуется узнать, сколько
квадратныхъ аршинъ заключается въ площади пола ком¬
наты. Для этого достаточно смерить линейнымъ арпш-
номъ длину и ширину комнаты и полученныя числа
перемножить. Пусть, напр., длина комнаты равна 10 ар-

— 76 —
шинамъ, а ширина 7 аршинамъ. Разд'Ьлимъ длину пола
на 10, а ширину на 7 равныхъ частей, а загЬмъ прове-
демъ лиши, какъ указано на чертеже; тогда площадь
пола разделится на кв. аршины, которыхъ будетъ 7 ря-
довъ по 10, т. е. 10Х 7 = 70.
10
7
92.	Какъ найти единичное отношеше двухъ
квадратныхъ мЪръ. Чтобы найти единичное отноше-
Hie двухъ квадратныхъ мЪръ достаточно помножить само
на себя единичное отношеше двухъ линейныхъ мЪръ тЬхъ
же назвашй.
Напр., ед. отношеше между квадр. саженью и квадр.
аршиномъ равно 3X3=9. Для объяснены этого вообра-
зимъ два квадрата та-
кихъ, чтобы у одного
сторона была въ ар¬
шинъ, а у другого въ
сажень; тогда менышй
квадратъ будетъ квад¬
ратный аршинъ, а боль-
ппй — квадратная са¬
жень. Если разделшгь
болышй квадратъ наЗ
равныя полосы, то каждая полоса, имея ширину въ

— 11 —
1 арш., а длину въ 3 аршина, будетъ содержать, оче¬
видно, 3 малыхъ квадрата; значить, болышй квадратъ
будетъ содержать ихъ 3 раза по 3 или 9.
Такимъ образомъ составляется следующая
Таблица нвадратныхъ мЪръ:
квадр. миля=49 кв. верст. (7X7=49)
„	верста=250000 кв. саж. (500X500=250000)
„	сажень=9 кв. арш. (3X3=9)
„	„	=49	кв.	фут. (7X7=49)
„ аршивъ=256 кв. верш. (16X16=256)
„ футъ=144 кв. дюйма (12X12=144)
„ дюймъ=100 кв. литй (10XJ 0=100)
92а. Десятина. Для изм'Ьрешя поверхности полей
употребляется десятина, содержащая въ себ'Ь 2400 кв.
60
40
US'
4 N
р
• • •
301 '
4
сажень и равная, слгЬд., площади прямоугольника, им'Ь-
ющаго въ длину 60 сажень, а въ ширину 40 саженъ, или
же прямоугольника, им'Ьющаго въ Длину 80 саженъ, а
въ ширину 30 саженъ (умноживъ 60 на 40 или 80 на
30, получимъ одно и то же число 2400).
93.	М'Ьры объем о въ. Для изм'Ьрешя объемовъ
употребляются м'Ьры, называемый кубическими, такъ
какъ онЬ им'Ьготъ форму куба. Ку-
бомъ наз. объемъ, ограниченный со
вс'Ьхъ сторонъ 6-ью одинаковыми
квадратами. Каждый квадратъ на¬
зывается стороною куба; лиши, по
которымъ пересекаются две смеж¬
ный стороны, называются ребрами

— 78 —
куба. ВсЬ ребра куба имЬютъ одинаковую длину. Кубъ,
у котораго каждое ребро въ дюймъ, называется куби-
ческимъ дюймомъ; кубическими футомъ назыв. такой
кубъ, у котораго каждое ребро равно линейному футу,
и т. п.
94.	Изм,Ьрен1е н'Ькоторыхъ объемовъ. Если
объемъ представляетъ собою форму, ограниченную 6-ю
прямоугольниками, то его легко измерить. Пусть,
напр., требуется узнать, сколько куб. аршинъ заклю¬
чается въ объеме комнаты. Для этого достаточно изме¬
рить линейнымъ аршиномъ длину, ширину и высоту
комнаты и полученный числа перемножить. Пусть, напр.,
длина комнаты будетъ 10 аршинъ, ширина — 7 арш.,
а высота — 8 арш. Умноживъ 10 на 7, мы узнаемъ,
что на полу комнаты поместится 70 квадр. аршинъ. Оче¬
видно, что на каждомъ изъ этихъ 70 квадр. арш. можно
поставить одинъ куб. аршинъ, а на всемъ полу ихъ
установится 70. Тогда получится слой кубовъ въ одинъ
аршинъ высоты (какъ изображено у насъ на рисунке);

— 79 —
но комната им’Ьетъ въ высоту 8 арш., слЪд., можно въ
ней поместить одинъ на другой 8 слоевъ. Тогда веЬхъ
куб. арш. окажется 70 X8» т.-е. 560, или произведете
трехъ чиселъ: 10Х7Х8-
Такъ же можно узнать объемъ ящика, сгЬны, ямы
съ отвесными станками и съ прямоугольнымъ основа-
н1емъ и т. п.
95.	Кань найти единичное отношете двухъ
нубическихъ мtръ. Чтобы узнать единичное отноше-
Hie двухъ кубичеснихъ Mtpb, достаточно повторить сомно-
жителемъ 3 раза единичное отношеше линейныхъ мЪръ
тЪхъ же назвашй.
Такъ, единичное отношеше между куб. саженью и куб.
аршиномъ равно ЗХ8Х3> т.-е. 27. Для объяснения
этого представимъ себ’Ь тате 2 куба, чтобы у одного
ребро было въ аршинъ, а у другого—въ сажень; тогда
менышй кубъ будетъ куб. аршинъ; а болытй — куб.
сажень. Очевидно, что на днЪ большего куба устано¬
вится 9 меныпихъ кубовъ (потому что дно большаго куба
содержитъ въ себ^ 9 квадр. аршинъ). Но высота боль¬
шаго куба равна сажени, а высота меныпаго куба равна
аршину, поэтому на первый слой малыхъ кубовъ можно
будетъ еще положить 2 слоя, и тогда выйдетъ 3 слоя
по 9 кубовъ, т.-е. всего 27 куб.

— 80 —
Такимъ образомъ составляется следующая
Таблица нубичеснихъ нгёръ.
куб. миля=343 куб. верст. (7Х7Х7)
„ верста=125000000 куб. саж. (500X500X600)
„ сажень=27 куб. арш. (3X3X3)
—343 куб. футамъ (7><7Х7)
„ аршинъ—4096 куб. вершк. (16X16X16)
„	футъ=1728 куб. дюйм. (12X12X12)
„ дюймъ=1000 куб. лишямъ (10ХЮХЮ)
96.	Меры объемовъ жидкихъ те л ъ. Основная
мера—ведро, имеющее объемъ, равный приблизительно
750 куб. дюймамъ; въ этомъ объеме помешается 30
фунтовъ чистой воды*).
Бочка=40 вед., ведро = 10 штофамъ, штофъ =2 по¬
луштофами, полуштофъ=б чаркамъ.
Меры сыпучихъ телъ (т.-е. ржи, пшеницы, овса
ит. п.). Четверть = 2 осминамъ=8 четверикамъ (или
мерамъ), четверикъ = 8 гарнцамъ (гарнецъ вмещаетъ
въ себе 8 фунтовъ чистой воды *).
Четверикъ есть сосудъ, котораго вместимость немного
менее куб. фута (1601 куб. дюймъ).
Замечаше. Слова „четверикъ" и „четверть" пи¬
шутъ сокращенно такъ: „чк.“ и „чт.“.
Меры торговаго веса:
Пудъ=40 фунтамъ.	Лотъ=3 золотникамъ.-
Фунтъ=32 лотамъ=96 золот. Золотникъ=96 долямъ.
Меры аптекарскаго веса. Аптекарсый фунтъ
меньше торговаго фунта на одну восьмую часть; онъ
равенъ 28 лотамъ или 84 золоти, торговаго вЬса.
*) при температур* 16*/8° Цельзш.

— 81 —
Ап фунтъ=:12 унщямъ.	I Драхма=3 скрупуламъ
Унщ'я=8 драхмамь.	I Скрупулъ-20гранамъ*).
МЬры цЬны (деньги). Какъ мЬры цЬны употребля¬
ются или металлическая монеты, или кредитные билеты.
1) Монеты употребительны золотыя, серебряный и
мЬдныя.
Золотая монета чеканится изъ сплава, содержащаго
9 вЬсовыхъ частей золота и 1 весовую часть мЬди. Въ
настоящее время обращаются слЬдуюгщя золотыя моне¬
ты: въ 15 рублей (импер1алъ), въ 10 руб., въ 7 руб.
50 коп. (полуимпер!алъ) и въ 5 руб.
Серебряная монета въ 1 рубль, въ 50 коп. и въ
25 коп., чеканится изъ сплава, содержащаго на 9 в'Ьсо¬
выхъ частей серебра 1 вЪсовую часть мЬди, а серебря¬
ная монета въ 20 коп., 15 коп., 10 коп. и 5 коп., чека¬
нится изъ сплава, содержащаго на б вЬсовыхъ частей
серебра 5 частей мЬди.
МЬдная монета чеканится въ 5 коп., 3 коп., 2 коп.,
1 коп., въ пол копейки и въ четверть копейки.
2) Кредитные билеты употребляются: въ 500 р.,
100 руб., 50 руб., 25руб., Юруб., 5 руб., 3руб. и 1руб.
‘МЬры бумаги. Стопа = 20 дестямъ, десть = 24
листамъ.
97.	МЬры, времени. Есть д^Ь основныя мЬры вре¬
мени: сутки и годъ. Сутки представляютъ приблизительно
то время, въ течете котораго земля совершаетъ полный
оборотъ около оси; онЬ раздЬляются на 24 часа, считае¬
мые отъ 1 до 12 и затЬмъ опять отъ 1 до 12. За на¬
чало сутокъ принимаютъ полночь, т.-е. 12 часовъ ночи.
НедЬля — 7 суткамъ.	Часъ = 60 минутамъ.
Сутки = 24 часамъ.	Минута = 60 секундамъ.
*) Въ настоящее время въ аптека хъ применяется также и метри¬
ческая система вЪса; см. объ этомъ выноску въ концъ § 209.
6 Заказ № 5456

— 82 —
Годъ представляетъ собою приблизительно то время, въ
течете котораго земля совершаетъ полный оборотъ кру-
гомъ солнца. У насъ принято считать каждые 3 года въ
365 дней, а четвертый въ 366 дней. Годъ, содержаицй
въ себе 366 дней, называется високосными, а года, содер¬
жание по 365 дней, — простыми. Къ четвертому году
добавляютъ одинъ лиштй день по следующей причин!..
Время обращетя земли кругомъ солнца содержитъ въ
себе не ровно 365 сутокъ, а 365 сутокъ и 6 часовъ (при¬
близительно). Такимъ образомъ простой годъ короче
истиннаго года на 6 часовъ, а 4 простыхъ года короче
4-хъ истинныхъ годовъ на 24 часа, т.-е. на оде!, сутки.
Поэтому, къ каждому четвертому году добавляютъ одн'Ь
сутки (29-е февраля). Случилось такъ, что годъ, отъ
котораго мы ведемъ наше л’Ьтосчислеше (т.-е. годъ Рож¬
дества Христова), былъ високосный; поэтому следуюицо
затЬмъ високосные годы были: 4-й, 8-й, 16-й, 20-й...
вообще таме годы, которыхъ числа делятся на 4 безъ
остатка; такъ, 1908-й годъ былъ високосный (1908 делится
на 4 безъ остатка), года же 1907,1906,1905 были простые.
Годъ разделяется на 12 неравныхъ частей, называе-
мыхъ месяцами. Вотъ назвашя месяцевъ по порядку:
январь (31 день), февраль (28 пли 29), мартъ (31), апрель
(30), май (31), iiOHL (30), ноль (31), августъ (31), сен¬
тябрь (30), октябрь (31), ноябрь (30) и декабрь (31).
ЛЬтосчислеше, по которому три года считаются въ 365
дней, а четвертый въ 366, было установлено КХгпемъ Це-
заремъ (въ 46 году до Р. Хр.) и потому наз. кшанснимъ.
Оно принято у насъ въ Poccin. Въ западной Европе счи-
таютъ несколько иначе, а именно тамъ счетъ идетъ на
13 дней впереди нашего; такъ, когда мы считаемъ 1-е
января, тамъ считаютъ 14-е января.
98.	Григорзанское летосчислен)е. Время, про¬
текающее отъ одного весенняго равноденстгйя до следую¬
щего весенняго равноденств!я, называется солнечнымъ
или тропическимъ годомъ; время, считаемое за годъ

— 83 —
по гражданскому л^тосчисленпо, называется г р а ж д а н с к и м ъ
годомъ.
Такъ какъ перемены времеыъ года зависать отъ положешя
земли относительно солнца, то солнечный годъ представляеть
такой промежутокъ времени, въ течете котораго вполне за¬
вершаются перемены вреыенъ года. Поэтому желательно,
чтобы годъ гражданскШ по возможности совпадалъ съ годомъ
солнечнымъ; только при этомъ условш времена года будутъ
приходиться въ одни и гЬ же месяцы. Л^тосчислеше, вве¬
денное Юлземъ Цезаремъ, достигаетъ этого не вполне. По
этому счисленпо гражданский годъ считается въ 365 дней и
6 часовъ, тогда какъ солнечный годъ содержитъ (приблизи¬
тельно) 365 дней 5 часовъ 48 минуть 48 сек., такъ что годъ
кшанскаго счислешя длиннее солнечнаго (приблизительно)
на 11 мин. 12 сек., что въ 400 л-Ьть составляетъ почти
3 дня. Юл1анское лйтосчислеше исправлено было впервые
папою Григор1емъ XII I-м ъ въ 1582 году. Къ этому году
разница между гражданскимъ счислешемъ времени и солнеч¬
нымъ составляла 10 сутокъ, такъ что считали, напр., 1-е
сентября, когда следовало бы по солнечному времени считать
11-е сентября. Чтобы уравнять гражданское время съ солнеч¬
нымъ, ГригорШ XIII пове.тЬлъ вместо 5 октября въ 1582 г.
считать 15-е октября. Но такъ какъ подобное запаздываше
должно было повториться и впосл4дствш, то ГригорШ XIII
установилъ, чтобы на будущее время каждыя 400 л!зтъ гра-
жданскаго счислешя были сокращены на 3-е сутокъ. Это
сокращеше должно было производиться такимъ образомъ. По
юлианскому счисленш тЬ годы, которыхъ числа представляютъ
полныя сотни, считаются високосными, напр, годы 1600-й,
1700-й и т. п. должны считаться по кшанскому счисленш
въ 366 дней. Но Григорш XIII повелЪдъ, чтобы тате
годы считались простыми,.кромФ тЪхъ, у которыхъ число
сотенъ делится на 4. Всл4дств1е этого, по счисленш
папы Григор1Я, годъ 1600-й долженъ былъ считаться ви-
сокоснымъ (16 делится на 4), а годы: 1700,1800,1900—про¬
стыми, тогда какъ по кшанскому счислетюъеЬ эти 4 года счита¬
лись високосными. Такимъ образомъ каждыя 400 л'Ьтъ сокраща¬
ются на 3-е сутокъ. Счислеше, установленое Григор1емъ XIII,
пз'в'Ьстно подъ именемъ григор!анскаго. Оно въ насто¬
ящее время принято по всей Европа, кром4 Россш й Грецш.
Григор1анское счислеше называется иначе новымъ сти-
лемъ, а кшанское—старымъ стилеыъ. Такъ какъ въ
1582 году новый стиль подвинулся впередъ отъ стараго стиля
6*

— 84 —
на 10 дней, а послЬ того еще на 3 дня (въ 1700, 1800 и
1900 годахъ), то въ настоящее время старый стиль отстаетъ
отъ новаго на 13 дней.
99. Именованное число. То, что получается
послЬ измЬрешя величины (результата измЬрешя), наг
зываюта числомъ. Число наз. именованными, если при
немъ оставлено назваше единицы измЬрешя, напр. 7
сажень. Число лаз. отвлеченными, если при немъ не
поставлено назвашя единицы, которою производилось
измЬреше; таково, напр., число 7.
Именованное число наз. простыми, если оно составлено
изъ единицъ только одного назвашя, напр., 13 фунтовь.
Именованное число называется составными, если оно со¬
ставлено изъ единицъ разныхъ назвашй, напр.: 13 фун-
товъ 5 лотовъ 2 золотника.
Если составное именованное число правильно образо¬
вано, то всякое отдельное число въ немъ не должно
составлять ни одной единицы слЬдующаго высшаго
разряда; напр., такое число:
2 пуда 85 фунтовь
неправильно составлено, потому что 85 фунтовь боль-
ще 40 фунтовь и, значить, 85 фунтовъ содержать въ
себЬ нисколько пудовъ (именно 2 пуда 5 фунт.). Пра¬
вильно составленное число будетъ 4 пуда 5 фунт.
100. Двойное опр е д Ь л е н i е числа. Въ начала этого
учебника число было определено, какъ собран!е единицъ (§ 1).
Теперь числу дано другое определеше, а именно: число
есть результатъ измЬрен1я. Заметимъ, что первое определе¬
ше представляетъ собою частный случай второго; напр.,
собраше, называемое числомъ 3, можно разсматривать, какъ
результатъ измерешя такого значешя величины, въ которомъ
другое значеше, принятое за единицу, повторяется разъ, да
еще разъ, да еще разъ. Значить, первое определение заклю¬
чается во второмъ. Но нельзя сказать того же о второмъ
определены: не всяюй результата измерешя есть число въ
смысле собрашя, потому что часто случается, что въ резуль¬

— 85 —
тат4 измерешя получается не одно число, а совокупность
многихъ чиселъ. Значить, второе определение даетъ числу
более широкое значете, чемъ первое; оно обнимаетъ собою
и числа целыя, и числа дробныя.
IT. Преобразован1е именованыаго
числа.
101. Иогда именованныя числа считаются
равными. Если два именованныя числа выражаютъ
собою одно и то же вначеше величины, то говорятъ, что
ташя именованныя числа равны между собою; напр.,
составное имен, число 2 саж. 1 арш. равно простому
имен, числу 7 арш., потому что оба эти числа выража¬
ютъ' одну и ту же длину.
. Есть два преобразовали одного именованнаго
числа въ другое, равное ему: раздроблен1е и пре-
вращеше.
102. Раздроблен!е. Раздроблемемъ наз. преобразо¬
вало именованнаго числа въ единицы одного какого-нибудь
низшаго разряда.
Примерь: 5 пуд. 4 фунта 15 лотовъ выразить только
въ золотникахъ.
Чтобы решить этотъ вопросъ, узнаемъ сначала, сколь¬
ко въ 5 пуд. заключается фуятойъ; къ полученному
числу приложимъ 4 фунта; загЬмъ узнаемъ, сколько во
всЬхъ фунтахъ заключается лотовъ; къ полученному
числу приложимъ 15 лотовъ; наконецъ узнаемъ, сколько
во всЬхъ лотахъ заключается золотниковъ. Действ1я рас-
полагаютъ такъ:
5 пуд. 4 фун. 15 лотъ.
Х*о
200 	 фунтовъ въ 5 пудахъ.
+ 4
204 	 фунта въ 5 пуд. 4 фу*.

— 86 —
204
Х32
408
612
6628 	 лотовъ въ 5 пуд. 4 фун.
Ч~
6543	....	лота въ 5 пуд. 4 фунт. 15 лот.
_Х!
19629	....	золотниковъ	въ 5 пуд. 4 фунт. 15 лот.
103.	Превращен!е. Превращежемъ называется преоб¬
разовала именованнаго числа въ единицы высших^ разря¬
довъ.
Прим'Ьръ: 19629 золотниковъ выразить въ мЪрахъ
выпшихъ разрядовъ.
Чтобы решить этотъ вопросъ, узнаемъ сначала, сколько
въ 19629 золотникахъ заключается лотовъ; потомъ, сколько
въ полученномъ числЬ лотовъ заключается фунтовъ;
потомъ—въ этихь фунтахь сколько пудовъ.
ДЬйств1я располагаютъ такъ:
19629 |3
181]
6543
32
1б!
6411
204
40
15!
143
200
5 пуд.
12
128
4 фун.
12 j 15 лот.
9
9
О' зол.
19629 8ол.*= 5 пуд. 4 фун. 15 лот.

— 87 —
Ш. Д'ЁйствХя надъ именованными чис¬
лами.
104.	Смыслъ дЪйствШ надъ именованными числами. Сум¬
мой нЪсколькихъ данныхъ значетй одной и той асе величины
наз. новое вначеше той асе величины, составленное изъ ча¬
стей, соответственно равныхъ даннымъ вн&четямъ. Та¬
кимъ образомъ, напр., можетъ быть сумма нЪсколькихъ дан¬
ныхъ длинъ, сумма нЪсколькихъ данныхъ вЪсовъ и т. п.
Понятте о суммЪ слуасить основашемъ для опредЪлеш'я
дЪйств1й надъ вначешями величины. Эти опре-
дЪлеш’я слЪдующ)я:
ДЪйств1е, посредствомъ котораго отыскивается сумма, назы¬
вается слоасен1емъ.
. ДЪйств1е, посредствомъ котораго по данной суммЪ и од¬
ному слагаемому отыскивается другое слагаемое, наз. вычи-
тан1емъ.
ДЪйствсе, посредствомъ котораго данное значеше величины
повторяется слагаемымъ столько разъ, сколько въ данномъ
числ'Ь ерть единицъ, наз. умножешемъ.
ДЪйств1е, посредствомъ котораго по данному произведение
и одному изъ сомножителей отыскивается другой сомножитель,
наз. дЪлен1емъ.
Когда значенш величины измЪрены, то они выражаются
именованными числами; тогда дЪйств1я надъ значешями вели¬
чины становятся дЪйств!ями надъ именованными
числами; но смыслъ дЪйствШ отъ этого не измЪняется.
Если бы именованныя числа всегда выражались при помощи
одной и той же единицы, то дЪйствгя надъ ними ничЪмъ Н9
отличались бы отъ дЪйствШ надъ числами отвлеченными; такъ,
складывать 215 пуд. и 560 пуд. надо совершенно такъ же,
какъ складываются 215 какихъ угодно единицъ съ 660
такими же единицами. Но именованныя числа часто выра¬
жаются при помощи единицъ различныхъ названШ; тогда дЪй-
CTBiH нйдъ ними производятся по ннымъ правиламъ, чЬмъ
дЬйств1я надъ числами отвлеченными. Разсмотримъ эти правила.

— 88 —
Сложен1е именованныхъ чиселъ.
105.	Для удобства подписываютъ слагаеыыя одно подъ
другимъ такъ, чтобы единицы одного назвашя стояли въ
одномъ вертикальномъ столб'Ь. Начинаютъ сложеше съ
единицъ низшаго разряда; загЬмъ переходятъ посл'Ьдо-
вательно къ сложешю единицъ сл’Ьдующихъ высшихъ
разрядовъ. Напр.:
5
вер...
490 саж..
6 фут.
11 дюйм.
10
»
432 .
Б „
10 „
—i_ .
8
я
460 „
4 „
9 „
2
я
379 „
3 ..
И
3
я
446 ,,
2 1
10 „
28
вер.
2207 саж.
20 фут.
51 дюйм.
32
вер.
210 саж.
3 фут.
3 дюйм.
Посл'Ь сложешя получилось (подъ первою чертою) не¬
правильно составленное именованное число; подъ нимъ
проводить вторую черту и превращаютъ 51 дюймъ въ
4 ф. и 3 д.; 3 д. подписываютъ подъ второю чертою
на мЬстЬ дюймовъ, а 4 ф. прикладываютъ къ 20 ф.;
24 ф. превращаютъ въ 3 саж. и 3 ф.; 3 ф. подписы¬
ваютъ подъ второю чертою, а 3 саж. прикладываютъ
къ 2207 саж. и т. д.
Можетъ случиться, что въ одномъ или н'Ьсколькихъ
слагаемыхъ н'Ьтъ единицъ такихъ назвашй, кашя есть
въ остальныхъ слагаемыхъ; тогда на ы'Ьстахъ недостаю-
щихъ единицъ пишутъ нули. Напр.:
1	1
300	вер...	О	саж... О	арш...	8	вершк.
250	„	...	80	„	2	.	...	12	„
30	.	1	„	...	о	„
+
550 вер... 111 саж... 1 арш... 4 вершк.
(Зд'Ьсь превращен1я сд'Ьланы въ ум’Ь).

— 89 —
Вычитан1е именованныхъ чиселъ.
106.	Пусть требуется вычесть 2 версты 80 саж. 2 арш.
5 вершк. изъ 9 вер. 50 саж. 2 арш. Подписываемъ въ
изв'Ьстномъ порядк'Ь вычитаемое подъ уменьшаемымъ
и проводимъ черту:
Чтобы вычесть 5 вершковъ, беремъ отъ 2-хъ аршинъ
1 аршинъ (въ знакъ чего ставимъ точку надъ 2 арш.);
взятый аршинъ раздробляемъ въ вершки; получаемъ 16
вершк.; пишемъ 16 надъ 0 вершк. и вычитаемъ 5 вершк.
пзъ 16 вершк.; оставнпеся 11 вершк. пишемъ подъ чер¬
тою. 2 арш. изъ 1 арш. вычесть нельзя, беремъ отъ
50 саж. одну сажень (въ знакъ чего ставимъ точку
вадъ числомъ саженъ); раздробляемъ взятую сажень въ
аршины и прикладываемъ къ 1 &рш. уменыиаемаго;
получаемъ 4 аршина; пишемъ 4 вадъ числомъ аршинъ.
Теперь вычитаемъ 2 арш. изъ 4-хъ арш.; остатокъ 2
пишемъ подъ чертою. Продолжаемъ такъ действ до
конца.
Вотъ еще примерь вычитанш:
549	4	16
6 вер... 469 саж... 2 арш... 11 вершк.
40	32	3
5 пуд... О фунт. О лот. О зол.
		16	24	,	2	„
16
24
О зол.
4 пуд... 23 фунт. 7 лот. 1 зол.

— 90 —
Умножеше именованныхъ чиселъ.
107.	Такъ какъ множитель означаетъ, сколько разъ
множимое должно быть повторено слагаемымъ, то онъ
всегда есть число отвлеченное. Поэтому надо только
разсмотрЗуть умножен1о именованнаго числа
на отвлеченное.
Прим^ръ 1. Пусть требуется умножить 5 ласт.
4 чт. 7 чк. 3 гарн.	на 6. Расположимъ	дМствге такъ:
5 ласт.	4	чт....	7	чк....	3	гарн.
	Х6
30 ласт.	24	чт....	42	чк....	18	гарн.
32 л....	5	чт....	4	чк....	2	гарн.
Умноживъ на 6 отдельно гарнцы, четверики, четверти,
ласты, получимъ (подъ первою чертою) неправильно
составленное именованное число: 30 ласт. 24 чт. 42 чк.
18 гарн. Чтобы преобразовать его въ правильно соста¬
вленное именованное число, превращаемъ (въ ум'Ь или
на сторон-Ь) 18 гарн. въ 2 чк. и въ 2 гарн.; 2 гарнца
подписываемъ подъ второго чертою, а 2 чк. приклады-
ваемъ къ 42 чк., отчего получаемъ 44 чк.; превраща¬
емъ эти 44 чк. въ 5 чт. и 4 чк.; 4 чк. подписываемъ
подъ второю чертою, а 5 чт. прикладываемъ къ 24 чт.;
продолжаемъ такъ до конца.
Прим-Ьръ 2. Когда множитель состоять изъ двухъ
и бол4е цыфръ, то лучше производить на сторонЬ какъ
умножеше отдЬльныхъ чиселъ множимаго, такъ и пре-
вращеше. ДЬйств1е въ этомъ случа-Ь полезно распола¬
гать такъ, какъ это сделано на сл'Ьдующемъ прим’Ьр’Ь:

— 91 —
26 пуд.... 38 фун.... 84 зол.
X78
2103 пуд
... 32 фун.... 24 зол.
84
38
26
Х78
Х78
Х?8
672
304
208
588
266
182
6552 [96
2964
2028
576 68
+68
+ 75
792
3032
40
2103 пуд.
768
280
75
24 зол.
232
200
32фуй.
ДОлвн1е именованныхъ чиселъ.
108.	Дйлеше именованныхъ чиселъ, какъ и отвле-
ченныхъ, имйетъ двоякое значеше: 1) узнать, сколько
разъ одно число содержится въ другомъ (т. е. найти
множителя по данному произведенш и множимому), или
2)	разложить число на равныя части (т. е. найти мно¬
жимое по данному произведешю и множителю). Въ
первомъ случай именованное число дйлится на именован¬
ное, во второмъ—именованное дйлится на отвлеченное.
1)	Дйлеше именованнаго числа на именованное.
Пусть требуется узнать, сколько разъ 8 ф. 2 л. со¬
держатся въ 3 п. 18 фунт. Для этого раздробимъ дй-
лимое и дйлителя въ мйры одного назвашя, и притомъ
I

— 92 —
въ самыя мелюя, кагая есть въ дЬлимомъ и въ дЬли-
телЬ, т.-е. въ нашемъ примЬрЬ въ лоты:
3 п.... 18 фун.	8	ф....	2	л.
Х40	Х32
120	256
+ 18	+2
138	258	лотовъ.
Х32
276
414
4416 лотовъ.
Теперь узнаемъ, сколько разъ 258 лот. содержатся въ
4416 лотахъ:
4416 | 258
258	17
1836
1806
30
Мы узнали такимъ образомъ, что 258 лот. (т.-е. 8 ф.
2 л.) содержатся въ 4416 лот. (т.-е. въ 3 п. 18 ф.) 17
разъ, причемъ 30 лот. остается ьъ остаткЬ.
При дЬленш имен, числа на \ ыенованное частное есть
число отвлеченное, потому что оно означаетъ, сколько
разъ д'Ьлитель содержится въ дЬлимомъ.
2)	ДЬлеже именованнаго числа на отвлеченное.
Пусть требуется 18 верстъ 137 саж. 2 арш. разделить
на 14 (равныхъ частей). Для этого раздЬлимъ 18 верстъ
на 14 (равныхъ частей); оставиляся отъ дЬлешя вер¬
сты раздробимъ въ сажени; приложимъ 137 саженъ; раз¬
дЬлимъ получившееся число саженъ на 14 (равныхъ ча¬
стей); оставпшся сажени раздробимъ въ аршины; прило¬
жимъ 2 арш.; наконецъ, разд’Ьлимъ получившееся число
аршинъ на 14 (равныхъ частей).

— 93 —
ДЬЯствЬт располагаются такъ:
18 в... 137 саж... 2 ар. j 14
14
4... версты въ остатка.
Х&00
2000
4- 137
2137... саженъ.
73:
37
9... саж. въ остаткЪ.
X?
27
Ч~2
29... аршинъ.
1... арш. въ остатк'Ь.
XII
16... вершковъ.
2... верш, въ остатк-Ь.
Задачи на вычислен1е времени.
109.	Задача 1.Пароходъ вышелъ изъ гавани
27-го апреля, въ 7 часовъ утра. Когда паро-
ходъ возвратился въ эту гавань, если онъ
пробылъ въ плаван1и 6 лгЬс. 8 дней 21 часъ
40 мин.?
Первое ptiueHie. Когда говорятъ, что отъ такого-то
числа такого-то месяца прошелъ 1 1гЬсяцъ, то это зна¬
чить, что наступило такое же число сл'Ьдующаго ме¬
сяца. Если, напр., отъ 27-го апреля (7 часовъ утра)
прошелъ 1 мЪсяцъ, то это значить, что наступило 27-е
мая (7 часовъ утра). Зам'Ьтивъ это, будемъ решать на¬
шу задачу такъ:
Возвращеше парохода произошло позже его отбыт 1я
на 6 мЬс. 8 дней 21 ч. 40 м. Это значить, что посл’Ь
1 в. 152 с. 2 ар. 1 вер.
При дбленш именован-
наго числа на отвлеченное
частное должно быть чи¬
сломъ именованнымъ, такъ
какъ оно яредставляетъ
собою одну изъ равныхъ
частей д'Ьлимаго.

— 94 —
его отбытая прошло сначала 6 мЬс., потомъ 8 дней,
затЬмъ 21 часъ 40 м. и тогда пароходъ возвратился *).
Когда отъ 27-го апрЬля (7-ми часовъ утра) прошелъ 1
мЬсяцъ, то наступило 27-е мая (7 час. утра); когда
прошелъ другой М'Ьсяцъ, наступило 27-е шня (7 час.
утра); продолжая такъ прикладывать по 1 мЬсяцу 6
разъ, получимъ 27-е октября (7 час. утра). ПослЬ этого
прошло еще 8 дней. Такъ какъ въ октябрь 31 день,
то изъ этихъ 8 дней 4 дня приходились на октябрь, а
остальные 4 дня на ноябрь. Значить, наступило 4-е
ноября (7 часовъ утра). Потомъ прошло еще 21 часъ.
Если бы протекло 24 часа, то было бы 5-е ноября
7 час. утра. Но 21 часъ менЬе 24-хъ на 3 часа; зна¬
чить, было Б-е ноября 4 часа утра; наконецъ, прошло
еще 40. мин. и тогда пароходъ возвратился. Итакъ,
возвращеше парохода было 5-го ноября въ 4 часа 40
мин. утра того же года.
*) Въ такомъ поряди* считают* обыкновенно. И во всяком* слу
чае должно предварительно условиться относительно порядка слВ-
довашя годовъ, месяцев* и дней, такъ какъ величина промежутка
времени, выраженнаго въ такихъ, не вполне постоянных* единицах*,
зависит* отъ порядка ихъ. Напр., промежутокъ времени, сл’Ьдуюпцй
за 27-мъ апреля и равный 6 мес. -)- 8 дней, не равен* промежутку
времени, следующему тоже за 27-ыъ апреля, но равному 8 дн.-}-6 мес.
Это видно изъ следующей таблицы:
27-е апреля.
Прошло 6 м*с	27-е окт. I Прошло 8 дней	 5-е мая
Прошло 8 дней . ,... 4-е ноябр. | Прошло 6 м*с	5-е	ноябр.
Такимъ образомъ оказывается, что промежутокъ, следуюндй за
27 апреля и равный 6 м.-}-8 дн., короче промежутка 8 дн.-)-6 мес.
Причина будетъ ясна изъ следующаго расчета:
я—27 авг.
v/ «а сш •—
6) 27 сент.-
30
дн.
1)
5
мая—5 шня
.. 31 д.
31
Д-
21
5
шня—5 шля
30
дн.
3)
5
шля—5 авг.
.. 31 д.
31
Д-
4)
5
авг.—5 сент
.. 31 д.
31
Д-
5)
5
сент.—5 окт
.. 30 дн.
30
дн.
6)
5
окт.—5 ноябр. ..
.. 31 д.
183
184

— 95 —
Такъ обыкновенно и решаются подобный задачи, если
промежутокъ времени, протекций отъ одного события до
другого (напр., отъ отбытая парохода до его возвраще-
шя), не великъ. Въ противномъ случай удобнйе будетъ
слйдующШ пргемъ.
Второе рЪшеже. Предварительно узнаемъ, сколько вре¬
мени прошло съ начала года, т.-е. съ 1-го января до
27-го апрйля 7-ми часовъ утра. Прошло 3 мйсяца: ян¬
варь, февраль и мартъ, и 26 дней апрйля; такъ какъ
отбытае произошло въ 7 часовъ утра, то, значить, про¬
шло еще 7 часовъ слйдующаго дня (27 апрйля). Всего
съ начала года до отбыпя парохода прошло 3 мйс. 26
дней 7 час. Теперь приложимъ къ этому числу 6 мйс.
8 дней 21 час. 40 мин.:
,3 мйс....	26	дн....	7	час.
'6 „	...	8	„ ...	21	„ ...	40	мин.
9 мйс....	34	дн....	28	час...	40	мин.
10 мйс....	4	дн....	4	час...	40	мин.
Превращая 35 дней въ мйсяцы, мы должны задаться
вопросомъ, во сколько дней считать мйсяцъ. Для этого
обратимъ внимаше, что отъ начала года прошло 9 мй-
сяцевъ; значить, изъ 35 дней долзйенъ составиться 10-й
мйсяцъ, а 10 мйсяцъ (октябрь) содержитъ 31 день;
поэтому изъ 35 дней осталось 4 дня, а 31 день со¬
ставили 1 мйсяцъ (который мы приложили къ 9 мйся-
цамъ) *).
Мы узнали, что отъ начала года до возвращетя па¬
рохода прошло 10 мйс. 4 дня 4 часа 40 мин. Но это
не окончательный отвйтъ на вопросъ, потому что тре¬
*) Разсмотр-Ьвъ внимательно сложеше, которое намъ пришлось вы¬
полнить въ этой задач'Ь, мы легко залгЪтимъ, что въ немъ сохраненъ
тотъ порядокъ слДцовашн (дни 8а месяцами), о которомъ мы говорили
въ предыдущей выноскЪ. Въ самомъ д’Ьл'Ь, 35 дней мы прибавляемъ
послгь того, какъ прибавлены 6 мЪсяцевъ, а не раньше.

— 96 —
бовалось узнать, когда пароходъ возвратился, а не сколь¬
ко времени прошло отъ начала года до возвращешя па¬
рохода. Поэтому передЬлаемъ ответь такъ, чтобы онъ
отвечали на вопросъ „когда?® Если прошло 10 м’Ьсяцевъ,
то, значить, начался 11-й м'Ьсяцъ: ноябрь. Если про¬
шло 4 дня этого месяца, то, значить, началось уже 5-е
число ноября. Итакъ, пароходъ, возвратился 5-го ноября
въ 4 часа 40 мин. утра.
Задача 2. Путешественникъ возвратился
домой Б-го ноября въ 2 часа 10 мин. попо¬
лудни. Когда онъ отправился въ путеше-
CTBie, если его отсутств1е изъ дома продол¬
жалось 4 мес. 25 дн. 19 час.?
Первое ptiueHie. Какъ понимать, что отсутеше путе¬
шественника продолжалось 4 мес. 25 дней 19 часовъ?
Это надо понимать такъ: после отправлешя въ путеше-
ств1е прошло сначала 4 мес., потомъ прошло еще 25
дней, загЬмъ еще 19 часовъ, и тогда путешественникъ
возвратился, т.-е. тогда наступило 5-е ноября 2 часа
10 мин. пополудни. Поэтому, чтобы определить время
отбыт путешественника, отсчитаемъ отъ „5-го ноября
2 часа 10 мин. пополудни" сначала 19 часовъ, потомъ
25 дней и, наконецъ, 4 месяца. Если бы отсчитать не
19 часовъ, а 24 часа, то получилось бы 4-е.ноября 2
часа 10 мин. пополудни. Но 19 часовъ менее 24-хъ ча¬
совъ на 5 час.; след, получимъ 4-ое ноября 7 час. 10
мин. пополудни. Теперь отсчитаемъ 25 дней. Отсчи-
тавъ 4 дня, получимъ 31 октября; отсчитавъ еще 21
день, получимъ 10-е октября 7 час. 10 мин. пополудни.
Теперь отсчитаемъ 4 месяца. Получимъ 10-е шня 7 час.
10 мин. пополудни*).
*) И въ этой задач* получился бы другой ответь (9 тоня), если бы мы
отсчитывали сначала 4 мЬсяца, потомъ 25 дней, потомъ 19 часовъ, т.-е.
если бы мы понимали продолжительность путешемтая не какъ сумму
4 м*с.-|-25 дней-|-19 час., а какъ сумму 19 час.-)-25 дней-}-4 мЬсяца

- 97 —
Когда промежутокъ времени, который надо отнять,
выражается большими числами, то удобнее решать за¬
дачу слЬдующимъ пр1емомъ.
Второе ptmehie. Узнаемъ, сколько времени прошло отъ
начала года до 5 ноября .2 час. 10 мин. пополудни.
Прошло 10 мЬсяцевъ (январь, февраль... октябрь), 4
дня (ноября) и нисколько часовъ и минуть. Чтобы уз¬
нать, сколько часовъ и минутъ, примемъ во внимаше,
j	что за начало дня считается полночь. Отъ полуночи до
I	полудня прошло 12 часовъ; но возвращеше совершилось
въ 2 часа 10 мин. пополудни; значить, отъ полуночи до
возвращешя прошло 14 час. 10 мин. Всего отъ начала
года до возвращешя путешественника прошло 10 мЬс.
4 дня 14 час. 10 мин.
Теперь вычтемъ изъ этого числа то время, которое
путешественникъ пробылъ въ путешествш:
34	38
10 мЬс...	4 дня...	14	час...	10	мин.
~ 4	„ ...	25	, ...	19	. ...	О	.
5 мЬс...	9 дн ....	19	час...	10	мин.
При вычитанш дней намъ пришлось занять одинъ
М'Ьсяцъ и раздробить его въ дни. ^ъ такихъ случаяхъ
надо сообразить, какой мЬсяцъ раздробляемъ въ дни,
потому что не всЬ мЬсяцы содержать одинаковое число
дней. Въ нашей задачЬ 3 дня уменыпаемаго принад¬
лежать ноябрю (потому что 10 мЬс., начиная съ на¬
чала года, уже прошли); такъ какъ 25 дней вычитае-
(	мага	нельзя отнять отъ этихъ 3-хъ дней ноября, то
приходится часть ихъ отнимать отъ 10-го мЬсяца, т.-е.
отъ октября; октябрь имЬетъ 31 день; прибавивъ 31 день
къ 3 днямъ ноября, получимъ 34 дня.
СдЬлавъ вычиташе, мы узнали, что отъ начала года
до отправлетя путешественника въ путь прошло Б мЬс.
9 дней 19 часовъ 10 мин. Но это не окончательный
7 Заказ № 5456

— 98 —
ответь, потому что требовалось узнать, когда произошло
отправлеше. Передйлаемъ отвйтъ такъ, чтобы онъ от-
вйчалъ на вопроеъ: „когда?" Если прошло 5 мйс., то,
вначить, наступилъ 6-й мйсяцъ, шнь; если 9 дней этого
мйсяца прошли, то, значить, наступило 10-е шня; при-
томъ 10-го шня прошло уже 19 час. 10 мин.; значить,
часы будутъ показывать 7 час. 10 мин. пополудни.
Итакъ, путешественникъ отправился въ путь 10-го шня
въ 7 час. 10 мин. пополудни того же года.
Задача 3. Императоръ Александръ I всту-
пилъ на престолъ 12-го марта 1801-го года и
скончался 19-го ноября 1825-го года. Сколько
времени парствовалъ Императоръ Алек¬
сандръ I?
Первое ptuieHie. Отъ 12-го марта 1801 года до 12-го
марта 1825 года прошло ровно 24 года. Отъ 12-го марта
1825 года до 12-го ноября того же года прошло 8 мйся-
цевъ; наконецъ, отъ 12 ноября до 19 ноября прошло 7
дней; значить, Александръ I царствовалъ 24 года 8 мйс.
и 7 дней.
Второе рйшеше. До 12 марта 1801 года отъ Р. Хр.
прошло 1800 лйтъ 2 мйсяца и 11 дней, а до 19-го но¬
ября 1825-го года прошло 1824 года ЮмЪс. 18 дней.
Для рйшешя задачи надо, очевидно, вычесть изъ по-
слйдняго числа первое:
1824	года....	10 мйс.... 18	дней
"	1800	„ ....	2 „ .... 11	„
24	года....	8 мйс.... 7	дней.
Это будетъ окончательный отвйтъ, потому что въ за-
дачй требовалось узнать, сколько времени царствовалъ
Императоръ Александръ I.
109,а. Точный счетъ времени. Въ описанныхъ при-
кЬрахъ рйчь идетъ о такъ называемомъ календарномъ
зчетЬ времени, по которому промежутокъ времени выражается
зъ единицахъ, не вполнй постоянныхъ, т.-е. въ годахъ и
мйсяцахъ. По точному счету промежутокъ времени дол-

— 99 —
ясень быть выраженъ въ постоянный, едшидахъ, т.-е. въ
недЪляхъ, дняхъ и подразделетяхъ дня. Календарный счегь
употребляется во многихъ вопросахъ практической жизни,
когда не важно знать точный размерь какого-нибудь проме¬
жутка времени, а только число календарныхъ годовъ и ме-
сяцевъ, заключавшееся въ немъ (напр., при уплате жалова¬
нья, разсчитываемаго обыкновенно по месяцамъ).
Покажемъ вдЬсь на двухъ примерахъ, какъ слЬдуетъ по¬
ступать въ тЬхъ случаяхъ, когда р’Ьчь идетъ о точномъ
счете времени.
Предварительно заметимъ, что по календарному счету
промежутокъ времени отъ какого-нибудь момента даннаго
года до такого же момента следующего года (напр., отъ
полудня 15-го марта 1896 г. до полудня 15-го марта 1897 г.)
принимается равнымъ году; подобно этому, промежутокъ
отъ какого-нибудь момента одного месяца до такого же мо¬
мента следующего месяца (напр., отъ 2 часовъ дня 13-го
мая до 2 часовъ дня 13-го йоня того же года) принимается
за месяцъ. Годовой промежутокъ содержитъ въ себе 366
дней или 365, смотря по тому, было ли въ этомъ проме¬
жутке 29-е число февраля, или не было. Напр., годъ отъ
15-го йоня 1895 года до 15-го йоня . 1896 года содержалъ
въ себе 366 дней, такъ какъ въ этомъ промежутке было
29-е февраля (1896 годъ високосный); промежутокъ же отъ
15-го йоня 1896 года до 15-го йоня 1897 года имелъ 365
дней, такъ какъ февраль въ 1897 году содержалъ только
28 дней. Месячный промежутокъ можешь содержать въ себе
28, 29, 30 и 31 день, смотря по тому,*будетъ ли въ этомъ
промежутке последнее число месяца 28-е, или 29-е, или 30-е,
или 31-е. Напр.:
Месячный промежутокъ	Содержитъ
времени:	въ	себе:
отъ	до
■(въ февр. 29) 29 дн.
(въ февр. 28) 28 дн.
(въ март. 31) 31 дн,
(въ апр. 30) 30 дн.
20 февр.	1896	г.	20	март.	1896	г.	f
20 февр.	1897	г.	20	март.	1897	г.	"
20 март	20	апреля  з
20 апреля	 20	мая 	“
Заметивъ это, решимъ следу юнце примеры.
Примерь 1. Начало событая 13-го сентября 1890 г.
Конецъ собьтя  2-го йоня	1897 г.
Определить точную величину продолжительности его.
7*

32
Отъ Р. Хр. до конца собыпя прошло 1696 л. 5 м. 1 д.
„	„	„	„ начала „	„	1889	л.	8	м. 12 д.
Продолжительность собьтя по кал. счету 6 л. 8 м. 20 д.
Выразимъ теперь найденный промежутокъ времени въ
дняхъ. Предположимъ сначала, что каждый годъ имЬегь
365 дней, а каждый мЬсяцъ 30 дней. Тогда число дней будетъ:
365.6-|-30.8-f-20=:2190+240-]-20=2450.
Теперь исправимъ этотъ счетъ. Bo-первыхъ, разсчитаемъ,
сколько изъ 6-ти годовъ нашего промежутка было високос-
ныхъ. 29-е февраля приходилось въ 1892 г. и въ 1896 г.
Значить, число дней должно было увеличено на 2. Во-
вторыхъ, опредЬлимъ поправку на месяцы. Когда отъ 13
сентября 1890 года прошло 6 лЬтъ, то наступило 13 сен¬
тября 1896 года; затЬмъ еще прошли 8 мЬсяцевъ. Значить,
эти 8 м’Ьсяцевъ обнимаютъ собою промежутокъ времени отъ
13 сентября 1896 года до 13 мая 1897 г. За этотъ проме¬
жутокъ 31-ое число приходилось 4 раза: въ октябре, 'де¬
кабре, январЬ и мартЬ; кромЬ того, въ этомъ промежутке
былъ февраль. Такъ какъ это февраль 1897 года (годъ
простой), то онъ содержалъ въ себЬ 28 дней. Значить,
число дней въ нашихъ 8 мЬсяцахъ должно быть увеличено
на 4—2, а число дней во всемъ нашемъ промежутке должно
быть увеличено на 2-J-4—2, т.-е. на 4, и потому оно должно
быть 2454.
ПрингЬръ 2. Некоторое собыйе продолжалось 800 дней
20 час. 13 мин. Начало этого собыпя было въ 7 час. 40 м.
вечера 18 февраля 1893 года. Определить моментъ, въ ко¬
торый собыпе окончилось.
Считая годъ въ 365 дней и мЬсяцъ въ 30 дней, найдемъ,
что 800	дней составляютъ	2 года 2	мЬс.	10 дней;	значить:
800 д.	20	ч. 13 м. =2 г.	2 м.	10	д. 20 ч. 13 м.	(прибли¬
зительно).
Отъ Рожд. Хр. до начала собыпя прошло 1892 г. 1 мЬс.
17 дней 19 час. 40 мин. Прибавимъ къ этому времени
приблизительную величину даннаго промежутка:
.1892 г. 1 м.	17 д.	19	час.	40 мин.
2 г. 2 м.	10 д.	20	час.	13 .мин.
1894 г. 3 м.	28 д.	15	час.	53 мин.
Теперь сдЬлаемъ поправки, т.-е. опредЬлимъ, насколько
мы ошиблись, допустивъ, что 800 д.=2 года 2 мЬс. 10 дн.

— 101 —
Эти 2 года следовали за 18 февр. 1893 года по 18 февр.
1895 года. Въ этомъ промежутка високосныхъ годовъ ве
было; значитъ, въ нашемъ предположен^, что годъ—365 дн.,
не было ошибки. 2 месяца следовали за 18 февр. 1895 г.;
значитъ, это были месяцы:
1) Отъ 18 февраля 1895 г. до 18 марта 1895 г. 28 дней.
2) Отъ 18 марта 1895 г. до 18 апрЪля 1895 г. 31 день.
59 дней.
Мы предполагали, что эти 2 ыйсяца содержать 60 дней,
а на самомъ дЬл’Ь они имйли на 1 день меньше; значитъ,
800 дней составляютъ не 2 года 2 м-fec. 10 дн., а 2 года
2 мйс. 11 дн.; поэтому въ найденной суммй мы должны уве¬
личить число дней на 1. СдЬлавъ это, найдемъ, что отъ
Рожд. Христ. до конца событш прошло
1894 года 3 мйс. 29 дн. 15 час. 53 мин.
и, вначитъ, конецъ событая произошелъ въ 1895 году
апреля 30-го въ 3 часа 53 мин. пополудни.

— 102 —
ОТДЪЛЪ ТРЕТ1Й.
О дЪлимости чиселъ.
Зам4чан1е. После именованныхъ чиселъ естественно
было бы перейти къ разсмотренш дробныхъ чиселъ, такъ
какъ эти числа, подобно первымъ, представляютъ собою
результата измерешя, но въ более общемъ виде. Однако
обстоятельное разсмотрете свойствъ дробныхъ чиселъ мо¬
жетъ быть выполнено только тогда, когда предварительно
уяснены некоторый свойства целаго числа. Эти свойства
главнымъ образомъ относятся до условШ, при которыхъ
одно число делится на другое безъ остатка. Поэтому отделъ
этотъ озаглавливается „О делимости чиселъ“.
I. Признаки делимости.
110.	Основ ныя истины. Когда одно число де¬
лится на другое безъ остатка, то для краткости речи
говорить просто, что первое число делится на второе.
Такъ, говорить: 15 делится на 3, но не делится на 4
Существуютъ признаки, по которымъ легко узнать, не
производя делешя на самомъ деле, делится или не де¬
лится данное число на некоторый друпя числа. Нахо-
ждеше этихъ признаковъ делимости основано на сле¬
дующими истинахъ:
1)	Если каждое слагаемое делится на одно и то же
число, то и сумма разделится на это число.
Возьмемъ, напр., сумму: 15-j-20-j-40, въ которой каж¬
дое слагаемое делится на 5. Это значить, что каждое

— 103 —
изъ этихъ чиселъ можетъ быть составлено сложешемъ
пятерокъ; такъ, сложивъ 3 пятерки, получимъ 15; при-
ложивъ еще 4 пятерки, получимъ 15+20; наконецъ,
добавивъ еще 8 пятерокъ, получимъ 15+20+40; зна¬
чить, сумма эта можетъ быть составлена сложешемъ
пятерокъ; поэтому она делится на 5.
ЗамЬтимь, что если слагаемыя не делятся на какое-
нибудь число, то изъ этого нельзя еще заключить, чтобы
сумма не делилась на это число; напр., 17 и 8 не де¬
лятся на 5, но сумма 174-8, т.-е. 25, делится на 5.
2)	Если одно изъ двухъ слагаемыхъ дЪлится, а другое
не дЬлится на какое-нибудь число, то сумма не разделится
на это число.
Возьмемъ, напр., числа: 20 и 17; изъ нихъ первое
делится, а второе не делится на 5. Это значить, что
20 можно составить сложешемъ пятерокъ, а 17 нельзя.
Въ такомъ случае очевидно, что сумма 20-{-17 не мо¬
жетъ быть составлена сложешемъ пятерокъ; значить, эта
сумма не делится на 5.
111.	Признакъ делимости на 2. Заметимъ, что
все числа, которыя делятся на 2, наз. четными, а те,
которыя не делятся на 2, наз. нечетными.
Десятокъ делится на 2; поэтому сумма какого угодно
числа десятковъ делится на 2. Всякое число, оканчи¬
вающееся нулемъ, есть сумма десятковъ; напр., 430
есть сумма 43 десятковъ. Значить, всякое число, окан¬
чивающееся нулемъ, делится на 2.
Возьмемъ теперь два числа, изъ которыхъ одно окан¬
чивается нечетною, а другое четною цифрою, напр., 337
и 328. Ихъ можно представить въ виде суммъ такъ:
327=320+7;	328=320+8.
Число 320 оканчивается нулемъ и потому делится
на 2; 7 не делится на 2; потому 327 не разделится

— 104 —
на 2 (если одно изъ двухъ слагаемыхъ делится, а дру¬
гое не делится на какое-нибудь число, то сумма не
разделится на это число). Слагаемое 8 делится на 2;
поэтому 328 раздйлится на 2 (если каждое слагаемое
делится на одно и то же число, то и сумма разделится
на это число). Изъ этого следуетъ:
на 2 делится тольно такое число, ноторое оканчивается
нулемъ или четною цыфрою.
112. Признакъ делимости на 4. Сотня делится
на 4; поэтому сумма какого угодно чйсла сотенъ де¬
лится на 4. Всякое число, оканчивающееся двумя ну¬
лями, есть сумма сотенъ; значитъ, всякое число, окан¬
чивающееся двумя нулями, делится на 4.
Возьмемъ теперь два числа такихъ, чтобы у одного
сумма десятковъ съ единицами не делилась на 4, а у
другого делилась, напр., 2350 и 2348. Ихъ можно пред¬
ставить въ виде суммъ такъ:
2350=: 2300+50;	2348 =2300+48.
Число 2300 оканчивается двумя нулями и йотому де¬
лится на 4; 50 не делится на 4; поэтому 2350 не раз¬
делится на v4 (если одно слагаемое делится, а другое
не делится, то.4..); 48 делится на 4, поэтому 2348 раз¬
делится на 4 (если каждое слагаемое делится, то...).
Изъ этого следу етъ:
на 4 делится тольно такое число, ноторое оканчивается
двумя нулями или у нотораго две последшя цыфры выра-
жаютъ число, делящееся на 4 *).
113. Признакъ делимости на 8. Тысяча де¬
лится на 8; поэтому сумма какого угодно числа ты¬
сячъ делится на 8. Значитъ, всякое число, оканчива¬
ющееся тремя нулями, делится на 8.
*) Подобпымъ же образомъ можно вывести аналогичный прнавакъ
дЬлиыости на 25.

— 105 —
Возьмемъ теперь два числа такихъ, чтооы у одного
сумма сотенъ, десятковъ и единицъ не делилась на 8, а
у другого делилась, напр., 73150 и 73152. Ихъ можно
представить въ виде суммъ такъ:
73150=73000-f-150;	73152=73000-1-152.
150 не делится, а 152 делится на 8. Изъ этого за-
ключаемъ, что 73150 не делится, а 73152 делится
на 8. След.:
на 8 делится только такое число, которое оканчивается
тремя нулями или у котораго три последшя цыфры выра-
жаютъ число, делящееся на 8 *).
114. Пр изнаки делимости на 5 и на 10. Де¬
сятокъ делится на 5 и на 10; поэтому число, составлен¬
ное изъ десятковъ, т.-е. оканчивающееся нулемъ, де¬
лится на 5 и на 10. Если число не оканчивается нулемъ,
то оно не делится на 10, а на 5 оно разделится только
тогда, когда последняя его цифра будетъ 5, потому что
изъ всегь однозначныхъ чиселъ 5 есть единственное
число, делящееся на 5. Итакъ:
на 5 делится только такое число, которое оканчивается
нулемъ или цыфрою 5;
на 10 делится тольно такое число, ноторое оканчивается
нулемъ.
115. Признаки делимостщна 3 и на 9. Пред¬
варительно	заметимъ, что	и на 3,	и на 9 делится	всякое
число,	написанное посредствомъ	цыфры 9, т.-е.	9,	99,
999 и т. п. Действительно:
999 : 3=333;	9999 :	3=3333;
999 : 9=111;	9999 :	9=1111; и т. д.
Заметнвъ это, возьмемъ какое-нибудь число, напр.
2457, и разложимъ его на единицы различныхъ разрядовъ:
2457=1000-f-1000
+ lOO-j-lOO-flOO-flOO
4- lo-i-io-fio-fio-i-io
  	  	4*	^
*) Подобнымъ же образомъ можно вывести аналогичный признакъ
ДЬлимости на 125.

— 106 —
Разложимъ каждую тысячу на 999 и 1, каждую сотню
на 99 и 1, каждый десятокъ на 9 и 1. Тогда вместо
2 тысячъ получимъ 2 раза по 999 и 2 единицы; вместо
4 сотенъ получимъ 4 раза по 99 и 4 единицы; вместо
6 десятковъ—5 разъ по 9 и еще 5 ед. След.:
2457=999+999	+2
99+99+99+99+4
9+9+9+9-|-9+5
+7
Слагаемыя 999, 99 и 9 делятся на 3 и на 9; значить,
делимость даннаго числа на 3, или на 9, зависитъ толь¬
ко отъ суммы 2+4+5+7; если эта сумма делится или
не делится на 3, или на 9, то и данное число делится
или не делится на эти числа. Сумма 2+4+Б+7 есть
сумма чиселъ, выражаемыхъ цифрами даннаго числа,
написанными отдельно; для краткости говорятъ, что это
есть сумма цыфръ даннаго числа. Поэтому можемъ сказать:
на 3 делится только такое число, у котораго сумма цыфръ
делится на 3;
на 9 делится только такое число, у нотораго сумма цыфръ
делится на 9.
Въ нашемъ примере сумма цйфръ равна 18; 18 де¬
лится на 3 и на 9; значить, 2457 тоже делится и на 3,
и на 9.
116.	Признакъ делимости на 6. Предвари¬
тельно заметимъ, что если число делится на 6, то оно
должно разделиться и на 2, и на 3, т.-е. на те числа,
на которыя делится 6. Действительно, если число де¬
лится на 6, то, значить, его можно разложить на
шестерки, т.-е. представить его въ виде суммы:
6+6+6+6+
Но каждую шестерку можно разложить и на двойки,
и на тройки; значить, и данное число можно разложить
и на двойки, и на тройки; след., данное число должно
делиться и на 2, и на 3.

— 107 —
Йзъ этого сл'Ьдуетъ, что если какое-нибудь число
не делится на 2, или не делится на 3 (напр., число
45, которое не делится на 2, или число 50, которое
не делится на 3), то такое число не ыожетъ разде¬
литься на 6, такъ какъ если бы оно делилось на 6, то
разделилось бы и на 2, и на 3.
Возьмемъ теперь какое-нибудь число, напр., 534, ко¬
торое делится па 2 и на 3; разъяснимъ, что оно разде¬
лится и на 6.
Если 534 делится на 3, то его можно разложить на 3
равныя части. Предположимъ, что оно разложено на
эти части и что 2 части соединены въ одну группу;
тогда 534 представится въ виде суммы двухъ слага¬
емыхъ такъ:
534
HzTcS+a '
Первое слагаемое, состоящее изъ двухъ равныхъ ча¬
стей, конечно, делится на 2. Если бы второе слагаемое
не делилось на 2, то тогда и сумма 534 не делилась
бы на 2 (если одно слагаемое делится, а другое не
целится на какое-нибудь число, то сумма не разде¬
лится на это число). Но 534 делится на 2; значитъ, и
второе слагаемое должно делиться на 2; а второе сла¬
гаемое есть третья часть числа 584; если же третья
часть делится на 2 равныя части, то все число мо-
жетъ разделиться на 6 равныхъ частей*).
*) Если учапуеся имЬютъ уже представлете о просгЬйшихъ дро-
бяхъ, то достаточность признака дЬлимости на 6 можно разъяснить
такъ: если данное число делится на 2 и въ то же время на 3, то
это значить, что половина его есть цЬлое ‘число и третья часть
также цЬлое число; но въ такомъ случаЬ и разность между полови¬
ною числа и его третью частью тоже должна быть числомъ цЪлымъ;
1	1	3	1	2\
а эта разность составляетъ -g числа (такъ какъ ^- = -g-, a-g- = -g-l.
Если же -g- даннаго числа есть число цЬлое, то, значитъ, данное
число делится на 6 безъ остатка.

— 108 —
Теперь можемъ утверждать: на 6 делится тольно та¬
кое число, которое делится на 2 и на 3, которое, слЬд.,
оканчивается нулемъ или четною цифрою и у котораго,
кроме того, сумма цыфръ делится на 3.
117. Подобнымъ же образомъ можно вывести следую-
цце признаки делимости на 12, на 18 и на 15 *):
на 12 делится только такое число, которое делится
на 3 и на 4;
на 18 делится только такое число, которое делится
на 2 и на 9;
на 15 делится только такое число, которое делится
на 3 и на 5.
118. Выводъ признаковъ делимости на камя угодно
составныя числа основывается на слЬдующихъ теоремахъ.
Теорема 1. Если произведен1е о,а2 делится
па р, и Oj не имЬетъ съ р общихъ делителей,
кроме 1, то о2 делится на р.
Предположимъ сначала, что а^>р. РаздЬлимъ а1 вар и
назовемъ частное и остатокъ отъ этого делешя соответ¬
ственно q и г. Тогда
ai=PQ-\-r (1).
Убедимся относительно остатка г, что онъ во 1) не ра-
венъ 0 и во 2) не имЬетъ общихъ делителей съ р, кроме 1
*) Съ иебольшимъ, впрочемъ, измЪнещемъ для числа 15, для ко¬
тораго достаточность признака дЪлимости можно вывести такъ:
пусть какое-нибудь число, напр. 75, д'Ьлится на 3 и на 5; требуется
доказать, что оно д’Ьлится на 15. Если 75 Д'Ьлится на 5, то, значить,
число это можно разложить на 5 равныхъ частей. Сгруппируемъ эти
5 частей въ 2 группы такъ: одна группа въ 3 части, другая группа
въ 2 части. Такъ какъ сумма ихъ (75) д’Ьлится, по условно, на 3,
и группа въ 3 части, очевидно, д’Ьлится на 3, то другая группа (въ
2 части) должна дЪлиться на 3. ЗамЪтивъ это, соединимъ теперь всЪ
5 частей въ 3 группы: 2 части, 2 части и 1 часть. Группы, состоя¬
ния изъ 2-хъ частей, какъ сейчасъ разъяснено, дЪлятся на 3; зна¬
чить, и третья группа, въ 1 часть, должна дЪлиться на 3; но если
пятая часть числа дЪлится на 3 ранныя части, то Есе число должно
раздЪлиться на 15 равныхъ частей.

— 109 —
Действительно, если бы 7=0, то at=pq и тогда Oj дели¬
лось бы на р, а это противоречить допущешю, что о, и р
ве имеютъ общихъ делителей, кроме 1. Предположимъ да¬
лее, что р и г имеютъ какого-нибудь общаго делителя Г>1.
Тогда о, делилось бы на t и, след., о, и р имели бы общаго
делителя £>1, что противоречить допущение.
Если г не равенъ 1, то раздблимъ у? на г и назовемъ частное
и остатокъ отъ этого дблешя д, иг,. Тогда
p=rqY+rx (2)
Такъ какъ риг суть числа, не имеющая общихъ дели¬
телей, кроме 1, то изъ равенства (2) убеждаемся, подобно
предыдущему, что во 1) г, не равно 0 и во 2) г и г, не
имеютъ общихъ делителей, кроме 1. Если г, неравно 1, то
раздблимъ г на г,, отчего получимъ остатокъ 7,, не равный
нулю и не имеющШ общихъ делителей съ г, кроме 1. Если
7, не равенъ 1, то раздблимъ г, на и т. д.; тогда поду-
чимъ рядъ равенствъ:
Щ=РЯ -fr
Р=Щ -
r=rtqt-
rt —'
г*
изъ которыхъ убеждаемся, что остатки г, г,, 7, и т. д. не
равны нулю. Такъ какъ при всякомъ дбленш остатокъ дол-
женъ быть меньше делителя, то 7<j?,	и т- Д-
Поэтому, произведя достаточное число дблетй, мы, наконецъ,
дойдемъ до такого остатка, который равенъ 1. Пусть 1.
Тогда
7„_2=7n_,g„-fl.
Умножимъ почленно каждое изъ получевныхъ равенствъ
о,о2=у?до2
Pat =rQ&
га, =7,g,o,
-го,
-7,0,
¥п— ^n—lQn
Обращая внимание на первое изъ этихъ равенствъ, разсу¬
ждаемъ такъ: такъ какъ о,о2, по условш, делится на у?, то и
сумма pqa%-\-T о, делится на у?; первое слагаемое этой суммы
дблится на р; след., и второе слагаемое, т.-е. 70,, дблится
J

— 110 —
на р. Перейдя аатЬмъ къ равенству второму, находимъ, что
сумма pas и одно изъ слагаемыхъ (га2)д, делятся на р, от¬
куда ваключаемъ, что и второе слагаемое, г,а,, делится на р-
Перейдя ватбмъ къ равенству (3), отъ (3) къ (4), отъ (4)
къ (5) ит. д., дойдемъ,. наконецъ, до послЪдняго равенства,
изъ котораго заключимъ, что а% делится на р.
Если o,<j9, то мы раздЪлимъ р на аи затЪмъ о, на
остатокъ; после первый остатокъ на второй и т. д.; тогда
получимъ тагая равенства:
р =atq-\-r	Къ этимъ равенствамъ, очевидно, можпо*
al=rql -j-r,	применить те же разсуждешя, каюя были
г =г^%-\-г% и т. д. изложены выше; значитъ, и въ этомъ
случае дойдемъ до заключешя, что аг
делится нар.
Теорема 2. Если а делится порознь на числа
р и q, причемъ р и q не имеютъ общихъ делите¬
лей, кроме 1, то а делится на произведете pq.
Для доказательства назовемъ частное отъ делешя а на р
черезъ Q; тогда a=pQ... (1). Такъ какъ, по условш, а
делится на q, то изъ равенства (1) заключаемъ, что pQ
делится на q. Но р не имеетъ съ q общихъ делителей,
кроме 1; значитъ, согласно теореме 1-ой, Q должно делиться
на д. Пусть частное отъ этого делетя будетъ Qt; тогда
Q=qQl... (2). Вставивъ въ равенство (1) наместо Q равное
ему произведете, получимъ:
o^=P(gQl)=iPQ)Ql
откуда видно, что а есть произведете двухъ множителей:
(pq) и Qti значитъ, а делится на pq.
Изъ этой теоремы выводимъ: если число делится
на 2 и на 3, то оно делится на 6; если число
делится на 3 и на 4, то оно делится на 12; и т. п.
119.	Общм признакъ делимости на 7, 11 и 13. Чтобы
узнать, делится ли данное число на 7, или на
11, или на 13, достаточно, зачеркнувъ въ числе
три последуя цыфры, вычесть изъ оставша-
гося числа зачеркнутое (или на оборотъ); если
остатокъ равенъ 0, или делится на 7, или 11,
или 13, то и данное число разделится на 7, или
11, или 13.
Для доказательства заметимъ, что 1000-|-1 делится и на 7,
и на 11, и на 13, въ чемъ можно убедиться непосредственно

— Ill —
дЬлешемъ. ПослЬ этого положимъ, что въ данномъ числЬ
всЬхъ тысячъ а, а Ь будетъ часть его, состоящая изъ со¬
тенъ, десятковъ и единицъ; тогда данное число можно пред¬
ставить: а.1000-\-Ь, что равно а.1001-\-Ь—а. Если а^>Ь, то
последнее выражеше можно представить такъ:
а. 1001—[а—Ь)
л когда 6>а, то оно равносильно выражешю:
а. 1001-\-(Ь—а)
И въ первомъ, и во второмъ случаЬ для дЪлимости числа
на 7, или 11, или на 13 необходимо и достаточно, чтобы
а—Ь, или Ъ—а дёлил9сь на 7, или на 11, или на 13, или
же равнялось 0, такъ какъ а. 1001 д'Ьлится всегда и на 7,
и на 11, и на 13.
Пусть, напр., требуется узнать, дЬлится ли на 7 число
11673207. Зачеркиваемъ три послЬдтя цыфры и изъ остав-
апагося числа вычитаемъ зачеркнутое:
11673 m
—207
11466
Чтобы узнать, дЬлится ли это число на 7, поступаемъ съ
еимъ точно такъ же:
11 Ш
— 11
455
455 дЬлится на 7; значить, и данное число дЬлится на 7,
120.	Признакъ дЬлимости на 37. Чтобы узнать, дЬ¬
лится ли данное число на 37, достаточно, за-
черкнувъ въ числЬ три послЬдн1я цыфры, сло¬
жить оставшееся число съ зачеркнутымъ; если:
полученная отъ этого суммадЬлится на 37, то и
данное число раздЬлится на 37.
Для доказательства замЬтимъ, что 1000—1, т.-е. 999.
дЬлится на 37, въ чемъ можно убЬдиться непосредственно.
Пусть данное число будеть а. 1000-\-Ь, гдЬ Ь есть часть,
состоящая изъ сотенъ, десятковъ и единицъ. Тогда данное
число можно представить такъ: а. 999-\-ф-\-а)', такъ какъ
41. 999 всегда дЬлится на 37, то дЬлимость даннаго числа
на 37 зависитъ лишь отъ Ь-\-а, что и требуется доказать.

— 112 —
П. Числа простыя и составныя.
121. ОлредЬлеюя. 1) Число, ноторое дЬлится только
на единицу и на само себя, наз. простымъ *); таково,
напр., число 7, которое д'Ьлится только на 1 и на 7.
2) Число, которое дЬлится не только на единицу и на
само себя, но еще и на -друпя числа, наз. составнымъ;
таково, напр., число 12, которое дЬлится не только на
1 и на 12, но и на 2, на 3, на 4 и на 6.
Есть 26 простыхъ чиселъ, меныпихъ 100, а именно:
1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Въ концЬ этой книги приложена таблица, въ которой
выписаны всЬ простыя числа, не превосходяпця 6000.
122. Теорема. Всякое составное число делится
на некоторое простое число, большее 1
Пусть N есть составное число. По определенно, N дЬ-
лится на некоторое число t, большее 1 и меньшее N. Если
t есть число простое, то теорема доказана; если же t число
составное, то оно, въ свою очередь, делится на некоторое
число большее 1 и меньшее t. Въ такомъ случае и N
делится на tt. Если tx есть число простое, то теорема до¬
казана; если же tx число составное, то оно делится на t2,
которое больше 1 и меньше t2. Такимъ образомъ убедимся,
что N делится на некоторое простое число большее 1
123. Теорема. Существуетъ безчисленное мно¬
жество простыхъ чиселъ.
Допустимъ обратное, т. е., что простыхъ чиселъ ограни¬
ченное число. Въ такомъ случае должно существовать наи¬
большее Простое число. Пусть такое число будетъ а. Тогда
все простыя числа должны заключаться въ ряду: 1, 2, 3,
5, 7,11	 а.	Чтобы опровергнуть это допущеше, составимъ
новое число N такимъ образомъ:
1V=(1.2.3.5.7	а)+1,
*) Употребительны также назвашя: „абсолютно—простое*, „перво¬
начальное* число.

— 113 —
т.-е. перемножимъ вс-Ь простыя числа отъ 1 до а и къ про¬
изведение) приложимъ еще 1.
Такъ какъ N, очевидно, больше а, и а, согласно предпо-
ложешю, есть наибольшее изъ простыхъ чиселъ, то N дол¬
жно быть числомъ составнымь. Но составное число, по до¬
казанному выше, делится на некоторое простое число, боль¬
шее 1. Сл’Ьд., N делится на некоторое число изъ ряда: 2,
3, 5, 7, 11	 а.	Но этого быть не можетъ, такъ какъ N
есть сумма двухъ слагаемыхъ, изъ которыхъ первое (1. 2.
3. 5.. а) делится на всякое число изъ ряда: 2, 3, 5.... а, а
второе (1) не делится ни на одно изъ этихъ чиселъ. Итакъ,
нельзя допустить, чтобы существовало наибольшее простое
число; а если н!>тъ наибольшаго простого числа, то рядъ
простыхъ чиселъ безконеченъ.
124.	Составлеже ряда послЪдовательныхъ простыхъ чи¬
селъ. Самый простой способъ составлетя ряда послЬдова-
тельныхъ простыхъ чиселъ состоять въ томъ, что изъ ряда
натуральныхъ чиселъ отъ 1 до а (число, которымъ жела-
ютъ ограничить рядъ) выключаютъ сначала всЬ числа, дб-
ляпцяся на 2, потомъ всЬ числа, д^ляпцяся на 3, затЬмъ
числа, дЪляпцяся на 5, на 7, на 11 и т. д. Это делается
очень просто: выписавъ рядъ нечетныхь чиселъ отъ 1 до а,
зачеркиваютъ въ немъ каждое 3-е число после 3-хъ, ка¬
ждое 5-е число после 5, каждое 7-е после 7-ми и т. д. Для
объяснетя этого npieMa предположимъ, что желаютъ за¬
черкнуть все составныя числа, дЬляпуяся на 7. Наимень¬
шее число, делящееся па 7, есть само 7. Но 7 простое
число и потому не должно быть зачеркнуто. Такъ какъ не¬
четный числа отличаются одно отъ другого на 2, то-сле¬
дующая за 7-ю числа будетъ: 7-j-2, 7-f-(2 . 2), 7-f-(2 . 3),
7—(—(2. 4) и т. д. Изъ нихъ первое число, делящееся на 7,
есть, очевидно, 7—(2 . 7); это будетъ 7-е число после 7.
Также только 7-е число, следующее за 7-}-(2. 7), будетъ
делиться на 7; однимъ словомъ, кратнымъ 7-ми будетъ ка¬
ждое 7-е число после 7-ми и никакое иное.
Описанный npieMb изв’Ьстенъ подъ именемъ рЪшета Эра-
тосеена (cribrum Eratosthenis). АлександрШсюй математикъ
Эратосеенъ, живппй въ 3-мъ в’Ьк'Ь до Р. Хр., писалъ числа
на дощечке, покрытой воскомъ, и прокалывалъ дырочки
надъ теми числами, который делятся на 2, на 3, на 5
ит. д.; отъ этого дощечка уподоблялась решету, сквозь
которое какъ бы просеивались составныя числа.
8 Звквз № 5456

— 114 —
Въ настоящее время имЬются таблицы всЬхъ послЬдова-
тельныхъ простыхъ чиселъ, менышхъ 9 ООО ООО*).
Ш. О д'Ьлителях'ъ составного числа.
I.	Разложен1е составного числа на простыхъ
множителей.
125. 0предЬлен1е. Разложить составное число на
простыхъ множителей значить представить его въ видЪ
произведешя нЪсколькихъ простыхъ чиселъ.
Напр., разложить 12 на простыхъ множителей значить-
представить 12 такъ: 12=2.2.3.
126. Объяснено разложен1я. Пусть требуется
разложить на простыхъ множителей какое-нибудь со¬
ставное число, напр., 420. Для этого находимъ, по при-
знакамъ дЪлимости, наименьшее простое число (кромЬ 1),
на которое д'Ьлится 420. Такое число есть 2; раздЬлимъ
420 на 2:
420 : 2 = 210; откуда 420=210 . 2	(1).
Теперь находимъ наименьшее простое число (кромЬ 1),
на которое дЬлится составное число 210. Такое число
есть 2; раздЬлимъ 210 на 2:
210 : 2 = 105; откуда 210 = 105 . 2
ЗамЬнимъ въ равенствЬ (1) число 210 равнымъ ему
произведешемъ:
420 = 105 . 2 . 2	(2).
Наименьшее простое число, на которое дЬлится со¬
ставное число 105, есть 3; раздЬлимъ 105 на 3:
105 : 3 = 35; откуда 105 = 35 . 3
ЗамЬнимъ въ равенствЬ (2) число 105 равнымъ ему
произведешемъ:
420 = 35 . 3 . 2 . 2
*) Наибольшее простое число, навЪстное до сего времени, есть
2в1—1—2 305 843 009 213 693 951; это число было найдено священ-
никомъ о. Тоанномъ Иервуитнымъ въ 1883 г.

— 115 —
420
2
210
2
105
3
35
5
7
7
1
Наконецъ, въ последнее равенство подставимъ на ме¬
сто 35 равное ему произведете простыхъ чиселъ 5.7;
тогда получимъ требуемое разложеше:
420 = 5 . 7 . 3 . 2 . 2
Такъ какъ произведете не изменяется отъ перемены
месть множителей, то можно писать ихъ въ какомъ
угодно порядке; обыкновенно пишутъ ихъ отъ меныпихъ
къ большимъ, т.-е. такъ; 420 = 2 . 2 . 3 . 5 . 7.
127.	Какъ располагаютъ нахожден1е про¬
стыхъ множителей. Разложеше на простыхъ мно¬
жителей располагаютъ обыкновенно такъ:
т.-е. пишутъ данное составное число и проводятъ
справа отъ него вертикальную черту. Справа отъ
черты помещаютъ наименьшее простое число, на
которое делится данное составное, и делятъ на
него это данное число. Цыфры частнаго под¬
писываютъ подъ делимымъ. Съ этимъ частнымъ
поступаютъ также же, какъ съ даннымъчисломъ. Дейсття
продолжаютъ до тЬхъ поръ, пока въ частномъ не полу¬
чится 1. Тогда все числа, стояндя направо отъ черты,
будутъ простыми множителями даннаго числа.
Вотъ еще примеры
8874 2 Дойдя до частнаго 493, мы затрудняемся ре-
4437 3 шить, на какое число оно дЬлится. Въ такихъ
1479 3 случаяхъ обращаемся къ таблицЬ простыхъ
493 17 чиселъ (въ концЬ этой книги). Если въ ней
29 29 встрЬтится число, поставившее насъ възатруд-
1 неше, то оно дЬлится только на само себя. 493
не находится въ таблицЬ простыхъ чиселъ; значитъ, это
число—составное и потому должно дЬлиться на какое-
нибудь простое число, большее 1. Пробуемъ дЬлить его
на 7, на 11, на 13.. и т. д. до тЪхъ поръ, пока не дой¬
демъ до дЬлешя безъ остатка. Оказывается, что 493
дЬлится на 17, при чемъ въ частномъ получается 29.
Теперь можемъ окончить разложеше.

—116 —
128. Сокращенные пр1емы разложен!я. 1)Если
данное составное число не велико, то его
простыхъ множителей прямо выписываютъ
въ строку. Наир.:
72 = 2 . 2 . 2 . 3 . 3
При этомъ говорятъ такъ: 72 равно 2, умноженнымъ
на 36 (2 пишемъ, а 36 запомиеаемъ); 36 равно 2. умно¬
женнымъ на 18 (2 пишемъ, а 18 запоминаемъ); 18 равно
2, умноженнымъ на 9; и т. д.
Если данное число легко разлагается на
какихъ-нибудь составныхъ множителей, то
полезно разложить его сначала на этихъ
множителей, а потомъ каждаго изъ нихъ
разложить на простыхъ. НапримЬръ:
14000 = 1000 .14 = 10 .10.10 .14 = 2 . 5.2.5.2.5.2. 7
ЗамЬчаме. Когда въ разложенш одинъ и тотъ же мно¬
житель повторяется нисколько разъ, то можно писать
сокращенно, употребляя то обозначенie степени, ко¬
торое мы указали прежде (§ 62). Такъ, вмЬсто строки:
14000 = 2 .2.2.2.5.5.5.7 пишутъ короче:
14000 = 2‘. 53. 7
ЗдЬсь показатели степени 4 и 3, поставленные
надъ числами 2 и 5, означаютъ, сколько разъ эти числа
должны быть повторены множителями.
129. Важное свойство разложен!я. Всякое
составное число разлагается только въ одинъ рядъ прос¬
тыхъ множителей.
Напр., число 14000, какимъ бы способомъ мы его не
разлагали на простыхъ множителей, всегда даетъ такой
рядъ, въ которомъ множитель 2 повторяется 4 раза,
множитель 5 повторяется 3 раза, а множитель 7 входить
только одинъ разъ (конечно, множители эти могул
стоять въ какомъ угодно порядк-Ь).
Для доказательства этого предложешя, допустимъ, что какое-
вибудь число N дало два ряда простыхъ множителей:

— 117 —
N=abc.... и .№=0,6,с,....; откуда: abc.... = а,й,с,....
Л’Ьвая часть послЬдняго равенства делится на а; значить,
и правая часть должна делиться на а Но а. число простое,
поэтому произведете <1,6,0,.... только тогда разделится на а,
когда одинъ изъ его множителей делится на а\ для этого
нужно, чтобы одно изъ чиселъ: а,, 6,, с,.... равнялось а.
Пусть а,=а. Разделивъ обе части равенства на а, получимъ:
йс....=й,с,....
Подобно предыдущему убедимся, что одинъ изъ множи¬
телей: й,, с,,.... равенъ Ь. Пусть й,=й; тогда cd...=c1d1...
Продолжая эти разсуждешя далее, увидимъ, что все мно¬
жители перваго ряда входятъ также и во второй рядъ. Раз¬
деливъ обе части равенства на о,, убедимся, чтовъпервомъ
ряду есть множитель а,. Такимъ образомъ, подобно преды¬
дущему, найдемъ, что все множители второго ряда входятъ
и въ первый рядъ. Отсюда следуетъ, что оба эти ряда мо¬
гутъ отличаться только порядкомъ множителей, а не самими
множителями,,—другими словами, что два эти ряда пред¬
ставляюсь на самомъ деле только одинъ рядъ.
2.	Нахождете дЪлителей составного числа.
130.	Определен! е. Если одно число делится на дру¬
гое безъ остатка, то это другое число наз. дЬлителемъ
перваго числа. Такъ, заметивъ, что 40 делится на 8 безъ
остатка, мы можемъ число 8 назвать дЬлителемъ 40-а.
Всякое простое число, наир, число 11, имЬетъ только
двухъ делителей: 1 и само себя.
Всякое составное число имЬетьболЬе двухъ дЬлителей;
напр., число 6 имЬетъ 4-хъ делителей: 1, 2, 3 и 6; изъ
нихъ первые три простые, а послЬдтй составной.
ДЬлители даннаго составного числа могутъ быть най¬
дены по следующему правилу. .
Правило. Чтобы найти всЬхъ делителей даннаго со¬
ставного числа, предварительно разлагаютъ его на про¬
стыхъ множителей; каждый изъ этихъ множителей будетъ
лростымъ дЬлителемъ даннаго числа, составные же де¬
лители получаются перемножен!емъ простыхъ множителей
по два, по три, по четыре и т. д.
8*

— 118 —
Пусть, напр., требуется найти дЬлителей числа 420.
Для этого разложимъ это число на простыхъ множителей:
420=2 . 2 . 3 . 5 . 7 .
Легко понять, что 420 дЬлится на каждаго изъ сво-
ихъ простыхъ множителей; напр., это число дЬлится на
5, потому что его можно представить въ видЬ произ-
ведетя: (2 . 2 . 3 . 7) . 6 = 84.5. Значить, простые
множители составного числа служатъ также и его про¬
стыми дЬлителями.
Чтобы найти составныхъ дЬлителей, примемъ во вни¬
мание, что множителей произведешя можно соединять
въ различный группы. Соединимъ ихъ, положимъ, такъ:
420=(2 . 3) . (2 . 5 . 7) = 6. 70.
Теперь 420 представляеть собою произведете двухъ
множителей: 6 и 70; слЬд., 420 дЬлится и на 6, и на 70.
Соединяя множителей въ иныя группы, увидимъ такимъ
же образомъ, что 420 дЬлится на произведете какихъ
угодно своихъ простыхъ множителей.
ЗамЬчан1е. Чтобы найти частное отъ дЬлешя дан¬
наго составного числа на какого-нибудь его дЬлителя,
достаточно изъ разложешя составного числа выключить
тЪхъ множителей, которые входятъ въ дЬлителя, и
оставшихся множителей, перемножить. Напр., чтобы
найти частное отъ дЬлешя 420 на 70, выбросимъ изъ
разложешя 420=2. 2.3.5 . 7 множителей 2, 5 и 7, про¬
изведете которыхъ составляетъ 70, и оставппеся множи¬
тели 2 и 3 перемножимъ (получимъ 6).
131.Теорома. Составное число неимЬетъ иныхъ
делителей, кромЬ тЬхъ, которые получаются
по указанному выше правилу.
Пусть Р есть делитель числа N. Назвавъ частное огь
дЬлешя N на Р черезъ Q, получимъ: N=PQ. Разложись

— 119 —
числа Р и Q на простыхъ множителей и вставимъ въ ра¬
венство N=PQ на м^сто Р и Q ихъ разложешя; тогда мы
получимъ разложеше числа N. Такъ какъ другого разло-
жешя число N не имеетъ, то заключаемъ, что все простые
множители Р входятъ въ разложеше числа N.
IV.	ОбшДй наиболыпШ делитель.
132. Определен!е. ОбщимънаибольшимъдЬлителемъ
несколькихъ данныхъ чиселъ называется самое большее
число, на которое делятся все эти данныя числа.
Напр., общШ наибольший делитель трехъ чиселъ: 18,
30 и 24 есть 6, потому что 6 есть самое большее число,
на которое делятся все эти числа.
Два числа, для которыхъ обир'й наиболышй делитель
есть 1, наз. взаимно простыми*). Таковы, напр., числа
14 и 15.
Укажемъ два способа для нахождешя общаго наиб,
делителя несколькихъ чиселъ.
1.	Нахождеже общаго наибольшего делителя посродствомъ
разложежя на простыхъ множителей.
133. Правило. Чтобы найти общего наибольшего дели¬
теля несколькихъ данныхъ чиселъ, разлагаютъ эти числа
на простыхъ множителей и перемножаютъ между собою
техъ изъ этихъ множителей, которые общи всемъ чи-
сламъ **).
*) Или первыми между собою.
**) Если учащееся освоились съ употреблетемъ показателя стеиеии,
то это правило лучше выразить бодЪе точно такъ: чтобы иаКти общаго
наиб. дЬлителя нЪсколыиигь данныхъ чнселъ, разлагаютъ эти числа на
простыхъ множителе! и загЬмъ составляютъ произаеден1е изъ всЪхъ
разлнчныхъ множителей, общихъ даннымъ числамъ, беря иащдаго множи¬
теля съ наименьшимъ показателемъ, съ накинь онъ входить еъ составь
данныхъ чиселъ.

— 120 —
Пусть, напр., требуется найти общаго наиб. дЬли¬
теля двухъ чиселъ 180-и и 126-и. Для этого предвари¬
тельно разложимъ эти числа на простыхъ множителей:
180=2 . 2 . 3	3 . 5	126=2	.	3	.	3	. 7.
Сравнивая между собою множителей этихъ чиселъ,
замЬчаемъ, что между ними есть общ1е, а именно: 2,
3, 3. Каждый изъ этихъ общихъ множителей будетъ и
общимъ дЬлителемъ 180-ти и 126-ти. Чтобы получить
составныхъ общихъ дЬлителей, надо перемножить об¬
щихъ множителей по два и по три. НаиболыпШ общШ
дЬлитель, очевидно, получится, если перемножимъ всЬхъ
общихъ множителей:
2.3. 3 = 18.
Пусть еще требуется найти общаго наиб. дЬлителя
трехъ чиселъ: 210, 1260 и 245. Разложимъ эти числа
на простыхъ множителей:
210
2
1260
2
245
5
105
3
630
2
49
7
35
5
315
3
7
7
7
7
105
3
35
5
7
7
Теперь видимъ, что общШ наиб. дЬлитель этихъ чи¬
селъ равенъ произведетю общихъ множителей 5' и 7,
т.-е. равенъ 35.
2.	Нахождеше общаго наибольшего дЬлителя посред¬
ствомъ послЬдовательнаго дЬлешя.
134.	Этотъ способъ, въ примЬнети къ двумъ дан-
нымъ числамъ, основанъ на слЬдующихъ двухъ исти-
нахъ:
1)	Если большее изъ двухъ данныхъ чиселъ дЬлится
на меньшее, то меньшее изъ нихъ есть общш наиболышй
дЬлитель.

— 121 —
Напр., возьмемъ два числа: 54 и 18, изъ которыхъ
большее делится на меньшее. Такъ какъ 54 делится на
18 и 18 делится на 18, то значитъ 18 есть обЩ1й де¬
литель чиселъ 54 и 18. Этотъ делитель есть въ то же
время и наиболышй, потому что 18 не можетъ де¬
литься на число, большее 18.
2) Если большее изъ двухъ данныхъ чиселъ не делится
на меньшее, то ихъ обирй наиболышй делитель равенъ
общему наибольшему делителю другихъ двухъ чиселъ, а
именно: меньшаго изъ данныхъ чиселъ и остатка отъ
дележ'я большаго изъ нихъ на меньшее.
Пусть, напр., даны два числа: 85 и 30, изъ которыхъ
большее не делится на меньшее. Разделивъ первое на
второе, получимъ: 85:30 = 2 (ост. 25). Разъяснимъ, что
обпцй наиболышй делитель чиселъ 85 и 30 долженъ
быть также общимъ наибольшимъ делителемъ другихъ
двухъ чиселъ, а именно 30 и 25.
Такъ какъ делимое равно делителю, умножен¬
ному на частное, плюсъ остатокъ, то:
85 = (30. 2) + 25
Такимъ образомъ, число 85 представляется намъ, какъ
сумма двухъ слагаемыхъ: одно слагаемое равно 30.2,
а другое 25. Заметивъ теперь, что если число 30 де¬
лится на кашя-нибудь числа, то и произведете 30.2
делится на эти числа, мы можемъ изъ написаннаго
выше равенства вывести тагая два заключетя:
1) все обдце делители чиселъ 85 и 30, деля сумму
(85) и одно слагаемое (30.2), должны делить и другое
слагаемое (25) *);
2) все общ1е делители чиселъ 30 и 25, деля каждое
слагаемое (30.2 и 25), должны делить и сумму (85).
Значитъ, две пары чиселъ: (85 и 30) и (30 и 25) имеютъ
однихъ и техъ же общихъ делителей; след., у нихъ дол¬
женъ быть одинъ и тотъ же общШ наиболышй делитель.
*) Если бы другое слагаемое не разделилось, то не разделилась
бы и сумма.

— 122 —
Посмотримътеперь, какъ можно пользоваться этими
двумя истинами для нахождетя общаго наиб, делителя
двухъ чиселъ. Пусть требуется найти общаго наиболь-
391	|	299	шаго делителя чиселъ 391 и 299.
299	1	Раздблимъ 391 на 299, чтобы узнать.
299	92	не будетъ ли 299 общимъ наиб;
276	3	дЬлителемъ	(на	основанш	истины
92 23	1-ой).	Видимъ,	что	399	не	делится
92	4	на 299, поэтому 299 не есть обнцй
О	наиб, делитель. На основанш исти¬
ны 2-й утверждаемъ, что обидй наиб, делитель чиселъ
391 и 299 есть также обицй наиб, дЬлитель 299 и 92.
Станемъ искать общаго наиб, делителя этихъ чиселъ. Для
этого дЬлимъ 299 на 92, чтобы узнать, не будетъ ли 92
общимъ наиб. д'Ьлителемъ (истина 1-я). Видимъ, что 92
не есть обицй наиб. дЬлитель. Теперь опять, на основа-
ши истины 2-ой, говоримъ, что обшдй наиб. дЬлитель
чиселъ 299 и 92 есть также обицй наиб. дЬлитель чиселъ
92 и 23. Станемъ искать этого дЬлителя. Для этого дЬлимъ
92 на 23. Видимъ, что 23 есть обпдй наиб. дЬлитель
пары чиселъ 92 и 23, слЬд. и пары чиселъ 299 и 92,
слЬд. и пары 391 и 299.
Правило. Чтобы найти общаго наиболыиаго дЬлнтеля
двухъ чиселъ по способу лослЬдовательнаго дЪлемя, надо
дЬлить большее изъ нихъ на меньшее, потомъ меньшее на
первый остатонъ, загЬмъ первый остатокъ на второй,
второй на трепй и т. д. до гЬхъ поръ, лона не получится
въ остаткЬ 0; лослЬдмй дЪлитель будетъ общимъ наиболь-
шимъ дЬлителемъ.
Способъ этотъ полезно применять тогда, когда дан¬
ныя числа не легко разлагаются на простыхъ множи¬
телей.
135.	ПримЬнен1е этого способа къ тремъ
и болЬе даннымъ числамъ. ПримЬнимъ этотъ
способъ къ нахождетю общаго наиб. дЬлителя трехъ

— 123 —
чиселъ, напр., 78, 130 и 195. Для этого найдемъ сна¬
чала общаго наиб. делителя только двухъ изъ нихъ,
напр., 78-ми и 130:
130 |_78
78	1
78 [ 52 Обицй наиб. делитель этихъ чи-
52	1	селъ оказывается 26.
52 [J26
52 ~2
О
Теперь отыщемъ общаго наибольшаго делителя 26-и
и третьяго даннаго числа 195-и:
Полученное такимъ образомъ число
195 | 26	13 и есть обицй наиб, делитель трехъ
182	7	данныхъ чиселъ. Действительно, 26,
26
26
13	будучи общимъ наиб, делителемъ
2	130 и 78, содержитъ всЬхъ простыхъ
О	множителей,	общихъ	этихъ	числамь;
13, будучи общимъ наиб, делителемъ
26 и 195, содержитъ всЬхъ простыхъ множителей, общихъ
этимъ числамь. След., 13 содержитъ всехъ простыхъ
множителей, общихъ тремъ числамь: 130, 78 и 195; зна¬
чить, 13 есть обпдй наиб, делитель этихъ чиселъ.
Подобными же образомъ, если требуется найти общаго
наиб, делителя 4-хъ или более чиселъ, то сначала
находятъ общаго наиб, делителя двухъ первыхъ чиселъ,
загЬмъ—общаго наиб, делителя между найденнымъ де-
лителемъ и третьимъ числомъ, далее общаго наиб, де¬
лителя между последнимъ делителемъ и четвертымъ
числомъ и т. д.
V. Наименьшее кратное число.
136.	О пределен! я. 1) Нратнымъ числомъ даннаго
числа наз. всякое число, которое делится на данное безъ
остатна.

— 124 —
Для каждаго даннаго числа можно найти безчислен-
ное множество кратныхъ чиселъ; стоитъ только данное
число умножить на 1, на 2, на 3, на 4 и т. д. Такъ,
для числа 9 кратными будутъ: 9X1 = 9, 9X2 = 18,
9X3 = 27, 9X4 = 36 и т. д.
2) Наименьшими кратными числомъ нЪсколькихъ данныхъ
чиселъ называется самое меньшее число, которое делится
на каждое изъ зтихъ чиселъ.
Такъ, для трехъ чиселъ: 6,15 и 20 наименьшее крат¬
ное есть 60, такъ какъ меньше 60-и никакое число не
делится на 6, на 15 и на 20, а 60 делится на эти числа.
Наименьшее кратное данныхъ чиселъ находится по
следующему правилу:
Правило. Чтобы найти наименьшее нратное несноль-
нихъ чиселъ, сначала разлагаютъ все эти числа на лро-
стыхъ множителей; затемъ, взявъ одно изъ нихъ, припи-
сываютъ къ нему недостающихъ множителей изъ другого
числа; къ этому произведена прилисываютъ недостающихъ
множителей изъ третьяго числа и т. д. *).
Пусть, напр., требуется найти наименьшее кратное
чиселъ 100, 40 и 35. Сначала разложимъ каждое изъ
етихъ чиселъ на простыхъ множителей:
100 = 2 .2.5.5; 40 = 2 .2.2.5; 35=5 . 7.
Чтобы какое-нибудь число делилось на 100, на 40 и
на 35, необходимо, чтобы въ него входили все простые
множители этихъ делителей. Выпишемъ всехъ множи¬
телей числа 100 и добавимъ къ нимъ техъ множителей
числа 40, которыхъ недостаетъ въ разложенш 100. Тогда
*) Если учапцеся освоились съ употреблетемъ показателя степени,
то правило это можно выразить такъ:
Чтобы найти наименьшее нратное кЬскольиихъ чиселъ, разлагаютъ ихъ
на простыхъ множителей и загЬмъ составляютъ произведете изъ всЬхъ
различныхъ множителей, входящихъ въ разложен1я данныхъ чиселъ, беря
наждаго множителя съ наибольшимъ показателемъ, съ канимъ онъ вхо-
дитъ въ составъ данныхъ чиселъ.

— 125 —
получимъ произведете 2 . 2 . 5 . 5 . 2, делящееся и
на 100, и на 40. Добавимъ теперь къ этому произведение
техъ множителей числа 35, которыхъ въ произведенщ
недостаетъ. Тогда получимъ число:
2 . 2 . 5 . 5 . 2 . 7 = 1400,
делящееся и на 100, и на 40 и на 35. Это и есть наимень¬
шее кратное число, потому что, выключивъ изъ него
хотя бы одного сомножителя, мы получимъ число, ко¬
торое не разделится на какое - нибудь изъ данныхъ
'шселъ.
Замечай!е. Найдя наименьшее кратное и помно-
живъ его на какое угодно число, мы получимъ тоже
кратное число, но не наименьшее. Напр., для 100, 40
и 35 общими кратными, помимо 1400, будутъ:
1400.2	1400.3	1400.4	1400.5 и т. д.
137.	Некоторые частные случаи. Разсмотримъ
два случая, въ которыхъ наименьшее кратное можетъ
быть найдено весьма просто.
Случай 1-й, когда никакая пара данныхъ
чиселъ не имеетъ общихъ множителей.
Пусть, напр., даны три числа: 20, 49, 33, изъ кото¬
рыхъ, какъ видно изъ разложешй:
20=2.2.5; 49 = 7.7; 33 = 3.11
никакая пара не имеетъ общихъ множителей.
Применяя къ этому случаю общее правило, придемъ
къ заключенш, что все данныя числа надо пере¬
множить:
20 . 49 . 33 = 32340.
Такъ же надо поступить, когда отыскивается найм,
кратное простыхъ чиселъ; напр., найм, кратное чиселъ
3, 7 и 11 равно: 3.7. 11 = 231.
Случай 2-й, когда большее изъ данныхъ
чиселъ делится на все остальныя. Тогда
наибольшее число и есть найм, кратное. Пусть, напр.,

— 126 —
даны четыре числа: 5, 12, 15 и 60, изъ которыхъ боль¬
шее 60 дЬлится на 5, на 12, на 15; такъ какъ оно при
этомъ, конечно, дЬлится и на само себя, то оно и есть
наименьшее кратное.
138.	Другой способъ нахожден1я наимень-
шаго кратнаго. Можно находить найм, кратное, не
разлагая данныхъ чиселъ на простыхъ множителей (что
иногда бываетъ затруднительно). Для этого, въ при-
мЬнеши къ двумъ даннымъ числамъ, поступаютъ по
следующему правилу:
Чтобы найти наименьшее нратное двухъ чиселъ, предва¬
рительно находятъ ихъ общаго наибольшего дЬлителя,
затЪмъ дЪлятъ на него одно изъ чиселъ и полученное
частное умножаютъ на другое число.
Пусть, напр., требуется найти найм, кратное чиселъ
391 и 85. Находимъ (способомъ послЬдовательнаго дЬ-
летя) ихъ общаго наиб. дЬлителя; онъ равенъ 17. Те¬
перь раздЬлимъ одно изъ данныхъ чиселъ, напр., 85,
на 17; получимъ 5. Умноживъ 5 на другое данное число,
т.-е. на 391, найдемъ 1955; это и есть найм, кратное 391
и 85. Действительно, частное 85 :17 должно содержать
въ себЬ тЬхъ простыхъ множителей числа 85-ти, которые
не входятъ въ 391; поэтому произведете 391 . (85 : 17)
должно содержать въ себЬ всЬхъ простыхъ множителей
числа 391 и еще тЬхъ множителей числа 85, которые не
входятъ въ 391, а это, какъ мы видЬли, и составляешь
найм, кратное чиселъ 391 и 85.
Чтобы найти этимъ способомъ найм, кратное трехъ,
четырехъ и болЬе данныхъ чиселъ, достаточно найти
сначала найм, кратное двухъ изъ нихъ, потомъ найти
найм, кратное этого найм, кратнаго и третьяго числа
и т. д.

ОТДЪЛЪ ЧЕТВЕРТЫЙ.
Обыкновенный дроби.
I. Основныя ПОНЯТ1Я.
139. Доли единицы. Если какую-нибудь единицу,
напр., аршинъ, раздЬлимъ на несколько равныхъ частей,
то каждая часть получаетъ назваше, указывающее,
сколько такихъ частей содержится въ целой единице.
Такъ, когда единица разделена на 12 равныхъ частей,
то каждая часть называется двенадцатою частью;
разделивъ единицу на 40 равныхъ частей, иолучимъ
сороковыя части и т. п. Вторая часть называется иначе
половиной, третья часть—третью, четвертая часть-
четвертью.
Части единицы, получаемый отъ делешя ея на не¬
сколько равныхъ частей, называются долями единицы.
140. Дробное число. Одна доля или сображе нй-
сколькихъ одинаковыхъ долей единицы называется дробью.
Напр., 1 десятая, 3 пятыхъ, 12 седьмыхъ суть дроби.
Цйлое число вместе съ дробью составляетъ смешанное
число; напр., 3 целыхъ 7 восьмыхъ.
Дроби и смешанный числа называются дробными чис¬
лами въ отлич1е отъ целыхъ чиселъ, составленныхъ изъ
целыхъ единицъ.

— 128 —
141.	Изображено дроби. Принято изображать
дробь такъ: пишутъ число, показывающее, сколько
долей содержится въ дроби; подъ нимъ проводятъ черту,
горизонтальную или наклонную; подъ чертою ставятъ
другое число, показывающее, на сколько равныхъ частей
разделена единица, отъ которой взята дробь. Напр.,
дробь 3 пятыхъ изображаютъ такъ;
Число, стоящее надъ чертою, называется числителемъ;
оно показываетъ число долей, изъ которыхъ составлена
дробь. Число, стоящее подъ чертою, называется знаме-
нателемъ; оно означаетъ, на сколько равныхъ частей
была разделена единица. Оба эти числа вместе назы¬
ваются членами дроби.
Смешанное число изображаютъ такъ; пишутъ целое
число и къ нему, съ правой стороны, приписываюгь
дробь; напр., число три и две седьмыхъ изображается
такъ: 3? или 3*/7.
142.	Происх ождеПе дробныхъ чиселъ отъ
измерен я. Положимъ, мы желаемъ измерить какую-
нибудь длину помощью вершка; допустимъ, что вер¬
шокъ въ этой длине укладывается 7 разъ, причемъ полу¬
чается остатокъ, менышй вершка. Чтобы измерить этотъ
остатокъ, подыскиваемъ такую долю вершка, которая,
если возможно, уложилась бы въ остатке безъ новаго
остатка. Пусть окажется, что восьмая доля вершка укла¬
дывается въ остатке ровно 5 разъ. Тогда говоримъ, что
измеряемая длина равна 7в/8 вершка.
Подобно этому дробныя числа могута получаться при
измереши в^са (напр., 2*/4 зол.), при измерены времени
(напр., 7/ie часа) и вообще при измеренш значетя
какой бы то ни было величины.
Такимъ образомъ, всякое дробное число (равно какъ
и всякое целое) можно разсматривать, какъ результата
измеретя.
3
— или
5

— 129
Число (ц-Ьлое или дробное) наз. именованнымъ, если
оно сопровождается назватемъ той единицы, которая
употреблялась при изм'Ьрети, или доли которой упо¬
треблялись при изм'Ьреши, напр., 3Д вершка; въ про-
тивномъ случай число наз. отвлеченнымъ, напр. 3Д.
143. Происхожден1е дробныхъ чиселъ отъ
д'Ьленхя ц'Ьлаго числа на равныя части.
Пусть требуется раздЬлить 5 яблокъ между 8 учени¬
ками поровну. Мы можемъ выполнить это д’Ьлете такъ:
разр'Ьжемъ одно яблоко на 8 равныхъ частей и дадимъ
каждому ученику по одной части; за'гЬмъ сд'блаемъ то же
самое со вторымъ яблокомъ, третьимъ и т. д. Тогда каж-
дый ученикъ получить по 5 восьмыхъ яблока. Значить,
восьмая часть 5-и яблокъ (и вообще 5-и какихъ-нибудь
единицъ) равна 5/8 яблока (и вообще 5Д одной еди¬
ницы).
Возьмемъ другой примъръ: пусть требуется умень¬
шить въ 5 разъ число 28, т.-е. требуемся вместо 28-и
взять пятую часть 28. Найти пятую часть 28-и мы мо¬
жемъ такъ: пятая часть одной единицы есть 7Б; пятая
часть другой единицы есть также 1/6; если такимъ обра-
зомъ возьмемъ по пятой части отъ каждой изъ 28 еди¬
ницъ, то получимъ *8/б.
Изъ этихъ прим’Ьровъ мы можемъ вывести следующее
правило, которое полезно запомнить:
Чтобы уменьшить цЪлое число въ нисколько разъ, до¬
статочно взять это число числителемъ дроби, а знаменате-
лемъ написать другое число, показывающее, во снольно
разъ уменьшается цЪлое число.
144. Равенство и неравенство чиселъ. Два
числа считаются равными или неравными, смотря по
тому, равны или неравны значешя величины, выра-
:каемыя этими числами, при одной и той же единиц'Ь.
Такъ, мы говоримъ, что 3/4=6/8; этнмъ мы хотимъ сказать,
9 Закез Кб 5456

— 130 —
что два значешя величины (наср., две длины), изъ
которыхъ одно состоять изъ 3 четвертей единицы, а
другое—изъ 6 восьмыхъ той же единицы, равны между
собою.
Изъ двухъ неравныхъ чиселъ болынимъ считается то,
которое выражаетъ большее значеше величины при
одной и той же единице. Такъ, если мы говоримъ, что
У5>/8, мы желаемъ этимъ выразить, что значеше ве¬
личины, равное V* какой-нибудь единицы, больше зна¬
чешя величины, равнаго У8 той же единицы (напр., */5
фунта больше У8 фунта).
145. Дробь правильная и неправильная.
Дробь, у которой числитель меньше знаменателя, наз
правильною; дробь, у которой числитель равенъ или
больше знаменателя, наз. неправильною. Очевидно, пра
вильная дробь меньше 1, а неправильная равна ей или
больше ея; напр., 7/8<0, */8=1, 8/8>1.
146. 0бращен1е целаго числа въ непра¬
вильную дробь. Цйлое число можно выразить въ
нанихъ угодно доляхъ единицы. Пусть, напр., требуется
выразить 8 въ двадцатыхъ доляхъ. Въ одной единице
заключается 20 двадцатыхъ; след., въ 8 единицахъ ихъ
будетъ 20X8, т.-е. 160. Значить:
20.8 160
8 =
20 20 '
гг	100	-inn 1700
Примеры:	—	100 =
целое число иногда бываетъ полезно изобразить въ
виде такой дроби, у которой числитель равенъ этому це¬
лому числу, а знаменатель есть 1. Такъ, вместо 5 пишутъ
иногда ВД. Чтобы придать смыслъ такимъ выражешямъ,
условливаются, что разделить единицу на одну- равную
часть значить оставить единицу безъ изменешя.

- 131 —
147. Обр ащен1е смЬшаннаго числа въ не¬
правильную дробь. Пусть требуется обратить 83/„
въ неправильную дробь. Это значитъ: узнать, сколько
пятыхъ долей заключается въ 8 цЬлыхъ единицахъ и
3-хъ пятыхъ доляхъ той же единицы. Въ 8 единицахъ
пятыхъ долей содержится 5Х8> т.-е. 40; значитъ, въ
8 ед. и 3-хъ пятыхъ ихъ будетъ 40-J-3, т.-е. 43. Итакъ,
8V* = W/*.
тт	о? 31 лп1 41 О*2 177
Примеры: 3—==—; 10^=—; 25^=-^--
Правило. Чтобы обратить смешанное число въ непра¬
вильную дробь, умножаютъ цЪлов число на знаменателя и
нъ произведена прибавляютъ числителя; полученное отъ
этого число берутъ числителемъ искомой дроби, а знаме¬
нателя оставляютъ прежняго.
148. 0бращен1е неправильной дроби въ
смешанное или цЬлое число. Пусть требуется
обратить неправильную дробь 10% ъъ смешанное число,
т.-е. узнать, сколько въ этой дроби заключается Ц’Ьлыхъ
единицъ и сколько еще восьмыхъ долей, не составляю-
щихъ единицы. Такъ какъ единица заключаегь въ себЬ
8 восьмыхъ, то въ 100 восьмыхъ содержится столько
единицъ, сколько разъ 8 восьмыхъ содержатся въ 100
восьмыхъ. 8 восьмыхъ въ 100 восьмыхъ содержатся 12
разъ, при чемъ 4 восьмыхъ остаются. Значитъ, 100 вось¬
мыхъ содержать 12 цЬлыхъ единицъ и еще 4 восьмыхъ
доли.
Итакъ, 10% = 12VS.
69	_3	314	14 85	„25
ПримЬры:	8— 8;	25	12 2g; 17	’ 25	•
Правило. Чтобы обратить неправильную дробь въ смЪ-
шанное или цЬлое число, дЬлятъ числителя на знаменателя;.
цЬлое частное отъ этого дЬлежя означаетъ, сколько еди¬
ницъ въ дроби, а остатокъ—снолько долей единицы.
9*

— 132 —
Обращение неправильной дроби въ смешанное или
цфлое число называютъ иначе исключешемъ Ц'Ьлаго числа
изъ неправильной дроби.
П. Изм’ЬнегНе величины дроби съ изм'Ь-
нен!емъ ея членовъ.
149. Съ увеличемемъ числителя дробь увеличивается;
напр., 7»>V*j потому что об-Ь дроби составлены изъ
одинаковыхъ долей, но число ихъ въ первой дроби
больше, ч'Ьмъ во второй.
Съ увеличемемъ знаменателя дробь уменьшается; напр.,
7ю<7», потому что об^ дроби им'Ьютъ одинаковое
число долей, но доли въ первой дроби мельче, чЪмъ
во второй.
Отсюда сл'Ьдует.'Ъ, что
съ уменыпетемъ числителя дробь уменьшается;
съ уменыпетемъ знаменателя дробь увеличивается.
150. Если числителя дроби увеличимъ въ нЪснолько разъ,
то дробь увеличится во столько же разъ.
Напр., увеличимъ числителя дроби */ю въ ТРИ раза;
получимъ 1S/10- Эта дробь больше прежней въ 3 раза,
потому что число долей въ ней больше прежняго въ 3
раза, а доли остались тЬ же.
Если знаменателя дроби увеличимъ въ нисколько разъ
то дробь уменьшится во столько же разъ.
Напр., увеличимъ знаменателя дроби */10 вь 5 разъ,
получимъ 4/бо- Эта дробь меньше прежней въ 5 разъ,
потому что въ ней число долей осталось прежнее, но
доли сд'Ьлались мельче прежнихъ въ 5 разъ.
Отсюда сл'Ьдуетъ, что
если числителя дроби уменьшимъ въ нисколько разъ
то дробь уменьшится во столько же разъ;
если знаменателя дроби уменьшимъ въ нисколько разъ,
то дробь увеличится во столько же разъ.

— 133 —
151.	Если оба члена дроби увеличимъ или уменьшишь въ
одинаковое число разъ, то величина дроби не изменится.
Напр., уменынивъ оба члена дроби */м въ 2 раза,
мы получимъ новую дробь -j6. Эта дробь равна прежней,
потому что если мы уменыпимъ только одного числителя
въ два раза, то дробь уменьшится въ 2 раза; если же загЬмъ
уменыпимъ еще и знаменателя въ 2 раза, то эта умень¬
шенная въ 2 раза дробь увеличится вдвое и, след.,
сделается равной прежней дроби.
Вообще изм’Ьнете дроби вполне сходно съ изм'Ьне-
темъ чаетнаго, при чемъ числитель зам'Ьняетъ собою
делимое, а знаменатель—делителя.
152-Какъ увеличить или уменьшить дробь
въ нисколько разъ. Зная, какъ изменяется дробь
съ изменетемъ ея числителя и знаменателя, мы можемъ
вывести слецукшця правила:
1) Чтобы увеличить дробь въ несколько разъ, доста¬
точно увеличить во столько же разъ ея числителя или умень¬
шить во стольно же разъ ея знаменателя.
2) Чтобы уменьшить дробь въ нЪснольно разъ, доста¬
точно уменьшить во столько же разъ ея числителя или
увеличить во столько же разъ ея знаменателя.
ПримЪры.
Увеличить 7/и въ 5 разъ; получимъ 8S/1S.
Увеличить 7/ls въ 6	разъ;	„	**/,*	или 7/8
Уменьшить 8/и въ 7	разъ;	„	8/вз
Уменьшить 8/э въ 4	раза;	„	*/3е	или */»
Замечаню. Эти правила можно применять и къ це¬
лому числу, если только целое число будемъ разематри-
ватъ, какъ дробь, у которой знаменатель равенъ 1, а
числителемъ служить это целое число. Пусть, напр.,
требуется уменьшить 5 въ 8 разъ. Представимъ число 5
подъ видомъ дроби */i и применимъ правило объ умень-
к

— 134 —
шеши дроби; тогда получимъ в/№ что, какъ мы видели
раньше (§ 143), действительно меньше 5-и въ 8 разъ.
153. Отъ прнбавлен1я нъ членамъ дроби одного и того же числа
правильная дробь увеличивается, а неправильная уменьшается, при чемъ
та и другая приближаются къ 1.
Напр., прибавимъ къ членамъ правильной дроби % по 3;
получимъ 8/10. Первая дробь меньше 1 на дв4 седьмыхъ, а
вторая меньше 1 тоже на две, но не седьмыхъ, а десятыхъ.
Но 2/io<C2Ai значитъ. вторая дробь ближе къ 1, чЬмъ первая,
и потому Vio>Vj- Возьмемъ теперь неправильную дробь,
напр., */5, и прибавимъ къ ея членамъ по какому-нибудь
числу, напр., по 4; тогда получимъ la/s. Первая дробь больше
1 на 3 пятыхъ, а вторая больше 1 тоже на 3, но не пятыхъ,
а девятыхъ; но 8/в<С3/бэ значитъ, вторая дробь ближе къ 1,
ч£мъ первая, и потому 1а/»<С8/в-
111. Сокращен1е дробей.
154. Определена. Сокращешемъ дроби называется
приведете ея къ более простому виду посредствомъ раз¬
делами числителя и знаменателя на одно и то же число
(отъ чего, какъ мы видЬли, величина дроби не изме¬
няется).
Конечно, сокращать можно только такую дробь, у
которой члены имЬютъ какого-нибудь общаго делителя,
большаго 1; напр., дробь 8/13 можно сократить на 4,
отъ чего получимъ дробь 2/з меньшимъ числителемъ
и знаменателемъ.
Дробь, которая не можетъ быть сокращена, наз. несо¬
кратимою. Такова, нанр., дробь 9/*0-
155. Сокращать дробь можно двумя способами.
Первый способъ (последовательное со¬
кращено) состоитъ въ томъ, что отыскиваютъ по при-
знакамъ делимости какого-нибудь общаго делителя чле-
новъ дроби и сокращаютъ на него; полученную дробь,
если можно, сокращаютъ снова; продолжаютъ такое по¬

— 135 —
ел'Ъдовательное сокращеше до тЬхъ поръ, пока не по¬
лучится дробь несократимая. Напр.:
А X
84 21  7
360 ~'90 — 30
Для памяти надписываютъ надъ дробью то число, на
которое сокращаютъ.
Второй способъ (полное сокращено) упо¬
требляется тогда, когда по признакамъ делимости нельзя
определить, сократима ли дробь, или н’Ьтъ. Тогда оты-
скиваютъ (способомъ посл’Ьдовательнаго дЬлешя) общаго
наиболыпаго делителя для числителя и знаменателя
дроби, а зат'Ьмъ делятъ оба члена дроби на этого де¬
лителя. Напр., пусть требуется сократить 891/S27- Для
этого находимъ общаго наиболыпаго делителя чиселъ
391 и 527 (онъ равенъ 17) и потомъ на него сокращаемъ:
391 _ 391 : ~17 23
527“527 :"17	31
Въ этомъ случае после сокращешя получается дробь
несократимая. Действительно, общ1й наиб, делитель
числителя и знаменателя долженъ содержать въ себе
всехъ общихъ простыхъ множителей, входящихъ въ
составь числителя и знаменателя; поэтому, когда на
него раздЬлимъ числителя и знаменателя, то получен-
ныя частныя уже не могутъ содержать въ себе ника-
кихъ общихъ множителей и, след., не будутъ иметь
никакихъ общихъ делителей.
156.	Теорема. Если две дроби равны и одна изъ
нихъ несократима, то члены другой дроби въ
одинаковое число разъ кратны соответствую-
щихъ членовъ несократимой дроби.
Для доказательства положимъ, что дробь ~ несократима,!, е.
числа а и 6 не имеютъ общихъ делителей, кроме 1. Пусть

— 136 —
другая дробь -j- равна первой дроби. Умножимъ оба члена
второй дроби на 6, а первой—на Ъ1; такъ какъ значетя дро¬
бей огь этого не изменятся, то получимъ равенство:
а. Ъ оЪ,	,	,	...
~Ь$ = Щ' 0ткуда: aib = abi (!)■
Правая часть этого равенства делится на а; значить, его
лйвая часть тоже делится на а; но Ъ, по условию, есть число
взаимно простое съ а\ значить, надо, чтобы а, делилось на а
(§ 118). Обозначивъ частное отъ дЬлетя а, на а буквой от,
можемъ положить: а, = am, посл’Ь чего равенство (1) даетъ:
amb=abl
откуда, раздЬливъ об'Ь части равенства на а, получимъ
mb = й,. Итакъ: а, = am и й, = bm; а это значить, что а,
и 6, въ одинаковое число разъ кратны соответственно а и Ь.
Сл'Ьдств1Я. 1) Две несокрауимыя дроби могутъ
быть равны другъ другу только тогда, когда у
нихъ равны числители и равны знаменатели.
2)	Умножеше членовъ дроби на одно и то же
число есть единственный способъ преобразо-
ван1я несократимой дроби.
ГУ. Приведен1е дробей къ общему на¬
именьшему знаменателю.
157.	Основываясь на томъ, что дробь не изменить
своей величины, если оба ея члена умножимъ на одно
и то же число, мы всегда можемъ выразить данныя-
дроби въ одинаковыхъ доляхъ единицы или, какъ го¬
ворить, привести ихъ къ общему знаменателю. Укажемъ
способъ, посредствомъ котораго можно приводить дроби
не только къ общему, но притомъ и къ наимень¬
шему знаменателю.

— 137
Пусть требуется привести дроби 1/,г и 7/ls къ наимень¬
шему общему знаменателю. Разсуждаемъ такъ: Е/1г есть
дробь несократимая, поэтому, кроме 12-хъ долей, ее
можно выразить только въ доляхъ 24-хъ, 36-хъ, 48-хъ и
т. д., т.-е. знаменатели всехъ дробей, которымъ можетъ
равняться дробь */14, должны быть числами кратными
12-ти *); подобно этому, знаменатели всехъ дробей, кото¬
рымъ можетъ равняться дробь 7/16, должны быть чис¬
лами кратными 15-ти; след., общШ знаменатель этихъ
двухъ дробей долженъ быть общимъ кратнымъ числомъ
12-ти и 15-ти, а наименьппй обпщй знамена¬
тель долженъ быть наименыпимъ кратнымъ
числомъ 12-ти и 15-ти. Найдемъ наименьшее кратное
этихъ чиселъ:
12 = 2 .2.3
15 = 3 . 5
н. кр. = 2 . 2 . 3 . 5 = 60.
Это и будетъ найм, обпцй знаменатель дробей в/» и 7/16.
Чтобы выразить каждую изъ этихъ дробей въ 60-хъ
доляхъ, надо найти для ихъ знаменателей такъ назы-
ваемыхъ дополнительныхъ множителей, т.-е.
для каждаго знаменателя найти то число, на которое его
надо умножить, чтобы получить щаим. кратное. Сравни¬
вая между собою разложешя 12-ти, 15-ти и 60-ти, нахо
димъ, что для получешя 60-ти надо умножить 12 на 5,
а 15 на 2 . 2, т.-е. на 4. Чтобы не изменились вели¬
чины дробей, надо умножить числителя каждой дроби
на то же число, на которое умножаемъ ея знаменателя:
5	5	.	5	25	7	7_	. 4	28
12 12 . 5 “60	15	15	. 4 “60*
Пусть еще требуется привести къ наименьшему общему
знаменателю три дроби: */90, 7/40 и Первая изъ
*) Строгое доказательство этого утверждешя представляетъ тео¬
рема § 156-го.

— 138 —
нихъ после сокращешя даетъ 2/«> остальныя дроби но-
сократимыя. Отыщемъ наименьшее кратное 45, 20 и 76
45 = 3.3.5	доп.	мн.	для	45 = 2.2.5 = 20
20=2.2.5	„	„	,,	20=3.3.5 = 45
,75=3.5.5	„	в	„	75 = 2.2.3 = 12
н. кр. =3.3.5.2.2.5 = 900.
Теперь умножимъ оба члена каждой дроби на допол-
нительнаго множителя для ея зйаменателя:
2	2 . 20	40 7	7	.	45 315 8	8	.	12	96
45—45 . 20 —900’ 20—20 . 45~~9бб’ 75~75 . 12 —900*
Правило. Чтобы привести данный дроби къ наимень¬
шему общему знаменателю, предварительно, если можно,
ихъ сокращаютъ, затЬмъ находятъ наименьшее кратное
всехъ знаменателей и умножаютъ оба члена каждой дроби
на дополкительнаго множителя для ея знаменателя.
Некоторые частные случаи.
158.	Случай 1-й, догда никакая пара зна¬
менателей не содержитъ общихъ множите¬
лей. Напр. */т> Vie, */*• Въ этомъ случа-Ь найм, крат¬
ное знаменателей равно произведенш ихъ: 7.15.8. Сл'Ьд.,
оба члена первой дроби придется умножить на 15.8=120,
второй—на 7.8 = 56 и третьей—на 7.15 = 105:
3 3 .120 360 4 4 . 56 224 5 5 .105 525
7 7 .120~84б’ 15~15 756“840’ "8“ 8 .105~840‘
Правило. Чтобы привести къ наименьшему общему зна¬
менателю ташя несократимыя дроби, у которыхъ никакая
пара знаменателей не содержитъ общихъ множителей, до¬
статочно оба члена наждой дроби умножить на произведе¬
те знаменателей всЪхъ остальныхъ дробей.
Такъ же поступають, когда знаменатели—числа про¬
стыя.
ЗамЪчаше. Это правило можно прилагать во всЬхъ
случаяхъ, но тогда общШ знаменатель не всегда будетъ

— 139 —
наименышй. Если, напр., знаменатели данныхъ дробей
будутъ числа: 6, 8 и 9, то, взявъ произведете ихъ,
получимъ число 432; между тЬмъ наименьшее кратное
этихъ чиселъ есть 72.
Случай 2-й, когда наибольппй изъ знаме¬
нателей дЬлится на каждаго изъ осталь-
ныхъ, напр., %> 7/ib 8/з15- Знаменатель 315 д’Ьлится
на 7, на 15 я на самого себя. Въ этомъ случаЬ наиболь-
шй знаменатель есть наименьшее кратное всЬхъ знаме¬
нателей; значить, он*ь долженъ быть общимъ знамена-
телемъ:
Доп. мн.	для	7=45;	Доп.	мн.	для	15=21
3	3 . 45	135	7	7	.	21	147	8	8
7	7 . 45	315’	15	15	.	21“	315’ 315“ЖЕ'
158,а. Сравнено дробей. Приведен1е дробей къ
общему знаменателю облегчаетъ сравнете ихъ повели-
чинЬ. Пусть, напр., требуется узнать, равны или не
равны дроби */7 и */is» и если не равны, то которая изъ
нихъ больше. Для этого приведемъ ихъ къ общему
знаменателю:
5	5	.	13	65	9	9	. 7	63
7	7	.	13 —91	13	13	. 7	91
Теперь видимъ, что данныя дроби не равны, и первая
больше второй, такъ какъ у нея числитель больше.
V.	Нахожден1е дроби даннаго числа и
обратный вопросъ.
1.	Нахождеше дроби даннаго числа.
159.	ЗамЬчаше. Выражеше „найти дробь числа1* часто
можно заменить другимъ выражешемъ: „найти часть числа1*,
именно тогда, когда данная дробь меньше 1; напр., если тре¬
буется найти 7/* какого-нибудь числа, то, понятно, мы най-

— 140 —
демъ часть этого числа, такъ какъ 7/g меньше ц^лаго; но
если требуется найти 8/, какого-нибудь числа, то это не зна¬
чить, что отыскивается часть этого числа, такъ какъ 8/7 пре¬
восходить ц-Ьдое.
Находить дробь даннаго числа приходится при р'Ьшети
очень многихъ задачъ. Прим’Ьромъ могутъ служить задачи,
въ родЬ сл'Ьдующихъ:
По^здъ въ часъ проходить 40 верстъ; сколько верстъ онъ
жроходитъ въ 7/8 часа?
Аршинъ матерш стоить 8 руб.; сколько рублей стоять 7/t
аршина? и т. п.
160.	Ум’Ья увеличивать и уменьшать число въ ни¬
сколько разъ, мы легко можемъ находить данную дробь
всякаго числа.
ПримЪръ 1-й. Найти */* числа 26-и.
Для этого сначала найдемъ */* числа 26-ти, т.-е.
уменыпимъ 26 въ 4 раза, а потомъ полученную четверть
увеличимъ въ 3 раза:
1 26
числа 26-ти составляетъ —	(§	143).
*	3	о*	26	•	3	78 -о 1
слъд., — числа 26-ти составляютъ —=^-=19 —
Примерь 2-й. Найти 8/в числа 5/в.
Для этого найдемъ сначала */* числа */в, т.-е. умень-
шимъ */в. въ 3 раза, а загЬмъ результатъ увеличимъ
въ 8 разъ:
15	5
числа —составляетъ
V 8	5	5.8	40	„2
слъд., числа -з- составляютъ г-—з = т^ = - тг
о	о	о	.	о	1о	У

— 141 -
2.	Нахожден1е неизвЪстнаго числа по данной его
161.	Замечаше. Находить неизвестное число по данной его
дроби приходится при решети очень многихъ задачъ; приме-
ромъ могуть служить задачи, подобный следующимъ:
Въ часа поездъ проходить 30 верстъ; сколько верстъ
онъ проходить въ часъ?
За ls/4 арш. (т.-е. за 7Д арш.) матерш заплатили 14 руб.;
сколько стоить аршинъ этой матерш? и т. п.
Примеръ 1-й. Найти число, ко то par о 3/в
составляютъ 5.
Такъ какъ въ 5 заключаются 3 восьмыхъ искоыаго
числа, то, уменыпивъ 5 въ 3 раза, мы найдемъ Vs ис'
комаго числа, а увеличивъ результатъ въ 8 разъ, полу¬
чимъ 8/в искомаго числа, т.-е. целое искомое число.
Выразимъ это строчками:
примеръ 2-й. Найти число, котораго 8/з
составляютъ 22/а, т.-е. 2%.
Выразимъ ходъ разсуждешя строчками:
дроби,
—неизв. числа составляютъ 5;
О
след., —неизв. числа составляетъ—,
О	О
8
20
-тг неизв. числа составляютъ -7Г:
3	9
1 20
след., -д-неизв. числа составляетъ^-,
20
3
а -д неизв. числа составляютъ
20 . 3 60	5
9 . 8" 72 ~6

— 142 —
VI.	Д'Ьйств1я надъ отвлеченными
дробями.
162.	Смыслъ дЬ Н CTBifi надъ дробными чис¬
лами. Такъ какъ дробный числа выражаютъ некоторый зна-
четя величины, то дЬйств1я надъ нивга имЬютъ тотъ же
смыслъ, какъ и д,Ьйств1я надъ именованными числами (см.
§ 104). Такъ, сложить три дроби: 3/i+7/m+*/ie значить найти
число, выражающее сумму трехъ значешй величины, изъ
которыхъ одно состоитъ изъ 3-хъ четвертей, другое изъ
7 десятыхъ и третье изъ 9 шестнадцатыхъ долей одной и
той же единицы (напр., найти число, выражающее сумму
трехъ длинъ: */* аршина, 7/м аршина и */« аршина). КромЬ
того, для обобщетя нЬкоторыхъ вопросовъ, въ курс* дро¬
бей допускаютъ еще два особыя дЬйстшя: умножеше на
отвлеченную дробь и дЬлеше на отвлеченную дробь.
С л о ж е н I е.
163.	ЗамЬтимъ, что назвашя чиселъ, какъ данныхъ,
такъ и искомаго, при каждомъ ариеметическомъ дЬй-
ствш, а также и знаки этихъ дЬйствШ, остаются для
дробныхъ чиселъ гЬ же сакыя, что и для цЬлыхъ.
Определен! е. Сложеше есть ариеметическое дЪйств1е,
посредствомъ нотораго нЪсколько данныхъ чиселъ соеди¬
няются въ одно число, называемое ихъ суммой *)•
Пусть требуется сложить дроби съ одинаковыми
знаменателями, напр, таия:
- + - + -
11 11 11
Очевидно, что 7 одиннадцатыхъ, да 3 одиннадцатыхъ,
да 5 одиннадцатыхъ какой-нибудь единицы составляютъ
*) Общее опредЪлен1е суммы чиселъ. Суммою н-Ьсколышхъ данвыхъ
чиселъ наз. новое число, выражающее сумму ееличинъ, измЪряемыхъ
данными числами, при одной и той же единиц!* изыЪренш.

— 143 —
7+3+5 одиннадцатыгь той же единицы. Значить, чтобы
найти искомую сумму, надо сложить числителей и подъ
ихъ суммой подписать общаго знаменателя:
7 | 3	5 7+3+5 15  4
11+11+11	11	11	1 11
Пусть теперь требуется сложить дроби съ разными
знаменателями, напр, тамя:
-+-+-
4 ‘10 '16
Приведемъ всЬ эти дроби къ общему знаменателю и
сд'Ьдаемъ сложеше, какъ въ первомъ случа-Ь:
20	^	^
3	Г	9 _ 60+56+45 _ 161	1_
4	10-*	16	80	“	80	— 280"
Число, поставленное надъ каждою данною дробью,
есть доп. множитель, на который должно умножить члены
дроби, чтобы привести ее къ общему знаменателю.
Правило. Чтобы сложить дроби, достаточно привести
ихъ къ общему знаменателю, затЪмъ сложить числителей
и подъ суммою ихъ подписать общаго знаменателя.
Пусть, наконецъ, требуется сложить см'Ьшанныя
числа:
4 4 - 4
Сначала сложимъ дроби:
■1.	Л
2+ 9 . Б _ 4+27+25 _ 56	26	13
15 + 10+ 6 ~	30	— 30— 30	15
Теперь сложимъ цЬлыя числа и къ сумм!, ихъ доба-
вимъ 1, получившуюся отъ сложешя дробей:
4+8+3+1=16
13
Значить, полная сумма равна 16 jg.

— 144 —
ЗамЬчан1е. Основное свойство суммы, указанное
нами раньше для цЬлыхъ чиселъ (§ 29), принадлежите
также и дробнымъ числамъ, т.-е. сумма не зависите оте
того порядка, въ какомъ мы соединяемъ единицы и доли
единицъ слагаемыхъ.
В ы ч и т а н i е.
164.	Определен!е. Вычитаже есть ариеметическое
дЬйстше, посредствомъ котораго по данной суммЬ и од¬
ному слагаемому отыскивается другое слагаемое.
Другими словами, вычиташе есть д'Ъйсттае, посред¬
ствомъ котораго узнается, какое число останется оте
уменыдаемаго, если оте пего отд'Ьлимъ часть, равную
вычитаемому.
Пусть	даны	для	вычиташя дроби	съ	одинако¬
выми знаменателями, напр, тагая:
 7 з
8 8-
7	3
Если оте уменьшаемаго g отд'Ьлимъ часть въ g, то
останется, очевидно, 7—3 восьмыхъ. Поэтому, чтобы
найти искомый остатокъ (или разность), надо изъ числи¬
теля уменьшаемаго вычесть числителя вычитаемаго и
подъ остаткомъ подписать того же знаменателя:
7	3	7-3	4	1
8	8 — 8	8 ~ 2	'
Пусть	теперь данныя дроби имЬютъ	разныхъ	зна¬
менателей:
11 3^
15	8*
Приведя эти дроби къ общему знаменателю, сдЬлаемъ
вычиташе, какъ было объяснено раньше:

— 145 —
Л 15
11	3	88—45	43
15	8 “ 12(Г— ~Ш>	*
Правило.	Чтобы	вычесть дробь изъ	дроби,	достаточно
привести ихъ	нъ общему знаменателю,	загЬмъ	изъ	числи¬
теля уменьшаемаго вычесть числителя вычитаемаго и подъ
ихъ разностью подписать общаго знаменателя.
Если нужно вычесть смешанное число изъ дру¬
гого смЬшаннаго числа, то, если можно, вычнтаютъ
дробь изъ дроби, а цйлое изъ цЬлаго. Напр.:
8»	54=8§-б|=зА
11	4	44	44	44
Если же дробь вычитаемаго больше дроби уменьша¬
емаго, то берутъ одну единицу изъ цЬлаго числа умень¬
шаемаго, раздробляютъ ее въ надлежащая доли и при-
бавляютъ къ дроби уменьшаемаго. Напр.:
* 5	*п18	е55	о84	к55—/29
1 11 в 66	66“ 66	66	66
Такъ же производится вычитате дроби изъ цЬ-
лаго числа; напр.:
,_2|=в1_2| = 4|
5	о	5	5
17	' 17 17“" 17
ЗамЬчан1е. При вычитанш дробныхъ чиселъ, такъ
же какъ и цЬлыхъ чиселъ (§ 29), вычитаемое не можетъ
быть больше уменьшаемаго, а должно быть меньше его,
или равно (въ послЬднемъ случай остатокъ принимается
равнымъ 0).
165.	ИзмЬнен1е суммы и разности. Сумма и
разность дробныхъ чиселъ изменяются при измЬнеши
данныхъ чиселъ совершенно такъ же, какъ сумма и
разность цЬлыхъ чиселъ, г.-е.:
10 Заказ № 5456

— 146 —
1) Если увеличивается (или уменьшается) слагаемое,
то и сумма увеличивается (или уменьшается) на столь¬
ко же.
2) Если увеличивается (или уменьшается) уменьша¬
емое, то и разность увеличивается (или уменьшается)
на столько же.
3) Если увеличивается (или уменьшается) вычитаемое,
то разность уменьшается (или увеличивается) на столь¬
ко же.
У м н о ж е н i е.
Задача. Аршинъ сукна стоить 5 руб. Сколько стоять
мьсколько аршинъ этого сукна?
Для рЬшешя вопроса мы должны умножить 5 руб. на число
аршинъ, когда это число ц№лое (напр. 10 арш.), и мы
должны найти дробь 5-ти руб., когда число аршинъ дробное
(напр., 13/2 арш.).
Чтобы въ подобныхъ вопросахъ можно было давать одинъ
ответе, условились расширить поште объ умроженш, на¬
вивая этимъ словомъ также и нахождеше дроби числа.
166.	Определен!е. Умножить какое-нибудь число
(множимое) на ц’Ьлое число (множитель) значитъ повторить
множимое слагаемымъ столько разъ, сколько во множитвлЪ
единицъ.
Умножить какое-нибудь число (множимое) на дробь (мно¬
житель) значитъ найти эту дробь множимаго.
Такъ, умножить 7/8 на 5 значитъ повторить 7/s сла_
гаемымъ 5 разъ, другими словами, найти сумму: 7/8-f-
V+Ve+Ve+Vs ’ умножить 5 на 7/8 значитъ найти
семь восьмыхъ 5-ти единицъ. Такимъ образомъ нахож¬
дете дроби даннаго числа, разсмотр'Ьнное нами раньше
(§160), мы будемъ теперь называть умножешемъ на дробь.
Указанное определение умножешя на дробь можно приме¬
нять и къ умноженш на ц1>лое число, если только это д'Ьлое
число предварительно обратить въ какую-нибудь неправильную
дробь (§ 146). Но въ такомъ случай возникаете вопросъ,
не будете ли опредйлеше умножешя на дробь противоречить
опредйлешю умножешя на цйлое число. Положимъ, напр.,

— 147 —
требуется умножить 5 на 3. По опреД’Ьлепда умножетя на
цЬлое число это значить повторить 5 слагаемымъ 3 раза.
Если же мы вместо цЬлаго множителя 3 возьмемъ какую-
нибудь неправильную дробь, равную 3, напр. 80/,0з и станемъ
5 умножать не на 3, а на *°/10, то, согласно определенно
умножетя на дробь, мы должны будемъ найти 80/10 числа 5.
Такъ какъ 10/1() числа 5 составляютъ равно 5, то 30/,0 чи¬
сла 5 составляютъ 5, повторенное слагаемымъ 3 раза; след.,
будемъ ли мы 5 умножать на 3, или на *°/10, результата умно¬
жешя окажется одинъ и тота же. Такимъ образомъ, умно-
жете на дробь не противоречить умноженио на целое число.
ЗамЪчан1я. 1) Отъ умножешя на правильную дробь
число уменьшается, а отъ умножешя на неправильную дробь
число увеличивается, если эта неправильная дробь больше
1, и остается безъ изменешя, если она равна 1.
Напр., произведете 5. 7/8 должно быть меньше 5-и,
такъ какъ оно означаетъ только 7/8 пяти; произведен!е
5. % должно быть больше 5-и, потому что оно означа¬
етъ */8 пяти; и, наконецъ, произведете 5. 8/s, т. е. 8/8
пяти, равно 5.
2)	При умноженш дробныхъ чиселъ, такъ же какъ и
цЪлыхъ (§ 45), произведете принимается равнымъ 0, если
какой-нибудь изъ сомножителей равенъ 0; такъ, 0.7/8 = О
и 7/8.0=0.
167.	При умноженш чиселъ могутъ представиться
сл’Ьдуюпце б случаевъ:
1) Умножен1е ц'Ьлаго числа на ц Ъ л о е. Этотъ
случай былъ разсмотр'Ьнъ въ ариеметшсЬ ц’Ьлыхъ чиселъ.
2) Умножен1е дроби на ц'Ьлое число. Пусть
требуется 8/10 умножить на 5. Это значить: повторить
8/10 слагаемымъ 5 разъ, иначе сказать, увеличить 8/10
въ 5 разъ. Чтобы увеличить какую-нибудь дробь въ
5 разъ, достаточно увеличить ея числителя или умень¬
шить ея знаменателя въ 5 разъ (§ 152). Поэтому:
3 . .	3.5	15	3	...	3	3
JO X 5 — jo = 1О ИЛ!и 10 X ° — ioT5 — 2
10*

— 148 —
Правило. Чтобы умножить дробь на цЪлое число,
достаточно умножить на это цЪлое число числителя или
разделить на него знаменателя дроби.
3) Умножен1е цЪлаго числа на дробь.
Пусть дано умножить 7 на '/,. Это значить: найти */*
семи единицъ. Для этого найдемъ сначала 7Э семи еди¬
ницъ, а потомъ */*•
1	7
Такъ какъ	числа 7 составляешь -гг-;
У	J
а больше въ 4 раза,
4	_	7.4
то	числа 7 составляютъ
q	_ч.4	7.4	28
Значить:	7Х~д	~ "д" = "д ■
Правило. Чтобы умножить цълое число на дробь, до¬
статочно ц’Ьлое число умножить на числителя дроби и это
произведете сдЬлать числителемъ, а знаменателемъ под¬
писать знаменателя дроби.
4) Умножен1е дроби на дробь. Пусть надо
умножить s/s на У а- Это значить: найти 7/„ числа s/s*
Для этого сначала найдемъ ‘/s. а затбмъ 7/8 числа */-.
W	1	3	3
1акъ какъ -к- числа -гг составляетъ
о	5	5.0
7	1
а -7Г- больше въ 7 разъ,
О	О
7	3	3.7
то -т.- числа —	составляютъ	-г-н
8	о	5.8
_	3	7	3.7	21
Значить:	T><-8=0=46
Правило. Чтобы умножить дробь на дробь, достаточно
умножить числителя на числителя и знаменателя на зна¬
менателя и первое произведете сделать числителемъ, а
второе знаменателемъ.

— 149 —
Зам,Ьчан1е. Это правило можно применять и къ
случаямъ умножешя дроби на ц^лое ■ число и ц'Ьлаго
числа на дробь, если только ц'Ьлое число будемъ раз-
сматривать, какъ дробь съ знаменателемъ 1. Такъ:
3 V - _ 3 v 5 — 3.5 15  3
10 X ° — io X т — Ш —10 “ Т
7у1—Гу i—
X 9	1 X 9 ~ 1.9	9 -
5)	Умножен1е см'Ьшанныхъ чиселъ Чтобы
умножить см’Ьшанныя числа, достаточно обратить ихъ
въ неправильный дроби и умножить по правиламъ умно-
жешя дробей. Напр.:
о 3 У 4 2 _ 13V14_13.14_ 182	2
5X^3— 5X3— 53 — 15 — а^15
Впрочемъ, обращеше см’Ьшанныхъ чнселъ въ непра¬
вильный дроби не составляетъ необходимости. Напр.,
чтобы умножить 7 на б8/*, можно 7 повторить слагае¬
мымъ 5 разъ и къ полученной суммЬ приложить 8Д 7-и:
7.64 = (7X6) + (7Xt)=36+t=40T
168.	Сокращен1е при умножен1и. При умноженш
дробныхъ чиселъ иногда можно делать сокращение. Напр.:
оч16v 5 _ 16X5 _4Х5_ 20
21^28	21X28	21.7	147
Такое сокращеше возможно делать потому, что величина
дроби ве изменяется, если числителя и знаменателя ея умень-
шаеыъ въ одинаковое число разъ.

— 150 —
Изъ приведенныхъ примЬровъ видно, что при умноженш
цЬлаго числа на дробь или дроби на цЬлое число можно
сокращать цЬлое число съ знаменателемъ дроби, а при умно-
женш дроби на дробь можно сокращать числителя одной дроби
съ внаменателеыъ другой.
169. Пр оизведеше нЬсколькихъ дробей.
2	7	5
Пусть дано перемножить три дроби:	Умио-
2-7
живъ две первыя, получимъ:	^	;	умноживъэто число
2.7.5	70	_
па третью дробь, найдемъ: _g~g'g-= УуГ- Значитъ:
Чтобы перемножить нисколько дробей, достаточно пере¬
множить ихъ числителей между собой и знаменателей между
собою и первое произведете сделать числителемъ, а второе
знаменателемъ.
Если въ числ’Ь множителей есть см’Ьшанныя числа,
то ихъ обращаютъ въ неправильный дроби.
Замечай! е. Это правило можно применять и къ
такимъ произведешямъ, въ которыхъ некоторые множи¬
тели числа целыя, потому что целое число можно рас¬
сматривать, какъ дробь, у которой знаменатель 1. Напр.:
2V6vA-lvAу£-£-5-^- £2- 25_з-1
4А А6—4А1А6	4.1.6	4.2	—	8	8'
170. Свойства произведен!я.	ТЬ	свойства про¬
изведешя, которыя были нами указаны для цЬлыхъ
чиселъ (§§ 59, 60 и 61), примЬняются и къ произведенш
дробныхъ сомножителей:
1)	Произведете не измЬняется отъ перемЬны мЬстъ
сомножителей.
„	2 .	5 . . 3	5	3 .	, 2
Напр.:	зХ¥Х1=1Х7Х-3-
Действительно, первое произведете равно дроби
2 5 3	5	3	2
а второе равно дроби —■~3. Но эти дроби рав¬

— 151 —
ны, потому что ихъ члены отличаются только поряд-
комъ ц’Ьлыхъ сомножителей, а произведете цЪлыхъ чи¬
селъ не изменяется при перемене месть сомножителей.
2) Чтобы умножить наное-нибудь число на произведете,
достаточно умножить это число на перваго сомножителя,
полученное число на второго и т. д.
Пусть, напр., надо умножить число 10 на произведе¬
те — — I т е на — ь разъяснимъ, что для этого
4' 7 \ ’	'	28/
3
достаточно умножить 10 на а потомъ полученное
5
число умножить еще на у. Когда мы умножимъ 10 на
3	3	3
то найдемъ — десяти; если затемъ эти у десяти
5	5
умножимъ еще на -у, то получимъ -у трехъ четвертей
5
10-и. Но -j трехъ четвертей (чего либо) составляютъ
3	5	15
у, т. е. щ (этого чего либо); значитъ, посл'Ь двухъ
• 3 5
умноженЮ 10-ти на — и полученнаго числа на —, мы
найдемъ тотъ же самый результатъ, какъ и отъ одного
15
у множен) я 10-ти на Подобнымъ же образомъ можно
разъяснить, что для умножешя какого-либо числа на
3 2 1
произведете у.у.-g-. достаточно умножить это число
3	2
на у, полученное число умножить на у и результатъ
1
умножить еще на -g-.
3) Чтобы вычислить произведете нбскольнихъ сомножи¬
телей, можно разбить ихъ на группы, сдЪлать умножеше въ
наждой rpynnt отдельно и полученныя числа перемножить.
5 3 2 1	/ 5 3\ /2 1\	5	2	1
Напр.: 6 4 7 5	^б4/Д75у	8	35	28

— 152 —
Д t л е н i е.
171. Определен!е. дележе есть ариеметичесное дЬй-
CTBie, посредствомъ нотораго по данному произведена и
одному изъ сомножителей отыснивается другой сомножитель.
Напр., разделить 7/8 на 3/в значить: найти такое число,
которое надо умножить на 3/Б, чтобы получить ’/в?
или: найти такое число, на которое надо умножить
3/5, чтобы получить 7/g.
Въ первомъ случае частное представляетъ собою иско¬
мое множимое, во второмъ случае—искомаго множителя.
Такъ какъ множимое и множитель могутъ меняться
местами, то при данныхъ делимомъ и делителе вели¬
чина чаетнаго не зависитъ отъ того, означаетъ ли оно
множимое или множителя.
Изъ определешя дейсшя делешя следуетъ:
1) Нахождеже неизвЬстнаго числа по данной его дроби,
раземотренное нами прежде (§ 161), можетъ быть выпол¬
няемо посредствомъ дележя.
Такъ, если требуется найти такое число, котораго
7/8 составляютъ 5, то это, другими словами, значить:
найти такое число, которое составить 5, если его умно¬
жимъ на 7/8; значить, 5 есть произведете, 7/8 множи¬
тель, а отыскивается множимое; а это делается посред¬
ствомъ делешя 5 на 7/s.
2) Отъ дЬлетя на правильную дробь число увеличивается,
а отъ дележя на неправильную дробь число уменьшается,
если эта неправильная дробь больше 1, и остается безъ
изменетя, если она равна 1.
Напр., частное 5: 7/8 доляшо быть больше 5-ти, потому
что 5 составляетъ только 7/8 этого чаетнаго; частное 5 : */8
должно быть меньше 5-ти, потому что 5 составляетъ
9/8 его, и, наконецъ, частное 5 : % должно быть равно 5.
172. При дЬленщ могутъ представиться следу юхще 5
случаевъ:
1)	Делен1е целыхъ чиселъ. Этотъ случай былъ

— 153 —
разсмотр-Ьнъ въ ариеметикЬ ц'Ьлыхъ чиселъ. Но тамъ точ¬
ное д^леше не всегда было возможно, такъ какъ д'Ьлимое
не всегда есть произведете дЬлителя на ц-Ьлое число;
поэтому приходилось разсматривать Д’Ьлегпе съ ос¬
таткомъ. Теперь же, допустивъ умножеше на дробь, мы
всяйй случай Д'Ьлешя ц'Ьлыхъ чиселъ можемъ считать
возможнымъ. Пусть, напр., требуется разд'Ьлить 5 на 7,
т.-е. найти число, котораго произведете на 7 даетъ 5. Та¬
кое число есть дробь 6/j, потому что */7- 7 = 5. Точно такъ
же 20: 7=20/7, потому что 20/7. 7=20. Такимъ образомъ;
Частное отъ дЪлежя двухъ цЪлыхъ чиселъ всегда можно
выразить дробью, у ноторой числитель равенъ дЪлимому, а
знаменатель—дЪ лите лн>.
2). Д’Ьлеше дроби на ц'Ьлое число. Пусть
требуется разделить 8/э на 4. Это значить: найти число,
которое надо умножить на 4, чтобы получить 8/9. Но
отъ умножешя на 4 всякое число увеличивается въ 4
раза; значить, искомое число, увеличенное въ 4 раза,
должно	составить	®/9	и потому,	.чтобы	найти	его,	надо
8/в уменьшить	въ	4 раза. Чтобы	уменьшить	дробь	въ	4
раза, достаточно уменьшить въ 4 раза ея числителя или
увеличить въ 4 раза ея знаменателя; поэтому:
8	.	8:4	2
ТГ:4=—о	‘-0
8 . 8 8 2
0,110	9	9.4	36	9
Правило. Чтобы раз дЪ лить дробь на цЪлое число, до¬
статочно раздЬлить на это цЪлое число числителя дроби
или умножить на него знаменателя дроби.
3) Д'Ьлен1е Ц'Ьлаго числа на дробь. Пусть
надо разд'Ьлить 3 на 2/g. Это значить: найти такое
число, которое надо умножить на 2/s, чтобы получить 3.
Но умножить какое-нибудь число на 2/6 значить найти
2/'в этого числа; поэтому:
2
— неизв. частнаго = 3,

1	3
слЬд.	—	неизв.	частнаго	—-jr
5	2
5	3	к 3.5
а	—	неизв.	частнаго	= -г.5=
о	2	2
о	о 2	3.5
Значитъ:	3: —=-гг-
э 2
Правило. Чтобы разделить цЪлое число на дробь,
достаточно умножить это цЬлое число на знаменателя дроби
и произведете разделить на числителя дроби.
4)	Д Ь л е н ie дроби на дробь. Пусть дано в/6 : 7/и-
Это значить: найти число, которое, умноженное на7/ц>
составить в/в. Но умножить какое-нибудь число на 7/п
значитъ найти 7/п этого числа; поэтому:
7	5
тт неизв. частнаго = тг
11	о
1	5
слъд.	—	неизв. частнаго
11	5.11
а	неизв. частнаго — ъ—-п
11	6.7
5	7	5.11	55	13
Значить:	7	:11=677=42 =1	42
Правило. Чтобы разделить дробь на дробь, доста¬
точно умножить числителя первой дроби на знаменателя
второй, а знаменателя первой дроби на числителя второй
и первое произведете разделить на второе.
ЗамЬчан1е. Подъ это правило можно подвести и
случаи 2-й и 3-й, т. е. дЬлете дроби на цЬлое число
и дЬлете цЬлаго числа на дробь, если только ц'Ьлое
число будемъ разсматривать, какъ дробь съ знаменате-
лемъ 1. Такъ:
8 . .	8	4	8.1	8	2

— 155 —
5)	ДЪленхе см'Ьшанныхъ чиселъ. Обративъ
смешанный числа въ неправильная дроби, делятъ ихъ
но правиламъ делешя дробей. Напр.:
Я •	1
'	6	' 6 — 23 — 23“	23
3	1 31 _ 11 31.. 2 31.  9
4	2	4	" 2 ~~4.11~22	22'
173.	Общее правило делен1я. Если переста-
вимъ въ данной дроби числителя на место знаменателя,
и наоборотъ, то дробь, получившаяся после этой пере¬
становки, называется обратною по отношешю къ дан¬
ной. Такь, для 7/в обратная дробь будетъ 8/7. Целое
число также имеетъ обратную дробь; напр., для 5 или
для 6Д обратная дробь будетъ Vs- Условившись въ этомъ,
можемъ высказать такое общее правило делешя:
Чтобы разделить одно число на другое, достаточно де¬
лимое умножить на дробь, обратную делителю.
Въ верности этого правила легко убедиться изъ
следующего примернаго сравнешя:
1-5-1
8 40
и
-X-
8 Л'5
II
©1
к 7 40
5:~8=Т
и
5X4
51е”
II
2.4 10
3 : 5 12
и
2	о
3	А 4
10
12
174. Сокращеюе при делен1и. При деленш дроб¬
ныхъ чиселъ иногда можно делать сокращете. Напр.:
4
„	12.±=™1=*Л=“=1в1
х> 1 И 8 2 2 2
2
_§.	?.7—U—?8—1 1
9 : 7 9 ё —9.3—27	27
6
1	7	5.18^5.3^_ 15 . 1_
'	12 ! 18 — 12.7^2.7“ 14~	14

I
— 156 —
Такое сокращеше возможно делать потому, что величина
дроби не изменяется, если числителя и знаменателя ея умень-
шаемъ въ одинаковое число разъ.
Изъ приведенныхъ примере въ видно, что при деленш це-
лаго числа на дробь и дроби на целое можно сокращать це¬
лое число съ числителемъ, а при деленш дроби на дробь
можно сокращать числителя съ числителемъ, знаменателя съ
знаменателемъ.
175.	Примеры задачъ, решаемыхъ деле-
Н1емъ. Делете употребляется во всехъ гЬхъслучаяхъ,
когда одно изъ данныхъ чиселъ возможно разсматривать
какъ произведете, а другое, какъ множимое или мно¬
жителя. Приведемъ примеры:
Задача 1. Во сколько часовъ путешественникъпрой-
детъ путь въ 347/8 версты, если каждый часъ онъ про¬
ходить по 4*/2 версты?
Для решетя задачи надо узнать, сколько разъ 4‘/2
версты следуетъ повторить слагаемымъ, чтобы получить
347/g версты; т.-е. надо отыскать, на какое число следуетъ
умножить 4‘/2, чтобы получить въ произведенш 347/8.
Здесь 347/8 есть произведете, 4‘/2 — множимое, а тре¬
буется найти множителя; это выполняется делешемъ:
0. 7	1	279	9	31	„3
34 — * 4 — 	• — — — =7
8	2	8	’2	4	4
Частное показываетъ, что если 4‘Д версты повторить
слагаемымъ 7 разъ и къ результату добавить еще */*
отъ 4'/2 верстъ, то получится 347/8 версты; значить,
347/8 версты будутъ пройдены въ 73/, часа.
Задача 2. Сколько аршинъ сукна можно купить на
6 руб., если каждый аршинъ стоить 7‘Д рублей?
Очевидно, на 6 руб. нельзя купить ни одного аршина
сукна, стоимостью въ 7*/2 руб.; но можно купить неко¬
торую часть аршина. Чтобы узнать, какую именно, до¬
статочно определить, на какую дробь следуетъ умножить
71/*, чтобы получить 6. Здесь 6 произведете, 7*/2
множимое, а отыскивается множитель; поэтому вопросъ
решается делешемъ:

— 157 —
я . 7 1 _«.15_12_ 4
2 — ' 2	15	5
Частное показываетъ, что ‘/б числа 7*/4 составляютъ
6; значитъ, на 6 руб. можно купить ‘/в арш., стои¬
мостью въ 7*/а руб. за аршинъ.
Задача 3. За 73/, фунта чаю заплачено 183/е рубля.
Сколько стоить фунтъ чаю?
Для р'Ьшетя задачи надо найти такое число, которое,
повторенное слагаемымъ 73/4 раза*), составить 183/в. Здесь
183/5 произведете, 73/4 множитель, а отыскивается мно¬
жимое; значитъ, задача решается делешемъ:
-iw 3 .п	3	93 _ 31	93 . 4	12	п 2
5	4	5"	4	5. 31	5	5
Фунтъ чаю стоить 2а/в руб., т.-е. 2 руб. 40 коп.
Задача 4. За 7/8 аршина матерш заплачено 14 руб.
Сколько стоить аршинъ этой матерш?
Очевидно, за аршинъ матерш заплачено такое число,
котораго 7/в составляютъ 14 руб., т.-е. такое число, кото¬
рое сл'Ьдуетъ умножить на 7/„, чтобы получить 14 руб.
Здесь 14 произведете, 7/8 множитель, а отыскивается
множимое:
Аршинъ матерш стоить 16 рублей.
ИзнгЬнеше произведешя и частнаго.
176.	Произведете и частное дробныхъ чиселъ изменяется
такъ же, какъ произведете и частное цЪлыхъ чиселъ.
Эти изменения полезно вьфазить теперь въ более общемъ
виде, чемъ мы выражали прежде, и именно такъ:
Если умножимъ одного изъ сомножителей на каное-либо число, то
произведете умножится на то же число.
*) Сокращенное выражеше: „повторить какое-нибудь число сла¬
гаемымъ 73Д раза“ (и тому подобный) означаетъ „повторить какое-
нибудь число слагаемымъ 7 разъ и къ суммЪ добавить еще 3/4 этого
числа*.
I

— 158 —
Такъ, если въ примере:
Е 2 10
6-Т=7
7	.	„	/	7\	2
умножимъ множимое на —, то произведете будетъ 15. — J. —,
•	г-	7	2
что выражаетъ то же самое, что и призведете	5 .	—. —.
7	2
Переставивъ въ этомъ произведенш сомножителей -т- и
4	«5
отчего произведете не изменится, мы получимъ:
— JL— 10 7
• Т ’ Т ~ "3 • Т'
7
Такимъ образомъ, произведете умножилось тоже на —.
Такъ какъ множимое и множителя можно поменять ме¬
стами, то сказанное относится и ко множителю.
Если раздЬлимъ одного изъ сомножителей на какое-либо число, то про¬
изведете разделится на то же число, потому что разделить на ка¬
кое-либо число все равно, что умножить на обратную дробь.
177. Если умножимъ делимое на какое-нибудь число, то и частное
умножится на то же число.
Действительно, делимое есть произведете, а делитель и
частное—сомножители; значить, умножая делимое и оставляя
делителя безъ перемены, мы умножаемъ произведете и оста-
вляемъ безъ изменетя одного сомножителя; а это возможно
только тогда, когда другой сомножитель, т.-е. частное,
умножится на то же число.
Если умножимъ делителя на какое-либо число, то частное разделится
на то же число.
Действительно, умножая делителя и оставляя делимое
безъ перемены, мы умножаемъ одного сомножителя и оста-
вляемъ безъ изменетя произведете; а это можетъ быть
только тогда, когда другой сомножитель, т.-е. частное, раз¬
делится на то же число.
Подобный же заключетя можно вывести относительно д£-
лешя делимаго и делителя на какое-либо число.

— 159 —
VII.	Д-Ьйств1я надъ именованными
дробями.
178.	Раздроблен1е. Пусть требуется ’/# пуда
раздробить въ золотники. Для этого раздробля¬
емъ 7/» пуда сначала въ фунты, а потомъ въ золотники:
7/9 пуда раздробляемъ въ фунты. 1 пудъ им'Ь-
етъ 40 фунтовъ; сл’Ьд., 7/, пуда содержать 7/9 сорока
фунтовъ; чтобы найти 7/9 сорока, надо умножить 40 на
7/в (или 7/9 на 40):
7	280
-9-Х40=-д- (Фунта)
фунта раздробляемъ възол. 1 фунтъим'Ьетъ
«й	А	*	280 ^	280	Ой
96 золоти., след. —д- фунта содержать -д-числа96зол.;
280 280
чтобы найти —Q— числа 96-ти, надо 96 умножить на
9
(	280	Ой\
| или —g - на 96 J:
Х96=	=	2986	(золоти.).
Изъ этого примера видимъ, что раздроблете дробнаго
именованнаго числа производится танъ же, какъ и цЪлаго
числа, т.-е. посредствомъ умножешя на единичное отношеше.
179.	Превр ащенiе. Пусть требуется 3/4 арш. пре-
вратить въ версты, т.-е. узнать, какую часть
версты составляютъ */* арш. Для этого превратимъ ихъ
сначала въ сажени, а потомъ—въ версты:
*/* арш. превращаемъ въ сажени. Это значитъ
узнать, какую часть сажени или 3-хъ аршинъ состав¬
ляютъ */» аршина; другими словами: на какую дробь
надо умножить 3, чтобы получить а/х. Это узнается дЪ-
лешемъ:
т=»=4
4	4
I

— 160 —
Значить, 3/t арш. составляютъ */д сажени.
V, сажени превращаемъ въ версты, т.-е.
узнаемъ, какую часть версты, или 500 саженъ, состав¬
ляетъ V* сажени. Для этого надо разделить ‘/* на 500;
500= , „
4	2ОО0
1
след., ’/» саж- составляетъ ^qqq версты.
Изъ этого примера мы видимъ, что превращеме дроб-
наго именованнаго числа производится такъ же, накъ и
цЪлаго числа, т.-е. посредствомъ дЪлежя на единичное
отношеше
180.	Задача 1. Обратить въ составное име-
7
нованное число-^^ версты.
oUU
Это значить узнать сколько въ вер. заключается
оОО
саженъ, аршинъ и т. д. Это делается посредствомъ
раздроблетя:
7	7	35
^ версты въ сажени: — Х500 = 18 =478 (саж.).
Оставляя въ стороне 4 сажени, раздробимъ:
3/8 саж. въ аршины: 3/8Х3=в/8 = 178 (арш.).
Оставляя въ стороне 1 арш., раздробимъ:
‘/в арш. въ вершки: 78Х16 = 2 (вершка).
7
Следовательно, ggg версты = 4 саж. 1 арш. 2 верш.
Задача 2. Какую часть сутокъ составля¬
ютъ 3 часа 75/8 мин.?
Эта задача решается посредствомъ превращешя:
61 61
7в/8 мин. превращаемъ въ часы: -g- :bO = |gg
часа.

—161 —
Пржбавляемъ 3 часа: ^)-}-3=:	(часовъ).
1501	1501	1501
часа превращаемъ въ сутки:: 24=-^^
(сутокъ).
181.	Сложеше, вычитате, умножеше и д’Ьлете дроб¬
ныхъ именов. чиселъ можно производить двоякимъ пу-
темъ: 1) или, выразивъ всЬ данныя имен, числа въ
мЬрахъ одного и того же назвашя, поступаютъ съ ними,
какъ съ дробями отвлеченными; 2) или, обративъ всЬ
данныя въ составныя имен, числа, поступаютъ съ ними,
какъ съ целыми именов. числами. Напр.:
1)	Сложить: % версты+ 2 в. 15% саж.-{-101 саж.
I арш. 21/* вершка.
% версты превращаемъ въ составное име¬
нованное число:
%X500 = 1^2=214% (саж).; %Х3 = % (арш.).
QA
% X16=у=13% (вершк.).
Сл'Ьд., */7 в. = 214 саж. 13% вершк.
% саж. превращаемъ въ составное имено¬
ванное число:
7tX3 = */t = 27* (аРш-), 7tX16 = 4 (вершк.).
Сл'Ьд., 15% саж. =15 саж. 2 арш. 4 верш.
Теперь сложимъ, какъ складываются д’Ьлыя состав¬
ныя именованныя числа:
214 саж	13%	вершка.
-f 2 версты 15 „ 2 арш	4	„
 101 , 1 „	■ ■ ■ . 2%
2 версты 330 саж. 3 арш	20%t	вершка.
2 версты 331 саж. 1 арш	43/и	вершка.
II Заказ № 5456

— 162 —
Можно было бы выразить всЬ данныя въ вершкахъ
или иныхъ мерахъ одного и того же назвашя и по¬
томъ складывать, какъ дроби отвлеченныя. Полученное
отъ сложены простое именованное число можно было
бы, въ случае надобности, обратить въ составное.
2)	Умножить 4 пуда 6*/, фунта на */,.
Чтобы умножить на 4/7» надо умножить на 4 и раз¬
делить на 7;
4 п. 6% ф.
X4
16 п. 26*/,
14
2
Х4Ю
14	О	320 * О	-.КБ	Л.
Т“	2Г~Ф‘= пУДа j57« Ф-
80
+ 267.
106*/, —
3) Разделить 2 стопы 12г/г дест. на 2 Е/* дести.
Обращаемъ оба данныя числа въ дести:
2 X 20 = 40 (дест.);	40+ 127, = 527, (дести).
Теперь производимъ делете:
827,: 2*/. = ^ : F=1-St2 =2° (раЗЪ)-
4) Разделить 5 боч. 7*/* ведра на */,.
Чтобы разделить на */,, надо умножить на 3 и раз¬
делить на 2:
5 боч. ls/i ведра
ХЗ
15 боч. 237* ведра 1
~т	ор:о
1	7	боч.	-^—в.	=	7	боч.	31®/8	в.
Х40	8
40
+ 28V.	053

отдълъ пятый
Десятичныя дроби.
I.	Главн,Ьйш1я свойства десятичных'ъ
дробей.
182. Десятичныя доли. Доли, получаемыя отъ
делешя единицы на 10, на 100, на 1000 и вообще на
такое число равныхъ частей, которое выражается 1 съ
однимъ или нисколькими нулями, называются десятич¬
ными долями.
Такимъ образомъ, десятичныя доли, последовательно
у меньшаюндяся, будутъ следуюпця:
1111 1 1
10’ 100’ 1000’ 10000’ 100000’ 1000000 и Т' Д'
Изъ двухъ неодинаковыхъ десятичныхъ долей большая
называется десятичною долею высшаго разряда, а мень¬
шая — десятичною долею низшаго разряда. Каждая де¬
сятичная доля содержитъ въ себе 10 десятичныхъ до¬
лей следующаго низшаго разряда. Такъ:
1 10 1 10 1 10
!б—юо’ 100-1000’ Шо_юоооо ит‘д'
183. Де сятичная дробь. Всякая дробь, у которой
знаменатель есть 1 съ однимъ или несколькими нулями,
(и которая состоять, след., изъ десятичныхъ долей) наз
десятичной (или десятичнымъ числомъ); таковы, напр.,
3	27	27401	_	1
дроби: 10 , 100 , 1000 , 3 10(Ю и т. п.
Въ отлич1е отъ десятичныхъ те дроби, которыя мы раз-
сматривали до сего времени, т.-е. дроби, имевлщя ка-
кихъ-угодно знаменателей, наз. обыкновенными.
11*

— 164 —
Десятичныя дроби представляютъ много удобствъ
сравнительно съ обыкновенными. Поэтому свойства ихъ
и дЗ>йств1я надъ ними полезно разсмотрЬть особо отъ
дробей обыкновенныхъ.
184.	Изображен1е десятичной дроби безъ
знаменателя. Въ изображенш цЬлаго числа изъ
двухъ рядомъ стоящихъ цыфръ. правая всегда озна¬
чаетъ единицы въ 10 разъ меньппя, нежели л'Ьвая.
Условимся распространить это значеше мЬстъ и на тЪ
цыфры, которыя могутъ быть написаны вправо отъ про¬
стыхъ единицъ. Положимъ, напр., что въ такомъ изобра¬
женш:
6 3, 4 8 2 5 9...
цыфра 3 означаетъ простыя единицы. Тогда цыфра 4
означаетъ единицы, въ 10 разъ менытя, нежели простыя
единицы, т.-е. десятыя доли; 8 означаетъ сотыя доли,
2 — тысячныя, 5 — десятитысячный, 9—стотысячный и
т. д. Чтобы не ошибиться въ значенш М'Ьстъ, условимся
отделять занятою цЬлое число отъ десятичныхъ долей.
На мЬста недостагощихъ долей, а также и на м’Ьсто
щЬлаго числа, когда его иЬтъ, будемъ ставить нули.
Напр., при такихъ услов1яхъ выражеше 0,0203 озна¬
чаетъ: 2 сотыхъ 3 деслтитысячныхъ.
Цыфры, стояпця направо отъ запятой, называютъ
десятичными знанами.
Зам’Ьтивъ это, мы легко можемъ изобразить всякую
десятичную дробь безъ знаменателя. Пусть, напр., дана
32736
десятичная дробь - Сначала исключимъ изъ нея цЬ-
736
лое число; получимъ 32 -^qqq • Теперь представимъ ее такъ:
32736 ;32 ТОО 30	6	=№, 7,3,6
1000 1 1000 ~ 1000 ’ 1000 1 10 1 100 ' 1000
Значить, дробь эту можно изобразить такимъ образомъ:
3?7^_32 736
ToW-32’736

— 165 —
Это легко проверить, раздробивъ въ числе 32,736
целое число и все десятичныя доли въ доли самыя мел-
шя (въ тысячныя), что можно сделать такъ: 32 целыхъ
составляютъ 320 десятыхъ; приложивъ къ нимъ 7 деся-
тыхъ, получимъ 327 десятыхъ. Такъ какъ каждая деся¬
тая содержитъ въ себе 10 сотыхъ, то 327 десятыхъ со¬
ставляютъ 3270 сотыхъ; приложивъ къ нимъ 3 сотыхъ,
получимъ 3273 сотыхъ. Такъ какъ 1 сотая = 10 тысяч-
нымъ, то 3273 сотыхъ=32730 тысячныхъ; приложивъ къ
этому числу еще 6 тысячныхъ, получимъ данную дробь
32736 тысячныхъ.
Пусть еще дана дробь jqqqqq- Представимъ ее такъ:
578	500	70	8
100000 “ 100000 + ЮОООО юоооо —
5,7.8
1000 1 10000 1 100000
След., дробь эта изобразится такимъ образомъ:
i«=°-0U5T8
Теперь мы можемъ вывести следующее правило:
Правило. Чтобы данную десятичную дробь написать
безъ знаменателя, пишутъ ея числителя и отдЬляютъ въ
иемъ запятою съ правой стороны столько десятичныхъ зна-
новъ, сколько есть нулей въ знаменателе (для чего иногда
съ левой стороны числителя приходится написать не¬
сколько нулей).
185.	Какъ читается десятичная дробь, на¬
писанная безъ знаменателя. Сначала прочиты-
ваюгь целое число (а когда его нетъ, то говорятъ:
„нуль целыхъ11); затемъ читаготъ- число, написанное
после запятой, какъ бы оно^было целое, и прибавляють
названхе техъ далей, которыми дробь оканчивается;
напр., 0,00378 читается: 0 целыхъ 378 стотысячныхъ.
Значить, дробь, написанная безъ знаменателя, прочи¬
тывается такъ, какъ если бы она была изображена при
помощи числителя и знаменателя.

—166 —
Впрочемъ, дробь, у которой очень много десятичныхъ зна¬
ковъ, предпочитаютъ читать такъ: разбиваютъ все десятич¬
ные знаки, начиная отъ запятой, на грани, по 3 знака въ
каждой грани (кроме последней, въ которой можетъ быть
одинъ и два знака); зат'Ьмъ читаютъ каждую грань, какъ
целое число, добавляя къ названю числа первой грани слово
„тысячныхъ“, второй грани — „миллюнныхъ", третьей—„бил-
люнныхъ“ ит. д.; къ назвашю числа последней грани до-
бавляютъ назваше долей, выражаемыхъ последнею дыфрою
дроби. Такимъ образомъ, дробь: 0,028 306 ООО 07 читается
такъ: 0 цЬлыхъ, 28 тысячныхъ, 306 миллюнныхъ, 0 бил-
люнныхъ, 7 стобиллюнныхъ.
186. Заметнмъ, что прилисываше нулей справа
или	слева десятичной дроби,	изображен¬
ной	безъ знаменателя, не изменяетъ	ея	ве¬
личины. Напр., каждое изъ чиселъ:
7,05	7.0500	007,05
выражаетъ одну и ту же дробь: 7 целыхъ, 5 сотыхъ,
такъ какъ 500 десятитысячныхъ равно б сотымъ, а
007 выражаетъ просто 7.
187. Сравнен1е десятичныхъ дробей. Пусть
желаемъ узнать, какая изъ следующихъ дробей больше:
0,735 и 0,7349987
Для этого къ дроби, у которой десятичныхъ знаковъ
меньше, припишемъ (хотя бы только мысленно) съ правой
стороны столько нулей, чтобы число десятичныхъ знаковъ
въ обеихъ дробяхъ оказалось одно и то же:
0,7350000	0,7349987
Такимъ образомъ мы привели обе дроби къ общему
знаменателю и видимъ, что первая дробь содержитъ
7350000 десятимиллюнныхъ, а вторая 7349987 десятимил-
люнныхъ; такъ какъ 7350000 больше 7349987, то первая
дробь больше второй.
Подобнымъ образомъ легко убедиться, что вообще изъ
двухъ десятичныхъ дробей та больше, у которой число
ц'Ълыхъ больше; при равенстве пфлыхъ — у которой число
десятыхъ больше; при равенстве целыхъ и десятыхъ—у ко¬
торой число сотыхъ больше, и т. д.

— 167 —
188. Изменен1е десятичной дроби отъ пе-
ренесешя запятой. Перенесемъ въ дроби 3,274
запятую на одинъ знакъ вправо; тогда получимъ новую
дробь 32,74. Въ первой дроби цыфра 3 означаетъ про¬
стыл единицы, а во второй—десятки; след., значеше ея
увеличилось въ 10 разъ. Цыфра 2 означаетъ въ первой
дроби десятыя доли, а во второй—простыл единицы;
след., ея значеше тоже увеличилось въ 10 разъ. Такъ
же увидимъ, что значеше и прочихъ цыфръ увеличи¬
лось въ 10 разъ. Такимъ образомъ: отъ перенесения за¬
пятой вправо на одинъ знакъ десятичная дробь увеличи¬
вается въ 10 разъ.
Отсюда следуетъ, что отъ перенесешя запятой вправо
на 2 знака десятичная дробь увеличивается въ 100 разъ,
на 3 знака—въ 1000 разъ и т. д.
Обратно: отъ перенесешя запятой влево на одинъ знакъ
десятичная дробь уменьшается въ 10 разъ, и, след., на
2 знака—въ 100 разъ, на 3 знака—въ 1000 разъ и т. д.
189. Пусть требуется увеличить дробь 0,02 въ 10000
разъ. Для этого достаточно перенести въ ней запятую
на 4 знака вправо. Но въ данной дроби имеется всего
два десятичныхъ знака. Чтобы было 4 знака, припишемъ
съ правой стороны 2 нуля, отчего величина дроби не
изменится. Перенеся потомъ запятую на конецъ числа,
получимъ целое число 0200 или просто 200.
Пусть требуется уменьшить ту же дробь въ 100 разъ.
Для этого достаточно перенести въ ней запятую на 2
знака влево. Но въ данной дроби влево отъ запятой
имеется только одинъ знакъ. Чтобы было два знака,
припишемъ съ левой стороны 2 нуля (одинъ для це-
лаго числа), отъ чего величина дроби не изменится.
Перенеся потомъ запятую на два знака влево, полу¬
чимъ 0,0002.
Всякое целое число можно разсматривать, какъ деся¬
тичную дробь, у которой вправо отъ запятой стонтъ

— 168 —
сколько угодно нулей; поэтому увеличеше и уменыпеше
цЬлаго числа въ 10 разъ, въ 100 разъ, въ 1000 разъ
и т. д. совершается такъ же, какъ и десятичной дроби.
Напр., если уменьшимъ ц’Ьлое число 567,000... въ
100 разъ, получимъ 5,67.
II.	Д,Ьйств1я надъ десятичными дробями.
Сложеше десятичныхъ дробей.
190.	Сложеше десятичныхъ дробей производится танъже,
канъ и сложеше цЪлыхъ чиселъ. Пусть, напр., требуется
сложить: 2,078 -|— 0.75 —[—13,5602. Подпишемъ эти дроби
другъ подъ другомъ такъ, чтобы ц'Ьлыя стояли подъ
ц'Ьлыми, десятыя подъ десятыми, сотыя подъ сотыми
н т. д.:
2,078	2,0780
+ 0,75	-f	0,7500
13,5602	13,5602
16,3882	16,3882
Начинаемъ сложеше съ наименынихъ долей. Отъ сло¬
жетя десятитысячныхъ получимъ 2; пишемъ эту цыфру
подъ чертою. Отъ сложетя тысячныхъ получимъ 8; пи¬
шемъ 8 подъ чертою. Отъ сложешя сотыхъ получимъ 18;
но 18 сотыхъ = 10 сотыхъ-[-8 сотыхъ; десять сотыхъ
составляютъ одну десятую; запомнимъ ее, чтобы прило¬
жить къ десятымъ долямъ слагаемыхъ, а 8 сотыхъ на-
пишемъ подъ чертой. Продолжаемъ такъ цЬйств1е до
конца.
Чтобы не ошибиться при подписывали, полезно урав¬
нять нулями числа десятичныхъ знаковъ во веЬхъ сла¬
гаемыхъ (какъ это сд’Ьлано у насъ при вторично^гь сло¬
жены).

— 169 —
Вычитате десятичныхъ дробей.
191. Вычитаже десятичныхъ дробей производится такъ же,
какъ и вычитаже цЪлыхъ чиселъ. Пусть, напр., тре¬
буется изъ 5,709 вычесть 0,30785. Подпишемъ вычитае¬
мое подъ уменыпаемымъ такъ, чтобы разряды одного
назвашя стояли другъ подъ другомъ:
5,709	Чтобы	вычесть послед шя две цыфры вы-
0,30785	читаемаго, возьмемъ изъ 9 тысячныхъ 1 ты-
5,40115 сячную и раздробимъ ее въ десятитысячныя;
получимъ 10 десятитысячныхъ. Изъ нихъ
возьмемъ одну и раздробимъ ее въ стотысячный; тогда
вместо 10 десятитысячныхъ получимъ 9 десятитысячныхъ
и 10 стотысячныхъ. Значитъ, цыфру 5 вычитаемаго надо
вычесть изъ 10, цыфру 8 —изъ 9, а цыфру 7 — изъ 8.
Такъ же производится вычитате десятичной дроби
изъ целаго числа; напр.:
3	Отъ	3	беремъ	1	и	раздробляемъ	ев	въ	деся-
1,873 тыя; отъ нихъ беремъ 1 десятую и раздроб-
\ 127 ляемъ ее въ сотыя; отъ сотыхъ беремъ 1 со¬
тую и раздробляемъ ее въ тысячныя. Отъ этого
вместо 3 целыхъ получимъ: 2 цЬлыхъ, 9 десятыхъ, 9
сотыхъ и 10 тысячныхъ. Значитъ, цыфру 3 вычитаемаго
придется вычесть изъ 10, цыфры 7 и 8 — изъ 9, а
■цыфру 1—изъ 2.
Можно также предварительно уравнять нулями числа
десятичныхъ знаковъ въ уменынаемомъ и вычитаемомъ
и затемъ производить вычитате:
_5,70900	 3,000
0,30785	1,873
5,40215	1,127
Умножеше десятичныхъ дробей.
192. Разсмотримъ два случая: первый, когда одинъ
изъ сомножителей целое число, второй—когда оба сомно¬
жителя дроби.

— 170 —
Примерь 1.	Примерь 2.
3,085X23	8,375X2,56
Если бы въ этихъ пртгЬрахъ мы изобразили десятич¬
ныя дроби при помощи числителя и знаменателя и про¬
извели действ1е по правилу умножешя обыкновенныхъ
дробей, то получили бы:
1)	3085	3085X23	_	70955
* 1000*	1000 — 1000	— <и’9°5
8375	256:=^Х_256_21М000_
’ 1000^100	1000 ХЮ0— 100000
След., для обоихъ случаевъ мы можемъ вывести сле¬
дующее общее правило:
193.	Правило. Чтобы умножить десятичныя дроби, доста¬
точно, отбросивъ запятыя, перемножить полученныя целыя
числа и въ произведены отделить запятою съ правой сто¬
роны столько десятичныхъ знановъ, сколько ихъ есть во
множимомъ и во множителе вместе.
Цейств1е всего лучше располагать такъ:
3,085	8,375
X 23	Х2,56
9255	50250
6170	41875
70.955	16750
21,44
При этомъ запятыя не отбрасываются, а на нихъ только
не обращаютъ внимашя при умноженш целыхъ чиселъ.
Дйлеше десятичныхъ дробей.
194.	Разсмотримъ два случая: первый, когда делитель
целое число, второй—когда делитель десятичная дробь.
1 случай, когда делитель целое число.
Приближенное частное.
Пусть требуется разделить 39,47 на 8. Расположимъ

— 171 —
дЬйствге такъ, какъ оно располагается при дЬленш
Ц'Ьлыхъ чиселъ:
39,47) 8	ДЬлимъ	39	ц'Ьлыхъ	на	8; получимъ
74	4,93	B>b частномъ 4 ц'Ьлыхъ, и въ остаткЬ
27	7 цЬлыхъ. Раздробляемъ остатокъ въ
—~	десятыя доли и сносимъ 4 десятыхъ
дЬлимаго; получаемъ 74 десятыхъ. ДЬ¬
лимъ 74 десятыхъ на 8; получимъ въ частномъ 9 де¬
сятыхъ и въ остаткЬ 2 десятыхъ. Раздробляемъ оста¬
токъ въ сотыя доли и сносимъ 7 сотыхъ дЬлимаго;
получаемъ 27 сотыхъ. РаздЬливъ ихъ на 8, получимъ
въ частномъ 3 сотыхъ и въ остаткЬ 3 сотыхъ.
Положимъ, что мы на этомъ прекратили дЬйств1е. Тогда
получимъ приближенное частное 4,93. Чтобы узнать, на
сколько оно разнится отъ точнаго частнаго, сравнимъ его
съ этимъ частнымъ. Чтобы получить точное частное, доста¬
точно къ числу 4,93 приложить дробь, которая получится
отъ дЬлешя остатка (3 сотыхъ) на 8. Отъ дЬлешя 3 еди¬
ницъ на 8 получимъ s/s единицы; оть дЬлешя 3 сотыхъ на
8 получимъ ®/8 сотой. Значить, точное частное равно суммЬ
4,93-j-s/s сотой. Отбросивъ % сотой, мы сдЬлаемъ ошибку,
которая меньше одной сотой (*/„ сотой меньше цЬ-
лой сотой). Поэтому говорятъ, что 4,93 есть прибли¬
женное частное съ точностью до у100. Если вмЬсто того,
чтобы отбрасывать */« сотой, мы дополнимъ эту дробь
до цЬлой сотой (увеличивъ ее Па */8 сотой), то сдЬлаемъ
ошибку, тоже меньшую ‘/юо5 тогда получимъ другое
приближенное частное: 4,93-)-0,01, т.-е. 4,94, тоже
съ точностью до !/100. Число 4,93 меньше, а 4,94
больше точнаго частнаго; поэтому говорятъ, что первое
число есть приближенное частное съ недостаткомъ, а
второе—съ избыткомъ.
Если станемъ продолжать дЬйств1е дальше, обращая
остатки въ десятичныя доли, все болЬе и болЬе мел-
юя, то будемъ получать приближенныя частныя съ
большею точностью. Такъ если обратимъ остатокъ 3

— 172 —
СОТЫХЪ БЪ тысячныя долп и разд’Ьлимъ 30 тысячныхъ
прибл. частное 4,933 (съ недостат-
комъ) или 4,934 (съ избыткомъ), при-
чемъ ошибка менЬе 7моо-
Продолжая дЬлеше далЬе, мы
можемъ иногда дойти до остатка О
(какъ въ нашемъ примЬрЬ); тогда
получимъ точное частное. Въ про-
тивномъ случаЬ приходится доволь¬
ствоваться приближеннымъ част-
нымъ, причемъ ошибку можно сде¬
лать какъ угодно малого. Если, напр., мы желаемъ найти
приближенное частное съ точностью до одной миллионной,
то прекращаемъ дЬлеше тогда, когда въ частномъ по¬
лучилась цыфра мшшонныхъ долей.
Такимъ образомъ дЬлен1е десятичной дроби
на цЬлое число производится такъже, какъ
и дЬлен1е цЬлыхъ чиселъ, причемъ остатки
обращаютъ въ десятичныя доли, все болЬе
и болЬе мелк1я, и дЬйств1е продолжаютъ
до тЬхъ поръ, пока или не получится точ¬
ное частное, или въ приближенномъ част¬
номъ не получится цыфра тЬхъ десятич¬
ныхъ долей, которыми хотятъ ограничиться.
Такъ же поступаютъ при дЬлен1и цЬлаго числа
на цЬлое, если желаготъ получить частное въ видЬ
десятичной дроби.
30	|	7	Напр.,	дЬля	30	на	7	и	прекра-
20	4 2857... тивъ дЬлеше на цыфрЬ десяти-
тысячныхъ, получимъ приближен-
—	ное частное 4,2857 (съ нед.) или
—	4,2858 (съ изб.) съ точностью
—	До Sioooo-
1
195.	Какъ получить приближенноечастное
съ точностьюдо 7, десятичной доли даннаго
на 8, то получимъ
39, 47j	8
74	4,	93375
27
30
60
40
О

— 173 —
разряда. Полезно заметить, что изъ двухъ прибли-
женныхъ частпыхъ, одно съ недостаткомъ, а другое съ
избыткомъ, какое-нибудь одно оказывается точнымъ до
V* десятичной доли последняго разряда, а именно такимъ
частнымъ будетъ частное съ недостаткомъ, если остатокъ
меньше */* делителя, и частное съ избыткомъ, если
остатокъ больше делителя. Для объяснешя раз¬
смотримъ делеше 39,47 : 8. Положимъ, мы беремъ при¬
ближенное частное 4,93, при которомъ остатокъ 3 меньше
39, 47|	8	половины делителя (т.-е. меньше 4).
74	4,93375 Тогда точное частное будетъ 4,93-4-%
~27	сотой; значить, оно отличается: отъ
числа 4,93 на 3/8 сотой (меньше */*
’ —	сотой), а отъ числа 4,94 на % сотой
—	(более !/а сотой); въ этомъ случае,
значить, выгоднее взять частное съ
О	недостаткомъ.
Возьмемъ теперь въ томъ же примере приближенное
частное 4,933, при которомъ остатокъ 6 больше поло¬
вины делителя. Точное частное будетъ 4,933-|-6/8 ты¬
сячной; значить, оно отличается отъ числа 4,933 на в/'8
тысячной (более ‘/а тысячной), а оть числа 4,934 на а/8
тысячной (менее ‘/а тысячной); въ этомъ случае, зна¬
чить, выгоднее взять частное съ избыткомъ.
Правило. Чтобы получить приближенное частное съ
точностью до ‘/а Десятичной доли даннаго разряда, продол-
жаютъ дележе до техъ поръ, пока въ частномъ не получится
цыфра этого разряда, причемъ эту цыфру увеличиваютъ
на 1, если получившыся при этомъ остатокъ больше ‘/2 дели¬
теля; въ противкомъ случае ее оставляютъ безъ изменетя.
2 случай, ногда делитель десятичная дробь.
196.	Этотъ случай сводятъ на первый следующимъ
образомъ. Пусть требуется разделить 3,753 на 0,85.
Чтобы разделить какое-нибудь число на 8Б/100, доста¬

- 174 —
точно это число умножить на 100 и результата разде¬
лять на 85. Умноживъ дЬлимое на 100, получимъ 375,3.
Остается разделить это число на 85. Такимъ образомъ мы
приходимъ къ дЬлетю десятичной дроби на цЬлое число:
375,3 : 85 = 4,415...
Точно такъ же поступаютъ при дЬлеши цЬлаго числа
на десятичную дробь; напр.,
7 : 0,325 = 7000 : 325 = 21,538...
Правило. Чтобы разделить какое-нибудь число на деся¬
тичную дробь, отбрасываютъ въ делителе запятую и увели-
чиваютъ делимое во столько разъ, во сколько увеличился де¬
литель; затемъ дйлятъ по правилу дЬлежя на целое число.
1П. Обращен1е обыкновенныхъ дробей
въ дееятичныя.
197. Такъ какъ дЬйсшя надъ десятичными дробями
производятся проще, чЬмъ надъ дробями обыкновенными,
то часто бываетъ полезно обыкновенный дроби обратить
въ дееятичныя *)• Укажемъ два способа такого обрахцешя.
198. Первый способъ: посредствомъ разложежя зна¬
менателя на простыхъ множителей. Пусть требуется обра¬
тить 7,овъ десятичную дробь. Для этого зададимся вопро-
сомъ: нельзя ли привести дробь 7,о къ такому знамена¬
телю, который выражался бы 1-ею съ нулями? Чтобы
привести несократимую дробь къ другому знаменателю,
надо оба ея члена умножить на одно и то же число.
Чтобы узнать, на какое число надо умножить 40 для
получешя 1 съ нулями, примемъ во внимаше, что число,
выражаемое единицею съ нулями, разлагается только
*) ЗамЪтимъ, что при совершети вычислений надъ дробями деся¬
тичными и обыкновенными совместно не всегда необходимо приво¬
дить эти дроби къ одному виду; если, напр., требуется 0,567 умно¬
жить на г,7, то нЪтъ надобности обращать 3/7 въ десятичную дробь;
можно 0,507 умножить на 3 и результатъ разделить на 7.

— 175 —
на множителей 2 и 5, причемъ оба эти множителя вхо¬
дятъ въ разложеше одинаковое число разъ, именно
столько разъ, сколько стоить нулей при 1. Напр.:
1000 = 10.10.10=2.5.2.5.2.5
10000=10.10.10.10 = 2.5.2.5.2.5.2.5 и т. п.
Зам'Ьтивъ это, разложимъ 40 на простыхъ множителей:
40 = 2.2.2.5
Изъ этого разложешя видимъ, что если умножить 40 два
раза на 5, то посл'Ь умножешя получится такое число, въ
которое 2 и 5 будуть входить множителями одинаковое
число разъ (по 3 раза); значитъ, тогда получится 1 съ
нулями (съ 3 нулями). Чтобы дробь не изменила своей
величины, надо и числителя ея умножить 2 раза на 5:
7	7.5.5	175
40	40.5.5	1000'
0,175
-ч?	7	7.5.5.5	875
Прим-Ьры: 1) g 2.2.2	2.2.2.5.5.Б—1000	’
2)-i— ±- — 4~2-2-2 - 32 - 0 032
;125~~5.5.5— 5.S.5.2.2.2	1000	5
оч11_ И _ И.5 _ 55
20	2.2.5	2.2.5.5	100
Изъ разсмотрЪн1я этого способа слЪдуетъ:
1. Если знаменатель обыкновенной дроби не содержитъ
никанихъ иныхъ множителей, кромЪ 2 и 5, то таная дробь
обращается въ десятичную.
2. Если знаменатель обыкновенной дроби содержитъ въ
себЬ нанихъ-либо множителей, отличающихся отъ 2 и 5,
и эти множители не сокращаются съ числителемъ, то такая
дробь не можетъ обратиться въ десятичную.
Возьмемъ, напр., дробь 36/sit въ которой знамена¬
тель содержитъ множителей 3 и 7. Посмотримъ прежде
всего, не сокращаются ли эти множители съ числите¬
лемъ. Одинъ изъ нихъ, именно 7, сокращается; посл'Ь
сокращетя полумиль 6/i°- Такъ какъ 12 содержитъ мно¬
жителя 3, то эта дробь не обращается въ десятичную,

— 176
потому что на каюя бы целыя числа мы ни умножали
знаменателя ея, никогда не получимъ 1 съ нулями.
Ташя дроби можно обращать лишь въ приближенный
десятичныя, какъ увидимъ после.
3.	Десятичная дробь, получающаяся изъ обыкновенной,
имеетъ столько десятичныхъ знаковъ, сколько разъ въ зна¬
менателе обыкновенной дроби, после сокращежя ея, повто¬
ряется тотъ изъ множителей 2 и 5, который входитъ въ
него большее число разъ.
Пусть, напр., въ знаменателе обыкновенной дроби,
после ея сокращешя, больше повторяется множитель 2
и пусть этотъ множитель входитъ 4 раза. Тогда при¬
дется добавлять множителя 5 и столько разъ, чтобы
после добавлешя оба множителя входили по 4 раза;
значить, после умножешя въ знаменателе получится 1
съ 4-мя нулями, а потому и десятичная дробь будетъ
иметь 4 десятичные знака. Напр.:
7	7	_	7.5.5.5 _ 875 _0ftq
80	2.2.2.2.5	80.5.5.5	10000
199.	Второй способъ: посредствомъ делешя числи¬
теля на знаменателя. Этотъ способъ более употребителенъ,
чемъ первый, такъ какъ онъ применимъ и къ такимъ
обыкновеннымъ дробямъ, которыя обращаются только
въ приближенныя десятичныя доли.
Пусть требуется обратить дробь *3/8 въ десятичную.
Число *3/3 можно разсматривать, какъ
23 | 8	частное отъ делешя 23 на 8 (§ 172). Номы
70 2,875	видели, что частное отъ делешя целыхъ
чиселъ можно найти въ внде десятич-
——	ной дроби, точно или приближенно. Для
 	этого надо только обращать остатки отъ
0	делешя въ десятичныя доли, все более
и более мелгая, до техъ поръ. пока не получится въ
остатке нуль, или пока не получатся въ частномъ доли того
разряда, дальше котораго не желаютъ итти. Въ нашемъ
примере получилось точное частное; след., **/,—2,875.

— 177 —
Пусть еще требуется обратить */ц въ десятичную
дробь. Такъ какъ эта дробь несократима и знамена¬
тель ея содержитъ простого множителя 7, отличнаго отъ
2 и 5, то £е нельзя обратить въ десятичную; однако,
можно найти такую десятичную дробь, которая прибли¬
зительно равняется 3/и и притоыъ съ какою угодно
точностью. Если, напр., мы желаемъ найти десятичную
дробь, которая отличалась бы отъ */ц менЬе, чЬмъ на
‘/юоог 10 достаточно найти 3 десятичные знака отъ дЬ-
летя 3 на 14:
Приближенное частное 0,214 или
30 | 14	0,215 отличается отъ точнаго частнаго,
20 0,214...	т.-е. отъ */«. менЬе, чЬмъ на 71000.
р]сли продолжать дЬлеше дальше, то
—£	степень приближетя становится все
больше и больше. Однако 'дЬлеше ни¬
когда не можетъ окончиться, потому
что въ противномъ случаЬ мы получили бы десятичную
дробь, которая въ точности равнялась бы ’/,,, что не¬
возможно; такимъ образомъ, продолжая дЬлеше, мы мо¬
жемъ получить въ частном ь сколько угодно десятич¬
ныхъ знаковъ.
200. Конечный и безконечныя десятичныя
дроби. Десятичная дробь, у которой число десятич¬
ныхъ знаковъ можетъ быть какъ угодно велико, наз.
безконечною, а та, у которой число десятичныхъ зна¬
ковъ опредЬленное, наз. конечною дробью.
Можно сказать, что обыкновенная дробь, которая не
можетъ обратиться въ конечную десятичную, обращается
въ безконечную десятичную.
201. Пер1одическ1я дроби. Безконечная деся¬
тичная дробь, у которой одна или нЬсколько цыфръ
неизмЬнно повторяются въ одной и той же послЬдова-
тельности, называется перюдическою десятичною дробью,
а совокупность повторяющихся цыфръ называется nepio-
домъ этой дроби.
12 Заказ № 5456

— 178 —
Перюдичесгая дроби бываютъ чистыя и смешанный.
Чистою перюдическою дробью называется такая, у кото¬
рой перюдъ начинается тотчасъ после запятой, напр.;
2,36 36 36	;	смешанною—такая, у которой между
запятой и первымъ перюдомъ есть одна или нисколько
цыфръ, не повторяющихся, напр.: 0,5 23 23 23 Пе-
рюдичесгая дроби пишутъ сокращенно такъ:
вместо 2, 36 36	 пишутъ:	2,(36)
. . О, 5 23 23..	„	0,5(23)
и читаютъ ихъ такимъ образомъ: (первая) 2 ц'Ьлыхъ,
36 въ перюд'Ь, (вторая) 0 цЬлыхъ, 5 до периода, 23 въ
nepiofl’fe.
.202. Безконечная десятичная дробь, получаемая отъ обра-
щешя обыкновенной дроби, всегда перюдическая.
Убедимся въ этомъ на какомъ-нибудь прим'Ьр'Ь Пусть
желаемъ обратить въ десятичную дробь **/,. Такъ какъ
знаменатель 7 не составленъ изъ множителей 2 и 5 и
эта дробь несократима, то она не можетъ обратиться
въ конечную десятичную. Сл'Ьд., она обратится въ без-
конечную десятичную. Чтобы получить нисколько ея
знаковъ, станемъ делить 19 на 7. Такъ какъ д’Ьлеше
не можетъ окончиться, то всевозможныхъ остатковъ
должно быть безконечно много. Но остатки всегда мень¬
ше делителя; поэтому различныхъ остатковъ не мо¬
жетъ быть больше 6 сл'Ьдующихъ: 1, 2, 3, 4, 5, 6.
Изъ этого сл'Ьдуетъ, что при доста-
19 |_7	 точномъ продолжеши дЬ>лешя остат-
50 2,71428571 ки непременно начнутъ	повто-
То	р ять с я. Действительно:	7-й оста-
~30	токъ оказался такой же какъ и пер-
~20	вый- Но если повторился	остатокъ,
00	то, приписавъ къ нему 0,	мы полу-
—чимъ такое же делимое, какое было
-=г	раньше (50); значить, въ частномъ
начнутъ получаться те же цыфры,
_	кагая были раньше, т.-е. въ частномъ
®	получится перюдическая дробь.

— 179 —
IV.	Обращен1е пер!одическихъ дробей въ
обыкновенный.
203. Пр едварител ьное зам,Ьчан1е. Сначала
разсмотримъ, каыя перюдичестя дроби получаются отъ
обращешя такихъ обыкновенныхъ, у которыхъ числи¬
тель есть 1, а знаменатель—цыфра 9, написанная одинъ
или нисколько разъ сряду:
3
999
1
1
9
99
10 | 9
100 | 99
1000
1000
1
30 0,111...
10
1
100 0,0101...
1
~ =0,111...
«7
1=0.0101-
1
999
999
0,001001...
= 0,(001).
Изъ разсмотр'Ьшя процесса этихъ д'Ьлешй легко вы¬
вести, что въ такихъ перюдическихъ дробяхъ пер1одъ со-
стоитъ или изъ 1, или изЪ 1, предшествуемой нулями,
причемъ въ перюд-Ь столько цыфръ, сколько разъ въ
зваменател'Ь дроби повторяется цыфра 9.
204 Обращение чистой пер1одической дро¬
би въ обыкновенную. Пусть жецаемъ найти обык¬
новенную дробь, отъ которой происходить чистая пе-
рюдическая 0, 23 23... Для этого сравнимъ ее съ дру¬
гою, бол-fee простою, у которой перюдъ им-Ъетъ столько
же цыфръ, но состоитъ изъ 1, предшествуемой нулями:
О, 23 23 23
О, 01 01 01
Первая дробь содержитъ: 23 сотыхъ, 23 десятитыс., 23
миллюнныхъ и т. д.; вторая дробь содержитъ: 1 сотую,
1 десятитыс., 1 миллшнную и т. д. Значить, въ первой
дроби содержится десятичныхъ долей этихъ разрядовъ
въ 23 раза бол-Ье, ч-Ьмъ во второй. Поэтому, если суще-
ствуетъ обыкновенная дробь, отъ обращешя которой

— 180
получается пергодическая 0, (23), то она должна быть
въ 23 раза более обыкновенной дроби, отъ которой
происходить О, (01); но дробь 0, (01) происходить, какъ
1
мы видели, отъ gg; след., дробь 0, (23) должна про-
23
исходить отъ gg. И действительно:
230 ! 99
198	0,23...
320	23
297	gg	—0,	23 23 23...
23
Правило. Чтобы обратить чистую перюдическую дробь
оъ обыкновенную, достаточно ея перюдъ сделать числите-
лемъ, а знаменателемь написать цыфру 9 столько разъ
сколько цыфръ въ nepioAt *).
Примеры: 0, (7)—-^ ; 2, (05) = 2^; 0, (063)=^—^
Замечангя. 1. Чистая перюдическая дробь 0,999... не
можетъ получиться отъ обращешя въ десятичную какой-
либо обыкновенной дроби, такъ какъ, если бы такая
обыкновенная дробь существовала, то она должна была
бы равняться ®/*5 а число это, равное 1, не обра¬
щается въ безконечную десятичную дробь.
2.	Знаменатель обыкновенной дроби, получаемой отъ
обращежя чистой перюдической, не содержитъ множителей
2 и 5.
Действительно, этотъ знаменатель до сокращешя окан¬
чивается цыфрою 9 и потому не делится ни на 2, ни
*) Данная перюдическая дробь получается отъ обращешя не только
такой обыкновенной дроби, которая указана въ этомъ правил*, но
также и всякой другой обыкновенной дроби, равной указанной; напр ,
~	63	7	63
О, (063) получается отъ обращешя не только ggg. но иу-pj = ggg. Отъ
какой-либо обыкновенной дроби, не равной указанной въ правил*,
данная перюдическая получиться не можетъ.

— 181 —
на 5; Сл’Ьд., онъ не делится на эти числа и после со-
крпщешя дроби.
205.	0бращен1е смешанной пер1одической
дроби въ обыкновенную. Пусть требуется найти
обыкновенную дробь, отъ которой происходить сме¬
шанная перюдическая 0,3(52). Для этого перенесемъ въ
ней запятую до перваго перюда; тогда получимъ чистую
перюдическую дробь 3,(52), которая происходить отъ
52
обыкновенной 3 —. Но, перенеся запятую на одинъ знакъ
вправо, мы увеличили значеше каждой цыфры въ 10 разъ;
52
след , дробь 3— должна быть въ 10 разъ более той,
УУ
отъ которой произошла 0,3(52). Поэтому, чтобы найти
52
эту дробь, достаточно 3gg разделить на 10. Такимъ об-
59	349	зло
разомъ: 0,35252....=3,(52): 10= 3^: 10 = ’w:10 = ш
И действительно:
3490	990
2970	0,352...
5200	349	—	3525252
4950	990	’
“2500
1980
520
Можно вывести очень удобное правило для обращешя
смешанной перюдической дроби въ обыкновенную; для
этого обратимъ внимаше на то, какъ можно выполнить
д*лен1е оАпшшаго числа 31 на 10. Сначала обра-
тимъ смешанное число въ неправильную дробь. Для
этого следуетъ 3 умножить на 99 и приложить потомъ
52. Но вместо того, чтобы умножить 3 на 99, мы можемъ

— 182 —
умножить 3 на 100 и уменьшить результата на 3.
Такимъ образомъ:
52	3.99+52	3.100	- 3 + 52
99	99	~	99
Вместо того, чтобы вычесть 3, а потомъ приложить
52, можно сначала приложить 52, а потомъ вычесть 3.
Сл'Ьд.:
„52 3.10G+ 52 — 3  352 — 3
99	99	—	99
Остается	уменьшить эту дробь въ	10 разъ,	т.-е.	при¬
писать	къ	ея знаменателю 0;	тогда	мы получимъ	ту
обыкновенную дробь, отъ которой происходить перюди-
ческая 0,3(52). Такимъ образомъ:
352-3	349
О, 35252...:
990	990
Разсуждая подобно предыдущему, также найдемъ:
5,7868... = 5l^l=5H
к_ссо 578-57	521	.	71
ИЛИ	5, /888... = —gQ— = — = о -
Правило. Чтобы обратить смешанную перюдическую
дробь въ обыкновенную, достаточно изъ числа, стоящего
до второго переда, вычесть число, стоящее до перваго
пер1ода, и полученную разность взять числителемъ, а зна¬
менателемъ написать цыфру 9 стольно разъ, снолько цыфръ
въ перюдЬ, со столькими нулями, сколько цыфръ между
запятой и перюдомъ *).
3aMfeчанiя. 1. Смешанная перюдическая дробь съ
перюдомъ 9 не можетъ получиться отъ обращешя въ де¬
сятичную какой-либо обыкновенной дроби. Возьмемъ,
напр., дробь 0,36999... Если бы существовала обыкно¬
*) Къ этому правилу можно сделать то же дополнеше, которое
мы высказали въ выноскЪ къ правилу § 204-го

— 183 —
венная дробь, отъ обращешя которой получается эта
перюдическая, то она должна была бы равняться дроби:
369—36_ 36.10 + 9— 36 _ 36.10 — 36 + 9_ 36. 9 + 9 _
900	— 90СГ —	900"	~	900	—'
_ (36 + 1) 9 _ 37
—	900	—100
37
Но дробь jqq обращается въ конечную десятичную
0,37, а не въ безконечнуго.
2 Знаменатель обыкновенной дроби, получаемой отъ
обращемя смешанной перюдической, содержитъ множителя
2 или 5, или того и другого.
Действительно, этотъ знаменатель до сокрагцешя окан¬
чивается нулемъ и потому делится и на 2 и на 5.
Оба эти множителя могли бы сократиться съ числите-
лемъ только тогда, если бы числитель оканчивался тоже
нулемъ. Но числитель получается отъ вычитания числа,
стоящаго до перваго перюда, изъ числа, стоящаго до
второго перюда; такъ какъ последняя цыфра перюда не
можетъ оказаться одинаковою съ последнею цыфрою до
перюда (если перюдъ взять верно), то очевидно, что
числитель не можетъ оканчиваться нулемъ; поэтому и
после сокращешя въ знаменателе останется множитель
2 или 5, или тотъ и другой вместе.
Kaxifl обыкновенных дроби обращаются въ чистый
пер1одическ1я и нак!я — въ смешанный-
206.	1. Обыкновенная дробь, знаменатель которой не
содержитъ множителей 2 и 5, обращается въ чистую пе¬
рюдическую
Напр.: 1=0, (428571);	= 0,(6); ^ = 0, (45)
Действительно: во 1) такая дробь должна обратиться
въ какую-нибудь перюдическую (§ 202); во 2) эта перю¬
дическая дробь не можетъ быть смешанною, потому что

— 184 —
смешанная перюдическая дробь, какъ мы видЬли, обра¬
щается въ такую обыкновенную дробь, знаменатель ко¬
торой содержитъ множителей 2 и 5. Сл'Ьд., она должна
обратиться въ чистую периодическую.
2.	Обыкновенная дробь, знаменатель которой, послЬ со¬
кращен, вмЬстЬ съ другими множителями, содержитъ мно¬
жителей 2 или 5, обращается въ смешанную перюдическую.
QK К	О	110
Напр.: ^ = -=0,8 (3); — = 0,5 (3); ^=0,26 (4) и т. д.
ДЬйствительно: во 1) такая дробь должна обратиться
въ какую-нибудь перюдическую; во 2) эта перюдическая
дробь не можетъ быть чистою, потому что чистая nepio-
дическая дробь, какъ мы видЬли, происходитъ отъ такой
обыкновенной, знаменатель которой не содержитъ мно¬
жителей 2 и 5. Сл'Ьд., она должна обратиться въ смЬ-
шанную перюдическую.
Пределы десятичныхъ перюдическихъ дробей.
207. Строгая теорш перюдическихъ дробей основана на
понятш о пределе. Издожимъ вкратце эту теорйо.
Определена. Число наз. постоянными, .если оно
пмЬетъ одно определенное значеше, и переменными, если
оно способно принимать безчисленное множество различныхъ
значенШ. Такъ, дробь 0,83 есть число постоянное, дробь же
0,83333..., у которой число десятичныхъ знаковъ предпола¬
гается неопределенно возрастающимъ, есть число переменное,
такъ какъ оно принпмаетъ безчисленное множество различ¬
ныхъ значенШ, а именно:
0,8: 0,83; 0,833; 0,8333; 0,83333; и т. д.
Если переменное число, изменяясь по опре¬
деленному закону, приближается къ некото¬
рому постоянному числу такъ, что разность
между этимъ постояннымъ числомъ и перемен¬
ны мъ делается и остается меньше какого
угодно даннаго числа, какъ бы мало это число
ни было, то это постоянное число наз. преде-
ломъ переменнаго.

— 185 —
Напр., переменное число 0,999..., въ которомъ число десят.
внаковъ предполагается неопределенно возрастающимъ, имеетъ
пределомъ 1, такъ какъ разность 1 —0,999.. при достаточиомъ
числе десятичныхъ знаковъ въ дроби 0,999... делается,
и, при дальнейшемъ уведиченш числа десятичныхъ знаковъ,
остается меньше какого угодно даннаго числа, какъ бы
мало это число ни было (напр., меньше 0,000001).
Без конечная десятичная дробь, получаю¬
щаяся отъ обращения обыкновенной дроби,
при неограниченномъ увеличен^ числа ея де¬
сятичныхъ знаковъ стремится къ пределу, а
именно къ той обыкновенной дроби, отъ обра-
щен1я которой она происходить. Пусть, напр.,
мы нашли, что отъ обращешя 3/„ получилась такая безко-
нечная дробь: 0,214285... Тогда, какъ мы видели (§ 199),
отъ */и разнятся: 0,2 менее, чемъ на 'До, 0,21 менее, чемъ
на 'Д00, 0,214 менее, чемъ на 'Д000 и т. д.; значить, раз¬
ность */„—0,214285... при неограниченномъ увеличенш числа
десятичныхъ знаковъ въ вычитаемомъ делается и остается
меньше какого угодно малаго даннаго числа. Равенство
*/„=0,214285... и должно понимать въ томъ смысле, что
*/,, есть пределъ переменнаго числа 0,214285..., такъ что
правильнее это равенство писать такимъ образомъ:
Чи=пред. 0,214285...
где пред. есть сокращеше слова „пределъ“.
Можно считать очевиднымъ, что одно и то же переменное
число не можетъ иметь двухъ различнъС^ъ пределовъ.
208 Существуешь несколько пр^емовъ нахождешя предела
перюдическихъ десятичныхъ дробей. ’Разсмотримъ одинъ
изъ нихъ.
Теорема 1. Чистая перюдическая десятичная дробь,
при неограниченномъ увеличенш * числа ея пер1одовъ,
нмЪетъ пределъ. равный обыкновенной дроби, у которой
числитель есть першдъ, а знаменатель—цыфра 9, написан¬
ная столько разъ сряду, сколько цыфръ въ перюдЪ.
Для доказательства возьмемъ какую-нибудь чистую nepio-
дическую десятичную дробь, напр., 0,2323... Обовначимъ
черезъ хп величину этой дроби въ томъ случае, когда въ ней

— 186 —
возьмемъ только п первыхъ перюдовъ, отбросивъ всЬ осталь¬
ные. Тогда будемъ им^ть равенство:
Жп_0,23 23 23 --23— ЮО-^ 100*	1003
Умноживъ об'Ё части этого равенства на 100, получимъ:
п—1
Ч	OQ	OQ	24
100жпг=23, 23 23...23 = 23 + —+^+... + ^^(2)
Вычтя (1) изъ (2), найдемъ:
ддх — 23 — 23
уаж„ —а* 100„
23	23
откуда:	хп=,
99	99.100»
Изъ этого равенства видно, что по м'Ьр'Ь увеличешя числа
перюдовъ, т.-е. п, переменное число хп приближается къ
23
постоянному числу gg такъ, что разность между ними, равная
99 100” ’ Д^лается и остается какъ угодно малой; значитъ,
23
Осесть предЬлъ перюдической дроби 0,(23).
Теорема 2. Смешанная перюдическая десятичная дробь,
при неограниченномъ увеличены числа ея перЫдовъ,
имЪетъ предЬлъ, равный обьжновенной дроби, у которой
числитель есть разность между числомъ, стоящимъ до вто¬
рого перюда, и числомъ, стоящимъ до перваго перюда, а
знаменатель — цыфра 9, написанная столько разъ сряду,
сколько цыфръ въ перюдЪ, со столькими нулями на конце,
сколько цыфръ между запятой и первымъ перюдомъ.
Возьмемъ какую-нибудь смешанную перюд. десят. дробь,
напр., 0,52(375), и положимъ, что
52 ,	375
а:п = 0,52 375 375...375:
375
• 1)
100 ‘ 100.1000'
375	.	„	375
100.1000* ‘ 1 100.1000"

— 187 —
Умноживъ обе части этого равенства сначала на 100, по¬
томъ на 100.1000, получимъ?
Э7К	Q7K
100^=52+1Ш+"-+Шб^-	«
100000^ = 52375 + ^+^ + ... + ,-5^-. (3)
Вычтя (2) изъ (3), вайдемъ:
375
99900% = (52375 - 52) - 1да;
52375 — 52	375
откуда:	хп—	99900	99900.1000"'
Изъ этого равенства видно, что по мере увеличешя числа
перюдовъ, т.-е. п, разность между постоянною дробью
52375	52
— в п и переменною величиною десятичной дроби де-
уууии
лается и остается какъ угодно малой; эначитъ, эта постоян¬
ная дробь есть предЬлъ данной смешанной перюдической
дроби *).
V.	Метрическая система м’Ьръ.
209.	Изъ системъ именованныхъ меръ, употребляе-
мыхъ въ друтигь государствахъ, особенно замечательна
своею простотою французская или метрическая система
мере, принятая во многихъ странахъ.
За единицу длины въ этой системе принята одна деся-
тимиллтнная часть четверти земного мерщцана; эта еди¬
ница называется метръ (metre означаетъ мера) **).
Метръ разделяется на 10 равныхъ частей, 7ю часть
*) Изложенный дв-6 теоремы легко доказываются также при по¬
мощи указываемой въ алгебр-6 формулы, опредбляющей сумму чле-
новъ геометрической убывающей безконечной прогрессш.
**) ВслЪдств1е нЪкоторыхъ погрешностей при изм-бренш дугимери-
Д1ана употребляемый въ практик-6 метръ не вполн-6 равенъ десятимил-
люнной дол-Ь четверти меридаана (нарижскаго, какъ предполагалось).

— 188 —
метра—еще на 10 равныхъ частей, */юо метра, въ свою
очередь, на 10 равныхъ ча¬
стей ит. д. Съ другой сто¬
роны употребляются мЪры въ
10 метровъ, 100 метровъ и
т. д. Чтобы назвать деся¬
тичныя подразд'Ьлетя метра,
присоединяютъ къ слову
„метръ“ латинсйя слова:
деци (для обозначения 1/1(
центи (/|оо), милли
такъ, дециметръ озна¬
чаетъ 7,о часть метра, ц е н-
тиметръ—7,00 часть метра, миллиметръ—7юоо
часть метра. Центиметръ наз. часто сантиметръ.
МЪры, кратныя метра, называются при помощи гре-
ческпхъ словъ: дэка (10), гекто (100), кило (1000); такъ,
декаметръ означаетъ 10 метровъ, гектометръ —
100 метровъ, километръ —1000 метровъ.
!!1ф!П
lilijllll
iililil!
lilijllll
lilijllll
lilijllll
niljllTT
lilijllll
lilijllll
lilijllll
0
4
S
3
4
s
в
7
И
8 le
1 дециметръ, разделенный на 10 сантиметровъ, изъ которыхъ каж¬
дый подраздбленъ на половины и миллиметры.
Таблица метрическихъ мЪръ длины:
1 метръ = 10 дециметрамъ = 100 сантиметрамъ = 1000
миллиметрамъ;
10 метровъ = 1 декаметру, 100 метровъ = 1 гектометру;
1000 метровъ = 1 километру.
Полезно заметить сл'Ьдуюцця приблизительный соотно-
шешя метрическихъ мЪръ съ русскими:
1 метръ = 2274 вершка=1,4 аршина=37, фута;
1 дюймъ = 27, сант.; 1 верш, немного короче 4*/г еант.
1 километръ на 94 аршина короче версты *).
*) Точнее: 1 метръ = 22,4976 вершка = 1,4061 арш. = 3,2809 фута;
1 аршинъ = 0,7112 метра.

— 189 —
Назван1я метрическихъ меръ принято сокращенно обо¬
значать такъ:
метръ	м.
дециметръ . . дцм.
сантиметръ. .	см.
миллиметръ. .	мм.
километръ. . .	км.
Для измерешя поверхностей употребляются квадратный
м^ры:	кв.	метръ, кв. декаметръ	и т.	п.	Каждая	изъ	та-
кихъ меръ	содержитъ въ себе	100	меръ	следующаго
низшаго разряда; такъ, кв. дециметръ содержитъ 100
кв. сантиметровъ.
Для измерешя площади полей употребляется аръ и
гектаръ. Аръ есть квадратный декаметръ, гектаръ ра-
венъ 100 арамъ. Гектаръ приблизительно равенъ 0,9
нашей десятины*).
Для измЬрешя объемовъ служатъ кубичесгая меры:
куб. метръ, куб. дециметръ и т. д. Каждая изъ этихъ
меръ содержитъ въ себе 1000 меръ следующаго низшаго
разряда; такъ, кубичесгай метръ содержитъ 1000 куб. деци-
метровъ. Объемъ, равный куб.метру, называется стеръ,если
онъ служить для измерешя количества дровъ, угля и т. п.
Для измерешя вместимости сосудовъ (и объемовъ жид-
кихъ и сыпучихъ телъ) употребляется литръ. Литръ есть
объемъ, равный одному кубическому Дрциметру. На наши
меры онъ приблизительно равенъ 0,3 гарнца**). Упо¬
требительны также децилитръ и центилитръ, декалитръ
и гектолитръ.
Единицею веса служить граммъ. Это есть (почти
точно) весъ одного кубическаго сантиметра чистой пе¬
регнанной воды при температуре 4° Целься (или 3,2®
Реомюра) въ безвоздушномъ пространстве. На наши
меры граммъ равенъ приблизительно 227* долямъ***),
*) Гектаръ = 0,91533 десятины; десятина = 1,0925 гект.
**) Литръ = 0,3049 гарнца = 61,0237 куб. дюйма.
***) Грамыъ=22,505долей=0,2344золотн. золотн.=4,2657 грам.

— 190 —
т.-е. около Yi золотника. Граммъ подразделяется на деци¬
граммы, сантиграммы и миллиграммы; веса, кратные
грамма, суть: декаграмыъ, гектограммъ и килограммъ.
На наши меры килограммъ приблизительно равенъ 21/2
фунтамъ *). Употребительна еще мера тонна, равная
1000 килограммовъ (приблизительно 61 пудъ).
Монетною единицею служить франкъ. Это есть сере¬
бряная монета, весящая ровно 5 граммовъ и содержа¬
щая приблизительно на 9 частей чистаго серебра 1 часть
меди**). Десятая часть франка называется децимъ, а
сотая—сантимъ. 5 сантимовъ составляютъ 1 су. На наши
деньги 1 франкъ приблизительно равенъ 37 */* коп.
210.	Всл’Ьдстае того, что единичное отношеше меръ
метрической системы равно основанш нашей системы
счислешя, все действ1я надъ именованными числами,
выраженными по этой системе, выполняются проще,
чемъ по какой-либо другой системе.
Пусть, напр., требуется раздробить въ метры 2 килом.
5 гекгоы. 7 декам. 3 метра 8 децим. 4 сантим, и 6
миллим. Такъ какъ километры—это тысячи метровъ, гекто¬
метры — сотни метровъ ит. д., то очевидно, данное со¬
ставное именов. число выразится въ метрахъ такъ:
2573,846 метровъ. Перенося въ этой десятичной дроби
*) Килограммъ = 2,4419 фунта; фунтъ^О, 40951241 килогр.
Въ настоящее время метрическая система применяется
также и въ аптекахъ. Нашимъ Торговымъ Уставомъ установлено
следующее соотношеше между мерами аптекарскаго веса и метри¬
ческими:
1 аптек. фунтъ=358,32336 граммамъ;
1	„ гранъ= 62,208916 миллиграммовъ;
1 килограммъ = 2,7907754 аптек, фунта;
1 граммъ = 16,074866 аптек, грана.
**) Въ настоящее время серебряный монеты, стоимостью меньше
б фр., приготовляются изъ сплава, содержащаго на 835 тысячныхъ
чистаго серебра 165 тысячныхъ меди; монета въ 5 франковъ делается
изъ сплава, въ которомъ на 9 частей чистаго серебра приходится
1 часть меди.

— 191 —
запятую вправо или влево, найдемъ, что: 2573,846 мет.=
= 257,3846 декам.=25,73846 гектом.=2,573846 килом.=
=25738,46 децим. = 257384,6 сантим. = 2573846 миллим.
Такъ же легко совершается превращеже простого име¬
нованнаго числа въ составное. Пусть, напр., требуется
превратить 2380746 ыилиграыыовъ въ меры высшихъ
разрядовъ. Такъ какъ граммъ=1000 миллигр., то:
2380746 миллигр.= 2380,746 грам. = 2 килогр. 3 гектогр.
8 декагр. 7 децигр. 4 сантигр. 6 миллигр.
ДЬйсттая надъ метрическими именованными числами
совершаются такъ, какъ надъ десятичными дробями.
211.	Удобствк метрической системы. Изъ
сказаннаго о метрической системе можно заключить, что
она обладаетъ следующими тремя важными удобствами:
1)	меры различныхъ величинъ находятся въ простой
зависимости отъ основной меры, метра; 2) единичное
отношеше мЪръ одно и то же для всехъ разрядовъ и
всехъ величинъ (кроме, конечно, поверхностей и объе-
ыовъ); 3) это единичное отношеше равно основанш на¬
шей системы счислешя, вследств1е чего дейсттая надъ
именованными числами значительно упрощаются.

ОТДМЪ ШЕСТОЙ.
Отношете и пропорuiя.
I.	Отношен1е.
212.	Определен!е. Отношешемъ одного значен!я ве¬
личины нъ другому значежю той же величины наз. отвле¬
ченное число, на которое надо умножить второе значеже,
чтобы получить первое.
Такъ, отношеше длины 15 арш къ длине 3 арш.
есть число 5, потому что 15 арш =3 арш. X5; отноше-
Hie веса 3 фунт, къ весу 15 фунт есть число •/,, такъ
какъ 3 ф. = 15 ф. X Vs.
Можно разсматривать отношен!е и двухъ
отвлеченныхъ чиселъ; такъ, отношеше числа 25
къ числу 100 равно i/l, потому что 25=100X7*-
Значен1я величины, между которыми разсматривается
отношеше (или числа, которыми выражены эти значе-
Hifl), наз. членами отношешя; первое значеше есть пре-
дыдуицй членъ, второе значеше — последующа членъ.
Когда отношеше есть целое число, то оно показываетъ,
сколько разъ предыдущей членъ содержитъ въ себе
последующей; такъ, отношеше 2 пудовъ къ 10 фунтамъ
равно целому числу 8 (т. е. -2 пуда=10 фунт.Х8); это
значитъ, что 2 пуда содержать въ себе 10 фунт. 8 разъ.
Когда отношеше есть дробь, то оно означаетъ, какую
дробь последующаго члена составляетъ предыдущей.

— 193 —
членъ; напр., отношеше 10 фунт, къ 2 пудамъ равно
дроби ‘/* (т.-е. Ю фунт.=2 пуд.Х1/*); это значить, что
10 фунт, составляютъ Vs часть 2-хъ пудовъ.
Изъ того, что предыдуыцй членъ равенъ последую¬
щему, умноженному на отношеше, следуетъ, что пре-
дыдущШ членъ можно разсматривать, какъ делимое,
последующ! й членъ, какъ делителя (въ смысле мно¬
жимаго), а отношеше — какъ частное (въ смысле мно¬
жителя). Поэтому нахождеше отношешя принято обо¬
значать знакомъ делешя; напр., отношеше 2 пудовъ
къ 10 фунтамъ обозначаютъ такъ:
2 пуда : 10 фунт. или:
Отношен1е именованныхъ чиселъ всегда
можетъ быть заменено отношешемъ отвле-
ченныхъ чиселъ. Для этого достаточно выразить
именованныя числа въ одной и той же единице и взять
отношеше получившихся отвлеченныхъ чиселъ. Напр.,
отношеше 10 фун. 16 лот. къ 3 лот. равно отношешю
336 лот. къ 3 лот., а это отношеше равно отношешю
отвлеченныхъ чиселъ 336 къ 3.
Въ последующемъ изложенш мы будемъ большею
частью говорить только объ отношенш отвлеченныхъ
чиселъ.
213.	Зависимость между членами отноше-
н1я и самимъ отношешемъ та же самая, какая суще-
ствуетъ между делимымъ, делителемъ и частнымъ. Такъ;
1) ПредыдущШ членъ равенъ последующему, умно¬
женному на отношеше (делимое равно делителю, умно¬
женному на частное).
2) ПоследующШ членъ равенъ предыдущему, делен¬
ному на отношеше (делитель равенъ делимому, делен¬
ному на частное).
3) Отношеше увеличивается (или уменьшается) во
столько разъ, во сколько увеличивается (или умень¬
шается) предыдущей членъ.
13 Заказ N° 5456

— 194 —
4)	Отношеше уменьшается (или увеличивается) во
столько разъ, во сколько увеличивается (или умень¬
шается) послЪдующШ членъ.
б) Отношен1е не изменяется, если оба члена отношешя
увеличены или уменьшены въ одинаковое число разъ.
214. НахоЖден1е неизвестнаго члена. Если
въ отношенш неизвестенъ одинъ предыдущШ членъ,
то онъ находится умножешемъ (зависимость 1); если
же неизвестенъ одинъ последующи, то онъ получается
делешемъ (завис. 2); напр.:
1) х : 7*/2 = 2;	отсюда:	х—ЧЧ„У^2 = 1Ь.
2) 15 : х=2;	„	х=15 : 2 = 7‘/,.
215.	Сокращен1е	отношен1я. Если оба члена
отношешя делятся на	одно и	то же число, то мы	ыо-
жемъ сократить ихъ на это число, отчего отношеше не
изменяется (завис. 5); напр.:
отношеше 42 : 12 равно отношенш 7:2.
216. У ничтожеше дробныхъ членовъ. Если
умножимъ оба члена отношешя на одно и то же число,
то отношеше не изменится (завис. 4). Пользуясь зтимъ
свойствомъ, мы можемъ всякое отношеше, у котораго
одинъ или оба члена дробные, заменить отношешемъ
целыхъ чиселъ. Пусть, напр., дано отношеше 7/« • 5.
Умножимъ оба члена этого отношешя на 3; тогда оно
заменится отношешемъ целыхъ чиселъ 7 : 15,
Если оба члена отношешя — дроби, то достаточно
привести ихъ къ общему знаменателю и затеыъ его от¬
бросить; напр., отношеше 7u : f7.» после приведешя
дробей къ общему знаменателю, обратится въ такое:
»/„ : м/и. Откинувъ знаменателя, мы увеличимъ оба
члена въ 42 раза, отчего отношеше не изменится;
тогда получимъ отношеше целыхъ чиселъ 15 : 20 или
3 : 4.
217. Обратный отношен1я. Два отношешя на¬
зываются обратными, если предыдущШ членъ одного

— 195 —
изъ нихъ служить ПОСЛ'Ьдующимъ членомъ другого и
обратно. Таковы, напр., отношешя: 10 : б и б : 10.
Такъ какъ отношеше можетъ быть изображено въ
вид*Ь дроби, то обратное отношеше все равно, что об¬
ратная дробь.
II.	Пропорц1я.
219. OnpeAtneHie. Равенство, выражающее, что одно
отношеже равно другому отношение, наз. пролорц!ей.
Зам'Ьтивъ, напр., что каждое изъ двухъ отношешй
8 пуд. : 4 пуда и 20 арш. : 10 арш. равно одному и
тому же числу 2, можемъ написать пропорщю:
8 пуд. : 4 пуда=20 арш. : 10 арш.
Зам'Ьнивъ въ ней бба отношешя именованныхъ чиселъ
отношешями отвлеченныхъ чиселъ, получимъ пропорщю
отвлеченныхъ чиселъ:
8 : 4 = 20 : 10
8 20
(что пишется еще и такъ: -g = jq).
Пропорщя читается различно; напр., написанную
выше пропоршю можно читать такъ:
отношеше 8 къ 4 равно отношенш 20 къ 10;
или 8 относится къ 4 такъ, как^> 20 относится къ 10.
4 числа, составляющая пропорции ваз. лролорц(ональ-
ными числами; изъ нихъ первое и последнее называются
крайними, второе и третье—средними членами пропорщи.
Мы буреыъ предполагать дал"Ье, что всЬ члены про¬
порщи отвлеченный числа.
220. Изм,Ьнен1е членовъпропорц1ибезъ н'а-
рушеHifl ея. Бели изы'Ьнимъ члены пропорщи тага»
что первое отношеше останется равнымъ второму, то го-
ворятъ, что пропорщя не нарушена. Легко убедиться, что
1)	Если оба члена перваго или оба члена второго отно-
шен!я увеличимъ или уменьшимъ въ одинаковое число разъ,
то пролорц1я не нарушится,
13*

— 196 —
потому что отъ этого не изменится ни первое, ни вто¬
рое отношеше; напр.:
12 : 6 = 48 : 24
36 : 18 = 48 : 24
12 : 6 = 16 : 8
2) Если оба предыдуире или оба послЬдуюцре члена
увеличимъ или уменьшимъ въ одинаковое число разъ, то
лролорц1я не нарушится,
потому что отъ этого каждое отношеше изменится оди¬
наково; напр.:
12 : 6= 48 : 24
36 : 6 = 144 : 24
12 : 2= 48 : 8
3) Если ect члены увеличимъ или уменьшимъ въ одина¬
ковое число разъ, то лролорщя не нарушится,
потому что отъ этого не изменится ни первое, ни вто¬
рое отношеше; напр.:
12 : 6 = 48 : 24
6 : 3=24 : 12
Такимъ образомъ, не нарушая пропорцш, мы можемъ
увеличивать или уменьшать въ одинаковое число разъ
каждый крайнШ съ каждымъ среднимъ.
221. Сокращен1е пропорц!и. Если какой-нибудь
изъ крайнихъ членовъ имеетъ общаго дЬлителя съ какимь-
нибуць ивъ среднихъ членовъ, то эти члены можно сокра¬
тить на ихъ общаго дЬлителя (каждый крайнШ съ каждымъ
среднимъ можно уменьшать въ одинаковое число разъ).
Напр.:
х : 20=35 : 25
х :	4=35 :	5
х :	4= 7 :	1
222. Уничтожено дробныхъ членовъ. Пока-
жемъ на трехъ примЬрахъ, какъ молено это сдЬлать:
1)	10 : £ = 2 : %
Откинемъ въ 4-мъ членЬ знаменателя; отъ этого мы уве¬
личимъ его въ 5 разъ; чтобы пропорция не нарушилась,
надо увеличить въ 5 разъ какой-нибудь изъ среднихъ чле¬
новъ (каждый	крайнШ съ	каждымъ	среднимъ	можно	увели¬
чивать	въ	одинаковое число разъ).	Умножимъ	на	5	второй

— 197 —
или третчй члены; тогда получимъ дв'Ь пропорщи съ це¬
лыми членами: 10 : 15=2 : 3 и 10 : 3 = 10 : 3.
2)	8 : 7, = 10 :
Приведеыъ ofrfe дроби къ "общему вйаменателю и откинемъ
его; этимъ мы увеличимъ въ одинаковое число разъ край-
шй и среднШ члены, отчего пропорция не нарушится:
8 : 28 = 10 : 35.
3)	3 : 7, = »/, : *«■/,„.
Приведемъ всЬ члены къ общему знаменателю и отбро¬
симъ его; этимъ мы увеличимъ вс4 члены въ одинаковое
число разъ, отчего пропорция не нарушится:
432 : 126 = 408 : 119.
223.	Важное свойство лропорц1и. Произведе¬
те нрайнихъ членовъ пропорщи равно произведешю сред-
нихъ ея членовъ.
Такъ, въ пропорщи 8 : 4=20 :10 произведете край-
нихъ 8.10 равно произведешю среднихъ 4.20.
Чтобы доказать это свойство для всякой пропорции, *)
обозначимъ члены пропорщи такимъ образомъ:
1 чл. : 2 чл. = 3 чл. : 4 чл.
По свойству отношен!я мы можемъ написать:
1 членъ=2 чл. X отношеше;
3 членъ=4 чл. X отношеше;
причемъ оба отношешя, входяпця въ эти равенства,
должны быть равны между собою (по опред’Ьлешю про¬
порщи).
Умножимъ об'Ь части пердаго равенства на 4-й членъ
а об’Ь части второго равенства на 2-й членъ:
1 чл. X4 чл. = 2 чл. Хотн. X4 чл-
3 чл-Х2 чл. = 4 чл.Хотн-Х2 чл-
*) Предполагается при этомъ, что въ пропорщи веб 4 члена суть
числа отвлеченныя, или, по крайней мбрб, такими'числами выра¬
жаются оба члена какого-нибудь одного изъ отношешй, составдяю-
щихь пропорщю. Напр., къ пропорщи пудъ: фунтъ = 40:1 приме¬
нимо разематрнваемое свойство, но, конечно, такимъ свойствомъ не
обладаетъ пропорщя пудъ: фунтъ = 40 арш.: 1 арш., въ которой
нбтъ отвлеченныхъ членовъ.

— 198 —
Правыя части этихъ равенствъ состоять изъ одина*
ковыхъ множителей и потому равны другъ другу; зна¬
читъ, равны и л"Ьвыя части равенствъ, т.-е.:
1 чл.Х4 чл. —3 чл. X2 чл.
Но 1-й и 4-й члены суть крайше, а 3-й и 2-й сред-
Hie; значитъ, произведете крайнихъ равно произведе-
Hiio среднихъ.'
224.	Обратное предложен!е. Если произведете
двухъ канихъ-нибудь чиселъ равно произведена двухъ
другихъ чиселъ, то изъ этихъ 4-хъ чиселъ можно составить
пропорщю, беря сомножителей одного произведежя за
нрайн!е, а сомножителей другого произведежя за средже
члены пропорщи.
Возьмемъ, напр., дв*Ь пары чиселъ: 4 и 21, 7 и 12
татя, что произведете первой пары равно произведение
второй пары. т.-е.
4Х21 = 7Х12-
Чтобы превратить это равенство въ пропорщю, разд'Ь-
лимъ обЪ части его на каждое изъ слЬдующихъ 4-хъ
произведетй: 4X7, 4X12, 21X7, 21X12, т.-е. на
каждое изъ такихъ произведетй, въ которыхъ одинъ
сомножитель взять изъ перваго произведешя (4 X 21), а
другой—изъ второго произведешя (7X12):
4 Х21 7 Х12_ 4X21	7X12.	4Х21_7Х12
4X7 — 4><7; 4X12“ 4X12’ 21 X 7	21 X 7
4X21 _ 7 X12
21 Х12 — 21X12
Сокративъ эти равенства, получимъ:
21 12	21	_4_12.	4	 7^
7“ 4’	12	4’	7 —21’	12	21
Каждое изъ этихъ 4-хъ равенствъ есть пропорщя, въ
которой крайше члены суть сомножители одного изъ
данныхъ произведетй, а средте члены—сомножители
другого даннаго произведешя.
На этомъ основаши, чтобы пов-Ьрить пропорщю, до-

— 199 —
етаточно убЬдиться, что произведете крайнихъ равпо
произведен!*) среднихъ членовъ ея; напр., пропорщя
4 : 7 = 868 : 1519 вЬрна, потому что 1519. 4 = 6076 и
868 . 7 = 6076.
225. Нахожден1е неизвЬстнаго члена про-
пор ц1и. Возьмемъ пропорцш: 8 : 0,6 = а; : */*» въ
которой неизв’Ьстенъ одинъ изъ среднихъ членовъ, обо¬
значенный буквою х. Въ ней произведете крайнихъ чле-
новъ=8Х */«=6^ значить, произведете ея среднихъ
членовъ тоже должно быть 6; но одинъ изъ среднихъ
членовъ есть 0,6; значить, другой среднШ получится,
если 6 раздЬлимъ на 0,6:
х—6 : 0,6 = 60 : 6 = 10
Такимъ образомъ, среднШ членъ равенъ произведежю
крайнихъ, дЬленному на другой среджй.
Подобно этому крайнШ членъ равенъ произведена сред¬
нихъ, дЪленному на другой крайнШ.
226. Перестановки членовъ пропорц1и. Въ
каждой пропорцш можно переставить: 1) средше члены,
2)	крайте члены и 3) крайте на мЬсто среднихъ и
наоборотъ. Оть такихъ перестановокъ пропоршя не
нарушится, потому что не нарушится равенство между
произведен!ями крайнихъ и среднихъ членовъ. Пусть,
напр., иыЬемъ пропорцш:
1) 4 : 7 = 12 : 21
Переставим, въ ней средше члены, получимъ:
2) 4 : 12 = 7 : 21
Переставимъ въ каждой изъ этихъ пропоршй крайте
члены; тогда получимъ еще двЬ пропоршй:
3)	21 : 7 = 12 : 4	4) 21 : 12 = 7 : 4
Наконецъ, переставимъ въ каждой изъ полученныхъ
4-хъ пропоршй средше на мЬсто крайнихъ и наоборотъ,
тогда получимъ еще 4 пропоршй:
5) 7 : 4 = 21 : 12	7)	7	: 21 = 4 : 12
6) 12 : 4 = 21 : 7	8)	12	: 21 = 4 : 7

— 200 —
Можно было бы въ каждой изъ этихъ 8-ми пропоршй
переставить отношешя, т.-е. поставить второе отношеше
первымъ, а первое вторымъ; но отъ такой перестановки
не получится новой пропорцш, въ чемъ легко убЬдить¬
ся непосредственно. Если, напр., въ пропорцш 5-й
переставимъ отношешя, то получимъ не новую пропор-
цш, а ту, которая была получена ранЬе, именно подъ
Ms 4. СлЬд., путемъ всевозможныхъ перестановокъ можно
получить вмЬсто одной пропоршй 8 пропоршй.
227.	Непрерывная пропорц1я. Пропорщя на¬
зывается непрерывной, если оба средше или оба крайте
ея члена равны другъ другу. Таковы, напр., пропорцш:
32 : 16 = 16 : 8	20 : 5 = 80 : 20
Если въ послЬдней пропоршй переставимъ второе от
ношеше съ первымъ, то получимъ: 80 : 20=20 : б; от¬
сюда видно, что непрерывную пропоршю всегда можно
представить такъ, что одинаковы будутъ оба средше ея
члена.
ПовторяющШся членъ непрерывной пропоршй назы¬
вается среднимъ геометрическимъ числомъ двухъ другихъ
членовъ пропорщи. Такъ, 16 есть среднее геометри¬
ческое 32 и 8.
Пусть требуется найти среднее геом. двухъ чиселъ а и Ь.
Назвавъ его черезъ х, получимъ, по опредЬленш, такую
пропорцш: а : х—х : Ъ\ откуда имЬемъ: x2—db, x — \fab7
Исходя изъ этой формулы, можемъ определить среднее гео¬
метрическое двухъ чиселъ, какъ корень квадратный
изъ произведешя ихъ. Это опредЬлеше расширяютъ
и на тотъ случай, когда данныхъ чиселъ болЬе двухъ. Сред¬
нимъ геометрическимъ п данныхъ чиселъ на¬
зывается корень n-овой степени изъ произве¬
ден! я этихъ чиселъ.
Разсматриваютъ иногда среднее ариеметическое двухъ,
трехъ и болЬе данныхъ чиселъ.
Среднимъ ариеметическимъ нЬснолькихъ чиселъ называет¬
ся частное отъ дЬлешя суммы этихъ чиселъ на число ихъ.

— 201 —
Такъ, среднее ариеметическое б-и чиселъ: 10, 2, 18, 4
и 6 равно:
10 + 2 + 18 + 4+6
	5	~8-
Сложныя лролорцм.
228.	Изъ двухъ или болЬе пропорщй можно соста¬
вить новыя пропорщи, вазываемыя сложными, основы¬
ваясь на сл’Ьдующихъ истинахъ:
1) Если соответственные члены неснольнихъ пропорщй
перемножимъ, то получимъ новую пропорщю.
Пусть, напр., им-Ьемъ две пропорщи:
40 : 10 = 100 : 25
4 : 2 = 10 : 5
Перемножимъ соответственные члены этихъ пропорщй;
тогда получимъ такую новую пропорщю:
(40 . 4) : (10 . 2) =(100 . 10) : (25 . 5)
т.-е.	160 : 20=1000 : 125
У такой пропорщи каждое отношеше равно произве-
детю отношетй данныхъ пропорщй.
2) Если члены одной пропорщи разделимъ на соответ¬
ственные члены другой пропорщи, то получимъ новую про¬
порщю.
Напр., если разделимъ соответственные члены про¬
порщй:
*0 : 10 = 100 : 25
8 : 4=10 : 5
то получимъ такую новую пропорщю:
40 10	100	25	к	..	_
Т:Т=к>:Т>т--е-6:2/>г=10:5
У этой пропорщи каждое отношеше равно частному
отъ делешя отношешй данныхъ пропорщй.

— 202 —
Производныя пропорц!и.
229- Изъ одной пропорцш можно получить нисколько
другихъ пропорщй, называемыхъ производными, осно¬
вываясь на сл'Ьдующихъ соображешяхъ.
Возьмемъ какое-нибудь отношеше, напр., 21 : 7.
Если къ предыдущему его члену приложимъ послЪдую-
щШ, то получимъ новое отношен1е: (21 + 7) : 7, ко¬
торое, очевидно, больше прежняго на одну единицу.
Если же изъ предыдущаго члена вычтемъ посл’ЬдунмцШ,
то получимъ отношеше: (21 — 7) : 7, которое меньше
прежняго на одну единицу.
Зам'Ьтивъ это, возьмемъ какую-нибудь пропорцш:
21 :. 7 = 30 : 10
и составимъ изъ нея новую пропорщю такимъ образомъ:
(21 + 7) : 7 = (30+ 10) : 10	(1)
Эта пропорцш B-Ьрна, потому что каждое отношеше
въ ней больше отношешй данной пропорцш на одно и
то же число, именно на 1. Составленную нами про¬
порщю можно высказать такъ:
Сумма членовъ перваго отношешя относится нъ его по¬
следующему члену, какъ сумма членовъ второго отношешя
относится къ его последующему члену.
Составимъ теперь изъ данной пропорщи такую:
(21 — 7) : 7 = (30 — 10) : 10	(2)
Эта пропорщя верна, потому что каждое отношеше
въ ней меньше отношешй данной пропорщи на одно и
то же число, именно на 1. Составленную нами про¬
порщю можно высказать такъ:
Разность членовъ лерваго отношешя относится къ его
последующему члену, накъ разность членовъ второго отно¬
шешя относится къ его последующему члену.
Переставимъ средше члены въ первой производной
пропорщи и въ данной:
(21 + 7) : (30 + 10) = 7 : 10
21 : 30 = 7 : 10

— 203 —
Въ зтигь двухъ пропорщяхъ вторыя отношешя оди¬
наковы; значитъ, первыя отношешя должны быть равны:
(21 + 7) : (30 +10) = 21 : 30
Переставивъ средше члены, получимъ:
(21 + 7) : 21 =(30 +10) : 30	(3)
т.-е. сумма членовъ перваго отношешя относится нъ его
предыдущему члену, нанъ сумма членовъ второго отноше¬
шя относится къ его предыдущему члену.
Переставимъ средше члены во второй производной
пропорщи и въ данной:
(21 — 7)	:	(30 —	10) = 7	:	10
21	:	30 =	7 : 10
Откуда:	(21	—	7) : (30 — 10) = 21	:	30	(4)
или:	(21	—	7) : 21 =(30 —10)	:	30
т.-е. разность членовъ перваго отношешя относится нъ его
предыдущему члену, нанъ разность членовъ второго отно¬
шешя относится нъ его предыдущему члену.
Переставимъ средше члены въ первой и второй про-
изводныхъ пропорщяхъ:
(21 +7)	:	(30 +	10) = 7	:	10
(21 — 7)	:	(30 —	10) = 7	:	10
Откуда: (21	+ 7) :	(30 +10) = (21 - 7)	:	(30-10)
или:	(21	+ 7) : (21 - 7) = (30 +10)	:	(30 -10)	(5)
т.-е. сумма членовъ перваго отношешя относится нъ ихъ
разности, какъ сумма членовъ второго отношешя относится
къ ихъ разности.

ОТДЪЛЪ СЕДЬМОЙ.
НЪкоторыя задачи на пропорцюнальныя
величины.
I.	Простое тройное правило.
Величины прямо пропорцюнальныя.
231.	Задача. 8 аршинъ сукна стоять 30 руб.
Сколько стоять 16 арш. этого сукна?
Числа: 8 арш. и 16 арш. представляютъ собою два
8начешя одной и той же величины, именно количества
аршинъ сукна; числа; 30 руб. и искомое число руб. суть
тоже два значешя одной и той же величины, именно
стоимости сукна. Значить, въ предложенной задаче
говорится о двухъ величинахъ: о количестве аршинъ
сукна и о стоимости ихъ. Эти величины зависятъ одна
отъ другой, потому что съ изменешемъ одной изъ нихъ
изменяется и другая. Разсмотримъ эту зависимость
подробнее.
Пусть количеству аршинъ сукна мы дали два произ¬
вольный значешя, напр.: 10 арш. и 25 арш. Тогда
стоимость ихъ получить тоже два значенья, но не про¬
извольный, а вполне определенныя, находящаяся въ
соответствш со взятыми значениями количества аршинъ.
Иоложимъ, мы не знаемъ, сколько стоять 10 аршинъ и
сколько стоять 26 аршинъ сукна. Но, и не зная этого,

— 205 —
мы можемъ, однако, утверждать, что 25 арш. сукна сто¬
ять болЬе, чЬмъ 10 арш. этого сукна, и притомъ во
столько разъ бол'Ье, во сколько разъ 25 арш. болЬе 10
арш.; другими словами, мы можемъ утверждать, что
отношеше стоимости 25-ти арш. сукна къ стоимости 10-ти
арш. этого сукна должно быть такое же, какъ и отно¬
шеше 25-ти арш. къ 10-ти арш., т.-е.
Стоимость 25-ти арш.  25 арш
Стоимость 10-ти арш.	10 арш.
Действительно, отношеше 25-ти арш. къ 10 арш.
есть число 2*/а; и отношеше стоимости 25-ти арш. къ
стоимости 10-ти арш. тоже равно числу 272.
Кагая бы два значешя количества аршинъ мы ни
взяли, всегда найдемъ, что имъ соотвЬтствують два
определенный значешя стоимости, и что отношеше
этихъ значешй количества аршинъ равно отношешю
соответствующихъ значешй стоимости.
Если две величины зависятъ одна отъ другой такъ, что
каждому значение одной изъ нихъ соответствуете одно
определенное значеше другой, причемъ отношеше наждыхъ
двухъ значешй одной изъ нихъ равно отношешю двухъ
соответствующихъ значешй другой, то таюя величины на¬
зываются прямо пропорциональными {или просто пропорщ-
ональными).
Такъ, количество аршинъ сукна пропорщонально сто¬
имости ихъ (или стоимость сукна пропорщональна коли¬
честву аршинъ сукна).
Весьма простой признакъ пропорциональности двухъ ве¬
личинъ состоите въ слЬдующемъ:
Если съ увеличешемъ произвольная значешя одной вели¬
чины въ 2 раза, 3 раза, 4 раза и т. д. соответствующее
значеше другой величины увеличивается тоже въ 2 раза,
3 раза, 4 раза и т. д., то ташя величины пропорциональны*).
*) Въ ариеметикб можно этотъ признакъ принять безъ доказа-
телъства.

— 206 —
Такь, если произвольное число аршинъ сукна увели¬
чимъ въ 2, 3, 4 и т. д. раза, то стоимость ихъ уве¬
личится тоже въ 2, 3, 4 и т. д. раза; это величины
пропоршональныя.
232. РЪшеже способомъ приведежя къ единице. Уяснивъ
зависимость двухъ величинъ нашей задачи, выразимъ
ходъ решетя ея следующими строчками.
Такъ какъ 8 арш. стоять 30 руб
и стоимость сукна пропорцюнальна числу аршинъ его,
30 «
то	1	аршинъ	стоить	-g руб.
30
след.,	16	аршинъ	стоять	-g . 15 = 56*/,	руб.
Способъ, которымъ мы решили эту задачу, наз. при-
ведежемъ къ единице, такъ какъ по этому способу одно
изъ условШ задачи приводится къ 1 (такъ, въ приведен¬
ной задаче мы узнали стоимость 1 аршина).
Величины обратно пропоршональныя.
233. Задача. 6 человекъ рабочихъ оканчиваютъ не¬
которую работу въ 18 дней; во сколько дней окончатъ
ту же работу 9 человекъ, работая такъ же успешно,
какъ и первые?
Въ этой задаче тоже говорится о двухъ величинахъ:
о количестве рабочихъ и о продолжительности работы
ихъ. Эти величины зависать одна отъ другой, потому
что съ изменешемъ одной изменяется и другая. Но эта
зависимость иная, чемъ въ задаче 1-ой. Тамъ отноше¬
ше двухъ произвольныхъ значешй одной величины было
равно отношенш двухъ соответствующихъ значешй дру¬
гой величины; здесь же, какъ сейчасъ увидимъ, отно-

— 207 —
шеше двухъ произвольныхъ значенШ одной величины
равно обратному отношешю соотв'Ьтствующихъ зна¬
чешй другой величины. Возьмемъ, напр., два ташя про-
извольныя значешя количества рабочихъ: 6 чел. и 12
чел. Имъ соотвЬтствують два значешя продолжитель¬
ности работы, но не произвольныя, а находящаяся въ
соотвётствш со взятыми значешями количества рабо-
чпхъ; причемъ, очевидно, большему количеству
рабочихъ соотвётствуеть меньшее число дней рабо¬
ты, а именно число дней во столько разъ должно быть
меньше, во сколько разъ число рабочихъ больше; такъ,
если 6 чел. оканчиваюсь работу въ 18 дней, то 12 чел.
скончать работу въ 9 дней.
Значить, отношенье 6 чел. къ 12 чел. равно обратному
отношешю 18 дней къ 9 днямъ, т.-е.
6 чел.	9 дней
12 чел.	18 дней
Если двё величины зависятъ одна отъ другой такъ, что
каждому значешю одной изъ нихъ соотвётствуетъ одно
определенное значеше другой, причемъ отношеше каждыхъ
двухъ значешй одной изъ нихъ равно обратному отношешю
соотвётствующихъ значешй другой, то ташя величины на¬
зываются обратно пропорцюнальными.
Такъ, продолжительность работы обратно пропорщо-
нальна количеству рабочихъ (при одинаковыхъ прочихъ
услов1яхъ, т.-е. при одинаковомъ размёрё работы и оди¬
наковой степени успешности работы каждаго рабочего).
Весьма простой признанъ обратной пропорщональности
двухъ величинъ состоитъ въ слёдующемъ:
Если съ увеличешемъ произвольнаго значешя одной ве¬
личины въ 2 раза, 3 раза, 4 раза и т. д. соответствующее
значеше другой величины уменьшается тоже въ 2 раза,
3 раза, 4 раза и т. д., то ташя величины обратно пропор-
цюнальны.
I
j

- 2Ш.—
Такъ, съ увеличешемъ количества рабочихъ въ не¬
сколько разъ, продолжительность работы уменьшается во
столько же разъ; это величины обратно пропорщональныя.
234. PtmeHie способомъ приведежя нъ единице. Уяснивъ
зависимость между двумя величинами нашей задачи,
решимъ ее приведешемъ къ единице.
Такъ какъ 6 человекъ оканчиваютъ работу въ 18
дней, и число дней обратно пропорцюнально числу ра¬
бочихъ, то
1 чел. окончить работу въ 18.6 дней;
18 6
след., 9 чел. окончить	работу	въ	—^	=12	дней.
235. Простое тройное правило.	Въ	каждой изъ	приве-
денныхъ эадачъ речь шла только о двухъ величинахъ,
прямо пропорщональиыхъ (какъ въ первой задаче),
или обратно пропорщональиыхъ (какъ во второй задаче);
при этомъ въ каждой задаче дано было по одному соот¬
ветствующему значенда обеихъ величинъ:
1-я задача.	2-я задача.
Колич. сукна... 8 арш.	Колич.рабочихъ. 6 чел.
Стоимость ихъ.. 30 руб,	Продолж. работы. 18 дней
а требовалось узнать, какое значеше приметь одна изъ
величинъ, если другая получить новое данное значеше:
1-я задача.	2-я задача.
Колич. сукна ... 15 арш.	Колич. рабочихъ. 8 чел.
Какова ихъ стоимость?	Какова продолж. работы?
Способъ решать таюя задачи наз. простымъ тройнымъ
правиломъ.
235, a. PtmeHie посредствомъ пропорщи. Мы указали
наиболее простой способъ решетя: приведен)е къ
единице. Но можно задачи на простое тройное пра¬
вило решать и посредствомъ пропорщи. Напр., при
решенш задачи о стоимости сукна можно разсуждать
такъ: стоимость еукна пропорщональна числу аршинъ
его; поэтому 15 аршинъ стоять более 8-ми аршинъ

— 209 —
во столько разъ, во сколько 15 более 8; значить, обо-
значивъ искомую стоимость черезъ х, получимъ про¬
порцш: х : 30 = 15 : 8, откуда: х = (30 X15) : 8 =
= 567, руб.
Для рЬшешя задачи о рабочихъ можно разсуждать
такъ: число дней работы обратно пропорщонально числу
рабочихъ; поэтому 9 чел. окончатъ работу въ меньшее
число дней, чЬмъ 6 чел., и во столько разъ меньшее,
во сколько 6 меньше 9; значить, искомое число х дней
должно удовлетворять пропорцш х : 18 = 6 : 9, откуда:
ж = (18Х6) : 9=12 дней.
II.	Сложное тройное правило.
236.	Задача. Для освЬхцешя 18 комнатъ въ 48 дней
издержано 120 фунт, керосину, причемъ въ каждой
комнате горело по 4 лампы. На сколько дней доста-
петъ 125 фунт, керосину, если освещать 20 комнагь
и въ каждой комнате будетъ гореть по 3 лампы?
Расположимъ даяныя зтой задачи въ две ташя строчки
(неизвестное число поставимъ въ последнемъ столбце):
18 ком.—120 фун.—4 лам.—48 дней
20 . -125 а —3 „ -х „
Для penienifl задачи разсуждаемъ такъ: искомое число
дней было бы 48, если бы число комнатъ было 18,
число фунтовъ керосину было 120 и число лампъ въ
каждой комнате было 4. Но все эти числа заменены
въ вопросе задачи новыми, отчего, вероятно, изменится
и число дней изъ 48 въ какое-нибудь иное. Чтобы
удобнее узнать, какъ именно изменится число дней,
предположимъ, что сначала только одно число верхней
строчки заменено новымъ числомъ, а потомъ и другое,
и третье. Такъ, допустимъ, что сначала число комнатъ
изменено изъ 18 въ 20, потомъ число фунтовъ. йзме-
14 Заказ N° 5456

— 210 —
нено изъ 120 въ 125 и, наконецъ, число лампъ изме¬
нено изъ 4 въ 3.
Когда измёнимъ число комнатъ изъ 18 въ- 20, а
прочш числа оставимъ тё же самыя, то мы получимъ
упрощенную задачу, которую можно высказать такъ:
для освёщешя 18 комнатъ керосину достаеть на 48
дней; на сколько дней достанетъ керосину для освё¬
щешя 20 комн. (при одинаковыхъ прочихъ условьяхъ,
т.-е. если керосину идетъ 120 фунт, и въ каждой ком-
натё будетъ горёть по 4 лампы)?
Эта задача на простое тройное правило. Рёшимъ ее
приведешемъ къ 1.
Число дней обратно пропорщрпально числу комнатъ;
поэтому, если при освёщенш 18 комнатъ керосину до-
стаетъ на 48 дней, то при освёщенш только одной
комнаты его достанетъ на 48.18 дней, а при освёщенш
48 18
20 комнатъ число дней окажется —(что равно 43%
дня, но вычислять эту формулу теперь безполезно).
Замёнимъ теперь 120 фунт, керосину 125-ю фунт
Тогда получится такая задача на простое тройное правило:
юл *	48-18
120 фунт, керосину	сгораетъ въ 2Q -	дней;	во	сколько
дней сгоритъ 125	фунт, керосину (при	одинаковыхъ
прочихъ услов1яхъ)?
Число дней прямо пропорщонально числу фунтовь;
- , 48-18
поэтому 1 фунгь керосину сгоритъ въ 20120 дней* а
Ю* л	48.18.125
125 ф. сгорятъ въ	2Q120 дней.
Наконецъ, замёнимъ 4 лампы 3-мя лампами. Тогда
получится такая задача на простое тройное правило"
если въ каждой комнатё горять 4 лампы, то керосину
48.18.125
достанетъ на —on -.v- дней: на сколько дней доста-

— 211 —
нетъ керосину, если въ комнате будетъ гореть по 3
лампы (при одинаковыхъ прочпхъ услов1яхъ)?
Число дней обратно пропорщонально числу лампъ;
поэтому если будетъ гореть одна лампа, то дней ока-
48.18.125.4	.	.	„
жется —20" 120—’ а ПРИ Г0Р™Ш 3"хъ лампъ ихъ
48.18.125.4
должно быть:	ao.iao.s'	'
Теперь приняты во вниман!е все услов1я вопроса;
остается вычислить полученную формулу: а;=60 дней.
Въ этой задача говорилось о 4-хъ величинахъ: о ко¬
личестве комнатъ, о продолжительности осв'Ьщетя, о
количеств’! керосину и о количеств’! лампъ, причемъ
каждая пара этихъ величинъ находится между собою въ
пропорщональной зависимости прямой или обратной (если
ве! проч1я величины не изменяются); при этомъ дано
было по одному соответствующему значенш ве!хъ ве¬
личинъ:
18 комн.—120 фунт.—4 лампы—48 дней
а требовалось* найти, какое значеше приметь одна изъ
величинъ, если все nponiH получать некоторый новыя
данныя эначешя:
20 ком.—125 фунт.—3 лампы—а; дней
Способъ решать татя задачи, когда данныхъ величинъ
более двухъ, наз. сложнымъ тровнымъ лравиломъ.
III.	Задачи на проценты.
238.	Определен!е. „Проценту каного-либо числа
означаетъ сотую часть этого числа; след., два, три...
процента какого-нибудь числа означаютъ две, три...
сотыхъ этого числа *).
*) Слово „проценть" происходить отъ латинскаго выражетя
„pro-centum", что означаетъ „со ста", или „на сто*.
14*

— 212 -
Такъ, если говорить, что въ такомъ-то учебяомъ за-
веденш число успевающихъ учениковъ составляетъ 75
процентовъ всего числа учащихся, то это значите, что
первое число составляетъ 75 сотыхъ второго числа (или,
что все равно, на каждыхъ 100 учениковъ приходится
75 успевающихъ и 25 не успевающихъ).
Чаще всего слово „проценте" употребляется въ ком-
мерческихъ вопросахъ, когда речь идете о прибыли или
убыткЬ. Напр., говорятъ, что торговецъ получилъ 20
процентовъ прибыли на затраченный имъ капиталь. Это
надо понимать такъ, что онъ получилъ прибыли 20 со¬
тыхъ затраченнаго капитала (иначе сказать, 20 рублей
на каждые затраченные 100 рублей, или 20 коп. на
каждый затраченныя 100 коп.).
Проценте обозначается знакомь %; напр., 5% озна¬
чаете 5 процентовъ.
Большинство задачъ на проценты бываютъ коммер-
ческаго характера. О такихъ задачахъ мы и будемъ го¬
ворить по преимуществу. Предварительно условимся
относительно смысла некоторыхъ выражений.
Когда одно лицо занимаете у другого деньги, то при
етомъ часто ставится услов!емъ, чтобы должнинъ упла-
чивалъ заимодавцу определенные ежегодные проценты.
Если, напр., говорятъ, что некто занялъ 500 руб. по
7°/0 (или изъ 7%) годовыхъ, то это значите, что дол-
жникъ обязался, во 1-хъ, уплатить по истеченш у слов-
леннаго срока эти 500 руб., а, во 2-хъ, сверхъ этой
суммы уплачивать заимодавцу ежегодно до конца срока
по 7 сотыхъ этого капитала, т.-е. по 35 руб. Заметимъ.
что заимодавецъ называется иначе нредиторомъ-
Случается, что лица, имеюиця свободныя деньги,
отдаюте ихъ въ баннъ. Въ такомъ случае банкъ уплачи¬
ваете этимъ лицамъ за пользовате ихъ деньгами опре¬
деленные ежегодные проценты. Въ свою очередь, банкъ
выдаете ссуды за известные ежегодные проценты.

— 213 —
Капихадъ, отданный на проценты, называется началь¬
ными шоиталомъ; число процентовъ (иначе прибыль,
получаемая въ течете одного года на 100 рублей,-вы¬
раженная . въ рубляхъ) называется процентною таксою;
прибыль на весь капиталъ—процентными деньгами; на¬
чальный капиталъ, сложенный съ процентными деньга¬
ми, называется наращеннымъ капиталомъ. Если, напр.,
200 рублей отданы въ ростъ *) на 1 годъ по 5°/0, то
начальный капиталъ—это 200 руб., процентная такса—
5, процентныя деньги за годъ—10 _руб., наращспный
капиталъ—210 руб.
239. Полезно заметить, что процентныя деньгй про-
порцюнальны времени м напиталу, при одинаковыхъ про¬
чихъ условьяхъ. Если, напр., капиталъ 100 руб. и
процентная такса 5°/0, то процентныя деньги за 1 годъ
будутъ 5 р., за 2 года—10 р., за 3 года—15 руб.
и т. д., т.-е. при неизмённомъ капиталё онё возраста-
ютъ пропорцюнально времени, а если время 1 годъ и
такса 5°/0, то процентныя деньги со 100 руб. будутъ
б руб., съ 200 руб.—10 руб., съ 300 руб.—15 руб. и т. д.,
т.-е. при неизмённомъ времени онё возрастаютъ про¬
порщонально капиталу.
Наращенный капиталъ не пропорцюналенъ времени.
Если, напр., капиталъ 100 руб. и процентная такса
б%> то черезъ 1 годъ наращенный капиталъ будетъ
106 руб., а черезъ 2 года 110 руб., а не 210 руб.
240. Различный группы задачъ на процен-
т ы. Задачи на проценты можно разбить на 4 группы,
соотвётственно тому, что неизвёстно изъ слёдующигъ
4-хъ величины а) процентныя деньги (или наращенный
капиталъ), Ь) начальный капиталъ, с) процентная такса
и d) время, въ теченье котораго капиталъ находится въ
ростё; при этомъ задачи второй группы бываютъ двоя-
*) Т.-е. отданы въ бывгь илн частному лицу на проценты1.

— 214 —
каго рода; въ однЬхъ даются процентныя деньги, въ
другихъ—наращенный капиталъ. Какъ решаются задачи
во веЬхъ этихъ случаяхъ, будетъ видно изъ «гЬдующихъ
5 прюгЬровъ.
Задача 1. Найти процентныя деньги съ капитала
7285 р., отданнаго въ ростъ по 8% на 3‘/2 года.
Такъ какъ 8°/0 какого-нибудь числа означаютъ 8 со¬
тыхъ этого числа, то:
8	728^	8
7285 руб. въ годъ приносятъ 7285 • ^	руб.
7285 руб. въ -1 года „	^W^ = 2039 Р> 80 К'
Замечашя. 1) Если время содержитъ месяцы или
дни, то надо найти процентныя деньги за 1 м’Ьсяцъ или
за 1 день, а потомъ и за данное число м'Ьсяцевъ илп
дней. При этомъ надо иметь въ виду, что въ номмер-
ческикъ вопросахъ, для удобства вычислен^, принято счи¬
тать годъ въ 360 дней, а мЬсяцъ въ 30 дней.
2) Если бы въ задаче требовалось определить нара¬
щенный капиталъ, то надо сначала вычислить-процент¬
ныя деньги, а потомъ приложить их/ь къ начальному
капиталу.
Задача 2. Какой капиталъ, отданный въ ростъ по
63/4%, принесетъ въ 6 л-Ьтъ 8 м'Ьсяцевъ 3330 руб. про-
центныхъ денегъ?
Процентныя деньги за 1 годъ составляютъ 63/4 (т.-е.
27/i) сотыхъ капитала, а за 6 л. 8 мес. (=80 мес.)
27 80
оне составятъ -£~j2 сотыхъ капитала, что по сокра
щеши, равно 45 с о т ы м ъ капитала. Эти 45/100 капитала,
согласно условш задачи, должны равняться 3330 руб.,
значить, здесь дана дробь неизвестнаго числа (капи¬
тала), а требуется найти целое неизвестное число; это

— 215 —
45
находится дЬлешемъ (§171).Начал. капиталъ=3330
= 7400 р.
Задача 3. Какой капиталъ, отданный по 5%, обра¬
тится чрезъ 6 лЬтъ въ 455 руб.?
Въ 455 руб. заключаются начальный капиталъ и про¬
центный деньги съ него за 6 лЬтъ. За 1 годъ процент¬
ный деньги составляютъ 5/юо капитала, слЬд., за 6 л'Ьтъ
онЬ составятъ 5/100 . 6 = 30/ю0 = 3/ю капитала. Такимъ
образомъ, въ 455 руб. заключаются начальный капиталъ
и еще 3/io ег°. т--е- 13/ю начальнаго капитала; значить:
13	4550
нач. капиталъ = 45о : — = -у^-=350 (руб.).
Задача 4. По какой таксЬ процентовъ надо отдать
капиталъ 15108 руб., чтобы въ 2 года 8 мЬсяцевъ по¬
лучить 2417 руб. 28 коп. процептныхъ денегъ?
Чтобы узнать таксу процентовъ, достаточно опредЬ-
лить, сколько копеекъ въ течен1е года получается
со 100 коп. или съ 1 рубля.
Такъ какъ 15108 руб. въ32мЬс. принос. 241728 коп.,
* к» *	241728.12	_
то 1 руб. въ 12 мЬс. принос. -^5108~32= К0П'
Если 1 рубль приносить въ годъ 6 коп., то, зна¬
чить, капиталъ отданъ по 6°/0-
ЗамЬчаше. Если въ задачахъ подобнаго рода
вмЬсто процентныхъ денегъ данъ наращенный капиталъ,
то слЬдуетъ изъ него вычесть начальный капиталъ;
тогда получимъ процентный деньги.
Задача 5. На сколько времени надо отдать 2485 р.
по 7°/0, чтобы получить 139 руб. 16 коп. процентныхъ
денегъ?
Такъ какъ въ 1 годъ 2485 руб. приносить (2485.7/10о)
руб., то:
л оп л с тисе 7 л 13916	4.
неизв. время = 139,16: (2485.	=	-=	(года)	=
= 288 дней.
[

— 216 —
241.	Простые и сложные проценты. Про¬
центы (или процентныя деньги) бываютъ простые и
сложные. Чтобы понять разницу между тёми и дру¬
гими, возьмемъ примёръ. Положимъ, что кто-нибудь
отдалъ въ банкъ 100 руб. по 5°/0. Если это лицо по
прошествш года не возьметъ своыхъ 5 руб. процент-
ныхъ денегъ, то его капиталъ обратится въ 105 руб.
Можетъ быть поставлено условие, чтобы въ течете вто¬
рого года проценты нарастали не только на начальный
капиталъ, т.-е. на 100 руб., но еще и на тё 5 руб.,
которые наросли въ теченье перваго года; также и въ
слёдуюьще года. Или же можетъ быть условлено, чтобы
въ течете второго и слёдующихъ годовъ проценты счи¬
тались только на начальный капиталъ, т.-е. на 100 р.,
хотя бы лицо, положившее каыиталъ, и не брало еже¬
годно процентныхъ денегъ.
Когда проценты считаются не только на начальный
капиталъ, но и на проценты съ него, образовавьшеся
отъ прошлыхъ лётъ и присоединяемые къ капиталу, то
они называются сложными; если же проценты счи¬
таются только на начальный капиталъ, то они называ¬
ются простыми.
Во всёхъ задачахъ, которыя были приведены выше,
предполагались простые проценты; это всего чаще бы-
ваетъ въ дёйствительности *).
241а. Задачи на простые проценты могутъ быть рёшаемы
помощью слёдующихъ общихъ формулъ. Пазовемъ начальный
капиталъ—а руб., процентную таксу—р, время—t лётъ, про¬
центный деньги—х руб., наращенный капиталъ—А руб. Чтобы
найти зависимость между этими величинами, разсуждаемъ такъ:
Р
такъ какъ процентныя деньги за годъ составляютъ капи¬
*) Сложные проценты съ капитала ва данное число л-Ьтъ вычи¬
сляются или способомъ, указываемымъ въ алгебрЪ, или же такъ:
сначала находятся простые проценты за первый годъ; эти проценты
прикладываются къ капиталу и на полученную сумму вычисляются
простые проценты за второй годъ; эти проценты прикладываются
къ капиталу, бывшему за второй годъ, и съ полученной суммы вы¬
числяются простые проценты эа третШ годъ и т. д.

— 217 —
тала, то а руб. въ годъ принесугь руб.; въ t лЬть эта
величина возрастетъ въ t разъ; значитъ:
apt .	.	,	apt
Х==-ЩГ и ^=в+*=«+Тбо--
IV.	Задачи на у четь векселей.
242.	Определен!я. Когда одно лицо занимаетъ у
другого деньги подъ проценты, то обыкновенно долж-
никъ выдаетъ своему кредитору письменное обязательство
въ томъ, что онъ къ известному сроку уплатить заня¬
тую сумму вместе съ причитающимися на нее процен¬
тами. Такое обязательство, написанное на гербовой бу¬
маге и по установленной форме, называется венселемъ.
Положимъ, напр., что должникъ занялъ у кредитора
1000 руб. на 1 годъ по 10% и заемъ былъ сделанъ
1-го января 1908 года. Тогда, разсчитавъ, что черезъ
годъ 1000 руб. должны обратиться въ 1100 р., должникъ
выдаетъ кредитору, примерно, такой вексель:
Москва (назвате города), 1-го января 1908 года.
Вексель на 1100 руб. Отъ сего 1-го января
1908 года, черезъ двенадцать месяцевъ, по
сему моему векселю повиненъ я заплатить
(такому-то), или кому онъ прикажетъ, тысячу
сто рублей, которые я отъ него получилъ
наличными деньгами. (Сдедуетъ подпись долж¬
ника) *).
Въ векселе не пишется ни сумма, занятая въ дей¬
ствительности, ни процентъ, по которому сделанъ былъ
*) На практикЬ при выдач!» векселя проценты обыкновенно удер¬
живаются впередъ; если, напр., заняты 1СЮ0 руб. на годъ по 10%, то
вексель пишется въ 1000 руб., а занимагопцй получаетъ только 900р.;
100 руб. кредиторъ удерживаетъ впередъ, какъ процентныя деньги.

— 218 —
заемъ; но выставляется сумма денегъ, которую надо
уплатить, и срокъ, въ который должна быть сдёлана
уплата. Сумма, записанная въ векселё, называется век¬
сельною суммою или валютою векселя. Валюта есть за¬
нятый капиталъ вмёстё съ причитающимися на него про¬
центами за время, на которое быль сдёланъ заемъ.
Кредиторъ, имёюицй вексель, не можетъ требовать отъ
должника уплаты ранёе срока, назначеннаго въ векселё.
Однако, можетъ случиться, что самъ должникъ поже-
лаетъ уплатить по векселю ранёе срока. Положимъ, напр.,
что должникъ желаетъ заплатить за полгода до срока по
своему векселю въ 1100 руб. Ему нётъ расчета пла¬
тить теперь же 1100 руб., потому что онъ могъ бы поль¬
зоваться въ течете полугода процентными деньгами съ
тёхъ денегъ, которыя оиъ теперь предлагаетъ къ уплатё.
Между кредиторомъ и должнпкомъ въ такихъ случая хъ
происходить соглашенье, по которому кредиторъ долженъ
получить нёсколько менёе вексельной суммы. Это согла-
шете выражается въ формё нёкотораго числа процен-
товъ вексельной суммы, которое кредиторъ предоставля-
етъ должнику удержать изъ нея; условленная такса про-
центовъ обыкновенно относится къ году. Если, напр.,
между кредиторомъ и должникомъ произошло соглаше-
Hie, по которому должникъ, уплачивая по векселю ранёе
срока, имёетъ право удержать 8%, то это значить, что
если онъ платить за годъ до срока, то можетъ удержать
въ свою пользу 8/100 веьссельной валют (значить, 8 коп.
съкаждаго рубля валюты); если же онъ платить за 72 года
до срока, то можетъ изъ каждаго рубля валюты удер¬
жать только 4 коп.; платя за 1 мёсяцъ до срока, удержи-
ваетъ изъ каждаго рубля только *Д* ели % коп. и т. п.
Сумма, вычитаемая изъ валюты, когда по векселю
уплачивается ранёе срока, называется учетомъ или
диснонтомъ векселя; опредёлить учетъ за данное время
по данному проценту значить учесть или дисконтировать
вексель.

- 219
Учитывать вексель приходится еще и тогда, когда кре-
диторъ продаетъ вексель своего должника постороннему
лицу (или банку); въ этомъ случае покупатель удержи-
ваетъ въ свою пользу ту сумму, которая придется по
условленному годовому % за все время, остающееся до
вексельнаго срока.
243. Различныя группы задачъ на учетъ
векселей. Подобно задачамъ на проценты, задачи на
учетъ векселей могутъ быть разделены на 4 группы со¬
образно тому, что неизвестно изъ слЬдующихъ 4-хъ ве¬
личинъ: а) учетъ (или сумма, уплачиваемая по вексе-
лю), Ь) валюта векселя, с) процентная такса, по кото¬
рой сдЬланъ учетъ и d) время, остающееся до срока
векселя; при этомъ задачи, въ которыхъ неизвестна ва¬
люта, могутъ быть двоякаго рода: въоднЬхъ дань учетъ,
въ другихъ — сумма, уплачиваемая по векселю.
Такъ какъ учетъ векселя есть ничто иное, какъ про¬
центный деньги съ валюты, причитаюпцяся по усло¬
вленной годовой таксе за все время, недостающее до
срока векселя, то задачи на учетъ векселей нияЬмъ
не отличаются отъ соответственпыхъ задачъ на про¬
центы.
Приведемъ некоторые примеры.
244. Задача 1. Вексель въ 5600 руб. уплатили за
б месяцевъ до срока съ учетомъ по 6%- Какой сделанъ
былъ учетъ по этому векселю?
Искомый учетъ представляетъ собою процентный день¬
ги, при читавшаяся съ 5600 р. за 5 месяцевъ, считая
по 6°/0 годовыхъ. Поэтому
5600.6.5	,
учетъ = 10о712~	(ру	*
8амЬчан1я. 1) Если приходится вычислять учетъ
за несколько дней, то принимаютъ годъ въ 360 дней,
а мЬсяцъ въ 30 дней.

— 220 —
2) Если бы въ этой задаче требовалось отыскать не
учетъ, а сумму, которую нужно заплатить по векселю,
то можно сначала найти учетъ, а потомъ вычесть его
изъ данной валюты.
Задача 2. За два года до срока проданъ вексель съ
учетомъ въ 148 рублей. Определить валюту векселя,
если учетъ былъ сдЬланъ по 8°/0.
Задача эта равносильна такой задаче на проценты:
определить начальный капиталъ,' съ кото-
раго процентныя деньги за 2 года, считая
по 8% годовыхъ, составляютъ 148. руб.
Решается такъ, какъ задача 2-я стр. 201-й.
Задача 3. За два года до срока уплатили по век¬
селю 777 руб. Найти валюту этого векселя, если изве¬
стно, что у четь былъ сделанъ по 8%.
Эта задача равносильна такой задаче на проценты:
какъ великъ начальный капиталъ, если,
вычтя отъ него процентныя деньги, причи¬
тающаяся съ этого капитала за 2 года, счи¬
тая по 8% годовыхъ, мы получимъ 777 р.
За 2 года процентныя деньги составляютъ 1е/100 на-
чальнаго капитала; значить, если ихъ вычтемъ изъ него,
останется 8i/100 капитала; эти м/100 капитала должны рав¬
няться 777 руб.; след., искомый капиталъ = 777 : 8У100 =
= 925 руб.
245.	Математически учетъ. Учетъ, описанный
въ предыдущихъ параграфахъ, называется коммерче-
снимъ. Есть еще особаго рода учетъ, называемый мате¬
матическими. Чтобы понять разницу между ними, возь¬
мемъ примерь. Определить учетъ по 6% съ век¬
селя въ 800 рубл., уплачиваемаго за 10 мес.
до срока. Предварительно узнаемъ, сколько процен-
товъ за 10 месяцевъ составить 6% годовыхъ. Окажется
5°/0. Итакъ, за недостающее время придется учесть, удер¬
жать 5°/0.До сего времени мы считали, что эти 5% озна-
чаютъ 5 сотыхъ валюты векселя, т. е., что съ каждаго

— 221 —
рубля валюты удерживается 5 коп. Но можно понимать
учетъ въ 5°/0 иначе. Можно думать, что за вексель въ
800 руб. уплачена теперь такая сумма, которая, будучи
отдана въ ростъ по 5%5 обращается къ концу срока век¬
селя въ 800 руб. Понимаемый въ такомъ смысле учетъ
называется математическимъ. Съ перваго раза можетъ
показаться, что нетъ разницы между коммерческимъ и
математическимъ учетами. Однако, если ближе всмотримся
въ вопросъ, заметимъ разницу. Мы предположили, что
сумма, уплачиваемая теперь за вексель, должна обра¬
титься въ 800 р., считая по 5%; но каждый рубль, при¬
нося 5°/с, обращается въ 1 р. 5 коп.; поэтому въ800р.
должны повторяться столько разъ 1 руб. 5 коп., сколько
разъ въ сумме, уплачиваемой теперь, повторяется 1 рубль.
Значитъ, при новомъ нашемъ предположены придется
учитывать по 5 коп. изъ каждыхъ 105 коп. валюты, а не
изъ каждыхъ 100 коп., какъ это делается при коммер-
ческомъ учете. Такъ какъ въ валюте 105 коп. повто¬
ряются меньшее число разъ, чемъ 100 коп., то, значитъ,
математичесжй учетъ меньше коммерчьскаго. Действи¬
тельно, коммерчесюй учетъ за«годъ съ 800 руб. по 5%
лп *	■*	г чу 80000
равенъ 40 руб., а математичесюй учетъ = 5Х-1Лг —
lUt)
= 3809 ^j-коп. = 38 руб. 9U/S1 к.
Итакъ, математичесюй учетъ отличается отъ коммер-
ческаго темъ, что проценты, причитаюнщеся за
время, остающееся до вексельнаго срока,
учитываются не изъ рубля валюты, какъэто
делается при коммерческомъ учете, а изъ
суммы рубля съ процентными деньгами, при¬
читающимися на него за оставшееся время
(т.-е. съ наращеннаго рубля).
На практике производится учетъ коммерческий, и
такса процентовъ условливается въ предположен! и, что
учеть будетъ сделанъ съ рубля, а не съ наращеннаго

— 222 —
рубля; если бы между заинтересованными лицами про¬
изошло соглашеше—производить учетъ математичесый,
то, конечно, процентная такса была бы условлена иная,
ч^мъ для учета коммерческая.
245,а. 8адачи на учетъ векселей могутъ быть решаемы
при помощи слЬдующихъ общихъ формулъ. Пусть А будетъ
валюта векселя, р—процентная такса, по которой произво¬
дится учегь, t — время до срока, выраженное въ какихъ-нибудь
одинаковыхъ единицахъ: годахъ, м!зсяцахъ или дняхъ, х—
учегь, и а—сумма, уплачиваемая за вексель (А, х и а вы¬
ражены, положимъ, въ рубляхъ). Прежде всего мы находимъ
число процентовъ, приходящееся за время t. Если t означаетъ
г о д ы, то число процентовъ, очевидно, будетъ pt\ если t озна-
чаетъ месяцы, то число процентовъ будетъ потому что
Р
ва 1 М'Ьсяцъ приходится —г%;еслиtозначаетъ дни, то число
1а
pt
процентовъ будетъ ~q %, потому что за 1 день приходится
Р
°/0. Назовемъ, для краткости, число процентовъ за время t
черезъ q. Тогда получимъ слЬдуюшдя формулы:
Со 100—|—д рублей учитывается q рублей; въ валютЬ 100-}-?
Учетъ коммерчески.
Учетъ равенъ q сотымъ валюты; слЬд.:
Учетъ математичесшй.
рублей повторяются
А
разъ; слЬд.:
100-fg
10,-f-g
и а —А —
100 + q
Aq

Правило сроковъ.
246. Иногда предстоять вадобность решать следующее
вопросы: 1) нисколько сроковъ уплаты долга заменить однимъ
ерокомъ: 2) одинъ срокъ уплаты заменить нисколькими;
•!) нисколько сроковъ заменить нисколькими другими.
Такъ какъ при этомъ не должны пострадать ни интересы
заимодавца, ни интересы должника, то подобные вопросы
могутъ быть решаемы на основанш слфдующихъ двухъ
истины
I. Процентныя деньги не изменяются, если капиталъ уве¬
личимъ, а время уменьшимъ въ одинаковое число разъ, или
наоборотъ. Напр., проц. деньги съ 1000 руб. за 8 мес. тЬ
же самыя, что и съ 2000 руб. за 4 Misc., или съ 500 за
16 мес.
То же самое можно сказать о коммерческомъ учете. Напр.,
коммерчески} учетъ съ 250 руб. за 9 мес. тогь же, что и
съ 50 руб. за 45 месяцевъ.
II. Сумма процентныхъ денегъ съ несколькихъ одинако¬
выхъ капиталовъ за разныя времена равна процентнымъ
деньгамъ съ одного такого напитала за сумму всехъ отдЪль-
ныхъ временъ. Напр., процентныя деньги съ 50 руб. за 8 мес.,
сложенныя съ процентными деньгами съ 50 руб. за 10 мес.,
равны процентнымъ деньгамъ съ 50 руб. за 10-]—8 месяцевъ.
То же самое можно сказать о коммерческомъ учегб съ
одинаковыхъ валютъ за разныя времена.
247. На основанш этихъ истинъ решимъ для примера
следующая задачи:
Задача 1. Некто долженъ по тремъ векселямъ: 4200
руб. черезъ 6 мес.', 3500 р. черезъ 7 мес. и 2000 р. черезъ
9 мес. Онъ желаетъ заменить эти три векселя однимъ на
сумму 4200-)—3500-j-2000, т.-е. на 9700 руб. На какой срокъ
онъ долженъ написать вексель?
Очевидно, должникъ долженъ написать такой вексель,
действительная стоимость котораго была бы равна сумме
действительныхъ стоимостей трехъ векселей. Такъ какъ
валюта одного векселя, срокъ котораго отыскивается, равна
сумме валютъ трехъ данныхъ векселей, то для сказаннаго
веобходимо, чтобы учетъ (предполагается коммерчесшй) съ

— 224 —
9700 руб. за неизвестное время былъ равенъ сумме учетовъ
съ трехъ данныхъ векселей. Для удобства вычислешя при-
ведемъ три векселя къ какой-нибудь одной валюте, налр.,
къ 100 р., разсуждая такъ: учетъ съ 4200 руб. за 5 мес.
равенъ учету съ 100 р. за 5+42, т.-е. 210 мес.; выразимъ
это сокращенно такъ:
4200 руб. 5 мес. =100 руб. 210 мес.
Подобно этому:
3500 р. 7 м.=100 р. 245 м. и 2000 р. 9 мес.=100 р. 180
мес. Но 100 р. 210 м.+ 100 р. 245 м.+100 р. 180 м. =
= 100 р. 635 м. Съ другой стороны:
100 р. 635 м.=9700 р. ^ м. = 9700 р. 6 м. 16 дн.
У /
(приблизительно).
След., вексель на 9700 руб. долженъ былъ нашсанъ на
6 м. и 16 дщй (или 17).
Задача 2. некто по условно долженъ былъ уплатить.
3000 р. черезъ 9 мес.; но онъ уплачиваетъ 1500 руб. черезъ
2 мес. и 1000 рублей черезъ 5 мес. Спрашивается, черезъ
сколько времени онъ долженъ уплатить остальные 500
рублей.
Для соблюден1я интересовъ заимодавца необходимо, чтобы
процентныя деньги съ	3000 руб. за	9	мес. были	равны
сумме процентныхъ денегъ съ 1500 руб.	за 2 мес., съ 1000
руб. за 5 мес. и съ 500 р. за искомое время. Такъ какъ:
1500 р. 2 м. =500 р.	6 м. и 1000 р.	5	м. = 500 р.	10 м.
то	1 1500 р.	2 м. +1000 р.	5	м. = 500 р.	16 ы.
Съ другой стороны: 3000 р. 9 м.=500 р. 54 м.
След., остальные 500 руб. должны быть отданы черезъ
54—16=38 мес. отъ совершешя займа.
V.	Ц’Ьпное правило.
248.	Задача. Сколько пудовъ составятъ 100 гермап-
скихъ фунтовъ, если известно, что 18,36 герм, фунта
равны 99/60 килограмма, а 18,75 килограмма равны 45%
русскаго фунта?

— 225 —
Для удобства решетя расположимъ данныя такъ:
Сколько пудовъ въ 100 герм, фунтахъ,
если 18,36 герм. ф. =99/Б0 килогр.
„ 18,75 килогр. = 453Д русск. ф.
40 русск. ф. = 1 пуду.
(Первая строчка содержитъ вопросъ задачи, а каждая
изъ остальныхъ начинается такими мерами, которыми
оканчивается предшествующая; последняя строка должна
оканчиваться назван!емъ меры, о которой говорится въ
вопросе).	•
Решить задачу можно различными способами. Наи¬
более удобный способъ следуюнйй.
Обращая вниман1е на последнюю строку, а затемъ
переходя оть нея постепенно къ следующимъ верхнимъ
строчкамъ, разсуждаемъ такъ:
Если 40 русск. ф. = 1 пуду,
то 1 русск. ф. = 7и пуда,
лкч	К	1-453/*
a 45s/i русск. Ф- = - 40~* пуда.
Но 453/t русск. ф. составляютъ 18,75 килограмма;
значитъ:
1-45»/*
1 килогр. =-40718 7Г ПуДа’
а 9а/60 килогр. = 1.45»/1.9»/и
40.18,75 ЩД0ВЪ
Но 99/50 килогр. составляютъ 18,36 герман. фунта;
значить:
1 45*^ 9е/
1 геРм- ф- =ТоЗб^18Ж ПУЛ0ЕЪ-
1 453/ О9/ 100
а 100 герм. ф. = 40-	18,36 Пуд0ВЪ’ I1!
183.459.100.100 100
= 4.50.40.1875.1836 — 'Б0 ПуДа‘
15 Заказ № 5456

— 226 —
Разсматривая формулу [1], легко зам'Ьтимъ следую¬
щее правило: расположивъ вопросъ и условия задачи
такъ, какъ было указано выше, следуетъ произведете
чиселъ, которыми оканчиваются строчки, разделить на про¬
изведете чиселъ, которыми оне начинаются.
Правило решать подобныя задачи наз. цепнымъ, по¬
тому что, располагая данныя, какъ было указано выше,
мы получаемъ изъ всехъ строчекъ подоб1е цепи (прп-
чемъ строчки уподобляются отдельнымъ звеньямъ). Пра¬
вило это лучше называть правилось перевода, потому
что въ задачахъ на это правило меры одного государ¬
ства требуется перевести на меры другого.
VI.	Задачи на пропорциональное
д,Ьлен1е.
249.	Задача 1. Разделить 84 на три части пропор¬
ционально числамъ 7, 5 и 2.
Это надо понимать такъ: разделить 84 на татя три
части, чтобы первая часть относилась ко второй, какъ
7 къ 5, а вторая къ третьей, какъ 5 къ 2. Назовемъ
искомыя части буквами xt, х3 и хъ. Въ задаче требуется,
чтобы эти части могли удовлетворить следующимъ двуыъ
пропорщямъ:
гс,.: х2 = 1 : 5.. (1) х2 : ац = 3 : 2.. (2).
Изъ этихъ пропорщй можно вывести такое заключеше:
если число х1 разобьемъ на 7 равныхъ долей, то такихъ
долей въ х„ должно быть 5, потому что только при этомъ
условш отношеше хг къ хп_ равно отношешю 7 : 5; та¬
кихъ же долей въ хг должно быть 2, потому что только
при этомъ условш отношеше х2 къ х3 равно отношешю
5:2. Отсюда следуетъ, что седьмая доля х1 въ сумме:
a?i —j— —(— х2 содержится 7 —|— 5 —2 раза, т.-е. 14 разъ.

— 227 —
Но сумма: ж, -f- ж2 + хг Должна составлять 84; значить,
седьмая доля ж, равна 84 ; 14 = 6. Такихъ долей заклю¬
чается 7 въ хх, 5 въ xi и 2 въ х3; Сл'Ьд.
хх = 6.7 = 42, х.г = 6.5 = 30; х3 = 6.2 = 12.
Зам t чаше. Изъ пропорщи (1) и (2) можно вывести
такую третью пропорцш:
Действительно, мы видели, что если хх разбить на 7
равныхъ долей, то такихъ долей въ х3 должно быть 2;
поэтому отношеше хх къ хг равно отношенш 7:2.
Три написанныя выше пропорщи можно написать со¬
кращенно такъ:
Правило. Чтобы разделить число на части пропорщо-
нально несколькимъ данными числами, достаточно . раз¬
делить его на сумму этихи чисели и частное умножить на
наждое изи этихи чисели.
250.	Задача 2. Разделить 968 на 4 части пропор-
щонально числами:
Прежде всего заменимъ данный рядъ дробныхъ чи¬
селъ рядомъ целыхъ чиселъ. Для этого привелемъ все
дроби къ общему знаменателю и обратить смешанную
дробь въ неправильную:
Если откинемъ общаго знаменателя, то увеличимъ ка¬
ждую дробь въ одинаковое число разъ (именно въ 40 разъ);
отъ этого отношешя между ними не изменятся; след.:
хх : х, : х3 -=1 : 5 : 2
13	2	3
\ — •   *   •
2 ' 4 ’ 5 ‘ 8
11 . 3	2 , 3	■ 16 • —
2~ '' Т ' 5~ ' Ъ"	40 ‘ 40 ' 40 ' 40
3
4
5 ' S
: -^-=60 : 30 : 16 : 15
15*

— 228 —
Теперь задачу можно выразить такъ: разделить 968
на 4 части пропорщонально числамъ 60 : 30 :16 : 15.
Эта задача решается такъ, - какъ и 1-я.
251. Способъ, посредствомъ котораго можно разделить
число на части пропорщонально несколькимъ даннымъ
числамъ, называется правиломъ пропорцюнальнаго де¬
лежя. Есть очень много задачъ, къ которымъ приме¬
няется это правило. Напр.:
Задача 3. Три купца составили товарищество для
ведешя некотораго торговаго дела. Первый купецъ
внесъ для этой цели 15000 руб., второй —10000 руб.,
третШ—12500 руб. По окончанш торговаго дела они по¬
лучили общей прибыли 7500 р. Спрашивается, сколько
изъ этой прибыли придется получить каждому купцу?
Такъ какъ прибыль на каждый внесенный рубль
должна получиться одинаковая, то прибыль каждаго
участника въ товариществе пропорщональна капиталу,
внесенному имъ. Поэтому задача сводится на такую:
разделить 7500 на три части пропорщонально числамъ
15000, 10000 и 12500; а это есть задача на пропор-
цюнальное делете. Чтобы решить ее, прежде всего за-
метимъ, что числа ряда 15000 : 10000 : 12500 можно
разделить на одно и то же число (на 2500); отъ этого
не изменятся отношешя между ними. Сокративъ, полу¬
чимъ 6:4:5. Теперь разделимъ 7500 на три части
пропорщонально 6:4:5. Разсуждая такъ, какъ было
объяснено въ задаче 1, найдемъ:
6=3000; х2=~~. 4=2000; гс3=^. 5=2600
1Э	15	1о
Правило пропорцюнальнаго делешя называется иногда
правиломъ товарищества, потому что помощью этого пра¬
вила решаются, между прочимъ, татя задачи, въ ко¬
торыхъ, подобно сейчасъ решенной, требуется разделить
общую прибыль между несколькими лицами, составивши¬
ми товарищество для общаго коммерческаго предпр1япя.

— 229 —
252.	Задача 4. На железной дороге работало 3
артели рабочихъ; въ первой артели было 27 рабочихъ,
во второй—32, въ третьей—15; первая артель работала
20 дней, вторая —18, третья—16; все три артели полу¬
чили за работу 4068 руб. Сколько рублей придется по¬
лучить каждой артели?
Если бы каждая артель работала одинаковое число
дней, то плата каждой артели была бы пропорщональна
числу рабочихъ въ ней; поэтому преобразуемъ услов1я
нашей задачи такимъ образомъ, чтобы число дней ра¬
боты для каждой артели было одинаково. Напр., пред¬
положимъ, что каждая артель работала бы по одному
дню; тогда, конечно, уменьшилась бы плата каждой ар¬
тели; для того, чтобы эта плата не изменилась, надо,
чтобы число рабочихъ въ каждой артели увеличилось
во столько разъ, во сколько число дней уменьшилось.
Такъ, чтобы первой артели получить за 1 день ту же
плату, какую она получаетъ за 20 дней, надо, чтобы
въ этой артели рабочихъ было не 27, а 27 X 20; также
во второй артели должно быть рабочихъ не 32, а
32 X18, чтобы эта артель получила за 1 день такую
же плату, какъ и за 18 дней; въ третьей артели должно
быть рабочихъ 15 X18» чтобы и эта артель получила
ту же плату за 1 день, какъ и за 16 дней. Теперь по¬
лучаемъ таюе два ряда чиселъ:
числа рабочихъ (27 X 20): (32 X18): (15 X18)
дней	111
Остается разд’Ьлить 4068 на части пропорцюнально
числами рабочихъ. Сокративъ предварительно эти числа
(на 3 и на 4), найдемъ, что 4068 нада разд'Ьлить про-
порщопально 45 : 48 : 20. Обозначивъ искомыя части
буквами ж1, xt и хг, получимъ, какъ было прежде объ¬
яснено;
4068 . 45	4068 .45
ч	—=36 •46=le20<Py6-)-

— 230 —
4068 . 48
= 30 . 48= 1728 (руб.)
113
4068 . 20
113
- = 36 . 20 = 720 (руб.).
Вместо того, чтобы приводить къ 1 числа дней, мы
могли бы привести къ 1 числа рабочихъ; тогда мы
должны были бы задаться вопросомъ: если бы вместо
каждой артели было только по одному рабочему, то
сколько дней долженъ былъ бы работать этотъ рабочШ,
чтобы получить ту же самую плату? Очевидно, что ра¬
бочШ, заменяющШ первую артель, долженъ былъ бы ра¬
ботать (20X^7) дней, вторую—(1&Х 32) дней, третью—
(16X15) дней. Тогда пришлось бы 4068 делить на части
пропорщонально только числу дней.
Можетъ случиться, что въ задаче даны 3 и бол-fee
ряда чиселъ,' пропорщонально которымъ требуется раз¬
делить данное число. Если бы, напр., въ предыдущей
задаче сказано было, что первая артель работала еже¬
дневно столько-то часовъ, вторая столько-то и третья
столько-то, то пришлось бы плату делить пропорщо¬
нально: во-1) числамъ рабочихъ, во-2) числамъ дней
и' въ-3) числамъ часовъ. Тогда нужно было бы два
ряда чиселъ привести къ 1, напр., предположить, что
каждая артель работаетъ 1 день по 1 часу.
253.	Задача 5. Разделить число а на 3 части обратно
пропорщонально числамъ ш, пар.
Это значитъ, что число о требуется разделить на таюя
3 части, чтобы первая часть относилась ко второй, не какъ
т къ п, а какъ п : т, а вторая къ третьей не какъ
тр, а какъ р: п. Назвавъ искомыя части ж,, х2 и х3, мо¬
жемъ выразить требования задачи такими пропорщями:
Но* отношеше	п	:	т	mojkho	заменить	равнымъ ему	отноше-
11	.11;
шемъ — : —;	точно такъ же	р	:	п	можно	заменить	— . —
плл	м '	'И	71
ж, : х., = п : т
ж„ : ж,=р : п.
т п
п р

— 231 —
тогда получимъ:
—JL. _!
1 ‘ 2 т ' п
х,: X,— — : —
2	3	п	р
откуда видно,	что	части xt, х2 и хг должны	быть	прямо
111
пропорщональны числамъ — : — : —. Итакъ, чтобы разде¬
лить число на части обратно пропорцюнально даннынъ числанъ, надо
разд'Ьлить его пряно пропорцюнально числамъ, обратнымъ даннынъ.
Прим'Ьромъ задачъ подобнаго рода можетъ служить такая:
Капиталъ въ 10150 руб. раздЪленъ на 3 части и каждая
часть отдана въ роетъ: первая часть по 5°/0, вторая по 6°/0,
а третья по 6‘/о0/0. Какъ велики эти части, если известно,
что каждая часть приносить ежегодно одинаковый доходъ?
Такъ какъ проц. деньги за годъ одинаковы	для	всЬхъ
частей, то очевидно, что искомыя части обратно пропор-
шональны процентнымъ таксамъ. Значить, 10150 руб. надо
разделить на 3 части обратно пропорцюнально числа'мъ
112
5:6: 6'Д или прямо пропорцюнально числамъ -g- : -g- : jg.
Приведя эти дроби къ общему знаменателю и откинувъ по-
с.т£днш, получимъ цЪлыя числа 78:65:60, пропорщонально
которымъ надо разделить 10150 руб.
254.	Задача	6.	Разделить 125 на тайя 4 части,
чтобы первая	часть относилась ко второй,	какъ	2: 3,
вторая къ третьей, какъ 3 : 5, а третья къ четвертой,
какъ 5 : 6.
Задача 7. Разделить 125 на тайя 4 части, чтобы
первая часть относилась ко второй, какъ 2 : 3, вторая
къ третьей, какъ 4 : 5, а третья къ четвертой, какъ 6 :11.

— 232 —
Въ каждой изъ этихъ задачъ даны отношешя между
частями и сумма частей, а отыскиваются самыя части.
Однако есть существенная разница между этими зада¬
чами. Въ первой задаче отношешя:
2:3,	3:5	и	5:6
таковы, что последующей членъ перваго отношешя ра¬
венъ предыдущему члену второго, а последуюнцй членъ
второго отношешя равенъ предыдущему члену третьяго.
Вследств1е этого можно сказать, что въ первой задаче
требуется 125 разделить на 4 части пропорщонально
числамъ 2 : 3 : 5 : 6. Значить, эта задача ничемъ не
отличается отъ задачи 1-й.
Во второй задаче отношешя между частями
2:3,	4:5	и	6 : 11
таковы, что последующШ членъ одного отношешя не
равенъ предыдущему члену следующаго отношешя.
Однако этотъ случай легко привести къ первому;
укажемъ для этого два способа.
Способъ 1-й. Обозначивъ искомыя части буквами
хх, х9, хг и xt, можемъ написать следующая три про¬
порцш:
хх : х.2 = 2 :	3
х3 : xz = 4 :	5
хъ : xt = 6 :11
Изъ первой пропорцш видимъ, что если хх разобьемъ
на 2 равныя доли, то такихъ долей въ xt должно быть
3.	Узнаемъ теперь, сколько такихъ же долей должно
содержаться въ хг и въ хх. Изъ второй пропорцш ви¬
димъ,	что	xt	составляетъ */* х2'->	но	въ	х2	заключаются
3 равныя доли;	значить, въ х3	такихъ	долей	будетъ
ЗХв/4,т.-е. 15/,. Изъ третьей пропорцш видимъ, что хх
составляетъ 11/в хг\ но въ х» заключается равныхъ долей
18Д; значить, въ хх такихъ долей будетъ 18/»Хп/в» т-'е-

233
вв/8. Итакъ, въ х4 содержится 5B/g такихъ равныхъ долей,
какихъ	въ	хг	содержится 1в/4, въ	х2	сод.	3, а	въ	хх сод.
2.	Значитъ,	для	рЪшешя задачи	достаточно	число 125
разделить на 4 части пропорщонально числамъ:
2 • s • — • —
1 ■ 6 ■ 4 •	8
или, умножая вебхъ ихъ на 8:
16 : 24 : 30 : 55
Такимъ образомъ задача приводится къ задача 1-й.
Способъ 2-й. xt : х0 = 2
х2 : хг = 4:
х. : xh = 6 :
3
5
11
=48
=72
=90
х,:х.: =48: 72 : 90
72
90
165
165
Чтобы уравнять 2-й членъ 1-го отношешя съ 1-мъ членомъ
2-го отношешя, умножимъ оба члена 1-го отношешя на 4,
а второго на 3 (эти числа выписаны направо отъ отношешй,
за чертою). Чтобы уравнять 2-й членъ 2-го отношешя съ
1-мъ членомъ 3-го отношешя, умножимъ оба члена 2-го отно¬
шешя на 6, а третьяго на 5. Оба члена 1-го отношешя умно¬
жимъ также на 6, а 3-го на 3 (веб эти множители выписаны
за чертой). -Послб умножешя получимъ татя отношешя, ко¬
торый можно выписать въ одинъ рядъ, и, следовательно,
задача приводится къ 1-й.
Зам,Ьчан1е. Если бы члены данныхъ отношешй
были выражены дробными числами, то полезно эти от¬
ношения предварительно заменить отношешями ц1>лыхъ
чиселъ.
VII.	Задачи на сьгЬшейе и сплавы.
255.	СмЪшвмб 1-го рода. Задача. Смешано три сорта
муки: 15 фунт, по 8 коп., 20 фунт, по 7 коп. и 25 фунт,
по 4 коп. за фунт. Что стоить фунтъ см'Ьси?
Узнаемъ сначала, что стоять веЬ фунты 1-го сорта,
всЬ фунты 2-го сорта и веЬ фунты 3-го сорта; потомъ—
16 Гк.к.и № 5456

— 234 —
что стоить вся смЬсь; затЬмъ—сколько фунтовъ во всей
смЬси, наконецъ—цЬну	одного	фунта смЬси:
15 ф. по	8 коп.	стоять	8.15 = 120	коп.
20 ф. по	7 коп.	„	7.20 = 140	„
25 ф. по	4 коп.	„	4.25 = 100	„
Вся см'Ьсь стоить  360 „
ВсЬхъ фунтовъ въ смЬси: 15-|-204-25=60.
ЦЬна одного фунта смЬси: 360: 60=6 коп.
Подобнымъ образомъ рЬшаются тагая задачи, въ кото¬
рыхъ даны цЬна и количество каждаго сорта смЬши-
ваемыхъ веществъ, а отыскивается цЬна единицы смЬ¬
си. Тагая задачи называются задачами на смЬшеше
1-го рода.
256.	СмЬшеше 2-го рода. Задача. Изъ двухъ сортовъ
чаю составлено 32 фунта смЬси; фунтъ перваго сорта
стоить 3 руб., фунтъ второго сорта—2 руб. 40 коп.
Сколько фунтовъ взято отъ того и другого сорта, если
фунтъ смЬшаннаго чаю стоить 2 р. 85 к. (безъ прибыли
и убытка)?
Способъ 1-й. Продавая дорогой сортъ по 2 р.
85 к., продавецъ будетъ получать убытка на каждомъ
фунтЬ 15 коп. (3 р.—2 р. 85 к.); продавая дешевый
сортъ по 2 р. 85 к., продавецъ будетъ получать при¬
были на каждомъ фунтЬ 45 к. (285—240). Если бы
убытокъ отъ фунта дорогого сорта былъ равенъ при¬
были отъ фунта дешеваго сорта, тогда, чтобы убытокъ
покрылся прибылью, надо было бы взять дорогого сорта
столько же, сколько и дешеваго. Но въ нашей задачЬ
убытокъ отъ фунта дорогого сорта меньше прибыли отъ
фунта дешеваго сорта; изъ этого надо заключить, что,
для покрьтя убытка прибылью, дорогого сорта должно
взять болЬе, чЬмъ дешеваго, и во столько разъ, во
сколько разъ 45 больше 15. Значить, 32 фунта надо
разделить на двЬ части пропорщонально 45 : 15 (или

г
— 235 —
3 : 1); первая часть покажетъ, сколько фунтовъ должно
взять отъ дорогого сорта, а вторая—сколько фунтовъ
должно взять отъ дешеваго сорта. Обозначивъ число
фунтовъ дорогого сорта черезъ хи а число фунтовъ
дешеваго сорта черезъ хг, будемъ имЬть, по правилу
пропорщональнаго дЬлешя:
90
=	3 = 8.3 = 24; z2 = S.l=8
Итакъ, для того, чтобы при смЬшенш не имЬть ни
прибыли, ни убытка, количества двухъ смЬшиваемыхъ
сортовъ должны быть обратно пропорцюнальны числамъ,
показывающимъ прибыль или убытокъ на единицЪ каждаго
сорта.
Способъ 2-й. Предположимъ, что веб 32 фунта взяты
отъ какого-нибудь одного сорта, напр., отъ i-го. Тогда смЬсь
будетъ стоить дороже, чЬмъ требуется, потому что соста¬
влена только изъ дорогого сорта. Узнаемъ, на сколько до¬
роже. Одинъ фунтъ 1-го сорта дороже фунта требуемой
смЬси на 15 коп. (потому что 3 руб. больше 2 р. 85 к. на
15 коп.); значитъ, 32 фунта 1-го сорта будутъ стоить до¬
роже 32 фун. требуемой смЬси на 15)х(32, т.-е. на 480 коп.
Чтобы понизить стоимость смЬси, надо нисколько фунтовъ
дорогого сорта заменить столькими же фунтами божбе де¬
шеваго сорта. Если одинъ фунтъ 1-го сорта замЬеимъ фун-
томъ 2-го сорта, то стоимость смЬси понизится на 60 коп.
(3 р.—2 р. 40 к.=60 к.); значитъ, чтобы понизить стоимость
смЬси на 480 к., надо заменить столько фунтовъ 1-го сорта
вторымъ сортомъ, сколько разъ 60 к. содержится въ 480 к.,
т.-е. 8 фунтовъ (480 : 60=8). Если 8 фунтовъ 1-го сорта
замЬнимъ вторымъ сортомъ, то перваго сорта останется
32—8, т.-е. 24 фунта. Итакъ, для составления см'Ьси надо
взять 24 ф. 1-го сорта и Б ф. 2-го сорта.
Задачи, въ которыхъ дана цЬна~ единицы каждаге
смЬшиваемаго вещества, цЬна единицы смЬси и коли¬
чество см'Ьси, а отыскивается количество смЬшиваемыхъ
веществъ, называются задачами насмЬшеше 2-го рода.
ВмЬсто цЬны единицы смЬси можетъ быть дана стои¬
мость всей смЬси; но это обстоятельство не можетъ

— 236 —
измЬнить npieMa рЬшешя, потому что, зная количество
смЬси и ея стоимость, легко опредЬлимъ (дЬлетемъ)
цЬну одной единицы смЬси.
ЗамЬтимъ, что задачи на смЬшеше 2-го рода воз¬
можны только тогда, когда цЬна единицы смЬси заклю¬
чается между цЬною единицы 1-го рода и цЬною еди¬
ницы 2-го рода. Напр., было бы невозможно составить
смЬсь чаю, безъ прибыли и убытка, цЬною по 3 руб.
20 к. за фунтъ изъ двухъ сортовъ чаю, цЬною по
3 руб. и по 2 руб. 40 к. за фунтъ.
257. НеопредЬленныя задачи на CMbmeHie.
Если въ задачахъ на смЬшеше 2-го рода дано для смЬ-
шешя болЬе двухъ сортовъ веществъ, то задача становится
неопределенною, т.-е. такая задача допускаетъ безчислен-
ное множество рЬшетй. Это станетъ понятнымъ изъ слЬ-
дующаго примЬра: составить смЬсь вина въ 40 ведеръ, цЬ¬
ною но 5 руб. 50 коп. за ведро, изъ трехъ сортовъ вина:
по 6 руб., по 5 руб. и по 4 р. 80 к. за ведро. ЦЬна од¬
ного ведра смЬси заключается, какъ видно, между цЬною
ведра 1-го сорта и цЬною ведра 2-го сорта; съ другой сто¬
роны она заключается между цЬною ведра 1-го сорта и цЬ¬
ною ведра 3-го сорта. Поэтому мы можемъ составить тре¬
буемую смЬсь, смЬшивая вино 1-го сорта со вторымъ или
вино 1-го сорта съ третьимъ. Допустимъ, что мы какую-
нибудь часть 40 ведеръ составили смЬшетемъ первыхъ
двухъ сортовъ, а оставшуюся часть 40 ведеръ составили
смЬшетемъ 1-го и 3-го сортовъ; смЬшавъ обЬ эти смЬси,
получимъ требуемую смЬсь. И такъ, вотъ щиемъ для рЬше-
шя предложенной задачи: надо разбить 40 ведеръ на кагая-
нибудь двЬ части, и одну изъ этихъ частей составить смЬ-
щеше 1-го сорта со 2-мъ, а другую—смЬшетемъ 1-го
сорта съ 3-мъ. Такь какъ дЬлить на двЬ части 40 ведеръ
мы можемъ безчисленпымъ множествоыъ способовъ, то оче¬
видно, что предложенная задача неопредЬленная.
258. Задачи на смЬгцеше жидкостей. Если
говорятъ: „вино въ 48 градусовъ", то это надо пони¬
мать такъ, что въ каждыхъ 100 объемныхъ частяхъ этого
вина содержится 48 частей • чистаго спирта, а осталь-
ныя 52 части составляетъ вода; значить, число граду-

— 237 —
совъ означаетъ процентное объемное содержало чистаго
спирта; иначе сказать, оно означаетъ, сколько сотыхъ
долей объема смЬси приходится на чистый спиртъ. За¬
дачи на смЬшете такихъ жидкостей, которыхъ каче¬
ство выражается числомъ градусовъ, можно подраздЬ-
лить тоже на 2 рода, подобно задачамъ, разсмотрЬннымъ
выше. Приведемъ примеры.
Задача 1. 30 ведеръ вина въ 48 градусовъ смЬшано
съ 24 ведрами вина въ 36 градусовъ. Сколько градусовъ
въ смЬси?
Въ каждомъ ведрЬ 1-го сорта заключается 48 сотыхъ
ведра чистаго спирта. Значитъ, въ 30 ведрахъ 1-го сорта
чистаго спирта содержится 48X30, т.-е, 1440 сотыхъ
ведра. Въ 24 ведрахъ 2-го сорта чистаго спирта заклю¬
чается 36X24, т.-е. 864 сотыхъ ведра. Во всей см’Ьси
чистаго спирта будетъ 1440-}-864, т.-е. 2304 сотыхъ
ведра. Такъ какъ всЬхъ ведеръ вина въ смЬси 30-}-24,
т.-е. 64 ведра, то въ каждомъ ведрЬ смЬси чистаго
спирта будетъ 2304 : 54, т.-е. 42% сотыхъ ведра. Зна¬
читъ, смЬсь окажется въ 42% градуса.
Задача 2. Желаютъ составить смЬсь изъ вина
двухъ сортовъ: въ 48 град, и 36 град. Сколько надо
взять того и другого, чтобы составить 10 ведеръ вина
въ 45 град.?
Такъ какъ ведро 1-го сорта содержитъ спирта на 3
сотыхъ' ведра болЬе, а ведро 2-го сорта на 9 сотыхъ
менЬе, чЬмъ требуется, то 1-го сорта должно взять
болЬе, чЬмъ 2-го, во столько разъ, во сколько 9 бо¬
лЬе 3. Значитъ, 10 ведеръ надо раздЬлить на 2 части
пропорщонально числамъ 9:3 или 3:1. 1-го сорта надо
10	„	„1	„	Ю	.	„1
взять: gq-j . 3 = 7-; 2-го сорта: g-pj .1 = 22-

— 238 —
259.	Задачи на сплавы металловъ. Золото и
серебро, по причине своей мягкости, не употребляются
на изд,Ьл1я въ чистомъ виде, но сплавляются съ ка¬
кими-либо другими болЬе твердыми металлами (чаще
всего съ медью). Сплавленные съ золотомъ или сере-
бромъ посторонн1е металлы называются лигатурой. Ко¬
личество чистаго золота или чистаго серебра выражается
пробой. У насъ чаще всего принято, что проба озна¬
чаетъ, сколько вЬсовыхъ частей чистаго металла содер¬
жится въ 96 вЬсовыхъ частяхъ сплава.
Напр., золото 56-й пробы есть такой сплавъ, въ ко-
торомъ на 96 вЬсовыхъ частей приходится 56 частей
чистаго золота, а остальныя части—лигатура. Такъ какъ
въ фунтЬ 96 золотниковъ, а въ золотнике 96 долей,
то можно сказать, что проба означаетъ, сколько золот¬
никовъ чистаго металла содержится въ фунте сплава,
или сколько долей — въ одномъ золотнике.
Задачи на сплавы металловъ, которыхъ качество вы¬
ражается пробой, можно подразделить на 2 рода, подобно
задачамъ на смЬшете, разсмотрЬннымъ выше. Пркве-
демъ прпм-Ьры.
Задача 1. 25 фун. серебра 84-й пробы сплавлены
въ 12l/s фун. серебра 72-й пробы. Какой пробы сплавъ?
Въ каждомъ фунтЬ 1-го сорта заключается 84 золот.
чистаго серебра. Въ 25 фунтахъ того же сорта содер¬
жится 84X25, т.-е. 2100 зол чистаго серебра. Въ
127, фунтахъ 2-го сорта чистаго серебра заключается
72 X1272, т:-е. 900 зол. Значитъ, во всемъ сплавЬ
чистаго серебра будетъ 2100-|- 900, т.-е. 3000 зол.
Такъ какъ всЬхъ фунтовъ въ сплаве 25-}-127в, т.-е.
377*, то въ каждомъ фунте сплава чистаго серебра бу¬
детъ 3000 : 3772, т.-е. fcO зо.аи,анковъ. След., сплавъ
окажется 80 й пробы.

г
— 239 —
Задача 2. Сколько нужно взять золота 91-й и 8772
пробы, чтобы составить слитокъ въ 2 фунта 8 золотни-
ковъ 88,9 пробы?
Такъ какъ \ золотникъ 1-го сорта содержитъ чистаго
золота бол'Ье, ч'Ьмъ требуется, на 2,1 доли, а 1 золот¬
никъ 2-го сорта содержитъ мен^е на 1,4 доли, то 1-го
сорта надо взять меньше 2-го въ отношенш 1,4:2,1.
Значить, 200 золотниковъ надо разделить на 2 части
пропорщонально 1,4:2,1, или 14:21, или 2:3.

ПРИЛ0ЖЕН1Е.
Приближенный вычислен1я.
1. Иногда случается, что, производя какое-либо дЬй-
CTBie надъ десятичными числами, мы не интересуемся
точнымъ результатомъ этого дЬйстйя, ажелаемъ полу¬
чить только нисколько первыхъ его десятичныхъ зна¬
ковъ; въ такомъ случае вместо данныхъ чиселъ можемъ
брать друпя, выраженныя меньшимъ числомъ цыфръ,
и производить дЬйств1я сокращеннымъ способомъ. Цель
этой главы — указать сокращенные способы сложешя,
вычиташя, умножешя и дЬлешя десятичныхъ чиселъ.
2. Определежв. Если, желая получить приближен¬
ный результата дЬйств1я, мы вместо числа А беремъ
другое о, то последнее наз. приближен!емъ числа
А съ недостаткомъ если а <[ А, и съ избыт¬
ке мъ, если а^>А. Число А, по отношенш къ своему
приближешю, наз. тогда точнымъ числомъ.
Погрешностью приближешя наз. разность между
этимъ приближешемъ и точнымъ числомъ *). Такъ, по¬
грешность чиселъ 52 и 56, разематриваемыхъ, какъ
приближешя числа 54, есть 2.
Часто случается, что точная величина погрешности
остается неизвестной, а известно только, что она меньше
дроби Цп; тогда говорить, что это приближеше точно
до Vп.
3. Когда имЬють дЬло съ десятичными числами, то при¬
ближешя ихъ обыкновенно берута съ точностью до деся¬
тичной единицы какого-либо разряда: до Vie, до 1/1М, и т. д.
*) Такая погрешность наз. абсолютной въ отлише отъ относитель¬
ной погрешности, подъ которою разуы’Ьютъ отношеше абсолютной
погрешности къ точному числу.

— 241 —
и даже съ точностью до '/* десят. единицы. Тагая при-
ближетя легко находятся по слЬдующимъ лравиламъ:
1) Чтобы получить приближеюе съ недо¬
статкомъ даннаго десятичнаго числа (съ
конечными или безконечнымъ числомъ де¬
сятичныхъ знаковъ) съ точностью до одной
десятичной единицы какого-либо разряда,
достаточно отбросить въ числ'Ь всЬ цыфры,
стояния вправо отъ той, которая выражаетъ
единицы этого разряда.
Такъ, приближете съ недостаткомъ числа 3,14159265...
съ точностью до 7юо есть 3,14, потому что во-1) пО-
слЬднее число меньше даннаго, и во-2) погрЬшность,
равная 0,159265... сотой, меньше0,99999... сотой, т.-е.
меньше 1 сотой.
Если желаемъ получить приближете съ точностью
до одной цЬлой единицы какого-либо разряда (до 1,
до 10, до 100 и т. п.), то, отбросивъ всЬ цыфры,
стоящ1я вправо отъ той, которая выражаетъ единицы
этого разряда, мы должны заменить нулями гЬ изъ
отброшенныхъ цыфръ, которыя выражаютъ цЬлыя еди¬
ницы, десятки, сотни и т. п. Такъ, приближете числа
5835,2173... съ точностью до одной сотни есть 5800.
2) Чтобы получить приближен1е съ избыт¬
комъ даннаго десятичнаго числа съ точ¬
ностью до одной десятичной единицы ка¬
кого-либо разряда, достаточно, отбросивъ
въ числ'Ь всЬ цыфры, стояния вправо отъ
той, которая выражаетъ единицы этого раз¬
ряда, увеличить на 1 посл-Ьднюю изъ удер-
жанныхъ цыфръ.
Такъ, приближете съ избыткомъ числа 3,14159265..
съ точностью до 0,001 есть 3,142, потому что во-1) по-
слЬднее число больше даннаго и во-2) погрЬшность его
меньше 0,001.

— 242 —
3)	Чтобы получить приближение даннаго
десятичнаго числа съ точностью до •/* деся¬
тичной единицы какого-либо разряда, до¬
статочно, поступивъ такъ, какъ было выше
сказано въ правиле 1-мъ, увеличить на 1
последнюю изъ удержанныхъ цыфръ, если
первая изъ отброшенныхъ цыфръ есть 5
или больше 5-ти, а въ противномъ случае
оставить ее безъ изменен1я.
Такъ, приближеше (съ нед.) числа 3,141592... съ точ¬
ностью до 7а сотой есть 3,14, такъ какъ погрешность
менее 0,5 сотой; приближеше того же числа (съ изб.)
съ точностью до 7а тысячной есть 3,142, такъ какъ
погрешность, равная 1—0, 592... тысячной, очевидно,
меньше 0,5 тысячной.
4.	НЬноторыя теоремы о погрешностях!». Заметить,
что если а есть приближеше числа А, причемъ погреш¬
ность равна а, то А—а-\-а., если приближеше взято
съ недостаткомъ, и А —а — а, если оно взято съ
избыткомъ.
I.	Если все слагаемыя взяты съ недостат¬
комъ или все съ избыткомъ, то погреш¬
ность суммы равна сумме погрешностей
слагаемыхъ.
Такъ, если А, В я С суть точныя числа, а а, Ъ и с
ихъ приближешя, все съ недостаткомъ или все съ из¬
быткомъ, причемъ соответствующая погрешности будутъ
«, М Т» То’
А — а + а.,	В=Ъ±$,	С=с±	-у.
С. .д.,	А-\-В-\-C={a-\-b-\-d)db(a-f-P-f-T)-
Отсюда видно, что суммы А-\-В-\-С и o-f-6-f-c раз¬
нятся между собою на <х —J— /3 —J—
Если некоторый слагаемыя взяты съ недостаткомъ
а друпя съ избыткомъ, то погрешность суммы, оче
видно, менее суммы погрешностей слагаемыхъ.

г
— 243 —
П. Если уменьшаемое и вычитаемое взяты
оба съ недостаткомъ или оба съ избыткомъ,
то погрешность разности равна разности
погрешностей уменыпаемаго и вычитае-
маго.
Такъ, если 4 = а + а и Б=й±|3, то
А — Б = о а — Ь —(- /3 = (о — 6) ~4~ а —j- р.
Отсюда видно, что разности А —В и а — Ъ разнятся
между собою на а — /3 или на р —а (если /з<^а).
Заметимъ, что въ этомъ случае остается неизвест-
нымъ, будетъ ли приближенная разность съ недостат¬
комъ, или съ избыткомъ.
Когда одно изъ приближетй взято съ недостаткомъ,
а другое съ избыткомъ, то погрешность разности равна
сумме погрешностей данныхъ чиселъ; значить, въ слу¬
чае, когда характеръ приближеый неизве-
стеръ, можно только утверждать, что по¬
грешность разности не более суммы по¬
грешностей данныхъ чиселъ.
Ш. Если одинъ изъ двухъ сомножителей
есть число точное, а другой приближенное,
то погрешность произведеыя равна про¬
изведена погрешности прибл иженнаго
сомножителя на точнаго сомножителя.
Такъ, если А —а ±а, то Am ~ am ±	откуда видно,
что Ат и am разнятся между собою на am.
Произведете окажется съ недостаткомъ, если прибли¬
женный сомножитель взять съ недостаткомъ, и съ из¬
быткомъ въ противномъ случае.
IV. Если делитель есть число точное, а
делимое приближенное, то погрешность
чаетнаго равна частному отъ делешя по¬
грешности делимаго на делителя.

— 244 —
m	.	Л.	CL	,	CL
1акъ, если A —a A-a,	to	—=	1	;	откуда видно,
— mm— m	>
 	A	a	a
что частный	— и	—	разнятся	между собою	на	—.
Частное окажется съ недостаткомъ, если делимое взято
сь недостаткомъ, и съ избыткомъ въ противномъ случае.
Приближенное сложеше.
5.	Правило. Чтобы получить сумму несколь-
кихъ десятичныхъ чиселъ съ точностью до
одной единицы даннаго разряда, достаточ¬
но, когда слагаемыхъ не более 11, въ каж¬
домъ изъ нихъ отбросить все цыфры, сле¬
дующая за темъ разрядомъ, единицы ко¬
тораго въ 10 разъ менее единицы дан¬
наго разряда, сложить полученныя прибли-
жен1я, отбросить последнюю цыфру резуль¬
тата и увеличить на 1 предпоследнюю его
цыфру.
8,14188.
9,869В.-
3,183... Такъ, поступая по этому правилу въ дан-
34,557812
13,011... номъ примере, получимъ приближенную
31,7736
95,534 сумму 95,54 съ точностью до 0,01.
95,54.
Объяскеше. Отбрасывая десятичные знаки, начи¬
ная съ 4-го, мы делаемъ въ каждомъ слагаемомъ по¬
грешность меньшую 0,001, и беремъ приближешя все
съ недостаткомъ. Въ такомъ случае погрешность при¬
ближенной суммы 95,534, равная сумме погрешностей
слагаемыхъ, будетъ менее 11-ти тысячныхъ, если сла¬
гаемыхъ не более 11-ти. Отбросивъ въ результате по¬
следнюю цыфру, мы еще уменьшаемъ сумму, но не

— 245 —
более, какъ на 9 тысячныхъ; значить, наибольшая по-
грешность числа 95,53 менее 11 + 9 тысячныхъ, т.-е.
менее 20 тыс. или 2 сотыхъ. Увеличивъ цыфру сотыхъ
на 1, мы увеличиваемъ сумму на 1 сотую; значить, на
столько же уменынаемъ погрешность; вследаятае этого,
погрешность числа 95,54 менее 2 — 1 сотой, т.-е. ме¬
нее 1 сотой.
Когда слагаемыхъ более 11, но менее 102, то въ
каждомъ изъ нихъ должно отбросить все десятичные
знаки, следующее за гЬмъ разрядомъ, единицы котораго
въ 100 разъ меньше единицы даннаго разряда.
Приближенное вычиташе.
6. Правило. Чтобы получить разность двухъ
десятичныхъ чиселъ съ точностью до одной
единицы даннаго разряда, достаточно от¬
бросить въ данныхъ числахъ все цыфры,
следующая за единицами этого разряда, и
найти разность полученныхъ приближе¬
на.
5,084... Напр., поступая по этому правилу въ дан-
~2,773... номъ примере, получимъ приближенную
2,311 разность 2,311 съ точностью до 0,001.
Объяснен!е. Отбрасывая всф десятичные знаки,
начиная съ 4г-го, мы делаемъ въ каждомъ числе по¬
грешность, меньшую 0,001, и беремъ приближешя оба
съ недостаткомъ. Въ такомъ случае погрешность раз¬
ности, равная разности погрешностей уменыпаемаго и
вычитаемаго, очевидно, меньше 0,001.
7. Правила приближеннаго сложешя и вычитатя
позволяютъ решить следующШ важный въ практиче-
скомъ отношеши вопросъ:
Найти сумму или разность данныхъ при-
ближенныхъ десятичныхъ чиселъ съ воз¬

— 246 —
можно большею точностью и определить
пределъ погрешности.
Пусть, напр., даны числа: 7,358..., 0,0274., и 3,56..,
изъ которыхъ первое точно до ‘/ioooj вт0Р°е Д° 7юоо* и
третье до 1/100; требуется найти ихъ сумму съ наиболь¬
шею точностью. Применяя правило сокращеннаго сло-
жешя, мы легко заметимъ, что сумма можетъ быть
найдена только съ точностью до */10 и потому, производя
сложеше, безполезно брать въ данныхъ числахъ (первомъ
и второмъ) цыфры, стоянця направо отъ цыфры сотыхъ.
Пусть еще требуется найти съ возможно большею
точностью разность чиселъ: 3,1415.. и 2,034.., изъ
которыхъ первое точно до ‘/юооо> а второе до */io*o> и
вба числа взяты съ недостаткомъ. Применяя правило
приближеннаго вычиташя, заметимъ, что разность мо¬
жетъ быть найдена только до '/1С00 (и потому въ пер-
вомъ числе безполезно брать цыфру 5).
Приближенное умножеше.
8.	Правило. Чтобы получить произведете
двухъ десятичныхъ чиселъ съ точностью
до одной единицы даннаго разряда, подпи¬
сываютъ подъ множимымъ цыфры множи¬
теля въ обратномъ порядке (справа налево)
такъ, чтобы цыфра его простыхъ единицъ
стоцла подъ тою цыфрою множимаго, кото¬
рая выражаетъ единицы, въ 100 разъ меньппя
единицы даннаго разряда. Затемъ умножа¬
ютъ множимое на каждую значащую цыфру
множителя, не обращая при этомъвнимашя
на цыфры множимаго, стояния вправо отъ
той цыфры множителя, на которую умножа¬
ютъ. Все эти частныя произведешя подпи¬
сываютъ одно подъ другимъ такъ, чтобы

— 247 —
первыя справа ихъ цыфры стояли въ од-
номъ вертикальномъ столбца, после чего
ихъ складываютъ. Въ сумме отбрасываютъ
две цыфры справа и увеличиваютъ на 1 по¬
следнюю изъ оставшихся цыфръ. Наконецъ,
въ получившемся такимъ образомъ числе
ставятъ запятую такъ, чтобы последняя его
справа цыфра выражала единицы даннаго
разряда.
Правило это требуетъ изменетя въ случаяхъ, о ко¬
торыхъ будетъ сказано ниже.
Прим. Найти произ. 314,159265358... X 74, 63254392G
съ точностью до 0,001.
314,1592658§&- • -
6%934 523647
2199 114855 погрешность	<^7	стотыс.
125 663704	„	<4
18 849552	в	«	<6
942477	„	<3
62830	„	<2
15705	,,	<5
1256	,,	<4	„
93	„	<3	„
27	<9	*
23446,50499
23446,505
Поступая по данному правилу, найдемъ приближен¬
ное произведете 23446,505, точное до 0,001 съ (недо¬
статкомъ или избыткомъ).
Объяснете. Во-1) объяснюсь, что все частныя
произведешя выражаютъ единицы одного и того же
разряда, именно во 100 разъ менышя единицы даннаго
разряда (въ нашемъ примере—стотысячный доли). Дей¬
ствительно, умножая на первую цыфру 7 число 314159265,
мы умножаемъ миллюнныя доли на десятки; значитъ,

— 248
получаемъ въ произведенш стотысячный доли. Да¬
лее, умножая на 4 число 31415926, мы умножаемъ стоты¬
сячный доли на простыя единицы; значить, получаемъ
снова въ произведенш стотысячный доли, и т. д.
Изъ этого следуетъ, что сумма 2344650499 выражаетъ
стотысячный доли, т.-е. она есть число 23446,50499.
Во 2) объяснимъ, что погрешность въ окончатель-
номъ результате менее 0,001.
Действительно, такъ какъ часть множимаго, написан¬
ная направо отъ цыфры 7 множителя, меньше 1 мил-
люнной, то, пренебрегая произведешемъ этой части на
70, мы уменьшаемъ результатъ на число, меньшее 7
стотысячныхъ. Далее, такъ какъ часть множимаго, на¬
писанная направо отъ цыфры 4 множителя, меньше 1
стотысячной, то, пренебрегая произведешемъ этой части
на 4 простыя единицы, мы уменьшаемъ результатъ ва
число, меньшее 4 стотысячныхъ. РаЗсуждая подобнымъ
образомъ относительно всехъ прочихъ цыфръ множи¬
теля, на которыя приходится умножать, заметимъ, что
мы уменьшимъ результатъ на число, меньшее 7 + 4+
+6+3 +2+Б + 4 + 3 + 9 стотысячныхъ. Наконедъ, такъ
какъ множимое меньше 1 тысячи, а часть множителя,
написанная влево отъ множимаго (на которую, след.,
не приходится умножать вовсе) меньше 2 + 1 стимил-
лшнныхъ, то, пренебрегая произведешемъ множимаго
на эту часть множителя, мы еще уменьшаемъ резуль¬
татъ на число, меньшее 2+1 стотысячныхъ. Следова¬
тельно, беря вместо точнаго произведешя число
23446,50499, мы уменьшаемъ первое на число, мень¬
шее (7+4+6+3+2+5+4+3+9)+2+1 стотысячныхъ,
т.-е. вообще меньше 101 стотысячной, если только
сумма цыфръ множителя, на которыя приходится умно¬
жать, увеличенная на первую изъ отбрасываемыхъ его
цыфръ, не превосходить 100 (что въ большинстве

— 249 —
случаевъ и бываетъ *). Кроме того, отбрасывая две
последшя цыфры результата, мы снова уменыпаемъ
произведете на число, не превосходящее 99 стотысяч-
ныхъ. Поэтому все уменьшеше будетъ менее 101-f-99
стотысячныхъ, т.-е. менее 2 тысячныхъ; если же по¬
следнюю цыфру увеличимъ на 1, т.-е. на 1 тысячную,
то результата 23446,505 разнится отъ точнаго произ-
ведешя менее, чемъ на 2—1 тысячной, т.-е. менее
1-й тысячной (причемъ остается неизвесшымъ, будетъ
ли онъ съ избыткомъ или съ недостаткомъ).
Изъ этого объяснешя следуетъ, что данное правило
(известное подъ назвашемъ правила Утрехта) можетъ
быть применяемо безъ всякаго изменешя только тогда,
когда сумма цыфръ множителя, на которыя
приходится умножать, увеличенная на пер¬
вую изъ его отбрасываемыхъ цыфръ, непре-
вышаетъ 100. Когда эта сумма заключается между
100 и 1001, то въ правиле надо сделать два изменешя:
1) цыфру простыхъ единицъ подписывать подъ тою
цифрою множимаго, которая выражаетъ единицы, въ
1000 разъ менышя единицы даннаго разряда, и 2) въ
результате, вместо двухъ, отбросить три последшя
справа цыфры.
Когда же эта сумма не превыщаета 10, то достаточно
написать цыфру простыхъ единицъ множителя подъ тою
цыфрою множимаго, которая выражаетъ единицы, въ 10
разъ менышя единицъ даннаго разряда, и въ результате
отбросить одну цыфру справа:
ЗамЪчаше. Увеличивать на 1 последнюю изъ удер-
жанныхъ цыфръ произведешя не всегда необходимо.
Это нужно было сделать въ разсмотренномъ примере,
потому что тамъ погрешность произведешя (до увеличе-
шя на 1 последней цыфры его) менее суммы
(7—4—J—6—)—3—)—2—J—5—)—4—)—3—}—9) —j—2-|—1 —}—99 стотыс.,
*) Это всегда ингЬетъ ыбсто, если число частный» произведет®
не превосходитъ 10.
17 Заказ № 5456

— 250 —
которая заключается между 100 и 200 стотысячныхъ.
Но если бы отбрасываемый 2 цыфры были не 99, а,
напр., 25, то погрешность произведешя оказалась бы
меньше суммы
(7-j-^6+3+2-f-5-|-4+3-f9)+2+l+2o стотыс.,
т.-е. меньше 71 стотыс., что въ свою очередь меньше
100 стотыс., т.-е. меньше 1 тысячной. Значитъ, тогда
не нужно было бы увеличивать последнюю цыфру на 1.
Въ этомъ случае произведете было бы съ недостат¬
комъ.
9.	Сколько десятичныхъ знаковъ должно
взять въ данныхъ сомножителяхъ, чтобы
получить произведете съ требуемою точ¬
ностью. Въ применепш правила Утрехта мы необра-
щаемъ никакого внимашя на те цыфры множимаго, ко¬
торый стоять вправо отъ множителя, и на те цыфры
множителя, которыя стоять влево отъ множимаго; и те
и друпя мы можемъ совсемъ отбросить. Такимъ обра-
зомъ, во множиыомъ и во множителе нужныхъ цыфръ
должно быть одно и то же число; не трудно заранее
определить, сколько ихъ должно быть, чтобы произве¬
дете было съ заданною точностью. Разъяснимъ это на
примере.
Пусть требуется вычислить до 7юо произведете
1000 т. (|/5—1)
где тт есть отношеше окружности къ диаметру, равное
3, 1415926535... Обращай внимаше на последнее умно¬
жеше, разсуждаемъ такъ: искомое произведете должно
быть вычислено до 1 сотой; значитъ, цыфра простыхъ
единицъ множителя (т.-е. |/ 5—1) должна стоять подъ
4-мъ десятичнымъ знакомь множимаго; съ другой сто¬
роны, во множителе (i/~5—1) нетъ разрядовъ выше
простыхъ единицъ; изъ этого заключаемъ, что больше
4-хъ десят. знаковъ во множичомъ, т.-е. въ 1000 -к
безполезно вычислять. Значить, 1000 -к надо взять

— 251 —
равнымъ 3141,5926; сл'Ьд., и во множителЪ, т.-е. въ
>/5-1, надо вычислить 8 цыфръ. Извлечешемъ нахо¬
димъ, что >/5 = 2,2360679 и сл’Ьд. >/5 — 1 = 1,2360679.
Д,Ьйств1е выполняется такъ:
1000 тс = 3141,592 6
9760 632,1 = >/5—1
3141 592~6
628 318 4
94 247 7
18 849 О
188 4
21 7
2 7
3883 220 5
3883, 22
Пусть еще требуется вычислить it* съ точностью до
0,01. Такъ какъ тс3 = и*-гс, и въ Ц'Ьлой части числа тс
только одна цыфра, то тс* должно вычислить до 4-го
десят. знака. Такъ какъ и*=тс. к, то, для нахождешя
етого произведешя до 4-го десят. знака, надо взять число
* съ 6-ю десят. знаками. ДЬйсше расположится такъ:
71 = 3,141592
9,8696
2 951413
5 1413
9 424776
29 6088
314159
9869'
125660
3944
3141
98
1570
45
279
31 0044
6
31 , 01 =7Г!
9 869591
71*=9,8696
10.	Правило Утрехта позволяетъ решить сл’Ьдуюпцй
вопросъ: найти произведете данныхъ при-
ближенныхъ чиселъ съ возможно большею

— 252 —
точностью и определить пред^лъ погреш¬
ности. Пусть, напр., даны два числа: 25,34627... и
8,3794..., изъ которыхъ первое точно до 1 стотысяч¬
ной, а второе—до 1 десятитысячной, и требуется вы¬
числить ихъ произведете съ возможно большею точ¬
ностью. Напишемъ сначала то число, у котораго всехъ
цыфръ менее, т.-е. 8,3794, а подъ нимъ подпишемъ
въ обратномъ порядке цыфры другого числа такъ, чтобы
цыфра высшаго его разряда приходилась подъ послед¬
нею цыфрою множимаго:
8,37 94
726 43,52
Теперь видимъ, что цыфра простыхъ единицъ множи¬
теля приходится подъ тысячными долями множимаго;
след., по правилу Утрехта, произведете получится съ
точностью до одной единицы, большей тысячной доли
во 100 разъ, т -е. до l/i0 (оно будетъ 212,3 съ не¬
достаткомъ).
Приближенное дележе.
11.	Лемма. Если делителя, болыпаго еди¬
ницы, заменимъ его целою частью, то уве¬
личимъ частное на число, меньшее этого
частнаго, деленнаго на целую часть дели¬
теля.
Для доказательства положимъ, что делимое есть М,
делитель А и дробная часть делителя а. Тогда целая
часть делителя есть А—а и
М	М
точное частное = —з, прибл. частное=
Jx СС
М М МА-МА4-Ма
увеличеше частнаго=2-^ j= (А_а) А --■=
Ма. Ма , .	.
= й--«М=1Г: (^~а)

— 253
Такъ какъ а<1, то Мл М\ поэтому
М
увеличенхе чаетнаго : (А — а),
Л.
т.-е. меньше точнаго чаетнаго, дЬленнаго на цЬлую
часть дЬлителя.
Напр., замЬнивъ дЬлителя 367,28 его цЬлою частью
367, мы сдЬлаемъ ошибку, меньшую 1/п1 точнаго част-
наго.
12.	Правило. Чтобы найти частное двухъ
десятичныхъ чиселъ съ точностью до одной
единицыданнагоразряда, находятъ прежде
всего высшiй разрядъ чаетнаго и затЬмъ
число его цыфръ и. ДалЬе отдЬляютъвъдЬ-
лител'Ь слЬва наименьшее число цыфръ, ка¬
кое потребно для того, чтобы выражаемое
ими число было не меньше числа и, сопро¬
вождаемая п нулями. Остальныя цыфры
дЬлителя отбрасываютъ. Въ дЬлимомъ от-
дЬляютъ сл'Ьва столько цыфръ, чтобы выра¬
жаемое ими число содержало въ себЬ полу¬
ченная делителя менЬе 10 разъ. Осталь¬
ныя цыфры дЬлимаго отбрасываютъ.
РаздЬливъ это дЬлимое на делителя, на¬
ходятъ первую цыфру чаетнаго и зат'Ьмъ
первый остатокъ.
ПослЬ этого дЬлятъ первый остатокъ на
делителя, зачеркнувъ въ послЬднемъ одну
цыфру справа; отъ этого получаютъ вторую
цыфру чаетнаго и зат'Ьмъ второй остатокъ.
Второй остатокъ делить на дЬлителя, за¬
черкнувъ въ немъ еще одну цыфру справа;
отъ этого находятъ третью цыфру чаетнаго
и трет1й остатокъ.

— 254 —
Про должаютъ такъ действ1е до техъ порь
(зачеркивая въ делителе при каждомъ
частномъ делен1и одну цыфру справа), по¬
ка не получатъ всехъ п цыфръ частнаго.
Наконецъ, в”Ъ полученномъ частномъ ста¬
вятъ запятую такъ, чтобы последняя спра¬
ва цыфра выражала единицы даннаго раз¬
ряда.
Пусть, напр., требуется найти съ точностью до 0,01
частное:
31415,92653589	432,6394825...
Такъ какъ делимое больше делителя, умноженнаго
на 10, но меньше делителя, умноженнаго на 100, то
высшШ разрядъ частнаго—десятки. Съ другой стороны,
последняя цыфра въ частномъ должна выражать сотыя
доли, согласно требовант; изъ этого заключаемъ, что
число цыфръ въ частномъ должно быть 4.
Первыя слева цыфры делителя, выражаюиця число,
не меньше 40000, будутъ 43263. Остальныя цыфры
делителя отбрасываемъ. Делимое, согласно правилу, бу¬
детъ 314159. Остальныя цыфры делимаго отбрасыва¬
емъ. Тогда дейстае выполнится такъ:
314159 | 43263
302841	72,61
11318
8652
2666
2592
74
 43
31
Объяснеме. Прежде всего приведемъ вопросъ къ
отыскашю частнаго съ точностью до целой еди¬

— 255 —
ницы, причемъ делитель былъ бы число, не меньшее
40000.
Для этого достаточно:
во-1) увеличить делимое во сто разъ, отчего уве¬
личится во столько же разъ частное, а следов, и по¬
грешность его;
во-2) перенести въ делимомъ и делителе запятую
вправо на одно и то же число цыфръ (отчего частное
не изменится), именно на столько, чтобы делитель сде¬
лался не меныпимъ 40000.
Тогда вопроеъ приводится къ нахождению частнаго:
314159265,3...: 43263,9...
съ точностью до целой единицы.
Заменимъ теперь делителя целою его частью; отъ этого,
по доказанному, мы увеличимъ частное на число, меньшее
этого частнаго, деленнаго на целую часть делителя. Но
частное, содержа въ целой части 4 цыфры, менее 10‘, а
целая часть делителя не меньше 40000, вследсте этого
мы увеличимъ частное на число, меньшее 10‘: 40000,
т.-е. меньшее 7«- Запомнивъ это, будемъ находить частное
314159265,3...: 43263
Чтобы найти число единицъ высшаго разряда част¬
наго, т.-е тысячи, достаточно разделить число тысячъ
делимаго на делителя. Это мы и сделали, получивъ въ
частномъ цыфру 7. Остатокъ отъ точнаго делимаго бу¬
детъ 11318265,3... Этотъ остатокъ должно разделить
на 43263, чтобы пополнить приближенное частное,
определяемое теперь съ точностью до г/4. Разделивъ
оба эти числа на 10, приведемъ вопроеъ къ деленш
1131826,53... на 4326,3.
Это частное имеетъ въ целой части только 3 цыфры;
значить, оно меньше Ю3. Заменивъ делителя целою его
частью, которая более 4000, мы увеличимъ частное на
число, меньшее 103:4000, т.-е. меньшее 7»- Запомнивъ
это, будемъ находить частное 1131826,53...:4326.

— 256 —
Чтобы найти первую цыфру этого чаетнаго, т.-е. сотни,
достаточно число сотенъ делимаго разделить на делителя.
Это мы и сдйлали, получивъ въ частномъ цыфру 2.
Продолжая эти разеуждешя далйе, увидимъ, что при
получеши каждой цыфры чаетнаго мы его увели чиваемъ
на число, меньшее 7*- Такъ какъ вейхъ цыфръ въ ча¬
стномъ 4, то въ результат^ мы увеличимъ частное на
число, меньшее . 1.
Съ другой стороны, не дйля остатка 31.. на послйд-
няго дйлителя 43, мы уменьшаемъ частное на число,
меньшее 1. Значить, мы увеличили его на число, мень¬
шее 1, и уменьшили на число, меньшее 1; слйд., по¬
лученный результатъ, во всякомъ случай, точенъ до1.
Перенеся теперь запятую въ дйлимомъ на прежнее
мйсто, т.-е. раздйливъ его на сто, мы будемъ имйть
частное 72,61, съ точностью до 7юо-
Замйчаше. Приведенное правило и его объяснеше
не требуетъ никакого измйнешя въ томъ частномъ случай,
когда какое-нибудь дйлимое содержитъсоотвйтствующаго
дйлителя 10 разъ. Тогда ставимъ въ частномъ число 10
(въ скобкахъ). Продолжая дйлеше, увидимъ, что вей слй-
дуюцуя цыфры чаетнаго должны быть нули. Пусть, напр.,
требуется найти частное 485172,923...: 78,254342... съ
точностью до 1. Примйняя правило, найдемъ:
485172 | 78254 Третье дйлимое (7823) содержитъ
469524	61(10)0 соотвйтствующаго дйлителя (782)
15648	6200	десять разъ; пишемъ въ частномъ
7825	число 10. Слйдующая цыфра въ
7823	частномъ оказалась 0. Искомое част-
7820	ное есть число 61 (10)0, т.-е. 6200.
3~
Въ этомъ случай приближенное частное
больше точнаго чаетнаго. Дййствительно, цыф¬
ры чаетнаго, найденный раньше, чймъ представился
этотъ случай, не могутъ быть меньше, чймъ бы слй-

— 257 —
довало, такъ какъ мы при каждомъ частномъ деленш
брали делителей, которые меньше точнаго делителя.
Значитъ, первыя две цыфры точнаго частнаго должны
выражать число, не больше 61, поэтому оно меньше
числа 6200.
13.	Правило сокращеннаго делешя позволяетъ решить
следующШвопросъ: найти частное отъ д е л е н i я
данныхъ приближенныхъ десятичныхъ чи¬
селъ съ возможно большею степенью точ¬
ности и определить пределъ погрешности.
Пусть, напр., даны два числа: 56, 42375... и 6,237..., изъ
которыхъ первое точно до 1 стотысячной, а второе—до 1
тысячной, и требуется найти частное отъ делешя пер-
ваго на второе съ возможно большею точностью. Раз¬
суждаемъ такъ: предположимъ, что, применяя правило
сокращеннаго делешя, мы могли бы въ частномъ найти 4
цыфры. Тогда делитель долженъ быть больше 40000.
Но въ нашемъ делителе не дано достаточнаго числа
цыфръ, чтобы можно было образовать (по правилу деле¬
шя) число, большее 40000. Значитъ, 4-хъ цыфръ въ
частномъ получить мы не можемъ. Посмотримъ, можемъ
ли получить 3 цыфры. Тогда делитель долженъ быть
более 3000. Изъ нашего делителя мы можемъ образо¬
вать число, большее 3000; это будетъ 6237. Съ другой
стороны, и изъ нашего делимаго мы можемъ образовать
число, большее 6237. Значитъ, цы можемъ найти въ
частномъ 3 цыфры, не более. Такъ какъ высшШ раз-
рядъ частнаго, очевидно, простыя единицы, и всёхъ
цыфръ въ немъ 3, то оно будетъ точно до '/100.
Если бы делимое было только 66,42, а делитель
прежшй 6,236, то тогда мы не могли бы получить въ
частномъ и 3-хъ 'цыфръ, потому что въ делимомъ не
дано достаточнаго числа цыфръ, чтобы изъ нихъ обра¬
зовать число, большее 6237. Въ этомъ случае мы мог¬
ли бы найти только 2 цыфры частнаго. Действительно,

— 258
тогда, делитель долженъ быть более 200, т.-е. 623, а
делимое более 623, что возможно.
14.	ПримЬромъ примЬнешя предыдущихъ правилъ можетъ
служить следующая задача.
Задача. Вычислить съ точностью до одной
сотой выражеше:
j/348 —1/127
Х~ |/2 + j/3 + |/б — |/12
Это выражеше есть частное; поэтому прежде всего опре-
делимъ, сколько должно быть цыфръ въ этомъ частномъ,
а для этого надо знать высшш разрядъ его. Начавъ извле¬
чете |/348 и |/127, мы увидимъ, что первый корень въ
целой своей части содержитъ 18, а второй 11; след., чис¬
литель равенъ приблизительно 7; знаменатель равенъ при¬
близительно 2. Значитъ, высппй разрядъ въ частномъ—про¬
стыя единицы. Такъ какъ частное требуется вычислить до
сотыхъ долей, то въ немъ должно быть 3 цыфры. Поэтому
знаменатель мы должны вычислить настолько точно, чтобы
изъ него можно было (по правилу сокращеннаго дЬлешя)
образовать число, большее 3000, для чего достаточно вы¬
числить 5 его цыфръ, а для этого необходимо (по правилу
сокращеннаго сложетя) найти отдельные корни знаменателя
съ 6-ю цифрами. Производя извлечете, найдемъ:
}/2=1,41421; ]/3=1,73205; |/б=2,23606; j/l2=3,46410
и затемъ: у/2	|/3 -)- |/5 — |/12 = 1,9183 (до 7twoo)*
Теперь надо вычислить числителя съ такою точностью,
чтобы изъ первыхъ его цыфръ можно было образовать число,
большее 19183. Такъ какъ числитель равенъ приблизительно
7, то сверхъ целаго числа въ немъ потребуется вычислить
еще 4 десятичные знака, а такъ какъ числитель есть раз¬
ность, то уменьшаемое и вычитаемое надо вычислить также
до 4-го десятичнаго знака. Извлечешемъ ваходимъ:
|/348=18,6547	|/127=11,2694
j/348 — |/127=7,3853
Остается разделить по правилу сокращеннаго дЪлетя 73853
на 19183, посл'Ь чего получимъ
0=3,85 (до 71в0).

— 259 —
Задачи:
1. Вычислить до ‘/100 выражеше у=ах*-\-Ьх, если а—
—2,71856.., 6=1,605043.. и ж=0,04271...
2. При тЬхъ же вадашяхъ вычислить съ наибольшею точ¬
ностью выражеше:
ахА-1
У Ь-\-х
3. Вычислить до V10000 выражеше Vй-
тс
4. Вычислить -—'7; съ 13 десятичными знаками.
u4oUU
5. Вычислить до Vioo произведете
■к.37,54832709.637,8324926.
6. Прямоугольникъ им^етъ измерешями: 6=38,32... и
6=6,687... Вычислить его площадь съ возможно большею
точностью и указать предЬлъ погрешности.
7. Вычислить съ точностью до 1 миллиметра окружность,
описанную около квадрата:, котораго сторона равна 1 метру.
8. Вычислить до 0,001 выражеше:
11	1
2+ — -+-	h Ч
1.2 ~ 1.2.3.	1.2.3.4.5.6.7.
9. Вычислить съ 6-ю десятичными знаками сторону квад¬
рата, равновеликаго кругу, котораго рад^усъ равенъ 1.
10. Вычислить до 0,001 выражеше 1^2,5 — |/1,25
Указанге. По правиламъ алгебры» чтобы найти приближен¬
ное значеше квадр. корня съ точностью до 1/п, надо умно¬
жить подкоренное число ва п*, изъ полученнаго произведе¬
шя извлечь корень съ точностью до 1 и результатъ разде¬
лить на п. След., вопросъ приводится къ вычисление выра¬
жешя:
j/2500000 — ЮООООО^/ТЖ
съ точностью до 1. Для этого достаточно извлечь корень
съ точностью до 1 изъ цгьлой части подкоренного числа.
Итакъ, разность 2500000—1000000 у/1,25 надо вычислить
до 1; значитъ, вычитаемое надо вычислить тоже до 1; по¬
этому |/ 1,25 придется находить до 1 миллюнной.

— 260 —
IX. Таблица простыхъ чиселъ,
НЕ ПРЕВОСХОДЯЩИХЪ 6000.
2
179
419
661
947
1229
1523
1823
2131
3
181
421
673
953
1231
1531
1831
2137
5
191
431
677
967
1237
1543
1847
2141
7
193
433
683
971
1249
1549
1861
2143
11
197
439
691
977
1259
1553
1867
2153
13
199
443
701
983
1277
1559
1871
2161
17
211
449
709
991
1279
1567
1873
2179
19
213
457
719
997
1283
1571
1877
2203
23
227
461
727
1009
1289
1579
1879
2207
29
229
463
733
1013
1291
1583
1889
2213
31
233
467
739
1019
1297
1597
1901
2221
37
239
479
743
1021
1301
1601
1907
2237
41
241
487
751
1031
1303
1607
1913
2239
43
251
491
757
1033
1307
1609
1931
2243
47
257
499
761
1039
1319
1613
1933
2251
53
263
503
769
1049
1321
1619
1949
2267
59
269
509
773
1051
1327
1621
1951
2269
61
271
521
787
1061
1361
1627
1973
2273
67
277
523
797
1063
1367
1637
1979
2281
71
281
541
809
1069
1373
1657
1987
2287
73
283
547
811
1087
1381
1663
1993
2293
79
293
557
821
1091
1399
1667
1997
2297
83
307
563
823
1093
1409
1669
1999
2309
89
311
569
827
1097
1423
1693
2003
2311
97
313
571
829
1103
1427
1697
2011
2333
101
317
577
739
1109
1429
1699
2017
2339
103
331
587
853
1117
1433
1709
2027
2341
107
337
593
857
1123
1439
1721
2029
2347
109
347
599
859
1129
1447
1723
2039
2351
113
349
601
863
1151
1451
1733
2053
2357
127
353
607
877
1153
1453
1741
2063
2371
131
359
613
881
1163
1459
1747
2069
2377
137
367
617
883
1171
1471
1753
2081
2381
139
373
619
887
1181
1481
1759
2083
2383
149
379
631
907
1187
1483
1777
2087
2389
151
383
641
911
1193
1487
1783
2089
2393
157
389
643
919
1201
1489
1787
2099
2399
163
397
647
929
1213
1493
1789
2111
2411
167
401
653
937
1217
1499
1801
2113
2417
173
409
659
941
1223
1511
1811
2129
2423

261 —
2437
2833
3259
3659
4073
4507
4943
5393
5801
2441
2837
3271
3671
4079
4513
4951
5399
5807
2447
2843
3299
3673
4091
4517
4957
5407
5813
2459
2851
3301
3677
4093
4519
4967
5413
5821
2467
2857
3307
3691
4099
4523
4969
5417
5827
2473
2861
3313
3697
4111
4547
4973
5419
5839
2477
2879
3319
3701
4127
4549
4987
5431
5843
2503
2887
3323
3709
4129
4561
4993
5437
5849
2521
2897
3329
3719
4133
4567
4999
5441
5851
2531
2903
3331
3727
4139
4583
5003
5443
5857
2539
2909
3343
3733
4153
4591
5009
5449
5861
2543
2917
3347
3739
4157
4597
5011
5471
5867
2549
2927
3359
3761
4159
4603
5021
5477
5869
2551
2939
3361
3767
4177
4621
5023
5479
5879
2557
2953
3371
3769
4201
4637
5039
5483
5881
2.579
2957
3373
3779
4211
4639
5051
5501
5897
2591
2963
3389
3793
4217
4643
5059
5503
5903
2593
2969
3391
3797
4219
4649
5077
5507
5923
2609
2971
3407
3803
4229
4651
5081
5519
5927
2617
2999
3413
3821
4231
4657
5087
5521
5939
2621
3001
3433
3823
4241
4663
5099
5527
5953
2633
зон
3449
3833
4243
4673
5101
5531
5981
2647
3019
3457
3847
4253
4679
5107
5557
5987
2657
3023
3461
3851
4259
4691
5113
5563
2659
3037
3463
3853
4261
4703
5119
5569
2663
3041
3467
3863
4271
4721
5147
5573
2671
3049
3469
8877
4273
4723
5153
5581
2677
3061
3491
3881
4283
4729
5167
5591
2683
3067
3499
3889
4289
4733
5171
5623
2687
3079
3511
3907
4297
4751
5179
5639
2689
3083
3517
3911
4327
4759
5189
5641
2693
3089
3527
3917
4337
4783
5197
5647
2699
3109
3529
3919
4339
4787
5209
5651
2707
3119
3533
3923
4349
4789
5227
5653
2711
3121
3539
3929
4357
4793
5231
5657
2713
3137
3541
3931
4363
4799
5233
5659
2719
3163
3547
3943
4373
4801
5237
5669
2729
3167
3557
3947
4391
4813
5261
5683
2731
3169
3559
3967
4397
4817
5273
5689
2741
3181
3571
3989
4409
4831
5279
5693
2749
3187
3581
4001
4421
4861
5281
5701
2753
3191
3583
4003
4423
4871
5297
5711
2767
3203
3593
4007
4441
4877
5303
5717
2777
3209
3607
4013
4447
4889
5309
5737
2789
3217
3613
4019
4451
4903
5323
5741
2791
3221
3617
4021
4457
4909
5333
5743
2797
3229
3623
4027
4463
4919
5347
5749
2801
3251
3631
4049
4481
4931
5351
5779
2803
3253
3637
4051
4483
4933
5381
5783
2819
3257
3643
4057
4493
4937
5387
5791

0ГЛАВЛЕН1Е.
Цыфры означаютъ нумера страницъ.
Передъ статьями, напечатанными мелкимъ шрифтомъ, постановлена
ввЬздочка.
Иредислов1е стр. 111.
О Т Д Ъ Л Ъ I.
Отвлеченный цЪлыя числа.
L Счислеше. Пошше о числЬ, 1. Естественный рядъ чиселъ, 1.
Счетъ, 2. Словесное счисленie до тысячи, 2. Письменное счислеше
до тысячи, 3. Словесное счислеше чиселъ, большихъ тысячи, 4.
Письменвое счислеше чиселъ, большихъ тысячи, 4. Разряды и классы
единицъ, 6. Сколько въ числЬ заключается всЬхъ единицъ даннаго
разряда, -7. *Различныя системы счислешя, 7.
II. Сложен1е. ОпредЪлеше, 10. Основное свойство суммы, 11. Сложе-
Bie двухъ одновначныхъ чиселъ, И. Сложеше двузначнаго числа съ
однозпачнымъ, 11. Сложение многозначныхъ чиселъ, 11. Сложеше
большого числа слагаемыхъ, 13. Увеличеше числа на другое число, 14.
III. Вычиташе. ОпредЬлеше, 14. Вычиташе одвозначваго числа, 15.
Вычитате многозначнаго числа, 15. ПовЬрка вычиташя, 17. Умень-
шев!е числа ва другое число, 17. Сравнеше двухъ чиселъ, 18. Обратыыя
дЬйстшя. 18.
IV. Славянсная и римская иумеращя, 18.
V. ИзмЬнеше суммы и остатка, 20
VI. Знаки дЬйствм, скобки, формулы, 22.
VII. Умножеше. ОпредЬлешя и разъяснешя, 24. Увеличеше числа
въ нисколько разъ, 26. НеизмЪняемость произведен1я отъ перемены
мЬстъ сомножителей, 26. Умножеше однозначнаго числа ва одно¬
значное, 27. Умножев1е многозначнаго числа на однозначное, 26.
Умвожеше на единицу съ вулями, 29. Умножеше на значащую цыфру
съ нулями, 30. Умножеше на многозначное число, 31. Умножеше
чиселъ, оканчивающихся нулями, 33. Умножеше въ порядк’Ь, обрат-
номъ принятому, 34. ПовЬрка умножешя, 35 Произведете вЬсколь-
кихъ сомножителей, 35 Какъ умножить на произведете нЬсколькихъ
чиселъ, 37. Сомножителей произведешя можно соединять въ группы,
38 Степень, 39.
VIII ДЬлеше. Предварительное за мЬ чаше. 39. ОпредЬлеше, 40. Свой¬
ство частнаго, 41. ДЬлеше съ остаткомъ, 41. Когда употребляетсн
дЬлеше, 43. ДЬлеше посредствомъ сложев1я. вычиташя и умножешя.
44 Какъ узнать, будетъ ли частное однозначное или многозначное.
45. Частное однозначное, 45. Частное многозначное. 48. Другое объ-
яснеше дЬлешя, 50. Правило дЬлешя, 51. Сокращенное дЬлеше. 51.
Упрощешя дЬлешя въ томъ случаЬ, когда дЬлитель оканчивается
нулями, 52. ПонЬрка дЬлешя, 54. Какъ можно раздЬлить ва произ¬
ведете, 54.
IX. ИзиЬнен1е произведешя и частнаго, 55.

— 263 —
ОТДЪЛЪ II.
Именованный целый числа.
I. ИзмЬрвше велнчинъ. Понят1е о величинЬ, 60. Значеше величины
61. ИзмЬреше значешя величины, 61. МЬры, употребляемый въ Ро<>
era, 62. Имевованное число, 72.
II. Преобразовало именованнаго числа. Раздроблеше, 72. Превраше-
Hie 73.	^
III. ДЬйств'ш надъ именованными числами. "Смыслъ дЬйств!й иадъ
именованными числами, 75. Сложеше, 76. Вычитан!е, 77. Умноже-
Bie, 78. ДЬлеше, 79.
IV. Задачи на вычислена времени. 81. Точный счетъ времени, 86.
О Т Д -В Л Ъ III.
О делимости чиселъ.
I. Признаки дЬлкмости. Основныя истины, 90. Пригнакъ делимости
на 2, 91. Признака дЬлимости на 4, 92. Признакъ делимости на 8, 92.
Признаки делимости на 5 и на 10, 93. Признаки делимости на 3 и
на 9, 93. Признаки дЬлимости на 6, 94. "Теоремы, 96. *Лризнаки
дЬлимости на 7, 11 и на 13, 98. "Признакъ дЬлимости на 37, 99.
II. Числа простыя и составныя. ОпредЬлешя, 100. *Теоремы, 101.
"Составлеше ряда послЬдовательныхъ простыхъ чиселъ. 101.
III. О дЬлителяхъ составного числа. Разложеше на простыхъ множи¬
телей 102. "Важное свойство разложешя, 104. Нахождев1е дЬлителей
составного числа, 105. "Теорема, 106.
IV. ОбщШ наиболышй делитель. ОпредЬлеше, 107. Способъ 1-й: по¬
средствомъ разложешя на простыхъ множителей, 107. Способъ 2-й
посредствомъ послЬдовательнаго дЬлешя, 108.
V. Наименьшее кратное число. ОпредЬлеше, 111. Частные случаи,
113. Нахождеше наименьшего кратнаго при помощи общаго наиболь¬
шего дЬлителя, 114.
О Т Д -В Л Ъ IV.
Обыкновенный Дроби.
I. Основныя понят1я. Доли единйцъ, 115. Дробное число, 115. Изо-
Сражеше дроби, 116. Происхождеше дробныхъ чиселъ отъ измЬре-
шя, 116 11роисхождев1е дробныхъ чиселъ отъ дЬлешя, 117. Равенство
и неравенство дробныхъ чиселъ, 117. Дробь правильная и непра¬
вильная, 118. Обращеше цЬлаго числа въ дробь. 118. Обращеше
смЬшаннаго числа въ неправильную дробь, 119. Обращеше непра¬
вильной дроби въ смЪшанное число, 119.
II. ИзмЬнен1е величины дроби съ измЬнемемъ ея члеяовъ, 120.
Ill Сокращен^ дробей, 122.
IV. Приведете дробей нъ общему знаменателю, 124.
V. Нахожден1е дроби даннаго числа « обратный вопросъ, 127.
VI. ДЬйств1я надъ обыкн отвлечен, дробями. Сложеше. 130. Вычита-
ше, 132. ИзмЬнеше суммы и разности 133 Умножеше, 134. Дьле-
ше, 139. ИзмЬненш произведевГя н частнаго, 145.
VII. ДЬйств1я надъ именованными дробями, 147.

— 264 —
О Т Д Ъ Л Ъ V.
Десятичныя дроби.
I. ГлавнЪйш1я свойства десятичиыхъ дробей. Десятичныя доли, 151.
Десятичная дробь, 151. Изображете десятичной дроби безъ знамена¬
теля. 152. Чтев1е десятичной дроби,153. Сравнев1е десятичныхъ дробей,
154. Перенесев1е запятой, 155.
II. ДЬйств1я надъ десятичными дробями. Сложеше, 156. Вычитание,
157. Умножеше, 157. ДЬлеше, 158.
III. 0бращен1е обыкновенныхъ дробей въ десятичныя, 162.
IV. 0бращен1е пер1одичеснихъ дробей аъ обыкновенные, 167. Кашя
обыкновенныя дроби обращаются въ чистыя першдичбскш и кашя—
въсмЬшанныя, 171.*ПредЬлы першдичоскихъ десятичныхъ дробей, 172.
V. Метричесная система мйръ, 175.
О Т Д Ъ Л Ъ VI.
Отношеше и пропорщя.
I. Отношен1е. ОпредЬлеше, 180. Зависимость между членами отно¬
шешя, 181. Нахождете неизвЬстнаго члена, 181. Сокращеше отно-
шев1я, 182. Уничтожеше дробныхъ членовъ, 182. Обратный отно¬
шешя, 182.
II. Пропорщя.- ОпредЬлеше, 183. *ИзмЬнете членовъ пропорщи
беэъ нарушен1я ея, 183. *Сокращете пропорщи, 184. *1 ничтожете
дробныхъ членовъ, 184. Произведете крайнихъ равно произведенш
среднихъ и обратное предложеше, 185. Нахождете неизвЬстнаго
члена, 187. Перестановки членовъ пропорцш, 187. Непрерывная
пропорщя, 188. Сложныя пропорщи, 189. Производныя пропорщи, 190.
О Т Д -В Л Ъ VII.
НЪкоторыя задачи на пропорцюнальныя величины.
I. Простое тройное правило, 192.
II. Сложное тройное правило, 197.
III. Задачи на проценты, 199.
IV. Задачи на учетъ векселей, 205. ‘Правило сроковъ, 211.
V. ЦЬлное правило, 212.
VI. Правило лропорц1ональнаго дЬлен1я, 214.
VII. Задачи на смЪшен1е и сплавы, 221.
ПРИЛОЖЕНА.
Приближенный вычислешя, 228. Таблица простыхъ чиселъ, не пре-
восходящихъ 6000, 248.
Оглавлеше, 250.