Author: Иванов Г.С.
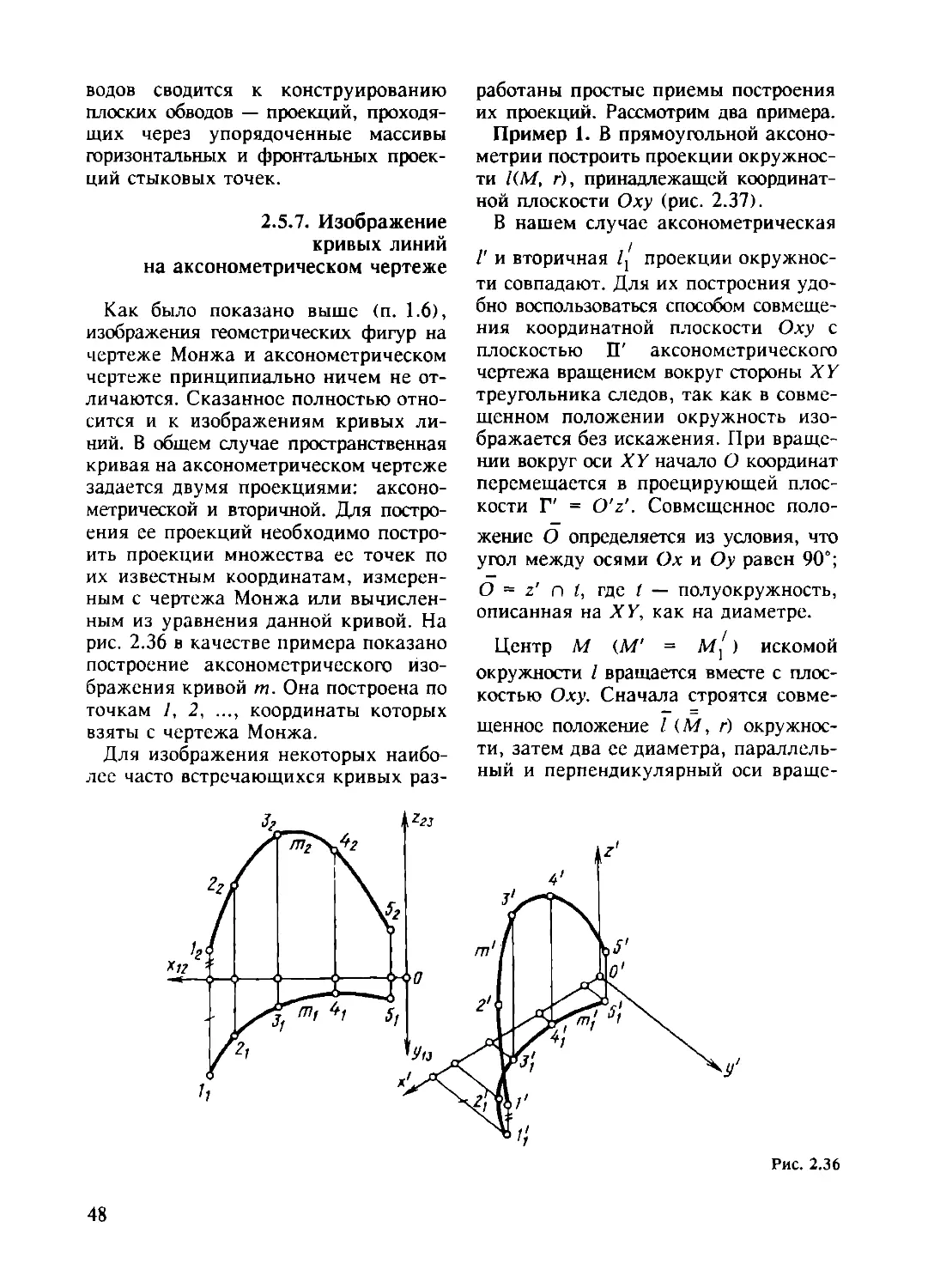
Tags: математика геометрия топология черчение инженерная графика
ISBN: 5-217-02058-Х
Year: 1995
Text
Г. С. ИВАНОВ
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ
Рекомендовано Государственным комитетом
Российской Федерации по высшему образованию
в качестве учебника для студентов
высших технических учебных заведений
Москва «Машиностроение» 1995
ББК 22.151.3я73
И 20
УДК 515(075)
Рецензент проф. С.А. Фролов
Иванов Г.С.
И20 Начертательная геометрия: Учебник для вузов. М.: Машино-
строение, 1995. — 224 с.; ил.
ISBN 5-217-02058-Х
В учебнике дано подробное наложение теории построения обратимых изобра-
жений трехмерного пространства, а именно чертежей основных геометрических
фигур, способов преобразования изображений, теории и способов решений
позиционных и метрических задач.
Предназначен для студентов машиностроительных специальностей вузов.
И ^2^0000Ч)22 523^5
038(01)-95
ББК 22.151.3я73
Издание выпущено в счет дотации, выданной Комитетом РФ по печати.
ISBN 5-217-02058-Х © Издательство "Машиностроение” 1995
Оглавление
Предисловие.............................................................6
Принятые обозначения....................................................8
Глава 1. Начертательная геометрия, ее предмет и основной метод......... 10
1.1. Проецирование — конструктивный способ отображения
пространства на плоскость ........................................ 10
1.1.1. Центральное проецирование и его свойства ............ 11
1.1.2. Параллельное проецирование и его свойства ........... 12
1.1.3. Прямоугольное проецирование и его свойства........... 13
1.2. Требования, предъявляемые к чертежу ........................ 14
1.3. Метод двух изображений моделирования пространства .......... 15
1.4. Чертеж Монжа — основной вид обратимого изображения.......... 16
1.4.1. Двухкартинный чертеж Монжа........................... 16
1.4.2. Трехкартинный чертеж Монжа........................... 17
1.5. Аксонометрия — вид наглядного обратимого изображения ....... 18
1.5.1. Основные понятия и определения ...................... 18
1.5.2. Прямоугольная аксонометрия и ее свойства .............20
1.6. Сравнение свойств чертежа Монжа и аксонометрии ..............21
1.7. Другие виды обратимых изображений............................22
1.7.1. Перспектива ..........................................23
1.7.2. Проекции с числовыми отметками........................23
1.7.3. "Федоровские” векторные чертежи.......................24
1.7.4. Циклография Фидлера—Федорова..........................24
Упражнения и вопросы для самопроверки ............................25
Глава 2. Основные геометрические образы. Изображение их
на чертеже...............................................................26
2.1. Задание прямой линии на чертеже .............................26
2.1.1. Прямые частного положения.............................26
2.1.2. Следы прямой .........................................28
2.1.3. Взаимное положение двух прямых........................29
2.2. Задание плоскости на чертеже. Родство........................30
2.2.1. Плоскости частного положения .........................31
2.2.2. Следы плоскости ......................................33
2.3. Аналитическое задание прямых и плоскостей....................33
2.3.1. Уравнения плоскостей общего и частного положения......34
2.3.2. Уравнения прямых общего и частного положения .........34
2.3.3. Задачи на определение взаимного положения точек,
прямых и плоскостей ................................. 35
2.4. Многогранники ...............................................35
2.4.1. Основные понятия и определения ..................... 35
2.4.2. Изображение многогранников на чертеже.................36
2.5. Кривые линии и обводы....................................... 37
2.5.1. Основные понятия и определения .......................37
2.5.2. Конические сечения. Прямоугольная проекция
окружности........................................... 40
2.5.3. Пространственные кривые и свойства их проекций........42
2.5.4. Цилиндрическая винтовая линия.........................43
2.5.5. Обводы............................................... 44
2.5.6. Практические способы построения обводов...............45
2.5.7. Изображение кривых линий на аксонометрическом
чертеже.............................................. 48
2.6. Поверхности ................................................ 49
2.6.1. Основные понятия и определения .......................50
2.6.2. Поверхности параллельного переноса....................53
2.6.3. Поверхности вращения..................................57
2.6.4. Винтовые поверхности .................................61
2.6.5. Линейчатые поверхности .............................. 64
3
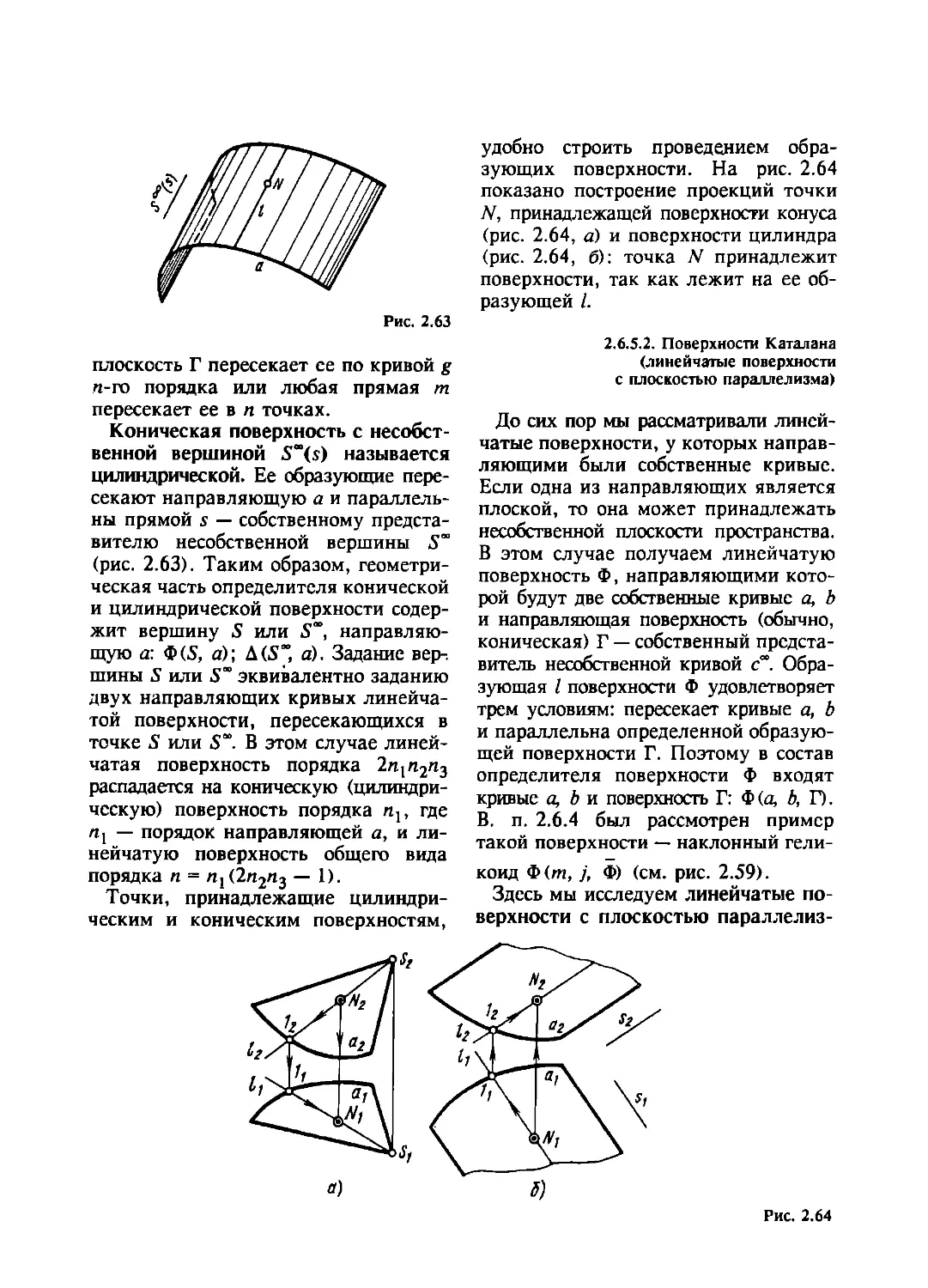
2.6.5.1. Конические и цилиндрические поверхности ......65
2.6.5.2. Поверхности Каталана (линейчатые поверх-
ности с плоскостью параллелизма)......................66
2.6.5.3. Инженерный способ задания линейчатых
поверхностей ..........................................68
2.6.5.4. Торсовые поверхности..........................69
2.6.5.5. Вывод уравнений линейчатых поверхностей ......70
2.6.6. Циклические поверхности................................71
2.6.7. Поверхности зависимых сечений..........................74
Упражнения и вопросы для самопроверки...........................75
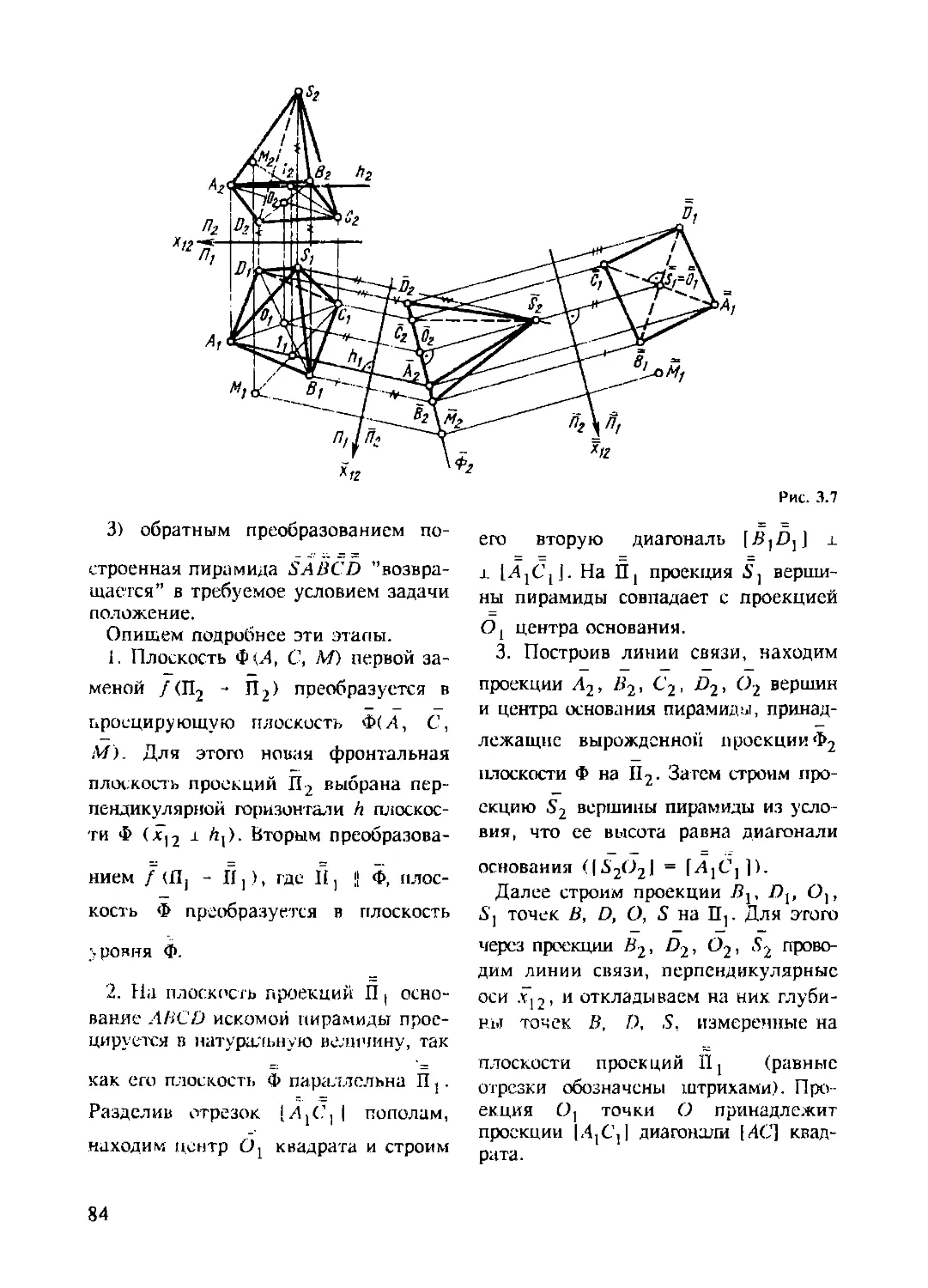
Глава 3. Способы преобразования чертежа ................................78
3.1. Основные понятия и определения................................78
3.2. Способ замены плоскости проекций..............................79
3.2.1. Алгоритм замены плоскостей проекций ...................80
3.2.2. Алгоритмы решения основных задач ......................81
3.3. Способ плоскопараллельного движения ..........................85
3.3.1. Алгоритмы решения основных задач ......................86
3.4. Способ вращения вокруг проецирующей прямой....................88
3.4.1. Алгоритмы решения основных задач ......................88
3.4.2. Выводы................................................ 90
3.5. Способ вращения вокруг прямой уровня .........................91
3.5.1. Способ совмещения .....................................92
3.6. Способ дополнительного проецирования..........................92
3.7. Способы преобразования аксонометрического чертежа.............95
3.7.1. Способ совмещения .....................................95
3.7.2. Способ замены плоскости проекций.......................97
Упражнения и вопросы для самопроверки...............................98
Глава 4. Теория и алгоритмы решения позиционных задач ............99
4.1. Классификация позиционных задач ........................99
4.1.1. Положение фигуры относительно плоскостей
проекций..................................................... 100
4.1.2. Взаимное положение двух фигур........................ 101
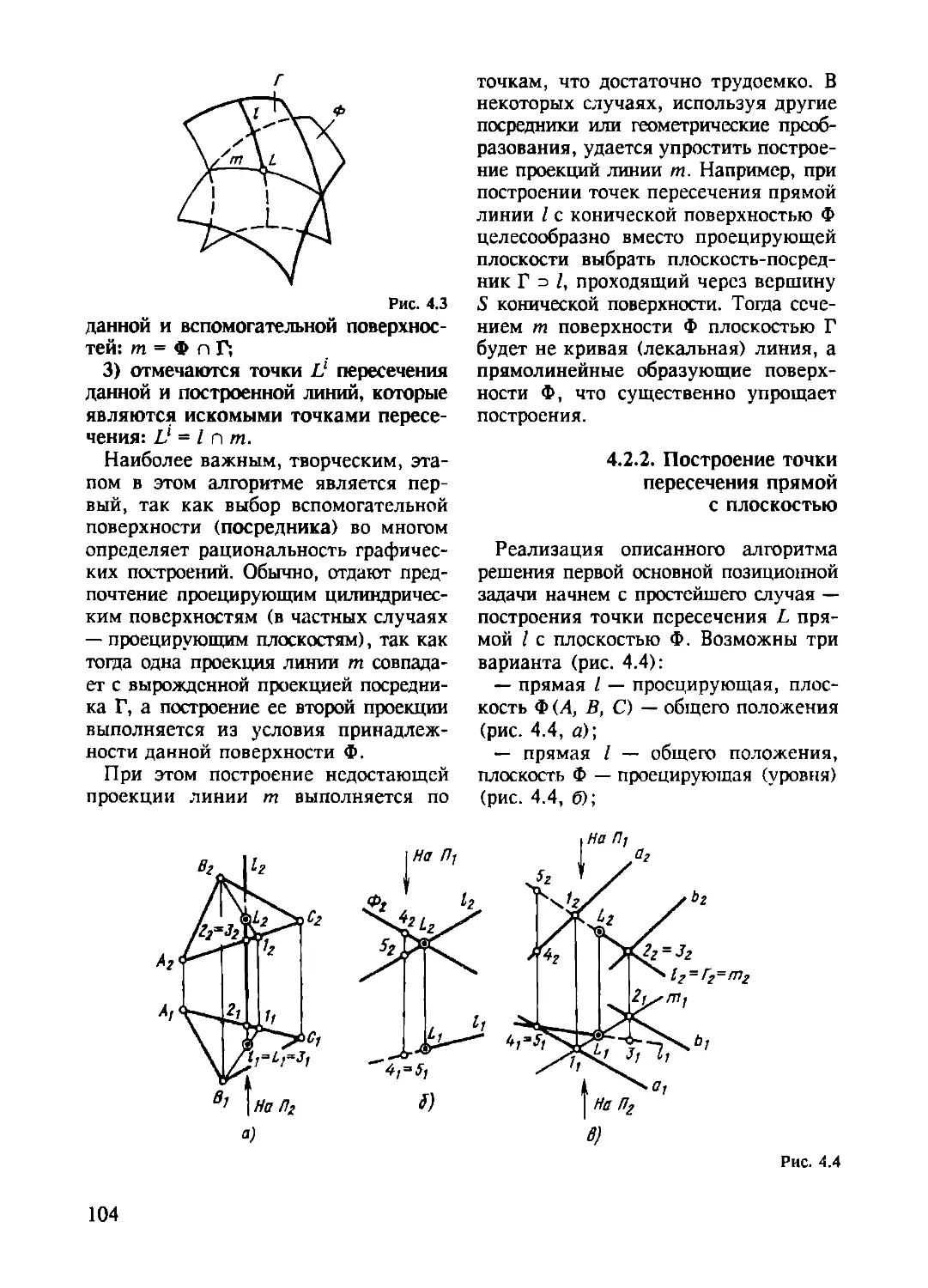
4.2. Построение точек пересечения линии с поверхностью............ 103
4.2.1. Алгоритм решения первой основной позиционной
задачи...................................................... 103
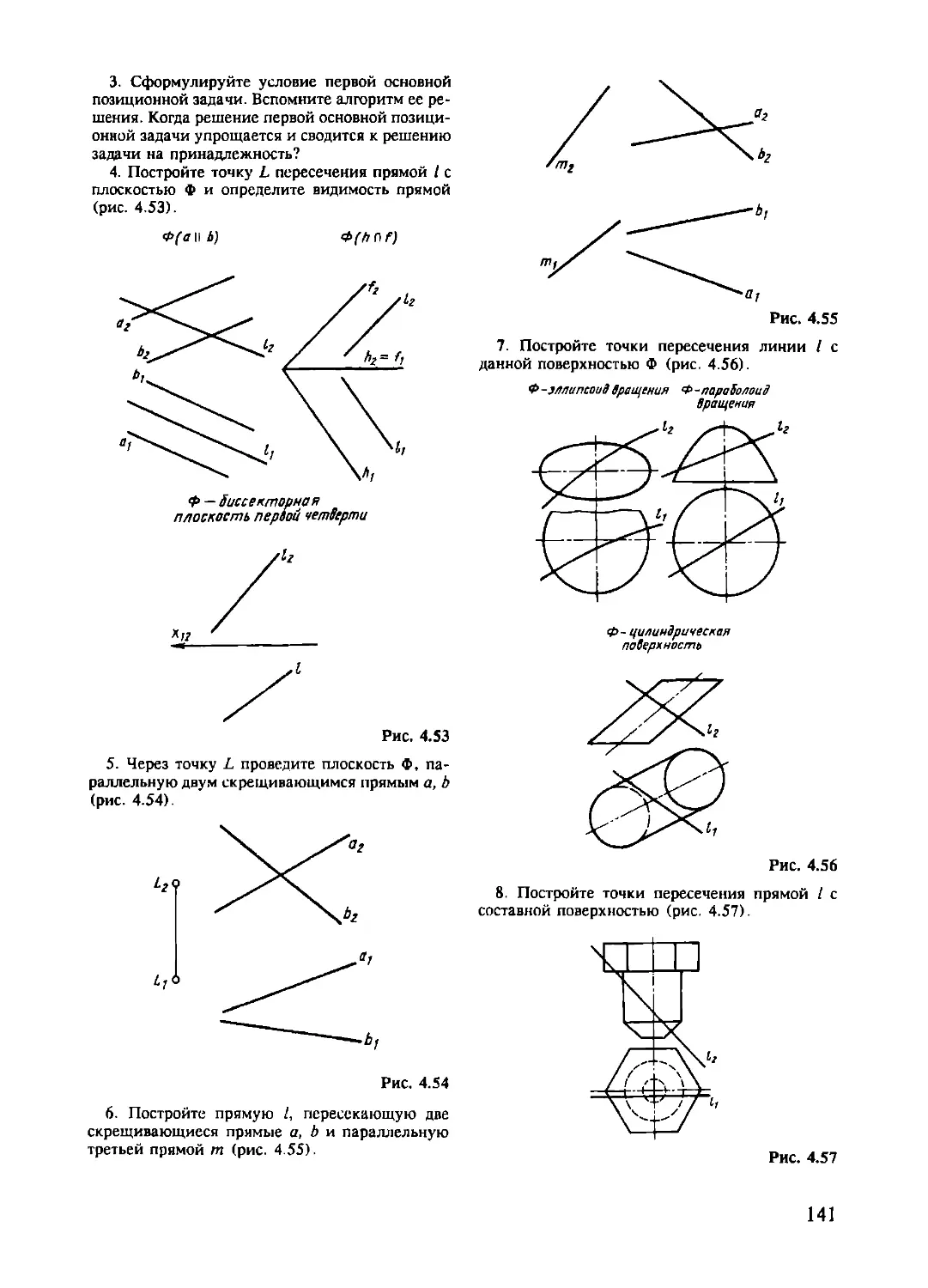
4.2.2. Построение точки пересечения прямой с плоскостью...... 104
4.2.2.1. Параллельность прямой и плоскости........... 106
4.2.3. Построение точек пересечения линии с поверхностью .... 107
4.2.4. Построение точек пересечения линии с составной
поверхностью................................................. 108
4.3. Алгоритм построения линии пересечения поверхностей........... 110
4.4. Способ вспомогательных плоскостей .......................... 111
4.4.1. Построение линии пересечения двух плоскостей.......... 112
4.4.1.1. Параллельность двух плоскостей ............. 114
4.4.2. Сечение многогранника плоскостью...................... 115
4.4.3. Построение линии пересечения поверхностей двух
многогранников............................................... 116
4.5. Способ плоскостей уровня .................................... 119
4.5.1. Сечение поверхности плоскостью........................ 120
4.5.2. Построение линии пересечения двух поверхностей ....... 122
4.6. Способ вращающейся плоскости................................. 122
4.7. Способ вспомогательных сфер.................................. 125
4.7.1. Способ концентрических сфер........................... 126
4.7.2. Способ эксцентрических сфер........................... 128
4.8. Аналитические алгоритмы решения задач на пересечение......... 129
4.9. Случаи распадения линии пересечения поверхностей............. 132
4.10. Касание — частный случай пересечения ........................ 134
4.10.1. Касание линии и поверхности.......................... 135
4.10.2. Касание поверхностей в точке......................... 135
4.10.3. Касание поверхностей вдоль линии .................... 139
Упражнения и вопросы для самопроверки.......................... 140
4
Глава 5. Теория и алгоритмы решения метрических задач ............... 144
5.1. Классификация метрических задач............................ 144
5.2. Определение натуральной величины отрезка .................. 146
5.3. Перпендикулярность прямых и плоскостей..................... 147
5.31. Перпендикулярность прямой и плоскости............... 149
5.3.2. Перпендикулярность двух плоскостей.................. 150
5.3.3. Построение нормали поверхности ..................... 151
5.4. Линии наибольшего наклона.................................. 152
5.4.1. Линии наибольшего наклона плоскости ................ 152
5.4.2. Линии наибольшего наклона поверхности............... 154
5.5. Алгоритмы решения типовых метрических задач ............... 155
5.5.1. Положение фигуры относительно плоскостей
проекций............................................. 155
5.5.2. Метрика фигуры ..................................... 160
5.5.3. Взаимное положение фигур............................ 162
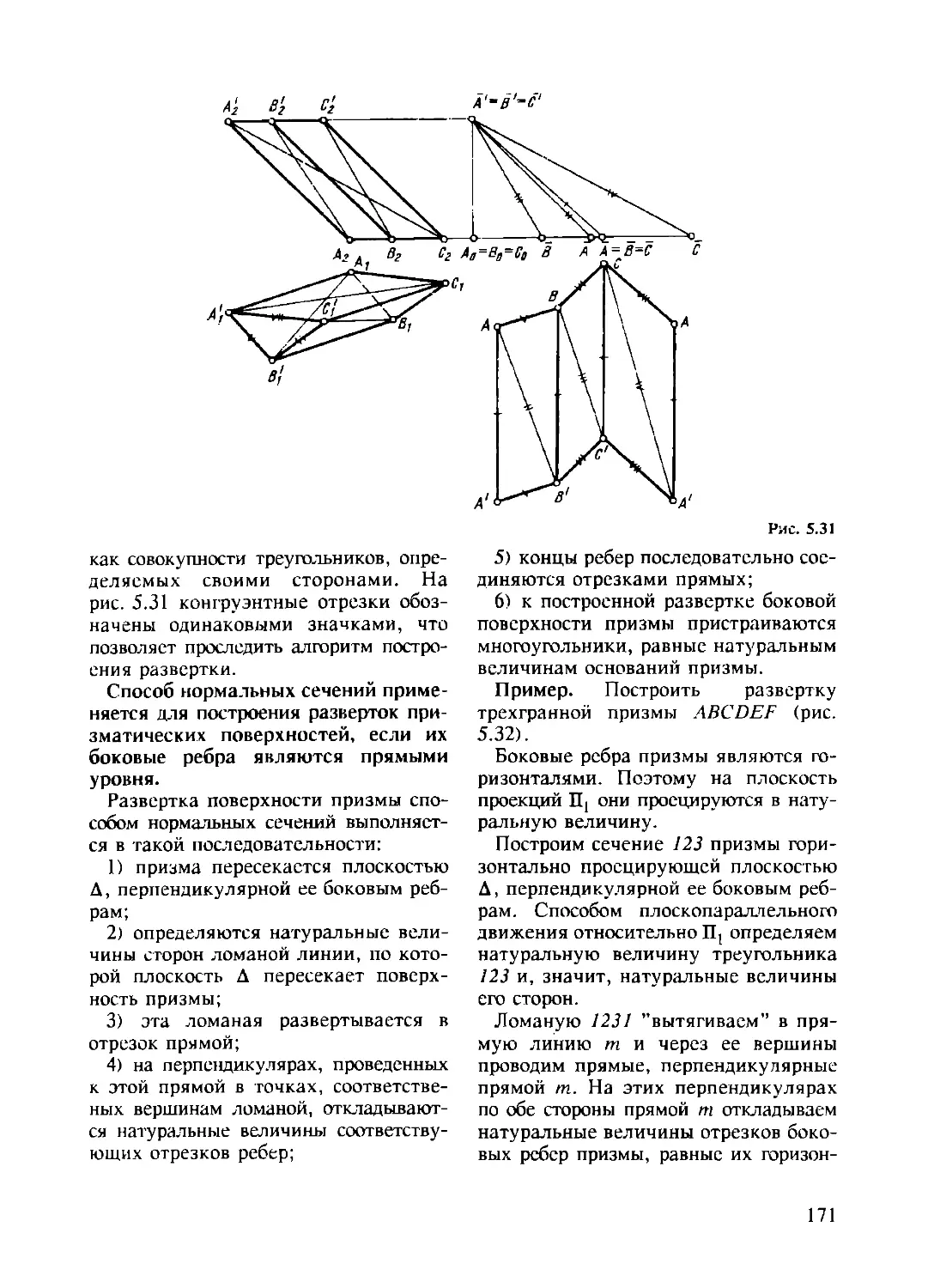
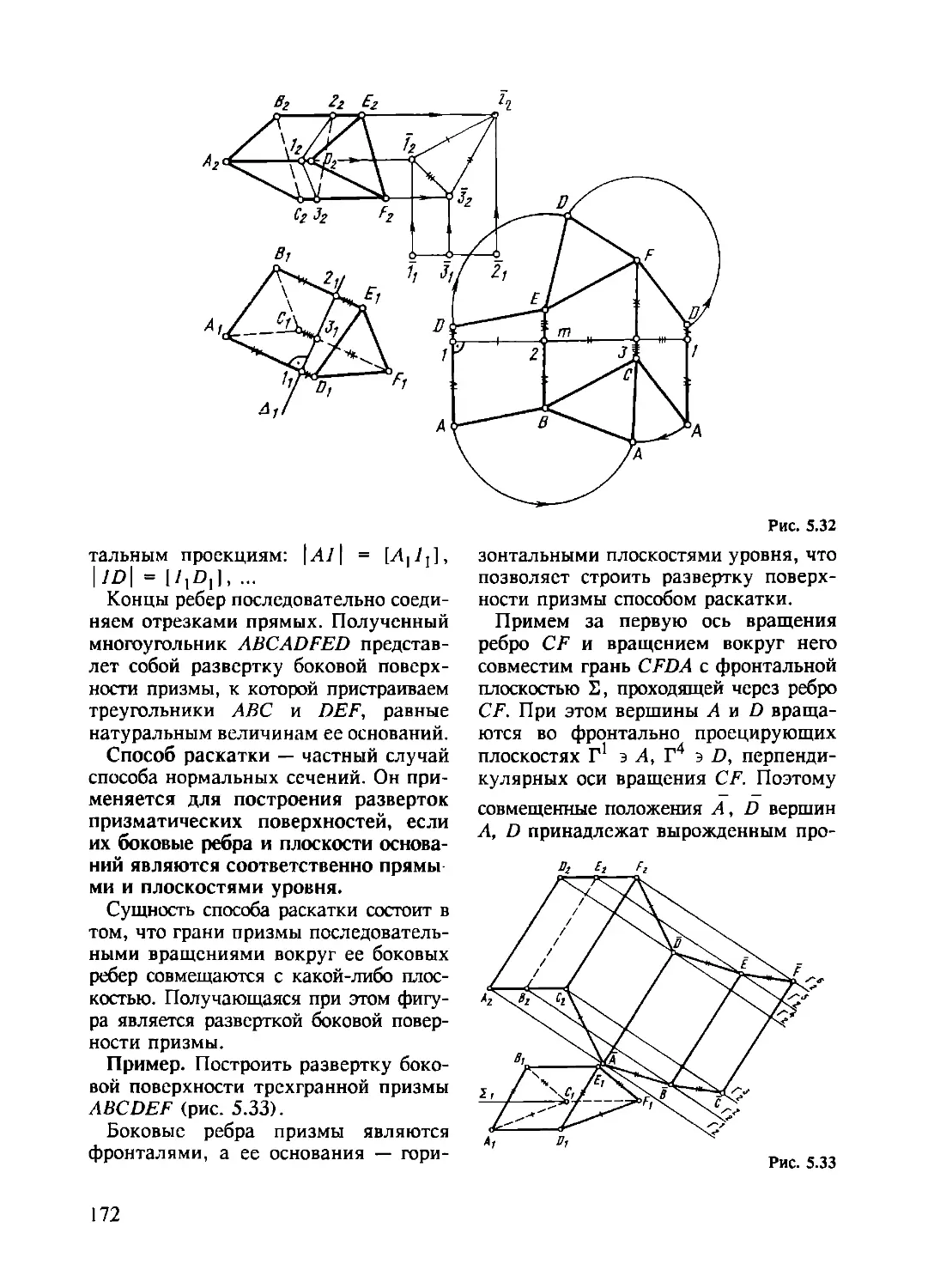
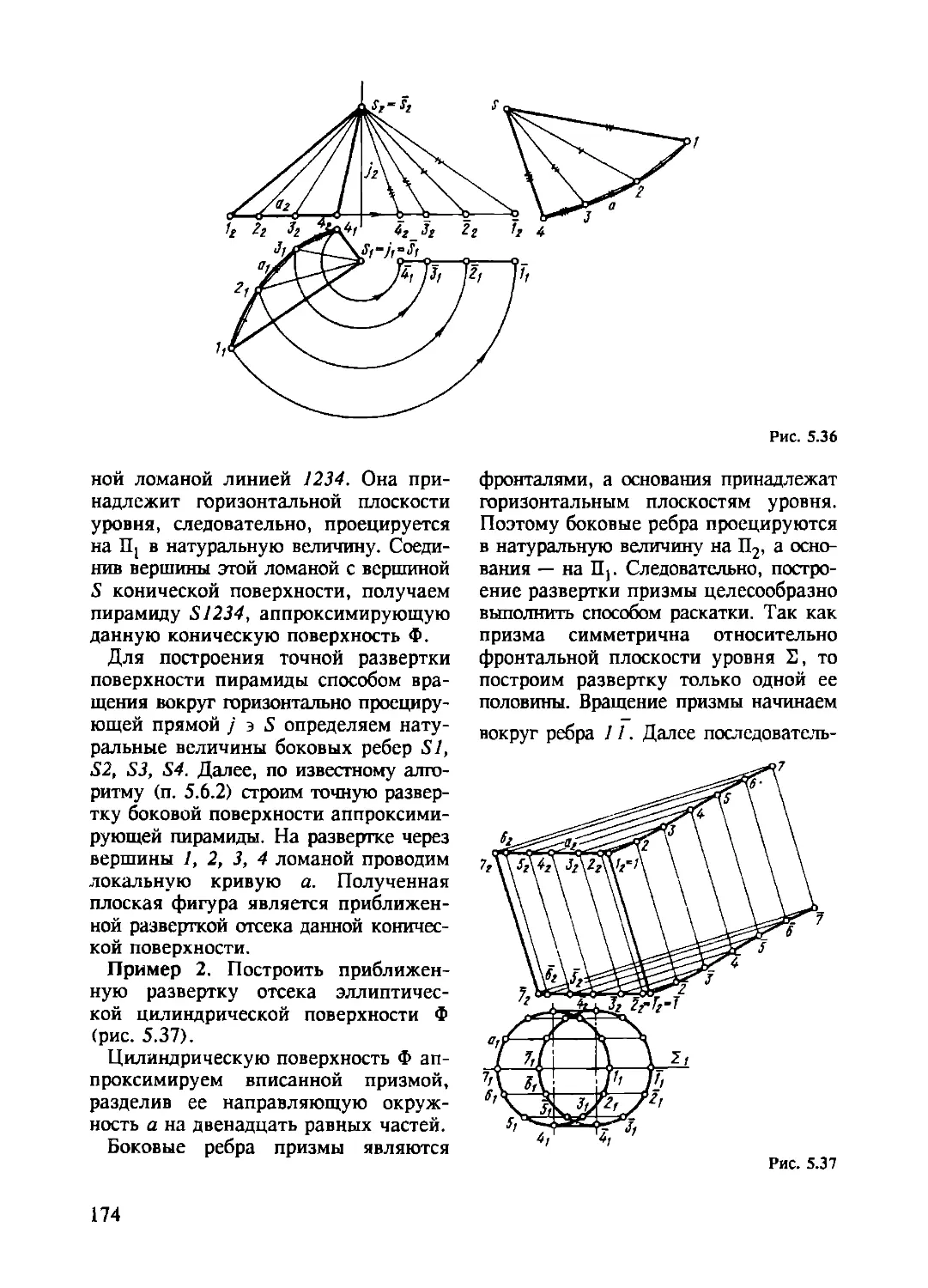
5.6. Развертки поверхностей. Основные понятия и алгоритмы
построения разверток............................................ 167
5.6.1. Основные понятия и определения ..................... 168
5.6.2. Алгоритмы построения точных разверток многогран-
ных поверхностей..................................... 169
5.6.3. Алгоритмы построения приближенных разверток раз-
вертывающихся поверхностей ................................. 173
5.6.4. Алгоритмы построения условных разверток нераз-
вертывающихся поверхностей .......................... 176
5.7. Метрические задачи, решаемые построением разверток......... 179
5.8. Задачи на геометрические места и принципы их решения........ 180
Упражнения и вопросы для самопроверки....................... 184
Глава 6. Учебно-исследовательские задачи в курсе начертательной
геометрии............................................................. 186
6.1. Обобщенные виды проецирования и их применение для
решения позиционных задач....................................... 186
6.1.1. Построение косой проекции прямой на моно-
проекционном чертеже................................. 187
6.1.2. Построение точек пересечения кривой линии
с поверхностью вращения..................................... 190
6.1.3. Возможные обобщения метода двух изображений ........ 192
6.2. Аналитический способ построения наглядных изображений....... 192
6.3. Родство — модель плоскости на чертеже Монжа................ 197
6.4. Моделирование поверхностей второго порядка на чертеже
Монжа............................................................ 200
6.5. Стереографическое проецирование в моделировании
поверхностей..................................................... 204
6.5.1. Исследование свойств однополостного гиперболоида..... 204
6.5.2. Моделирование сферы инверсией............. 206
6.6. Нелинейные преобразования плоскости и их применение для
конструирования кривых линий ................................... 209
6.6.1. Задание центральных нелинейных преобразований
плоскости ........................................... 209
6.6.2. Конструирование и исследование свойств алгебра-
ических кривых высших порядков.............................. 213
6.7. Нелинейные преобразования пространства и их применение
для конструирования поверхностей................................ 215
6.7.1. Задание нелинейных преобразований пространства
как совокупности преобразований пучка плоскостей .... 215
6-7.2. Применение нелинейных преобразований простран-
ства для конструирования поверхностей ............... 217
6.8. Решение позиционных и метрических задач посредством
геометрических преобразований ............................. 219
Список литературы ................................................... 222
Предметный указатель................................................. 223
5
Предисловие
Учебник предназначен для студентов инженерно-технических специальностей
вузов (кроме архитектурных и строительных) и соответствует программе курса
начертательной геометрии.
Широкое внедрение в производство и образование электронно-вычислительной
техники требуют внесения корректив как в содержание общеинженерных дисцип-
лин, так и в методику их преподавания. Начертательная геометрия как учебная
дисциплина должна способствовать глубокому усвоению учащимися ее сущности
как науки, изучающей методы геометрического моделирования пространств
различного числа измерений и структур, так как построение геометрических или
математических моделей является одним из важных этапов автоматизированного
проектирования и расчета современной техники, оптимизации технологических
процессов, организации и управления производством.
Отказ от узкого понимания предмета и цели изучения начертательной
геометрии лишь как теоретической базы курса черчения привел к пересмотру ее
структуры с целью систематизации изучаемого материала, разработки способов
конструирования и изображения геометрических фигур, решения общегеометри-
ческих и прикладных задач. Учебник призван способствовать самостоятельно-
му изучению предмета студентами, являясь средством организации учебного
процесса, подчеркивая единство и взаимосвязь методов начертательной и анали-
тической геометрии как базы для автоматизации решения задач прикладной
геометрии.
Структура учебника способствует реализации постановления ’’Основные
направления перестройки высшего и среднего специального образования в
стране”: ’’...осуществить решительный поворот от массового, валового обучения
к усилению индивидуального подхода, развитию творческих способностей
будущих специалистов, опираясь на их самостоятельную работу, активные
формы и методы обучения...”. В связи с этим настоящий учебник имеет двух-
уровневую структуру изложения материала.
Рис. 0.1
6
Первый уровень (рис. 0.1), реализованный в первых пяти главах учебника,
отражает современное состояние преподавания начертательной геометрии как
учебной дисциплины, изучающей теорию методов отображения пространства
на плоскость и графического решения стереометрических задач на чертеже.
Структура и содержание этой части учебника определились в результате анализа
двухвековой истории начертательной геометрии, существующих учебных про-
грамм и опыта преподавания предмета в ведущих вузах страны, дискуссий и
обсуждений на научно-методических семинарах и конференциях.
Современные требования, предъявляемые к учебным курсам начертательной
геометрии, соответствуют идеям Г. Монжа, которыми он руководствовался при
создании начертательной геометрии. Формулируя предмет начертательной
геометрии ([7], с. 13), он выделяет две цели:
1) ’’...дать методы для изображения на листе чертежа, ...любых тел приро-
ды...”,
2) ”...дать способ на основании точного изображения определять формы тел
и выводить все закономерности, вытекающие из их формы и их взаимного
расположения ”.
Кроме того, в разделе ’’Сравнение начертательной геометрии с алгеброй”
он отмечает: ’’Следует пожелать, чтобы обе эти науки изучались вместе...”
(с. 28).
Особенность изложения материала состоит в параллельном изучении способов
задания геометрических фигур на комплексном и аксонометрическом чертежах,
графических и аналитических алгоритмов решения позиционных и метрических
задач.
Второй уровень, реализованный в шестой главе, рассчитан на развитие
творческих способностей студентов, активизируя самостоятельную работу по
линии УИРС и НИРС. В этой главе изложен материал об обобщенных методах
отображения, получения непрерывных моделей поверхностей, конструирования
кривых линий и поверхностей посредством нелинейных преобразований и т.д.
Изложение материала не детализируется, а освещаются лишь общетеорети-
ческие и принципиальные стороны вопроса, оставляя для самостоятельного
изучения конкретные задачи, сформулированные в виде тем для исследования.
Материал этой главы в достаточной мере отражает актуальные проблемы при-
кладной геометрии, решаемые научными и инженерно-техническими работ-
никами.
Автор приносит искреннюю благодарность профессорам Виницкому И.Г.,
Фролову С.А., доцентам Боровикову И.Ф., Желонкину Е.И., Халдееву И.М.
за замечания и советы, направленные на улучшение содержания учебника.
Для совместного использования с настоящим учебником издано учебное
пособие ’’Сборник задач по начертательной геометрии” (авторы Иванов Т.С.,
Желонкин Е.И.). По вопросам приобретения учебного пособия следует обращать-
ся на кафедру прикладной геометрии Московского авиационного института по
адресу: 125871, Москва, Волоколамское шоссе, 4.
7
Принятые обозначения
В учебнике используются общепринятые в математике в частности, в курсе
геометрии средней школы обозначения и символы. Имеющиеся особенности
связаны со спецификой курса начертательной геометрии, оперирующей проекци-
ями геометрических фигур.
1. Точки обозначаются прописными буквами латинского алфавита: А, В, С,
D, ... или арабскими цифрами: 1, 2, 3, ...; центр проецирования обозначается
буквой S.
2. Прямые и кривые линии, произвольно расположенные относительно
плоскостей проекций, обозначаются строчными буквами латинского алфавита:
а, Ь, с, d, ...
Линии, занимающие особое положение, обозначаются:
h — горизонтальная прямая уровня (горизонталь);
/ — фронтальная прямая уровня (фронталь);
р — профильная прямая уровня;
х — ось абсцисс;
у — ось ординат;
z — ось аппликат;
к — постоянная прямая чертежа (эпюра) Монжа;
$ — направление параллельного проецирования.
Для линий применяются также следующие обозначения:
АВ — прямая, определяемая точками А и В\
[АВ] — отрезок прямой, ограниченный точками А и В;
АВ — вектор;
[АВ] — дуга, ограниченная точками А и В;
|АВ | — натуральная величина отрезка [АВ];
ех> еу> ez или е ПРИ ех = еу~ ez~ единичные (масштабные) отрезки.
3. Поверхности обозначаются прописными буквами греческого алфавита: Г —
гамма, Д — дельта; 0 — тета, Л — ламбда, Е — кси; П — пи, Е — сигма, Ф — фи,
ф — пси, Q — омега.
Для указания способа задания поверхности рядом с их буквенными обозначе-
ниями в круглых скобках пишутся обозначения задающих их элементов: Г (А, В,
С); Д(а, М)\ Ф(/,/)...
Плоскости проекций обозначаются буквой П с добавлением нижнего или
верхнего индекса:
Щ — горизонтальная плоскость проекций,
П2 — фронтальная плоскость проекций,
П3 — профильная плоскость проекций,
П' — аксонометрическая плоскость проекций.
4. Углы обозначаются строчными буквами греческого алфавита: а, р, у, 8—
Применяются также следующие обозначения:
Z АВС — угол с вершиной в точке В;
Л
а, Г — угол между прямой а и плоскостью Г.
8
5. Проекции точек, линий, вырожденные проекции плоскостей и цилиндричес-
ких поверхностей обозначаются теми же буквами или цифрами, что и сами
точки, линии и плоскости с добавлением нижнего индекса, а в аксонометричес-
ких проекциях добавляется верхний индекс ’’штрих":
ЛрВр.. ьх„. мГр Фр. .. — горизонтальные проекции;
^2’ ^2>" а2, Ь2,.. Г2, Ф2„ .. — фронтальные проекции;
A3, в3„. а3, Ь3,.. Г3, Ф3„ .. — профильные проекции;
а; в;... ; а', Ь',... ; Г', Ф',... — аксонометрические проекции.
Вторичные проекции в аксонометрии имеют в обозначении нижний индекс,
соответствующий индексу натуральной плоскости проекций:
А1 , В2 , С3 aj , b2 , С3 Tj, Ф2, Д3>...
Совпадающие проекции осей координат обозначают двойными индексами: х12
вместо Xj = х2, z23 вместо z2 = z3, у13 вместо У[ = у3.
6. Последовательность геометрических элементов (точек, линий, плоскостей)
обозначается следующим образом: А, А, А; а, а,, а; П, П, П; х, х, х или А, А1,
А2, А3; а, а1, а2.
Для обозначения несобственных элементов (точек, линий, плоскостей)
используется верхний индекс °°: А”, Г”. В случае необходимости указания
способа задания несобственных элементов в скобках даются обозначения их
собственных представителей: 5”(5), а“(Г),...
7. Также используются следующие символы:
6 — принадлежность точки (элемента множества) геометрической фигуре
(множеству): А е т, В с Ф;
с — принадлежность (включение) геометрической фигуры (подмножества)
данной фигуре {множеству): т <= Г; Д => Z;
и — объединение множеств: [АВ] и [ВС] — ломаная АВС;
л — пересечение множеств: а л Г, Ф л Д;
= — совпадение, результат операции, присвоение: At = Вр А = т л Г;
а — конгруэнтность: [АВ] “ [СО];
--подобие: Д АВС - Д АВС;
|| — параллельность: а || т, т || Г;
± — перпендикулярность: пг ± к, t ± Г;
-— обозначение скрещивающихся прямых: а — Ь;
- — отображение, преобразование: а - at, at - at;
— — логическое следствие: т || п -» || пр т2 II п2.
Если символы перечеркнуты наклонной чертой, то это означает наличие
частицы ”не”:
А $ I — точка А не принадлежит прямой Z;
а | b — прямые а, b не параллельны.
9
Глава 1
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ,
ЕЕ ПРЕДМЕТ И ОСНОВНОЙ МЕТОД
Начертательная геометрия, являясь
одним из разделов математики, изуча-
ет методы отображения пространства
на плоскость и способы графических
решений стереометрических задач на
чертеже.
Многообразие геометрических фигур
трехмерного пространства и отношения
между ними составляют предмет на-
чертательной геометрии.
Геометрические фигуры делятся на
линейные (точка, прямая, плос-
кость) , нелинейные (кривая линия,
поверхность) и составные (многог-
ранники, одномерные и двумерные
обводы).
Основным элементом пространства
принято считать точку, а все геометри-
ческие фигуры можно представить как
множества точек.
Возможны следующие отношения
между фигурами:
позиционные (принадлежность, пе-
ресечение, параллельность), метричес-
кие (расстояние, угол).
Известны три основных способа ото-
бражения пространства: конструктив-
ный, аналитический и аксиоматичес-
кий.
При конструктивном способе между
фигурами пространства и их изображе-
ниями устанавливается непосредствен-
ная связь с помощью проецирующих
линий и поверхностей.
При аналитическом способе отобра-
жения (моделирования) пространства
точкам ставятся в соответствие их
координаты, линиям и поверхностям —
соответственно системы уравнений и
уравнения.
При аксиоматическом способе связь
между фигурами пространства и их
изображениями устанавливается по-
средством систем аксиом.
В курсе начертательной геометрии
рассматривают конструктивные спосо-
бы отображения. Поэтому основным
методом начертательной геометрии
является метод проецирования.
1.1. Проецирование —
конструктивный способ
отображения пространства
на плоскость
Проецирование точки пространства
на плоскость можно выполнять линией
(прямой) или поверхностью (плос-
костью). В первом случае точка про-
ецируется на плоскость в точку
(рис. 1.1, а) или в точки (рис. 1.1, б).
Рис. 1.1
10
Во втором случае проекцией точки
является линия (рис. 1.1, в). Широкое
применение получили проецирования
прямыми, проходящими через фикси-
рованную точку (центральное проеци-
рование) , или проецирование множес-
твом параллельных прямых (парал-
лельное проецирование).
1.1.1. Центральное
проецирование
и его свойства
Центральное проецирование (рис.
1.2) состоит из центра проецирования
5 и плоскости проекций Пр которую
иногда называют плоскостью изобра-
жения или картинной плоскостью. Для
построения проекции Ai некоторой
точки А пространства выполняют сле-
дующие операции:
— строят проецирующую прямую 5А;
— определяют точку Л- пересечения
прямой 5Л с плоскостью П(.
Точку At называют центральной
проекцией точки А.
Отметим основные свойства
центрального проецирования:
1) проекцией точки является точка:
А - Л,-;
2) прямая проецируется в прямую:
т -> Щр так как проецирующая плос-
кость Г(5, т) пересекает плоскость
проекций П( по прямой т(;
3) сохраняется принадлежность:
А е т - Л, е
В проектной геометрии доказывается
еще одно важное свойство центрально-
го проецирования:
4) сохраняется сложное отношение
четырех точек: (ASCD) = (А^С^),
которое представляется как отношение
двух простых отношений трех точек:
(АВС) _ (А&С^
(ABD) (A^D;)
или в развернутом виде
[АС] . |ЛВ] _
[ВС] ‘ [BD]
(1.1)
[Л.-С,] [Л,/),]
= T^CJ : вдГ
В евклидовом пространстве сущес-
твуют точки, которые не имеют цен-
тральных проекций, и наоборот, в
плоскости П( есть точки, которые в
пространстве не имеют оригиналов.
Действительно, точка К прямой т, в
которой она пересекается с плоскостью
П, проходящей через центр проециро-
вания 5 и параллельной плоскости
проекций Пр не имеет проекции, так
как проецирующая прямая SK парал-
лельна П, и, следовательно, ее не пере-
секает. Другими словами, все точки
плоскости П не имеют центральных
проекций на Пг.
С другой стороны, для точки про-
екции mt прямой т на последней нет
оригинала, так как проецирующая
прямая SNi параллельна самой пря-
мой т, следовательно, ее не пересе-
кает.
Для исключения подобных случаев
евклидово пространство расширяют
введением несобственных (бесконечно
удаленных) точек. Такое пространство
называется расширенным евклидовым
пространством. Оно получается допо-
лнением:
— евклидовой прямой одной не-
собственной точкой: а + А*\
11
— евклидовой плоскости одной несо-
бственной прямой: Ф + и“;
— евклидового пространства одной
несобственной плоскостью: Е3 + Г°°.
В расширенном евклидовом
пространстве справедливы следующие
аксиомы соединения (принадлежнос-
ти):
1) две прямые, принадлежащие од-
ной плоскости, пересекаются в точке
(собственной или несобственной);
2) прямая и плоскость пересекаются
в точке (собственной или несобствен-
ной);
3) две плоскости пересекаются по
прямой (собственной или несобствен-
ной).
В расширенном евклидовом про-
странстве все параллельные прямые
имеют одну общую несобственную
точку и образуют связку прямых с
несобственным центром, а все парал-
лельные плоскости имеют общую несо-
бственную прямую и образуют пучок
плоскостей с несобственной осью.
Из принятого дополнения евклидово-
го пространства несобственными эле-
ментами следует способ их изображе-
ния (задания) на чертеже. В этом слу-
чае говорят, что несобственные эле-
менты задаются их собственными
представителями:
— несобственная точка А°° — прямой
а, т.е. Л“(а);
— несобственная прямая g° — плос-
костью Г, т.е. g“(D.
1.1.2. Параллельное
проецирование
и его свойства
Параллельное проецирование явля-
ется частным случаем центрального
проецирования, когда центр проеци-
рования 5 становится несобственным.
Поэтому обычно вместо несобственного
центра проецирования 5“ говорят о
направлении проецирования s (рис.
1.3).
Рис. 1.3
Первые три свойства центрального
проецирования, сформулированные в
п. 1.1.1, будут справедливыми и в слу-
чае параллельного проецирования.
Четвертое свойство требует уточнения,
так как между центральным и парал-
лельным проецированиями имеется
существенное отличие в изображении
несобственных элементов. В общем
случае при центральном проецирова-
нии несобственная точка (например,
№ на рис. 1.2) проецируется в
собственную точку, так как проециру-
ющая прямая всегда является
собственной и пересекает плоскость
проекций в собственной точке. В слу-
чае же параллельного проецирования
проекцией несобственной точки всег-
да будет несобственная точка, так как
проецирующая прямая является несо-
бственной и, следовательно, пересекает
плоскость проекций обязательно в
несобственной точке. Отсюда следуют
еще три свойства параллельного прое-
цирования:
4) сохраняется простое отношение
трех точек: (АВС) = (Л^-Ср или в
развернутом виде
MCI _ • (1.2)
[ВС] [5,0,] ’
5) сохраняется параллельность:
а II b - || bf,
6) отношения длин проекций отрез-
ков параллельных прямых к длинам
самих отрезков постоянны:
12
[АС] [ВС] ’
(1.3)
Формула (1.2) следует из (1.1) при
условии, что точка D (а значит и £>г)
AD “
будет несобственной. Тогда ------- =
BD°°
Формула (1.3) получается из (1.2)
перестановкой крайних членов пропо-
рции.
Из приведенных свойств вытекают
следующие теоремы:
1. Проекцией центрально симмет-
ричной фигуры также будет централь-
но симметричная фигура (рис. 1.4).
Рис. 1.4
2. Плоские фигуры, параллельные
плоскости проекций, проецируются на
последнюю без искажения (рис. 1.5).
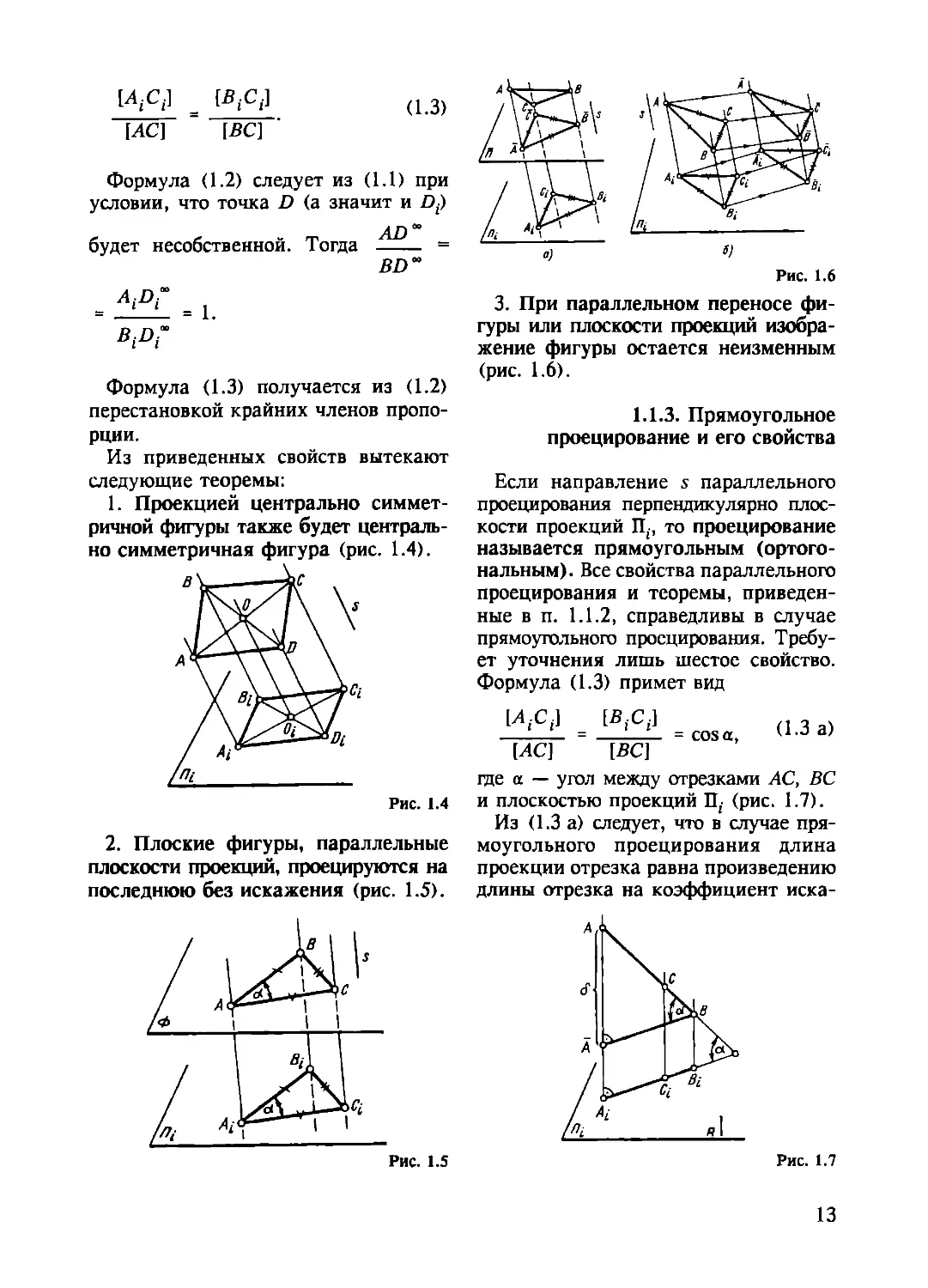
3. При параллельном переносе фи-
гуры или плоскости проекций изобра-
жение фигуры остается неизменным
(рис. 1.6).
1.1.3. Прямоугольное
проецирование и его свойства
Если направление s параллельного
проецирования перпендикулярно плос-
кости проекций Пр то проецирование
называется прямоугольным (ортого-
нальным). Все свойства параллельного
проецирования и теоремы, приведен-
ные в п. 1.1.2, справедливы в случае
прямоугольного проецирования. Требу-
ет уточнения лишь шестое свойство.
Формула (1.3) примет вид
И,-С,.]
[лс]
[вс]
где а — угол между отрезками АС, ВС
и плоскостью проекций П(- (рис. 1.7).
Из (1.3 а) следует, что в случае пря-
моугольного проецирования длина
проекции отрезка равна произведению
длины отрезка на коэффициент иска-
Рис. 1.7
13
жения (косинус угла наклона отрезка
к плоскости проекций):
[Л(С,] = [AC] cos а.
При решении ряда метрических за-
дач (см. разд. 5) необходимо уметь
решать обратную задачу: имея проек-
ции отрезка, определить его натураль-
ную величину. Из рис. 1.7 ясно, что
натуральную величину, например,
отрезка АВ можно определить исполь-
зуя свойства прямоугольного треуголь-
ника АВА, где АВ fl Afii.
1) [АВ] - [XjB,]: cosa;
2) натуральная величина отрезка АВ
равна гипотенузе прямоугольного
треугольника AS Л, один катет кото-
рого равен проекции [ЛД] = [АВ]
отрезка на П{, а второй катет — раз-
ности расстояний d = [A4J - [BSJ
концов отрезка до этой плоскости
проекций.
Последнее утверждение называют
правилом прямоугольного треуголь-
ника.
Важное значение для решения мет-
рических задач имеет изучение взаи-
мосвязи величины угла и его проек-
ции. Произвольный плоский угол прое-
цируется без искажения при выполне-
нии условия теоремы 2 (см. п. 1.1.2).
Прямой угол проецируется в натураль-
ную величину при менее жестком
ограничении, которое определяется
теоремой:
прямоугольной проекцией прямого
угла является также прямой угол,
если одна его сторона параллельна
плоскости проекций, а другая не пер-
пендикулярна ей.
Рассмотрим чертеж на рис. 1.8. Сто-
рона АВ прямого угла АВС параллель-
на плоскости проекций П(, а сторона
ВС не перпендикулярна Пг. Тогда
AjBt V АВ; прямая АВ перпендикуляр-
на плоскости Г(ВСпВВр, так как
АВ ± ВС (по условию угол АВС пря-
мой) , АВ х BBi (направление проеци-
Рис. 1.8
рования s = ВВ( перпендикулярно П(-, а
сторона АВ || П(). Отсюда следует пер-
пендикулярность проекции А^ сторо-
ны АВ плоскости Г. Поэтому Afit пер-
пендикулярна любой прямой плоскости
Г и, в частности, проекции В(С( сто-
роны ВС данного прямого угла, т.е.
Л(В(- ± В(С(. Теорема доказана.
1.2. Требования,
предъявляемые к чертежу
Из определения начертательной гео-
метрии, данного в начале этой главы,
к чертежу предъявляются следующие
требования: обратимость, точность,
простота, наглядность.
Последние три требования не нужда-
ются в пояснениях. Раскроем понятие
обратимости чертежа: чертеж называ-
ется обратимым, если по изображе-
нию фигуры можно восстановить ее
форму, размеры и положение в про-
странстве. Очевидно, чертеж будет
обратимым только в том случае, если
между множествами геометрических
фигур пространства и их изображений
установлено взаимно однозначное со-
ответствие. Так как любая геометри-
ческая фигура представляется как
множество точек, то сформулирован-
ный признак обратимости можно уточ-
нить так: чертеж будет обратимым,
если трехпараметрическому множес-
тву точек пространства соответствует
14
трехпараметрическое множество их
изображений.
Множество точек пространства трех-
параметрично, так как любая точка
определяется однозначно тремя коор-
динатами, что принято обозначать так:
°°3. Аналогично, точек на плоскости
будет двупараметрическое множество
°° , а на прямой — однопараметричес-
кое множество «в1.
Очевидно, что чертеж фигуры, полу-
ченный путем проецирования на одну
плоскость проекций, не будет обрати-
мым, так как множества точек прос-
транства и плоскости не равны: “>3 *
* “2. Действительно, на рис. 1.2 по
проекции А(. невозможно восстановить
положение оригинала в пространстве:
в точку Ai проецируется все однопара-
метрическое множество (в»1) точек
прямой 5А(.
Таким образом, одна из основных
задач начертательной геометрии как
научной дисциплины состоит в разра-
ботке способов получения обратимых
чертежей. Известно множество таких
способов, наиболее распространенные
из которых получаются по схеме мето-
да двух изображений.
1.3. Метод двух изображений
моделирования пространства
Метод двух изображений предназна-
чен для моделирования точечного про-
странства, т.е. пространства, в котором
основным элементом является точка, а
все остальные фигуры представляются
как множества точек .
Аппарат классического метода двух
изображений состоит из основного цен-
В геометрии также рассматриваются абстрак-
тные пространства, основными элементами кото-
рых являются соответственно прямая, окруж-
ность, сфера и т.п. Пространство, основным
элементом которого является прямая, называется
линейчатым. Такое пространство моделируется
по схеме классического метода двух следов.
Рис. 1.9
тра проецирования 5, плоскости изо-
бражения П, двух вспомогательных
плоскостей проекций Пр П2 и двух
вспомогательных центров проецирова-
ния S], S2 (рис. 1.9). Центры проеци-
рования S, Sp S2 принадлежат одной
прямой I, которая пересекает плоскость
изображения П в исключенной точке F.
Произвольная точка А пространства
изображается на чертеже двумя проек-
циями Ар А2, лежащими на одной
прямой (колинейными) с точкой F.
Для их получения точка А из вспомо-
гательных центров Sp S2 проецирует-
ся на вспомогательные плоскости про-
екций Пр П2 соответственно в точки
Ар А2, которые затем из основного
центра проецирования 5 перепроеци-
руются в точки Ар А2 на плоскость
изображения П.
Полученное изображение является
обратимым, так как по известным про-
екциям Ар А2 можно восстановить
положение оригинала А в пространст-
ве. С точки зрения исчислительной
геометрии обратимость полученного
изображения объясняется тем, что °°3
точек пространства изображается °°3
парами точек Ар А2. Действительно,
пары точек Ар А2, колинейные с точ-
кой F, составляют трехпараметричес-
кое множество, так как одну точку,
например
выбрать из
А11
на плоскости П можно
ее точек, а другую — из
15
°»1 точек, принадлежащих лишь пря-
мой ГАр Поэтому пары точек Ар А2
будут составлять тоехпараметрическое
множество °°3 = °° «в1.
Большинство известных обратимых
чертежей, используемых в инженерной
практике (эпюр Монжа, аксонометрия
и перспектива), получаются по схеме
классического метода двух изображе-
ний.
1.4. Чертеж Монжа —
основной вид
обратимого изображения
Развитие производства потребовало
разработки таких обратимых изобра-
жений, которые отличались бы высо-
кой точностью и простотой, были бы
приспособлены для изображения дета-
лей машин и механизмов. Француз-
ский математик и инженер Гаспар
Монж (1746 — 1818 гг.), систематизи-
ровав и обобщив накопленные к тому
времени знания по теории и практике
построения изображений предметов
пространства, предложил получать их
изображения путем прямоугольного
проецирования на две или три взаимно
перпендикулярные плоскости проек-
ций. В зависимости от этого такие
чертежи называют двухкартинными
или трехкартинными.
1.4.1. Двухкартинный
чертеж Монжа
Рассмотрим получение двухкартин-
ного чертежа (рис. 1.10, а). Одна из
плоскостей проекций всегда располага-
ется горизонтально. Она называется
горизонтальной плоскостью проекций
и обозначается буквой Пр Другая
плоскость, вертикальная, называется
фронтальной плоскостью проекций и
обозначается буквой П2. Линию их
пересечения принимают за ось Ох де-
картовой системы координат, ось Оу
принадлежит Dj, ось Oz — П2. Прямоу-
гольные проекции Aj, А2 оригинала А
на плоскости проекций Пр П2 соответ-
ственно называются горизонтальной
проекцией А] и фронтальной проекци-
ей А2 точки А.
Вращением вокруг оси Ох плоскость
Щ совмещается с плоскостью П2. При
этом проекции Ар А2 точки А будут
расположены на прямой Ар А2, пер-
пендикулярной оси Ох и называемой
линией связи (рис. 1.10, б). Получен-
ное изображение называется эпюром
(чертежом) Монжа или комплексным
чертежом.
Плоскости проекций Пр П2 делят
пространство на четыре части, называ-
емые четвертями. В зависимости от
расположения точки А в той или иной
Рис. 1.10
16
четверти ее проекции Л2 могут
занимать различное положение относи-
тельно оси Ох.
Очевидно, что полученный чертеж
является обратимым, так как по нему
можно определить координаты точки А
в пространстве (см. рис. 1.10, а и б).
Отсюда следует, что на двухкартинном
чертеже можно решать любые позици-
онные и метрические задачи.
С позиций классического метода
двух изображений чертеж Монжа по-
лучается при совмещении плоскости
изображения П с фронтальной плос-
костью проекций П2, горизонтальная
плоскость проекций П( перпендикуляр-
на П2 = П (см. рис. 1.10, а). Центры
проецирования S, Sp S2 являются
несобственными. При этом точка S\
находится в направлении, перпендику-
лярном П], точка 52 — перпендикуляр-
ном к П2. Точка 5 является не-
собственной точкой прямой s, перпен-
дикулярной оси Ох = П] п П2 и состав-
ляющей с плоскостью изображения П =
= П2 угол 45°.
В этой конструкции прямая /, инци-
дентная несобственным точкам 5,
52, пересекает плоскость изображения
П в несобственной точке F°°. Поэтому
носители проекций А{, А2, называемые
линиями связи, параллельны между
собой.
1.4.2. Трехкартинный
чертеж Монжа
В ряде случаев, например, в маши-
ностроении используют трехкартинный
чертеж Монжа (рис. 1.11). Он получа-
ется из двухкартинного путем добавле-
ния третьей плоскости проекций П3,
перпендикулярной оси Ох (рис. 1.12).
Эта плоскость называется профильной
плоскостью проекций.
Рис. 1.11
Заметим, что на трехкартинном чер-
теже третья проекция фигуры является
зависимой, т.е. она однозначно строит-
ся, если известны две другие проекции
фигуры. Трехкартинные чертежи стро-
ят для изображения сложных фигур,
если на двухкартинном чертеже появ-
ляются трудности в чтении чертежа
Рис. 1.12
17
фигуры. Например, на рис. 1.11 по
проекциям детали на плоскости проек-
ций П], П2 невозможно однозначно
определить форму выемки на проуши-
нах (прямоугольная, круглая, эллипти-
ческая) , если чертеж не дополнен раз-
мерами или специальными обозначе-
ниями. Наличие проекции на П3 дает
полное представление о ее форме.
Плоскости проекций Пр П2, П3 делят
пространство на восемь частей, назы-
ваемых октантами. Первые четыре
октанта располагаются левее профиль-
ной плоскости проекций П3. Их нуме-
рация показана на рис. 1.12. Плоскость
проекций Щ является плоскостью сим-
метрии для 1 и 5, 2 и 6, 3 и 7, 4 и 8-го
октантов.
Для получения трехкартинного чер-
тежа Монжа плоскости проекций Пр
П3 вращением соответственно вокруг
осей Ox, Oz (рис. 1.12, а) совмещаются
с фронтальной плоскостью проекций
П2. Проекции Лр А2, А3 произвольной
точки А пространства расположены на
линиях связи, перпендикулярных соот-
ветствующим осям координат: AjA2 ±
Л12, -^2^3 -1- z23 Фис- 1-12, б). Построе-
ние третьей (зависимой) проекции
точки по двум независимым проекци-
ям показано на рис. 1.12 б. Для этого
удобно использовать постоянную ли-
нию чертежа к, проходящую через
начало координат и составляющую с
осью Ох угол 45°.
Отметим, что в ряде случаев на чер-
теже Монжа не указываются проекции
осей координат (см. рис. 1.11). Такие
чертежи принято называть безосными.
1.5. Аксонометрия —
вид наглядного
обратимого изображения
В инженерной практике также широ-
ко применяется другой тип обратимого
чертежа, называемый аксонометрией.
Отличительной особенностью аксоно-
Рис. 1.13
метрического изображения является
наглядность. На рис. 1.13 дано аксоно-
метрическое изображение детали,
трехкартинный чертеж которого приве-
ден на рис. 1.11. Сравнение этих ри-
сунков позволяет оценить достоинства
и недостатки приведенных изображе-
ний. Для объективной оценки изучим
способ получения аксонометрического
чертежа.
1.5.1. Основные понятия
и определения
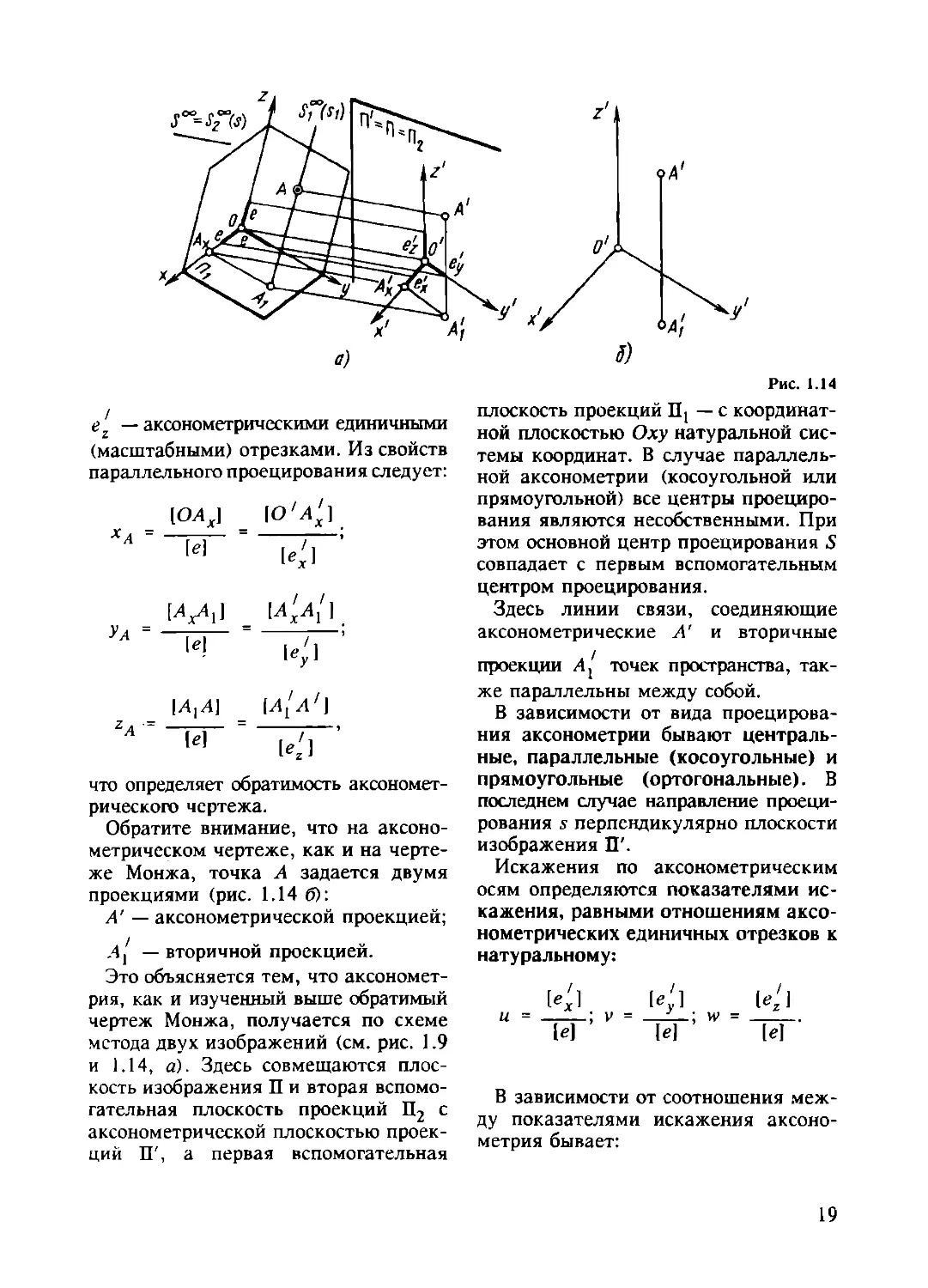
Аксонометрическое изображение
получится в результате проецирования
фигуры (в нашем примере — точки Л),
отнесенной к натуральной системе
координат Oxyz, на аксонометрическую
плоскость проекций П' (рис. 1.14 а).
Точка А связывается с системой коор-
динат Oxyz посредством натуральной
координатной ломаной АА^АХО, где
[ОЛХ] = хА, [А^А,] = ул, [AtA] = zA
суть координаты точки А, измеренные
натуральным единичным (масштаб-
ным) отрезком е.
Проекция А' точки А на IT называ-
ется аксонометрической проекцией,
. / .
проекция Aj точки А] — вторичной
проекцией, проекция O'x'y'z' — ак-
сонометрической системой координат,
A'A^A^O' — аксонометрической ко-
/ /
ординатнои ломаной, проекции <?, ev,
л у
18
Рис. 1.14
е1 — аксонометрическими единичными
(масштабными) отрезками. Из свойств
параллельного проецирования следует:
[ОЛХ] |ОХЛ^1
хА = ------ = -------;
|Л,Л] [а'л']
что определяет обратимость аксономет-
рического чертежа.
Обратите внимание, что на аксоно-
метрическом чертеже, как и на черте-
же Монжа, точка А задается двумя
проекциями (рис. 1.14 б):
А’ — аксонометрической проекцией;
. /
Л] — вторичной проекцией.
Это объясняется тем, что аксономет-
рия, как и изученный выше обратимый
чертеж Монжа, получается по схеме
метода двух изображений (см. рис. 1.9
и 1.14, а). Здесь совмещаются плос-
кость изображения П и вторая вспомо-
гательная плоскость проекций П2 с
аксонометрической плоскостью проек-
ций П', а первая вспомогательная
плоскость проекций Ht — с координат-
ной плоскостью Оху натуральной сис-
темы координат. В случае параллель-
ной аксонометрии (косоугольной или
прямоугольной) все центры проециро-
вания являются несобственными. При
этом основной центр проецирования S
совпадает с первым вспомогательным
центром проецирования.
Здесь линии связи, соединяющие
аксонометрические А' и вторичные
. /
проекции /Ц точек пространства, так-
же параллельны между собой.
В зависимости от вида проецирова-
ния аксонометрии бывают централь-
ные, параллельные (косоугольные) и
прямоугольные (ортогональные). В
последнем случае направление проеци-
рования s перпендикулярно плоскости
изображения П'.
Искажения по аксонометрическим
осям определяются показателями ис-
кажения, равными отношениям аксо-
нометрических единичных отрезков к
натуральному:
le!x] [е'] {e'z\
и = ---; v = —w =____________
Id Id Id
В зависимости от соотношения меж-
ду показателями искажения аксоно-
метрия бывает:
19
1) изометрическая (все показатели
искажения равны);
2) диметрическая (два показателя
искажения равны, но не равны тре-
тьему) ;
3) триметрическая (все показатели
искажения различны).
При построении аксонометрических
изображений необходимо знать, на-
сколько произвольно могут быть выб-
раны аксонометрические оси и аксоно-
метрические единичные отрезки. На
этот вопрос отвечает основная теорема
аксонометрии, называемая также тео-
ремой Польке. Она утверждает, что в
косоугольной аксонометрии выбор
аксонометрических осей и единичных
отрезков е', е', е/ совершенно про-
изволен.
Таким образом, на основании этой
теоремы мы можем утверждать, что
фигура, полученная заданием на плос-
кости П' трех произвольных лучей
О'х', О'у', O'z' и отложением на
/ / /
них трех отрезков er, ev, е. произ-
Л у Z
вольной длины (см. рис. 1.14), может
рассматриваться как параллельная
проекция трех взаимно перпендику-
лярных осей системы координат Oxyz
с отложенными на них равными еди-
ничными отрезками е.
1.5.2. Прямоугольная
аксонометрия и ее свойства
Теорема Польке несправедлива для
прямоугольной аксонометрии, так как
задание направления проецирования
s(OO') х IT (рис. 1.15) оставляет на
выбор положения начала О натураль-
ной системы координат Oxyz только
одну степень свободы (О е s) вместо
двух степеней свободы в случае парал-
лельной аксонометрии. Поэтому необ-
ходимо знать ограничения, накладыва-
емые на выбор аксонометрической
системы координат О 'х 'у 'z ’ и единич-
/ / /
ных отрезков ех, еу, ez , которые
следуют непосредственно из свойств
прямоугольной аксонометрии.
1. Треугольник следов XYZ, по кото-
рому натуральная система координат
пересекается с плоскостью изображе-
ния П', является остроугольным
(рис. 1.15).
Это свойство очевидное: декартова
система координат пересекается с лю-
бой плоскостью, отличной от коорди-
натной, по остроугольному треуголь-
нику.
2. Аксонометрические оси О'х',
О'у', O'z' являются высотами треу-
гольника следов XYZ.
Справедливость этого свойства следу-
ет из теоремы о проецировании прямо-
го угла (см. п. 1.1.3); например, пря-
мые Oz, XY перпендикулярны, при
этом XY с П' (или XY || IT), поэтому
их проекции O'z', X'Y' = XY также
будут перпендикулярными.
3. Сумма квадратов показателей
искажения равна двум:
2 2 2 т
U + V + W = 2.
(1.4)
Эта формула называется основной
формулой прямоугольной аксономет-
рии.
20
Докажем справедливость основной
формулы. Так как s ± П', то треуголь-
ники ОО'Х, OO'Y, OO'Z прямоуголь-
ные. Поэтому а' = 90° — а, Р' = 90° —
— Р, у' = 90° — у. Известно, что сумма
квадратов косинусов направляющих
углов прямой равна единице. Поэтому
cos2az + cos2pz + cos2yz =1.
Действительно (рис. 1.16), имеем
(ОО7)2 = (ОО*)2 +
+ (ООу)2 + (ОО')2,
где ООХ = OO'cosa', ООу =
= OO'cosP', ООХ = OO'cosy'.
Формулу (1.5) перепишем, заменив
косинусы углов синусами их дополни-
тельных углов:
sin2 a + sin2p + sin2 у = 1
или
(1 - cos2 a) + (1 - cos2p) +
+ (1 - cos2 у) = 1.
Отсюда
cos2a + cos2p + cos2y = 2,
где
[e'l „
cos a = --- = u; cosp = —— = v;
И [e]
[ezZ]
cosy = ---- = w,
и
т.е. получили основную формулу (1.4)
прямоугольной аксонометрии.
Так как О <> и, v, w < 1, то в прямо-
угольной аксонометрии нельзя выби-
рать произвольно показатели искаже-
ния.
Таким образом, для задания в пря-
моугольной аксонометрии аксономет-
рической системы координат сначала
выбирают остроугольный треугольник
следов (свойство 1), затем строят его
высоты, которые принимают за аксоно-
метрические оси координат (свойство
2), и, наконец, задаются показателями
искажения, удовлетворяющими основ-
ной формуле (1.4), в которой О <. и, v,
W < 1 (свойство 3).
1.6. Сравнение свойств
чертежа Монжа
и аксонометрии
Наибольшее распространение среди
обратимых чертежей получили чертеж
Монжа и аксонометрия. Они использу-
ются для изображения деталей и узлов
в машиностроении, а также строитель-
ных конструкциях. Применяя тот или
иной способ изображения, необходимо
знать их достоинства и недостатки.
Сравнение изображений точки А на
чертеже Монжа (рис. 1.17 а) и на ак-
сонометрическом чертеже (рис. 1.17,
б), а также изображений детали (см.
рис. 1.11 и 1.13) позволяет сделать
следующие выводы:
1) изображения геометрических фи-
гур на чертеже Монжа и на аксономет-
рическом чертеже принципиально ни-
чем не отличаются, так как указанные
21
чертежи получаются по единой схеме
метода двух изображений: фигура на
обоих чертежах изображается двумя
проекциями;
2) чертеж Монжа проще и точнее
аксонометрического чертежа, так как
на чертеже Монжа все единичные
(масштабные) отрезки изображаются
без искажения, а в аксонометрии с
искажением;
3) аксонометрический чертеж
нагляднее чертежа Монжа, так как
проекции координатных плоскостей
являются невырожденными, а на двух-
картинном чертеже Монжа изображе-
ние координатной плоскости Oyz вы-
рождается в прямую.
Из вышесказанного вытекают два
важных следствия:
1) алгоритмы графического решения
позиционных задач на чертеже Монжа
и на аксонометрическом чертеже оди-
наковы;
2) алгоритмы графического решения
метрических задач значительно проще
на чертеже Монжа.
В следующей главе будут рассмотре-
ны вопросы задания геометрических
фигур как на чертеже Монжа, так
и на аксонометрическом чертеже.
Предпочтение будет отдано чертежу
Монжа как наиболее простому и точ-
ному. Аксонометрические проекции
будут строиться в случае необходи-
мости получения наглядных изобра-
жений.
Рис. 1.17
1.7. Другие виды
обратимых изображений
Было отмечено, что для решения
прикладных задач моделирования про-
странства был разработан ряд способов
получения обратимых чертежей. Наи-
более древним из них является способ
построения перспективных изображе-
ний. Этот способ широко используется
для построения изображений крупно-
размерных сооружений (строительных,
архитектурных), так как позволяет
передавать кажущиеся изменения ве-
личины и формы объекта, вызванные
его расположением и удаленностью от
наблюдателя (рис. 1.18). Теория по-
строения перспективных изображений
изучается в архитектурных и стро-
ительных вузах [4]. Здесь же бу-
дут приведены лишь сведения о гео-
метрических основах теории перспек-
тивы.
22
1.7.1. Перспектива
Перспективные изображения начали
применять при решении практических
задач строительства еще в древнем
Египте. В трактате римского архитек-
тора Марка Витрувия (I в. до н.э.)
’’Десять книг об архитектуре” имеется
ряд сведений, относящихся к построе-
нию перспективных изображений. Ос-
новы теории перспективы были разра-
ботаны в эпоху возрождения итальян-
цем Альберти (1404 — 1472 гг.), не-
мцем Дюрером (1471 — 1528 гг.) и
многими другими зодчими и художни-
ками.
С позиций метода двух изображений
построение перспективы выполняется
по следующей схеме (рис. 1.19 а).
Плоскость изображения П совмещает-
ся с картинной плоскостью П2> а вто-
рая вспомогательная плоскость проек-
ций Пр называемая предметной, выби-
рается перпендикулярной картинной
плоскости П2. Обычно картинная плос-
кость располагается вертикально. Пер-
вый вспомогательный центр проециро-
вания Sj расположен в бесконечности
в перпендикулярном направлении к
предметной плоскости П]. Второй вспо-
могательный центр S2 совпадает с ос-
новным центром проецирования 5 и
называется точкой зрения.
На рис. 1.19 а дополнительно пока-
зана плоскость горизонта Г, которая
проходит через точку зрения 5 и па-
раллельна предметной плоскости Пр
Она пересекает картинную плоскость
П по линии горизонта Л, параллельной
основанию картины t = П п Пр Основа-
ние Р перпендикуляра, опущенного из
точки 5 на плоскость П, называется
главной точкой картины.
Произвольная точка А пространства
на перспективном чертеже изобража-
ется двумя проекциями (рис. 1.19, б):
Л2 — перспективой точки А,
УЦ — вторичной проекцией точки А.
1.7.2. Проекции
с числовыми отметками
Приведем также краткие сведения о
способах построения обратимых черте-
жей, основанных на прямоугольном
проецировании и предназначенных для
изображения объектов, у которых вы-
сота значительно меньше их длины и
ширины. К таким объектам относятся
котлованы под фундаменты всевозмож-
ных строительных и гидротехнических
сооружений, насыпи и выемки в до-
рожном строительстве и мелиорации,
горные выработки в добывающей про-
мышленности и т.д. Широкое распро-
странение для изображения перечис-
ленных объектов получили проекции с
числовыми отметками, ’’федоровские”
векторные чертежи, циклография Фид-
лера-Федорова. Эти способы основаны
Р h
"------------
-ч > —I------
Pf t
S)
Рис. 1.19
23
п,
°At(4)
1 гз 4
Рис. 1.20
Рис. 1.21
на том, что положение точки в про-
странстве относительно плоскости про-
екций будет вполне определено, если
наряду с ее прямоугольной проекцией
будет каким-либо образом задана ее
высота, т.е. ее расстояние до плоскости
проекций.
Проекции с числовыми отметками
получаются так:
1) какая-либо плоскость простран-
ства, обычно горизонтальная, прини-
мается за плоскость проекций IIj
(рис. 1.20);
2) точка А пространства прямоуголь-
но проецируется на плоскость ГЦ в
точку Лр
3) определяется высотная (числовая)
отметка точки А, которая равна высоте
4) проекция уЦ точки А снабжается
числовой отметкой, значение которой
указывается в круглых скобках.
На чертеже указывается масштаб.
Точки, расположенные под плоскостью
проекций П1, имеют отрицательные
числовые отметки. Оценивая обрати-
мость, точность и простоту чертежей с
числовыми отметками, следует отме-
тить их недостаток — отсутствие на-
глядности.
1.7.3. ’’Федоровские”
векторные чертежи
Этот способ получения обратимых
чертежей предложен академиком
Е.С. Федоровым (1853 — 1919 гт.)
с целью усовершенствования проек-
ций с числовыми отметками.
Здесь высотные отметки заменены
векторами, чьи модули равны аппли-
катам (высотам) изображаемых точек
(рис. 1.21). Направление векторов
выбирается произвольно, но они до-
лжны быть параллельными между
собой. Точки с отрицательными число-
выми отметками изображаются проти-
воположно направленными векторами.
"Федоровские” проекции отличаются
от проекций с числовыми отметками
большей наглядностью и отсутствием
на чертеже несвойственных для графи-
ки числовых отметок.
1.7.4. Циклография
Фидлера—Федорова
Этот способ также возник при усо-
вершенствовании проекций с числовы-
ми отметками. Здесь числовая отметка
точки равна радиусу окружности (цик-
ла) , построенной с центром в прямоу-
гольной проекции Aj изображаемой
точки А (рис. 1.22). В зависимости от
знака аппликаты изображаемой точки
моделирующей окружности приписы-
вается та или иная ориентация.
Рис. 1.22
24
Упражнения и вопросы
для самопроверки
1. Что составляет предмет начертательной гео-
метрии?
2. Перечислите свойства центрального проеци-
рования.
3. Может ли центральной проекцией окруж-
ности быть эллипс, парабола, гипербола?
4. Дайте определение расширенного евклидо-
вого пространства.
5. Вспомните свойства параллельного проеци-
рования.
6. Может ли параллельной проекцией окруж-
ности быть парабола, гипербола?
7. Сформулируйте правило прямоугольного
треугольника определения натуральной величи-
ны отрезка.
8. Сформулируйте теорему о прямоугольной
проекции прямого угла.
9. Сформулируйте признак обратимости чер-
тежа.
10. Постройте проекции следующих точек на
двухкартинном чертеже Монжа: А (10, 20, 30);
В (20, 0, 40); С (30, -40, 20); D (40, - 30,
- 30); Е (50, 20, - 20); F (60, 40, 0).
11. На двухкартинном чертеже Монжа
постройте проекции точки А, симметричной
точке А (30, 40, 50) относительно горизонталь-
ной плоскости проекций П|, фронтальной плос-
кости проекций П2, оси Ох.
12. На трехкартинном чертеже Монжа по-
стройте проекции следующих точек: А (10, 20,
30); В (30, - 40, 20); С (- 40, 30, 50); D
(-50, 20, - 30).
13. Определите положения точек в простран-
стве по их проекциям на двухкартинном чертеже
14. Вспомните схему получения аксонометри-
ческого изображения.
15. Что называется показателем искажения по
аксонометрической оси?
15. Перечислите свойства прямоугольной аксо-
нометрии.
17. Перечислите достоинства и недостатки
чертежа Монжа и аксонометрического чертежа.
18. Где используются перспективные изобра-
жения?
Глава 2
ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ.
ИЗОБРАЖЕНИЕ ИХ НА ЧЕРТЕЖЕ
Эта глава посвящена изображению
основных геометрических образов
(прямая, плоскость, многогранник,
кривая линия и поверхность) на черте-
же Монжа и на аксонометрическом
чертеже. Построение изображений
каждого геометрического образа начи-
нается с изложения основных понятий
и определений, завершается выводом
их уравнений. Параллельное рассмот-
рение графических и аналитических
способов задания геометрических обра-
зов является необходимым условием
для получения их изображений (визуа-
лизации) на экранах дисплеев и гра-
фопостроителях, а также решения
прикладных задач с использованием
вычислительной техники.
2.1. Задание прямой
линии на чертеже
При изучении свойств центрального
проецирования было показано, что
проекцией прямой линии является
прямая. Таким образом, на двухкар-
тинном чертеже прямая т изображает-
ся двумя проекциями (рис. 2.1):
горизонтальной и фронтальной
~ на чертеже Монжа;
„ , „ /
аксонометрической т и вторичной т1
— на аксонометрическом чертеже.
Так как прямая т однозначно опреде-
ляется двумя точками Л и В, то ее
проекции определяются проекциями
этих точек. Проекции прямой в силу
сохранения принадлежности при прое-
цировании проходят через одноимен-
ные проекции точек: т^рВ]);
т2(А2, В2); т'(А',В')\ т^(.А^,В^).
И обратно точка А принадлежит пря-
мой т, если проекции принадлежат
одноименным проекциям прямой:
А е т, если Л, 6 mlt А2 е т2;
А е т , А{ е т1 .
2.1.1. Прямые частного
положения
Прямая, расположенная произволь-
но относительно плоскостей проек-
ций, называется прямой общего поло-
жения. Прямая, параллельная какой-
либо плоскости проекций, называется
Рис. 2.1
26
прямой уровня. На чертеже Монжа
различают (рис. 2.2):
— горизонтальную прямую уровня
(горизонталь) А;
— фронтальную прямую уровня
(фронталь) /;
— профильную прямую уровня р.
Все точки прямых уровня имеют
равные или глубины (фронталь), или
высоты (горизонталь), или широты
(профильная прямая уровня). Поэтому
соответствующие проекции линий
уровня параллельны проекциям опре-
деленных осей координат:
/1 II ^2 Л л12’
Pl II У13- Р2 II z23‘
Так как обе проекции р2 любой
профильной прямой уровня перпенди-
кулярны оси х12, то для однозначности
ее задания необходимо указать на
чертеже проекции двух любых ее то-
чек.
Согласно теореме 2 (см. п. 1.1.2)
отрезки прямых уровня проецируются
без искажения на соответствующую
плоскость проекций:
[ЛВ] е/ =>\АВ\ = |Л2В2|,
[ЛВ] е h - |ЛВ| = I,
[ЛВ] Ер -|ЛВ| = |Л3В3|.
Построение проекций М^, М2 точки
М, принадлежащей профильной пря-
Профильная прямая
уровня (р\\П3)
Аг
Вг
В,
М,
А,
Рис. 2.2
мой уровня р, выполняется из условия
сохранения простого отношения трех
точек (см. свойство 4 п. 1.1.2):
(AjBjAfj) = (Л2В2М2).
Один из графических алгоритмов
построения фронтальной проекции М2
точки М е р по заданной горизонталь-
ней проекции М] показан на рис. 2.2:
через проекции точек А, В проводятся
параллельные прямые и отмечаются
точки Л^, Во пересечения соответ-
ственных прямых; точки Ло, Во опре-
деляют ’’ось преломления” р0; затем
через Afj проводится прямая II
|| а через точку Мо пересечения
M^Mq с AqBq проводится прямая
MqM2 || AqA2; точка М2 = MqM2 п
п А2В2 будет искомой. Аналогично
строится горизонтальная проекция
точки М е р по заданной фронтальной
проекции М2.
Применительно к построению аксо-
нометрических изображений можно
также говорить о прямых общего поло-
жения и прямых уровня. К последним
можно отнести прямые, параллельные
аксонометрической плоскости проек-
ций П' и граням П^Оху), П2(Охг),
П3 (.Oyz), натуральной системы коорди-
нат Oxyz. Но обычно такой классифи-
кации не придерживаются, так как
чертежи таких прямых в отличие от
чертежа Монжа не имеют очевидных
27
Рис. 2.3
особенностей. Только аксонометричес-
кий чертеж прямой, параллельной
координатной плоскости П^Оху), име-
ет отличительную особенность: аксоно-
метрическая и вторичная проекции
прямой всегда параллельны. Сказанное
справедливо и для чертежей прямых,
параллельных координатным плоскос-
тям П2 (Oxz), П3 (Oyz), если их вторич-
ные проекции принадлежат этим гра-
ням.
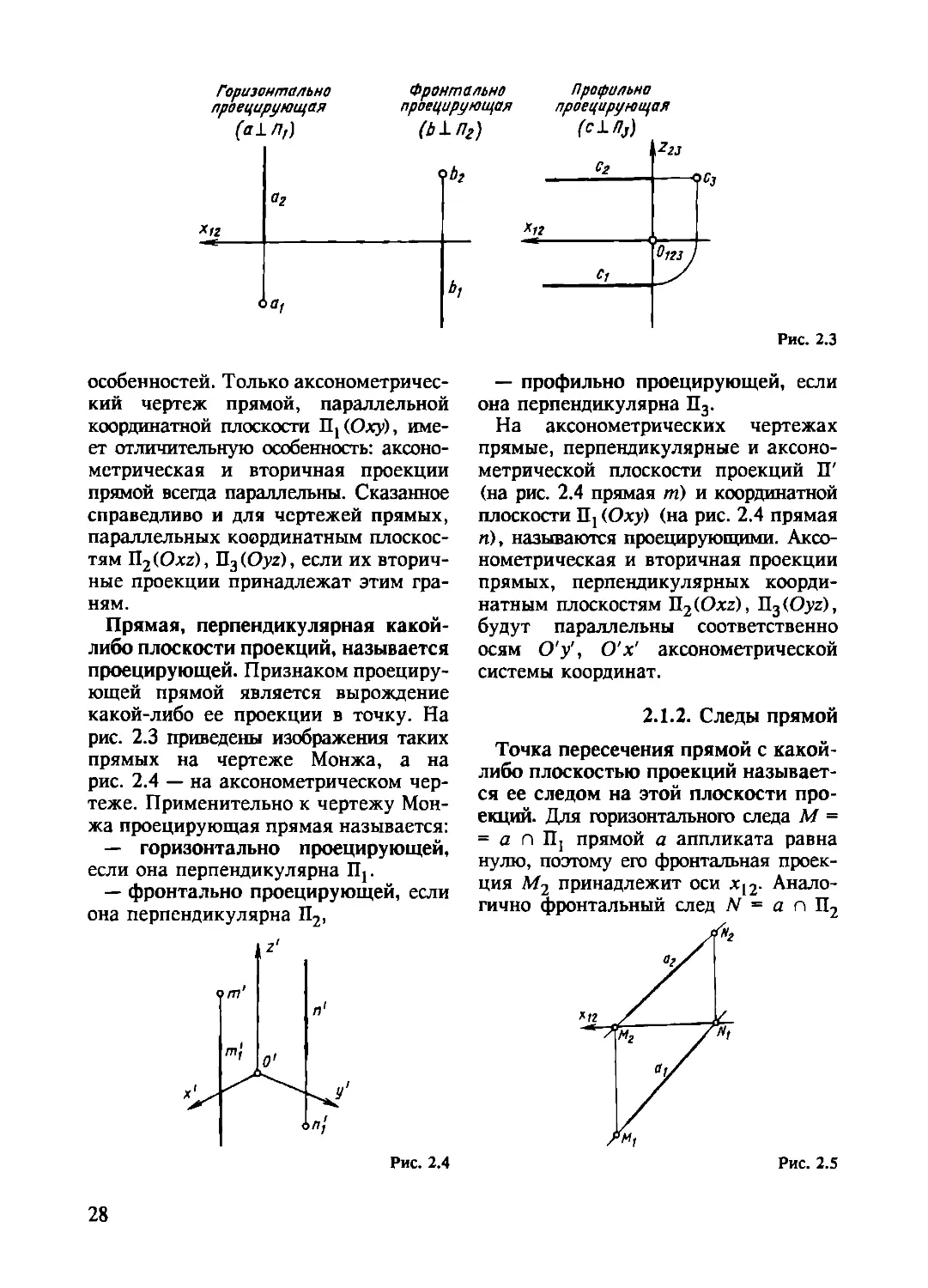
Прямая, перпендикулярная какой-
либо плоскости проекций, называется
проецирующей. Признаком проециру-
ющей прямой является вырождение
какой-либо ее проекции в точку. На
рис. 2.3 приведены изображения таких
прямых на чертеже Монжа, а на
рис. 2.4 — на аксонометрическом чер-
теже. Применительно к чертежу Мон-
жа проецирующая прямая называется:
— горизонтально проецирующей,
если она перпендикулярна Пр
— фронтально проецирующей, если
она перпендикулярна П2,
— профильно проецирующей, если
она перпендикулярна П3.
На аксонометрических чертежах
прямые, перпендикулярные и аксоно-
метрической плоскости проекций П'
(на рис. 2.4 прямая т) и координатной
плоскости П! (Оху) (на рис. 2.4 прямая
п), называются проецирующими. Аксо-
нометрическая и вторичная проекции
прямых, перпендикулярных коорди-
натным плоскостям П2(Oxz), П3(Oyz),
будут параллельны соответственно
осям О'у', О'х' аксонометрической
системы координат.
2.1.2. Следы прямой
Точка пересечения прямой с какой-
либо плоскостью проекций называет-
ся ее следом на этой плоскости про-
екций. Для горизонтального следа М =
= а п П] прямой а аппликата равна
нулю, поэтому его фронтальная проек-
ция Л/2 принадлежит оси х12. Анало-
гично фронтальный след N = а п П2
Рис. 2.4
Рис. 2.5
28
Рис. 2.6
имеет ординату, равную нулю, следо-
вательно, его горизонтальная проекция
?/] принадлежит оси х12 (рис. 2.5). На
аксонометрическом же чертеже просто
строится лишь след М прямой Ь на
координатной плоскости Dj(Оху): аксо-
нометрическая М' и вторичная
м[ проекции точки М совпадают, т.е.
(Л/' = ) - Ь' л А/ (рис. 2.6). Для
построения следов прямой на коорди-
натных плоскостях П2 (Oxz), П3 (Oyz)
надо предварительно построить ее вто-
ричные проекции на этих плоскостях
проекций. Построение следа N прямой
Ь на аксонометрической плоскости
проекций П' сводится к решению зада-
чи нахождения точки пересечения
данной прямой b с плоскостью П',
заданной треугольником следов XYZ.
2.1.3. Взаимное положение
двух прямых
В трехмерном пространстве две
прямые могут быть пересекающимися,
параллельными и скрещивающимися.
Две пересекающиеся прямые имеют
общую точку. Поэтому на чертеже
точки пересечения их фронтальных и
горизонтальных проекций (аксономет-
рических и вторичных проекций) яв-
ляются проекциями их общей точки
(рис. 2.7, а):
а П b = М -at П b\ = Mv
а2 ^2 = ^2
Две скрещивающиеся прямые не
имеют общей точки. Поэтому точки
пересечения их горизонтальных и
фронтальных проекций (аксонометри-
ческих и вторичных проекций) явля-
ются совпадающими проекциями двух
различных точек (рис. 2.7, в). Такие
точки называются конкурирующими и
применяются для определения види-
мости при рассмотрении взаимного
положения двух фигур. На П2 точка В
закрывает собой точку А, так как она
расположена ближе к наблюдателю (ее
горизонтальная проекция дальше
расположена от оси х12). Аналогично
Рис. 2.7
29
на П] точка С закрывает собой точку
D, так как точка С расположена выше
точки D (С2 расположена дальше от
оси х12).
2.2. Задание плоскости
на чертеже. Родство
Построение чертежа плоскости имеет
принципиальные особенности. Если
точка и прямая изображаются на чер-
теже своими проекциями, то проециро-
вание точек некоторой плоскости на
какую-либо плоскость проекций приво-
дит к установлению соответствия меж-
ду точками данной плоскости и плос-
кости проекций. В случае параллель-
ного (в частном случае, прямоугольно-
го) проецирования это соответствие
обладает следующими очевидными
свойствами, непосредственно вытекаю-
щими из свойств параллельного прое-
цирования (рис. 2.8):
Рис. 2.8
— прямой а соответствует прямая af,
— сохраняется принадлежность (М е
6 а — 6 а,);
— сохраняется параллельность (а Ц
b « а, II bt);
— сохраняется простое отношение
трех точек ({MNK) =
Точечное соответствие, обладающее
перечисленными свойствами, называ-
ется перспективно-аффинным или
родственным.
При проецировании точек А1 плос-
кости Ф на две плоскости проекций П],
П2 устанавливается взаимно однознач-
ное соответствие Т между полями го-
ризонтальных и фронтальных (в аксо-
нометрии — между полями аксономет-
рических и вторичных) проекций
П, (Л/) - П2(Л2 ), которое также обла-
дает перечисленными свойствами. Та-
ким образом, на любом чертеже, по-
лученном по схеме метода двух изо-
бражений посредством двух парал-
лельных проецирований, плоскость
моделируется (изображается) род-
ственным соответствием.
Так как плоскость однозначно опре-
деляется тремя точками, точкой и
прямой, двумя пересекающимися или
параллельными прямыми, то родство Т
или, что то же самое, плоскость Ф за-
дается проекциями указанных трех
точек, точки и прямой, двух пересека-
ющихся или параллельных прямых.
Впредь способ задания плоскости бу-
дем указывать обозначениями соответ-
ствующих элементов, заключенных в
круглые скобки и записанных после
обозначения плоскости. Например,
Ф(А,В,С) — плоскость Ф, заданная точ-
ками А, В, С, или ее модель — родство
Т, заданное тремя парами соответ-
ственных точек - Л2, Bj - В2, Cj -
- С2 (на чертеже Монжа) (рис. 2.9),
30
или А' ~ Ау , В' ~ , Cj - с{ (на
аксонометрическом чертеже).
Прямая принадлежит плоскости,
если имеет с ней две общие точки. На
рис. 2.9 горизонталь h принадлежит
плоскости Ф(Д В, О, так как они име-
ют две общие точки А, К.
Точка принадлежит плоскости, если
она принадлежит какой-либо прямой
этой плоскости. На рис. 2.9 точка М
принадлежит плоскости Ф (А, В, С), так
как она принадлежит горизонтали h
этой плоскости. Построение недостаю-
щей проекции точки, прямой по задан-
ной их одной проекции из условия
принадлежности данной плоскости
называют также построением соответ-
ственных точек и прямых в родстве.
Для упрощения таких построений
целесообразно иметь прямую d\ = d2,
проходящую через три точки пересече-
ния проекций сторон треугольника
АВС: = 2)2) = ^2-®2> ^^1 =
= 2Г2) = А В2С2, (2*1 = Fq) —
= А{С{ а А2С2. Прямая dt = d2 назы-
вается осью родства и представляет
собой совпавшие проекции линии
пересечения данной плоскости Ф (А, В,
С) с биссекторной плоскостью четных
четвертей. Проекции всех прямых
плоскости Ф(А, В, С) (соответственные
прямые родства Т) пересекаются в
точках, принадлежащих оси родства,
например,
BxMi П В2М2 = W! = 1V2) е (<Zj = d2).
2.2.1. Плоскости
частного положения
Плоскость, произвольно располо-
женная относительно плоскостей
проекций, называется плоскостью
общего положения.
Плоскость, перпендикулярная ка-
кой-либо плоскости проекций, назы-
вается проецирующей, а параллельная
ей — плоскостью уровня.
Различают горизонтально, фрон-
тально и профильно проецирующие
плоскости (рис. 2.10). У проецирую-
щих плоскостей одна проекция вырож-
дается в прямую. Поэтому соответству-
ющая проекция фигуры, принадлежа-
щей такой плоскости, вырождается в
прямую. Проецирующая плоскость
однозначно задается на чертеже своей
вырожденной проекцией. При изобра-
жении профильно проецирующей плос-
кости на двухкартинном чертеже в
системе плоскостей проекций Пр П2
необходимо помнить, что горизонтали
Рис. 2.10
31
и фронтали такой плоскости являются
профильно проецирующими прямыми.
Признаком проецирующих плоскос-
тей является вырождение (превраще-
ние) каких-либо двух из трех линий
уровня в проецирующие прямые (см.
рис. 2.10). Это согласуется с призна-
ком перпендикулярности двух плоскос-
тей: проецирующая плоскость перпен-
дикулярна плоскости проекций, так
как содержит проецирующую прямую.
Относительно аксонометрического
чертежа проецирующие плоскости
бывают двух видов:
— плоскости, перпендикулярные
координатным плоскостям IIj (Оху),
П2(Oxz), П3(Oyz) (соответственно па-
раллельные осям Oz, Оу, Ох) нату-
ральной системы координат;
— плоскости, параллельные направ-
лению проецирования s (см. рис.
1.14, а).
У первого вида проецирующих плос-
костей вырождаются их вторичные
проекции на соответствующие коорди-
натные плоскости, а у второго вида —
аксонометрические проекции. Тс и
другие виды плоскостей принято назы-
вать проецирующими без конкретиза-
ции направления проецирования. На
рис. 2.11 приведены аксонометричес-
кие чертежи плоскости общего положе-
ния Ф(А, В, С), заданной тремя точка-
ми; плоскости Г, перпендикулярной
координатной плоскости П](Оху), и
плоскости Д, параллельной направле-
нию 5 проецирования.
Плоскости уровня являются частны-
ми случаями проецирующих. Они, как
и проецирующие плоскости, обычно
изображаются своими вырожденными
проекциями. На рис. 2.12 представле-
ны изображения плоскостей уровня на
чертеже Монжа. Фигура, принадлежа-
щая плоскости уровня, проецируется
на соответствующую плоскость про-
екций в натуральную величину.
Относительно аксонометрического
чертежа плоскости уровня бывают
двух видов:
— плоскости, параллельные коорди-
натным плоскостям П](Оху), П2(Oxz),
П3 (Oyz);
— плоскости, параллельные аксоно-
метрической плоскости проекций П'.
Первые плоскости удобно задавать
на чертеже двумя пересекающимися
прямыми, параллельными соответству-
Гориоонтальная
плоскость уровня
(011 /77)
Фронтальная Профильная
плоскость уровня плоскость уровня
(ДНП2) (Г\\Л3)
Рис. 2.12
32
ющим аксонометрическим плоскостям
(аксонометрические и вторичные про-
екции таких прямых параллельны
соответствующим аксонометрическим
осям). Второй вид плоскостей уровня
удобно задавать двумя пересекающи-
мися прямыми, параллельными любым
двум сторонам треугольника следов.
2.2.2. Следы плоскости
Рассматривая задания плоскостей на
чертеже, отметим, что решения многих
задач упрощаются, если плоскости
заданы следами — линиями их пересе-
чения с плоскостями проекций. Дру-
гими словами, следы плоскости — это
линии "нулевого” уровня.
Из этого определения следуют алго-
ритмы их построения. На чертеже
Монжа (рис. 2.13) построение следов
A0, J° плоскости Ф (Л, В, С) выполняет-
ся в такой последовательности:
1) горизонтальный след hq определя-
ется горизонтальными следами М и N
прямых АВ и ВС;
2) фронтальный след /0 проходит
через точку схода следов = £>2) =
, о
= л1 ПХ|2 и параллелен произвольной
фронтали / плоскости Ф (А, В, С).
Относительно аксонометрического
чертежа следами плоскости называют
прямые ее пересечения с координатны-
Рис. 2.13
ми плоскостями натуральной системы
координат. На аксонометрическом
чертеже (рис. 2.14) построение следов
А, /, р плоскости Ф(а п А) выполняется
в такой последовательности:
1) след А = Ф п П^Оху) строится по
следам N, М прямых a, b; (N' = n[ ) =
= a' n а[ , (М' = ) = b' п ;
2) след /= Ф п П2 (Oxz) строится по
точке X' = х( схода следов на оси Ох
и следу К прямой а на П2 (Oxz);
3) след р = Ф п П3 (Oyz) строится по
точкам Y' = y( , Z сходов следов на
осях Оу и Oz или по следу L прямой b
на П3 (Оу?) и одной из указанных точек
сходов следов.
Заметим, что соответствующие следы
проецирующих плоскостей совпадают
с их вырожденными проекциями.
2.3. Аналитическое
задание прямых
и плоскостей
Как было уже отмечено, решение
графических задач на ЭВМ требует их
аналитической интерпретации. Поэто-
му кратко изложим известные из курса
2 Зак. 871
33
аналитической геометрии сведения о
задании прямых и плоскостей, об усло-
виях принадлежности и взаимном по-
ложении.
2.3.1. Уравнения плоскостей
общего и частного положения
Плоскость общего положения в декартовых
координатах аналитически описывается линей-
ным уравнением с тремя переменными:
Ах + By + Cz + D = 0. (2Л)
Как было показано выше, проецирующие
плоскости однозначно определяются своими вы-
рожденными проекциями. Следовательно, их
уравнения эквивалентны уравнениям соответ-
ствующих вырожденных проекций — уравнени-
ям прямых, принадлежащих соответствующим
координатным плоскостям (плоскостям проек-
ций) :
1) горизонтально проецирующая плоскость
Ах + By + С = 0; (2-2)
2) фронтально проецирующая плоскость
Ах + Bz + С = 0; (2-3)
3) профильно проецирующая плоскость
Ay + Bz + С = 0. (2-4)
Плоскости уровня как параллельные соответ-
ствующим координатным плоскостям имеют для
всех своих точек равные значения тех или иных
координат:
1) горизонтальная плоскость уровня
Az + В = 0 или z = Н; (2 5)
2) фронтальная плоскость уровня
у = Q; (26)
3) профильная плоскость уровня
r = G (2.7)
2.3.2. Уравнения прямых
общего и частного
положения
Прямая пространства представляется как ли-
ния пересечения двух плоскостей Поэтому ана-
литически она задается системой двух линейных
уравнений (2.1). Если в качестве указанных
плоскостей взять проецирующие, то система
уравнений
Ах + By + С = 0
(2.8)
Мх + Nz +D = 0
эквивалентна графическому заданию прямой на
чертеже Монжа посредством двух прямоуголь-
ных проекций.
Прямые уровня удобно задавать как линии
пересечения проецирующей плоскости с плос-
костью уровня:
1) горизонталь Л
' z = Н
(2.9)
Ах + By + С = 0;
2) фронталь f
Г у = Q
(2.10)
Ах + Bz + С = 0;
3) профильная прямая уровня р
х = G
(2.11)
Ay + Bz + С = 0.
Любая проецирующая прямая определяется
как линия пересечения двух проецирующих
плоскостей, в частном случае — плоскостей
уровня, например:
1) горизонтально проецирующая прямая
х = G
(2.12)
у = Q;
2) фронтально проецирующая прямая
х = G
(2.13)
z = Н-,
3) профильно проецирующая прямая
(у = Q
(2.14)
z = Н.
Очевидно, что системы уравнений (2.12),
(2.13), (2.14) эквивалентны заданию координат
точек — вырожденных проекций данных прое-
цирующих прямых, которые их однозначно
определяют.
2.3.3. Задачи на определение
взаимного положения точек,
прямых и плоскостей
Точка принадлежит плоскости, если ее коор-
динаты при подстановке в уравнение (2.1) плос-
кости превращают его в тождество. Для построе-
ния точки, принадлежащей плоскости, задаются
любыми ее двумя координатами (задаются ее
одной проекцией) и, подставив их в (2.1), вы-
числяют значение третьей неизвестной коорди-
наты.
Точка принадлежит прямой, если ее коорди-
наты удовлетворяют системе уравнений (2.8).
Для построения точки, принадлежащей прямой,
задаются любой одной ее координатой и, подста-
вив ее в систему (2.8), вычисляют значения двух
других неизвестных координат.
Прямая, определяемая системой (2.8), при-
надлежит любой плоскости, уравнение которой
имеет вид
Ах + By + С +
(2.15)
+ к(Мх + Nz + D) = О
ИЛИ
(Л + кМ)х + By +
+ XWz + С + kD =• О,
где А — произвольное число.
Две плоскости будут параллельными (пере-
секаются по несобственной прямой), если в
их уравнениях коэффициенты при одноимен-
ных неизвестных будут пропорциональными.
В противном случае эти плоскости пересека-
ются.
Две прямые, определяемые двумя системами
(2.8), в общем случае будут скрещивающимися,
так как система четырех линейных уравнений с
тремя неизвестными в общем случае не имеет
решения. Если же эта система имеет решение,
то данные две прямые будут пересекающимися.
И, наконец, эти прямые будут параллельны,
если попарно параллельны задающие их плос-
кости.
Следы плоскости описываются системами двух
уравнений, состоящими из (2.1) и уравнения
соответствующей координатной плоскости.
Координаты следов прямой вычисляются
решением системы трех уравнений, состоящей
из двух уравнений, задающих саму прямую, и
уравнения соответствующей координатной плос-
кости.
2.4. Многогранники
Поверхности многогранников явля-
ются составными геометрическими
фигурами пространства. Многогранные
формы широко распространены в при-
роде (кристаллические решетки раз-
личных веществ, пчелиные соты), в
технике (детали машин и механизмов,
поверхности и конструкции складыва-
ющихся антенн, концентраторов со-
лнечной энергии), в строительстве и
архитектуре (складчатые покрытия
зданий, фрагменты зданий и их ко-
нструктивные элементы) и т.д. При
расчетах сложных технических повер-
хностей численными методами, воспро-
изведении их на станках с числовым
програмным управлением, визуализа-
ции на экранах графических дисплеев
и т.д. они заменяются (аппроксимиру-
ются) вписанными или описанными
многогранными поверхностями.
2.4.1. Основные понятия
и определения
Поверхности многогранников состоят
из конечного числа плоских многоу-
гольников, называемых гранями. Две
смежные грани пересекаются по реб-
ру — общей стороне смежных многоу-
гольников, а три грани или более име-
ют общую вершину. При этом любые
две вершины многогранника соединя-
ются ломаными, состоящими только из
его ребер.
Совокупность всех вершин и ребер
многогранной поверхности называется
ее сеткой. Многогранная поверхность
называется замкнутой, если каждое
ребро принадлежит двум ее граням.
Тело, ограниченное замкнутой многог-
ранной поверхностью, называется мно-
гогранником.
Из всего многообразия многогранни-
ков наибольший интерес представляют
призмы, пирамиды, правильные мно-
гогранники.
35
Рис. 2.15
Рис. 2.17
Многогранник, две грани которого
являются n-угольниками, лежащими
в параллельных плоскостях, а осталь-
ные грани — параллелограммами,
называется n-угольной призмой (рис.
2.15). Эти многоугольники называются
основаниями призмы, параллелограм-
мы — боковыми гранями.
Многогранник, одна из граней кото-
рого — произвольный многоугольник,
а остальные грани — треугольники,
имеющие общую вершину, называется
пирамидой (рис. 2.16). Многоугольная
грань пирамиды называется основани-
ем, треугольные — боковыми гранями.
Общая вершина треугольников называ-
ется вершиной пирамиды.
Рис. 2.16
Часть пирамиды, ограниченная ее
основанием и плоскостью, параллель-
ной основанию и не проходящей через
вершину, называется усеченной пира-
мидой (рис. 2.17).
Многогранник называется метричес-
ки правильным, если все его грани
являются правильными многоугольни-
ками, и все многогранные углы —
конгруэнтными правильными многог-
ранными углами. К ним относятся
(рис. 2.18): тетраэдр (а), октаэдр (б),
a) i) в)
Рис. 2.18
икосаэдр (в), куб (г), додекаэдр (д).
Правильные многогранники исследовал
Платон. Поэтому они также называют-
ся платоновыми многогранниками.
2.4.2. Изображение
многогранников
на чертеже
На чертеже многогранники изобра-
жаются проекциями своих сеток, т.е.
проекциями вершин и ребер. На рис.
2.19 дан чертеж трехгранной пирамиды
на эпюре Монжа, а на рис. 2.20 —
36
аксонометрический чертеж трехгран-
ной призмы. Показано построение
проекций точек, принадлежащих по-
верхностям данных многогранников.
Чертеж многогранной поверхности, на
котором можно построить проекции
любой принадлежащей ей точки, назы-
вается полным. На таком чертеже
можно решить любые позиционные
Так как многогранная поверхность
определяется совокупностью граней, то
ее математическую (аналитическую)
модель можно представить как систему
уравнений и неравенств. Уравнения
описывают плоскости ее граней, а не-
равенства определяют пределы измене-
ния координат точек, принадлежащих
каждой грани.
2.5. Кривые линии
и обводы
Невозможно найти такую область
деятельности человека, где бы он не
встречался с кривыми линиями в виде
абстрактных геометрических образов
или в виде их физических (материаль-
ных) моделей. И траектория движения
небесных тел и линия, проведенная на
листе бумаги, являются одномерными
геометрическими фигурами.
В прикладной геометрии при матема-
тическом описании всевозможных тех-
нических кривых, которыми являются
траектории движения точек машин и
механизмов, силовые линии магнитных
полей, оси дорог, трубопроводов, кана-
лов, каждую из них рассматривают
как дугу одной какой-либо математи-
ческой кривой или как одномерный
обвод — составную линию, представ-
ляющую собой последовательность
дуг различных кривых.
2.5.1. Основные понятия
и определения
Кривая — это множество точек про-
странства, координаты которых явля-
ются функциями одной переменной:
х = /1 (р)
Z =/3(р).
Термин кривая в разных разделах
математики определяется по-разному.
В начертательной геометрии кривую
37
рассматривают как траекторию движу-
щейся точки, как проекцию некоторой
кривой, как линию пересечения двух
поверхностей и т.д.
В основу классификации кривых
положен вид их уравнений. Кривые
подразделяются на алгебраические и
трансцендентные соответственно то-
му, являются ли их уравнения в пря-
моугольной системе координат алгеб-
раическими или трансцендентными.
Семейство алгебраических кривых, в
свою очередь, подразделяется на подсе-
мейства в зависимости от порядка
кривой. Графически порядок кривой
определяется числом точек пересече-
ния ее с прямой, если она плоская,
или с плоскостью, если она простран-
ственная. При этом надо иметь в виду,
что в число точек входят как действи-
тельные, так и мнимые точки. Напри-
мер, плоская кривая третьего порядка
т. может пересекаться с прямой: в трех
различных действительных точках; в
двух совпавших (касается здесь) и
одной отличной от них точке; в одной
действительной и двух мнимых точках.
Поэтому для правильного определения
порядка кривой необходимо выбрать
такую прямую или плоскость, которая
пересекала бы кривую в действитель-
ных различных точках.
Кривая называется плоской, если
все ее точки принадлежат некоторой
плоскости, в противном случае она
называется пространственной.
Кроме этого, плоская алгебраическая
кривая характеризуется классом и
жанром. Класс кривой равен степени
ее уравнения, записанного в так назы-
ваемых тангенциальных координатах.
Графически класс кривой определяет-
ся числом касательных, проведенных
к ней из точки, не лежащей на кри-
вой. Касательные здесь также могут
быть действительными и мнимыми.
Жанр р плоской алгебраической
кривой равен разности между воз-
можным для данного порядка п и
существующим dc числом двойных
точек:
(п - 1) (п - 2)
При этом следует иметь в виду,
что к двойным точкам относятся
узловые (рис. 2.21, а), изолирован-
ные (рис. 2.21, б) и точки возврата
(рис. 2.21, в). Через двойную узловую
точку проходят две различные ветви
кривой, через изолированную точку —
две мнимые ветви, а в точке возврата
ветви кривой касаются друг друга.
Кривые нулевого жанра называются
рациональными. Они находят широкое
применение для описания всевозмож-
ных аэро- и гидродинамических про-
филей.
На чертеже кривая линия задается
своими проекциями. Аналитический,
эквивалент такого задания кривой
получается, если в системе уравнений
(2.16) освободиться от параметра р:
У = Ф1 <-к)
z = Фг(х).
(2.17)
Другими словами, кривая линия
задается как линия пересечения двух
проецирующих цилиндрических повер-
хностей. В общем случае простран-
ственная кривая линия представляется
как пересечение двух поверхностей:
38
ф(х, у, z) =0
(2.18)
Д(х, у, z) = 0.
Если одна из них будет плоскостью,
то кривая линия будет плоской.
В некоторых случаях при изображе-
нии кривой линии, кроме проекций
кривой, необходимо задать по крайней
мере проекции одной ее точки. Дей-
ствительно, на рис. 2.22, если бы не
были указаны проекции точки А, не-
возможно было бы однозначно постро-
ить горизонтальную проекцию В} точ-
ки В по ее фронтальной проекции В2,
так как линия связи пересаекает гори-
зонтальную проекцию кривой в двух
точках. Наличие проекций точки А
позволяет, обходя кривую в выбранном
направлении, однозначно построить
В общем случае по чертежу кривой
можно без дополнительных построений
определить, пространственная она или
плоская. На рис. 2.22 кривая а про-
странственная, так как имеет пары
конкурирующих точек С, D и М, N.
Однако, если даны проекции дуги кри-
вой или проекции не имеют особых
точек, то необходимо выполнять допо-
лнительные построения. Надо на кри-
вой выбрать три произвольные точки и
проверить, лежит ли любая четвертая
точка кривой в плоскости, определяе-
мой первыми тремя. Кривая т(т^,
т2), изображенная на рис. 2.23, про-
М2) кривой не лежит в плоскости Ф (Л,
В, С), определяемой некоторыми тремя
точками А, В, С этой кривой.
Для исследования локальных (диф-
ференциальных) свойств кривой в
окрестности выбранной точки строят
касательную и нормаль. Касательной
прямой t в точке М кривой т называ-
ется предельное положение секущей
MN, когда точка N стремится вдоль
линии т к точке М (рис. 2.24). Нор-
малью п к плоской кривой в точке М
называется прямая, перпендикулярная
касательной /, построенной в этой
точке. Пространственная кривая имеет
в каждой точке бесчисленное множес-
тво нормалей, принадлежащих нор-
мальной плоскости. Нормаль плоской
кривой принадлежит ее плоскости.
К локальным свойствам кривой отно-
сится также понятие кривизны. Пре-
дельное положение / окружности Г,
проходящей через точку М кривой и
две другие ее близкие точки N и Р,
когда N - М-, Р - М (рис. 2.25), назы-
вается кругом кривизны. Центр (? и
39
радиус R окружности I называются
соответственно центром и радиусом
кривизны. Величина к = — называет-
ся кривизной кривой в точке М.
2.5.2. Конические сечения.
Прямоугольная проекция
окружности
Кривые второго порядка называют-
ся также коническими сечениями, так
как получаются сечением конической
поверхности вращения некоторой
плоскостью. Как известно, кривые
второго порядка бывают: неприводи-
мые (окружность, эллипс, парабола и
гипербола), приводимые или распав-
шиеся (две действительные или мни-
мые пересекающиеся прямые, две со-
впавшие прямые, две действительные
или мнимые параллельные прямые).
Окружность и эллипс, как замкнутые
кривые, не содержат несобственных
точек. Парабола имеет одну несобст-
венную точку, а гипербола — две несо-
бственные точки (несобственные точки
ее асимптот).
Следовательно, если секущая плос-
кость Г пересекает все образующие
конической поверхности, то получает-
ся эллипс, кривая второго порядка, не
имеющая несобственных точек. В час-
тном случае, когда плоскость Д пер-
пендикулярна к оси конической повер-
хности, в сечении получается окруж-
Рис. 2.26
ность. Если секущая плоскость Ф па-
раллельна одной образующей коничес-
кой поверхности, то получается пара-
бола. Если же плоскость 6 параллельна
двум образующим, то — гипербола,
кривая второго порядка, имеющая две
несобственные точки (рис. 2.26).
Если секущая плоскость проходит
через вершину конической поверхнос-
ти, то кривая второго порядка распада-
ется на две пересекающиеся прямые.
Они будут действительными различны-
ми, если плоскость пересекает телес-
ный угол, определяемый конической
поверхностью. Эти прямые совпадут,
если плоскость касается конической
поверхности, и будут мнимыми, если
секущая плоскость находится вне те-
лесного угла. И, наконец, указанные
прямые будут параллельными, если их
точка пересечения (вершина коничес-
кой поверхности) является несобствен-
ной, т.е. коническая поверхность будет
вырожденной в цилиндрическую.
При выполнении машиностроитель-
ных чертежей часто возникает необхо-
димость построения прямоугольных
проекций окружности. Прямоугольной
проекцией окружности является эл-
липс. В большую ось эллипса проеци-
руется диаметр окружности, лежащий
на прямой уровня, а в малую ось —
диаметр, составляющий наибольший
угол с плоскостью проекций.
Рассмотрим три случая.
40
1. Окружность / лежит в плоскости
уровня Ф. Естественно, она проециру-
ется на одну из плоскостей проекций в
натуральную величину, а на другую
плоскость проекций — в отрезок, со-
впадающий с вырожденной проекцией
2. Окружность I лежит в проецирую-
щей плоскости Д (рис. 2.28). Одна ее
проекция вырождается и совпадает с
вырожденной проекцией плоскости,
вторая проекция — эллипс. Построение
проекций /|, /2 ясно из чертежа.
3. Окружность, лежащая в плоскости
общего положения, проецируется на
обе плоскости проекций в эллипсы.
Пример. Построить проекции Zj, /2
окружности 1(0, R), лежащей в плос-
кости Г(Л п /), где О = h A f (рис.
2.29).
Выше было отмечено, что большие
оси эллипсов /[, /2 принадлежат лини-
ям уровня, соответственно горизонтали
h и фронтали /, и по величине равны
диаметру окружности I. Поэтому боль-
шую ось Л]#! эллипса 1Х на ГЦ откла-
дываем на горизонтальной проекции
горизонтали Ар а большую ось Л/2.У2
эллипса Z2 — на фронтальной проекции
фронтали /2. Вторые проекции Л2, В2,
Л/|, соответственно точек А, В, М,
N находим из условий принадлежности
горизонтали и фронтали.
Для построения малых осей и
P2Q2 проводим прямые П\ а А\В\, п2 а
M2N2. Эллипс теперь определен
большой осью направлением
малой оси и двумя точками М\,
Этих условий достаточно для графи-
ческого определения величины его
малой оси (см. рис. 2.28; 2.29):
— через точку искомого эллипса
/| проводим прямые, параллельные
AlBi и И];
— отмечаем точку 2 пересечения
прямой, параллельной Пр с окруж-
ностью v, описанной на /ЦВр как на
диаметре;
— отмечаем точку / = О}2 п и
получаем отрезок О}1, определяющий
величину малой полуоси эллипса Zj.
41
Аналогично определяется величина
малой полуоси эллипса /2 — фронталь-
ной проекции окружности I.
2.5.3. Пространственные кривые
и свойства их проекций
Исследование свойств кривой вклю-
чает в себя исследование кривой в
целом и исследование ее дифференци-
альных свойств (в окрестности ее точ-
ки). При исследовании свойств кривой
в целом необходимо установить общие
свойства кривой и се проекции. Естес-
твенно, они связаны со свойствами
проецирования.
Сформулируем и докажем основные
проекционные свойства пространствен-
ных кривых. Они будут справедливыми
и для проекций плоских кривых.
1. Несобственная точка кривой
проецируется в несобственную точку
ее проекции.
Это свойство — следствие свойств
параллельного проецирования, которое
представляет собой отображение, ста-
вящее в соответствие несобственные
точки пространства несобственным
точкам плоскости проекций.
2. Касательная к кривой проециру-
ется в касательную к ее проекции,
если направление проецирования не
параллельно касательной.
Как известно, касательная — это
секущая, пересекающая кривую в двух
совпавших точках (рис. 2.30). При
параллельном проецировании точкам
кривой однозначно соответствуют
точки ее проекции. Следовательно,
двум совпавшим точкам пересечения
касательной с кривой соответствуют
две совпавшие точки пересечения про-
екции касательной и проекции кривой.
Это свойство дает возможность уста-
новить способ построения касательной
t кривой т в ее точке М. Для этого
необходимо провести касательные Z(, /2
в точках Му, Л/2 соответственно к
проекциям Шу, ш2 кривой т. Прямые
Z], (2 будут проекциями искомой каса-
тельной.
3. Порядок проекции алгебраичес-
кой кривой равен порядку самой кри-
вой.
Проведем некоторую проецирующую
плоскость Ф, которая данную кривую I
п-го порядка пересечет в п точках
d(j= 1, 2,..., п). Согласно однознач-
ности параллельного проецирования
точки U проецируются в точки L-
плоскости проекций П(, принадлежа-
щие прямой а( = Ф п П(. Т.е. прямая а,
пересекает проекцию /( кривой I также
в п точках.
В частных случаях проекция может
распадаться и иметь меньший, чем у
кривой, порядок. Например, кривая
второго порядка, лежащая в проециру-
ющей плоскости, проецируется в пря-
мую, считаемую дважды, так как каж-
дая проецирующая прямая пересекает
оригинал не в одной точке, как это
было в общем случае, а в двух точках.
Если же каждая проецирующая пере-
секает пространственную кривую п-го
порядка в к точках, то порядок про-
екции равен п : к.
Еще один частный случай имеет
место при нахождении центра проеци-
рования на кривой. Например, кривая
второго порядка из какой-либо своей
точки проецируется в прямую линию.
В этом случае порядок проекции на
единицу меньше порядка оригинала. В
общем случае, если центр проецирова-
ния совпадает с Л-кратной точкой
42
пространственной кривой n-го поряд-
ка, то порядок проекции равен п — к.
4. Жанр проекции кривой равен
жанру самой кривой. На .этом свой-
стве основано правило для определения
жанра пространственной кривой, если
известен жанр ее проекции (см. п.
2.5.1).
Исследование дифференциальных
(локальных) свойств кривой в окрес-
тности некоторой ее точки производит-
ся путем построения ее проекций на
грани сопровождающего трехгранника
(трехгранника Френе).
Сопровождающий трехгранник состо-
ит из трех ребер — касательной, нор-
мали и бинормали и из трех граней —
соприкасающейся, нормальной и
спрямляющей плоскостей (рис. 2.31).
Все плоскости, проходящие через
касательную t к кривой т в ее точке
М, называются касательными. Среди
них содержится одна, называемая со-
прикасающейся плоскостью 0, являю-
щейся предельным положением неко-
торой плоскости б (Л/, М, М при
стремлении точек М, М вдоль кривой
к точке М. В дифференциальной гео-
метрии показывается, что соприкасаю-
щаяся плоскость 0 наилучшим образом
приближается в окрестности точки М
к кривой т. Поэтому кривую т в
окресности точки М рассматривают
как плоскую.
Как было выше отмечено, плоскость
Г э М, перпендикулярная касательной
t, называется нормальной. Плоскость
t|r => t, перпендикулярная плоскости 0,
называется спрямляющей. Прямая п ~
= Г п 0 называется главной нор-
малью, а прямая b = Г п <р — бинор-
малью.
Таким образом, зная определения
ребер и граней сопровождающего трех-
гранника, можно без особых труднос-
тей построить их на чертеже в случае
графического задания исследуемой
кривой.
2.5.4. Цилиндрическая
винтовая линия
Наиболее часто встечающаяся в ин-
женерной практике пространственная
кривая — это цилиндрическая винто-
вая линия.
Цилиндрическая винтовая линия
представляет собой траекторию точ-
ки, совершающей равномерное посту-
пательное движение вдоль некоторой
прямой т, которая в свою очередь
равномерно вращается вокруг парал-
лельной ей оси /.
Расстояние h, на которое точка М
перемещается вдоль образующей за
один ее оборот, называется шагом
винтовой линии. Описываемая при
этом точкой М дуга называется вит-
ком (рис. 2.32).
и Л
Число р = — называется парамет-
2л
ром винтовой линии и определяет
поступательное перемещение z точки
М вдоль прямой т за время поворота
последней на угол <р, равный одному
радиану.
Радиус г цилиндра, описываемого
прямой т вращением вокруг оси у,
называется радиусом, а ось j — осью
винтовой линии.
При совмещении оси Oz системы
координат Oxyz с осью j винтовой ли-
нии ее уравнения в параметрической
форме имеют вид
43
X = r COS ф,
у = г sin ф,
Z = рф.
(2.19)
Исключая параметр ф из (2.19), по-
лучаем уравнение ее горизонтальной
проекции (ГЦ х у) — окружности
х2 + у2 = г2 (2.19а)
и фронтальной проекции (П2 => j) —
косинусоиды
х = г cos _. (2.196)
Р
Очевидно, винтовая линия однознач-
но определяется своей осью у, шагом h
(или параметром р) и радиусом г. Поэ-
тому для построения проекций /2
винтовой линии I на чертеже задаем
цилиндр вращения осью у, радиусом г
и откладываем на оси j отрезок, рав-
ный шагу Л (см. рис. 2.32).
Вырожденная проекция цилиндра
есть горизонтальная проекция дан-
ной винтовой линии. Для построения
фронтальной проекции /2 делим
окружность /j и отрезок h на равное
число частей (на рассматриваемом
чертеже — 12 частей). Фронтальные
проекции точек винтовой линии нахо-
дим как точки пересечения одноимен-
ных горизонтальных и вертикальных
прямых, проведенных через точки
деления.
Винтовая линия может быть правой
или левой. Она называется правой,
если наблюдатель смотрит вдоль оси
винтовой линии и видит ее закручива-
ющейся при подъеме против движения
часовой стрелки.
Угол а, составленный касательной к
винтовой линии с плоскостью Г х у,
постоянен для любой ее точки и назы-
вается углом подъема винтовой ли-
нии.
Нетрудно показать, что кратчайшая
линия, соединяющая две точки повер-
хности цилиндра, будет винтовой ли-
нией.
В технике также встречаются винто-
вые линии, принадлежащие коничес-
ким поверхностям и другим поверхнос-
тям вращения.
2.5.5. Обводы
Решение ряда задач требует построе-
ния линий, проходящих через упорядо-
ченный массив точек или через данные
точки и имеющие в них наперед за-
данные положения касательных, кру-
гов кривизны и т.д. Иногда требуется
какую-либо графически или аналити-
чески заданную кривую заменить дру-
гой кривой. Например, при обработке
результатов эксперимента по получен-
ным дискретным значениям изучаемой
зависимости требуется вывести се ана-
литическое выражение, т.е. необходи-
мо вывести уравнение кривой, прохо-
дящей через экспериментально полу-
ченные точки. Другой пример: кон-
структор графически задал некоторый
аэродинамический профиль, для выпо-
лнения аэродинамических расчетов
44
или для воспроизведения на экране
дисплея необходимо его перезадать
аналитически.
Все задачи такого типа сводятся к
замене (аппроксимации) одной функ-
ции, заданной дискретно, графически
или аналитически, другой функцией
определенного вида. Имеется три ос-
новных метода аппроксимации функ-
ций:
1) интерполирование функций;
2) приближение функций;
3) конструирование обводов.
Интерполирующая кривая проводит-
ся через выбранные точки исходной
кривой, называемые узлами интерпо-
лирования. При приближении исход-
ной функции fix) новой функцией
<р (х) на множестве точек (хг-, yt) (i = О,
1, ... п) в качестве меры приближения
обычно минимизируют сумму квадра-
тов разностей
п
minS = - /Ос,)]2.
/и
Если исходна кривая задана большим
числом точек, то выбор новой кривой,
качественно аппроксимирующей исход-
ную, требует выполнения сложных
вычислений. Для упрощения решения
задачи в качестве аппроксимирующей
линии конструируют составную кри-
вую — обвод.
Обводом называется линия, состав-
ленная из дуг кривых выбранного
вида, которые в стыковых точках име-
ют определенный порядок соприкос-
новения.
В инженерной практике в качестве
составляющих обводов обычно исполь-
зуют отрезки прямых, дуги кривых
второго и третьего порядка. Порядок
соприкосновения составляющих в сты-
ковых точках определяет порядок
гладкости обвода. Если смежные со-
ставляющие имеют в стыковых точ-
ках общие касательные, то составная
линия называется обводом первого
порядка гладкости. Составная линия
представляет собой обвод второго
порядка гладкости, если график изме-
нения кривизны по ее длине будет
непрерывным. С этих позиций лома-
ная линия представляет собой обвод
нулевого порядка гладкости.
2.5.6. Некоторые способы
построения обводов
Разработано множество способов
конструирования обводов. Приведем те
способы, которые отличаются просто-
той и получили широкое применение.
1. Радиусографический способ
Через упорядоченный массив точек
A1 Ц = 1, 2, ..., п) проводится обвод
первого порядка гладкости, составлен-
ный из дуг окружностей (рис. 2.33).
Рис. 2.33
Построение составляющих обвода осно-
вано на простых свойствах окружнос-
тей. Первая составляющая т' одно-
значно определяется первыми тремя
точками Л1, Л2, Л3. Центр О1 окруж-
ности ш1 строится как точка пересече-
ния перпендикуляров р1, р2, восстав-
45
ленных из середин С1, С2 ее хорд
а'а2, а2а3.
Вторая и последующие составляющие
т2, т3, ... определяются двумя точка-
ми и касательной, построенной к пре-
дыдущей составляющей в стыковой
точке. Центр О2 второй составляющей
т" определяетя как точка пересечения
прямой ОХА3, соединяющей центр О1
предыдущей окружности со стыковой
точкой А3, с перпендикуляром р3, вос-
ставленным из середины С3 хорды
А3А4. Аналогично строятся все после-
дующие составляющие т1 (j= 1, 2,
п-2).
2. Способ кривых
второго порядка
Этот способ имеет ряд модификаций.
Ниже описан алгоритм построения
точек обвода, заданного упорядочен-
ным массивом точек A' (t = 1, 2, ..., п)
и положениями касательных t‘ в этих
точках (рис. 2.34).
Как известно, кривая второго поряд-
ка однозначно определяется заданием
пяти точек. Это следует из того, что ее
уравнение в декартовых координатах
имеет вид
Ах2 > By2 + Сху + (2 2())
+ Dx + Еу + 1 = 0.
Подставив в это уравнение последо-
вательно координаты пяти точек, по-
лучаем пять линейных уравнений с
пятью неизвестными А, В, С, D, Е.
Решение полученной системы урав-
нений определяет значения указан-
ных коэффициентов в уравнении
(2.20).
На практике обычно кривую второго
порядка задают тремя точками и каса-
тельными в двух точках или двумя
точками А1, А2, касательными ?,
О
г в этих точках и так называемым
инженерным дискриминантом d =
[ВС]: [ТС] (рис. 2.34), где Т — точка
пересечения качательных ?, t2, по-
строенных в точках А1, А2 кривой вто-
рого порядка т1; ТС — медиана треу-
гольника А1 ТА2. Если d < 0,5, то щ1
будет дугой эллипса, при d = 0,5 —
дугой параболы, при d > 0,5 — дугой
гиперболы. Таким образом, выбирая
значение инженерного дискриминанта
d, управляют формой кривой второго
порядка.
Построение обвода первого порядка
гладкости из дуг кривых второго по-
рядка начинают с выбора значений
инженерного дискриминанта d для
каждой составляющей, исходя из ви-
зуальной оцени данного массива точек
и касательных, обеспечения требуемой
формы конструируемого обвода. После
этого для каждой составляющей т‘
обвода по известному значению дис-
криминанта dl строится третья точка
В, которая вместе с точками А', А1+1 и
касательными t1, ?+1 однозначно ее
определяет. Этих данных достаточно
для вычисления коэффициентов урав-
нения (2.20), описывающего составля-
ющую т1 обвода, или для графическо-
го построения множества точек сосгав-
Рис. 2.34
46
ляющей т1, которые строятся последо-
вательно (см. рис. 2.34):
— на первом этапе строятся точка В
и касательная Г, параллельная хорде
A A j
— на втором этапе по аналогии с
алгоритмом построения точки В стро-
ятся относительно треугольников
А1 ТВ и ВТ'А2 точки В, В' и каса-
тельные t,
— эти точки и касательные порожда-
ют четыре новых треугольника, отно-
сительно которых строятся четыре
новые точки составляющей щ1.
Этот процесс продолжается до тех
пор, пока не будет получено достаточ-
ное число точек каждой составляющей
т‘ конструируемого обвода.
3. Сплайн-аппроксимация
Для проведения кривой через данные
точки часто в качестве лекала исполь-
зуется гибкая рейка (spline). Аналити-
чески ось изогнутой рейки приближен-
но можно описать полиномиальным
уравнением третьей степени
у =А0 + + А2х2 + А3х3. (2.21)
График этой функции показан на
рис. 2.35. Эта кривая называется куби-
ческой параболой. Она однозначно
определяется заданием четырех точек,
двух точек и касательных, проведен-
ных в этих точках и т.д.
Рис. 2.35
Разработано множество способов по-
строения обводов первого и второго
порядков гладкости из дуг кубических
парабол. Например, если обвод задан
массивом точек и касательными в них
М ‘<х(, yz, у/)*,
где у1 =— = А, +2А2х +ЗАэХ2, (2.22)
dx 1 £ °
то построение составляющей т1 обвода
[определение коэффициентов Ло, Лр
Л2, А3 ее уравнения (2.21)] сводится к
решению системы четырех линейных
уравнений с четырьмя неизвестными
Ао, Ар А2, Аэ:
yi = A0 + Alxi + A2xl2 + A3xi3
2 3
Vivi =А0 + А1х,И + A2xi^A3xi>l
I 7
у;. =A1+2A2xj + 3A3x.
/А1=Л1+2Л2х/ + 1+злзхАг
где xjr yi — координаты стыковой точки
М‘\ *1+1 > >'г+1 — координаты стыковой
точки Af,+1; у/ — угловой коэффици-
ент касательной в точке М';у/н1 — уг-
ловой коэффициент касательной в точ-
ке А/,+|.
Отметим, что в настоящее время в
прикладной геометрии наибольшее
применение получил метод сплайн-ап-
проксимации. Он обобщен на констру-
ирование двумерных обводов — состав-
ных поверхностей из отсеков бикуби-
ческих сплайнов.
В заключение заметим, что построе-
ние одномерных пространственных об-
Напомним. что геометрическим смыслом пер-
/
вой производной у. является значение углового
коэффициента касательной, построенной к кри-
вой в се точке М‘(х,, у).
47
водов сводится к конструированию
плоских обводов — проекций, проходя-
щих через упорядоченные массивы
горизонтальных и фронтальных проек-
ций стыковых точек.
2.5.7. Изображение
кривых линий
на аксонометрическом чертеже
Как было показано выше (п. 1.6),
изображения геометрических фигур на
чертеже Монжа и аксонометрическом
чертеже принципиально ничем не от-
личаются. Сказанное полностью отно-
сится и к изображениям кривых ли-
ний. В общем случае пространственная
кривая на аксонометрическом чертеже
задается двумя проекциями: аксоно-
метрической и вторичной. Для постро-
ения ее проекций необходимо постро-
ить проекции множества ее точек по
их известным координатам, измерен-
ным с чертежа Монжа или вычислен-
ным из уравнения данной кривой. На
рис. 2.36 в качестве примера показано
построение аксонометрического изо-
бражения кривой т. Она построена по
точкам /, 2, ..., координаты которых
взяты с чертежа Монжа.
Для изображения некоторых наибо-
лее часто встречающихся кривых раз-
работаны простые приемы построения
их проекций. Рассмотрим два примера.
Пример 1. В прямоугольной аксоно-
метрии построить проекции окружнос-
ти /(Л/, г), принадлежащей координат-
ной плоскости Оху (рис. 2.37).
В нашем случае аксонометрическая
I' и вторичная // проекции окружнос-
ти совпадают. Для их построения удо-
бно воспользоваться способом совмеще-
ния координатной плоскости Оху с
плоскостью П' аксонометрического
чертежа вращением вокруг стороны XY
треугольника следов, так как в совме-
щенном положении окружность изо-
бражается без искажения. При враще-
нии вокруг оси XY начало О координат
перемещается в проецирующей плос-
кости Г' = O'z'. Совмещенное поло-
жение О определяется из условия, что
угол между осями Ох и Оу равен 90°;
О = z' п t, где t — полуокружность,
описанная на XY, как на диаметре.
Центр М (М' = м[) искомой
окружности I вращается вместе с плос-
костью Оху. Сначала строятся совме-
щенное положение I (М, г) окружнос-
ти, затем два ее диаметра, параллель-
ный и перпендикулярный оси враще-
Рис. 2.36
48
ния XY. При обратном вращении они
преобразуются в оси эллипса /' = // —
проекции данной окружности I.
Пример 2. В прямоугольной аксоно-
метрии построить проекции цилиндри-
ческой винтовой линии т (j = Oz, г, h)
n t 1
Построение проекции т , тх ци-
линдрической винтовой линии выпо-
лним, используя ее свойства и способ
построения ее проекции на чертеже
Монжа (см. п. 2.5.4 и рис. 2.31).
Сначала построим вторичную проек-
/
цию тх , для чего воспользуемся спо-
собом совмещения (см. пример 1). Со-
вмещенную проекцию т делим на
определенное число равных частей (в
нашем случае — 12) и обратным вра-
щением точек деления находим вто-
ричные проекции 1Х , 2Х, ..., 12х ,
7J] = на тх .
Далее строим аксонометрические
проекции указанных точек. Для этого
шаг h делим на такое же число равных
частей. На линиях связи, проходящих
через вторичные проекции, откладыва-
ем пропорциональные углам поворота
высоты точек I, 2, ..., 12, 13: 1{ = Г,
2Х2' = 7 —, з'х3' =2 — , 4Х4’ = 3 — ,
1 12 1 12 1 12
..., = /2_L. На рис. 2.38 пока-
зан другой прием построения аксоно-
метрических проекций точек 1, 2,
13: через точки деления шага А, отло-
женного на оси j винтового движения,
проведены горизонтали, аксонометри-
ческие проекции которых параллельны
их вторичным проекциям 011Х , 012Х,
..., О113xj точки пересечения аксоно-
метрических проекций этих горизонта-
лей с соответствующими линиями свя-
зи будут аксонометрическими проек-
циями Г, 2', ..., 13' точек цилиндри-
ческой винтовой линии т.
В заключение отметим, что построе-
ние изображений кривых линий имеет
первостепенное значение при изучении
образования и задания на чертеже
поверхностей.
2.6. Поверхности
Поверхности составляют обширное
многообразие нелинейных фигур трех-
мерного пространства. Любое тело
ограничивается своей поверхностью.
49
Нет ни одной области деятельности
человека, где бы он не сталкивался с
поверхностями в виде материальных,
физических и т.д. моделей.
Инженерная деятельность связана
непосредственно с конструированием,
расчетом, изготовлением различных
технических поверхностей. Большин-
ство задач прикладной геометрии сво-
дится к автоматизации конструирова-
ния, расчета и воспроизведения слож-
ных технических поверхностей.
2.6.1. Основные понятия
и определения
Наиболее сложными геометрически-
ми фигурами трехмерного простран-
ства являются поверхности — двупара-
метрические множества точек. Про-
стейшими из них являются плоскости,
любая точка которых однозначно опре-
деляется заданием двух координат.
Аналогично любая точка поверхности
также определяется заданием двух
криволинейных координат и, v
(рис. 2.39). Другими словами, повер-
хность — это множество точек про-
странства, координаты которых явля-
ются функциями двух переменных:
X = f\(и, v)
у = f2(u, v) (2.23)
z = f3(u, v)
Уравнения (2.23) называются пара-
метрическими уравнениями поверхнос-
ти и выражают декартовы координаты
точек поверхности через их криволи-
нейные координаты.
Из рис. 2.39 следует другое опреде-
ление поверхности. Если точка М пе-
ремешается по кривой т, параллель-
ной координатной оси Ov, то ее коор-
дината им останется неизменной, т.е.
линия т определяется заданием одной
координаты им, а поверхность Ф пред-
ставляет собой однопараметрическое
множество линий т‘. Иначе, поверх -
ность Ф можно рассматривать как не-
прерывную совокупность последова-
тельных положений линии т, которая
в процессе перемещения не меняет
свою форму или же меняет ее по неко-
торому закону.
Такой способ образования поверхнос-
тей называется кинематическим. Ли-
ния т называется образующей. Зако-
ны распределения положений образую-
щей в пространстве и изменения ее
формы задаются обычно направляю-
щими линиями. Кинематический спо-
соб образования поверхностей доста-
точно нагляден и прост. Он получил
широкое применение при конструиро-
вании технических поверхностей. В
специальных разделах математики и
некоторых отраслях техники рассмат-
ривают другие способы образования
поверхностей, отличающиеся от кине-
матического.
Говоря о кинематичеком способе об-
разования, вводят понятие определите-
ля поверхности, как совокупности
независимых условий, однозначно
определяющих эту поверхность. Опре-
делитель поверхности состоит из двух
частей: геометрической и алгоритми-
ческой. Например, сфера Ф однозначно
определяется заданием ее центра О и
радиуса R, что записывается так: Ф(О,
R). Точка О и радиус R составляют
геометрическую часть определителя, а
алгоритмическая часть формулируется
50
словами: сфера — эго множество точек
пространства, удаленных от точки О
на данное расстояние R.
Очевидно, одна и та же поверхность
может иметь несколько определителей.
Например, сфера Ф может быть образо-
вана вращением окружности т вокруг
ее диаметра /:Ф(4 ги). Или сфера одно-
значно определяется заданием четырех
ее точек: Ф(А, В, С, D). Здесь же умес-
тно вспомнить о способах задания
плоскости: тремя точками Г(А, В, С),
точкой и прямой Г(А, а), двумя пере-
секающимися Г(а п Ь) и параллельны-
ми прямыми Г(а Ц Ь).
Такие поверхности, как поверхность
фюзеляжа самолета, кузова автомоби-
ля, лопатки турбины и т.д., имеют
сложный закон образования. Их опре-
делители чрезвычайно сложны и раз-
нообразны. Поэтому выработали уни-
версальный определитель, геометри-
ческую часть которого составляет дис-
кретный каркас (множество) образую-
щих, а алгоритмическую часть — алго-
ритм уплотнения каркаса (перехода от
дискретного каркаса к непрерывному).
Например, в топографии рельеф зем-
ной поверхности задают семейством
горизонталей — сечений поверхнос-
ти горизонтальными плоскостями
(рис. 2.40).
Построение проекционных изображе-
ний поверхности вызывает определен-
Рис. 2.41
ные трудности. Если точка и линия
изображаются на чертеже своими про-
екциями, то проецирование точек не-
которой поверхности на какую-либо
плоскость проекций приводит к уста-
новлению соответствия между точками
данной поверхности и плоскости про -
екций. Это соответствие будет неод-
нозначным, так как несколько точек
поверхности могут иметь одну и ту же
проекцию, и нелинейным, так как
прямой линии плоскости проекций бу-
дет соответствовать кривая линия дан-
ной поверхности (рис. 2.41).
При проецировании точек поверхнос-
ти на две плоскости проекций Пр П2
между полями проекций П[(А], В(, ...);
П2(А2, В2, ...) точек поверхности Ф(.4,
В, ...) устанавливается некоторое мно-
гозначное нелинейное соответствие
rClj-Ao), которое является моделью
данной поверхности. Напомним (см.
п. 2.2), что плоскость моделируется
взаимно однозначным линейным соот-
ветствием — родством.
Однако такое толкование задания
поверхности на двухкартинных черте-
жах в силу его сложности и отсутствия
наглядности не нашло применения в
инженерной практике. Обычно кине-
матические поверхности задаются
проекциями элементов геометричес-
кой части определителя. Чертеж по-
верхности является обратимым (по-
лным) , если относительно любой точ-
ки, заданной на том же чертеже, мож-
но однозначно ответить, принадлежит
51
она данной поверхности или нет. Чаще
критерий полноты задания поверхнос-
ти формулируют так: чертеж повер-
хности является полным, если по
одной проекции ее точки можно по-
строить вторую проекцию.
Построение проекции точки, принад-
лежащей поверхности, основано на
следующем признаке: точка принадле-
жит поверхности, если она принадле-
жит какой-либо линии этой поверх-
ности. При графическом построении
проекций точки, принадлежащей по-
верхности, необходимо постараться
провести через нее такую линию по-
верхности, проекции которой были бы
графически простыми. На рис. 2.42
показано построение фронтальной
проекции Л/2 точки М, принадлежа-
щей сфере Ф(О, Л), по заданной ее
горизонтальной проекции Через
точку М на сфере Ф можно провести
бесчисленное множество окружностей,
которые будут проецироваться на ГЦ и
П2 в эллипсы. Только окружности,
расположенные во фронтальной и го-
ризонтальной плоскостях уровня, име-
ют графически простые проекции. На
рис. 2.42 через точку М проведена
окружность т, расположенная во
фронтальной плоскости уровня. Поэто-
му она на П1 проецируется в отрезок
И],анаП2-в натуральную величи-
ну. Задача имеет два решения: -
Рис. 2.42
При построении проекций точки,
принадлежащей сложной поверхности,
заданной дискретным каркасом образу-
ющих, через точку проводят произ-
вольную линию поверхности (обычно
плоскую кривую, расположенную в
проецирующей плоскости). Вторую
проекцию кривой строят по ее точкам
пересечения с дискретным каркасом
образующих. При графическом реше-
нии задачи искомую проекцию строят
с помощью лекала, а при аналитичес-
ком решении или необходимости выпо-
лнения высокоточных построений —
одним из известных способов аппрок-
симации кривых (см. п. 2.5.6).
Аналитически признак принадлеж-
ности точки некоторой поверхности
выражается в том, что при подстановке
координат данной точки в уравнение
поверхности последнее превращается в
тождество 0=0. Для этого целесообраз-
но параметрическое уравнение (2.23)
поверхности путем освобождения от
параметров и, v представить в явной
форме:
z = <р(х, у) (2.24)
или в неявной форме:
у(х, у, г) = 0. (2.25)
Если уравнения (2.24) и (2.25), за-
писанные в декартовых координатах,
представляют алгебраический многоч-
лен n-й степени, то они определяют
алгебраическую поверхность п-го
порядка. В противном случае повер-
хность является трансцендентной.
Очевидно, плоскость, описываемая
многочленом первой степени (2.1),
является алгебраической поверхностью
первого порядка.
При подстановке в уравнение (2.25)
алгебраической поверхности и,-го по-
рядка координат х, у горизонтальной
проекции некоторой точки или коорди-
нат х, z фронтальной проекции какой
либо точки получается в общем случае
52
алгебраическое уравнение л-й степени
от одной переменной, которое, как
известно, имеет и решений. Графичес-
ки это означает, что проецирующая
прямая, проходящая через данную
проекцию точки поверхности, пересе-
кает последнюю в и точках. Поэтому
задача построения недостающей про-
екции точки поверхности л-го порядка
имеет в общем случае л решений. Эти
решения могут быть действительными
различными, некоторые из них могут
быть мнимыми или совпавшими в раз-
личных комбинациях. Отсюда следует
графический способ определения по-
рядка алгебраической поверхности: он
равен числу точек пересечения повер-
хности с произвольной прямой. Заме-
тим, что бесконечное множество точек
пересечения прямой линии с поверх-
ностью является признаком трансцен-
дентности этой поверхности.
Чертеж поверхности, заданной про-
екциями элементов геометрической
части ее определителя, не отличается
наглядностью. Для придания чертежу
поверхности наглядности его дополня-
ют очерковыми линиями. Множество
проецирующих прямых, огибающих
данную поверхность Ф, образует прое-
цирующую цилиндрическую поверх-
ность Д (рис. 2.43). Линия t, вдоль
которой поверхность Ф касается цилин-
дрической поверхности Д, называется
контурной линией. Проекция кон-
турной линии t как след проецирую-
щей цилиндрической поверхности Д на
плоскости проекций П( называется
очерковой линией поверхности Ф на П;.
Проекция той же линии t на другую
плоскость проекций называется линией
видимости по отношению к П(-.
На рис. 2.42 чертеж сферы Ф допо-
лнен очерковыми линиями tt, к2 на
плоскостях проекций Пр П2 и линиями
видимости t2, Aj относительно плоскос-
тей проекций П], П2, что придает чер-
тежу определенную наглядность и
позволяет решать задачи на видимость.
Многообразие поверхностей требует
их систематизации. При рассмотрении
кинематического способа образования
поверхностей в основе ситематизации
лежат два признака: вид образующей
и закон ее перемещения. По виду об-
разующей принято различать линейча-
тые (образующая — прямая), цикли-
ческие (образующая — окружность) и
поверхности зависимых сечений (об-
разующая — плоская кривая), по зако-
ну перемещения образующей — повер-
хности параллельного переноса, вра-
щения и винтовые.
Такая систематизация является до-
статочно условной, ибо одна и та же
поверхность может быть отнесена од-
новременно к различным видам. На-
пример, коническая поверхность вра-
щения относится к линейчатым и по-
верхностям вращения. Или любую
перечисленную группу поверхностей
можно считать поверхностями зависи-
мых сечений, так как, пересекая их
семейством плоскостей, получаем мно-
жество плоских сечений, характерис-
тики которых взаимозависимы.
2.6.2. Поверхности
параллельного переноса
Поверхность, образованная парал-
лельным перемещением образующей
/ по направляющей т, называется по-
верхностью параллельного переноса.
Форму поверхности параллельного
переноса имеет, например, канавка,
53
Рис. 2.44
получаемая на заготовке фасонной
фрезой на трехкоординатном фрезер-
ном станке, где фреза, кроме враще-
ния вокруг своей оси, совершает не-
прерывные перемещения вперед-назад,
вправо-влево и вверх-вниз.
Если линия I совершает параллель-
ное перемещение (рис. 2.44), то векто-
ры ММ1, NN1, КК1, ..., соединяю-
щие соответственные точки двух ее
смежных положений I, Г, будут рав-
ными. Поэтому закон движения обра-
зующей I однозначно определяется за-
данием траектории (направляющей) т
движения одной ее точки М. Следо-
вательно, геометрическая часть опре-
делителя поверхности параллельного
переноса состоит из направляющей т
и образующей /: Ф(щ, /).
Из рис. 2.44 видно, что для повер-
хности параллельного переноса образу-
ющая и направляющая линии взаимо-
заменяемы, т.е. при движении линии I
по линии т или, напротив, линии т
по линии I образуется одна и та же
поверхность Ф. Действительно, из па-
раллелограмма MNN'M' следует, что
точка У' получается переносом точки
/V на вектор ММ1 или переносом точ-
ки М' на вектор MN. Отсюда очевид-
но, что поверхность параллельного
переноса содержит два семейства кон-
груэнтных линий: семейство образую-
щих I, I", ... и семейство на-
правляющих (линий хода) т, п, к, ...
На чертеже поверхность параллель-
ного переноса задается проекциями
элементов геометрической части опре-
делителя, т.е. проекциями образующей
/ и направляющей т (рис. 2.45). Для
проверки полноты задания необходимо
уметь строить недостающую проекцию,
например, At точки А, принадлежащей
поверхности Ф (т, I), если ее фронталь-
ная проекция А2 известна. Простей-
ший способ построения состоит в пред-
варительном построении по точкам
каркаса образующих /, Г, Г, ...; про-
ведении через Л, фронтальной проек-
ции а2 какой-либо линии а поверхнос-
ти Ф; построении ее горизонтальной
проекции по точкам пересечения с
каркасом образующих и нахождении
искомой проекции Л] точки Л. Однако
этот способ трудоемок и графически
неточен.
Построения можно упростить, если
воспользоваться так называемой кри-
вой ошибок I (см. рис. 2.45). Для
определения вектора NA = ММ1
параллельного переноса на фронталь-
ной проекции 12 образующей берем ряд
54
торы М212, М222, •••’ противополож-
ные векторам Л2?2, А222, •••’ к0141^
/2, 22, ..., которых определяют кри-
вую ошибок t . Точка М2 пересечения
кривой ошибок t с фронтальной проек-
цией т2 направляющей определяет
фронтальную проекцию Л/2Л/2 иско-
мого вектора ММ1 = NA. На 12 стро-
им точку N2 из условия противополож-
ности векторов М2М2 , A2N2. Нахо-
дим по линиям связи горизонтальные
проекции , N1 точек М', /Уина
линии связи находим искомую проек-
цию Л] точки А из условия A^Aj =
Поверхности параллельного переноса
обычно образуются движением плоской
кривой I по плоской направляющей те,
принадлежащих проецирующим плос-
костям (рис. 2.46). Здесь построение
недостающей проекции, например, А]
точки А по ее заданной фронтальной
проекции А2 существенно упрощается:
А2 F A2N 1 || т2; Л/2 ~ 12 । < А,Л^2; А2 £
е Л-)М2 || N2M2, М2 = Л2М2 п тг
м/ emi; М/ 6 Л//.4! || At =
= А2Л] гт м'л,.
Очевидно, поверхности параллельно-
го переноса можно классифицировать
по виду образующих. Они будут ли-
нейчатыми, точнее цилиндрическими,
ости образующей является прямая
линия; циклическими, если образую-
щей будет окружность: поверхност ями
зависимых сечений, если образующей
является некоторая линия Повер-
хность параллельного переноса будет
алгебраической, если ее направляю
щая и образующая будут алгебраичес-
кими кривыми. В противном случае
она будет тансцендентной. Справедли-
ва следующая теорема: если образу-
ющей и направляющей поверхности
параллельного переноса являются
алгебраические кривые порядков н(,
п2, пересекающиеся в одной точке, то
порядок п поверхности равен произве-
дению порядков ее направляющей и
образующей:
и = П[П2. (2.26)
Докажем эту теорему. Пусть ради
простоты образующей I будет плоская
кривая порядка и(. Тогда плоскость Г
образующей пересекает направляю-
щую т порядка п2 в >г2 точках М1,
через каждую из которых в плоскости
Г проходит по одной образующей
Значит, некоторая прямая Л, принад-
лежащая плоскости Г, пересекает каж-
дую из этих п2 образующих в г.] точ-
ках, а всю поверхность Ф — в п,п2
точках.
В частном случае образующая I мо-
жет перемещаться в пространстве,
пересекая направляющую т не в од
ной точке, а в j точках. Тогда поря
док поверхности параллельного пере
55
Рис. 2.47
носа вычисляется по следующей фор-
муле:
(2.27)
Выведем уравнение поверхности
параллельного переноса. Для простоты
в качестве ее направляющей и образу-
ющей примем плоские кривые, распо-
ложенные в координатных плоскостях
(рис. 2.47). Пусть их уравнения, запи-
санные в явной форме, имеют вид
Z:z=/(jc.); 22g
т: z = у(у).
По условию кривые I, т должны
пересекаться. Поэтому уравнения
(2.28) при подстановке значений х = О,
у = 0 должны иметь равные значения
аппликат. Наиболее просто это требо-
вание обеспечивается при прохожде-
нии кривых I, т через начало коорди-
нат. В этом случае в уравнениях (2.28)
отсутствую! свободные члены.
Из рис. 2.47 видно, что высота NtN
произвольной точки N образующей/
равна сумме высоты этой точки в
начальном положении и высоты
М\М точки М пересечения образую-
щей I с направляющей т в процессе
движения:
[/V]A1 = lVrV] + [Л^М].
Отсюда уравнение поверхности Ф в
явной форме имеет вид
z = f(x) + у(у). (2.29)
Пример 1. Вывести уравнение по-
верхности параллельного переноса,
образованной движением окружности
/ по направляющей параболе т
(рис. 2.48л
Рис. 2.48
Окружность /, принадлежащая коор-
динатной плоскости Oxz и проходящая
через начало координат, имеет уравне-
ние
х2 + <z - Я)2 = А2. (2-3и>
Парабола т с вершиной О и верти -
кальной осью, принадлежащая коорди-
натной плоскости Oyz, имеет уравне-
ние
у2 = 2pz. (2-31)
Записав уравнения (2.30), (2.31) в
явной форме и подставив в (2.29),
получаем уравнение алгебраической
поверхности четвертого порядка [см.
формулу (2.26)] в явной форме:
z = У Я 2 - х1 R + ~
2р
или в неявной форме:
у4 - 4p(z - R)y2 +
4р2(х2 <• z2) - 8p2/?z = 0.
56
Пример 2. Вывести уравнение повер-
хности параллельного переноса, обра-
зованной движением параболы I с Oxz
по другой параболе т <- Oyz.
Рассмотрим два случая:
1) параболы I, т ’’раскрыты” в одну
сторону (рис. 2.49):
2) параболы I, т ’’раскрыты” в раз-
ные стороны (рис. 2.50):
раболе, а перпендикулярной оси Oz —
по эллипсу.
Во втором случае образуется повер-
хность второго порядка, называемая
гиперболическим параболоидом:
z = *z - zi.
2р 2q'
Эта поверхность пересекается с плос-
костями, параллельными координат-
ным плоскостям Oxz, Oyz, по парабо-
лам, а плоскостями, параллельными
Оху, — по гиперболам. С плоскостью
Оху она пересекается по гиперболе,
распавшейся на две пересекающиеся
прямые.
В этом случае в отличие от предыду-
щего образуется поверхность второго
порядка, так как данные образующая
и направляющая пересекаются в двух
точках [см. формулу (2.27)]: в
собственной точке О и несобственной
точке оси Oz.
В первом случае образуется повер-
хность второго порядка, называемая
эллиптическим параболоидом;
С любой плоскостью, проходящей
через ось Oz, она пересекается по па-
2.6.3. Поверхности вращения
Поверхность, образованная враще-
нием некоторой линии (образующей)
вокруг какой-либо прямой называ-
ется поверхностью вращения.
В природе существует множество
тел вращения: планеты и звезды; дета-
ли машин и механизмов; предметы
быта.
Поверхность вращения однозначно
определяется осью / и образующей./.
Поэтому ее определитель записывается
так; Ф(/, /).
На чертеже поверхность вращения
Ф(/, D задастся проекциями оси j и
образующей I (рис. 2.51). Построение
проекций точки А е Ф целесообразно
выполнять проведением окружности т
— сечения поверхности Ф плоскостью
Г, перпендикулярной ее оси j. Окруж-
ность т определяется центром О -
= j п Г и радиусом [OL], где L = I о Г.
Сечения поверхности вращения плос-
57
костями, перпендикулярными ее оси,
называются параллелями. Параллель,
радиус которой больше радиусов смеж-
ных параллелей, называется эквато-
ром. Параллель, радиус которой мень-
ше радиусов смежных параллелей,
называется горловой окружностью
(горловиной).
Сечения поверхности вращения плос-
костями, проходящими через ее ось,
называются меридианами. Меридиан,
принадлежащий плоскости уровня,
называется глазным.
Семейства параллелей и меридианов
образуют прямоугольный сетчатый
каркас поверхности вращения. Через
произвольную точку А поверхности
вращения проходят единственные па
раллсль и меридиан, пересекающиеся
под прямым углом. Касательные, по-
строенные к меридиану в точках его
пересечения с экватором или горловой
окружностью, параллельны оси повер-
хности вращения.
Если образующая I — алгебраическая
кривая, го поверхность вращения Ф(/Л
также будет алгебраической. Порядок
поверхности вращения зависит от по-
рядка се образующей.
Теорема 1. При вращении алгеб-
раической кривой n-го порядка вок-
руг произвольной прямой образует-
ся поверхность вращения поряд-
ка 2п.
Действительно, образующая п-го
порядка пересекается с плоскостью Г,
перпендикулярной оси вращения, в п
точках. Каждая из этих п точек опи-
сывает в плоскости Г окружность.
Поэтому любая прямая т плоскости Г
пересекает каждую окружность в двух
точках, а все п окружностей — в 2л
точках. Следовательно, прямая т
пересекает поверхность вращения в
2п точках, что определяет ее по-
рядок.
В качестве примера рассмотрим об-
разование широко распространенной в
технике поверхности тора (кольца).
Тор образуется вращением окружности
I вокруг оси /, расположенной в плос-
кости этой окружности (рис. 2.52).
Показано построение горизонтальных
,1.2,3.4
проекции Л) , ./Ц , , Л] некоторой
точки А поверхности тора по заданной
. - , 1 , 2
се фронтальной проекции Л2 = А2 =
= Л23 = А2 . Задача имеет четыре ре-
шения: фронтально проецирующая
прямая а э А пересекает поверхность
тора в четырех точках.
Следствие. При вращении прямой I
вокруг второй прямой j образуется
Рис. 2.52
58
линейчатая поверхность вращения
второго порядка:
если I n j — коническая поверхность
вращения,
если I || j — цилиндрическая повер-
хность вращения,
если I - j — однополостный гипер-
болоид вращения.
Первые две поверхности известны из
программы средней школы. Образова-
ние однополостного гиперболоида вра-
щения не так очевидно. Поэтому ниже
будет рассмотрено построение его глав-
ного меридиана, который дает четкое
представление о форме этой по-
верхности.
Теорема 2. При вращении кривой ti-
ro порядка, имеющей плоскость сим-
метрии, вокруг оси, лежащей в этой
плоскости, образуется поверхность
вращения п-го порядка.
В этом случае каждые две точки
пересечения образующей I с плос-
костью Г, перпендикулярной оси j вра-
щения, описывают одну окружность,
так как они равноудалены от центра
О = Г n j. Обще число окружностей
равно -2. Поэтому произвольная пря-
мая т плоскости Г пересекает каждую
из них в двух точках, а всего точек
пересечения будет п, что определяет
порядок получаемой поверхности вра-
щения.
Следствие. При вращении кривой
второго порядка вокруг ее оси обра-
зуется поверхность вращения второго
порядка:
окружность вокруг любого диаметра
— сфера;
эллипс вокруг малой оси — сжатый
эллипсоид вращения;
эллипс вокруг большой оси — вытя-
нутый эллипсоид вращения;
парабола вокруг оси — параболоид
вращения;
гипербола вокруг мнимой оси —
однополостный гиперболоид враще-
ния;
гипербола вокруг действительной
оси — двуполостный гиперболоид вра-
щения.
Чертеж поверхности вращения, за-
данной проекциями элементов геомет-
рической части определителя, не отли-
чается наглядностью. Так как форма
поверхности вращения наглядно опре-
деляется ее меридианом, то чертеж
поверхности дополняют изображением
главного меридиана, если ее ось явля-
ется проецирующей прямой. В общем
случае строят очерковые линии повер-
хности.
Пример 1. Построить главный мери-
диан однополостного гиперболоида
вращения Ф(у, I) (рис. 2.53).
Главный меридиан т строится как
множество точек 1, 1 ; 2; 2 , ... пере-
сечения параллелей, описываемых
точками 1, 2, ... образующей Z, с плос-
костью S / главного меридиана. При
этом точка 1 образующей I, ближай-
шая к оси вращения /, описывает гор-
ловую окружность q. Однополостный
гиперболоид симметричен относитель-
59
I
Рис. 2.54
но плоскости горловой окружности q.
Поэтому для построения точек главно-
го меридиана достаточно взять точки
на полупрямой /.
Однополосгный гиперболоид Ф содер-
жит два семейства прямолинейных
образующих — последовательных поло-
жений образующей I и симметричной
ее прямой Г. Очевидно, образующие
одного семейства между собой не пере-
секаются, а образующие разных се-
мейств пересекаются между собой. Это
свойство образующих однополостных
гиперболоидов было использовано та-
лантливым русским инженером, почет-
ным членом Академии наук СССР
Шуховым В.Г. (1853—1939 гт.) для
проектирования легких и жестких
конструкций радиомачт, башен, гради-
рен и т.д. (рис. 2.54).
Пример 2. Построить проекции очер-
ковых образующих поверхности конуса
вращения Ф(/, Г) с наклонной осью
(рис. 2.55).
Пусть ось j является фронталью.
Тогда угол а, составленный образую-
щей I и осью j, проецируется на П2 в
натуральную величину. Поэтому на П2
проекции /2, /2 очерковых образую-
щих составляют с фронтальной проек-
Рис. 2.55
цией j2 оси угол а, на 1^ их проекции
совпадают: = // = ц.
Для построения на П] проекций
очерковых образующих выберем про-
извольную параллель к (к2 ± /2) и по-
строим вспомогательную сферу Д, ка-
сающуюся поверхности конуса Ф по
этой параллели к. На П[ проекции 11,1 ]
искомых очерковых образующих каса-
ются очерковой окружности сферы
Д. Точками касания являются проек-
ции , К\, точек К, К пересечения
двух окружностей k, t, принадлежащих
вспомогательной сфере Д. Фронтальные
проекции Z2 = S2K2, Z2 ~ $2^2 этих
очерковых образующих определяют
линию видимости поверхности конуса
относительно Пр
Приведенный алгоритм обобщается
на построение очерковых линий пове-
рхности вращения с наклонной осью.
Для этого в поверхность вращения
вписываются вспомогательные сферы и
очерковые линии строятся как огибаю-
щие проекций этих сфер (рис. 2.56).
60
Рис. 2.56
Уравнение поверхности вращения
выводится очень просто, если она зада-
на осью /, совмещенной с осью Oz сис-
темы координат Oxyz, и меридианом /,
принадлежащим координатной плос-
кости Oxz или Oyz (рис. 2.57).
Пусть меридиан имеет уравнение
= [AfAfJ = [Л/, О] = х или в коорди-
натной форме:
X = ^х2 + у2 .
(2.33)
Поэтому, подставив значение х из
(2.33) и z = Z в уравнение (2.32) обра-
зующей, получаем уравнение повер-
хности вращения
Z = /((/л2 + у2 )
или
Z = f(^x2 + у2 ).
Пример. Вывести уравнение эллип-
соида вращения, образованного враще-
нием эллипса х2/а2 + z^/b2 = 1 вокруг
оси j = Oz.
В уравнение образующей вместо х
/ Э
подставляем ух + у . Получаем
Рассмотрим его произвольную точку
М(х, z), где х = [OAfJ, z = [Л/Af,] =
[OMZ], При вращении образующей I
вокруг оси Oz = } высота точки М не
изменяется: [AfA/J = [ОД^21 =
[Л/М,] = z.
Также не меняется расстояние точки
М до оси вращения: [MMJ = [Л/; О] =
х2 + у1 + z2 = |
а2 Ь2 '
— уравнение эллипсоида вращения,
который будет сжатым, если а > Ь, и
вытянутым, если а < Ь. При а = b эл-
липсоид вырождается в сферу, описы-
ваемую уравнением
2 2 2 2
х + у +z = а .
2.6.4. Винтовые поверхности
Поверхность, образованная винто-
вым движением некоторой линии,
называется винтовой поверхностью.
Винтовые поверхности нашли широ-
кое применение в технике. Это — по-
верхности деталей резьбовых соедине-
ний (гаек, болтов, винтов и т.д.), вин-
товых зубчатых колес, деталей червяч-
ных и винтовых передач, шнеков,
гребных и воздушных винтов и многих
других механизмов.
61
Движение линии называется винто-
вым, если каждая точка этой линии
описывает цилиндрическую винтовую
линию (см. п. 2.5.4). Таким образом,
ча винтовой поверхности имеется два
семейства линий, составляющих ее
сетчатый каркас: семейство образую-
щих и семейство линий ходов (винто-
вых параллелей).
Если при своем движении образую-
щая I пересекает ось j винтового дви-
жения, то поверхность называется
закрытой, в противном случае — от-
крытой. Если образующей является
прямая линия, то винтовая поверх-
ность называется геликоидом. Гелико-
ид называется прямым, если образую-
щая / перпендикулярна оси j винтово-
го движения, в противном случае —
наклонным. Закрытый наклонный
геликоид также называется архимедо-
вым, так как его сечением плоскостью,
перпендикулярной оси j винтового
движения, является кривая, называе-
мая спиралью Архимеда.
Если образующие открытого гелико-
ида являются касательными некоторой
цилиндрической винтовой линии, то
геликоид называется эвольвентным,
так как его нормальное (перпендику-
лярное оси Д сечение представляет
эвольвенту окружности. Эвольвентный
геликоид является частным видом кон-
волютного геликоида, который отно-
сится к группе открытых наклонных
геликоидов. Такие геликоиды образу-
ются винтовым движением прямой,
касающейся цилиндрической повер-
хности вращения, ось которой совпада-
ет с осью j винтового движения, и со-
ставляющей с осью у угол, отличный от
прямого.
Винтовые поверхности являются
трансцендентными, так как закон дви-
жения образующей определяется ци-
линдрической винтовой линией, пред-
ставляющей собой трансцендентную
кривую (см. уравнение 2.19а).
Из приведенных определений следу-
ет, что в состав геометрической части
определителя винтовой поверхности
входят:
цилиндрическая винтовая линия т,
определяющая винтовое движение;
ось j винтового движения для закры-
тых поверхностей и соосная цилиндри-
ческая поверхность Д для открытых
винтовых поверхностей;
угол а, составленный осью геликоида
и его образующей, или его эквивалент
(плоскость параллелизма, направляю-
щая коническая поверхность и т.д.).
Кроме того, для винтовых поверхнос-
тей общего вида в состав определителя
входит образующая I, свойства которой
существенно влияют на форму и свой-
ства винтовой поверхности.
Рассмотрим задание на чертеже про-
стейших винтовых поверхностей —
прямого и наклонного геликоидов.
Прямой закрытый геликоид Ф обра-
зуется винтовым движением прямой I,
пересекающей под прямым углом ось j
винтового движения. Условие перпен-
дикулярности прямых /, j эквивалентно
условию параллельности образующих
некоторой плоскости (на рис. 2.58
плоскости проекций П, ± у). Винтовое
62
Рис. 2.59
движение на чертеже удобно задавать
проекциями направляющей цилиндри-
ческой винтовой линии т. Поэтому
определитель прямого геликоида запи-
сывается так: Ф(у, т, П]).
На рис. 2.58 построен каркас образу-
ющих, пересекающих ось /, винтовую
линию т и параллельных плоскости
проекций Пр Здесь же показано по-
строение фронтальной проекции А2
точки А, принадлежащей поверхности
прямого геликоида Ф, по заданной ее
горизонтальной проекции ЛР Для это-
го через точку А проведена образую-
щая I поверхности Ф.
На рис. 2.59 задан наклонный закры-
тый геликоид Ф(/, т, а). Его образую-
щие составляют с осью j заданный угол
а, что эквивалентно условию их па-
раллельности соответствующим обра-
зующим направляющей соосной кони-
ческой поверхности вращения Ф(/, I).
Поэтому для построения каркаса об-
разующих наклонного геликоида Ф
делим его направляющую винтовую
линию т и направляющую линиют
конической поверхности Ф на некото-
рое равное число частей. Тогда соот-
ветственные образующие поверхностей
Ф, Ф, проходящие через точки линий
т, т с одинаковыми индексами, будут
параллельными (на П] их проекции
совпадают, а на П2 — параллельны).
Каркас образующих наклонного ге-
ликоида можно построить и без приме-
нения направляющей конической по-
верхности. Фронтальные проекции
образующих 1—1, 13—13 составляют
с /2 угол а, так как в силу параллель-
ности этих образующих плоскости
проекций П2 он изображается на по-
следней без искажения. Поэтому дугу
1—13 винтовой линии т и отрезок
[/—/3| оси у винтового движения
делим на некоторое число равных час-
тей. Соединив соответственные точки
линий т, j, получаем каркас образую-
щих наклонного геликоида.
На рис. 2.59 построена очерковая
линия к2 наклонного геликоида на П2
как огибающая линия фронтальных
проекций каркаса образующих. По
точкам касания очерковой линии к2 с
фронтальными проекциями образую-
щих построена ее горизонатльная про-
екция к}, являющаяся линией види-
мости наклонного геликоида на Пр На
этом же рисунке показано построение
недостающей проекции произвольной
точки А поверхности Ф. Для этого че-
рез точку А проведена некоторая ли-
ния I, принадлежащая поверхнети Ф.
Ее проекции (р t2 построены по точ-
кам пересечения с каркасом образую-
щих.
Вывод уравнений винтовых повер-
хностей продемонстрируем на приме-
рах вывода уравнений прямого и на-
клонного геликоидов. Для простоты ось
Oz системы координат Oxyz совместим
63
с осью j винтового движения. Тогда
параметрическое уравнение направля-
ющей винтовой линии т имеет вид
(2.19).
Положение произвольной точки А на
поверхности прямого геликоида
(рис. 2.58) однозначно определяется
полярным углом <р, составленным обра-
зующей I геликоида и координатной
плоскостью Oxz, и радиус-вектором р
— расстоянием от точки А до оси j
винтового движежния (до оси Oz).
Поэтому декартовы кординаты про-
извольной точки А прямого геликоида
выражаются через параметры <р, р
следующим образом:
X = pcoscp,
у = psincp, (2.35)
Z = РФ,
где р — параметр направляющей ци-
линдрической винтовой линии т. Фор-
мулы (2.35) определяют уравнения
прямого геликоида в параметрической
форме.
Для вывода аналогичных уравнений
наклонного геликоида следует заме-
тить, что высота z его произвольной
точки А равна сумме высоты z = рф
точки М винтовой линии т, через ко-
торую проходит образующая МА гели-
коида, и высоты А" = (г — p)ctga точки
А, соответственной точке А и находя-
щейся на поверхности направляющего
конуса Ф (рис. 2.59). Тогда параметри-
ческие уравнения наклонного геликои-
да имеют вид:
X = рсовф,
у = рзтф, (2.36)
z = РФ + (г - p)ctga.
В заключение заметим, что прямой
и наклонный геликоиды служат рабо-
чими поверхностями деталей (болтов,
гаек, шпилек, винтов) резьбовых сое-
динений, червячных передач, винто-
вых транспортеров (шнеков).
2.6.5. Линейчатые поверхности
Поверхность, образованная движе-
нием прямой линии по заданному
закону, называется линейчатой.
Линейчатые поверхности широко
используются в технике. Это — повер-
хности крыльев, оперения, отсеков
фюзеляжа, пилонов самолета, цилин-
дрических и конических зубчатых
колес, покрытия и ограждения архи-
тектурных сооружений.
Закон движения образующей обычно
задается направляющими линиями.
Определим их число для задания ли-
нейчатой поверхности общего вида. Из
определения поверхности (см. п. 2.6.1)
следует, что линейчатая поверхность
представляет собой однопараметри-
ческое множество прямых.
Множество прямых трехмерного про-
странства четырехпарамстрично, так
как произвольную прямую простран-
ства можно задать системой уравне-
ний:
У = кгх + Ьх
z = + А2,
в которой имеются четыре независи-
мых коэффициента (параметра) Aj, к2,
А], Ь2. Поэтому для получения одноп-
араметрического множества прямых
пространства необходимо ’’связать”
любые три из этих четырех парамет-
ров. Это можно выполнить многими
способами. Например, условием пере-
сечения прямой с какой-либо кривой в
одной точке или касания прямой ка-
кой-либо поверхности в одной точке
’’связывается” один параметр. Есть
условия, которые эквивалентны ’’свя-
зыванию” двух параметров, например,
пересечение с кривой линией в двух
точках, прохождение через фиксиро-
ванную точку и т.д.
Таким образом, линейчатая поверх-
ность общего вида задается таким чис-
64
лом направляющих, которые все вмес-
те ’’связывают” три параметра. Таких
направляющих может быть не более
трех. Линейчатые поверхности, имею-
щие максимальное число направляю-
щих линий, называются поверхностя-
ми с тремя направляющими. Геомет-
рическая часть их определителя
включает в себя эти направляющие:
Ф(а, Ь, с).
Если направляющими линейчатой
поверхности являются алгебраические
кривые а, Ь, с соответственно поряд-
ков Пр и2, п3, сама поверхность Ф(а,
Ь, с) также будет алгебраической п-го
порядка, равного удвоенному произ-
ведению порядков направляющих:
п = 2и] n2n3. (2.37)
В качестве примера рассмотрим ли-
нейчатую поверхность, определяемую
тремя прямолинейными направляющи-
ми а, Ь, с (рис. 2.60). Через каждую
точку любой направляющей проходит
единственная образующая I. Например,
через точку А е а проходит образую-
щая I — линия пересечения двух плос-
костей Д(Л, Z>); Г(Л, с). Плоскость А
пересекает поверхность Ф(а, Ь, с) по
двум пересекающимся прямым b, I.
Значит, данная поверхность Ф является
поверхностью второго порядка. Она
называется эллиптическим однополос-
тным гиперболоидом и содержит два
семейства прямолинейных образующих
(рис. 2.61): семейство направляющих
а, Ь, с, ... и семейство образующих I,
I', ...
Рис. 2.61
Поверхность Ф будет нераспавшейся,
если се направляющие не имеют об-
щих точек. В противном случае она
распадается на составляющие, сумма
порядков которых будет равна
Далее рассмотрим некоторые виды
линейчатых поверхностей.
2.6.5.1. Конические
и цилиндрические поверхности
Коническая поверхность общего
вида образуется движением прямой I
(образующей), проходящей через
фиксированную точку 5 (вершину) и
пересекающей направляющую кривую
а (рис. 2.62). Если направляющей яв-
ляется алгебраическая кривая п-го
порядка (плоская или пространствен-
ная), то и порядок конической повер-
хности Ф будет равен п, т.е. любая
65
Рис. 2.63
плоскость Г пересекает се по кривой g
п-го порядка или любая прямая т
пересекает ее в п точках.
Коническая поверхность с несобст-
венной вершиной £“($) называется
цилиндрической. Ее образующие пере-
секают направляющую а и параллель-
ны прямой s — собственному предста-
вителю несобственной вершины 5“
(рис. 2.63). Таким образом, геометри-
ческая часть определителя конической
и цилиндрической поверхности содер-
жит вершину 5 или 5°°, направляю-
щую а: Ф(5, а); Д(5”, а). Задание вер-,
шины 5 или 5” эквивалентно заданию
двух направляющих кривых линейча-
той поверхности, пересекающихся в
точке 5 или 5“. В этом случае линей-
чатая поверхность порядка 2n1n2«3
распадается на коническую (цилиндри-
ческую) поверхность порядка и1( где
— порядок направляющей а, и ли-
нейчатую поверхность общего вида
порядка п = nl(2n2n3 — 1).
Точки, принадлежащие цилиндри-
ческим и коническим поверхностям,
удобно строить проведением обра-
зующих поверхности. На рис. 2.64
показано построение проекций точки
N, принадлежащей поверхности конуса
(рис. 2.64, а) и поверхности цилиндра
(рис. 2.64, б): точка У принадлежит
поверхности, так как лежит на ее об-
разующей I.
2.6.5.2. Поверхности Каталана
(линейчатые поверхности
с плоскостью параллелизма)
До сих пор мы рассматривали линей-
чатые поверхности, у которых направ-
ляющими были собственные кривые.
Если одна из направляющих является
плоской, то она может принадлежать
несобственной плоскости пространства.
В этом случае получаем линейчатую
поверхность Ф, направляющими кото-
рой будут две собственные кривые а, b
и направляющая поверхность (обычно,
коническая) Г — собственный предста-
витель несобственной кривой с“. Обра-
зующая I поверхности Ф удовлетворяет
трем условиям: пересекает кривые а, b
и параллельна определенной образую-
щей поверхности Г. Поэтому в состав
определителя поверхности Ф входят
кривые а, Ь и поверхность Г: Ф(о, b, D.
В. п. 2.6.4 был рассмотрен пример
такой поверхности — наклонный гели-
коид Ф(т, j, Ф) (см. рис. 2.59).
Здесь мы исследуем линейчатые по-
верхности с плоскостью параллелиз-
Рис. 2.64
llЛ a = A\
11ПЬ = 01
li\\r(llnc°°=Cl°‘’)
ма, которые также называют повер-
хностями Каталана (Е. Catalan). Об-
разующие / этих поверхностей пересе-
кают направляющие кривые а, b и
параллельны плоскости параллелизма
Г — собственному представителю несо-
бственной направляющей прямой с“
(рис. 2.65).
В зависимости от вида направляю-
щих а, b поверхность с плоскостью па-
раллелизма называется цилиндроидом,
коноидом и косой плоскостью.
Цилиндроидом называется линейча-
тая поверхность с плоскостью парал-
лелизма, у которой направляющими
являются кривые линии.
Каркас образующих цилиндроида на
комплексном чертеже строится весьма
просто, если в качестве плоскости па-
раллелизма принята одна из плоскос-
тей проекций или проецирующая плос-
кость. На рис. 2.66 построен каркас
образующих цилиндроида с направлю-
щими кривыми а, b и плоскостью па-
раллелизма Пр Образующие цилиндро-
ида являются горизонталями.
Построение горизонтальной проек-
ции Xj по заданной фронтальной про-
екции А2 точки А, принадлежащей
цилиндроиду, осуществлено проведени-
ем образующей I э А. Для построения
фронтальной проекции В2 по заданной
горизонтальной проекции точки В
на поверхности проведена произволь-
ная кривая т. Ее фронтальная проек-
ция т 2 построена по точкам пересече-
ния с образующими цилиндроида.
Если направляющими цилиндроида
являются алгебраические кривые по-
рядков Пр п2 (порядок несобственной
направляющей прямой равен единице),
то порядок п цилиндроида определяет-
ся по формуле (2.37), где п3 = 1:
п = 2п^п2. (2.38)
Коноидом называется линейчатая
поверхность с плоскостью паралле-
лизма, имеющая криволинейную и
прямолинейную направляющие.
На чертеже коноид задается анало-
гично цилиндроиду. Построение карка-
са образующих и точек, принадлежа-
щих поверхности, не отличается от
соответствующих построений для ци-
линдроида, рассмотренных выше.
Если криволинейная направляющая
коноида есть алгебраическая линия
порядка Ир то его порядок п определя-
ется подстановкой в формулу (2.38)
значения п2 = 1:
п = 2/ij. (2.39)
На рис. 2.67 приведен чертеж конои-
да, получившего название ’’прямой
67
У!
Рис. 2.67
клин”. Направляющими коноида явля-
ются эллипс а и прямая Ь, плоскость
параллелизма П3 перпендикулярна
прямой b и плоскости Д эллипса. Эта
поверхность, будучи алгебраической
поверхностью четвертого порядка,
содержит в плоскостях Г1 || Д каркас
эллипсов. Несобственная прямая Г => Д
является для этого коноида двукрат-
ной. Поэтому плоскость Г* => Г пере-
секает его по дважды считаемой пря-
мой Г и эллипсу т1.
Косой плоскостью называется ли-
нейчатая поверхность с плоскостью
параллелизма и прямолинейными
направляющими. Из формулы (2.39)
при П] = 1 следует, что косая плос-
кость — поверхность второго порядка.
Она больше известна под названием
гиперболический параболоид, так как
несет на себе каркас не только
прямых, но также гипербол и парабол
(см. рис. 2.50). Гиперболический пара-
болоид содержит два семейства пря-
мых, параллельных двум плоскостям
параллелизма.
2.6.5.3. Инженерный способ
задания линейчатых поверхностей
Задание линейчатой поверхности Ф
двумя направляющими а, b и взаимно
однозначным соответствием Т, уста-
новленным между точками этих на-
правляющих, называется инженерным
способом задания. Образующие такой
поверхности проходят через соответ-
ственные точки. Определитель повер-
хности в этом случае записывается
так: Ф(а, b, Т).
Этот способ задания линейчатой
поверхности получил широкое распро-
странение в технике. Например, ука-
занным способом задастся линейчатое
крыло самолета. Два сечения крыла
принимают за направляющие а, Ь.
Хорды этих сечений делят на сто час-
тей. Через точки деления проводят
прямые, перпендикулярные хорде, и
отмечают их точки пересечения с вер-
хней и нижней дужками сечения. Этот
процесс называется процентной раз-
бивкой сечений крыла. Точки верхней
и нижней дужек сечений а, Ь, распо-
ложенные ”на одном проценте”,
считаются соответственными и опреде-
ляют каркас образующих поверхности
крыла.
Если направляющие а, b являются
алгебраическими кривыми порядков
Ир п2, то порядок п линейчатой по-
верхности, заданной инженерным
способом, вычисляется по формуле
Клебша:
п = И] + п2- (2.40)
Из этой формулы следует, что для
получения линейчатой поверхности
второго порядка (гиперболического
параболоида) необходимо задать
прямолинейные направляющие а, b
(рис. 2.68). Взаимно однозначное соот-
ветствие можно задать условием ра-
„ [АМ]
венства простых отношении =
= [CWJ
[£W] ’
Соответственные точки М ~ N опре-
деляют образующую I данной повер-
хности.
Для построения каркаса образующих
следует разделить отрезки |ЛВ|, [CZ)]
направляющих а, b на равное число
68
Рис. 2.68
частей и точки с одинаковыми индек-
сами принять за соответственные. По-
строение проекций произвольной точки
К поверхности выполняется с помощью
некоторой линии t поверхности, проек-
ции /|, которой строятся из условия
пересечения с каркасом образующих.
2.6.5.4. Торсовые поверхности
Линейчатая поверхность, образован-
ная множеством касательных к про-
странственной кривой, называется
торсовой или поверхностью с ребром
возврата (рис. 2.69).
Направляющая кривая а поверхности
Ф называется ребром возврата, так как
произвольная плоскость Г пересекает
поверхность Ф по кривой т, имеющей
точку возврата М = а п Г.
Геометрическая часть определителя
торсовой поверхности Ф состоит лишь
из ребра возврата а : Ф(а).
Задание ребра возврата ’’связыва-
ет” три параметра четырехпараметри-
ческого множества прямых простран-
ства. Это можно объяснить следующим
образом. Пусть линейчатая поверх-
ность Ф определена двумя конгруэн-
тными пространственными кривыми а, а
(рис. 2.69) и взаимно однозначным
соответствием Т, установленным меж-
ду точками Л', А' этих кривых. Пред-
положим, что кривые а, а непрерывно
приближаются друг к другу и в преде-
ле совпадают так, что совпадают по-
парно соответственные точки А‘, А1.
Таким образом, в пределе образующие
А‘А‘ поверхности Ф становятся каса-
тельными f к пространственной кривой
а. Из приведенного толкования способа
образования торсовой поверхности сле-
дует, что она выделяется из двупара-
метрического множества хорд (бисе-
кант) кривой а требованием, что обра-
зующими f торсовой поверхности яв-
ляются лишь те хорды, которые каса-
ются ребра возврата а (пересекают его
в двух совпавших точках Л' = Л').
Если направляющей а торсовой по-
верхности Ф является рациональная
алгебраическая кривая порядка пр то
порядок п поверхности Ф вычисляется
по формуле
п = (Hj - I)2. (2.41)
На чертеже торсовая поверхность Ф
задается проекциями ребра возврата
(рис. 2.70). Для построения точки
И f Ф по одной заданной се проекции,
например М\, проводим горизонталь-
ную проекцию образующей э М},
касающуюся пр Отмечаем точку каса-
69
ния /] е а1г строим ее фронтальную
проекцию 12 6 а2 и проводим фрон-
тальную проекцию образующей t2 э
12, касающуюся а2 в точке 12. Фрон-
тальная проекция М2 точки М принад-
лежит t2.
2.6.5.5. Вывод уравнений
линейчатых поверхностей
Вывод уравнений линейчатых повер-
хностей выполняется в такой последо-
вательности:
1) записываются уравнения образую-
щей в той или иной форме;
2) выражая коэффициенты уравне-
ний образующей через параметры
уравнений направляющих, получают
уравнение поверхности.
Пример 1. Вывести уравнение повер-
хности конуса Ф(5, а), если известны
координаты ее вершины 5(0, 0, 10) и
уравнения направляющей а:
х2 * у2 = 16
Z = 0
(2.42)
Из условия задачи следует, что вер-
шина 5 поверхности конуса принадле-
жит оси Oz системы координат, на-
правлющая окружность а лежит в ко-
ординатной плоскости Оху.
Запишем уравнения произвольной
образующей I как прямой, проходящей
через две точки 5, А 6 а:
х ~ *' = Y ~У| = z ' *' (2.43)
*2 - *i Уг - У| z2 - zi
В уравнение (2.43) вместо хр ур
подставляем координаты точки 5 и
значения х2, z2 из уравнений (2.42).
Имеем
х _ _у _ z ~ 10
’ ’10 '
Освобождаемся от параметра у2 и
получаем уравнение конической повер-
хности Ф(5, а) в неявной форме:
25 (X 2 + У2) - 4(Z - 10)2 = 0.
Пример 2. Вывести уравнение ’’пря-
мого клина” Ф(а, Ь, П3), заданного
прямолинейной направляющей Ь'
[у =0
(2.44)
z = 10;
эллипсом а\
9х2 + 1 бу 2 = 144 (2.45)
z = 0
и плоскостью параллелизма П3 (см.
рис. 2.67).
Запишем уравнения прямой Z, прохо-
дящей через две точки Л(хр ур
Zj) е а, В(х2, у2, z2) е b и параллель-
ной П3:
У - у, Z - z,
. Уг - У1 z2 “ 2i (2.46)
X = %1 = х2.
В уравнения (2.46) подставим значе-
ния yj, Zj из (2.45) и у2, z2 из (2.44):
70
4У - у/144 - 9Х2 _ Z
-у/144 - 9Х2 10
или после упрощений:
(144 - 9X2)(Z - 10)2 - (2 47)
- 1600 У2 = 0.
Получили алгебраическое уравнение
четвертой степени, значит, ’’прямой
клин” есть поверхность четвертого
порядка. Эта поверхность плоскостями
r'CZ = const) пересекается по эллип-
сам, в чем нетрудно убедиться, подста-
вив в формулу (2.47) вместо Z какое-
либо число.
Пример 3. Вывести уравнение косой
плоскости Ф([АВ], [CD], 77, заданной
инженерным способом. Пусть точки А,
В, С, D заданы своими координатами
4(4, 0, 0), В(2, 0, 0), С(0, 2, 6), D(0,
6, 10), а соответствие Т определяется
отношением
Им'] = [C./V']
[ВМ ' ] [DN ‘ ]
(2.48)
В уравнение (2.43) образующей I
подставим координаты точек Ml; N1,
выраженные через координаты исход-
ных точек А, В, С, D и удовлетворяю-
щие отношению (2.48):
хм
< + + 1Ув.
1 + X ’ Ум 1 + X ’
+ A.Zn хг + XxD
Zl/ “ Хаг =
м 1 + X ‘ 1 + X
Ус * >-Уо zc + XzD
yN = 1 + X ‘ ZN = 1 + X
После подстановки значений коорди-
нат данных точек имеем
4 + 2Х
Z
6 + юх ’
1 + X
В уравнении (2.49) освобождаемся от
параметра к и после элементарных
упрощений получаем уравнение косой
плоскости
4X(Z-V) + (5Z-7У) (Z - У-4) =0,
т.е. косая плоскость является повер-
хностью второго порядка.
2.6.6. Циклические поверхности
Поверхность, образованная движе-
нием окружности постоянного или
переменного радиуса, называется
циклической.
Примером циклической поверхности
могут являться стебли растений, в
технике — всевозможные трубопрово-
ды. Поверхности вращения составляют
подкласс циклических поверхностей,
имеющих прямолинейные центровые
линии.
Из определения следует,'что цикли-
ческая поверхность содержит однопа-
раметрическое множество окружнос-
тей. Закон движения образующей
(окружности) или, что то же самое,
выделение однопараметрического мно-
жетва образующих из шестипарамет-
рического множества окружностей
трехмерного пространства определяется
различными геометрическими условия-
ми. К ним относятся, например, на
правляющие линии, определяющие
траектории движения центра или ка-
ких-либо точек образующей; условия
Произвольная окружность в пространстве
определяется заданием ее плоскости Е (три
степени свободы), центра О е Е (две степени
свободы) и радиуса R (одна степень свободы).
71
принадлежности, параллельности, пер-
пендикулярности и т.д., определяющие
положение плоскости образующей в
пространстве; линии или графики, за-
дающие закон изменения радиуса об-
разующей. Всевозможные комбинации
этих условий будут определять цикли-
ческую поверхность общего вида, если
их суммарное параметрическое число
будет равно пяти.
Комбинаций пятипараметрических
геометрических условий очень много.
Поэтому невозможно установить еди-
ную форму записи определителя цик-
лической поверхности общего вида.
Наибольшее распространение получи-
ли циклические поверхности с плос-
костью параллелизма, каналовые и
трубчатые.
Если все образующие циклической
поверхности расположены в паралле-
льных плоскостях, то она называется
циклической поверхностью с плоско-
стью параллелизма. Эти поверхности
относятся к классу так называемых
поверхностей пучковых сечений. Плос-
кости образующих таких поверхностей
проходят через фиксированную пря-
мую, называемую осью пучка плоскос-
тей. Очевидно, в случае поверхностей
с плоскостью параллелизма ось пучка
будет несобственной прямой.
Циклическая поверхность называет-
ся каналовой. если плоскости ее обра-
зующих перпендикулярны траектории
движения центра образующей.
Каналовая поверхность называется
трубчатой, если она содержит каркас
конгруэнтных образующих.
Приведем примеры задания цикли-
ческих поверхностей на комплексном
чертеже.
Пример 1. Построить каркас образу-
ющих и очерковые линии циклической
поверхности с плоскостью параллелиз-
ма Ф </, а, П]) (рис. 2.71).
Поверхность Ф образуется движением
окружности /, центр Q которой пере-
мещается по центровой линии у, плос-
кость образующей параллельна Пр
закон изменения радиуса R = [QA]
задается кривой линией (параметроно-
сителем) а.
Для построения каркаса образующих
проводим семейство горизонтальных
плоскостей, которые пересекают цен-
тровую линию j в точках Q', парамет-
роноситель а — в точках А1. Образую-
щие I1 проецируются на П, в окруж-
ности //(Q/, Rl = [Q/a/]), а на П2 —
в отрезки 1^ , равные 27?'. Соединив
концы отрезков 1-^ лекальной кривой
(2, ^2> получаем очерковую линию
поверхности Ф на П2. Очерковую ли-
нию и,, поверхности Ф на П] стро-
им как огибающую окружностей if.
Горизонтальная проекция t\,t\
очерковой линии (2, 72 поверхности Ф
на П2 строится как лекальная кривая,
проходящая через концы горизонталь-
ных диаметров окружностей //. Линия
(j является линией видимости по-
72
всрхности Ф на Пр Линия видимости
/л2, т2 поверхности Ф на П2 строится
по фронтальным проекциям точек
касания очерковой линии т^, с
окружностями /]'.
Построение точки, принадлежащей
циклической поверхности, выполняет-
ся по общей методике. На рис. 2.71
показано построение горизонтальной
проекции К] точки К, расположенной
на видимой стороне циклической по-
верхности Ф, по заданной ее фронталь-
ной проекции К2. Для этого через
точку К проведена образующая /' по-
верхности Ф. Если построение образую-
щей, проходящей через данную точку,
затруднительно, то через данную точ-
ку проводят произвольную линию по-
верхности. Ее проекции строят по точ-
кам пересечения с каркасом образую-
щих.
Пример 2. Построить каркас образу-
ющих и очерковые линии трубчатой
поверхности Ф(/, Г) (рис. 2.72).
Поверхность Ф образуется движением
окружности I постоянного радиуса,
центр Q которой перемещается по
центровой линии /, а плосксть образу-
ющей перпендикулярна линии j.
Так как центровой линией j является
фронталь (/ параллельна П2), то плос-
кости образующих перпендикулярны
П2. Следовательно, окружности I1 прое-
цируются на П2 в равные отрезки 12 , а
на П] — в эллипсы с равными боль-
шими осями.
Очерковая линия Z2, t2 поверхности
Ф на П2 строится как лекальная кри-
вая, проходящая через концы отрезков
12. Очерковая линия поверх-
ности Ф на П) огибает эллипсы . В
рассматриваемом случае она касается
эллипсов /[' в концах их больших
осей.
Построение проекций X,, К2 точки
К, принадлежащей каналовой повер-
хности, выполняется по общей методи-
ке.
Уравнение циклической поверхности
выводится так:
1) записываются уравнения образую-
щей (проекций окружности);
2) параметры, входящие в уравнения
образующей, выражаются из уравне-
ний направляющих линий (параметро-
носителей) .
В качестве примера выведем уравне-
ние циклической поверхности с плос-
костью параллелизма, изображенной
на рис. 2.71.
Произвольная образующая описы-
вается системой уравнений
(X - х0)2 + (У -у0)2 = R2 (250)
Z = zQ,
где х0, у0, zQ — координаты центра
Q‘ окружности I1; R — радиус окруж-
ности
Пусть центровая линия j определяет-
ся системой уравнений
73
х = kz + Ь
(2.51)
у = qz + с,
а параметроноситель а — системой
уравнений
[ 2 3
\ х =A0+Aiz+A2zz+А3гл (2.52)
I У = D.
Координаты х0, у0, zQ центра Q'
окружности I1 удовлетворяют системе
уравнений (2.51). Радиус R образую-
щей /' выражается формулой
/ 2 2
R = ]/ (хА - х0) + (ул - у0) ,
где хА, уА удовлетворяют системе
(2.52).
Поэтому уравнение циклической по-
верхности будет.
(X - kZ - b)2 + (У - qZ - с)2 =
= (Ло + AXZ + A2Z2 + 43Z3 -
- kZ - 5)2 + (D - qZ - c)2.
Получили алгебраическое уравнение
шестой степени. Следовательно, повер-
хность Ф является алгебраической по-
верхностью шестого порядка.
2.6.7. Поверхности
зависимых сечений
Поверхность, образованная движе-
нием плоской кривой переменной
формы, называется поверхностью
зависимых сечений.
Следует отметить, что приведенное
определение достаточно условно и не
является общепринятым. Оно введено
проф. И.И. Котовым, чтобы подчер-
кнуть их отличие от вышерассмотрен-
ных групп поверхностей, содержащих
каркас конгруэнтных (подобных — для
циклических поверхностей) сечений.
Некоторые авторы такие поверхности
называют непрерывно-топографически-
ми, другие — сложными. К сожалению,
все эти названия не раскрывают сущ-
ности данных поверхностей в силу их
большого многообразия в природе и
технике. Попытки более детальной
классификации этих поверхностей не
дали положительных результатов. Все
это говорит о невозможности единой
(универсальной) формы записи их
определителей, следовательно, и спосо-
ба задания их на чертеже.
Очевидно, из общей схемы образова-
ния данных поверхностей их опреде-
лители должны содержать три компо-
ненты:
1) исходную образующую;
2) условия, задающие однопарамет-
рическое множество (пучок) плоскос-
тей образующих в пространстве (нали-
чие плоскости параллелизма, оси пуч-
ка, условие перпендикулярности ка-
кой-либо пространственной кривой и
т.д.);
3) условия, задающие законы изме-
нения параметров образующей в про-
цессе ее движения (направляющие
линии для се характерных точек, гра-
фики изменения некоторых парамет-
ров и т.д.).
В качестве примера возьмем ранее
рассмотренную поверхность — прямой
клин (см. п. 2.6.5.2, рис. 2.67). Теперь
эту поверхность определим как повер-
хность зависимых сечений, образован-
ную параллельным перемещением
эллипса а переменной формы. При-
мем, что поверность Ф ’’прямого кли-
на” образуется параллельным движе-
нием эллипса а, плоскость которого
остается параллельной Пр Центр О
эллипса перемещается по прямой ON,
его большая полуось не меняет своей
величины, а малая полуось изменяется
по линейному закону, заданному пря-
мой MN (см. рис. 2.67). Поэтому опре-
делитель такой поверхности можно
записать так: Ф(а, Пр ON, MN).
74
Покажем аналитически, что полу-
ченная таким образом поверхность
тождественна коноиду, уравнение
(2.47) которого было выведено в
п. 1.6.5.5.
Эллипс
X2 + г2
т2 п2
Z = О,
(2.45а)
где т = 4, и = 3 [см. формулу (2.45)],
перемещаясь в пространстве, изменяет
значение п малой полуоси по линейно-
му закону, заданному прямой MN:
у - у.
Уг - У\
Z - *,
z2 “ zl
(2.53)
где Af(yj =3, Z[ =0), N(y2 ~ 0> z2 ~
= 10).
Подставим в (2.53) координаты точек
М, N и запишем уравнение прямой
MN в виде
у _ 3 ( 1 0 ' Z) . у __ Q
” Го ’
Подставив в уравнение (2.45а) обра-
зующей постоянное значение т = 4
большой полуоси и вместо п перемен-
3(10 - Z)
ное значение п = у = -------- малой
J ю
полуоси, получим уравнения повер-
хности ’’прямого клина” как поверх-
ности зависимых сечений:
(10 - Z)2(9X2 - 144) + (2.54)
+ 1600У2 = 0.
Уравнения (2.47) и (2.54) эквивален-
тны, что подтверждает получение од-
ной и той же поверхности.
В заключение отметим, что на черте-
же поверхности зависимых сечений в
силу их сложного закона образования
обычно изображаются дискретным кар-
касом образующих.
Упражнения и вопросы
для самопроверки
1. Постройте горизонтальную проекцию
A(B|C| треугольника АВС, принадлежащего
плоскости Д(/п т) (рис. 2.73).
2. Через точку А проведите горизонталь h под
углом 45" к плоскости проекций П2 и фронталь
/ под углом 30° к плоскости проекций Пг По-
стройте следы этих прямых.
3. Через точку А проведите горизонтально
проецирующую плоскость Д под углом 45' к
плоскости проекций П2 и фронтально проециру-
ющую плоскость Г под углом 30° к плоскости
проекций Пр
4. Через данную прямую общего положения /
проведите какую-либо плоскость общего поло-
жения Д, горизонтально проецирующую плос-
кость Г и фронтальнопроецирующую плоскость
Ф. Постройте следы этих плоскостей.
5. В плоскости Ф(А, В, С) общего положения
постройте горизонталь h, отстоящую от П, на
30 мм, и фронталь /, отстоящую от П2 на 40 мм.
6. Определите взаимное положение двух пря-
мых (рис. 2.74).
Рис. 2.74
7. Постройте на чертеже .Монжа и в косоу-
гольной аксонометрии проекции некоторой пи-
рамиды SABCD, основанием которой является
квадрат ABCD, принадлежащий плоскости про-
екций Пг Высота [SA/J пирамиды равна диаго-
нали [АС] основания, где М — центр квадрата.
75
Постройте проекции некоторой точки N. при-
надлежащей грани SAH.
8. Вспомните характеристики плоских алгеб-
раических кривых и способы их определения.
9. Может ли парабола быть параллельной
проекцией гиперболы?
10. Конической поверхности вращения при-
надлежит пространственная кривая zi-го порядка.
В кривую какого порядка она спроецируется из
вершины 5 конической поверхности на произ-
вольную плоскость? Почему?
11. Дайте определение порядка гладкости
обвода.
12. Какая кривая проецируется на плоскости
проекций Пр И2 в окружности, имеющие равные
радиусы?
13. Постройте проекции окружности 1(0, R)
на Л,, П2, Пч. Окружность I принадлежит про-
фильно проецирующей плоскости, составляющей
с плоскостью проекций П, угол 30°.
14. Постройте обвод из дуг окружностей, за
данный упорядоченным массивом точек /I1, А2,
..., Л8 (рис. 2.75).
16. Постройте горизонтальную проекцию а,
линии с(а2), принадлежащей поверхности па-
раллельного переноса Ф(т, /) (рис. 2.77).
17. Постройте фронтальную проекцию ^ли-
нии п(а,), принадлежащей поверхности враще-
ния Ф (/, I) (рис. 2.78).
18. Постройте, проекции конуса вращения Ф(у,
Г), заданного проекциями оси /, образующей /,
если его основание принадлежит фронтально
проецирующей плоскости Г(Г2) (рис. 2.79).
О47
а А6
Рис. 2.75
15. Постройте изображение кривой т в произ-
вольной косоугольной аксонометрии по извес-
тным се проекциям на чертеже Монжа
(рис. 2.76).
19. Постройте каркас образующих прямого
открытого геликоида Ф(Д, т, П,). Постройте
фронтальную проекцию а2 линии а (а,), принад-
лежащей поверхности геликоида (рис. 2.80).
20. Постройте каркас образующих /' однопо-
лостного эллиптического гиперболоида Ф(а, Ь, с),
заданного направляющими а, Ь, с (рис. 2.81).
76
21. Постройте каркас образующих косой плос-
кости Ф(а, Ь, П2) и горизонтальную проекцию т,
линии т(т2), принадлежащей данной повер-
хности (риг. 2.82).
22. Постройте каркас образующих линейчатой
поверхности Ф(а, Ь, Т), заданной инженерным
способом. Постройте горизонтальную проекцию
т, линии принадлежащей данной повер-
хности (рис. 2.83).
23. Постройте фронтальную проекцию т2
линии т(Щ|), принадлежащей торсовой повер-
хности Ф(с) (рис. 2.84).
24. Постройте очерковые линии трубчатой
поверхности, образованной движением сферы,
центр О которой перемещается по цилиндричес-
кой винтовой линии т (рис. 2.85).
Рис. 2.85
25. Постройте каркас образующих поверхнос-
ти зависимых сечений с плоскостью параллелиз-
ма П,, образованной движением эллипса /, центр
О которого перемещается по линии у. Закон
изменения величины его большой полуоси задан
кривой а, малая полуось эллипса / постоянна
(рис. 2.86).
Рис. 2.84
Рис. 2.86
77
Глава 3
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА
Способы преобразования чертежа
применяются для приведения геомет-
рических фигур в частное положение
относительно плоскостей проекций.
Графические алгоритмы решения пози-
ционных и метрических задач значи-
тельно проще, если геометрические
фигуры занимают частное положение
относительно плоскостей проекций.
Например, построение сечения т ка-
кой-либо поверхности Ф плоскостью Г
выполняется очень просто, если плос-
кость Г будет проецирующей. В этом
случае одна проекция линии пересече-
ния т совпадает с вырожденной проек-
цией плоскости Г, а построение недо-
стающей проекции выполняется из
условия принадлежности линии т
поверхности Ф.
3.1. Основные понятия
и определения
Термин ’’преобразование” имеет
строгое математическое определение.
Если даны два множества -¥(х', х2, ...),
У(у\ у2, ...) и указано правило, по
которому каждому элементу х‘ мно-
жества X ставится в соответствие опре-
деленный элемент У множества Y, то
говорят, что множество X отображает-
ся на множество Y.
При этом элемент У называется об-
разом элемента х‘. Например, парал-
лельное (центральное) проецирование
точек пространства на плоскость явля-
ется отображением: любой точке А
пространства соответствует ее проек-
ция А •.
Отображение называется преобразо-
ванием, если множежства X, Y совме-
щены, т.е. не только элементу У соот-
ветствует определенный элемент У, но
и обратно, элементу У соответствует
определенный элемент х1.
В этом случае говорят, что множес-
тво X отображается на себя X = Y.
Например, центральная симметрия
точек пространства относительно неко-
торой точки О есть преобразование
пространства.
Произвольное преобразование про-
странства обозначим буквой /. Если /
отображает точку А на точку А, то это
принято записывать так: А = /(Л).
Преобразование, отображающее точку Л
на Л, называется обратным и обозна-
чается : Л = f~] (Л).
Последовательное выполнение двух
преобразований /, f называется ком-
позицией (произведением) преобразо-
ваний
/ = 7 -7
Если А = /(Л), Л = f (Л) то Л =
= 7 <л) =7(7<л».
Аналитически в пространстве преоб-
разование / задастся уравнениями:
X = а(Х, У, Z);
У = Р(Х, У, Z); (ЗЛ)
Z = у(Х, У, Z).
Эти уравнения по Ф. Клейну можно
истолковать двояко.
1. В системе уравнений (3.1) X, У, Z
— координаты некоторой точки А про-
странства относительно системы отне-
78
Рис. 3.1
ссния Oxyz, а X, Y, Z — координаты
той же точки А относительно системы
отнесения Oxyz (рис. З.1.). В этом
случае уравнения (3.1) называются
формулами преобразования коорди-
нат, т.е. одна система координат пре-
образуется в другую, а фигура остается
в покое.
2. В системе уравнений (3.1) X, Y, Z
— координаты некоторой точки А, а X,
У, Z — координаты точки А относи-
тельно данной системы отнесения
Oxyz = Oxyz (рис. 3.2). В этом случае
уравнения (3.1) называются формула-
ми преобразования пространства, т.е.
одна фигура преобразуется в другую,
а система координат остается в покое.
В зависимости от такого толкования
функций (3.1) способы преобразования
чертежа разделяются на две группы.
1. Преобразование системы коорди-
нат:
а) способ замены плоскости проек-
ций;
б) способ дополнительного проециро-
вания;
2. Преобразование пространства:
а) способ плоскопараллельного дви-
жения;
б) способ вращения вокруг проециру-
ющей прямой;
в) способ вращения вокруг прямой
уровня.
В настоящей главе будут рассмотре-
ны все перечисленные способы приме-
нительно к преобраованию чертежа
Монжа. Для преобразования аксоно-
метрического чертежа обычно приме-
няются лишь способы замены плоскос-
ти проекций и вращения вокруг пря-
мой уровня (способ совмещения).
Все задачи, решаемые преобразова-
нием комплексного чертежа, сводятся
к решению следующих четырех основ-
ных задач:
1) преобразовать прямую общего
положения в прямую уровня;
2) преобразовать прямую общего
положения в проецирующую;
3) преобразовать плоскость общего
положения в проецирующую;
4) преобразовать плоскость общего
положения в плоскость уровня.
Рассмотрим перечисленные выше
способы преобразования чертежа и
алгоритмы решения основных задач.
3.2. Способ замены
плоскости проекций
Сущность этого способа состоит в
замене исходных плоскостей проекций
на новые с тем, чтобы данная геомет-
рическая фигура заняла частное поло-
жение относительно новых плоскостей
проекций. При этом графическое и
аналитическое решения поставленных
задач значительно упрощаются, если
преобразование / одной системы плос-
костей проекций (координат) Oxyz в
другую Oxyz представить как компо-
зицию (произведение) двух преобразо-
ваний: f (Oxyz - Oxyz), f (Oxyz -
Oxyz).
79
3.2.1. Алгоритм замены
плоскостей проекций
Преобразование /= f • f, представ-
ляемое как последовательная замена
плоскостей проекций /(П|, П2 - П|,
П2), f (П|,П2 - Пр П2), будем вы-
полнять, соблюдая следующее ограни-
чение: одна из новых плоскостей про-
екций совмещается с одноименной
"старой” плоскостью проекций (П| =
= П] или П2 = П2, П2 = П2 или П[ =
= 111) и, как следствие, новая
плоскость проекций выбирается пер-
пендикулярной остающейся "старой”
плоскости проекций.
Покажем вывод формул преобразова-
ния на примере замены горизонталь-
ной плоскости проекций IIj на новую
П( или, что то же самое, замены сис-
темы координат Oxyz на Oxyz, когда
координатные плоскости Oxz иOxz
являются совмещенными (рис. 3.3).
Для упрощения переход от системы
координат Oxyz к системе Oxyz пред-
ставлен в виде композиции преобразо-
ваний: вращения вокруг оси Оу
(Oxyz - O'x'y'z') параллельного пе-
реноса на вектор ОО (O'x'y'z' -
- Oxyz).
Абсцисса х точки А в новой системе
ОАХ = ОС + САХ = к + О' Ах =
= к + О1 М + МЛ'К = к + O/tzsina +
+ A2A_cosa = к т zsina + Acosa.
В рассматриваемых преобразованиях
ордината точки А остается неизменной:
У =>,'=>'•
Аппликата z точки А в системе
Oxyz равна отрезку
OAZ - OB + BA. = I + О! А1. =
= I + О ’ N - A'z N = I + (Xt.cosa -
- A2A2sina = I + zcosa - Asina.
Таким образом, искомые формулы
замены Hj -» П, имеют вид
х = xcosa + zsina + к\
у = у- (3.2)
z = -Asina + zcosa - /,
где a — угол, составленный новой
П] и исходной П| плоскостями проек-
ций; к. I — координаты точки О отно-
сительно системы координат Oxz.
Аналогично выводятся формулы за-
мены фронтальной плоскости проекций
П2 на новую П2:
а = Acosp + у sin р + с;
у = -Asinp + ycosp + t/; (3.3)
где р — угол, составленный плоскостя-
ми проекций П2, П2; с, d — координа-
ты точки О относительно системы
Оху.
Из формул (3.2) и (3.3) непосред-
ственно следует правило (алгоритм)
пост|юения проекции данной точки на
80
новую плоскость проекций (рис. 3.4):
при замене горизонтальной плоскос-
ти проекций на новую остается неиз-
менной ордината (глубина) данной
точки (см. рис. 3.4, а);
при замене фронтальной плоскости
проекций на новую остается неизмен-
ной аппликата (высота) данной точки
(см. рис. 3.4, б).
Формулы преобразования f (Oxyz -
- Oxyz):
х = /1 (х, у, Z );
у = /2(7, й *); (3.4)
z = /3(х, у, Z )
будут аналогичны формулам (3.2) и
(3.3). Формулы результирующего пре-
образования f = f f (Oxyz - Oxyz)
получаются подстановкой значений х,
у, z из формул (3.2) или (3.3) в фор-
мулы (3.4) преобразования / . Напри-
мер, при такой последовательности
замен плоскостей проекций / (П] •
- IIj), f (П2 - П2) формулы резуль-
тирующего преобразования имеют вид
Рис. 3.4
х - (xcosa + zsina + £)cosp +
+ ysinp * с;
у = -(xcosa + zsina + (3.5)
+ £)sinP + ycosp + d',
z = - xsina + zcosa + I.
Для другой последовательности за-
мен плоскостей проекций формулы
результирующего преобразования вы-
водятся аналогично. Очевидно, реше-
ния некоторых задач требуют выпо-
лнения замены только одной плоскости
проекций. Решения других задач могут
потребовать выполнения замен обеих
плоскостей проекций.
3.2.2. Алгоритмы решения
основных задач
Сначала рассмотрим алгоритмы ре-
шения четырех основных задач.
Задача 1. Преобразовать прямую АВ
общего положения в прямую уровня
или, другими словами, определить
натуральную величину отрезка [Л/?].
Для решения этой задачи выбираем
новую плоскость проекций параллель-
но данной прямой. На рис. 3.5 новая
фронтальная плоскость проекций П2
выбрана параллельно АВ, т.е. новая
ось х12 выбрана параллельно горизо-
нтальной проекции прямой АВ.
81
Проекция А 2В 2 на новой плоскости
проекций П2 определяется проекция-
ми А 2, В 2 се точек А, В, построенны-
ми по алгоритму, приведенному на
рис. 3.4, б.
Очевидно, эта задача также легко
решается заменой горизонтальной пло-
кости проекций П( на новую плоскость
проекций П j. Для этого новую ось
Х[2 = П2 п Пj нужно выбрать парал-
лельно фронтальной проекции Л2В2
данной прямой. Построение новых
проекций А ।, В1 точек А, В выполня-
ется по схеме (см. рис. 3.4, а).
Аналитическое решение этой же задачи
Пусть прямая АВ задана системой уравнений
(рис. 3.5):
. У = к1х + bi (3.6)
z = кгх + Ь2.
Заменим фронтальную плоскость проекций П2
на новую плоскость П2, параллельную прямой
АВ. Плоскость П2 определяется уравнением
у = к'Х.
Отсюда
Рис. 3.5
Подставив найденные значения sina. cos а в
формулы (3.3) и выразив х, у, z через х. у, z,
получаем формулы обратного преобразования:
Z - Z.
(3.7)
Подставив значения х, у, z из формул (3.7) в
(3.6), получаем уравнения прямой АВ в новой
системе координат:
У =
ЦУ -
+ ь2.
(3.8)
z
Таким образом, прямая АВ стала параллель-
ной координатной плоскости Ox z = П2 новой
системы отнесения (у - const).
Задача 2. Преобразовать прямую АВ
общего положения в проецирующую
прямую.
Очевидно, эта задача при наложен-
ных выше ограничениях на выбор но-
вых плоскостей проекций не решается
заменой одной плоскости проекций.
Действительно, новую плоскость про-
екций нельзя выбрать одновременно
перпендикулярной прямой АВ и одной
из плоскостей проекций исходной сис-
темы отнесения.
Поэтому задачу решаем двумя пре-
образованиями (см. рис. 3.5). Преобра-
зованием f (П2 - П2) прямую АВ пре-
образуем в прямую уровня в си-
стеме Пр П2 (см. задачу 1). Вто-
рым преобразованием / (П[ - П)), где
новая плоскость проекций П] выбира-
ется перпендикулярно прямой
А6(Л2В2 ± х21), в системе П1,П2
получаем проецирующую прямую.
82
Задача 3. Преобразовать плоскость
общего положения в проецирующую
(рис. 3.6).
По условию задачи новая плоскость
проекций должна быть перпендикуляр-
ной данной плоскости Ф(Л, В, С). Это
условие будет выполнено, если она
будет перпендикулярна горизонтали h
плоскости Ф при замене П2 на П2 или
фронтали f плоскости Ф при замене IIj
На рис. 3.6 показано решение этой
задачи заменой горизонтальной плос-
кости проекций П[ на горизонтальную
плоскость проекций П1. Здесь Ф ± П],
так как П( х / <= Ф (х12 ± /2). Постро-
ение новых проекций At, В{, С] то-
чек А, В, С плоскости Ф ясно из рисун-
ка.
Напомним, что две плоскости Ф, П] или ф,
П2 перпендикулярны, если одна из них (Ф)
содержит прямую, перпенидкулярную второй
'П| или П2) Поэтому Фс Пр если / с Ф
перпендикулярна Пр Ф1П2, если h с Ф пер-
пендикулярна п2 (см. рис. 2.10).
Задача 4. Преобразовать плоскость
общего положения Ф(Л, В, С) в плос-
кость уровня. Другими словами, опре-
делить натуральную величину треу-
гольника АВС (см. рис. 3.6).
Нетрудно показать, что решение
этой задачи требует последовательною
выполнения двух замен плоскостей
проекций (композиции преобразова-
ний), так как невозможно выбрать
новую плоскость проекций, которая
была бы одновременно параллельной
плоскости Ф и перпендикулярной одной
из плоскостей проекций исходной сис-
темы П[, П2.
Поэтому первой заменой / Ш[ - Пр
плоскость Ф преобразуем в проецирую-
щую в системе П2, ГЦ (см. задачу 3),
а второй заменой f (П2 - П2), где
П2 | Ф, приводим ее в положение
плоскости уровня в системе ГЦ , П2.
Последние три основные задачи, как
и первая, легко реализуются аналити-
чески. Поэтому их решение с примене-
нием ЭВМ не вызывает затруднений.
В заключение приведем пример ре-
шения комплексной задачи. Пусть
дана плоскость общего положения Ф (Л,
С, М). Требуется построить пра-
вильную четырехгранную пирамиду
SABCD, основанием которой является
квадрат ABCD, принадлежащий плос-
кости Ф. Пусть высота [5OJ, где О —
центр квадрата ABCD, равна диагона-
ли \АС] основания (рис. 3,7).
Задача решается в три этапа:
1) плоскость Ф(Л, С, М) общего по-
ложения преобразуется в плоскость
уровня Ф (см. задачу 4);
2) на плоскости уровня Ф по усло-
вию задачи ’’надстраивается" пирами-
да 5 Л BCD;
83
3) обратным преобразованием по-
его вторую диагональ [#]£]] ±
строенная пирамида SABCD ’’возвра-
щается” в требуемое условием задачи
положение.
Опишем подробнее эти этапы.
1. Плоскость Фц4, С, М) первой за-
меной /(П2 - П2) преобразуется в
проецирующую плоскость Ф(Л, С,
М). Для этого новая фронтальная
плоскость проекций П2 выбрана пер-
пендикулярной горизонтали h плоскос-
ти Ф (х)2 1 hx). Вторым преобразова-
нием f (И) - II ]), где II; || Ф, плос-
кость Ф преобразуется в плоскость
уровня Ф.
2. На плоскост ь проекций П ( осно-
вание ABCD искомой пирамиды прое-
цируется в натуральную величину, так
как его плоскость Ф параллельна П j.
Разделив отрезок (Лjt?, | пополам,
находим центр квадрата и строим
а. [Л jCj J. На П] проекция S] верши-
ны пирамиды совпадает с проекцией
О; центра основания.
3. Построив линии связи, находим
проекции Л2, Д2, С2, Z>2, О2 вершин
и центра основания пирамиды, принад-
лежащие вырожденной проекции Ф2
плоскости Ф на II2. Затем строим про-
екцию S2 вершины пирамиды из усло-
вия, что ее высота равна диагонали
основания <(S2O2j = [Л]С] ]).
Далее строим проекции Др Ор
S] точек В, D, О, S на П]. Для этого
через проекции В2, D2, О2, S2 прово-
дим линии связи, перпендикулярные
оси ,?12, и откладываем на них глуби-
ны точек В, D, 5, измеренные на
плоскости проекций II [ (равные
отрезки обозначены штрихами). Про-
екция О] точки О принадлежит
проекции h4|Cj| диагонали |4С] квад-
рата.
84
Для построения фронтальных проек-
ций В2, D2, S2 точек В, D, S через их
горизонтальные проекции проводим
линии связи, перпендикулярные оси
х12, и откладываем их высоты, изме-
ренные на плоскости проекций П2.
Решение задачи завершается постро-
ением проекций ребер пирамиды и
определением их видимости.
3.3. Способ
плоскопараллельного
движения
В отличие от способа замены плос-
костей проекций, которым данная фи-
гура преобразуется в фигуру частного
положения путем изменения системы
отнесения, способом плоскопараллель-
ного движения фигура приводится в
частное положение в результате ее
перемещения в пространстве относи-
тельно неподвижной системы отнесе-
ния. В теории преобразований пока-
зывается, что движение / фигуры в
пространстве можно представить как
композицию двух плоскопараллельных
движений / •/ относительно взаимно
перпендикулярных плоскостей.
Определение. Движение фигуры в
пространстве называется плоскопа-
раллельным, если все ее точки пере-
мещаются в параллельных плоскос-
тях.
Впредь будем рассматривать плоско-
параллельные движения фигур относи-
тельно плоскостей проекций. Пусть не-
который треугольник АВС совершает
плоскопараллельное движение относи-
тельно горизонтальной плоскости про-
екций П[ (рис. 3.8). Тогда его вершины
перемещаются в горизонтальных плос-
костях, значит, фронтальные проекции
вершин перемещаются по горизонталь-
ным прямым. Очевидно, угол наклона
плоскости треугольника к плоскости
проекций П[ остается неизменным.
Рис. 3.8
Поэтому при перемещении горизон-
тальная проекция треугольника свою
форму не меняет. Следовательно,
справедлива теорема: при плоскопа-
раллельном движении фигуры относи-
тельно горизонтальной плоскости
проекций фронтальные проекции ее
точек перемещаются по прямым, пер-
пендикулярным линиям связи, а гори-
зонтальная проекция фигуры остается
конгруэнтной самой себе.
Справедлива аналогичная теорема о
плоскопараллельном перемещении
относительно П2: при плоскопарал-
лельном движении фигуры относи-
тельно фронтальной плоскости проек-
ций горизонтальные проекции ее то-
чек перемещаются по прямым, пер-
пендикулярным линиям связи, а
фронтальная проекция фигуры оста-
ется конгруэнтной самой себе.
Приведем вывод формул плоскопараллельного
движения. Пусть фигура совершает плоскопа-
раллельное движение относительно плоскости
проекций П, (см. рис. 3.8). Плоскопараллельное
движение треугольника АВС можно разложить-
на два преобразования:
— вращение вокруг оси OZ на угол а (АВС -
А'В'С')-,
— параллельный перенос на вектор А А
(А'В'С - АВС).
При принятых на рис. 3.8 обозначениях для
вывода формул вращения вокруг оси Oz необхо-
димо заметить, что [O5J - [ОВ{ ];
[OSJ = — = -2L;
cosy siny
85
[ОВ(] = _____= yl ;
cos(y - a) sin(y - a)
[В,Я] = [B'B'] (z = z').
Отсюда имеем
[ов/1 = *—
cos (у - а)
cosy cosa + sinysina
Последовательное выполнение преобразований
(3.9) и (3.10) дает формулы плоскопараллельно-
го движения относительно П,
х = xcosa + ysina + с;
у = - xsina + ycosa + d\ (3.11)
z - z.
Аналогично выводятся формулы плоскопарал-
лельного движения относительно П2. Они имеют
вид
х - xcosa «• zsina + к\
X V
_______cosa + z sin a
[OflJ__(OBJ
или после упрощений
x - xcosa + ysina.
Аналогично,
Ю*,'] = Т-/-------Г
sin (у - а)
У
siny cosa + cosy sina
= __________Г____________
у X
—- cosa + _______ sina
[OBJ [OBJ
или после упрощений
у - - Jtsina + уcosa.
Таким образом, формулы вращения
Oz имеют вид
= л cos a + ysina;
у - - xsina + у cos a;
(3.9)
z - z.
Формулы параллельного переноса
ABC) имеют вид
+ c;
У = У *d-,
вокруг оси
(A'B'C -
(3.10)
z = z',
где c, d — координаты горизонтальной проекции
Л] точки А.
z - - xsina + zcosa + /.
Сравнение формул (3.11) и (3.3),
(3.12) и (3.2) плоскопараллельного
движения и замены плоскостей проек-
ций показывает их полную идентич-
ность, что подтверждает справедли-
вость двоякого истолкования функций
(3.1) по Ф. Клейну: независимо от то-
го, перемещается ли фигура относи-
тельно плоскостей проекций или фи-
гура остается в покое, а изменяется
положение плоскостей проекций, фор-
мулы преобразований имеют один и
тот же вид.
3.3.1. Алгоритмы решения
основных задач
Идентичность формул плоскопарал-
лельного движения и замены плоскос-
тей проекций означает, что графичес-
кие алгоритмы решения задач тем и
другим способом должны быть принци-
пиально одинаковыми. Проследим это
на примерах решения основных задач.
Задача 1. Преобразовать прямую
общего положения в прямую уровня —
фронталь (рис. 3.9).
Выполним плоскопараллельное пере-
мещение прямой АВ относительно
горизонтальной плоскости проекций.
Так как прямая АВ должна быть
фронталью, то ее горизонтальную про-
86
Эта задача решается двумя преобра-
зованиями.
Сначала плоскопараллельным движе-
нием относительно П, прямую АВ пре-
образуют во фронтальную прямую
уровня АВ (см. задачу 1). Затем плос-
копараллельным движением относи-
тельно П2 прямую АВ преобразуют в
горизонтально проецирующую прямую
скцию XjjB] расположим перпендику-
лярно линиям связи. При этом соглас-
но сформулированной выше теореме
горизонтальные проекции
|.4 j 5| 1 отрезка [Л/?] и его образа [Лб]
должны быть конгруэнтны.
Фронтальные проекции Л2, В2 точек
А, В перемещаются соответственно по
прямым Ф2, Д2 — вырожденным проек-
циям горизонтальных плоскостей уров-
ня Ф, Д, в которых перемещаются точ-
ки Л. В.
В результате выполненного плоско-
параллельного перемещения определя-
ются натуральная величина отрезка
АВ (| АВ | = [ Л2В2 ]) и угол у его на-
клона к горизонтальной плоскости
проекций.
Задача 2. Преобразовать прямую АВ
общего положения в горизонтально
проецирующую прямую Л В (рис. 3.9).
АВ. При этом [Л2б21 = М2В2] . го-
ризонтальные проекции Л], В{ точек
А, В перемещаются по прямой в] —
вырожденной проекции фронтальной
плоскости уровня 0, в которой переме-
щаются точки А, В.
Задача 3. Построить центр О окруж-
ности т, описанной около треугольни-
ка АВС (рис. 3.10).
Для решения этой задачи необходи-
мо плоскость АВС общего положения
преобразовать в плоскость уровня,
построить здесь искомую точку и об-
ратным преобразованием найти ее про-
екции на исходном чертеже.
Очевидно, одним плоскопараллель-
ным движением плоскость общего по-
ложения нельзя преобразовать в плос-
кость уровня. Напомним, что эта зада-
ча способом замены плоскостей проек-
ций также решалась в два этапа. Вы-
At
вг
*2
Л=6
Рис. 3.10
87
полним последовательно два плоско-
параллельных перемещения треу-
гольника АЙС: сначала относительно
фронтальной плоскости проекций,
затем относительно плоскости проек-
ций Ifj.
При первом плоскопараллельном
движении ф плоскость треугольника
ЛЙС преобразуем в проецирующую
плоскость. Для этого фронтальную
проекцию А2В2С^ образа расположим
так, чтобы Фронталь /(/], f2) стала
горизонтально проецирующей. При
этом согласно сформулированной выше
теореме фронтальные проекции треу-
гольников АИС и ЛВС должны быть
конгруэнтны (| Л2В2С2 I |A2^2^-2^’
а горизонтальные проекции А,, В}. С]
вершин Л, В. С треугольника опишут
соответственно прямые Ф,, Л,, Г) —
вырожденные проекции фронтальных
плоскостей уровня, проведенных через
эти вершины.
Вторым плоскопараллельным движе-
нием <р относительно П[ треугольник
АВС преобразуем в треугольник АВС,
расположенный в горизонтальной
плоскости уровня. При этом отрезки
I^CJ конгруэнтны и по-
следний располагаем перпендикуляр-
но линиям связи. Поэтому фронталь-
ная проекция А2В2С2 определяет на-
туральную величину треугольника
АВС
Известными построениями находим
фронтальную проекцию ()2 центра О
искомой окружности, по линии связи
строим его горизонтальную проекцию
и(. Обратными преобразованиями
ф 1 , ф-1 (последовательность постро-
ений на рис. 3.10 показана стрелками)
находим проекции О], О2 центра О
окружности, описанной вокруг треу-
гольника АВС.
3.4. Способ вращения
вокруг проецирующей
прямой
При вращении фигуры вокруг прое-
цирующей прямой каждая ее точка
описывает окружность, расположенную
в соответствующей плоскости уровня.
Поэтому этот способ является частным
случаем способа плоскопараллельного
движения, когда точка описывала не-
которую плоскую кривую, форма кото-
рой не влияла на алгоритм решения
той или иной задачи. Отсюда следует,
что графические и аналитические ал-
горитмы построения соответственных
точек способами плоскопараллельного
движения и вращения вокруг проеци-
рующей прямой должны отличаться
лишь в деталях, оставаясь однотипны -
ми по существу.
Например, формулы преобразования
вращения вокруг проецирующей пря-
мой имеют тот же вид, что и (3.11),
(3.12). Теперь в этих формулах с, d н
к, I определяют координаты вырожден-
ных проекций соответственно горизон-
тально проецирующей и фронтально
проецирующей осей вращения, а « —
угол поворта вокруг оси.
Графический алгоритм построения
соответственных точек способом вра-
щения вокруг проецирующей прямой
отличается лишь тем, что здесь указы-
ваются обе проекции траектории дви-
жения точки, в то время как в способе
плоскопараллельного перемещения на
чертеже строилась лишь одна проекция
траектории движения точки.
3.4.1. Алгоритмы решения
основных задач
Рассмотрим алгоритмы решения ос-
новных задач способом вращения вок-
руг проецирующей прямой.
Задача 1. Определить натуральную
величину отрезка [АЯ1 или, другими
88
словами, преобразовать прямую АВ
общего положения в прямую уровня.
Для упрощения графического реше-
ния этой задачи горизонтально прое-
цирующую ось вращения i выберем
проходящей через точку В (рис. 3.11).
Тогда точка В останется в покое (В\ =
= , В2 = В2) и нужно построить
лишь повернутое положение точки А.
Точка А описывает окружность а,
плоскость Ф которой параллельна Пр
Поэтому а2 = Ф2, а1 ~ окружность с
центром в ip радиус которой равен
отрезку А\В}.
Отрезок А2В2 определит натураль-
ную величину если [ АВ ] будет
фронталью (его горизонтальная проек-
ция [/ЦТ?] ] будет перпендикулярна
линиям связи).
Задача 2. Преобразовать прямую АВ
общего положения в проецирующую.
Рассмотренными выше способами эта
задача решалась в два этапа. Очевид-
но, ее решение способом вращения
вокруг проецирующей прямой также
требует двух преобразований. Сначала
вращением, например, вокруг горизон-
тально проецирующей оси i прямую
АВ преобразуем в прямую уровня АВ
— фронталь (см. рис. 3.11). Вторым
вращением вокруг уже фронтально
проецирующей оси / фронталь АВ
преобразуется в горизонтально проеци-
рующую прямую АВ. На рис. 3.11 для
упрощения графических операций ось
j выбрана проходящей через точку А
прямой АВ.
Задача 3. Плоскость общего по ложе-
ния Ф(Д, В, С) преобразовать в гори
зонтально проецирующую плоскостьФ
(А, В, С) (рис. 3.12).
Для решения этой задачи необходи-
мо задать ось вращения и определить
величину угла, на который должен
быть повернут треугольник АВС. При
выборе оси врашения следует помнить,
что при вращении вокруг горизонталь-
но проецирующей прямой (плоскопа-
раллельном движении относительно
П() угол наклона фигуры к П) остается
неизменным. При преобразовании
плоскости общего положения Ф(Л, В,
С) в горизонтально проецирующую
плоскость Ф(Д. В, С) угол наклона
плоскости Ф к Л] изменяется от какого-
то исходного значения у до прямого
(у = 90"). Поэтому в качестве оси
вращения необходимо выбрать фрон-
тально проецирующую прямую /. Для
упрощения графических операций
желательно, чтобы она проходила че-
рез одну из вершин треугольника АВС
(рис 3.12).
Рис. 3.12
89
Угол а поворота определяют, исполь-
зуя признак проецирующих плоскостей
(см. п. 2.2.1). Для того чтобы плос-
кость ФС4, В, С) стала горизонтально
проецирующей, ее необходимо повер-
нуть на такой угол а, чтобы ее фрон-
таль / после поворота стала горизон-
тально проецирующей прямой /. От-
сюда следует алгоритм преобразования
плоскости Ф общего положения в про-
ецирующую плоскость Ф:
— выбирается проецирующая ось
вращения i, проходящая (условие же-
лательное, но необязательное) через
одну из вершин треугольника АВС;
•— в плоскости Ф строится фронталь /,
если ось i перпендикулярна П2, или
горизонталь й, если ось i перпендику-
лярна Пр
— построенная фронталь / (горизон-
таль Л) поворачивается вокруг оси i до
проецирующего положения / (Л);
— все точки фигуры поворачиваются
на угол а, составленный исходным и
повернутым положениями фронтали
(горизонтали).
При неудачном выборе оси вращения
происходит наложение проекций ис-
ходного и повернутого положений фи-
гуры, что затрудняет чтение чертежа.
Для устранения этого недостатка необ-
ходимо выбрать другую ось вращения,
пересекающую построенную в плоскос-
ти фигуры фронталь или горизонталь.
Задача 4. Плоскость общего положе-
ния Ф(Л, В, С) преобразовать в плос-
кость уровня Ф(Л, В, С), другими
словами, определить натуральную
величину треугольника АВС (см.
рис. 3.12).
Эта задача способом вращения вок-
руг проецирующей прямой, как и изу-
ченными выше способами замены
плоскости проекций, плоскопараллель-
ного движения решается в два этапа:
1) вращением вокруг первой оси i,
например, перпендикулярной П2, плос-
кость Ф(Л, В, С) преобразуете? в прое-
цирующую плоскость Ф(Л, В, С) (см.
задачу 3);
2) вращением вокруг второй дси /,
перпендикулярной другой плоскости
проекций, проецирующая плоскость
Ф(Л, В, С) преобразуется в плоскость
уровня Ф(Л, В, С).
Вторую ось вращения j также целе-
сообразно выбрать проходящей через
одну из вершин треугольника АВС
или во избежание наложения проек-
ций исходного и повернутого положе-
ний фигуры — в плоскости данной
фигуры. Величина угла поворота опре-
деляется условием задачи — необходи-
мостью получения плоскости уровня
Ф(Л, В, С).
3.4.2. Выводы
Рассмотрев алгоритмы решения че-
тырех основных задач тремя вышеиз-
ложенными способами преобразования
чертежа Монжа; можно сделать следу-
ющие выводы:
— первая и третья основные задачи
всеми способами решаются одним пре-
образованием — заменой одной плос-
кости проекций, одним плоскопарал-
лельным движением или одним враще-
нием вокруг проецирующей прямой;
— вторая и четвертая основные зада-
чи решаются с помощью двух преобра-
зований, причем последовательность
выполнения графических операций в
принципе одна и та же;
— во всех трех способах проекции
данной фигуры и ее образа на одну из
плоскостей проекций конгруэнтны (в
способе замены плоскостей проекций
они совпадают);
— все три преобразования аналити-
чески задаются одними и теми же фор-
мулами; сравните (3.2) и (3.11), (3.3)
и (3.12).
90
Таким образом, область применения
всех рассмотренных преобразований
одна и та же. Использование их в каж-
дом конкретном случае зависит от
дополнительных условий. Например,
способ плоскопараллельного перемеще-
ния позволяет удобно располагать про-
екции фигуры на всем поле чертежа и
избежать наложения проекций В спо-
собе замены плоскостей проекций про-
екция фигуры и ее образа на одной
плоскости проекций тождественны
(совпадают), что уменьшает число
вспомогательных построений. В спосо-
бе вращения вокруг проецирующей
прямой также выбором положения оси
вращения удается уменьшить число
вспомогательных построений.
3.5. Способ вращения
вокруг прямой уровня
Вращение вокруг прямой уровня
применяется, как правило, для реше-
ния четвертой основной задачи — пре-
образования плоскости общего положе-
ния в плоскость уровня. В этом случае
в отличие от рассмотренных выше спо-
собов задача решается одним преобра-
зованием, что и определяет предпочти-
тельность такого решения.
В качестве примера рассмотрим
определение натуральной величины
Рис. 3.13
треугольника АВС вращением вокруг
его горизонтали (рис. 3.13). Для удо-
бства горизонталь h проведем через
вершину А данного треугольника. В
этом случае точка А, а также точка
I = h л ВС, как находящиеся на оси
вращения, останутся в покое: А = А,
J = Г.
Вершины В, С, вращаясь вокруг оси
Л, опишут окружности, плоскости S, Г
которых будут горизонтально проеци-
рующими, так как они перпендикуляр-
ны горизонтали Л:
В е £ х h (В, е Е] х Л,>;
С е Г х h (С, е Г, х Л,).
Вначале построим повернутое поло-
жение В точки В из условия, что тре-
угольник АВС в повернутом положе-
нии будет горизонтальной плоскостью
уровня Ф(Ф2 = Л2). Точка В, вращаясь
вокруг оси h, описывает в пространстве
окружность. Центр О этой окружности
определяется как точка пересечения
оси вращения h с плоскостью 2. Так
как плоскость 2 является горизонталь-
но проецирующей, то горизонтальная
проекция О] точки О есть точка пере-
сечения горизонтальной проекции
оси вращения и вырожденной проек-
ции 2j плоскости 2. Фронтальная про-
екция О2 точки О принадлежит й2.
Радиус вращения точки В равен отрез-
ку [OB] (OjBp О2В2).
Повернутое положение В точки В
будет принадлежать горизонтальной
плоскости уровня Ф( Ф2 = /ь). Поэтому
горизонтальная проекция Bi точки В
будет принадлежать вырожденной про-
екции 2] плоскости 2 и отстоять от О|
на расстояние [Oj ], равное нату-
ральной величине радиуса вращения
[ОВ]. Натуральную величину отрезка
91
ОВ можно определить любым изучен-
ным выше способом. На рис. 3.13 она
определена по правилу прямоугольного
треугольника (см. п. 1.1.3): | ОВ | =
= [OjBj] = [OjBq] , где [OjBq] — гипо-
тенуза прямоугольного треугольника
O^B^Bq, построенного на горизонталь-
ной проекции lOjBJ, как на катете;
второй катет равен разности
высот 5Z концов отрезка [ОВ].
Повернутое положение С вершины С
построено из условия принадлежнос-
ти точки С плоскости Г и повер-
нутому положению прямой Bl : Ci =
= Г] n Bj/p Фронтальные проекции
вершин А, В, С принадлежат вырож-
денной проекции Ф2 плоскости повер-
нутого треугольника (на рис. 3.13 они
не показаны).
3.5.1. Способ совмещения
Если за ось вращения принимается
линия нулевого уровня (линия уровня,
принадлежащая плоскости проекций),
то рассматриваемый способ вращения
вокруг линии уровня называют спосо-
бом совмещения, так как при враще-
нии вокруг линии нулевого уровня
плоская фигура совмещается с какой-
либо плоскостью проекций.
В качестве примера рассмотрим по-
строение натуральной величины се-
чения ABCDE пятигранной призмы
фронтально проецирующей плоскостью
Ф(Ф2) способом совмещения с го-
ризонтальной плоскостью проек-
ций (рис. 3.14). Секущая плоскость
Ф — фронтально проецирующая, по-
этому фронтальная проекция сече-
ния Л2В2С2£>2£'2 принадлежит вырож-
денной проекции Ф2 плоскости. Данная
призма является горизонтально прое-
цирующей (ее боковые грани и ребра
перпендикулярны П|), поэтому гори-
зонтальная проекция се-
чения совпадает с проект"'и основа-
ния призмы на Пр
Для определения натур льной вели-
чины сечения выбираем в качестве оси
вращения горизонталь нулевого уровня
/г(Лр Л2) — след плоскости Ф и Пр В
рассматриваемом примере горизонталь
h является фронтально проецирующей
прямой. Поэтому окружности, описы-
ваемые вершинами сечения, проециру-
ются на П2 в натуральную величину, а
на П] — в виде прямых, перпендику-
лярных следу h плоскости Ф, т.е. прак-
тически в этом примере способ совме-
щения эквивалентен способу вращения
вокруг фронтально проецирующей
прямой.
3.6. Способ
дополнительного
проецирования
Под способом дополнительного прое-
цирования понимают совкупность при-
емов приведения линейных (прямых и
плоскостей), нелинейных (кривых
линий и поверхностей) фигур в прое-
цирующее положение путем измене-
ния направления проецирования, вы-
бора новой плоскости или поверхности
проекций, заменой прямоугольного
проецирования параллельным, цен-
тральным или криволинейным проеци-
рованием. Заметим, что проецирование
называется криволинейным, если в
92
качестве проецирующих линий выби-
раются плоские или пространственные
кривые линии. При решении ряда за-
дач могут одновременно выбираться
новые плоскости проекций и виды
проецирования. Обычно способ допо-
лнительного проецирования применя-
ется при решении позиционных задач
(см. гл. 4). Решение основывается на
преобразовании геометрической фигу-
ры общего положения или вида в прое-
цирующую. Приведем несколько при-
меров преобразования геометрических
фигур в проецирующие.
Пример 1. Прямую а(а1( а2) общего
положения способом дополнительного
проецирования преобразовать в прое-
цирующую относительно П] = ГЦ
(рис. 3.15).
Задача решается, если прямоуголь-
ное проецирование на П] заменить
параллельным проецированием на
ЕЦ = IIj в направлении s || а. Это рав-
носильно замене прямоугольной систе-
мы координат Oxyz на косоугольную
систему Oxyz, у которой ось Oz па-
раллельна направлению дополнитель-
ного проецирования s || а, а коорди-
натная плоскость Оху совпадает с
кординатной плоскостью Оху исходной
системы (см. рис. 3.1). В этом случае
дополнительная проекция а1 прямой а
на плоскость Щ = П вырождается в
точку, т.е. данная прямая относитель-
но IIj стала проецирующей. Заметим,
что построение дополнительной проек-
ции <2] прямой а графически эквива-
лентно построению ее горизонтального
следа (сравните с рис. 2.5).
Пример 2. Плоскость 2 (а п />) об-
щего положения преобразовать с
проецирующую относительно II2 = П2
(рис. 3.16).
Алгоритм решения этой задачи
должен реализовать следующее оче-
видное положение: данная плоскость 2
станет проецирующей относительно
П2 - П2, если направление s дополни-
тельного проецирования параллельно
плоскости 2. Это утверждение следует
из определения проецирующей плос-
кости (см. п. 2.2.1): плоскость называ-
ется проецирующей, если она парал-
лельна направлению проецирования.
Как известно, прямая $ будет парал-
лельна плоскости 2, если она парал-
лельна какой-либо прямой этой плос-
кости. Поэтому для решения данной
задачи можно выбрать бесчисленное
множество направлений дополнитель-
ного проецирования. Например, на-
правление .S' может быть параллельным
прямой а или Ь, входящей в определи-
тель плоскости 2. На рис. 3.16 направ-
ление s дополнительного проецирова-
ния выбрано параллельным горизонта-
93
ли h плоскости S. Вырожденная допо-
лнительная проекция Е2 плоскости Е
на П2 = П2 в направлении s проходит
через следы В(В2), Л(Л2), Я(Я2) соот-
ветственно прямых Ь, a, h на П2.
Пример 3. Определить: пересекает
ли прямая I в действительных точках
коническую поверхность Ф(5, а)
(рис. 3.17).
Рис. 3.17
Рассмотрим алгоритм решения дан-
ной задачи, основанный на идее допо-
лнительного проецирования. Другой
алгоритм решения этой задачи будет
рассмотрен в следующей главе.
Взаимное положение прямой I и по-
верхности Ф станет очевидным, если
построить их дополнительные проек-
ции на какую-либо плоскость проек-
ций, чтобы относительно этой плоскос-
ти проекций коническая поверхность Ф
была проецирующей. Отсюда вытекает
следующая схема решения данной
задачи:
— необходимо воспользоваться допо-
лнительным центральным проецирова-
нием с центром 5, совмещенным с вер-
шиной конической поверхности Ф (тог-
да коническая поверхность будет
проецирующей, так как ее образую-
щие проходят через центр проециро-
вания);
— целесообразно в качестве плоскос-
ти проекций принять плоскость £ на-
правляющей а конической поверхности
Ф (тогда дополнительная проекция ко-
нической поверхности Ф совпадает с ее
направляющей а).
Таким образом, решение задачи
сводится к построению дополнительной
центральной проекции I прямой I на
плоскость £ основания а конической
поверхности Ф. На рис. 3.17 плоскость
Ф основания а совпадает с горизонталь-
ной плоскостью проекций Пр Поэтому
дополнительная центральная проекция
Z (/], /2) прямой I из точки S опреде-
ляется горизонтальным следом /(/,,
/2) прямой I и следом 2(2t, 22) прое-
цирующей прямой SM, где М — произ-
вольная точка прямой I. Так как в
рассматриваемом случае дополнитель-
ные центральные проекции а(а1; а2)
конической поверхности Ф и I прямой
I из точки S на плоскость £ = ГЦ не
пересекаются в действительных точках
(Zj то в пространстве прямая /
и коническая поверхность Ф также не
пересекаются в действительных точ-
ках.
Пример 4. Определить: принадлежит
ли точка А(Л], Л2) поверхности тора
Ф(/, D (рис. 3.18).
94
Одно из возможных решений этой
задачи в несколько иной формулиров-
ке было рассмотрено в п. 2.6.3 (см.
рис. 2.52). Здесь же предложим другую
интерпретацию схемы решения, осно-
ванную на идее дополнительного прое-
цирования.
Очевидно, что некоторая точка при-
надлежит проецирующей поверхности,
если соответствующая ее проекция
принадлежит вырожденной проекции
данной поверхности. Говорят, что вы-
рожденная проекция проецирующей
поверхности (плоскости) обладает ’’со-
бирательным” свойством, т.е. она
как бы собирает на себя проекции
всех точек и линий, принадлежа-
щих проецирующей поверхности
(плоскости).
Отсюда вытекает следующая схема
решения задачи:
— принимая семейство параллелей т
поверхности тора Ф в качестве проеци-
рующих линий криволинейного
(окружностного) проецирования, пред-
ставим поверхность Ф проецирующей
(тогда се вырожденной проекцией Ф
будет образующая Z: Ф] = Zj);
— построим дополнительную кри-
волинейную проекцию Л(А1, Л2)
точки А на плоскость Г образующей Z.
Криволинейная проекция А точки А
строится как след проецирующей
окружности т, проходящей через точ-
ку А, на плоскости Г образующей Z.
Заметим, что проецирующими окруж-
ностями в данном примере являются
все окружности, центры которых при-
надлежат оси / поверхности Ф, а их
плоскости перпендикулярны оси /.
Если криволинейная проекция А
принадлежит вырожденной проекции
Ф = Z, то точка А принадлежит повер-
хности Ф. На рис. 3.18 А £ Ф, поэтому
точка А не принадлежит поверхности
тора.
3.7. Способы преобразования
аксонометрического
чертежа
Способы преобразования аксономет-
рического чертежа, как и чертежа
Монжа, применяются для упрощения
решений позиционных и метрических
задач путем преобразования геометри-
ческих фигур общего положения в
фигуры частного положения. Обычно в
учебных курсах начертательной гео-
метрии рассматривают два способа
преобразования прямоугольного аксо-
нометрического чертежа: способ совме-
щения и способ замены плоскости про-
екций.
3.7.1. Способ совмещения
Способ совмещения был рассмотрен
в п. 2.5.7 на примере построения про-
екций окружности на прямоугольном
аксонометрическом чертеже (см.
рис. 2.37). Если дана геометрическая
фигура, расположенная в какой-либо
координатной плоскости натуральной
системы, то она вращением вокруг
соответствующей стороны треугольни-
ка следов совмещается с плоскостью
аксонометрических проекций. При
этом данная фигура изображается в
натуральную величину, что позволяет
упростить решения ряда позиционных
и метрических задач с ее участием. К
таким задачам можно отнести:
1) определение метрических характе-
ристик (размеров) фигуры, принадле-
жащей плоскости натуральной системы
координат и заданной своими проекци-
ями на аксонометрическом чертеже;
2) построение фигуры, принадлежа-
щей какой-либо плоскости натураль-
ной системы координат и удовлетворя-
ющей наперед заданным метрическим
и позиционным требованиям.
Пример 1. Определить натуральную
величину треугольника АВС, принад-
95
лежащего координатной плоскости Oxz
натуральной системы (рис. 3.19).
Данную задачу решим способом со-
вмещения координатной плоскости Oxz
с плоскостью изображения П' прямо-
угольной аксонометрии вращением
вокруг стороны XZ треугольника сле-
дов. Для упрощения построений ось
вращения XZ проводим через вершину
С треугольника АВС: С' е XZ ± О'у'.
Далее, строим совмещенное положе-
ние Oxz системы координат Oxz, для
чего предварительно находим совме-
щенное положение О начала коорди-
нат. Точка О, вращаясь вокруг оси XZ,
описывает в пространстве окружность,
принадлежащую проецирующей плос-
кости Г = О'у'. Поэтому О принадле-
жит плоскости Г. С другой стороны,
треугольник OXZ прямоугольный, так
как его стороны ОХ и OZ лежат на
осях натуральной декартовой системы
координат. Значит, точка О находится
как точка пересечения вырожденной
проекции Г' плоскости Г и окружности
I, описанной на отрезке XZ, как на
диаметре (угол XOZ, опирающийся на
диаметр XZ окружности t, является
прямым).
Треугольник АВС с Oxz вращается
вместе с координатной плоскостью Oxz
до совмещения с плоскостью изображе-
ния П'. Точка С, как принадлежащая
оси вращения XZ, остается в покое
С = С. Совмещенное положение вер-
шины А находится из условия ее при-
надлежности оси Oz : А' е O'z' ~А
е Oz, А'А || Г'. Для построения со-
вмещенного положения В точки В
продолжаем сторону АВ до пересече-
ния с осью Ох в точке J, находим ее
совмещенное положение 1 и на А1
определяем точку В. Построенный
треугольник АВС есть натуральная
величина данного на чертеже тре-
угольника АВС.
Пример 2. Построить ромб ABCD,
принадлежащий координатной плос-
кости Оху, если известны его центр
= М'), вершина Ж/Ц7 = А') и
длина т его сторон (рис. 3.20).
Совместим координатную плоскость
Оху вращением вокруг стороны XY
треугольника следов с плоскостью П'
аксонометрического изображения. Для
этого на отрезке XY, как на диаметре,
описываем полуокружность t и отмеча-
ем точку О пересечения O'z' с t:Oxy
— совмещенное положение координат-
96
ной плоскости Оху. Строим совмещен-
ные положения: А, Л/ данных точек
А, Л/, для чего продолжаем прямую
А^Л/{ = А'М' до пересечения с аксо-
нометрической осью О'у' в точке 2' и
осью вращения XY в точке Г. Совме-
щенные образы 1 = 1', 2(2 е Ох)
точек Г, 2' определяют совмещенные
положения А £ 12, М Е 12 точек Л,
Л/ и совмещенное положение АС
([АЛ/]) = [Л/С]) диагонали АС иско-
мого ромба.
Далее строим на диагонали АС со-
вмещенный образ ABCD ромба:
— через точку Л/ проводим прямую
Л/3, перпендикулярную диагонали
АС;
— из точки А, как из центра, описы-
ваем окружность радиусом т и отме-
чаем точки В, D ее пересечения с
прямой Л/3.
Обратным вращением построенного
ромба ABCD вокруг оси XY получаем
его аксонометрическую проекцию
A'B'C'D' = a'b[c(d[, где (С/ =
= С') е А'Л/', (в{ = В'), (D[ =
= D') е Л/'З'. Очевидно, в силу
свойств параллельного проецирования
аксонометрической проекцией ромба
ABCD является параллелограмм
A'B'C'D' = a'b'c'd' .
3.7.2. Способ замены
плоскости проекций
Этот способ предназначен, в основ-
ном, для определения натуральных
величин отрезков, принадлежащих
аксонометрическим осям. Такие задачи
возникают при определении показате-
лей искажения в прямоугольной аксо-
Рис. 3.21
нометрии, когда по известным нату-
ральным единичным (масштабным)
отрезкам требуется построить соотве-
тствующие аксонометрические отрезки.
Рассмотрим на конкретном примере
решение подобной задачи. Пусть пря-
моугольная аксонометрия дана своими
аксонометрическими осями (рис. 3.21).
Требуется построить аксонометричес-
/
кии единичный отрезок ez , если из-
вестен соответственный натуральный
единичный отрезок ez.
Задачу решим способом замены
плоскости проекций. Новую плоскость
проекций П выберем параллельно про-
ецирующей плоскости Г, проходящей
через ось Oz натуральной системы ко-
ординат. Плоскость Г пересекает аксо-
нометрическую плоскость проекций П'
по прямой ZM, а натуральную систему
координат Oxyz — по оси Oz и прямой
ОЛ/, где Л/ — точка пересечения плос-
кости Г со стороной XY треугольника
следов XYZ. Треугольник ОЛ/Z, обра-
зованный указанными прямыми, пря-
моугольный, так как ось Oz перпенди-
кулярна координатной плоскости Оху.
Он ортогонально проецируется на но-
вую плоскость проекций П в треуголь-
ник ОЛ/Z. Так как плоскости Г,П
параллельны, то треугольники ОЛ/Z
и ОЛ/Z конгруэнтны.
97
Поэтому построение треугольника
OMZ выпоняется в такой последова-
тельности.-
— вершины М, Z, как принадлежа-
щие плоскости изображения П', прое-
цируются на П в точки М, Z, принад-
лежащие вырожденной проекции плос-
кости П;
— точка О определяется как точка
пересечения линии связи О'О с полу-
окружностью t, описанной на отрезке
MZ, как на диаметре.
Ось Oz проецируется на вспомога-
тельную плоскость П без искажения.
Поэтому на Oz откладываем натураль-
ный единичный отрезок ez и обратным
проецированием получаем на аксоно-
метрической оси O'z' аксонометричес-
кий единичный отрезок e'z . При необ-
ходимости с помощью аналогичных
построений получают аксонометричес-
/ /
кие единичные отрезки е , е .
Упражнения и вопросы
для самопроверки
1 Дайте определения понятий преобразова-
ние, композиции преобразований. Вспомните
классификацию преобразований чертежа, исходя
из двоякого истолкования уравнений (3.1).
2. Вспомните теорию способа замены плоскос-
ти проекций и алгоритм построения соответст-
венных точек.
3. Сформулируйте теоремы о плоскопарал-
лельном движении фигуры относительно П| и П2.
4. Покажите на чертеже графический алго-
ритм построения соответственных точек способом
вращения вокруг проецирующей прямой.
5. Решите четыре основные задачи каждым из
следующих способов: замены плоскости проек-
ций, плоскопараллельного движения, вращения
вокруг проецирующей прямой. Сопоставьте алго-
ритмы решения каждой задачи перечисленными
способами и сформулируйте их общие и отличи-
тельные свойства.
6. Определите натуральную величину угла
АВС способом вращения вокруг линии уровня
(рис. 3.22).
7. Определите натуральную величину угла
АВС способом совмещения (вращения вокруг
линии нулевого уровня) (рис. 3.22).
8. Вспомните теорию способа дополнительного
проецирования. Способом дополнительного прое-
цирования преобразуйте плоскость АВС в гори-
зонтально проенирукнцую (рис. 3.22).
9. Способом совмещения постройте аксономет-
/ /
рические единичные отрезки ех . ez , если
даны аксонометрические оси прямоугольной
аксонометрии и натуральный единичный отрезок
е (рис. 3 23).
Рис. 3.23
10. Вычислите показатели искажения и, v, w
по аксонометрическим осям в прямоугольной
аксонометрии, если даны натуральный единич-
ный отрезок е и аксонометрические оси
(рис. 3.23). Аксонометрические единичные от-
III „ ,
резки е, , е., , е_ построите способом замены
дуг
плоскости проекций.
98
Глава 4
ТЕОРИЯ И АЛГОРИТМЫ
РЕШЕНИЯ ПОЗИЦИОННЫХ ЗАДАЧ
Как было отмечено в первой главе, в
курсе начертательной геометрии рас-
сматривается два типа отношений
между геометрическими фигурами:
позиционные и метрические. Соответ-
ственно этому решаются два типа за-
дач. Изучение теории и алгоритмов
решения позиционных задач в трех-
мерном расширенном евклидовом про-
странстве направлено на развитие
’’пространственного мышления” уча-
щихся для дальнейшего чтения и со-
ставления чертежей трехмерных объ-
ектов как на бумаге, так и на экранах
дисплеев. Некоторые из них (построе-
ние касательных плоскостей, соприка-
сающихся поверхностей) имеют непо-
средственное значение и составляют
основу при составлении математичес-
ких моделей технических форм в про-
цессе их автоматизированного проек-
тирования и воспроизведения на обо-
рудовании с числовым программным
управлением.
Следует заметить, что любая форма
детали машины или механизма, строи-
тельной конструкции или природного
объекта состоит из дуг и отсеков аб-
страктных геометрических фигур (пря-
мых и кривых линий, плоскостей,
сфер, цилиндров, конусов и т.д.). Поэ-
тому для их конструирования, изобра-
жения, варьирования формой и разме-
рами необходимо уметь синтезировать
их из абстрактных геометрических тел,
строить линии пересечения ограничи-
вающих деталь поверхностей, опреде-
лять принадлежность тех или иных
точек и линий граням и поверхностям
детали и т.д.
При решении позиционной задачи
необходимо придерживаться следую-
щего:
— внимательно прочитав условие
задачи, представить ее исходные дан-
ные в пространстве, используя при
необходимости их физические модели
(мелок или резинку в качестве модели
точки, карандаш или линейку в качес-
тве модели прямой и т.д.);
— пользуясь материалом настоящей
главы, наметить алгоритм решения
задачи в пространстве и реализовать
его на чертеже.
4.1. Классификация
позиционных задач
В начертательной геометрии пози-
ционными задачами принято называть
такие, в которых требуется опреде-
лить положение фигуры относительно
плоскостей проекций и взаимное по-
ложение (принадлежность, параллель-
ность, пересечение и непересечение)
двух или более фигур. В случае пере-
сечения двух фигур необходимо уметь
строить их общую часть (точку или
точки, линию).
Из определения следует, что все
позиционные задачи можно отнести к
двум группам (см. рис. 4.1):
— задачи на чтение чертежа фигуры
или, другими словами, задачи на опре-
деление положения фигуры относи-
тельно плоскостей проекций;
— задачи на определение взаимного
положения двух фигур .
Определение взаимного положения трех и
более фигур сводится к рассмотрению их попар-
ного положения. Например, при определении
общих точек трех поверхностей скачала строят
линию пересечения любых двух поверхностей, а
затем — точки пересечения этой линии с третьей
поверхностью.
99
Позиционные
задачи
Рис. 4.1
4.1.1. Положение фигуры
относительно
плоскостей проекций
Задание геометрических фигур на
чертеже было подробно рассмотрено во
второй главе. Поэтому здесь, говоря о
чтении чертежа фигуры, в частности,
об определении ее положения относи-
тельно плоскостей проекций, кратко
повторим изложенное во второй главе.
Геометрическая фигура относительно
той или иной плоскости проекций мо-
жет занимать произвольное (общее)
или частное положение. Принято счи-
тать, что геометрическая фигура за-
нимает частное положение относи-
тельно плоскости проекций, если не-
которые элементы геометрической
части ее определителя занимают час-
тное положение относительно этой
плоскости проекций. Например, если
ось поверхности вращения перпендику-
лярна или параллельна какой-либо
плоскости проекций, то эта поверх-
ность имеет частное положение отно-
сительно этой плоскости проекций. В
противном случае она будет поверх-
ностью общего положения.
При рассмотрении прямых линий и
некоторых поверхностей, в частности,
плоскостей эти фигуры подразделяют
на проецирующие и уровня. Геометри-
ческая фигура (прямая, плоскость и
цилиндрическая поверхность) будет
проецирующей относительно какой-
100
либо плоскости проекций, если она
представляет собой прямую или одно-
параметрическое множество прямых,
перпендикулярных этой плоскости
проекций. Проекции таких фигур на
эту плоскость являются вырожденны-
ми. На рис. 4.2 приведены чертежи
горизонтально проецирующих прямой
а, плоскости S и цилиндрической по-
верхности Ф. Такие фигуры на чертеже
однозначно определяются заданием
только вырожденной проекции (см.
чертеж плоскости Е), хотя в ряде слу-
чаев для наглядности изображают их
проекции на другую плоскость проек-
ций (см. чертежи прямой а и цилин-
дрической поверхности Ф). Прямые и
плоскости могут занимать еще одно
частное положение, когда они парал-
лельны плоскости проекций. Тогда
соответствующая координата всех их
точек имеет одно и то же значение.
Такие прямые и плоскости, как извес-
тно, называются прямыми и плоскос-
тями уровня.
Однако ни одна поверхность, кроме
плоскости, не может быть поверх-
ностью уровня. Но любая поверхность
содержит три семейства линий уровня
— семейства кривых, получающихся
при сечении поверхности тремя семей-
ствами плоскостей уровня. Например,
на рис. 2.40 изображена топографичес-
кая поверхность с каркасом горизонта-
лей.
При решении задач этой группы
обычно нет необходимости в выполне-
нии каких-либо построений, так как
по чертежу фигуры можно сразу же
определить ее положение относительно
той или иной плоскости проекций,
если на чертеже имеется проекция
фигуры на ту или иную плоскость
проекций.
Однако в некоторых случаях такие
построения необходимы. Например,
пусть требуется определить положение
плоскости 0(4, В, С). Так как эта
плоскость может быть или плоскостью
общего положения, или профильно
проецирующей, то строим какую-либо
ее линию уровня, например горизон-
таль h. Если горизонталь h не вырож-
дается в профильно проецирующую
прямую (см. рис. 2.9), то плоскость 0
занимает общее положение. Если же
горизонталь h будет к тому же про-
фильно проецирующей (см. рис. 2.10),
то и плоскость 0 будет профильно про-
ецирующей. Конечно, положение плос-
кости 0 можно было определить и по-
строением профильной проекции
Л3В3С3 задающего ее треугольника
АВС.
4.1.2. Взаимное положение
двух фигур
Остановимся более подробно на
рассмотрении задач второй группы
(рис. 4.1), связанных с определением
взаимного положения двух геометри-
ческих фигур трехмерного расширен-
ного евклидова пространства.
Сначала напомним некоторые сведе-
ния из геометрии. Геометрическая фи-
гура характеризуется размерами (дли-
ной, шириной и высотой). Точка как
геометрическая фигура, нс имеющая
размеров, является нульмерной. Пря-
мые и кривые линии, характеризую-
щиеся только длиной, являются одно-
мерными фигурами. Плоскости или
поверхности имеют два измерения,
поэтому являются двумерными.
Известна формула для подсчета раз-
мерности г пространства (фигуры)
пересечения двух каких-либо про-
101
странств (фигур) размерностей р, q,
расположенных в данном операцион-
ном пространстве размерности п: г =
= р + q — п. В нашем случае п = 3,
поэтому эта формула примет вид г =
= р + q-3.
Из этой формулы следует, что
— две поверхности (плоскости) (р =
= q ~ 2), расположенные в трехмерном
пространстве, всегда пересекаются по
линии (г = 2 + 2 — 3 = 1);
— поверхность (плоскость) (р = 2) и
линия (^=1) всегда пересекаются в
точке(ах) (г = 2 + 1 — 3 = 0);
— две произвольные линии (р = q =
Г) трехмерного пространства не имеют
пересечения, так как г = 1 + 1 — 3 =
= — 1, т.е. отсутствие пересечения
характериустся отрицательным значе-
нием размерности г.
Если же две линии (р = q = 1) при-
надлежат одной поверхности (л = 2),
т.е. уже расположены не в трехмер-
ном, а двумерном пространстве, то они
пересекаются в гочке(ах) (г = 1 + 1 —
— 2 - 0). Однако есть исключения.
Например, общеизвестно (см. пп. 2.6.3,
2.6.5), что образующие одной серии
однополостного гиперболоида между
собой не пересекаются. Эти вопросы
детально изучаются в алгебраической
геометрии.
Из сказанного следует, что две пря-
мые трехмерного пространства (см.
рис. 2.7, л) являются скрещивающими-
ся, т.е. не имеют общей точки, в то
время как две прямые, принадлежащие
одной плоскости, пересекаются в точке
(см. рис. 2.7, а) или параллельны (пе-
Здесь речь идет о пересечении d алгебраи-
ческом смысле, т.е. линия пересечения всегда
существует, но она может быть действительной
или мнимой. Например, две сферы в трехмерном
пространстве всегда пересекаются по окружнос-
ти, которая будет действительной, если межцен-
тровое расстояние меньше суммы их радиусов, и
мнимой, если межцентровое расстояние будет
больше суммы их радиусов.
ресекаются в несобственной точке)
(см. рис. 2.7, б).
Таким образом, при изучении взаим-
ного положения двух фигур, располо-
женных в одном трехмерном простран-
стве, следует рассмотреть три возмож-
ности:
— принадлежность одной фигуры
другой;
— пересечение двух фигур;
— отсутствие пересечения двух фи-
гур.
К первой подгруппе относятся задачи
на определение принадлежности точки
данной линии или поверхности, а так-
же линии данной поверхности. Алго-
ритмы решения задач этой подгруппы
были детально изучены во второй гла-
ве. Третья подгруппа содержит лишь
одну задачу, так как в трехмерном
пространстве не имеет пересечения
только пара произвольно расположен-
ных линий .
Вторая подгруппа содержит наиболь-
шее число задач. Здесь необходимо в
первую очередь различать, когда в ре-
зультате пересечения получаются со-
бственные и несобственные фигуры.
Как известно, если две геометричес-
кие фигуры имеют только несобствен-
ное пересечение (бесконечно удален-
ную общую часть), то они называют-
ся параллельными.
В трехмерном пространстве рассмат-
ривают параллельность двух прямых
(п. 2.1.3), прямой и плоскости
(п. 4.2.2.1), двух плоскостей
(п. 4.4.1.1). Спрашивается: почему не
говорят о параллельности двух кривых
линий или двух поверхностей? Объяс-
нение простое: две кривые линии, при-
надлежащие одной поверхности, пере-
секаются в точках, которые в общем
случае не могут быть все одновременно
Сказанное не следует понимать так, что в
трехмерном пространстве отсутствуют пересека-
ющиеся линии. Их бесчисленное множество. Но
в этом случае они занимают частное взаимное
положение
102
несобственными, так как не могут ле-
жать в одной несобственной плоскости
трехмерного пространства. Аналогично,
линия пересечения двух поверхностей,
будучи пространственной кривой, не
может принадлежать несобственной
плоскости трехмерного пространства.
Задачи, когда пересечение двух фи-
гур является собственным, бывают
трех типов:
— построение линии, пересекающей
в данной (ых) точке (ах) вторую линию;
— построение точек (ки) пересечения
линии с поверхностью;
— построение линии пересечения
двух поверхностей.
Предельным (частным) случаем пе-
ресечения является касание фигур.
Поэтому к позиционным задачам отно-
сятся задачи на построение касающих-
ся линий; линии, касающейся повер-
хности; двух касающихся поверхнос-
тей. При этом две поверхности могут
касаться в одной или одновременно
нескольких точках и, наконец, касать-
ся вдоль некоторой линии.
Заметим, что задачи на построение
касающихся линий и поверхностей
имеют важное прикладное значение.
Например, оси трубопроводов, предна-
значенных для транспортировки газов,
жидкостей и сыпучих материалов (пе-
сок, опилки, стружка и т.д.), выполня-
ют в виде составной линии (одномер-
ного обвода), состоящей из отрезков
прямых, дуг окружностей, плоских и
пространственных кривых, касающихся
в стыковых точках. Сама поверхность
трубопровода представляет при этом
гладкий двумерный обвод, состоящий
из отсеков цилиндрических и цикли-
ческих поверхностей, соприкасающих-
ся вдоль их общих (стыковых) окруж-
ностей. По указанному принципу кон-
струируются сложные технические
поверхности, например, поверхности
кузовов легковых автомобилей, фю-
зеляжей самолетов, лопаток турбин
и т.д.
4.2. Построение точек
пересечения линии
с поверхностью
Задачу построения точек пересече-
ния кривой линии с поверхностью
принято называть первой основной
позиционной задачей, так как алго-
ритмы решения многих позиционных и
метрических задач включают в себя
процедуру ее решения.
При решении этой задачи с участием
алгебраических кривых и поверхнос-
тей необходимо помнить основную
теорему алгебры, которая примени-
тельно к решению данной задачи фор-
мулируется так: алгебраическая кривая
п-го порядка и алгеброическая повер
хность порядка т пересекаются я пт
точках. В число этих точек входят как
действительные, так и мнимые точки.
Если данная кривая линия, или повер-
хность, или одновременно обе являют-
ся трансцендентными, то число точек
их пересечения будет бесконечно боль-
шим.
При решении практических задач
обычно строят точки пересечения дуги
кривой с отсеком поверхности. Оче-
видно, в этом случае число точек их
пересечения будет значительно мень-
ше. Болес того, возможен вариант,
когда в пределах данной дуги кривой
или отсека поверхности отсутствует
точка пересечения.
4.2.1. Алгоритм решения
первой основной
позиционной задачи
Построение точек L1 пересечения
линии I с поверхностью Ф выполняет-
ся в три этапа (рис. 4.3):
1) данная линия I заключается в
вспомогательную, обычно, проециру-
ющую цилиндрическую поверхность
Г: /<= Г;
2) строится линия т пересечения
103
Рис. 4.3
данной и вспомогательной поверхнос-
тей: и = Ф л Г,
3) отмечаются точки L1 пересечения
данной и построенной линий, которые
являются искомыми точками пересе-
чения: [} = I г\т.
Наиболее важным, творческим, эта-
пом в этом алгоритме является пер-
вый, так как выбор вспомогательной
поверхности (посредника) во многом
определяет рациональность графичес-
ких построений. Обычно, отдают пред-
почтение проецирующим цилиндричес-
ким поверхностям (в частных случаях
— проецирующим плоскостям), так как
тогда одна проекция линии т совпада-
ет с вырожденной проекцией посредни-
ка Г, а построение ее второй проекции
выполняется из условия принадлеж-
ности данной поверхности Ф.
При этом построение недостающей
проекции линии т выполняется по
точкам, что достаточно трудоемко. В
некоторых случаях, используя другие
посредники или геометрические преоб-
разования, удается упростить построе-
ние проекций линии т. Например, при
построении точек пересечения прямой
линии I с конической поверхностью Ф
целесообразно вместо проецирующей
плоскости выбрать плоскость-посред-
ник Г э I, проходящий через вершину
S конической поверхности. Тогда сече-
нием т поверхности Ф плоскостью Г
будет не кривая (лекальная) линия, а
прямолинейные образующие поверх-
ности Ф, что существенно упрощает
построения.
4.2.2. Построение точки
пересечения прямой
с плоскостью
Реализация описанного алгоритма
решения первой основной позиционной
задачи начнем с простейшего случая —
построения точки пересечения L пря-
мой I с плоскостью Ф. Возможны три
варианта (рис. 4.4):
— прямая I — проецирующая, плос-
кость Ф (Л, В, С) — общего положения
(рис. 4.4, а);
— прямая I — общего положения,
плоскость Ф — проецирующая (уровня)
(рис. 4.4, б);
Рис. 4.4
104
— прямая I и плоскость Ф(а | Ь) —
общего положения (рис. 4.4, в).
Решения первых двух вариантов не
вызывают затруднений. В первом слу-
чае прямая I — горизонтально проеци-
рующая. Поэтому горизонтальные про-
екции любой ее точки, в том числе и
искомой точки L пересечения с плос-
костью Ф(Я, й, С), совпадают с се вы-
рожденной проекцией: L\ = /(. Постро-
ение фронтальной проекции Д2 точки
L выполняется из условия принадлеж-
ности точки L плоскости Ф: точка L
принадлежит плоскости Ф, так как она
принадлежит прямой В1 плоскости Ф.
Во втором случае плоскость Ф —
фронтально проецирующая. Поэтому
фронтальная проекция L2 искомой
точки определяется как точка пересе-
чения вырожденной проекции Ф2 плос-
кости Ф с фронтальной проекцией /2
данной прямой I. Горизонтальная про-
екция Л, строится из условия принад-
лежности точки L прямой L
В третьем, общем, случае построение
искомой точки L пересечения прямой
I с плоскостью Ф(а || Ь) выполнено по
описанному в п. 4.2.1 алгоритму:
1) прямая I заключена во фронталь-
но проецирующую вспомогательную
плоскость Г: /2 = Г2;
2) построена линия пересечения т
плоскостей Ф и Г: w2 = Г2 = /2; гори-
зонтальная проекция /Н] построена из
условия се принадлежности данной
плоскости Ф(то с Ф, так как т, Ф име-
ют две общие точки 1 и 2);
3) точка L пересечения прямых Z, т
является искомой точкой пересечения
прямой I с плоскостью Ф.
Для придания чертежу большей на-
глядности на рис. 4.4 определена види-
мость с помощью конкурирующих
точек (см. п. 2.1.3). Считая плоскость
Ф непрозрачной, невидимая относи-
тельно плоскости Ф часть прямой I
изображена штриховой линией. Види-
мость на П| определена с помощью
конкурирующих точек 4, 5 (4{ = 5,),
где 4 в Ф, 5 Е I. На рис. 4.4, б точка 4
плоскости Ф расположена выше точки
5 прямой I. Поэтому точка 4 закрывает
собой точку 5, значит, часть проекции
1\ прямой / на II] от точки пересечения
L в сторону точки 5 закрыта плос-
костью Ф и является невидимой. На
рис. 4.4, в напротив, точка 5 прямой I
расположена выше точки 4 плоскости
Ф. Поэтому на П| часть проекции Z,
прямой I от точки L в сторону точки 5
является видимой.
Видимость на П2 определена с по-
мощью конкурирующих точек 2, 3
(22 = 32), где 2 е Ф, 3 е I. На
рис. 4.4, а и в точка 3 прямой / распо-
ложена ближе точки 2 плоскости Ф.
Поэтому на П2 часть проекции /2 пря-
мой I от точки пересечения L в сторо-
ну точки 3 будет видимой.
Необходимо отметить, что, исполь-
зуя описанные в третьей главе преоб-
разования чертежа, общий случай
взаимного расположения прямой I и
плоскости Ф можно привести к одному
из частных вариантов. Это достигается
преобразованием плоскости Ф или пря-
мой Z общего положения в проецирую-
щую. Однако такое решение, как пра-
вило. графически сложнее решения
этой задачи по общему алгоритму.
Целесообразно применять то или иное
преобразование чертежа, построенного
в системе плоскостей проекций П|, П2,
если прямая КМ, N) является про-
фильной прямой уровня (рис. 4.5).
В этом случае вспомогательная плос-
кость Г => I является профильной плос-
костью уровня. Линия т пересечения
данной плоскости Ф(сг || Ь) с посредни-
ком Г также будет профильной прямой
уровня, поэтому одноименные проек-
ции прямых Z, т совпадают. Для по-
строения точки их пересечения (L =
= I л т) необходимо преобразовать
чертеж так, чтобы образы I , т этих
прямых занимали общее положение.
На рис. 4.5 это достигнуто заменой
105
горизонтальной плоскости проекций П]
на новую, произвольно выбранную,
горизонтальную плоскость проекций
Пр В частности, новую плоскость
проекций П[ можно совместить с про-
фильной плоскостью проекций П3(П] =
= П3).
Другой способ решения данной зада-
чи: прямая I заключается не в проеци-
рующую плоскость, как это делалось
до сих пор, а в плоскость общего поло-
жения. Для этого достаточно вне пря-
мой / взять какую-либо точку К. Тогда
вспогательная плоскость Г будет опре-
деляться точкой К и прямой I. Правда,
в этом случае несколько усложнится
построение линии т пересечения плос-
костей Ф и Г, так как они обе будут
плоскостями общего положения. Алго-
ритм решения такой задачи будет рас-
смотрен ь п. 4.4.1.
4.2.2.1. Параллельность
прямой и плоскости
В частном случае при построении
точки пересечения прямой линии с
плоскостью может оказаться, что дан-
ная прямая / параллельна линии т
пересечения данной и вспомогательной
плоскостей (/П| J на рис. 4.4, в,
/, | й| на рис. 4.5). Это означает,
что прямая ! параллельна данной плос-
кости Ф. Такое утверждение следует из
известного условия параллельности
прямой и плоскости: прямая парад
лельна плоскости, если она парад
лельна какой-либо прямой этой плос
кости.
Поэтому построение прямой /. парад
дельной плоскости Ф. выполняется п<
такому алгоритму:
— в плоскости Ф строится произволь-
ная прямая т\
— через данную точку А проводите}
прямая /, параллельная т.
Пример. Через точку А провеете
прямую /. параллельную плоскость
проекций П] и плоскости Ф(а ] Ь)
(рис. 4.6).
Так как искомая прямая I должна
быть параллельна П], то она является
горизонталью. Чтобы она была парал-
лельна и плоскости Ф. она должна быть
параллельна горизонтали h этой плос-
кости. Поэтому сначала строим гори-
зонталь А, принадлежащую плоскости
Ф: /1 с ф (а | J), так как А, Ф имеют
общие точки 1, 2. Затем через точку А
проводим прямую Z, параллельную
построенной горизонтали.
Другое решение этой задачи основа-
но на утверждении: прямая одновре-
менно параллельна двум плоскостям,
если она параллельна линии их пере-
сечения. Поэтому можно было постро-
ить горизонтальный след А плоскости
Ф (линию пересечения плоскостей Ф,
Пр и параллельно этому следу А (го-
ризонтали нулевого уровня) провести
прямую /.
106
4.2.3. Построение точек пересечения
линии с поверхностью
Построение точек пересечения кри-
вой линии с поверхностью выполняется
по общему алгоритму (см. п. 4.2.1).
Покажем это на примере построения
точек пересечения £' пространственной
кривой I с отсеком цилиндроида Ф (а, Ь,
Пр (рис. 4.7).
Кривую I заключаем во фронтально
проецирующую цилиндрическую по-
верхность Г(Г2), которая пересекает
цилиндроид Ф по кривой т. Так как
ап с Г, то ее фронтальная проекция т2
совпадает с вырожденной проекцией Г2
вспомогательной поверхности Г: т2 =
= Г2. Горизонтальную проекцию
линии пересечения т строим по точ-
кам из условия принадлежности ци-
линдроиду Ф. Линии I vl т, принадле-
жащие поверхности цилиндра Г, пере-
секаются в искомых точках L1, I?.
Приведенное решение является типо-
вым. В ряде случаев для более точного
построения линии пересечения данной
и вспомогательной поверхностей или
для упрощения построений целесооб-
разно использовать другие виды вспо-
могательных поверхностей или способы
преобразования чертежа. Приведем
примеры.
Пример 1. Построить точки пересе-
чения прямой / с конической повер-
хностью Ф(5, а) (рис. 4.8).
Здесь целесообразно прямую / за-
ключить в плоскость Г общего поло-
жения, проходящую через вершину 5
конической поверхности Ф. Тогда Г
пересечет Ф по образующим, что из-
бавляет от построения лекальной кри-
вой и позволяет более точно по-
строить искомые точки. Для этого
строим линию 12 пересечения плоскос-
ти Г (/ л SM) с плоскостью 2 основа-
ния а конической поверхности, где
1 = I n Е, 2 = SM л S.
Направляющая а поверхности Ф и
прямая 12 лежат в плоскости 2 и поэ-
тому пересекаются между собой: в
нашем случае 3, 4 = а г> 12; через
точку 3 проходит образующая S3, а
через точку 4 — образующая S4 кони-
ческой поверхности Ф. Таким образом,
линия пересечения т = Ф л Г распа-
лась на две прямые S3, S4. Точки L1,
L2 = m(S3, S4) л I являются иско-
мыми.
Выполненные выше построения мож-
но объяснить с позиции теории способа
дополнительного проецирования (см.
п. 3.6, пример 3). Используя дополни-
тельное центральное проецирование с
центром 5 на плоскость 2, коническую
поверхность Ф отображаем на се на-
правляющую а, прямую I — на прямую
Риг. 4.8
107
12. Точки 3 и 4 пересечения линий а,
12 являются дополнительными проек-
циями из S на S искомых точек Ll, L2
пересечения прямой I с конической
поверхностью Ф.
Пример 2. Построить точки L) пере-
сечения прямой / со сферой Ф(О, R)
(рис. 4.9).
Прямую I заключаем в горизонталь-
но проецирующую плоскость Г, кото-
рая пересекает сферу Ф по окружности
т. Чтобы не строить фронтальную
проекцию ш2 окружности т, являю-
щуюся эллипсом, выполним замену
плоскости проекций П2 на П2, где
П2 || Г. Тогда на новую плоскость
проекций П2 окружность т спроеци-
руется в натуральную величину ш2;
новая проекция /2 прямой I перссека-
.-1 “2
ется с w2 в проекциях L2, L2 иско-
мых точек £?, L2. По линиям связи
строим их проекции на исходных плос-
костях проекций.
4.2.4. Построение точек
пересечения линии
с составной поверхностью
Отличительной особенностью алго-
ритма построения точек пересечения
линии с составной поверхностью (по-
верхностью многогранника или дву-
мерным обводом) является то, что
линия пересечения посредника с дан-
ной поверхностью также будет состав-
ной (многоугольником или одномер-
ным обводом). Сказанное проиллюс-
трируем на примерах построения точек
пересечения прямой I с многогранной
поверхностью.
Многогранную поверхность прямая
может пересекать в нескольких точ-
ках, различных или совпавших. Число
к точек пересечения зависит от взаим-
ного положения прямой и многогран-
ной поверхности. При этом О < к < п,
где п — число граней многогранной
поверхности. Например, прямая, про-
ходящая через противоположные вер-
шины куба, пересекает все шесть его
граней в двух по три совпавших точ-
ках.
Пример 1. Построить точки пересе-
чения прямой I с трехгранной призмой.
На рис. 4.10 показан алгоритм реше-
ния этой задачи. Реализация этого
алгоритма на чертеже Монжа показана
на рис. 4.11. Прямая I заключена во
вспомогательную фронтально проеци-
рующую плоскость Г(Г2). Она пересе-
кает призму АВС АВС по треугольни-
ку DEF, с которым данная прямая I
Рис. 4.10
108
Рис. 4.11
пересекается в искомых точках Ll, L2.
В ряде случаев решение получается
графически проще и точнее, если дан-
ную прямую заключить в плоскость
общего положения. Обычно, это имеет
место, если данная прямая или часть
ребер поверхности многогранника яв-
ляются профильными прямыми уровня.
Данную прямую также целесообразно
заключать в плоскость общего поло-
жения, если в этом случае сечение
многогранника имеет значительно
меньше вершин по сравнению с сече-
нием многогранника проецирующей
плоскостью.
Пример 2. Построить точки пересе-
чения прямой I с поверхностью пира-
миды SABCD (рис. 4.12).
Два ребра SB, SD пирамиды являют-
ся профильными прямыми уровня.
Поэтому определение проекций точек,
принадлежащих им, требует вспомога-
тельных построений.
Чтобы избежать вспомогательных
построений, заключим прямую I в
плоскость общего положения Г, прохо-
дящую через вершину S пирамиды.
Для удобства построений плоскость
Г(5, /) зададим пересекающимися пря-
мыми I, S1, где 1 — произвольная точ-
ка прямой I.
Рис. 4.12
Плоскость Г пересекается с плос-
костью основания Д (ABCD) пирамиды
по прямой 23 (2j3], 2232), где 2 -
- I п S, 3 = S1 п Д, или, точнее, плос-
кость Г пересекает основание ABCD
пирамиды по отрезку 45, где 4 =
= 23 п АВ, 5 = 23 п ВС. Так как плос-
кость Г проходит через вершину 5
пирамиды, то она пересекает послед-
нюю по треугольнику 4S5. Далее, от-
мечаем искомые точки встречи Л1 (Л]1,
. 1. ,2, , 2 .2.
L2 ), L (L\ , L2 ) прямой I с треуголь-
ником 4S5.
В заключение отметим, что до сих
пор все примеры решения первой ос-
новной позиционной задачи были вы-
полнены на чертеже Монжа. В п. 1.6
было показано, что алгоритмы графи-
ческого решения позиционных задач
на чертеже Монжа и на аксонометри-
ческом чертеже совершенно одина-
ковы. Для иллюстрации этого постро-
им точки пересечения прямой / с по-
верхностью трехгранной пирамиды
SABC на аксонометрическом чертеже
(рис. 4.13).
Задача решается по описанному вы-
ше алгоритму. Прямую КГ, ) за-
ключаем в проецирующую плоскость
109
Г(Г'). Она пересекает пирамиду SABC
по треугольнику 123(1'2'3', /]2|3]).
Прямая I пересекает треугольник 123
в двух точках L(L', l(), М(М',
которые являются искомыми.
Таким образом, решение первой
основной позиционной задачи на чер-
теже Монжа и на аксонометрическом
чертеже выполняется по единому алго-
ритму.
4.3. Алгоритм построения
линии пересечения
поверхностей
Построение линии пересечения по-
верхностей является наиболее интерес-
ной и часто встречающейся в инженер-
ной практике позиционной задачей.
Эту задачу принято называть второй
основной позиционной задачей. Она
решается введением вспомогательных
поверхностей Р, называемых посред-
никами. При выборе посредников ис-
ходят из того, чтобы они пересекали
данные поверхности по графически
простым линиям — прямым и окруж-
ностям. Правильный выбор вспомога-
тельных поверхностей определяет ра-
циональность последующих графичес-
ких построений.
Рис. 4.14
Алгоритм решения второй основной
позиционной задачи представим в виде
схемы (рис. 4.14) и поясним рисунком
(рис. 4.15). Учитывая вид данных по-
верхностей Ф, Д и их взаимное распо-
ложение, выбирают вид посредника Г
(блок 2). В качестве посредников мо-
гут использоваться различные повер-
хности. Для построения линий пересе-
чения простейших поверхностей в
качестве посредников обычно исполь-
Рис. 4.15
НО
зуют плоскости и сферы. Поэтому
различают способ плоскостей и спо-
соб сфер, которые в свою очередь тоже
подразделяются.
I. Способ плоскостей:
1) способ плоскостей уровня;
2) способ вращающейся плоскости.
II. Способ сфер:
1) способ концентрических сфер;
2) способ эксцентрических сфер.
Следует заметить, что при построе-
нии линии пересечения более сложных
поверхностей в качестве посредников
используют конические и цилиндри-
ческие поверхности.
Построение линии пересечения по-
верхностей начинают с определения ее
опорных точек, к которым относятся
экстремальные точки и точки види-
мости.
Точки линии пересечения называют-
ся экстремальными, если они принад-
лежат граничным посредникам в пре-
делах области их использования. Экс-
тремальные точки определяют пределы
изменения 6 параметра посредника
(см. рис. 4.14, блок 3). Экстремальные
точки могут быть построены точно,
если данные поверхности Ф, Д имеют
общую плоскость симметрии S: общие
точки поверхностей Ф, Д и их плоскос-
ти симметрии S будут экстремальны-
ми. В противном случае они строятся
приближенно.
Точки видимости отделяют види-
мую часть линии пересечения от не-
видимой и находятся на очерковых
линиях пересекающихся поверхнос-
тей. В этих точках проекция линии
пересечения касается очерковой линии
той или другой из пересекающихся
поверхностей. Поэтому для построения
точек видимости выбирают такие по-
средники, которые пересекали бы одну
или обе данные поверхности по их
очерковым линиям. Полученные точки
принадлежат очерковым линиям дан-
ных поверхностей и являются точками
видимости.
Учитывая желаемую точность по-
строения (расчетов), определяют число
i посредников Г*. Число i определяет
шаг х изменения параметра посредника
(блок 4): s = А, где б — расстояние
i
между граничными посредниками.
Построение точек (расчет их коорди-
нат) линии пересечения с помощью
каждого посредника выполняется в та-
кой последовательности (см. рис. 4.14,
блок 4; рис. 4.15):
1) строится линия пересечения
посредника Г' с поверхностью Ф;
2) строится линия d‘ пересечения
посредника Г' с поверхностью Д;
3) отмечаются точки L11 пересечения
линий (11 между собой, которые
принадлежат искомой линии пересече-
ния I.
Эти операции выполняются со всеми
посредниками; множества проекций
полученных точек определяют проек-
ции /р /2 искомой линии пересечения
I (блоки 6, 7, 8). При построении про-
екций /р /2 линии пересечения после-
довательно соединяют точки L‘J, распо-
ложенные на соседних посредниках,
начиная с какой-либо экстремальной
точки. В точках видимости проекция
линии пересечения касается очерковой
линии той или иной поверхности и из-
меняет свою видимость, т.е. здесь ви-
димая часть проекции линии пересече-
ния стыкуется гладко с ее невидимой
частью. Видимая часть проекции ли-
нии пересечения плавно переходит в
видимую часть очерковой линии по-
верхности, а ее невидимая часть — в
ту часть очерковой линии, которая в
результате пересечения поверхностей
исчезает вместе с ’’вырезаемым” отсе-
ком поверхности.
4.4. Способ
вспомогательных плоскостей
Способ вспомогательных плоскостей
применяется для построения линии
пересечения таких пар поверхностей,
которые пересекаются с семейством
111
посредников по графически простым
линиям (прямым и окружностям).
Такие пары поверхностей составляют:
— две плоскости;
— плоскость и поверхность многог-
ранника;
— две многогранные поверхности;
— плоскость и линейчатая поверх-
ность;
— плоскость и поверхность враще-
ния;
— две поверхности вращения с па-
раллельными осями;
— две конические (коническая и
цилиндрическая, две цилиндрические)
поверхности;
— две линейчатые поверхности с
общей плоскостью параллелизма и
некоторые другие пары поверхностей.
Таким образом, область применения
способа вспомогательных плоскостей
достаточно обширна.
4.4.1. Построение
линии пересечения
двух плоскостей
Две плоскости в трехмерном расши-
ренном евклидовом пространстве пере-
секаются по прямой. Так как прямая
однозначно определяется двумя точка-
ми, то для построения линии I пересе-
чения двух плоскостей Ф и А доста-
точно определить две их общие точки
М, N.
Задача решается графически просто,
если хотя бы одна из пересекающихся
плоскостей является проецирующей. В
этом случае одна проекция линии I
совпадает с вырожденной проекцией
проецирующей плоскости, а вторая
проекция строится из условия принад-
лежности второй из пересекающихся
плоскостей. Например, на рис. 4.4, в
фронтально проецирующая плоскость
Г(Г2) и плоскость общего положения
Ф(<2 || />) пересекаются по прямой т,
фронтальная проекция дп2 которой
совпадает с вырожденной проекцией Г2
плоскости Г. Горизонтальная проекция
т1 прямой т построена из условия
принадлежности плоскости Ф: т с Ф,
так как т, Ф имеют две общие точки 1
и 2.
Если обе данные плоскости Ф, Д яв-
ляются проецирующими или плоскос-
тями уровня, то возможны два вари-
анта:
— плоскости Ф, Д одноименно прое-
цирующие, т.е. они перпендикулярны
одной плоскости проекций;
— плоскости Ф, Д разноименно прое-
цирующие, т.е. перпендикулярны двум
различным плоскостям проекций.
В первом случае линия / пересечения
плоскостей Ф, Д также будет проециру-
ющей (рис. 4.16). Во втором случае
плоскости Ф, Д пересекаются по прямой
/, проекции /], /2 которой совпадают с
вырожденными проекциями соответ-
ственно плоскостей Ф, Д (/j = Фр /2 =
= Д2) (рис. 4.17).
Построение линии пересечения двух
плоскостей общего положения можно
выполнить различными приемами в
зависимости от способа их задания.
Однако сущность всех этих приемов
едина: с помощью двух плоскостей-
посредников Г, Г определяются две
точки М, N искомой линии пересече-
ния I. Рассмотрим несколько примеров.
Пример 1. Построить линию пересе-
чения I плоскостей Ф(а n b), А(т 1| и)
(рис. 4.18).
В качестве посредников выберем
какие-либо две параллельные проеци-
рующие плоскости Г, Г (на рис. 4.18
112
плоскости Г, Г — горизонтально прое-
цирующие). Плоскости Г, Г пересека-
ют плоскость Ф по двум параллельным
прямым g(g\, g2), g(g\, §2^ плоскость
Д — по параллельным прямым d(d^,
d-2>, d(d{, d2), Прямые g, d, принад-
лежащие плоскости Г, пересекаются в
точке М — общей точке трех плоскос-
тей Ф, Д и Г. Аналогично, прямые g,d
пересекаются в точке N — общей точке
трех плоскостей Ф, Д и Г. Точки М, N,
как принадлежащие данным плоскос-
тям Ф и Д, определяют их линию пере-
сечения /(/], 12).
Очевидно, для решения этой задачи
с успехом можно использовать в качес-
тве посредников фронтально проециру-
ющие плоскости, горизонтальные и
(или) фронтальные плоскости уровня.
Пример 2. Построить линию пересе-
чения / плоскостей Ф(А, В, С), Ь(Е, F,
G). Определить видимость (рис. 4.19).
Точки М, N, определяющие искомую
линию пересечения I, найдем как точ-
ки пересечения каких-либо двух сто-
рон данных треугольников АВС и EFG
с плоскостью другого треугольника. На
рис. 4.19 точка М построена как точка
пересечения стороны АС с плоскостью
Д, a N — как точка пересечения сторо-
ны ВС с плоскостью Д, т.е. дважды
решена первая позиционная задача по
алгоритму, описанному в п. 4.2.2. Для
построения точек М(М\, М2), ЛЧАр
N2) использованы две вспомогательные
горизонтально проецирующие плос-
кости Г, Г. Построенные точки М, N
определяют линию пересечения I = MN
данных плоскостей Ф и Д. На рис. 4.19
выделен отрезок KN линии пересече-
ния I, находящийся в пределах нало-
жения проекций треугольников АВС и
EFG, так как плоскости Ф и Д считают-
ся ограниченными этими треугольни-
ками.
Очевидно, выбор сторон треугольни-
ков и проходящих через них вспомога-
тельных плоскостей достаточно произ-
волен. Предпочтение отдается тем
сторонам и вспомогательным плоскос-
тям, которые не требуют выполнения
каких-либо дополнительных построе-
ний или построений, выходящих за
пределы листа. С этих позиций на
рис. 4.19 все стороны треугольников
АВС и EFG равноправны, так как они
при продолжении пересекают постро-
енную прямую I в пределах листа.
Здесь также нс играет роли выбор
горизонтально или фронтально проеци-
рующих вспомогательных плоскостей
Г, Г. Напротив, попытка проведения
на рис. 4.18 вспомогательных проеци-
рующих плоскостей через прямые а, b
или т, п привела бы к небходимости
их продолжения за пределы листа.
Поэтому здесь в качестве посредников
выбраны такие проецирующие плос-
кости Г, Г, которые в пределах листа
113
пересекают прямые а, b и т, п, задаю-
щие данные плоскости.
Определение видимости непрозрач-
ных треугольников АВС и EFG на
рис. 4.19 выполнено с помощью конку-
рирующих точек:
2 и 5 — относительно горизонтальной
плоскости проекций (точка 5 располо-
жена выше точки 2; поэтому на П]
часть треугольника АВС, расположен-
ная в сторону точки 5, закрывает со-
бой часть треугольника EFG, располо-
женную от линии пересечения в сторо-
ну точки 2);
6 и 7 — относительно фронтальной
плоскости проекций (точка 7 треуголь-
ника EFG расположена ближе точки 6
треугольника АВС; поэтому фронталь-
ная проекция части треугольника EFG,
расположенная от /2 в сторону точки
72, закрывает собой фронтальную про-
екцию части треугольника АВС, распо-
ложенную от /2 в сторону точки 62).
Пример 3. Построить линию пересе-
чения I плоскостей Ф (Л° п /°),
Д (h 0 п / 0), заданных следами
(рис. 4.20).
Построение проекций 1Х, /2 линии
пересечения I для такого варианта
задания плоскостей Ф, Д выполняется
наиболее просто, так как на чертеже
присутствуют проекции линий пересе-
чения данных плоскостей с плоскостя-
ми-посредниками. Их роль здесь выпо-
лняют плоскости проекций Пр П2.
Плоскость П| пересекает данные
плоскости Ф, Д по горизонталям нуле-
вого уровня (следам на П,). Поэтому
точка Л/(Мр М2) их пересечения яв-
ляется горизонтальным следом искомой
прямой I. Аналогично, плоскость П2
пересекает плоскости Ф, Д по фронта-
лям нулевого уровня (следам на П2).
Поэтому точка N(NX, N2) их пересече-
ния является фронтальным следом
прямой I. Таким образом, прямая Z(/p
/2) однозначно определяется точками
М и N: Z] = M}N}, l2 = M2N2.
4.4.1.1. Параллельность
двух плоскостей
В частном случае две плоскости Ф, Д
могут пересекаться по несобственной
прямой Г. Например, если бы на
рис. 4.19 прямая АС оказалась парал-
лельной прямой 12, а прямая ВС —
параллельной 34, то точки М и N их
пересечений были бы несобственными.
Значит, прямая / = MN также была бы
несобственной. Такие плоскости, когда
две пересекающиеся прямые одной
плоскости параллельны двум пересе-
кающимся прямым второй плоскос-
ти, называются параллельными
(рис. 4.21):
Ф(£П d) ||Д(# А 7) -g||f, d\\d.
Из этого определения следует алго-
ритм построения плоскости Д, парал-
лельной данной плоскости Ф. Пусть
плоскость Ф дана двумя параллельны-
ми прямыми g, т. Через точку А тре-
буется провести плоскость Д, парал-
лельную Ф (рис. 4.22).
Рис. 4.21
114
В плоскости Ф строим какую-либо
прямую d, пересекающую прямые g,
т. Затем через точку А проводим пря-
мую g, параллельную g, и прямую d,
параллельную d. Построенные пересе-
кающиеся прямые g, d определяют
искомую плоскость Д, параллельную Ф.
4.4.2. Сечение
многогранника плоскостью
Сечением многогранной поверхности
плоскостью является многоугольник.
Различают два способа построения
сечения многогранника плоскостью:
1) способ ребер — определяются
вершины многоугольника сечения;
2) способ граней — определяются
стороны многоугольника сечения.
При первом способе вершины много-
угольника определяются многократным
решением первой позиционной задачи
— построением точек пересечения ре-
бер многогранника с секущей плос-
костью (см. п. 4.2.2). Этот способ пред-
почтителен, если некоторые ребра
многогранника являются проецирую-
щими.
Второй способ сводится к многократ-
ному решению второй позиционной
задачи — построению линий пересече-
ния граней многогранника с секущей
плоскостью. Этот способ целесообразно
применять, если некоторые грани мно-
гогранника являются проецирующими
плоскостями. Конечно, в ряде случаев
бывает целесообразным комбинирован-
ное применение обоих способов.
Число сторон сечения (С) удовлетво-
ряет неравенству М <. С < Г, где Г —
число граней многогранника, М —
минимальное число граней многогран-
ника, проходящих через одну из его
вершин (М 3).
Например, в зависимости от положе-
ния секущей плоскости сечениями тет-
раэдра могут быть четырехугольники и
треугольники (рис. 4.23).
Определенные затруднения при по-
строении сторон и вершин многоуголь-
ника-сечения вызывает то обстоятель-
ство, что ребра и грани многогранника
являются соответственно отрезками
прямых и отсеками плоскостей. Может
случиться, что точка пересечения ка-
кого-либо ребра с секущей плоскостью
находится на продолжении ребра. На-
пример, на рис. 4.23 точка D =
= GH л Д. Такие точки полезно ис-
пользовать или для проверки точности
решений — точки L, М, D и К. N, D
должны лежать на одной прямой, если
точки М, N уже построены, или для
нахождения недостающих вершин се-
чения М = LD л SG, N = KD л /6,
если они еще не построены.
Подобное имеет место и в случае,
если линия пересечения секущей плос-
кости с плоскостью грани многогранни-
ка проходит вне самой грани (многоу-
гольника).
Проиллюстрируем это на приме-
ре построения сечения пирамиды
115
SABCDE плоскостью общего положе-
ния Д(т 1| и), заданной двумя парал-
лельными прямыми т, п (рис. 4.24).
Анализ расположения ребер и граней
данного многогранника относительно
плоскостей проекций показывает, что
ребро SE — горизонтально проецирую-
щая прямая;
грани ABCDE, ABS — фронтально
проецирующие плоскости;
грани ASE, DSE — горизонтально
проецирующие плоскости.
Так как многогранник содержит че-
тыре проецирующие грани, то в пер-
вую очередь найдем линии их пересе-
чения с секущей плоскостью А.
Основание ABCDE данной пирамиды
пересекается с плоскостью А по прямой
/2(7121, /222), отрезок KN(K\NV
K2N2) которой есть одна из сторон
многоугольника-сечения.
Вторая фронтально проецирующая
грань ABS пересекается с плоскостью
Д по прямой 34(3 ^4}, 3242), отрезок
KL(KXL}, K2Lj) которой также нахо-
дится во внутренней области треуголь-
ника ABS, и поэтому является сторо-
ной искомого многоугольника-сечения.
Заметим, что точка К(К{, К2) была
построена ранее, поэтому она является
теперь контрольной: прямая 34 должна
проходить через точку К.
Далее строим линии пересечения
секущей плоскости Д с горизонтально
проецирующими гранями. На рис. 4.24
показано построение прямой 56 =
= Д и SDE. Прямая 56 не пересекает
внутреннюю область треугольника
SDE. Следовательно, эта грань нс пе-
ресекается с плоскостью Д. Также не
пересекается с плоскостью Д грань
ASE, ибо из предыдущих построений
выяснилось, что ребра [AS], [ЛЕ],
[SE] не пе.ресекают плоскость Д.
Так как оставшиеся не рассмотрен-
ными грани BSC, CSD суть плоскости
общего положения, то найдем точку
пересечения их общего ребра SC с
секущей плоскостью. Для этого ребро
SC заключаем во фронтально проеци-
рующую плоскость Г, строим прямую
78(7{8\, 7282) = Д п Г и получаем
недостающую вершину AfGWj, М2)
искомого многоугольника-сечения
KLMN.
4.4.3. Построение линии
пересечения поверхностей
двух многогранников
Две многогранные поверхности в об-
щем случае пересекаются по простран-
ственной замкнутой ломаной линии. В
частных случаях эта ломаная может
распадаться на две и более замкнутые
ломаные линии. Вершинами ломаной
являются точки пересечения ребер
одного многогранника с гранями друго-
го. Стороны ломаной представляют
собой отрезки прямых, по которым
пересекаются грани многогранников.
116
Отсюда следуют два способа построе-
ния линии пересечения поверхностей
многогранников:
1) способ ребер — построение вер-
шин ломаной как точек пересечения
ребер первого многогранника с граня-
ми второго и ребер второго многогран-
ника с гранями первого; при этом най-
денные точки соединяются в опреде-
ленной последовательности, соблюдая
следующее правило: прямыми соеди-
няются проекции лишь тех точек,
которые принадлежат одной грани;
2) способ граней — построение сто-
рон ломаной как отрезков прямых
попарного пересечения граней данных
многогранников.
Выбор одного из этих способов или
их комбинации зависит от свойств
данных многогранников. Построения
будут более простыми, если вершины
ломаной определяются для проецирую-
щих ребер, а стороны ломаной — для
проецирующих граней. При выборе
вспомогательных плоскостей для по-
строения вершин и сторон ломаной с
участием ребер и граней общего поло-
жения необходимо руководствоваться
рекомендациям и, сформулированными
в пп. 4.2.2, 4.4.1.
При построении линии пересечения
поверхностей двух пирамид, призмы и
пирамиды, двух призм целесообразно
в качестве вспомогательных плоскос-
тей выбирать плоскости общего поло-
жения:
1) если строится линия пересечения
поверхностей двух пирамид, то вспо-
могательные плоскости должны прохо-
дить через вершины пирамид;
2) построение линии пересечения
поверхностей пирамиды и призмы
упрощается, если вспомогательные
плоскости проходят через вершину
пирамиды и параллельны боковым
ребрам призмы;
3) для построения линии пересече-
ния поверхностей двух призм следует
использовать вспомогательные плос-
кости, параллельные боковым ребрам
обеих призм.
Указанные плоскости пересекают
поверхность пирамиды по прямым,
проходящим через ее вершину, а по-
верхность призмы — по прямым, па-
раллельным ее боковым ребрам. Это
существенно сокращает объем графи-
ческих построений и позволяет заранее
определить те грани одного многогран-
ника, с которыми пересекаются ребра
другого многогранника.
Рассмотрим конкретные примеры.
Пример 1. Построить линию пересе-
чения трехгранной пирамиды SABC с
профильно проецирующей прямоуголь-
ной призмой (рис. 4.25).
Грани призмы являются плоскостями
уровня. Поэтому построение линии
пересечения поверхностей многогран-
ников выполним способом граней. Сна-
чала строим сечение пирамиды плос-
костью Г верхней грани призмы. Из
полученного треугольного сечения
выделяем ломаную 1234, располо-
женную в пределах верхней грани
призмы. Затем строим треугольное
сечение пирамиды плоскостью Г ни-
117
жней грани призмы, на котором выде-
ляем участки 5 6 7 и 9 10, располо-
женные в пределах нижней грани.
Точки 4, 5 принадлежат одновремен-
но грани SBC пирамиды и передней
грани призмы, значит отрезок 4 5 яв-
ляется линией их пересечения. Анало-
гично, по отрезку 1 10 пересекаются
грань SAB пирамиды и передняя грань
призмы. Точки 7, 9 принадлежат за-
дней грани призмы, но различным
граням SAC и SAB пирамиды. Поэтому
необходимо найти точку 8 пересечения
задней грани призмы с ребром SA пи-
рамиды. Горизонтальная проекция 3]
точки 8 определяется как точка пере-
сечения SiAj с вырожденной проекци-
ей задней грани призмы, так как эта
грань является фронтальной плос-
костью уровня.
Замкнутая пространственная лома-
ная 12 3 456789 10 1 представляет
собой искомую линию пересечения
поверхностей данных многогранников.
Пример 2. Построить линию пересе-
чения поверхностей горизонтально
проецирующей четырехгранной приз-
М2 Lz Kz
Рис. 4.26
мы и трехгранной пирамиды SABC
(рис. 4.26).
Так как боковые грани призмы явля-
ются горизонтально проецирующими
плоскостями, то определение точек
пересечения ребер 5А, SB, SC пирами-
ды с гранями призмы выполняется
просто: горизонтальные проекции этих
точек получаются в результате пересе-
чения горизонтальных проекций ука-
занных ребер с вырожденными проек-
циями граней призмы.
Из боковых ребер призмы только
ребро NN пересекается с поверхностью
пирамиды. Для определения точек 5, 8
ее пересечения с поверхностью пира-
миды через нее проводим плоскость Г,
проходящую через вершину S пирами-
ды. Плоскость Г пересекает грани SAB
и SAC пирамиды по прямым S10 и S9,
которые, пересекаясь с AW, определя-
ют недостающие вершины 8, 5 искомой
линии пересечения. Она состоит из
двух замкнутых ломаных 12 3 1,45
6 7 84.
Пример 3. Построить линию пересе-
чения двух трехгранных пирамид
SABC, TEFG (рис. 4.27).
Основания АВС и EFG данных пира-
мид принадлежат одной горизонталь-
ной плоскости S. Поэтому точки 1, 2,
3, 4 пересечения сторон этих треуголь-
ников являются вершинами искомой
линии пересечения пирамид.
Для определения остальных вершин
ломаной линии пересечения выберем
плоскости-посредники, проходящие
через вершины S, Т пирамид. Эти
плоскости будут проходить через пря-
мую ST и пересекать общую плоскость
Е их оснований по прямым, проходя-
щим через точку М пересечения пря-
мой ST с плоскостью S. Тогда вспомо-
гательная плоскость Г, проходящая
через какое-либо боковое ребро пира-
миды, например ребро TG пирамиды
TEFG определяется двумя пересекаю-
щимися прямыми ST и MG.
118
Если прямая MG пересекает ос-
нование ЛВС (MXG\ n XjBjCj) вто-
рой пирамиды (в нашем случае
MG п ЛВС = 5, 6), то плоскость
Г<5Т n MG) пересекает пирамиду
SABC по прямым S5, S6. Ребро TG и
прямые S5, S6 принадлежат вспомога-
тельной плоскости Г, поэтому пересе-
каются между собой в точках 7, 8 —
вершинах искомой ломаной линии
пересечения пирамид.
Из рис. 4.27 видно, что ребра ТЕ, TF
не пересекаются с пирамидой SABC, а
ребра 5Л, SC нс пересекаются с пира-
мидой TEFG, так как их горизонталь-
ные проекции не накладываются на
горизонтальные проекции соответст-
венно пирамид SABC и TEFG. Гори-
зонтальная проекция ребра SB
накладывается на проекцию
пирамиды TEFG. Поэтому надо про-
верить, не пересекает ли ребро SB
пирамиду TEFG. Для этого про-
водим вспомогательную плоскость
Г (ST п МВ) = SB, которая не пересе-
кает основание EFG пирамиды TEFG
(М\ВХ E\F\G\). Значит, ребро SB не
пересекается с пирамидой TEFG.
Таким образом, данные пирамиды
пересекаются по двум треугольникам
1 2 7 1,3 4 8 3.
В заключение необходимо заметить,
что в случае пересечения поверхностей
пирамиды и призмы вспомогательные
плоскости Г' проводятся через прямую,
проходящую через вершину пирамиды
и параллельную боковым ребрам при
змы. Если же строится линия пересе-
чения поверхностей двух призм, то
предварительно задается плоскость
параллелизма Г°, определяемая двумя
пересекающимися прямыми, парал-
лельными боковым ребрам призм.
Вспомогательные плоскости Г' выбира-
ются параллельными Г°. Они пересе-
кают плоскость Е оснований призм
по параллельным прямым (примеры
см. в [51).
4.5. Способ плоскостей
уровня
В предыдущем разделе при построе-
нии линий пересечения плоскостей и
многогранников выбор вспомогатель-
ных плоскостей осуществлялся доста-
точно произвольно. Это объясняется
тем, что любая вспомогательная плос-
кость пересекается с данными плоскос-
тями и многогранниками по прямым
линиям. Если же одной из пересекаю-
щихся фигур является криволинейная
поверхность, то на выбор вспомога-
тельных плоскостей накладывается
дополнительное условие: семейство
вспомогательных плоскостей должно
пересекать данную поверхность по
графически простым линиям (прямым
и окружностям). Поэтому плоскости
не всегда могут быть использованы в
качестве посредников. Если же приме-
нение плоскостей-посредников возмож-
но, то на выбор их положения сущес-
твенно влияют свойства данной повер-
119
хности. Например, если одной из пере-
секающихся фигур является поверх-
ность вращения общего вида, то плос-
кости-посредники должны быть обяза-
тельно перпендикулярны ее оси. Толь-
ко в этом случае она будет пересекать-
ся с посредниками по окружностям.
4.5.1. Сечение
поверхности плоскостью
Способом плоскостей уровня можно
построить сечения линейчатых и цик-
лических поверхностей с плоскостью
параллелизма. Семейство посредников
Г2, параллельных плоскости паралле-
лизма, пересекает такую поверхность
Ф по графически простым линиям £
(прямым или окружностям), а секу-
щую плоскосгь Д — по прямым dl. Точ-
ки пересечения линий dl, принадле-
жащих одной плоскости Iv, определяют
искомую линию / = Ф п Д.
Пример 1. Построить сечение I по-
верхности вращения Ф(у, т) плос-
костью общего положения Д(а || Ь),
заданной параллельными прямыми а,
b (рис. 4.28).
Построение линии пересечения I
начнем с определения ее опорных то-
чек. Сначала построим экстремальные
точки, которые принадлежат общей
плоскости симметрии 0 данных повер-
хностей Ф и Д. Для поверхности враще-
ния Ф любая плоскость, проходящая
через ее ось, будет плоскостью симмет-
рии, а для секущей плоскости Д —
любая перпендикулярная ей плоскость.
Поэтому их общей плоскостью симмет-
рии будет горизонтально проецирую-
щая плоскость 6, проходящая через ось
вращения j и перпендикулярная плос-
кости Д. Из курса геометрии средней
школы известно, что две плоскости Д
и 0 перпендикулярны тогда, когда од-
на из них содержит прямую, перпен-
дикулярную второй. Так как плоскость
0 э j является горизонтально проеци-
рующей, то она должна быть перпен-
дикулярной горизонтали h плоскости Д.
Поэтому в плоскости Д строим про-
извольную горизонталь (на рис. 4.28
Рис. 4.28
120
построена горизонталь нулевого уровня
Л°) и плоскость 0 проводим перпенди-
а 1.°
кулярно этой горизонтали: 0] г пл .
Для простоты построения экстре-
мальных точек выполняем замену
плоскости проекций П2 - П2, где
П2 || 0. Относительно новой системы
плоскостей проекций Пр П2 данная
плоскость А будет фронтально проеци-
рующей. Поэтому ее вырожденная
проекция Д2 пересекает очерковую
линию т2 и граничную параллель к2
в проекциях А2, В2 = С2 на П2 экс-
тремальных точек. По линиям связи
находим проекции Лр А2; В^, В2; Ср
С2 экстремальных точек на исходных
плоскостях проекций.
Считая плоскость А прозрачной, а
поверхность Ф непрозрачной, найдем
точки видимости. Все точки отсека
поверхности Ф относительно П] види-
мы. Поэтому горизонтальная проекция
/[ искомого сечения будет полностью
видимой. Относительно П2 часть линии
пересечения /, расположенная ближе
плоскости 2 главного меридиана т,
является видимой, а другая часть —
невидимой. Поэтому для определения
точки видимости на П2 проводим вспо-
могательную плоскость 2. Она пересе-
кает поверхность вращения Ф по глав-
ному меридиану т(т{, т2>, а плос-
кость А — по прямой t2). Точка
М = т n t будет искомой точкой види-
мости.
Построение случайных точек сечения
I выполняем с помощью горизонталь-
ных плоскостей уровня Г'. Исходя из
требуемой точности построений рассто-
яние между верхней Л и нижними
точками В, С линии пересечения де-
лим на определенное число частей,
через которые проводим плоскости-по-
средники Г'.
На рис. 4.28 показаны построения,
свяанные с одним из посредников.
Плоскость Г пересекает поверхность
вращения Ф по параллели g(g}, g2), a
секущая плоскость А — по горизонтали
A(A[, А2). Точки /, 2 пересечения этих
линий g, h являются случайными точ-
ками искомой линии пересечения I.
Выполнив описанные построения с
участием каждой плоскости Г', получа-
ем множество точек. Через их горизон-
тальные и фронтальные проекции про-
водим лекальные кривые — проекции
/], 12 искомого сечения I. При по-
строении проекций Zj, 12 необходи-
мо помнить, что в точках видимости
они изменяют свою видимость и каса-
ются здесь очерковой линии т повер-
хности Ф.
Пример 2. Построить сечение / отсе-
ка коноида Ф(а, Л, П2) плоскостью об-
щего положения А, ограниченной треу-
гольником АВС (рис. 4.29).
В качестве посредников Г' выбираем
фронтальные плоскости уровня, так
как они, будучи параллельны плоскос-
ти параллелизма П2 коноида Ф, пересе-
кают последний по образующим. Плос-
кость-посредник Г пересекает коноид Ф
по образующей g(g}, g2), а секущую
121
плоскость Д — по прямой d(dl, d2).
Точка J пересечения прямых g, d при-
надлежит искомой линии пересечения
1Щ. 12).
Экстремальные точки М, N линии
пересечения строятся проведением
посредников, проходящих через гра-
ничные образующие коноида.
Отсек данного коноида ограничен
двумя образующими и дугами направ-
ляющих. В состав его границы не вхо-
дит очерковая линия. Поэтому линия
пересечения не содержит точек види-
мости: ее проекции на И) и П, являют-
ся видимыми. На рис. 4.29, считая
отсеки коноида Ф и плоскости Д непро-
зрачными, определена видимость:
— на IIj по конкурирующим точкам
2, 5;
— на П2 по конкурирующим точкам
4, 5.
4.5.2. Построение линии
пересечения двух поверхностей
Способ плоскостей уровня применя-
ется для построения линии пересече-
ния поверхностей, имеющих однои-
менные графически простые линии
уровня (прямые или окружности).
На рис. 4.30 показано построение
линии I пересечения конической по-
верхности вращения Ф(/, т) со сферой
Л (О, R). Обе поверхности в качестве
горизонталей содержат семейства
окружностей, поэтому посредниками
б'/дут горизонтальные плоскости уров-
ня Г'
Экстремальные (высшая и низшая)
точки А. В линии пересечения опреде-
ляются проведением общей плоскости
симметрии Е(/, СУ) данных поверхнос-
тей Точками видимости на П2 будут
эти же точки, так как они принадле-
жат очерковым линиям поверхности
конуса и сферы на П2. Точки видимос-
ти £>,, О]7 на П] определяются прове-
дением посредника Г, проходящего
Рис. 4 30
через центр сферы. В этом случае
плоскость Г пересекает сферу по
окружности d, проекция d{ которой
на Щ будет очерковой.
Случайные точки 1, Г линии пере-
сечения I определяются проведением
горизонтальных плоскостей уровня Г:
Г (\ Ф = g, Г п Д = d, g n d = J, Г.
Так как общая плоскость симметрии
S данных поверхностей параллельна
П2, го на П2 видимая и невидимая вет-
ви проекции 12 .линии пересечения сов-
падают. На П] проекция дуги DAD'
линии пересечения видима, а проекция
дуги D'BD — невидима; в точках D^,d[
горизонтальная проекция линии
пересечения касается очерковой .линии d\
сферы.
4.6. Способ
вращающейся плоскости
Этот способ применяется для по-
строения линии пересечения двух
конических, конической и цилиндри-
ческой, двух цилиндрических повер-
хностей.
122
Рис. 4.31
Способ состоит в том, что множество
(пучок) плоскостей-посредников Г!,
проходящих через вершины S, S' дан-
ных конических поверхностей Ф, Д,
пересекает последние по образующим
(рис. 4.31). При этом прямая s = SS'
является осью пучка плоскостей-по-
средников. Очевидно, название способа
связано с кинематическим образовани-
ем пучка плоскостей Г1, проходящих
через фиксированную прямую 5.
Если направляющие а, b конических
поверхностей Ф(5, a), &(S', А) принад-
лежат одной плоскости S, то плоскость
Г1 определяется двумя пересекающими-
ся прямыми: фиксированной прямой s
и переменной прямой т‘, принадлежа-
щей плоскости Е и проходящей через
точку М пересечения прямой s с плос-
костью Е. Поэтому каждая плоскость Г'
определяется заданием прямой т1.
Так как направляющие а, b коничес-
ких поверхностей Ф, Д и прямая т1
принадлежат плоскости S, то через
точки А1 = а п т\ В‘ = b п т' прохо-
дят образующие £ = 5Л' = Ф п Г', dl =
= 5 'В1 = Д п Г1 конических поверхнос-
тей. Эти образующие, попарно пересе-
каясь между собой, определяют точки
Ll] = SA1 n 5 'В1 искомой линии пересе-
чения I.
Пример. Построить линию пересече-
ния I отсеков конических поверхностей
Ф(S, а), Д (5Ь), направляющие а, b
которых принадлежат одной плоскости
£ (рис. 4.32).
1. Строим прямую $ = 55' и находим
точку М ее пересечения с плоскостью
£ направляющих а, b данных коничес-
ких поверхностей.
2. Находим экстремальные точки
L (Lj, Л2) и Z(Llt линии пере-
сечения /(/р /2). Для этого в плоскости
S через точку М проводим такие пря-
мые т, т, которые проходили бы
через концы дуги одной направляю-
щей и пересекали бы вторую направ-
ляющую. В нашем случае А 6 т п Ь,
Рис. 4.32
123
A e m n b. Если направляющие a, b
являются замкнутыми кривыми, то
надо проводить такие прямые, которые
касаются одной направляющей и пере-
секают вторую направляющую (см.
рис. 4.31). Прямые т, т (плоскости
Г(х n т), T(s п in)) задают пределы
изменения положения посредника Г*.
Плоскость Г пересекает коническую
поверхность Ф по граничной образую-
щей SA, а поверхность Д — по образу-
ющей S'В. Точка L = SA п 5'В пе-
ресечения этих образующих определя-
ет одну из экстремальных точек L.
Аналогично определяется вторая экс-
тремальная точка L.
3. Строим случайные точки линии
пересечения. Для этого угол туту
делим на несколько частей прямыми
т/ (на рис. 4.32 показана одна из
таких прямых ту). Плоскость-по-
средник Г($ п т) пересекает кони-
ческие поверхности Ф, Д соответст-
венно по образующим SACSjA], S^A-j),
S 'B(Sy By, S2 B2), где A = Г n a (Aj =
= n й|), В = Г n b (By = my n by).
Точка L(Ly, L2) пересечения прямых
SA, S 'В будет случайной точкой иско-
мой линии I пересечения конических
поверхностей Ф, Д.
4. Определяем видимость на с
помощью конкурирующих точек 1, 2,
а на П2 — точек 3, 4.
Описанный алгоритм справедлив и
для построения линии пересечения ко-
нической и цилиндрической, двух ци-
линдрических поверхностей. Имеются
лишь некоторые особенности: в случае
пересечения конической и цилиндри-
ческой поверхностей (рис. 4.33) пря-
мая s проводится через вершину S
конической поверхности параллельно
Рис. 4.33
образующим поверхности цилиндра. В
случае построения линии пересечения
двух цилиндрических поверхностей
(рис. 4.34) прямая s будет несобствен-
ной, так как их ’’вершины” являются
несобственными точками. В этом слу-
чае посредники Г' будут параллельны-
ми: плоскость параллелизма Г°(т°)
определяется двумя прямыми TD, TG,
проходящими через произвольную точ-
ку Т пространства и параллельными
образующим данных цилиндрических
поверхностей. Плоскость Г° пересекает
плоскость Е направляющих по прямой
т°. Поэтому на чертеже плоскости
посредники Г! задаются прямыми т‘,
принадлежащими плоскости S и парал-
лельными прямой т°.
В заключение отметим некоторые
возможные варианты в задании пересе-
кающихся поверхностей Ф, Д.
124
1. Направляющие а, b поверхностей
Ф, А не лежат в одной плоскости 2.
Тогда предварительно строят сечение,
например, а поверхности Ф плоскостью
2 направляющей b второй поверхности
А. Далбе задачу решают, принимая в
качестве направляющей поверхности Ф
кривую а. Возможно другое решение
задачи для такого варианта задания
поверхностей Ф, А. Строят точки М,
М' пересечения прямой s с плоскостя-
ми 2, 2' направляющих а, Ь. Тогда
плоскость-посредник Г будет пересе-
каться с плоскостью 2 направляющей
а по прямой т, проходящей через
точку М, а с плоскостью 2' на-
правляющей b — по прямой т', прохо-
дящей через точку М‘. При этом пря-
мые т, пг', принадлежащие одному
посреднику Г, пересекаются в точке
М° на прямой t пересечения плоскос-
тей 2, 2'.
2. Направляющие а, b поверхностей
Ф, А являются пространственными кри-
выми. Тогда выбирается произвольная
проецирующая плоскость или плос-
кость уровня 2. Строятся сечения а',
Ь' поверхностей Ф, А плоскостью 2.
Эти сечения далее принимаются в ка-
честве направляющих данных повер-
хностей.
3. В частном случае ось s пучка
плоскостей Г1 может быть проецирую-
щей прямой. Тогда, очевидно, посред-
ники Г* также будут проецирующими.
Поэтому в способе вращающейся
плоскости в качестве посредников
используются не только плоскости
общего положения, но и проецирую-
щие плоскости. Если же ось х пуч-
ка плоскостей Г1 будет несобствен-
ной прямой уровня, то плоскости
также будут плоскостями уровня.
Это говорит о том, что способ
плоскостей уровня является частным
случаем способа вращающейся плос-
кости.
4.7. Способ
вспомогательных сфер
Использование сфер в качестве по-
средников основаны на справедливости
следующей теоремы и ее следстия.
Теорема. Две соосные поверхности
вращения Ф(/, а), А (7, h), где i = j,
пересекаются по окружностям (па-
раллелям), проходящим через точки
пересечения их меридианов.
Действительно (рис. 4.35), общие
точки 1, 2, ... = а о. b этих меридианов
описывают общие для данных повер-
хностей Ф, А параллели с/1, с/2, ...
Рис. 4.35
Следствие. Сфера, центр которой
принадлежит оси поверхности враще-
ния, пересекается с последней по
окружностям.
Плоскости этих окружностей перпен-
дикулярны оси j поверхности враще-
ния. Поэтому их проекции (одна или
Рис. 4.36
125
Рис. 4.37
o5et будут графически простыми лини-
ями лишь тогда, когда ось j будет про-
ецирующей (рис. 4.36) или линией
уровня (рис. 4.37).
4.7.1. Способ
концентрических сфер
Способ концентрических сфер при-
меняется для построения линии пере-
сечения двух поверхностей вращения,
имеющих общую плоскость симмет-
рии, которая должна быть плоскостью
уровня.
В этом случае оси г, / данных повер-
хностей Ф, Д принадлежат общей плос-
кости симметрии Е и поэтому пересе-
каются в точке О — центре вспомога-
тельных сфер Г' . Вспомогательные
сферы Г2 пересекаются с данными по-
верхностями Ф, Д по окружностям.
Если плоскость симметрии Е является
плоскостью уровня, то оси /, j также
будут прямыми уровня или проециру-
ющими. Тогда указанные окружности,
плоскости которых будут проецирую-
щими или уровня, проецируются на
одну из плоскостей проекций в отрезки
прямых. Поэтому, если общая плос-
кость симметрии Е данных поверхнос-
тей Ф, Д не является плоскостью уров-
ня, то предварительно надо выполнить
преобразование чертежа с тем, чтобы
плоскость Е стала плоскостью уровня.
Если точка О является несобственной (при
i I Л, то радиусы вспомогательных сфер будут
бесконечно большими, т.е. они вырождаются в
плоскости; получается частный случай — способ
плоскостей.
Рис. 4.38
Алгоритм способа концентрических
сфер рассмотрим на примере построе-
ния линии пересечения 1(11, /2) повер
хности вращения Ф (i, а) с конической
поверхностью вращения Д(/, Л)
(рис. 4.38).
Отмечаем точку О = i п / — центр
вспомогательных сфер-посредников Г'.
Поверхности Ф, Д имеют общую плос-
кость симметрии Е || П2, которая пере-
секает данные поверхности по очерко-
вым линиям на П2, точки пересечения
А, В, С, D которых принадлежат иско-
мой линии I. Точка А наиболее удале-
на от точки О, поэтому отрезок ОА
определяет Лгаах одной граничной сфе-
ры Г (Лтах — верхний предел измене-
ния параметра (радиуса) вспомогатель-
ных сфер).
Для определения /?mjn другой гранич-
ной сферы Г из точки О2 строим нор-
мали на очерковые линии данных по-
верхностей: больший из двух отрезков
нормалей определяет /?min, т.е. вспомо-
гательная сфера Г радиуса 7?min будет
126
касаться одной из поверхностей и пе-
ресекать другую. Радиусы R1 вспомога-
тельных сфер Г1 должны удовлетворять
неравенству
^min * s -^тах’
В этом случае сферы Г1 позволяют
получать действительные точки линии
пересечения (точки, проекции которых
расположены в пределах наложения
проекций пересекающихся поверхнос-
тей).
На рис. 4.38 граничная сфера Г ра-
диуса /?тах = [ОЛ] не построена, так
как она определяет лишь построенную
ранее точку Л (Л], Л2). Другая гранич-
ная сфера Г радиуса Z?mjn касается
поверхности вращения Ф по окружнос-
ти g (#i, g2) и пересекает коническую
поверхность по двум окружностям d,
d1. Эти окружности попарно пересе-
каются в двух действительных точках
1, Г и в двух мнимых точках, фрон-
тальные проекции которых находятся
за пределами очерковых линий данных
поверхностей.
Здесь следует обратить внимание на
два момента.
1. Ту из двух данных поверхностей
Ф, Д, которой касается вспомогательная
сфера Г минимального радиуса J?mjn,
назовем для наглядности ’’толстой”, а
другую — ’’тонкой”. На рис. 4.38 по-
верхность вращения Ф (z, а) будет ’’тол-
стой”, а коническая поверхность Д(/, Ь)
— ’’тонкой”. Очевидно, ’’тонкая” по-
верхность Д по одной замкнутой кри-
вой ’’входит” в ’’толстую” поверхность
Ф и по другой замкнутой кривой ’’вы-
ходит” из нее. Такое наглядное пред-
ставление помогает строить проекции
линии пересечения после построения
множества точек искомой линии пере-
сечения.
2. Реальная (действительная) линия
пересечения I поверхностей Ф, Д не
проходит через мнимые точки пересе-
чения окружностей g, d, т.е. физичес-
ки проекции линии пересечения могут
находиться лишь в пределах наложе-
ния проекций пересекающихся повер-
хностей. Но математической проекци-
ей линии пересечения I на плоскость
симметрии S или ей параллельную
плоскость проекций является не дуга
кривой, а вся кривая в целом, т.е.
линия, проходящая через проекции
как действительных, так и мнимых
точек. Это можно объяснить так: ли-
ния I пересечения поверхностей Ф, Д
является линией пересечения не толь-
ко для данных двух поверхностей, но
и бесчисленного множества других по-
верхностей, среди которых обязательно
находятся три проецирующие цилин-
дрические поверхности, задаваемые
проекциями /], Z2, /3 линии I на плос-
кости проекций Uj, П2, П3. Поэтому
мнимые точки линии пересечения ис-
пользуются для более точного построе-
ния ее проекции на той плоскости
проекций, которая параллельна общей
плоскости симметрии S.
На рис. 4.38 показаны все построе-
ния, выполнение для одного посредни-
ка Г2. Она пересекает поверхность Ф по
окружностям g, g', а поверхность Д —
по окружностям d, d'. Эти окружнос-
ти, попарно пересекаясь, определяют
действительные 2 = 2', 3 = 3' и мни-
мые точки искомой линии I. Горизон-
тальные проекции действительных
точек построены из условия принад-
лежности поверхности Ф: 2, 2', 3,
3' f g <= Ф. Мнимые точки пересечения
этих окружностей использованы для
более точного построения фронтальной
проекции Z2 линии I.
В силу параллельности плоскости
симметрии S фронтальной плоскости
проекций видимая и невидимая ветви
фронтальной проекции Z2 линии пере-
сечения Z накладываются друг на дру-
га. Поэтому на чертеже Z2 изображает-
ся линией видимого контура.
127
Видимость на П] ограничивает кони-
ческая поверхность Д. Для определения
точек видимости Л/j, Л//,
построены фронтальные проекции (см.
п. 2.6.3) т2 = т2 очерковых образую-
/
щих т}, т} конической поверхности
Д. Горизонтальные проекции точек М,
N = I л tn, т' {М2, N2 = т2 п 12) на
П] разделяют видимые и невидимые
участки горизонтальной проекции Zj
искомой линии /.
4.7.2. Способ
эксцентрических сфер
Этот способ применяется для по-
строения линии пересечения цикли-
ческой поверхности с поверхностью
вращения, если они имеют общую
плоскость симметрии, которая
должна быть плоскостью уровня.
Алгоритм построения линии пересе-
чения I поверхностей Ф, Д способом
эксцентрических сфер включает сле-
дующие основные операции.
1. Построение экстремальных точек
линии пересечения, используя в качес-
тве посредника общую плоскость сим-
метрии S данных поверхностей Ф, Д.
2. Построение случайных точек ли-
нии пересечения с помощью вспомога-
тельных сфер, центры которых при-
надлежат оси поверхности вращения.
Построения с участием каждого по-
средника выполняются в такой после-
довательности:
— на циклической поверхности Ф
выбирается окружность g, расположен-
ная между построенными ранее экс-
тремальными точками;
— через окружность g проводится
вспомогательная сфера Г, центр О
который принадлежит оси j поверхнос-
ти вращения Д;
— строятся окружности <1, <1, ..., по
которым посредник Г пересекается с
поверхностью вращения Д;
Рис. 4.39
— отмечаются точки 1, 12, 2'
пересечения окружностей g и d,d, ....
3. Построение точек видимости ли-
нии пересечения.
На рис. 4.39 приведен пример по-
строения проекций линии пересечения
/ циклической поверхности Ф (г, п, Пр
с плоскостью параллелизма П( и кони-
ческой поверхности вращения Д(/, т).
Плоскость симметрии Е поверхностей
Ф, Д пересекает их по очерковым лини-
ям на П2, которые, пересекаясь между
собой, определяют экстремальные точ-
ки А, В, С, D линии пересечения I.
Для построения случайных точек 1, Г
линии I на циклической поверхности Ф
выбрана произвольная образующая —
окружность g. Через центр окружности
g перпендикулярно се плоскости прове-
дена прямая Z и отмечена точка О ее
пересечения с осью j конической по-
верхности Д. Из точки О, как из цен-
тра, описана вспомогательная сфера Г,
проходящая через выбранную окруж-
ность g. Сфера Г пересекает поверх-
ность конуса Д по двум окружностям
128
d, d, которые пересекают окружность
g в точках J, Г (действительных,
мнимых), принадлежащих искомой
линии пересечения /). Горизонтальные
проекции найденных точек строим из
условия их принадлежности поверхнос-
ти Ф:
1,1' е £ <= Ф.
Используя несколько сфер-посредни-
ков, получаем случайные точки, кото-
рые достаточно точно определяют про-
екции /р /2 искомой линии пересече-
ния.
Видимость на фронтальной плоскости
проекций ограничивает общая плос-
кость симметрии S данных поверхнос-
тей: видимая и невидимая части фрон-
тальной проекции 12 линии пересече-
ния совпадают, так как плоскость S
параллельна П2.
Для определения видимости горизон-
тальной проекции /j линии пересече-
ния необходимо сопоставить взаимное
положение фронтально проецирующей
цилиндрической поверхности 0, прохо-
дящей через центровую линию цикли-
ческой поверхности,и горизонтальной
плоскости уровня Л, проходящей через
ось конической поверхности. Правая
часть линии пересечения полностью
закрывается цилиндрической повер-
хностью 0 (расположена на невидимой
относительно П] стороне циклической
поверхности Ф), поэтому ее горизон-
тальная проекция будет невидимой,
если поверхность Ф продолжается неог-
раниченно вправо. На рис. 4.39 имеем
лишь отсек поверности Ф и правая
часть ее линии пересечения с Д распо-
ложена так, что ’’просматривается”
через верхнее основание п поверхности
Ф. Поэтому горизонтальная проекция
правой части линии пересечения пол-
ностью видима.
Левая часть линии пересечения на П]
частично видима (дуга так
как расположена выше поверхности 0
и плоскости Л, а ее дуга М1А1М^
невидима, так как расположена на
невидимой относительно П] части ко-
нической поверхности.
4.8. Аналитические
алгоритмы решения
задач на пересечение
Решение позиционных задач на ЭВМ требует
аналитического описания графических опера-
ций. используемых при их решении. С этой
целью дадим краткое изложение осноп аналити-
ческого решения рассмотренных выше задач.
Аналитически определение точек пересечения
линии / с поверхностью Ф сводится в общем слу-
чае к решению системы трех нелинейных урав-
нений с тремя неизвестными. Эта система состо-
ит из уравнения поверхности Ф, записанного в
явной (2.24) или в неявной форме (2.25), и сис-
темы двух нелинейных уравнений с тремя неиз-
вестными, записанных в форме (2.17) или (2.18)
и задающих линию /. В общем случае, как из-
вестно, такая система решается методами вычис-
лительной математики.
В частных случаях при определении коорди-
нат точек пересечения простейших линий и
поверхностей получаются достаточно простые
системы, которые решаются известными из сред-
ней школы методами. Например, определение
координат точки L пересечения прямой I с плос-
костью Ф сводится к решению системы трех ли-
нейных уравнений с тремя неизвестными. Эта
система состоит из уравнения (2.1) плоскости Ф
и системы уравнений (2.8), описывающих пря-
мую /. Решение такой системы не вызывает за-
труднений.
Пример. Определить координаты точки L
пересечения прямой /, заданной системой урав-
нений
2х + 4у - 1 =0
Зх - 2z + 4 = 0
с плоскостью Ф общего положения
5х - 2у + 3z - 5 = 0.
Координаты точки L являются решением сис-
темы уравнений
129
2х + 4у - 1 =0
Зх - 2z + 4 = 0
5х - 2у + 3z - 5 = 0.
Как известно, такая система имеет единствен-
ное решение, если определить системы
то эти плоскости параллельны. Таким образом,
если коэффициенты при неизвестных в уравне-
нии плоскости Фив одном из уравнений, задаю-
щих прямую /, пропорциональны, то прямая I
будет параллельна плоскости ф.
Аналитическое решение первой основной по-
зиционной задачи сводится в итоге к решению
алгебраического уравнения n-й степени от одной
переменной. Здесь п определяет число точек
(действитсльньсх, мнимых, совпавших) пересече-
ния линии с поверхностью. Например, пусть
требуется найти точки пересечения прямой /,
определяемой системой
2х + Зу + 4 = 0
Зх - 4z + 5 = 0,
не равен нулю. В нашем случае А = — 84.
Координаты точки L вычисляются по форму-
лам
Д, Д2
— у = _; z = —,
Д А А
со сферой Ф, описываемой уравнением
(х - 2)2 + (у + I)2 + (Z - 4)2 = 25.
Выразив у и z через х в уравнениях прямой /
и подставив их в уравнение сферы, получаем
квадратное уравнение от одной неизвестной х:
где
-1 4 0
\ = 4 0 -2 = -4;
-5 -2 3
(х - 2)2 + j ~2* ~ 4 + 1 |2 +
4)2"25
или после упрощений
д2
2-10
3 4-2
5-5 3
23;
161х2 - 1362х - 2079 = 0.
2 4-1
3 0 4
5 -2 -5
162.
Решив это квадратное уравнение, получаем
значения абсцисс точек пересечения L, L пря-
мой I со сферой Ф. Подставив найденные значе-
ния абсцисс в уравнения прямой /, вычисляем
ординаты и аппликаты точек L, L.
Как известно, в радикалах решаются лишь
уравнения до четвертой степени. Поэтому при
и г 5 решения уравнений выполняются прибли-
женно методами, изучаемыми в вычислительной
математике. В вычислительных центрах имеются
стандартные программы, реализующие указан-
ные приближенные методы.
Анализируя изученные выше графические
способы построения линий пересечения повер-
хностей, следует отметить, что области их при-
менения достаточно узки. Изучаемыми способа-
ми невозможно даже построить линию пересече-
ния двух поверхностей второго порядка общего
вида, ибо плоскости-посредники пересекают их
по кривым второго порядка, а подобрать вспомо-
162 \
~ ’м’/'
23
84’
4
. 84 ’
В частном случае определитель системы А
Имеем
L
может быть равен нулю. Это возможно тогда,
когда пропорциональнй! элементы каких-либо
двух строк. Из аналитической геометрии извес-
тно, что если коэффициенты при неизвестных в
уравнениях двух плоскостей пропорциональны,
130
гательные сферы, которые пересекали бы их
одновременно по окружностям, невозможно.
Поэтому обычно инженерные задачи, связанные
с построением линии пересечения поверхностей
и требующие точных результатов, решаются ана-
литически.
Аналитическое решение второй основной по-
зиционной задачи реализует лишь способ плос-
костей уровня. Это объясняется, во-первых, про-
стотой вычислений при реализации способа
плоскостей уровня, а во-вторых, необходимостью
выполнения ряда вспомогательных аналитичес-
ких выкладок при реализации способа сфер, и,
конечно, ограниченностью области их примене-
ния.
Аналитически расчет кординат точек £'' линии
пересечения I двух поверхностей Ф(х, у, z) - О,
Д(х, у, z) - 0 выполняется в такой последова-
тельности:
1) вводятся плоскости-посредники Г', парал-
лельные какой-либо координатной плоскости,
например, Оху:
z = Z
2) подставив в уравнения поверхностей Ф, А
значение z - z*, получают уравнения кривых g\
d‘ — сечений данных поверхностей плоскостью
Г':
g(x, у) = О
</(х, у) = 0;
3) методами, изучаемыми в вычислительной
математике, решается полученная система двух
нелинейных уравнений с двумя неизвестными и
вычисляются координаты точек [У искомой ли-
нии пересечения.
Вычисления последнего этапа выполняются
просто, если кривые s', d' являются прямыми и
окружностями. Тогда вычисление координат
точек l!2 сводится к решению квадратного урав-
нения.
Рассмотрим пример. Пусть требуется постро-
ить линию пересечения (вычислить кординаты
точек линии пересечения) конической повер-
хности Ф, образованной вращением прямой а:
Ах + Bz + С = 0
вокруг оси Oz и сферы А, заданной своим цен-
тром Л/(хм, ум, zM) и радиусом R.
Система уравнений
А^х2 + у2 + Bz + С = 0
(х - х„)2 + (у - ум)2 + (z - zM)2 = R2
описывает линию I пересечения данных повер-
хностей.
Для изображения этой линии на графопостро-
ителе или на экране дисплея необходимо вычис-
лить кординаты ее точек. С этой целью будем
присваивать переменной z какие-либо конкрет-
ные численные значения z - z1, что равносильно
выбору множества плоскостей-посредников Т“,
параллельных координатной плоскости Оху.
Подставив значение z - z' в данную систему,
получаем систему двух квадратных уравнений с
двумя неизвестными:
х2 + у2 + О = 0
(х - хм)2 + (у - ум)2 + К = 0,
где D - + J?; К - - z )2 — Л2.
А
Выразив из первого уравнения у - V ~D ~
и подставив во второе, после некоторых элемен-
тарных упрощений получаем квадратное уравне-
ние от одной переменной:
Ex2 + Fx + G = 0,
2 2 2 2
ще£-4(Хм + ум ); F - - 4хм( Хм + Ум + Ю;
2 2 2
G- (Х + Ум +Ю2 + 4> D.
Решаем полученное квадратное уравнение
-F ± \]F2 - AEG
Абсциссы Х|, х2 точек L‘J будут действительны-
ми, если дискриминант F2 — AEG будет положи-
тельным числом. Подставив значения х,, х2 в
уравнение кривой £ или d‘, получаем координа-
ты двух точек l!'(х,, у,, ?), La(xlf уг, zO линии
пересечения I.
Варьируя значением z - ?, где zmjn s ? 4
s zmax, вычисляем координаты множества точек
l!2 линии пересечения /. Аппликаты znlln и zmax
определяют экстремальные точки линии пересе-
чения, для которых дискриминант F2 — AEG
равен нулю. При ?, равном zmin и zmax, окруж-
ности s', d‘ касаются друг друга, а для zm]n s
s z's zmax они пересекаются в действительных
точках и, наконец, для z' > zmax и ? < zmjn они
пересекаются в мнимых точках.
131
4.9. Случаи распадения
линии пересечения
поверхностей
Ранее основное внимание было уде-
лено теории способов и алгоритмам
построения линии пересечения повер-
хностей. Теперь рассмотрим некоторые
вопросы алгебры, относящиеся к по-
строению линии пересечения алгебраи-
ческих поверхностей.
Основная теорема алгебры примени-
тельно к пересечению поверхностей
читается так: две алгебраические по-
верхности порядков п, т пересекают-
ся по пространственной кривой по-
рядка пт.
Следствие: две поверхности второго
порядка пересекаются по простран-
ственной кривой четвертого порядка.
Для графической реализации алго-
ритмов построения линии пересечения
поверхностей существенное значение
имет следующая теорема: если алгеб-
раические поверхности порядков п, т
имеют общую плоскость симметрии,
то линия их пересечения прямоуголь-
но проецируется на эту плоскость
или ей параллельную в кривую по-
рядка .22.
Следствие: если две поверхности
второго порядка имеют общую плос-
кость симметрии, то линия их пересе-
чения прямоугольно проецируется на
эту плоскость или ей параллельную в
кривую второго порядка.
Важное значение для решения при-
кладных задач имеют случаи, когда
линия пересечения двух поверхностей
распадается на две или более составля-
ющих. Возможны случаи, когда две
или более составляющих совпадают,
что ведет к касанию данных поверх-
ностей вдоль этих составляющих. Для
конкретности рассмотрим такие случаи
применительно к пересечению двух
поверхностей второго порядка.
Рис. 4.40
Линия пересечения двух поверхнос-
тей второго порядкда в случае их час-
тного взаимного положения может
распадаться в следующих вариантах:
1)4=1+3;
2) 4 = 1 + 1 + 2;
3)4 = 1 + 14-1 + 1;
4) 4 = 2 + 2.
Первые три варианта возможны
лишь при пересечении линейчатых
поверхностей второго порядка, так как
в состав их линии пересечения входят
прямые. Первый вариант получается,
если пересекающиеся поверхности
второго порядка имеют одну общую
образующую. На рис. 4.40 показан
пример пересечения двух конических
поверхностей Ф(5, a), A(S, b) имею-
щих общую образующую SS. Поэтому
линия их пересечения состоит из этой
образующей и пространственной кри-
вой третьего порядка /. Построение
линии I удобно выполнить способом
вращающейся плоскости (см. п. 4.6).
132
Второй вариант распадения можно
проиллюстрировать следующим приме-
ром (рис. 4.41). Пусть пересекаются
однополостный гиперболоид Ф и кони-
ческая поверхность Д(5, а). При этом
вершина S конической поверхности Д
принадлежит поверхности Ф, а ее на-
правляющая а проходит через следы
М, N образующих т, п гиперболоида,
проходящих через точку 5. Тогда пря-
мые т, п будут общими для поверх-
ностей Ф, Д, которые дополнительно
пересекаются по кривой второго поряд-
ка I. Здесь линию / также удобно стро-
ить способом вращающейся плоскости.
При этом за ось пучка вспомогатель-
ных плоскостей можно брать любую из
прямых т, п.
Третий вариант распадения можно
представить так: две конические по-
верхности второго порядка с общей
вершиной (две цилиндрические повер-
хности с параллельными образующи-
ми) всегда пересекаются по четырем
образующим, которые могут быть дей-
ствительными различными, мнимыми
и совпавшими в различных вариантах.
На рис. 4.42 показаны три случая пе-
ресечения:
1) все образующие действительные
различные;
2) две действительные образующие
совпали, две другие — различные;
3) две образующие действительные
различные, две другие — мнимые.
Во втором случае конические повер-
хности касаются вдоль совпавших об-
разующих.
Большой теоретический и приклад-
ной интерес представляет четвертый
вариант распадения линии пересечения
двух поверхностей второго порядка на
две кривые второго порядка. Есть ряд
известных теорем, относящихся к это-
му варианту распадения.
Теорема: если две поверхности вто-
рого порядка имеют общую кривую
второго порядка, то они пересекают-
ся еще по одной кривой второго по-
рядка.
Пример. Построить линию пересе-
чения b двух конических поверхнос-
тей Ф(5, а), Д(5, а), имеющих об-
щую направляющую окружность а
(рис.4.43).
Рис. 4.43
133
Данные поверхности Ф, Л имеют об-
щую фронтальную плоскость симмет-
рии Г. Поэтому линия их пересечения
проецируется на П2 в соответствии с
вышеприведенным следствием в рас-
павшуюся кривую второго порядка,
так как сама линия пересечения явля-
ется распавшейся на две кривые вто-
рого порядка. Плоскость Г пересекает
данные поверхности по очерковым
образующим, через точки /2, 22, J2, 42
пересечения которых проходит фрон-
тальная проекция линии пересечения.
Так как фронтальная проекция линии
пересечения представляет собой рас-
павшуюся на две прямые кривую вто-
рого порядка, где одна из прямых а2
проходит через точки /2, 32, то вторая
прямая Ь2 будет проходить через точки
22’ 42‘
Горизонтальная проекция искомой
недостающей составляющей линии
пересечения строится из условия при-
надлежности одной из данных кони-
ческих поверхностей.
Отметим, что кривые второго поряд-
ка а, Ь, принадлежащие обеим кони-
ческим поверхностям Ф, Д, пересекают-
ся в двух точках М, N. Эти точки мо-
гут быть действительными различными
(см. рис. 4.43), совпавшими или мни-
мыми. Это утверждение справедливо
для любых двух кривых второго поряд-
ка, принадлежащих одной поверхности
второго порядка. Действительно, плос-
кости этих кривых пересекаются по
прямой, которая пересекает поверх-
ность второго порядка всегда в двух
точках (действительных различных,
совпавших или мнимых). Через эти
точки, очевидно, проходят указанные
кривые второго порядка.
Другие теоремы, относящиеся к рас-
падению линии пересечения двух по-
верхностей второго порядка на две
кривые второго порядка, будут расмот-
рены в следующем разделе.
4.10. Касание — частный
случай пересечения
В курсе математического анализа
касательной t к кривой т в ее точке М
называется предельное положение MN*
секущей MN, которое она занимает
при стремлении точки N вдоль кривой
т к точке М (см. рис. 2.24). Другими
словами, касательная t — это такая
секущая (хорда), которая пересекает
кривую т в двух совпавших точках
М = V. Это определение распространя-
ется и на касание кривых линий, плос-
ких и пространственных. Так как две
кривые могут пересекаться в несколь-
ких точках, то в пределе могут сов-
пасть две, три и более точек. Поэтому
говорят о двухточечном, трехточечном
и т.д. касаниях. Например, две кривые
второго порядка могут иметь двухто-
чечное, трехточечное и четырехточеч-
ное касания. На языке математическо-
го анализа это означает, что в случае
двухточечного касания координаты
совпавших точек удовлетворяют урав-
нениям обеих кривых, а также в этой
точке равны первые производные, взя-
тые от уравнений этих кривых. В слу-
чае трехточечного касания дополни-
тельно равны вторые производные, а в
случае четырехточечного касания рав-
ны и третьи производные. В инженер-
ной практике принято называть двух-
точечное, трехточечное и т.д. касания
соответственно касаниями первого,
второго, и-го порядка гладкости. Кри-
вые, составленные из дуг касающихся
кривых, называются обводами (см. пп.
2.5.5.—2.5.6).
Указанные понятия распространяют-
ся в соответствтующей интерпретации
и на касания поверхностей. Как
было отмечено выше, вопросы построе-
ния касающихся кривых и поверхнос-
тей имеют важное прикладное значе-
ние. Поэтому рассмотрим подробнее
некоторые теоретические аспекты и
134
алгоритмы решения задач на по-
строение касающихся кривых и повер-
хностей.
4.10.1. Касание линии
и поверхности
Задача построения линии, касающей-
ся данной поверхности, является вспо-
могательной при построении двух ка-
сающихся поверхностей. Линия т
касается поверхности Ф в точке А,
если она касается в этой точке какой-
либо линии а, в частности, прямой
данной поверхности.
Практическое значение имеет по-
строение прямой т, касающейся по-
верхности Ф.
Пример 1. В точке А сферы Ф(О, R)
построить какую-либо касательную
прямую т (рис. 4.44).
Рис. 4.44
Задача имеет множество решений,
так как через точку А на поверхности
Ф можно провести бесчисленное мно-
жество кривых линий. На рис. 4.44
через точку А проведена горизонталь-
ная окружность а. Прямая
касающаяся в точке А окружности а,
будет касательной и к сфере Ф.
Пример 2. Из точки С, не принадле-
жащей поверхности конуса вращения,
провести к последней какую-либо ка-
сательную (рис. 4.45).
Эта задача также имеет бесчислен-
ное множество решений. На рис. 4.45
построена одна из возможных каса-
тельных t:
— через точку С проведена горизон-
тальная плоскость уровня Г, перпенди-
кулярная оси i поверхности конуса
вращения;
— плоскость Г пересекает коничес-
кую поверхность по окружности
а(ар а2);
— в плоскости Г через точку С к
окружности а проведена она из воз-
можных касательных t.
Точка А — точка касания касатель-
ной t к поверхности конуса вращения.
4.10.2. Касание поверхностей
в точке
Две поверхности, имеющие в их
общей точке общую касательную
плоскость, называются соприкасаю-
щимися в этой точке. Таким образом,
построение двух соприкасающихся в
данной точке А поверхностей Ф, Д сво-
дится к построению касательной плос-
кости Т.
В дифференциальной геометрии по-
казывается, что множество касатель-
ных ?, проведенных к поверхности Ф
в некоторой ее точке А, принадлежит
плоскости Т, если точка А является ее
регулярной (обыкновенной) точкой.
Если же точка А является особой точ-
кой поверхности Ф, то множество каса-
135
тельных t образует коническую повер-
хность т с вершиной в этой точке.
Так как касательная плоскость т од-
нозначно определяется двумя прямы-
ми, то алгоритм ее построения состоит
из следующих этапов:
— через данную точку А поверхности
Ф проводятся какие-либо две ее линии
а, Ь;
— в точке А строятся касательные ?,
Z2 к выбранным линиям а, Ь; пересека-
ющиеся прямые Z1, t2 определяют
плоскость Т, касающуюся поверхности
Ф в точке А.
Этот алгоритм лежит в основе анали-
тического способа построения каса-
тельной плоскости Т поверхности Ф в
ее точке А. Если в уравнение Ф(х, у,
z) = 0 поверхности подставить значе-
ния х = хА, у = уА, z = zA , то получа-
ем уравнения сечений а, Ь, с повер-
хности Ф плоскостями, проходящими
через точку А и параллельными соот-
ветственно координатным плоскостям
Oyz, Oxz, Оху. Частные производные
дФ(х, у, z) ЭФ(х, у, z) ЭФ(х, у, z)
дх ’ ду ’ dz
точке Л(хА, уА, zA) суть угловые коэф-
фициенты касательных t2, прове-
денных в точке А к кривым а, Ь, с.
Уравнение касательной плоскости Т
имеет вид
дФ , , дФ . .
(х - *Л> + 37 <у - Уа> +
Эх ду (4.1)
Рис. 4.46
Л(й], h2), а другая — фронталью f(J\,
f2). Искомая плоскость Т определяется
этими прямыми уровня.
Пример 2. Построить плоскость Т,
касающуюся поверхности конуса вра-
щения Ф и проходящую через данную
точку М f Ф (рис. 4.47).
Рис. 4.47
Рассмотрим примеры графического
построения касательных плоскостей.
Пример 1. Построить плоскость Т,
касающуюся сферы Ф(О, R) в точке
А е Ф (рис. 4.46).
На сфере Ф через точку А проводим
две окружности а, Ь, расположенные в
плоскостях уровня. К этим окруж-
ностям в точке А строим касательные,
из которых одна будет горизонталью
Так как искомая плоскость Т касает-
ся поверхности конуса Ф по образую-
щей, то она проходит через вершину S
конуса, следовательно, и через прямую
SM. Строим точку М пересечения
прямой SM с плоскостью Г основания
а конуса Ф. Из точки М проводим ка-
сательные ?, Z2 к основанию а конуса
и отмечаем точки касания А, В.
Задача имеет два решения: через
точку М проходят две плоскости
136
Рис. 4.48
TSM n SA), T (SM n SB), касающиеся
поверхности конуса вдоль ее образу-
ющих 5Л и SB.
Ранее неоднократно отмечалось, что
касание является предельным (част-
ным) случаем пересечения. Касатель-
ная плоскость, касаясь поверхности в
заданной точке, пересекает ее, как и
любая произвольная плоскость, по
некоторой кривой, действительной или
мнимой. При этом точка касания для
линии пересечения будет всегда двой-
ной (узловой, возврата или изолиро-
ванной ). На чертеже (рис. 4.48) пока-
заны сечения поверхности вращения
Ф(1, Z) тремя фронтально проецирую-
щими плоскостями Г, Д, S, касающи-
мися поверхности вращения соответ-
ственно в точках А, В, С. Точки каса-
ния А, В, С для соответствующих сече-
ний а, Ь, с являются узловой, возврата
и изолированной. Заметим, что в диф-
ференциальной геометрии такие точки
принято называть соответственно
гиперболическими, параболическими
Двойная точка кривой линии называется изо-
лированной (см. п. 2.5.1), если через нее про-
ходят две мнимые ветви. Координаты этой точки
удовлетворяют уравнению кривой, хотя точка
визуально может и не принадлежать действи-
тельной ветви этой кривой.
и эллиптическими. Поверхности, со-
стоящие только из гиперболических
точек, являются вогнутыми и назы-
ваются поверхностями отрицательной
кривизны (например, эллиптический и
параболический гиперболоиды).
Поверхности, состоящие только из
параболических точек, называются
поверхностями нулевой кривизны. К
таким поверхностям относятся цилин-
дрические, конические и торсовые.
Поверхности, состоящие только из
эллиптических точек, являются вы-
пуклыми и называются поверхностя-
ми положительной кривизны (напри-
мер, сфера, эллипсоид, параболоид
и т.д.).
Поверхности, содержащие все виды
точек, называются поверхностями
двоякой кривизны (например, повер-
хность тора).
В заключение приведем теорему о
соприкасающихся поверхностях второ-
го порядка и примеры решения задач
на построение соприкасающихся по-
верхностей.
Теорема о двух точках соприкосно-
вения: если две поверхности второго
порядка имеют две точки соприкосно-
вения, то линия их пересечения рас-
падается на две кривые второго по-
рядка, пересекающиеся в указанных
точках.
Как было отмечено, две поверхности
второго порядка в общем случае пере-
секаются по пространственной кривой
четвертого порядка. Точки соприкосно-
вения поверхностей для этой кривой
должны быть двойными. Но простра-
нственная кривая четвертого порядка
не может иметь более одной двойной
точки. Наличие двух двойных точек,
которые могут быть действительными
различными, совпавшими или мнимы-
ми, является признаком распадения
этой кривой на две кривые второго
порядка.
Пример 1. Сферу Д(О, R) вращением
вокруг горизонтально проецирующей
137
Рис. 4.49
прямой /(q, z2) привести в соприкасаю-
ющееся положение (с внешней сторо-
ны) с поверхностью конуса вращения
Ф(/, I) (рис. 4.49).
Множество центров О1 сфер радиуса
R, соприкасающихся с поверхностью
конуса вращения Ф с внешней стороны,
образует внешнюю эквидистантную
(равноотстоящую) коническую повер-
хность Ф. Поэтому для нахождения
повернутых положений О', О", центра
О данной сферы Д необходимо найти
точки пересечения траектории (окруж-
ности т), описываемой центром О
сферы Д, с эквидистантной конической
поверхностью Ф. Плоскость Г окруж-
ности т пересекает поверхность Ф по
окружности п, которая с окружностью
т пересекается в точках О', О" —
центрах искомых повернутых положе-
ний сферы Д. Точки М(М}, М2), N(N^,
jV2) являются точками соприкоснове-
ния поверхности конуса Ф со сферами
Д'(О', R), &"(О", R). Они построены
как основания перпендикуляров, про-
веденных из точек О', О" к поверх-
ности конуса Ф. Для их графического
построения точки О', О” предвари-
тельно повернуты вокруг оси j конуса
Ф в положение О и найдены поверну-
тые положения М = N точек сопри-
косновения на очерковой образующей
поверхности конуса Ф. Так как очерко-
вая образующая конической поверх-
ности является фронталью, то в соот-
ветствие с теоремой о проекции прямо-
го угла (см. п. 1.1.3) прямой угол,
составленный прямыми ОМ = ON и
SM = SN, проецируется в натураль-
ную величину на П2.
Пример 2. Построить круговые се-
чения эллиптического конуса Ф
(рис. 4.50).
138
Рис. 4.50
Для решения задачи воспользуемся
теоремой о двух точках соприкоснове-
ния. Построим вспомогательную сферу
Д(О, Л), имеющую с поверхностью
эллиптического конуса две точки со-
прикосновения А(А2, А3), В(В2, В3)
(эти поверхности в точках А, В имеют
соответственно общие касательные
плоскости Г', Г"). В соответствии с
теоремой о двух точках соприкоснове-
ния линия пересечения поверхностей
Ф, Д распадается на две кривые вто-
рого порядка, которые будут окруж-
ностями, так как они принадлежат
сфере.
Поверхности Ф, Д имеют общую про-
фильную плоскость симметрии S. Поэ-
тому их распавшаяся линия пересече-
ния будет проецироваться на профиль-
ную плоскость проекций П3 в распав-
шуюся кривую второго порядка а3 п Ь2
(см. п. 4.9), проходящую через точки
/3, 23, 53, 43 пересечения их очерко-
вых линий и профильные проекции
А3 = В3 точек соприкосновения. Сече-
ния эллиптического конуса профиль-
но проецирующими плоскостями, па-
раллельными плоскостям окружнос-
тей а, Ь, являются его круговыми
сечениями.
4.10.3. Касание поверхностей
вдоль линии
Конструирование поверхностей, ка-
сающихся вдоль заданной линии, явля-
ется распространенной инженерной
задачей при создании математических
моделей сложных технических повер-
хностей в процессе их автоматизиро-
ванного проектирования и воспроизве-
дения на оборудовании с числовым
программным управлением.
В геометрической интерпретации
методика конструирования поверхнос-
тей, касающихся вдоль некоторой ли-
нии, сводится к поиску таких повер-
хностей, линия пересечения которых
распадается на несколько конгруэн-
тных (равных) составляющих. При
совпадении двух или более составляю-
щих эти поверхности вдоль совпавших
линий будут иметь определенный по-
рядок соприкосновения.
Для простоты и конкретности рас-
смотрим указанные вопросы примени-
тельно к поверхностям второго поряд-
ка. Например, если центр О сферы Д
принадлежит оси поверхности конуса
вращения Ф, то они пересекаются по
двум окружностям а, b (рис. 4.51).
При непрерывном уменьшении радиуса
сферы радиусы окружностей а, b не-
прерывно изменяются и в пределе
Рис. 4.51
139
становятся равными, т.е. в пределе
окружности а, b станут конгруэнтными
и совпадут, а поверхности Ф, Д' будут
соприкасаться вдоль окружности а‘ =
Ь‘. Другими словами, поверхности Ф, Д'
будут пересекаться по двум совпавшим
окружностям.
Необходимое и достаточное условие
касания двух поверхностей второго
порядка вдоль кривой второго порядка
формулируется теоремой о трех точ-
ках соприкосновения: если две повер-
хности второго порядка имеют три
точки соприкосновения, то они каса-
ются по кривой второго порядка,
проходящей через эти точки.
Следствие: очерковой линией повер-
хности второго порядка является
кривая второго порядка.
Действительно, при центральном
(параллельном) проецировании неко-
торой поверхности второго порядка
огибающая проецирующая коническая
(цилиндрическая) поверхность касает-
ся оригинала вдоль кривой второго
порядка. Поэтому проецирующая по-
верхность в соответствии с теоремой
будет поверхностью второго порядка и
пересекает плоскость проекций по
кривой второго порядка — очерковой
линии оригинала на этой плоскости
проекций.
И, наконец, сформулируем теорему
Монжа, в условии которой фигурируют
соприкасающиеся вдоль кривой повер-
хности второго порядка.
Теорема Монжа: если две поверх-
ности второго порядка вписаны в
третью поверхность второго порядка
или описаны вокруг нее, то линия их
пересечения распадается на две кри-
вые второго порядка.
На рис. 4.52 изображены две кони-
ческие поверхности вращения, описан-
ные вокруг сферы. Конические повер-
хности касаются со сферой по окруж-
ностям а, Ь, которые как принадлежа-
щие одной сфере пересекаются в двух
точках М, N. Очевидно, эти точки
Рис. 4.52
могут быть действительными различ-
ными, совпавшими или мнимыми.
Точки М, N для конических поверх-
ностей являются точками соприкосно-
вения. Следовательно, теорема Монжа
есть частный случай теоремы о двух
точках соприкосновения. Отсюда сле-
дует, что кривые второго порядка I, к,
по которым пересекаются данные ко-
нические поверхности, будут прохо-
дить через точки М, N.
Завершая изложение теоретических
основ и алгоритмов решения позицион-
ных задач, отметим, что многообразие
таких задач велико. Их графическое
решение с участием кривых линий и
поверхностей высших порядков неце-
лесообразно и в большинстве случаев
невозможно. Но на изложенных алго-
ритмах базируются аналитические и
численные методы решения таких за-
дач с применением современной вы-
числительной техники. Поэтому без
овладения изложенными алгоритмами
немыслимо решение прикладных за-
дач.
Упражнения и вопросы
для самопроверки
1. Какие задачи называются позиционными?
2. Вспомните классификацию позиционных
задач.
140
3. Сформулируйте условие первой основной
позиционной задачи. Вспомните алгоритм ее ре-
шения. Когда решение первой основной позици-
онной задачи упрощается и сводится к решению
задачи на принадлежность?
4. Постройте точку L пересечения прямой / с
плоскостью Ф и определите видимость прямой
(рис. 4.53).
Ф(а\\ Ь)
ф — диссекторная
плоскость первой четверти
Рис. 4.55
7. Постройте точки пересечения линии I с
данной поверхностью Ф (рис. 4.56).
Ф-зллипсоид вращения Ф-параболоид
вращения
Ф- цилиндрическая
поверхность
5. Через точку L проведите плоскость Ф, па-
раллельную двум скрещивающимся прямым а, b
(рис. 4.54).
Рис. 4.54
6. Постройте прямую /, пересекающую две
скрещивающиеся прямые а, b и параллельную
третьей прямой т (рис. 4.55).
Рис. 4.56
8. Постройте точки пересечения прямой I с
Рис. 4.57
141
9. Вспомните алгоритм решения второй основ-
ной позиционной задачи. Какие поверхности
обычно используются в качестве посредников
при построении линии пересечения поверхнос-
тей? Вспомните области применения способов
плоскостей уровня, вращающейся плоскости,
концентрических и эксцентрических сфер.
10. Постройте линию I пересечения следую-
щих пар плоскостей Ф, Д (рис. 4.58).
Ф(АВС) , A(EFD)
12. Постройте сечение многогранной поверх-
ности фронтально проецирующей плоскостью Г
и способом совмещения определите натуральную
величину сечения (рис. 4.60).
Рис. 4.60
13. Постройте на трехкартинном чертеже
Монжа и аксонометрическом чертеже линию
пересечения данных призматических поверхнос-
тей (рис. 4.61).
О
Ф(апЬ), А - виссекторна»
плоскость первой четверти
11. Постройте параллельные плоскости Ф, Д,
проходящие через данные скрещивающиеся
прямые а, b (рис. 4.59).
Рис. 4.61
14. Постройте линии пересечения данных
многогранной и криволинейной поверхностей
(рис. 4.62).
Рис. 4.59
142
15. Постройте линии пересечения данных кри-
волинейных поверхностей Ф, Д (рис. 4.63).
Ф(а,Ь, П,) - косая плоскость Ф(!,о)-ояяаптаткт конус
Рис. 4.63
16. Приведите примеры распадения линии
пересечения двух поверхностей второго по-
рядка.
17. Две кривые второго порядка принадле-
жат одной поверхности второго порядка. Имеют
ли эти кривые общие точки? Если да, то
сколько?
18. Постройте недостающую составляющую
линии пересечения поверхностей конуса и ци-
линдра, имеющих общее основание (рис. 4.64).
Рис. 4.64
19. Сформулируйте условие касания линии и
поверхности.
20. Дайте определение условия касания плос-
кости и поверхности, двух поверхностей.
21. Какие точки поверхности называются эл-
липтическими, параболическими и гиперболи-
ческими? Приведите примеры поверхностей,
состоящих из эллиптических, параболических и
гиперболических точек. Существуют ли пове-
рхности, содержащие все типы точек?
22. Сформулируйте теорему о двух точках
соприкосновения.
23. Постройте линии перехода отсека трубоп-
ровода (рис. 4.65).
Рис. 4.65
143
Глава 5
ТЕОРИЯ И АЛГОРИТМЫ
РЕШЕНИЯ МЕТРИЧЕСКИХ ЗАДАЧ
В этой главе систематизируются мет-
рические задачи, решаемые в курсе
начертательной геометрии, концен-
трированно излагаются теория и алго-
ритмы их решения. Метрические зада-
чи отличаются своим разнообразием,
что ведет к определенным трудностям
при изучении алгоритмов их решения.
В инженерной практике встречается
множество метрических задач как на
этапе проектирования и расчета техни-
ческих форм, так и на этапе их изго-
товления (воспроизведения).
При решении той или иной метри-
ческой задачи следует придерживаться
следующей схемы:
- внимательно прочитав условие
задачи, представьте ее исходные дан-
ные в пространстве, используя при
необходимости мелок, резинку в качес-
тве модели точки, карандаш или ли-
нейку в качестве модели прямой и т.д.;
— наметьте последовательность реше-
ния этой задачи в пространстве, пред-
ставьте алгоритм ее решения как набор
алгоритмов решения типовых задач, на
которые можно разложить данную
задачу;
— наметьте алгоритм решения задачи
на чертеже, обратив внимание на вы-
бор рационального решения с точки
зрения простоты и числа графических
построений.
5.1. Классификация
метрических задач
Задачи называются метрическими,
если требуется определить метричес-
кие свойства данной фигуры (длина,
площадь и т.д.) или метрические
свойства, обусловленные ее положе-
нием относительно плоскостей проек-
ций, или, наконец, взаимным положе-
Рис. 5.1
144
нием двух и более фигур (угол между
прямыми и плоскостями, расстояние
между фигурами и т.д.).
В соответствии с этим определе-
нием все метрические задачи, решае-
мые в курсе начертательной геомет-
рии, можно разбить на пять групп
(рис. 5.1).
Первую группу составляют задачи,
связанные с определением метрических
свойств положения данной фигуры от-
носительно плоскостей проекций (рас-
стояние, угол), определяющие пара-
метры положения фигуры. Например,
положение точки относительно плос-
костей координат (проекций) опреде-
ляется ее координатами, положение
прямой можно определить координата-
ми ее следов на плоскостях проекций
или координатами следа на какой-либо
плоскости проекций и углами наклона
к двум плоскостям проекций. В случае
задания плоскостей и поверхностей в
качестве параметров положения высту-
пают метрические характеристики
определяющих их элементов (геомет-
рической части определителя повер-
хности). Например, сфера имеет три
параметра положения — координаты ее
центра. За параметры положения плос-
кости можно принять три отрезка,
отсекаемые плоскостью на осях систе-
мы координат.
Во вторую группу объединены зада-
чи, связанные с определением метрики
фигуры: длины отрезка или дуги, раз-
меров плоской, фигуры, параметров
формы поверхности. Параметрами
формы поверхности принято называть
те ее элементы, которые однозначно
определяют ее форму и размеры. На-
пример, для сферы и цилиндра враще-
ния параметром формы является ве-
личина радиуса, а для трехосного
эллипсоида — величины его полуо-
сей.
В третью группу объединены задачи
по определению взаимного положения
фигур: определение расстояния и угла
между двумя фигурами. Решение боль-
шинства задач этой группы требует
построения нормалей (перпендикуля-
ров) к прямым, плоскостям и повер-
хностям.
Четвертая группа задач связана с
построением разверток поверхностей
(точных, приближенных и условных).
Построение разверток поверхностей
имеет как самостоятельное значение с
точки зрения изготовления их из ли-
стового материала, так и вспомогатель-
ное значение при решении ряда метри-
ческих задач на построение отдельных
линий или сетей линий на поверхнос-
ти. К ним относятся задачи на по-
строение кратчайших (геодезических)
линий, криволинейных фигур с задан-
ными метрическими свойствами, при-
надлежащими той или иной повер-
хности.
В пятую группу выделены задачи на
построение геометрических мест (мно-
жеств) точек, удовлетворяющих опре-
деленным метрическим требованиям. В
трехмерном пространстве такие задачи
сводятся к нахождению точки (точек),
линии или поверхности.
Структурная схема (см. рис. 5.1)
позволяет наглядно и достаточно ин-
формативно представить комплекс
метрических задач, алгоритмами реше-
ния которых должен владеть студент
технического вуза. Решения этих за-
дач сводятся к решению простейших
(базовых) задач. К ним в первую
очередь следует отнести:
— определение натуральной величи-
ны отрезка, заданного своими проек-
циями (определение расстояния меж-
ду двумя точками);
- построение проекций прямой,
перпендикулярной данной плоскости,
или обобщенно - определение угла
между двумя прямыми.
Поэтому изложение теории и алго-
ритмов решения метрических задач
начнем с рассмотрения сформулиро-
ванных задач.
145
5.2. Определение
натуральной
величины отрезка
Теория и алгоритмы решения этой
задачи были рассмотрены ранее:
— способ прямоугольного треугольни-
ка (см. п. 1.1.3 и рис. 1.7);
— способ замены плоскостей проек-
ций (см. п. 3.2.2 и рис. 3.5);
— способ плоскопараллельного дви-
жения (см. п. 3.3.1 и рис. 3.9);
— способ вращения вокруг проециру-
ющей прямой (см. п. 3.4.1 и рис. 3.11).
Перечисленные способы применяют-
ся для определения натуральной вели-
чины отрезка, заданного на чертеже
Монжа. Решение этой задачи на аксо-
нометрическом чертеже выполняется
способами совмещения и замены плос-
кости проекций (см. п. 3.7).
Способ прямоугольного треугольни-
ка представлен в п. 1.1.3 в виде
правила. Конкретизируем это прави-
ло применительно к двухкартинному
чертежу Монжа и рассмотрим пример
(рис. 5.2):
1) натуральная величина отрезка
равна гипотенузе прямоугольного тре-
угольника, построенного на его гори-
зонтальной проекции как на катете:
второй катет этого треугольника ра-
вен разности высот концов отрезка
(рис. 5.2, б);
2) натуральная величина отрезка
равна гипотенузе прямоугольного тре-
угольника, построенного на его фрон-
тальной проекции как на катете; вто-
рой катет этого треугольника равен
разности глубин концов отрезка
(рис. 5.2, б).
Попутно при решении этой задачи
определяются углы наклона данной
прямой к плоскостям проекций:
а — угол наклона прямой АВ к гори-
зонтальной плоскости проекций Пр
Р — угол наклона прямой АВ к фрон-
тальной плоскости проекций П2-
Это правило следует из известного
по программе средней школы опреде-
ления угла наклона прямой к плоскос-
ти как угла, составленного прямой и ее
прямоугольной проекции на эту плос-
кость.
Аналитически длина d отрезка АВ
определяется по формуле
Рис. 5.2
146
d = ^(x2-x1)2 + (y2-y1)2 + (z2-zt)2.
(5.1)
Вывод этой формулы очевиден (см.
рис. 5.2): натуральная величина d =
= LAj В] или d = [Л2В] отрезка АВ
определяется по теореме Пифагора:
d2 = [Л^]2 + [fi]B]2 или d2 =
= [А2В2]2 + [В2В]2, где [AjBj]2 =
= (*2 - Xi)2+ (У2 - У])2; [^В] = z2 -
— Zp ~~ ^2 — + ^2 ’
[В2В] = у2 - У].
5.3. Перпендикулярность
прямых и плоскостей
Алгоритмы построения перпендику-
лярных прямых, прямой и плоскости,
двух, плоскостей основаны на теореме
о прямоугольной проекции прямого
угла (см. п. 1.1.3). Применительно к
двухкартинному чертежу Монжа она
формулируется так:
1) прямой угол проецируется в на-
туральную величину на горизонталь-
ную плоскость проекций Пр если одна
его сторона является горизонталью, а
другая сторона не перпендикулярна
2) прямой угол проецируется в на-
туральную величину на фронтальную
плоскость проекций П2, если одна его
сторона является фронталью, а дру-
гая сторона не перпендикулярна П2.
Пример 1. Построить прямую а,
проходящую через данную точку А
и перпендикулярную горизонтали h
(рис. 5.3).
Так как прямой угол, составленный
прямыми a, h, проецируется в нату-
ральную величину на Пр то построе-
ние проекций искомой прямой а начи-
наем с ее горизонтальной проекции аР
а1 перпендикулярна и проходит
через горизонтальную проекцию А]
точки А.
Положение фронтальной проекции
прямой является неопределенным, так
как задача имеет бесчисленное мно-
жество решений: все прямые, проходя-
щие через точку А и лежащие в гори-
зонтально проецирующей плоскости Ф,
удовлетворяют условию задачи. Среди
них есть только одна прямая а(а^ а2),
пересекающая горизонталь й в точке 1,
а все остальные прямые йЧй/, й2),
удовлетворяя условию задачи, горизон-
таль й не пересекают.
Пример 2. Построить прямую а,
проходящую через данную точку
А и перпендикулярную фронтали /
(рис. 5.4).
Рис. 5.3
147
Рис. 5.4
Так как прямой угол, составленный
прямыми а, /, проецируется в нату-
ральную величину на П2, то построе-
ние проекций искомой прямой а начи-
наем с ее фронтальной проекции а2: ai
перпендикулярна /2 и проходит через
фронтальную проекцию А2 точки А.
Положение горизонтальной проекции
искомой прямой является неопределен-
ным, так как задача имеет бесчислен-
ное множество решений: все прямые,
проходящие через точку А и лежащие
во фронтально проецирующей плоскос-
ти Г, удовлетворяют условию задачи.
Среди множества этих прямых только
одна прямая а(а1У а2) пересекает
фронталь / в точке 1, а все остальные
прямые ft1 (ft/, ft/), удовлетворяя усло-
вию задачи, фронталь / не пересекают.
Рассмотренные примеры можно ис-
толковать так же, как решения следу-
ющих задач:
1) построение проецирующих плос-
костей Ф и Г, проходящих через точку
4 и перпендикулярных соответственно
данной горизонтали h и фронтали /;
2) построение прямых уровня h и /,
перпендикулярных соответственно
проецирующим плоскостям Ф и Г.
Аналитически условие перпендику-
лярности двух прямых в пространстве
следует из свойств скалярного произве-
дения двух векторов. Напомним, что
скалярным произведением двух векто-
ров а , ft называется произведение их
модулей на косинус угла между ними:
а • ft = |а | - |ft | • cos(a ft).
Если данные векторы перпендикуляр-
ны, то cos(a ft) = 0. Поэтому векторы
a(xj, У], zp, ft(x2, у2, z2) будут пер-
пендикулярными, если
а • ft = хгх2 + У]У2 + z{z2 = 0.
Например, прямая а с направляю-
щим вектором а (Хр ур Zj) будет пер-
пендикулярна горизонтали h с направ-
ляющим вектором h (х2, у2, 0), если
*1*2 + JV2 13 °' (5’3)
Так как в условие (5.3) не входит
координата z( вектора а (она может
принимать любое значение), то через
произвольную точку А можно провести
бесчисленное множество векторов {а},
перпендикулярных h (см. рис. 5.3).
При этом перпендикулярность векто-
ров а, h однозначно определяется
перпендикулярностью их проекций на
148
П] (координатную плоскость Оху), так
как в формулу (5.3) входят лишь аб-
сциссы и ординаты этих векторов.
5.3.1. Перпендикулярнсть
прямой и плоскости
Из курса геометрии средней школы
известно, что прямая перпендикуляр-
на плоскости, если она перпендику-
лярна двум любым пересекающимся
прямым этой плоскости.
Это условие нельзя непосредственно
реализовать на чертеже, так как пря-
мые углы, составленные искомым пер-
пендикуляром и произвольными пря-
мыми данной плоскости, не будут про-
ецироваться на П] и П2 в натуральную
величину. Среди этих углов имеются
два, которые спроецируются на плос-
кости проекций П], П2 в натуральную
величину:
1) угол, составленный искомой пря-
мой и горизонталью данной плоскости,
проецируется в натуральную величину
на Пр
2) угол, составленный искомой пря-
мой и фронталью данной плоскости,
проецируется в натуральную величину
на П2.
Поэтому при решении данной задачи
в качестве двух пересекающихся пря-
мых плоскости выбирают не произ-
вольные прямые, а горизонталь h и
фронталь / (рис. 5.5). Тогда условие
перпендикулярности прямой и плос-
кости на чертеже Монжа формулиру-
Рис. 5.5
ется так: прямая перпендикулярна
плоскости, если ее горизонтальная
проекция перпендикулярна горизон-
тальной проекции горизонтали, а
фронтальная проекция — фронталь-
ной проекции фронтали этой плос-
кости.
Это утверждение можно символичес-
ки записать так:
I х Е - Z] х А], 12 1 /2, (5.4)
где h, f с £.
Пример. Построить прямую I э Л,
перпендикулярную плоскости S (а || Ь)
(рис. 5.6).
Рис. 5.6
Сначала в плоскости Е проводим
горизонталь h(hx, h2) и фронталь f(J\,
/2), а затем строим проекции lx х hx и
l2 х /2 искомой прямой Z, где 1Х эЛр
^2 э ^2-
Выполненное решение можно интер-
претировать как построение плоскости
Е, проходящей через точку 1 и перпен-
дикулярной данной прямой Z. Искомая
плоскость S определяется горизонталью
h х Z и фронталью / х Z.
Для аналитической записи условия
перпендикулярности прямой и плос-
кости целесообразно перейти от урав-
нений (2.8) прямой в проекциях к
уравнениям прямой, проходящей через
две данные точки М(хх, У|, z(), 7V(jc2,
Уг> z2>-
149
* = У - У. = 2_±. (5.5)
х2 - *1 У2 - >1 г2 - Z1
Если в уравнениях (5.5) ввести обоз-
начения Z = x2 — Хр т = у 2 — У1. п =
= z2 — 2р то уравнения
х ~ xi = у -У| = z ~ г, (5.6)
I т п
называются симметричными уравнени-
ями прямой. Здесь I, т, п являются
координатами направляющего вектора
прямой MN.
Аналитически условие перпендику-
лярности прямой (5.6) и плоскости
(2.1) записывается так:
L = ™ = 2 (5.7)
АВС
Уравнения прямой, проходящей через
данную точку M(x0, у0, zq) и перпен-
дикулярной плоскости (2.1), имеют
вид
X - = У - Уо = z - zo (5.8)
А В~~ С ’
а уравнение плоскости, проходящей
через точку Л/(х0, у0, zQ) и перпенди-
кулярной прямой (5.6), имеет вид
/(х-х0) + т(у -у0) + n(z -zQ) =0. (5.9)
5.3.2. Перпендикулярность
двух плоскостей
Как известно, две плоскости перпен-
дикулярны, если одна из них прохо-
дит через прямую, перпендикулярную
к другой (рис. 5.7).
Очевидно, через прямую а, перпен-
дикулярную плоскости Г, можно про-
вести к последней бесчисленное мно-
жество плоскостей. Они образуют пу-
чок плоскостей с осью а.
Отсюда следует, что через произ-
вольную точку М пространства прохо-
дит бесчисленное множество плоскос-
Рис. 5.7
тей Ф', перпендикулярных данной
плоскости Г. Они составляют пучок с
осью а, проходящей через точку М и
перпендикулярной плоскости Г. Для
однозначного решения задачи о по-
строении перпендикулярных плоскос-
тей необходимо потребовать, чтобы
искомая плоскость была задана каки-
ми-либо двумя исходными условиями,
например:
— проходила через две заданные
точки;
— проходила через данную прямую;
— была параллельна данной прямой
и проходила через заданную точку и
т.д.
Пример. Построить плоскость Ф,
проходящую через данную прямую а и
перпендикулярную плоскости V(D, к)
Задачу решают в такой последова-
тельности:
1) на прямой а выбирают произволь-
ную точку А;
150
2) через точку А проводят прямую Ь,
перпендикулярную плоскости Г (см.
п. 5.3.1, рис. 5.6);
3) пересекающиеся прямые а, b опре-
деляют искомую плоскость Ф(а г Ь).
Уравнение плоскости Ф, проходящей
через прямую а, заданной симметрич-
ными уравнениями (5.6), и перпенди-
кулярной плоскости Г, заданной урав-
нением вида (2.1), имеет вид
х - х, у - У! Z - Z]
, _ о <5.Ю)
I т п = v.
А В С
Заметим, что если в рассмотренном
примере построить линию а пересече-
ния плоскостей Г и Ф (см. п. 4.4.1), то
прямую а можно считать прямоуголь-
ной проекцией данной прямой а на
плоскость Г. Аналитически прямая а
определяется системой уравнений (2.1)
и (5.10).
5.3.3. Построение
нормали поверхности
Нормалью поверхности называется
перпендикуляр, проведенный к ее
касательной плоскости в точке каса-
ния с поверхностью.
Построение нормалей поверхностей
является распространенной инженер-
ной задачей. Расчет на прочность все-
возможных поверхностей резервуаров,
архитектурно-строительных оболочек
и т.д.; разработка управляющих про-
грамм сверления, фрезерования торцо-
выми фрезами технических поверхнос-
тей; расчет кинематики и динамики
движения тел по направляющим по-
верхностям и многие другие задачи
требуют построения нормалей повер-
хностей.
Графическое построение нормали п
поверхности Ф в некоторой ее точке А
сводится к последовательному реше-
нию двух задач:
1) построение в точке А поверхности
Ф касательной плоскости Т (см.
п. 4.10.2);
2) восставление из точки А плоскос-
ти Т перпендикуляра п (см. п. 5.3.1).
Пример. Построить нормаль п в точ-
ке А сферы Ф(О, R) (рис. 5.9).
Рис. 5.9
Сначала через точку А проводим
касательную плоскость Т к данной
сфере Ф (см. п. 4.10.2, пример 1)*.
Плоскость Т определяется горизон-
талью Л(ЛР Л2) и фронталью /(/р /2),
касающимися в точке А соответственно
окружностей а, b — сечений поверхнос-
ти Ф плоскостями уровня, проходящи-
ми через точку А. Затем в точке А
восставляем перпендикуляр п(п1 ±
п2 ± /2) к плоскости Т. Прямая п явля-
ется искомой нормалью.
Уравнение нормали п имеет вид
(5.8), где х0, у0, — координаты точ-
ки А, удовлетворяющие уравнению
сферы Ф:
Заметим, что в этом примере в силу простоты
данной поверхности не было необходимости в
выполнении всех описанных построений. Оче-
видно, что все нормали сферы проходят через ее
центр О. Поэтому достаточно было построить
проекции нормали как прямой, проходящей
через точки О и А.
151
2 2 2 п 2
x + у +z = R ,
А, В, С — коэффициенты при неизвес-
тных в уравнении (4.1) касательной
плоскости Т.
В нашем случае А = = 2х0, В =
= = 2у0, С = = 2z0. Таким обра-
зом, уравнение искомой нормали п
имеет вид
х - х0 = у - >'о z - z0
~ Уо ~~о
5.4. Линия
наибольшего
наклона
Как было отмечено во второй главе,
поверхности (плоскости) содержат се-
мейства линий, характеризующие их
положение относительно плоскостей
проекций. Это — семейства линий
уровня поверхностей (плоскостей), ко-
торые получаются в результате их
сечения плоскостями уровня. Кроме
линий уровня положение поверхности
(плоскости) относительно плоскостей
проекций характеризуют линии наи-
большего наклона. Например, любая
плоскость общего положения содержит
прямые, которые составляют с той или
иной плоскостью проекций наиболь-
ший угол. Аналогично, через произ-
вольную точку какой-либо поверхнос-
ти в общем случае проходят три ли-
нии, каждая из которых составляет с
соответствующей плоскостью уровня
наибольший угол. Точнее, касатель-
ные, проведенные в данной точке к
указанным кривым, составляют с соот-
ветствующими плоскостями проекций
максимальный угол. Такие линии (в
частности, прямые) называются линия-
ми наибольшего наклона поверхности
(плоскости) к той или иной плоскости
проекций.
Линия наибольшего наклона к гори-
зонтальной плоскости проекций назы-
вается линией ската или линией наис-
корейшего спуска. Эти названия под-
черкивают их физическую сущность:
например, траектория шарика, катя-
щегося по поверхности под воздействи-
ем его веса, является линией ската.
Линии наибольшего наклона имеют
широкое применение в различных
областях науки и техники. Например,
в курсе начертательной геометрии с их
помощью определяют углы наклона
данной плоскости к плоскостям проек-
ций; в математическом программиро-
вании при решении всевозможных
задач оптимизации (метод наискорей-
шего спуска) они применяются для
определения максимумов или миниму-
мов функций многих переменных; в
инженерной практике они применяют-
ся при прокладке осей дорог, трубопро-
водов и т.д.
5.4.1. Линии наибольшего
наклона плоскости
Алгоритм построения линии наиболь-
шего наклона плоскости основан на
справедливости следующей теоремы.
Теорема. Прямые плоскости, пер-
пендикулярные ее линиям уровня,
являются линиями наибольшего на-
клона к соответствующим плоскостям
проекций.
Теорема утверждает, что линии наи-
большего наклона плоскости к П1 пер-
пендикулярны ее горизонталям, линии
наибольшего наклона к П2 — фронта-
лям и, наконец, линии наибольшего
наклона к П3 — профильным прямым
уровня.
Докажем справедливость этой теоре-
мы применительно к линиям наиболь-
шего наклона к Пр Пусть в плоскости
Ф через ее точку А проведены две пря-
мые: прямая АВ, перпендикулярная
горизонтали Л с Ф, и произвольная
прямая АС (рис. 5.10). Покажем, что
152
Рис. 5.10
угол 0, составленный прямой АВ с
плоскостью проекций П], больше угла
у наклона прямой АС к П., т.е. прямая
АВ является линией наибольшего на-
клона плоскости Ф к плоскости проек-
ций Пр
Как известно, углы 0 и у составлены
данными прямыми АВ, АС и их прямо-
угольными проекциями АуВ^, на
Пр На рис. 5.10 точки В, С совпадают
с их проекциями Blt С1( так как они
выбраны на горизонтали нулевого
уровня Л“ = Ф п Пр
По теореме о проецировании прямого
угла (см. п. 1.1.3) прямой угол, состав-
ленный перпендикулярными прямыми
АВ и h°, проецируется на П] в нату-
ральную величину: /А1В1С1 = 90°.
Повернем прямоугольный треуголь-
ник АА}В вокруг его катета АА^ до
совмещения с плоскостью треугольника
А4]С. Совмещенное положение В
вершины В находится внутри отрезка
/ЦСр так как в прямоугольном треу-
гольнике А^В^С) катет [AjBJ = [тЦВ]
меньше гипотенузы [AjCJ. Отсюда
следует, что угол 0 = /.АВА} будет
больше угла у = ZACAt как внешний
угол треугольника АС В. Теорема до-
казана.
Аналогично доказывается, что пря-
мая плоскости Ф, перпендикулярная
фронтали f <= Ф или профильной пря-
мой уровня р <= Ф, является линией
наибольшего наклона плоскости Ф со-
ответственно к П2 или П3.
Пример. В плоскости Ф (А, В, С) по-
строить линию I наибольшего наклона
к П2, проходящую через точку В
(рис. 5.11).
Искомая линия I в соответствии с
доказанной теоремой должна быть
перпендикулярной фронтали / плоскос-
ти Ф. Поэтому алгоритм решения зада-
чи состоит из следующих операций:
1) в плоскости Ф строим фронталь
/(ГР/2>;
2) через точку В в плоскости Ф про-
водим прямую I, перпендикулярную
фронтали /: В2 е /2 ± /2, /2 = B}2V
Аналитически линии наибольшего
наклона плоскости определяются сис-
темой двух уравнений:
1) уравнения (2.1) данной плоскости
Ф;
2) уравнения (5.9) плоскости, пер-
пендикулярной соответствующей пря-
мой уровня (5.6) и проходящей через
данную точку.
При этом в уравнении (5.6) прямой
уровня одна из координат направляю-
щего вектора будет равна нулю (в
случае горизонтали — п = 0, фронтали
— «1 = 0, профильной прямой уровня —
I = 0). Кроме того, координаты х,, у,,
Zj точки, через которую проходит тре-
буемая по условию задачи линия уров-
ня, и координаты х0, у0, z0 точки,
153
принадлежащей искомой линии наи-
большего наклона, должны удовлет-
ворять уравнению (2.1)данной плос-
кости Ф.
5.4.2. Линии наибольшего
наклона поверхности
Линии наибольшего наклона повер-
хностей представляют собой в общем
случае пространственные кривые. Гра-
фически они строятся по точкам. Су-
ществующие вычислительные способы
их построения реализуют графические
алгоритмы.
Алгоритм построения состоит из сле-
дующих операций:
1) на поверхности строится семей-
ство соответствующих линий уровня;
их число определяется исходя из за-
данной точности построения точек ис-
комой линии;
2) в данной точке поверхности к
проходящей через нее линии уровня
строим перпендикуляр, который теоре-
тически лежит в касательной плоскос-
ти, проведенной к поверхности в дан-
ной точке:
3) допуская, что каркас линий уров-
ня построен достаточно плотно, нахо-
дим точку пересечения построенного
перпендикуляра с соседней линией
уровня ;
4) в построенной точке выполняем
операции п. 2; этот процесс продолжа-
ется до тех пор, пока не будут по-
строены точки искомой линии наи-
большего наклона на всех линиях
уровня данной поверхности.
Сказанное проиллюстрируем на кон-
кретных примерах.
Пример 1. Построить на косой плос-
кости Ф(о, Ь, Пр линию наибольшего
Теоретически указанные линии не пересека-
ются. Для практической реализации алгоритма
перпендикуляр, принадлежащий касательной
плоскости, заменяют хордой (секущей) данной
поверхности.
Рис. 5.12
наклона I к горизонтальной плоскости
проекций, проходящую через точку
М е Ф (рис. 5.12).
Сначала построим каркас образую-
щих данной поверхности, которые
являются ее горизонталями. Поэтому
построение линии наибольшего накло-
на начинаем с построения ее гори-
зонтальной проекции, так как пря-
мые углы, составленные образующими
поверхности и хордами искомой ли-
нии наибольшего наклона, проеци-
руются на IIj в натуральную вели-
чину.
Горизонтальную проекцию иско-
мой линии строим как ломаную
... стороны которой перпенди-
кулярны горизонтальным проекциям
образующих косой плоскости, проходя-
щих через соответствующие вершины
ломаной. Фронтальная проекция Z2
строится из условия принадлежности
линии наибольшего наклона I данной
поверхности Ф.
Пример 2. На циклической повер-
хности Ф(/, т, П2) построить линию
наибольшего наклона I к фронтальной
плоскости проекций, проходящую че-
рез точку М е Ф (рис. 5.13).
Данная поверхность образована дви-
жением окружности т постоянного
радиуса, центр О которой перемещает-
ся по кривой /, а плоскость окружности
остается при ее движении параллель-
154
Рис. 5.13
ной П2. На рис. 5.13 построен каркас
окружностей {т}.
Построение проекций /2 искомой
линии наибольшего наклона сводится
к построению заменяющей (аппрокси-
мирующей) ее ломаной линии М12...
Каждая сторона этой ломаной должна
быть перпендикулярной соответствую-
щей образующей поверхности, точнее,
касательной Z, проведенной к образую-
щей в вершине искомой ломаной.
Так как образующие т‘ поверхности
Ф являются ее фронталями, то прямые
углы, составленные сторонами ломаной
и касательными проецируются без
искажения на П2. Поэтому сначала
строим фронтальную проекцию
М2/222... искомой ломаной:
— сторона Л/2/2 перпендикулярна
касательной /2, проведенной к проек-
ции т2 образующей в точке М2 (пря-
мая М212 проходит через центр О2
окружности т2);
— фронтальную проекцию 12 следую-
щей вершины ломаной получаем как
точку пересечения прямой О2М2 с
проекцией соседней образующей.
Аналогично строим фронтальные
проекции остальных вершин ломаной
М12. Ее горизонтальную проекцию
строим из условия принадлежности
вершин ломаной данной поверхно-
ти Ф.
В заключение заметим, что построе-
ние линий наибольшего наклона слож-
ных поверхностей, встречающихся в
инженерной практике, выполняется
по описанному алгоритму с примене-
нием современной вычислительной
техники.
5.5. Алгоритмы
решения типовых
метрических задач
В этом разделе рассмотрим алгоритм
решения метрических задач, относя-
щихся к первым трем группам класси-
фикации (см. рис. 5.1).
5.5.1. Положение фигуры
относительно
плоскостей проекций
Метрические задачи, включенные в
эту группу, сводятся к определению
расстояний от данных фигур или их
элементов до плоскостей проекций,
осей и начала координат, а также
углов наклона данных фигур к плос-
костям проекций и осям координат.
Очевидно, можно говорить о расстоя-
нии геометрической фигуры до плос-
кости проекций, если она является
фигурой уровня, т.е. речь может идти
лишь о расстоянии точки до плоскости
проекций, прямой и плоскости уровня
до соответствующей плоскости проек-
ций. Таким образом эти задачи связа-
ны лишь с чтением чертежа и решают-
ся без вспомогательных построений:
— измерением координат данной точ-
ки относительно выбранных плоскос-
тей проекций (см. рис. 1.10; 1.14);
— измерением расстояния прямой
или плоскости уровня до соответствую-
щей плоскости проекций;
155
— измерением расстояния проециру-
ющей прямой до двух плоскостей про-
екций.
Расстояние от прямой уровня до
соответствующей плоскости проекций
на чертеже Монжа определяется изме-
рением расстояния от соответствующей
оси координат до параллельной ей
проекции линии уровня. Расстояние от
прямой уровня до соответствующей
плоскости проекций на чертеже Монжа
определяется измерением расстояния
от соответствующей оси координат до
параллельной ей проекции линии
уровня. Расстояние между плоскостью
уровня и соответствующей плоскостью
проекций измеряется между вырож-
денной проекцией плоскости и парал-
лельной ей осью координат. Расстоя-
ние от проецирующей прямой до соот-
ветствующих плоскостей проекций
измеряется между се вырожденной
проекцией и осями координат, лежа-
щими в соответствующей плоскости
проекций.
Пример 1. В плоскости 2(а || Ь) по-
строить линию, отстояющую от гори-
зонтальной плоскости проекций на
Искомой линией является горизон-
таль Л. Ее фронтальная проекция Л2
параллельна оси Ох и отстоит от нее
на данное расстояние 20 мм. Горизон-
тальную проекцию Л] строим из усло-
вия принадлежности прямой h плоскос-
ти 2: h с S «• h, S э 1, 2.
Пример 2. На конической поверхнос-
ти Ф(5, а) построить точку М, абсцисса
хм и ордината ум которой известны
Горизонтальную проекцию точки
М строим по ее известным координа-
там. Фронтальную проекцию М2 стро-
им из условия принадлежности точки
М поверхности конуса Ф: М е Ф М е
е S1 с Ф.
При решении некоторых задач тре-
буется определить расстояния от точки
до какой-либо оси координат или нача-
ла координат, от прямой или плоскос-
ти до начала координат, от проециру-
ющей прямой или плоскости до соот-
ветствующей (параллельной) оси коор-
динат. Часть этих задач решается до-
статочно просто. Например, расстояние
от точки до какой-либо оси координат
измеряется длиной отрезка, соединяю-
щего начало координат с проекцией
точки на перпендикулярной данной
оси плоскости проекций. Расстояние
между проецирующей прямой и парал-
лельной ей осью координат равно дли-
не отрезка, соединяющего ее вырож-
денную проекцию с началом коорди-
нат. Определение расстояния от точки
до начала координат сводится к по-
строению натуральной величины от-
резка.
Сложнее решаются задачи на опре-
деление кратчайшего расстояния от
прямой или плоскости до начала коор-
156
динат. Для этого необходимо из точки
О опустить перпендикуляр на данную
прямую или плоскость, найти основа-
ние А перпендикуляра и определить
натуральную величину отрезка О А.
Графическое решение таких задач бу-
дет рассмотрено в п. 5.5.3.
Аналитически расстояние от начала
кординат О до плоскости, заданной
уравнением вида (2.1), вычисляется по
формуле
d = |Р| (5.11)
у/а1 + в2 + с2
а до прямой, заданной уравнениями
вида (5.6), — по формуле
а а у у
АЛАА
/ЦП2, /П[ =/2х12’/^3 = -^2 z23'
Положение геометрической фигуры
или ее элементов относительно плос-
костей проекций характеризуется так-
же углами, составленными фигурой с
плоскостями проекций или с осями
координат. В трехмерном пространстве
к таким фигурам относятся прямые и
плоскости.
Угол между прямой а и плоскостью
проекции П( измеряется углом, состав-
ленным данной прямой а и ее проек-
цией а, на эту плоскость проекций.
Проецирующая прямая, как следует
из ее определения, перпендикулярна
одной из плоскостей проекций и па-
раллельна двум другим. Прямая уров-
ня параллельна одной плоскости про-
екций. Поэтому углы, составленные ею
с другими плоскостями проекций, про-
ецируются без искажения на парал-
лельную плоскость проекций:
Р Р Y Y
АЛЛА
Л ||Пр ЛП2 = Aj Х|2, ЛП3 = Л] у13
(рис. 5.16);
а а Р Р
АЛАА
р || П3, рП| = р3у31, рП2 -- p3z32.
Построение натуральной величины
угла, составленного прямой общего
положения и какой-либо плоскостью
проекций, можно выполнить:
1) способом прямоугольного треу-
гольника (см. п. 5.2 и рис. 5.2);
2) преобразованием данной прямой в
прямую уровня способами замены
плоскости проекций (п. 3.2), плоско-
параллельного движения (п. 3.3) и
вращения вокруг проецирующей пря-
мой (п. 3.4).
Аналитически величина угла у, со-
ставленного прямой общего положе-
ния, заданной уравнениями (5.6), и
какой-либо плоскостью проекций, вы-
числяется по формуле
siny
| Al + Вт + Сп |
yjl2 + т2 + п2
(5.13)
в которой А = В = О, С = 1 — в случае
горизонтальной плоскости проекций
ПрА = С = 0, В = 1 — в случае П2; А =
= 1,В = С = 0 — в случае П3.
157
Определение угла между данной
прямой I и какой-либо осью координат,
которые в общем случае являются
скрещивающимися, выполняется в
такой последовательности:
1) через начало координат проводит-
ся прямая I, параллельная данной
прямой I;
2) прямая I вращением вокруг оси
координат, угол наклона к которой
определяется, совмещается с одной из
плоскостей проекций, проходящих
через эту ось;
3) угол <р, составленный совмещен-
ной прямой / и осью вращения, будет
искомым.
На рис. 5.17 показано определение
по описанному алгоритму натуральной
величины угла ф, составленного пря-
мой общего положения I с осью коор-
динат Оу.
Рис. 5.17
Следует заметить, что описанный
алгоритм является графически самым
простым, но не единственным. Он
лишь реализует один из возможных
вариантов определения угла ф, состав-
ленного двумя скрещивающимися пря-
мыми а, Ь. Как известно, искомый угол
Ф равен углу между пересекающимися
прямыми а, Ь, параллельными дан-
ным. Поэтому выбор положения пря-
мых а, b и способа определения нату-
ральной величины угла ф, составленно-
го ими, многовариантен и зависит от
факторов, влияющих на простоту гра-
фических построений.
Аналитически углы а, р, у, образуе-
мые прямой общего положения соот-
ветственно с осями Ох, Оу, Oz, вычис-
ляются по следующим формулам:
I
cosa = —----------------;
x]l2 + т2 + п2
п т
cosp = ; (5.14)
jl2 + т2 + п2
п
cosy = ——— .
Jl2 + т2 + п2
Угол наклона i|r данной плоскости Ф
к какой-либо плоскости проекций П(-
определяется предварительным постро-
ением в плоскости Ф линии наибольше-
го наклона т к этой плоскости проек-
ций П-. Угол, составленный линией
наибольшего наклона и ее проекций на
Пр является линейным углом искомого
двугранного угла т|г между плоскостью
Ф и плоскостью проекций П;. Поэтому
алгоритм определения угла состоит из
следующих операций:
1) в плоскости Ф строится линия
наибольшего наклона т к плоскости
проекций П(;
2) любым известным способом опре-
деляется натуральная величина угла
наклона ф прямой т к плоскости про-
екций Пр
3) угол ф является искомым углом
наклона плоскости Ф к плоскости про-
екций Пр
На рис. 5.18 показан пример постро-
ения натуральной величины угла ф на-
клона плоскости Ф (А, а) к горизонталь-
ной плоскости проекцй Пр
Сначала в плоскости Ф построена ли-
ния наибольшего наклона А2 к Пр
A]2j j. Л] с Ф. Затем способом прямоу-
158
Рис. 5.18
гольного треугольника определена
натуральная величина \2^А | отрезка
А2 построеной линии наибольшего
наклона. Угол т|г, составленный прямой
А2 и ее проекцией А^2{ на Пр равен
искомому двугранному углу, состав-
ленному плоскостями Ф и Пр
Если же данная плоскость Ф является
проецирующей, то она перпендикуляр-
на одной плоскости проекций П,, а
углы наклона к двум другим плоскос-
тям проекций определяются без вспо-
могательных построений: они равны
углам, составленным ее вырожденной
проекцией Ф( с осями координат, лежа-
щими в плоскости проекций П-. Поэто-
му определение угла наклона плоскос-
ти общего положения Ф к какой-либо
плоскости проекций П(- можно выпо-
лнить преобразованием данной плос-
кости в проецирующую. При этом
плоскость Ф надо сделать проецирую-
щей относительно любой плоскости
проекций, отличной от П;-.
Аналитически углы наклона плоскос-
ти Ф, заданной уравнением вида (2.1),
к плоскостям проекций Пр П2, П3 вы-
числяются по формулам:
cos а = ± — ;
у/а2 4 в2 + С2
cos0 = ± ——-д — ; (5.15)
у/А2 + в2 + с2
cosy = ± — .
у)А2 + в2 + с2
И, наконец, рассмотрим алгоритм
определения углов наклона плоскости
общего положения Ф к осям координат.
Эту задачу можно решить нескольки-
ми способами. Наиболее простыми
являются два.
Первый способ основан на построе-
нии прямоугольных проекций осей
координат на данную плоскость и из-
мерении углов, составленных осями
координат и их прямоугольными про-
екциями на эту плоскость. Этот способ
состоит из следующих операций:
1) решая первую позиционную зада-
чу, строим точки X, Y, Z пересечения
плоскости Ф с осями координат Ох, Оу,
Oz;
2) из начала координат О опускаем
перпендикуляр q на плоскость Ф и
находим его основание Q = q л Ф на Ф;
3) любым известным способом (см.
главу 3) определяем натуральные ве-
личины искомых углов а = LOXQ, Р =
= LOYQ, у = ZOZQ.
Примеры графического решения за-
дач такого типа будут рассмотрены в
разделе 5.5.3.
Второй способ основан на преобразо-
вании данной плоскости в проецирую-
щую вращением ее вокруг осей коор-
динат, ибо в повернутом положении
искомый угол будет составлен вырож-
денной проекцией плоскости и осью
вращения.
Проиллюстрируем этот способ на
примере определения угла наклона у
плоскости общего положения Ф(А л t)
к оси Oz (рис. 5.19).
Сначала построим точку Z пересече-
ния оси Oz с плоскостью Ф. Для этого
найдем следы 1 = h л П2, 2 = t л П2
прямых h и t на П2 и, значит, след 12
плоскости Ф на П2: 12 = Ф л П2. Прямая
12 пересекает ось Oz в искомой точке
Z = Oz л Ф.
159
Рис. 5.19
Затем вращением вокруг оси Oz
плоскость Ф сделаем фронтально про-
ецирующей. Для этого необходимо
повернуть горизонталь h с Ф во фрон-
тально проецирующее положение
А х П2 (А| х -*12)- Тогда плоскость Ф
станет фронтально проецирующей и ее
вырожденная проекция Ф2 проходит
через точки Z2 = Z и К. Угол у, со-
ставленный z2 и Ф2, будет искомым.
Аналитически углы а, р, у наклона
плоскости Ф, заданной уравнением
вида (2.1), соответственно к осям коор-
динат Ох, Оу, Oz вычисляются по фор-
мулам:
sin а = т А — ;
7л2 * в2 + с2
sinp = т -; (5.16)
у/А2 + В2 + С2
sin у = т — — —,
у/a2 + В2 + С2
где верхние знаки берутся, если в
уравнении (2.1) свободный член боль-
ше нуля, а нижние, если свободный
член меньше нуля.
5.5.2. Метрика фигуры
Задачи по определению размеров
(метрики) геометрической фигуры
можно разбить на три подгруппы (см.
рис. 5.1):
1) определение длины отрезка (сто-
роны многоугольника, ребра многог-
ранника и т.д.);
2) определение размеров плоской
фигуры (площади, величины угла и
др.);
3) определение параметров формы
геометрических фигур (поверхностей,
многогранников и т.д.).
В эти группы не включены задачи по
вычислению объемов тел, площадей
отсеков поверхностей, так как они
выполняются по известным формулам
курса стереометрии или методами диф-
ференциального и интегрального ис-
числения, изучаемыми в курсе матема-
тического анализа. Например, задача
вычисления объема V и площади 5
поверхности шара сводится к определе-
нию его радиуса R, так как они вычис-
ляются по известным формулам: V =
= 5 = 4яЛ2. Таким образом,
решение такого типа задач сводится к
определению параметров формы или,
другими словами, размеров определяю-
щих фигуру элементов с последующи-
ми аналитическими расчетами.
Алгоритмы графического и аналити-
ческого решения задач первой под-
группы были рассмотрены в разде-
ле 5.2. Решения задач второй подгруп-
пы выполняются изученными в треть-
ей главе способами преобразования
чертежа. Алгоритмы решения задач
третьей группы сводятся к алгоритмам
решения типовых метрических задач,
связанных с построением перпендику-
лярных прямых и плоскостей, опреде-
лением натуральных величин отрезков
и плоских фигур.
Пример 1. Построить центр О опи-
санной вокруг треугольника АВС
окружности (рис. 5.20).
160
Рис. 5.20
Способом плоскопараллельного дви-
жения (см. п. 3.3.1) плоскость треу-
гольника АВС преобразовываем в плос-
кость уровня. Построив биссектрисы
двух углов треугольника, находим
точку О (C>i, О2 > их пересечения —
центр вписанной окружности. Обрат-
ным преобразованием находим сначала
проекции О], О2 > а затем проекции
Ор О2 искомой точки на исходном
чертеже. На втором этапе обратного
преобразования для построения гори-
зонтальной проекции Oj точки О через
нее в плоскости треугольника проведе-
на прямая А2 (на рис. 5.20 построены
лишь ее горизонтальные проекции
А^2j, Х|2|).
Пример 2. Определить величину
радиуса R сферы Ф с центром О, каса-
ющейся данной плоскости Т(а n Z>)
(рис. 5.21). Построить очерковые ли-
нии сферы.
Радиус R для сферы Ф является пара-
метром формы. Для решения задачи
необходимо из точки О опустить пер-
пендикуляр / на плоскость Т, построить
точку пересечения М = I n Т и опреде-
лить натуральную величину отрезка
[СШ] = R.
Задачу решим способом замены
плоскостей проекций (см. п. 3.2.2).
Плоскость Т общего положения преоб-
разуем в проецирующую плоскость
заменой фронтальной плоскости проек-
ций П2 на новую П2. Для этого новую
фронтальную плоскость проекций П2
выбираем перпендикулярно горизонта-
ли h плоскости Т(Л] ± х)2). Из проек-
ции О2 центра О на П2 опускаем пер-
пендикуляр Z2 на вырожденную проек-
цию Т2 плоскости Т на П2. Отрезок
Рис. 5.21
161
ральной величине радиуса R искомой
сферы Ф.
Очерковые линии сферы Ф на Пр П2
описываем из проекций Ор О2 центра
О радиусом R = [ О2М2 ].
5.5.3. Взаимное
положение фигур
В этой подгруппе объединены задачи
на определение расстояний между
точкамй, прямыми и поверхностями
(плоскостями) и углов, составленных
прямыми, кривыми линиями, плоскос-
тями и поверхностями.
Определение расстояний между дву-
мя точками; точкой и прямой; точкой
и плоскостью; между параллельными
прямыми, параллельными прямой и
плоскостью, двумя параллельными
плоскостями сводится к определению
натуральной величины отрезка, состав-
ленного данными точками; точкой и
основанием перпендикуляра, опушен-
ного из точки на данную прямую или
плоскость; основаниями общего пер-
пендикуляра, проведенного к данным
параллельным прямыми и плоскостям.
Когда говорят об определении рассто-
яния между двумя скрещивающимися
прямыми, имеют в виду построение
кратчайшего расстояния между бли-
жайшими точками данных прямых,
т.е. между основаниями их общего
перпендикуляра. Распространенной
задачей является определение точки
(точек) какой-либо поверхности Ф,
наиболее близко расположенной к
данной точке М или расположенных
на данном расстоянии от данной точки
М. Когда рассматривают взаимное
положение линии и поверхности или
двух поверхностей, которые не пересе-
каются в действительных точках или
по действительным линиям, возникает
задача определения их минимального
расстояния, под которым понимается
расстояние между их ближайшими
точками. Например, подобная задача
решается при управлении воздушным
движением в районе аэропорта — во
избежание столкновения самолетов
контролируется минимальное расстоя-
ние между областями (трехосными
эллипсоидами) вероятного их располо-
жения.
Определение углов между двумя
пересекающимися или скрещивающи-
мися прямыми, прямой и плоскостью,
двумя плоскостями сводится к построе-
нию натуральной величины плоского
угла, составленного соответственно
данными пересекающимися прямыми
или пересекающимися прямыми, па-
раллельными данным скрещивающим-
ся прямым, прямой и ее прямоуголь-
ной проекцией на данную плоскость,
прямыми, по которым пересекаются
данные плоскости с перпендикулярной
им плоскостью.
Когда говорят об углах, составлен-
ных кривыми линиями и поверхностя-
ми, имеют в виду углы, образованные
касательными прямыми и плоскостями.
Так, например, угол между двумя
кривыми линиями в их общей точке
измеряется углом, составленным каса-
тельными прямыми, проведенными в
их общей точке к данным кривым ли-
ниям. Угол между кривой линией и
поверхностью в их общей точке равен
углу, составленному касательными
прямой и плоскостью, построенными в
этой точке соответственно к кривой
линии и поверхности.
Рассмотрим примеры решения мет-
рических задач, характеризующих вза-
имное положение двух геометрических
фигур.
Пример 1. Определить расстояние
от точки О до плоскости Т(а п Ь)
(рис. 5.22).
Простейшее решение этой задачи
состоит из следующих этапов:
1) через точку О проводим прямую
I, перпендикулярную данной плоскости
Т (см. п. 5.3.1);
162
2) строим точку М пересечения пря-
мой I с плоскостью Т (см. п. 4.2.2);
3) способом прямоугольного треу-
гольника определяем натуральную
величину [О2М'] отрезка ОМ (см.
п. 5.2).
Другое решение этой задачи, осно-
ванное на использовании способа заме-
ны плоскости проекций, было показано
на рис. 5.21. Здесь упрощение построе-
ний достигнуто предварительным пре-
образованием данной плоскости общего
положения Т в проецирующую плос-
кость. Очевидно, этот же эффект до-
стигается применением других рас-
смотренных в гл. 3 способов преобразо-
вания чертежа.
Аналитически расстояние d от точки
О(Х[, ур Zj) до плоскости Т(Лх + By +
+ Cz + D = 0) вычисляется по фор-
муле
d , w. •».-5'. •-£! (5Л7)
Ул2 + в2 + с2
Ранее приведенная формула (5.11)
является частным случаем форму-
Рис. 5.22
лы (5.17), в которой = у, = zt =
= 0.
Пример 2. Определить расстояние от
точки А до прямой т (рис. 5.23).
Эта задача без применения преобра-
зований чертежа решается в такой
последовательности:
1) через данную точку А проводим
плоскость Д(й п /), перпендикулярную
даной прямой m(h{ ± mlt f2 J- т2);
2) строим точку пересечения М пря-
мой т с построенной плоскостью Д;
3) отрезок АМ(А,МХ; А2М2) будет
искомым; на рис. 5.23 его натуральная
величина [А'М2] построена способом
прямоугольного треугольника.
Очевидно, для решения этой задачи
можно использовать рассмотренные в
гл. 3 преобразования. Тогда возможны
два варианта решения.
1. Преобразовав данную прямую
общего положения в прямую уровня,
имеем возможность непосредственного
построения проекций отрезка, опре-
деляющего расстояние от данной точки
до данной прямой, с последующим
определением его натуральной вели-
чины.
163
ного треугольника определяем его на-
туральную величину [А'М2].
2. Преобразовав любым известным
способом плоскость, определяемую
данными точкой и прямой, в плоскость
уровня, решаем на преобразованном
чертеже простую планиметрическую
задачу определения расстояния от
точки до прямой.
Аналитически длина перпендикуля-
ра, опущенного из данной точки А(х0,
у0, z0) на данную прямую, представ-
ленную уравнениями вида (5.6), вы-
числяется по формуле
На рис. 5.24 показано решение этой
задачи способом замены плоскости
проекций. Выбрав новую фронтальную
плоскость проекций П2 параллельно
данной прямой m(x12 II wij), строим
проекции А2 и т2 данных фигур на
плоскость П2. Так как в системе Щ —
— П2 прямая т является линией уров-
ня, то непосредственно строим проек-
ции А2М2, A}Mi отрезка AM, опреде-
ляющего расстояние от точки А до
прямой т. Обратным преобразованием
находим фронтальную проекцию
этого отрезка и способом прямоуголь-
Эта формула обобщает ранее приве-
денную формулу (5.12), в которой х0 =
= Уд = zo = °-
Пример 3. Определить кратчайшее
расстояние между двумя скрещиваю-
щимися прямыми АВ, CD (рис. 5.25).
Решение задачи сводится к построе-
164
нию общего перпендикуляра MN к
данным скрещивающимся прямым. Эта
задача решается на проекционном
чертеже в том случае, если одна из
данных прямых будет проецирующей.
Поэтому на рис. 5.25 прямые АВ и CD
способом плоскопараллельного переме-
щения без нарушения их взаимного
положения преобразованы так, что
после двух последовательных переме-
щений (сначала относительно П{, а за-
тем относительно П2) прямая АВ стала
горизонтально проецирующей, а пря-
мая CD осталась прямой общего поло-
жения.
На преобразованном чертеже по-
строен общий перпендикуляр MN
к данным прямым: х С] Dp так
как CD является горизонталью,
M2N2 х А2В2, так как АВ параллель-
на фронтальной плоскости проекций.
Искомый отрезок MN проецируется
без искажения на Пр так как он па-
раллелен Пр Обратным преобразовани-
ем отрезок MN последовательно ото-
бражается на MN и далее на MN (на
рис. 5.25 перемещения точек М -
- М - М и Л' - Д' - Л' показаны
стрелками).
Аналитически кратчайшее расстоя-
ние d между двумя скрещивающимися
прямыми, заданными уравнениями:
х - X, _ у - у, z - z,.
X - х2 = у - у2 = z - z2
12 «2 ’
вычисляется по формуле
d =
Кг2 ~
l/fal х а2)2
(5.20)
где rj (%р ур zp, r2 (Xj, у2, z2) — ради-
усы-векторы каких-либо точек, при-
надлежащих соответственно данным
прямым; (/р Щр пр, а2(12, т2, п2)
— направляющие векторы данных пря-
мых.
Пример 4. Определить кратчайшее
расстояние между точками сферы Ф(О,
R) и конической поверхности враще-
ния ДО, о) (рис. 5.26).
Отрезок MN, где М е Д, N е Ф, сое-
диняющий ближайшие точки данных
поверхностей, лежит в их общей плос-
кости симметрии Г(О, j) и принадле-
жит прямой, проходящей через центр
О сферы и перпендикулярной образую-
щей а конической поверхности Д, где
а = Д л Г. Заметим, что из двух обра-
зующих, по которым плоскость Г пере-
секает коническую поверхность Д,
выбирается та, которая ближе к
точке О.
Решение этой задачи упрощается,
если воспользоваться способом враще-
ния вокруг проецирующей прямой.
Вращением вокруг оси j конической
165
поверхности Д плоскость Г преобразуем
в плоскость уровня Г. Тогда плоскость Г
пересекает сферу по очерковой окруж-
ности I, а коническую поверхность А
— по очерковой образующей а. Пер-
пендикуляр [ ОМ ], проведенный через
центр О повернутой сферы Ф к очер-
ковой образующей а конической по-
верхности Д, пересечет эти поверхнос-
ти в ближайших точках М е Д, N е
Ф. Искомое кратчайшее расстояние
проецируется без искажения
на П2. Обратным вращением отрезка
MN получаем проекции
\M2N^ искомого отрезка MN на ис-
ходном чертеже.
Пример 5. Определить натуральную
величину угла а, составленного двумя
скрещивающимися прямыми а, Ъ (рис.
Угол между двумя скрещивающими-
ся прямыми равен углу, составленному
пересекающимися прямыми, парал-
лельными данным. Поэтому на прямой
Ъ выбираем произвольную точку К и
через нее проводим прямую с, парал-
лельную прямой а. Тогда задача сво-
дится к определению натуральной
величины угла, составленного пересе-
кающимися прямыми с n Ъ = К. Эта
задача проще всего решается способом
вращения вокруг линии уровня (см.
п. 3.5).
В качестве оси вращения выбираем
горизонталь A: h п с = 1, h n b = 2.
При вращении угла 1К2 точки /, 2
остаются в покое. Необходимо постро-
ить лишь повернутое положение К
точки К. Для этого способом прямоу-
гольного треугольника находим нату-
ральную величину радиуса вращения
|OXl = [О] К'] точки К вокруг оси А.
Повернутое положение К точки К
принадлежит плоскости Г ± А е
е Г,), ее горизонтальная проекция
отстоит от точки О] на расстоянии,
равном натуральной величине радиуса
вращения: [OjXJ = [OjK']. Угол а,
составленный прямыми с], , будет
искомым.
Аналитически угол а между двумя
скрещивающимися прямыми, заданны-
ми уравнениями (5.19), вычисляется
по формуле
'А ♦ тл * "Л
cos а = -
(5.21)
Пример 6. Определить угол наклона
а прямой b к плоскости Ф (рис. 5.28).
Простейшее решение этой задачи
состоит из следующих операций.
1) строится точка В пересечения
прямой b с плоскостью Ф (см. п. 4.2.2);
2) из произвольной точки К прямой
b опускается перпендикуляр с на плос-
кость Ф (см. п. 5.3.1);
Рис. 5.28
166
3) строится точка С пересечения
прямой с с плоскостью Ф;
4) любым известным способом стро-
ится натуральная величина угла а =
= LKBC.
В построенном треугольнике угол
ВКС является дополнительным до 90°
к искомому углу а. Это положено в
основу более рационального алгоритма
решения сформулированной задачи,
который включает в себя следующие
операции:
1) из произвольной точки К прямой
Ь опускается перпендикуляр с на плос-
кость Ф;
2) способом вращения вокруг линии
уровня строится натуральная величина
угла ВКС, который будет дополнитель-
ным до 90° к искомому углу а =
= LKBC (см. пример 5, рис. 5.27).
Аналитически величина угла накло-
на а прямой, заданной уравнениями
вида (5.6), к плоскости, заданной
уравнением (2.1), вычисляется по фор-
муле
sina = ---- (5.22)
у/А2* В2* С1
Пример 7. Определить величину
двугранного угла а, образованного
плоскостями Ф, А (рис. 5.29).
Как известно, двугранный угол изме-
ряется соответственным ему линейным
углом, получающимся сечением двуг-
ранного угла плоскостью Г, перпенди-
кулярной его ребру I. Отсюда следует
алгоритм решения данной задачи:
1) строим прямую / пересечения
данных плоскостей Ф, Д (см. п. 4.4.1);
2) через произвольную точку L пря-
мой I проводим плоскость Г, перпенди-
кулярную прямой /;
3) строим линии g, d пересечения
данных плоскостей с плоскостью Г: g =
= Ф п Г, tZ = Д п Г;
4) любым известным способом опре-
деляем натуральную величину угла a,
составленного пересекающимися пря-
мыми g, d.
Следующий алгоритм является более
рациональным. Он состоит из следую-
щих операций (см. рис. 5.29):
1) через произвольную точку К про-
странства проводим перпендикуляры Ь,
с к данным плоскостям Д, Ф;
2) способом вращения вокруг линии
уровня определяем натуральную вели-
чину угла, составленного пересекаю-
щимися прямыми Ь, с; искомый угол
а будет дополнительным до 180° к по-
строенному углу.
Аналитически величина угла а, со-
ставленного плоскостями
А^х + В]У+ C]Z + Dj =0,
А2х + В^у + C2z + Z>2 = 0,
вычисляется по формуле
А,А, + В,В, <• С,С, _
cosa = ± 12 12 12 . (5.23)
^А2*В2*С2 ^а^в^с2
5.6. Развертки поверхностей.
Основные понятия
и алгоритмы
построения разверток
В этом разделе рассмотрим основные
понятия и определения, относящиеся к
построению разверток поверхностей, а
также алгоритмы решения метричес-
167
ких задач, связанных с построением
различных видов разверток и отнесен-
ных к четвертой группе в классифика-
ции (см. рис. 5.1).
5.6.1. Основные понятия
и определения
Если абстрактную математическую
поверхность представить в виде тон-
кой, гибкой и нерастяжимой пленки,
то некоторые из поверхностей можно
путем изгибания совместить с плос-
костью без разрывов и складок. По-
верхности, обладающие этим свой-
ством, называются развертывающи-
мися, а фигура, полученная в резуль-
тате совмещения поверхности с плос-
костью, называется разветкой.
Построение разверток представляет
важную техническую задачу, так как
множество изделий различных отрас-
лей промышленности изготавливаются
из листового материала путем изгиба-
ния. Это — обшивки самолетов и су-
дов, всевозможные резервуары и тру-
бопроводы в нефтехимической и газо-
вой промышленности, изделия швей-
ной и кожевенной промышленности и
т;д.
Одним из основных этапов проекти-
рования таких изделий является по-
строение разверток. С целью упроще-
ния изготовления изделий со всевоз-
можными отверстиями, проемами,
окнами и т.д. предварительно с боль-
шой точностью выполняют их развер-
тку с тем, чтобы после гибки получить
готовые изделия, удовлетворяющие
всем исходным требованиям.
Имеется также ряд прикладных за-
дач, в которых необходимо построить
на развертке линии и фигуры с опре-
деленными свойствами, например,
геодезические линии, которые задают-
ся двумя точками или точкой и на-
правлением. Эта задача является рас-
пространенной при изготовлении тех-
нических поверхностей намоткой и
выкладкой из тканых композиционных
материалов.
Представление поверхности в виде
тонкой, гибкой и нерастяжимой плен-
ки достаточно наглядно, но оно не
позволяет исследовать необходимые и
достаточные условия развертываемости
поверхностей и свойства их разверток.
Знание этих условий и свойств необхо-
димо для разработки алгоритмов по-
строения разверток поверхностей и
решения соответствующих задач. Поэ-
тому данную поверхность Ф и ее раз-
вертку Ф целесообразно рассматривать
как соответственные множества точек
(Л) и (Л). Тогда можно сказать, что
развертка Ф поверхности Ф является
образом поверхности Ф в некотором
отображении Т.
Отображение Т ставит в соответствие
точке Л е Ф определенную точку Л
развертки Ф, а множество точек (Л)
отображается на множество (Л). Из
понятия отображения непосредственно
следует, что линия I поверхности Ф
отображается на линию I развертки Ф.
Очевидно, замкнутая линия, простая
или составная, отображается в замкну-
тую линию, также простую или со-
ставную.
Из физической модели процесса раз-
вертывания поверхности на плоскость
следует, что площадь отсека поверх-
ности, ограниченная замкнутой лини-
ей, равна площади отсека плоскости,
ограниченной образом этой линии на
развертке. Другими словами, отобра-
жение имеет в качестве инвариантно-
го (неизменного) свойства — свойство
сохранения площадей соответствен-
ных фигур.
Такие отображения называют изо-
метрическими. Поэтому разверткой
Ф поверхности Ф следует называть ее
плоский образ в изометрическом ото-
бражении.
168
Свойство сохранения площади в рас-
сматриваемом изометрическом отобра-
жении влечет за собой справедливость
следующих двух свойств:
1) длины соответственных линий
поверхности и ее развертки равны;
2) углы, образованные линиями
поверхности, равны углам, составлен-
ным их образами на развертке.
Из этих свойств вытекают следствия:
1) прямая поверхности отображает-
ся на прямую развертки;
2) параллельные прямые поверхнос-
ти отображаются на параллельные
прямые развертки.
Аналитически отображение Т задает-
ся формулами х =/1(х, у, z), у = f2(x,
у, z) где х, у, z — координаты произ-
вольной точки поверхности Ф; х, у —
координаты соответственной точки
развертки Ф. Функции /], /2, связыва-
ющие координаты соответственных
точек, являются интегральными. Поэ-
тому в этом разделе будем расматри-
вать лишь графические алгоритмы по-
строения разверток.
В дифференциальной геометрии по-
казывается, что к развертывающимся
криволинейным поверхностям относят-
ся только поверхности нулевой кривиз-
ны (поверхности, состоящие исключи-
тельно из параболических точек). Эти
поверхности составляют подмножество
линейчатых поверхностей, для которых
касательная плоскость, построенная в
какой-либо точке поверхности, касает-
ся ее во всех точках прямолинейной
образующей, проходящей через эту
точку. Иными словами, у развертыва-
ющихся (линейчатых) поверхностей
касательные плоскости, проведенные
во всех точках одной образующей,
совпадают.
Указанным признаком развертывае-
мости на плоскость обладают лишь
три группы линейчатых поверхностей:
цилиндрические, конические и тор-
совые.
Для этих поверностей строятся при-
ближенные развертки, ибо они в про-
цессе построения развертки заменяют-
ся (аппроксимируются) вписанными
или описанными многогранными по-
верхностями. Необходимость аппрокси-
мации вызвана тем, что спрямление
направляющих линий указанных по-
верхностей основано на их замене
вписанными или описанными многоу-
гольниками. Точные развертки ап-
проксимирующих многогранных повер-
хностей принимаются за приближен-
ные развертки развертываемых повер-
хностей.
Хотя все остальные поверхности
теоретически не развертываются на
плоскость, но инженерная практика
тем не менее требует построения их
’’разверток”. Для этих поверхностей
строятся так называемые условные
развертки.
5.6.2. Алгоритмы построения
точных разверток
многогранных поверхностей
Разверткой многогранной поверх-
ности называется совокупность кон-
груэнтных ее граням многоугольни-
ков, расположенных в одной плоскос-
ти, если указано соответствие сторонам
и вершинам многоугольников ребер и
вершин данной многогранной повер-
хности.
Из этого определения следует, что,
имея многогранную поверхность, мы
можем всегда построить ее развертку.
Для этого достаточно построить в ка-
кой-либо плоскости совокупность мно-
гоугольников, конгруэнтных граням
многогранника.
Рассмотрим построение точных раз-
верток наиболее распространенных
многогранных поверхностей — повер-
хностей пирамид и призм.
Так как у пирамиды боковые грани
— треугольники, то построение ее раз-
вертки сводится к построению нату-
169
ральных величин этих треугольников,
для чего необходимо найти натураль-
ные величины всех ребер пирамиды.
Пример. Построить развертку повер-
хности пирамиды SABCD (рис. 5.30).
Рис. 5.30
Основание ABCD пирамиды лежит в
горизонтальной плоскости уровня.
Поэтому его стороны на П, проециру-
ются в натуральную величину. Для
определения натуральных величин
боковых ребер воспользуемся способом
прямоугольного треугольника. Так как
разности высот концов всех боковых
ребер равны, то построим прямоуголь-
ные треугольники с общим катетом
550. Вторые катеты этих треугольни-
ков равны длинам горизонтальных
проекций этих ребер. Для удобства
построение натуральных величин боко-
вых ребер вынесено на свободное поле
чертежа. Совокупность треугольников
550Л, SS0B, SSqC, SSqD с общим
катетом SS0 называется диаграммой
натуральных величин.
Построение развертки поверхности
пирамиды ясно из приведенного черте-
жа, на котором конгруэнтные отрезки
обозначены одинаковыми значками. К
развертке боковой поверхности пира-
миды пристраиваем ее основание, ко-
торое предварительно разбиваем с
помощью диагонали BD на два треу-
гольника.
Построение развертки поверхности
призмы выполняется тремя способами:
1) способом треугольников (триангу-
ляции),
2) способом нормальных сечений,
3) способом раскатки.
Способ треугольников является наи-
более универсальным. Он пригоден для
построения точных разверток любых
многогранных поверхностей, а также
для построения приближенных и ус-
ловных разверток линейчатых повер-
хностей.
По способу треугольников (триангу-
ляции) развертка призмы строится в
такой последовательности:
— в каждой грани призмы проводится
диагональ, которая разбивает ее на два
треугольника;
— определяются натуральные вели-
чины сторон этих треугольников;
— на плоскости строятся последова-
тельно треугольники, конгруэнтные
данным.
Способ основан на свойстве ’’жес-
ткости” треугольника — три отрезка
определяют единственный треугольник.
В то время как четыре, пять, ... отрез-
ков определяют бесчисленное множес-
тво четырех-, пяти-, ... угольников.
Пример. Построить развертку боко-
вой поверхности трехгранной призмы
АВСА'В'С' (рис. 5.31).
В каждой из боковых граней призмы
проводим диагональ и построением на
свободном поле чертежа диаграммы
натуральных величин определяем на-
туральные величины боковых ребер
\АА<1 = | ВВ11 = |CCZ| и построен-
ных диагоналей , | ВС11 ,
| СА11 . Основания призмы параллель-
ны горизонтальной плоскости проек-
ций, поэтому они проецируются на Щ
в натуральную величину.
Имея натуральные величины ребер
призмы и трех диагоналей, строим раз-
вертку боковой поверхности призмы
170
как совокупности треугольников, опре-
деляемых своими сторонами. На
рис. 5.31 конгруэнтные отрезки обоз-
начены одинаковыми значками, что
позволяет проследить алгоритм постро-
ения развертки.
Способ нормальных сечений приме-
няется для построения разверток при-
зматических поверхностей, если их
боковые ребра являются прямыми
уровня.
Развертка поверхности призмы спо-
собом нормальных сечений выполняет-
ся в такой последовательности:
1) призма пересекается плоскостью
А, перпендикулярной ее боковым реб-
рам;
2) определяются натуральные вели-
чины сторон ломаной линии, по кото-
рой плоскость А пересекает поверх-
ность призмы;
3) эта ломаная развертывается в
отрезок прямой;
4) на перпендикулярах, проведенных
к этой прямой в точках, соответстве-
ных вершинам ломаной, откладывают-
ся натуральные величины соответству-
ющих отрезков ребер;
Рис. 5.31
5) концы ребер последовательно сое-
диняются отрезками прямых;
6) к построенной развертке боковой
поверхности призмы пристраиваются
многоугольники, равные натуральным
величинам оснований призмы.
Пример. Построить развертку
трехгранной призмы ABCDEF (рис.
5.32).
Боковые ребра призмы являются го-
ризонталями. Поэтому на плоскость
проекций П| они проецируются в нату-
ральную величину.
Построим сечение 123 призмы гори-
зонтально проецирующей плоскостью
А, перпендикулярной ее боковым реб-
рам. Способом плоскопараллельного
движения относительно определяем
натуральную величину треугольника
123 и, значит, натуральные величины
его сторон.
Ломаную 1231 ’’вытягиваем” в пря-
мую линию т и через ее вершины
проводим прямые, перпендикулярные
прямой т. На этих перпендикулярах
по обе стороны прямой т откладываем
натуральные величины отрезков боко-
вых ребер призмы, равные их горизон-
171
Рис. 5.32
тальным проекциям: |А7| = [Л|/]],
|/D| = U^il, ...
Концы ребер последовательно соеди-
няем отрезками прямых. Полученный
многоугольник ABCADFED представ-
лет собой развертку боковой поверх-
ности призмы, к которой пристраиваем
треугольники АВС и DEF, равные
натуральным величинам ее оснований.
Способ раскатки — частный случай
способа нормальных сечений. Он при-
меняется для построения разверток
призматических поверхностей, если
их боковые ребра и плоскости основа-
ний являются соответственно прямы
ми и плоскостями уровня.
Сущность способа раскатки состоит в
том, что грани призмы последователь-
ными вращениями вокруг ее боковых
ребер совмещаются с какой-либо плос-
костью. Получающаяся при этом фигу-
ра является разверткой боковой повер-
ности призмы.
Пример. Построить развертку боко-
вой поверхности трехгранной призмы
ABCDEF (рис. 5.33).
Боковые ребра призмы являются
фронталями, а ее основания — гори-
зонтальными плоскостями уровня, что
позволяет строить развертку поверх-
ности призмы способом раскатки.
Примем за первую ось вращения
ребро CF и вращением вокруг него
совместим грань CFDA с фронтальной
плоскостью S, проходящей через ребро
CF. При этом вершины А и D враща-
ются во фронтально проецирующих
плоскостях Г1 э А, Г4 э D, перпенди-
кулярных оси вращения CF. Поэтому
совмещенные положения A, D вершин
A, D принадлежат вырожденным про-
Рис. 5.33
172
екциям Г^, плоскостей Г1, Г4 и
отстоят от точек С, F на расстоянии
[С2А] = [F2D] = IC011 = l^W-
Далее, последовательными вращени-
ями вокруг осей AD, BE совмещаем с
плоскостью S грани ABED, BCFE.
5.6.3. Алгоритмы построения
приближенных разверток
развертывающихся поверхностей
Построение приближенных развер-
ток развертывающихся поверхностей
(конических, цилиндрических и тор-
совых) сводится к построению точных
разверток многогранных поверхнос-
тей, вписанных в данные поверхности
или описанных около них. Таким
образом, построение приближенных
разверток выполняется в такой после-
довательности:
1) данную развертывающуюся повер-
хность Ф заменяют (аппроксимируют)
многогранной поверхностью Ф;
2) строят точную развертку ф мно-
гогранной поверхности Ф;
3) точную развертку Ф аппроксими-
рующей многогранной поверхности Ф
принимают за приближенную развер-
тку данной развертывающейся повер-
хности Ф.
Точность построения приближенных
разверток зависит от точности аппрок-
симации направляющих линий данных
поверхностей. Аппроксимация направ-
ляющих линий поверхности ломаной
линией, составленной хордами данной
кривой, называется способом малых
хорд.
При построении разверток поверх-
ностей цилиндра и конуса вращения
нет необходимости в их аппроксима-
ции многогранными поверхностями,
так как существуют весьма простые
аналитические зависимости между па-
раметрами поверхности и развертки.
Разверткой отсека поверхности ци-
линдра вращения (рис. 5.34) радиуса г
и высотой h является прямоугольник с
размерами сторон h и 2лг.
Разверткой отсека поверхности кону-
са вращения (рис. 5.35) является сек-
тор радиуса R = ^г2 + Л2 , угол кото-
рого
2пг 2пг
а ~ ,
где г — радиус направляющей окруж-
ности конуса; h — высота конуса.
Рассмотрим примеры построения
приближенных разверток отсеков раз-
вертывающихся поверхностей.
Пример 1. Построить приближенную
развертку отсека конической повер-
хности Ф(5, а) (рис. 5.36).
Дугу направляющей а конической
поверхности аппроксимируем вписан-
173
Рис. 5.36
ной ломаной линией J234. Она при-
надлежит горизонтальной плоскости
уровня, следовательно, проецируется
на в натуральную величину. Соеди-
нив вершины этой ломаной с вершиной
S конической поверхности, получаем
пирамиду S1234, аппроксимирующую
данную коническую поверхность Ф.
Для построения точной развертки
поверхности пирамиды способом вра-
щения вокруг горизонтально проециру-
ющей прямой j э S определяем нату-
ральные величины боковых ребер S1,
S2, S3, S4. Далее, по известному алго-
ритму (п. 5.6.2) строим точную развер-
тку боковой поверхности аппроксими-
рующей пирамиды. На развертке через
вершины 1, 2, 3, 4 ломаной проводим
локальную кривую а. Полученная
плоская фигура является приближен-
ной разверткой отсека данной коничес-
кой поверхности.
Пример 2. Построить приближен-
ную развертку отсека эллиптичес-
кой цилиндрической поверхности Ф
(рис. 5.37).
Цилиндрическую поверхность Ф ап-
проксимируем вписанной призмой,
разделив ее направляющую окруж-
ность а на двенадцать равных частей.
Боковые ребра призмы являются
фронталями, а основания принадлежат
горизонтальным плоскостям уровня.
Поэтому боковые ребра проецируются
в натуральную величину на П2, а осно-
вания — на П]. Следовательно, постро-
ение развертки призмы целесообразно
выполнить способом раскатки. Так как
призма симметрична относительно
фронтальной плоскости уровня S, то
построим развертку только одной ее
половины. Вращение призмы начинаем
вокруг ребра 11. Далее последователь-
Рис. 5.37
174
ным вращением (перекатыванием)
вокруг соответствующих ребер совмес-
тим все грани призмы с фронтальной
плокостью уровня S, проходящей через
ребро 11. Полученная фигура являет-
ся приближенной разверткой заданной
цилиндрической поверхности.
Пример 3. Построить развертку
отсека торсовой поверхности (рис.
5.38).
Отсек данной торсовой поверхности
ограничен дугой АЕ ребра возврата а,
дугой АЕ плоской кривой т и отрезка-
ми АА. ВВ двух се образующих.
Впишем в дугу АЕ ломаную ABCDE.
Через вершины ломаной проведем
образующие торсовой поверхности.
Теоретически эти образующие между
собой не пересекаются, так как ребро
возврата является пространственной
кривой. Однако при замене торсовой
поверхности вписанной многогранной
поверхностью ее смежные ребра при-
нимаются пересекающимися. Другими
словами, дуга АЕ ребра возврата ап-
проксимируется ломаной ABCDE, сто-
роны которой принадлежат ребрам
аппроксимирующего многогранника.
В нашем примере кривая т располо-
жена в горизонтальной плоскости
уровня, поэтому стороны ломаной
ABCDEF проецируются на П, в нату-
ральную величину. Для определения
натуральных величин ребер вписанно-
го многогранника и сторон ломаной
ABCDE построена диаграмма нату-
ральных величин, основанная на ис-
пользовании способа прямоугольного
треугольника.
Здесь на горизонтальной оси отложе-
ны длины горизонтальных проекций
ребер АА ([ОЛ] = [Л^ ]), ЯЙ(1О/?] =
= [5]В[ ]) и т.д. На вертикальной оси
отложены разности высот концов ре-
бер. Для упрощения построений гори-
зонтальная ось расположена в плоскос-
ти кривой т.
По найденным значениям натураль-
ных величин ребер аппроксимирующей
многогранной поверхности построена
ее точная развертка, которая принима-
ется за приближенную развертку отсе-
ка данной торсовой поверхности.
175
5.6.4. Алгоритмы построения
условных разверток
неразвертывающихся
поверхностей
Как было отмечено выше, для нераз-
вертывающихся поверхностей строят-
ся условные развертки. Построение
условной развертки Ф данной повер-
хности Ф выполняется в такой последо-
вательности:
1) исходя из требуемой точности
построения развертки данная повер-
хность Ф разрезается на несколько рав-
ных или примерно равных частей Ф‘;
2) отсеки Ф' данной поверхности Ф
аппроксимируются отсеками разверты-
вающихся поверхностей Ф1;
3) по уже рассмотренной методике
(п. 5.6.3) выполняются приближенные
развертки Ф' отсеков поверхностей Ф',
совокупность которых принимается за
условную развертку данной поверхнос-
ти Ф.
Пользуясь описанной методикой,
рассмотрим примеры построения раз-
верток линейчатых поверхностей и
поверхностей вращения, наиболее ши-
роко применяемых в инженерной
практике.
Пример 1. Построить условную раз-
вертку отсека цилиндроида Ф(а, Ь, П2)
(рис. 5.39).
Отсек цилиндра, изображенного на
приведенном рисунке, применяется для
соединения двух цилиндрических тру-
бопроводов с пересекающимися осями.
Так как поверхность Ф имеет плос-
кость симметрии Г, то построим раз-
вертку лишь одной ее половины. На-
правляющие окружности а, b цилин-
дроида конгруэнтны, поэтому цилин-
дроид Ф плоскостями Г' разбиваем на
равные по ширине части Ф', ограничен-
ные двумя образующими и дугами
направляющих а, Ь. Например, между
Рис. 5.39
176
плоскостями Г и Г' расположены два
отсека цилиндроида, ограниченные
соответственно образующими АА',
ВВ' и GG', FF', дугами АВ, А'В' и
GF, G'F' окружностей а, Ь.
Плоскости Г* проходят через верши-
ны ломаной ABCDEFG, вписанной в
окружность а по способу малых хорд.
Каждый отсек Ф' цилиндроида ап-
проксимируем отсеками двух коничес-
ких поверхностей Ф1, Ф'. Для этого
соединяем любые две противополож-
ные вершины криволинейных четырех-
сторонников, ограничивающих отсек
Ф!. ’’Диагонали” этих четырехсторон-
ников не принадлежат данной повер-
хности Ф, так как они не параллельны
ее плоскости параллелизма П2. Таким
образом, конические поверхности Ф',Ф'
определяются вершинами четырехсто-
ронников, через которые проходят их
’’диагонали”, и направляющими —
дугами окружностей а, Ь. Все образую-
щие этих конических поверхностей за
исключением тех, которые параллель-
ны плоскости параллелизма П2, не
принадлежат данной поверхности Ф.
Так как направляющие конических
поверхностей Ф‘, Ф! — дуги окруж-
ностей а, b — выбраны достаточно ма-
лыми и обеспечивающими заданную
точность построения развертки, то они
заменяются стягивающими их хордами
— сторонами ломаных ABCDEFG и
A'B'C'D'E'F'G'. Таким образом, по
существу развертка данного цилиндро-
ида выполняется способом триангуля-
ции.
Стороны ломаных ABCDEFG и
A'B'C'D'E'F'G', образующих АА',
ВВ', ... цилиндроида проецируются в
этом случае в натуральную величину
на соответствующие плоскости проек-
ций. Натуральные величины ’’диагона-
лей” АВ', ВС', CD', ... определяются
способом прямоугольных треугольни-
ков путем построения диаграммы нату-
ральных величин.
Развертка Ф цилиндроида ф пред-
ставляет собой фигуру, состоящую из
треугольников АВА', А'ВВ' ..., нату-
ральные величины которых построены
по трем сторонам и состыкованы вдоль
смежных сторон.
Пример 2. Построить условную раз-
вертку Ф отсека поверхности враще-
ния Ф(/, Г) (рис. 5.40).
Условные развертки неразвертываю-
щихся поверхностей вращения выпо-
Рис. 5.40
177
лняются в основном двумя способами:
способом цилиндров и способом кону-
сов.
При построении условной развертки
способом цилиндров данная поверх-
ность Ф ’’разрезается” плоскостями Г1,
проходящими через ее ось j (обычно на
двенадцать равных частей Ф1). Каждую
часть заменяют отсеком касательной
цилиндрической поверхности Ф', кото-
рая касается Ф' вдоль ее среднего мери-
диана. Поверхность цилиндра Ф' как
и часть поверхности вращения ограни-
чена плоскостями Г*.
При этом дуги параллелей повер-
хности Ф аппроксимируются отрезка-
ми образующих поверхностей цилин-
дров Ф'.
На рис. 5.40 поверхность Ф ’’разреза-
на” на шесть частей. Одна из частей,
средним меридианом которой является
главный меридиан 5Л, заменена фрон-
тально проецирующей цилиндрической
поверхностью Ф', образующие которой
ограничены плоскостями Г, Г'.
Для приближенного построения раз-
вертки отсека поверхности цилиндра
Ф' ее направляющая AS, являющаяся
одновременно нормальным сечением,
аппроксимирована ломаной ABCDES.
Развертку отсека поверхности цилин-
дра Ф' строим по способу нормальных
сечений, для чего спрямляем ломаную
ABCDES в отрезок прямой ABCDES.
Через точки А, В, С, ... проводим
прямые перпендикулярные Л5, на
которых откладываем отрезки каса-
тельных, проведенных к соответствую-
щим параллелям и ограниченных плос-
костями Г, Г'.
Для построения развертки поверх-
ности вращения способом конусов дан-
ная поверхность Ф ’’разрезается” плос-
костями Д', перпендикулярными ее
оси, на несколько частей — ’’поясов”.
Для определения числа ’’поясов” мсри-
диан поверхности вращения аппрокси-
мируется ломаной ABCS, через верши-
ны которой проводятся секущие плос-
кости Д' (рис. 5.41).
Плоскости Д' пересекают поверхность
вращения Ф по параллелям — направ-
Рис. 5.41
178
ляющим а, Ь, с, ... аппроксимирующих
поверхностей конусов Ф1, а стороны
АВ, ВС, CS ломаной ABCS пересекают
ось j поверхности в точках S", S',
S — вершинах конических поверхнос-
тей Ф‘.
Построение условной развертки Ф
данной поверхности Ф сводится, таким
образом, к построению разверток по-
верхностей конусов Ф1, что не вызыва-
ет никаких затруднений. На рис. 5.41
длины дуг окружностей, описанных
7 —”2. Я —3
радиусами R и R , R и R , равны,
так как они соответствуют параллелям
Ь, с поверхности Ф.
В заключение следует заметить, что
выбор способа построения условной
развертки поверхности вращения в
реальном проектировании во многом
зависит от конкретных размеров по-
верхности и размеров листового мате-
риала, из которого изготавливается
поверхность.
5.7. Метрические
задачи, решаемые
построением разверток
Все метрические задачи, связанные с
построением криволинейных фигур,
принадлежащих данной поверхности Ф,
решаются построением развертки Ф
(точной, приближенной или условной).
Такой подход основан на свойстве
изометричности (см. п. 5.6.1) повер-
хности и ее развертки, т.е. на свойстве
сохранения площади, а следовательно,
длины и угла.
Распространенной инженерной зада-
чей является построение линии повер-
хности, удовлетворяющей определен-
ным требованиям.
Например, требуется соединить две
точки А, В поверхности Ф кратчайшей
линией I. Такая линия поверхности,
как известно, называется геодезичес-
кой. На плоскости кратчайшей линией
между двумя точками является отрезок
прямой. Поэтому для решения постав-
ленной задачи строят развертку Ф
данной поверхности Ф. На развертке
находят образы А, В данных точек
поверхности. И, наконец, находят в
обратном отображении 7 1 на повер-
хности Ф геодезическую [ЛД] как
образ отрезка АВ развергки Ф.
Другой пример: линия, принадлежа-
щая поверхности вращения и пересека-
ющая все меридианы этой поверхности
под постоянным углом а, называется
локсодромой (локсодромией). Форму
локсодромы имеет путь корабля ь оке-
ане или самолета над земной повер-
хностью при постоянном истинном
курсе а. Проведение локсодромы также
можно выполнить путем построения
развертки поверхности.
По описанной методике решаются
также задачи на построение двумер-
ный фигур, принадлежащих поверх-
ности и удовлетворяющих определен-
ным метрическим требованиям.
Пример. Па поверхности прямого
кругового конуса Ф построить равнос-
торонний криволинейный треугольник
АВС, если дана его сторона АВ, при-
надлежащая образующей (рис. 5.42).
Задача решается в такой последова-
тельности:
1) строим развертку Ф отсека повер-
хности конуса Ф в виде кругового сек-
_ /о . э
тора радиуса к = \ir + п с цент-
2яг
ральным углом а - —-------, где г —
радиус основания конуса, h — высота
конуса;
2) отложив на образе SM образую-
щей натуральную величину стороны
[АВ ] = [Л2В2] треугольника, строим
179
Рис. 5.42
(в силу
его образ АВС на развертке
свойства изометричности треугольник
АВС также будет равносторонним);
3) строим проекции Л^Ср Л2В2С2
искомого треугольника; для этого сна-
чала находим проекции Ср С2 верши-
ны С, соответственной точке С на
развертке Ф:
— проводим образ SN образующей
SW э С;
— из условия [ ] = [MN] или
у = Р ------- (см. рис. 5.42) строим
Г
проекции S2W2 образующей,
которой принадлежит вершина С иско-
мого треугольника;
— на очерковой образующей конуса
откладываем отрезок 5250 = SC и вра-
щением вокруг оси конуса находим
проекции С2, С] вершины С (на
рис. 5.42 построения показаны стрел-
ками) ;
— для построения проекций сторон
АС, ВС искомого треугольника дугу
MN развертки Ф и соответственную ей
дугу M{N^ основания конуса Ф делим
на равное число частей и отмечаем
точки пересечения образов SI, S2,S3
образующих со сторонами АС, ВС,
которые по аналогии с построением
проекций С2, Сеточки С отображаем
на проекции соответствующих образу-
ющих SI, S2, S3.
Соединив проекции полученных то-
чек лекальными кривыми, получаем
проекции искомого криволинейного
треугольника.
5.8. Задачи
на геометрические места
и принципы их решения
Любая задача начертательной гео-
метрии сводится к построению иско-
мых фигур (точек, линий, поверхносг
той, ...), удовлетворяющих определен-
ным позиционным или метрическим
условиям. Каждому метрическому ус-
ловию в пространстве соответствует
180
множество фигур, которые образуют
геометрические места (ГМ) точек,
прямых и т.д. Большинство метричес-
ких условий сводится к следующим
четырем:
— расстояние,
— угол,
— равноудаленность,
— равнонаклоненность.
Общеизвестны определения кривых
второго порядка как геометрических
мест точек:
а) окружность — это геометрическое
место точек, удаленных от данной
точки О (центра) на заданное расстоя-
ние Л;
б) эллипс — это геометрическое мес-
то точек плоскости, сумма расстояний
которых до двух фиксированных точек
Г1, F2 (фокусов) постоянна;
в) гипербола — это геометрическое
место точек плоскости, разность рас-
стояний которых до двух фиксирован-
ных точек Fl, F2 (фокусов) постоянна;
г) парабола — это геометрическое
место точек плоскости, равноудален-
ных от данной точки F (фокуса) и
данной прямой d (директрисы).
Перечислим определения наиболее
часто встречающихся в пространстве
геометрических мест:
1) геометрическое место точек, уда-
ленных от данной точки О на расстоя-
ние R, есть сфера Ф(О, /?);
2) геометрическое место точек, уда-
ленных от данной прямой j на расстоя-
ние R, есть поверхность цилиндра вра-
щения ф(/, R) ;
3) геометрическое место точек, уда-
ленных от данной плоскости Г на рас-
стояние d, образует две плоскости Г1,
Г2 параллельные Г;
4) геометрическое место точек, сум-
ма расстояний которых до двух фикси-
рованных точек F1, F2 постоянна, есть
эллипсоид вращения с осью F1 F2;
5) геометрическое место точек, раз-
ность расстояний которых до двух
фиксированных точек F , F2 постоян-
на, есть двуподостный гиперболоид
вращения с осью Г1/’2;
6) геометрическое место прямых,
составляющих с данной прямой у угол
а, это множество прямых, параллель-
ных поверхности конуса вращения Ф(/,
а)*;
7) геометрическое место прямых,
составляющих с данной плоскостью Г
угол а, это множество прямых, парал-
лельных поверхности конуса вращения
Ф(/, 90°— а), где / х Г;
8) геометрическое место точек, рав-
ноудаленных от двух данных точек А,
В, есть срединная плоскость, перпен-
дикулярная АВ;
9) геометрическое место точек, рав-
ноудаленных от точки А и прямой А,
есть параболический цилиндр, образу-
ющие которого параллельны Ь;
10) геометрическое место точек, рав-
ноудаленных от точки А и плоскости
Д, есть параболоид вращения с осью /,
где А е j ± Д;
11) геометрическое место точек, рав-
ноудаленных от двух прямых а, Ь,
есть:
— гиперболический параболоид, если
прямые а, b скрещивающиеся;
— две биссекторные плоскости, если
прямые а, b пересекающиеся;
— срединная плоскость, если прямые
а, b параллельные;
12) геометрическое место точек,
равноудаленных от прямой а и плос-
кости S, есть:
— поверхность эллиптического кону-
са, если a n S и az S;
— поверхность конуса вращения,
если a l S;
— параболический цилиндр, если
а II S;
13) геометрическое место точек,
равноудаленных от плоскостей Г, Д,
есть:
Прямая называется параллельной поверхнос-
ти конуса, если она параллельна какой-либо ее
образующей.
181
— срединная плоскость, если Г || А;
— две биссекторные плоскости, если
Г I А;
14) геометрическое место прямых,
равнонаклоненных к двум данным пря-
мым а, Ь, есть множество прямых, па-
раллельных биссекторным плоскостям
линейного угла ab. где а || a, b fl b;
15) геометрическое место прямых,
равнонаклоненных к прямой а и плос-
кости Г, есть множество прямых, па-
раллельных поверхности эллиптичес-
кого конуса;
16) геометрическое место прямых,
равнонаклоненных к двум данным
плоскостям Г, А, есть множество пря-
мых, параллельных биссекторным
плоскостям двугранного угла Г А.
При решении задач на геометричес-
кие места как и любых метрических
задач, полезно знать основные правила
их решения:
— правило упрощения,
— правило разложения,
— правило приращений.
Правило упрощения реализуется
приведением исходных фигур в час-
тное положение.
Преобразованием исходных фигур
общего положения, входящих в усло-
вие задачи, в проецирующие или фи-
гуры уровня часто удается стереомет-
рическую задачу свести к планиметри-
ческой. что существенно упрощает
графические построения.
Например, пусть требуется построить
геометрическое место точек, равноуда-
ленных от вершин треугольника АВС.
Нетрудно установить, что искомое гео-
метрическое место точек представляет
прямую /, проходящую через центр О
описанной вокруг треугольника АВС
окружности и перпендикулярную плос-
кости А АВС.
Задачу можно решить несколькими
способами. Сначала рассмотрим алго-
ритм ее решения ”в лоб":
а) строим середины М и N любых
двух сторон треугольника АВС, напри-
мер, сторон АВ и ВС: [AM] = [МВ],
[ВАЛ = [7VC];
б) строим плоскости А и Г, проходя-
щие соответственно через точки М и N
и перпендикулярные прямым /1В и ВС:
М е A j. АВ, N е Г ± ВС;
в) строим искомую прямую I как
линию пересечения плоскостей А и Г:
I = А п Г.
Этот алгоритм требует выполнения
достаточно громоздких графических
построений и развитого пространствен-
ного представления и не базируется на
опыте решения планиметрических за-
дач, полученном в средней школе.
Следующий алгоритм лишен указан-
ных недостатков:
а) используя любой способ преобра-
зования чертежа, плоскость треуголь-
ника АВС общего положения преобра-
зуется в плоскость уровня АВС;
б) известным из планиметрии спосо-
бом находится центр О окружности,
описанной вокруг треугольника АВС;
в) искомая прямая I проходит через
точку О перпендикулярно плоскости
треугольника АВС.
Таким образом, выбор рационального
алгоритма является важным этапом в
решении задач.
Правило разложения условий задачи
заключается в том, что все условия,
которым должна отвечать искомая фи-
гура, рассматриваются отдельно. Каж-
дому условию тогда отвечает какое-
либо геометрическое место, а искомая
фигура получается как "пересечение”
всех геометрических мест.
Рассмотрим конкретный пример.
Пусть требуется построить прямую I,
пересекающую две данные прямые а и
b и составляющую с ними соответст-
венно углы аир.
Геометрическое место прямых, со-
ставляющих с прямой а угол а, есть
182
множество прямых, параллельных
поверхности некоторого конуса враще-
ния Ф(п, а). Аналогично геометричес-
кое место прямых, составляющих с
прямой b уголр, есть множество пря-
мых, параллельных поверхности второ-
го конуса вращения A (Z>, Р). Если ко-
нусы Ф и Д имеют общую вершину S,
то ’’пересечением” указанных двух
геометрических мест будет множество
прямых пространства, параллельных
двум общим образующим I, I этих
поверхностей.
Это образующие 1, 7 будут действи-
тельными различными, если а + р > у,
где у — угол, составленный прямыми а
и Ь; совпавшими, если а + р = у, и
мнимыми, если а + р < у. В первом
случае конусы Ф и Д пересекаются по
двум различным образующим, во вто-
ром случае касаются, а в последнем
случае не пересекаются. Поэтому в
первом случае задача имеет два реше-
ния, во втором — одно решение, а в
третьем задача не имеет решения.
Наконец, остается построить иско-
мую прямую I, параллельную I или I
и пересекающую данные прямые а, Ь.
Таким образом, сложную метрическую
задачу привели к достаточно простой
позиционной задаче.
Алгоритм решения данной задачи
включает следующие этапы:
— через произвольную точку 5 пря-
мой а проводим прямую Ь, параллель-
ную данной прямой Ь;
— принимая точку 5 за вершину,
прямые а, b за оси, строим конические
поверхности вращения Ф(а, а), Д(5, 0),
образующие которых составляют с
осями соответственно углы « и Р;
— строим общие образующие 1,7
конических поверхностей: I, I =
= Ф п Д;
— строим точки В, В пересечения
прямой h с плоскостями Г (и о I) и S
(а г, 7);
— через точку В в плоскости Г про-
водим прямую Г, параллельную I, и
отмечаем точку А = Г п о;
— через точку В в плоскости S про-
водим прямую Z", параллельную 7. и
отмечаем точку А = I" о а.
Прямые Г - АВ, Г = ЛВ являются
искомыми.
Правило приращений составляет
базу графического способа построения
некоторых геометрических мест. Суть
этого способа состоит в том, что при
построении геометрических мест, удо-
влетворяющих двум условиям (равноу-
даленность. равнонаклоненность и
др.), их численным значениям даются
последовательные приращения и иско-
мая фигура строится как множество
точек, линий, получаемых после каж-
дого приращения.
Известен графический способ постро-
ения параболы как геометрического
места точек, равноудаленных от точки
F и прямой d (рис. 5.43).
Другой пример этою принципа при-
веден на рис. 5 44, где показана идея
способа построения геометрического
18.3
5. Сформулируйте теорему о прямоугольной
проекции прямого угла.
6. Когда прямой угол проецируется без иска-
жения на горизонтальную плоскость проекций?
7. Когда прямой угол проецируется без иска-
жения на фронтальную плоскость проекций?
8. Постройте равнобедренный треугольник
АВС с основанием [ВС] на горизонтали /1, если
[ВС] = 1,5]ЛО], где [АО] — высота треугольни-
ка (рис. 5.46).
места точек, равноудаленных от пря-
мой а н плоскости Г.
Искомое геометрическое место точек,
представляющее собой поверхность
эллиптического конуса Ф, строится как
однопараметрическос множество эл-
липсов получаемых как
сечения поверхностей Д' соосных ци-
линдров вращения плоскостями 0',
параллельными данной плоскости Г.
При этом приращения радиусов ци-
линдров Д' и расстояний от плоскостей
0' до плоскости Г пропорциональны.
Упражнения и вопросы
для самопроверки
1. Какие задачи называются метрическими?
2. Вспомните классификацию метрических
задач.
3 Какие способы существуют для определения
натуральной величины отрезка?
4. [Кктройте горизонтальную проекцию отрез-
ка АВ, если известна его натуральная величина,
равная 40 мм (рис. 5.45).
Рис. 5.46
9. Сформулируйте условие перпендикулярнос-
ти прямой и плоскости на чертеже Монжа.
10. Постройте недостающую проекцию точки
К, удаленной от заданной плоскости Е (Л, В, С)
на 25 мм (рис. 5.47).
Рис. 5.47
11. Сформулируйте условие перпендикуляр-
ности двух плоскостей.
12. Дайте определение нормали поверхности.
13. На поверхности конуса вращения по-
стройте точку М, ближайшую к данной точке А
(рис. 5.48)-.
Рис. 5.45
Рис. 5.48
184
14. Дайте определение линии наибольшего
наклона. Вспомните их назначение. Сформули-
руйте теорему.
15. В плоскости Е(А, В, С) постройте линию
наибольшего наклона к горизонтальной плоскос-
ти проекций, проходящую через точку В (см.
рис. 5.47).
16. Постройте отрезок, определяющий крат-
чайшее расстояние между прямой общего поло-
жения m(mt, nvj и осью Ох.
17. Постройте прямую CD, проходящую через
точку С и пересекающую прямую АВ под углом
Ф - 30". Сколько решений имеет данная задача?
18. Постройте прямоугольную трапецию
ABCD с большим основанием [ЯС] на прямой
т, если [AD] - [АВ], a [DC] - 1,2[АВ]
(рис. 5.50).
19. Постройте фронтальную проекцию точки
С, чтобы плоскость Е(А, В, С) составляла с
плоскостью проекций П, угол 60° (рис. 5.51).
Сколько решений имеет данная задача?
20. Постройте сферу минимального радиуса с
центром в данной точке О, внутри которой нахо-
дится данный треугольник АВС (рис. 5.52).
21. Дайте определение развертки поверхности.
Вспомните основные свойства разверток. Какие
поверхности являются развертываемыми? Для
каких поверхностей строятся точные, прибли-
женные и условные развертки?
22. Дана треугольная пирамида SABC коорди-
натами своих вершин 5(0, 0, 50), А(0. 0, 0),
В(30, 0, 0), С(20, 40, 0). Постройте ее развер-
тки так, чтобы:
а) длина ломаной, по которой "разрезается”
пирамида, была минимальной;
б) лист прямоугольной формы, из которой
выкраивается развертка, имел минимальную
площадь;
в) развертка уместилась на листе прямоуголь-
ной формы, имеющем ширину 50 мм и мини-
мальную длину; подсчитайте площадь получен-
ного листа и сравните с площадью листа в слу-
чае (б);
г) постройте на одной из полученных при
решении предыдущих задач разверток точку D,
соответственную точке D(20, 20, ?), принадле-
жащей грани SBC данной пирамиды;
д) нанесите на развертки, полученные при
решении задач (а), (б), (в), линию, соответст-
венную многоугольнику, по которому данная пи-
рамида пересекается с плоскостью, заданной
своим уравнением 2х + z — 2 - 0.
23. Постройте проекции прямой т, параллель-
ной данной прямой а и равноудаленной от точек
С, D, и прямой а (рис. 5.53).
Рис. 5.53
24. В плоскести Е(а п Ь) постройте геометри-
ческое место точек, равноудаленных от данных
точек А, В (рис. 5.54)
Рис. 5.54
185
Глава 6
УЧЕБНО-ИССЛЕДОВАТЕЛЬСКИЕ ЗАДАЧИ
В КУРСЕ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Целью настоящей главы является
изложение вопросов, направленных на
развитие творческих способностей сту-
дентов на основе активизации их са-
мостоятельной исследовательской рабо-
ты. Предлагаемый материал не следует
расценивать как систематизированный
курс ’’высшей” начертательной геомет-
рии. В раздел включены лишь некото-
рые вопросы общетеоретического ха-
рактера, в той или иной мере развива-
ющие и обобщающие отдельные зада-
чи, способы, методики, рассмотренные
в первых пяти главах.
При отборе материала автор руко-
водствовался опытом проведения науч-
но-исследовательской работы студентов
на кафедре прикладной геометрии
МАИ, а также стремлением отразить
как теоретические, так. и прикладные
вопросы актуальных проблем, решае-
мых научными и инженерно-техничес-
кими работниками.
Конечно, нереально детальное осве-
щение в учебнике всех вопросов. Поэ-
тому изложение материала каждого
раздела завершается перечнем тем и
задач, выносимых на самостоятельное
исследование, которые наряду с тема-
ми для самостоятельных исследований,
имеющимися на каждой кафедре на-
чертательной геометрии и инженерной
графики, должны способствовать под-
готовке высококвалифицированных
творческих инженеров.
6.1. Обобщенные
виды проецирования
и их применение для решения
позиционных задач
Как было уже отмечено в п. 1.1,
проецирование точек можно выполнять
линиями и поверхностями. Детально
были изучены свойства центрального
проецирования и его частных видов:
параллельного и прямоугольного. При
этом множество проецирующих пря-
мых проходит через центр проецирова-
ния, который может быть собственным
или несобственным.
Центральное проецирование прямы-
ми линиями достаточно просто обобща-
ется заменой прямых линий кривыми
линиями или множествами более об-
щего вида. В первом случае проециро-
вание называется криволинейным. В
качестве проецирующих линий широко
используются окружности (окружное -
тное проецирование), цилиндрические
винтовые линии (винтовое проецирова-
ние) и другие линии, например, кони-
ческие винтовые линии, кривые второ-
го порядка, пространственные кривые
третьего порядка и др. При этом мно-
жества проецирующих линий задаются
определенным образом в каждом кон-
кретном случае для обеспечения при-
надлежности данной точке оригинала
одной проецирующей линии.
Множествами прямых, обобщающих
связки прямых, т.е. прямых, проходя-
щих через фиксированную точку, яв-
ляются конгруэнции прямых. Наибо-
лее просто конгруэнции прямых зада-
ются их фокальными линиями а, Ь.
Множество прямых пространства, пе-
ресекающих две фиксированные фо-
кальные линии, образует двупарамет-
рическое множество прямых — конгру-
энцию. Если фокальные линии а, Ь
являются алгебраическими, то конгру-
энция также является алгебраической.
Алгебраическая конгруэнция характе-
ризуется порядком п и классом к.
Порядок п конгруэнции равен числу
прямых конгруэнции, проходящих
через произвольную точку простран-
186
Рис. 6.1
ства, а класс к — числу прямых кон-
груэнции, принадлежащих произволь-
ной плоскости пространства.
Например, множество прямых (/'),
пересекающих две скрещивающиеся
прямые а, Ь, образует конгруэнцию
первого порядка и первого класса
Кг(1,1). Действительно (рис. 6.1),
через произвольную точку М про-
странства проходит единственная пря-
мая Г, пересекающая фокальные пря-
мые a, b: I' = Г(Л/, а) п Л (Л/, Л). А в
произвольной плоскости Е лежит одна
прямая Г = АВ конгруэнции, где А =
= апЕ,5 = Ап£. С этих позиций
связка прямых является конгруэнцией
первого порядка и нулевого класса
Кг(1,0).
Очевидно, что в качестве множества
проецирующих прямых целесообразно
использовать конгруэнции первого
порядка. Тогда через произвольную
точку протранства будет проходить
единственная проецирующая прямая.
Такие конгруэнции задаются в общем
случае фокальной прямой а и фокаль-
нои пространственной кривой b по-
рядка Ир имеющей с прямой a — 1
фиксированных точек А‘ (рис. 6.2). В
этом случае произвольная точка М с
прямой а определяют плоскость Г, а с
кривой b — коническую поверхность
Д порядка И]. Плоскость Г, как прохо-
дящая через вершину М конической
поверхности Д, пересекает последнюю
по образующим Z'+1, из которых z =
Рис. 6.2
= И] — 1 образующих МА1 проходят
через фиксированные точки А‘ = а п Ь,
а одна является свободной. Она прини-
мается в качестве проецирующей пря-
мой, проходящей через точку М.
Отметим, что проецирование кон-
груэнциями прямых называется косым
проецированием.
Далее приведем примеры примене-
ния обобщенных видов проецирования
для решения позиционных задач.
6.1.1. Построение косой
проекции прямой
на монопроекционном чертеже
Рассмотрим построение косой проек-
ции q на плоскость Щ некоторой пря-
мой с, получаемой проецированием
прямыми конгруэнции Кг(1,1). Пусть
конгруэнция Кг (1,1) задана двумя
скрещивающимися фокальными пря-
мыми а, b (рис. 6.3). Построения будем
187
выполнять на необратимом чертеже,
получаемом путем прямоугольного
проецирования точек пространства на
плоскость проекций Пр Такие изобра-
жения называются монопроекционны-
ми чертежами или, короче, монопро-
екциями.
Для однозначного выполнения гра-
фических построений монопроекцион-
ный чертеж должен быть позиционно
полным. Это означает, что каждая
геометрическая фигура должна быть
задана определяющими ее элементами
с указанием их положения в простран-
стве. В нашем случае для получения
позиционно полного изображения не-
обходимо указать точки пересечения
Лр Bp Ci прямых о, Ь, с с плоскостью
проекций П], а также точки А, В пе-
ресечения прямых а, b с некоторой
плоскостью 0 проходящей через дан-
ную прямую с. Плоскость 0 определим
двумя пересекающимися прямыми с,
d, где d — прямая пересечения плос-
костей 0, Пр Отсюда следует, что пря-
мая d проходит через точку Ср
Таким образом, задача построения
косой проекции Cj прямой с сводится
к построению множества проецирую-
щих прямых I1, пересекающих данные
три прямые а, Ь, с, и нахождению то-
чек С/ их пересечения с плоскостью
Пр Точки С/ определяют искомую
косую проекцию Ср Но множество
прямых /' составляет одно семейство
образующих однополостного гипербо-
лоида Ф (см. п. 2.6.5). Поэтому проек-
цией будет сечение проецирующего
однополостного гиперболоида Ф плос-
костью Пр Значит, линия q будет
кривой второго порядка, т.е. при косом
проецировании прямая линия проеци-
руется в кривую линию. Заметим, что
начертательная геометрия, основанная
на косом проецировании, называется
нелинейной.
Графическое построение следов С\
проецирующих прямых /1 на плоскости
проекций П] выполняется просто. На
прямой с выберем произвольную точ-
ку С1 (см. рис. 6.3). Она вместе с
прямой а определяет плоскость Г, ко-
торая пересекается с плоскостью 0 по
прямой С‘А, а с плоскостью П[ — по
прямой 7Ц/, где 1 = С'А nd. Точка
С1 вместе с прямой b определяет плос-
кость Д, которая пересекается с плос-
костью 0 по прямой С'В, а с плос-
костью IIj — по прямой Bj2, где 2 =
= С ‘В n d. Плоскости Г, Д пересека-
ются по проецирующей прямой /!,
проходящей через точку С‘ и пересе-
кающей плоскость П] в точке =
= A1/nBJ2. Множество точек ,
построенных таким образом, определя-
ет искомую косую проекцию Cj данной
прямой с.
Если на рис. 6.3 убрать линии, огра-
ничивающие плоскости П], 0 и прида-
ющие чертежу ’’объемность”, а также
оставить лишь точки At, А прямой а,
ТОЧКИ Вр В прямой Ь, то получим
конструктивный аппарат квадратично-
го преобразования Т2 между совме-
щенными полями точек П; (С^), 0(С1).
В этом преобразовании прямой с одно-
го поля соответствует кривая второго
порядка С[ второго поля.
Построение соответственных точек
С/ - С1, выполняется одной линей-
кой, если дана инвариантная прямая d
преобразования и по две фиксирован-
ные точки Лр Bj и А, В соответствен-
но полей Пр 0. Алгоритм прямого пре-
образования Т2(Су ~ С‘): А\С}‘ n d =
188
= 1, n d = 2, C‘ = Al n B2.
Аналогично, алгоритм обратного пре-
образования Tjl (С‘ ~ С/) состоит из
следующих операций: AC1 n d = 1,
ВС1 nd = 2, С/ = Aj 1 л Вх2.
Заметим, что полученное квадратич-
ное преобразование с позиций начерта-
тельной геометрии истолковывается
как монопроекционная модель плос-
кости 6 на плоскости изображения ГЦ.
Из теории нелинейных алгебраичес-
ких преобразований известно [3], что
квадратичные преобразования в каж-
дом поле имеют три исключенные, так
называемые фундаментальные точки.
Для этих точек нарушается однознач-
ность соответствия. Каждой из них в
другом поле соответствует прямая,
называемая принципиальной.
Тема для исследования
Завершая конспективное изложение
материала этого раздела, сформули-
руем ряд задач для самостоятельного
исследования.
1. Найдите фундаментальные точ-
ки полей П/, в и соответственные им
принципиальные прямые полей в, П{.
2. Взяв произвольные прямые mt
с к с в, графическим построением
их образов т - т2, кt - к убедитесь,
что кривые второго порядка т и к{
проходят через все три фундамен-
тальные точки соответствующих
полей. Также убедитесь, что любой
прямой поля П], проходящей через
одну из фундаментальных точек это-
го поля, в поле в соответствует кри-
вая второго порядка, распавшаяся на
принципиальную прямую и собственно
образ.
3. Возьмите в любом поле в качес-
тве прообраза кривую второго поряд-
ка. Но точкам постройте ее образ в
другом поле. Убедитесь, что образом
является кривая четвертого порядка,
имеющая двойные точки, которые
совпадают с фундаментальными точ-
ками этого поля. Выясните, как вли-
яет взаимное положение прообраза и
принципиальных прямых этого поля
(их пересечение в двух действитель-
ных различных точках, в двух совпав-
ших точках и в двух мнимых точках)
на вид двойной точки образа в другом
поле. Обратите внимание, что двой-
ная точка может быть узловой, воз-
врата и изолированной.
Изучите свойства образов кривых
второго порядка, проходящих через
одну, две и три фундаментальные
точки.
4. На рис. 6.3 задайтесь системой
декартовых координат, общей для
полей П](Оху) и в(Оху), т.е. Оху =
= Оху. Для простоты ось Ох =Ох
можно совместить с инвариантной
прямой d, а ось Оу = Оу выбрать
произвольно. Аналитически описав
операции графического алгоритма
построения соответственных точек
С^(х, у) - С1 (х,у ), выведите форму-
лы прямого преобразвания Т2 в виде
£ = />(Л^); (6.D
У f2 (X, у)
и формулы обратного преобразова-
ния Т2 1 в виде
х = Ф1(х, у); (62)
У = <₽2(х> у '>•
Убедитесь, что функции f], f2, <Pj, <р2,
Являются дробно-квадратичными,
т.е. их числители и знаменатели
являются квадратными многочле-
нами.
Формулы (6.J), (6.2) преобразова-
ния Т2, будучи аналитическими экви-
валентами алгоритма построения
соответственных точек, служат
базой для программной реализации
преобразования Т2 и применения его
189
для автоматизированного конструи-
рования и исследования свойств ал-
гебраических кривых высших порядков.
5. Используя выведенные формулы
преобразования, выполните аналити-
ческие исследования задач, сформули-
рованных в пп. 2, 3.
6. Все вышеизложенное в этом раз-
деле повторите для случая косого
проецирования прямыми конгруэнции
Кг (1,2), заданной фокальной прямой
а и фокальной окружностью Ь, кото-
рые имеют одну общую точку М.
Обратите при этом особое внимание
на получение позиционно полного
моноизображения.
6.1.2. Построение точек
пересечения кривой линии
с поверхностью вращения
Использование криволинейного прое-
цирования покажем на примере по-
строения точек пересечения кривой
линии с поверхностью вращения. Та-
кая задача решается по алгоритму,
описанному в п. 4.2.3. Обычно, в ка-
честве вспомогательной поверхности,
которая проводится через данную кри-
вую линию, выбирается цилиндричес-
кая проецирующая поверхность. В
нашем случае, когда необходимо по-
строить точки пересечения кривой I с
поверхностью вращения Ф, целесооб-
разно через данную кривую I провести
вспомогательную поверхность враще-
ния Г, соосную с данной поверхностью
Ф. Тогда в соответствии с теоремой о
пересечении двух соосных поверхнос-
тей вращения (см. п. 4.7) данная и
вспомогательная поверхности Ф, Г пе-
ресекаются по их общим параллелям,
проходящим через точки пересечения
их главных меридианов.
Таким образом, данная задача сво-
дится к построению главных меридиа-
нов данной и вспомогательной повер-
хностей вращения или только главного
меридиана вспомогательной поверхнос-
ти Г, если в состав определителя дан-
ной поверхности Ф входит в качестве
ее образующей главный меридиан. Но
построение главного меридиана т сво-
дится к проведению через точки обра-
зующей / множества параллелей и на-
хождению их точек пересечения с
плоскостью S главного меридиана (см.
рис. 2.53 и п. 2.6.3). Другими словами,
построение главного меридиана т
можно истолковать как построение
криволинейной проекции образующей
I на плоскости Е, когда проецирование
осуществляется множеством окружнос-
тей.
Пример. Построить точки L1 пере-
сечения кривой линии I с поверх-
ностью вращения Ф (у, а) (рис. 6.4).
В соответствии с алгоритмом реше-
ния кривую I заключаем в вспомога-
тельную поверхность вращения Г(/, /),
соосную с данной поверхностью Ф.
Затем строим главный меридиан т(тх,
т2) вспомогательной поверхности Г,
как линию ее пересечения с горизон-
тальной плоскостью S, проходящей
через ось j поверхностей Ф, Г. Другими
словами, строим криволинейную про-
екцию т на плоскость S данной линии
/, проведя через ее точки проецирую-
щие окружности.
Дуги главных меридианов а, т по-
верхностей Ф, Г пересекаются в точ-
Рис. 6.4
190
,ке L(L\, L2) — криволинейной проек-
ции на S искомой точки L(L^, L2) пе-
ресечения кривой I с поверхностью
вращения Ф.
Задачи для исследования
1. Постройте криволинейные проек-
ции прямой I, окружности т, эллипса
к на плоскость уровня S, проходящую
через ось j, и на проецирующую плос-
кость Л, параллельную оси j, проеци-
рованием множеством окружностей,
центры которых принадлежат оси j,
а их плоскости перпендикулярны оси
j. Убедитесь, что криволинейные про-
екции данных линий являются алгеб-
раическими кривыми, порядки кото-
рых в 2 раза больше порядков данных
линий. Докажите справедливость
этого результата.
2. Постройте криволинейную проек-
цию I j данной кривой линии I на пло-
скость проекций П] проецированием ее
точек множеством цилиндрических
винтовых линий, соосных с данной
винтовой линией т (рис. 6.5). При
этом все проецирующие винтовые
линии должны иметь один и тот же
шаг h и отличаться друг от друга
лишь радиусами. Разработайте гра-
фический алгоритм построения кри-
волинейной проекции Ll точки Lei,
Рис. 6.5
исключающий построение проецирую-
щей цилиндрической винтовой линии.
Другими словами, построение криво-
линейной проекции I] можно истолко-
вать как построение сечения винто-
вой поверхности Ф(], т, I) плос-
костью П{.
3. Используя идею вспомогательно-
го проецирования множеством соос-
ных цилиндрических винтовых линий
с равными шагами, постройте точки
пересечения кривой tflj, 12) с цилин-
дрической винтовой поверхностью Ф,
образованной винтовым движением
окружности т (рис. 6.6). Винтовое
Рис. 6.6
движение задано цилиндрической вин-
товой линией t(tj, t2). Плоскость
окружности т при ее движении оста-
ется параллельной П].
4. Разработайте графический спо-
соб построения винтовых линий на
поверхностях вращения, основанный
на предварительном построении соос-
ной цилиндрической винтовой линии и
ее отображении на поверхность вра-
щения проецированием множеством
прямых, пересекающих ось винтовой
линии под прямым углом. Убедитесь,
что это множество проецирующих
прямых составляет конгруэнцию
Кг (1,1), определяемую фокальными
191
прямыми: осью цилиндрической вин-
товой линии и несобственной прямой
плоскости, перпендикулярной этой
оси.
Используйте полученные винтовые
линии для построения криволинейных
проекций каких-либо данных линий,
разработайте графические алгорит-
мы построения криволинейных проек-
ций, исключающие построение прямо-
угольных проекций проецирующих
винтовых линий.
6.1.3. Возможные обобщения
метода двух изображений
Классический метод двух изображе-
ний, описанный в п. 1.3 (см. рис. 1.9),
позволяет получать линейные модели
пространства: прямая линия простран-
ства отображается также в прямую
линию плоскости проекций.
Аппарат классического метода двух
изображений может быть легко обоб-
щен с целью получения нелинейных
моделей путем:
1) замены центрального проецирова-
ния криволинейным проецированием
или проецированием прямыми конгру-
энции первого порядка и k-vo класса:
2) заменой вспомогательных плоскос-
тей проекций и (или) плоскости изо-
бражения поверхностями проекций.
Необходимость таких обобщений вы-
зывается потребностями теории и
практики построения обратимых изо-
бражений сложных поверхностей, по-
вышения художественной выразитель-
ности изображений (построение собс-
твенных и падающих теней, панорам-
ная и купольная перспектива, широко-
форматное и панорамное кино), по-
строением теории специальных видов
фотосъемок и расшифровки изображе-
ний (щелевая аэрофотосъемка, двух-
средная фотосъемка) и т.д.
Аналогичные обобщения возникают,
например, при съемке неподвижного
объекта подвижной камерой. Подобные
задачи возникают при проектировании
всевозможных тренажеров, предназна-
ченных для подготовки или повышения
квалификации водителей и пилотов.
При этом на экране тренажера возни-
кает изображение, аналогичное тому,
которое видит водитель машины или
пилот самолета при их движении с
определенной скоростью.
Подобных задач можно перечислить
достаточно много. В своей основе их
решение сводится к построению точек,
линий пересечения проецирующих
линий, поверхностей с плоскостями
или поверхностями проекций. Поэтому
в качестве подготовительных задач для
самостоятельного исследования можно
рекомендовать построение проекций
(центральных, косых, криволинейных)
простейших фигур (прямых, окружнос-
тей, дуг каких-либо кривых, треуголь-
ников, прямоугольников и т.д.) на по-
верхности проекций (плоскости, сферы
или полусферы, отсеки цилиндричес-
ких и конических поверхностей враще-
ния).
6.2. Аналитический
способ построения
наглядных изображений
Аналитические алгоритмы построе-
ния наглядных изображений служат
базой для их реализации средствами
машинной графики при автоматизиро-
ванном проектировании. Хотя в специ-
альной литературе по машинной гра-
фике при построении наглядных изо-
бражений пишут о построении перс-
пективных или аксонометрических
изображений, однако не следует их
отождествлять с машинными реализа-
циями описанных в первой главе аксо-
нометрических (см. п. 1.5) и перспек-
тивных (см. п. 1.7.1) чертежей. В кур-
се начертательной геометрии под аксо-
нометрическими и перспективными
чертежами понимают наглядные обра-
192
тимые изображения. Поэтому чертеж
фигуры кроме перспективной или ак-
сонометрической проекции содержит
еще вторичную проекцию. В трехмер-
ной машинной графике под перспек-
тивными или аксонометрическими
чертежами обычно понимают лишь
наглядные изображения [8]. Поэтому
на экране дисплея или на графопостро-
ителе строятся лишь перспективные
(центральные) или аксонометрические
(параллельные) проекции. Таким об-
разом, в литературе по машинной гра-
фике под терминами перспективное
или аксонометрическое изображение
имеют в виду наглядное необратимое
изображение фигуры, полученное пу-
тем ее центрального или параллельно-
го проецирования на картинную плос-
кость.
Аналитический способ построения
наглядных изображений с позиций
машинной графики сводится к вычис-
лению координат и, v проекции неко-
торой точки оригинала по ее извест-
ным координатам х, у, z;
u=Mx,y,z)- (63)
V = /2(^
где и, v — координаты проекции неко-
торой точки в системе координат Ouv,
выбранной на картинной плоскости; х,
у, z — координаты точки фигуры в
пространственной системе координат
Oxyz.
Вывод формул (6.3) можно выпол-
нить несколькими способами. Дадим
краткое изложение двух из них.
1. Пусть наглядное изображение на
картинной плоскости П' получается
параллельным проецированием в на-
правлении s {к, I, т) (ри. 6.7), где к, I,
т — направляющие коэффициенты
вектора s. Тогда натуральная система
координат Oxyz проецируется в аксо-
нометрическую систему координат
O'x'y'z', с осью O'z' которой совмес-
тим ось O'v декартовой системы, вы-
бранной в плоскости IT.
Для вывода формул отображения
(6.3) необходимо через данную точку
А(х, у, z) провести проецирующую
прямую АА'
X - х _ Гу _ z - z
(6.4)
к I т
и построить точку А' ее пересечения с
картинной плоскостью 1Г
АХ + BY + CZ. + D = 0. (65)
Координаты х', у', z' точки А' =
= АА'пП' определяются совместным
решением систем уравнений (6.4),
(6.5):
/ _ х(В1 + Cm) - к(Ву + Cz + D) .
” Лк + В! < Ст ’
/ _ у(Ак + Ст) -l(Ax *Cz + D) . {(у
У Ак + В1 > Ст ’
z / _ х(Ак + Вт) - т(Ах + By + D)
Ак * Bl + Ст
Теперь точку А'(х', у’, z') необхо-
димо отнести к системе координат
193
О 'uv. Для этого сначала запишем
уравнение оси O'z' = O'v как прямой,
проходящей через точки О', Т =
= Oz с П'. Координаты точки О'
получаются подстановкой в форму-
лы (6.6) значений координат точки
0(0, 0, 0):
и
х> = - kD
0 Ак + Bl + Ст ’
у/ = ~lD •
0 Ак + В1 + Ст ’
(6.7)
/
20
- mD
Ак + В1 + Ст
Координата v точки А’ равна расстоя-
нию от точки А' до оси О'и (до плос-
кости Г) и вычисляется по формуле
А координаты точки Т получаются
совместным решением уравнения (6.5)
с уравнениями оси Oz: X = 0; У = 0:
х = 0; у = 0; z = - £. (6.8)
т -'Т Т с
Уравнения прямой O'v = О'Т имеют
вид
хо - хт Уо - Ут zo - ZT
Уравнения оси О'и представляют
систему, составленную из уравнений
(6.5) плоскости П' и плоскости Г, пер-
пендикулярной оси O'v и проходящей
через точку О':
(Xq - ХТ)(Х “ Xq) +
+ (Уо -Ут^У -Уо) + (6Л0)
+ (Zq - zT)(Z - Zq) = 0.
Тогда координата и точки А' относи-
тельно системы О 'uv равна расстоянию
от точки А' до оси O'v и вычисляется
по известной формуле [2]
к^о - Хт)(х' - +
- хт)2 +
+ (Уо Ут)(у/ Уо) + (*0 zt)(z' *о)1
4— ... ___________________—
+ (Уо - Ут)2 + (ZoZ - ip)2
(6.12)
Если в формулы (6.11), (6.12) под-
ставить значения х', у', z' из (6.6),
Xq , уд , zq из (6.7), хт, ут, zT из (6.8),
то получим формулы отображения
(6.3), по которым непосредственно
вычисляются значения координат и, v
параллельной проекции А' данной
точки А(х, у, z).
Очевидно, аналогичными выкладка-
ми можно вывести формулы (6.3) для
расчета координат точек некоторой
фигуры, получаемой центральным
проецированием оригинала на картин-
ную плоскость П'.
Читателю предлагается вывести
эти формулы самостоятельно и,
задавшись какой-либо пространствен-
ной фигурой (куб, параллелепипед с
вырезами и т.д.), построить ее па-
раллельную и центральную проекции
194
на какую-либо плоскость П', т.е.
вычислить, пользуясь выведенными
формулами, координаты проекций
вершин данного многогранника.
2. Описанный выше способ вычисле-
ния координат параллельных и цен-
тральных проекций точек в системе
координат O'uv плоскости изображе-
ния достаточно громоздок и мало при-
способлен для машинной реализации.
Дело в том, что при машинной реали-
зации необходимо учитывать дополни-
тельные ограничения [8]:
— изображается лишь часть про-
странства, расположенная по одну
сторону от центра проецирования;
— телесный угол, в пределах которо-
го располагаются проецирующие лучи,
ограничен.
Аппарат получения наглядного изо-
бражения состоит (рис. 6.8) из точки
зрения (проецирования) S, картинной
плоскости IT. Прямая SO', перпенди-
кулярная картинной плоскости П',
называется главным лучом зрения,
точка О' = SO' п П' — главной точ-
кой картины, длина d отрезка SO' —
дистанционным расстоянием.
На картинной плоскости П' выбира-
ется система координат O'uv, ось О'и
которой горизонтальна, а ось O'v —
вертикальна. Площадь картинной
плоскости П' ограничивается кадро-
вым окном — рабочим полем картин-
ной плоскости, имеющим форму квад-
рата со стороной 2д. Пирамида с вер-
шиной в точке 5, основанием которой
является кадровое окно, называется
пирамидой видимости.
Если начало пространственной систе-
мы координат 5xsyszs совмещено с
центром проецирования 5, ось 5zs
выбрана вертикальной (Szs || О 'v), ось
Sxs — горизонтальна (Sxs || О'и), а
ось Sys совмещена с главным лучом
зрения, то координаты и, v проек-
ции А’ некоторой точки A(g, I, h) вы-
числяются по простым формулам (см.
рис. 6.8):
и = v = (6.13)
Z /
Если аппарат центрального проеци-
рования расположен произвольно отно-
сительно пространственной системы
координат Oxyz (рис. 6.9), то для вы-
вода формул отображения (6.3) необ-
ходимо выполнить ряд преобразований
координат. Пусть центр 5 проецирова-
ния имеет координаты х0, у0, z0, а
главная точка О’ картины — коорди-
наты Хр Ур Zp
Выполниим параллельный перенос
системы координат Oxyz на вектор OS,
т.е. систему координат Oxyz преобразу-
ем в систему Sx'y'z'. Тогда произ-
вольная точка А(х, у, z) в новой систе-
ме координат будет иметь кординаты
А(х', у', z'), где
195
х1 = х - х0; у' = у - у0; (6 ,4)
Z 1 = Z - Zq.
Затем вращением вокруг оси Sz' на
некоторый угол а систему координат
Sx'y'z' преобразуем в систему коор-
динат Sx"y"z". Здесь а — угол, состав-
ленный осью Sy' с вертикальной плос-
костью Д, проходящей через главный
луч зрения SO'. Значение угла а
определим из прямоугольного тре-
угольника MNO', катеты O'N, NM
которого параллельны соответственно
осям Оу, Ох и равны |OW| = У] — у0,
I MN | = х1 — х0. Гипотенуза |О'Л/| =
= /(X! - х0)2 + (у, - у0)2.
Отсюда
У<х1 - хо>г * <У1 - У©)2
Хл
cosa = - (6.15)
7<*i - V + (У1 - у©)2
Формулы этого преобразования име-
ют вид
xz/ = xzsina - у1 cosa;
у" = х7cosa + у zsina;
подставив в которые значения коорди-
нат х', у', z' точки А из (6.14), полу-
чим ее координаты х", у", z" в новой
системе
хи = (х - x0)sina - (у - y0)cosa;
у" = (х - x0)cosa + (у - y0)sina;
z" = z - z„. <6.16)
И, наконец, вращением вокруг оси
Sx" на некоторый угол р, где р —
угол, составленный осью Sy" с глав-
ным лучом SO’ зрения, систему кор-
динат Sx"y"z" преобразуем в си-
стему координат Sxsyszs. Значе-
ние угла Р определяем из прямо-
угольного треугольника SMO', катеты
SM, МО' гипотенуза SO', которого
равны | SM | = Z] — zq, |Л/О'| =
= /(x1-x0)2 + (yl-y0)2, I SO' I
= ^(x1-x0)2+(y1-y0)2+(z1-z())2.
Отсюда имеем
sinP = 1 ;
У(х1 - *о)2 + 61 - У©)2 + <zi - Ч)2
cosp = А-^1<У1^_
У(х, - X©)2 + (У! - То)2 + (Zj - Zq)2
(6.17)
Формулы этого преобразования име-
ют вид
г - г " •
Xs - X ,
ys = z " sinp + у11 cosP;
zs = zn cosp - y/z sinp,
подставив в которые значения х", у",
z", из (6.16) получаем координаты g, I,
h точки А в системе Sxsyszs:
g = xs = (х - x0)sina - (у - y0)cosa;
Z=ys = (z-z0)sinp + l(x- (618)
-x0)cosa + (у -y0)sina]cosp;
h = zs = (z - z0)cosp - 1 (x -
-x0)cosa + (y -y0)sina]sinp.
196
И, наконец, подставив значения g, /,
h. из (6.18) в (6.13), получаем форму-
лы отображения:
, <х - x0)sina -
и = а----------------------------
(z - zo)sin0 + [(х - x0)cosa +
- (у - y0)cosc
<• (у - yo)sina]cos0 ’
(6.19)
(z - z0)cosp - | (x - x0)cosa +
V = d---------------------------- -
(z - z0)sinp + ((x - x0)cosn ♦
+ (y - y0)sina]sinp
+ (y - y0)sine]cosp
Эти формулы достаточно просты, так
как здесь значения sina, cosa, sin0,
cos (J постоянны для выбранного аппа-
рата отображения.
Приведенные в этом разделе выклад-
ки позволяют аналитически ’’строить”
параллельные и центральные проекции
геометрических фигур на картинной
плоскости, отличающиеся нагляд-
ностью. Такие изображения, получен-
ные на экране дисплея, создают эф-
фект объемности, позволяют оценить
конструктивные и эстетические до-
стоинства изображаемых фигур. Прав-
да, для получения машинных изо-
бражений необходимо еще решить ряд
задач:
1) отсечение частей изображае-
мой фигуры пирамидой видимости
или коррекция масштаба изображе-
ния;
2) удаление невидимых линий и т.д.
Принципы решения этих задач до-
ступно изложены в справочнике |8|.
Там же можно познакомиться с основ-
ными идеями и задачами машинной
графики в системах автоматизирован-
ного проектирования. Они представля-
ют богатый материал для самостоя-
тельных исследований.
6.3. Родство —
модель плоскости
на чертеже Монжа
При рассмотрении задания плоскости
на чертеже Монжа (п. 2.2) было пока-
зано, что моделью плоскости является
родственное (перспективно-аффинное)
соответствие, устанавливаемое между
полями горизонтальных и фронталь-
ных проекций точек данной плоскости.
При этом были сформулированы его
основные свойства, непосредственно
вытекающие из свойств параллельного
проецирования. Было отмечено, что
родство имеет двойную прямую d{ =
d2, называемую осью родства. Она
представляет собой совпавшие проек-
ции линии пересечения данной плос-
кости с биссекторной плоскостью чет-
ных четвертей. Отсюда следует широко
используемый способ задания родства
парой соответственных точек А} ~ А2
и осью родства t/j = d2, что равносиль-
но заданию плоскости S точкой А и
прямой d. Тогда построение точки М2,
соответственной точке Л/(, выполняет-
ся в такой последовательности
(рис. 6.11):
— проводится прямая А1М1 и отмеча-
ется точка = AlMl п
— точка М2строится как точка пере-
сечения прямой /2/l2l с ПРЯМ°Й Л4]Л/2,
параллельной направлению родства
Родство, будучи частным случаем
аффинных преобразований, не сохра-
Рис. 6.10
197
няет длину отрезка и величину угла.
Однако родство в каждой плоскости
имеет два направления, называемые
изометрическими. При этом отрезки
соответственных прямых, параллель-
ных этим направлениям, конгруэнтны
(рис. 6.10). Из алгоритма построения
соответственных точек следует, что
одно направление параллельно оси
родства d\ = d2. Действительно, отре-
зок HjBj, параллельный оси родства,
преобразуется в конгруэнтный отрезок
А2В2, так как они являются противо-
положными сторонами параллелограм-
ма А^А^^^. Соответственные прямые
Л]В[ - А2В2, будучи параллельными
оси родства = d2, пересекаются с
последней в несобственной точке 3“.
Для нахождения другого изометри-
ческого направления выполним следу-
ющие построения:
— найдем середину С отрезка AtA2;
— построим прямую t, перпендику-
лярную AjA2 в точке С;
— из точки О пересечения прямой t
с осью родства, как из центра, опишем
окружность I радиуса [OAJ = [ОЛ2].
Очевидно, конгруэнтные отрезки
ОЛ[, О А 2 являются соответственными
в родстве. Они определяют вторые
изометрические направления родства в
плоскостях и П2.
Из выполненных построений следует
(см. рис. 6.10), что прямые Л]/, А21 и
И]2, А22 соответственны в родстве.
Кроме того, они взаимно перпендику-
лярны, т.е. прямому углу 1Ау2 в род-
стве соответствует прямой угол 1А22.
Таким образом, в плоскости Щ сущес-
твуют два перпендикулярных направ-
ления 1А} ± А]2, которым в плоскости
П2 также соответствуют перпендику-
лярные направления 1А2 ± А22. Эти
направления называются главными
направлениями родства.
Рассмотренные выше свойства род-
ства можно исследовать аналитически,
если вывести формулы преобразова-
ния. Для этого в совмещенных плос-
костях П[ = П2 выберем систему коор-
динат Оху (рис. 6.11) и выведем фор-
мулы преобразования, связывающие
координаты х, у текущей точки Л/1
плоскости П1 с координатами х', у'
соответственной точки М2 плоскос-
ти П2.
Пусть плоскость S имеет уравне-
ние
АХ + BY + CZ + D = 0. (620)
Из способа получения эпюра Монжа
следует, что
X = х = х', Y = - у, Z = у1. (6‘21)
Подставив значения х, х', у, у' из
(6.21) в (6.20), получим формулы пря-
мого преобразования:
(6.22)
и формулы обратного преобразования:
(6.23)
Эти формулы позволяют по известным
координатам х, у горизонтальной про-
екции Мх точки М вычислять коорди-
наты х', у' фронтальной проекции М2
и обратно. Имея эти формулы, можно
аналитически осущетвлять исследова-
ние свойств родства и решения задач
198
на эпюре с участием модели плос-
кости.
В качесте примера покажем, что
прямой т1 плоскости П] соответствует
в плоскости П2 также прямая т2. Для
этого в уравнение
Nx + Му + К = О
произвольной прямой mt подставим
значения х, у из (6.23). После элемен-
тарных выкладок получаем линейное
уравнение
1и+™\х'+^у'*^+К=0,
\ в I в в
определяющее прямую т2 — образ
прямой пг1 в родстве.
С позиций начертательной геометрии
построение образа т2 прямой mY в
родстве эквивалентно построению про-
екций т2 линии пересечения гори-
зонтально проецирующей плоскости
rtmp с данной плоскостью S, модели-
руемой на чертеже Монжа родством.
Обобщая это утверждение, можно ска-
зать, что построение образа т2 ^ти к\
некоторой линии тх или к2 в родстве
равносильно построению недостающей
проекции ш2(Л|) линии пересечения
т(к) плоскости S с горизонтально про-
ецирующей ГОн,) или фронтально
проецирующей Д(А2) цилиндрической
поверхностью.
Выполняя самостоятельные исследо-
вания, связанные с построением ука-
занных линий, следует обратить вни-
мание на равенство порядков соответ-
ственных линий - т2, Aj - А2, так
как родство является линейным преоб-
разованием. В ряде случаев целесооб-
разно помнить о наличии у родствен-
ных преобразований главных и изомет-
рических направлений. Например, при
построении эллипса как образа окруж-
ности в родстве целесообразно предва-
рительно построить его главные на-
правления, проходящие через центры
этих кривых. Тогда диаметры окруж-
ности, совпадающие с главными на-
правлениями родства, преобразуются в
оси эллипса. Наличие осей значитель-
но упрощает построение эллипса.
Приведем еще один пример. Пусть
требуется в поле П] построить квадрат,
образом которого в поле П2 будет не
параллелограмм как в общем случае, а
ромб. Как известно, у ромба диагонали
взаимно перпендикулярны. Поэтому в
качестве его прообраза надо брать та-
кой квадрат, у которого диагонали
будут параллельны главным направле-
ниям родства в поле П1. Если же тре-
буется построить ромб, стороны кото-
рого равны сторонам квадрата, то тогда
необходимо воспользоваться существо-
ванием изометрических направлений.
При выполнении таких исследований
целссообрано проводить их графически
и аналитически, чтобы полнее уяснить
взаимосвязь методов начертательной и
аналитической геометрии. Такое ’’па-
раллельное” исследование полезно при
решении следующей задачи.
Как было показано, плоскость обще-
го положения Е моделируется род-
ством, которое удобно задавать парой
соответственных точек - А2 и осью
dl -= d2 родства (см. рис. 6.10). В об-
щем случае направление .402 родства
не перпендикулярно оси d^ = d2 род-
ства и отрезки А}4, А24, где 4 = А{А2
n d Wj = с/2), не равны.
Известно, что частными случаями
родства являются: косая симметрия,
когда [Aj4] = [А24] (рис. 6.12, а);
прямая осевая симметрия, когда
AjA2 idu [А 14] = ]А24] (рис. 6.12,
б); сдвиг, когда AtA2 / d (рис. 6.12,
в); параллельный перенос, когда ось d
родства является бесконечно удален-
ной прямой (рис. 6.12, г).
Требуется выяснить положение
плоскости S в пространстве, чтобы
ее моделями были перечисленные пре-
образования. Необходимо записать
уравнения таких плоскостей и вывес-
ти формулы моделирующих их преоб-
199
d
в)
А29
разований. Графические алгоритмы
построения соответственных точек
в указанных преобразованиях надо
получить соответствующим приспо-
соблением алгоритма построения
соответственных точек в родстве
для конкретного частного случая его
задания.
6.4. Моделирование
поверхностей второго порядка
на чертеже Монжа
В современной начертательной гео-
метрии рассматривают кинематический
способ образования поверхностей (см.
п. 2.6.1). При этом на чертеже повер-
хность изображается проекциями эле-
ментов геометрической части опреде-
лителя или проекциями линий карка-
са. Такой способ образования и зада-
ния поверхностей отличается просто-
той и наглядностью. Однако в силу
дискретности задания поверхности
существенно усложняются вопросы
исследования ее свойств в целом.
В терминах начертательной геомет-
рии дискретный каркас составляет
геометрическую часть определителя
поверхности, а алгоритмическая часть
включает в себя закон непрерывного
изменения параметров линий каркаса,
обеспечивающий получение непрерыв-
ного каркаса поверхности, включаю-
щего в себя исходный дискретный кар-
кас. В связи с этим известные способы
Рис. 6.12
конструирования поверхностей пред-
ставляют собой по существу способы
перехода от дискретного каркаса к
непрерывному. Таким образом, кон-
струирование поверхности сводится к
построению линий каркаса или мно-
жества точек, принадлежащих линиям
каркаса.
Как известно, дискретный каркас не
определяет поверхность однозначно,
ибо построение точек поверхности, не
лежащих на данных линиях каркаса,
может быть осуществлено различными
способами. В связи с этим поверхнос-
ти, заданные одним и тем же исход-
ным дискретным каркасом, но полу-
ченные различными способами ’’уплот-
нения” каркаса, могут отличаться друг
от друга существенно. Поэтому детали
или изделия, изготовленные на раз-
личных предприятиях по одному и
тому же чертежу технической повер-
хности, могут оказаться не взаимоза-
меняемыми.
Исследование свойств поверхности в
целом выполняется достаточно просто,
если она задана на чертеже непрерыв-
ной моделью. Последняя в методе двух
изображений представляет собой соот-
ветствие, порождаемое между полями
первых и вторых проекций точек по-
верхности. Например, как было пока-
зано в пп. 2.2; 6.3, плоскость на черте-
же Монжа моделируется перспективно-
аффинным соответствием (родством).
Построение непрерывных моделей
поверностей в методе двух изображе-
200
ний устанавливает тесную связь между
начертательной и алгебраической гео-
метриями. Целью настоящего и следу-
ющих трех разделов является изучение
этих связей применительно к изобра-
жению (моделированию), конструиро-
ванию и исследованию поверхностей.
Начнем с рассмотрения простейших
поверхностей — поверхностей второго
порядка.
На чертеже Монжа поверхность, как
и плоскость, моделируется соответст-
вием Т, устанавливаемым между поля-
ми горизонтальных и фронтальных
проекций точек данной поверхности Ф.
На рис. 6.13 сфера Ф2 моделируется
дву-двузначным квадратичным соот-
„,2-2
ветствием Т2 , установленным между
полями горизонтальных (Л]) и фрон-
тальных (А2) проекций точек А е Ф2.
Действительно, точке А1 поля П] в
поле П2 соответствуют две точки А2,
А2 — фронтальные проекции точек А,
А, в которых горизонтально проециру-
ющая прямая АА пересекает сферу Ф2
Аналогично, точке А2 поля П2 в поле
П] соответствуют две точки Ар At .
Прямой поля П1 в поле П2 соответ-
2
ствует эллипс а2 — проекция окруж-
2
ности а , по которой горизонтально
Рис. 6.13
Рис. 6.14
проецирующая плоскость Д э пере-
секает сферу Ф2.
При этом произвольной точке Aj
прямой а1 на П2 соответствуют две
различные действительные точки А2,
А2, если точка А( находится внутри
очерковой линии сферы (рис. 6.14).
Точкам Ср D} пересечения прямой
с очерковой окружностью на П] со-
тветствуют совпавшие точки С2 = С2,
D2 = D2. И, наконец, точке е
расположенной вне очерковой линии,
соответствуют на П2 две мнимые точки
В2, В2 (на рис. 6.14 они условно изо-
бражены крестиками). Таким образом,
2-2
рассматриваемое соответствие Т2
может ставить в соответствие действи-
тельной точке одного поля две
действительные различные, две дей-
ствительные совпавшие и две мнимые
точки второго поля.
Образом прямой одного поля в дру-
гом поле будет эллипс, касающийся
соответствующей очерковой линии
сферы в двух точках, расположенных
на одной линии связи: на рис. 6.14
прямой Я] соответствует эллипс а2,
201
касающийся очерковой окружности т2
в действительных различных точках
Л/2, М2. Эти точки будут мнимыми,
если на П[ прямые at, т1 пересекаются
вне очерковой линии /j. Они будут
совпавшими, если alt mt пересекаются
в точке, принадлежащей очерковой
линии сферы на Пр
С позиций теории многозначных ал-
гебраических соответствий линии Zj и
т2 называются линиями касания, так
как образы прямых и кривых линий
касаются их в точках, попарно распо-
ложенных на линиях связи.
Линии «ip 12 называются двойными
(но не инвариантными), так как они
являются носителями двойных точек —
двух совпавших точек одного поля,
соответственных одной точке второго
поля.
Соответственные совпавшие точки
разных полей, например = К2, на-
зываются инвариантными . В нашем
случае множество инвариантных точек
принадлежит мнимому эллипсу d^ = d2
— совпавшим проекциям окружности
d, по которой сфера Ф2 пересекается с
биссекторной плоскостью четных чет-
вертей (окружность d является мни-
мой, так как сфера Ф2 расположена в
первой четверти и с биссекторной
плоскостью четных четвертей не пере-
секается) .
Для аналитического построения соот-
ветственных точек, получения уравне-
ний образов данных линий и т.д. выве-
2-2
дем формулы соответствия Т2 —
модели сферы Ф2 на чертеже Монжа. В
совмещенных полях П| = П2 выберем
систему координат Оху = О'х'у' (см.
рис. 6.14). Произвольной точке
поля П( присвоим текущие координаты
х, у, а соответственной точке А2 поля
П2 — координаты х', у’.
В теории однозначных соответствий термины
"двойной” и ’’инвариантный” являются синони-
мами.
Пусть сфера Ф2 описывается уравне-
нием
(X - а)2 + (У - Z>)2 + (Z - с)2 = Л2,
где а, Ь, с — координаты ее центра; R
— радиус сферы. Из выбора простран-
ственной и плоской систем координат
следует: X = х = х', Y = — у, Z = у'.
Подставив эти значения в уравнение
сферы, получаем формулы прямого
соответствия:
/
У
и
______________________(6.24)
7 = ± уЯ 2 - (х - а)2 - (у - Z02 + с
формулы обратного соответствия:
X
_____________________________(6.25)
у = ± /л2- (х7-о)2- (у'-с)2 - b .
2-2
Полученное соответствие Т2 как
модель сферы на чертеже Монжа
удобно использовать для конструиро-
вания и исследования свойств алгеб-
раических кривых высших порядков.
Можно порекомендовать строить об-
разы кривых второго и высшего по-
рядков в данном соответствии. Рас-
сматривая всевозможные взаимные
положения прообраза aj относитель-
но характерных линий т{, lt соот-
ветствия, исследовать свойства об-
раза а2, обратив внимание на его
порядок, наличие особых точек и т.д.
Особый интерес представляет кон-
струирование кривых с наперед задан-
ными свойствами: инцидентность
каким-либо данным точкам; получе-
ние кривой данного порядка, наперед
заданной формы и т.д.
Например, с целью математического
моделирования технических кривых
типа ’’шпангоут” фюзеляжа самолета
или вертолета необходимо уметь кон-
струировать замкнутые выпуклые кри-
вые, имеющие в своих экстремальных
точках (верхней и нижней, левой и
202
Рис. 6.15
правой) параллельные касательные.
Кроме того, способ их конструирова-
ния должен позволять управлять ’’по-
лнотой” кривой.
Такие кривые удобно получать с
2-2
помощью Т2 — модели цилиндра
вращения (рис. 6.15). Левая С2 и пра-
вая D2 точки определяют диаметр
вспомогательной цилиндрической по-
верхности. Профильные проекции А3,
В3 двух других экстремальных точек
А2, В2 и С3 = £>3 точек С2, D2 одно-
значно определяют дугу окружности
2-2
а3. Образ а2 дуги а3 в Т2 отве-
чает части наперед заданных усло-
вий, предъявляемых к ’’шпангоуту”.
Формой (’’полнотой”) кривой а2
можно управлять несколькими спо-
собами:
1) вместо дуги окружности а3 можно
брать дугу эллипса или другой более
сложной кривой;
2) вместо цилиндра вращения брать
эллиптический цилиндр;
3) кривую а3 представить как обвод,
составленный из двух дуг В3С3, С3А3
окружностей или эллипсов.
Таким образом, имеется достаточно
широкий спектр возможностей для
управления формой конструируемой
кривой и удовлетворения требований
прохождения через дополнительные
точки.
С позиций начертательной геометрии
построение кривой а2 как образа
окружности а3 (см. рис. 6.15) можно
истолковать как построение фронталь-
ной проекции линии пересечения да-
ной горизонтально проецирующей
цилиндрической поверхности вращения
с профильно проецирующей цилиндри-
ческой поверхностью, заданной своей
направляющей линией а3.
В заключение отметим, что самос-
тоятельные исследования можно
выполнить как с целью получения
непрерывных моделей различных по-
верхностей второго и высшего поряд-
ков, так и использования полученных
моделей для конструирования кривых
высших порядков и исследования их
свойств, решения задач на пересече-
ние с проецирующими цилиндрически-
ми поверхностями.
Обобщая рассмотренные выше при-
меры на моделирование алгебраичес-
кой поверхности Ф” м-го порядка в
методе двух изображений, можно ска-
зать, что она будет моделироваться
(и * п)-значным соответствием/^
n-го порядка. Как известно, теория
многозначных соответствий сложна и
мало изучена, поэтому в классической
начертательной геометрии при изуче-
нии сложных поверхностей стремятся
так выбрать аппарат отображения,
чтобы поверхности моделировались
взаимно однозначными соответствия-
ми. Эти вопросы более подробно будут
рассмотрены в последующих разделах.
Построение непрерывной модели
поверхности путем ее отображения на
плоскость в отличие от се задания
дискретным каркасом позволяет иссле-
довать свойства поверхности по ее
модели. Это утверждение проиллюс-
трируем построением взаимно одно-
значной модели однополостного гипер-
болоида путем его стереографического
проецирования на плоскость.
203
6.5. Стереографическое
проецирование
в моделировании поверхностей
Понятие о стереографическом прое-
цировании возникло применительно к
моделированию сферы. Вначале стере-
ографическим проецированием называ-
ли центральное проецирование точек
сферы Ф из ее точки 5 на плоскость П,
касающуюся сферы в точке О, диамет-
рально противоположной центру S
проецирования. В настоящее время под
стереографическим проецированием
понимают центральное проецирование
точек алгебраической поверхности Ф”
n-го порядка из ее (и—1)-кратной точ-
ки S на произвольную плоскость IT. В
этом случае произвольная проецирую-
щая прямая 5Л, где А е Ф”, пересекает
поверхность Ф” и плоскость проекций
Я каждую лишь в одной точке, уста-
навливая между ними взаимно одно-
значное (перспективное) соответствие.
Наличие такого соответствия позволя-
ет исследовать свойства поверхности в
целом (!) в отличие от дифференци-
альных свойств (свойств поверхности в
малом), изучаемых в курсах диффе-
ренциальной геометрии.
Исследование свойств поверхности в
целом осуществляется методами ал-
гебраической, начертательной и анали-
тической геометрий. В начертательной
и аналитической геометрии поверхнос-
ти исследуют способом сечений, когда
поверхность рассекают семействами
плоскостей, параллельных координат-
ным плоскостям, и рассматривают
динамику изменения параметров сече-
ний: порядки кривых; их распадения;
наличие особых точек, асимптот и т.п.
При этом обычно не исследуются про-
странственные кривые, принадлежа-
щие поверхности.
Наиболее полное исследование
свойств поверхности в целом осущес-
твляется методами алгебраической
геометрии путем отображения повер-
хности на плоскость. Семейства линий
поверхности отображаются на семей-
ства линий плоскости, где устанавли-
ваются их инциденции (принадлеж-
ность) — число и кратность их точек
пересечения, инцидентность опреде-
ленным исключенным (фундаменталь-
ным) точкам, пересечение с исключен-
ными линиями. Зная эти инциденции
и свойства аппарата отображения,
судят о свойствах семейств линий на
поверхности.
6.5.1. Исследование свойств
однополостного гиперболоида
Сказанное выше рассмотрим на при-
мере исследования свойств в целом
однополостного гиперболоида Ф путем
стереографического проецирования ее
точек из точки S 6 Ф на плоскость Ф'
(рис. 6.16). При таком проецировании
между точками А е Ф, А' е Ф' за не-
которым исключением устанавливается
взаимно однозначное соответствие Т,
так как каждая проецирующая прямая
5Л пересекает поверхность Ф в одной
свободной точке А и плоскость Ф' — в
точке А'. Нарушение однозначности
имеет место для точки S и двух обра-
зующих Sf( , 5^2 поверхности Ф,
204
инцидентных точке 5. Действительно,
при А = S положение проецирующей
5.4 будет неопределенным, так как в
качестве 5А можно принять любую
прямую, касающуюся поверхности Ф в
точке 5. Поэтому проекцией точки А =
= 5 следует считать след /' плоскости
Т, касающейся поверхности Ф в точ-
ке 5.
Плоскость Т пересекает Ф по двум
образующим SF(, SF^, все точки
которых проецируются на Ф' соответ-
ственно в точки f( , F^ Поэтому
точки f[ , F} и прямая /' будут в
плоскости Ф' исключенными (фунда-
ментальными), так как для них нару-
шается однозначность: 5 - Sf{ -
- .F|/, SF2 - f£ Аналогично, на
поверхности Ф исключенными являют-
ся точка 5 и прямые Sf[ , SF^ .
Соответствие Т является квадратич-
ным, так как плоскость Ф' отображает-
ся на поверхность второго порядка Ф.
Теперь изучим семейства линий
поверхности Ф как образы определен-
ных семейств линий плоскости Ф'.
Произвольная прямая а' плоскости Ф'
отображается в кривую второго поряд-
ка ст поверхности Ф, так как проеци-
рующая плоскость Г(5, а') пересекает
Ф по кривой второй порядка п2. При
этом а1 инцидентна точке 5, так как
a' n ]' = а Г - 5 в силу того, что
j' - 5. Поэтому двупараметрическое
множество прямых плоскости Ф' ото-
бражается в двупараметрическос мно-
жество кривых второго порядка повер-
хности Ф, инцидентных точке 5. Пучок
прямых (А') отображается в пучок
кривых второго порядка поверхности
Ф, инцидентных двум точкам A, S.
Если какая-либо прямая Ь' плоскос-
ти Ф' инцидентна точке f{ , то ей на
Ф соответствует кривая второго поряд-
ка, распавшаяся на прямую SF^ , СООТ-
ветсгвенную точке А] , и непо-
средственно на образ b данной прямой
Ъ'. Значит, пучок прямых (-f/) ото-
бражается в семейство прямолинейных
образующих поверхности Ф. Все эти
образующие пересекают прямую Sf[ ,
но между собой не пересекаются, так
как центр f[ пучка прообразов ото-
бражается не в точку, а в целую пря-
мую SF(. Аналогично, пучок (F^)
прямых плоскости Ф' отображается в
другое семейство прямолинейных обра-
зующих поверхности Ф, которые пере-
секают прямую 5 ^2 > но межДУ собой
не пересекаются.
Таким образом, получили известное
свойство линейчатых поверхностей
второго порядка: линейчатая повер-
хность второго порядка содержит два
семейства действительных прямоли-
нейных образующих, при этом образу-
ющие одного семейства между собой не
пересекаются, но каждая образующая
одного семейства пересекает все обра-
зующие другого семейства. Последняя
часть утверждения справедлива пото-
му, что в плоскости Ф каждая прямая
пучка (Fj7) пересекает все прямые
пучка (Е27) и обратно.
Теперь изучим семейства линий
поверхности Ф, соответственные семей-
ствам кривых второго порядка плоскос-
ти Ф'. Любая кривая второго порядка
т' плоскости Ф' отображается в кри-
вую четвертого порядка с узловой
(двойной) точкой 5 поверхности Ф, так
как соответствие Т квадратичное и
кривая т' пересекается с прямой /' в
двух точках (действительных различ-
ных, совпавших или мнимых). Так как
любые две кривые второго порядка на
плоскости Ф' пересекаются в четырех
205
точках, то их образы на Ф пересекают-
ся в четырех простых точках и имеют
общую двойную точку S.
Если кривая второго порядка плос-
кости Ф' инцидентна точке f{ или
F^, то ей на Ф соответствует простран-
ственная кривая третьего порядка
(нормкривая), инцидентная точке S,
так как ее прообраз пересекает /' в
одной свободной точке, отличной от
F^ или F^ . При этом любые две кри-
вые второго порядка, проходящие че-
рез точку f{ , пересекаются между
собой еще в трех точках, поэтому их
образы на Ф будут пересекаться в че-
тырех точках: в точке S и образах
указанных трех точек. Если же одна
кривая второго порядка инцидентна
точке f{ , а другая — точке F^ , то
они пересекаются в четырех точках.
Значит, их образы на Ф будут пересе-
каться уже в пяти точках: в точке S и
образах указанных четырех точек.
Таким образом, на Ф существует два
семейства нормкривых. При этом нор-
мкривые одного семейства пересека-
ются между собой в четырех точках, а
разных семейств — в пяти точках.
Рассмотрим еще одно интересное
свойство семейств нормкривых. Произ-
вольная кривая второго порядка плос-
кости Ф', инцидентная точке f{ , пе-
ресекается с каждой прямой пучка
(г/) в одной свободной точке, а с
каждой прямой пучка ( F^ ) — в двух
точках. Следовательно, каждая нор-
мкривая одного семейства пересекается
с каждой прямолинейной образующей
одной серии в одной точке, а с каждой
образующей второй серии — в двух
точках.
Очевидно, любая кривая второго
порядка плоскости Ф', инцидентная
одновременно точкам F^ , F^ , отобра-
жается в кривую второго же порядка
поверхности Ф, ибо пространственная
кривая четвертого порядка в этом слу-
чае распадается на прямые Sf[ - г/ ,
SFj ^2 и собственно образ — на
указаную кривую второго порядка.
Повторяя приведенные выше рас-
суждения с семействами кривых вы-
сших порядков плоскости Ф', можно
получить их образы на исследуемой
поверхности Ф и изучить их свойства
(порядок, наличие особых точек и их
виды) и взаимное положение (число
точек пересечения с прямолинейными
образующими, кривыми второго и
высшего порядков). В качестве самос-
тоятельного исследования можно
также рекомендовать повторить
приведенные выше выкладки по по-
строению модели нелинейчатой по-
верхности второго порядка. Напри-
мер, отображение параболоида враще-
ния Ф можно выполнить прямоуголь-
ным проецированием ее точек на
плоскость Ф ’, касающуюся поверхнос-
ти Ф в ее вершине. Очевидно, в этом
случае центр S проецирования будет
несобственной точкой данного пара-
болоида. Здесь желательно выяснить,
что у параболоида, как и у других
нелинейчатых поверхностей второго
порядка, есть два семейства прямоли-
нейных (но уже мнимых!) образую-
щих.
6.5.2. Моделирование
сферы инверсией
Построенная выше монопроекцион-
ная модель однополостного гиперболо-
ида обеспечивает возможность исследо-
вания свойств поверхности в целом. Но
она, будучи необратимой, не отвечает
требованиям, предъявляемым к чер-
тежу в начертательной геометрии (см.
п. 1.2). Для устранения этого недостат-
ка достаточно воспользоваться двумя
стереографическими проецированиями.
206
Рис. 6.17
Для определенности рассмотрим кон-
кретный пример построения обратимо-
го чертежа сферы Ф путем ее отобра-
жения на картинную плоскость П дву-
мя стереографическими проецировани-
ями из центров S], Х2 е В качестве
центров проецирования S2 выберем
диаметрально противоположные точки
сферы Ф, а в качестве плоскости изо-
бражения П — плоскость, проходящую
через центр О сферы и перпендику-
лярную прямой SjS2 (рис. 6.17).
При двух стереографических проеци-
рованиях точек сферы на плоскость П
на плоскости изображения получаем
два поля Пр П2 проекций: поле П] —
проекции точек сферы из центра
поле П2 — проекции точек сферы из
центра S2. Между полями Пр П2 уста-
навливается взаимно однозначное со-
ответствие: точка Л) поля П[ из X]
проецируется в единственную точку А
сферы Ф, которая из центра Х2 также
проецируется в единственную точку А2
поля П2. Это соответствие будет квад-
ратичным. Действительно, прямая ах
поля П; проецируется из точки 5] на
сферу Ф в окружность а — сечение
сферы Ф проецирующей плоскостью
При этом окружность а прохо-
дит через центр X] проецирования.
Окружность а из центра S2 проециру-
ется эллиптической конической по-
верхнстью 0(Х2, а), сечением а2 кото-
рой плоскостью П будет кривая второго
порядка. Так как прямой ах поля ГЦ в
поле П2 соответствует кривая второго
порядка а2, то соответствие Т2
(П[ - П2) является квадратичным.
Покажем, что в преобразовании Т2
прямой одного поля всегда соответсву-
ст окружность второго поля. На самом
деле, проецирующая коническая по-
верхность 0(Х2, а) пересекается со
сферой Ф по пространственной кривой
четвертого порядка (2-2 = 4), которая
распадается на окружность а и еще на
одну кривую второго порядка (4—2 =
= 2). Последняя, как принадлежащая
сфере Ф, является также окружностью.
Эта окружность ’’стянулась” в точку
S2 (ее радиус равен нулю), точнее, она
распалась на две мнимые прямые,
пересекающиеся в действительной
точке S2. Другими словами, эта рас-
павшаяся окружность представляет
собой общее сечение сферы Ф и кони-
ческой поверхности 0 плоскостью Т,
касающейся сферы Ф в точке S2. Плос-
кость Т параллельна П, так как
П ± XjX2. Поэтому сечение конической
поверхности 0 любой плоскостью, па-
раллельной Т, в том числе и плос-
костью изображения П, является
окружностью. Таким образом, произ-
вольной прямой одного поля в преоб-
разовании Т2 соответствует в другом
поле окружность, проходящая через
центр О преобразования (0 => SXS2,
SXS2 п П = 0).
Проведя аналогичные операции,
покажите, что произвольной окруж-
ности одного поля преобразование Т2
в другом поле ставит в соответст-
вие также окружность, не проходя-
щую через центр О преобразования. В
частности, окружность d2 — сечение
сферы Ф плоскостью П — соответ-
ствует сама себе, т.е. является двой-
ной (инвариантной). Это преобразо-
вание называется инверсией.
Алгоритм построения соответствен-
ных точек Л] - А2 инверсии Т2
(рис. 6.18), вытекающий из аппарата
моделирования сферы Ф (XjAj п Л2 =
= A, п ОАХ = А2, где к2 — сечение
сферы Ф плоскостью Д(Хр Х2, Ар), не
207
Рис. 6.18
совсем удобен, так как используются
точки S2, не принадлежащие плос-
кости П модели. Этот недостаток мож-
но легко устранить. Рассмотрим подо-
бные треугольники О52Л2 и
оа2 _ os.
~os'1
или
[0Л1][0Л2] = Л2,
где /?= [05)1 = (OS2].
Далее, из /Ц проведем касательную
Л]Л/ к окружности к2 и из точки М
касания опустим перпендикуляр Л/Л2
на прямую ОЛ[. Имеем также подо-
бные треугольники ОМАГ, ОА2М:
ОМ = 0Аг
04^ ОМ
или
[ОЛ]]-[С>Л2] = л2,
где R = [ОМ].
Но окружности к2 (см. рис. 6.18) и
d2 (см. рис. 6.17) равны как сечения
одной и той же сферы Ф плоскостями,
проходящими через ее центр О. По-
этому вместо к2 можно использовать
инвариантную окружность <12. Тогда
построение соответственных точек
Л, - Л2 в инверсии Т2 выполняется
’’без выхода в пространство” (см.
рис. 6.19);
1) через данную точку Л[ проводим
касательную At М к инвариантной
окружности d2, если Л] расположена
вне окружности d2, или восставляем
Рис. 6.19
перпендикуляр А2М к 0Л2, если точка
Л2 расположена внутри окружности с/2;
2) из точки М касания опускаем
перпендикуляр МА2 на прямую OAt
(через точку М проводим касательную
Л/Л] к окружности d2);
3) отмечаем точку пересечения пря-
мых: Л2 = ОЛ] п МА2 или Л] =
= Л/Л] п 0Л2.
Полученная модель Т2 сферы Ф при-
годна для решения различных позици-
онных задач с участием данной сферы.
Например, на рис. 6.19 показано по-
строение проекций точек В, N пересе-
чения прямой /(/j, /2) со сферой Ф(Т2).
Первая проекция /] прямой I отнесена
к полю П] модели Т2 данной сферы:
/] = //. Затем, построена окружность
12 — образ прямой /]7 в инверсии Т2.
Для этого предварительно построена
точка Л2 — образ точки Л] в инверсии
Т2, где Л] — основание перпендикуля-
ра, опущенного из центра О преобра-
зования на прямую /]7. Окружность
12 построена на отрезке ОЛ2, как на
диаметре. Вторая проекция 12 прямой
/, пересекаясь с окружностью /2 , опре-
деляет вторые проекции В2, N2 иско-
мых точек В, N = I п Ф. Их первые
проекции В], 7V] определяются как
точки пересечения прямых (линий
связи) ОВ2, ON2 с первой проекцией /]
данной прямой I.
208
Задачи для исследования
1. Выведите формулы преобразова-
ния (инверсии) Т2, аналитически опи-
сав выполненные графические опера-
ции алгоритма построения соответ-
ственных точек. Графически и анали-
тически изучите образы различных
кривых второго порядка в инверсии.
Покажите, что произвольной кривой
второго порядка в инверсии соответ-
ствует кривая четвертого порядка.
Выясните, когда центр О будет для
этой кривой узловой точкой, точкой
возврата и изолированной точкой?
Покажите, что кривой второго по-
рядка (кроме окружности), проходя-
щей через центр О, соответствует
кривая третьего порядка.
2. Сопоставьте алгоритмы опреде-
ления точек пересечения прямой ли-
нии со сферой, описанные в этом
разделе и в разделе 4.2.3. Есть ли
между ними принцииальные отличия?
Какой алгоритм графически проще и
почему?
3. Выбрав вместо сферы другую
поверхность второго порядка (враще-
ния или общего вида), попробуйте по
аналогии с вышеизложенным полу-
чить ее модель путем двух стереогра-
фических проецирований. Для этого
предварительно изучите материал
раздела 6.3 монографии [3]. Заметим,
что, моделируя поверхности высших
порядков путем двух стереографичес-
ких проецирований, можно получить
центральные нелинейные преобразова-
ния плоскости и изучить их свойст-
ва. Другой подход к их заданию осве-
щается в следующем разделе.
6.6. Нелинейные
преобразования плоскости
и их применение для
конструирования кривых линий
В различных разделах математики
плоскую кривую линию рассматривают
как:
1) график функции f(x, у) = 0 или
<р(р, а) = 0, заданной в декартовых или
полярных координатах;
2) геометрическое место точек плос-
кости, удовлетворяющее некоторым
метрическим условиям (например,
окружность — множество точек, уда-
ленных от точки О на данное расстоя-
ние Л);
3) проекцию (центральную, парал-
лельную, косую и т.д.) некоторой про-
странственной или плоской кривой
(например, кривые второго порядка —
центральные проекции окружности);
4) множество точек пересечения
соответственных линий двух пучков
(например, окружность — множество
точек пересечения двух пучков пер-
пендикулярных прямых);
5) образ данной линии в некотором
преобразовании плоскости (например,
эллипс — образ окружности в родстве).
Заметим, что этот перечень не явля-
ется полным. Он содержит лишь наи-
более распространенные способы кон-
струирования плоских кривых линий.
В этом разделе рассмотрим конструир-
ование кривых посредством нелиней-
ных центральных преобразований
плоскости, которые будем представлять
как совокупность преобразований пря-
мых = I- , проходящих через центр S
преобразования Т. Такие преобразова-
ния называются расслаивающимися в
пучке прямых.
6.6.1. Задание центральных
нелинейных
преобразований плоскости
Центральное нелинейное преобразо-
вание Т будет задано однозначно, если
на любой прямой = I. , проходящей
через центр S, будет установлено вза-
имно однозначное соответствие. На
прямой Z(- = I- можно установить вза-
имно однозначные соответствия трех
типов: проективные, аффинные и мет-
рические.
209
Проективные соответствия удобнее
всего задавать их двойными точками
D = D', D = D1, которые впредь бу-
дем обозначать буквами Z>, D. Тогда
любая пара, соответственных точек А,
А' составляет с точками D, D одно и
то же сложное отношение
(DDA4 z) = (££Л) = £1: £11 = А.
(DDA,~) DA DA1
Если Л. * —1, то соответствие на пря-
мой 1=1' будет неинволюционным, в
противном случае — инволюционным.
В неинволюционном соответствии ка-
кой-либо точке прямой I = Г соответ-
ствуют различные точки в зависимости
от того, к какому ряду (/ или Г) она
отнесена, т.е. точке М = N' соответ-
ствуют точки М' и N, которые не
совпадают. В инволюционном же пре-
образовании точке М = N' соответст-
вует одна и та же точка М' = N..
Неинволюционное соответствие на
прямой I = Г, когда Л * —1, задается
двойными точками D, D и одной па-
рой соответственных точек А - А' или
значением Л сложного отношения.
Инволюционное соответствие на пря-
мой 1=1', когда А = —1, задается лишь
двойными точками.
Если на прямой I = Г одна из двой-
ных точек, например, D будет несо-
бственной, то проективное соответст-
вие становится аффинным, а сложное
отношение (DD^AA') = А вырождается
в простое отношение трех точек
(DAA1) = _£1_ = Л.
DA1
При А # —1 нд прямой I = Г устанав-
ливается неинволюционное аффинное
соответствие, а при А = —1 — инволю-
ционное. В последнем случае все пары
А - А', В ~ В', ... соответственных
точек являются симметричными отно-
сительно двойкой точки D.
И, наконец, если на прямой 1 = 1'
обе двойные точки будут несобствен-
ными, то имеем метрическое соответ-
ствие — параллельный перенос на век-
тор АА'. Очевидно, это соответствие
однозначно задается парой соответст-
венных точек А - А'. Оно является
неинволюционным.
Таким образом, для получения цен-
трального нелинейного преобразования
Т с центром S необходимо на каждой
прямой = I- пучка (5) задавать
двойные точки D, D и пару соответ-
ственных точек А - А'. Указанные
точки удобно получать как точки пере-
сечения некоторых кривых d, d, а, а'
с прямыми /,• = I- пучка (5). Так как
каждая из перечисленных кривых до-
лжна пересекаться с любой прямой
пучка (5) только в одной свободной
точке, то остальные точки пересечения
должны совпадать с точкой S. Поэтому
кривые d, d, а, а' должны быть алгеб-
раическими кривыми некоторого по-
рядка nc (п — 1)-кратной точкой S.
Двойные точки D, D проективного
соответствия на прямой Ц = I- совер-
шенно равноправны. Поэтому их мож-
но получать как точки пересечения
прямых lj = I- с некоторой кривой d.n
n-го порядка с (л — 2)-кратной точкой
S. Если же на прямых /г- = I- устанав-
ливаются аффинные соответствия, то
кривая dn должна быть распавшейся на
кривую <Zn-1 порядка п— 1 с (и—2)-
кратной точкой S и несобственную
прямую d1.
Очевидно, можно предложить доста-
точно много вариантов задания цен-
тральных нелинейных преобразований,
варьируя положением центра S преоб-
разования (точка 5 может быть собст-
210
венной и несобственной), выборов вида
и характеристик кривых d, d, а, а',
их взаимного положения. Рассмотрим
несколько конкретных примеров зада-
ния преобразования Т и вывода его
формул.
Пример 1. Пусть преобразование Т
расслаивается в пучке прямых 5(Z) на
параллельные переносы (рис. 6.20).
Мгновенные векторы АА' параллель-
I 11
ного переноса на прямых = /г- опре-
деляются точками их пересечения с
данными прямыми а, а' — носителями
соответственных точек А ~ А'.
Совместим начало О декартовой
системы координат Оху с центром S
преобразования Т. Пусть прямые а, а’
имеют в этой системе соответственно
уравнения
У = gx * Ъ ;
у = tx + с.
(6.26)
Выведем формулы преобразования Т..
Из алгоритма преобразования следует
х‘ - х = Ад' - хА;
/ - У = У\'~ Ук,
(6.27)
где хА, yA — координаты точки А пере-
сечения прямых I = /', а; хА/, уА/ —
координаты точки А' пересечения
прямых I = Г, а'; х, у — координаты
точки-прообраза М; х', у' — координа-
ты точки-образа М'.
Координаты точек А, А' определим
совместным решением уравнений
(6.26) прямых а, а' с уравнением
у = кх или у! = кх1
прямой 1=1' — носителя соответствен-
ных точек. Имеем
\ к - g к - g I
u t к - 11
или, освобождаясь от параметра к =
= Z = 2L, получаем
А {-Iх.
\ У - gx у - gx I
\ у - tx у - tx I
Подставив координаты точек А, А' в
уравнения (6.27), получаем формулы
прямого преобразования:
х / _ х -b(y - tx) +с(у- gx) + (у - gx) (у - tx)
(у - gx)(y - tx)
(6.28)
/ _ у -6(у - tx) + с(у - gx) + (у - gx) (у - Гх)
(у - gx) (у - tx)
и формулы обратного преобразования:
г = хZ (у‘ ' Sx'Xy' -tx') ♦
(6.29)
+ b<y'-ix') - с(.у'-gx') .
X (у7 - tx')
,___,/ (у1 -gx'Xy' -tx') +
У-У----------------------
(у' gx') х
+ bty' - tx')-cty' - gx')
X (у1 - tx')
211
Алгоритм построения соответствен-
ных точек М - М' в рассматриваемом
преобразовании можно упростить,
совместив точку А (см. рис. 6.20) с
центром S преобразования, что имеет
место при прохождении прямой а че-
рез точку S. В этом случае координаты
точки А будут равны нулю, а формулы
преобразования примут вид
(6.30)
(6.31)
Пример 2. Пусть центральное преоб-
разование 7' расслаивается в пучке
S(l = /') прямых на параллельные
переносы, мгновенные векторыАА1
которых определяются точками А'
пересечения прямых = /г- с окруж-
ностью а', а начало А этих векторов
совпадает с центром 5 преобразования
(рис. 6.21).
При выбранной системе координат
Оху окружность а' описывается урав-
нением
(х - R)2 + у2 = R2, (6>32)
где R — радиус окружности.
Из алгоритма построения соответ-
ственных точек М ~ М' следует
х1 - X = ХКГ,
у' - У = УА7’
где координаты хА/, уА/ точки А' =
= I п а' определяются совместным
решением уравнения (6.32) окружнос-
ти а' и уравнения носителя I = Г соот-
ветственных точек:
/ ( 2Rx2 2Rxy 1
V х2 + у1 х2 + у2 J
Формулы прямого преобразования
имеют вид
/ х2 * у2 + 2Rx,
X =х---------------
х2 + v2
У (6.33)
/= х2 + У2+ 2Ях
Х2+у2
Формулы обратного преобразования
имеют вид
х = х / (х7)2 + (у7)2 - 2Rx'.
{ ’ у (6.34)
у = у/ (Л')2 + 2RX>
(х7)2 * (у7)2
На рис. 6.22 и 6.23 заданы нелиней-
ные преобразования, расслаивающиеся
в пучке прямых на симметрии с цен-
трами D = I n d. На рис. 6.22 центр S
преобразования является собственным,
а на рис. 6.23 — несобственным. Инва-
риантная линия d должна пересекать-
ся, как было отмечено выше, с любой
прямой I = Г пучка (S) лишь в одной
свободной точке. Поэтому при задании
преобразований с несобственным цен-
тром S”, принадлежащим оси Оу сис-
темы координат Оху, в качестве кри-
212
Рис. 6.23
вых d можно выбирать параболы вы-
сших порядков, уравнения которых
имеют вид
у =А0 +А^ +А2х2 +А3х3 +..., (6.35)
или кривые, описываемые дробно-ра-
циональными функциями:
у = (6.36)
Во + В^х + Вгх 2 + ... + ДЛ_|Х
В качестве тем для самостоятель-
ного исследования можно предложить
сконструировать аппараты цент-
ральных нелинейных преобразований
плоскости с собственными или несо-
бственными центрами, расслаиваю-
щимися в пучке прямых на проектив-
ные, аффинные и метрические соот-
ветствия. Аналитическим описанием
графических операций алгоритма
построения соответственных точек
нужно вывести их формулы преобра-
зования. Графическими построениями
и аналитическими выкладками необхо-
димо исследовать свойства получен-
ных преобразований: порядок, инволю-
ционность, наличие инвариантных
(двойных) точек и линий, наличие
точек и линий, для которых наруша-
ется однозначность соответствия.
Знание этих свойств позволяет ис-
пользовать полученные преобразова-
ния для конструирования кривых вы-
сших порядков и исследования их
свойств.
6.6.2. Конструирование
и исследование свойств
алгебраических кривых
высших порядков
Нелинейные преобразования нашли
широкое применение в конструирова-
нии кривых высших порядков и иссле-
довании их свойств. Это основано на
том, что простым линиям (прямым,
кривым второго порядка и т.д.) они
ставят в однозначное соответствие
кривые высших порядков. Например,
преобразование Т, полученное в пре-
дыдущем разделе в примере 2, произ-
вольной прямой (рис. 6.21)
Ах' + By' + С = 0 (6'37)
ставит в соответствие кривую т' тре-
тьего порядка, уравнение которой по-
лучается подстановкой в (6.37) значе-
ний х', у' из (6.33):
(Ах + Ву)(х2 + у2 + 2Rx) з
(о.Jo)
+ С(х2+ у2) = 0.
Эта кривая в начале координат име-
ет двукратную точку. Действительно,
при подстановке в (6.38) значения х =
= 0 получаем
у2(Ву + С) =0,
т.е. ось Оу пересекает кривую т' в
точке О(у( 2 = 0), считаемой дважды,
с
и в точке D(0, — _ ).
в
213
Отмеченные свойства кривой т'
можно легко прогнозировать, если
предварительно изучить свойства дан-
ного преобразования Т.
1. Ось Оу для преобразования Т яв-
ляется инвариантной, т.е. все ее точки
являются двойными: D = D' или х =
= х', у = у'. Действительно, при под-
становке в (6.33) значений х = х', у =
= у' имеем 2Rx = 0 или х = 0, т.е.
Оу(х = 0) состоит из двойных точек,
для которых X = х', у = у'.
Отсюда следует, что прямая m и ее
образ т' обязательно пересекаются в
точке D, принадлежащей оси Оу (коор-
Q
динаты 0, — —, точки D удовлетвряют
уравнениям (6.37) и (6.38)).
2. Центр S преобразования является
фундаментальной точкой. Ей в поле П'
соответствует не одна точка S', а це-
лая окружность а'. Действительно,
при подстановке в (6.34) значений х =
= 0, у = 0 имеем
(х' - R)2 + (yz)2 = R2.
Этой же точке, отнесенной к полю
П', в поле П соответствует также
окружность s, симметричная окруж-
ности а' относительно начала коорди-
нат. Действительно, при подстановке
в (6.33) значений х' = 0, у' = 0
имеем
(х + Л)2 + у2 = R2.
Поэтому прямой т, пересекающей
окружность s в двух точках (действи-
тельных различных, совпавших или
мнимых), соответствует кривая третье-
го порядка т', имеющая двукратную
точку О = S', которая на т' может
быть узловой, возврата или изолиро-
ванной.
Убедитесь в справедливости этого
утверждения графическим построе-
ние. 6.24
нием образов т', т', т 1 трех пря-
мых т, т, т, пересекающих
окружность s соответственно в двух
различных, совпавших и мнимых точ-
ках.
Таким образом, знание свойств пре-
образования позволяет прогнозировать
свойства конструируемых кривых или
даже конструировать кривые с наперед
заданными позиционными и метричес-
кими свойствами. Например, преобра-
зование, заданное на рис. 6.23, облада-
ет замечательным свойством — экви-
формностью, т.е. сохранением площа-
дей соответственных фигур, ограничен-
ных замкнутыми линиями. Действи-
тельно, площади фигур, ограниченных
соответственными линиями т ~ т',
т - т1, т ~ т' (рис. 6.24), равны,
так как в пределе будут равны площа-
ди элементарных трапеций, на кото-
рые разбиваются эти фигуры верти-
кальными прямыми (носителями соот-
ветственных точек) при неограничен-
ном увеличении их числа.
При этом достаточно просто мож-
но управлять формой конструируемых
кривых путем изменения параметров
прообраза и инвариантной кривой <1.
Рекомендуем выполнить такие иссле-
дования самостоятельно.
214
6.7 Нелинейные
преобразования пространства
и их применение для
конструирования поверхностей
В современных курсах начертатель-
ной геометрии изучается в основном
кинематический способ образования
поверхностей, когда поверхность обра-
зуется в результате перемещения не-
которой линии постоянной или пере-
менной формы. При всех своих несо-
мненных достоинствах (простота, на-
глядность) этот способ имеет сущес-
твенные недостатки, связанные со
сложностью исследования свойств по-
верхности в целом. Этого недостатка
лишен способ конструирования повер-
хностей посредством нелинейных пре-
образований пространства.
Достоинства кинематического спосо-
ба и способа преобразований в конст-
руировании поверхностей суммируются
и дополняют друг друга, если исполь-
зовать для этих целей расслаивающи-
еся преобразования пространства,
представляющие собой совокупность
некоторых однотипных преобразований
в пучке плоскостей а-, проходящих
через некоторую прямую и.
6.7.1. Задание нелинейных
преобразований пространства
как совокупности преобразований
пучка плоскостей
Задание расслаивающихся нелиней-
ных преобразований пространства вы-
полняется просто:
I) задается пучок плоскостей и(а^
своей осью и;
2) в пространстве задаются некото-
рые линии и (или) поверхности, кото-
рые, пересекаясь с плоскостями <rt- рас-
слоения, устанавливают в них одно-
типные преобразования Т(.
Совокупность преобразований Т\
плоскостей а(- порождает нелиней-
ное преобразование пространства.
При задании таких преобразований
необходимо так выбрать линии и (или)
поверхности, входящие в аппарат пре-
образования, чтобы они в каждой
плоскости а(. расслоения обеспечивали
однозначное задание преобразования
Т\. Например, при задании нелинейно-
го преобразования пространства, рас-
слаивающегося в пучке плоскостей
и(аг) на центральные симметрии, необ-
ходимо в качестве носителя s центров
5( симметрии в плоскостях а;- выбрать
такую кривую, которая пересекалась
бы с каждой плоскостью «г только в
одной свободной точке Sr Этому усло-
вию удовлетворяют произвольная пря-
мая s, не параллельная оси и пучка
плоскостей; любая кривая второго по-
рядка, пересекающая ось и в одной
фиксированной точке; ..., алгебраичес-
кая кривая s’1 п-го порядка, пересека-
ющая ось и в п— 1 фиксированных
точках. Все эти линии с каждой
плоскостью а- расслоения пересека-
ются лишь в одной свободной точ-
ке 5(, остальные точки принадлежат
оси и и из рассмотрения исключа-
ются.
Если в аппарат преобразования Г(-
плоскости а у расслоения входит неко-
торая линия djt то ее носителем в про-
странстве будет поверхность Д. При
этом поверхность Д должна пересекать-
ся с каждой плоскостью а(- только по
кривой d? Например, если поверхность
Д должна пересекаться с каждой плос
костью а( по прямой, го она может
быть плоскостью; линейчатой повер-
хностью второго порядка, проходящей
через ось и; ...; линейчатой поверх
ностью n-го порядка с (n—1) -кратной
прямой и.
Очевидно, варьированием положения
оси и пучка плоскостей, видов преоб-
разований Т; и способов их задания в
плоскостях dj расслоения можно полу-
чить большое многообразие преобразо-
ваний пространства. Рассмотрим два
примера.
215
Пример 1. Пусть преобразование
пространства расслаивается в пучке
плоскостей а( с осью и = Оу на цен-
тральные симметрии Т(-, определяемые
центрами Х(- пересечения некоторой
прямой х с Oxz с плоскостями а .
Произвольной точке М (х, у, z) ста-
вим в соответствие точку М'(х', у',
z') по следующему алгоритму:
— точка М выделяет из пучка (и)
плоскость at(u, М);
— плоскость а( пересекает прямую s
в точке Sp
— строим точку М‘ е а(-, симметрич-
ную точке М относительно точки 5(:
[Л5(] = [Х^'Ь
Выведем формулы преобразования.
ПЛОСКОСТЬ Ир
Z = tx
пересекает прямую $:
z = кх + Ь\
у = О
в точке Х((—А_, О, -2L_J. Тогда из
условия [А5(] = [Х^А'] имеем
ь
Т~к
ь .
ГИГ
О - у = у' - 0; (6 39)
JL. - z = z' - JL.
t - к t - к
В уравнениях (6.39) освобождаемся от
параметра t = — и получаем формулы
X
прямого преобразования в виде
у1 = У,
(6.40)
/ 2b - z + кх
Z = 2-----------
z - кх
Формулы обратного преобразования
имеют симметричный вид, что говорит
об инволюционности полученного пре-
образования. Оно является квадратич-
ным, так как ставит в соответствие
произвольной плоскости Ф'
Ax' + By' + Cz' + £> = 0
линейчатую поверхность второго по-
рядка
(Ах + Cz) (2b - z + кх) +
+ (By + D)(z - кх) = 0.
Пример 2. Пусть преобразование
пространства расслаивается в пучке
параллельных плоскостей а; на куби-
ческие преобразования Т3, получаемые
в плоскостях а(- по схеме рис. 6.21.
Для задания преобразований Т3 в
плоскостях af-, параллельных коорди-
натной плоскости Оху, необходимо
задать окружности и точки Si
(рис. 6.25). Пусть носителем окруж-
/
ностеи а(- является коническая повер-
хность Е(0, а'), а носителем точек Х;
— прямая s, совпавшая с осью Oz сис-
темы координат. При этом прямая $
должна быть образующей конической
поверхности S.
216
Выведем уравнение конической по-
верхности Б, если ее направляющая а'
имеет уравнения
г = Р-
Запишем уравнения произвольной
образующей поверхности Е как пря-
мой, проходящей через две точки 0(0,
О, 0) и А', координаты х2, у2, z2 = р
которой удовлетворяют уравнениям
(6.41):
X _ у _ Z
~1 Ъ Р
или
х У _ £
- (Xj - г)2 р'
Освобождаясь от параметра х2, получа-
ем уравнение конической поверхности
Е в виде
р(х2 + у2) - 2rxz = 0. (6.42)
Так как плоскости а- пересекают
коническую поверхность по окружнос-
тям различного радиуса, то для полу-
чения формул прямого преобразования
необходимо подставить в формулы
(6.33) значение R = f(z), выраженное
из уравнения (6.42). Для этого в (6.42)
подставляем у = 0. Имеем
рх - 2rz = 0.
Отсюда R = _ = Подставив в
2 Р
(6.33) значение R = —, получаем фор-
р
мулы прямого преобразования
/ _ Р<х2 ► у2) + 2rxz.
р<х~*у2} ’
/ р(х2 + у2) < 2rxz. (6.43)
р(х2 ♦ у2) ’
Аналогично выводятся формулы обрат-
ного преобразования.
В полученном преобразовании произ-
вольной плоскости
Ах1 + By1 + Cz1 + 25 = 0
соответствует поверхность Ф3 третьего
порядка
(Ах + Ву)[р(х2 + у2) + 2rxz] +
+ p(Cz + D)(x2 + у2) = 0.
Таким образом, получили кубичес-
кое преобразование пространства. Оче-
видно, выбирая в качестве поверхности
Е циклические поверхности с плос-
костью параллелизма Оху, проходящие
через прямую s = Oz, можно получить
преобразования более высоких поряд-
ков.
6.7.2. Применение
нелинейных преобразований
пространства для
конструирования поверхностей
В девятой главе монографии [3]
приведены примеры конструирования
достаточно сложных технических по-
верхностей посредством расслаиваю-
щихся нелинейных преобразований
пространства. Здесь же мы приведем
простой пример конструирования тех-
нической поверхности, несущей каркас
аэродинамических профилей С.А. Чап-
лыгина.
Требуется вывести уравнение повер-
хности Ф, проходящей через два аэро-
динамических профиля т1у т2, распо-
ложенных в параллельных плоскостях
а1 = Оху, а2 (рис. 6.26). Как из-
вестно, аэродинамические профили
С.А. Чаплыгина представляют собой
217
Рис. 6.26
алгебраические кривые четвертого
порядка, являющиеся образами пара-
бол второго порядка в инверсии.
Пусть профиль т1 является образом
параболы :
у’ = Во + BlX' + В2(х')2,
а профиль т2 — образом параболы
/
w2 :
у- = Ао + Лгг7 + Л2(л7)2
в инверсиях относительно окружностей
J1 <= Оху, d2 <= а2, центры которых
принадлежат оси Oz системы коорди-
нат, а их радиусы равны соответствен-
но R2. Пусть плоскость а2 отстоит
от плоскости ctj = Оху на расстоянии Л.
т.е. z2 ~ й.
Так как по условию поверхность Ф
должна содержать в плоскостях at, па-
раллельных Оху, профили Чаплыгина,
то целесообразно ее получить как об-
раз поверхности Ф', несущей в плос-
костях а(- каркас парабол второго по-
рядка т- , в преобразовании простран-
ства, расслаивающейся в плоскостях ai
на инверсии. С этой целью выведем
предварительно формулы этого преоб-
разования и уравнение поверхности-
прообраза Ф'.
Для вывода формул преобразования
пространства необходимо в формулах
инверсии
/ R2x
X - ___________
X 4- V
? (6.44)
задать закон изменения радиуса R
инвариантной окружности по высоте,
т.е. R = /(z). Пусть для простоты R
изменяется от Л] до R2 по линейному
закону:
й - R2 - Лр
z - R2,
т.е. Я,= 2 (Л2-Л1).
* п
Подставив в (6.44) вместо R значе-
ние Л(, получим формулы кубического
преобразования, расслаивающегося в
пучке параллельных плоскостей на
инверсии:
, _ (R2 - R^xz2
h2(x2 + у1)
, = (R2 -Rt)2yz2 (6.45)
h2(x2 + у2) ’
Уравнение поверхности-прообраза
Ф', проходящей через параболы гп{ ,
/
т2 , выведем также из допущения, что
коэффициенты их уравнений изменя-
ются по высоте пропорционально.
Имеем
(6.46)
* (А2 - B2)(X7)2J.
Тогда уравнение конструируемой по-
верхности Ф получается подстановкой
в уравнение (6.46) прообраза Ф' значе-
218
ний х', у', z' из (6.45). После элемен-
тарных упрощений имеем
(А2 -В2) (Л2 -7?,)4x2z4 +Л2(Я2 -
-flj)2(x2+y2)z[G4! -Bx)xz-hy\ +
+ А4С4о -В0)(х2 + у2)4 = 0.
Таким образом, искомой поверх-
ностью является алгебраическая повер-
хность шестого порядка.
Описанная методика пригодна для
вывода уравнений поверхностей, кон-
струируемых с помощью расслаиваю-
щихся преобразований пространства.
В качестве тем для самостоятельно-
го исследования рекомендуется рас-
смотреть получение с помощью та-
ких преобразований поверхностей, пр
своей форме напоминающих те илй
иные технические поверхности (все-
возможные каналовые поверхности с
переменными сечениями, поверхности
лопаток турбин, лопастей винтов и
т.д.). Предварительно необходимо
научиться получать сечения таких
поверхностей, разработать способы
управления их формой путем измене-
ния параметров прообраза, аппарата
преобразования и их взаимного поло-
жения.
6.8. Решение позиционных
и метрических задач
посредством геометрических
преобразований
Геометрические преобразования на-
шли также широкое применение при
решении позиционных и метрических
задач. Решение задачи состоит из трех
основных этапов:
1) исходные данные (геометрические
фигуры, условия, параметры) с по-
мощью определенного преобразования,
выбранного исходя из условий задачи,
преобразуются в новые данные, кото-
рые проще по сравнению с исходными;
2) по известным алгоритмам решает-
ся задача в преобразованном (упро-
щенном) варианте;
3) обратным преобразованием реше-
ние задачи отображается на исходные
данные.
Эта методика многократно исполь-
зовалась при решении ряда задач в
3—5 главах. В настоящем разделе про-
демонстрируем се применение для
решения трех нетривиальных, но до-
статочно простых задач. Другие при-
меры решения задач с помощью гео-
метрических преобразований можно
найти в [10].
Пример 1. Через точку А провести
касательные /, t к эллипсу т, задан-
ному своими осями, и построить точки
касания (рис. 6.27).
Построение очерка эллипса по дан-
ным его осям с последующим проведе-
нием искомых касательных, например,
построением кривой ошибок (см. [5])
достаточно трудоемко и неточно. Поэ-
тому предварительно преобразуем эл-
липс т и точку А посредством родст-
венного преобразования в окружность
т' и точку А'.
Ось d родства совместим с большой
осью MN эллипса, а направление род-
ства — с малой осью CD. На отрезке
MN, как на диаметре, описываем
окружность т', точки С', D' пересе-
219
чения которой с прямой CD будем счи-
тать соответственными в родстве точ-
кам С, D эллипса. Таким образом,
родство определяется осью d и парой
соответственных точек С ~ С'. Строим
точку А' — образ данной точки А в
родстве: AC n d = 1, 1С п АА' = А',
где АА’ || СС. Из точки А' проводим
касательные f, t! к окружности т' и
отмечаем точки L', К' их касания с
т'. Обратным преобразованием строим
искомые касательные t, t к эллипсу т
и точки L, К их касания с т, соответ-
ственные прямым t', t' и точкам L',
К' в родстве.
Пример 2. Дана плоскость Д и две
точки А, В, расположенные по одну
сторону от плоскости Д (рис. 6.28).
Требуется построить точку М, принад-
лежащую плоскости Д, чтобы ломаная
АМВ имела минимальную длину.
Если бы точки А, В были расположе-
ны по разные стороны от плоскости Д,
то искомой ломаной был бы отрезок
АВ, а точкой М — точка его пересече-
ния с плоскостью Д. Отсюда следует
алгоритм решения этой задачи:
1) строим точку А', симметричную
точке А относительно плоскости Д;
2) строим точку М пересечения пря-
мой А 'В с плоскостью Д;
3) ломаная АМВ будет искомой, так
как длины симметричных отрезков AM
и А'М равны, а кратчайшее расстоя-
Рис. 6.28
ние между точками АВ есть отрезок
[А'В] = [А'М] + [МВ].
Пример 3. Построить точки пересе-
чения прямой I с эллиптическим па-
раболоидом Ф (рис. 6.29).
Для упрощения построений предва-
рительно преобразуем эллиптический
параболоид Ф в параболоид вращения
Ф'. Это можно сделать преобразовани-
ем родства с двойной плоскостью Д —
фронтальной плоскостью симметрии
параболоида и направлением родства,
перпендикулярным плоскости Д. На
чертеже это преобразование сводится к
построению окружности а1 — образа
эллипса а, одного из сечений повер-
хности Ф горизонтальной плоскостью
уровня. При этом прямая / преобразу-
ется в прямую Г: их фронтальные
проекции /2, /2 совпадают, а горизон-
тальные проекции соответствен-
ны в родстве, заданном вырожденной
проекцией Д] двойной плоскости Д и
любой парой соответственных точек
кривых at ~ а[ (на рис. 6.29 в качес-
тве этих точек выбраны точки пересе-
чения /] пар п а[).
Рис. 6.29
220
Дальнейшие построения общеизвес-
тны: заключив прямую /' во фронталь-
но проецирующую плоскость Г, строим
сечение т (т^ , т2) поверхности Ф
плоскостью Г и отмечаем точки К', L'
пересечения линий т', Г. Так как
сечением т' является эллипс, его
/
горизонтальная проекция т1 построе-
на ПО ОСЯМ И
Искомые точки К, L = I п Ф построе-
ны как образы точек К' L' в установ-
ленном родственном соответствии.
В заключение заметим, что изложен-
ные в этой главе вопросы составляют
лишь небольшую часть актуальных
проблем, решаемых современной на-
чертательной геометрией. Нерассмот-
ренными остались вопросы моделиро-
вания многомерных, неэвклидовых и
неточечных пространств; решения
задач начертательной геометрии на
ЭВМ; прикладной геометрии, связан-
ные с моделированием технических
форм и объектов, технологических
процессов и т.д. Представление о мно-
гообразии таких задач теоретического
и прикладного характера, а также о
способах, методиках и алгоритмах их
решения можно получить по многочис-
ленным публикациям в научных, на-
учно-методических сборниках по на-
чертательной (прикладной) геометрии
и инженерной графике.
Список литературы
I. Бубенников А.В. Начертательная геометрия М.: Высшая школа,
1985. 288 с.
2. Выгодский М.Я. Справочник по высшей математике. М.: Наука,
1964. 870 с.
3. Иванов Г.С. Конструирование технических поверхностей (мате-
матическое моделирование на основе нелинейных преобразований).
М.: Машиностроение, 1987. 192 с.
4. Короев Ю.И. Начертательная геометрия. М.: Стройиздат, 1987.
319 с.
5. Курс начертательной геометрии / Н.Ф. Четверухин, В.С. Ле-
вицкий, З.И. Прянишникова и др.; Под ред. Н.Ф. Четверухина. М.:
Высшая школа, 1963. 420 с.
6. Курс начертательной геометрии (на базе ЭВМ) / А.М. Тевлин,
Г.С. Иванов, Л.Г. Нартова и др.; Под ред. А.М. Тсвлина. М.: Высшая
школа, 1983. 175 с.
7. Монж Г. Начертательная геометрия. М.: Изд. АН СССР, 1947.
291 с.
8. Справочник по машинной графике и проектированию /
В.Е. Михайленко, В.А. Анпилогова, Л.А. Кириевский и др.; Под ред.
В.Е. Михайленко, А.А. Лященко. К.: Будивельник, 1984. 184 с.
9. Фролов С.А. Начертательная геометрия. М.: Машиностроение,
1983. 240 с.
10. Фролов С.А. Методы преобразования ортогональных проекций.
М.: Машиностроение, 1963. 144 с.
Предметный указатель
Аппроксимация 45
Бинормаль 43
Геликоид
— наклонный 62
— прямой 62
Гиперболоид
— двухполостный 59
— однополостный 59
Диметрия 20
Изометрия 20
Инверсия 206
Каркас
— дискретный 51, 200
— непрерывный 200
Кривая
— алгебраическая 38, 213
— коробовая 45
— ошибок 54
— трансцендентная 38
Кривизна
— кривой 40
— поверхности 137
Линия
— видимости 53
— винтовая 43. 49
— геодезическая 179
— наибольшего наклона 152, 154
— очерковая 53, 59, 60, 72, 140
Нормаль
— главная 43
— кривой 39, 43
— поверхности 151
Обвод 44, 1 34
Определитель поверхности 50
Параболоид
— вращения 59
— гиперболический 57, 181
— эллиптический 57, 220
Плоскость
— касательная 43
— нормальная 43
— соприкасающаяся 43
— спрямляющая 43
Поверхность 49
— алгебраическая 52
— многогранная 35
— развертываемая 168, 169
— топографическая 51
— торсовая 69
— трансцендентная 52, 62
Показатель искажения 19
Преобразование 78
— изометрическое 168
— нелинейное 209, 215
— расслаивающееся 209, 215
— родственное 30, 197
— эквиформные 214
Проецирование 10
— косое 187
— криволинейное 92, 94, 190
— параллельное 12
— прямоугольное 13
— стереографическое 204
— центральное 11
Развертка поверхности 167
— приближенная 169, 173
— точная 169
— условная 169, 176
Ребро возврата 69
След
— плоскости 33
— прямой 28
Теорема
— Монжа 140
— о двух точках соприкосновения 137
— о трех точках соприкосновения 140
— Польке 20
— о проецировании прямого угла 14
Точка
— видимости 111
— возврата 38
— гиперболическая 137
— двойная 38
— изолированная 38, 137
— конкурирующая 29
— параболическая 38, 137
— узловая 38
— эллиптическая 137
Треугольник следов 20
Трехгранник Френе (сопровожда-
ющий) 43
Триметрия 20
Эллипсоид вращения 59
223
Учебник
Геннадий Сергеевич Иванов
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Редактор Н.В. Скугаревскал
Художественный редактор С.Н. Голубев
Технический редактор О.В. Рожкова
Корректор Л. В. Тарасова
ИБ №7531
Лицензия ЛР № 080003 от 15.08.91.
Сдано в набор 25.03.93. Подписано в печать 31.01.95. Формат 70*100/16.
Бумага офсетная. Гарнитура литературная. Печать офсетная.
Усл. печ. л. 18,20. Усл. кр.-отт. 18,20. Уч.-изд.л. 16,83.
Тираж 10000 экз. Заказ 8f1• „С”
Ордена Трудового Красного Знамени издательство ’’Машиностроение’’,
107076, .Москва, Стромынский пер., 4
Отпечатано в московской типографии N? 4
Комитета Российской Федерации по печати,
129041, Москва, Б.Переяславская ул., 46