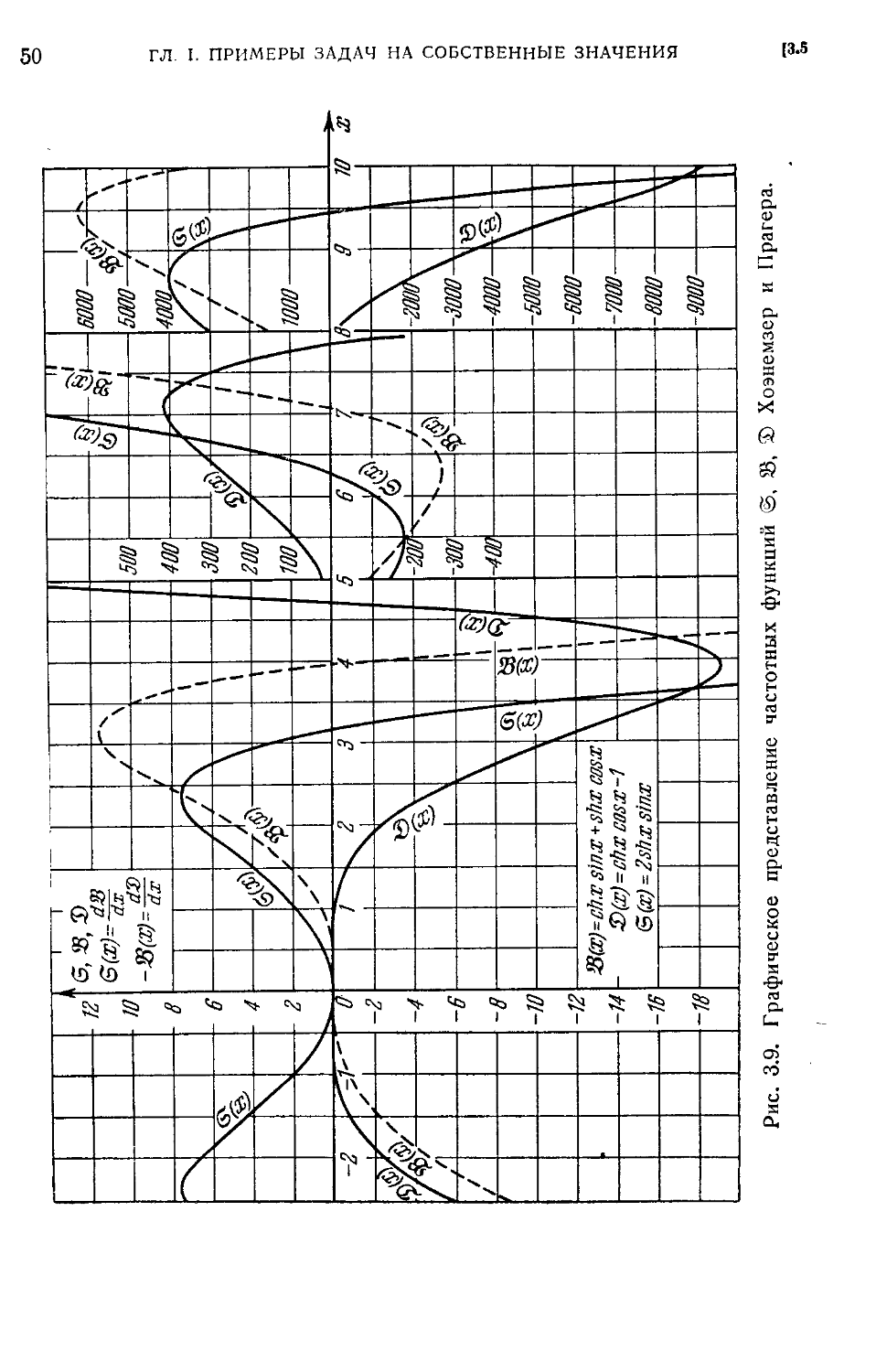
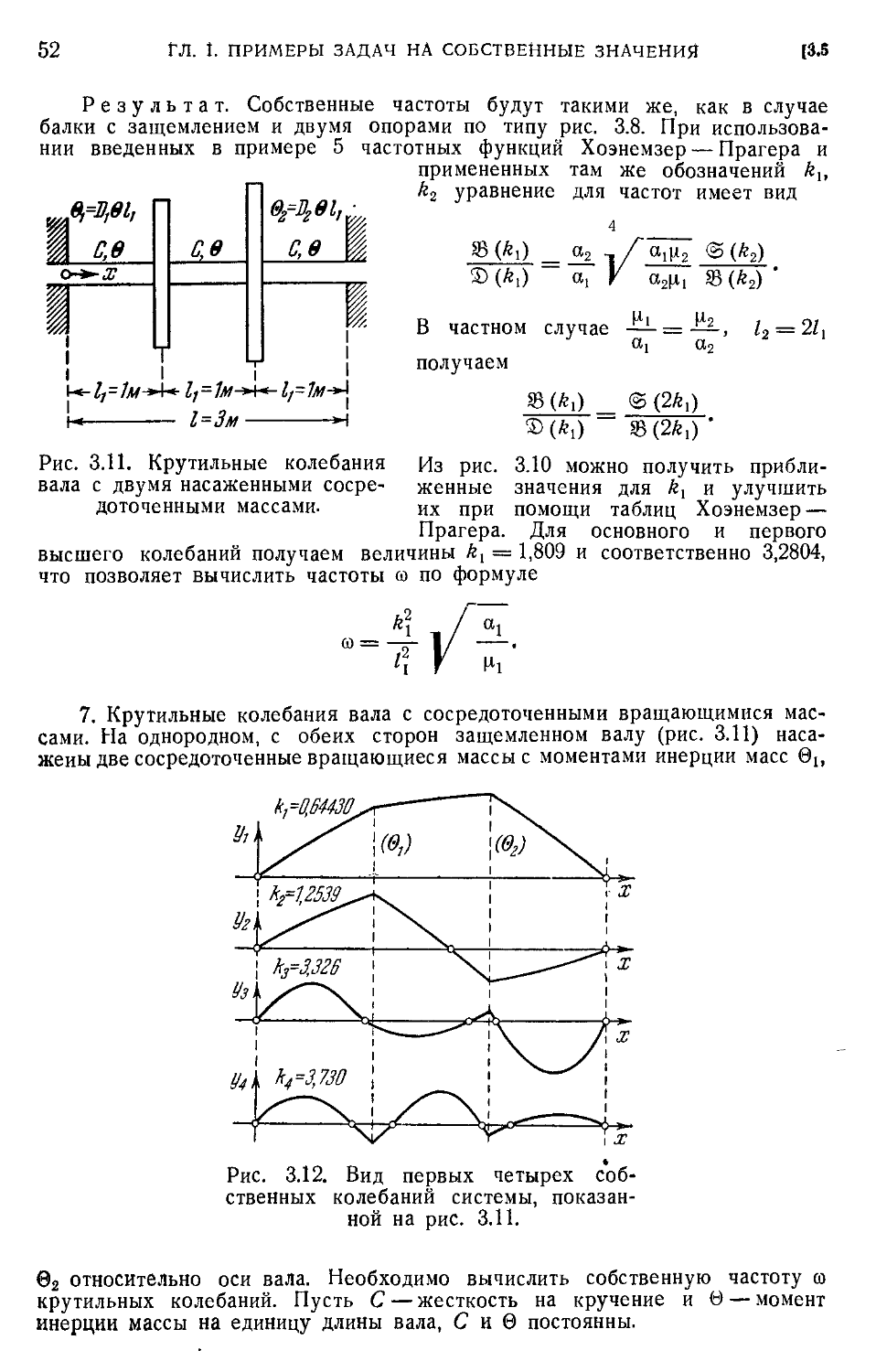
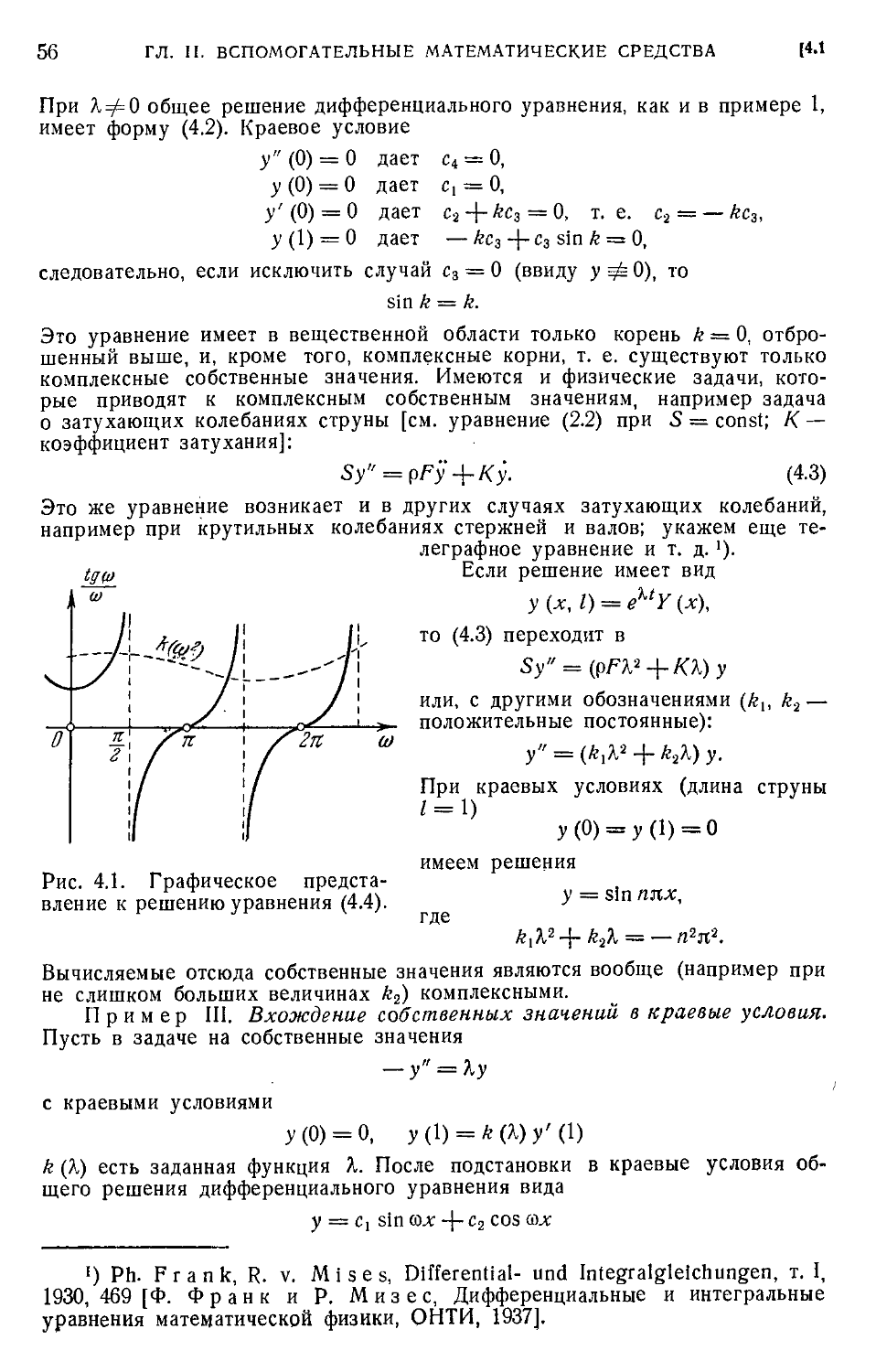
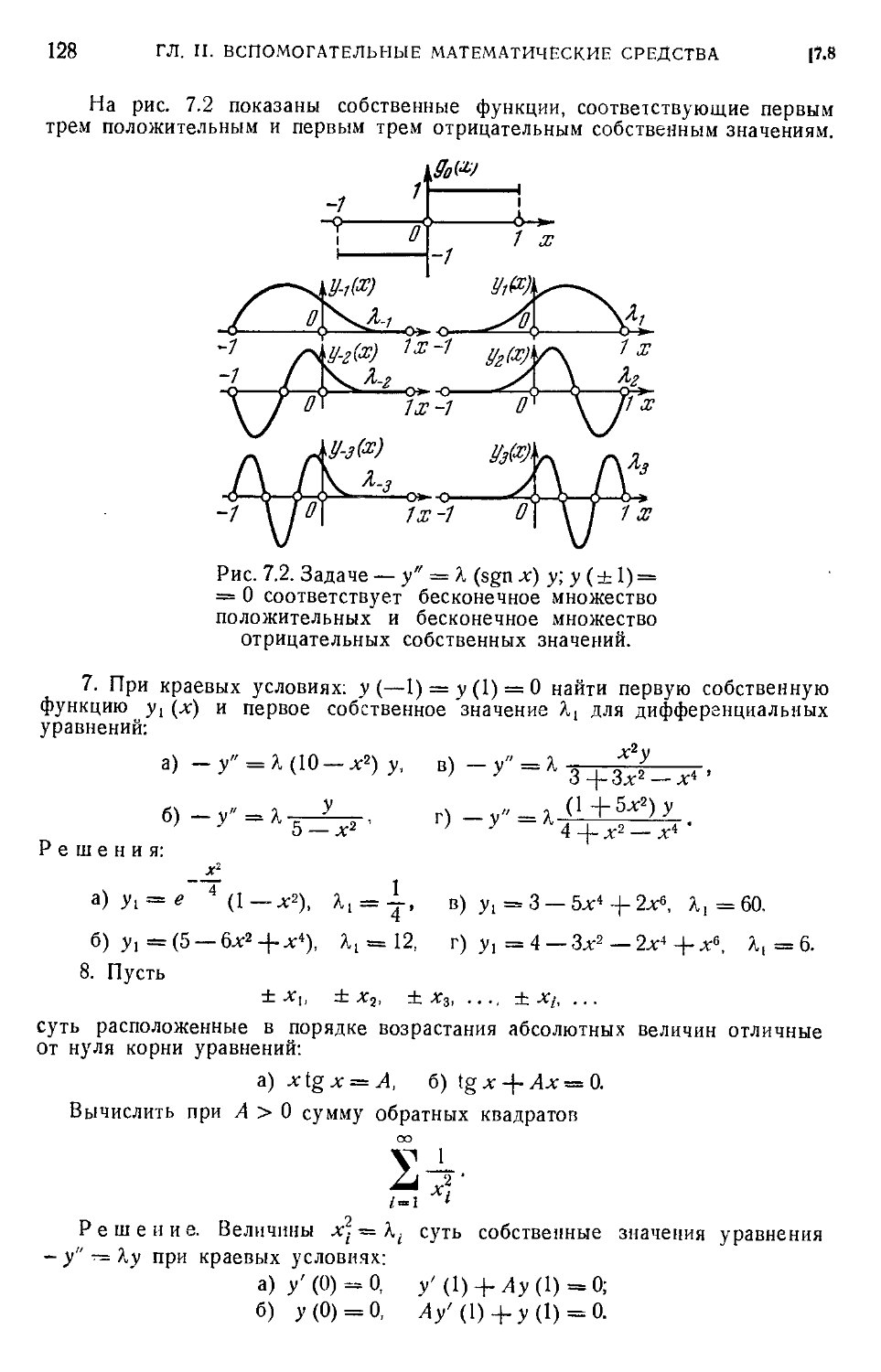
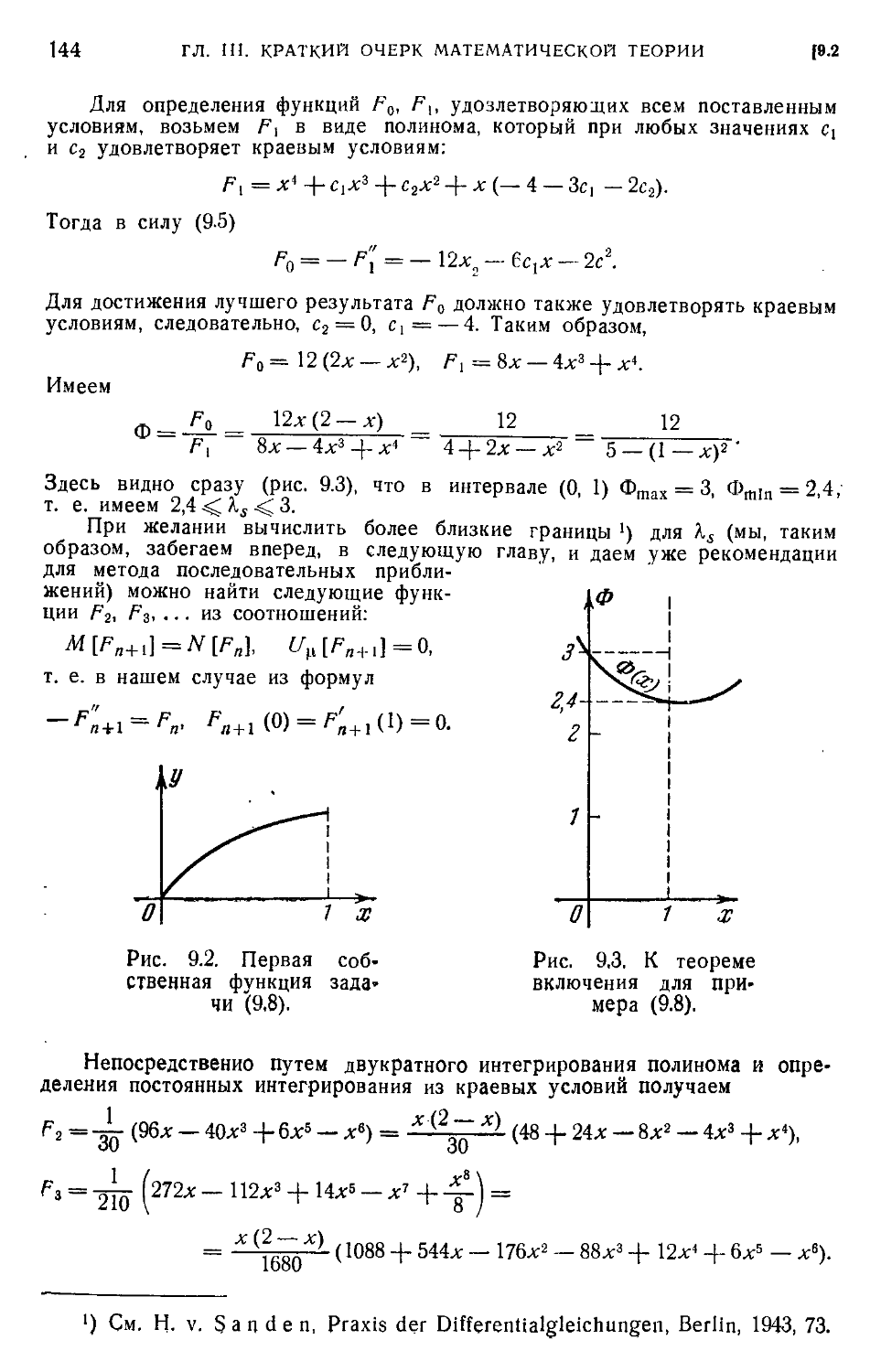
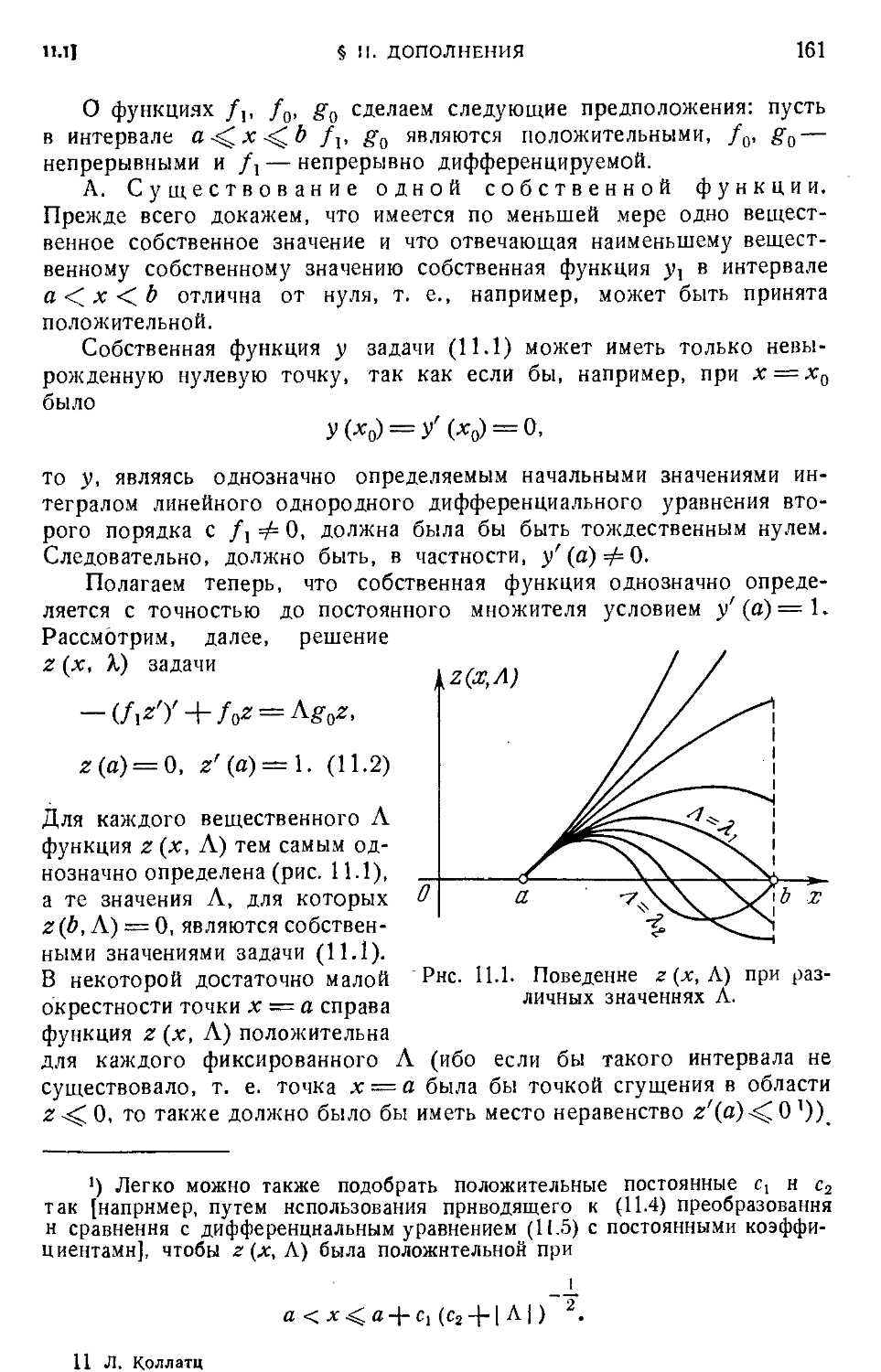
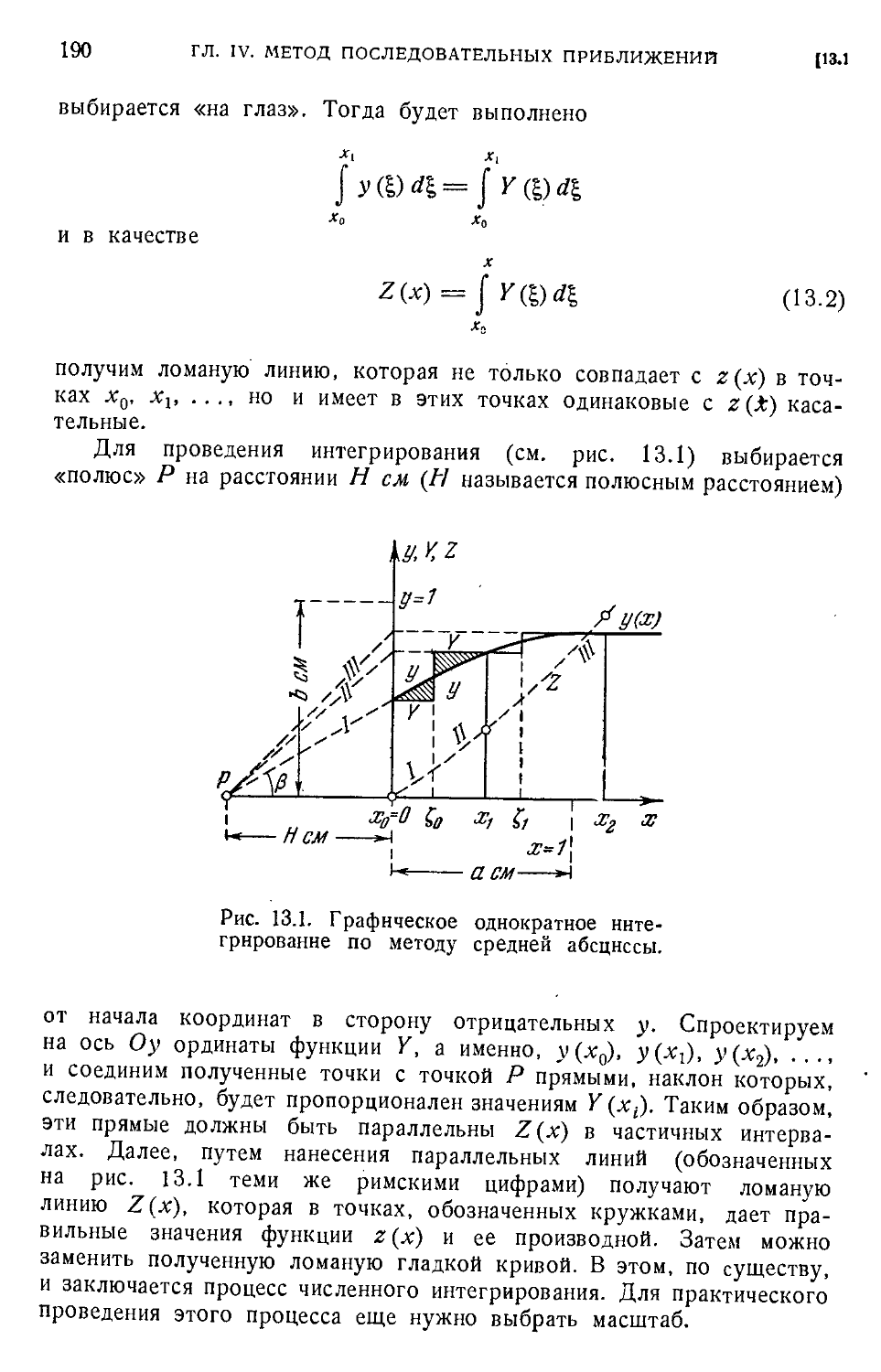
Text
EIGENWERTAUFGABEN
MIT TECHNISCHEN
ANWENDUNGEN
von Dr. Dr. h. с LOTHAR COLLATZ
MIT 137 ABBILDUNOEN UND 15 TAFELN
2. DURCHGESEHENE AUFLAOE
№33 ' 7}
ИИ2Х8Д8£ i
! HE БОЛЕЕ 1И
i ОДНИ РУКИ И2Х8Д8£ I
БИБЛИОТЕКА
СЕЛЬСКАЯ
НОЙЬ
LEIPZIG 1963
AKADEMISCHE VERLAQSQESELLSCHAFT
OEEST & PORT1O K- —O.
Ф из и ко -
Математическая
Библиотека
Инженера
Л. КОЛЛАТЦ
ЗАДАЧИ
НА СОБСТВЕННЫЕ
ЗНАЧЕНИЯ
С ТЕХНИЧЕСКИМИ ПРИЛОЖЕНИЯМИ
Перевод со второго
немецкого издания
под общей редакцией
В. В. НИКОЛЬСКОГО
ИЗДАТЕЛЬСТВО «НАУКА*
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1968 -,
518
К 60
УДК 518.0
Задачи на собственные значения (с техническими
приложениями). Коллатц Л.
Автор книги Лотар Коллатц является известным специали-
специалистом в области прикладной математики, относящейся главным
образом к задачам технической механики. В данной книге рас-
рассматриваются задачи на собственные значения, связанные с про-
проблемой потери устойчивости, упругими колебаниями и др. При
этом акцент делается не на физическое, а на математическое
содержание задач; особое внимание уделяется вычислительным
методам.
Рассмотрение общей теории (функции Грина, интегральные
уравнения, теорема разложения, вариационные принципы) про-
проведено в простой форме и содержит ряд оригинальных черт.
Значительное внимание уделяется развитому автором методу
последовательных приближений, численной реализации вариа-
вариационных принципов, задачам для матриц. Излагаются конечио-
разностные и другие методы, представляющие интерес для лиц,
занимающихся задачами на собственные значения.
Таблиц 15, иллюстраций 137, библ. 72 названия.
2-2-4
ОГЛАВЛЕНИЕ
Перечень таблиц 9
Предисловие редактора перевода 11
Из предисловий автора к первому и второму изданиям 13
Введение и краткий обзор 15
ГЛАВА ПЕРВАЯ
ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
ИЗ ТЕХНИЧЕСКОЙ МЕХАНИКИ
§ 1. Проблема устойчивости 18
I.I Продольный изгиб стержня, защемленного на одном конце A8). 1.2. Продольный
изгиб стержня, защемленного на одном конце и шарнирно опертого иа другом B0).
1.3. Продольный изгиб стержня с учетом собственного веса B1). 1.4. Сжатый стержень
на упругом основании B2). 1.5. Опрокидывание консольной балки при изгибе B3).
1.6. Кручение и опрокидывание двутавровой балки B5). 1.7. Сжатие и кручение вала B6).
1.8. Выпучивание круговой арки B8).
§ 2. Задачи о колебаниях 30
2.1. Колебания свободно подвешенного каната C0). 2.2. Крутильные колебания стерж-
стержней C3). 2.3. Изгибиые колебания стержня C4). 2.4. Пример физической задачи с отри-
отрицательными собственными значениями C6). 2.5. Колебания стержня с учетом влияния
собственного веса C8). 2.6. Критическое число оборотов вала с гироскопическим эффек-
эффектом C9). 2.7. Крутильные колебания диска D1).
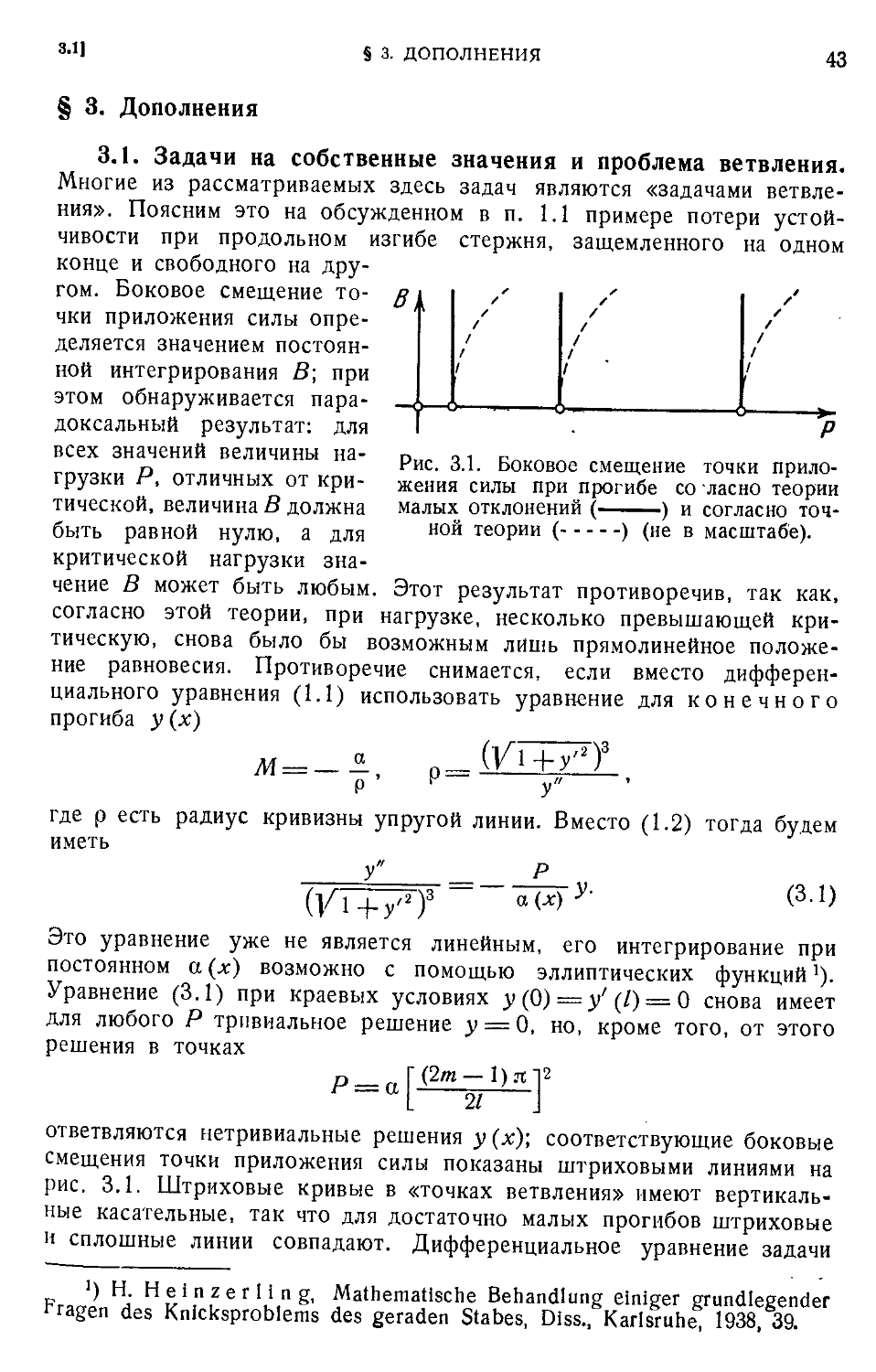
§ 3. Дополнения 43
3.1. Задачи на собственные значения и проблема ветвления D3). 3.2. Системы диф-
дифференциальных уравнений D4). 3.3. Другие краевые условия, соотношение между значе-
значениями иа обоих концах D5). 3.4. Задачи на собственные значения для уравнений с част-
частными производными D5). 3.5. Упражнения D7).
ГЛАВА ВТОРАЯ
ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
§ 4. Основные сведения о задачах на собственные значения .... 54
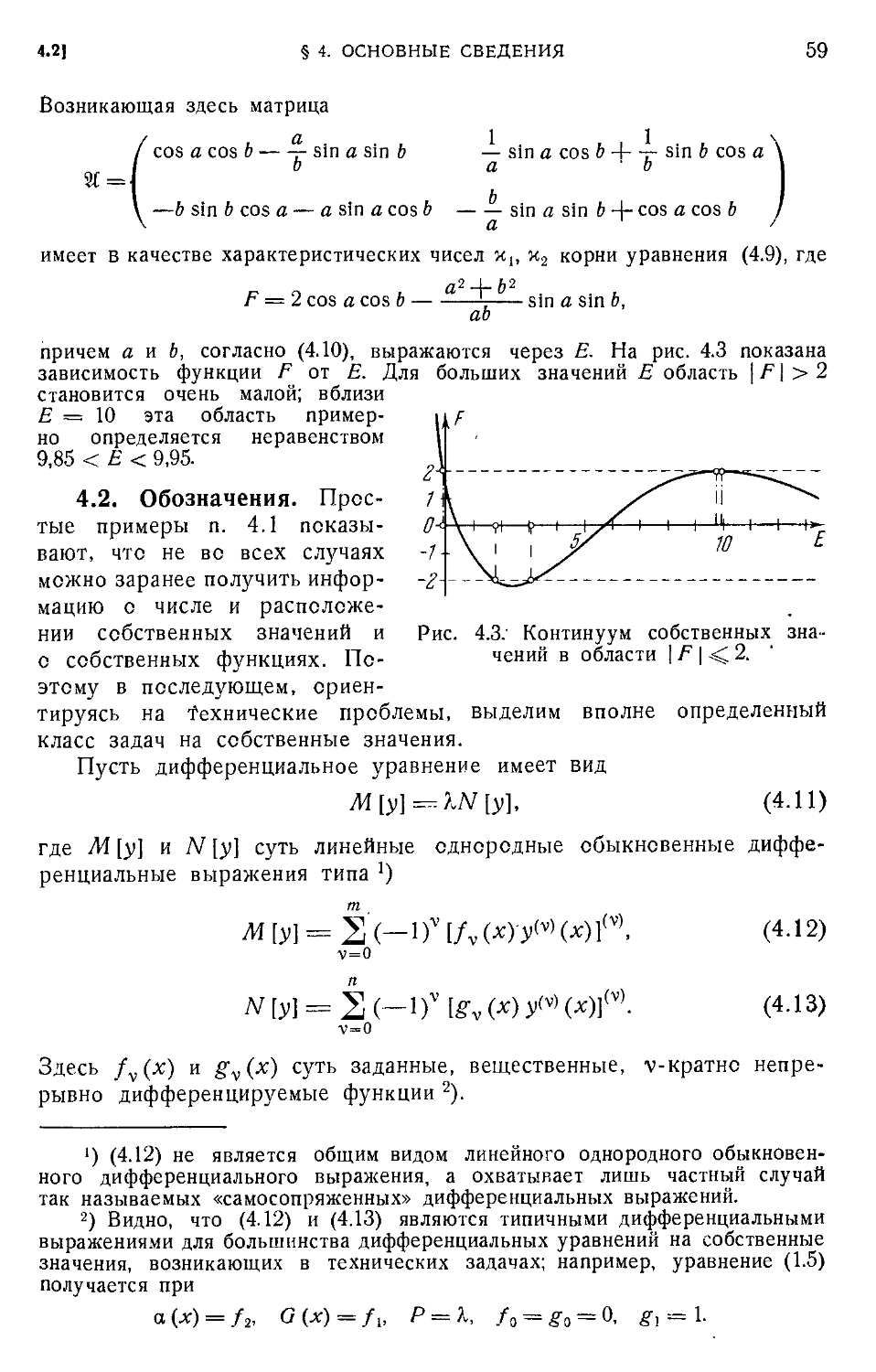
4-1. Различные случаи распределения собственных значений E4). 4.2. Обозначения E9).
4.3. Самосопряженность F1). 4.4. Обобщенная ортогональность F4). 4.5. Вещественность
6 ОГЛАВЛЕНИЕ
собственных значений F6). 4.6. Формула Дирихле F8). 4.7. Одночленный класс F9).
4.8. Пример самосопряженной задачи с невещественными собственными значениями G0).
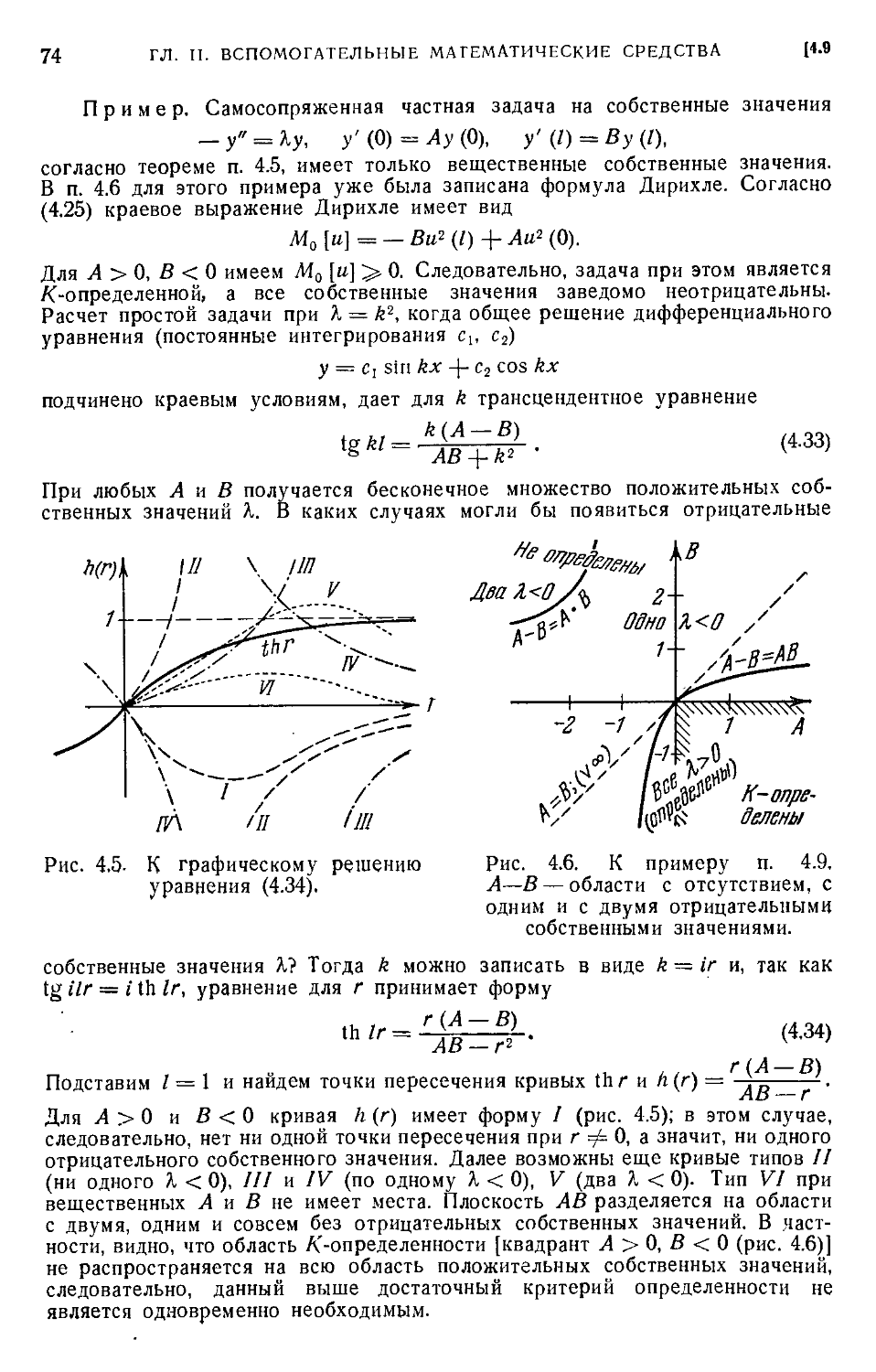
4.9. Определенность задачи на собственные значения G1).
§ 5. Функция Грина для обыкновенных дифференциальных урав-
уравнений 75
5.1. Определение функции Грина G5). 5.2. Вывод формулы решения для краевой за-
задачи G7). 5.3. Построение функции Грина нз фундаментальной системы G8). 5.4. Сим-
Симметрия функции Грина О (х, |) = О(|, л:) для самосопряженной краевой задачи (82).
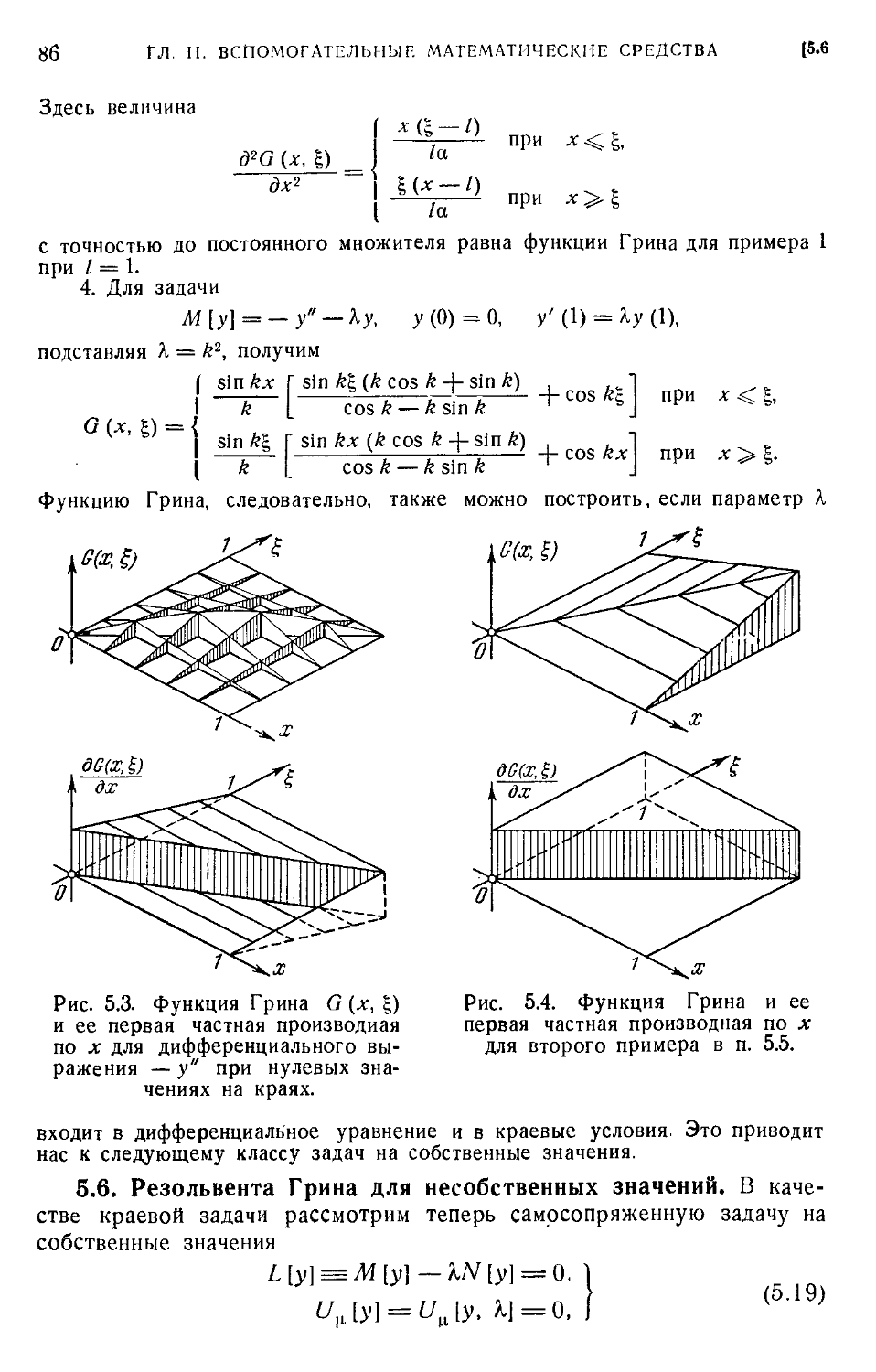
5.5. Простые примеры функции Грнна (85). 5.6. Резольвента Грина для несобственных
значений (86). 5.7. Условия существования собственных значений (87). 5.8. Поведение
резольвенты Грииа в точках собственных значений К (90). 5.9. Кратные собственные
значения (92). 5.10. Полуопределенные задачи на собственные значения (95).
§ 6. Функция Грина для уравнений с частными производными . . 95
6.1. Основные понятия (96). 6.2. Частный класс задач (97). 6.3. Функция Грнна, предвари-
предварительные замечания A00). 6.4. Решение краевой задачи прн помощи функции Грина A02).
6.5. Другие типы уравнений с частными производными A04).
§ 7. Связь с интегральными уравнениями 105
7.1. Одночленный класс и интегральные уравнения A05). 7.2. Выводы из теорнн инте-
интегральных уравнений A08). 7.3. Применение к одночленному классу A11). 7.4. Интегральные
уравнения и дифференциальные уравнения с частными производными A13). 7.5. Одно-
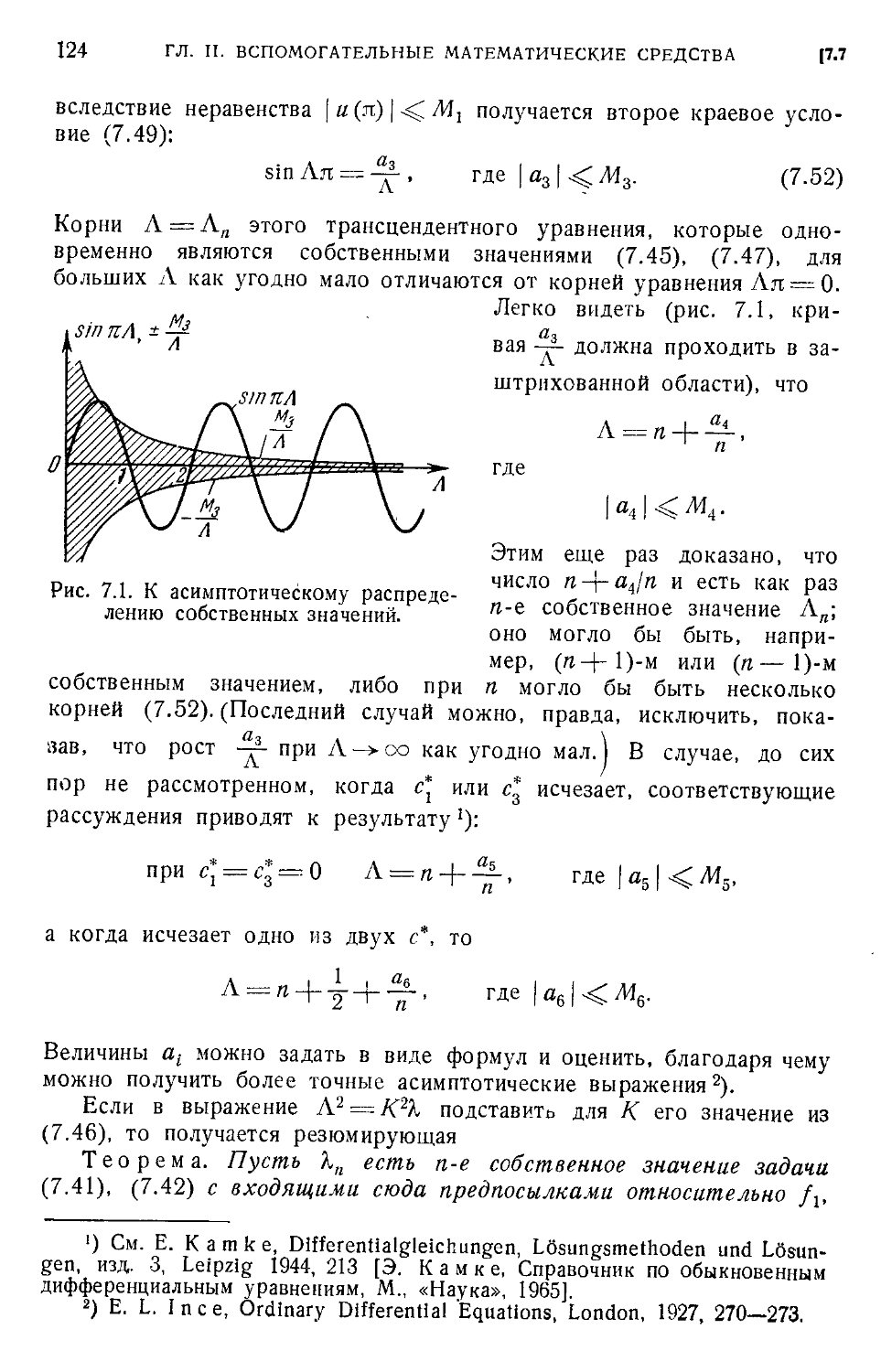
Одночленный класс и интегральное уравнение Вольтерра A16). 7.6. Пример A20). 7.7. Асимпто-
Асимптотическое распределение собственных значений A21). 7.8. Упражнения A25).
ГЛАВА ТРЕТЬЯ
КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ
§ 8. Минимальные свойства собственных значений 131
8.1. Минимальное свойство наименьшего собственного значения A31). 8.2. Проведение
доказательства A32). 8.3. Минимальные свойства высших собственных значений A35).
8.4. Мннимаксимальный принцип Куранта A38). 8.5. Теорема сравнения A40).
§ 9. Теорема включения 142
9.1. Формулировка теоремы A42). 9.2. Пример к теореме включения A43). 9.3. Доказа-
Доказательство теоремы включения A45). 9.4. Сравнение с задачами, разрешимыми в замкну-
замкнутом виде A46).
§ 10 Теорема о разложении 147
10.1. Предварительные замечания A47). 10.2. Коэффициенты Фурье A48). 10.3. Формула
Парсеваля A49). 10.4. Вспомогательная теорема о некоторых рядах по собственным
функциям A52). 10.5. Сходимость ряда Фурье A0.5) A55). 10.6. Теорема о разложении.
Доказательство в случае п=-0 A56). 10.7. Замечание A57). 10.8. Теорема о разложении.
Завершение доказательства для п>0 A59).
§ 11. Дополнения 160
11.1. Элементарное обоснование минимальных свойств в случае уравнений второго по-
порядка A80)." 11.2. Минимальные свойства собственных значений в случае уравнений
с частными производными A66). 11.3. Двупараметрические задачи на собственные зна-
значения, криаые собственных значений A70). 11.4. Упражнения A71).
ОГЛАВЛЕНИЕ 7
ГЛАВА ЧЕТВЕРТАЯ
МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
§ 12. Постоянные Шварца 176
12.1. Метод последовательных приближений в общем случае A76). 12.2. Введение по-
постоянных Шварца а^ н отношений ц^ A77). 12.3. ц^ образуют монотонную невозра-
стающую последовательность A80). 12.4. Нижняя граница для первого собственного
значения A81). 12.5. Практическое проведение метода A85). 12.6. Примеры применения
метода последовательных приближений A87).
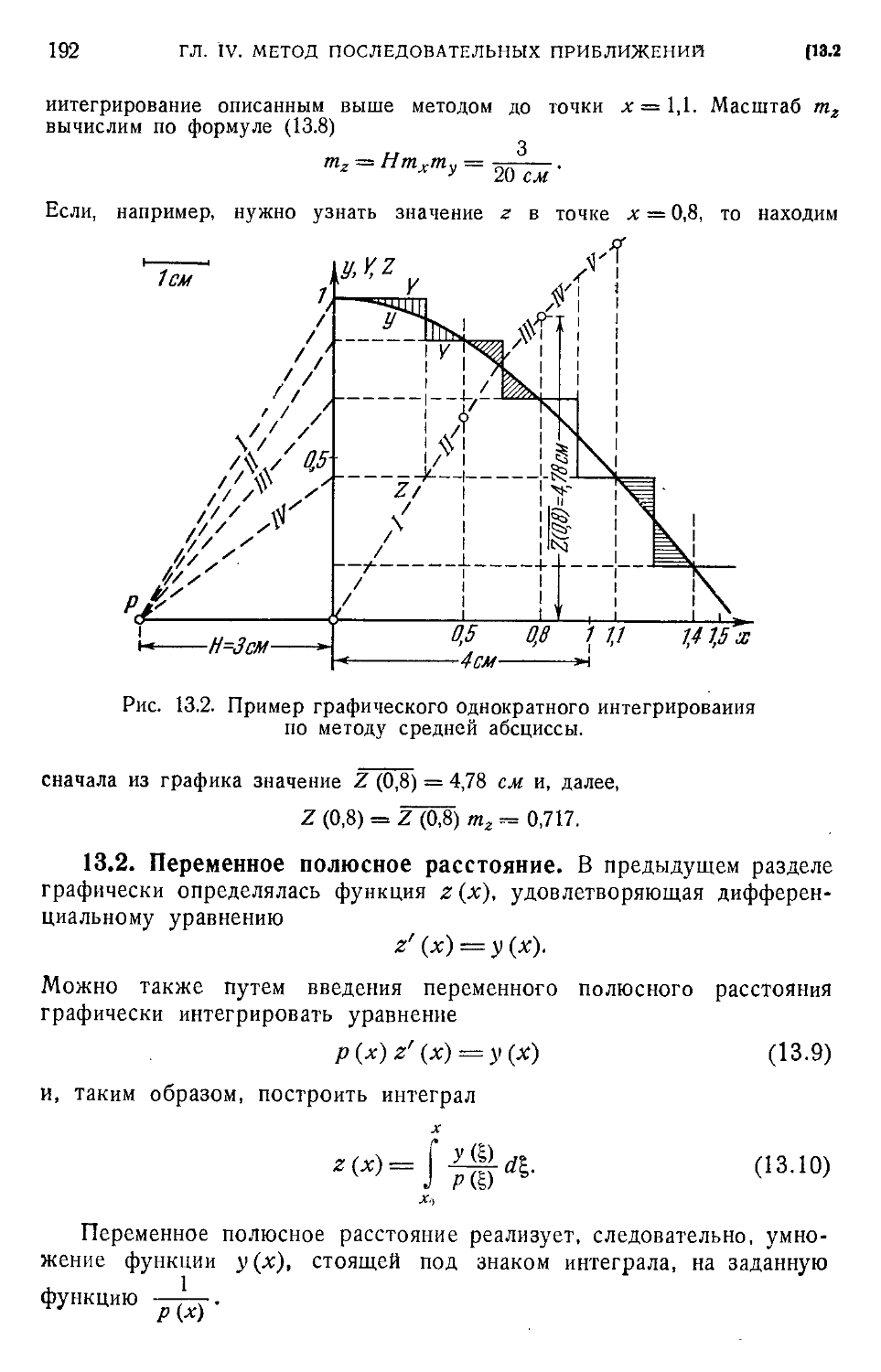
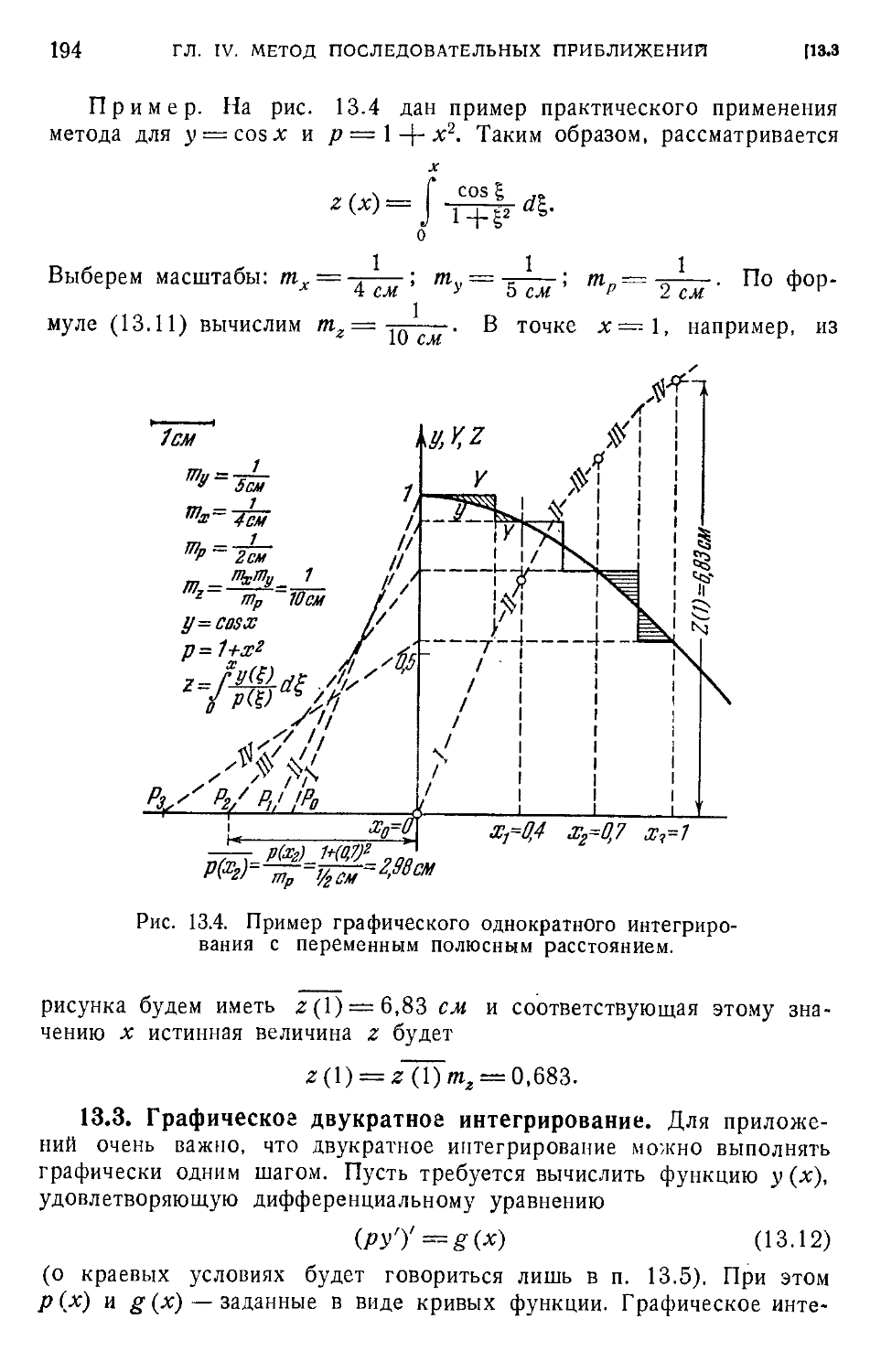
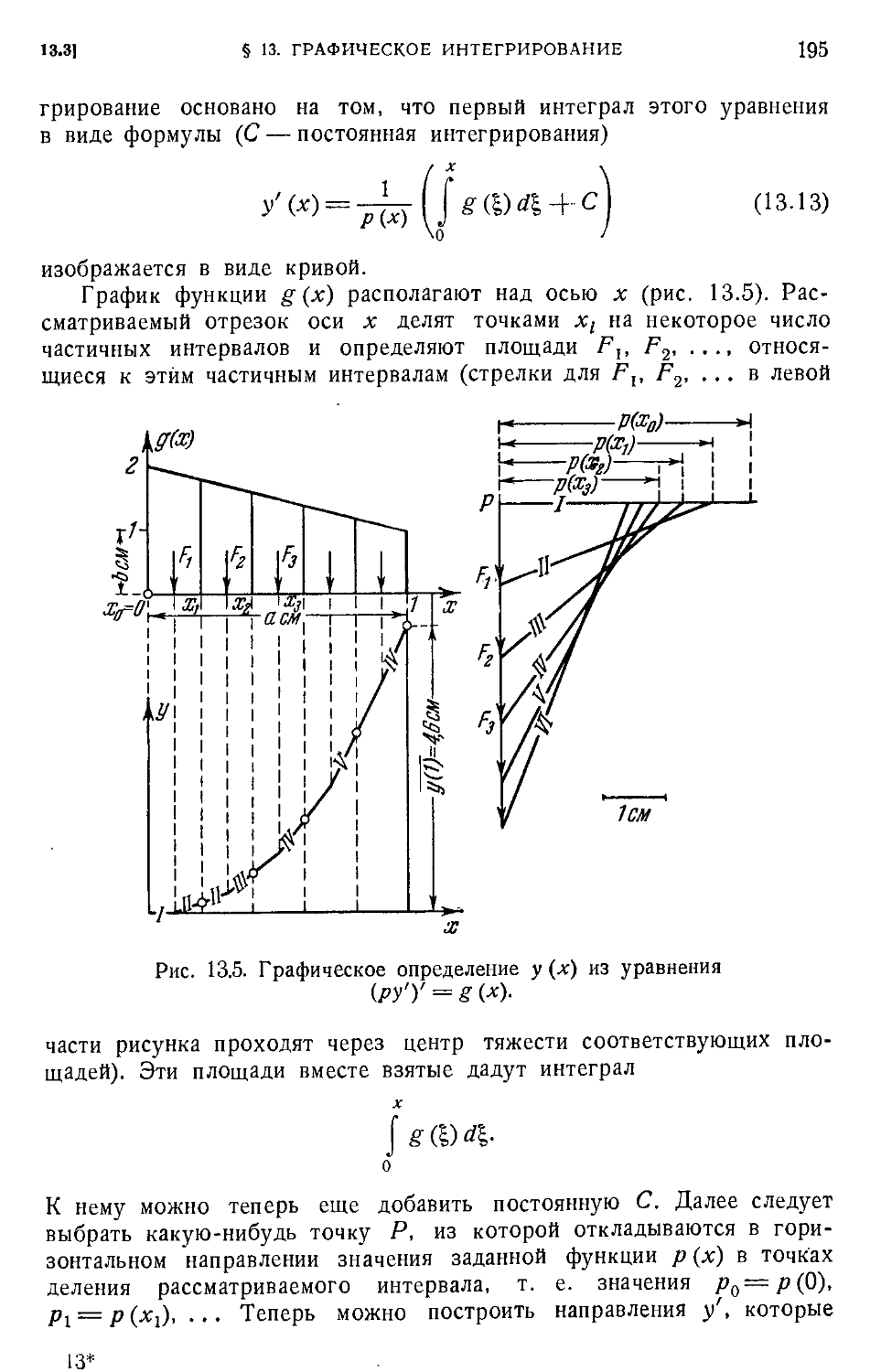
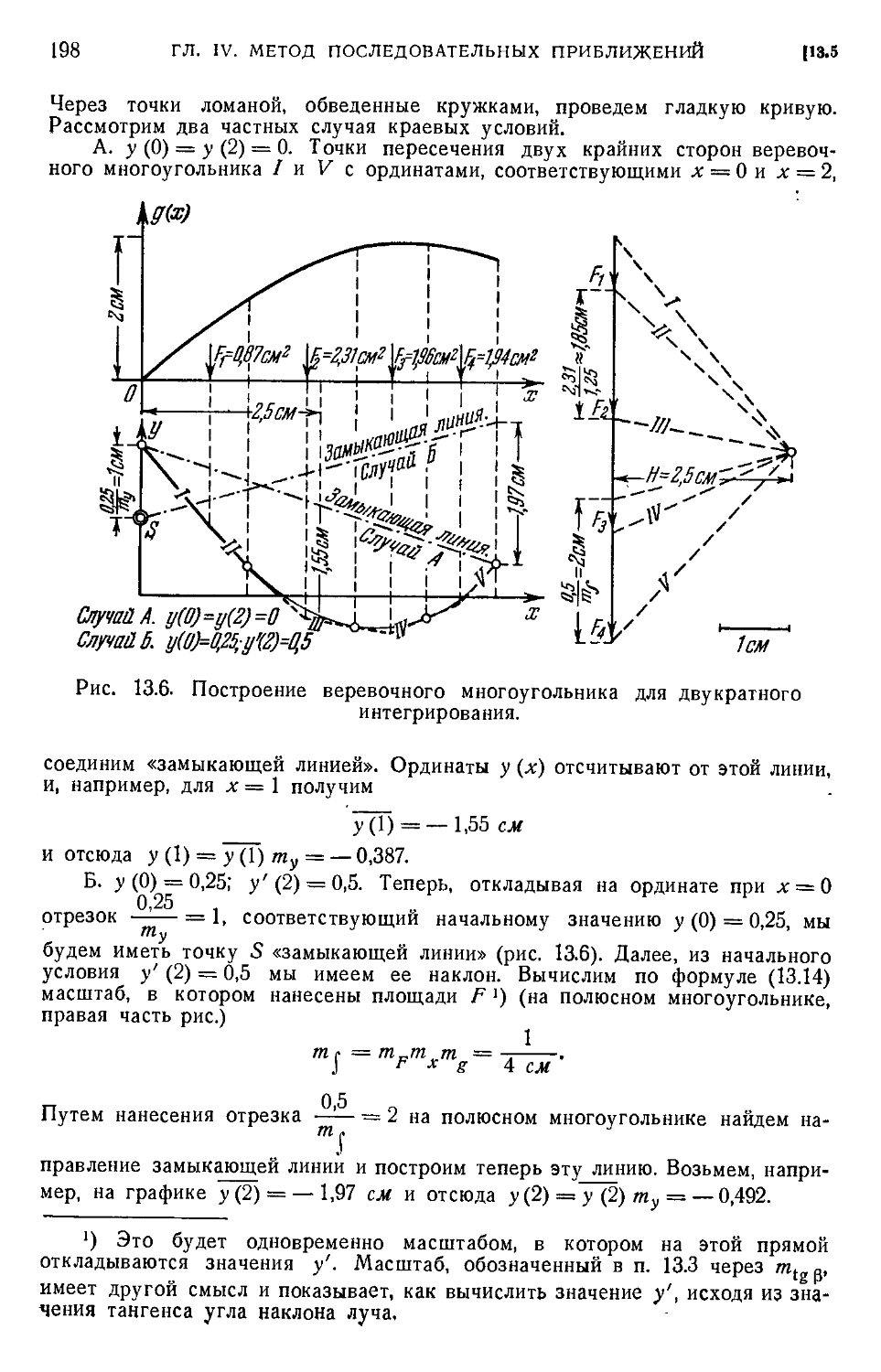
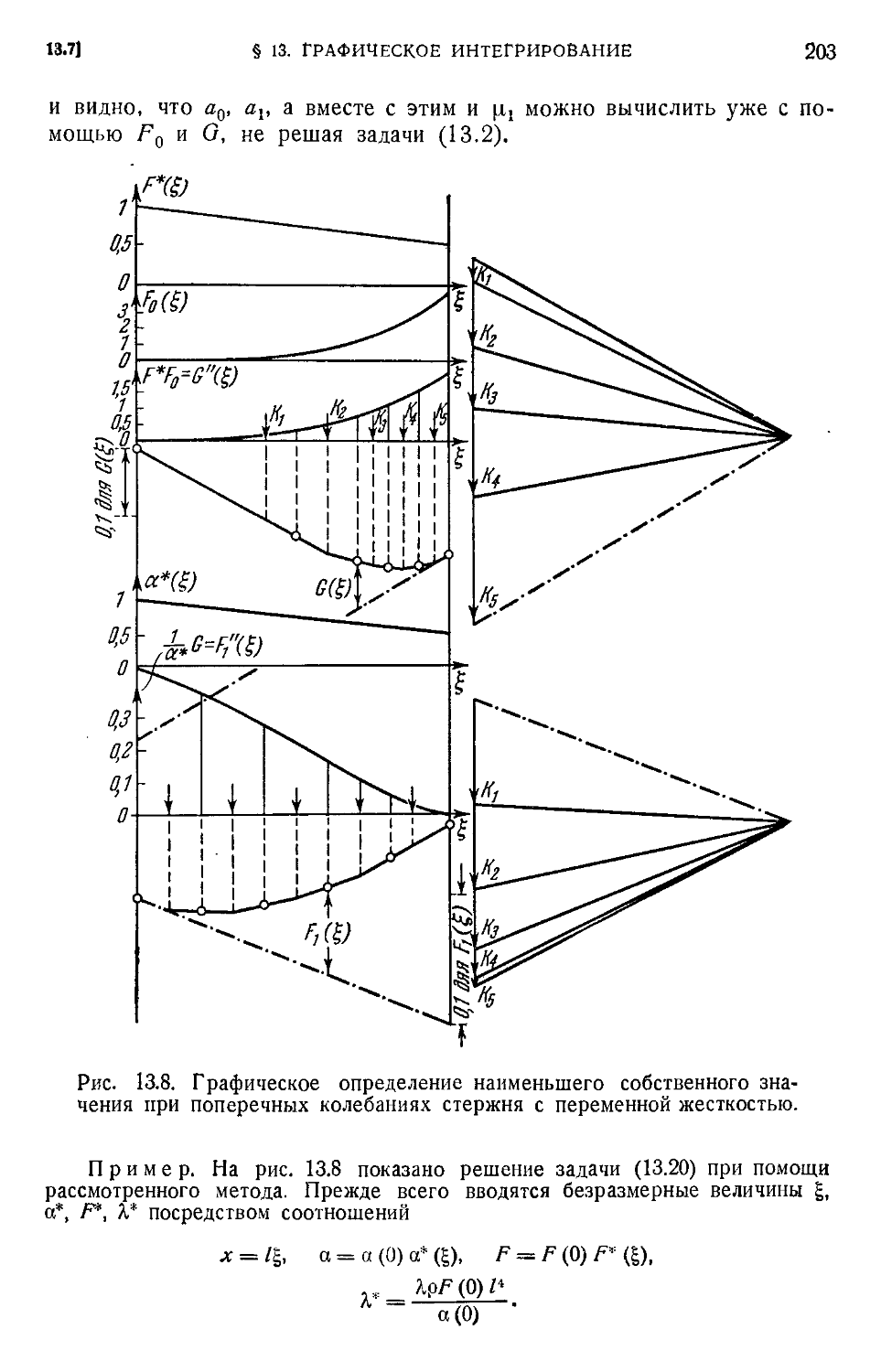
§ 13. Графическое интегрирование 189
13.1. Графическое однократное интегрирование A89). 13.2. Переменное полюсное рас-
расстояние A92). 13.3. Графическое двукратное интегрирование A94). 13.4. Особый случай
обыкновенного веревочного многоугольника A97). 13.5. Учет краевым условий A97).
13.6. Графическое проведение метода последовательны): приближений A99). 13.7. Гра-
Графическое определение цг B01).
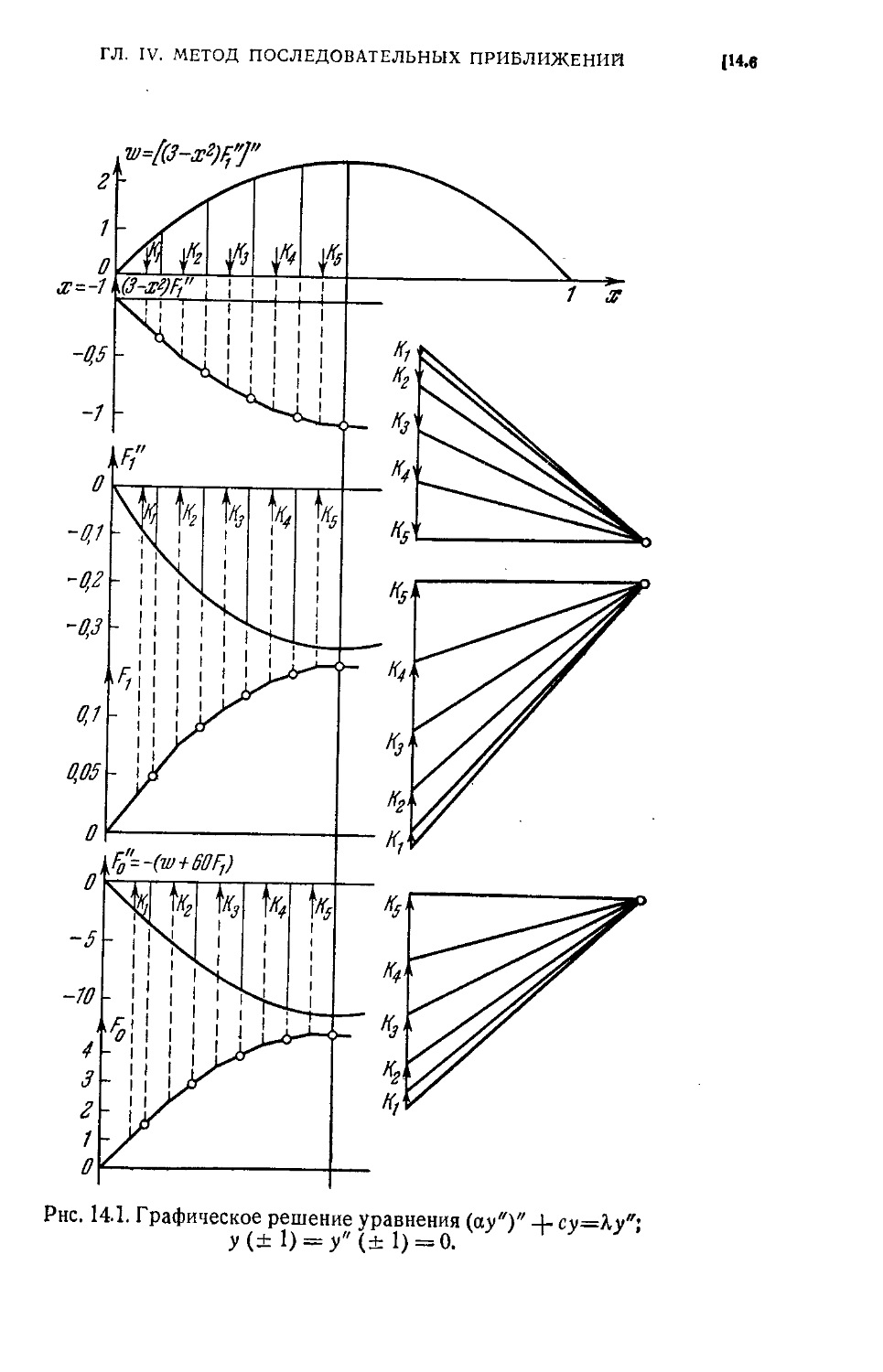
§ 14. Дополнения 204
14.1. Метод последовательные приближений для дифференциальным уравнений с част-
частными производными B04). 14.2. Теорема включения Крылова—Боголюбова для одно-
одночленного класса B06). 1.4.3. Доказательства основной формулы A2.19) при помощи тео-
теоремы о разложении B09). 14.4. Сходимость итерационного процесса для краевых залач
B12). 14.5. Метод" КЪх& для' высших собственных "значений B14).' 14.6. Упражнения B15).
ГЛАВА ПЯТАЯ
ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
§ 15. Основы метода Ритца 221
15.1. Три минимальных принципа B21). 15.2. Общий метод Рнтца B24). 15.3. Уравнения
Галеркииа B25) 15.4. Сведение к вековому уравнению B27). 15.5. Линейное представле-
представление в случае минимального принципа Камке B31). 15.6. Уравнения Граммеля B32). 15.7.
Численные примеры B34). 15.8. Приближения Ритца для высших собственных значений
238).
§ 16. Дальнейшее развитие метода Рита 240
16.1. Вариационные уравнения Эйлера B40). 16.2. Пример. Задача на собственные зна-
значения B44). 16.3. Обратная постановка задачи и метод Ритца B45). 16.4. Энергетический
метод для задач о колебаниях B46). 16.5. Изгибные колебания B48). 16.6. Пример. Кру-
Крутильные колебания B50). 16.7. Энергетический метод для дифференциальных уравнений
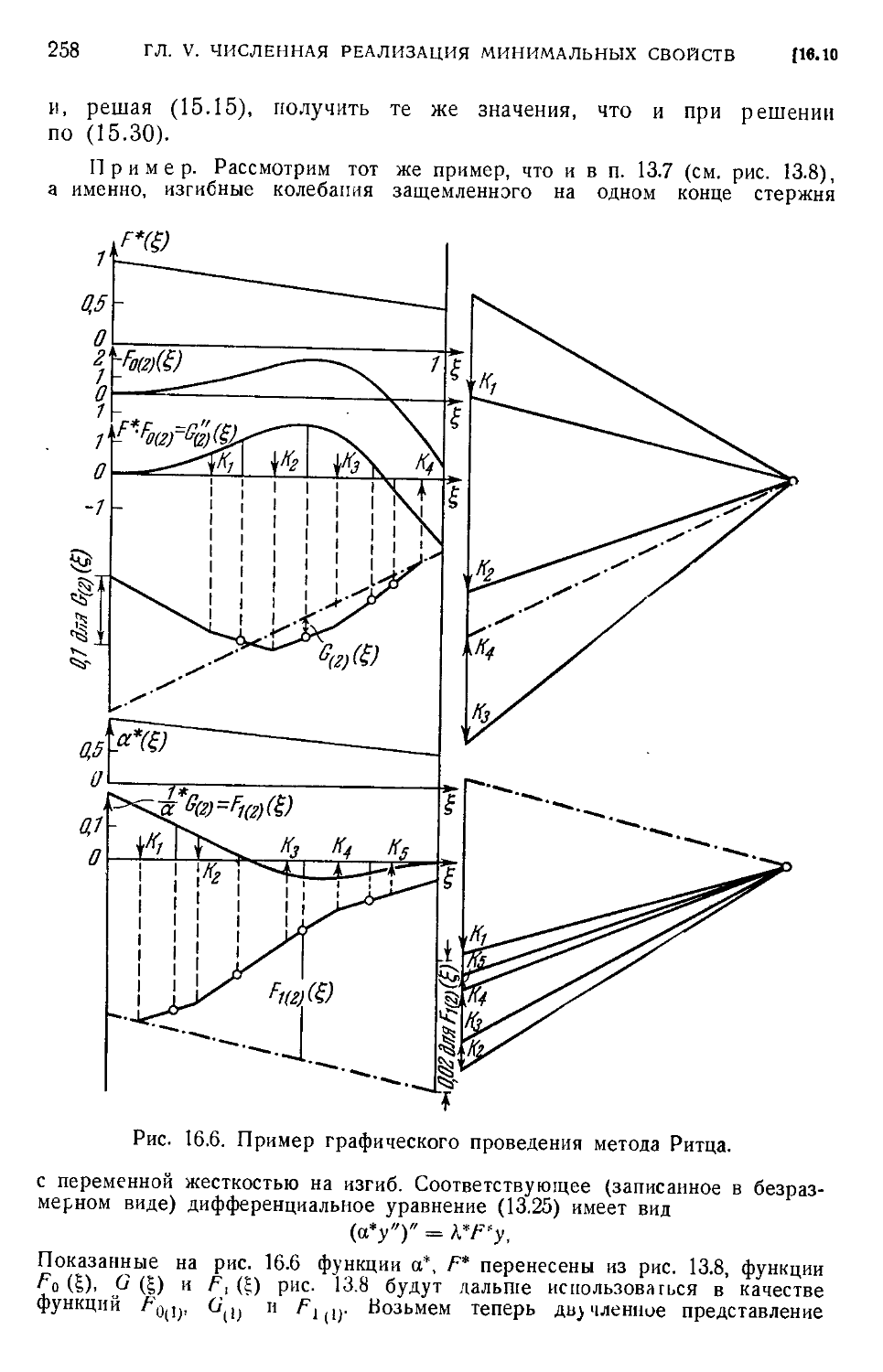
с частными производными B53). 16.8. Проблема потери устойчивости B55). 16.9. Графи-
Графическое проведение метода Ритца B55). 16.10. Графическое получение уравнений Грам-
Граммеля B56). 16.11. Упражнения B60).
ГЛАВА ШЕСТАЯ
ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
§ 17. Основные сведения о задачах на собственные значения для
матриц • 267
17.1. Обозначения B67). 17.2. Матрицы с особыми свойствами B68). 17.3. Квадратичные
н эрмитовы формы B69). 17.4. Вещественность характеристических чисел B75). 17.5.
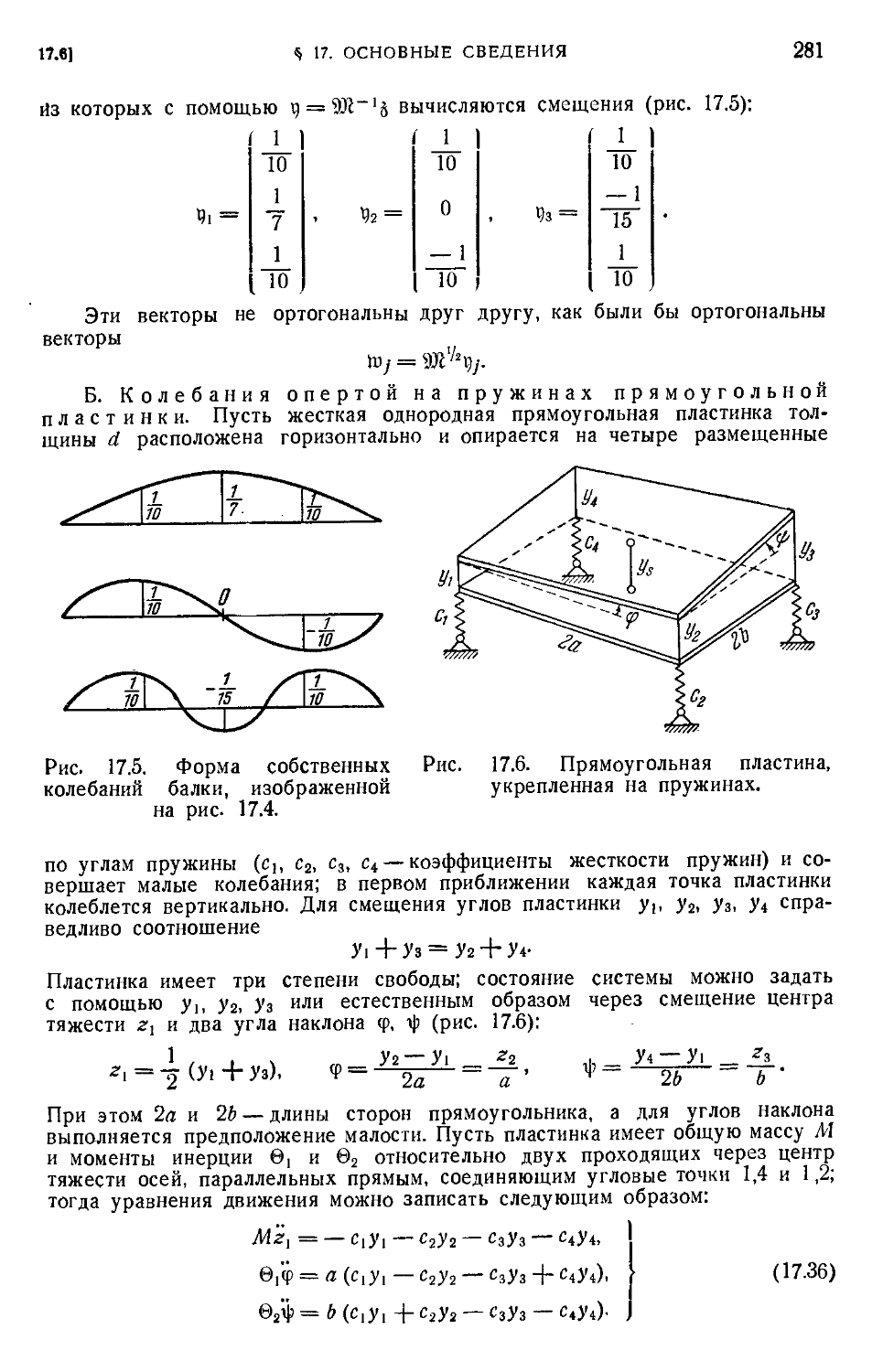
Обобщенная унитарность собственных векторов B77). 17.6. Примеры промежуточных
g* ОГЛАВЛЕНИЕ
задач на собственные значения из механики B78). 17.7. Примеры общих задач на соб-
собственные значения из механики B84). 17.8. Эрмитова самосопряженность в случае нн-
тегро-дифференциальных уравнений B 91).
§ 18. Экстремальные свойства характеристических чисел 295
18.1. Определение характеристических чисел при помощи задач на максимум B96). 18.2.
Приведение к главным осям B98). 18.3. Выводы и оценки C 01). 18.4. Одновременное
приведение к главным осям двух эрмитовых форм C04). 18.5. Пример. Геометрическая
интерпретация собственных векторов двух квадратичных форм C08). 18.6. Мииимакси-
мальный принцип Куранта C09). 18.7. Теорема включения C11). 18.8. Численное приме-
применение теоремы включения C13).
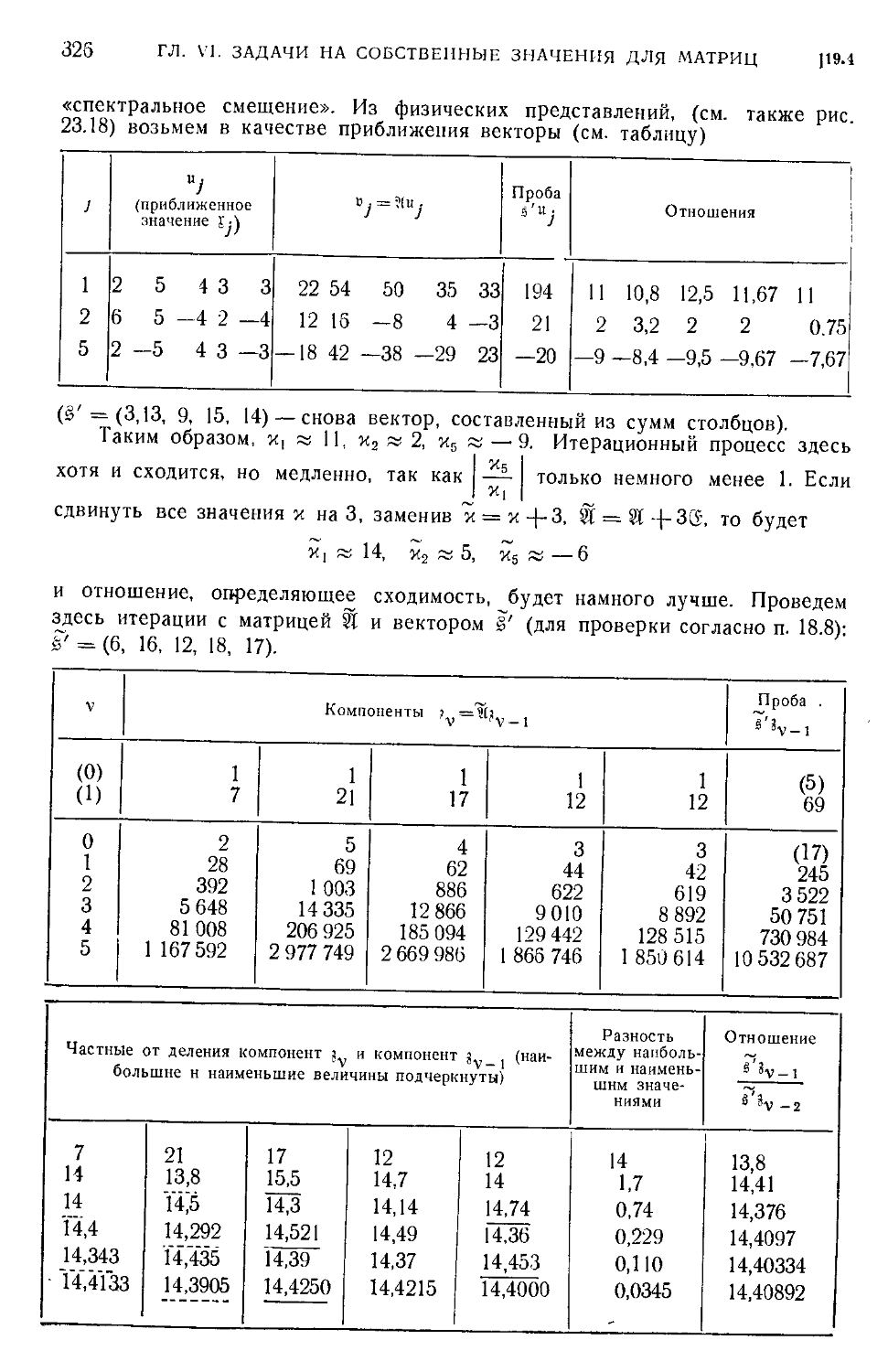
§ 19. Итерационный метод и главные векторы 315
19.1. Итерационный метод в общем случае C15). 19.2. Нижняя и верхняя границы для
характеристических чисел C21). 19.3. Понижение порядка C23). 19.4. Численный при-
пример C25). 19.5. Введение главчых векторов C28). 19.6. Доказательство теоремы
о разложении C30) 19.7. Сходимость итерационного метода для частных задач на соб-
собственные значения C32). 19.8 О степенях матрицы C33). 19.9. Системы обыкновенных
линейных дифференциальных уравнений C34). 19.10. Постоянные коэффициенты и глав-
главные векторы C37).
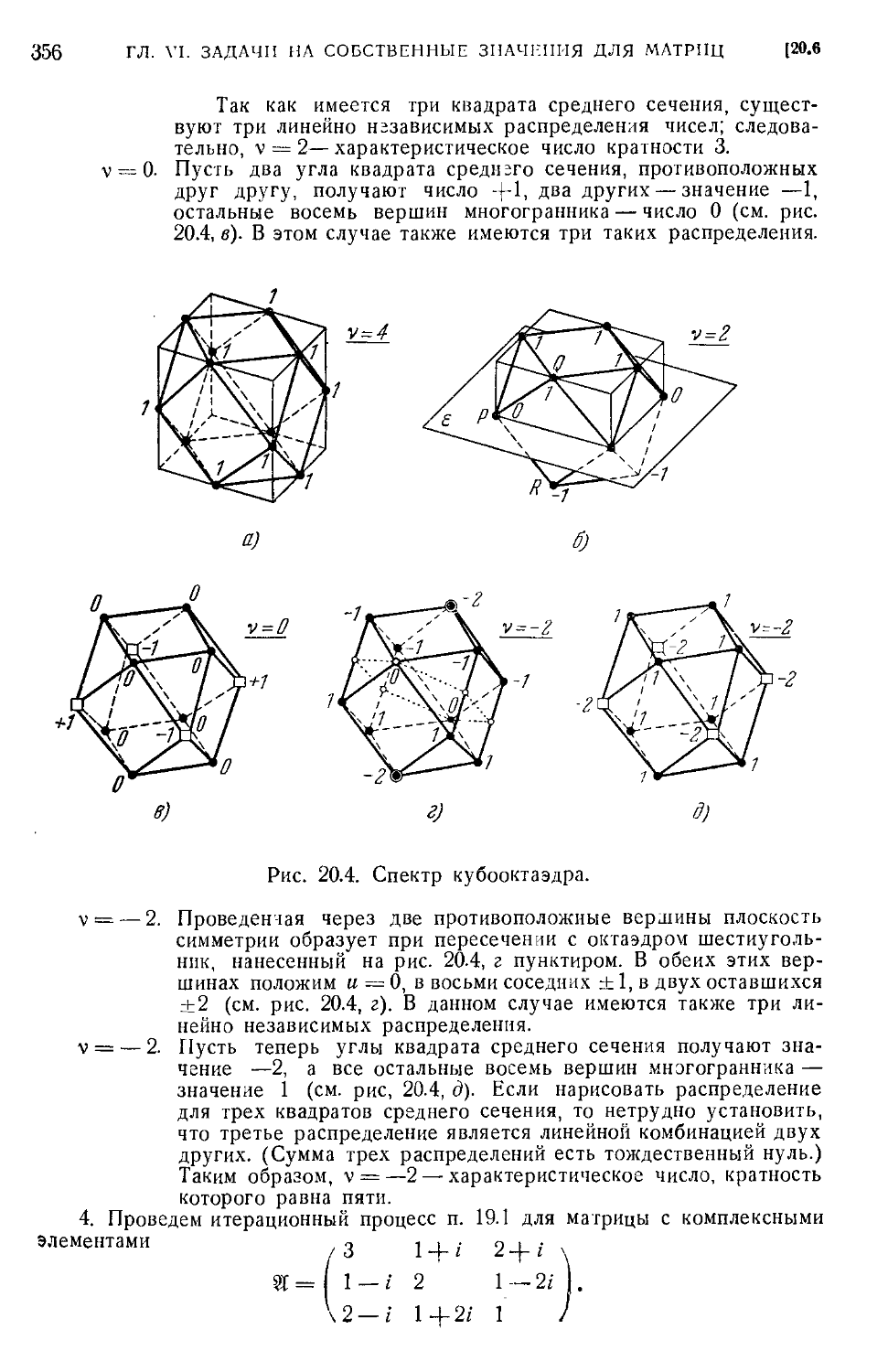
§ 20. Дополнения 339
20.1. Матричные полиномы и уравнение Кэли C39). 20.2. Функции матриц и степенные
ряды матриц C42). 20. 3. Приближенные решения систем линейных уравнений C45). 20.4.
Оценки характеристических чисел матриц C48). 20.5. Особые методы получения харак-
характеристического уравнения C52) 20.6. Упражнения C54).
ГЛАВА СЕДЬМАЯ ..
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
§ 21. Метод конечных разностей первого приближения для обыкно-
обыкновенных дифференциальных уравнений 359
21.1. Описание, метода конечных, разностей C59). 21.2. Пример для дифференциального
уравнения второго порядка C61). 21.3. Пример для дифференциального уравнения чет-
четвертого порядка C63). 21.4. Прямые методы для разностных уравнений C65).
21.5. Минимальное свойство наименьшего собственного значения в методе конечных
разностей C67).
§ 22. Улучшение метода конечных разностей 368
22.1. Конечные выражения C69). 22.2. Метод конечных разностей повышенной точ-
точности C71). 22.3. Пример ила разностного метода повышенной точности C72).
22.4. Вспомогательные формулы для многоточечного метода C72). 22.5. Пример C75).
22.6. Метод в общем случае C76).
§ 23. Метод конечных разностей для уравнений с частными произ-
производными 378
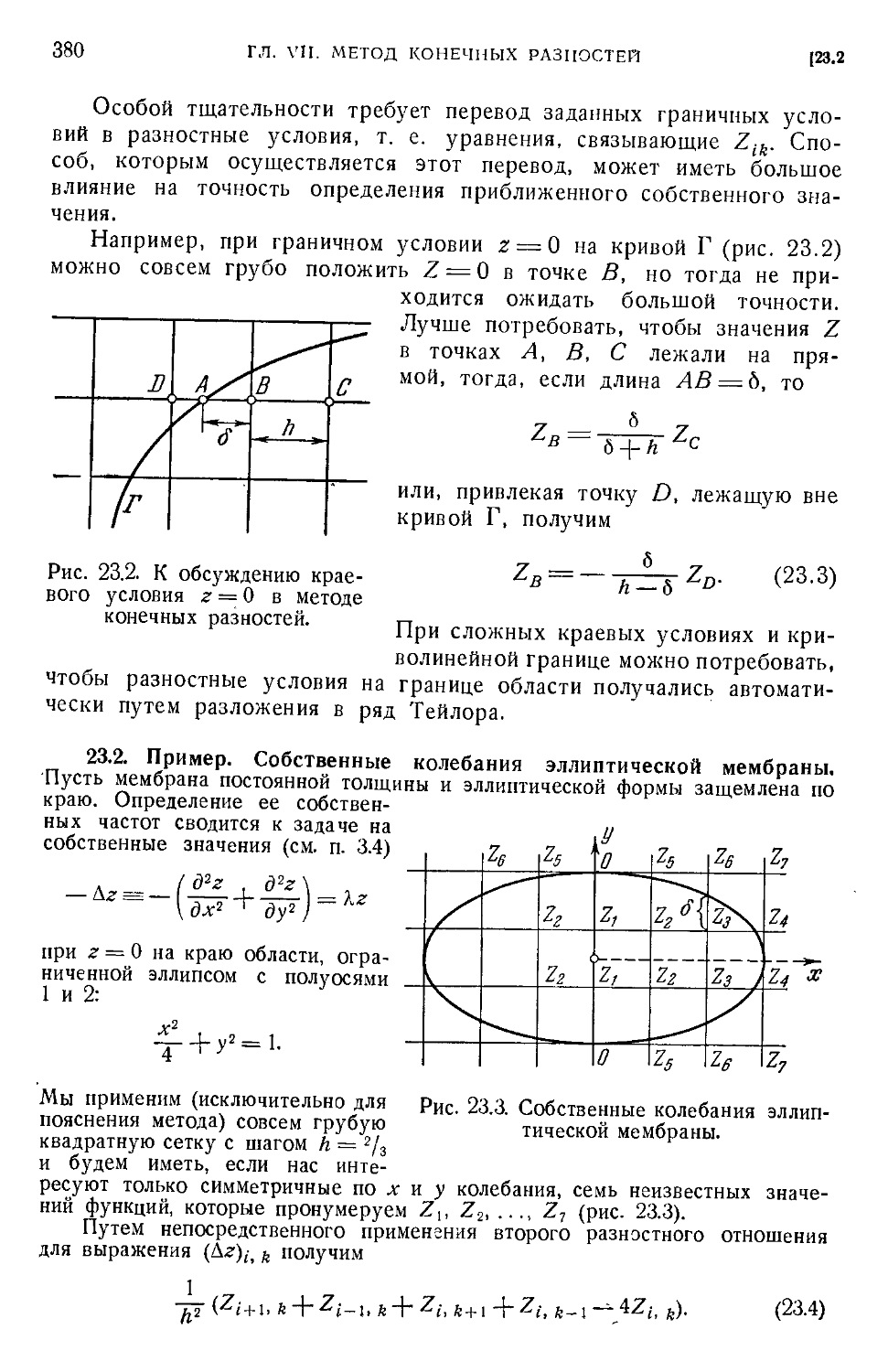
23.1. Обыкновенный метод конечных разностей i-л.ч метод первого 'приближения C7S).
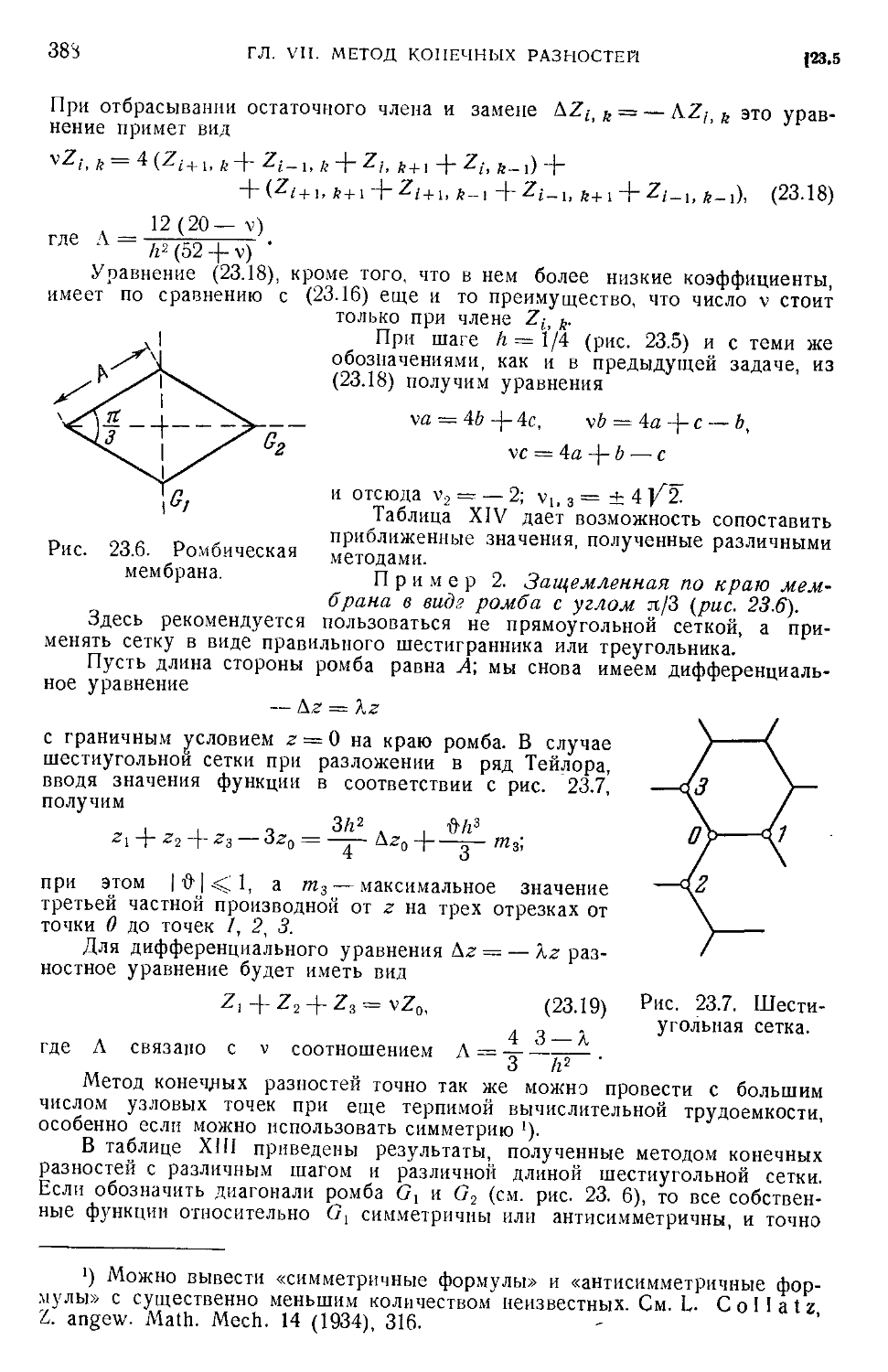
23.2. Пример. Собственные колебания эллиптической мембраны C80). 23.3. Метод ко-
конечных разностей повышенной точности C81). 23.4. Многоточечный метод C83).
23.5. Примеры. Колебания мембраны C86). 23.6. Упражнения C93).
ОГЛАВЛЕНИЕ 9
ГЛАВА ВОСЬМАЯ
РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ
§ 24. Метод возмущений 401
24.1. Описание метода D01). 24.2. Кратные собственные значения D05). 24.3. Связь
с принципом Рэлея D07). 24.4. Пример к методу возмущений. Продольный изгиб
тяжелых стержней D09).
§ 25. Другие методы 411
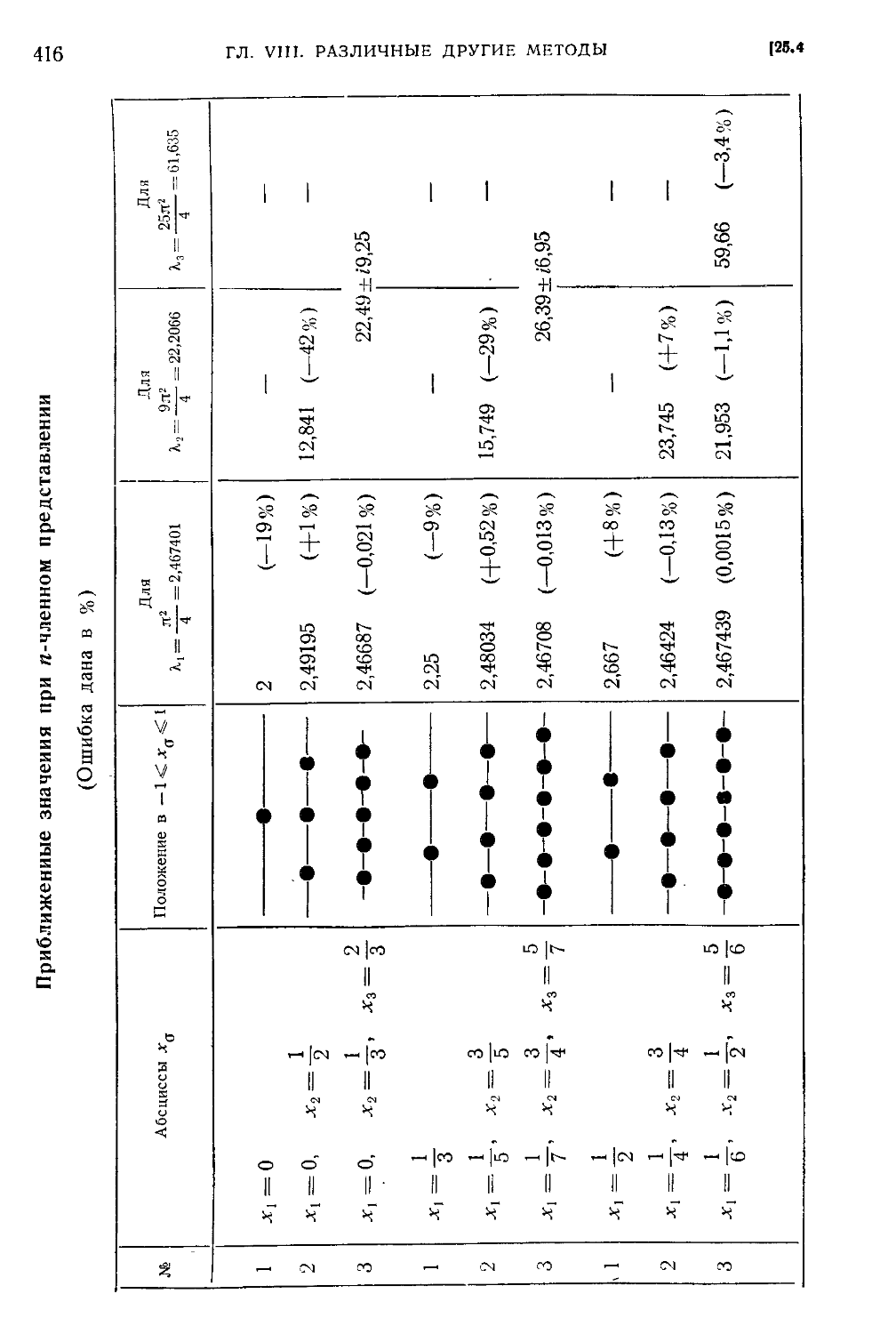
25.1. Формула Данкерлея для сложных систем D11). 25.2. Формула Саусвелла D12).
25.3. Минимум среднеквадратичной ошибки D13). 25.4. Метод коллокаций D14).
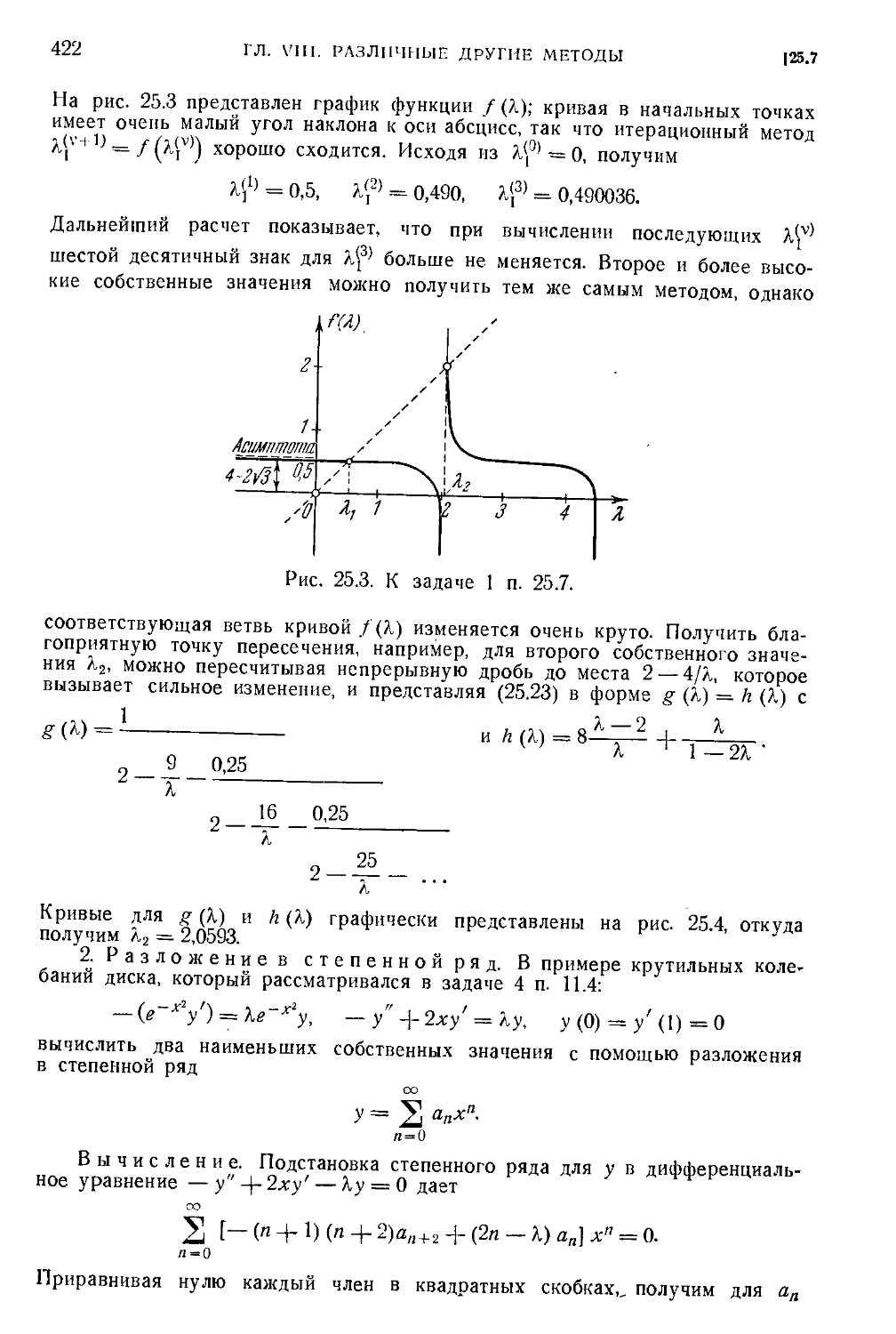
25.5. Разложение в непрерывную дробь. Дифференциальное уравнение Матье D17).
25.6. Представление в виде ряда D20). 25.7. Упражнения D21).
Рекомендации по выбору методов приближенного вычисления собствен-
собственных значений 427
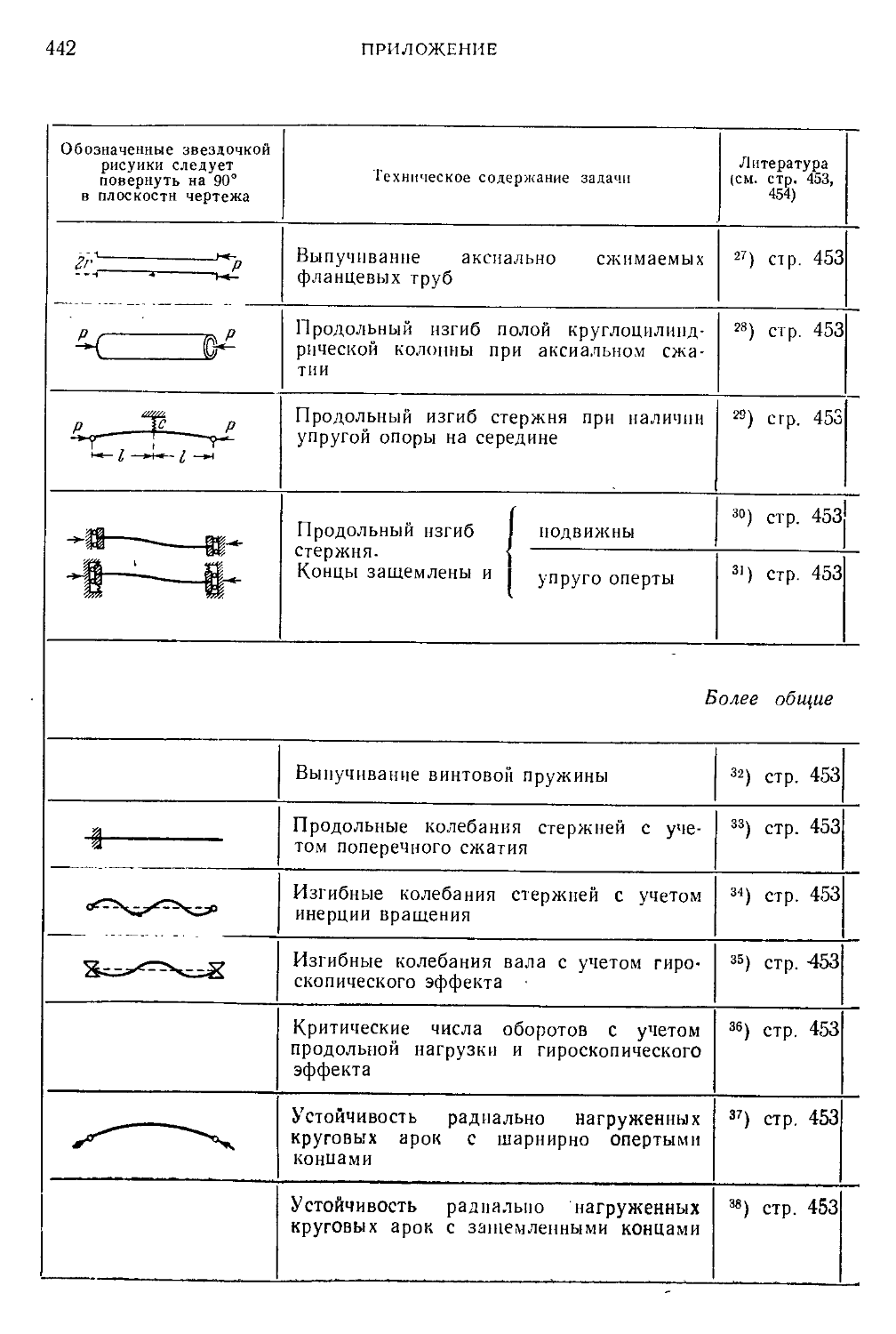
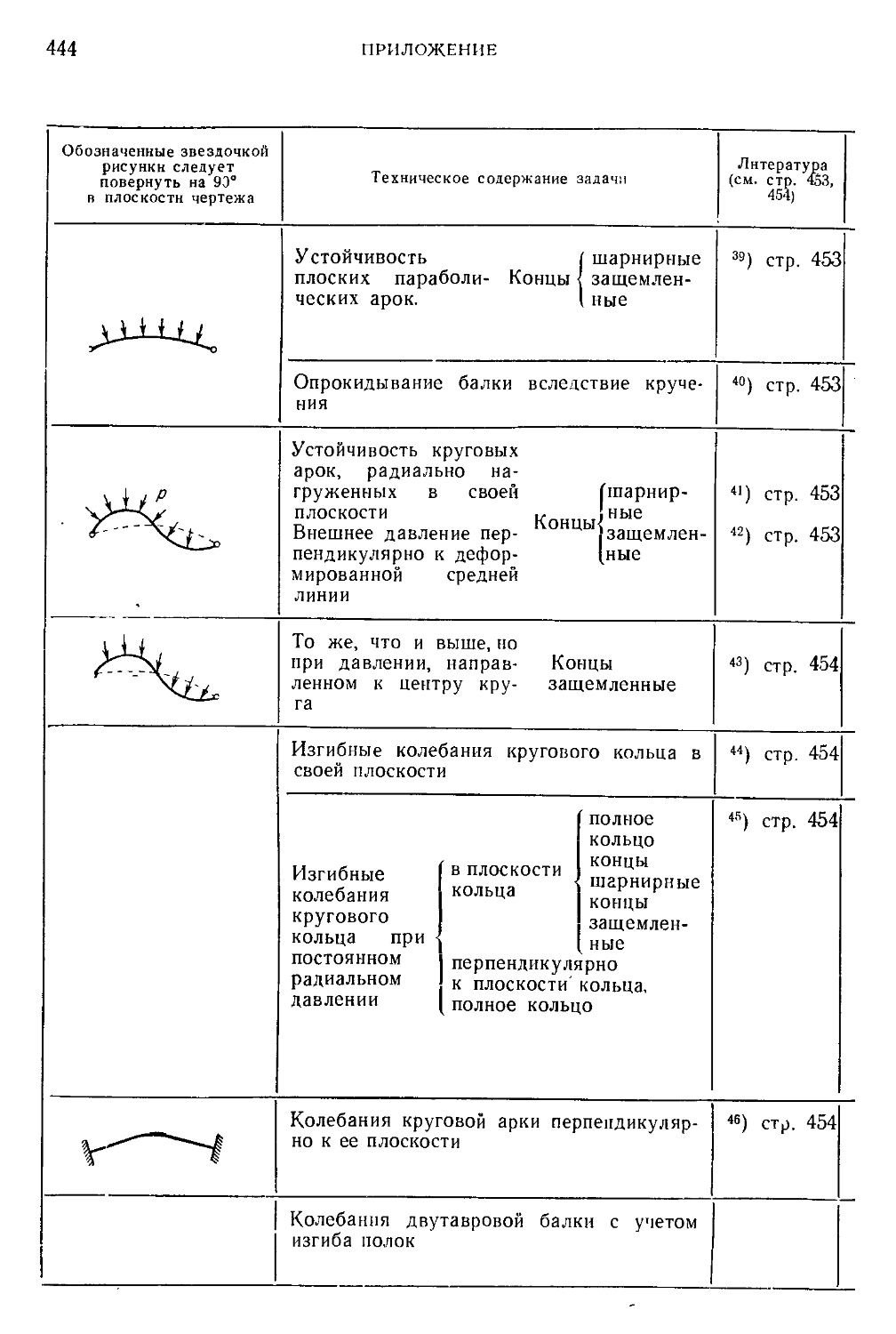
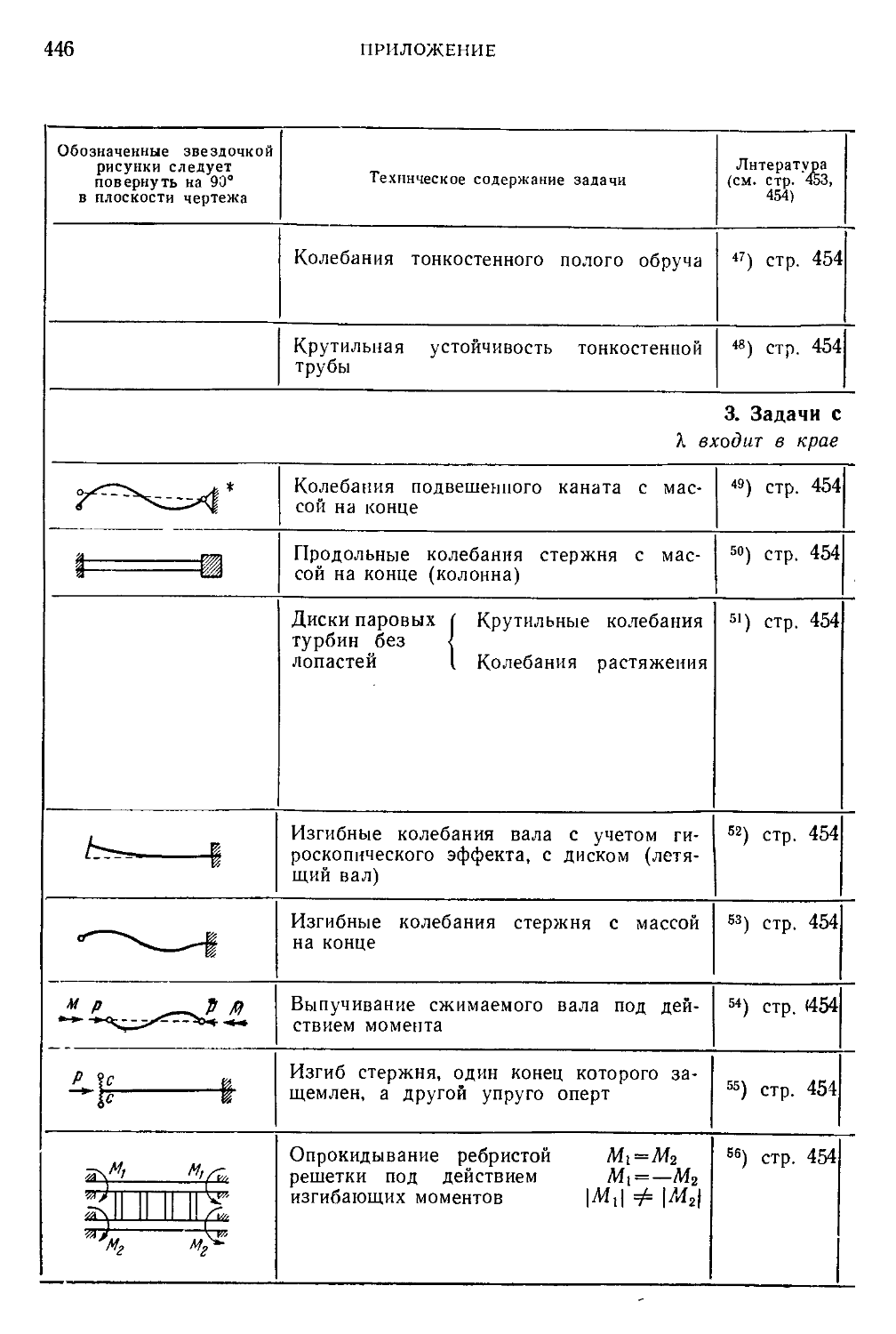
Приложение. Перечень рассмотренных примеров. Таблицы 429
Дополнительная литература 501
ПЕРЕЧЕНЬ ТАБЛИЦ
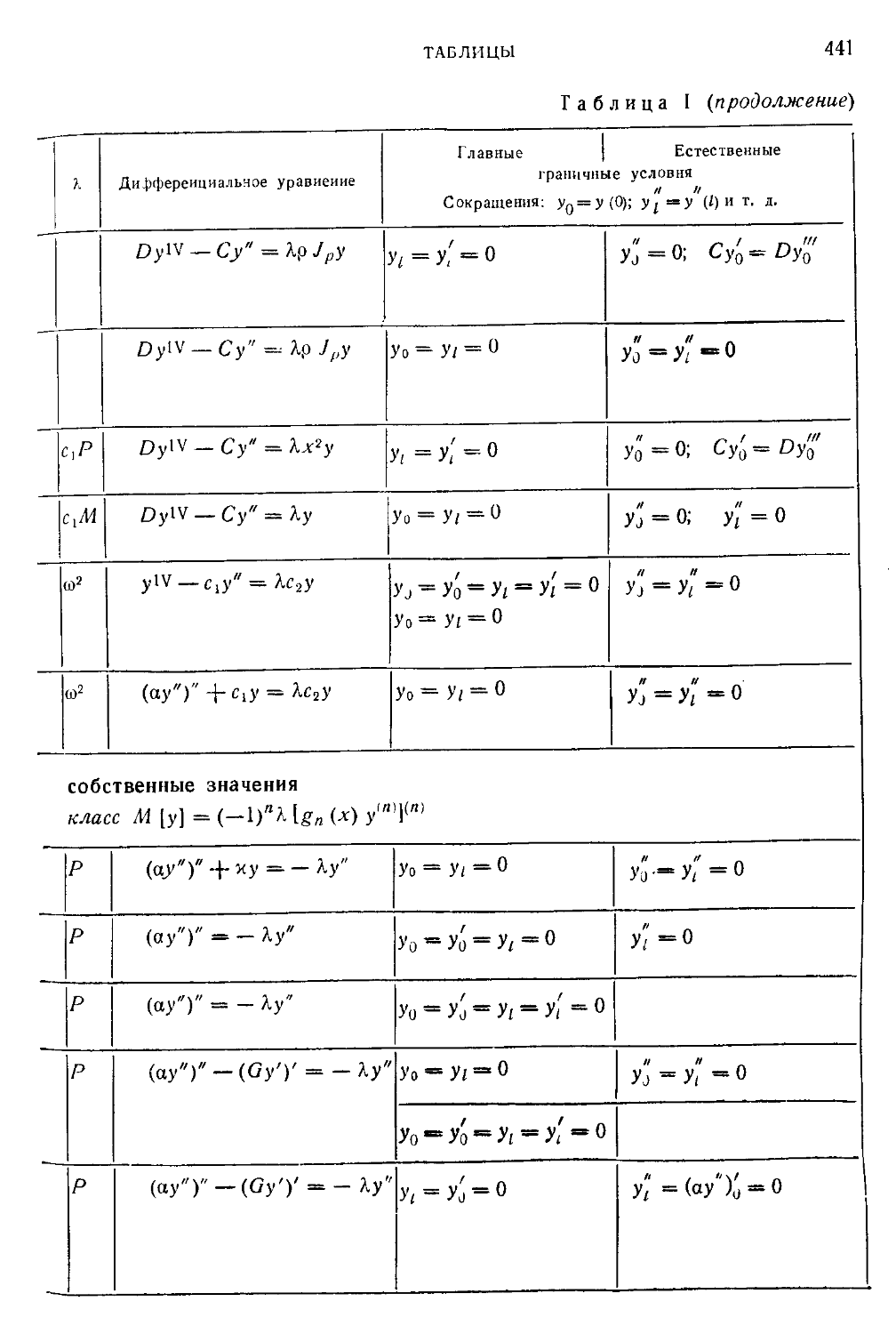
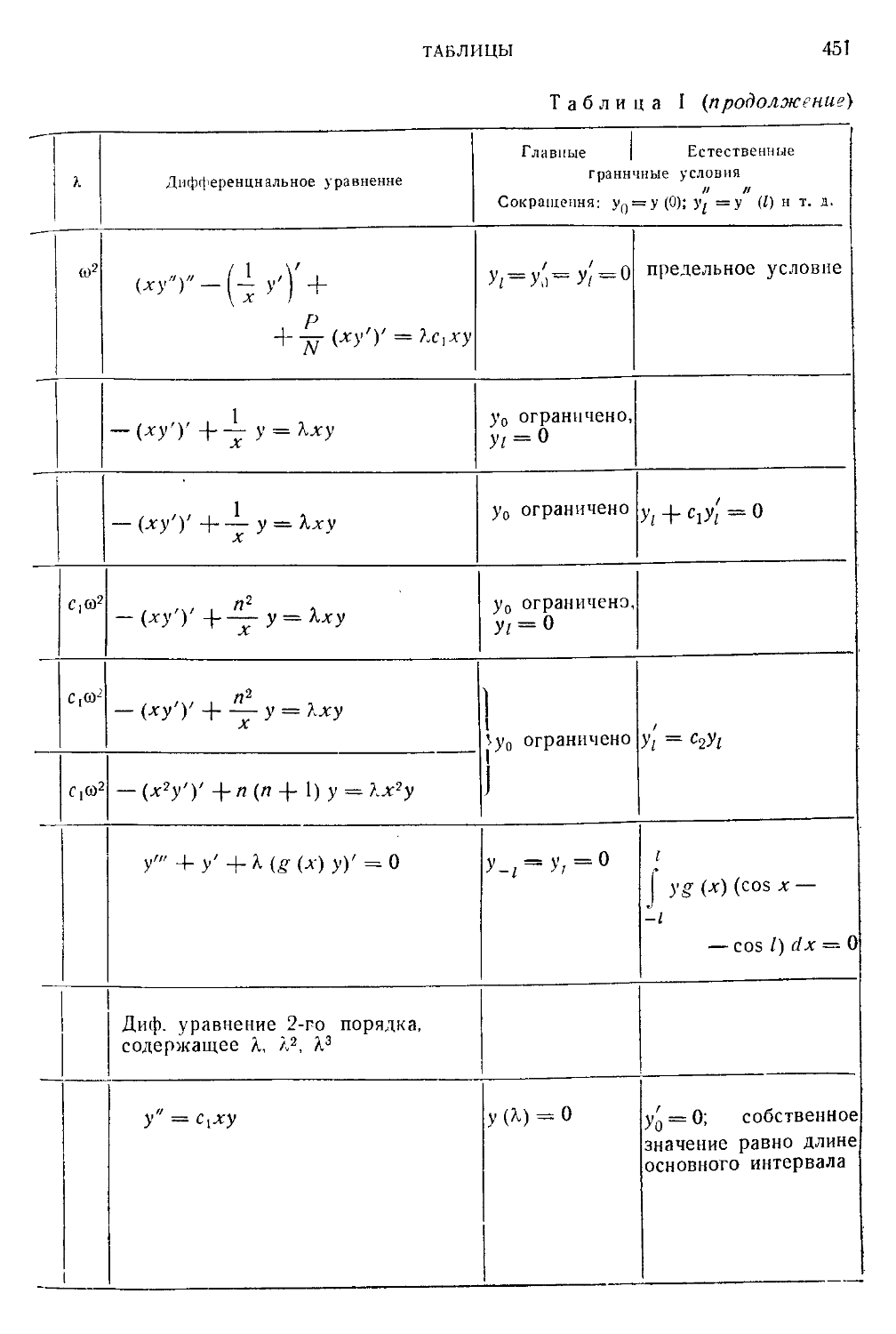
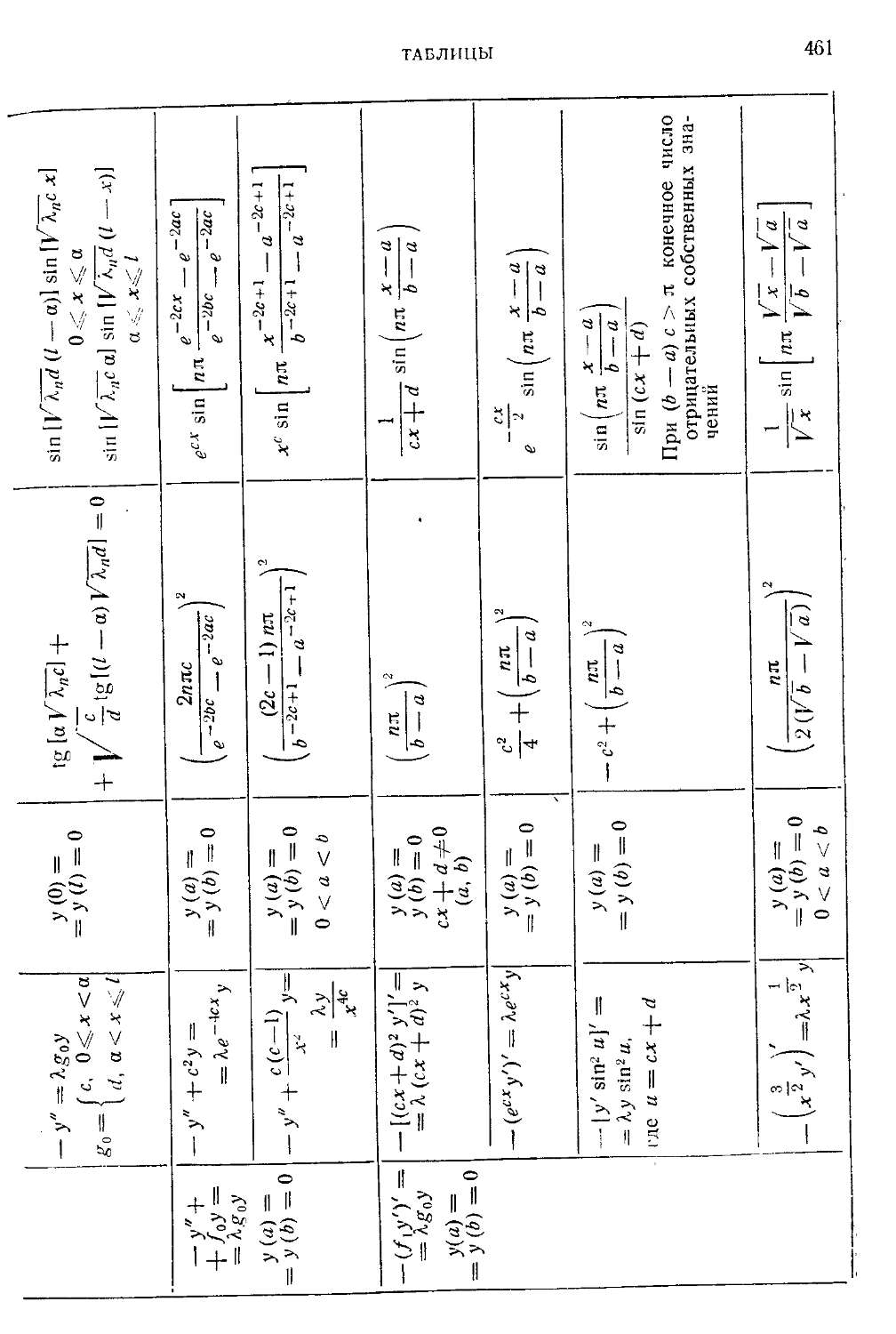
Таблица I. Простые примеры технических задач на собственные зна-
значения для обыкновенных дифференциальных уравнений 436
Таблица II. Простые примеры технических задач на собственные зна-
значения для дифференциальных уравнений с частными производными . . 455
Таблица III. Краевые выражения Дирихле 457
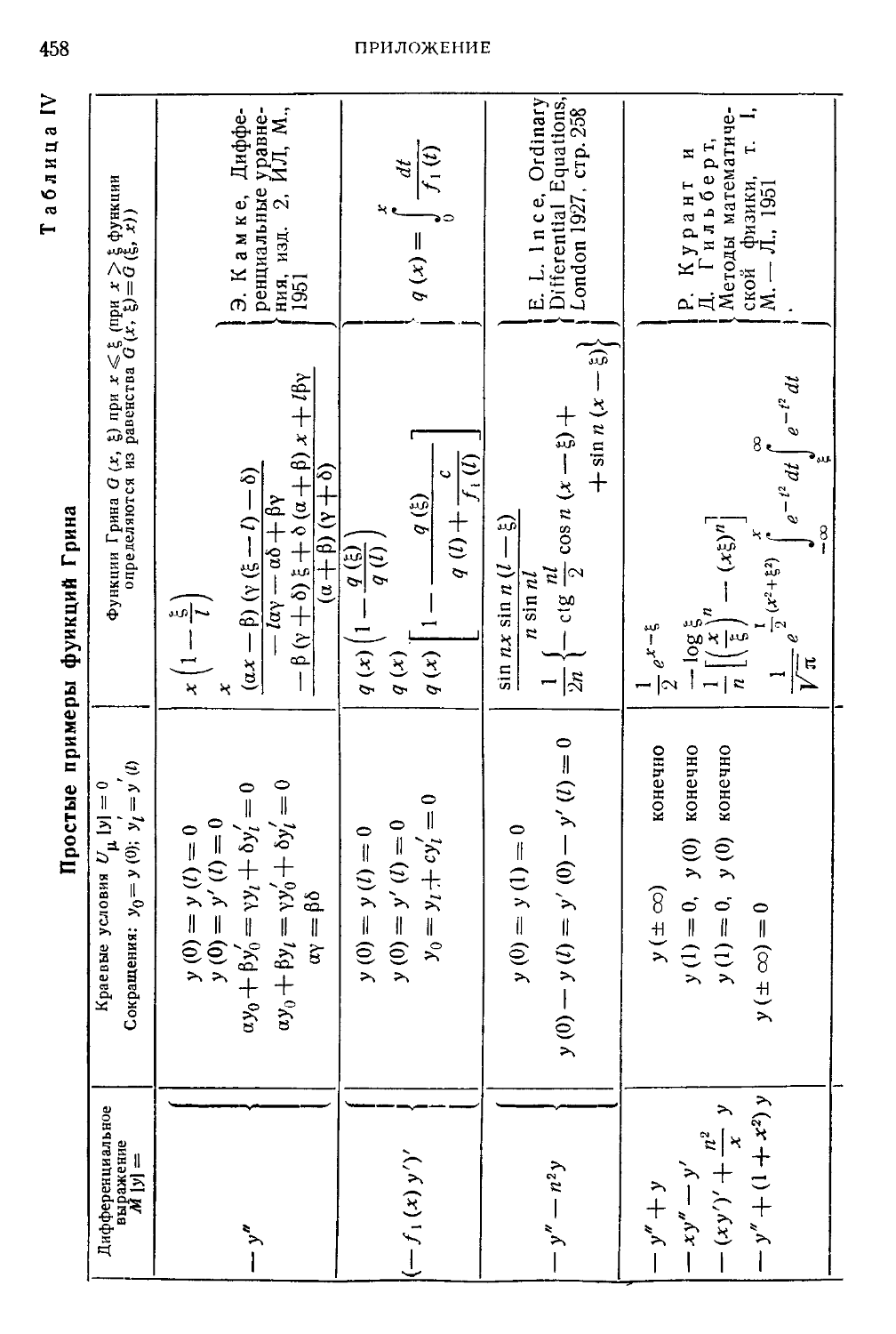
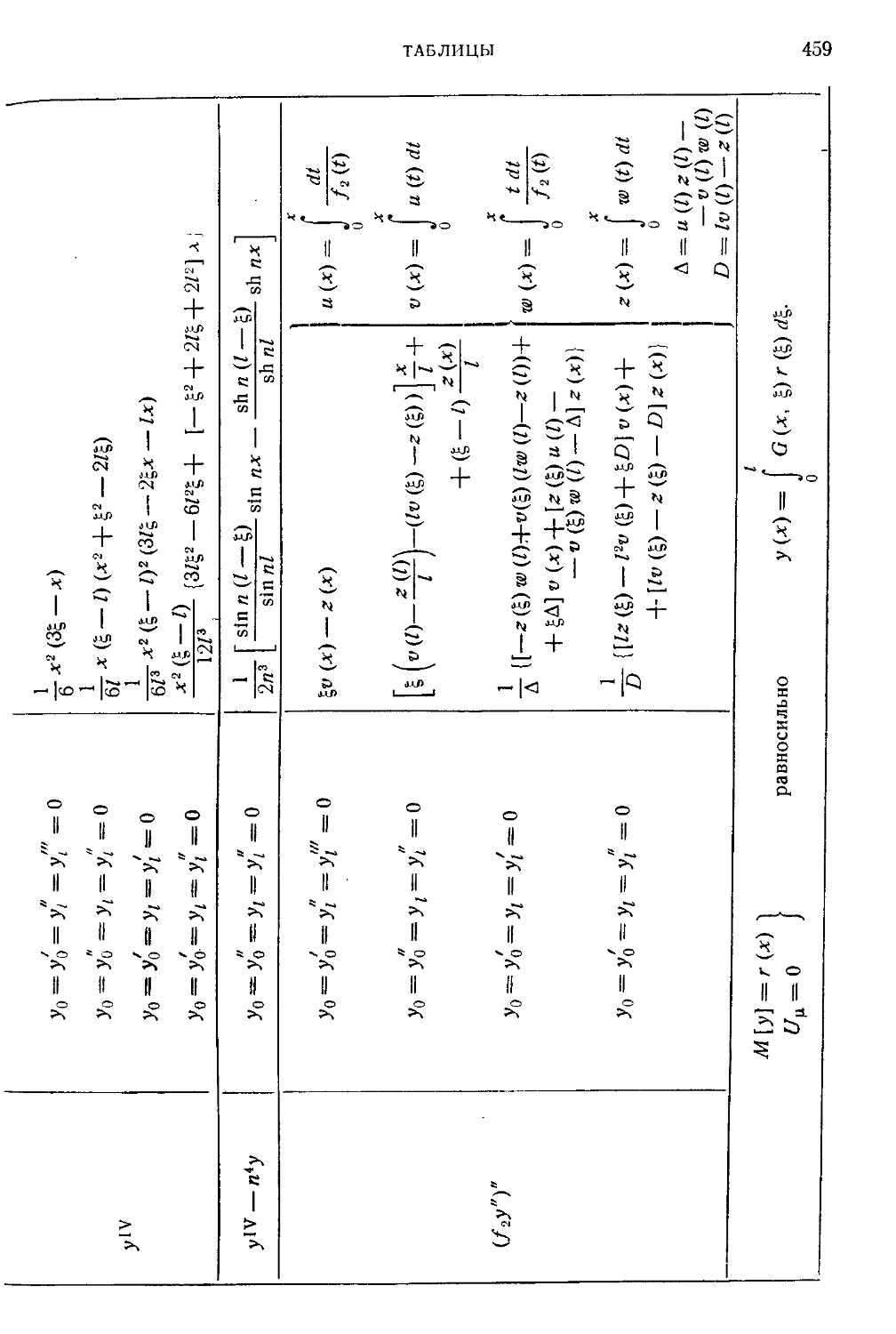
Таблица IV. Простые примеры функций Грина 458
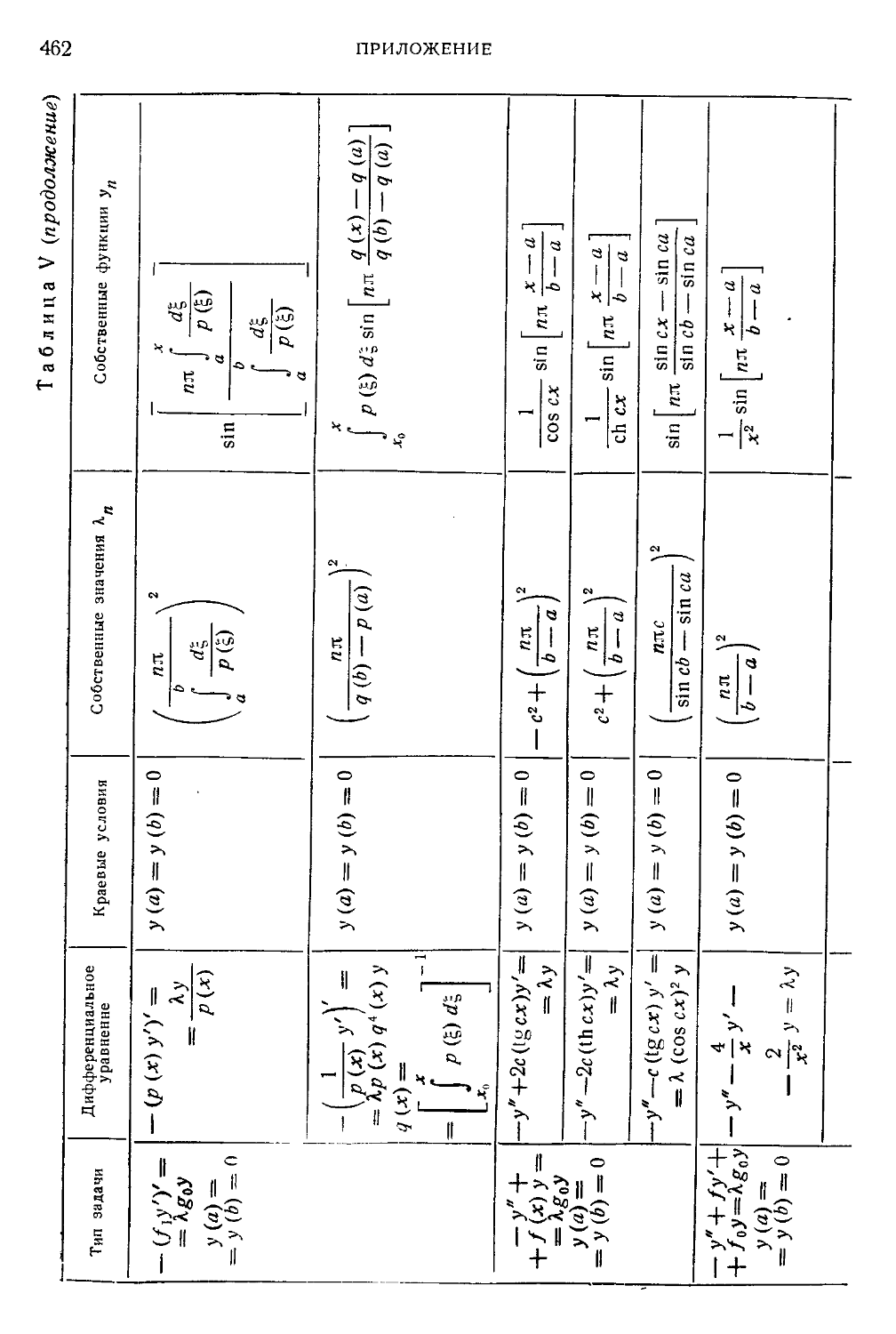
Таблица V. Некоторые разрешимые в замкнутой форме задачи на
собственные значения для дифференциальных уравнений второго порядка 460
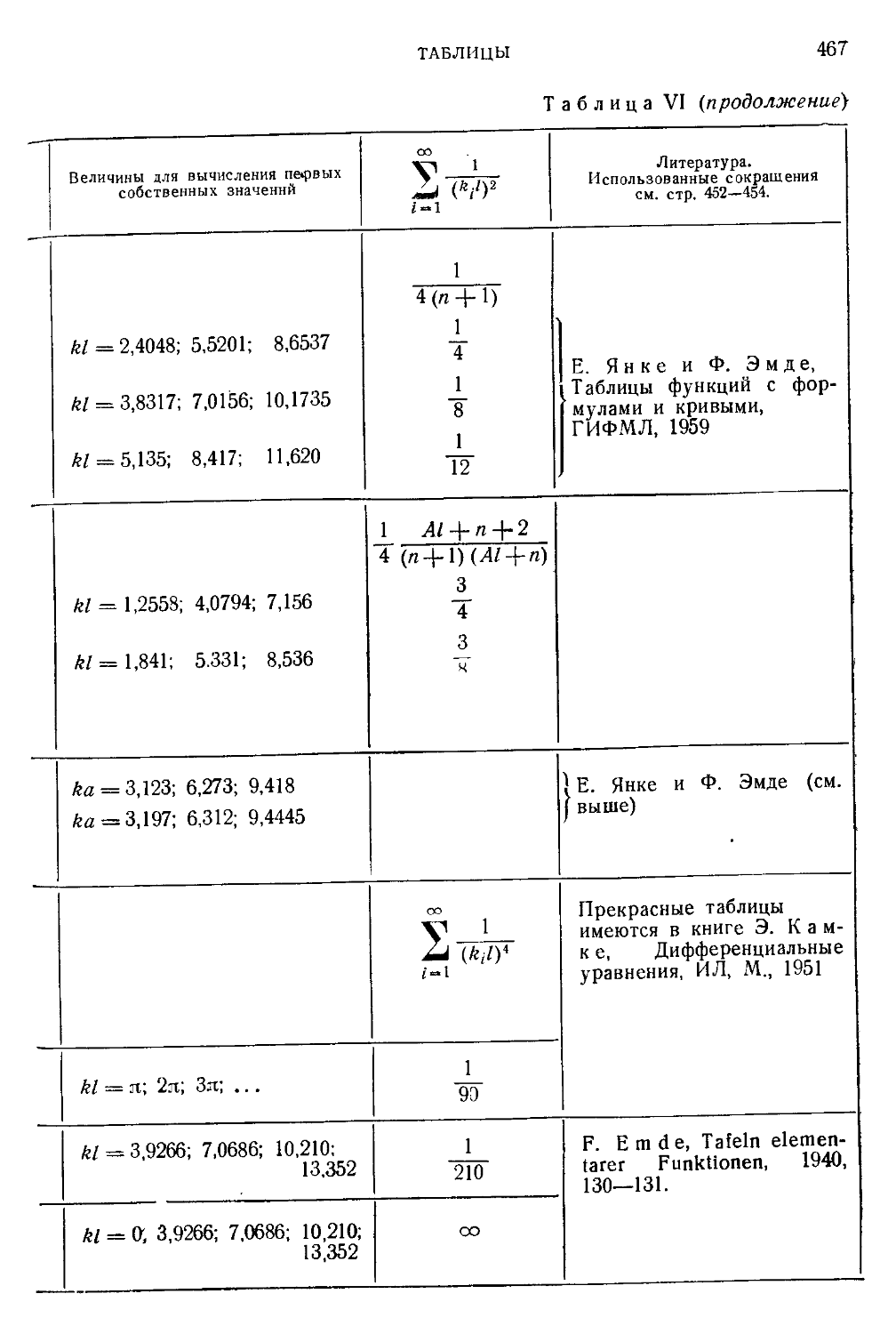
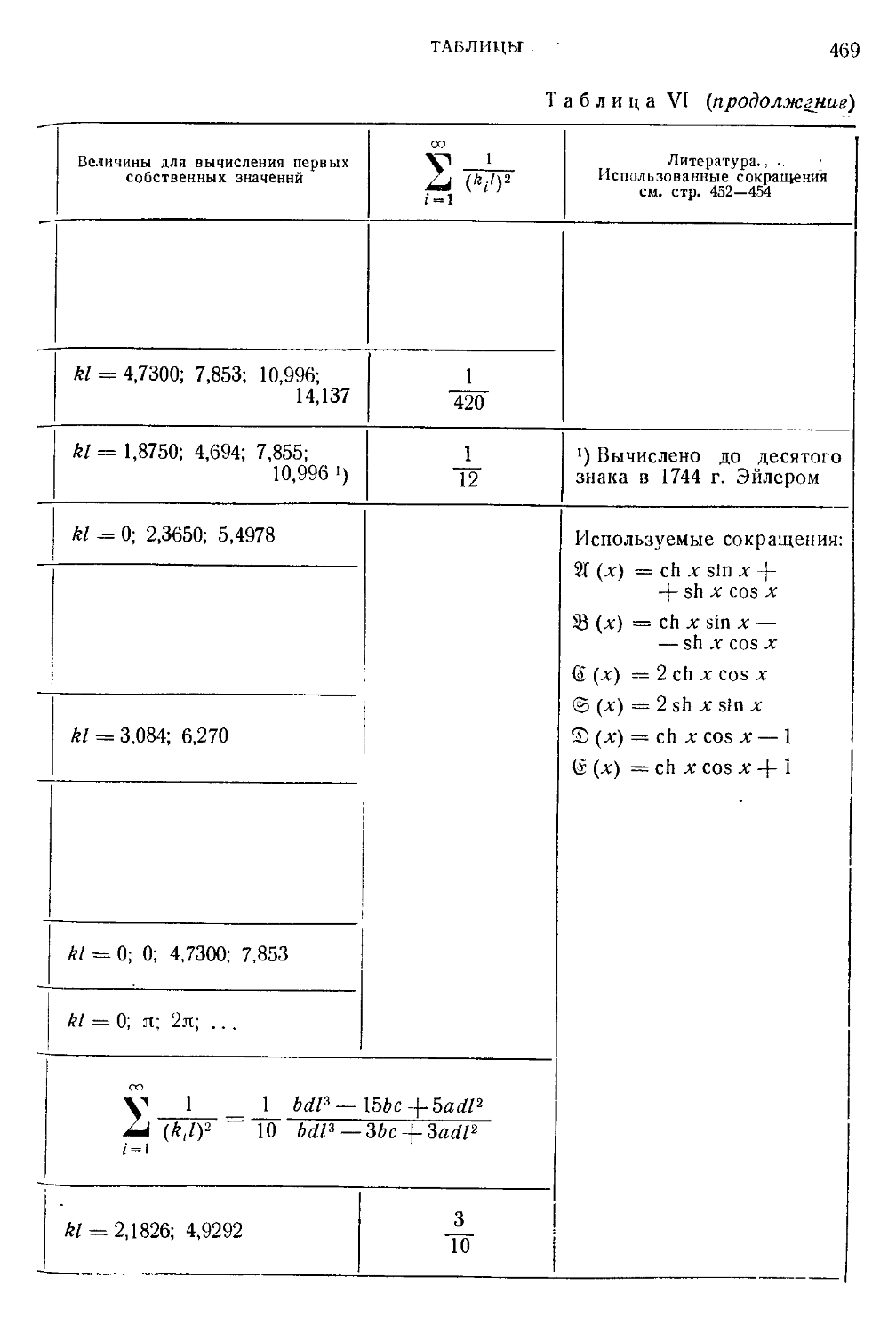
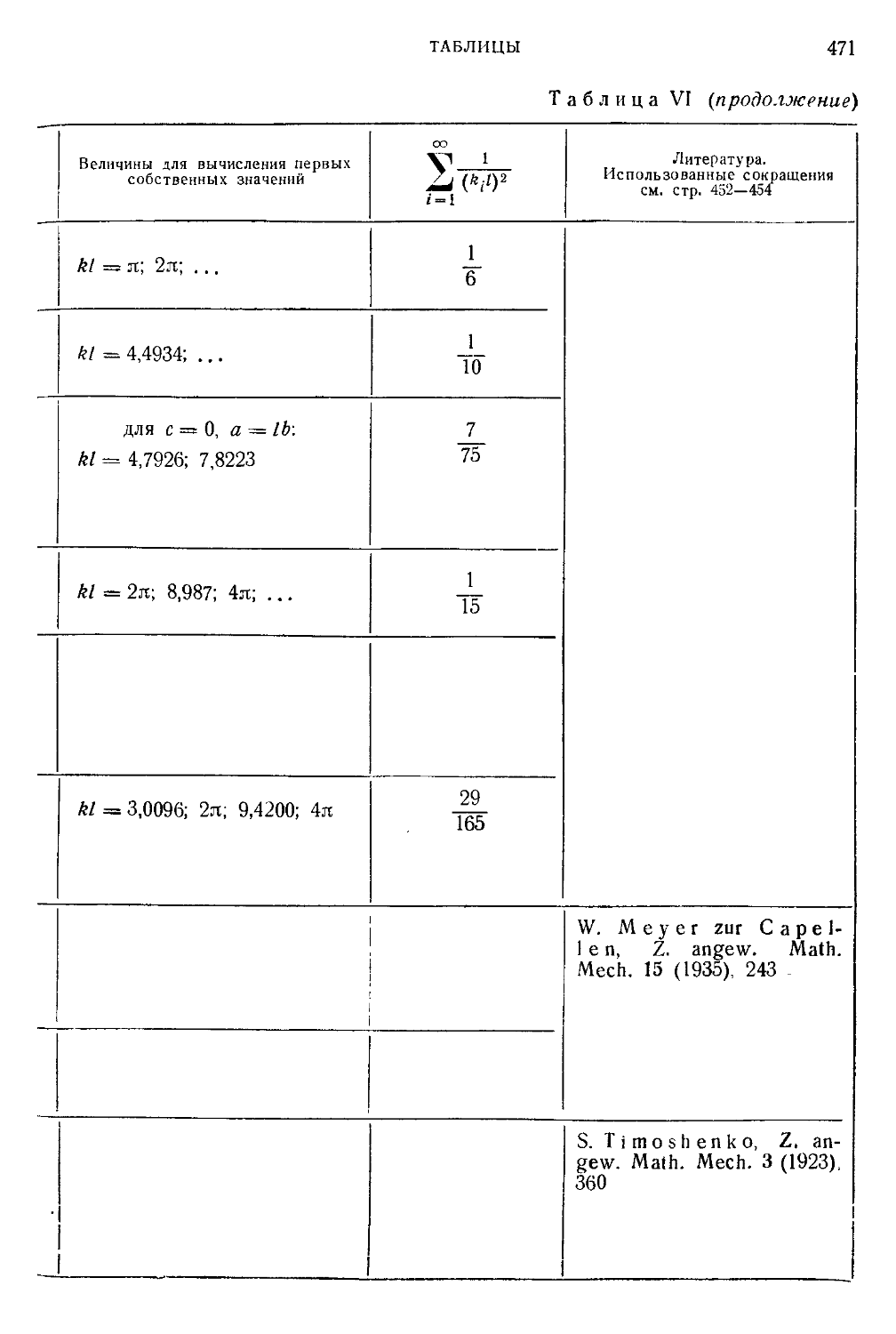
Таблица VI. Трансцендентные уравнения для собственных значений
простейших задач 464
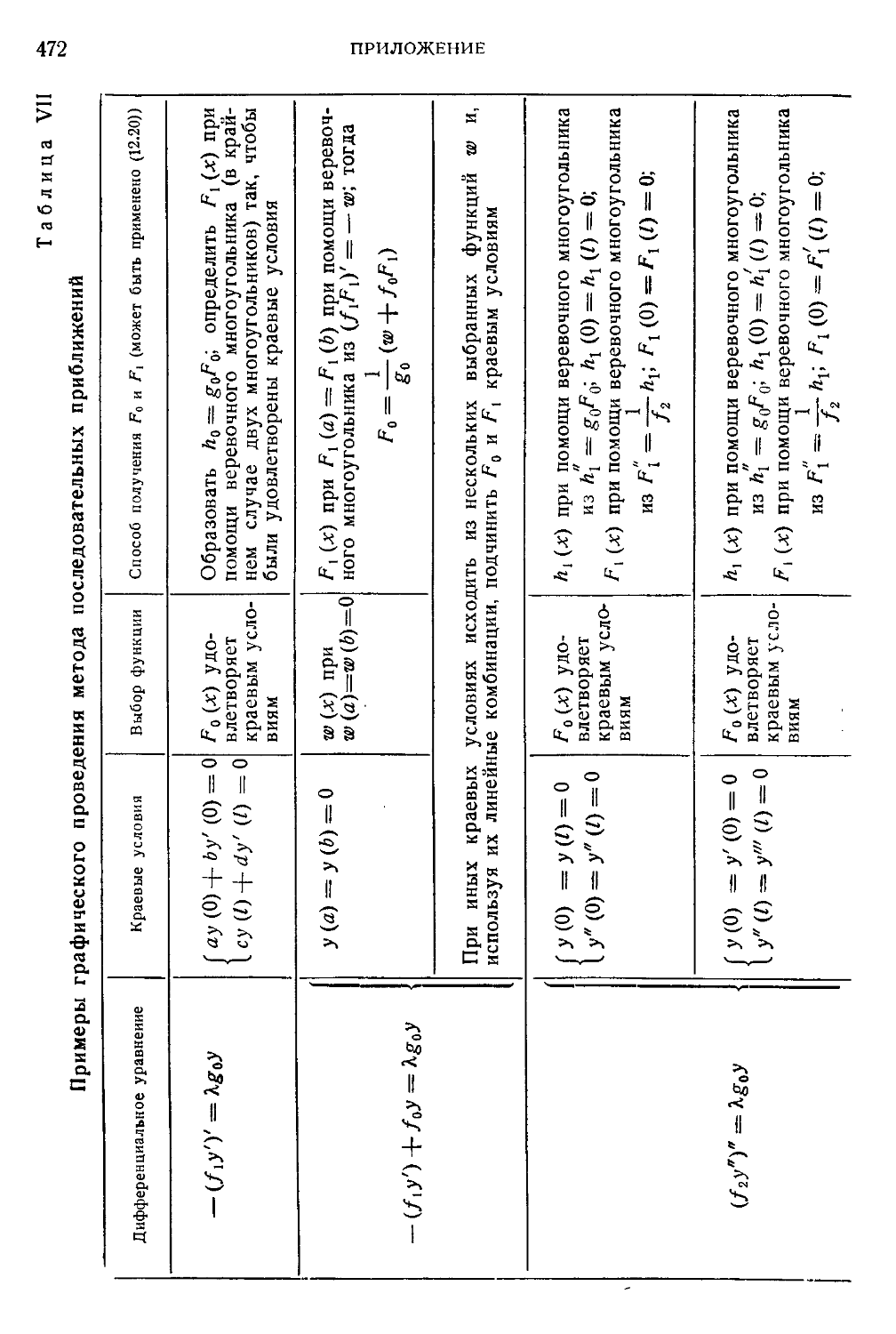
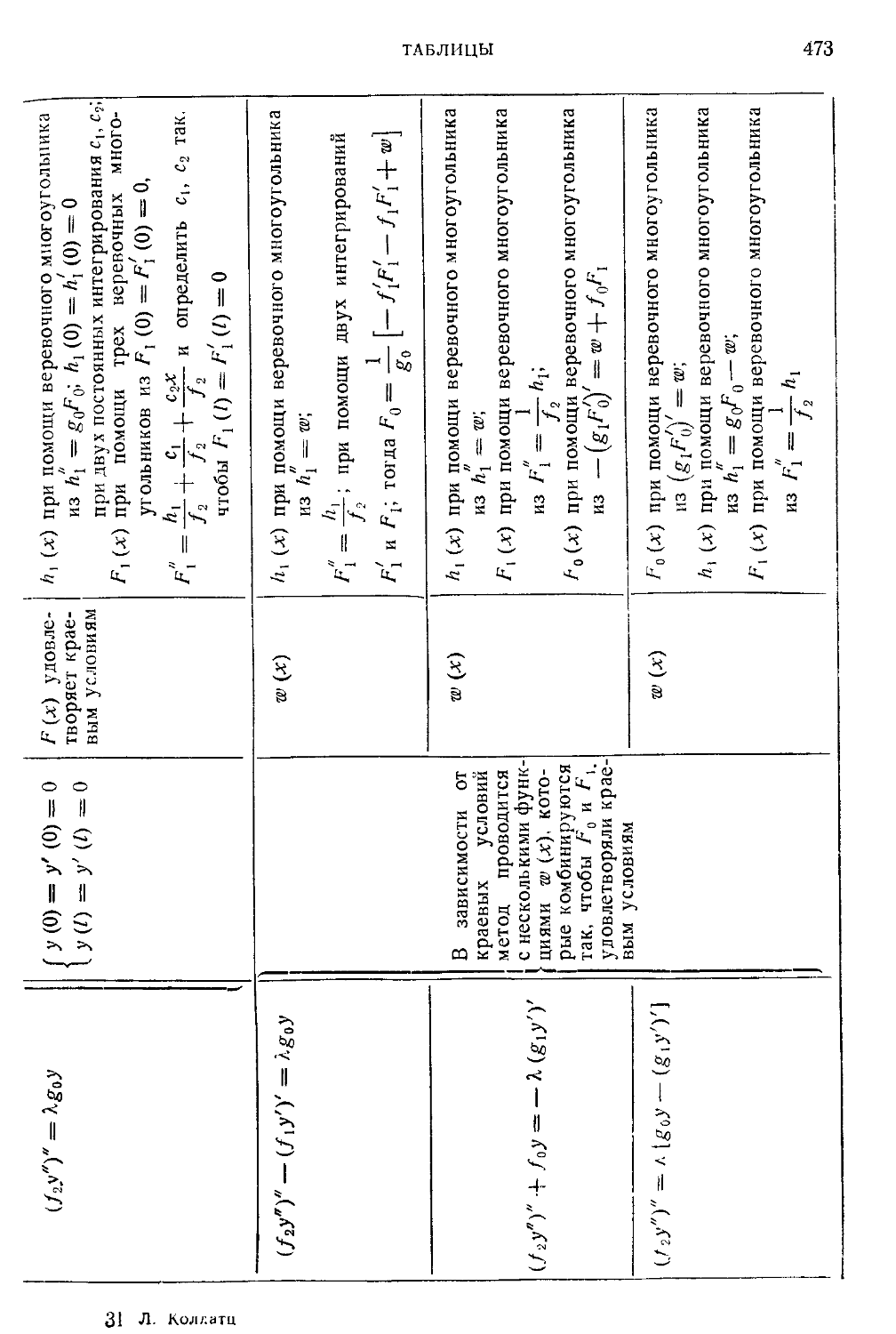
Таблица VII. Примеры графического проведения метода последова-
последовательных приближений 472
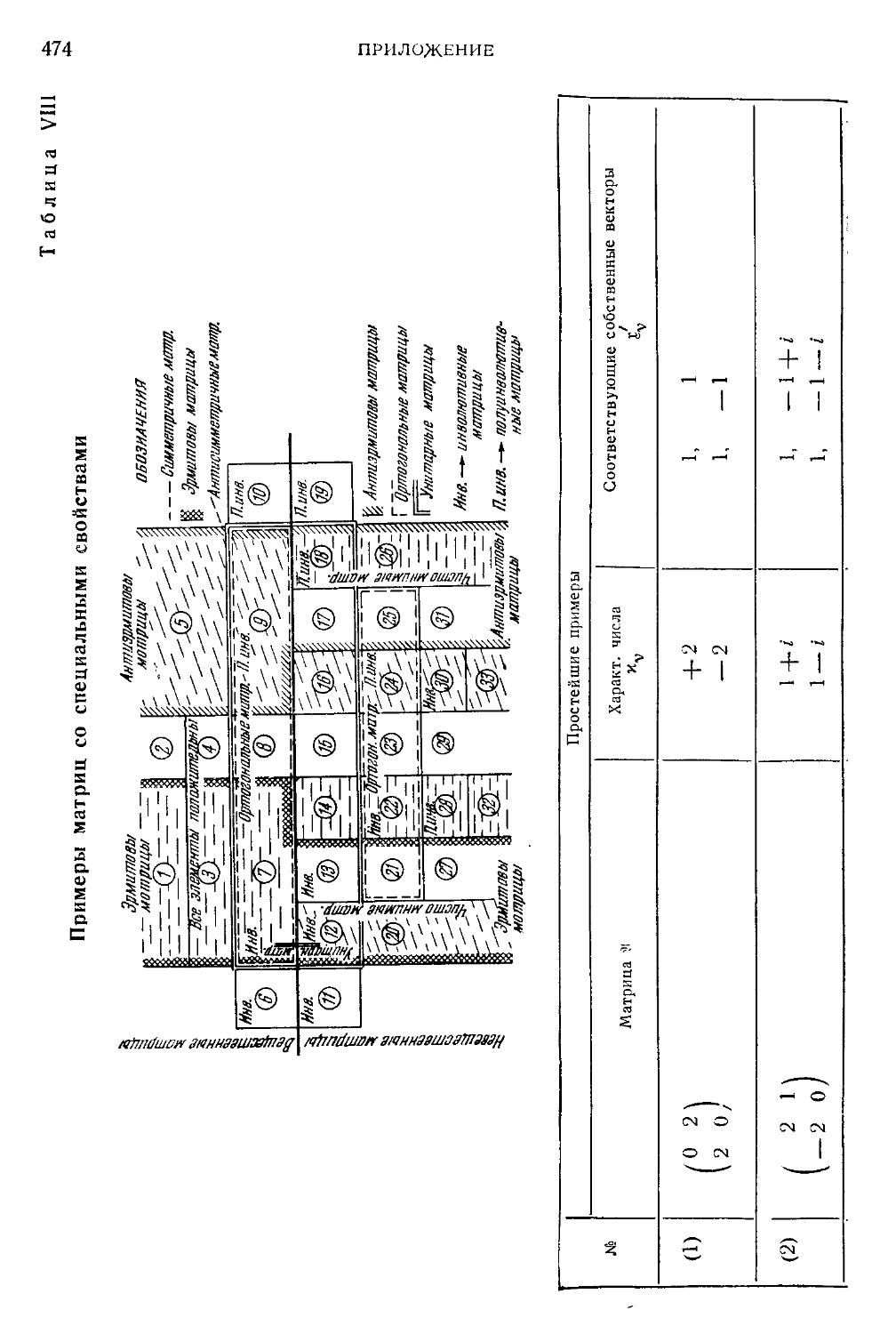
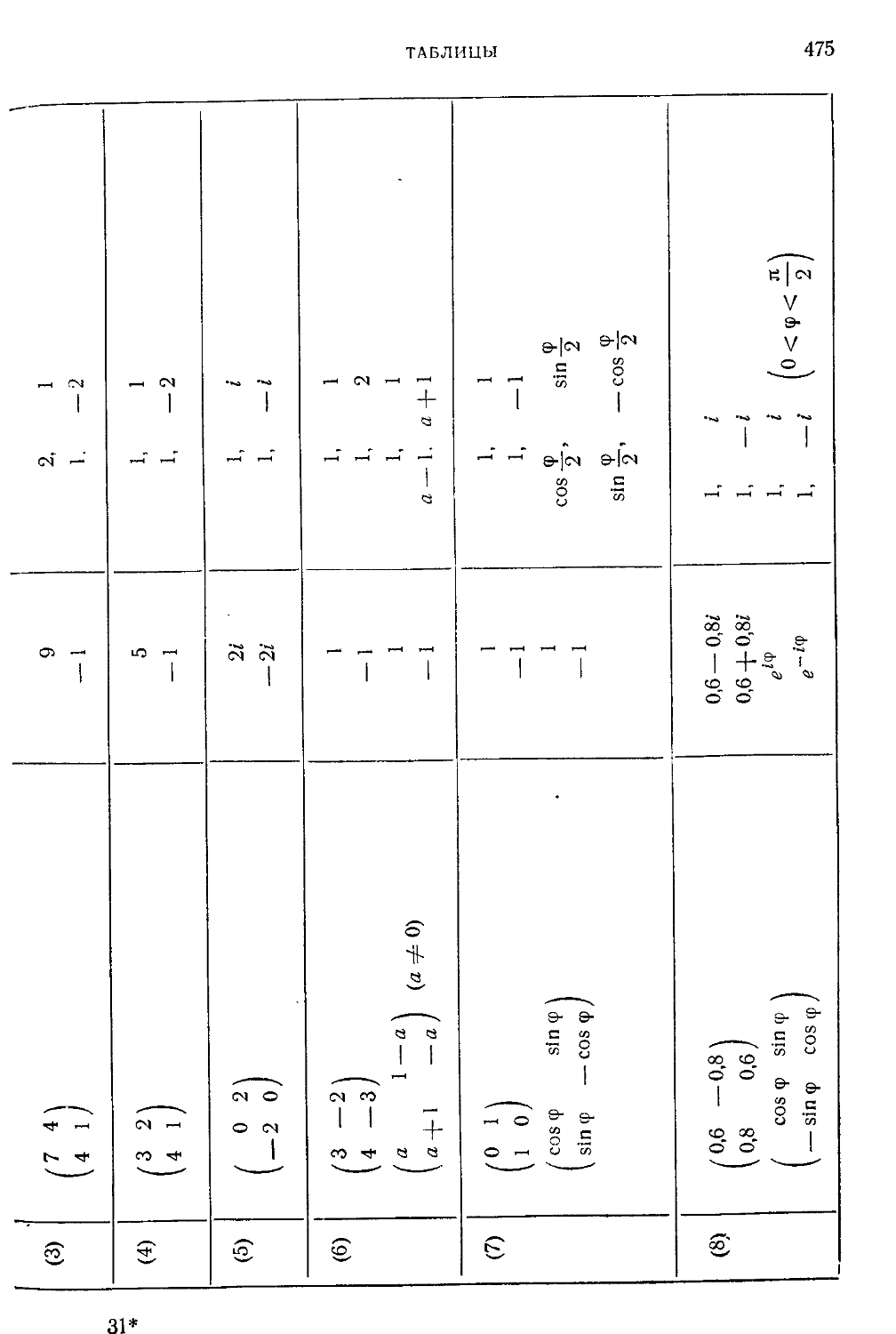
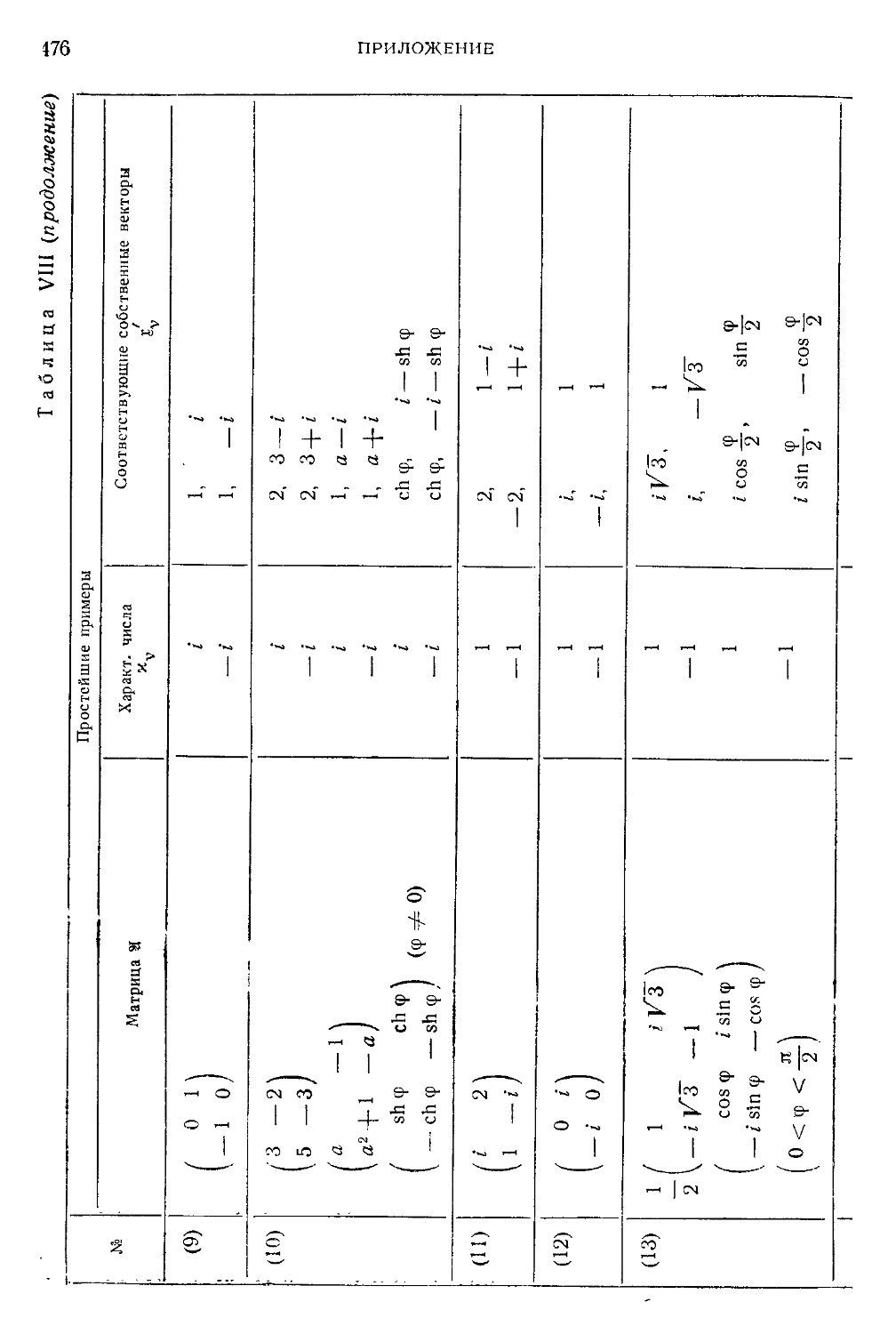
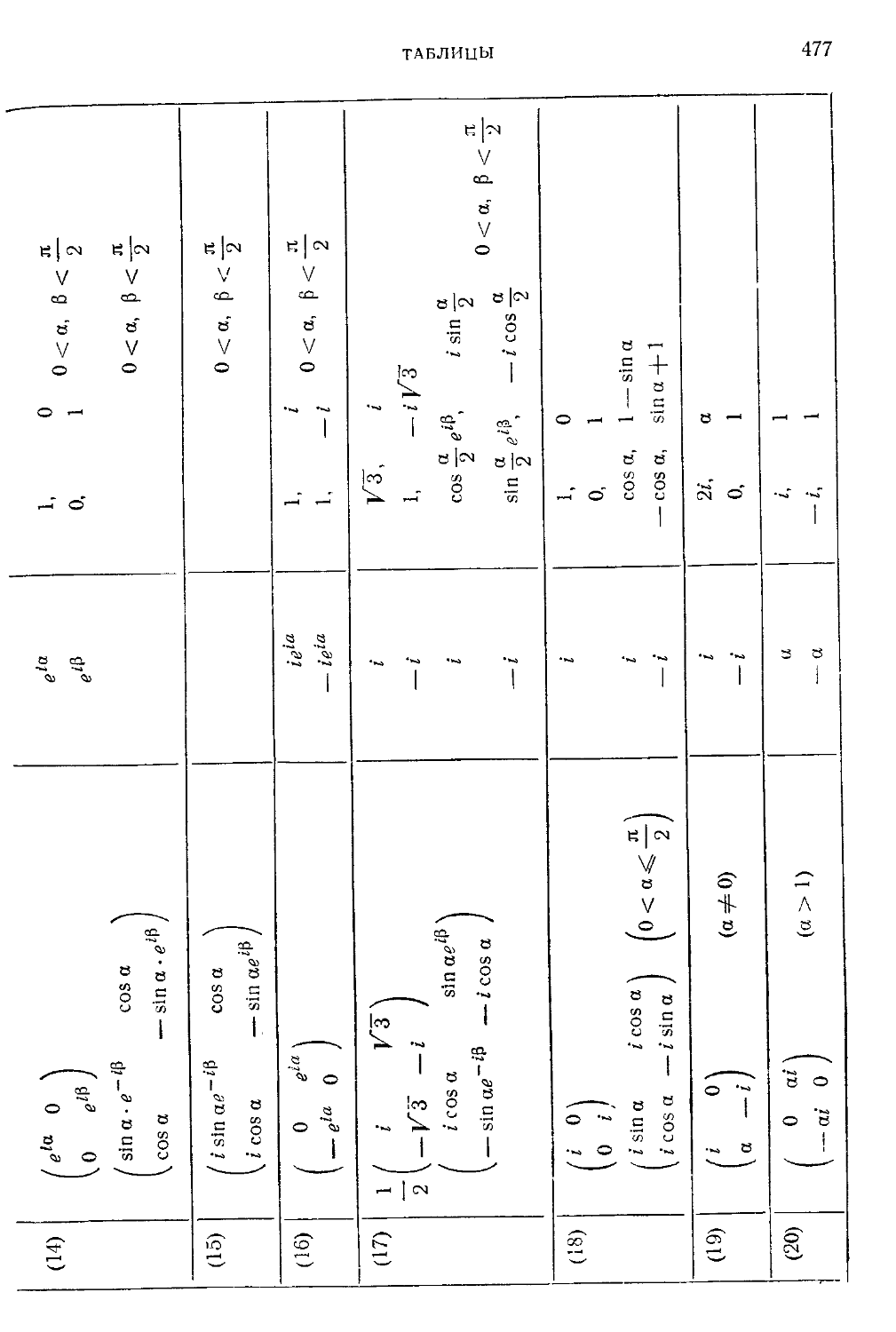
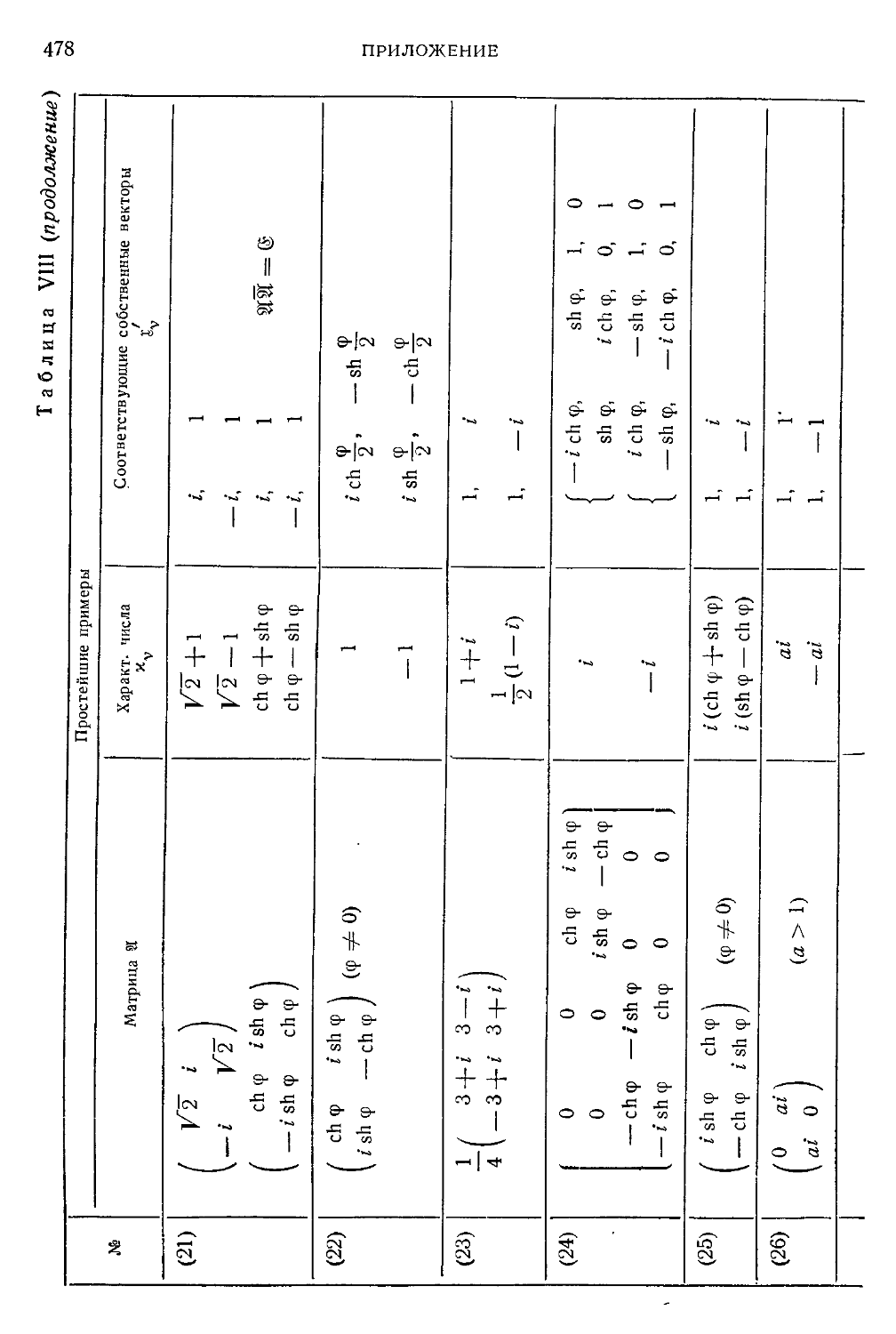
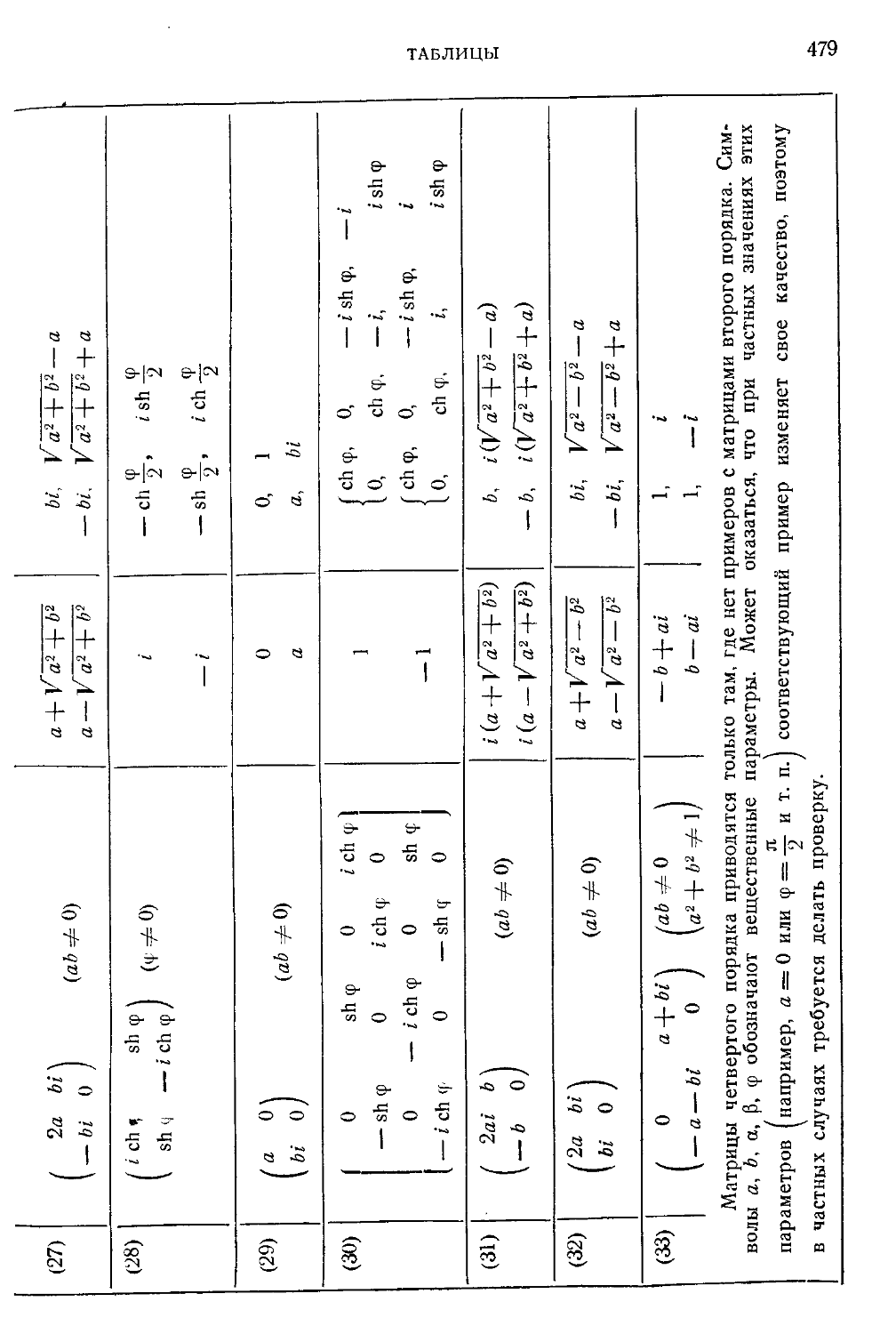
Таблица VIII. Примеры матриц со специальными свойствами .... 474
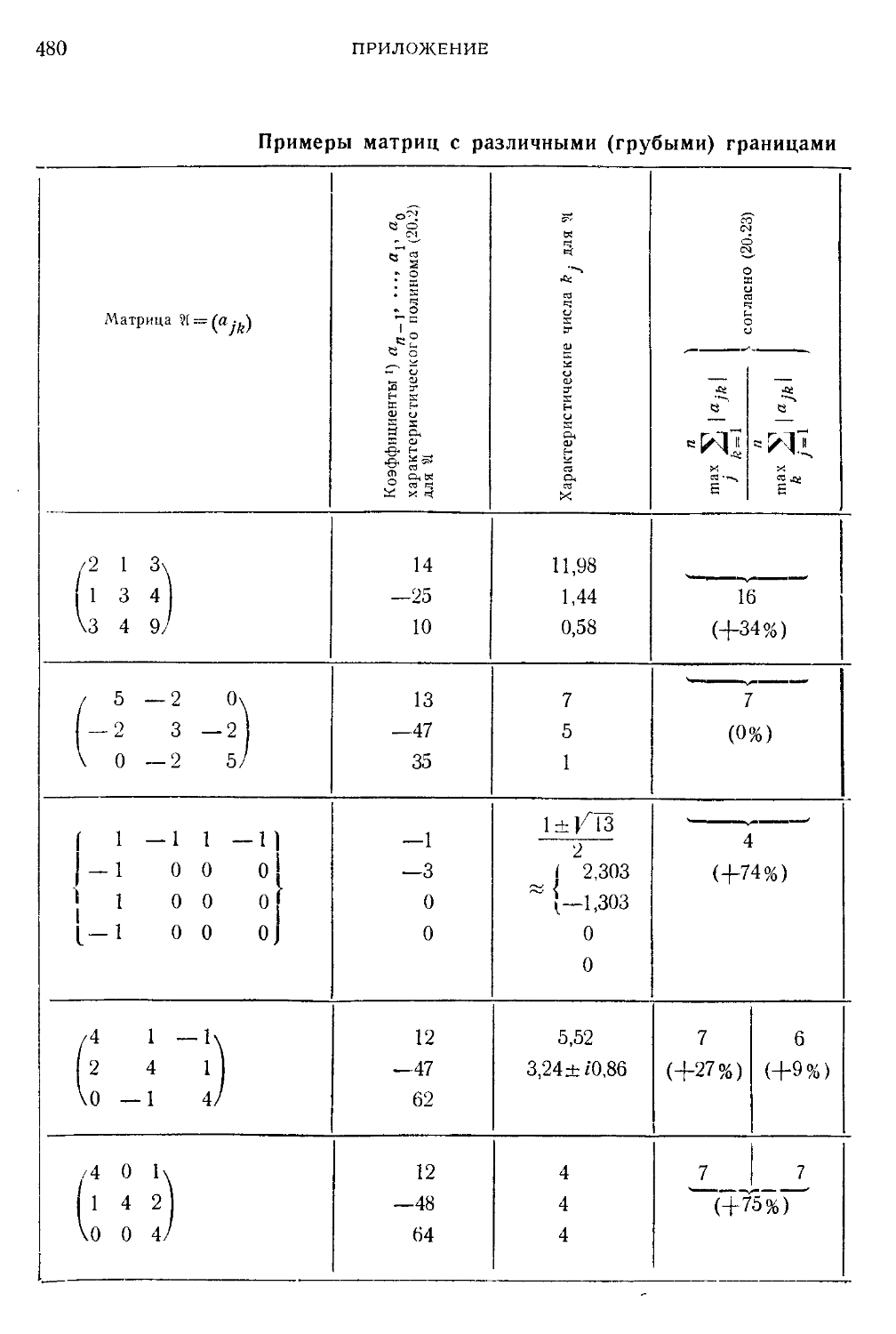
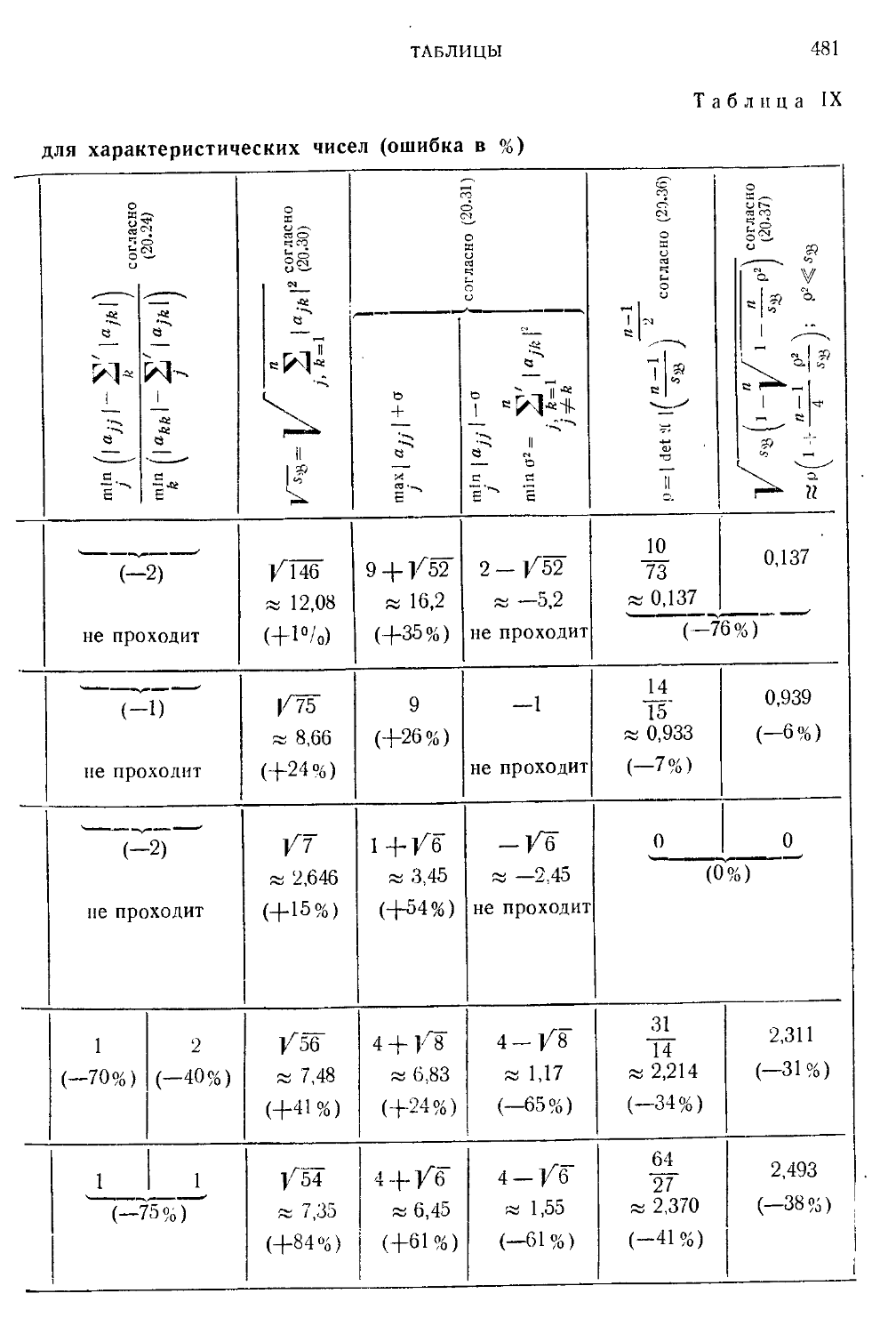
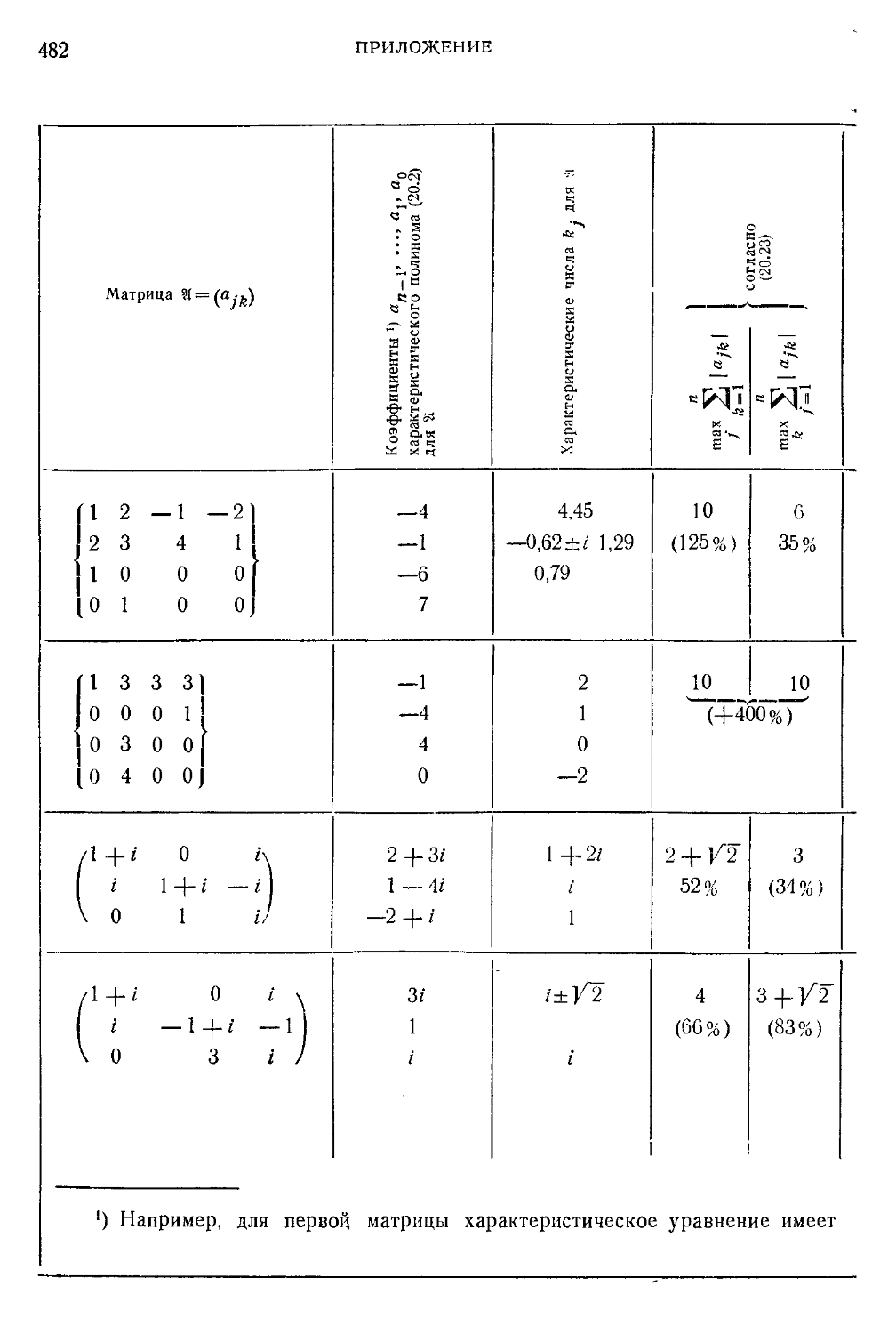
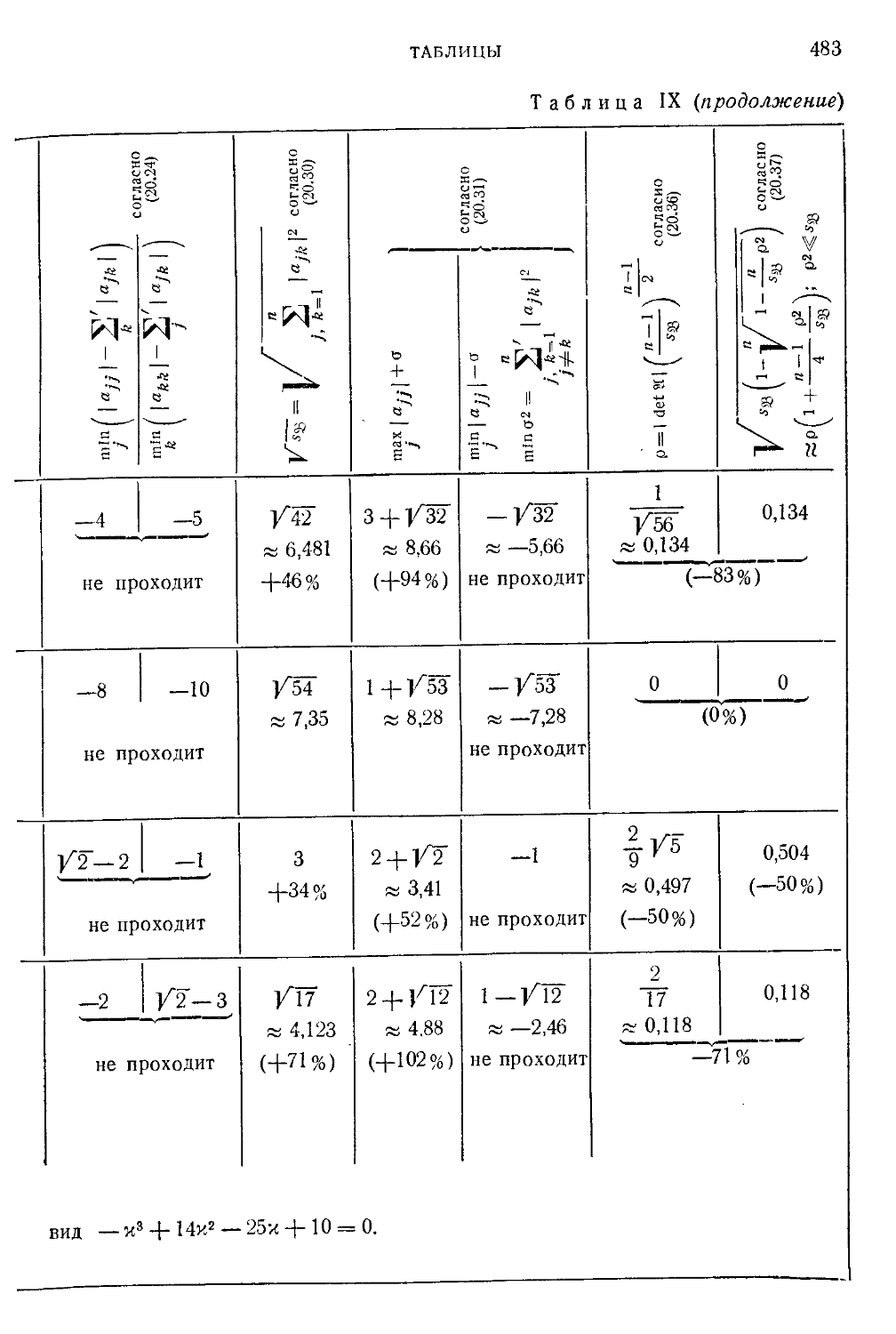
Таблица IX. Примеры матриц с различными (грубыми) границами
для характеристических чисел 480
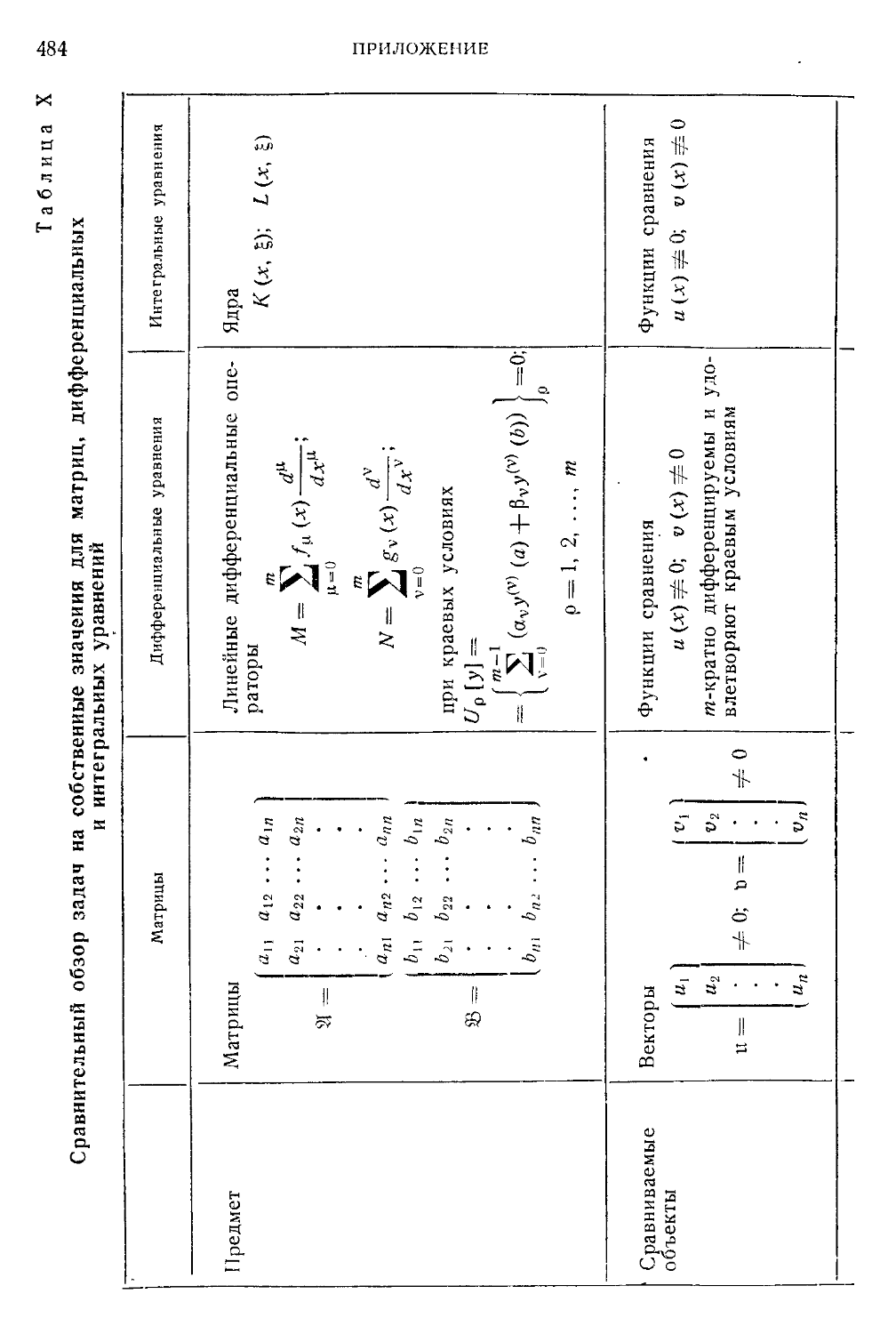
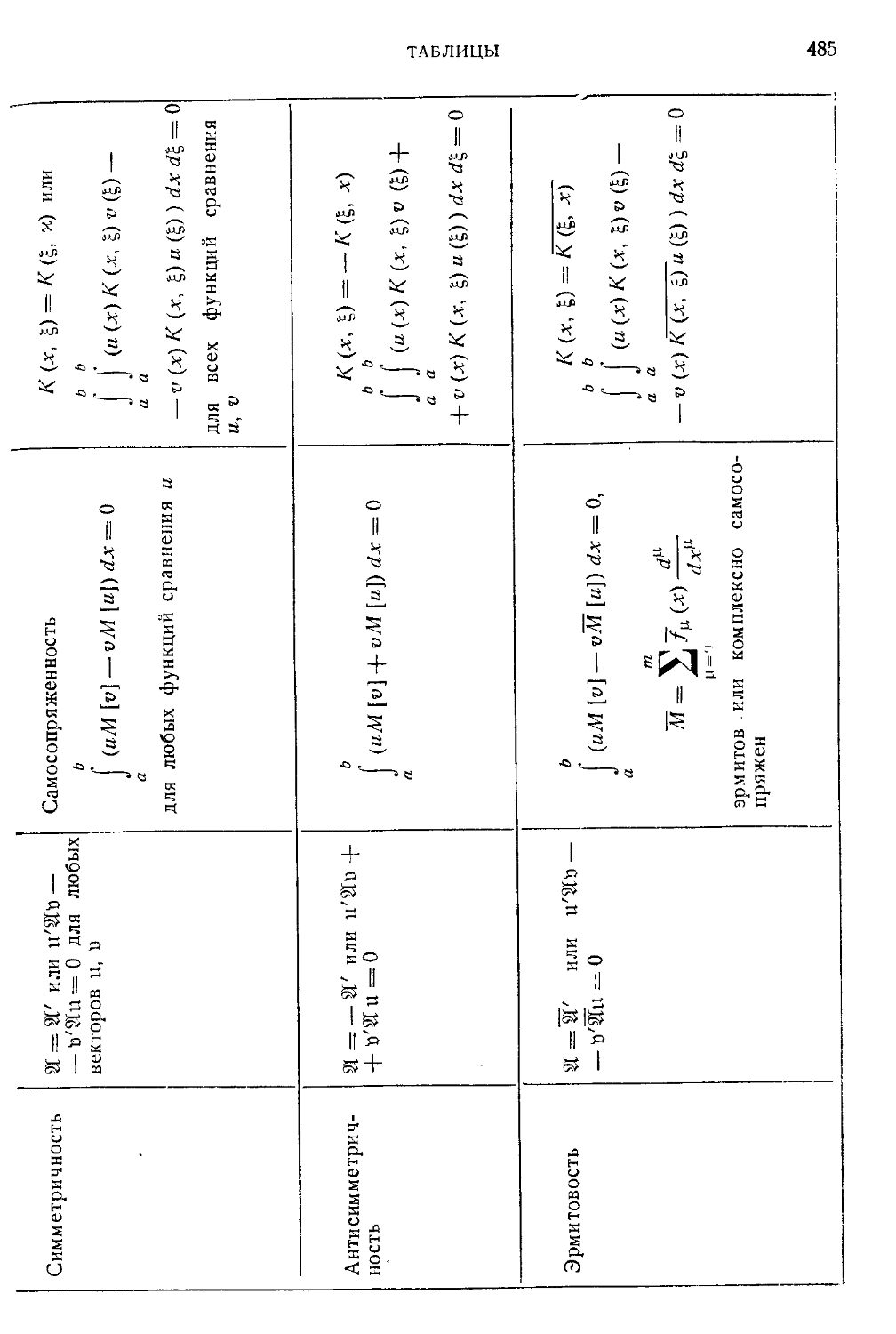
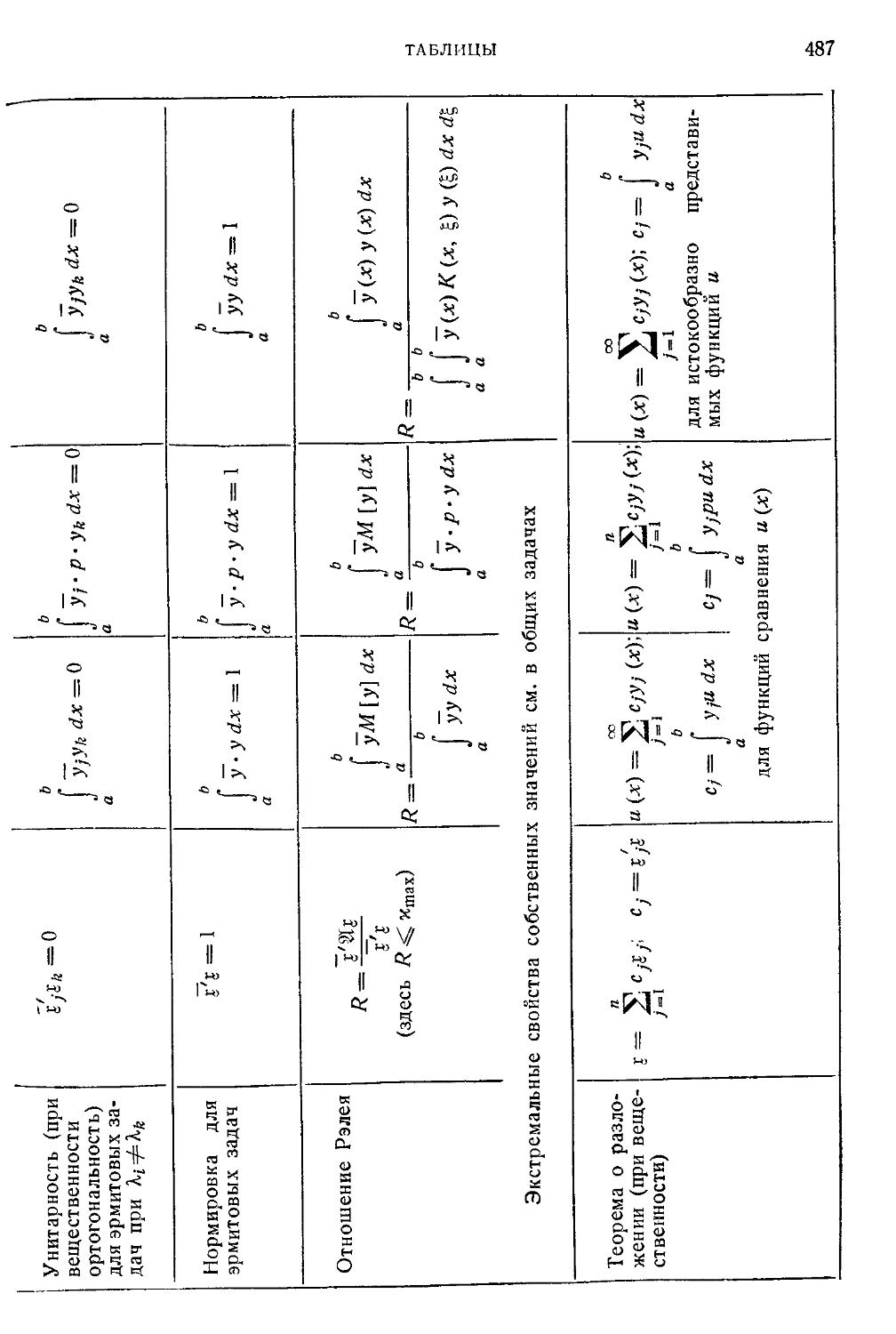
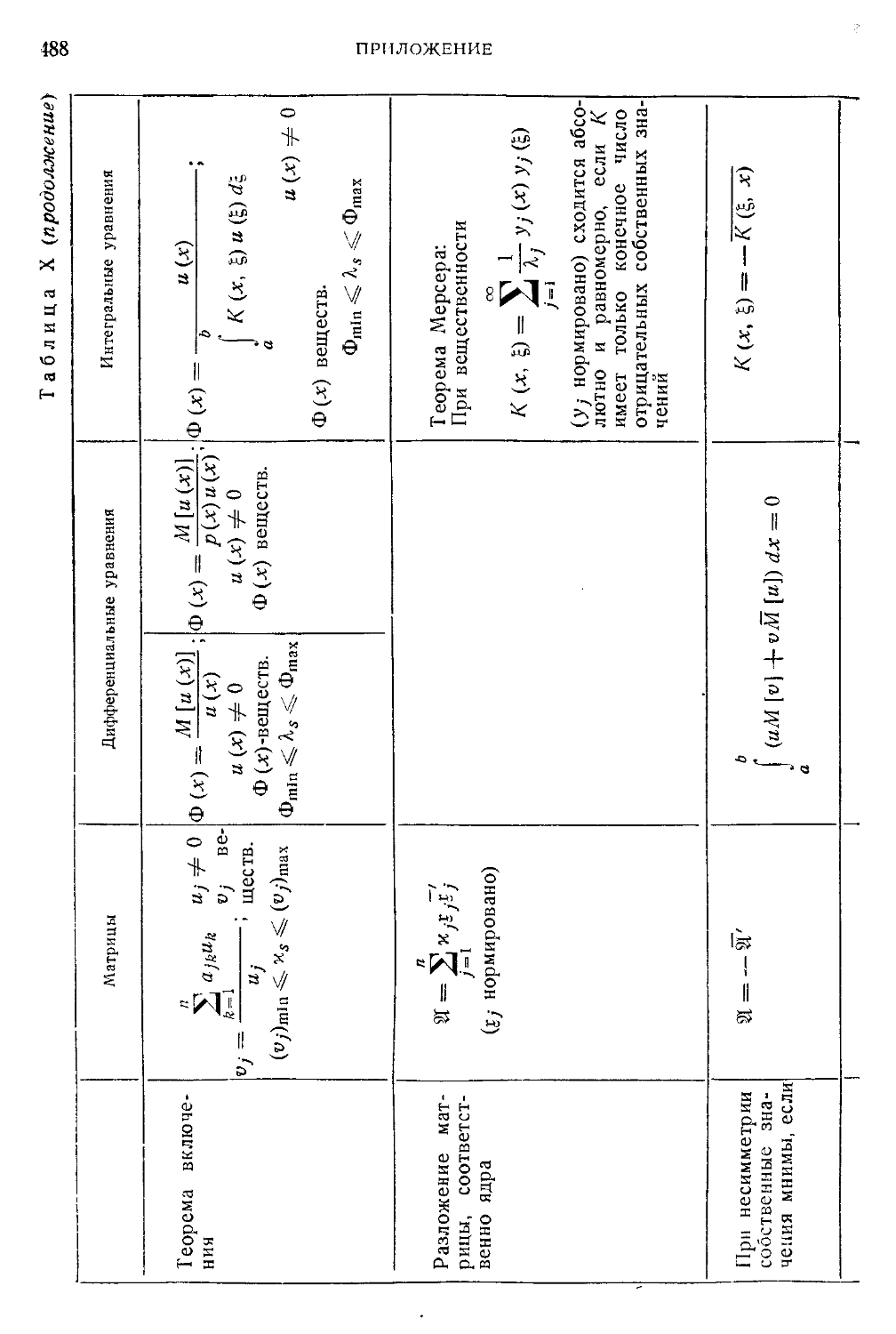
Таблица X. Сравнительный обзор задач на собственные значения для
матриц, дифференциальных и интегральных уравнений 484
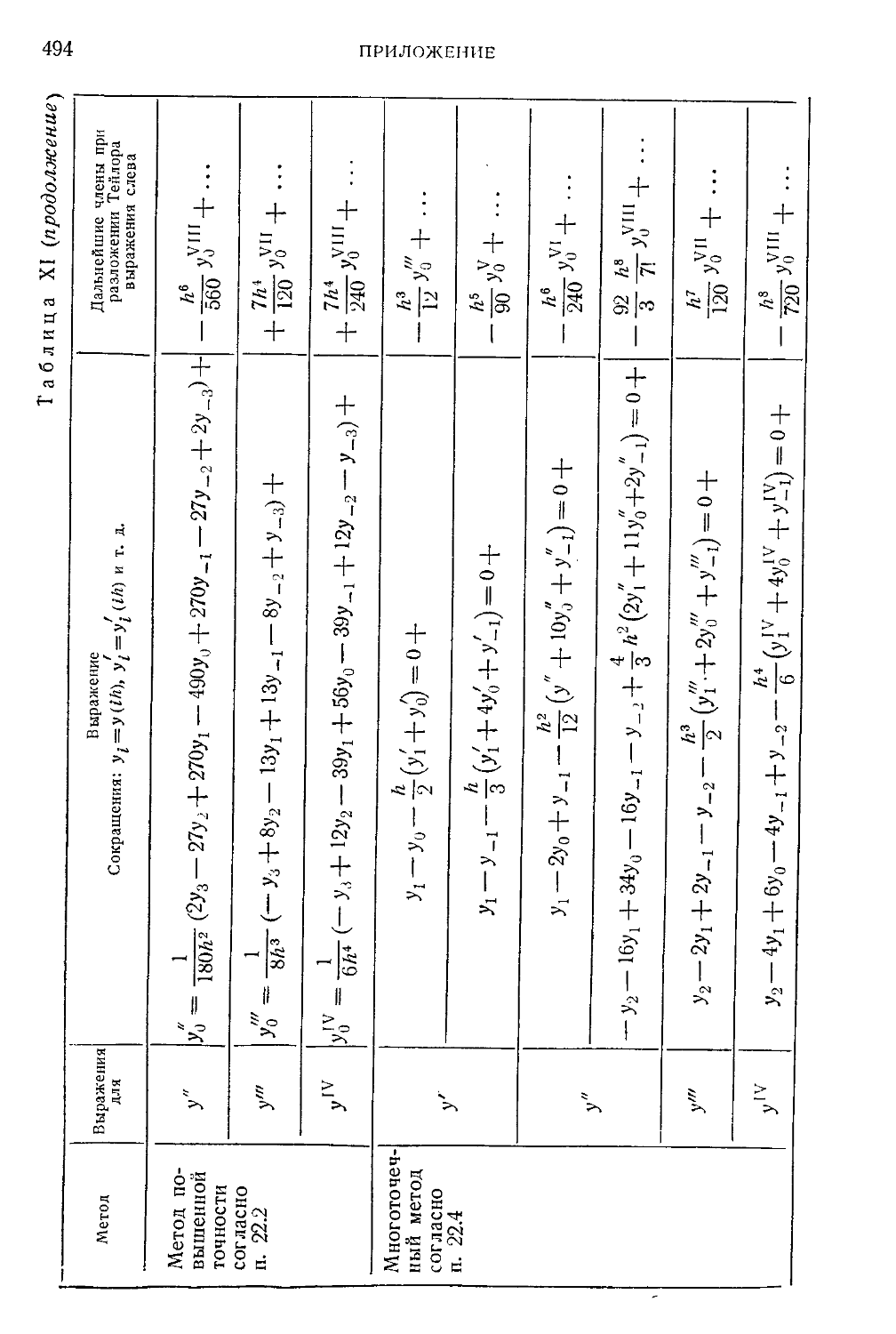
Таблица XI. Выражения конечноразностиого метода для производных 493
Таблица XII. Выражения коиечноразностного метода для операто-
операторов Д и ДД 495
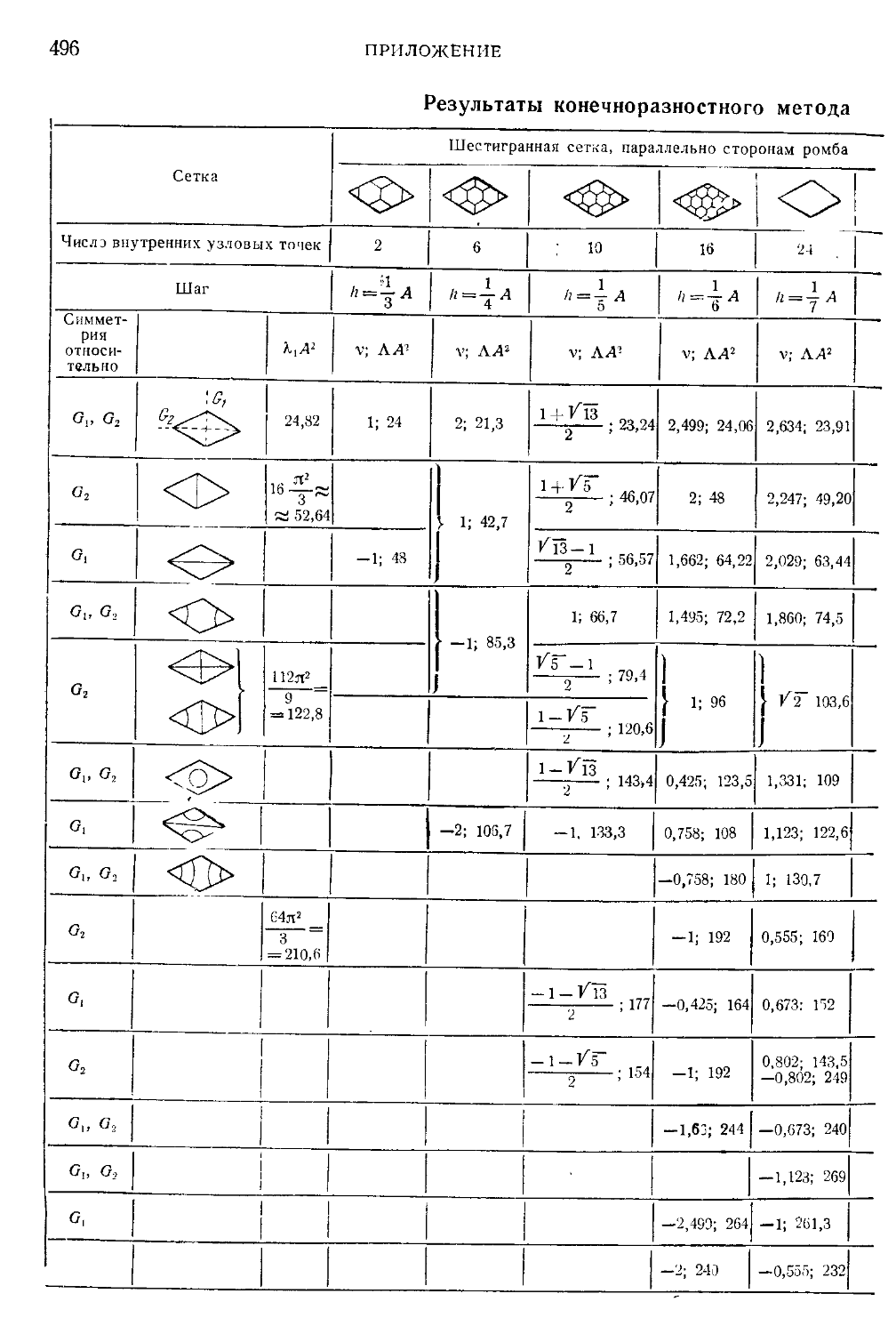
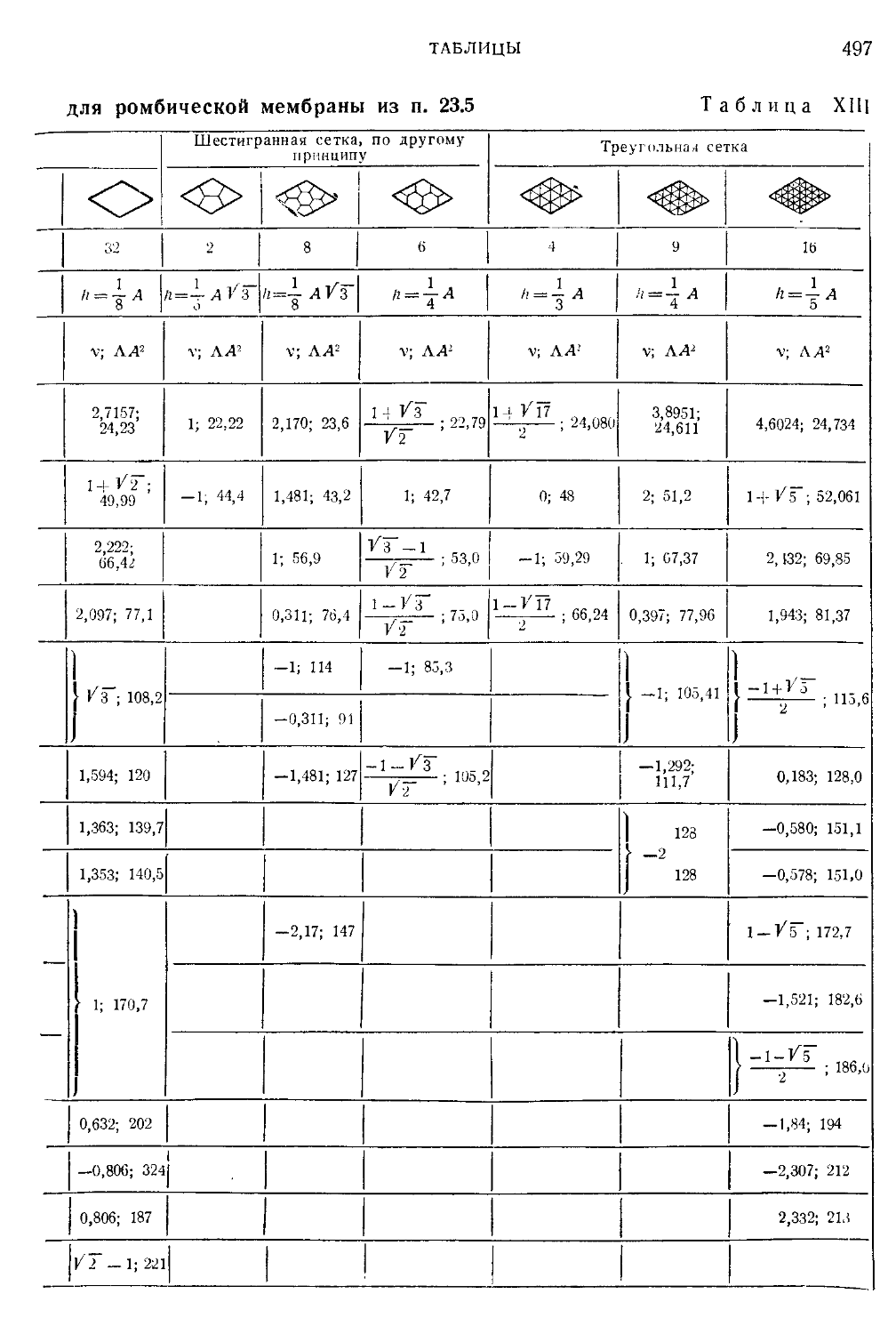
Таблица XIII. Результаты конечноразностного метода для рдмбиче-
ской мембраны из п. 23.5 496
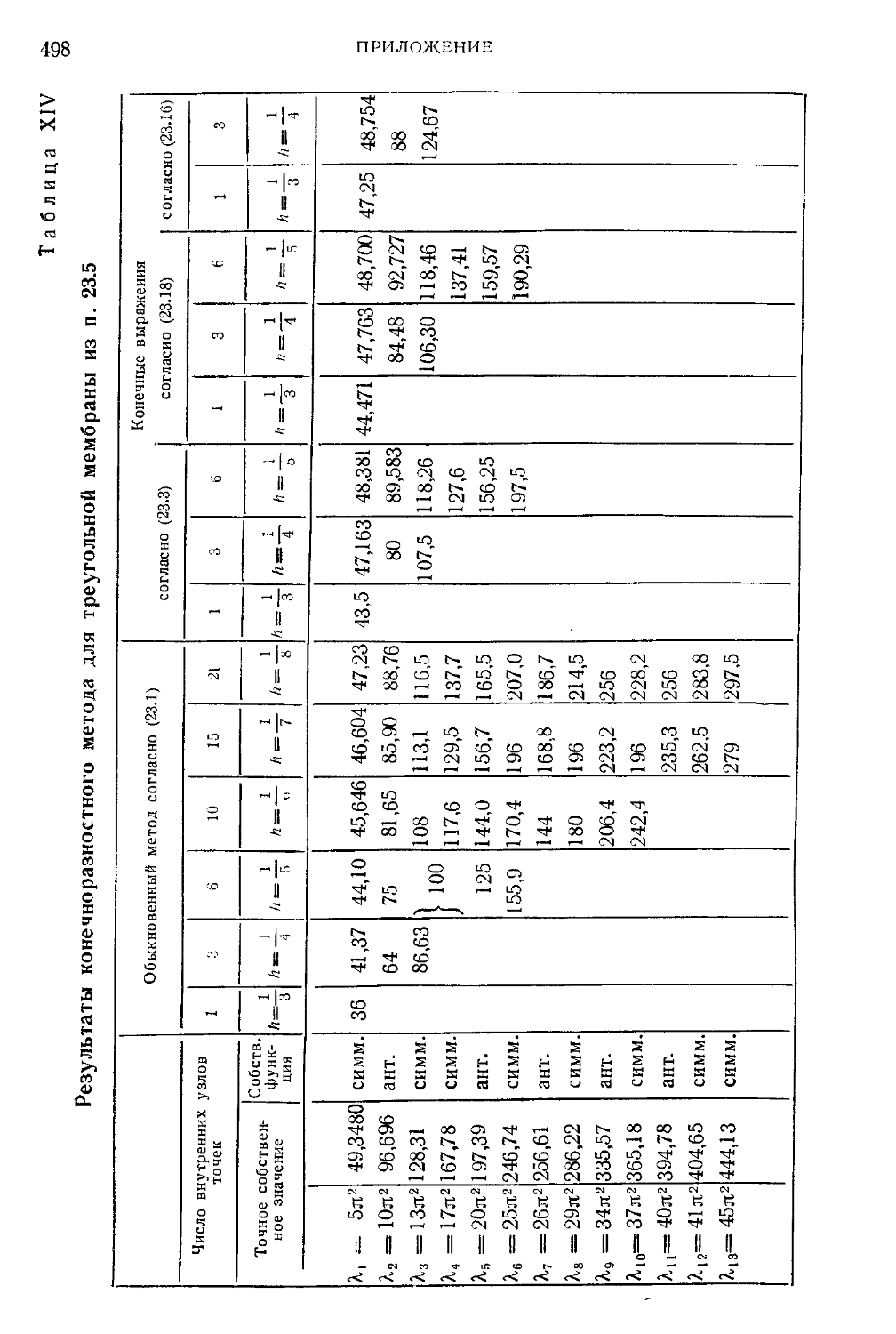
Таблица XIV. Результаты конечноразностного метода для треуголь-
треугольной мембраны из п. 23.5 498
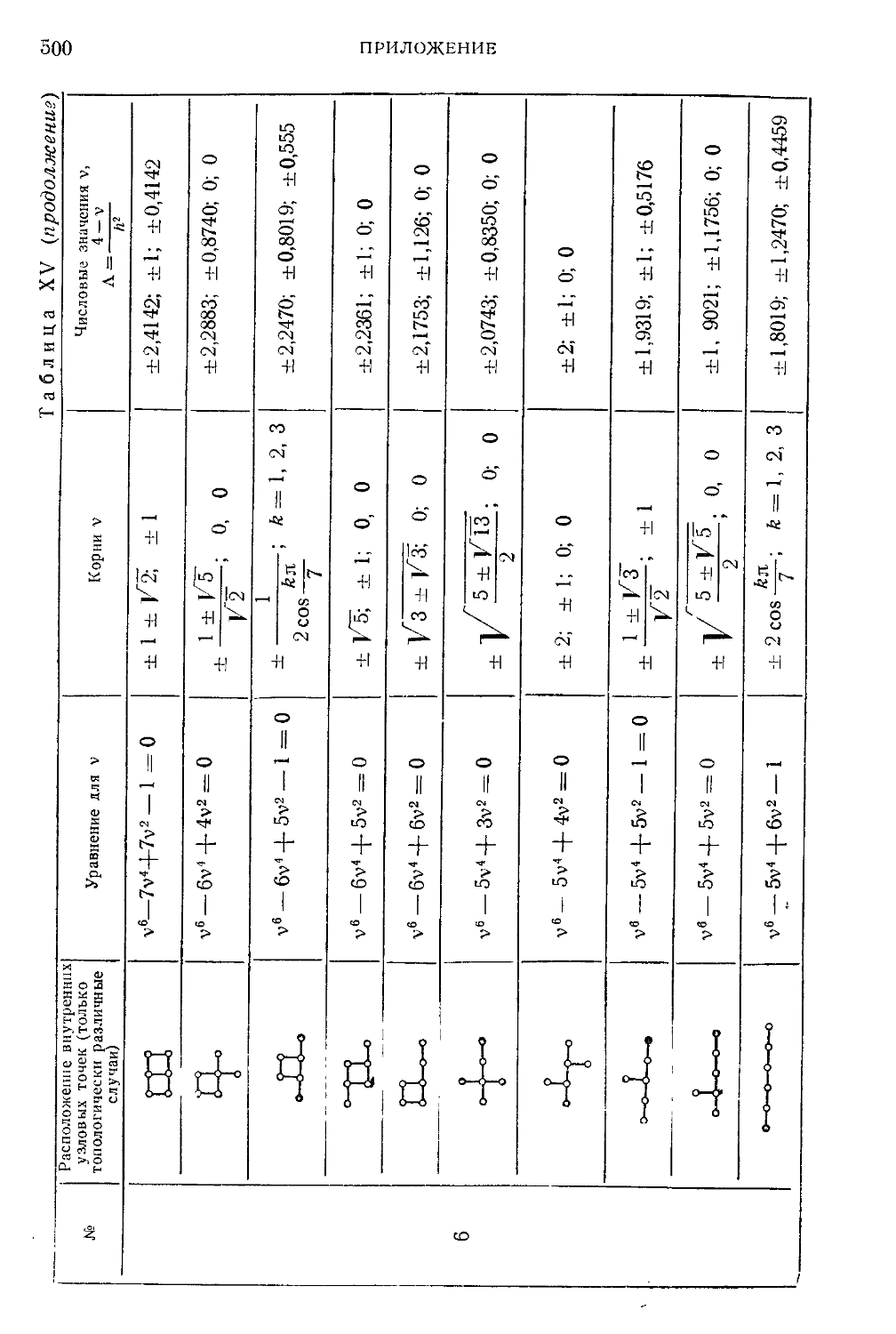
Таблица XV. Спектры сеточных областей (до шести внутренних
точек включительно) 499
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Лотар Коллатц широко известен как специалист в области при-
прикладной математики. Еще в 1953 г. в русском переводе появилась
его книга «Численные методы решения дифференциальных уравнений».
Теперь предлагается перевод книги Л. Коллатца, посвященной
проблеме собственных значений. Он выполнен со второго издания
этой книги, вышедшего в 1963 г. в Лейпциге.
Лейтмотивом книги является мысль автора о важности проблемы
собственных значений в физике и технике, это определяет и ее ма-
математическое содержание. Располагая огромным опытом, Л. Коллатц
почти не прибегает к компиляции, что делает его книгу в высокой
степени оригинальным произведением, но ограничивает область рас-
рассматриваемых приложений почти исключительно задачами механики.
Книга и начинается обзором некоторых задач технической механики,
приводящих к проблеме собственных значений (устойчивость и коле-
колебания). Этот материал иллюстрирует математические особенности
задач на «технически осязаемых» примерах. Он интересен и поучи-
поучителен для лиц, занимающихся задачами на собственные значения не
только механического, но и, например, электродинамического проис-
происхождения. Причины лежат здесь как в принципиальной общности,
так и в историческом происхождении различных задач.
Вводные математические сведения относятся в основном к теории
линейных дифференциальных операторов в элементарном изложении,
хотя функционально-аналитическое понятие оператора прямо и не ис-
используется: автор говорит о «дифференциальном выражении» и крае-
краевых условиях задачи. Точно так же прямо не используется понятие
функционала,, несмотря на то, что экстремальные свойства функцио-
функционалов играют в изложении значительную роль. Вводимая система по-
понятий вообще несколько отличается от общепринятой, однако при
переводе она не подверглась изменениям, поскольку это потребо-
потребовало бы недопустимых отступлений от оригинала в ущерб манере,
а возможно, и замыслу автора. Но иногда во избежание недоразу-
недоразумений делались примечания.
Основное содержание книги посвящено вычислительным методам.
Излагаются вариационные принципы и связанные с ними оценки
12 ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
собственных значений, а также метод Ритца, конечноразностные методы.
Специально рассмотрены задачи на собственные значения для матриц.
При этом автор отдает предпочтение тем направлениям, в разработку
которых им самим внесен существенный вклад.
По своему характеру книга близка к запросам инженеров, зани-
занимающихся вычислениями и осваивающих вычислительную математику,
а также аспирантов и научных работников в области техники. Но надо
отметить, что и лица, хорошо знакомые с распространенными руко-
руководствами по вопросам вычислительной математики, смогут извлечь
для себя пользу из книги Л. Коллатца, поскольку многие из сообщае-
сообщаемых автором сведений относятся к малоизвестным. Это касается, на-
например, вопроса о существовании собственных значений, применения
минимаксимального принципа и двусторонних оценок собственных
значений на основе итерационного процесса. Не все в книге равно-
равноценно. Подробно рассматриваемые графоаналитические приемы, по-
видимому, уже не имеют прежнего значения. В то же время нигде
прямо не говорится о применении ЭЦВМ, хотя, разумеется, книга
нужна в первую очередь именно тем, кто пользуется современными
вычислительными средствами.
Работа по переводу была распределена следующим образом: пре-
предисловие, введение и гл. 1 — III — Д. И. Корниенко, гл. IV, VII, VIII
и приложение (таблицы) —В. Г. Феоктистов, гл. V, VI—В. П. Орлов.
Примечания переводчиков и редактора даны в виде подстрочных
сносок, отмеченных звездо4ками (сноски автора снабжены номерами).
Оригинальная библиография сохранена; при наличии русского пере-
перевода последний указывался в квадратных скобках. Если русский пе-
перевод отсутствовал, то по возможности указывался отечественный
эквивалент (также в квадратных скобках, снабженный вводными сло-
словами: «см., например»). Кроме того, библиография дополнена отдель-
отдельным перечнем в конце книги. Были исправлены замеченные опечатки.
В. В. Никольский
ИЗ ПРЕДИСЛОВИЙ АВТОРА
К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
Предлагаемая книга может служить лишь введением в обширную
область задач на собственные значения и их численного решения. При
этом не было стремления к полноте, так как объем литературы как
по математической теории, так и по прикладным вопросам в послед-
последние десятилетия сильно возрос. В частности, практические приложения
ограничиваются главным образом областью механики; некоторые инте-
интересные классы задач, например задачи на собственные значения для
дифференциальных уравнений с частными производными, для инте-
интегральных уравнений, при бесконечной основной области и т. д., могли
быть затронуты либо только в виде отдельных примеров, либо в крат-
кратких вводных параграфах.
Наряду с задачами на собственные значения для дифференциаль-
дифференциальных уравнений в особой главе рассматриваются также подобные зчдачи
для матриц; глава эта, однако, изложена более сжато, чем другие и
должна способствовать выявлению аналогий в методах и результатах
задач на собственные значения для матриц и дифференциальных урав-
уравнений; это, возможно, наиболее отчетливо сказывается в теории,
основанной на экстремальных свойствах. Одновременно мной руко-
руководила идея путем введения многочисленных примеров из механики
побудить читателя к более интенсивному использованию матричных
методов.
Книга возникла на основе лекций, прочитанных мной в летнем
семестре 1942 г. для дипломированных инженеров и интересующихся
студентов; эти лекции были изданы под названием «Задачи на соб-
собственные значения и их численное решение».
После того как предыдущее издание быстро разошлось, увеличи-
увеличилось число запросов на книгу. Между тем был достигнут прогресс
во многих направлениях, прежде всего в теоретическом отношении,
в то время как основы численного решения регулярных задач на соб-
собственные значения не изменились столь значительно. В ближайшее
время вследствие сильной загруженности я не смог бы, пожалуй,
в теоретической части отдать должное большему изяществу совре-
современной математической теории, которого можно было бы достигнуть
14 ИЗ ПРЕДИСЛОВИЙ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
главным образом путем большего привлечения методов функциональ-
функционального анализа. Поэтому во втором издании сохранен (вплоть до п. 10.7)
текст предыдущего издания; это позволяет использовать книгу в ка-
качестве инструмента всем тем, кто имеет дело с вычислением соб-
собственных значений в механике и в других областях физики и техники.
Однако для облегчения любителям математической теории ознакомле-
ознакомления с новейшим развитием предмета составлен библиографический
перечень некоторых новых работ, естественно, не претендующий на
полноту и предназначенный лишь служить указанием для дальнейшего
изучения; во многих из приведенных работ можно найти дальнейшие
ссылки.
Ганновер, июнь 1949 Гамбург, апрель 1962
Лотар Коллатц
ВВЕДЕНИЕ И КРАТКИЙ ОБЗОР
Одной из наиболее ранних, досконально исследованных задач на
собственные значения является рассмотренная Леонардом Эйлером
в 1744 г. проблема определения критической нагрузки (так называе-
называемая «эйлерова сила при продольном изгибе») для гибкого стержня,
работающего на сжатие и подверженного опасности потери устойчи-
устойчивости. В XIX веке при построении классической математической фи-
физики возникли многочисленные задачи на собственные значения для
колебаний. За последние десятилетия в самых различных отраслях
физики и техники появились задачи на собственные значения в таком
изобилии, что в этой книге невозможно предусмотреть все примене-
применения. В главе первой поэтому выделяется узкая область — механика;
уже здесь возникают разнообразные задачи на собственные значения,
что дает возможность хорошо проследить их характерные свойства.
В частности, оказывается, что если несколько десятилетий назад огра-
ограничивались главным образом так называемыми «частными задачами на
собственные значения» для дифференциальных уравнений в форме
М[г] = Хр-г,
то ныне необходимо рассматривать «общие задачи на собственные
значения»
Здесь Z — неизвестная собственная функция, А, —собственное значение,
р — заданная функция, независимая от координат, М и N—заданные
линейные дифференциальные выражения *). К ним добавляются еще
некоторые краевые условия. Особую роль играют задачи на соб-
собственные значения для обыкновенных дифференциальных уравнений;
они исследованы значительно полнее, чем для уравнений с частными
производными. Отказываясь от систематического обсуждения задач
Для уравнений с частными производными, будем говорить о них лишь
" той мере, как это необходимо для их численного решения.
*) Автор не пользуется понятием «дифференциальный оператор» и не вво
Дит в определение М и N краевые условия.
16 ВВЕДЕНИЕ И КРАТКИЙ ОБЗОР
Существуют различные методы развития теории задач на собствен-
собственные значения; три важнейшие из них используют:
1) дифференциальные уравнения,
2) интегральные уравнения,
3) вариационное исчисление.
Каждый из этих методов имеет свои особые преимущества. Клас-
Классическая теория интегральных уравнений Фредгольма, Гильберта,
Е. Шмидта и др. предлагает очень изящный подход к теории соб-
собственных значений. При достаточной компактности она дает много
фактического материала (например, теорема о разложении произволь-
произвольной функции) и с одинаковым успехом приводит к цели как в случае
обыкновенных дифференциальных уравнений, так и в случае уравне-
уравнений с частными производными. Трудности при этом переносятся на
предварительную стадию, а именно на составление уравнений. В теории
предполагается существование функции Грина, а следовательно, и ядра
интегрального уравнения, но на вопрос о существовании решения эта
теория в общем виде ответа не дает. В рамках теории интегральных
уравнений решаются задачи одночленного класса (§ 7); общие задачи
на собственные значения приводят к интегро-дифференциальным урав-
уравнениям, которые математикой освоены недостаточно.
Вариационное исчисление использует минимальные свойства соб-
собственных значений. В этом случае дифференциальные уравнения и
краевые условия выступают в качестве необходимых условий Эйлера
для минимума. Эти минимальные свойства дают для численного ре-
решения задач на собственные значения весьма плодотворную основу,
понятую в ее полном значении Ритцем. Зато в классическом вариа-
вариационном исчислении остаются открытыми вопросы о существовании
минимума, о виде экстремума в случае высших собственных значе-
значений и т. д.
Метод дифференциальных уравнений, согласно теории Камке,
является наиболее эффективным для обыкновенных дифференциальных
уравнений. В этой книге он описан более подробно, чем другие ме-
методы. В случае самосопряженной (п. 4.3) и полностью определенной
(п. 4.9) общей задачи на собственные значения на этом пути можно
непосредственно обосновать минимальные свойства собственных зна-
значений; метод доказательства при этом для некоторых читателей, воз-
возможно, непривычен, но он прост. Можно было бы также дать ответ
на вопросы о существовании минимума отношения Рэлея, о суще-
существовании бесконечного множества собственных значений и о мини-
минимальных свойствах высших собственных значений.
К минимальным свойствам естественно примыкает метод последо-
последовательных приближений (глава четвертая). Здесь приводится фунда-
фундаментальная формула A2.19), применение которой, правда, связано
с некоторыми дополнительными предпосылками (см. теорему в п. 12.4).
Однако если эти предпосылки выполнены, что во многих прикладных
случаях имеет место, то из формулы A2.19) ценой относительно не-
ВВЕДЕНИЕ И КРАТКИЙ ОБЗОР 17
сложных вычислений получают достаточно точные для прикладных
целей верхнюю и нижнюю границы первого собственного значения.
Глава шестая должна выявить аналогию в методах и результатах
задач на собственные значения для дифференциальных и интегральных
уравнений, с одной стороны, и для матриц, — с другой. В главах
седьмой и восьмой приводятся некоторые методы приближенного на-
нахождения собственных значений, которые применимы довольно уни-
универсально (при слабых предпосылках), но относительно которых нельзя
с уверенностью сказать (в большинстве же случаев вообще неизвестно),
являются ли получаемые приближенные значения слишком большими
или слишком малыми. Эти методы, как, например, разностный, при-
применяются в случаях, когда при малой вычислительной работе хотят
получить представление о порядке величины собственного значения,
либо когда описанные в предыдущих главах методы неприменимы
из-за невыполнения предпосылок. Техника применения различных ме-
методов будет поясняться по мере надобности на примерах (последние
приводятся в конце книги). Численные примеры имеются также в моем
сообщении (Z. angew. Math. Mech. 19 A939), 224). Рекомендации
по применению разных методов в конкретных случаях будут даны
в обзоре (тоже в конце книги).
ГЛАВА ПЕРВАЯ
ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
ИЗ ТЕХНИЧЕСКОЙ МЕХАНИКИ
Рассмотрим прежде всего некоторые примеры из техники, при-
приводящие к проблеме собственных значений. При этом оказывается,
что даже в случае совсем простых механических ситуаций возникают
сложные математические вопросы. Механическая сущность будет
затрагиваться, по мере надобности, лишь кратко, подробное изложе-
изложение можно найти в учебниках по технической механике.
§ 1. Проблема устойчивости
1.1. Продольный изгиб стержня, защемленного на одном конце.
Рассмотрим в качестве простейшей задачи на собственные значения
защемленный на одном конце гибкий стержень длины /, на другой —
свободный — конец которого в центре тяжести концевой площади
действует сжимающая сила Р, направленная вдоль оси стержня.
Поперечные сечения стержня не обязательно одинаковы, но главные
оси инерции всех сечений должны лежать в двух фиксированных
направлениях. Для каждого значения Р возможен такой случай положе-
положения равновесия, когда ось стержня остается прямолинейной. Известно,
однако, что имеется критическое значение Р, выше которого прямо-
прямолинейное положение нестабильно, равновесие является неустойчивым;
при устойчивом же положении равновесия стержень имеет изогнутую
форму. Нас будет интересовать начало потери устойчивости при про-
продольном изгибе, т. е. мы рассмотрим положение равновесия стержня,
незначительно отличающееся от прямолинейной формы. Для этого
положения (см. рис. 1.1, где дана также ориентация координатных
осей х и у; начало координат расположено в точке приложения
силы Р) уравнение упругой линии при малых отклонениях у{х)
имеет вид
М = Яу = —£.//' = —оу". A.1)
Здесь применены обычные обозначения: М—изгибающий момент,
Е—модуль упругости, J—осевой момент инерции сечения, а = £7—
жесткость на изгиб; штрихи означают производные по х.
1.1]
§ 1. ПРОБЛЕМА УСТОЙЧИВОСТИ
19
Итак, в качестве дифференциального уравнения задачи имеем
Р
У '=■
а(х)
A.2)
Здесь не учитываются явление укорочения стержня в результате сжа-
сжатия и возможное неупругое поведение материала стержня. Кроме
дифференциального уравнения к математической фор-
формулировке задачи относятся еще краевые условия,
которые в данном случае зависят от способа закреп-
закрепления стержня. Из рис. 1.1 непосредственно выте-
вытекают геометрические условия у@) = 0, у'(/) = 0.
Далее ищется решение дифференциального урав-
уравнения с учетом краевых условий. Возьмем в качестве
примера стержень постоянного поперечного сечения
(а = const) и положим Я/а = % — Ы1. Тогда решение
дифференциального уравнения имеет вид
у = A cos kx -j- В sin kx.
Произвольные постоянные интегрирования А и В
определяются из граничных условий. Из условия
у@) = 0 следует, что Л = 0.
Второе краевое условие дает
/ (t) — kB coskl = 0.
V///////////////A
Рис. 1.1. Про-
Продольный изгиб
стержня, за-
защемленного на
одном конце и
свободного на
другом.
Это означает либо
1) k = 0, т. е. отсутствие нагрузки, этот случай не представляет
интереса; либо
2) 5 = 0, что дает
это решение соответствует прямолинейному положению равновесия,
оно, конечно, возможно, однако сейчас также не представляет инте-
интереса; либо
3) cos &/ = (),
kl = n/2, Зя/2, 5я/2. ...
Данным значениям k соответствуют критические нагрузки
т —1) I2 , о .
^j 12 )
и каждому из этих особых значений соответствует вполне опреде-
определенная (с точностью до постоянного множителя В) функция прогиба
у (х) = Bsinkx (рис. 1.2).
Еще раз определим математическое содержание проблемы: рас-
рассматривается линейное однородное дифференциальное уравнение
с однородными краевыми условиями у @) = у' (I) = 0.
2*
20
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[1.2
Для любого значения А эта краевая задача имеет «тривиальное»
решение ysO. Кроме того, имеются еще определенные значения А,
а именно бесконечное счетное мно-
\ti жество значений
Рис. 1.2. Первые четыре собствен-
собственные функции (возможные поло-
положения равновесия) призматиче-
призматического стержня при продольном
изгибе с соответствующими кри-
критическими нагрузками.
где т—\, 2, ..., для которых за-
задача имеет не равные тождественно
нулю («нетривиальные») решения
у(х). Эти значения А называются соб-
собственными значениями задачи, и
для каждого собственного значения
имеется определенная с точностью
до постоянного множителя разре-
разрешающая функция у (х), называемая
собственной функцией. Определение
собственных значений и собственных
функций и есть подлежащая реше-
решению задача, которая представляет интерес с физико-технической точки
зрения. Решение этой задачи может натолкнуться на большие труд-
трудности, так как решение в замкнутой форме, с которым мы сейчас
познакомились, особенно в случае дифференциальных уравнений с пере-
переменными коэффициентами, часто невоз-
невозможно. В данной главе мы будем до-
довольствоваться сведением рассматривае-
рассматриваемых проблем к задачам на собственные
значения и к математической формулировке
последних, отложив численное решение
до следующих глав.
1.2. Продольный изгиб стержня, за-
защемленного на одном конце и шарнирно
опертого на другом. Пусть теперь при-
примерно так, как показано на рис. 1.3,
верхняя- точка стержня находится на одной
вертикали с его нижней точкой. При этом
на верхнюю, шарнирно укрепленную точ-
точку, кроме силы Р, действует еще неиз-
неизвестная горизонтальная сила Н. Поэтому изгибающий момент теперь
равен
М = Ру — Нх = — EJy" = — ay".
Исключим из полученного соотношения неизвестную силу Н посред-
посредством двукратного дифференцирования; в результате получим диф-
дифференциальное уравнение
(ау ) = — Ру ч U »ч)
Рис. 1.3. Продольный изгиб
стержня, защемленного на
одном конце и шарнирно
опертого на другом. •
1.31
ПРОБЛЕМА УСТОЙЧИВОСТИ
21
Так как это уравнение четвертого порядка, то нам необходимы также
четыре краевых условия (внизу защемление, вверху нулевой изги-
изгибающий момент):
у @) = 0, у @ = 0,
у"@) = 0. /@ = 0.
Искомая критическая нагрузка Р появляется как собственное значе-
значение % задачи четвертого порядка. Заметим, что собственное значе-
значение X входит уже умноженным не на у, как в A.2), а на его вторую
производную у".
1.3. Продольный нзгиб стержня с учетом собственного веса.
При рассмотрении случая потери устойчивости прямолинейного стержня
(см. п. 1.1) можно учесть еще собственный вес
стержня'). Тогда действующая внизу сила давле-
давления Р равна сумме приложенной вверху силы Ро
и полного веса Go стержня (см. рис. 1.4). В основу
рассмотрения, как к в п. 1.1, будет положено
отличное от прямолинейного, слабо изогнутое по-
положение равновесия стержня. Изгибающий момент
М (х) в сечении стержня х определяется теперь
как силой Ро, так и распределенным собственным
весом верхней части стержня; на элемент стержня
длиной hi, на расстоянии | от верхнего конца
(рис. 1.4) действует сила тяжести yF A|, где F
обозначает площадь поперечного сечения стержня
и у — удельный вес. Теперь можно определить
изгибающий момент в произвольном сечении стерж-
стержня и получить вместе с тем уравнение упругой
линии
у FAS
Af =
? F)
- у
, = -ay"
Рис. 1.4. Продоль-
Продольный изгиб защем-
защемленного одним кон-
концом стержня при
учете собствен-
собственного веса.
Интеграл устраняется с помощью дифференцирования. Согласно
общему правилу дифференцирования интеграла по параметру2)
Ф (х) ф (х)
■Ь J <><*•»«- J *£*«+
ф(дг) Ф(дг)
, ф (x)W(x)—0(x, Ф(х))ср'(х)
') F г. A. W i 11 е г в, Das Knicken schwerer Oestange, Z. angew. Math.
Mech. 21 A941), 43; R. Or an Olsson, Ing.-Archiv 13 A942) 162.
2) K. Knopp, Einfuhrung in die h6here Matheraatik, т. Ill, Leipzig, 1933,
319; Hfltte, des Ingenieurs, изд. 27, т. I, Berlin, 1942, 118 [см., например,
В.И.Смирнов, Курс высшей математики, т. II, М. — Л., Гостехиздат, 1952].
22 ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ П.4
получаем
х
РоУ' + / 4F (I) У' (х) dl = — (ay")'
о
или
X
(Р- О0) у' + у' (х) J у/7 (I) d£ = - (a/')'.
о
Если обозначить через О (х) вес стержня от нижнего конца до точки х
I X
O(x)=j yF (I) dl = Qo— J yF (I) dl,
x 0
то последнее выражение можно записать так:
(a/O' + P/ —O(jc)./ = 0. _ A.4)
Повторное дифференцирование приводит к так называемой само-
самосопряженной форме (объяснение см. в п. 4.3) дифференциального
уравнения
(а/7' — (Оу')' =Ру". A-5)
При этом Р является снова собственным значением X. Этому диф-
дифференциальному уравнению четвертого порядка сопутствуют четыре
краевых условия (последнее условие следует из A.4) для х = 1):
1.4. Сжатый стержень на упругом основании. Пусть стержень
длины /, подвергающийся действию осевой сжимающей силы вели-
величины Р, лежит на упругом осно-
> ^У z^*— вании (железнодорожный рельс).
Р " r^Y- -*T*^i ^ Примем гипотезу Винклера о том,
Л f \ <f \ \ I чт0 сида Р (х), действующая на
l/fyl единицу длины стержня при про-
прогибе на величину у, пропорцио-
Рис. 1.5. Сжатый стержень на упру- нальна величине прогиба у, т. е.
гом основании.
р (х) = Ку.
К называется коэффициентом постели. Тогда при малом продольном
изгибе (рис. 1.5) уравнение упругой линии имеет вид
Ky(l)(x — l)di = -ay".
б
Дифференцирование дает
1.5J
§ 1. ПРОБЛЕМА УСТОЙЧИВОСТИ
23
и в результате повторного дифференцирования получаем дифферен-
дифференциальное уравнение
-Py". A.6)
Краевые условия при шарнирном закреплении имеют вид
У @) = у @ = 0, у" @) = у" @ = 0.
1.5. Опрокидывание*) консольной балки при изгибе1). На
рис. 1.6 показанау становленная на ребро балка, защемленная на одном
конце и несущая на другом груз Р; таким образом, предполагает-
предполагается, что /у велик по сравнению с
Jz (Jy^$>Jz)- Система координат
ориентирована относительно балки
так, что ось х совпадает с осью
балки до деформации, ось z совпа-
совпадает с направлением приложенной
силы Р, а ось у направлена в сто-
сторону отклонения.
Если груз Р мал, то возни-
возникает только изгиб. Когда же сила
Р превышает определенную кри-
критическую величину («опрокиды-
(«опрокидывающая нагрузка»), то на этот
изгиб накладывается боковое оп-
опрокидывание: изгиб относительно
осей у и z и кручение (это можно
наблюдать при аналогичном изгибе
рейсшины). Для определения кри-
критической величины груза рассмот-
рассмотрим слабое опрокидывание, когда
боковое отклонение у незначи-
незначительно и угол закручивания Ь мал.
При этом необходимо обратить
особое внимание на обозначения.
Напомним кратко некоторые правила обозначений, употребляемых
в дальнейшем: момент Tt силы j? вводится как вектор:
Рис. 1.6. Боковое опрокидывание
балки, установленной на ребро, под
действием изгибающей сосредоточен-
сосредоточенной нагрузки Р.
На рисунках вектор-момент, в отличие от вектора-силы, будет всегда
обозначаться двумя стрелками. Вращающее действие момента такое же,
*) Применяется еще термин «потеря плоской устойчивости».
') L. P r a n d 11, Dissertation, Mlinchen, 1899. A. und L. F 0 p p 1, Drang
und Zwang, т. II, изд. 2, MUnchen und Berlin, 1928, 323-352 [А. Феппль
и Л. Феппль, Сила и деформация, т. II, ОНТИ, 1936]; К. Federhofer,
Z. angew. Math. Mech. 6 A926), 43; Handbuch der Physik, т. VI, Berlin.
1928, 284.
24
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[1.5
что и эквивалентной пары сил. При изгибе (в правой системе коор-
координат) изгибающий момент, направленный параллельно оси z, счи-
считается положительным, а поперечная сила считается положительной,
если она направлена в отрицательном направлении оси у (рис. 1.7).
Вследствие этого вектор изгибающего момента Mz (изгиб в плос-
плоскости (х, у)) будет считаться положительным в положительном
направлении оси г, в то время как вектор-момент Му (изгиб в плос-
плоскости (х, z)) положителен в отрицатель-
отрицательном направлении оси у, как это показано
на рис. 1.6. (Система осей х, у, г является
правой, как и система х, z, —у.)
Уравнения упругой линии (с учетом
указанного правила знаков) имеют вид
Му = -ауг", Мг = -ау. A.7)
При этом ay = EJy, az=EJz, где Jy, Jz
обозначают моменты инерции поперечного
сечения относительно осей у и z. Учитывая
оговоренное выше условие о том, что
/у 3>> Jz, приведем следующие упрощаю-
упрощающие соображения.
Компоненты момента силы Р по осям у
и х имеют вид Рх и Р (у0 — у) соответ-
соответственно (рис. 1.6). Компоненту Р (у0 — у)
из-за ее малости можно считать направленной вдоль оси стержня. В про-
противоположность этому составляющая изгибающего момента Рх вслед-
вследствие своей относительно большой величины должна быть разложена
на составляющие в направлении новой (деформированной) оси стержня
и в перпендикулярном к нему. Компонента Рх вдоль нового напра-
направления стержня равна —Рху' (рис. 1.6), а компонента вдоль новой
вертикальной оси равна РхЬ. Итак, в качестве уравнения изгиба имеем
_ а2у" = — РхЪ.
Из-за наличия компоненты момента в направлении стержня имеем еще
уравнение кручения, которое в общем виде формулируется так:
Крутящий момент равен жесткости при кручении, умноженной на
относительный угол закручивания').
(Относительным углом закручивания называется угол закручивания
на единицу длины; этот угол определяется при произвольном изме-
изменении ft (x) как ■9/=-т—.1 Здесь, следовательно, имеем
Рис. 1.7. Ориентация изги-
изгибающего момента и попе-
поперечной силы.
') С. В. В 1 е z e n о, R. О г a m m e I, Technische Dynamik, Berlin, 1939,
116 [К. Б. Б и цен о и Р. Г р а м м е л ь, Техническая динамика, т. 1, Гос-
техиздат, 1950].
1.6] § I. ПРОБЛЕМА УСТОЙЧИВОСТИ 25
где С—жесткость при кручении. Дифференцирование этого уравне-
уравнения дает
— Ру' -f Ру' + Рху" = - {СЪ'У.
Используя уравнение изгиба, можно исключить отсюда у"; тогда
в качестве дифференциального уравнения задачи получаем
J A.8)
с краевыми условиями:
=0 (у защемления угол закручивания равен нулю), "I
■&' @) = 0 (на свободном конце момент равен нулю). J
Здесь С и az — заданные функции от х, а Р2 есть собственное зна-
значение к.
Более строгое проведение выкладок приводит к дифференциаль-
дифференциальному уравнению для ft, в которое войдет также и другой момент
инерции Jz:
= Ц=£. (Pxf О.
В рассмотренных до сих пор случаях задачи на собственные значе-
значения (по крайней мере для стержней постоянного поперечного сечения)
легко допускали решение в замкнутом виде с помощью элементарных
функций. Здесь же мы имеем дифференциальное уравнение, решение
которого даже в случае стержня постоянного поперечного сечения
не выражается через элементарные функция в замкнутом виде, а при-
приводит к цилиндрическим функциям ]).
В уравнении A.8) Рх есть изгибающий момент М{х) от силы Р;
при других видах нагрузок его место занимает изгибающий момент
от соответствующих сил. При некоторой распределенной нагрузке
имеем, следовательно, дифференциальное уравнение
д Iм <*>1 » . A.10)
1.6. Кручение и опрокидывание двутавровой балки. Если рас-
рассмотренный в п. 1.5 стержень является двутавровой балкой, то вместо
дифференциального уравнения второго порядка A.8) возникает урав-
уравнение четвертого порядка 2). В этом случае крутящий момент больше
не равен Си', к нему добавляется член третьего порядка. Кручение
') L. Р г a n d 11, Kipperscheinungen, ein Fall von instabilem elastischem
Qleichgewicht, Dissertation Miinchen, 1899 (рассмотрены также другие типы
закрепления и нагрузок)
2) Л. u n d L. Foppl, Drang und Zwang, т. II, изд. 2, Mflnchen und
Berlin, 1928, 339 [А. Феппль и Л. Феппль, Сила и деформация, т. II,
ОНТИ, 1936].
26
ГЛ. I ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[1.7
tf
отдельного элемента двутавровой балки (рис. 1.8) связано с изгибом
полок; при повороте поперечного сечения на малый угол Ф центры
тяжестей полок сдвигаются на отрезок у = — $, где h есть расстоя-
расстояние между обоими центрами тяжести. Если ft не постоянно, а является
некоторой функцией х, то это равносильно изгибу полок вокруг
стенки балки, т. е. «вокруг
высокого ребра». В расчет
входит также момент инерции
-p-v-f полки относительно
оси z, т. е. относительно ее
малой оси. С изгибом по-
полок связана поперечная сила
Q=—(а,у")', которая соз-
создает момент, совпадающий
по направлению с крутящим
моментом. Подробные вы-
выкладки показывают, что при
кручении двутавровой балки
крутящий момент С^' должен
быть заменен выражением
A.11)
Q+AQ
Рис. 1.8. Кручение элемента двутавровой
балки.
При опрокидывании балки двутаврового сечения уравнение A.10)
должно быть заменено следующим:
A.12)
A.13)
Так как порядок этого уравнения вдвое выше, чем уравнения A.10),
то необходимо добавить еще два краевых условия. В случае сосредо-
сосредоточенной нагрузки на свободном конце х = 0, как в п. 1.5, вместо A.9)
имеем краевые условия:
#(/) = 0, ft"@) = 0 (из-за у" = 0),
ft'(/) = 0 (защемленная полка, следовательно, у'=0),
Г_ СЪ' -f- -^- (а Л")'] = 0 (крутящий момент = 0
для х = 0).
1.7. Сжатие и кручение вала1). При действии достаточно боль-
большого вращающего момента провод пли вал длины / может потерять
') J. Ratzersdorfer, Knickfestigkeit von Staben und Stabwerken,
Wien, 1936, 35; С. В. В i e z e n о, R. Q r a m m e 1, Technisclie Dynamik, Berlin,
1939, 545 [К. Б. Бицено и Р. Грамме ль, Техническая динамика, т. I,
Гостехиздат, 1950].
1.7]
§ 1. ПРОБЛЕМА УСТОЙЧИВОСТИ
27
устойчивость в форме винтообразной линии: с ростом крутящего
момента вначале имеет место только скручивание, затем, при опре-
определенном «критическом» крутящем моменте М, ось винтообразно
деформируется. Если вал к тому же подвергается действию осевой
сжимающей силы Р (рис. 1.9), то эта винтообразная деформация
наступает раньше, т. е. уже при меньшей величине крутящего мо-
момента М.
Рассмотрим вал в слабо изогнутом состоянии, т. е. при малых у
и z. Моменты Pz и Ру пренебрежимо малы. Крутящий момент М,
напротив, имеет относительно
большую величину и должен
быть разложен на компоненты
My' и Mz' по осевым направ-
направлениям (рис. 1.9). Поэтому,
согласно принятым в п. 1.5 (ср.
рис. 1.7) обозначениям, имеем
уравнения изгиба:
— az" = Pz— My',
— ay"'= Ру -f- Mz''.
м
Рис. 1.9. Вал под действием сжатия и
кручения.
Здесь принято ау = аг и по-
поэтому жесткость на изгиб обо-
обозначена просто через а; первое уравнение дает при дифференциро-
дифференцировании
(—az"y = Pz'—Mf = Pz'+ — y+ — z'. A-14)
Ct СО
Умножение на а и повторное дифференцирование соотношения A.14)
— [a (az")'Y = P (az1)' -f M2z" -f MPy'
приводят к дифференциальному уравнению
[a (az")'Y -f P [{az')'4 az"] -f M2z"
с краевыми условиями:
=-0
(последние два уравнения следуют из A.14) при у = 0).
Если вал имеет постоянное поперечное сечение, т. е. a — const,
то дифференциальное уравнение имеет вид
A.15).
28
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[1.8
Если М задан и ищется критическая осевая сжимающая сила Р, то
собственное значение входит в дифференциальное уравнение квадра-
квадратично. При заданной силе Р и неизвестном критическом моменте М
собственное значение X = Мг, как и прежде, входит в первой сте-
степени. В случае отсутствия осевой силы дифференциальное уравнение
можно привести к самосопря-
самосопряженной форме:
(аг'Т = —>И2(-^)' • A-16)
В качестве другой особенности
следует упомянуть о вхожде-
вхождении собственного значения в
краевые условия.
1.8. Выпучивание круго-
круговой арки1). Пусть изогнутый
тонкий стержень постоянного
сечения, ось которого является
дугой с радиусом а и цен-
Рис. 1.10. Выпучивание кругового стерж- тральным углом 2E, подвержен
действию равномерного одно-
одностороннего внешнего давле-
давления р. В качестве простого слу-
случая изучения потери устойчивости может быть вычислено критическое
давление, при котором стержень может выпучиваться в своей пло-
плоскости. При этом принимается, что давление после деформации на-
направлено также перпендикулярно к искаженной средней линии. Введя
полярные координаты г, ц> (рис. 1.10), можно охарактеризовать новое
положение частицы А заданием ее смещений v, w, рассматриваемых
как малые, в тангенциальном и радиальном направлениях. Новое
положение А' в прямоугольных координатах дается следующими
выражениями:
х =(а — w) siti(p-\-v cos ф, у = {а — w) cos ф — ■у sin ф.
Смещения v и w обусловливают тангенциальные растяжения — —z—
и соответственно. Сделаем теперь следующее допущение о не-
нерастяжимости средней линии, т. е. что полное тангенциальное растя-
растяжение et равно нулю:
dv „ dv
ня в его плоскости под действием внеш-
него давления.
ссе,
= 0, или w =
Для изгиба слабо искривленного стержня действителен закон: изги-
изгибающий момент М равен жесткости на изгиб а, умноженной на изме-
■)J. Ratzersdorfer Knickfestigkeit von Staben und Stabwerken,
Wien, 1936, 305.
1.8]
§ 1. ПРОБЛЕМА УСТОЙЧИВОСТИ
29
нение кривизны К*. Здесь К* = есть изменение кривизны
в результате деформации. Новая кривизна К вычисляется по извест-
известной формуле
где штрихи означают производные по величине s = axp (s— длина
дуги до деформации). Пренебрегая квадратичными членами в v, w
и используя условие w = av', получаем
ах' =acos(p — (v-\- aw')sin(fi,
ay' =— asincp — (v -\- aw') cos ф,
a2x" = (— a — av' — aV) sin ф — (v-f- aw') cos ф,
a2y" = (— a — av' — a2w") cosfp-^-iv-^-aw
2 2 = 1, a3 (y'x" — x'y") = a2 A + v'
и тем самым в силу
Используя соотношение между изгибающим моментом и изменением
кривизны
имеем
После этого предварительного геометри-
геометрического рассмотрения выделим элемент
стержня длины As и составим условие
равновесия для действующих на этот эле-
элемент сил и моментов. Действующими на
являются поперечная сила Q, нормальная
сила N, изгибающий момент М и вне-
внешняя нагрузка р As. Силы Q, N и изгибающий момент М, как
это видно по направлению стрелок на рис. 1.11, считаются положи-
положительными; например, положительный момент увеличивает кривизну.
Пусть г|з есть угол касательной к деформированной оси стержня
с фиксированным в пространстве направлением, и, таким образом,
А-ф — угол, который образуют друг с другом нормали к концевым
сечениям выделенного элемента. Уравнения равновесия всех сил
Рис. 1.11. Силы и моменты
элементе кругового
стержня.
30 ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ I2-1
в проекции на радиальное и тангенциальное направления имеют вид
Q — р As — (Q -\- AQ) -f- N -J- + (N -f- AN) -^- = 0,
А* ..._п.
уравнение моментов относительно точки пересечения касательных
к оси стержня в конечных точках элемента
Q + @ + AO)
Переходя в этих уравнениях к пределу при Дгр —> 0 и учитывая, что
K="J==~3st полУчаем
— Q' — р-1гЫК = 0, A.19)
— QK— N' = 0, A.20)
Q-f Ж' = 0. A.21)
Так как М = аК*, то из A.21) следует, что Q = — а (К*)' = ~ а/С'
(К* и /С отличаются на постоянную); затем из A.19) и, далее, из
A.20) получаем
/С/С'" — /С'/С"+— /С'4 /С3/С' = 0. A.22)
Если, наконец, выразить кривизну /С через смещение г; и оставить
только линейные относительно v члены, то получим искомое диф-
дифференциальное уравнение шестого порядка:
v + I^o. A.23)
В качестве краевых условий добавляются:
на шарнирно закрепленных концах v = w — М = 0 или v = v' =
= гГ = 0
и на защемлении г» = w = w' = 0 или ^=^'=^" = 0.
Собственным значением здесь является критическое давление р.
§ 2. Задачи о колебаниях
2.1. Колебания свободно подвешенного каната. Рассмотрим
малые колебания абсолютно гибкого тяжелого нерастяжимого каната
длины /, подвешенного за один конец. Начало координат совпадает
с точкой подвеса, ось х направлена вниз (рис. 2.1). Предполагается,
что колебания происходят в плоскости х, у; боковое отклонение у
и угол отклонения у' принимаются малыми (arctgу' =5= у'). На выде-
выделенный элемент длины Ах действуют силы натяжения 5 и 5 -\-AS,
сила тяжести pgF Ах и (согласно принципу Даламбера) сила инерции
2.1] i
§ 2. ЗАДАЧИ О КОЛЕБАНИЯХ
31
— pF Axy (где р есть плотность, F — площадь поперечного сечения,
g — ускорение свободного падения, штрихи обозначают производные
по длине х, а точки — по времени t). Разлагая силы натяжения на
горизонтальные и вертикальные со-
составляющие и заменяя AS по фор-
формуле Тейлора на S''Ax, получаем
условия равновесия:
S' Ax-\- pgF Ах = 0,
(Sy')'-PFy=0
или
(Sy'Y=9F'y.
B.1) Лх
B.2)
Рис. 2.1. Малые колебания сво-
свободно подвешенного гибкого ка-
каната.
Первое из этих уравнений означает,
что уменьшение силы натяжения
с ростом х обусловлено влиянием
собственного веса каната. Без до-
дополнительного рассмотрения можно
понять случай, когда канат нагру-
нагружен внизу сосредоточенной массой М
с весом О = Mg. Тогда сила натя-
натяжения в точке х равна сумме весов нижележащей части каната и под-
подвешенного груза О. Для однородного каната (р и F постоянны),
например:
S=Q+9gF(l—x).
Сила натяжения 5, следовательно, может счи-
считаться известной. Тем самым B.2) является диф-
■%-(ОгуA) ференциальным уравнением колебаний каната;
это — уравнение с частными производными для
неизвестной функции у (х, t). Для однородного
нагруженного каната это уравнение имеет вид
[(О +-9gF{l-x))y'\'=pF"y. B.3)
Из всей совокупности возможных колебательных
процессов нас в данный момент интересуют син-
синхронные колебания, так называемые собственные
колебания, т. е. вопрос о том, обладает ли диф-
дифференциальное уравнение с частными производ-
производными решением вида
у (х, t)^Y (х) cos со (t —10), B.4)
где t0 есть постоянная. При таком виде движения все частицы каната
колеблются с одинаковой круговой частотой со й в одной фазе, но
с разными амплитудами К. При решении вида B.4) имеем
у = — а2у,
Рис. 2.2. К выводу
краевых условий
при колебаниях ка-
каната с массой на
конце.
32 ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ [2-1
и в результате получаем обыкновенное дифференциальное уравнение')
[(О 4- pgF {I — х)) y'Y = - p/Vy. B.5)
Это уравнение даже при постоянном pF не может быть проинтегри-
проинтегрировано элементарно из-за множителя (/ — х) и решение этого уравне-
уравнения приводит к функциям Бесселя. Краевые условия имеют вид
1) у@) = 0, 2) у'(/) = -^у(/). B.6)
Второе краевое условие получается из рассмотрения равновесия сил,
приложенных к подвешенному грузу (рис. 2.2); сила тяжести и сила
инерции должны давать равнодействующую, которая уравновешивает
силу натяжения и которая, следовательно, наклонена под углом у'
к вертикали, т. е.
, О
Таким образом, это краевое условие не зависит от величины веса О
и действительно также для О = 0. (Вместо условия 2) можно также
записать у"A) = 0.)
Круговые частоты со являются искомыми. Ищутся, таким образом,
те значения параметра со, для которых уравнение B.5) с краевыми
условиями B.6) имеет тождественно не равное нулю («нетривиальное»)
решение. Снова имеем задачу на собственные значения, как и в § 1.
Величина со2 является собственным значением X; как ив п. 1.3 здесь
имеет место та особенность, что собственное значение входит в крае-
краевые условия (именно во второе уравнение B.6)). Собственные коле-
колебания имеют особое значение при рассмотрении общего решения
уравнения в частных производных B.3). Известно, что имеются
основное колебание, т. е. собственное колебание с наинизшей кру-
круговой частотой со,, и последовательность высших колебаний с частотами
а>2, w3, . . . Пусть а>1 расположены по порядку возрастания их вели-
величин; каждой частоте (О; соответствует определенная (с точностью
до постоянного множителя) собственная функция у{. Так как урав-
уравнение B.3) линейно и однородно, то сумма двух решений есть также
решение. Можно составлять линейные комбинации нескольких и даже
бесконечного числа решений («наложение»), т. е. выражение
со
у (х, t)= 2Л (х) (Av cos aJ -f 5v Sin wv*)
V-I
является также решением при любых постоянных Av, Bv, поскольку
Av и Bv убывают так быстро, что ряд, полученный путем двукрат-
') Можно в B.5) заменить у на У. Как амплитудная функция Y (х), так
и колебательная функция у (х, t) при любом фиксированном / (т. е. в каждый
момент времени) удонлетворяют уравнению B.5). Вместо у (.£, /) здесь будет
кратко писаться у (х).
8 HE БОЛЕЕ ГИ КНИГИ В
} ОДНМ РУКИ И 2ХВ ДВЕ
§ 2. ЗАДАЧИ О КОЛЕБАНИЯХ
33
ного почленного дифференцирования по х и по t, равномерно схо-
сходится. Это решение для ^ = 0 удовлетворяет определенным начальным
значениям:
v-l
= y(x. 0)=
v=l
B.7)
Пусть теперь для проблемы собственных значений можно доказать
так называемую тео^му_о_£азложенЕИ,^.т. .е.- ухтаао.вихь., что «про-
«произвольную» Функцию jp (л;)_можно разложить п© соёетвенным- -функ-
-функциям yjjx). В рассматриваемом случае это означает, например, что
для" "любых заданных функций g (x) и h(x) найдутся постоянные
(коэффициенты) Av и Bva>v соответственно такие, что соотноше-
соотношения B.7) будут иметь место. Тогда оказывается, что бесконечный
ряд для у (х, t) представляет общее решение дифференциального
уравнения с частными производными,
так как любое решение этого урав-
уравнения определяется его начальными
значениями g (x) и h (x). Следова-
Следовательно, любое движение каната мо-
может быть представлено как суперпо-
суперпозиция собственных колебаний.
2.2. Крутильные колебания
стержней. Рассмотрим крутильные
колебания прямого (но не обяза-
обязательно постоянного сечения) стержня
длины / относительно своей оси.
Предположим, далее, что он за-
защемлен на одном конце и свободен
на другом. Ось х направим от
Рис. 2.3. Моменты, действующие
на элемент стержня при крутиль-
крутильных колебаниях.
свободного конца, где поместим начало координат, к защемленному
вдоль неизогнутой оси стержня. Пусть $ = $(х, t) есть угол пово-
поворота поперечного сечения в точке х к моменту t относительно по-
положения равновесия. (Мы не учитываем здесь то обстоятельство, что
все сечения, исключая круговые и кольцевые, при кручении не остаются
плоскими, но искривляются.) Если обозначить жесткость стержня
при кручении в точке х через С = С(х) (как и в п. 1.5), то кру-
крутящий момент определяется выражением
М =С~=СЪ'
' dx
При крутильных колебаниях на элемент стержня действует слева
момент Mt и справа Mt -\- AMt (рис. 2.3), так что &Mt определяет
3 Л. Коллатц I RBT с; ПЧЖп-птпжг ж I
34 ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ I2-3
угловое ускорение элемента. Имеем
ДМ, = УрР Дх&,
где р — плотность и Jp—полярный момент инерции поперечного се-
сечения в точке х. Тем самым для '©■(л;, t) получаем дифференциальное
уравнение движения в частных производных
Взяв снова решение для собственных колебаний вида B.4)
ft (x, t) = D (x) cos at
и положив Ф = — со2&, получаем обыкновенное дифференциальное
уравнение
_ (С^'У = coVpft B.9)
с краевыми условиями:
ф(/)=0 (угол поворота защемленного сечения равен нулю),
У @) = 0 (равенство нулю крутящего момента на свободном конце).
В случае балки двутаврового сечения, как в п. 1.6, порядок диф-
дифференциального уравнения повышается; если, как в A.11), дополнить
Ах член С^' слагаемым ^-(суЕК')', то
B.9) переходит в
U I "--" 4г- (а /У)" ~ (.С^У = рЛсо2^ B.10)
-pFAxy c такими же краевыми условиями,
как в A.13):
Рис. 2.4. Колебания изгиба О @ = 0. <К (Q = 0. У @) = 0,
защемленного стержня. Г Л2 . „„ , „.,] .
Условие У(/) = 0 определяется изгибом полок, так как для защем-
защемленных полок имеет место у'=0 (ср. п. 1.6). Для балки без полок
в общем случае У @) ф 0.
2.3. Изгибные колебания стержня. Стержень длины / с прямо-
прямолинейной осью, закрепленный каким-нибудь образом, например заще-
защемленный одним концом, как на рис. 2.4, может, кроме исследован-
исследованных в п. 2.2 крутильных колебаний, также совершать изгибные
колебания. Пусть ось х совпадает с прямой осью стержня, а ось у
направлена в сторону предполагаемого отклонения от положения рав-
равновесия; отклонение полагается малым, Рассмотрим вначале колеба-
колебательный процесс при условии, что каждый элемент стержня колеблется
как твердая частица параллельно оси у. Остаются неучтенными, таким
образом, все побочные влияния, обусловленные тем, что в действи-
действительности из-за изменения наклонов упругой линии при колебаниях
2.3]
§ 2. ЗАДАЧИ О КОЛЕБАНИЯХ
35
каждый элемент стержня поворачивается с некоторым угловым уско-
ускорением и что элементы стержня не сохраняют свою форму и вслед-
вследствие изменения углов возникают напряжения сдвига и т. д. Рас-
Рассматривая затем при обычных обозначениях (плотность р, площадь
сечения F, жесткость на изгиб а) силу инерции — pFy в качестве
нагрузки р, из известного уравнения изгиба стержня
непосредственно получим уравнение движения
(а/0" = — 9F'y- B-П)
Отсюда, взяв решение уравнения для собственных колебаний в виде
у — у (х, f) — Y (х) cos Ш, ,*
получим обыкновенное дифференциальное урав- А
нение
(а/0" = Р^2У • B-12)
В зависимости от вида закрепления концов
стержня имеем различные краевые условия; вы-
выделим несколько примеров (см. рис. 2.5).
1. Стержень слева защемлен, справа сво-
свободен:
у(О) = /(О) = о. у" @ = /"(О = о.
2. Стержень закреплен с обеих сторон шар-
шарнирно:
У @) = у @ = 0, у" @)= у" @ = 0.
3. Осуществлено с обеих сторон упругое
закрепление стержня.
Здесь при опускании левого конца стержня на величину у@)
возникает поперечная сила Q = cy @) (где с — коэффициент жесткости
пружины), следовательно, на левом конце
Рис. 2.5. Различные ви-
виды закрепления колеб-
колеблющегося стержня.
На правом конце возникает опорная реакция —Q = (ау")'х=1 = су (I).
Таким образом, имеем краевые условия:
у"@) = 0, (ау")о+су(О) = О,
у" @ = 0, (а/'); —су @=0.
4. Стержень слева закреплен шарнирно, справа—упругое закреп-
закрепление:
у(О) = у"(О) = О, /'@ = 0, («/О/— су @ = 0
3*
36 ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ [2.4
(нижние индексы показывают, что имеются в виду производные
в точках х = 0, х = 1 соответственно).
2.4. Пример физической задачи с отрицательными собствен-
собственными значениями. Если в приведенных выше случаях 3 и 4 закре-
закрепления концов стержня при его изгибных колебаниях коэффициент
жесткости является отрицательным (т. е. при малых отклонениях на
концах действует сила, увеличивающая отклонение, что физически
можно легко реализовать), то собственные значения могут оказаться
отрицательными. С целью облегчения вычислений выберем только
одну опору упругой, другую же — в виде жесткого шарнира. Пусть
стержень имеет постоянное сечение; тогда уравнение B.12)
CtylV = р/7(о2у) B.13)
если ввести ради краткости обозначения
k=^=.k\ B.14)
принимает вид
yiv = %у = tfy. B.15)
Общим решением этого уравнения для k = 0 будет
у = A sinkx-\- В cosfex -\-С sh kx ~\- D ch kx,
где Л, В, С, D — произвольные постоянные.
Из первых двух краевых условий
имеем
Два других краевых условия
при k Ф О означают
А {— /г3coskl — — smkl\4- С (/г3chkl — — sh kl\ = 0.
Это — система двух линейных однородных уравнений для А и С,
которая имеет решение, отличное от Л = С = 0, если определитель,
составленный из коэффициентов этой системы, обращается в нуль:
— sin fe/ shkl
— k3coskl — — sinkl ti6 ch kl — — sh kl
a a
= 0.
2.4]
§ 2. ЗАДАЧИ О КОЛЕБАНИЯХ
37
Вычисление этого определителя дает
трансцендентное уравнение для k (и
собственного значения X):
после деления на sinklshkl
тем самым одновременно для
cthhl-ctgU
Из графического представления
обеих частей этого уравнения,
(рис. 2.6) видно, что как при по-
положительных, так и при отрица-
отрицательных с существует бесконечно
много вещественных точек пере-
пересечения кривых cth kl — ctg kl и
—£- для положительных k; таким
образом, согласно B.14), суще-
существует бесконечно много положи-
положительных собственных значений-^.
Имеются ли также и отрица-
отрицательные собственные значения К?
Для ^<0 представим k, согласно B.14), как корень четвертой сте-
степени из отрицательного числа в виде k = s(l-\-i), где s вещественно.
Пусть, далее, 1=1; подстановка k = s(l-\-i) в B.16) и использо-
использование соотношений
sinfe==sinschs-(~^ cos s sh s,
cos k == cos s ch s — i sin s sh s,
~~S= >- sh fe = coss sh s-4-isinschs,
ch k — cos s sh s -4- i sin s sh s
Рис. 2.6. Вещественные корни
трансцендентного уравнения B.16);
С == 2 ^
-1
Рис. 2.7. Графическое представле-
представление комплексных корней уравне-
уравнения B.16); С = -J-.
после коротких преобразований дает
новое уравнение для s:
с sin 2s — sh 2s
2as3
' ch 2s — cos 2s
Графическое представление правой
части этого уравнения (рис. 2.7)
показывает, что для положительных с нет ни одной вещественной,
а при отрицательных с имеется одна вещественная точка пересечения.
Таким образом, для с < 0 имеется одно отрицательное собственное
значение к. Соответствующее ему движение не может быть названо
«собственным колебанием», самое большее его можно назвать «соб-
«собственным движением»:
у (х, t) = Y (x) cos at = Y (x) cos
yi±t = Y (x)ch
38
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[2.3
функция у(х, t) имеет, следовательно, для отрицательного Я, возра-
возрастающий со временем множитель. Прочие собственные значения X,
которые являются положительными, соответствуют обычным колеба-
колебаниям; однако рассматриваемая система является нестабильной; имею-
имеющаяся в наличии даже очень малая компонента собственного движе-
движения, соответствующая отрицательному собственному значению, растет
со временем неограниченно. Если осуществлено упругое закрепление
обоих концов стержня (способ крепления 3 в п. 2.3, рис. 2.5), то
при I = 1 для k получается трансцендентное уравнение
Первый множитель уже подробно исследован выше, второй снова
дает бесконечно много положительных собственных значений и для
отрицательного с еще одно отрицательное собственное значение; при
k = s(\-\-i) он дает уравнение
__ с sin 2s 4 sh 2s
2a!3 ~ cos 2s -f- ch 2s '
Правая часть представлена гра-
графически на рис. 2.8. При таком
способе закрепления, следовательно,
для с < О возникают два отрица-
отрицательных и бесконечное множество по-
положительных собственных значений.
2.5. Колебания стержня с уче-
учетом влияния собственного веса.
Рассмотрим изгибные колебания за-
защемленного на одном конце вер-
вертикального стержня (например, высокой дымовой трубы1)) при тех же
допущениях, что и в п. 2.3. Пусть ось х совпадает с неотклоненной
осью стержня и направлена вертикально вниз, боковое (малое) откло-
отклонение обозначается через у. На элемент стержня в отклоненном
положении теперь, кроме силы инерции, действует еще сила
тяжести (рис. 2.9), так что выражение для изгибающего момента
будет иметь вид
х х
М=—ау" = — J 1—pF'y (£)] (х — l)dl—j pgF [у (|) — у (х)] d\.
о о
Дифференцирование дает
X X
М' = - (ay")' = | pFy (I) dl -f- J pgFy' (x) d\.
Рис. 2.8. Графическое представле-
представление в случае отрицательных соб-
собственных значений колеблюще-
колеблющегося стержня, упруго закреплен-
закрепленного на обоих концах; С = ■=—.
M. G. Puwein, Beton und Eisen 39 A940), 162.
2Л] § 2. ЗАДАЧИ О КОЛЕБАНИЯХ 39
Второй интеграл имеет величину у' (х) О (х), где G (х) = pgF dl,—
о
вес стержня от верхнего конца до точки х. Таким образом, после
повторного дифференцирования имеем
B.17)
или снова с учетом выражения для собственных колебаний B.4):
(а/'/' -|- (О/)' = pFco2y. B.18)
Для случая стержня постоянного поперечного сечения О = pF gx,
следовательно, и в этом случае дифференциальное уравнение имеет
переменные коэффициенты и собственное значение
Я, = со2 невозможно найти просто в замкнутой форме, ■%
как в случае уравнения с постоянными коэффициен- -pFjj^ \\х
тами. Краевые условия имеют вид """ \ \
у @ = /@ = 0. /'@) = /"@) = 0.
2.6. Критическое число оборотов вала с ги-
гироскопическим эффектом!). «Летящим валом» на-
называют вращающийся с угловой скоростью со вал,
защемленный с одной стороны и несущий на другом,
свободном, конце диск. Здесь при вычислении кри-
критического числа оборотов в общем случае нельзя fHC- 2.9. Коле-
, . . бания изгиба
пренебрегать гироскопическим эффектом, вызывае- стержня с уче-
мым наклоном диска и частиц вала. Вследствие том собствен-
наклона диска ось вращения больше не является глав- ного веса.
ной осью инерции, вектор момента количества дви-
движения J (кинетический момент) поэтому не совпадает с направле-
направлением оси вращения, а вращается вокруг нее. Изменение момента
количества движения (точнее, его производная по времени) равно
действующему на диск моменту.
Пусть наклон диска характеризуется малым углом ф = /. Пусть,
далее, диск имеет момент инерции А относительно его оси симме-
симметрии и В относительно перпендикулярной к ней оси. Компоненты
угловой скорости относительно обеих этих осей тогда равны
(рис. 2.10) со cos ф и со sin ф или, вследствие малости ф, со и соф,
а компоненты вектора момента количества движения будут: У, = Лео
и У2 = 5соф. Из этих компонент можно построить полный момент
количества движения J; конец вектора кинетического момента нахо-
находится от оси вращения на «расстоянии»
а = ]х sin ф — J2 cos ф =%s ^ф — 7_, = (А — В) соф = Ссоф,
') С. В. Biezeno, R. Gramrael, Technische Dynamik, Berlin, 1939,
80S-806, 821 [К. Б. Бицено и Р. Г р а м м е л ь, Техническая динамика,
1 II, Гостехиздат, 1950].
40
ГЛ. 1. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[2.6
где подставлено С = А — В. Вследствие равномерности вращения
производная по времени
dJ \ /-• о
-тг = J= ЙСО = ССО'Чр.
Это есть момент, с которым вал действует на диск1).
Момент, с которым диск действует на вал, таким образом, равен
АГ = — Ссо2ф. B.19)
Далее, возникают центробежные силы: — my = -{-mai2y, где у (х, f) =
= Y{х)соъЫ, причем ffi=p/v-ecTb масса вала на единицу длины.
Рис. 2.10. К выводу дифференциального
уравнения летящего вала.
Если Жо есть масса диска и с—разность моментов инерции на еди-
единицу длины вала (соответствующая С), то изгибающий момент имеет
вид
х
М == - а/ = - J
0 центробежная сила вала
х
гироскопический " вала
эффект диска,
Дифференцирование дает
X
М' == (- а/')' = - J pF<»2y (I) dl —
B.20)
- ссо2у' (*), B.21)
') Этот вектор-момент направлен перпендикулярно к плоскости, опре-
определяемой со, Ji и Л. и на рис. 2.10 показан в перспективе как —-.
2.71
§ 2. ЗАДАЧИ О КОЛЕБАНИЯХ
41.
и повторное дифференцирование приводит к дифференциальному
уравнению задачи
(а/')" = «2 [9Fy + (су'У\. B.22)
В точке защемления х = I имеем, как в п. 2.3, краевые условия:
у (I) = у'(I) — 0; краевые условия для х = 0 получаем, подставляя
в B.20) и B.21) х = 0:
а/'(О) = Со)У @),
(а/)о = Муу @) +
("О).
B>23)
В этой задаче собственное значение а»2 также входит в краевые
условия.
2.7. Крутильные колебания диска1). В насаженном на вал вра-
вращающемся диске, толщина у (г) которого зависит от расстояния г
до оси вращения, под влиянием измене-
изменения числа оборотов могут иметь место
колебания кручения и растяжения в своей
плоскости, которые связаны между собой,
Силы связи, однако, количественно малы
по сравнению с обусловливающими коле-
бания силами инерции, и при вычислении
собственных частот можно пренебречь
связью2), а также производить расчет для
невращающегося диска. Поэтому в даль-
нейшем радиальное растяжение не рас
сматривается; вал принимается защемлен-
ным на концах (рис. 2.11). При крутильных
колебаниях концентрические окружности диска сдвигаются друг отно-
относительно друга и нанесенная первоначально на диске прямая переходит
в кривую, характеризуемую углом закручивания ф = ф(г) (рис. 2.12).
Это дает связь между относительным сдвигом у (изменение первона-
первоначально прямого угла) и напряжением сдвига т. Из рис. 2.12 непо-
непосредственно получается
Дш
у = г -7г-
схема.
или в пределе, если штрихом обозначать производную по г,
Здесь О есть модуль сдвига.
B.24)
') R. Grammel, Z. angew. Math. Mech. 5 A925), 193—200; С. В. Bie-
z e n о, R. Grammel, Technische Dynamik, Berlin, 1939, 652 [К. Б. Бицено
и Р. Грамме ль, Техническая динамика, т. II, Гостехиздат, 1950].
2) С. В. Biezeno, R. Grammel, Technische Dynamik, Berlin, 1939,
655 [К. Б. Бицено и Р. Граммель, Техническая динамика, т. И, Гостех-
Гостехиздат, 1950J.
42
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[2.7
Выделим теперь в диске кольцо в пределах от г до г + Дг. Все
напряжения сдвига создают в итоге моменты относительно оси вала
(различные внутри и снаружи; внутри момент М, а снаружи
М -|~ДЖ); разность ДМ обусловливает ускорение вращения кольца.
Напряжения сдвига действуют на поверхности величиной 1ягу> они
дают, следовательно, момент
dM
. М = 2лгхуг внутри, М -)—-j—Д/- снаружи.
Выделенное кольцо имеет момент инерции
где р есть плотность; следовательно, для него уравнение движения
имеет вид
г At,
^ — dr г — р яг
или
(г2ху)' = р/уф,
и если вместо т подставить его величину
согласно B.24), то
О (г W)' = рг3уф-
При ф(г, 0 = Ф (/") cos ©^
циальное уравнение имеет вид
B.25)
дифферен-
B.26)
Рис. 2.12. Деформация диска На внутренней границе г = г0 имеем крае-
при крутильных колеба- вое условие:
ниях.
т. е. напряжение сдвига пропорционально углу закручивания; постоян-
постоянная с вычисляется на основе конструктивных данных и была бы,
к примеру, другой, если бы вал был защемлен с одной стороны.
На свободном внешнем крае г = R напряжение сдвига т = 0 и
поэтому
Если же на краю имеется еще инертная масса, что-нибудь вроде
турбинных лопаток, то напряжения сдвига привносят момент, кото-
который обусловливает угловое ускорение лопаток. Тогда—т(/?) =
= ф(/?) • const, и имеем краевое условие ф' (/?)== С,со2ф (/<!). Здесь Сх
есть положительная постоянная и ш2 — собственное значение.
3.1)
§ 3. ДОПОЛНЕНИЯ
43
защемленного на одном
§ 3. Дополнения
3.1. Задачи на собственные значения и проблема ветвления.
Многие из рассматриваемых здесь задач являются «задачами ветвле-
ветвления». Поясним это на обсужденном в п. 1.1 примере потери устой-
устойчивости при продольном изгибе стержня,
конце и свободного на дру-
другом. Боковое смещение то-
точки приложения силы опре-
определяется значением постоян-
постоянной интегрирования В; при
этом обнаруживается пара-
парадоксальный результат: для
всех значений величины на-
Рис. 3.1. Боковое смещение точки прило-
приложения силы при прогибе со ласно теории
малых отклонений ( ) и согласно точ-
точной теории ( ) (не в масштабе).
грузки Р, отличных от кри-
критической, величина В должна
быть равной нулю, а для
критической нагрузки зна-
значение В может быть любым. Этот результат противоречив, так как,
согласно этой теории, при нагрузке, несколько превышающей кри-
критическую, снова было бы возможным лишь прямолинейное положе-
положение равновесия. Противоречие снимается, если вместо дифферен-
дифференциального уравнения A.1) использовать уравнение для конечного
прогиба у{х)
М = —
где р есть радиус кривизны упругой линии. Вместо A.2) тогда будем
иметь
у" Р
-1 z^^ —— ————— \) /О 1 \
Это уравнение уже не является линейным, его интегрирование при
постоянном а (х) возможно с помощью эллиптических функций!).
Уравнение C.1) при краевых условиях у@) = у'(/) = 0 снова имеет
для любого Р тривиальное решение у = 0, но, кроме того, от этого
решения в точках
ответвляются нетривиальные решения у(х); соответствующие боковые
смещения точки приложения силы показаны штриховыми линиями на
рис. 3.1. Штриховые кривые в «точках ветвления» имеют вертикаль-
вертикальные касательные, так что для достаточно малых прогибов штриховые
и сплошные линии совпадают. Дифференциальное уравнение задачи
') Н. Heinzerling, Mathematische Behandlung einiger grundlegender
Fragen des Knicksproblems des geraden Stabes, Diss., Karlsruhe, 1938, 39.
44
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[3.2
на собственные значения A.2) получается из C.1) путем «линеари-
«линеаризации», т. е. путем разложения по у и его производным и отбрасы-
отбрасывания всех нелинейных членов. Места ветвления при этом схваты-
схватываются точно. Вычисление собственных значений дает, следовательно,
места ветвления точно поставленной задачи, учитывающей конечные
деформации.
3.2. Системы дифференциальных уравнений. Постановка технических
задач на собственные значения часто приводит (ср. примеры в пп. 1.7,
1.8, 2.1) к системе обыкновенных
дифференциальных уравнений со
многими неизвестными, которые
можно свести к одному диффе-
дифференциальному уравнению высшего
порядка путем исключения неиз-
неизвестных. Назовем здесь в каче-
качестве другого примера задачу оп-
определения предела опрокидыва-
опрокидывания ребристой решетки '), нагру-
нагруженной изгибающими моментами
м2 м2
Ми М2 (рис. 3.2).
Для бокового отклонения т|
и обоих углов опрокидывания р,
и р2 при введении безразмерных
величин получаются дифференциальные уравнения
Рис. 3.2. Опрокидывание решетки под
воздействием изгибающих моментов.
= 0,
C.2)
где Af1 = |i,c3, Л12 = ц2Сз- При этом сь с2, с3 — заданные постоянные, зави-
зависящие от геометрических размеров, жесткости обоих брусьев и ребер. Не-
Независимой переменной является координата Ъ, в направлении одного из бру-
брусьев, штрихи означают производные по \. Если принять концы брусьев
с обеих сторон жестко защемленными, то имеем краевые условия:
р2 = 6, можно придать дифференциальным
i — На) б" + 4^1 V = 0,
Вводя величины Pi+p2 = Y. Pi —
уравнениям форму
Ci (Hi
с, (Ц. — Из) Ч" — 6" + с26 = 0.
Теперь у и 5 можно легко исключить и для ц получается уравнение вось-
восьмого порядка
+ r,vi (_ 4с2
(Зс2 -
- $ - 0. C.4)
') J. W e i n h о 1 d, Ober Kipplasten eines Holm — Rlppenrostes, Ing.-Arch.
9 A938), 411-419. S
3.41
§ 3. ДОПОЛНЕНИЯ
45
В граничных точках | = О и | = 1 выражения
г,, г,'. 2л'V + (ц? +14) V, 2r,VI + (ц? + $ Л1 V + 2с2 (ц? + HiH2 + $ < C-5)
то |ij выступает в качестве
равны нулю. Если подставить ц2 = const
собственного значения Я.
В то время как в случае системы C.2) собственное значение Я не вхо-
входит в краевые условия C.3), в случае дифференциального уравнения вось-
восьмого порядка собственное значение появляется в краевых условиях C.5).
В случаях |л, = |А2 и ц, = — и2 порядок уравнения снижается до шестого.
Для ц, = (.12 = К Л получается уравнение
C.6)
И ДЛЯ
— |Л2 = V к
В обоих случаях имеем шесть краевых условий:
Л @) = л' @) = г, A) = л' A) = T|IV @) + Л-п" @) = riiv A) + Яг," A) = 0.
3.3. Другие краевые условия, соотношение между значениями на
обоих концах. Могут иметь место различные краевые условия, отличные
Рис. 3.3. Краевые условия другого вида.
от содержащихся в §§ 1 и 2, например такие, которые вносят связь между
обоими краями. Если, скажем, при помощи каната, растянутого силой S,
задать равные амплитуды на краях в случае изгибных колебаний стержня
(рис. 3.3 слева), то краевые условия будут иметь вид
уф) = -уA), у" @) = у" (I) = 0,
Если в канат включить еще пружины и концы закрепить упруго (рис. 3.3
справа), то получим краевые условия:
У" @) = у" (I) = 0,
(ay"U_o = (Со + С2) у @) + С2у @; - (ау")'х=,, = (С, + С2) у (I) + С2у @).
3.4. Задачи на собственные значения для уравнений с част-
частными производными. Здесь кратко перечисляются некоторые типич-
типичные примеры без сколько-нибудь подробных выводов.
46 ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ C-4
Поперечные колебания однородной мембраны удовлетворяют урав-
уравнению d2w
с ^W==~W ( )
При этом да = да(л;, у, t) есть отклонение мембраны в точке х, у
в момент t; средняя плоскость мембраны в положении равновесия
перекрывает данную область 23 плоскости (х, у). Далее, с2 = р/р
есть частное от деления действующего в мембране напряжения р на
плотность р, a А =-г-j--|~ "XT— оператор Лапласа. Если, как в п. 2.1,
для собственных колебаний примем форму w(x, у, t) = z(x, у)еш,
где а» является круговой частотой, то при
получаем дифференциальное уравнение
— kz = Xz. C.9)
Кроме того, в качестве краевых условий имеем: в случае защемлен-
защемленного края 2=0, в случае упруго закрепленного края az -(-{5 -г— =0,
где аир — заданные на краях функции и п означает направление
внешней нормали.
При эллиптической форме мембраны целесообразно ввести эллип-
эллиптические координаты. Тогда возникает дифференциальное уравнение 1)
— Az = X (sin2 х -f sh2 у) z,
причем собственная функция z входит в правую часть, будучи ум-
умноженной на некоторую функцию веса.
В случае неоднородной массы или неравномерно напряженной
мембраны 2) имеем дифференциальное уравнение
- (Azx + Bzy)x — (Bzx + Czy)y = -Кг. C.10)
где А, В, С—заданные функции х, у; здесь нижние индексы х, у
означают дифференцирование, т. е., например, zx=-~—.
Дифференциальное уравнение четвертого порядка возникает,
в частности, в случае плоских колебаний:
Простейшими являются краевые условия:
2 = 0, -j- = 0 при защемлении
и 2 = 0, Аг = 0 в случае свободного опирания многоугольной об-
области.
') F. Pockels, Uber die partielle Differentialgleichung ku-\-№n-
Leipzig, 1891.
2) Handbuch der Physik, т. VI, Berlin, 1928, 381.
3.5]
§ 3. ДОПОЛНЕНИЯ
47
Вместо дальнейшего перечисления примеров укажем на подборку
их в таблице II, которая, равно как и таблица I, ограничивается
задачами нз механики. Рассмотрение других крупных прикладных
областей физики, таких как задачи на собственные значения в аку-
акустике, аэродинамике, учении об электричестве, ядерной физике и т. д.,
завело бы нас слишком далеко; назовем лишь в качестве одной из
наиболее известных задачу на собственные значения для уравнения
Шредингера i):
Дф_|_ £*£.[*,_£/(*. у. *)]ф = 0. C.11)
где т, h — постоянные, U (х, у, z) — потенциальная энергия, являю-
являющаяся заданной функцией координат, г|э — собственная функция и
% — собственное значение энергии. В качестве краевого условия имеем
равенство нулю ф на бесконечности.
В таблице II применяются те же обозначения, что и в'таблице I.
3.5. Упражнения. 1. Сформулировать задачу на собственные значения,
в частности, краевые условия, в случае сжатого стержня заземленного на
одном конце, при упругом закреплении на другом (х = 0J), '
см. рис. 3.4. Пусть с есть коэффициент жесткости упру-
гого закрепления, а (лг) — жесткость на изгиб стержня,
Р — искомая критическая сила. Собственным весом пре-
пренебречь.
Решение. Дифференциальное уравнение A.3) с крае-
краевыми условиями
у (/) = у' (I) = у" @) = 0; Ру' @) + су @) + (ау")^о = °-
Собственное значение % = Р появляется в последнем
из них.
2. Опертый на концах стержень длины / с постоян-
ной жесткостью на изгиб а и постоянной массой ц на еди-
ницу длины нагружен на расстоянии а от опоры массой М
(рис. 3.5) (мотор на балке). Составить трансцендентное
уравнение для собственных частот изгибных колебаний
(как в п. 2.3., пренебрегая побочными влияниями, напри-
мер продольными колебаниями и т. д.).
Решение3). Если обозначить прогиб в левом пролете у, (лг), в пра-
правом у2 (лг), то при % = —— = ft4 функции
у, = А{ sin kx-\-B{ sh kx, y2 = A2 sin k (I — лг) -j-S2 sh k (I — лг)
Рис. 3.4. Сжа-
тый стержень,
защемленный
на одном конце
и УпРУгОц за-
крепленный на
другом.
') Подробнее см. G. Joos, Lehrbuch der theoretischen Physik, изд. 3,
Leipzig, 1939, 605; Frank u. v. M i s e s, Differential u. lntegralgleichun-
gen, т. 11, изд. 2, Braunschweig, 1935, 992—1044 [Ф. Франк и Р. М и з е с.
Дифференциальные и интегральные уравнения математической физики, ОНТИ,
1937].
2) A. FOppl, L. FOppl, Drang und Zwang, т. 11, изд. 3, Munchen—
Berlin, 1928, 311 [А. Феппль и Л. Феппль, Сила и деформация,
т. II, ОНТИ, 1936] (там, правда, другой подход).
3) Подобная задача есть в книге К. Hohenemser, W. Prager,
Dynamik der Stabwerke, Berlin, 1933, 139, там она ставится, но не дово-
доводится до уравнения C.12).
48
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[3.5
удовлетворяют дифференциальному уравнению и краевым условиям. По-
Постоянные А\, б[, Аъ В2 исключаются при помощи переходных условий:
(«) = у2 (<*);
И ==
Ma2'
a >
Обозначая b = / — а, получаем для k характеристическое уравнение
sin ka sin kb sh &a sh kb 2ц
sin W sh kl ~ Mk '
Для а = 6 получается более простое уравнение
C.12)
3. Призматический стержень длины /, закрепленный на концах, как по-
показано на рис. 3.6, в середине и на правом конце подвергается действию
осевой силы Q. Вычислить критическое значение Q, т. е. значение, при пре-
превышении которого наступает потеря
устойчивости при продольном изгибе.
Решение. Поскольку стержень
имеет постоянную жесткоеть на изгиб а,
Рис. 3.5. Колебания изгиба
балки с сосредоточенной на-
нагрузкой.
Рис. 3.6. Задача о продольном
изгибе стержня при наличии двух
сжимающих сил Q.
дифференциальное уравнение упругой линии в каждом из двух про-
пролетов слева и справа от срединной нагрузки можно проинтегрировать
в замкнутом виде при помощи тригонометрических функций; исключение
постоянных интегрирования из краевых и переходных условий дает для
величины о = 1/ -2- -=• трансцендентное уравнение
бет ctg а + 3 У2а ctg (У2а) = 1.
Первые два корня a,, ff2. соответствующие собственным значениям, были
приближенно вычислены способом, отличным от приведенного здесь, в ра-
работе '):
2А2^1
= 6,506,
25,2.
4. Рассмотрим предыдущий пример, предположив, что в середине дейст-
действует сила Р вместо Q (следовательно, левая опорная реакция равна P + Q
') С. В. Biezeno, R. О г a m m e 1, Technische Dynamik, Berlin, 1939,
512 — 516 [К. Б. Бицено и Р. Граммель, Техническая динамика,
т. II, Гостехиздат, 1950].
3-51 § 3. ДОПОЛНЕНИЯ 49
вместо 2Q). Установим соотношение между Р и Q, необходимое для начала
потери устойчивости при продольном изгибе.
Ход решения как в предыдущем примере. Полагая
получаем
Q BР + Q) а2 ctg ff2 + (P + Q) (P + 2Q) °i ctg a, = P\
5. Составить трансцендентное уравнение для собственных частот в слу-
случае изгибных колебаний балки на трех опорах с длинами пролетов /, и /2
(рис. 3.7). Жесткость на изгиб а и масса ц на единицу длины на каждом
пролете постоянны, посторонними влияниями, как и в примере 2, пренебречь.
Результат. Применяя обо-
значения
Xf
можно записать искомое уравнение
в форме:
Рис. 3.7. Колебания изгиба балки на
трех опорах.
Здесь использованы введенные Хоэнемзер и Прагером ') табулированные
вспомогательные функции, которые оказываются пригодными во многих ко-
„ a лебательных задачах для отдельных
балок и целых стержневых систем:
Ж (х) = ch х sin x -f- sh x cos x,
58 (х) = ch х sin x — sh x cos x,
V2- \Х) = z ch х cos x>
<3 (х) = 2sh х sin л:,
35 (х) = ch jc cos л: — 1,
@ (jc) = ch x cos jc -|- 1.
C.14)
На рис. 3.9 и ЗЛО графически пред-
представлены функции @, 58, 3) и часто
Рис. 3.8. Колебания изгиба рамы. sg @
встречающиеся отношения -яг- и -тй-.
6. На рис. 3. 8 показана рама с жестким углом с высотой стойки /, и
длиной перекладины /2. Пусть на одном конце рама защемлена, а на дру-
другом закреплена шарнирно. Заданные жесткости на изгиб а,, а2 и массы
щ, ц2 на единицу длины полагаются постоянными. Определить сначала
в общем виде, а затем для частного случая — = —, /2 = 2/, собственные
Ct[ Ct2
частоты изгибных колебаний, снова пренебрегая, как в примере 2, посто-
посторонними влияниями.
') К. Hohenemser, W. Prager, Dynamik der Stabwerke, Berlin,
1933, 127 и далее. Там имеется также много других просчитанных примеров
для балок и систем стержней.
4 Л. Коллатц
50
ГЛ. I. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[3.5
X
у
?
да
7
1
/
/
/
/a>'
\
\
Ь
0
7
с
Ц
9
О
1
0
- 1
0
, о
5
я
I 7
Г
f
\
1
Ж^9 -/ihxsinx-shxcasx
У
\
\
1
/
/
1
D(x)=chx cosx-
6(x)=Zshxsinx
\
1
T
e
да'
P"
/
f
-^
I
\
\
1
\
/
/
t
;
\
x
x?
5
SB
f
/
/
t
? \
\
IK
7
\
6
1
33
/
1
SB
£
f
1
v
A
Рис. ЗЛО. Графическое представление функций -=г и -^-,
А) до
52
ГЛ. 1. ПРИМЕРЫ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
[3.5
Результат. Собственные частоты будут такими же, как в случае
балки с защемлением и двумя опорами по типу рис. 3.8. При использова-
использовании введенных в примере 5 частотных функций Хоэнемзер — Прагера и
примененных там же обозначений й,,
й2 уравнение для частот имеет вид
С,в
В частном случае -=-i- =
1 «.
получаем
а2
1=3м
н
8B*,)"
Рис. 3.11. Крутильные колебания
вала с двумя насаженными сосре-
сосредоточенными массами.
Из рис. 3.10 можно получить прибли-
приближенные значения для й, и улучшить
их при помощи таблиц Хоэнемзер —
Прагера. Для основного и первого
высшего колебаний получаем величины й, = 1,809 и соответственно 3,2804,
что позволяет вычислить частоты <в по формуле
k\ fa,
■~тк ^'
7. Крутильные колебания вала с сосредоточенными вращающимися мас-
массами. На однородном, с обеих сторон защемленном валу (рис. 3.11) наса-
насажены две сосредоточенные вращающиеся массы с моментами инерции масс 0t,
Рис. 3.12. Вид первых четырех соб-
собственных колебаний системы, показан-
показанной на рис. 3.11.
02 относительно оси вала. Необходимо вычислить собственную частоту со
крутильных колебаний. Пусть С — жесткость на кручение и в — момент
инерции массы на единицу длины вала, Сив постоянны.
3.51 § 3. ДОПОЛНЕНИЯ 53
Результат. Обозначая ради краткости
&2ы\ е, е2
-=% = &, л,=-7-, л2 = -Н7-)
с ■ "'"в/,
получаем для k трансцендентное уравнение
3 — 4 sin2 ft —|
Численный пример: Л, = 1, Л2 = 2. Тогда первые четыре корня уравнения
будут
ft, =0,64430, ft2 = 1,2539, ft3 = 3,326, ft4 = 3,730
н
Я, =0,41512, Я2 = 1,5721, Я3 = 11,06, Я4 = 13,91.
На рис. 3.12 показаны соответствующие им первые четыре типа собст-
собственных колебаний (угол у (х), на который поворачивается поперечное се-
сечение вала в точке х из положения равновесия). В точках крепления со-
сосредоточенных масс кривая у (х) терпит изломы. На концах у = 0. В слу-
случае основного колебания у всюду, кроме концов, отлично от нуля, первое
высшее колебание обнаруживает один, а второе — ровно три узла; замеча-
замечательно, что в данном примере отсутствует тнп собственного колебания
с двумя внутренними узлами.
ГЛАВА ВТОРАЯ
ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
Параграфы 4 и 5 содержат некоторые основные определения и
простые теоремы из теории задач на собственные значения и све-
сведения о функции Грина для обыкновенных дифференциальных урав-
уравнений, постоянно используемые в последующих главах. §§ 6 и 7
являются в основном обзорными и должны ознакомить читателя с не-
необходимыми сведениями из теории дифференциальных уравнений
в частных производных и интегральных уравнений.
§ 4. Основные сведения о задачах на собственные значения
Общее определение задачи на собственные значения'). Пусть
задано линейное однородное (обыкновенное или в частных произ-
производных) дифференциальное уравнение относительно функции z
одного или многих переменных х, хг. Коэффициенты, с кото-
которыми функция z и ее производные входят в дифференциальное урав-
уравнение, являются заданными функциями переменных хь ..., хт и па-
параметра К. Далее, на z налагается некоторое число линейных
однородных краевых условий, т. е. уравнений, которые являются
линейными и однородными относительно значений z и ее производ-
производных в каких-нибудь данных точках х, хг. Ищется значение
параметра Я^_ для которого существует некоторая тождественно не
равная нулю функция z, удовлетворяющая всем краевым условиям и
дифференциальному уравнению. Задачи такого типа называются зада-
задачами на собственные значения.
Вначале рассмотрим обыкновенные дифференциальные уравнения2).
4.1. Различные случаи распределения собственных значении.
В первой задаче на собственные значения, рассмотренной в п. 1.1,
') Говорят также о «собственных значениях» в случае матриц, интег-
интегральных уравнений и вообще других линейных однородных задач; здесь,
однако, в первую очередь и почти исключительно речь пойдет о собствен-
собственных значениях применительно к дифференциальным уравнениям.
2) В обыкновенных дифференциальных уравнениях вместо г будем ис-
использовать букву у.
4.1] § 4. ОСНОВНЫЕ СВЕДЕНИЯ 55
была получена бесконечная последовательность вещественных и даже
положительных собственных значений. Эта ситуация имеет место
в большинстве технических задач на собственные значения. Следую-
Следующие простые примеры показывают, однако, что отнюдь не в любой
задаче возникает такое «нормальное» распределение собственных зна-
значений; наличие такого распределения обеспечивается только при оп-
определенных предпосылках. Таким образом, указанный вопрос нуж-
нуждается в более подробном математическом исследовании.
Пример I. Случай отсутствия собственных значений. Рассмот-
Рассмотрим задачу на собственные значения
Здесь у (х) — искомая функция, штрихи означают производные по х1).
Внешне эта задача лишь незначительно отличается от задачи об изгибных
колебаниях стержня или продольного изгиба.
В случае дифференциального уравнения вида y'V = Ху мы имели
бы в точности уравнение изгибных колебаний стержня, защемленного
в точке х = 1 и свободного на другом конце {х = 0). Рассматриваемое
же дифференциальное уравнение D.1) и три из четырех краевых условий
такие же, как в задаче о продольном изгибе для такого стержня
(формулировка иная, чем в п. 1.1). Только четвертое краевое условие
у'" @) = 0 должно быть заменено условием (ау")^._0 =— Ху @) или, так как
у" @) = 0, условием ау0 = Ху^ \ В обеих названных физических задачах
мы, естественно, имеем нормальное распределение собственных значений,
в рассматриваемой же задаче, напротив, вообще нет собственных значений!
Итак, уже незначихельное. изменение условий задачи, мажет полностью из-
м£нить__распределение _србствешшхГГзнач¥нйи.
ДлТХ^ГТГ дифференциальное уравнение y'V = 0 имеет решение у = со+
-f- CiX-\-c2x2 -\-с3х3; при заданных краевых условиях это решение дает у=0
и потому отпадает. Для ХфО общее решение рассматриваемого дифферен-
дифференциального уравнения при X = k2 имеет вид
у = с, -)-с.2х -(— с3 sin kx-\-Ci cos *-*• D-2)
Краевое условие у" @) = 0 требует с4 = 0, а условия: у'" @) = 0, у' A) = 0,
у A) = 0 — требуют равенства нулю с3, сг и Ci соответственно, т. е. нет ни
собственных значений, ни собственных функций.
Пример II. Случай комплексных собственных значений. Рассмот-
Рассмотрим то же самое дифференциальное уравнение D.1), но с другими краевыми
условиями:
yiv = - Ху", у @) = у' @) = у" @) = у A) = 0.
При X = 0 имеем решение дифференциального уравнения снова в виде по-
полинома третьей степени, но краевые условия выполняются только для у = 0.
') Знак при X не имеет значения. Но вообще целесообразно записывать
дифференциальное уравнение так, чтобы у, y'V, ... имели положительные
знаки, а у", yvl, ... —отрицательные; тогда собственные значения в случае
«нормального» их распределения, как правило, положительны.
2) Пфлюгерв качестве проблемы продольного изгиба называет задачу
для стержня постоянного поперечного сечения, защемленного в точке х = 1
и свободного в точке х = 0, нагруженного на свободном конце силой, дейст-
действующей всегда в направлении касательной, т. е. силой, которая при откло-
отклонении изменяет направление и называется «следящей силой».
56
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
[4.1
При ХфО общее решение дифференциального уравнения, как и в примере 1,
имеет форму D.2). Краевое условие
у" @) = 0 дает с4 = 0,
у @) = 0 дает с, = 0,
у'@) = 0 дает c-2-{-kc3 — 0, т- е- c.2 = — kc3,
уA) = 0 дает —kc3 -\~c3 sin & = 0,
следовательно, если исключить случай с3 = 0 (ввиду у ф 0), то
sin k = k.
Это уравнение имеет в вещественной области только корень k = 0, отбро-
отброшенный выше, и, кроме того, комплексные корни, т. е. существуют только
комплексные собственные значения. Имеются и физические задачи, кото-
которые приводят к комплексным собственным значениям, например задача
о затухающих колебаниях струны [см. уравнение B.2) при 5 = const; К —
коэффициент затухания]:
Sy" = pFy -\-Ky. D.3)
Это же уравнение возникает и в других случаях затухающих колебаний,
например при крутильных колебаниях стержней и валов; укажем еще те-
телеграфное уравнение и т. д.').
Если решение имеет вид
у (х, I) = еиУ (х),
то D.3) переходит в
ш
или, с другими обозначениями (*,, k2 —
положительные постоянные):
у" = (А,Я2 + к.гХ) у.
При краевых условиях (длина струны
1 = \)
у@) = уA)=0
имеем решения
у = sin пях,
где
Рис. 4.1. Графическое предста-
представление к решению уравнения D.4).
Вычисляемые отсюда собственные значения являются вообще (например при
не слишком больших величинах k2) комплексными.
Пример III. Вхождение собственных значений в краевые условия.
Пусть в задаче на собственные значения
с краевыми условиями
У @) = 0, у A) = k (Я) у' A)
k (X) есть заданная функция Я. После подстановки в краевые условия об-
общего решения дифференциального уравнения вида
у = с, sin тх -f- c2 cos азх
') Ph. F r a n k, R. v. M i s e s, Differential- und Integralgleichungen, т. 1,
1930, 469 [Ф. Франк и Р. М и з е с, Дифференциальные и интегральные
уравнения математической физики, ОНТИ, 1937].
4.Ц
§ 4. ОСНОВНЫЕ СВЕДЕНИЯ
57
(здесь взято Л = со2) получаем трансцендентное уравнение для «
■ = k (a2).
D.4)
Точки пересечения
tgto
кривых -2— и
k (to2) дают собственные значения
(рис. 4.1). В зависимости от свойств функции k (Я) можно получить либо
бесконечное, либо конечное множество собственных значений, либо даже
ни одного (например, когда &(<в2)= — lj.
Пример IV. Появление кусочного спектра. Рассмотрим уравнение
Шредингера C.11) в частном случае одномерного периодического сило-
силового поля
у* +(£_£/(*)) у = 0. D.5)
Постоянный множитель при Е — U здесь принят равным единице, что воз-
возможно, если соответственно подобрать масштаб по оси х. Пусть потен-
потенциальная энергия U (х) есть заданная кусочно-непрерывная вещественная
периодическая функция с периодом а:
U (х -f a) = U (х).
Ищется собственное значение энергии Е, для которого дифференциальное
уравнение обладает тождественно не равным нулю решением у (х) и которое
при всех (вещественных) х остается ограниченным.
Используем ради наглядности матричное исчисление. Пусть гх-{х),
г2(х) — система фундаментальных функций уравнения D.5). Тогда в силу
периодичности дифференциального уравнения zx{x-\-a), z2(x-\-a) — также
решения; их можно, следовательно, представить как линейные комбина-
комбинации гх (х), z2 (x):
гх (х + а) = anzx (x) -f al2z2 (х),
г2 (х-\-а) = a2lzl (x) -\- a22z2 (х).
Вронскиан этой системы имеет независимую от х и отличную от нуля
величину
[ (■*) г2 (х)
г\(х-\-а) г'2{х~
следовательно,
Если ввести вектор-столбец
i
и матрицу коэффициентов
то D.6) можно записать так:
D.6)
z[ (х) z'2 (x)
— я12а21 = 1.
1
D.7)
\z2(x+ka)j
«21 «22
D.8)
St есть невырожденная матрица; D.8) действительно для всех целочислен-
целочисленных (также отрицательных) значений k.
Пусть х,, х2 есть характеристические числа матрицы St, т- е. в силу D.7)
корни уравнения
х2 — Fv. -\- 1 = 0, где F = au-\-a22. D.9)
Тогда из теорем матричного исчисления можно вывести:
и
1
~0
ч
1
' '
, ,
3
1
1
4\ х
|
, 1
58 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [4Л
1. Если l^l = | йц+а221 > 2, то корни х,, х2 вещественны, их произ-
произведение равно 1, т. е., например, если | х, | > 1, то | х21 < 1; 3tftfo при k ->со
или k -> — со неограниченно; соответствующая величина Е не является
в этом случае собственным значением.
2. Если | F | < 2, то хь х2 являются комплексно сопряженными, | v.x | =
= | х21 = 1; 8tftj0 при любом j0 остается ограниченным; каждое решение
уравнения D.5) является собственной
функцией; соответствующие величины Е
являются двукратно вырожденными соб-
собственными значениями.
3. При | F | = 2, т. е. при F = ± 2,
имеем xt = х2 = ± 1; имеется по мень-
меньшей мере один вектор $0, удовлетво-
удовлетворяющий равенству 41 j0 = ± з0, т- е-
решение у (х) уравнения D.5), обла-
обладающее свойством: у (х -\- а) = ± у (х).
Тогда имеет место равенство у (х-\-2а)=
Рис. 4.2. Периодический кусочно- = у (х).
постоянный потенциал. Обозначим непрерывную функ-
функцию F (Е) через F; области, в кото-
которых | F | < 2 и которые, следовательно, содержат континуум собственных
значений, будут ограничены величинами Е, при которых F = ± 2, и, таким
образом, существуют периодические решения с периодом а или 2а '). В каче-
качестве примера возьмем потенциал (см. рис. 4.2):
f 1 при 0< х < 1,
U(x) — { —1 при 1<х<2,
( £/ (.* -f- 2) при всех х
Введем сокращенные обозначения ук, у'к для у (й), у' (й), а также обо-
обозначим
а2 = £—1, 62 = £+1. D.10)
Тогда можно из у0 и у^ вычислить величины yv уь а затем и у2, у2:
У1 = Уо cos е-) sin a,
У[ = — уоа sin a~\-y'o cos а,
!
у2 = yt cos Ь -(- -т- sin 6 =
sin 6 cos а
/ , а \ /sin а cos 6 .
= у0 I cos а cos о г- sin а sin 6 Ы~ Уо i 1
= — y1b&inb-\-y[ cos b —
= y0 (— b sin b cos а — a sin a cos 6) -(- >'g I sin a sin b -\- cos a cos b I.
') В работе H. A. Kramers, Das Eigenwerlproblem im eindlmenslo-
nalen periodischen Kraflfelde, Physika, т. II, 1935, 483—490, доказывается,
что существует бесконечно много таких отдельных областей; см. также при-
пример в работе R. d e. L. К г о n i g, W. О. Р е n e e у Quantum Mechanics
of Electrons in Crystal Lattices Proc Royal Soc. London'A 130 A931), 499—513.
4.21
§ 4. ОСНОВНЫЕ СВЕДЕНИЯ
59
Возникающая здесь матрица
' а
cos a cos b — sin a sin b
b
II
— sin a cos b 4- -r s>n b cos a
—b sin b cos a — a sin a cos b sin a sin b 4- cos a cos b
a '
имеет в качестве характеристических чисел %ь х2 корни уравнения D.9), где
г = 2 cos a cos 6
ab
sin a sin b,
причем а и Ь, согласно D.10), выражаются через Е. На рис. 4.3 показана
зависимость функции F от Е. Для больших значений Е область \F\>2
становится очень малой; вблизи
Е = 10 эта область пример-
примерно определяется неравенством
9,85 < Е < 9,95.
4.2. Обозначения. Прос-
Простые примеры п. 4.1 показы-
показывают, что не во всех случаях
можно заранее получить инфор-
информацию с числе и расположе-
расположении собственных значений и Рис. 4.3: Континуум собственных зна-
с собственных функциях. По- чений в области 1F |< 2.
этому в последующем, ориен-
ориентируясь на технические проблемы, выделим вполне определенный
класс задач на собственные значения.
Пусть дифференциальное уравнение имеет вид
М [у] — XN [у], D.11)
где М [у] и N [у] суть линейные однородные обыкновенные диффе-
дифференциальные выражения типа ])
М[у]= S(—l
v=0
С4-12)
[у] == i (-l)v [gv (x)
v-0
(x)
f\
D.13)
Здесь fv(x) и gv(x) суть заданные, вещественные, v-кратнс непре-
непрерывно дифференцируемые функции 2).
') D.12) не является общим видом линейного однородного обыкновен-
обыкновенного дифференциального выражения, а охватьшает лишь частный случай
так называемых «самосопряженных» дифференциальных выражений.
2) Видно, что D.12) и D.13) являются типичными дифференциальными
выражениями для большинства дифференциальных уравнений на собственные
значения, возникающих в технических задачах; например, уравнение A.5)
получается при
a(x) = /2, G (*) = /„ /> = Я, /о = #о = О. #1 = 1-
60 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА D.2
Пусть т^> п; тогда, следовательно, 2т есть порядок дифферен-
дифференциального уравнения, а 2л — порядок выражения, умножаемого на X.
Далее предполагается
В зависимости от того, будет ли п = 0 или п > 0, рассмотрим
следующие два случая.
1. Случай га = 0: тогда N [у]=gQy. К этому случаю относятся
две группы задач в таблице I. Эти задачи назовем «частными зада-
задачами на собственные значения» ]).
2. Случай п > 0: в таблице I это — задачи третьей и четвертой
групп, которые называются «общими задачами на собственные зна-
значения».
К дифференциальному уравнению порядка 2т прибавляются еще 2т
линейных однородных краевых условий
^[)>]=0 (ц = 1, 2 2т). D.14)
Это—линейные однородные уравнения относительно значений у и
его производных вплоть до порядка Bт—1) в двух фиксированных
точках х=а и х = Ь.
Одно из этих условий имеет вид
2m-l
2 (avyW(a)-{-$vyW(b))=0,
где av и pv суть заданные вещественные, не равные одновременно
нулю постоянные (или также некоторые заданные функции собствен-
собственного значения X). 2т краевых условий D.14) должны быть линейно
независимыми.
Краевые условия подразделяются на главные и естественные 2):
Определение. Постараемся из возможно большего числа 2т
данных краевых условий D.14) устранить производные т-го и
высших порядков посредством линейных комбинаций этих усло-
условий. В результате получим k краевых условий, которые содержат
производные порядка не выше (т—1) и которые назовем «глав-
«главными краевыми условиями», в то время как ни из одного
из Bт — k) оставшихся краевых условий все производные т-го
и высших порядков не устраняются; последние называются «есте-
«естественными краевыми условиями».
') Здесь предполагается, что ^0 (х) Ф 0. В литературе обсуждается
также «полярный» случай, когда непрерывная функция ^0 (■*) меняет знак;
например, в работе Е. Кашке, Math. Z. 45 A939), 759.
2)Е. Катке, Math. Z. 48 A942), 67—100.
4.3] § 4. ОСНОВНЫЕ СВЕДЕНИЯ 61
Если, например, в некоторой задаче второго порядка1) (т = \)
имеют место краевые условия у (а) -\-у' (а) = 0, у ф)-\- 2у'(а) = О,
то можно посредством линейных комбинаций вывести новое краевое
условие. 2у(а) — уф) = 0, в котором первая производная больше не
встречается; однако нельзя установить никакие другие краевые усло-
условия, линейно независимые от только что названных, которые не
содержали бы никаких производных. В этом случае имеем, следова-
следовательно, главное краевое условие, а именно 2у (а) — у(Ь) = О, и есте-
естественное краевое условие, например у (а) -\- у' (а) = 0.
Содержащиеся в таблице I краевые условия уже разделены на
эти две группы.
Для удобства терминологии целесообразно в дальнейшем ввести
классификацию встречающихся функций. Установим следующие три
класса вещественных функций, из которых каждый последующий
представляет сужение (подмножество) предыдущего.
1. «Д опустим ые функции»-— удовлетворяют главным
краевым условиям и т-кратно непрерывно дифференцируемы.
2. «Функции сравнения»—удовлетворяют всем краевым
условиям и 2т-кратно непрерывно дифференцируемы.
3. «Собственные функции»—удовлетворяют всем крае-
краевым условиям и дифференциальному уравнению. Функция и ^ 0
при этом из всех трех классов исключается.
Примечание. Понятия «допустимые функции» и «функции сравне-
сравнения» устанавливаются здесь только для случая, когда собственное значение Я.
не входит в краевые условия.
4.3. Самосопряженность. Принятые до сих пор ограничения
все еще не являются достаточными. В примерах I- и II п. 4.1 диф-
дифференциальные уравнения имеют форму, определяемую выражениями
D.11) — D.13); однако мы не имели там нормального распределения
собственных значений. В обоих примерах причина этого лежит
в краевых условиях; в них нарушается свойство, называемое
') Для частных задач в литературе встречаются еще следующие обо-
обозначения:
В случае дифференциального уравнения второго порядка (т = 1) усло-
условия носят названия:
у (а) — у (Ь) = 0 краевых условий первого рода,
у' (а) = у' (Ь) = 0 краевых условий второго рода,
С\У (о) -\- С2>'' (о) — dvy (b) -f- d2y' (b) = 0 краевых условий третьего рода или
также условий Штурма.
В книге С. В. В i e z e n о. R. Gramme!, Technische Dynamik, Berlin,
1939, 136 [К. Б. Б и цен о и Р. Г р а м м е л ь, Техническая динамика, т. I,
Гостехиздат, 1950] в задачах второго и четвертого порядка в связи с меха-
механическими представлениями главные краевые условия названы геометри-
геометрическими, а естественные — динамическими.
62 ГЛ. П. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА И-3
в последующем «самосопряженностью». Это свойство в дальнейших
исследованиях будет очень часто использоваться ').
Пусть а, Ъ есть интервал, в котором, рассматривается дифферен-
дифференциальное уравнение задачи. Обычно х—а и х — Ь являются точками,
которые входят в краевые условия. Тогда имеем
Определение самосопряженности. Рассматриваемая
задача на собственные значения D.11), D.14) называется само-
самосопряженной, если для двух любых функций сравнения и, v
справедливо
ь ь
\ (uM[v] — vM[u])dx = 0, J (uN[v] — vN[u])dx = O. D.15)
Является рассматриваемая задача на собственные значения само-
самосопряженной или нет, легко установить при помощи интегрирования
по частям.
Например, задача на собственные значения
является самосопряженной; здесь А и В — заданные числа. А именно,
для двух функций и, v, удовлетворяющих граничным условиям, имеем
i i
J {и (—v") — v(— и") dx = [— uv'-i- vu'\[ + J (u'v'-v'u')dx = 0,
о
так как если подставить
и' @) = Аи @), и' (I) = Ви (I),
то все сокращается.
Вообще самосопряженность можно дополнительно проверить при
помощи интегрирования по частям следующим образом.
Образуем на основе D.15) выражение
b m
J uM [v] dx = J и 2 (-l)v [Д (х) vWf> dx.
a- v=>0
') Название «самосопряженный» происходит из теории, в которой
каждому обыкновенному линейному дифференциальному уравнению сопо-
сопоставляется его «сопряженное» уравнение. Мы здесь не будем углубляться
дальше в эту теорию.
4.3] § 4. ОСНОВНЫЕ СВЕДЕНИЯ 63
Выделяем один из членов суммы и применяем v-кратное интегриро-
интегрирование по частям:
ь
(-Dv J B[/v(*)tKv>]<v>rf* =
a
b
(v-1)]* + (-l)v-1 J u'[fv
b
+ J u.Wfv(x)vWdx. D.16)
a
b
Точно так же преобразуем соответствующий член в vM [и] dx и,
а
так как интегралы справа взаимно сокращаются, получим в правой
части только краевой член ]):
ь
(-1)V | {и [/vtKv>f> _ „ [/vB(v)](v)} dx =
а
rv-1 6
= S(-1)V+Pf"(P) l/vW^r1"'1-^1 [/,W«M]M"P|1 •
Lp-o Ja
Такие суммы должны быть образованы для каждого члена диффе-
дифференциального выражения и просуммированы по v. Тогда получается
так называемое преобразование Дирихле 2)
ь
\ (иМ [v] — vM [и] )dx =
а
Г т v-1 -|й
Lv-o p-o Ja
D.17)
') Как это обычно принято в записи сумм, сумма для v = 1 означает
только член с р = 0, а для v = 0 сумма является пустой и заменяется
нулем.
2) П. Г. Дирихле, немецкий математик, родился 13 февраля 1805 г.
в семье почтового служащего в Дюрене (район Аахена), жил долгое время
(до 1822 г.) в Париже, в 1827 г. стал доцентом университета в Бреслау,
в 1829 г. переселился в Берлин, в 1832 г. стал экстраординарным и в 1839 г.
ординарным профессором математики Берлинского университета; с 1832 г.—
член Берлинской академии наук, после смерти Гаусса в 1855 г. — профессор
в Геттингене, где умер 5 мая 1859 г.
64 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [4.4
Если краевые условия таковы, что сумма обращается в нуль как для
дифференциального выражения М, так и для N, то задача является
самосопряженной. *
Большинство задач таблицы I самосопряженные, но не все. Исклю-
Исключение составляет, например, задача об изгибных колебаниях «летя-
«летящего» вала с гироскопическим эффектом, снабженного диском на
конце.
Далее, все задачи таблицы VII, поскольку краевые условия ого-
оговариваются, являются самосопряженными, и нет необходимости для
каждой задачи этого типа делать проверку на самосопряженность.
Обсудим некоторые простые следствия самосопряженности.
4.4. Обобщенная ортогональность. Будем исходить из пред-
предположения, что задача на собственные значения D.11), D.14) имеет
собственные значения X и собственные функции у и является само-
самосопряженной. Пусть Х[ и Xk — два различных собственных значения
с соответствующими им собственными функциями yt и yk. Таким
образом,
M
Тогда, имея в виду, что собственные функции являются и функциями
сравнения, из самосопряженности получаем
а
или, используя дифференциальное уравнение для собственных функций,
ь ь
[yk] dx-lij ykN [yt] dx.
О = h J
Оба интеграла равны (опять же вследствие самосопряженности), сле-
следовательно,
а
Таким образом, в силу того, что 'kk=/='kl, следует
ь
J ytN [yk\ dx = 0, li=f=%k. D.18)
a
Две заданные в интервале а, Ъ интегрируемые функции ty(x), ф(х)
ь
называются «ортогональными», если <po]? £/дг = 0. Так как в нашем
4-41 § 4. ОСНОВНЫЕ СВЕДЕНИЯ 6!>
случае имеем не просто
ь ь
\ У(Ук d* = 0. но J y,N \yk] dx = 0,
a a
то говорят, что функции yt и yk являются «ортогональными
в обобщенном смысле».
Если заменить в случае Xk Ф 0 в D.18) N[yk] на у— /И[)к], то
получим
J = 0, h^K- D.19)
Это равенство действительно также в случае Xk = 0, так как тогда
Теорема. £сли задача на собственные значения М \у] = XN \у]
с краевыми условиями U^ [у] = 0 является самосопряженной и
имеются два не равных друг другу собственных значения Xt, lk
с соответствующими им собственными функциями yt, уъ, то
последние ортогональны в обобщенном смысле, т. е. для них
действительны соотношения D.18), D.19).
Частные случаи. В частных задачах на собственные значе-
значения М [у] = XgQ(x)y соотношение ортогональности имеет вид
ь
\ O, К + Ч- D-20)
Здесь, следовательно, функции К^о!-^ и VlS'oli'ft ортогональны
в обычном смысле.
Если N [у] имеет частный вид [gn (x) Уп>](п) и в краевые условия
входит требование, чтобы у, у' y(«-]) были равны нулю на обоих
краях а и Ь, то в результате «-кратного интегрирования по частям
получаем
ь ь
Q, lt^lk. D.21)
В этом случае, таким образом, функции |Л gn I yW ортогональны
в обычном смысле.
Пример обобщенной ортогональности. Задача о про-
продольном изгибе двусторонне защемленного стержня длины / = 1 (см. п. 1.2)
формулируется в виде yiv = — Ху"; у @) = у' @) = у A) = у' A) = 0.
Нечетные собственные значения А,, А3, А5, ... определяются формулой
(г=1, 2, 3, ...)
5 Л. Коллатц
66
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
14.5
а четные — соответственно формулой
л. — Az1 (г — 1 2 3 1
где гг суть положительные корни трансцендентного уравнения tg г = г.
Собственные функции, соответствуюдие нечетным собственным значе-
значениям, не меняют знак в основной области; здесь, таким образом, орто-
ортогональность в обычном смысле уже не имеет места. Например, уь у3 явно
не ортогональны. Однако вполне
справедливо D.18):
1
Г "
В этом случае в силу условий
у. @) = у. A) = 0 можно записать
1
J у'Ук dx = 0,
о
Рис. 4.4. К задаче о продольном из- f
гибе. Функции у, и у] образуют ор- т- е- У,- образуют ортогональную си-
тогональные системы. стему^ функций (рис. 4.4). Кроме того,
все у; по той же причине ортого-
ортогональны функции и = 1. Равенство D.19) показывает, что функции у; также
образуют ортогональную систему.
4.5. Вещественность собственных значений. Выясним, может ли
зздчча на собственные значения D.11), D.14), которую мы пред-
предполагаем самосопряженной и в которой, как и во всех ранее рас-
рассмотренных задачах, все коэффициенты дифференциального уравне-
уравнения и краевых условий вещественны, иметь комплексные собственные
значения.
Некоторой вещественной собственной функции у, для которой
N [у] ф 0, обязательно соответствует вещественное собственное зна-
значение. Поэтому комплексному собственному значению X = s-\-lt (где
s, t вещественны, гФ§) при Ы[у]фО обязательно соответствует
комплексная собственная функция у (х) = и (х)-\-tv (х) (где и, v —
вещественны). Тогда вследствие вещественности коэффициентов диф-
дифференциального уравнения и постоянных краевых условий комплексно
сопряженная величина X = s — it является также собственным значе-
значением, соответствующим собственной функции у = и — iv. Вследствие
предполагаемой самосопряженности имеем
ь
0 = J (yM[y\~yM\y])dx.
а
Поскольку имеют место соотношения
M[y]=lN[y], М[у] = Ш[у],
«•51 § 4. ОСНОВНЫЕ СВЕДЕНИЯ 67
ТО
ft ft
О = 1 J yN [у] dx — kjy~N [у] dx
а а
или, опять в силу самосопряженности,
ft
0 = (k—X)^yN\y]dx. D.22)
а
Кроме того, имеем
%-% = — Тй.
Значит, если интеграл yN [у] dx Ф О, то из этого следует t = О,
а
т. е. собственные значения могут быть только вещественными. В силу
условия
N [и — iv] = N\u] — IN [v]
этот интеграл можно представить так:
ft
J (и + Iv) N \и — (V] dx =
а
ft ft ft
= J uN [и] Лс -И J («Л/ [м] — uN [v] )dx-\- \ vN [v] dx.
a a a
Здесь мнимое слагаемое равно нулю, так как и вещественная и, и
мнимая v части у являются функциями сравнения. Рассматриваемый
интеграл, следовательно, имеет вид
yN [у] dx = | («W [и] + z>N [z/]) dx.
a
В частной задаче на собственные значения, когда N [y]=go(x)y, он
принимает значение
и, так как тождественное равенство нулю и и v исключается, он
отличен от нуля, если go(x) имеет постоянный знак. Тогда все
собственные значения вещественны. Вообще действительна
Теорема. Если задача на собственные значения D.11), D.14)
имеет вещественные коэффициенты, является самосопряженной
68
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
[4.6
b
и интеграл uN [и] dx для всех функций сравнения сохраняет
а
один и тот же знак, то все ее собственные значения вещественны.
Последняя предпосылка выполняется, например, в частной задаче
на собственные значения, если gn(x) имеет постоянный знак.
4.6. Формула Дирихле. Для более подробного исследования
предпосылки, появившейся в последней теореме, естественно напра-
напрашивается мысль об общем рассмотрении интегралов
ь ь
\ иМ [и] dx и | uN [и] dx.
а а
Их можно преобразовать, точно так же как интеграл в D.15), при
помощи интегрирования по частям. М [и] означает сумму D.12), и
из этой суммы, как в п. 4.3, выделяется один член. Результат инте-
интегрирования по частям имеет вид [он содержится уже в D.16), если
там подставить и = v]
ь
(-If
Tv-1 -j* S
= 2j (~1)V+P uip) [/v«'v)i(v p) + J
Lp-0 Ja a
При суммировании по v получается так называемая формула Дирихле
Ь ь т
J иМ [в] dx = J J] /v(вМ)*rfx-f MQ [u].
D.23)
где
о v-0
Г т v-1
VI VI
Мо \и] называется краевым выражением Дирихле.
Точно так же для N [и] можно вывести формулу
ь ь п
J uN [и] dx = J ^ ^v («MJ dx -+- Wo [в],
D.24)
a v—U
где Nn [и] — краевое выражение Дирихле, образованное так же,
как и Мо [и].
Пример. Для уже рассмотренной в п. 4.3 задачи на собственные
значения
— у" = Ау. у'@) = Ауф), у'A)=*ВуA)
можно получить путем однократного интегрирования по частям в качестве
1.71 § 4. ОСНОВНЫЕ СВЕДЕНИЯ 69
результата формулу Дирихле
J м(— u")dx= [м (—«')](,— [ — u'u'dx = Г u'2 dx — But (/) + Ли2 @).
о оо
D.25)
При этом Af0 [и] = — fiu2 (/) -)- Ли2 @) есть краевое выражение Дирихле.
При более простых краевых условиях (у или у' на краях равно нулю)
оно бы исчезло, но здесь это выражение появляется (н должно быть, напри-
например, принято во внимание при применении метода Ритца, см. § 15).
4.7. Одночленный класс. Вещественность собственных значений
гарантируется, согласно теореме п. 4.5, если, кроме самосопряжен-
ь
ности задачи, выполняется еще предпосылка, что uN [и] dx coxpa-
а
няет постоянный знак для всех функций сравнения. Эта предпосылка
выполняется не только в случае частных задач на собственные зна-
значения, но и в случае более обширного класса задач, так называемого
«одночленного класса». Эти задачи образуют важный особый класс
общих задач на собственные значения, с которым мы часто будем
встречаться.
Определение одночленного класса. Задача на соб-
собственные значения вида D.11)— D.14) принадлежит к одночлен-
одночленному классу, если: 1) дифференциальное выражение N [у], кото-
которое является множителем при собственном значении X, состоит
только из члена
() D-26)
и 2) краевые условия D.14) таковы, что для двух любых функций
сравнения и, v действительно равенство
ь ь
j uN [v] dx= J gn (x) a(«W> dx. D.27)
a a
Пояснение. Таким образом, в случае одночленного класса
дифференциальное уравнение имеет вид
M[y]=l(-l)"[gn(x)y("n{n). D-28)
Условие D.27) в каждом отдельном случае всегда может быть легко
проверено при помощи интегрирования по частям (преобразование
Дирихле согласно п. 4.3); например, D.27) наверняка выполняется,
если краевые условия таковы, что на краях y(i) [g„y{n)f" =0
при / = 0, 1, 2 я— 1.
Одночленный класс, естественно, содержит частные задачи на
собственные значения, т. е. задачи М [у] = Xgoy с любыми краевыми
70 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [4.8
условиями; далее, задачи М [у] = — h(gx (х)у')', если краевые усло-
условия таковы, что уу' на краях равно нулю. В таблице I задачи
третьей группы принадлежат к одночленному классу.
Согласно формуле Дирихле D.24) в задачах одночленного класса
краевые выражения Дирихле, относящиеся к дифференциальному
выражению N [и], равны нулю, и из D.27) непосредственно следует
J uN [и] dx= [ gn (uWf dx
для всех функций сравнения а. Так как в соответствии с пред-
предпосылкой, принятой в п. 4.2, функция gn(x) имеет постоянный знак,
справедлива
Теорема. В случае самосопряженных задач одночленного
класса, в которых для любых функций сравнения и^фО1), все
собственные значения вещественны.
4.8. Пример самосопряженной задачи с невещественными
собственными значениями. В примерах п. 4.1, в которых появляются
невещественные собственные значения, задачи были несамосопряжен-
несамосопряженными. В теоремах пп. 4.5 и 4.7 о вещественности собственных зна-
значений самосопряженность была существенной предпосылкой. На вопрос
о том, может ли самосопряженная задача вообще иметь только веще-
вещественные собственные значения, следует ответить отрицательно. До-
Докажем это при помощи построения обратного примера. Возьмем
в качестве дифференциального уравнения для самосопряженной задачи,
не принадлежащей к одночленному классу, следующее:
(ЛуТ - (/УУ + /оу = ^ {- (gy)' +£оуЬ D-29)
Чтобы обеспечить самосопряженность подходящими краевыми усло-
условиями, положим
У(—!) = /(-!) = УA) = У'О) = 0.
Этим краевым условиям, например, удовлетворяет функция
y = (x2—\Jh(x),
где h (x) четырежды непрерывно дифференцируема во всем замкнутом
интервале (—1, -|-1). Функция h (x) должна быть комплексной, если
собственное значение к будет комплексным. Выберем h (х) == х2 -\-i;
таким образом,
') Как показывает пример II п. 5.7, нельзя отказаться от требования,
что для всех функций сравнения и.(п)ф0. Там и'гзО для функции сравне-
сравнения и = 1 и каждое число К (в том числе любое комплексное число)
является собственным значением,
4.S) § 4. ОСНОВНЫЕ СВЕДЕНИЯ 1\
Теперь можно легко указать уравнение типа D.29), которому удовле-
удовлетворяет у, представляя /v и gv в виде полиномов. Вычисление пока-
показывает, что у удовлетворяет следующему уравнению с невеществен-
невещественными собственными значениями'):
1 Г/—146 , , о1 „ _\ ,Л" . 1 Г/1891
[(x4 + 21v2 5)у "J +
_\ ,Л" . 1 Г/1891 2 ,\ ,1'
— 5)у "J + 2"Ц-ГХ ')у J
121)yT+189y}.
4.9. Определенность задачи на собственные значения. Опре-
Определение. Задача на собственные значения называется «опре-
«определенной», если все собственные значения являются веществен-
вещественными и имеют один и тот же знак. Она называется «положительно
определенной», если все X > О, и «отрицательно определенной»,
если все X < 0. Задача называется «полуопределенной», если среди
собственных значений встречается также число нуль, но все
остальные собственные значения имеют один и тот же знак.
Введем, далее, понятие «полностью определенной за-
задач и».
Определение. Задача на собственные значения с уравне-
уравнением D.11) называется полностью определенной, если-для каждой
функции сравнения и выполняются неравенства
ь ь
[ uM[u]dx>0 и [ uN[u]dx>0. D.30)
а а
В этом случае верна
Теорема. Полностью определенная задача на собственные
значения является положительно определенной.
Например, если Xk есть собственное значение полностью опре-
определенной задачи, соответствующее собственной функции yk, то ра-
равенство
тождественно выполняется для всех х, и из этого равенства путем
■) В этом примере принятое в п. 4.2 требование gn (x) Ф 0 выполняется
в основном интервале —1<л;<1. Если отказаться от этого требования,
то то же самое положение вещей имеет место в следующем примере
(сообщенном мне Виландтом): самосопряженная задача на собственные зна-
значения
имеет собственные значения Я = i, соответствующие собственным функциям
у = /-(- cos х.
72 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
интегрирования обеих частей в интервале a, b получаем
I dx
J Vй [У*]'
у а
у JV [у. | dx
J
а
При названных предпосылках отношение
ь
Г иМ [и] dx
Г uN [и] dx
D.31)
которое называют «отношением Рэлея»'), может принимать только
положительные значения, если и есть некоторая функция сравнения *).
А так как все собственные функции являются функциями сравнения,
то в силу равенства R [ук] = Х,А все собственные значения поло-
положительны.
Если к интегралам отношения Рэлея применить формулу Ди-
Дирихле, то получим
Ь т
J У^/А^\^х + М0[и]
a v-0
Из этого представления можно непосредственно получить достаточные
условия определенности задачи, полагая, например, слагаемые в чис-
числителе и знаменателе порознь положительными. Это дает2) следующее
Определение. Самосопряженная задача на собственные зна-
значения D.11) — {АЛА) называется К-определенной, соответственно
') Джон Вильям Стретт (с 1873г. лорд Рэлей) родился
12.XI 1842 г. в Лэнгфорд Гров (Эссекс), с 1869 г.—член «Тринити колледжа»
в Кэмбридже; в 1879 г. стал преемником Максвелла в качестве профессора
экспериментальной физики в Кэмбриджском университете. В 1877 г. завер-
завершил работу «Теория звука». С 1873 г. — член Лондонского королевского
общества. Умер 30. VI 1919 г.
*) Выражение R [и] сопоставляет каждой функции сравнения и неко-
некоторое число и, следовательно, согласно современной математической терми-
терминологии, является функционалом.
2) Е. Kamke, Math. Z. 48 A942), 71.
1.91 § 4. ОСНОВНЫЕ СВЕДЕНИЯ 73
К-полуопределенной, если все функции Д, и gv неотрицательны
и краевые выражения Дирихле Мо [и] и N0[u], рассматриваемые
как квадратичные формы относительно значений и, и', и", . ..
[(см. D.23), D.24)], принимаемых ими на краях, являются
положительно определенными, соответственно полуопределен-
полуопределенными.
В этом случае действителен
Достаточный критерий. К-определенная задача на соб-
собственные значения является одновременно определенной.
/С-определенность легко проверяется.
Кроме формулы Дирихле, имеются также другие преобразования,
при помощи которых может быть проверена определенность задачи.
Например, задача о колебаниях балки, изогнутой по дуге окруж-
окружности (см. таблицу I),
— yvi -f 2yiv — у" = I (— у" + у)
с краевыми условиями
у (а) = у' (а) = у" (а) = у ф) = у' ф) = у" ф) = О
или
у (а) = у' (а) = у"' (а) = у (Ь) = у' ф) = у'" ф) = О
является положительно определенной, ибо с учетом краевых условий
интегрирование по частям дает
ь ь ь
J иМ [и] dx = J и (— Bvi -f 2«iv — и") dx = I" (и'" — u'f dx > 0.
d a a
Знак равенства может иметь место только при условии и'"— и'^0.
Следовательно, и должно быть решением этого дифференциального
уравнения и иметь, таким образом, форму
и == cl -f-
где С], с2, с3 — постоянные. Но тогда вследствие краевых условий
и==0. Поэтому для каждой функции сравнения имеет место нера-
неравенство ,
ь
J uM[u]dx>0,
а
Так как одновременно
ь
[ uN\u}dx>0,
а
то отсюда следует положительная определенность задачи.
74
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
D.9
Пример. Самосопряженная частная задача на собственные значения
- у" = Ау, у' @) = Ау @), у' (t) = By (t),
согласно теореме п. 4.5, имеет только вещественные собственные значения.
В п. 4.6 для этого примера уже была записана формула Дирихле. Согласно
D.25) краевое выражение Дирихле имеет вид
M0M=>-But(l)+Au*@).
Для А > 0, В < 0 имеем Мо [и] > 0. Следовательно, задача при этом является
/(-определенной, а все собственные значения заведомо неотрицательны.
Расчет простой задачи при А = k2, когда общее решение дифференциального
уравнения (постоянные интегрирования сь с2)
у = с, sin kx -\- c2 cos kx
подчинено краевым условиям, дает для k трансцендентное уравнение
U 1 Л D\
D.33)
При любых А и В получается бесконечное множество положительных соб-
собственных значений А. В каких случаях могли бы появиться отрицательные
/Г-т/ге-
Велены
Рис. 4,5- К графическому решению Рис. 4.6. К примеру п. 4.9,
уравнения D.34). А—В — области с отсутствием, с
одним и с двумя отрицательными
собственными значениями.
собственные значения А? Тогда k можно записать в виде k = ir и, так как
tgi7r = ith/r, уравнение для г принимает форму
Подставим / = 1 и найдем точки пересечения кривых thr и h(r) = -^ '-.
Для А > 0 и В < 0 кривая Л (/-) имеет форму / (рис. 4.5); в этом случае,
следовательно, нет ни одной точки пересечения при г Ф 0, а значит, ни одного
отрицательного собственного значения. Далее возможны еще кривые типов //
(ни одного к < 0), /// и IV (по одному к < 0), V (два А < 0). Тип VI при
вещественных .Д и В не имеет места. Плоскость АВ разделяется на области
с двумя, одним и совсем без отрицательных собственных значений. В част-
частности, видно, что область Д'-определенности [квадрант А > 0, В < 0 (рис. 4.6)]
не распространяется на всю область положительных собственных значений,
следовательно, данный выше достаточный критерий определенности не
является одновременно необходимым.
5.1] § 5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИЙ 75
§ 5. Функция Грина для обыкновенных
дифференциальных уравнений
Для дальнейшего понадобятся некоторые сведения о функциях
Грина. Ниже они будут кратко рассмотрены и, для начала, вне зави-
зависимости от задач на собственные значения').
6.1. Определение функции Грина. Пусть
v E.1)
v=o
есть некоторое линейное дифференциальное выражение, порядок кото-
которого k может быть четным или нечетным. Функции pv(x) предпола-
предполагаются непрерывными и pk{x) для всех х отличны от нуля. Пусть,
далее, рассматривается неоднородная краевая задача, в которой при
заданной непрерывной функции г (х) надо найти решение неоднород-
неоднородного дифференциального уравнения
Цу] = г(х), E.2)
которое удовлетворяет краевым условиям, как в D.14):
^[У]^0 (И=1. 2 k). E.3)
Попытаемся построить функцию G (х, £), так называемую «функцию
Грина»2) (именуемую также «функцией влияния»), которая разрешает
краевую задачу в форме
ь
\,l)r{l)dl E.4)
для любой заданной функции г (х).
Функция Грина G (х, |) определяется посредством следующих
условий:
1. G как функция | при фиксированном х из интервала
а < | < b удовлетворяет однородному дифференциальному урав-
уравнению L [G] = 0 при всех х Ф |. В каждой из двух треугольных
областей а^.х<^£<!# и а^^^х^.Ь (рис. 5.2) G обладает
частными производными
= 0. I. 2.....A).
и эти производные в каждой из "этих областей являются не-
непрерывными функциями х и \.
') Литература к § 5: Е. L. I n с е, Ordinary Differential Equations, London,
1927, 205; E. К a m k e, Math. Z. 46 A940), 234, 244; E. К a m k e, Differen-
tlalgleichungen: L6sungsmethoden und LOsungen, т. I, изд. 3, Leipzig, 1944,
188. [Э. Камке, Справочник по обыкновенным дифференциальным урав-
уравнениям, М., «Наука», 1965; см., например, Ф. М. Морс и Г. Фешбах,
Методы теоретической физики, т. I, ИЛ, 1958. ]
2) Грин Джордж A793—1841) — английский физик-теоретик.
76
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
E.1
2. G как функция х удовлетворяет краевым условиям
UVL[G] = O.
3. G для х = | при а < £ < b непрерывна со своими производ-
производными по х вплоть до (k — 2)-го порядка, в то время как про-
производные (k—\)-го порядка испытывают скачок на величину —тгт.
Обозначив
dv0 (х, l)
dxv
E.5)
имеем
G(x, I), G'(x, I) G{k-2)(x, I)
непрерывны при х = |
e->0
tj"'
или, в более краткой записи,
Рис. 5.1. Коэффициент
влияния (прогиб в точ-
точке х под влиянием еди-
единичной нагрузки в точ-
точке I) в качестве функ-
функции Грина.
E.6)
Вопрос об условиях существования функ-
функции Грина G(x, |), удовлетворяющей всем
выдвинутым здесь требованиям, будет иссле-
исследован в п. 5.3.
Пример. В некоторых физических задачах почти непосредственно
очевидно, как получить функцию Грина. Рассмотрим в качестве при-
примера балку длины / на двух опорах, нагруженную на расстоянии % от
левой опоры единичной силой (рис. 5,1). Тогда функция Грина О (дг, \) равна
прогибу у\ (х): О (х, |) =» г\ (х) при единичной нагрузке в точке | есть «функ-
«функция влияния» е (х, I). Поперечная сила Q » — (aTf)' в точке нагрузки х => g
испытывает скачок единичной величины, или прн постоянном а, т)'" испы-
испытывает скачок на величину 1/а, в то время как т), г|', ц" в точке * = £
непрерывны. Дифференциальное уравнение для прогиба г\ (х) при плотности
нагрузки р (х) имеет вид
(алТ »/><*)•
Краевые условия: т| и г\" равны нулю при х = 0 и х = /. r\ == G (x, g) удо-
удовлетворяет однородному дифференциальному уравнению (aTi")" = 0, за исклю-
исключением точки приложения нагрузки х = £, и краевым условиям.
Если вместо единичной силы действует нагрузка р (£) Д£, то прогиб
равен О (лг, £)/>(£) Л£, а если по всей балке распределена нагрузка с интен-
интенсивностью р (£), то полный прогиб будет
Л (■*)
= J °
Р (I)
т. е. становится очевидным, что при помощи функции Грина можно полу-
получить решение неоднородной краевой задачи в указанной интегральной форме.
5.21 § 5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ УРАВНЕНИЙ
77
5.2. Вывод формулы решения для краевой задачи. Положим,
прежде всего, что для нашей краевой задачи E.2), E.3) имеется
функция Грина О(х, |), которая удовлетворяет выдвинутым в п. 5.1
условиям, и покажем, что тогда функция F{x), определяемая инте-
интегралом
ft
есть решение у(х) указанной задачи. Дифференцируя эту функцию
и используя обозначение E.5), имеем
* ь
F' (х) = J О' (*, I) r (I) <Ц. F" (х) = J G" (х, I) r (I) dl, ...
ft
J
При последующем дифференцировании необходимо учитывать, что
G^k~x\x, \) в точке х = \ испытывает скачок, соответственно чему
интервал интегрирования от а до b точкой х подразделяется на два
интервала:
Здесь [Gik~l)(x, i)]j-Jt_(, есть предельная величина, причем I меньше,
чем х, и стремится к х слева. Для этого предела можно также
записать [О'**^, 4)]^._t+0. так как (к— 1)-я производная О по х
в области а <! | <! х ^.Ь предполагается непрерывной функцией х
и | (эта производная для х = \ принимается «односторонней»). Теперь
можно использовать соотношение разрывности E.6), из чего следует
/=■(*) (х) =
(х,
При подстановке в дифференциальное уравнение E.1) получаем
v=U
Pv(x)
v-0
dxv
78 ГЛ. It. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА E.3
Интеграл в правой части исчезает, так как О удовлетворяет одно-
однородному дифференциальному уравнению L [О] = О Х); следовательно,
имеем L[F] = r(x). Далее, F(x), так же как и О(х, |), удовлетво-
удовлетворяет всем краевым условиям и фактически является, таким обра-
образом, решением рассматриваемой краевой задачи. Вместе с тем,
однако, еще нельзя сказать, является ли F(x) единственным решет.ем
задачи.
Если имеется несколько, т. е. по крайней мере два, различных
решений, например Fx (х) и F2(x), то их разность г(х) = /71(х) —
— F2(x) является тождественно не равным нулю решением анало-
аналогичной E.2), E.3) однородной задачи:
L{z] = 0. и^1г]=0.
Если бы можно было показать, что эта однородная задача имеет
только решение z = 0, то тем самым было бы доказано, что не-
неоднородная задача E.2), E.3) может иметь лишь единственное
решение. Этот вопрос обсуждается в следующем пункте.
5.3. Построение функции Грина из фундаментальной системы.
В данном пункте исследуется остававшийся до сих пор открытым
вопрос о существовании и единственности функции Грина, причем
применяется метод, который одновременно может служить способом
для построения функции Грина.
Однородное дифференциальное уравнение
L [у] = 0 E.7)
имеет фундаментальную систему из k линейно независимых решений
Zj, z2 zk. (Решения обозначены zt, а не y[t так как у{ ниже
обозначают собственные функции.) Итак, имеем
Тогда общее решение уравнения E.7) имеет вид
к
где ct — произвольные постоянные.
Так как функция Грина точно так же должна удовлетворять одно-
однородному дифференциальному уравнению, то с необходимостью сле-
следует возможность построения ее в каждой из двух областей х -^ \
и х ^-1 из решений z., взятых с разными коэффициентами с. и с*
') G удовлетворяет дифференциальному уравнению L [G] = 0, за исклкь
еннем точки х = |, но при интегрировании по | это не имеет значения.
5.3]
§ 5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИЙ
79
в каждой области (см. рис. 5.2):
к к
О (х, £) = 2 c,zt (х) = Л (в, 4 &,) *, (х),
х
i-i
E.8)
Здесь с. и с* заменены соответственно на ai-\-bi и at — bt (ai и bt—
пока неизвестные функции |). Прежде всего, можно определить bl
из переходных условий в точке х = |.
Условие непрерывности функций О(х, |), О'(х, |) G(ft)(x, |)
дает
2*.Mv)(l) = 0 (v = 0, 1 k — 2). E.9)
i = i '
Наконец, условие скачка E.6) для G( ~ (х, |) требует
1
2Рь (I) '
E.10)
Таким образом, для k неизвестных bt (|) по-
получено А линейных уравнений, из которых
всегда можно вычислить bit так как опреде-
определитель системы этих уравнений
E.Ц)
Рис. 5.2. Две области,
л: <".4 и х~^-\, в случае
функции Грина,
неравен нулю; это «определитель Вронского»
для функций zt. Он отличен от нуля вследствие того, что zt пред-
предполагаются линейно независимыми1).
После того как bt найдены, at вычисляются из краевых условий.
Последние имеют вид
= 1. 2 к).
Верхний знак применяется в том случае, если в краевых условиях
рассматривается левый край х = а; при рассмотрении правого края
') J. Horn, Oewohliche Differentialgleichungen, изд. 2, Berlin — Leipzig,
1927, 57 [см., например, В. И. Смирнов, Курс высшей математики, т. II,
М- —Л., Гостехиздат, 1952].
80 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [5.3
х = Ь берется нижний знак. Вследствие линейности U^ получаем,
таким образом, для k неизвестных at столько же уравнений:
к к
2fl£f/Azi] = + ^Ь(и {zL\ (ц=1, 2 k). E.12)
Определитель этой системы уравнений имеет вид
M*iL Ui[z2\. .... Utlzk]
M*il. Uk[z2] Uk[zk]
E.13)
Если | f/u [zt] | Ф 0, a; можно вычислить; в этом случае функция
Грина существует, причем находится однозначно.
Если | U^ [z(] | = 0, ai из E.12) либо не могут быть вычислены,
либо находятся неоднозначно; в п. 5.7 при рассмотрении задачи на
собственнные значения показывается, что в этом случае равенство
|t/(i[z;]| = 0 как раз представляет условие существования для соб-
собственных значений.
Согласно E.8) можно, таким образом, в случае, если \U [zt]\=£0,
записать функцию Грина в форме
х<с,
x>| E.14)
o, (x, i) a2 (x, i)
причем Gj(x, |) непрерывно, a G2(x, |) имеет разрыв (k — 1)-й
производной.
Функция Грина, следовательно, составляется из двух частей;
первая часть Gj(x, |) k раз непрерывно дифференцируема по х,
другая часть О2(х, I) испытывает скачок (k—1)-й производной.
Элемент G2 всегда определен, так как определитель системы
уравнений для t>l не обращается в нуль; в противоположность этому
элемент Gj существует лишь в случае, когда определитель | U^ [zt] |
не равен нулю. Согласно правилу Грамма при вычислении at этот
определитель появляется в знаменателе и можно записать
причем числитель И(х, |) существует всегда, а именно, Н(х, |)
как линейная комбинация . из zt (x) при постоянном \ есть решение
однородного дифференциального уравнения: L[H] =0. G2 не зависит
от краеьых условий, зато Gx зависит от них,
5.3| § 5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИИ 81
Определитель E.13) появляется также при рассмотрении вопроса
о том, имеет ли аналогичная E.2), E.3) однородная краевая задача
L[y]=0. £/ц[у]=0
нетривиальное (тождественно не равное нулю) решение у. Такое ре-
решение у должно допускать представление его в виде
п
у (*) = 2 £/*<(*)•
где С1 — постоянные, удовлетворяющие системе уравнений:
п
SC^^^O G*=l, 2 к).
Определителем этой системы уравнений снова является определи-
определитель E.13). Числа С; не равны одновременно все нулю, а однород-
однородная краевая задача имеет нетривиальное решение тогда и только
тогда, если | £/ц \zt] | = 0- Если же \Uyi[zl\\=fc 0, однородная задача
имеет только решение у = 0; в этом случае решение неоднородной
задачи находится однозначно.
Итак, в результате получается
Теорема. Пусть zl (х) zk (х) есть фундаментальная
система (k линейно независимых решений) обыкновенного линей-
линейного однородного дифференциального уравнения k-го порядка
/,[у]=0. Если в точках х = а и х = Ь налагаются k (линейно
независимых) линейных однородных краевых условий U -[у] = о
(ц=1, 2, ..., k), то в случае, когда \ U^lZj] | Ф 0, имеется
однозначно устанавливаемая при помощи трех названных в я. 5.1
требований функция Грина О(х, |). Она разрешает краевую за-
задачу L[y]z=r (х), £/ц[у]=0 при произвольной правой части г (х)
посредством формулы решения E.4), причем решение это является
единственным. В случае же, если определитель \ U^ [zt] | равен
нулю, однородная краевая задача L [у] = 0, ' U^ [у] = 0 имеет
тождественно не равное нулю решение.
Подробно просчитанный пример построения функции Грина со-
согласно описанному методу дан в п. 7.8, упражнение 2.
Дополнение. Частные производные g' при
-j- a -^ k — 2 являются непрерывными функциями х и \.
Именно, если эти производные о5разованы от О в форме E.8),
то можно показать, что в точке х = | элементы, полученные из
h
2 bt (|) zt (x), исчезают. Дифференцируя первое уравнение E.9),
() Л. Коллатц
82 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [5.4
представляющее тождество относительно |, получаем:)
т. е. вследствие второго уравнения E.9)
dG (x, I) ,,
следовательно, ' непрерывна; аналогично, дифференцируя вто-
второе уравнение E.9), получаем
4H(»=o. EЛ6)
<1
d2G (х, ?) d3G (x, I) dk~2G (x, g)
т. e. • ■■- b/ , и точно так же- ' ■, ..., г-^—^-, не-
дхд% дх2д1 dxk~zdl
прерывна. Далее, дифференцируя E.15) с учетом E.16), получаем
т. е. ' *' непрерывна, а при дифференцировании E.15) подтвер-
d3G (х £)
ждается непрерывность -—. ' и т. д.
5.4. Симметрия функции Грина О (х, |) = О (|, х) для само-
самосопряженной краевой задачи. Пусть теперь краевая задача E.2),
E.3) является самосопряженной2); это значит, что: 1) дифферен-
дифференциальное уравнение имеет четный порядок k = 2т и записывается
в виде
L[y] = M [у] = S (-l)v [/„(*) y<v)(*)]<v} = r (x)
v=0
и 2) краевые условия U^ [у] = 0 таковы, что для любых функций
сравнения «, х>
ь
') В последующем доказательстве используется то обстоятельство, что
Функции bi (|) обладают непрерывными производными до (k — 2)-го порядка,
то обеспечено, если функции pv (x) предположить не только непрерыв-
непрерывными, как в п. 5.1, но даже (k — 2) раз непрерывно дифференцируемыми.
Этой дополнительной предпосылки можно, однако, избежать, см. Е. Катке,
Math. Z. 46 A940), 272.
2) До сих пор понятие самосопряженности вводилось только в случае
задач на собственные значения,
5.4) § 5. ФУНКЦИЙ ГРННЛ ДЛИ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИЯ g3
При помощи преобразования Дирихле (см. п. 4.3) этот интеграл
в общем случае трансформируется в краевое выражение порядка
2т— 1:
ь
j(uM[v]— vM[u])dx = [S(u, v)]ba. E.17)
a
Здесь
m v—1
v=0 p-0 V V
есть билинейная форма относительно а, и и их производных до
Bт—1)-го порядка, а именно, согласно D.17) производные Bт—1)-го
порядка w т~ , v т~ появляются в сумме только при р = 0, v — m,
так что можно записать
S(u, v) = (—l)m{fm{,avBn-1) — viPn-ly)} + низшие производные.
Предположим теперь, что для рассматриваемой краевой задачи
функция Грина существует, и образуем эту функцию для двух про-
произвольных, однако в дальнейшем фиксированных точек | = |j и |=|2
при а < |j, |2 < Ь\ обозначим эти функции ОA) и G^y.
Тогда имеем
Г (ОA)Ж [0B)] — GB)M [О;,,]) dx = О,
так как
т. е. потому, что О, за исключением точки х = |j и соответственно
х = |2. удовлетворяет дифференциальному уравнению [но не вслед-
вследствие самосопряженности, так как ОA) и ОB) из-за разрывности
Bw — 1)-й производной не являются функциями сравнения]. С дру-
другой стороны, приведенный выше интеграл можно оценить путем:
а) разбиения интервала интегрирования а, Ь на три частичных ин-
интервала: от а до |, — е, от |, -f е до |2 — е и от |2 -f e до Ь\
б) применения в каждом из этих частичных интервалов преобразова-
преобразования E.17) и в) устремления е к нулю. Таким образом, получается
/
\,+0 |2+0
= [5@,,,. О<2,)]!Г0
84 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [5.4
Далее, вследствие допущения о самосопряженности задачи имеем
Точно так же в выражении [5(ОA), ОB))]^'+° исчезают все вели-
величины, содержащие производные порядка ниже, чем 2т—1, так как
они непрерывны; лишь в производных Bт — 1)-го порядка вслед-
вследствие соотношения разрывности E.6)
о%- \и + о) - o'ff»(El _ о) =
остается
Соответственно в выражении [5(GA), GB))]|!+° остается
Обе величины в сумме дают нуль, т. е. на самом деле имеем
G(h, |2) = О(|2, £,). E.18)
Это равенство утверждает свойство симметрии функции Грина.
Другое доказательство1) симметрии функции Грина О(х, |) для
самосопряженной задачи E.2), E.3) основано на использовании не-
непосредственно формулы решения E.4). Пусть г (х) и s(x) — две
непрерывные, а в остальном произвольные, заданные в основном ин-
интервале а^.х^.Ь функции, а и(х) и соответственно v(x) — реше-
решения краевых задач:
L[u] = r(x) ^[и] = 0,
L[v] = s (х) £/й [v] ш* 0.
Согласно формуле решения E.4) это означает
ь ь
и(х)= j O(x, l)r(\)dl, v(*)— j O(x, l)
а а
В силу допущения о самосопряженности имеем
ь
[ (uL [v] — vL [и] )dx = 0
или, подставляя выражения для и, v, L[u], L[v\:
ь ь
J J (G(x, £)— G(|, x))r(l)s(x)dldx = 0;
') Это доказательство сообщил мне Г. 3 е й ф е р т.
5.51 § 5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИИ 85
при этом во втором члене х и | меняются местами. Вследствие про-
произвольности функций г (х) и s (х) это равенство требует обращения
в нуль множителя
<р(х, 1) = О(х. 1)-О(%, х);
так как если ф(х, |) в некоторой точке квадрата а < х, |<#
отлично от нуля, например положительно при х = х0, | = |0, то
в силу непрерывности О оно было бы положительно в малом
квадрате |х — х01 <^ 6, ||—|01 <С 6. Если при этом взять непрерыв-
непрерывные функции s (х) и г(х) положительными при | х — х01 < 6 и
I — 1о I < ^ соответственно (исключая значения s(x)^0 и /■(!)=()),
то двойной интеграл не был бы равен нулю. Имеем, следовательно,
Q(x. l) = Q(l. x).
5.5. Простые примеры функции Грина. 1. Функцию Грина для диф-
дифференциального уравнения М [у] — — у" и краевых условий у @) = у A) = 0
можно легко найти при помощи метода, приведенного в п. 5.3:
;A— x) При
На рис. 5.3 G н -т— как функции х и \ нанесены в аксонометрической
проекции.
2. Для задачи
функция Грина имеет вид
G (х £ч = / х ПРИ Х<Ь,
' U при лг> £.
Рис. 5.4 демонстрирует те же G и -г— как функции .* и | в аксонометри-
аксонометрической проекции.
Можно утверждать: функция Грина G (х, |) симметрична относительно
биссектрисы х = |.
Напротив, функция " ■' I ' ■■ ■ уже не симметрична! Кроме того, видно,
что скачок -5— в g-направлении имеет обратный знак по сравнению со скач-
ОХ
ком в л>направленни:
G' (х, -*-+-()) — G' (х, х — 0)= 1, G' (x-\-0, x)~G' (х — 0, лг)== — 1.
3. Для задачи
М [у] = ayIV, у @) = у" @) = у (/) = у" (/) = 0,
где а постоянно, функция Грина просто равна прогибу (рис. 5.1); пример
аналогичен приведенному в п. 5.1.
I
G (х, I) = {
ПРИ
8б ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА E.6
Здесь величина
д2О (х, I) _
дх*
la
х -1)
при х
la
при
с точностью до постоянного множителя равна функции Грина для примера 1
при / = 1.
4. Для задачи
М[у] = -у"-Ху, у@)=,0, у'A) = Яу A),
подставляя А = k2, получим
( sin б* Г sin &!(&cos £ + sin k)
5A-z ь—z—-
cos ^ — & sin &
Ц ' ^
. "I
+ cos kl при x < E,
"I
J
cos
при л:
I A [ cos к — к sin к
Функцию Грина, следовательно, также можно построить, если параметр X
Рис. 5.3. Функция Грина G (х, I)
и ее первая частная производная
по х для дифференциального вы-
ражения — у" при нулевых зна-
значениях на краях.
Рис. 5.4. Функция Грина и ее
первая частная производная по х
для второго примера в п. 5.5.
входит в дифференциальное уравнение и в краевые условия. Это приводит
нас к следующему классу задач на собственные значения.
5.6. Резольвента Грина для несобственных значений. В каче-
качестве краевой задачи рассмотрим теперь самосопряженную задачу на
собственные значения
6.7] § 5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИЙ 87
в которой, возможно, выполняются предпосылки п. 4.2; единственное
отличие от пп. 5.1—5.4 состоит в том, что здесь появляется пара-
параметр к. Функция Грина будет теперь зависеть еще и от к:
О(х, 1) = О(х. 1,1).
Функцию Грина О(х, |, к) называют тогда также «резольвентой
Грина». При этом под к понимается параметр, который может при-
принимать любые значения, за исключением собственных. (Согласно тео-
теореме п. 5.3 функция Грина существует, если однородная краевая за-
задача имеет только решение у = 0, т. е. если к не является соб-
собственным значением.) Тогда, следовательно, величина
ь
= J 0{x. £, k)r(l)dl E.20)
есть решение краевой задачи
L[y] = M [у] - Ш [у] = г (х),
Ull[y,l]=0.
5.7. Условия существования собственных значений. В задаче
на собственные значения E.19) функции z£ (x) фундаментальной си-
системы (см. п. 5.3) дифференциального уравнения М [у] — kN[y] — Q
зависят также от к: zt (x) = zt (x, к). Линейные комбинации их должны
давать собственные функции у:
2т
При этом Ct должны быть определены так, чтобы были удовлетво-
удовлетворены краевые условия
2т
S С,£/ [г„ к] = 0 (ц = 1. 2 2т). E.22-)
Это — 2т линейных однородных уравнений для 2т неизвестных Ci%
которые имеют нетривиальное решение в том случае, когда опреде-
определитель из коэффициентов равен нулю. Это есть как раз определи-
определитель, уже фигурировавший в E.13):
u[zl, к] | = 0. E.23)
Последнее уравнение есть условие существования чисел Ci ф 0, т. е.
существования собственных функций. Итак, уравнение E.23) есть
уравнение для собственных значений к.
Теперь, если воспользоваться сведениями из аналитической теории
обыкновенных дифференциальных уравнений, можно сделать некото-
некоторые общие заключения о локализации собственных значений. В этом
и в последующих пунктах привлекаются поэтому теоремы из это-'!
88 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [5.7
теории. Используем, во-первых, теорему о зависимости решений диф-
дифференциального уравнения от параметров.
Если коэффициенты дифференциального уравнения и начальных
условий являются дифференцируемыми функциями некоторого пара-
параметра X и, следовательно, с рассматриваемой точки зрения являются
аналитическими функциями X, то решения также суть аналитические
функции X!). V ' '"<
Параметр X входит в дифференциальное уравнение E.19) линейно,
следовательно, решения zt (х, X), которые могут быть определены
постоянными, не зависящими от X начальными условиями, являются
регулярными функциями X, а именно, zt(x, X)—целые функции X
для фиксированного х из области а^х ^.Ь.
Если X входит в краевые условия аналитически, то А (X) также
является аналитической функцией X. В примерах таблицы I X встре-
встречается в краевых условиях, если оно вообще в них входит, всегда
лишь в первой степени, т. е. U^ [zt] является целой функцией X.
Значит, А (X) также есть целая функция X; поэтому справедливо сле-
следующее утверждение:
Либо А(X) есть тождественный нуль, тогда каждое X яв-
является собственным значением, либо уравнение А (X) = 0 обла-
обладает, самое большее, бесконечным счетным множеством изоли-
изолированных нулевых точек без точки сгущения в конечной области.
В этом случае собственные значения можно расположить в по-
порядке возрастания их модулей:
Пример I. Каждое Я является собственным значением.
В задаче на собственные значения
L [у] = — у" — Ху = 0, <7( [у] =? у @) — у A) = О, £/2 [у] — у' @) -(- у' A) = О
функции
Zx =5= Sin ^Jf, ^2 =5 COS fejf,
где Я = к2 Ф 0, образуют фундаментальную систему2). Уравнение E.23) здесь
будет
A(l+cosfe) —
') J. Horn, GewOhnliche Differentialgleichungen, изд. 2, Berlin—Leip-
2ig, 1927, гл. 8 [см., например, Н. М. Матвеев, Дифференциальные урав-
уравнения, изд. ЛГУ, 1965].
2) Фундаментальная система из целых функций X: г{ = -j=r sin /Я х,
г2 — cos УХх, удовлетворяет свободным от Я начальным условиям:
*j@)=0, г\ф) = 1, г2@)=1, г!г@)=0.
5.7) § 5. ФУНКЦИЙ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИЙ
89
Это равенство выполняется для каждого к, значит, все значения (не должны
исключаться также комплексные числа А и А = 0) являются собственными
значениями. Им отвечают собственные функции y = cosk[x—^-1.
Пример II. Задача о продольном изгибе. В случае продольного
изгиба стержня постоянного сечения с защемленными, но подвижными кон-
концами (рис. 5.5), имеем задачу на
б
1
Y
собственные значения вида
/@) = /"@) = /(/) =/"@=0.
р
Здесь А = •— (где Р есть сжи-
сжимающая сила и а — жесткость на
изгиб) и краевые условия озна-
означают равенство нулю наклона и
поперечной силы на краях. Каж-
Каждое значение А является собствен-
собственным значением, соответствующим собственной функции у = const, и стержень
может сдвигаться параллельно самому себе. Кроме того, имеется последова-
последовательность собственных значений
Рис 5.5. Задача о продольном изгибе
для стержня с защемленно-подвижными
концами.
(га=1, 2, 3, ...),
плх
эти собственные
соответствующих собственным функциям уп = cos
значения, таким образом, являются «двукратно вырожденными».
Дополнение о двукратно вырожденных собственных значениях.
В последнем примере появился термин двукратно вырожденные соб-
собственные значения. Определение вырожденных собственных значений
дано в п. 5.9. Здесь скажем только: число X называется двукратно
вырожденным собственным значением, если ему отвечают две линейно
независимые собственные функции. Докажем используемую в п. 5.8
теорему: если Xj — двукратно вырожденное собственное значение,
то производная возникающего в E.23) определителя А (А) обращается
в нуль в точке X = X*')
к=к,
E.24)
Одному такому собственному значению Xj отвечают, согласно выше
данному определению, две линейно независимые собственные функции
уA), уB\ а значит, две линейно независимые системы решений С(Д Cf
системы уравнений E.22). Так как постоянные множители при С1
произвольны, можно положить С\^ = С\' =1 [возможно, после
') Теорема может быть также обращена и обобщена на многократно
вырожденные собственные значения. Вырожденность собственного значения Ау
в случае самосопряженной задачи совпадает с кратностью, которую имеет Лу
как нулевая точка Д (А). См. сноску на стр. 94.
90 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [5.8
перенумерации zx, z2 z2m, если при первоначальной нумерации
С1!1' или С22) должны обратиться в нуль; при этом у определителя E.23),
самое большее, изменится знак]. Сложим теперь в определителе E.23)
[он выписан в E.13)] элементы i-х столбцов для i = 2, 3, ..., 2т,
умноженные на С\ , с элементами первого столбца и элементы г'-х
столбцов для 1 = 1, 3, 4, ..., 2т, умноженные на С/2), с элементами
второго столбца; тогда в первом и втором столбцах E.13), со-
согласно E.22), останутся одни нули. Если теперь продифференциро-
продифференцировать определитель, дифференцируя нужные столбцы и складывая по-
получающиеся определители, то производные для к = kt обратятся
в нули, так как каждый из определителей содержит по меньшей мере
один нулевой столбец, т. е. действительно E.24).
5.8. Поведение резольвенты Грина в точках собственных зна-
значений к. Пусть к = кх есть собственное значение, а именно простой
корень характеристического уравнения E.23)
Имеем А(А,) = (А,— X,j) А* (Л,), и А* (А,) есть аналитическая функция к,
причем A*(^) Ф 0.
Функция Грина согласно E.14) имеет вид
G(x, I, X) = G1(x, I. *) + G2(x, I, к)=И(^Х) +О2(*. 1, к).
Здесь Н и G2—целые функции к, поэтому G(x, \, к) является «ме-
роморфной» функцией к, т. е. G во всей А,-пло;кости, исключая по-
полюсы, регулярна, а именно О имеет полюсы в точках собственных
значений kt; умножение на (к — кг) дает
О (х, 1, к) (к - кх) = -U*;^X) +(к- к,) 0.2 (х, I, к). E.25)
Выражение в левой части при к = кх не определено, так как в этом
случае функция Грина не существует. Выражение же в правой части
имеет вполне определенный предел, когда к стремится к кх. При
этом отношение /У/А* остается регулярным, второй член в правой
части стремится к нулю, следовательно, левая часть G(x, |, к)(к — A,t)
при k—>ki имеет предел
она является, в частности, регулярной при k = kt, если ее рассмат-
рассматривать как функцию к при любых, но фиксированных х и |. Теперь
утверждается, что эта предельная функция —\-t v* . - есть соответ-
соответствующая ^ собственная функция. Н (х, |, к) является 2т раз не-
непрерывно дифференцируемой и, согласно E.3), как линейная комби-
комбинация решений фундаментальной системы удовлетворяет во всем им-
r.8J § 5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИЙ 91
тервале а^х^Ь дифференциальному уравнению E.19) при Я.=Я,,
Далее, для каждого %ФХ1 функция G(x. \, X) удовлетворяет крае-
краевым условиям £/^ = 0, т.е. имеет место
^[О(х, I, Я,) (Я, — Я,,)] = 0 при кфк,,
а значит, и в пределе!)
UA lim О(х, I, Я,) (Я, — Я,)] = 0,
т. е. Н (х, £,, Х{) равным образом удовлетворяет краевым условиям.
Функция Н(х, £,, Хх), таким образом, при фиксированном | является
соответствующей Хх собственной функцией, и так как, согласно
п. 5.7, в случае невырожденного собственного значения не суще-
существует двух линейно независимых, отвечающих этому значению соб-
собственных функций, можно записать Н(х, £,, X1)=const-y1 (x), где ух
есть некоторая выделенная фиксированная собственная функция, со-
соответствующая Х-у. Постоянная, которую обозначим через С, может
зависеть еще от |; таким образом, имеем Н(х, £,, Хг) = у^ (х) С (|).
Функция Грина G(x, |, X) для значений X, не являющихся соб-
собственными, согласно п. 5.4, симметрична относительно х и |. Сле-
Следовательно, и G(x, |, X) (X — Х{) при X Ф Ху, а значит, и предельная
функция при X Ф Ху и вместе с ней и Н(х, |, XJ симметричны отно-
относительно х и |. Последняя функция должна, следовательно, иметь
вид
Н(х, |. Х,) =
при этом постоянная С* теперь больше не зависит от х или от |.
Можно, таким образом, для любого X записать
И (х, |. X) = у, (х) у, (I) С*+(Х- Я.,) Н\
С*
где Н* — опять целая функция X. При Сх^= .t .. , следовательно.
имеем
G (х, 1, X) =- С]У^1^1) + О;(х, \, X), E.26)
причем G\ есть мероморфная, но в точке Х — Ху регулярная функ-
функция X. Точно так же можно поступать с другими точками собствен-
собственных значений Х2, Х3 пока эти Xt являются невырожденными;
тогда, если у2, у3, ... суть соответствующие указанным собственным
значениям собственные функции, получаем
G(x, 1, X) =-- 2 Cvylil\yJil) + G*s (x, 1. I), E.27)
V-I
') Согласно E.14) G (x, |, А,) есть конечная сумма Zj, значит, разрешена
перемена местами операций дифференцирования и предельного перехода.
92 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [5.9
где Gs — мероморфная, но в точках А,, А2, ..., А, регулярная функция,
имеющая полюсы в точках следующих собственных значений As+I, As+2, • ■■
5.9. Кратные собственные значения. Определение. Соб-
Собственное значение А называют r-кратно вырожденным, или гово-
говорят, что оно имеет кратность г, если имеется ровно г линейно
независимых собственных функций у,, у2 уг, соответствую-
соответствующих этому собственному значению:
M[yl]=W[yl], UVL[yi] = Q (/=1.2 г). E.28)
Это определение точно так же действительно и в случае диффе-
дифференциальных уравнений в частных производных, где необходимо
только у{х) заменить на z(x, у, . . .).
Приведем в качестве простого примера самосопряженную задачу
о сжатом стержне на упругой опоре:
yv_j_4y=-ay. у @) = у" @) = у (л) = у" (л) = 0. E.29)
Здесь наименьшее собственное значение А, = 5 является двукратно
вырожденным, ему соответствуют две линейно независимые собствен-
собственные функции у! = sin л;, y2 = sin2x. Самосопряженная задача
_ yiv_ 49/ = XA4ylv-h 36y),
y = y" = y'v = 0 при х = 0 и х — п
имеет А. = 1 в качестве трехкратно вырожденного собственного зна-
значения с собственными функциями yk=s\nkx, где k=\, 2, 3. Можно
легко привести примеры собственных значений с любой кратностью
вырождения г, например построить задачи
v-I v=0
у = у" = . . . = уBт-2) _0 при Х = 0 И Х = Л
с постоянными коэффициентами /v, gv, в которых sinx, sin 2x, ...
.. ., sinrx суть собственные функции, соответствующие одному и
тому же собственному значению.
При появлении вырожденных собственных значений можно, в сущ-
сущности, воспользоваться результатами для случая отсутствия вырож-
вырождения, однако доказательства усложняются и требуют более обшир-
обширных вспомогательных средств. Поэтому ограничимся здесь сообщением
результатов, а при необходимости некоторых доказательств—указа-
доказательств—указанием литературы.
Если линейно независимые функции у,, у2, .. ., у, в качестве
собственных функций самосопряженной полностью определенной за-
задачи на собственные значения D.11) — D.14) отвечают л-кратно вы-
вырожденному собственному значению А, то функции
5.9J
5. ФУНКЦИЯ ГРИНА ДЛЯ ОБЫКНОВЕННЫХ ДИФФ. УРАВНЕНИЙ
93
при любых постоянных ара также являются собственными функциями,
отвечающими тому же самому собственному значению %. В частности,
можно ар(Т определить так, что функции Y р будут ортогональны
в обобщенном смысле:
*
Г YpM[Ya]dx = 0 прирост, E.30)
а
а постоянный множитель при Yp можно с точностью до знака опре-
определить так, что КР будут «нормированными», т. е.
*
YpN[Yp]dx=] при р=1, 2, .... г.
E.31)
Что можно найти постоянные аро с такими свойствами и осуществить
такой «процесс ортонормировки»,. доказывается с другой точки зре-
зрения в п. 15.4; это можно видеть, однако, и непосредственно, под-
подставляя
у
/7
ytN\yi]dx
а другие Y вычисляя по рекуррентным формулам'):
К+х (*) =
К+х
- j Yo (*) j Yo (I) N [y,+I (I)] d\.
O-I
E.32)
Вследствие предположения о линейной независимости функций ур
ни одна из величин К* тождественно не равна нулю, поэтому все
числители в E.32) отличны от нуля.
Полагая процесс ортонормировки уже выполненным, будем писать
снова у вместо Y. Точно так же могут быть нормированы собствен-
собственные функции, соответствующие другим собственным значениям, и
ортонормированы, поскольку они соответствуют вырожденным соб-
собственным значениям, так что формула D.18) принимает вид
t @ при I ф k,
y,N[yk]dx = { E.33)
J ( 1 при i — k.
') R. Courant, D. H 11 b e r t, Methoden der mathematlschen Physlk,
т. I, изд. 2, Berlin, 1931, 42 [P. Курант и Д. Гильберт, Методы ма-
математической физики, т. I, ГИТТЛ, 1951].
94 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [5.9
Теорема. В случае самосопряженной полностью определен-
определенной задачи на собственные значения D.11) — D.14) имеется нор-
нормированная, в обобщенном смысле ортогональная система соб-
собственных функций yt. Для нее существует соотношение E.33).
Пусть теперь G(x, |, X) есть, как в п. 5.6, резольвента Грина,
которая, следовательно, разрешает неоднородную краевую задачу E.21)
посредством формулы E.20). Если Х^ есть л-кратно вырожденное
собственное значенге, то можно G(x, |, X) записать в форме, соот-
соответствующей E.27):
G(x, lt ц
где G* мероморфна относительно X и при Х = ХХ регулярна. Функ-
Функции ур принимаются ортогональными в обобщенном смысле. Это пред-
представление резольвенты Грина может быть доказано средствами тео-
теории вычетов !).
Суть предыдущего можно выразить следующим образом: пред-
представление E.27) резольвенты Грина верно также в случае вырожден-
вырожденных собственных значений, поскольку собственные функции, соответ-
соответствующие таким Xj, выбраны ортогональными в обобщенном смысле.
Из E.34) можно вывести важную теорему о разрешимости не-
неоднородной краевой задачи
M[u] — XN[u]=k(x). 1^[и]=0 E.35)
при X = Xj. Эта задача разрешима не для любых правых частей,
а только для определенных функций h(x), а именно всегда, если h(x)
ортогональна ко всем собственным функциям ух, у2 уг, соот-
соответствующим собственным значениям Xf.
ь
J yp(x)h(x)dx--=0 (p=l. 2 г), E.36)
а
т. е. если подставить выражение E.34) для резольвенты Грина в фор-
формулу решения E.20), то в силу E.36) в правой части остается только
член
ь
j G*(x, I, X)h(l)dl.
a
Так как G* при X = Xj является регулярной, то для X^Xj получаем
ь
cr(x.l,kj)h(Qdl. E.37)
') Е. Kamke, Definite selbstadjungierte Eigenwertaufgaben, Math. Z,
46 A940), 242—250.
S.10) § б ФУНКЦИЯ ГРИНА ДЛЯ УР-НМй С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 95
Тот факт, что таким способом найденная предельная функция и (х)
на самом деле разрешает краевую задачу E.35), нуждается в более
подробном доказательстве, которое здесь не может быть приведено;
общее решение E.35) получается кз E.37) путем аддитивного допол-
дополнения собственных функций, соответствующих Xj.
5.10. Полуопределенные задачи на собственные значения. В случае
полуопределенной задачи на собственные значения D.11)—D.14)
в числе прочих собственных значений, согласно определению п. 4.9, по-
появляется также число нуль. Например, в задаче об изгибных колебаниях
призматического, свободного на обоих концах стержня
встречается собственное число А, = 0, а именно, в качестве двукратно выро-
вырожденного собственного значения с собственными функциями у = 1 и у = х.
Появление собственного значения X = 0 означает, согласно пп. 5.3 и 5.7,
что для краевой задачи
М[у] = г(х), ^[у]=0 E.38)
функция Грина не существует. Можно, однако, построить так называемую
«обобщенную функцию Грина», при помощи которой задача на собственные
значения, поскольку она вообще имеет решение, разрешается посредством
формулы, аналогичной E.4):
ь
у (х) = J G (х, I) r (I) d\.
Теория, представленная в § 8 и далее, также может быть распространена
на полуопределенные задачи на собственные значения, но более глубокое
рассмотрение здесь не проводится '). \
§ 6. Функция Грина для уравнений
с частными производными
Общая теория уравнений с частными производными сложна и не
может рассматриваться как законченная. Приведем, однако, некото-
некоторые краткие сведения о функции Грина и о задачах на собственные
значения в простейших случаях 2), а именно только те, которые позже
(в пп. 7.4, 11.2, 14.1 и в § 23) потребуются.
') Более подробно в книге Е. Kamke, Differentialgleichungen: L6sungs-
methoden und Losungen, изд. 7, Leipzig, 1961, 191 [Э. Камке, Справочник
по обыкновенным дифференциальным уравнениям, «Наука», 1965], а также
Math. Z. 46 A940), 231—286; далее в книге R. Co ur a n t, D. Hilbert,
Methoden der mathematischen Physik, т. 1 изд. 2, Berlin, 1931, 306
[P. Курант и Д. Гильберт Методы математической физики, т. I,
ГИТТЛ, 1951].
2) Более строгое и подробное рассмотрение см. R. С о и г а п t, D. Hil-
Hilbert, Methoden der mathematischen Physik, т. 1, 11, Berlin, 1931, 1937
[P. Курант и Д. Гильберт, Методы математической физики, т. 1 и II,
ГИТТЛ, 1951].
96 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСкИЕ СРЕДСТВА f6.1
6.1. Основные понятия. Формальное распространение основных
понятий, рассмотренных в § 4, на уравнения с частными производ-
производными не представляет затруднений. Пусть дифференциальное уравне-
уравнение имеет вид
M[z] = XM[z], F.1)
где z — неизвестная функция, М и N — заданные линейные однород-
однородные дифференциальные операторы для функций нескольких незави-
независимых переменных х, у, . . .; X — собственное значение. К этому
добавляются краевые условия:
UtlW = 0 (И=1. 2 k). F.2)
Здесь и^[г\ — линейные однородные дифференциальные выражения
относительно г, взятые на некоторой заданной граничной кривой
(или граничной поверхности) области 93, которую назовем основной
областью. Числа X, для которых имеются тождественно не равные
нулю удовлетворяющие краевым условиям решения уравнения F.1)
(«собственные функции»), называются собственными значениями
задачи.
Тождественно не равные нулю функции и независимых перемен-
переменных х, у, .. . называются «функциями сравнения», если они удо-
удовлетворяют краевым условиям U^ [и] = 0 и обладают непрерывными
частными производными такого высокого порядка, как это необхо-
необходимо для образования М[и] и N [и]. Задача на собственные значения
называется самосопряженной, если для любых двух функций срав-
сравнения и, w всегда имеет место
Г (иМ [w] — wM [и]) dv = 0, f (uN [w] — wN [и]) dv = 0. F.3)
a sb
Здесь интегралы берутся по основной области 93, dv — dxdy...
означает элемент объема.
Задача на собственные значения называется определенной, если
все собственные значения kt вещественны и имеют один и тот же
знак, и полуопределенной, если все ^ вещественны, не меняют знака
и среди них имеется число нуль.
Задача на собственные значения называется полностью опреде-
определенной, если для любой функции сравнения всегда выполняются не-
неравенства
Г иМ [и] dv > 0, J uN [и] dv > 0. F.4)
6.2J § 6. ФУНКЦИЯ ГРИНА ДЛЯ УР-НИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 97
Тогда имеем: полностью определенная задача на собственные значе-
значения является определенной и все ее собственные значения положи-
положительны. Это следует из того, что г есть собственная функция, отве-
отвечающая собственному значению X, и поэтому всегда
f zM [z] dv
iо. F.5)
k
zN[z\dv
Если в первом неравенстве F.4) вместо знака > допустить
знак ^-, то таким же образом получается, что задача на собственные
значения является определенной или полуопределенной.
В то время как из полной определенности следует вещественность
собственных значений, нельзя ожидать, что одна только самосо -
пряженность обусловливает вещественность собственных значений,
изо это не имеет места даже в случае обыкновенных дифференциаль-
дифференциальных уравнений, как показано в примере п. 4.8. Предпосылки само-
самосопряженности и полной определенности проверяются в отдельных
случаях, как и при обыкновенных дифференциальных уравнениях,
путем применения интегрирования по частям или соответствующих
вспомогательных средств, как, например, интегральной теоремы
Гаусса и т. д. (см. проведение проверки в п. 6.2). Поскольку, как
уже отмечалось, столь же общая теория, как в случае обыкновенных
дифференциальных уравнений, здесь в настоящее время не может
быть дана, выделим в последующем — до некоторой степени в качестве
примера — частный класс задач.
6.2. Частный класс задач. Рассмотрим задачу на собственные
значения следующего типа при двух независимых переменных х, у.
Пусть дифференциальное уравнение (его называют «эллиптическим»)
имеет вид
М\г] = — (pzx)x — (pzy)y ■+ qz = kN [z] == Xgoz. F.6)
Здесь z = z(x, у) — неизвестная собственная функция, X — собствен-
собственное значение, р(х, у), q(х, у) и go(x, у) — заданные непрерывные
функции; кроме того, р и g0 положительны и р имеет непрерывные
частные производные по х и у. Индекс х или у означает частное
дифференцирование по соответствующей переменной, т. е., например.
Пусть в плоскости независимых переменных х, у задана замкнутая,
односвязная область 23, которая ограничивается кусочно-гладким кон-
контуром Г (рис. 6.1). На Г функции z(x, у) подчинены краевому
7 Л. Коллатц
98
ГЛ. П. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
[6.2
условию !):
F.7)
Здесь а и р — заданные на Г, непрерывные, не равные одновременно
нулю функции длины дуги s, измеряемой от некоторой выбранной
фиксированной точки контура.
При этом п означает направление
внешней нормали (рис. 6.1); если (п, х)
и соответственно (п, у) суть углы между п
и направлениями осей х и у, то для лю-
любой непрерывно дифференцируемой функ-
функции w(x, у) имеем
w cos (п x)+wcos(n' У)-
F.8)
= ~Ш ~ w* cos
Вспомогательным средством, соответ-
соответствующим интегрированию по частям в слу-
случае обыкновенных дифференциальных
уравнений, здесь является интегральная
теорема Гаусса, которая для любой функ-
функции f(x, у), имеющей непрерывные частные производные по х, может
быть записана в виде 2)
Рис. 6.1. Область S3, поло-
положительно ориентированный
контур Г, внешняя нор-
нормаль п.
J дПдхУ) dxdy = \ f (*■ У) cos (»■ x) ds-
F.9)
Направление обхода контура Г при этом должно быть выбрано
положительным.
Если аир имеют одинаковые знаки и q(x, у) > 0, то задача,
как легко проверить посредством интегрирования по частям, является
полностью определенной. Необходимо для этого лишь исследовать
первый из двух данных в F.4) интегралов, так как неравенство
J uN [и] dv= f f gou2 dxdyyO
') Это краевое условие не так безобидно, как кажется на первый взгляд.
Помимо того, что в возможных точках излома контура дг!дп не определена,
вообще нельзя в случае уравнений в частных производных требовать, чтобы
все разрешающие функции удовлетворяли краевым условиям во всех точках
контура. О более подробной формулировке краевых условий см. R. Сои-
rant, D. H i I b e r t, Methoden der mathematischen Physik, т. II, изд. 2,
Berlin, 1931, 508 [P. Курант и Д. Гильберт, Методы математической
физики, т. II, ГИТТЛ, 1951].
2) К. Knopp, Einfiihrung in die hOhere Mathematik, т. Ill, Leipzig,
1942, 347 [см., например, В. И. Смирнов, Курс высшей математики, т. II,
М.—Л., Гостехиздат, 1952].
6.2] § 6. ФУНКЦИЯ ГРИНА ДЛЯ УР-НИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 99
выполняется. Указанный интеграл равен
J иМ [и] dv = JJ [— и {рих)х — и {риу)у -f qu2) dx dy.
й аз
Член Г qu2 dx dy положителен вследствие положительности q. Пер-
аз
вый член можно преобразовать, если к функции / = и(рих), имеющей
производную fх = и[ри^х-\ ри2х, применить теорему F.9). Получаем
— Г Г и (рих)х dx dy = J J pux dx dy — J puxu cos (re, x) ds.
в в г
Точно так же для второго члена
— \ \ и (риу)у dx dy — Г J ри^ dx dy — Г рииу cos (re, у) ds.
в в г
В силу F.8)
их cos (re, x) -f- йу cos (re, y) = un,
поэтому имеем
J J «Ж [и] tfx йГу = j j \qu2-\- p(u2x-\- и')] й?дг tfy — J р«йл d*.
в а г
Отсюда видно, что условия F.4) выполняются, так как контурный
интеграл в силу краевого условия F.7)
сш = —
неотрицателен; для р ф 0 подынтегральное выражение удовлетворяет
соотношению
а для р = 0 оно исчезает, так как и равно нулю.
Если положить также равным нулю q, то из рассмотрения сле-
следует, что все собственные значения неотрицательны:
Тогда может случиться, что число нуль также является собственным
значением (например, в случае сс = О, т. е. краевых условий вида
ип = 0, число нуль является собственным значением с собственной
функцией и = const).
Далее, при помощи интегральной теоремы Гаусса F 9) легко
проверяется и самосопряженность задачи на собственные значения
F.6), F.7).
7*
100 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [в.З
Если в F.6), F.7) подставить
f = puxw — puwx, т. е. ^ =
то имеет место
J \ KP"x)xw—(Pwx)x "I dx аУ =
в
= j [pwux cos (n, x) — pwwx cos (n, x)] ds;
г
аналогично
J J l(puy)y w — (pwy)y "Idx dy =
в
= j [pwuy cos (n, y) — puwycos(n, y)]ds.
г
Сложив эти два равенства и F.8), получим
[ [ {—wM[u] + uM[w})dxdy= Г р(wun — uwn)ds. F.10)
в • г
Это — так называемая «формула Грина» (аналог «формулы
Дирихле» в случае обыкновенных дифференциальных уравнений).
При краевых условиях F.7) интеграл, стоящий в правой части,
исчезает, так как для р =/= 0 имеем
а а
ип = — —и, wn = — jw,
следовательно, wun—йи>л —0; а для р = 0
и = tw = 0,
т. е. краевая задача F.6), F.7) является самосопряженной.
6.3. Функция Грина, предварительные замечания. Этот пункт еще не
содержит доказательств и служит лишь введением в теорию функции Грина
для уравнений в частных производных. Целью является, как и в случае
обыкновенных дифференциальных уравнений, решение краевой задачи при
неоднородном уравнении посредством функции Грина.
При любой непрерывной правой части <р (х, у) дифференциального урав-
уравнения, в котором М [г] имеет вид F.6),
М [г] = Ф (*, у) F.11)
и однородных краевых условиях az -\- $zn = 0 на контуре Г решение можно
представить в форме
Х' у) = J 1 ° (Х' У' 1 ^ ф (l 11) dl d% FЛ2)
где G(x,y\ |, т|) есть функция Грина, которая и здесь выражает «функцию
влияния».
6.3] § 6. ФУНКЦИЯ ГРИНА ДЛЯ УР-НИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 101
Чтобы получить представление о функции влияния, рассмотрим сначала
в качестве примера случай />=1, <? = 0, т. е. уравнение Пуассона
дх2 ду2 '
с краевым условием z = 0 на Г. Тогда z (x, у) можно истолковать как про-
прогиб равномерно нагруженной мембраны, защемленной по контуру Г, причем
Ф (х, у) есть произведение плотности на-
нагрузки Ф (х, у) на постоянный множитель С,
зависящий от толщины и упругих свойств
мембраны. Если взять теперь единичную
нагрузку, равномерно распределенную на
малой круговой площадке радиуса р с цен-
центром в точке |, т), в то время как остальная
часть мембраны не нагружена, то возникает
прогиб z (х, у), который зависит от вели-
величины выбранной площадки. Если, далее,
устремить р к нулю (сохраняя нагрузку
единичной), т. е., образно выражаясь, при-
приложить игольчатую нагрузку, то соответ-
соответствующий прогиб сходится к функции вли-
влияния, которая в данном случае, точно так
же как в п. 5.1 для нагруженного стержня,
представляет функцию Грина G (х, у; |, т|).
Однако в противоположность случаю на-
нагруженного стержня прогиб в рассматри-
рассматриваемом примере не остается конечным; при
приближении к точке приложения нагрузки
он логарифмически стремится к бесконеч-
Рис. 6.2. Функция Грина
G (х, у; |, т|) к дифференциаль-
дифференциальному выражению Az с краевым
условием z = 0 при х2 -(- у2 = 1.
ностн. Пусть, например, задана функция Грина для круговой мембраны еди-
единичного радиуса
О {х, у; I, г,) = - -L In г + -^ In [A - х\ - уцJ + (хт\ - у®*], F.13)
-L
где
на рис. 6.2 в аксонометрии показана функция Грина при фиксированных |,
т| в зависимости от х н у.
Функцию Грина G можно определить посредством следующих требова-
требований: G (х, у; |, г]), как функция х, у при фиксированных |, т|, удовлетворяет
краевым условиям и дифференциальному уравнению М [G] = 0 вплоть
до точки х-=\, у = т). (При этом точка (£, т|) пусть будет внутренней
точкой SB.) В этой точке G имеет особенность, а именно, должно быть
lim
р-*э
2лр
——ds = —
>J On
1
Р F. Ч)'
F.14)
Это равенство соответствует условию скачка E.6) в случае обыкновенных
дифференциальных уравнений. Интегрирование производится по малому
КРУГУ радиуса р вокруг точки |, т| (рис. 6.3), а затем должен быть выполнен
dG
предельный переход р->0. Следовательно, -т— может стать неограниченной;
например, прн р = 1, q = 0, т. е. в случае оператора Лапласа
102 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [в.4
при любой области 58 функция Грина имеет вид
О = -д— 1пг-\- непрерывная функция, где г = V(x — |J + (У — Ю2 •
Выражение F.13) дает пример функции Грина для круговой области 23
и Р = 0. При этом
да 1 ,
-г— = — -я (-непрерывная фзгнкция.
Таким образом, имеем
2яр
J ~дп s ~~
о
причем R ограничено; значит, в пределе при р -> 0 остается только число —1,
как этого требует F.14).
6.4. Решение краевой задачи при помощи функции Грина.
И в случае общего дифференциального уравнения F.6), рассмотрен-
рассмотренного нами, G имеет логарифмическую особенность:
где а и Ь — непрерывные функции, имеющие непрерывные вторые
частные производные, причем д(|, г); |, г))^—1. Сложный вопрос
о существовании функции Грина здесь не рассматривается'). Напро-
Напротив, здесь принимается, что задана функция G(x, у; |, г]), которая
удовлетворяет краевым условиям F.7) и дифференциальному урав-
уравнению и которая в окрестности точки х = |, у = г) может быть пред-
представлена в виде F.15). Тогда выставленное вначале требование F.14)
о предельном значении малого контурного интеграла
2яр
1
Г да
-з—
as —
удовлетворяется само собой.
Введенная таким способом функция Грина G(x, у; |; ту) решает
краевую задачу. Чтобы понять это, подставим в формулу Грина F.10)
w — Z, т. е. М[хт]=(р, и u — G(x, у; |, г]) и проинтегрируем по
заданной области, вырезав при этом малый круг радиуса р вокруг
точки (|, т]). Область интегрирования заштрихована на рис. 6.3.
В качестве контура области интегрирования теперь, кроме контурной
') R. С our ant, D. Hilbert, Methoden der mathematischen Physik,
т. I, изд. 2, Berlin, 1931, 320; т. II, 1937, 471. Там же подробно обсуждается
вопрос о допустимой области S3 [Р. Курант и Д. Гильберт, Метбды
математической физики, т. I, 11,-ГИТТЛ, 1951].
6.41 § 6. ФУНКЦИЯ ГРИНА ДЛЯ УР-НИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 103
кривой Г, выступает еще контур С малого круга. Чтобы подчеркнуть,
что в последующих уравнениях направление обхода контура С должно
быть отрицательным (рис. 6.3), определим границу как Г — С. В пол-
полной области интегрирования М [О] — 0, и остается
у; |, i))<p(x.y)dxdy= j P(z^—Q§
т-с
Так как z n О удовлетворяют однородным краевым условиям F.7),
интеграл по внешнему контуру Г отпадает, как и в п. 6.2. При ин-
интегрировании по круговому контуру С и
У
при переходе к пределу при р = 0 имеем
■О
-с
дг „ ,
p—Qds-
^ дп
pz
да
дп
Если при этом взять логарифмическую
особенность, то О растет как ]пр, длина
пути интегрирования есть 2яр, a plnp
при р—>0 стремится к нулю. Имеем, сле-
следовательно,
х
G(x, y; \.
, у) dxdy =
Рис. 6.3. К особенности функ-
функции Грина.
Это есть общая формула решения; надо только еще поменять местами
х, у и |, т). Функция Грина при этом не меняется; покажем сим-
симметрию
О(х. у; £, ц) = 0A, п; *. у). F.16)
Для этого рассмотрим две различные точки
|р r)j и ^2> Лг- назвав соответствующие им
функции Грина кратко О,, G2:
G1 = G(x, у; lv цг), G2 = G(x, у, £2, ц2).
Рис. 6.4. К симметрии
функции Грина.
Подставим эти функции в формулу Грина
F-10)- положив и = О, и w = Q2, и про-
интегрируем по заданной области 23, причем
обе взятые точки вырежем малыми кругами
радиуса р, Область интегрирования заштрихована на рис. 6.4; имеем
три контура Rv R2, /?з> ПРИ этом направление обхода контурных
кривых Л?, и /?2 является отрицательнъш. Тогда
{- G2M [О,] + Q,M [G2]} dx dy = 0,
104 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [6.5
так как Gx и G2 (за исключением этих точек) удовлетворяют урав-
уравнению М [G,] = М [G2\ = 0. Согласно формуле Грина поэтому имеем
Интеграл по /?3 исчезает в силу того, что G, и G2 удовлетворяют
краевым условиям F.6). Из интеграла по — /?j при предельном пере-
переходе р -> 0 получаем
jpQ^ds-^0 и _ JPO2^</*->-0,F,. т|,;&,.ть).
-R, -Ri
Если те же соображения применить к интегралу по /?2, то получим:
6.5. Другие типы уравнений с частными производными. Соображения
пп. 6.2 и 6.4 можно в принципе перенести на уравнение
Af|>] = — (Ргх1) —(Ргх2) —(Ргх) ~Ь Чг = hgQz, F.17)
где г (хь хъ х3) есть некоторая функция трех независимых переменных хх,
х2, х3. При краевых условиях F.7) на граничной поверхности можно дока-
доказать самосопряженность, а для ар > 0 и полную определенность задачи, как
это было проделано в п. 6.2 только при двух независимых переменных х, у.
Основное отличие состоит в том, что функция Грина G (хи х2, х3; £,, |2, |3)
имеет теперь другую, не логарифмическую особенность, а именно:
~ п (-^ii Х2) Х3\
где
Здесь Hi — непрерывные со своими производными до второго порядка
включительно функции, которые определяются посредством следующих тре-
требований: G должна удовлетворять, кроме точки г = 0, соответствующему
F.17) однородному уравнению М [G] = 0 и краевым условиям. К вопросу
о существовании функции Грина здесь опять нет возможности подойти.
Симметрию G, напротив, точно так же как в п. 6.4, можно легко доказать.
Функцию Грина можно построить также и в случае уравнений в частных
производных более высокого порядка. Для уравнения
от двух независимых переменных х, у функция Грина имеет вид
О(х,у;%, г\) = — -^-гПпг-\-Ь{х, у; |, ц),
гда г2 — (х — |J -f- (у — г]J. Функция * (х, у; |, т|), непрерывная с ее ча-
частными производными до четвертого порядка включительно,, должна быть
Определена так, чтобы G (кроме точки г = 0) удовлетворяла уравнению
ДД(? = 0 и краевым условиям.
7.1) § 7- СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 105
§ 7. Связь с интегральными уравнениями
7.1 Одночленный класс и интегральные уравнения. Пусть
G(x, |). как и в п. 5.4, есть функция Грина для дифференциального
выражения М [у] при краевых условиях:
*УЯ = 0 (ц = 1. 2, .... 2т).
Она, согласно п. 5.6, существует как раз тогда, когда Я, —0 не
является собственным значением задачи D.11) — D.14), что мы и пред-
предполагаем здесь. Решение краевой задачи М [у] — г (х), i/^[y] = 0
при любом непрерывном г (х) дается общей формулой решения E.4).
Так как для собственной функции действительно дифференциальное
уравнение D.11), то из E.4) при г (х) = ХМ [у] возникает для соб-
собственной функции у (х) соотношение
*
(l)]dl. G.1)
Выражение такого типа для п > 0 (см. 4.13) называют линейным одно-
однородным «интегро-дифференциальным уравнением».
Для ге = 0, т. е. для частного класса задач N\y\ =zgQ{x)y, при
положительном go(x) и при
для (f(x) получаем уравнение
b
Это — так называемое линейное однородное интегральное уравнение
второго рода. Если задача на собственные значения является само-
самосопряженной, то G (х, |), а вместе с тем и «ядро» К (х, |) симме-
симметричны относительно х и |.
Задачи подобного типа в более общем виде получают для одно-
одночленного класса (п. 4.7); в этом случае N[y], согласно D.26), имеет
вид (—I)" [gn (х)у^п\ а формула решения G.1) переходит в сле-
следующую:
ь
J(х, I)\gn(|)yW(|)](л)dl.
В силу предпосылки D.27), сделанной в случае одночленного класса,
интеграл в правой части путем «-кратного интегрирования по частям
может быть преобразован к виду
= Я, J
i) d\.
106 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА G.1
Здесь и-кратное дифференцирование под знаком интеграла допу-
допустимо '), так как производные
dxv dl" '
согласно дополнению к п. 5.3 (имеем п < т, т. е. выполняется соот-
соотношение v-f-rt<^2/?z — 2), при O^v^rt являются непрерывными
функциями. Итак, получаем
ъ
У(л) (*) = Я. / д'"д%%1) ёп (I) У(л) (I) d%.
а
Если в случае положительной функции gn (x) подставить
x)y(n)(x) = V(x) G.2)
К(х, 1)=
то для ф снова получим обычное линейное однородное интегральное
уравнение второго рода:
ь
Ядро К(х, I) симметрично, если симметрична G (х, I).
Зададимся обратным вопросом: является ли тождественно не ра-
равное нулю решение ф(лг) интегрального уравнения
ь
= х J д2пд%р] У>„ (*) g,, (В ф (В<*& G-4)
собственной функцией у (х) соответствующей задачи одночленного
класса. Для этого исследования примем дополнительные предпосылки:
1. Пусть Зи < 2т — 1.
2. В числе краевых условий U^ [у] = 0 встречаются такие:
Для частных задач на собственные значения п = 0, и тогда допол-
дополнительные предпосылки отсутствуют. . .
') К. К п о р р, Einfuhrung in die hOhere Mathematik, т. Ill, изд. 7, 1942,
317 [см., например, В. И. Смирнов, Курс высшей математики, т. II,
М.—Л., Гостехиздат, 1952].
7.1} § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 107
Во-первых, из требования Зи < 2т — 1 следует, что производные
д3па (х, I) „ . .
^—}г~ все еще непРеРьшны- Если ф(л;) есть непрерывное реше-
решение G.4), то и-кратное дифференцирование G.4) обеспечивает суще-
существование непрерывных производных ф("'(л;). Мы можем, следова-
следовательно, образовать функцию
ь
y(x)=J0(х, I)-^(УёТШ) Ф(S)) dl G.6)
а
и доказать, это эта функция является собственной функцией задачи
одночленного класса. Уравнение G.6), согласно E.4), эквивалентно
следующей задаче:
M[y]=(VgB(x)<p(x))ln\ и^[у) = 0;
следовательно, у удовлетворяет всем краевым условиям. Далее, так
как О (х, I) удовлетворяет дополнительно наложенным краевым усло-
условиям G.5), из G.6) путем и-кратного интегрирования по частям по-
получается
ь
у (х) = (-1).» J д'Ю^ 1) У¥Ш Ф (i) d\.
а
/г-кратное дифференцирование по х при использовании G.4) дает
и, таким образом,
Значит, у удовлетворяет также дифференциальному уравнению и
является поэтому собственной функцией.
Теорема. Самосопряженную задачу на собственные значения
D.28), D.14), для которой Х = 0 не является собственным зна-
значением и функция gn{x) в основном интервале a, b имеет по-
постоянный знак, при помощи функции Грина можно трансформи-
трансформировать в линейное однородное интегральное уравнение второго рода
с вещественным симметричным непрерывным ядром. Каждому
решению у(х) одночленного класса можно, согласно G.2), сопоста-
сопоставить решение интегрального уравнения G.4). При дополнительных
предпосылках G.5) можно также, обратно, из каждого решения
интегрального уравнения, согласно G.6), построить собственную
функцию задачи одночленного класса.
108 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА |М
7.2. Выводы из теории интегральных уравнений. Ограничимся
здесь приведением без доказательства следующих выводов из теории
интегральных уравнений 'J). Относительно вещественного тождественно
не равного нулю ядра К{х, £) линейного однородного интегрального
уравнения второго рода
ь
= a,J/с (*, |)ф (!)<*! G.7)
при а ^ х, | -^ b предполагается следующее:
1) симметричность, т. е. К (х, Q — K(l, x);
2) квадратичная интегрируемость, т. е. интегралы
ь ь
JK(x,l)dx,
а
b
J K2(x, l)dx, J j K2(x, Ddxdl
а а
Ь Ь
существуют и, поскольку они зависят еще от |, являются ограни-
ограниченными;
3) непрерывность в среднем, т. е. для всех х выполняется
условие:
ь
lim f [K{x, l)-K{xv l)]2dl = 0. G.8)
Если К(х, I) непрерывно, то предпосылки 2) и 3) выполняются
автоматически.
Далее, имеем определение:
Число X, для которого G.7) имеет тождественно не равное нулю
квадратично интегрируемое решение (р(х), называется собственным
значением, а отвечающее ему решение — собственной функцией.
') Доказательство можно найти, например, в книгах: G. H a m e I, Inte-
gralgleichungen, Berlin, 1937, 51—91 hR. Courant, D. Hllbert, Methoden
tier mathematischen Physik, Berlin, 1931, т. I, 96—130 [P. Курант и Д. Гиль-
Гильберт, Методы математической физики, т. I, ГИТТЛ, 1951].
2) Существенным прогрессом теория интегральных уравнений обязана
Гильберту.
Давид Гильберт после Гаусса был наиболее значительным, весьма
многосторонним математиком. Теория задач иа собственные значения обязана
ему больше, чем это можно выразить в отдельных замечаниях.
Д. Гильберт родился 23.1 1862 г., в Кенигсберге, где он в 1884 г. защитил
докторскую диссертацию. В 1895 г. Феликс Клейн пригласил его в Геттин-
ген, где Д. Гильберт работал вплоть до своей смерти, последовавшей
14.11 1943 г. [См. некролог G. H a m el, Z. angew. Math. Mech. 23A943), 128.]
7.2] § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 109
Собственная функция ф называется нормированной, если
ь
Ф2 (х) dx=l.
Функция и(х) называется истокообразно пред ставимой, если
имеется такая квадратично интегрируемая функция v(x), что действи-
действительно равенство
и(х)=$К(х.
При названных предпосылках имеет место следующая теорема:
Все собственные значения X уравнения G.7) являются веще-
вещественными; очевидно, что Х=0 не есть собственное значение.
Имеется минимум одно собственное значение X и максимум
счетное бесконечное множество собственных значений, которые
могут быть расположены поэтому в виде последовательности
Xlt X2, ... и которые в конечной области не имеют точки сгу-
сгущения; далее, кратность вырождения собственного значения,
которая указывает число линейно независимых собственных функ-
функций, отвечающих этому собственному значению, может быть
только конечной.
Число собственных значений при непрерывном ядре конечно в том
случае, когда ядро «вырождено», т. е. когда оно может быть представлено
в виде конечной суммы произведений некоторой функции х на некоторую
функцию |:
г
К (х, I) = 2 а* (*) bk (|).
k-i
Собственные функции, соответствующие различным собственным
значениям, ортогональны:
ь
(x)dx = 0, X^Xk.
Г
Собственные функции, соответствующие вырожденному собственному
значению, могут быть ортогонализованы (см. п. 5.9), так что если
вырожденные собственные значения в последовательности Хх, Х2, ...
повторяются соответственно кратности вырождения, то существует
надлежащая система нормированных ортогональных собственных функ-
функций ф1( ф2, .... так называемая «ортонормированная система», для
которой
г , I 0 при i Ф k,
J [ 1 при i — k.
ПО ГЛ. П. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА 1?.2
Всякую истокообразно представимую функцию и (х) можно разложить
в ряд по таким образом нормированным и ортогонализованным соб-
собственным функциям (Рь(х), который сходится абсолютно и равно-
равномерно:
2). G.10)
причем коэффициенты разложения ck определяются формулой
ь
ck= j u(x)yk(x)dx. G.11)
a
«Итерированное ядро» K2(x, |)
ь
К2(х, £) = j К(х, р)К(р,
можно разложить в ряд, сходящийся абсолютно и равномерно no x
и по |:
а.2(х, §;—
"
*
и действительно соотношение
ь ь ь
f К,(х. x)dx = jj[K(x, l)]2dxdl = ^jy. G.12)
a a a k *
Если К (х, |) непрерывно и все собственные значения Kk поло-
положительны или только конечное число их отрицательно, то имеет
силу абсолютно и равномерно сходящееся разложение (теорема
Меркера):
К(х, 1) = %®
k
и
j K(x, x)dx = ^i~. G.13)
a k
Соответствующее G.7) неоднородное интегральное уравнение
D
= к J К{х, I) Ф (У </6 -f / (*) G.14)
7.31 § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ ]]1
имеет, поскольку X не является собственным значением, однозначно
определяемое решение
*
Ф (х) = f (х)
*г - п
a L / — 1 J
G.15)
При этом бесконечный ряд сходится равномерно по л: и по | для
всех >., не являющихся собственными значениями.
Далее, действительна теорема включения1): Если v(x) не-
непрерывна, а функция
Ф(х) = — ^ G.16)
К (х, £) v (I) dl
заключена между конечными границами Фт1п и Фтах и имеет
постоянный знак, то между Фт1п и Фтах расположено по мень-
меньшей мере одно собственное значение Xk:
х- G-17)
Собственные значения можно определять из вариационного прин-
принципа. Так и-ое,положительное собственное значение Хп (поскольку
оно существует) определяется соотношением
ь ь
y- = max K(x, l)w(x)w{l)dxdl, G.18)
а а
причем w (х) пробегает область всех квадратично интегрируемых
функций 2), которые удовлетворяют дополнительным условиям:
ь ь
\w1{x)dx=\, (w(pidx = 0 (/ = 1,2 и—1); G.19)
а а
здесь фг есть /-я собственная функция вышеупомянутой ортонорми-
рованной системы.
7.3. Применение к одночленному классу. Применим теперь эти
теоремы к интегральному уравнению G.4) для задач одночленного
класса (п. 7.1). Ядро G.3) вещественно, непрерывно, симметрично и
удовлетворяет, следовательно, всем требуемым в описанной теории
предпосылкам. Теория обеспечивает вещественность собственных
') L. Kollatz, Math. Z. 47 A941), 395.
2) Соотношения G.18), G.19) сохраняют силу также и в том случае,
если w (х) пробегает только область непрерывных или кусочно-непрерывных
функций, см. R. С о u r a n t, D. H i I b e г t, Methoden der mathematischen
Physik, т. I, изд. 2, Berlin, 1931, 104 [P. Курант и Д. Гильберт,
Методы математической физики, т. I, ГИТТЛ, 19511
112 ГЛ. И. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [7.3
значений в соответствии с теоремой п. 4.7; соотношение ортогональ-
ортогональности G.9) при представлении собственных функций yk задачи в форме
дифференциального уравнения с помощью равенства ф,- (х) =
= Vsn(x) уТ (*) (см- G-2)) переходит в
*
/ gn (x) yf (х) yj*> (х) dx = 0 при X, Ф Xk G.20)
а
в соответствии с D.21); формулы G.12) и G.13) при выполнении
дополнительных предпосылок G.5) означают
* = 1
no * *
Sir
G.21)
причем верхняя формула доказывается только для случая, когда по-
появляется, самое большее, конечное число отрицательных %k [см., на-
например, (8.2), когда отрицательных собственных значений нет].
При применении теоремы разложения G.10), G.11) возникает
вопрос: какие функции и{х) являются истокообразно представимыми?
Для ответа на него примем предпосылки, приводившиеся уже в G.5):
среди краевых условий U^[y]=0 могут присутствовать и такие:
... =у(п-Ц ф) = 0, G.22)
выполняется неравенство 3« < 2т — 1 и % = 0 не является собствен-
собственным значением. Пусть, далее, w(x) есть любая функция сравнения.
Тогда соотношением М[1И]=Ц)(х) определяется некоторая функ-
функция ф(л;) и, согласно E.4), действительно равенство
w(x)= JQ(x, £) ф (£)<*£•
Так как G(x, |) удовлетворяет краевым условиям G.22), то путем
я-кратного интегрирования по частям получаем
7.4] § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 113
где Ф(х) есть функция, удовлетворяющая уравнению -р^- =
= (—1)"ф(лг). Дифференцируя под знаком интеграла п раз, что до-
допустимо, получаем
/
Согласно G.3) поэтому имеем
*
Это есть функция u{x) = w^{x) \fgn(x), истокообразно представи-
мая посредством непрерывной функции v (£) = . и, следова-
V gn (£)
тельно, она может быть разложена в ряд
«*»>(*) = 2 с*у£°(*)
по собственным функциям G.2)
Этот ряд сходится абсолютно и равномерно. При я-кратном по-
почленном интегрировании от а до л: получается, что каждую функцию
сравнения можно разложить в ряд по собственным функциям ук (х)
[постоянные интегрирования отпадают в силу краевых условий G.22)]
со
w(*)= 2 **У*(«) G-23)
и что этот ряд можно почленно п раз дифференцировать. Аналогич-
Аналогичная теорема разложения будет доказана в п. 10.5 другим способом
(без интегральных уравнений); там получается, что ряд G.23) может
дифференцироваться почленно даже (т—1) раз.
Несмотря на изящество и большую прозрачность методов инте-
интегральных уравнений, мы не будем изучать их подробнее, потому что
они достаточны лишь для задач одночленного класса, а общие задачи
на собственные значения сводятся к интегро-дифференциальным ура-
уравнениям G.1), которые математически освоены еще слишком мало.
7.4. Интегральные уравнения и дифференциальные уравнения
с частными производными. Интегральные уравнения играют полез-
полезную роль не только при изучении обыкновенных дифференциальных
уравнений (при этом теория интегральных уравнений, правда, не так
глубока, как представленная в §§ 4, 5, 8, 12 прямая теория диффе-
дифференциальных уравнений). Они особенно полезны при анализе уравнений
§ Л. Коллатц
114 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА р.4
с частными производными. Большим преимуществом теории инте-
интегральных уравнений является то, что выводы теории одинаково при-
применимы как при одной, так и при многих х, у, . .. независимых
переменных. Например, при двух независимых переменных х, у вместо
интегрирования по основному интервалу (а, Ь) следует всего лишь
интегрировать по основной области 33 плоскости (х, у). Покажем это
на примере приведенного в п. 6.2 частного класса задач на собствен-
собственные значения уравнения второго порядка с частными производными F.6)
M[z] = — (pzx)x — (pzy)y-lrqz = 'kgoz в области 33
с граничными условиями F.7)
az-\-fizn = 0 на контуре Г.
Как и в п. 6.4, предполагаем существование функции Грина
G (х, у; |, г|), которая разрешает краевую задачу F.11), F.7)
в форме F.12). Для собственной функции z(x, у) выполняется F.11)
при cp = XgQz; тогда формула решения F.12) принимает вид
г(х, y) = ljJG(x, у; £, т|)£о(&. Л) * (I Л) <*£*!■
Следовательно, если подставить (полагая g0 положительным)
К(х, у; I. ч) = О(х, у; %, т1)У>0(*, y)go(l ц) G.24)
и [ф теперь означает иное, чем в F.11)]
Ф(*. y) = z(x, y)Ygo(x, у), G.25)
то ср есть собственная функция однородного интегрального уравнения
второго рода:
jJ(x, у; I, тОф(|. rj)dldr\.
Ядро К(х, у; |, т]) удовлетворяет названным в п. 7.2 пред-
предпосылкам; оно вещественно и симметрично, так как функция Грина
является, согласно F.16), симметричной. Далее, оно не является
ни непрерывным, ни ограниченным, так как функция Грина имеет
логарифмическую особенность, однако оно квадратично интегрируемо,
потому что в силу строения F.15) функции Грина можно записать
К{х, у; I i\) = A(x, у; \, т]Iпг + Д(*, у; I, Ц), G.26)
где
г = Y(x—lf+(y—i\y.
Здесь А и В — непрерывные функции, которые обладают даже не-
непрерывными частными производными второго порядка, если ими об-
обладает go(x, у).
7.4] § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ Ц5
Так, если образовать интеграл
\\К{х, у; I vfrdxdy,
аз
то особенность при х = \, у = Ц не сказывается. Действительно,
если ввести полярные координаты
* = !-f-p cos ft, _y = r)-f- p sin ^",
то dx dy переходит в pdpdft, а интеграл по малому кругу радиуса г
вокруг точки х — \, у = ц при достаточно малом г дает сколь угодно
малый вклад, так как г In г стремится к нулю при г—»0. И г (In гJ
также стремится к нулю при г—»0, т, е. все приведенные в пред-
предпосылке 2 п. 7.2 интегралы существуют и являются ограниченными.
Легко видеть, наконец, что ядро К(Х, у; %, ц) обладает непреры-
непрерывностью в среднем. Так как сумма двух непрерывных в среднем ядер
есть также непрерывное в среднем ядро !), то достаточно проверить
непрерывность в среднем члена А(х, у; |, цIпг ядра К G.26).
При образовании интеграла G.8) вырежем из области 33 малый круг
радиуса г вокруг точки х = \, у — Ц', точка х1: у^ лежит уже в этой
круговой области. Вклад круговой области стремится к нулю, потому
что r(lnrJ->0 при г->0.
Ядро К{х, у; %, т|) вида G.26) удовлетворяет, таким образом,
всем предпосылкам для применения теории интегральных уравнений.
Тем самым доказывается, прежде всего, существование по меньшей
мере одного и вещественность всех имеющихся собственных значе-
значений. Соотношение ортогональности G.9) в силу G.25) переходит
в следующее:
\\ Q приЯг^ЯА. G.27)
') Если ядра К (х, £) и К* (х, £) непрерывны в среднем, т. е. если для
них выполняется G.8), то G.8) выполняется также для ядра S (х, I) =гК-\-К*,
ибо имеем
*
lira f [S (x, £) — S (xu £)P dl = lim Д + lim Д
! > X
J [S (x, l) — S (xu DY dl = lira Д + li
где
+ 2lira J [K(x, 1)-К(хь ШКЧх, l)-K*(xu £)J rf|,
a
b b
Д = J [K (x,l) - К (xlt l)Y dl; Д* = J [K* (x, I) - K* (xu i)]' d%
a a
Согласно предпосылкам Аи А' стремятся к нулю при хх -* х, а третий член
в правой части, оцениваемый по абсолютной величине при помощи неравен-
неравенства Шварца как У"ДД*. точно так же стремится к нулю.
116
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
G.5
Теорема разложения G.10), G.11) обеспечивает разложение в ряд
по собственным функциям любой, удовлетворяющей краевым усло-
условиям F.7) и обладающей непрерывными частными производными до
второго порядка включительно, функции и(х, у). Дальнейшие при-
применения теории интегральных уравнений к дифференциальным уравне-
уравнениям в частных производных обсуждаются в пп. 11.2 и 14.1.
Также и в других названных в п. 6.5 типах задач на собствен-
собственные значения особенности функций Грина, а значит, и ядра соответ-
соответствующего интегрального уравнения, не являются помехой. Приведен-
Приведенные в предпосылке 2 п. 7.2 интегралы, как легко видеть, существуют
и ограниченны. Теория интегральных уравнений, таким образом, имеет
очень обширные возможности применения; мы, однако, не рассма-
рассматриваем ее более подробно, так как уже вопрос о существовании
функции Грина, как указывалось в п. 6.4, выходит за рамки данной
книги.
7.5. Одночленный класс и интегральное уравнение Вольтерра.
Интегральные уравнения вида
Ф (*) =
X
J К(х, I)Ф(I)d%.
G.28)
в которых, следовательно, верхним пределом интегрирования служит
переменная х, называются интегральными уравнениями Вольтерра
второго рода, а именно, при /(х)фО — неоднородными и при
/(лг)^О— однородными. Любое обыкновенное дифференциальное
уравнение &-го порядка L[y]=r(x) можно трансформировать не-
непосредственно в интегральное уравнение Вольтерра второго рода при
помощи формул
= ф (х),
*) (х) =
ф (I) d\.
p=0
(p=0, 1 k—l),
G.29)
где c0, cl c*-i> xo—постоянные. Если применить этот метод
к задаче на собственные значения
M[y]=XN[y], , G.30)
то собственное значение Я появится в уравнении Вольтерра вообще
в различных местах и не только просто в качестве множителя при
интеграле, как в G.28).
7.51
7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ
117
Однако в задачах одночленного класса можно построить несколько
иного типа уравнение Вольтерра, в котором собственное значение Я,
выступает, точно так же как в G.28), в качестве множителя при
интеграле и нигде больше. Построение этого интегрального уравне-
уравнения связано с методом вариации коэффициентов для получения част-
частного интеграла неоднородного дифференциального уравнения
М[у]=г(х). G.31)
Пусть 2j, z2 zk есть фундаментальная система, т. е. k линейно
независимых решений уравнения /И [у] = 0, и пусть рк {х) есть коэф-
коэффициент 1) при высшей производной yW(x). Решение G.31), как
известно 2), имеет тогда вид
k
y='%yl(x)zl(x). G.32)
i-i
Если ввести y't (х) = С. (х), то С1 (х) определяются из уравнений:
j-1
i = l
(*) Ct (x) = О,
G.33)
Эта система уравнений имеет однозначно определяемое решение,
так как ее определитель, будучи вронскианом фундаментальной си-
системы zt(x), отличен от нуля. В силу этих уравнений из G.32)
путем последовательного дифференцирования получаем
(*=1. 2 k—l).
t-1
G.34)
') В D.11), D.12) коэффициент при высшей производной обозначался
(—l)m fm(x)- Здесь мы пишем ри(х), так как соображения данного пункта
действительии не только для самосопряженных выражений вида D.11), D.12),
ио и для дифференциальных выражений типа E.1).
2) J. Horn, QewOhnliche Differentialgleichungen, изд. 2., Berlin — Leip-
Leipzig, 1927, 67 [см., например, Н. М. Матвеев, Дифференциальные уравне-
уравнения, нзд. ЛГУ, 1965].
118 ГЛ. И. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА |7.5
При подстановке G.32) в G.31) в силу M[zL] = 0 тотчас полу-
получается, что М [у] = г (х), т. е. у(х) является интегралом G.31).
Если обозначить решение системы G.33) в случае г = \ через Di{x),
то имеем Cl{x) = r (x)Dl(x), причем Dt(x) не зависит от г(х).
Поэтому общее решение G.31) можно записать в форме
* к х
У (*) = 2 c,zt (x) 4- 2 *, (х) / Dt (I) r (I) <Ц. G.35)
i=l 1=1 а
Здесь с,, с2 сь — произвольные постоянные.
В системе G.33), за исключением последнего уравнения, С{(х)
можно заменить через D-t (x). Эти уравнения тогда совпадают с урав-
уравнениями E.9), E.10) для величин bt (x). Поэтому, применяя после-
последовательное дифференцирование уравнений G.33):), точно как в п. 5.3,
приходим к следующему:
и
% zf (x) D(!v)(х) = 0 при ii-f- v<£ — 2. G.36)
/-1
Применим теперь формулу решения G.35) к уравнению на соб-
собственные значения однрчленного класса или вообще к уравнению вида
G.37)
где p-\-q-^.k — 2, причем g(x) пусть непрерывно дифференцируема
как р раз, так и q раз.
В качестве общего решения этого уравнения имеем
4яЛ J Jmm
/=1 a i=I
При интегрировании по частям интеграл в правой части приводится
к виду
f~l)
, (x) D'.{1) [g (I) yW (l)
Краевое выражение исчезает при | = jc в силу G.36), а при | = а
оно является линейной комбинацией zt (x) и, следовательно, может
') При этом требуется, чтобы Dt (|) имела непрерывные производные
до (k — 2)-го порядка. О bt (g) следует сказать дословно то же самое, что
и в сноске ') на стр. 82.
7.5] § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 119
быть добавлено к первой сумме в G.38). Итак, с новыми постоян-
постоянными citV имеем
ft х к
У (х) = 2 с/, 1*, (*) — * J 2 *i(х) D/ G> [Z F) У(р) (i)lG~!) <*|.
j=l a (=1
Точно так же получаем, q—1 раз интегрируя по частям:
ft X ft
i-l а (=1
Учитывая, что, согласно G.36),
2 zt [Dfg] ' = gi ZlDft4+1) + g 2 ^e = 0
ii ii ji
и, равным образом,
2*i №>*]' = о
i-l
и т. д., применяя вторично /^-кратное интегрирование по частям,
получаем для у (х) (если постоянные снова обозначить ct) неоднород-
неоднородное интегральное уравнение Вольтерра второго рода:
* х и
У (*) = 2 Vi (*) + (- 1)"+? Я. J 2 ** W [^ E) g A)Г У (I) dt
i-l а «=1 G.39)
Дальнейшие рассуждения приводятся без доказательства (впрочем, легко
выполняемогоI). В случае ограниченного непрерывного ядра К, т. е.
\К(х, |)|<С при а<|<л;<*,
решение ф(х) неоднородного уравнения G.28) существует; оно одно-
однозначно определяется посредством G.28) и может быть найдено ме-
методом последовательных приближений. Если у0 (х) есть произвольная
интегрируемая функция, то функции уп (х), определяемые соот-
соотношением
«+1
. l)yn(l)dl (« = 0,1,2,...), G.40)
сходятся в интервале а, Ь равномерно к решению ц>(х).
В случае уравнения G.39) положение несколько иное, так как
постоянные с{ и Я неизвестны. Несмотря на это, можно применить
метод последовательных приближений, данный формулой G.40),
') О. Н a m e I, Integralgleichungen, Berlin, 1937, 32.
120 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА G.6
а именно следующим образом (при этом, правда, ничего нельзя сказать
о сходимости метода): исходим из произвольно выбранных, наперед
заданных краевых условий, которым функция уо(х) по возможности
уже удовлетворяет, и определяем постоянные ct, которые при вычи-
вычислении yn+i(x) еще выбираются свободно, а также величину Я,
которую затем рассматриваем в качестве приближенного собственного
значения, таким образом, чтобы у„+] удовлетворяла краевым усло-
условиям и была бы величиной одного порядка с уп. Множитель же
при yn+i еще не зафиксирован, и мы используем какое-нибудь усло-
условие нормировки, например: уп (х0) = уп+, (*0) или ^(*0) =K + i (Л>
Детали см. в следующем примере.
7.6. Пример. Изгибные колебания защемленного на одном конце и сво-
свободного на другом стержня постоянного сечения длины / = 1 приводят,
согласно п. 2.3 (рис. 2.5), к задаче на собственные значения:
yiv = Ay, у @) = у' @) = у" A) = у'" A) = 0.
В силу G.29) при k = 4, р = 3 можно сразу записать соответствующее
интегральное уравнение Вольтерра
y(x) = 2ucPx +l J 3! ^HS-
p=o о
Из краевых условий у @) = у' @) = 0 получаем со = Ct — 0; из других двух
краевых условий с2 и с3 так просто выразить нельзя.
Для решения интегрального уравнения итерационным методом, согласно
G.40), исходим из функции у0 {х):
у0 (х) = 6л-2 — 4л-3 + х\
удовлетворяющей всем краевым условиям, и получаем
Множитель при Я может быть непосредственно найден путем четырехкрат-
четырехкратного интегрирования у0 (х); например, из 6х2 получаем
6л-5 хе
3 ■ 4•5 • 6 60
Далее, yi (x) должно удовлетворять краевым условиям. Произвольный
пока множитель при у{ (х) устанавливается, согласно рекомендации в заклю-
заключении п. 7.5, так, чтобы у0 и ух были величинами одного порядка; наиболее
просто потребовать yo(l)=Vi(l). Из трех уравнений
у\ A) = 2с2 + 6с3 + у = °' У"A) = 6сз + X = °'
Уо A) - У. О) = 3 - с2 - с, —^ = 0
находим
312 144 . 720 1оопо4
С = Ж< «. = —59-- ^ = -39- =12,2034
вместо точного значения Я = 12,362.
7.7] § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 121
Улучшенное приближенное значение получаем, проделывая следующие
итерационные шаги. Так как постоянный множитель при у^ не зафикси-
24
рован, разделив наиденные величины на -щ, имеем
v-6 y7 V-8
у, (*) = 13^-6^+4" —Т+ 'SB-
Тогда у2 (х) будет
. ._ 2 . з, Я / 13-у6 9х7 х"> х" . х" \
у,(х)-с2х +с3х + 45 ^-g 28~ + 2Т~ Ц.112 + 112 - 132 J"
Из трех линейных уравнений у A) = у" A) = ух A) _ у2 A) = 0 получаем
для неизвестных с2, с3. ^ значения:
сел 1 о 14ft fiSA
^ С Л ^ 123581 (ошибка —0,0396) ')•
7.7. Асимптотическое распределение собственных значений.
При помощи интегрального уравнения Вольтерра G.51) можно опре-
определить асимптотическое распределение собственных значений в случае
дифференциального уравнения второго порядка2)
G.41)
и краевых условий Штурма
сУ(а)+с2У(«) = 0. с3у' ф) -f с4у F) == 0. G.42)
Пусть /, >0, ^о>°> fv /о- ё'о непрерывны, /j и g0 дважды непре-
непрерывно дифференцируемы. Вначале дифференциальное уравнение G.41)
путем введения новой переменной трансформируется к более простой
форме при помощи преобразования, полезного и в других случаях.
Вводятся новая независимая переменная
^^Yf;dx G-43)
а
и новая зависимая переменная
и = ву, где e = (gof1)'/t. G.44)
Постоянная К подлежит определению позже. Здесь это преобра-
преобразование ради краткости дается готовым, его можно, разумеется,
проводить при любых функциях в и z (х)\ в и z (х) можно
') «Ошибка» приближения \ к «истинной величине» х в литературе
вводится, к сожалению, различными способами: | — х, х — | или || — х \.
Здесь, следуя F. Kohlrausch, Praklische Physik, т. I, Leipzig und Berlin, 1943,
стр. 12, она определяется как g — х, так что имеем: приближенная величина
равна истинной величине плюс ошибка и истинная величина равна прибли-
приближенной величине плюс «поправка». Относительная ошибка выражается
в процентах истинной величины.
2) Е. L. In ce, Ordinary Differential Equations, London, 1927, 270-273
122 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [7.7
определить из требования, чтобы дифференциальное уравнение имело
простое строение G.45).
Из G.43) и G.44) следует
1L— ±(£±\Ъ— _1JE!
dx — К \ f J * К /,
и
t_dy__d_lu\d£\\_du Ji^
— —1
и dz\'
,,,,, \ d \ du n del dz If d2u л d261 в2
(f \\' V (м) // (н) //
К1\У > — к dz [dzU U dz J dx ~ K2 [dz*U U dz2 \ /, •
Дифференциальное уравнение G.41) переходит, таким образом,
в следующее:
-g+[Л2-?(*)]« = О, G.45)
где
Л» = ±^ ^
Постоянная К связана с длиной нового основного интервала; он
равен л для
ь
^Yjdx. G.46)
Краевые условия G.42) принимают вид
^(■§H+^(°)=°- cl{ti+c>^-°- G-47>
Пусть сначала с*фО, с*фО; тогда G.47) можно записать в форме
G-48)
G.49)
Свободный пока множитель при «(г) может быть определен посред-
посредством начальных условий'):
тогда G.48) удовлетворяется. Решение G.45) можно теперь сразу
получить описанным в п. 7.5 методом вариации коэффициентов. Если
d2u
положить в G.31) М [у\ — -рт -{-Аи, г (z) = q (z) и (z) и в качестве
') и @) не может быть равным нулю, так как в противном случае,
согласно G.48), было бы равным нулю и и' @), а значит, и(х)^0 — реше-
решение G.45) при начальных условиях и = «' = 0.
7.71 § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 123
фундаментальной системы Wi = cosA.2> K2 = sinA.2, то формула
решения G.35) дает
г
u(z) = A cos Az -|- В sin Az + ~ Г sin (Л (z — t)) q (t) и (t) dt.
о
Что эта функция на самом деле удовлетворяет дифференциальному
уравнению G.45), легко установить путем подстановки. Из начальных
условий G.50) получаем постоянные интегрирования: Л = 1, 5 =-г-.
Таким образом, интегральное уравнение Вольтерра для и (z) имеет вид
г
±- \
о
— t))q(t)u(t)dt. G.51)
Решение и (z) исходной краевой задачи G.45), G.50) в интервале
0 <С z <^л при заданном Л устанавливается однозначно и является
непрерывным. Пусть М есть максимальное абсолютное значение и(х)
в этом интервале, которое соответствует точке z — Z\. Тогда при
о
посредством оценки интеграла в G.51) получаем для М неравенство
Функция cos Az-\- -r-sin Az представляет относительно z колебания
с амплитудой
имеем, таким образом,
или
1
при |A|>Q.
Итак, М ограничено для всех | Л | > Q, а значит, для всех веще-
вещественных Л
Жj, а в дальнейшем Ж2, Ж3, ... означают независимые от Л по-
постоянные. Таким образом, из G.51) следует
jj = —AsinAn-\-a2, где | а21< Ж2;
124
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
[7.7
вследствие неравенства \и(п)\-^.М1 получается второе краевое усло-
условие G.49):
sin Лл =
А '
где | а3 |
G.52)
Корни Л = Лл этого трансцендентного уравнения, которые одно-
одновременно являются собственными значениями G.45), G.47), для
больших А как угодно мало отличаются от корней уравнения Лл —0.
Легко видеть (рис. 7.1, кри-
кривя
вая -~- должна проходить в за-
заштрихованной области), что
где
Этим еще раз доказано, что
_,_,,, , число п-\-а,1п и есть как раз
Рис. 7.1. К асимптотическому распреде- тйгтпеннпе чнячение Л ■
лению собственных значений. "'е собственное значение л„,
оно могло бы быть, напри-
например, (ra-p-l)-M или (я—1)-м
собственным значением, либо при п могло бы быть несколько
корней G.52). (Последний случай можно, правда, исключить, пока-
показав, что рост -^- при Л->оо как угодно мал.) В случае, до сих
пор не рассмотренном, когда с* или с* исчезает, соответствующие
рассуждения приводят к результату'):
при с* = с* = 0 Л:
f- -г-, где I а, I < Ж,,
а когда исчезает одно из двух с , то
А . , 1 , ЙВ
где
Величины аг можно задать в виде формул и оценить, благодаря чему
можно получить более точные асимптотические выражения2).
Если в выражение А2 = К21 подставить для К его значение из
G.46), то получается резюмирующая
Теорема. Пусть Хп есть п-е собственное значение задачи
G.41), G.42) с входящими сюда предпосылками относительно /1р
') См. Е. Kamke, Differentialgleichungen, Losungsmethoden und Losun-
gen, изд. 3, Leipzig 1944, 213 [Э. К а м к е, Справочник по обыкновенным
дифференциальным уравнениям, М., «Наука», 1965].
2) Е. L. I n с е, Ordinary Differential Equations, London, 1927, 270—273.
7 8] § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 125
/о и So- Тогда имеет силу закон асимптотического распределе-
распределения собственных значений
lim —£■ =
!/•
G.53)
Порядок величины собственных значений, таким образом, вовсе
не зависит от коэффициентов cv и функций /0, входящих в краевые
условия G.42) и в G.41) соответственно.
7.8. Упражнения. 1. Рассмотрим особые случаи распределения собствен-
собственных значений. Решить следующие несамосопряженные задачи на собствен-
собственные значения (найти все собственные значения с соответствующими собствен-
собственными функциями):
а) у" = Ху'; у @) = у (I) = 0.
б) - у" = Ху; у @) = у' @) = 0.
в) —у" —Ху; у @) = у' A) — Лу'(О) = О.
TV
Д) yIV = — Ху"; у" @) = у'" @) = у" A) = /" A) = 0.
Решения:
а) Имеются только комплексные собственные значения: Х^ =—-—>
ук = е " — 1 (я = 0, +1, ±2, ± ...).
б) Нет никаких собственных значений.
в) При X = k2 для k получается трансцендентное уравнение cos k = k2;
оно имеет в вещественной области два отличающихся только знаками корня
и, кроме того, бесконечное множество комплексных (а не чисто мнимых)
корней; имеется, следовательно, одно вещественное положительное и беско-
бесконечное множество комплексных собственных значений. Положительное соб-
собственное значение: X = 0,6792.
При краевых условиях у @) = у' A) — Хау' @) = 0 трансцендентное
уравнение имеет вид cos k = ak2. В этом случае, задаваясь любым положи-
положительным целым числом г, можно надлежащим выбором постоянной а достичь
того, что будут иметь место ровно г вещественных собственных значений.
г) Имеется только одно невырожденное собственное значение: Я,=0
при у, = х.
д) Каждое число X является двукратно вырожденным собственным зна-
значением с у [ == 1 и у 2 = х.
2. Построить функцию Грина для краевой задачи
L 1У] = У1У + Ь2у" = г (х), у @) = у' @) = у A) = у' A) = 0.
Это одновременно пример для резольвенты Грина, если положить k2 = z.
Для контроля вычислить
1
f G (х, l)dl=h (x)
и убедиться, что h (x) разрешает краевую задачу при г=1.
Вычисление по методу, данному в п. 5.3:
126 ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА [7.8
Фундаментальную систему уравнения £[у] = 0 образуют функции
2, =«= 1, гг = х, гъ — sin Ах, zt = cos kx.
Уравнения E.9), E.10) для ft,- здесь имеют вид
Ь\ + Ы + Ь3 sin kl -\- ft4 cos k\ = О,
ft2 + Aft3 cos k\ — Aft4 sin fcg = 0,
— A2ft3 sin AS; — A2ft4 cos Ag = 0,
а их решения
— A3ft3 cos A| + £3ft4 sin Ag = — -i,
1,1.,, 1
*2 = -от2-. ft3 =-огз-cos Ag, ft4 = -_sin,
Теперь необходимо решить систему уравнений E.12) для a-v Она имеет
вид
п\ -\- ft, -[- а4 -[- ft4 = О,
й2 -|- ft2 -J- А (л3 -[- ft3) = О,
&\ — ftj -}- Й2 — ft2 ~г~ (^з — ^з) sin А ~|- (й4 — ft4) cos A = О,
д2 — ft2 -(- А (й3 — *з) cos А — А (д4 — ft4) sin A = О
и имеет единственное решение, если определитель
D = А B — 2 cos А — A sin A)
ие равен нулю. Ради краткости обозначим: sinA = s и cos A = с. Тогда
для в; получаются выражения:
Da, = ft, AJs + 2ft2 (s — Ac) -f 2ft3A (s — Ac) -f 2ft4A (As + с — 1),
£>a3 = 2ft, As -f 2ft2 (As + с — 1) + ft3AJs + 2ft4As,
Da4 = 2ft,A (c — 1) 4- 2ft2 (Ac — s) + 2ft3A (Ac — s) — ft4A2s.
Согласно E.8) функция Грина может быть построена непосредственно
при помощи ai и bt. Если в выражения для й; подставить значения ft/, то
после упорядочивания и группировки членов получаем
A2 DG (х, I) = (Ах — sin Ах) [— s (kl — sin Ag) + (с — 1) A + cos kl) -f As] -f-
+ A — cos Ax) [A — c) (kl -f sin Ag) -f (kc — s) A — cos kl) — As sin kl]
при x-^g; при x^-| функцию Грина получаем из условия симметрии
G (x, I) = G (I, х). Для проверки вычисляется
1 X 1
- J +J =
О х
[A Dx2 -\-k(k + kc — 2s) (I — cos Ax) — D (kx — sin kx)].
Эта функция фактически разрешает краевую задачу при
3. Определить функцию Грина G (х, |) для задачи
Ответ.
G (*, 6) = ХЧ\^ХУ [Юё2 - bxl Cg + 1) + х* F|2 + 3g + 1)]
7.8] § 1. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 127
при -*:<;£; при -v>£ функция G (х, I) получается путем перемены ме-
местами X И %.
4. Вырожденные собственные значения. Если задано любое целочислен-
целочисленное k > 0, то можно указать собственное значение Xj самосопряженной
определенной задачи
d2z d2z
Аг = Ix2 + If = "" •
z = 0 на контуре квадрата со стороной длины я, которое является по мень-
меньшей мере /%-кратно вырожденным.
Д оказательство. Если стороны квадрата заданы уравнениями
х = 0, х = я, у = 0, у = л, то собственные функции
г = sin mjfsin ny
при целочисленных т, п соответствуют собственному значению X = Хтп =
Используем теперь k различных точек (jf,, у,); (х2, у2);...; (-*:#, у^)
с рациональными координатами в первом октанте единичного круга, т. е.
х\-\-^=\ (/ = 1,2 к),
О < yi < xt.
Если представить себе все 2k дробей хь у, х/,, ук отнесенными
к общему знаменателю R, то собственному значению X = R2 соответствуют
k линейно независимых собственных функций
z = sin {Rxtx) sin (Ryty) (i = 1, 2 6).
5. Двукратно вырожденное собственное значение. Наименьшее собствен-
собственное значение задачи
yIV + ^р- у = - */'. у (°) = у' @) = у (I) = у' (I) = о
является двукратно вырожденным. Какие собственные функции ему соот-
соответствуют?
Ответ. Собственному значению X = Юл2/'2 соответствуют
„ ях . Зял: ях Зях
у, = 3 sin —-. sin —-— и у2 = cos — cos —-—.
6. Если в задаче на собственные значения — у" = Xg0 (x) у; у (а) =
= у (Ь) = 0 непрерывная функция g0 (x) в интервале a<jf<ft принимает
как положительные, так и отрицательные значения, то существует беско-
бесконечное множество отрицательных собственных значений (см. сноску ') на
стр. 60). Просчитать в качестве примера, разрешаемого в замкнутом виде,
случай [в котором, правда, предпосылка о непрерывности g0 (x) не выпол-
выполняется]
—1 при —1^х<!0,
1 при 0 < л:< 1.
Результат. Если ц.,, ц2, ... — положительные корни уравнения
tgn-f thfi = O (|i, = 2,3650, ц2 = 5,4978, F. Emde, Tafein eiementaren Funk-
tionen, 1 £40, стр. 131), то собственные значения Я, суть ± ц?, где « = 1,2, ...,
а соответствующие им собственные функции имеют вид
| sin Y~X~i sh (VTj" (x -\- 1)) при л: < 0,
1 sh /Я7 sin (/Я" A — х)) при х > 0.
128
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
[7.8
На рис. 7.2 показаны собственные функции, соответствующие первым
трем положительным и первым трем отрицательным собственным значениям.
Рис. 7.2. Задаче — у" = X (sgnx) y;y(±l) =
= 0 соответствует бесконечное множество
положительных и бесконечное множество
отрицательных собственных значений.
7. При краевых условиях: у (—-1) = у A) = 0 найти первую собственную
функцию у! (л:) и первое собственное значение Х^ для дифференциальных
уравнений:
а) — у" = X A0 — л:2) у, в)— у" = Х-
3-|~3х2 —
б) -у"-
5 — х2 '
г) -у" =
Решения:
а) У1 = е 4 A—Л),
б) у,=E-6л-2+л-4),
8. Пусть
4 4- х2 — х4 '
==—, в) у! = 3 — 5л:4 4- 2л-6, X, =60,
■ 1 = 12, г) у, =4 — Зх2— 2х4+х6, Я,
= 6.
± X/, .. .
суть расположенные в порядке возрастания абсолютных величин отличные
от нуля корни уравнений:
a) xtgx = A, б) tg х -)- Ах = 0.
Вычислить при А > 0 сумму обратных квадратов
У —
Решение. Величины x-t = Л; суть собственные значения уравнения
-/' — Ху при краевых условиях:
а)/@) = 0, у'A) + ЛуA)=0;
б) у@) = 0, Л/(
7.8] § 7. СВЯЗЬ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ 129
Так как функцию Грина для этой задачи можно найти (см. таблицу IV),
то уравнение G.13), соответственно G.21), дает непосредственно в качестве
суммы обратных квадратов:
в случае а)
^ х2, "J
1-1 ' О
А +1 — Ах . 1 , 1
! dx = ,
А 2 А
• = I [x-— Wx = l_
в случае б)
В таблице VI найти в качестве примера результаты для нескольких зна-
значений А-
9. Проверить следующие примеры ') задач на собственные значения,
в которых собственные функции, отвечающие разным собственным значе-
значениям, отличаются друг от друга как угодно мало. Пусть е есть произволь-
произвольная, в частности как угодно малая постоянная. Самосопряженная задача
имеет для XX = Q собственную функцию у, == 1 и для Я2 = 1—собственную
функцию у2 = 1 + е sin x. Задача не принадлежит к рассмотренному в § 4
классу задач, так как функция g0 в интервале 0 < х < 2я меняет знак и
нарушается принятая в п. 4.2 предпосылка gtt Ф 0.
Уравнение
с неоднородными краевыми условиями у^ @) = у'v* Bя), v = 0, 1, 2, 3,
9 • 1
н случае комплексной функции £i=34 е~1Х для Я1=-рг- имеет собст-
венную функцию ух = е1х и для Я = 1/8 собственную функцию у2 = elx -\- ze2ix.
10. Сопоставить системе2) дифференциальных уравнений первого по-
порядка относительно двух функций у (х), z (л:)
£L = b(x)y+Xc(x)z, 4L =
путем исключения z дифференциальное уравнение второго порядка относи-
относительно у.
') Оба примера сообщены мне Виландтом.
2) Подробную теорию собственных значений, вытекающую из так назы-
называемой канонической системы
(/=1, 2, ..., n)
dzj _ ■yi .
можно найти у Е. Holder, Math. Ann. 119 A943), 21—66.
130
ГЛ. II. ВСПОМОГАТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
[7.8
Результат. При Хг = ц получаем для у дифференциальное уравне.
ние в самосопряженной форме D.11), D.12)
Ь
11. Определить собственные значения и собственные функции интеграль-
интегрального уравнения с симметричным вырожденным ядром от двух независимых
переменных х, у
г{х, у) = \ J
-1 -1
Указание. Правая часть есть полином второй степени относительно х
и у, т. е. z имеет вид
г = ав + п\Х + а2у -f a3x2 -f a^xy + й6у2.
Если подставить этот полином г в обе части, то путем сравнения коэф-
коэффициентов для шести неизвестных av получим систему шести линейных
однородных уравнений с определителем (подставлено \л. = 1/4Я.):
о
о
1
—2
1
О
_2_
3
о
о
о
о
2
1
2
О
О
О
л
45
Л
45
0
0
-и
2
" 3"
1
3
0
0
0
— и
0
0
0
1
3
1
= 0.
Шесть корней этой системы уравнений (расположенных по порядку
возрастания абсолютной величины Я):
Соответствующие им собственные функции:
•г-ii з== ±4У ТЗ" +^х~^2; г2 = -^ —у; г4 = х + у; г5 = л:2 — у2;
гв = —10-j- 15 (х2 4-у2)-f- 12xy. Начертить узловую линию (zv = 0) в квад-
квадрате — 1<аг, у<1 и проверить соотношения ортогональности G.9) и фор-
формулы G.12), G.13) для
J J J J C*-6-
-i Ji -i -i
ГЛАВА ТРЕТЬЯ
КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ
В § 8 будут обоснованы минимальные свойства собственных значе-
значений. Эти свойства составляют основу для развитых в § 9 и в гл. IV и V
численных методов. В § 10 дается доказательство теоремы о раз-
разложении, которая не обладает такой же степенью общности, как
минимальные свойства, однако распространяется на одночленный класс.
Доказательство этой теоремы предполагает у читателя несколько
большую математическую подготовку, чем предыдущие параграфы,
но в силу центрального положения этой теоремы оно дается по воз-
возможности полно. Формулировка теоремы понятна и для менее мате-
математически подготовленных читателей.
Для часто встречающегося частного класса задач на собственные
значения второго порядка
У(а)=у(Ь) = 0
— независимо от прочих исследований этой главы — элементарное
доказательство важнейших фактов будет дано в п. 11.1.
§ 8. Минимальные свойства собственных значений
8.1. Минимальное свойство наименьшего собственного значе-
значения. При исследовании определенности задачи на собственные значе-
значения нам уже встречалось [см. D.31)] отношение Рэлея
ь
иМ [и] dx
5
Г uN [и] dx
Это число R [и], поскольку знаменатель не обращается в нуль, может
быть образовано для любых функций сравнения и, т. е. (см. п. 4.2)
для функций и ф 0, которые 2/я-кратно непрерывно дифференцируемы
и удовлетворяют краевым условиям.
Сделаем следующие предположения:
9*
132 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [8.2
Пусть задача на собственные значения D.11)—D.14)
М[у)-Ш[у}=0, ^[у]=0
является самосопряженной (см. п. 4.3) и вполне определена, т. е.
в соответствии с D.30)
ь
[ иМ [и] dx > 0,
а
b
J uN[u]dx->0
для всех функций сравнения. (8.2)
Проверка этих предположений в каждом отдельном случае может
быть легко осуществлена методами, изложенными в § 4.
Тогда, как будет доказано в п. 8.2,
/?[и]>Л, (8.3)
т. е. образованное с некоторой функцией сравнения и отношение
Рэлея R [и] никогда не будет меньше наименьшего собственного зна-
значения A,j. Если же в качестве и используется первая собственная
функция Ух, то /?[yil==^i. Таким образом, справедлива
Теорема. Пусть задача на собственные значения D.11)—D.14)
является самосопряженной, а условия полной определенности (8.2)
выполнены. Тогда первая собственная функция у; разрешает
вариационную задачу нахождения минимума отношения РэлеяфЛ),
если и пробегает всю область функций сравнения. Соответст-
Соответствующий минимум есть первое собственное значение Kt.
8.2. Проведение доказательства. Пусть теперь и — некоторая
фиксированная функция сравнения. Мы полагаем, что R[u] получено
при помощи этой функции; отношение R[u] есть, таким образом,
определенное число.
Для доказательства утверждения (8.3) строится вспомогательная
функция т)(лг) путем подстановки в дифференциальное уравнение и
вместо у и R вместо X:
M[u\ — RN[u\ = 4\{x). (8.4)
Если выбранная функция и совпадает с собственной фунцией yt,
то R = %i и ц(х) = 0. Если же совпадение приблизительно, то воз-
возникает «функция ошибки» ti(x), принимающая лишь малые значения.
Обратно: если т](л;) = 0, то и — решение уравнения
т. е. и — собственная функция, соответствующая собственному зна-
значению R. В этом случае соотношение R J> ^, несомненно, верно.
Поэтому случай т]^0 можно исключить из рассмотрения.
8.2) § 8- МИНИМАЛЬНЫЕ СВОЙСТВА СОБСТВЕННЫХ ЗНАЧЕНИЙ 133
При фиксированном и также и ч\{х) есть некоторая определенная
непрерывная функция. Сформулируем следующую краевую задачу:
M[v] — W[v] = y\(x), L^N=0, (8.5)
где X— параметр, возрастающий от нуля, Таким образом, это — не-
неоднородная краевая задача с заданной правой частью г\ (х). Решение
зависит еще от параметра X, v=^-v(x, X), и для тех X, которые не
являются собственными значениями, может быть сразу же указано
при помощи резольвенты Грина на основании E.20), E.21):
O(x, I. XO](£)dl. (8.6)
В соответствии с п. 5.8 резольвента Грина — мероморфная функ-
функция X; она имеет полюсы в местах собственных значений X = Х^ и
в остальной области регулярна. Поэтому и v(x, X) также непрерывна
и регулярна относительно X, за исключением, быть может, точек
Х = ХГ Построим еще одну вспомогательную функцию
*
А(Я)=| t\(x)v(x, X)dx. (8.7)
а
Эта функция вводится потому, что с использованием (8.5) она может
быть записана в форме
ь
h (X) = J (v (х, X) М [v (х, X)] — Xv (х, X) N [v (х, X)]) их. (8.8)
а
Как видно, здесь появляются фигурирующие в исходных условиях
выражения ь ь
[ vM [v] dx и f vN [v] dx.
a a
Вместе с v(x, X) функция h(X) также непрерывна и регулярна отно-
относительно X, за исключением точек X = Xt. Чтобы наглядно описать
функцию h (X), вычислим ее для некоторых частных случаев.
1. А, = /?. В этом случае дифференциальное уравнение (8.5) от-
относительно v переходит в дифференциальное уравнение (8.4) относи-
относительно и (х), причем граничные условия оказываются как раз такими,
которым должна удовлетворять функция и, т. е.
v(x, R) — u(x)
и в силу (8.8)
* ь ь
h (R) = \ (иМ [и] — RuN [и]) dx = \ иМ [и] dx — R \ ttN [u\dx -■■ Q%
134
ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ
[8.2
так как R, согласно (8.1), определено именно как отношение обоих
интегралов. Итак, констатируем: h(R)—0.
2. Х = 0. В силу полной определенности задачи Х = 0 не является
собственным значением, так что этот выбор возможен. При этом,
согласно (8.5), v(x, 0) есть решение краевой задачи
M[v] = i\(x), £/„[©] = <). .
С определенной таким образом функцией ввиду условий (8.2)
имеем b
h @) = Г vM [v] dx > 0.
Докажем еще, что производная dh/dX везде
положительна. Это значит, что h(X) выгля-
дит> как Эт0 показано на рис. 8.1: h(X)
имеет при Я = 0 положительное значение, а
при X = R значение нуль; h (к) везде непре-
непрерывна и дифференцируема, за исключением
Рйс. 8.1. График вспомо- точек X = Kl; h(k) везде (кроме точек Я = Я;)
гательнои функции Л (Я), возрастает. Если бы между точками 0 и R
не было собственных значений, выполнялось
бы неравенство й(/?)>й(О), что не имеет места. Отсюда следует,
что между нулем и R лежит по меньшей мере одно собственное зна-
значение. Итак, R ^ Я].
Для доказательства положительности производной вычислим раз-
разность двух значений функции h в точках X и V. В соответствии
с (8.7)
ь
h(X) — h (X*) = { {v (x, X) r\(x) — v (x, X*) ц (х)} dx.
а
В подынтегральном выражении первый раз полагаем
ц(х) = М [v (х, Х*)\ — k*N [v (х, X*)]
и второй раз
ц(х) = М [v (х, X)} — XN [v (х, X)]
[согласно (8.5) оба выражения действительно равны заданной функ-
функции ц(х)]. Тогда
ь
h(X) — h (X*) = | [v (x, X) М [v (x, X*)] — v (x, X*) М [v (х, X)} —
а
— k*v(x, l)N[v(x, X*)]^rXv(x, X*)N[v(x, X)}} dx.
Первые два слагаемых справа при интегрировании взаимно уничто-
уничтожаются з силу предполагаемой самосопряженности, а интегралы от
8.3) § 8. МИНИМАЛЬНЫЕ СВОЙСТВА СОБСТВЕННЫХ ЗНАЧЕНИЙ 135
вторых слагаемых, не считая множителя X, равны друг другу,
опять-таки из-за самосопряженности. Таким образом,
h(X)—h{X*) = {X — X") v(x, X)N[v(x, X*)]dx. (8.9)
a
Отсюда следует, что в пределе при X*—>Х в силу (8.2)
4r= lim k (Л? ~ г*Х ) = v(x- X)N[v(x, X)]dx>0. (8.10)
a
Этим доказательство неравенства R^>XX завершено. Одновременно
доказано существование по крайней мере одного собственного зна-
значения.
8.3. Минимальные свойства высших собственных значений1).
Точно так же и второе собственное значение Х2 можно определить
при помощи вариационной задачи. А именно, оказывается, что оно
является наименьшей величиной, которую принимает отношение Рэлея,
когда и пробегает область не всех функций сравнения, а только тех
из них, которые ортогональны первой собственной функции у; в обоб-
обобщенном смысле (или ортогональны N [yj в обычном смысле).
Мы исходим из функции и, которая, как функция сравнения,
удовлетворяет таким же условиям, как и в п. 8.1, и, сверх этого,
удовлетворяет еще «дополнительному условию»
J и (х) N [yi (x)] dx = 0. (8.11)
а
Теперь уже и (х) не может быть, например, собственной функцией,
отвечающей Xt. Вопрос о существовании такой функции и (х) не рас-
рассматривается. Если, например, w(x) — какая-нибудь функция срав-
сравнения, которая не должна быть первой собственной функцией у], то
условию (8.11) будет удовлетворять функция
Ух (I) N [у, (I)]
') Приведенную в заключение этого пункта теорему о минимальных
свойствах (s-(-l)-ro собственного значения Ks±x мы доказываем при до-
дополнительном предположении, что %,, %2< ^з. •• •■ Xs+i являются невырожден-
невырожденными собственными значениями. Теорема, однако, верна также в случае
вырождения и формулируется здесь в общем виде. Доказательство для по-
последнего случая имеется в статье Е. Kamke, Math. Z. 46 A940), 251—286.
136 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [8.3
Для обоснования минимальных свойств второго собственного зна-
значения снова положим, что и (х) — фиксированная функция, тогда от-
отношение Рэлея R [и] также есть некоторое определенное число.
Построим, подобно (8.4), вспомогательную функцию Ц(х):
(8.12)
Если ti(x) = 0, то и (х) является собственной функцией, и
так как она не может быть первой собственной функцией, то
это — вторая или одна из высших собственных функций. Тогда,
следовательно, верно неравенство R^X2. Поэтому достаточно до-
доказать истинность утверждения R ^> Х2 при условии ц(х)фО.
Аналогично (8.5) сформулируем краевую задачу
решение которой v = v (x, X) можно найти непосредственно при по-
помощи резольвенты Грина:
ь
v(x, Я)= J О(х. I, А,) л (£)</£.
а
Резольвента Грина имеет полюс при Я, == A,lt и можно, согласно
E.26), записать ее в виде
и(х, |, л)=—х — х ги\{х< s. л),
причем Gi(x, |, X) в точке Х = Х1 регулярна. Имеем поэтому
ь ь
v(х, X) = J С'У'хA)/1'F) Л (I)dl + J О\(х, |, Х)цA)сЦ.
а а
Первый интеграл обращается в нуль, так как из предпосылки, что «
ортогональна N [yj, в силу самосопряженности следует
ь
J uN [yj] dx = J yfl [u] dx = 0.
Далее имеем
ь
J uN [yj] dx = J и M^l] dx = -j- J yiM [u] dx = 0.
a a a
Следовательно,
t> ь
J yxM [и] dx = J yj/V [и] йл: == 0,
8.3]
§ 8. МИНИМАЛЬНЫЕ СВОЙСТВА СОБСТВЕННЫХ ЗНАЧЕНИЙ
137
и, таким образом, в силу (8.12)
Итак, остается
Ь
v(x, Я)= J О*(х, I Я) т](£)</£.
(8.13)
Особенность при X = Xlt таким образом, выпала, v(x, X) может быть
определена с помощью этого уравнения также и в этом случае.
При Х = ХХ функция v(x, X) регулярна, она является сингулярной
только в случае более высоких собствен-
собственных значений Xt. В дальнейшем доказа-
доказательство идентично таковому в п. 8.2.
Вспомогательная функция, построенная
аналогично (8.7),
ь
h(X)= | 4(x)v(x, X)dx
при X = R
чения:
и X =
имеет частные зна-
знаРис 8.2. К доказательству
минимального свойства вто-
второго собственного значения.
h(Xl)= J {v(x, Xx)M\v(x, Xtf — XiVix, X})N[v(x,
e(jf, K{)N[V(X,
Здесь оба множителя положительны'), первый согласно пред-
предпосылке (8.2), второй в силу уже обоснованных минимальных свойств
первого собственного значения ^ следовательно, h (Х{) > 0.
В остальной области h(X) имеет, как в (8.10), положительную
производную и, таким образом, вид, как на рис. 8.2. Значит, h (к)
не для всех к из интервала Xl^.X^.R может быть регулярной, т. е.
в этом интервале локализовано следующее собственное значение.
Тем самым доказаны утверждение R^-X2 и одновременно существо-
существование второго собственного значения. Вообще точно таким же образом
доказывается, что:
') При этом используется то обстоятельство, что v (х, X) является функ-
функцией сравнения также и при Х = ХЬ что можно доказать на основе (8.13).
Для более подробного представления об этом см. сноску на стр. 135.
138 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [8.4
Если функция сравнения и удовлетворяете дополнительным условиям
J uN [yt (x)\ dx = 0 (/=1,2 s), (8.14)
a
то имеет место
Так как при u — ys+1 отношение Рэлея принимает значение Я,и,
то обосновано минимальное свойство для собственного значения Я,4 v
Теорема. Пусть задача на собственные значения D.11), D.14)
является самосопряженной и условия (8.2) полной определенности
выполняются. Тогда существует бесконечное множество веще-
вещественных положительных собственных значений Хх, Я2> ... При
этом {s-\- \)-e собственное значение равно минимуму, который
принимает отношение Рэлея (8.1), когда и пробегает область
всех тех функций сравнения, которые ортогональны в обобщен-
обобщенном смысле первым s собственным функциям [т. е. выполняются
дополнительные условия (8.14)]; при этом вырожденные собствен-
ные значения должны перечисляться согласно их кратности.
Одновременно следует, что собственные значения Ks растут не*
ограниченно;
Яу—> со при s —*оо,
так как, согласно п. 5.7, собственные значения К в конечной области
не могут иметь точки сгущения.
8.4, Минимаксимальный принцип Куранта '). При обсуждении
в п. 8.3 минимальных свойств E-)-1)-го собственного значения
в дополнительные условия (8.14) вошли s первых собственных функ-
функций. Ниже собственное значение ks+l определяется «независимым»
способом, при котором нет надобности обращаться к низшим соб-
собственным функциям. Возьмем s линейно независимых интегрируемых
функций
wv w2 ws
и рассмотрим только те функции сравнения и, которые ортогональны
в обычном смысле к этим 5 выбранным функциям и которые, следо-
следовательно, удовлетворяют дополнительным условиям
ь
[uwadx = 0 @=1,2 s). (8.15)
') R. Courant, D. Hilbert, Methoden der mathematischen Physik,
т. 1, изд. 2, Berlin, 1931, 352 [P. К у р а н т и Д. Г и л ь б е р т,. Методы мате-
математической физики, т. 1, ГИТТЛ, 1951].
8.4J § 8. МИНИМАЛЬНЫЕ СВОЙСТВА СОБСТВЕННЫХ ЗНАЧЕНИЙ 139
Минимум1) отношения Рэлея (8.1) для допустимых теперь функций и
имеет величину, зависящую еще от выбранных функций wa:
min R [и] — M(wl, w2 ®s).
и
В этом случае собственное значение Я1$+1 является максимумом этой
функции M(w1, w2 ~ii>s). когда wa пробегает совокупность инте-
интегрируемых функций:
^54l — maxM (да,, w2 ws). (8.16)
В качестве резюме получается
Теорема. Пусть задача на собственные значения D.11), D.14)
является самосопряженной и полностью определенной [т. е. удо-
удовлетворяется (8 2)]. Пусть, далее, M(wv w2 ws) есть мини-
минимум или нижняя граница отношения Рэлея (8.1), когда и пробе-
пробегает область всех функций сравнения, ортогональных s данным
линейно независимым интегрируемым функциям wx, w2 ws.
Тогда (s-f- \)-e собственное значение Я5+1 равно наибольшей вели-
величине, которую принимает M(wb w2 ws), когда w0 пробегает
совокупность всех рассматриваемых систем функций.
Доказательство. Пусть, сначала, wb w2, ..., w^—фикси-
w^—фиксированные функции. Покажем, что имеются допустимые функции
(ортогональные, следовательно, всем w0), которые могут быть по-
построены как линейные комбинации из первых (s -\- 1) собственных
функций уа:
0-1
Условия ортогональности требуют
* 5+1 ft
О = ■[ uwp dx = V а0 { wpy0 dx при р=1,2 s.
0 — 1 а
Это — s линейных однородных уравнений относительно (s-f- 1) коэф-
коэффициентов аа; следовательно, всегда найдутся а0, не все равные
нулю.
Для функций м, построенных с этими аа, согласно (8.17), исполь-
используя D.18) или E.33), получаем
Ь 5+1 5+1
J иМ [и] dx = J ]£ аауа ^ ахМ [yx] dx =
s+l s+l
.^V [yx] dx.
а 0—1 т—1
5+1 S+l
= J
t —1
') Или нижняя граница. В вариационной задаче может случиться, что
нижняя граница не достигается ни при какой функции сравнения.
140 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [8.5
В силу обобщенной ортогональности собственных функций от инте-
интегралов остаются только члены с а —т:
* s + l Ь
J иМ [и] dx = ]£ а\\ J y0N [y0] dx
а 0 = 1 а
и соответственно
* s+l b
j uN [a] dx = ^al jy0N[yg)dx.
0 = 1 a
Стоящие в правых частях интегралы, согласно предпосылке (8.2),
положительны, т. е. в силу того, что Яа-^Я5+ь можно получить
оценку:
ь
Г иМ [и] dx < Xs+1 f uN [u] dx
и тем самым
Искомый минимум /? может быть лишь еще меньше, чем определен-
определенное таким образом R [а], значит, и подавно
Итак, доказано, что
Теперь варьируем wb w2, .... ws\ если взять, в частности,
то имеем прежнюю минимальную задачу для высших собственных
значений, и тогда M = ks+V Значит, ks+i есть максимум М при
вариации wa, или, пользуясь одной символической формулой:
\ min/?[a] ]
ks+1= max i u у. (8.18)
(«>,,..., ws) [ дополнит, условия (8.15) j
8.5. Теорема сравнения. Она является прямым следствием мини-
максимального принципа и гласит:
Теорема. Если рассматриваются две самосопряженные за-
задачи на собственные значения вида D.11), D.14)
M[y] = KN[y], M[y] = k*N*[y] (8.19)
S.5) § 8. МИНИМАЛЬНЫЕ СВОЙСТВА СОБСТВЕННЫХ ЗНАЧЕНИЙ 141
при одном и том же М[у] и с одинаковыми краевыми условиями
Up [у] — 0 и если для всех функций сравнения
ь
J иМ [и] dx > О,
а
Ь Ь
J uN [и] dx > J иМ* [и] dx > 0, (8.20)
а ■ а
то для всех собственных значений Xs и )JS обеих задач (8.19) имеем
К <J К при s=l, 2, ...
В силу предпосылки (8.20)
и это неравенство имеет место также для всех минимумов и макси-
максимумов, т. е. ks^ks при всех s.
Теорему сравнения часто можно использовать для быстрой оценки
собственных значений. Если, например, имеем уравнение
yiv = ^(i+x)y
с краевыми условиями
то в качестве задач сравнения берем самосопряженные полностью
определенные задачи с теми же краевыми условиями:
yiv == х*у, yiv = 2ГУ
Имеем
1 1 1
J и A + х) udx = |A+*)«2Лс> J и2 dx.
0 0 0
Следовательно, теорема сравнения применима. Из нее получаем
>^S <^ ^s ^" r*s ,
Таким образом, имеем задачи сравнения, решения которых (диффе-
(дифференциальные уравнения имеют постоянные коэффициенты)
Хп == (пп) , Хп = ^
значит, все собственные значения заключены в границах
142 ГЛ. 111. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ (9.1
§ 9. Теорема включения
9.1. Формулировка теоремы. Дальнейшее применение минимакси-
мального принципа п. 8.4 представляет теорема включения; она рас-
распространяется на задачи одночленного класса с дифференциальным
уравнением D.28)
M[y\^XN[y]w(-\)nX[gn{x)y^\(n) (9.1)
и краевыми условиями U^ [у] = О согласно D.14).
Правда, должны быть приняты несколько более сильные предпо-
предпосылки, чем в п. 4.7. Теорема гласит1):
Теорема включения. Пусть задача одночленного класса
(9.1), D.14) удовлетворяет предпосылкам:
а) она является самосопряженной,
ь
б) для каждой функции сравнения иМ [и] dx > О,
а
в) функции gn {x) в основном интервале а, Ь имеют постоян-
постоянный знак,
г) для двух любых функций сравнения и, v и п раз непре-
непрерывно дифференцируемой функции g(x)
ь ь
(—1)" J и [gv(n>](n> dx= J gu(n>v(n) dx.
a a
Если имеем функцию сравнения Рг и 2п раз непрерывно диф-
дифференцируемую функцию Fo, которые удовлетворяют соотношению
M[F1] = N[F0], (9.2)
и если функция
£^1 (9.3)
F[n)(x)
лежит в интервале a, b между конечными границами и не
меняет там знак, то между максимумом и минимумом функ-
функции Ф локализовано по меньшей мере одно собственное значение
задачи (9.1), D.14):
Если, например, Fa есть собственная функция yt, то в силу (9.2)
F1 = -j- Fo, и для частного Ф получаем, согласно (9.3), Ф = lt — const.
Если теперь Fo отличается от yt, то Ф(х) в интервале a, b уже не
■)Г. Виландт показывает, что данная теорема включения, теорема
включения Крылова — Боголюбова в п. 14.2, формула A2.19) и др.
могут рассматриваться как частные случаи общей теоремы включения.
9.2]
§ 9. ТЕОРЕМА ВКЛЮЧЕНИЯ
143
остается постоянной (см. рис. 9.1), однако между наибольшей и наи-
наименьшей величинами Ф остается заключенным по меньшей мере одно
собственное значение.
Предпосылка г) в каждом отдельном случае может быть легко
проверена при помощи интегрирования по частям и требует от крае-
краевых условий, чтобы краевые выражения,
проявляющиеся при интегрировании по
частям, исчезали. Приведенные в таблице I
задачи одночленного класса все удовлет-
удовлетворяют выдвинутым здесь более сильным
предпосылкам.
Согласно теореме п. 8.3 все собствен-
собственные значения Xs, а значит, в силу теоремы
включения также и Ф, имеют тот же знак,
что и функция gn {х).
В случае частных задач на собствен-
собственные значения (я = 0) условия для Fo и Ft Рис- 9Л- к теореме вклю-
можно сформулировать несколько проще').
Здесь достаточно исходить из какой-нибудь функции сравнения Fx
и подставить
Ь x
Тогда
и имеем
_Г0_ M[FX] _ M[F{]
' - F - N{F}
/max
(9.5)
(9.6)
(9.7)
Функция Fo не обязательно должна удовлетворять краевым усло-
условиям, однако стараются Fo и Fr выбирать так, чтобы Fo удовлетво-
удовлетворяла по возможности большему числу этих условий, с тем чтобы
она приближалась к собственной функции, а пределы (9.4) не были бы
слишком грубыми.
9.2. Пример к теореме включения. Прежде чем провести доказатель-
доказательство теоремы включения, рассмотрим простейший пример задачи частного
класса (рис. 9.2):
-у" = Ху, у@) = /A) = 0. (9.8)
') Теорема включения в случае частных задач на собственные значения
для первого собственного значения доказана в работе О. Temple, Proc.
Lond. math. Soc. B) 29 A929), 257—280.
Оценки для всех собственных значений сверху и снизу в случае диф-
дифференциального уравнения (не обязательно линейного относительно А)
— у" = Q (х, Л) у с краевыми условиями Штурма имеются в работе
W. Quade, Math. Z. 51 A948), 92—125,
144
ГЛ. Ш. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ
[9.2
Для определения функций Fo, F{, удовлетворяющих всем поставленным
условиям, возьмем Z7, в виде полинома, который при любых значениях Ci
и с2 удовлетворяет краевым условиям:
/=•, = л:4
Тогда в силу (9.5)
-f с2х2 + х (— 4 — Зс, — 2с2).
• 6с,аг — 2с .
Для достижения лучшего результата Fo должно также удовлетворять краевым
условиям, следовательно, с2 = 0, с, = — 4. Таким образом,
Имеем
/=•„= 12 Ba: — j
12* B — л:)
8л: — 4л:3 4- х
= 8л: — 4л:3 -(- л:4.
12 12
4+2л:
5 — A — л:J'
Здесь видно сразу (рис. 9.3), что в интервале @, 1) Фтах = 3, ФтШ = 2,4,
т. е. имеем 2,A^,XS ^3.
При желании вычислить более близкие границы ') для Ks (мы, таким
образом, забегаем вперед, в следующую главу, и даем уже рекомендации
для метода последовательных прибли-
приближений) можно найти следующие функ- \ф
ции F2, Ft, ... из соотношений:
M[Fn+l]=N[Fnl t/ц [/'„+,] = О,
т. е. в нашем случае из формул
г 2,4-
1
0
У
f" I
1
1
1
1
1
7
X
О
1
Рис. 9.2. Первая соб-
собственная функция зада-
задачи (9,8).
Рис. 9,3. К теореме
включения для при-
примера (9.8).
Непосредственно путем двукратного интегрирования полинома и опре-
определения постоянных интегрирования из краевых условий получаем
4г (96* — 40л:3
— л:6) =
D8 + 24* — 8л:2 — 4л:3 + л4),
Ю
|272л:-
= х B~Х) A088 + 544* — 176а:2 — 88л:3 + 12*4 + 6л:5 — л:6).
') См. Н. v. 3 a n d e n, Praxis der Differentialgleichungen, Berlin, 1943, 73.
9.31 § 9. ТЕОРЕМА ВКЛЮЧЕНИЯ 145
ту
Частное Фл = "~* , если ради краткости обозначить 1х — х2 = р = 4v, при-
• п
мет вид
30D + Р) _ 15 A + у)
2 48 + 12Р+Р2 2C+3v_|_v2)
Фт.п = Ф2A) = -^- = 2,4590, Фтах = Ф2@)=-| =
итак, теперь уже имеем 2,459 <; Xs <; 2,5. Далее,
_ 56 D8 -f 12р + Р2) _ 14 C + 3v + у2)
3~
1088 + 272р + 24р2-f р3 ~ 174" 17v 4v2 4" v3
Фтш = Фз A) = -^| = 2,4664, Фтах = Ф3 @) = -g- = 2,4706.
Теперь, следовательно, 2,4664 < Xs < 2,4706.
Такая точность для многих технических задач достаточна. Точное значение
Л, =-^ = 2,4674011.
В рассмотренном примере удалось удобным способом вычислить следую-
следующие функции F2, Fs и тем самым повысить точность. В более сложных
задачах вычисление следующих Fn часто наталкивается на большие практи-
практические трудности, и в этих случаях метод последовательных приближений
на основе одних только Fo и /•', в состоянии дать значительно более точные
границы для первого собственного значения, чем это возможно при помощи
теоремы включения.
9.3. Доказательство теоремы включения. Согласно (9.1), (9.2)
в теореме включения применяются две функции Fo, Fv удовлетво-
удовлетворяющие соотношению
М [FJ =р N [FQ] = (-1)" [g,( (x) F{on)}in).
Если из (9.3) подставить сюда
то получим, что Fx удовлетворяет дифференциальному уравнению
М [FJ = (-1)" [gn (х) Ф (х) F\n)}{n), (9.9)
т. е. F] есть собственная функция этого дифференциального уравне-
уравнения при краевых условиях U^ [F^ — 0.
Построим теперь три задачи сравнения:
2. M[y] = (-iri"[gn(x)<U(x)y(nn{n). \ (9.10)
3. М [у] = (-\)п%'" [gn (х) Фтзху(п>]{п)
(при одних и тех же краевых условиях £/ [у] = 0).
146 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ (9.4
Вторая задача имеет собственную функцию y = F\, с собственным
значением 1, причем пусть 1 есть s-e собственное значение этой
задачи:
Первая и третья задачи имеют собственные функции у—у „с соб*
ственными значениями ks, hs , а именно:
где Xs есть s-e собственное значение исходной задачи (9.1), D.14),
т. е.
Теперь предпосылки теоремы сравнения из п. 8.5 выполнены.
Необходимо еще дополнительно проверить неравенство (8.20)
J uN [и] dx > J uN* [и] dx.
Здесь, как выясняется при помощи /t-кратного интегрирования по
частям, для всех функций сравнения и в силу предпосылки г) теоремы
п. 9.1 [мы могли бы без ограничения общности считать gn(x) положи»
тельной]:
J «( ) IS"n ш
a
» ft »
J " max ^ J " J " "
а а
т. е., согласно теореме сравнения, имеем
следовательно, (9.4) доказано.
9.4. Сравнение с задачами, разрешимыми в замкнутом виде.
Часто при помощи теорем включения и сравнения удается указать
границы для всех собственных значений. Если, например, рассматри-
рассматривается задача
-у" = Хр(х)у, у@)
то ее следует сравнить с некоторой аналогично построенной задачей
10.11 § 10. ТЕОРЕМА О РАЗЛОЖЕНИИ 147
с теми же краевыми условиями, собственное значение %*п которой-
известно. Например, в случае
Ф>0. с>0)
имеем (согласно таблице V) собственные значения
с собственными функциями
/ пп In
In
a-\-b
Если применить у* в качестве Fx в теореме включения, то в силу
(9.6)
п р
и имеем границы
Чем лучше р* можно «подогнать» к р, тем ближе сходятся границы,
причем относительные границы для всех собственных значений оди-
одинаково близки. Таким образом, хорошо иметь возможно больший
набор разрешимых в замкнутом виде задач на собственные значения.
В таблице V приведено несколько простых, разрешимых в замкну-
замкнутом виде случаев.
§ 10. Теорема о разложении
10.1. Предварительные замечания. В § 8 для полностью опре-
определенных самосопряженных задач на собственные значения в форме
D.11)—D.14) было доказано существование бесконечного множе-
множества вещественных положительных собственных значений к^ Соб-
Собственные значения снова считаем расположенными в порядке возра-
возрастания их величин: 0 <С Х1 <С ^2 <С ^3 • ■ • *> каждому собственному
значению к( соответствует собственная функция уь; собственные
функции можно полагать нормированными и ортогональными в обоб-
обобщенном смысле (см. E.33)):
0 при I Ф k,
1 при i — k.
и
iO*
и
\
148 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ A0.2
Тогда в силу равенства M[yk]=kkN[yk] также
ь
0 при i Ф k,
1 при / = fc A0,2)
а
Зададимся, далее, вопросом, можно ли произвольную функцию
сравнения и (х) «разложить» по собственным функциям ук (х), т. е.
имеет ли место представление
СО
и м = 2 в»у» (*). (ю.з)
где ак — постоянные. К такой постановке вопроса мы уже подхо-
подходили в п. 2.1, а так называемая «теорема о разложении» является
важнейшим вспомогательным средством, которым мы будем пользо-
пользоваться в разных местах.
10.2. Коэффициенты Фурье. В случае простого примера задачи
на собственные значения
собственным значениям Xk = k2 соответствуют собственные функции
yk = 1/ —%'mkx. Из теории рядов Фурье известно, что каждая
функция сравнения и {х), т. е. каждая дважды непрерывно диффе-
дифференцируемая функция и(х) при условиях: и@) = и(я) = 0, посред-
посредством соотношения и (— х) = — и {х) дополняется до некоторой не-
нечетной, определенной в интервале — я ^ х <^ я, функции и может
быть разложена в тригонометрический ряд1), здесь, в частности, по
синусам:
со
При этом «коэффициенты Фурье» bk определяются формулой2)
X
2 Г
Ьк — — и (л:) sin их dx.
я ^
о
') К. Knopp, EinfQhrung in die h6here Mathematik, Leipzig, 1942 [см.,
например, В. И. Смирнов, Курс высшей математики, т. II, М. — Л., 1952].
Предпосылка непрерывной двукратной дифференцируемое™ для разложи-
разложимости в тригонометрический ряд не требуется, достаточно уже того, что
а(х) — непрерывная функция ограниченной вариации (К п о р р, т. II, 519);
даже требование непрерывности может быть ослаблено.
2) К. Knopp, Einfiihrung in die hohere Matheniatik, Leipzig, 1942 [см.,
например, В. И. Смирнов, Курс высшей математики, т. II, М. — Л., 1952].
10.3] § 10. ТЕОРЕМА О РАЗЛОЖЕНИИ 149
4
Если подставить sin&jc^l/ ~yk и ак=-ЬкЛ/ 4-, то получим
где
ак = | а (х) ук (х) dx.
На этом простом примере теория рядов Фурье показывает воз-
возможность разложения любой функции сравнения и по собственным
функциям ук. Зададимся теперь вопросом о разложимости в •случае
более сложных задач на собственные значения.
Считая равенство A0.3) справедливым, умножим обе его части
на Ny^x)] и получившийся при этом ряд почленно проинтегрируем
в интервале (а, Ь). Тогда, в силу A0.1), все члены рядал кроме
одного (при k=l), обращаются в нуль, и мы имеем
ь
J и.(х) N [yt (x)] dx = at. A0.4)
а
Такое эвристическое рассмотрение дает
Определение. В качестве коэффициентов Фурье at заданной
непрерывной функции и(х), применительно к задаче на собственные
значения D.11)—D.14), вводятся величины A0.4).
С этими величинами at можно формально построить ряд
и возникают вопросы:
1. Сходится ли ряд A0.5)?
2. Если ряд A0.5) сходится, то представляет ли он тогда функ-
функцию и(х), с которой образованы коэффициенты a{i
10.3. Формула Парсеваля. В дальнейшем будем считать, что
и{х) есть функция сравнения. Прежде всего, можно показать, что
для формально составленного ряда A0.5) сумма
всегда сходится, т. е. что ас в любом случае с ростом i стремится
к нулю *).
*) Сходимость ряда 2 а1 — более сильный факт, чем стремление
оо
1 V1 1
к нулю а;. Например, -т=г-->0 при п ->■ оо, но ряд /, — расходится.
150 ГЛ. 111. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [W.3
Для доказательства этого введем «остаток» i"p{x) ряда A0.5) и
положим
г„(х) = в(х)-2в/У/(х). A0.61
В любом случае гр{х) является функцией сравнения. Если гр = 0
для некоторого числа р, то и есть линейная комбинация собствен-
собственных функций у1 ур\ тогда в силу (ЮЛ) и A0.4) ap + i — ap+2—
= ... =0 и поэтому все последующие остатки гр+-1, гр+2< •••
равны нулю — вопрос о сходимости является тривиальным. Положим
поэтому грф 0.
Если бы мы смогли показать, что гр{х) с ростом р для всех х
из области а^.х-^.Ь стремится к нулю, то на поставленные в за-
заключение п. 10.2 вопросы о сходимости мы получили бы утверди-
утвердительные ответы.
Функция гр(х) ортогональна в обобщенном смысле р первым
собственным функциям ylt у2 ур, так как, используя A0.1) и
A0.4), получаем
* * р ь
\ rpN [yk\ dx = \uN [yk\ dx~^ at J ytN[yk]dx = ak-ak = 0
a a f-1 a
при k—l, 2 p. A0.7)
Точно так же в силу равенства М [yk\ = XkN [yk\ имеем
rpM[yk]dx = 0 при ft = 1, 2 p. A0.8)
a
Поэтому, согласно теореме п. 8.3, отношение Рэлея, построенное
с функцией гр, является верхней границей для (р -\- 1)-го собствен-
собственного значения Яр+1:
Далее, в отношении Рэлея
Zp=^rpM\rp\dx и Np=jrpN[rp}dx,
а
числитель является ограниченным. На самом деле в силу A0.8) и
(Ю.2)
ь I p
J uM[u]dx= J I^+Je^l Af r^+JJe^ \dx =
a a ^ /-1 / L f=i J
p \ \ " Л p
10.31 § Ю. ТЕОРЕМА О РАЗЛОЖЕНИИ 151
в левой части стоит фиксированное число
J иМ [и] dx,
следовательно, Zp для всех р ограничено. Из того, что R[rp]^-kp+v
получаем
Z
Так как Zp остается ограниченным, a ^pi.\ с ростом р неограни-
неограниченно растет, Np с ростом р стремится к нулю. Аналогично A0.9)
в силу A0.7) и A0.1) имеем
а \ /-1
Ь I Р
\ X
Итак, для р—>ро получаем так называемую формулу Парсеваля
N\u\dx, A0.11)
1-Х
Из нее легко вывести также часто употребляемую формулу, которая
связывает две функции сравнения и(х), v(x) и их коэффициенты
Фурье at, bt. Если запишем формулу Парсеваля для функции
u(x)-tv(x)
1-Х
= | «jV [и] dx + 2 J иЛГ [v] dx-\- | vN [v] dx
и вычтем отсюда формулы Парсеваля для функций и и к, то полу-
получим:
со Ъ
j£ a fit = f uN [v] dx. A0.12)
i = l a
Дополнение!. При несколько более слабых предпосылках
можно вместо равенства Парсеваля A0.11) получить неравенство
152 ГЛ. 111. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [10.4
Парсеваля A0.13)*). Для этого вводится понятие «полудопустимой»
функции. Чтобы функция и(х) при любой заданной функции срав-
сравнения v удовлетворяла условиям
ь ь
\ uN [и] dx>0, J (uN \v] — vN [и] )dx = 0,
a a
в общем, не обязательно, чтобы и сама была функцией сравнения;
достаточно, чтобы и была 2га раз непрерывно дифференцируема и
удовлетворяла части наперед заданных краевых условий и^и]—®
(какие это и сколько краевых условий, можно всегда легко установить
посредством интегрирования по частям, см. пп. 4.3 и 4.9). Функцию,
которая удовлетворяет этим краевым условиям и для которой суще-
существует иBЛ), следует называть полудопустимой. Для такой функции
A0.7) выполняется, а уравнение A0-10) дает для нее в силу Np^-Q
неравенство Парсеваля
оо Ь
2) а) < J uN [и] их. A0.13)
1-Х а
Дополнение. 2. В качестве дополнительного результата из
A0.9) в силу Zp^0 получаем сразу так называемое неравенство
Бесселя**) то ь
V? J <**• A0.14)
r-l a
Как резюме результатов этого пункта может быть сформулиро-
сформулирована еще одна
Теорема. Пусть задача на собственные значения является
самосопряженной и полностью определенной, причем и (х) — неко-
некоторая функция сравнения и й(- — ее коэффициенты Фурье согласно
СО оо
A0.4). Тогда ряди ^ а2, и 2 ^(а? сходятся, а именно, действие
тельны равенство Парсеваля и неравенство Бесселя:
i-l a i-1
Если и не является функцией сравнения, а только полудопусти-
полудопустимой функцией, то имеет место неравенство Парсеваля A0.13).
10.4. Вспомогательная теорема о некоторых рядах по соб-
собственным функциям. В дальнейшем нам понадобится снова для
самосопряженной полностью определенной задачи на собственные
*) По общепринятой терминологии, неравенство Бесселя.
**) Термин нэ является общепринятым.
10.41 § ю. ТЕОРЕМА О РАЗЛОЖЕНИИ 153
значения D.11) — D.14) сходимость ряда
^11 „_„., ._,,, A0.,5)
ft-1 *
представляющего собой сумму квадратов v-x производных собствен-
собственных функций ук, деленных на собственные значения '); v в дальней-
дальнейшем пусть будет фиксированным.
Для доказательства сходимости рассмотрим функцию w(x), ко-
которая т раз непрерывно дифференцируема и должна удовлетворять
краевым условиям
w (a) = w' (а) = ... =щ>(т-1) (а) = w (b) = w' ф) =
= ... =wlm-V(b)=0; A0.16)
в остальном она может быть совершенно произвольной. Получим при
помощи этой функции числа ak:
Zr—w(x)dx. A0.17)
a
Эти числа ak можно считать коэффициентами Фурье некоторой
функции сравнения v(x), определенной как решение краевой задачи
Эта краевая задача, поскольку к= 0 не является собственным зна-
значением, имеет однозначно определяемое решение v(x), представимое
посредством функции Грина, согласно E.20), E.21):
ь
j
а
Теперь легко вычисляются коэффициенты Фурье v(x):
ъ ь ь
J v{x)N\yk (x)\ dx= J -g-M \yk\ dx = J f-M [v] dx =±
= (—l)v Г
J
a
v-кратное интегрирование по Частям с учетом A0.16) подтверждает,
что коэффициенты Фурье функции v совпадают с величинами ak ив
A0.17).
') Последующее доказательство дано в статье Е. Kamke, Math. Z. 46
A940), 273.
154 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ П0.4
Неравенство Бесселя A0.14) для функции сравнения v.(x) и для
какого-нибудь натурального числа р имеет вид
ft -J2
ь
*=■!
k — l a a
С другой стороны,
b b b b
f vM [v] dx = (—l)v f irazKv> dx — \ \ О (х, |) w^ (x) ?iy(v> (|) dx d\.
J J D J
a a a a
В силу A0.16) v-кратное интегрирование по частям как по х, так
и по | дает
ь ь ь
a a a *
гак как, согласно дополнению к п. 5.3, в силу 2v-^2m —2 част-
частные производные
d2vG (х, I)
dxv d%v
существуют и являются непрерывными функциями х и £. Если срав-
ь
нить оба результата для vM [v] dx друг с другом, то получим
( <J2vG (л:, I) -Л ylv> (x) ylv) (|) )
JJ S \wWw®dxdl>0. A0.18)
Г Г ( <J2vG (л:, I) -Л ylv> (x) y
ft-l
Так как это неравенство должно быть действительным для каждой
функции w(x), которая только т раз непрерывно дифференцируема
и которая должна удовлетворять краевым условиям A0.16), то для
х = \ получается
г
Это следует из того, что если бы з A0.18) величина в фигурных
скобках имела отрицательное значение в точке х = \ = *0, то вслед-
вследствие непрерывности она была бы отрицательной и в достаточно
малом квадрате
I* — I
10.51 § 10. ТЕОРЕМА О РАЗЛОЖЕНИИ J55
Тогда можно было бы функцию w(x) выбрать так, что она для
| х — х01 < е принимала бы положительные значения, а в остальной
области исчезала и неравенство A0.18) было бы нарушено.
Неравенством A0.19) утверждаемая сходимость доказана.
10.5. Сходимость ряда Фурье A0.5). Теперь мы можем ответить
на первый из двух поставленных в п. 10.2 вопросоз о сходимости.
Теорема. Пусть задача на собственные значения D.11) —
D.14) является самосопряженной и полностью определенной.
Пусть и есть функция сравнения и с ней образованы коэффи-
коэффициенты Фурье at согласно A0.4). Тогда, согласно A0.5), постро-
построенный с этими at ряд и ряд, полученный путем его почленного
v-кратного дифференцирования (у может принимать значения
0, 1, 2 т— 1)
сю
2ia.yf(x), A0.20)
сходятся; сходится равномерно в интервале a, b даже ряд, со-
составленный из абсолютных величин членов.
Это видно непосредственно из неравенства Шварца ')*); согласно
последнему, для двух натуральных чисел р, q
Здесь первая скобка в правой части в силу неравенства Бесселя
A0.14) стремится к нулю при р, q->0 (независимо от х), а вторая
скобка, согласно формуле A0.19), остается ограниченной равно-
равномерно по х. Следовательно, также
ч
Д) I a.y<v> (х) I -> 0 при р, q—>oo
i-P
равномерно для всех х из интервала а ^ х ^ Ь, т. е. ряд A0.20)
Сходится абсолютно и равномерно по х.
') К. Knopp, Einfuhrung in die hohere Mathematik, Leipzig, 1942,
т. I, 106, 133 [см., например, В. И. Смирнов, Курс высшей математики.
т. I I, M. — Л., 1952]. Неравенство Шварца означает: если си с2, ..., сп и
d\, d2 dn — любые вещественные числа, то имеем
Это неравенство непосредственно следует из тождества
*) В отечественной литературе принят термин «неравенство Коши».
156 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ Ц0.6
10.6. Теорема о разложении. Доказательство в случае я = 0.
Теперь необходимо исследовать, какова сумма ряда A0.5). Для этого
привлекаем обобщенную формулу Парсеваля A0.12), в которой %>
является какой-нибудь функцией сравнения с коэффициентами
Фурье Ь(.
со Ъ
* V afii = Г uN [v] dx.
1 = 1 а
Если подставить сюда значения коэффициентов Фурье
ь ь
bt= [ vN[yt]dx= f ytN[v]dx (t=l. 2, .. .),
a a
то получим (изменение порядка суммирования и интегрирования в силу
со
доказанной в п. 10.5 равномерной сходимости ряда 2 аЛ законно)
и (х) — У, а,у; (х) }■ N [v] dx = 0.
Й J
Положив
со
(J (х} = и (х} ^ (х• v• Гх) (\0 21 "^
имеем, таким образом, для всех функций сравнения v(x)
ь
С U (x)N[v]dx = 0. A0.22)
а
О функции U (х) мы знаем следующее: она (т—1) раз непрерывно
дифференцируема и удовлетворяет из краевых условий (согласно
разделению краевых условий в п. 4.2) всем главным краевым усло-
условиям (так как и и yt удовлетворяют этим условиям). Если бы мы,
кроме того, знали, что U (х) непрерывно дифференцируема даже 2т
раз и является функцией сравнения, то A0.22) означало бы, что
все коэффициенты Фурье ир функции U (х) равны нулю. Тогда,
согласно формуле Парсеваля A0.11), должно было бы быть
UN[U\dx = Q.
и в силу предположения (8.2) мы имели бы [/ = 0. Тем самым тео-
теорема о разложении для любой функции сравнения и (х) была бы
доказана.
10.7J § Ю. ТЕОРЕМА О РАЗЛОЖЕНИИ 157
Во многих случаях к заключению о том, что (У(х) = 0, можно
было бы прийти на основании приведенных выше свойств U (х), не
опираясь на недоказанное утверждение, что U (х) есть функция
сравнения. Ограничимся здесь только случаем задач одночленного
класса, хотя можно было бы обсуждать и несколько более общие
случаи 1).
Пусть дифференциальное уравнение имеет вид D.28)
М \у] = XN [у] = Я. (— 1)" [gn (х) yWf\
где gn (х) > 0, а в числе краевых условий должны быть (главные
краевые условия)
у(а) = у'(а) = ... = y(«-i) (с) = у (*) = /(*)= ...
= 0. A0.23)
В случае я = 0, т. е. в частных задачах на собственные значения
М[у] =^go(x).y, никакие предпосылки A0.23) о краевых условиях
не нужны. В этом случае из A0.22) и без того следует, что
ь
J g0Uvdx = 0, A0.24)
а
значит, U должно быть тождественным нулем, так как если бы U
было отлично от нуля, например U > 0 в некоторой точке х0, то
в силу непрерывности U также и в некотором малом интервале
|х — -^ol^8 Функция U была бы положительной и, выбрав v до-
достаточно гладкой, положительной в |х — хо|<е и равной нулю
в остальной области, мы получили бы нарушение A0.24).
Тем самым в случае п = 0 теорема о разложении доказана. Для
п > 0 необходимо некоторое вспомогательное рассмотрение; дока-
доказательство теоремы о разложении завершается только в п. 10.8.
10.7. Замечание. В случае некоторого произвольного п в диффе-
дифференциальном уравнении D.28) из A0.22) при принятых предпосыл-
предпосылках путем и-кратного интегрирования по частям следует
ь
Г gnU{n)v(n) dx = 0. A0.25)
i)
а
£/ существует в силу п^т—1 и является непрерывной.
Это равенство действительно для всех функций сравнения v; по-
последние удовлетворяют краевым условиям A0.23). Из этого можно
заключить2), что функции gnU , обозначаемые для краткости у,
!) Е. Kamke, Math. Z. 46 A940), 276 — 280. Пробел, имеющийся
в приведенном там доказательстве, восполнен здесь в п. 10.7.
") За краткое доказательство этого автор признателен Теодору
Букку, Штутгарт.
153
ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ
[10.7
являются полиномами Pn-i степени (га—1):
Ф(х)= J ... J yW^^-^-
gyi) = Pn^(x). A0.26)
Для доказательства этого вводится вспомогательная функция ф(х)
A0.27)
причем /?2я-1 (х) еСТЬ полином степени не выше Bга — 1), определен-
определенный так, что ф(х) удовлетворяет краевым условиям A0.23). Это, как
известно, всегда возможно, так как для 2га неизвестных коэффи-
коэффициентов данного полинома имеем систему 2га уравнений, получаемых
из A0 23), определитель которой Ап отличен от нуля. Для доказа-
доказательства можно, без ограничения общности, принять а = 0, b = 1,
тогда
1
1
0
0
0
0
0
0
TP
г
0
1
1
1
0 1
0 1
0
0
—
0
1
0
2
•2
• 2
0
0
1
га
га
;»-
0 .
1 .
0 .
3 .
0 .
3-2.
0 .
0 .
(га-
-1)!
0
1
0
.. (л-1)
0
..(я_2)(я_
.. (л-1)!
.. (л-1)!
1
(п
1)...2 (га-
1
га
я(я-1)..
.
4
.3
0
1
0
Bл-2)
.. Bл-
0
2)Bл-3)
0
..Bл—2)Bл—3)....-л Bл-
1)
)л ...3
1
л4-1
(«41)«
10 0 ...
ОНО ...
0 0 2! ...
0 0 0 ... (л
... 1
... 2л—1
0
1
0
Bл —1
Bл-
0
1)Bл
0
-1)Bл-2)-
0
0
0
-1)!
. . . Bл—1)Bл —2). .
... 1
... 2га — 2
.. .4. . .Bга—2)
•6„.
)
-2)
....(л+1)
A0.28)
.(«4-1).
• ••(«41)
• •
/
-1
ГТ ..1
v-0
—
¥=0.
10.8J § 10. ТЕОРЕМА О РАЗЛОЖЕНИИ 159
Для функций ф(лг), определенных согласно A0.27), тогда имеем
<!*»>(*) = Y (*) — ?„_!(*). A0.29)
где qn-i(x) есть некоторый полином степени (п—1). Далее, ф<"> ор-
ортогональны <?„_], так как для хг, где 0<^г<^га, из интегрирования
по частям с учетом краевых условий A0.23), которым ф удовлет-
удовлетворяет, следует
<«>хгйх = 5J(— W-p-l)r(r— 1) ... (r_p-f 1)хг-р =0;
Lp»o Ja
таким образом, из A0.25) при ■Р = ф получаем
* ь ь ь
0 = J у (х) ф("> (х) й?х = J [ф(п>]г й?х + J ф(л)^„-1 их = J [qjf»>]8 tfx,
а о а а
т. е. ф<">(х) = 0, или в силу A0.29) Y(x) =^,(_[ (х) есть полином
степени (п — 1).
10.8. Теорема о разложении. Завершение доказательства
для я^-0. Теперь начатые в п. 10.6 рассуждения могут быть
быстро доведены до конца. Проведенные в предыдущем пункте
вспомогательные рассмотрения дали следующий результат: пусть и(х)
есть функция сравнения и V (х), согласно A0.21), — отличие этой
функции сравнения от формально построенного для нее ряда Фурье.
Тогда посредством A0.29) доказано, что функция y(x) = gnUln) есть
полином Р„_[ степени (п — 1), см. A0.26). Поэтому га-кратное диффе-
дифференцирование у(х) дает
Функция U удовлетворяет этому дифференциальному уравнению
и 2я краевым условиям A0.23) и должна быть, таким образом, тож-
тождественно равной нулю, ибо в противном случае она была бы собст-
собственной функцией самосопряженной удовлетворяющей условиям (8.2)
задачи
с краевыми условиями A0.23), т. е. она соответствовала бы собст-
собственному значению 1 = 0. Эта задача, однако, будучи полностью оп-
определенной задачей на собственные значения, имеет только положи-
положительные собственные значения. Таким образом, имеет место1)
>) Расширение границ применимости теоремы разложения дано у
Н. Schubert, «Ober die Entwlcklung zulMsslger Funktlonen nach den
Eigenfunktlonen bei definlten selbstadjungierten Elgenwertaufgaben», Slt«
zungsberlchte der Heldelberger Akademle der Wlsgenscnaften, Mafiiematlsch -*
Naturwlssenschaftllche Klasse, 1948, вып. 8, 22.
160 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ IH-'
Теорема о разложении. Пусть задача на собственные
значения D.11) — D.14) удовлетворяет предпосылкам:
1. N [у] имеет частный вид Л/[у] = (—1)" [gn (х) yn>](n>, где
^„(■О>0-
2. Задача является самосопряженной и условия (8.2) полной
определенности выполняются.
3. В числе краевых условий присутствуют условия A0.23):
у (й) = у' (а) = . .. = У"-1) (а) = уф) = у'ф)=...= уС'-1) ф) = 0.
Тогда любую функцию сравнения и (х) можно разложить в ряд
по собственным функциям, абсолютно и равномерно сходящийся
в интервале (а, Ь):
оо
причем at определяются посредством A0.4), и этот ряд можно
(от—1) раз почленно дифференцировать.
В случае частного класса задач можно показать, что не только
функции сравнения, но все кусочно-непрерывные функции с квадра-
квадратично интегрируемыми первыми производными могут быть разложены
в ряды по собственным функциямх).
§ 11. Дополнения
11.1. Элементарное обоснование минимальных свойств в слу-
случае уравнений второго порядка. Для частных задач на собствен-
собственные значения вида
с краевыми условиями у(а)=уф) — 0 минимальные свойства наи-
наименьшего собственного значения k-у, которые описываются теоремой
п. 8.1, могут быть обоснованы совершенно элементарно (без исполь-
использования функции Грина и т. д.) на основе тождества A1.6), полез-
полезного также для многих других доказательств. Так как минимальные
свойства составляют основу метода Ритца, а A1.1) — очень часто
встречающееся дифференциальное уравнение, то здесь доказательство
будет повторено, хотя результат содержится уже в п. 8.2.
О распространении метода доказательства на уравнения четвер-
четвертого порядка см. второе упражнение в п. 11.4.
Чтобы сохранить элементарный характер доказательства, здесь
дополнительно обосновываются моменты, которые опытному чита-
читателю хорошо известны.
') См. сноску 2) на стр. 111.
и.Ц
§ II. ДОПОЛНЕНИЯ
161
О функциях /,, /0, g0 сделаем следующие предположения: пусть
в интервале а<[х<;# /,, g0 являются положительными, /0, g0 —
непрерывными и /, — непрерывно дифференцируемой.
А. Существование одной собственной функции.
Прежде всего докажем, что имеется по меньшей мере одно вещест-
вещественное собственное значение и что отвечающая наименьшему вещест-
вещественному собственному значению собственная функция ух в интервале
а < х < b отлична от нуля, т. е., например, может быть принята
положительной.
Собственная функция у задачи A1.1) может иметь только невы-
невырожденную нулевую точку, так как если бы, например, при х = х0
было
то у, являясь однозначно определяемым начальными значениями ин-
интегралом линейного однородного дифференциального уравнения вто-
второго порядка с /\ФО, должна была бы быть тождественным нулем.
Следовательно, должно быть, в частности, у'(а)=£0.
Полагаем теперь, что собственная функция однозначно опреде-
определяется с точностью до постоянного множителя условием у' (а)=1.
Рассмотрим, далее, решение
z (х, X) задачи
(/!*')'
* =
= 1. A1.2)
Для каждого вещественного Л
функция z (х, Л) тем самым од-
однозначно определена (рис. 11.1),
а те значения Л, для которых О
zip, Л) = 0, являются собствен-
собственными значениями задачи A1.1).
В некоторой достаточно малой
окрестности точки х = а справа
функция z (х, Л) положительна
для каждого фиксированного Л (ибо если бы такого интервала не
существовало, т. е. точка х = а была бы точкой сгущения в области
z<;0, то также должно было бы иметь место неравенство ''
Рнс. 11.1. Поведенне z (х, Л) при раз-
различных значениях Л.
') Легко можно также подобрать положительные постоянные с{ н с2
так [например, путем использования приводящего к A1.4) преобразования
и сравнения с дифференцнальным уравнением A1.5) с постоянными коэффи-
коэффициентами], чтобы z (х. Л) была положительной при
| Л|
11 Л. Коллатц
162 ГЛ. Ш. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [11.1
Для очень больших отрицательных значений Л функция z(x, Л)
положительна во всем интервале а<х^Ь; так как для
)mla
разность /0—Ag0 положительна; если бы z(x, Л) не была положи-
положительной при всех х > а, то z (x, Л) должна была бы иметь в этом
интервале нулевую точку при х = | > а, там было бы z' < 0, в то
время как из A1.2) путем интегрирования от а до \ следовало бы
I
txz' (I) = h (a) • 1 -+- / (Л - Л§-0) z (х) dx > 0.
а
Далее, z (x. Л) является непрерывной (даже дифференцируемой)
функцией Л и для каждого фиксированного Л — дважды непрерывно
дифференцируемой функцией х. Если рассмотреть z(x, Л) для Л,
растущего от — оо, то вначале при
я < х <! b функция z положительна. Мы-
Мыслимы следующие два случая:
I. z (х, Л) положительна для всех Л
х при а < х Ь
Л
a b x II. z (x, А) положительна не для всех Л
и х при а < х ^.Ь.
Рис. 11.2. К доказательству jai< как для достаточно больших от-
отрицательных Л [например, для Л из A1.3)]
z > 0 при а < х <^ Ь, то во втором случае
вследствие непрерывности z и z' no x и Л должно быть наименьшее
Л^Л^ для которого ^ впервые становится нулем при х = х0, где
я < х0 <С £; следовательно, 2 (х0, Л]) = 0 и 2 (х, Л) > 0 при Л < Л1
и а < х ^.Ь. [Если лгд означает первую после а нулевую точку
z(х, Л), то z (х\, Л) < 0, т. е. х\ при Л—>Л1 не может как угодно
близко подойти к а вследствие непрерывности z' и условия z' (а, Л)=1.]
В этом случае возможно лишь хо = Ь, т. е. z (b, Л,) = 0, и
z (х, Л]) > 0 при а < х < Ь, значит, Л] есть наименьшее собствен-
собственное значение Хх, а отвечающая ему собственная функция положи-
положительна при а < х < Ь. Действительно, если бы z (x0. Л,) было равно
нулю при а < х0 < Ь, как на рис. 11.2, то вследствие того, что
z(х, Л^^-О для всех других х интервала а<х^.Ь, производная
z' (х, Л) должна была бы быть равной нулю. Однако г и г' не
могут одновременно обращаться в нуль в одной и той же точке х0,
как это выше разъяснялось для у.
Итак, необходимо только еще показать, что случай I исключается.
Введем вместо х новую независимую переменную |
dt
/i @ "
H.1J § II. ДОПОЛНЕНИЯ 163
При этом интервал a, b из-за положительности fx (x) однозначно
преобразуется в интервал 0, | ф) на оси \. .Если положить
то задача A1.2) в силу соотношений -—-==/, (х) = Fl(Q и —рг- =
= fx (x) z' (x) принимает вид
w" = -s (I) w (I) = Fx (I) [Fo (I) - ЛО0 (I)] w (I),
= 0, w' @) = Fx @), J (U )
где штрихи означают производные по \. В случае I WQ,, Л) должна
быть положительной для всех Л и I из 0 < I ^ l(b); мы, однако,
покажем, что это не так для больших положительных Л. Для этого
сравним w(l, Л) с решением v(Q = -? /='1(O)sin k\ дифференциаль-
дифференциального уравнения
v" = — k4 , A1.5)
с такими же начальными условиями г/@) = 0, v' @) = Fx @).
Ближайшая за \ = 0 следующая нулевая точка v (|) есть £ = я/А.
Рассмотрим теперь еще интервал 0^|^я/А, который обозначим J,
и выберем А > пЦ ф), так что J содержится в 0, \ ф).
Выберем, далее, Л таким большим, что s (|) > k2 для всех £ из
интервала У, для чего следует лишь положить
Л
•^ min (F,O0)
Если умножить первое уравнение A1.4) на v, a A1.5) на w, то их
разность дает
w"v — v"w = — (s (|) — k2) vw.
Если бы да было положительным для всех \ внутри У, то правая
часть последнего уравнения была бы там отрицательной, а поэтому
также и интеграл по этому интервалу от 0 до |:
I
w'v — v'w = — Г (s (I) — k2) vw d\ < 0 (при | > 0 из У).
о
Для £ = 4г вследствие того, что v = 0, v' — — F,@)<0; из этого
И,
следует, что w (я/А) < 0, в противоречии с предположением w > 0.
Следовательно, wfe. Л), а значит, и z (x, Л) не могут быть поло-
положительными для всех х из интервала а<^х^.Ь и для всех Л. Тем
самым доказано существование наименьшего вещественного собствен-
собственного значения Хх и положительной в интервале а < х < b первой
собственной функции.
164 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ 111.1
Б. Минимальные свойства наименьшего собствен-
собственного значения. Доказательство минимальных свойств А,, основы-
основывается на следующем тождестве для некоторых трех функций и, /, у,
для которых лишь должны существовать и', /', у" в рассматривае-
рассматриваемой точке х и у (х) Ф 0:
\ у ) у \ J Jy \y
Это тождество подтверждается вычислением:
_ и» ffsy . 2uu'fy' 2
(/У Л"
у у
= f (//)' +«'7-/(«'2-
из чего A1.6) следует непосредственно.
Пусть теперь и есть любая «допустимая функция», т. е. тожде-
тождественно не равная нулю, удовлетворяющая краевым условиям и (а) =
= и ф) = 0, непрерывно дифференцируемая функция [было бы даже
достаточно вместо непрерывной дифференцируемости потребовать,
чтобы и была кусочно-непрерывно дифференцируемой и чтобы суще-
существовали и' (а) и и' (Ь)\. Далее, положим в A1.6)/ = /, и у — равным
первой собственной функции у,, существование которой уже дока-
доказано. Тогда в силу A1.1)
f X,
Если проинтегрировать A1.6) в интервале а, Ь, то левая часть
обратится в нуль. На самом деле, у'г на краях не исчезает, следова-
следовательно, к/у, на краях имеет конечные значения, а краевые значения
й2/у( равны нулю. В правой части У Л —) =и' — У[-~ имеет на
краях конечные значения, так что интеграл существует. Таким обра-
образом, при интегрировании получаем
ь ь ь
J и* (/0 - ^0) dx 4- J «''Л dx-j fiy2 [Л^2 dx = о.
а а а
Так как yj, кроме точек х = а и х = Ь, нигде в интервале
интегрирования не обращается в нуль, как это было показано выше,
то третий интеграл имеет конечную и неотрицательную (так как /1 > 0)
величину. Третий интеграл равен нулю тогда и только тогда, когда
(и у
—) =0, т. е. когда и сама есть первая собственная функция.
11.11 § II. ДОПОЛНЕНИЯ 165
Если опустить третий интеграл, то тогда знак равенства следует за-
заменить на знак ^-, и получается
ь
С11-7)
dx
т. е. наименьшее собственное значение Х1 одновременно является наи-
наименьшей величиной, которую принимает частное в правой части A1.7),
когда и пробегает область всех допустимых функций. Знак равенства
будет иметь место только в том случае, если и сама является первой
собственной функцией.
Для второго собственного значения Х2 при помощи описанного
здесь метода доказательства получается формулировка: Если | является
лежащей внутри интервала a, b нулевой точкой второй собственной
функции у2, т. е. У2(|) = 0. то Х2 является минимумом, который
принимает частное в правой части A1.7), если от допустимых функций
дополнительно потребовать, чтобы они обращались в нуль в точке |,
т. е. и(!) = 0. Дополнительные условия теперь, следовательно, иные,
чем в теореме п. 8.3.
В. Теорема включения для первого собственного
значения. Присоединяем данное Барта') элементарное доказа-
доказательство для частного случая теоремы включения, которое использует
несколько отличающееся от A1.6) тождество A1.8). Последнее для
трех функций а, /, у, для которых должны лишь существовать
и", /', у" в некоторой рассматриваемой точке х и и(х)фО, имеет вид
(ОТ = £ (/«')' -i-lf (и'у - «/)]'. (Ц.8)
и
В правильности этого тождества легко убедиться путем дифференци-
дифференцирования выражения в квадратных скобках.
Пусть теперь и есть произвольная функция сравнения, т. е. дважды
непрерывно дифференцируемая функция с и(а) = и (Ь) = 0, которая,
однако, внутри интервала принимает только положительные значения:
и (х) > 0 при а < х < Ь.
Далее, подставим в A1.8) вместо / функцию fl из A1.1) и вместо у
первую собственную функцию yv о которой мы уже знаем, что она
внутри интервала не обращается в нуль, т. е., например, уг > 0 при
а < х < Ь. Тогда, согласно A1.1),
>) J, В art a, Ing.-Arch. 8 A937), 35-37.
166 ГЛ. Ш. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ 1И.2
и A1.8) после деления на gny1 принимает вид
^=Л_1Л-ТЧ.^_. A1.9)
1 go gou. ^ gauy1 к '
где
Z=Z(x)=[fl(u'yl-uy[)]'. A1Л 0)
Если теперь для данной функции и при а < х < b ввести вспо-
вспомогательную функцию
ф,,.л -(f^'Y+fpU _ М[и]
( ' ~~ gou — N [и] '
то A1.9) принимает форму
Я, =Ф(а:L-—^—• A1-И)
1 v ' gouyi V
Теперь Z (х) в силу A1.10) есть непрерывная функция, интеграл
которой по основной области из-за краевых условий для к и у,
обращается в нуль:
Следовательно, либо Z^O, либо Z при а < х < b принимает
вначения обоих знаков. Так как g0, a, yY при а < х < b положи-
положительны, функция либо тождественный нуль, либо принимает
значения обоих знаков. Таким образом, в A1.11) функция A,j — Ф(х)
не при всех х из а < х < b всегда положительна или всегда отри-г
цательна, т. е. имеем
Это есть формулировка теоремы включения п. 9.1 для первого соб-
собственного значения Хг задачи A1.1).
11.2. Минимальные свойства собственных значений в случае
уравнений с частными производными. Пусть
M[z] = Xgoz A1.12)
«сть уравнение с частными производными для функции z двух или
.более независимых переменных х, у, .... a g0—заданная непре-
непрерывная положительная функция этих переменных и на z на краях
некоторой области 33 налагаются, как в F.2), краевые условия
£/й[2] = 0 (|i=l, 2 k). A1.13)
Пусть Эта задача на собственные значения является самосопряженной
и полностью определенной (см. F.3) и F.4)) и существуют функция
11.2. § П. ДОПОЛНЕНИЯ 167
Грина1) О (х, у, ...; |, ц, ...) и связанное с ней, согласно G.24),
ядро
К(х, у, ...; |, ть ...)=
= О(х, у, ...; I, У], ...)Ygo(x, y,...)go(l, Ti. ...). (П.14)
которое симметрично, квадратично интегрируемо и непрерывно в сред-
среднем, так что приведенная в п. 7.2 теория интегральных уравнений
применима.
При этих предпосылках всю изложенную в пп. 8.1—8.4 теорию
минимальных свойств собственных значений можно почти дословно
перенести на уравнение с частными производными A1.12). Мы можем
поэтому быть краткими. Пусть и(х, у, . . .) есть некоторая функция
сравнения, т. е. (см. п. 6.1) имеющая столько частных производных,
сколько необходимо для образования М[и], и пусть £/^[и] = 0,
и фО. Тогда с этой функцией можно построить отношение Рэлея
иМ [и] dxdy ...
A1.15)
I £o dxdy ...
58
и соответствующую2) (8.4) функцию ц*
М [и] — Rgou = if (x, у). A1.16)
Для доказательства неравенства R[u]^-Xl можно снова положить
rf^O. Тогда решение краевой задачи, соответствующей (8.5):
имеет вид
v(x, у, Я,)= J J О(х. у; I,
т. е. функция V(х, y) = v(x, у, ^)Y^o(x' У) есть однозначно опре-
определяемое решение неоднородного интегрального уравнения
V(x, y) = lj JK(x. у; I, ц)УA, v[)dldi\+f(x, у),
') То есть уИ [г] = г (х, у, ...), £/ц[г] = 0 эквивалентно уравнений
г{х, у ,...)= | G(x, у, ...; |, ц, ...)dldx\ ...
2) Мы пишем if вместо т) как в (8.4), так как здесь, например, в A1.14)
ц применяется в другом значении. В дальнейшем для экономии места, опу-
опускаем многоточие за х, у, соответственно за £, ц.
}68 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ 111.2
где
f(x, y)=jJ0(x, у; I, tOWoC*. y)i\'a< 4)dldt\, A1.17)
поскольку X не является собственным значением. Именно, V(x, у),
согласно общей формуле решения G.15), которая действительна и
в случае функций многих переменных, можно прямо записать в виде
v(x. у,
A1.18)
причем zt(x, y)Y&o(x' У) есть собственная функция ядра К; следо-
следовательно, zt(x, у)—собственная функция задачи A1.12), A1.13).
Далее, можно, точно так же как в (8.7), построить функцию
h (X) = Г j ц* (х, у) v(x,y, I) dx dy
S3
и дальнейшее доказательство вести при N [а]= goa, как в п. 8.2.
Точно так же на рассматриваемый случай можно перенести дока-
доказательство минимальных свойств второго собственного значения Х2,
данное в п. 8.3; дополнительному условию (8.11) здесь соответствует
условие
J J. y)go(x, у)гг(х. y)dxdy^0. A1.19)
Однако доказательство того, что вследствие этого дополнительного
условия обходится особенность функции Грина в точке А, = А,1, надо
проводить, руководствуясь формулой решения A1.18). В последней
при А, = А,[ в сумме выпадает неограниченно возрастающий член, если
имеет место условие
г (I, л) Vgo(l ц)/A, Ю d\ dn = 0. A1.20)
Далее, A1.20) фактически есть следствие из A1.19), так как в силу
равенства M[zl] = X1gQzl имеем, согласно A1.19) и предполагаемой
самосопряженности:
J J. и (х, у) М [zx (х, у)] dx dy=- J J гх (х, у) М [и (х, у)] dx dy = 0,
S3 S3
и в силу A1.16) и A1.19)
J J zx (х, у) ч* (х, у) dx dy = 0.
11-21 5 И. ДОПОЛНЕНИЯ 169
Подставив сюда вместо zx ее значение, вытекающее из A1.12),
zx{x, y) = Xxjj G(x, у; |.
SB
получаем уравнение
X
[J
которое с учетом A1.17) непосредственно переходит в A1.20).
Вообще для «-го собственного значения ^л имеем: Хп является
минимумом отношения Рэлея A1.15), когда и пробегает область всех
функций сравнения, ортогональных (п— 1) первым собственным фун*
кциям Zi (x, у), умноженным на g0:
(/=1,2 n — 1). A1.21)
Этому вариационному принципу можно сопоставить еще второй.
Приведенный в п. 7.2 для случая интегральных уравнений вариа-
вариационный принцип в силу G.18) означает
Г да2 (х, у) dx dy
5A1.22)
J J J J л<<x' y; ^' ^w ^' y^w ^' ^^rfA: dy d^ dr]
причем w пробегает область непрерывных (ненормированных) функций.
Для w определяется функция сравнения Fx (x, у), которая удовле-
творяет дифференциальному уравнению
w — -tL^ M [F,\, i 11.23)
Vg0 '
т. е.
F](x, y) = j $ К(х, у, Ь nl^M^Ldldn. A1.24)
Таким образом,
J $ Fl(x,y)M[Fl]dxdy
причем Fx пробегает область всех функций сравнения,
A1.25)
170 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ [Н.З
Отношение в правой части имеет форму, отличную от A1.5).
К соотношению этих двух минимальных принципов ]) мы еще вернемся
в п. 14.1.
Теорему включения § 9 можно также непосредственно распро-
распространить и на уравнения в частных производных. Используем для этого
формулы G.16), G.17) теории интегральных уравнений и положим,
как в A1.23),
v{x) M[F]
Тогда G.16) принимает вид
Это отношение можно образовать для произвольной функции сравне-
сравнения Fi(x, у). Если Ф в области 33 имеет постоянный знак и заклю-
заключено между пределами Фт1п и Фтах, то между Фт1п и Фтах имеется
по меньшей мере одно собственное значеняе Xk.
11.3. Двупараметрическиг задачи на собственные значения,
кривые собственных значений. Бывает иногда, что в задаче на
собственные значения появляются два параметра, например, при
исследовании влияния некоторой величины а, присутствующей
в дифференциальном уравнении, на собственное значение X или что-
нибудь подобное. Если обозначить оба параметра через Хг и Х2, т. е.
в только что приведенном случае, например, Х = Х1 и а = Х2, то
вообще для каждого Х1 имеется счетное бесконечное множество зна-
значений Х2, и при графическом представлении в плоскости Х1, Х2 полу-
получается счетное бесконечное множество ветвей «кривых собственных
значений»2). (Способ обозначения здесь иной, чем раньше,—в п. 5.7
XL обозначало i-t собственное значение.)
В качестве примера3) рассмотрим защемленный на обоих концах
сжатый стержень на упругом основании, когда коэффициент постели
') На наличие двух минимальных принципов указывается в книге
G. Н а ш ш е I, Integraigleichungen, Berlin, 1937, 88.
2) В частных случаях свойства кривых собственных значений иссле-
исследуются у Н. Schaefer, Beitrag zur Berechnung des kieinsten Eigenwertes
eindimensionaier Eigenwertaufgaben, Diss., Hannover, 1937, E.
3) В технической литературе имеется много примеров двупараметри-
ческих задач на собственные значения; назовем лишь задачу о потере устой-
устойчивости при кручении однородного вала (С. В. Biezeno, R. Grammel,
Technische Dynamik, Berlin, 1939, 547 [К. Б. Бицено и Р. Граммель.
Техническая динамика, т. II, Гостехиздат, 1950]). В этом примере крутящий
момент W и осевая сжимающая сила Р— два параметра. Условием потери
устойчивости является квадратичное соотношение между IF и Я, а так
называемая диаграмма потери устойчивости, являющаяся параболой в пло-
плоскости (Р, W), есть ветвь кривой собственных значений.
11.4]
§ 11. ДОПОЛНЕНИЯ
171
взят как переменный параметр. Задача в этом случае имеет вид:
yiv = я,,у - 2l2f, у @) = у' @) = у (I) = у' (/) = 0.
Множитель 2 перед Х2 добавлен только из соображений удобства
при вычислениях. Решение задачи приводит к трансцендентному
уравнению, которое при
распадается на два:
tg a th т
а т '
0 tg а = — т th т.
На рис. 11.3 показаны пер-
первые три ветви соответствующей
кривой собственных значений.
ПА Упражнения. 1. Прове-
Проверить формулу Парсеваля A0.11)
и неравенство Бесселя A0.14)
в примере: — у" = Ху, у @) =
= у (я) = 0 для функции сравнения
и = пх — х2.
Проверка. Как уже указывалось в п. 10.2, здесь имеются собствен-
собственные значения Яд = «2 с нормированными собственными функциями
-30
К
3804
поп
600,5
SL
0
700
л,
\
п
\
7 2)
Л
Я
\
Л4
г1г
\
г*
--9
Щ
г*
\
\
(
ч
л
i
N
Лг
\
7rf
\
\
\
64т
100
12=1ОП2
1 1 1
\
Рис. 11.3. Кривые собственных значе-
значей v X 2Х"
р
ний для задачи yiv
0) '0) (/)
— 2Х2у",
0"
/~
у. = 1/ — sin kx. Коэффициенты Фурье функции и (х) вычисляются по
формуле
я я
Г /"Т Г
aft=J u{x)yk(x)dx= у — I (ях —.
о ■ о
sin kx dx =
V л k3
2_
я
О
при нечетных k,
при четных k.
Поэтому
1
ч-\
г=1
Bг - 1)в
30
32
г-1
172 ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ JIM
Эти величины совпадают с
я
J uN[u]dx = J (пх — х*)* dx =-^
о
я
n
uM [и] dx = 2 (пх — -
о о
2. Распространить описанный в п. 11.1 элементарный метод обоснования
минимальных свойств наименьшего собственного значения на задачу четвер-
четвертого порядка:
(Лу'У = Я^оу, у (а) = у" (а) = у F) = у" (Ь) = 0.
Пусть при этом g0, /2 положительны, g0 непрерывна, /2 дважды непрерывно
дифференцируема.
Указание. Вместо тождества A1.6) использовать здесь тождество
+ ^£- (и'У - "У'J - -£■ («"у - «у"J - ■— (/У)" + /«;
подставить « в качестве «допустимой функции», т. е. дважды непрерывно
дифференцируемой функции, удовлетворяющей главным краевым условиям
ГП f t t t t t t
Рис. 11.4. Сжатый стержень на упругом основании.
и(а) = и (Ь) = 0; / = /2 и у = у,. При этом у, есть первая собственная функ-
функция, следующие свойства которой надо использовать: ух > 0 и у'[ < 0 при
а < лс < b\ yt и yt не обращаются в нуль на краях а, Ъ. Такое доказатель-
доказательство (при других обозначениях) проведено в работе «Deutsche Mathematik»,
т. II, 1937, 205.
3. Теорема включения. Найти верхнюю и нижнюю границы кри-
критической нагрузки Р для сжатого стержня на упругом основании (коэффи-
(коэффициент постели К = 60с), шарнирно закрепленного в точках х = ± 1, и имею-
имеющего переменную жесткость на изгиб а = сC — х2) (рис. 11.4).
При Р=сХ задача, согласно п. 1.4, имеет вид
М [У] = [C - *2) У"]" + бОу = - Лу",
У (-1) = У" (~1) = У (+1) = У" (+1) = 0.
Взяв два полинома Fa (x) и Z7, (х), которые удовлетворяют краевым усло-
условиям и находятся в соотношении ЛГ[/71] = — F'o, получаем
I СП 27Ъ
UFa = 5 C433 — 4032л:2 + 546ж4 -f 56а;6 — За:8). / К '
11.4] § 11. ДОПОЛНЕНИЯ
Согласно (9.3) построим отношение
р', „ч 30 D8 — 13л-2 — 2л-4 + 4- хЛ
173
" F[(x) 45—Юл-2 —Злг4
Ф (лг) принимает свои экстремальные значения прн л: = 0 и дг = ± 1:
Ф @) = 32,
TJ « 31,07.
Итак, в силу (9.4) имеем 31,07 < Я <32.
Более близкие границы для этого примера вычисляются по формуле
A2.19) в задаче 2 п. 14.6.
4. Теорема включения. Задача на собственные значения
возникает при крутильных колебаниях диска переменной толщины. Краевые
условия соответствуют закрепленному внутреннему и свободному внешнему
краям. Этим краевым условиям удовлетворяет фуикция
да = е2 sin anx,
если числа ап выбраны так, что tg ап -\- ап — 0.
Согласно (9.6) вычисляем
, —(e~x'w) 2 i 2 ,
2
w
н отсюда в силу (9.7)
Для первых четырех собственных значений получаем такие границы:
л
1
2
3
4
ап
2,029
4,913
7,978
11,09
Нижняя
границь
3,116
23,14
62,65
121,9
Верхняя
для Кп
4,116
24,14
63,65
122,9
Границы для более высоких собственных значений вычисляются всегда
относительно более точно. Для двух первых собственных значений ср. за-
задачу 2 п. 25.7 или Z. angew. Math. Mech. 19 A939), 304, 306.
5. Теорема включения. Нахождение критической нагрузки для
сжатого стержня постоянного сечения на упругом основании, закрепленного
шарнирно, приводит к задаче
yiv + Ay = - Яу", у (-1) = у" (-1) = у A) =» У" A) = 0.
Найти границы для Я, прн А = 20.
Решение. Для определения двух функций Ро (х) и F, (х), удовлетво-
удовлетворяющих всем краевым условиям и соотношению f]4 -jr AFl=- ~ FQl исходим
174
ГЛ. III. КРАТКИЙ ОЧЕРК МАТЕМАТИЧЕСКОЙ ТЕОРИИ
111.4
из некоторой функции F{ (х), причем Fv F'[ и F\v обращаются в нуль
в граничных точках х = ± 1 (так как из условия Z7, = FQ = 0 следует также
равенство нулю F^X Полином наинизшей степени, удовлетворяющий этим
условиям, определяется с точностью до постоячного множителя выражением
Fy (х) = 61 — 75л-2 + 15л:4 — хв = A — л:2) F1 — 14л:2 + л:4).
Тогда
— F'o = 120 (Зл- — л:3) + А (б1х — 25л-з -|- Зл:* — ^Л.
Требуется найти не Fo, а, согласно (9.3), отношение
р' 20 C — л:2) -f -i А [б1 — 25л:2 + Зл:4 — у л:6\
ф==_ — _____ .
Ниже в таблице для нескольких значений А даны Фтт, ФШах, средние
значения -^ (Фшах + Фтт) с максимальной ошибкой
Фтях — Фтт
Фшах + фтт
и для сравнения соответствующие точные собственные значения. Фактическая
ошибка среднего значения, особенно при А = 40, значительно меньше макси-
максимальной. При А = 20 Fl представляет приближение для первой, а при
А = 40 — для второй собственной функции, так как при А = 40 стержень
изгибается скорее по полной синусоиде (с узлом в середине), чем по полу-
полусинусоиде.
А
10
20
40
90
фт1п
6,466
10,533
18,66667
38,928
фтах
6,548
10,595
18,69047
39
Среднее значение
Т(фтах + Фтт)
6,507
10,564
18,67857
38,964
Теоретические
границы ошибки,
%
0,63
0,3
0,064
0,1
Точное
собственное
значение
Я,= 6,5202
Я, = 10,5731
Я2 = 18,67879
Я3 = 38,9430
6. Метод Ф. Кисе л инга (Z. angew. Math. Mech. 10 A930), 594). Гра-
Границы в теореме включения сближаются введением в функции Fo (x), F\ (x)
из п. 9.1 дополнительного параметра р, который подбирается таким образом,
что пределы (9.4) располагается возможно ближе. Провести это в примере
Для
— у" _ Я A -\- sin л:) у, у @) = у (я) = 0
Fi (х) = sin х -\- р sin Зле.
Результат.
Ф(л-) =
(sin х -\- р sin Зл:) A -\- sin x)
11.4] § И. ДОПОЛНЕНИЯ 175
Если представить Ф(х) для разных значений р графически, то различ-
различные кривые проходят через некоторую фиксированную точку, в данном слу-
случае через точку
х = ~, Ф = 2B —/3~) и 0,5359.
о
Фт1п становится наибольшим, если р определяется из условия: Ф'|-т-)=0,
У Я 2
т. е. при р = г ■ « —0,01118; при этом Фт1п = 0,5359.
Фтах становится наименьшим, именно Фтах = 0,5673, если р определяется
из условия: Ф @) = Ф (-£■). т. е. при р = -д=- B9 — /868) я — 0,01710.
2 i> 1. »-. "F" г— 27
Итак, имеем границы:
Xi> 0,5359 (ошибка —0,7%),
Я, < 0,5673 ( » +5,1%)-
Без параметра р, т. е. при р = 0, получились бы лить весьма грубые гра-
границы: 0,5 < Х{ < 1.
ГЛАВА ЧЕТВЕРТАЯ
МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
Описанный здесь метод последовательных приближений (называе-
(называемый также итерационным процессом) применим не только для задач
на собственные значения, но и во многих других задачах, связанных
с дифференциальными уравнениями, и имеет большое значение как
для теории, так и для численных расчетов. Прежде всего, он пред-
представляет стандартный метод для приближенного вычисления наимень-
наименьшего собственного значения самосопряженных задач вида D.11)—D.14)
(при некоторых дополнительных условиях, см. теорему п. 12.4), а сле-
следовательно, для большого числа проблем, встречающихся в технике.
При небольшой вычислительной трудоемкости метод позволяет полу-
получить часто очень близкие верхнюю и нижнюю границы для первого
собственного значения. Практическое применение метода подробно
излагается в пп. 12.5 и 13.6.
§ 12. Постоянные Шварца
12.1. Метод последовательных приближений в общем случае.
Метод последовательных приближений применим при очень общих
предположениях, а именно, если собственное значение X входит ли-
линейно в дифференциальное уравнение и краевые условия (процесс при-
применим также и для дифференциальных уравнений в частных произ-
производных, см. п. 14.1). В основу будут положены дифференциальные
уравнения D.11) и краевые условия D.14).
В общем случае метод заключается в следующем. Исходя из произ-
произвольно выбранной функции F0(x), определяют последовательность
функций Fu F2 при этом Fk получают из Fk_x, решая краевую
задачу. Во всех членах дифференциального уравнения и краевых усло-
условий, содержащих Я в качестве множителя, Ху заменяют на Fk_1,
а в членах, свободных от к, заменяют у на Fk. Например, для задачи
— у" — 1у; у(\) = 0; 1у'(О) — у(О) имеЛи бы
12.2] § 12. ПОСТОЯННЫЕ ШВАРЦА 177
Процесс упрощается, если X не входит в краевые условия. Тогда,
исходя из F0(x), функции Fv F2, . . . определяют, решая краевые
задачи
М[/%]= Л/[/%_,],
Можно ожидать, что в случае сходимости Fn с ростом п все более
принимают вид собственной функции ys. Тогда \ "\ должно при-
ближенно равняться соответствующему собственному значению ks. Это
отношение зависит еще от х. За приближенное собственное значе-
значение Л принимают величину
образованную по способу отношения Рэлея D.31). Ниже при под-
подробном исследовании мы ограничимся более узким классом задач1).
12.2. Введение постоянных Шварца ак и отношений цй. Пусть
задача на собственные значения вида D.11)— D.14) самосопряженная,
выполнены условия полной определенности (8.2) и собственное зна-
значение к не входит в краевые условия.
Начальная функция /^(л:) может быть выбрана произвольной,
однако так, чтобы выполнялись следующие условия: функция должна
быть непрерывной вместе со своими 2ге производными. Она может
не удовлетворять всем граничным условиям, достаточно, чтобы для
') Более общие результаты приводятся в работе: Н. W i e I a n d t, Das
Iterationsverfahren bei nicht-selbstadjungierten Eigenwertaufgaben, Math. Z. 50
A944), 93—143. В частности, на стр. 134 показывается, что если, например,
а) наименьшее по модулю собственное значение Х{ не вырождено, отлично
от нуля н в известном смысле прнчастно к Fo; б) не существует другого
ъ
собственного значения с тем же самым модулем, что и Я,; в) у,// [yt] dx=f 0
а
для собственной функции у,, принадлежащей к собственному значенню Я,, то
и функции Fn прн подходящей нормировке равномерно сходятся вместе
со своими 2т производными к собственной функции у(.
178 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ [12.2
любой функции сравнения и имело место!)
ь ь
Г (F0N[u] — uN[F0])dx = O и Г /yV [Fo] dx > 0. A2.3)
С помощью преобразования Дирихле D.17) можно в каждом От-
Отдельном случае легко установить, каким краевым условиям должна
удовлетворять Fo для выполнения A2.3). Например, в случае
N[y] = goy, т. е. для частного вида задачи на собственные значения,
условия A2.3) выполняются автоматически. Функция Fo не должна при
этом удовлетворять каким-либо краевым условиям и может быть лю-
любой непрерывной функцией, тождественно не равной нулю. Если же
само Fo удовлетворяет всем 2т краевым условиям, то вследствие
самосопряженности, разумеется, будет выполнено и условие A2.3).
Для получения точных границ выбирают обычно Fo так, чтобы
были уже выполнены все краевые условия. Однако иногда для удоб-
удобства вычисления подчиняют Fo только некоторым краевым условиям,
и тогда лишь функции Flt F2, ..., определяемые из A2.1), удовле-
удовлетворяют всем 2т краевым условиям. (Для практических целей часто
ограничиваются F:.)
С помощью Fп, найденных таким образом из решения краевой
задачи, образуют введенные Шварцем2) постоянные ak (постоянные
Шварца):
ь
ak = | FiN[Fk.l]dx, 0<*<A, £ = 0,1,2,... A2.4)
a
Они только внешне зависят от i, так как, используя итерационное
правило A2.1) и самосопряженность, можно получить
ь ь
ak= f FlM[Fk_i+l]dx= f Fk_!+1M[Fi]dx =
a a
b b
= J PH-i+iN[Fl.l\dx=\Fl.lN[Fk_l+l\dx. A2.5)
a a
b
т. е. интеграл Г FtN [Fk_t] dx зависит только от суммы i-\-(k—i),
a
а следовательно, только от k. Например,
ь ь ь
a2= Г F2N [Fo] dx= Г Ffl [FJ dx = Г F0N [F2] dx. A2.6)
a a a
') To есть Fa (x) по терминологии п. 10.3 (см. дополнение 1) должна быть
полудопустимой функцией.
2)Карл Герман Амандус Шварц A843—1921) — немецкий
математик.
12.21 § 12. ПОСТОЯННЫЕ ШВАРЦА 179
В силу (8.2) все ak положительны, так как
ь ь
a2k=JFkN[Fk]dx>0, aM_,= j FkM[Fk]dx > 0. A2.7)
а а
Используя постоянные Шварца ak, можно вычислить отношения
Шварца
Ввиду A2.7) все \ik положительны. Отношения ц2к с четным индексом
можно записать в виде отношений Рэлея D.31)
ь
J FkM [Fk] dx
ц =£**=!=« = R[Fk]. A2.9)
J FkN [Fk\ dx
a
Пример. Пусть дана задача на собственные значения
- У" = Я,у, у @) = у A) + у' A) = 0.
От функции Fu (x) здесь требуется только непрерывность. Мы можем поло-
положить, например, Fo (x) = 1. По итерационному правилу A2.1) Ft (x) опреде-
определим из задачи
Интегрируя уравнение, найдем Ft= Ci-^-c^x—=- х2, причем постоянные ин-
интегрирования С! и с2 определим так, чтобы Z7, подчинялась краевым усло-
условиям. Находим
FCx22)
Вычислим теперь постоянные Шварца ай, в,, а2 и отношения [1, и [i2:
i I i
а0 24 а, 25
fll==^T = -; |l2 = ^=":
аналогично найдем /^г, F3 и F4
1440/7з= 50л:— 35л:3 + 9л:5 — 2хв,
241 920F4 = 2035л: — 1400л:3 + 294л:5 — 36л:7 -f 6л:8.
12*
180 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
Следующая таблица содержит первые а^ и (яй.
[12.3
k
0
1
2
3
Л
с
fi
Ч
1
5
24
1
20
163
28-480
1069
315-1152
653
3168 ■ 288
108281
3003 • 207360
H
^1-48
5
^- = 4,1667
4401 1П603о
1069
94072
22855
891345
216562 Vioaaa-J
0,6333
0^L40
0,00577
0,000896
0,0001476
С помощью приведенной в дальнейшем основной формулы A2.19) и
найденных значений jij можно вычислить первое собственное значение до
пятого знака включительно
Я, = 4,1159.
В качестве /2 при этом было взято второе собственное значение уравнения
9я2
— у" = Яу, у @) = у' @) = 0, равное —j-. Найденное собственное значение Я,
может быть точно вычислено как наименьший положительный корень транс-
трансцендентного уравнения tg k = — k (Я = k2).
12.3, \ik образуют монотонную невозрастающую последова-
последовательность. Это легко установить, если принять во внимание, что
ввиду (8.2) для любой функции сравнения и
ь ь
Q, = J uM[u]dx>0, <?2 = J uN [и] dx > 0.
Мы положим теперь
U (Jjli 1 Г Ь
/6 + 1'
Эта функция и, когда ифО, для & = 0 является полудопустимой,
а для &>0 — функцией сравнения. Возможно также, что и=0,
например, если Fo является собственной функцией, поэтому в даль-
дальнейшем мы будем писать Q1 J>0, Q2 ^ 0.
12.4J § 12. ПОСТОЯННЫЕ ШВАРЦА 181
Далее, используя A2.4) и A2.5), получим
ь
dx =
— *» + A*-l —
<?2 = «2* («2AJ+2 ~ < + l) > 0 (A = 0. 1, 2, . . .)•
Ввиду A2.7) можно оба эти неравенства разделить на #2fta!ft+i или
на O2fta2ft+ia2ft+2' B результате будем иметь
(ft=l. 2. ...). 1
Следовательно, jxft монотонно убывают. Согласно A2.9) ц2А является
отношением Рэлея R[Fk]. По теореме в п. 8.1 /?[/%] ^-Л,ь по-
поэтому все (Aft больше или равны hv
Итак, имеет место
Теорема. Пусть задача на собственные значения D.11)—D.14)
является самосопряженной, выполнены условия полной определен-
определенности (8.2) и собственное значение X не входит в краевые усло-
условия. Если начальная функция Fo удовлетворяет условию A2.3),
то отношения Шварца \xk, вычисленные согласно A2.1), A2.4),
A2.8) с помощью Fo, образуют монотонно убывающую, ограни-
ограниченную снизу первым собственным значением Хг и, таким образом,
сходящуюся последовательность
Hi>H2>Me> ••• Ж- A2.11)
Отсюда вытекает существование нижней границы последователь-
последовательности |j,ft, но ничего нельзя сказать о величине этой границы, кроме
того, что она больше или равна kv Если, например, F0(x) является
s-й собственной функцией ys, то \xk = Xs для всех k. Граница в этом
случае равна Xs. Таким образом \x,k могут быть очень далеки от X,.
Для вычислений очень важно, что при известных добавочных усло-
условиях \xk могут быть достаточно близки к 1, и что даже можно
Оценить величину ошибки | [ik — Xt |.
12.4. Нижняя граница для первого собственного значения.
В этом параграфе в случае простого первого собственного значения
будет оценена сверху ошибка \ik — Хр и таким образом будут уста-
установлены верхняя и нижняя границы для hv Результатом явится фор-
формула A2.19). Эта важная формула будет в п. 14.3 выведена еще раз
другим путем, с помощью теоремы разложения.
182 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ [12.4
Для доказательства1) формулы A2.19), именно только для дока-
доказательства, а не для численных расчетов, используется, кроме исход-
исходной функции F0(x), еще вспомогательная функция Н0(х), которая
является линейной комбинацией из Fo и первой собственной функ-
функции Ух2):
H0 = F0-cyi. (W. 12)
Она в обобщенном смысле ортогональна первой собственной функ-
функции уг:
ь
J H0M[yl]dx=0. A2.13)
Первую собственную функцию у-^ (х) мы будем считать нормирован-
нормированной в виде
ь
j y1N[yl]dx=l. A2.14)
а
Тогда из требования A2.13) найдем с
ь ь
;,] dx = с угЫ \ух] dx = c
и, таким образом, полностью определим функцию Но. Она ортого-
ортогональна к N [уг] и, как говорят, не содержит компоненты первой
собственной функции. Представим себе теперь, что с помощью метода
последовательных приближений A2.1) определеР1ы последующие функ-
функции сравнения Нх, Н2, ... по правилу М [Нп] —N [#„_,] при
U^ [Нп] = 0, т. е. аналогично тому, как из Fo определяются Fп 3).
') Формула A2.19) для частного вида задач на собственные значения
доказана у О. Т е ш р 1 е, Proc. Lond. math. Soc. B) 29 A929), 257—280,
а также у О. Temple und W. О. Bickley, Rayleigh's Principle and
its Application to Engineering, London, 1933.
2) Если Fo (x) является первой собственной функцией, то все (ift = Xi и
в A2.19) будет иметь место знак равенства. В дальнейшем мы исключим
этот тривиальный случай, тогда Н0ф0.
8) Подобно Fo функция #о является также полудопустимой функцией.
ь
Из Г H0N [Яо] dx>0 следует, в частности, N [ЯО] = М [Я,] ^0, стало быть,
а
точно так же Н^фО для всех k._
12.4] § 12. ПОСТОЯННЫЕ ШВАРЦА 183
Тогда также все последующие Ht будут ортогональны к N [ух\, так
как
ь ь ь
J HXN \yy] dx = -±- J НУМ [у,] rfjc = -jL J у,Л1 [Я,] Ac =
а а а
J у,Л/ [Яо] rfjf --= i- J
а
Точно так же
ь
J Я,Л/ [у,] ^= р- J «o^tyil rfx =0- A2Л5)
а ' я
Если мы теперь образуем отношение Рэлея R[Hk\ для k^l, то
по теореме из п. 8.3 оно будет верхней границей для второго соб-
собственного значения к2, так как в силу A2.15) дополнительное условие
(8.14) (при k— 1) выполнено. Стало быть, R [Hk] ~^-h2 для k ^ 1. По-
Построим с помощью функций Я,, постоянные Шварца bk и отношения vk:
= 0. 1, 2, ...)•
Тогда vft образуют монотонно убывающую числовую последователь-
последовательность с vk ^> А,2.
Функции Яй определенным образом связаны с F^. Так, например,
поскольку с учетом A2.12)
i"" хг yJ=м [Fi1 ~ i м ш=^ [F°] ~cN ш=N [H°]
и функция Z7, т~Ух удовлетворяет, таким образом, уравнению, ко-
торому должна удовлетворять функция Нх:
Точно так же можно показать, что вообще
184 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ {12.4
Между постоянными Шварца ak и bk также существует определенная
связь:
ak = ^ F0N [Fk\ dx = J (tfo+ cyi) N \нк +^ y, j dx =
a a L 1 J
ft ft
=^ J H0N [Hk\ dx + jz $H0N [y,] dx +
a ' a
ft ft
+ с J yiN [Hk] dx+~j yiN[y,j dx.
l
Поэтому вследствие A2.13), A2.14) и вытекающего из A2.15) ра-
равенства
получается
г2
ak — bk-\-— (k = 0, 1, 2, ...).
Это равенство перепишем также для
и, ислючая с2, придем к соотношению
= *ft —Ма-н (* = 0, 1, 2, ...)•
Используя это равенство, мы можем установить связь между отно-
отношениями Шварца i*ft и vk:
Iх* —
, йй + 1—А1 / ЙА + 1—Al Oft — A|Oft + ,
bk—i—ЛцЬ/г Vft — Л]
Теперь можно оценить
и, таким образом, из A2.16) получим
1161 . § 12. ПОСТОЯННЫЕ ШВАРЦА 185
или в случае ^2>^4i (на этом условии мы еще остановимся в даль-
дальнейшем, оно требует к2 > А,, и таким образом, чтобы >*, было невы-
невырожденным собственным значением) имеем
!X!X A2.18)
1
M-A + l
Неравенство A2.17) остается в силе, если в нем %2 заменить его
нижней границей 12. Это важно, потому что во многих случаях вто-
второе собственное значение неизвестно, но может быть задана нижняя
граница для него. Для перехода к A2.18) нужно потребовать в таком
случае, чтобы 12 > цй+1. Таким образом, получен следующий результат.
Теорема. Пусть для задачи на собственные значения
D.11) — D.14) выполнены условия:
а) самосопряженности,
б) полной определенности Л, Яг
(8.2), а также Рн Им и "и *~v* у~
в) собственное значение X н ~ &г **' Л **' А
входит в краевые условия, 7**7г
г) наименьшее собственное
значение Я,, невырожденное. Рис- 1\1- „Локализация собственных
.. , ' _ ^ значении и отношении Шварца.
Исходя из 2п-кратно непре-
непрерывно дифференцируемой функ-
функции F0(x), которая удовлетворяет такому количеству краевых
условий, что справедливо A2.3), с помощью метода последова-
последовательных приближений A2.1) найдем функции Flt F2, . . . и далее
постоянные Шварца A2.4) и отношения \ik A2.8). Если при этом 12
удовлетворяет условию
то для первого собственного значения А,, справедлива оценка
12.5. Практическое проведение метода. В методе последова-
последовательных приближений исходят из выбранной функции F0(x) и каждую
последующую функцию F\(x), F2{x), ... получают, решая краевую
задачу. Если рассматриваемое дифференциальное уравнение имеет
достаточно простое строение, то можно, как это показано в при-
примере 12.2, вычислить некоторое число функций Fk(x). Однако
в случае более сложной задачи на собственные значения (при более
сложном дифференциальном уравнении) повторное решение краевой
задачи наталрсивается часто на большие трудности. Поэтому важно,
186 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ Р2.5
что для многих задач с достаточной для прикладных целей точностью
можно обойтись только функциями F0(x) и Fx(x).
Вычислительный процесс состоит из следующих трех шагов.
1. Находим две функции F0(x) и Fx(x) такие, что М [Fj] = N[F0].
При этом Fx{x) удовлетворяет всем краевым условиям, a F0(x) —
только такой их части, чтобы выполнялось A2.3).
Во многих случаях такие две функции Fo и /•", можно определить
графическим интегрированием. Подробнее об этом см. п. 1Э.6. Для
специальных задач на собственные значения, когда N [F0] = g0F0,
можно исходить из одной функции Fv которая удовлетворяет всем
краевым условиям, a Fo вычислять на основании равенства g0F0 = M [F:].
Обычно к F: можно прибавить удовлетворяющие краевым условиям
функции ij),-, умноженные на константы ct, выбрав последние так,
чтобы функция Fo удовлетворяла краевым условиям. При этом часто
получают существенно более благоприятные результаты, причем во-
вообще результат тем лучше, чем ближе Fo и Fx к первой собствен-
собственной функции.
2. Вычисляют постоянные Шварца A2.4) и отношения A2.8)
«о = J FoN [/"о! dx. а, = J F,N [FQ] dx, a2= J FtN [Fr] dx,
a a a A2.20)
Тогда, как известно,
3. Чтобы вычислить нижнюю границу для Xh необходимо знать
нижнюю границу 12 для второго собственного значения к2, хотя бы
совсем грубо, но все же так, чтобы выполнялось неравенство /2 > ц2-
Часто нижнюю границу для собственных значений удается установить
путем сравнения с задачей на собственные значения, коэффициенты
которой постоянны. Далее, для практических целей часто бывает
достаточно погрешность от ji2 знать приближенно (знать, какой деся-
десятичный знак может быть еще использован) В этом случае за /2
принимают приближенное значение для к2, вычисленное методом
Ритца, методом конечных разностей, либо каким-нибудь другим ме-
методом. Хотя этот прием не совсем точен и не всегда правилен
(т. е. /2 не будет нижней границей А,2), но имеет известное оправда-
оправдание вследствие того, что оценки A2.19) мало зависят от 12, если /2
не лежит вблизи \ikii- Тогда в силу A2.19)
(Xj
12.6]
§ 12. ПОСТОЯННЫЕ ШВАРЦА
187
12.6. Примеры применения метода последовательных приближений.
1. Пример. Шарнирно опертый сжатый стержень. Пусть имеется
сжатый стержень (рис- 12.2) длины / = яис переменной жесткостью
^не-
^некоторый шарнирно оперт на обоих концах х = 0 н х = п.
Для нахождения критической нагрузки Р нужно решить следующую
задачу:
. р
где Я = —.
с
Мы исходим из удовлетворяющей краевым усло-
условиям функции
Fx — sin x
и определяем Fo согласно A2.1) из уравнения
-/^ = A+sin *)/>„,
тогда
sin х
0 1+sin.*
Найдем постоянные Шварца
я
Рис. 12.2. Продольный
изгиб стержня с пере-
переменной жесткостью.
о
а, = I A -}- sin х) F<fx dx =
oJ о
я
J
0
и отношения
2 , я . 4
1 х dx = -7г- 4- -я-
• = 0,54088.
= Jf!L = JL_2 = 0,54648,
а, я
Прн этом в силу A2.11) ц, >> jx2!> Я,. Для установления нижней границы Я,
нужно оценить Л2 снизу. Это мы сделаем путем сравнения с задачей, коэф-
коэффициенты которой постоянны.
Если заменить 1 -\- sin x числом 2, то, согласно п. 9.4, все собственные
значения уменьшатся (если заменить l-(-sinA: единицей, то все собствен-
собственные значения увеличатся). Вспомогательная задача
188
ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
[12.6
имеет собственные функции уп = sin пх с собственными значениями
Ял==~т-
Так как Я2 >12 > 2, то 12 — 2 будет нижней границей для Я2.
Из A2.19) получаем оценки
0,53880 < Я, < 0,54088.
Среднее значение Я, и 0,5398 и, следовательно, ошибка не больше 0,2%.
2. Пример. Защемленный на одном конце, шарнирно опертый на дру-
другом сжатый стержень.
Задача изгиба для стержня, защемленного с одной стороны ичшарнирно
опертого с другой (рис. 12.3), длины I = 1 и с переменной жесткостью
а = сB — х) приводит, согласно A.3), к диффе-
дифференциальному уравнению
или, если положить
Р
Я = —,
к уравнению
{{2-х) /'}" = -Я/'
с краевыми условиями
Рис. 12.3. Продольный
изгиб стержня, защем-
защемленного на одном конце
и шарнирно закреплен-
закрепленного — на другом.
Для нахождения Fo и Fu удовлетворяющих
A2.1), положим
Fi = д2л:2 -|~ п$х^ -|- п$х* -|- ядл:5.
Здесь также целесообразно исходить из Fx. Так
как Fx — полином пятой степени, то М [Fi] =
= N [Fo] = — Fq — полином второй степени и
Fo — полином четвертой степени. Постоянные
интегрирования и величины а; определим так,
чтобы Fo удовлетворяло трем главным краевым условиям Fo @) = Fo @):
= /?0A) = 0, a Fx — всем четырем краевым условиям.
Получим
F, = 24л:2 — 4л:8 — 47л:4 -f 27л:5,
FI = 12 D — 2л: — 47лг2 + 45лг3),
Fo = 12 (92лг2 — 137л:8 -f 45л:4).
Теперь согласно A2.4) определим постоянные Шварца
1
Qfi
у-4978,1 «288-237,052,
F0Fq dx
- Г
о
1 i
- J fV' dx = - J
16 026
144 • 15,8988,
о
Контроль!
X
^-45,2=\2- 6,45714
13.1] § 13. ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ 189
и отношения
ц, = ^2- = 29,8201, ц2 = -2L = 29,54646.
а, а2
Грубую нижнюю границу для Х2 найдем, решив вспомогательную задачу
с постоянными коэффициентами. Для этого в исходном уравнении заменим
функцию B — х) постоянной величиной, и притом наименьшим ее значением
в интервале 0<^л:<^1, равным 1,
/iv = -!/".
Собственное значение этого уравнения при заданных краевых условиях
(см. таблицу VI) получим из трансцендентного уравнения
при Я = к*.
Первые корни этого уравнения будут
Я, =20,19, Я2 = 59,68.
Таким образом, получим грубую границу 12 для Я2
Я2 > 59,68 = 12
и из A2-21) получим оценки для Я,
29,275 < Я, < 29,5465.
Среднее значение Я « 29,41 имеет ошибку не более 0,5%.
§ 13. Графическое интегрирование
13.1. Графическое однократное интегрирование. Графическое
интегрирование функции у{х), заданной в виде кривой, читателям
должно быть хорошо известно'). Мы кратко изложим здесь основные
моменты, которые понадобятся в дальнейшем. Остановимся на осо-
особенно удобном «методе со средней абсциссой».
Функция у(х) изображена на рис. 13.1. Интеграл от этой функ-
функции запишем в виде
X
=J у
Рассматриваемый отрезок оси х разделим на некоторое число
частичных интервалов точками xt, x2. ■■■ Функцию у{х) в каждом
частичном интервале, например [х0, х,], заменим кусочно-постоянной
функцией Y (х) равной у(%) слева от £0 и У{Х\) справа от Со- Назы-
Называемая «средней абсциссой», £0 выбирается так, чтобы части поверх-
поверхности, заштрихованные на рис. 13.1, имели равные площади. Обычно £q
') См., например, F г. A. W i 11 e r s, Methoden der praktischen Analysis,
Berlin —Leipzig 1928 [см. также Д. Н- Головнич, Графическдя матема-
математика, ОНТИ, 1934].
190 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
выбирается «на глаз». Тогда будет выполнено
[13.1
*1
и в качестве
A3.2)
получим ломаную линию, которая не только совпадает с z{x) в точ-
точках х0, хх но и имеет в этих точках одинаковые с z(X) каса-
касательные.
Для проведения интегрирования (см. рис. 13.1) выбирается
«полюс» Р на расстоянии Н см {tl называется полюсным расстоянием)
Р У(х)
а см
Рис. 13.1. Графическое однократное инте-
интегрирование по методу средней абсциссы.
от начала координат в сторону отрицательных у. Спроектируем
на ось Оу ординаты функции К, а именно, у(х0), y^i). У(х2), ■■-,
и соединим полученные точки с точкой Р прямыми, наклон которых,
следовательно, будет пропорционален значениям У (Xj). Таким образом,
эти прямые должны быть параллельны Z{x) в частичных интерва-
интервалах. Далее, путем нанесения параллельных линий (обозначенных
на рис. 13.1 теми же римскими цифрами) получают ломаную
линию Z(x), которая в точках, обозначенных кружками, дает пра-
правильные значения функции z(x) и ее производной. Затем можно
заменить полученную ломаную гладкой кривой. В этом, по существу,
и заключается процесс численного интегрирования. Для практического
проведения этого процесса еще нужно выбрать масштаб.
13.11 § . ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ 191
Масштаб может быть введен как отношение')
,. - действительная величина ,,„ „,
Масштаб т = -, г тт— A3.3)
(величина изображения в см (на чертеже)) v '
Тогда для взятой на чертеже величины изображения в сантиметрах
действительное значение находится умножением на масштаб:
Действительная величина = величине изображения в см X масштаб т.
A3.4)
Прежде всего, мы используем масштаб по осям х и у при по-
построении кривой у (х), выбирая единичную длину по оси х равной а см,
а по оси у — равной b см. Тогда
Величину изображения будем отличать от истинной чертой сверху,
так например, Y (х0) будет представляться длиной Y(x0) см, таким
образом,
Появившаяся здесь величина mz есть искомый подлежащий вычисле-
вычислению масштаб, с помощью которого мы по найденной Z-ординате
вычислим истинное значение z.
Из рис. 13.1 найдем
С другой стороны (см. ломаную Z),
So m£°
Сравнивая оба выражения для tgp и учитывая равенство Z(t^) =
= £0К(л;0), получим
mz = Hmxmy. A3.8)
Пример. На рис. 13.2 графически изображена функция у = cos x.
Выберем масштабы
_ 1 __ 1
х 4 см у Ъ см'
В качестве точек деления возьмем точки с абсциссами хх = 0,5; х2 = 0,8;
лг3=1,1| х4 — 1,4 и заменим кривую у = cos x кусочно-постоянной функ-
функцией Y. Положим полюсное расстояние Н = 3 см и проведем графическое
') См., например, Th. Pose hi, Lehrbuch der Technischen Mechanik,
т. II, Berlin, 1936, 82 и К. К letter, Einfuhrung in die teclinische Schwin-
gungslehre, Berlin, 1938, 9.
192
ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
[13.2
интегрирование описанным выше методом до точки л: = 1,1. Масштаб тг
вычислим по формуле A3.8)
тНтт
Если, например, нужно узнать значение г в точке х — 0,8, то находим
1,41,5 х
Рис. 13.2. Пример графического однократного интегрирования
по методу средней абсциссы.
сначала из графика значение Z @,8) = 4,78 см и, далее,
Z @,8) = Z @,8) тг = 0,717.
13.2. Переменное полюсное расстояние. В предыдущем разделе
графически определялась функция z (x), удовлетворяющая дифферен-
дифференциальному уравнению
Можно также путем введения переменного полюсного расстояния
графически интегрировать уравнение
p(x)z'{x) = y(x) A3.9)
и, таким образом, построить интеграл
p(l)
A3.10)
Переменное полюсное расстояние реализует, следовательно, умно-
умножение функции у(х), стоящей под знаком интеграла, на заданную
Функцию -ущ.
13.2|
§ 13. ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
193
Выберем масштаб тр для функции р{х) и отложим на отрица-
отрицательной оси х (рис. 13.3) вместо фиксированного до сих пор полюс-
полюсного расстояния Н отрезки
Р (•*<) ,
p{xt) ==■
1, 2,
Последующий процесс точно такой же, как и в п. 13.1, только
теперь используется не фиксированный полюс Р, а полюсы Ро, Рг, ....
соответствующие xt. Вместо равенства A3.6) получим теперь
_ П^) _ Y (х0) тр
р{х0) р (х0) ту
и равенство A3.8) для масштаба тг перейдет в
тхту
т„
A3.11)
Подобно предыдущему полученную ломаную заменяют гладкой кри-
кривой, проведенной через точки, обозначенные кружками. Правда, теперь
Рис. 13.3. Графическое однократное интегрирование
с переменным полюсным расстоянием.
из равенства заштрихованных поверхностей не следует, что указанные
точки принадлежат z(x); можно лишь утверждать, что с уменьше-
уменьшением частных интервалов (xt, x^{) функции z(x) и Z(х) могут
быть сделаны как угодно близкими. При практическом проведении
интегрирования точки деления не следует выбирать слишком часто,
чтобы не допустить накопления неизбежных неточностей чертежа.
Если требуется большая точность, то лучше построить по точкам
функцию -у х'^ и интегрировать по методу, указанному в п. 13.1.
13 Л. Коллатц
194
ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
[13.3
Пример. На рис. 13.4 дан пример практического применения
метода для y = cosx и р — 1 -J- x2. Таким образом, рассматривается
Г cos I
dl.
Выберем масштабы: тх = -^j ; my = -g-^-; mp = -^-^ ■ По фор-
формуле A3.11) вычислим mz
-r=
. В точке x~l, например, из
Рис. 13.4. Пример графического однократного интегриро-
интегрирования с переменным полюсным расстоянием.
рисунка будем иметь z(l) —6,83 см и соответствующая этому зна-
значению х истинная величина z будет
13.3. Графическое двукратное интегрирование. Для приложе-
приложений очень важно, что двукратное интегрирование можно выполнять
графически одним шагом. Пусть требуется вычислить функцию у (х),
удовлетворяющую дифференциальному уравнению
(Py')'=g(x) A3.12)
(о краевых условиях будет говориться лишь в п. 13.5). При этом
р(х) и g (x) — заданные в виде кривых функции. Графическое инте-
13.3]
§ 13. ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
195
грирование основано на том, что первый интеграл этого уравнения
в виде формулы (С — постоянная интегрирования)
A3.13)
изображается в виде кривой.
График функции g (х) располагают над осью х (рис. 13.5). Рас-
Рассматриваемый отрезок оси х делят точками х1 на некоторое число
частичных интервалов и определяют площади F}, F2, ..., относя-
относящиеся к этим частичным интервалам (стрелки для Z7,, F2, ... в левой
Р(Хд)-
Рис. 13.5. Графическое определение у (х) из уравнения
(РУ'У = g (•*)•
части рисунка проходят через центр тяжести соответствующих пло-
площадей). Эти площади вместе взятые дадут интеграл
К нему можно теперь еще добавить постоянную С. Далее следует
выбрать какую-нибудь точку Р, из которой откладываются в гори-
горизонтальном направлении значения заданной функции р (х) в точках
деления рассматриваемого интервала, т. е. значения ро=р(О),
рх = р (л:)), ... Теперь можно построить направления у', которые
13*
196 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ ЦЗ.З
находятся по формуле A3.13), и получить путем их переноса ломаную
линию для у (л:). Значения этой ломаной в точках xt (на рис. 13.5
эти значения обозначены кружочками) используют для построения
гладкой кривой.
Теперь нужно еще вычислить масштаб, в котором получены зна-
значения кривой у (х). При построении кривой g (х) сначала выбирают
масштаб для х и g (рис. 13.5):
1 1
т т
•* а см s b см
Далее измеряются и наносятся в виде отрезков площади графика g(x),
для этого выбирается поверхностный масштабный множитель
К см*
/га*
1 см
Если, например, поверхность в 4 см2 представляется 1 см, то
4 см2
тР = Т7м-
Далее выбирается масштаб для построения значений функции р (х)
1
С помощью этих масштабов нужно теперь вычислить аналогичный
масштаб ту.
Прежде всего определяют масштаб тл, в котором наносится зна-
значение интеграла. При этом каждый сантиметр в соответствии с выше
принятым масштабом означает тр см2, и так как см2 площади кри-
кривой g (х) в действительности равен тх • mg, то каждый сантиметр
значения интеграла равен mFmxmg; таким образом,
т f =mFmxmg. A3.14)
В этом масштабе следует наносить также постоянную интегри-
интегрирования С, если она задана. Наклон кривой, как видно, будет искажен
в отношении масштабов, т. е.
т.. „ = ■
и отсюда следует, наконец, масштаб для у:
или
m2j.
13.5] § 13. ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ 197
Пример. Рис. 13.5 представляет одновременно пример практического
проведения интегрирования для функций Р=тШ—' 8~^ —х- При вы-
выбранных масштабах т —т = 1/4 см, т =1/1 см, от = 1,2 см2/1 см
03 е
вычисляют, согласно A3.15), ту — ~—. Так, в точке х = 1 из рисунка
I СМ
получаем
у A) = 4,6 см;
отсюда уA) = отууA) = 1,38.
В то же время точное решение
1 _ 1 ,
удовлетворяющее краевым условиям у @) = у' @) = 0, принимает в точке
х =1 значение у A) = 1,375.
13.4. Особый случай обыкновенного веревочного многоуголь-
многоугольника. В качестве важного особого случая следует рассмотреть случай,
когда р—1 (рис. 13.6). При этом, следовательно, интегрируют
дифференциальное уравнение
f = g(x). A3.16)
Вся р-шкала свертывается в одну точку и получается конструк-
конструкция обыкновенного веревочного многоугольника'). При этом
1 1 __1_
р с см расстояние до полюса Н
и из A3.5) находим формулу для масштабного множителя
A3,17)
Пример будет рассмотрен в следующем пункте.
13.5. Учет краевых условий. Для уравнения y" = g(x) соответ-
соответствующее однородное уравнение у" = 0 имеет решение y = Ci~\-c2x.
Следовательно, к решению неоднородного уравнения можно добавить
любую линейную функцию, и ординату у можно отсчитывать не
от оси х, а от произвольной прямой, всегда получая решение диф-
дифференциального уравнения A3.16). Эта прямая («замыкающая линия»)
выбирается так, что у или у' удовлетворяют заданным краевым
условиям.
Пример. На рис. 13.6 показано построение веревочного многоуголь-
многоугольника для уравнения у" = g (x) = sin x в интервале 0<л:<2. Полюс может
быть выбран в любой точке. Возьмем следующие масштабы:
т= 1/2 см, тх — 1/2,5 см, Н = 2,5 см, тр=1,25 см2/1 см.
Тогда по формуле A3.17) найдем
mv —
4 см'
') См„ например, W. S с h I i n k, Technische Statik, Berlin, изд. 3, 1946, \\\,
198
ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
|13.5
Через точки ломаной, обведенные кружками, проведем гладкую кривую.
Рассмотрим два частных случая краевых условий.
А. у @) = у B) = 0. Точки пересечения двух крайних сторон веревоч-
веревочного многоугольника / и V с ординатами, соответствующими х = 0 и х = 2,
i Жх)
Случай В. у@НДу'(Ю=Ц5
Рис. 13.6. Построение веревочного многоугольника для двукратного
интегрирования.
соединим «замыкающей линией». Ординаты у (х) отсчитывают от этой линии,
и, например, для х = 1 получим
у A) = — 1,55 см
и отсюда у A) = у A) ту — — 0,387.
Б. у @) = 0,25; у'B) = 0,5. Теперь, откладывая на ординате при х = 0
О 25
отрезок —:— = 1, соответствующий начальному значению у @) = 0,25, мы
ТПу
будем иметь точку 5 «замыкающей линии» (рис. 13.6). Далее, из начального
условия у' B) = 0,5 мы имеем ее наклон. Вычислим по формуле A3.14)
масштаб, в котором нанесены площади F ') (на полюсном многоугольнике,
правая часть рис.)
mс =m^m^m
г х g 4 см
0,5
Путем нанесения отрезка —— = 2 на полюсном многоугольнике найдем на-
направление замыкающей линии и построим теперь эту линию. Возьмем, напри-
например, на графике у B) = — 1,97 см и отсюда у B) = у B) ту = — 0,492.
') Это будет одновременно масштабом, в котором на этой прямой
откладываются значения у'. Масштаб, обозначенный в п. 13.3 через mtg^,
имеет другой смысл и показывает, как вычислить значение у', исходя из зна-
значения тангенса угла наклона луча,
13.61 § 13. ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ 199
Не так нагляден учет краевых условий при графическом интегри-
интегрировании уравнения (ру'У = g (х), обсуждавшемся в п. 13.3. Здесь
линейная функция с} -f с2х при р Ф const не является решением
однородного уравнения (ру'У =0, и поэтому нет такой удобной
возможности учесть краевые условия путем подходящего расположе-
расположения замыкающей линии. Имеются две возможности:
1. Расположить точку Р на произвольной высоте.
2. Начинать с у(х0) на произвольной высоте.
Если имеется одно краевое условие для у' и одно для у, то
процесс прост. Из краевого условия для у' устанавливают первый
или последний полюсный луч и, перенося его в правую часть ри-
рисунка, определяют высоту точки Р. Если же даны другие краевые
условия, например у@) = у(а) = 0, то нужно построить два вере-
веревочных многоугольника для двух различных точек Р и взять линей-
линейную комбинацию полученных таким образом функций
У
Условие у@) = 0 будет выполняться тогда, например, при у,@) =
= у2 @) = 0, а отношение с, : с2 выбирается так, чтобы было у (а) = 0.
13.6. Графическое проведение метода последовательных при-
приближений. Для метода последовательных приближений, описанного
в § 12, используют, согласно п. 12.5, две функции F0(x) и F} (x)
такие, что М [Fx] = N [Fo]. При этом Fx удовлетворяет всем краевым
условиям, a Fo—некоторой их части.
Во многих прикладных задачах две такие функции можно опреде-
определить графическим интегрированием. Мы рассмотрим, прежде всего, про-
простейшие случаи частной задачи на собственные значения М [у] = Xgoy.
При этом функцию Fo выбирают так, чтобы она по возможности
передавала ожидаемый ход первой собственной функции у,, а функ-
функцию Fx определяют путем графического интегрирования с помощью
веревочного многоугольника. Для задач с M[y]=(f2y")" или
М [у] = (/уу'У это удается сделать сразу. В качестве примера рас-
рассмотрим колебания шарнирно опертого с обеих сторон стержня
с заданной переменной жесткостью на изгиб а(х) и с заданным рас-
распределением массы go(x) (рис. 13.7). Тогда
Теперь выбирается Fo и строится кривая g0F0. Путем двукратного
интегрирования (первый веревочный многоугольник) получают отсюда
сначала Fx и, интегрируя еще двукратно, получают Fx (второй вере-
веревочный многоугольник). Следует заметить, что графически всегда
только интегрируют, но не дифференцируют. Затем вычисляют
200
ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
[13.6
постоянные Шварца и отношения по формулам A2.4) и A2.8):
* *
dx
-/
i dx' a2=
dx
— J
dx.
Необходимое при этом интегрирование производят графически с по-
помощью планиметра или численно по формулам Симпсона. Для опре-
определения верхней и нижней границ для наименьшего собственного
значения Х± используются формулы A2.21), как это описано в п. 12.5'.
Рис. 13.7. Графическое интегрирование уравнения
(ау")" = Xgoy.
Обратимся снова к более общим случаям. Нахождение двух функ-
функций Fo и Fb удовлетворяющих поставленным в § 12 условиям,
удается осуществить в общем случае для задач в форме
f\ A3.18)
A3.19)
\fm(x)yl-m)tm)=lN\y].
Уравнение A3.18) относится к одночленному классу (см. п. 4.7).
Мы полагаем его в основу при последующем изложении, в случае
уравнения A3.19) можно действовать аналогично.
13.71 § 13. ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ 201
При A3.18), таким образом, должно выполняться
В выражении М [Fx] наивысшую производную будет иметь член
Далее обычно поступают так:
а) Выбирают наивысшую производную Fv т. е. Ffm\ и все более
низкие производные определяют путем интегрирования.
б) Затем образуют М [F^ и получают уравнение
в) Интегрируют п раз функцию М [F^ и находят, таким обра-
образом, gn(X) f["\ ■-;
г) Путем деления на glt(x) получают F^P и, наконец, посредством
«-кратного интегрирования определяют FQ.
Теперь нужно учесть краевые условия; F должно удовлетворять
всем краевым условиям, Fo—в общем случае только некоторой их
части. Во многих случаях (см. таблицу VII) их можно учесть сразу
при интегрировании (например, при помощи подходящей замыкающей
линии), иногда, однако, наталкиваются при этом на трудности. Все же
эти трудности можно преодолеть, применяя наложение, которое
в силу линейности задачи всегда возможно. Проводят весь процесс
для нескольких функций F[A)), F[B)) F\{r)) и определяют в вы-
выражении 1)
v=l
коэффициенты cv так, чтобы Fx и Fo удовлетворяли всем краевым
условиям, которые еще должны быть выполнены.
В таблице VII для некоторых часто встречающихся задач указы-
указывается, как можно определить две удовлетворяющие заданным тре-
требованиям функции.
13.7. Графическое определение ц\. В пп. 12.5 и 13.6 описы-
описывался графический метод, в котором оба отношения Шварца jllj и [х2
являются верхними границами для первого собственного значения hlt
причем с их помощью по формуле A2.19) можно найти также и ниж-
нижнюю границу для A,j. Вместо этого можно во многих случаях с мень-
меньшей затратой труда (в основном посредством графически проведен-
проведенного интегрирования) находить только (ij, которое во всяком случае
1) Верхние индексы в двойных скобках означают не производные, а служат
для обозначения функций.
202 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ [13.7
даст нижнюю границу для Я^. Число (Xj обеспечивает меньшую точ-
точность, чем \12, и, кроме того, ничего нельзя сказать о погрешности
[i] — Я,!, но для многих технических целей реализуемая точность до-
достаточна, в особенности если функция F0(x), которая является при-
приближением для первой собственной функции у1(х), выбрана удачно.
В качестве примера рассмотрим поперечные колебания стержня
с переменной жесткостью на изгиб а (л:), длины Z, с плотностью р
и площадью поперечного сечения F (х). Пусть стержень закреплен
на одном конце и свободен на другом. Тогда (см. п. 2.3) будем иметь
задачу на собственные значения
у @) = /@) = у" (I) = у'"{1) = 0. A3.20)
По методу последовательных приближений будем исходить из функ-
функции F0(x), которая передает ожидаемый ход первой собственной
функции и, в частности, удовлетворяет главным краевым условиям
(в обозначениях п. 4.2)
С помощью Fo методом последовательных приближений путем гра-
графического интегрирования определяют Flt которая удовлетворяет
уравнению и условиям:
(aFi)" = 9FF0, Ft @) = F[ @) = F\ (I) = F'" (I) = 0.
Именно, сначала из
G"=zpFF0, о (/) = G'(/) = 0 A3.21)"
с помощью первого веревочного многоугольника определяют
G(x) = aFi, а затем из
F" ^=- — G (x\ F @) = F* (()} = 0 ^13 22^
с помощью второго веревочного многоугольника находят Fv
Далее, по формулам A2.4), A2.8) вычисляют отношения Шварца
M-i и \h:
а0 а,
где
/ i i
ао= Г pFFldx, а,== J pFFGFldx, a2= J pFFJdx. A3.23)
0 0 0
Теперь ах можно записать также в форме
щ = Г G"Fl dx=\ Gl- '[dx=\ -i G2 dx, A3.24)
13.7]
§ 13. ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
203
и видно, что а0, аь а вместе с этим и \у,х можно вычислить уже с по-
помощью Fo и О, не решая задачи A3.2).
Рис. 13.8. Графическое определение наименьшего собственного зна-
значения при поперечных колебаниях стержня с переменной жесткостью.
Пример. На рис. 13.8 показано решение задачи A3.20) при помощи
рассмотренного метода. Прежде всего вводятся безразмерные величины |,
a*, F*, Я* посредством соотношений
* = /§, а=а@)а*(|), F = F@) F* Ц),
Я'= '«@) '
204 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ [14Л
Уравнение A3.20) при этих обозначениях будет иметь вид
( '* /f\ff - * ~* /10 ЛГ\
ay ) = KFy. A3.25)
Штрихи обозначают теперь производные по \. На рис. 13.8 даны графики а*
и F* как функций |.
Исходя из функции Fo (g), которая должна быть близкой к первой соб-
собственной функции, найдем функцию G путем графического интегрирования
согласно A3.21):
G" = F*FB, G A) = G' A) = 0.
Точки ломаной линии, обозначенные кружками, являются истинными точками
кривой G (|), ломаную линию, впрочем, нужно заменить гладкой кривой, <ко-
торая на рис. 13.8 ие показана во избежание нагромождения.
Масштабы можно вычислить нгпосредственно из A3.17). На рис. 13.8
нангсена вместо масштаба вычисленная сообразно с ним шкала. С помощью
Fa и G можно теперь по формулам A3.23) и A3.24) определить постоянные
Шварца аа и а,. Измеряя ординаты и приближенно вычисляя по формуле
Симпсона интегралы, получим ')
ао= 1,337, а, =0,0620, ц, =-^- = 21,6.
а.
Более точное значение можно получить после графического интегриро-
интегрирования уравнения A3.22)
F[ = ~G, /'1@) = /?1'@)=0
и определения Fx.
Тогда по формуле A3.23) получим а2 — 0,00322 и верхнюю границу для
первого собственного значения \к2 = —- = 19,25.
а2
§ 14. Дополнения
14.1. Метод последовательных приближений для дифферен-
дифференциальных уравнений с частными производными. Как уже указы-
указывалось в п. 12.1, метод последовательных приближений можно при-
применять принципиально для любой задачи на собственные значения для
дифференциальных уравнений с частными производными
M[z]=W[z]. A4.1)
Функции Fo, Flt F2, ... многих независимых переменных х, у, ...
можно вычислить по правилу A2.1) и с их помощью по формуле A2.2)
находить приближенные значения Л для собственного значения К.
Но для того, чтобы сделать определенные заключения о Л, нужны
дальнейшие предположения, а именно, примем те же самые предполо-
предположения, что и в п. 11.2. Пусть дифференциальное уравнение имеет вид
M[z] = lgoz A4.2)
') Приведенный здесь пример довольно груб и служит только для по-
пояснения метода. Путем построения большего чертежа и более тщательного
выбора исходной функции /^ (х) можно значительно улучшить результат.
14-11 § 14. ДОПОЛНЕНИЯ 205
для функции z двух или большего числа независимых переменных х,
у, ...; ради простоты будем писать только х, у. Предположим, что
функция go(x, у) непрерывна и положительна, причем краевые условия
и„(г) = 0 0i=l. 2 А), A4.3)
как и в F.2), заданы на контуре Г области 23. Пусть, далее, для
задачи на собственные значения (ср. F.3) и F.4)) выполнены условия
самосопряженности и полной определенности и имеется функция Грина
О(х, у; |, т]), причем ядро
• К(х, у; I. т]) = О(ж, у; |, Т1)У>О(*. y)S0(t Л) A4.4)
симметрично, квадратично интегрируемо и непрерывно в среднем,
т. е. применима теория интегральных уравнений из п. 7.2. Исходя
из функции сравнения F0(x, у) (т. е. такой не равной тождественно
нулю функции, которая удовлетворяет краевым условиям U^ [Fo] = 0
и с которой можно образовать М [Fo]), определяют последующие
функции сравнения F'„:
M[Fn\ = g0Fn_l, ty/M^O (л=1. 2, ...). A4.5)
Затем находят постоянные Шварца
J I vFf^idxdy (я = 0. 1. 2, ...) A4.6)
и отношения
И„=^ (л=1. 2, ...). A4.7)
Тогда неравенство
Иг>ц2>ц3> ...>1г A4.8)
И ОСНОВНУЮ формулу A2.19) При
а„ = J
можно доказать почти дословно так же, как и в § 12, поскольку
для доказательства монотонного уменьшения цп необходимы только
самосопряженность и полная определенность задачи!).
Отношения ц2п с четными индексами 2л можно снова записать
как отношения Рэлея, и даже, согласно A1.15), в виде A2.9)
Ввиду минимальности наименьшего собственного значения (ей. п. 11.2)
\i2n, следовательно, и все цп, являются верхними границами для Xv
') Факт монотонного уменьшения \к„ имеет место для любого дифферен-
дифференциального уравнения М [z] = XN [z], если соответствующая краевая задача
самосопряженна и полностью определенна.
206 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ [14.2
Этим доказано A4.8). Отношения [Х2я_1 с нечетными индексами свя-
связаны с минимальным принципом A1.25) для наименьшего собствен-
собственного значения, который в п. 11.2 назван вторым. Отношение, стоящее
в правой части A1.25), равно \ilt и соответственно оно будет равно j.i2n.
если записать F п вместо Fv
Доказательство A4.9) можно провести точно так же, как в п. 12.4,
ь
положив вместо у, N[y], ... dx соответственно z, goz,
.. . dx dy.
sb
14.2. Теорема включения Крылова — Боголюбова для одно-
одночленного класса'). Эта теорема использует теорему разложения из
п. 10.8 и справедлива с той же степенью общности. Итак, пусть
имеется самосопряженная вполне определенная задача из одночленного
класса D.28), D.14) для дифференциального уравнения
М [у] = Ш [у] = (— \)п% lgnyWf>
с £■„ (х) =£ 0, и в числе краевых условий встречаются
у (а) = у' (а) — . . . = уС-1) (а) = уф)==у'ф)= ... = уС-1» ф)=0.
A4.10)
Тогда имеет место
Теорема включения Крылова — Боголюбова. Пусть
при выполнении предпосылок теоремы разложения из п. 10.8 для
двух функций F0(x) и Ft(x) вычислены отношения jij и \х2 A2.20),
причем F0(x), согласно дополнению \ в п. 10.3, есть полудопу-
полудопустимая, a F\ (x) — функция сравнения и они связаны соотношением
Тогда между числами
М-2— /(Mi — ^2) М-2 « М-2+ V(M-i — М-2)М2 A4.11)
лежит по меньшей мере одно собственное значение рассматри-
рассматриваемой задачи.
Для задачи на собственные значения частного вида M[y] = Xgoy
можно исключить предпосылку A4.10) и условие полудопустимо-
полудопустимости F0(x), так как тогда любая непрерывная функция F0(x) полудо-
полудопустима, и частная форма теоремы гласит:
') Для специального случая эта теорема, часто называемая в литературе
по имени Вайиштейна, приводится у Н. Крылова и Н. Боголюбова, Бюлл.
Акад. наук СССР, сер. физ.-мат., Ленинград A929), 47L Для специальных
задач на собственные значения теорема доказана Г. Д. Вайнштейиом [см.
Н. D. Weinstein, Proc. nat. Acad. Sci. Washington 20 A934), 529] и при
более слабых предположениях Е. Камке, Math. Z. 45 A939), 788.
14.2] § 14. ДОПОЛНЕНИЯ 207
Пусть при функции сравнения F1 (x) образованы числа
ь ь
а
Ь
а
Тогда между границами A4.11) лежит по крайней мере одно соб-
собственное значение.
Доказательство. По условию функции Fo и Fx связаны соот-
соотношением
М [FJ = N [Fo].
Fx удовлетворяет краевым условиям и является функцией сравнения.
По теореме п. 10.8 она может быть разложена в (т—1)-кратно
почленно дифференцируемый ряд по нормированным собственным
функциям ур
где (согласно A0.4))
причем ряд абсолютно и равномерно сходится в интервале a, b (это
касается и дифференцированных рядов). Образуем с помощью Fo и F1
по A2.20) постоянные Шварца а0, ах а2 и отношения ц1 и ц2. Тогда
с учетом самосопряженности будем иметь
ь
J (Hj^i - Fo) № [Л1 - N [Л,]) dx
Ь
JFaN[F0]dx
A4.12)
Выражение, стоящее в левой части равенства, можно преобразовать.
208 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ [14.2
Если для сокращения записи обозначить 1ф = ц2/71 — Fo, то числитель
примет вид
J ipN [гр] dx.
причем для этого выражения будет выполняться неравенство Парсе-
валя A0.13)"
Ь со
где через ср обозначены коэффициенты Фурье функции тр. Тогда
ь ь ъ
J /yv \ур\ dx=j ypN [Fo] tfx = J ypM [F,] dx =
= J F,M [yp] dx = Xpj F,N [yp] = lpb
b
a a
и, следовательно,
cp = bP (M-2 — V-
Таким образом, для числителя левой части A4.12) справедливо
p=i
в то время как знаменатель можно вычислить следующим образом
(ряд для F\ вследствие п^т — 1 почленно дифференцируем п раз):
ь ь ь
J FXN \FX\ dx = JFt (- 1)" [gnFffn) dx=j FWgnFW dx =
a a a
b со b со со
= J 2 bpyfgnFW dx=\^ bpFxN [yp] dx = ^ Vp.
a p=\ a p-1 p—\
Если же не только п -< т — 1, но и 2я <С т — 1, то ряд для Fx
можно почленно дифференцировать In раз, и последний результат
можно получить короче:
b со b со
р, q = \ а р-1
14.3J § Н. ДОПОЛНЕНИЯ 209
Таким образом, A4.12) дает
A4ЛЗ)
Если теперь Kj ближайшее к \i2 собственное значение (или одно из
возможных одинаково удаленных), то для всех р
и из A4.13) следует
(М-2 — М2 < (М-1 — М-г) М-2
или, как утверждалось в A4.11),
М-2 — /(М-i — М-г) М-2 < ^ < М-2 + V(M-i — М-2) М-2-
14.3. Доказательство основной формулы A2.19) при помощи
теоремы о разложении. Формулы § 12 для метода последователь-
последовательных приближений очень удобно и наглядно можно доказать с помощью
теоремы разложения (§ 10). Этот способ проведения доказательства
будет кратко изложен в дальнейшем. В § 12 был использован более
сложный, но зато и более общий метод. Там рассматривалась общая
проблема на собственные значения, в то время как теорема разложе-
разложения пока связывается с задачами из одночленного класса. К тому же
предположение, что FQ есть функция сравнения, необходимое для
применимости теоремы разложения, в прикладных задачах часто не
выполняется или трудно выполнимо. Пусть для задач на собственные
значения D.11) — A4.14) выполнены условия теоремы включения,
в частности, рассматривается дифференциальное уравнение вида
]" A4.14)
и, кроме того, 2я <; m — 1 :). Функцию сравнения Fo можно разло-
разложить в ряд по собственным функциям yt
оо
Л>=2'/У/ A4.15)
и ряд можно почленно (т—1) раз дифференцировать. Ряд A4.15),
а также ряды, полученные почленным дифференцированием A4.15),
сходятся абсолютно и равномерно. Поэтому
A4-16)
') Это предположение для частных задач на собственные значения всегда
выполняется.
14 Л. Коллатц
210 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ П4-3
Сумма A4.15) начинается при этом с номера i—r, где г ~У>> 1. Поэтому
можно допустить, что Fo не имеет компонент первых (г — 1) соб-
собственных функций. В A4.15) тогда сгФ0.
Ряд
i=r
удовлетворяет уравнению
м м=2 с< J^rri=2
и краевым условиям D.14), т. е. <р(х) равна функции Fl(x), которая
получается в методе последовательных приближений из Р0(х). Точно
так же для последующих функций F2(x), F3(x), ... получим
= 0. 1. 2. ...)• A4.17)
Теперь сразу можно вычислить постоянные Шварца. При сделанных
предположениях ряды можно перемножать и почленно интегрировать.
Для ак с учетом E.33) получим
^22^
' j=r i-r '
Для отношений Шварца A2.8) отсюда будем иметь
-^Г = -ё^-*> Г ""^.(^О... 2....). 04.19)
Так как все К: положительны и rki^-Xr, то монотонное уменьше-
уменьшение \ik и их ограниченность, согласно A2.11), т. е. в данном случае
факт
*• ... >К, A4.20)
14.3] § 14. ДОПОЛНЕНИЯ 211
можно установить непосредственно из следующих соотношений:
=l. 2. ...). 04.21)
■
i=r
Из A4.19) следует, далее, сходимость \ik к собственному значению Кг
(также и в случае вырожденного КГ), а из A4.17) следует сходимость
( Хг\
функции Fh с подходящим множителем [например, с —I к r-й соб-
ственной функции ут(х) при &->со (в случае вырожденного %г
г+Р .
т. е. если Kr = lr^l= ... lr+p, к 2 с1Уг (х) •
Из A4.21) следует
£1 «5
A4-23)
В суммах выпадает член с i = r\ поэтому значения отношений A4.23)
можно уменьшить, положив в знаменателе lr+i^i~l вместо Xt, где
^r+i^^r+i- Тогда 1г+1 можно вынести за знак суммы; числитель и
знаменатель после этого будут иметь общий множитель, сократив на
который, получим
14»
212 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ [14.4
Нижнюю границу 1г+1 при переходе к следующей формуле A4.25)
нужно выбрать так, чтобы 1г+1 > \ik. (Если hr+1>Xr, то из-за схо-
сходимости \1к к \ при достаточно большом k всегда будет выполнено
lr+l > цк , j.) Тогда из A4.24) получим
или
И _J£n!±*±L<A¥<li A4.25)
'Г+1 J
что для случая, когда %г есть первое собственное значение A,lf сов-
совпадает с A2.19)').
14.4. Сходимость итерационного процесса для краевых задач.
Начнем с простого примера. Краевая задача
. . , cos ax ,-.
имеет вполне определенное решение у(х)=\ . Оно суще-
существует, если cosa=£0, т. е. если а не равно числам ± л/2, ± Зл/2,
± 5я/2, ...
Для решения этой краевой задачи можно применить следующий
итерационный процесс: исходя из произвольно выбранной непрерыв-
непрерывной функции У0(х), определяют последовательность функций Y1(x),
Y2 (x), ... как решений краевых задач
Для исследования сходимости этого итерационного процесса вводится
отклонение Yп (х) от точного решения у (х)
zn(x)=Yn(x) —
Тогда zn(x) удовлетворяет соотношениям
(л = 0, 1, 2, ...).
z\ (x) — дважды непрерывно дифференцируемая функция, удовлетво-
удовлетворяет краевым условиям, и ее можно, следовательно, разложить в ряд
Фурье
v-I
') Дальнейшие формулы для оценок см. в Math. Z. 46 A940), 698—702.
14.41 § 14. ДОПОЛНЕНИЯ 213
Тогда
v=l
Почленно дифференцируя выражение для z2 (в данном случае это
можно делать), получим z = — a2z^, кроме того, z2 удовлетворяет
краевым условиям. Точно так же следует
2 '
т. е. для | a | < л/2 2„ стремится к нулю. Итерационный процесс
сходится. При | а | > я/2 2„->сх), если Cj =£ 0. Итерационный про-
процесс при этом в общем случае расходится.
Пусть теперь
£&rr~'w}
есть самосопряженная краевая задача и для соответствующей одно-
однородной краевой задачи
М[у]-Ш[у] = 0, и^[у] = Ъ A4.27)
выполнены условия, требуемые в теореме разложения п. 10.8. Исходя
из произвольно выбранной непрерывной функции YQ(x), вычислим
последующие функции Yп по формулам
M[Yn+1] = aN[Yn]-\-r(x), £7^ [Кя+1] = 0 (п = 0, 1, ...). A4.28)
Для исследования сходимости снова введем отклонение от истинного
решения
Тогда справедливо
M[zn+1]=aN[zn], и^[га+1]>=0 (п =0, 1, 2, . ..).
При принятых предположениях z1 (x) можно разложить в ряд по
собственным функциям yt(x) задачи A4.27)
Тогда
1-1
есть решение краевой задачи
214 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ J14.5
и в общем случае
со
*л+1 (х) = 2] (■£-)" ciVi (■*)• A4-29)
Таким образом, итерационный процесс сходится при любом С[, если
модуль а меньше наименьшего собственного значения: |a|<A,j; если
же \a\^-Xv итерационный процесс при сх Ф 0 в общем случае
расходится.
14.5. Метод Коха для высших собственных значений1). При-
Применение теоремы разложения для исследования метода последова-
последовательных приближений в п. 14.3 показало: если исходная функция F0(x)
в обобщенном смысле ортогональна к первым г — 1 собственным
функциям, но не ортогональна к r-й собственной функции, то отно-
отношения Шварца \ik сходятся к r-му собственному значению Хг. Если,
в частности, F0(x) ортогональна только к первой собственной функ-
функции у1 (-"О, то \ik сходятся в общем случае ко второму собственному
значению Х2. Поэтому второе собственное значение Х2 можно при-
приближенно вычислить, исходя из функции Н0(х), ортогональной в обоб-
обобщенном смысле к последней функции Fп (х), которая была опреде-
определена при вычислении первого собственного значения и которая является
лучшим приближением для ух (х). Но так как Fn (x) не точно совпа-
совпадает с >'i (х), то Но (х) все же будет иметь небольшую компоненту
первой собственной функции, и в целях осторожности на каждом
шаге итерации отнимают компоненту функции Fu (х), которая является
лучшим приближением для первой собственной функции. Таким обра-
образом, функция Hk вычисляется по следующему правилу:
М [Hi] = N [//,_,], Ulx[Hl] = 0,
Г IF mi ri%
A4.30)
Hk = Hi g ^ J Hi (I) N [Fn ®] d%
J FnN [Fn] dx a
и приближенное значение для Х2 получают по формуле
ь
A4.31)
') J. J. Koch, Verhandl. 2 internat. Kongr. f. Techn. Mech., Zurich,
1926, 213—218.
14.6]
§ U. ДОПОЛНЕНИЯ
215
Аналогично можно определить и третье собственное значение, вычитая
после каждого шага метода компоненты первой и второй собствен-
собственных функций1) (см. задачу 4 в п. 16.11).
14.6. Упражнения. 1. Согласно примеру в п. 12.2 провести метод после-
последовательных приближений для краевой задачи
исходя из функции Fo (х) = 1 (по сравнению с п. 12.2 здесь изменено только
первое краевое условие).
Результат. Из A2.1) получим
2!/>,= 3 — х2,
4!/?2 = 49— \8х* + х\
6! F3 = 1987 — 735л;2 + 45а:4 — *».
По формулам A2.4) и A2.8) получим для а и |Л. значения
k
0
1
2
3
л
ak
1
9
T
•766
315
9314
2835
230698
51975
••
—
1 = 0,75
-^ = 0,740741
coy
-22i-= 0,7402089
766
n74fi17fin8
4657
256135 _07l0l710oo
346047 °'7m7/l0Ji
—
—
0,009259
0,0005319
П ППЛПЧ9ЙП
0,000002056
H-2-H-X
—
—
—
12,89
12,00
11 Rn
Для первых двух собственных значений будем тогда иметь
Я, =0,740174, Х8 я 11,8.
Точные собственные значения можно получить как корни уравнения
* tg * = 1.
Из таблицы VI Я2 = 11,73.
2. Найти границы для первого собственного значения задачи, рассмо-
рассмотренной в задаче 3 из п. 11.4,
у (±
У" (± 1) ==0.
') Другие методы для приближенного определения высших собственных
значений можно найти в работе А. Т г а е n k ! e, Ing.-Arch. 1 A930), 499—526.
ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
A4.6
Рнс. 14.1. Графическое решение уравнения (ау")" + су=Ау";
A) 'A) 0
14.6] § 14. ДОПОЛНЕНИЯ ,217
Решение. Две функции сравнения, связанные требуемым в A2.1)
соотношением, уже даны в A1.27). По формулам A2.4), A2.8) вычислим теперь
ао = 3 761 275; а1 = 119 950,9; а2 = 3825,593
и отсюда
ц! = -^ = 31,35679; ц2 = -^- = 31,35485.
Нижнюю границу 12 для второго собственного значения Я2 (при рас-
рассмотрении только симметричных собственных функций) получим путем
сравнения с задачей, коэффициенты которой постоянны. Заменив функцию
3 — х2 ее наименьшим значением 2, найдем
/2 = 60f-^-
и получим по формуле A2.19) границы более близкие, чем в п. 11.4,
31,35096 < Я; < 31,35485.
3. Решить задачу 2 графически по методу § 13.
Будем исходить из функции w (х) = |Хз — х2) Р"\\', которая изображена
на рис. 14.1. Функция w равна нулю на концах интервала [—1, 1] и симме-
симметрична, поэтому в дальнейшем можно будет ограничиться правой частью
интервала [—1, 1]. Первый веревочный многоугольник дает C — х2) F\, раз-
разделив иа 3 — х2, найдем функцию F'[, которая с помощью второго веревоч-
веревочного многоугольника приводит к Fv Затем вычислим функцию — Fo =
= w + бО/7! и отсюда с помощью третьего веревочного многоугольника
найдем F0(x). Масштаб для F'[, Fx, Fo получим сразу По формуле A3.17).
На рис. 14.1 приведена шкала. Интегралы
для постоянных Шварца вычисляют по фор- ,,,_г/_ с х=П
муле Симпсона Х=0 2+cosx
ао = 71,5, а; = 2,28, а2 = 0,073.
Отношения Шварца (лх = —- и \i}--
а] а2
отличаются друг от друга в пределах точно- Рис. 14.2. Продольный изгиб
сти чертежа и имеют значение приблизи- стержня к задаче 4 п. 14.6.
тельно 31,3,
4. Найти по A2.19) критическую нагрузку шарнирно опертого на обоих
концах стержня (рис. 12.2) длины I = я и с переменной жесткостью
а = тт-р^ (рис. 14.2).
2 + cos х уу '
При Р = сЯ имеем
- у" = Я B + cos x)y = Xg-oy, у @) = у (я) = 0.
Решение. Две функции Fu, Fh удовлетворяющие краевым условиям
и связанные соотношением — F, = g0F0, легко найти, положив
cos x
Константу с можно выбрать любой. Но для того, чтобы получить хоро-
хороший результат, потребуем, чтобы Fo и Fit которые должны быть прибли-
приближениями для первой собственной функции, по возможности были близкими.
218 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ [14.6
При этом Fo можно грубо оценить значением в середине интервала /М-н-)
и значением производных на концах интервала Fo @), Fo (я).
Чтобы функция F\ была бы близкой к Fo, потребуем выполнения равенств:
Fo @): F[ @) = Fo (-J) :Fi(j) (значение с = 10),
'a (я) : F[ (я) = ^о (т):/?1 (т) (значение с = 14).
Таким образом, не удается достигнуть очень хорошего совпадения, и для
получения возможно лучшего совпадения положим с = 12. Тогда по фор-
формулам A2.4) и A2.8) найдем *
я я
J gofo dx = 16jt D - V~S), Й1 = J goFoFi dx = 74Jt>
о
о
n
= Г
J
о
Ac - 15bt, |i! = -gg- = 8 D 77|A1) = 0,4903674,
|X2 = -21 = -j^i- = 0,4900662.
a2 151
Нижнюю границу 12 для Я2 можно получить, заменив gu(x) максимальным
значением 3. Решая полученную краевую задачу, найдем
я2 4
<я - з ■ '2- з
и отсюда по формуле A2.19)
0,489891 < Я! < 0,490066
(см. также задачу 1 из п. 25.7).
5. Найти для задачи 5 из п. 11.4 (стр. 173)
ylv + 2Oy = -ly", у(±1) = /(±1)=0
два первых собственных значения Х^ и Я2.
Результат. Применим, как и в п. 11.4, в качестве исходной функции
ДЛЯ Я!
F, (х) — 61 — 75л-2 + 15л:4 — Xs.
Тогда
Fo (х) = 644 ~ — 790л2 + 155л;4 — Юл;6 + jr^,
1 1
0Fu dx = 1 027 294, al = - J Fof'i dx = 97 160,652,
-l -i
i
a2 = - j F/[dx = 9189,4026,
-i
Hi = — = 10,573148, цг = 10,573120 (ошибка -f 0,00024%).
14.6] § 14. ДОПОЛНЕНИЯ 219
Для нахождения второго собственного значения Я,2 будем исходить из
нечетной функции Z7, (х), которая, таким образом, кроме условия Р1(±1) =
= р" (±1) = f\v (±1), удовлетворяет еще условию Р} @) = 0 (что равно-
равносильно обобщенной ортогональности к первой собственной функции:
^ 1У1 dx = 0 I ; имеем
-1 /
Fx = 31л: — 49л-3 -f 21л:5 — Зл:7,
Ро = А D30л- — 628л-3 + 210л-5 — 12л-7 + х\
1
ао = ~ j F0Fq dx = 141 082,65, в, = И 779,580,
-1
а2 = 989,62786, ц, = ^- = 11,97688,
|л2 = -^- = 11,90304 (ошибка +0-06%).
а2
Точные собственные значения
20+ [Щ
(«=1.2,...),
Я, = 10,573096, Я,2 = 11,896028, Я,3 = 23,10724.
6. Вычислить несколько функций Fn (x) для краевой задачи
Решение. Исходя нз Fo {х) = 1 — Л, получим
12F, (л-) = A — л-2J, ЗбО^ (л-) = A — л-2J C — л-2),
■60480/7з (л-) = A — л-2J E1 — 22л-2 + Зл:4),
8 8 16 8
ао__, «1=15"' Й2 = "945' аз-уТб75'
1 />
Д4= 231-405' |Л1 = 15' 1*2=10-5'
Из = Ю, ц4 = 9Д Я,, = я2 = 9,8696.
7. Вычислить верхние границы |Ль |Л2 для наименьшего собственного
значения Я,! краевой задачи
yIV + А [A - х) у']' = Ху, у @) = у' @) = у" A) = у'" A) = 0
при А = 2, применяя в методе последовательных приближений для /^ (л-)
и Z7! (л-) многочлены возможно более низкой степени, такие, чтобы функ-
функция F0(x) удовлетворяла главным, a F^(x) — всем краевым условиям.
Решение. С помощью функций
Ро = 6л-2 + 28л-3 — 15л-4, /=•, = -ij- (ЗОЛ-2 — Юл:3 — 5л-4 + Зл:5)
(если А отлично от 2 или 6, то нужно для Fo и F^ применить полином
соответственно пятой и шестой степени) получим постоянные Шварца и
220 ГЛ. IV. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ A4.6
отношения
= -^. = 69,4857, а, = ~ = 7,40935, а2 = -ЦЦ- = 0,803579,
^ЗШ=9>37789, й,-^- 9,2206a
8. Для нелинейной задачи на собственные значения (собственное значе-
значение Я входит в квадрате)
— у" = Яу + Х*х*у, у(±1) = 0
определить по правилу
несколько приближенных функций F^ и приближение для соответствующего
собственного значения (члены дифференциального уравнения, которые со-
содержат в качестве множителя Хр, соответствуют в итерационном правиле
членам Fu-p)-
Решение. В качестве двух исходных функций, удовлетворяющих крае-
краевым условиям, выберем
р0 = о, F{ = 1 — х2
и получим
12F2 = 5 — 6х2 -+- х\
ШР3 = 79 — 75x2 _ 15^4 + 1 i*e
20 l60Ft = 2239 — 2212л:2 — 350л:4 -4- 364л — 4Ь8.
Из отношения двух последующих функций *+1 получим приближенное
собственное значение Я,, « 1,94.
ГЛАВА ПЯТАЯ
ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
Рассматриваются три минимальных принципа. К каждому из них
можно применить «схему Ритца»; таким образом получают соответ-
соответственно уравнения Галеркина, Камке, Граммеля. Параграф шестна-
шестнадцатый посвящается практическому, численному и графическому, приме-
применению метода Ритца и, кроме того, таким технически важным случаям,
в которых не полностью выполнены принимавшиеся до сих пор в этой
книге допущения, но в которых с помощью энергетического рассмо-
рассмотрения можно составить экстремальные выражения и затем применить
к ним процесс Ритца. В отдельных доказательствах в пп. 15.3, 15,4
и 15.8 будет использовано несколько простых фактов из теории мат-
матриц. Те, для кого эти факты непривычны, могут пропустить соответ-
соответствующие доказательства; в гл. VI о матрицах, независимо от пред-
представленного в гл. V материала, сообщаются все необходимые сведения.
§ 15. Основы метода Ритца
15.1. Три минимальных принципа. Возьмем самосопряженную
задачу на собственные значения D.11) — D.14), у которой собствен-
собственное значение к не фигурирует в граничных условиях. Пусть условия
полной определенности (8.2)
ь ь
j uM[u]dx>0, J uN\u]dx>0
a a
выполняются для всех функций сравнения. Тогда справедливы сле-
следующие минимальные принципы.
1. Минимальный принцип Рале я. По теореме п. 8.1 наимень-
наименьшее собственное число Х1 есть минимум, который принимает отноше-
отношение Рэлея (8.1),
f иМ [и] dx
R\u] = ^~b , A5.1)
b
f uN [и]
dx
если и пробегает область всех функций сравнения,
222 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ [15.1
2. Минимальный принцип Камке. Область функций и можно
расширить по сравнению со случаем минимального принципа Рэлея,
что при практическом решении часто дает большие преимущества.
При этом, правда, сверх полной определенности нужно предполагать
А"-определенность (см. п. 4.9). Так как доказательство сравнительно
длинно, приведем только результат; за доказательством следует обра-
обратиться к оригинальной работе Камке ').
Если применить к отношению Рэлея в соответствии с п. 4.6 фор-
формулу Дирихле, то R [и] перейдет в
Ь т
Ь п
a v-0
При этом вследствие принятой самосопряженности можно исключить
с помощью краевого условия U^ [и] = 0 в краевых выражениях Ди-
Дирихле Мо [и] и No [и] производные и порядка т и выше, так что
в A5.2) останутся только и и производные и до порядка (т—1)
включительно. В таблице III в явном виде выписаны выражения Мо [и]
и No [и] для важнейших классов задач.
Теорема Камке тогда гласит, что Хг есть минимум отношения
К [и], если и пробегает область допустимых функций, которые по
определению в п. 4.2 должны быть только т раз непрерывно диф-
дифференцируемы и удовлетворять лишь главным краевым условиям.
3. Минимальный принцип для частных задач на собственные
значения2). Для случая N[у] = g0(x)у получается еще один принцип
из метода последовательных приближений (см. п. 12.1). Пусть
и (х) — произвольная функция сравнения; ее можно понимать как
функцию Fx (x) итерационного процесса и для нее образовать функцию
^ A5.3)
Тогда отношение Рэлея A5.1) можно записать, как отношение
Шварца (х2 (согласно A2.9))
R [и] = R [FJ = jv
') Е. Kamke, Ober die definiten selbstadjungierten Eigenwertaufgaben,
IV, Math. Z. 43 A942), 67—100.
2) L. CoMatz, Z. angew. Math. Mech. 19 A939), 228.
15.Ц § 15. ОСНОВЫ МЕТОДА РИТЦА 223
Но так как, согласно A2.11), цк монотонно убывает, то fii^-V
Теперь легко (ij выразить через F^
ь ь
J /yv [Fo] dx J F0M [F,] dx
J
a a
значит, в соответствии с A5.3), если вместо Fx снова написать и,
получается ь
—W (м ^ *2 dx
И!==- т . A5.5)
Г
иМ [и] dx
Минимум этого отношения (ij для и, пробегающих область всех функ-
функций сравнения, есть наименьшее собственное значение X. В общем
/? [и] есть лучшее приближение, чем (ij при той же функции сравне-
сравнения, однако ц1 часто вычисляется быстрее, см. пп. 13.7 и 16.10')•
Пример. Сравним три рассмотренных выше принципа на примере
следующей задачи:
— у" = Ху, у @) = 0. у' A) + Су A) = 0, С>0.
В соответствии с принципом Рэлея A5.1) имеем
1
— Г ии" dx
Я; = min j ,
Г и2 dx
о
причем и пробегает область функций сравнения, т. е. всех дважды непре-
непрерывно дифференцируемых функций, для которых и @) = и' AL" Си A) = 0.
Согласно принципу Камке A5.2), учитывая D.25), получим
« . о
А, = 1ШП —
J (u')*dx + C[u(lW
a2 dx
') Новый экстремальный принцип и получающиеся из него верхние и
нижние границы для собственных значений представлены в диссертации Ле-
мана (J. Lehmann, Beitrage zur numerischen L6sung litiearer Eigenwertpro-
bletne, Dresden, 1948).
224 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ П5.2
где и пробегает область допустимых функций, т. е. всех непрерывно диф-
дифференцируемых функций с и @) = 0 (необходимо удовлетворить лишь глав-
главным краевым условиям). Для третьего минимального принципа A5.5)
Я, = min
I
(м"J
о
— им"
dx
и пробегает область функций сравнения.
Численный пример для отношения Рэлея. Задача
-у" = Яу, /@) = уA)=0
в качестве первой собственной функции имеет
е собственным значением
У\ = cos -£. х
Я. ,=-^1 = 2,4674...
В качестве пробной функции, для которой выполняются граничные условия,
возьмем, например, полином, а именно полином наинизшей степени, удовле-
удовлетворяющий краевым условиям:
и = 1 — хК
Тогда в соответствии с A5.1) получим
J* 2 A — лег»)
о
I
J
. dx
R [ы] = А_ = ^L == А = 2,5 > Л, = 2,4674.
Таким образом, уже с этой совсем простой пробной функцией можно полу-
получить для Хх значение с превышением всего на 1,5%.
15.2. Общий метод Ритца. Напрашивается мысль ввести функ-
функцию и, зависящую от параметров av a2, ..., ар:
и = и(х; av а2 ар),
и варьировать их так, чтобы образованное с помощью этой функции
минимальное выражение, например отношение Рэлея
Я [«] = /?[«(*; av a2 ар)\,
15.3] § 15. ОСНОВЫ МЕТОДА РИТЦА 225
принимало наименьшее значение. Тогда можно предположить, что это
наименьшее значение R будет близким к Хх (Вальтер Ритц, 1908)').
При нахождении минимума R как функции ах, а2 ар в каче-
качестве необходимых условий выступают равенства
dR „ dR dR „ ,_ .
-з— = 0, -з— = 0 з— = 0. A5.6)
дах да2 дар у '
Они представляют собой р уравнений для определения величин ах,
а2 ар. Точно так же можно и в двух других приведенных
в п. 15.1 минимальных выражениях К [и] и (Xj [«] взять и, зависящую
от параметров аи а2 ар, и получить уравнения, подобные A5.6).
Рассмотрим теперь три введенных в п. 15.1 минимальных прин-
принципа более подробно.
15.3. Уравнения Галеркина*). К удобным уравнениям можно
прийти, если вместо произвольной (нелинейной) зависимости и от ах,
а2, ..., ар использовать линейное представление
e = a1t»1(*) + fl2t»2(*)+ ••• + apvp{x). A5.7)
При этом V\, v2, ..., vp должны быть линейно независимыми функ-
функциями сравнения, так что м = 0 только при ах = а2= ... =ар = 0.
Этот случай исключается. Таким образом, и также является функ-
функцией сравнения. При подстановке и в A5.1) получается2)
ь р р
aTvT (x) \ asM [vs (x)] dx
р
(х) У^ asN [vs (x)} dx
а т=\ s-\
Для краткости введем величины mrs и nrs:
ь ь
mrs= j vr(x)M[vs(x)]dx, nrs = J vr (x) N [vs (x)] dx. A5.9)
') Вальтер Ритц, немецкий физик-теоретик, родился 22 февраля
1878 г. в семье художника в Швейцарии, учился с 1899 по 1902 г. в Цю-
Цюрихе и Геттингене.
Его основные работы, которые здесь следует назвать, — это диссертация
о новом методе решения некоторой вариационной задачи математической
физики, а также J. f. reine u. angew. Math. 135 A908), 1 и Annalen d. Phy-
sik 28 A909), 737. Умер Ритц в 1909 г.
*) Б. Г. Галеркин A871—1945) — выдающийся русский математик и
инженер, специалист по строительной механике.
2) При практическом проведении процесса часто бывает лучше ие за-
задаваться функциями vr (x) и из них образовывать М [vr (x)], а выбирать
функции М [vr] и из них интегрированием получать vr. При графическом
проведении метода такой обратный порядок действий прямо-таки необходим,
см. пп. 16.9 и 16.10.
15 Л. Коллатц
226 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ [15.3
Их можно понимать также как элементы двух квадратных матриц
Ж и «Я:
/тп ... mlp\ {tin ... п1р-
зи=|
тр1 ... трр/ \пр1 ... прр
Ввиду принятой самосопряженности задачи обе эти матрицы симмет-
симметричны:
mrs = msr< nrs = nST. A5.10)
Тогда R имеет вид отношения двух квадратичных форм Z и N
(можно не опасаться, что читатель спутает знаменатель с дифферен-
циальным оператором, обозначенным той же буквой N): R [и] = -j-=-,
где
Z= 2 mrsaras. N= 2 nTsaTas. A5.11)
T, S=l Г, S-l
Числитель и знаменатель в соответствии с (8.2) могут принимать
только положительные значения (случай а1=а2== ... =ар—0
исключается), таким образом, Z и N — положительно определенные
квадратичные формы. Необходимые условия минимума тогда имеют вид
1. 2 р.
... г
Минимум R обозначим через Л; он принимается в качестве прибли-
приближенного значения для первого собственного значения А^:
Л = min R [и (х; av a2 ар)\. A5.12)
Согласно принципу Рэлея A5.1) A.^%Y. Это Л одновременно является
значением ZJN в точке минимума. Поэтому уравнения для ар упро-
упрощаются
-7Г- — Л-^- = 0. A5.13)
даг даг ч
В соответствии с A5.11)
р
Отсюда следует
р р
• = 2 Л, mrsas, -г- = 2 V гаг А.
Из A5.13) поэтому имеем
р
2 as(mrs — Anrs) = 0, /-=1,2 р. A5.14)
s-l
15.4| § 15. ОСНОВЫ МЕТОДА РИТЦА 227
Эти уравнения называют уравнениями Галеркина *). Они представляют
собой р линейных однородных уравнений для as и имеют нетри-
нетривиальное (т. е. не.равное тождественно нулю) решение, когда ма-
матрица коэффициентов уравнений имеет равный нулю определитель
п —Длц . . . mlp—Anlp
det (mrs
m2l — Лп21 ... т2р —
трр—Апрр
= 0. A5.15)
Это — алгебраическое уравнение /?-й степени относительно Л; оно
имеет р корней Л,, Л2, .... Ар; так как обе матрицы 3R и Щ сим-
симметричны и действительны и соответствующая Щ квадратичная форма Л/
положительно определена, все корни Лг, согласно известной теореме
алгебры, действительны1). Мы можем расположить их в порядке воз-
возрастания Л, -^ Л2 ^ ... <С Ар, и рассматривать эти числа в качестве
приближенных значений первых р собственных чисел Я,,, %2 ^р.
В п. 15.8 показано, что все они являются верхними границами для
собственных значений: Ai^-Ki.
Уравнениям A5.14) можно дать еще одно толкование. Отношение
/?—Z/Л/ не меняет своего значения, если все аг умножить на одну
и ту же постоянную С Ф 0. Можно поэтому представлять себе аТ
«нормированным» и рассматривать только такие системы чисел ах,
а2 ар, для которых знаменатель N принимает определенное
значение, например значение, равное 1:
р
• 2 nrsaras=l. A5.16)
Г, S-1
Тогда /J=Z и можно исследовать минимум квадратичной формы Z
при дополнительном условии A5.1 бJ).
15.4. Сведение к вековому уравнению. Если используемые
в представлении A5.7) функции vr(x) ортогональны и нормированы
в обобщенном смысле, т. е. имеют место соотношения
[ 0 при г ф s,
r s A5.17)
*) По-видимому, автор имеет в виду связь уравнений A5.14) с методом
Галеркина, в котором они получаются независимо от проблемы минимизации
функционала. В знак того, что эти уравнения выражают основной результат
как метода Галеркина, так и метода Ритца, их целесообразно назвать урав-
уравнениями Галеркина — Ритца.
1) По теореме в п. 18.4; см. также О. Perron, Algebra, Berlin — Leip-
Leipzig, 1927. [См Д. К. Фаддеев, В. Н. Фаддее в а, Вычислительные методы
линейной алгебры, Физматгиз, изд. 2, 1963.]
2) Отсюда можно сделать заключение о существовании минимума Л; по
теореме Вейерштрасса Z как непрерывная функция а{, а2,..., ар на замк-
замкнутом ограниченном множестве, заданном с помощью A5.16), достигает ми-
минимума по крайней мере в одной точке.
15*
228
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[15.4
то уравнение A5.15) для приближенных значений
вековое уравнение
тп— Л т12 ... т1р
— обыкновенное
ш22 — Л
ttlr.
трр—А
= 0.
A5.18)
Тогда Л; — собственные значения (характеристические числа) ма-
матрицы Tt, и для их нахождения имеются специальные методы *).
Если же исходные функции vr(x) не удовлетворяют уравне-
уравнениям A5.17), то с помощью линейного преобразования
w2 = c2lvx -f- c22v2.
, = cplvx -f- cp2v2 4- ...
CPPVP
A5.19)
можно перейти к новой системе функций, ортогональных и норми-
нормированных в обобщенном смысле. Этот переход называется ортогонали-
зацией ■). Сначала определяют сп из
Г 10гЫ [wx] dx ^=
так что
с2 =■
J VlN[Vl]dx
а
Согласно (8.2) знаменатель отличен от нуля; знак числа сп выби-
выбирается произвольно, так как функции wr (x) определяются только
с точностью до знака. Затем определяют два числа с*2Х и с^, не равных
одновременно нулю, так, чтобы функция
была ортогональна к wv т. е. должно быть
ь
c*2l J
dx
с22
[г/2] dx == 0.
*) См. гл. VI, подробнее см. Д. К. Ф а д д е е в, В. Н. Ф а д д е е в а.
Вычислительные методы линейной алгебры, Физматгиз, изд. 2, 1963.
') Ортогонализация в п. 5.9 была проведеиа с помощью готовых фор-
формул E.32), однако ввиду ее важности этот процесс будет здесь повторен
8 несколько иной форме.
16.41
§ 15. ОСНОВЫ МЕТОДА РИТЦА
229
Так как v{ и v2 линейно независимы, w*2 не может быть тождественно
равна нулю; теперь можно определить еще одну постоянную С2 так,
чтобы w2z=C2w*2 удовлетворяло условию нормировки
ь
Г w2N [w2] dx — \.
а
При этом положим с21 = С2с*21 и с22 = С2с*2.
Теперь определим три не равных одновременно нулю числа таких,
чтобы функция w*3 = Cgjfj -(- c*32v2-4 Сзз^з была ортогональна wl и w2:
ь ь ь
С1х J W1N [Vl] dX + С32 J ™1^ N dX + С33 J ^1^ Ы d* = °'
«Ы
Ввиду линейной независимости vv v2, v3 функция та* не может быть
тождественно равна нулю, так что ее можно умножить на постоян-
постоянную С3 такую, чтобы для w3==C3w3 выполнялось условие
Г w3N [w3] dx = 1.
Продолжая таким образом, получаем
г
\wT
0 для г ф s,
1 для r = s.
A5.20)
Функции «>г (л:) линейно независимы, так как из соотношения
р
г-1
с помощью умножения на N [wq] и интегрирования по интервалу
от а до b мы получили бы, что 0^ = 0 для ^—1, 2, ..,, р. Со-
Согласно A5.9) можно vr выразить через w/.
vx = — wn = duwlt
i'2= ^i™! 4-
dp2^>2 H
A5.21)
230
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[15.4
т. е. в преобразовании A5.19) си не равны нулю; действительно,
если бы было cQ9 — 0 при не равных нулю си, с22 cq_l^q_l,
то в q-м уравнении из A5.19) возникло бы линейное соотношение
между wy, w2 iwq с не равными одновременно нулю коэффи-
коэффициентами, что невозможно.
Напишем теперь с только что полученными путем ортогонализа-
ции функциями wr(x) представление, подобное A5.7),
и = 2 brwr(x),
A5.22)
получим, далее, уравнения Галеркина и вычислим корни соответ-
соответствующего векового уравнения, которые обозначим через Л; (звездочка
имеет здесь другое значение, нежели раньше).
Тогда Л, = Л*; действительно, совокупность функций и при
использовании представления A5.7) та же, что и при A5.22), поэтому
минимум Лх для R [и] в обоих случаях один и тот же. Но и осталь-
остальные корни вековых уравнений A5.15) для представлений с vr и с wr
совпадают
Л; = Л*, 1=1, 2 р. A5.23)
Это легко видеть, если записать уравнения Галеркина в матричной
форме. Введем матрицы
(dn О
а2
ар
Ь =
ь2
•=(<*«)=
... 0
rf2i d00 ... О
d22
dpl
dPP>
тогда можно оба представления A5.7) и A5.22) сравнить между собой,
пользуясь A5.21):
р р р р р
и = 2 ал= 2 2 asdsrwr — 2 bTwT, где bT = 2 dsras,
s-\ s-l r-l r=I s«l
или
Ь = ©'а,
причем ЗУ обозначает матрицу, транспонированную к £).
Обозначим числа, образованные по аналогии с A5.9) при помощи
wr(x) вместо vr(x), через
ь ь
m*s = Г wfM \ws] dx, n*s = Г wrN \w} dx
и будем понимать их как элементы матриц Ж" и 9Г; очевидно,
15.61 § 15. ОСНОВЫ МЕТОДА РИТЦА 231
9T = S — единичная матрица; подстановка A5.21) в A5.9) дает
р р
mrs = к 2 г <VXr nrs = ft2 drkdsk,
или
и уравнения Галеркина A5.14)
EК — ЛЯ) а = О
переходят в
Умножая слева на 2) , получаем
(ЗГ - Л<5) (ЗУа) — ЭГ6 — ЛЬ = 0.
Но это — уравнения Галеркина для представления A5.22) с wr(x).
Если Л—значение, для которого уравнения A5.14) имеют нетри-
нетривиальное решение, то мы имеем для того же самого значения
Л = Л* нетривиальное решение для уравнений Галеркина с пред-
представлением A5.22).
15.5. Линейное представление в случае минимального прин-
принципа Камке. Здесь по аналогии с тем, как это делалось в п. 15.3,'
применим представление
р
и = 2 arvr(x)
r-l
к минимальному принципу Камке A5.2). Функции vr(x) должны быть
допустимыми функциями и удовлетворять главным граничным усло-
условиям, удовлетворение естественным граничным условиям не требуется.
Обозначив краевые значения и и производных и в граничных точ-
точках а и b
и (а), и1 {а) «('"-•'(а); и(р), и'ф) и^т~^ ф)
через
«1. «2- • • • ■ Чт-
получим для краевых выражений Дирихле в A5.2) MQ [и] н Л/0[и]-
следующие квадратичные формы относительно и1 и2т:
1т 2т
М0[и]= 2 bklukult NQ[a]= 2 cklukuv A5.24)
ft, /~i k, /-1
Выражения Мп[и] и N0[u] для ряда практически важных случаев
приведены в таблице III. Минимальное выражение К [и] при под-
подстановке представления и (точно так же как в предыдущем пункте
232
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[15.6
выражение /?[«]) станет отношением двух квадратичных относи-
относительно ат форм:
где
и (m*s и n*TS имеют другой смысл, нежели в п. 15.4) если краевые
значения функции vr (x)
Vr (a), V'r (а) • x;(m-l> (fl). ^ ф), v' ф) v(m-l
обозначить через vrl, vr2 vTim< имеем далее
Ъ m / р \ I р \ 2т р
a v=0
s=l
P
причем m*s симметрична по записи, т. е. m*s = m*sr, так что
J
a v-0
Точно так же
* п
a v=0
ft,i=l
2m
fe, г-1
Дальнейший ход рассуждений такой же, как в п. 15.3, только
R[u], Z, N здесь заменяются К [и], Z*, N*. Тогда для первых р
собственных значений описанный здесь способ дает приближения Л,
получаемые как корни уравнения
\2 - An*l2 .. . m\p - An\p
m*pl - AflPl
\P - AflP
lPP
= 0.
A5.27)
15.6. Уравнения Гаммеля. Точно так же как в пп. 15.3 и 15.4,
введем теперь линейное представление
р
и = 2 arvr (х)
15.61
§ 15. ОСНОВЫ МЕТОДА РИТЦА
233
в третье из записанных в п. 15.1 минимальных выражений A5.5),
а именно в ц, [и]. При этом сначала примем, что обсуждается част-
частная задача на собственные значения для дифференциального урав-
уравнения
Здесь vT (х) должны образовывать систему р заданных функций
сравнения, следовательно, как и в п. 15.3, они должны удовлетворять
всем краевым условиям, не только главным. Тогда будет (в точном
соответствии с п. 15.3)
Л / Р \ ( Р \
= J j±fi I Yi arM [*V (*I I 2 а*М [vs (x)}) dx =
где
и соответственно этому
p
Г, 5=1
Ps = J j^- M [vr (x)] M [vs (x)} dx;
A5.28)
= j vr(x)M[vs(x)]dx.
A5.29)
Величины reS совпадают с величинами mrs в A5.9). Результаты даль-
дальнейших вычислений перенесены из п. 15.3, только величины Z, N, mrs
и nrs отмечены значком . Уравнениям A5.14) здесь соответствуют
уравнения Граммеля1):
S
■=!. 2, ....
A5.30)
и приближенные значения Л для первых р собственных значений
получаются как корни уравнения
det(«D_A/lD)=:
Q
П
П
= 0. A5.31)
') Р. Граммель, Ein neues Verfahren zur LOsung technischer Eigen-
wertprobleme, Ing.-Arch. 10 A939), 35—46. Уравнгния там были получены
другим способом,
234 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ [15.7
При реализации метода удобно исходить не из vr (х), а из Ж [vr (х)]
и определять vr{x) из них путем интегрирования, см., например,
п. 16.10.
Если рассматривается общая задача на собственные значения для
дифференциального уравнения М [у] = A,7V[y], то вместо A5.5) следует
вернуться к первоначальному выражению величины цх A5.4) (см,
также A2.20)), дающему верхнюю границу для кг. Положим
и выберем функцию FQ так, чтобы в соответствии с A2.1) было
М [FJ — N [Fo]. При этом FQ должна быть полудопустимой, т. е.
удовлетворять тем краевым условиям, которые необходимы для выпол-
выполнения A2.3). (Требование A2.3) относится ко всем функциям срав-
сравнения, а не только к примененным здесь специальным функциям
и=2 arvr-) Для того чт°бы получить FQ, определим для каждой из р
функций vr (x) соответствующую ей полудопустимую функцию wr (x)
с помощью равенства М [vr] = /V [wr] *). Тогда можно положить
F0(x)=J,arwr(,x).
za
Проварьируем теперь ат так, чтобы отношение A5.4) щ ——ту стало
минимальным; числитель имеет теперь вид
ь I р \ / р \ р
И 21 а*м [v°(x)] )dx = 21
a
в то время как знаменатель не изменился в сравнении с A5.29).
Формула A5.28) должна быть теперь заменена равенством
m?s= j wr(x)M[vs(x)]dx,
а
в то время как A5.29), A5.30) и A5.31) остаются без изменений.
15.7. Численные примеры. Частная задача на собственные значения.
Рассмотрим теперь обсуждавшийся в п. 12.2 пример:
с помощью трех минимальных принципов. Для этого в минимальных выра-
выражениях, приведенных в конце п. 15.1, нужно только положить С = 1.
Для всех трех принципов используем представление Ритца A5.7) с сохране-
') Следовательно, для п ;> 1 wr (x) определяется как решение краевой
задачи. Мы предполагаем, что эти краевые задачи разрешимы для г — 1,
2, ...,/?, в противном случае vT(x) видоизменяются подходящим образом.
15.7]
§ 15. ОСНОВЫ МЕТОДА РИТЦА
235
нием двух членов, в качестве которых используются два подходящих про-
простейших полинома.
А. Уравнения Галеркина. Будем применять функции vu v2,
которые удовлетворяют всем граничным условиям. Полиномами низшей
степени, удовлетворяющими этим условиям, будут
I/, = Зх — 2х2, щ =. 2х — хг.
Тогда М [«,] = 4, М [v2] — 6х. Производя с ними вычисления в соответ-
соответствии с A5.9), получим
1 1
«11=
; = 4CJC —
J
0
1
/и,2= f v,M[v2]dx = ( 6х (Зх — 2х2) dx = 3
и точно так
т2.
Уравнение
Положив Л
же
= -
14
5 ' '
г,, =
4
«.» =
[15.15) тогда примет вид
10
Зз
= 7 г, получим
50 —
45 —
84г
77z
-Л
45-
42-
4
и
15
-77г
-71г
-1
0
с
14
5
== с
uxv2 dx = -
Л И
Л 105
15 ' 2
= 0.
5г2 — 148г -[- 75 = 0.
71
105"
Корни этого квадратного уравнения г = -^-G4 ± /2851) дают верхние гра-
границы для обоих собственных значений
] ( 4,1211 (ошибка +0,13%),
Л,, 2 = д-G4 ± У 2851) = | 2547д (ошибка ц_5,5%).
Точные собственные значения определяются по таблице VI с Я = k2 из транс-
трансцендентного уравнения tgft = — k. Я, =4,11586, Я2 = 24,14 (ft, =2,02876,
ft2 = 4,913).
О приближенных значениях, появляющихся при применении представле-
представления Ритца с двумя функциями, как мы здесь это делали, можно утверждать
следующее. Пусть Aj и Л^ (пронумерованные в порядке возрастания Aj < Л2)
суть отношения Рэлея, образованные с помощью координатных функций vl
и v2 в качестве пробных функций, а А, и А2 — приближенные значения,
полученные при двучленном представлении и — a\Vx -j- a2v2, тогда для само-
самосопряженной задачи на собственные значения, для которой выполняются
условия (8.2), имеют место неравенства
0
А[
А2-
A5.32)
236 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
Действительно,
A5.7
«22
а уравнение A5.15), принимая во внимание симметричность A5.10), можно
привести к виду
(A-AIHA-A^^-^2.
Приближения Л,, Л2, полученные при использовании двучленного предста-
представления, удовлетворяют этому уравнению. В силу предположения (8.2) я,, > 0,
п22 > 0 н, следовательно, правая часть неотрицательна н обращается в нуль
только прн Л =
«12
-. Относительно
«1
ничего сказать нельзя, в нашем
численном примере
«12
< А.,. Если
Рис. 15.1. Расположение нулей для
двучленного представления Ритца.
обе части уравнения как функции Л
представить графически (рис. 15.1),
то получим две параболы, из которых
одна принимает между Л* и Л2 отри-
отрицательные значения, следовательно,
между Aj и Л2 нет точек, общих с дру-
другой параболой, т. е. справедливо A5.32)'). Пусть, например, v2 дает хорошее
приближение для собственной функции у2 и Л2 немного больше Я2, тогда новое
приближенное значение Л2 окажется хуже! (Л2>Л2>Л2.)
Б. Минимальный принцип Камке. Теперь возьмем функции vx
и v2, являющиеся только допустимыми, следовательно, удовлетворяющие
лишь главным краевым условиям. Из краевых условий у @) = 0 есть главное,
а у A)-|-у'A) = 0 — естественное. Простейшие полиномы vu v2 с t/^ @) = 0
суть vx = х н v2 = х2; таким образом, мы получаем представление
и = а,х -\- а2х2. Теперь можно согласно A5.25) и A5.26) вычислить mrs и n*s,
но можно нх также получить подстановкой представления и в минимальное
выражение
1
иЫх
') Это можно доказать также следующим образом. Согласно A5.12) ми-
минимум отношения Рэлея R при вариации аи а2 есть число Л = А,, и это
число есть корень уравнения A5.15). Точно так же максимум R тоже должен
быть корнем A5.15) и равен Л2. И следовательно, Л2<Л2. [Примечание ред.
Автор имеет в виду R[axvx-\-a2v2\-\
15.7]
§ 15. ОСНОВЫ МЕТОДА РИТЦА
237
Тогда будет
1
dx + (al
2а1
следовательно,
Соответств енно
/ип=2,
1
=
1,1
= -д-. «12 = "' «22 = "g"
Уравнение для Л A5.27) при этом имеет вид
-7Л 2"ТА
2-1л 1--1
22
= 0.
Это квадратное уравнение имеет корни Л = -=- F4 ± 4 Kl66) или
о
Л., =4,1545, Л2 = 38,512.
В. Уравнения Граммеля. В данном случае функции vx, v2, взятым
в качестве функций сравнения, должны снова удовлетворять всем краевые
условиям; в качестве первого грубого приближения возьмем те же функции
что и в п. А:
v{=3x — 2x2, v2 = 2x — х3,
для которых
М [t>,]= 4, М [v2] = 6х.
Здесь ga(x) имеет значение, равное 1, поэтому из A5.28), A5.29) получаем
/яЯ=16, пп = пп = 12, nQ = -^-, n°=3, 2 = ^-
и уравнение A5.31)
16 12. А 12-ЗА
О
имеющее корни
12 —ЗА
12 ,
12—
А
= 0,
4,2120,
238 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ [15.8
Лучшие приближения можно было бы получить, если исходить не из vT (x),
а из функций М [v2 (x)\, например M[vx\ — x, M [v2] = х2, и применением
итерации получить удовлетворяющие граничным условиям функции t/,, v2 ').
15.8. Приближения Ритца для высших собственных значений.
В соответствии с идеей Ритца (см. A5.12)) разыскивается минимум
отношения Рэлея R; совершенно очевидно, что все корни At, кото-
которые получаются из A5.15), суть верхние границы для первого соб-
собственного значения Я,,. Если представить себе At расположенными
в порядке их возрастания, как в п. 15.3, то, кроме того, высшие
приближения Ритца окажутся верхними границами для соответствую-
соответствующих высших собственных значений, т. е. справедлива следующая
Теорема. Пусть задача на собственные значения D.11)—D.14)
самосопряженная и полностью определенная (что означает выпол-
выполнение (8.2)) и собственные значения X не входят в краевые
условия. С помощью линейно независимых координатных функций
vv v<2 vp метод Ритца проводится в форме Галеркина, т. е.
по A5.9) могут быть вычислены постоянные mrs и nrs, а также р
корней уравнения A5.15) AL. Все AL действительны; их можно
расположить в порядке возрастания: Л, -^ Л2 -^ ... ^ Ар, так
что они будут представлять собой верхние границы для соот-
соответствующих собственных значений:
Л,- >А,г, 1=1, 2, .... р. A5.33)
Доказательство достаточно провести здесь только для второго
собственного значения Л2 ^> Я,2, для остальных оно выглядит анало-
аналогично. Итак, пусть задана определенная система функций vb v2 vp,
с помощью которой мы получаем представление Ритца
р
U = 2 arvr-
Систему функций можно считать ортонормированной в обобщенном
смысле
ь
0 для г Ф s,
1 для г — s.
Действительно, в п. 15.4 было показано, что если vr(x) линейно
независимы, то всегда можно перейти к другой системе ws(x), для
которой выполняются A5.20) и с которой получаются те же Л, что
и с vT (x). Тогда Л,- суть корни векового уравнения или характе-
') Практическая применимость уравнений Граммеля показана на различных
технических примерах, см. Е. М a i e r, Biegeschwingungen von spannungslos
verwundenen Staben, insbesondere von Luflschraubenblattern, Ing. — Archiv II
AP40), 73—98; R. Orammel, Gber die Losung technischer Eigenwertproblerae,
Forschungsh. Qebiet Stahibau, 6 A943), 36—42.
l"j.e] § 15. ОСНОВЫ МЕТОДА РИТЦА 239
ристические числа симметричной матрицы Tl = (mlk), или также хара-
характеристические числа квадратичной формы
р
z = 2 mrsaras.
г, s = \
Отношение Рэлея, согласно A5.8), A5.11) и A5.17), принимает вил.
р
2 mTsaras
R\u] = ^=^-p =Q.
Доказательство утверждения Л2 ^ Х2 апеллирует к минимаксималь-
ному принципу Куранта для квадратичных форм 1). Сообразно с этим
сначала утверждается: минимум Q = AV т. е. минимум Q при варьи-
варьировании av дает значение А{. Обозначим теперь через /и = m (cr),
где Cj, с2, ..., ср — произвольно заданные постоянные, минимум Q
при дополнительном линейном однородном условии
тогда минимаксимальный принцип Куранта гласит: Л2 будет равно
максимуму m (cr) при варьировании с/.
max/min Q\ = Л2.
Этот принцип в точности соответствует минимаксимальному прин-
принципу, изложенному в п. 8.4.
Обозначим теперь, как в п. 8.4, минимум отношения Рэлея R [и]
при дополнительном условии
Г wu dx = О
а
через M(w), тогда в соответствии с принципом Куранта в п. 8.4
maxAmin R [и] \ = Х2,
w \ и )
т. е. Я,2 есть максимум М (w), если w пробегает область всех инте-
интегрируемых функций.
Теперь мы докажем, что для произвольно выбранной функции w
всегда М (w) <; Л2. Если это доказано, то это неравенство должно
быть справедливо также для максимального значения, которое при-
принимает M(w), т. е. будет А,2^Л2. Итак, пусть w—произвольная,
') В соответствии с п. 186; см. также R. Сои г ant и. D. Gilbert,
Methoden der mathematischen Physik, т. 1, изд. 2, Beriin, 1931 [P. Ку-
Курант, Д. Гильберт, «Методы математической физики», т. 1, изд. 2, ГТТИ,
М. —Л., 1951].
240 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ A6.1
но в дальнейшем фиксированная функция. Мы вычислим для нее
постоянные сг по правилу
b
сг = wvr dx
а
и образуем т (сг), т. е. минимум Q (одновременно минимум R) при
варьировании аг с дополнительным условием
Это условие идентично условию
р Ь Ь
2jar wvrdx = wudx = 0,
r-l a a
Р
следовательно, ш{сг) есть минимум R для функций и= 2 arvr ПРИ
г=1
р
условии 2crarr=0. и эти функции составляют подмножество допу-
г=1
стимых для M(w) функций. Таким образом,
m (cr) ^> M (w).
Теперь А2 = тахте (сг), следовательно, m(cr) ^ Л2, а отсюда следуют
М (w) ^ Л2 и утверждение Х2 ^ Л2.
Для высших собственных значений лишь привлекается соответ-
соответственно больше дополнительных условий (о более подробном дока-
доказательстве см. примечание на стр. 222).
§ 16. Дальнейшее развитие метода Ритца
16.1. Вариационные уравнения Эйлера. Общая теорема в п. 15.8,
которая дает строгое обоснование метода Ритца, связана с несколь-
несколькими предположениями (например, должно выполняться условие полной
определенности (8.2))'). Имеются задачи технического происхождения,
для которых эти предположения не выполняются, но в которых тем
не менее метод Ритца применим. Во многих из этих случаев может
быть составлено некоторое выражение J. Рассматриваемые в вариа-
вариационном исчислении необходимые условия минимума J, так называе-
называемые уравнения Эйлера2) с их граничными условиями, совпадают
') Могут быть сформулированы более сильные теоремы.
2) Леонард Эйлер, выдающийся математик, родился ~в 1707 г.,
в семье священника в Базеле. В 1727 г. приехал в Петербург, где в 1730 г.
стал профессором физики, а в 1733 —профессором математики. В 1741 г.
он был приглашен в качестве профессора математики в Берлин, а в 1766 г.
вернулся обратно в Петербург. Умер в 1783 г.
\в.1-| § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 241
с заданными дифференциальными уравнениями и их граничными усло-
условиями. Вычислители-практики в этих случаях порой применяют метод
Ритца, ожидая, что нижняя граница отношения Рэлея будет одно-
одновременно приближением для наименьшего собственного числа краевой
задачи. Ясности ради необходимо подчеркнуть, что уравнения Эйлера
дают лишь необходимые, но не достаточные условия минимума. Из-за
этой трудности «классического» подхода метод Ритца в § 15 был
введен вне связи с вариационным исчислением; подход, примененный
в §§ 4, 5, 8, 12, 15, позволяет ответить на оставшийся открытым
в классическом вариационном исчислении вопрос о существовании
минимума.
Дадим краткий вывод1) уравнений Эйлера и применим их к задаче
на собственные значения.
Пусть задана вариационная задача о нахождении наименьшего
значения выражения J:
ь
j=J[u}= J F(x, и, и', и" u^)dx-\-
а
-\-А(и(а), и'(а), и" (а) и{т~'[)(а))-\-
+ В(иф), и'ф), и"ф) и{т-1)ф)) = тт. A6.1)
При этом F — заданная, непрерывная функция от х, и, и', ..., м(т)
с непрерывными частными производными до (/»-(- 1)-го порядка вклю-
включительно; А и В — непрерывные, с непрерывными частными произ-
производными по всем аргументам функции краевых значений от и,
и' и^т~]\ и пусть в качестве функций сравнения допустимы
все 2т раз непрерывно дифференцируемые функции и (х), которые
удовлетворяют некоторым заданным однородным линейным краевым
условиям
V^[u] = 0, [1=1, 2 k. A6.2)
Пусть эти краевые условия будут того же типа, что и написанные
раньше в D.14) f/(i[y] = O, пусть они линейно независимы и не со-
содержат частных производных порядка выше т. — 1 (главные краевые
условия). Положим, что J имеет минимум и что среди допустимых
функций и имеется одна функция у (х), которая доставляет минимум
J[y]<J[u]. A6.3)
Пусть т)(х) — допустимая функция; тогда можно с помощью пара-
параметра е ввести однопараметрическое семейство функций
A6.4)
') Для более подробного ознакомления см., например, R. Courant,
D. Gilbert, Methoden der mathematischen Physik, тт. 1, 11, изд. 2, Beriin,
1931. [P. Курант, Д. Гильберт, Методы математической физики, тт. Г,
11, ГИТТЛ, изд. 2, М. —Л., 1951.]
16 Л Коллатц
242 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ A6.1
и установить для него неравенство A6.3). Для этого семейства функ-
функций У [и] будет непрерывно дифференцируемой^ функцией е, так что
У[и] —Ф(е). Эта функция будет принимать минимум для е = 0 только
тогда, когда ее производная Ф' @) = 0 (если, следовательно, «первая
вариация» еФ' @), которую обозначают также 6У, обращается в нуль).
Вычисления дают
dx 4
e=O
При этом нижними индексами обозначаются частные производные,
например
F - dF
Теперь преобразуем интеграл путем интегрирования по частям отдель-
отдельных слагаемых подынтегральной функции до тех пор, пока в подынте-
подынтегральном выражении вместо ц^ не появится ц:
b
Fy,r)' dx = lr\Fy>
a
b
b
J
a
'y dx,
h
J Prf dx = ^Fy _ ц *_ p^ + J ц ^_ Fyl, dx>
a a
и так же для последующих слагаемых. Из равенства Ф' @) = 0
в соответствии с A6.5) следует
A6.6)
16.1] § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 243
с краевым выражением
5 = [r\Fy. + (ц'/V - г] JL F
. A6.7)
Функция т](х) может быть произвольной допустимой функцией; по-
поэтому A6.6) может быть выполнено только тогда, когда выражение
в прямоугольных скобках подынтегральной функции тождественно
равно нулю, что следует из такого косвенного доказательства: если бы
выражение в прямоугольных скобках не обращалось в нуль, напри-
например, было больше нуля в некоторой точке х0, а < х0 < Ь, то это
выполнялось бы и в достаточно малой окрестности |х— хо|<^6
этой точки; тогда, если A6.6) выполняется для функции r\ — yf, то
для ц=ц** оно должно было бы нарушаться при подстановке
„( Ч*+(х — х0— 6Jm+1(x — xo+6Jm+1 для |х —хо|<6,
1 Ц* для | х — х01 > 6.
Таким образом, должно быть
Это — так называемое уравнение Эйлера вариационной задачи A6.1),
A6.2); оно представляет собой необходимое условие, которому должно
удовлетворять решение задачи у(х), и имеет порядок 2т.
При обращении в нуль выражения в квадратных скобках из A6.6)
обращается в нуль и краевое выражение 5. Предположим теперь для
нашей задачи на собственные значения, что фигурирующие в A6.1)
функции F, А и В суть квадратичные формы и и ее производных;
тогда S — билинейная однородная форма, т. е. линейная однородная
форма краевых значений как у и ее производных, так и г\. Пусть у
и т) удовлетворяют краевым условиям A6.2). С помощью A6.2) k
из 2т краевых значений т)(а), г]' (а), ..., r\(m~^(a); f](b), ц'(b), ...
..., vfm~^(b) могут быть выражены через остальные. Эти остальные
2т — k краевых значений могут быть названы <<свободными краевыми
значениями» ') и их произвольную последовательность можно обозна-
обозначить г]], х\2< %> ■••• Щт-k- Если выразить в 5 все краевые значения
от т] через «свободные краевые значения», то 5 примет вид
2т-к
v-1
') Е. Камке, Math. Z., 48 A942), 70.
16*
244
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
|1в.2
причем Wv [у] линейна и однородна относительно у в краевых зна-
значениях. Так как t]v может быть выбрана произвольно и для каждой t]v
имеется соответствующая допустимая функция, из A6.9) следует
Wv[y] =
v=l. 2
2m —k.
A6.10)
Это 2т — k необходимых условия на решение у вариационной за-
задачи A6.1), A6.2), которые в общем должны быть отличны от k
краевых условий A6.2), так что, вообще говоря, для функции, удо-
удовлетворяющей дифференциальному уравнению
порядка 2т, должно быть 2т краевых усло-
условий. О разрешимости этой краевой задачи,
однозначности решения и о различии краевых
условий A6.2) и A6.10) при данной степени
общности ничего не утверждается.
16.2. Пример. Задача на собственные
Рис. 16.1. Изгибные ко- значения. Для изгибных колебаний защемлен-
лебания закрепленного ного одним концом стержня длины /, свобод-
свободна одном конце стержня ный конец которого нагружен точечной мас-
с сосредоточенной мае- „ ,* ,-
сой сой М и для которого жесткость на изгиб
равна а, а масса на единицу длины ц, посто-
постоянна (рис. 16.1), вариационная задача, как будет более подробно
обосновано в п. 16.4, имеет вид
J = J (аи — Х\ш§ dx — ХМи (If = экстремум A6.11)
с главными краевыми условиями
A6.12)
Выражение Ф' @), представляющее собой с точностью до множи-
множителя е первую вариацию и обращающееся в нуль, здесь, как это
тотчас получается интегрированием по частям, имеет вид
i
0 = [dJ[ydt^] = J [(«/)"-Я^у] л dx + S, A6.13)
] = J
где
S = m'ay"Y0 - [г] (ау")% - Шу (I) т, (/) =
= т, @) (а/О',,о — Л' @) Ао
Н- Л @ [~ («/)' - Шу]х_, + Ц' {I) (а А.г
Здесь т|@) и т]'@) обращаются в нуль согласно A6.12). Итак, из
16.3] § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 245
S — 0 следует и обращение в нуль множителей при т](/) и т]'@>
и для у получаются краевые условия
{(ау")'-\-1Му]х=[=>0, у" (/) = 0.
К этим краевым условиям добавляются еще у @) = у'@) = 0. Диф-
Дифференциальное уравнение для у получается приравниванием нулю вы-
выражения в прямоугольных скобках в A&. 13), что дает
(«/')" = Яцу;
X получается как собственное значение этой краевой задачи.
Уравнения этой задачи на собственные значения можно также по-
понимать как необходимые условия другой вариационной задачи.
Пусть к входит, по предположению, линейно и функции F, А, В
из A6.1) суть квадратичные формы и и производных от и; тогда
выражение J из A6.1) может быть представлено в виде J=Jl-\-XJ2,
причем У] и J2 уже не зависят от к. Тогда необходимые условия
A6.8) и A6.10) эквивалентны отысканию минимума выражения Jx
с дополнительным условием J^—cofisi (в частности, У2=1) или
отысканию минимума отношения1)
16.3. Обратная постановка задачи и метод Ритца. В п. 16.1
для данной вариационной задачи A6.1), A6.2) были указаны в ка-
качестве необходимых условий её решения дифференциальное урав-
уравнение Эйлера A6.8) и краевые условия A6.10). На обратную
постановку вопроса: найти для заданных дифференциального уравне-
уравнения и краевых условий соответствующую вариационную задачу, для
которой они выражают необходимые условия, налагаемые на реше-
решение, ответить не так легко; не для всякой краевой задачи имеется
соответствующая вариационная задача, она, например, не может быть
поставлена, когда порядок дифференциального уравнения нечетный;
но и при четном порядке уравнения не всегда имеется вариационная
формулировка, соответствующая данной задаче.
Дифференциальное уравнение в самосопряженной форме
всегда можно записать как уравнение Эйлера A6.8), нужно только
в A6.1) подставить
v=0 v-0
') О правилах вариационного исчисления для задачи с дополнительными
условиями см. R. С о u r a n t, D. Gilbert, Methoden der mathematischen
Physik, т. I, II, изд. 2, Berlin, 1931 [P. Курант, Д. Гильберт, Методы
математической физики, тт. I, II, ГИТТЛ, изд. 2, М. — Л., 1951].
246 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ Цв.4
В качестве A6.2) применяют главные краевые условия. Затем пы-
пытаются так задать две квадратичные формы А и В в A6.1), чтобы
A6.10) соответствовало естественным краевым условиям; вопрос
о том, когда это возможно, здесь вообще не исследуется. Для само-
самосопряженных полностью определенных задач на собственные значения,
у которых X не входит в краевые условия, в § 15 были получены
соответствующие вариационные задачи, а для подавляющего боль-
большинства задач, возникающих в физике и технике, соответствующие
вариационные задачи часто могут быть получены более коротким пу-
путем из энергетического рассмотрения. Несколько примеров этого
будет дано в пп. 16.4 и 16.5.
Пусть для некоторой задачи дано подлежащее минимизации вы-
выражение J[u] вида A6.1), тогда можно, как в § 15, применить ме-
метод Ритца. Подставим представление (обычно линейное) A5.7)
в A6.1) и получим с помощью
о6-15)
■\j\aiVi(x)]
1Щ 1 = 0,
да к=\, 2 р, A6.16)
уравнения метода Ритца. В качестве vt(x) применяют линейно неза-
независимые, удовлетворяющие главным краевым условиям, достаточное
число раз дифференцируемые функции.
16.4. Энергетический метод для задач о колебаниях. Пусть
задана произвольная колебательная система, совершающая малые ко-
колебания около положения равновесия. Если для некоторого собствен-
собственного колебания принять синусоидальную форму движения каждой
отдельной частицы, то получим, что отклонение1) из положения равно-
равновесия в зависимости от времени будет у (t)—Y sin (at. При этом при-
примем, что все частицы колеблются в одном ритме, т. е. с одинаковой
круговой частотой со и одинаковой фазой; все частицы проходят одно-
одновременно положение равновесия и в одно время достигают своего
наибольшего отклонения (амплитуда К). Это значение К зависит от
конкретной частицы, т. е. является функцией места.
Составим теперь выражения кинетической энергии Т и потен-
потенциальной U- Обозначим через р плотность, а через dv элемент
объема тел, тогда
Т = Т (t) = -1 Г py'2dv — ^ Г рсо2К2 cos2 cot dv = Гсо2 cos2 at. A6.17)
') у (t) зависит от положения выделяемой частицы, характеризуемой ко-
координатами xit х2,,.., хт. Вместо y(t) можно бы было писать y(t, xlt хг,,.., хг).
6.41 § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 247
При этом
Т* = 4- { pV2dv A6.18)
— так называемая «приведенная кинетическая энергия».
Выражение для потенциальной энергии зависит от рассматривае-
рассматриваемого тела и не может быть выписано в общем виде. Потенциальная
энергия представляет собой работу, которую надо совершить, чтобы
вызвать изменение положения отдельных частиц, заданных с помощью
y{t) (например, работа против внешних сил, работа деформации и
т. д.). Она для каждой рассматриваемой системы должна считаться
известной и зависит указанным образом от смещений у.
Будем рассматривать колебательные процессы без затухания.
Тогда по закону сохранения энергии Е = Т (t)-\-U (t) в любой мо-
момент времени, т. е. при максимальном Т потенциальная энергия U
будет минимальна и наоборот. Определим произвольную постоянную
при U так, чтобы в положении равновесия было G = 0; тогда пол-
полная энергия Е = Ттах = £/тах, т. е. при колебаниях имеет место пол-
ный обмен между кинетической и потенциальной энергиями.
Тогда, согласно A6.17), Гтах = со2Г*, следовательно,
©2=i^L. A6.19)
Если известна форма колебаний, т. е. распределение амплитуды К
по объему тела, то по этой формуле можно вычислить соответствую-
соответствующую круговую частоту со.
Сформулируем теперь «рэлеевский принцип» механики: если под-
подставить в A6.19) справа вместо К произвольно выбранную, но воз-
возможную, т. е. совместную с краевыми условиями, функцию, описы-
описывающую форму колебаний, то получившееся значение будет больше
или равно квадрату наименьшей собственной частоты со2 или, выражаясь
иначе, со2 есть минимум отношения Рэлея A6.19), если использовать
для сравнения все распределения амплитуды, совместные с краевыми
условиями.
Этот принцип часто обосновывают следующим образом *): пусть
Y* — произвольно выбранное, но удовлетворяющее граничным усло-
условиям распределение амплитуды; заданная система сравнивается с дру-
другой, которая имеет лишь одну степень свободы и для которой рас-
распределение амплитуды имеет форму у = сУ*, причем с зависит только
от t, но не от координат. Дополнительные условия связи, в общем,
увеличивают жесткость тела и вместе с тем частоту основного
колебания.
') S. Timoshenko, Schwingungsprobleme der Technik, Berlin, 1932
[С. П. Тимошенко, Колебания в инженерном деле, Физматгиз, 1962].
248 ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ A6.5
Конечно, это заключение не является строгим обоснованием мини-
минимальных свойств coj; минимальные свойства трудно обосновать с такой
общностью с помощью подобных простых рассуждений. Все же
минимальный принцип выполняется строго в большом числе случаев,
например, когда рассматриваемая задача приводит к задаче на соб-
собственные значения, для которой выполняются предположения теоремы
в п. 15.8; в этом случае выражение A6.19) соответствует отношению
Рэлея D.31). Постулируем теперь механический принцип Рэлея также
для тех технических задач, для которых минимальные свойства со2
не могут быть обоснованы строго, и используем его как основание
метода Ритца при приближенном вычислении а1.
Метод Ритца тогда проводится уже описанным в § 15 и в заклю-
заключении п. 16.3 способом; составляют представление
р
Y=^iaivi, A6.20)
i-h
где at — постоянные, a vt — допустимые амплитудные функции. Вместо
того чтобы находить минимум отношения —Щг-, можно в соответ-
соответствии с правилом вариационного исчисления использовать требова-
требование (со2 = Я.)
J=Um^ — %T*= экстремум A6.21)
и далее составить уравнения метода Ритца в форме
-^- = 0, /=1,2 р. A6.22)
16.5. Изгибные колебания. Если при вычислении собственных
частот изгибных колебаний ферм, рам, стержней и т. д. пренебре-
жимы побочные влияния продольных колебаний, инерции вращения
и сил сдвига, то приведенная кинетическая энергия Т* и потенциаль-
потенциальная энергия U должны задаваться выражениями:
= I J p/V
ds, A6.23)
uds. A6.24)
При этом, как обычно, обозначаем: р плотность, F — площадь попе-
поперечного сечения, а —жесткость на изгиб, М—изгибающий момент,
s — длина дуги и, наконец, и — амплитуда (ранее обозначавшаяся
через К). Интеграл берется по всему телу, например, по всему стержню.
В качестве примера рассмотрим балку постоянного сечения, нагруженную
сосредоточенной массой М. Пусть длина балки 3 м. Конфигурация и размеры
системы показаны на рис. 16.2. Пусть М составляет две трети от общей
16.5]
§ 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА
249
массы балки, равной pFl. Выражения для A6.23) и A6.24) для энергий Т*
и f^max здесь имеют вид
J
= -2-J аи dx.
2
Подставляя M = -1r-pFlt из A6.19) получим
о
udx
_ о
Рис. 16.2. Изгибные колебания
опертой концами балки, на-
нагруженной сосредоточенной
массой.
Краевые условия здесь и @) = и" @) = и C)=и" C) = 0. В помещенной ниже
таблице в первой строке в качестве и приведена функция и = sin -9- х,
удовлетворяющая всем граничным условиям, которая для основного коле-
колебания дает меньшее, следовательно, более точное значение R [и], чем стоя-
стоящая во второй строке функция и=Ъх—л:2, удовлетворяющая только главным
краевым условиям и @) = и C) = 0. В третьей строке приведены результаты
двучленного, в четвертой строке трехчленного представления Ритцадля R[u]
и
Sin-5-ЛГ
о
Зх—х2
ах sin -5-Jf+
-f- а2 sin —q- л:
V* „• VJlx
v-l, 2, 4
Z
Jt О
"8T'T
12
re4
■8TX
X|K + I6al)
rt4 2 2
81 v*1 1 2 1
+ 256ai)
N
! , 2.1 _3
-jq + 2 • 4 =-Jq-
/222
\ 1 1 ^1 4'
-^-■0,5 = 0,60129
ТбТ = °'7453
*;.|A7±/я1)-
л4 f 0,49193
81 \ 10,84 ~
f 0,59159
~ 113,03
I 0,59097
| 12,94
{ 233
250
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[16.6
16.6. Пример. Крутильные колебания. В качестве следующего при-
примера ') будет рассмотрен вал кругового сечения с насаженными на него
дисками (рис. 16.3).
Ось х направим по оси цилиндра; жесткость при кручении С и момент
инерции в на единицу длины цилиндра пусть будут постоянны. В точках
х = It, /=1, 2, ..., п, насажены вращающиеся массы с моментами инерции
относительно оси, равными в^. Концевые точки х = 0 и х = / будем считать
,и— h—Ч
■If
в.
с, в
в"
Ш,
Рис. 16.3. Крутильные колебания вала с на-
насаженными дисками.
защемленными, а через <р (х, t) обозначим угол, на который откло-
отклоняется от положения равновесия сечение х в момент времени t; тогда для
ф (х, t) = Ф (х) sin &t приведенная кинетическая энергия может быть запи-
записана в виде
г г -,
r = i-\ |(ФМJе(х)^4-Увг(Ф(;())!
A6.25)
а максимальная потенциальная энергия будет
I
U ты = j
(Ф' (х) у dx.
A6.26)
(Здесь для общности написаны еще С (х) и Ф (х).)
Вводя
получают, согласно A6.21), соответствующую вариационную задачу (фигури-
рующее здесь X* отличается от Я, в A6.21) множителем —);
/ Г I п П
/* = Г (Ф' (х) J dx — X* I" (Ф (х) J dx -f- V D* (Ф (/(.) J = экстремум.
° ° '"' A6.27)
') Из-за разрывности производных (см. A6.28)) теоремы, сформулирован-
сформулированные в этой книге, не могут быть доказаны для рассматриваемого случая.
Это пример технического происхождения (см. п. 16.4), в котором все же
можно получить вариационную задачу A6.29) на основе метода Ритца.
В остальном изложенная в книге теория легко переносится на имеющиеся
случаи, подобные этому, см., например, замечания в конце этого пункта;
далее см. О. Temple, W. О. В i с к 1 е у, Rayleigh's Principle and its Appli-
Application to Engineering, London, 1933.
1в.в] § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 251
Так как концы считаются защемленными, в качестве главных краевых усло-
условий имеем Ф @) = Ф (/) = 0, при незащемленных концах было бы Ф' @) =
= ф' (I) = 0.
Далее учитывают переходные условия в точках х= 1^. В то время как Ф
непрерывно в точках х = 1[, Ф' делает там скачок. Условия скачка можно
получить непосредственно из уравнений движения для вращающихся масс в;,
можно их также получить из вариационной задачи в соответствии с мето-
методом п. 16.1; продемонстрируем это. Если подставить Ф = у -(- щ в A6.27) и
проинтегрировать по частям, то при /0 = 0, ln+l = l из-за
I " li+i п li+\ и
=2 J у'л'<*■* = -2 J
о / о /
получим в качестве множителя при е уравнение (первая производная при-
приравнивается нулю)
Г л (-У"-
\-у'
При этом уже использовано г| @) = г| (I) = 0, а у' (li — 0), соответственно
y'(/j-(-O), обозначает, как это принято, значение у' в точке lt при прибли-
приближении к ней справа и слева. Из последнего уравнения непосредственно
получаются дифференциальное уравнение — у" = Х*у и условия скачка
/ С/ + 0) - / ('< - °) = - *"D> (/;)■ A6.28)
Численный пример. Возьмем уже обсуждавшуюся в задаче 7
п. 3.4 систему (см. рис. 3.11). При этом /, = 1 м, I2 = 2llt [= I3 = 3lt.
Вводятся «безразмерные» величины
х = 1гЬ Di = -[^, <Р (Е) = У ft!), ф'A) = //(*), i.^i.*l\.
Тогда вариационная задача A6.27) будет иметь вид
з г з -|
У[ф]= f у'2 dl — ),\ Г Ф2^ + О,фA J + О2ф BJ = экстремум A6.29)
3 Г 3
0 Lq
с главными краевыми условиями
ф @) = ф C) = 0 A6.30)
и следующими из A6.28) условиями скачка:
A6.31)
Для случая D, = 1, О2 = 2 может быть применено следующее двупарамет-
рическое представление Ритца:
Я\1 ДЛЯ \ < 1,
(^i — а2) C — I) для 2<
252
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[16.6
Подставляя ф в A6.29), получаем уравнение относительно Л для вычисления
приближенных значений Я,:
J = 2 (а\ - аха2 + д|) - -^ (\4а\ - Па\а2
Уравнения -^— = 0, -=— = 0 тогда дают для -~- = ц
0 =
2 — 28ц 1 —17ц
= 3A — 18ц + 53ц*)
Л- ±
Л~" 53
Двучленное представление Ритца
1 — 17ц 2—16ц
1,6179 (ошибка +2,9%).
приводит к
. я „ , , 2л
= ах sin -g- g -f- a2 sin -y-
дающему худшие, чем в предыдущем случае, приближения
0,4330 (ошибка +4%),
1,8517 (ошибка +18%).
Представление Ритца с линейными функциями, проведенное вначале, лучше
описывает изломы кривой <р (см. рис. 3.12).
пред
_ (
Рис. 16.4. К замене функций фг, ортогональных
с весом, функциями ф/, ортогональными в обыч-
обычном смысле.
В случае распределенных и в случае сосредоточенных масс можно теорию
собственных значений построить в полном соответствии с гл. II и III, здесь
мы лишь приведем пример свойств ортогональности. Пусть Фг и ф^ — две
собственные функции — ф" = А<р, подчиненные условиям A6.30) и A6.31)
с различными собственными значениями, тогда можно вычислить
j9. A) Ф^ A)
B) ф^ B) = 0
16.71 § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 253
и характеризовать это соотношение как «ортогональность с весом». С по-
помощью отрезков длины Dv в которых функции <р. постоянны, можно соста-
составить функции ф., ортогональные в обычном смысле. Возникающее таким
образом из рис. 3.12 представление дано на рис. 16.4.
16.7. Энергетический метод для дифференциальных уравне-
уравнений с частными производными. Описанные в п. 16.4 энергетиче-
энергетические методы без всяких оговорок применимы и для дифференциальных
уравнений с частными производными. Мы поясним их на классическом
примере однородной мембраны толщины h и плотности р, совершаю-
совершающей поперечные колебания. Поверхность мембраны в состоянии покоя
покрывает односвязную область 23 плоскости (х, у); пусть мембрана
закреплена по периметру и равномерно натянута; это означает, что
если сделать произвольное сечение мембраны, перпендикулярное к ее
средней плоскости, то в плоскости сечения не будет напряжений
сдвига, а будет лишь всюду одинаковое нормальное напряжение о.
Если обозначить через z (x, у, t) отклонение мембраны из пло-
плоскости (х, у) в момент времени t, то получим, учитывая
z(х, у, t) — Z(x,
согласно A6.18) выражение для приведенной кинетической энергии
T* = \ph J \z\x, y)dxdy.
Потенциальная энергия U определяется увеличением площади мем-
мембраны !), т. е. при малых отклонениях посредством выражения
Круговая частота со, соответствующая собственному колебанию Z(x, у),
задается тогда, согласно A6.19), выражением
A6.32)
J J
Z2 (x, у) dx dy
!
Краевое условие Z =0 на контуре Г позволяет записать интеграл
в числителе в виде (согласно преобразованию п. 6.2 для р=1, q = 0)
— j J ZbZdxdy, A6.33)
') S. T i m о s h e n k о, Swingungsprobleme der Technik., Berlin, 1932.
[С. Тимошенко, Колебания в инженерном деле, физматгиз, 1959.]
254
где
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
116.7
Д =
а2
дх2
д2
ду2
— оператор Лапласа.
Если вид функции собственного колебания неизвестен, можно,
как в A6.20), A6.22), вычислить круговую частоту с помощью метода
Ритца.
Пример. Эллиптическая мембрана1). Пусть контур мем-
мембраны Г описывается эллипсом (рис. 165)
J-2
Рис. 16.5. Эллиптическая мембрана.
Собственные колебания Z (х, у) мо-
могут быть представлены с помощью
функций Матье, т. е., вообще говоря,
сложным образом. Приближенно соб-
собственные значения можно здесь опре-
определить с помощью трехчленного пред-
представления Ритца
з
Z = 2 aivi (*. У)-
1=1
В качестве г>; (х, у), если рассматривать лишь симметричные относительно
осей хну обращающиеся в нуль на Г собственные функции, используем
следующие функции:
г>! (х, у) = 4 — х2 — 4у2, i»2 (х, у) = x2vx (х, у), v3 (х, у) = y2v{ (х, у).
Тогда AZ = — 10а, -f 4 B — 5*2 — 2у2) а2 + 2 D — х2 — 25у2) а3. При прове-
проведении метода появляется интеграл I x2my2m dx dy. На основании симмет-
рии можно для всех интегралов ограничиться заштрихованной на рис. 16.5
областью Е эллипса. Тогда интегралы
х2ту2п dx dy
легко вычисляются:
«00 = 72. «02 :
I = 7г5б>
«20 = 7
«40= 1. «42 = 78,
«60 = 6А>, «62 = 74,
«80 = 7.
«22 = 7l2, «24 = 7з2, «26 = 7б4.
«44 =
С помощью этих интегралов можно
J = _ Г Г (Z AZ) dx dy — к Г Г Z2 dx dy
') Е. Trefftz, Ober Fehlerabschatzung bei Berechnung von Eigenwerten-
Math. Ann. 108 A933), 595-602.
16.9]
§ 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА
255
выразить через аь а2, а3 и получить из условия совместимости A6.22) урав-
уравнение для Л, дающее приближения собственных значений к:
10 —8/3Л 20/з-4/зЛ 5/з—7зЛ
го/3-4/3Л 46/з-8/5Л 5/б-2/15Л
5/з-7зЛ 5/б-:
Заменяя 2Л = 5 B — v), получаем
— 1 -f2v v v
5v 11 -J-6v l+2v
l
ЛоА
=0.
= 4 Fv3 -f 73v2 -[- 124v — 96) = 0.
5v l+2v 35-f6v
Решая это кубическое уравнение, находим
Л =
3,5692,
12,045,
29,803.
При проведении метода Ритца с двучленным представлением, при котором
отбрасывается член с v3 (x, у), получается
Ю —8/3Л2о/з
20
^7Л46/
«/3Л
= 0
и отсюда
16.8. Проблема потери устойчивости. Для этих задач также
можно получить подлежащие минимизации выражения и, с помощью
энергетического подхода, установить возможность применения метода
Ритца, однако входить в детали мы здесь не будем ')•
16.9. Графическое проведение метода Ритца. Метод Ритца
во всех случаях, когда в согласии с п. 13.6 можно провести гра-
графически метод последовательных приближений, точно так же удобно
реализовать графически. Это имеет место в таких важных случаях,
когда уравнения имеют вид A3.18) или A3.19):
О6-34)
) = lN[y]. A6.35)
В дальнейшем мы ограничимся уравнениями A6.34); в случае урав-
уравнения A6.35) поступают вполне аналогично. В п. 13.6 было показано,
') В задаче о продольном изгибе прямого стержня метод применен
в работах: J. Ratzersdorfer, Die Knickfestigkeit von Staben und Stab-
werken, Wien, 1936; K. Marguerre, Ober die Behandlung von Stabilitats-
problemen mil Hiife der iinergetischen Methode, Z. angew. Math. Mech. 18
A938), 57-73; DVL-Jahrbuch, 1938, 252—262.
256
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[16.10
как с помощью только интегрирования (избегая графических
дифференцирований) можно составить две функции F0(x) и Z7, (х),
которые удовлетворяют условиям метода последовательных приближе-
приближений и для которых, в частности, справедливо
MlF1] = H(x) = (-l)a[ga(x)F£)f). A6.35)
При использовании р-членного представления Ритца A5.7)
р
u=^arvr(x), A6.36)
r = I
метод последовательных приближений проводят р раз (с линейно
независимыми функциями) и составляют функции /""ofi), ^0B). •••. ^о(р).
/^(i). ^iB) ^i(p)- Mi)- ^B) Мр)! эти Функции связаны
друг с другом соотношениями
=1' 2.
Р.
и удовлетворяют необходимым краевым условиям. В соответствии
со сказанным выше это возможно благодаря численному интегри-
интегрированию.
Далее, функции F\(r) можно использовать в качестве исходных
функций vT{x) в представлении Ритца A6.36) и определить посред-
посредством численных или графических квадратур величины A5.9)
ь
A6.37)
Подставляя эти величины в A5.15), получим уравнения для опреде-
опреде/}!!
во ВТО"
ления приближений Ритца Л. Дифференцирование [
ром уравнении A6.37) только кажущееся, так как в п. 13.6 было
описано, как можно, исходя из высших производных Fi™\, получить
все низшие производные F^s) с v < 1т с помощью интегрирования;
выражение [g"^!"!]'"' можно, следовательно, найти из уже имею-
имеющихся F^s) без дифференцирования. Пример приведен в п. 16.10.
16.10. Графическое получение уравнений Граммеля. В п. 13.7
было показано, что в методе последовательных приближений при
получении верхних границ ц, и [i2 и нижней границы для первого
собственного числа X,j во многих случаях можно, проделав вдвое
меньшую работу, составить верхнюю границу [X,, точность которой
достаточна в технических задачах, особенно если исходные функции
подобраны удачно.
16.10] § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 257
Это соответствует тому, что в этих случаях при проведении ме-
метода Ритца точно так же (во всяком случае, что касается составле-
составления уравнений Ритца) можно сократить работу, минимизируя, как
в п. 15.1, не \i2, a \iv Тогда получают уравнения Граммеля A5.30).
Поясним это, как и в п. 13.7, на примере изгибных колебаний
защемленного на одном конце стержня (с теми же обозначениями,
что и в п. 13.7)
у @) = /@) = /(/) =/"(/) = ().
Исходя из р линейно независимых функций Fo(r), г—1, 2 р
удовлетворяющих главным краевым условиям
Fo (Г) = Fq (п = 0 для х = 0,
определяют графически при помощи р веревочных многоугольников
функции G(r) из
G(r) = pFFoif), G(r) = G('n = 0 для х = 1.
Для уравнений Галеркина A5.14) еще раз вычерчивают р веревоч-
веревочных многоугольников и определяют F\ (г) из
К(г)=-^)"О(Г), Fi (г) = F[ (г) = 0 для * = 0.
Для уравнений Граммеля A5.30) нужны только первые р веревоч-
веревочных многоугольников и не нужны функции F\ (r), так как величины
mQ и «Q уже выражены через FQ } и G Если заменить vr(x)
на Fur), то получим, согласно A5.28) и A5.29),
— J
0
/
'ur)G(s)dx =
i i
= j f'[ (r)G(s) dx == j — G{r)G{s) dx.
и о
Следовательно, можно составить уравнения Граммеля A5.30).
Сравнительно легко определить также функции Ft (rj при помощи
построения последующих веревочных многоугольников, так что
по A5.9) можно найти величины
/ i
"irs = J pFvrF0 (s) dx - Bg, nrs = J pFvrv6 dx
о о
17 Л. Кпллатц
258
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
{16.10
и, решая A5.15), получить те же значения, что и при решении
по A5.30).
Пример. Рассмотрим тот же пример, что и в п. 13.7 (см. рис. 13.8),
а именно, изгибные колебания защемленного на одном конце стержня
F*i
Рис. 16.6. Пример графического проведения метода Ритца.
с переменной жесткостью на изгиб. Соответствующее (записанное в безраз-
безразмерном виде) дифференциальное уравнение A3.25) имеет вид
(а*у")" = K'F'y,
Показанные на рис. 16.6 функции a*, F* перенесены из рис. 13.8, функции
Fo (I), G (I) и F, (I) рис. 13.8 будут дальше использоваться в качестве
функций FOb, О',.' и f, и. Возьмем теперь дь> членное представление
16.10)
§ 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА
259
Ритца; для этого применим еще раз графическое интегрирование с другой
фй Ру Функции Fo ,2) и Fo A) должны быть линейно независимыми
функцией ) (
и первая из них на рис. 16.6 задана произвольно так, как представляют
первое высшее колебание. Совершенна не требуется, чтобы Fo B) переда-
передавало форму высшего колебания; в действительности графическое построение
показывает, что Р^л) имеет заметную компоненту в направленли первого
собственного колебания (основного тона); конструируемая с помощью Fq,^
функция Fl B, по своей форме близка к основному колебанию, в частности,
F1m\ не имеет больше нулевых точек на отрезке 0 < | < 1.
Первый веревочный многоугольник дает функцию О2 (£)'• смысл построе-
построения и масштаб те же, что и в примере п. 13.7. Теперь могут быть соста-
составлены уравнения Граммеля. Из п. 13.7 возьмем величины
тО = ай = 1,337, nfj = я, = 0,0620.
Заново определим численное значение интегралов (вычисленных здесь по
методу Симпсона)
1
= J ^0 A)^
„а
Ч12
0 B)
?(DGB) '
г-i С * 1
— 0,174, m22J = J F F'o Bj dl = 1,678,
о
i
1,0151, ng = j --rG
= 0,00642.
Из уравнений Граммеля тогда получаем
1,337 —0.0620Л —0,174 —0.0151Л
— 0,174 —0.0151Л 1,678—0.00612Л
= 0
и отсюда
19,3,
Г 19,3
= {б74.
Интегрируя G.2) с помощью второго веревочного многоугольника, найдем F} (-,y
теперь можно составить уравнения Галеркина A5.15). Для этого, кроме уже
известных величин mrs = л^ (г, s = l, 2) и ип = я2 = 0,00322, заново вы-
вычислены интегралы
i i
я,2 = J F*FX (})Fl B) dg = 0,000824, п,л = J F*F\ B) dg = 0,000216.
Тогда из уравнений A5.15)
0,0620 — 0,003220Л 0,01510 — 0ДЮ824Л
0,0151 — 0,000824Л 0,00642 — 0,000216Л
0 =
и отсюда
Л =
19,20,
535,0.
17*
260
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[16.11
16.11. Упражнения. 1. Вычислить приближенное значение собственной
частоты основного тона и первого высшего для изгибных колебаний балки,
изображенной на рис. 16.7 (см. также задачи 5, 6 п. 3.5). Как и в п. 3.5,
введем сокращение
й£ 4 г'.
Тогда получим
■1г=2м-
К
dx
Рис. 16.7. Изгибные колебания за-
защемленной на одном конце балки
с двумя опорами.
= inin ■
J-
dx
где и пробегает область допустимых функций, т. е. удовлетворяет краевым
условиям (рис. 16.7):
и @) = и B) = и C) = и1 C) = 0,
и' B) непрерывна.
Расчет. В качестве двух допустимых функций возьмем, например,
ях „ 2лх , . Зялг . \пх
v, = sin —тг 2 sin—г \- sin —-; sm—^—,
О 0 0 6
. ях . с, . Зял: . . 5ях
v2 — sin -,—(-2 sin—^ (-sin fi
Если принять
и учесть, что
и = c,v, -\-c2v2.
315я
J
. кях . 1пх ,
sin —j— sin —r^- dx =
О для k — / четных, k Ф I,
■у ДЛЯ k = /,
Г *-/-! к + 1-i
(-1)
(-1)
я
k — l
то A5.15) дает
402 — 552а — ц G — 12а) 163 — 940а — ц C — 10а)
163—940а —цC—10а) 950 —6ц
откуда получаем
146,74,
1775,0
для k — / не-
нечетных,
= 0,
_ С
1,8224 (ошибка -f-0,7%),
3.3990 (ошибка + 3,0%).
2. Применить для приведенного в конце п. 15.1 примера
~у" = ку, / @) ~ у A) = 0
16.11)
§ 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА
261
двучленное представление Ритца
и = a,w, (х) + a2v2 (x)
с функциями сравнения г», = 1 — х2, v2 = 1 — л:3.
Результат. Уравнение A5.15) для этого случая имеет вид
!± _8_д
3 15
12
9 .
Л
= 0
и его корни
2'4в8Ю
Л = 6/65 A41 ±/13056) = \ *'™W ^иика+О.ОЗ*),
' . I 23,563 (ошибка+ 6,0%).
3. Вычислить для отдельных допустимых функций отношения Рэлея и
применить двучленное представление Ритца для случая продольного изгиба
шарнирно опертого с одной стороны и защемленного — с другой стержня
(рис. 12.3, стр. 188) с переменной жесткостью на изгиб
[B- х) у"]" = - Ху", у @) = у' @) = у A) = у" A) =0
(см. пример 2 п. 12.6).
Результат. Согласно A5.2) отношение
1
B —л:) u dx
1
u'2dx
задано в следующей таблице для некоторых функций и:
Функция и
х* — х3
Зх2 — 5л:3 + 2л:4
sin пх —jj- sin 2ял:
Выпол-
Выполнение
краевых
условий
только
главные
все
все
Числитель
Z*
5
57
5
-СГ-?)
Знаме-
Знаменатель
N*
2
15
12
35
л2
7*
*«1=-^5-
f = 37,5
(ошибка+ 28%)
ifl = 33,25
(ошибка +13%)
15 32
"Т "9"= '
(ошибка +14%)
Представление Ритца и(х)^ alvl(x)-\-a2v2(x) с удовлетворяющими
только главным краевым условиям функциями
V, (х) = а:2 — л:3, v2 =■ л:3 — ^4
262
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[16.11
в соответствии с A5.27) приводит к
2 . 23
23
1
27 3
5Л
= 0,
откуда
Рассмотренные здесь представления еще очень грубы, и полученные
результаты хуже, чем в п. 12.6.
4. Для рассмотренной в примере 4 п. 14.6 задачи (см. рис. 14.2, стр. 217)
_ у" = X B -f cos х) у, у @) = у (я) = 0
ввести п-членное представление Ритца
л
sin
v-1
Результат. Здесь
[и'2 _ я B -f cos *) и2] их = ^] (v2 - 2Л) а2 -
0 v=l v-1
и уравнение A5.15) после отбрасывания постоянных множителей примет вид
2 —4Л — Л 0 ... 0
— Л 8—4Л —Л ... 0
0 _ Л 18 —4Л ... 0 =°-
0 0 0 ... 2л2 — 4Л
При п ->• оо можно перейти к уравнению, полученному в п. 25.6 методом
цепных дробей. По рекуррентной формуле
Fn=Bn2_4A)/V,-A2/V2, я = 3, 4, 5, ...
можно вычислить полиномы высоких степеней Fn и исследовать сходимость
приближений Ритца. Для я<4 получим следующие приближенные зна-
значения.
Приближенные значения при n-членном представлении Ритца
л
1
2
3
4
Для /.,
0,5
0,490059
0,49003570
0,49003562
Для ?.,
2,17660
206120
2,05936
Для Хъ
.—
5,09162
4,67187
Для 1,
_
—
—
9,3529
Из таблицы видно, что, вообще говоря, высшие приближенные значения
получаются неудачно; следовательно, например, для того чтобы получить
приближение для собственного значения Я3, необходимо не трехчленное,
16.11J § 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА 263
а по меньшей мере четырехчленное представление Ритца. Однако можно
при вычислении высших собственных значений избежать дополнительных
вычислений, связанных с увеличением числа свободных параметров, если
использовать представление, которое требует ортогональности к низшим,
уже вычисленным с определенной степенью точности собственным функ-
функциям. Пусть в рассматриваемом примере в качестве приближения первой
собственной функции у, получена функция К,:
V, = sin х + е sin 2х, е = -j (/То — 3) = 0,0081139;
применим теперь две функции представления
и, = а, F sin х + sin 2х), и2 = а2 sin Зх,
которые удовлетворяют условию ортогонализации
л
f B + cos х) Г, (х) uj (x) dx = 0 для ] = 1 и 2.
и
I + 4е
Это дает 6 = -——= — 4е = —0,324556. Получаемое с этим предста-
влениеы уравнение
262 + 8 — Л D62 + 26 + 4) — Л
— Л 18 —4Л
дает
2,06122,
5,0892,
т. е. приблизительно такую же точность, как трехчленное представление без
обращения к ортогонализации ').
5. Для задачи на собственные значения
ввести представление Ритца
V-1
для колебаний симметричной формы.
Результат. Для р = 1 получаем с и — I —х2 отношение Рэлея
^ = 4 = 2,5.
Для р = 2 приближенные по Ритцу собственные значения будут следующие:
= 0
при точных значениях
А,, = -^- = 2,46740110027, 12 =-- -^-р = 22,206610.
') См. VV. J. D u n k a n, D. D. L i n d s а у. Methods for Calculating the
Frequencies of Overtones, Reports and Memoranda № 1888 D207), Aeronau-
Aeronautical Research Commitee, 1938.
264
ГЛ. V. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МИНИМАЛЬНЫХ СВОЙСТВ
[16.11
При трехчленном представлении (р — 3) получаем, положив Я=—«-t-,
кубическое уравнение для \х |а3+210|л2+6735|а=440 и для Я, исключительно
хорошее значение Xf = 2,4674011087.
6. Решить с помощью представления Ритца и = atx2-\-а2хг пример
yiv = Ху, . у @) = у' @) = у" A) = у'" A) = 0.
Результат. Корни уравнения
[--t-A 6 — -i-Л
5 6
Л2
1260
,0
получаются следующие:
_ Г 12,4802 (ошибка + 1 %),
А = ( 1211,52.
7. Для обсуждавшегося в задаче 5 п. 11.4 и задаче 5 п. 14.6 сжатого
стержня введем удовлетворяющее всем краевым условиям представление
Ритца
yiV+20y = — Ху", у (± 1) = у"(± 1) = 0,
и = а, E — б*2 + х4) + а2 (9х2 — 14а-4 + 5хв).
При обозначении pi = — Л получим для |х уравнение
8899 — 561ц 2014—121ц
2014 — 121(А -рз- • 17911— 281ц
= 0
Г 10,
■= I 24;
10,5730968 (ошибка +0.00001%),
24,036371 (ошибка +0,4%).
Если бы пример решался только с а,, то отношение Рэлея дало бы результат
Л = -^- = 10,57516 (ошибка + 0,02%).
loo
8. Для задачи
yiv + АЦ1- х) у']' = Ху, у @) = у' @) = у" (/) = у'" (/) = 0
применить представление Ритца и = atx2 + агхъ и сравнить значения, по-
полученные для .Л = 2, I = 1 с соответствующими результатами задачи 7 из
п. 14.6.
Результат. Корни уравнения
/3 + Л/4 б
дадут приближения собственных значений
Л = 1. (8С - 102 ± J/9984 - 1072С + 29С2),
16.11]
§ 16. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДА РИТЦА
265
здесь обозначено С — -ут- АР; для А = 2, I = 1 получается
9,31706
. 1195,5.
9. Для задачи
yiv = Ху, у @) = у' @) = у" A) = у'" A) = 0
ввести нелинейное, удовлетворяющее главным граничным условиям пред-
представление Ритца
и = 1 — cos ах.
Результат. Имеем
" dx
о a4 Ba + sin 2a)
\«
— 8sina-fsin2a'
Подставляя вместо а разные значения, например а=1, 2, 3, получают при
интерполяции наименьшее значение R для а и 1,85 и соответствующее
R= 12,89 (ошибка +4%).
10. Применить метод Ритца к интегро-дифференциальному уравнению ')
+ i
— 20y"-\-k ( у dx = l(l—x2) у, у (± 1) = /'
= 0.
-1
Решение. В отношение Рэлея
R[u] =
r I V Y
(u + 20u'u)dx + k\ udx)
-l V-i /
+ 1
= min
-l
вводится представление и = A—хг) (а -|- Ьхг) и получается
23 , 2 16
Т^Х 105
^-k -La
45 315Л
72 8 661 2
~3~ + 5 Й~15 Т05+25й
32
3465
Л
= 0;
для k = 200
331,73,
1165,7.
') К. KlOppel, К- Н. L i e, Lotrechte Schwingungen von Hangebrucken.
Ing. Arch.,13 A942), 211—266.
ГЛАВА ШЕСТАЯ
ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
В этой главе в большей степени, чем в других, у читателя пред-
предполагаются знания математики и навык математического мышления.
Последующее изложение не является введением в теорию матриц,
а должно лишь показать тем, кто уже немного знаком с матрицами,
аналогию между задачами на собственные значения для дифферен-
дифференциальных уравнений, интегральных уравнений и матриц.
Так, будут предполагаться известными основные понятия элемен-
элементарной матричной алгебры, такие, например, как понятие произведе-
произведения двух матриц, квадрата матрицы 212, произведения двух квадрат-
квадратных матриц, обратной матрицы Я и т. д. *). Предполагается также,
что понятие ортогональности, эрмитовости и унитарности частично
знакомы читателю; однако определения этих понятий будут в краткой
форме даны еще раз. Почти всегда будут рассматриваться комплексные
матрицы, хотя для многих приложений можно было бы ограничиться
матрицами с действительными элементами. Но как раз в последнее
время комплексные матрицы появились в различных областях прило-
приложений, например, при исследованиях устойчивости линейных коле-
колебательных систем со сдвинутыми по фазе силами, в квантовой физике,
и т. д., так что в основу изложения для общности положены комп-
комплексные матрицы. Кроме того, благодаря этому изложение становится
значительно более законченным. Однако тот, кто интересуется только
действительными матрицами, может каждой теореме, сформулирован-
сформулированной для комплексных матриц, легко сопоставить соответствующую
теорему для действительных матриц, используя тот факт, что для
действительных матриц совпадают понятия симметричности и эрми-
эрмитовости и понятия ортогональности и унитарности. Впрочем, пони-
понимание материала должны облегчить приводимые примеры.
*) Подробнее о матрицах см., например, Ф. Р. Г а н т м а х е р, Теория
матриц, изд. 2, «Наука», 1966; А. П. Мишина и И. В. Проскуряков,
Высшая алгебра, СМБ, изд. 2, «Наука», 1965; Д. К. Фаддеев, В. Н. Фад-
Фаддее в а, Вычислительные методы линейной алгебры, изд. 2, Физматгиз, 1963.
17.1]
§ 17. ОСНОВНЫЕ СВЕДЕНИЯ
267
§ 17. Основные сведения о задачах на собственные значения
для матриц
17.1. Обозначения. Матрицы мы будем обозначать готическими
буквами, например
а также сокращенно: 21 = (а;й). Элементы матрицы могут быть как
действительными, так и комплексными. Если все ujk действительны,
матрица называется действительной, в противном случае —комплексной.
В дальнейшем мы будем рассматривать только квадратные ма-
матрицы, т. е. матрицы, у которых совпадают число строк и число
столбцов. Нам, кроме того, встретятся матрица-строка (я=1) и
матрица-столбец (т. = 1). Оба последних типа матриц мы будем также
называть векторами и обозначать строчными готическими буквами.
Матрица, получающаяся из 21 заменой строк столбцами (для
квадратной матрицы — отражением относительно главной диагонали),
называется транспонированной (или «отраженной») относительно 21
и обозначается штрихом:
ап а21
а,
22
|, или, короче, %' = (akJ).
а1т •••
Так, например, матрицы
Г -—
2, .... Хп)
A7.0
транспонированы друг относительно друга.
Замена в матрице 21 всех элементов а1ь комплексно сопряжен-
сопряженными ajk коротко обозначается чертой над 91:
Квадратную матрицу 6 называют единичной матрицей я-го пот
рядка, если все элементы главной диагонали равны единице, а осталь-
остальные равны нулю:
1 для j = k,
где б.-ь =
О для J Ф к.
268 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ П?-2
Квадратную матрицу называют вырожденной (соответственно
невырожденной), если ее определитель
det9l = |c;j
равен нулю (соответственно не равен нулю). Для каждой невыро-
невырожденной матрицы 91 существует обратная ей однозначно определенная
матрица 9Р1 такая что
матрица 9Р1 такая, что
Имеют место следующие соотношения:
—i _ A7.2)
', (9t) = (t)~1, j
справедливые для любых квадратных матриц; последние три равен-
равенства верны при дополнительном условии невырожденности 91 и 58.
17.2. Матрицы с особыми свойствами. Матрица 91 называется
симметричной, если она равна своей транспонированной, т. е. если
она при зеркальном отображении относительно главной диагонали
переходит сама в себя: 91 = 91'.
При переходе к комплексным матрицам оказывается, что большее
значение имеет понятие «эрмитовой» ') матрицы, а не «симметричной»,
а именно, матрица 91 называется эрмитовой, если она при транспо-
транспонировании переходит в комплексно сопряженную:
91'= 91 или также 91' =31;
следовательно, попарно симметричные относительно главной диаго-
диагонали элементы матрицы комплексно сопряжены друг другу, а на
главной диагонали стоят только действительные числа. Например,
матрица
/2 1 + ЗА
91 = 1 I эрмитова.
\1 61 1 /
В действительной области понятия симметричности и эрмитовости
совпадают.
Матрица 91 называется кососимметричной (антисимметричной), если
91 = —31',
если, следовательно, при отражении относительно главной диагонали
матрица переходит в саму себя, умноженную на —1; на главной
диагонали тогда стоят нули.
') Ш. Эрмит (Charles Hermitе) родился 24 декабря 1822 г.
в Лотарингии. Его основные работы посвящены теории чисел, алгебре, эл-
л.шгическим и другим специальным функциям. Особенно известно его дока-
доказательство трансцендентности числа е. Умер в 1901 г.
17.31 § I?. ОСНОВНЫЕ СВЕДЕНИЯ 269
Матрица 21, обладающая свойствами
%=- 21' или 31' = —t,
называется «антиэрмитовой»; у антиэрмитовой матрицы на главной
диагонали стоят чисто мнимые числа (или нули); например, матрица
0 1 + ЗЛ
1 + 3/ -2t) антиэРмитова-
Матрица 21 называется инволютивной, соответственно полуинво-
лютивной, если ее квадрат 212 равен единичной матрице 6, соответ-
соответственно — Й. Для полуинволютивной матрицы 214 = (§.
Матрица 21 называется ортогональной, если
2Г=2Г1 или, следовательно, 2121' =Щ'21 = @.
Понятием, имеющим в комплексной области такой же смысл,
как ортогональность матрицы в действительной области, является
понятие унитарности матрицы. Матрица 21 называется унитарной, если
27' = 2Г\ или 2l2T' = 2l'2X = (S.
Так как модуль определителя матрицы 21 не изменится, если перейти
к комплексно сопряженной матрице 21 или к транспонированной
матрице 21', то из
det 21 det 21' = 1 или det 21 ■ det Я' = 1
следует, что как ортогональная, так и унитарная матрицы имеют не
равный нулю определитель с модулем 1.
Названные здесь свойства позволяют составить «звезду свойств»
такую, что соединенные по три одинаковыми линиями свойства неко-
некоторой матрицы связаны между собой в том смысле, что из любых
двух с необходимостью вытекает третье; например, связаны вместе
действительность матрицы, ортогональность и унитарность, или орто-
ортогональность, полуинволютивность и кососимметричность и т. д.
(см. рис. 17.1).
В таблице VIII сопоставлены названные здесь свойства и приве-
приведены соответствующие примеры.
Для дальнейшего примем, что матрица называется нормальной, если
ЭЩ' = Ш"$Х. Все эрмитовы, кососимметричные и унитарные матрицы нор-
нормальны.
17.3. Квадратичные и эрмитовы формы. Мы разовьем неко-
некоторые понятия, руководствуясь геометрическими представлениями для
симметричных матриц, а затем дадим определения для произвольных
матриц.
270
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
117.3
В аналитической геометрии рассматривают общие уравнения кри-
кривых (я=2) и поверхностей (и—3) второго порядка в прямоугольных
Ннео-
лютиеные
матрицы
'Эрмитовы
матрицы
у
ЧСимметртны
1 матрицы
21=21'
зональные
матрицы
Лнти-
эрмитавы
матрицы
ar=-af'
Циста-
мнимые
матрицы
Рис. 17.1 Звезда свойств матриц.
координатах хх, х2,
= 1, ajk =
A7.3)
С помощью матричного произведения это уравнение можно за-
записать как матричное уравнение
причем 31 — симметричная матрица данных коэффициентов 21 =(a;-ft) =
= (akJ), а х/ и г имеют тот же смысл, что и в A7.1). Предпола-
Предполагается, что 21 невырождена.
17.31
§ 17. ОСНОВНЫЕ СВЕДЕНИЯ
271
При этом особый интерес представляет нахождение главных осей,
т. е. таких векторов % кривой или поверхности, которые параллельны
нормали it в точках пересечения с поверхностью (кривой), п||г
(рис. 17.2). В качестве компонент вектора нормали можно, согласно
известным теоремам, взять компоненты градиента Q:
= @9- М. dQ )
' с, дх2 ' дхп)'
grad С,
или, учитывая
dx;
xk, J=\. 2, .... я,
■4kAk
k-\
так как множитель 2 не изменяет направления нор-
нормали:
In
и' = 2
\
k=\
2 <hkXn 2 ankxk .
Рис. 17.2. К опреде-
определению главных осей
(Согласно A7.1) матрицу-строку мы обозначаем и'.) Для главных
осей должно быть n||j или
п = «5 A7.4)
с множителем пропорциональности %. Более подробно:
в матричной форме эти уравнения означают
SVfv v» /1 7 Ч\
г, G' \ '*-*
Это п линейно независимых уравнений для хх, х2 хп; необхо-
необходимое и достаточное условие существования нетривиального решения
j;- — равенство нулю определителя матрицы коэффициентов
— ^ «12 ••• «1«
«21 «22 — * • • • «2л
Ф (%) = det (Я — %s) =
■*я1
= 0. A7.6)
Корни щ, %2 и„ этого алгебраического уравнения, которое
называется «характеристическим уравнением матрицы 91» или также
«вековым» уравнением, называются «характеристическими числами»
матрицы 21. Уравнение A7.6) применяется также для определения
характеристических чисел несимметричных "и произвольных комплекс-
комплексных матриц.
272 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ 117-3
Для дальнейших определений матрица 31 не обязательно должна
быть симметричной; только применительно к поверхностям второго
порядка матрица 31 будет предполагаться симметричной.
Обратные величины Xs —— называют «собственными значениями»
матрицы 31 *), они являются корнями уравнения
det (Ж — й) =
ги — 1
Хап1 ка„2 ... ка„„ — 1
= 0. A7.7)
В то время как уравнение A7.6) для % всегда имеет степень п, урав-
уравнение A7.7) для X только для невырожденных матриц имеет степень п.
Иногда говорят, что у вырожденных матриц появляются собственные
значения Х = оо.
Вектор £, являющийся решением A7.5), в случае, когда его ком-
компоненты не все равны нулю одновременно, называется «собственным
вектором» матрицы 31.
Каждый собственный вектор ^ принадлежит определенному характе-
характеристическому числу %s, в то время как каждому характеристическому
числу %s принадлежит по крайней мере однопараметрическое семей-
семейство пропорциональных друг другу собственных векторов. Из этого
семейства можно выбрать два отличающихся лишь знаком различных
«нормированных» собственных вектора. При этом вектор называется
нормированным, если
2
= 21 Xj p =
Если имеется q связанных с собственным числом %г линейно не-
независимых векторов, то говорят, что %г имеет кратность q (^-кратно
вырождено)').
Для поверхности второго порядка характеристические числа свя-
связаны с главными осями as.
Из семейства собственных векторов выберем вектор £s, соответ-
соответствующий точке на поверхности:
S'2l5=l.
и если эта точка находится на расстоянии а от начала координат
*) Обычно собственными значениями называют Щ.
') Это приведенное здесь определение удобно для эрмитовых матриц;
для произвольных матриц кратность характеристического числа определяют
по кратности корня х,г уравнения A7.6) (это может давать другое число
кратности).
17.3] § 17. ОСНОВНЫЕ СВЕДЕНИЯ 273
то из A7.5) следует
и, = -у = Т-- О7-8)
as ^s
Таким образом, собственные числа равны квадратам длин главных
осей. Положительные характеристические числа означают действитель-
действительные главные оси. Характеристические числа кратности два появляются,
например, в случае эллипсоида вращения.
В комплексной области квадратичным формам соответствуют эрми-
эрмитовы формы
п
H=^iaJhxJxk. A7.9)
где должно быть a;-ft —aft;-, в остальном а^ и Xj могут быть произ-
произвольными комплексными числами; тогда можно коротко записать
Следовательно, 21 предполагается эрмитовой матрицей 51'=51. Такая
эрмитова форма для произвольных комплексных векторов принимает
всегда только действительные значения; поскольку Н есть просто
число, т. е. матрица из одного элемента, равная, очевидно, своей
транспонированной матрице, то, согласно A7.2), имеем
н = н' = (ъ'щу = j'a'j. A7.Ю)
Если образуем комплексно сопряженное к Н' число Н = Н' =
= (j'5l/;i;) —Е'^% то с помощью равенства 21 =51' получим Н = Н,
т. е. И — действительное число.
Пусть И может быть положительным числом только при г/х, > 0
и, следовательно, Я = 0 только при £ = 0, тогда эрмитова форма и
принадлежащая ей матрица называются «положительно определен-
определенными». Соответственно Н и 21 называются «отрицательно определен-
определенными», когда
f<0 для foX).
j = о для ~gi = 0.
Если Н может принимать оба знака, то Н и 21 называют «не-
«неопределенными». При Н^-0 для всех % (Н = 0 для некоторых
векторов jc, при х'л > 0), Н и 21 называют «положительно полуопре-
делемными»; соответственно объясняется понятие «отрицательная полу-
полуопределенность».
Матрица называется положительной, когда все ее элементы по-
положительны; положительно определенная матрица не обязательно
18 Л. Коллатц
274 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [17.3
/2 —1\
положительна, например, 91—1 ) положительно определенная,
/1 2\
но не положительна. Наоборот, матрица 91=1 I положительна, но
не положительно определенная.
В различных приложениях возникают следующие задачи на соб-
собственные значения для матриц:
1. Частные задачи на собственные значения
Задана матрица 91, требуется найти характеристические числа к, для
которых уравнение имеет нетривиальное решение £.
2. Промежуточная задача
91jc = k£>jc. A7.11)
Кроме матрицы 91, задана еще диагональная матрица 55, у которой
не равны нулю только элементы главной диагонали:
'dx О ... О
О d2 ... О
О 0 ...dn
Кроме того, предполагается еще dj > 0. Тогда можно с помощью
диагональной матрицы
0 ... 0
0 УТ2... 0
о о утя
у которой все корни выбираются положительными, свести задачу
к частной задаче на собственные значения для ty = 5) j:
% 'А9 = »«9. A7.13)
при этом S эрмитова, если эрмитова 91.
3. Общая задача на собственные значения
A7.14)
Здесь задаются две матрицы 91, 33. Характеристические числа
X], к2, ..., кя, для которых A7.14) имеет отличные от нуля соб-
17.41 § 17. ОСНОВНЫЕ СВЕДЕНИЯ 275
ственные векторы в качестве решений, являются здесь корнями
«характеристического уравнения»
«11 — 5**11 «12 — **12 • • • «1я —
««1 - *Ьп\ ап2—%Ьп2 • • • «ял —
=0. A7.16)
17.4. Вещественность характеристических чисел. Пусть для
общей задачи на собственные значения A7.14) 91 и 33 — эрмитовы
матрицы. Допустим, что задача имеет характеристическое число х и
принадлежащий ему собственный вектор jc. Умножим обе части урав-
уравнения слева на j':
Согласно A7.10) обе части этого уравнения действительны, так как 21
и 23 по предположению эрмитовы. Если матрица 23 положительно
определенная, то j'23j Ф 0 и из
I L=l3- A7.16)
следует, что х тогда тоже должно быть действительным. Через R [£]
обозначено отношение Рэлея, которое будет использовано ниже.
Разумеется, если вместо 23 положительно определенной является 21,
то можно перейти к обратным величинам и заключить, что все имею-
имеющиеся характеристические числа действительны, может быть, беско-
бесконечны. Аналогично получается, если 21 или 23 отрицательно опреде-
определены. Но если 21 и 23 неопределенны, то может случиться, что для
какого-то собственного вектора х'Щ = i;'23j = 0 и х не действительно.
Приведем простой пример.
'—I 0\ /I 21
Матрицы 21=1 1 и 23 = 1 I действительны и симмет-
симметричны, следовательно, также эрмитовы, но обе неопределенны. Для
задачи A7.14) один из собственных векторов равен
v у з +
тогда будет j;'2l;i; = :t'23x = 0. и характеристические числа, получаю-
щиеся как корни уравнения
= 0, равны к, 9= ±-?=,
2% 1 х т/о
т. е. не действительны.
Если 23—единичная матрица, т. е. рассматривается частная задача
на собственные значения, то для действительности собсгзенных чисел
достаточно, чтобы 21 была эрмитовой (в случае действительных мат-
матриц— симметричной), так как единичная матрица (S, конечно,
18*
276 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ |П.4
положительно определенная. Для частной задачи на собственные значе-
значения при комплексной матрице % действительные собственные значения
получаются не в случае симметричной, а в случае эрмитовой матрицы.
/1 2/ \
Так, пусть дана симметричная, но не эрмитова матрица 21 = I,
_ \ — /
ее характеристические числа xIi2== i /]/ не действительны.
Если в общей задаче на собственные значения 23 не вырождена,
то можно A7.14) умножить слева на 33 ~ :
и действительность характеристических чисел имеет место в соответ-
соответствии с только что доказанным, если (J = 33~ 91— эрмитова матрица,
т. е.
С другой стороны, если 51 и 33 предполагаются эрмитовыми, то имеют
место равенства
Таким образом, матрица (£ эрмитова в том случае, если
Ъ~\=%Ъ~1 A7.lV)
или (умножая на 33 справа и слева обе части равенства) если 9133 = 3321,
т. е. 91 и 33 — перестановочные матрицы.
Резюмируя, получаем
Теорему о действительности характеристических
чисел. Пусть в общей задаче на собственные значения
матрицы 91 и 33 эрмитовы. Если, кроме того, матрица 33 опре-
определенна либо не вырождена, причем 21 и 33 перестановочны, то
все характеристические числа действительны. В промежуточной
задаче на собственные значения 2tt = jcSg для действительности
характеристических чисел достаточно, чтобы матрица 91 была
эрмитова и имела положительные элементы, и, наконец, для
частной задачи достаточно эрмитовости 21. Последний случай
включает также действительную симметричную матрицу.
Пример. Обе матрицы % = I, ) и 33 = | ) для действи-
\\ a-\-b) \d c-\-bd!
литовы и перестановочны. I
[, например, для а = 1, b = —
«-Q--U
тельных а, Ь, с, d эрмитовы и перестановочны. В общем случае они не
являются определенными, например, для а = 1, b = — 1, с = I, d = 2 матрицы
17.51 § I?. ОСНОВНЫЕ СВЕДЕНИЯ 277
неопределенны; в соответствии с теоремой корни уравнения
_х 1 _ 2х
1 — 2х у.
= 0 действительны:
: х1>2 = -2-A ± 1/ -р-1.
17.5. Обобщенная унитарность собственных векторов. Примем,
что в общей задаче на собственные значения A7.14) с эрмитовыми
матрицами 91, 23 (матрица 23 положительно определена) имеются два
собственных вектора Jr, x,s, принадлежащих двум различным характе-
характеристическим числам кг и и,. Запишем
Умножая первое уравнение слева на j/ и второе на %', получим после
вычитания
7,4 -.Л = *£Ч ~ КА'«?.. A7.18)
Пусть теперь z = ^91^ — число, которое можно представить как
одноэлементную матрицу, равную своей транспонированной:
Так как 21'= 21 и 23' = 2Т, получаем
?,Ч = ХЩ,- S's4 = fMs- C17.19)
Тогда A7.18) перейдет в
следовательно,
i^23rr = O для nr^Ks. A7.20)
Если умножить
слева на ^, то, учитывая A7.20), получим
Введем следующие
Определения.
Два вектора j, t) называются
ортогональными друг другу, если j^ = 0, A7.22)
унитарными друг относительно друга, если j'v = O A7.23)
и обобщенно унитарными относительно задачи на собственные
значения 2lj = кЩ (или, коротко, обобщенно унитарными), если
?23» = О. A7.24)
278 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [17.в
Из A7.22) сразу следует
(;'9)' = V'S = O.
а из A7.23)
из A7.24), согласно A7.19), поскольку 33 эрмитова, имеем
?33j = O. A7.25)
При 33 = 6 обобщенная унитарность A7.24) переходит в обыч-
обычную унитарность A7.23); если хотя бы один из векторов j, ty дейст-
действителен, то унитарность и ортогональность A7.22) равносильны.
С помощью введенных обозначений может быть сформулирована
следующая
Теорема. Пусть общая задача на собственные значения
91j=:k33j имеет два собственных вектора ir, is, принадлежащих
двум различным собственным числам нг, hs, и пусть 21, 33 эр-
эрмитовы матрицы, а 33 — положительно определенная матрица;
тогда гг, £, обобщенно унитарны, т. е. имеют место равенства
A7.20) и A7.21).
При 33 = 6, т. е. для частной задачи на собственные зна-
значения 21 j = щ, векторы, принадлежащие двум различным кг, %s,
унитарны: ~/ п
«А — и- »
17.6. Примеры промежуточных задач на собственные значения из
механики.
А. Колебания балки с сосредоточенными массами.
Пусть балка длины / нагружена в точках, отстоящих от левой опоры
на расстояния хи..., хп, сосре-
/77; тг гл„ доточенными массами тъ ..., тп
(рис. 17.3). Оба конца балки шар-
нирно оперты; можно рассматри-
рассматривать и другие способы крепления,
при этом изменятся только коэф-
коэффициенты СВЯЗИ Ufk-
Рассмотрим малые изгибные
„ ,_о .. , , , колебания, т. е. малые отклонения
Рис. 17.3. Изгибные колебания балки уунагруженных точек бал-
. с п сосредоточенными массами. ^. пр/»том н„'римеМ1 чт0 массой
балки по сравнению с массами
от,, тг, ..., тп можно пренебречь, и будем учитывать только жесткость на
изгнб балки EJ.
Нагрузка Р в точке Xj вызывает в точке х^ прогибу у* = Paj^. Для
шарнирно опертой на обоих концах балки при постоянной жесткости на
изгиб EJ ')
х){1-.
а'" ПЕЛ
(tfcj = Ct/# ДЛЯ
*/)
всех
V х
j,k.
1
xk
-х)
4
x){l-Xj)
A7.26)
О См. Hutte, Инженерный справочник, т. I, ГИТТЛ, 1932.
17.8]
§ 17. ОСНОВНЫЕ СВЕДЕНИЯ
279
В'соответствии с принципом Даламбера при колебаниях добавляются силы
инерции — "ijyj, имеющие смысл нагрузки, так что, складывая прогибы,
полученные от суммарного действия п сил, получим
У1 = —
У п. = —
Введя матрицы
а12 ... а
= l а21 а22 ... а2п
— m2y2ai2 — ... — mnynaln,
— «гУг^пг — ... — mnynann.
'от, 0 ... 0
,_| 0 m2 ... 0
A7.27)
va
Л1 аЯ2
а„
О О
Ул
можно коротко записать A7.27) в следующем виде:
9 = _ mx'i A7.29)
Будем теперь рассматривать собственные колебания, при которых все
массы колеблются в одном ритме, т. е. с одной круговой частотой со и оди-
одинаковой фазой:
У/ = Yj cos at,
т. е.
или t) = — c
Отсюда следует
здесь
A7.30)
A7.31)
A7.32)
таким образом, получается частная задача на собственные значения
%Щ = Щ A7.33)
с матрицей S13K, в общем случае несимметричной.
10кг 21кг Юнг
Рис. 17.4. Балка с тремя сосредоточен-
сосредоточенными массами.
Для 501») = з получается, однако, промежуточная задача на собственные
значения
9tS = xaR-1S A7.34)
с симметричной матрицей St.
Наконец, введя, как в A7.13), обозначение 3K'/2q = W, получаем частную
задачу на собственные значения
Gft> = ЭД'/22Ш'/2№ A7.35)
с симметричной матрицей S.
280
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
117.6
Например, можно выбрать .*,• = /—> у = 1, 2, 3, и rtij = '• О, =
G3 = 10 кг; О2 — 21 кг (рис. 17.4).
Матрицы 81 и Ш здесь получаются следующие:
= ц 0 21 0 , ц = ^^.
к 1
Уравнение A7.34) с обозначениями к* = — =
дующему вековому уравнению:
приводит к еле-
9--Т7Г И
16 —
11
21
И
9- —
У 10
Н2-£
V*
16—gj- 22
11
у?_
"Ж
_ , и* \ и*2 — 496х* + 2940
~u-7oj 210 ~°-
Его корни:
к}: = 490 (основное колебание),
к| = 20 A-е высшее колебание),
Kg = 6 B-е высшее колебание).
Теперь легко также найти форму собственных колебаний; например
Яд = 6 дает для компонент Zj вектора $ однородную систему уравнений
(легко выписываемую по определителю)
Решение с точностью до постоянного множителя будет
г, = 1, г-2 = —1,4, г3=1.
Соответственно для других колебаний получаем собственные векторы (не
нормированные)
17.81
17. ОСНОВНЫЕ СВЕДЕНИЯ
281
из которых с помощью X)
1
10
1
7
1
То
= Ж~'§ вычисляются смещения
Ч2 =
1
Тб"
0
— 1
"То"
9з =
1
10
_ 1
Т5"
1
Тб"
Эти векторы не ортогональны друг другу, как были бы ортогональны
векторы
Б. Колебания опертой на пружинах прямоугольной
пластинки. Пусть жесткая однородная прямоугольная пластинка тол-
толщины d расположена горизонтально и опирается на четыре размещенные
7-
Рис. 17.5. Форма собственных
колебаний балки, изображенной
на рис. 17.4.
Рис. 17.6. Прямоугольная пластина,
укрепленная на пружинах.
по углам пружины (с, с2, с3, с4 — коэффициенты жесткости пружин) и со-
совершает малые колебания; в первом приближении каждая точка пластинки
колеблется вертикально. Для смещения углов пластинки У), у2, у3, У4 спра-
справедливо соотношение
У\ + Уз = У2 + У4-
Пластинка имеет три степени свободы; состояние
с помощью у,, у2, уз или естественным образом
тяжести г1 и два угла наклона <р, \р (рис. 17.6):
системы можно задать
через смещение центра
1 / . ч
ту (У1 + Уз).
У2 —У1 . 22
2а ~ а '
У4 — У\
При этом 2л и 26 — длины сторон прямоугольника, а для углов наклона
выполняется предположение малости. Пусть пластинка имеет общую массу М
и моменты инерции G, и в2 относительно двух проходящих через центр
тяжести осей, параллельных прямым, соединяющим угловые точки 1,4 и 1,2;
тогда уравнения движения можно записать следующим образом:
Mz, = — с,у, — с2у2 — с3уз —
6,'ф = а (с,у, — с2у2 —
&Л = * (с,у, + с2у2 —
A7.36)
— с4у4).
282
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[17.8
Введя 0, = М -w-, 02 = М ■
О
(для выступающих пластинок были бы соот-
A7.37)
ветственно другие значения), при обозначениях
У2 = г\ -\- г2 гЗ У>> — г\ Z2 ~Г" гЗ
получим уравнения
— Мг, = Czx + (С — 2с, — 2с4) z2 + (С — 2с, — 2с2) z3,
м ■■
- -Tz2 = (С - 2с, - 2с4) г, + Cz2 + (С - 2с2 - 2с4) z3,
± z3 = (С - 2с, - 2с2) г, + (С - 2с2 - 2с4) z2 + Cz3.
При этом С = с, -\-с2
матричного уравнения
где
с2
с4. Эти уравнения можно записать в виде
..
Щ = — Ш$,
— с, + с2 + с3 — с4 — с, — с2
— С4
С,—
— С4
. —С,—
М О
о 4^
A7.38)
0 ° TJ
Подход к собственным колебаниям, соответствующий A7.30), дает з= —ffl25,
откуда следует промежуточная задача на собственные значения
Щ = ffl2i(Rj. A7.39)
Пример. Пусть будет с{~с, с2 = Зс, с3 == 2с, с4 = 4с; тогда
10 0 2\
0 10 — 4 J.
2-4 10/
Введя обозначение ft = , вместо A7.39) получим уравнение для частот
0 2
у! = Я*
о
2
)__ _4
= —yi (ft3 — 70ft2 -f- 1344ft — 7200) = 0. A7-40)
Уравнение имеет следующие корни:
ft, = 42,198, ft2 = 18,672, k3 — 9,1402.
Соответствующие собственные векторы получаются путем решения системы
линейных однородных уравнзний, например, для А3 — 9,1402:
0,8598г, + 2гз = 0,
6,9533.г2 — 4zs = 0,
2г, — 4*2 +■ 6,9533^3 = 0.
17,6]
§ 17. ОСНОВНЫЕ СВЕДЕНИЯ
283
Из этой системы получаем z3—l, z, = — 2,326, z2 = 0,575. В рассматривае-
рассматриваемом случае, когда определитель A7.40) содержит два нуля, наиболее удобно
определять собственные векторы 5у и числа kj с помощью интерполяции,
при которой задаются числом k, взяв г3= 1, из первых двух уравнений на-
находят гх и г2 и подставляют их в третье уравнение.
Таким образом, получается таблица
k
9,15
9,14
2
г'= ft-10
—2,353
—2,32558
4
10-1*
0,5755
0,57527
2г,-4г2 + ^10-— \z3
—0,058
+0,00111
0,231 \
1,059 |,
1,0 /
Зз =
\
( - 2,326
0,575
V 1,0
и далее собственные векторы
/ 0,00621 \
3, = - 0,984 , Ь2 =
V 1,0 /
Каждому этому собственному вектору соответствует собственное колебание
с определенной узловой линией, которую получают, определяя из A7.37) уу
и находя вдоль периметра пластинки
_ точ-ки с нулевым отклонением, поль-
пользуясь интерполяциями (рис. 17.7). Точки
пересечения трех узловых линий суть
три узловые точки Рь Р2. Ра- Отклонения
Рис. 17.7. Узловые линии соб-
ственых колебаний прямоуголь-
прямоугольной пластинки.
Рис. 17.8. Вал с насаженными дис-
дисками.
в трех узловых точках — это так называемые «главные координаты». Если
преобразовать уравнения движения к главным координатам, то они окажутся
полностью «развязанными»:
xj = — а)хр } = 1, 2, 3.
В. Вал с вращающимися массами. Пусть на валу насажено
несколько дисков с моментами инерции вь в2 в„ (рис. 17.8). Отрезок
вала между дисками с моментами инерции 6;-_, и 0у имеет длину /;-, жест-
жесткость при кручении GJj = Cj = Djlj и пренебрежимо малый момент инерции
284
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
117.7
по сравнению с 0.. Обозначим через q>. (t) угловое отклонение у'-го диска
относительно произвольно определенного в пространстве направления в мо-
момент времени t. Если концы вала могут свободно вращаться в опорах, то
уравнения движения запишутся следующим образом:
0/фу4-£>;-+1(Ф;-ф;Ч1) + £>;(Фу-фу-1) = О> у = 1, 2,..., п,
причем должно быть положено <ро = ф и фя+1 =<ря. Используя свойства соб-
собственных колебаний A7.30)
получают промежуточную задачу на собственные значения
где
Ъ\ —
н
ф]
Ф2
Фл
D,
~D2
0
, ft =
— £»2
D2 + D
-D3
/0i
/ '
Г
Vo
—
D3
0 ..
e2 ..
0 ..
0
-D3
+ D<
. 0
. 0
• 0/
...
...
0
0
0
о
о
о
По вращательным колебаниям имеется обширная литература.
17.7. Примеры общих задач на собственные значения из механики.
А. Малые колебания системы без затухания. Пусть задана
в потенциальном поле с помощью обобщенных координат qb q2, ..., qn
голономная и склерономная механическая система без трения, имеющая п
степеней свободы. Система совершает малые колебания около положения
равновесия, определяемого координатами
9j. = 0, у =. 1, 2, ..., п.
Пусть точка системы с координатами q, в момент времени t занимает поло-
положение, определяемое радиусом-вектором
Тогда ее скорость d будет
0 =
1
'«Г
и ее кинетическая энергия
где
Sm
— V
/. ft-I
A7.41)
A7.42)
причем значок S означает суммирование по всем массам-
17.71 § 17. ОСНОВНЫЕ СВЕДЕНИЯ 285
Все b ,k суть функции от qk, но при малых колебаниях их можно счи-
считать постоянными (равными значению функции при qr = 0). Таким образом,
кинетическая энергия Т является положительно определенной квадратичной
формой относительно скоростей by с постоянными коэффициентами.
Потенциальная энергия может быть разложена в ряд Тейлора в точке
причем волнистая линия означает, что должно быть взято значение в под-
подходящей промежуточной точке. Так как значение V определяется с точ-
точностью до постоянного слагаемого, примем V @, ..., 0) = 0.
Поскольку точка qr — 0 должна быть положением равновесия,
=1,2 п.
Если заменить в первом приближении, как было сделано при вычислении
кинетической энергии, функцию -^—г— значением в точке qr = 0
w dq.dqk
, л , A7.43)
то для потенциальной энергии получим также квадратичную форму
п
v
а именно, положительно определенную форму, если положение равновесия
является устойчивым.
Уравнения Лагранжа второго рода для системы
— (——\ =0, L = T— V, У=1, 2 л, A7.45)
dt \dq.) dqf
принимают вид:
п
С помощью матриц
ап ...
) J A7.46)
апп> -Ь1П ... Ъ1Ш1 у
это можно записать короче
58A-4-Sfq = 0. ■ A7.47)
Для собственных колебаний соответственно A7.30)
q. = Q . cos at, ii = — co2q; A7.48)
в результате получим общую задачу на собственные значения
Щ = хЩ, ш2 = х. A7.49,1
286
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
117.7
Б. Система с затуханием. Если учесть также силу сопротивле-
сопротивления, пропорциональную скорости, то уравнения движения примут вид ')
п
2 (V*
i
V*
kqk-\-ajkqk) = O, /=1,2 л,
или при помощи матрицы £, определенной по аналогии с A7.46):
Принимая, что
получаем
= 0.
31) q = 0.
Тогда х определяются как корни уравнения
A7.50)
A7.51)
A7.52)
A7.53)
A7.54)
^ппп ~Г апп
Так как матрица 33 не вырождена, можно перейти также к части эй задаче
на собственные значения с матрицей Ш порядка 2л. Для A7.51) можно за-
записать
_, _, A7-55)
Введя матрицу Ш и вектор с 2л компонентами
Ч\> • •■■. Чп'< Ч\ Чп- /
о к \ /<,;
= I. A7.56)
сппх
получим
A7.57)
В. Пример системы без затуха-
затухания. Пусть сложный, например тройной, ма-
маятник с пружинной связью (рис. 17.9) состав-
составлен из стержней с длинами /,, /2, /3 с закреп-
закрепленными массами ти тъ т3 и имеет пру-
Жину, коэффициент жесткости которой с.
Колебания, возникающие при отклонениях
стержней на углы Фь ф2, фз от положения
равновесия, будем считать малыми. Тогда, согласно A7.41), кинетическая
энергия
Рис. 17.9. Сложный маятник
с пружинной связью.
/2ф2J
ф, + г2ф2 + /3ФзJ =
') См., например, Р h. F r a n k, R. v. Mises, Differential-und Integral-
gleichungen der Mechanik und Physik, т. II, изд. 2, Braunschweig, 1935
[Ф. Франк, Р. Мизес, Дифференциальные и интегральные уравения мате-
математической физики, ОНТИ, М., 1937].
17.71
§ 17. ОСНОВНЫЕ СВЕДЕНИЯ
287
причем коэффициенты 6у# образуют матрицу 33 (см. A7.41), A7.42)):
тз)
11т
1тз
. A7.58)
1 1 + '2Ф2) +
с матрицей коэффициентов ayft:
Потенциальная энергия составляется из энергии положения в поле тяготения
и энгргии деформации пружин
V = Т [(
• = («/ft) =
A7.59)
Рассмотрим численный пример
/, = /2 = 1 м, 13 — 2м, niig = 2 кГ, m2g = m3g = 1 кГ, с = 1 .
При этом
Введя
согласно A7.49)
33
будем
2
— — м к
[ = 2 м кГ-
иметь
33*. 33* =
%*, Ж* =
1 Л
/2
1
Vi
/4
2
\2
1
1
1
2
3
2
1
1
2
2
2
3
Легко получить, далее, следующее уравнение:
4_2ft 2— ft 2—ft
2_ft 3--ft 2 — ft
2 — ft 2 — A 3 — 2*
2
1
1
2 —ft 3—ft 2 —ft
B — ft) = B — ft) (ft2 — 6ft f- 6) = 0,
2_ft 2 —ft 3—ft
корни которого ft, = 3 ^- ^ 3 , ft2 = 2, ft3 = 3 —1
288
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[17.7
Вычисляя соответствующий kx собственный вектор из системы
- 2 A + /3 ) <р, — A + /З") ф, - A+ VD ф3 = О,
получаем
Фз =
и, таким образом, собственные векторы
jO+УЮ
— 2 —У
1
j(l
-2 + УЗ
1
Рис. 17.10 показывает форму соответствующих колебаний. Низшая ча-
частота принадлежит k3; соответствующее колебание может классифициро-
классифицироваться как основное и имеет узел в об-
области 3-го стержня, в то время как 1-е выс-
высшее колебание не имеет узлов. При этом
колебании стержни между массами т1 и
т2 и массами т2 и т3 колеблются вместе,
как твердое тело.
Г. Колебания балки с массами
и пружинами. Пусть на произвольно
опертой балке находится несколькб сосредо-
сосредоточенных масс тх, т2,..., тп, которые связа-
связаны с жестким основанием пружинами, имею-
имеющими коэффициенты жесткости с,, с2, ..., сп,
/77?
т„
Первое Второе
Основное высшие
колебание колебания
Рис. 17.10. Форма собствен-
собственных колебаний сложного
маятника.
Рис. 17.11. Балка с сосредоточен-
сосредоточенными массами и пружинами.
как это изображено на рис. 17.11. Массу балки будем считать малой по
сравнению с массами /п,, т2, ..., тп.
Введем, как в п. 17.6, коэффициенты влияния а/п и получим тогда урав-
уравнения движения
у= 1, 2 п.
A7.60)
k=\
Для собственных колебаний, согласно A7.30), получается общая задача на
собственные значения
п . п
«2 V а ,„ у,= у.+ Уа.Ау., У =1.2 п, A7.61)
§ 17. ОСНОВНЫЕ СВЕДЕНИЯ
289
или с использованием матриц
с, ... О
О ... сп
3 =
ап ... а,„\
а„, ... а„
A7.62)
С помощью g данную задачу можно привести к промежуточной задаче
на собственные значения
ш29Лц = (д-1-(-е)ц. A7.63)
В качестве примера рассмотрим расположенную на двух опорах балку
с постоянной изгибной жесткостью EJ, несущую четыре расположенные на
т
Рис. 17.12. Балка на двух опорах с че-
четырьмя массами на пружинах.
равных расстояниях а = -=-1 массы (рис. 17.12). Матрица коэффициентов
о
а3
влияния g с i= . будет следующая:
32 45 40 23
45 72 68 40
40 68 72 45
23 40 45 32
обратная матрица равна
= («д) = А
1045Л
344 —331 144 —36
—331 488 —367 144
144 —367 488 —331
_36 144 —331 —344
1
: 777., -JI
0,4
А '
Пусть, в частности,
Тогда A7.63) перейдет в частную задачу на собственные значения с н
Щ = XX),
1180 -331 144 —36
-331 906 —367 144
144 —367 906 -331
_36 144 —331 762
В п. 18.8 этот пример исследуется численно.
где
81 =
A7.64)
1Q Л. Коллати
290
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[17.7
Д. Балка с подвешенными на пружинах массами..
Можно дать множество других механических примеров, ведущих к общим
задачам на собственные значенля. Рассмотрим еще конструкцию, изображен-
изображенную на рис. 17.13. На произвольно опертой балке расположены сосредоточен-
сосредоточенные массы ти тъ ..., тф соединенные пружинами, коэффициенты жесткости
которых с,, с2, ..., cq, с другими массами т9 + 1, ..., m2q. Масса балки
ул т1 тг щ у, ■
Рис. 17.13- Балка, нагруженная сосре-
сосредоточенными и подвешенными на
пружинах массами.
пусть будет опять пренебрежимо мала. При введении, как в п. 17.6А, коэф-
коэффициентов влияния ajk уравнения движения примут вид:
= 2
-у*))-
/=1.2 q- A7.65)
Теперь могут быть введены матрицы порядка q:
"■99
... m
... о
0 ... c
' У
О
■У2Ц
Тогда уравнения движения с учетом соотношений A7.30) можно запи-
записать так:
Введя матрицы порядка 2q:
Ж:
о
о
— е е/ \ о т2)
Можно записать общую задачу нт собственные значения
A7.67)
или в случае, если р существует и известна, можно получить Промежу-
Промежуточную задачу на собственные значения
A7-68)
17.81 J 17. ОСНОВНЫЕ СВЕДЕНИЯ 291
17.8. Эрмитова самосопряженность в случае интегро-диффе-
ренциальных уравнений. Настоящий параграф выпадает из общего
содержания главы о матрицах и имеет целью проиллюстрировать тот
факт, что различные понятия матричного исчисления легко перено-
переносятся на интегро-дифференциальные уравнения.
Рассмотрим симметричную матрицу 21 = 21' и два произвольных
вектора U, to; тогда
и'Яи='(п'Я»)' = Ь/Я/и = »/Яц; A7.69)
если, наоборот, для какой-либо матрицы 21 для любых векторов u, to
имеет место соотношение
u'2tto— b'2lu = 0, A7.70)
то матрица 21 является симметричной; действительно, выберем
в качестве ц и to единичные векторы (см. A8.9)) таким образом, что
у и у-я, а у to k-я компоненты равны 1, а остальные равны нулю;
тогда получим из A7.70)
a-jk = Н;-
Следовательно, условие A7.70) означает симметрию матрицы 21.
В случае дифференциальных уравнений A7.70) соответствует само-
самосопряженности D.15). Аналогично
u'Stb — ti'3lu = 0 обозначает эрмитову матрицу Щ,
lt'Stb -j- b'Stu = 0 обозначает антисимметричную матрицу Щ,
и'ШЬ -j- Й'Йи = 0 обозначает антиэрмитову матрицу St.
Определим теперь общую самосопряженность не только для
задач на собственные значения, но и для дифференциальных выра-
выражений.
Определение. При заданных действительных краевых
условиях D.15)
^[у] = 0. ц=1. 2 г, A7.71)
дифференциальное выражение E.1)
k
My] = 2/>v(*)y(v)(*) A7.72)
v-0
называется самосопряженным, соответственно эрмитово само-
самосопряженным, если для двух произвольных функций сравнения
и(х), v(x) имеет место
ь
I
a
соответственно
ь
J (uL [v] —
292 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ \П.Ь
При этом функция и(х) называется функцией сравнения, если
она отлична от нуля, удовлетворяет краевым условиям и k раз не-
непрерывно дифференцируема. Через L обозначено комплексно сопря-
сопряженное к L дифференциальное выражение
2
V-0
Так, например, при краевых условиях
= у(д)= ... = уС") ф) = 0 A7.73)
2{[2(i f [2jl+1 ^+1]] A7.74)
— эрмитово самосопряженное дифференциальное выражение, при
условии, что все функции ро(х), рг(х) Р2тп(х) являются дей-
действительными (и дифференцируемыми столько раз, сколько нужно
для образования выражения L); подробнее:
[у] = р^> + (р2у'У
/'+ Р'3У'У + i{2p5y'"+ p'5y")'+ ...;
после ^-кратного интегрирования по частям следует требуемое ра-
равенство (^
ъ
J
ft
= (-1)? 2/ J -^
= (-1)* 2t [p2q+lu«W)]ba = 0
Аналогично можно ввести антисимметричность и антаэрмато-
вость.
Определение. Дифференциальное выражение A7.72) с кра-
краевыми условиями A7.71) называется антисимметричным, соот-
соответственно антиэрмитовым, если для всех функций сравнения и, v
имеют место равенства
ъ
J (uL[v]-i-vL[u])dx = Q
17.8|
и соответственно
§ 17. ОСНОВНЫЕ СВЕДЕНИЯ 293
ь
J (uL[v\ + vL[a]) dx = 0.
Точно так же как это было сделано выше, можно показать, что при
краевых условиях A7.73) выражение
о{[
будет антиэрмитовым.
Пусть теперь задано интегро-дифференциальное уравнение !)
в форме
Ф [У] = *,¥[?]. A7.75)
где
Ф [у] = Л1
[у] =
$F(x.
[у] =
2 i
р-0
), А/ [у] = 2 vp
р-0
A7.76)
Пусть функции \ip(x), vp(x) — заданные в интервале а-^х-^Ь не-
непрерывные комплексные функции х; F(x, \) и G (х, |) заданы
в я <^ х, £,<^Ь и также являются непрерывными функциями х и |,
а Я- — отыскиваемое собственное значение, принадлежащее собственной
функции у(х). Пусть т^-п; т называется порядком интегро-диф-
ференциального уравнения, соответственно этому к A7.75) доба-
добавляется т линейных, однородных, линейно независимых действитель-
действительных краевых условий
^[у] = 0, ц=1. 2, ..., т. A7.77)
Обычные интегральные уравнения понимаются тогда как интегро-
дифференциальные уравнения нулевого порядка, к которым не тре-
требуется добавлять краевые условия; к интегро-дифференциальным
уравнениям нулевого порядка относятся также такие уравнения, как,
') Задачи на собственные значения для ингегро-дифференциальных и
общих функциональных уравнений рассмотрены в работе: R. С о u r a n t,
Uber die Anwendungen der Variationsrechnung in der Tiieorie der Eigen-
schwingungen und iiber neue Klassen von Funktionalgleichungen, Acta щ*
thematica 49 A926), I—68,
294 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ . |17.8
например,
j K(x — l)y®dl = k J L(x—l)y(l)dl A7.78)
a a
с заданными функциями К(х), L(x).
Оператор Ф называется эрмитово самосопряженным, если М [у]
эрмитово самосопряжено и ядро F эрмитово, т. е. если
F(x,l)^F&, х). A7.79)
Тогда для всех функций сравнения и(х), v(x) будет
Г (иФ [v] — г/Ф [и] )dx = 0. A7.80)
а
Оператор Ф называют положительно определенным, если для всех
функций сравнения и (х)
ь
J пФ[и]ёх>0. A7.81)
а
Аналогичное утверждение справедливо для XF.
Точно так же как в пп. 4.4 и 4.5, можно показать при предпо-
предполагаемой эрмитовой самосопряженности Ф и Ч? и положительной
определенности VF вещественность Я, и свойства ортогональности.
Пусть дано собственное значение Я, и принадлежащая ему собствен-
собственная функция у. Тогда из A7.75) следует
*
J УФ [у] dx
X = R[u] = ^b , A7.82)
причем R [и] имеет смысл отношения Рэлея. Знаменатель положи-
положителен. Числитель вследствие эрмитовой самосопряженности Ф дей-
действителен: так как
ь ь
Z=
a a
следовательно, все имеющиеся собственные значения Я, действительны.
Если, кроме того, Ф—положительно определенный оператор, все
собственные значения положительны. Пусть, далее, у;-, ук—соб-
ук—собственные функции, соответствующие двум различным собственным
18.Ц § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 295
значениям kj, кк,
Следовательно, также
где
Ф[и]=М[и\+$ F(x, l)u{l)dl
а
Таким образом, получаем
* ь ь
\ (Укф lyj] - Ур Ы ) dx = kj J yft4r lyj] dx-\k\ .v/F [yfti dx.
a a a
Так как yj и yk — функции сравнения, из-за эрмитовой самосопря-
самосопряженности следует, что левая часть равна нулю, а оба интеграла
в правой части равны друг другу; тогда
ь
или, если использовать действительность собственных значений:
\yJX\yj\dx = Q A7.83)
а
при kj Ф кк.
Пример. Для
у" + ,у = Ху, у (—1) = у A) =0
М [у] = у"-\- iy' при данных краевых условиях эрмитово самосопряжен,
а N [у] = у, кроме того, положительно определен, следовательно, все соб-
собственные значения действительны. Так как здесь общее решение дифферен-
дифференциального уравнения может быть задано в виде экспоненциальной функции,
собственные значения легко вычисляются; получаем
1 - nW
Ап = т . п = 0, 1, 2, ...
§ 18. Экстремальные свойства характеристических чисел
Ниже дается новое определение характеристических чисел'), обо-
обозначаемых через и*, и далее показывается, что х* совпадают с опре-
определенными согласно A7.6) ку Максимальные свойства и теорема
') В этом параграфе мы следуем книге R. С о u r a n t, D. Gilbert,
Methoden der mathematischen Physik, т. I, II, изд. 2, Berlin, 1931 [P. Ку-
Курант, Д. Г и л ь б e p г, Методы математической физики, тт. I, II, ГИТТЛ,
изд. 2-е, М-—Л., 1951].'
296
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[18.1
включения дают основу для различных численных методов нахожде-
нахождения собственных значений матриц.
18.1. Определение характеристических чисел при помощи
задач на максимум. Пусть дана эрмитова форма
= J Ч = . 2j ajkXjXk
A8.1)
с эрмитовой матрицей 21 = 51'. Наглядности ради читатель может
оперировать с частным случаем действительной симметричной матрицы
и при Н—\ представлять себе уравнение поверхности второго по-
порядка. Эти геометрические представления помогут также при даль-
дальнейших определениях и образовании новых по-
понятий. А именно, для таких поверхностей
наименьшую и наибольшую главные оси можно
определить через расстояния до точек поверх-
поверхности с минимальным, соответственно макси-
максимальным, удалением от центра, т. е.
H=l.
max,
min.
Рис. 18.1. К определе-
определению главных осей при
помощи задачи на
экстремум.
Точно так же оба эти направления главных
осей можно задать с помощью соотношения
min,
max.
Обозначим через хл и jn решения этих задач.
Вторая по величине главная ось может быть
найдена путем определения наименьшего расстояния до поверхности
на направлениях, перпендикулярных к первой главной оси (рис. 18.1),
следовательно,
я
if ~— 1 х I Xi. X ~—* ' 1 х . ^==z min,
и так же можно найти другие главные оси.
От этих наглядных представлений мы переходим к решениям
экстремальной задачи для эрмитовой матрицы %
Н = 1'Щ~ max
с дополнительным условием
A8.2)
A8.3)
Согласно A7.10) Н принимает только действительные значения.
Наверняка имеется вектор £,, являющийся решением этой задачи на
18.11 § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 297
максимум, так как по теореме Вейерштрасса непрерывная функция
на ограниченном замкнутом множестве достигает своего наибольшего
(а также наименьшего) значения по крайней мере в одной точке
области. Этот максимум обозначим через и*.
Можно легко задать также границы для Н на мнэжестве точек j'j=^1
(и вместе с тем для х*). Пусть максимальный модуль a :k есть А:
\ajk\<A, j, k= 1, 2, ..., п,
тогда будет
п
', 2 I aJ" II *1 I I хк К
и, далее, по неравенству Шварца (см. подстрочное примечание 1 в п. 10.5
стр. 155)
Итак, // — ограниченная и непрерывная функция.
Максимум и* для Я достигается при jc = ji.
Будем теперь разыскивать максимум Н при двух дополнительных
условиях
?5=1, ?Si = 0; A8-5)
таким образом, к сравнению допускаются только нормированные и
унитарные к ?л (см. A7.23)) векторы. Снова по теореме Вейерштрасса
должен существовать вектор % = ;г2, на котором достигается новый
максимум, обозначаемый через и*. Компоненты векторов jCj и J2
будут xjV Xj2 соответственно.
Теперь составляются третья задача на максимум
Н = max
при дополнительных условиях ^'jc=l, j'jj== j'j2 = 0, решение ко-
которой # = к* для $ = $з' и общая г'я задача на максимум
при дополнительных условиях j'j=1, jc'j5 = O, для 5=1, 2, 3, ...
..., г—1. Для /•<;« наверняка найдутся такие векторы;, пусть j —
линейно независимый относительно jlf jc2 Sr-i вектор, тогда
г-1 _
„* , 'V /7'v "> v
* — 5 — —. Ь кр> 5р
унитарен к j.^, j2' •••> Sr-i и S* не может быть тождественно равен
нулю, так как иначе вектор j был бы линейно зависим относительно
298
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
118.2
gj, jc2 x,r_v Умножением на подходящий множитель С можно
нормировать j* к х, = Су.\ Процесс оканчивается при г — п га-й за-
задачей на максимум, для которой Н = х\ Далее видно, что после-
последовательно найденные решения xk линейно независимы. Из условия
= О
умножением слева на x.j получаем, что все <х;- должны быть равны
нулю.
18.2. Приведение к главным осям. Компоненты xJr вектора £г,
найденного по указанному выше методу, запишем теперь в виде
матрицы 11
х\п
Xnl Xn2
утверждается, что U — унитарная матрица, которая для
я,
Х2п
X
пп
A8.6)
A8.7)
эрмитову форму переводит в чисто квадратичную. Форма Н пере-
переходит в новую форму (так как в данном случае путаницы можно
не опасаться, сохранена буква И):
Я — $% =
где
A8.8)
и можно показать, что (Е — диагональная матрица. Пусть в норой
координатной системе уР Щ, ,.., ^—единичные векторы:
1
0
0
0
0
1
0
0
A8.9)
При преобразовании A8.7) i)f переходит в х,г
Прежде всего, следует, что U унитарна; действительно, записывая
векторы jj, х,'2 Х.'п как строки матрицы 11', вследствие
1 при г — s,
О при г Ф s
A8.10)
18.21 § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 299
получаем
1141 =
(si
4-1
fan
1 0 ... О
О 1 ... О
О 0 ... 1
Преобразованная эрмитова форма имеет вид
A8.11)
Вместо A8.8) можно писать также 6 = U~131U. При унитарных
преобразованиях A8.7) сохраняется квадрат модуля вектора или его
«норма»:
l'l = i/U'Up =?V A8.12)
(в действительной области унитарным преобразованиям соответствуют
ортогональные преобразования, при которых сохраняется длина век-
вектора).
Полученная из 31 новая матрица 6 эрмитова, так как
)' = U'f'U = U'2lU = 6, A8.13)
A8.14)
Можно показать, что 6 имеет диагональную форму, т. е. что Cjk = O
для j Ф k. Так как вектор jt был определен из требования Н = max = к*
для $'$ = 1, то в преобразованной форме Н принимает максимум %*
при р = ^; подставим, согласно A8.9), I)! в A8.14), тогда получим
сп = Яшах^%*. Далее утверждается, что cI2 = 0. Для доказательства
применительно к \I используем действительную вариацию е такую,
что —1<е<1, и перейдем к некоторому вектору \fv который
остается допустимым вектором, удовлетворяющим дополнительному
условию 1)* 1)*= 1:
Е
О
A8.15)
Для этого вектора # = %*A—е2) -j- (cl2 -f- с21) е У1 — е2 |- с22е
Согласно A8.13) матрица 6 эрмитова, т. е. с21-=с12, следователь^
зио
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
A8.2
при е = 0 эта функция должна принимать максимум х*; для поведе-
поведения при малых е существенным является линейный относительно е
член, и Н только тогда принимает максимум, когда обращается
в нуль производная
ldH\
—;—
т. е. когда исчезает множитель при е:
следовательно, с]2 должно быть чисто мнимым. Если повторить теперь
рассуждения с
1 -е2
/е
О
6
A8.17)
— е2 -f с22г2 следует, что
то из Л/(у**) = х*A — е2L (с12— с2^1гУ\ — е -f с22г
с12 = с2\ = с]2, т. е. с12 должно быть действительно. На основании
первого равенства с12 должно быть чисто мнимым, следовательно,
i2 21
Соответствующие рассуждения можно применить ко всем
/ ф k. Например, для с23
О
I — е*
е
О
О
соответственно рГ =
о
Тогда при
к* до-
довыполняются также и необходимые для определения #тах
полнительные условия 1)*\)[ == 0 и соответственно Х)*2"'хI = 0. Таким
образом, показывается, что в преобразованной форме все смешанные
произведения cJkyjyk для j ф k исчезают и Н принимает вид
л
/=-i
■i=S«yy,y,=
/ -1
2
=- I
A8.18)
18.3| § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 301
Как видно, 6 имеет характеристические числа и*; тогда
или, согласно A8.8),
»,= *>,. s=b 2 «•
Умножая слева на U и учитывая, что £5 = и^, получаем в соответ-
соответствии с A8.7)
Таким образом, jts суть собственные векторы матриц 21, соответ-
соответствующие характеристическим числам х5 = и*.
Теорема. Пусть 21 — некоторая эрмитова матрица, имею-
имеющая п действительных характеристических чисел щ, х2 х„:
«1>К2>...>хя. A8.20)
Эрмитова форма Н = j'2ljc достигает максимума щ для j = jtlt
когда J пробегает область всех нормированных (j'j=1) п-компо-
нентных векторов, и максимума кг при J = 5/- ^с-^«. кроме норми-
нормировки j'js=1, наложить еще дополнительные условия $'54 = 0,
s=l, 2 г —1. Решения $,, j2 jn задачи на максимум
одновременно являются собственными векторами матрицы 31
я/ш характеристических числах щ, к^ к„. Э/ии нормирован-
нормированные собственные векторы образуют унитарную матрицу U:
!*=»(&. S2 5я).
которая при j = Up преобразует армитову форму к диагональному
л
Если бы в A8.2) разыскивался не максимум, а минимум Я при
дополнительных условиях A8.3), то аналогичное рассмотрение пока-
показало бы, что минимальное значение Н является характеристическим
числом матрицы, т. е., согласно A8.20),
Нт\п = №йпш = ия при ?;с = 1.
18.3. Выводы и оценки. В случае, если Н при j'j > 0 оказы-
оказывается всегда положительным, все максимумы jtj, x2 х„ будут
положительными; таким образом, справедлива следующая
Теорема. Эрмитова матрица 31 тогда и только тогда поло-
положительно определена, когда все ее характеристические числа
положительны.
Так как Н и j'j; суть однородные эрмитовы формы, можно
для чисел к, и х„, обозначаемых далее (к.ц)тах и (хя)т1п, записать
302 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [18.3
следующие неравенства
(K«t)min -?S<?2tr <(х,л)тах .5% "A8.21)
причем удовлетворение дополнительному условию j'j = 1 больше не
требуется.
Для произвольной неэрмитовой матрицы 21 матрица
33 = 21'21
эрмитова; она является положительно определенной при невырожден-
невырожденной матрице 21 и положительно полуопределенной при вырожденной 31.
Действительно, 33'= 21'21 = 93, и если заменить j на Ш), получим
^ = ?93у>0, A8.22)
где t)'93l) при невырожденной матрице 21 обращается в нуль только,
когда J = 0. Обозначим теперь (неотрицательные) характеристические
числа матрицы 93 = 21'21 через (и^(J:
х« = + j/xg,,, = + Yn. A8.23)
Для эрмитовой матрицы 21
х* = |хи1 A8.24)
и для положительно определенной эрмитовой матрицы
В случае произвольной матрицы, введя для хя и хя обозначе-
J Itlin П1ЭХ
ния |21| и |2l|, получим соотношения1)
Щ<1*я|<Щ A8.25)
так как J есть собственный вектор, соответствующий характеристи-
характеристическому числу к, то имеет место соотношение
xj = 2ij, xjT=j"r
и |x|2j'5 = 5'2I'2lj = 5'935. В соответствии с A8.21) теперь получаем
(*®)т1п ?I < I и Р ?S < (х«)шаХ S'S-
откуда, сокращая на j'jc, непосредственно приходим к A8.25). Если
применить векторную форму записи для модуля
') Эти обозначения применялись Виландтом.
18.3] § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 303
то неравенство A8.21) с учетом A8.22) даст
ИЛИ
При этом в левой, соответственно правой, части будет знак ра-
равенства, если заменить I) собственным вектором задачи %'Щ = (к?(J р,
принадлежащим |2l|, соответственно |91|.
Теорема. Для линейного преобразования Ш) = j справедлива
оценка
причем в качестве знаменателя выступает наибольшее, соответ-
соответственно наименьшее, число A8.23), или
ШМ- A8-27)
Если 21 — эрмитова матрица, то
\Щ j-'s < | $Щ | < 2tjj.
Введем несколько неравенств, которые понадобятся в дальнейшем.
Пусть 91 и 23 — заданные матрицы и l)t — принадлежащий | 31 —(— ЭЗI
собственный вектор задачи
, A8.28)
Тогда, используя равенство
согласно A8.27) получим
1+18р« К
Далее, пусть ря — принадлежащий j QX —(— 33 f собственный вектор A8.28).
Тогда
Итак, имеют место соотношения
"" ~^ ' A8.29)
Эти-неравенства можно наглядно изобразить на числовой оси к
(рис. 18.2),
304 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [18.4
18.4. Одновременное приведение к главным осям двух эрми-
эрмитовых форм. Для общей задачи на собственные значения преобразо-
преобразование к главным осям происходит совершенно аналогично случаю
Область значений для х ш
Щ\ Ш Ш Ш
Ш Ш
х
Границы для 191+33\ Границы для
\ /
Область значений для х m+SB
Рис. 18.2. Границы для собственных чисел.
частной задачи, поэтому все изложенное выше будет повторено более
кратко. Пусть снова поставлена задача
21 и 23—эрмитовы матрицы и 33,—кроме того, положительно опре-
определенная матрица, тогда
$'33j > 0 для всех j, для которых j'j > 0. A8.^0)
В этом случае все характеристические числа 23 положительны. Вместо
имевшейся раньше нормировки g'j = 1 выступает нормировочное усло-
условие с матрицей 33;
?93Х=1. A8.31)
Каждый не равный тождественно нулю вектор \ можно умножением
на постоянную С перевести в вектор ^ = С\, для которого справед-
справедливо A8.31). Будем опять исходить из задач на максимум. Сначала
составим максимум
на множестве векторов с $'Щ = 1, Этот максимум х* достигается
при j = jlf
Максимум существует, как и ранее, на основании теоремы Вейерштрасса;
можно легко сделать оцен<у для Н: по теореме из п. 18.3 следует
Таким образом, форма Н при дополнительном условии A8.31) является огра-
ограниченной,
18.4| § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 305
Вторая задача на максимум
Н = max
с дополнительными условиями ^г'ЗЗг = 1, £'58г2 = О имеет решение
5 = 52 при /У = х*; вообще J = Jr при # = х*— решение задачи
Н = max
с дополнительными условиями ~р'Ву.= \, ;c'58;r,j=O для s=l, 2, ...
..., г—1. Найденные последовательно векторы, являющиеся реше-
решениями задачи, линейно независимы, так как из равенства
«iSi + <hh +•••- + %*.q = 0
после умножения слева на £'.23 следует a. — 0, так что все постоян-
постоянные должны обращаться в нуль.
Пусть l есть линейно независимый по отношению к j^, g2> • • • ■ Ъг-\
(г^п) вектор; тогда имеет место равенство
x*=j-S№pMp
р=1
с дополнительными условиями ;c*23jC[ = O для 0=1, 2 г—1,
и после умножения £* на постоянную С можно удовлетворить также
условию A8.31), так как j* не равен тождественно нулю из-за пред-
предполагаемой линейной независимости. Итак, для всех п задач на мак-
максимум имеются допустимые векторы, а вместе с тем и векторы
So h' •••• £/<• являющиеся решениями задачи.
Как в A8.6) составим из полученных таким образом векторов-
решений матрицу преобразования Ж, которая больше не должна быть
унитарной:
хи х12 • ■ • Х\
X2l X22 • • • Х2п
ПП .
A8.32)
Вследствие линейной независимости jr det X ¥= 0; таким образом X
не вырождена.
При преобразовании
5 = #> A8.33)
векторы j:r переходят в единичные векторы \)г (см. A8.9)).
Вместо A8.10), A8.11) здесь появляются (для s>r в соответ-
соответствии с A7.25))
f 1 для г = 5,
« <18-34>
308 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ A8.4
И
1 ... О
0 ... 1
= <S. A8.35)
При преобразовании A8.33) эрмитова форма Н переходит в
с
A8.36)
Так как дополнительные условия g'5B$= I, j'23j5 = 0 переходят здесь,
согласно A8.33), A8.35), в
то доказательство факта, что (£ — диагональная матрица с элемен*,
там и х*
х* 0 ... О
о х;... о
о о...*;
буквально такое же, как в п. 18.2; необходимо только выступавшие
там дополнительные условия £'$=1, j'$r = 0 заменить на j'S$=l,
Х'¥5%г = 0. Таким образом, обе эрмитовы формы j'Slj и j'23j перей-
перейдут в
п п
~1[г Х^ * ~" ~/ ^1 —
Следовательно, ® опять имеет в качестве характеристических чисел х*,
т. е.
или по A8.35), A8.36)
18.4] § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 307
Умножением слева на (X') {Х несингулярна, следовательно, (S')~l
существует) получают в соответствии с A8.33)
т. е. вектор-решение js одновременно является собственным вектором
общей задачи на собственные значения A7.14) с характеристическими
числами к;5 = х*.
Теорема. Пусть 91, 33— две эрмитовы матрицы и 33 поло-
положительно определена. Общая задача на собственные значения
имеет тогда п действительных характеристических чисел
Щ, •■-. и„
^ > к2 > .. . х„, A8.37)
обладающих максимальными свойствами: эрмитова форма Н=%'Щ
достигает максимума щ при g = je1, когда j пробегает область
векторов с j'33j= 1, и максимума хг при J = jr, если, кроме тег?,
наложить дополнительные условия %'%5$S—Q для s—1, 2 г—1.
Решения задачи на максимум одновременно являются собствен-
собственными векторами задачи Щ — kSjc с характеристическими числами
2«
Эти нормированные посредством равенства g'Sj = 1 собствен-
собственные векторы образуют матрицу
которая при 1==Щ приводит к диагональному виду сразу обе
эрмитовы формы j'2lj и j'%:
л л
2j %}У]У) и 2j У}У}*
)-\ j-l
т. е.
%Г для r = s
_ A8.38)
О для г 4= s
-{
Как и в A8.21), здесь тоже можно, введя обозначения для щ и
>Cn («si, s)max и (ия, s)mm соответственно, перейти к неравенствам
и отказаться от дополнительных условий j'93j=1.
9fi*
308
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[18.5
18.5. Пример. Геометрическая интерпретация собственных
векторов двух квадратичных форм. Пусть заданы две действительные
эрмитовы (квадратичные) формы
Нг = Ах] - Ах{х2 — 2x1 = S'%
Ъх\ =
A8.40)
с матрицами
21 =
4 —2
—2 —2
23 =
3 1
1 3
г =
*1
Здесь 23 положительно определена, % неопределенна. Поставим
задачу — привести одновременно обе формы с помощью линейного
преобразования к чисто квадратичному виду.
Характеристические числа и соответствующей задачи на собст-
собственные значения A7.14) определяются из A7.15)
det B1 — к23) =
4 —Зк —2— и
—2 — и —2 — Зк
= 8х2—Юи —12 = 0,
«I = 2; х2= г-- Теперь можно определить соответствующие соб-
собственные векторы. Для «i==2 имеем уравнения
/ 2а\ \
следовательно, 11= . причем произвольную постоянную а опре-
делим так, чтобы выполнялось условие нормировки A8.34):
Ж'
3 -4а2+2. 2а(— а) + 3(— аJ=1, откуда а =
соответственно второй нормированный вектор будет
$2 =
5
2/22
Из собственных векторов составляется матрица преобразования
в соответствии с A8.32), A8.33)
2 1 )
0,603 0,106 4
A8.41)
2/22
5
/ГГ 2/ТГ
—1
-0,302 0.532/'
так что записанные подробно формулы преобразования имеют вид
2,1 —1 5
I ,/-тт- У it' глАТГ -*'2' 2 " .ат-г ^1 "Г п.^л?г
18.6| § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 309
Это преобразование действительно переводит Н^ и Н2, согласно
A8.40), одновременно в две чисто квадратичные формы
Матрица A8.41) не унитарна (здесь — в действительной области —
не ортогональна), т. е. если хх, х2 толковать как прямоугольные
координаты, после преобра-
преобразования получаются косо-
косоугольные координаты у], у2.
На рис. 18.3 показаны кри-
кривые #j=l (гипербола) и
ц.г = 1 (эллипс). Новые глав-
главные оси у], у2 не совпадают
ни со старыми главными
осями еъ е2 эллипса, ни
с осями hv h2 гиперболы,
видно, что касательные в точ-
точках пересечения одной из
новых осей с эллипсом и ги-
гиперболой параллельны друг
другу и другой оси. Отно-
Относительно этих косоугольных
координат оба конических
сечения будут «аффинно-
симметричными» к этим осям
у,, у2. (Новые оси суть со-
сопряженные сечения как для
эллипса, так и для гиперболы). Вследствие нормировки обе единичные
точки лежат на эллипсе.
18.6. Минимаксимальный принцип Куранта.
В общих задачах на собственные значения для матриц можно так же,
как в п- 8.4 для дифференциальных уравнений (с учетом сделанных в п. 18.4
допущений), найти собственные числа х5 «независимым» путем, без исполь-
использования собственных векторов $,, $2, .... j5-i- В качестве основной геомет-
геометрической идеи могло бы служить представление, что, например, для трех-
трехосного эллипсоида длины главных осей могут быть найдены независимо
друг от друга, как будет показано для средней оси. Пусть q — произвольный
вектор, тогда Ъ (а) — максимальное удаление центра от точек эллипсоида,
лежащих в плоскости, проходящей через центр и перпендикулярной к век-
вектору а (рис. 18.4). Минимум всех значений Ъ при вариации q есть искомая
вторая главная ось. Он реализуется, когда q имеет направление наиболь-
наибольшей оси.
Составим для общей задачи A7.14) задачу на экстремум
A8.42)
Рис. 18.3. Главные оси двух конических
сечений.
Н =
= max
при дополнительных условиях
= l, 2, .... г —1,
A8.43)
310
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[18.6
причем cfs =
4ns
— произвольнэ заданные линейно независимые векторы.
Максимум М -от Н зависит от выбранных векторов д: М(ць..., цг_{).
Утверждается, что r-е характеристическое число %г является минимумом М,
когда qs пробегает совокупность всех систем г — 1 векторов.
Теорема. Пусть 21 и 33 — две произвольные
эрмитовы матрицы и 23 положительно опреде-
определена. Пусть Ж (if,, .... qr_i) — максимум эрми-
эрмитовой формы Н = j'2lj при произвольно заданных
векторах С|,,
qr_i, если на г, налагаются
дополнительные условия j/23;e=1( q^j: = 0, s—1,
2 г — 1. Тогда r-е характеристическое число хг
общей задачи на собственные значения 2l;c —x23j
есть минимум М, когда (\s пробегает совокуп-
совокупность всех систем г — 1 линейно независимых
векторов.
Для проведения доказательства будем считать
Рис. 18.4. К ми- собственные векторы J, %п известными. Опре-
нимаксимально- делим сначала вектор
му принципу г
Куранта. „ _ V, г ,г.
принадлежащий r-й экстремальной задаче, т. е. удовлетворяющий
дополнительным условиям A8.43):
'j\
= 0,
s=\, 2 г — 1.
Последние г — 1 уравнений суть однородные линейные уравнения
для г неизвестных ср с2 сг и, следовательно, всегда имеют
нетривиальное решение, а один общий множитель всегда можно опре-
определить так, чтобы выполнялось первое нормировочное условие
j'58j=1 (при использовании A8.34)):
= 1.
A8.44)
При подстановке вектора j эрмитова форма Н принимает вид (при
использовании A8.34))
И = . 2 f
Вследствие A8.37) и A8.44) Н ^ кг
18.71 § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 311
Искомый максимум может быть только больше, следовательно,
имеет место неравенство
Но значение кг можно вычислить также непосредственно по тео-
теореме п. 18.4, а именно, если положить q;- = Q3'j^ для j=\, 2, ...
. . ., г — 1.
Таким образом, хг есть минимум М, как утверждалось. Можно
снова освободиться от нормировочного условия j'58j=1, отыскивая
вместо максимума Н максимум отношения
J- = £«L. A8.45)
Одновременно из этого отношения видно, что в двух задачах
2lj = x23j, 2lj = x*23% A8.46)
для которых предположения предыдущей теоремы выполняются и
i'93s>s'99's A8.47)
для всех j, отношение 1//? первой задачи всегда меньше или равно
отношению 1//? второй задачи при том же самом j; это неравенство
справедливо для всех максимумов и соответствующих минимумов, т. е.
иг<и* для г=1, 2 « A8.48)
18,7, Теорема включения. Теорема легко доказывается для
задачи A7.11) (промежуточнрй), но, вероятно, справедлива и в более,
широкой области. Она гласит:
Теорема. Пусть в промежуточной задаче
51 эрмитова, а 2)—диагональная матрица с положительными
элементами dj. Пусть и — вектор с не равными нулю компонен-
компонентами Uj, из которого образуем далее вектор to = 9tu с компонен-
V)
тами Vj. Если все отношения qj = —— лежат в интервале J
действительной оси, то J содержит по меньшей мере одно харак-
характеристическое число xs.
Для доказательства введем диагональную матрицу О.:
<?, О 0 ... О
О q.2 0 ... О
О О O...?J
A8.49)
312 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [18.7
Тогда по определению
b = &Du = 2lu, A8.50)
т. е. к —собственный вектор задачи, соответствующий характеристи-
характеристическому числу и=1: 2Ij = kO.£)j.
Будем различать два случая.
1-й случай. Все q-; положительны.
Сопоставим три задачи сравнения:
I. 21 j =
н. ^ =
причем q и Q пусть будут наименьшим (соответственно наибольшим)
из чисел qj (предполагаемых действительными).
Задачи I и III имеют собственные векторы j;-, соответствующие
характеристическим числам
v.\j = — , соответственно Ищу = -^-.
Задача II имеет одно собственное число (например, s-e)
Теперь, так как для любого £ имеет место соотношение
применима теорема сравнения A8.47), A8.48):
или
9<*s<Q- 08-51)
2-й случай. Не все qj положительны. Этот случай сводится
к предыдущему.
Пусть имеется число N такое, что все q*i~q ,-{-N становятся
положительными. Произведем замену
= Г, СЧ-#(£ =
так что будет иметь место B1 -f~ МЪ) п = D* = Cl*Du и для задачи
с величинами, снабженными звездочками, все отношения будут поло-
положительны. Задача 2Tj = k*®j; имеет собственные векторы j;-, соот-
соответствующие характеристическим числам
и* = к. -)- N.
18.81 § 18. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 313
Интервал q* имеет по меньшей мере одно характеристическое число
х* = х^ + Л/, следовательно, интервал для qj включает по крайней
мере одно %s.
Сформулируем еще одну теорему включения при других предположениях.
Теорема. Пусть в задаче
Щ. (не обязательно симметричная) —матрица с неотрицательными эле-
элементами ajk^-Q и I) — диагональная матрица с положительными эле-
элементами dj главной диагонали; и — вектор с положительными компо-
компонентами uj, из которого образуем вектор ti = Slit с компонентами vj.
Vj
В интервале J, между наибольшим и наименьшим из п чисел <7.=
1
лежит наибольший корень щ задачи Щ = к£>$.
Для доказательства используем теорему, восходящую к Фробениусу ').
При сделанных предположениях задача Шх = x£>j имеет одно действительное
неотрицательное характеристическое число кь которое называется макси-
максимальным корнем, и нет другого характеристического числа, превосходящего его
по абсолютному значению. Имеется собственный вектор, соответствующий кь
все компоненты которого неотрицательны. С Щ. связана также транспониро-
транспонированная матрица Щ.'', ЭГ$ = k£)j имеет те же характеристические числа и
такой же максимальный корень, что и Щ = x35j. Пусть jt — собственный
вектор задачи Sl'j = x£>j, соответствующий максимальному корню иь который
имеет неотрицательные компоненты ZjX. Введем, как в A8.49), матрицу Ъ,
тогда получим, согласно A8.50),
0 = »'j, - to'Si = u'S'D'j, - и'Щ'з, = u'Q£>3, — и'х,£>з, = u' (Q - x,®) Щ{.
(Для диагональных матриц ЗУ£У = 35О = ОЗ).) Здесь все Uj > 0, все dj > 0,
все 2у(>0, но не все 2^ = 0; стоящее справа выражение может не обра-
обратиться в нуль, если для всех J величины Qj — %\ все положительны или все
отрицательны. Следовательно, должно быть
min q. < к, < max^..
/ 1 j 1
18.8. Численное применение теоремы включения. Численное нахожде-
нахождение характеристических чисел будет произведено на примере собственных
колебаний балки с массами и пружинами, взятом из п. 17.7Г. Итак, зададимся
частной задачей на собственные колебания A7.5) с матрицей (см. A7.64))
1180 —331 144 —36
—331 906 —367 144
144 -367 906 —331
{ —36 144 —331 762
Сначала оценим грубо собственный вектор для основного колебания
и' = A, 2, 2, 1),
откуда следует ti' = (STu)' = G70, 891, 891, 352); при получении ti = Stu реко-
рекомендуется проверка сумм столбцов; образуют вектор сумм столбцов матрицы ~й:
ё' = (957, 352, 352, 539);
%■■
') О. Frobenius, Sitz.-Ber. PreuB. Akad. Wiss., Math.-phys. K1-, Ber-
Berlin, 1912, ч. 1.
314
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[18.8
тогда сумма компонент и должнл быть равна ё'п:
ё'и = 2904 = 770 + 891 -f 891 + 352.
Вычисляя отношения qj, имеем числа: 770; 445,5; 445,5; 352. Простым варьиро-
варьированием компонент можно быстро сблизить отношения; целесообразно при-
применить схему, содержащую поправки компонент Uj н обусловленные ими
поправки компонент vj, которые получаются непосредственно, и тогда отно-
отношения могут быть вычислены с помощью логарифмической линейки. При
этом важно сначала уравнять друг с другом отношения при компонентах
с большими модулями, тогда можно будет легко скорригировать компонгнты
с относительно малыми модулями.
Процесс вычислзний понятен из приведенной таблицы.
с
Вектор и
текущими
поправками
и,
1
—0,5
0,5
0,5
0,5
—0,08
0,42
«2
2
2
2
2
2
«3
2
2
-Н
3
3
3
и,
1
1
+1
2
+0,2
2,2
2,2
С
Вектор
текущими
поправками,
обусловленными изменением и
V,
770
—59Э
183
+ 108
288
—7,2
283,8
—94,4
186,4
891
+ 165,5
1056,5
—223
833,5
+28,8
862,3
+26,48
888,78
V.
891
-72
819
+575
139;
—66,2
1327,8
-11,52
1316,28
VA
352
+ 18
370
+431
801
+ 152,4
953,4
+2,88
956,28
v,/u,
770
360
576
562
444
Этиошення q
V2/U2
446
528
417
431
445
»М
446
410
465
443
439
352
370
401
4,33
434
Теперь согласно теореме включения
434 < х < 445;
очевидно, точность можно легко повысить, продолжая процесс; можно избе-
избежать проб, находя вектор Ь из системы линейных уравнений. Опишем
сначала метод в общих чертах. Пусть задан вектор, являющийся приближен-
приближенным решением задачи Sir = хЩ. Приближенное собственное значение опре-
определяется нз отношения Рэлея
it
tt'Su
A8.52)
а Ь находится из системы уравнений Я (и + Ь) = х83 (и +- Ь), т., е. из
(% — х5В) Ь =* f * Й3и — Slit. A8.53)
Это — система я линейных уравнений для такого же числа неизвестных,
причем определитель системы практически равен пулю, так как х является
хорошим приближением для и. Приравняем одну компоненту b нулю, напри-
например у-ю, если модуль Uj достаточно велик; если и было хорошим приближе-
приближением, то п уравнений для оставшихся (п — 1) неизвестных с удовлетворительной
точностью будут совместны.
19.1] § 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ 315
Для частной задачи на собственные значения (§8 = S) процесс упро-
упрощается:
й = 5Гн, 'к=41Д, (й- н©) b = f = xu —t>. A8.54)
n'n
В данном примере и и и взяты как заданные векторы, стоящие в послед-
последней строке приведенной выше таблицы:
х =-^- = 438,961, х = -^- = 438,988.
н'и to и
Положим х = 438,9 и d2 — 0.
Для вектора b получается тогда система:
741,ldi+ 144d3— 36d4 = — 2,06,
—ЗЗЫ, — 357d3 -f 144tf4 = — 10,98,
+ 467,1^3— 331cf4 = 0,42,
— ЗЗЫ3 + 323,Ы4= 9,30;
ее решение
d,*—0,016, d3x 0,095, dt = 0,128.
Компоненты векторов (после округления) будут следующие:
и'= @,404; 2; 3,10; 2,33),
■о' = A77,24; 876,096; 1361,546; 1022,816).
Отношения qj равны: 438,7; 438,16; 439,2; 439,0 и к = -^Д = 438,8969;
х = -^- = 438,8974.
Таким образом, приближенное значение
х = 438,897,
а верхняя и нижняя границы следующие:
438,16 <х< 439,2.
Этот процесс применим точно так же и для других характеристических
чисел (описанный в § 19 итерационный процесс мог бы сходиться к вектору,
принадлежащему не основному колебанию, а высшему).
§ 19. Итерационный метод и главные векторы
19.1. Итерационный метод в общем случае. Точно так же как
для дифференциальных уравнений (см. гл. IV), для матриц имеется
опробованный приближенный метод определения собственных векто-
векторов и характеристических чисел задач на собственные значения типа
Щ = кЩ. A9.1)
Образуем, отправляясь от произвольно выбранного начального век-
вектора lQ =£ 0, последовательность векторов $0, J,, ..., Js, ... согласно
правилу
%_! = %, 5 = 1.2 A9.2)
316 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ |1».1
и соответственно для частной задачи %х — щ — по правилу
%-i = 3*. s=l. 2, ... A9.3)
При исследовании сходимости может быть использована
Теорема о разложении. Пусть дана общая задача на
собственные значения Щ — х23;с с заданными матрицами ?1 и 23
порядкапсразличными характеристическими числами хР х2, .... х„,
причем 23— невырожденная матрица, или % и 23 эрмитовы и
93 — положительно определенная матрица. Тогда имеется п
собственных векторов glF j2 ;ся, таких, что произвольный
вектор I может быть представлен в виде линейной комбинации rv
с коэффициентами cv:
и
S = 2cvJv A9.4)
v-l
Для этого нужно доказать, что имеется я линейно независимых векто-
векторов Xi- У.2' ■■■' In- Для эрмитовых матриц 91 и 23 и положительно
определенной матрицы 93 это уже было выполнено в п. 18.1. Пока-
Покажем теперь, что при невырожденной матрице 23 собственные векторы,
принадлежащие различным характеристическим числам, линейно не-
независимы. Если имеет место линейная зависимость, должно суще-
существовать наименьшее число s~^>2 собственных векторов, для которых
где все as Ф 0. Так как 93 не вырождена, существует 93, и каж-
каждый собственный вектор удовлетворяет уравнению
®5/ = иу5/> J=l> 2 s>
где (S^Srt.
Умножим A9.5) слева на К, тогда получим
Из этого уравнения и из A9.5) можно исключить jj и прийти к ли-
линейной зависимости (s—1) векторов
а2(х2 — иО&г-Ь ..• +as(Ks — *i)L = 0,
что находится в противоречии с предположением о минимальном
числе линейно зависимых векторов s.
Сформулированная теорема о разложении позволяет при итера-
итерационном процессе представлять начальный вектор через собственные
ректоры
ао=2*г&- A9.6)
19.1] § 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ 317
При этом ст — постоянные, не все равные нулю. Из A9.2) следует
и после умножения слева на ЗЭ
: 2 c,w,sr
Таким образом, на каждом шаге итерационного процесса постоян-
постоянные ст умножаются на характеристические числа яг.
После s-ft итерации получают
r-\ ' ' '
Расположим v.r в порядке убывания модулей:
\Щ\>\Щ\> ... >К|. A9.8)
Возможны два случая.
1-й случай. Принадлежащее первому не равному нулю cq ха-
характеристическое число Ку по модулю больше, чем последующие
или Cj Ф 0 и | и, | > | и,-1 для 7 = 2. 3, .... «, ]
или с, = с,= ... = с„_! = 0, с„¥=0, [ A9.9)
Вторая возможность содержит первую в качестве частного случая.
Из A9.7) тогда следует (х? Ф 0)
п
('К \s
— ) стремится к нулю, и тогда получается
т. е. векторы %s, умноженные на подходящие постоянные, сходятся
к ^-му собственному вектору.
2-й случай. Соответствующее первому не равному нулю cq число ■кд
равно по модулю числу х и. Тогда, в общем, отсутствует сходи-
сходимость итерационной последовательности, а также последовательности
n~sis. Рассмотрим два частных случая.
318 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ |19.1
Случай 2а: nq — — k?+i! I Kff I > I Kq+2| J> 0. В этом случае векторы $s
при четном s и при нечетном s сходятся к разным пределам:
Iim K-Bff+1»j — с г — с г I A9.12)
Случай 26. Пусть кя+1 = кA; cq ф 0; | kq | > | к?+2|> 0. Пусть
также 0 %q — A-\-tB, где А и В действительны. В A9.10)
сумма справа сходится к нулю при s->oo. Поэтому для достаточно
большого s
Запишем это приближенное равенство для s, s-j--l, s-\- 2 и умно-
умножим на
тогда при суммировании j? и j?+I исчезают, так что
Заменим здесь s на s-f 1, тогда получим два приближенных равен-
равенства для определения величин и -f-x =2Л, и?х? = A2-f-В2:
\%q + %) (hh + 2 %s + lh+l) "^ C^i+3 ^ + 1^ + 2)'
— , A9.15)
ИЛ EА+ 2 h + lh + \) "^ (h+ l5s + 3 h+2h+2)-
Если линейная зависимость трех векторов $s, ji+1, ji+2, согласно
A9.14), выполняется с достаточной степенью точности, то A9.14)
справедливо для каждой компоненты вектора, например, для у'-й ком-
компоненты Zjt s вектора $4, так что A9.15) переходит в
где
■) W. J. D u n к a n, A. R. С о I I a r, Matrices applied to the Motions of
Damped Systems, Philos. Magazine 19, 7 A935), 197—219.
19.1]
§ 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ
319
Пример. Механическая система с затуханием. Для системы, изо-
изображенной на рис. 19.1, с массами ти т2, пружинами с коэффициентами
жесткости с,, (г и с учетом сил сопротивления, пропорциональных скоростям
///////////////////////////////л
Рис. 19.1. Механическая система
с затуханием.
с коэффициентами пропорциональности ku k2, уравнения движения для малых
угловых отклонений ф[, ф2 имеют вид
/И2ф2 = С2 (ф! — ф2) -f- 4k2 (ф1 — ф2)
(сила тяжести здесь не учитывается). Допуская, что
1
полагая
~сг С\ = с2, 4/И[ = /и2, 4^1'
(fj (t) = Ф)вг1, фу = ;
н вводя обозначения
/ГПо • -. / С2 ь
С2 F ш-2
получаем частную задачу на собственные значения
где
О 0 1 01
0 0 0 1
-3 1—2 1
1-1 1-1
£' = (-2, 0, 0, 1).
Так же как в п. 18.8, 8'—вектор, полученный суммированием столбцов Я. Итера-
Итерационный процесс начнем с вектора A, 1, 0, 0), причем можно вынести за скоб»
ку множитель 2, так как начиная со следующей итерации все векторы jv
получают этот множитель. Приведенная на стр. 320 таблица содержит век-
векторы j0, j,, ...,Si2, появляющиеся при итерациях. Столбец с компонентами
320
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[19.1
to. см
t-T см"
LO
LO
см"
о
о
со
to
LO
см"
3
LO
CM
s
CM
о
CM
to
LO.
cm"
.1
CM OO
t^ oo
to o_
см" со со"
CM
LO
OO CM ^ CD
.-<. CM. CM. CM
со со со" со"
LO
см" a> cr>
g [О CO CO
CO СЭ
OO О LO
f- см см a>
Я g § 3
I I I I
LO
O" .-H
а
a>
•^* 00
см a>
CM (--
T 7 "
00 a>
00 ^-< со со
^* 00 см о
t— to CO О
LO
о см
LO LO
0O r4
CM CM
tD ^ч J?
t-- со
со о
CO ^*
CM (--
CO CD
см a>
t-- со
to
00 CO ^*
00 to to
О LO f-
r-i tr- to
t» i-l 0
со a> 00
CM CM CO
CM CM to
I CO CM
LO f CO ■*
CO (M Ю r-
I 4
О i-t CM CM
I I
CD О CM CD
CM CM
о" о о
2 8
о о — см см
О — <N CO ■*
О) О IN
см см
CO i~* ^5
7 °* T
32 LO ■*
19.2| $ 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ 321
sv, соответствующий вектору gv, используется, согласно п. 18.8, для про-
иерки с помощью суммирования
Согласно A9.16) вычислены приближенные значения
х -f к = 2А = — 2,562, хх = Л2 -f В2 = 3,265.
Из уравнения х2 -}- 2,562х -|-3,265 = 0 находим величины
хь2 = А ± iB = — 1,281 ± П.274,
определяющие частоту и затухание колебания (здесь — для первого обертона).
Нетрудно определить также частоту и затухание для основного коле-
колебания, так как сразу находятся след матрицы Ш Sa = Xj -f- *2 + хз ~Ь х4 = — ^
и ее определитель det Ж = Х|Х2х3х4 = 2. При к, -f- Х2 = — 2,562 и х,х2 = 3,265
можно найти х3 + х4 = — 0,438; Х3Х4 = 0,6126 и тогда получается
х3,4 = — 0,219 ± Ю.751.
19.2. Нижняя и верхняя границы для характеристических
чисел. Как в § 12, и в случае матриц можно при итерационном
процессе A9.2) получить постоянные Шварца ak и отношения vk,
а затем границы для характеристических чисел. Пусть матрицы 21 и S
эрмитовы и 23 — положительно определенная; для полученной согласно
A9.2) последовательности векторов j4 образуем числа
4 = 0,1.2....;
тогда из A9.7) и A8.38) следует
п п
Расположим Иу, как в A9.8), в порядке убывания модулей; при этом
некоторые с могут быть равны нулю (не все); тогда
Первое не равное нулю с пусть равно сг и относится к числу хг=^0.
Тогда, следовательно,
e*s=2kJ2»'J. 09-17)
Дальше образуются отношения
V* =—— =-
21 Л. Коллатц
, ft=l, 2, ... A9.18)
322 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
Тогда
я
I с
k-l
q-r
; A9.20)
далее
A9.21)
Из A9.19) при k -> оо следует
lim va = k,. A9.22)
Различают два случая.
1-й случай. Все kq неотрицательны, тогда выражения в A9.19),
A9.20) неотрицательны, vA, монотонно возрастая, стремится к кг
при k—>oo:
V, <V2< ... <КГ
В A9.21) из суммы выпадает член с q = r. Пусть 1г + 1 — верхняя
граница для %r+i, которая все же меньше vft:
Vft>', + i>>Wi (>и? для ? = г + 2, г 4-3. ...),
тогда
и далее следует
19.3] § 19, ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ 323
поэтому
и
=l. 2, ...
• —1
A9.23)
2-й случай. и? имеют различные знаки. Тогда проводят вычи-
вычисления только с 52ft с четным индексом:
*»=£• 4 = 0.1.2
величины а* определяются согласно
Введя обозначения х2 = х* и v2ftv2ft + 1 = v*, получим
п *
V, ., *ft * a2k ak
ah= У, с гх , vh = = -j—
[19.24)
A9.25)
?-/■
т. е. имеют место соотношения A9.17), A9.18), в которых вели-
величины ak, xq> vk заменены величинами со звездочками, и справедливы
дальнейшие преобразования до A9.23), так как все к* неотрицательны.
Неравенства A9.23), например, имеют вид
zlL — I
причем Г+1 теперь есть верхняя граница для х2г
A9.27)
19.3 Понижение порядка. Если в обшей задаче на собственные
значения
%1 = хЪ?, A9.28)
известны одно характеристическое число хх и принадлежащий ему
собственный вектор jj, то можно его «отщепить» и тем самым по-
порядок задачи п понизить на 1. (В этом разделе хх не означает наи-
наибольшего по модулю характеристического числа.) Запишем векторы
Хо
91*
324 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ A9.3
где \j не могут быть все равны нулю. Пусть \х Ф 0 (при \х = 0, но
£. =И= 0 последующие рассуждения могли бы быть проведены с #-м
столбцом).
Умножим столбцы определителя A7.15) последовательно на хх,
х2 хп и заменим первый столбец суммой всех умноженных на х„
столбцов
(an—nbn) хх -f- • • • + (au—v.bln) хп ап — vbn . . . au—
(a„i— %bnl)xx-{- . .. +(aaa—xbna)xnaa2- nbn2 . . . ann —
Вследствие 9(j, = х,93(Г] можно в первом столбце заменить
0;Л + • • • + а]пх„ = щ фпхх + . . . + b]axn) =
и вынести из первого столбца множитель щ — х:
= 0.
(щ — и)
In an2 —
= 0. A9.29)
Таким образом, полином л-й степени относительно х представляется
в виде произведения (х1 — и) на полином (л—1;-й степени.
В оставшемся определителе вычтем из q-й строки (для q^>>2) первую
строку, умноженную на ^'^j тогда в первом столбце окажутся только
нули, за исключением числа |j ф 0, и можно отбросить первую строку
и первый столбец
«22 — ^^22 |f- (« — ^*> a — Kb —
an2 - *bn2 — ¥- («12 — ^12) • • • ann — 4» — T"
61 si
= 0.
A9.30)
Таким образом, задача Щ = кЩ переходит в подобную задачу
21У = х93у, A9.31)
но с матрицами (л—1)-го порядка 21*, 23*.
В частной задаче на собственные значения
A9.30) упрощается, так как 93 = (£ и л;у- = |;-; новое уравнение A9.30)
снова оказывается вековым уравнением. Оно соответствует новой
частной задаче
19.11
§ 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ
325
с матрицей (л—1)-го порядка
«12 ап3 — ■
. A9.32)
Установим зависимость между каким-либо собственным
ром $2- принадлежащим х = к,, с компонентами (х12, х22,
векто-
■- хп2)
для A9.28) и собственным вектором г* с (л—1) компонентами
(х*г х*32 л;*2) для A9.31). Переход к определителю A9.29) со-
соответствует введению новых неизвестных
хп х\
х
12'
X
22
X • X*
2 1
X
22'
12
A9.33)
т. е. A9.29) является определителем новой системы уравнений для
х ,,
J2'
первая строка соответствует уравнению
(и, — иг
A9.34)
Из этого уравнения для к2 Ф щ вследствие \Y Ф О при известных х*-2
для j > 1 можно вычислить величину х*2 и затем согласно A9.33)
Xj2 для всех у. Конечно, можно еще найти собственные векторы
путем решения получающейся при к = к2 однородной системы ура-
уравнений.
Можно также составить соответствующие формулы для к] = к21)-
19.4. Численный пример. Рассмотрим пример акустической задачи
из п. 23.5, в которой разыскиваются характеристические числа матрицы
(—2 4 0 2 0
4 0 4 8 2
0 4 0 2 8
14 1—14
0 14 4 0
Итерационный процесс здесь сходится тем лучше, чем больше модуль харак-
характеристического числа я,, превышающего остальные, поэтому сначала пред-
представим себе расположение характеристических чисел и выберем подходящее
') Н. W i е 1 a n d t, Das Iterationsverfahren bei nicht — selbstadjungier-
ten linearen Eigenwertaufgaben, Math. Z. 50 A944), 93—143.
325
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
119.4
«спектральное смещение». Из физических представлений, (см. также рис.
23.18) возьмем в качестве приближения векторы (см. таблицу)
J
1
2
5
2
6
2
Kj
(приближенное
значение
5 4
5 -4
-5 4
3 3
2 —4
3 —3
22
12
-18
54
15
42
50
—8
—38
'j
35
4
—29
33
—3
23
Проба
s'u.
194
21
—20
11
2
—9
10,8
3,2
—8,4
Отношения
12,5
2
-9,5
11,67
2
—9,67
11
0.75
-7,67
(§' = C,13, 9, 15, 14) — снова вектор, составленный из сумм столбцов).
Таким образом, я, и 11, и2 да 2, х5 и—9. Итерационный процесс здесь
хотя и сходится, но медленно, так как — только немного менее 1. Если
сдвинуть все значениях на 3, заменив x = x-f-3, Ж = Я -{-3S, то будет
я, як 14, я2 и 5, х6 и —6
и отношение, определяющее сходимость, будет намного лучше. Проведем
здесь итерации с матрицей Я и вектором §' (для проверки согласно п. 18.8):
ё' = F, 16, 12, 18, 17).
V
@)
A)
0
1
2
3
4
5
Компоненты ? =1fijv j
1
1
7
2
28
392
5 648
81008
167 592
2
С
бе
100Г
14 33J
206 92Е
2 977 74£
)
1
17
4
65
88£
12 866
185 094
2 669 981
>
[
1
12
3
44
622
9010
129 442
1 865 746
1
12
3
42
619
8 892
128 515
1 850 614
Проба .
«4-1
E)
69
A7)
245
3 522
50 751
730 984
10 532 687
Частные от деления компонент jv
7
14
14
14,4
14,343
14,4133
И
компонент
, (наи-
21
13,8
U',5
14,292
14,435
14,3905
17
15,5
14,3
14,521
14,39
14,4250
12
14,7
14,14
14,49
14,37
14,4215
12
14
14,74
14,36
14,453
14,4000
Разность
между наиболь-
наибольшим значе-
ниями
14
1,7
0,74
0,229
0,110
0,0345
-
Отношение
3 Ц? -2
13,8
14,41
14,376
14,4097
14,40334
14,40892
19.41
§ 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ
327
При этом мы сначала исходили из (^) = A, 1, 1, 1, 1), получили (jj) =
= G, 21, 17, 12, 12) и, так как эти числа относятся приблизительно как
2:5:4:3:3, взяли эти числа в качестве компонент $„, Можно, так же как
в п. 19.2, составить таблицу из величин ak и отношений v^:
a■m
'О, 1, 2,
0
1
2
3
4
Ч
63
907
13089
188481
2714714
V* "к - i
14,397
14,4311
14,4000
14,40312
5
6
7
8
"к
3,9099665 • 107
5,631738- 10«
8,114250- 10э
1,1691138- 10"
14,40287
14,40355
14,40807
14,40816
Примем во внимание, что теперь больше не выполняется ak~bjbk-j'<
для произвольных j, например, теперь имеет место
6o5d= 188 141 ф 3^2=188 481,
матрица 31 здесь не эрмитова; кроме того, отношения vA не обнаруживают
монотонной сходимости, например, если вычислены v4, v6, v6 и оказалось,
что они почти равны друг другу, то из этого еще нельзя заключить, что
дальнейшие vft сохранят это значение.
Прервем итерации на fe; тогда в качестве собственного век гора следует
принять:
£, = A; 2,550; 2,287; 1,599; 1,585).
С хх = 1 получаются непосредственно нужные для A9.32) отношения, на-
например лг2/аГ[ = 2,550; эти числа согласно A9.32) дают матрицу
—7,2 4 2,9 2
—5,148 3 —2,574 8
—2,396 1 —1,198 4
—5,34 4 0,83 3
Можно было бы исходить из произвольного вектора, однако процесс
ускоряется путем пересчета вектора
(х12; х22; х32; xi2; х52) = B; —5; 4; 3; —3)
согласно A9.33) в вектор
D2; 4; 4: -4; 4) = B; -id; -0,574; -0,2; -6,17).
Так как, однако, и2 и и5 близки по модулю, сделаем для ускорения сходи-
сходимости обратный сдвиг
UI =ЗГ— 3S, ё'' = (—23,084, 9; -3,042; 14)
328
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[19.5
и получим тогда из итерационного процесса (последний столбец дает при-
приближенное значение для х5):
(округлено)
—10,1 —0,574 —0,2 —6,17
_87,8 —3,15 —0,2 —51,5
_78 —3,9 —0,4 —45,6
—68,7 —3,8 —0,2 —40
Сумма
—17,04
—142,7
—127,9
—112,7
V
0
1
2
3
87,80
780,5
687,6
605
3,15
39,48
37,77
34,18
X
—0,215
—0,38
2,27
1,645
51,47
456,42
400,5
351,5
Сумма
'v
142,21
1276,0
1128,1
992,3
0
1
2
3
—8,70
—8,90
—8,93
—8 80
Отношения
компонент
-5,5 -+-1
—12,5 +1,9
—9,7 —5,7
—8,99 —8,22
—8,32
—8,86
—8,78
—8,79
'v
sv
-8,35
—8,96
—8,83
—8 805
19.5. Введение главных векторов. При исследовании сходи-
сходимости итерационного процесса выше была использована теорема о
разложении, по которой произвольный вектор начального приближения
$0 может быть представлен с помощью собственных векторов jy. Но это
не всегда возможно. Имеются примеры, когда не существует ни одного
собственного вектора, и представление с помощью собственных век-
векторов невозможно. В таких случаях используются главные векторы.
Пример 1. Частная задача на собственные значения с одним собствен-
собственным вектором. Матрицы
2 2 0\ / 3 4 0\
— 2 5 2 )
7 -10 —5 /
имеют х = 0, соответственно и'= 1, в качестве трехкратно вырожденного
характеристического числа и обладают однопараметрическим семейством соб-
собственных векторов
4 2 I или 31* = Ш, + @
10 —6 /
19.51
19. ИТЕРАЦИОННЫ!! МЕТОД И ГЛАВНЫЕ, ВЕКТОРЫ
329
Пример 2. Общая задача на собственные значенля без собственнэго
вектора. Задача A7.14) для
Н'ЛУ -С!)
= —1
(?J и S3 обе симметричны и неопределенны) не имеет характеристических
чисел; определитель
1-х 2-х
2-х 3-х
не обращается в нуль ни для ка-
какого х.
Определение глав-
главного вектора. Вектор ф
называется главным вектором
частной задачи на собствен-
собственные значения
(91 —Jt(S)j = O, A9.35)
если для некоторого целого
г > О имеет место
(91 — kS/IJ = O; A9.36) Рис. 19.2. Плоскость Е главных векто-
при этом § называется глав-
главным вектором степени г, если
г — наименьшая степень, при которой
нию A9.36).
Собственные векторы суть главные векторы 1-й степени.
Пример.
Для приведенного выше примера 1 уравнение главных векторов 2-й сте-
степени I; = 1J для матрицы Я с и = 0 имеет следующий вид:
■—4 24 8\ ■ /А,-
ров 2-й степени,
удовлетворяет уравне-
= 0, где
Для компонент I) получают условие
А, —6А2 —2А3
Все векторы
6 + 2
и 1)
\ А3 /
двупараметрического семейства с произвольными А2, А3 суть главные век-
векторы степени г<;2, а именно 2, поскольку они не являются собственными
векторами и не могут иметь степень 1. Вследствие того, что Ш3 = 0, все
векторы с тремя компонентами, не являющиеся главными векторами степе-
степеней 2 или 1, суть главные векторы степени 3. Собственные векторы, прове-
проведенные из фиксированной точки, образуют прямую g, а главные векторы
степени 2 — плоскость, проходящую через эту прямую, но не содержащую
ее (рис. 19.2.)
330 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ A9.9
Для главных векторов справедлива следующая простая теорема:
Главный вектор l)r r-Pi степени удовлетворяет одновременно всем
уравнениям высших степеней г {- 1, г -\ 2 как непосредственно
видно из равенства
Очевидно,
(91 - кйУ Ьг = br~q
для q < г есть главный вектор степени г—q и, следовательно, для
9 = г — 1 — собственный вектор.
Введение главных векторов не добавляет новых характеристиче-
характеристических чисел; но если для некоторого числа я имеется главный вектор
степени г, то для того же числа и имеется также собственный век-
вектор г; нужно только сделать замену
1^ = г A9.37)
для того, чтобы получить (% — х(£);г = 0 (не может быть t = 0. так
как иначе t)r было бы степени -^ г—1).
В тех случаях, когда, как в приведенном выше примере 2, от-
отсутствуют характеристические числа, нет и главных вектороь. Однако
имеет место следующая
Теорема о разложении. Для частной задачи на соб-
собственные значения с произвольной матрицей всегда имеется по
меньшей мере одно характеристическое число и главные векторы
такие, что произвольный вектор j0 может быть представлен как
сумма
k
Ho=SV С19'38)
(Здесь индекс при \) не означает степени главного вектора.)
19.6. Доказательство теоремы о разложении. Для доказатель-
доказательства будем вектор j@ понимать как начальный вектор последователь-
последовательности итераций, образованных согласно A9.3),
^ = ^-1 = 21%. *=1. 2. ... A9.39)
Полученная после п итераций последовательность из (п -f- 1) векторов
не будет линейно независимой в пространстве размерности п, следо-
следовательно, имеет место соотношение
т т
0=Iic^=^ic(in%, A9.40)
где не все cq = Q\ в частности, можно положить стФ0, а именно
ст=\; может быть т — п, но также может быть и т < п. Введем
теперь полином
in
/>W=2v,. A9.41)
0
19.61 § 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ 331
Пусть он имеет корни |], |2, ..., \k кратности гь г2, ..., /у.
к
р (х) = (х- &,/1 (х - 12)г> ...{х- lk)rk =Л(х- lk)r),
причем rj-f r2-\- ... -f- rk = т.
Образуем, далее, k вспомогательных функций рх (х) Pk(x),
каждая из которых не содержит множителя (х—|;):
Pj(x)= P(X\., у=1.2 к, A9.42)
(* — I]) '
и которые в своей совокупности являются взаимно простыми. Со-
Согласно известной теореме алгебры1) тогда имеются полиномы
q-i{x) 4k(x) такие, что
1 == рх (х)qx (х) + Р2(х) д2(х)+ ••• + Pk (х)qk(х)-
Теперь в каждом таком тождестве степени х можно заменить степе-
степенями матрицы 91, а х° через 91° — б; так как степени матрицы %J, 91*
перестановочны друг с другом, матричные полиномы можно вычи-
вычислять алгебраически, как обычные полиномы. Следовательно, имеет
место
Умножение этого равенства справа на 50 дает
к
h = li Ь]. где 1}J *= Pj (9t) qj (9t) у
J-i
Введенные здесь векторы fyj являются главными векторами. Действи-
Действительно, из A9.42) следует
(х - |// Pj (х) q, (х) == qj (х) • р (х).
Если, далее, заменить х матрицей 21
B1 - lj&)r> Pi (Щ Я, (Щ = Ч} B1) р B1)
и учесть, что согласно A9.40), A9.41)
то после умножения на $0 справа получим
(Я-!,(£//&, = О,
т. е. i)j — главный вектор матрицы 91 степени г;- и принадлежит
характеристическому числу \у Этим доказана возможность представ-
представления Jo с помощью главных векторов.
1) О. Perron, Algebra, т. I, Berlin— Leipzig, 1927, 185 [см. А. Г. К у-
р о ш, Курс высшей алгебры, Физматгиз, 1963].
332 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ 119.7
19.7. Сходимость итерационного метода для частных задач
на собственные значения.
Пусть снова 21 — произвольная киадратная матрица, а д5—итера-
д5—итерационная последовательность, полученная при произвольном начальном
векторе согласно A9.39). На основании A9.38) $0 можно представить
как сумму главных векторов фу, причем j0 и l)j не равны тожде-
тождественно нулю. Тогда имеет место соотношение
к к
h = 2 ъ% = 2 (Я - и/И- к/>у f)j.
Пусть l)j — главный вектор степени Лу, принадлежащий характери-
характеристическому числу y.j. По формуле бинома Ньютона
j=i a
Согласно определению главного вектора
собственный вектор г, для a==rf—1,
таким образом, сумма A9.43) распространяется только на а от 0
до Гу—1. В подробной записи сумма A9.43) имеет вид
^Г} A9-44)
Пусть теперь s неограниченно возрастает.
Как и в п. 19.1, будем различать несколько случаев:
1-й случай. Среди различных характеристических чисел Kj,
принадлежащих векторам ^, ..., [)к, имеется одно, например кь пре-
превосходящее по модулю остальные: | кх | > | Ку | для у = 2, 3 п.
(Все «!, к2 к„ различны, так как согласно доказательству
в п. 19.6 i)h §2 bk в теореме о разложении принадлежат исклю-
исключительно различным характеристическим числам.) Тогда в A9.44)
при s—>оо преобладающим становится последний член
т. е.
^= (9l-K1e)ri-1n1 = s,; A9.45)
\ 1 I
при этом j, есть принадлежащий кх собственный-вектор.
19.81 § 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ 333
1-й случай, в частности, имеет место, если каждые попарно от-
отличные друг от друга собственные числа (которые могут повторяться
многократно) имеют также различные модули.
2-й случай. Пусть существуют два различных характеристи-
характеристических числа X], щ, равных по модулю, таких, что
| щ | = | х21 > | %j | для у > 3.
Тогда сходимость вообще отсутствует; как и в п. 19.1, можно рас-
рассмотреть ряд частных случаев').
19.8. О степенях матрицы. Из A9.44) можно вывести важные
факты о степенях матрицы 21. Если мы выберем в качестве j0 у-й еди-
единичный вектор (все компоненты $0 равны нулю, за исключением у'-го,
который равен 1), то полученный из итерационного процесса A9.39)
вектор ls = Wlo равен у'-му столбцу матрицы 91". Пусть, далее, все
характеристические числа %q по модулю меньше 1, тогда согласно
A9.44) is сходится к нулю, т. е. у-й столбец 91 * стремится поэле-
поэлементно к нулю при s—>оо. Это справедливо для каждого у. сле-
следовательно, все п2 элементов 9F по отдельности стремятся к нулю.
Если, с другой стороны, имеется хотя бы одно характеристиче-
характеристическое число uq с модулем |и?|^>1, то все элементы 915 не могут
стремится к нулю. Действительно, для принадлежащего кд собствен-
собственного вектора j? имеет место равенство
и правая часть не стремится к нулевому вектору при s->oo.
Теорема. Только в случае, когда все характеристические
числа матрицы 91 по модулю меньше 1, последовательность
матриц 9t5 при s->oo сходится поэлементно к нулевой матрице.
Используем одно простое следствие теоремы. Пусть все | %q \ •<
<а<1, тогда матрица —91 = 91* имеет характеристические числа
п* = —и, которые также все по модулю меньше 1, | х? | < а < 1
и согласно теореме %*s сходится поэлементно к нулю, т. е. все
элементы а*/ь матрицы 91*E^ ограничены:
|а*.<>)| < А для всех у, k, s.
Для элементов aW матрицы 915 тогда имеет место соотношение
< аМ для всех у, к, s.
') Н. W i e I a n d, Das Iterationsverfaliren bet nicht-selbsiadjungierten
Higenwertanfgaben, Math. Z. 50 A944), 93— 144.
334
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
119.9
Пусть вектор J имеет компоненты zx, z2 zn с | z,
векторный ряд
Тогда
J .. A9.46)
сходится, так как ряд для у-й компоненты можорируется следую-
следующей геометрической прогрессией: z-\- naAz-\- na?Az -j- .. .
Если же 91 имеет характеристическое число к^ с модулем ^-1,
соответствующее собственному вектору j , то ряд
если выбрать J = j . Таким образом, справедлива
2
V=>0
расходится,
Теорема. Ряд
2
v=0
сходится для произвольного вектора $
только тогда, когда все характеристические числа матрицы 91
по модулю меньше 1. Сходимость в этом случае абсолютная,
со
и ряд ^ ^V также сходится абсолютно.
19.9 Системы обыкновенных линейных дифференциальных
уравнений. Обсудим некоторые применения матричного исчисления
к системам дифференциальных уравнений. Пусть задана система ли-
линейных дифференциальных уравнений:
dy, . \
-jl- = yi = ah(t)yl + a]i(t)y2+ ••• +aJn{t)yn + r,(t). [ ?)
У=1. 2 п, |
причем ujk{t) и гj{i) — заданные непрерывные и ограниченные функ-
функции времени, и ставится задача отыскания решений этой системы.
Для отыскания решений этой системы зададимся начальным условием:
Ууо = М°) для t==0'
Как известно, каждое линейное дифференциальное уравнение «-го
порядка можно переписать в виде системы A9.47).
Применим матрицы
au al2
У\
У2
;
Уп
>'2
•
*
Уп.
Г2
■
*
, 91 =
i
■"•22
а„
а„
а„
тогда A9.47) будет иметь вид
р = 2li) +г. A9.48)
При г=0 система называется однородной, при г ф 0 — неоднородной.
Представим себе, что с помощью различных начальных условий оп-
19.91
§ 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ
335
ределеньг п линейно независимых решений однородной системы.
Эти п векторов р;- образуют «фундаментальную систему»:
У1я
= ' »„ =
Ун
У21
Уя1.
У12
У22
Уяя
В качестве примера можно считать, что система решений задается
начальными условиями
У] @) = 1.
Система решений удовлетворяет для каждого у =1, 2, ... п урав-
уравнениям
ViJ = %X)j. A9.49)
Векторы t)y для некоторого значения t—t0 линейно независимы, если
образованная при этом матрица
(Уи Уи ••• Уи\
sjj = (pj, р2> ..., t)fl)= A9.50)
\ Ул1 Уя2 • • • Уяя /
не вырождена, т. е. если Д = det ЭД ф 0. Далее справедливо следую-
следующее утверждение: если система 1)у линейно независима для какого-
либо t — t0, то она линейно независима для любых t. Для произ-
производной определителя, дифференцируя по столбцам, получим из
A9.49)
«пУи4 ••• ~
Уй
Уи
- • • • 4 аяяуЯ1 Уя2 • • • У
Уи О-пУпЛ- ••■ + «1яУя2 У13
4-..
... 4 аппуп2 уя, ... уля
УпУ12 ••• У1, я-1 «пУы'т- ••• 4 а\пУпп
Уя.я-i ол]у]я
336
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
|19.9
Здесь каждое а.-, имеет множитель Д, например множитель при аи
Ун
У22
УЛ2 • • • Упп
У12
У21 У23 • • • У2п
Уп\ УпЗ
Упп
4 •••
У21 У22 ••• У2./1-1
Уя1 У «2 •■• Уя, л-1
= А.
в то время как все ajk при у Ф k имеют множитель 0, например
множитель при а12
У12
У22
У«2 • • • Уп
— У22
У21 У23
Уя1 У«3 • • • Уяя
У21 У22 ••• У2.Я-1
У«2
Уп,п-\
так как совпадают две строки.
Обозначим, через s% след матрицы 91:
У21 У22 • • • У2«
У21 У22 • ' • У2п
Уя1 У«2 • ■ • Уя
= 0,
тогда имеет место соотношение
Д = $% • Д
или
t
J s%l(t)dt
* A9.51)
т. ё. или Д = 0, или Д отличен'от нуля для все* t. При системе
решений l)j, ..., 9Я вектор
Ъ = У)-с A9.52)
также порождает систему решений, причем вектор
содержит а' произвольных постоянных Cj. Как видно, A9.52)
янляется общим решением однородной системы, так как оно может
19.101 § 19. ИТЕРАЦИОННЫЙ МЕТОД И ГЛАВНЫЕ ВЕКТОРЫ 337
быть связано с произвольными начальными условиями X) @) = 1H,
нужно только положить
я)~ существует, так как Д = det *JJ Ф 0.
Так же как в случае отдельного дифференциального уравнения,
для нахождения частного решения неоднородной системы A9.48)
здесь можно применить метод вариации постоянной.
Запишем
и = 3)-с@. A9.53)
где Cj{t) — функции, подлежащие определению. Подставляя A9.53)
в A9.48), получаем
Теперь согласно A9.49)
*j) = (!),, tJ \)п) =
таким образом,
или
с =
о
причем с* — вектор с константами с*, с* с*. Таким образом,
получаем общее решение неоднородной системы
(t \
с* + [ ty~\dt\. A9.54)
о /
19.10. Постоянные коэффициенты и главные векторы. Пусть
в A9.47), в частности, коэффициенты a-)k постоянны; тогда для
однородной системы, так же как и в случае одного уравнения, можно
получить представление
где j — постоянный вектор, ах — подлежащая определению постоян-
постоянная. Так как
то после сокращения на не равный нулю множитель ем получаем
Щ = Ч-
Если 31 имеет различные характеристические числа и;- с соответствую-
соответствующими им собственными векторами г,, то с помощью неопределенных
338 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [19.10
коэффициентов Cj общее решение однородной системы уравнений
p = ?U) можно записать следующим образом:
При кратных характеристических числах появляется небольшое услож-
усложнение. Для однородного линейного дифференциального уравне-
уравнения ге-ro порядка с постоянными коэффициентами в случае дву-
двукратно вырожденного корня характеристического уравнения реше-
решением дифференциального уравнения, помимо еп/, будет также teKt;
здесь же, однако, tr^f' вообще не будет у-м решением при дву-
двукратно вырожденных характеристических числах и приходится рас-
рассматривать главные векторы fy. Пусть \)г есть главный вектор сте-
степени г, принадлежащий характеристическому числу и матрицы %.
Введем дальше векторы
с помощью соотношений
(Я - х(£П), = СД — х®) $,_,«., = &г_,. 5 = 1,2 г. A9.55)
Вместо неприменимого представления
(а$-\-aft + ... +аг_/-1г>'"
введем представление с главными векторами
р=(ао(>, -f а,%_, Н~а2^,_2-т- ... +аг-/-\)е*'
и попытаемся определить aj таким образом, чтобы 1) удовлетворяло
однородным уравнениям. При подстановке I) в равенство y=5U) и
после сокращения на множитель ея' получаем
aoxf), -f a,x^,_, -f- ... ■+■ ar-.xy.tr~\ -f a,^_, 4 2a2^,_2 +- ...
Если сравнить коэффициенты при одинаковых степенях t, например
при t4, то имеем с учетом A9.55)
9 = 0, 1 г —2
или
Я<7 Я<7-1 00
~ (q+\)q
Следовательно,
lO.11 § 20. ДОПОЛНЕНИЯ 339
есть решение однородной системы. С помощью линейных комбинаций
решений такого рода можно, используя теорему о разложении, удо-
удовлетворить любым начальным условиям, следовательно, это есть наи-
наиболее общее решение однородной системы.
Простой пример. Пусть задана система
^':ЗУ'-У2'} A9.57)
Здесь
-(! -;)
имеет только одно характеристическое число и = 2 как корень уравнения
g ^ I
= и2 — 4и-)-4 = 0 с однопараметрическим семейством соб-
1 1 — х
ственных векторов J = с I ]• Решением A9.57) будет, следовательно,
I) = ce2t (Л, но не 8 = с ■ t ■ e2t I J , так как j = с ■ e2t ( ^ ~[ ) ф Щ =
Bt\
1. Найдем главные векторы fJ 2-й степени: (Щ. — 2SJ tj2 = 0; здесь
(Я — 2@J = 0, следовательно, любой вектор 1J = I ) есть главный вектор
\Ь I
и при
согласно A9.56)
, (a+t(a~b)\ 2<
есть общее решение A9-57), как можно проверить непосредственно подста-
подстановкой.
§ 20. Дополнения
20.1. Матричные полиномы и уравнение Кэли. Если 51 имеет
в качестве характеристических чисел щ кп, то характеристиче-
характеристическими числами 912 будут к2 к2п, так как из равенства <р(х) =
= detCl — x(S) = 0 следует ф(х)ф(— к)= det (91—xg) detCt-f x6)=
= det Bt2 — x26) = 0. (В случае кратных характеристических чисел Ху
матрицы 51 высказанные соображения еще ничего не говорят относи-
относительно кратности хЯЛ Далее, если 51 не вырождена, обратная ма-
пг-1 -1-1 _1
трица Д имеет характеристические числа xi , xq , ..., хя , как
видно из следующего соотношения: detfSl 6) =х~я det2t~ X
Xdet(K©— 51) = 0. Теперь можно поставить вопрос о вычислении
характеристических чисел произвольного матричного полинома.
99*
340 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ B0.1
Пусть
т г
h (х) = 2 *v*v = А, П (* — *Р)
v=0 p=l
— заданный полином относительно х с коэффициентами Av (напри-
(например, hT ф 0 для rj>l) и корнями хр, тогда полином h C1) относи-
относительно некоторой заданной матрицы 31 определяется так:
* (Я) = 2 Av3lv = А, П C1 - хрй), B0.1)
v-0 р=1
причем 51° = S. Если, как в A7.6),
п п
ф (%) = det C1 — хй) = П К — «) = 2 avvy B0.2)
0=1 v=0
— характеристический полином матрицы 31 с характеристическими
числами х0 в качестве корней, то из B0.1) следует после перехода
к определителям
det h C1) = hnT П det C1 - ир6) = h* Д П («0 - «P) =
P-I p-l 0-1 .
П(гП(«о-«р))=Па(«<1)- B0.3)
В частности, если сделать замену h(x) = g(x) — %, то получим важ-
важное и удивительно простое соотношение
п
det (g B1) - xg) = П (е («о) - «)• B0-4)
0-1
Теорема. Пусть 31 — произвольная матрица с характери-
характеристическими числами X], х2 и„ и §"(х)—заданный полином х.
Тогда матрица g C1) имеет характеристические числа g (щ),
§"(н2) §"(^г)- «Э/ио справедливо и в случае кратных характе-
характеристических чисел.
Для степеней матрицы 31 имеет место примечательное соотноше-
соотношение— уравнение Кэли, или Гамильтона — Кэли')•
') Артур Кэли, английский математик, родился в 1821 г. После
окончания Кэмбриджского университета становится адвокатом и одновре-
одновременно занимается математическими исследованиями. В этот период (до 1863 г.)
им было написано около 300 статей. В 1863 г. Кэли стал профессором мате-
математики в Кэмбридже. Умер в 1895 г.
Вильям Роуэ н Гамильтон родился в 1805 г- в Дублине. Уже
в 1827 г. он становится профессором астрономии в Дублинском университете
и отновременно директором обсерватории. Гамильтону принадлежит много
работ по механике и математике, в частности, им были открыты кватер-
кватернионы. Умер Гамильтон в Дублина в 1865 г.
20.1] § 20. ДОПОЛНЕНИЯ 341
Для матрицы 23(x) = 3t— x(S, которая для произвольного х
в общем случае не вырождена, можно образовать обратную матрицу
/ Ап(к) А,,(х) ... Аа1(х)\
l i
(
фМ \А1п(х) А2п(х) ... Ааа(х)
Здесь
я
Ф (х) = det 23 = det B1 — кЩ = 2 avxv,
v=o
как и в B0.2), — характеристический полином матрицы 31, a AkJ(%)~
алгебраические дополнения элементов матрицы 23, следовательно,
полиномы относительно х, имеющие наивысшую степень (п—1).
Таким образом, можно ф(хJ3~ (х) записать в виде
причем матрицы 23О, 23, 23n_, не содержат величин к. При
умножении справа на 23 = 31 — х® в правой и левой частях равенства
окажутся полиномы /г-й степени:
а сравнение коэффициентов и последующее перемножение с задан-
заданными степенями 31
1= 2303l
n К S» SW S»
• 31
при сложении дает
так как с правой стороны все члены взаимно уничтожаются.
Теорема. Пусть ф(х) — характеристический полином ма-
матрицы 31, т. е. ф (х) = det Bt — хб); тогда 31 удовлетворяет своему
характеристическому уравнению, уравнению Гамильтона — Кэли:
фC1) = 0. - B0.6)
С помощью уравнения Кэли B0.6) можно выразить п-ю и высшие
степени матрицы 31 через 6, 31, 3t2, .... 31""' с помощью линейной
комбинации.
Пример.
/012ч /58 13 ч /34 60 99 ч
Щ=|1 2 3 ], Ж2=( 8 14 23), Щ3= 60 105 173 ).
\2 3 5/ V 13 23 38 / V 99 173 285/
342 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАГРИЦ J2C2
Коэффициенты уравнения Кэли а0, ах, аг
можно определить без вычисления характеристического определителя из пер-
первых строк матриц; получаем
—60 = 0-f-«1 • 1
—99 = 0-f a,-2 + «2-13.
и отсюда ао=1, а, = — 4, а2 = — 7; таким образом,
Высшие степени можно получить умножением этого уравнения на SC, Щ.2, ...,
например
/ 258 451 743 \
Щ* = 7Ж3 + Ш2 — Ш = 53W2 + 27Щ — 7® = I 451 789 1300 1.
\743 1300 2142/
* су
Умножением на Ж , Щ. , ... получаются отрицательные степени, например
я_1=4е+7м2 г; -; j
V 1 —2 1
20.2. Функции матриц и степенные ряды матриц. Матричные
полиномы часто бывает удобнее вычислять с помощью интерполя-
интерполяционных формул Лагранжа. Эти формулы позволяют с помощью
«вспомогательного полинома Лагранжа» *)
(•* — xt)(x — х2) ... (х — xq_x)(x — хд+1) ... (х — х„)
M-*)=(v; —XUX —X) (X —X YOT^X \ П Т\ B0'7)
\Лд Л1) уЛд Л$) . . . \Лд Лд_ ]) \Л д Л д _{. | ) . . . \Х д X п)
задать полином f (х) степени не выше (я— 1), который в заданных я
точках Х\, х%, .... хп принимает заданные значения функции / {х{).
/(*а) /(*„)■•
f(x)=42iJ(xq)Lq(x). B0.8)
Справедливость этой формулы непосредственно видна из соотношения
1 для s = q,
0 для s ф q.
Если потребовать, чтобы для всех я значений функции было f(xq)= 1,
получим /(х)= 1:
*) Термин в русской литературе не употребляется; интерполяционным
полиномом Лаграижа называют / (х) B0.8).
20.2] § 20. ДОПОЛНЕНИЯ 343
Заменим в B0 7), B0.8), B0.9) х матрицей %, характеристические
числа которой и,, х2 хя все отличны по модулю, и выберем
эти v.q в качестве точек xq, тогда получим
L(%) = ~ '-A- -. ч-^-Ц чт ' / 2IL, B0.10)
n
t(ty\ . "S^ f (y^ \ ^ (Щ) Г20 11^
9-1
n
<S=S^A). B0.12)
Пусть теперь g(x) — заданный полином л-й степени относительно х,
который мы разложим по степеням (х — Ху) в точке х=Ху:
g(x) = g (х;.) — 2 «г (* ~ ty)r.
Умножим это уравнение на Lj(x) и заменим х на 91:
g (91) £у (91) = g(y.j) Lj (91) — 2 ar (91 — х ,(S)r Lj(%). B0.13)
Сумма, фигурирующая в написанном равенстве, равна нулю, так как
каждый член содержит множитель Ф(91), который обращается в нуль,
как это следует из уравнения Кэли B0.6); например,
(91 — щ®,) Lx (91) = -. РЩ == 0.
(и, —х2) ... (х, — v.n)
Если просуммировать B0.13) по у, то уравнение упростится вслед-
вследствие B0.12):
~ B0.14)
Таким образом, если известны характеристические числа матрицы 31
и составлен интерполяционный полином Лагранжа Lj(%) согласно
B0.10), то можно образовать полином любой степени g(9t) без вы-
вычисления высоких степеней 91.
Пусть s(x) — функция, представимая с помощью частичных сумм
степенного ряда
s (х) = lim s (х) = 2 стх'•
#->оо г-0
где
344 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [20.2
Тогда, согласно B0.14), имеет место соотношение
я
Если степенной ряд сходится для всех значений х — и,, то предель-
предельный переход q—>co дает
причем матрица s B1) определяется с помощью равенства
г-о"Г
Теорема. Пусть матрица 21 имеет различные характери-
характеристические числа и,, и2, ..., и„. Пусть также имеется степен-
степенной ряд s(x)
00
« (X) = 2 СГХГ,
r-0
а все характеристические числа %q находятся в области схо-
сходимости степенного ряда, тогда сходится также степенной
ряд матриц
г-0
и для матрицы, определяющей сумму ряда, имеет место соот-
соотношение
2
r-0
2
/-1
B0.15)
причем Lj(%) определяются согласно B0.10).
Пример. Для матрицы
/ 2 -1 U
Щ= 1—13
\-2 11/
характеристические числа получаются из уравнения
2-х. ■ —1 1
<Р(к) =
1
—2
—1-я 3
1 1-х
х, = 2; х„ =
l)=0,
= — 1.
20.3| § 20. ДОПОЛНЕНИЯ 345
Согласно B0.10) имеем
причем
Проверка по B0.12) подтверждает правильность вычислений.
Согласно B0.14), B0.15) тогда, к примеру, получается
Я2 о?
— 2Я»= B"> — 2-2') ■ „ —1— A'° — 3 - 1э)
О
sin (лЯ) = 0;
cos (пЩ) = I, (W) — Ц (Ж) — L3 (ЗД
cos2 (я?Г) = @.
Для всегда сходящихся степенных рядов, соответствующих таким функ.
циям, как cos x, sin *, e*, ch jf, sh д; н т. д., можно просто составить ма-
матричные ряды для функций cosSl, sin St, £Я, ch Щ, sh Щ и т. д. согласно B0.15),
если матрица Щ имеет различные характеристические числа. Сходимость
геометрического ряда
оо
или (в"
г-0
имеет место в том случае, если все числа у.] различны и по модулю меньше
единицы. Сходимость ряда при иаличии кратных иу, модули которых, однако,
меньше 1, следует из теоремы п. 19.8.
20.3. Приближенные решения систем линейных уравнений.
Системам линейных уравнений и приближенным методам их решения
посвящено большое количество работ, в которых с успехом исполь-
используются матрицы и характеристические числа. Здесь будут даны лишь
несколько оценок применимости характеристических чисел и матриц
к системам уравнений.
1. Систему уравнений
п
346
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
[20.3
можно коротко записать в матричном виде, согласно п. 17.1, как
2lj = r. B0.16)
Пусть р — приближенное значение вектора j, а матрица 21 вследствие
ошибок округления преобразуется в матрицу 21 4 23. Если образо-
образовать выражение B14 S3)p, то справа к вектору г добавится вектор
ошибки ^: B14 8)9 = г-г-f. B0.17)
Возникает задача оценки этой ошибки l) — j по известным величи-
величинам 21, 23, «, г, f.
Вычитанием B0.16) из B0.17) получаем
B14 23) (р — S) = f— 23j.
Согласно A8.27) можно дать оценку
19-5 |<
а из B0.16)
|23г.|<|23||$|<
При использовании A8.29) имеет место1)
Теорема. Если для линейной системы уравнений 21 j = г
известно решение «.близкой системы-» B1 4 23) I) = г -f f. яю ло-
дуль вектора разности может быть оценен следующим образом-.
Щ -1 © I
предполагается, что знаменатель положителен.
При 23 = 0 будет
B0.18)
19-SKjiq-- B0.19)
2. Для приближенного решения системы линейных уравнений B0.16)
с преобладающими элементами главной диагонали а;/=£0 часто исполь-
используется итерационный метод. Заменим в матрице 21 нулями сначала
элементы ajk с j < k, затем ajk с j ^ k, тогда получим две ма-
матрицы 23 и (£:
B0.20)
23 =
«п
«21
«я,
Вследствие
0
«22
CL
ап
0
0
«яЗ
... 0
... 0
... ап<1
del iS Ф (
. S
). т. е
=
0
0
0
не
«12
0
0
«13
«23 •••
0 ...
вырождена.
а
а2
0
') Н. W it i in ey er, Z. angew. Math. Mech. 18 A938),
20.3) § 20. ДОПОЛНЕНИЯ 347
В названном итерационном методе определяют последовательность
приближенных векторов t(I>, £<2), . . . %№ исходя из некоторого
произвольно выбранного вектора j'0) по правилу
sBrfv+D-l-g^^r, v = 0,1,2.... B0.21)
Для исследования сходимости этого метода вводятся векторы при-
приращения s(v):
j(v) __ -(v + 1) j(v).
Они удовлетворяют уравнению
или, с введением D = — 23 К,
f+^==^) = I)Y-1)= ... =DV+1J(O).
Теперь рассмотрим ряд
частные суммы которого суть непосредственно приближенные решения
т@) Y(l) tB)
Согласно второй теореме п. 19.8 ряд сходится для произвольного
вектора $@) в том случае, если все характеристические числа яд
матрицы 2), а следовательно, корни уравнения
det (£> — пЩ = det (— 23~'(Е — x(S) = det (— S3) det (иЗЗ-f 6) = 0.
по модулю меньше 1.
Пусть $*0) и j;@) связаны друг с другом соотношением 93j'0) -\-
~\- Щ}0) = г, так что при невырожденной матрице 31 каждому 5@)
соответствует определенный вектор j*0). Тогда справедлива следующая
Теорема. Пусть 91 — невырожденная матрица, у которой
элементы главной диагонали не все равны нулю. Итерационный
метод B0.20), B0.21), дающий приближенное решение линейной
системы B0.16), сходится для произвольного начального век-
вектора % @) только тогда, когда все корни уравнения и
det (иЗЗ + К) =
•лап аХ2 аш ... аХп
на,
22 «23 • • • л
па1
= 0 B0.22)
1п пап2 иа„3 ... яап
по модулю меньше единицы.
Если 91 предполагается действительной и симметричной, то можно
дать другие критерии сходимости; имеется обширная литература1)-
') R. v. Mlses ц. Н. Р о 11 ас г ek-0 ei r i n ger, Praktlsche Verfahren
der Oleichungsaufl6sung, Z. angew. Math. Mech. 9 A929), 58—77, 152—164.
348 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ |20.4
20.4. Оценки характеристических чисел матриц.
А. Пусть характеристическому числу и матрицы 21 принадлежит
собственный вектор т с компонентами хх, х2, ..., хп. Среди них
имеется одно, наибольшее по модулю, например /га-е: | хт \ ;> | Xj |,
для у'=1 п. В /га-м уравнении, соответствующем этой ком-
компоненте,
я
(X -атт)Хт= Ъ' amkxk
А 1
(Здесь штрих обозначает исключение из суммы члена с индексом k — tn)
можно построить оценки:
Hi\mk\\h\ 2
*mk
Так как хт Ф 0, то можно разделить обе части неравенства на | х
Левая часть оценивается снизу, причем имеется две возможности:
п
К 2
Так как неизвестно, какое значение имеет /га, нужно выбрать наибо-
наиболее неблагоприятный случай; тогда получаются оценки:
я
B0.23)
B0.24)
т \ k-l
Поскольку матрица 01 и транспонированная матрица W имеют оди-
одинаковые характеристические числа, можно в этих формулах заме-
заменить amk на ahm.
Б. Другая оценка связана с неравенством A8.25):
При этом согласно A8.23) *п—-\-Укш'ну Матрица S = 3t'2l, со-
согласно п. 18.3; положительно определенная или, в случае выро-
вырожденной матрицы 91, положительно полуопределенная. В первом
случае все и.8>0, во втором случае х .я, ^> 0. Назовем теперь
«следом» некоторой матрицы Ъ = ф1к) сумму элементов главной
диагонали
п
sm = 2 bjj. B0.25)
20.4)
§ 20. ДОПОЛНЕНИЯ
349
В характеристическом уравнении
Ьп — х
П
— у. ... Ь.
•in
= (— 1)" fx« — ^.x"-1]^ ... 4- det 23 = 0 B0.26)
след является множителем при х", так что по теореме Виета
п п п
J I J I J s== 1
В данном случае элементами главной диагонали матрицы 33 ='Л'31
являются числа
*пк
и след равен
B0.28)
Для эрмитовой матрицы, следовательно, имеет место, согласно A8.24),
соотношение
х r-j = 2^ ajj'
и для произвольной матрицы 31
у*
B0.29)
Таким образом,
B0.30)
В. Выведенная Эрхардом Шмидтом оценка использует разложение
матрицы 31 на диагональную £) и остаточную 33:
й„ 0 ... 0
^1 0 а22 ... 0
33 =
,0 0 ... аи
' 0 а,2 . .. а,„ '
ая1 ап2 ... 0
Тогда, согласно A8.25) и A8.26). имеют место соотношения
350 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ B0.4
Диагональная матрица!) имеет, очевидно, характеристические числаа^.
Тогда
35 = а
41
гЦ Imln
и согласно B0.30)
К Д','•"
Д,'
причем штрих у знака суммы вновь обозначает исключение члена
с J — k.
Таким образом,
/ п
]k \
ajk p.
B0.31)
Г. Можно также оценить отдельно мнимую и действительную
части характеристического числа.
Из равенства Щ — щ следует
J -o-J — XJ J, ^ZU.OzJ
а из 3ljc = xj получается
при переходе к транспонированным величинам в
Если положить
где а и р — действительные числа, то сложением (соответственно
вычитанием) B0.32) и B0.33) получим
где
= 1C1-ft').
При этом 5[ = §-|-/C представляется как сумма эрмитовой ма-
матрицы § и антиэрмитовой матрицы jo; © снова оказывается эрми-
эрмитовой. Из A8.21) непосредственно следуют оценки:
20.4)
§ 20 ДОПОЛНЕНИЯ
351
Возьмем в качестве простого примера матрицу
2 2"
3( =
Эрмитова составляющая 31 будет
а антиэрмитова
—2 3
2 О
О 3.
О 2
—2 О
Для этих матриц и^ = (■*]; и^= ± 2, откуда для х.ч —а4 О по-
V3/
лучаем ifi
2<а<3, —2<р<2.
В этом прямоугольнике плоско-
плоскости (а, р) лежат характеристические
числа матрицы 31 (рис. 20.1):
4
-1
1 Z
Q..
а:
Д. Хорошая оценка снизу мо- -^
дулей характеристического числа
матрицы простыми средствами без Рис 2о.1. Оценка вещественной и
использования значения определи- мнимой частей характеристиче-
теля матрицы 31 вряд ли возмож- ского числа,
на, так как при 21=0 имеется
также характеристическое число х = 0. Пусть теперь det?l =£0, Если
образовать снова соответствующую матрице 21 матрицу 23 = 31'21,
то все иув будут положительны, и согласно B0.27) имеет место
соотношение
B0.34)
Среднее геометрическое положительных чисел не больше среднео
их арифметического
У H2S3 •
(И2!В -f- Кда 4 • • •
— к,»).
следовательно,
| det ЭД
352 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ [20.5
Более грубая оценка %—ицз <^ s-a дает1)
«-1
I хл 1П1щ > | ^ 1 = У>^~^ > 1 det % [ • (j;i7^") 2 * B0-36)
Несколько более точную оценку можно дать с помощью биномиального
разложения, так как ss — хт и xi3 неотрицательны:
sn _ /5) х _L .х \1 ^ /s х )" -4- Я fS4 X , )"~ ' X , •
следовательно, согласно B0.35),
и, решая это неравенство относительно х1а , получаем
I^ILn^ffl^lJSJ^-/4-"(«-!)"-'det 33. B0.37)
Эта оценка имеет место для любой положительно определенной эрмитовой
матрицы $3 н любой матрицы Щ, если s^ и det 53, согласно B0.28) и B0.34)
выражены через элементы Я. При неэрмитовых матрицах Я увеличение вы-
вычислительных затрат не окупается большей частью увеличением точности по
сравнению с B0.36).
Таблица IX показывает на многих примерах, что среди различных оце-
оценок, полученных в этом пункте, иногда оказываются подходящими одни,
иногда — другие.
20.Г,. Особые методы получения характеристического уравнения.
Уравнение Кэлн B0.6) также используется для построения метода соста-
составления 2) характеристического уравнения <р (х) = 0 матрицы Щ; исходя из
произвольного начального вектора, образуем, согласно A9.3), последователь-
последовательность итераций j0, g,, $2 д„; тогда из B0.5) после умножения на з0 справа
следует
Это векторное уравнение с п компонентами представляет собой при изве-
известном 3V систему уравнений для п отношений —-, —-,..., п~х . Видоиз-
ап ап ап
менение этого метода было предложено Хессенбергом 3).
Метод последовательного повышения порядка. Опи-
Описанным ниже методом можно составить характеристическое уравнение сим-
симметричной матрицы Щ л-го порядка, если для подматрицы (п—1)-го порядка
ап-\,п-\
') Оценки до B0.37) были получены в диссертации Н. Wittmeyer,
EinfluB der Anderung einer Matrix..., Darmstadt, 1934.
2) R. A. Frazer, W. J. D u n k a n, A. R К о 11 a r, Elementary Matrices,
London, 1946. [P. Фрезер, В. Дункан, А Кол л ар, Теория матриц
н ее приложения к дифференциальным уравнениям и дннамнке, ИИЛ, М.,
1950.]
3) К. Hessenberg, Auflosung linearer Eigenwertaufgaben mit der
Hilfe der Hamilton — Cayleyschen Qleichung, Diss., Darmstadt, 1941.
Метод реферирован в работе L. С о 11 a t z, Qrafische und Numerische Ver-
fahren, Fiat Review, 1948, Angewandte Math., I.
20.S]
§ 20. ДОПОЛНЕНИЯ
353
известны все характеристические числа х,, к2, ..., v.n..\ с принадлежащими
им собственными векторами. При введении вектора а'=(ап1, апъ ..., а„, „_,)
характеристическое уравнение для матрицы St имеет вид ')
Л 1
\
/ j
B0.38)
Эта форма уравнения часто бывает удобна при итерационных методах
нахождения к.
При описанном здесь методе образуют характеристические числа и соб-
ственные векторы, например, для матрицы второго порядка
ап а,
затем
можно перейти к матрице третьего порядка и для нее согласно B0.38) опре-
определить характеристические числа и из решения однородной системы уравне-
уравнений— относящиеся к ним собственные векторы и т. д., чтобы путем после-
последовательного повышения порядка матрицы подойти к заданной матрице.
Рассмотрим для пояснения метода один простой пример:
A4 10 9\
\ ~ /14 10\ ~ г ( 23,0499,
10 12 4 j, Я-(ю i2j, x,,2 = 13± 101=| ад5Ш_
S,' = (l; 0,90499), 52 = A; —1.10 499), а' = (9; 4),
а'j, = 12,6200, a'j2 = 4,5800;
уравнение B0.38) тогда имеет вид
87,555
^"
9,447
23,050-я^" 2,9501 — и
4- х — 3 = 0.
Процесс решения этого уравнения по методу Ньютона иллюстрируется
легко обозримой схемой, причем приближенные значения могут быть полу-
получены с помощью логарифмической линейки.
х —3
87,555 : B3,050 — х)
9,4447: B,9501 — х)
/ (х) = сумме
87,555 : B3,050 — хJ
9,4447: B,9501 — хJ
/' (к) =■ сумме -j- 1
уточнение = — / (х): /' (к)
новое значение
27
24
—22,2
—0,39
1,4
5,62
0,02
6,64
-0,21
26,79
26,79
23,79
—23,410
—0,396
-0,016
6,26
0,02
7,28
+0,002
26,792
= х,
4,5
1,5
4,720
—6,094
0,126
0,25
3,94
5,19
-0,024
4,476
= х2
-2,3
—5,3
3,454
1,799 ■
—0,047
0,14
0,34
1,48
0,032
—2,268
= х3
') Доказательство и пример матрицы 12-го порядка, элементы которой
суть 5—6-разрядные числа, дани в работах J. Morris and J. W. Head,
On an «Escalator» Method for the Numerical Solution of Lagrangian Frequency
Equations, Aircraft Engineering, Nov. 1942; Coupled Flexural Vibrations of the
Blades of a Propeller and Torsional Vibration of an Engine Crankshaft System,
Reports and Memoranda № 2011 F348), Aeronautical Research Council, 1942.
354
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ
20.6. Упражнения. 1. Показать, что все характеристические числа -л уни-
унитарной матрицы 81 равны по модулю 1.
Решение. Из Щ — щ следует 8[j = j<$ и 1"й' = щ'. Вследствие
М'Щ. = E получаем
т
т
Таким образом, как утверждалось, хх = 1.
2. Пусть на защемленной на одном конце балке с жесткостью на изгиб EJ
(собственной массой балки можно пре-
пренебречь) на расстоянии 1а и За от
конца закреплены две массы, свя-
связанные пружинами (с — коэффициенты
жесткости) с двумя другими массами т
(рис. 20.2). Требуется найти собствен-
собственные частоты. Пусть
с — -
1 3EJ
Рис. 20.2. Колебания системы
«балка — массы — пружины».
Решение. Составим сначала в соответствии с п. 17.7Д матрицу коэф-
коэффициентов связи §. Получим
о /8
tf Ли
следовательно,
*
14\
27}'
1
20,4
47
—14
—20
0
i 1
21 —
20Л \—14
—14 —20
28
0
—20
0
20
0
0
—20
0
20
Вычтем из диагональных элементов число 20; тогда получим задачу
Щ = у.% где ® = 20 (АЖ* — E) и к = 20 (ю2тЛ — 1).
Характеристическое уравнение для @
• 27 —к —14 —20 0
—14 8 —х 0 —20
—20
0
0
—20
■у.
0
0
,_i2P._27 14
14
У. !
= 0
400
400
можно путем замены v. == г перевести в квадратное уравнение для г,
решения которого будут
В таблице, приведенной ниже, даны найденные значения Ку и принадлежащие
им собственные решения \)f, вид соответствующих собственных колебаний
изображен на рис. 20.3.
20.6]
§ 20. ДОПОЛНЕНИЯ
355
1
2
3
4
г ,
0,58108
34,4189
= z\
= z2
X;
1
-19,7116
—9,175
20.293
43,594
и . + 20 =
= 20 Amtif
0,2884
10,825
40,293
63 594
1
1
1
1
27- Zj
У-'- 14
1,8871
-0,530
1,8871
—0,530
20
KJ
1,0146
2,180
—0 986
—0,459
20
y4 — y2
1,9147
—1,155
—1,860
0,243
3. Назовем распределением чисел на многограннике такое упорядочение
чисел и,, «2. •••• и1 в вершинах Ри Р2, ..., Pi, что для каждой вершины Р-}
v-кратное числа Uj, соответствующего вершине, равно сумме чисел, сопо-
сопоставляемых соседним вершинам. Число v называется тогда характеристиче-
характеристическим числом многогранника, а все возмож-
возможные числа v образуют «спектр» много- '4
гранника (см. также задачу 5 п. 23.6). v есть
характеристическое число матрицы ЭГ = (ajk),
сопоставляемой многограннику, такой, что ее
элементы а^ равны 0 или 1 в зависимости от
того, имеют вершины Pj и Ри общее ребро
или нет; ujj = 0.
Вычислим спектр кубооктаэдра '), т. е.
такого многогранника, который получается со-
соединением середин 12 ребер куба (рис. 20.4). ioz
Результат. Соответственно 12 углам
октаэдра получают матрицу *й 12-го порядка,
характеристическое уравнение которой можно у.
получить непосредственным вычислением М -
Ф (v) = det (Щ. — v(S) = v12 — 24V1» — 16v9 +
со,
+ 192v8 + 192v7 — 640v6 — 768v5+ —i
-\- 768v4 -f- 1024v3 = (v — 4) (v —■ 2)з v3 (v -f- 2M.
Тот, кто обладает хорошим простран-
пространственным воображением, может представить
себе 12 распределений чисел непосредственно
из рисунка и получить полином без составле-
ния матрицы и раскрытия определителя.
В результате:
v = 4. Все вершины имеют одно и то же Рис 20.3. Форма собст-
число uj = const, например и} = 1 венных колебаний системы,
(см. рис. 20.4, а). изображенной на рис 20.2.
v = 2. Плоскость е, проведенная по-
посредине между двумя параллельными гранями куба, рассекает
кубооктаэдр в «квадрате среднего сечения» (см. рис. 20.4, б).
Вершины многогранника располагаются в четырех точках Р
квадрата среднего сечения и по четыре точки Q и R в двух
квадратных гранях. Положим в точках Р число и равным 0,
в точках Q«=1hm = —1 в точках R, тогда получим рас-
распределение чисел, соответствующее v = 2.
') Пример U. Sinogowitz'aK нашей совместной работе о спектрах
графов.
356
ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗИАЧННИЯ ДЛЯ МАТРИЦ
[20.6
Так как имеется три квадрата среднего сечения, сущест-
существуют три линейно независимых распределения чисел; следова-
следовательно, v = 2—характеристическое число кратности 3.
v = 0. Пусть два угла квадрата среднего сечения, противоположных
друг другу, получают число -(-1, два других — значение —1,
остальные восемь вершин многогранника — число 0 (см. рис.
20.4, в). В этом случае также имеются три таких распределения.
v=4
v=Z
S)
Рис. 20.4. Спектр кубооктаэдра.
v = — 2. Проведенчая через две противоположные вершины плоскость
симметрии образует при пересечении с октаэдром шестиуголь-
шестиугольник, нанесенный на рис. 20-4, г пунктиром. В обеих этих вер-
вершинах положим и = 0, в восьми соседних ±1, в двух оставшихся
+ 2 (см. рис. 20.4, г). В данном случае имеются также три ли-
линейно независимых распределения.
v = — 2. Пусть теперь углы квадрата среднего сечения получают зна-
чгние —2, а все остальные восемь вершин мнэгогранника —
значение 1 (см. рис, 20.4, д). Если нарисовать распределение
для трех квадратов среднего сечения, то нетрудно установить,
что третье распределение является линейной комбинацией двух
других. (Сумма трех распределений есть тождественный нуль.)
Таким образом, v = —2 — характеристическое число, кратность
которого равна пяти.
4. Проведем итерационный процесс п. 19.1 для матрицы с комплексными
элементами Q , , . 0 , .
St= 1
1—2/
2 —/ 1+2/
20.61
§ 20. ДОПОЛНЕНИЯ
357
Решение. Исходя из jo=(l, 1, 1)_ далее получаем приведенные
в таблице векторы jv. В пятой колонке даны результаты проверки с век-
векб ё' F 21 4 + 3/ 4—/) согласно п. 18.8.
в алце р jv
тором сумм столбцов ё' = F — 21;
0
1
2
3
1
6 4- 2/
32 4~ 13/
187-j-80/
К
1
4— 3/
22— 17/
125—105/
1
4+ /
28 4- 4/
1614-25/
Сумма
компонент
3
14
82
473
1 Ч-12
3
82
2766
94 565
Ошибка
K-.iu)
5,2281 (—11%)
5,80790 (—0,7%)
5,84708 (—0,04%)
Характеристическое уравнение здесь имеет вид
Ф (х) = det {Ж — хй) = — я3 -f 6х2 + х — И = 0
и имеет корни
5,84947,
1,44865,
—1,29812.
Рис. 20.5 показывает, как на комплексной плоскости многоугольники (здесь
треугольники), соответствующие
собственным векторам, делаются
постепенно похожими друг на друга
и приближаются к виду много-
многоугольника, представляющего соб-
собственный вектор.
5. Сколько значений имеет ко-
корень квадратный X из матрицы
второго порядка Ю Пусть задана
матрица ЭГ = I I. Сколько
d I
(е f\
различных матриц X =
\у h)-
летворяют равенству X2 = ЭГ?
Решение. Из е2 4- fg = a,
СоВстеенный
штор
шЬ
1удов-
Рис. 20.5. Сходимость итерационного ме-
метода для комплексной матрицы.
получается X = ±
1
Jrfg=d исключением /, g, h по-
получаем уравнение 4-й степени для
е, в котором е4 имеет коэффи-
коэффициент А = (а — dJ -f- 46с. В слу-
случае АфО имеются, вообще говоря,
четыре различные матрицы X, на-
например, для матрицы Ш = I _
/3—1
и 3f,.4=±B _2
Мы здесь откажемся от полного (легко проводимого) обсуждения различ-
различных возможностей и отметим еще только, что для матрицы Ж= ±(£ суще-
существует бесконечно много решений,
—1
2
/17
11 —1
2 6
358 ГЛ. VI. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МАТРИЦ |12.6
Для Ж = (J можно в .? = , а для Ж = — S в 1=
V fb + \)
утг^л -ъ
величины о я с выбирать произвольно.
с —Ybl]
6. Матрицу 91 = (ajk) назовем «равностолбцовой», если все столбцы
имеют постоянную сумму q
п
Ч = 2 a)k-
7-1
В теории вероятностей ') особую роль играют «стохастические матрицы»,
т. е. матрицы с действительными неотрицательными элементами и постоян-
постоянными суммами столбцов q = 1. Нижеследующие теоремы справедливы и для
матриц с постоянными суммами строк.
Покажем: а), что сумма и произведение двух равностолбцовых матриц
Ж и 33 с суммами столбцов q^, q,A суть снова равностолбцовые матрицы
с суммами строк (в очевидных обозначениях)
(равностолбцовые матрицы образуют «кольцо»); б) что для равностолбновой
матрицы q есть характеристическое число; в) что обратная к *й матрица Ж~1
есть также равностолбцовая матрица, если Ж не вырождена. (Равностолбцо-
(Равностолбцовые невырожденные матрицы образуют пеабзлеву группу с умножением
в качестве группового сложения. Группа имеет различные подгруппы, на-
например, подгруппу матриц с рациональными элементами или матриц с опре-
определителем — 1 и т. д.)
Доказательство, а) непосредственно вычисляется; б) соответству-
соответствующий собственный вектор Ж' есть г'=A, 1, ..., 1); в) матрица Я удовлетво-
удовлетворяет своему уравнению Кэли B0.5)
причем предполагается
ao = d
Отсюда получаем
Ж'1 = - — (в,® + • • • + апЖп~х).
Согласно а) все матрицы правой стороны (§, Ж, Ж2, ..., Жп~{, следовательно,
и вся правая часть равностолбцовые, что и требовалось доказать; последнее
можно пояснить также следующим образом2): для вектора j, согласно б)
имеет место равенство qi = SCj или SC-1j = —j, т. е. Ж~
ную сумму столбцов l/q.
>) Например, G. S с h u I z, Zur Theorie des Galtonschen Brettes, Z. f. Phy-
sik 92 A936), 747—754; Grenzenwertsatze fur die Wahrscheinlichkeiten verket-
teter Ereignisse, Deutsche Math. I A936), 665—669.
2) Частное сообщение Г, Виландта.
ГЛАВА СЕДЬМАЯ
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
§ 21. Метод конечных разностей первого приближения
для обыкновенных дифференциальных уравнений
В методе конечных разностей используется замена всех диффе-
дифференциальных соотношений разностными. Это возможно не только для
задач на собственные значения, но и для любых задач, связанных
с решением дифференциальных уравнений.
В п. 21.1 этот метод излагается в общих чертах, независимо
от задач на собственные значения.
21.1. Описание метода конечных разностей. Интервал (а, Ь),
в котором требуется найти решение у (х) какой-либо задачи для диф-
дифференциального уравнения, разби-
разбивают на п одинаковых частей дли-
длины h:
Ь — а
h =
п
х0^
Уо
h
У,
h
-ах, х
Уг
f-•
z
ч
—>.
ч
у„
h называется шагом. Таким обра-
образом получают точки деления х1 =
= a + lh. Значение функции в Рис. 21.1. К методу конечных разно-
точке деления отмечают индек- стей.
сом. Так, например, yt есть зна-
значение у(х) в точке хг (см. рис. 21.1) и Yt — приближенное значе-
значение величины yt.
В методе конечных разностей рассматривают дифференциальное
уравнение в точке х = xt и заменяют в ней определенным образом
все дифференциальные соотношения разностными, таким образом по-
получают систему линейных уравнений для определения приближенных
значений Y\.
Так, например, производную у' {xt) заменяют через
B1.1)
360 ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
и вторую производную y"(Xi) — через
9
Далее вводится оператор Л для любой функции f (х) по правилу
Д/(*) = /(*-г *)-/(*)
и оператор Д*
Д*/ (*) = Д (Д*-1/ (^)) = Д*-1/ (^ 4- Л) ~ Д*/ (*). ft = 1. 2, ...
(с Д°/(*) = /(*))•
Так, например,
Тогда в общем случае можно дать следующее правило для замены
производной yk(Xi) разностными отношениями:
Производную y"(Xi) четного порядка k можно заменить k-м раз-
разностным соотношением
а производную ур(х) нечетного порядка р — средним арифметическим
/7-х разностных соотношений
Таким образом, дифференциальное уравнение в точке х{ можно за-
заменить так называемым «разностным уравнением», т. е. уравнением
для конечного числа приближенных значений V/. Начальные или
краевые условия также заменяются разностными соотношениями. На-
Например, для краевой задачи четного порядка k с k краевыми усло-
условиями, заданными в точках х = а и х = Ь, в каждой точке деле-
деления xt (i = 0, I и) составляют разностное уравнение и каждому
краевому условию соответствует во всяком случае одно разностное
уравнение. Таким образом, получают п 4- k -f- 1 уравнений для такого же
количества неизвестных
Y к . У k ,..., У и-
Эти уравнения линейны, если линейны дифференциальное уравнение
и краевые условия, в противном случае получается нелинейная си-
система уравнений.
О разрешимости этой системы уравнений при той степени общ*
ности, которая здесь принята, ничего сказать нельзя.
21.2]
§ 21. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
361
Дополнение. Часто можно применять еще и другие способы
замены дифференциального соотношения разностным и получать, та-
таким образом, различные разностные уравнения. Например, в выра-
выражении {/у')'х-жХ можно сначала произвести дифференцирование и ис-
использовать описанный здесь способ замены для каждой производной;
тогда получилось бы выражение
2ft
ft2
или можно было сделать замену согласно B1.1) каждой из обеих
производных. В этом случае получилось бы выражение
Yj — Yi_2
-fi-i 2ft
2h
2ft
Третье выражение будет получено в п. 21.5. Уравнения, полученные
различными способами, в общем случае отличаются друг от друга и
приводят к различным результатам (см. задачу 7 в п. 23.6).
21.2. Пример для дифференциального уравнения второго порядка.
В качестве примера мы рассмотрим продольный изгиб шарнирно опертого
с обеих сторон стержня, жесткость которого на изгиб для правой половины
равна У, а для левой равна -я J. Уравнение изгиба
путем введения безразмерных величин можно свести
к следующей задаче на собственные значения:'
B1.5)
B1.6) у=
у @) = у A) = о,
где g0 есть функция, показанная на рис. 21.2,
Тогда критическая нагрузка
X
EJ
/2 '
Рис 21.2. Продольный
изгиб стержня.
В это выражение подлежащее вычислению собственное значение Я[ входит
вместо известного из формулы Эйлера множителя я2.
Будем производить вычисления с шагом /г = 1/3. В силу краевых усло-
условий Yo = К3 = 0 получается только два неизвестных значения функций Y,
и Г2 (рис. 21.2).
Дифференциальному уравнению в точке х = Х[ соответствует теперь
разностное уравнение
Y 2Y + Yl
362
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[21.2
Вместо X записано приближенное значение Л. Если обозначить Л/г2 = ц,
то уравнение перейдет в
Положив теперь г = 1 и / = 2, с учетом краевых условий получим два ли-
линейных однородных уравнения:
К2-2К,+и2Г,=0,
Эта система имеет нетривиальное решение, если определитель, состав-
составленный из ее коэффициентов, равен нулю
3 1 ,/-5-
откуда следует ]х=-к ±уГо, или
5,7058 (ошибка— 11%),
21,294 (ошибка —25%).
Чтобы получить более точные значения, повторим вычисления с меньшим
шагом h — 1 '5 (рис. 21.3). В силу краевых условий Ко = К5 = 0. Разностные
уравнения в этом случае будут
*У К2 —2К, +2цК, =0,
Рис. 21.3. Вычисления с
шагом.
где опять положено Л/г2 = ц.
меньшим Здесь также можно было вычис-
вычислить определитель, однако более про-
просто Y2, Y3, K4 последовательно вы-
выразить через К,. Последнее уравнение дает тогда искомое алгебраическое
уравнение для Л •
ГГ22
Г, (V — 24ц3 -f 45ц2 — 30ц -f 5) = 0.
Корнями этого уравнения 4-й степени будут
ц, = 0,24605, ц2 = 1, цз = 1,62218, ц4 = 3,13177
и отсюда при Л = 25ц найдем
Л, =6,1513 (ошибка — 4%), Л3 = 40,55 (ошибка—31%),
Л2 = 25 (ошибка— 12%), Л4 = 78,29 (ошибка—30%).
Точное решение можно получить из трансцендентного уравнения
|/2"tg^-f-tg(^)/~) = 0, при Я = 4г2.
Первыми четырьмя корнями этого уравнения будут
г, = 1,2657, г3 = 3,833,
г2 = 4,6663, г4 = 5,263,
откуда
Я, =6,4075, %ъ = 58,78,
Я2 = 28,437, Я4 = 110,8.
21.3]
§ 21. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
363
21.3. Пример для дифференциального уравнения четвертого порядка.
При решении дифференциальных уравнений выше второго порядка нужно
использовать значения функции К,- внз заданного интервала, как это уже
указывалось в п. 21.1. Эти значения должны быть исключены с помощью
заданных краевых условий.
В качестве примера возьмем рассмотренную в п. 12.6 задачу о сжатии
стержня, описываемую дифференциальным уравнением
[B-.*)/']" =-Яу"
при краевых условиях у @) = у' @) = у A) = у" A) = 0.
Краевые условия при шаге h = 1/л следующим образом соответствуют
условиям для Yi (рис. 21.4):
у@) = 0,
у'@) = 0,
уA)=0,
у"A)=0,
Ya = 0,
= 0,
Последнее условие полу-
получено из равенства К„+1 —
Теперь дифференциальное
уравнение заменяется разно-
разностным. Для этого можно сна-
сначала произвести дифференциро-
дифференцирование в уравнении и потом у".
'" IV
у , у заменить по отдельности соответствующими разностными соотноше-
соотношениями или, что более удобно, действовать следующим образом, который для
наглядности описан при шаге h = 1/5. В конечноразностном методе отдель-
отдельным выражениям у, у", ... соответствуют значения:
Рис. 21.4. Метод конечных разностей при
продольном изгибе стержня, защемленного
на одном конце и шарнирно закрепленного
на другом.
X
]
5
0
1
5
2
5"
3
5"
4
5
1
6
V
К,
0
г.
Y2
Y3
Y,
0
-у*
2К,
Y2 — 2К, = а
Y3-2Y2+ K,=p
Yt-2Y3+ K2 = Y
-2Yt+ Г3 = б
0
2-х
10
9
5
8
5
7
5"
6
5
5
T
5li2B-x) у"
20Г,
9K2— 18К,
8Г3— 16К2 + 8К,
7К4 —14К3 + 7К2
-12К4-6Г3
0
364
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
|21.3
где
Дифференциальному уравнению [B — х)у']"— — ^У" в точке л:=1/5
будет тогда соответствовать разностное уравнение
B0У.) - 2 (9К2 - 18У.) + (8Кз - 16К2 +8Г,) = |i (Уя - 2 У,),
ц = — 5/г2Л.
Можно было бы для точек xi = -=-(< = 1, 2, 3, 4) написать четыре раз-
о
ностных уравнения, однако несколько удобнее в качестве неизвестных рас-
рассматривать не К;, а вторые разности, которые для краткости обозначены
через а, р, Y. б, и уже с этими величинами провести описанную выше схему.
Теперь нужно еще К, выразить через а, р\ y. б:
Таким образом, имеем теперь следующие значения:
X
0
1
2
5
3
5
4
1
Ыу"
_ .2. Dа + 3Р + 2Y + б)
а
CCL
Y
6
0
Ъ№ B - х) у"
— 16а — 12р — 8y—46
9а
8Р
7Y
66
0
/гМ5Л2B--с)у"]"
— 34а — 4р — 8у — 46
9а — 16р + 7Y
8P-14y4-66
7Y—126
Разностные уравнения будут иметь вид
— 19а — 4р — 8y — 46 = — ра.
= — рб
где 5/г2Л = р 4~ 15-
Из равенства нулю определителя
1—194-р —4 —8 —4
9 — 1 4-Р ^ О
О 8 1 -4-Р б
0 0 7 34-р
= р* _ 1бр3 + 120р2 + 1320р + 1335 = 0
21.4]
§ 21. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
365
следует
— 9,541
— 0,942
8,073 и Л==
18.4
27,30 (ошиока
70,29
115,4
167
-7%)
21.4. Прямые методы для разностных уравнений. Чтобы из-
избежать решения систем алгебраических уравнений высоких порядков,
которые получаются при применении метода конечных разностей
с мелким шагом, часто используют прямые методы (см. гл. VI) для
приближенного нахождения ха-
характеристических чисел ').
Мы поясним это на примере
задачи о крутильных колебаниях
диска (задача 4 п. 11.4):
-
Y0=0
0
У
Уг
1
Уз
X
/ЛЧ Рис .21.5 Метод конечных разностей
с краевыми условиями у @) = при крутильных колебаниях диска.
= у'A) = 0.
Дифференциальному уравнению, согласно B1.1), B1.2), соответ-
соответствует при шаге h—\jn разностное уравнение (обозначения см. на
рис. 21.5)
1
1
7=1. 2 я),
2
Из краевых условий получим
Прежде всего произведем вычисления с шагом Л = 1 /3.
Из уравнений
8Y2=\iYlt 11Ki + 7K3 = (J,K2
получим путем исключения
HIi3=±/2l4. (X2 = O
') Эти методы отчасти совпадают с методом релаксации, который под-
подробно описан в учебниках: R. V. Southwell, Relaxation methods for engi-
engineers, London, 1940, Relaxation methods in theoretical physics, London, 1946
[см. также М. В. Николаева. О релаксационном методе Саусвелла (кри-
(критический обзор), Груды Матем. ин-та им. В. А. Стеклола, АН СССР, XXVIII
1949].
366
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
121.4
и отсюда
Л, = 3,371, Л2=18, Л3= 32,63.
Y
Y
Y
Y
Y
1
2
3
4
5
И 31 =
При меньшем шаге h = 1/5 разностные уравнения в матричной
записи будут иметь вид
311) = |х»
при
О 24 О О О
27 0 23 О О
\)= Y3 и 31 = 0 280220
О 0 29 0 21
О 0 0 50 О
Теперь для нахождения формы основного колебания воспользуемся
решением задачи, полученным при шаге h =1/3, добавляя к нему
(приближенно, методом графической интерполяции) промежуточные
ординаты.
Таким образом, получим приближенный вектор для t>
u' = @,286 0,555 0,779 0,931 1);
отсюда
Btu)' = b' = A3.32 25,64 36,11 43,59 46,75)
и отношения
■^-=D6,6 46,3 46,4 46,7 46.75).
Из того, что эти отношения остаются почти постоянными, можно
заключить, что собственная функция найдена достаточно хорошо. Но
для собственного значения точность еще не достаточна, так как нужно
найти Л = 50—Ц- Можно указать на различные способы повышения
точности, как, например, дальнейшие итерации или внесение попра-
поправок Rj в компоненты вектора, с тем чтобы сделать отношения более
близкими.
В этом простом случае уравнения второго порядка скорее всего
приводит к цели последующая интерполяция. Положим первую ком-
компоненту вектора «х = 1 и последующие компоненты ап вычислим из
уравнений 21и = цн. Ошибка в последнем уравнении 50а4 — ца5 = 0
является мерой ошибки в вычислении приближенного значения ц.
В результате многократного проведения вычислений с различными
значениями ц и интерполяции легко можно получить \i = 46,485;
Л =3,515.
21.5] § 21. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
На таблице показано проведение вычислений.
367
Приближения
для \х
46,5
46,6
46,485
Приближения
для ц
46,5
46,6
46,485
и,
1
1
1
г>, = ци8 —28и2
73,3091
74,2527
73,16801
„-д..
46,5
46,6
46,485
1
3,33233
3,37512
3,325819
1,9375
1,94167
1,936875
„-и,.-».,
75,3958
77,2387
75,12096
г>3 = ц«г-27и,
63,0938
63,4817
63,03563
1
3,59028
3,67803
3,577187
23 V'
2,74321
2,76007
2,740680
0,336
2,640
—0,00537
Так как метод конечных разностей дает только приближенное
значение, то не имеет смысла получать Л с большой точностью. При
заданном шаге последняя строка таблицы необязательна, она только
показывает, как легко ц и Л могли бы быть вычислены с точностью
до следующих 2—3 десятичных знаков.
21.5. Минимальное свойство наименьшего собственного зна-
значения в методе конечных разностей. Для разностных уравнений
можно построить такую же теорию, как и для дифференциальных
уравнений. Ради простоты поясним это на примере уравнения второго
порядка:
— (//)' + qy = bgy. У @) = у @ = 0 B1.7)
при />0 и ^>0.
При шаге h = l/n задача B1.7) соответствует разностным уравне-
уравнениям
г-Л-
1 B1.8)
при /. 1 =/
<ч
h
Точно так же как наименьшее собственное значение Хг задачи B1.7)
согласно § 8 можно найти, решая проблему минимума, и для наи-
наименьшего собственного значения Aj задачи B1.8) имеется соответ-
соответствующая минимальная проблема:
л-1
л-1
л(,'"<-
л-1
B1.9)
368 ГЛ. VII. МЕТОЛ КОНЕЧНЫХ РАЗНОСТЕЙ 122.
При этом Uj могут быть какими-нибудь действительными удовле-
удовлетворяющими краевым условиям uQ = ull = 0 числами с Uj ф 0. В B1.9)
знак равенства имеет место, если Uj являются компонентами собствен-
собственного вектора Yj разностного уравнения B1.8). При п -> оо B1.9)
переходит в соответствующее минимальное выражение для первого
собственного значения задачи B1.7) (ср. A1.7)).
Если обозначить числитель и знаменатель выражения B1.9) соот-
соответственно через Z и Л/, то отношение ZjN принимает все значения,
которые оно вообще может принимать, уже для значений и-ь, удовле-
удовлетворяющих дополнительному условию Л/= 1. По теореме Вейер-
штрасса, согласно которой функция, непрерывная в ограниченной
замкнутой области, принимает наименьшее значение по крайней мере
в одной ее точке, разрешимость минимальной проблемы Z — m'm
при Л/=1 гарантирована.
Для нахождения минимума, согласно правилам дифференциального
исчисления, должны быть выполнены необходимые условия:
-A^=0 (,= 1.2 я-1). B1.10)
но эти условия совпадают с уравнениями B1.8).
Путем более точного сравнения минимальных выражений для Х1
и Л*"' можно показать1), что Л|л) при га->оо сходится к ^ и ошибка
с уменьшением h стремится к нулю 2) как ti2:
IU — М'] | < const • /z2. B1.11)
§ 22. Улучшение метода конечных разностей
При применении описанного в § 21 «обыкновенного» метода
конечных разностей с большим шагом h, а следовательно, при отно-
относительно нетрудоемких вычислениях, можно получить вполне при-
пригодное для многих целей представление о порядке величины собствен-
собственного значения и о поведении собственной функции. Для получения
более точного решения приходится повторять этот процесс с более
') L. С о 1 1 a t z, Deutsche Mathematik, т. II A937), 189—215; там обсу-
обсуждаются также задачи для уравнгний четвертого порядка. Дальнейшая лите-
литература по теории метода конечных разностей: М. Plancherel, Le passage
a la limite des equations aux differences aux equations differentielles dans les
problemes aux limites, Bull. Sci. math. B) 47 A923), 153—160, 170—177.
2) Как улучшенные приближенные значения Aj в работе Н. В U с к п е г,
«Ober Konvergenzsatze, die sich bei der Anwendung eines Differenzenver-
fahrens auf ein Sturm — Liouvillesches Eigenwertproblem ergeben», Math.
Zeitschr. 51 A948), 423—465, применяются
где С — легко вычисляемая постоянная.
22.1]
22. УЛУЧШЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ
369
мелким шагом, однако из-за очень медленной сходимости данного
метода при уменьшении h объем вычислительной работы растет много
быстрее, чем точность. В этом параграфе описаны различные виды
улучшения обыкновенного метода разностей.
22.1. Конечные выражения. Основой для описанного в п. 22.2
метода конечных разностей повышенной точности являются опреде-
определенные «конечные» выражения. Они представляют линейные комбина-
комбинации значений функции y( + v, которые приближенно, но по возможности
хорошо, совпадают со значением взятой вперед производной у(*>
в точке х-г Так, например, при небольшом шаге h следующие выра-
выражения в общем случае дают лучшие приближения для первой и второй
производной y'(Xi) и y"{Xj), чем примененные в § 21 разностные
отношения B1.1), B1.2),
у.
Т2Л
{гг.г)
Эти выражения легко получаются с помощью формулы Тейлора.
Пусть, например,
где ср
подлежат определению. Разложим каждый член этой суммы
муле Тейлора:
р р
по формуле Тейлора:
Таким образом,
2 2 2 2
y-i 2л ср +Щ 2л р^-г--^ Zu рср+зг-< 2j
Р--2
Р--2
р=-2
Р--2
Если потребовать, чтобы выражение, стоящее в правой части послед-
последнего равенства, с точностью до членов порядка /z5 совпадало с yj, то
получается пять линейных уравнений для пяти неизвестных ср
2 2 2 2 2
р„_2
р--2
р_-2
р--2
Решение этой системы дается конечным выражением, стоящим в пра-
правой части равенства B2.2).
Примененные в этом примере методы можно обобщить. Сначала
мы дадим следующее
370 ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ B2.1
Определение. Пусть дано однородное линейное дифферен-
дифференциальное выражение k-го порядка относительно у с заданными
непрерывными функциями pv(x)
k
M>'] = 2/\(*)v(v)- B2.3)
v=o
Линейная комбинация
S СА), B2.4)
р
р--р
где Ср — некоторые постоянные, а р и q — целые числа, назы-
называется конечным выражением r-го приближения для дифферен-
дифференциального выражения L [у] в точке х = xt, если разложение А
в ряд Тейлора в точке xt содержит производные yv (xt) при v <^ k
с множителями pv (xt) и не содержит производных yW (xt) при
Тогда для любой (k-\- r -\- 1) раз непрерывно дифференцируемой
функции у(х) будет справедливо разложение
2
v-0
B2.5)
Здесь i^l^l, D — не зависящая от у константа, | y(*+r+1) |max —
максимальное абсолютное значение производной y(k+r+l'i в некото-
некотором интервале, содержащем все точки xt-\-ph.
Теорема. Для любого заданного линейного дифференциаль-
дифференциального выражения B2.3) и для любого неотрицательного целого
числа г в каждой точке х — xt существует конечное выражение
r-го порядка точности. Таких выражений существует бесконечно
много.
Для доказательства разложим выражение B2.4) в ряд Тейлора.
Получим
А= y{xt)[ C_p+..
B2.6)
причем остаточный член R при | Ф | <^ 1 можно записать в виде
22.2) § 22. УЛУЧШЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ 371
Согласование разложения B2.6) с B2.3) дает для Ср систему
k-\-r-\-l уравнений
<<■
0, A;+l<>c</fe-br.
Эта система линейных уравнений в случае q-\- p^> k-{- r, т. е. в том
случае, когда имеется достаточно много абсцисс xt-\-()h, а следова-
следовательно, и достаточное количество неизвестных, всегда разрешима.
Если количество неизвестных Cp(p-\-q-\-\) больше, чем количество
уравнений (k-\- r-\- 1), то (p-\-q—k — г) неизвестных можно поло-
положить равными нулю, а остальные вычислить из системы уравнений
B2.8). Действительно, определитель этой системы есть определитель
Вандермонда и как произведение разностей отличных друг от друга
чисел всегда отличен от нуля.
В таблице XI приведены простые конечные выражения для низших
производных. С их помощью можно составить конечные выражения
для любого дифференциального оператора до четвертого порядка
включительно.
22.2. Метод конечных разностей повышенной точности. Этот
метод вполне аналогичен рассмотренному в § 21 обыкновенному
методу конечных разностей, который можно рассматривать как метод
конечных разностей первого приближения. Разница состоит в том,
что теперь дифференциальные соотношения заменяются при помощи
конечных выражений, приведенных в п. 22.1 и в таблице XI. Поясним
этот метод в r-м приближении, используя обозначения п. 21.1, при
этом ограничимся случаем нечетного r — 2s-\-l.
Заменим каждое дифференциальное отношение в точке xt разно-
разностным выражением г-го приближения, которое использует только
точки, симметрично расположенные относительно xt, от xi_m_s до
xi-\m+s (пусть 2т— порядок дифференциального уравнения). Тогда
можно для каждой из двух граничных точек и для (я—1) внутрен-
внутренних точек, т. е. для точек х0, Х\, х2 хп, записать разностное
уравнение, соответствующее дифференциальному уравнению, и полу-
получить для п -f- 2т -\- 2s-\- l неизвестных значений К(., а именно зна-
значений от К_т_5 до Ynjm+S, (я-j- 1) уравнений. Далее, каждое из 2т
краевых условий дает одно разностное уравнение.
Не хватает еще 2s уравнений. Поэтому необходимо присоединить
еще 2s конечных уравнений более низкого приближения, что можно
сделать по-разному, например, можно для каждой из двух гранич-
граничных точек х0 и хп добавить соответствующие дифференциальному
уравнению разностные уравнения 1, 3 Bs—1)-го приближения.
Этот способ будет проиеден на последующих примерах. Если в крае-
краевых условиях не встречаются Bт — 1)-е производные, то разностные
уравнения r-го приближения, записанные для точек х0 и хп, можно
372
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[22.4
опустить, тогда будут иметь место только значения от Y_m_s+1 до
у
пл-тл s—\'
Ч.Ч..Ъ. Пример для разностного метода повышенной точности. Мы
используем пример, приведенный в п. 21.2 при демонстрации обыкновенного
метода конечных разностей (продольный изгиб стержня, рис. 21.2). Таким
образом, имеет место задача на собственные значения B1.5), B1.6). При
шаге h = 1/3 получим для неизвестных значений функции Y_u Ya, Yu ..., Y4
(рис. 22.1) в точках х\, x<l два разностных уравнения третьего приближения
I Д Оу __ Q
ХШ + Л1К2 = 0.
В силу краевых условий Yo—Y3 — 0.
Для того чтобы исключить значения Y_t и К4 вне интервала [0, 1) нужно
привлечь еще уравнения более низкого приближения. Поэтому мы запишем
для х0 и х3 обыкновенные разно-
у стные уравнения
-У»
-j-
+
16К2
16К3
— зок.
12/г2
— 30К2
4-
+
16К0
16К,
— Y-i
, у
УО=О
ч
Рис. 22.1. Значения функции вне интер-
интервала [0, 1].
= — У2. Если положить
и
нения:
16К2 —29К, + 2иК, =0,
16К, —29К2+ цК2 = 0.
Приравнивая нулю определитель этой системы
— 29 + 2ц 16
16
найдем
и = ~ (87 ± /2889)
Они упрощаются, так как вслед-
вследствие краевых условий Ко = К3 = 0
и в силу симметрии К_, = — Y\
\i = 12АЛ2, получатся следующие урав-
0 =
= 2jx2 — 87ц + 585 = 0,
А =
или
6,2345 (ошибка —2,7%),
26,39 (ошибка — 7%).
Сравнение с результатами обыкновенного метода конечных разностей
в п. 21.2) показывает, что здесь с большим шагом h = '/з результат лучше,
чем там с шагом h = l/6.
22.4. Вспомогательные формулы для многоточечного метода.
Методы, о которых будет рассказано в пп. 22.4—22.6, в случае
простых дифференциальных уравнений часто приводят к хорошим
результатам, хотя их применение иногда бывает довольно сложным.
Улучшение по сравнению с обыкновенным методом конечных раз-
разностей состоит в том, что каждое отдельное разностное уравнение
22.4] § 22. УЛУЧШЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ 373
учитывает соответствующую задачу на собственные значения в большем
количестве точек. Этот метод основан на использовании выражений
следующего вида:
ч-р
B = v?jp(avyv+Avym), B2.9)
являющихся линейными комбинациями значений у и значений произ-
производных некоторого фиксированного порядка k функции в соседних
точках xv; при этом постоянные av, Av определены так, чтобы при
разложении выражения в ряд Тейлора в точке xt производные до
возможно более высокого порядка получили множитель нуль.
Мы поясним это на примере производной второго порядка (& = 2).
Для нее известно обыкновенное разностное отношение второго по-
порядка, и можно записать приближенное равенство
При разложении этого выражения в ряд Тейлора в точке х1 оказы-
оказывается, что первый поправочный член *) будет порядка /г4 yiv. Легко
видеть, что если использовать y"L и у_1, то можно получить
выражение, в котором поправочный член будет еще более высокого
порядка по h. Положим при I = О
В = a_ly_l + aoyo+ alVl 4- Л_у_, + Vo + AJi
и разложим это выражение в ряд Тейлора:
5= у0 ( a.x-f- ao+
+ Ч (-«-1 +
Если приравнять выражения в круглых скобках нулю, то получим
1 h2 1
Л Л Л
Таким образом, получится формула
В И?
4- члены шестого порядка B2.10)
(в силу симметрии члены с yv отсутствует).
*) Имеется в виду поправка, делающая приближенное равенство точным.
374 ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ [22.4
Совершенно аналогично можно рассмотреть общий случай с про-
твэдной любого порядка k. Разложение выражения В в ряд Тейлора
в точке xt будет иметь вид
1+р
\-=i-P
-f А (У*} + (v — 0 /гУ*+1> + (v — if -^ yib+V -f- ... I \; B2.
av и Av должны быть определены так, чтобы у., у'., у"., ... до про-
производной возможно более высокого порядка, скажем до порядка
(k-\-r) включительно, получили бы множитель нуль.
Для этого коэффициенты av и величины
B2.12)
должны удовлетворять системе уравнений:
2 flv(v —0" = 0, и = 0, 1, 2, ...,£—I,
2
v=i —
i + P
(
\-i-p
% = k, k-\-
B2ЛЗ)
Будем искать такое выражение В вида B2.9), в котором не все av
и bv равны нулю. Это будет гарантировано в случае, если потре-
потребовать, чтобы коэффициент bL в точке разложения xt был отли-
отличен от нуля. Так как выражение В определяется с точностью
до произвольного множителя, можно положить bi=\. Тогда B2.13)
есть неоднородная система (&-f г-\- 1) уравнений для неизвестных av
и bv. Если выбрать р достаточно большим и иметь достаточное
количество неизвестных, то система будет иметь любое количество
решений (существование бесконечного множества решений следует
уже из того, что каждому конечному выражению, которое можно
составить способом, указанным в B2.1), соответствует решение си-
системы B2.13)).
В таблице XI приведены выражения вида B2.9) для производных
до четвертого порядка включительно.
Для случая, когда используются точно три значения Ь_г, b0, b{,
в задаче 6 п. 23.6 даны в явном виде выражения для производных
любого порядка. Наконец, еще представляет интерес следующий
специальный случай. Пусть k и г — четные числа, k = 2p, r—'2q
11 0 < q <; р. Мы сохраним только bv с |v—'i\^q и, таким
22.51 § 22. УЛУЧШЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ
образом, положим
375
Мы утверждаем, что система уравнений B2.13) будет иметь един-
единственное решение, если нормировка выбрана так, что bt = 1 при аь = 1.
В этом случае число уравнений будет совпадать с числом неиз-
неизвестных и будет равно k-\- г-\- \\ нам нужно еще, таким образом,
показать, что определитель D системы B2.13) в данном случае
не равен нулю. Он имеет вид
1
-р
р2
(~р)*-'
(-V
<-р>*+>
1
— 1
1
...(-1)*-
... (-1)*
1
1
1
11
1
... 1
... р
..V
...р*-1
...р*+1(
0
0
0
0
1
...
...
* • .
...
(-<?) ... 1
0
0
0
0
I
0
0
0
0
1
.) <>(■
0
0
0
0
1
Т)-(А
0
0
0
0
1
''V)q
B2.14)
Легко видеть, что определитель B2.14) равен произведению двух
определителей
1 ... 1 1 ... 1
B2.15)
и
1 ... 1
D2 =
Оба они не равны нулю, так как D, есть определитель Вандермонда
(см. п. 22.1), a D2 переходит в определитель Вандермонда, если
вынести из каждой строчки множители
(k+2\
\ )
(
\ k
Ik+r
\ k
22.5. Пример. Мы снова рассмотрим задачу о продольном изгибе из пп. 21.2
и 22.3 (см. рис. 21.2) с уравнениями и граничными условиями B1.5) и B1.6):
У" = -^оУ, у @) == у A) =0.
При шаге h — '/з мы имеем значения функций Ко, Кь К2, Y3 (обозначения
см. на рис. 21.2).
Воспользуемся формулой B2.10), пренебрегая членами шестого порядка
(в этом случае мы должны вместо точных значений функции у. и значений
376 ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 122.6
производных y"t записать приближенные значения Yt и Кг), в точках хх — */3:
г2 - 2к,+г0 - -& (К + юг;+К)=о,
Г3 - 2Г2 + Г, - ~ (Гз + ЮГ2 + г;') = 0.
Краевые условия дадут Ко = Y3 = 0. Согласно диффгренциальному уравнению
Таким образом,
Л2
Г, - 2Г, + -jg- Л (К2 + 20Г,) = 0,
/,2
- 2К2 + Г, + -1. Л A0Г2 + 27,) = 0,
где положено
Л2 .
Из условия равенства нулю определителя этой системы
получим квадратное уравнение для ц = —
1+2ц —2+10[х
[е для ц = —
v2 — 21v + 66 = 0,
откуда
_ | 6,2966 (погрешность — 1,7%),
~{ 28,067 (погрешность —1,3
Эти значения существенно точнее в сравнении с полученными обыкно-
обыкновенным методом разностей в п. 21.-2 и точнее, чем значения, полученные
разностным методом в третьем приближении. ,
22.6. Метод в общем случае. Рассмотрим дифференциальное
уравнение
M{y] = W[y].
Наивысшая производная пусть будет уBт>. Воспользовавшись фор-
формулой B2.9), запишем, таким образом, уравнение
i+P
2 (avYv+AvY{*m>) = 0 B2.16)
v=i-p
для всех внутренних точек.
Используя дифференциальное уравнение, заменим везде Y[m) через
низшие производные Y^m~l\ К*,2'"' v'v, Yv. Эти Y(s) будут
выступать как дополнительные неизвестные. Запишем теперь для всех
производных, входящих в дифференциальное уравнение, формулы
22.6)
§ 22. УЛУЧШЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ
377
типа B2.9) во всех внутренних точках (соответствующие коэффи-
коэффициенты av< Лv мы отметим штрихами):
=0.
B2.17)
Особого внимания требуют краевые точки. Для исключения всех
излишних неизвестных здесь может оказаться необходимым примене-
применение «односторонних» формул. Мы
поясним это на примере.
Пример. Крутильные колебания
диска. Задача 4 в п. 11.4 приводит к диф-
дифференциальному уравнению
_(,
-*■/)'
или
/)'= *,-
2лгу' — Ху
Уо=0
0
у
/
Г
г
1
*•*
4
7
—.
у3-уг
t Т х
... ...
с краевыми условиями у @) = у' A) = 0.
При решении этой задачи методом
Рис. 22.2. Метод конечных разно-
разностей для примера крутильных
колебаний п. 22.6.
конечных разностей мы применим (рис 22.2) грубый шаг h =
образом, -J^—
2
Тогда формула B2.10), записанная для точек х = -г
таким
2
X =
При
шем
-=-, дает
5
у-1
-у,
> + у 1(у>
этом были использованы краевые
будет учтена
еще
симметрия, из
2 + ЮК"
1 1 Г»1/
J ~Т^ "' 2
условия
которой
+ У'о) =
+о-
следует
= 0,
0.
у*
К
= К3 (в дальней-
= — y'X Теперь
согласно дифференциальному уравнению B2.18) с приближенным значе-
значением Л вместо К
Запишем еще формулы для у'. С помощью таблицы XI для
получим уравнения
и х = -=■■
5
378
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[23.1
Нужно еще исключить К„. Для этого применяется согласно таблице XI
следующее соотношение
Теперь имеется достаточное количество уравнений для исключзнчя неизвест-
неизвестных значений функций.
Решая полученную систему уравнений, найдем
218Л2 — 5423Л — 16 329 = О
или
3,5049 (ошибка —2,5%),
21,371 (ошибка—11%).
Л =
§ 23. Метод конечных разностей для уравнений
с частными производными
Как уже указывалось в § 21, метод конечных разностей приме-
применим для очень широкого класса задач. Для уравнений с частными
производными при сложной форме
границы этот метод является един-
единственным практически пригодным,
так как при применении других
методов учет граничных условий
весьма затруднителен.
Ради удобства изложения мы
ограничимся случаем двух незави-
независимых переменных х, у, хотя
метод можно точно так же при-
применять и для большего числа не-
независимых переменных.
23.1. Обыкновенный метод
конечных разностей или ме-
метод первого приближения. Мы
с
b
1
\
\
1
Уо\
\
1
\
•*—
ih
—^
—-^
/
i,h\
/
/
\
1
— X
Рис. 23.1. Прямоугольная сетка к ме-
методу конечных разностей для диф-
дифференциальных уравнений с частными
производными.
введем прямоугольную сеть с ша-
шагом h по горизонтали и / по вертикали (см. рис. 23.1). Точки с ко-
координатами
С*-». ±>.±*....>
называются узлами.
Выбор начальной точки х0, у0 и величин h и / произволен; но
все же большей частью для лучшего удовлетворения краевым усло-
условиям стремятся к тому, чтобы возможные прямолинейные участки
границы совпадали с прямыми сетки B3.1) или в случае криволиней-
криволинейной границы особенно характерные точки совпадали с узлами сетки.
Можно применять и другие, отличные от прямоугольной, сетки,
по при этом разностные выражения усложняются и- становятся не-
23.11 § 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 379
удобными для численных расчетов, особенно если применять сетку,
которая не переходит в себя при параллельном переносе. В пода-
подавляющем большинстве случаев используется квадратная сетка.
Значения функции в точках x-v yk мы обозначим индексами /, k:
так например, ziyk есть значение искомой функции z(x, у) в точ-
точках х = Х;, y = yk и Zlik—приближенное значение дЛя zlyk.
Дифференциальному уравнению и граничным условиям соответ-
соответствуют, точно так же как и в случае обыкновенных дифференциаль-
дифференциальных уравнений, разностные уравнения. Разностные соотношения и
конечные выражения можно легко получить с помощью «операторов
сдвига» Ех и £у, применение которых к любой функции g (х, у) уве-
увеличивает аргумент х или у на величину шага. Таким образом,
y) = g(x + h. у), Eyg (х, y) = g (x, у + /),
» р„ B3.2)
Операторы можно возводить в любую целочисленную (положительную
или отрицательную) степень')
ExE™g{x, y) = g(x-+kh, y + ml).
С этими операторами можно действовать формально как с алгебраи-
алгебраическими величинами и ими можно заменить дифференциальные опе-
операторы.
Как пример для вычислений с помощью этих операторов запишем раз-
ностное отношение для , 2°. ■. Согласно таблице XI, отбрасывая остаточ-
остаточный член, при h = / будем иметь
7H, о ~ ~2Л" ^°-' ~ ^°- "!) = ~2h
Окончательно получим
= "газ- (^i, 1 — 2^о, 1 + ^-1, 1 — ^i, -1 + 2^о, -1 ~ 8-1, -0'
Так, любому дифференциальному уравнению можно сопоставить
разностное уравнение. Это производится для каждой «внутренней»
узловой точки, т. е. для каждой узловой точки, которая вместе со
своими четырьмя соседними точками xi+1, yk\ xt_x, yk\ xt, у^+\\ х^
ук_1 находится внутри или на границе Г области 93 задачи.
J. F. Steffensen, Interpolation, Baltimore, 1927.
380
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[23.2
Особой тщательности требует перевод заданных граничных усло-
условий в разностные условия, т. е. уравнения, связывающие Zik. Спо-
Способ, которым осуществляется этот перевод, может иметь большое
влияние на точность определения приближенного собственного зна-
значения.
Например, при граничном условии z = 0 на кривой Г (рис. 23.2)
можно совсем грубо положить Z = 0 в точке В, но тогда не при-
приходится ожидать большой точности.
Лучше потребовать, чтобы значения Z
в точках А, В, С лежали на пря-
прямой, тогда, если длина АВ = 6, то
или, привлекая точку D, лежащую вне
кривой Г, получим
Рис. 23.2. К обсуждению крае-
краевого условия z = 0 в методе
конечных разностей.
7 —
ГЛ"^1
B3.3)
При сложных краевых условиях и кри-
криволинейной границе можно потребовать,
чтобы разностные условия на границе области получались автомати-
автоматически путем разложения в ряд Тейлора.
23.2. Пример. Собственные колебания эллиптической мембраны.
Пусть мембрана постоянной толщины и эллиптической формы защемлена по
краю. Определение ее собствен-
собственных частот сводится к задаче на у
собственные значения (см. п. 3.4) iR 2$ ' п
X
при z = 0 на краю области, огра-
ограниченной эллипсом с полуосями
1 и 2:
Рис. 23.3. Собственные колебания эллип-
эллиптической мембраны.
Мы применим (исключительно для
пояснения метода) совсем грубую
квадратную сетку с шагом к = 2/3
и будем иметь, если нас инте-
интересуют только симметричные по х и у колебания, семь неизвестных значе-
значений функций, которые пронумеруем Zj, Z2, ..., Z7 (рис. 23.3).
Путем непосредственного применения второго разностного отношения
для выражения (Д^),-, k получим
, k+\
—4Z;,
B3.4)
3.3]
23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
381
Если Л есть приближенное собственное значение А, вычисленное методом
конечных разностей, то разностное уравнение будет иметь вид
ft + i -\-Zi, ft-i = vZ,-, ft, B3.5)
где введено обозначение v = 4 — Ah2.
В данном случае при ц = v— 1
Если теперь грубо положить Z4 = Z5 = Z6 = О (Z7 здесь не учиты-
учитывается), то получится уравнение ц (ц2 — 3) = 0 и отсюда приближенные зна-
значения для Hi, приведенные в первом столбце таблицы, помещенной ниже.
Более точные значения можно получить, если Z4, Z5, Z6 исключить согласно
B3.3), но и при этом ошибка из-за небольшого числа узловых точек будет
все же довольно значительной. Согласно рис. 23.3
6 =
— 1 , _ 1— VT _
• таким образом, Z6 = ^ Z3;
точно так же получим
7 -
Z -
4—
и для определения jx будем иметь следующее уравнение:
(ц + 0,82514) (цг -|- 0,09384ц — 2) = ц.
Корни этого уравнения ц,-, найденные по ним приближенные значения Л;,
а также значения, вычисленные многоточечным методом (см. п. 23.4) с учетом
Z7 = — tj- Z3, приводятся в следующей таблице:
Корни \it и приближенные значения Лг
Обыкновенный метод конечных разносте
Краевые условия Z4, Z5, Z6=0
/з
0
-VT
2,853
6,75
10,65
й п. 23.1
Многоточечный метод п. 23.4
Краевые значения исключены по B3.3)
1,5839
- 0,528
— 1,976
3,186
7,94
11,20
И,-
7,694
— 3,245
— 9,825
3 52
9,85
15,10
23.3. Метод конечных разностей повышенной точности. В этом
методе, подобно тому как это было сделано в п. 22.1—22.3 для
обыкновенных дифференциальных уравнений, разностное отношение
заменяется конечным выражением, разложение которого в ряд Тейлора
давало бы лучшее совпадение с заданным дифференциальным выра-
выражением (т. е. до членов более высокой степени), чем разложение
в ряд Тейлора разностного отношения. Для вывода конечного вы-
выражения такого рода имеются два способа: 1) операторный способ
и 2) непосредственное разложение в ряд Тейлора,
382
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[23.3
Достаточно описать, как для одного из членов
произволь-
дха ду$
ного дифференциального выражения находится конечное выражение
(а именно «конечное выражение r-го приближения», в разложении
Тейлора которого, кроме члена —-—^- имеются только члены s-ro
порядка, где s = a-\- P-(~ r -\~1).
При операторном способе используются снова введенные посред-
посредством B3.2) операторы сдвига Ех и Еу. По теореме п. 22.1 для
производной а-го порядка имеется конечное выражение (/- —|— р —j— 1)-го
приближения, которое с помощью оператора
в виде
. . р
I даг\ _ V4 ^ „о , л ^ dsz
Ех можно записать
\дх°
dx»
При этом г ^> 0 есть любое наперед заданное число, s = t-\-q.-\$-\-\,
l^il^l, D и р — зависящие от г числа. Соответственно имеются
такие константы Ср, D , р , что при | ^ | ^ 1 справедливо
dsz
dys
Вместе с тем следующие операторные уравнения справедливы, если
операторы применяются к целым рациональным функциям z(x, у),
которые содержат х и у в степени не выше (s— 1) и для которых,
таким образом, остаточный член отсутствует:
дха
•-Р
Р--Р*
Так как для рассматриваемого класса функций дифференцирование
и сдвиг являются перестановочными операциями, то можно записать
дха
Q.
• — р
Теперь образуем для произвольной функции g (x, у), имеющей не-
непрерывные частные производные до s-ro порядка включительно, вы-
выражение
р р'
у)кk= Ц S cf°gtxi■+ph' у*+ol)
P--P <У-=-р*
23.4| § 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 383
и при разложении в ряд Тейлора с точке xt, yk получим
а + Ь <
при этом | g(s) |max означает максимальное значение суммы всех
частных производных s-ro порядка в области | х—x^^sh; | у—yft|<^s/;
|^1, a D' — постоянная.
Константы Yo, ь для всех рассматриваемых функций одни и те же.
Если g есть целая рациональная функция степени не выше (s— 1)
по обеим переменным вместе, то правая часть в выражении B3.6)
исчезает.
Если положить g = {х — Xj)a (у — yk)b при a^-Q, b^O, a-\-
то Qg(x,y) есть искомое конечное выражение для
у)
дха дуР
Число s при этом может принимать любое значение (произвольно),
т. е. имеются конечные выражения любого приближения1).
Конечное выражение с той же степенью приближения, как и
в выражениях операторного метода, часто можно получить более
просто (используя меньшее число узловых точек), делая непосредст-
непосредственную замену
( Г*Ч ) = У Ср, „£(*, + ?*. yft + a/) + *D|^)U B3.7)
\ дхаду? //, й ~
и определяя отсюда неизвестные еще константы Ср а так, чтобы при
разложении в ряд Тейлора имело место совпадение суммы, стоящей
в правой части B3.7), до членов (s—1)-го порядка включительно.
В таблице XII приводятся конечные выражения для часто употребляемых
дифференциальных операторов
о.*2 ' ду2 ох* дх2 ду2 ду*
23.4. Многоточечный метод. Метод, описанный в пп. 22.4—22.6,
можно распространить и на дифференциальные уравнения с частными
производными. Здесь в еще большей мере справедливо замечание, что
этот метод позволяет получить хорошие результаты при простом
строении дифференциальных уравнений, в то время как в случае
сложных уравнений проведение этого метода гораздо более затруд-
затруднительно, чем метода п. 23.3.
') Подобный же операторный метод можно провести при любом числе
независимых переменных.
384 ГЛ. Vil. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ [23.4
Воспользуемся опять прямоугольной сеткой B3.1). Пусть диф-
дифференциальное уравнение, как в F.1), имеет вид
M[z] = lN[z], B3.8)
где М [z] — дифференциальное выражение s-ro порядка
^ч £ T ^Г/р ■ B3-9)
a>0, C>0
при этом Яц/р1—заданные функции х, у. Мы будем различать два
случая.
Случай I.Коэффициенты Р^ наивысшего члена Ms [z] по-
постоянны. Образуем выражение типа B2.9)
В=Ъ (а,, „г,, „+ Аш (Ms [г] ),, й), B3.10)
где число узлов, по которым производится суммирование, подлежит
уточнению. Коэффициенты alk и Aik — константы. Разложим теперь
выражение В в некоторой узловой точке по формуле Тейлора. Коэф-
Коэффициенты alk и Alk определяются тогда из требования, чтобы при
разложении в ряд Тейлора коэффициенты при
дха
обращались в нуль для а-|-р<> + г (а^>0, Р^>0). При этом
нужно выбирать г > 0. В случае г = 0 можно в качестве В исполь-
использовать обыкновенные разностные отношения. В построенном таким
образом выражении В Ms [z] выражаются с помощью дифференциаль-
дифференциальных уравнений B3.8) и B3.9) через низшие производные. Так, для
приближенных значений Zt k получается уравнение
o. B3.li)
В этом уравнении в качестве неизвестных выступают Zt к и значе-
ния Z) ь , являющиеся приближениями к I г-) . Уравнения
\dxady^J
типа B3.11) записываются для каждой внутренней узловой точки.
Теперь нужно еще исключить Z;%p) при a-f E>0. Это возможно
благодаря тому, что можно построить выражение вида
i,
23_41 5 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 385
ла+Ь.,
причем при разложении в ряд Тейлора коэффициенты при —.
дх ду
для a-^b^s-f-r равны нулю. Тогда уравнения В* = О (с заменой
г{ Ана Z^ k) реализованы для всех производных g-, входящих
в B3.8). Точно так же как и дифференциальному уравнению,
краевым условиям сопоставляются соответствующие уравнения для
Zt, k и Z(j%P). При этом часто для краевых условий нужно добавлять
уравнения низшего приближения, для того чтобы получить одина-
одинаковое количество уравнений и неизвестных.
Случай II. Коэффициенты Р*£$ наивысшего члена Ms [z] в B3.9)
не постоянные, а являются функциями от х и у.
Тогда можно действовать двояко. Или построить уравнения в форме
В* = 0 B3.12) для всех производных, встречающихся в дифферен-
дифференциальном уравнении, а также и для производных 5-го порядка, и
записать, кроме того, дифференциальные уравнения для всех внут-
ренних узловых точек с Z) ft' вместо к , или применить
\dxadyvJik
выражение вида
я** = 2«;^+л!;(жи)^).
При этом коэффициенты a**k, Л** теперь в каждом полученном урав-
уравнении нужно вычислять заново, так как из-за переменных коэффи-
коэффициентов Р'^Р (которые сами должны быть разложены в ряд Тейлора)
разложение в ряд Тейлора нужно производить заново для каждой
внутренней точки. Проведение метода из-за этого может быть очень
утомительным.
Мы поясним этот случай на примере уравнения (ср. п. 6.2)
М[г\= — (ргх)х — (ргу)у + qz = kgoz, B3.13)
которое можно также записать в виде
, , Рх Ру . Я . So _„ , ..
bz = zxx+zyy = zx -г^-г-%~г. B3.14)
Теперь члены с наивысшими производными гхх и гуу имеют посто-
постоянные коэффициенты. Используя симметрию, для Дг получим в уз-
узловой точке Xj, yk выражение вида B3.10) с еще неизвестными коэф-
коэффициентами с,, с2 сб (h = l)
■+ c5(hzi+h ft-f Дг,.,, ft+ Д«;, S-, i +л^г, ft-i) +
-i^(^,u-,it • 4 r- ■)• B3.15)
386
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
23.5]
При этом, кроме четырех соседних точек (/-)- 1, к), (I—1, к),
(/, k-\- 1), (/, k— 1), обозначенных на рис. 23.4 квадратиками ■,
которые уже использовались при выводе обыкновенных разностных
отношений B3.4), были привлечены еще точки (/+ 1, £-)-1),
(/4- U k— 1), (/—1, k-if-l), (i— 1, k— 1) (обозначенные на рис. 23.4
кружочками О)-
При разложении выражения B3.15) в ряд Тейлора легко видеть,
что все члены до частных производных пятого порядка включительно
можно положить равными нулю, и при этом остается еще свобода
М
р у р
выбора. Можно, например, положить с6 = 0 и
получить
с\ — 5с2 = 20 с3 — -££■ с4 = -р-
или, записывая еще раз подробно:
4Qzik - 8
zlt ft_,) —
= остаточный член 6-го порядка. B3.16)
Формулы такого рода удобно иллюстрировать наглядными схемами,
в которых около значков о записывают число-
числовые коэффициенты перед Zt k и (курсивом)
перед AZt к
— 2. —8., —2.
-D
i.h
40., -:
-2. —I
— 2.
Рис. 23.4. Схема со-
составления выраже-
выражения &z.
ф Щ точки, используемые
в обыкновенном методе
конечных разностей,
О Ш D точки, используе-
используемые в метоле п. 23.3 (ко-
(конечное выражение),
в Я О точки, используе-
используемые в многоточечном ме-
метоле конечных разностей
п. 23.4.
Если представить себе теперь уравнение
B3.16), записанное для каждой внутренней
узловой точки с заменой z на Z при отбра-
отбрасывании остаточного члена, а также заменить
в нем Az по разностному уравнению B3.14),
то получатся уравнения для Z(i k и приближен-
приближенных значений
Z(/,'ft0)
для
дг\
ду l
п
Для последних можно использовать
формулы из таблицы XI для обыкновенных
производных. Таким образом, например, для у — направления
1,1г
О
и еще нужно записать такое количество краевых условий, чтобы
получить количество уравнений, равное количеству неизвестных.
23.5. Примеры. Колебания мембраны. Пример 1. Защемленная на
краю мембрана в виде прямоугольного равнобедренного треугольника.
23.5] § 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Для этого случая имеем дифференциальное уравнение
387
О
■1-
0
о
с краевым условием 2 = 0 на границе равнобедренного прямоугольного тре-
треугольника с катетом / = 1 (рис. 23. 5).
Этот пример с обыкновенным разностным
отношением и конечным выражением был ра-
разобран в работе '). Результаты приводятся
в таблице XIII. Ниже этот пример будет опи-
описан многоточечным методом согласно п. 23.4.
При шаге h — 1/4 (см. рис. 23.5) имеются
три внутренние точки. Значения функции
в этих точках мы обозначим через а, Ь, с. При
выводе разностных уравнений типа B3.16) по-
понадобятся также точки, лежащие вне треуголь-
треугольника. Так как на границе z-= О, то, таким
образом, Лг = 0, и на гипотенузе (в системе
координат £, г], показанной на рис. 23. 5) z^ = О,
вместе с тем также г^ = 0.
I
Рис. 23.5. Мембрана в форме
равнобедренного треуголь-
треугольника.
Продолжим z как нечетную функцию и
используем в качестве соответствующих зна-
значений функции — си — Ъ.
Можно теперь сразу записать разностные
уравнения B3.16). Уравнение, записанное, на-
например, для точки а, будет иметь вид 40а — 86 — 8с -+- 8Л2 (— Аа) +
+ К2 (— Ab — Ac) = 0.
Окончательно имеем уравнения
Аа
Ab
Ac
42c-8a-2ft-^-—^- =
В результате вычислений получим
Л2 = 88, Ль з = ^5Т<
г ч Г 48,7540,
1352) = { 124,665.
Для уравнения — Лг = "Kz можно построить еще и другое разностное
уравнение, обладающее той же степенью приближения, но намного благопри-
благоприятнее для численных расчетов. А именно, для этого можно использовать
имеющуюся в B3.15) свободу в выборе констант, чтобы отношения с2:с3 и
с5: с6 сделать равными друг другу. Тогда получится выражение
B,. | I . | . \ I "
■f 14(Д2', + 1, k + S.Z^u ъ-\-Ы-1, fe+i +AZ;,*-i) +
, ft + i+ ' ~Ь • + •)} = остаточный член 6-го порядка. B3.17)
l) G. S с h u I z Formelsammlung zur praktischen Mathematik, Sammlung
Goschen, Berlin — Leipzig, 1937.
38S
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
B3.5
При отбрасывании остаточного члена и замене Л2",-, ^ = — A.Z/, /, это урав-
уравнение примет вид
t-\,k-\), B3.18)
где Л =
12B0— v)
/z2E2-f v) '
Уравнение B3.18), кроме того, что в нем более низкие коэффициенты,
имеет' по сравнению с B3.16) еще и то преимущество, что число v стоит
только при члене 2"г, к.
При шаге h = 1/4 (рис. 23.5) и с теми же
обозначениями, как и в предыдущей задаче, из
B3.18) получим уравнения
ха = АЬ -\- 4с, хЬ = 4а -
хс = 4а -)- 6 — с
с — Ь,
Рис.
23.6. Ромбическая
мембрана.
и отсюда v2 = — 2; Vi, 3 = ± 4 У2.
Таблица XIV дает возможность сопоставить
приближенные значения, полученные различными
методами.
Пример 2. Защемленная по краю мем-
мембрана в видг ромба с углом я/3 (рис. 23.6).
Здесь рекомендуется пользоваться не прямоугольной сеткой, а при-
применять сетку в виде правильного шестигранника или треугольника.
Пусть длина стороны ромба равна А; мы снова имеем дифференциаль-
дифференциальное уравнение
— Д,г = Хг
с граничным условием г = 0 на краю ромба. В случае
шестиугольной сетки при разложении в ряд Тейлора,
вводя значения функции в соответствии с рис. 23.7,
получим
Z\ + г2 + z3 — 3z0 = -£- Л.г0 -j g- m3;
при этом |д|<1, а т3 — максимальное значение
третьей частной производной от г на трех отрезках от
точки 0 до точек /, 2, 3.
Для дифференциального уравнения Дг = — Xz раз-
разностное уравнение будет иметь вид
где Л связано с
соотношением
B3.19)
л — 1. 3~Х
3 ~hr~ ■
Рис. 23.7. Шести-
Шестиугольная сетка.
Метод конечных разностей точно так же можно провести с большим
числом узловых точек при еще терпимой вычислительной трудоемкости,
особенно если можно использовать симметрию ').
В таблице XIII приведены результаты, полученные методом конечных
разностей с различным шагом и различной длиной шестиугольной сетки.
Если обозначить диагонали ромба G, и О2 (см. рис. 23. 6), то все собствен-
собственные функции относительно G{ симметричны или антисимметричны, и точно
') Можно вывести «симметричные формулы» и «антисимметричные фор-
формулы» с существенно меньшим количеством неизвестных. См. L. С о I I a t z,
Z. angew. Math. Mech. 14 A934), 316.
23.5|
23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
389
Рис. 23.8. К симметрии фор-
формы колебаний.
так же относительно О2, не говоря о собственных функциях, относящихся
к вырожденному собственному значению, для которых можно построить нг-
симметричную форму колебаний с помощью линейной комбинации. Напри-
Например, форма колебаний на рис. 23.8, где обозначены узловые линии, отно-
относительно О2 ни симметрична, ни антисимметрична. Формы колебаний, анти-
антисимметричные относительно Оь одновре-
одновременно соответствуют собственным функ-
функциям равностороннего треугольника со сто-
стороной А. Они могут быть заданы в зам-
замкнутой форме и отвечают собственным зна-
значениям ')
' 4я \2
1а) а
где (i, p — любые положительные целые
числа.
Вообще формы колебаний, определяю-
определяющие приближенные собственные значения,
могут быть упорядочены, и оказывается,
что всякое собственное решение разностного уравнения есть приближение
для вполне определенного собственного решения дифференциального урав-
уравнения.
При рассмотрении таблицы XIII особенно бросаются в глаза следующие
два факта.
1. При п внутренних узловых точках полученные приближения \[п\
л£,л) Л^"' являются приближениями не для первых п собственных значе-
значений Ль Л2, ..., Л„, а для некоторых п
собственных значений X^i, Лд2, ..., Лдп.
Даже последовательность приближенных
собственных значений может быть со-
совсем иной, чем для точных собственных
значений (например, для шестиуголь-
шестиугольной сетки с ft = -ri приближения 143,4
о
и 133,3 для седьмого и восьмого собст-
собственного значения). Поэтому для более
высоких собственных значений сущест-
существует неопределенность в порядке следо-
следования, которую можно устранить только
путем более точных вычислений, в част-
частности, с меньшим шаго,м.
2. Сходимость собственных значе-
значений разностных уравнений Л1/1' к Х{
при возрастании п, как было уже установлено для первого собственного
значения, отнюдь не монотонна. При этом шестиугольная сетка располагается
в ромбе не произвольно, а совершенно определенным образом, так чтобы
конец наибольшей диагонали ромба был центром шестиугольника.
Вместо шестиугольной сетки можно также применить и треугольную
сетку. Значения функций обозначим, согласно рис. 23.9, через zu, zx z6.
С помощью разложения в ряд Тейлора получим
Рис. 23.9. Треугольная сетка.
(z, + z2 + z3 -f z, -f z, - 6z0) = i£i
') F Pockels Ober die partielle Differenzialgleichung
Leipzig, 1891, 148—155.
= 0,
390
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
B3.5
при | ■& | < 1; т4 — максимальное значение частной производной четвертого
порядка от z на отрезках длиной h от точки 0 до точек /, 2, ..., 6. Если
обозначить приближенное значение через Л*, а также заменить Д.г0 через
— Л*\г0, то разностное уравнение с Л* = —Ц^—- будет иметь вид
Z, + Z2 + Z3 + Z4 + Z5 + Z6 = vZ0.
При треугольной сетке можно также применять более точные методы.
В улучшенном методе конечных разностей, описанном в п. 23.4, исходят
из разложеиия в ряд Тейлора
6 /6
/
V z-t — 6z0 т£- V
1-1
-\- 18Дг0 I = остаточный член 6-го порядка.
Если теперь обозначить приближенное значение через Л**, а также заменить
-d
0
0
п
-а
/>
d
е
п
а
Ь
с
п
\
0
d
е
0
\
0
0
0
Рис. 23.10. Колебания воздуха в «домике».
6-v
hzi через — A**Z/, то разностные уравнения с Л** = -р- ^ _|_ ^, будут
иметь вид
S z' =
B3.20)
Разностные уравнения, значения v и собственные функции разностиого урав-
уравнения точно такие же, как и в случае обыкновенного метода конечных раз-
разностей, только приближенные значения Л* и Л** различны, а именно для
|v| < 6 (при краевом условии г = 0 из известной оценки характеристических
16 2
чисел матрицы ') следует | v | < 6) вследствие неравенства 1Q > —.
1о -4— v 3
Л** > Л*.
Пример 3. Акустическая задача. При колебании воздуха в замкну-
замкнутом объеме (домик в виде призмы, размеры которого даны на рис. 23.10)
уплотнение воздуха s удовлетворяет дифференциальному уравнению
Л2с гJс Л2о 1 Л2С
') Величина v есть характеристическое число матрицы, у которой со-
согласно B3.20) каждая строчка состоит из нулей и некоторого числа единиц,
а именно 6 единиц, если все соседние точки являются внутренними, а в про-
противном случае — менее шести. Отсюда следует | v | <; 6-согласно B0.23).
23.5]
§ 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
391
с краевым условием s = 0 на всей границе (р0 — плотность воздуха в сво-
свободном состоянии, а при колебании р = р0 A —j— s) )• После выделения вре-
временного множителя е
собственные значения
где
iat
и множителя sin —-— получим для и задачу на
д2и . dhi
дх2
= — )м,
__ СО2 Я2Я2
с условием и = 0 на границе области 5В.
Задачу следует решать улучшенным методом конечных разностей, исполь-
используя выражение B3.18).
Обозначая значения функции через а, 6, с, d, e (см. рис. 23.10), при
шаге h = -=- А для симметричной формы колебаний получим следующую си-
систему разностных уравнений:
46 + 2d — 2а = va, '
4а + 4с -f- 8rf -f 2<? = vb,
4b-\-8e-\-2d = vc,
46 4" 4<? -(- a 4" c — d — \d,
Ac 4- 4rf 4" * = v^>
которую монсно записать в матричном виде Ши = vu при
—2
4
0
1
0
4
0
4
4
1
0
4
0
2
8
2
1 —1
4
Здесь v связано с Л соотношением
\ —
4
12
0
2
8
4
0
н и =
20—v
а
b
с
d
е
52 4-'
Для того чтобы определить основную форму колебаний, мы оценим сначала
совсем грубо распределение u-значений в виде
и' = @,4 1 0,8 0,6 0,6);
образуем
BГи)' = 0' = D,4 10,8 10,7 6,6)
и получим как отношения компонент векторов 0 и и значения
A1 10,8 12,5 11,7 11).
Теперь легко видеть, как можно улучшить компоненты (например, третья
компонента и, равная 0,8, слишком мала и т. д.); путем изменения значений
методом, описанным в н. 18.8. получим улучшенный начальный вектор
и*' = @,39 1 0,9 0,63 0,62)
с
(%и*у = Vs' = D,48 11,44 10,22 7,14 7,12)
392
ГЛ. Vtl. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[23.5
й отношения A1,486 11,44 11,36 11,333 11,48); таким образом, известно:
ll,33<v,< 11,49
или
6,436 < ЛЛ2 < 6,569
(теорема включения п. 18.7 здесь
применима, если перейти к мат-
матрице Я 4" 2@, которая имеет только
неотрицательные элементы). Эта
точность для технических целей
часто вполне достаточна- Отноше-
Отношения Рэлея будут
= 11,4084 и
= 11,4087,
так что для \А2 получим прибли-
приближение 6,504.
Мы используем этот пример,
чтобы пояснить метод релаксации
(ср. п. 21.4) для обыкновенного
метода конечных разностей при
шаге h = '/з (РИС- 23.11).^ Будем
исходить из совсем грубой оцен-
оценки. Для значений слева вверху
О
/к
1
т
0
п
д
i
j
0
о
Г
ь
с
d
е
0
N
\
f
ff
I
J
0
\
I
m
0
\
а) с
0
n
n
oj
и
n
U
n
в)
n
n
и
^S1^
^^0,42
-0,05
0,44
0,30
0
0
^^0,37
0,44
0,30
0
0
S^0,375
0456
0,293
0
'^
1,16
2,76
1,44
3,27
0,97
3,23
^
1,20
3,24
1,47
334
0,97
3,23
^
1,236
3,296
1,506
3,3026
0,986
3,298
0
0,42
0,72
+0,04
0,72
+0,08
0,53
0
0
0,42
0,78
0,80
0,53
0
0
0,417
0,780
0832
0,53
0
^S
1,37
3,26
2,56
3,56
2,67
3,70
1,74
3,28
1,41
3,36
2,59
3,41
2,71
3,39
1,76
3,32
^
1.37Б
3,300
2,574
3,3
2,746
3,301
1,750
3,302
0,20
0,65
1
0,98
0,72
-006
0
0,
y^
0,20
0,65
1
0,98
0,66
0
A
0,1805
0,596
095
0,98
0,6/9
0
0,65^-
3,25
2,04
3,14
3,07
3,07
3,16
3,23
2,04
2,84
0,65**
3,25
2,04
3,14
3,15
3,15
3,2В
3,33
2,04
3,09
0,59ff^
3,302
19645
3,296
3,130
3,301
3,233
3,299
2,040
3,235ff
Рис. 23.11. Сетка в методе ко-
конечных разностей для акусти-
акустической задачи.
Рис. 23.12. Проведение метода
сации.
релак-
релакна рис. 23.12 в каждом узле, например, для £=0,42 образуем сумму сосед-
соседних значений и получим значение справа сверху для каждой узловой
точки, т. е. для k: g -J-/-f 0 + 0 = 0,72 -f 0,44 -j-0 -f-0 = 1,16. Теперь обра-
23.6]
§ 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
393
зуем отношения и вычислим числа, стоящие справа внизу, так для к полу-
получим значение ' „ = 2,76. Эти отношения суть приближения для v, они
должны по возможности совпадать. В нашем примере эти отношения коле-
колеблются между 2,76 и 3,7; оценка, таким образом, не очень хороша, но легко
видеть, что можно улучшить значения. Вносятся поправки в четыре осо-
особенно отличающихся числа. На рис. 23.12, а эти поправки подчеркнуты и
стоят слева внизу около каждой узловой точки. Улучшенная схема изобра-
изображена на рис. 23.12, (У. Колебание упало при этом на одну треть, так что
теперь 3,09 <^ v ^ 3,41. Повторяя этот процесс несколько раз, можно при
некотором навыке очень быстро сузить границы так, что они будут лежать
в пределах точности счетной линейки. Счетная линейка дает везде значение
отношений 3,30, в то время как вычислительная машина в точках е п I дает
соответственно значения 3,2955 и 3,3026. Между этими значениями должно
лежать v. Из соотношения v = 4 — Ah2 следует АА2 « 6,31.
23.6. Упражнения. 1. Вычислить собственные значения и собственные
функции задачи
У
приближенно обыкновенным методом
конечных разностей. Вычисления бу-
будем производить с шагом h = >/3-
Применим сначала симметричную
формулу Y (ih) = Y (— ih) и получим
тогда для Л = 81(j. уравнение
—2 + % 2 0
1 _2-|- 10ц 1
0 1 _2 -f 13ц
= 1170ц3 — 674ц2 -f 93ц — 2 = 0,
откуда
Л, = 2,1290, Л3 = 13,9, Л5 = 30,6.
В случае антисимметричной формулы
Л,=2,729
У
ОЛ
-7 0|Ч
/ X
А2=В,98
V
= 0,
получим
—24-Юц 1
1 -2 4- 13ц
откуда
Л = ^-B3±/Ш), Л2 = 6,98,
Л4 = 21,6.
-7
Рис. 23.13. Первые пять собственных
функций для задачи 1 из п. 23.6.
На рис. 23.13 показаны соответствующие пять собственных функций
разностного уравнения.
2. Сравнить приближенные значения Л, вычисляемые методом повышен-
повышенной точности в п. 22.2 (по формуле B2.2)) для задачи
-у" = Ау, у@) = у'A)=0
С точным решением-
394
ГЛ VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
|23.6
Вычисление с шагом h = '/4- Получим уравнение
4ц4 — 1028ц2 — 1024.il + 32 257 = 0,
где 2ц=-|-Л—30.
—14,0750
—6,8300
5,4158
15,489
Л
2,4667
21,787
54,44
81,30
К
я2
Я3
я4
Точное
-у
^z УЛ j
= 25Я,
== 49А.,
значение
= 2,46740
Ошибка по Л
—0,02696
-1,896
—1296
—3396
3- Вычислить первое собственное значение Я, задачи
обыкновенным методом конечных разностей § 21, методом повышенной точ-
точности (формула B2.2)) и многоточечным методом п. 22.4 (с использованием
формулы B2.10)).
Результат. Приближенные значения для Я, = 18,9563:
1
2
1
3
1
4
1
1
"
Обыкновенный метод
конечных
§
Л,
16
17,12
17,871
18,25
18,463
разностей
21
ошибка
-1696
—9,696
—5,7%
—3,796
—2,6%
Метод повышенной
точности B2.2)
Л,
18,67
18,703
18,858
18,9129
ошибка
-1,596
-1,396
—0,52%
—0,23%
Многоточечный
метод
Л, -
19,2
18,89
18,9288
п. 22.4
ошибка
+1,3%
-0,3596
-0,1596
4. Решить разностные уравнэнля § 21 и провести метод повышенной
точности п. 22.2 для задачи 6 п. 14.6
при произвольном шаге h = 2/н в замкнутой форме и сравнить с точным
решением.
23.81
§ 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
395
Результат. При шаге h = 2/п можно решение разностного урав-
уравнения
-L
-L
(г = 1, 2, ..., п_
с краевыми условиями
' о = ' л == 0; /
дать в замкнутой форме
Yt= I —cos knih
Ко, К,, ... при этом считаются от левого края х = —1 (рис. 23.14), а й = 1
означает первое собственное решение разностного уравнения, й = 2 — второе
собственное решение и т. д. до А =—~— •
=1, 2, ..., Г-^i-l V
Рис. 23.14. Совпадение Yi с точными значениями в точках x-v
Значения Yt совпадают со значениями, которые принимает собственная
функция
в точках xi — — 1 -+- ih — — 1 -| . Метод конечных разностей, таким об-
образом, позволяет получить в этом примере вид собственных функций без
ошибки. Собственное значение же разностного уравнения
п2 A — cos
дает отклонение от точного значения Xk = й2л2
Л^"'—Xk = уу (-члены с более высокой степенью Л2,
которое стремится к нулю пропорционально Л2.
При использовании конечных выражений пп. 22.2 и 22.3 получатся раз-
разностные уравнения
^ (Д<кг_2 - \ л^_3) = - л
±
с краевыми условиями
396
ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[23.6
Собственные функции разностного уравнения точно такие же, как и
полученные выше обыкновенным методом конечных разностей, но собствен-
собственные значения
(я)
;= 2A —COS
сходятся к точным собственным значениям Я# быстрее, отклонение
13
Лй"'—Xk — — -TjKrr k6n6h4 -f- члены более высокой степени по h2
Г
стремится к нулю пропорционально /г4.
5. Из всех защемленных по краю мембран с одинаковыми параметрами
(плотность, толщина, натяжение и площадь) наименьший основной тон имеет
круговая мембрана, но среди них нет мембраны
с наибольшим осноеным тоном. Для соответствую-
соответствующей разностной задачи, напротив, вопрос о наи-
наибольшем основном тоне имеет простой ответ.
Пусть в квадратной сетке (B3.1) при h = / = 1)
& есть конечная односвязная область, ограниченная
многоугольной границей Г, которая состоит из се-
сеточных отрезков прямых (соединительных отрезков
сеточных узлов). Узловые точки ® делятся на точки,
лежащие на границе Г, и точки, лежащие внутри
области. Далее, предположим, что внутренние точки
образуют связную область; поэтому область, пока-
показанная на рис. 23.15, исключается. Теперь все об-
области, удовлетворяющие вышеперечисленным пред-
предположениям и имеющие определенное постоянное
число N внутренних точек, сравниваются, и для
Рис. 23.15. К вопросу
о связности области
внутренних узловых
точек.
каждой области записывается разностная задача на собственные значения
согласно B3.5)
\Zit й = D — Ah2) Zit ft = сумме четырех значений Zit ft в точках,
соседних с точкой (г, к);
%1, к = 0 для граничных точек (/, к). B3.21)
Для каждой области @ тогда имеется вполне определенный спектр, т. е.
некоторое число собственных значений Ла разностного уравнения и, в част-
частности, наименьшее собственное зна-
значение А1 ((я).
Доказать, что Л] (е) будет наи-
наибольшим, если область © будет рас-
растянута, т. е. если каждый внутренний
узел имеет не больше двух сосед-
соседних внутренних узлов. На рис. 23.16
для N = 5 показаны эти «растянутые»
формы, выполненные двумя спосо-
способами, которые имеют одинаковый
спектр.
Доказательство можно провести, пользуясь минимальными свой-
свойствами Л] ,gj). Узловые точки в области ©, расположенные в какой-либо по-
последовательности, обозначим Яь Р2, ... ■ Если w есть функция, принимающая
какие-нибудь действительные значения во внутренних 'узловых точках и
Рис. 23.16. Сеточная область «растяну-
«растянутой формы» с наибольшим Л.
§ 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
39?
обращающаяся в нуль на границе, то, положив w (Р[) = аь, получим
2 (ш< — т>У
Р,, IJ,— смежные
*, < £ « B3 221
Знак равенства будет иметь место в том случае, если wi есть значение пер-
первой собственной функции разностного уравнения. Таблица XV дает значения
собственных функций разностного уравнения для сеточной области до N = 6
внутренних узловых точек, расположенных в
порядке убывания наименьшего собственного зна-
значения.
Соответственно можно для любого «графах
(рис. 23.17) установить «спектр» собственных
значений, пронумеровав узлы от 1 до N, обозна-
обозначив значения функций в узлах через Z , 2Г„, ...
..., ZN и выписав для каждого узла уравнение
vZj = сумме Z-значений в соседних узлах (/ = 1,
2 N).
Рис. 23.17. К «спектру»
B3.23) графа.
Если приравнять определитель этой системы нулю, то получим алге-
алгебраическое уравнение степени N для определения чисел v, которые обра-
образуют спектр.
6. Вывести для многоточечного метода, описанного в п. 22.4, выражение
вида B2.9) для любой производной порядка /г; при этом из а^„, ..., aj,p
Гk + 1 1 / k , k +'
берутся значения с р= —^— I т. е. р = у для четного k и р = —^—-
для нечетного k\ и из Av — значения Л;_,, Л,-, Л;+1-
Результат. Для четного k при разложении в ряд Тейлора получим
и для нечетного k
= Ckhk+iy<-k+i) -f- высшие производные
где Cft — постоянная.
7. Сравнить для задачи
1+х
= Ckhk+iy(k+A} -{- высшие производные,
= Я.у, у(О) = уA)=О
два способа обыкновенного метода конечных разностей; в первом случае,
производя дифференцирование и заменяя производные у', у" по формулам
B1.1), B1,2),.получить уравнения
-2у/ + >'»-. +р'. Ум-1-У<-1 +Лу, = 0 B3.24)
308
ГЛ. Vll. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
[23.6
в другом случае использовать, согласно B1.8), уравнения
Р \У1+\ — (Р 1+Р ЛУ1 + Р 1У1-1+ЛЛ2у,- = 0. B3.25)
/ + Т
i+Pt 1
Р 1У
l~~2
По формулам B3.25) получатся несколько улучшенные значения.
Л-
1
2
1
3
1
4
Вычисления
по B3.24)
Af = 5,333
Af = 6,075
Л23) = 18,23
Л(!4) = 6,371
Л24) = 21,35
Af = 37,50
Ошибка
—21%
—10%
-32%
—6%
—20%
-37%
Вычисления
по B3.25)
Af-5,486
Af = 6,150
Af = 18,47
Л(!4) = 6,415
Л24) = 21,50
Л^ = 37,81
Ошибка
-19%
—9%
-31%
—5%
-19%
-37%
8. Для колебаний воздуха в примере 3 п. 23-5 обыкновенным методом
конечных разностей получить узловые фигуры низших обертонов. Положить
при этом / = 2А
При обозначениях, принятых в п. 23.5 и на рис. 23.10, используя B3.5),
получим разностные уравнения для симметричной формы колебаний
va — b, xb = a -f- с -f- 2d, vc = 2e -+- b, vd = b -(- e, ve — с -\-d
при v = 4 — A2h2.
Отсюда найдем уравнение
v5 — 7v3 + 4v = 0
для определения частоты колебаний. Для отдельных корней vy решения изо-
изображены на рис. 23.18, куда добавлены оба решения, относящиеся к анти-
антисимметричной форме колебаний. Отсюда по формуле
можно вычислить приближенные значения более низких собственных частот
которые приведены в таблице
V
2,5244
1
0,7923
0
—0,7923
a-4D-v)
5,90
12
12,83
16
19,17
я2
°+ —
8,37
14,47
15,30
18,47
21,64
а'+л2
15,77
■21,87
9яа
*+—
28,1
23.6]
§ 23. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
399
Для
fv v
А
V
V? 1
v,=2,5244
v4=0
А
0
/,
0
1
Л593
1,497
2,524
2,186
v5=-0,7923/
Aw
/ 1
-0,792
-0,686
/ /
A.
0
0
V3=O,7923
ve=-1
/,
-1
Ao
0
0
Рис. 23.18. К задаче 8.
Рис. 23.19. Узловые поверхности при колебаниях воздуха (задача R)
400 ГЛ. VII. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ [28.6
и уже отсюда приближенно найти узловые фигуры несколькнх первых обер-
обертонов и пронумеровать их (рис. 23.19). Для большей достоверности рекомен-
рекомендуется повторить вычисления улучшенным методом, по возможности, с мень-
меньшим шагом.
9. Для симметричного типа колебаний из задачи 10 п. 16.11
i
iv ,„ " , , Г , » ,, , ,
у1»—20у -\-k у dx — А A -[- х2) у, у (± 1) = у (±1) = 0
применить обыкновенный метод конзчных разностей, вычисляя интеграл
по формуле Симпсона.
Результат. При шаге h — 1/2 будем иметь два неизвестных значения
функции а, Ь в точках х = 0 и х — -^-. Разностные уравнения
™ 2Ъ — 2а
4b + a
6
дают прн Л = 64ц, k = 96р
_ 10^2 — 72,ц -\- 47
Р~ 21ц— 134
для А = 200 получим
310,4,
_ ( 310,
= [ 431.
ГЛАВА ВОСЬМАЯ
РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ
§ 24. Метод возмущений
Метод возмущений может с большим успехом применяться, если
для задачи на собственные значения, решение которой нужно найти,
можно указать «близкую» задачу, решение которой известно, т. е.
задачу с теми же самыми граничными условиями и с не сильно от-
отличающимися коэффициентами в дифференциальном уравнении.
24.1. Описание метода. Рассмотрим дифференциальное уравнение
М[у] = Ш[у] B4.1)
с краевыми условиями
1/ц[у] = 0. A=1, 2 k. B4.2)
Ради простоты мы опишем этот метод для случая одной независимой
переменной х, он точно так же будет справедлив для дифферен-
дифференциальных уравнений с частными производными и для большего ко-
количества переменных, нужно только тогда интегрирование распро-
распространить на всю основную область.
Пусть известно решение другой задачи на собственные значения
M*ly] = X*N*ly], B4.3)
с теми же краевыми условиями, что и исходная задача, но с коэф-
коэффициентами дифференциального уравнения, несколько отличающимися
от коэффициентов уравнения B4.1). Пусть и-я собственная функция,
которую мы обозначим у* = ул 0 соответствует собственному значе-
значению Я* = %п 0. Задача с известным решением уп 0 называется тогда
«невозмущенной» задачей, а задача B4.1), B4.2), решение которой
нужно найти, «возмущенной» задачей с членами возмущения
М[у) = М\у] — М*{у\, N[y\ = N[y] — N*[y]. B4.4)
Относительно невозмущенной задачи B4.3), B4.2) предположим, что
она самосопряженна, так что выполняются условия D.15), и что для
402 ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ 124.1
собственных функций ул> 0 справедливо
Для возмущенной задачи в данном случае самосопряженности
не требуется.
Введем теперь параметр возмущения е и образуем однопарамет-
рическое семейство задач на собственные значения:
B4.5)
,= 1, 2, .... ft). '
Тогда е = 0 будет соответствовать невозмущенной задаче, а е=1 —
возмущенной.
Собственная функция уп новой задачи B4.5) рассматривается в за-
зависимости от е. Теперь мы сделаем предположение, в общем случае
трудно доказуемое, что я-е собствелное значение "кп и я-я собствен-
собственная функция уп могут быть разложены1) в степенные ряды по е и
эти ряды сходятся при 8=1, причем M[yn] и N [уп] могут быть
образованы путем их почленного дифференцирования. Итак,
B4.6)
') При довольно общих предположениях F. R е 11 i с h доказал возмож-
возможность разложения Хп и уп в степенные ряды по е, оценил их область схо-
сходимости и даже ошибку при обрывании ряда на k-м члене, им же был рас-
рассмотрен случай вырожденнэго собственного значения, Math. Ann. 113 A937),
600; 116 A939), 555; 117 A940), 356. В качестве примера его оценок (Math.
Ann. 117 A940), 361—378) рассмотрим следующую задачу:
- (/У У + (/о + ю) у = Яу, у @) = у (/) = 0,
/, непрерывно дифференцируема; /,hs непрерывны;
/, > 0, s (х) < S в 0 < х < /.
Пусть для невозмущенной задачи (для е = 0) dn выбраны так, что в ин-
интервале Ял, 0 — dn < л < ЯЛ| 0 -\- йп не содержится других собственных зна-
значений, кроме Ял, 0. Тогда ряды B4.6) сходятся для | е | < -jTh и справедливы
оценки (при соответствующей нормировке собственных и возмущенных функ-
функций) для k = 0, 1, 2, ...
-2'
V = 0
ft+1
fe+1
v-0
Оценку для у„ нужно понимать в смысле сходимости в среднем, так что
/ -р/2
|/(-*I = '
24.1] § 24. МЕТОД ВОЗМУЩЕНИЙ 403
Рассмотрим сначала случай, когда k,h 0 есть простое собственное
значение невозмущенной задачи. Случай многократного вырождения
собственного значения будет рассмотрен в п. 24.2.
Внося B4.6) в B4.5), получим
v-0 v-1
oo oo oo
= („Zj6 "n, vJv.^Je N [Уп, v\ -\~ 2* e '» [Ул, v-l] )•
v=0 v=-0 v—l
Формально перемножая ряды и приравнивая коэффициенты при
одинаковых степенях е, будем иметь
от е°: Ж* [у„, 0] = К, о^* [уя, о]. B4.7)
от е: Ж* [ул, i] + М [у„, о] = К, iN* [уя> 0] + Я„, „ [N* [уя, ,] +
+ ^[Ул, о]). B4.8)
от ev: Ж* [у„, v] + ж [Ул, v-i] = ^л, v^* [ул, о] +
-f iiK v-p(^ [У«, Р] + N [у„, p_j] ). B4.9)
Уравнение B4.7) совпадает с уравнением B4.3) и автоматически
выполняется. Вследствие предполагаемой самосопряженности невозму-
невозмущенной задачи неизвестные %,h ь ул, 1. ^л, 2. У л, 2. • • • можно определить
следующим образом1). Если умножить B4.8) на уЛH и проинтегри-
проинтегрировать по всей области, то, учитывая D.15), а также B4.7),
получим
*
b
= J У л, 1 (^* [У л. ol - К oN* [У», oD
откуда
B4.10)
') См. R. С о и г a n t, D. H i I b e r t, Methoden der math. Physik, т. 1,
изд 2, 1931 (Курант и Гильберт, Методы математической физики,
т. I, ГИТТЛ, М—Л., 1951).
404
ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ
[24.1
Аналогично из B4.9) при v = 2 найдем
ъ
Лп, 2—
B4.11)
Вычислительный процесс, таким образом, заключается в следующем.
При известных уп0 и Я,„10 вычисляют A,n>, из B4.10), для этого
потребуются (кроме дифференцирования и элементарных операций)
только квадратуры. После вычисления Я,п> 1 находят ylhV решая
краевую задачу, причем _уП) j должно удовлетворять дифференциаль-
дифференциальному уравнению B4.8), т. е. уравнению
М* [уа,,] - К, о^* Ьп, i\ = г (х) = - М[уп< 0] +
+ К,оМ[уп,0] + К А*\Уп,о) B4.12)
с краевыми условиями B4.2).
Эта неоднородная краевая задача имеет решение, так как соот-
соответствующая однородная задача есть невозмущенная задача на соб-
собственные значения B4.3), B4.2), и согласно п. 5.9 неоднородная
задача разрешима, если правая часть г (х) ортогональна к собственным
функциям уп<0
ъ
j0(x)dx = 0; B4.13)
но %т х было найдено таким образом, что это условие выполнено.
Функция упЛ определяется краевой задачей B4.12) не однозначно,
а с точностью до yni0 с постоянным коэффициентом, но мы можем
отбросить этот добавочный член при уп j, полагая, что он уже
учтен при разложении B4.6) в уп0.
Если уп< j -определено, то для вычисления "кп< 2 потребуются снова
только квадратуры, для вычисления же _уп2 опять нужно решить
краевую задачу: уп 2 должно удовлетворять дифференциальному
уравнению B4.9) при v = 2 и краевым условиям B4.2). Эта краевая
задача тоже имеет решение, так как выполнено соответствующее
условие B4.13). Аналогично находятся, далее, Я,Я1 ,•, уп< и Легко
можно вывести формулы для Я,Я|3, ... 1), но часто бывает достаточно
') W. М е у е г г и г С а р е 11 е n, Ann. Physik E) 8 A331), 301.
24.2) § 24. МЕТОД' ВОЗМУЩЕНИЙ 405
одного %п ,, так что для его нахождения не нужно решать крае-
краевых задач.
Мы получим тогда как улучшенное собственное значение для
задачи B4.1), B4.2) (т. е. для е=1) следующее:
24.2. Кратные собственные значения. Пусть теперь %п
есть а-кратно вырожденное собственное значение невозмущенной
задачи B4.3), B4.2); уп>0, уп+1<0 Уп+а-\,о~ относящиеся
к нему собственные функции, которые мы будем считать ортонор-
мированными в обобщенном смысле (см. п. 5.9). Это требование не
определяет однозначно систему уп 0 Уп+a-i, о> и> как будет
показано, для этого нужны еще дополнительные условия. Наиболее
поразительное явление при возмущении вырожденных собственных
значений — это «расщепление», т. е. такой факт, когда при внесении
небольшого возмущения возмущенная задача в общем случае уже
имеет не вырожденное собственное значение, а несколько близких
простых собственных значений. В примере E.29), рассмотренном
уже в п. 5.9,
j,iv_|_4j, = -*,/'.
наименьшее собственное значение Хг — 5 двукратно вырождено при
собственных функциях sinx и sin 2х. У возмущенной задачи
yiv _|_ D _|_ г)у = - %у"
с теми же самыми краевыми условиями sin x принадлежат собствен-
собственному значению 5 + е, a sin 2x — собственному значению 5-(-е/4;
двукратно вырожденное собственное значение Х1 = 5 «расщепилось»
на два простых собственных значения.
Схема, продолженная в п. 24.1, применима точно так же и здесь,
только теперь нужно при определении ynti из краевой задачи B4.12)
потребовать, чтобы правая часть г (х) была ортогональна ко всем
собственным функциям уп0 УЯ4а-1, о- Тогда согласно п. 5.9
краевая задача будет иметь решение.
Таким образом, должно удовлетворяться равенство
ь
J r(x)yn+lt0(x)dx = 0, / = 0,1 а—1, B4.14)
а
или, если положить
M[y]-K,ouly] = siyl
то
b Ь
j $ j *1Уп,о1Уп+иоах- B4-15)
406 ГЛ. Vllf. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ [24.2
Интеграл, стоящий в правой части равенства B4.15), при / = 0
отличен от нуля, а при 1=1, 2 а—1 исчезает вследствие
E.33). Поэтому yn+i,0 должны удовлетворять условию
ъ
sbn,<M>n+i, 0(x)dx = 0. t=l. 2 a —1.
Если yn+1 рассматривать как функцию от е и провести те же самые
рассуждения с уп+\ вместо уп, то получится аналогичное условие
разрешимости краевой задачи для уп+/, i:
ъ
S[yll+ho]yll+l>u{x)dx = Q, / = 0. 2, 3 a—1. B4.16)
В общем случае
ь
]ye+/iOd*=O. l*k< l' А=0. 1. 2 a—I. B4.17)
Если yn+tt о определены так, что, кроме условия ортогональности
E.33), выполнены еще требования B4.17), то без труда можно
использовать схему, описанную в п. 24.1, и, в частности, например,
получить
= 0. 1, 2 a—1). B4.18)
To, что всегда имеется система собственных функций, удовлетво-
удовлетворяющая требованиям E.33) и B4.17), следует из известной теоремы
алгебры. А именно, если и,, и2 иа есть любые линейно неза-
независимые собственные функции из B4.3), B4.2), то положим
г=1
Тогда при обозначениях
ь
а
:r (i = l, 2 а). B4.19)
NTS= JN*[ur]usdx, Srs=jS{ur]usdx;
а а
Ь Ь
"ik = J МЪп+1-1, ol Уп + k-l, 0 dX- Sik = J 5 [Уп + i-l, 0] Уп + k-l, 0dX<
24.3) § 24. МЕТОД ВОЗМУЩЕНИЙ 407
имеем
»«= 2 CirCksNrs, slk= S С/АА,- С24-2»)
г. s=\ г, s = l
Это — формулы, с помощью которых две квадратичные формы
Qi= 2 ^„ZrZ, и Q2= 2 SriZrZ,
Г, i=l Г, S=l
путем преобразования
Zr=IiCirxl B4.21)
можно перевести в новые формы:
а а
Qi= 2 «г**Л и <?2= 2 $«*/**•
г, ft-i i, ft=i
Согласно п. 18.4 имеется вещественное преобразование B4.21)
с не равным нулю определителем, при котором Q[ и Q2 содержат
только члены с х2., т. е. для которого nik = sik = 0 при / ф k, если
хотя бы одна из двух квадратичных форм, например Qj, является
знакоопределенной. Это предположение в данном случае выполнено,
а
так как и = 2 ^kuk есть собственная функция невозмущенной системы
ft-i
и поэтому
a ft Г а "I / а
r, i-1 aLr=l J \i-l
и Qj = 0 только для Zj = Z2= ... =Za = 0, т. е. Qj положительно
определена.
Таким образом, имеются числа Ctk, с помощью которых Qj и Q2
можно перевести в формы Qb Q2 с nlk — slk = 0 для t ф k, и
с помощью этих функций можно из любой выбранной системы соб-
собственных функций, согласно B4.19), перейти к системе уп> 0, ...
•••> .Ул4а-1, с которая ортогональна в обобщенном смысле, удо-
удовлетворяет условиям B4.17) и для которой можно провести схему
метода возмущений п. 24.1.
24.3. Связь с принципом Рэлея. В п. 24.1 было показано, что
про[.едение первого шага метода возмущения (вычисление %п^ {) не
связано с большой вычислительной работой и сводится к двум квад-
квадратурам; последующие же шаги довольно трудоемки: каждый раз
приходится решать краевуют задачу. Следует обратить внимание на
то, что приближение метода возмущений, полученное при учете лишь
линейного члена,
*«***,„, 0+*,„,, С24.22)
408 ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ [24.3
во многих случаях совпадает с отношением Рэлея
\уп, оМ[уп, 0]dx
J Уп, oN [Уп, о] dx
а
или находится в тесной связи с ним. Из B4.7) получаем
J Я, О
п, 0
J Уп, oN*[yn,o]dx
а
и с учетом B4.10)
ъ
| Уя, о {М- [Уп. о) — *я, оп[Уп, о]} dx
4o+4i = - Ъ ■ , B4-23)
J Уп, oN* [уя, 0] dx
а
Сравнивая B4.23) с выражением для R[yn<0], получим, приводя
дроби к общему знаменателю и используя B4.4):
* ь
J Уп, <Д \Уп, о) rf-« ] Уп>АМ [Уп, о] — ^я, (Д [Уя, о]} ^
J Уп, oN* [Уп. о] dx J уПг 0N [yn, 0] dx
а а
B4.24)
Частные случаи. Часто метод возмущений применяется в таких
случаях, когда для рассматриваемой краевой задачи B4.1), B4.2)
имеется близкая задача, у которой одно из выражений М или N не
изменено. Если, например, N = N* и отличаются лишь М и /И*,
т. е. /V^O, то формула B4.24) перейдет в
Ья,о+А'в,1 = Я[3'я,оЬ B4-25)
Если одновременно yn 0 является собственной функцией возму-
возмущенной задачи, как функции sin jc в примере п. 24:2, то не только
24.4] § 24. МЕТОД ВОЗМУЩЕНИЙ 409
выполняется B4.25), но тогда ^„,0 + ^n, i совпадает с точным соб-
собственным значением возмущенной задачи.
Если же изменилось только выражение /V, а М—М*, то из
B4.10) следует
ъ
J
J Уп, <sN [yn, a] .
[Уп, о] dx
' — ^n, 0— ^«, 0 ft ~^.0l' Я[УЯ, ,
и отсюда
A,Bt 0-|- Я,в> i = R — (/?~^"' °J . B4.26)
Если /? положительно, то улучшенное значение Хп< 0+^n, i меньше
отношения Рэлея R и совпадает с ним только тогда, когда ХЙ1 <, = /?.
В этом случае Xlh0 — R и, следовательно, улучшение Кп1=0. Как
видно, R играет здесь особую роль.
24.4. Пример к методу возмущений. Продольный изгиб тяжелых
стержней. Определение критической нагрузки Р при продольном изгибе
шарнирно опертого с обоих концов, вертикально расположенного стержня
длины / постоянного сечения при учете его собственного веса ') приводит
к задаче на собственные значения
yiv —е(д:у/)' = —Яу", 1
у@) = у"@) = у(/) = у"(О = 0. } B427>
Если а есть жесткость стержня на изгиб, то, зная наименьшее собственное
значение Я, задачи B4.27), по формуле
определим критическую нагрузку.
Для простоты введем безразмерные величины и положим /==1. Про-
Пропорциональная плотности стержня величина е является здесь параметром
возмущения. При е = 0 невозмущенная задача
M*[y] = X*N*[y], т. е. здесь у1У = _Я*у",
при тех же самых краевых условиях имеет собственные функции
уд_ 0 = sin плх
и собственные значения Я* = Я„, 0 = пглг.
Возмущением является член
М[у]=-(ху')',
в то же время
') Fr. A. W i I I er s, Das Knicken schwerer Oestange, Z. angew. Math.
Mech. 21 A941), 43.
410 ГЛ. VUI. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ [25.1
Улучшение Я„, , находим непосредственно из B4.10)
1 1
sin плх [—х (sin плх)']'dx x sin2 плх dx
А„, 1 — —:
sin njx-v (—л2я2 sin плх) dx I sin2 плх dx
о о
Улучшенное собственное значение по B4.27)
Если хотят получить член при е2, нужно определить уп< , из B4.12), решая
следующую краевую задачу:
Уп,1 + плУп, 1=>{хУп, о) —^^ o = "Itcos"Itj: + " я ^у - ^j sin «яд:,
У„, 1 @) = >£, 1 @) = Уп, 1 A) = У"п, 1 A) = 0.
Если отбросить не влияющие на Я„,, функции const • sin плх, то решение
будет
х — х* . Зх .
cos плх + Ты вт ппх +
Теперь для Яп, 2 из B4.11) с помощью квадратур получим
1
1
У д' Adx
J Уп.
Jy«,o>v,
или, подставляя найденные значения для уп 0 и уп }
I -П6Я6 Для почетных л,
( 0 для четных л.
Теперь можно из B4. 27) найти улучшенное собственное значение
Для е=1 и п= 1 получим отсюда Я, = 10,371 вместо соответствующего
значения Я,, 0 = я2 « 9,87 невозмущенной задачи.
2S.1] § 25. ДРУГИЕ МЕТОДЫ 411
§ 25. Другие методы
25.1. Формула Данкерлея для сложных систем. Пусть для за-
задач на собственные значения
М[у] =XN\y], Uti[y]=b B5.1)
выражение N [у] можно представить в виде суммы нескольких выра-
выражений /Vp [у]
N]y] = ^N[y], B5.2)
p-i
при этом для всех г частичных краевых задач
М [у] =--ЯрЛГр [у], U^ [у] = 0 (р = 1, 2 г) B5.3)
известно наименьшее собственное значение Я?-
Далее, пусть для всех частичных краевых задач B5.3) выполнены
условия самосопряженности и полной определенности, требуемые в
п. 8.1 для справедливости теоремы о минимальных свойствах Vr
Таким образом, справедливо
ь
\ иМ (и) dx
^P<hB5.4)
uNp (и) dx
если и есть какая-нибудь функция сравнения.
Тогда можно установить нижнюю границу для первого собствен-
собственного значения Я] сложной задачи (формула Данкерлея):
L B5.5)
^ ЯР
p-i 1
Если в качестве функции сравнения и в B5. 4) взять первую собствен-
собственную функцию У] краевой задачи B5.1), то получим
ь ь
yxM[y,)dx
412 ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ [25.2
ИЛИ
ь ь
-^ />'iWp Ы dx<-jjr J yiN Ш dx-
а 1 а
Если написать это уравнение для всех р и просуммировать по р от 1
до г, то вследствие B5.2) получится
L < V L
^к
Пример будет приведен в задаче 6 п. 25.7.
25.2. Формула Саусвелла '). Эта формула в известном смысле про-
противоположна формуле Данкерлея, она дает нижнюю границу для первого
собственного значения А^ краевой задачи B5.1), если М [у] может быть
представлено как сумма
г
М [^] =. ^ М. [у],
p=i
а для г частичных краевых задач
Mp[y]=XpN[yl ^[у]=0 B5.6)
выполнены условия самосопряженности и полной определенности. Из
свойства минимальности наименьшего собственного значения Я,? B5.6)
при использовании в качестве функции сравнения собственной функ-
функции Vi из B5.1) получим
ь
у,Л/р [yj dx
_.h\dx
а
Суммируя по р от 1 до г, будем иметь
ь
р ' ■• *TI->Adx
Отношение, стоящее в правой части равенства, равно A,j, таким
[) Q. Temple, Proc. Lond. math. Soc. B) 29 A929), 271.
25.31 § 25. ДРУГИЕ МЕТОДЫ 413
образом, отсюда получим неравенство Саусвелла
А,, >]£*?■ B5.7)
25.3. Минимум среднеквадратичной ошибки'). Метод будет
описан для случая одной независимой переменной х, но точно так
же применим и для случая многих независимых переменных. Для
собственной функции у краевой задачи M[y]=XN[y], U [у]=0
приближенно положим
y^s<w(x, сь с2, ..., ck) B5.8)
где w по возможности удовлетворяет краевым условиям. Если огра-
ограничиться нормированными функциями, то требование наименьшей средне-
среднеквадратичной ошибки примет вид
ъ
/■
(M [w] — AN [w] J dx = min.
a
Но для того чтобы не нужно было вводить условие нормировки,
приближенные значения Л и постоянные ct определяют из требования
ь
[ (М [w] — AN [w] у dx
F[w] = - ъ ==min B5.9)
a
Тогда для определения ct и Л получают уравнения
Если в простейшем случае в качестве w взять какую-нибудь функцию,
которая не зависит от параметров clf с2 то из уравнения -гт- = О
получим приближенное значение для Л
ь
J M [w] N [w] dx
А = -ь B5.11)
[ (N [w]J dx
a
Это значение совпадает для /V [у] = const • у с отношением Рэлея (8.1).
') М. N a s t a, Atti d. R. Accademia Nazionale dei Lincei F) 12 A930), 212;
W. OrObner, Jahresbericht der Deutschen Math. Vereinig. 48 A938), 22.
414 ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ [25.4
25.4. Метод коллокаций. Описанный ниже метод очень прост при
ручном счете'), не требует никаких специальных предварительных све-
сведений и в большинстве случаев при небольшой трудоемкости позво-
позволяет составить не только грубое представление о решении, но иногда
даже приводит к довольно точным результатам.
Применение метода не ограничивается обыкновенными дифферен-
дифференциальными уравнениями, а также задачами на собственные значения,
он может быть применен для любой краевой задачи, но для простоты
мы будем рассматривать только задачи на собственные значения.
Рассмотрим дифференциальное уравнение из п. 6.1
M[z]=KN[z]
с такими же краевыми условиями
^[«1 = 0 (ц=1. 2, .... К).
Для собственной функции z приближенно положим
р
z ^ а = 2 av
p-i
Функции сравнения vp выберем так, чтобы они удовлетворяли всем
краевым условиям. Значения параметров ар определим из условия,
чтобы при подстановке приближенного выражения и в дифференциаль-
дифференциальное уравнение это уравнение удовлетворялось в р точках. Эти р точек по
возможности распределяют равномерно по всему интервалу. Таким об-
образом, получается р линейных однородных уравнений для определе-
определения параметров ар. Приравненный нулю определитель этой системы дает
уравнение для нахождения приближенного собственного значения Л.
Пример I. Обыкновенное дифференциальное уравнение. Появление
комплексных приближений. Будем рассматривать симметричные собствен-
собственные функции уравнения
-у" = Ау, у (—1) = у A) = 0
из задачи 5 п. 16.11 и поэтому возьмем представление
P-I
удовлетворяющее краевым условиям. Подстановка его в дифференциальное
уравнение дает
j]яр [- 2р Bр - 1) *2р~2 + Л A - х2Р)] = 0.
Р-1
Потребуем, чтобы это уравнение удовлетворялось в точках ха, которые по воз-
возможности равномерно распределены в интервале (— 1, 1). Если выбрать р= 2
') R. A. F r a z е г, W. P. Jones, Sylvia W. S k a n, Approxi-
Approximations to Functions and the Solutions of Differential Equations, Reports and
Memoranda № 1799 B913), Aeronautical Research Committee, Ю37, 33.
25.41 § 25. ДРУГИЕ МЕТОДЫ 415
и взять, например л:, =0; х2 = '/2, то в силу симметрии дифференциальное
уравнение будет удовлетворено в точках х = —1/2, 0. '/а-
Уравнения будут иметь вид
для х = 0: я, (— 2 -j- Л) -|- я2Л = 0,
1 / 3 \ / 15
для x^y- [2+A)+[3 +
Из
— 2 + Л Л
получим
л _ 1 <<У\ + 1/941-) _ ( 2.492°.
В приведенной на стр. 416 таблице даны приближения для А,/, получающиеся
при />= 1, 2, 3 при трех различных выборах точек ха; при этом для высших
собственных значений получаются комплексные приближения, но для наимень-
наименьшего собственного значения Л, приближения довольно точны. Ошибка с ро-
ростом р уменьшается не монотонно.
Пример П. Те же самые приближенные значения, что и в методе
Ритца. Для проблемы продольного изгиба (см. задачу 4 п. 14. 6)
- у" = I B + cos х) у, у@) = у(я) = 0
положим
р
ухи— 2 flp s'n Рх-
(.,'=■1
Подставляя представление для и в дифференциальное уравнение, будем
иметь
р
2 яр sin рх (— р2 -\- Л B -f cos x)) = 0.
!
При /7=1, например, в точке л:, = -д- я получим
а, (—1+Л-2) = 0 или Л = -^;
при /7=2 для л:а = -^ по (а = 1 и 2) и при /7 = 2 для лга = — па (а = 1, 2, 3)
получим точно такие же уравнения для определения Л, а следовательно,
такие же приближенные собственные значения, как и в методе Ритца для
задачи 4 п. 16. 11, т. е довольно точные приближения
Пример III. Дифференциальное уравнение с частными производ-
производными, эллиптическая мембрана. Пусть, как и в п. 16.7, на границе эл-
эллипса Г
задано краевое условие z = 0; внутри эллипса
Аг -\- 1г = 0.
В качестве приближенного значения г возьмем удовлетворяющую граничным
условиям функцию
z и и {х, у) = D — х2 — \f) (я, + а2х< -j- а6у2).
416
ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ
[25.4
635
о
О! II
Ч
4 К
ю
(М
«г
2066
§ II
Ч "к
С)
—
^'
1
С£"
к г
V/
to
ч°
V/
7
ю
Положение
ч°
2
исс
Абсц
%
<
Г
с
1
1
1
1
т
1
<м
<
)
о
II
II
*7
с
1
1
00
с
-
•?
Ь
ю
с"
с
4
4
4
1—1
^"
>
1
Н
о"
II
|
,25
с
44
22,49;
1
1
1
1
П О2
h
о
1-
00
CD
С
С
<
<
1
D Ю
n" с
» 4
»
» 4
»
h
1
1
i?
fco
1
еч
о" ~*
II ■
1
■Г 5
СО
>
СО
т
с
с
с
(-
1
1
п
ю"
с
с
о
г;
V
8
00
с
4
4
4
4
СО
v
>
>
«
1
-;
ю
CD
и
26,39:
Я
СО
о
о"
1
00
о
5?
1»
О
•
О
•
ю
%
СО
™
1
1
Н
СП
\
1
1
i
1
00
-
t
г-
CD
CD
С
4
4
»
Я
+
CO"
с
?
СО
с
с
■л
с
4
4
4
4
СО
ь
1—1
)
>
»
1
?
"■*
й
с
—,
^_
СО
~*
ю
я
1
СО
ю
с
п
21,
а?
ю
о
о
с
с
п
3
,46
с
.
4
<
4
ю
ь
»
1
I
1
CD
|
1
™
"с,
"со
СО
25.5|
§ 25. ДРУГИЕ МЕТОДЫ
417
Тогда, как и в п. 16.7,
Дм =. — 10а, + 4 B — 5.x2 — 2у2) а2 -f 2 D — х2 — 25у2) а3.
В первом приближении при а2 = а3 — 0 возьмем л: = 1, у = 0. Тогда в силу
симметрии дифференциальное уравнение будет удовлетворяться в точках
х=±\, у =0:
— 10а, -f ЗЛа, =0,
л 10
откуда Л = -д-.
Качество приближения в очень
сильной мере зависит от вы-
выбора точек, в которых долж-
должно удовлетворяться дифферен-
дифференциальное уравнение. В таблице
(рис. 25.1) приведены прибли-
приближенные значения, полученные
для нескольких положений то-
точек коллокации.
25.5. Разложение в не-
непрерывную дробь. Диф-
Дифференциальное уравнение
Матье. Многие прикладные
задачи, например задачи тео-
теории потенциала, приводят
к дифференциальному урав-
уравнению Матье
_ у" = (к — 2/г2 cos 2х) у
B5.12)
с параметрами А. и А2. В плоскости к, ti2 можно найти «неустойчи-
«неустойчивые» и «устойчивые» области, а именно, говорят, что точка (kv h2)
относится к устойчивой области, если соответствующее дифферен-
дифференциальное уравнение B5.12) имеет при этих параметрах только такое
решение, которое остается ограниченным при возрастании х, в про-
противном случае эта точка относится к неустойчивой области *).
В точках (A-i, А2) на границе между этими областями уравнение
B5.12) имеет периодическое решение с периодом 2я. Эти периоди-
периодические решения B5.12) называются функциями Матье первого рода.
При заданном h они являются собственными функциями краевой зада-
задачи для дифференциального уравнения B5.12) с краевыми условиями
B5.13)
Положение точек
_,
V* о
ч^ •
V. .
у
—«.
1 J'x
. KJ
Ко'орди-
Ко'ординаты
точек
х,=1
х,=0,8
У 1=0,4
Уг'оА
Приближен-
Приближенные значе-
значения для Я
Л rff~???
Л -— *
~3,68
Л,=3,500
Л2=10,705
Рис. 25.1. Метод коллокации для опреде-
определения собственных колебаний эллиптиче-
эллиптической мембраны.
') Эти области представлены в книге М. J. О. S t r u 11, Lamesche, Ma-
thieusche und verwandte Funktionen in Physik und Technik; Ergebnisse der
Mathematik und ihrer Qrenzgebiete, т. I, Berlin, 1932, 230 [M. Д. О. С т р е т т,
Функции Ляме, Матье и родственные им в физике и технике, ОНТИ —ДНТВУ,
Харьков — Киев, 1935]. Там приведена подробная теория дифференциального
уравнения Матье.
7 Л. Коллатц
418 ГЛ VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ |25.5
Они могут быть разложены в ряд Фурье и делятся на четыре типа:
Сл (х) = 2 Ап, 2m + i cos Bm -j- 1) х, я = 1, 3, 5
т = 0
Cn (x) = 2 An, 2m cos 2mx, я = 0, 2, 4
5„ (x) = 2 ^n, 2m . i sin Bm -f- 1) x, it = 1, 3, 5, ...,
n (x) = 2 Я/i, 2m Sin 2/ИХ,
n = 0, 2, 4, ...
B5.14)
Собственные функции и граничные кривые могут быть хорошо
вычислены для всех четырех типов методом разложения в непрерыв-
непрерывную дробь. Для пояснения метода мы выберем sn с нечетным я. Под-
Подставив выражение для sn в дифференциальное уравнение B5.12),
используя формулу
cos 2x sin kx = -х [sin (k -|- 2) x -\- sin (к — 2) x],
получим после приравнивания коэффициентов перед sinx, sin Зх,
sin5x, . . .
множитель перед sin x: — Вп г -4- ХВп , -4- h2Blh , — h?Bn 3 = 0,
множитель перед sin Зх: — 9£?я> 3 + ^я, з — ^2^я, i — ^2^я, 5==
множитель перед sin 5х: — 25бЯ| 5 -)-- А,ВЯ_ 5 — ^2^я, з
Имеем бесконечную систему уравнений с определителем
Я, — 1 -+ А2 — А2 О О
— А2 Я, — 9 — А2 О
А==
О
О
0
%— 25 —А2
— А2 Я - 49 ...
B5.15)
такого вида, что Я входит только в диагональные члены и линейно
и только два соседних с диагональю ряда имеют не равные нулю
элементы. Такой определитель может быть представлен непрерывной
дробью. Так как подобные определители иногда встречаются, то мы
') Определитель здесь представлен чисто формально. Если взять в каче-
качестве приближения усеченный определитель, например, третьего порядка, то
это будет означать, что из бесконечной системы уравнений использованы
только три первых выписанных выше уравнения.
25.5|
§ 25. ДРУГИЕ МЕТОДЫ
419
выпишем определитель такого рода в общем виде
ап —
0
0
«12
0
0
«22
«32
0
— Ai>22
«23
«33
a
= 0 B5.16)
Определитель, полученный путем отбрасывания я первых строк и я
первых столбцов, мы обозначим через Ап. Разлагая его по элементам
первого столбца, получим
Л = (ап — kbn) А, — ака21А2 — 0.
Л, = (а22 — ^^22) ^2 — «23«32^3>
Л2 = («33 — ^ЗЗ) Л3 — «34«43Л4
Преобразование этих уравнений дает
Un = ап —
-^-, -£ = а22 — ХЬ^ — а23аг2 -^
и, таким образом,
1 h „
Кйп — ап
^12 ^21
Продолжая этот процесс до бесконечности, будем иметь
B5.17)
Вопрос о сходимости этой непрерывной дроби здесь не рассматри-
рассматривается.
Применяя B5.17) к определителю B5.15), получим
hB5.18)
~
_ 49 — ...
Решать уравнение B5.18) можно итерационным методом. Обо-
Обозначив правую часть через К (к), получим уравнение Х = К(К). Поло-
Положив в правой части приближенное значение К , получим в качестве
нового приближения X '
27*
420
ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ
[25.6
На рис. 25.2 Я, представлена как функция от X,(v). Вычисление
Я, происходит очень быстрой так как для вычисления непрерыв-
непрерывной дроби вследствие очень хорошей сходимости может быть взято
всего несколько членов. Из рисунка видно, что наименьший корень
вследствие очень малого наклона кри-
кривой К (Я.) может быть вычислен ме-
методом итераций очень точно. Напри-
Например, имеем для h = 1, исходя из Я,' ' = О,
а,<0> = 0, Я.A)=— 0,1116,
Я.{2) = —0,11023, Я.C) = — 0,110249.
Рис. 25.2. Определение соб- Вычисление следующих корней про-
ственных значений уравне- изводится не итерационным методом,
ния Матье. а вычислением точек кривой на рис. 25.2
и интерполяцией, что также из-за хо-
хорошей сходимости B5.18) не представляет больших затруднений (ср.
также задачу 1 в п. 25.7),
25.6. Представление в виде ряда. Часто применяемый метод
для приближенного решения краевой задачи состоит в том, что
собственная функция ищется в виде ряда (степенного, тригонометри-
тригонометрического и т. д.)
У С*) =
р=1
(■*)•
B5.19)
Возможность такого разложения предполагается.
О достоинствах и применимости такого рода представления при
той степени общности, в которой здесь данный метод изложен,
ничего сказать нельзя. Известны как примеры, для которых разло-
разложения в ряд при небольшой вычислительной работе дают пре-
превосходные результаты, так и примеры, в которых сходимость вообще
отсутствует, так что для вычислительных целей метод становится
неприменимым.
Здесь будет только кратко объяснено, как проводить такое раз-
разложение; применимость подобного разложения существенно зависит
от удачного выбора исходной системы функций г|зр (х) и от умелого
проведения метода.
Функции фр(х) по возможности выбирают так, чтобы они удо-
удовлетворяли краевым условиям.
Если подставить представление B5.19) в заданное дифференциаль-
дифференциальное уравнение и получившиеся функции М [i|)p] и /V [ij)p] разложить
в ряд снова по ij)p (или по другой полной системе функций)
[%\ = S dp
сг-1
B5.20)
25.71
§ 25. ДРУГИЕ МЕТОДЫ
421
то получим уравнение
э=1
с -id )
B5.21)
Приравнивая нулю выражения, заключенные в скобки, получим
бесконечную систему линейных уравнений для нахождения коэффи-
коэффициентов ар. Ее обычно решают приближенно, принимая в качестве
приближенных значений для k первых собственных чисел нули усе-
усеченного определителя, который является полиномом А:-й степени
относительно к.
си —
сп —
. — ыь
= 0. B5.22)
25.7. Упражнения. 1. Метод разложения в непрерывную
дробь. Вычислить критическую нагрузку при продольном изгибе стержня
для задачи 4 из п. 14.6 как наименьшее собственное значение кх
— у" = X B 4- cos х) у, у @) = у (я) = 0
методом разложения в непрерывную дробь, описанным в 25.5.
Результат. Полагая у — ^ ап sin nx и пользуясь формулой
2 cos х sin nx — sin (л -(- 1) x~\- sin (n — 1) x,
получим для коэффициентов ап бесконечную систему линейных уравнений,
определитель которой с заменой Х= 1/ц (см. задачу 4 в п. 16.11) имеет вид
1
Д =
2-й- -н-
2
о
о
2
2 —4ц
0
V 2-9ц ~
2" 2-16ц
= 0.
По формулам B5.16) и B5.17) получим соответствующее уравнение в виде
непрерывной дроби
Я = / (Я,);
/(*,) = .!
2 —
0,25
4 0,25
о 9 0,25
X
B5.23)
16
422
ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ
125.7
На рис. 25.3 представлен график функции / (Я); кривая в начальных точках
имеет очень малый угол наклона к оси абсцисс, так что итерационный метод
^(v+1) __ у A(v)~| ХОрОШО сходится. Исходя из Я^0' = 0, получим
Я'/) = 0,5, к[2) = 0,490, Я<3) = 0,490036.
Дальнейший расчет показывает, что при вычислении последующих Я^
шестой десятичный знак для Я^ больше не меняется. Второе и более высо-
высокие собственные значения можно получить тем же самым методом, однако
Рис. 25.3. К задаче 1 п. 25.7.
соответствующая ветвь кривой /(Я) изменяется очень круто. Получить бла-
благоприятную точку пересечения, например, для второго собственного значе-
значения Я2, можно пересчитывая непрерывную дробь до места 2 — 4/Я, которое
вызывает сильное изменение, и представляя B5.23) в форме g (Я) = h (Я) с
1
- я
0,25
о
16
Я
0,25
2 —
25
Я
и h (Я) = 8
Я —2
1—2Я •
Кривые для g (Я) и h (Я) графически представлены на рис. 25.4, откуда
получим Я2 = 2,0593.
2. Разложение в степенной ряд. В примере крутильных коле-
колебаний диска, который рассматривался в задаче 4 п. 11.4:
вычислить два наименьших собственных значения с помощью разложения
в степенной ряд
я=-0
Вычисление. Подстановка степенного ряда для у в дифференциаль-
дифференциальное уравнение — у" -\- 2ху' — Ху = 0 дает
[- (п + 1) (я + 2)ап+2 + Bл - Я) ап] х" = 0.
л-0
Приравнивая нулю каждый член в квадратных скобках,, получим для ап
25. ДРУГИЕ МЕТОДЫ
25.7]
рекуррентную формулу
Используя граничные условия, найдем
у' @) = а, = 1, у @) = а0 = 0.
Отсюда получим
423
3!
5!
—2) (Я —6) (Я —10)
7!
Второе краевое условие у'A) = 0 представляет собой трансцендентное урав-
уравнение для нахождения X
(X) = 1 -
, — 2 (Х — 2)(Х — 6) (Я—2) (А. —6) (Я. —10)
2!
4! 6!
(Л — 2) (Я — 6) (Я — 10) (X— 14)
+ 8!
Нули этой функции g (X) удобнее определять не путем обрывания ряда и
решения соответствующего алгебраического уравнения, а вычисляя g (X)
для нескольких значений X по хорошо схо-
сходящемуся ряду, затем посредством интер-
интерполяции можно найти точки пересечения
g (X) с осью абсцисс. Получим
А., =3,59692, А.2 = 23,518.
3. Вычислить наименьшее собственное
значение
\\+х)
Здесь более целесообразно разлагать в ряд
не у, а
у@)=уA) = 0.
4 ■
3
Z
1
0
-1
л,
4 Л35 Л
Подстановка степенного ряда в диффе-
дифференциальное уравнение дает рекурреншую Рис. 25.4. Метод разложения
формулу для Ьп=п\ап в непрерывную дробь для вто-
h I ,i ,„ 1ЧЛ ч рого собственного значения.
bn+\ = — X{bn+i — ("— 1)*л-2)
.(« = 2, 3, ...).
С Ьо = 1 получим Ьх = 0, 62 = 63 = — А,, 64 = А,2, Ьь = 4А,2, 66 = 4А,2—Я3, 67=
оо
=—9А,3, 68=—28Я3 -(- А,4, ... А из у A) = V "j_~9\| bn = 0.получим трансцен-
3 11
дентное уравнение -^ — -go
13
л-0
ТТЖ^ + ТТГЯ.4-'"-0'*3-
торого, как и в задаче 2 (не путем обрывания), получим в качестве первого
корня
Хх - 6,774.
424 ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ [25.7
4. Комбинация различных методов. Вычислить первые три
собственных значения для краевой задачи
= Яу, у @) = у A) = 0.
Теорема сравнения. Грубые границы для Я
■^-А:2л2<Я*<£2л2 (£=1,2,...)
можно получить путем сравнения с краевыми задачами —=- у" = Ху и —у" =
= Ху при тех же краевых условиях. Пользуясь теоремой сравнения из
п. 8. 5, получим написанное выше неравенство.
Теорема включения. С помощью удовлетворяющей краевым усло-
условиям функции
114- уЛ2«<-2
образуем по формуле (9.6) вспомогательную функцию
ф <*> -k^ (w^jj о + ^'' - тпг^Г B5-24)
Для л =. —, т. е. при 4/г —J— I ==- 0, получим границы
(ЫАJ -f-jlg- < А* < (£лЛJ + ~, А = ~ B/2 + 1) B5.25)
или
6,697 < Я, < 7,080, |
26,624 < Х2 < 27,008, \ B5.26)
59,836 < Х3 < 60,220. j
Границы, вычисленные в процентах, болге благоприятны для высших
собственных значений. Границы можно улучшить с помощью функции Грина
(по таблице IV)
а(х, g)
Тогда по формуле G.21) получим
0 0
Используя верхнюю границу для А2, Х3, Л4, Я5, вычисленную из B5.25), от-
отсюда найдем Я, > 6,7617.
25.7]
§ 25 ДРУГИЕ МЕТОДЫ
425
Сузить границы можно, кроме того, меняя в B5.24) величину п и опре-
определяя наилучшее значение путем интерполяции:
к
1
2
3
4л -1- 1
0,078
0,050
0,0206
0,013
0,0082
0,0056
Экстремальное
значение Ф
Фтах= 6,843
Фт,п= 6,764
Фтах = 26,782
Фт1п = 26,695
Фтах = 60,00
Фш.п = 59,91
Границы для собственных
значений
6,764 < Л, < 6,843
26,695 < Л2 < 26,782
59,91 <Л3< 60,00
Для высших собственных значений этот метод предпочтительнее всех
других.
Метод последовательных приближений.
Исходя из Fo (х) = 360 (*—х2), получим согласно п. 12.5
I = 34* -|- 17*2 — 60*3 — 15*4 ■-)- 24*5
4422 107494
и из A2.20)
[i, = 6,8385, ц2 = 6,7876.
Если из B5.26) взять /2 — 26,624, то A2.21) дает
6,770 < Л! < 6,788.
5. Показать, что для функционального уравнения на собственные значения
С краевыми условиями
у(-1)«уA)=*о
(у при х чя. 0 регулярно) существует счетное бесконечное множество поло^
жительных собственных значений К, ио которые возрастают не пропорцио»
нально л2, как в G.53), а экспоненциально с ростом л. С помощью разложе»
ния в степенной ряд вычислить первые три собственных значения.
Результат. Л„> Xi2n~i для л= 1, 2 Я, -2,091, Я2* 13,1. Я,}"»
« 51,6.
6. С помощью формулы Данкерлея B5.5) получить нижнюю границу для
первого собственного значения краевой задачи
есть
Решение. Наименьшее собственное значение краевой задачи
yIV = 10ЛA)у, у @) = у A) = у @) - у' A) = 0
,,1, D.73004L , ....
Ц1' = ч —'— (по таблице VI),
а для краевой задачи
y'v = - >-2у". у @) = у A) =
» 0
426 ГЛ. VIII. РАЗЛИЧНЫЕ ДРУГИЕ МЕТОДЫ [23.7
Отсюда по формуле B5.5)
Я, > ——1 — = 22,071 .
Верхнюю границу для собственного значзния Л, можно получить с по-
помощью отношения Рэлея
1
Л[«1=~Л
/<»•)'
10и2 -f и'2) dx
подставляя в качестве функции сравнения и = 1 — cos 2лх:
Л, < 22,432.
Среднее значение Xt « 22,25 отличается от точного не более чем на 1%.
7. Для задачи 8 из п. 14.6
— у" = Ху _|_Я2л:2у, у(±1)=0
определить несколько собственных значений, разлагая соответствующие
собственные функции в степенной ряд.
Результат. Подставив
оо
в дифференциальное уравнение, получим для коэффициентов ап рекуррентную
формулу
Имеются две системы собственных функций: симметричная (а, = а3 = • ■ • = 0)
и антисимметричная (а0 = «2 = а4 = • • ■ = 0).
Обозначая г — %х2, получим для симметричных собственных функций
_ £ £^_ 13г3 . 17г« _ 745г5
У — ys~ l~ 2! 41 ' 61 "*" 81 101 ' '"■
и для антисимметричных функций
y = ye = ^(i_j! i£L+."
у 7Г'+-
Краевог условие у A) = 0 представляет тогда трансцендентное уравнение
для собственных значений. Здесь возникает новое интересное явление: име-
имеются две основные формы колебаний.
Обе симметричные собственные функции, принадлежащие к собственным
значениям X = 1,9517 и % к—6,5, не обращаются в нуль внутри интервала
— 1 < х < 1.
РЕКОМЕНДАЦИИ ПО ВЫБОРУ МЕТОДОВ ПРИБЛИЖЕННОГО
ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ
Разумеется, невозможно раз и навсегда указать, какой из описан-
описанных в этой книге методов является наилучшим в данном конкретном
случае. В зависимости от личного вкуса вычислитель может предпо-
предпочитать одни методы другим, а при некотором навыке будет исполь-
использовать видоизменения и комбинации описанных здесь общих методов.
Напомним в краткой форме некоторые из важнейших методов, не
претендуя на полноту.
1. Решения в замкнутой форме
а) В случае обыкновенных дифференциальных уравнений с посто-
постоянными коэффициентами можно указать общие решения в замкнутой
форме. Постоянные интегрирования находятся из краевых условий.
б) В случае обыкновенных дифференциальных уравнений с непо-
непостоянными коэффициентами и дифференциальных уравнений с частными
производными решения в замкнутой форме удается получить редко.
Некоторые примеры таких случаев приведены в таблицах V и VI.
Вообще же для вычисления собственных значений применяются чис-
численные и графические методы.
2. Приближенное вычисление
а) При небольших требованиях к точности очень часто можно
получить границы для первого и даже для высших собственных зна-
значений с помощью теоремы сравнения (п. 8.5) или теоремы включения
(§ 9). При этом рассматриваемая задача сравнивается с другой, раз-
разрешимой в замкнутой форме, например, для обыкновенного диффе-
дифференциального уравнения с постоянными коэффициентами. Границы
собственных значений часто могут быть существенно улучшены путем
использования свободного параметра в теореме включения (см. задачу
6. п. 11.4).
б) Обыкновенный метод конечных разностей (§§21 и 23) при грубом
шаге и, следовательно, небольшой вычислительной работе дает пред-
представление о распределении низших собственных значений и поведении
собственных функций (см. задачу 1 п. 23.6). Если требуются более
точные значения, то вместо перехода к более мелкому шагу следует
воспользоваться одним из улучшенных разностных методов.
428 РЕКОМЕНДАЦИИ ПО ВЫБОРУ МЕТОДОВ
3. Более точное вычисление
а) Для первого собственного значения в случаях, когда выполнены
дополнительные предпосылки теоремы п. 12.4, наилучшим, пожалуй,
является метод последовательных приближений, дающих верхнюю и
нижнюю границы согласно A2.19); в зависимости от свойств задачи
результат получается численно или графически (§ 12 и 13, в част-
частности п.п. 12.5, 12.6, 13.6).
б) Большую область применения имеет метод Ритца (см. п. 16.1);
он дает также верхние границы для высших собственных значений.
Если высшие собственные значения требуется определить с большей
точностью, то в представлении Ритца берется достаточно большое
число членов, например, для вычисления второго собственного зна-
значения по крайней мере три. Точность приближенных собственных зна-
значений по Ритцу зависит от свойств выбранных функций. Поэтому
метод Ритца (обычно при графической реализации) проводят таким
образом, что выбранные собственные функции улучшаются итерационно.
Во многих случаях существует возможность ограничиться непол-
неполным интерационным шагом. Тогда при меньшей вычислительной
(соответственно графической) работе (в сравнении с полным итера-
итерационным шагом) и во всяком случае с меньшей точностью можно на-
написать уравнения Граммеля и из них найти приближения для собст-
собственных функций и собственных значений.
в) Еще шире область применения метода конечных разностей, ко-
который не связан с какими-либо дополнительными предположениями и
для некоторых задач, например, в случае дифференциальных уравне-
уравнений с частными производными, является единственным практически реа-
реализуемым методом приближенных вычислений. Методы повышенной
точности описаны в §§ 22 и 23. Однако в методе конечных разно-
разностей мало что можно сказать о приближениях; вообще неизвестно,
являются ли приближенные собственные значения слишком большими
или слишком малыми.
4. Прочие методы
Кроме этого, в распоряжении имеется много других методов, ко-
которые в различных частных случаях могут быть очень удобны. Не
стремясь к полноте, укажем только разложение в ряды (пп. 25.5 и
25.6), метод возмущений (§ 24) и метод интегральных уравнений (§ 7),
ПРИЛОЖЕНИЕ
ПЕРЕЧЕНЬ РАССМОТРЕННЫХ ПРИМЕРОВ. ТАБЛИЦЫ
Обозначения: В — некоторые пояснения, D — конечноразностныи метол,
Du— формула Данкерлея, Dv— улучшенный конечноразностныи метод,
е — точные решения, Е — теорема включения, G — функция Грина,
/—метод интегральных уравнений, It — итерационный метод,
К — метод непрерывных дробей, К1 — метод коллокащш,
Р—метод степенных рядов, R — метод Рэлея — Ритца,
S—метод последовательных приближений, St — метод возмущений,
V — теорема сравнения
Дифференциальное
уравнение
Краевые условия
Метод
и указание
страницы
Дифференциальные уравнения второго порядка
— у" = Л у
(см. также
таблицу VI)
Тип'
у (Л) = у'(й) = О
'0)-0
У' @) - c,j
У @) - у (
у' @) - Л.у @) « у' (/) - £у (/) ^
у @) — у' A) — Лу' @) =0
У@)-уA)-у'@) + У'A) =
0 85, е171,
R 263, К1Ш
е 19, G 85, £ 143,
R 261, S142,
£394, Dv 394
б 128, S 179,
R 223, 234,
б 128, S 214
е 56, 0 87
В 69, *74
£125
— у" = кр (л) у
у @) = у (а) = 0
£146
р(х) = 10 — х2 и
некоторые другие
примеры
— >'" = >■ sg nx ■ у
у (± 1) =0
у (± 1) = 0
е 127
430
ПРИЛОЖЕНИЕ
Продолжение
Дифференциальное
уравнение
„ BЯу для х < V2
—у—{
[Яу для х > у2
— у" = Я A -)- sin x) у
— у" — Я B -j- cos x) у
— у" = Ялу
-у" = ЯA+^)у
_ у" =
= A — 2/г2 cos 2л) у
у _|_ (А, ± 1) у = 0
у" —)- (Я — U (х)) у = 0
— У = Л_у —|- Л2^с2у
_(г-*У)' = Лв-^
С у' V ?у
у" + 'У = ^у
некоторые другие
Краевые условия
У @) = у (я) = 0
у @) = у (я) = 0
У@) = уA) = 0
у (± 1) = 0
Периодичность
Периодичность
у ограничено в бесконечности
у (± 1) = 0
,@)-,'A)-0
У @) = У A) = 0
У @) = у @ = 0
у (± 1) = 0
Метод
и указание
страницы
«362, D361,
£>t/372, 375
Е 174, S 187
S217, R 262,
К1 415, К 421
D394. D1/394,
Z, angew Math.
Mech. 19A939),
316
£>393
AT 417
«58
В 57
S220, Р426
£173, Dv377,
D 365, Р 422,
Z. angew. Math.
Mech. 19 A939),
304—308
D397, Р422,
V 424, £ 424,
G424, S425
«125
«295
случаи в таблицах V, VI и стр. 71, [25, 128, 130
ПЕРЕЧЕНЬ РАССМОТРЕННЫХ ПРИМЕРОВ
431
Продолжение
Дифференциальное
уравнение
Краевые условна
Метод
н указание
страницы
Дифференциальные уравнения порядка выше второго
yIV = Лу
(см. также табли-
таблицу VI)
y.v-Mi + *>y
(ay")" = А£0У
у1Ч+А({\-х)у'У=
yIV = _Ay"
yiv-f Ay = — Xy"
;;::!;:-:,
ylV = Aly-27l2y"
ylV = X (Юу — у")
ylV —e(jcy')'= — Ху"
[B-*) у 1 =-Ay
fC_^)yT +
-f60y = —Лу"
yjO) = y'jO) = y"(l) = y'"(l) = O
У @) + с,"у'" @) = У С) + С2У'" @ = °
у@)=у"@) = уA)=у"A) = 0
У @) = у' @) = у" @ = у'" @ = 0
у(± 1) = у'(± 1)= 0
у @) = у' @) = у A) = v' A) = 0
различные другие краевыз условия
у (± 1) — у" (± 1) =0
у @) = у" @) = у (я) = у" (я) = 0
у @) = у' @) = у' @ = у' @ = 0
у @) = у" @) = у A) = у" A) = 0
у(О) = у @) = уA)-у A)-0
у(± 1) = у(± 1) = 0
/ 120, R 264, 265
}<?36, 6 95
V 140
S202, #258
S219, #264
е 394, D 395,
Dv395
е№, S219
е 55, 56, 89,
125, Ta6fl.VI
£173, S218,
#264
е93, Stm
,170
#426, Dm 425
SM09
S 188, #261,
D363
£ 172, S 215
некоторые другие случаи в таблице VI и стр. 70, 129
432
ПРИЛОЖЕНИЕ
Продолжение
Дифференциальное
уравнение
yVI = г (х)
— yvi — 49у" =
_yvi+2yiv_y" =
= 4— у" + у)
Краевые условия
у, у', у" = 0 для х = 0 и 1
у, у", у1 v = 0 для х = 0 и л
у, у', у" или у, у', у'" = 0 при
х = а и х = b
Другие примеры
Продольный изгиб стержня от двух сил
Крутильные колебания вала с двумя сосредоточенными
массами
Изгибные колебания
точенной массой
Изгибные колебания
балки на двух опорах с сосредо-
балки на трех опорах или рамы
Метод
и указание
страницы
О 12S
«92
6 73
«48
«52, /?251
«48, #249
«49, 49, #259
Дифференциальные уравнения с частными производными
— Дг = Хг
(колебания мембраны)
525 d2s
дх2 ду2
d2s
Z = 0 на краю
квадрат
круг
эллипс
ромб
треугольник
пятиугольник, рис. 23.10
s = 0 на краю «домика»
«127, D 429
G 100
Л 254, D 380,
№415
D 388, 0« 389,
D386, Dt-387,
« 498, Z. angew.
Math. Mech.
19A939),
305—309
Dt/390, D391
6 390, D398
ПЕРЕЧЕНЬ РАССМОТРЕННЫХ ПРИМЕРОВ
433
Продолжение
Вид уравнения и краевые условия
Интегральн
1
-1
1 1
Г С
* (*, у) _ A, j j (
-1 -l
— у" (х) = А. у (-^ )
ые и функциональные
уравнения
у (± 1) = у" (± 1) = 0
у(±1) = 0
Метод
и указание
страницы
R 265, D 400
«130
Р495
Матрицы
Задачи
Степени матриц
Функции матриц
Оценки
Повышение порядка
Типы матриц
,0 12ч
«- 123
\2 3 5/
, 2-1К
«в 1-13
/14 10 9\
8Х = 10 12 4 |
V 9 4 3/
Метод
и указание
страницы
«342
е 344
В 351
б 353
434
ПРИЛОЖЕНИЕ
Продолжение
Задачи
Частные
Матрица системы
дифференциальных
уравнений
Пример с только
одним собственным
вектором и глав-
главными векторами
Балка на двух опо-
опорах с подпружинен-
подпружиненными массами
Балка с массами
и пружинами
Механическая си-
система с затуханием
Крутильные колеба-
колебания диска
Акустическая задача
задачи
5С =
gr
•Л —
31 =
QY
и =
Ctf
Щ —
31 =
31 =
Типы матриц
на собственные значения
C —1\
1 1/
/ 2 4 Ох
9 4 2
, :
V 7—10 —6/
1 180 —331
— 331 906 —
144 —367
— 36 144 —
14^
36'
90(
33
47 —14—20
— 14 28
3 -
— 20 0 20
0—20
0 0 1
0 0 0
-3 1 -2
1-1 1 -
0 24 0 0 0
27 0 23 0 0
0 28 0 22 0
0 0 29 0 21
0 0 0 50 0
—2 4 0 2 0
4 0 4 8 2
0 4 0 2 8
14 1—14
0 14 4 0
3
0
1
1
-1
1 -
г
0
-20
0
20
-36
144
331
762
Метод
и указание
страницы
«5 = Ч
е 339
е 339
5 289
£313
«■354
Л 319
//366
Л 325
£391
ПЕРЕЧЕНЬ РАССМОТРЕННЫХ ПРИМЕРОВ
435
Задачи
Комплексные эле-
элементы
/3
- 1_/
\2-1
Типы матриц
1+«
2
1+2/
2 + / ч
1-
1
Многогранник (кубооктаэдр), матрица 12-го
Дальнейшие примеры в
Промежуточные
Балка с сосредото-
сосредоточенными массами
Опертая на пружи-
пружинах прямоугольная
пластина
Общие задач
Тройной маятник
с пружинной связью
Главные оси кони-
конических сечений
Задача без собствен-
собственного вектора
Ш
и
Я
таблицах
задачи не
/ 9 11
= 11 16
V 7 11
/10
= 0 1
V 2 -
на с о б с
/4 2 2
= 232
\2 2 3
/ 4-
-и-
VIII и
IX
-2/
/
порядка
и собственные
Л
П|,
9/
0 2ч
0-4'
4 10^
т в е н
\
/
_2
35 =
•
н ы
i
=
\
ш =
'11
ll 1
значения
/10 0
-
V
35 =
0 21
0 0
/3 0
= 01
\0 0
е- з н а ч е
'2 1
1 1
vl 1
/3
1\
2/
з)
°)
о/
0
1/
Продолжение
Метод
и указание
страницы
//356
<?356
г 355
г 280
г 281
Н И Я vij === HSoj
«287
е 308
5 328
98*
436
ПРИЛОЖЕНИЕ
Простые примеры технических задач иа собственные
Обозначенные звездочкой
рисунки следует
повернуть на 90°
в плоскости чертежа
Техническое содержание задачи
Литература
(см. стр. 453,
454)
I. Частные задачи на собствен
Дифференциальные уравнения
Поперечные колебания струны, концы за-
закреплены
Поперечные колебания струны, один ко-
конец свободен
Поперечные колебания струны. Концы
упруго закреплены
1) стр. 453
2) стр. 453
Поперечные колебания струны па упру-
упругом основании
3) стр. 453
Продольные колебания стержня. Концы
закреплены
Продольные колебания стержня. Один ко-
конец свободен
*) стр. 453
Крутильные колебания стержня
Крутильные колебания стержня. Концы
в подшипниках
стр. 453
Продольный изгиб стержня. Концы шар-
нирно закреплены
Продольный изгиб стержня. Один коней
защемлен, другой свободен
9) стр. 453
Опрокидывание балки
7) стр. 453
{Крутильные колебания
Колебания растяжения
8) стр. 453
ТАБЛИЦЫ
437
Таблица I
значения для обыкновенных дифференциальных
г.
Дифференциальное уравнение
ные значения М\у\ — Ър(х)у
второго порядка
(О3
(О2
(О2
ш2
со2
(О2
со2
со2
р
р
р-1
с,»2
С!»2
-у" = Х^-у
-y" = Af-y
-y" = X^-y
— у" 4- с,у = ^с2у
— (Су')' = ^р-/рУ
— (Су')' =» ЯрУ^у
5
у ™» а
_у»»л!у
' а '
— (x3hy')' = Лх3йу
, / А' 1 \
Главные
Сокращения
Уо = У1 = 0
Уо = 0
Уо = У/ = 0
Уо = У; = 0
Уо = О
уг^0
Уо — Уг •» 0
Уо = О
У1-0
у,=0
^ уравнений
граничные
^0
= у@)
у' =
С.Уо
у'г-
Уо =
У/"
1
Рстественные
условия
; у, = у A) и т. д.
= 0
1 1
= 0
= 0
=■ у[ = о
.0
1
= У; j
438
ПРИЛОЖЕНИЕ
Обозначенные звездочкой
рисунки следует
повернуть на 90°
в плоскости чертежа
Техническое содержание задачи
Литература
{см. стр. 453,
454)
Выпучивание кругового кольца при по-
постоянном внешнем давлении р
Колебания маятника с вибрирующей точ-
точкой подвеса
Поперечные колебания кольцевой мембра-
мембраны (внутренний радиус Rt, внешний ра-
радиус Ra)
9) стр. 453
стр. 453|
■>) стр. 453
Изгибные колебания стержня, вращаю-
вращающегося около перпендикулярной ему оси
(с учетом только центробежных сил)
стр. 453
Устойчивость тонкостенных полых шаров
при равномерном внешнем давлении
|3)стр. 453
Дифференциальные уравнения
Изгибные колебания стержня. Конны
шарпирно оперты
стр
. 453
Изгибпые колебания стержня. Один ко-
конец свободен
Изгибные колебания стержня. Концы за-
защемлены
Изгибиые колебания стержня. Упругие
опоры
Изгибные колебания стержня. Совмеще-
Совмещение упругих опор с упругим защемлением
15) стр. 453
Из1ибные колебания сжимаемого стерж-
стержня
I6) стр. 453
Изгибпые колебания сжимаемого стерж-
стержня с учетом собственного веса (дымовая
труба)
стр. 453
ТА13ЛИЦЫ 439
Таблица I (продолжениг)
к
Р
(О2
(О2
UJ
Дифференциальное уравнение
— У" + У = Яс,у
— У" + g(*)y = Яс1у;
— (ху')' -| у = Ле^у
-[(^-х2)у'1'=4^
— у" — У' ctg л: +
+ у ctg2 х - Ху
Главные
граничн
Сокращения: у =5у
Естественные
ые условия
// //
С); У; = у С) и т- д-
периодичность
периодичность
У (Ri) = У (Л„) = 0
четвертого порядка
W2
(ау")" = Лр^у
(ay")" = IpFy
(ау")" = XpFy
(ау")" = XpFy
(ау")" = IpFy
(ау")" -j- ^У" = Яр/'у
(а_)-")" + (Gy')' = Wy
уа=У;=о
Уо = Уо = У( = У\ * °
Уо = У( = 0
Уо = У; = 0
Уо = Уи = °
Уо = y"i = °
" '"
У, =У( -0
у0 = у, = 0;
| Уо + с,Уо' ^= 0
II 1 II i
Уо ==г с1Уо' У; :== — ci>r/
v* — /* " '
// //
Уо = Уг = °
У( =У( =0
440
ПРИЛОЖЕНИЕ
Обозначенные звездочкой
рисунки следует
повернуть на 93"
в плоскости чертежа
Техническое содержание задачи
Литература
(см. стр. 453,
454)
Крутильные колебания двутавровых ба-
балок с учетом изгиба полок
Крутильные колебания двутавровых ба-
балок. Концы оперты
18) стр. 453
Опрокидывание двутавровых балок с уче-
учетом изгиба полок
Опрокидывание двутавровых балок под
действием моментов, концы оперты
|9) стр. 453
Колебания
сопротивляю-
сопротивляющегося изгибу
каната
Жесткое защемление
Безмоментное защемле-
20) сгр. 453
ние
Колебания стержня на упругом основа-
основании
«') стр. 453
2. Общие задачи на
Одночленный
Сжимаемый стержень на упругом основа-
основании
?-') стр. 453
Продольный изгиб стержня. Один конец
защемлен, другой — щарнирно оперт
и) стр. 453
Продольный изгиб стержня. Концы за-
защемлены
»«) стр. 453
Продольный (шарнирно-
изгиб тяжелых Концы I оперты, защем-
стержней. [лены
») стр. 453
Продольный изгиб стержня с учетом соб-
собственного веса
26) стр. 453
ТАБЛИЦЫ 441
Таблица I (продолжение)
1
с,Р
(О2
(О2
Дифференциальное уравнение
DylV — СУ' = ЛрУру
DylV — Су" =- Лр J/ty
DylV — Су" = Л*2у
DylV — Су" = Лу
у1У_С1у" = Лс2у
(ay")'' -J- Ciy = Лс2у
Главные
грани чнь
Сокращения: у^ = у
yt = у' = 0
уо = у; = О
у, = у[ = 0
Уо = У, = 0
yj = Уо = У; = У; = °
Уо= У( = 0
Уо=У, = О
Естественные
ie условия
/I It
@); У i =У №"'■ Д-
Уа = 0; Су0 = Dy0
" "
Уо = У/ — 0
Уо = 0; Суо = Dy0"
it ll
У;=у;'=о
собственные значения
класс М [у] = (—l)"X [gn (x) у""]'л)
р
р
р
р
р
(ЧУ*)' + *У «- - ^У"
(ау")" = - Лу"
(ау")" = — Лу"
(ау")" — (Gy')' = — Лу"
(ау")" — (Gy')' = — Лу"
Уо = У/ =°
Уо = Уо = У/ = 0
Уо = Уи = У; = У/' = °
Уо = У( = О
Уо-^-Л-у'-О
Уо'-уГ-О
у;=о
Уа'-уГ-О
у* =(ау")и = 0
442
ПРИЛОЖЕНИЕ
Обозначенные звездочкой
рисунки следует
повернуть на 90°
в плоскости чертежа
Техническое содержание задачи
Литература
(см. стр. 453,
454)
Выпучивание аксиально сжимаемых
фланцевых труб
7) стр. 453
Продольный изгиб полой круглоцилинд-
рнческой колонны при аксиальном сжа-
сжатии
28) стр. 453
Продольный изгиб стержня при наличии
упругой опоры на середине
crp. 45S
подвижны
Продольный изгиб
стержня. j
Концы защемлены и | упруго оперты
стр
. 453|
31) стр. 453
Более общие
Выпучивание винтовой пружины
стр. 453
Продольные колебания стержней с уче-
учетом поперечного сжатия
3) стр. 453
Изгибные колебания стержней с учетом
инерции вращения
34) стр. 453
Изгибные колебания вала с учетом гиро-
гироскопического эффекта ■
35) стр. 453
Критические числа оборотов с учетом
продольной нагрузки и гироскопического
эффекта
36) стр. 453
Устойчивость раднально нагруженных
круговых арок с шарнирно опертыми
кониами
37) стр. 453
Устойчивость радналыю нагруженных
круговых арок с защемленными концами
38) стр. 453
ТАБЛИЦЫ 443
Таблица I (продолжение)
к
р
СгР
Р
Р
Р
Дифференциальное уравнение
У1У+^у" + <мУ = -^2у"
y'V + c,y = -Xy"
(ay")" = - Лу"
(ay")" = - Лу"
(ay")" = — Лу"
Главные
граничные у<
Сокращения: уо = у(О);
Уо= У/ = 0
Уо = >7 = 0
Уо = у[ = °
Уо = Уг = О
Уо = У/ = °
Естественные
ловия
у" = у" @ и т. д.
" " Г,
Уо = Уг = °
Уо = У/' = °
Уо=О.
/ "\/ С
(«У )/ = -j У/
Уо =y; =0
Уо +с,У0 =
= У( +С2У;=0
задачи M[y] = XN[y]
Р
'Л
а2
а2
а2
- ay" = Л (у-с,у")
-£у" = Л(у-с,у")
ayiV = Л (р/=у — /ру")
(ay")" = Л (pFy + (су')')
(ау")" + Ру" = Л(су+с2у")
у1У + 2у" + у = Л(су-у")
»
Уо=У/ = О
Уо = О
Уо= У( = О
Уо = У/ = О
Уо=У/ = О
Уо=У/ = °
Уо = Уо = У/ = У; = О
У;=о
Уо=У; =0
Уо = У" = °
Уо = Уг == 0
Уо = У/ = °
444
ПРИЛОЖЕНИЕ
Обозначенные звездочкой
рисунки следует
повернуть на 90"
в плоскости чертежа
Техническое содержание задачи
Литература
(см. стр. 453,
454)
Устойчивость I шарнирные
плоских параболи- Концы | защемлен-
ческих арок. I ные
зэ) стр. 453
Опрокидывание балки вследствие круче-
кручения
0) стр. 453
("шарнир-
Устойчивость круговых
арок, радиально на-
нагруженных в своей
плоскости Концы^мыс
Внешнее давление пер- |защемлен-
пендикулярно к дефор- (ные
мированной средней
линии
4') стр. 453
42) стр. 453
То же, что и выше, но
при давлении, направ-
направленном к центру кру-
круга
Концы
защемленные
43) стр 454
Изгибные колебания кругового кольца в
своей плоскости
44) стр. 454
Изгибные
колебания
кругового
кольца при
постоянном
радиальном
давлении
в плоскости
кольца
полное
кольцо
концы
шарнирные
концы
защемлен-
защемленные
перпендикулярно
к плоскости кольца,
полное кольцо
45) стр. 454
Колебания круговой арки перпендикуляр-
перпендикулярно к ее плоскости
«) стр. 454
Колебания двутавровой балки с учетом
изгиба полок
ТАБЛИЦЫ 445
Таблица I (продолжение)
к
ш-
омент
s я
11
о s
СО
Д
раъ
а
рая
а
ра*
а
ю2
со2
со2
юг
СО*
со2
Дифференциальное уравнение
y|V + y" =
= А [4л:/" + B — Зл:2) у" — Аху'}
»
у1У = Л[-(л-2/)'+2у]
_ (yVi +2yiv + у") = I (yiv + у")
_ (yvi + 2yiv + у") = I (y'v + у")
_ (yvi-f 2yiv-f/') = A (y<v+2y")
- (yvi + 2yiv _/') = сМУ - У")
_[yvi+B + Cl)y'v + (l+c,)y"] =
= A[ylV-f B-c2)y"+(l+c2)y]
_ [yV) + B + c.) yiv + A + c,) y"l =
= A[yiv+B-c2)y" + (l+c2)y]
-[yVi-fB + c,)y'v+(l+C|)y"] =
= A[yiv + B-c2)y-(l+c2)y]
_[yVI+B + Cl)yIV + (l + Cl)y"] =
= ^.(У —c2y")
-(yV'+2yiv+/') =
= X(c,>-iv_c2>-» + c3>-)
уравнение 8-го порядка
Гланные
граничные ус
Сокращения: у0 = у(О);
Уо = У/ = 0
Уо = Уо = У( = У/ — 0
Уо = У/ = У/ = 0
Уа = Уо = У/ = y'i = 0
,'Уо = Уо = У л = 0
1У/ = У;' = y"i = 0
Ь^ = Уо = Уо=О
1У- = У\ = уГ = 0
Кстественные
лэвия
// п
^ =У @ и т. д.
у", = у", = о
уГ-о •
уГ = уГ = о
периодичность
периодичность
Уо = Уо = У/ = У/' = 0
к-Уо-Уо-О
1У/-У/=У/*-0
nt ttt _
Уо =У( =0
периодичность
|Уо = у{) = Уо = 0
[У/ = У/' = У;" = 0
446
ПРИЛОЖЕНИЕ
Обозначенные звездочкой
рисунки следует
повернуть на 90°
в плоскости чертежа
Техническое содержание задачи
Литератур
(см. стр. 4S
454)
Колебания тонкостенного полого обруча
47) стр. 454
Крутильная устойчивость тонкостенной
трубы
в) стр. 454
3. Задачи с
Я входит в крае
Колебания подвешенного каната с мас-
массой на конце
Продольные колебания стержня с мас-
массой на конце (колонна)
4Э) стр. 454
стр. 454
Диски паровых
турбин без
лопастей
Крутильные колебания
Колебания растяжения
51) стр. 454
Изгибные колебания вала с учетом ги-
гироскопического эффекта, с диском (летя-
(летящий вал)
52) стр. 454
Изгибные колебания стержня с массой
на конце
стр. 454
м р
Р Й
Выпучивание сжимаемого вала под дей-
действием момента
54) стр. D54
Р Чс
Изгиб стержня, один конец которого за-
защемлен, а другой упруго оперт
55) стр. 454
Опрокидывание ребристой
решетки под действием
изгибающих моментов
56) стр. 454
\МХ\ ф \Мг\
ТАБЛИЦЫ 447
Таблица I (продолжение)
к
Дифференциальное уравнение
4
- Уу1 + 2 ёу (*) y(v) = Я (у - у")
v-0
Уравнение 8-го порядка
Главные
граничные ус
Сокращения: у,. = у(О); )
Естественные
ловия
'г' = у'(О " т. д.
периодичность
особенностями
вые условия
i
ю2
с,ш2
С1«2
с,ш2
со2
со2
М2
р
— \{0 "г" gpFx) у']' = XpFy
— у" ^ Яу
1м h' 1 \ я
(аУГ-Х(^ + (сУ')')
(«/')" = Яр,у
сс ее
(ау")"=-Яу"
_ yVI -к-ЗСоУ^ ^ Д,уIV
_*_ yVI Д- СгУ^^ == Яу^
Уравнение 8-го порядка
у, = о
У/ = У/ = 0
У, =У/=0
Уо = Уг = 0
У/ = У/' - 0
(У1 - У/ =* 0
/
: у?-Чу,
У'(ЛГ|)=С2У(^1)
Уу = А.С[Уо
У,=0
(а2у'"
4-
4-Я)у')Оиг = о
Уо = О-о +
Г:
448
ПРИЛОЖЕНИЕ
Обозначенные звездочкон
рисунки следует
повернуть на 90°
в плоскости чертежа
Техническое содержание задачи
Дифференциальное
Опрокидывание балки под действием мас-
массы на конце с учетом собственного веса
57) стр. 454
D
Продольные колебания цилиндрических
оболочек
стр. 454
М Р
Затухающие колебания, например, каната
59) стр. 454
Р М
Выпучивание вращающегося вала под
действием сжатия
стр. 454
Изгибные колебания стержней с учетом
кручения и изменения угла элемента
стержня
61) стр. 454
Колебания упругого каната
стр. 454
Колебания замкнутых круговых оболочек
при равномерном внешнем давлении
3) стр. 454
Другие
Колебания свободно подвешенного кана-
каната
64) стр. 454
ТАБЛИЦЫ 449
Таблица I (продолжение)
к
Дифференциальное уравнение
Главные
грани
Сокращения: Уп
Естественные
чные условия
= у@); у" = у"A) и т. д.
уравнение содержит X и X2
Р
й2
Р
й2
Cjffl2
^2
_(CyT = iKWy
v"fl Cl \ Vv
Sy" = (p/'X2 + CiX) у
c,yiv -f Яу" -f X (X — 1) у = 0
+ («г 4- СзЯ) L [у] + (с«Я2 + с6Х + с6) у
Уо = Уг = 0
Уо=Уг = О
Уо = Уг = 0
Уо=Уг = О
Уо = Уг = 0
(o?yff/ ~\-
—|— (схА, —j— Л12) у')п и ;^=0
,;-,;-.
(У' + c3y'")i = 0
особенности
ш2
— [gpxy'Y — ^-ру
Уо ограничено,
450
ПРИЛОЖЕНИЕ
Обозначенные звездочкой
рисунки следует
повернуть на 90°
в плоскости чертежа
i
Техническое содержание задачи
Колебания сжимаемых круговых пластин
Полярно-симметричная 1 Край защемлен
потеря устойчивости <
круговой пластины ' Край оперт
Поперечные колебания круговой мембра-
мембраны
Радиальные колебания сплошного ци-
цилиндра
Радиальные колебания шара
Выпучивание криволинейных стержней
Колебания конической оболочки
Критическая длина при опрокидывании
стержня
Литература
(см. стр. 453,
454)
65) стр. 454
ss) стр. 454
67) стр. 454
68) стр 454
69) стр. 454
'<>) стр. 454
7i) стр. 454
ТАБЛИЦЫ 451
Таблица I (продолжение)
оо2
С|Ш2
с,ш2
Cjffl
Дифференциальное уравнение
<"">"- D >■')'+
+ дг(л:У')' = ;'-с1хУ
— (ХУ'У +— у = А.*у
— (-*у')'+ — у = Я*у
л2
— (■*>'')' +—у = ^у
— (-«у')' + ~ у = ^-«у
-(^2у')'+л(л + 1)у = ^2У
у'" + у' + К (g (л) у)' = 0
Диф. уравнение 2-го порядка,
содержащее X, /А X3
у" = ctxy
Главные
грани
Сокращения: yf.
у,=у,'=у,'=о
у0 ограничено,
у0 ограничено
у0 ограничено,
у, = 0
1
*у„ ограничено
Г
У_,= У, = О
у(Л) = О
Естественные
чные условия
= У @); 5'г'=у" @ н т. д.
предельное условие
У; + С1У( = °
У; = с2Уг
J yg(x)(cosx —
-1
— cos /) dx = 0
Уц = О; собственное
значение равно длине
основного интервала
452 ПРИЛОЖЕНИЕ
Пояснения к задачам на собственные значения для обыкно-
обыкновенных дифференциальных уравнений. В таблице I приведены не-
некоторые простые примеры задач на собственные значения из меха-
механики, упорядоченные по типу дифференциального уравнения, опре-
определяющего задачу. В первых двух группах собственное значение X
фигурирует, будучи умноженным на собственную функцию, но не на
ее производные, в третьей и четвертой группах X умножается и на
производные (общие задачи на собственные значения), дальнейшие
группы имеют особенности.
Подобное перечисление, конечно, не претендует на полноту. В про-
простейших случаях, например, для колебаний струны и стержня, для
продольного изгиба стержня, приводится несколько типов краевых
условий; подобным же образом можно увеличить число примеров,
меняя способы закрепления (соответственно краевые условия) и во
многих других приведенных случаях. Рассматривая более сложные
системы (например, составленные из нескольких частей), можно по-
построить любое число новых задач. Далее, многочисленные примеры за-
задач на собственные значения можно получить, привлекая другие раз-
разделы физики, в которые мы не вдаемся.
В таблице I используются обозначения:
с — коэффициент жесткости пружины,
с—разность моментов инерции,
С—крутильная жесткость,
С], с2 — постоянные,
D — постоянная полок,
Е — модуль упругости,
F—площадь поперечного сечения,
О — вес, функция веса,
g—ускорение свободного падения,
/ — длина стержня, струны и т. д.,
М — вращающий момент,
Р — сила сжатия,
S — сила натяжения,
х — независимая переменная,
у — собственная функция,
а — жесткость на изгиб,
х — коэффициент постели,
X— собственное значение,
р — плотность,
W — круговая частота.
Ниже, при указании литературы к таблице I, для экономии места ссылки
на следующие труды приводятся в сокращении:
Р. Курант и Д. Гильберт. Методы математической физики, тт.
1 и 2. ГИТТЛ, 1951;
Auerbach und Hort, Handbuch der physikalischen und technischen
Methanik, т. Ill, 1927, т. IV, 1931;
ЛИТЕРАТУРА К ТАБЛИЦЕ I 453
С. В. Biezeno, R. Qramrael, Technische Dynamik, Berlin, 1939
[К. Бицено и Р. Граммель, Техническая динамика, М. — Л., 1950];
J. Raizersdorfer Die Knieckfesiigkeii von Staben und Stabwerken,
Wien, 1936;
С. П. Т и м о ш е н к о, Колебания в инженерном деле. ГИФЛ, 1959;
Handbuch der Physik, т. VI, Berlin, 1928, статья F. Pfeiffer, 309—403.
ZaMM — Zeitschrift fur angewandte Mathematik und Mechanik
ЛИТЕРАТУРА К ТАБЛИЦЕ 1
1) Handbuch d. Physik, VI, 353, 355; Courant — llilbert 1, 250.
2) M. Biot, ZaMM 14 A934), 216.
3) K. Klotter, Ing.-Archiv 3 A932), 156.
4) Handbuch d. Physik VI, 357.
5) Handbuch d. Physik VI, 358.
6) 1 Ratsersdorfer A936), 22; Biezeno — Gramme 1, 502, 506.
7) L. Prandtl, Dissert. Miinchen, 1899; J. W e i n h о 1 d, ZaMM 14 A934),
380.
8) Biezeno — Gramme 1, 653, 657, 663.
9) Ing.-Archiv 1 A930), 301; T h. P 6 s с h 1, Techn. Mech. II A936), 185.
10) К I o 11 e r — К о t о w s k i, ZaMM 19 A939), 289.
11) Handbuch d. Physik VI, 379.
12) Handbuch d. Physik VI, 367.
13) E. Schwerin, ZaMM 2 A922), 84.
14) Handbuch d. Physik VI, 360, 368; С. П. Тимошенко, N. M о n о n о b e,
ZaMM 1 A921) 444; Cl Schaefer, Theor. Physik, 1 A937), 682.
15) Hohenemser — Prager, Dynamik der Stabwerke A933), 77.
16) Handbuch d. Physik VI, 365.
17) Puwein, Beton u. Eisen 39 A940), 162.
18) fop pi, Drang u. Zwang II A920), 355 [А. Феппль и Л. Ф е п n л ь.
Сила и деформация, т. 11, ОНТИ, 1936].
19) Foppl, Drang u. Zwang II A920), 359.
20) W. Meyer z u г С a p e 11 e n, ZaMM 15 A935), 243.
21) K. Klotter, Ing.-Archiv 3 A932), 156.
22) В iezeno —Gra m rnel, 521; 1. Ratzersdorfer A936), 142.
23) В i e z e n о — G r a m in e 1, 508.
24) H. H einzer li n g. Dissert., Karlsruhe, 1938.
25) Fr. A. Wilier s, ZaMM 21 A941), 43.
26) Auerbach— Hort IV, 101; n. 1.3 данной книги.
27) E. С h w a 11 a, ZaMM 10 A930). 74.
28) Handbuch d. Physik VI, 299, 302; Auerbach —Hort IV, 143.
29) A. Schleusner, Strenge Theorie d. Knickung u. Biegung, A937), 115.
30) n. 5.7 данной книги.
31) К lemperer —Gibbons, ZaMM 13 A933), 253.
32) Biezeno—Koch, ZaMM 5 A925), 280; Biezeno —Gramme 1, 550;
J. A. Haringx, Proc. Akad. Amsterdam 45 A942), 533, 650.
30 Л. Ко.ылц
454 ЛИТЕРАТУРА К ТАБЛИЦЕ 1
33) Auerbach — Hort III, 320.
34) Auerbach —Hort 111, 322; С. П. Тимошенко.
35) К. Karas, Ing.-Archiv 1 A930), 167; Biezeno —Gramme 1, 821.
36) K. Karas, Ing.-Archiv 1 A930), 167.
37) Auerbach - Hort IV, 127.
38) S. Tim oshenko, ZaMM 3 A923), 360
39) J. Ratzersdorfer A936), 314—320.
40) R. Sonntag, ZaMM 9 A929), 378.
41) J. Ratzersdorfer A936), 305—311.
42) P. Funk, ZaMM 4 A924), 143.
43) J. Ra tzersdor f er A936), 311—313.
44) Handbuch d. Physik VI, 374; Auerbach — Hort III, 342.
45) K. Federhof er, Ing.-Archiv 4 A933), 112, 115, 279, 283.
46) K. Federhof er, ZaMM 20 A940), 17.
47) K. Federhof er, Ing.-Archiv 10 A939), 129.
48) E. Schwerin, ZaMM 5 A925), 238.
49) G. H am el, Elementare Mechanik A912), 536—539. . .
50) K- Ludwig, ZaMM 14 A934), 361.
51) Biezeno — Gramme 1, 657
52) Biezeno—Gramme t, 803, 821.
53) F. G a ssm a n n, Ing.-Archiv 2 A932), 222.
54) J. Ratzersdorfer A936), 35.
55) стр. 47 данной книги.
56) п. 3.2 данной книги; J. W e i n h о 1 d, Ing -Archiv 9 A938), 412.
57) L. P r a n d 11, Dissert., Munchen, 1899, 46.
58) Handbuch d. Physik VI, 395.
59) Frank und v. M i s e s, Differentialgl. u. Integralgl. 1 A930) [Ф Франк
и Р. М и з е с, Дифференциальные и интегральные уравнения математи-
математической физики, ГИТТЛ, М. — Л., 1937].
60) J. Ratzersdorfer A936), 35.
61) Handbuch d. Physik VI, 359; С. П. Т и м о ш е н к о.
62) R. Hoger, ZaMM 14 A934), 361; 15 A935), 109.
63) К. Fed erhof er, ZaMM 15 A935), 27.
64) G. Ham el, Elementare Mechauik A912), 536.
65) Fr. A. Willehs, ZaMM 20 A940), 37.
66) Biezeno —Gram me 1, 585; A. N a d a i, Elastische Platten A925), 251.
67) Auerbach — Hort III, 355.
68) Handbuch d. Physik VI, 399, 402.
69) A. Lock shin, ZaMM 16 A936), 50.
70) K. Federhof er, Ing.-Archiv 9 A938), 293.
71) H. v. San den, Praxis d. Diff. — Gleichungen, Berlin, 1943, 51,
ТАБЛИЦЫ
455
Таблица II
Простые примеры технических задач на собственные значения
для дифференциальных уравнений с частными производными
Объяснение используемых обозначений на стр. 452 и 453
Техническая задача
Дифференциальное
уравнение
= дх2 ду2 ' х дх '
соответственно г , z и т. д.
у хх
Литература
Диффергнциальное уравнение второго порядка
Поперечные колеба-
колебания однородной мемб-
мембраны
Поперечные колеба-
колебания при введении дру-
других координат;
Например, эллипти-
эллиптическая мембрана
Поперечные колеба-
колебания неравномерно на-
напряженной мембраны
Поперечные колеба-
колебания мембраны на уп-
упругом основании
Выпучивание плас-
пластины с квадратично
изменяющейся жестко-
жесткостью
Поперечные колеба-
колебания быстро вращающе-
вращающегося тонкого диска
Дифф->ргнциальное
Изгибные колебания
тонкой пластины
Изгибные колебания
пластины на упругом
основании
— Дг = Xz
— Az = Xg (x, у) г
— Дг = X (sin2 лг+sh2 у) г
-{Azx + Bzy)x-
— (Bzx + Czy)y = Яг
-Дг + с,г = Яг
Ci 4- Со (х2 -f- у2)
х дх
1— с,*2 ,
Х2 -УУ '-
Auerbach - Hort,
III, 351
С. П. Тимошенко.
Ф. Франк и Р. Ми-
зес, Дифференц. и ин-
тегр. ур. матем. физи-
физики.
Handbuch d. Physik
VI, 381.
К. Klotter, Ing.-Ar-
chiv 3 A932), 156
R. Qran Olsson,
Ing.-Archiv9 A938), 206
Handbuch d. Physik
VI, 388
уравнение четвертого порядка М [г] = Xpz
Д Дг = Xz
Д Дг -(- с,г= Xz
С. П. Тимошенко
К. Klotter, Ing.-Ar-
chiv 3 A932), 156
an*
456
ПРИЛОЖЕНИЕ
Техническая задача
Изгибные колебания
пластины, сжимаемой
со всех сторон
Изгибные колебания
вращающегося диска
Таб
Дифференциальное
уравнение
()х2 Оу^ ' X ()х '
соответственно г , г и т. д.
у хх
Д Дг -j- с! Дг = Xz
ДД С) д г
/ 1 \ *
Диффёргнциальное у равнение вида N
Выпучивание пл;>-
стины при односторон-
одностороннем сжатии
Выпучивание пла-
пластины при сжатии, оди-
одинаковом со всех сто-
сторон
Выпучивание пла-
пластины при сдвиге
Выпучивание пла-
пластины с переменном
жесткостью
Выпучивание цилин-
цилиндрической оболочки
большого диаметра
Л Л -у _ 1
дх2
Д Дг = — X Дг
. d2z
Ох 0\
Д (Л' Дг) +
_l A _ v) BN t zx —
дг z дг г ,) =
= — X Дг
dbz dkz d6z
дхь ' ду* ~~ " дх6
лица II (продолжение}
Литература
К. Federhofer,
Ing.-Archiv 6 A935),
68
Handbuch d. Physik
VI, 388
G. I. Taylor, ZaMM
13 A933), 147
E. С h wall a, Ing.-
Archiv 5 П934), 54
О. Н. Faxen, ZaMM
15 A935), 268
E. T r e f f t z, ZaMM
15 A935), 339
E. Seydel, Ing.-Ar-
Ing.-Archiv A933) 4, 169
E. T r e f f t z—Fr. A.
W i 11 e r s, ZaMM 16
A936), 336
R. Gran Olsson, Ing.-
Arch. 9 A938), 205
Biezeno—Gramme
A939), 607
<[u\
Mo[u
(f*y")
R\u]
ft
f ,
I1
M
vof,"
i
Дифференциальное уравнение
и отношение Релея R \и\
— (/\У')'-Ь/оУ = Ь-КоУ
а
b
Г g0u2 dx
а
"-(/1У')' + /оУ= r r ■
-Ч-(^У) +go>]
/2«"*+/iM'2+/o«2)rf-< + 'Wo ["]
й
(ff\u' ~{~ £ои ) dx -{- N0[u\
а
0 = /И оа + Af Oft
] = [a°G2«")'°-/2«'«" -/,««']»
Кроме случая g-,^=0
lh
■
Краевые выражения Дирихле
(сокращения
Уа =
(
лг
! Уа =
1 у'ь =
/
V "«—• V —
•^ Q -' О.
У а = аУв:
Уь — 0;
(/гУ")б =
Уа =
/ /* \
(/2>'")а =
(Ау'Х =
f(/2y")ft =
{ (/2y")ft =
Краевые условия
Ув = У (a); /lft = /, i»). •■■)
у& = о
аУв; У* = — РУ*
J b* J la*a J ibJ b
аУа + У/1йУй
— Y/iaya — РУ&
= 0
Уа = аУа
(/2У")а = РУа + а(/2У")а
-0
Уй = — «У*
- РУо — а (/2У")&
= Уь> (fiy')a = (Лу')ь
' г
= «Уа + Р>'а
= УУв + (/1в —а)Уа
«У* — РУй
Yyft + (/ift —«)Уй
Таблица 111
Краевые выражения Дирихле М и N
мо =
Мп —
моа =
моь =
моь —
0
«/la
Л^оа
«/•2а
(«/l
Л^ог-
a/2ft
0
О
0
4 + p/i><4
+ 2yflaflbuaub
= 0
«a'. ^Oa-0
2 —Р)ц2; Л^Оа=а^аиа
= 0
/2
ц ; Л^ Q
;, — p) и*;; ЛГог, = a^lfta^
= 0
г2 _^ 2аиаиа + Рма2
Простые примеры функций Грина
Таблица IV
Дифференциальное
— у»
<-/iC*)y')'
-/'-„у
— у" Л-у
-ху'-у' 2
-(■«у')'+4- >
— y" + (i+*2)
г
У
Краевые условия U \у\ — 0
Сокращения:
У@) =
У@) =
аУо+РУо =
«Уо + РУ* =
ау —
У@) =
у@) =
Уо
У@)~
У(±
УA) =
У A) =
у(±оо) =
i
уо=у(О); уг = у @
у @ = о
у' @ = о
Yy; + бУг = 0
Yy^+6y; = o
У КЧ — и
у' @ = о
1 г\/ П
Угтт- Уг
У @)-У @ = о
оо) конечно
0, у @) конечно
0, у @) конечно
0
Функции Грина 0 (х, £)
при л: < | (при х > | функции
определяются из равенства 0 (лг
■* (^ —7")
X
— lay — аб -(- Py
— Р (y ~~f~ б) ^ ~1~ (^ ~{~ Р) *^"
(ot —{— р) (Y ~г~ о)
./. q A) \
1 Q A) I
Я(х)
1 ^1
L /I (I) J
sin nx sin/г (/ — £)
/г sin «/
М nl ,
+ sinn
1 ^_s
— log 1,
— I— I — (хъ)п 1
я L\ i / J
^ 1 ^~^2 ^y/ 1
-oo I
1
f'PY
I
(•* — i)|
~~t7 /if
%) = Q(%,x))
Э. Камке, Диффе-
ния, изд. 2, ИЛ, М.,
1951
J /.W
Е. L. I n с е, Ordinary
> Differential Equations,
London 1927, стр.258
P. Курант и
Д. Гильберт,
Методы математиче-
математической физики, т. I,
М. —Л.. 1951
Уо =
Уо =
Уо =
Уо
Уо
= У/
= У;
= Уг
= У<
= Уг
= 0
' = 0
= 0
-
12/3
=0
1 rsinn(/ —|) shn(l-i), I
sin nx > b/ sh nx
h / J
2n3 I sin nl
sh
/ " от
У У
= У/ =0
Уо = Уо = У; = У; = О
Уо = Уо = Уг = У; =0
\l (v @- ~]-(lv Й) -г (|) I у +
(дг)
и @ -
]
±
dt
X
v(x)= \ и i
«;(*) =
;rf/
дг) = J w (t) dt
0
A = и (I) z (I) —
— v(l)w (I)
D = lv(t)—2(t)
M [y] = r (x)
равносильно У (•<) = G (x, g) r (g) rfg.
Таблица V
Некоторые разрешимые в замкнутой форме задачи на собственные значения для дифференциальных
уравнений второго порядка
о
Тип задачи
Дифференциальное
уравнение
Краевые
условия
Собственные значения к =
Собственные функции у
при различных краевых условиях таблицы VI
у (а) =
й)
— у =
Я у
(X -f-CJ
у(а) =
= у(й)=0
х+сфО (а,Ь)
у(а) =
= у(*)=0
О < а < b
у" =
Яу
(С2 — X2J
у(а) =
= у(*) = 0
с < а < b < с
■ у =
У («) =
= у F) = О
— у =.
у@) =
()
у@) =
пл;
In
а -(-с
й-f с
плаЬ
а — b
2спл
In
с-\- b с — а
с — b с ~\- а
b t a
arctg arct" —
n (n -+- 1)
c)]
—
sin
плЬ
b — а
1——
х
—jc^ sin
In
In
г -f- jc с — a
с — x c-\-a
с -\- b с — a
с — b с -\- a j -
1
yc2 4- xi sin пл
, x a
arcfg arctg —
arctg arctg —
V x /, B У' Xnx) (функции Бесселя J{)
s ~/ Bx
ax' n y^l *
производная
сферической
функции
-y"+
У (а) =
_(/,у')' =
= ^£оУ
y(fl) =
= y(ft)=O
— >
->
[
(
= X
где
(
" = я*
Г с, 0
\d, а
" +с*у
= х
„ с (с
л
(cx + d)
X (сх\
?сху'У =
у' sin* и
у sin2 и
и = сх
- V
хгу>) =
У
<лг</
=
е ■*" у
-1) __
Ху
х*
2 у']'=
- «О2 у
= А.е«у
]' =
1
=А,х- у
У @) =
= у @ =
у(а) =
- У (Ь) -
у (fl) =
= У (*) =
0 < а <
У (я) =
у (ft) =
(fl, ft)
У (а) =
= у (ft) =
у(а) =
= У (*) =
У («) =
- у (ft) -
0 < а <
= 0
= 0
= 0
b
0
= 0
= 0
= 0
- 0
ft
/■—
+ \/ ^-tg[(/—а)У%5] =0
/ 2ляс у
/ Bс — 1) пл у
( пл у
U-flj
с2 / ля у
4 Ift flj
с I { пя )*
1 \b —a )
/ ля у
12 ((/"ft -(/а)/
\
sin \\rXnd (I — а)] sin Wxnc x]
0 < x < а
sin [(/^^„c a] sin [|^A,,rf (Z — A')]
a •;', jt<. /
Г e~2cx е~гасЛ
L e~ ° — e~ ac\
1 „,„(__ •« —я \
cjc 4- ^ V b — aj
ex
\ b — a )
\ 6 — a )
sin (cx-j-rf)
При (ft — а) с > я конечное число
отрицательных собственных зна-
значении
1 . Г /Г_УТ1
К* [ Vb -Va J
1
Таблица V (продолжение)
Тип задачи
Дифференциальное
уравнение
Краевые условия
Собственные значения X
Собственные функции у
-(/,>'')' -
— (Р (■*) У')'
у (а) = у (ft) = О
У (в) =
= у (ft) = О
/>(■*)
Г *S
(х)
()
у!
у (а) = у (й) = О
= J P (I) dl
у
■'
q(b)-p(a)
sin
dj
J'»'•*■
у (в) = у (й) = О
у()
у (*) = О
—у*—2c(thcx)y'=
у (а) = у F) = О
/ пл Y
ЛТ^а-)
COS СХ
■ Г •* —«1
sin пя -г
ch
■ Г х — аЛ
-sin пл -г
L Ь — а j
-y"—c(tgcx)y' =
= Х (cos схJ у
У (я) = у (ft) = О
/ яле \2
\ sin eft — sin ca )
sin
пл
sin ex — sin ca
sin eft — sin ca
У (fl) = У (ft) = 0
у(й) =
= у (ft) = О
1 . Г л: —а]
—5-sin ля -т
x2 L ft — a. J
— (/,y')' =
y'(a) =
— У (ft) — 0
Периодич-
Периодичность
У"
У
—
go —
I P
-[у'
где и
— 2сху' —
— с2*2 = Ху
Ху
1п2 v-212
(С X )'
Ху
О2 _1_ V2\2
(,С ~\-Х )
У" = ^оУ
(с; 0<;.*<а
U <!<*<*
1 Л'
(х) )
= А,р (jt) у
sin2 и]' =
sin2 и,
Ряд дальнейших примеров,
краевыми точками
рат физики,
У
У'
>
У'
У
у
(в) =
@) =
I /1 «-
1' 1 <
@) =
(а) —
(«)=
(а)=
y(ft) =
У@ =
.У \ /
у @ =
V (Ь) -
у уа+
1
у'( й+
разрешимых в
и с бесконечной основной,
Физматгиз, 1960.
-0
= 0
- и
= 0
- п
2я\
с /
— 1
С 1 1 и ~ 1
с, , /Bп-1)сд\2
V "с-/ j
^ , / Bп —1)сл\2
С Г I г 1
V 2агс1§7 j
tg [а /Цс] tg[(l—a)VK
/
/2п — 1 п
1 2 ь
\ а
с -(-с п
замкнутой форме задач на
областью) имеется в книге;
\
)
/
сх2
1
у
У с2-|-
sin |
cos
sin
п —
п >
Kin L
х — а~\
L ft —a J
v-2 priQ
VX~d(l
Vxnca
—
In — 1
2
_
1
(ex -\- d
Г in C
2 1пС
L 1п с
2 Л .
— a)] cos [V~Xn
sin tyXnd (I -
X ~
J p (s) dl
ч а
л b
a _
fsin
\ COS ^
— / -
5 С -
с*];
x)l
]
\
a
0 — простое собственное зна-
значение
0 — двукратно вырожденное
собственное значение
собственные значения (с сингулярными
Э. J
Маделунг,
Математический аппа-
454
ПРИЛОЖЕНИЕ
Трансцендентные уравнения для соб
Дифференциальное
уравнение
Краевые условия.
Сокращения:
у0-у(о>,у;~у'(о
СУ1 + аУ[ = 0
УО = У; = О
Уо = у\ = 0
у0 = у', = 0
Уо = У/ + Лу, = 0
а у. 4- 6у = 0
с>'/' + dy'o = 0
Частный
случай
а = с = 0
6 = rf = 0
. —0
А' = т
1
2
Л/=---1
6 = 0
Л/= 2
Л/ = 1
Л/ = —1
Л/= —2
b = — й
rf = -c
Трансцендентное уравнение
для собственных значений
(ad-bc)k
bd + aek*
sin ft/ = 0
sin ft/ = 0
cos ft/ = 0
A tg ft/ = — k
tg ft/ = - ft/
tg ft/ = — 2ft/
tor ft/ = ft/
fttgft/ = ^
ft/ tg ft/ = 2
ft/ tg ft/ = 1
ft/ tg ft/ = — 1
ft/ tg ft/ = — 2
ftv4 tg ft/ = 1
cos ft/ = 1
ТАБЛИЦЫ
453
Таблица VI
ственных значений простейших задач
Величины длч вычисления первых
собственных значений
оо
у 1 | | 1 ;
Ы (й,/J 2 ' 3/ аа
kl = л; 2л; Зл
kl = 0; л; 2л
fc/ л Зя 5я
2' 2 ' 2
« = 2,0288; 4,9132; 7,9787
kl = 1,8366; 4,8158; 7,917
« = 1,1656; 4,6042
kl - 0; 4,4934; 7,7253; 10,9041
«=1,0769; 3,646
kl = 0,8603; 3,4256; 6,4373
kl = i -1,1997; 2,7984; 6,1212
kl = i ■ 2,0653; 2,4587; 5,9594
kl = 0; 2л; 2я; 4я, 4л; ...
оо
$ас ~\- Pbd
— bc — lbd
1
6
со
1
2
Л/ -f-3
6 (Al -f-1)
1/3
7/18
5/6
со
1 I
2'Al
1
3/2
— 1/2
0
1
2 0-М)
oo
Литература.
Использованные сокращения
см. стр. 432—454
Ф. Франк и Р. Мизес,
Дифференциальные и ин-
интегральные уравнения ма-
математической физики,
ГИТТЛ, 1937
F. Emde, Tafeln elemen-
tarer Funktionen, 1940,
125—131
Biot, ZaMM, 14 A934),
217
F. E m d e, Tafeln elemen-
tarer Funktionen, 1940,
125—131
С. П. Тимошенко, Ко-
Колебания в инженерном деле,
ГИФМЛ, 1959
466
ПРИЛОЖЕНИЕ
Дифференциальное
уравнение
X X2
л = k> ~ ХУ'
~У"-х+-хТ =
= Яу;
А = А4'
Уо
У;
Vn
У<
У<г
Уо
СУ',
Уо =
Уо^
Уо =
Краевые условия.
Сокращения:
уо = у(О), y;'=y'@
конечно,
= 0
конечно
-J- Ayt = 0
= У, = 0
//
/ /
-|- Ьу 1 = 0
' + dyi = 0
It It
-,:-„-*->
-А-»-*-.
Частный
случай
п
п -
п --
П =
п -
А1--
п -
А1--
п = .
/ =
п —
1 =
п =
6 =
а =
= 0
= 1
= 2
Л = 0
= 0;
= 1
= 1;
= 0
4/ = 1
--2а;
-.0
-.2а;
-. 1
; = 0
,..
*-»
Трансцендентное уравнение
для собственных значений
У„ (kl) = 0
Уо (А/) = 0
У, (kl) = 0
У2 (W) = 0
Jn — функции Бесселя
k/n(kl) + AJn(kl)=0
У, (kl) = 0
— Ш, (*О + Л(*О = 0
*/У0 (*/) — У, (£/) = 0
Уо (kl) = 0
У„(*я)ЛГ„(«) =
= J (kl) N (ka)
Jn — функции Бесселя,
Nn — функции Неймана
(ack* -f- bd) 33 (*О —
— 6eA3G (AO +
tg kl = th A/
tgA/ = th A/
ТАБЛИЦЫ 467
Таблица VI (продолжение)
Величины для вычисления пецзвых
собственных значений
« = 2,4048; 5,5201; 8,6537
« = 3,8317; 7,0156; 10,1735
« = 5,135; 8,417; 11,620
« = 1,2558; 4,0794; 7,156
«=1,841; 5.331; 8,536
ka = 3,123; 6,273; 9,418
ka = 3,197; 6,312; 9,4445
kl = я; 2и; Зя; ...
« = 3,9266; 7,0686; 10,210;
13,352
« = (У, 3,9266; 7,0686; 10,210;
13,352
2л (VJ
1
4(п + 1)
1
1
8
1
12"
1 Al + n + 2
4 (n~+i)(Al + n)
3
4
3
V
Ал (kiiy
(-1
1
"90"
1
210
со
Литература.
Использованные сокращения
см. стр. 452—454.
Е. Янке и Ф. Эмде,
Таблицы функций с фор-
формулами и кривыми,
ГИФМЛ, 1959
Е. Янке и Ф. Эмде (см.
выше)
Прекрасные таблицы
имеются в книге Э. К а м-
к е, Дифференциальные
уравнения, ИЛ, М., 1951
F. Erade, Tafeln elemen-
tarer Funktionen, 1940,
130—131.
468
ПРИЛОЖЕНИЕ
Дифференциальное
уравнение
yiV^Ay;
I = А1
yIV = _X/'
Уо =
,7V "
Уо =
"■
Л-
(у =
!
1 *
1 Л>"
1 ^о
Г у =
1'Уо
Уо =
]«Уо
Уи5
yi-
Уо =
ау\
in
СУ1
Краевые условия.
Сокращения:
У0 = У @), >'/ = у'@
= Уо = О
4-by' — 0
-j- dy 1 =я 0
= Уо = У/ = у/ =
Г 1 III
~ Уо — У/ — У/ —
= у; = о
_j_ dy^ = 0
= у = 0
+ Уо = 'У/" + У/'
= У; = 0
_|_ 6у0 = 0
= Уо = У/ = У
= Уо = У, = У, *
= уо=О
4- *у;' = о
+ dyl = 0
°
= 0
0
-0
= 0
Частный
случай
в-е-о
a—c — l
b = d=\
a = lb
Трансцендентное уравнение
для собственных значений
ack^(kl) + bckm(kl)
— arfA5B (A/) +
+ bdl? (kl) = 0
cos kl ch A/ = 1
cos kl ch kl = — 1
tg kl + th kl = 0
+ A (arf — ftc) 33 (A/) = 0
(/)»(/)+ ( )
adkz> (kl)-\-cbk4 (kl)-\-
+ (acA4 — 6rf) 33 (A/) = 0
ch kl cos kl = 1
sinA/ = 0
6 (Asc + A/rf) cos A/ =
= d (k2la-\-b) sin kl
, ., ., 1 — A2/2
ТАБЛИЦЫ , 469
Таблица VI {продолжение)
Величины для вычисления первых
собственных значений
Ы = 4,7300; 7,853; 10,996;
14,137
kl = 1,8750; 4,694; 7,855;
10,996 1)
kl = 0; 2,3650; 5,4978
« = 3,084; 6,270
kl = 0; 0; 4,7300; 7,853
kl = 0; л; 2я; .. .
m
у 1 1 bdP —
СО
2j <vJ
i
20"
Т2
156с-f 5adl2
'-' (*'/)я 10 bdl3-3bc+3adl2
« = 2,1826; 4,9292
10
Литература., ..
Использованные сокращения
см. стр. 452—454
') Вычислено до десятого
знака в 1744 г. Эйлером
Используемые сокращения:
ЭГ (х) = ch х sin a: -f-
+ sh x cos jc
3} (x) = ch x sin x —
— sh x cos x
(&(x) = 2 ch л; cos л:
© (л;) = 2 sh x sin л:
S) (jc) = ch л; cos x — 1
6 (jc) = ch x cos jc —}— 1
470
ПРИЛОЖЕНИЕ
Дифференциальное
уравнение
Краевые условия.
Сокращения:
Уо = У @). J7=y'U)
Частный
случай
Трансцендентное уравнение
для собственных значений
Уо = Уо = Уг=У1 =°
Ь=с=О
sin kl =
Уо = Уо = >'/ = У'=° й=с=
tg kl
Уо = >'о = 0
Щ -{-by't=O
су)" + ^У, = О
Уо = Уо = У/ = У/'
йУо + *
'Уо = Уо=/У/'+У/=°
-\-kd(bl — a)]si
+ *2/«rf cos £/ —
— 2bd(\ —coskl)
kl . kl kl
T=0 и tg-g-^
+ ()X
X (kl caskl — sin W) -f-
46rf (A/sin A/— 2-f
+ 2 cos */) = 0
a=c=t
b=d=\
kl
sin —- = 0 и
kl
•~Ay" = ly
2—~A
Г 5
r t» ^ + s th — = 0 и
= 1,1,1
2 s 2
J. tt>r = —th s
_, = У_г=У/=У/=0
2+
1
/.2
■ slnWslis/
sk
— 2 cos klchsl = 0
ТАБЛИЦЫ 471
Таблица VI (продолжение)
Величины для вычисления первых
собственных значений
kl = it; 2я; ...
kl = 4,4934; ...
для с = 0, а = lb:
kl = 4,7926; 7,8223
kl = 2я; 8,987; 4it; ...
kl = 3,0096; 2я; 9,4200; 4я
ОО
i
6
i
10
7
75
1
Т5
29
165
Литература.
Использованные сокращения
см. стр. 452—454
W. Meyer zur С а р е 1-
1 е n, Z. angew. Math.
Mech. 15 A935), 243 -
S. T i m о s h en k о, Z, an-
angew. Math. Mech. 3 A923),
360
Примеры графического проведения метода последовательных приближений
Дифференциальное уравнение
-(/i/)+/oy = teoy
(/«У")" = ^оУ
Краевые условия
Г ау @) + 6у' @) = 0
\cy(l) + dy> A) =0
У (а) = у F) = 0
Выбор функции
F0(x) удо-
удовлетворяет
краевым усло-
условиям
w (х) при
w(a)=w{b)=Q
Способ получения Fq и /*"j (может быть применено A2.20))
Образовать ho — goFo; определить Fy (x) при
помощи веревочного многоугольника (в край-
крайнем случае двух многоугольников) так, чтобы
были удовлетворены краевые условия
Z7, (х) при F{ {a) = F{ (b) при помощи веревоч-
веревочного многоугольника из (.fiF{)' = — w\ тогда
/?o = ^(«» + /o/?i)
so
При иных краевых условиях исходить из нескольких выбранных функций w и,
используя их линейные комбинации, подчинить Fo и F, краевым условиям
ГУ @) = у(/) = 0
1 У" @) = У" (/) = 0
(УФ) =у'@) = 0
1 у" С) = У" A) = 0
F0(x) удо-
удовлетворяет
краевым усло-
условиям
F0(x) удо-
удовлетворяет
краевым усло-
условиям
hx (дг) при помощи веревочного многоугольника
из h[ = gQP0; hx @) = hx (/) = 0;
F\ (x) при помощи веревочного многоугольника
из F[ = -L h{, Fx @) = Fx (/) = 0;
/2
hx (x) при помощи веревочного многоугольника
из h" = g0F0; й1@) = Й1(/)=0;
F\ (дг) при помощи веревочного многоугольника
из/^у-Й!; ^@) = ^(/)=0;
(f2y")" = Xgoy
(/2уТ-(/1У')' = А£0у
\J гУ ) i /оУ л^s1У )
Г У @) = у' @) = 0
[ у A) = у' (Л = О
В зависимости от
краевых условий
метод проводится
с несколькими функ-
функциями да (х), кото-
которые комбинируются
так, чтобы Fo и /•',
удовлетворяли крае-
краевым условиям
F(х) удовле-
удовлетворяет крае-
краевым условиям
да (х)
w(x)
w(x)
ft \
F,
F\
Л,
и
F'x
Л,
F'
F*
Л,
F,
(X)
(X)
(X)
=
и
(JC)
(Jf)
(X)
(x)
(x)
при помощи
веревочного многоугольника
из h\ = ^0; Ai @) = А; @) = 0
при двух постоянных интегрирования с,, с5;
при помощи трех веревочных много-
многоугольников
f \ f \
чтобы Fy (/)
при помощи
из Aj = да;
из /?, @) = F\ @) = 0,
J— и определить с,, с2 так.
/ 2
= Л'(') = о
веревочного многоугольника
Л.
-р-1-; при помощи двух интегрировании
Pjj тогда Fg =
при помощи
из Aj = да;
при помощи
из F^ = —-
при помощи
из — {ei^o,
при помощи
из (giF^ =
при помощи
из Ai = ^о/7
при помощи
1
из f[ = -у-
= — — 1 \F\ — f]F] ~\~да
веревочного многоугольника
веревочного многоугольника
Ар
веревочного многоугольника
= да + /q^i
веревочного многоугольника
= да;
веревочного многоугольника
о — w<
веревочного многоугольника
А,
Таблица Vlll
Примеры матриц со специальными свойствами
Эрмитовы
%—_jtматрица/ ~~-^
Антиэрмитове/
матрицы
See элементы полажитедрны
ОБОЗНАЧЕНИЯ
Симметричные матр.
Зрмитовш матрицы
'Антисимметричныематр.
^ нтизрмитт/ матрицы
Г Ортогональные матрицы
« Унитарные матрицы
Ине.-
матрицы
П. ине. -
инволютивные
матрицы
*- полуинволштие-
ные матрицы
с
X
S
га
№
A)
B)
Простейшие примеры
Матрица ?!
/0 2^
У 2 0/
( 2 М
1-2 0/
Характ. числа
Kv
— 2
1-М
1 —г
Соответствующие собственные векторы
4
1, 1
1, —1
1, — 1-м
1, —1—/
ТАБЛИЦЫ
475
е- И
Q •§
00
о
1
to
о
00
о"
-f-
СО
о"
е-
■§■
1
.5 о
31*
Таблица VIII (продолжение)
: к°-
(9)
A2)
A3)
Простейшие примеры
Матрица К
1-1 <W
/3 -2\
\5 —3J
/а -П
\д2 + 1 _Д//
/ sh ф ch ф \
\ — ch ф — sh ф /
С -,)
i/i iVi\
~2\ — iV3 —I J
1 cos ф / sin ф \
\ — / sin cp — cos ф /
1
Характ. числа
Kv
— i
i
— i
i
i
1
— 1
1
— 1
1
1
— 1
Соответствующие собственные векторы
4
1, i
1, —i
2, 3 — i
2, 3+«
1, a—i
ch ф, / — sh ф
ch ф, — / — sh ф
2, \—i
— 2, 1 + i
U 1
— i. 1
/ Vs. i
-Vs
ф ф
( cos у , sin y
Ф Ф
is\n-~, — cos-i-
1
ТАБЛИЦЫ
477
V
ca
в"
V
о
V
CO.
в"
V
о
V
в"
V
о
V
в"
V
о
V
со.
в"
V
о
!со
|со
с 4-
В
С
в
V
о
о
в
л
s
и с
в о
о в
о
см
Таблица VIII (продолжение)
B1)
B2)
B3)
B4)
B5)
B6)
/
(
/
(
(
\
V2
— i
сЬф
— / sh q
ch?
г sh ф
l / зн
4 V—34
0
0
— С11ф
— г sh ф
^ — ch ф
@ ai\
{ai 0 )
Матрица
V2J
i sh ф \
ch ф /
/ sh ф \
1 (ф
— ch ф /
- г 3 — г \
0
0
— / sh ф
сЬф
сЬФ\
/ sh ф /
ш
Ф °)
ch ф
г sh ф
0
0
Ф
(а> 1)
г sh ф '
— ch ф
0
0
Простейшие примеры
Характ. числа
VT + i
/2-1
ch ф 4" sh ф
ch ф — sh ф
1
— 1
1+/
у A-0
г (ch ф 4" sh ф)
г (sh Ф — ch ф)
ai
— ai
I
i
— г
i
— i
i
i
1
1
r
I
r
I
1
1
1
1
Соответствующие собственные
i
l
l
i
chf. -s
Sh|, _C
i
— i
— i ch ф,
sh ф,
i ch ф,
— sh ф,
i
— i
r
h^
2
hT
sh ф,
г ch ф,
— sh ф,
— i ch ф,
= e
1,
0,
1,
0,
векторы
0
1
0
1
00
B7)
B8)
B9)
C0)
C1)
C2)
C3)
/ 1а
\
(
(
— Ы
i ch »,
sh ц
а 0\
ы oj
0
— sh
0
— i ch
1 2ai
' 2a bi
,bi 0
' 0
bi
0
Ф
o)
)
bi
\
)
sh ф \
i ch ф /
sh с
0
— /ch
0
(ab -/- <
(Ф
(ab
P
Ф
a -J- bi \
0 j
Матрицы четвертого
волы а,
b, a, p\
Ф
^C
ф(.
0
i ch
0
-sh
{at
(at
)
))
i ch ф
Ф 0
sh ф
Ф 0 J
ФО)
ФО)
tab ф 0
U2+62 ф 1
порядка
обозначают
параметров (например, а
в частных случаях
= 0
требуется
)
приводятся
вещественные
или
л.
Ф == "о" и
Т.
а + У а2 + б2
e-У а2+/;2
г
— г
0
а
Ца-У а*+Ъ*)
а —У а2— Ь2
— b + ai
b — ai
ы,
— bi.
— ch ~
0,
a,
|ch
to,
|ch
to,
b.
— b.
bi,
— bi,
1,
1,
только там, где нет примеров с
параметры. Может
п. J соответствующий
делать проверку.
оказаться,
пример
Уя2 + 62 —
У а? + б2 -f
-, <shf
-, г ch -|-
1
ft/
Ф, 0,
ch ф,
Ф, 0,
ch ф,
i(ya2 + b2
1 (у а2 _J_ b2
i
матрицами
\
а
а
— г" sh ф, — г
— г, i sh ф
— г sh ф, i
i, i sh ф
-a)
+ a)
второго порядка. Сим-
что при частных значениях этих
изменяет свое качество, поэтому
480
ПРИЛОЖЕНИЕ
Л1атрица
/2 1 3^
1 3 4
\3 4 9/
/ 5 —
1— 2
4 0 —
<■ 1
-1
1 1
1
1-1
/4 1
2 4
Vo -1
/4 0 Ц
14 2
\0 0 4У
и
2
3
2
1
1
0
0
0
)
= («;*)
°\
-2
5/
1
I
0
0
0
-ч
1)
4/
Примеры
i
0
0
0
матриц с
о??
Ǥ.
ион и
-в
^ с
- g
а ?
§ о.
К су
Коэй
хара
для
14
—25
10
13
—47
35
1
1
—3
0
0
12
—47
62
12
—48
64
различными (грубыми) границами
для '
А:
га
о
D-
О
ICTI
ктерр
Хара
11,98
1,44
0,58
7
5
1
1±|'Оз
2
1 2,303
~ {—1,303
0
0
5,52
3,24 ±/0,86
4
4
4
С-
§
О
а
Е-
С
Ь.
а;
^_
В ***
вНХ
в
16
(+34%)
7
@%)
(+74%)
7
(+27%)
7
6
(+9%)
7
(+75%1Г
ТАБЛИЦЫ
для характеристических чисел (ошибка в %)
481
Таблица IX
о
С
о
и
^
—
1
в
а,
с
,
О
i
1-
не проходит
• -*
не проходит
• ,
не проходит
1
(—70%)
1
2
(—40%)
1
(-75%)
о
к
соглас
B0.30)
II
р—
II
/146
=в 12,08
/75"
и 8,66
(+24%)
VT
та 2,646
(+15%)
/56
к 7,48
(+41%)
/54
яг 7,35
(+84%)
ь
+
9-4-/52"
а 16,2
(+35%)
9
(+26%)
1+/6
и 3,45
(+54%)
4 + /8
«6,83
(+24%)
4 + УТ
яв 6,45
(+61%)
СО
о
ласно
о
СЗ
■^ ||
в с,
с с
2-/52
и —5,2
не проходит
_!
не проходит
-/6
« —2,45
не проходит
4-/8"
я 1,17
(-65%)
4 —/6"
« 1,55
(-01%)
i
«
С
С
С
с
Z
ч
t
t.
7
"
Т;
10
73
0,
14
15
D
1
Э
J
3
■—s
137
О
1й
2\ СОГЛ
с
Ч.
в
\
Г
(-76%)
0,933
(—7%)
яз
0
31
14
@
2,214
(-34%)
64
27
2,370
(-41
96)
(
)
Я С
С
^ ?
0,137
0,939
я
п
2.
1
-6%)
0
2,311
(—31?
2,493
(-38?
)
)
482
ПРИЛОЖЕНИЕ
Матрица 5I=(
1 2
2 3
1 О
О 1
— 1 —2
4 1
О О
О О
—4
—1
—6
7
4,45
—0,62 ±/ 1,29
0,79
10
A25%)
6
35%
13 3 3)
О 0 0 1 '
0 3 0 0
[0400
—1
—4
4
О
2
1
О
—2
10
(~400%Т
Л+/ О
/ 1+
^ 0 1
I
— i
i
2 + 3/
1—4/
-2 + /
1+2/
52%
3
C4%)
Л
+г О
i -1+/
О 3
3/
1
/±/2
4
F6%)
3+/2
(83%)
') Например, для первой, матрицы характеристическое уравнение имеет
ТАБЛИЦЫ 483
Таблица IX (продолжение)
О
i
—4
-5
У2
« 6,481
не проходит
яз 8,66
(+94%)
—/32"
яз —5,66
не проходит
1
/56
в 0,134
0,134
(—83%)
—8
—10
У4
ss 7,35
:« 8,28
не проходит
— /53
и —7,28
не проходит
@%)
/2 — 2 —1
3
+34%
не проходит
!в 3,41
(+52%)
—1
не проходит
4 ук
« 0,497
(-50%)
0,504
(-50%)
—2 /2 — 3
не проходит
х 4,123
(+71%)
УГ2
s; 4.88
(+102%)
1—/12"
и —2,46
не проходит
2
If
0,118
0,118
—71%
вид _
Таблица X
Сравнительный обзор задач на собственные значения для матриц, дифференциальных
и интегральных уравнений
Предмет
Сравниваемые
объекты
Матрицы
Матрицы
91
аз
—
=
Векторы
и =
«1
U2
ап о12 . ..
^21 ^22 • * •
апХ ап2 ...
Ь21 #22 •••
*
^0; b =
.
•
V\
v2
Vn.
¥=0
Дифференциальные уравнения
Линейные дифференциальные опе-
операторы
т
» У1 f (v) ^ ■
N x\g {х) dV ■
при краевых условиях
и„ [у] =
= 2 («vy(v)(«)+Pvy(v)W) =0;
1 v = o Jp
р= 1, 2 т
Функции сравнения
и(х)фО; v(x)^Q
«-кратно дифференцируемы и удо-
удовлетворяют краевым условиям
Интегральные уравнения
Ядра
К {х, 1); L {х, 1)
Функции сравнения
и (х) ^0; v (х) ф. 0
1
Симметричность
Антисимметрич-
Антисимметричность
Эрмитовость
Я = Ж' или и'Яй —
— Ь'Яи = 0 для любых
векторов u, и
Я = — Я' или и'Яи -(-
+ й'Яи =0
Я = Я' или u'Slb —
— й'Яц = 0
Самосопряженность
b
[ (ыА1
для любых
b
[ (иМ
J
а
ъ
[ (аМ
J
а
м
[v]—vM
функций
[v] + vM
[v] — vM
т
[u])dx = Q
сравнения и
[a]) dx = Q
[a]) dx = 0,
эрмитов или комплексно самосо-
самосопряжен
К (х, 1) = /< A, и) или
1 I' (м (л:) /< (.г, |) t> (|) -
J J
— v (х) К (х, 1) а A) ) dx dl = 0
для всех функций сравнения
и, v
К (х, 1) = - /С A, х)
b b
J J (« (JC) /< (JC, I) V (I) +
-(- v (x) К (x, g) и (£)) dx d£, = 0
К (x, l) = K (|, JC)
й 6
J J (« (JC) /< {X, I) V (I) -
a a
— v (x) К (x, |) и (£)) dx dl, = 0
Таблица X (продолжение)
Положительная
определенность
при вещественно-
вещественности
при комплексности
Задача; собствен-
собственное значение Я,
характеристиче-
характеристическое число х = —
Я
Собственное ре-
решение
Собственные зна-
значения веществен-
вещественны, если
или при вещест-
вещественности
Матрицы
tt'Stu >
0
|u|>0
u'Uu > 0
J ИЛ1
x,s
x2s
xns
r = Я2Х^
к щ
Д'
К'
Дифференциальные уравнения
ь
[ иМ [и
а
Ъ
Г ~п.М [и
]dx> 0,
]dx>0
для любых функций сравнения и
М [у] = Яу
с Up [у] = 0
Уз (х) к Xs
b
r —
М [у] = Хр (х) у;
Р (х) > 0,
Up [у] = 0
ys (x) к Я^
(иМ [v] — vM [и]) dx = Q
а
I" (uM [v] — vM \u]) dx = 0
а
Интегральные уравнения
b b
а а
b Ь
\ и (х) К (х, 1) и (g) dx d\ > 0
для всех функций сравнения и
ь
у (х) = Я I К (х, 1) у (s) dc,
ys (х) к \s
К (х, 1) = К (ё, х)
Унитарность (при
вещественности
ортогональность)
для эрмитовых за-
задач При Xj=^A.£
Нормировка для
эрмитовых задач
Отношение Рэлея
-
(здесь R
Экстремальные свойства
Теорема о разло-
разложении (при веще-
вещественности)
п
= 0
= 1
>щ
< хтах)
собственны}
ь
\lflbdx~Q
а
b
у • у dx = 1
а
b
J уМ [у] dx
Р а
й
Г —
а
ь
\
а
Ь
\
а
р
yrp.ykdx = 0
у ■ р ■ у dx = \
ь
с _
уМ [у] dx
а
Ь
^y-p-ydx
а
. значений см. в общих задачах
со
«W = 2wW;
й
Cj = J у/Ц tfX
а
«(
п
х) = 2 С;'У/ (ХУ<
ь
Z] — У/ри dx
а
для функций сравнения и {х)
й
J У0k dx
а
й
J yydx =
а
b
г
J yWy
D a
b b
J J y(x)K{x,
a a
oo
7 = 1
для истокообразно
мых функций и
\
= 0
1
(x)rfx
1) у A) dx d\
b
Cj = yjU. dx
a
представи-
Таблица X (продолжение)
Теорема включе-
включения
Разложение мат-
матрицы, соответст-
соответственно ядра
При несимметрии
сооственные зна-
значения мнимы, если
Матрицы
п
к — \ ^') ^^"
v> Uj ' Ществ.
(Vj)mln <? *s <■ («/)max
n
(lj нормировано)
si = —sr
Дифференциальные уравнения
Af[u(jc)].
Ф (дг)-веществ.
Фтш < A.s < Фтах
й
М [и (х)] .
р (х) и (х)'
Ф (х) веществ.
С (иуИ [w] + vM [и]) dx = 0
а
Интегральные уравнения
Ф (ri U '■*'
^ W г, >
f /< (х t)u (I) dl
J l • y ^fe; ъ
a
Ф(х) веществ.
Фт1п < &s < Фтах
Теорема Мерсера:
При вещественности
оо
К (х, 1) = У -J- у;- (*) у;- (Е)
(у;- нормировано) сходится абсо-
абсолютно и равномерно, если К
имеет только конечное число
отрицательных собственных зна-
значении
К(х, 1) = — КA, х)
I
Теоремы суммиро-
суммирования для собст-
собственных значений
Задача
Собственные зна-
значения веществен-
вещественны, если
п
i-i
Х~1 9
j-l
= 2а;;
Я нормировано
Щ =
35 =
3t=l
xDr
rfj 0
•
0 dn
'; d;- > 0
(след Щ
о
, если
зеществ.
С помощью
G.21)
М
(ср. выше!)
М эрмитов;
функций Грина, см.
[у] = Ьр(х)у
[у] = 0
и(п) ф 0
р (х) > 0
СО ft
У 4-= f
^ A./ J
/ —1 a
ПО ft
j-l J a
M Г vl = (— 1)"
с Up \y\ = 0
при
ft
/<(
ft
J
a
м
Г „ [gv(n)]{n) dx =
= (-
Одночленный
/И эрмитов;
И<П) Е^ 0
l)r
x, x) dx
K2 (x, I) dx d\
g(x)y[n)\{m
ft
J ga{n)v{n) dx
a
■сласс
g(x)>0
Таблица X {продолжение)
Обобщенная уни-
унитарность (при ве-
вещественности
обобщенная орто-
ортогональность) и нор-
нормировка при
х j фу.^ или Яу=^=Я^
Теорема включе-
включения и теорема о
разложении
Задача
Собственные зна-
значения веществен-
вещественны, если
Матрицы
_, ( 0, j ф k
Дифференциальные уравнения
ft
yjPyk dx = \
Интегральные уравнения
а
справедливы при дополнительных предпосылках
Щ = хЗЗг
ЭГ и 33 эрмитовы; по
крайней мере 9£ или S3
положительно опреде-
определены
1
M [y] = XAf [y]; Up [у] = О
M я N эрмитовы; по крайней мере
М или Af положительно опреде-
определены
ft
J L {х, |) у (Е) dl =
а
ft
= Я. J К (*, £) у (£) ^
а
L н К эрмитовы; по меньшей
мере L или К положительно
определены
Частные задачи
при этом содер-
содержат
Обобщенная уни-
унитарность (при ве-
вещественности
обобщенная орто-
ортогональность) и
нормировка при
ху=^х£ соответст-
соответственно ^фХ^
Отношение
Рэлея R
_, Г 0, ]фк
ij Sk I 1, J = k
ц $Щ (S3—положит.
j/sgj опред.)
N[y]
b
J yjN [у*]
a
b
J yM
D a
K b
jyN
a
(N — положит
= у или ру
dx~{ 1, /.= к
[y]dx
[y]dx
опред.) Amin < R
K(x
=
t
b
I.
a a
n
(K
i) =
( °'
,. 1 l
lim •; -к—,
"I I
b
У}(x) L {x
b b
f Г
1 vW
a a
b b
\ fy»
a a
— ПОЛОЖИТ
a^l< x — e
1) yk (I) dx dl =
_ f 0; у ф к
L (x, l) у (I) dx dl
К {x, l) у (I) dx dl
опред.)
Таблица X (продолжение)
Матрицы
Дифференциальные уравнения
Интегральные уравнения
Экстремальные
свойства 1-го соб-
собственного значе-
значения
Я! = min H
при
* Далее веществ.
Н = Г уМ [у] dx ft ft
s-ro собственного
значения
J yN [у] dx = 1
А'(Х' l)y{l)dxdl
b Ь
при дополнительных условиях (У = 1, 2, ..., s — 1)
J y^V [У/] dx = 1
r, i)
= 0
Минимаксималь-
ный принцип
Куранта:
Xs '= max (min H)
Н нормировано, как и выше, при дополнительных условиях (у = 1, 2, ..., s—1)
£'£;= О,
J у^
ft ft
J
при этом г/, соответственно
), выбираются произвольно и ищется максимум
min ПРИ вариации Гу, соответственно г j (x)
Таблица XI
Выражения конечноразностиого метода для производных
Метод
Обыкновен-
Обыкновенный метод
согласно§21
Метод по-
повышенной
точности
согласно
п. 22.2
Выражения
для
ч'
У
у"
у'»
yIV
У"
Выражение
Сокращения: у^ = у((Л), y^ = y^(ih) и т. д.
У°^Ш(У1~ У-0 +
Уо=-7гтО'1-2>о+>'-1) +
уо = i (у2 - 2У1 + 2У _! - У _2) +
УоУ = -^(У,-4у1 + 6уо-4у_1+у_2) +
)'o = i(->'2 + 8yI-8y_1 + y_2) +
Уо = 5оТ (Хз — 9У2 + 45У1 — 45У-1 + 9У-2 — У-з) +
у" = w(~y2+16yi~30y°+16y-1~y-2) +
Дальнейшие члены при
разложении Тейлора
выражения слева
h a h2 nr
~Yya~Ty° ~ ■•■
h2 m A4 v
" Уо 120 Уо ~ ■ ■ •
6 Уо ~збоУо ""■••
A2 v A4 Vii
4 Уо 4оУо — •••
h\Vl A4vv...
-T- 30 >u I" •••
/j6 vvn4-
40 Уо "^ -" *
-Г 9оУо + •••
Таблица XI (продолжение}
Метод
Метод по-
повышенной
точности
согласно
п. 22.2
Многоточеч-
Многоточечный метод
согласно
п. 22.4
Выражения
для
у"
у'"
y'v
У
У
у">
ylv
Выражение
Сокращения: у^ = у(/Л), У(- = У^(»Л) и т. д.
Уо = -^ BУз - 27у2 + 270У1 - 490у0 + 270у_! - 27у_2 + 2у_3) +
Уо" = -щг (— Уз + 8Уг — 13?! + 13у_! — 8у_2 + у_3) +
yoV = 6F" (~ У.» + 12^ " 39У1 + 5б^о - 39У-1 + !2У-2 - У-з) +
У1 — Уо~у(>'1+>'о) = о +
У1— У_1 — -^ (У1 + 4Уо + yli) = 0 +
У1-2уо + У-1--^0 +ЮУо+)'_1)-О +
-У2-16у1+34Уо-16у_1-у_, + |-Л2Bу;' + 11Уо+2у'11) = О +
У2-2у1 + 2у_1-у_2-^(уГ.+ 2У;" + /:1) = О +
y2_4y1 + 6y0-4y_1 + y_2--^(y'v + 4y'v + yLV1) = 0 +
Дальнейшие члены при
разложении Тейлора
выражения слева
-т£г»?'" + ...
+ — yVI" +
-Г 240 Уо + ■ • •
/г3 /// ,
—Гг-Уо + •■■
"~Wy° + •••
240 у° ^ '- -
92 й8 vVI» О-
3 7! ^ "Г •••
120 У^" + • • •
/г8 vv"'-U
Выражения конечноразностного метода для операторов А и АА
Таблица XII
Метод
Обыкновенный
метод соглас-
согласно п. 23.1
Метод повышен-
повышенной точности
согласно п. 23.3
Многоточечный
метод согласно
п. 23.4
Выражение
Сокращения: г._ ft-z(tt, *Д); Д^ s = (-|L+-Щ^
y-ftft
= -J2-(^»+''», 1 +2-,, о+^о, -1—420, 0) +
Л Л / ^ 1 О ^ 1 ^ \
ааг0, о ^4 1- ^^2 1 dyi)oo
= -^-[20г0, 0—8B,, о + 2о,,+2-1, о+2о, _,)
+ 2 B,, i+Z,, _!+£_!, 1+2_,, _,) +
+ (г0, 2 + 22> о + 2-2, о + 20, _2)] +
А20, 0=-j2^- I" б0г0. 0+16 (гЬ 0+^0, 1+2_ь 0 + 20, -О —
— B2, о + 2о, 2+2-2,о+2о, _2) +
+ 14 B2, о + г0, 2 + 2_2, „ +2о, _2) —
— 77Bl, 0 + 20, 1+2_,,о + 2о, _,) +
—BЬ 2+22, 1+2,, _2+22,-1+2-,, 2+2-2, ,+2_ ь-2+2_2,_,)]+
40z0, о — 8(г,,о + го, i + 2_,,o + 2o, _,) —
— 2 (г,, , + г,, _, + г_,,+, + 2_,,-1)
+ 8А2 А20, о+ А2 (Аг,, о+ А^о, -, + Дг_,, 0 + Аг0, _,) =
14Ого,о—16(г,,0+20,,+г-,,о+го,_1+г,,,4-2!,-,+2_ ы+г-,,-,)
— 3 B2, о + 20, 2 + 2_2, о + 20, -г) +
+ |"^[46Дго,о + Ю(Аг,,о + А2о, , + А2-,,о + А2о, _,) +
+ Дг,, , + Дг,, _, + Дг_,, , + Дг_,, _,] =
Дальнейшие члены при разложении Тейлора
выражения слева; сокращение
/ rji + kz ^ dl + kz \
у = 0
12b0'* 360bUlb 20160Ua '"
h2
"с" (So, 6 + £2, 4) • • •
Ui /N
+ 90 t0>6 ' 1008 feo'8T- •••
+ 4§qA51So, 8 + ^6г2,6 + 30£4,4) 4- ...
-^C£o,6-5S2,4)+...
/,8
1^o-(-23£o,8+42£2>6) + ...
>
m
496
ПРИЛОЖЕНИЕ
Результаты конечноразностного метода
Сетка
Шестигранная сетка, параллельно сторонам ромба
I
Числэ внутренних узловых точек
Шаг
Симмет-
Симметрия
относи-
относительно
1..А-
v; Л Л'
v; ЛЛ2
v; ЛЛ'
v; ЛЛ2
v,- ЛА2
О„ О2
24,82
1; 24
2; 21,3
; 23,24
2,499; 24,06;
2,634; 23,91
„ G,
г! 52,64
—1; 48
О
112л2
= 122,8
- ; 46,07
2; 48 | 2,247; 49.20J
1; 42,7
/13-1
; 56,57
1,662; 64,22,
1; 66,7
1,495; 72,2
— 1; 85,3
/Г-1
; 79,4
1-/5
; 120,6
1; 96
2,029; 63,44
1,860; 74,5
/2 103,6
о„ о2
о,, о.
64л' __
3 ~
= 210,6
-~ ; 143>4|
0,425; 123,5
1,331; 109
-2; 108,7
— 1, 133,3
0,758; 108
1,123; 122,6;
—0,758; 180
1; 130,7
— 1; 192
0,555; 160
=^;177
—0,425; 164,
0,673:
-1-/Г
I 2
154
—1; 192
0,802- 143,5:
—0,802; 249|
О,, 02
g,, а.
— 1,63; 244
—2,493; 264
—'>■ 240
—0,673; 240[
— 1,123; 269
— 1; 261,3
—0,55г); 232|
ТАБЛИЦЫ
для ромбической мембраны из п. 23.5
497
Таблица X111
Шестигранная сетка, по другому
принципу
Треугольная сетка
=1лУз-
=-1 л Уз"
v; ЛЛ2
V; ЛЛ2
v; Л Л2
V; ЛЛ2
v; ЛЛ-'
v; AA'
V; Л Л2
2,7157;
24,23
1; 22,22
2,170; 23,6
И U
U-. 22,79
14
- ; 24,080
3,8951;
24,611
4,6024; 24,734
14-У 2 ;
49,99
— 1; 44,4
1,481; 43,2
1; 42,7
0; 48
2; 51,2
14-/5 ; 52,061
2 221-
66,li
1; 56,9
— _ ; 53,0 -1; 59,29
Y'l I
1; 07,37
2,132; 69,85
2,097; 77,1
0,311; 7d,4
>-pL., 66,24
0,397; 77,96
1,943; 81,37
—1; 114
-1; 85,3
/3 ; 108,2
—0,311; 91
I —1; 1С
105,41
; 115,6
1,594; 120
— 1,481; 127
^-; 105,2
2
V~i
-1,292;
111,7
0,183; 128,0
1,363; 139,7
123
—0,580; 151,1
1,353; 140,5
—2
128
—0,578; 151,0
—2,17; 147
1_/5 ; 172,7
1; 170,7
—1,521; 182,6
-1-VT
186,
0,632; 202
-1,84; 194
—0,800; 324
0,806; 187
/7 — 1; 2i\
—2,307; 212
2,332; 21.!
Результаты конечноразностного метода для треугольной мембраны из п. 23.5
Число внутренних
точек
Точное собствен-
собственное значение
X, = 5я2
Л2 = Юя2
Х3 = 13я2
Х4 =17я2
Хь = 20я2
Х6 = 25я2
Х7 = 26я2
Хь = 29я2
Я,9 = 34я2
Я,ш=37я2
Х,,= 40я2
Х12=41я2
Я,13=45я2
49,3480
96,696
128,31
167,78
197,39
246,74
256,61
286,22
335,57
365,18
394,78
404,65
444,13
1»ЗЛ0В
Собств.
функ-
функция
симм.
ант.
симм.
симм.
ант.
симм.
ант.
симм.
ант.
симм
ант.
симм
симм
1
36
Эбыкнов
3
-4
41,37
64
86,63
енный метод согласно B3.
6
44,10
75
L 1 пп
> ши
125
155,9
10
A«JL
45,646
81,65
108
117,6
144,0
170,4
144
180
206,4
242,4
15
*-т
46,604
85,90
113,1
129,5
156,7
196
168,8
196
223,2
196
235,3
262,5
279
1)
21
*-т
47,23
88,76
116,5
137,7
165,5
207,0
186,7
214,5
256
228,2
256
283,8
297,5
согласно B3.3)
1
1
т
43,5
3
*-т
47,163
80
107,5
6
A—L
О
48,381
89,583
118,26
127,6
156,25
197,5
Конечные выражения
согласно B3.18)
1
-4-
44,471
3
47,763
84,48
106,30
в
*-т
48,700
92,727
118,46
137,41
159,57
190,29
согласно B3.16)
1
47,25
3
л-Т
48,754
88
124,67
Спектры сеточных областей
(до шести внутренних точек включительно)
Таблица XV
1
2
3
4
5
Расположение внутренних
узловых точек (только
топологически различные
случаи)
о
о—о
о-тв-о
п
+
О—О—О—О
Уравнение для v
v = 0
v2 —1 =0
v3_2v = 0
V4 _ 4V2 = 0
V4 — 3v2 = 0
v4 3v2+l—0
v5 — 5v3 + 2v = 0
vs _ 4V3 = о
v5 — 4v3 + 2v = 0
vs _ 4v3 + 3v = 0
Корни v
0
± 1
±VT, о
±2, 0, 0
± Vs, о, о
1 ±/5"
± 2
+ УЪ±Р- °
± 2; 0, 0, 0
± Vе! + V~2, 0
± /37 ± l; о
Числовые значения v,
л 4-v
h2
0
±1
±1,4142; 0
±2; 0; 0
±1,7321; 0; 0
+ 1,6180; +0,6180
+2,1358; +0,6622; 0
+ 2; 0; 0; 0
±1,8478; ±0,7656; 0
±1,7321; ±1; 0
Таблица XV (продолжение)
О
Расположение внутренних
узловых точек (только
топологически различные
случаи)
ш
Н-о
О—О—о—О
&
o—<i—о—о—о
V6-
V6
V6
V6
V6
V6
V6
V*
V*
V*
Уравнение для
-7v<+7v2-l-
— 6v4+4v2 =
— 6v4 + 5v2 =
— 6v4-f6v2 =
— 5v4-f3v2 =
- 5v4-f 4v2 =
-5v4 + 5v2-
— 5v4 -f 5v2 =
^5v4+6v2-
V
= 0
0
1=0
0
0
0
0
1-0
0
1
±
±
±
±
±
±
+
±
Корни
1 ± /2; ±
i ± VW.
V2 '
1
2 cos —=-
V~5\ ± l;
V3±/3l
V
1
k =
0,
0;
n/ 5 ±/13
У 2
2; ± 1; 0;
1 ±/3~
2 cos—=—;
0
* =
п
-i,
0
0
o-
o,
= 1,
2, 3
0
0
2, 3
Числое
±2,4142;
±2,2883;
±2,2470;
±2,2361;
±2,1753;
+ 2,0743;
±2; ±1;
±1,9319;
ыа значения V,
4-v
ft2
±1; ±0,4142
±0,8740; 0; 0
±0,8019; ±0,555
±1; 0; 0
±1,126; 0; 0
+ 0,8350; 0; 0
0; 0
+ 1; +0,5176
±1, 9021; ±1,1756; 0; 0
±1,8019;
±1,2470; ±0,4459
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Ахиезер Н. И. и Глазман И М., Теория линейных операторов в гиль-
гильбертовом пространстве, изд 2, «Наука», 1966.
Aronszajn N., Rayleigh—Ritz and A. Weinstein methods for aproximation
of eigenvalues, I, II, Proc. Nat. Acad Sci. 34 A948), 470—480, 594—601.
Bauer F. L., Das Verfahren der Treppeniteration und verwandte Verfahren
zur Losung algebraischer Eigenwertprobleme, Z. angew. Math. Phys., 8
A957), 214—235.
Bauer F. L. und Householder A. S., Absolute norms and characteristic
roots, Num. Math. 3 A96Ц, 241—246.
Б л о х и н ц е в Д. И., Основы квантовой механики, изд. 4, М., «Высшая
школа», 1963.
Borsch-Supan W. und Bottenbruch H., Eine Methode zur Eingren-
zung samtlicher Eigenwerte einer hermiteschen Matrix mit tiberwiegender
Hauptdiagonale, Z. angew. Math. Mech. 38 A958), 169—171.
Borg G., Eine Umkehrung der Sturm — Liouvilleschen Eigenwertaufgabe.
Bestimmung der Differentialgleichung durch die Eigenwerte, Acta Math. 78
A946), 1—96.
Brown well F. H., Extended asymptotic eigenvalue Distributions for bounded
domains in «-space, Z. Math und Mech. 6 A957), 119—166.
Buckner H., Die praktische Behandlung von Integralgleichung (Ergebnisse
der Angewandten Mathematik, Heft 1), Berlin-Gottingen-Heidelberg, 1952, 127.
Bukovics E., Naturliche Eigenwertprobleme bei gewonlichen Differential-
gleichungen, Symposium on the Numerical Treatment of Ordinary Differen-
Differential Equations, Integral and Integro-Differential Equations, Basel, 1960,
355—361.
Causey R. L. und Hengici P., Convergence of approximate eigenvectors
in Jacobi methods, Numer. Math. 2 A960), 67—78.
Dettmar H. K-, Symmetrisierbare Eigenwertaufgaben bei gewohnlichen Dif-
ferentialgleichungen, Z. angew. Math. Mech. 34 A954), 284—287.
Dettmar H. K. und Schliiter A., Praktische Losung von Eigenwertauf-
Eigenwertaufgaben des Hartree—Fockschen Typs, Z. angew. Math. Mech. 38 A958),
220—236.
Diaz J. В., Upper and lower bounds for eigenvalues, Proe. Symp. Appl. Math.
8 A958), 53—78.
F a 1 k S., Einschliefiungssatz fur Eigenwerte und Vektoren normaler Matrizen-
paare, Wiss. Z. Techn. Univ. Dresden 10 A961), 1033—1039.
Гантмахер Ф. Р. и Крейн М. Г., Осцилляционные матрицы, ядра и
малые колебания механических систем, Гостехиздат, М. — Л., 1950.
Гельфанд И. М. и Костю ченко А. Г., О разложении по собственным
функциям дифференциальных и других операторов, ДАН СССР 103
A955), 349—352.
Haas H. L., Bestimmung der Eigenwerte des allgemeinen Eigenwertproblems,
Numer. Math. 2 A960), 341—343.
Heinrich H., Ein inverses Eigenwertproblem fur endliche Matrizen und
seine graphische Losung fur n = 3, Z. angew. Math. Mech. 40 A960),
62—64.
502 ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Householder A. S. und Bauer F. L., On certain methods for expanding
the characteristic polynominal, Numer. Math. 1 A959), 29—37.
Howay G., Biharmonic eigenvalue problem of the semi-infinite strip, Q. of
Appl. Math. 15 A957), 65—81.
Kato Т., On the upper and lower bounds for eigenvalues, J. Phys. §oc. Japan
4 A949), 415—438.
Kato Т., On positive eigenvectors of positive infinite matrices, Commun. Pure
Appl. Math., 11 A958), 573—586.
Klotter K., Analyse der verschiedenen Verfahren zur Berechnung der Tor-
sionseigenschwingungen von Maschinenwellen, Ing.-Arch. 17 A949), 1—61.
Klotter K-, Technische Schwingungslehre, 2 Bd., 2 Aufl, Berlin — Gottin-
gen — Heidelberg, 1960, 483.
Kneschke A., Differentialgleichungen und Randwertprobleme II, Leipzig,
1961, 628, в особенности стр. 436—622.
Kreyszig E., Die Ausnutzung zusatzlicher Vorkenntisse fur die Einschliefiung
von Eigenwerten beim Iterationsverfahren, Z. angew. Math. Mech. 35
A955), 89—95.
Laasonen P., On the simultaneous determination of several eigensolutions
of a selfadjoint system of differential equations, Math. Tables and other
Aids to Computation 15 A959), 13—20.
Lancaster P., A generalised Rayleigh quotient iteration for lambda matri-
matrices, Arch. Rational Mech. Anal. 8 A961), 309—322.
Lauchli P. und Waldburger H., Berechnung von Beulwerten mit Hilfe
von Mehrstellenoperatoren, Z. angew. Math. Phys. 11 A960), 445—454.
L e h m a n n N. J., Beitrage zur numerischen Losung linearer Eigenwert-
probleme, Z. angew. Math. Mech. 29 A949), 341—356; 30 A950), 1—16.
L e h m a n n N. J., Zusammenhang allgemeiner Eigenwertaufgaben bei Diffe-
Differentialgleichungen mit der Integralgleichungstheorie, Z. angew. Math.
Mech. 31 A951), 251—253.
Lotkin M., Characteristic values of arbitrary matrices, Q. of Appl. Math. 14
A956), 267—275.
Magnus K., Schwingungen, Stuttgart, 1961, 251.
Marguerre K., Neuere Festigkeitsprobleme des Ingenieurs, Berlin — Gottin-
gen — Heidelberg, 1950.
Meixner J. und Schafke F. W., Mathieusche Funktionen und Spharoid-
funktionen, Berlin — Gottingen — Heidelberg, 1954, 414.
Moser J., Singular perturbation of eigenvalue problems for linear Differential
equations of even order, Commun. Pure and Appl. Math. 8 A955), 251—278.
Muller H., Uber eine Klasse von Eigenwertaufgaben mit nichtlinearer Para-
meterabhangigkeit, Math. Nachr. 12 A954), 173—181.
Muller P. H. und Kummer H., Zur praktischen Bestimmung nichtlinear
auftretender Eigenwerte, Anwendung des Verfahrens auf eine Stabilitats-
untersuchung, Z. angew. Math. Mech. 40 A960), 136—143.
H а й м а р к М. А., Линейные дифференциальные операторы, ГИТТЛ, 1954.
Nitsche J. A., Einfache Fehlerschranken beim Eigenwertproblem symmetri-
scher Matrizen, Z. angew. Math. Mech. 39 A959), 322—325.
Nitsche J. A., Fehlerschranken bei Eigenwertproblemen normalisierbarer
Matrizen, Z. angew. Math. 31 A961), 320—324.
Osborne M. R., ^-Extrapolation in eigenvalue problems, Quart. Mech. and
Appl. Math. 13 A960), 156—168.
О s trow ski A. M., On the convergence of the Rayleigh quotient iteration
for the computation of the characteristic roots and vectors. 6 работ в Arch.
Rational Mech. Anal. A957—1960), 1:233—241- 2:423—428- 3:325—340;
3 : 341—347; 3 : 472—481; 4 : 153—165.
Payne L. F., Inequalities for eigenvalues of supported and free plates, Q. of
Appl. Math. 16 A958), 111—120.
Pf liiger A., Stabilitatsprobleme der Elastostatik, Berlin, 1950.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА 503
Redheffer R. M., Maximum principles and duality, Monatsh. Math. Wien
62 A958), 56—75.
Rutishauser H., Bestimmung der Eigenwerte und Eigenvektoren einer
Matrix mit Hilfe des Quotienten — Differenzen — Algorithmus, Z. angew.
Math. Phys. 6 A955), 387—401.
Rutishauser H., Ein quadratisch konvergentes Verfahren zur Eigenwert-
bestimmung bei unsymmertrichen Matrizen. I, Z. angew. Math. Phys. 12
A961), 568—571.
S a g a n H., Boundary and eigenvalue problems in mathematical physics, New
York —London, 1961.
Schmeidler W., Vortrage liber Determinanten und Matrizen, Berlin, 1949.
Schmeidler W., Integralgleichungen mit Anwendungen in Physik und Tech-
nik, Leipzig, 1950.
Schnell W., Berechnung der Stabilitat mehrfeldriger Stabe mit Hilfe von
Matrizen, Z. angew. Math. Mech. 35 A955), 269—284.
Schonhage A., Zur Konvergenz des Jacobi — Verfahrens, Num. Math. 3
A961), 374—380.
Schroder J., Fehlerabschatzungen zur Storungsrechnung fur linearen Eigen-
wertprobleme bei gewohnlicher Differentialgleichungen, Z. angew. Math.
Mech. 34 A954), 140—149.
Schroder J., Storungsrechnung bei Eigenwert- und Verzweigungsaufgaben,
Arch. Rational Mech. Anal. 1 A957—1958), 436—468.
Stiefel E. und Ziegler H., Naturliche Eigenwertprobleme, Z. angew. Math.
Phys. 1 A950), 111—138.
S z a b о J., Hohere technische Mechanik, 3 Aufl., Berlin — Gottingen — Heidel-
Heidelberg, 1960.
Szego Q., Inequalities for certain eigenvalues a membrane of given area,
J. Rat. Mech. Anal. 3 A954), 343—356.
Tithmarsch E. C, Eigenfunction expansions, Oxford, 1 A946), II A958).
T и т ч м а р ш Е. С, Разложения по собственным функциям, связанным
с дифференциальными уравнениями второго порядка. ИЛ, т. I, 1960;
т. II, 1961.
Unger H., Nichtlineare Behandlung von Eigenwertaufgaben. Z. angew. Math.
Mech. 30 A950), 281—282.
Unger H., Zur Praxis der Biorthonomierung von Eigen- und Hauptvektoren,
Z. angew. Math. Mech. 33 A953), 321—331.
Weinberger H. F., Upper and lower bounds for eigenvalues by finite diffe-
difference methods, Commun. Риге and Appl. Math. 9 A956), 613—624.
W e i n e 1 E., Torsionsbeulung eines Plattenstreifens, Z. angew. Math. Mech. 36
A956), 293—296.
Weinstein A., Bounds for eigenvalues and the method of intermediate
problems. Proc. Internat. Conference on Partial Diff. Equations, Math.
Reserach Center Madison, Wise, USA, 1961.
Wetter I ing W., Zum Einschliefiungssatz von Kryloff — Bogoliubov fur
Eigenwertaufgaben bei gewohnlichen Differentialgleichungen, Num. Math.
2 (I960), 18—21.
W i e 1 a n d H., Die Einschliefiungssatze von Eigenwerten normalen Matrizen,
Math. Ann. 121 A949). 234—241.
Wieland H., Einschliefiung von Eigenwerten hermitescher Matrizen naeh
dem Abschnittverfahren. Arch. Math, 5 A954), 108-114
Wittmeyer H., Berechnimg einzelner Eigenwerte eines algebraischen linea-
linearen Eigenwertproblems (lurch Storiteration, Z. angew. Math. Meeh. 35
A955), 441—452.
Ziegler H., Knickung gerader Stabe unter Torsion, Z. anaew. Math Phys.
3 A952), 9<i—119.
Zurmuhl R., Matrizen- Eine Ddrstellung fQr lngenieure, иад. 2, Benin, 1958.
Л. Коллатц
ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
(с техническими приложениями)
М., 1968 г., 504 стр. с илл.
Редактор И. А. Маркузон
Техн. редактор С. Я- Шкляр
Корректоры Н. Д. Дорохова, Г. И. Иванова
Сдано в набор 25/XI 1967 г. Подписано к пе-
печати 25/V 1968 г. Бумага бОХЭО'/щ. Физ. печ. л. 31,5.
Условн. печ. л. 31,5. Уч.-изд. л. 30,1. Тираж 18400 экз.
Цена книги 2 р. 37 к. Заказ Ws 1002.
Издательство «Наука».
Главная редакция
физико математической литературы.
Москва, В-71, Ленинский проспект, 15
Ленинградская типография № 2
имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров
СССР. Изм.-.йловский пр.. 29.