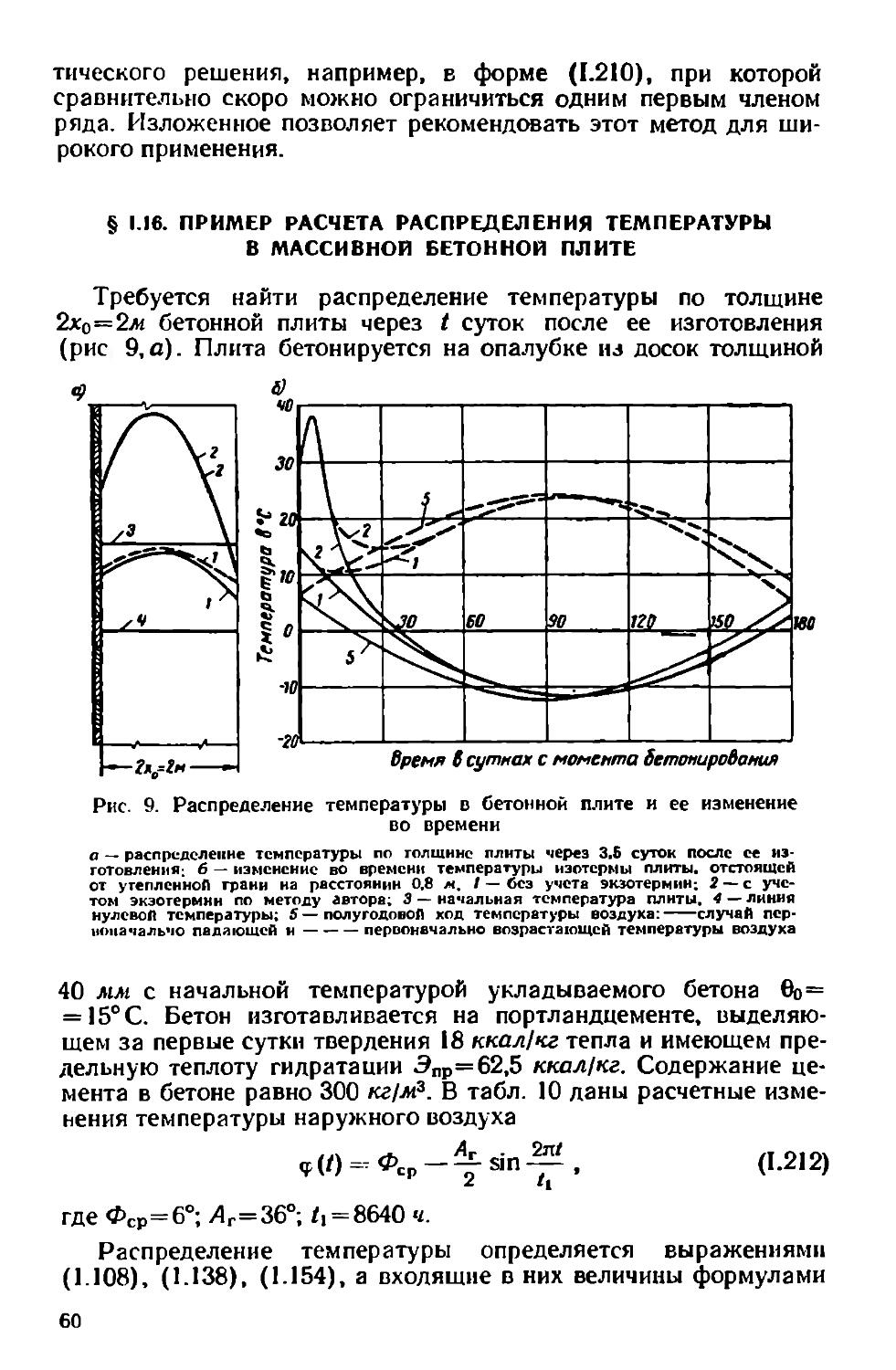
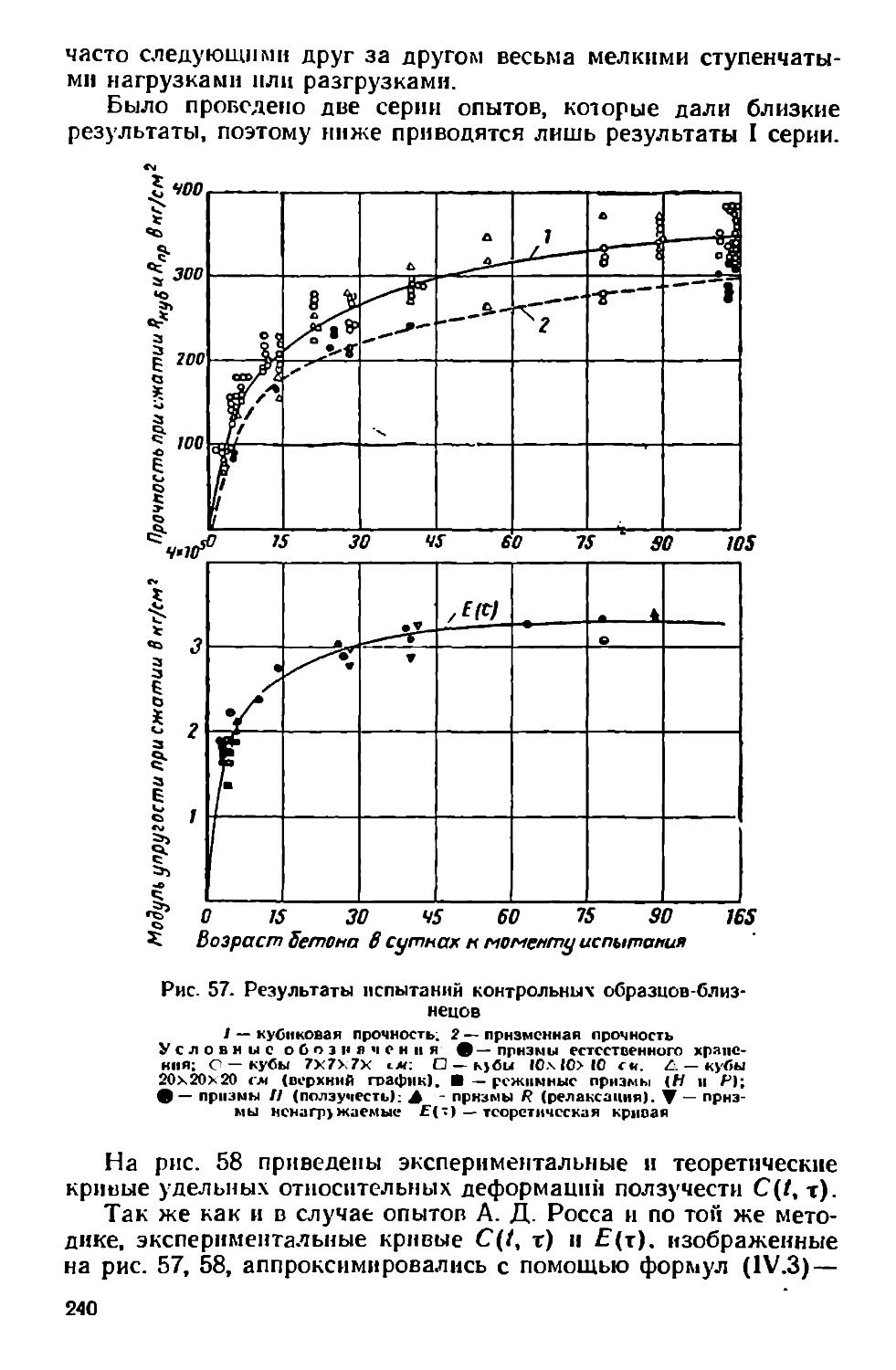
Author: Александровский С.В.
Tags: строительство инженерных сооружений железобетонные конструкции
Year: 1966
Text
£
< »*
БЕТОННЫХ .
И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
НА ТЕМПЕРАТУРНЫЕ 'И ВЛАЖНОСТНЫЕ ВОЗДЕЙСТВИЯ (С УЧ1ТОМ ПОЛЗУЧЕСТИ] < ”
f * * X-.. . - . ч .
..
г ;
. ;
'•A'
С. В. АЛЕКСАНДРОВСКИЙ д-р техн, наук
РАСЧЕТ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ
КОНСТРУКЦИЙ НА ТЕМПЕРАТУРНЫЕ И ВЛАЖНОСТНЫЕ ВОЗДЕЙСТВИЯ (С УЧЕТОМ ПОЛЗУЧЕСТИ)
СТРОЙИЗДАТ— 1966
УДК 624 012.3/.4.042 S
Книга посвящена весьма важной для строительства проблеме расчета бетонных и железобетонных конструкций на температурные н влажностные воздействия, с учетом ползучести.
На основе наиболее прогрессивной отечественной теории ползучести Г. Н. Маслова — Н. X. Арутюняна (теории упруго-ползучего тела) разработаны точные и практически удобные методы расчета этих конструкций с учетом ползучести на температурные и усадочные напряжения, соответствующие требованиям новых норм проектирования СНиП П-В.1-62 и СН 55—59.
Рассмотрен ряд практически важных инженерных задач о расчете распределения температуры и влажности и напряженно-деформированном состоянии брусьев (балок), плит, слоя (бесконечного полупространства), бетонных блоков, вызываемом изменениями их температуры и влажности. Особое внимание уделено повышению практической ценности получаемых при этом решений.
Приведены результаты больших экспериментальных исследований ползучести, влажностных и температурных деформаций бетона, а также температурно-усадочных напряжений в нем.
Книга содержит богатый иллюстративный материал и необходимые числовые примеры расчета, отвечающие требованиям новых норм проектирования обычных (СНиП П-В.1-62) и гидротехнических (СН 55—59) бетонных и железобетонных конструкций. Приводятся таблицы, облегчающие труд инженера, а также обширная библиография по рассматриваемой проблеме.
Работа представляет большой интерес для инженеров-строителей проектировщиков бетонных и железобетонных конструкций гражданских. промышленных и гидротехнических сооружений, мостостроителей, а также научных работников и аспирантов, работающих в области теории железобетона, теории ползучести и теории тепло- и влагопередачи в бетоне и тепловой обработки железобетонных конструкций.
ПРЕДИСЛОВИЕ
В обычных условиях работы бетонные и железобетонные конструкции неизменно подвергаются воздействиям не силового характера, вызывающим изменения их деформированного состояния, или, как говорят, претерпевают вынужденные деформации.
К вынужденным деформациям относятся деформации, связанные с изменением температуры и влажности бетона вследствие отсутствия термогигрометрпческого равновесия с внешней средой (разогрев от экзотермпи и последующее остывание, усадка, набухание, периодические изменения температуры и влажности, связанные с годовым циклом температуры и влажности воздуха), смещением (осадкой) опор, искусственным перераспределением усилий и т. п. Без учета возникающего при этом напряженно-деформированного состояния не возможен надежный и экономичный расчет бетонных п железобетонных конструкций гражданских, промышленных и гидротехнических сооружений. Он особенно необходим в связи с устранением излишних коэффициентов запаса при расчете этих конструкций на прочность, жесткость и трещи нестойкость по новым действующим нормам СНпП II.В. 1-62 и СН 55—59.
Изучение напряженно деформированного состояния, вызываемого вынужденными деформациями, требует учета изменчивости во времени физико-механических свойств бетона, а также его ползучести. Это связано с тем, что вынужденные деформации часто возникают в молодом возрасте бетона, с другой стороны, их действие обычно сохраняется весьма длительное время. Существенной же особенностью этих деформаций является то, что вызываемые ими напряжения, независимо от их величины, вследствие ползучести бетона обычно значительно уменьшаются во времени, даже в области линейной ползучести, в то время как напряжения, вызываемые действием внешней нагрузки, в этой области практически не изменяются и действие ползучести сказывается лишь на перемещениях (деформациях) конструкций.
Исследованию напряженно деформированного состояния бетонных и железобетонных конструкций при наличии вынужденных деформаций и при учете ползучести бетона и посвящена настоящая работа, при этом основное внимание в ней уделено температурным и влажностным напряжениям.
3
Это исследование проведено для стадий возведения и эксплуатации конструкций и сооружений, поэтому в монографии рассматриваются только задачи, связанные с устойчивым деформированием, характеризующимся затуханием скорости деформаций ползучести. Кроме того, имеется в виду линейная зависимость между напряжениями и деформациями бетона как упругими, так и полными, определяемыми с учетом ползучести.
В соответствии с этим также принято допущение о равенстве и постоянстве коэффициентов поперечной деформации: упругой Vjft) и деформации ползучести тъЦ, т) : vi(t) =v’2(/, r)=const. По малости vj(t) и v2(/,t) это допущение приводит к незначительным погрешностям.
Учтено также старение бетона, т. е. изменение с возрастом сю модулей упруго-мгновенных деформаций £(т) и G(t), а также меры ползучести Cv(t, т).
Указанные важные свойства бетона, т. е. его старение и наследственность, наиболее полно учитывает современная и наиболее совершенная теория ползучести — теория упруго-ползучего тела (наследственная теория старения) Г. Н. Маслова — Н. X. Арутюняна. На основах этой теории, но с учетом новых, более совершенных наследственных функций бетона, предложенных автором, в монографии рассмотрен ряд практически важных задач о напряженно-деформированном состоянии бетонных и железобетонных конструкций, вызываемом вынужденными деформациями бетона.
Особое внимание уделено задачам теории тепло- и влагопро-водности бетона при наличии источников тепла и стоков влаги, интенсивность которых зависит от температуры, а также упругомгновенным задачам теории упругости тел с модулями E(t) и <7(/), зависящими от возраста бетона. Полученные в монографии решения таких задач необходимы для исследования напряженно-деформированного состояния бетона, вызываемого изменениями температуры и влажности, с учетом ползучести на основе известного принципа Вольтерра — Н. X. Арутюняна.
Специальное исследование посвящено учету температурно-влажностных воздействий при расчете железобетонных конструкций при наличии трещин и без них в соответствии с новыми действующими нормами СНиП П-В.1-62.
ГЛАВА I
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ БЕТОНА
Решению задач о термонапряженном состоянии бетонных и железобетонных конструкций должно предшествовать определение температурных полей, возникающих в них в результате внешних температурных воздействий, отсутствия термометрического равновесия с окружающей средой и экзотермии бетона. Процесс диффузии тепла во влажном бетоне при этих условиях весьма сложен, так как наряду с теплообменом в нем происходит массообмен при наличии фазовых превращений. В результате этого тепловые потоки слагаются из двух составляющих: кон-дуктивной (перенос тепла за счет теплопроводности) и конвективной (перенос тепла движущейся жидкостью).
С другой стороны, потоки влаги в бетоне, переносящие тепло, в свою очередь, состоят из составляющей, связанной с влагопро-водностью, и составляющей, связанной с термовлагопровод-ностью, обусловленной неравномерным распределением температуры по объему высыхающего тела.
В аналогичных условиях находятся все влажные капиллярно-пористые коллоидные тела во время высыхания и особенно в процессе их искусственной сушки при высоких температурах. Основные законы переноса тепла и массы вещества в таких телах были сформулированы А. В. Лыковым [108], [109], которым предложена и теория тепло- и массообмена в процессе сушки материалов, не обладающих экзотермией. Эта теория вполне может быть применена и к бетону.
Однако в обычных условиях работы бетонных и железобетонных конструкции, которые мы и будем иметь в виду, температура и влажность бетона изменяются незначительно. Во всяком случае его температура редко превышает 60° С, и при том время, в течение которого сохраняются в нем наибольшие из наблюдаемых температур, непродолжительно. При этих условиях можно (это подтверждено рядом экспериментов [80], [55]) пренебречь влиянием составляющей теплового потока, связанной с переносом тепла движущейся жидкостью, и, соответственно, со-
5
ставляюшей потока влаги, обусловленной явлением термовлаго-проводности.
Куда более важным в этом случае является учет внутренних источников тепла, а именно экзотермии гидратируемого цемента, и внутренних стоков влаги, т. е. химического связывания свободной воды, интенсивность которых существенно зависит от температуры. Вопрос об интенсивности связанного с этим тепловыделения в бетоне и степени возможного разогрева последнего рассмотрен в § 1.4, 1.15 и 1.16, где показано, что они могут быть довольно значительными. Учтя эти обстоятельства, мы приходим к уравнениям теплопроводности (1.2) и влагопроводности (II.2), которые подробно и исследуются в дальнейшем.
Теории теплопроводности бетона в такой постановке без учета и с учетом экзотермии посвящены работы С. В. Александровского [3, 4, 6], Г. Д. Вишневецкого [57], А. А. Гвоздева [63], [65], Б. Г. Коренева [99—101], А. В. Лыкова [107], С. А. Миронова [124], Ю. А. Нплендера [134, 137], К. Ф. Фокина [187], В. М. Штейнберга, И. Е. Прокоповича и И. В. Гольдфарба [210], [211], С. А. Фрида [196] и многих других авторов.
Ниже рассматривается общая задача теории теплопроводности бетона при внутренних распределенных по объему тела источниках тепла, интенсивность которых зависит от температуры процесса
Получено соответствующее дифференциальное уравнение теплопроводности, одинаково пригодное как для положительных, так и отрицательных температур, и разработан аналитический метод его интегрирования. Этот метод, названный методом дополнительных фиктивных источников тепла, в случае переменных во времени граничных условий не требует применения теоремы Дюамеля и приводит к повышенной сходимости решений, полученных на его основе. Последнее обстоятельство очень важно для решения задач о термонапряженном состоянии неравномерно нагретых твердых тел.
§ 1.1. ТЕПЛОПРОВОДНОСТЬ. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ БЕТОНА
При неравномерном распределении температуры по объему тела его менее нагретым частям непрерывно передается тепло более нагретых зон. Такая передача тепла называется теплопроводностью.
У ряда материалов (например, у древесины) теплофизические свойства, связанные с теплопроводностью, изменяются от точки к точке по объему тела, а сама теплопроводность в одних направлениях лучше, чем в других. Теплофизические свойства материалов изменяются также в зависимости от их температуры. Однако в большинстве практически важных случаев эти изме-ь
нения не велики, поэтому обычно эти свойства считают независящими от температуры.
У некоторых материалов тепловой поток не только является следствием внешнего воздействия (нагрев или охлаждение), но связан также со свойством материала выделять или поглощать тепло. Примером может служить бетон, выделяющий в процессе твердения значительное количество тепла вследствие экзотермической реакции гидратации цемента. Это обстоятельство в больших массах бетона приводит к его разогреву и часто нежелательному появлению температурных трещин.
В дальнейшем мы и будем рассматривать тела, материал которых обладает экзотермией, имея в виду в первую очередь бетон. При этом будем считать последний однородным и изотропным телом с теплофизическимп свойствами, не зависящими от времени (возраста бетона) и температуры.
Первое из этих предположений носит условный характер. Однако хаотичность размещения заполнителей в бетоие позволяет думать, что он в больших объемах в общем является однородным и изотропным. Что касается остальных из перечисленных допущений, то они будут рассмотрены в § 1.3.
В теории теплопроводности показывается [93], что величина теплового потока в единицу времени через единицу площади поверхности в данной точке тела равна
Qy = -l~, (1.1)
dv
где Ф(х, y,z,t)—температура тела, X— коэффициент теплопроводности материала, v — внешняя нормаль к рассматриваемой поверхности.
Рассматривая условия теплопередачи через элементарный объем тела, с помощью выражения (1.1) можно получить следующее дифференциальное уравнение теории теплопроводности бетона [4]:
= (1.2)
di ус dt
в котором: ат — коэффициент диффузии тепла (коэффициент температуропроводности), равный
= —, (1.3)
у с
X — коэффициент теплопроводности; с— удельная теплоемкость; у — плотность бетона; Ц — содержание цемента в бетоне; Э — количество тепла, выделяемое к рассматриваемому моменту времени весовой единицей цемента.
Уравнение (1.2) представляет собой уравнение теплового баланса элементарного объема бетона и является основным в теории теплопроводности.
1
В общем случае температура бетона является функцией времени и всех трех координат точек тела. При этом мы будем иметь трехмерную по координатам задачу теории теплопроводности, решение которой определяет пространственное температурное поле в нем. Из общего случая пространственной задачи могут быть получены частные случаи плоской и линейной задач, осевой или полярной симметрии, соответствующие часто встречающимся задачам, в которых температурные поля зависят только от двух или только от одной координат. Некоторые из них мы рассмотрим в дальнейшем.
Решение основной задачи теории теплопроводности об отыскании температурной функции <P(x,y,z, t) требует интегрирования дифференциального уравнения (1.2) при граничных и начальном условиях, определяющих соответственно тепловой поток на поверхности тела и распределение температуры по его объему в начальный момент времени, и при заданном законе тепловыделения в бетоне Э(х, у, г, t) от экзотермии цемента. Для практического же использования решений этой задачи необходимо располагать численными значениями ряда коэффициентов, характеризующих собой теплофизнческие свойства бетона.
§ 1.2 ГРАНИЧНЫЕ И НАЧАЛЬНОЕ УСЛОВИЯ
Из встречающихся видов граничных условий наибольший практический интерес представляет случай свободного теплообмена на поверхности тела с подвижной средой (вода, воздух). Температура среды, окружающей тело, может изменяться по определенному закону, определяемому некоторой заданной функцией <р(/) времени Z. В этом случае потеря тепла с единицы поверхности тела в единицу времени пропорциональна разности температур поверхности и среды вблизи поверхности, т. с.
<?. = °нт1ф —*(01- (1.4)
Коэффициент пропорциональности ант в этом уравнении носит название коэффициента теплопередачи и зависит от формы тела, состояния и температуры его поверхности, а также ряда других факторов. Так как на поверхности тела тепло не может накапливаться, то количества подводимого к ней тепла (1.1) и тепла теряемого (1.4) равны между собой. Приравнивая выражения (1.1) и (1.4), получаем следующее граничное условие для рассматриваемого случая теплообмена с подвижной средой:
-^-+Л(Ф-ч>(0] =0. (1.5)
О V
В уравнении (1.5) величина
h - (1.6)
А>
8
представляет собой относительный коэффициент теплопередачи. Этот вид граничных условий встречается наиболее часто, и мы будем в дальнейшем им широко пользоваться, имея в виду свой заданный закон изменения температуры (0 со стороны каждой отдельной координатной поверхности с нормалью v, ограничивающей тело. Аналогичным образом могут быть получены выражения и для других видов граничных условий, встречающихся в приложениях.
Если поверхность тела поддерживается при заданной температуре ф(0, то граничные условия на этой поверхности имеют вид
Ф-=<р(0. (1.7)
Если поверхность тела непроницаема для тепла, то на ней
Отмети^, что граничные условия (1.7) и (1.8) являются частными случаями более общего условия (1.5) и получаются из него соответствующим предельным переходом.
Действительно, при бесконечно большом ацТ температура на поверхности тела будет мгновенно следовать за изменениями температуры внешней среды. Устремляя поэтому в уравнении (1.5) h ->со, мы и получим граничное условие для этого случая в виде (1.7).
Если поверхность тела непроницаема для тепла, то, независимо от Ф и <р(0, в уравнении (1.4) Q должно быть равно 0. Чтобы удовлетворить этому условию, мы должны положить в нем аТн=0. Устремляя поэтому в уравнении (I 5) h -> 0, мы получаем граничное условие для этого случая в виде (1.8).
Возможность указанных предельных переходов избавляет нас от необходимости в дальнейшем рассматривать особо задачи с граничными условиями (1.7) и (1.8). Достаточно будет получить лишь решения ряда задач с граничными условиями вида (1.5). Решения же аналогичных задач с другими граничными условиями мы получим из найденных решений, осуществив в них соответствующий из указанных предельных переходов.
При решении ряда нестационарных задач теории теплопроводности часто встречается случай утепления грани тела слоем термоизоляции; ее роль, например, может играть опалубка. Теплообмен на такой грани может быть оценен при помощи некоторого условного коэффициента теплопередачи оНт , равного [4]
а\=——, (1.9)
ИТ 4 । л „ ’ \
где Хт и бт — соответственно коэффициент теплопроводности и толщина термоизоляции, а ант — коэффициент теплопередачи на открытой поверхности.
9
Анализируя формулу (1.9), мы видим, что при 6т=0 (термоизоляция отсутствует) ант =ант- В этом случае имеет место свободный теплообмен на поверхности бетона. При 6Т= со (идеальная нетеплоемкая изоляция) атн=0. В этом случае поверхность раздела непроницаема для тепла. Для промежуточных значений 6Т каждого вида термоизоляции может быть построена кривая а*т =/(6т), представляющая собой ветвь гиперболы, асимптотой которой является ось бт.
Таким образом, при отыскании нестационарных температурных полей бетонных тел сложные граничные условия на их утепленных гранях практически могут быть заменены граничными условиями свободного теплообмена при некотором условном коэффициенте теплопередачи аНт, определяемом по формуле (1.9) и являющимся функцией толщины термоизоляции и ее теплозащитных свойств.
Начальное условие определяет распределение температуры бетона по объему тела в некоторый момент времени, принятый за начало отсчета. Оно может быть задано в виде некоторой непрерывной функции координат точки
Ф = /(х,у, z) при t 0. (1.10)
Это соответствует ряду практических задач, с которыми приходится иметь дело в приложениях. Имея, однако, в виду бетон, укладываемый в момент tu принятый за начало отсчета времени (Л=0), отметим, что в рассматриваемом случае начальное условие (1.10), записанное нами в общем виде, не имеет смысла.
Действительно, невозможно представить себе, чтобы бетонная смесь, перемешанная в бетономешалке и быстро уложенная в опалубку, имела бы температуру, неравномерно распределенную по объему тела при пока еще отсутствующей экзотермнп. Поэтому правильная постановка начального условия (1.10) в этом случае приводит нас к следующей его форме:
Ф 0о — const при t- 0, (1.11)
где 0о —начальная температура укладываемой бетонной смеси. Это начальное условие мы и будем иметь в виду в дальнейшем при определении температурных полей в молодом бетоне. Условием же (1.10) следует пользоваться только в случае необходимости расчета распределения температуры, вызываемого внешними воздействиями, возникающими в момент времени /2. условно принимаемым за новый нуль отсчета времени, когда тепловыделение в бетоне практически уже закончилось. Задачи подобного рода хорошо изучены в курсах классической теории теплопроводности [93], [107], и мы их здесь рассматривать не будем. При необходимости воспользуемся ими в их готовом виде.
ю
§ 1.3. ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА БЕТОНА
В уравнениях теории теплопроводности и решениях ее задач фигурируют следующие теплофизические характеристики бетона, знание которых для использования этих решении в приложениях необходимо: коэффициент теплопроводности X; коэффициент температуропроводности ат; удельная теплоемкость с; коэффициент теплопередачи амт; плотность у, относительный коэффициент теплопередачи h. Эти характеристики не являются, как известно, независимыми друг от друга и связаны соотношениями (1.3) и (1.6).
Коэффициент теплопроводности X (ккал/м • ч-град) определяет стационарные процессы теплопередачи в бетоне и представ ляет собой количество тепла (ккал), протекающее в единицу времени (ч) при установившемся тепловом режиме через единицу площади изотермической поверхности (м2), при единичном температурном градиенте (град/м).
Коэффициент температуропроводности а-; (м2/ч). наоборот, характеризует нестационарный режим теплопередачи в бетоне и выражает собой количество тепла (ккал), протекающее в единицу времени (ч) при неустановившемся тепловом режиме через единицу площади (м2) поверхности равного удельного теплосо-(ккалi чл \ ---------------------------------------------------/ '
Представляет также интерес удельная теплоемкость бетона с (ккал/кг• град), равная количеству тепла (ккал), необходимого для повышения температуры весовой единицы тела (кг) на 1°
Коэффициент теплопередачи с открытой поверхности в окружающую среду ант (ккал/м2 • ч*град) характеризует собой суммарный теплообмен на поверхности тела, максимальную роль в котором играет конвекция. Этот коэффициент представляет собой количество тепла (ккал), отдаваемое бетоном с единицы открытой поверхности (м2) в единицу времени (ч) при единичном перепаде температур поверхности теплообмена и окружающей среды (град).
Плотность у (кг/м3) характеризует степень заполнения объема материала веществом. В теории теплопроводности под плотностью обычно понимают величину, численно равную удельному весу бетона.
Теплофизические свойства бетона (в противоположность такому его свойству, как прочность) практически ие подвержены влиянию химических реакций, сопровождающих непрерывны ! процесс его твердения, а зависят только от вида материалов, составляющих бетон. В соответствии с этим, и это экспериментально установлено, они мало изменяются с возрастом бетона и практически их можно считать не зависящими от него. Наоборот, другие особенности бетона в большей степени влияют на его теплофизические свойства, и можно считать, что, в основном.
и
последние зависят от вида крупного заполнителя, водоцементного отношения и состава бетонной смеси, а также температуры бетона.
На рис. 1 приведены результаты опытов по исследованию влияния типа крупных заполнителей на теплофизические свойства бетона, проведенных в США при строительстве плотины Boulder.
Рис. 1 Зависимость тсплофизических свойств бетона от типа крупного заполнителя
Автором методом ква-зистационарного теплового режима были проведены исследования теплофизических свойств бетонов на отечественных цементе и заполнителях, в которых изучалось влияние на них водоцементного отношения и возраста бетона. Методика этих опытов изложена в работе [12], а их результаты приведены на рис. 2 и 3. С помощью метода регулярного теплового режима было также изучено влияние температуры на теплофизические свойства цементно-песчаного раствора. Методика этих исследований изложена в работе [4]; результаты
опытов приведены на рис. 4.
Исследование влияния
влажности и пористости (объемного веса) бетона на его теп.тофизические свойства проведено А. У. Франчуком, которым составлены таблицы теплотехнических показателей строительных материалов [188]. включающие в себя и соответст
вующие данные для бетона. Некоторые экспериментальные данные о коэффициенте температуропроводности гидротехнического бетона содержатся в работе Ц. Г. Гинзбурга [69]. Обобщая
результаты всех описанных опытов, можно отметить сле-
дующее.
Коэффициент теплопроводности бетона существенно зависит от вида крупного заполнителя. Бетоны на базальтовом и риолитовом заполнителях обладают наннвзшпм коэффициентом теп-лопровотностн. в то время как бетоны на кварцитовом заполнителе отличаются высокими значениями последнего.
12
Рис. 2. Зависимость коэффициента теплопроводности Л, объемной теплоемкости с и коэффициента температуропроводности ат бетона от водоцементного отношения. Сухой бетон состава (по весу) 1:2,1:4,9 на портландцементе активностью 475 кГ/см2.
Рис. 3. Зависимость коэффициента теплопроводности 1 и объемной теплоемкости с бетона от его возраста. Бетон состава (по весу) 1:2,1:4,9 на портландцементе активностью 475 кГ/см3, В/Ц=0А1.
Значения Киев начале опыта приняты за 100%
13
Водоцементное отношение влияет на коэффициент теплопроводности бетона в значительно меньшей степени, чем вид крупного заполнителя. При этом увеличение начального содержания воды в бетоне вызывает уменьшение его коэффициента теплопроводности. Так, при увеличении В/Ц на 32,5% (рис. 2) коэффициент теплопроводности снижается всего на 5,5%.
Рис. 4 Зависимость коэффициента температуропроводности ат и относительного коэффициента теплопередачи Л цементного раствора от температуры Раствор состава (по весу) 1:4,32. В)Ц = = 0,583 на портландцементе активностью 556 кГ/cms
Повышение температуры вызывает увеличение коэффициента теплопроводности бетона и притом в довольно ощутимой степени.
Теплоемкость бетона несколько повышается с ростом В/Ц, но в весьма малых пределах. Так, при увеличении последнего на 32,5% объемная теплоемкость бетона возрастает всего на 3,5% (рис. 2).
Минералогический состав крупного заполнителя оказывает незначительное влияние па теплоемкость бетона. Наибольшей теплоемкостью обладают бетоны па доломитовых заполнителях, а паинизшей—бетоны на кварцитовых и гранитных заполнителях.
Повышение температуры бетопа влечет за собой повышение его удельной теплоемкости; при значительных изменениях температуры это повышение может доходить до 20%, л
Тип крупного заполнителя оказывает значительное влияние на температуропроводность бетона. При этом наивысшей температуропроводностью обладают бетоны на кварцитовых заполнителях, а паннизшей — бетоны па базальтовых заполнителях.
Влияние водоцементного отношения сказывается на температуропроводности значительно меньше, чем влияние вида крупного заполнителя. С увеличением начального содержания воды в бетоне его температуропроводность несколько снижается. При этом повышение В/Ц на 32,5% уменьшает ее всего на 8,5%- При повышении температуры температуропроводность бетона также снижается.
Плотность бетона зависит в основном от удельного веса составляющих его материалов, состава смеси и ее пластичности. Тип заполнителя влияет на плотность бетона через состав смеси и свой удельный вес. Наибольшую плотность имеют бетоны на базальтовом крупном заполнителе. Бетоны на риолитовых заполнителях имеют меньшую плотность. Плотность бетона уменьшается при увеличении ВЩ, поскольку удельный вес воды значительно ниже удельного веса заполнителей. Так как температурное объемное расширение бетона весьма незначительно, то практически можно считать плотность бетона не зависящей от температуры.
Коэффициент теплопередачи с открытой поверхности бетона в окружающую среду а„т изменяется в широких пределах и зависит от характера поверхности тела, его формы, аэродинамических условий, в которых происходит теплообмен, свойств окружающей среды и температуры. Повышение температуры бетона вызывает значительное повышение относительного коэффициента теплопередачи h (рис. 4). В этом же направлении влияет на h и повышение В/Ц. Величина коэффициента теплопередачи ант существенно зависит от подвижности окружающей среды, например, от скорости воздуха. Ряд нормативных документов учитывает это, дифференцируя величину аНт в зависимости от скорости ветра [139].
Возраст бетона оказывает незначительное влияние на его теплофизические свойства. Проведенные исследования [12] на образцах, изолированных от влагопотерь, показали (рис. 3), что коэффициент теплопроводности такого бетона с увеличением возраста последнего снижается всего на 5—7%. Это связано с химическим связыванием воды замеса и происходящими в бетоне новообразованиями. По времени же изменение А исчерпывается 8—10 сутками, после чего теплопроводность невысыхающего бетона практически не изменяется. Изменение объемной теплоемкости бетона с изменением его возраста не превышает 5%.
Описанные выше исследования теплофизических свойств бетона показывают, что повышение температуры приводит к одновременному значительному снижению коэффициента температуропроводности и повышению коэффициента теплопередачи бе
15
тона. Следовательно, при экзотермическом разогреве бетонного массива, с одной стороны, снижается его способность к выравниванию градиентов температуры, с другой стороны, повышается его теплоотдача с открытых поверхностей. Сочетание этих обстоятельств оказывает неблагоприятное воздействие на напряженное состояние массива, повышая неравномерность распределения температуры в нем и способствуя развитию температурных напряжений.
С другой стороны, мы видели, что бетоны с малым В/Ц обладают большей способностью к выравниванию температур по объему, и температурные изменения в них протекают быстрее. По этой причине бетоны с низким водоцементным отношением более выгодны для изготовления бетонных массивов по сравнению с бетонами, имеющими большие ВЩ, с точки зрения величин температурных напряжений, развивающихся в них от экзо-термии цемента. По этой же причине для массивных сооружении выгодно применение медленно твердеющих бетонов, у которых снижение теплопроводности при старении проходит медленнее, и которые, следовательно, обладают большей способностью рассеивать тепло экзотермии в молодом возрасте.
Учитывая, в общем, небольшую изменчивость теплофизических свойств бетона, а также то, что расчет изменений его температуры, особенно при учете колебаний температуры внешней среды, носит довольно гипотетичный характер, в прикладных задачах теории теплопроводности принимают обычно некоторые постоянные осередненные значения характеризующих их коэффициентов, назначаемые по экспериментальным или справочным данным. Так, например, в СН 55—59 [139] на основании описанных выше опытов автора приведены следующие их величины:
м-ч град кг-град
г (112)
„ . п_з л2 ккал ' '
ат 3-10 —; <х11т--20--------------,
ч м~-ч-град
которыми и можно пользоваться при отсутствии специальных экспериментальных данных.
§ 1.4. ЭКЗОТЕРМИЯ БЕТОНА
Давно известно, что известь п цемент при гидратации выделяют значительное количество тепла. В конце прошлого века уже были описаны наблюдения за повышением температуры цементных растворов при их твердении [112]. Позже, когда применение бетонных и железобетонных конструкций значительно возросло, изучение величины и характера теплоты гидратации стало необходимостью. Этого требовала практика зимнего бетонирования и
16
особенно строительства массивных бетонных сооружении, у ко торых вследствие экзотермии обычно наблюдается резко нерав номерное распределение температуры.
В связи с ограничением теплопотерь наружными слоями бе
тона ядро таких сооружении шественно разогревается, что пературных напряжений. Последние, сочетаясь с напряжениями, вызываемыми колебаниями температуры внешней среды, и усадочными напряжениями, связанными с высыханием бетона, часто приводят к нежелательным температурно-усадочным трещинам.
На рис. 5 показано изменение во времени температуры внутри нижней и верхней частей вертикальных ступенчатых блоков бетонной плотины Upper Narrows.
Большая заслуга в изучении экзотермии цементов и бетонов принадлежит советским исследователям. Следует отметить опыты В. С. Лукьянова [105], С. А. Миронова [124, 125], П. Б. Будникова и Л. Г. Гулино-вой [44], В. А. Кинда, С. Д. Окорокова и С. Л. Вольфсона [96], И. П. Еременка [82], С. Д. Окорокова, И. Д. Запорожца и А. А. Пари некого [141], исследования Гипро-цемента по специализации цементов [97—98], а также
в начальный период их жизни су-приводит к развитию больших тем-
Рнс. 5. Изменение температуры бетона внутри плотины Upper Narrows
/ — среднегодовая температура воздуха; 2 — то же, воды
специальные исследования на Днепрострое, Волгострое, строительстве канала имени Москвы и ряде других крупных гидростроек.
Можно считать установленным, что наиболее важными факторами, влияющими на экзотермию бетона, являются: химический и минералогический состав цемента, крупность его помола, температура укладки бетона и окружающей среды, содержание цемента.
В табл. 1 приведены данные В. А. Кинда, С. Д. Окорокова и
17
С. Л. Вольфсона [96] о тепловыделении различных минералов цементного клинкера.
Таблица 1
Тепловыделение минералов портландцементного клинкера
Наимсниванмс минералов Количество выделяемого тепла в кал г в возрасте
3 лисп 7 днем 28 дней 3 месяцев
ЗСаО-А|2О3 141 157,6 208,6 221,7
ЗСаО-SiO» 96,6 109 116,2 124,3
5СаО ЗА12О3 56,5 96.6 171,4 214,5
4СаО- AlsO3Fe_.O3 22,3 59,6 90,3 99,4
2CaO-SiOs 5,1 24,8 39,6 43,9
Наиболее высокой экзотермичностью отличаются минералы СзА, а наиболее низкой — C2S. После трехмесячного возраста только 2CaO-SiO2 дает значительное приращение выделяемого тепла, а остальные минералы не дают существенного увеличения тепловыделения.
Наибольшая теплота гидратации присуща высокоалюминат-ным и высокоалитовым цементам. Наименьшее тепловыделение дают белитовые цементы. Алитовые и браунмиллеритовые цементы по экзогермичности занимают промежуточное место. Так, например, по данным Гипроцемента [97]—[98]. портландцементы с расчетными характеристиками, указанными в табл. 2, дают тепловыделение в соответствии с табл. 3.
Таблица 2
Расчетная минералогическая характеристика клинкеров
Наименование цемента C.S c:s CjA C.AF
в %
Белитовый ... . . . . 24 50 8 11
Алитовый . . . . . . 57 19 6 15
Высокоалитовый ... .... 65 10 6 14
Браунмиллеритовый 69 3 — 23
Высокоалюмииатный . . ... 41 32 15 10
Как следует из данных табл. 3, наибольшее количество тепла в лабораторных условиях выделяется в первые три дня твердения цемента.
С. А. Миронов [125] на основе лабораторных исследований и натурных наблюдений при температурах твердения бетона 15— 20°С рекомендует пользоваться данными о тепловыделении чистых клинкерных цементов в бетонных массивах, приведенными в табл. 4.
18
Таблица 3
Тепловыделение портландцементов
Наименование цементов Абсолютное значение тепловыделения в кал г Интенсивность тепловыделения в<> времени в % Сравнительное тепловыделение различных портландцементов в %
3 лней 28 лней 3 лней 28 дня дней 28 лней
Бслитовый 33 47 63 52 75 100 100 100 100
Алитовый 47 56 67 70 84 100 143 119 106
Высокоалитовый . . . 62 71 81 76 88 100 188 151 129
Браунмиллеритовый . . 51 64 74 69 86 100 155 136 118
Высокоалюминатный . . 61 71 84 73 85 100 185 151 133
Таблица 4
Тепловыделение чистых клинкерных цементов в бетоне в ккал/кг
Сорт цемента Марка цемента Продолжительность тверлення
3 лня 7 лней | 28 дней 180 дней
Глиноземистый (плавленый) 500—600 101 115 125 130
Глиноземистый 400 90 95 100 110
Портландцемент 600 72 90 120 130
» 500 60 75 100 115
400 48 60 80 100
» ...... 300 36 45 60 80
» 200 24 30 40 60
Пуццолановый портландцемент 400 35 45 60 80
» ... 300 25 35 45 60
» 200 20 25 35 45
Песчано-пуциолановый портландцемент 300 20 30 40 60
Введение в портландцемент гидравлических или инертных добавок приводит к снижению абсолютных значений тепловыделения. Величина этого снижения не пропорциональна, а меньше количества введенной добавки. Например, введение в портландцемент 25% диатомита снижает тепловыделение через 7 дней на 5-10% [97].
Удельное тепловыделение портландцемента при введении таких добавок повышается. Так, в указанном случае среднее удельное тепловыделение повысилось на 17—27%. Это объясняется увеличением реагирующей поверхности вследствие разъединения отдельных зерен портландцемента зернами добавки.
и
Топкость помола цемента и температура укладки бетона также влияют на экзотермию. Более тонкий помол цемента и более высокая температура повышают тепловыделение и бетон твердеет быстрее. При низких температурах, близких к температуре замерзания воды, гидратация цемента, а следовательно, и тепловыделение замедляются и практически прекращаются вовсе на период замораживания бетона.
Существенно влияет на величину тепловыделения содержание цемента в единице объема бетона: чем выше последнее, тем больше и эта величина. Большой расход цемента приводит к обильному тепловыделению и значительному повышению температуры, что следует всегда иметь в виду при подборе состава бетона для массивных сооружений.
§ 1.5. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ ПРИ СКОРОСТИ ЭКЗОТЕРМИИ, ЗАВИСЯЩЕЙ ОТ ТЕМПЕРАТУРЫ ПРОЦЕССА
Отыскание температурных полей в бетоне с учетом экзотермии требует задания в аналитическом виде скорости тепловыделения, входящей в правую часть уравнения теплопроводности (1.2).
Поскольку скорость экзотермии существенно зависит от температуры бетона, то и количество выделившегося тепла к данному моменту времени в различных его точках не одинаково. Если в начальный момент твердения бетона тепловыделение одинаково по всему его объему, то в последующие моменты времени вблизи поверхности тела оно начинает отставать от тепловыделения в ядре, поскольку в силу теплообмена распределение температуры по объему тела становится неравномерным. Поэтому функция экзотермии, характеризующая собой тепловыделение в бетоне, оказывается зависящей не только от времени, но и от координат точки Э=Э(х, у, z, t). Представить эту функцию в виде некоторого точного закона, учитывающего все обстоятельства, влияющие па тепловыделение в бетоне, не представляется возможным. Приходится учитывать только главные из них и довольствоваться приближенным выражением для нее, достаточно хорошо описывающим действительную картину тепловыделения в бетоне. С этой целью был сделан ряд предложений С. В. Александровским [4], Г. Д. Вишневецким [57], А. А. Гвоздевым [63], И. П. Еременком [82], И. Д. Запорожцем [85] п другими исследователями.
Понятно, что основным критерием приемлемости принимаемого приближенного выражения для экзотермии должен служить опыт. Так как экспериментально наплучшим образом изучен вопрос о тепловыделении цемента (бетона) в адиабатических условиях, рассмотрим в первую очередь именно этот процесс.
20
В соответствии с известными положениями физической химии скорость реакции гидратации цемента в бетоне зависит от концентрации реагирующих компонентов и особенно от температуры процесса. Поэтому, сочетая закон действия масс с уравнением Аррениуса, можно записать скорость экзотермии в следующем виде:
^=(Э„р-Э(/)|/(0), (1.13)
где Э(/) — количество тепла, выделяемое при гидратации 1 кг цемента к моменту времени t, Эпр—полное количество тепла, выделяемое 1 кг цемента за все время гидратации, а 6 — температура адиабатического процесса. В формуле (1.13) первый множитель можно рассматривать, как условную концентрацию реагирующих компонентов, а второй — как константу скорости, зависящую от температуры.
Выражение (1.13) является весьма гибким и при надлежащем выборе функции f( 6) хорошо описывает процесс адиабатического тепловыделения в бетоне. Оно было предложено А. А. Гвоздевым [63]. Будучи распространенным на неадиабатический процесс тепловыделения в бетоне, это выражение приводит к уравнению теплопроводности относительно температуры процесса Ф 163]
ал
—-^ат^2Ф +Ь/(Ф)е ° , (1.14)
аналитическое решение которого наталкивается на неопреодоли-мые трудности. Кроме того, область применения этого уравнения ограничена случаем неизменно положительных температур процесса на всем рассматриваемом интервале времени.
Практически часто встречается случай, когда бетон, уложенный при положительной температуре и вначале разогревающийся от экзотермии, подвергается затем действию волны холода и неодновременно по объему принимает отрицательную неравномерно распределенную температуру. Такой случай рассмотрен в §1.16. Будучи распространенным на этот случай, уравнение (1.14) может привести к «обратимости» процесса тепловыделения, т. е. к кажущемуся увеличению концентрации реагирующих компонентов. Поэтом} весьма важно, не отступая от экспериментальных данных, найти путь уточнения уравнения (1.14) и, с другой стороны, его упрощения, позволяющий получить аналитическое решение этого уравнения. Такой путь состоит в следующем.
Разлагая неопределенную пока еще функцию f(0) в ряд Мак-лорена и ограничиваясь двумя первыми членами разложения, имеем
/(0)^А + В0, (1.15)
21
где А и В — пока еще произвольные постоянные. Такая линейная аппроксимация функции f(0) вполне достаточна, так какобычно изменение температуры бетона от экзотермии не очень велико. Внося (1.15) в (1.13), находим
Рпр -3(0] [А 4- В0(/)]. (1-16)
Общеизвестно, что при нуле градусов твердение бетона, а следовательно, и тепловыделение в нем практически прекращаются. Для того чтобы удовлетворить этому условию, мы должны в уравнения (1.16) положить постоянную А равной нулю. Таким образом, мы получим
= В 0(0- (1.17>
Решение этого дифференциального уравнения имеет вид
5(0-Э11р[1-е * ] (1.18)
и, следовательно, в случае адиабатического тепловыделения
^--ВЭ^Офе 6 , (1.19)
где 0 (/) — общий интеграл у равнения теплопроводности, соответствующего адиабатическому процессу:
00(1^ = ВЭпг Ц. е (/) е и (1.20)
dt су
Здесь Ц — содержание цемента в бетоне, а С и у — соответственно его удельная теплоемкость н плотность.
Общий интеграл уравнения (1.20), удовлетворяющий начальному
0(/) = 0о при/-0 ~ (1.21)
и предельному
б(/)-011р при / оэ (1.22)
условиям, равен
0 (/) =------^пг-2-----, (1.23)
во + Юф-аде В0-пр'
где В— произвольная постоянная, 0о—начальная температура процесса, а 0пр— предельная температура адиабатического процесса в конце тепловыделения, причем
011р 0..-I (1.24)
22
В справедливости выражения (1.23) нетрудно убедиться непосредственной его подстановкой в (1.20) при учете (1.24).
Внося (1.23) в (1 19), окончательно получаем
£э„рВП|,в(/) 25)
* ~ 61)р 4 6U ( еВ ",||> z — 1)
Проанализируем соответствие этого выражения экспериментальным данным о тепловыделении цементов в бетоне в адиабатических условиях.
Используя зависимость (1.24) по формуле
5(Л ^-Ю(о-е0|, (1.26)
мы можем найти тепловыделение к текущему моменту времени адиабатического процесса. Оно будет равно
. во 4 (Опр- Йо)е пр J
и, следовательно,
*Э(0 = ^пр6оСе~ДПп:1/ (1 98)
Л [0о4 (0Пр-0о)е-В"":‘Т
Нетрудно видеть, что точка перегиба кривых (1.27), пли, что то же, максимум функции (1.28), имеет место при
'‘=7Г|п1гЧ с-29’
О “пр \ М) /
Максимальная же скорость тепловыделения при этом равна
L di Jm.ix (Опр 0и)
В уравнениях (1.27), (1.28) мы имеем три произвольных независимых постоянных — начальную температуру процесса ()„, предельную величину тепловыделения Эпр и параметр В. Как следует из формул (1.27) и (1.28), этот параметр при заданной предельной величине тепловыделения Эпр оказывает влияние лишь на скорость адиабатического процесса и время достижения ею максимальных значений и потому может быть назван параметром скорости адиабатического тепловыделения в бетоне. Таким образом, надлежащим выбором величины этого параметра на основе экспериментальных данных о тепловыделении чистого цемента, или цемента в растворе оандартного состава, можно характеризовать его сорт с точки зрения скорости твердения, т. е. классифицировать цементы на медленно твердеющие, обычные и быстро твердеющие. Надлежащим же выбором величины Э|1р можно характеризовать цемент по предельной величине экзотер
23
мин, т. е. классифицировать цементы на высокотермичпые, обычные и низкотермичные.
С помощью выражений (1.26) и (1.27) для параметра скорости адиабатического тепловыделения цемента в бетоне будем иметь формулу
Рис. 6 Кривые тепловыделения и скоростей тепловыделения цемента в Сетоне при различных его начальных температурах 60 и параметрах скорости тепловыделения В
а — при постоянном В 2 • 10“4 1'градч и переменном 6о : /—•t. — KTC; 2 —6„ 20' С. 3- 0, С; 4 — 6. • 4Сг С; 5 — 6 =50' С; б — при постоянном
6„ 20° С я переменном В- 6 — В 2 • 10—4 1/грод ч; 7 — В=2,5 • I0-4 Цград ч; 8 — В- 3.33 • 10—41/грсд • ч; 9 — В'-5- 10~4 Цград ч
по которой он и может быть всегда найден на основе экспериментальных данных о теплоте гидратации цемента Э(1). Выражение (1.27) наилучшим образом описывает экспериментальный характер адиабатического тепловыделения цемента в бетоне 3(1), если параметр В определен по формуле (1.31) для интервала времени, близкого к моменту времени /| наибольшей скорости адиабатического тепловыделения.
На рис. 6 приводятся кривые (1.27) и (1.28) при различных значениях 6о л В для бетона с удельным весом у=2400 кг/м3 на портландцементе марки 400 с содержанием 300 кг/м3. Удельная
24
теплоемкость бетона с принята равной 0,23 ккал/кг-град, а его предельная экзотермия оценена в 100 ккал/кг (см. табл. 4). Нетрудно видеть, что задание скорости экзотермии в форме (1.28) хорошо согласуется с экспериментальными данными, которые свидетельствуют о том, что при снижении начальной температу-
Рис. 7. Теплота гидратации и скорость тепловыделения портландцемента в растворе, исследованного в § 1.15
/, 2 — теоретические кривые, рассчитанные по формулам
(1.27) и (1.28).
ры бетона 6о выделение тепла замедляется; это же наблюдается и при переходе от быстро твердеющих к медленно твердеющим цементам [82], [96]. Кроме того, кривые, изображенные па рис. 6, хорошо согласуются с экспериментальными кривыми и по своему очертанию (рис. 7).
Перейдем теперь к случаю неадиабатического тепловыделения в бетоне. По аналогии с (1.17) будем считать скорость экзотермии в этом случае пропорциональной, но не температуре процесса Ф, а некоторой функции этой температуры положи
25
тельной при положительных температурах. Так как эга функция рока еще не определена, зададим ее в форме
Г(Ф) = <р(Ф)Ф(/). (1.32)
Тогда мы будем иметь уравнение
= в рпр - э (0] <р(Ф)Ф(о, (1.33)
общий интеграл которого равен
г -в[ <»(«)
5(0 = 3^ [1-е <5 ], (1.34)
и, следовательно,
9 -в(<р(ф)ф<ол
-ВЭ„л(Ф)Ф(/)е » . (1.35)
Кроме того;
—вГ<₽(ф) Ф(ол
Эпр-Э(0 = Эпре * . (1.36)
Нетрудно видеть, что при положительных температурах уравнения (1.35) и (1.36) определяют процесс с затухающими до нуля скоростью и концентрацией реагирующих компонентов. В случае же, когда температура тела под влиянием внешних воздействий в ходе процесса, начиная с некоторого момента времени, становится отрицательной, дальнейшее направление последнего зависит от вида функции <р(Ф) и будет исследовано позже.
Б уравнении (1.33) выражение В [Эпр—Э(/)]<р(Ф) можно рассматривать, как некоторую условную концентрацию реагирующих компонентов, при которой скорость тепловыделения линейно зависит от температуры процесса. Так как в соответствии с формулой (1.17) скорость адиабатического процесса также линейно зависит от его температуры, то на основании выражений (1.19) и (1.35) должно быть
-в|'е(/>л
вэП1,е(/)е °0(0 37)
' “ Ф(0'
-в|<г(Ф)Ф(/)Ш
ЯЭпр<НФ)Ф(Ое 0
Это дает уравнение
—Вf <f (Ф) Ф (О Ш - В [ в (/) л
ф(Ф)е ° = е й (1.38)
26
и начальное условие
<р[ф(0)] = 1 (1.39)
для отыскания функции <р(Ф).
Общий интеграл уравнения (1.38), удовлетворяющий начальному условию (1.39), равен
-Вр(/)Л
Ф (ф) = ------£-2—------------ , (1.40)
t —BjO(/)d/
1 — В [ Ф (t) е 0 at ь
в чем можно убедиться непосредственной подстановкой (1.40) в (1.38). Нетрудно видеть, что при Ф = 0 <р(Ф) = 1, а при Ф< 0 0«р(Ф)<1 для любого момента времени, в том числе и при t со.
Внося (1.40) в (1.35), получаем следующее простое и хорошо согласующееся с опытом выражение для скорости экзотермии в общем случае неадиабатического процесса
-Вр(/)Л
^-=ВЭ„рФ(0е u . (1.41)
Наконец, внося сюда (1.23), мы получаем окончательную форму этого выражения
d3(t) вэур е„рФ(о (1 42)
* ~ епр-00(1-еВ%')’
которой и будем в дальнейшем пользоваться.
Выражение (1.41) уже свободно от недостатков формулы (1.14), так как с течением времени благодаря наличию в нем
—Baindt
множителя е ° скорость экзотермии становится исче-
зающе малой, что и наблюдается в действительности. Поэтому перемена знака температуры вследствие возможной волны холода, сравнительно медленно проникающей в бетон, к этому моменту времени будет носить чисто формальный характер. Это видно на примере числовой задачи, рассмотренной в § 1.16.
Кроме того, выражения (1.41), (1.42) обладают еще одним важным достоинством — они позволяют получать решения сложнейших задач теории теплопроводности аналитическим методом даже в самых общих случаях двух- и трехмерных по координатам задач с переменными во времени граничными условиями, что не удается в случае, например, уравнения (1.14). Это показано в § 1.10—1.16.
Внося выражение (1.42) для скорости экзотермии в уравнение (1.2), с учетом (1.24) мы получаем следующее уравнение теп-
27
лопроводпостн при распределенных по объему тела источниках тепла, интенсивность которых зависит от температуры:
— = от¥2Ф + <о(/)Ф. (1-43)
dt где
к (/) = - (°"г , (1.44)
е11р + е0 (ев в,,рl- 1)
а v2 — оператор Лапласа, в общем случае трехмерной по координатам задачи, равный
В формуле (1.41) В (l/ч-град) — параметр скорости адиабатического тепловыделения данного цемента в бетоне заданного состава, определяемый по формуле (1.31), Эпр (ккал/кг)—предельная величина адиабатического тепловыделения цемента, 0пр —предельная температура адиабатического процесса твердения бетона, определяемая по формуле (1.24), 0о—начальная температура бетона.
Методами математической физики можно показать, что уравнение (1.43) принадлежит к уравнениям параболического типа, имеет единственное решение и что оно всегда существует. Мы найдем его ниже.
§ 1.6. КЛАССИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ ПРИ ИСТОЧНИКАХ ТЕПЛА, ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ
В соответствии с изложенным выше задача теории теплопроводности при источниках тепла, зависящих от температуры, имеющая однозначное решение, ставится следующим образом: требуется отыскать температурную функцию Ф(х, у, z, г), удовлетворяющую дифференциальному уравнению теплопроводности с источниками тепла, зависящими от температуры
=пт¥2Ф + «(0Ф (1-46)
при заданных граничных условиях, например, условиях вида
+ h [Ф — <р (/)] г-. О па поверхности, (1.47)
соответствующих случаю свободного теплообмена, и начальном j словии
Ф 0о при t = 0; (1.48)
функции со(/), <р(/) и начальная температура 60 заданы.
28
В силу линейности основного дифференциального уравнения (1.46) рассматриваемая задача Может быть сведена к двум более простым задачам. Действительно, представим искомую функ-
цию Ф в виде суммы двух слагаемых
Ф Ф1 (х, у, 2, t) + Ф2 (Д', у, 2, I). (1-49)
В качестве функции Ф1 выберем решение задачи:
= (1.50)
- ^ + ^Ф1~0 на поверхности; (1-51)
Ф1 - 0о при t - 0. (1.52)
Тогда функция Ф2 будет решением следующей задачи:
^- = 0т¥2Ф2 + со(ОФ2; (1.53)
at
^- + Л[Фо — <р(/)]=0 на поверхности; (1-54) д v
Ф2 — 0 при t = 0. (1.55)
Легко видеть, что, накладывая решения этих двух более простых задач, получим решение исходной задачи в первоначальной ее постановке.
Вспомогательная задача с однородными граничными условиями, определяемая уравнениями (1.50)—(1.52), представляет собой первую классическую задачу теории теплопроводности при источниках тепла, зависящих от температуры. Вторая же вспомогательная задача с однородным начальным условием, определяемая уравнениями (1.53)—(1.55), является второй классической задачей этой теории.
При наличии готовых решений первой и второй классических задач по формуле (1.49) всегда может быть составлено общее решение задачи теории теплопроводности при источниках тепла, зависящих от температуры, определяющее собой температурное коле при этих условиях. Ниже рассматриваются классические аналитические методы решения этих вспомогательных задач.
§ 1.7. ПЕРВАЯ КЛАССИЧЕСКАЯ ЗАДАЧА ТЕОРИИ ТЕПЛОПРОВОДНОСТИ
ПРИ ИСТОЧНИКАХ ТЕПЛА, ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ.
ОДНОМЕРНЫЙ ТЕПЛОВОЙ ПОТОК В ПЛИТЕ
Решение первой из указанных выше задач найдем методом Фурье. Представим искомую температурную функцию Ф\ в виде произведения четырех функций:
ф^тюхогоогг,). (1.56)
29
каждая из которых зависит только от одной своей переменной — времени t или координаты точки £, ц или £ соответственно. Внося (1.56) в уравнение (1.50) и разделяя переменные, будем иметь
+ +_v8Z(Oi
L ха) го» za) J T(ty
Левая часть этого равенства зависит только от координат точки, а правая — только от времени t. При этих условиях удовлетворить равенству (1.57) мы можем только, положив
у^--о»(0--/п2; (1.58)
. - a2- = - В2- viZ® = - v2 (I 59)
Ха) ’ F(n) za) V’
где а, р, у, in - произвольные пока постоянные числа, причем о,(а2 + р2 +у2) =/и2. (1.60)
Знаки у правых частей уравнений (1.58) — (1.59) выбраны по физическим соображениям, сущность которых будет ясна из дальнейшего.
Общее решение уравнения (1.58) имеет вид
t
— [ (пГ -<о (/)] dt
T(t)=Ae° , (1.61)
где А — произвольная постоянная интегрирования, пли, с учетом (1.44) и (1.60)
Т « == е'а % '" "" ' U-62)
О ("ll?- VI»)
Для процессов, которые мы рассматриваем, когда тело стремится к температурному равновесию с внешней средой и достигает его по истечении длительного промежутка времени (t -*• со), функция T(t) должна быть затухающей. По физическому смыслу уравнения (1.44) видно, что функция <о(/) всегда положительна, поэтому условию затухания процесса мы можем удовлетворить, лишь сохранив знак минус в правой части уравнения (1.58). В противном случае температура Ф1 будет при увеличении времени t неограниченно возрастать, что физически невозможно.
Нашей задачей является отыскание общего выражения для Ф1 одинаково пригодного и для ряда частных случаев распределения температуры по объему тела, например, когда температура Ф1 зависит только от одной из координат. Рассматривая этот случай, мы видим, что уравнению (1.57) можно удовлетворить, лишь сохранив знак минус в правой части первого из уравнений (1.59). Аналогичные рассуждения приводят пас к необходимости такого же знака в правых частях остальных уравнений (1.59).
зо
Как следует из уравнения (1.62), функция Т(/) с точностью до постоянного множителя А полностью определена, если известны постоянные а, 0 и у, представляющие собой так называемые характеристические числа задачи. При этих условиях, с точностью до произвольных постоянных интегрирования, всегда могут быть найдены и функции Х(£), У(1]), Z(0. входящие в уравнения (1.59), которые называются фундаментальными функциями. Вид этих функций определяется видом выбранной системы ортогональных координат 1], Так как уравнения (1.59) являются обыкновенными дифференциальными уравнениями второго порядка, то искомые фундаментальные функции Х(£), У(ц), Z(t) будут содержать в себе по две произвольных постоянных, поэтому в общем виде они могут быть записаны следующим образом:
X (Ю = КЛ (В) + е F2 (В); Y (п) = М ф, (ф + vife ft); (1.63)
Z(B) = ^g>i(O + pg>2(B),
где К, е,... — произвольные постоянные интегрирования, a Fi(B). f2(£). — — линейно независимые частные решения уравнений (1.59).
Таким образом мы будем иметь 10 независимых произвольных постоянных а, 0, у. А, К, М, N, е, v и ц.
Структура формулы (1.56) такова, что, не нарушая общности решения, мы можем произвольные постоянные интегрирования К, М к N положить равными единице. После этого останется всего 7 независимых произвольных постоянных: 3 характеристических числа а, 0, у и 4 произвольных постоянных интегрирования А, е, V, ц. Для их отыскания мы будем иметь одно начальное (1.48) и шесть граничных условий вида (1.47), из которых значения этих постоянных всегда могут быть однозначно определены.
Дальнейший ход решения первой классической задачи мы рассмотрим на конкретном примере одномерного теплового потока вдоль оси ох через плиту толщиной 2х0, имеющую практически неограниченные размеры в двух других направлениях. Задачи подобного рода встречаются при расчете распределения температуры по толщине плит, оболочек пли конструкций, составленных из них. В этом случае, очевидно, функции У(т]) и Z(Q тождественно равны единице, 0=у=О, а
Х(£) = Х(х) = cosax + esin ах, (1-64)
поэтому формула (1.56) с учетом (1.62) и (1.64) принимает вил
Фх(х, 0 = AF(t)(cosax -f-e sin ax)e й8,,р^ , (1.65)
где
F(0 --------------®2Е_
' / ЯП
Опр 4- 0о ( с 1
(1.66)
31
В рассматриваемом случае мы будем иметь два граничных условия:
дх
hi = 0 при х — — х0;
4- Ь2Ф1~ 0 при х —х0. дх
(1.67)
Здесь для общности принято, что относительные коэффициенты теплопередачи h на гранях плиты различны.
Внося (1.65) в (1.67), находим:
_______— ^2_________.
2а 4- (*! 4- fi2)tgax0 ’
(1.68)
(1.69)
ctg 2а х0
а2 — h^hi, а (^1 4" Ьг)
Характеристическое уравнение (1.69) хорошо исследовано в теории теплопроводности [93], где показано, что оно имеет бесчисленное множество корней а как отрицательных, так и положительных. Но так как его отрицательные корни по абсолютной величине равны положительным, не нарушая общности решения, (1.65) можно органичиться лишь положительными корнями этого уравнения — характеристическими числами ат. Тогда мы будем иметь бесчисленное множество постоянных
т 2am4-(fti 4 ft2)tgaOTx0 ’
а, следовательно, и бесчисленное множеств' > линейно независимых фундаментальных функций
(х) - cos ат х + ет sina^x, (1.71)
каждая из которых будет удовлетворять первому из уравнений (1.59). Поэтому общее решение уравнения (1.50) мы найдем в виде суммы его частных решений
ФДх.О F(0"'fX(cosa,nx4-E,nsina,nx)e“^T<,--BD-'₽) (1.72) Щ=1
Начальное условие (1.52) с учетом (1.72) дает нам
I /,n(cosa,nx 4-emsinamx). (1.73)
zn=l
Следовательно, постоянные Ат являются коэффициентами разложения заданной начальной температуры 0о в ряд по фундаментальным функциям (1.71) и поэтому равны
Дет =------------40'l_sil1Q"‘*'’----. (1.74)
(’ + Ет) 2агп *0 + 0 - Ет) sin 2am х0
32
Первые три корня характеристического уравнения ctg£ = hXf,
iiqg 382-
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.5
2.0
3.0
20,0
30.0
40.0
50,0
60,0
80,0
100,0
0.0000 0.0316 0,0447 0,0632 3.1416 3,1419 3,1422 3,1429 6,2832 6.2833 6.2835 6.2838
0,0774 3,1435 6.2841
0,0893 3,1441 6,2845
0,0998 3.1448 6.2848
0.1410 3.1479 6.2864
0,1987 3.1543 6,2895
0,2425 3,1606 6.2927
0,2791 3,1668 6.2959
0.3111 3,1731 6.2991
0,4328 3.2039 6.3148
0,5218 3.2341 6,3305
0.5932 3.2636 6.3461
0.6533 3.2923 6,3616
0,7051 3.3204 6,3770
0.7506 3,3477 6,3923
0.7910 3.3744 6.4074
0.8274 3.4003 6.4224
0.8603 3,4256 6,4373
0.9882 3.5422 6,5097
1.0769 3,6436 6.5783
1.1925 3.8088 6.7040
1.2646 3,9352 6,8140
1.3138 4.0336 6,9096
1.3496 4,1116 6,9924
1.3766 4.1746 7,0640
1.3978 4,2264 7,1263
1.4149 4,2694 7,1806
1,4289 4,3058 7,2281
1.4729 4,4255 7,3959
1.4961 4.4915 7.4954
1,5202 4,5615 7,6057
1.5825 4,5979 7.66-17
1,5400 4.6202 7,7012
1,5451 4,6353 7.7259
1.5514 4.6543 7.7573
1,5552 4.6658 7,7764
1.5708 4.7154 7.8540
33
Итак, решение рассматриваемой первой классической задачи для плиты определяется формулами (1.72), (1.66), (1.69), (1.70) и (1.74).
Отметим часто встречающийся важный случай симметричных граничных условий для плиты
Лд = Л2 = Л. (1.75)
В этом случае, в соответствии с выражением (1 70), в формулах (1.72) и (1.74) следует положить ет=0 и считать ctm равным
а,п=42-’ (Г76>
2х0
где — положительные корни характеристического уравнения
ctg£ = -^-, (1.77)
пх0
в которое преобразуется уравнение (1.69) при условии (1.75).
Первые три корня уравнения (1.77) приведены в табл. 5, заимствованной из книги А. В. Лыкова [107].
§ 1.8. ВТОРАЯ КЛАССИЧЕСКАЯ ЗАДАЧА ТЕОРИИ ТЕПЛОПРОВОДНОСТИ ПРИ ИСТОЧНИКАХ ТЕПЛА, ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ. ОДНОМЕРНЫЙ ТЕПЛОВОЙ ПОТОК В ПЛИТЕ
Решение второй задачи, определяемой уравнениями (1.53) -(1.55), представляет большие трудности, и нам придется рассмотреть его более подробно.
Вначале рассмотрим подсобную задачу об отыскании температурной функции F, удовлетворяющей уравнениям:
^- = aTv*F + v>(t)F; (1-78)
-^- + h(F—1) = 0 на поверхности; dv (1-79)
F — 0 при t = 0. (1-80)
Представляя F в виде суммы Г-Ф8 + Ф4, (181)
выберем в качестве Ф3 решение следующей задачи: (1.82)
+ h (Ф3— 1) — 0 на поверхности д v (1.83)
34
о стационарном распределении температуры при стационарных граничных условиях (1.79). Тогда для фУнкпии мы будем иметь уравнения
Ст v2 Ф4 + (0 (Ф3 + ф4); (1.84)
dt
^-+ ЛФ4 = О на поверхности; (1.85)
dv
Фй = —Ф3 при Ь О, (1.86)
в которых функцию Ф3 уже следует рассматривать как заданную.
Отыскание функций Ф3 и Ф4 с помощью уравнений (1.82) — (1.86) не вызывает затруднений. Таким образом, поставленную выше подсобную задачу об отыскании температурной функции F при стационарных граничных условиях (1.79) можно считать решенной. Теперь перейдем к рассмотрению исходной второй классической задачи.
Допустим, что температура среды равна нулю от 1=—со до /=0и равна 1 от t = 0 до t=t. Тогда начальная температура тела равна нулю, температура среды равна 1 и температура тела будет равна Г(£, »), £, t) при f>0, т. е. будет решением рассмотренной выше подсобной задачи. Поэтому, когда температура среды равна нулю от t=—со до f=X и 1 от t=“k до t = t, температура тела будет равна
— *) при />Х.
Точно таким же образом, когда температура среды равна нулю от t=—со до /=Х+ДХ и равна 1 от /=Х+ДХ до t=t, температура тела будет равна F(g, ц, £, t—X—ДХ) при />Х+ДХ. Отсюда следует, что если температура среды равна нулю от t=— со до f=X, 1 от /=Х до /=Х+ДХ и нулю от / = Х+ДХ до t—t, то температура тела будет равна
Г(&т\ЛЛ~*) — — Х-Д*) при t >Х.
При бесконечно малом интервале ДХ(ДХ ->0), очевидно, температура тела будет равна
— F(£, т], t — X)dX при t > X. dt
Если бы на интервале dX температура среды была бы равна не 1, а <р(Х), то температура тела была бы равна
<p(X)4-F(5,n,t,/ —X)dX при / > 0. dt
Следовательно, разбивая интервал времени от /=0 до t=t на бесконечно малые интервалы dX и суммируя соответствующие каждому такому интервалу результаты, мы найдем окончательно
35
решение второй классической задачи, когда температура среды равна <$>(/), в форме
Ф2-
f Ф(*)4 F& П,
(1.87)
где F (£, т], £, t) — решение указанной выше подсобной задачи, т. е. температура в момент времени t в точке (g, т), £) тела, начальная температура которого равна нулю, окруженного средой, имеющей температуру, равную единице.
Соотношение (1.87) есть обобщение известной теоремы Дюамеля [93] на наш более общий случай задачи теории теплопроводности при источниках тепла, зависящих от температуры. Таким образом, решение второй классической задачи, рассмотренной в § 1.6, можно всегда найти, пользуясь этой теоремой по формуле (1.87), если известно решение подсобной задачи (1.78)— (1.80).
Применение классического метода решения второй- классической задачи, основанного на теореме Дюамеля, мы проиллюстрируем на примере задачи об одномерном тепловом потоке в неограниченной плите, рассмотренной в § 1.7.
Вначале рассмотрим подсобную задачу, определяемую уравнениями (1.78)— (1.80), которые в данном случае принимают вид:
+<o(')F: (L88)
— — h^F—1) = 0 при к -—х0; дх
+ A2(F—1)--0 при х--х0;
(1.89)
F = 0 при t = 0.
(1.90)
Используя (1.82) — (1.83) для функции Ф3, будем иметь уравнения:
^ = 0;
(1.91)
(Фа~ 1) = 0 при х = —х0; dx
+ Л2(Ф8 — 1) = 0 при х х„,
решение которых будет равно
Ф,= 1.
(1.92)
(1.93)
36
На основании формул (1.84) — (1-86) с учетом (1.93) для функции Ф4 будем иметь уравнения:
= +*<);
dt ох2
— Л, Ф4 = 0 при х — х0;
дХ (1.95)
+ Л8 Ф4 = 0 при х — х0;
Ф4 = — 1 при t - 0. (1.96)
Эти уравнения весьма схожи с уравнениями первой классической задачи (1.50) — (1-52) для плиты неограниченных размеров, поэтому метод их решения будет таким же.
Представляя функцию (х, t) в виде ряда по фундаментальным функциям (1.71), имеем
Ф^х, Ё Qm (О (cos ат х + е,п sin am х). (1.97)
m=l
При этом граничные условия задачи (1.95) будут автоматически удовлетворяться.
Раскладывая 1 в области — х0-С х в ряд по этим же функциям,находим
1 = Ё Pm (cos ат х + е,л sin am х), (1.98)
m=l
где
₽„ - ---------. (1.99)
(‘ + '«) Н. 'о + 0 - е™) •!" Ч» «о
Внося выражения (1.97) и (1.98) в (1.94), для Qm(0 будем иметь обыкновенное дифференциальное уравнение
О)+[*x-Mo]Qm(o=<ow„. (moo)
общий интеграл которого, удовлетворяющий начальному условию (1.96), равен
0,(0 = (1- -(о,4_ ,1
оХ~В0пр I в(бпр-Оо)
Таким образом:
Р(х, 0 = 1+ Е Qm(0 (cos ат X + emsin ат х). т=1
(1.102)
37
Следовательно:
m=co
-?-F(x,t — k) = Qm(t — ‘k)(cosamx 4-emsinamx)
Ot Ot
т=Л
и поэтому окончательно m=® t
— ?v)dl](costtmx+emsinamx). (1.103) „1=1 о
Как следует из выражения (1.103), решение второй классической задачи, найденное с помощью теоремы Дюамеля, всегда получается в виде рядов, сходимость которых для различных точек тела различна и ухудшается по мере приближения точки к поверхности тела и, особенно, к его углам. Поэтому весьма важно найти метод решения задач теории теплопроводности, дающий улучшение сходимости этих решений. Это необходимо еще и потому, что, как это будет показано в главе V, отыскание температурных напряжений, например, в случае плоской задачи, производится по Лапласиану \/2Ф изменений температурного поля Ф, для определения которого требуется двойное дифференцирование этих решений, что ухудшает их сходимость. Такой метод, предложенный автором, дающий повышенную сходимость решений задач теории теплопроводности, излагается ниже.
§ 1.9. УПРОЩЕНИЕ ЗАДАЧИ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ ПРИ ИСТОЧНИКАХ ТЕПЛА, ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ.
МЕТОД АВТОРА
Рассмотрим другой метод интегрирования уравнений (1.46) — (1.48) теории теплопроводности при источниках тепла, зависящих от температуры. Этот метод, предлагаемый нами, мы назовем методом дополнительных фиктивных источников.
Введем в рассмотрение некоторые распределенные по объему тела дополнительные фиктивные источники тепла, зависящие от координат точки и времени, с интенсивностью
9 = Yc[<oWA-^l], (1.104)
где о)(О определяется выражением (1.44), а Ф1— пока произвольная функция.
Рассмотрим теперь задачу (1.46)—(1.48) для некоторой температурной функции Ф2 при наличии этих дополнительных источников (1.104), однородных граничных условиях вида (1.47)
38
и произвольном пока начальном условии (1.107). Основные уравнения этой вспомогательной задачи будут иметь вид:
ъ?2ф2 + (о№ + ; (1.105)
dt ot
^- + ЛФ., = 0 на поверхности; (1.106)
dv
Ф2 = е0 —ф^о) при t = о. (Lio?)
В этих уравнениях функцию Ф1 следует рассматривать как пока еще произвольную, но заданную функцию.
Подберем теперь эту функцию таким образом, чтобы решение Ф2 задачи (1.105) — (1.107), будучи сложенным с Фь дало бы нам общее решение Ф исходной задачи теории теплопроводности (1.46) — (1.48) с первоначально заданными действительными источниками тепла, зависящими от температуры.
Иными словами, подчиним функцию Ф1 условию
Ф^Ф^Ф. (1.108)
Внося (1.108) в уравнения (1-46) — (1.48), для функции Ф\ с учетом (1.105), (1.106), получаем следующие уравнения:
V2 Ф1 = 0; (1.109)
Лф.
—- + h 10!—<р(Л1=0 на поверхности (1.110) dv
Таким образом, функция Ф| должна быть решением третьей или смешанной граничной задачи эллиптического типа с граничными условиями (1.110), в которых время t рассматривается как параметр, а <р (О —температура среды, в общем случае различная со стороны каждого из координатных срезов, ограничивающих тело.
Общее решение уравнения (1.109) всегда может быть выражено через гармонические функции с коэффициентами (произвольными постоянными интегрирования), зависящими от времени t. Распоряжаясь этими коэффициентами должным образом, можно удовлетворить и граничному условию (1.110), тем самым указанная краевая задача будет решена, а функция Ф1 однозначно определена. Ниже будет показано, что решение задачи (1.109). (1.110), удовлетворяющее указанным условиям, всегда может быть найдено, и мы его получим для ряда практически наиболее важных случаев.
Вспомогательную задачу, определяемую уравнениями (1.109), (1.110), назовем первой основной задачей теории теплопроводности при источниках тепла, зависящих от температуры. Ее решение — температурная функция 0i — будет определять собой температурный режим тела в условиях свободного теплообмена
39
с внешней средой с заданной температурой ср (/) и при наличии распределенных по его объему источников тепла интенсивностью
9 = Y^- (1-111)
ОТ
Этот режим описывается гармоническими функциями координат точки с коэффициентами в виде постоянных интегрирования, зависящих от времени /. Такой температурный режим мы будем называть обобщенным к в а з и с т а ц и о парным температурным режимом. Таким образом, первая основная задача теории теплопроводности есть задача об обобщенном квазистационарном температурном режиме.
Вторую вспомогательную задачу с однородными граничными условиями, определяемую уравнениями (1.105)—(1.107), мы будем называть второй основной задачей теории теплопроводности при источниках тепла, зависящих от температуры. Эта задача будет определять собой температурный режим тела, находящегося в условиях свободного теплообмена со средней с нулевой температурой, имевшего начальную температуру 60—Ф)(0), и при распределенных по его объему источниках тепла, зависящих от температуры, интенсивностью
q =- ус [<о (0 (Ф,+ Ф2) - • (I-112)
Решение этой задачи также может быть всегда найдено аналитическим методом с применением обычных приемов классической теории теплопроводности.
Итак, мы видим, что предлагаемый метод дополнительных фиктивных источников обладает рядом несомненных преимуществ. Во-первых, этот метод позволяет свести сложную задачу теории теплопроводности при источниках тепла, зависящих от температуры, к двум более простым вспомогательным задачам; во-вторых, даже в самом общем случае нестационарных граничных условий он не требует применения теоремы Дюамеля и поэтому свободен в значительной своей части от указанных выше недостатков классических методов решения задач теории теплопроводности. Как будет показано ниже, решение первой основной задачи в большинстве практически наиболее важных случаев удается найти в замкнутом виде, что существенно улучшает сходимость всего решения в целом.
Само собой разумеется, что метод дополнительных фиктивных источников со всеми его преимуществами применим и в случае задачи теории теплопроводности без наличия источников тепла (экзотермии), т. е. при ее классической постановке. Такая задача будет представлять собой лишь частный случай более общей задачи, поставленной в § 1.6 и рассматриваемой в дальнейшем. Поэтому на примере такой более простой задачи в простейшем случае одномерного теплового потока можно провести
40
наглядное сопоставление двух сравниваемых методов: классического метода Дюамеля и метода дополнительных фиктивных источников. Это будет сделано позже в § 1.12, после того как с помощью последнего метода будет получено решение указанной задачи в общем случае источников тепла, зависящих от температуры.
При наличии готовых решений первой и второй основных задач по формуле (1.108) всегда может быть составлено общее решение задачи теории теплопроводности при источниках тепла, зависящих от температуры, определяющее собой температурное поле при этих условиях. Ниже рассматриваются аналитические методы решения этих вспомогательных задач.
§ 1.10. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ТЕПЛОПРОВОДНОСТИ. СЛУЧАИ ЗАМКНУТОГО РЕШЕНИЯ
Укажем случай, когда удается получить решение первой основной задачи теории теплопроводности об обобщенном квази-стационарном температурном режиме в замкнутом виде.
Рассмотрим задачу об одномерном тепловом потоке вдоль оси ох через плиту толщиной 2.v0, имеющую практически неограниченные размеры в двух других направлениях:
---Л1 [ф1 — <Pi (01 = 0 при х = — х0;
дФг (1.114)
— + Мф1 — <Рг(01 —0 прих = х0.
В этом случае
^(о-сдо + сао^-. (U15)
Внося (1.115) в (1.114), для функций Ci(/) и С2(/) будем иметь уравнения:
(1 — х0) Ci (0 4- hi х0С£ (0 = —hlxu <pi (0 ; |
(1 + h2xv)Ci(t) 4- Л2.гоСг(0 = h2x0<p2(t), J (IH6)
из которых находим:
С1(0 = <Р1(0 + ‘+/1*> сИ0; «I xo
c /а = Мг-МУгСП-ф, (/)|
2 /ц ! '2hth2x0 4- Л2
(1.117)
41
При других видах граничных условий функции G(0 и С2(0 имеют следующие значения:
а) при граничных условиях:
ф- —[Ф1 —<Р1(01 = 0 при х - — х0-дх
ф1 = Ч>2(0 прих = л0;
(1.118)
С1(0-Ф1(0+
Й1Х0
С = Mo 1<Р2 (О — <Р1 (01 .
2U I 4- 2/цхо
б) при граничных условиях.
“ — [А — Фя (0J =0 при х = — л0;
fW' О дх
при X = Хо,
а также при:
ф| “ Ф1 (0 при х = — х0;
дФ, Л
—— - 0 при х = х0;
дх
Ся(0 = Фя(0; С2(0-0;
в) при граничных условиях:
ф1 (0 = Ф1 (О при х = — х0; |
Ф1(0 = ф#(0 при х = х0; ( J
С (t) = (/) + ф2 (z) • С2 (0 = ФИО ~Ф1<0
(1.119)
(1.120)
(1.121)
(1.122)
(1.123)
(1.124)
В случае одномерного теплового потока вдоль радиуса г полого цилиндра практически неограниченной длины, но ограниченного поверхностями г=а и г=Ь (а<Ь) исходные уравнения имеют вид
-^- + — •^-=0; (1.125)
дгг г дг
—Ля[Ф,—<ря(01 =0 при г = а;
Яй> 0-126)
—1 + Л2 — «ЫО] =0 при г = Ь.
or
В этом случае
Фя (г, 0 - Ся (0 + С2(0 In . (1.127)
42
Внося (1.127) в (1.126), имеем:
С1(О = Ф1(0+—?- С2(0;
Л] о
= abhjht [ф2 (О — ф, (/)]
ahi+abhih2 In/—j+ bhs
(1.128)
При других видах граничных условий функции Ci(0 и С2(0 будут иметь следующие значения:
а) при граничных условиях
~Мф1 —<h(0] =0 при г = а; or Ф, =- ф2 (/) при г = Ь; (1.129)
С1(0 = Ф1(0+-?—С2(0; а Q _ c/,l |ф2 (0 — ф| (QI . 1 4-аЙ! Ini—J б) при граничных условиях: —Aj [0! —Ф1(0) =0 при dr = 0 при дг а также при: Ф1 = Ч>1 (0 при г = а; = 0 при г = Ь; дг С1(О-Ф1(0; С2(0 = О в) при граничных условиях: Ф, = Ф1(0 при г = а; ] Ф1 = ЧЧ>(0 при г — Ь~, \ га; г = А, • (1.130) (I.I31) (1.132) (1.133) (1.134)
Ci = чч (0; С2(0 = -^-г-(0 ф,(0 . '"(т) (1.135)
В случае сплошного цилиндра радиусом г=Ь мы будем иметь лишь одно второе условие. В этом случае, полагая
Ф. (г, 0==С1(0 + С2(01п
(1.136)
4*
43
найдем, что условиям (1.126) можно удовлетворить, положив
CJZ) 0; CJ0 = ф2(0 = Ф('). (1-137)
Таким образом, в рассматриваемом случае
<Л(0 = <₽(/). (1.138)
Аналогичным образом можно показать, что для всех твердых тел, у которых вся поверхность поддерживается при температуре ф(0, или у которых на всей поверхности происходит теплообмен со средой, температура которой равна <$>(/), всегда будем иметь условие (1.138).
§ 1.11. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ТЕПЛОПРОВОДНОСТИ. обобщенный квазистационарныи температурный режим прямоугольной призмы, случай незамкнутого решения
В более сложных задачах о двух- и трехмерных тепловых потоках в телах, грани которых поддерживаются при различных температурах или на гранях которых происходит свободный теплообмен со средой, имеющей различные температуры, решение первой основной задачи теории теплопроводности удается найти лишь в незамкнутом виде. Ниже приводится такое решение для прямоугольной призмы неограниченной длины, с размерами поперечного сечения 2дох2т/о при попарносимметричных граничных условиях на взаимно противоположных гранях. Рассматриваемая задача встречается при расчете распределения температуры по сечению длинных призматических стержней (колонн, балок, элементов рам, столбчатых бетонных блоков и т. п.). Исходные уравнения этой задачи имеют вид:
«УФ, д2Ф, дх2 + ду*
д v
1- Л, (Ф,-<й(0) =0
^--Л2(Ф1-ф2(/))=0 ду
^- + ^[^-^(01-0
— 0;
при X ~ —Хо\
при X = л0;
при у = ~ у0 ;
при у = уй.
(1.139)
(1.140)
Решение этой задачи имеет вид [3]
т=со
= 2 £ Q„, (0 cos атх ch <х„, у + т=1
+ 2 S A'n(t)ch0nxcospny, п=1
(1.141)
44
где
о ___________________4/i2 sin ат хп ф2 (/)_________
’*"* (2аот х0 + sin 2ит х0) [(Лл+атут) ch ат у0 +
4/12 s*n ат хо *Ps fQ . 0 142)
+ (ат + Mm) Sin ат Vol ’
N ___________________4Л1 Sin pn y0 <r, (/)____________
* K^l Pn^n) Ch Pn *<>+ (Pn+ Aj ^n) sh Pn XojX 4/i1sinPny0<h (0. (| 143)
x (2₽„ f/0 + sin 2₽„ ffo)
у________^2 ~}~ am )h am Уо .
m um r h2 th atn y0 ’
6 = *1 +PnthPr.ro 1 ’ 4
Pn + hi th ₽„ л0 (
a am, pn — положительные корни характеристических уравнений
ctg<xx0=—; (1.145)
hi
ctgPf/0 = -^. OHG)
/12
П одстановкам и
a = —; p=-^- (1.147)
Хо Уо
эти уравнения приводятся к уравнениям вида:
ctg£ = —; (1.148)
hi х0
ctgg = -^—. (1.149)
h^yo
Уравнение (1.148) хорошо исследовано в классической теории теплопроводности [93], [1С7]. Первые три корпя этого уравнения даны в табл. 5. Полагая в формулах (1.141) — (I.I49) h\ = h2=^h, <Pi(0=q>2(0=4)(0 и устремляя в них Л->со , мы-получим решение рассматриваемой задачи для случая, когда поверхность тела поддерживается при температуре ч>(/):
У (- 1)”--------------------------COS +
<2m+o«4to 2х»
m_0 (2m-j-1) я ch----------
।_______W)___________
/9 . .(2Л+1)Я*0
(2n + I) я ch--------
2j/o
X ch .<^±2)л* cos-ff1^1^
2у0
2у0
(1.150)
45
Ряды по гиперболо-тригонометрическим функциям в решениях (1.141), (1.150) весьма быстро сходятся, поэтому они удобны для их практических приложений. Например, ряд (1.150) в каждой точке тела быстро сходится к <р(/), в чем нетрудно убедиться численным методом. Поэтому вместо (1.150) можно пользоваться готовым решением (1.138). Это обстоятельство уже отмечалось в § 1.10.
§ 1.12. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ТЕПЛОПРОВОДНОСТИ ПРИ ИСТОЧНИКАХ ТЕПЛА, ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ. ОДНОМЕРНЫЙ ТЕПЛОВОЙ ЛОТОК В ПЛИТЕ
Рассмотрим вторую основную задачу теории теплопроводности при источниках тепла, зависящих от температуры, в случае одномерного теплового потока вдоль оси ох через плиту толщиной 2*0, имеющую неограниченные размеры в двух других направлениях. Решение первой основной задачи для этого случая мы нашли в § 1.10 в форме (1.115) и (1.117), поэтому исходные уравнения рассматриваемой задачи имеют вид:
w (/)ф>+ы & с> ю <0 + д/ ov®
+ {<п(/)С2(/)-С2(0]^.
—- — h. Ф., --- 0 при х = — л0; дх
дФ» , . ~
-у- + й2Ф2 -•= 0 при х = х„;
(1.151)
(1.152)
Ф2 0(0) —С,(0) —С,(0) — при / - 0. (1.153)
*0
В формулах (1.151) — (1.153) функции <•>(/), Ci(0 и Cz(t) заданы и определены выражениями (1.44) и (1.117).
В связи с однородностью граничных условий (1.152) общий интеграл уравнения (1.151) будем искать в виде ряда по фундаментальным функциям (1-71)
Ф2- Е Tm(/)(cosamx + E„,sina„,x); (1.154) m=l
тогда граничные условия задачи (1.152) будут автоматически чдовлетворены, если am—положительные корни уравнения (1.69).
Внося (1.154) в (1.151) и учитывая разложения в области
— х0 < х < л'о (1.99) и
*71 = 00 _
Е Qm(cosa,„x + е„, si net,,, л), Я1=1
(1.155)
JG
где
~q ______(sin ат х0 — ат х0 cos ат х0)_ 156)
%. [(’ +C^)2amXo+(1-Cn1)sin2amXo] ’
для Tm(t) получаем следующее дифференциальное уравнение: г;(о+г„(о[от^-И(0] =
~Р„ [»(()€,(/)-с;(0]+ [и(ОС2(О-С2(0]. (1.157)
общий интеграл которого, удовлетворяющий начальному условию (1.153), равен
'Г /л .. и\ I л— ( °т °т~ дппп) 1
Tm(t) - O)(0|fi(0iip -ад- е
- Х„ (О + °, «’ f Х„ © е"( ''“^1 • О -158)
о
где v ifx ________________ хо ?т Ci (/) + Qm Cz (О zt fcn\
- -------x(, w (0--• (1-lby)
При этих условиях выражение (1.154) удовлетворяет всем уравнениям задачи (1.151) — (1.153) и поэтому является ее общим решением.
В случае (1.75) решение (1.154) принимает вид
T^/Jcosa,,,*, (1.160)
m=l
где Tm(t) по-прежнему находится по формуле (1.158), в которой р =------------------------4sinamxu--
2am х0 + sin 2am х0
(1.162)
«(/)
а ат — по формуле (1.76), где £— положительные корни уравнения (1.77).
Подстановкой
a = — *0 формула (1.161) приводится к виду
~Г, ._______2sin ^,п__
' т
Em ’i S,H 5m COS
(1.163)
(1.164)
В силу уравнения (1.77) постоянные Рт, определяемые по формуле (1.164), зависят только от hx0 и номера т характеристического числа t/m и поэтому могут быть протабулированы в зависи-
47
Таблица 6
_ z am Ьп
Первые три значения постоянных Рт - —----:—т-----—
Ъп + Sin Im COS Im
hxc -P,
0 1 0 0
0,001 1,0002 0,0002 0
0,002 1,0004 0,0004 0,0001
0,004 1,0008 0,0008 0,0002
0,006 1,0012 0.0012 0,0003
0,008 1,0015 0.0016 0,0004
0,01 1,0020 0,0020 0,0005
0,02 1,0030 0,0040 0,0010
0.04 1,0065 0,0080 0.0020
0,03 1,0099 0,0119 0,0030
0,08 1,0130 0,0158 0,0040
0.10 1.0159 0,0197 0,0050
0,20 1,0312 0,0381 0,0190
0,30 1,0450 0,0555 0,0148
0,40 1.0581 0,0719 0,0196
0,50 1,0701 0,0873 0,0243
0,60 1,0813 0,1025 0,0289
0,70 1.0918 0.1154 0,0335
0,80 1.1016 0,1282 0,0379
0,90 1,1107 0,1403 0,0423
1 1,1192 0,1517 0,0466
1.5 1,1537 0,2013 0,0667
2 1,1784 0.2367 0,0848
3 1,2102 0.2881 0,1154
4 1.2287 0,3215 0,1396
5 1,2403 0,3442 0.1588
6 1,2478 0,3604 0,1740
7 1.2532 0,3722 0,1861
8 1.2569 0.3812 0.1959
9 1.2598 0.3880 0,2039
10 1.2612 0.3934 0,2104
15 1,2677 0,4084 0,2320
20 1.2699 0,4147 0,2391
30 1,2717 0,4198 0.2472
40 1,2723 0,4217 0,2502
50 1,2727 0,4227 0,2517
60 1.2728 0,4232 0,2526
80 1.2730 0,4237 0,2535
100 1,2731 0.4239 0,2539
°° 1.2732 0,4244 0,2546
48
мости от этих величин. В табл. 6 даны первые три значения этих постоянных.
Наконец, устремляя в выражении (1.160) Л-*оо , получим решение второй основной задачи, соответствующее случаю, когда грани плиты поддерживаются при заданных температурах <р( (Z) и<рг(О:
ф.= s<-1)CT^</)cos-w-4l)Ttx • m=0
в котором x»n(0. Рт определяются по формулам (1.161), (1.162) при
(2т 4- 1) Л
(1.165)
(1.158),
(1.166)
плиты
х= — Хо
a Ci(/) отыскивается по выражению (1.124).
Представляет интерес также случаи, когда х=х0 поддерживается при температуре <р2(0. а "а происходит теплообмен со средой, температура которой <р( (/). Решение рассматриваемой задачи при этом определяется формулами (1.154), (1.99), (1.119), (1.156) и (1.159) при
em = ctgamx0, (1.167)
в которых am — положительные корни характеристического уравнения
ctg2ax0 =----— . (1.168)
Подстановкой а = -£- (1.169)
ZXo
уравнение (1.168) приводится к виду
ctg£ =----(I.17O)
Это уравнение хорошо исследовано в теории теплопроводности [107]; три первых корня его даны в табл. 7.
Располагая теперь решениями первой и второй основной задач об одномерном тепловом потоке в плите, проведем сопоставление классического метода Дюамеля и предлагаемого метода дополнительных фиктивных источников на простейшем примере плиты, имеющей начальную температуру 0о, грани которой поддерживаются при температуре ф(0. когда внутренние источники тепла отсутствуют. Для удобства использования
49
Таблица 7
Первые три корня характеристического уравнения
Е. Е, Е,
0 1.5708 4,7124 7,8540
0,1 1,6320 4,7335 7.8667
0,2 1,6887 4,7544 7,8794
0.3 1.7414 4,7751 7,8920
0,4 1.7906 4,7956 7.9046
0.5 1.8366 4,8158 7.9171
0,6 1.8798 4,8358 7,9295
0,7 1,9203 4,8556 7.9419
0,8 1.9586 4,8751 7.9542
0,9 1.9947 4,8943 7.9665
1 2,0288 4,9132 7,9787
2,1746 5,0037 8,0385
2 2.2889 5,0870 8,0962
3 2,4557 5.2329 8,2045
4 2,5704 5,3540 8,3029
5 2,6537 5,4544 8,3914
6 2,7165 5,5378 8,4703
7 2,7654 5,6078 8,5406
8 2,8044 5,6669 8,6031
9 2,8363 5,7172 8,6587
10 2.8628 5,7606 8.7083
15 2.9476 5,9080 8.8898
20 2.9930 5,9921 9,0019
30 3,0406 6,0831 9,1294
40 3,0651 6,1311 9.1986
50 3.0801 6,1606 9,2420
60 3,0901 6,1805 9,2715
80 3,1028 6,2058 9,3089
100 3.1105 6,2211 9,3317
СО 3,1416 6,2832 9,4248
имеющегося с литературе готового решения этой задачи запишем ее уравнения в следующем виде: дФ _ д*Ф . dt ‘ °т дх2 ’
Ф — <* <0 при X — 0 и Л- — /;
Ф - 0о при / = 0.
(1.171)
(1.172)
(1.173)
Решение этой задачи по методу Дюамеля имеет вид (см. [93], стр. 81):
50
v. n Л X
X sin —-— e
(1-174)
Решение же рассматриваемой задачи по метолу дополнительных фиктивных источников мы получим на основе формул (1.138), (1.165) и (1.108), положив в них В = 0 и осуществив преобразование координаты х в связи с переносом начала координат из центра плиты на ее грань. Сделав это, будем иметь
. zj\ Г« о V П —(—!)"] - лях] .
* = »(0 11-2 1' ,,я ап — +
П=1 п=® /
+ 2 S 1'~(-||Л1 (о„ + f Ф(ОX
пл ( Р J J
П=1 О
агп"т:-1
Xsin-^p- е ~. (1.175)
Сопоставляя выражения (1.174) и (1.175), мы видим, что при ограниченном числе членов рядов, входящих в эти выражения, решения рассмотренной задачи существенно различны Степень этого различия постепенно снижается по мере увеличения числа учитываемых членов ряда и при учете их бесконечного числа сравниваемые выражения совпадают, поскольку
2y^(-insln^ = i пл е
(1.176)
в области разложения I. Различие выражений (1.174)
и (1.175) при ограниченном числе членов состоит в том, что решение (1.174) медленно сходится па поверхности плиты и вблизи нее, в то время как решение (1.175) сходится весьма быстро в каждой точке плиты и, особенно, у ее поверхности. Покажем
это на числовом примере.
Рассматривая для простоты случай <р(/) —<ро=-^-=const, на
основании формул (1.174) и (1.175) будем иметь: а) по методу Дюамеля
Л =00
VI ( °1nvl \
— = 2 / । -I1 — ( 1 + е » Isin —. (1.177)
Фо «л \ / I
Л=1
51
б) по метолу дополнительных фиктивных источников
— = 1 + 2 /, -Н~(~1)П| sin е 1‘ . (1.178>
q„ пл I
В табл. 8 для точек *1 = 0,125/, х2=0,25/ и х3=0,5/ плиты толщиной 1 = 2 м при ат=3-10-3 м2/ч дня моментов времени /| = 5 ч и 12=84 ч по формулам (1.177) и (1.178) вычислены ве-Ф ..
личины - при учете в них различного числа членов. Как сле-Фо
дует из этой таблицы, для получения результата, отличающегося от его верного значения не более чем на 5%, в рассматриваемом случае по методу Дюамеля требуется учет 5—6 членов ряда, в то время как по методу автора для этого требуется всего 1—2 члена.
Таблица 8
Сравнение решений задач об остывании бетонной плиты, найденных по методу Дюамеля (1.177) и по методу автора (1.178)
8Г8
Улучшение сходимости решений, достигаемое в методе дополнительных фиктивных источников, весьма существенно особенно для задач о термопапряженном состоянии неравномерно нагретых тел. Как известно, в основные уравнения этих задач входят производные от температуры по координатам точки, а при дифференцировании выражений, аналогичных (1.174), их сходимость ухудшается. Поэтому весьма важно с самого начала получить улучшенную сходимость решений задач теории теплопроводности, если не удается найти их в замкнутом виде. Это и достигается в предлагаемом метоле.
52
§ 1.13. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ТЕПЛОПРОВОДНОСТИ ПРИ ИСТОЧНИКАХ ТЕПЛА, ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ. ДВУХМЕРНЫЙ ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОЙ ПРИЗМЕ
Рассмотрим теперь вторую основную задачу теории теплопроводности при источниках тепла, зависящих от температуры, для прямоугольной призмы, исследованной в § 1.11. Исходные уравнения этой задачи имеют вид:
^=О,(^- + ^-)+т(0(Ф1+Фг)-^-; (1.179)
dt \ дхг ду1 j dt
---Л1Ф2 = 0 при х = — А'о;
^ + M>8 = 0 при Х = Х0; dx
— /г2Ф2 = 0 при у - — у0-,
+ Л2Ф2 = 0 при у = t/0;
Ф2 = 60 —Ф^О) при /-0, (1.181)
где Ф1 — решение первой основной задачи для нашей призмы, найденное нами в§ 1.11 в виде (1.141).
Следуя методике, изложенной в § 1.12, функцию Ф2 будем искать в виде двойного ряда
Ф2 = Tmn(t)cosитхcos(1.182)
Выбирая при этом в качестве ат и ₽п положительные корни уравнений (1.145), (1.146), мы удовлетворим автоматически граничным условиям задачи (1.180). Вил функции Tmn(t) найдем из уравнения (1.179), внеся тула (1.182). Предварительно представим решение (1.141) также в виде двойного ряда
Ф1 - Ё S Dmn(0cosamxcosp„y, (1.183)
8 ( Qm (О Pn (Cm COS pny0 sh amy0+pn s in pn ch amy0)
am + Pn I + sin
I A'n (')Qm (Pn cos ащХр sh pnx0 + am sin amx0 ch pnx0) j 2Cm*o 4- sin 2amx0 J *
53
Кроме того, будем иметь разложение в области —хе<л<х0 —уо<У<Уо-
1 = Ё £ стп cos атх cos fiay, (1.185)
где
с = ___________16sinamxnsin ___________
(2amx0 + sin 2amxn) (2₽п% + sin 2₽„t/0) ’
Внося теперь (1.182) и (1.183) в (1.179) для Ттп (/), будем иметь обыкновенное дифференциальное уравнение
Т'тП (0 + [ М + ₽п ) ~ " (0] Ттп (0 =
= (1.187)
сбщий интеграл которого, удовлетворяющий начальному условию (1.181), равен
Г™('> = “<'> + +
+ О.К + К) + (1.188)
При этих условиях выражение (1.182) удовлетворяет всем уравнениям задачи (1.179) — (1.181) и поэтому является ее общим решением Полагая в формулах (1.182) — (1.188) ht = h2=h, <Pi(О =фг(0 =<f(0 и устремляя Л->оо, получим решение рассматриваемой задачи для случая, когда поверхность тела поддерживается при температуре (О
"ff r„„«)cos |2"Х'11" • (И89>
в котором Ттп(1) по-прежнему определяется по формуле (1.188)
°" = ~(л;0~я~; ° <2"^11я ; (|,190)
; = <IJ9n
При возрастании чисел тип коэффициент Стп в формулах (1.188) и (1.191) быстро убывает, вследствие чего ряды (1.182) (1.189) также быстро сходятся, поэтому найденные решения удобны для практических приложений.
54
§ 1.14. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ТЕПЛОПРОВОДНОСТИ ПРИ ИСТОЧНИКАХ ТЕПЛА, ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ
Рассмотрим еще вторую основную осесимметричную задачу теории теплопроводности при источниках тепла, зависящих от температуры, для неограниченного кругового цилиндра радиусом го- В общем случае граничного условия, соответствующего теплообмену на поверхности цилиндра, исходные уравнения этой задачи имеют вид:
+ ЛФ2 = 0 при г. == г0; (1.193)
Ф2-Оо —ФДО) при/=0, (1.194)
где Ф! — решение первой основной задачи для нашего цилиндра, найденное нами в § 1.10 в замкнутом виде
Ф1=Ч>((). (1.195)
Следуя классической форме решения задач теории теплопроводности для цилиндра [93], функцию Ф2 будем искать в виде ряда по функциям Бесселя
Ф.» («»/). (1196)
Выбирая при этом в качестве ат положительные корни уравнения
hJ0 (аг0) - aJi (аго) = 0, (1.197)
мы автоматически удовлетворим граничному условию (1.194). Вид функции Tm(t) найдем из уравнения (1.192), внеся туда (1.196). Сделав это, с учетом разложения в области 0<г<го
1 =T^o(an/), (1.198)
где
______2ДтА (стгр)_____
['.(-„'J?
(1.199)
для функции Г„,(() будем иметь обыкновенное дифференциальное уравнение
Гп (0 + [ < - <> (0] Тт (t) = [<О (0 <Р (!) - <₽' (/)] Ст, (1.200)
55
общий интеграл которого, удовлетворяющий начальному усло-вию (1.194), равен
7 (Л = С <D(t) ! 0,1 е (°т<1т В°пр)/ ____________
7"Ю <«<»<') (в^-ад е „(О
т mJ <о(В) ’J
(1.201)
При этих условиях выражение (1.196) удовлетворяет всем уравнениям задачи (1.192) —(1.194) и поэтому является ее общим решением.
Устремляя в формулах (1.196), (1.199) и (1.201) Л-> со , мы получим решение рассматриваемой задачи для случая, когда поверхность цилиндра поддерживается при температуре ф(0- Это решение будег иметь тот же вид (1.196), где Тт(/) по-прежнему определяется по формуле (1.201) при
т amro^l (атго)
(1.202)
а а,п — положительные корни характеристического уравнения J0(arc) = 0. (1.203)
Подстановкой
(1.204)
формула (1.202) и уравнения (1.197), (1.203) приводятся соответственно к формуле
(£m)
(1.205)
и к уравнениям вида Лг<Л(В-ЬМЭ = 0; (1.206)
Л(£) = 0. (1.207)
Уравнения (1.206), (1.207) хорошо изучены в классической теории теплопроводности [1.93], [1.107] и их корни протабулиро-ваиы.
§ 1.15. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРИИ
Для экспериментальной проверки предлагаемого метода определения температурных полей в молодом твердеющем бетоне с учетом зависимости экзотермии цемента от температуры процесса были использованы результаты опытов автора 1949 г. [4]. Эта проверка проводилась сопоставлением теоретического решения соответствующей плоской температурной задачи, найденного
56
нс методу автора, с действительно наблюдаемым распределением температуры в средней по высоте части массивных образцов типа высоких пилонов.
Модель такого пилона представляла собой цилиндрическую массивную лепешку диаметром 1 м и высотой 30 см с теплоизо лированными торцами.
В качестве исследуемого материала был применен цементно песчаный раствор с удельным весом 2300 кг/м3 состава (по весу) I : 4,32, ВЩ=0,583 с содержанием цемента 390 кг/л3.
Портландцемент Вольского завода активностью 556 кПсм2 имел примерно следующий минералогический состав в %: C3S 56; C2S — 21; С3А — 7; C4AF — 14, удельный и объемный веса со ответственно 3000 кг/л3 и 1200 кг/л3.
Песок — нормальный Вольский, удовлетворяющий требованиям ОСТ 3083, с удельным и объемным весами соответственно 2625 кг/л3 и 1730 кг/л3 и средней крупностью зерен 0,63 мм
Вода —обыкновенная, водопроводная.
Тепловыделение примененного в опытах цемента в растворе в адиабатических условиях исследовалось термосным метолом путем измерения температуры раствора, твердеющего в сосуде Дюара с определенным коэффициентом теплоотдачи в термостат с постоянной температурой, равной 20° С.
Испытания проводились с двухкратной повторяемостью опыта и дали близкие результаты (табл. 9).
Таблица 9
Удельная теплота 1идратации в ккал/кг портландцемента в растворе, примененного в опытах (нарастающий итог)
W пробы Продолжительность твердения цемента в часах
3 б 9 12 15 •8 | 1 21 | 24 1 1 36
1 2.9 4,1 5,7 7,4 9,7 12,1 15,1 17,4 26,9
2 2,5 3,6 5,3 7,3 9,6 12,3 15,4 18,3 31,5
Среднее 2,7 3,9 5,5 7,4 9,7 12,2 15,3 17,9 29.2
Продолжение табл. 9
№ пробы Продолжительность твердения цемента в часах
48 | 1 72 96 120 | 1 144 1 | 168
1 34,9 41,9 46,0 48,6 51,0 52,9
2 39,7 49,9 57.4 62,3 65.0 65.6
Среднее 37,3 45,9 51,7 55,4 58.0 59.2
По данным этой таблицы с помощью формулы (1.31) для (=21 ч и (=24 ч определялись значения параметра скорости тепловыделения цемента в исследуемом растворе В. При этом пре-
57
чельная теплота гидратации была оценена в 62,5 ккал/кг (табл. 9), а удельная теплоемкость раствора принята равной с=0,21 ккал/кг-град. Эти значения В оказались близкими и равными:
В - 0,52-1 :~3 Мград-ч. (1.208)
На рис. 7 приведены экспериментальные данные о теплоте гидратации исследуемого цемента в растворе, взятые из табл. 9,
Рис. 8. Сопоставление теоретических и экспериментальных данных о разогреве массивного цилиндрического образца от экзотермии. Теоретические кривые изменения во времени температуры ряда изотерм образца
I — г 0. 2 г 0,5/•<>; 3— г—0.75 г<.,ООО - соответствующие экспериментальные точки
и построены теоретические кривые Э(Г) и Э'(/), рассчитанные по формулам (1.27) и (1.28) при найденном значении В.
Экспериментальное определение коэффициента температуропроводности ат и относительного коэффициента теплопередачи h раствора проводилось на малых цилиндрических образцах диаметром 20 см и высотой 50 см по данным наблюдений за их всесторонним остыванием после предварительного нагрева до некоторой постоянной температуры в водяной ванне. Результаты этих опытов приведены в § 1.3. На основании экспериментальных кривых зависимости и h от температуры раствора, изображенных на рис. 4, с учетом наблюдаемых в опытах изменений температуры поверхности массивных образцов (рис. 8) были приняты следующие средние значения от и й для исследуемого раствора
аг = 3.8- 10“3л<2/ч; h = 3,5 м~1. (1.209)
58
Экспериментальное определение температурных полей, вызываемых экзотермией в молодом бетоне, проводились на указанных выше моделях цилиндрических пилонов. Температура этих образцов в процессе их разогрева и остывания измерялась с точностью до О,Г с помощью предварительно заложенных в них термопар.
Действительное распределение температуры в массивных образцах сопоставлялось с теоретическим температурным полем, вычисленным по формулам (1.195), (1.196), (1.201) с учетом найденных значений В, аг и h (1.208), (1.209). Температурная функция Ф(г, t), определяющая это температурное поле, найденная таким образом, при <р (0 =<ро=0о= const имеет вид
Ф (г, /) = Фо +"f Тт (0 (а,лг), (1.210)
где
Тт(*) =
CTnA(e„p-0D)Cj е пр -е т
(«т <£-eenp) [% + (%- %) e"BV I
(1.211)
а остальные величины определяются по формулам (1.24), (1.199) и уравнению (1.197).
На рис. 8 приведено сопоставление рассчитанных таким образом теоретических кривых изменения во времени температуры указанных точек поперечного сечения пилона с соответствующими ее экспериментальными значениями.
При построении изображенных на этом рисунке теоретических кривых для моментов времени t < 24 ч в формуле (1.210) учитывался дополнительно и второй член ряда *.
Отметим, что на рис. 8 после 48 суток наблюдается некоторое «западание» экспериментальных точек. Объясняется это тем, что после прохождения пика температур с образца снимали стальную листовую опалубку. При этом теплоизоляцию верхнего торца приходилось приподнимать на короткий момент времени, в течение которого теплопотери образца несколько увеличивались. Это нашло свое отражение в том факте, что экспериментальные точки на этом рисунке после пика температур «западная» располагаются ниже теоретических кривых.
Как следует из рис. 8, предлагаемый метод определения температурных полей в молодом твердеющем бетоне с учетом зависимости экзотермии цемента от температуры процесса дает хорошее соответствие теоретических и экспериментальных данных. Кроме того, он обеспечивает быструю сходимость анали-
1 Уче1 второго члена ряда в данном примере требуется только при t <24 ч.
59
тического решения, например, в форме (1.210), при которой сравнительно скоро можно ограничиться одним первым членом ряда. Изложенное позволяет рекомендовать этот метод для широкого применения.
§ 1.16. ПРИМЕР РАСЧЕТА РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ В МАССИВНОЙ БЕТОННОЙ ПЛИТЕ
Требуется найти распределение температуры по толщине 2х0=2л1 бетонной плиты через t суток после ее изготовления (рис 9,а). Плита бетонируется на опалубке из досок толщиной
Рис. 9. Распределение температуры в бетонной плите и ее изменение во времени
а — распределение температуры по толщине плиты через 3.6 суток после се изготовления; б — изменение во времени температуры изотермы плиты, отстоящей от утепленной грани на расстоянии 0.8 м. I — без учета экзотермии; 2 — с учетом экзотермии по методу автора; 3 — начальная температура плиты. 4 — линия нулевой температуры; S — полугодовой ход температуры воздуха:--случай пср-
иоиачальчо падающей и------первоначально возрастающей температуры воздуха
40 мм с начальной температурой укладываемого бетона 6о= = 15°С. Бетон изготавливается на портландцементе, выделяющем за первые сутки твердения 18 ккал/кг тепла и имеющем предельную теплоту гидратации Эпр=62,5 ккал/кг. Содержание цемента в бетоне равно 300 кг/м3. В табл. 10 даны расчетные изменения температуры наружного воздуха
(1-212)
где Фср=6°; Дг=36°; 6 = 8640 ч.
Распределение температуры определяется выражениями (1.108), (1.138), (1.154), а входящие в них величины формулами
60
Таблица 10
Расчетные изменения температуры наружного воздуха <р (0 в град
/ В ч 42 84 168 360 720 1080 1440 2400 3360 4320
V (0 5.5 4.9 4.1 1.2 —3 -6.7 -9,6 —11.7 —5.6 6
(1.158), (1.70), (1.212). Принимая во внимание условия задач и ограничиваясь первым членом ряда в формуле (1.154), с учетом выражений (1.108), (1.138) для температуры плиты получим следующую формулу:
Ф(х,0 = <р(0 4-Т(/)Г(г), (1.213)
где
F(x) = cos ах 4- е sin ах; (1.214)
Т (0 Х1 «) [Л, + (0 + ЛзХз (I) +
4- Л«х«(0 + Ахв(01 -РФ(0. (1.215)
Здесь
<L2I6)
XtW’e^'"; (1.217)
Х3(П = е-Ввпр'; (1.218)
Х4 (f) = ara2 sin — — cos — ; (1.219)
6 6 6
Хв(0 [(ата*-В0Пр) sin^—^cos^-]X3(0; d-220)
Л1 = Фср0о; = JoOnp _Л1_ Аз +2л +0(Л.
a-rd* ата2
Л _ ^ср (блр — 6р) . д Лг00 .
’ г[(^ + (^]’ д /Мвпр-Оо)
5 Г 2л Ч ’ 2[(ата®-ВеПр)»4Ц— 1 j А . (1.221)
— 4 sin ахп
Р ~ (1 + в2) гахр + (1 - е2) si:- 2ахп ’
61
em определяется по формуле (1.70), а а — первый положительный корень уравнения (1.69).
Принимая для опалубки:
Хоп = 0,15 - к-™ а ; 6ОП = 0,04Л1 (1.222)
м*ч-град
и для бетона . . ккал ккал
Л ®нт 20 .
м-ч-град мг-ч-град
с=0,23-*-- ; ат = 3 10-3 —; у = 2400 —, кг-град ч ж8
находим для грани плиты х=—х0, укрытой опалубкой
* 0,15-20 о ккал
а =-----------------= 3.16--------
нт 0,15 + 0,04-20 м*-ч-град
и, следовательно, , 3,16 , ос -1 . 20 ,, -1
hx = -ру = 1,86 м ; Л2= — = 11,75.м .
(1.224)
(1.225)
Внося (1.225) в уравнение (1.69) и решая его методом подбора, находим
а, = 1,226 .и-1. (1.226)
Подстановка этого значения а в уравнение (1.69) для проверки дает нам
ctg(2-1,226) =
1 1,226(1,86+ 11,75) '
1,2127 = 1,2165 (ошибка 0,3%).
Таким образом:
sin ах0 = 0,9411; cos ах„ = 0,338; sin 2ах0 = 0,6363;
а2 = 1,503 м~2; 2а = 2,452 tg ал0 = 2,7844.
Параметр скорости тепловыделения цемента в бетоне найдем но формуле (1.31)
15+о^з'5й
62,5 300 \ 0,23 ’ 2400J
= 0,716-10-3-----!---
ч-град
Теперь находим:
е-=|5+^^=,6 + 33-96 = 48-96’-вепр = 0,716-10"3-48,96 = 35,055- КГ3 —;
62
ата2 = 3-1СГ3 1.2262 = 4,509-10-3 — ;
ч
ата2 — В8Гр = 4,509 • Ю-3 — 35,055 10-3 - — 30,546 10 1 - ;
2.452 Н 1,86 -Ь 11.75)2.7841
4-0.9411 ,
р=---------------------------------------- 1.174:
(1 4-0.2452) 1,226-2 Н-(1 —0.215-’) 0.6363
At =---6 v -19,96 • 103 (град2 «);
1 4,509-10~3
. 6(48,96— 15) с с_ 1Пз , , .
А3 =------—1= — 6,67 10 (гра >г ч);
3 30.546 10-3 '
Ал =-------------—--------------- - — 12943,42- 103(гра<Ач),
Аь =----------18(48.96-15) _ _ 654 76б. 103(гр^2.ч).
(30.540- КГ» Г + (^f
Л. =----------------—3’Нг = 627,597 (град-1)-,
4320 (4,509- IO”3 )2 + (—-) I
Г \ 4320 / ]
---15-48.96 _ w 10з 6 67 10з _ 15 б27 597 _ 4,509-10-3
_ 3^2 654,766-103 = 139,694 Наград2 *).
Далее вычисляем функции p<f>(t), Xi(O» — Xs(0 > а затем Т(1) (табл. 11—16).
Таблица И
Значения функции %г(0 для различных моментов времени t
( 0^=4,509.10-3-^
t в Ч 0 42 84 168 360 720 1080 1440 2400 и более
Ота*/ 0 0,1894 0.3788 0,7575 1,6232 3,2465 4.8697 6,4930 10.8216
Хг(О 1 0.8274 0,6847 0.4688 0,1973 0,0389 0,0076 0,0015 0
63
Таблица 12
Значения функции Хз(О Д-ля различных моментов времени t
В0пр=35.О55-1О-я -у)
t в Ч 0 42 84 168 360 и более
Абпр' 0 1,4723 2,9446 5,8892 12,62
ХзЮ 1 0,2293 0,05262 0,002769 0
Таблица 13
Значения функции х>(0 для различных моментов времени t (par а2 = 1.174 4,509- Ю^1 = 5,294-10-3 —)
» * Х.(О ®о + ( °пр-6о) Хз<'> в град х,(О,017^
0 1 33,96 48,96 0,108
42 0,2293 7,787 22,787 0,232
84 0,05262 1,787 16,787 0,315
168 0.002769 0.094 15,094 0,351
360 и более 0 0 15 0,353
Значения функции (О для различных моментов времени t (ота2 = 4,509-10-3 у; у- = 0,7272-1О-3 -у)
в ч 2nt G 2г/ cos G 2к 2r.t COS X h t, X 10» о — 1 м sin G а о3 sin —х Х10» в — X. (t) 10» в 1-
0 0 1 0,727 0 0 -0,727
42 0,0305 0,999 0,727 0,0305 0,138 —0,589
84 0,0611 0,998 0,726 0,0611 0,275 -0,451
168 0,122 0,993 0,722 0,122 0,550 —0,172
360 0,262 0,966 0,702 0,259 0,168 0,466
720 0,524 0,865 0.629 0.5 2,254 1,625
1080 0,785 0,707 0,514 0,707 3.188 2,674
1440 1.047 0.5 0,364 0,866 3,905 3,541
2400 1,745 —0.173 -0,126 0,985 4,441 4,567
3260 2,443 —0,766 -0,557 0,643 2,899 3.456
4320 3,142 —1 —0,727 0 0 0,727
64
Таблица 15
Значения функции Хз (О Для различных моментов времени t ( ат а2— В епр = — 30,546-10’ у; у = 0,7272-10~3 у)
t в ч 1 у a tOlx х — uis (duo ) -1 » 2> 4е — a sOl [ — 503 - )] X.U) /.(/) 10’в —
0 0 0,727 —0,727 1 -0,727
42 —0,932 0,727 -1.659 0,2293 —0,380
84 —1,866 0.726 —2,592 0,05262 -0,136
168 —3,727 0,722 —4,449 0,002769 —0,0123
360 и —7,911 0,702 —8,613 0 0
более
Таблица 16
Значения функции T(t) для различных моментов времени t
Ai Xj (О 10“3 в граР-ч А, у.» (t) 10~3 в epod’-w % ! 4 4sx*(0 Ю—3 в ерод’-ч [Л1+ Xi (/)]10-3 в град'-ч 7(0+ ₽<₽(/) в град & 1*. T (t) в град
0 139,694 -6,67 9,41 0,476 162,87 17,546 7.044 10,546
42 115,583 —1,529 7,624 0,249 141,887 32,918 6.457 26,461
84 95,648 -0,351 5,837 0,089 121.183 38,173 5,753 32,420
168 65.488 —0,018 2,226 0,008 87,582 30,741 4,461 26,280
360 27,562 0 — 6,031 0 41,491 14,646 1,560 13,086
720 5,434 0 —21,033 0 4,361 1,539 — 3,522 5,061
1080 1.062 0 —34,611 0 — 13,589 — 4,797 — 7,866 3,069
1440 0,21 0 —45,833 0 — 25,653 — 9,056 -11.270 2,214
2400 0 0 —59,113 0 — 39,153 — 13,821 -13,736 —0.085
3360 0 0 —44,723 0 — 24,763 — 8,741 — 6,574 —2,167
4320 0 0 — 9,41 0 10,55 3,724 7,044 —3,32
Теперь вычисляем значения функции F(x) (1.214) для различных точек плиты (табл. 17). После чего по формуле (1.213) находим температуру плиты в градусах в ее отдельных точках (табл. 18) с учетом экзотермии.
65
Таблица 17
Значения функции F(x) для различных точек плиты (0=1,226 ж-«: е=—0,2451)
Л В Л ах sin ах Esin ах cos ах F(x)
—1 —0,6 -0.2 0,2 0,6 1 Температура —1,2269 -0,7356 —0,2452 0,2452 0,7356 1,2260 Ф(х, /) в отд —0,9411 —0,6710 —0,2428 0.2428 0,6710 0,9411 ельных точка 0,2307 0,1645 0.0595 —0,0595 —0,1645 —0,2307 х плиты при 0,338 0,7414 0.9701 0.9701 0,7414 0,3380 Ts ее разогреве 0,5687 0,9059 1,0296 0,9106 0,5770 0,1073 з блица 18 и остывании
X в м
в сут. в ч - 1 -0.6 -0.2 0.2 0.6 1
0 1,75 3,5 7 15 30 45 60 100 140 180 0 42 84 168 360 720 1080 1440 2400 3360 4320 12 20,5 23,3 18,7 8,8 0 — 5 - 8,4 —11.7 - 6.8 11,6 29,5 34,3 27,6 13,2 1.6 - 3.9 — 7,6 -11,6 - 7,6 3 16.9 32,7 38,3 30,8 14,8 2.2 — 3,5 - 7,3 —11,6 - 7,8 2,6 15,7 29,6 34,4 27,7 13.2 1.6 — 3,9 — 7,6 —11,6 — 7.6 3 12,1 20.8 23,6 19 8,9 — 0,1 - 4,9 - 8,3 -11.7 - 6,8 4.1 7,1 8,3 8,4 6,6 2.7 — 2,5 — 6,4 — 9,4 — 11.7 — 5.8 5,6
Температуру плиты без учета экзотермии найдем по формуле (1.213), положив в ней бпр = 0о. Это дает нам:
А = А = о;
А = А —(в, - «.») + М.
OrCLz
и, следовательно,
ф (х, t) = <f (/) + {Mi + Ахг (0 + (01 — w (0} F (*)•
С помощью этой формулы и табл. 10, 11, 14 и 17 были найдены значения температуры Ф (л, /) и на их основе построены соответствующие кривые на рис. 9. Показаны распределение температуры в рассмотренной плите в момент ее наибольшего разогрева и изменение во времени температуры ее изотермы, отстоящей от грани, утепленной опалубкой, на расстоянии х=0,8 м.
66
рассчитанные без учета экзотермии и с учетом экзотермии по методу автора; на этом же рисунке рассмотрены случаи падающей (сплошные линии) и возрастающей (пунктирные линии) температуры воздуха по закону синусоиды (1.212).
Как видно из рисунка, плита вначале интенсивно разогревается от экзотермии, затем медленно теряет накопленное тепло. После этого температура ее отдельных точек начинает следить за изменениями температуры воздуха с определенным сдвигом фазы. Из изложенного следует, что учет экзотермии при расчете температурных полей таких массивных конструкций необходим
Отметим, что в начальный момент времени, в соответствии с данными табл. 18, мы получили неравномерное распределение температуры по толщине плиты, причем внутри ее температура оказалась примерно на 12,5% выше действительной начальной температуры бетона. Это объясняется тем, что для нахождения температуры бетона Ф (х, t) мы пользовались только одним первым членом ряда формулы (1.154), сходимость которой при 0 ухудшается.. Отмеченное обстоятельство, однако, не имеет практического значения, так как, начиная с некоторого малого момента времени, влияние последующих членов ряда формулы (1.154) становится пренебрежимо малым.
В табл. 19 показано распределение температуры в бетонной плите толщиной 0,2 м, симметрично остывающей при постоянной температуре воздуха 6° С, найденное с учетом (цифры в числителе) и без учета (цифры в знаменателе) экзотермии при условиях рассмотренного выше примера. Из таблицы следует, что превышение температуры отдельных точек плиты, найденной с учетом экзотермии, над соответствующей температурой, рассчи-
Таблица 19
Температура отдельных точек тонкой бетонной плиты при ее разогреве н остывании в град.
t X в м
в сут в« 0 | 0,025 0.05 0.075 0.1
16,2 15,9 15,2 13,9 12,2
16,2 15,9 15,2 13,9 12,2
0,25 9,2 9,1 8,8 8,4 7,9
8,5 8,3 8,2 7.8 7,4
0,5 12 7,3 7,3 7,2 7 6,8
6,6 6,5 6,46 6,4 6,3
24 6,6 6,6 6,5 6,5 6,4
6,1 6,1 6 6 6
5 120 6 С 6 6 6
и более 6 6 6 6 6
67
тайной без учета последней, не превышает Г. Поэтому учет экзотермии бетона при расчете полей температуры подобных немассивных конструкций не имеет практического значения; эти конструкции могут рассчитываться на температурные воздействия без учета экзотермии.
СНиП П-В.1-62 [174] в зависимости от модуля поверхности т разделяет конструкции на: массивные т<2, средней массивности 2<т<15 и пемассивные т >15.
Модуль поверхности плиты, рассмотренной в настоящем при-2 1 1 1 1П
мере т~~^—р = — = — = 0' т-е- эта плита принадлежит к категории плит средней массивности. Следовательно, изложенный выше вывод можно теперь сформулировать следующим образом: расчет и распределения температуры в конструкциях средней массивности и немассивных конструкциях можно производить без учета экзотермии.
Плита же, рассмотренная ранее, имеет модуль поверхности лг=-у-=1<2 м~1 и принадлежит к категории массивных конструкций. Для таких конструкций, как это следует из табл. 18, учет экзотермии при расчете температурных полей необходим.
ГЛАВА //
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ ВЛАГОПРОВОДНОСТИ БЕТОНА
Исследованию влажностных напряжений в бетоне должно предшествовать определение полей влажности, возникающих в нем вследствие внешних воздействий, отсутствия гигрометрического равновесия с окружающей средой и химического связывания воды в бетоне при гидратации цемента.
В главе 1 было показано, что при обычных условиях работы бетонных и железобетонных конструкций можно пренебречь влиянием температуры на диффузию влаги в бетоне и считать, что движение влаги в нем происходит в основном за счет градиента влажности.
Более важным является учет стока влаги в бетоне за счет химического связывания свободной воды. Учтя это обстоятельство, мы приходим к уравнению влагопроводности бетона (II.2), которое подробно и исследуется в дальнейшем.
Теории влагопроводности бетона в такой постановке, без учета и с учетом стока влаги посвящены работы С. В. Александровского [12], А. В. Белова [28, 30], А. И. Вейника [54], Г. Д. Вишневецкого [56, 57], А. В. Лыкова [108, 109], К. Ф. Фокина [187], А. У. Франчука [189, 190] и ряда других исследователей.
Ниже рассматривается общая задача теории влагопроводности бетона при внутреннем распределенном по объему тела стоке влаги, интенсивность которого зависит от температуры процесса. Получено соответствующее дифференциальное уравнение влагопроводности и дан аналитический метод его интегрирования, аналогичный методу дополнительных фиктивных источников тепла, рассмотренному в главе 1, и обладающий всеми его преимуществами.
§ 11.1. ВЛАГОПРОВОДНОСТЬ. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ВЛАГОПРОВОДНОСТИ БЕТОНА
При неравномерном распределении влажности по объему капиллярно-пористого тела влага в его менее влажные части непрерывно поступает из более влажных зон. Такая передача вла
69
ги происходит во всех твердых капиллярно-пористых телах, подверженных воздействию влажности, и называется ^лагопро-водностью.
У ряда материалов с ориентированными капиллярами (например, у древесины) влагофизические свойства, связанные с влагопроводностью, зависят от ориентации капилляров, а сама влагопроводность в одних направлениях лучше, чем в других. Влагофизические свойства материалов изменяются также в зависимости от их влажности. В большинстве практически важных случаев, однако, эти изменения не велики, поэтому обычно эти свойства считают не зависящими от влажности.
У некоторых материалов влагопередача является следствием не только внешнего воздействия (увлажнения или высушивания), но связана также с особым свойством материала связывать влагу. Примером этого может служить бетон, у которого в процессе твердения химически связывается значительное количество свободной воды.
В дальнейшем мы и будем рассматривать тела, материал которых обладает свойством связывать влагу, имея в виду в первую очередь бетон. При этом будем считать его однородным и изотропным телом с влагофизическими свойствами, не зависящими от возраста бетона и его влажности. Первое из этих допущений из-за хаотичного размещения микро- и макропор в бетоне вполне приемлемо; вторые два рассмотрены в § II.3.
Как и во всяком капиллярно-пористом теле, процесс влагопе-редачи в бетоне весьма сложен, а некоторые его закономерности не вполне изучены. До настоящего времени, например, не установлено, перемещается ли влага в бетоне преимущественно в виде пара или, наоборот, главным образом в виде жидкой фазы. По-видимому, однозначного ответа на этот вопрос не существует; все зависит от условий высыхания бетона, его влажности, температуры и размеров тела.
В опытах Г. А. Бужевича [45] изучался процесс испарения воды из бетонных кубов при их естественном высыхании на воздухе. Скорость испарения влаги из бетона сравнивалась со скоростью испарения с поверхности чистой воды. Оказалось, что вначале эти скорости были равны; это косвенно указывает на то, что процесс испарения влаги из бетона на данном отрезке времени происходил за счет миграции жидкости изнутри к поверхности и ее испарения на ней. Затем, через некоторое время, скорость испарения воды из бетона становилась большей, чем у чистой воды и оставалась таковой в течение некоторого времени. Это говорит о том, что величина поверхности испарения в бетоне возрастала за счет ее проникновения внутрь тела. Следовательно, в это время в его поверхностных слоях влага уже перемещалась в виде пара.
Наконец, процесс высыхания заканчивался при скорости испарения, меньшей, чем скорость испарения воды, постепенно
70
убывающей до нуля по мере уменьшения содержания в бетоне испаряемой воды. Следовательно, в конце периода высыхания влага в бетоне перемещалась только в парообразном состоянии.
В опытах автора [16] по изучению влияния масштабного фактора на влажностные деформации бетона было установлено, что у малых образцов критическая влажность 1 достигалась бетоном практически одновременно во всем их объеме, о чем свидетельствовало одновременное начало усадки в наружных и внутренних слоях тела. Это указывает на то, что к этому моменту времени поверхность испарения пронизывала всю толщу бетона.
В более же крупных образцах к моменту начала усадки в наружных слоях бетона его внутренние зоны имели еще некоторый запас свободной воды и не претерпевали усадочных деформаций.
Таким образом, соотношение между парообразной и жидкой составляющей влажностного потока в бетоне в данный момент ьремени высыхания и в данной точке его объема зависит от масштабного фактора и продолжительности высыхания.
Еще более интересные данные были получены в опытах А. И. Вейника и А. С. Шубина [55]. В этих опытах с помощью ра диоактивных изотопов был изучен процесс переноса тепла и влаги при конвективной сушке влажных капиллярно-пористых тел. Моделью такого тела служил песок, увлажненный насыщенным раствором радиоактивной соли до определенного начального влагосодержания. В процессе сушки образца мигрирующая жидкость переносила с собой эту соль, за движением которой следили с помощью счетчика Гейгера — Мюллера.
В случае внутреннего испарения влаги, а следовательно появления перообразной составляющей влажностного потока, радиоактивная соль выпадает в осадок и больше не перемещается. По изменению активности отдельных участков материала можно было судить о количестве влаги, перенесенной как в виде жидко сти, так и в виде пара.
Было установлено, что при сушке материала воздухом с обычной температурой некоторое количество влаги (—17%) испаряется внутри материала. Оказалось также, что на механизм процесса сушки и глубину зоны внутреннего испарения оказывает влияние величина массосодержания.
При низком начальном массосодержании (<2%) молярное перемещение отсутствует и сушка происходит за счет молекулярной диффузии парообразной влаги.
При высоких (>4%) массосодержаниях влага мигрировала к поверхности образца в жидкой фазе, где и происходило ее интенсивное испарение, о чем свидетельствовал бурный рост активности этой поверхности.
1 О критической влажности бетона см. § II 1.7.
71
Возвращаясь к бетону молодого возраста, отметим, что процесс его высыхания всегда начинается при наличии большого количества жидкой влаги, вводимой в бетонную смесь при ее изготовлении. Следовательно, такой бетон при высыхании последовательно проходит через все три стадии, подмеченные в описанных опытах Г. А. Бужевича.
В связи с тем, что в силу разнообразных условий, в которых может находиться бетон, невозможно четко разграничить, в какое время и в каких его зонах имеет место та или иная из этих стадий, представляется пока единственно верным исходить из единого для всех их закона влагопередачи по отношению к общему. суммарному потоку влаги, независимо от соотношения его составляющих — жидкой и парообразной влаги. Важно только, чтобы физические характеристики бетона, определяющие его влагофизические свойства, устанавливались экспериментальным путем в условиях опыта, близких к тем, которые наблюдаются при его естественном высыхании.
Именно таким подходом и отличается современная математическая теория влагопроводности, не учитывающая явление термовлагопроводности. Этой теорией мы и будем пользоваться, обобщив ее на случай учета распределенных по объему тела стоков влаги.
Пусть в твердом капиллярно-пористом теле распределение влажности U в момент времени t определяется выражением С(х, у, z, /).
Б математической теории влагопроводности показывается, что величина потока влаги через единицу площади любой поверхности в данноГ точке тела равна
(И1)
где U — влажность материала на этой поверхности, ав — коэффициент диффузии влаги, у — плотность материала, v — направление внешней нормали к поверхности в данной точке.
Рассматривая условия влагопередачи через элементарный объем капиллярно-пористого тела, с помощью выражения (II.1) можно получить следующее дифференциальное уравнение влагопроводности бетона [12]
в котором величины ав и у имеют указанный выше физический смысл, а Н (кг/м3) — функция гидратации бетона, определяющая собой количество химически связываемой влаги (кг) при гидратации цемента в единице объема бетона (л3).
Уравнение (И.2) представляет собой уравнение баланса влаги в элементарном объеме бетона и является основным в теории влагопроводности.
72
Решение основной задачи теории влагопроводпости бетона об отыскании функции влажности I/ (х, у, z. t) требует интегрирования дифференциального уравнения (II.2) при граничных и начальном условиях, определяющих соответственно поток влаги на поверхности тела и распределение влажности по его объему в начальный момент времени, и при заданном законе стоков влаги Н(х, у, г, t) за счет ее химического связывания. Для практического же использования решений этой задачи необходимо располагать численными значениями ряда коэффициентов, входящих в это уравнение, в том числе и определяющих собой влагофизические свойства бетона. Некоторые из них уже были рассмотрены в § 1.3, остальные будут изучены ниже.
Отметим, что существуют различные способы задания влажности бетона U. Она может быть задана в относительных единицах по объему— (jiz3/jit3) или по весу— {г/г}-, часто ее задают в процентах по объему—(м31м3) 100 или в процентах по весу — (г/г) 100.
В дальнешем мы будем пользоваться измерением влажности в относительных единицах по весу (г/г). Заданная таким образом относительная влажность будет определять собой количество влаги (г) в бетоне, отнесенное к единице его веса (г) в сухом состоянии. Она может быть определена как разность весов мокрого и сухого образца, деленная на вес сухого образца.
§ 11.2. ГРАНИЧНЫЕ И НАЧАЛЬНОЕ УСЛОВИЯ-РАВНОВЕСНАЯ ВЛАЖНОСТЬ БЕТОНА
В состоянии термодинамического и гигрометрического равновесия бетона с влажным воздухом его температура равна температуре окружающей среды. Поэтому граничные условия теплопередачи на открытой поверхности тела (1.5) предполагают, что потеря тепла с единицы такой поверхности в единицу времени пропорциональна разности температур поверхности и среды вблизи нее (1.4). Влагосодержание же бетона в рассматриваемом случае приобретает некоторое постоянное равновесное значение. Соответствующая ему относительная влажность бетона называется его равновесной относительной влажностью.
Относительная равновесная влажность бетона не равна относительной влажности окружающего воздуха. Поэтому потеря влаги с единицы открытой поверхности тела в единицу времени пропорциональна не разности влажностей поверхности бетона и окружающего воздуха, а разности относительных влажностей бетона: поверхностной U и равновесной ф(/) с окружающей средой
f = <WY[t/-1>(0]. (П.З)
Коэффициент пропорциональности анв в этом уравнении носит название коэффициента влагопередачи и зависит от формы
73
тела, состояния и влажности его поверхности, а также ряда других факторов.
Так как на поверхности тела влага не может накапливаться, то количества подведенной влаги (II. 1) и влаги потерянной (П.З) должно быть равны между собой. Приравнивая выражения (II. 1) и (П.З), получаем граничное условие для рассматриваемого случая влагопередачи
-^ + р[1/-ф(0]=0. (П.4)
В этом уравнении величина
Р (П-5)
ав
представляет собой относительный коэффициент влагопередачи. Этот вид граничных условий встречается наиболее часто, и мы будем широко пользоваться им в дальнейшем, имея в виду свой заданный закон изменения относительной равновесной влажности бетона ф, (t) на каждой из координатных поверхностей с нормалью V, ограничивающих тело. Аналогичным образом могут быть получены выражения и для других видов граничных условий, встречающихся в приложениях.
Если влажность бетона на поверхности тела поддерживается равной ф(х, у, z, I), то на этой поверхности граничные условия имеют вид
1/ = ф(х,р,2,0- (П.6)
Если поверхность тела непроницаема для потока влаги, то на ней
W=°- <"'7’
Отметим, что граничные условия (II.6) и II.7) являются частными случаями более общего условия (II.4) и получаются из него соответствующим предельным переходом.
Действительно, при бесконечно большом аив влажность бетона на поверхности тела будет мгновенно принимать значения равновесной влажности. Устремляя поэтому в уравнении (II.4) р -> со, мы получим граничное условие для этого случая вида (П.6).
Если поверхность тела непроницаема для потока влаги, то независимо от U и ф(/) в уравнении (П.З) должно быть д=0. Чтобы удовлетворять этому условию, мы должны положить в нем а„в = 0. Устремляя поэтому в уравнении (П.4) р-> 0, мы получаем граничное условие для этого случая в виде (II.7).
Возможность указанных предельных переходов избавляет нас от необходимости в дальнейшем рассматривать особо задачи с граничными условиями (П.6) и (П.7). Достаточно будет по-
74
лучить лишь решение ряда задач с граничными условиями вида (II.4). Решения же аналогичных задач с другими граничными условиями мы получим из найденных решений, осуществив в них
соответствующий из указанных предельных переходов.
Для практического использования граничных условий (П.4) необходимо располагать данными об относительной равновесной влажности бетона. Величина этой влажности зависит от температуры и влажности окружающего воздуха и от способа достижения бетоном гигрометрического равновесия с внешней средой. Если бетон, стремясь к такому равновесию, отда-дает влагу, то оно достигается путем его высыхания, или, как говорят, десорбции; если же бетон поглощал влагу, то равновесное состояние наступает в результате его увлажнения, или, как принято говорить, сорбции.
Графическая зави
Рис. 10. Изотермы сорбции и десорбции ря да строительных материалов а — изотермы сорбции шлакобетона- /—т = -1400 кг/м3, Г-20'С; 2—т-920 кг/м3. Г-0” С: 3 —1“920 кг1м\ f—35° С; б — изотермы сорбции пе 1'0Й?2.иа: 4~ Т“850 «г/л3; /-20е С; 5— Т “800 кг/м3-•=2Сг С; б—т—345 кг/м3, t -0 — 35" С: 7—Т =
—660 кг/м3- Г—20” С; в — изотермы десорбции-в — цемеитнопесчаиый раствор; 9 — бетон 1 : 2,1 : 4.9. В/Ц-0.575 (лаиные автора): 10 — расчетная изотерма десорбции бетона; г — изотермы сорбции и десорбции цементного камня- II — изотерма десорбции; 12 — изотерма сорбции
симость равновесной относительной влажности бетона от относительной влажности воздуха при постоянной температуре, изображенная в виде некоторой кривой, называется изотермой сорбции или десорбции, в
зависимости от того, к какому из двух указанных выше случаев достижения равновесного состояния она относится.
Обычно подобного рода кривые имеют S-образный вид (рис. 10), причем изотермы сорбции и десорбции совпадают
75
только в двух крайних точках: при <р=1 и <р=0, образуя своеобразные гистерезисные петли (рис. 10,г). Верхней ветвью таких петель всегда является изотерма десорбции. Объясняется это, по-видимому, тем, что гигрометрическое равновесие бетона наступает весьма медленно, поэтому экспериментально наблюдаемое равновесие является лишь кажущимся; с равновесным вла-госодержанием в бетоне меньшим истинного в случае сорбции и большим истинного в процессе десорбции.
Изотермы сорбции и десорбции бетона изучены слабо; для других же родственных бетону материалов они исследованы лучше [56, 86, 187, 200]. Результаты этих исследований позволяют считать, что на равновесную влажность бетона влияние температуры в области обычных положительных ее значений не велико1. При прочих равных условиях равновесная влажность бетона зависит от содержания геля в нем, степени дисперсности частиц и их адсорбционной способности, пористости, а также ряда других факторов.
По данным исследований автора (рис. 10, в), в обычных пределах положительных температур уравнение десорбции тяжело-ю бетона приближенно может быть представлено в виде линейной зависимости
ф(<р) = (20+1,5Ф)10“4, (II.8)
где <р—относительная влажность воздуха в процентах;
ф— равновесная весовая относительная влажность бетона в г/г.
При решении ряда нестационарных задач теории влагопро-водности часто встречается случай укрытия грани тела слоем влагоизоляции, ее роль, например, может играть опалубка. Вла-гообмен на такой грани может быть оценен при помощи некоторого условного коэффициента влагопередачи а*в, величину которого, по аналогии с выражением (1.9), можно находить по следующей приближенной формуле:
Таким образом, при отыскании нестационарных влажностных полей бетонных тел сложные граничные условия на их гидроизо-лированных гранях практически могут быть заменены граничными условиями свободного влагообмена при некотором условном коэффициенте влагопередачи а*0, отыскиваемом по формуле (II.9) и являющемся функцией толщины влагоизоляции бв и ее влагозащитных свойств, определяемых коэффициентами ав и aUD.
1 Это, например, следует из рис. 10, а, на котором изотермы сорбции шлакобетона объемным весом 920 кг/м3 при температурах 0 и 35е С мало отличаются друг от друга.
76
Начальное условие определяет распределение относительной влажности бетона по объему тела в некоторый момент времени, принятый за начало отсчета. Оно может быть задано в виде некоторой непрерывной функции координат точки
U = f(x,y,z,) при t Q. (11.10)
Это соответствует ряду практических задач, с которыми приходится иметь дело в приложениях. Однако, имея в виду изложенное в конце § 1.2, мы будем пользоваться более простой формой начального условия, а именно
U Uo — const при / = 0, (Н.П)
где Uo — начальная влажность бетона.
Если в качестве начального момента момент укладки бетона, то его начальная быть определена по формуле
Цо = В/Ц- , 0 1 +П + Ш
где В/Ц — водоцементное отношение, а П
сительные части песка и щебня соответственно в бетонной смеси.
времепи t=0 принят влажность Uо может
и Щ — весовые отно-
(11.12)
§ 11.3. ВЛАГОФИЗИЧЕСКИЕ СВОЙСТВА БЕТОНА
В уравнениях теории влагопроводности бетона и решениях ее задач кроме плотности у фигурируют еще коэффициент диффузии влаги ав и коэффициент влагопередачи анв.
Коэффициент диффузии влаги ав (м2/ч) представляет собой количество влаги (кг), протекающее через единицу площади (л2) поверхности изовлаги (поверхности равной влажности) в единицу времени (ч) при единичном перепаде концентрации вла-/ кг/м? \ ,
ги I—-—) в бетоне.
Коэффициент влагопередачи с открытой поверхности в окружающую среду ctUB ) численно равен количеству влаги (кг), отдаваемому влажным бетоном с единицы открытой поверхности (л2) в единицу времени (ч), при единичном перепаде концентраций влажности бетона: поверхностной и равновесной с окружающей средой (кг/л3).
Влагофизические свойства бетона практически не зависят от химических реакций, сопровождающих процесс твердения бетона, поэтому они мало подвержены влиянию возраста бетона. Другие же особенности бетона в большей степени влияют на его влагофизические свойства, которые в основном зависят от водоцементного отношения, состава бетонной смеси и влажности бетона.
77
Автором [12] по специальной методике, основанной на регулярном режиме сушки, было проведено экспериментальное изучение влагофизических свойств бетона.
В опытах было исследовано шесть серий бетонных и растворных образцов. В пяти из них изучалось влияние В/Ц и возраста бетона и раствора на их влагофизические свойства. В шестой серии исследовалось влияние содержания цемента. Образцы этой серии были изготовлены из бетона трех составов, в каждом из которых соотношение между весовыми частями заполнителей сохранялось неизменным, менялось лишь содержание цемента. В качестве вяжущего использовался портландцемент активностью 475 кГ/см2. Результаты описанных опытов приведены на рис. 11—13. Обобщая эти результаты, можно отметить следующее.
Коэффициент диффузии влаги в бетоне тем меньше, чем выше водоцементное отношение. Так, при увеличении последнего на 86% величина аи снижается на 9,5%. Величина же коэффициента влагоперехода аыв, наоборот, существенно повышается с ростом В!Ц, увеличиваясь в 4,3 раза при возрастании последнего в тех же пределах (рис. 11).
Установленная зависимость влагофизических свойств бетона от водоцементного отношения связана с тем, что характер пористости бетона существенно меняется при изменении ВЩ. Бетоны на больших ВЩ имеют более крупные поры и количество их больше, чем у бетонов с малым ВЩ\ в то же время известно, что движение жидкости по тонким смачиваемым капиллярам происходит быстрее, чем в случае толстых капилляров По-видимому, на влагопередачу в бетонах при больших ВЩ оказывает существенное влияние медленная диффузия влаги в крупных порах, объединенных в капиллярные трубки, не заполненные полностью жидкостью, стенки которых покрыты пленочной водой. В этих условиях влагопередача в большей части проходит за счет медленных процессов внутреннего испарения и диффузии пара, тогда как в случае мелких пор, заполненных влагой, она проходит быстрее в основном за счет миграции влаги. У бетонных образцов с большим ВЩ поверхность, на которой происходит влагообмен с внешней средой, имеет большое количество и размеры открытых пор; она более «ноздревата» и, следовательно, более развита. У таких бетонов влагоотдача происходит интенсивнее и коэффициент влагопередачи естественно выше.
Из изложенного следует, что с точки зрения опасности растрескивания от усадочных напряжений бетоны с большими водоцементными отношениями невыгодны. У них диффузия влаги замедленна и влагоотдача с поверхности ускорена. Это приводит к более быстрому высыханию поверхностных слоев, развитию больших градиентов влажности и, следовательно, усадочных напряжений.
78
aswt-
0.4 0.5 0.6 0.7 0.0 0.3
Водоцементное отношение
Рис. 11. Зависимость коэффициента диффузии влаги ав, коэффициента влагопередачи aHD и относительного коэффициента влагопередачи р бетона и цементного раствора молодого возраста от водоцементного отношения
1 — бетон состава (по весу) 1 : 2.1 : 4.9; 2 — цементный раствор состава (по весу) 1 : 2.1
79
Рис. 12. Зависимость коэффициента диффузии влаги ав, коэффициента влагопередачи анв и относительного коэффициента влагопередачи р бетона молодого возраста от содержания цемента. В/Ц=0,64. Экспериментальные точки (слева направо) соответствуют содержанию цемента 278, 324, 370 кг/м3 и составу бетона (по весу) соответственно 1 : 2.1 :4,9; I : 1,62:3,92 и I : 1,4:3,27
Примечание. Величины ав. анв н р даны в процентах от их средних значения, соответствующих содержанию цемента, равному 2/5 ке!м\
Рис, 13. Зависимость коэффициента диффузии влаги ав и коэффициента влагопередачи анв от возраста бетона. Бетон состава (по весу) 1 : 2,1: 4,9
/ - В/Ц = 0,7; 2 - В/Ц =0,82; 3 - B/U = 0,93
Примечание. Величины ов, анв даны в процентах от их средних значений, соответствующих началу высыхания образцов в возрасте 2 суток.
Из рис. 11 видно, что коэффициент влагопередачи апв весьма велик по сравнению с коэффициентом диффузии влаги ав, следовательно во влажном бетоне неизбежно быстрое высыхание поверхностных слоев, так часто приводящее к поверхностным усадочным трещинам, вероятность появления которых тем выше, чем выше относительный коэффициент влагопередачи р. Поскольку при возрастании В/Ц прочность бетона снижается, а величина р повышается, то у бетонов на больших В/Ц появление поверхностных усадочных трещин при отсутствии ограничения высыхания неизбежно.
Существенное влияние на влагофизические свойства бетона оказывает содержание цемента в нем. Так, с увеличением расхода цемента от 275 до 375 кг!м3 (на 36,5%) коэффициенты диффузии влаги пв и влагопередачи ацВ возрастали в среднем соответственно на 31 и 80% (рис. 12). По-видимому, увеличение содержания цемента, делая бетон более удобоукладываемым, уменьшает размеры и количество пор в нем, что, по аналогии с уменьшением ВЩ, повышает способность бетона к влагообмену В связи с тем, что изменения апв при этом более существенны, бетоны с большим расходом цемента быстрее высыхают с поверхности (величина относительного коэффициента влагопередачи р у них больше) и, при прочих равных условиях, имеют более неравномерное распределение влажности, следовательно, они менее выгодны с точки зрения величин усадочных напряжений.
Описанные данные позволяют рекомендовать для определения коэффициента диффузии влаги в бетоне с учетом весового водоцементного отношения и содержания цемента следующую эмпирическую формулу:
ав = 6 (1 — 0.2B/Z7) (1 4- юЛи2/ч, (11.13)
где Ц — содержание цемента в кг/м3.
С увеличением возраста бетона коэффициент диффузии влаги ап и коэффициент влагоперехода аив снижаются (рис. 13), следовательно, процессы влагопередачи и влагообмена с внешней средой у старого бетона протекают медленнее, чем у бетона в раннем возрасте
Интересно также отметить, что в то время как повышение температуры бетона снижает коэффициент диффузии тепла, приводя к замедлению теплообмена, увеличение его влажности повышает коэффициент диффузии влаги и ведет к ускорению влагообмена. Такое различие во влиянии температуры на теплообмен и влажности на влагообмен в бетоне связано с различием физических картин тепло- и влагообмена. В то время как теплообмен происходит молекулярным путем, т. е. главным образом за счет кондуктивной составляющей теплового потока, влагообмен связан с переносом массы поглощенного вещества в виде жидкости или пара.
81
При расчете распределения влажности в бетоне обычно исходят из некоторых средних значений св и анв, назначаемых по справочным или экспериментальным данным. Например, в СН 55—59 [139] на основе описанных опытов автора включены следующие средние значения этих коэффициентов:
cB=5-10~fi—; МО-4-. (П.14)
ч ч
§ 11.4. АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ДЛЯ СКОРОСТИ ГИДРАТАЦИИ, ЗАВИСЯЩЕЙ ОТ ТЕМПЕРАТУРЫ ПРОЦЕССА
При нормальных условиях твердения бетона непрерывно происходит процесс гидратации содержащегося в нем цемента, сопровождающийся химическим связыванием воды. В результате этого определенное количество воды затворения активно участвует в формировании новообразований в бетоне и, как говорят, прочно связывается в виде точных соотношений определенных кристаллогидратов. Связываемая таким образом вода в силу огромной энергии подобной связи в дальнейшем уже не участвует во влагопередаче в бетоне, поэтому этот процесс следует рассматривать как непрерывный сток влаги, распределенный по его объему, с определенной интенсивностью во времени.
Количество воды, химически связываемой различными минералами клинкера, а также цементами разных минералогических составов, изучалось в ряде работ [47, 73, 129, 199].
На основании этих исследований можно считать, что в среднем количество связываемой портландцементом воды в долях его сухого веса равно 15% в месячном возрасте бетона, 20% — к 3-месячному возрасту и 25—30% к концу его твердения.
Как и всякая химическая реакция, процесс гидратации будет существенно зависеть от температуры; следовательно, интенсивность стока влаги в бетоне самым тесным образом связана с полем температуры в нем. Поэтому нашей задачей является вывод аналитического выражения для скорости гидратации, зависящий от температуры процесса.
Так как химическое связывание воды в бетоне является непосредственным следствием экзотермической реакции гидратации цемента, то естественно предположить прямую пропорциональность количества связываемой воды количеству выделившегося тепла при его твердении
Я(/) = /щЭ(о, (11.15)
где Н{1) {кг/м3) —так называемая функция гидратации бетона, входящая в уравнение влагопроводности (II.2) и определяющая собой количество (кг) химически связываемой влаги при гидратации цемента в единице объема бетона (м3), 3(t){ ккал ]—
82
количество тепла (ккал), выделяемое одной весовой единицей цемента (кг) к тому же моменту времени при его гидратации в бетоне, Ц (—) — содержание цемента, К ( ) — коэффи-
\MSJ \ккалкг/
циент пропорциональности.
Коэффициент К физически представляет собой количество химически связываемой воды (кг) одной весовой единицей цемента (кг) при ее частичной гидратации в бетоне, во время которой выделяется 1 ккал тепла.
Указанное предположение высказывалось и ранее рядом исследователей. В частности, Г. Д. Вишневецкий [56] для сопоставления кинетики экзотермии нормального (по классификации С. Д. Окорокова [140]) портландцемента с кинетикой химического связывания воды при его гидратации составил специальную таблицу тепловыделения и содержания прочносвязанной воды к различным срокам твердения портландцемента примерно следующего минералогического состава: 60% Сз$+15% C2S + + 15% СзА+Ю% C4AF.
Эти данные, полученные обработкой результатов опытов В. А. Кинда, С. Д. Окорокова, С. Л. Вольфсона [96] и более поздних опытов С. Д. Окорокова, воспроизведены во втором и третьем столбцах табл. 20. В двух других столбцах этой таблицы на их основе подсчитаны значения коэффициента К для указанного цемента и выписаны их отклонения от соответствующего среднего значения.
Таблица 20
Значения коэффициента К для нормального портландцемента
^Возраст Т епловыдслсние Э (/>, в ккал!кг Количество прочносвязанной воды UW С (П кг кг в 10J ккал, кг Отклонение в % от среднего значения
3 ДНЯ 79,59 0,092 0,116 _7
7 дней 96,03 0,116 0,121 з
28 дней 106,8 0,147 0,138 + 10
Среднее . . 0,125
3 мес. 114,78 0,175 0,153 —1
6 мес. 121,1 0,188 0,155 0
I год 126,4 0,198 0,157 +1
Среднее . . 0,155
Как следует из табл. 20, зависимостть (11.15). в общем хорошо подтверждается опытом. Для ряда американских портланд
83
цементов она подтверждается также данными Т. Пауэрса и Т. Браунъярда [240]. Правда, значения К в табл. [20], подсчитанные для бетона 3-месячного — годичного возраста, несколько вы ше, чем для молодого бетона. Это объясняется, по-видимому, неодинаковым характером ошибок измерений в опытах U(t) и 3(f).
Величины U(t), как известно, определяются весьма точно методом количественного анализа. Тепловыделение же 3(f) определяется калориметрическим способом с неизбежными ошибками измерений за счет труднооцениваемых теплопотерь, тем большими, чем больше продолжительность опыта. Это обстоятельство. по-видимому, и приводит к вероятно кажущемуся увеличению коэффициента К с возрастом бетона. Таким образом, для обычных нормальных портландцементов среднее значение этого коэффициента может быть принято равным
К = 0,125-10—2 . (11.16)
\ ккал/кг /
Скорость химического связывания воды в бетоне на основании выражения (11.15) будет равна
^- = (11.17)
Следовательно, в твердеющем бетоне мы будем иметь сток влаги с интенсивностью
= = (11.18)
В § 1.5 было найдено хорошо согласующееся с опытом аналитическое выражение (1.42) для скорости экзотермии
С учетом этого выражения и формул (1.44) и (1.24) формула (11.18) может быть переписана следующим образом:
Qu (0 = - dJ^~= - (0 Ф (0- (II. 19)
Мы получили таким образом выражение для интенсивности стока влаги в твердеющем бетоне, устанавливающее ее зависимость от температуры процесса, которым и будем пользоваться в дальнейшем.
Выражение (11.19) обладает очень важным достоинством; оно позволяет получать решения сложнейших задач теории влагопроводности аналитическим методом даже в самых общих случаях двух- и трехмерных по координатам задач с переменными во времени граничными условиями. Это показано в § II.5—11.10.
84
§ 11.5. УРАВНЕНИЕ ВЛАГОПРОВОДНОСТИ ПРИ СТОКЕ ВЛАГИ, ЗАВИСЯЩЕМ ОТ ТЕМПЕРАТУРЫ. УПРОЩЕНИЕ И МЕТОД РЕШЕНИЯ ЗАДАЧИ ТЕОРИИ ВЛАГОПРОВОДНОСТИ
Внося (11.19) в выражение (П.2), мы приходим к следующему уравнению баланса влаги в элементарном объеме бетона:
= arfU — Кси (0 Ф, (П .20)
где Ф — его температура, а остальные величины имеют физический смысл, указанный в § 1.5, П.1. Это уравнение представляет собой уравнение влагопроводности со стоком влаги, зависящим от температуры бетона.
В соответствии с изложенным выше задача теории влагопро-годностп при стоке влаги, зависящем от температуры, имеющая однозначное решение, ставится следующим образом.
Требуется отыскать влажность бетона L'(x, у, z, t), удовлетворяющую дифференциальному уравнению влагопроводности со стоком влаги, зависящим от температуры:
= au\2U — Кси (0 Ф (11.21)
при заданных граничных условиях, например, условиях вида
+ — ф(0] = 0 на поверхности, (11.22)
соответствующих наиболее общему случаю свободного влагооб-мена,п начальном условии
U = U0 при / 0, (11.23)
функции со(0, Ф(*, У, 2, 0, ф(0 и начальная влажность Uo — заданы.
Уравнения (П.21) — (П.23) похожи на соответствующие уравнения (1.46) — (1.48) теории теплопроводности при источнике тепла, зависящем от температуры, поэтому применим для их решения метод, аналогичный методу дополнительных фиктивных источников. Этот метод мы будем называть методом дополни тельного фиктивного стока.
Введем в рассмотрение некоторый распределенный по объему тела дополнительный фиктивный сток влаги, зависящий от координат точки и времени, с интенсивностью
(П.24)
где Ui — пока произвольная функция. Рассмотрим теперь исходную задачу (11.21)— (П.23) для некоторой функции влажности 1>2 при наличии этого дополнительного стока (II.24), однородных
85
граничных условиях вида (11.26) и произвольном пока начальном условии (11.27). Основные уравнения этой вспомогательной задачи будут иметь вид:
(11.25}
+ pU2 — 0 на поверхности; (11.26)
U.^U^-U^O) при / = 0. (П.27)
В этих уравнениях функцию U\ следует рассматривать как пока еще произвольную, но заданную. Подберем теперь эту функцию таким образом, чтобы решение U2 задачи (11.25) — (11.27), будучи сложенным с U\, дало бы нам общее решение U исходной задачи теории влагопроводности (П.21) — (11.23) с первоначальным заданным действительным стоком влаги, зависящим от температуры. Иными словами, подчиним функцию условию
Ut + Ut = U. (II.28)
Внося (П.28) в уравнения (П.21) — (П.23) для функции Uit с учетом (11.25) — (П.27) получаем следующие уравнения:
V2t7i = 0; (11.29)
4- p[Ut— ф(0] - 0 на поверхности. (П.30)
Таким образом, функция U\ должна быть решением третьей или смешанной граничной задачи эллиптического типа с граничными условиями (П.30), в которых время t рассматривается как параметр, а ф(0 — равновесная влажность бетона, в общем случае различная на каждом из координатных срезов, ограничивающих тело.
Как показано в § 1.10, 1.11, общее решение уравнения вида (П.29) всегда может быть выражено через гармонические функции с коэффициентами (произвольными постоянными интегрирования), зависящими от времени t. Распоряжаясь этими коэффициентами должным образом, можно удовлетворить и граничному условию (11.30), тем самым указанная краевая задача будет решена, а функция U\ однозначно определена.
Вспомогательную задачу, определяемую уравнениями (П.29) — (II.30), назовем первой основной задачей теории влагопроводности при стоке влаги, зависящем от температуры. Ее решение — функция IJ\ — будет определять собой влажностный режим тела в условиях свободного влагообмена с внешней средой при переменной равновесной влажности ф(/) и при наличии распределенного по его объему стока влаги интенсивностью
86
описываемый гармоническими функциями координат точки с коэффициентами в виде постоянных интегрирования, зависящих от времени t. Такой влажностный режим мы будем называть обобщенным квазистационарным влажностным режимом. Таким образом, первая основная задача теории влагопроводности — есть задача об обобщенном квазистационарном влажностном режиме.
Вторую вспомогательную задачу с однородными граничными условиями, определяемую уравнениями (II 25) — (11.27), мы будем называть второй основной задачей теории влагопроводности при стоке влаги, зависящем от температуры. Эта задача будет определять собой влажностный режим тела, находящегося в условиях свободного влагообмена со средой при нулевой равновесной влажности, имевшего начальную влажность (7о—(0), и при распределенном по его объему стоке влаги, зависящем от температуры, интенсивностью
i = - у [Кеш (0 Ф - . (11-32)
Решение этой задачи также может быть всегда найдено аналитическим методом с применением обычных приемов классической теории влагопроводности.
Итак мы видим, что предлагаемый метод дополнительного фиктивного стока обладает рядом преимуществ. Во-первых, этот метод позволяет свести сложную задачу теории влагопроводности при стоке влаги, зависящем от температуры, к двум более простым вспомогательным задачам. Во-вторых, метод дополнительного фиктивного стока, основанный на рассмотрении обобщенного квазистационарного влажностного режима, даже в самом общем случае нестационарных граничных условий, не требует привлечения теоремы Дюамеля и поэтому свободен в значительной своей части от недостатков, основанных на при?ле-нении классических методов решения задач теории влагопроводности, связанных с плохой сходимостью этих решений. Для эффективной теории влагопроводности это обстоятельство особенно существенно, поскольку сходимость ее решений зависит от величин коэффициентов ав и ацВ- Так как эти величины значительно меньше величин коэффициентов ат и ант, то сходимость решений задач теории влагопроводности также значительно хуже, чем соответствующих решений теории теплопроводности.
Как будет показано ниже, решение первой основной задачи в большом числе практически наиболее важных случаев удается найти в замкнутом виде, что существенно улучшает сходимость решения всей задачи теории влагопроводности в целом.
Улучшение сходимости решений, достигаемое в методе дополнительного фиктивного стока, весьма существенно также для задач о влажностных напряжениях в неравномерно высыхаемых телах. Как известно, в основные уравнения этих задач входят
87
производные от влажности бетона по координатам точки (см. гл. V), а при дифференцировании выражений, аналогичных (1.72), (1.97), их сходимость ухудшается. Поэтому весьма важно с самого начала получить улучшенную сходимость решений задач теории влагопроводности. Это и достигается в методе дополнительного фиктивного стока.
Разумеется, метод дополнительного фиктивного стока со всеми его преимуществами применим и в случае задачи теории влагопроводности без наличия стока влаги, т. е. при ее классической постановке. Такая задача будет представлять собой лишь частный случай рассматриваемой более общей задачи.
При наличии готовых решений первой и второй основных задач по формуле (11.28) всегда может быть составлено общее решение задачи теории влагопроводности при стоке влаги, зависящем от температуры, определяющее собой поле влажности при этих условиях. Ниже рассматриваются аналитические методы решения этих вспомогательных задач.
§ 11.6. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ВЛАГОПРОВОДНОСТИ. СЛУЧАЙ ЗАМКНУТОГО РЕШЕНИЯ
Сопоставляя уравнения (11.29) — (11.30) с уравнениями (I.I09) — (1.110), мы видим, что с точностью до обозначений они вполне тождественны. Поэтому для того чтобы получить решения уравнений (11.29) — (11.30), достаточно в решениях уравнений (1.109) — (1.110), определяемых формулами (1.115), (1.117), (1.119), (1.122), (1.124), (1.127), (1.128), (1.130), (1.133), (1.135) — (1.138), заменить Ф] на ft на р и tp(t) на ф(0- Сделав это, будем иметь следующие формулы.
При одномерном потоке влаги вдоль оси ох через плиту толщиной 2х0, имеющую неограниченные размеры в двух других направлениях
UA*A) ~ В At) + В At) — , хо
причем
а) при граничных условиях:
—Р1[£Л —чМО] =0 прих-—х0;
^- + Р2^1-Ф2(О]=О при х = х0;
в At) = Ф1(')+ (1 + Р1Хо)в£(0;
Р1хо
щ = Р1Ргхо № (О - <1 (<)| .
Pi + %Р1Ргхо + Pi
(11.33)
(11.34)
(11.35)
88
б) при граничных условиях:
— Pi Н4 — Ф1(0] =0 прих = —х0;1
(71 = -фг(/) при х - х01 I
В1(0 = ’М0+— ^в2(0;] Р1ХО
в = Р1>'р №2 (О — (<)| .
И' 1 + 2Plx0
в) при граничных условиях:
— Pt [«/, — *1 (01 = ° при х = — хи;
dUi
-^-=0 прих=-х0,
а также при
Vi 4ч (0 при х = — х0, ]
-^- = 0 прих.х0, |
в2(0 = 0; (0 = 44(0;
(11.36)
(11.37)
(11.38)
(11.39)
(11.40)
г) при граничных условиях:
<4=t>(0 Ui = ф2(0 при X = — х0; | при х = х0, J (П-41)
Br(0= yI'MO + WI; fi2(0= (11-42)
Таким же путем могут быть получены и формулы для случая одномерного потока влаги вдоль радиуса г цилиндра.
В случае сплошного цилиндра, а также во всех случаях твердых тел, у которых вся поверхность поддерживается при заданной влажности бетона ф(0 или у которых на всей поверхности происходит влагообмен со средой, температуре и влажности которой соответствует равновесная влажность бетона ф(0.
^(0=Ф(0. (П-43)
§ 11.7. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ВЛАГОПРОВОДНОСТИ. обобщенный квазистационарный влажностный РЕЖИМ прямоугольной призмы, случай незамкнутого решения
В более сложных задачах о двух- и трехмерных потоках влаги в телах, грани которых поддерживаются при различных влажностях или на гранях которых происходит свободный вла-
89
гообмен со средой, температуре и влажности которой соответствуют различные равновесные влажности материала на отдельных гранях, решение первой основной задачи теории влагопроводности удается найти лишь в незамкнутом виде. Ниже приводится такое решение для прямоугольной призмы неограниченной длины с размерами поперечного сечения 2х0Х2г/0 с попарно симметричными граничными условиями на противоположных гранях. Рассматриваемая задача встречается при расчете распределения влажности бетона по сечению длинных призматических стержней (колонн, балок, элементов рам, столбчатых бетонных блоков и т. п.). Исходные уравнения этой задачи имеют вид:
(11.44)
dW, _Q
дх2 дуг
dUY дх -а КА -•Ф1(О] = о при X = — х0
dUt дх + аКА -Ф, (01 = о при X =-х0;
dUt ду -а КА — Фг(01 = ° при У = ~Уо,
dUj ду + Pi КА —ФИО] = о при У ~ Уо-
(11.45)
Сравнивая эти уравнения с уравнениями (1.139), (1.140) первой основной задачи теории теплопроводности для рассматриваемой призмы, устанавливаем их полное тождество с точностью до обозначений. Поэтому решение нашей задачи мы найдем в готовом виде, заменив в формулах (1.141) — (1.150) Ф1 на Ui, h, на Ри Ч>»(0 на ф,-(/), т на k,п на s и считана* и ps положительными корнями уравнений:
ctg ах0 = — ; ctg . (II .46)
Pl Pi
Учтя изложенное, мы не будем выписывать общего решения рассматриваемой задачи. При желании оно может быть всегда получено с помощью указанных выше последовательных замен.
$ 11.8. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ВЛАГОПРОВОДНОСТИ ПРИ СТОКЕ ВЛАГИ, ЗАВИСЯЩЕМ ОТ ТЕМПЕРАТУРЫ.
ОДНОМЕРНЫЙ поток влаги в плите
Рассмотрим вторую основную задачу теории влагопроводности при стоке влаги, зависящем от температуры, в случае одномерного потока влаги вдоль оси ох через плиту толщиной 2х0, имеющую неограниченные размеры в двух других направлениях.
90
Решение первой основной задачи для этого случая мы нашли в § П.6 в форме (11.33), (П.35), поэтому исходные уравнения рассматриваемой задачи имеют вид:
^ = ав ~ м ф -(° - &—* <п-47)
ОТ ОХх Хо
— р! иг = 0 при х = — х0;
7 (П.48)
-у5- + р2 (Jz = 0 при х = х0;
U„ = U0 — ВДО) — В2(0)— при t = 0. (П.49)
хо
Выражение
=_у[в;(0+ (П.50)
в уравнении (П.47) может рассматриваться, как дополнительный фиктивный сток влаги, зависящий от времени t и координаты точки х.
В формулах (П.47), (П.49) функции <o(Z), B\(t) и B2(t) заданы и определены выражениями (1.44), (П.35), а температура Ф(х, /) предполагается уже найденной. При этих условиях уравнение (П.47) будет представлять собой уравнение диффузии с известной правой частью в виде заданной функции координат точки тела и времени. Метод интегрирования таких уравнений предложен в работах автора [3], [4]. Применим этот метод для решения рассматриваемой задачи.
В связи с однородностью граничных условий (П.48) общий интеграл уравнения (П.47) будем искать в виде ряда по фундаментальным функциям (1.71):
= У 7\(0(cosaftx + eftsinaftx), (II.51)
Л=1
тогда граничные условия задачи (П.48) будут автоматически удовлетворены, если ал—положительные корни уравнения (1.69) при h\=p\ и Л2=р2-
Внося (П.51) в (П.47) и учитывая разложения в области —х <х<х0:
1 == У Рк (cos aft х + еЛ sin аь х);
(11.52)
Л=оо
х = У Qft(cosaftx + eftsin akx) (11.53)
91
и
(П.54)
(11.55)
(П.56)
(П.57)
(II.58)
л=®
ф (Л, t) = S (0 (cosa*x + е* sin a*x),
где
p _______________4 sin a*x0_________.
* (1 4-E*)2aftx0+(l-E^)sin2aftx0 ’
q = 4e* (sin ak x„ — a* x0 cos ak x0)
k a*[(1+£ft)2a*xo+(1-£*)sin2a*xo]
J Ф(х, Z)(cosa*x + e* sin a* x) dx
J (cos a* x + e* sin a* x)* dx
—*0
e ________Pl — Pt_______
k~ 2aft + (pi + Pt} tg a* xo
для Th (0 получаем следующее обыкновенное дифференциальное уравнение
П(о+«в «и,(о=-[₽.«;(<)+ 77в;<'>+
+ Ка, (t)S„ (01. (П.59)
Общин интеграл этого уравнения, удовлетворяющий начальному условию (П.49), равен:
t
Т„(1) = и„Р,е-“. — Хл(О + J f a.a’x»(6>-
О
- Кси (|)S* (0] е-“» “а <'-е><%, (П.60)
где
Хо(О = В, (0Рк + В2(0 . (П.61)
*Ь
При этих условиях выражение (П.51) удовлетворяет всем уравнениям задачи (П.47)—(П.49) и поэтому является ее общим решением.
При pi=p2=p решение (П.51) принимает вид
Л=со
U2 = У Tk (t) cos ak x, (П.62)
Л=1
где Th(t) по-прежнему находится по формуле (П.60), в которой
Р =------4sinafeX°-; (11.63)
2a* х04- sin2a*x0
Хл (0-^(0^, (П-64)
92
a ait — положительные корни первого из уравнений (11.46).
Подстановкой
= (1165)
*0 формула (11.63) приводится к виду
р =-------. (П .66)
+ SIn Ik cos
В силу уравнений (11.46) постоянные Рь, определяемые по формуле (П.66), зависят только от рх0 и номера k характеристического числа 1;/, и поэтому могут быть протабулированы в зависимости от этих величин. В табл. 6 даны первые три значения этих постоянных при h=p И Pm=Pk.
Наконец, устремляя в выражении (11.62) р -> оо , получим решение второй основной задачи, соответствующее случаю, когда грани плиты поддерживаются при заданных влажностях Ф1(О иф2(0:
£4= У(—l)*7\(/)cos (2fe+1)iTX t (Ц.67)
—J 2х0
Л=0
в котором Tk(t), и определяются по формулам (11.60), (11.61) и (11.55) при
(2л + 1)л (П.68)
2х0
а В|(0 отыскивается по выражению (11.42).
Представляет интерес также случай, ксгда грань плиты л = —х0 поддерживается при влажности ф2(0. а на грани х=х0 происходит влагообмен со средой, температуре и влажности которой соответствует равновесная влажность бетона ф((0. Решение рассматриваемой задачи при этом определяется формулами (П.51), (П.60), (П.61), (П.55) —(П.57) при
eft = ctgaftx0, (11.69)
в которых ед — положительные корни уравнения
ctg 2ax0 ----— . (II.70)
a
Подстановкой
a =4- (11.71)
уравнение (П.70) приводится к виду
ctg5 = -^-. (П.72)
Три первых корня этого уравнения даны в табл. 7 при h=p.
93
В заключение отметим, что в связи с тем, что функции <о(£) и -Sfc(lj) предполагаются уже найденными при расчете температуры Ф (х, t), интеграл
t
С 2
Кс J со ® S* (£) е % °*£ , (11.73)
входящий в формулу (11.60), проще всего вычислять с помощью планиметра по графику подынтегрального выражения или аналитически, но после аппроксимации последнего простейшими легко интегрируемыми функциями.
§ 11.9. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ТЕОРИИ ВЛАГОПРОВОДНОСТИ ПРИ СТОКЕ ВЛАГИ, ЗАВИСЯЩЕМ ОТ ТЕМПЕРАТУРЫ. ДВУХМЕРНЫЙ поток влаги в прямоугольной призме
Рассмотрим теперь вторую основную задачу теории влагопро-всдности при стоке влаги, зависящем от температуры, для прямоугольной призмы, исследованной в § П.7. Исходные уравнения этой задачи имеют вид:
— = ав(-^- + — КсаЩФ — (11.74)
dt в\ дх* ду* J v ' dt ’ ' '
dUt дх диг дх Pi — о + р, и2 = 0 при при х = — х0; Х = х0; (П.75)
ду р2 ^2 — 0 при у = — Уо;
dU2 ду 4- = 0 при у = Уи;
при t = 0, (П.76)
где — решение первой основной задачи для нашей призмы, найденное нами в § П.7.
Следуя мегодике, изложенной в § П.8, функцию U2 будем искать в виде двойного ряда
i/2= L Е r^(0cosaftxcosp5J/.
*=1 s=l
(П.77)
94
Выбирая при этом в качестве щ и ps положительные корни уравнений (11.46), мы удовлетворим автоматически граничным условиям задачи (11.75). Вил функции 7'fts(Z) найдем из уравнения (11.74), внеся туда (11.77) и учитывая разложения в области —х0<*Оо; —Уо <У< Уо-
Ui = Т S ^**(Ocosa*xcosP4y; (П.78) *=1 S=1
Ф = £ S DjjJ/JeosafcXeosPjy (П.79)
*=1 S- 1
yjCfticosa*xcos₽sf/, (11.80)
*=1 s=l
где
Ул
2<?* (О f cos у ch aft у dy
(0 ----------------=*-----------------------4-
Ус
( COS3Ps£/tft/ —Ус
*o
2 Ns (t) [ cos x ch ps xdx
+------------=5--------------------- (11.81)
f cos2 aft xdx
** У»
J J Ф(х, у, t) cos ak xcos psydxdy
Dks = -*~y' ----------------------------; (П.82)
J cos2aft xdx J cos2P5t/dt/ -*> —Уо
J» Уо
J cosaftxdx J cos2p5ytfj/
~xo—Ул
^>0 Уп
J cos2 a*xdx [ cos2 p5t/ dy
-*• —Уо
(11.83)
95
а функции Qk(t), Ns(t) определяются по формулам (1.142), (1.143) при замене в них tn на k, п на s, Л, на р,-, <Pi (/) на ф((0 и при ак и ps, являющимися корнями уравнений (11.46). Сделав это для Ths(t), будем иметь уравнение
T'hs (О + М “л + ₽s) Л. (О = - *«> (0 Dks (0 - A-ks (0, (11.84) общий интеграл которого, удовлетворяющий начальному условию (11.76), равен
Л.10 = Ц,С,, -4и(0 +
I
+ J [*.К + ФА.Ю-^0)(5)Dte(g)] X
о
X е"“в ( + Ф dl. (11.85)
При этих условиях выражение (11.77) удовлетворяет всем уравнениям задачи (П.74) — (11.76) и таким образом является ее общим решением. При возрастании чисел k и s коэффициенты ^fes(O. Cks, определяемые по формулам (11.81), (11.83), быстро убывают, вследствие чего ряды в решениях (П.77), (П.78) быстро сходятся, поэтому эти решения удобны для практических приложений Полагая в формулах (П.77), (II.78) Pi = p2=P. ф|(0 = =ф2(0=ф(0 и устремляя р-» со, мы получим решение рассмотренной задачи для случая, когда поверхность тела поддерживается при влажности бетона ф(0:
I/, = 1” ‘francos <a+""«cOs(2s + l>"i'. (4.86) -*о ^Уо
Л=о s=O
в котором Ths(t) по-прежнему определяется по формуле (11.85) при:
= (2k + 1)_л_ р = _12к + 1)л_ (п 87)
* 2х0 2%
(2А+ 1)(2s + 1) Л« ’ Aj (0 = Ф (0 • (П .88)
§ 11.10 ПРИМЕР РАСЧЕТА РАСПРЕДЕЛЕНИЯ ВЛАЖНОСТИ В МАССИВНОЙ БЕТОННОЙ ПЛИТЕ
Найдем распределение влажности в бетонной плите, рассмотренной в § 1.16, к текущему моменту времени t с учетом стока влаги. Бетон марки 200 состава (по весу) 1 :2, 1 :4,53, В/Ц = 0,5. Для простоты рассмотрим случай, когда температура внешней среды <р(0 и равновесная влажность бетона ф(0 постоянны и равны соответственно:
Ч>(0 = фср = 6°; ф(0 = фср = 1,25-10-2 (г/г). (11.89)
96
Распределение температуры Ф(х, t) по толщине плиты, соответствующее этому случаю, мы найдем, положив всюду в примере § 1.16 Л5=0. При этом мы будем иметь
Ф(х,0 = ФсР + 7'(0Г(х), (11.90)
где
T(t) = х, (01А + Лх2(0 + Лхз (01 - рФс₽. (П.91)
А = (П-92)
ат а2
а остальные величины определяются по формулам (П.89), (1.214), (1.216) —(1.218), (1.221), (1.226).
Учтя, что А2 = - -----19,96 • 103 + 6,67 • 103 = 149,583X
4,509-10—3
Х103 (град2-ч) и полагая в формуле (1.215) и табл. 16 Аа=А5= =Д6=0, по формуле (11.91) найдем T(t), соответствующее рассматриваемому случаю (табл. 21).
Таблица 21
Значения функции 7(Т) для различных моментов времени t
t в ч Аа х- (П и-3 в граИА-ч Ах» (О ю-3 в граИА-ч 1А+Ах»(') + +А>Х»(О] ю-3 в гра&^-ч т (/) 4- рфср в град Г(/) о град
0 149,583 —6,67 162,873 17,59 10,546
24 134,177 —2.875 151,262 27,067 20,032
42 123,766 —1,529 142,197 32,99 25,946
60 144,133 —0,814 133,279 36,785 29,741
84 102,42 —0,351 122,029 38.439 31,395
120 87,058 —0,0994 106,918 36,459 29.415
144 78,083 —0,0428 98 34.104 27.06
168 70,125 —0,018 90,067 31,614 24,57
360 29,513 0 49,473 17,464 10,42
720 5.819 0 25,779 9,1 2.056
1080 1,137 0 21,097 7,447 0,403
1440 0,224 0 20,184 7,125 0,081
2400 0 0 19.9G 7,044 0
Распределение влажности в (11.28), (11.43), (11.51), (11.60) и ряда, найдем в следующем виде:
плите на основании формул ограничиваясь первым членом
^(*,0 = ФсР + ^(06(х),
(11.93)
где
G(x) = cosp* + vsinp.r;
(11.94)
Я (0 = Хе (О [<7 (<4 ~ Фс₽) Ъ (О Л];
(11.95)
97
Й (0 = Х1 (0 х3 (0; S (0 = А [Л + Д10 т (0]; (11.96)
v (П= МО 5(0 (II.97)
х’ Хс(О ’
а 0 — первый положительный корень уравнения.
(II .98)
Р2 — Р1Рг
Входящие сюда величины равны:
(II.99)
Хв(0-е • 2p+(Pl + P2)tg₽x0 ’
л fiOnp (Опр — 00) . (II. 100)
Z17 ’
Рата
А = ъ (II.101)
‘ и (14-v2) 2р*0 + (1 - V2) sin 2рх0 ’
. _ 2ФСР sin рх0 . 9 р (II. 102)
л 1+ev . . о. , 1—ev . . , Ао- й sin(a Р)х0+ , Л sin(a + p)x0; (11.103)
а—р а+Р
— _ 4Д, sin рх0 q ~ 2р (11.104)
Принимая для опалубки:
ав = 6-10~6 м~)ч\ a1IB = 2-10~4 м/ч\ дв = 0,04 м (11.105)
и для бетона
ав = 5• 10~6 №/ч; <х11Э = 2 -10-4 м/ч.
(11.106)
по формуле (П.9) находим для грани плиты, укрытой опалубкой:
= —6-10-«-2-10^»-----= 0 857 j0-4 л/ч jj j07)
нв 6-10-е4-0,04 2-1G-4 ’
Следовательно [формула (П.5)]:
0,857-10—4 _i 2-10-4 -1 |ПО.
р, =------------= 17,14 м ; р~ =-------------— 40 м (II.108)
м 5-10-в ’ ’ 5-10-« ' 1
Внося (II. 108) в уравнение (11.98) и решая его методом подбора, находим
₽, = 1,1815 л-1.
(11.109)
Подстановка этого значения 0 в уравнение (П.98) для проверки дает нам
tg(2-1,1815) -^b2815<17-<+J0).t ’ 1,18152— 17,4-40
т. е. 0,9865 = 0,9867 (ошибка 0,02%).
98
Таким образом: ₽2 = 1,3959 л"2;
2₽ = 2,363 м~~ ; а — ₽ = 0,0445 л"1 ; а + ₽ = 2,4075 м1;
sin 0хо = 0,9252; cos ₽х0 = 0,3795;
tg0xo = 2,4377;
sin 2₽х0 = 0.7023; sin (а — 0) х0 = 0,04485; sin (а + ₽) v0 = 0,6699.
Теперь находим:
л8 =
17.14 — 40 п 1С1.
V = ----------------------------- — 0,1614;
2,363 + (17,14 + 40)2,4377 = 35,055.10—8 (48,96—-j5)_ = }
7 5,294-Ю—3
------------------£1^------------------ = о J_ .
(1 + 0,1614я) 2,363 + (1 — 0,16142)0,9252 м
л 2,6-0,9252 п one
° 1,1815
(1 + 0.245-0,1614) 04485 (1-0,245-0,1614)
0,0445 ’ 2,4075
X0,6699 = 1,314 м. - 4-0,76-0,9252 ,
о =----------------= 1,191 .
4 2,368
Начальную влажность бетона найдем по формуле (П.12) U0 =----------------------—---------= 6,55- Ю-2 г/г.
0 1 + 2,1 + 4,53
Л10 —
Далее (табл. 22) вычисляем функции хв(О> ы(0. S(t) и х?(0-На рис. 14 построен график функции х?(0. а в табл. 22 на его /
основе с помощью планиметра вычислены площади]’ I\z-о
лее в табл. 23 вычислены значения функции H(t) для различных моментов времени, а в табл. 24—значения функции G(x) для отдельных точек плиты. Наконец в табл. 25 приведены значения влажности бетона (7(х, /)> рассчитанные с помощью формулы (П.93) в процентах по весу (цифры в числителе).
Найдем теперь критическую влажность бетона, воспользО' вавшись формулой (П1.2) и данными табл. 34.
UKp = 0,00625 + 1,4 0,005 = 1,325-10 2 г/г.
Таким образом, критическая влажность бетона UKP составляет ~20% от его начальной влажности Uo.
Если обратиться к табл. 25, то мы увидим, что через месяц высыхания влажность бетона на поверхности и внутри плиты составляет ~ 87—91% от его начальной влажности и значительно
99
Таблица 22
Значения функций Х<ХО. со(О, S(Q, Х.;(0 и | Хт (ОЛ для различных моментов времени
+8-
§
24
42
60
84
120
144
168
360
720
0,0167
0,0293
0.0419
0,0586
0,0837
0,1005
0,1173
0,2512 0,5025
0,9998 0,9997 0.9996 0,9994 0,9992 0,999
0,9988 0,9975 0,995
108 77.149 53,198 33,688
16,575 5,081
2,234 0,972 О
О
24,315 17,349 11,963
7,575 3,727 1.143 0.502 0,219
13.857
26,322 34,093
39,08
41,253 38,651
35,557
32,285 13,692
2,702
23,253 35,718
43,489
48,476
50,649 48,047 44,953
41,681
23,088 12,098
17,672 27,146
33,052 36,842 38,493
36,516
34,164
31,678 17,546
9,194
429,695 471,056
395,52 279,189 143,55
41,771 17,167
6.946 О
О
О Ю, 18, 24, 29, 32, 32, 33, 33,
Таблица 23
Значения функции H(t) для различных моментов времени I.
q(LQ- фср)-1,191 (6,55-1,25) 10~:=- 63,123-КГ3 г/г
Кс = 0,125 1 О'3 0,23 = 0,2875 1 О'3 кг/град
t в « 1 17 (/) dt 10s в г/г - Ac J х7 (')<« ] 1О3 в г/г Н (/) 10s в г/г
0 0 63,123 63,123
24 3,112 60,011 59,999
42 5.236 57,887 57,87
60 7,187 55,936 55,914
84 8,53 54,593 54,56
120 9,306 53.817 53,774
144 9,484 53,639 53,585
168 9,671 53.452 53,388
360 9.723 53,4 53,266
720 9,812 53,311 53,041
Таблица 24
Значения функции G(x) для отдельных точек плнты
х в * еж sin рЖ * sin р х COS Р jr G(x)
—1 —1,1815 —0,9252 0,1493 0,3795 0,5289
-0,6 —0,7089 —0,6511 0,1051 0,759 0,864
—0,2 —0,2363 —0,2343 0,03781 0,9722 1,01
0,2 0,2363 0,2343 —0.03781 0,9722 0,9344
0.6 0,7089 0,6511 -0.1051 0,759 0,6539
1 1,1815 0,9252 —0,1493 0,3795 0,2302
100
выше критической влажности Uvp. Следовательно, за это время бетон потерял лишь часть свободной воды, главным образом за счет ее химического связывания, не достигнув эффективной влажности. Поэтому его высыхание на этом отрезке времени не сопровождалось усадкой и развитием усадочных напряжений. Из
Время В сутках
Рис. 14. График функции Х.(0=---
Хс(О
этого вытекает практически важный вывод о том, что развитие усадочных напряжений в массивных бетонных конструкциях возможно только в бетоне зрелого возраста.
Отметим, что в начальный момент времени, в соответствии с данными табл. 25, мы получили неравномерное распределение влажности по толщине плиты, причем внутри ее влажность оказалась примерно на 15% выше действительной начальной влажности бетона Uo. Объясняется это тем, что для нахождения влажности бетона U(x, t) мы пользовались только одним первым чле-
101
Таблица 25
Значения влажности бетона U(x, t) в отдельных точках плиты при ее высыхании в (г/г)102 (процентах по весу) с учетом и без учета стока влаги
f X п м
в сут. в ч —1 -О.6 | _ ~€'2 । 0,2 0,6 1
0 0 4,589 6,704 7,625 7,148 5,378 2,703
4,423 6,434 7,31 6,856 5,173 2,631
4,588 6,703 7,624 7,147 5,377 2,703
2,5 4,207 6,081 6,897 6,475 4,906 2,538
4,587 6,702 7,623 7,146 5.376 2,702
4,09-1 5,896 6,681 6,275 4,766 2,488
4,586 6,699 7,62 7,143 5,374 2,702
4,067 5,852 6,63 6,227 4,733 2Л76
4,58 6,69 7,609 7,133 5,367 2,699
4,055 5,333 6,607 6^206 4,718 2,471
4,572 6,677 7,594 7,119 5,357 2,696
пом ряда формулы (11.51), сходимость которого при (->0 ухудшается.
Здесь мы имеем полную аналогию с результатами расчета температуры плиты в примере § 1.16.
Интересно оценить влияние фактора стока влаги в бетоне на распределение его влажности в плите. С этой целью найдем последнее без учета этого фактора по формуле (П.93), положив в ней Л7=0. Это дает
(*. 0 = Фер + 9 (Uo - Фер) Хе (0 G (х). (II. 110)
Найденные по этой формуле с помощью табл. 22 и 24 значения влажности бетона в отдельных точках плиты указаны в табл. 25 цифрами в знаменателе.
Как следует из табл. 25, расхождения в величинах влажности бетона, вычисленных с учетом и без учета стока влаги, уже становятся весьма значительными и достигают 25%. Таким образом, учет стока влаги при определении полей влажности плиты и подобных ей конструкций необходим.
ГЛАВА III ТЕМПЕРАТУРНЫЕ И ВЛАЖНОСТНЫЕ ДЕФОРМАЦИИ БЕТОНА
В обычных условиях работы бетонных и железобетонных конструкций бетон непрерывно претерпевает изменения температуры и влажности, вызывающие появление в нем температурных и влажностных деформаций. Вследствие неравномерного распределения последних по объему тела, а также из-за ограничения деформаций внешними связями, их появление сопровождается развитием напряжений. Поэтому изучение характера, величин и особенностей температурных и влажностных деформаций бетона имеет большое практическое значение.
Исследованию температурных деформаций бетона посвящены работы Келлера [173], Дэвиса и Трокселла [173], Мейерса [237], Н. А. Мощанского [129], Ю. А. Нилендера [134—138], С. Г. Тахтамышева [177] и ряда других исследователей.
Особый предмет исследований составляют температурные деформации бетона при высоких температурах, например, жаростойких бетонов. Этот вопрос подробно освещен в специальной литературе [123, 133], обобщающей исследования, проведенные в НИИЖБ Госстроя СССР в этом направлении. Влажностные деформации бетона изучены в работах С. В. Александровского [7—10], [13—17], А. В. Белова [28, 29], Г. Д. Вишневецкого [56, 57], Г. Колоузека [231], Р. Лермита [104], В. В. Михайлова [126, 127], Н. А. Мощанского [129], Ю. А. Нилендера [134—138], Т. Пауэрса и Т. Брауньярда [240], 3. Н. Цилосани [200], А. Е. Шейнина [201—203] и многих других.
Ниже кратко излагаются экспериментальные данные о температурных деформациях, усадке и набухании бетона и результаты проведенного автором исследования некоторых особенностей его влажностных деформаций, существенных для проблемы влажностных напряжений в бетоне.
§ 111.1. ТЕМПЕРАТУРНЫЕ ДЕФОРМАЦИИ БЕТОНА
При изменениях температуры, связанных с нарушением термометрического равновесия, бетон претерпевает температурные деформации. Этот вид деформаций, например, неизбежен в ряде
103
массивных бетонных конструкций, обычно разогревающихся в молодом возрасте бетона от экзотермии, а затем медленно осты-ваемых с течением времени. Непрерывные температурные деформации свойственны также сооружениям, находящимся на открытом воздухе и подвергающимся атмосферным воздействиям, носящим периодический характер. Наконец, аналогичное влияние оказывают на конструкции технологические циклы, например в автоклавах, пропарочных камерах, горячих цехах и т. п.
Появление температурных деформаций при ограничении перемещений конструкций или в связи с неравномерным их распределением по объему бетона влечет за собой развитие температурных напряжений, которым часто сопутствует появление в нем температурных трещин. В указанном общем случае температурные деформации бетона слагаются из двух составляющих: свободной температурной деформации, пропорциональной изменению температуры, и так называемой напряженной деформации, вызываемой уже собственно температурными напряжениями.
Для расчета температурных напряжений и деформаций бетона в первую очередь необходимо располагать данными о величине свободных температурных деформаций. Величины этих деформаций обычно характеризуют коэффициентом линейного температурного расширения бетона а, который определяет собой свободную относительную деформацию бетона при равномерном изменении его температуры на один градус.
Установлено [173], [237], чго на величину коэффициента линейного расширения бетона существенное влияние оказывает вид крупного заполнителя (табл. 26) и состав бетона (табл. 27).
Таблица 2G
Влияние вида крупного заполнителя на коэффициент линейного расширения бетона а
(опыты Дэвиса и Трокселла)
Вил заполнителя
Кварц....................................
Песчаник ................................
Гравий ..................................
Гранит ..................................
Базальт .................................
Известняк ...............................
о-10° (град)—•
11.9
11.7
10.8
9.5
8.6
6.8
Наибольшим линейным расширением обладают жирные бетоны и бетоны на кварцевых заполнителях, а наименьшим — тощие бетоны и бетоны на известняковых заполнителях. Объясняется это тем, что сами заполнители имеют различные величины
104
Таблица 27
Влияние состава цементно-песчаного раствора на его коэффициент линейного расширения а
Состав по весу а 10" (град) ~1
опыты Келлера | | опыты Мейерса
1:0 12,6 18,4
1:1 11 13,3
1:2 10,1 —
1:3 — 11.2
1:4 10,4 —
1:6 9.2 10.4
1:8 9.5 —
этого коэффициента, как правило, меньшие, чем у чистого цементного камня (табл. 28). Поэтому отощение цементного раствора песком и щебнем снижает величину а.
Таблица 28
Коэффициент линейного расширения некоторых каменных материалов, применяемых в качестве заполнителей (опыты Келлера)
Материалы а-10® (град)
Кварц, перпендикулярно к оси кристаллов 13,3
Песчаник 12,4
Сланцы : . . . 10.1
Известняк : : : : = 9.1
Гранит 8,1
Кварц, параллельно оси кристаллов 7,9
Кирпич : ; . 4.5
Ощутимое влияние на величину коэффициента а оказывают возраст и режим-хранения бетона (табл. 29). Водоцементное же отношение [177] (табл. 29), а также изменение температуры в пределах 4—55° [173] не оказывают заметного влияния на него.
Из изложенного следует, что в бетоне, даже при равномерном изменении температуры, неизбежно возникают местные температурные напряжения. Это обусловливается различием в величинах коэффициента температурного расширения материалов, составляющих бетон.
Температурные деформации и коэффициент линейного расширения цементного камня и бетона при низких отрицательных температурах экспериментально были изучены В. М. Москвиным и М. М. Калкиным [128]. Эти исследования показали, что при изменении температур от —5 до —70° С в бетоне происходят необратимые изменения структуры цементного камня, которые при оттаивании бетона приводят к значительным остаточным дефор-
105
Таблица 29
Влияние возраста и условий хранения иа коэффициент линейного расширения бетона а [в (град.)-1 - 10е] (опыты С. Г. Тахтамышева)
Состав бетона (по несу) вщ Хранение а-10» (град) ~1
возраст бетона
3—4 сут. П-13 сут.
0,64 Горячее 8,8 8,3
. Q ЛД. А 0,64 Холодное 9,3 8,7
1 :о,ио:4, zi 0,72 Горячее 8,1 8
0,72 Холодное 9,2 9
0,64 Горячее 8,3 8,2
1 • *) АЙ Л *>А 0,64 Холодное 9,3 9.1
1 ZZjDo.^.Z^i 0,72 Горячее 7,8 8.3
0,72 Холодное 9,2 9,3
Примечание. Холодное храпение — влажное хранение при температуре +20° С, а горячее—влажное храпение при температуре +40° С.
маиням тем большим, чем больше величина водоцементного отношения.
При значительном нагреве бетона происходит так называемая температурная усадка — необратимая деформация, связанная с дополнительным высыханием цементного камня и его обезвоживанием. Однако этот вид деформаций не имеет практического значения для обычного бетона при обычных значениях температур. Температурная усадка велика лишь у жаростойких бетонов, претерпевших значительный разогрев, особенно у бетонов на жидком стекле [123]. Коэффициент линейного расширения таких бетонов находится в пределах (3,6-е-9) 1СГ6 (град)-1, увеличиваясь с повышением температуры у бетонов на портлендском и глиноземистом цементе и уменьшаясь — у бетонов на жидком стекле.
§ II 1.2. ВОДА В БЕТОНЕ
Классификация влаги во влажных капиллярно-пористых дисперсных телах может быть произведена по ряду классификационных признаков: по степени ее подвижности, изменениям кристаллической решетки материала при дегидратации, изменению физико-механических свойств материала в зависимости от степени его увлажнения и т. п.
Интересующие нас влажностные деформации бетона связаны с удалением из него влаги или, наоборот, с увеличением ее содержания. Эти процессы неизбежно сопровождаются затратой или соответственно накоплением энергии, зависящей от нарушения или восстановления определенных форм связи влаги с
106
материалом. Поэтому в основу классификации влаги в бетоне должна быть положена интенсивность энергии этой связи.
Именно по такому принципу построена схема акад. П. А. Ребиндера [156, 157], согласно которой все формы связи влаги с материалом делятся на три большие группы: 1) химическую связь; 2) физико-химическую связь и 3) физико-механическую связь. Применим эту схему к бетону.
Химическая связь воды в бетоне осуществляется в точных количественных соотношениях (стехиометрическая связь) в результате химической реакции гидратации цемента и образования кристаллогидратов при кристаллизации из пересыщенных растворов. При образовании такой связи определенная часть воды в бетоне исчезает и входит в состав новых веществ. Количества воды, химически связываемой отдельными клинкерными минералами и цементами различного минералогического состава, были указаны в § П.4.
Интенсивность энергии этой формы связи очень велика; она может быть нарушена только химическим воздействием или прокаливанием. В связи с этим химически связанная, или, как еще говорят, прочиосвязанная вода в бетоне в процессах влаго-обмена с внешней средой не участвует. Однако при расчете полей влаги в бетоне на основах теории влагопроводности химическое связывание воды следует учитывать как распределенный по объему тела внутренний сток влаги, интенсивность которого зависит от температуры процесса и времени. Один из методов такого учета изложен в § П.4.
Физико-химическая связь воды в бетоне осуществляется в различных не строго определенных соотношениях в виде адсорбционной связи в гидратных оболочках. Она возникает в бетоне вследствие диспергирования и растворения в воде вещества цементных зерен с образованием ионно-дисперсного и молекулярно-дисперсного раствора, а также в результате адсорбции влаги. Причиной возникновения этой связи как в том, так и в другом случае является молекулярное силовое поле; различие заключается лишь в том, какие из молекул принимают участие в возникновении этой связи.
При диспергировании и растворении образуются сольватные оболочки вокруг молекул вещества.
При адсорбции связь возникает в результате молекулярного силового поля молекул внешней и внутренней поверхностей мицелл, как это наблюдается у гидрофильных веществ, или молекул внешней поверхности вещества, как это имеет место у гидрофобных веществ.
Вода сольватных оболочек в бетоне находится в свободном состоянии и поэтому обладает всеми свойствами обычной воды.
Адсорбционно же связанная вода обладает рядом свойств, отличающих ее от обычной воды, что используется при разработке различных методов ее количественного определения. К
107
числу этих свойств относится: неспособность к растворению его электролитов и ряда других растворимых в обычной воде веществ, практически равная нулю электропроводность, удельная теплоемкость меньше единицы, повышенная плотность, в связи с чем эта вода имеет свойства упруго-твердого тела и ее тонкие пленки толщиной < 0,1ц обладают расклинивающим действием.
Не вся адсорбционно связанная вода имеет одинаковые свойства. Наиболее прочно связан мономолекулярный слой воды, свойства которого в наибольшей степени отличны от свойств обычной воды. Последующие слои связанной воды удерживаются с ослабевающей силой и их свойства постепенно приближаются к свойствам обычной воды. Толщина такого полимолекул ярного слоя адсорбционной воды примерно равна нескольким стам диаметров ее молекул.
К физико-химически, в частности, адсорбционно связанной воде относят также цеолитную воду. Цеолитами называет группу минералов, представляющих собой водные алюмосиликаты кальция и натрия. Кристаллические решетки цеолитов состоят из каркасов с полостями, содержащими молекулы воды, слабо связанной с жесткой кристаллической основой. При известных условиях вода цеолитов может удаляться, а затем вновь поглощаться без разрушения кристаллической структуры. Поэтому содержание воды в цеолитах зависит от температуры и влажности окружающей среды.
Физико-химическая связь кроме адсорбционно связанной воды присуща также осмотической воде. В бетоне, однако, содержание этой воды практически невелико, особенно в его зрелом возрасте.
Поверхность раздела твердой и жидкой фаз в бетоне огромна; по данным Н. А. Мощанского [129], эта поверхность в свежезатворенной бетонной смеси выражается цифрой порядка 500 м21м3. В отвердевшем же бетоне годичного возраста благодаря разрыхлению она еше больше и равна около 1 км2/м3. В связи с этим количества адсорбционно связанной воды в бетоне также велики, а их роль в поведении бетона под влиянием внешних воздействий среды и нагрузки весьма существенна.
Сведения о количествах физико-химически связанной воды в бетоне ограничены. По опытным данным Г. Н. Сиверцева [168], количество адсорбционно связанной воды цементом за 24 ч составляло 600—1700 мг/г. Для бетона же месячного возраста, по данным Н. А. Мощанского [129], это количество составляет около 50% от веса воды затворения.
Адсорбционная связь в бетоне относится к числу связей средней интенсивности, которые могут быть разрушены испарением воды из сольватных оболочек, десорбцией внешних и межмнцел-лярных поверхностей и дезадсорбцпей. Даже при обычных температурах и влажностях воздуха при отсутствии гпгрометри-
108
ческого равновесия эти процессы происходят в бетоне сравнительно легко, хотя для этого и требуется довольно продолжительное время. Таким образом, эта категория физико-химически связанной воды принимает активное участие во влагообмене бетона с внешней средой.
Физико-механическая связь в бетоне осуществляется в неопределенных количественных соотношениях. К этой форме связи относится свободная вода, захваченная в ячейках кристаллизационной структуры, и вода в микро- и макрокапиллярах ’.
Структурная связь возникает в бетоне при захвате воды в результате образования геля. В этом случае вода удерживается механически, за исключением мономолекулярпого слоя, где она связана силами адсорбции. Эта связь довольно слабая и легко нарушается испарением, отжатием воды, давлением или нарушением структуры.
Связь в микрокапиллярах возникает в результате непосредственного соприкасания бетона с водой или поглощения им паров воды из влажного воздуха и последующей капиллярной конденсацией (сорбционная влажность). В таких капиллярах вода пгевдосвязана капиллярными силами и легко удаляется испарением.
В макрокапиллярах физико-химическая связь возникает только за счет непосредственного соприкасания бетона с водой. Так как давление насыщенного пара в таких капиллярах практически равно его давлению над плоскостью, то они не могут сорбировать влагу из воздуха и капиллярная конденсация в них не может иметь места. В макрокапиллярах вода удерживается механически, за исключением адсорбционно связанных пристенных слоев, и легко удаляется испарением или искусственным созданием давления больше капиллярного (например, вакуумированием пли центрифугированием).
Проследим теперь за кинетикой высыхания некоторого малого объема увлажненного цементного камня, достаточно малого для того, чтобы его высыхание можно было бы считать равномерным по объему. Испарение влаги из такого объема начинается в первую очередь из крупных пор и капилляров за счет нарушения физико-механических связей и удаления так называемой свободной воды. Этот процесс не сопровождается изменением объема (усадкой) цементного камня.
После испарения воды из крупных пор и капилляров начинается ее испарение из микропор и мелких капилляров; прогрессирующе развиваются силы капиллярного сжатия, в связи с чем цементный камень претерпевает деформацию сжатия. Возни-
1 По классификации А. В. Лыкова [108], к микрокапиллярам относятся капилляры с радиусом менее 10-5 см. Капилляры с большим радиусом принято называть макрокапиллярами.
109
кающую вследствие этого усадку мы будем называть капиллярной.
После удаления капиллярной воды начинается удаление структурно связанной и адсорбированной воды. Вначале удаляется вода структурных ячеек, образованных мельчайшими кристалликами продуктов гидратации цемента (субмикрокристалликами геля) и полимолекулярно адсорбированных слоев. Наконец последней удаляется вода, адсорбированная в виде мономолекул ярных слоев. Дальнейшее высушивание цементного камня возможно только в сушильном шкафу, где удаляется вода, адсорбированная в целях молекулярных размеров, образующихся в местах сцепления субмикрокристаллов геля.
Удаление структурносвязаниой и адсорбированной воды сопровождается значительным сжатием цементного камня. Развивающую при этом усадку называют адсорбционной.
Капиллярная и адсорбционная составляющие усадки бетона составляют в сумме его так называемую влажностную усадку.
Следует различать еще контракционную усадку. Эта составляющая усадки бетона носит физико-химический характер и связана с уменьшением объема системы «цемент — вода» при возникновении новообразований в процессе схватывания и начального периода твердения бетона, имеющих объем меньший, чем объем исходных продуктов. Контракционный эффект также связан с физико-химическим процессом адсорбции воды поверхностью цементных зерен и кристаллов новообразований, при котором происходит уплотнение воды в тонких адсорбционных слоях, а следовательно, и сжатие системы.
Наконец, существует еще карбонизационная усадка, являющаяся следствием уменьшения объема затвердевшего цементного камня в бетоне при разложении находящихся в напряженном состоянии кристаллов гидроокиси кальция в результате их химического взаимодействия с углекислым газом, содержащимся в воздухе. Эта составляющая усадки бетона таким образом также носит физико-химический характер. Необходимым условием для возникновения карбонизационной усадки является наличие напряженного состояния кристаллов гидроокиси кальция, которое неизбежно возникает в бетоне вследствие влажностной усадки и действия внешней нагрузки.
Рассмотренная выше схема высыхания цементного камня, конечно, существенно упрощена. В действительности, особенно в бетоне, этот процесс протекает значительно сложнее. Некоторые его особенности мы еще рассмотрим ниже. Сейчас нам важно подчеркнуть то, что удаление влаги из малых объемов бетона происходит по вполне четкому закону, вначале удаляются категории воды, обладающие наименьшей энергией связи, а затем остальные виды воды с очередностью по возрастающей интенсивности этой энергии.
ПО
§ 111.3. УСАДКА БЕТОНА
При отсутствии гигрометрического равновесия с воздухом влажный капиллярно-пористый бетон высыхает, уменьшая свой объем. Вследствие малости коэффициента диффузии влаги его высыхание происходит неравномерно по объему — в бетоне возникают градиенты влажности и. даже при отсутствии внешних ограничений деформаций, усадочные напряжения.
Как уже было указано выше, усадка бетона связана с химическими и физическими процессами, происходящими при взаимодействии цемента с водой, изменением влажности цементного камня при его высыхании и карбонизацией и слагается из контракционной, влажностной и карбонизационной составляющих. Для оценки сравнительных величин этих составляющих усадки и их роли в рассматриваемой нами проблеме обратимся к некоторым экспериментальным данным.
Одно из первых изучений контракционной усадки бетона было проведено Ю. А. Нилендером [134—138], как один из этапов широкой программы исследования, связанных с испытанием Днепровской плотины. Проведенные по оригинальной методике опыты выявили, что эта усадка бетона, называемая им «собственно усадкой», оказалась в 5—10 раз меньше влажностной усадки, связанной с его высыханием. В зависимости от вида цемента относительные линейные деформации «собственно усадки» цементного камня через 40—50 суток достигали значения, равного 20-10-5, в то время как на открытом воздухе обычная усадка того же цементного камня составляла от 50-10-0 до 107-10-s.
Шпиндель [247], исследуя усадку цементного теста, начиная с момента его затворения, получил характерные кривые усадки портландцементов с различной тонкостью помола в первые сутки твердения. Им было установлено, что большая часть контракционной усадки происходит до конца схватывания цемента; она значительно превышает усадку за месячный срок твердения, измеряемую на образцах-близнецах, начиная с суточного возраста. При этом цементы более тонкого помола давали большую усадку, чем такие же цементы более крупного помола.
В американских опытах [214] запаянные образцы из раствора на различных цементах имели к трем месяцам хранения относительные деформации в 3—15 раз меньше, чем у образцов-близнецов, высыхающих на воздухе, и после раскрытия и дальнейшего хранения их на воздухе давали значительную относительную усадку, равную (30-г-55) Ю-5 .
Интересное исследование контракционного эффекта при взаимодействии гидравлических вяжущих с водой было проведено В. В. Некрасовым [131, 132], который установил, что этот эффект пропорционален степени гидратации цемента. На ход контрак
111
ции влияют химический состав цемента, степень его измельчения, исходное соотношение между весами цемента и воды в смеси, а также некоторые добавки. В. В. Некрасов считал, что в основном контракционный эффект имеет чисто химическую природу и связан с образованием силикатов кальция.
Аналогичные опыты были проведены Н. А. Мещанским [129], который кроме усадки цементов изучил также контракцию некоторых инертных материалов. Им была установлена контракция таких внешне расширяющихся материалов, как гипс и расширяющийся цемент. В отличие от В. В. Некрасова Н. А. Мощанский трактует контракцию цементного теста более глубоко и считает, что она вызывается целым комплексом физико-химических процессов.
Б. Г. Скрамтаев высказал предположение, что контракцпон-ный эффект должен сопровождаться появлением вакуума в твердеющем цементном камне и бетоне, и последний действительно был обнаружен в значительных пределах [172]. В специально поставленных опытах им было установлено, что наибольшее разрежение достигается за первые 2—4 суток твердения и оно тем больше, чем больше тонкость помола цемента и чем выше его активность.
Подводя итоги сказанному, можно считать, что контракщюн-ная усадка, несомненно играющая существенную роль в технологии бетона, не имеет практического значения для рассматриваемой нами проблемы усадочных напряжений в бетоне. Она, во-первых, мала по величине сравнительно с влажностной усадкой, во-вторых, развивается в значительной своей части в весьма раннем возрасте бетона, когда последний обладает большой пластичностью, т. е. повышенными реологическими свойствами. По этой причине усадочные напряжения, развивающиеся в бетоне в это время, невелики и к тому же с течением времени значительно релаксируют.
Влажностная усадка бетона изучалась многими исследователями и продолжает интенсивно изучаться в настоящее время. Объясняется это, с одной стороны, сложностью рассматриваемого явления, с другой стороны, появлением новых сортов вяжущих и видов бетонов, например, мелкозернистых, песчаных бетонов для вибропрокатных изделий.
Установлено, что эта составляющая усадки зависит от множества технологических и физических факторов, а также среды, в которой находится бетон.
Высокосортные, тонкомолотые и высокоалюминатные цементы обладают большой усадкой, особенно в начальный период твердения. Так, например, в опытах Гленвиля [226] (табл. 30), в которых сравнивалась усадка трех сортов цемента, глиноземистый цемент за 7 дней твердения давал усадку, равную почти 40% полуторагодичной, тогда как усадка портландских цементов не превышала за это время 8% от полуторагодичной усадки.
112
Таблица 30
Влияние copra цемента на его усадку
Сорт цемента Усадка цементного раствора (ма/а.и)-10* в возрасте
7 дн. 28 дн. 3 мес. 6 мес. 12 мес. 18 мес.
Обыкновенный портландский . . 2 9 20 25 32 37
Высокосортный портландский . . 3 10 25 34 38 40
Глиноземистый 16 21 31 36 40 42
Следовательно, при прочих равных условиях в таком же соотношении примерно находится и усадка бетонов, приготовленных на этих цементах [129].
Большое влияние на усадку бетона оказывает минералогический состав цемента. В соответствии со структурной теорией усадки А. Е. (Лейкина [201—203] последняя тем больше, чем больше объем геля в единице объема, цементного камня и, следовательно, чем меньше объем кристаллического сростка. Отношение между этими структурными составляющими определяется структурным коэффициентом [203], величина которого непосредственно зависит от минералогического состава цемента. Чем меньше для него этот коэффициент, тем при прочих равных условиях больше усадка бетона, приготовленного на данном цементе. Это убедительно доказано прямыми опытами.
Существенное влияние на величину усадки раствора и бетона оказывает также содержание в них цементного теста (состав бетона). Чем жирнее раствор или бетон, т.е. чем больше содержится в них цементного камня, тем выше их влажностная усадка. Весьма показательны в этом отношении опыты Н. А. Монтанского [129], а также опыты автора [9] (рис. 15) с бетонными образцами, высыхающими через торцы.
Заполнитель (песок, щебень) уменьшает усадку цементного теста. Хотя сами каменные материалы, применяемые в качестве заполнителей, вследствие их пористости обладают определенной способностью к усадке при высушивании [250], их влажностные деформации значительно меньше, чем у цементного теста, поэтому они оказывают сдерживающее влияние на усадку бетона, причем степень последнего существенно зависит от вида заполнителя. Об этом, например, говорят опыты Р. Дэвиса, который сравнивал влияние различных заполнителей на влажностные деформации бетона состава 1:2:3 при В/Ц = 0,9. Во всех образцах мелкая фракция заполнителя состояла из того же материала, что и крупная, а модуль крупности оставался постоянным и равным 5,58. Результаты этих опытов приведены в табл. 31. Обращает на себя внимание малая усадка бетона на гранитном и известняковом щебне по сравнению с бетоном на гравии и песчанике.
из
Рис. 15. Влияние содержания цемента (состава бетона) на усадку бетона при его высыхании. Бетой 4-суточного возраста к началу высыхания на портландцементе активности 475 кГ/см2, ВЩ-O.GD. Состав бетона (по весу)
1 - 1 2.1 : 4.9. Д-273 кг/м\ 2 - I 1.68 : 3.92. Д-319 кг/м3-.
3 — 1 : 1.4 : 3.27. И' 359 кг/м’
Сдерживающее влияние заполнителя зависит также от его упругих свойств: оно тем сильнее, чем выше его модуль упругости. Это подтверждается опытами Штутгарской лаборатории с бетонами одного количественного состава, но с применением различных заполнителей. Усадка этих бетонов находилась воб-
114
Таблица 31
Влияние вида заполни гелей на влажностные деформации бетона
Вид заполнителя Усадка из возтухе (мм/ши)1(Р Набухание в воде (/rx/HAjK?
Гравий - 79 7.4
Песчаник 75 5.5
Известняк 39 5
Гранит 37 13,1
ратной зависимости к модулю упругости заполнителя (за исключением базальта) (табл. 32).
Таблица 32
Зависимость усадки бетона от модуля упругости заполнителя
Род заполнителя Модуль упругости заполнителя в к Г/см' Усадка бетона в воз растс 6G дней (мм мм) W*
Базальт 1015000 39
Доменный шлак 960000 27
Известняк 721 000 31
Гранит Пестрый известняк 168 000 49
71000 68
Таблица 33
Зависимость усадки цементного раствора от ВЩ
В‘Ц Относительная усадка цементного раствора (л<н лтл«)10= к возрасте
35 дней | 2 мсс. 3 мес. 4 мсс.
0.3 75 1 151 182 200
0,4 104 | 220 253 285
На величину усадки бетона оказывает влияние также гранулометрический состав заполнителя и, в частности, его модуль по верхности, так как он обусловливает относительный размер цементной оболочки, обволакивающей зерна заполнителя. В ряде опытов можно найти подтверждение этому обстоятельству [216]
Заметное влияние на усадку цементного раствора и бетона оказывает водоцементное отношение: чем выше ВЩ, тем больше и усадка этих материалов. Это видно из табл. 33, составление!! по данным опытов Карлсона [216] с цементным раствором, и из рис. 16, где изображены результаты опытов автора [9] с бетой ными образцами, высыхающими через торцы. Характер этой
115
зависимости, по-видимому, связан с различными прочностью и пористостью у бетонов с разным В/Ц.
Чем выше В/Ц, тем ниже прочность бетона и выше его пористость, тем интенсивнее происходит у него влагообмен с внешней средой и тем слабее сопротивление кристаллического сростка объемным изменениям геля. И, наоборот, при малых
в сутках
Рис. 16. Влияние волонементного отношения на высыхание и усадку бетона. Бетой 4-суточного возраста к началу высыхания состава (по весу) 1.2, 1 :4,9 на портландцементе активности 475 кГ/см2
1— В/Ц-0,545; 2 — В/Ц-0.595; 3 — В/Ц-0.745; 4 —В/Ц-0.845
В/Ц больше прочность бетона и меньше его пористость, поэтому указанные обстоятельства действуют в обратном направлении и усадка его оказывается меньшей
Возраст бетона к началу высыхания также оказывает значительное влияние на влажностную усадку. Чем позже начинается высыхание бетона, тем больше его прочность к этому моменту времени, тем, следовательно, меньше усадка.
Влажностная усадка в значительной степени зависит от масштабного фактора. В больших образцах или в бетонных кон-
116
Рис 17. Влияние на высыхание и усадку бетона а — длины образцов одного и того же сечения, высыхающих через горцы, длиной: 1—21 см: 2 — 17,5 см: 3—11.5 см: 6 — размеров поперечного сечения образцов одной и то же длины, высыхающих через боковую поверхность, сечением 4 — 10х 10 гл; £ — 7X7 СМ: 6 — 5X5 см. Бетон 4-суточного возраста к началу высыхания состава (по весу) 1:2,12:4,9 на портландцементе марки 400 кГ/сл5, ВЩ—0.678 - 0.638
117
струкциях усадочные деформации оказываются значительно меньшими, чем в малых образцах, на которых обычно проводят лабораторные опыты. Это подтверждается опытами К. С. Карапетяна с бетонами на легких заполнителях [89], а также специальными опытами автора по изучению влияния масштабного фактора на усадку обычного тяжел жо бетона [16] (рис. 17). В
Рис. 18. Влияние характера высыхания образцов на усалку бетона. Бетон состава (по весу) I : 2.13: 4.9 на портландцементе марки 400 кПсм2, ВЩ = 0,567. Высыхание с 4-суточного возраста
/ — с боковой поверхности; 2 — через торны
этих последних опытах было установлено, что усадка малых образцов не только развивается быстрее, но оказывается и значительно большей, чем у больших образцов по достижении равновесного состояния сравниваемыми образцами. В этих же опытах по специальной методике было проведено также сравнительное изучение усадки наружных и внутренних слоев бетона в образцах, высыхающих через торны, причем оказалось, что они больше у наружных слоев не только в любой момент времени высыхания, но и в конце его. Причины этого рассмотрены в работе автора [16].
Характер высыхания образцов также оказывает существенное влияние на ход усадки и ее величины. В специально поставленных опытах автора [18] (рис. 18) было отмечено, что усадка
118
призматических образцов, высыхающих только через боковую поверхность, развивается интенсивнее и ее величина больше, чем у образцов-близнецов, высыхающих только через торцы. Причины такого различия в усадке сравниваемых образцов те же, что и в случае образцов разных размеров.
Большое влияние на усадку бетона оказывает его температура. Повышение температуры увеличивает коэффициент влагопередачи бетона и, следовательно, интенсифицирует процесс высыхания. При неравномерном же распределении температуры по объему тела, как это, например, имеет место при разогреве бетона от экзотермии, к некоторому ускорению высыхания проводит также явление термодиффузии влаги {108]. В конечном счете все это влечет за собой увеличение усадки бетона.
При высоких температурах в бетоне может произойти разрушение части кристаллогидратов и его дополнительное высушивание, сопровождающееся увеличением усадки. Особо ведут себя в этом случае жароупорные бетоны, которые при этих условиях обнаруживают значительную температурную усадку, особенно при первичном нагревании [123].
Наконец, значительное влияние на усадку бетона оказывает внешняя среда — ее влажность и температура. С уменьшением влажности воздуха в соответствии с изотермой десорбции (§ 11.2) равновесная влажность бетона снижается, следовательно, суммарные влагопотери бетона к моменту достижения им равновесного состояния увеличиваются, а это, в свою очередь, приводит к увеличению его предельной усадки. Повышение температуры воздуха действует в том же направлении, так как обычно приводит к уменьшению его относительной влажности.
Усадка бетона при циклически изменяющихся невысоких положительных температурах больше усадки при соответствующей средней постоянной температуре. Так, в опытах А. В. Путанса [153] на диапазоне температур от +30 до +50°С она была при этих условиях в 2-5-3 раза больше, чем у бетона с постоянной температурой +40° С, а ее предельная величина уменьшалась с увеличением возраста бетона к началу высыхания.
По своей абсолютной величине влажностная усадка, как правило, во многом превосходит контракционную усадку. Об этом можно судить по приведенным выше опытным данным. Она может быть довольно значительной и достигать величины (70 -е--5- 100) 10-5 мм/мм, как это наблюдалось в опытах П. И. Глужге [70]. В обычных условиях лабораторных опытов [7, 9, 16] автор также наблюдал большую усадку исследуемых бетонов, достигающую 70 • 10~5 мм/мм. Это значительно выше, чем величина предельной усадки бетона, равная 15*10“5 мм/мм, рекомендованная для расчетов старыми нормами. Поэтому эта составляющая представляет наибольший интерес для проблемы усадочных напряжений в бетоне.
119
Физическая природа влажностной усадки бетона вскрыта недостаточно полно. Об этом говорят различные гипотезы о природе объемных изменений цементного камня и бетона, вызванных изменениями их влажности. Довольно полный обзор этих гипотез и взглядов различных исследователей на природу усадки дан в монографии 3. Н. Цилосани [200].
Некоторые из исследователей целиком [195] или главным образом [144, 225] считают основной причиной усадки бетона капиллярные явления. Другие, отрицая ведущую роль этих явлений, объясняют усадку бетона иными причинами, носящими физико-химический характер. Часть этих исследователей, например, считает основной причиной усадки удаление межкристаллической воды [39, 104, 233, 240]; другая часть [7, 9, 201] — объемные изменения гелевой структурной составляющей цементного камня, обусловленные изменением содержания в геле связанной силами адсорбции воды, при высыхании бетона.
Ряд исследователей придерживается компромиссных взглядов Некоторые из них, разделяя взгляды А. Е. Шейнина, признают в некоторых случаях ощутимую роль капиллярных явлений [8, 13, 129, 231] и привлекают дополнительно к рассмотрению расклинивающее и стабилизирующее влияние тонких пленок воды в межзерновом пространстве [129]. Другие [231] объясняют усадку бетона действием как капиллярных сил, так и сил, возникающих при удалении из цементного теста «межслойной» воды из слоев, образованных между кристаллами новообразований цементного камня.
Рядом работ советских ученых [7, 9, 200, 201—204, 209] доказано, что капиллярная составляющая усадки цементного камня, связанная с изменениями молекулярного давления лишь вследствие микроскопических искривлений поверхности жидкости на границе раздела фаз, не велика и носит второстепенный характер. Поэтому попытка развития капиллярной теории усадки бетона, предпринятая Е. Фрейсинэ [195], в настоящее время признана несостоятельной.
Наибольшим признанием среди советских специалистов пользуется структурная теория усадки бетона А. Е. Шейнина. Однако, по-видимому, наиболее полно природа этого сложного явления может быть раскрыта с дополнительным привлечением к этой теории ряда физико-химических представлений. Заслуживает внимания механизм влажностной усадки, сформированный на основе анализа богатых экспериментальных данных, в том числе и своих собственных опытов, 3. Н. Цилосани [200].
Карбонизационная усадка изучалась многими исследователями. Ранние исследования этого явления выполнены Ф. М. Ли [233]. Позже этот вид усадки изучался в ряде работ западных [213, 232, 234, 251] и отечественных ученых [169, 170]. Наиболее логично физико-химическая природа этого явления была объяс-
120
йена Т. С. Пауэрсом [242]. Его причины кратко рассмотрены нами в § II 1.2.
Величина карбонизационной усадки существенно зависит от размеров образца и может быть довольно большой. Так, в опытах Вербека [251] она была почти равна влажностной усадке, а суммарная усадка оказалась примерно в два раза больше усадки только от одного высыхания. Аналогичные данные сообщались и рядом других авторов.
Из сказанного следует, что карбонизационная составляющая усадки также имеет значение для проблемы усадочных напряжений. Так как обычно влажностная и карбонизационная усадка в опытах наблюдается одновременно, то имеющиеся экспериментальные данные об усадке бетона, высыхающего на воздухе, уже относятся к сумме этих ее составляющих. Поэтому в изучаемом нами случае нет необходимости рассматривать раздельно эти явления и вполне допустимо учитывать лишь эффект их совместного действия.
§ II 1.4. НАБУХАНИЕ БЕТОНА
Увлажняясь в результате атмосферных воздействий или прямого контакта с водой, бетон естественной влажности набухает, увеличивая свой объем.
Вследствие низкого значения коэффициента диффузии влаги в бетоне его увлажнение, а следовательно, и набухание происходят неравномерно по объему — в бетоне возникают градиенты влажности и, даже, при отсутствии внешнего ограничения деформаций, влажностные напряжения набухания. Исследование деформаций и напряжений набухания имеет большое значение для бетонных конструкций и, в частности, гидротехнических, работающих в условиях переменного влажностного режима. Однако в настоящее время этот вопрос изучен еше довольно слабо как теоретически, так и экспериментально.
Установлено, что набухание бетона, так же как и усадка, зависит от ряда технологических и физических факторов.
Бетоны на высокосортных тонкомолотых цементах имеют большие деформации набухания и большую скорость набухания. Здесь мы имеем полную аналогию с соответствующими закономерностями усадки бетонов на таких цементах [129, 226].
Известное влияние на набухание бетона оказывает содержание в нем цементного теста (состав бетона). Чем жирнее бетон, тем больше его деформации набухания при увлажнении. Это обстоятельство нашло свое подтверждение в опытах автора [10] (рис. 19). При этом одним и тем же изменениям весовой относительной влажности у бетонов с малым содержанием цемента соответствуют большие деформации набухания, чем у бетонов с большим его расходом. Причиной указанного различия в де-
121
Рис. 19 Влияние содержания цемента (состава бетона) на набухание бетона при его увлажнении. Бетон 98-суточного возраста к началу увлажнения на портландцементе активности 475 кГ/смг, В/Ц—0,69. Состав бетона (по весу)
I — I : 2,1 : 4.9. Ц-273 кИм\ 2 - I : 1.68 : 3,92, Z/-3I9 кг/*’;
3 - 1 : 1.4 : 3.27. Ц-35Э кг/м3
122
формациях набухания бетонов с разным содержанием цемента является разница в количестве цементного теста, при которой одно и то же изменение влажности бетона вызывает разную степень увлажнения геля: меньшую у бетона с большим содержанием цемента и большую при его малом расходе. Разным степеням увлажнения геля соответствуют и разные по величине деформации набухания.
Обычные каменные заполнители (гранит, базальт, известняк) оказывают сдерживающее влияние на набухание бетона, причем степень последнего существенно зависит от вида заполнителя и его гранулометрического состава (см. табл. 31).
Значительное влияние на набухание бетона оказывает водоцементное отношение. В области не слишком больших ВЩ его набухание тем больше, чем выше водоцемептпое отношение, как это, например, наблюдалось в опытах автора [10].
Причины этого, вероятно, те же, что и в случае усадки бетона. Характер влияния ВЩ на деформации набухания бетона в этих опытах был таков, что одним и тем же изменениям влажности образцов на разных ВЩ при увлажнении соответствовали разные по величине деформации набухания. Последние были тем больше, чем меньше было ВЩ. Так, у образцов из бетона с ВЩ—0,545 при одной из той же степени увлажнения они в среднем были в два раза больше, чем у образцов из бетона с ВЩ— =0,895. Объясняется это различной пористостью бетонов на малых и больших ВЩ. По-видимому, у бетона с малым ВЩ, имеющем меньшую пористость, чем у бетона с большим ВЩ, одно и то же изменение влажности в сторону ее увеличения освобождает большие по величине капиллярные силы, развивающиеся в его порах при высыхании, и создает более благоприятные условия для набухания геля. При этом в нем развиваются и значительно большие по величине деформации набухания.
На набухание бетона влияет также его возраст к моменту начала увлажнения. Чем старее бетон, тем меньше степень его увлажнения и деформации набухания. Интересно отметить, что молодой бетон, защищенный от высыхания, будучи погруженным в воду, также дает значительные деформации набухания. Так, например, в опытах Р. Дэвиса с бетоном на гранитном щебне наблюдалось изменение длины и веса образцов, погруженных в воду в возрасте двух дней. При этом их относительное удлинение росло медленно и достигало за шесть месяцев хранения в воде величины 14-10-5, а увеличение веса составляло при этом 1.6%, причем значительная доля его происходила в первые несколько суток после замачивания. Аналогичная картина наблюдалась и в опытах автора (рис. 20).
Существенное влияние на набухание бетона оказывает масштабный фактор. Это было подтверждено специальными опытами автора по изучению этого влияния на влажностные деформации обычного тяжелого бетона [16] (рис. 21). В этих опытах бы
123
ло установлено, что набухание больших образцов не только развивается медленнее, но и оказывается в равновесном состоянии меньшим, чем у малых образцов-близнецов. Было также найдено, что набухание наружных слоев бетона при его увлажнении больше, чем во внутренних слоях, не только в любой момент времени увлажнения, но и в конце его.
0/ 23456789
Продол/кителъность опыта 6 сутках
Рис. 20. Влияние возраста бетона на его относительные деформации набухания ен и увеличение весовой относительной влажности Д1/н ври увлажнении
а — увлажнение, начиная с 3-суточного возраста; б — увлажнение, начиная с 28-суточного возраста
Примечание. До увлажнения образцы были гидро-иэолирсваны от высыхания.
Причины этого рассмотрены в работе автора [16]. По своей абсолютной величине набухание бетона значительно меньше, чем его усадка. Это видно из результатов упомянутых выше опытов Р. Девиса (табл. 31), в которых величина усадки образцов на воздухе после предшествующего 28-дневного хранения во влажном песке за полгода их высыхания в 6 раз была выше их полугодичного набухания в воде, а потеря веса—в 3 раза большей, чем его увеличение при хранении в воде. Об этом говорит так
124
же сравнение результатов опытов автора по усадке и набуханию бетонов, приведенных выше и в § III.3, а также некоторые их результаты, обсуждаемые в § II 1.6, II 1.7.
Можно думать, что физическая природа набухания бетона аналогична природе его усадки, мало зависит от капиллярных
Рис. 21. Влияние на увлажнение и набухание бетона длины образцов, увлажняемых через торцы. Бетон 6-месячного возраста к началу увлажнения состава (по весу) 1 :2,12: 4,9 на портландцементе активности 385 кГ/см2, £/£1=0.638. Длины образцов:
I — 21 сл<; 2—17,5 слц 3 — 11,5 Он
явлений и связана в основном с набуханием гелевой структурной составляющей цементного камня при увлажнении. Однако имеются и некоторые существенные различия в физической картине процессов усадки и набухания бетона. Эти различия будут рассмотрены в § II 1.7.
§ 111.5. ФИЗИЧЕСКИЕ СВОЙСТВА БЕТОНА, СВЯЗАННЫЕ С ЕГО ВЛАЖНОСТНЫМИ ДЕФОРМАЦИЯМИ
При изменениях влажности, связанных с нарушением или отсутствием гигрометрического равновесия с внешней средой, непосредственным увлажнением и т. п., бетон претерпевает влаж-
125
постные деформации. Этот вид деформаций неизбежен для сооружений, находящихся на открытом воздухе, гидротехнических конструкций, а также конструкций отапливаемых гражданских зданий и промышленных цехов с сухим или, наоборот, влажным климатом.
Появление влажностных деформаций при ограничении перемещений конструкций или в связи с неравномерным распределением их по объему бетона влечет за собой возникновение влажностных напряжений, которые часто вызывают появление в нем нежелательных трещин, например усадочных. В указанном случае влажностные деформации бетона слагаются из свободной влажностной деформации, при известных условиях пропорциональной изменению его влажности, и напряженной деформации, называемой уже собственно влажностными напряжениями.
Для расчета влажностных напряжений и деформаций бетопа в первую очередь необходимо располагать данными о величине его свободных относительных удельных влажностных деформаций усадки и набухания. Величины этих деформаций бетона, по предложению автора [9, 10], принято характеризовать соответственно коэффициентом линейной усадки 0 и коэффициентом линейного набухания ц, являющимися аналогами его коэффициента линейного температурного расширения а.
Коэффициенты Р и т] имеют размерность мк^мм. j и физически представляют собой относительные деформации бетона (в мм/мм), вызываемые изменением его весовой относительной влажности (в г/г) на единицу, соответственно при равномерных высыхании (или гигроскопическом увлажнении) и увлажнении жидкой влагой. Графически эти коэффициенты могут быть интерпретированы как тангенс угла наклона кривых соответственно усадки или набухания бетона к оси изменений его весовой относительной влажности на графиках, вычерченных в осях «относительная деформация (.мл/лш) — изменение весовой относительной влажности (г/г)» (см., например, правые верхние графики на рис. 16—17 и 19—21).
Экспериментально коэффициенты р и rj у бетона изучены довольно хорошо [9. 10, 15]. Установлено, что величина коэффициента линейной усадки бетона р довольно стабильна и у бетонов на одном и том же цементе мало изменяется при варьировании водоцементного отношения, содержания цемента, начальной влажности бетона и его возраста (рис. 22). Это находит свое выражение в том, что кривые усадки бетона в осях «относительная усадка — уменьшение весовой относительной влажности» при изменении этих параметров остаются почти параллельными друг ДРУГУ (см. Р,,с- 15—17). Коэффициент же линейного набухания бетона т], в отличие от его коэффициента линейной усадки р, за-
126
"7 ,
Ч‘Ю'г
Рис. 22. Влияние на коэффициенты линейной усадки р и линейного набухания т) возраста бетона и технологических факторов
а — зависимость коэффициента линейкой усадки от водоцементного отношения, содержания цемента (состава бетона) н возраста бетона; ь — зависимость коэффициента линейного набухания ц от ВЩ н содержания цемента (состава бетона)
Примечание. На нижнем графике (рис 22, с) значения Р даны в процентах от величины Р , соответствующей возрасту бетона к началу высыхания, равному трем суткам.
127
висит существенно от влажности бетона и водоцементного отношения, но практически не зависит от содержания цемента и его величина значительно меньше величины 0 (рис. 22,6).
Учитывая малую изменчивость коэффициента 0 и еще пока недостаточную изученность факторов, влияющих на коэффициент г], на основании описанных выше опытов, по предложению автора, в СН 55—59 [139] и СНиП П-В.1-62 [174] включены следующие средние значения этих коэффициентов для обычного тяжелого бетона:
—2 Л.И/Л1Л
0 — 3-10
_ , з мм!ММ г] = 5-10 --------
2/2
(II1.1)
2.2
Этими средними значениями коэффициентов 0 и т] указанные нормы и разрешают пользоваться при расчете бетонных и железобетонных конструкций на изменения их влажности.
§ 111.6. ВЛИЯНИЕ ДЛИТЕЛЬНОГО ВНЕШНЕГО НАГРУЖЕНИЯ НА РЕЖИМ ВЫСЫХАНИЯ И УСАДКУ БЕТОНА
Бетон представляет собой капиллярно-пористое тело, состоящее из твердого скелета, образованного заполнителями, склеенными цементным камнем, и большого количества пор различных размеров, образуемых за счет несовершенства уплотнения бетонной смеси при ее укладке н наличия в ней воды замеса, постепенно расходуемой на гидратацию цемента и испарение. Длительное нарушение гигрометрического равновесия, вызванное избытком воды, непрерывно поддерживаемое изменениями температуры и влажности внешней среды, приводит к развитию в высыхающем бетоне объемных сил, действие которых сопровождается его усадкой. В тесной связи с усадкой бетона находится его ползучесть, одной из причин которой служат также явления, происходящие в высыхающем геле. Эга связь находит свое выражение в зависимости ползучести бетона от его влажности, а также во влиянии масштаба образцов на их деформации при одинаковых условиях загружения.
Большое влияние на происходящие в бетоне явления, связанные с усадкой и ползучестью, оказывает также длительное его нагружение, которое вызывает изменение плотности бетона, особенно в раннем возрасте, вследствие его большой пластичности. При соблюдении известных условий это приводит к упрочнению бетона — практически важному обстоятельству, подробно изученному А. В. Саталкиным и Б. В. Сенченко [167]. Известно также, что коэффициент Пуассона у бетона существенно возрастает с увеличением напряжений, что объясняется повышением его поперечной деформативности за счет пор и появления микротрещин [36—38].
128
Длительное нагружение бетона приводит также к изменению размеров пор в нем, что изменяет режим его высыхания и, следовательно, должно влиять на усадку. Между тем часто полагают, что усадка нагруженного и ненагруженного бетона одинакова. Такое допущение, например, обычно используют при обработке экспериментальных данных о ползучести бетона. Специальное экспериментальное исследование этого вопроса, проведенное автором [8, 13, 18], показало, что такое предположение неправильно, а ошибки, связанные с ним, существенны, трудно оценимы и переменны по величине.
В этих исследованиях было установлено, что изменения влажности бетона по мере его высыхания у нагруженных н ненагру-женных образцов-близнецов неодинаковы. Длительно нагруженные образцы как при сжатии, так и при растяжении, как правило, высыхают быстрее, что видно из рис. 23, иллюстрирующего некоторые результаты этих опытов на образцах, высыхающих с боковой поверхности.
По осн ординат на этом рисунке отложены превышения изменений весовой относительной влажности длительно нагруженных образцов над ее изменениями у образцов ненагруженных, найденные непосредственным определением разности в весах сравниваемых образцов и отнесенные к единице приложенных напряжений.
Из рассмотрения рис. 23 следует, что длительно растянутые образцы вслед за приложением нагрузки во всех случаях высыхали быстрее ненагруженных. При этом, например, у больших нагруженных бетонных образцов превышение изменений относительной влажности над ее изменениями у образцов ненагруженных доходило до 5% на 1 кГ1см7 напряжений.
Сжатые же образцы вели себя по-разному: малые образцы с большим модулем поверхности вслед за приложением нагрузки высыхали медленнее ненагруженных образцов-близнецов; боль шие же образцы с малым модулем поверхности, наоборот, высыхали быстрее контрольных образцов (превышение изменений относительной влажности у них доходило до 2% на 1 кГ/см* напряжений). Средние образцы занимали промежуточное положение: вначале сжатые образцы высыхали быстрее контрольных ненагруженных, а затем медленнее их. Таким образом, имеет место очевидное влияние внешнего длительного нагружения бетонных образцов на режим их высыхания. Причины этого рассмотрены ь работе автора [8].
Поскольку экспериментально доказано, что влажностная усадка бетона при известных условиях прямо пропорциональна изменениям его влажности [7, 9], то, следовательно, нагружение бетона оказывает влияние не только на его высыхание, но одновременно и на его усадку, увеличивая ее. Это обстоятельство подробно исследовано в работах автора [8, 13, 18].
129
Рис. 23. Сравнительные данные о режимах высыхания длитсаыю нагруженных и нснагруженных образцов
а — растяжение; 6 — сжатие: I — образцы сечением 1Х2 см. из раствора состава (по весу) 1 : 3 ВЩ -0,33; 2 — образцы сечением 2.7Х2.7 см. из раствора состава (по весу) 1 : 3 В/77’0,33; 3 — образцы сечением 5x5 см. из бетона состава (по весу) 1 : 2,1 : 4,9 ВЩ 0.71
130
§ 111.7. НЕКОТОРЫЕ ОСОБЕННОСТИ УСАДКИ И НАБУХАНИЯ БЕТОНА. СУЩЕСТВЕННЫЕ ДЛЯ РАСЧЕТА ВЛАЖНОСТНЫХ НАПРЯЖЕНИИ
Поскольку усадка и набухание являются следствием изменений вл а госодержан и я в бетоне для расчета связанных с ними влажностных деформаций и напряжений, необходимо располагать данными о зависимости усадки и набухания бетона от изменений его относительной влажности. Опыты автора [7, 9, 10], проведенные в этом направлении, выявили ряд некоторых особенностей влажностных деформаций бетона, важных для расчета бетонных и железобетонных конструкций па изменения их влажности. Изучение этих особенностей стало возможным благодаря применению новой методики экспериментального изучения усадки и набухания. Эта методика состояла в следующем.
Образцы в виде бетонных призм изготавливались в стальных формах. После распалубки, обычно в возрасте 2 суток, в течение которых образцы хранились укрытыми влажными опилками, они гидронзолировались по боковой поверхности нитрокраской п парафином. Далее на них устанавливались рычажные тензометры на двух взаимно противоположных гранях на базе, практически равной длине образца. Для этого использовались специально заложенные в образцы металлические пластинки. Торцы образцов в течение всего опыта оставались открытыми, поэтому их высыхание или искусственное увлажнение с помощью ватных фитилей проходило только через торцы. Таким образом в опыте искусственно создавались направленные (осевые) высыхание или увлажнение образцов.
Такая методика выгодно отличается от обычно применяемой еще со времен Консидера методики изучения деформацип бетона на образцах, подверженных всестороннему высыханию или увлажнению. Осевые высыхание и увлажнение образцов исключают неравномерное распределение влажности по их сечению, возникающее при всестороннем высыхании пли увлажнении, которое сопровождается развитием напряженных деформаций, накладывающихся на «чистые» деформации усадки или набухания и затемняющих их1. Кроме того, она также почти исключает влияние случайных кратковременных колебаний влажности воздуха в помещении. Происходит это потому, что эти колебания, обычно имея малую длину волны, при гидроизолироваииой боковой поверхности образца проникают в него лишь на незначительную глубину со стороны открытых торцов, малую сравнительно с его длиной.
Наконец, что также важно, гидропзолированный с боков об-
1 При осевых высыхании или увлажнении образца в нем возникает неравномерное распределение влажности лишь вдоль его продольной оси. Связанные с этим влажностные напряжения в образце имеют второй порядок малости по сравнению с напряжениями, появляющимися в нем при его всесторонних высыхании или увлажнении.
131
разец с точки зрения влагообмена и влажностных деформаций моделирует пластины и плиты, а также поверхностные слон массивных сооружений, у которых преобладают потоки влаги в одном направлении.
Образцы систематически взвешивались на весах с точностью до 0,01 г для определения изменений в весе вследствие высыхания или увлажнения. Одновременно с точностью (0,5: 1)10 5по тензометрам велись наблюдения за их относительными деформациями. Высыхание образцов происходило в естественных условиях, для чего образцы хранились подвешенными и взвешивались на весах в таком же положении. Увлажнение образцов выходило за границы гигроскопической влажности бетона, как это, например, имеет место в сооружениях, соприкасающихся с водой, и осуществлялось с помощью ватных фитилей через торцы призм.
Для феноменологической теории усадочных напряжений и деформаций бетона большое значение имеет выяснение зависимости между усадкой бетона и уменьшением его влажности при высыхании. Эта зависимость устанавливает связь между изменениями поля влажности бетона и полем его усадочных деформаций и без нее нельзя перейти к расчету усадочных напряжений.
Графически рассматриваемая зависимость изображается экспериментальными кривыми свободной, не стесненной усадки бетона при его одномерном (см. выше) высыхании в осях: «Изменения весовой относительной влажности — относительная усадка». Учитывая большое практическое значение этих кривых, необходимо иметь единую методику их построения. Практически эти кривые имеют вид S-образных кривых, подобных изображенным на рис. 24 и относящимся к одному из бетонов, исследованных в опытах автора. Такой вид кривых усадки не случаен.
После установки на высыхание бетонного образца, достаточно влажного для того, чтобы в его порах имелась свободная вода, и имеющего температуру, равную температуре окружающего воздуха (сухого термометра), начинается процесс влагообмена с внешней средой. Вначале, интенсивно испаряясь, удаляется свободная вода, причем зона ее испарения постепенно проникает в глубь образца. Испарение свободной воды не сопровождается усадкой бетона, однако при этом его температура в зоне интенсивного испарения снижается до температуры мокрого термометра и образец в этой зоне, а также на близлежащих участках, куда проникает волна охлаждения, претерпевает температурное сокращение. Этот процесс, протекающий во времени, связан с одновременным изменением веса образца и соответствует начальному восходящему участку на кривой его деформаций.
После того как в зонах, прилегающих к открытой поверхности образца, свободная вода испарится, бетон этих зон постепенно принимает температуру сухого термометра, претерпевая при этом температурные расширения. Этот процесс соответствует ни-
132
сходящему участку на кривых усадки (рис. 24). Развивающееся вслед за этим дальнейшее высыхание образца связано уже с испарением адсорбированной воды геля, сопровождается интенсивной усадкой бетона, накладывающейся на предшествующие деформации и дающей резко выраженную восходящую ветвь на кривой усадки.
из бетона на мелком щебне состава (по весу) 1 :2,1 :4,9 на портланд цементе активности 475 кГ/ся?, ВЩ=0,7^. Возраст бетона к началу высыхания
1 — 3 суток; 2 — 7 суток; 3—14 суток; 4 — 28 суток
Следует отметить, что в том случае, когда начальная влажность бетона такова, что в нем пет запаса свободной воды, кривые усадки не имеют ни S-образного вида, ни начального участка практически нулевой усадки. В этом случае кривая усадки начинается с начала координат и последняя однозначно связана с изменением влажности бетона. Это подтверждается экспериментами автора [9] и отчетливо видно, например, на кривых усадки, изображенных на рис. 25 и относящихся к подсушенным призмам.
Интересны в этом отношении также опыты, описанные Менделем [241], результаты которых изображены па рис. 26. Кривые
133
усадки на этом рисунке относятся к образцам, изготовленным из цементного теста, разбавленного порошкообразным кремнеземом в различных соотношениях: от чистого цемента до смеси из 25% цемента и 75% кремнезема. Образцы выдерживались в течение недели при температуре 2ГС.
Рис- 25. Влияние начальной влажности бетона на его усадку при высыхании. Бетон состава (по весу) ! : 2,1 :4,9 на портландцементе активности 475 кГ/сл2, ВЩ --0,545
1 — подсушенный бетон; 2 — бетон естественной влажности;
3 — бетон, вымоченный в воде
Как видно из рисунка, усадка образца из чистого цемента с самого начала прямо пропорциональна влагопотерям, что указывает на то, что в этом образце практически отсутствуют поры и капилляры и, следовательно, нет и свободной воды.
134
Рис. 26. Экспериментальные кривые зависимости усадки от влагопотерь цементного камня с различным содержанием (в про центах по весу) тонкомолотого кремнезема.
При наибольших содержаниях кремнезема вид кривой усадки ясно указывает на наличие пор и свободной воды в образце. По мере увеличения содержания кремнезема, по этой причине, кривые усадки все более и более принимают указанный выше S-образный вид. К концу периода высыхания образцов приращения удельной усадки, т. е. усадки, отнесенной к единице веса потерянной влаги, у всех образцов одинаковы.
В раннем возрасте бетона восходящий начальный участок на кривых усадки бетона может быть полностью погашен или даже перекрыт деформациями температурного расширения, связанными с экзотермическим разогревом образца (см., например, кривую усадки на рис. 24, относящуюся к началу высыхания образца в 3-дневном возрасте).
Как следует из рис. 24, температурные деформации па начальном периоде удаления из бетона свободной воды не велики. В описываемых опытах они не превышали (1 н-2)10 5 мм/мм при общей усадке порядка (50 75) 10-5 мм/мм,
поэтому практически их можно не принимать во внимание. В соответствии с этим, имея в виду «чистую» усадку не затемненную этими температурными деформациями, следует за начало этой усадки принимать момент, соответствующий напнизшей точке начальной нисходящей ветви на кривой усадки (рис. 24).
Приняв за пуль отсчета усадки деформацию образца в этот момент времени, мы будем иметь кривую чистой усадки бетона, аналогичную кривым, изображенным на рисунках в § 1П.З. При этом мы получим, что до этого момента времени удаление свободной воды не сопровождается усадкой бетона, что
135
согласуется с современными представлениями о ее физической природе.
Рассмотренный прием и был положен в основу обработки экспериментальных кривых усадки в опытах автора, обсуждаемых в настоящей раб> тс.
Рис 27. Типичные кривые влажностных Деформаций бетона и изменений его влажности при попеременных высушиваниях и увлажнениях. Восходящие вегви — усадка (высыхание); нисходящие — набухание (увлажнение). Бетон 4-суточного возраста к началу испытаний состава (по весу) 1 :2,1 ; 4.9 на портландцементе активности 475 кГ/см2, /3/7/=0,545
Исследования влажностных деформаций бетона, проведенные автором по описанной выше новой методике, свидетельствуют о необратимости в широком смысле слова объемных изменений бетона при его повторных попеременных высыханиях и увлажнениях. Характер этой необратимости усадки п набухания бетопа з условиях осевых сушки и увлажнения образцов весьма типичен.
На рис. 27 изображены гистерезисные петли влажностных деформаций бетона, наблюдавшиеся в опытах автора, имеющие характерный арфообразный вид, н типичные кривые изменений
136
во времени его весовой относительной влажности и относительных деформаций. Восходящие ветви кривых, изображенных на этом рисунке, соответствуют высушиванию образца, а нисходящие ветви — его увлажнению. Поскольку увлажнение бетона во времени протекает значительно быстрее его высыхания, кривые изменений влажности и деформаций образцов на рис. 27 изображены с использованием переменного масштаба по оси времени с увеличением его на отрезках этой оси, соответствующих увлажнению образца.
Интересно отметить, что при повторных циклах высушивания и увлажнения бетона его деформации постепенно затухают, что проявляет себя в последовательном уменьшении длин восходящих ветвей усадки и нисходящих ветвей набухания образца на рис. 27. Это связано с изменением структуры и физико-механических свойств бетона во времени при его старении и, в первую очередь, с развитием упругой кристаллической составляющей цементного камня и старением геля, с одной стороны, и уменьшением его пористости, с другой. Описываемые опыты начинались с 4-суточного возраста бетона, поэтому эти изменения были существенными, особенно на первом цикле высушивания.
Так как степень увлажнения образца в опыте превышала начальную естественную влажность бетона после распалубки, то нисходящие ветви набухания на рис. 27 пересекают вертикаль его начальной влажности и значительные участки этих ветвей расположены слева от нее.
Одной из причин наблюдаемого гистерезиса влажностных деформаций является неоднозначная зависимость усадки и набухания бетона от изменений его влажности. Эта неоднозначная зависимость между деформациями бетона, связанными с его высыханием или увлажнением, и наблюдаемыми при этом изменениями его относительной влажности видна па рис. 25, относящемся к случаю усадки бетонных призм-блнзпеиов в условиях их осевой сушки при гидронзолированной боковой поверхности, имеющих различную начальную влажность.
Из рис. 25 следует, что при достаточно большой начальной влажности влагопотери образцов в начале высыхания не сопровождаются усадкой. Усадка начинает развиваться лишь по достижении влагопотерями определенных значений тем больших, чем больше начальная влажность призм.
Следствием этого является неоднозначная зависимость усадки бетона от уменьшения его относительной влажности: одному и тому же по величине уменьшению влажности образцов-близнецов, вымоченных, естественной влажности и подсушенных соответствуют разные по величине деформации усадки. Наоборот, одна и та же усадка у них является следствием различных изменений относительной влажности — больших у вымоченных призм, меньших у призм естественной влажности и еше меньших у призм подсушенных. Эта неоднозначность объясняется тем, что
137
в начале высыхания влажного бетона сначала удаляется свободная вода из крупных пор цементного камня, что не вызывает усадки отвердевшего бетона [7, 9, 201]; только после потери всей или большей части свободной воды в образце начинаются высыхание и объемные изменения геля, сопровождающиеся усадкой бетона.
Второй, не менее важной причиной гистерезиса влажностных деформаций бетона является существенное различие в физической картине процессов его усадки и набухания, и связанное с этим различие в величинах коэффициентов линейной усадки и линейного набухания.
При высыхании бетона в малых объемах из пего вначале удаляется в основном вся свободная вода, обладающая меньшей энергией связи, чем связанная вода геля [7, 9, 201]. Удаление воды геля в зонах, прилегающих к открытой поверхности высыхания, задерживается транзитом свободной воды из внутренних более влажных зон бетона, поэтому высыхание геля начинается лишь после ее удаления.
При набухании же бетона процесс увлажнения раздваивается. Наряду с транзитом жилкой свободной воды в его внутренние более сухие зоны происходит увлажнение геля в зонах, лежащих на ее пути, сопровождающееся переходом части этой свободной воды в связанную волу геля.
В соответствии с изложенным деформации бетона при высыхании п увлажнении не могут быть обратимы, так как кривая его усадки соответствует изменениям влажности, связанным лишь с потерей связанной воды геля при его высыхании после предшествующего удаления свободной воды, в то время как кривая набухания соответствует изменениям влажности, связанным как с увлажнением геля, так и с одновременно происходящим заполнением пор бетона свободной водой. Следствием изложенного является существенное различие в кривых набухания и усадки бетона.
Если типичная кривая усадки высыхающего бетона представляет собой монотонную кривую, являющуюся прямой линией, за исключением небольшого начального участка, то типичная кривая набухания бетона при увлажнении имеет более сложное очертание. Для нее характерен начальный пологий участок, которому, как правило, предшествует некоторый участок почти нулевых деформаций набухания, и крутая восходящая ветвь в конце увлажнения после изменения знака кривизны кривой (рис. 28).
Помимо необратимости процессов усадки и набухания бетона в координатах «изменение влажности — деформации» имеет место также необратимость этих процессов во времени. Это находит свое выражение в том, что время увлажнения и набухания бетона неизмеримо мало по сравнению со временем его высыхания и усадки. Так, в описываемых опытах первое из них составляло
138
не более 10 суток, в то время как второе достигало почти трех месяцев.
Такое различие во времени достижения равновесного состояния при высыхании (усадке) бетона и его увлажнении (набухании) объясняется указанным выше существенным различием в физической картине усадки и набухания.
Рис. 28 Типичные кривые влажностных деформаций и изменений влажности бетона при одномерных (осевых) высыхании и увлажнении образцов. Бетон состава (по весу 1:2,1:4.9 на портландцементе активности 475 кГ/см2, ВЩ=0.545
/ — усадка (высыхание) начиная с возраста 4 суток; 2 — набухание (увлажнение) после предшествующего высыхания
Интересно отметить, что при длительном цикле попеременных повторных высушиваний и увлажнений постепенно уменьшаются по величине и стабилизируются во времени не только деформации бетона, но и наблюдаемые при этом изменения его влажности. Это говорит о том, что наряду с изменением механических свойств бетона во времени происходит также и изменение его физических свойств, т. е. структуры. Таким образом, как следует из рис. 27, по мере старения бетона меняется не только характер его пористости, но и количественное соотношение между содержанием в единице объема его гелевой и кристаллической структурных составляющих.
139
Изучение особенностей усадки и набухания бетона позволяет сделать ряд некоторых общих выводов, важных для теории влажностных напряжений. Прежде всего мы уже видели выше, что деформации бетона, связанные с изменением его влажности, необратимы в широком смысле этого слова. Такая необратимость деформаций существенно затрудняет установление аналитической связи между полями изменения влажности бетона и влажностных деформаций, или напряжений в нем, особенно при его попеременных периодических высыханиях и увлажнениях, на широком диапазоне изменения влажности. Между тем эти процессы протекают в бетоне не только под влиянием атмосферных воздействий, но часто являются обычными для работы конструкций, как это, например, имеет место в зонах переменных уровней гидротехнических сооружений, цехах с мокрой технологией, а также в периодически наполняемых водой и опоражниваемых конструкциях (емкости, шлюзы, доки т.п.).
С другой стороны, неучет такого характера деформирования бетона при изменениях его влажности может привести к ошибочным расчетным значениям деформаций и напряжений от усадки или набухания. Поэтому эффективная теория влажностных напряжений в бетоне должна отражать в какой-то мере эти особенности действительной картины его усадки и набухания.
Выше мы вплели, что лишь часть полных изменений влажности бетона, связанная с уменьшением влажности собственно геля, сопровождается его усадкой. Изменение же влажности бетона за счет уменьшения лишь содержания в нем свободной воды усадки не вызывает, что особенно хорошо видно на рис. 27.
Поскольку усадка бетона при достаточно большой его начальной влажности начинается лишь после некоторого начального высыхания, необходимо сосредоточить внимание на том значении эффективной влажности бетона, начиная с которого в нем развивается усадка. Эффективной влажностью бетона L'3 мы будем называть часть его полной влажности, представляющую собой меру содержания в нем адсорбционпо связанной воды геля, удаление которой сопровождается его усадкой. Остальная часть полной влажности бетона представляет собой меру содержания в нем свободной воды, удаление которой не вызывает его усадки.
Если назвать предельную величину эффективной влажности бетона, при которой гель имеет максимальную степень увлажнения при отсутствии в бетоне свободной воды, критической вл а ж н о с т ь ю бетона Uup, то тогда можно сказать, что усадка бетона связана лишь с изменениями его эффективной влажности, меньшей ее критического значения UKp. А эти изменения влажности бетона уже будут однозначно связаны с его усадкой.
Величины изменений эффективной влажности в опытах, результаты которых изображены па рис. 15—17 и нм подобных, равны величинам проекций кривых усадки на ось изменений ве-
но
совой относительной влажности бетона. При полном высушигг-нии бетона до нулевой влажности предельные величины этих проекций численно будут равны критической влажности бетона.
Величина критической влажности бетона зависит от сорта цемента, водоцементного отношения, содержания цемента (состава бетона) и его возраста. Характер этой зависимости в настоящее время экспериментально изучается. Данные уже проведенной
Рис. 29. Зависимость критической влажности бетона 1/кр от содержания цемента (состава бетона) и В/Ц. Естественное высыхание на воздухе с относительной влажностью 70% до равновесной влажности U7. Бетон 4-суточного возраста к началу высыхания на портландцементе активности 475 кГ/смй. Состав бетона (по весу)
а — на верхнем графике для отдельных групп экспериментальных точек (слева направо) I : 2.1 : 4.9; I ' 1.68 3.92;
I : 1,4 : 3,27; б — па нижнем графике 1 • 2.1 : 4.9
автором части этих исследований показывают, что величина критической влажности бетона возрастает с ростом В/Ц и содержания цемента в линейной зависимости примерно на 15% на каждые 25 кг цемента в кубическом м^тре бетона и каждую 0,1 В/Ц (рис. 29). Поэтому для ее определения автором была предложена формула
С7кР=и7+^кр» (III.2)
учитывающая влияние на критическую влажность бетона указанных параметров, а также масштабного фактора [16].
14!
Здесь IV’—расчетная равновесная влажность бетона в конструкции, соответствующая относительной влажности воздуха 70%, равная:
0,0125 г/г — для немассивных конструкций и 0,00625 г/г — для конструкций массивных;
С'*р — расчетная избыточная сверх равновесной влажности IV’ критическая влажность бетона, равная: 0,01 г/г —для немассивных конструкций и 0,005 г/г — для конструкций массивных;
k — коэффициент, определяемый по формуле
k = 0,7 + 0,15 р-~ 225 + В/^~°»4Л (1П.З)
\ 25 0,1 /
в зависимости от содержания цемента Ц в кг/м3 бетона и водоцементного отношения ВЩ.
Таблица 34
Зависимость коэффициента k в формуле (111.2) от марки бетона
Марка I00 150 2QQ
300 400 500 600
k 1,6 1,5
1.3 1,2 1,1 1
При отсутствии данных о Ц и ВЩ коэффициент k в формуле (II 1.2) можно принимать по табл. 34 в зависимости от марки бетона.
Для конструкций средней массивности величины IV’ и 17*р находятся по интерполяции.
В зависимости от модуля поверхности, открытой для высыхания, т [л-1] (отношения поверхности элемента, открытой для высыхания, к его обьему) бетонные и железобетонные конструкции могут быть разделены на: а) массивные конструкции т <2, б) конструкции средней массивности 2</и<15 и г) конструкции немассивные т>15 [174].
Итак, пути развития эффективных методов расчета влажност пых напряжений в бетоне, отражающие рассмотренные выше особенности его усадки п набухания, состоят, во-первых, в учете указанной неоднозначной зависимости усадки бетона от изменений его влажности с помощью введения в рассмотрение эффективной и критической влажностей и, во-вторых, в использовании разных по величине коэффициентов линейной усадки н линейного набухания бетона (§ 111.5).
Располагая данными о критической влажности бетона, а также величинами коэффициентов его линейной усадки £ и линейного набухания •»], всегда можно уже рассчитать свободные влажностные деформации и перемещения бетонных и железобе
142
тонных элементов, необходимые для расчета влажностных усилий и напряжений в статически неопределимых конструкциях.
Например, свободные линейные относительные деформации прямолинейного элемента при усадке вследствие равномерного высыхания от начальной влажности, большей, чем его критическая влажность 1
МО = IW- ^(01- (Ш.4)
Если же имеется в виду случай, когда начальная влажность бетона Uo ниже С/кр, то [9]
МО = ₽1^о-С/(Ob (Ш.5)
В этом случае усадка развивается с самого начала высыхания бетона и зависимость между деформациями усадки и уменьшением его влажности при высыхании однозначна.
Для расчета свободных линейных относительных деформаций набухания бетона МО. с учетом зависимости коэффициента линейного набухания от влажности, может быть предложена следующая формула:
С(/)
е.,'0 ~ \ri(U)dU. (III.6)
с,
Если в качестве т) (L7) принять его некоторое среднее значение, то формула (1П.6) принимает вид [10]
МО = - n|t/(O-U1 • (Ш-7)
По аналогии могут быть получены и обшие формулы для деформаций (перемещений) от усадки и набухания бетона для плоской системы, составленной из брусьев или плит. Эти формулы приведены в главе IX.
При ограничении изменений длины элемента в рассмотренных выше случаях в нем могут возникнуть упругие влажностные напряжения усадки:
МО ~mp-M01£(0; (Ш-8)
МО - PK'o-MOlMO (Ш.9)
или набухания:
С(О
он(/) .-E(Z)fn(t/)dL/; (Ш.10)
М0 = -ч[М0-Ц,|£(0- (Ш.11)
В действительности же за счет ползучести бетона величины этих напряжений существенно снижаются (см. главы VII и VIII),
1 Для того чтобы в последующем получить знак плюс у растягивающих усадочных напряжений, деформации укорочения от усадки здесь и в дальнейшем считаются положительными, а деформации удлинения от набухания, по аналогии, — отрицательными.
143
поэтому при их расчете учет ползучести бетона обязателен. Методы учета ползучести бетона при расчете температурных н влажностных напряжений изложены в главе VIL
Наиболее часто встречаются случаи неравномерного изменения температуры и влажности бетона по сечениям элементов конструкций. Определение температурных и влажностных напряжений в этом случае требует привлечения методов теории упругости.
Однако в подавляющем числе случаев применяемые бетонные и железобетонные статически неопределимые конструкции представляют собой либо стержневые системы, составленные из брусьев (неразрезные балки, рамы сборных промышленных цехов и т. д.), либо пространственные конструкции, составленные из плит, с расчетными схемами в виде плоских элементов, работающих по схеме стержневых конструкций (туннельные конструкции, многопролетные покрытия и т. д.). Для определения температурных и влажностных деформаций (перемещений) и нормальных напряжений (усилий), действующих в подобных конструкциях в сечениях, перпендикулярных к продольной оси их элементов, можно воспользоваться гипотезой плоских сечений. Основанные на этом допущении методы расчета упругих температурных напряжений в бетонных брусьях разработаны Г. Н. Масловым [117, 119]. В дальнейшем мы воспользуемся имя, распространив их на расчет влажностных деформаций (перемещений) и напряжений (усилий) и обобщив их на случай учета ползучести бетона.
ГЛАВА IV
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ ПОЛЗУЧЕСТИ БЕТОНА
Уже давно было замечено, что поведение бетона под нагрузкой не соответствует идеализированной схеме Гуковского упругого тела. Действительно, даже при неизменных во времени нагрузках деформации бетона продолжают развиваться, т. е. «ползти» с течением времени, а напряжения, при известных условиях.
могут уменьшаться, или, как говорят, релаксировать.
Эти особенности бетона отчетливо проявляются при наблюдении за деформациями бетонных призм, загруженных осевыми постоянными напряжениями, или за величиной приложенного к
ним усилия, которую следует поддерживать для сохранения постоянной во времени первоначально сообщенной им деформации.
В свете современных
представлений, развитых О. Я. Бергом [36, 38] на основании обобщения многочисленных экспериментальных данных, в том числе и своих собственных опытов, зависимость между напряжениями и деформациями бетона при нагружении и разрушении его, например, одноосным сжатием представляется весьма сложной и выглядит (рис. 30) в виде кривой, имеющей экстремум и восходящую и нисходящую ветви. Полная деформация е при этом слагается
Рис. 30. Типичная зависимость между напряжениями и деформациями при осевом сжатии бетона
из некоторой начальной деформации ео, упругой деформации еу, деформации ползучести еп, развивающейся во времени без нарушения сплошности бетона, пластической деформации второго рода Ei и псевдопластической деформации е2
е -- Ео 4- Еу -| Е„ 4- 4- Ео
(IV. 1)
145
Деформацией е0 в связи с ее малостью обычно пренебрегают. Деформации еу и еп линейно связаны с напряжениями и составляют предмет исследования линейной теории ползучести бето-иа. В этой области деформации ползучести при постоянных напряжениях всегда затухают во времени, т. е. имеет место устойчивое деформирование [158, 162].
Пластические деформации ei связаны с развитием несмыка-ющихся микроразрывов при о>/?т и нелинейно зависят от напряжений.
Псевдопластические деформации е2 развиваются при высоком уровне напряжений, связаны с самоускоренным процессом образования дефектов структуры за счет накопления микроразрушений и также нелинейно зависят от напряжений.
Сумму деформаций еп, Ei и Ей называют деформациями нелинейной ползучести; она исследуется в нелинейной теории ползучести бетона. В области нелинейной ползучести при напряжениях, достигающих уровня, при котором развиваются деформации Е| и е2, скорость деформации после загруження первое время затухает, затем в течение некоторого периода может оставаться постоянной, после чего увеличивается вплоть до разрушения образца. В этом случае имеет место неустойчивое деформирование [162].
Возможен случай, когда напряжения вызывают пластические деформации второго рода ei, но их величина недостаточна для развития псевдопластических деформаций е2- При этом скорость деформации после некоторого периода затухания становится постоянной. Этот случай безразличного деформирования [162] может привести к разрушению бетона с течением времени, т. е. к необеспеченной его длительной сопротивляемости.
Ползучесть и связанная с ней способность к релаксации напряжений являются важными свойствами бетона, которые приходится учитывать при рассмотрении длительных воздействий па пего нагрузки, изменений температуры или влажности. Кроме того, бетон обладает еще способностью «стареть», т. е. изменять во времени характеристики своих физико-механических свойств: прочность, модули упругих продольных деформаций п сдвига, коэффициент поперечной деформации н т. д.
При учете ползучести и старения бетона связь между его деформациями и напряжениями становится более сложной, чем в случае идеально упругого тела, для которого, как известно, эта связь выражается сравнительно простым обобщенным законом Гука.
Установлением аналитической связи между деформациями и напряжениями с учетом ползучести и старения бетона, анализом этой связи и решением на ее основе ряда прикладных задач н занимается теория ползучести.
Современная теория ползучести бетона представляет собой феноменологическую теорию, т. е. теорию, основанную на отра-
116
женин объективных экспериментальных данных без глубокого проникновения в физическую сущность самого явления ползучести. Произошло это потому, что даже до настоящего времени физическая природа ползучести бетона еще не раскрыта полностью, п, как известно, существуют различные, порой несовместимые взгляды на сущность этого явления и его причины (см. § 1V.1).
Экспериментальные основы теории ползучести бетона были заложены в ранних работах западных ученых Дэвиса, Дютрона, Глэнвилля, Шенка н др. Однако бурное развитие эта теория, как самостоятельная область науки о напряженно деформированном состоянии упруго-ползучих тел. полечила лишь в исследованиях советских ученых, которым принадлежат все наиболе значительные работы по этой проблеме. К их числу относятся исследования Б. Л. Абрамяна, Н. X. Арутюняна, П. И. Васильева, А. А. Гвоздева, И. И. Гольденблата, М. А. Задояпа, А. К. Мал-мейстера, М. М. Манукяна, Г. Н. Маслова, Н. Я. Панарина, С. В. Полякова, И. Е. Прокоповича, Ю. Н. Работнова, А. Р. Ржа-нпцына, М. И. Розовского. И. II. Улицкого, С. Е. Фрайфельда и многих других авторов. В частности, Н. X. Арутюняном была разработана получившая всеобщее признание у нас и за рубежом отечественная теория упруго-ползучего тела (наследственная теория старения), наиболее полно отражающая основные свойства бетона, интенсивно развиваемая в настоящее время в трудах школы АН Арм. ССР. а также П. И. Васильева, А. А. Гвоздева, Н. Я. Панарина, И. Е. Прокоповича, М. И. Розовского и ряда других советских ученых.
Ниже рассматриваются некоторые вопросы линейной теории ползучести бетона, важные для проблемы температурных и влажностных напряжений, и предлагаются новые аналитические выражения для наследственных функций теории упруго-ползучего тела, при которых эта теория наилучшим образом согласуется с результатами опытов.
§ IV.1. ПОЛЗУЧЕСТЬ БЕТОНА
На способность бетона к неупругим деформациям впервые обратил внимание Консндер [217] в своих исследованиях деформаций бетона при растяжении в условиях непродолжительной выдержки нагрузки. Однако самое раннее исследование собственно ползучести бетона принадлежит, по-видимому. Вульсопу (254], отметившему увеличение во времени прогибов под нагрузкой испытанных им железобетонных балок, Подмеченное нм свойство бетона он назвал термином «flow», т. е. «течением» (ползучестью), ставшим вслед за этим обиходным в специальной литературе.
Некоторое время этому свойству не придавалось значения, но интерес к нему продолжал расти и вскоре после ряда разрозпеп-
И7
ных экспериментальных работ начинается глубокое систематическое исследование влияния различных факторов на ползучесть бетона [218].
Из числа наиболее интересных зарубежных работ следует назвать работы Дэвиса, Дютрона, Глэнвилля, Лермита, Росса, Фрейденталя, Шенка и других авторов. В СССР этому вопросу посвящены экспериментальные исследования С. В. Александровского, В. В Цлинкова, П. И. Васильева, А. А. Гвоздева, К. С. Карапетяна, Н. И. Катина, С. В. Полякова, И. Е. Прокоповича. А. В. Саталкина, В. И. Скатынского, И. И. Темнова, И. И. Улицкого, С. Е. Фрайфельда, В. А. Харламова, 3. Н. Цилосанп, А. Е. Шейкина, А. В. Яшина и др.
Установлено, что на ползучесть бетона существенное влияние оказывает ряд технологических и физико-механических факторов, а также среда, в которой он находится. Результаты опытов Глэнвилля [227] и Росса [243] указывают на то, что деформации ползучести бетона последовательно возрастают, если применять цементы в такой последовательности: глиноземистый, высокосортный, портландский, обыкновенный портландский. Это объясняется тем, что бетоны на высокосортных цементах имеют большую начальную прочность, с другой стороны, эти цементы имеют повышенное содержание минералов С3А и C4AF, что приводит к увеличению содержания кристаллической структурной составляющей в единице объема цементного камня в бетоне [201, 165] и, в свою очередь, к его большей сопротивляемости деформациям.
С увеличением В/Ц ползучесть бетона при прочих равных условиях возрастает [218]. Объясняется это тем, что при увеличении В/Ц гель, разжижаясь, становится менее вязким и его содержание в единице объема бетона возрастает, бетон же становится менее прочным, а следовательно, и более деформируемым. При прочих равных условиях (в особенности при равных В/Ц) ползучесть бетона возрастает также с ростом содержания цемента [218]. Таким образом, жирные бетоны, имеющие большее содержание цементного теста в единице объема, имеют большую ползучесть, чем тощие. При одинаковом же составе бетона и прочих равных условиях, но разных В/Ц более пластичные бетоны обнаруживают большую ползучесть, чем менее пластичные.
Значительное влияние на ползучесть бетона оказывает вид заполнителя— чем жестче последний, тем меньше ползучесть бетона [219]. Могут быть, однако, и исключения из этого правила, так как на ползучесть бетона существенное воздействие оказывает гранулометрический состав заполнителя, его пластические свойства, а также способность к водопоглощению и адсорбции.
Многочисленными опытами установлено, что с ростом величины напряжений ползучесть бетона возрастает.
Исследование ползучести бетона при высоких напряжениях, проведенное Н. И. Катиным [94], (рис. 31), показало, что даже
148
при невысоких напряжениях связь между скоростями деформаций ползучести и напряжениями нелинейна. Однако при напряжениях, составляющих небольшую долю от призменной прочности бетона, эта зависимость уже через небольшой промежуток времени становится линейной, особенно в бетоне молодого возраста.
Рис. 31. Влияние величины напряжений на ползучесть бетона при сжатии (опыты Н. И. Катина). Бетон состава (по вес}) 1 :3;4,5 на портландцементе активностью 422 кГ[смг, В/Ц=б,62. Сжатие в возрасте 28 суток
Принято считать, хотя это и не точно, что до уровня напряжений, не превышающего половины призменной прочности бетона, связь между напряжениями п деформациями ползучести при сжатии линейна. В случае же растяжения бетона, как это подтверждается опытами Н. И. Катина [94], П. И. Васильева [50], К. С. Карапетяна [88], А. Е. Шейнина и В. Л. Николаева [207] и ряда других авторов, эта линейная связь сохраняется почти вплоть до его разрушения.
Знак напряжений также оказывает влияние на ползучесть бетона. Однако данные различных исследователей о соотношении величин деформаций ползучести при его сжатии и растяжении весьма противоречивы. Так, в опытах Глэнвилля п Томаса [226— 229] ползучесть бетона при растяжении оказалась одинаковой с его ползучестью при сжатии, а в опытах П. И. Васильева [50] и
1-19
Б. В. Блинкова [41] она была выше последней в 1,5 раза. В аналогичных опытах Н. И. Воронкова [61] эта цифра была уже равна 3, а у А. В. Саталкина [166] доходила даже до 5. Причины этого, связанные с несовершенством общепринятой методики эксперимента, рассмотрены подробно в работе автора [18].
Наибольшую ясность в этот вопрос вносят опыты Н. И. Катина [94], проведенные на гидроизолированных от высыхания растворных образцах молодого возраста. Эти опыты показали, что при численно равных по величине напряжениях ползучесть бетона при растяжении на 20—30% выше, чем при сжатии.
Объясняется это влиянием микродефектов структуры бетона, неизбежно возникающих в нем при растяжении в молодом возрасте. У бетона зрелого возраста в аналогичных опытах А. Е. Шейнина и В. Л. Николаева [207] наблюдалась практически одинаковая ползучесть при сжатии и растяжении.
Возраст бетона к моменту загружения существенно влияет на величину деформаций ползучести, которые оказываются тем большими к данному моменту времени наблюдения, чем моложе был бетон в момент загружения. В такой же зависимости находятся и предельные деформации ползучести бетона, загруженного в разном возрасте.
Сказанное хорошо видно на рис. 32, а и б как в случае непрерывно высыхающего бетона (опыты Шенка [245]), так и в случае гидроизолированного бетона, искусственно защищенного от высыхания (опыты С. В. Александровского и Э. Я. Багрия).
Такой характер влияния возраста бетона на его ползучесть вполне понятен. Чем старше бетон к моменту загружения, тем он прочнее и тем меньше содержит он геля, следовательно, при прочих равных условьях тем меньше и его ползучесть.
В опытах Девисов [219], Дютрона [224] и позже рядом других исследователей было выявлено существенное влияние на ползучесть бетона влажности среды, в которой находится незащищенный от высыхания бетон во время опыта как до, так и после его загружения (рис. 33, а и б). Результаты этих опытов косвенно указывают па то, что по мере высыхания бетона его ползучесть должна увеличиваться, однако методика этих опытов не позволяет непосредственно выявить характер влияния степени влажности самого бетона на его ползучесть.
Дело в том, что все эти опыты проводились либо на незащищенных от влагопотерь образцах-близнецах, высыхающих на всем протяжении эксперимента (например, в исследованиях Шейка), либо на полностью изолированных от влагопотерь образцах, не высыхающих на протяжении всего опыта (в опытах С. В. Александровского и Э. Я. Багрия) (рис. 32).
В первом случае все образцы-блнзпецы, начиная с момента распалубки, высыхали подобно и в равной степени, так что их кривые ползучести также подобно и в равной степени искажались с течением времени за счет высыхания бетона. Во втором
150
Возраст Бетона в сутках к моменту наблюдения
Рис. 32. Зависимость полных деформаций и предельных деформаций ползучести бетона при сжатии от его возраста к моменту загружения а — полные удельные относительные деформации; б — предельные удельные относительные деформации ползучести; 1 — бетон, непрерывно высыхающий па воздухе на протяжении всего опыта, начиная с момента распалубки образцов (опыты Шенка); 2 — бетон, изолированный от высыхания па протяжении всего опыта, начиная с момента распалубки образцов (опыты С. В. Александровского и Э. Я. Багрия)
151
Рис. 33. Влияние влажности среды твердения до и после загруже-ния бетона на его ползучесть при сжатии и степени влажности самого бетона на его ползучесть и релаксацию напряжений при растяжении
а — опыты Дютрона: / — 60 суток до эагружения — в воде, после загруже-ння - на воздухе с относительной влажностью 50%; 2 - до н после загру-жения — на воздухе с относительной влажностью 50%; 3 — 60 суток до за-гружения на воздухе с относительной влажностью 50%, после загруження в воде; 4 — до и после эагружения в воде; б — опыты Девиса: до загруження 28 суток - во влажном песке, после загруження — на воздухе с относительной влажностью: 5 — 50%; 6-70%; 7—100%; 8 — в воде; в - опыты автора. Бетон, высыхающий до данного момента времени загруження и изолированный от высыхания на протяжении всего дальнейшего опыта, начиная с момента загруження. Вверху — кривые удельных полных и упруго-мгновенных деформаций (деформации отнесены к единице приложенных напряжений); внизу-кривые релаксации удельных напряжений и кривая мгновенных удельных напряжений (напряжения отнесены к единице сообщенных упруго-мгновенных напряжений)
№раст Бетона 6 сутках н моменту маБтодения
же случае кривые ползучести не искажались вовсе, так как бетон не претерпевал высыхания.
Для прямого исследования влияния на ползучесть влажности высыхающего бетона при одновременном его старении автором по оригинальной методике были проведены специальные опыты, в которых, помимо ползучести, изучалась также релаксация напряжений в бетоне. Образцы в этих опытах представляли собой призмы, высыхающие с момента их распалубки в 4-суточном возрасте до момента их загружения.
Перед загруженном в данном возрасте бетона каждый из устанавливаемых под нагрузку образцов полностью защищался от последующего высыхания нанесением гидроизоляционного покрытия в виде нитрокраски и парафина. Таким образом, исследуемый бетон, загружаемый последовательно в разных возрастах, имел к моментам загружения различную, но остающуюся уже неизменной с момента загрузки влажность
Характер высыхания образцов до их загружения в описываемых опытах был следующим. Образцы были гидроизолирова-ны по большей части своей боковой поверхности и высыхали через открытые участки вблизи торцов. Таким образом, на среднем участке длин образцов бетон находился в условиях одномерного (осевого) высыхания. Этим исключалось на этих участках неравномерное по сечению высыхание бетона, всегда сопровождающееся значительными напряженными деформациями.
Результаты опытов, относящихся к случаю растяжения бетона, изображены на рис. 33, в, где на верхнем графике представлены кривые удельных (т. е. отнесенных к единице приложенных напряжений) относительных деформаций растяжения, а на нижнем— кривые релаксации удельных (т. е. отнесенных к единице сообщенных упруго-мгновенных деформаций) напряжений. Из рисунка следует, что ползучесть бетона и связанная с ней его способность к релаксации напряжений повышаются при его высыхании, перекрывая в описываемых опытах с некоторого момента времени даже обратное по своему характеру влияние старения бетона. В частности, кривые удельных относительных деформаций на этом рисунке в начале были такими же, как в указанных выше опытах Шейка и автора (рис. 32), ио по истечении некоторого времени, когда высыхание бетона становилось уже существенным, начинали постепенно по величине ординат обгонять друг друга (рис. 33,в). Таким образом, степень влажности бетона оказывает прямое и существенное влияние на его ползучесть.
Приведенные выше данные о влиянии влажности среды и бетона на его ползучесть относятся к случаю его осевого нагружения. При изгибе же в опытах 3. Н. Цилосани [200] наблюдалась обратная картина. Все испытанные им цемептно-песчаные образцы состава (ио весу) 1 :3. ВЩ — 0.5. прошедшие термообработку, предварительно высушенные, находящиеся в пиромет-
154
рпческом равновесии со средой и предварительно насыщенные водой, увеличивали прогиб по мере увеличения влажности среды, п он был наибольшим у балочек. испытанных в воле. Автор объясняет это облегчением возникновения и развития пол па-грузкой микродефектов структуры цементного камня во влажной среде, в частности в воле, за счет адсорбционных и иных явлений. Действительно, можно думать, что в малых предварительно высушенных образцах, которые были испытаны 3. Н. Цн-лосапн, сечением всего 2x3 см эти явления могли играть значительную роль.
Существенное влияние на ползучесть высыхающих пол нагрузкой образцов оказывает масштабный фактор. Опытами В. С. Булгакова [46], Дэвиса [218. 219], К. С. Карапетяна [89. 90], И. И. Темнова [178], И. И. Улицкого [186] и ряда других авторов показано, что ползучесть незащищенного от высыхания бетона как при кратковременном, так и при длительном действии нагрузки тем больше, чем меньше поперечное сечение образца. На рис. 34, а приведены соответствующие данные опытов В. С. Булгакова.
По-видимому, между влияниями масштабного фактора и влажности бетона на его ползучесть имеется тесная связь: малые образцы высыхают быстрее больших; в любой момент времени влажность бетона в них меньше, чем в больших образцах, поэтому они и ползут пол нагрузкой больше. Большие же образцы всегда более влажные и ползучесть их меньше.
Наконец, значительное влияние на ползучесть бетона оказывает характер его загруження, т. е. вид напряженного состояния и его повторяемость. Кроме ползучести при осевых сжатии ч растяжении бетон обладает также ползучестью при внецент-ренном сжатии, изгибе, сдвиге и кручении.
При кратковременном действии нагрузки краевые деформации внецентренно сжатых бетонных призм на более напряженной грани превышают деформации при центральном сжатии [11].
В опытах К. Э. Таля и Е. А. Чистякова [176] по исследованию влияния длительной нагрузки на несущую способность гибких железобетонных колонн ползучесть бетона существенно увеличивала прогибы последних, приводя при достаточно высоком уровне напряжений к разрушению колонн через некоторое время, продолжительность которого зависела от отношения величин разрушающих нагрузок: длительной н кратковременной.
Большая ползучесть при изгибе бетонных брусьев по сравнению со сжатыми образцами неизменно наблюдалась и в ряде опытов автора [24], в частности, описанных в § VI 11.5.
Влияние характера загруження бетонных образцов при длительном действии центрального сжатия, внецентренного сжатия и изгиба специально изучено в опытах И. И. Темнова [178]. На рис. 34,6 приведены кривые мер ползучести исследованных в этих опытах образцов сечением 7X7 см и 14X14 см, вычислен-
155
ных для виецентренно сжатых и изогнутых образцов по краевым деформациям сжатых граней, отнесенным к единице напряжений, найденных по формулам сопротивления материалов. Из этого рисунка видно, что ползучесть при впеиентренном сжатии незначительно отличается от ползучести при чистом сжатии, превышая ее; при изгибе же развивается значительно большая ползучесть.
Специальные исследования ползучести бетона при кручении, проведенные В. В. Блинковым [40] и К. С. Карапетяном [91], установили, что при одинаковых напряжениях ползучесть бетона при кручении и осевом растяжении практически одинакова и что связь между напряжениями и деформациями ползучести бетона при кручении линейна почти до его разрушения.
Имеются также некоторые данные о ползучести бетона при сложном напряженном состоянии [37, 223, 248]. Некоторые из них рассмотрены в § IV.4.
Повторяемость нагружения бетона (нагрузки и разгрузки, вибровоздействия) оказывает существенное влияние на его ползучесть. Многочисленными опытами по простому (спокойному) нагружению и разгружению бетона [41, 50, 94, 212, 244] показано, что деформации обратной ползучести (последействия) бетона после разгрузки меньше, чем деформации ползучести образца-близнеца, впервые загруженного теми же напряжениями, в том же возрасте и той же продолжительности действия (рис. 35). Это обстоятельство послужило поводом для критики принципа наложения воздействий в теории ползучести (см. § IV.5) и ряда предложений для его уточнения [41, 50, 66].
При большой частоте чередования нагрузок возникает эффект виброползучести. Он состоит в том, что ползучесть бетонных образцов, подвергаемых попеременным загружениям и разгруже-ниям с большой частотой, оказывается большей, чем у образцов-близнецов при постоянно*, (непрерывном) загружении теми же напряжениями.
Так, в опытах Р. Лермита [104] ползучесть образцов попеременно сжимаемых и разгружаемых напряжениями 126 кГ/см2 при частоте 500 циклов в минуту через 24 ч (720000 циклов) была такой же, как у образцов-близнецов, непрерывно сжатых такими же напряжениями в течение 28 суток, а 14 суток действия цикличной нагрузки (10100000 циклов) оказались эквивалентными в отношении величины деформации ползучести 600 суткам выдерживания образцов-близнецов под постоянной нагрузкой. В этих же опытах было установлено, что бетон, подвергнутый длительному постоянному нагружению, практически уже не обладает ползучестью при последующих циклических нагрузках.
Аналогичный эффект повышения ползучести за счет вибровоздействий с разными частотами и амплитудами, но при одновременном действии и статической нагрузки был огмечен и в специ
157
альных опытах А. К. Малмейстера [110, 111] и К. К. Шкербелиса [208] с железобетонными балками, прогибы которых возрастали при увеличении частоты и амплитуды вибровоздействий.
Причины виброползучести еще не ясны и в настоящее время это свойство бетона продолжает интенсивно изучаться.
Рис. 35 Деформации ползучести при нагрузке, деформации последействия после разгрузки и модуль упругости при за-гружении и при разгрузке призм (опыты А. В. Яшина). Бетон состава (по весу) 1 :3; 4,5 на портландцементе активностью 350 кПсм\ В/Ц=0.(8
1 — при за гружении призм. 2 — при разгрузке призм после длительной выдержки их под нагрузкой; 3. 5. 11. 12. 13. 15 — номера призм
Примечание. Заштрихованные участки со знаком «минус» ограничены кривой ползучести, а участки со знаком «плюс» — кривой упругого последействия.
Кроме обычного тяжелого бетона свойством ползучести обладает также и ряд других родственных ему материалов: легкие, ячеистые и силикатные бетоны, кирпичная кладка, пластбетон и т.п. В качестве примера можно указать на ползучесть ряда
155
силикатных материалов, исследованных в опытах В. И. Скатын-ского [171].
Обстоятельное исследование ползучести кирпичной кладки, выполненное С. В. Поляковым [148], также показало, что законы ее поведения при длительном нагружении близки к законам деформирования бетона. В связи с этим рекомендованные им аналитические выражения для наследственных функций кирпичной кладки вполне применимы и к бетону.
Физическая природа ползучести бетона в настоящее время не раскрыта полностью, и существуют различные взгляды на сущность этого явления.
Ряд авторов (Е. Фрейсинэ, В. Гелер и др.) объясняет ползучесть бетона действием сил капиллярного давления. Некоторые исследователи считают главной причиной ползучести бетона механическое вязкое выдавливание под нагрузкой жидкой влаги из структуры цементного камня (Р. Дэвис, Р. Лермпт и др.).
Другие отдают предпочтение вязкому течению под нагрузкой геля — одной из структурных составляющих цементного камня (А. Невилль, И. И. Улицкий, А. Е. Шейкин и др.).
Следующая группа исследователей объясняет ползучесть бетона главным образом пластической деформацией его кристаллической структуры, особенно в зрелом возрасте (А. К. Малмей-стер, А. Я. Столяров и др.).
Наконец, имеется группа ученых, которые связывают ползучесть бетона с неизбежным непрерывным возникновением и развитием в нем мнкротрещин и других микродефектов (Д. Глюк-лнх, О. Я. Берг).
Существуют и компромиссные взгляды, при которых считается, что ползучесть бегона является следствием ряда причин в их различных сочетаниях. Например, К. С. Карапетян считает, что при низких напряжениях ползучесть бетона является следствием вязкости гелевой составляющей цементного камня и капиллярных явлений. При высоких напряжениях кроме этих причин существенную роль играет уже образование и развитие микротре-шин в бетоне. Относительная же роль этих причин в процессе ползучести бетона зависит от ряда факторов: уровня напряжений, возраста бетона, температуры и влажности внешней среды н т. д.
С. В. Александровский, А. А. Гвоздев, И. Е. Прокопович и ряд других исследователей придерживаются таких же взглядов, но считают важным также и изменение влажности геля в процессе его высыхания и особенно вследствие механического воздействия длительно приложенной нагрузки.
Хороший обзор существующих взглядов на физическую природу ползучести бетона дан в работах А. Невилл я [238] и 3. Н. Цилосани [200]. Проанализировав многочисленные опытные данные по ползучести бетона и своих собственных опытов с цементно-песчаным раствором, последний пришел к выводу, что
159
ползучесть бетона определяется главным образом постепенным возникновением и развитием микротрещин и разрывов в кристаллизационной структуре бетона и межкристаллическим вязким течением. Остальные из рассмотренных выше факторов носят сопутствующий характер.
Ползучесть бетона может играть как положительную, так и отрицательную роль в работе бетонных и железобетонных конструкций. Она приводит к значительному снижению величин напряжений в бетоне, вызываемых вынужденными деформациями (температурных, усадочных и т.п.), и иногда к выгодному перераспределению напряжений. В железобетонных изгибаемых элементах она отдаляет момент образования трещин.
Вместе с тем, ползучесть приводит к увеличению деформаций конструкций под нагрузкой, например прогибов плит, балок и внецентренно сжатых гибких элементов, к перегрузке облицовок стен п колонн и т.д.
§ 1V.2. РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ В БЕТОНЕ
В тесной связи с ползучестью бетона находится его способность к релаксации напряжений при сообщенных ему вынужденных деформациях. Это свойство бетона обнаруживается лучше всего при измерении усилия, необходимого для поддержания неизменной во времени первоначально сообщенной бетонной призме осевой деформации. Оказывается, что вследствие развивающейся ползучести бетона необходимые для этого напряжения постепенно уменьшаются во времени до некоторого предела опр, значительно меньшего, чем начальные напряжения о(Шч.
Степень релаксации напряжений существенно зависит от возраста бетона к моменту сообщения ему вынужденной деформации и может быть довольно значительной для молодого бетона.
Кривые, графически изображающие закон падения напряжений вследствие релаксации, называются кривыми релаксации. На рис. 52 приведены такие кривые для бетона, высыхающего на протяжении всего времени наблюдения. Аналогичные кривые для молодого бетона, высыхающего только до момента загружения, полученные в опытах автора, были приведены в § IV.1 (см. рис. 33,в).
Ползучесть и релаксация напряжений в бетоне, как уже отмечалось выше, тесно связаны друг с другом, поэтому кривые релаксации напряжений всегда могут быть построены теоретическим путем на основе экспериментальных кривых ползучести, и наоборот, теоретические кривые ползучести могут быть построены по экспериментальным кривым релаксации напряжений.
Способность бетона к релаксации напряжений, вызываемых вынужденными деформациями, является весьма ценным свойством, помогающим ему в статически неопределимых конструкци
160
ях более спокойно переносить воздействия температуры, влажности, осадки опор и изменения усилий, связанные с их искусственным перераспределением. Благодаря ей напряжения в бетоне, возникающие от действия .-них факторов, значительно снижаются с течением времени.
Вместе с тем релаксация напряжений может играть и отрицательную роль. Например, вследствие ее возникают нежелательные потери натяжения арматуры в предварительно напряженных железобетонных конструкциях [78, 185J или искусственно созданных усилий обжатия бетона в гидротехнических конструкциях [27].
§ IV.3. УПРУГО-МГНОВЕННЫЕ ДЕФОРМАЦИИ БЕТОНА
При кратковременном нагружении бетона его деформации при прочих равных условиях зависят от скорости нагружения. Это подтверждается опытами М. С. Боришапского и Е. А. Троицкого [42, 180], а также исследованиями О. П. Квирикадзе [95]. По этой причине величина модуля упругости бетона также зависит от скорости его нагружения и убывает с уменьшением последней. Поэтому упругие деформации бетона линейно связаны с напряжениями лишь при достаточно быстром загружении. В связи с этим в теории ползучести бетона говорят о модуле «упругомгновенных» деформаций, т. е. деформаций, развивающихся при весьма быстром его нагружении.
При этих условиях упругие деформации бетона при сжатии и растяжении [49, 50, 94, 151, 207], а также сдвиге и кручении [40, 91] линейно зависят от величины напряжений, модули продольных упруго-мгновенных деформаций при сжатии и растяжении равны между собой и между модулем упруго-мгновенной деформации сдвига G(t), модулем упруго-мгновенной продольной деформации Е(т) и коэффициентом упруго-мгновенной поперечной деформации vi(t) существует обычная связь [25].
В дальнейшем для сокращения записи вместо терминов «модуль упруго-мгновенной деформации» и «коэффициент упругомгновенной поперечной деформации» мы будем применять всюду термины «модуль упругости» и «коэффициент поперечной деформации», имея в виду соответствующие упруго-мгновенные деформации.
Экспериментально последние определяются с помощью определенных методических правил (см., например, §IV.13), как суммарные деформации, слагающиеся из упругих деформаций на отдельных кратковременных ступенях загруження, между которыми соблюдаются определенные выдержки во в; емени. Дефор
161
мации, натекающие во время этих выдержек, относятся к деформациям ползучести и в упругие деформации не включаются.
Многочисленные опыты показали, что упругие деформации бетона, а следовательно, и модули упругости и коэффициент упругой поперечной деформации изменяются с возрастом бетона т к моменту его загружения, асимптотически приближаясь к
с- По опытам НИИ£
е!с}нГ/с^г
збодн.
£(гАиГ/с~1
cfti=3*ws{t-o,4c~e'eet)
З'ИГ 2*!QS- О 1Ч05 i
кГ/см*_^-------;------------;----
£&*3,73Ч05Ц D.47Be°o”st)
][ । । о-ПоопытамДнепросгпроя
714 26 56 I6Z 274
ЗбОдн.
£1^)нГ/см о-По опытам Шенна
714 26 56
274 ЗбОдн
Рис. 36 Кривые изменения во времени модуля упругости бетона по данным различных опытов
соответствующим постоянным величинам, относящимся к бетону весьма зрелого возраста.
Например, на рис. 36 [25] показано изменение с возрастом бетона его модуля упругости при сжатии, наблюдаемое в ряде экспериментов. По предложению Н. X. Арутюняна это изменение модуля £(т) удобно аппроксимировать зависимостью
£(т) = £0 (1 — £ е-'^) . (IV.3)
где £о — предельное значение модуля упругости для бетона зрелого возраста, а
Р и | — некоторые параметры, подбираемые из опыта.
162
Аналогичные зависимости могут быть предложены и для 6(т) и vi(t); однако следует помнить, что из трех функций Е(т), G(t) и V! (т) только две можно выбрать в качестве независимых, третья будет выражаться через них с помощью выражения (IV.2).
Поскольку, в силу известных зависимостей, между модулем упругости Е(т) и пределом прочности бетона имеется определенная связь, условия твердения бетона оказывают значительное влияние на величину этого модуля. Например, с увеличением температуры твердения бетона скорость нарастания его модуля упругости во времени увеличивается.
На изменение модуля Е(т) оказывает влияние также и длительное загружение его внешней нагрузкой, которое вызывает изменение плотности бетона, особенно в раннем возрасте, вследствие его большой пластичности’.
Величина модуля упругости при сжатии зависит от напряжений, при котором измерены деформации. С ростом напряжений вплоть до разрушения бетона она падает, причем уменьшается модуль упругости быстрее у бетонов с большим В/Ц и с малым содержанием цемента [102].
Учесть одновременно зависимость модуля упругости от напряжений и от возраста бетона весьма трудно. В направлении этого в настоящее время сделаны лишь робкие попытки. Поэтому современная теория ползучести бетона учитывает только изменение модуля во времени обычно в форме (IV.3).
Поскольку температурно-влажностные воздействия часто носят циклический характер, для проблемы температурно-влажностных напряжений в бетоне важным является вопрос о его поведении при действии повторных нагрузок. Еще в опытах Йошида [230] было показано, что при этих условиях бетон ведет себя по-разному в зависимости от величины напряжений.
Если напряжения не велики (менее 40—50% предела прочности), то после нескольких циклов повторения нагрузки диаграмма деформаций сжатия бетона становится прямолинейной, а величины деформаций стабилизируются, т. е. бетон внешне приобретает свойства упругого тела (рис. 37,а).
При более высоких напряжениях при первичном нагружении зависимость между деформациями и напряжениями нелинейна: деформации возрастают не пропорционально напряжениям и быстрее их. После нескольких циклов повторения нагрузки на некоторое время эта зависимость становится линейной и полные деформации стабилизируются. Затем после определенного большого числа повторений нагрузки полные деформации вновь растут и линейная зависимость между деформациями и напряжениями нарушается. Описанный процесс закапчивается разрушени-
1 В известных опытах Роша было отмечено уменьшение пористости бетонных призм с 26 до 12% при существенном увеличении прочности бетона после их всестороннего обжатия.
163
2
Рис. 37, а. Зависимость между напряжениями и продольными и поперечными деформациями бетона при сжатии при ограниченном (малом) числе циклов нагружения (опыты Йошида)
Рис. 37. б. Зависимость между напряжениями и продольными и поперечными деформациями бетона при сжатии при многократно повторных нагрузках
8?
ем бетона вследствие прогрессирующего развития микротрещин (рис. 37,6) и характерен для напряжений, превышающих предел выносливости (усталости) бетона, составляющий примерно половину предела прочности статического сжатия бетона [11].
В литературе нет данных об усталостном разрушении бетона, вызванного только цикличными изменениями температуры и влажности на диапазоне их обычных изменений. Поэтому принято считать, что упругие деформации бетона, вызываемые температурно-влажностными напряжениями, линейно зависят от величины последних и в отношении их бетон ведет себя целиком как упругое тело.
§ IV.4. ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ БЕТОНА
При действии нагрузки наряду с продольными бетон претерпевает и поперечные деформации. Вопрос о поперечных деформациях бетона весьма существен для теории ползучести в целом и, в частности, для проблемы температурно-влажностных напряжений, поскольку последние, как правило, распределяются неравномерно по объему тел. Раскрытие связанной с этим внутренней статической неопределимости тел при решении задач теории ползучести требует привлечения физических уравнений, устанавливающих связь между напряжениями и деформациями бетона, в которые кроме модулей упругости продольной деформации £(т) и деформации сдвига G(t) входят коэффициенты упругой поперечной деформации vi(t) и поперечной деформации ползучести vz(t, т).
Обширное исследование поперечных деформаций бетона при действии кратковременных нагрузок было проведено О. Я. Бергом [36, 38] Они показали, что в области линейной ползучести (о</?т) коэффициент упругой поперечной деформации Vi(t) постоянен и для зрелого бетона примерно равен 0,13-*-0,22. (В среднем v( = =0,167.)
Вопрос о коэффициенте поперечной деформации ползучести т) также мог бы быть решен на основании данных экспериментов. Однако задача эта не из легких, так как экспериментальных работ по исследованию ползучести бетона в условиях сложного напряженного состояния крайне мало. Кроме того, результаты их подчас противоречат друг другу.
Так, Фрейсинэ [195] утверждает, что ползучесть бетона при чистом сдвиге равна нулю, в то время как Дюк и Дэвис [223] на основании проведенных ими опытов считают, что ползучесть бетона при сдвиге вдвое превышает его ползучесть при осевом сжатии.
Н. X. Арутюняном [25] в предположении одинаковой ползучести бетона при растяжении и сжатии без каких бы то ни было
166
ограничений для коэффициента v2(f, т) было получено условие
<о (/, т) = 2 (Ц- v2 (/, т)] С (Л т), (I V.4)
устанавливающее связь между мерами ползучести при чистом сдвиге <х>(/, т) и осевом сжатии С(/, т). Обращаясь к этому условию, видим, что, по Фрейсинэ, мы должны были бы иметь т2(/, т) =—1, а, по Дюку и Дэвису, v2(f, т) =0.
В опытах И. Е. Прокоповича [151] в течение 100 суток наблюдения за образцами-близнецами, подвергнутыми только сжатию и только кручению, сохранялось условие ы(/, т)<2С(/, т), следовательно, оказалось v2(f, т)<0, что физически необъяснимо.
Немногочисленные опыты Девисов и Броуна [220, 221], а также Глэнвилля и Томаса [229] по исследованию поперечных деформаций бетона при длительном сжатии, по мнению авторов, показали, что v2(t, т) меньше vi (т).
В работе [248] приведена таблица, составленная А. Д. Россом на основании экспериментальных данных по длительному двухмерному напряженному состоянию бетона, показывающая, что в процессе ползучести изменение поперечного расширения практически не наблюдается; при этом вновь фигурируют опыты Дюка и Девиса [223].
Таким образом, многие исследователи склоняются к тому, что v2(/, т)~0, а вовсе не близок к 0,5, как это, например, требуется в классической теории пластичности. Между тем имеются и другие сведения.
Так, по данным Р. Лермита [104], в Мюнхене было найдено, что поперечная деформация ползучести бетона достигает значительной величины.
Н. Г. Корсаком [102] в области линейной ползучести проведены опыты по определению коэффициента Пуассона для бетона в возрасте 30 дней. Величины коэффициентов Пуассона в этих опытах оказались равными по полным деформациям 0,18; по упругим деформациям 0,14. Это указывает на то, что в данных опытах v2(/, t)>v1(t).
В. А. Бушковым [48] описаны опыты над бетоном состава 1 :6 при ЯПр=147 кГ/см2. Приведенные им данные об упругих поперечной и продольной деформациях и общих поперечной и продольной деформациях показывают, что при возрастании напряжений от 70 до 110 кПсм2 V|(t) возрос от 0,154 до 0.242, в то время как v2(/, т) вырос соответственно от 0,334 до 0,667, оставаясь в ходе опытов все время больше vi(t).
Из сказанного следует, что в настоящее время вопрос о поперечной деформации ползучести бетона еще не исследован в должной мере. Поскольку имеются противоречивые данные, при которых у одних авторов v2(/, т) был больше, а у других, наоборот, меньше vi(t), можно считать, что условие v2(/, т) =/=
167
=}= vi(t) еще не доказано, поэтому удобно пока пользоваться равенством
v2(t, т) = Vj (т) = v = const. (I V.5)
Можно ожидать, что по малости vz(t, т) и vi(x) это допущение приведет к малым погрешностям даже в том случае, если окажется, что условие (IV.5) на самом деле не имеет места. Действительно, как показал И. Е. Прокопович [151], возможные погрешности в величинах октаэдрических напряжений в бетоне при трехмерном напряженном состоянии с учетом (IV.5) не превышают 5—6%.
Принятие условия (IV.5) автоматически приводит к пятой из гипотез, рассмотренных ниже в § IV.5. Действительно в современной теории ползучести Н. X. Арутюняна фигурируют следующие полные единичные (удельные) деформации бетона [25]:
осевая деформация
6(/’т)=Т^Г + С(/’т): (IV-6)
поперечная деформация
61 (/’г)=Ж+Vz (Л т) с (i> т): (i v7)
деформация сдвига
МЛ т) = 7ТТ+ <»('.*). (IV .8)
G (т)
Внося (IV.5) в (IV.7) и (IV.8), находим
(/, т) = v6 (t, т); 62 (t, т) - 2 (1 + v) 6 (I, т). (I V.9)
Таким образом, принятие условия (IV.5) приводит к постулированию одинаковой зависимости от времени всех трех удельных деформаций бетона 6(/,т), 6i(/,t) и 6г(Лг), т. е. к пятой рабочей гипотезе, рассмотренной в § IV.5.
Допущение (IV.5) крайне удобно, так как при его соблюдении система основных совместных интегральных уравнении теории ползучести, описывающих напряженно деформированное состояние упруго-ползучего тела, распадается на независимые и притом более простые уравнения [25] (см. также § 1V.9). Это обстоятельство имеет огромное практическое значение, так как открывает большие возможности для решения задач теории ползучести доступными инженеру методами. Условием (IV.5) мы и будем пользоваться в дальнейшем.
§ IV.5. РАБОЧИЕ ГИПОТЕЗЫ СОВРЕМЕННОЙ ЛИНЕЙНОЙ ТЕОРИИ ПОЛЗУЧЕСТИ БЕТОНА
Современная теория ползучести бетона представляет собой феноменологическую теорию, основанную на объективных экспериментальных данных о поведении бетона под действием длн-168
тельных нагрузок. Как и всякая феноменологическая теория, эта теория исходит из ряда основных рабочих гипотез, сформулированных на основании обобщения этих экспериментальных данных и положенных в основу ее математического аппарата. Эти рабочие гипотезы формулируются следующим образом:
1) бетон рассматривается как изотропный и однородный материал;
2) между полными деформациями бетона (мгновенно-упругими деформациями и деформациями ползучести) и напряжениями в нем существует линейная зависимость;
3) абсолютные величины деформаций (упругих и неупругих) принимаются не зависящими от знака напряжений;
4) для деформаций ползучести применим принцип наложения воздействий.
Как известно, этот принцип формулируется следующим образом. Полная (суммарная) деформация ползучести при переменных (ступенчато изменяющихся) напряжениях может быть найдена, как сумма приращений деформаций ползучести, вызванных соответствующими приращениями напряжений. При этом считается, что вызываемая данным приращением напряжений Да, величина соответствующего приращения деформаций ползучести Aen,i, накапливаемая к некоторому моменту времени наблюдения t сверх деформации ползучести ЕДвп-i-i. вызванной другими (предшествующими) приращениями напряжений Дсп, .... AOi-i, зависит только от величины и длительности действия этого приращения, но не зависит от величины и длительности действия остальных и, в том числе, предшествующих ему приращений напряжений;
5) принимается одинаковая зависимость от времени всех видов полных единичных относительных деформаций, а именно: удельной осевой деформации 6 (Л т), удельной поперечной деформации 61 (,,т) и удельной деформации сдвига 6г(/,т) (см. § IV.4).
Первая из этих гипотез носит условный характер. Однако хаотичность размещения заполнителей в бетоне позволяет думать, что он в больших объемах, в общем, является однородным и изотропным. Правда, исследованиями К- С. Карапетяна [92] и И. Е. Прокоповича [151] показано, что величина деформации ползучести зависит от направления действия усилия относительно слоев укладки бетона при изготовлении образцов, т. с. что бетон относительно деформаций ползучести ортотропен. Однако степень этой ортотропности невелика. Например, в опытах И. Е. Прокоповича образцы, изготовленные из обычного тяжелого вибрированного бетона, имели деформации ползучести при сжатии перпендикулярно слоям укладки всего на 7% больше, чем в случае сжатия вдоль этих слоев. В связи с этим рассматриваемая гипотеза выглядит вполне приемлемой.
169
Отметим, что для однозначности решения задач теории ползучести эта гипотеза должна быть дополнена требованием отсутствия начальных напряжений при отсутствии внешней нагрузки и предшествующих изменений температуры и влажности бетона. Таким образом, первую рабочую гипотезу теории ползучести бетона следует формулировать следующим образом.
Бетон рассматривается как изотропный и однородный материал, у которого при отсутствии внешней нагрузки и предшествующих изменений его температуры и влажности отсутствуют и начальные напряжения.
Вторая гипотеза основана на многочисленных опытных данных, указывающих на ее справедливость, но в определенных пределах величин напряжений. Например, доказано (см. § IV.1), что при растяжении такое допущение справедливо вплоть до разрушения бетона, а при сжатии — до напряжений, равных примерно 0,5 его призменной прочности.
Третья из указанных предпосылок могла бы быть наиболее легко обоснована экспериментально. Однако, как было показано в § IV. 1, имеющиеся в литературе по этому вопросу данные весьма разноречивы. Возможные причины этого связаны с методикой эксперимента и подробно рассмотрены в работе автора [18]. Опыты Н. И. Катина [94], А. Е. Шейкина и В. Л. Николаева [207], проведенные на гидроизолнрованных образцах и потому связанные с минимальными погрешностями, возникающими обычно вследствие неаддитивности усадки и ползучести, убеждают в приемлемости этой предпосылки.
Наиболее дискуссионной является четвертая из указанных гипотез, постулирующая применимость принципа наложения воздействий, особенно в случае знакопеременных нагрузок. Опа оспаривается рядом исследователей, причем поводом для этого послужили опыты П II. Васильева [50], А. Д. Росса [244], А. В. Яшина [212] и некоторых других авторов по изучению деформаций бетонных образцов после их полной или частичной ступенчатой разгрузки.
На рис. 35 воспроизведены результаты указанных опытов А. В. Яшина. Как видно из рис. 35, модуль упруго-мгновенной деформации при разгрузке призм был примерно на 33% выше, чем при первичной нагрузке призм-блнзнецов. Примерно на столько же деформации последействия при разгрузке образцов были меньше деформаций ползучести призм-близнецов, впервые загруженных теми же напряжениями, в том же возрасте и той же продолжительности действия. Так как в описываемых опытах не наблюдалось повышения прочности бетона у призм, выдерживаемых под нагрузкой, по сравнению с ненагруженнымн призмами [212 (стр. 54)], то это можно отчасти объяснить начальными пластичностью и неоднородностью бетона, устраняемыми при первом же нагружении.
170
Рис. 38. Применение принципа наложения воздействий при ступенчатых нагрузках и разгрузках (опыты А. Д Росса)
/ — экспериментальная кривая полных деформаций; 2 — теоретическая кривая по принципу наложения воздействий
Эти и подобные им экспериментальные данные позволяют думать, что применение принципа наложения в его обычной форме может привести к некоторым погрешностям. В связи с этим П. И. Васильевым [50], В. В. Блинковым [41] и А. А. Гвоздевым [66] сделаны предложения по усовершенствованию этого принципа путем введения в рассмотрение различных по величине наследственных функций бетона при сжатии и при растяжении. Эти предложения весьма заманчивы, но приводят к существенному усложнению и без того сложной теории ползучести бетона, поэтому отказ от обычной формы принципа наложения воздействий крайне нежелателен. Кроме того, это, по-видимому, и не требуется, так как опыты показывают, что применение принципа наложения воздействий вполне оправдано. Это хорошо видно из рис. 38, воспроизводящего результаты опытов А. Д. Росса [244] по проверке применимости этого принципа, а также опытов С. В. Александровского и Э. Я. Багрия, описанных в § IV.13 (см. рис. 63).
Сказанное выше ни в коем случае не следует рассматривать как отказ от дальнейших экспериментальных исследований в направлении оценки погрешностей и области применимости принципа наложения воздействий. Наоборот, исследования такого рода крайне желательны, так же как и дальнейшее изучение других особенностей ползучести бетона. Однако методика этих исследований должна быть более совершенной, чем та, которая применяется в настоящее время. Некоторые пути разработки такой методики указаны в работе автора [18].
Последняя из пяти указанных выше гипотез не является обязательной. Она была предложена Г. Н. Масловым [120] в его варианте теории упруго-ползучего тела и существенно упрощает ее уравнения. Это упрощение состоит в том, что система совместных основных интегральных уравнений этой теории при этом распадается на отдельные независимые интегральные уравнения и компоненты тензора напряжений определяются независимо друг от друга, каждая из своего самостоятельного уравнения по соответствующей компоненте тензора напряжений упруго-мгновенной задачи (см. § IV.9).
Н. X. Арутюнян отказался от этой гипотезы и разработал наиболее общую теорию ползучести бетона, относящуюся к случаю неодинаковой зависимости от времени указанных единичных деформаций ползучести. Эта теория нашла свое окончательное завершение в его фундаментальной монографии [25]. В настоящее время эта теория является наиболее общей и наилучшим образом описывает все наиболее важные свойства бетона, характеризующие его поведение под длительной нагрузкой. Она получила всеобщее признание как в нашей стране, так и за рубежом и интенсивно развивается в трудах большой группы советских учетных.
На основании всего изложенного можно утверждать, что пер
172
вые четыре из указанных выше пяти рабочих гипотез современ-1 ной линейной теории ползучести бетона вполне приемлемы и в настоящее время нет оснований для отказа от любой из них. Пятая из этих гипотез не обязательна, но крайне удобна, и мы ее также будем иметь в виду в дальнейшем.
Анализ имеющихся в литературе экспериментальных данных, проведенный в § IV.4, подтверждает приемлемость этой гипотезы. Связанные с нею возможные погрешности невелики и на основании приведенных там данных И. Е. Прокоповича могут быть оценены в 5—6%.
§ IV.6. ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ ПОЛЗУЧЕСТИ БЕТОНА Г. Н. МАСЛОВА—Н. X. АРУТЮНЯНА.
ОДНОМЕРНАЯ ЗАДАЧА ПРИ НАЛИЧИИ ВЫНУЖДЕННЫХ ДЕФОРМАЦИЙ
Рассмотрим основные уравнения линейной теории ползучести бетона Г. Н. Маслова — Н. X. Арутюняна применимо к проблеме температурно-усадочных напряжений. Вначале ограничимся одномерной задачей осевого сжатия (растяжения) бетонного бруса. В этом случае рассматриваемая теория исходит из экспериментальных кривых удельной осевой относительной деформации бетона 6(/, т), которые предполагаются заданными (рис. 39,а).
Функция 6(/, т) определяет собой полную относительную деформацию призматического бруса, наблюдаемую к текущему моменту времени I, вызываемую единичными напряжениями, приложенными в некотором возрасте бетона т. Деформация 6(/, т) таким образом включает в себя соответствующие деформации: упругую и деформацию ползучести, развивающуюся за время t—т, отнесенные к единице напряжения.
Будем считать, что брус претерпевает еще дополнительно относительную деформацию укорочения (удлинения) е°(/), вызываемую некоторыми дополнительными факторами не силового характера, например, изменениями температуры (температурное сокращение) или влажности (усадка) за время t—т. Такую деформацию мы будем в дальнейшем называть вынужденной. Тогда в соответствии с первой и второй рабочими гипотезами, рассмотренными в § IV.5, для полной относительной деформации бруса будем иметь выражение1
е(0 = е°(0 + а(т1)6(/,т1)+ [^-6(/,T)dT, (IV.10)
J dr
1 Знак вынужденной деформации €°(0 считается в данном случае совпадающим со знаком деформации силовой е(/) —е°(0, т. е. деформации, вызываемой действием напряжений g(ti).
173
Рис. 39. Типичные кривые осевых деформаций и напряжений бетонного бруса
а — кривые единичных (удельных) деформаций: / — Упруго-мгновенных, возникаю-
щих в момент загружения | кривая-----|: 2 — полных, развивающихся во времени
\ £(’)'
вследствие ползучести; 3 — случай загружения бруса — постоянные по времени напряжения; 4 — то же. переменные напряжения; б — кривые единичных (удельных) напряжении 1 — упруго-мгновенных, возникающих в момент создания деформации (кривая £(?)), 2 — полных развивающихся во времени вследствие релаксации;
3 — случай деформированного бруса — постоянная во времени напряженная деформация; 4 — то же, переменная напряженная деформация
Уравнения (IV.10), (1V.12) выражают собой в интегральной форме сформулированный выше принцип наложения воздействий и для случая температурной деформации были получены Г. Н. Масловым [120].
Из уравнения (IV. 12) следует, что полная продольная напряженная деформация бруса е(/)—е°(/) слагается из упругой деформации
у Е(0
(IV. 13)
174
и деформации ползучести
еп(/) - -fa(T)-^6(Z,T)dc. (1V.14)
Так как в соответствии с правилом знаков, принятым в уравнении (IV.10), в интервале времени т( < t < со — 6(/,т) имеет знак, обратный знаку напряжений о(т), то деформация ползучести, вычисленная по формуле (IV.14), всегда положительна. Таким образом, полная продольная деформация бруса вследствие ползучести бетона всегда больше его соответствующей упругой деформации.
Уравнение (IV.12) часто называют интегральным уравнением Вольтерра второго рода относительно искомых неизвестных напряжений о(/) и его решение записывают в форме
а (0 = [е (0 - en (/)| Е (t) + j (е (г) - е° (т)] Р (I, т) dx. (IV. 15)
При этом функцию P(t,x) считают резольвентой ядра ^(/,т) = - -^—6(/,т) уравнения (IV.12). Строго говооя, уравнение (IV.12) от
в записанном таким образом виде не является интегральным уравнением Вольтерра, а функция P(t, т) в уравнении (IV.15) не есть резольвента его ядра. Это вытекает из того факта, что, как известно из теории интегральных уравнений, ядро уравнения Вольтерра L(t, т) и его резольвента R(t, т) должны быть связаны соотношением (64]
^(/.г)- /?(/,т)^ f/?(Lx)L(Z,|)de, (IV.16)
из чего следует, что ядро L(t, т) и резольвента /?(/, т) должны иметь одну п ту же размерность. Функции же K(t, т) и Р(/, т), как нетрудно видеть, имеют разную размерность, а именно:
1; l₽((,r)J=[—1.
[ кГ-сут J ( см2-сут J
Поэтому, чтобы удовлетворить этому требованию, уравнения (1V.12) и (IV.15) следует записывать в виде;
f-££Li(z,t)dT; (IV.17)
*- V/ J (V
= е 10 - (О- j [е(t) - е° (т)] R (/, т) dx. (IV.18)
175
где ядро
L((,t)=-E(t)^6(Z,t). (IV. 19)
ОХ
При такой форме записи (IV.17), (IV.18) основных уравнений теории ползучести первое из них уже будет интегральным уравнением Вольтерра второго рода относительно упругих деформаций а ФУНКЦИЯ Я(/, т) будет резольвентой его ядра Z. (/, т); обе эти функции будут иметь одну и ту же размерность
= [Я(/, т)]=[—1 (IV.20)
LcpnJ
и удовлетворять соотношению (IV. 16).
Запись основных уравнений теории ползучести в форме (IV. 17) и (IV. 18) свободна от указанных выше недостатков. Она была предложена А. А. Гвоздевым [64] и стала теперь общепринятой
Ввиду важности уравнений (IV.17) и (IV.18) укажем другой возможный путь их построения.
По аналогии с полной единичной напряженной деформацией 6(/, т) (рис. 39, а) введем в рассмотрение полные единичные напряжения р(/, т) (рис. 39,6) [21]. Под полными единичными напряжениями p(t, т) будем понимать напряжения, которые в любой момент времени наблюдения t необходимо иметь в призматическом бетонном брусе для поддержания неизменной во времени его полной единичной относительной напряженной деформации, сообщенной ему в возрасте бетона т.
Допустим, что призматическому брусу в момент времени, совпадающий с возрастом бетона т=ть с помощью напряжений сообщена напряженная деформация е(т()—е°(Т|), которая в последующем сохраняется неизменной (рис. 39,6). Тогда в соответствии с первой и второй рабочими гипотезами, рассмотренными в § IV.5, для полных напряжений в брусе мы будем иметь
о (/, Х1) = [е (Т1) - е° (tJJ р (t, тх), (IV.21)
где Е°(() —вынужденная деформация бруса одного из указанных выше типов.
Рассмотрим теперь другой случай, когда в момент времени Tt с помощью напряжений брусу сообщена напряженная деформация е(Т|)—е°(Т1), которая затем под их влиянием изменяется с течением времени по закону е(/)—е°(/) (рис. 39,6).
Разбивая интервал времени /—Ti на равные промежутки Дт и заменяя кривую напряженных деформаций е(()—е°(0 ступенчатоломаной линией (рис. 39,6), будем иметь
е(/)-е°(0 = е(Т1) —е°(т!)+ % А [е (г,) — е° (т,)]. (IV.22)
176
Так как приращения напряженных деформаций Д[е(т,) — е°(т,)] происходят в различных возрастах бетона, то полные напряжения в брусе к текущему моменту времени t на основании второй и четвертой рабочих гипотез § IV.5 мы найдем также в виде суммы
о(0=[е(т1)-ео(т1)]р(/,т1)+ 2 AH^-e^i,)] р(/, т,). (IV.23) т<— Ti
Устремляя Дт -»0 и переходя к пределу, получим формулу для полных напряжений о(0, относящуюся к случаю непрерывно изменяющихся напряженных деформаций е(/)—ес(0:
а(0 = [е(т1)-е«(т1)]р(/,т1)+ f £ [е (т)-е° (т)] р (/, т) dr, (IV.24) или, интегрируя по частям и принимая во внимание, что p(t, t) = =EV),
О (0 = 1е (0 - Е° (ОJ Е (/) - J [е(т) - Е° (т)]-А р(/, Т) dr. (IV.25)
ч
Наконец, вводя обозначение
(IV26)
перепишем уравнение (IV.25) в виде
-|g- = e(n-EO(/)-J [е (т)-е®(т)1 R(t.T)dT, (IV.27)
что полностью совпадает с (IV. 18). Рассматривая это уравнение, как интегральное уравнение Вольтерра второго рода, найдем его решение в виде
е (О - е° (0 = L (t, т) dr, (IV.28)
£ V/ J & v*
совпадающим с (IV.17), где Е(/,т)—резольвента ядра R(t,x), отыскиваемая на его основе по уравнению (IV.16).
Таким образом, функции L(t, т) и R(t,x) попарно взаимны и
каждая из них может рассматриваться как ядро или как резольвента соответствующего интегрального уравнения (1V.27) или (IV.28) в зависимости от того, какая из двух входящих в них функций и е(0—е°(/) задана, а какая является искомой.
I? о (О
Вели заданы относительные напряжения и отыскиваются
177
относительные деформации е(/)—е°(/), ядром является функция а резольвентой функция если же заданы деформации e(Z)—е°(/) и отыскиваются напряжения то« наобо
рот, ядром служит функция Lit,т), а резольвентой функция R(t,T).
Интегральные члены в уравнениях (IV.27) и (IV.28) являются функционалами, т. е. отражают всю историю деформирования или нагружения бруса на интервале времени /—ть или, лучше сказать, наследуют к данному моменту наблюдения t эффект этих процессов на всем этом отрезке времени. При заданном законе деформирования или нагружения бруса степень этого эффекта зависит от физических особенностей материала, отражаемых функциями L(t, т) и R(t, т), поэтому эти функции мы будем называть н а сл е д ст ве н н ы м и функциями бетона со-
ответственно п е р в о г о и второго рода.
Наследственная функция первого рода L(t,x) всегда может быть найдена на основании зависимости (IV. 19) по экспериментальным кривым полной удельной осевой относительной деформации бетонного бруса 6(/,т). Аналогичным образом па основании зависимости (1V.26) по экспериментальным кривым полных единичных напряжений р(/,т) всегда может быть найдена наследственная функция бетона второго рода /?(/,т).
Из выражений (IV.19) и (IV.26) следует, что эти функции не зависят ни от величин, ни от характера изменений напряжений и деформаций бетона, а являются физическими характеристиками его упруго-ползучих свойств. В связи с тем, что наследственные функции бетона А(/,т) и /?(/,т) играют огромную роль в теории ползучести, ниже в § IV.7 особо рассмагривается их физический
смысл.
§ IV.7. ФИЗИЧЕСКИЙ СМЫСЛ НАСЛЕДСТВЕННЫХ ФУНКЦИЙ БЕТОНА L(t ,т) и R(t, т)
Для того чтобы выяснить физический смысл наследственной функции влияния первого рола L(t, т), обратимся к простейшему случаю деформирования призматического бруса. Сообщим этому брусу в момент времени т продольную единичную относительную упругую деформацию е(т) = 1, выдержим неизменной эту деформацию в течение некоторого малого отрезка времени Дт и, полностью сняв ее в момент времени т+Дт. будем наблюдать полную деформацию бруса в текущий момент времени />т+Дт, вызванную действием этого единичного импульса 1-Дт упругой деформации.
Вследствие малости Дт можно пренебречь изменением упругих свойств тела на этом отрезке времени п считать, что Ё(т + + Дт) =С(т). При этом, для того чтобы осуществить указанную
178
операцию, мы должны будем приложить к брусу осевые напряжения о(т)=Е(т) в момент времени т, выдержать их неизменными в течение указанного малого отрезка времени Дт л снять их полностью в момент времени т + Дт.
Введем в рассмотрение некоторую функцию L, определяющую собой эффект действия рассмотренного единичного импульса предшествующей упругой деформации 1 • Дт на полную дсфор-
Рис. $0. Напряжения и деформации бруса при действии единичного импульса 1-Дт
а — упругой деформации; б - полкой деформации
манию бруса, наблюдаемую в текущий момент времени / и выражающую эту деформацию в долях от указанного упругого импульса.
Вначале предположим, что материал тела идеально упруг. Тогда, очевидно, полная деформация тела в момент времени т + Дт будет равна упругой деформации, сообщенной ему в момент времени т
е (т 4-Дт) = е‘(т) = 1, (IV.29)
поэтому после снятия этой деформации в любой момент времени />т+Дт деформация тела будет равна нулю (рис. 40,а), а следовательно будет равна нулю н функция L. Таким образом, для идеально упругого тела функция L тождественно равна нулю.
179
По-иному в этих условиях будет обстоять дело в случае упруго-ползучего тела, каковым является бетон, обладающий свойствами ползучести и последействия. При сохранении неизменной в течение отрезка времени Дт упругой единичной деформации, а следовательно, неизменных напряжений = в нем к моменту времени т+Дт разовьется некоторая деформация ползучести еп(т+Дт), таким образом, к этому моменту времени мы будем иметь полную деформацию бетона
Еполн (Т + Дт) = 1 + вп (т + Дт) =£= еу (т). (I V.30)
Поэтому при снятии единичной упругой деформации в момент времени т+Д/ в нем останется остаточная деформацияеп(т+Дт), которая затем вследствие последействия начнет изменяться (убывать) с течением времени (рис. 40,а).
пня t будет отлична от пуля и ее величина будет определяться функцией L, уже не равной в этом случае пулю. Таким образом, введенная нами в рассмотрение функция представляет собой функцию влияния, связанного с ползучестью бетона, единичного импульса предшествующей упругой деформации, действовавшего в возрасте бетона т, на его полную деформацию, наблюдаемую в момент времени t.
При фиксированном т величина функции L будет зависеть от длины промежутка t—т, т. е. от t, а при выбранном t по тем же соображениям она будет зависеть от т, таким образом, в общем случае упруго ползучего тела, свойства которого не инвариантны относительно начала отсчета времени (стареющий бетон), мы будем иметь
L=L(t,z), (1V.31)
т. е. функция L в явном виде одновременно будет зависеть и от времени наблюдения t и от возраста бетона т.
Зная L(t,x), мы можем всегда определить полную деформацию в момент времени t, вызываемую рассмотренным выше импульсом 1 - Дт упругой деформации, по формуле
Деп(/)=/.(/, т) -1-Дт. (IV.32)
Рассмотрим теперь случай, когда предшествующая упругая деформация еу(/) на всем интервале t—т отлична от нуля и пе
180
ременна (рис. 41). Очевидно этому случаю соответствует загру-жение бруса напряжениями =ey(t)E(f).
Разбивая интервал t—х на малые равные отрезки Дт и представляя кривую изменения предшествующей упругой деформа-
ции в виде непрерывного ряда последовательных упругих им-о (т.) . , , о (т.)
пульсов & * " Дт интенсивностью еу(т,) = по принципу на-
ложения воздействий суммарную полную деформацию в момент наблюдения t, вызываемую эффектом действия предшествую-
щих упругих импульсов, найдем в следующем виде:
(1V.33)
Устремляя Лт -> 0 и переходя к пределу, получим следующую формулу для указанной суммарной деформации еп(0. относящуюся к случаю непрерывно изменяющихся упругих деформаций, или, что то же, непрерывно изменяющихся напряжений о (О
<1Х--34)
Если мы хотим подсчитать полную деформацию бруса в момент наблюдения t, то мы должны еще учесть упругую деформацию, происходящую в это время
= (lv-35)
Таким образом, полная продольная деформация e(t) бетонного бруса в момент времени наблюдения t будет равна
= (lv36)
Действительно, если бы наше тело было бы идеально упругим, то предшествующие импульсы упругой деформации не влияли бы на величину полной деформации в момент времени t и она была бы целиком равна упругой деформации (IV.35) в этот момент времени. Так как наше тело обладает ползучестью, то предшествующие упругие импульсы дадут дополнительную составляющую этой деформации (IV.34) и мы получим поэтому полную деформацию в текущий момент времени t в виде суммы (IV.36).
Сравнивая уравнения (IV.17) и (IV.36), мы видим их полное тождество в случае отсутствия вынужденной деформации [е°(0 = =0]. Это позволяет нам теперь дать следующее определение фи
181
зического смысла наследственной функции первого рода
«Наследственная функция первого рода L(t,r) представляет собой функцию влияния единичного импульса 1 • dx предшествующей упругой деформации, действовавшего в возрасте бетона т на полную деформацию бетона, наблюдаемую в момент времени />т». Именно такое определение этой функции было дано А. А. Гвоздевым [64], который назвал ее «функцией памяти» (erinnerungsfunldion).
Величина деформации Деп(О. вызываемая действием единичного импульса 1 -dx предшествующей упругой деформации еу(0. зависит от величины деформации ползучести еп(0» натекающей за время dx при за гружении бруса этим импульсом в возрасте бетона т, и поэтому оказывается тем большей, чем меньше т. Кроме того, она зависит от степени эффекта последействия и поэтому возрастает при уменьшении t—т. В связи с этим функция L(t, т) при фиксированном / = /, = const графически должна изображаться кривой L = L(/„t), имеющей вид провисшей нити с крутовосходящнми левой и правой ветвями. Позже мы увидим, что это действительно так.
Теперь, применив аналогичные рассуждения, выясним физический смысл наследственной функции второго рода Сообщим брусу в момент времени т единичный импульс 1 • Дт, но уже не упругой, а полной продольной деформации е(0 = 1, выдержим эту деформацию неизменной в течение малого отрезка времени Дт и, полностью сняв ее в момент времени т + Дт (рис. 40,6), будем наблюдать за упругой деформацией бруса в текущий момент времени />т + Дт, вызванной действием этого единичного импульса полной деформации. Как и прежде, будем полагать £(т+Дт) =Е(т).
Для того чтобы создать единичную деформацию в момент времени т, мы должны будем в это время приложить к брусу напряжения о(т)=Е(т). Так как мы на этот раз в течение времени Дт сохраняем уже неизменной не упругую, а полную деформацию е(/) = 1, то эти напряжения на этом отрезке времени Дт будут уменьшаться (релаксировать).
Для снятия полной единичной деформации е(0 = I в момент времени т+Дт мы должны будем приложить к брусу осевые напряжения о(т)=£(т) обратного знака, часть которых погасит оставшуюся долю первоначально приложенных напряжений о(т)=Е(т). в результате мы получим в брусе некоторые напряжения обратного знака. Так как в дальнейшем мы предполагаем полную деформацию бруса неизменной, т. е. закрепленной на уровне е(/)=0, то эти напряжения в свою очередь будут релаксировать и в момент времени t от них останется только некоторая доля о(/) (рнс. 40,6).
Если мы разделим текущие ординаты полученного графика напряжений о(/) на текущее значение модуля Е(0. то получим подобный ему график упругих деформаций бруса еу(/) (рис.
1£2
40,6), поскольку между ними и напряжениями о(0 существует связь (IV. 13).
Введем теперь в рассмотрение некоторую функцию R, определяющую собой эффект действия рассмотренного единичного импульса предшествующей полной деформации 1 - Дт на упругую деформацию бруса, наблюдаемую з текущий момент времени t, и выражающую эту деформацию в долях от указанного импульса.
Для идеально упругого тела полные деформации равны деформациям упругим, поэтому в этом случае функция R совпадает с функцией влияния L и, как было уже показано выше, тождественно равна нулю.
Для бетона, обладающего свойствами ползучести и релаксации напряжений, функция R отлична от нуля и представляет собой функцию влияния, связанного с релаксацией напряжений, единичного импульса предшествующей полной деформации, действовавшего в возрасте т, на его упругую деформацию, наблюдаемую в момент времени t.
Нетрудно видеть, что функция R, так же как и функция L, в общем случае упруго-ползучего тела, свойства которого не инвариантны относительно начала отсчета времени (стареющий бетон), в явном виде будет зависеть от времени наблюдения t и возраста бетона т
R R(t,x). (IV.37)
Зная R(t, т), мы можем всегда определить упругую деформацию в момент времени t, вызванную рассмотренным выше импульсом 1 - Дт полной деформации, по формуле*
Деу(Л = — R(t,x) I Дт. (IV.38)
Рассмотрим теперь случай, когда предшествующая полная деформация е(/) на всем интервале t—т отлична от нуля и переменна. Разобьем интервал t—т па малые равные отрезки Дт и представим кривую изменения предшествующей полной деформации в виде непрерывного ряда последовательных импульсов интенсивностью е(т,), аналогично тому, как это сделано на рис. 41. Тогда по принципу наложения воздействий суммарную упругую деформацию в момент наблюдения I, вызванную эффектом действия этих предшествующих импульсов, найдем в следующем виде:
еу (0 = - S е<г.) Я (Л D-1 • Дт. (IV.39)
Т=Ч
Устремляя Дт->0 и переходя к пределу, получим следующую формулу для указанной суммарной упругой деформации еу(/),
1 Знак минус в формуле (IV.38) введен потому, что упругая деформацнч Деу(0 и предшествующая полная деформация е(т) = 1 имеют разные знаки (рис 40,6).
183
относящуюся к случаю непрерывно изменяющейся полной деформации е(0
еу (t) = - j е (т) R (t, т) dr. (IV-40)
Полная упругая деформация в момент времени t, с учетом (IV.40), численно равная будет равна
= (IV.4I)
Действительно, если бы наше тело было бы идеально упругим, то предшествующие импульсы полной деформации не влияли бы на величину полной упругой деформации в момент времени t и она была бы численно равна полной деформации е(0 в этот момент времени. Так как наше тело обладает свойством релаксации напряжений (упругих деформаций), то предшествующие импульсы полной деформации уменьшат эту деформацию на величину (1V.40) и мы получим поэтому полную упругую деформацию в текущий момент времени t в виде алгебраической суммы (IV.41).
Сравнивая уравнения (IV. 18) и (IV.4I), мы видим их полное тождество в случае отсутствия вынужденной деформации [е°(0=0]. Это позволяет нам теперь дать следующее определение наследственной функции второго рода R(t, т). Наследственная функция второго рода /?(/, т) представляет собой функцию влияния единичного импульса 1 -dr предшествующей полной деформации, действовавшего в возрасте бетона т, на упругую деформацию бетона, наблюдаемую в момент времени />т.
Величина деформации Деу(0. вызываемая действием единичного импульса предшествующей полной деформации е(т), зависит от степени релаксации напряжений (упругой деформации) за время dr при загружении бруса этим импульсом в возрасте бетона т и поэтому оказывается меньшей, чем меньше т. Кроме того, она зависит от степени эффекта релаксации на интервале времени t— (т+<?т) и потому возрастает при уменьшении t — т. В связи с этим функция /?(/, т) при фиксировании /=/j= = const графически должна изображаться кривой /?=7?(/,-,т), имеющей вид нити, закрепленной в точке т=0 и приподнятой за правый конец т=/,; ниже мы убедимся в этом.
Геометрически функции влияния L(t, т) и /?(/,т) можно интерпретировать как пространственные поверхности влияния в соответствующих трехмерных пространствах (L, t, т) и (R, t, т), имеющие вид, изображенный на рис. 42. Существенной особенностью этих поверхностей является то, что они ограничены двумя сходящимися на осях L или R плоскостями: координатной г=0 и биссекторной /=т, образующими бесконечно простираю
184
щийся клин в положительном направлении осей t, т. За пределами биссекторной плоскости /=т, т. е. при т>/, по своему физическому смыслу функции L(/, т) и Я(/,т) тождественно равны пулю.
Кривые £(т) и ₽(т) при / = const, представляющие собой линии пересечения поверхностей влияния L(t, т) и R(t, т) с семейством плоскостей t = ti=const, условно совмещенные на одном плоском графике, показаны на рис. 43. В таком виде эти кривые экспериментальным путем были получены А. В. Яшиным [212]. Они относятся к невысыхающему бетону состава (по весу)
Рис. 42. Поверхности влияния
а — первого роде 1(/, ч); б — второго рода Я(Г, х)
1:3:4,5, В/Ц = 0,62 на портландцементе Воскресенского завода активностью 350 кГ/см2.
Своеобразное очертание поверхностей влияния L(t, т) и 7?(/, т), изображенных на рис. 42, указывает па то, что напряжения, действовавшие на бетон, или сообщенные ему деформации, совсем недавно, а также те, которые были приложены или, соответственно, сообщены ему в молодом возрасте, оставляют значительный след к данному моменту времени наблюдения, тогда как влияние напряжений, прикладываемых в промежуточный период, или деформаций, создаваемых в это время, в значительной степени стирается. На это важное обстоятельство неоднократно указывал А. А. Гвоздев [64].
Интересен вопрос о конечности аппликат поверхностей влияния £.(/, т) и R(t, т) на бессекторной плоскости 1 = т (рис. 42). Экспериментально выяснить это обстоятельство чрезвычайно трудно. Однако имеются соображения, указывающие на то, что эти аппликаты (или, что то же, правые восходящие хвосты на кривых L(ti, т) и R(tit т) на рис. 43) у бетона должны быть конечными. Действительно, экспериментально доказано [50, 88, 94], что ползучесть бетона даже при очень высоких напряжениях.
185
близких к разрушающим, носит затухающий характер. Это обстоятельство накладывает на функции влияния L(t, т) и /?(/, т) определенные требования, а именно: величины интегралов
J L (t, т) d т и /₽ (/, т) dr (IV.42)
должны быть конечными при любых />т и, в частности, при t -*• 03 , а следовательно, в общем случае должны быть конеч-
Возраст Ветопа Г В сутках
Рис. 43. Наследственные функции влияния бетона по экспериментальным данным А. В. Яшина
а — функция влияния первого рода L(t. г ); б — функция влияния второго • рода Я («, т )
ними и ординаты !=г на кривых рис. 43*. Несоблюдение этого условия может привести к постулированию незатухающей ползучести, что не наблюдается у бетона.
1 В некоторых случаях можно допустить у функций L(t, т) и R(t, т) особенность в точке /=т Однако характер этой особенности должен быть таким, чтобы выполнялось указанное выше условие для интегралов (IV.42). В этом случае функции £(/. т) и /?(/, т) буд>т инвариантными относительно возраста бетона т. что возможно только у старою и высохшего (или невысыхающего) бетона Этот прием, например, используется в теории наследственности [158, 162].
186
Например, функция влияния академика Ю. Н. Работиова [154]
хорошо описывающая ползучесть металлов, к бетону неприменима, ибо интеграл
(/-г)'- (IV.43)
при t -> оэ расходится.
В заключение настоящего параграфа отметим, что уравнения (IV.17) и (1V.I8) получены с помощью принципа наложения воздействий на основе полной единичной относшельной деформации б(/, т) рассматриваемого бруса, поэтому указанный физический смысл наследственных функций бетона L{t, т) и R(t, т) в широком смысле слова связан с применимостью этого принципа и утрачивается, если она отвергается.
§ IV.8. ОБЩАЯ ТРЕХМЕРНАЯ ЗАДАЧА ЛИНЕЙНОЙ ТЕОРИИ УПРУГО-ПОЛЗУЧЕГО ТЕЛА ПРИ НАЛИЧИИ ВЫНУЖДЕННЫХ
ДЕФОРМАЦИЙ
Выяснив физический смысл функций влияния L(t, т) и R(t. т), перейдем к уравнениям линейной теории ползучести, относящимся к случаю сложного напряженного состояния бетона при вынужденных деформациях.
При исследовании этого напряженного состояния методами теории ползучести приходится вводить в рассмотрение коэффициенты поперечной деформации vi(t) и v2(f, т) соответственно для упругой и неупругой частей деформации. При этом для общности полагают, что коэффициент vi (т) зависит только от возраста т бетона, а коэффициент v2(Z, т) —как от возраста т, так и от продолжительности действия нагрузки t—т. В этих случаях также кроме модуля осевой упруго-мгновенной деформации Е(т) и полной единичной продольной деформации 6(/, т) (IV.6) приходится рассматривать еще модуль упруго-мгновенных деформаций сдвига (IV.2) и полные единичные поперечную деформацию б|(/, т) (IV.7) и деформацию сдвига б2(/, т) (IV.8).
При vi(t)=^v2 (/, т) уравнения совместности деформаций тела в теории ползучести получаются весьма сложными [25] и, главное, образую! собой совместную систему интегро-дифференциальных уравнений, решение которой при современном уровне знаний наталкивается па большие математические трудности. Поэтому удобно пока пользоваться условием (IV.5), принятие
1Я7
которого, во-первых, как это было показано в § 1V.4, приводит к незначительным погрешностям, во-вторых, существенно упрощает решение задач теории ползучести, поскольку при этом указанная выше система совместных уравнений теории ползучести распадается па независимые и более простые уравнения.
Используя условие (IV.5) и вытекающие из него соотношения (1V.9), выпишем основные уравнения линейной теории упруго-ползучего тела при наличии вынужденных деформаций, относящихся к случаю его сложного трехосного напряженного состояния.
Для того чтобы составить эти уравнения, необходимо кроме гипотез линейной теории ползучести, сформулированных в§ IV.5, ввести еще дополнительно следующие рабочие предпосылки:
1) напряженные деформации е* (О, ..... у*у (0, вызываемые действием собственно напряжений, и деформации вынужденные (0. ••••» Yxy (0. ••• малы и не зависимы друг от друга;
2) упругие характеристики материала v, Е(т) и G(t) не зависят от величин вынужденных деформаций и причин, их вызывающих (температуры, влажности и т.п.);
3) скорости вынужденных деформаций невелики, в связи с чем ускорениями перемещений и, v и w точек тела можно пренебречь.
Применение первой предпосылки вполне обосновано, т. к. обычно указанные деформации бетона невелики, что позволяет применять для анализа его напряженно деформированного состояния математический аппарат линейной теории ползучести и алгебраически суммировать напряженные и вынужденные деформации.
Вторая гипотеза также вполне применима к бетону, если в соответствии с первой предпосылкой рассматривать весьма малые вынужденные деформации, не приводящие к микронарушениям сплошности материала и вызывающие напряжения, не превышающие его предела упругости, а также исключить из рассмотрения значительные изменения температуры и влажности бетона, как мы условились выше.
Наконец, третья гипотеза также применима к бетону, так как вследствие низких значений величин его тепло- и влаго-физических характеристик (см. § 1.3 и 11.3) изменения температуры и влажности бетона происходят очень медленно, вследствие чего инерционным эффектом упругих сил вполне можно пренебречь.
В дополнение к изложенному условимся в дальнейшем считать, что поверхностные и объемные силы отсутствуют, сосредоточив свое внимание лишь на напряжениях и деформациях тела, вызываемых только его вынужденными деформациями.
При указанных предпосылках напряженно деформированное
188
состояние рассматриваемого упруго-ползучего тела будет определяться напряжениями 1 ।
<(0, °у(0. <(0; ]
<„(') = фМ <,(0 - «о. = <„(') I (IV'41>
и деформациями
<(0, е;(0, <(0;
Сю. vuo. y;z(o-.
2<о;(о, 2w;(o,
(IV-45)
(IV.46)
— средние вращения, a v*(t) и tc *(0 - перемещения точек тела в направлении координатных осей х, у и z соответственно.
При этом между деформациями и напряжениями существует следующая связь [21, 25]2:
(I +*)<(') — *-$*(0
<(') = *!(') + ---------------— +
.................• • • • • Jt.s.z); (IV47) С(0 = ^(0 + г[ (l+^~ +
.......................(x,y,Z),
1 Здесь и всюду в дальнейшем знак звездочки у напряжений, деформаций и смешений указывает, что имеются в виду напряжения, деформации и смешения, отыскиваемые с учетом ползучести.
2 Здесь и всюду в дальнейшем символом . . . (х, у, г) указывается, чго остальные однотипные зависимости получаются последовательной круговой заменой х на у, у на г и г на х.
189
где
s* (/) = и; (о + а* (о + ст: (п (I v.48)
п L(t, т)—наследственная функция второго рода (IV.19), деформации удовлетворяют обычным уравнениям совместности:
а-е*(О .
ду2 дх2 дхду
...................(Х.У.2)-,
2 дУх(/) = д Г д¥у*г(0 ^:г(0+^:у(0].
дудг дх [ дх ду дг J’
......................(x,y.z)
и связаны с перемещениями формулами:
(IV.49)
<(0- «;<о=^. «О <IV50>
Л дх у оу 02
Ъ>Л' ду дх ’ ^) = -^Г + -7Г‘ * - д“*& I ^*(0
(IV-51)
и напряжения удовлетворяют обычным уравнениям равновесия а<(0 , ^<(0 , <?<(') _ 0. ]
дх ду дг ' Г (IV-52)
........................(Х.у.2). J
Кроме того, должны удовлетворяться соответствующие граничные условия.
В тех случаях, когда решение задачи о напряженно деформированном состоянии упруго-ползучего тела проводится в напряжениях, необходимо располагать уравнениями совместности, выраженными в напряжениях. Эти уравнения можно получить, если внести в уравнения совместности (1V.49), выраженные в деформациях, значения деформаций, взятые из закона Гука. Мы их выпишем в готовом виде, так как они нам понадобятся в дальнейшем. Эти уравнения имеют вид:
[I + V, (/)] ---Е(П J(v'«r)X
X-Мб (Л г) + г)1 + ^ • X
dx ох£ их J
xdr =йх(0;
(IV.53)
(х.у, Z);
190
[i+v,(O]Vr;>(o + ^>—
- e m [ {v2 ю [«о+«1 ('. Т»+
dxdy dr ) *
.......................(X.y.Z), !
(IV.54)
где
Qx(0 =
E(0 f^^y(0 v ^2v°x(O
1 — vx(/) I dxdy 1 dydz dzdx
dy2
<?2e°(0 _ t <?2e$(') dx2 ' dz2
d2e°z(t)
cPe°x{t) d2^)
dz2 dx2 ’
(IV. 55)
(x, y, z);
О (t) - Г + ^V°xz(() -ху{,~ 2 L dxdz + dydz
<?Vvy(') 2 1.
dz2 dxdy J ’
............................(x, y, z).
(IV.56)
Уравнения (IV.53), (IV.54) выписаны для общего случая vi (т)=/= v2((, т).
В заключение отметим следующее. Полные напряжения, деформации и смещения в общем случае всегда являются функциями координат точек х, у, z и времени t. Начиная с этого параграфа, мы, как это принято [25, 151], для сокращения записи будем указывать только их зависимость от времени t и снабжать их звездочкой, т. е. писать о* (/), ..., е* (/), ... ...
Это делается для того, чтобы отличить эти длительные полные напряжения о* (х, у, z, t), ...., деформации е* (х, у, z, t),... и перемещения и *(х, у, z, t), .... связанные с ползучестью бетона, от соответствующих кратковременных напряжений
Ох(х, у, z, t), ..., деформаций Ех(х, у, z, t), ... и перемещений и(х, у, z, I)...упруго-мгновенной задачи, рассмотренной в
главах V и VI, не зависящих от ползучести и отыскиваемых по уравнениям теории упругости.
191
§ IV.9. НЕКОТОРЫЕ ОБЩИЕ ЗАМЕЧАНИЯ
ПО ПОВОДУ МЕТОДА РЕШЕНИЯ РАССМАТРИВАЕМЫХ ЗАДАЧ ЛИНЕЙНОЙ ТЕОРИИ ПОЛЗУЧЕСТИ
В современной линейной теории упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна весьма важным является понятие об упруго-мгновенных напряжениях и деформациях, являющихся решением так называемой упруго-мгновенной задачи теории упругости. Эту задачу и связанную с ней терминологию ввел в рассмотрение в своей монографии [25] Н. X. Арутюнян. Он предложил упруго-мгновенной задачей теории упругости называть задачу о напряженно-деформированном состоянии идеально упругого и. следовательно, не обладающего ползучестью тела, с упругими коэффициентами, зависящими от времени, вызываемом воздействием поверхностных и объемных сил или вынужденных деформаций, считая при этом действие этих сил статическим, т. е. рассматривая время как параметр.
Н. X Арутюнян показал, что для такой задачи сохраняются обычные уравнения равновесия, граничные условия и уравнения совместности, выраженные в напряжениях, для чисто упругого тела, в их обычной форме при условии, что в последних уравнениях упругие коэффициенты (постоянные) Е и v заменяются функциями £(/) и v(t). Например, в случае простого одноосного сжатия обычная связь между напряжениями и деформациями в форме закона Гука
е = (1V.57)
полностью сохраняется, но переписывается в форме
е(0 = т^г (IV58)
и т. д.
Большая заслуга Н. X. Арутюняна состоит в том, что он, введя в рассмотрение указанную упруго-мгновенную задачу, обобщил известный принцип Вольтерра на случай упруго-ползучего тела, одновременно обладающего свойствами наследственности и старения, и показал, что при некоторых условиях напряженно деформированное состояние такого тела, вызываемое факторами, связанными с изменением его деформаций (температурными воздействиями, усадкой и т.п.), однозначно определяется с учетом ползучести и изменяемости модуля упруго-мгновенной деформации полными напряжениями о* (/), ...,т*у(/), •••• отыскиваемыми на основе соответствующих напряжений от(0. •••. Txi/(O. -- упруго-мгновенной задачи для этого же тела.
Сравнив правые и левые части уравнений совместности упруго-ползучего тела (1V.53), (IV.54) и воображаемого идеально упругого тела, не обладающего ползучестью (V.9) при одних и
192
тех же заданных вынужденных деформациях, Н. X. Арутюнян получил следующую систему совместных интегро-дифференциальных уравнений [25]:
|1 + (0) V2ox(/) + д-^= [1 + г, (0] (0 +
+ (IV59)
................................ (*, у, 0;
[1 + Vj(t)| v*Txy(0+ = [1 + V, (0] v2<y(0 +
w.*>+m^i+ (IV №}
.......................................(*, У, z), где
S* (0 = ux (0 + a* (0 + a* (0; S(0 = ux(t) + Oy (0+ oz(0; (IV.6I)
6i (0 t) = [Vi (0 - vc (t, 0] + v2 (0 t) 6 (t, т) (I V.62)
и, кроме того,
S*(0 = S(0 + f 3*(t)£ [26(/.t) + 6, (Z,r)] dr. (IV.63) 2 + vi (0 J or
Кроме уравнений (IV.59), (IV.60) и (IV.63) напряжения (0, ..., т’у (0, ... должны еще, очевидно, удовлетворять однородным уравнениям равновесия (IV.52) и граничным условиям
о* (0 cos (Мх) 4- т^.у (/) cos (Ny) t*rz (0 cos (Wz) = 0; т‘х (0 cos (Nx) + o* (0 cos (My) + (0 cos (Mz) = 0;
(0 cos (Mx) + v^y (t) cos (My) + a* (0 cos (Mz) = 0.
(IV.64)
На основе уравнений (IV.59), (IV.60), (IV.52), (IV.64) H. X. Арутюнян пришел к указанному выше выводу о том, что полные напряжения о* (/), .... т*у (t), , вызываемые факто-
рами, связанными с изменением деформаций тела, как, напри-
193
мер, температурными воздействиями, осадкой опор, усадкой и т. д., с учетом ползучести и изменяемости модуля E(f) определяются через соответствующие напряжения ох(0» ...
упруго-мгновенной задачи для этого же тела системой этих уравнений. При условии (IV.5) решение системы (IV.59), (IV.60), (IV.63) будет удовлетворять граничным условиям (IV.64) и уравнениям равновесия (IV.52) только в том случае, если оно будет иметь следующий общий вид:
<(/) f <(т)Л(/,т)Л = ох(0: .................(х,у,г)-,
..................{X,y,z).
(IV.65)
Только в этом случае, внося о* (0- • ••-. (т), ..... выра-
женные таким образом, в уравнения (IV.52) и (1V.64), мы получим однородные интегральные уравнения Вольтерра:
Г('» н дх*ху (О । _
[ дх Чу ' dz J
- Г + + jК{1, т)л = 0;
J L дх ду дг | . . .' .ч........................................ (х,У,г);
[ о* (0 cos (Nx) + Т*у (0 cos (Ny) + t*z cos (/Vz)] —
~ J [ °х (T) C0S (Nx) + Txy CO C0S +
+ Ххг (О C0S (Л<г)| * (z« О dx °;
[ Тух (О C0S ’О C0S 'Ь Tyz (О C0S (^] —
— J [ Тух (О C0S (Nx) + °у (О COS (^)+
+ хуг СО cos (Nz)] V' dr 0;
[ т;х (/) cos (Nx) 4- Ггу (/) cos (Ny) 4- а* (/) cos (Nz)] —
— j [ TLr (0 cos (Nx) + т'у (т) cos (Ny) 4-
4- о* (t) cos (/Vz)| К (t, t) dr -- 0,
(IV.66)
(IV.67)
194
имеющие единственные решения (IV.52) и (IV.64), и, следова
тельно, удовлетворим автоматически уравнениям равновесия и
граничным условиям.
Внося (IV.65) в систему (IV.59), (IV.60), (1V.63), получим
условия:
К{1-г) = Г+^w' £,в('’т> + 61 (/’т,1:
(IV.68)
К(/,т) -Е(1)-^6(/.г).
которые с учетом (1V.5) вполне совместимы и дают нам
W.z)- E(t ^б(Лт).
(IV.69)
При этом система (IV.59), (IV.60) распадается на мые интегро-дифференциальные уравнения:
Vе < (О - J Vе < (т) Е (/) ± б (t, т) dz = V2 ок (0;
независи-
............................................ (х, у, Z);
Vs (0 - [ Vе (т) Е (0 б (/, т) dx = v2 (0;
.........................•..................(Х,у,2)
пли
< (Л - f < ft) £ (0 £ б (t, т) dr ? ах (t) + ох (0;
............................................(х,У,г);
(0— J (т) Е (t) б (/, т) di xxiz (Z) 4- тху (/);
............................................(x.y.Z),
(IV.71)
где cx(t),....xxv(t),...., — некоторые пока произвольные
гармонические функции, удовлетворяющие уравнениям:
V2 (0 = 0;
.... (x,y,zy, V2rxiz(0 = 0;
(IV.72)
. (х,у, z).
Разрешая уравнения (IV.71) относительно напряжений
Ох(0,--.-, тХ1/(0 ...внося их в граничные условия упруго-
195
мгновенной задачи (V.10) и принимая во внимание (IV.72), найдем, что напряжения ох(/), .... ti1z(0. .. на контуре тела должны удовлетворять нулевым граничным условиям, аналогичным (IV.64), и, следовательно, в силу известной теоремы об экстремальных значениях гармонических функций тождественно должны быть равны нулю во всей области тела.
Принимая это во внимание, мы и получим уравнения:
< (0 ~ < (т) Е (t) ± 6 ((, т) dr = Од (0;
..............................(x,y.z)-,
J (Т) Е (/) 6 (/’Т) dX = T*v
..............................(x.y.z)
или с учетом (IV. 19):
<!l+f<^L(z,T)dT = ^L; E(t) J £(т) £(О
• ... ?...............(x.y.zy,
J f Т*У I (f Tx ят _ (0 .
E(0 +J E(T) L^dX~ E(t)’
......................(x,y,z).
(IV.73)
(IV.74)
найденные для этого случая Н. X. Арутюняном, решения которых автоматически будут удовлетворять всем уравнениям задачи. Таким образом, указанный выше весьма важный вывод Н. X. Арутюняна в случае (1V.5) существенно упрощает решение рассматриваемой задачи.
Отметим, что этот вывод доказан лишь для случая, когда граничные условия заданы в напряжениях, т. е. имеют вид (IV.64) [25]. Важным поэтому является вопрос о его справедливости в случае, когда граничные условия заданы в перемещениях. Рассмотрим этот вопрос.
В начале ограничимся случаем, когда поверхность тела в каждой точке жестко закреплена в пространстве, т. е. когда на каждую точку его контура наложены абсолютно жесткие связи. В этом случае вдоль каждой из линий контура:
у = yk = const, z = zk = const; 1
x = xk = const; z = zk = const; I (IV.75)
x = xk = const; z = yk == const J
!96
соответственно:
(IV.76)
“*(*. yk,^k, 0 = 0;] v* (Xk, у, zk, 0 = 0; | w*(xk, yk, z,t) = Q J
и, следовательно, в любой точке поверхности тела du* (?) = ди* (?) = dw*{t) = 0 дх ду дг
С помощью формул (IV.47), (IV.50), (IV.51) эти граничные условия для тела с жестко закрепленным контуром мы раскроем в следующей форме:
, <ну><(0-уГот ,
' £(<)
J[<.'±!y:<<b-vyw]L(([t)dT = o.
(IV.77)
{x.y.z).
Так как условия (IV.77) соблюдаются в любой момент времени t, то они будут справедливы и для упруго-мгновенной задачи, для которой эти условия, аналогично (IV.77), запишутся в форме:
eo(f)+(Hv)0H/)-vS(/)=0;| ..............(x,y.z).J
(IV.78)
Если мы теперь внесем сюда (IV.74), то получим уравнения, полностью совпадающие с (IV.77), следовательно, полные напряжения о* (/), .... (/), .... найденные в форме (IV.74), будут
тождественно удовлетворять и граничным условиям (IV.77) жесткого закрепления контура тела. В этом состоит доказательство применимости указанного выше принципа Н. X. Арутюняна и в этом случае граничных условий, а следовательно, и в общем случае смешанных граничных условий.
Иначе будет обстоять дело, если на контур тела наложены упругие связи, податливость которых зависит от величины напряжений. Например, когда на контурной координатной плоскости тела х=const
“*М "‘Ю = №><«<'>• 0V.79)
В этом случае решение задачи в форме (IV.74), где напряжения упруго-мгновенной задачи удовлетворяют на этой плоскости аналогичным условиям:
« (0 = ”. т. 11« = ‘?7. Ъ. W; ® (0 = Д г„ (П, (IV.80)
МЧ
197
приводят к условиям па контуре:
^T-(0+te<'(T,£(ct)d’“l’(',;
><-m+fe(t“w£(£t)dt=‘“(')-
Поэтому на этом контуре мы будем иметь условия: £*1) < (0 =- U (/) ~ J “ Ю Я Т)
(0 =v (О — Jv со я & о dT;
(0 - № (0 - -ft* (О R V, т) dx, совпадающие с (IV.81) только в том случае, если: и* (0 = и (0 — и (т) R (t, т) dx;
v* (0 V (t) — j V (т) R (/, т) dx;
w* (0 = w (t)~ f w (t) R (t, т dx.
(IV-81)
(IV.82)
(IV.83)
что, как это будет сейчас показано, не совместимо с (IV.79). Таким образом, рассматриваемый принцип Н. X. Арутюняна на случай упруго-податливых связей на контуре тела не распространяется. Это обстоятельство в предположительной форме впервые, по-видимому, было отмечено И. Е. Прокоповичем [151] при рассмотрении плоской задачи теории ползучести.
Отметим, наконец, одно очень важное обстоятельство.
Имея в виду рассмотренный выше принцип Н X. Арутюняна, в случае (IV.5) мы, с учетом уравнений (IV.47), (IV.73) и (IV.74), находим
198
«О- +<(,);
................(х.у.г); v; от=?т?гтх>от+?:,('*
(IV.84)
..............................(Х,У,2),
что совпадает с (V.4). Таким образом, в этих случаях полные деформации тела равны его упруго-мгновенным деформациям и, следовательно, ползучесть бетона не оказывает влияния на его деформации, а изменяет лишь величину напряжений в нем.
Теперь вернемся к случаю (1V.79). Так как из уравнений (IV.84) следует
| (IV.85)
.... (x,y,z), I
du*(t) _ du(t) . dv*(t) _ dv't) dw(f)
dx dx ’ dy dy ' dz dz
в то время как. согласно уравнениям (IV.83), должно быть:
ди* [Г) дх ди(0 ' ’ дх S^rR(i’T)dT;
*>*(0 ду _ dv(t) ду (IV.87)
dw*(t) dz dw(t) dz
Из несовместимости уравнений (IV.86), (IV.87) следует доказательство неприменимости принципа Н. X. Арутюняна к случаю упруго-податливых связей на контуре тела.
Резюмируя сказанное, можно теперь принцип Н. X. Арутюняна сформулировать следующим образом.
Если напряженное состояние тела вызвано его вынужденными деформациями, то в случае отсутствия на контуре тела упруго-податливых связей и при v2(/, т) =V|(/) =v=const с учетом ползучести и изменяемости модуля Е(т) его полные деформации е*(0....у*у (0, ... равны деформациям МО. YxV(0.
соответствующей упруго-мгновенной задачи для этого же тела, а полные напряжения о* (0,....тху (/), .... определяются через упруго-мгновенные напряжения этой задачи МО...........
199
txv(O. с помощью независимых интегральных уравнений (IV.74), в которых L(t, т)—наследственная функция бетона первого рода.
Этот результат имеет огромное практическое значение, так как, во-первых, существенно упрощает рассматриваемую задачу и, во-вторых, позволяет использовать для ее решения имеющийся набор готовых решений соответствующих задач теории упругости.
На основании всего изложенного выше может быть сформулирован следующий метод последовательного решения рассматриваемых задач о температурных и влажностных напряжениях в бетоне.
Вначале методами теории тепло- или соответственно влагопроводности определятся изменения температурного поля или поля влажности данного тела. Для бетона молодого возраста соответствующие методы определения полей температуры и влажности при наличии внутренних распределенных источников тепла (экзотермии) и стока влаги (химического связывания) с учетом влияния на их интенсивность температуры процесса развиты в главах 1 и П настоящей работы.
Для бетона зрелого возраста, когда внутренние источники тепла и стоки влаги практически отсутствуют, для этой цели можно воспользоваться имеющимися готовыми решениями соответствующих классических задач теории тепло- и влагопроводности (12, 30, 93, 107].
Затем на основе найденных изменений полей температуры и влажности бетона методами теории упругости решается соот-вествующая упруго-мгновенная задача для воображаемого идеально-упругого тела с модулями £(/) и C(t), причем как обычно G(0= 2^/+ )' ДЛЯ этого МОГУТ быть использованы, например, имеющиеся готовые решения задач термоупругости.
Большое число таких задач рассмотрено в курсах теории упругости, а также в работах О. Е. Власова [79], Б. Г. Коренева [101]. Н. Н. Лебедева [103], Г. Н. Маслова [118, 119]. А. В. Белова [31, 33—35], Э. Мелана и Г. Паркуса [122], Г. Паркуса [147] и других исследователей. В главе VI некоторые из этих задач уточнены и дополнены. Там же рассмотрены и некоторые новые упруго-мгновенные задачи.
После этого по найденным напряжениям упруго-мгновенной задачи и при заданных модуле упругости бетона Е(т) и наследственной функции второго рода R(t, т) с помощью квадратур отыскиваются уже искомые полные (с учетом ползучести) напряжения в рассматриваемом теле.
Полные же деформации принимаются равными деформациям упруго-мгновенной задачи.
Эту последовательность решения рассматриваемых задач теории ползучести мы и используем широко в дальнейшем.
200
Методы отыскания полных напряжений с учетом ползучести по напряжениям упруго-мгновенной задачи развиты в главе VII, где показано, что эта операция сводится к умножению соответствующих составляющих тензора упругих напряжений заменяющей упруго-мгновенной задачи па коэффициент приведения H*(t, Ti). Для вычисления этого коэффициента достаточно располагать данными о наследственной функции бетона второго рода R(t, т) и законе развития во времени ею вынужденной деформации, который всегда известен.
§ 1V.10. О НАСЛЕДСТВЕННЫХ ФУНКЦИЯХ ТЕОРИИ ПОЛЗУЧЕСТИ БЕТОНА
Выше мы видели, что в основные уравнения теории ползу чести входят наследственные функции L(t. т) и /?(/, т) соответственно первого и второго рода. В § IV.7 был рассмотрен физический смысл этих функций и дано их точное определение, как соответствующих функций влияния. Теперь укажем пути их эк-
спериментального определения.
Функции L(t. т) и R(t, т) с помощью формул (IV.19) и (IV.26) однозначно выражаются через полною удельную относительную продольную деформацию т) и полные удельные относительные напряжения p{t, т), поэтому определение этих функций требует построения экспериментальных кривых 6(/, т) и p(t, т). Они имеют вид семейства кривых, изображенных на рис. 39, а и б.
Обычно кривые 6(/, т) и p(t, т) строятся в осях (б, /) или (р, t) и каждая из них относится к заданному фиксированному возрасту бетона т в момент загружения. Поэтому для нахождения па нх основе функции L{t, т) и R(t, т) с помощью формул (IV.19) и (IV.26) эти кривые необходимо перестроить в осях (б, т) и (р, т) так, чтобы каждая из них соответствовала заданному фиксированному моменту наблюдения /*, а затем продифференцировать их (например, графически) по т. Перестроенные таким образом кривые 6(/, т) и р(/, т) имеют вид, изображенный на рис. 44. Обычно эту операцию производят аналитически, аппрок-
симируя предварительно соответствующими выражениями кривые 6(/, т) и р(/, т), построенные в осях (6, /) и (р, t).
Так как поведение бетона при кратковременном (мгновенноупругом) и длительном загружении не равнозначно, то удобно из полной удельной деформации 6(/, т) выделить отдельно упруго-мгновенные деформации и деформации, развивающиеся во времени вследствие ползучести бетона. Сделать это можно по-
разному:
а) выделить упруго-мгновенные деформации вующие только моменту загружения т и
1 ----------,соответст-Е(т)
201
б) выделить текущие упруго-мгновенные деформации
E(t) ’
соответствующие текущему моменту времени наблюдения t.
Первый путь предложен Г. Н. Масловым [120] и был общепринятым до настоящего времени [25, 49, 50, 151]. В этом случае по предложению Г. Н. Маслова считают, что
6(Лт,=тЬ’+с(Л т)>
(IV .88)
где С(/, т)—некоторая удельная деформация ползучести, изображающая собой часть полных деформаций 6(/, т), натекающую во времени сверх первоначальной упругой деформации
в момент загружения. Поскольку сама упругая деформация
изменяется во времени, функция С(/, т) в действительности представляет собой лишь часть деформации ползучести, меньшую, чем сама деформация ползучести.
Второй путь был предложен автором [18] и предполагает деформацию 6 (/, т) равной
6('’т)=_Нтг + с*('’т)’
(IV.89)
где C*(t, т) —удельная деформация ползучести, изображающая собой часть полных деформаций 6(/, т), натекающую во времени сверх текущей упругой деформации - и представляющую собой чистую деформацию ползучести.
Вопрос об определяемой таким образом чистой деформации ползучести был поднят Уитпеем [253] и позже еще раз обсуждался Мак-Генри [236], который называл ее «истинной» ползучестью. Однако тогда он не вызвал интереса у специалистов. После указанного выше предложения автора, облеченного в конкретную аналитическую форму, и сделанного на его основе критического анализа некоторых результатов непоследовательного использования выражения (IV.88) [18] интерес к этому вопросу вновь возрос и в настоящее время он снова обсуждается в ряде работ.
Смысл и различие двух представлений 6(/, г) (IV.88) и (1V.89), а также функций C(t, т) и С*(/, т) ясен из рис. 45, а.
Поскольку имеются в виду одни и те же экспериментальные кривые полных деформаций 6(С т), обе формы записи (1V.88) и (IV.89) равноценны и приводят к одним и гем же функциям L(t, т), определяемым с помощью формулы (IV. 19), а следовательно, к однозначному решению задач теории ползучести о полных деформациях и полных напряжениях в бетоне.
203
[18]. Лишь в случае неизменного
По-иному обстоит дело, если требуется на основе выражений (IV.13) п (IV.14) подсчитать только упругие деформации и напряжения упруго-мгновенной задачи или только деформации ползучести и только степень уменьшения упругих напряжений за счет ползучести бетона (коэффициент релаксации упругих напряжений). В этом случае весьма важно разобраться в том, что собой представляют функции С(Г,т) и С*(/,т) и каков их физический смысл. Это тем более необходимо потому, что физический смысл функции С(/,т) неточно трактуется многими авторами, а сама функция С(/,т), следуя Г. Н. Маслову, неправильно называется мерой ползучести бетона, т. е. единичной (удельной) относительной деформацией ползучести к моменту времени t. Такое определение функции С(Г,т) неточно и в ряде указанных случаев может привести к ошибкам [120].
В действительности функция С(?,т) в уравнении (IV.88) представляет собой не меру ползучести, а лишь ее часть, получаемую уменьшением единичной относительной деформации чистой ползучести на переменную величину ууу — — представляющую собой разницу упругих единичных деформаций бетонного бруса в момент приложения напряжений т и в момент времени наблюдения t (рис. 45) . . J ______________ во времени модуля упругости Е
(«старый» бетон) функция C(t,x) является его мерой ползучести С*(Лт).
Таким образом, между функцией удельных деформаций С(/.т) и мерой ползучести бетона C*{t, т) имеется следующая зависимость:
Рис 45. Кривые осевых относительных деформаций 6(Л т ) бетонного бруса, загруженного постоянными по величине единичными напряжениями (а), и осевых напряжений p(t, т) в бетонном брусе с сообщенной ему единичной деформацией (б)
/ — упруго мгновенные деформации, возникающие в момент вагружения, полные деформации, развивающиеся no i.peMi ни вследствие ползучести: 3 — упруги мгновенные напряжения, возникающие п момент создании деформации. J — полные напряжения, развивающиеся во времени вследствие релакса-
С* (/,т) = —-----------—+ С(/,т).
' ’ ’ Е(т) Е(0 ’
(IV.90)
204
Следовательно, для упругого тела, не обладающего ползучестью,
Сф(Г,т)-0, (IV.9I)
а С(/,т) = —----------------------------— (IV.92)
£(/) £(т)
и не равно нулю. Внося (IV.92) в (IV.17), мы и получим единственно верное в этом случае соотношение (IV.58), лежащее в основе упруго-мгновенной задачи и принципа Н. X. Арутюняна, рассмотренного в § IV.9. Условие же
С(/,т) О, (IV.93)
применяемое некоторыми авторами при переходе к предельному случаю упругого тела, является ошибочным.
Ошибку подобного рода, например, допустил Г. Н. Маслов при рассмотрении температурных напряжений в теле с переменным модулем упругости £(/) и не обладающим свойством ползучести. Н. Н. Маслов [120], используя условие (1V.93), получил при этом для любой составляющей этих напряжений Q(x, у, г, /) при постоянном во времени температурном перепаде Т=Т0 неверную формулу
Q(x, у, z,t) = u(х, у, z) Тп Ео, в которой о(л, у, z) —напряжения упруго-мгновенной задачи при £=1 и Г=1, а £0=const. В действительности же, с учетом (IV.92), в этом случае должно быть
Q (X, у, z,t)—с (Л, у, z) Т0£ (/).
Укажем также, что хотя в фундаментальной монографии Н. X. Арутюняна [25] функция C(t, т) по традиции и называется мерой ползучести бетона, однако в пей имеется и четкое разделение полных деформаций бетона на упруго-мгновенные (IV.13), подчиняющиеся линейному закону, и деформации ползучести (IV.14) ([25], стр. 16), при этом предельный переход (IV.93) нигде не применяется.
В соответствии с изложенным выше взамен выражения (1V.88) для полной осевой относительной единичной деформации бетонного бруса, входящей в уравнение (IV. 19), автором было предложено выражение (IV.89), в котором функция C*(t, т) уже представляет собой действительно полную меру ползучести бе
тона.
Экспериментальное определение меры ползучести C*(t, т) производится на основе выражения (IV.90) и не сложнее определения функции удельных деформаций С(1, т), поскольку для построения кривой единичных упругих деформаций , не-
205
обходимой для этого, никаких новых опытных данных не требуется.
Графически мера ползучести C*(t, т) весьма похожа на функцию удельных деформаций C(t, т), поэтому^ для ее аналитического выражения пригодны в равной степени все обычно рекомендуемые в литературе выражения для С(/, т), но, конечно, при других значениях, входящих в эти выражения параметров. Это. гидно из рис. 46, на котором в качестве примера мера ползуче-7540 7
Рис. 46. Кривые меры ползучести С*(/, т) и функции удельных деформаций С(/, т) бетона, исследованного в опытах С. В. Александровского и Э. Я. Багрня. Бетон состава (по весу) 1 : 1,9-4,4. В/Ц=0,65 на портландцементе активностью 567 кГ/см2
------С (t.-h-----с* (Т.п
сти C*(t, т) изображена в виде обычных кривых, построенных на основе экспериментальных данных С. В. Александровского и Э. Я. Багрня.
Неправильно думать, как это делают некоторые, что введение в рассмотрение меры ползучести C*(f, т), т. е. переход от выражения (IV.88) к выражению (IV.89), приводит в итоге к завышению релаксационной способности бетона и иному характеру' перераспределения усилий в железобетонных элементах.
Сравниваемые выражения отличаются лишь различным соотношением входящих в них двух слагаемых при неизменной их сумме. По этой причине применение формулы (IV.89) взамен выражения (IV.88) в полном виде приводит к идентичным результатам, но избавляет нас от ошибки при предельном переходе к материалу, не обладающему ползучестью, а также при исчислении только упругих деформаций н напряжений упруго-мгно
206
венной задачи или только деформаций ползучести и только степени уменьшения упругих напряжении за счет ползучести бетона (коэффициента релаксации упругих напряжений).
Кроме того, применение указанного выше принципа Воль-терра-Арутюняпа требует строгого определения смысла напряжений упруго-мгновенной задачи для стареющею бетона с переменным модулем E(t). Такое единственно верное определение этих напряжений, например, по уравнениям (IV.36) и (IV.4I) мы получаем только при условии (IV.91), т. е. при L(l, т) = =/?(/, т)=0.
Рассмотрим вопрос о полных удельных напряжениях p(t, т), введенных в § IV.6. Под этими напряжениями мы условились понимать напряжения, которые в любой момент времени наблюдения необходимо иметь в призматическом бетонном брусе для поддерживания неизменной во времени полной единичной относительной деформации, сообщенной ему в возрасте бетона т. Очевидно, для p(t,r) мы будем иметь формулу
р(/,т) =. Е(т) (IV.94)
в которой Е(т)—модуль упруго-мгновенной деформации в момент загружения бетона т, a r{t, т) — некоторая функция удельных напряжений, изображающая собой закон падения во времени начальных удельных напряжений за счет ползучести бетона. Таким образом, первое слагаемое в формуле (IV.94) представляет собой начальные упругие удельные напряжения, необходимые для сообщения бетону в возрасте т единичной деформации, а второе слагаемое—степень уменьшения этих напряжений во времени.
Функцию r(t, т) по аналогии с функцией С(/, т) можно было бы назвать мерой релаксации напряжений или просто мерой релаксации, однако по соображениям, аналогичным высказанным в начале параграфа о функции C*(f, т), это было бы неправильно, так как r(t, т) представляет собой лишь часть меры релаксации r*(t, т). Лучше напряжения p(t, т) представить в виде (рис. 45,6)
р(Г,т) (IV.95)
При такой форме записи входящая сюда функция г*(/, т) уже будет представлять собой полную меру релаксации. Таким образом, функция удельных напряжений r(t, т) и мера релаксации r*(Z, т) связаны соотношением
г(/. т) = г*(/. т) + Е (т) - Е(t). (IV.96)
Мера ползучести C*(t, т) и мера релаксации r*(t, т), введенные нами в рассмотрение, представляют собой вторую пару наследственных функций бетона, которые мы будем соответственно называть наследственными функциями третьего и четвертого рода.
207
Пользуясь интегральным уравнением (IV.16), устанавливающим взаимосвязь между наследственными функциями L(t, т) и /?(/, т), можно получить аналогичное уравнение для второй пары наследственных функций C*(t, т) и r*(t, т). Эго уравнение, в чем легко убедиться с помощью формул (1V.19), (IV.26), (IV.89) и (IV.95), имеет вид [21]
Е <т> £ С*<' т> - тЬг • £ г* <'• т> -
ОХ С (t) ох
~ г* (В, т) (t, В) <%. (IV.97)
J дт д£
С помощью этого интегро-дифференциального уравнения одна из наследственных функций, входящая в него, может быть всегда найдена по заданной другой.
Таким образом, при соблюдении условий пятой из рассмотренных в § 1V.5 рабочих гипотез линейной теории ползучести бетона мы имеем полный класс наследственных функций бетона, образующих взаимные пары в указанном выше смысле
Ut);
Если отказаться от гипотезы об одинаковой зависимости от времени всех видов полных единичных деформаций бетона, как это сделано в обобщенной теории ползучести, развитой Н. X. Арутюняном [25], то число наследственных функций соответственно возрастает. Необходимые сведения по этому вопросу можно найти в работах [63, 64]. Однако, как это было показано в § 1V.4, для рассматриваемой нами проблемы температурно-влажностных напряжений такое усложнение теории не требуется и мы ограничимся случаем применения указанных четырех наследственных функций.
Из этих четырех функций только одну можно выбрать в качестве независимой; остальные же будут выражаться через выбранную последовательными зависимостями (IV.16), (1V.19), (IV.26), (IV.89) и (IV.95).
§ IV.11. ОБ ОСНОВНЫХ РАЗНОВИДНОСТЯХ современной теории ПОЛЗУЧЕСТИ БЕТОНА И НАСЛЕДСТВЕННЫХ ФУНКЦИЯХ, ФИГУРИРУЮЩИХ В ИХ УРАВНЕНИЯХ
Среди ряда различных направлений современной теории ползучести бетона различают три основные ее разновидности:
теорию упругой наследственности, предложенную Больцманом [215] и Вольтерра [252], получившую в дальнейшем свое существенное развитие в работах А. К. Малмейстера [111], А. Р. Ржаницына [159—162] и др.;
208
теорию старения, разработанную Дишингером [222] и Унтне-ем [253], значительно развитую в работах Н. А. Буданова [43], Глэнвилля [226—229], Я. В. Столярова [173] п особенно И. И. Улицкого [181—186];
теорию упруго ползучего тела (наследственную теорию старения), разработанную Г. Н. Масловым [120] и Н. X. Арутюняном [25, 26], получившую свое дальнейшее развитие в работах Б. <П. Абрамяна [1], П. 11. Васильева [49—53], А. А. Гвоздева [63—66], М. А. Задояна [83], [84], М. М. Манукяна [115—116], Н. Я. Панарина [146], С. В. Полякова [148], И. Е. Прокоповича [149]—[151], М. И. Розовского [163—164] и многих других.
Для всех этих теорий в их линейной трактовке общими являются основные рабочие гипотезы теории ползучести, рассмотренные в § IV.5. Отличие же их состоит в различном подходе к вопросу об обратимости его деформаций ползучести при частичной пли полной разгрузке, что находит свое выражение в различной физической и математической интерпретации этого вопроса.
Теория старения полностью отрицает обратимость деформаций ползучести. Этим самым постулируется параллельность кривых ползучести у образцов раннего и позднего загружения *. Математически это выражается в том, что функция удельных деформаций ползучести принимается в виде
C{t, т, tJ = С (f, Ti) — С (т, tJ, (IV.98)
причем C(t, ti) задается обычно в форме
С (Г, rj = С(оо, tJ [1-е-т('-т,)]. (IV.99)
Здесь Т| — момент времени загружения, принятый за начало отсчета и определяющий собой выбор исходной кривой ползучести (IV.99).
Нетрудно понять, что задание C(t, т, п) в виде (IV.98) постулирует нулевую ползучесть в возрасте бетона т, значительно большем, чем принятый за начало отсчета времени. При длительных интервалах времени наблюдения1 2 это обстоятельство должно приводить к существенным погрешностям в задачах, где напряжения (деформации) претерпевают значительные изменения в моменты времени t, отдаленные от выбранного начала его отсчета ть тем большие, чем больше t—т:.
Принимая C(t, т, ti) в форме (1V.98) и имея в виду случай «стареющего» бетона с переменным модулем упругости £(т),
1 Т. е. подразумевается, что кривая ползучести бетонного бруса, загруженного единичными осевыми напряжениями, в более позднем возрасте получается из кривой ползучести образца, загруженного такими напряжениями ранее, параллельным смещением соответствующей ее части вдоль оси ординат (оси деформаций). Гипотеза об указанной параллельности кривых ползучести была предложена Уитнеем (253].
2 Имеются в виду длительные процессы.
209
найдем входящие в основные уравнения теории (1V.17), (IV.18) и (1V.94) наследственные функции теории старения в следующем виде:
кроме того, мы будем иметь
- f Г(т) ~~ С (т. т,) rfx
р(/,т)-£(т)е т . (IV.101)
На рис. 47, а построены кривые C(t, т, tJ, r(t, т, Ti), Цт, т,) /?(Л т, Ti) и p(t, т, Т|), рассчитанные по формулам (IV.98), (IV.100), (IV. 101), т. е. в таком виде, как они фигурируют в теории старения. За начало отсчета времени ть определяющее собой выбор исходной кривой ползучести, в этих формулах принято Ti = 2 сут. Все эти кривые рассчитаны для бетона, экспериментальные кривые ползучести и модуля упругости которого описываются уравнениями:
С (t, т) = (ct + [ 1 —е1 ('-т)]; (IV. 102)
£(т) = £п (I—е-,1т) (IV. 103)
при значениях параметров:
= 0,975 • 10~5 (кГ смг)~\ — 4,62 • 10~® (; )
\*Г/см-) | (IV. 104)
у = 0,03 (су/п)-1; Ео = 2,6- 105(кГ/сл1г); р 0,206 (сут)~\ |
рекомендованных для бетона Н. X. Арутюняном [25]. Выражение экспериментальных кривых С(/, т) и £(т) в форме (1V.102), (IV. 103) удобно для последующего сопоставления функций C(t, т), r(t, т), L(t, т), R(t, т) и p(t, т) теории старения с соответствующими функциями теории наследственности и теории упруго-ползучего тела.
Нетрудно видеть, что при принятых выражениях для C(t, т) (IV. 102) и £(т) (IV.103)
С (t, т, tJ = + Y-) [ е-т(т-т,) (IV. 105)
210
L (t, т, т,) =- E(t) -I Y (C, + ; (1V. 106)
-т(с> + .у) [Е(т)е1(1~т,,^т
Хе ' . (IV.107)
Теория наследственности постулирует полную обратимость деформаций ползучести. Этим самым предполагается полное тождество кривых ползучести бетона, загружаемого в разные сроки Математически это выражается в том, что мера ползучести задается в виде
С* (Л т) - С(t, т) = С (/ — т). (IV. 108)
При этом С(/—т) принимается обычно в форме
C(t — т) С, (IV.109'
где Ci = const.
Физически это означает, что имеется в виду бетой с физико-ме хапическимн свойствами, инвариантными относительно абсолют кого значения времени наблюдения. В соответствии с этим в этой теории принимается также Е(т) — Ео = const.
Следовательно, теория наследственности применима лишь к «старому» высохшему или невысыхающему бетону, наследственные функции этой теории поэтому имеют вид [21]:
L (t — т) = Ео С, уе-т</-т>; (IV. 110)
Я (t — т) = Ео Сх у е-т (1 +FX>’' (IV. 111)
г*(/—т) = г( -т) = £°С' [1—е-т(,+£"с,)('-т>], (IV. 112) 1 4- £0С|
т. е. тоже зависят только от t—т. Функция p(t, т) также будет зависеть только от t—т и равна
Р('-т) 1 Дс; + £°C1 е~т(1+£С,)('~т)] • (IV.113)
На рис. 47, б построены кривые наследственных функций C(t—т), r(t—т), L(t—т), R(t—т) и кривые полных удельных напряжений p(t—т) теории наследственности, рассчитанные по формулам (IV.109), (IV.1I0) — (IV.113), причем для Сь Е(, и у по-прежнему приняты их значения, взятые из формул (IV. 104).
1 Т. е. подразумевается, что кривые ползучести бетонных образцов, загружаемых единичными осевыми напряжениями в разные сроки, получаются переносом одной и гой же кривой ползучеегн вдоль оси абсцисс (оси времени).
211
Теория упруго-ползучего тела учитывает частичную обратимость деформаций ползучести, вызванную влиянием старения бетона. Таким образом, наследственные функции этой теории, помимо Е(т), включают в себя еще и функцию старения <р(т). Математически это выражается в том, что функция удельных деформаций ползучести C(t, т) задается в виде
С(/, т) = ф(т)С (/— т), (IV.114>
при этом обычно ф(т) и C(t—т) принимаются равными:
так что для C(t, т) получают формулу (1V.102). Наследственные функции этой теории имеют вид [21]:
г (t, т) = уЕ (т) ф (т) ст,(т) J Е (т)е-т,(т) А; (IV. 116) £(/,т) = £(т) |ф'(г) — [ф'(т) + Уф(т)] е~т('-Ч -(IV.117) Е (I, т) = — {у [ф (т) Е (т) е’,(т)]' J Е (т)е“’,(т) А —
— Е'(т) — уф (т) Е® (т)|, (IV. 118)
где
’I(t) = у J [1 + ф(т)£(т)] A, (IV.119)
a Ti — произвольный момент времени, назначаемый из удобства вычисления интеграла в формулах (IV.116), (IV.118).
На рис. 47,в построены кривые С(/,т), r(t, т), L{t, т), R(t, т), рассчитанные по формулам (1V.102), (1V.116) — (IV.118), и кривые р(/, т), найденные по выражению
p(t, т) = Е (0 [1 — j R(t, т) А ] (IV. 120)
на основе формул (1V.102), (IV.103), (IV. 118) при значениях входящих в них параметров (1V.104), рекомендованных в теории упруго-ползучего тела Н. X. Арутюняном.
Переходя к сравнительному анализу наследственных функций С(/, т), r(t, т), L(t, т), /?(/, т) рассмотренных трех разновидностей современной теории ползучести бетона, будем иметь в ви
212
ду хорошо известные экспериментальные кривые его ползучести д релаксации напряжений, а также кривые L(t, т) и R(t, т), построенные экспериментальным путем для бетона в опытах Д. В. Яшина [212] (рис. 43).
Сравнивая кривые C(Z, т) на графиках рис. 47, мы видим, что все три теории в современной их трактовке исходят из кривых C(t, т), плохо согласующихся с экспериментальными данными. Все они имеют общие для всех теорий недостатки, состоящие в том, что, пользуясь формулами (1V.98), (IV.102) и (IV.109), нельзя достичь хорошего соответствия теоретических и экспериментальных величин деформаций ползучести одновременно при малых и больших значениях времени наблюдения t, особенно для образцов, загружаемых в ранних возрастах бетона.
Эти формулы не отражают также наблюдаемое в опытах быстрое натекание деформаций ползучести во времени их наблюдения, близкому к моменту загружения образцов. Начальные участки теоретических кривых ползучести, построенных на основе этих выражений, не имеют характерного крутого подъема, которое всегда наблюдается в опытах не только над молодым, но и над старым бетоном [50, 94, 212]. Это приводит к тому, что найденные на их основе кривые функций влияния L(t, т) и /?(/, т) не имеют правых круто восходящих ветвей при т близком или равном t. Как было указано Л. А. Гвоздевым [64], функции L(t, т) и R(t, т), обладающие этим недостатком, не применимы для решения задач, в которых мы имеем дело с быстроменяю-щимися во времени напряжениями (деформациями), что в известной мере суживает область применения рассматриваемых теорий ползучести. Для устранения этого недостатка мы должны в формулах (IV.98), (IV.102) и (IV.109) придать у большие значения, но при этом мы получаем быстро затухающую ползучесть, что не наблюдается в опытах. При малых же значениях у мы имеем медленно развивающуюся ползучесть, как это и наблюдается в действительности, но не получаем начального крутого подъема кривых ползучести сразу же после загружения. Приходится выбирать среднее из двух зол и назначать параметр скорости ползучести у средним по величине. При этих условиях скорость ползучести, особенно в молодом возрасте бетона, оказывается заниженной.
Мера ползучести теории старения (1V.98), кроме того, имеет еще и тот недостаток, что приводит к нулевой ползучести в возрасте бетона, далеко отстающем от возраста Т|, выбранного за начало отсчета времени. Это равносильно предположению о том, что ползучесть бетона быстро исчерпывается и приводит к релаксационной задаче с первоначально созданной деформацией в момент времени Ti или близкий к нему к чрезмерно интенсивной релаксации напряжений. Кривые релаксации весьма скоро выходят на горизонтальную асимптоту. Это хорошо видно на рис. 47, а.
213
Plt.t.t)! В нГ/смг flit,?,?,) в(сутнах)'1 Llt.t,) Blcymnaxl'1 rlt.T.tJB кГ/см* С(В,Г,Р,)в(»Г/смг/^
Рис 47.а. Наследственные функции и кривые релаксации удельных напряжении в теории
старения
214
215
Рис. 47,в. Наследственные ф\ нкции и кривые релаксации удельных напряжений в теории упруго-ползучего тела Г. В Маслова — Н. X. Арутюняна
/-Т 2. 2-Г-4- 3-- б. 4-Т-10: 5-т -20: 6-Z-2; 7 - I 4. 8 - t 6; 9 - f- 10. 10 — Z- 20. II — Z-40 (Z H В
216
Так как, с другой стороны, теория старения полностью отрицает обратимость деформаций ползучести, а, следовательно, и эффект последействия, то погашение натекающих деформаций ползучести в релаксационной задаче мы должны производить только за счет деформаций упругого возвращения при частичной разгрузке. Это приводит не только к интенсификации процесса релаксации напряжений во времени, но и к существенному завышению самой степени релаксации, особенно при начальном загружении бетона в молодом возрасте и в возрасте, близком к Ть Происходит это еще и потому, что упругие деформации разгрузки в старом возрасте бетона при одной и той же ступени напряжений значительно меньше по величине, чем деформации загружения в молодом возрасте, поэтому для их осуществления в поздние сроки требуется сброс напряжений в значительных пределах.
Степень релаксации напряжений, возникающих в возрасте бетона т, в теории старения зависит от выбора начала отсчета времени п. Это хорошо видно на примере старого бетона, для которого она определяется по последней из формул (IV.100). Действительно, при Т| =/=т и значительно меньшим, чем т, как уже отмечалось выше,
С(/,т1)-С(т,т1)^0, (IV. 121)
поэтому в этом случае и г(/, т) ~0.
При Т1 = т степень релаксации напряжений оказывается наибольшей и равной
г (I. т) = Ev [1-е£С('~т)], (IV. 122)
где С(/—т) —кривая ползучести старого бетона.
Это обстоятельство приводит к существенным и неоднозначным погрешностям в оценке степени релаксации в задачах, где напряжения (деформации) претерпевают изменения на всем интервале времени наблюдения t—п. А именно: для воздействий близлежащих к выбранному началу отсчета времени т( она оказывается значительно завышенной, а для воздействий, происходящих в отдаленные от п моменты времени, t — наоборот, значительно заниженной и практически равной нулю, если t—ti велико. Поэтому безоговорочное суждение о том, что теория старения всегда приводит к завышению степени релаксации напряжений, в широком смысле слова наверно.
Существенным недостатком теории старения является также то, что функция влияния L{t, т) этой теории не зависит от времени наблюдения /. Таким образом, согласно этой теории, эффект действия напряжений в заданном возрасте т один и тот же для любого момента времени наблюдения t, т. е. остается неизменным во времени. Это является следствием полного отрицания обратимости деформаций ползучести.
217
Указанные недостатки теории старения делают ее мало пригодной для описания длительных процессов, при которых напряжения или деформации претерпевают значительные изменения в моменты времени, отдаленные от выбранного начала его отсчета. Поэтому она неприменима, например, к процессам с интенсивным нарастанием напряжении (деформаций) после предшествующего сравнительно спокойного периода их развития и при наличии интенсивных повторных и переменных кратковременных или длительных воздействий. Эта теория может дать приемлемые результаты при решении задач теории ползучести, отличных от указанных выше, для непродолжительных интервалов времени наблюдения или в случае рассмотрения длительных результатов кратковременного или однократного (импульсного) воздействий. Таким образом, применение теории старения вполне оправдано для решения всякого рода релаксационных задач указанного типа (отпуск и потери натяжения арматуры, однократная осадка опор и т. д.) Именно для такого рода задач эта теория главным образом и используется широко И. И. Улицким и его учениками.
Мера ползучести теории наследственности (IV. 109), помимо указанных выше общих недостатков, так же как и все остальные наследственные функции этой теории, инвариантна еще относительно абсолютного значения возраста бетона. Это делает ее применимой только к кругу задач теории ползучести для «старого» и высохшего (пли невысыхающего) бетона, физико-механические свойства, в том числе и влажность которого уже не изменяются во времени. Для такого рода задач эта теория и применяется широко А. Р. Ржаницыным и его школой.
Функция удельных деформаций ползучести теории упруго-ползучего тела (IV. 102), применяемая в настоящее время, помимо рассмотренных выше общих недостатков, в состоянии описать лишь кривые ползучести с ординатами, возрастающими во времени значительно медленнее, чем это наблюдается в опыте. При этом скорость этих деформаций у бетона молодого возраста, спустя значительное время после загружения образцов, остается большей, чем в загруженных позднее образцах (рис. 47,в). Математически это вытекает из того факта, что производная
-аС^’-т)- = п (т) е—»<*-’> (IV. 123)
зависит в явном виде от возраста бетона т к моменту загружения, а функция <р(т) с ростом т имеет быстро затухающий характер. Поэтому оказывается, что для образцов-близнецов из молодого бетона, загружаемых в близкие моменты времени п и 1'2(т2>Т1). в любой момент времени наблюдения t имеет место неравенство
при t > тг (IV. 124)
21В
или с учетом (IV. 114) и (IV. 115)
<Р(Т») > Ф(т2)
(IV. 125)
Рис. 48 Графическое доказательство существования неравенства (IV.I24) для молодого бетона
^(т.) .______fT(xa—
На рис. 48 построены графики левой и правой частей неравенства (IV.125), рассматриваемых как функции длины интервала времени т2— ть При этом для функции <р(т) принято выражение (IV. 115) и значения параметров Сь At и у (IV.104), рекомендованные для бетона Н. X. Арутюняном. Из рис. 48 следует, что для молодого бетона (ti=2 сут., Ti=4 сут., Т| = 6 сут.) неравенство (IV.125) соблюдается для значительных интервалов времени т2—ti. Многочисленными же экспериментальными исследованиями установлено, что скорости деформаций ползучести образцов, загруженных в различных, по близких друг к другу возрастах не слишком большими напряжениями, спустя некоторое время после загружения сравнительно быстро становятся почти одинаковыми. Это находит свое выражение в кажущейся параллельности экспериментальных кривых ползучести, за исключе-
нием некоторых их начальных участков (см., например, рис. 32).
Выражение (IV.114) не отражает также наблюдаемое в опытах быстрое натекание деформаций ползучести вслед за за гружением образцов. При этих условиях скорость ползучести, особенно в молодом возрасте бетона, оказывается заниженной.
Так как функцию старения <р(т) =С| + — в формуле (IV.102)
подбирают независимо от у, стремясь к хорошему соответствию теоретических и экспериментальных скоростей старения, то оказывается, что для бетона молодого возраста мы, пользуясь этой формулой, обычно получаем скорость старения больше, чем скорость ползучести. Это приводит к неравенству (IV. 125). которое эквивалентно условию, что деформации последействия после полной разгрузки имеют тот же знак, что и деформации ползучести, т. е. что после полной разгрузки образца в нем, хотя и с меньшей интенсивностью, но продолжают развиваться деформации ползучести, а не последействия.
В действительности же деформации последействия после полной разгрузки всегда имеют знак, обратный знаку предшествую
2IS
щих деформаций ползучести. Указанный недостаток выражения (1V.102) приводит к завышению степени релаксации напряжений в молодом возрасте и иногда даже к искажению качественной картины этого процесса. Подтверждением этому является нижний график на рис. 47, в, из которого видно, что кривые релаксации напряжений в молодом возрасте бетона, рассчитанные на основе выражения (IV.102), пересекают ось времени, переходя в область отрицательных значений напряжений, что физически невозможно.
Происходит это потому, что из-за получаемого отсутствия последействия в обычном смысле этого слова в молодом бетоне при соблюдении постоянства первоначально сообщенной деформации приходится погашать натекающие деформации ползучести, так же как и в рассмотренном выше случае теории старения, только за счет упругого возвращения при частичной разгрузке. Так как модуль упругости молодого бетона интенсивно возрастает во времени, то в конечном итоге для этого потребуется сброс напряжений по величине больший, чем первоначально приложенные напряжения Но по этой причине сохранение постоянной деформации образца в конце процесса релаксации становится возможным только при приложения напряжений обратного знака.
Наследственные функции L(t, т) и R(t, т), применяемые в настоящее время в теории упруго ползучего тела, противоречат также, в некотором смысле, физической сущности процесса ползучести бетона.
Действительно, из рис. 47, в видно, что кривые L(t, т) для малых моментов времени t располагаются ниже аналогичных кривых для более поздних t, т. е. имеют меньшие ординаты. Поэтому эффект действия напряжений в заданном возрасте бетона т оказывается большим не для близлежащих моментов времени t, а для более поздних моментов наблюдения. В действительности же в эксперименте наблюдается совершенно обратная картина (рис. IV.43).
Далее, кривые /?(/, т) на рис. 47, в, особенно в молодом возрасте бетона, имеют нисходящий характер с падающими ординатами при приближении т к /. Это приводит к тому, что эффект действия вынужденной деформации тем больше, чем дальше он отдален от моментов его наблюдения, что также противоречит экспериментальным данным. Характер этой погрешности значительно более существен, чем той, которая была отмечена выше у функции L(t, т), и приводит, в частности, к искажению указанного выше характера физической сущности кривых релаксации напряжений.
В то же время выражение (IV. 102) обладает очень существенным достоинством: оно сравнительно просто и, главное, позволяет свести решение основных интегральных уравнений теории ползучести (1V.17), (IV.18) к решению линейных дифференци
220
альных уравнений второго порядка с переменными коэффициентами и, при том, не содержащих самих искомых функций, а включающих в себя лишь их производные [25] Это позволяет удобно выражать решения задач теории ползучести в квадратурах и успешно применять для их вычислений быстрорешающие электронно-счетные машины Именно это обстоятельство позволило Н. X. Арутюняну впервые получить решение ряда сложных задач теории ползучести для молодого бетона, проанализировать их и сформулировать ряд важных теорем этой теории о соотношении между полными напряжениями в бетоне, найденными с учетом ползучести, и соответствующими напряжениями упругомгновенной задачи [25]. В частности, им было показано, что при условии (IV.5) в области линейной зависимости между деформациями и напряжениями ползучесть не изменяет величин напряжений в бетоне, вызываемых действием внешней нагрузки, но существенно уменьшает напряжения, вызываемые изменением его деформаций (см., например, § IV.9)
Из всего изложенного выше следует, что из всех существующих разновидностей современной теории ползучести старение и наследственность — эти важные свойства бетона — наиболее полно отражает теория упруго-ползучего тела Н. Г. Маслова — Н. X. Арутюняна [25, 120]*. Поэтому эта теория и используется в дальнейшем для изучения интересующей нас проблемы температурно-влажностных напряжений в бетоне. Однако степень соответствия экспериментальным данным расчетных величин деформаций и напряжений, отыскиваемых на ее основе, зависит от того, насколько удачно выбраны аналитические выражения для наследственных функций этой теории. Применяемые в настоящее время для этой цели выражения находятся в противоречии с результатами опытов и требуют существенной корректировки.
Очень важно поэтому попытаться, сохранив указанное преимущество выражения (IV. 102) для С(I, т), уточнить последнее с тем, чтобы устранить полностью или в значительной степени описанные выше его недостатки. В соответствии с этим ниже в § IV. 12 предлагаются новые аналитические выражения для наследственных функций теории упруго-ползучего тела, свободные от указанных выше недостатков и, вместе с тем, позволяющие свести решение основных уравнений этой теории (IV 17), (IV. 18) к квадратурам. Основанная на этих наследственных функциях теория ползучести Г. Н. Маслова — Н. X. Арутюняна наилучшим образом будет отражать все наиболее важные физико-механические свойства бетона и давать результаты, близкие к тому, что наблюдается в опыте.
Отметим, что в литературе имелись попытки синтеза теории
1 Эту теорию по предложению И. И. Гольденблата [71. 72] часто называют также наследственной теорией старения.
221
старения и теории наследственности для устранения указанных выше их недостатков.
Первая из таких попыток принадлежит Мак-Генри [236], который, сохраняя общепринятые у нас обозначения, предложил с этой целью функцию C(t, т) задавать в следующей форме:
С (t, т) = Со [1 - е-ь(/-')] + Ле"т‘т - . (IV.126)
Нетрудно видеть, что при 73=72 выражение (IV. 126) принимает вид
С (t, т) = Со [ 1 — е-ъ(/~т>] 4-А (— е(/), (IV. 127) т. е. сочетает в себе меры ползучести теории наследственности и теории старения, а при 73=71
С(/,т) = (Со + Ле“Н [1 -е-т,(/ Ч (IVЛ28)
и, в частности, при 73=72 = 71=7
С(/, т) = (Со 4- Ле“г) [1 — е_1(,_т)], (IV. 129) т. е. принимает вид видоизмененной меры ползучести теории упруго ползучего тела.
Однако сам Мак-Генри признает свою попытку неудачной, так как произведенное им сопоставление выражения (1V.126) с результатами своих собственных, а также и чужих опытов показало, что даже при yi =#у2 =£= "Уз. т. е. при максимальном числе независимых параметров, это выражение, как пишет Мак-Генри [236], «дает неудовлетворительное решение» для бетона молодого возраста и «является неточным» при длительных загружениях бетона. При меньшем числе независимых параметров в выражении (IV.126), т. е. в случаях (IV.128) или (IV 129), сходимость с результатами опытов будет еще худшей, однако простота этих выражений все еще сохраняет интерес к ним и побуждает к их дополнительному изучению. Это изучение в настоящее время интенсивно проводится И. Е. Прокоповичем и И. И. Улицким [151, 152].
Вторая попытка аналогичного вида была сделана А. В. Яшиным [212]; им было предложено выражение
С (/, т) = Ф (т) Ф (/ - т) 4- F (т) - F (О,
или в раскрытом виде
С(/,т)=(14--^)[Со|1-е-т‘(/-т,] +
4- В [ 1 - е-*'-’’] 1 4- А ( — e-Tl'), (IV. 130)
в какой-то мере устраняющее недостатки формулы (IV.102), но вместе с тем и ее достоинства, поскольку указанное выше приведение построенных на его основе интегральных уравнений теории ползучести (IV.17), (IV.18) к соответствующим линейным
222
дифференциальным уравнениям становится невозможным. Это обстоятельство является также общим для всех без исключения аналитических выражений наследственных функций теории упруго-ползучего тела, рекомендованных и другими исследователями. Поэтому мы не будем их подвергать здесь подробному критическому обзору.
Выражение (IV.130), кроме того, сохраняет в себе важный недостаток формулы (IV.I02), состоящий в том, что скорость ползучести
- ^(т)-^Ф(/-т)-Г(/), найденная на его основе, по-прежнему зависит в явном виде от возраста бетона т. Это обстоятельство было подробно рассмотрено выше.
Отметим, что при К=В = 0 выражение (IV.130) принимает уже известный нам вид (IV.127), пользуясь которым при у: =Л уг нельзя найти наследственную функцию второго рода /?(/, т) и получить решение задачи теории ползучести в замкнутом виде. Это удается сделать только при У1 = у2 = у, но тогда выражение (IV.127) приобретает вид (IV.129), мало чем отличающийся от выражения (IV.102) и содержащий в себе те же его основные недостатки.
§ IV.12. НОВЫЕ АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ НАСЛЕДСТВЕННЫХ ФУНКЦИЙ ТЕОРИИ ПОЛЗУЧЕСТИ БЕТОНА
Проведенные нами исследования [18, 20, 21] показали, что функция удельных деформаций ползучести C(t, т) может быть задана в виде
С(/, т) = ф(т)-ф(0 (^2^) + Д (т) 11 ~ е“с(/ 7)], (IV. 131) где
а»у>0; 0<Д2<1, (IV.132)
а ф(т) и Д(т) — функции, быстро убывающие с ростом т, подобные функции старения <р(т) в теории упруго-ползучего тела (IV.114).
Выражение (IV.131) удобно для дальнейшего представить в форме
С(/,т) = v(t) — F(t) (er — А2) — Д (т) е-о</~т’, (IV. 133) где
<р(т) ф(т) F-A(t), (IV. 134)
а
fw- <1V135>
223
Проанализируем выражение (IV.131). Нетрудно видеть, что С(/,т) = 0; С(со,т) = ф(т) (IV. 136)
и при достаточно большом т (старый бетон)
С (/, т) = С (t - т) = А3 [1 - е-*'-”] 4- А [1 - е“а('-т)], (IV-137) где
Д3 - ф (оо) = const и А = Д (со) = const.
Таким образом, выражение (IV.131) обладает теми же достоинствами, что и функция (IV. 102), но улучшает ее применимо к старому бетону, поскольку наличие второго слагаемого в формуле (IV. 131) при условиях (IV. 132) обеспечивает начальный крутой подъем кривых ползучести при малых t—т.
Переписывая выражение (IV. 131) в виде
С (/, т) = ф (т) - ф (П ( 1~Zge~-^ е-т(/-” + \ 1-Л2е-т' /
4-Д (г) [1 — е-а(/~’)], (IV. 138)
мы видим, что начальный крутой подъем кривых ползучести при малых t—т, который обеспечивается наличием третьего слагаемого в формуле (IV.138), в молодом возрасте бетона увеличивается с убыванием т потому, что при этом возрастает функция Д(т).
Далее, сравнивая сумму двух первых слагаемых в формуле (IV.138)
t (т) - ф (о (IV-139)
с правой частью выражения (IV.102)
Ф(т)-Ф(т)е-Т('-Л (IV. 140)
мы видим, что при фиксированном т вычитаемое в выражении (IV.139) с ростом t убывает значительно быстрее, чем вычитаемое в формуле (IV. 140), потому что с ростом t в этом случае функция ф(/) и дробь -*~Ае— быстро убывают, в то время
l-Xse-i'
как функция <р(т) остается неизменной.
Все указанное в итоге приводит к тому, что кривые ползучести (IV. 131) как в молодом, так и в старом возрасте бетона при малых t—т п при прочих равных условиях подымаются значительно круче, чем кривые (IV. 102), что и должно быть.
Вычисляя далее производную
дС^-т- = F (0 ( ег - А) 4- аД (т) е-а('“т> (IV. 141)
224
и составляя неравенство (IV. 124)
Г(О (еп‘ - 4) + «Л (т,)е-я(/-т*> > Г (t) (е^’-А2) +
Рис. 49. Сопоставление применяемого в настоящее время выражения (IV.102) и рекомендуемого выражения (IV.133) для функции СЦ.х ). рассчитанной по формуле (IV.102)—сплошные линии и по формуле (IV.133) — пунктирные линии. Возраст бетона к моменту загружения
/ — I сутки; 2 — 3 суток; 3 — 1 суток; 4 — И суток; 5 — 28 суток; 6 — кривая Л(т)
(IV.131) при применении принципа наложения воздействий обеспечивает наличие последствия после разгрузки в обычном смысле этого слова.
На рис. 49 приведено сопоставление выражений (IV.102) и (IV.131) при
Д(т)-т + пе-" (IV. 143)
и
т = 0,25 • 10-5 (кГ/сл2)-’; п = 0,99 • 10-5 (кГ/сти2)-1;
а = 0,275 (сут)-1. (IV. 144)
Причем в обоих случаях функция <р(т) принята равной (IV.115) при значениях входящих в нее параметров (IV.104), рекомендованных для бетона Н. X. Арутюняном. Как следует из рис. 49, выражение (IV.131) значительно лучше, чем выражение (IV.102), описывает характер экспериментальных кривых ползучести, особенно для бетона молодого возраста, и обеспечивает
225
обычно наблюдаемую кажущуюся параллельность этих кривых.
На основе формулы (IV.131) автором [21] были найдены следующие выражения для наследственных функций L(t, т) и R(t, т):
L (0 т) = Е(т) (т) + YF(0 ег +
+ [Д' (т) + аД (т)] е~а('-т)); (IV. 145)
R (t, т)« - {/<* (т) F (т) (ег - Л2) - К' (т) -
- к СО (етт - Аг) е-ч(т)]' J К (т) F (т) е*’> dr +
+ В, (0 е”*'* (IV. 146)
Ва (О = F (0 (е* - А) [Е2 (0 - Ля (0] -
— аЕ2 (О Д (0 4- К' (0 — Е' (ty, (IV. 147)
Р (О = {в; (0 + YeV F (01В2 (0 - Л* (0] -
- F* (О (е’' - А2 )2 [Е3 (0 - К3 (0) - аЕ (0 [Е (0 Д (0]' -
- а2Е3 (0 -A11L + -L F (0 (ет' -AJ IE2 (0 - К2(/)]' + л (О *
+ 2аЕ3 (0 Д (0 F' (t) ( ет' — Л2 )}; (IV. 148)
X (П = ------£19-----. (IV. 149)
1 + Д(ОЕ(/)
т] (0 = f К (т) Г (т) (ег — AJ dr, (IV. 150)
a Ti — произвольный момент времени, принимаемый из удобства вычисления интеграла (IV. 150).
Имея выражение для R(t, т) (IV. 146), можно по формуле (IV.120) и выражению
г(0т) = Е(т)-Е(0 {1-J Я(/,0* ) (IV.151)
найти функции p(t, т) и r(t, т).
Отметим, чго структура выражения (1V.146) такова, что оно весьма удобно для вычисления интегралов в формулах (IV.I20) и (1V.151), а также для выполнения квадратур в уравнении (IV.18). Происходит это потому, что интеграл от третьего сла
226
гаемого в выражении (IV.146) легко берется по частям, а функции Вз(0 и р(0. входящие в четвертое слагаемое этого выражения, зависят только от времени наблюдения Z. Действительно, нетрудно убедиться в том, что при R(t, т), найденной в форме (IV. 146)
]>(*, г)Л =-{X (г)- К (0 +
+ К (т) (е" - Л,) е-*” j К (т) Р (т)е'"> Л +
+ [|_(IV.152)
Рис. 50. Графики функций B3(t) и ц(0. определяемых по формулам (IV.147) и (IV.148)
I — кривая В3(0: 2 — кривая и (О; 3. 4. 5 — средние значения И (0 на данном промежутке t
На рис. 50 построены кривые Bs(t) и p(Z), рассчитанные по формулам (IV.147) и (IV. 148) с учетом (IV.115) и (IV.I04), (IV.143), (IV.144). Как видно из этого рисунка, функция p(Z) с ростом t изменяется весьма мало, поэтому в формуле (IV.146) вместо р (/) можно пользоваться средним значением
Нср = т-^- -- (IV. 153)
для интервала времени Ц—ть
227
Для старого бетона, т. е. при
£ (tj = Е0 = const; Л (Г) - Ло = const; |
А (0 =~- До = CC-nst; ф (/) = ф0 = const; I
£ (/- т) Е0 [тфое~1<'“’> 4- аЛие“°(/^)]; (IV. 155)
R (t — т) - A е“м'~х> + As е“₽’('“т>, (IV. 156) 1де
A= V-'pi' ; аЛо) |£° (Y^°+ аЛ°^ ~ р2^+
+ а*До + тЧо}; (IV.157)
А - Ло (уфо 4- аД0) - А, (IV. 158)
a pi и pa — корни характеристического уравнения
р2 + |у(1 + Еофо) + Р 4 атЛ0 (ф0 + = О, (IV. 159)
равные
Р1,3= -у {“4-т+ £o(y4’o 4- аД0) +
+ 1^£и (Y’l’o + аДо)2 + (а — v)2 -2£о М'о — аДо) (а — Y)}- (!V. 160)
На рис. 51 построены кривые наследственных функций С(£т), £(/, т) и R(t, т) стареющего бетона, рассчитанные по формулам (IV.131), (IV.145) и (1V.146) при
11>(т) = Сз4-^-; Д(т)-С1-С,+ ; (IV.16I)
Е(т) = £0 (1-е-к) (IV. 162)
и значениях параметров
Яд = 4,62- Ю-5/^-); С, = 0,975- ЮЛкГ/сл2)-1; \кГ,1смг)
А = 1;
А = 3,416 10~5 (^;2); С3 = 0,756 10~\кГ/см*Г\
е^2-вю'(^
а = 6 (сут)“ ’; Р = 0,206 (сут.)-1; у = 0,03 (сут.)-1.
(IV. 163)
рекомендованных Н. X. Арутюняном [25] для бетона. Как видно из этого рисунка, все эти кривые очень похожи на соответствующие экспериментальные кривые. Для того чтобы убедиться в этом, достаточно обратиться к рис. 43.
228
Рис. 51. Рекомендуемые для теории упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна наследственные функции С(/, т), L(t.x) н )
Примечание, т и / — в сутках.
229
На рис. 52 изображены кривые полных удельных напряжений (кривые релаксации напряжений) в бетонном брусе при сообщенной ему постоянной единичной относительной деформации. Эти кривые рассчитаны с помощью формулы (IV. 120) численным методом на электронно-вычислительной машине «Урал-4»
Рис. 52. Кривые полных удельных напряжений р(/, т) (кривые релаксации), рассчитанные с помощью формулы (IV.120) на основе новых наследственных функций
вид, обычно наблюдаемый в экспериментах, и даже для очень молодого бетона не переходят в область отрицательных значений напряжений р(/, т), как это было в случае C(t, т), принятой по Г. Н. Маслоьу — Н. X. Арутюняну в форме (IV.102) и при тех же самых значениях параметров (IV.163).
Все изложенное выше дает право рекомендовать применение наследственных функций (IV.131), (IV.145), (IV. 146) и (IV.15I). При этих условиях теория упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна, как это показано ниже, наилучшим образом будет отражать все наиболее важные физико-механические свойства бетона и давать результаты весьма близкие к тому, что наблюдается в опыте даже в самом общем случае кратковременных быстро изменяющихся воздействий.
Для спокойных, плавно изменяющихся, однократных или редко чередующихся воздействий можно рекомендовать и другие более простые приближенные выражения для наследственных функций, также приводящие в задачах теории ползучести стареющего бетона к хорошей степени соответствия экспериментальным данным. Эти выражения рассмотрены в работе автора [21].
23С
§ 1V.I3. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ОБЛАСТЕЙ ПРИМЕНИМОСТИ ОСНОВНЫХ РАЗНОВИДНОСТЕЙ теории ПОЛЗУЧЕСТИ БЕТОНА И ПРОВЕРКА НОВЫХ АНАЛИТИЧЕСКИХ ВЫРАЖЕНИИ ДЛЯ НАСЛЕДСТВЕННЫХ ФУНКЦИИ
Для экспериментальной проверки предложенных выше новых аналитических выражений для наследственных функций бетона необходимо располагать данными об экспериментально установленной связи между напряжениями и деформациями бетона при длительных и в первую очередь переменных нагрузках. Такие данные имеются в литературе, но в довольно ограниченном объеме. Кроме того, подавляющее их число относится к случаю постоянных напряжений и лишь некоторые из них получены в условиях ступенчатых нагрузок и разгрузок с длительными выдержками их отдельных ступеней. Поэтому наряду с использованием имеющихся экспериментальных данных для указанной цели автором совместно с инж. Э. Я. Багрием были поставлены специальные опыты, в которых изучалось поведение бетона при переменных режимах его загружения.
Результаты этих опытов, а также описанных в литературе наиболее интересных опытов А. Д. Росса [244] позволили не только проверить предложенные в § IV. 12 новые аналитические выражения для наследственных функций бетона, но и подкрепить соображения об области применимости основных разновидностей современной теории ползучести, высказанные в предположительной форме в § IV.11, а также получить дополнительные данные о применимости принципа наложения воздействий. Ниже приведены результаты указанных исследований.
Опыты А. Д. Росса
Исследования А. Д. Росса [244] проводились на высокопрочном вибрированном бетоне состава (по весу) 1 : 1,6 : 2,8, ВЩ = =0,375 на быстротвердеющем портландцементе. Бетонные кубы с ребром 4"(~10 см) имели в возрасте 28 дней прочность 672 кГ/см2. Образцами служили бетонные цилиндры диаметром 45/в" (~12 см) и длиной 12" (~30 см) с прочностью на сжатие равной примерно 0,7 R^yc-
Исследовались деформации образцов при длительных нагрузках в условиях ступенчатых нагрузок, разгрузок и чередующихся нагрузок и разгрузок. Опыты проводились в области линейной ползучести с наибольшей величиной напряжений, не превышающей 0,5 Rup.
Параллельно с указанными переменными режимами загружения исследовалась ползучесть образцов в разном возрасте бетона при постоянных напряжениях сжатия. Результаты этой части опытов позволили построить кривые C(t, т) удельных относительных деформаций ползучести. Эти кривые изображены на
231
Рис. 53. Обработка результатов опытов А. Д. Росса по теории старения и теории упруго ползучего тела при С(/.т ) Н. X. Арутюняна (IV.102) и автора (IV.133) Кривые удельных относительных деформаций ползучести C(t, т)
------ экспериментальные кривые; — И — 0 — II — по теории старения; ------по теории упочгополэучего тела при С(«. т) Н X Арутюняна;
------по теории упругоползучего тела при С(/, т) автора (нижний график)
232
рис. 53, где также нанесены теоретические кривые C(t, т), рассчитанные по теории старения, а также теории упруго-ползучего тела по формуле Н. X. Арутюняна (IV. 102) и по формуле автора (IV.133). Для построения экспериментальных кривых C(t, т) из экспериментальных кривых полных единичных деформаций 6 (/, т), полученных А. Д. Россом, вычитались упругие единичные деформации.
Необходимая для этого экспериментальная кривая Е (т) изображена на рис. 54, где нанесена также теоретическая кривая Е(т) (IV.3) при
Ео = 4,73 -105 ; 5 - 0,3; ₽ - 0,06 (сут.)"1 . (IV. 164)
\ см- /
Рис. 5-3. Опыты А. Д. Росса. Экспериментальная и теоретическая кривые модуля упругости бетона Е(т)
/ — экспериментальная кривая; ’—теоретическая кривая по формуле (IV3) с учетом (IV 164)
В связи с тем, что описываемые опыты проводились на молодом «стареющем» бетоне (загружение образцов в ряде режимов начиналось с восьмисуточного возраста бетона), область применения теории наследственности не исследовалась, так как последняя к такому бетону не применима. Исследовались лишь аналитические выражения для C(t, т) по теории старения [184]
С(/, т) -- <р (Т1) [ e-1(T-Tj - e-T('-Tj] (IV. 165) и по теории упруго-ползучего тела в двух вариантах: на основе формулы, предложенной Н. X. Арутюняном (IV. 102), и на основе нового предложения автора (IV. 133).
Подбор функций и параметров, входящих в эти формулы производился исходя из требований как можно лучшего приближения теоретических кривых к экспериментальным.
Значения найденных таким способом функций и параметров, входящих в выписанные выше аналитические выражения для С(/, т) сравниваемых теорий ползучести, оказались равными:
233
п формуле (IV. 165)
(IV. 166)
(pf-q) 21,7-10 1 'при т, = 8 сут. (рис. 55, fl, в); ^(тО— 17,15-10-7^'~-) ' »ри Т| — 28 сут. (рис. 55,6); у — 0,05 (сут.)-1
в формуле (IV. 102)
С, = 9,714- ; А. = 135,7- 10-7 (—V'; ]
\см I \с"*/ [(IV. 167)
у = 0,05 (сут.)-1; J
в формуле (IV. 133)
Л (г) •= (-у- I- 2,714) 10-7 (—г)1 сутках);
<р(т) - (2,971 + 20еОЛ,,,8т Д 1,428 е~°-1х) Ю~7(^-) ’
(т—в сутках) (IV. 168)
Л 0,3; у = 0,03 (сут.)-1; а = 5 (сут.)-1. (IV. 169)
Для построения теоретических кривых С(1, т) по теории старения на рис. 53 за начальную кривую естественно принята кривая, соответствующая началу отсчета времени, равному 8 суткам. Из этого рисунка хорошо видны погрешности принимаемой этой теории дополнительной рабочей гипотезы о параллельности кривых ползучести бетона, загружаемого в разном возрасте. Уже для образцов, загруженных в возрасте 28 суток, наблюдается резкое несоответствие теоретической кривой экспериментальным данным. Для более поздних кривых это расхождение еще больше увеличивается и для кривой, соответствующей т=91 суткам, ползучесть бетона согласно этой теории в рассматриваемом случае практически исчерпывается.
Из рис. 53 следует, что лучше всего описывают экспериментальные данные теоретические кривые C(t, т), полученные на основе предложения автора (IV. 133). Причем это хорошее соответствие соблюдается на всем диапазоне времени наблюдения, т. е. теоретические кривые как качественно, так и количественно хорошо отражают все особенности ползучести бетона как в молодом, так и в старом возрасте.
Хуже согласуются с опытом кривые C(t, т), построенные на основе формулы (IV.102). Это особенно наглядно видно на кривых ползучести образцов, загруженных в раннем возрасте бетона. Начальные участки этих кривых С(/, т) не имеют необходимого характерного подъемистого очертания, что наблюдается также и на кривых ползучести старого бетона.
Недостатки и преимущества сравниваемых аналитических
234
выражений для функции удельных деформаций ползучести C(t, т) лучше видны на результатах теоретической обработки на их основе экспериментальных кривых деформаций ползучести, полученных А. Д. Россом при разнообразных режимах загружения, осуществленных им в различных возрастах бетона.
Рис. 55а. Опыты А. Д. Росса. Случай ступенчато возрастающих напряжений
На рис. 55 представлены некоторые экспериментальные кривые полных деформаций ползучести бетона, наблюдаемые в описываемых опытах при ступенчатых нагрузках и разгрузках, и соответствующие им теоретические кривые, найденные на основе сравниваемых аналитических выражений для С(1, т).
Указанные экспериментальные кривые были получены некоторой перестройкой (отбрасывались упругие деформации в моменты нагружений или разгрузок отдельными ступенями напряжений) экспериментальных кривых полных деформаций, полученных А. Д. Россом.
Для сравнения были выбраны лишь три наиболее характерных режима нагружения в соответствии со схемами, показанными в верхней части графиков рис. 55. (Обозначения кривых даны в соответствии с рис. 53; кружочками показаны экспериментальные точки.)
Так как напряжения на каждой из ступеней нагрузок поддерживались постоянными, то теоретические значения деформаций ползучести в любой момент времени наблюдения t вычислялись как алгебраическая сумма произведений приращении
235
Рис. 556. Опыты А. Д. Росса. Случай ступенчато падающих напряжений
236
напряжений на ординаты теоретических кривых удельных деформаций ползучести C(t, т), соответствующих данному приращению напряжений.
Как видно из рис. 55, лучше всего экспериментальным данным соответствуют теоретические кривые деформаций ползучести, вычисленных на основе выражения для С(Л т) (1V.133). Эти кривые качественно и количественно хорошо согласуются с соответствующими экспериментальными кривыми на всем диапазоне изменений напряжений, особенно в случае чередующихся нагрузок и разгрузок.
Из рассмотрения рис. 55 следует, что теория упруго-ползучего тела, основанная на применении выражения (IV.102) для С(/, т), предложенного Н. X. Арутюняном, качественно правильно описывает процесс ползучести при ступенчатых нагрузках и разгрузках. Однако недостатки этого выражения для C(t, т), рассмотренные выше в § IV.I1, здесь сказываются в выпуклом виде. Теоретически вычисленные на его основе значения относительных деформаций ползучести для моментов времени наблюдения, близких к моменту приложения прирашений напряжений, плохо соответствуют экспериментальным значениям. Кроме того, накапливающиеся при этом отклонения теоретических значений относительной деформации ползучести от ее экспериментальных значений к концу периода наблюдения составляю! довольно значительную величину. Даже после полной разгрузки образцов, например в возрасте бетона, равном 120 суткам (рис. 55), деформации ползучести, вычисленные с учетом теоретической кривой С(/, 120), с ординатами, значительно превышающими ординаты соответствующей экспериментальной кривой C(t, 120) для этого возраста загружения (рис. 53), не могут полностью компенсировать сумму накопившихся отклонений, в результате чего остаточная теоретическая деформация ползучести получилась все же еще больше экспериментальной.
На рис. 55 также хорошо видны погрешности теории старения, о которых уже говорилось выше. Кривые деформаций ползучести, рассчитанные по этой теории, по истечении месяца, начиная с момента первичного загружения образцов, уже не реагируют на последующие нагрузки и разгрузки.
Опыты С. В. Александровского и Э. Я. Багрия
Автором совместно с инж. Э. Я. Багрием были проведены специальные опыты по исследованию связи между напряжениями и деформациями бетона при переменных режимах его загружения и разгрузки. Исследовался вибрированный бетон состава (по весу) 1 : 1,9 : 4,4, -^-=0,65.
Для изготовления этого бетона применялись следующие материалы.
237
Цемент портландский Белгородского завода, активности 567 кГ/см2, выдерживающий пробу на равномерное изменение объема и дающий нормальную консистенцию теста 25%, с началом и концом схватывания соответственно 3 ч 10 мин и 5 ч 28 мин. Тонкость помола цемента характеризовалась прохождением через сито 4900 отв!см2 96,1% навески.
Песок речной с объемным и удельным весами соответственно 1562 и 2640 Кс/м2, средней крупности 0,33 мм, с объемом пустот 41% и содержанием глины, определяемым 1,2% потери в весе при отмучивании.
Щебень мелкий известковый с удельным и объемным весами, соответственно равными 2490 и 1328 кг!м?, с объемом пустот 47%, просеянный через специально изготовленное сито с отверстиями диаметром 15 мм. Содержание глины в щебне характеризовалось потерей в весе при отмучивании 1,9%.
Вода обычная водопроводная специальным исследованиям не подвергалась.
Образцы в виде бетонных призм 7X7x60 см с оголовками из стальных плиток изготавливались в стальных формах и хранились укрытыми влажными опилками. В возрасте 3 суток они распалубливались, гидроизолировались парафином, техническим вазелином и полиэтиленовой пленкой и подвергались испытаниям на центральное сжатие в специальных рычажных установках с реверсивным приспособлением с помощью чугунных грузов, начиная с 4 суточного возраста ’.
Измерение деформаций производилось по четырем граням с точностью 0,4-10-5 с помощью индикаторов часового типа с ценой деления 2-10~3 мм.
Опыты проводились в камере со стабильными температурой и влажностью воздуха, средние значения которых были соответственно равны +14,5° С и 70%.
Наибольшие отклонения температуры и относительной влажности воздуха в камере от их средних значений в ходе опыта не превышали соответственно +2,5° С и ±5%.
На рис. 56 показан общий вид образцов во время их испытания.
Одновременно с рабочими призмами, подвергаемыми основным испытаниям, изготавливалось большое количество контрольных образцов-близнецов, хранящихся в идентичных условиях (кубы и призмы). Результаты испытания этих образцов, приведенные иа рис. 57, позволяют судить о хорошей степени однородности исследуемого бетона.
Часть основных рабочих призм испытывалась на ползучесть при постоянных напряжениях в различных возрастах бетона, а
1 Испытания на гидронзолированных призмах проводились с целью иг ключения усадки бетона и погрешностей в определении деформаций ползучести, связанных с неаддитивностью усадки и ползучести [18].
238
часть — на переменный режим нагружения и разгрузки для установления экспериментальной связи между напряжениями и деформациями бетона при этих условиях.
Рис. 56. Общий вид образцов во время испытания Опыты автора
Каждый из указанных режимов испытания проводился одновременно на двух образцах-близнецах, которые во всех случаях показали весьма схожие результаты.
Все испытания проводились на сжатие в области линейной ползучести при напряжениях, не превышающих 0,45 /?Пр, назначаемых по предварительным испытаниям контрольных образцов-близнецов. Переменные режимы загружения осуществлялись
239
часто следующими друг за другом весьма мелкими ступенчатыми нагрузками пли разгрузками.
Было проведено две серии опытов, которые дали близкие результаты, поэтому ниже приводятся лишь результаты I серии.
Рис. 57. Результаты испытаний контрольных образцов-близнецов
1 — кубиковая прочность. 2 — призменная прочность Условные обозначения ® — призмы естественного храпения; О — кубы 7Х7Х7Х т: □ — kj6u Ю.\10>10 сч. Л — кубы 20x20x20 см (верхний график). — режимные призмы (Н и Р); ® — призмы П (ползучесть); £ - призмы R (релаксация). ▼ — призмы ненагружаемые £(~) — теоретическая кривая
На рис. 58 приведены экспериментальные и теоретические кривые удельных относительных деформаций ползучести C(t, т).
Так же как и в случае опытов А. Д. Росса и по той же методике, экспериментальные кривые С(/, т) и E(t). изображенные на рис. 57, 58, аппроксимировались с помощью формул (1V.3) —
240
241
(1V.165), (1V.102), (IV.133). В этом случае значения функций и параметров, входящих в эти формулы, оказались равными:
в формуле (IV.165)
«рСц) = 51Ю-7^-) при Tj = 4 сут.; у = 0,06 (сут.р' ; (IV. 170) в формуле (IV. 102)
Cj = 27,61-10-7|/—V А,- 109,7 • 10-7 (———Г‘ ; 1
\кГ) \см*сут] I (IV. 171)
у = 0,06 (сут.)-1; j
в формуле (IV. 133)
Д (т) = (11,2 + 34e-0J251) 1(т — в сутках); (IV. 172)
<р(т) = (24,5 + Юе-0-“31 + 43,2е-0Л275т —Збе-0,35^-7^)
(т —в сутках); (IV. 173)
Д, = 0,85; у =- 0,02 (сут.)-1; а = 5 (сут.)-1; (IV. 174) в формуле (IV.3)
3,310Б—; £ = 0,575; ₽ = 0,072(сут.)-1. (IV. 175) см2
Для построения теоретических кривых C(z, т) по теории старения (рис. 58) за начальную кривую естественно принята кривая, соответствующая возрасту бетона Ti=4 сут., начиная с которого осуществлялись переменные режимы загружения режимных призм.
На рис. 58 изображены результаты указанной аппроксимации экспериментальных кривых C(Z, т).
Рис. 59 иллюстрирует степень соответствия сравниваемых теоретических значений предельной меры ползучести <р(т) экспериментальным данным.
В теории старения удается согласовать лишь начальное значение (Ti), соответствующее кривой ползучести образца, загруженного в возрасте бетона ть Остальные значения <р(т) получаются уже автоматически единственным образом.
В теории упруго-ползучего тела это удается сделать лучшим образом. При C(t, т), заданной в форме (IV. 102), этого можно достичь только приближенно из-за наличия в выражении для ср(т) всего двух параметров At и Сь Указанные выше их величины (IV.171) подбирались по способу наименьших квадратов.
При С (/, т) же, заданной в форме (IV. 133), и (т) и Д (т), выписанных в виде (VI. 172) и (IV. 173), достигается высокая степень этого соответствия, приводящая к практически полному совпадению теоретических п экспериментальных значений <р(т).
242
На рис. 60 показана схема режимов загружения режимных образцов I серии опытов, испытанных при переменных напряжениях.
Рис. 59. Соответствие сравниваемых теоретических значений предельной меры ползучести <р(т) экспериментальным данным
I — экспериментальная кривая; 2 — по формуле (IV.173); 3— по формуле (IV 102) при (—т=«, с учетом (IV.170); 1 — по формуле (IV.I65) при I— т,—- со и ч(т,) -"51 • 10-' (кГ/сл2)—1
Рис. 60. Схема режимов загружения образцов I серии опытов, испытанных при переменных напряжениях
На рис. 61—62 изображены экспериментальные кривые напряжений и относительных деформаций ползучести режимных призм Н и Р, испытанных при переменных режимах нагружения и разгрузок в соответствии со схемами, показанными на рис. 60. Как следует из этих рисунков, деформации призм-близнецов до тех пор, пока эти образцы оставались близнецами (примерно до
243
Рис. 61а. Сопоставление экспериментальной и теоретических кривых деформаций ползучести образцов, подвергнутых действию переменных напряжений. Режимы Р-1, Р-3
Рис. 616. Сопоставление экспериментальной и теоретичес ких кривых деформаций ползучести образцов, подвергнутых действию переменных напряжений. Режимы Р-2 и Р-4
/ —экспериментальная кривая; 2 — по теории старения на основе выражения (IV. 165); 3 —по теории упруго-ползучего тела на основе выражения (IV.102) Н. X. Арутюняна; 4 — то же, на основе выражения (1V.I33) автора
г=40 сут.), мало отличались друг от друга. В последующем же, когда образцы по режиму нагружения переставали быть близнецами, характер их деформирования существенно различался.
Результаты описываемых экспериментов, изображенные на рис. 61—62, и были подвергнуты соответствующей обработке.
Для построения теоретических кривых относительных деформаций ползучести режимных образцов Н и Р экспериментальные кривые напряжений и(/) в этих образцах, изображенные на верхних графиках рис 61—62, аппроксимировались с помощью соответствующих элементарных функций (экспоненциальных и линейных). После чего с помощью квадратур
еп (0 = ~ J ° (т) £ С (I, т) dr (IV. 176)
с учетом этих аппроксимирующих функций о(/), выражений (IV.165), (IV.102), (IV.133) и формул (IV.170) —(1V.174) находились теоретические значения относительных деформаций ползучести еп(0 и на рис. 61—62 строились соответствующие теоретические кривые.
Сопоставление экспериментальных и теоретических кривых еп(0. найденных по всем сравниваемым теориям, проведенное на рис. 61—62, полностью подтвердили соображения, изложенные в § IV.11. В связи с этим нет необходимости вновь подробно останавливаться на анализе областей применимости сравниваемых теорий ползучести. Отметим лишь наиболее важные результаты теоретического (см. § IV.11) и экспериментального (см. § IV. 13) изучения этого вопроса.
Теория старения наихудшим образом описывает поведение бетона при переменных, не монотонно изменяющихся напряжениях. В частности, она не может отразить и не отражает эффект воздействий, развивающихся или появляющихся спустя длительное время после начального загружения (третий этап опытов т> 40 суток).
Для монотонно изменяющихся воздействий, непродолжительных во времени (I и II этапы опытов 4 40 суток), теория
старения и теория упруго-ползучего тела, основанные на мере ползучести Н. X. Арутюняна (1V.102), дают близкие между собой результаты, но существенно отличающиеся от результатов опыта, особенно в случае падающих напряжений после первичного загружения (рис. 61) и на отрезке времени, близком к моменту загружения.
На основании проведенных анализов результатов опытов А. Д. Росса, С. В. Александровского и Э. Я. Багрия, а также всего изложенного выше, для описания поведения бетона под длительной нагрузкой, особенно в случае ее сложных режимов, рекомендуется к широкому применению теория упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна, основанная на мере
245
Рис. 62. Сопоставление экспериментальной и теоретических действию перемен
а — режимы Н-1 и Н-3, 6 — режимы
246
кривых деформаций ползучести образцов, подвергнутых ных напряжений
Н-2 и Н-4. Обозитчеиня см. на рис. 61
ползучести (IV.133), предложенной автором. Применение этой теории в таком виде особенно оправдано для учета температурно-влажностных воздействий при расчете бетонных и железобетонных конструкций. Именно с этой целью она широко и используется ниже.
Результаты описанных опытов С. В. Александровского и Э. Я. Багрия представляют еще одну возможность для проверки принципа наложения воздействий в теории ползучести, использованного при их обработке.
с Продолжительность наблюдения в суткам с начала (t\40cym) повтор-ным переменным воздействий
Рис. 63. Экспериментальные кривые абсолютных прирашений деформаций ползучести образцов, подвергнутых действию переменных напряжений, с начала повторных переменных воздействий
Действительно, если обратиться к рис. 61—62, то мы можем выделить группы призм, которые не были образцами-близнецами по условиям загружения на 1 этапе, но стали ими в этом смысле на III этапе загружения (т>40 суток) после предшествующих отдыха без нагрузки или выдержки ее. Такими образцами являются следующие группы призм: Н-1 и Н-3; Н-2 и Н-4; Р-1 и Р-3; Р-2 и Р-4.
На рис. 63 изображены кривые абсолютных приращений деформаций ползучести этих образцов, начиная с момента их повторного нагружения или разгрузки (т=40 суток). Из этого рисунка следует, что, несмотря на существенное различие в режимах загружения этих образцов в пределах каждой из их групп на 1 этапе (4 < т < 24 сут.), эти приращения деформаций ползучести у образцов одинаково загруженных на Ill этапе (т >40 сут.) оказались практически одинаковыми.
Таким образом, основное положение принципа наложения, положенное в основу 4-й рабочей гипотезы теории ползучести (см. § IV.5), нашло свое подтверждение в этих опытах.
248
Необходимо подчеркнуть, что в данном случае речь идет о приращениях деформаций ползучести, а не о их абсолютных величинах. Поэтому было бы неправильно думать, как это делают некоторые, что величина полной деформации к данному моменту времени наблюдения t>x, за вычетом ее прирашения, вызываемого приращением напряжений, действовавшим за время t—т, не зависит от предыстории загружения на промежутке 0 <7 < т и попросту равна деформации, натекшей к моменту времени т.
Следует, однако, отметить, что в описываемых исследованиях, так же как и в других известных в литературе опытах, деформации ползучести при разгрузке образцов оказались меньше примерно на 30%, а иногда даже и несколько более чем деформации ползучести образцов-близнецов, впервые загружаемых в том же возрасте. С этой точки зрения применение принципа наложения приводит к некоторым погрешностям.
Однако при использовании новых аналитических выражений для наследственных функций бетона (IV.145), (IV.146) и, в частности, для меры ползучести С (t, т) (IV. 133), погрешности эти невелики. Это наглядно видно на рис. 55 и 61, 62, особенно в случае сложных чередующихся воздействий.
Таким образом, применение принципа наложения в теории ползучести бетона, значительно упрощающего решения многих практических задач, является вполне оправданным.
В заключение следует отметить, что применение принципа наложения в его обычной форме, как это следует из рис. 61 и 62, приводит к некоторому преувеличению эффекта ползучести (последействия) как при нагрузках, так и при разгрузках. В связи с этим даже лучшая из современных теорий ползучести бетона — теория упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна — и притом основанная на новых эффективных аналитических выражениях для наследственных функций бетона предложенных выше все же дает некоторое расхождение с опытом.
Степень этого расхождения невелика и поэтому в большинстве случаев этой уточненной теорией можно вполне удовлетвориться. Для получения же еще большей точности придется уже произвести более глубокий ее пересмотр, связанный с тем или иным осложнением ее математического аппарата.
ГЛАВА V
УПРУГО-МГНОВЕННАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ ПРИ НАЛИЧИИ ВЫНУЖДЕННЫХ ДЕФОРМАЦИИ. ОБЩИЕ УРАВНЕНИЯ И МЕТОД РЕШЕНИЯ
§ V.I. ОБЩАЯ ТРЕХМЕРНАЯ УПРУГО-МГНОВЕННАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
В соответствии с определением упруго-мгновенной задачи теории упругости, данным в § IV.9, напряженно-деформированное состояние рассматриваемого ею упругого тела определяется напряжениями:
°* (О» оу(0, МО;
^.(O-bx(0; Tje(0-TZJf(0; v(0 = t,y(0 и деформациями:
где
8ж(0; ег(0; Y<y(0; уМ ¥уг(0;
2(dx(0; 2(Dy(0; 2cdz(0,
„ н\- 1 ldK,<z) dt>(0 1. ю'<°-т|^г —J’
ш (0=J_f*£W _^OT1
> 2 [ dz dx J
(V.l)
(V.2)
(V.3)
i !&>(/)
2 [ dz dy J
<*z(0 =
— средние вращения, a u(t), v(t), w(t) —перемещения точек тела в направлении координатных осей х, у и z соответственно. Зависимость между деформациями и напряжениями устанавливается обобщенным законом Гука:
(О = [(1 + v) а, (/) - vS (0] + (0;
...........................................(*,!/,*);
. - - ..................................{x,y,z).
(V.4)
250
где
$(0 = Ох(0 + м0 + МП;
(V.5)
деформации удовлетворяют уравнениям совместности: ^ех(О . ^(0 = ^(0 .
др® дх® дхду
.......................................• . • (х, у, г);
2 ^х(0 = д Г ^.-(') . <?Vx--(0 . ^УхУ(П | .
дудг дх [ дх ду дг J ’
...............................................(x,lj,Z)
и связаны с перемещениями формулами:
М0=^;
MO-***-; v,(0-^- + ^.
(V-6)
(V.7)
а напряжения удовлетворяют уравнениям равновесия:
(О , (О дгх. (/) = ।
дх ду дг ’I (V.8)
.........................U, У, ?) |
Кроме того, должны удовлетворяться соответствующие граничные условия.
Решение рассматриваемой упруго-мгновенной задачи можно проводить в напряжениях или в перемещениях.
В первом случае в первую очередь отыскиваются напряжения (V.i), а затем деформации (V.2) и перемещения. Последовательность решения задачи при этом следующая.
Вначале отыскиваются напряжения (V.1), удовлетворяющие уравнениям равновесия (V.8) и уравнениям совместности (V.6), выраженным в напряжениях [25]:
(i+v)v2ox(0+^ = fix(0;
.............(X, у, г);
(i+v)v4,(0+^-«Mh
.............(*,$/, г),
(V.9)
251
где Qx(O и £ixv(t) определяются по формулам (IV.55), (IV.56)
при условии (IV.5) и граничным условиям:
ох (0 cos (Nx) + тху (0 cos (Ny) + тхг (t) cos (Nz) 0; j
туХ (t) cos (Nx) + a у (t) cos (Ny) -f- туг (t) cos (Nz) = 0; [ (V. 10)
тгх (0 cos (Nx) + тгу (t) cos (Ny) -f- uz (t) cos (Nz) = 0. J
Затем по формулам (V.4) отыскиваются деформации тела и далее по уравнениям (V.7) с учетом характера закрепления тела в пространстве определяются уже его перемещения. В силу линейности уравнений (V.8) и (V.9) их решение можно искать в виде суммы:
М0 = %(0 + о«,(0; +
........ .(*.», г); .................(•«,!/. Z), I
где ох (О, —. tap (0 — общие интегралы однородных уравнений (V.8) и (V.9), соответствующие случаю отсутствия вынужденных деформаций тела, а (t), .... txyi (0, ... — любое из возможных частных решений уравнений (V.8), (V.9), соответствующее их заданным правым частям.
Общие решения уравнений (V.8) и (V.9) могут быть найдены по методу трех независимых бигармонических функций, предложенному Б. Г. Галеркиным, в соответствии с которым эти решения имеют вид:
X РфИО + + _ 2 (1—V) — v2q>i (0;
[ дх ду дг J дх
х -2(1
М'Н-^+^-с-^х
+ «ает + _ 2 (1 _V) Л ^„(0;
[ дх ду дг J дг
„ Г«*Р. (О . . ар3(/)| ,
дг ] +
L ду дх ]
г ... [ар, (/) , д<рг (о , <?фз (Qi
ХУ^=—№Т7Г + ~^-+ дг ] +
(V.12)
(V.13)
252
+ (!-*) V’l^ + ^1; I dz dy J
/A _ d* P<MO [ <M') , Дф»(01
4 дхдг [ dx + dy + dz J
+ (1 + [ dz dx ]
(V.13)
где<р1(/), фг(О» фз(0—независимые бигармонические функции, включающие в себя время t в качестве параметра, являющиеся решениями уравнения
v2v2( ) = о
(V.14)
и принимаемые в соответствии с требованиями, накладываемыми на напряжения и перемещения тела граничными условиями.
Частные решения оХа(/),..., тху (/) ...определяются видом вынужденных деформаций е® (/),...,уху(0 ... Пути их отыскания будут указаны ниже.
В тех случаях, когда наряду с напряжениями требуется отыскание перемещений точек тела, на'пример, когда граничные условия заданы в перемещениях, решение задачи удобно проводить в перемещениях. Необходимые для этого уравнения можно получить следующим образом.
Принимая во внимание формулы (V.7), с помощью уравнений (V.4) найдем:
’><'>=7^[d7e<'>(°]; °' <'» = гЧ - «? (О-т^е. со]
ху 2(1+v) [ ди дх ху J
(V.15)
(V.16)
где
6° (О = е« (0 + е«(0 + е« (0; (V. 17)
е(0 = ех(О + еу(О + ег(0. (V.18)
253
После чего, внося (V.15) и (V.16) в уравнения равновесия (V.8), будем иметь
+ (, _ 2v) а и (/) _ (j _ 2v)[^l+2412. +
дх L °У дг
_2*------L 1
дх l-2v дх К/]’
+(1-2v)V2i-(0-(1-2v)[^412-+^4^- +
" 0 L * & (V19)
+ 2^12- + -^-------f-e°(o|;
ду 1 — 2v ду J
02 ох ох
+ 2^ф2_ + _^г------
дг 1 — 2v дг J
Таким образом, ход решения задачи в перемещениях следующий.
Вначале по уравнениям (V. 19) отыскиваются перемещения u(t), v(t), w(t), затем по уравнениям (V. 15) и (V.16), по заданным вынужденным деформациям е° (/),... ,У°ху (0. — и найденным перемещениям находятся напряжения, а затем по формулам (V.4) и деформации тела.
В силу линейности уравнений (V.19) их решения можно искать в виде:
«(П = М0 + М); ] w(t) = wf (/) 4- uy2(O, J
(V.20)
где vi(t) и wi(t) —общие решения однородных уравнений (V.19), соответствующие случаю отсутствия вынужденных деформаций, a u2(t), v2(t), w2(t) —любое из возможных частных решений уравнений (V.19), соответствующее их заданным правым частям.
Общие интегралы однородных уравнений W| (0
всегда могут быть найдены по методу Б. Г. Галеркина с помощью трех независимых бигармонических функций в следующем виде:
251
„ /М » + v f д [Эф,(Г) , г<мо ,/Фз(0] “1{п = ~ + + “1Г"]“
— 2(1 — v)v2q>i(0};
v (f} = — 1 + v I д Г а<Р« Ю -L дЧ”-У} 4- 1 _
1 Е (/) I ду [ дх ду дг J
— 2 (1 — v)V2<p2(0};
г« /л- 1+v г г г а<Р1 <0 I а<М0 , дфз«) 1
L-аГ" + -ЪГ + -5Г-] -
- 2(1 - v) V293(0}.
(V.21)
Вид частных решений ц2(0. «2(0. ^г(0 определится видом вынужденных деформаций. Некоторые из них будут рассмотрены ниже.
При отыскании перемещений «(О. «(О и «40 входящие в них произвольные функции интегрирования определяются с помощью граничных условий, которые также всегда могут быть выражены в перемещениях.
Ниже будут рассмотрены решения некоторых упруго-мгновенных задач термо-упругого равновесия тел, которые нам понадобятся в дальнейшем. В этих задачах вынужденные деформации связаны с изменениями температуры тела и в соответствии с гипотезой Дюамеля — Неймана равны:
Здесь Ф(0 —температурная функция, определяющая собой расчетные изменения температурного поля тела, в общем случае зависящая от координат его точек и времени, а а — коэффициент линейного расширения.
При условиях (V.22) большинство из выписанных выше уравнений упруго-мгновенной задачи упрощается и принимает следующий вид [118]: закон Гука —
Вх (0 = [(1 + ?) Ох(0 - VS(/)] + аФ (t) ;
..............................(*,«/,*);
..............................у, Z),
(V.23)
255
ИЛИ
г (П Е& ГЭц(') I
ху( 2(1+v) L ду + дх J’
т (л^_ЁЮ_Г*40 +
yz( ' 2(1 +v) I dz ду ]’
уравнения равновесия —
+ (1 - 2v) vMO =2а(1 + v)^> ; дх дх
+ (1 - 2v) V2v (0 =2а (1 + v) ; ду ду
-^ + (l-2v)V2^(0=2a(l 4-v)^-; dz dz
уравнения совместности —
(l + v)vaajr(O + ^^- = =_uE(O[l±rv20(n + _^Ol;
|_1—v дх* J
...............................(x,ty,z}-, (l+v)Vr,W + -^-— oE(0^;
* дхду dxdy
.............................(X,y,z).
(V.24)
(V.25)
(V.26)
§ V.2. ПЛОСКАЯ УПРУГО-МГНОВЕННАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
Рассмотрим особо случай плоской упруго-мгновенной задачи о напряженно деформированном состоянии тела при наличии вынужденных деформаций. Такое состояние возникает в телах определенной конфигурации вследствие изменения температуры, усадки и т. п Например, в случае изменения температуры тела по закону Ф(х,у.г, t) составляющие его вынужденных деформаций будут равны (V.22).
25С
Эта задача может ставиться в двух вариантах: в виде задачи о плоской деформации длинных призматических тел и в виде задачи о плоском обобщенном напряженном состоянии тонких призматических дисков. Займемся первой из них.
Рассмотрим длинное призматическое тело с полностью защемленными торцами ось oz совместим с его продольной осью.
Будем иметь в виду случай, когда граничные условия, распределение напряжений и вынужденных деформаций не зависят от координаты z, отсчитываемой вдоль образующей. При этих условиях часть тела, выделенная на значительном расстоянии от его торцов, находится в условиях плоской деформации. Вследствие этого компоненты напряжений и деформаций будут зависеть только от двух координат точки к, у и времени I. Таким образом, в рассматриваемом случае:
«(0 = «(*•. 4/. О; vtf) = v(x,y,t)- и\0 = О, (V.27) т. е.
e.v (О = £л (*, У, t) \ ev (0 = ev ( v, у, t); уХу (t) = уху (х, у, 0; | V„(0-Yyz(0~e,(0 = 0 /
и, кроме того,
оД0 = ox(x,y,t); a„(O=o,(x,y,0-, Txy(t) = Txy(x,y,f) ;) = tv.(0 = 0; j
ог (О = v [ ux(0 + uy (/)] - 8» (0 E (0. (V.30)
Имея в виду напряжения, вызываемые вынужденными деформациями, будем считать, как и прежде, поверхностные и объемные силы равными нулю.
Вначале рассмотрим метод решения рассматриваемой задачи в напряжениях.
При сделанных выше предположениях напряженное состояние тела будет описываться следующими уравнениями. Компоненты напряжений будут удовлетворять двум уравнениям равновесия;
. дгху (/) = .
дх ду
&Сух (О j dtTy (0 __ g ( )
к ду
и однородным условиям на поверхности:
(0 cos (Л'х) + tXv (0 cos (Ny) = 0; | _
туА. (0 cos (/Vx) 4- av (0 cos (Ny) = 0. J
1 Имеется в виду отсутствие поворота и продольных смещений торцовых сечений тела.
257
Кроме того, они должны удовлетворять еще условиям совместности (V.9), из числа которых в силу условий (V.27) и (V.29) останется только одно
Г
L *£/’
дх2
(V.33)
V2 К (0 + оу(0] =-^у(0 , 2 с
—е'
По аналогии с функцией напряжений Эрп введем в рассмот-
рение функцию напряжений упруго-мгновенной задачи <p(f), такую, что тогда, очевидно:
V2 К (0 + оу (/)] - V2 V2 <Р (0,
(V.34)
(V.35)
где
(V.36)
(V.37)
дх* дх2ду2 ду*
Таким образом, уравнение совместности (V.33) примет вид:
дхду 2 |
После введения функции <jp(O уравнения равновесия (V.31) будут тождественно удовлетворены, а условия на поверхности (V.32) перепишутся следующим образом:
— cos(Nx)---- £ - cos(Ny) = 0;
ду2 дхду
— —-^^-cos(/Vx) — ф-- cos(M/) = 0.
дхду дх2
(V.38)
Итак, решение рассматриваемой задачи о плоской деформации сводится к интегрированию дифференциального уравнения совместности (V.37) при граничных условиях (V.38).
Отыскав функцию напряжений упруго-мгновенной задачи <г(0, удовлетворяющую уравнению (V.37), и граничным условиям (V.38), по формулам (V.34) найдем компоненты напряжений упруго-мгновенной задачи, которыми полностью определяется искомое напряженно деформированное состояние рассматриваемого тела, поскольку напряжения аг(О с помощью формулы (V.30) однозначно выражаются через напряжения ax(t) и cv(t).
258
а деформации ех(0» ву(О и Уху(0 на основе выражений (V.4) с учетом (V.29) также будут однозначно выражаться через эти напряжения по формулам:
(0 = [(1 — v) (0 - voy (Z)J + (1 + v) е® (0;
еу (0 - [(1 _ V) Оу (f) _ vax (/)] + (1 + v) е® (/);
Yxy(0=^^-Txy (0 + ^(0-
(V.39)
Однозначно будут определены также и смещения точек тела, поскольку они связаны с деформациями соотношениями (V.7).
Рассмотрим случай, когда
^(0 = е;(0-8«(0^ае0(П; |
V’,(0-vb(O“^(O=o. |
Такой случай, например, имеет место при температурных деформациях тела, усадке, набухании и т. п. При этом постоянная а может рассматриваться как коэффициент соответствующей линейной деформации, например коэффициент линейного температурного расширения, а функция е°(/) —как поле вызывающих ее изменений соответствующей характеристики состояния материала, например поле изменений температуры тела. Если при этом ввести в рассмотрение новые физические характеристики материала
£i(O=-j^r; a, = (l+v)a (V.41)
и учесть, что
1 + У! 1 4-v
£1(0 £(0 ’
(V.42)
то все основные уравнения задачи о плоской деформации, выписанные выше, перепишутся следующим образом:
а) уравнение совместности
vV«₽(') = -a1Ei(OV2e°(O; (V.43)
б) граничные условия:
cos (Nx) —со s (Ny) = 0;
ду2 дхду
— cos(^х) + -2соs(Ny) = 0;
(V.44)
259
в) связь между деформациями и напряжениями е. (/) к* (0 ~ Ъ оу (0] + О1 е° (0;
®У (0 = [оу (0 - vt ох (0] + а, (0;
Тху(О--2(‘|^,)-ТхУ(0:
г) связь между смещениями н деформациями: ^=М0;
(V.45)
(V.46)
Теперь рассмотрим тонкий призматический диск со свободными торцами и боковой поверхностью, сохранив выбранное ранее направление осей координат и по-прежнему считая, что объемные силы отсутствуют, а вынужденные деформации не зависят от координаты г. Вследствие этого, как и прежде, компоненты напряжений, перемещений и деформаций будут зависеть только от двух координат точки х, у и времени t. Таким образом, в рассматриваемом случае мы будем иметь
и = и(х, у, t)-, v = v (х, у, t), (V.47)
т. е.
ех (0 =- ел (х, у, 0; еу (П - еу (х, у, t)-, уХу (0 = уХу (х, у, 0; | Y«(0-YvJO = O J
и, кроме того,
а* (0 = ох (х, у, t); Оу (f) - оу (х, у, t); тм, (0 =тХу (х, у, 0; | т«(0 = туС(0 = ог(О = О. J '
При сделанных предположениях диск находится в плоском обобщенном напряженном состоянии, которое будет описываться следующими уравнениями. Компоненты напряжений по-прежнему будут удовлетворять двум уравнениям равновесия (V.31) и однородным условиям на боковой поверхности (V.32). Кроме того, они должны удовлетворять еще уравнениям совместности (V.9), из числа которых, в силу условий (V.48) и (V.49), останется только одно
<V.5O)
L ду‘ дх2 дхду J
где <г(/) — по-прежнему функция напряжений, связанная с напряжениями формулами (V.34).
260
Итак, решение рассматриваемой задачи о плоском обобщенном напряженном состоянии сводится к интегрированию дифференциального уравнения совместности (V.50) при граничных условиях (V.32).
Отыскав функцию напряжений упруго-мгновенной задачи <р(0, удовлетворяющую уравнению (V.50) и условиям (V.32), по формулам (V.34) найдем компоненты напряжений, которыми полностью определяется искомое напряженно деформированное состояние тела, поскольку его деформации на основе выражений (V.4) с учетом (V.49) будут однозначно выражаться через эти напряжения по формулам:
М0 = + «');
(V.51)
а смещения будут связаны с этими деформациями выражениями (V.7).
Рассмотрим теперь случай (V.40). Выписанные уравнения примут вид: а)
основные
б)
в)
уравнение совместности
V2 V2 <Р (0 = (О V2 е° (0;
граничные условия:
cos (Mt)--- cos (Ny) = 0;
— j. Ф (О cOSуч+ *9(0 cosj Q дхду ' dx2
связь между деформациями и напряжениями:
=тЬг ® ~va>' +ае°
S (0 -= К (0 ~ VQ. (О] + ае° (0;
=
(V.52)
(V.53)
(V.54)
г)
связь между смещениями и деформациями:
^+^ = ^(0-
(V.55)
261
Сравнивая уравнения (V.52) — (V.55) с уравнениями (V.43)— (V.4G), мы видим, что эти группы уравнений с точностью до постоянных a, v и функции E(t) совершенно идентичны, поэтому мы приходим к следующему практически весьма важному выводу.
В случае, когда вынужденные деформации тела заданы в форме (V.40), как это, например, имеет место при изменениях температуры или влажности бетона, решения упруго-мгновенных задач о плоской деформации и о плоском обобщенном напряженном состоянии с точностью до постоянных a, v и функции £(/) совпадают. Поэтому достаточно решить лишь одну последнюю задачу с физическими характеристиками материала а, v и £(/). Ес решение для случая плоского обобщенного напряженного состояния будет окончательным. Решение же соответствующей задачи о плоской деформации мы получим, заменив в найденном решении а на щ, v па и E(t) на Ei(t), вычисленные по формулам (V.41).
Для полноты последнего решения необходимо будет еще по формуле (V.30) найти напряжения о2(0, которые будут соответствовать рассмотренному выше случаю жестко защемленного по торцам тела. Их равнодействующие:
/V(/) = Jaz(/)dF;
^uz(t)xdF
(V.56)
будут представлять собой реакции заделки. Здесь F — площадь поперечного сечения тела.
Наконец, рассмотрим один важный случай, когда вынужденные деформации заданы в форме:
^(l)=A(l)+B(t)x + C(t)l/, )
где A(t), B(t), C(t) —некоторые функции только одной переменной t. Он понадобится нам в дальнейшем для решения задачи о плоской деформации бруса со свободными торцами. В этом случае правая часть уравнения (V.50) тождественно равна нулю, поэтому
VV<PW = O. (V.58)
Поскольку функция <jp(O в рассматриваемом случае должна к тому же удовлетворять еще однородным граничным услови-262
ям (V.38), то, очевидно, она тождественно равна нулю, следовательно, равны нулю и напряжения:
<тДП = оу(0 = тду(0 = 0. (V.59)
Поэтому с учетом (V.30), (V.59) и (V.57)
oz (t) = — E (/) [Л (0 + В (0 х + С (/) у\. (V .60)
Реакции заделки при этом будут равны:
N(t)--A(t)E{t)F0- ]
/И,(П= — C(t)E(t)Jx’, (V61)
My{f) ——B(t)E(t)Jy, J
где Fo — площадь, a Jx и Jy — моменты инерции поперечного сечения тела относительно его главных центральных осей.
До сих пор мы рассматривали длинное призматическое тело с жестко защемленными торцами. Рассмотрим теперь такое же тело, свободное от защемлений по концам. Решение упруго-мгновенной задачи о плоской деформации для рассматриваемого случая мы получим, накладывая решение (V.59) — (V.61) только что изученной задачи на решение соответствующей задачи для защемленного по торцам бруса, рассмотренной выше, и подбирая функции Л(0» E(t), C(t) таким образом, чтобы в каждом отдельном случае было бы
/V (0 = Мх (/) - Му (/) = 0. (V.62)
Это всегда удается сделать. Например, в случае температурных деформаций, как мы видели в г.здве I.
е°(0-еО(0 = £°(0 = аТ(0Х(х) Y(y), (V.63)
поэтому в этом случае достаточно принять •
Л(0 = В(0=.С(0 = 7’(0. (V.64)
При этих условиях напряжения ox(t), oy(t) и xxy(t) останутся неизменными, напряжения же az(0, определяемые по формуле (V.30), изменятся на величину (V.60) и будут равны
°г(0 = v [ (0 + ау (0] ~ е°г(0 Е (!) -
~Е(!)[А(/) + В(1)х + С(!)у], (V.65)
где A(t), B(t) и C(t) будут уже известными функциями t, равными
Л(о = IV [ W + °> (°] ~ (')] ;
В<!~> = lv [ <'* + а> <')] - <4(0 Е (0) xdF;
С(0 = ^77 j{'• [«,(0 + »,(0] -<4(0Е(0| UdF.
(V.66)
263
Отметим, что на торцах тела напряжения oz(t) в рассмотренном случае будут сняты лишь, как говорят, с точностью до главного вектора и главного момента. Таким образом, задача о не-защемленном по торцам брусе решена нами в духе принципа Сен-Венана. Более точное решение ее пока еще не найдено.
Аналогичным образом могут быть получены решения рассматриваемой задачи и для других условий на торцах тела. Например, для случая, когда торцовые сечения тела не могут поворачиваться, но не закреплены по отношению к продольным смещениям, мы будем иметь В(/)=С(/)=0, а /!(/) определяется по первой из формул (V.66). В случае же, когда, наоборот, торцы тела могут поворачиваться, но длина его оси остается неизменной А (0=0, a B(t) и С(0 определяются по формулам (V.66).
§ V.3. ПЛОСКАЯ УПРУГО-МГНОВЕННАЯ ЗАДАЧА. МЕТОД РЕШЕНИЯ
Рассмотрим метод решения плоской упруго-мгновенной задачи теории упругости, а именно, задачи о плоском обобщенном напряженном состоянии, ограничившись случаем, когда вынужденные деформации заданы в форме (V.40). В § V.2 мы видели, что в этом случае решение задачи сводится к интегрированию уравнения (V.52) при граничных условиях (V.53) с последующим отысканием напряжений, деформаций и смещений тела по формулам (V.34), (V.54) и (V.55) с обязательным удовлетворением третьему из уравнений (V.55).
Полный интеграл уравнения (V.52), как известно, состоит из общего интеграла соответствующего однородного уравнения
Vs Vs Ч> (0 = 0 (V.67)
и удобного частного решения уравнения (V.52) с правой частью.
Общий интеграл уравнения (V.67) можно всегда найти в виде бигармонической функции координат точки х и у с произвольными постоянными интегрирования, являющимися функциями времени t.
Практически, однако, функция е°(/), входящая в правую часть уравнения (V.52), (см. главы I и II) обычно задана в виде
e“(t) = X(x)Y(y)T(t), (V.68)
поэтому и функцию <р(0 удобно искать в форме произведения
<г(О = а<р(х,г/)Т(/)£(0. (V.69)
Таким образом, задача сводится к отысканию общего интеграла уравнения
V2 V2<p(*,«/) = 0. (V.70)
264
Этот интеграл удобно в общем случае записывать в виде ря^ да:
Ф (А У) = у Ах- + BXI/ + -L Ctf+
П~=О П=со
+ S fn (У) cosl„ х + 2 ф„ (у) sin со,, х , (V.71)
Л=1 Л=1
где
Л (У) = A„ ch у + Вп sh Хп у + С„ Хл у ch у +
+ D„X„yshX„i/; (V.72)
фл (!/) = Л. ch у + Gn sh <оп у + Pn <o„ i/chwn^ +
+ Qnw„i/sh(o„!/ (V.73)
общие интегралы дифференциальных уравнений четвертого порядка:
// (у) - 2Хл2/ (У) + ttfn (У) = 0; (V.74)
<р'п (у) — 2(0и фл (у) 4- ®л фп (у) = 0. (V.75)
Входящие в решение (V.71) произвольные постоянные А, В, С, Ап, .... Fn, ... определяются из граничных условий и условий равновесия тел. В этом решении предполагается, что грани у=0 и у=Н являются продольными кромками тела, а грани х= ±1 — его поперечными кромками.
Функции (V.71) соответствуют следующие выражения для напряжений и смещений1
сЛ0 = аТ(0Е(0[С+£Л(у)со5Ьвх +
+ Еч>№)яп®ях];
Л=1
оу(0 = vT(t)E(t) [А-^\2пШ^пх-~
— Ё ®*Ф„(!/)51П(опх];
(0 = — аТ (/) Е (t) [В—£ Хп Д (f/)si n V+ + Е ®„^,(!/)cosw„x];
(V.76)
Имеется в виду случай плоского обобщенного напряженного состояния.
265
и (t) = аТ (/) + Ь3 у + (С - v4) х + 2В (1 + v) у +
4- /„(!/)+ АЛО/)]sinМ“
<р'п (!/) + VtD„ Ф„ (у} ] cos (rt„ Л ] ;
v (о = аТ (о К - ba X 4- (Л - vC) у +
(V.77)
гп(у)~ (2 + ^Ш
cosXnx +
+ S <G/) — (2 1 v)<p;(i/)l sin<onx
Входящие в формулы (V.7I), (V.76) и (V.77) постоянные bi, b2 и Ьз выбираются из условий закрепления тела в пространстве как целого жесткого, а постоянные Х„ и соп— в зависимости от граничных условий на поперечных кромках тела х=±1, а именно:
а) если на этих кромках ох(/)=0, а гхь(/)=/=0, то:
’» = eL57ii: «>» = “• (V.78)
б) если на них од(/)=±=0, а тк-„(/)=0, то:
Х,,л=^---(?-~12л- ; <»ял = у+^; (V.79)
в) если на них ох(/)=/= 0, и т.гу=#0, то:
*я = «>й = у. (V.80)
Переходим теперь к отысканию ряда практически важных частных решений уравнения (V.52), при этом будем иметь в виду случай (V.68).
В соответствии с видом общего интеграла (V.71) функцию е°(/), заданную в формуле (V.68), удобно также представить в виде ряда
(0 = [g + Y* (!/)] {а + bx + V е„ со< А„ х +
+ "v duSin(rt Jt(0, (V.8I)
266
где
н
Г YlyWy
Ё=~Г~ (V-82)
— среднее значение функции Y (у), Y*(y) = V(i/)-g; (V.83)
еп = J [X (х) — а — bx] cos Х„ xdx; (V.84)
dn = -у- J |Х (х) — а — bx] sin со,, xdx, (V.85)
а а и b — пока произвольные постоянные, смысл которых мы сейчас же выясним.
В случае (V.78) должно быть:
О = -у [X(/) + Х(- /)]; b = ± (X (/) - Х(— /)]; (V.8G)
в случае (V.79):
a-y-j X(x)dx; b = X'(l); (V.87)
в случае (V.80):
а= y-J X(x)dx; 6 =-у [X(/) — Х(—/)]. (V.88)
Представив теперь выражение (V.81) в виде
е°(0 = |(a+Mg+(a + M*'*(i/) + [g+ S encosX„x +
( П=1
+ [g + (i/)l Ё dn ЯП со,, Т (х), (V.89)
найдем частные решения уравнения (V.52), соответствующие каждому из слагаемых фигурной скобки в выражении (V.89).
Так как
V2 (a + bx)gT (0 = О, (V.90)
то частное решение, соответствующее первому из этих слагав-, мых, такз^е равно нулю. Для учета этого слагаемого нам придется ввести дополнительный частный интеграл однородного
267
уравнения (V.70). Метод отыскания таких интегралов мы изложим ниже.
Частное решение, соответствующее второму слагаемому, выпишем сразу в простой форме
Чг (0 = аЕ (!) Т (!) (а + М J J У* (У) dy dy, (V.91)
ему будут соответствовать следующие значения напряжений и смещений1:
ал. (!) = -аЕ (!) T(i)(a+bx)Y* (у)-, Оу (!) = 0;
тЛ).(0 = -aE(i)T(i)b^Y*(y)dy,
й (!) = - (1 + v) аТ (!) b J |J У* (у) dy + 2 j У* (y)dy j dy, v(t) - (1 + v)aT(i)(a + bx) J V (£/)
о
(V.92)
(V.93)
Частные интегралы <рз(О и фДО, соответствующие третьему и четвертому слагаемым формулам (V.89), будем искать в форме:
<Рз(0 = — аЕ(!)Т (!) £ д>3„ G/) cos х; л=1
(!) — — аЕ (!) Т (!) £ (у) sinш„ х,
(V.94)
тогда для функций <p3n(t/) и q>m(y) будем иметь уравнения:
Ъп(у)- ы2п(!/)+^Фзп(!/) -{У*’(у)-^2п te+^O/)]); 1 (v.95)
—2^’ф^)+^Ч>4Я (y)=d„ {^* (у)—^п [g4-*'*G/)]|. J
Поскольку общие интегралы (V.72), (V.73) уравнений (V.74), (V.75) без правой части известны, частные решения этих урав-
1 Здесь и в дальнейшем при определении перемещений u(t) и к(0, соответствующих частным решениям, опущены произвольные функиии интегрирования, определяющие смещение тела как целого жесткого, поскольку такие
функции уже содержатся в формулах (V.77), отвечающих общему интегралу бигармонического уравнения.
268
пений ФзДу) и ЧЧп(у) найдем методом Коши. Следуя этому методу, подчиним интегралы (V.72), (V.73) условиям:
А (0) = А (0) =fn (0) = 0; А (0) = 1; |
<рп(О) = ф;(О)^ф;,(О)=О;<гп”(О)= 1.)
это сделает их равными:
(у)= 4"3 У^г.У—^ К У>,
мп (у}=^ -т (<•>« у ch у ~sh “п ^)-
2<о*
Тогда частные решения уравнений (V.95) будут равны:
Фз„ (У) = еп J Nn(y — П) {У*" 01) ~ + У* (’1)1) ;
<Р4п (у) = dn J Мп (У— П) (Г*Я 01) — ©n [g+r* (П)1} <01-
(V.97)
(V.98)
Например, при
У (у) --^g + У* (У) = С, + С2у;
(V.99)
<Рзп (у) = - -V Ка Мъ у sh К у + 2 (1 - ch Хл I/)] +
+ С2 [Х„ у (2 + chX„ у) - 3 sh Xn I/]}; (V. 100)
(у) ----------Ч- {С1 у sh соп у 4- 2 (1 — ch we £/)] -}-
20)3
4-С2 [со,,у(2 4- chw„i/) — 3shco„y]}. (V. 101)
Отметим, что в силу условий (V.96) любое из частных решений (V.98) удовлетворяет условиям
Ф (0) = ? (0) = ф" (0) = ф- (0) = 0, (V. 102)
что существенно упрощает уравнения для отыскания произвольных постоянных функций напряжений, получаемые из граничных условий. _
Имея выражения (V.98) для функций фзп(у) и <₽4«(у), по формулам (V.94) всегда можем определить искомые частные решения ф3(0 и <рч(О- Этим частным решениям в их совокупности будут соответствовать следующие выражения для напряжений и смещений:
269
(0 = —аЕ (0 Т (t) (у) cos 4-
+ S ?;п(»)яп®п х
Оу (0 = «£ (О Т (/) £ Л2^ (у) COSXn X +
П—а> __ I
+ S <M0)-in®»х ;
Lo (0 = — «£ (0 т (0 | £ Лп (у) sin Х„ X +
+ £ ^nte' COSW" Л-«=|
ь (I) = — аТ (/) { £ ц2п (y)+vk„ ф3л (iy)j sin л„ х —
~ S [“ + VW" f!/)] COS“n Л} ;
* (0 = — аТ (t) I v j”J_ (у) _ (24- V) ф3„ (у)Jcos Х„ г4
+ S [у (у) — (2 + V) ф4п (u)l sin u>„ л! .
(V.103)
(V.I04)
В некоторых случаях удобно проводить решение рассмотренной плоской задачи в перемещениях, поэтому ниже мы кратко рассмотрим и эту возможность, ограничившись случаем плоского обобщенного напряженного состояния, при вынужденных деформациях, заданных в форме (V. 40). При таком метоле решения задачи достаточно, как известно, найти обшее решение следующих уравнений равновесия, выраженных в перемещениях [118]:
[А, (0+р (0] ^-+ р (0 V2 «(0 = 2 [X, (/) 4- р (0J а 1М04-Р(01^ +М(ОУ2«(О = 2[М0+Н(О]
(V.1C5)
270
где
в(/)_ «±!Д + «^>. дх ду
? //) = JHZLMZL = vE{t}
'* ' X (/}-+-2|Л(/) 1— v«*
a k(t) и р(0 —«постоянные» Ламе, равные
(l+v)(l-2v) ’ 2(1+V) *
Если ввести среднее вращение 2£2 (Z) по формуле 2Q(0 = ^_2M(l. dx
(V.106)
(V.107)
(V.108)
д«/
то уравнения (V.105) перепишутся следующим образом:
(О + 2^(0] - 2М(0 ^=2[МО + Н(0]а^;
ох оу ох
(V.109)
Hi (О + 2И(/)]^ + 2ц(/)^£>- =2[X1(0+u(0]a^p-.
(V.110)
Полные интегралы этих уравнении могут быть представлены в виде суммы общих интегралов t»i(0 однородных уравнений (V.I10) без правой части и удобных частных решений и2(0 и ^2(0 полных уравнений (V.110):
и (О = (0 + «2 (0; f (0 = (0 + v2(0. (V. 111)
Общие интегралы щ(/) и vt (t) однородных уравнений хорошо известны в курсах теории упругости. Они были получены Файлоном в общем виде, который выразил их через известные алгебраические и трансцендентные функции. Одна из удобных для нас форм общих интегралов ui(/) и th (О была выписана нами выше в виде формул (V.77). Поэтому здесь мы ограничимся лишь рассмотрением некоторых частных решений и2(0 и в2(0-
Это полезно сделать для некоторых простейших случаев задания вынужденных деформаций еи(0, например, для которых V2e°(/)=0, и поэтому даже при решении задачи в напряжениях все равно приходится отыскивать перемещения с тем чтобы получить это решение в полном виде. Именно этому случаю как раз и соответствует первое слагаемое в фигурных скобках формулы (V.89).
Одно из частных решений уравнений (V.110) может быть найдено по методу Лява [118], если положить, что 0(0=0. В этом случае, очевидно
0а(0 = (1 +v)ae° (0, (V.112)
271
a u2(t) и v2(t) —частные решения уравнений:
+ e(1 + v)aep(0;
дх ду
dw2(t) 6M')__0 дх ду
(V.113)
Помножая второе равенство на i и складывая с первым или соответственно вычитая, приводим их к виду
£К(0 + *2(')]-i/y [М'Ж’МО] = (Ж)ае°(0; 4 l«2(0~w2(0] + 1-7- IMO-'MO] =(14-v)ae*’(0-
Произведем замену переменных по формулам:
В = х -J- iy\ T) = x—iy; (V.l 15)
х = 4й+',): = (v.ii6)
предварительно отметив соотношения:
дУ(х,у) = 1]) Л]_.
дх дБ ' dx di) ’ dx ’
дф(*. У> _ дф(Б. 1]) , дф(Б, ф
ду дБ dy di) dy ’
а также
дф(х. У) | f- дф(*. У) = 2 frHE. *1) .
dx dy di)
У) _ д<Г(х. У) _ 2 frME. Ч)
дх ду дБ
Обозначая:
«s(0 — iv2(t) = V(х, у, t), )
приводим равенства (V.114) к виду:
—= 4(1 +v) ae°(l’ ч-0; <?s 1
= 4 (1 +v) ae" (В, 4.0
и, следовательно:
t/(B,V)=4(1+v)aJ е0(Ьп’
V (£, 1), t) = 4(14- V) a J E" (В, 4, /) d»).
(V.l 17)
(V.l 18)
(V.l19)
(V.l20)
(V.121)
272
после чего находим:
и2 (0 = -у (!+v) а [] еп (В, 11. f) dl 4- f En (В, ii, /) dti]; «JO = [f e°(B, 4. 0<*B-Je°(B,4. ОЛ1]-
(V.122)
После выполнения интегрирования в формулах (V.122) следует произвести обратную замену переменных В и ч на х и у по формулам (V.115).
Например, при
&(Г) = ахуТ(1) (V.123)
с учетом формул (V.U6)
4
таким образом:
J е° (В, ч. 0 dB= - 4- ш (у - Ч2 5) Т (0;
J Е° (В, Ч. 0 d’l=-«* (чВ2-----Ч3) Т (/);
J е® (В. ч, t) <*В + J Еп (В, ч. 0 d4= у а(Ъ?у + if) T(t)-
J Е« (В, Ч. 0 <*В - J (В, ч, 0 <*ч= 4 ai + *0 т
Следовательно:
u2(t)= -^(1 + v)a(3x2y + y^)aT(0; v2 (0 = 4 (! +v) a (3xif + x3) aT (/)-
(V.124)
Часто при простых способах задания е°(О частные решения уравнений (V.113) легко выписать сразу. Например, при
^4t)=Y(y)T(t) (V.125)
«2 (0 = 0; V. (0 = (1 + v) aT (t) J У (у) dy, Xi
(V.126)
а при
е°(0 = X(x)T(f) (V.127)
«2(0 = (1 + v)aT(t)^X(x)dx; vz(t) = 0. (V.128)
273
где х1 и j/i—произвольные числа, выбираемые из соображений удобства, например, из условий максимального упрощения уравнений для определения произвольных постоянных функции напряжений. Часто из этих соображений удобно принять Xi = f/i = 0.
Таким образом, в случае
ео (t) = T (<), (V.129)
как это, например, будет при равномерном нагреве тела, возможны три формы частных решений:
1) и2 (/) = 0; п2 (t) = (1 + v) ay Т (/); (V. 130)
2) (0 = (1 + v) ахТ (ty, v2 (t) = 0; (V. 131)
3) М') = y(l+v)«T(0; t-2(0 = -j- d 4-v)ay T (t). (V.132)
Здесь принято условие Xi = //i=0, так как исключается смещения тела, как целого жесткого.
Перемещениям (V.126), (V.128) будут соответствовать напряжения:
оЛ (0 = — а£ (0 Т (t)Y(yy, Oy(t) = тЛу(t) = 0, (V.133)
или соответственно
(МП = гд¥ (Г) = 0; ov (/) = - аЕ (/) Т (t) X (л), (V. 134)
а перемещениям (V.I30) — (V.132) —напряжения:-
1) аД/) = -аЕ(ОГ(0; ov(/) = тжу(/) = 0; (V.135)
2) о л (0 = (/) = 0; иу (0 = - аЕ (t) Т (/); (V. 136)
3) оЛ (О = ov (0 = ~ -у аЕ & Т (0; (0 =0. (V. 137)
В зависимости от вила граничных условий удобно принимать ту или иную форму частных решений (V.130) — (V.132). Например, если поперечные кромки свободны от напряжений, удобно принять частное решение в форме (V. 131). Если же торцовые кромки закреплены а продольные свободны—то удобно принять частное решение (V.130).
Некоторые из этих частных решений мы используем в дальнейшем.
Например, слагаемому
^>(t) = (a + bx)eT(t) ‘ (V.133)
формулы (V.89) на основании изложенного выше будут соответствовать перемещения
ц2(0 = (1 + v)agT(t)[ax+ v2(t) = 0 (V.139)
и напряжения:
од (0 = (0 = 0; a, (Z) = - аЕ (/) Т (0 g (а + bx). (V. 140)
274
Просуммировав формулы для напряжении или соответственно перемещений, полученные выше, отвечающие всем рассмотренным частным решениям и общему интегралу Ангармонического уравнения, мы получим формулы для полных напряжений и смешений тела рассматриваемой задачи о его плоском обобщенном напряженном состоянии. Мы сделаем это ниже в § V.4.
Отметим, что, распоряжаясь должным образом постоянными и функцией Y*(y) в формуле (V.89), мы можем получить из рассмотренного выше общего решения ряд практически важных частных случаев. Например, положив
f> = en = d„ = F*G/) = O (V.141)
и считая е°(0 температурой тела, получим случай его равномерного разогрева, исследованный при некоторых частных граничных условиях Г. Н. Масловым [117]. Ниже мы рассмотрим этот случай более подробно.
§ V.4. ПОВЫШЕНИЕ ТОЧНОСТИ РЕШЕНИЙ ПЛОСКОЙ УПРУГО-МГНОВЕННОЙ ЗАДАЧИ
Как мы видели в § V.2, решение плоской упруго-мгновенной задачи сводится к интегрированию бигармонического уравнения с правой частью (V.50) относительно функции упруго-мгновенных напряжений <р(/).
Обшее решение этого уравнения обычно получают в рядах по гиперболо-тригонометрическим функциям типа (V.71), с помощью которых, не удается строго удовлетворить всем граничным условиям задачи. Поэтому на некоторых из кромок тела эти условия удовлетворяются только в духе принципа Сен-Венана, что приводит к тому, что часто, в тех случаях, когда на свободных кромках должны полностью отсутствовать напряжения, они снимаются лишь в интегральном смысле, т. е. с точностью до главного вектора и главного момента этих напряжений в пределах указанных кромок. Получаемые при этом решения оказываются практически применимыми лишь для вытянутых в должном направлении контуров и относятся только к их средней части, где погрешности указанного выше вида, в соответствии с принципом Сен-Венана, не велики.
Для повышения точности подобных решений может быть предложен следующий метод, основанный на идее метода Ме-наже.
Прибавим к общему интегралу (V.71) однородного Ангармонического уравнения (V.70) частный интеграл лого уравнения в виде полинома по степеням х и у
<Р2(*,!/)=Х (V.142)
<•* (*•)
275
Матрица коэффициентов aih этого полинома будет иметь вид
G00 Q01| G02 аоз| a0i aV5 °0б| • • • °10 I G11 °12 °1з| аи °1б|.............
G20 G21| G22 G£3 °24 |.................
°30 °31| °32 °3з1......................
ai0 а41 °Дз1...........................
G50 °51 |..............................
Geol...................................
(V.l 43)
Три коэффициента этой матрицы в верхнем левом углу, очевидно, будут соответствовать смещению тела как целого жесткого при напряжениях, равных нулю, поэтому они не представляют интереса и могут быть опущены.
Средняя очерченная область коэффициентов уже будет давать напряжения, отличные от нуля. Эти коэффициенты могут быть выбраны совершенно произвольно, так как эта часть полинома тождественно удовлетворяет бигармоническому уравнению (V.70).
Правая область матрицы также дает напряжения, отличные от нуля, но ее коэффициенты уже должны удовлетворять определенным соотношениям, лишь при соблюдении которых эта часть полинома (V.142) будет удовлетворять уравнению (V.70). Например, ограничиваясь случаем выписанного треугольника коэффициентов матрицы, мы будем иметь 6 таких условий:
3^04 + G22 + Зпао = 0;
5Qoo + g32 + Gu = 0;
5^05 + G23 + G« = 0;
5сь1 + За33 4- 5а15 = 0;
15aoe + а42 4- 2ам — 0;
15о6С 2а42 4- а24 ~ 0.
(V.144)
С учетом дополнительного слагаемого (V.142) функции (V.71), ограниченного выписанным выше треугольником коэффициентов полинома, полные напряжения и смешения тела в случае его плоского обобщенного напряженного состояния, рассмотренного в § V.3, будут выражаться следующими формулами при обязательном соблюдении условий (V.144):
ох (/) = аЕ (0 Т (/) [2а02 4- 6ссз// + 12<W 4- 20о05^ 4-4- 30aO6f/4 4- 2а12л 4- 2а22л2 4- 2а32х3 4- 2aasx4 4- 6а13лч/ 4-4- 12а14лт/2 4- 20а15>У 4- 6а23х2// 4- 12амхУ 4- 6а33х3// —
276
— (о + bx) Y* (y)+ j [ fn (y) — (f/)J cosM 4-
+ S [ ф’п (У) —<h„ (f/)] sin b)nx ); (V. 145)
(t) = аЕ (0 T (f) {2^20 + 2a21y + 2a+ 2 a23y3 4-
4- 2a24t/4 + 6ago* 4- 12a40x® 4- 20a5Oxs 4- 3Oaeox4 4-
4- 6a3ixy 4- Ca^xt/2 4- 6а33лт/3 4- I2a41x2y 4- 12a42x2y2 4-
4- 20а51Л/ — g (a 4- bx) — £ X2 [/„ (y) — ?3n (t/)j cos V ~
— Ё <•£ [<Pn (У) — <P4n (!/)] sin ): (V-146)
by (0 = — aE (0 T(t) {аи 4- 2a12y 4- 3a13t/ 4- 4altys 4- 5a13f/4 4-
4- 2a21x 4- За^л2 4- 4a41x3 4- Se^x* 4- 4a22xj/ 4- 6a23xy2 4-
4- Ъа^ху3 4- 6a32x2y 4- Oa^f/2 4- 8a*x*y 4-
4- b f Y* (y) dy— £ Xn [/; (у) — (у)] sin X„x -|-
y n=l
+ jf<on [ 4>n (y)—44n (£)] cosЬ>пх ]; (V. 147)
a (/) = aT (Г) {2л [a02— va20 4- (3a03 — va21) у 4-
4- (6a«)4 — va^f/2 4- (10au6—va23) ys 4- (15aCe — va21) y* 4-+ -y (Gi2 — 3va30) x+ -1- (a22 — 6vaw) x2 4- -J- (aK — 10va50) л3 | + -y (c42 — 15vae0) x4 4- -1 (a13 — va3l)xy 4- (2aw — va32) xy2 4-
4- у (10a15 — 3va33)xf/34- (a2s — 2va41) x2y 4- 2 (a£4 — va42) x2if 4-
+ (3as3— 10va51) x3y] — I3aso 4-2(14- v)a12] y2 —
— Ia31 4- (2 4- v) a13] if — -j- la32 4- 2 (2 4- v) a14] y' —
~~^[^зз+ 10(2 4-v)a15]^4-(l 4-v)g(ax4-^)~ y н
- (1 4- V) b J [ [ Y * (y) dy 4- 2 J Y * (y)dy] dy + b, + b3y +
277
+ S [77 (/n (У) - <h„ (у)) + (/n (y)-<p3n (y))j sin X„x-
— S [~ К ~ %n &))+VU)n ( Фп 0/) — ?4n (y)) ] <»nx J ; (V. 148)
v (f) = uT (!) |2f/ |a20 — vaC2 4- (a21 — 3va03) у +
+ у (a22 —6vaM)^ 4- ^(сгз~ IO^oJ!/3 4-
4- -y (a24 — 15veoe) у* 4- (Зада — val2) t 4- (6a4O — va22) x2 4-
-i- (10aM — vas2) xs 4- (15c60 — va42) x' + (a34 — va13) xy 4-
+ (a32 — 2vci<) Xlf + -у (З033 — 10vc15) xt? 4-
4- (2a4I — vfl2s) x2y 4- 2 (a42 — va24) x2if 4-
4- у (10adl — Згой) x^y ] — [3o03 4- (2 4- v) c2I] x2 —
— 1^13 4- (2 4- v) o31] x9 — ± [o23 4 2 (2 4- v) g41] x* —
-yj [Зп33 4- 10(2 4-v)asl] x3 4-(1 4-v)(a4-M J y4‘j)dy +
4- b2 + btx + £ [ ± (/; (y) - (!/))-
-(2 4- v) (fn(y)~4in(y)) )cosX„x 4-
4- У, [ Jr « (!/) - (!/)) - (2 4- v} («j,;, (у) — (у)) J sin % x J.
(V.149)
Входящие в формулы (V.148), (V.149) постоянные b\, b2, b3, bA определяются из условий закрепления тела в ирос1ранстве как целого жесткою, при этом должно соблюдаться условие
b3 + ^4-(1 4-v)au = (>. (V.150)
Таким образом, произвольно распоряжаться постоянными bt, b2t b3, b4 мы не можем.
278
Всего в формулах (V.145) —(V.149) мы имеем 25 постоянных А„, Вт,, С„, Dj,, Fn, Gn, Рп, Qn и altt, из числа которых, в силу условий (V.144), только 19 независимых. Распоряжаясь ими должным образом, мы сумеем полностью удовлетворить граничным условиям на продольных кромках тела и приближенно выполнить условия на торцовых (поперечных) кромках с большой степенью точности, значительно большей, чем это обычно получается.
Это увеличение точности решения получается, например, в случае свободных торцовых кромок за счет того, что в силу большого числа постоянных мы можемснять на них напряжения с точностью до их главного вектора и главного момента не только в пределах всей высоты этих кромок, но и в пределах их отдельных участков, а также строго снять эти напряжения в ряде их характерных точек, в которых они должны быть равны нулю при точном решении задачи. Кроме того, удается повысить и практическую ценность решения (V.71) в случае, когда используется ограниченное число членов ряда в нем.
Связанные с этим практические приемы рассмотрим ниже в § VI.7, 8 на конкретных примерах.
§ V.5. ОДНОМЕРНАЯ УПРУГО-МГНОВЕННАЯ ЗАДАЧА ДЛЯ БЕСКОНЕЧНОГО ПОЛУПРОСТРАНСТВА
Исследуем одномерную упруго-мгновенную задачу для бесконечного полупространства, имеющую место при вынужденных деформациях, заданных в формуле (V.40):
(/) = е° (/) at0 (t, z); |
— О, ( (V15I)
т. е. в случае, когда е°(/, г) зависит только от времени и только от одной координаты г, отсчитываемой от поверхности слоя вглубь.
В рассматриваемой задаче по условиям симметрии равны нулю все деформации сдвига и касательные напряжения. Кроме того, должно быть равно нулю нормальное напряжение ог(/), так как граничную поверхность слоя 2 = 0 мы будем считать незагруженной. Наконец, из условия безграничности слоя и постоянства напряжений и деформаций вдоль осей х и у горизонтальные напряжения ох(/) и cv(t), а также деформации fx(Z) и должны быть инвариантными относительно координат х и у и полные деформации вдоль этих осей к тому же должны быть равны нулю. Все эти рассуждения приводят нас к уравнениям:
У,у (0 = Y« (0 = ytJi (0 = (/) = (t) = 0; 1
ТХ„ (П = тдг (t) = туг (!) = о2 (t) = 0; J (V-152)
Од (0 = о„ (0 = о (Z, г) = - е® (/, z). (V. 153)
279
Нетрудно убедиться в том, что при напряжениях и деформациях, заданных в форме (V.151) — (V.153), уравнения равновесия (V.8), совместности (V.6) и закона Гука (V.4) тождественно хдовлетворяются; последнее из них, кроме того, дает
ег (t,z) = а ('.*)• (V.154)
Наконец, из уравнений (V.7) находим:
и (0 х - v (0 = 0; w (t,z) - а ( J е® (/, г) dz. (V-155)
Уравнения (V.152) — (V.155) полностью определяют напряженно деформированное состояние слоя при заданном законе его вынужденных деформаций (V.I51). Из их рассмотрения следует, что напряжения и деформации в слое пропорциональны этим вынужденным деформациям и получаются умножением последних на соответствующие множители, величины которых ясны из формул (V.153) и (V.154). Отметим, что в рассматриваемом случае мы имеем следующие очевидные равенства:
6 (t, z) = а Е° (Л ^); S (/, г) = — е° (/, z). (V. 156)
§ V.6. ОДНОМЕРНАЯ УПРУГО-МГНОВЕННАЯ ЗАДАЧА ДЛЯ ПРЯМОГО БРУСА
Рассмотрим наконец одномерную упруго-мгновенную задачу для прямого длинного призматического прямоугольного бруса при его вынужденных деформациях, заданных в форме:
й.<0 = = 1
eJ(O-e;(O = £»(<) = (о+ МТ(0, |
где а и b — некоторые константы, а г отсчитывается вдоль оси бруса от его левого торца. В этом случае линейного распределения вынужденных деформаций вдоль длины бруса удается найти точное решение упруго-мгновенной задачи, удовлетворяющее строго ее граничным условиям.
Действительно, применяя обратный метод теории упругости, найдем, что уравнения равновесия и совместности будут тождественно удовлетворены, если положить:
г,,(О = г„(О-т„(0 = аЛО = «ДО = О; 1
M0-CE(OTW. |<V158)
После чего, пользуясь законом Гука (V.4), сразу находим:
Yxz(/) = Yxy(0 = YyJ0=0; ]
ex(0 = ^(0 = -vCT(0-|-a(e + te)T(/); (V.159)
ei(0 = CT’(/) + a(a + M7’(0. J
280
Далее, применяя обычные приемы, с помощью уравнений (V.7) найдем перемещения точек бруса:
и (/) = [а (а + bz) — vC| лТ (/);
v(0 = [а (а 4- bz) — vC] уТ(/); (V. 160)
w (t) = |С-Ь а (о + z zT\t).
При этом предполагается неподвижно закрепленной в пространстве точка бруса x=z/=z=0.
Формулы (V.158) — (V.160) полностью определяют напряженно деформированное состояние бруса с точностью до произвольной постоянной С. Эту постоянную мы определили из граничных условий.
Из формул (V.158) следует, что боковая поверхность бруса полностью свободна от напряжений, поэтому обратимся к его торцам.
Если брус имеет свободу продольных перемещений, то равнодействующая напряжений ог(0, а следовательно, и сами напряжения должны быть равны нулю. Поэтому в этом случае С=0 и, следовательно:
еЛ (0 = (0 = ег (/) = а (а + bz) Т (f); (V. 161)
G (0 - За (а + bz) Т (/); (V. 162)
u(t) = a(a + bz)xT(t)-,
v(t) = a(a + bz)yT(t); (V.163)
иу(0=а(а + ^-z ^T’(Z),
т. е. брус остается ненапряженным и неискривленным; но отдельные его точки испытывают перемещения (V.163), связанные с расширением и удлинением бруса.
Если брус закреплен от продольных смещений, то его длина I остается неизменной, поэтому
\ez(t)dz = w(l) -0. (V.164)
о
Это дает нам
С=-а(а+А/ ). (V.165)
После чего в рассматриваемом случае имеем:
(t) = - а (а + I ) Е (0 Т (/); (V. 166)
ех(0 = %(t) = 1(а + ) v + {а + bz) 1 аТ^/); 1
ab (V. 167)
ег(0 = - ^-(l-2z)T(t)-,
281
u(t)= + -у I ) V + (a + bz) j aT(t)x-,
vlf) = [(a 4- у I ) v + (a 4- bz) J aT(t)y;
w(t) = ~a±-T(t)(l-z)z.
(V.168)
Таким образом, в этом случае при T(t)>0 в брусе возникает равномерное сжатие, но он по-прежнему остается неискривлен-ным, испытывая расширение вдоль осей х и у и сгущение вдоль оси г без изменения своей длины. Последнее, как это следует из второй формулы (V.167), приводит к деформации сжатия бруса на его участке 0 < z < -у и деформации растяжения на второй
I половине его длины .
2
Отметим, что в рассматриваемом случае мы будем иметь:
е (t) = a [a (1 + 2v) 4- ь (v/ - 4 + *)} T(/); (V.169)
S(0 = -a(a4- -у* (V17°)
ГЛАВА VI
НЕКОТОРЫЕ УПРУГО-МГНОВЕННЫЕ ЗАДАЧИ О ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ
В сопротивлении материалов и теории упругости рассмотрено большое число задач о температурных напряжениях в брусьях, плитах, оболочках и объемных телах. Наиболее интересные исследования принадлежат: А. В. Белову [31], [33—35]; С. Г. Гутману [75, 76], Г. Н. Маслову [117, 118, 119]; В. Г. Орехову [142, 143] и ряду других авторов. Соответствующие классические задачи рассмотрены в курсах теории упругости, а также в ряде специальных монографий Б. Г. Коренева [101], Н. Н. Лебедева [103], В. М. Майзеля [121], Э. Мел а на и Г. Паркуса [122, 147].
На основе этих готовых решений могут быть сконструированы указанным в § IV.9 способом решения соответствующих упруго-мгновенных задач.
Поэтому нет необходимости их здесь подробно выписывать. Ниже рассматриваются лишь некоторые важные упруго-мгновенные задачи, в решения которых удалось внести уточнения или дополнения.
Температура тел в общем случае в этих решениях предполагается изменяющейся по закону
Ф (х, у, z,t)^T (I) X (х) Y (у) Z (г), (VI. 1)
т. е. с одинаковым масштабом во времени для всех точек тела. В главе I мы видели, что в таком виде обычно находят решения задачи теории теплопроводности. Эти решения получаются в виде ряда по произведениям функций, подобным (VI.1), поэтому достаточно исследовать именно этот случаи.
Более общее решение задачи может быть получено всегда суммированием соответствующих ее простейших решений, аналогичных тем, которые мы сейчас рассмотрим.
§ VI.1. НАПРЯЖЕНИЯ В БЕСКОНЕЧНОМ ПОЛУПРОСТРАНСТВЕ ПРИ НЕРАВНОМЕРНОМ ИЗМЕНЕНИИ ЕГО ТЕМПЕРАТУРЫ
ПО ГЛУБИНЕ
Исследуем составляющую температурных напряжений в бесконечном полупространстве в предположении, что температура слоя изменяется лишь по его глубине и во времени по закону
283
&(z,t)=T(t)Z(z). (VI.2)
Полагая в формулах § V.5
е° (/, z) = Г (/) Z (z), (VI.3)
в рассматриваемом случае найдем следующие формулы для напряжений, деформаций и смещений точек слоя:
«»(<) = %(0=«(<) = T(/)Z(Z); | (vt4>
Yxy (') = Yjrz (0 = Ууг (0 = Ex (0 = ty (0 = 0; |
е2 (0 = е (0 = а ) Т (О Z (z); | (VL5)
а(/) = о(/) = 0; 1
“'W=а (ттт)7’(Z)f Z(z)dz- J (VI6) Кроме того, будем иметь
0(/,z) = а (l±I)Ta)Z(z); (VI.7)
S (t, z) = - T (/) Z (z). (VI .8)
Например, в случае гармонических колебаний температуры поверхности слоя по закону
<р(/) = 4nsin<onf (VI.9)
изменение температуры его точек, как известно из теории теплопроводности [93], определяется выражением
Ф (t,z) = Ап е~1«г Sin (unt- lnz), (VI. 10)
где ______
ат — коэффициент температуропроводности материала слоя. Поэтому, пользуясь формулами (VI.4) и (VI.5), напряжения и деформации слоя найдем в следующем виде:
С (/, z) = — Ane~>nZ sin ((О,/ — xnz);
/1+?\ -).z
e (Л z) = a n siп (ы„/ — X„z).
Из этих формул следует, что напряжения и деформации слоя будут также гармоническими функциями с амплитудами, неограниченно затухающими с глубиной.
284
Решение рассмотренной задачи имеет практическое значение для расчета расстояний между температурными швами (надрезами) в массивных бетонных сооружениях с открытыми поверхностями большой площади, подверженными воздействиям температуры воздуха. Эта задача рассматривалась с указанной целью П. И. Васильевым [51, 52] и А. Р. Ржаницыным [159].
§ VI.2. НАПРЯЖЕНИЯ В ПРЯМОМ БРУСЕ ПРИ ЛИНЕЙНОМ РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ ВДОЛЬ ЕГО ОСИ
Рассмотрим напряженно деформированное состояние призматического бруса длиной I с прямоугольным сечением в случае, когда изменения его температуры заданы в виде
<D(t,z) = (a + bz)T(t). (VI. 12)
С помощью формул § V.6 в этом случае найдем следующие выражения для напряжений, деформаций и смещений бруса:
а) если торцы бруса свободны от закреплений:
МО = МО = = МО = оДО = МО 0; (VI. 13)
Уху (0 = Ухг (0 = Yyz (0 = 0; | (V1.14)
(0 = (0 = Ъ (0 = е (0 = a (a +bz) Т (/); J
и (I) = а (а + bz) хТ (/);
v (/) = а (а + bz) уТ (0; . (VI. 15)
щ(0=а(а+ -^-z ^zT(t)-,
б) когда торцы бруса закреплены от продольных смещений: (') = Ъг (0 = ту2 (t) = (0 = оу (/) = 0; ]
М0 = ~« (Q + -yZ )£(07’(0; | (VI16)
Yxy(0 = YM0 = Yyz(0 = 0;
МО = еу (0 = [(а + у I } v + (о + bz) ]аТ(0;
М0 = ~ ^-(/-2г)Т(0;
н(0= [(°+ )v + (a4-M ]аТ(0х;
»(0= [(a+TZ + +
w{t) = —a-LT(t)(l~z)z.
(VI.17)
(VI. 18)
285
Анализ напряженно деформированного состояния бруса дан в § V.6, где показано, что в обоих случаях брус остается прямолинейным.
§ VI.3. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ПРИЗМАТИЧЕСКОМ БРУСЕ СО СВОБОДНЫМИ ГРАНЯМИ ПРИ НЕРАВНОМЕРНОМ РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ ПО ЕГО СЕЧЕНИЮ
Исследуем температурные напряжения в длинном прямоугольном призматическом брусе сечением 2х0х2^0 с продольными гранями, свободными от напряжений при изменении его температуры по закону:
Ф(х, y,t) = T(О F (х, у), (VI. 19)
аналогичному (VI.I). Точное решение этой задачи на основах плоской задачи теории упругости, как это, например, показано в § V.2, требует интегрирования уравнения
vV<P (*, у. О = - V20 (X, у, /) (VI .20)
при граничных условиях:
при »= ±9й
допрИх^±х,;
ду2
А Я ~ ' 0 ПРИ Х = 212 А'°: ± ^0-
(VI.21)
В работе [5] показано, что эта задача аналогична задаче о прогибах тонкой пластинки того же очертания, что и поперечное сечение бруса, с цилиндрической «жесткостью»
D = -1^ , (VL22)
загруженной поперечной «нагрузкой»:
9(х, y,t) = ~E (/) (х, у, t)
(VI.23)
и жестко защемленной по контуру. Точное решение ее неизвестно, поэтому приходится довольствоваться приближенным решением.
Такое приближенное решение, например, может быть получено по вариационному методу Б. Г. Галеркина. Таким путем оно было найдено Г. Н. Масловым [118], а затем в более общем виде А. В. Беловым [35]. Нам предстоит лишь его обобщить на случай произвольно заданной температуры в форме (VI. 19) н переменного модуля упругости Е(1).
286
Будем искать функцию напряжений <р(х, у, t) в следующем виде:
Ф (х, y.t) = - Т (О Р (х, у).
1 — V
(VI.24)
Тогда с учетом (VI.19) и (VI.20) для функции Р(х, у) будем иметь уравнение
У) = ^2F{x,y) (VI.25)
и граничные условия
= 0 при у = ± £/0; = ° при х = + х0; *^--0ПрИХ=±хо; j,= ±ifc (V1.26)
Зададим функцию Р(х, у) в виде полинома
Р(х, У) = (xl — Xi)2 (у2 — у2)2 £ £ alkvyk, i=0 Л=0 (VI.27)
где aih — пока произвольные постоянные. Нетрудно убедиться в том, что функция Р(х, у), заданная в таком виде, автоматически удовлетворяет граничным условиям (VI.26).
Для определения постоянных aift воспользуемся методом Б. Г. Галеркина. Подставляя (VI.27) в (VL25) и умножая полученное равенство последовательно на (х2—х2)2(у2—aihx ,ук и интегрируя его затем в пределах от —х0 до хс и от —у0, до ус, получим надлежащее число уравнений для определения постоянных aih.
Ограничиваясь тремя первыми членами ряда (VI.27), будем иметь:
Р(х,У) = (*г— *о)2 — 4/о)2 (аоо + + °oi*' )• (VI.28)
Внося (VI.28) в (VI.25), получим уравнение
Чх Р (Й - Й)’ + 4 (Зй - Й) (3*! - Й) + 3 (^ - ЙГ] + + ою х [15 - й)2 + 4 (&/ - й) (5Х2 - Эл® + 3 (х2 - х2)2) +
+ Ч«!/Р(Й-Й)2 + 4(3*8-Й)(5Й-ЗЙ) + 15 (х2 - х2)2| =
= (•».») (VI.29)
Применив указанный выше прием отыскания коэффициентов flih, найдем:
287
1575 J J V2 F (x, y) (x2 — roy (y2 — dx dy
2205 J J V2F(x, y) p—^)2(l/2—t^yxdxdy
(VI.30)
2205 J J v2F (x.y) (x2-^)2 (y2-^)2 ydxdy
Тем самым функция Р(х, у) будет полностью определена.
С учетом (VI.24) и формул (V.34) найдем напряжения в призме в следующем виде:
а (/) = _T(t)д2-{х' У}; 1—v дуг
оУ(0
т ,0=«<ОГ(0Щ^. '’V' 1-V " дхду
г_________ . -____-,... : .
E,m=o(i+v) ?(/) {f(x, 9)_ у)]);
e//)=a(l+v)T(0{F(x, у)---^Лх.у)]};
После чего для деформаций призмы будем иметь формулы:
Например, в случае (VI.28):
°- ('>=- т (0 4 ~w I °” <зи ~ +
+ У.., (Зу* - $ + % У (Sir - ЗУ?)];
о, Г (0 4 (у2 - у’)= [ ам (Зх® - лЭ +
+ а10 х (5л® — Эх’) + Оц1 у рл _ Х2)];
Тжу (0 = Т (i) 4 (X2 - х2) - У2) [4aw ху +
+ а10 у (бх2 - х2) + gw х (5/ - $].
(VI.31)
(VI.32)
(VI.33)
288
Кроме напряжений (VI.31) в брусе будут еще действовать напряжения оДО
Если торцы бруса полностью защемлены, то эти напряжения равны
ог (0 = v кг (0 + оу (01 - «Е (0 Т (О F(х, у). (VI.34)
где оЛ(0 н а„(О определяются по формулам (VI.31).
Если же торцы бруса свободны, то главный вектор и главный момент напряжений о-(0 в любом сечении призмы должны быть равны нулю.
Учтя это, в соответствии с изложенным в § V.2, найдем:
о2(0 = v К(0 + 0У(01 +<iE(t)T(t) [А+ Вх +
+ Cy — F(x,y)],
где
А - у- J J F(x,y)dxdy;
В=Т$ S E(x,y)xdxdy;
V -Хс —Уо
(VI.35)
(VI.36)
С = у- j j F (х, у) ydxdy.
Здесь Fo — площадь поперечного сечения бруса, a Jx и Jlt — моменты инерции этого сечения относительно его главных центральных осей.
Эффективность рассмотренного приближенного решения зависит от степени его сходимости. Г. Н. Маслов [118] исследовал ее для случая симметричного распределения температуры 1
Ф(л,£/,/) = Т(0со§ — с<Д (VI.37)
2*'о "{/и
и нашел, что разница в величинах напряжений, вычисленных при учете одного и трех членов ряда, соответствующих симметричному виду функции (VI.27), не превышает 8—10%. Таким образом, вполне достаточно ограничиться малым числом членов ряда (VI.27), а именно: одним членом, соответствующим коэффициенту Доо, в случае симметричного распределения температуры
1 В таком виде получается решение задачи теории теплопроводности об симметричном остывании бруса. См., например, главу I настоящей работы.
289
относительно обеих координатных осей; двумя членами ряда, соответствующими коэффициентам аоо и “ю. при симметричном распределении температуры только относительно оси оу и тремя членами ряда с коэффициентами аоо, сю, о0| в общем случае несимметричного распределения температуры.
В частности, Г. Н. Маслов [118] при симметричной функции Ф(х, у, t), заданной в форме (VI.37), при E(t)=E0 и Т(/)=7’о на основе одного первого члена ряда нашел следующие формулы для напряжений:
и показал, что при разогреве бруса наибольшие растягивающие нормальные напряжения возникают в середине более длинной стороны копира поперечного сечения и равны, например, при х0=2у0 0,78 . При этом брус вытянутого сечения оказыва-
ется более напряженным, чем, например, брус с х0=у0, у которого соответствующие напряжения были равны всего 0,59°Г-£о.
А. В. Белов [35] дополнил этот анализ и показал, что также велики, и даже несколько больше, напряжения ог, действующие вдоль ребер бруса. Поэтому при разогреве, например от экзотермии, в нем могут появиться продольные трещины в середине более широких граней и поперечные трещины, надрезающие его ребра, причем появление последних даже более вероятно.
290
§ VI.4. НАПРЯЖЕНИЯ В ПРИЗМАТИЧЕСКИХ ПРЯМОУГОЛЬНЫХ БРУСЬЯХ ПРИ ИЗМЕНЕНИЯХ ИХ ТЕМПЕРАТУРЫ, РАВНОМЕРНЫХ ПО ДЛИНЕ
И НЕРАВНОМЕРНЫХ ПО ВЫСОТЕ БРУСА
Рассмотрим прямой призматический прямоугольный брус с высотой поперечного сечения A/=2z0 (рис. 64) и исследуем температурные напряжения, возникающие в нем при отсутствии поверхностных и объемных сил при изменении его температуры по закону
(VI.39)
Ф (z, t) = T(t)Z(z).
Для удобства в дальнейшем координатные оси направили так, как это показано на рис. 64. Иными словами, исследуем случай
Рис. 64
изменения температуры бруса с одинаковым масштабом во времени для всех его точек равномерно по длине и ширине, но неравномерного по его толщине.
В гл. I мы видели, что в таком виде часто находятся решения одномерных по координатам задач теории теплопроводности.
Практическая ценность такого решения очевидна. Например, в таких условиях, с точки зрения распределения температуры, или близким к ним находятся элементы каркасных стен и другие подобные им конструкции, у которых преобладает тепловой поток в одном направлении.
Не налагая пока никаких ограничений, подобных гипотезе плоских сечений, применим обратный метод решения задач теории упругости и зададим напряжения в брусе в следующем виде:
(0 (0 = ryz (0 - ог (0 = 0;
о> (0 = [Q 4- Сл - Z(z)];
0>(0 = [Сз + г— Z(z)],
(VI.40)
где С], С2, С3, С4 — некоторые пока еще произвольные постоянные. Нетрудно убедиться, что эти напряжения тождественно удовлетворяют уравнениям равновесия (V.8) и совместности (V.26), поэтому это решение будет общим, если с помощью пос
291
тоянных Ci, С4 нам удастся удовлетворить граничным условиям задачи.
Напряжениям (VI.40), как нетрудно установить с помощью уравнений (V.23) и (V7), соответствуют деформации:
Yxy (0 = YJZ (0 = Y*.- (О = 0;
® - TZ7- vC«+~ vC^ 21;
(° = Т=7[Cs ~ vC1 + (С‘ - vC?2) z]: (VL41)
Ъ (/) = ~ {v [Q + Сз + (С* + С*}
и перемещения:
“(0 = ^-[G-vC3 + (C2-vC4)z]x;
v & = TZ71е* ~ vCi + <?* ~ vC=H у>
~ [<ci + сз)г + т +
+ -^(c2-vc4)^ + A(C4_^2)^_!±YjZ(z) dzj.
(VI.42)
Из выражений (VI.42) следует, что независимо от вида функции изменения температуры (VI.39) и граничных условий бруса, перемещения u(t) и v(i) являются линейными функциями от г, следовательно, его вертикальные сечения x=const и f/=const все время остаются плоскими.
Перейдем теперь к рассмотрению граничных условий.
Из уравнений (VI.40) следует, что грани бруса г=±г0 свободны от напряжений, а напряжения сх(1) не зависят от координаты х, поэтому снять их на боковых гранях строго не удается. Следовательно, можем снять на этих гранях лишь главный вектор и главный момент напряжений оЛ(0- Для этого достаточно определить постоянные С! и С2 из условий
J оА. (0 dz = J оЛ (0 zdz =-- 0, (VI.43)
——г»
что даст
f Z(z)dz, C2 = 4f Z(z)zdz. (VI.4-1)
2го J 2г3 J
-До ° -До
Постоянные С3 и С4 подлежат определению из граничных условий на торцах бруса.
292
При свободных торцах, не закрепленных от поворотов и смещений, должно быть
J cy(t)dz = J ov(/)zdz-0. (VI.45)
—Zr —Zu
Эти условия дают нам:
С3 = СА; С4 - С2, (VI.46)
где Ci и С2 определяются по формулам (VI.44). Таким образом, в рассматриваемом случае
М0 = <М') = ^ +^г-^-Ф(2,0, (VI.47)
где
F
M(t)=<^^&(z,t)zdF
(VI.48)
— некоторые фиктивные продольная сила и изгибающий момент, приложенные, к торцам бруса, a F и J — соответственно площадь и момент инерции поперечного сечения бруса относительно его горизонтальной центральной оси.
Деформации, отличные от нуля, и смещения бруса будут
равны:
“-тйгНг1+-Т
1-у I ЛЧО . M(t) [ f J
(VI.49)
« (Z) =-.
v(0=._ _L2L(2L(O_ ЖП V E(t) [ F J
(VI.50)
(VI.51)
W = - 2 +
Угол поворот? сечений бруса:
Ф(0=^..-±=21. ЛЦО у
4 д? E(t) J
Перемещение v(t) осевой линии у торцов бруса и угол поворота <р(/) его торцовых сечений будут равны:
и(0- ф(/)_ (VI.52)
' E(t) F ’ 44 ' E(t) J V ’
293
Прогиб осевой линии бруса:
(VL63)
Перемещение концов осевой линии бруса по отношению к ее средней точке равно
«-(d (VIS4)
|у= + 1 Zt {•) J
Для верного толкования выведенных здесь формул следует условиться о знаках температурных воздействий (знаках фиктивных продольной силы N(t) и изгибающего момента M(t) и способе закрепления бруса в пространстве, как целого жесткого. В этих формулах и дальше всюду принято:
1) положительные фиктивные силы N(t), M(t) соответствуют случаю равномерного разогрева (удлинения) бруса и большему нагреву его нижних волокон (изгибу выпуклостью в положительном направлении оси г) соответственно;
2) неподвижно в пространстве закреплена точка бруса с координатами х=0; у = 0\ 2=0.
В связи с последним обстоятельством прогибы осевой линии бруса, определяемые по формулам (VI.53) и (VI.54), при положительном фиктивном моменте M(t) всегда отрицательны.
При торцах бруса, имеющих свободу поступательных продольных перемещений, но закрепленных против поворота, должно быть
j cv(t)dz = 0;
Из этих условий следует:
С3 - Сь
Сл — vC2,
(VI.55)
(VL56)
где С, и С2 находятся по формулам (V1.44). В связи с этим будем иметь:
ох (/) = г — & (z, I)- (VI.57)
Oy(t) = 2^_ + 1^)г_^ф(г,0; (VI.58)
ед(/) = ^Г2^ + (1+ч,)^) 21;
А ' Е (/) L F J J
ev(Z)==(lz21.^;
' E(t) F
+(1+V)^ zl;
1—V L (t) L Г J J
(VI.59)
294
"(О-
1 —v N(l) v(t) = ----. — -у,
V ' E(t) F J
(VI.60)
Так как 1 ’ =0, то в рассматриваемом случае первоначально прямолинейный брус сохраняет свою прямолинейную форму п после изменения температуры.
При полностью защемленных торцах должно быть
v(d =^| =0. (VI.61)
1у=.‘.1 дг |у=±/
Это дает нам:
C3 = vCi; C4 = vC2. (VI.62)
Поэтому:
Ол(/)=^ + «£>г_2££!ф(г,0;
s-w=^[T+i!r-zH('>-0;
..0 = £аФ(г,0-[^+ «<'> ф
+ т(г. + Ь^.
(VI .63)
(VI.64)
(VI.65)
В настоящем примере, так же как и в предыдущем, смещения v(t) не зависят от г, поэтому, независимо от вида температурной функции Ф(г, /), первоначально прямой брус остается прямолинейным и после температурного воздействия.
Возможны и другие граничные условия для бруса; решения для них могут быть получены аналогичным образом, и мы их здесь уже рассматривать не будем.
295
В заключение отметим, что Г. Н. Маслов, рассмотрев настоящую задачу [119] с учетом гипотезы плоских сечений при постоянном модуле и стационарном тепловом режиме, получил для напряжений и перемещений бруса следующие формулы, отличные от тех, которые были получены выше:
а) для бруса со свободными торцами:
= (1 — v) (-у 4- -у z) — аЕ Ф (z);
v
(VI.66)
-.-If,
2Е
где N и М определяются по формулам (VI.48) при Е= const и Ф-Ф(г);
б) для бруса с жестко защемленными торцами:
су = — аЕФ(z); v = 0. (VI.67)
Сравнивая эти формулы Г. Н. Маслова с соответствующими формулами (VL47), (VI.50) и (VL63), (VI.65), видим, что формулы для перемещений с точностью до знака у прогибов оси бруса w совпадают1.
По-иному обстоит дело с напряжениями. Для них сравниваемые формулы дают совпадающие результаты только при линейном распределении температуры по закону
Ф(а)=Ф0(1 +az), (VI.68)
в этом случае свободный брус оказывается ненапряженным: (ox=Oi/=0) и лишь искривляется по параболе
te’|v=r -o = у аФ0 аУ^ (VI-69)
а брус с полностью защемленными торцами остается прямолинейным, но испытывает лишь напряжения (о*- = 0)
<т„--аЕФ0(1 + аг). (VI .70)
При произвольном (нелинейном) распределении температуры сравниваемые формулы дают уже существенное расхождение в величинах напряжений.
Для свободного бруса напряжения, вычисленные по формуле Г. Н. Маслова (VI.66), меньше в j— раз, т. е. для бетона, например на 25—30%. в зависимости от величины v.
1 При выбранном Г. Н. Масловым положительном направлении вертикальной осн бруса положительный фиктивный момент М вызывает его искривление выпуклостью вниз, поэтому при закрепленной неподвижно в пространстве точке х=</=г=0 прогибы бруса должны быть отрицательными. В связи с этим в формуле Г Н. Маслова для прогибов изогнутой осн бруса (;о|х =г_0 ) стоит неверный знак.
296
Для защемленного бруса разница в напряжениях вычисленных по полученным выше формулам и по формулам Г. Н. Маслова, как нетрудно видеть, равна
А^’(т + Тг) (VI.71)
1» может быть самой различной в зависимости от величин площади и статического момента площади эпюры Ф(г, t).
Таким образом, решение рассмотренной задачи о термоупругом равновесии бруса, полученное в свое время Г. Н. Масловым, дает верные с точностью до знака значения его перемещений и неточные значения напряжений'.
Происходит это потому, что без учета напряжений сх=су решение Г. Н. Маслова не удовлетворяет уравнениям совместности (V.26). Таким образом, например, в случае жестко защемленного по торцам бруса он допустил на его свободных гранях х= = const наличие напряжений их с главным вектором и главным моментом, отличными от нуля, рассмотрев по существу задачу о температурных напряжениях в брусе при неуравновешенных поверхностных силах. В соответствии с этим рекомендуется пользоваться более точными формулами для напряжений, найденными выше.
§ VI.5, НАПРЯЖЕНИЯ В ПЛИТЕ ПРИ НЕРАВНОМЕРНОМ ИЗМЕНЕНИИ ТЕМПЕРАТУРЫ ПО ЕЕ ТОЛЩИНЕ
Рассмотрим плиту высотой 2z0 (рис. 65) и исследуем температурные напряжения, возникающие в ней при изменении ее температуры по закону (VL2).
Именно в таком виде обычно находится решение задач теории теплопроводности для плит, вытяну-
тых в двух направлениях и относительно тонких (см. главу I).
В § VI.4 мы, рассмотрев аналогичную задачу для бруса, нашли ее решение в форме (V1.40), (VI.41), (V1.42). После определения значений постоянных С(, С2, С3 и С4, входящих в это решение, из соответствующих граничных условий оказалось, что оно не содержит в себе размеров бруса в плане и поэтому является одновременно и решением
1 Для перемещений Г. Н. Маслов получил верные формулы потому, что нашел их прямым путем, а не через неточные значения напряжений.
297
соответствующей задачи для плиты той же высоты 2г0, с теми же граничными условиями на боковых гранях. Однако возможные комбинации этих условий у плиты шире и нам придется рассмотреть дополнительно еще некоторые наиболее важные их сочетания.
Итак, для плиты, свободной по всем четырем граням, решение задачи определяется формулами (VI.47), (V1.48), (V1.49), (VI.50). Из последней из формул (VI.50) следует, что при M(t)=f=O плита искривляется по поверхности второго порядка.
Такое же решение получим и в случае, когда две смежные грани боковой поверхности плиты закреплены полностью или частично от нормальных смещений, а две другие противоположные им смежные грани свободны от напряжений с указанной выше степенью точности.
Для плиты с гранями х=const, свободными от закреплений, и с гранями у=const, имеющими свободу продольных перемещений, но закрепленными против поворотов, для напряжений, деформаций и смещений, будем иметь формулы (VI.57), (VI.58), (VI.59), (VI.60). Из последней из формул (VI.60) следует, что в этом случае плита искривляется по цилиндрической поверхности второго порядка с прямолинейной образующей, направленной вдоль оси у.
Такое же решение мы получили и в случае, когда грани i/=const закреплены указанным способом, одна из граней х = = const свободна, а другая закреплена от продольных смещений произвольным образом.
Для плиты с гранями x=const, свободными от закреплений, и с гранями у— const, полностью закрепленными от продольных смещений, решение задачи будет определяться формулами (VI.63), (VI.64), (VI.65).
В этом случае плита также искривляется по цилиндрической поверхности указанного выше вида.
Такое же решение будем иметь и в случае, когда грани плиты r/ = const полностью закреплены, одна из граней x=const свободна, а другая закреплена произвольным образом.
Наконец, в случае, когда вся боковая поверхность плиты закреплена от перемещений по нормалям к соответствующим боковым граням, произвольные функции ...» С4(/) в формулах (VI.40), (VI.41) и (VI.42) следует найти из условий:
и (/) — - “ = 0 на гранях х =- const;
v(i) =. — 0 на гранях у const.
Это дает нам:
(VI.72)
(VI.73)
(VI.74)
298
и, следовательно, тдг(0-т}Л0 = тгу(0-пг(0-0; ]
о,(0 o>(()-a(0--^T(0Z(z); | <VI 75>
Yry (0 ~ У» (П = У(,г (О е* (0 = By (0 = °; )
— | (VL76)
и (/) = о (0 — 0; ]
u,^ = rZ7ar(0JZ(z)d2- ) (VL77)
Из найденного решения следует, что в случае защемленной плиты помимо вертикальных сечений плоскими остаются и ее горизонтальные сечения, независимо от вида функции изменений температуры (VI.39), т. е. плита в рассматриваемом случае, оставаясь плоской, не искривляется, а испытывает лишь сжатие в горизонтальных направлениях напряжениями (VI.75).
Из всех рассмотренных решений вытекает, что независимо от вида закона изменения температуры (VI.39) и граничных условий плиты перемещения и(1) и v(t) ее точек являются линейными функциями от г; следовательно, вертикальные сечения плиты x=const и t/=const все время остаются плоскими.
Во всех полученных решениях фигурируют фиктивные продольная сила и изгибающий момент M(t), определяемые по формулам (VI.48). В этих формулах, так же как и во всех формулах для напряжений деформаций и смещений, под площадью F и моментом инерции / этой площади удобно понимать соответствующие величины, отнесенные к полоске любого поперечного сечения плиты единичной ширины.
Решение рассмотренной задачи для некоторых частных случаев стационарных тепловых потоков при Е=const для плит, полностью защемленных или полностью свободных по всему контуру, было получено Г. Н. Масловым [118].3десь оно обобщено на случай нестационарного теплового потока при переменном E(t), а также даны соответствующие решения для плит с иными граничными условиями.
§ VI.6. НАПРЯЖЕНИЯ В ДЛИННОМ ПРЯМОУГОЛЬНОМ ГЛОКЕ, ЖЕСТКО ЗАЩЕМЛЕННОМ ПО ОСНОВАНИЮ ПРИ РАВНОМЕРНОМ РАЗОГРЕВЕ (ТОРЦЫ БЛОКА ЗАКРЕПЛЕНЫ ОТ ТАНГЕНЦИАЛЬНЫХ СМЕЩЕНИИ)
Исследуем температурные напряжения в длинном прямоугольном призматическом блоке в случае его неравномерного разогрева во времени, но ра номерного от точки к точке. Этому
299
случаю соответствует изменение температуры блока по закону
Ф(/) = 7(0.
(VI.78)
Предположим, что продольная сторона блока у—0 (рис. 66) связана с неупругим основанием таким образом, что все принадлежащие ей точки лишены возможности вертикальных перемещений v и горизонтальных и, а торцы блока, имея свободу горизонтальных перемещений и в направлении оси Ох, лишены возможности вертикальных перемещений v.
Рис. 66
Как было показано выше, для решения такой задачи о плоской деформации длинного блока достаточно рассмотреть задачу о плоском обобщенном напряженном состоянии соответствующего плоского диска.
Эта последняя задача, применимо к указанным выше граничным условиям, для случая E=const и 7=const была решена Г. Н. Масловым [117]. В связи с тем, что опубликованное им решение содержит ряд досадных опечаток, а также ошибки в формулах для произвольных постоянных, приведем это решение в готовом виде, свободное от указанных недостатков и относящееся вместе с тем к случаю переменного модуля £(/) и изменений температуры (VI.78).
Это решение имеет вид:
их (0 = а Е (О Т (0 * 2* [(3/4k 4 Ck 4- 2Х* Bk ij) ch X* n +
4- (3B* 4- Dk 4- 21* Ak i]) sh Ml cosX*B; (VI.79)
cv (0 = аЕ (0 T (t) |Т[(Л ~ Ck - 21* Bk n) chM 4
+ (B* - Dk - 2X* /4* П) sh M] cos M - 11; (VI.80)
tX), (0 - а E (0 T (О? [(B* 4- Dk + 21* Ab л) ch X* n 4-
+ + Ck 4- 2X* B/{ rj) sh X*i)] sin X* £; (V1.81)
300
«(O = a/T(/){(l+v)g+ £ JL|(4A(3-v) +
+ (1 4- v) (Ck + 2ХЛ В* i])) ch XftT] 4-
+ (Bk (3 - v) + (1 4 v) (D* 4- 2Xft Ak л)) sh Ml sin Ц; (VL82)
о (/) = a IT (t) £ ± {[B* (3 - v)4-( 1 4- v) (Dk 4- 2Xft A„ ij)] ch M + *=i
4- M* (3 — v) — (1 4- v) (C* 4- 2Xft Bk i])] sh Xatj} cos В, (VI .83) e
£ = f; ’1=f: (VL84)
Xft= -(2-*-1)п-, (V1.85)
a
A‘~ <.\~v^'lt-|2eh^ + (1+V)X
X(X»nshXrfi-dftrfO—(VI.86)
B„ = ,/Z '.FT-12(1 - v)sh V + (I + v) X
0 4- v) л* Aft
X (2Xftp — 2Хлр. ch X41 4- sh 2Хлр)] ; (Vl-87)
= (-1)^4 Г 2C3-v)_ ch _
* (I4-v)AftAft Г 14-v
— (3 — v) ( sh u 4- ch2 A,* ,u) ~ 2 (1 4- v) l2k u2]; (VL88)
* (14-v)XftAft [14-v
— 2X41 ch V 4- Sh 2Хлц 4- 2Xji]. (VI.89)
В этих формулах:
И = ; (V1.90)
4*"4[ff7di’‘>i‘+4i'+^7]- <VI-91>
На рис. 67, а показаны эпюры напряжений ах для сечений блока £=0; £=0,25; £=0,5; £=0,75 и напряжений ау и тжи для сечения у=г]=0, рассчитанные для случая
»‘=т;т“4’ (VL92)
301
бу при у*0
Рис. 67. Эпюры напряжений в бетонных блоках при равномерном разогреве от экзотермни а- блок с защемленными торцами:---------ау по формуле (IV 80) (цифры D скобках),-а по тон же фор-
муле. но с 1 входящей в нес. разложенной в ряд по cos(цифры без скобок); б — блок со свободными тор-
на основе пяти членов ряда в формулах (VI.79) — (VI.81). Ординаты этих эпюр даны в долях от величины aE(t) T(t), так что истинные значения температурных напряжений находятся умножением этих ординат па aE(t)T(t).
Из рассмотрения рис. 67, а следует, что наибольшие нормальные напряжения возникают в плоскости сопряжения блока с основанием, где они достигают величины, близкой к aE(t)T(t), практически мало изменяясь на всем протяжении шва. Лишь вблизи торцов блока они быстро снижаются, обращаясь непосредственно в нуль на самих торцах х=±1.
Напряжения по подошве блока знакопеременны. При разогреве блока они стремятся оторвать от основания его среднюю часть и прижать к нему приторцовые участки шва, где напряжения Gv достигают наибольшей величины.
Касательные напряжения txv по подошве блока не велики, но по мере приближения к его торцам быстро возрастают, стремясь в крайней точке к бесконечности по мере увеличения числа членов ряда, учитываемых в формуле (VI.81). Это означает, что в этой точке блок испытывает большие местные напряжения, которые приводят к пластическим деформациям материала в этой зоне или локальному нарушению связи блока с основанием.
При разогреве блока на 1° в молодом возрасте бетона, т. е. при
Г(/) = ГС; а=1 • IO 5 (град)-' и £(/) = (1-^2) • 105 к Г/см2, в нем в средней части шва сопряжения с основанием возникнут небольшие напряжения отрыва
Оу~1 • I • 10-5(1-н2) • 105• 0,212 — 0,212 : 0,424 кГ/сл2.
Кроме того, эти напряжения существенно снижаются еще за счет ползучести бетона, поэтому, по-видимому, опасность отрыва блока от основания при его разогреве, например, от экзотермии в молодом возрасте, при хорошем качестве шва невелика.
Как следует из формул (V.79) — (VI.91), в решение задачи с рассмотренными граничными условиями абсолютные размеры блока не входят. Его напряжения, деформации и смещения зависят лишь от соотношения его сторон и не изменяются у блоков с различными размерами, но одним и тем же их соотношением.
Этот вывод остается справедливым до тех пор, пока жесткость блока остается несоизмеримо меньше жесткости основания. В том случае, когда эти жесткости равны или соизмеримы, необходимо учитывать податливость основания. При этом мы приходим к граничным условиям по подошве блока, соответствующим случаю упруго-податливых связей.
Задача о термонапряженном состоянии блока с учетом ползучести при таких граничных условиях различной модификации рассматривалась Б. Л. Абрамяном [I], Н. X. Арутюняном и Б. Л. Абрамяном [26] и И. Е. Прокоповичем [150]. Ими было по
303
казано, что при учете податливости основания напряженно деформированное состояние блока уже зависит от его абсолютных размеров.
Отметим, что в своем опубликованном решении Г. Н. Маслов [117] по неизвестной причине при тех же величинах р и v (VI.92) получил значения краевых ординат эпюры су, равные —0,727, не вытекающие даже из его собственных формул.
§ V1.7. НАПРЯЖЕНИЯ В ДЛИННОМ ПРЯМОУГОЛЬНОМ БЛОКЕ, ЖЕСТКО ЗАЩЕМЛЕННОМ ПО ОСНОВАНИЮ ПРИ РАВНОМЕРНОМ РАЗОГРЕВЕ (ТОРЦЫ БЛОКА СВОБОДНЫ ОТ НАПРЯЖЕНИЙ)
Для иллюстрации метола решения плоской упруго-мгновенной задачи, изложенного в § V.3, исследуем температурные напряжения в длинном прямоугольном бетонном блоке (рис. 66), жестко защемленном по основанию, возникающие в нем при его равномерном разогреве по закону (VI.78).
В § V.2 было показано, что для этого достаточно получить решение аналогичной задачи для тонкого диска. Заменив затем в нем физические характеристики материала a, v и E(t) соответственно на си, vi и Ex(t), вычисленные по формулам (V.41), получим интересующее нас решение. Поэтому рассмотрим в первую очередь задачу об обобщенном плоском напряженном состоянии тонкого диска того же очертания. На ее примере проиллюстрируем метод решения плоской задачи, изложенный в § V.3, V.4, и выясним его преимущества по сравнению с обычными методами ее решения.
Примем для диска следующие граничные условия:
Од (х, у, t) =-- 0 = о
ТдДа-, у, t) = 0 \>(х, yJ) = Q
и (х, у, t)0 о (*. У, t) = о
при х — + I; при у = Н\ при у г Н; при х ± /; при у — 0; 1
при у = 0. I
(VI.93)
(VI. 94)
Учитывая симметричное распределение температуры, напряжений, деформаций и смешений в диске, а также его равномерный разогрев, мы должны в формулах (V.145)—(V.149) положить-
°11 - °12 — °13 — °14 °15 — °30 — а31 — °32
= Озз ai0 = ait = FK = Gn — Рп = Qn -
= Ь = ея=а^Г*(^) = 0;
a - g - 1.
(VI.95)
304
Кроме того, из условий заделки блока следует, что
= =u(Z) = r(/)^0 при х- </ = 0; (VI.96)
дх ду
это дает дополнительно
Ь2 = Ь2= Ь3 = Ь4 = 0. (VI.97)
Теперь обратимся к граничным условиям (VI.93). Для того
чтобы удовлетворить строго первому из i рекомендациями § V.3 положим: них, в соответствии с
. _ (2fe — 1) л Хк п 21 ' 1 , (VI.98)
где
, (2fe—1)л 2 ’ (VI.99)
а также:
«оз «се = 0;
«02+ «гг^2 + ~ 0; (VI. 100)
«оз + «23 р = 0; «04 "F «24 I2 ~ 0»
кроме того, с учетом (V.144) и (VI. 100) должно быть: Зе»» + с-лг + 3cjo ~ 0;
а-з + = 0;
«42 + 2а2« — 0;
15ceo + 2а42 + а24--=0.
(VI.101)
Условий (VI.98), (VI.100), (VI.101) достаточно, чтобы полностью снять напряжения ах(0 на поперечных кромках.
Из всей матрицы коэффициентов aih у нас осталось лишь 12 коэффициентов:
«02» «03» «О4> «20» «21» «22» «23 > «24» а4»г «41» «42» «60, (VI. 102)
ио только 5 из них в силу условий (V.100), (VI.101) независимы. Выбрав в качестве них коэффициенты
«60, «40» «±3, «20 И «21
и положив для упрощения решения а6о=0, исключим все остальные с помощью формул:
«.и - 0; о02 = За4012 ~ 5ас01\ а03 = - а23Г~ (VI. 103)
«22 — I5rtc0/“ Цц = «га» (VI.104)
305
вытекающих из (VI.100) и (VI.101). Кроме того, для удобства в формуле (V.71) примем:
А.- В„„-±-(£>Л-ВД (VI.105)
Z2 7-п
Сп= Bk\ Dr^^-Ak. (V\AM)
После этого для напряжений п смещений будем иметь формулы: од (0 а Е (0 Т (/) {6(1- £2) (at - а2 ч) +
Ч- 2 ((ЗЛk + Ch + 2лй Bk i]) ch Xfti] 4~
! (3Bk [ Dk + 2Xft Ak П) Sh M COS M); (VI. 107) <jv (/) - a E(t) T(t) {2 [a4 -f- 6a, £2 4- i] (ao — 6a2 £2) —
-if (3ax -1) O2)] - 1+ V [(Л * - Ch - 2X* Bk i)) ch 1Л1) +
+ (Bk -Dk~ 2Xft Akij)sh cosХ,Л); (VI. 108) rxy(t) u.E(t)T(t){2t,{2a2£2 - a5 4- 3tj(2a, -цaJJ +
4- + Dk + 2Xft Ak i)) ch Xfti) +
+ (Ak + Ск -1- 2кк Вк n)sh sin ; (VI. 109)
u(t) = aT(/) {2g/ ((З-^^-Дзч)-гц2в1е + a4)-
— vi) (a5 — 2a2 Б2— 3a, i] -f- a21]2) + (1 + v) +
+ S X? K^(3-v)+(l +v)(Cft+ 2MOchM +
+ {Bk (3 - v) + (1 + v) (Dk + 2lh Aki))) sh 1ЛП] sin £}; (VI. 110)
V(/) =. a T(f)(2П / [a4 + 6a, £2+ ~ 4(a3 - 6a2£2) +
+ if (y a21] — a,)] — vt) I (1 — £2) (6a, — 3a21]) +
+ |21 [3a£ - (2 + v) a5] + -1- a2 Z (3 + 2v) +
+ S Yk I(B*(3 ~ V) + (1 1 v) (D/i + 2M Л*)} Ch +
Л=1
+ (^(3-v)-(l+v)(Cft + 2Xfti1BA))shXjti1]cosXA.B). (VI. 111)
306
Эти формулы при щ = a2 = at = a5 = 0; E{t)=E = const и T(t) = = То=const с точностью до пока еще произвольных постоянных Аь, В,., С/{ и Dh полностью совпадают с аналогичными формулами рассмотренного выше в § VI.6 решения Г. Н. Маслова [117]. В них введены безразмерные постоянные
«1 = ; а., = а23/3; at - п20; «5 = «211 (VI. 112)
и безразмерные координаты £ и i] (VL84).
Всего имеем 8 независимых постоянных аь ...» «5, Ah.Di;,
с помощью которых мы должны удовлетворить граничным условиям.
С помощью формул (VI. 107). (VI.84) устанавливаем, что первое из граничных условий (VI.93) тождественно удовлетворено; 2 и 3 из этих условий, а также условия (VI.94) дадут нам четыре уравнения для определения произвольных постоянных, входящих в формулы (VI.107) — (VI.111). После разложения в соответствующие ряды полиноминальных слагаемых, входящих в формулы (VI.108) — (VI.111), эти уравнения получим в следующем виде:
A* (ch 1*|* — 21ji sh 1*ц) 4 Bk (sh 1*|* — 21*j* ch 1/гр) — -C.dlXrf.-D.shirf. + H ir'Ja, [(2-4] + + a, |(M!- 6)>.= + 12] + O) JL + a5-fc 1} „ 0; (VI.113)
>4*(shl*p. + 21*|* ch 1*^) 4- B* (ch 1*|* 4- 21*|*sh l*u) 4-
+ C* sh 1*|* i Dk ch l*fi +
+ (~ I)*'1 {«*[(2 - ^)12- 4] - as A-| = 0; (VI. 114) 4*(3-v) + C*(l + v) 4- (- I)*"' fO1-^ (1 4- 2v -v!2) -
-Д*7Г + ??(-J' V4 = 0; (VI.115)
*-k j
(3 - v) B„ - (1 + v) D„ + (- 1 )•-’ {Л- ( Ц - 2) +
+ [ 4 - 12 (4 - 2)1} - (- ‘E’ X
x£1V2i-(^-2)‘,s = 0- (VI.U6>
В этих уравнениях введено обозначение (VI.90).
30/
Четвертому граничному условию (VL93) мы удовлетворить строго не можем, но у нас осталось еще 4 произвольных постоянных, с помощью которых это можно сделать приближенно, но с достаточно большой степенью точности. Для этого распорядимся ими так, чтобы максимально приблизить приближенное решение к точному
При точном решении должно быть
Чг»(О = 0 при А = ±у = °- '(VI.117)
Это лает нам дополнительное уравнение для определения произвольных постоянных следующего вида:
2 | (- If (В, + D,) + 24а, f ( XJ - 2) - as-i-} = 0. (VI. 118)
У нас осталось 3 произвольных постоянных. Распорядимся ими следующим образом. Разобьем высоту поперечной кромки на три равных участка и потребуем, чтобы в пределах каждого из этих участков равнодействующая напряжений тхуЦ) была равна пулю
mH
\xxy(t)dy = 0 при х = + I. (VI. 119)
пН
Это дает нам еще три уравнения вида:
(- I)*-1 {Л [2 (b sh b - a sh а) - (ch b - ch а)] +
+ Вк ^2 (b ch ХЛ b — a ch a) — -1- (sh 7.kb — shXfta)j +
Ck(ch b — ch 7.k a) + Dky- (sh 7.k b — sh X* a) +
+ (- 1)*"’ pt ~ a2) + Ъ (6 ( X’ - 2) (b - a) -
_ (fc3 _ a3)) + a3 (3 (3X2 _ 8)(b2 _ q2) _ X2 (fc4 _ fl4)) _
(<’-“)]} = 0. (VI.120)
где
(VI.121)
308
соответственно для следующих трех пар значений /и и п:
п 0; т - 1; 1 n=\,tn=2- (VI.122)
л = 2; т =.: 3. J
Выписанных нами уравнений (VI.113) — (VI.116), (VI.118), (VI. 120) вполне достаточно для определения всех произвольных постоянных, входящих в формулы (VI.107) — (VI.111). Эти уравнения образуют собой систему совместных алгебраических уравнений, число которых возрастает по мере увеличения числа учи тываемых членов ряда на четыре единицы на каждый его член. Так, при учете одного члена ряда нужно решить систему, состоящую из 8 уравнений, двух членов ряда — из 12 уравнений и т. д. При современном состоянии вычислительной техники это не вызывает затруднений.
Структура систем уравнений (VI.113), (VI.120) для случая учета пяти членов ряда показана в табл. 35, где черными точками указаны коэффициенты уравнений и свободные члены только отличные от нуля. Эта структура такова, что при осуществлении программы вычисления неизвестных, относящейся к данному случаю учета 5 членов ряда, по системе алгоритма Гаусса попутно можно получить значения неизвестных, относящихся к случаю учета 1, 2, 3, 4 и 5 членов ряда.
Система уравнений, схематически представленная в табл. 35, была решена с учетом соотношений (VI.92) и по найденным значениям произвольных постоянных и формулам (VI. 107) (VI. 109) рассчитаны напряжения в блоке для тех же точек, что и в примере § V1.6. Найденные эпюры напряжений изображены на рис. 67,6, на котором ординаты этих эпюр даны по-прежнему в долях от величины aE(t)T(t).
Из рассмотрения рис. 67,6 следует, что наибольшие нормальные напряжения сжимающие при разогреве блока, возникают в плоскости сопряжения блока с основанием, где они достигают величины близкой к aE(t)T(t), практически мало изменяясь на всем протяжении шва и лишь вблизи торцов быстро снижаясь обращаются в нуль на самих торцах.
Напряжения uv{t) по подошве блока неравномерны и знако-переменны. При разогреве блока они на средней части длины шва сопряжения растягивающие, а у торцов блока — сжимающие. Анализ найденного решения рассматриваемой задачи показывает, что при приближении к торцу блока величина сжимающих напряжений ov(t) сильно возрастает, стремясь в крайней его точке к бесконечности по мере увеличения числа членов ряда, учитываемых в формуле (VI.108). Это означает, что вблизи этой точки блок испытывает большие местные напряжения, приводящие к пластическим деформациям материала.
309
“ Таблица 35
° Структура системы алгебраических уравнений для определения произвольных постоянных Ai„..4s. сц,.. ,а$
i 1 Л Смысл уравнения ч Q ч" С d’ J? ч' CJ а" ч и Q ч: ч CJ а е А
1 2 3 4 тху (0=0 »,н :• (Orfx/=o j При x=±l nH при х=±1;у=0 п=0;/п=1 и=1;/и=2 п=2; ш=3 • • • • • • • • • • • • • •
5 6 7 8 a4(t)=O при y-H Tfy(/)=0 при у=п u(t)=O при у—0 о (0=0 при w=0 К=1 • • • • • • • •
9 10 11 12 <ту(0=0 при у=Н т,у(О=0 при у—Н при у-г-0 «(0=0 при у—0 К=2 • • • • • • • •
• • •
. . > . . . . • •
• • • •
. . • . . • . .
• • • ... ...
. . .
.
.
.
• . .
...
• • .
...
• • • •
...
. . .
...
7 7 "и
Cv (/)=0 при у=Н Т*У (0=0 при у=Н и (0=0 при у=0 с (0=0 при t/=0 (Гу (0=0 при у=Н т,у(0=0 при у=п и (0=0 при у=0 v(t)=0 при у=0 Пу (0=0 при у=п Т*У (0=0 при у=Н и (0=0 при у=0 v(O=0 при у=0
СО Ч* to о 2 ® 2 й сЗ С1 сч сч
311
При разогреве блока на Г напряжения отрыва блока от основания Cv(t) в средней его части в бетоне молодого возраста могут достичь = 1 • 1 • 10~s(1-^-2 ) 105 - 0,336 = 0,336 -* 0,672 кГ/см2. Таким образом, при разогреве блока от экзотер-мии на 25—35° С уже вполне вероятно образование продольной трещины по шву сопряжения блока с основанием. Возможность этого впервые была отмечена Ю. А. Нилендером на основе анализа экспериментальных данных испытания Днепровской плотины еще в 1937 г. Здесь она нашла свое теоретическое подтверждение.
В связи с этим представляет практический интерес задача о температурных напряжениях в блоке со свободными верхней и торцовыми гранями, сопряженном с основанием таким образом, что на плоскости сопряжения вследствие наличия продольной трещины и сил трения
ау(0 = 0; «(/) = 0 при у = 0. (VI 123)
Эта задача на основах линейной теории упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна по предложению Ю. А. Ни-лендера была решена автором в 1952 г. [5].
Сравнивая решения задач о температурных напряжениях в блоках, рассмотренных в § VL6 и VI.7, видим, что освобождение от закреплений торцов блока приводит к существенному увеличению напряжений uv(l) по его подошве и большей неравномерности их распределения. Поэтому блок со свободными торцами напряжен более невыгодно, чем в случае, когда его торцы закреплены от тангенциальных смещений.
§ VI.8. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В БЛОКЕ, ЗАЩЕМЛЕННОМ ПО ОСНОВАНИЮ И ИМЕЮЩЕМ СВОБОДНЫЕ ТОРЦЫ,
В ОБЩЕМ СЛУЧАЕ ЕГО НЕРАВНОМЕРНОГО РАЗОГРЕВА
Обратимся теперь к общему случаю неравномерного разогрева блока, рассмотренного в § VI.7.
Представляя в соответствии с рекомендациями § V.3 заданный закон изменений температурного поля блока в форме (V.89), получим соответствующие формулы для напряжений и смешений блока в виде выражений (V.145)— (V.149). Остается только определить из граничных условий входящие в них произвольные постоянные.
Дальнейшие рассуждения ограничим случаем симметричного распределения температуры блока относительно его оси Оу. Условившись об этом, мы должны положить в формуле (V.89)
b = d„ = O. (VI. 124)
312
Это дает нам для изменений температуры следующее выражение:
Ф(/) = Т(1)4- aY* (у) + g 2 ek cosM +
+ Г*(у)ТеЛсо81л}. (VI. 125)
Проанализируем эту формулу.
Первый из множителей в ней Т(1) устанавливает заданный масштаб изменения температуры блока во времени, получаемый из решения соответствующей задачи теории теплопроводности и связанный с условиями остывания блока.
Второй множитель, заключенный в фигурные скобки, определяет закон распределения изменения температуры по сечению блока.
Каждое из четырех слагаемых фигурной скобки соответствует определенной части объемной эпюры изменения температуры блока.
Первое слагаемое определяет случай равномерного разогрева блока на некоторую величину agT(t), устанавливаемую с помощью формул (V.86) и V.82).
Второе слагаемое выражает равномерное изменение температуры блока вдоль оси ох и неравномерное — вдоль оси оу по закону aY*(y)T(t). Масштаб этой части эпюры изменения температуры устанавливается по формулам (V.86) и (V.83).
Третье слагаемое определяет случай равномерного разогрева блока вдоль оси оу и неравномерного вдоль оси ох по закону Т(/)gZe/jCOsXfeg. Масштаб этой части устанавливается по формулам (\Л82) и (V.84).
Наконец, четвертое слагаемое определяет часть объема эпюры изменения температуры блока, связанную с его неравномерным разогревом вдоль обеих осей по закону Y*(y)T(t) SefccosZft£, масштаб которой устанавливается с помощью формул (V.83) и (V.84).
Выше мы видели, что каждой из этих частей эпюры изменения температуры соответствует свое частное решение уравнения (V.52), которые мы нашли в § V.3. С учетом этих частных решений полные формулы для напряжений и смещений блока в рассматриваемой задаче на основе выражений (V.145)— (V.149) и данных § VI.6, VI.7 будут иметь вид:
ох (0 = а Е (О Т (/) {б (1 - В2) (Й1 - а2 П) - аК* (/П)+
+ Е Л) ch \ 11 +
313
+ (VI.126)
Cy (0 a E (0 T (0 {2 [a4 + 6at ? 4- n (a5 - 6a2 £2) - 3a4 42 +
+ a2Tl3 aS £ Ck — 2Xft t]) ch Хлт]+
+ (Вк~Dk- 2ХЛ Ак4)shXftn - A(/1|)] cosХд|; (VI. 127) тдД0 -a£(/) T(t) |2g [2a Д2 -a6 + 6aP] -3c2t]2] +
+ £ J(Bft — Dk + 2?4. Ak t]) ch Хлт] + (Ак + Ск +
+ 21к Вк tj) sh ХлП - (Л))] sin ХД) ; (VI. 128)
и (/) == a IT (0 {2£ [(3 - g2) (at - а2 4) - va4 - 2^ vg2 -
— v»] (а5 — 2а2 £2) + vi]2 3at —i]3v а2 + (1 + v) ag +
+ S ^-[(^(3-v) + (H-v)(Cft + 2XftB^))chX^+
+ (Вк (3 - v) + (1 + v) (Dk + 2%л Ak ч)) sh Xft4 -
— <Йл(/т1) — Фза(^1)] sinZ^}; (VI.129)
v (0 = alT (t) ^2tj + 6аД2 + -^- •»] (as — 6c2 S2) —
— if ax -Ь у i]3 a2] — vt] (1 — £2) (6a1 — 3a2 4) +
+ £2 [3a2— (2 + v) a5] + a2 g«‘(3 + 2v) +
+a(l +v) (* V* (Z4)*l+ S ^[(B*(3-v)-(l +v)X
X (Dk + 2Xft Ak q)) ch XftT) + (Ak (3 — v) —
— (1 + v) (Ck 4- 21a. Bk 4)) sh XA.i] — <j 'A (/4) +
+ z* (2-+ 4- — %* (/T1)] cos •
(VI. 130)
314
В этих формулах: £ и т] — безразмерные координаты, определяемые формулами (VI.84); — безразмерная величина, отыс-
киваемая по выражению (VI.85); а и g— постоянные, определяемые по формулам (V.86) и (V.82); — заданная функция,
отыскиваемая по выражению (V.83),
фЭЛ(/П) = /0) {Г*"(/0)~ци+г*(/е)]}40, (VI. 131)
о
ек = j [Х(Ф - а - Ы £1 cos^dg, (VI. 132)
—1
а производные функции <р3п(lij) и Y*(/0) берутся по аргументам /т] и /0 соответственно.
Выражения для напряжений (VI. 126) — (VI. 128) и перемещений (VI.129) — (VI.130) удовлетворяют уравнениям совместности и равновесия, поэтому для полноты решения нам осталось только удовлетворить граничным условиям (VI.93), (VI.94).
Полагая в (VI.126) g=l, видим, что на поперечных кромках блока действуют напряжения
(0|5= ,, - - « Е (0 Т (1) nF* (Z rj), (VI. 133)
отличные от нуля в общем случае криволинейного распределения его температуры вдаль оси оу. Таким образом, строго удовлетворить первому граничному условию мы не можем. Заметим, однако, что в силу равенств (V.82) и (V.83)
=0, (VI. 134)
поэтому первое из граничных условий (VI.93) и удовлетворяется в интегральном смысле, т. е. с точностью до принципа Сен-Ве-нана.
Остальным граничным условиям (VI.93), (VI.94) мы можем удовлетворить с той же степенью точности, что и для блока, рассмотренного в § VI.7. Это дает нам необходимое число аналогичных уравнений для определения произвольных постоянных Л*. Bh, Ск, Dh, ai, ..., а5 и приводит к однозначности решения рассматриваемой задачи. Эти уравнения будут иметь те же левые части, но их правые части (свободные члены) будут иными.
Для удобства применения этих уравнений в отдельных частных случаях отсутствия тех или иных слагаемых объемной эпюры распределения температуры (VI. 125) их правые части, соответствующие каждой из ее составляющей, вычислены отдельно н собраны в табл. 36. Пользуясь данными этой таблицы, мы охватим все возможные частные случаи распределения температуры. Например, учитывая только один ее первый столбец и полагая в
315
CO О Таблица 36 Правые части уравнений для определения произвольных постоянных • Ah ,Bh, Ck, Dh, прн различных законах изменения температуры блока
№ уравнения Физический смысл уравнения При изменении температуры по закону:
W)-agT(t) 1"(П= =aY4lr,)T(t') k=9 t4n=gT(t) £ ₽ftcos>,ftE 4=1 A>=® ,'(/)=У’(/т,)Т(/) £ **cos>.^ *=1
1 <7,(/) = 0 при у = Н {- О*"’ А* 0 -2(chXAfi-l)] *1- - ФЭЙ (WIc=o
2 Хху (Л = 0 при у = Н 0 0 - y(MchXftti-shX*n) 7" Фз* (ZH) lg=o
3 u{t) = Q при 0 = 0 (-.)*» А* 0 0 0
4 о(0=0 при 0 = 0 0 0 0 0
5 f Gy (t) dX = Q -! прн 0 = 0 ag 0 0 0
6 7 (п = 0; т = 1) Ъу (0 = о при X ~ ± 1 и 0=0 mH 0 0 £(-1)*-'yfzx x(^-eh^) + 0 S(-1)-^X
8 (л = 1; f r.vj,(/)tf0=O 0 0 4=1
т = 2) 9 (л=2; m =3) ПН при X = ± 1 +x‘(Tsh2TL-
нем a=g=l, получим случай равномерного разогрева блока, подробно рассмотренный в § VI.7.
Принимая же во внимание все столбцы табл. 36, получаем решение задачи для общего случая неравномерного разогрева блока.
Из табл. 36 следует, что все свободные члены выписанных уравнений, соответствующие случаю
z°(t) = aY*(y)T(t), (VI. 135)
равны нулю, поэтому и все произвольные постоянные для данного случая также равны нулю. Это означает, что мы нашли решение задачи, соответствующее этому случаю в замкнутом виде и притом не требующее полиноминальных слагаемых для функций напряжений.
Компоненты напряжений и перемещений в этом случае, как вытекает из формул (V.92), (V.93), равны
ах (0 = - аЕ (0 Т (0 аУ* (у); оу (0 = тХу (0 - 0; (VI. 135)
u(0 = O; о(0 = (1 4-v)a7'(0a\Y*(y)dy. (VI.137) i)
Они вошли в формулы (VI. 126) — (VI. 130) в готовом виде.
Выше был рассмотрен случай симметричного разогрева блока относительно его оси оу. Не представляет труда получить теперь решение и для произвольного распределения температуры относительно обеих осей блока. Формулы для напряжений и смещений блока, соответствующие этому случаю, имеют вид (V.145)— (V.149).
Для определения входящих в них постоянных из рассмотрения граничных условий можно всегда составить необходимое число уравнений, подобных (VI.113) —(VI.116), (VI.118),(VI.120), и тем самым однозначно решить рассматриваемую общую задачу о температурных напряжениях в блоке. Мы не будем здесь выписывать эти уравнения, но обратим лишь внимание па необходимость соблюдения рекомендаций 11 § V.3 при их составлении.
В заключение отметим, что все выписанные нами формулы для напряжений, смешений и уравнения для определения входящих в них произвольных постоянных относятся к случаю плоского обобщенного напряженного состояния. Соответствующей заменой в них a, v и E(t) на щ, v, и Ei(t) (см. § V.2) можно легко получить все необходимые формулы и уравнения, относящиеся к случаю плоской деформации.
§. VI.9. НЕКОТОРЫЕ ЗАМЕЧАНИЯ ПО ПОВОДУ РАССМОТРЕННЫХ УПРУГО-МГНОВЕННЫХ ЗАДАЧ
В настоящей главе был рассмотрен ряд упруго-мгновенных задач, относящихся к случаю температурных напряжений. Решения этих задач могут Гыть непосредсть<-нно использованы в их
317
ютовом виде н для расчета влажностных напряжений в телах, если для последних имеет место линейная зависимость между изменениями влажности материала и его влажностными деформациями вида
е° (0 = ^(0, (VI. 138)
где £—коэффициент линейной влажностной деформации (усадки или соответственно набухания), a U(t)—изменение поля влажности.
Для этого достаточно в этих решениях заменить коэффициент линейного расширения а коэффициентом линейной влажностной деформации £, а изменение ноля температуры Ф(х, у, г, t) —изменением поля влажности U(x, у, z, I).
Для некоторых капиллярно-пористых коллоидных материалов зависимость (VI.138) неоднозначна, поэтому для них указанная возможность оказывается неприемлемой. К числу таких материалов относится, например, бетон, у которого деформации набухания связаны с увеличением влажности более сложной зависимостью (III.6), а деформация усадки в общем случае неоднозначно зависят от уменьшения его влажности.
Однако в § 1П.7 были указаны практические пути для преодоления этих затруднений, состоящие, во-первых, в учете указанной неоднозначной зависимости усадки бетона от изменений его влажности с помощью введения эффективной и критической влажностей бетона, во-вторых, в применении в практических расчетах среднего значения коэффициента линейного набухания бетона, и в-третьих, — в использования разных по величине коэффициента линейной усадки 0 и среднего коэффициента линейного набухания ц бетона.
При этих условиях для расчетных влажностных деформаций бетона будем иметь формулы:
еу (/) = fW’ (0; е„ (0 -: - T]t/ (0, (VI. 139) в которых U* (0 — изменение эффективной влажности бетона, a U(t) —изменение его полной влажности.
Смысл введенного понятия об эффективной влажности бетона разъяснен в § II 1.7, где также указано, как она выражается через полную и критическую влажность бетона. Необходимые дополнительные разъяснения содержатся в главе IX.
Сравнивая формулы (VI. 138) и (VI.139), видим их полное внешнее тождество, из чего следует, что полученные решения ряда практически важных упру го-мгновенных задач о температурных напряжениях могут быть непосредственно использованы в их готовом виде для расчета влажностных напряжений в бетоне. При этом в случае расчета напряжений набухания в них следует заменить коэффициент линейного расширения а средним коэффициентом линейного набухания бетона i], а изменение температурного поля Ф(х, у, z, t) — изменением поля его полной
318
влажности U(x, у, z, t). В случае же расчета усадочных напряжений в этих решениях а нужно заменить коэффициентом линейной усадки бетона 0, а Ф(х, у, z, t) —изменением поля его эффективной влажности L/3 (х, у, z, t).
В связи с указанным простым приемом мы не будем особо выписывать формулы для влажностных напряжений и перемещений рассмотренных выше упруго-мгновенных задач, имея в виду, что они всегда могут быть найдены из решений, полученных в настоящей главе указанным выше простым путем.
Методика отыскания расчетных изменений поля эффективной влажности бетона U3 (х, у, z, t) состоит в следующем.
Вначале методами теории влагопроводности, развитыми в главе II, отыскиваются поля влажности бетона в рассматриваемые моменты времени его высыхания /1 и t2. Затем они сравниваются с полем критической влажности бетона
U(x,y,z,t)^UKp, (VI. 140)
определяемой методом, изложенным в § III.7.
Если в любой точке объема тела влажность бетона в моменты времени t\ и t2 оказывается меньше критической влажности t/Kp. го эти поля влажности одновременно являются и полями его эффективной влажности. Поэтому расчетные изменения влажности бетона, вводимые в расчет усадочных напряжений, развивающихся в нем за время t2—flt в данном случае будут равны
U3(x, У. z, t) = U(х, у, z, t2) — U(x, у, z, tj. (VI. 141)
Если влажность бетона в моменты времени /| и t2 оказывается больше его критической влажности в некоторой части объема тела, то тогда следует в этих частях его объема принять:
U3 (х, У, г, *i) = ^кР | (V1.142)
при х < Xj; у < «!; z^z (хи yj |
и
U3(x,y,z,t2) = UKp 1 (VI. 143)
при х < х£; у<у2; а<г(х2, у2),|
где
z = z(xi,yl) при* = ^
и
z = г(х2>у2) при t = t2
(VI. 144)
(VI. 145)
— уравнения поверхностей изовлаги, на которых влажность бетона равна его критической влажности t/Kp, а
X < Xj ; у<у1\ z <z(xl,yl) при t = ; (VI.146)
и
*<х2; У<У1\ z<z(x2,y2) при t = t2 (VI.147)
319
— области тела, где /
U(x,y,z,t)>UKp. (VI. 148)
В остальной части объема тела, где
U(x,y,z,t)<UKp, (VI. 149)
следует считать U3 (х, у, z, t) равной его действительной влажности U(x, у, z, t).
Определив таким образом поля эффективной влажности бетона, можно составить их расчетное изменение
U3 (х, у, z, I) --= U3 (х, у, z, Q — U3 (х, у, z, /,) (VI. 150) и далее уже ввести его в расчет усадочных напряжений. Этот случай на примере одномерной задачи распределения влаги по сечению тела более подробно рассмотрен в § IX.5.
Интересен случай, когда на периоде высыхания бетона t2—Ц во всем его объеме влажность, уменьшаясь, остается все же большей UKp. Это может, например, наблюдаться на раннем периоде высыхания бетонного тела, имеющего большую начальную влажность (молодой бетон с высоким В/Ц или бетою предварительно увлажненный). В этом случае
U3 (х, у, z,tx) U3 (х, у, z, t2) = UKp. (VI. 151)
и поэтому расчетное изменение эффективной влажности бетона (VI. 150) равно нулю. Следовательно, при этих условиях за время t2—1\ в бетоне не возникают усадочные напряжения, что экспериментально доказано в опытах автора, описанных в § VII 1.5.
Из изложенного и, особенно последнего примера, следует, что ранее применяемая методика расчета усадочных напряжений по изменениям полной, а не эффективной влажности бетона приводит к их существенному преувеличению. Поэтому, по предложению автора, она заменена описанной выше новой методикой, основанной на понятиях эффективной и критической влажности бетона, вошедшей в СНиП П-В.1-62 [174], и поясняющие их материалы [19].
ГЛАВА Vll
УЧЕТ ПОЛЗУЧЕСТИ ПРИ РАСЧЕТЕ НАПРЯЖЕНИИ В БЕТОНЕ, ВЫЗЫВАЕМЫХ ЕГО ВЫНУЖДЕННЫМИ ДЕФОРМАЦИЯМИ
§ VII.1 ОБЩИЕ УКАЗАНИЯ
В § IV.9 мы видели, что прн условии (IV.5) полные напряжения в бетоне а*(0. т*у (0, отыскиваемые с учетом ползучести, определяются через соответствующие упруго-мгновенные напряжения стд(/), .... т.Г!/(0,... с помощью независимых интегральных уравнений (IV.74), решения которых могут быть записаны сразу в готовом виде:
£(/) E(t) J £(П
• —...............................(х,У,г)
JjrJO _ С r-"JT) R(t, T) dr, £(/) E(t) J E(T)
................................(*, У, 2),
(VII.1)
где R(t, т) — наследственная функция бетона вюрого рода. Таким образом, отыскание напряжений ползучести о* (/),..., т£у(0, ... сводится к вычислению квадратур (VII.1), поскольку напряжения упруго-мгновенной задачи предполагаются уже найденными (см. главы V и VI), а функция R(t, т) — известной (см. § IV.12).
Дальнейшее упрощение задачи получим, если учтем, что вынужденные деформации бетона обычно задаются в форме (V.40), а поле изменений соответствующей характеристики состояния материала е°(/) (температуры или влажности бетона) всегда
321
отыскивается методами теории тепло- или влагопроводности (см. главы I и II) в виде произведения
eO(t) = toT(t)F(x,y,z), (VI 1.2)
где eo = const, a T(t) и Г( х, у, г)—некоторые безразмерные функции, одна из которых зависит только от времени /, а другая — только от координат точек тела х, у, г. В соответствии с этим напряжения упруго-мгновенной задачи (см. главы V и VI) всегда находятся также в виде произведений
°* (0 - Geo Т (?) Е (0 Fx (х, у, г); ...........................
тлу (0 с/.е0 Т (I) Е (0 Fxy (х, у, z)\
...........................(x,y.z)
(VII-3)
аналогичной структуры.
Введем теперь в рассмотрение вспомогательную упруго-мгновенную задачу, решение которой имеет вид:
ax(t) = ае0Е (t)Fx(x, y,z); ..................(x,y,z)-, Txy(t) -- aEbE(t)Fxy(x,y,z)-..................(X, у, Z),
(VII.4;
т. e. получается из решения исходной упруго-мгновенной задачи при = Такую вспомогательную задачу будем называть заменяющей упруго-мгновенной задачей. Тогда решение исходной упруго-мгновенной задачи может быть записано следующим образом: _ •
Ол(0 = ал(0Т(/у,
.............(X, у, Z);
-- тХу (t)T(t).
............(X,y,z).
(VII.5)
В этих формулах функцию Т(0 можно рассматривать как коэффициент приведения упругих напряжений заменяющей задачи к напряжениям исходной упруго-мгновенной задачи.
Будем теперь по аналогии с (VII.5) искать полные напряжения о* (/), ..., т*у (0, ... в форме
од’(0=--ад(0//’(Лт1);
...............(х, у, z);
ТжУ(0 = t.iv (0//* (/,tj) ; .................(x,y,z).
(VII.6)
222
где H*(t, л)—коэффициент приведения упругих напряжений заменяющей задачи к искомым полным напряжениям, отыскиваемым с учетом ползучести.
Внося (VII.4) и (VI1.6) в (VII.I), для И* (t, xi) получаем следующую формулу;
Н* (/, Т1) - Т (0 - J Т (т) R (t, т) dx. (VII.7)
Итак, отыскивание полных напряжений о* (0, .... х*у (0, ... с учетом ползучести сводится к нахождению напряжений о*(0,..., хЛу(0, .... заменяющей упруго-мгновенной задачи и коэффициента приведения H*(t, х0. Отыскав эти напряжения (VII.4) и коэффициент H*(t, ti) (VII.7), по формулам (VII.6) всегда можем составить выражения для искомых полных напряжений <(0,....<у (0,...
Рассмотрим случай стационарной вынужденной деформации. В этом случае
Т (0 — Т (х) = 1 (VII.8)
и напряжения упруго-мгновенной задачи совпадают с напряжениями заменяющей задачи. При этом
Н* (t, х,) = 1 — J R (t, x) dr. (VII.9)
Из определения функции R(t, x) (см. § IV.7) вытекает, что всегда
J R(t,x)dx > 0 при Xi <t (VII.10)
и стремится к определенному пределу lim $R(t, x)dx<l. Поэтому функция Н* (t, ti), определяемая формулой (VII.9), затухающая от
Н* (6 т1) = I ПрИ t Ti до
0 < Н* (t, Xi) = 1 — lim j /?(0 т) Jx < I при t -» со .
В связи с этим и учитывая структуру формул (VI 1.6), функцию H*(t, ti) в рассматриваемом случае можно интерпретировать, как коэффициент затухания (релаксации) упругих напряжений за счет ползучести бетона к данному моменту времени наблюдения /.
323
Нетрудно видеть, что с учетом (VH.6) введенный нами коэффициент приведения H*(t, равен
т. е. представляет собой отношение полных напряжений о*(t, ti) в данный момент времени наблюдения t, исчисленных с учетом ползучести, к упругим напряжениям а(£ Ti) заменяющей упруго-мгновенной задачи в тот же момент времени t, найденным в предположении отсутствия ползучести бетона, причем оба эги напряжения о*( t, п) и c(t, п)отыскиваются для соответствующей вынужденной деформации, начинающей развиваться, или соответственно возникающей с одного и того же момента времени / = Т1-
Для тела, не обладающего ползучестью R(t, т) =0, поэтому для него
я* (Л-4) = ПО- (VII. 12)
Иными словами, полные напряжения в нем равны упругим напряжениям, отыскиваемым на основе упруго-мгновенной задачи. Чем больше ползучесть материала (выше степень релаксации упругих напряжений), тем больше текущие значения R(t, т) и тем меньше, следовательно, коэффициент H*(t, Ti).
Из изложенного следует, что учет ползучести при расчете напряжений в бетоне, связанных с его вынужденными деформациями, сводится к определению коэффициента приведения //*(/, Ti) упругих напряжений по формуле (VII.7) и самих напряжений ползучести по выражениям (VII.6) умножением на этот коэффициент соответствующих упругих напряжений заменяющей упруго-мгновенной задачи. Поскольку функции T(t) и R(t, т) предполагаются известными, нахождение H*(t, Т|) по формуле (VII.7) сводится к вычислению квадратур, которое может быть всегда выполнено наиболее доступными способами машинного и численного интегрирования или непосредственно аналитическим методом.
В § VI 1.2 изложена наиболее удобная практическая методика вычисления коэффициента приведения H*(t, ti) напряжений заменяющей упруго-мгновенной задачи, основанная на применении готовых таблиц функции R(t, т).
§ VIIJ2. МЕТОДИКА УЧЕТА ПОЛЗУЧЕСТИ ПРИ РАСЧЕТЕ НАПРЯЖЕНИИ, ВЫЗЫВАЕМЫХ ВЫНУЖДЕННЫМИ ДЕФОРМАЦИЯМИ
’ Вычисление коэффициента приведения упругих напряжении H*(t, ti) существенно упрощается, если составить таблицы значений наследственной функции второго рода R(t, т) для различных бетонов. Желательно иметь такие таблицы для бетонов раз
324
ных составов и марок на различных вяжущих. Это — дело ближайшего будущего.
Однако проведенный анализ изменчивости значений функции R(t, т) в зависимости от величин параметров, определяющих меру ползучести бетона и его модуль упругости, для ряда различных бетонов показал, что эта изменчивость носит довольно вялый характер. Объясняется это тем, что в выражения для R(t, т) (IV.146) модуль упругости £(/) и составляющие ф(/) и Д(0 предельной меры ползучести бетона входят лишь в виде произведений Е(0ф(0 и Е(0Д(0. Для того чтобы убедиться в этом, проще всего обратиться к выражению R(t—т) (IV.156) для старого бетона.
Так как с увеличением, например, прочности (марки) бетона величины Е(0 и ф(0, А (0 изменяются в обратных направлениях, то их произведения оказываются мало изменчивыми, что и приводит к указанному выше обстоятельству.
Подмеченное свойство R(t,x) позволяет упростить табулирование этой функции, ограничась составлением ее таблиц для «среднего» бетона, характеризуемого некоторыми средними значениями параметров функций E(t), ф(0 и Д(0.
Анализ имеющегося в литературе экспериментального материала о деформациях бетона при кратковременных и длительных загружениях, существенно облегченный уже имеющейся систематизацией соответствующих экспериментальных данных, проведенной И. И. Улицким [186], показал, что для такого бетона могут быть приняты следующие средние значения параметров функций E(t), ф(0 и Д(0, входящих в формулы (IV.3), (IV.145), (IV.146):
Ео = 2,6 • 105 кГ/см2; I = 1; ₽ -0,206 (сут.)-1;
Фо = 0,756 IO"5 (см21кГ j; ih = 3,416 • 10~5сут/кГ/czt2 ;
До= 0,219- 10"W/kT; = 1,204• 10-5 сут1кГ1см2 ;
(VII. 13)
(VII.14)
At = 1; а = 6 (сут.) 1; у = 0,03 (сут.) 1.
Параметрам (VII.13) — (VII.14) соответствуют следующие значения параметров меры ползучести C(t,r) (IV.102):
= 0,975-10-5 см2!кГ,
А, = 4,62 КГ5
у = 0,03 (сут.) ’,
[сут/кГ/см2 j;
(VII. 15)
в свое время рекомендованные в качестве средних для обычного тяжелого бетона Н. X. Арутюняном [25] ра основе, по-видимому, аналогичного обобщения экспериментальных данных о ползучести бетона.
325
Й Tm+i Таблица 37
Формулы для интегралов f Т (т) /? (I, т) dr
m—1
Лт1 = \п - T"-l ; ДТ2 = Т,п+> - тт •• - ДТ, + ДТ2 = Т(и+1 - тт_.
Квадратная парабола Rftt * f) Tm+1 f T(r)R(t, T)dr Tni—t
Квадратная парабола 7/Г/п-гД 1 7/Тт/>| 7(ttn * г/ Т/п-г Ъп *”,*t 1 rft^yffr^f} Ъп-t Tm + 1 гл* 2 * ’ 1Л('’ T'n-i ) AT! (2T (t«-i )A^(10At’-5AtAT1 + At2) + 60Дт{ — Arj + т (Tm+1) Дт, (ЮДт, дт2 - ЗДт2) -f- 7 ( tJ Дт2 (ЗДт, - 2Дт2)] + -+/?(/, Tffl) Ат2 [7 ( тт_, ) Дт8 (5Дт, - 2Дт) + 7 (+1) Дт, (ЗДт - 5Дт,) -f-+ 2Г ( тот) Лт’| + R (<, т,„+1 ) Ат, [7 (тт_, ) Дт2 (ЮДт, Дт2 - ЗДт2) -|-+ Т ( Tffl) Дт2 (ЗДт - 5Дт,) + 27 ( тт+1 ) Ат, ( ЮДт2 + ОДт2 - 15ДтДТ1)] ]
Трапеция 7-Г ТП1*1 12ДП дт2 Т"'-1) F ( Т—’ ХЗАТ1 - АТ2> Ат2 + Г ( Т-+* ХАТ1 - дт,) ДТ2] +/?(/, т J Дт2 [7 ( Тт_1) + 7 ( Tm+1)] + + R (< • Wl F ( Tm-1) (АТ2 ~ Лт1) ЛТ1 + Т ( W1 )(3лт2 - Ат1) Ат11}
Рекомендуемое значение параметра£0 (IV.13) близко к среднему значению начального модуля упругости бетона марок 300— 500 на мелком заполнителе по данным приложения 1 СНиП [174], как и должно быть, если учесть, что имеющиеся экспериментальные данные о деформациях бетона, положенные в основу рекомендуемых параметров (VII.13), (VII.14), относятся именно к бетонам на мелком заполнителе.
Для «среднего» бетона, определяемого параметрами (VII.13), (VI 1.14), по заданию автора счетно-вычислительной станцией ЦНППСК Госстроя СССР были составлены таблицы R(t,x), приведенные в приложении I. Числовые значения R(t, т), содержащиеся в этих таблицах, найдены численным решением по шагам уравнения (IV.16) с учетом (IV. 145) на электронно-вычислительной машине «Урал-4» с заменой интеграла конечной суммой.
При наличии готовых таблиц функции R(t,x) для определения коэффициента H*(t, Ti) приведения упругих напряжений к данному моменту времени t удобнее всего пользоваться следующей простой методикой:
1) выбирается таблица функции R(t,x), соответствующая данному моменту времени наблюдения t, для которого определяется коэффициент приведения Я*(Л п);
2) значения функции R(t,x), содержащиеся в этой таблице, умножаются на известные переменные значения заданной функции Т(х), зависящей от т;
3) любым доступным методом вычисляется площадь
jT(T)fl(/fT)dT (VII.16)
криволинейной трапеции, ограниченной кривой
F(t,x) = T(x)R(t,x), (VII. 17)
осью абсцисс (времени т) и ординатами x=t и х=Ть
4) вычитанием этой площади из T(t) по формуле (VI 1.7) находится коэффициент H*(t,xi) приведения к данному моменту наблюдения t напряжений заменяющей упруго-мгновенной задачи, возникающих с момента Ti.
Для вычисления площади (VII.16) можно пользоваться, например, планиметром, предварительно вычертив в нужном масштабе кривую (VI 1.17). Удобно также аппроксимировать эту кривую простейшими интегрируемыми функциями, после чего выполнить квадратуру (VI 1.16) непосредственно. Последний прием наиболее прост и удобен. В связи с этим составлена готовая табл. 37 интегралов (VII. 16) для простейших случаев аппроксимации функций Т(т) и R(t,x) в виде отрезков квадратных парабол на заданном промежутке Дт.
Задавая различные соотношения между Т(тт_1), Т(хт), Г(тж+|) и Дт1э Дт2, в частности полагая некоторые из них равны
327
ми нулю, с помощью этих таблиц можно получить готовый набор интегралов (VII.16) для ряда простейших случаев, сочетая которые с одновременным варьированием Дть Дтг и Дт всегда можно вычислить эти интегралы при любом очертании кривых Т(т). Для этого достаточно разбить заданную кривую 7"(т) на характерные участки, подобрать в табл. 37 соответствующие случаи их аппроксимации и воспользоваться отвечающими им готовыми значениями интегралов (VI 1.16), после чего произвести их суммирование. Последние могут быть всегда вычислены с большой степенью точности, поскольку имеются весьма подробные готовые таблицы R(t, т) (см. приложение I).
В § VII.3 и VII.4 на ряде примеров проиллюстрировано применение рекомендуемой методики учета ползучести при расчете напряжений в бетоне, вызываемых его вынужденными деформациями.
§ VI 1.3. СЛУЧАЙ СТАЦИОНАРНОЙ ВЫНУЖДЕННОЙ ДЕФОРМАЦИИ
Рассмотрим один важный частный случай вынужденной деформации и вычислим соответствующий ему коэффициент приведения упругих напряжений.
Допустим, что в некотором возрасте бетона п в нем появляется некоторое поле вынужденных деформаций, приводящее к возникновению напряжений, которое затем остается неизменным по времени. В этом случае стационарных вынужденных деформаций, очевидно, имеет место условие (VIL8).
Такой случай, например, мы получим, если создадим в свободном от внешних связей брусе или плите стационарный температурный перепад, а затем наложим внешние абсолютно жесткие связи, устраняющие температурное искривление элемента, и в дальнейшем будем неизменно сохранять его прямолинейную форму. При этих условиях напряжения в брусе, а следовательно, и реакции в этих связях вследствие ползучести будут затухать во времени по закону коэффициента приведения H*(t,ti) с учетом (V1I.8) равного (VII.9).
Принимая во внимание (IV.152), для H*(t, т) получаем следующую формулу:
(Ст.) - 1—+ +
£ V) I ЩО
+ К (тх) ( е1Г' - А2) е~ГЛх-> J К (т) F (т) е'(т) dx|. (VII. 18)
Для бетона, характеризуемого средними значениями параметров (VIIJ3), (VII.14), по формуле (VII.18) были вычислены коэффициенты H*(t,ti) для различных t и ть Значения этих коэффициентов приведены в табл. 38.
Э2в
Таблица 38
Коэффициенты затухания Я*(/,т1 ) упругих напряжений при стационарной вынужденной деформации t — возраст бетона в сутках к моменту наблюдения; Tt— возраст бетона в сутках в момент загружения.
Ti=2 сут., Ti =5 сут. Ti —10 сут., Tj—20 сут.
t Н*Ц. -|) 1 H»(t. Т,) • H'(t. т.) /
2 1 5 1 10 1 20 1
2.25 0,426 5,25 0,510 10,25 0.551 20.25 0,592
2.5 0.342 5.5 0,443 10,5 0.499 20,5 0.549
2.75 0.304 5,75 0,110 10,75 0,476 20,75 0,534
3 0,278 6 0,383 11 0,457 21 0,521
0.225 7 0.296 12 0,392 22 0,473
5 0,199 8 0.262 14 0.30S 25 0,367
10 0,187 10 • 0,228 18 0,251 30 0,301
20 0.186 20 0,215 20 0.238 40 0.253
30 0.185 30 0,208 30 0,214 50 0,252
оэ 0,186 0.200 оэ 0,210 оо 0,251
С помощью аналогичных таблиц могут быть построены так называемые кривые релаксации удельных напряжений р(/,Т|), необходимых для поддержания неизменной во времени осевой продольной деформации бруса е(/) = 1, начиная с его возраста ть Поскольку для этого в упругом брусе необходимо было бы иметь упругие напряжения
с(0^Е(/), (VII. 19)
искомые напряжения p(f,xi), очевидно, будут равны р(/,т1) = /7*(/,т1)Е(0, (VII.20)
где И* (t, ti) определяется по формуле (VII.18) или (VI 1.9).
Из табл. 38 видно, что ползучесть приводит к существенной релаксации напряжений в бетоне молодого возраста; степень релаксации начальных упругих напряжений в рассматриваемом случае составляет 81,4% — для кривой n=2 сут., 80%—для кривой Ti = 5 сут., 79% — для кривой xi^lO сут. и 74,9% — для кривой xi=20 сут.
Отметим, что рассмотренный нами случай (VI 1.8) относится не только к равномерной по объему тела вынужденной деформации. Он одинаково применим к любому закону ее распределения, лишь бы она была стационарной во времени.
§ VI 1.4. КОЭФФИЦИЕНТ ПРИВЕДЕНИЯ УПРУГИХ НАПРЯЖЕНИЙ В СТАРОМ БЕТОНЕ
Для бетона зрелого возраста и практически уже не стареющего вычисление коэффициента приведения напряжений заменяющей упруго-мгновенной задачи существенно упрощается, по
329
скольку у него модуль упругости постоянен и в выражение для наследственной функции второго рода R(t,v) возраст бетона в явном виде не входит. В этом случае формула (VI 1.7) принимает вид
Я*(/,т) = //*(/) = Т(/)—j T(t)R(1 — т)<1т. (VII.21)
Для такого бетона R(t—т) определяется по формуле (IV.I56). С ее учетом и с помощью выражения (VII.21), например, при стационарной вынужденной деформации будем иметь
Я*(1) = 1--(1 — е~р‘е~рг/), (VII.22)
Р> Р2
где Ai, А2, pi п р2 находятся по формулам (IV.157) — (IV.160).
В табл. 39 приведены значения коэффициента H*(t), найденные по формуле (VIL22) для старого бетона при средних значениях параметров (VII.13), (VII.14).
Таблица 39
Коэффициенты затухания H*(t) упругих напряжений при стационарной вынужденной деформации в старом бетоне
(сут.) 0 0.25 0,5 0,75 1 3 10 20 40
1 0,667 0,626 0,617 0,611 0.570 0,462 0,374 0,306 0,283
Предельное значение H*(t)
Я*(оо)х= 1——(VII 23) Pl Р2
при соответствующих значениях постоянных:
А1 -= 0,023701 (сут.)-1; А2 = 3,451670 (сут )“’; | 24)
Pl - 0,067419 (сут.)~1; р2 - 9,43797 (сут.)-', )
равно
Я*(со) = 0,28273. (VII.25)
Следовательно, степень релаксации напряжений в старом бетоне при стационарной вынужденной деформации составит 71,7% и по-прежнему является довольно значительной.
При отсутствии ползучести материала R(t,x)=0 (Л1=Л2=0 или pi=p2= 00 ). поэтому H*(t) = l. Следовательно, в любой момент времени наблюдения напряжения в теле в рассматриваемом случае равны начальным упругим напряжениям.
330
Рассмотрим теперь некоторые практически важные случаи нестационарной вынужденной деформации. Вначале предположим, что
Т(/)= 1—с"3'. (VII-26)
Этот случай, например, имеет место при регулярном режиме остывания илп высыхания [12] призматического тела. Внося (VII.26) в (VII.21), с учетом (IV.156) найдем:
— l _е-р/ —-A(l—е"₽,/)- —(l-e-₽J') + Р1 Р2
+ (е“₽' — е-₽*') + (е-р/ — е-м). (VI 1.27)
Pi — ₽ Рг — Р
Предельное значение Н* (/), как нетрудно видеть, совпадает с (V1I.23). Таким образом, в рассматриваемом случае полная степень релаксации упругих напряжений такая же, как и в случае стационарной вынужденной деформации, однако закон релаксации этих напряжений во времени иной.
Упругие напряжения в бетонном брусе с защемленными торцами, остывающем, например, по закону (VI 1.26) на То градусов, равны (см. § V1.4)
о (/) = аТ0 £ (1 — е-₽') . (VII.28)
Следовательно, напряжения заменяющей упруго-мгновенной задачи
o(t) = aT0E. (VI 1.29)
Поэтому полные напряжения в нем с учетом ползучести отыскиваются по формуле
о*(/)-аГ0££*(/), {VII.30)
в которой H*(t) берется из выражения (VI 1.27).
Интересен случай, когда брус с защемленными торцами внезапно разогревается на То, а затем медленно остывает по закону
Т(/)-е“₽' (VI 1.31)
до первоначальной температуры. Соответствующий этому случаю коэффициент приведения H*(t) найдем по формуле (VI1.27), опустив в ней члены, не содержащие р, и изменив знаки у оставшихся слагаемых
(/) - е*-----(е-* - е--') -
Р1 — р
(VII.32)
331
Упругие напряжения в брусе будут равны
с(() = ~аТ0Ее~^, (VII.33)
напряжения заменяющей упруго-мгновенной задачи
a(0--aTo£, (V1I-34)
а полные напряжения с учетом ползучести
о» (!) = - аТ, Е j е-”----(е-” - е’”') -
I Р1 -₽
-------(VII.35) Р2— Р J
Их предельное значение
о*(оэ)=0, (VII.36)
а характер изменения во времени зависит от соотношения р>, рг и р, т. е. от соотношения скоростей релаксации напряжений и остывания тела. При малых скоростях остывания бруса (Р<ЗС Pi< <р2) напряжения о*(0, затухая во времени, сохраняют первоначальный знак; при больших скоростях остывания (р 3>рг>Р1) вследствие относительного замедленного последействия возможна перемена знака напряжений с последующим их полным затуханием. В этом случае мы имеем аналогию с действием импульса полной деформации, исследованного в § IV.7 при выяснении физического смысла функции влияния /?(/,т) (рис. 40,6).
Теперь рассмотрим случай гармонической вынужденной деформации, при которой
T(/)sinco,17. (VII.37)
Он возникает, например, при воздействии на защемленный бетонный брус периодических колебаний температуры или влажности окружающей среды. С учетом формул (V1I.21) и (VI1.37) в этом случае найдем
/7* (7) = sin со?, t-(Р1 sin со,, t —
Pi + 4.
— со„ cos con t + co,, e~p‘')-;-Л-- (p2 sin co,, t —
РгН-41
— con cosco,, t co,, e“₽,/) . (VII.38)
При достаточно большом t получаем асимптотическое значение
/7* (/) sin со,, 7-Al (pj sin со„ t ~ со„ cos co,, 0 —
P? + “n
-------A- (p2 sinco„ t — co„ cosco,, 7). (VI 1.39) P2 + 4i
Упругие напряжения в рассматриваемом брусе при изменении 332
его температуры по закону (VII.37) с амплитудой То и начальным разогревом будут равны
и(/) = — аТ0Еsinco„ t. (VII.40)
Напряжения заменяющей упруго-мгновенной задачи определяются формулой (VI 1.34), поэтому асимптотическое значение полных напряжений с учетом ползучести
а* (/)-- аТ, Е Г11--------------sin <о„ / +
IA «I»: «^-1 о
<VIL4,)
Из формулы (VI 1.41) следует, что полные напряжения о*(0, так же как и упругие напряжения о(<), изменяются по гармоническому закону, но с другим периодом и с иной амплитудой.
При T(t), заданном в виде
T(t) - coscont, (VI1.42)
аналогичным образом найдем у,
Н* (I) = COS СО n t-- (Pi cos con t 4- si n t —
Pi4-“л
— Pi e-’’19----—— (p. cos<ont + co,, sin co— p»e~₽i/) . (VII.43)
Pi+^n
При достаточно большом t
H* (/) COSCOn t---- 1 - (pl COSCOj -I- co„ sin ro„ 0 —
Pi И»
----- (p2 cos co„ t + co,J sin co n t). (VII .44) P5 + “n
Упругие напряжения в брусе при изменении его температуры по закону (VII.42) с амплитудой То и начальным разогревом в этом случае будут равны
=_ — aT0Ecoswnt. (VII.45)
Напряжения заменяющей упруго-мгновенной задачи по-прежнему определяются формулой (VII.34). Асимптотические значения полных напряжений
Из этой формулы следует, что полные напряжения о*(О, так же как и упругие напряжения (VII.45), изменяются по гармоническому закону, но с другим периодом и иной амплитудой.
ГЛАВА VIII
НЕКОТОРЫЕ ЗАДАЧИ О ТЕМПЕРАТУРНЫХ И УСАДОЧНЫХ НАПРЯЖЕНИЯХ В БЕТОНЕ
При строительстве массивных бетонных сооружений часто наблюдается появление трещин, возникающих в них иногда даже до приложения эксплуатационной нагрузки, например, в американских плотинах Оуахи, Гренд Кули, Боулдер [214], а также в прискальных зонах в период строительства отечественных плотин Бухтарминской, Братской и Макмаканской ГЭС [2].
Типичные трещины иногда появляются также в бетонных и железобетонных конструкциях ряда промышленных сооружений (градирни, резервуары, промышленные цехи и т. п.).
Причинами образования подобных трещин являются усадка бетона и его температурные деформации, развивающиеся вследствие экзотермин цемента, на величину которых оказывают также влияние изменения температуры и влажности внешней среды. При этом в немассивных сооружениях главную роль играют усадка и внешние температурные воздействия, в то время как основной причиной образования трещин в массивных сооружениях являются повышение температуры бетона при его твердении от экзотермин и последующее понижение ее при остывании затвердевшего массива, вызывающие значительные температурные напряжения. В таких сооружениях усадка может служить лишь причиной образования неглубоких поверхностных трещин, которые впоследствии либо закрываются, либо развиваются уже от других причин.
Температурные напряжения, возникающие в массивных сооружениях от экзотермии цемента и, в частности, в бетонных блоках, на которые они разрезаются в процессе возведения, крайне нежелательны. Механизм их развития таков, что в начальный период, измеряемый несколькими днями и характеризующийся значительным разогревом блока, его ядро претерпевает температурные расширения, значительно превышающие деформации поверхностных слоев бетона, ограничивающих блок. По этой причине ядро массива в период его разогрева оказывается сжатым, а наружные, свободные слои бетона могут испытывать растяжение. При некоторых условиях (массивный столбча
334
тый блок, высокотермнчный цемент, большое содержание цемента, быстрое возведение) это может привести к образованию поверхностных температурных трещин в бетоне, появлению которых способствуют усадка его открытых слоев и колебания температуры внешней среды.
Так как неглубокие поверхностные трещины, появляющиеся в раннем возрасте бетона, впоследствии при его остывании закрываются, то опасными являются только трещины, проникающие глубоко внутрь бетонного массива.
В последующем наступает длительный период охлаждения массива, в течение которого более значительные деформации затвердевшего остывающего ядра, противоположные по знаку начальным температурным расширениям, вызывают перераспределение усилий в бетоне. Наружные свободные слои, ограничивающие высокий столбчатый блок, оказываются сжатыми, а его ядро испытывает растяжение. При известных условиях (значительный начальный разогрев в период твердения, короткий период остывания, бетон с низкой ползучестью) это может привести к образованию внутренних температурных трещин в ядре массива и в совокупности с глубокими трещинами на поверхности — к его сквозному растрескиванию.
У низких вытянутых блоков, деформации которых стеснены скалой или ранее изготовленными блоками, на которые они уложены, в этот период могут возникать значительные растягивающие температурные напряжения. Именно поэтому в прискальных зонах бетонных сооружений и наблюдается наибольшее число вертикальных температурных трещин [2].
Для предупреждения растрескивания, а также из соображений удобства работ массивное бетонное сооружение в процессе его возведения приходится разрезать на отдельные блоки и устраивать температурные швы. Размеры блоков при этом назначаются в зависимости от производительности механизмов, изготавливающих и укладывающих бетон, и из условий предотвращения появления трещин. Таким образом, при высокой производительности бетонных работ оба эти условия вступают в противоречие друг с другом, поскольку первое из них требует у величення размеров блока, а второе эти размеры ограничивает. Следовательно, необходимо научно обосновать оптимальные размеры бетонных блоков. Эта задача по существу все еще остается нерешенной с достаточной полнотой. Размеры блоков обычно назначаются по производственным соображениям на основе существующего опыта и часто не удовлетворяют второму требованию. Поэтому необходимо развитие и совершенствование практических способов борьбы с образованием температурных трещин в массивных бетонных сооружениях (применение специализированных низкотермичных цементов, искусственное охлаждение бетона, специальные способы производства работ и т. п.).
335
Серьезные неприятности могут причинить температурные трещины в бетонных и железобетонных статически неопределимых конструкциях промышленных сооружений, вызываемых колебаниями температуры воздуха или технологическими причинами. Поэтому и здесь приходится уделять большое внимание конструктивным мерам: устройству температурно-усадочных швов, надлежащему армированию, выбору рациональных конструктивных схем сооружений и т. п.
Исследованию температурных напряжений в бетоне посвящены работы Б. Л. Абрамяна [1], С. В. Александровского [5, 17, 19, 22, 23], Н. X. Арутюняна [25, 26], А. В. Белова [31, 33—35], П. И. Васильева [51—53], О. Е. Власова [79], А. А. Гвоздева [63, 65], М. М. Гришина [74], К. И. Дзюбы [77], Л. И. Дятловиц-кого и Л. Б. Рабиновича [81], М. А. Задояна [83, 84], М. М. Манукяна [115, 116], Г. Н. Маслова [117—120], Ю. А. Нилендера [134— 138], В. Г. Орехова [142, 143], Н. Я- Панарина [145, 146], И. Е. Прокоповича [150, 151], А. Р. Ржаницына [159, 160], М. И. Розовского [163], С. Е. Фрайфельда [194], С. А. Фрида [196] и многих других авторов.
Интересные исследования термонапряженного состояния элементов гидротехнических сооружений, в том числе и натурные, проведены в НИС Гидропроекта им. С. Я. Жука. Краткий обзор результатов этих исследований, выполненных только за последние годы, дан К- И. Дзюбой [77]. Эти исследования позволили сделать ряд важных выводов и дать рекомендации, используемые при проектировании гидротехнических конструкций и сооружений.
Усадочным напряжениям в бетоне также посвящено много исследований, среди которых следует, в первую очередь, указать па оригинальные работы Н. X. Арутюняна [25], А. В. Белова [28, 29, 30], А. А. Гвоздева [63, 65], Ю. А. Нилендера [134—138], Т. Пауэрса и Т. Браунъярда [240], Д. Пикетта [239], А. Р. Ржаницына [161], И. И. Улицкого [182]—[184] и А. Е. Шейнина [201— 204]. Широкое исследование усадки и усадочных напряжений в бетоне было проведено в течение последних лет в НИИЖБ Госстроя СССР [7-10, 13, 19].
В связи с актуальностью проблемы температурно-усадочных напряжений в бетоне необходимо уточнение и совершенствование надежных методов их расчета, учитывающих в полной мере изменчивость во времени его физико-механических свойств и ползучесть. Поэтому развитие эффективной теории температурно-усадочных напряжений, подкрепленной экспериментом, по-прежнему является важной задачей, решение которой связано с большими трудностями из-за отсутствия надежных приборов для непосредственного измерения напряжений в бетоне, что осложняет прямую экспериментальную проверку этой теории. Ближайшей задачей является разработка методики экспериментального изучения температурно-усадочных напряжений. Этому во
336
просу в значительной своей части посвящены списываемые в § VIII.4. и VII 1.5 исследования.
Ниже также на основах линейной теории упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна при уточненных выражениях для наследственных функций бетона и в соответствии с рекомендациями, изложенными в главах IV и VII, рассмотрены ряд одномерных и плоская задачи о температурных напряжениях в бетоне. При указанных условиях исследованы температурные напряжения и деформации в бетонных брусьях, полубеско-нечпом слое (бесконечном полупространстве) и бетонном блоке на основе соответствующих задач, рассмотренных в главе VI.
§ VIII.I. НЕКОТОРЫЕ ОДНОМЕРНЫЕ ЗАДАЧИ О ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ В СТАРОМ БЕТОНЕ С УЧЕТОМ ЕГО ПОЛЗУЧЕСТИ
В начале исследуем составляющую напряжений в бесконечном полупространстве, вызываемую изменениями его температуры по закону (VI.10), соответствующему гармоническим колебаниям температуры поверхности слоя. Упругие напряжения в слое при этих условиях мы нашли в § VI.1 равными (VI.11) или, что то же:
o(t,z) =o1(/,z) + o2(/,z) -
?Afl е~*п г sin 7 n z E (t) cos con t —
-^2- e-’n 2cos z E (t) sin o)n t.
(VIII.I)
Полные напряжения с учетом ползучести бетона и принципа положения воздействий будут равны:
о (t, z) = щ (/, г) И* (I, Т1) + о2(/, z) М (/, Т1)
(VIII.2)
где <Ti(/,z) и 02(t,z) —напряжения соответствующих заменяющих упруго-мгновенных задач
°* Ее "2 sin 2 ’
О 2 (Л Z) = — £ (/) e-’ n *cos Z,
(VIII.3)
а Н\ (Z,T|) и Н2 (/, Ti) —коэффициенты приведения этих напряжений, определяемые по формуле (V1I.7) для двух случаев T(t), соответственно равных:
Л (0 = cos соп /; Т2(0 = sinco„/.
(VIII.4)
337
Таким образом:
(/, тг) ~ cosant— j cosco„ т R(t, x)dx; (VIII.5)
(/, Tj) = sin <on t — sin сопт7? (/, т) dx. (VIII.6)
Входящая в эти формулы наследственная функция второго рода R(t, т) определяется по формуле (IV.146) или с помощью таблиц приложения I.
Для случая годовых гармонических колебаний температуры поверхности слоя с амплитудой Лп=18о и периодом 7=8640 ч (= 0,7272 • 10~3 1/ч) при а=1 • 10“5 градл\ v = 0,25; ат= = 3* 10~3 л2/ч, т.е. при Лп = 0,3482 м~', и ti = 1 сут. были рассчитаны упругие и полные (с учетом ползучести) напряжения в слое для бетона, характеризуемого параметрами (VII.13) и (VII.14).
Вначале с помощью табл. 37 и таблиц приложения I для /?(/, т) вычислялись интегральные члены в формулах (VII1.5) и (VII 1.6). При этом интервал времени t—ij разбивался на неравные промежутки (начиная от t) с шагом 0,1 сут., затем с шагом 0,3; 0,5 п 1 сут.
После этого вычислялись коэффициенты (f, ti) и //*(/, ti). Значения этих коэффициентов, найденных таким способом, приведены в табл. 40, где даны также значения модуля E(t).
Далее по формулам (VIII.3) при E(t) = \ вычислялись упругие относительные напряжения щ(Лг) и cs(l,z) (табл. 41). После этого по формуле (VIII.2) были найдены полные напряжения в слое о*(f,г).
Таблица 40
Модуль упругости и коэффициенты приведения Н*} (Лт,) и Н*2 (/. т,) упругих напряжений заменяющей задачи
t в сут. С (О 10-5 в кГсл’ n](t. *,) н*> (/,
2 0,8788 0,135550 0,007030
6 1,8446 2,2686 0.062411 0,021353
10 0,047943 0.045944
20 2,5578 0,012732 0,092525
40 2,6000 —0,098716 0,164470
120 2,6000 -0,512600 0.096594
На рис. 68 показаны эпюры упругих и полных напряжений в слое, найденных с учетом ползучести. Как видно из рисунка, ползучесть бетона, особенно в раннем возрасте, приводит к существенному снижению температурных напряжений.
338
Таблица 41
Относительные упругие напряжения (при £(/) = !) О1(/, z) и о2(/, z)
Z ВЛ °. (/. Z) °, (Л г)
0 0 24
0,5 3.4926 19,8605
I 5,7813 15,9274
2 7,6724 9.1772
3 7,3033 4,2416
5 4,1464 —0,7127
10 —0,2464 —0,6956
20 0,01428 0,01763
Рассмотренная задача в общем виде для старого бетона на основе теории наследственности была решена А. Р. Ржапицы-ным [159]. Здесь получено ее решение по теории упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна на основе нового аналитического выражения для С(/, т) в форме (IV.133) для стареющего бетона с переменным модулем упругости.
Исследуем теперь напряжения в защемленном по торцам бетонном брусе старого возраста высотой 2г0 при вынужденной деформации (VII.26), соответствующей, например, его равномерному остыванию или высыханию при температуре или, соответственно, эффективной влажности бетона, изменяющихся во времени по этому закону до предельной величины То (см.,например, § VIII.5).
Принимая во внимание вторую из формул (VI.63), условия задачи, а также формулы (VI.48), упругие осевые напряжения в брусе 1 найдем равными:
ау(() = а£Т0 (1 — е-3/) • (VI И.7)
Напряжения заменяющей задачи
оу(/) = аЕТ0. (VII 1.8)
Коэффициент приведения соответствующий случаю
(VII.26), был найден в § VII.4 и равен (VII.27). Таким образом, полные напряжения в брусе с учетом ползучести будут равны
а; (/) = аЕТ0 ГI - е-” - 4- (1 - <.-»') - (1 - е"*') +
У L Pi Рг
1 Напряжения ох(0, как нетрудно убедиться с помощью первой из формул (VI.63), тождественно равны нулю.
339
Их предельное значение совпадает с (VI 1.23) и при значениях параметров (VII.24) для «среднего» бетона составляет всего 28,3% от предельных значений упругих напряжений (VIII.7).
Из формулы (VIII.9) следует, что при весьма большом р, т.е. в случае, например, внезапно возникающего температурного перепада полные напряжения равны
<(0 =0ЕТ0[1--^-(1-е-*')--^- (1 — е“₽’')] - (VIII.10)
Их предельное значение равно (VII.23) и при значениях параметров (VII.24) для «среднего» бетона составляет те же 28,3%
Рис. 69. Температурные напряжения в бетонном брусе при его равномерном разогреве по экспоненциальному закону
/ — упругие напряжения; 2 — полные напряжения с учетом ползучести
На рис. 69 показаны кривые упругих и полных напряжений в рассматриваемом брусе, рассчитанные по формулам (VII 1.7) и (VIII.9) при а=1-Ю-5 град-1- т0=18°; ₽0,206 сут.-‘, Е= = 2,6-105 кГ/см2 и значениях параметров Alt Аг, pi и рг (VII.24) резольвенты R(t—т) для старого бетона.
Как видно из рис. 69, ползучесть бетона нс только существенно снижает величины температурных напряжений, но и изменяет характер их развития во времени. Если упругие напряжения монотонно возрастают, стремясь к некоторому пределу, то полные напряжения, возрастая, проходят через свой максимум, а затем начинают релаксировать, постепенно затухая во времени.
§ VIII.2. НАПРЯЖЕНИЯ В БЕТОННОЙ ПЛИТЕ ОТ ЭКЗОТЕРМИИ ПРИ УЧЕТЕ ИЗМЕНЕНИЙ ТЕМПЕРАТУРЫ НАРУЖНОГО ВОЗДУХА
Исследуем с учетом ползучести температурные напряжения в замыкающем блоке-плите толщиной 2z0=2 м перекрытия отсасывающих труб (или водоприемных отверстий) гидростанции (рис. 70), развивающиеся в нем от экзотермии и последующего остывания.
341
Распределение температуры в плите с учетом изменения температуры наружного воздуха было найдено в примере § 1.16 и определяется формулой (1.213).
Упругие температурные напряжения в плите найдем в соответствии с указаниями § VI.5 по формулам (VL63) § VI.4, имея в виду, в силу условий симметрии, полное защемление ее торцовых граней у = const в ранее уложенные смежные блоки перекрытия. Грани плиты x=const будем считать свободными от закреплений.
Расчетные изменения температуры плиты с учетом формулы (1.213) равны
Ф(г, О - ф(/) - ф(т>) + [Т( 0 - Т(Т1)] F(z), (VIII. 11)
Рнс. 70. Схема очередности бетонирования водоприемных отверстий или отсасывающих труб гидростанции
— забетонированная часть сооружения; 2 — замыкающий блок-плита; 3—подвесная опалубка
где T1 — возраст бетона, начиная с которого в нем могут развиваться температурные напряжения, отсчитанный с момента окончания бетонирования плиты. Учитывая большие сроки схватывания портландцементов и некоторую их условность, примем п равным одним суткам.
С помощью формул (VIII.11), (1.214) и (VL48) для погонного метра ширины плиты имеем:
W = {[<р(0-<p(ti)l 2zo+ [7(0- ЦГд)]^-] ; (VIII.12)
м ю 17 ю ~ т -=-(яп^«-
— az0cosaz0). (VIII.13)
И, далее, с учетом формул (VI.63), (VIII.11), (VIII.12), (VIII. 13), находим следующие выражения для упругих напряжений в плите:
(0 = (Г (0 - Т (тж)] ф, (г);
ау (0 = (0 + <2) (0 = [Г(0 - Т ( т,)] ф^г)-
-оЕ(/)|ф(0-ф(т1)],
(VIII.14)
342
— az0 cos az0) j — F(г);
, , . vsinuz0 . 3ve / . -W = —4- 7=-^- (sin <^0 —
иг0 (azoF
— azo cos ciz0) — F (г);
z0 — толщина плиты, а
(VIII. 15)
F(z) = cosaz + e sin az. (VIII. 16)
Напряжения заменяющей упруго-мгновенной задачи будут равны:
= ^(0=оГ(0 + ^2’(0, (VIII.17)
где
ё(у2,(0 = -оЕ(0- (VIII.18)
Полные напряжения в плите с учетом ползучести по принципу наложения воздействий найдем по формулам:
a‘y (0 = Оу1’ (О я; (Л TJ + о(у2) (/) Нг (t, т,), I предварительно вычислив коэффициенты приведения //, (Лп) и Н*2 (/,Т1) по выражению (VI 1.7) для двух случаев T(t), входящих в формулы (VIII.14), а именно для
Т1(1) = Г(/)-Т(т1); Т2(П = Ф(О-Ф(Г1). (VIII.20) Входящие сюда значения Т(п) и <p(ti) равны:
ТМ - 21,8е ; vfa) = 5,685° , (VIII.21) а текущие значения ф(/) и Т(/) берутся из табл. 10 и 16.
Графики функций T\(t) и T2(t) приведены на рис. 71; в табл. 42 даны их некоторые значения, необходимые в дальнейшем.
Таблица 42
Значения функций Tt(t) и T2(t) в град для некоторых моментов времени наблюдения /
1 в сут. 1 2 3 3.8 4 120
7*1(0 0 6,3 9,200 10,300 10,485 -23,075
МО 0 -0,315 -0,627 -0.845 —0,945 -15.285
343
Для вычисления интегралов (VII.16), входящих в формулу (VIL7) и соответствующих функциям Ti(t) и Тг(О> воспользуемся методикой, изложенной в § VI1.2.
Разбивая кривые Л(0 и T2(t) на характерные участки, удобные для применения таблиц приложения 1, принимая во внимание данные этих таблиц и пользуясь формулами табл. 37, найдем значения коэффициентов приведения Н\ (/, т>) и Н* (/, Ti) для двух моментов времени наблюдения: 1—4 сут., соответствующего
Рис. 71. Графики функций Tt(t) и Т2(0 а — функция Г(/); б — функция v (О
наибольшему разогреву плиты от экзотермии, и /=120 сут. после ее длительного остывания. Ниже в качестве примера приводится порядок вычисления коэффициента (/,т1) для /=4сут. Разбивая промежуток t—Ti на четыре интервала 4—3,8;
3,8—3; 3—2 и 2—1 сут., заменяя непрерывную кривую Tj (/) кусочно ломаной, составленной нз прямых, а кривую — ку-
сочно ломаной, составленной из ветвей квадратной параболы, Л
вычисляем последовательно интегралы f 7\ (x)R(t, x)dx с по-
мощью формулы последней строки табл. 37.
4
f Г,(г)Л(/, г) dr = |г °-|0 | [0,884824 X
3 8
(Дт1=Дт£—0,1 сут.)
344
X 10,30(3 0,1 —0,1)0,1 } 2,083471 0,22 (10,3+ 10,485) +
+ 5,64944-10,485(3 0,1 —0,1)0,1] = 5,16526 град.
Аналогично находим:
3.8
J Л (т) R (Л Т) dr = 2,25914 град-, з
з
\TY(x)R(t,x)dv -= 1,024857град;
2 2
J Л (т) R (*» т) & = 0,258445 град.
Поэтому
4
j 7\ (т) R (t, т) dr = 5,16526 + 2,25914 + i
+ 1,024857 + 0,258445 = 8,707702 град.
Далее, с учетом (VI 1.7), находим
ЯМ = 10,485 — 8,707702 = 1,777298 град.
Итак, при /=4 сут.
= lJ77298epad. (VIII.22)
Аналогично найдем:
при t = 4 сут. Н*2 (t, т,) — — 0,253103 град. (VIII.23) при /= 120 сут.
Н\ (z. Ti) =— 6,449986 град-, /Л‘ (/, ^) = — 2,05785 град. (VI11.24)
В табл. 40 даны значения модулей упругости £(/) для «среднего» бетона, вычисленных по формуле (1V.3) при параметрах (VII.13), а в табл. 43 значения функций ф1(2) и фг(г) для ряда характерных точек плиты, найденные с учетом формул (VIII.15), (VIII.16) и табл. 17 при
а - 1 10—5 (град)-’; v = 0,25. (VII 1.25)
Наконец, в табл. 44 даны значения упругих напряжений заменяющей задачи Су1’^). ОуЧО и ож(0, найденных с помощью формул (VIII.17) и (VIII.18), табл. 40 и 43 с учетом (VIII.25) для двух выбранных моментов времени.
На рис. 72 показаны эпюры упругих оя(0, av(/) и полных °* (0. Оу (О напряжений в плите, найденных по формулам (VIII.19) с учетом (VIII.22) — (V1II.25) и данных табл. 44, в рассматриваемые моменты времени.
345
Таблица 43
Значения функций ф> (г) и фч (г) в отдельных точках плиты
г в л -1 -0.6 -0,2 0 0,2 0.6 1
Ф. (2) 0,45657 0,016301 -0,21047 -0,23240 -0,19453 0,035999 0,40263
Фг (г) -0,31238 -0,67535 -0,82482 -0,80810 -0,731583 -0,423750 0,020183
Примечание. Нижняя грань плиты г=—г0 утеплена опалубкой; верхняя грань открыта.
Таблица 44
Напряжения в кГ/см1 • град заменяющей упруго-мгновенной задачи в отдельных точках сечения плиты
2 В М -I -0,6 -0.2 0 0.2 0,6 1
Н 5'”(0 -0,60768 -1,31378 -1,60455 —1,57202 -1,42317 -0,82433 0,039262
-1,45900
!1 ох (/) 0,88818 0,031711 -0,40943 -0,45209 -0,37842 0,070030 0,78325
Н ^(П -1,08292 -2,34122 -2,85938 -2,80142 -2,53616 —1,46900 0,069968
сч 'й'Лп -2,60000
ot (/) 1,58278 0,056510 -0,72963 -0,80565 —0,67437 0,12480 1,39579
Из рис. 72 следует, что плита в направлении оси Оу вследствие закрепления граней у=const вначале испытывает сжатие почти по всему сечению, а затем, после длительного остывания, существенное растяжение. В направлении оси Ох напряжения в плите знакопеременны, самоуравновешены и незначительны по величине. Ползучесть существенно снижает напряжения о„(/),
6u(t)
t-4cym t-tZOcgm.
(0,439) 1.790 (4,899) 38,126
(-1,096} 1 -7,264 (14J75) \ 73,63в\
(-7,160) 1 \ 98,763 \
1 104.384 \
(~2fi25) _L -15.104(23,419)
1 1 t05,721 |
(-7,482) -15,445(73,793)
1 1 / 1 / 1 93,765 /
(-1,966) -12(396(70,451)
/ /
(-о.71й\ -4,993, (17,335) / / f у/
6*(t)
f c 4cym. t- ftOcym
(1.397) 8,217 (-9,003) -37,708
(0,174)- j 0,734 (-0,805)X -7,880
(-OJ672) (4.350)
(-OJ8O4) \-4,740 (5,196) H 18.590
(-0,778) -4,293 (4,706) 4-416,836 П
(0,0564) r 0.337 (-0,364)у 7 -1,304
1 VW? / 1 (-10.2^ J, -36,523
Puc. 72. Эпюры нормальных напряжений в плите через 4 и 120 суток после бетонирования (цифры без скобок—упругие напряжения, цифры в скобках — напряжения, рассчитанные с учетом ползучести)
но в конце периода остывания плиты эти растягивающие напряжения все же довольно велики, что может привести к сквозной трещине в обычно более слабом шве сопряжения с ранее уложенными ''локами.
§ VI 11.3. НАПРЯЖЕНИЯ В БЕТОННЫХ БЛОКАХ ПРИ ИХ РАЗОГРЕВЕ ОТ ЭКЗОТЕРМИИ
Воспользуемся решениями задач § VI.6 и VI.7 об упругих напряжениях в массивных бетонных блоках для приближенной оценки с учетом ползучести температурных напряжений, развивающихся в них вследствие экзотермии.
Будем иметь в виду лишь первое слагаемое формулы (VI.125), соответствующее изменению средней температуры блока при его разогреве, положив для определенности
ф (0 = agT (t) = 7\ (t) = T(t)-T (Tt) (VI11.26)
и приняв T'i(Z) по рис. 71 и табл. 42. при Ti = l сут.
Таким образом, речь идет об оценке основной составляющей полных напряжений в блоке, вызываемой изменением его сред
347
ней температуры, подобным изменению температуры массивной плиты, рассмотренной в § 1.16 и VIII.2.
Ограничимся рассмотрением блока с торцами, закрепленными от тангенциальных смещений, изученного в § VI.6. Аналогично всегда могут быть исследованы и напряжения в блоке со свободными торцами (§ VI.7).
Упругие напряжения в блоке найдем умножением ординат эпюр, изображенных на рис. 67, а на аЕ(/) [Т(/)—T'(-ti)], приняв а=1-10~5 град-1, Е(/) по табл. 40 и = T(t)—T'(ti) в соответствии с данными табл. 16 и 42. Выполнив это, найдем:
при /=4 сут.
(0|w~M/)|T-=()^“1 1 ’ 10~5’1’459’106 • 1°.485=1 — 15,298 кПсм2--,
(*1=0(01,=0 1 • 1 Ю-5 -1,459-105 =
‘ b = ii
=-. — 1,459 ЛГ/СЛ‘2 ; град
при /=120 сут.
°х (0|, = о^о (/)Ч=11~_1.1.10-6 -2.6Х Ц =о у Д=о
X 105(— 23,075) = 59,995 кГ/cjw2;
ёх (01Т1=о~Ч (0,4=0 1-1-Ю-» -2,6-10» =
|t=o |е=н
__ 2 6
град
(VHI.27)
(VIII.28)
Коэффициенты приведения /Л*(/, Ti) напряжений заменяющей упруго-мгновенной задачи, соответствующие были найдены в § VIII.2 равными (VIII.22) и (VIII.24). Умножая напряжения (VIII.27) и (VIII.28) соответственно на эти коэффициенты, найдем следующие значения полных напряжений в рассматриваемых точках блока:
при / = 4 сут.
о* (/)|т=о о* (/)|т=о — — 1,459 • 1,777 = —2,593 кПсмг-, (VI11.29) 6=0 у Е=±1
при /=120 сут.
а*(/)|Т1=о~о*(/)|т1=о ~ — 2,6(— 6,45) = 16,77кГ/см2. (VIII.30)
Е=0 у Е=л1
Сравнивая эти напряжения с упругими напряжениями, видим, что ползучесть приводит к существенной релаксации температурных напряжений от экзотермии, особенно в бетоне молодого возраста. При длительном остыван-ии блока напряжения
348
<^(O|v-o н °у(О|ч=о меняют знак и становятся растягивающими. Их величина довольно велика, так что даже при благоприятном действии ползучести возможно появление вертикальной сквозной трещины по середине блока и его отрыв от основания в приторцовых зонах. Сказанное относится и к блоку со свободными торцами (§ VI.7), поскольку эпюры напряжений cx(t) и ctv(/) в нем весьма схожи с эпюрами этих напряжений в рассмотренном блоке.
§ VII 1.4. ЭКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИИ В БЕТОНЕ
Для экспериментального изучения температурных напряжений в бетоне автором совместно с инж. О. М. Попковой были поставлены специальные опыты. Объектом для эксперимента служил призматический брус (блок), жестко заделанный по торцам, с заданным температурным режимом. Таким образом, в опыте искусственно создавались условия наиболее простой одномерной температурной задачи. Жесткая заделка блока осуществлялась с помощью специальной рычажной установки [23].
Заданный температурный режим создавался специальной циркуляционно-нагревательной системой с насосом и регулированием температуры водяной ванны, в которой во время опыта находился блок.
Блок с призматической частью 25X50X140 см имел форму восьмерки. Для создания простых граничных условий защемления по торцам он укладывался на пружинное основание в виде «матраца», не препятствующее его смещениям. Опалубка боковых граней призматической части блока набиралась из отдельных досок, удаляемых перед заливкой ванны. В процессе испытания блока производилось измерение: температуры его отдельных точек, усилий в нем и деформаций его призматической части.
В опытах была избрана наиболее простая схема испытания блока, а именно: равномерный разогрев блока до заданной температуры без ограничения деформаций и последующее его остывание при полностью стесненных деформациях. Неизменность длины блока в процессе охлаждения обеспечивалась периодическими догрузками (подтяжками) блока с помощью рычажной системы; величина этих догрузок определялась по тарировочным данным рычагов. Таким образом экспериментально определялись температурные усилия в блоке в любой момент времени наблюдения в условиях его жесткой заделки. Концом эксперимента считался разрыв блока (как это было в двух из трех испытанных блоков) или его остывание до начальной температуры. Состав бетона (по весу) для блоков и контрольных образцов-близнецов 1:1,9:3,18, B/ZZ=0,6. Для приготовления бетона применялись следующие материалы: портландцемент Воскресенского (для
349
блока № 1) и Брянского (для блоков № 2, 3) заводов с практически одинаковой активностью 590 кГ[см2-, песок речной средней крупности (-—-0,33 мм), одинаковый для всех блоков, с объемным весом 1520 кг/jw3 и удельным весом 2640 кг/м3-, щебень подбирался нз двух фракций 5—10 и 10—20 мм в соотношении 1:1; вода — обычная водопроводная, специальным исследованиям не подвергалась.
Прочность бетона в среднем оказалась равной: 390, 460 и 400 кГ/см2 соответственно в блоках № 1, 2, 3.
Для сопоставления экспериментальных и теоретических значений температурных усилий в блоках необходимо было располагать сведениями о физико-механических свойствах исследуемого бетона. С этой целью была разработана методика ряда побочных исследований [23], к числу которых относится изучение следующих его свойств: ползучести и релаксации напряжений при растяжении, предела прочности при сжатии, осевом растяжении и растяжении при изгибе, модуля упруго-мгновенной деформации при растяжении. Эти свойства изучались на контрольных образцах-близнецах, находящихся в ванне вместе с блоком и проходящих тот же цикл разогрева. Перед запиранием блока в рычажной системе образцы извлекались из ванны и после остывания до комнатной температуры подвергались соответствующим испытаниям. Эти образцы именуются в дальнейшем образцами горячего хранения. Образцами холодного хранения назывались образцы-близнецы, хранившиеся в естественно-влажных условиях, не подвергавшиеся разогреву.
Основные результаты испытаний бетонных блоков приведены в табл. 45. На рис. 73—75 результаты испытания одного нз блоков (№ 2) изображены графически. Разогрев и охлаждение по сечениям и по длине блока были столь равномерными, что в масштабе рис. 73 не представлялось возможным нанести отдельные экспериментальные точки. В соответствии с этим показана лишь одна кривая разогрева и охлаждения блока, построенная по средним из показаний всех 17 термопар, заложенных в блок.
Термопары размещались группами в трех сечениях блоков: в середине его длины, в конце призматической части блока п в четверти ее длины (см. рис. 75).
На рис. 74 показаны эпюры изменений температуры блока № 2 в период его охлаждения на отдельных этапах опыта, а на рис. 75 — графики изменения во времени усилий, передаваемых тягами на блок, продольной силы и изгибающих моментов в нем, развивающихся в период его охлаждения в условиях стесненной деформации. На этом рисунке Мх — момент относительно горизонтальной, а Му — относительно вертикальной оси поперечного сечения блока.
На нижнем графике рис. 75 нанесена кривая относительных осевых деформаций блока в периоды его разогрева и остывания.
350
Таблица 45
Из этого рисунка следует, что в период остывания блока не удалось строго достичь постоянства его длины.
Некоторое укорочение блока эквивалентно упругой податливости связи, наложенной на него, которая учитывалась в дальнейшем при определении теоретических значений температурных напряжений.
Результаты наблюдений за температурой отдельных точек блока и его деформациями во время разогрева позволяли определить величину коэффициента линейного расширения бетона а, необходимую для нахождения расчетной теоретической кривой свободных температурных деформаций при охлаждении блока.
Она оказалась равной:
для блока №> 1 а = 1,03-10~® (град)—1;
для блока №>2 а = 1,01-10~5 „
для блока №3 а= 1,04-10~® „
(VIII.31)
Наблюдение за бетонными блоками во время их остывания позволяло к данному моменту времени получить следующие экспериментальные данные: 1) среднюю температуру оси блока; 2) относительную осевую деформацию блока; 3) продольную си-
351
352
Рис. 75. Усилия в тягах, продольные силы, изгибающие моменты и действительная осевая деформация блока № 2 на периоде его остывания
353
лу в блоке или соответственно температурные напряжения в нем; 4) фактический модуль деформации блока на отдельных ступенях его догружения (подтяжки); 5) предел «длительной» прочности бетона на растяжение в условиях водяной ванны, прошедшего цикл значительного (до 60° С) разогрева и охлаждения.
Изменения средней температуры оси блока № 2 в процессе его разогрева и охлаждения приведены на рис. 73. Ординаты ДГ изображенной там расчетной кривой, отсчитанные от горизон-
Лродолжительностъ б сушка» ость!Ьания блока, с номента его запирания
Рис. 76. Кривые осевых деформаций блока Ms 2 на периоде его остывания
I — кривея свободных температурных деформаций; 2 — кривая непогашенных деформаций; 3 — кривая расчетных деформаций
тальной пунктирной прямой, соответствующей абсолютному значению средней температуры блока в момент его закрепления, определяют кривую изменений температуры блока при его охлаждении, начиная с этого момента времени. Будучи умноженными на соответствующую величину коэффициента линейного расширения бетона (VI 11.31), ординаты этой кривой дают свободные температурные деформации при остывании блока, которые возникали бы, если бы блок не был закреплен от деформаций (кривая / на рис. 76). В действительности условие постоянства длины блока строго не выполнялось. Как уже отмечалось, длина блока уменьшалась вследствие не полностью погашаемых деформаций во время его догружений при остывании. Эти деформации блока при построении расчетной кривой его вынужденных деформаций вычитались из свободных температурных деформаций, найденных указанным выше способом. Графически деформации недотяжки блока Де изображены штрих-пунктирной расчетной кривой на нижнем графике рис. 75 с ординатами, отечн-
354
тываемыми от горизонтальной пунктирной прямой на этом рисунке, соответствующей абсолютному значению относительной осевой деформации блока в момент его закрепления. На рис. 76 эта кривая обозначена цифрой 2.
Кривые расчетных вынужденных деформаций блока, полученные алгебраическим сложением ординат кривых 1 и 2, обозначены на рис. 76 цифрой 3. Эти кривые и были положены в основу определения теоретических значений температурных напряжений в рассматриваемом блоке; для этого они аппроксимировались выражением
в (/ - Tl) = В 11 - j + A siп — (f~T1-) , (VII1.32) А/о
причем: В = 51,4-10~5 (мм/мм)~, л4=4- 10—5 (мм/км); 0 = 0,073 (сут.-1); Д/о=12 (сут.); т1 = 2,81 (сут.).
Экспериментальные значения температурных напряжений в блоке находились делением продольной силы в нем к данному моменту наблюдения на площадь его поперечного сечения. Температурные изгибающие моменты вследствие их малости не учитывались*. Найденные таким образом значения напряжений, отнесенные к серединам интервалов между двумя догружениями блока, изображены графически на рис. 80 в виде пунктирных кривых 3 и соответствующих экспериментальных точек.
Модуль деформации растяжения блока находился как частное от деления приращения напряжений в нем на приращение его осевой деформации на каждой ступени догружения.
На рис. 77, а нанесены отдельные значения этого модуля для блока № 2 п по ним построена осредненная кривая его изменений в ходе опыта (кривая /). Возле каждой экспериментальной точки указана продолжительность соответствующей ей ступени догружения блока.
На рис. 77,6 изображена зависимость величины модуля деформации растяжения от продолжительности ступени догружения блока в минутах. Из рисунка следует, что величина модуля деформации с ростом ступени догружения снижается, что объясняется развивающейся во времени ползучестью бетона.
С помощью кривой, изображенной на рис. 77,6, была построена кривая изменения модуля деформации в ходе опыта, приведенная2 к продолжительности ступени догружения блока, равной 15 мин, показанная на рис. 77, а (кривая 2). На рисунке видна тенденция к повышению модуля деформации с увеличением
* Краевые напряжения, найденные с учетом этих моментов (см. табл. 45), отличались от средних напряжений, вычисленных без их учета, не более чем на 7%.
2 Приведение производилось пропорционально ординатам кривой, изображенной на рнс. 77,6; при этом ее ордината, относящаяся к 15-лшн ступени догружения блока, прии/.та за единицу приведения.
355
продолжительности опыта, что вполне объяснимо в связи с уменьшающейся температурой бетона при остывании блока.
За расчетное значение модуля деформаций блока была принята его величина, соответствующая 15-минутной ступени догружения блока, равная Fcp=0,88- 105 кГ/см?_
Продолжительность ступени нагружения 6 нинутак
Рис. 77. Экспериментальные данные о модуле деформации при растяжении блока № 2 на периоде его остывания
а — изменение модуля деформации в ходе опыта; б — зависимость модуля деформаций от продолжительности ступени догружения блока; 1 — экспериментальная кривая; 2 — кривая, приведенная к продолжительности ступени догружения блока, равной 15 мин
356
На рис. 77, а нанесено также среднее значение модуля деформации неразорвавшегося блока № 2, найденное при его разгрузке после окончания опыта; оно оказалось несколько выше принятого значения и равным 1 • 105 кПсм2.
Расчетные значения модулей деформаций растяжения для остальных блоков были равны: для блока № 1 ЕСр=0,843Х Х105 кГ/см2 и для блока № 3 Еср=0,77-105 кГ/см2.
Усилия в блоках № 1 и 3, при которых произошел их разрыв, позволяли найти предел прочности при растяжении исследуемого бетона в горячей воде. Для блока № 1 этот «длительный» предел прочности на растяжение оказался равным <тр=14,1 кГ/см2, т. е. 30
в -^-j=2,12 раз меньшим, чем кратковременная прочность контрольных образцов горячего хранения, испытанных на воздухе при комнатной температуре. Соответственно для блока № 3 ар=18,3 кПсм2 и ар.к=39 кГ/см2, т. е. для него ар было в —- = 18,3 =2,14 раза меньше ар.к.
Блок Ке 2 не разорвался при остывании до комнатной температуры, но напряжения в нем, судя по ряду признаков, были близки к разрушающим. В конце опыта они были равны ар = = 15,4 кГ/см2, в то время как арк=37,5 кГ1см2. Таким образом, у z* 37,5 « .
этого блока в конце опыта было —= —— —2,4.
ар 15,4
Имеется много экспериментальных данных, относящихся в основном к ползучести бетона при постоянной (комнатной) температуре. Влияние температуры бетона на его ползучесть изучено главным образом для специальных жаростойких бетонов, нормальные условия работы которых характеризуются весьма высокими температурами [198].
Влияние температуры в пределах до 100е С на ползучесть обычных бетонов изучалось в опытах К. Ли [235], А. Тэйера [249] и И. Серафима [246]. Результаты этих опытов показывают, что скорость деформации ползучести существенно зависит от температуры среды, особенно в моменты времени, близкие к моменту загружения [249]. Однако кратковременность большинства из этих опытов, продолжавшихся всего несколько суток, не позволяет сделать окончательных выводов. Представляющие наибольший интерес опыты А. Тэйера (рис. 78) вместе с тем содержат и некоторые противоречия. Как видно из рис. 78, при одних и тех же температурах «влажные» образцы претерпевают большие деформации ползучести, чем «сухие», и меньшие, чем «полусухие».
Несмотря на известную противоречивость этих опытов, можно все же на основании их с уверенностью сказать, что повышение температуры мокрого бетона даже в незначительных пределах существенно увеличивает скорость его ползучести, а следовательно, и абсолютные значения деформаций ползучести на ог-
357
раниченном интервале времени их наблюдения. Так, по данным А. Тэйера, ползучесть образцов при повышении температуры бетона от 10 до 50° С за трое суток наблюдения увеличилась в 10,5 раз (образцы с /? = 200 кГ/см2) и в 2,6 раза (образцы с /? = 480 кГ/см2). В среднем образцы с 7? = 415 кГ/см2, т. е. с Я близким к наблюдаемому у бетона блоков № 2 и 3, в соответст-
Рис. 78. Ползучесть бетона различной влажности при разных температурах. Опыты Л. Тэйера
1 — «сухой» бетой; 2 — «полусухой» бетон; 3—«влажный» бетон. ®—R-200 кГ/с*’. О—Л-» -480 «Г/сти-
вии с изложенным должны были бы увеличить свою ползучесть в 4,4 раза (по линейной интерполяции). Очевидно, что при этих условиях нужна была новая методика построения кривых ползучести исследуемого бетона, учитывающая влияние его температуры на ползучесть.
Так как непосредственно экспериментальным путем получить кривые ползучести исследуемого бетона в горячей воде не представлялось возможным, была принята следующая методика построения расчетных кривых ползучести.
На основании анализа
указанных опытов можно предложить следующую гипотезу: при сравнительном экспериментальном исследовании ползучести насыщенного водой бетона практически зрелого возраста при комнатной и повышенной температурах, неизменных в ходе опыта, в любой момент наблюдения, начиная с некоторого малого интервала времени, отношение скорости деформаций ползучести «горячего» еР и «холодного» ех образцов постоянно и равно отношению их полных, начальных кратковременных деформаций
= const,
(V1II.33)
¥
где EJJ и Er — модули полных начальных кратковременных деформаций соответственно холодного и горячего образцов. Эта гипотеза и была положена в основу построения расчетных кривых ползучести горячего бетона.
358
Интегрируя уравнение (VII 1.33), получим
Ек
ег + С, =-- ех + С2; (VIИ.34)
начальное условие дает нам С| = С2, поэтому в любой момент времени
er=Fx-|^. (VIII.35)
Таким образом, в соответствии с изложенной гипотезой расчетная кривая ползучести горячего бетона получается из кривой ползучести холодного бетона искажением ее ординат путем их умножения на постоянный для данной кривой коэффициент приведения К, равный отношению указанных модулей холодного £х и горячего Е* образцов.
При обработке экспериментальных данных модуль на основании результатов опытов на образцах-близнецах холодного хранения принимался равным:
для блока № 1 Е* = 3,5 • 1 СР кПсм2-, для блока №2 Ej =.- 3,75-105 „
для блока № 3 Е* = 3,47 • 103 „
(VII 1.36)
За расчетные же значения модуля Е* принимались указанные выше значения модулей деформаций испытанных блоков, соответствующие наименьшей (15-минутной) ступени их догружения. Таким образом, коэффициенты приведения кривых ползучести оказались равными:
Л ХР 4 1Г 3,5-10® . 1ГО
для блока № 1 л. = —:-------------=4,152:
1 0,843- 10®
.. хр о гл 3,75-10® . лл.
для блока №2 л2 =-----------------=4,261:
2 0,88-10®
для блока №3 К3 = 3,47 10 =-4,506.
3 0,77-10®
(VIII 37)
Интересно отметить, что эти цифры весьма близки к коэффициенту увеличения ползучести горячего бетона /(=4,4, полученного в опытах А. Тэйера (см. стр. 358).
Расчетные кривые мер ползучести для бетона испытанных блоков, полученные умножением ординат кривых мер ползучести соответствующих контрольных образцов на коэффициенты приведения Ki, К2, Кз, изображены на рис. 79. Эти кривые C(t—т) аппроксимировались аналитической зависимостью (IV.137). На
359
пример, для блока № 2 параметры, входящие в выражение (IV. 137), оказались равными:
= 0,426 • 10-5 (сяг/кГ)-, Л = 0,682 • 10-5 (см2/кГ)-,
Y ~ 0,2 (сут.)~’ ; а = 2 (сут.)—1 .
(VIII. 38)
На рис. 79 нанесены также расчетные точки, найденные по
Рис. 79. Расчетные кривые мер ползучести бетона, приведенные к модулю деформаций блоков
1 — блок № I; 2 — блок J& 2; 3 — блок № 3
(IV. 137) хорошо описывает расчетные кривые ползучести для исследованного «горячего» бетона.
Расчетные теоретические значения температурных напряжений в испытанных блоках к моменту времени наблюдения t находились по формуле, аналогичной (IV.18):
t
u*(t — TJ = £ср[е(/— Tj)—Je(r —Ti)/?(/— r)drj, (VIH.39)
в которой:
Ecp—расчетный модуль деформации растяжения блока; е(/—ti) — расчетная вынужденная деформация блока, например (VIП.32), определяемая, как это описано на стр. 354;
Ti — момент времени, соответствующий закреплению блока.
360
При этом имелось с виду, что R(t—т), —т() о*(/—ti) являются функциями лишь продолжительности опыта, так как последний производился на бетоне зрелого возраста, прошедшем разогрев. По этой же причине модуль деформации ЕСр считался не зависящим от возраста бетона.
Наследственная функция второго рода /?(/—т) находилась на основе соответствующей расчетной кривой ползучести, определяемой, как это указано на стр. 359, по формуле (IV. 156) с учетом выражений (IV. 157)—(IV. 158), в которых
Е0 = Еср; фв = Л8; V = 4 (VIII.40)
Входящие в формулы (IV.157), (IV.158) параметры А3, А< уь у2 берутся из выражений, аналогичных (IV. 160).
Например, при значениях (VIII.38) этих параметров расчетной кривой ползучести (IV. 137) постоянные Аь /2, pi и р> для блока № 2 оказались равными:
А, = 0,0138(сут.)-‘; Л8 - 1,231 сут.-»; |
Pj = 0,227 (сут.)-1; р2 = 3,218 сут.-1 ./
Теоретические кривые температурных напряжений, рассчитанные с учетом и без учета ползучести, изображены на рис. 80; на этих же рисунках показаны экспериментальные (пунктирные) кривые напряжений, измеренных в период остывания блоков. Между теоретическими кривыми температурных напряжений, рассчитанных с учетом ползучести бетона, и экспериментальными кривыми этих напряжений имеется хорошее соответствие. Учет ползучести приводит к существенному снижению температурных напряжений в бетонных блоках в среднем на 35%.
Теоретические значения температурных напряжений, найденные на основе данных о ползучести и модуле упругости «холодного» бетона, т. е. контрольных образцов, прошедших тот же цикл разогрева и охлаждения, но испытанных на воздухе и прн комнатной температуре, оказались значительно в (4 5 раз)
больше экспериментальных значений температурных напряжений в блоках. Такое расхождение нельзя объяснить ни чем иным, как существенно более высокой ползучестью мокрого «горячего» бетона по сравнению с ползучестью бетона «холодного» [249], что учитывалось при построении расчетных кривых ползучести «горячего» бетона.
Наконец, из изложенного следует, что указанная выше гипотеза о методике построения расчетных кривых ползучести бетона при повышенных температурах, несмотря на ее очевидную приближенность, дает харошие результаты при оценке температурных напряжений.
Интересны также и некоторые другие результаты описанных исследований температурных напряжений в бетоне.
Прочность бетона на растяжение у восьмерок горячего хранения оказалась ниже, чем у соответствующих образцов-близнецов
361
Растягивающие температурные напряжения в блоке в кГ/см?
25
.362
холодного хранения, всего на 17%. (Образцы, извлеченные из горячей водяной ванны, быстро подсыхали в результате термо-диффузии во время остывания. Поэтому их влажность в момент испытания на прессе была низкой).
Прочность же на растяжение бетонных блоков, испытанных непосредственно в горячей воде, значительно снизилась по сравнению с контрольными образцами холодного хранения: у блока № 1 в 2,12 раза и у блока № 3 в 2,14 раза.
Столь существенное снижение прочности бетона на растяжение в горячей воде происходило не только по указанным выше причинам, но и в результате расклинивающего действия водных пленок, адсорбционного понижения прочности бетона, поглощения воды некоторыми кристаллогидратами, в частности трехкальциевым алюминатом, с последующим их размягчением, а также в результате снятия упрочняющих давлений менисков жидкости в микропорах и капиллярах.
Здесь мы имеем полное соответствие известным опытам А. 3. Басевича [27], К. А. Мальцева [ИЗ, 114] и Н. А Мещанского [129, 130]. Напомним, что снижение прочно;ти на растяжение бетона, находящегося в воде, составляло в опытах А. 3. Басевича 2—2,2 раза, а в опытах К- А. Мальцева 1,87—2,14 раза.
Снижение прочности бетона при растяжении должно было наблюдаться при деформировании блока в ванне во время его догружений (подтяжек). Действительно, большое снижение модуля деформации растяжения, так же как и прочности при растяжении, отмечалось у блоков, растягиваемых усилиями догрузок в горячей воде. Значения этих модулей деформации у всех трех испытанных блоков были меньше 1 • 105 кГ/см2 и меньше модулей деформации контрольных образцов в среднем в 4.3 раза.
Такое значительное снижение модуля деформации в горячей соде было связано не только с указанным эффектом снижения прочности бетона в воде, по и с существенным «размягчением» мокрого бетона при повышении его температуры подобно тому, как эго наблюдалось в опытах К- Ли [235] и А. Тэйера [249].
Бетон исследуемых блоков в горячей воде обладал значительной ползучестью, существенно превышающей по величине ползучесть контрольных образцов холодного хранения. Это полностью согласуется с опытами К- Ли и А. Тэйера. Напомним, что в соответствии с данными А. Тэйера ползучесть бетона с R--=415 кПсм\ т. е. близким тому, что наблюдалось у всех трех испытанных блоков, при разогреве от 10 до 50° С возрастает примерно в 4,4 раза. В исследуемом бетоне это увеличение примерно составляло от 4,1 до 4,3 раз.
Причины столь существенного увеличения ползучести бетона в горячей воде нуждаются в дополнительных экспериментальных исследованиях.
Развивающиеся при остывании бетонного блока в условиях стесненной деформации температурные напряжения достигали
363
прочности бетона на растяжение и в двух случаях из трех привели к разрыву блоков.
В результате повышенной ползучести горячего бетона наблюдалось и существенное снижение температурных напряжений по сравнению с их теоретическими значениями, найденными без учета ползучести. В среднем за 10 суток наблюдения оно составило 35%, т. е. примерно было равно тому, что в обычном бетоне при комнатной температуре наблюдается на значительно более длительных интервалах времени. Таким образом, ползучесть бетона играет важную роль, существенно снижая температурные напряжения в нем.
§ VIII.5. ЭКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ УСАДОЧНЫХ НАПРЯЖЕНИИ В БЕТОНЕ
Экспериментальное изучение усадочных напряжений, развивающихся в бетоне при его высыхании, проводилось на призматических брусьях, жестко заделанных по торцам и гидроизолиро-
Рис. 81 Установка для экспериментального изучения усадочных напряжений в бетоне
1 — испытуемый образец; 2 — поддерживающие образец рамки; 3 — постамент;
4 — рабочие тарированные рычаги. 5 — рычаги; б — распорка; 7 — тяги;
3 — рамки для крепления подвесок. 9 — ножевые опоры; 10 — крючья, заделанные в образец; 11 — мсссуры
364
ванных по боковой поверхности. Тем самым в опыте были искусственно созданы условия одномерной задачи осевых высыхания и усадки образца. Жесткая заделка образца производилась на специальной рычажной установке [24], изображенной на рис. 8J. Усилия на брус передавались четырьмя (с каждого торца) тягами, заделанными в образец на части его длипы. Таким образом торцы бруса оставались открытыми для высыхания. Степень последнего в любой момент времени определяли взвешиванием на весах образца вместе с установкой. Поддержание постоянства длины образца контролировалось с помощью тензометров, а необходимые для этого усилия определялись по тарировочным данным рычагов. В ходе эксперимента на основании этих данных определялись продольная сила и изгибающие моменты в образце, с помощью которых затем рассчитывались усадочные напряжения в нем.
Зная физико-механические свойства бетона, из которого изготовлялись рабочие образцы, и результаты их испытаний, можно было в любой момент опыта определить экспериментальное значение усадочного усилия в них и сравнить его с расчетной теоретической величиной.
По мере развития усадки, обнаруживаемой по изменению показаний тензометров, укоротившийся образец принужденно возвращался к своей первоначальной длине, тем самым погашалась усадочная деформация. С течением времени усилие, необходимое для этого, прогрессирующе возрастало и в конце концов становилось равным разрывному усилию в данном возрасте бетона. В этот.момент образец разрывался.
Параллельно испытывались также образцы-близнецы в условиях одномерных (осевых) высыхания и усадки без ограничения деформаций. Эти образцы имели те же размеры и однотипную гидроизоляцию, но не испытывали препятствий свободной усадке. Взвешиванием образцов и наблюдением за их деформациями устанавливались связь между усадкой и изменением влажности бетона и ход свободной усадки во времени, необходимые для теоретического рассмотрения напряженного состояния от усадки в рабочих образцах.
Ползучесть бетона при растяжении изучалась па бетонных призмах сечением 5x5 см.
До начала испытания образцы хранились гидроизолирован-ными по боковой поверхности на длине, равной 21 см, а также на некоторых участках вблизи их торцов.
У концов призм имелись участки, по площади равные площади торца и не имеющие гидроизоляции, через которые проходило высыхание образцов. Указанная методика хранения призм моделировала характер высыхания, аналогичный для основных рабочих образцов. Перед загружепием, для исключения дальнейшего развития усадочных деформаций, призмы полностью гидр*>изолир< вались п - всей поверхности.
365
Такая методика изучения ползучести бетона была принята по следующим соображениям. Обычно применяемая методика изучения ползучести высыхающего бетона на неизолированных образцах приводит к существенным погрешностям [18]. Причиной является допущение об одинаковой величине усадки нагру-
C(t,T)
C(t,T)
возраст бетона к иоиенту наблюдения
Старение\Амсы*ониг бето*а\рспсутст6ие Ьы-и отсутствии гысыкани* </ ста-
пебгтв- ’ старения \рспия бетона
Рис. 82. Типичные кривые предельной меры ползучести <р(т). влагопотерь Д1Г(/) [изменений весовой относительной влажности AU(/)], мер ползучести C(t. т ) и полных удельных деформации 6 (/, Т ) бетона, наблюдаемые в опытах
---------стареющий и непрерывно высыхающий бетон;---------стареющий бетон, вы-
сыхающий только до момента его загруже-
ния
AW ft) kvft)]
женных и ненагруженных об разцов, что в действительности не имеет места. От этих погрешностей можно было бы избавиться, перейдя к изучению ползучести на изолированных образцах. Однако, в данном случае, такая методика была неприемлема, поскольку само исследование усадки и усадочных напряжений производилось на непрерывно высыхающих образцах - близнецах. Поэтому и была принята описанная выше методика, при которой исключались также указанные ошибки в оценке деформаций ползучести отдельных загружаемых образцов, связанные с различием в усадке нагруженного и нена-груженного бетона. Целесообразность такой методики эксперимента ясна из следующего.
На рис. 82 показаны обычно наблюдаемые в опыте кривые предельной меры ползучести <р(т), влагопотерь ДИ7(т) [или, в другом масштабе, изменении весовой относительной влажности Дн (/)], мер ползучести C(t, т) и полных удельных деформаций б(/,т) стареющего и непрерывно высыхающего бетона, а также стареющего бетона, высыхающего только до момента загружения. Из этого рисунка видно, что в условиях естественного высыхания бетона имеются три характерных периода: 1) начальный, па котором бетон и стареет и высыхает; 2) промежуточный, на котором бетон высыхает, но практически уже не стареет, и 3) конечный, на котором бетон практически уже и не стареет и не высыхает.
366
Из рис. 82 следует, что для третьего периода построенные па основе описываемой методики кривые ползучести для практически уже не высыхающего бетона зрелого возраста будут весьма близки к достоверным. Для второго периода обсуждаемая методика позволяет получить лишь начальные участки кривых ползучести, близкие к аналогичным кривым непрерывно высыхающих образцов. Но поскольку предельные ординаты последних будут такими же, как и у кривых ползучести третьего периода, мы можем получить достоверные кривые ползучести для второго периода, как огибающие кривые с известными начальными участками и с теми же асимптотами. Для первого периода принятая методика не позволяет получить достоверные кривые ползучести, но в данном случае это не требуется, так как усадочные напряжения в защемленных образцах начинали развиваться лишь на втором периоде их высыхания. На первом же периоде высыхание образцов было связано с удалением лишь свободной воды и не сопровождалось усадкой.
Описанная методика позволила получить необходимые кривые ползучести, начиная с некоторого возраста бетона, с малыми погрешностями, близкие к кривым ползучести непрерывно высыхающих образцов.
Методика опытов по изучению релаксации напряжений в бетоне при его растяжении была схожа с описанной методикой опытов на ползучесть. Отличие состояло лишь в том, что после начального загружения образцов в заданном возрасте во времени сохранялось постоянной не усилие в образце, а сообщенная ему загружепием деформация.
Предел прочности бетона на растяжение определялся испы танием на осевое растяжение до разрыва вытянутых бетонных восьмерок сечением 5x5 см с призматической частью 23,5 см.
После распалубки до момента испытания восьмерки хранились запарафиненными на части боковой поверхности, аналогично призмам, подвергаемым испытаниям на ползучесть.
Такие условия храпения обеспечивали высыхание образцов во времени, подобное тому, которое имело место в основных образцах, испытываемых на рычажной установке.
Предел прочности при сжатии определялся в разных возрастах бетона испытанием бетонных кубиков 7x7x7 см. Кроме того, модуль упругости бетона определялся так же и при загру-жении бетонных призм в опытах на ползучесть и релаксацию напряжений, которое проводилось ступенями по той же методике. На рис. 83 изображены кривые упруго-мгновенных деформаций нескольких испытанных призм II серии опытов. В верхнем левом углу каждого из графиков указан возраст образца в сутках к моменту испытания, а в правом нижнем углу — полученное из опыта значение модуля упругости в (кГ1см2) • IO5.
Одновременно исследовались: ход развития во времени и величины свободней нестесненной усадки и усадочных папря-
367
жеиий в бетоне, пределы прочности бетона при осевых сжатии и растяжении, а также модуль упругости при растяжении бетона, как функции его возраста. Указанный комплекс опытов по изучению усадочных напряжений, усадки и связанных с ними
Рис. &3 Кривые упруго-мгновенных деформаций при растяжении призм II серии
Таблица 46
Основные сведения о бетоне исследованных I—V серий
№ серии Состав бетона (по весу) В/Ц Прочность бетона в кГ/см! прн Модуль упругости бетона при растяжении в кГ/сле 10~5
сжатии растяжении
I 1:2,2:4,9 0,66 273 212 гТб*-1’8’ 18,5 йГб(+5,6) 2,20 2-^-10’2)
I! 1:2,1:4,9 0,67 271 233 2Тб"7-9) 20.9 1ч1(+6,6) 2,81 М5(+14-7)
III 1:2,2:4,9 0,67 273 227 ^5J> 19,1 1Гб(-2-5) 2,42
IV 1:2,1:4,9 0,74 269 190 й6<-‘2’ 19,2 ад'-2) 2,57 Й51+’’9'
V 1:1,9:4,9 0,82 268 220 “-(+2) 19,6* 1 ^(-8.2) 2,45' ’
Примечания: I. Приведенные данные механических испытаний относятся к 28-дневному бетону
2. Прочность на растяжение бетона II серии найдена по линейной интерполяции соответствующих данных для бетона в возрасте 21 и 39 суток.
368
Как следует из табл. 46, во всех пяти сериях удалось получить однородный и сравнимый по физико-механическим свойствам бетон *.
Для изготовления бетона применялись следующие материалы: портландцемент Воскресенского завода активностью 475 кГ/см2 с началом и концом схватывания соответственно 2 ч 52 мин и 4 ч 34 мин\ песок речной мелкий средней крупности (— 0,33 мм) со средним объемом пустот 43,4%, средним удельным весом 2604 кг/м3 и объемным весом 1502 кг/ти3; щебень мелкий в виде дробленого гравия удельным весом 2660 кг/м3 подбирался из двух фракций 2,5—5 и 5—10 мм в соотношении 1:1; вода — обычная водопроводная, специальным исследованиям не подвергалась.
Результаты механических испытаний образцов описываемых пяти серий опытов изображены на рис. 84 На всех графиках наряду с экспериментальными точками нанесены соответствующие средние для всех испытанных образцов кривые изменений во времени физико-механических свойств бетона При этом кривая роста во времени модуля упругости аппроксимирована экспоненциальной зависимостью (1V.162) при
Ео = 2,6 • 10Б кГ!см\ 0 = 0,206 сут.-1 . (VI11.42)
На рис. 85, а в качестве примера приведены экспериментальные кривые удельных (т. е. отнесенных к единице приложенных напряжений) относительных деформаций призм I серии опытов, подвергнутых испытаниям на ползучесть при растяжении. Го-
ризонтальными черточками в начале кривых отмечены упруго-
мгновенные относительные деформации призм в момент их за-
гружепия. На рисунке нанесена также средняя для всех испы-
танных серий образцов кривая удельных упругих относительных
деформаций растяжения бетона »
рассчитанная с помощью
формулы (IV.162) и с учетом (VIII.42).
На рис. 85, б изображены экспериментальные кривые релаксации удельных (т. е. отнесенных к единице сообщенных призмам мгновенно-упругих деформаций) напряжений при растяжении призм той же серии опытов. На этом же рисунке нанесена средняя для всех испытанных серий образцов кривая мгновенных удельных напряжений растяжения, численно равных Е(т), рассчитанная по формуле (1V.162) с учетом (VIII.42). Вертикальные отрезки у начала кривых, изображенных на рис. 85. б, численно равны напряжениям, которые необходимо приложить к
1 В столбцах табл. 46, где содержатся три цифры, последние имеют следующий смысл: цифра в числителе означает среднее для соответствующих образцов-близнецов данной серии, а в скобках — наибольший процент отклонения, наблюдающийся в данной серии, от среднего для всех соответствующих образцов-близнецов всех пяти серий, которое указано в знаменателе.
369
Рис. 84. Сводные кривые изменений во времени прочности при сжатии и растяжении и модуля упругости при растяжении бетона по данным испытания кубов, восьмерок и призм I—V серий опытов
Ф — V серия Залитые знаки соответствуют
Салочкам и призмам, а псзалитыс — восьмеркам
370
призмам, чтобы сообщить им единичную мгновенно-упругую относительную деформацию растяжения.
Сводные осредненные кривые удельных деформаций и релаксации удельных напряжений по всем сериям испытанных образцов приведены на рис. 33, е, они и были положены в основу расчета теоретических значений усадочных напряжений в исследуемых бетонных образцах.
Рис. 85. Экспериментальные кривые удельных относительных деформаций и релаксации удельных напряжений при растяжении призм
I серии опытов
а — удельные относительные деформации призм, подвергнутых hi питаниям на ползучесть при -постоянных напряжениях. 6 — удельные напряжения в призмах, испытанных на релаксацию напряжений при постоянной деформации
На рис. 86 приведены результаты наблюдений за рабочими образцами III серии. Цифрами указаны значения усилий в заделанных образцах в момент их разрыва; цифрами в скобках — среднее значение продольной силы и сумма изгибающих моментов в образце соответственно в момент его разрыва. Нз двух моментов для каждого из образцов указан только один, имевший в опыте наибольшую величину; для другого момента указана лишь его величина в момент разрыва образца.
Обращает на себя внимание необычный характер кривой усадки свободных образцов, имеющей вид почти прямой линии. Такой вид этой кривой объясняется тем, что образцы вблизи каждого из торцов, примерно на длины, были армированы
371
Рис. 86. Результаты наблюдения за образцами III серии, претерпевающими свободную усадку и испытываемыми в рычажно-упряжных установках
а — кривая усадки свободных образцов; б — влагопотери образцов; в — усадочные усилия в защемленных образцах
ф — нагруженные образцы: С. А. О — нснагруженные образцы
тягами-крючьями, сдерживающими усадку в начале процесса ее развития, что в условиях одномерного высыхания образцов только через их торцы «выпрямляло» кривые усадки, изображаемые на графиках в осях «усадка — время».
372
Развитие усадки во времени начиналось у всех серий образцов сравнительно поздно (в среднем в возрасте бетона, равном 12—16 суткам), т. е. на 7—11-й день после начала их высыхания, которое было замедлено вследствие гидроизоляции их боковой поверхности. Аналогичным образом развитие усадочных напряжений в заделанных образцах начиналось практически также в эти сроки, по тем же причинам отдаленные от начала их высыхания.
Некоторые начальные значительные влагопотери образцов в результате удаления свободной воды не сопровождались ни развитием усадки, ни возникновением усадочных напряжений. Это обстоятельство неоднократно подчеркивалось ранее и наблюдалось и в прежних экспериментах автора [7, 9].
Во всех сравниваемых сериях опытов напряженные образцы имели заметно большие величины влагопогерь, чем их ненагру-женные образцы-близнецы, претерпевающие свободную усадку (см. рис. 87). Соответствующие средние превышения влагопо-терь у нагруженных образцов к моменту их разрыва при этом были равны: 3,6 г — у образцов I серии, 2,9 г — у образцов III серии, 2,7 г у образцов IV серии и 1,1 г у образцов V серии, что составляет соответственно 13,2; 9,7; 10,1 и 4,4% от влагопотерь к этому моменту времени у ненагруженных образцов. Это объясняется влиянием на высыхание бетона развивающихся в нем усадочных напряжений, что согласуется с результатами прежних опытов автора [8, 13].
Поскольку экспериментально установлено [7, 9], что усадка бетона прямо пропорциональна его влагопотерям (изменению влажности), можно утверждать, что усадка нагруженных образцов была также большей, чем у ненагруженных образцов.
Так как деформация усадки еу бетона линейно зависит от изменений ег > весовой относительной влажности
е (т) = 0ДС/(т), (VI 11.43)
то, следовательно, она линейно зависит и от его влагопотерь во время высыхания Дб(т). Следовательно:
е«(т) = е„„(т)^Ц^-. (VI1I.44)
По этой формуле с помощью данных об усадке ненагруженных образцов еНн(т) их влагопотерях Дб|т(т) и влагопотерях Дбн(т) нагруженных образцов, получаемых непосредственно из опыта, и рассчитывались средние приведенные теоретические кривые усадки ен(т) нагруженных образцов. Эти кривые построены на верхнем графике рис. 87, где для сравнения построены аналогичные кривые для ненагруженных образцов.
Наконец, на рис. 88 изображены сводные осредненные кривые усадки, изменений весовой относительной влажности и усадочных напряжений нагруженных образцов сравниваемых се
373
рий опытов. Пунктиром нанесены также соответствующие средние кривые, которые и были положены в основу определения теоретических значений усадочных напряжений в защемленных образцах при заданном законе развития во времени усадки в них. Эти значения в любой момент t можно найти из условия совместности деформаций в форме
ен (/) + еу.н (0 - О (VIII.45)
Рис 87. Кривые усадки и влагопотерь нагруженных (защемленных от усадки) и ненагруженных (свободно деформирующихся) образцов, начиная с момента развития усадочных напряжений в защемленных образцах
------иенагрчжеииые образцы, на которых исследовалась сводная усадка;--- нагруженные образцы, на ко-
торых исследовались усадочные напряжения, t — I серия;
2 — III серия; 3—IV серия; 4 —V серия
по формуле 1
t
-^7^- = еу.н(/,Т1) ~ (VIII.46)
где E(t) — модуль упругости бетона; Су.н(/, Ti) —закон развития во времени усадки в нагруженном образце.
Функция R(t, т) определяется по формуле (IV.26).
Развитие усадки и усадочных напряжений в образцах начиналось с того момента, после которого модуль упругости бетона практически уже не изменялся. Поэтому было принято E(t) =
1 В формуле (VI 11.46) знак напряженных деформаций принят обратным знаку усадки.
374
Рис. 88. Сводные приведенные кривые усадки, изменений весовой относительной влажности н усадочных напряжений в защемленных образцах сравниваемых серий опытов
--------приведенные кривые для отдельных серий опытов,-осредненпыс по всем сравниваемым сериям опытов расчетные кривые. 1 — I серия опытов.
2- III серия; 3—IV серия; 4 —V серия
Пр и м е ч а н и е. Пунктиром показаны соответствующие средние кривые
375
= Eo = const и выбрано в качестве Ео его предельное значение (VI 11.42).
Закон развития во времени средних относительных деформаций усадки нагруженных образцов (рис. 88) аппроксимировался зависимостью
еу.и(Лт1) = е0(/-т1)г (VIII.47)
Рис. 89. Сопоставление расчетных и осредненных экспериментальных кривых релаксации полных удельных напряжений для высыхающего бетона зрелого возраста
где
е0 = 0,286-10-5 лии/лии, т, = 16 сут. (VI11.48)
Внося (VII 1.47) в (VII 1.46), интегрируя по частям, принимая во внимание (IV.26) и учитывая, что е(ть Ti) =0, найдем
°(Лт1) = еи [ р(/,т)^т. (VIII,49)
Входящая сюда функция p(t, т) в нашем случае задана в виде экспериментальных кривых релаксации удельных напряжений, изображенных на рис. 33, в. Однако эти кривые относятся к бетону, не высыхающему с момента загружения. Поэтому их следует несколько видоизменить с. учетом последующего высыхания образцов-близнецов, подвергнутых испытаниям на усадочные напряжения.
Из рис. 33,е вытекает, что кривые релаксации образцов, загруженных в более поздние сроки (26, 28 и 29 сут.), по истече
376
нии большого интервала времени выходят на одну горизонтальную асимптоту. Это означает, что влияние высыхания на ползучесть бетона к этим срокам его загружения уже практически исчерпывается. Поэтому мы можем кривые релаксации непрерывно высыхающего бетона более ранних сроков загружения представить огибающими кривыми, выходящими на ту же асимптоту и изображенными на рис. 89 пунктирными линиями.
Эти кривые аппроксимировались формулой
P(t, т) = Ео - (Вх - В3 е-*') [1 - -
-В2[1— е_₽1('_т)], (VIII.50)
при Ео = 2,6-1О5 кГ!см\ Bt = 0,6 105 кПсм\ В3 = 0,82 105 кГ1см\ В3 = 14,8 1О5 кГ!см\ Р1 = 0,61 (сут.)-1; р2 = 2,5 (сут.)-1;
р. = 0,17(сут.)-‘.
(VIII.51)
Для сравнения на рис. 89 нанесены точки, ординаты которых найдены для отдельных моментов времени по формуле (VI 11.50) с учетом (VI 11.51). Как видно из рисунка, сравниваемые расчетные и экспериментальные кривые имеют хорошее совпадение.
Внося (VIII.50) в (VIII.49), находим
о (t, тх) = Еоеу.н (t — {1 — y (Bv 4- B2 — B3 e-’z —
1’ - [• - ^'-”1) • <VI!1-52>
На рис. 90 нанесена рассчитанная по формуле (VIIL52) с учетом (VIII.51) теоретическая кривая усадочных напряжений в защемленных образцах. Там же показаны экспериментальная кривая этих напряжений и теоретическая кривая упругих усадочных напряжений, рассчитанных без учета ползучести. На рисунке указаны также сроки разрыва исследуемых образцов во время их испытания. Как видно из рис. 90, экспериментальная и теоретическая кривые усадочных напряжений пересекаются в точке, близкой к среднему моменту времени разрыва образцов, и дают при этом напряжения, близкие к пределу прочности на растяжение исследуемого бетона. Напряжения разрыва, соответствующие точке пересечения этих кривых, составляют — 18 кГ/см2, т. е. примерно всего на 8% ниже средней кратковременной прочности бетона на растяжение, равной ~ 19,6/сГ/слг2 (см. табл. 46). Физически это вполне объяснимо, так как известно, что предел длительной прочности Гег-на несколько ниже его кратковременной прочности.
Нужно иметь в виду, что в момент разрыва образцов в них имелись некоторые, хотя и незначительные изгибающие моменты (см., например, рис. 86, е). По этой причине, а также вслед-
377
стопе неоднородности бетона разрывы большего числа образцов наступали несколько ранее теоретического времени разрыва, соответствующего случаю осевого растяжения однородного бетона, который и имеется в виду при построении теоретической кривой усадочных напряжений.
Из изложенного следует, что полученная теоретическая кривая усадочных напряжений в защемленных образцах количественно согласуется с экспериментальными данными о предель-
«> 1В
t
2. > б-18 к Чен*
4 —
F В ш 110 г у
Нонснты разрыва образцов
ю го зо to so ы го во
Возраст бетона б суткаж к ноненту наблюбения
Рис. 90. Экспериментальная и теоретические кривые усадочных напряжений в защемленных бетонных образцах
/ — теоретические упругие напряжения; 2 — экспериментальная кривая напряжений; 3 — теоретическая кривая полных напряжений, найденных с учетом ползучести бетона; 4 — образец разорвался преждевременно у крюка тяги
ных величинах напряжений разрыва от усадки бетона. Вместе с тем экспериментальная кривая усадочных напряжений по своему очертанию отличается от теоретической, т. е. наблюдается некоторое качественное несоответствие кривых. Это связано с принятой методикой экспериментального изучения усадки и усадочных напряжений, при которой, в силу необходимости, при-торцовые участки рабочих образцов были армированы хорошо заанкеренной проволокой (р= 1,9%), передающей растяжение образцу. При этих условиях возникающую в образце деформацию усадки приходилось погашать в опыте усилием, хотя и действующем на всей длине образца, но вызывающем его удлинение в основном за счет растяжения средней неармированной части.
Совершенно очевидно, что для погашения деформации, развившейся на всей длине образца, его растяжением на меньшей базе (т. е. части его длины) в эксперименте требовались большие напряжения, чем в случае расчетной теоретической схемы, когда предполагается равномерное удлинение бетонного образ
378
ца на всей его длине. В соответствии с этим экспериментальная кривая усадочных напряжений на рис. 90 в начале процесса располагается выше соответствующей теоретической кривой.
Незадолго до разрыва образца в нем образуются прогрессирующие микронадрывы и дефор мативность его повышается. При этих условиях для погашения соответствующих ступеней деформаций усадки в опыте требовались уже меньшие значения напряжений. По этой причине экспериментальная кривая напряжений на рис. 90 начинает загибаться вправо; наступает как бы «текучесть» бетона, заканчивающаяся разрывом образца. В конце процесса поэтому требуется приложение все меньших и меньших дополнительных напряжений, и экспериментальная кривая усадочных напряжений в это время располагается 5 же ниже теоретической.
Возвращаясь к результатам описанных исследований, мы видим, что экспериментальные значения усадочных напряжений значительно ниже теоретических упругих напряжений, найденных в предположении отсутствия ползучести бетона. К моменту разрыва образцов полные напряжения в них были примерно в 2 раза ниже теоретических упругих. Таким образом, ползучесть существенно снижает напряжения в бетоне от усадки. На основании этого можно сделать вывод, что рекомендации о снижении расчетных величин усадочных напряжений в бетоне за счет его ползучести, содержащиеся в СН 55—59 [139], подтвержаются экспериментами.
Указанные рекомендации позволяют в большом числе случаев отказаться от применения противоусадочной арматуры в виде сеток у открытых поверхностей массивных сооружений, что приводит к большой экономии стали.
Проведенные исследования усадки и усадочных напряжений позволяют сделать еще следующие выводы.
Теория упруго-ползучего тела Г. Н. Маслова — Н. X. Арутюняна при надлежащем выборе аналитического выражения для наследственной функции второго рода R(t, т) в форме (IV.26) с учетом (VI11.50) дает хорошее соответствие результатам эксперимента и правильно оценивает величины усадочных напряжений в высыхающем бетоне.
Выражение (VIII.50) для полных удельных напряжений р(/, т) и получаемое на его основе с учетом (IV.26) выражение для функции влияния второго рода R(t, т)
Я(/-т)=^-{Р1(В1-В3е-’к') е-₽‘(/-т) +
+ B2p2e-₽l('-T)| (VII 1.53)
для практически нестареющего, но высыхающего бетона хорошо согласуется с результатами эксперимента и может быть рекомендовано для применения.
ГЛАВА IX
УЧЕТ ТЕМПЕРАТУРНО-ВЛАЖНОСТНЫХ ВОЗДЕЙСТВИИ ПРИ РАСЧЕТЕ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
В обычных условиях работы бетонных и железобетонных конструкций температура и влажность бетона непрерывно изменяются во времени. В связи с низкими значениями коэффициента диффузии тепла и, особенно, коэффициента диффузии влаги у бетона изменения его температуры и влажности происходят неравномерно по сечениям конструкций: быстрее высыхают и изменяют температуру наружные открытые слои бетона; медленнее— его внутренние зоны. Это обстоятельство, а также ограничение свободных деформаций бетона внешними связями приводят к развитию в нем температурно-влажностных напряжений, которые следует учитывать при расчете прочности, трещиностой-кости, раскрытии трещин и деформаций бетонных и железобетонных конструкций.
Например, в жестко защемленном бетонном брусе при его равномерных охлаждении на 1° и высыхании на 0,1 % (при изменении весовой относительной влажности на 1 • 10-3 г/г) в предположении его упругой работы могут возникнуть температурные Gt и усадочные оу растягивающие напряжения:
о/ = а£Д7' = 1 -10-5-3-10ь-1 = 3 кГ/см2- ] ,1V ..
О Q I (***•0
оу-- рЕДС/ = 3-10“2-3-10’’-1 10-3 = ЭкГ/см2. J
Эти величины напряжений столь велики, что при обычно на-
блюдаемых изменениях температуры и влажности все бетонные статически неопределимые конструкции, например, находящиеся на открытом воздухе, должны были бы иметь сквозные температурно-усадочные трещины. Действительно, в опытах автора, описанных в § VII1.5, усадочные напряжения в защемленных высыхающих бетонных брусьях с течением времени достигали длительной прочности бетона на растяжение и все образцы, несмотря на благоприятное действие ползучести, райо или поздно разрывались.
В железобетонных статически неопределимых конструкциях температурно-усадочные трещины хотя и встречаются довольно 380
часто, но в большинстве случаев из-за благоприятного действия армирования и ползучести не носят такого угрожающего характера, и инженеры уже научились с ними бороться различными конструктивными мероприятиями. К их числу относятся: устройство температурно-усадочных швов, надлежащее армирование, выбор рациональной конструктивной схемы сооружений, регулирование их температурно-влажностного режима и т. п. Однако все эти мероприятия могут быть действенными только тогда, когда они основаны на надежном расчете величин усилий в конструкциях, вызываемых изменениями их температуры и влажности. Кроме того, встречаются и специальные железобетонные конструкции, для которых основными расчетными воздействиями являются именно изменения температуры и влажности бетона.
В соответствии с этим ряд нормативных документов [139, 179] содержит рекомендации по учету усадки и изменений температуры при расчете бетонных и железобетонных конструкций. Аналогичные указания включены и в СНиП П-В.1-62 [174]. Ниже кратко излагаются основные положения, касающиеся учета температурно-влажностных воздействий в соответствии с требованиями этих норм.
§ IX.1. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
В подавляющем числе случаев железобетонные статически неопределимые конструкции представляют собой либо стержневые системы, составленные из брусьев (неразрезные балки, рамы сборных промышленных цехов и т. д.), либо пространственные конструкции, составленные из плит с расчетными схемами в виде плоских элементов, работающих по схеме стержневых конструкций (туннельные конструкции, многопролетные покрытия и т. д.).
Исследование методами теории упругости напряженного состояния прямоугольных брусьев и плит, вызываемого неравномерным распределением температуры по их высоте (см. § VI.4 и IV.5), показывает, что их сечения, плоские до деформации, остаются плоскими и после температурных воздействий. Поэтому для определения температурных деформаций (перемещений) и нормальных напряжений (усилий), действующих в подобных конструкциях в сечениях, перпендикулярных к их продольной оси, можно воспользоваться гипотезой плоских сечений.
В соответствии с этой гипотезой взаимные сближение А/т концов осевой линии и угол Л<рт поворота торцовых сечений прямого бруса, имеющего свободные торцы, длиной /, вызываемые изменением температуры Т(х) точек его поперечного сечения,
381
неравномерным по высоте h=2x0 (рис. 91,а), на основе выражений (VI.52) и (V1.48) находятся по формуле
| T(x)dx \l(x)xdx
= а/ ----------- Д(р _ а/ . (1Х.2)
чг
Здесь а—коэффициент линейного расширения бетона.
Заменим изображенную на рис. 91, а заданную действительную эпюру ABDFG изменения температуры Т(х) условной (рас-
Рис. 91. Эпюры Т(х) изменений температуры точек поперечного сечения элемента (а) н U(x) распределения влажности бетона по его сечению (б)
/—действительная эпюра Г(л) (ABDFG): 2 —условная трапецеидальная эпюра Г(х) (АСЕС). учитываемая в расчетах; 3 — действительная эпюра U(x) (ACDFK). 4 —условная трапецеидальная эпюра l/(x) 1АВНК). учитываемая в расчетах
четной) трапецеидальной эпюрой ACEG, равновеликой ей по площади и статическому моменту площади относительно осевой линии бруса. Исходя из этих условий найдем:
f T(x)dx
^7---------= “ ДГср; (1Х.З)
J Т (х) xdx
—= &Т* (1Х.4)
и, следовательно:
Д/, = а/ДТср; Д<р, = а/ДТ*. (1Х.5>
Нетрудно видеть, что величины ДГСр п ДУ*, входящие в формулы (IX.3) — (IX.5), представляют собой соответственно изменения средней расчетной температуры ГСр и расчетного перепала
382
температуры Г*, вычисляемые по указанной выше условной трапецеидальной эпюре. В соответствии с этим в п. 4.25 СНиП 1 и введены понятия средней расчетной температуры (влажности), расчетного перепада температуры (влажности) и условной (расчетной) трапецеидальной эпюры, распределения температуры (влажности) по сечению элемента. С помощью формул (IX.5) всегда могуг быть найдены свободные температурные члены канонических уравнений метода сил при расчете статически неопределимых стержневых конструкций на изменение их температуры.
При отыскании величин &Тср и ДГ*. входящих в формулы (IX.5), можно поступить двояким путем:
1) по заданным действительным эпюрам распределения температуры, соответствующим двум рассматриваемым моментам времени ti и найти соответствующие условные трапецеидальные эпюры распределения температуры и по ним свои величины Тер и Т'(<); затем отыскать расчетные изменения ЛТср и АТ* по формулам:
АТср = Тер1 — Тер; АТ = (IX.6)
или:
2) по указанным двум заданным действительным эпюрам распределения температуры сразу найти действительную эпюру изменений АТ температуры Т, по ней условную трапецеидальную эпюру этих изменений, а затем по последней отыскать уже значения АТср и ДТ*.
Оба указанных пути равноценны и дают одни и те же результаты. Однако, как это будет указано ниже, в случае отыскания аналогичными способами расчетных изменений At/cp и At/* влажности бетона методически верным является лишь первый из них. Поэтому именно только эт- т, первый способ, и рекомендуется для применения.
Экспериментальные исследования влажностных деформации бетона, проведенные автором, выявили ряд особенностей этих деформаций, представляющих практический интерес. Наиболее важные нз них рассмотрены в § III.7 и учтены при составлении СНиП.
В пп. 4.25 и 4.26 СНиП введены понятия об эффективной и критической влажностях бетона и дано указание при учете изменений средней расчетной влажности п расчетного перепада влажности по толщине элемента принимать во внимание лишь те из них, которые связаны с изменениями эпюры распределения эффективной влажности по его сечению. Приведены формула и необходимые справочные данные для определения критической влажности бетона, а также физических характеристик бетона,
1 Здесь и далее, если это не оговорено особо, под СНиП понимается СНиП П-В.1-62 [I74J.
383
связанных с его температурными и влажностными деформациями: коэффициентов линейного расширения а, линейной усадки р и линейного набухания тр Введена классификация бетонных и железобетонных конструкций по степени массивности в зависимости от модуля поверхности т элемента конструкции и даны практические рекомендации по учету влпян-ня масштабного фактора на влажностные деформации этих конструкций (критическую влажность бетона) (см. § Ш.7).
Рассмотрим изображенную на рис. 91,6 заданную в момент времени п действительную эпюру (ACDFK) распределения влажности бетона по сечению элемента. В отличие от эпюры изменений температуры, показанной на рис. 91, а, эта эпюра относится к абсолютным значениям влажности бетона в отдельных точках сечения, а не их изменениям, которые нам предстоит еще вычислить. Для общности будем полагать, что на этой эпюре имеется участок (MEFK) (рис. 91,6, справа) с ординатами, превышающими критическую влажность бетона UKp.
Отсекая часть этой эпюры (EFG), лежащую выше UKp, мы найдем эпюру эффективной влажности (ACDEGK). Далее, заменяя эту эпюру эквивалентной в указанном выше смысле трапецеидальной эпюрой (АВИК), получим расчетную эпюру распределения влажности, по которой, пользуясь формулами, аналогичными (IX.3) и (IX.4), найдем:
UV+UW uP-U™
£/<>> = ; ГО = 2 h 1 . (IX.7)
Поступая аналогичным образом с другой действительной эпюрой распределения влажности бетона по сечению элемента в момент времени т2, точно так же найдем
t/<2’ + 1/<2> - и™
U™ = -1 2 ; и*ю= ------------—. (IX.8)
СР 2 ’ h ' ’
После чего, по формулам
AL^*’ = t/O — Up’; AL'*<?,,) = U*™ - и4" (1Х.9)
отыщем уже значение изменений средней расчетной влажности ЛГСр1) и расчетного перепада влажности бетона за время Т2—Т1-
Нетрудно сообразить, что описанный метод отыскания величин АГС2,1’ и Afy^2-1) является единственно верным, так как только он позволяет манипулировать с эпюрами распределения эффективной влажности бетона. Если же мы по заданным действительным эпюрам распределения влажности бетона по сечению элемента в моменты времени т2 и п сразу нашли бы по их разности эпюру изменения влажности бетона в отдельных точках его сечения за время т2—ть то получили бы эпюру изменений действительной, а не эффективной влажности и не смогли бы
364
выделить из нее изменения влажности за счет удаления свободной воды из бетона, не вызывающего усадки. Это особенно очевидно в случае, когда интервал времени тгп мал и ординаты получаемой таким способом эпюры изменения влажности бетона будут заведомо меньше его критической влажности UKp. Поэтому, как уже отмечалось выше, расчетные эпюры изменения влажности следует всегда находить по соответствующим эпюрам распределения не действительных, а эффективных влажностей бетона.
Располагая данными об изменениях средней расчетной влажности At/cp и расчетного перепада влажности Al/*, можно по формулам, аналогичным формулам (IX.5), найти перемещения, вызываемые изменениями влажности элементов конструкции. Эти формулы имеют вид:
а) при высыхании (усадке) бетона
А1у ₽/А1/ср; Афу = р/Al/*; (1Х.10)
б) при увлажнении (набухании) бетона
А/н = т]/Д^сР; Дф.. = П/ДС/*. (IX. 11)
В этих формулах р—коэффициент линейной усадки и т) — коэффициент линейного набухания бетона (см. § III 5).
Необходимые данные о распределении температуры и влажности по сечениям элементов бетонных и железобетонных конструкций для отыскания расчетных изменений температуры и влажности бетона находятся методами теории тепло- и влаго-проводности при учете рассмотренных выше особенностей температурно-влажностных деформаций бетона (см. главы 1 и II).
Определение усилий от температурно-влажностных воздействий в элементах бетонных и железобетонных конструкций, з которых по условиям эксплуатации не допускается образование трещин, производится как для однородных упругих систем с учетом работы бетона сжатой и растянутой зон и ползучести бетона, если рассматриваются длительные температурно-влажностные воздействия.
Железобетонные конструкции, в которых допускается образование трещин, рассчитываются с учетом неупругих деформаций и наличия трещин в растянутом бетоне, т. е. по повышенным кривизнам (пониженным жесткостям) их элементов. Поскольку при этом жесткости элементов и усилия в них оказываются взаимосвязанными, этот расчет приходится вести методом последовательных приближений.
Отметим, что при расчете бетонных и железобетонных конструкций па температурно-влажностные воздействия возможны: а) расчет существующего сооружения с учетом известного заранее его температурно-влажностного режима и б) предварительный расчет еще не существующего сооружения на гипотетические изменения его температурно-влажностного режима.
385
Первый случай встречается очень редко, например, при выяснении причин аварии эксплуатируемого сооружения с учетом фактических данных о его температурно-влажностном режиме *.
Второй случай, обычный для инженера-проектировщика, носит некоторый условный характер. Здесь приходится исходить из осредпенных данных многолетних наблюдений за метеорологическими условиями местности предполагаемого района строительства, анализа технологического режима подобных и уже эксплуатирующихся сооружений и т. п. Имея в виду известную гипотетичность подобных расчетов, не следует стремиться к их большой точности. В соответствии с этим в указанном выше методе последовательных приближений достаточно ограничиться двумя, максимум тремя, приближениями, включая и первоначальный расчет сооружения, как упругой системы (см. § IX.6).
§ IX.2. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ НА ИЗМЕНЕНИЯ ИХ ТЕМПЕРАТУРЫ И ВЛАЖНОСТИ
Температурно-влажностные воздействия на железобетонные конструкции следует учитывать при установлении расстояний между температурно-усадочными швами, а также в особых случаях расчета конструкций, подверженных значительным изменениям температуры или влажности, например, при: а) резко неравномерном распределении температуры или влажности по сечениям элементов; б) периодическом воздействии на конструкции производственно-технологических тепловыделений; в) устойчиво низкой влажности окружающей среды; г) расчете конструкций, находящихся на открытом воздухе в первом климатическом районе (см. табл. Б и рис. 8, п. 8.1 СНиП II-A.6-62 [175] и в сухих и устойчиво сухих районах (см. приложение И).
Можно не учитывать усадку бетона в элементах сборных железобетонных конструкций, а также в конструкциях, с раннего возраста защищенных от высыхания грунтом или лакокрасочными покрытиями.
При расчете в необходимых случаях на изменения температуры и влажности железобетонных конструкций, рассматриваемых как системы, состоящие из брусьев или плит (балочные, рамные, арочные и другие системы), необходимо пользоваться следующими указаниями.
При определении вызываемых изменениями температуры и влажности усилий и перемещений (деформаций) железобетонных статически неопределимых конструкций, у которых допускается наличие трещин, учитываются лишь изменения средней расчетной температуры (влажности) их элементов и расчетного
1 Например, данных метеорологических сводок за некоторый истекший период времени или результатов непосредственного измерения температуры и влажности на месте, анализа технологического режима сооружения и т. п.
386
перепала температуры (влажности) по толщине сечений элементов, отыскиваемые на основе соответствующей условной трапецеидальной эпюры изменений температуры (влажности) (см. § IX. 1, IX.4, IX.5). Расчет таких конструкций производится с учетом неупругих деформаций и наличия трещин способом последовательных приближений (см. § 1X 3), принимая во внимание длительность рассматриваемых воздействий.
В статически неопределимых железобетонных конструкциях, у которых наличие трещин не допускается, при расчете по образованию трещин (см. п. 4.1 СНиП) учитывается вся эпюра изменения температуры (эффективной влажности). Такие конструкции рассчитываются как однородные упругие системы, при этом жесткости их элементов определяются по указаниям п. 9.8 СНиП.
В статически определимых конструкциях изменения температуры или влажности вызывают лишь напряжения, эпюры распределения которых по их сечениям статически эквивалентны нулю. Поэтому у конструкций этого вида, у которых допускается наличие трещин, учет температурно-влажностных воздействий производится только при вычислении перемещений (деформаций). При этом учитываются лишь изменения средней расчетной температуры (влажности) их элементов и расчетного перепада температуры (влажности) по сечению элементов (см. § IX. 1, IX.4, IX.5).
В статически же определимых железобетонных конструкциях, у которых наличие трещин не допускается, расчет по образованию трещин производится по разности эпюр изменения температуры (эффективной влажности): действительной (криволинейной) и условной трапецеидальной.
Необходимые для расчета железобетонных конструкций величины средних расчетных температуры и влажности их элементов, а также расчетных перепадов температуры и влажности по толщине сечений элементов определяются в соответствии с указаниями § IX. 1, IX.4, IX.5.
При определении усилий, возникающих от изменений температуры и влажности в элементах статически неопределимых конструкций, должны учитываться их деформации (перемещения) в соответствии с указаниями § IX. 1, IX.3.
Температурно-влажностные усилия в железобетонных конструкциях, отыскиваемые в соответствии с рекомендациями настоящего параграфа, принимаются одинаковыми при расчете этих конструкций по всем трем предельным состояниям.
Расчет статически неопределимых железобетонных конструкций на тем перату рио-влажностные воздействия, рассматриваемых как системы, составленные из массивных брусьев или пли г, или представляющих собой сочетание массивны хи пемассивных элементов (балки, рамы, арки и т. п.). на основах строительной механики лучше всего проводить по способу последовательных
387
приближений (см. § IX.3) методом сил с учетом влияния продольных деформаций и деформаций сдвига на перемещения основной системы. При этом следует широко применять различные упрощающие приемы расчета, а именно: рациональный выбор основной системы, группирование лишних неизвестных, разложение нагрузки, на косо- и прямосимметричные составляющие, применение статически неопределимых основных систем, исполь-
Рис. 92 Действительная и расчетная схема массивной железобетонной рамы а — действительная схема; 6 — расчетная схема
зование симметрии расчетных схем и введение жестких консолей для надлежащего переноса лишних неизвестных в упругий центр.
Расчет статически неопределимых балочных, рамных или арочных систем, составленных из немассивных или средней массивности элементов, вполне допустимо производить без учета влияния продольных деформаций и деформаций сдвига па перемещения основной системы. Можно также не учитывать деформации сдвига при расчете массивных конструкций, обладающих симметрией геометрических размеров, условий опирания и распределения жесткостей, на симметричные воздействия температуры, влажности и внешней нагрузки. При определении степени массивности элемента конструкции следует пользоваться указаниями п. 4.26 СНиП.
Массивность конструкций следует учитывать также при выборе расчетной схемы сооружения, подлежащего расчету. На-
388
пример, сооружение, изображенное схематически на рис. 92. а, нельзя рассматривать как обычную раму с длинами составляющих ее стержней, равными их продольным размерам в осях. Ясно, что такой выбор расчетной схемы привел бы к завышенным значениям внутренних усилий и превышению запаса прочности всего сооружения в целом. При выборе расчетной схемы такого сооружения следует учитывать разгружающее влияние па деформации изгиба и сдвига составляющих его элементов их концевых участков, опирающихся на массивные, примыкающие к ним смежные элементы. Поэтому правильной расчетной моделью рассматриваемого сооружения, учитывающей массивность его элементов, будет служить рама с приузловыми участками ее стержней, бесконечно жесткими по отношению к их сдвигу и изгибу (рис. 92,6).
Практически это означает, что при учете деформаций изгиба и сдвига при вычислении перемещений (метод сил) или реакций (метод деформаций) основной системы следует исходить из длин элементов I, «в свету» и их пролетной жесткости. Поскольку приузловые участки элементов, составляющих сооружение на их продольные деформации разгружающего влияния не оказывают, то при учете последних следует исходить уже из действительных длин элементов т. е. из их размеров «в осях» и их пролетных жесткостей.
Расчет железобетонных конструкций на изменения их температуры и влажности в необходимых случаях производится: в период строительства при отсутствии эксплуатационных нагрузок и в период эксплуатации с учетом последних.
В первом случае расчет железобетонных конструкций на указанные воздействия следует производить, как правило, в предположении их упругой работы, т. е. по жесткостям, соответствующим сплошному приведенному сечению их элементов без наличия трещин в них. При этом жесткость при изгибе назначается в соответствии с рекомендациями п. 9.3 СНиП. В период эксплуатации железобетонные конструкции, в которых по условиям эксплуатации появление трещин недопустимо (предварительно напряженные элементы 1-й и 2-й категории трещипостойкости. слабо армированные элементы и т. п.), также должны рассчитываться аналогичным образом.
При расчете обычных и предварительно напряженных железобетонных конструкций 3-й категории трещиностойкости в период эксплуатации следует учитывать наличие трещин в растянутом бетоне и исходить из повышенных кривизн, назначаемых а соответствии с рекомендациями п. 9.7 СНиП и продольных осевых деформаций, определяемых в соответствии с указаниями § IX.3. При этом жесткость на сдвиг при расчете массивных кон струкций назначается соответствующей сплошному сечению эле ментов без учета трещин в них. В тех же случаях, когда в массивной конструкции возможно появление косых трещин при
ЗЯ9
соответствующем обосновании, допускается также снижение жесткости ее элементов на сдвиг на 10%.
При расчете железобетонных элементов с трещинами на длительные воздействия нагрузки, температуры или влажности их кривизны и продольные осевые деформации вычисляются в соответствии с рекомендациями п. 9.7 СНиП и указаниями § IX.3. При этом отношение v упругой части деформации крайнего волокна сжатой грани сечения к полной его деформации, в зависимости от условий работы конструкции, принимают: при сухом режиме работы конструкции v = 0,l; при нормальном режиме т = 0,15; при влажностном режиме v = 0,2.
Классификация режима работы конструкций, находящихся на открытом воздухе, по указанному признаку может производиться в соответствии с влажностно-климатическим районированием территории СССР [87], приведенным в приложении II.
Необходимые для расчета распределения температуры и влажности бетона по сечениям элементов, а также температурных и влажностных деформаций и усилий средние величины физических характеристик тяжелого бетона можно принимать по данным СН 55—59 [139] и СНиП П-В.1-62 [174].
При расчете железобетонных элементов на изменения их влажности расчетные значения коэффициентов лин€йной усадки и линейного набухания могут приниматься сниженными и равными величинам 0 и т] для бетона, умноженным на коэффициент т*
— 1 /и = ----,
1-1 пц
I де
(IX. 12)
(IX. 13)
Указанная в [139] и [174] средняя величина коэффициента линейного набухания т] относится к случаям набухания бетона за счет его контакта с водой (наполнение емкостей, затопление конструкций и т. п.). При расчете деформаций бетона, вызываемых его гигроскопическим увлажнением за счет адсорбции водяных паров из воздуха (деформации бетона, связанные с увеличением относительной влажности воздуха в суточном, месячном или годовом цикле), расчетную величину коэффициента линейного набухания т] следует принимать равной указанной там же величине коэффициента линейной усадки 0.
* Формулы (IX.12), (IX. 13) даны в обозначениях СНиП [174].
390
§ IX.3. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИИ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИИ ПРИ ИХ РАСЧЕТЕ НА ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ И ВЛАЖНОСТИ
Перемещения (линейные смещения и углы поворота) железобетонных конструкций, рассматриваемых как плоские системы. состоящие из брусьев или плит (балочные, рамные, арочные системы и т. п.). следует вычислять, определяя их жесткости или кривизны по рекомендациям пп. 9.3, 9.7, 9.10 СНиП применимо к рассматриваемому случаю.
При определении перемещений железобетонных конструкций в необходимых случаях должна учитываться длительность воздействия нагрузок, температуры и влажности.
Расчетные изменения температуры и влажности конструкций, находящихся на открытом воздухе, связанные с колебаниями температуры и влажности воздуха, за исключением специально оговариваемых случаев их кратковременных (например, суточных или декадных) изменений, относятся к категории длительных воздействий. К ним относятся также изменения температуры и влажности конструкций, связанные со стационарными технологическими режимами (конструкции кондиционируемых зданий, пропарочных камер непрерывного действия и т.п.). К категории кратковременных воздействий относятся изменения температуры и влажности конструкций автоклавов, нестационарных пропарочных камер и т. д.
Перемещения плоской статически определимой системы, состоящей из т железобетонных элементов, вызываемые изменениями температуры и влажности бетона, в общем случае могут быть определены по формулам:
Д„ = S J MfiWds + S f /V,aA.'cpds; 1
Д.У=Е f M,.₽Al/*ds+ X [M₽Al/cpds; nx)4.
•J v I I Z\ .1*1
AiH=S J Mi4At/*ds+S
(m>( Lm) ™ (4r.)
где Дп, Ату. Ajh — перемещения заданной системы в i-м направлении, вызываемые соответственно изменениями температуры, усадкой и набуханием бетона, М,, N, — изгибающие моменты и продольные силы в заданной системе от действия в t-м направлении соответствующей единичной обобщенной силы;
Цп — длина элемента т системы «в осях»;
а, ₽, т] — соответственно коэффициенты линейного температурного расширения, линейной усадки и
391
линейного набухания, средние значения которых были указаны выше;
Л/ср. Д^ср — соответствующие изменения средних расчетных температуры и влажности элементов, вычисляемые на основании указаний § IX.4 и 1Х.5;
Д/*, &U* — соответствующие изменения расчетных перепадов температуры и влажности по толщине сечения элементов, отыскиваемые с помощью рекомендаций тех же параграфов.
В формулах (IX.14) суммирование распространяется на все т элементов всей заданной системы.
Для массивных брусьев или плит в формулах (IX. 14) в первом слагаемом длину L,n следует принимать равной длине элементов «в свету»
Вызываемые нагрузкой перемещения плоской статически определимой системы, состоящей из брусьев или плит (балочные, рамные, арочные системы и т. п.), в которых не допускаются трещины в растянутой зоне или появление их мало вероятно (предварительно напряженные элементы 1-й и 2-й категории трещино-стойкости, слабо армированные элементы), определяются как для сплошного упругого тела по жесткости Вк, уменьшенной в случае длительного действия нагрузки в С раз (см. п. 9.4 СНиП). В общем случае перемещения таких систем, составленных из массивных элементов, вызываемые кратковременным действием нагрузки, определяются с учетом продольных деформаций и деформаций сдвига и указаний § IX.2.
Для немассивных и средней массивности брусьев или плит следует учитывать перемещения, вызываемые только изгибом элементов, с учетом их длин «в осях».
Перемещения плоской статически определимой системы, состоящей из брусьев или плит, изгибаемых, внецентренно сжатых и внецентренно растянутых с большими эксцентрицитетами, в которых при нагрузках, соответствующих стадии определения перемещений, могут появиться трещины в растянутой зоне (т. е. выполняемых без предварительного напряжения, а также предварительно напряженных 3-й категории трещиностойкостн), вызываемые внешней нагрузкой, находят, пользуясь методами гг 1
строительной механики. При этом значения кривизн — элементов определяются учетом уточнений зоны [67]
Р
в соответствии с указаниями п. 9.7 СНиП и с формулы для относительной высоты сжатой
£
1 । 1.5+у< 1+5(14 7)“ е, 1.8+ * — П.5Т-Т5
10|1н h0
В общем случае таких систем, составленных из массивных
(IX. 15)
392
элементов, перемещения определяются с учетом продольных деформаций и деформаций сдвига по формуле
4»=S + Е pv.Ms)* + S р-™- *• <1Х |6>
Здесь-------кривизна данного внецентренно сжатого пли вне-
Рк(з)
центрен'но растянутого с большим эксцентрицитетом элемента (с предварительным напряжением пли без него), определяемая для его отдельных сечений с учетом указаний п. 9.7 СНиП и формулы (IX.15);
Eft(s) — осевая деформация данного элемента с трещинами, определяемая для его отдельных сечений по формуле 1
I
Е Zu Р
</И3 — Nczi) 1]>а
(1Х.17)
а остальные величины имеют тот же смысл, что и в выражениях (IX.14).
В формуле (IX.17): г0—расстояние от центра тяжести площади сечения всей арматуры, расположенной в растянутой зоне, до осп элемента;----кривизна элемента в данном сечении, оп-
Р
ределяемая по формуле (173) п. 9.7 СНиП с учетом выражения (IX.15), а остальные величины имеют тот же смысл, что и в формуле (173) п. 9.7 СНиП.
При вычислении первого слагаемого в выражении (IX.16) можно пользоваться формулой
f М,—— ds
J Рк (S)
( 'т)
(%)
MtMkds ~~Вп
(IX. 18)
где п — число характерных участков эпюры моментов
ап — длины этих участков, в сумме составляющие длину /гп;
Вп — условная жесткость участка п.
Под характерными участками эпюры моментов понимаются ее участки, на длине которых в рассматриваемом элементе имеются или, наоборот, не имеются трещины. Границы этих участков имеют ординаты, равные моменту Мт соответствующего знака. Условные жесткости Вп этих участков принимаются равными: в пределах участка без трещин — жесткости Вк,
1 В обозначениях СНиП (174].
393
уменьшенной в случае длительного действия нагрузки в С раз (см. п. 9.4 СНиП); в пределах участка с трещинами
Мп
в 2тах (!Х ,19)
(7.)
Здесь Мятах—наибольший момент эпюры Mk на ее участке с 1
трещинами п, — — кривизна в сечении, где действует момент Рл
Л/япах, определяемая с учетом длительности действия нагрузки. Второе слагаемое в формуле (IX.16) в запас прочности можно вычислять по формуле
£ [ Л',!7(s)* =£ j (1Х.ЭД
При вычислении перемещений в соответствии с указаниями настоящего параграфа, используемых для определения усилий в статически неопределимых конструкциях, в запас прочности границы участков с трещинами определяются из расчета по образованию трещин по моменту Л-1Т, найденному по рекомендациям СНиП при замене /?т на /?£.
Для немассивных и средней массивности брусьев или плит в формуле (IX 16) можно ограничиться только одним первым слагаемым и полагать в нем lm=Lm, т. е. вычислять перемещения с учетом длин элементов «в осях» и без учета влияния продольных деформаций и деформаций сдвига.
При расчете железобетонных конструкций на изменения температуры и влажности для элементов постоянного сечения на
1
каждом участке с трещинами кривизна — вычисляется только Р
для наиболее напряженного сечения. В остальных сечениях такого участка вполне допустимо принимать кривизну изменяющейся пропорционально изменению значений изгибающего момента.
Перемещения плоских статически определимых систем, состоящих из брусьев (плит) различной степени массивности и работающих в разных условиях, в зависимости от случаев, рассмотренных выше, отыскиваются с помощью надлежащего сочетания соответствующих формул для каждого данного элемента или группы элементов системы.
Для отыскания перемещений плоских статически неопределимых систем, состоящих из железобетонных брусьев или плит, на основах строительной механики эти системы сначала рассчитываются по способу последовательных приближений методом сил с учетом, в необходимых случаях, влияния продольных де
394
формаций и деформаций сдвига на их перемещения. После отыскания таким способом усилий в их элементах последние рассматриваются уже как статически определимые конструкции, искомые перемещения которых определяются с помощью указаний настоящего параграфа.
Способ последовательных приближений состоит в следующем. Вначале статически неопределимая конструкция рассчитывается на действие заданных внешней нагрузки или изменений температуры и влажности, как упругая система в соответствии с рекомендациями настоящего параграфа. Затем на основании данных этого расчета для ее элементов на участках с трещинами в зависимости от полученного упругим расчетом случая и с учетом приведенных выше рекомендаций определяются новые жесткости (кривизны) элементов па этих участках; жесткости элементов на участках без трещин остаются прежними. После этого последовательно, до достижения хорошей степени приближения, повторяется расчет исходной статически неопределимой конструкции с учетом нового распределения жесткостей (кривизн). Данные этого расчета используются, как указано выше, для непосредственного определения окончательных жесткостей (кривизн), необходимых для вычисления искомых перемещений.
Имея в виду известную гипотетичность расчетов на изменения температуры и влажности, как уже отмечалось выше, не следует стремиться к их слишком большой точности. В соответствии с этим в указанном способе последовательных приближений достаточно ограничиться максимум тремя приближениями, включая и первоначальный расчет сооружения, как упругой системы.
§ IX.4. РАСЧЕТ РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ БЕТОНА ПО СЕЧЕНИЮ ЭЛЕМЕНТОВ КОНСТРУКЦИИ И ВЫБОР СРЕДНЕЙ РАСЧЕТНОЙ ТЕМПЕРАТУРЫ И РАСЧЕТНОГО ПЕРЕПАДА ТЕМПЕРАТУРЫ
Распределение температуры по сечениям элементов массивных и средней массивности железобетонных конструкций, находящихся на открытом воздухе или подверженных воздействиям периодических технологических изменений температуры, отыскивается методами теории теплопроводности с учетом технологических данных (см., например, § 1.16).
Нельзя, как это часто делается, расчет распределения температуры по сечениям элементов таких конструкций производить в предположении их стационарного (не зависящего от времени) теплового режима.
Необходимая для расчета распределения температуры по сечениям конструкций, находящихся на открытом воздухе,
395
расчетная температура наружного воздуха <р(т) может быть найдена по формуле
<р(т) =
2~У (IX.21)
где т - время в часах; Т| = 8640— число часов в году; /щах. /min— расчетные температуры наружного воздуха соответственно самого холодного и самого жаркого месяца года для данной местности, назначаемые на основе соответствующих обоснований и в соответствии с указаниями СНиП II-A.6-62 [175]; р —числовая величина, принимаемая по табл. 47, в зависимости от начала отсчета времени т.
Начальное распределение температуры по сечению элемента зависит от начальных условий изготовления конструкции и ее предшествующего температурного режима. Если рассматривается температурный режим элемента конструкции, начиная с момента ее изготовления, то его начальную температуру можно считать постоянной и равной температуре укладываемого бетона. При необходимости рассмотрения температурного режима конструкции лишь па отдельном периоде ее работы (например, на отрезке времени с начала замыкания конструкции до приложения эксплуатационной нагрузки) начальное и часто уже неравномерное распределение температуры по сечениям элементов конструкции в начале этого периода должно приниматься на основе соответствующих данных (например, равным заданной температуре бетона в момент замыкания конструкции) или на основе рассмотрения предшествующего этому моменту времени температурного режима конструкции.
В соответствии с формулой (IX.3) средняя расчетная температура /ср элемента, изменения которой вызывают его осевые деформации удлинения или укорочения, равна лежащей на оси этого элемента ординате условной трапецеидальной эпюры распределения температуры по сечению элемента. Расчетный же перепад температуры t* по сечению элемента в рассматриваемом направлении, изменения которого вызывают искривления его оси, на основании формулы (IX.4) равен взятому с соответ-
396
ствующлм знаком тангенсу угла наклона в заданном направлении наклонной стороны этой условной трапецеидальной эпюры распределения температуры к поперечному сечению элемента. Правило знаков для /Ср, /*, Д/Ср и (рис. 93) устанавливается следующим образом.
1. Изменение средней расчетной температуры (влажности) элемента и расчетного перепада температуры (влажности) по сечению элемента находятся как разности соответствующих величин, найденные вычитанием их значений для предыдущего момента времени из их значений для последующего момента времени
U*(K)*tg<£>0 U*(i)=O
= (к) -1 *(i) >0; & t = t •("'i-t *(i)< 0;
Рис. 93. Правило знаков для расчетного перепада температуры (влажности) и изменений средней расчетной температуры (влажности) и расчетного перепада температуры (влажности)
2. Положительные изменения средней расчетной температуры (влажности) соответствуют разогреву (увлажнению) элемента.
3. Положительный расчетный перепад температуры (влажности) соответствует случаю, когда на грани х=х0 элемента с высотой поперечного сечения 2х0 температура (влажность) бетона больше, чем на его грани х=—х<1 (см. рис. 93).
4. Положительное изменение расчетного перепада температуры (влажности) по сечению элемента соответствует случаю, когда вызываемое им искривление элемента обращено выпуклостью в сторону положительного направления оси ординат, лежащей в плоскости его поперечного сечения (рис. 93).
Условная трапецеидальная эпюра распределения температуры по высоте 2х0 прямоугольного сечения бетонного (слабо армированного) элемента находится из условий ее равенства по площади и статическому моменту площади относительно оси элемента действительной эпюре распределения температуры
2xofcp = F/; (IX.22)
397
396
Условная трапецеидальная эпюра распределения температуры по сечению железобетонного элемента должна быть по площади и статическому моменту площади относительно оси элемента отлична от действительной эпюры распределения температуры на некоторые величины, в связи с тем, что для такого элемента нужно исходить из его приведенного сечения. В случае прямоугольного элемента с симметричным распределением арматуры в направлении его толщины условная трапецеидальная эпюра распределения температуры находится при этом из условий:
Ч = Л - (" - О S /1° [ 'ер + 'Ч" -' (Ч")|; ’ f V’ OSA'»*.'’ I '«,+
(IX.23)
т. е. должна быть по площади и статическому моменту площади относительно оси элемента меньше или больше, чем действительная эпюра распределения температуры, на некоторые величины в зависимости от знака сумм, в формулах (IX.23). Входящие в выражения (IX.22) — (IX.23) величины имеют тот же смысл, что и в формулах (IX.24) (IX.26).
Средняя расчетная температура /Ср и расчетный температурный перепад /* по сечению прямоугольного железобетонного элемента в общем случае криволинейного распределения температуры в направлении высоты 2.г0 его сечения, когда температура элемента по его толщине 2у0 не изменяется и арматура расположена симметрично относительно оси Ох сечения (рис. 94,а), на основании выражений (IX.23) находятся по формулам:
*ср = К {(л — 1) — (п — 1) ада] 4-
+ 2у0 [JnFt-(п - 1)ЗД]}; (IX.24)
** = К '(и — 1) [FnS,a- (n - 1) 4-
4- 2^ [FaSt-(n-DS.FJ), (IX.25)
где
(IX.26)
Jn, Fn — соответственно момент инерции относительно оси Оу и площадь приведенного сечения элемента; F—площадь бетонного сечения элемента; Fa—площадь всей учитываемой арматуры, Sa, /а — соответственно статический момент и момент инерции относительно оси Оу площади всей учитываемой арматуры; Vta — часть объема заданной эпюры распределения температуры
399
по сечению элемента, выделяемая боковой поверхностью всех учитываемых арматурных стержней
«А =17аЛ.; (IX.27)
О’»
Sla — статический момент части объема заданной эпюры распределения температуры по сечению элемента, выделяемой боко-
вой поверхностью всех учитываемых арматурных стержней, относительно осн Оу его поперечного сечения
= (IX.28)
(/>
п — коэффициент приведения площади арматуры к бетону (модульное число), S/, Ft — соответственно статический момент относительно оси Оу и площадь заданной эпюры распределения температуры по сечению элемента, fa> — площадь /-го стержня учитываемой арматуры; х31— взятое с соответствующим знаком расстояние от центра тяжести поперечного сечения i-го стержня учитываемой арматуры до оси Оу поперечного сечения элемента, tai — ордината заданной эпюры распределения температуры по сечению элемента, лежащая над центром тяжести поперечного сечения i-го стержня учитываемой арматуры. Для бетонного
•100
(слабо армированного) элемента формулы (IX.24) — (IX—25) принимают вид:
*ср —; = (IX.29)
Р 2х„ 2x2
В формулах (IX.27) — (IX.28) суммирование производится по всем учитываемым арматурным стержням сечения элемента, число которых предполагается равным I.
Для железобетонных элементов с прямолинейным или близким к нему распределением температуры по высоте поперечного сечения, а также элементов, имеющих только конструктивную арматуру, вполне допустимо среднюю расчетную температуру элемента /ср и расчетный температурный перепад I* по сечению элемента определять по формулам (IX.29), как для бетонных (слабо армированных) элементов.
Площадь Ft и статический момент St плоской эпюры распределения температуры по сечению элемента в случае, когда распределение температуры задано в табличной форме (графически^ (рис. 95), приближенно можно отыскивать по формулам:
Л-^-(/<,+2 (n-I,2,...,m-I); (1Х.30)
(«)
(IX.3I)
Здесь т — четное число равных участков, составляющих высоту элемента 2х0, a to, ti, ..., Z,n-i, tm — ординаты заданной эпюры распределения температуры на границах этих участков. Вычисление площади Ft эпюры распределения температуры по сечению элемента в случае ее графического задания удобно производить также с помощью планиметр-!.
§ IX.5. РАСЧЕТ РАСПРЕДЕЛЕНИЯ ВЛАЖНОСТИ БЕТОНА ПО СЕЧЕНИЮ ЭЛЕМЕНТОВ КОНСТРУКЦИИ И ВЫБОР средней расчетной влажности
И РАСЧЕТНОГО ПЕРЕПАДА ВЛАЖНОСТИ
Распределение влажности бетона по сечениям элементов массивных и средней массивности железобетонных конструкций, находящихся на открытом воздухе или подверженных воздействиям периодических технологических изменений влажности, отыскивается методами теории влагопроводности с учетом технологических данных (см., например, § П.10). Нельзя, как это
401
иногда делают, расчет распределения влажности по сечениям элементов таких конструкций производить в предположении их стационарного (не зависящего от времени) влажностного режима.
Необходимая для расчета распределения влажности бетона по сечениям конструкций, находящихся на открытом воздухе, расчетная равновесная относительная влажность бетона может быть найдена по формуле
ф(т) = |^20 4- 1,5 + +
+ 1 CoS + J 10~4 г/г, (1Х.32)
где t/max и t/щщ — соответственно максимальная и минимальная среднемесячные относительные влажности наружного воздуха в процентах для данной местности, назначаемые в соответствии с табл. 3 п. 3.2 СНиП II-A.6-62 [175]; т. Г] — величины, имеющие тот же смысл, что и в формуле (IX.21) для температуры наружного воздуха; р — числовая величина, имеющая те же значения, что и в формуле (IX.21), но с нулевым значением, отнесенным не к июлю месяцу, а к месяцу максимальной среднемесячной относительной влажности наружного воздуха для данной местности, и соответствующей сдвижкой по месяцам остальных ее значений.
Расчетная равновесная относительная влажность бетона в конструкциях, находящихся в закрытом помещении, находится по формуле
ф(т) = 120 4- 1,51/ (т)] 10-4 г/г, (1Х.ЗЗ)
где £/(т) —технологическая относительная влажность воздуха в 'смещении в процентах, в общем случае являющаяся заданной функцией времени т.
Начальное распределение относительной влажности бетона по сечению элемента зависит от начальных условий изготовления конструкции и ее предшествующего влажностного режима. Если рассматривается влажностный режим элемента конструкции, начиная с момента ее изготовления, то начальную относительную влажность бетона можно считать постоянной н равной ее начальной влажности (11.12).
Прн необходимости рассмотрения влажностного режима конструкции лишь на отдельном периоде ее работы (например, на периоде, соответствующем отрезку времени с начала замыкания конструкции до приложения эксплуатационной нагрузки) расчетное начальное и часто уже неравномерное распределение влажности бетона по сечению элемента конструкции в начале этого периода должно отыскиваться на основе рассмотрения предше-
402
ствующего этому моменту времени влажностного режима конструкции.
Средняя расчетная влажность Ucp элемента, изменения которой вызывают его осевые деформации укорочения или удлинения, равна лежащей на оси этого элемента ординате условной трапецеидальной эпюры распределения относительной влажности бетона по сечению элемента.
Расчетный перепад влажности U* по сечению элемента в рассматриваемом направлении, с изменениями которого связаны искривления его оси, равен взятому с соответствующим знаком тангенсу угла наклона в заданном направлении наклонной стороны этой условной трапецеидальной эпюры распределения относительной влажности бетона к поперечному сечению элемента. Правило знаков для Ucp, U*, и (рис. 93) см. на стр. 397.
При отыскании условной трапецеидальной эпюры распределения относительной влажности бетона возможны два расчетных случая.
Случай первый — имеются в виду изменения средней расчетной влажности и расчетного перепада влажности бетона при высыхании элемента (расчет на усадку бетона) или гигроскопическом увлажнении за счет адсорбции водяных паров из воздуха (расчет влажностных деформаций бетона, связанных с колебаниями влажности наружного воздуха). Случай второй — имеются в виду изменения средней расчетной влажности и расчетного перепада влажности бетона при увлажнении элемента за счет контакта с водой (расчет на набухание бетона).
В первом расчетном случае условная трапецеидальная эпюра распределения относительной влажности бетона по высоте 2х0 сечения бетонного (слабо армированного) элемента находится из условий ее равенства по площади и статическому моменту площади относительно оси элемента эпюры распределения эффективной относительной влажности бетона
9
2*0^^; (1X34)
Условная трапецеидальная эпюра распределения относительной влажности бетона по сечению железобетонного элемента в первом расчетном случае должна быть по площади и статическому моменту площади относительно оси элемента отлична от эпюры распределения эффективной относительной влажности бетона на некоторые величины, в связи с тем, что для такого элемента нужно исходить из его приведенного сечения. В случае прямоугольного элемента с симметричным распределением арматуры в направлении его толщины условная трапецеидальная эпюра распределения относительной влажности бетона находится при этом из условий
403
•^.p - <n - о s л° i^p+
(«•)
2 (IX35)
4 w = SJ, - (n -1) 2л-’ 4" [<4p + («•)
4- <7*x<o _ <y« (xu>)],
т. e. должна быть по площади и статическом}' моменту площади относительно осн элемента меньше или больше, чем эпюра распределения эффективной относительной влажности бетона, на некоторые величины в зависимости от знака сумм в формулах (IX.35).
Входящие в выражения (IX.35) величины имеют тот же смысл, что и в формулах (IX.36) — (IX.40), а величины Fu, St; иэ(х[‘}) относятся к эпюре распределения эффективной относительной влажности бетона.
Во втором расчетном случае условная трапецеидальная эпюра распределения относительной влажности бетона находится аналогичным путем, по по полной эпюре распределения действительной относительной влажности бетона. Формулы (IX.34), (IX.35) справедливы и в этом случае, но в них вместо F3b, Sb, U3(xla°) берутся соответствующие величины, найденные по подпой действительной эпюре распределения относительной влажности бетона.
Эпюра распределения эффективной относительной влажности бетона находится из эпюры распределения его действительной относительной влажности по сечению элемента, отсечением и отбрасыванием ее частей, лежащих выше критической относительной влажности бетона
Определения эффективной и критической влажностей бетона даны в § 111.7; там же указаны методы их отыскания.
Средняя расчетная влажность 1/ср и расчетный перепад влажности U* по сечению прямоугольного железобетонного элемента в общем случае криволинейного распределения влажности в направлении высоты 2л'о его сечения, когда влажность элемента по его толщине 2уо не изменяется и арматура расположена симметрично относительно оси Ох сечения (рис. 94,6) в первом расчетном случае, указанном выше, находятся по формулам:
а) если вся кривая распределения действительной влажности бетона по высоте сечения элемента лежит выше критической влажности бетона (JKf>:
^р = Л".р|-'.Л + («-1)[-',Л-("-0]5;|; 0; (IX.36)
б) если на кривой распределения действительной влажности бетона по высоте сечения элемента имеется лишь участок
401
b < с, лежащий выше критической влажности бетона £/ир: = * |(«- -
- 2yuSa 10,5 м< р (с* - fe*) - SJ) +
+ 21/0(7,, H/K?(c-6)-Fd-(n - 1)ЗД/+ JnFu)]-, (IX.37)
U* = Л' {(и- 1) [£„$»,-(п- l)Savb-2y0Sa(UKp(c-b)-Fu)] 4-
+ 2f/o(^n [O.S^p^-^-SoH-FnSo-^-DSa^)}; (IX.38) в) если вся кривая распределения действительной влажности бетона по высоте сечения элемента лежит ниже критической влажности бетона (7кр:
^ср - |(« - 1) ^а-(« - 1)ада] +
+ 2f/o 17,,^-(и - l)SaSJ); (1Х.39>
U* = к {(и - 1) [Fn S’a - (и - 1) Sa^a] 4-
4- 2у0 [F„ Sv- (п - 1) Sa Fv]}. (IХ.40)
В формулах (IX.36) —(IX.40):
t»^a — часть объема эпюры распределения эффективной влажности бетона по высоте сечения элемента, выделяемая боковой поверхностью всех учитываемых арматурных стержней
(IX.41)
(<)
Sua — статический момент части объема эпюры распределения эффективной влажности бетона по высоте сечения элемента, выделяемой боковой поверхностью всех учитываемых арматурных стержней, относительно оси Оу его поперечного сечения
(ix.42)
«о
Sv и Fu — соответственно статический момент относительно оси Оу и плошадь заданной эпюры распределения действительной влажности бетона по сечению элемента;
Su и Fv — соответственно статический момент относительно оси Оу и площадь участка b < х < с заданной эпюры распределения действительной влажности бетона по сечению элемента, ограниченного абсциссами х—Ь и х=с\
—ордината эпюры распределения эффективной влажности бетона по сечению элемента, лежащая пад центром тяжести поперечного сечения i-ro стержня учитываемой арматуры, а остальные постоянные имеют тот же смысл, что и в формулах (IX.24) — (1Х.26).
При определении ординаты L/’, возможны два случая:
405
а) ордината заданной эпюры распределения действительной влажности бетона, лежащая над центром тяжести поперечного сечения рассматриваемого i-ro стержня учитываемой арматуры, больше или равна критической влажности бетона (УцР; в этом случае Uh принимается равной UKp и
б) ордината заданной эпюры распределения действительной влажности бетона, лежащая над центром тяжести поперечного сечения i-ro стержня учитываемой арматуры, меньше UKp, в этом случае Uh принимается равной этой ординате.
В формулах (IX.41), (1Х.42) суммирование производится по всем учитываемым арматурным стержням сечения элемента, число которых предполагается равным I.
Для бетонного (слабо армированного) элемента формулы (IX.36), (IX.40) принимают вид:
а) если вся кривая распределения действительной влажности бетона по высоте сечения элемента лежит выше критической влажности бетона Uup:
t/cp-^кр; ^* = 0; (1Х.43)
б) если на кривой распределения действительной влажности бетона по высоте сечения элемента имеется лишь участок
х лежащий выше критической влажности бетона Uup:
Ucp 1^- - h 4 и*р (<?- *)]; (1Х 44)
t/* - А 0,5икр(<*-d2)]; (IX.45)
2*о
в) если вся кривая распределения действительной влажности бетона по высоте сечения элемента лежит ниже критической влажности бетона U„p:
(7ср-^ ; (У* . . (1Х.46)
2т0 9*3
Средняя расчетная влажность (Уср и расчетный перепад влажности U* для железобетонного элемента во втором расчетном случае, указанном выше, находится по формулам (IX.39)— (IX.40). Для бетонного (слабо армированного) элемента в этом случае следует пользоваться формулами (IX.46).
В формулах (IX.36)- (IX.40) конструктивную арматуру можно не учитывать.
Для железобетонных элементов с прямолинейным или близким к нему распределением действительной влажности бетона по высоте поперечного сечения, а также элементов, имеющих только конструктивную арматуру, вполне допустимо среднюю расчетною влажность Uip и расчетный перепад влажности U* определять по формулам (IX.43)— (IX.46), как для бетонного (слабо армированного) элемента. ।
406
Площадь Fv и статический момент Sy эпюры распределения действительной влажности бетона по сечению элемента отыскиваются аналогично площади Ft и статическому моменту 5f эпюры распределения температуры по сечению элемента (см. § IX.4). Части Fv и S(/ соответственно площади Fv и статического момента Su эпюры распределения действительной влажности бетона находятся по формулам:
?</--= Fu-UKfJ (c—b); Su = Sb-0,5L’Kp (c2-^). (IX.47)
§ IX.6. ЧИСЛОВОЙ ПРИМЕР РАСЧЕТА ЖЕЛЕЗОБЕТОННОЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ НА ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ И ВЛАЖНОСТИ БЕТОНА*
Рассчитать железобетонную раму погонного метра зоны изотермического прогрева стационарной пропарочной камеры двухтуннельного типа (рис. 96) па изменения температуры и влажно-
Рис. 96 Схема стационарной пропарочной камеры двухтупнелыюго типа
сти ее элементов, связанные с переходом к длительному несимметричному циклу пропаривания изделий в одном (правом) из ее отсеков. Имея в виду худший случай работы рамы, поворотом ее фундаментов пренебрегаем.
Температура и влажность воздуха L’i со стороны внешнего контура рамы и в ее левом отсеке, а также температура /2 и влажность U2 воздуха в правом отсеке рамы соответственно равны: /, = 15° С; f7i = 60%; /2 = 80°С; £72 = 100%.
1 Пример составлен совместно с инж. О. М. Попковой. Расчетный объект в виде пропарочной камеры был предложен Гипротисом Госстроя СССР.
407
Ригель рамы несет полезную равномерно распределенную нагрузку, расчетное значение которой 9 = 2,5 Т/ле2.
Все элементы рамы выполнены из бетона марки 200 кГ/см2 и первоначально предполагаются симметрично армированными горячекатаной арматурой 0 12 А III с шагом 200 мм.
Определяем модуль поверхности элементов рамы (см. приме-
чание 2 к п. 4.26 СНиП):
f,,
iiiiiiimiiiiimiiniiiii1
— 5,72 At-1.
t, = 15" u, = eo%
t^SO° !
Ut--!00% |
и.
По I I
COO-435
coo
435
Рис. 97 Расчетная схема (а), основная система моментов в основной системе от сил Х| = 1
§
m —
2.1.1
1-1-0,35
(6) и эпюры изгибающих и нагрузки q (в)
с)
Так как 2<гл<15, то рама принадлежит к конструкциям средней массивности.
В соответствии с указаниями § IX.2 упругий расчет рамы производим по методу сил без учета продольных деформаций и деформаций сдвига, а ее расчетную схему (рис. 97, а) и основную систему (рис. 97, 6) выбираем с учетом длин элементов рамы в осях с групповыми лишними неизвестными, перенесенными в упругий центр.
По заданным расчетным влажностям воздуха U\ н Uz находим расчетные относительные равновесные влажности граней элементов рамы по формуле (IX.33), принимая во внимание, что в рассматриваемом стационарном состоянии
408
а) левые ригель и стойка —
= ф2 = (20 + 1.5 Ut) Ю-4 = (20 + 1,5 - 60) Ю4 = 1,1 • 10~2 г/г;
б) правый ригель, средняя и правая стойки —
ф» = (20 + 1,5-60) I0-4 =1,1-Ю“2 г/г;
ф2 = (20 + 1,5-100)10“4 = 1,7-10~2 г/г.
В соответствии с указаниями § II 1.7 находим относительную критическую влажность бетона £7Кр но формуле (III.2).
По линейной интерполяции, как для конструкции средней массивности, имеем:
U7 = (0.0125 - 0.00625) 2_2) + 0,00625 0,803- Ю 2 г/г;
15—2 '
(()>()1i^02-005) (5,72 — 2) + 0,005 = 0,643- ю " г/г
Так как данные о Ц и В/Ц отсутствуют, для определения коэффициента k формулы (II 1.2) пользуемся табл. 34, по которой находим, что k= 1,4. Тогда
U=W + ни' = 0,808-10~2 -{- 1,4-0,643-10 2 1,7-10“2 г/г.
Так как в рассматриваемом случае ф1<£/кр и ф2<£/кр, то изменения средней расчетной влажности Д17Ср и расчетного перепада влажности Д1/* по сечениям элементов рамы находим по действительным влажпостям ф1 и фг (§ IX.5).
Учитывая симметричное армирование рамы и линейное распределение расчетной влажности вследствие ее стационарного влажностпог-' режим': в соответствии с указаниями § IX.5, имеем:
а) до перехода к несимметричному циклу пропаривания для всех элементов рамы —
£/*> = 1,1-10-2 г/г; £/*(,) =0; Ср ’ ’ ’
б) после перехода к несимметричному циклу пропаривания для левых стойки и ригеля
t/‘2) = 1,1- 1(Г2 г/г; t/*(2) = 0;
для правой и средней стоек, а также правого ригеля — ^=(1±ьц^=1,4.10-г/г.
t/’(2)=-. (1,7~;1о!;)1()~2 = 1,713- кг2—.
Таким образом, расчетные изменения средней расчетной влажности Xt/cp и расчетного перепада влажности ДС'* будут равны:
409
для левых стойки и ригеля —
0; MJ'=u'o,-u'w = 0;
для средней и правой стоек, а также правого ригеля —
At/cp = 1,4- 1(Г2— 1,1-10-2 =0,3-10“2 г/г;
AL/* = 1,713-10-2 — 0 = 1,713-10-2—.
Аналогичным образом находим расчетные изменения средней расчетной температуры А/ и расчетного перепада температуры А/*:
для левых стойки и ригеля —
Д/ср = 0; А/* = 0;
для средней и правой стоек, а также правого ригеля —
А/ср = 32,5 град-, At* — 185,7 град!.к.
В соответствии с указаниями § IX.2 находим расчетные значения коэффициентов линейной усадки 0* и линейного расширения а бетона.
Из формулы (IX.12) при FK=Fn =0 и Еа = Еа=5,65 см2 имеем
т - —— =------------?-------= 0,97;
1|пц , , 2-10« 2-5,65
+ 2,65-106 ’ 100-35
0* = шр = 0,97-3-10-2 = 2,910-10-2
г/г
а= по-5—.
град
В первом приближении расчет рамы производим без учета наличия трещин по кратковременной жесткости ее элементов, сниженной за счет пластической деформации бетона на 15% [СНиП, п. 9.3, формула (170)] .
Предварительно находим:
2-106 „ гг
п =--------= 7,55;
2,65-105
/„ = ^+2(П-1)£,(^—«)’=
100 ЗУ +(7 55_ 1)2-5,65(17,5 —З)2 = 3729- Ю-6^;
Вк = 0,85E6Jn = 0,85-26,5- 10s-3729- Ю-6 = 0,0840-105 Гл2-
Пользуясь найденными значениями коэффициентов а, 0* и жесткости jBk, в соответствии с указаниями § IX.3 находим перемещения CiA, А,р, Ап, А,р основной системы. В качестве примера
410
приведем вычисление перемещении по направлению действия сил Х|. На рис. 97, в приведены необходимые для этого эпюры изгибающих моментов в основной системе от сил Х| = 1 и от нагрузки q-.
h_
2
6,
[4.Л Jl _L 2
[ 2 2 2 3
4,I75S (4,175 + 3-4,35) ----- 595,710-10
6-0.084-10*'
2 J 6ВК
м - ±(—L X -/-А . 2) =
6К 3 8 2 / 24 Вк
2,5-4,175-4,35s .сс 5
=:-------:-----— = — 426,155-10 м;
24-0,084.10*
Ди = А -/-а-А/* + 1-/-а-Л'ср - al (А ы* + д/ср) =
= 1 • Ю-’М.Зб (А2?5 185,7 + 32,б) -- 1828,1 • 10-5 м-
Д1,= y •/•Г-At'* + 1 -/-Г-Д^ср = ₽*/(-у + At/cp) -
= 2,91 -10“2-4,351,713- IO-2 + 0,30- IO-2)- 488,62- 10~s лг.
Аналогичным образом вычисляем перемещения по направлению остальных лишних неизвестных.
Далее составляем канонические уравнения для лишних неизвестных Xi вида:
+ ^12 Х2 + • • • + А1р + Ац/ + Дц, =- 0;
Система этих уравнений представлена в матричной форме в табл. 48. Значения лишних неизвестных, найденные решением этой системы уравнений, даны в табл. 49.
На рис. 98 приведены эпюры суммарных изгибающих моментов, поперечных и продольных сил в раме от полезной нагрузки, изменений температуры и влажности ее элементов, полученные в первом приближении.
Пользуясь данными упругого расчета рамы и принимая F -=5,65 см1 (50 12), находим необходимую площадь растянутой арматуры в ее элементах из расчета по прочности.
Так как для стоек рассматриваемой монолитной железобетонной рамы, жестко заделанных в фундамент (при /0=/=4 л«), оказывается, что m9,Rn = 0,999 и т] = 1,022 (см. п. 7.51 СНиП), то влияние гибкости ее элементов и длительного воздействия нагрузки на их несущую способность можно не учитывать.
411
Таблица 48
Канонические уравнения метода сил для лишних неизвестных основной системы (первое приближение)
№ Значение коэффи циентов системы канонических уравнений при неизвестных Свободные члены
Состояние системы уравнения X, х, X, X, xt X, от полезной нагрузки от измене-ниП температуры от изменений влажно-
Прямосимметричное 1 595,710 0 -216,200 0 0 0 -426,155 1828,100 488,620
2 0 633,550 -216,200 0 0 0 -1278,464 1550,600 414,519
3 -216,200 -216,200 202,980 0 0 0 -791,940 -1583,100 -423.207
Кососимметричное 4 0 0 0 884,520 0 -216,200 0 - 1828,100 -488,620
5 0 0 0 0 1574,000 216,200 0 1550,600 414,519
6 0 0 0 -216,200 216,200 401,790 0 3133,700 337,726
Рис. 98. Эпюры суммарных изгибающих моментов, продольных и поперечных сил в раме от нагрузки и изменений температуры и влажности
Примечание. Моменты — в Ли; силы в Т
Таблица 49
Лишние неизвестные первого приближения
Состояние системы Лишние неизвестные в Т и Тм От полезной нагрузки От изменения температуры От изменения влажности Суммарные
Прямоснмметричпое Kj —0,723 —0,276 —0,0738 — 1,073
х2 0,666 0,178 0,0476 0,892
Хз —3,962 7,696 2,057 5,791
Кососимметричное X, 0 0,173 0,0462 0.219
х5 0 0,0793 0,0212 0,100
Хе 0 — 7,749 —2,071 -9,820
Правый ригель:
М =-- 25,94 Тм; N = 1,292 7;
h0 = 0,32 м; е0 — 20,08 л;
е = 20,08 + °’32~ °-РЗ 20,22 л;
Ne - Ru bx ( Ло- - Яас 7; (Ло - а') =
= 1292- 2022 — 100 • 100 х (32 — 0,5 х) — 3400 - 5,65 (32—3) = 0, откуда, как и должно быть:
х = 7,23 см < 0,55 Ло = 0,55 • 32 — 17,6 см.
Поэтому (см. п. 7.48 СНиП)
Rubx I Rai F’ — N 100 100-7,23-| 3400-5,65—1292 o_ r „
ra =------------------ -----------—------------=- 26,5 cm2.
Ra 3400
Таким образом, принимаем:
Fa = 26,6 см2 (7022); F3 - 5,65 см2 (5012);
Правая стойка:
М = 22,498 Тм; N = 4,646 7;
Ло = 0,32 м; е0 ~ 4,85 м;
. ос . 0,32 — 0,03 с
е = 4,85 Ч—-—-—:— == 5 м.
По аналогии с расчетом правого ригеля находим:
х - 6,09 см < 0,55 Ло — 17,6 см;
Fa = 22,8 си2 (6 0 22); F = 5,65 см2 (5 0 12).
414
В связи с возможным случаем перехода к несимметричному циклу пропаривания в одном левом отсеке камеры армирование левых стойки и ригеля рамы принимаем соответственно таким же, как для правых, а среднюю стойку армируем симметрично; при этом имеем:
средняя стойка
М = 20,118 Тм\ N 12,658 7;
Ло = 0,32 м; ес=1,59л;
е = 1,59 + 0,15= 1,74 м.
Так как
N 12658 . «с о с
х =----=----------= 1,26 см < 2а = 2-3 = 6 см,
bRu 100-100
то площадь сечения арматуры находим по уравнению
р _ N(e — (hn—a')\ = 12 658 [ 1,74—(32—3)[ =
а‘ а Яа(Ло—а') 3400(32—3)
Принимаем
Fa = F’a = 19 см* (5022).
Для расчета рамы во втором приближении определяем кривизны ее элементов в сечениях наибольших моментов.
Правый ригель:
Гп = 100 -35 4- 7,55 (26,6 4- 5,65) = 3743 см2-,
Sn = 100-35 • у- 4- 7,55 (26,6-3 4- 5,65 (35—3)] = 632’5 он3,
Sn 63215
у = — =-------= 16,9 см-
s Fa 3743
Jn = 4- 100-35(17,5—16,9)24-7,55-26,6(16,9 —З)2 4-
4- 7,55 5,65 (35 — 16,9 — З)2 = 395 500 см4;
Г0=А = 395500 = 234(Ю у 16,9
U70 23 400 rtic
rK = — =-------= 6,25 см.
Fn 3743
По табл. 34 приложения II СНиП у=1,75
U7T1 = уЦ7п 1,75 • 23 400 = 40 900 см3-,
Мп = Яр U7T1 = 16-40 900 = 655 000 кГсм = 6,55 Тм-,
N = _Мт1_ =-------6Л5-----= 0 327 т
т е0—гя 20,08 — 0,0625
Ms = N(е0 4- у — а) = 1,292 (20,08 4- 0,169 — 0,03) =26,16 Тм-,
415
/И3г = (е0 + у — а) = 0,327 (20,08 4- 0,169 — 0,03) = 6,62 Тм;
М3 2 616 000
= 0,142; 100-32г.180
L =
г _ ^Зт
, nF'a у' =.---- =
vbh0
662 000 - = 0,0362;
100-322-180
7-55'5,66 = 0,0296;
0,45-100-32
1 —
1----= 0,0268;
32/
е.
Fan bh9 =
N
М»
NT
26,6-7,55 100-32
26,16
1,292 ~
_ 6,62 _ “ 0,327 ~
= 0,0628;
20,25 м;
20,24 м;
«1
1 , Д.5 4- У' =1 .
14 4L + 7) 14-5(0,142 4-0,0268)
’ h 10цл ’h0 * + 10-0,00831-7,55
_L5_i 0,0296 = Ж = 2^3 = 0 J
,20.25 _ h0 32
0,32
1 . 1.54 У' _________________1___________ .
14-5(£т--7) „ , 1-^-5(0,0362 + 0.0268)
’ + Юрп ’° ho ’ + 10 0,00831-7,55
'.б+о.огм ,,0 258>^=2_з =
П.5^1-5 32
0,32
z, =-- /70 1
2-3
— 0,0296 4- 0,214®
32________
2(0.02964-0,214) .
— 28,6 см;
ТУ'+^ ho
2(Т'4-£т) J
2-3
— 0,02964 0,258®
2(0,0296+0.258) .
= 28 см;
^зт—?1Т Кт _ 6,62 — 0,28-0,327 /И3—?!N ~ 26,16-0.286-1,292
Я>а = 1,3 — Sm----= 1,3 — 0,8-0,253----------1 °’25^— = 0,944;
6-4,5m ’ ’ 6—4,5 0,253
416
Кривизна при длительном действии нагрузки при v=0,2 (случай влажного режима):
1 = М3 Г Фа ,________________Фб_______1 _ ТУ фа
Р Ло г, [ £а Fа (у' + О bh0 Е6 v J Ло Еа Fa
= 2 616000 Г 0,944 ._________________0,9_________________
~ 32 28,6 [г-Ю- гб.б^ (0,0296 | 0,214) 100 32 2,65.103-0,2
1292-0,944
32 2- КХ-25,6
116,3-10"® — =11,63-10^ — . см м
Далее, аналогично предыдущему, находим: правая стойка —
— = 9,544-10"3 — ;
р м
средняя стойка —
— = 8,52-10"3-— . р м
Так как трещины имеются по всей длине элементов правого отсека рамы (М>МТ), то, пользуясь указаниями § IX.3, находим условные длительные жесткости Вп элементов рамы:
а) правый ригель, В,.= = —5-^-40- =0,0223- 10s Тм2-,
’ v и J_ П.63-10-3
Р
б) правая стойка Вп = —=0,0236- 10s Тм2-, 9,544- 10 3
в) средняя стойка Вп= 1 =0,0237- 10s Тм2.
В связи с возможностью указанного выше случая перехода к несимметричному циклу пропаривания в одном левом отсеке рамы и чередования несимметричных циклов, кривизны, а следовательно, и условные жесткости левых стойки и ригеля принимаем такими же, как для правых стойки и ригеля соответственно.
Учитывая, что найденные условные жесткости очень близки по величине, в расчет рамы по второму приближению вводим среднюю для всех ее элементов условную жесткость
В (0.0223+0.0236+0.0237) IO-- = 1()5
3
_ 0,0840-106
Так как-^- — =3,621, то расчет рамы во втором при-
ближении сводится к пропорциональному снижению лишних неизвестных первого приближения, вызванных изменениями температуры и влажности, в 3,621 раза. Лишние же известные, вызванные полезной нагрузкой, остаются неизменными.
В табл. 50 приведены найденные таким способом лишние неизвестные второго приближения, а на рис. 98 — соответствую-
417
щие ему суммарные эпюры изгибающих моментов, поперечных и продольных сил.
Таблица 50
Лишние неизвестные второго приближения
Состояние системы Лишние неизвестные в Т и Тм От полезной нагрузки От изменения температуры От изменения влажности Суммарные
Прямосимметричное Х1 —0,723 —0,0762 —0,0204 —0.820
хг 0,666 0,0492 0,0132 0,728
Хз —3,962 2,125 0,568 —1,269
Кососимметричное X, 0 0,0478 0,0128 0,0606
х5 0 0,0219 0,00585 0,0248
хв 0 —0,140 —0,672 —2,712
Пользуясь данными расчета рамы во втором приближении, подбираем ее армирование из расчета по прочности.
а) ригели:
М = 10,716 Тм-, N = 0,881 7;
F = 10,7 сл2; F' = 5,65 сл2;
б) крайние стойки:
714 = 7,674 7л; N = 4,738 Т\
Fa = 7,06 сл2; F* = 5,65 сл2;
в) средняя стойка:
М = 5,555 7л; К = 12,33 7;
Fa = F't = 5,65 сл2.
Далее производим расчет рамы в третьем приближении.
Для элементов рамы по усилиям второго приближения определяем Л4Т: 1
а) ригель —
7П = 100-35 + 7,55(10,7 + 5,65) = 3623 сл2;
Sn= 100-35-у + 7,55 [ 10,7 -3 + 5,65 (35—3)]-=62 805 сл3;
Sn 62805 у — — =------- = 17,3 сл.
л Fn 3623
ion ЗЯ»
Jn •-= - + 100-35(17,5— 17,3)2 +
+ 7.55 • 10,7 (17,3 — З)2 + 7,55 • 5,65 (35 — 17,3 — З)2 = 382 860 см1;
- А _ 382860 = 22 1 00 сл3;
у 17,3
418
u/o 22 100 _ ,
Гя = — =--------- - 6,1 CM;
F„ 3623
V/ri~ Л = 1,75-22 100 =-• 38 700 сл:3;
Л4т =R” U7T1 Ч- Nr* -16 • 387004-881 6,1 624 574 кгсм=6,246 Тм
По аналогии находим:
б) крайние стойки —
/Ит = 6,301 Тм;
в) средняя стойка —
Л4Т -6,704 Тм.
Определяем длины участков элементов рамы с трещинами и без трещин. Границы этих участков показаны на рис. 99. На этом
Рис. 99. Границы участков с трещинами в элементах правого отсека рамы и эпюры условных жесткостей В
же рисунке изображены эпюры условных жесткостей В на этих участках, вычисленных аналогично второму приближению. Пользуясь этими эпюрами, вновь повторяем расчет рамы в третьем приближении. Значения лишних неизвестных, полученных в результате этого расчета, приведены в табл. 51, а суммарные эпюры изгибающих моментов, поперечных и продольных сил — на рис. 98.
419
Лишние неизвестные третьего приближения
Состояние системы Лишние неизвестные в Т и Тм От полезной нагрузки От изменений температуры От изменений влажности Суммарные
Прямосимметричное X, —0,503 0,639 0,169 0,305
х2 0,541 0,261 0,0691 0,871
Х3 —4,665 3,722 0,986 0,043
Кососимметричное Х4 0 —0,596 —0,158 —0,754
Xs 0 —0,351 —0,093 —0,444
Хе 0 —3,981 —1.054 —5.035
Сравнивая эпюры моментов второго и третьего приближений, находим, что моменты в правом ригеле для этих приближений различаются незначительно, а моменты в стойках несколько завышены по сравнению с их вероятной конечной величиной, так как они получены при жесткостях, превышающих действительные конечные жесткости стоек рамы. Истинные значения этих моментов будут находиться между их значениями во втором и в третьем приближении, т. е.
5,555 Тм </ИП1ач < 15,149 Тм (средняя стойка);
5,921 Тм < Afmax < 10,342 Тм (крайняя стойка).
Принимая приближенно
Мтах = + = ю 352 Тм
для средней стойки и
10,342-1-5,921
Мтах =------------------= 8,142 Тм
2
для крайней стойки, получаем моменты, близкие к максимальному моменту ригеля в третьем приближении A7max= = 11,64 Тм, который и принимаем за расчетный для всех элементов рамы. Расчетные же значения продольных сил принимаем по третьему приближению.
В соответствии с принятыми значениями моментов п продольных сил подбираем арматуру в элементах рамы по прочности:
а) ригели —
М = 11,64 Тм, Л'= 1,059 7;
Г - 12,3 см2 (8 0 14); Г = 5,65 см2 (5 0 12);
б) крайние стойки —
Л4= 11,64 7л; W = 4,12 7;
Fa - 12,3 c-H2(8 0 14); F'a = 5,65 см2 (5 0 12);
420
в) средняя стойка —
М = 11,64 Тм; 12,62 Т;
Га = Гл = 12,3 ел:2 (8 0 14).
Поперечная арматура в элементах рамы устанавливается конструктивно, так как удовлетворяется условие (п. 7.30 СНиП)
Q = 6,75 Т< Rpbh0 - 7,2-100 -32 = 23000 кГ = 23 Т,
где Q = 6,75 Т — максимальное значение поперечной силы из трех приближений для всех элементов рамы Так как
<2= 6,75 Т< 0,25 R„ bhv --= 0,25• 100-100 32 = 80000 кГ =80 Т,
то условие (58) п. 7.25 СНиП также удовлетворяется.
Далее по окончательно принятым расчетным значениям усилий следует произвести расчет элементов рамы по деформациям п по раскрытию трещин, после чего расчет рамы можно считать законченным. Эти расчеты показывают, что даже при учете расчетной полезной нагрузки раскрытие трещин в наиболее напряженном сечении рамы с наибольшим моментом и наименьшей продольной силой (в месте примыкания правого ригеля к средней стойке) составляет 0,29 мм, т. е. меньше величины 0,3 мм, допускаемой нормами при учете нормативной полезной нагрузки. Наибольший прогиб наиболее напряженного правого ригеля рамы даже при учете расчетной полезной нагрузки также оказывается значительно меньше допускаемого нормами.
ПРИЛОЖЕНИЕ I
ТАБЛИЦЫ НАСЛЕДСТВЕННОЙ ФУНКЦИИ БЕТОНА ВТОРОГО РОДА
т /?(/. t) т Z? (/. -Г) т /г (/. -г)
t—2 суток
2 6,59306010 1,075 0.18471021 3.325 0,22322229
1,975 5,11022750 1.050 0.17914047 3,300 0.21890892
1,950 3,98590270 1,025 0,17384154 3,275 0,21482407
1,925 3,13267040 1 0,16880591 3,250 0,21092379
1,900 2,48442090 0,950 0,15940217 3,225 0,20717465
1,875 1,99164200 3,200 0,20355126
1,850 1.61510460 /—4 3,175 0,20003429
1,800 1,10726520 3,150 0,19660903
1,775 0,93756848 4 5,64943980 3,125 0,19326429
1,750 0,80624754 3,975 4.36630360 3,100 0,18999152
1,725 0,70398496 3,950 3,39055460 3,075 0,18678419
1,700 0,62374222 3,925 2,64831770 3,050 0,18363732
1.675 0,56020312 3,900 2,08347110 3,025 0.18054706
1,650 0,50935277 3.875 1,65338020 3 0,17751047
1,625 0,46815947 3,850 1,32565810 2,950 0.17146472
1,600 0,43433414 3,825 1,0757021 2,900 0,16567551
1,575 0,40614846 3,800 0,88482388 2,850 0,16010729
1,550 0,38229763 3,775 0,73882766 2,800 0,15473899
1,525 0,36179648 3,750 0.62693074 2,750 0,14955787
1,500 0,34390110 3,725 0,54094299 2,700 0.14455593
1,450 0,31381754 3,700 0,47464369 2,650 0,13972792
1,425 0.30088391 3,675 0.42330804 2,600 0.13507013
1,400 0,28900587 3,650 0,38334754 2,550 0,13057972
1,375 0.27799946 3,625 0,35203681 2,500 0,12625432
1,350 0,26772504 3,600 0,32730596 2,450 0,12209186
1,325 0,25807642 3,575 0,30758307 2,400 0,11809037
1,300 0,24897254 3,550 0,29167432 2,350 0,11424796
1,275 0,24035131 3,525 0,27867313 2,300 0,11056276
1,250 0,23216482 3,500 0,26789102 2,250 0,10703286
1,225 0.21437596 3,475 0,25880518 2,200 0,10365636
1,200 0,21695559 3,450 0,25101857 2,150 0.10043131
1,175 0.20988064 3.425 0,24422969 2,100 0.097355740
1,150 0.20313258 3,400 0,23820960 2,050 0,094427625
1,100 0,19055904 3,375 0,23278440 2 0,091644897
3,350 0,22782206 1,900 0,086127191
422
Продолжение
т RU. t) RU. ’)
1,800 0,081493893 5,050 0.15098101 /=11 ] суток
1,700 0,077493252 5,025 0,14837374
1,600 0,074032592 5 0,14778830 10 5,0156228
1,500 0,071069455 4,950 0,14455268 9,975 3,8600671
1,400 0,068576758 4,900 0,14144194 9,950 2,9772604
1,300 0,066531624 4,850 0,13842468 9,925 2,3028063
1,200 0,064911811 4,800 0,13548267 9,900 1,7875079
1,100 0,063694557 4,750 0,13260536 9,875 1,3937816
1 0,062856123 4,700 0,12978657 9,850 1,0929166
0,5 0,054642791 4,650 0,12702269 9,825 0,86298076
4,600 0,12431156 9,800 0.68722038
4,550 0,12165186 9,775 0.55283815
Л=( 5 суток 4,500 0,11904277 9,750 0,45005897
4,450 0,11646107 9,725 0,37141648
6 5,34935117 4,400 0,11240014 9,700 0.31120792
5,975 4,12027240 4,350 0,11182247 9,675 0,26507767
5,950 3,18471960 4,300 0,10829196 9,650 0.22969914
5,925 2,47245070 4,250 0,10686080 9,625 0,20253167
5,900 1,93007560 4,200 0,10450745 9,600 0,18163498
5,875 1,51696830 4,150 0,10221941 9,575 0,16552728
5,850 1,20221660 4,100 0,099989415 9,550 0,15307697
5,825 0,96229951 4,050 0,097882178 9,525 0,14341993
5,800 0,77832053 4 0,095460657 9,500 0,13589626
5,775 0,63966297 3,900 0,091414363 9,475 0,13000211
5,750 0.53296665 3,800 0,087244661 9,450 0,12535268
5,725 0,45134923 3,700 0,083484789 9,425 0,12165422
5,700 0,38881374 3.600 0 079980604 9,400 0,11868240
5,675 0,34079768 3,500 0,076680530 9,375 0,11626594
5,650 0,30283000 3.400 0,073566554 9,350 0.11427407
5,625 0,27527003 3.300 0,070630886 9,325 0,11260698
5,600 0,25210886 3,200 0,067872450 9,300 0,11118842
5,575 0,23581825 3,100 0,065285977 9,275 0,19996021
5.550 0,22223562 3,000 0,062870238 9,250 0.10887792
5.525 0,21147660 2,900 0,060624273 9,225 0,10790764
5,500 0,20286845 2,800 0,058544526 9.200 0,10702348
5,475 0,19589942 2,700 0,056629385 9,175 0,10620567
5,450 0,19018024 2,600 0,054876470 9,150 0,10543913
5,425 0,18541483 2,500 0,053283362 9,125 0.10471235
5,400 0,18137794 2,400 0,051847513 9,100 0.10401652
5,375 0,17789828 2,300 0,050566216 9,075 0,10334494
5,350 0,17484554 2,200 0,049436705 9,050 0,10269250
5,325 0,17212060 2,100 0,048456031 9,025 0,10205527
5,300 0,16964808 2 0,047521111 9 0,10143027
5,275 0,16737064 1,900 0,046828714 8,950 0.10011613
5,250 0,16524467 1,800 0,046375456 8,900 0,098870826
5,225 0,16323700 1,700 0,045957749 8,850 0,097669901
5,200 0,16122239 1,600 0,045671899 8.800 0,096499104
5,175 0,15948164 1,500 0,045513952 8.750 0,095350117
5,150 0,15770017 1,400 0,045479816 8.700 0.094218196
5,125 0,15596686 1,200 0,045287733 8,650 0,093100439
5,100 0,15427326 1 0,045095650 8,600 0,091995229
5,075 0,15261294 0,5 0,044999609 8,550 0,090901604
423
t т R (Л х) т R(t. х)
8,500 0.089818999 19,550 0,10099561 15,250 0,032761039
8,450 0,088747076 19,525 0,091318268 15 0,031789665
8,400 0,087685632 19,500 0,083809218 14,750 0,030849486
8,350 0,086634546 19,475 0,077973612 14,500 0.029940253
8,300 0,085593737 19,450 0,073429534 14,250 0,029061736
8.250 0,084563153 19,425 0,069882229 14 0,028213726
8.200 0.083542757 19.400 0,067104221 13,750 0,027396039
8.150 0,082532523 19,375 0,061919957 13,500 0,026608511
8.100 0,081532426 19,350 0,063193959 13,250 0,025851004
8.050 0,080542449 19,325 0,061821676 13 0,025123401
8 0.079562575 19,300 0,060722431 . 12,750 0,024425614
7,750 0,070374717 19,275 0,059833964 12,500 0,023757577
7,500 0,066242053 19,250 0,059108236 12,250 0,023119254
7,250 0,062560841 19,225 0,058508174 12 0,022510634
7 0,059093069 19.200 0,058005176 11,750 0,021931736
6,750 0,055826613 19,175 0,057577168 11,500 0,021382609
6,500 0,052761092 19,150 0,057207122 11,250 0,020863332
6,250 0,049896871 19,125 0,056881897 11 0,020374019
6 0,047234487 19,100 0,056591356 10,750 0,019914816
5,750 0,044774635 19,075 0.056327676 10,500 0,019485904
5,500 0,042518150 19,050 0,056084821 10,250 0,019087504
5,250 0,040463060 19,025 0,055858137 10 0.018719873
5 0,039619356 19 0,055644031 9,750 0,018383314
4,750 0,036979442 18,950 0,055193196 9,500 0.018078169
4,500 0,035547682 18,900 0,054787668 9,250 0,017804829
4,250 0,034325624 18,850 0,054409806 9 0,017563732
4 0,033314949 18,800 0,054049117 8,750 0,017355372
3.750 0,032517474 18,750 0,053693696 8,500 0,017180294
3,500 0,031935151 18,700 0,053356824 8,250 0.017039105
3.250 0,031570065 18,650 0,053019301 8 0.016932473
<3 0,031424438 18,600 18,550 18,500 0,052685474 0,052354562 0,052026095 <7,750 0,016861138
/=2 0 суток 18,450 18,400 0,051699792 0,051375487 t=4 0 суток
20 4,46763110 18,350 0,051053074 40 3,98442990
19.975 3,46280510 18,300 0,050732494 39,975 3.11697490
19,950 2,68705390 18.250 0,050413704 39,950 2,40073800
19,925 2,08815790 18,200 0,050096679 39,925 1,91186790
19.900 1.62579820 18,150 0,049781402 39,900 1,49969270
19,875 1,26884560 18,100 0,049467861 39,875 1,17805850
19,850 0,99326595 18,050 0,049156046 39,850 0.92707460
19,825 0,78050422 18 0,048845949 39,825 0,73121973
19,800 0,61623518 17.750 0,044464959 39,800 0,57838217
19.775 0,48939957 17,500 0,042971357 39,775 0,45911085
19.750 0,39145973 17,250 0,041692586 39,750 0.36603096
19,725 0,31582473 17 0,040459473 39,725 0.29338786
19.700 0,25740666 16,750 0,039260981 39,700 0,23669116
19.675 0,21227791 16,500 0,038096039 39,675 0,19243702
19.650 0,17740665 16.250 0,036964219 39,650 0,15789143
19,625 0.15045260 16 0,035865149 39,625 0,13092106
19,600 0,12960930 15,750 0,034798479 39,600 0,10986132
19,575 0,11348239 15,500 0,033763879 39,575 0,093413379
424
Продолжение
t R (*.x) 1 RU. t) t R (t.t)
39,550 0,080563784 35,250 0,022846657 /=120 суток
39,525 0,070521783 35 0.022369052
39,500 0,062670387 34,750 0.021901062 120 3,63644440
39,475 0,056528188 34,500 0,021442529 119.975 2,86583211
39,450 0,051719567 34,250 0,020993299 119.950 2,25961890
39,425 0,047951454 34 0,020553219 119.925 1,78273100
39,400 0,044995184 33,750 0.020122142 119,900 1,40757731
39,375 0,042672349 33,500 0,019699921 119.875 1,11245330
39,350 0,040843748 33,250 0,019286416 119.850 0,88028497
39,325 0,039400776 33 0,018881484 119,825 0,69764470
39,300 0,038258698 32,750 0,018484990 119.800 0,55395514
39,275 0,037351403 32,500 0,018096800 119,775 0,42091606
39,250 0,036627312 32,250 0,017716782 119,750 0,35198525
39,225 0,036046182 32 0,017344810 119,725 0,28201916
39.200 0,035576617 31,750 0.016980757 119,700 0.22697172
39,175 0,035194124 31,500 0,016624499 119,675 0,18366002
39,150 0,034879591 31,250 0,016275918 119,650 0,14958025
39,125 0,034618109 31 0,015934896 119.6n5 0,13276274
39,100 0,034398046 30,750 0,015601319 119.600 0,10165811
39,075 0,034210329 30,500 0,015275075 119,575 0,085047482
39,050 0,034047676 30.250 0,014956054 119,550 0,071972071
39,025 0.033905167 30 0,014644151 119,525 0,061677631
39 0,033777891 29,750 0,014339261 119.500 0,055570841
38,950 0,033528912 29,500 0.014041282 119,475 0,047184968
38,900 0.033321204 29,250 0,013750118 119,450 0.042152857
38,850 0,033138827 29 0,013465671 119.425 0.038185686
38,800 0,032972082 28,750 0.013187848 119,400 0,035050257
38,750 0,032815070 28,500 0,012916559 119,375 0,032585845
38.700 0,032664201 28,250 0.012651715 119,350 0,030633857
38,650 0.032517293 28 0.012393231 119,325 0.029089697
38.600 0,032373017 27,500 0,011895013 119.300 0,027866365
38,550 0,032230564 27 0,011421274 119,275 0,026895413
38,500 0,032089441 26,500 0,010971423 119,250 0,026122037
38,450 0.031949348 26 0,010544914 119,225 0,025506856
38,400 0,031810101 25,500 0.010141241 119,200 0,025013566
38,350 0,031671589 25 0.0097599452 119,175 0,024616962
38,300 0,031533374 24,5 0,0094006088 119,150 0,024296429
38.250 0,031396515 24 0,0090628613 119,125 0.024035752
38,200 0,031259886 23,5 0.0087463743 119,100 0,023822172
38,150 0,031123834 23 0,0084508837 119,075 0,023645657
38.100 0,030988349 22,5 0,0081761512 119.050 0,023498313
38,050 0,030853424 22 0.0079220059 119,025 0,023373929
38 0,030719053 21 0,0074750496 119 0,023267621
37,750 0.028334122 20,5 0.0072821690 118,950 0,023076782
37.500 0,027616311 20 0,0071097419 118,900 0,022928734
37,250 0,027034426 19,5 0,0069578917 118,850 0,022807257
37 0,026473082 19 0,0068268116 118,800 0,022702320
36,750 0,025923433 18,5 0,0067167699 118,750 0,022607714
36.500 0,025384645 18 0.0066281147 118,700 0,022519602
36.250 0,024856490 17 0.0065167917 118,650 0,022435609
36 0,024338785 16,5 0.0064952771 118.600 0.022354264
35,750 0.023831358 <16 0.0064737625 118,550 0,022274657
35,500 0,023334038 118,500 0,022196229
425
Продолжение
т R(t. t)
118,450 0,022118629
118,400 0,022042641
118.350 0,021965131
118,300 0,021889017
118,250 0,021813247
118,200 0,021737788
118,150 0,021662621
118,100 0,021587731
118,050 0,021513111
118 0,021438756
117,750 0.019920857
117,500 0,019498853
117,250 0,019116728
117 0,018848738
116,750 0,018536095
116,500 0,018228675
116,250 0,017926344
116 0,017629014
115,750 0,017336602
115,500 0,017049029
115,250 0,016766215
115 0,016488081
114,750 0,016214550
114,500 0,015945548
114,250 0,015681000
114 0,015420832
113,750 0,015164973
113,500 0,014913354
113,250 0,014665902
113 0,014422551
112,750 0,014183232
112,500 0,013947879
122,250 0,013716429
112 0,013488817
111,750 0,013264979
111,500 0,013044853
111,250 0,012828379
111 0,012615497
110,750 0,012406148
110,500 0,012200273
110,250 0.011997816
100 0,011798721
109,750 0,011602932
109,500 0,011410395
т R (f. x)
109,250 0,011221057
109 0,011034864
108,750 0,010851766
108,500 0,010671712
108,250 0,010494652
108 0,010320536
107,750 0,0101493166
107,500 0,0098094512
107,250 0,0098153755
107 0,0096525617
106,750 0,0094924584
106,500 0,0093350210
106,250 0,0091802058
106 0,0090279696
105,750 0,0088782702
105,500 0,0087310659
105,250 0,0085863154
105 0,0084439788
104,750 0,0083401621
104,500 0,0081663887
104,250 0,0080310579
104 0,0078979860
103,750 0,0077671360
103,500 0,0076384713
103,250 0,0075119560
103 0,0073875548
102,750 0,0072652331
102.500 0,0071449565
102,250 0,0070266915
102 0.0069104051
102,750 0,0067960646
101,500 0,0066836382
101,250 0,0065730945
101 0,0064644025
100,750 0.0063575316
100,500 0,0062524521
100,250 0.0061491344
100 0,0060475497
99 0,0034749900
98 0.0033017826
97 0,0031361387
96 0,0029791474
95 0,0028303721
94 0,0026833999
T Rtt.*>
93 0,0025558389
92 0,0024293176
91 0,0023094835
90 0,0021960023
89 0,0020885572
88 0,0019868476
87 0,0018905886
86 0,0017995101
85 0,0017133565
84 0,0016318851
83 0,0015548663
82 0,0014820826
81 0,0014133282
80 0,0013484081
79 0,0012871379
78 0,0012293434
77 0,0011748598
76 0,0011435314
75 0.0010752113
74 0,0010297608
73 0,00098704937
72 0,00094695388
71 0,00090935869
70 0,00087415515
69 0,00084124134
68 0,00081052189
67 0,00078190774
66 0.00075631591
65 0,00073066934
64 0,00070789674
63 0.00068693246
62 0.00066771637
61 0.00065019382
60 0,00063441205
59 0,00062003464
58 0,00060731891
57 0,00059613154
56 0,00058644521
55 0.00U57823793
54 0,00057149345
53 0,00056620152
52 0,00056235817
51 0,00055996601
<50 0,00055903471
426
ПРИЛОЖЕНИЕ II
LZ4
КЛИМАТИЧЕСКОЕ РАЙОНИРОВАНИЕ ТЕРРИТОРИИ СССР
ЛИТЕРАТУРА
1. Абрамян Б. Л. О температурных напряжениях в прямоугольном бетонном блоке. Известия АН Арм. ССР. Серия физико-математических и естественных наук, т. VII, А® 3, 1954.
2. Ад а мович А Н., Л а м к и н М. С. Обследование трещннообразова-1;ия в бетоне плотины Братской ГЭС путем бурения специальных скважин Труды координационных совещаний по гидротехнике, вып. IV. Совещание по вопросам термонапряженного состояния бетонных гидротехнических сооружений. Госэнергоизтат, 1962.
3 Александровский С. В. Теория температурных полей массивных бетонных тел с учетом экзотермии. Труды НИИ по строительству, вып. 1, Минмашстройнздат. 1949.
4. А л е к с а н д р о в с к и й С. В. Теория теплопроводности бетона. Исследования Массивные и стержневые конструкции. Труды НИИ по строительству. Госстрой изд ат, 1952.
5. Александровский С. В. Температурные напряжения в массивных бетонных блоках от экзотермии цемента. Исследования. Массивные п стержневые конструкции. Труды НИИ по строительству. Госстройиздат. 1952.
6 Александровский С. В., Соколова 3. Г. Расчет температур в массивных бетонных блоках аналитическим методом. Исследования. Железобетонные конструкции. Госстройиздат, 1955.
7. А л е к с а и д р о в с к и й С. В. О гистерезисе деформаций усадки и набухания бетона при его попеременных высушиваниях и увлажнениях. «Бетон и железобетон». № 9. 1958.
8. А л с к с а н д р о в с к и и С. В. О влиянии длительного действия внеш ней нагрузки на режим высыхания и усадку бетона Исследование свойств бетона и железобетонных конструкций. Труды НИИЖБ. вып, 4. Госстройн.з-дат, 1959.
9. Александровский С. В. Некоторые особенности усадки бетона. «Бетон и железобетон». № 4. 1959.
10. Александровский С. В. О набухании бетона при его увлажнении «Бетон н железобетон», № 10. 1959
11. Александровский С. В., Таль К. Э. Основные физико-механические свойства бетона. Справочник по сборному железобетону. Госстройиздат. 1959.
12. А л е к с а н д ро в с к и й С. В. О тепло-влагофнзических свойствах бетона, связанных с тепло- и влагообменом Исследование свойств бетона и железобетонных конструкций. Труды НИИЖБ. вып. 4 Госстройиздат. 1959.
13. Александровский С. В. О влиянии длительного действия внешнего растяжения на режим высыхания и усадку бетона. Труды НИИЖБ, ьып. 17 Госстройиздат, I960.
14 Александровский С. В. О необратимости усадки и набухания бетона. Исследования по теории железобетона. Труды НИИЖБ, вып. 17. Госстройиздат, 1960.
15. А л е к с а и д р о в с к и й С. В. Об усадке и набухании мелкозернистого бетона для вибропрокзтных изделии Технология п свойства бетонов и изделий, изготавливаемых методом впбропроката. Труды НИИЖБ, вып 20. Госстройиздат, 1961.
428
16. А л е к с а н д р о в с к н й С. В. О влиянии масштабного фактора на влажностные деформации бетона. Расчет железобетонных конструкций. Экспериментально-теоретические исследования по усовершенствованию расчета. Труды НИИЖБ, вып. 17. Госстройиздаг, 1961.
17. Александровский С. В. Некоторые вопросы теории температурных и влажностных деформаций и напряжений в бетонных и железобетонных конструкциях и сооружениях. Труды координационного совещания по гидротехнике, вып IV. Совещания по вопросам термонапряженного состояния бетонных гидротехнических сооружений. 1 осэнергоиздат. 1962.
18. Александровский С. В. О методике исследования ползучести и влажностных деформаций бетона. Методика лабораторных исследований деформаций и прочности бетона, арматуры и железобетонных конструкций. Госстройиздат, 1962.
19. Александровский С. В. Учет температурно-влажностных воздействий при расчете бетонных н железобетонных конструкций. Расчет и конструирование элементов железобетонных конструкций. Стройиздат, 1964.
20. Александровский С. В. О разновидностях современной теории ползучести бетона и наследственных функциях, фигурирующих в их уравнениях. Ползучесть строительных материалов и конструкций. Стройиздат, 1964.
21. А л е к с а и д р о в с к и й С. В. О наследственных функциях теории ползучести стареющего бетона Ползучесть строительных материалов н конструкций. Стройиздат, 1964.
22. Александровский С. В. Плоская задача при наличии вынужденных деформаций тела, обладающего ползучестью. «Строительная механика и расчет сооружений» № 6, 1964.
23. Александровский С. В, Попкова О. М. Экспериментально-теоретическое исследование температурных напряжений в бетоне. Трещино-стойкость и деформатнвность обычных и предварительно напряженных железобетонных конструкций. Стройиздат, 1965.
24. Александровский С В. Экспериментально-теоретические исследования усадочных напряжений в бетоне. Состав, структура, прочность и деформации бетонов. Стройиздат, 1965.
25. Арутюнян Н. X. Некоторые вопросы теории ползучести. Гостек-теоретиздат, М., 1952.
26. А р у т ю н я н Н. X., А б р а м я н Б. Л. О температурных напряжениях в прямоугольных бетонных блоках. Известия АН Арм. ССР, серия фнз.-мат., ест. и техн, наук, т. VIII, вып. 4, 1955.
27. Б а с е в и ч А. 3. Массивные гидротехнические сооружения с искусственным обжатием бетона. Госстройиздат, 1957.
28. Белов А. В. К вопросу об исследовании напряженного состояния б бетоне при его усадке. Известия НИИГ, т. 29, 1941.
29. Белов А. В. Опыт математической теории усадки бетона. Известия НИИГ, т. 35, 1948.
30. Белов А. В. Экспериментальное определение коэффициента диффузии влаги в цементном растворе при его высыхании. Известия ВНИИГ, т. 43, 1950.
31. Белов А. В. Температурные напряжения в бетонной плите при гармонических колебаниях температуры. Известия ВНИИГ, т. 45, 1951.
32. Белов А. В. О влиянии арматуры на величину усадочных напряжений в бетоне. Известия ВНИИГ, т. 45, 1951.
33. Белов А. В. Температурные напряжения в бетонной призме i рямо-угольного поперечного сечения. Известия ВНИИГ, т. 51, 1954.
34. Белов А. В. К определению предельной толщины бетонной плиты из условия прочного сопротивления ее температурным растягивающим напряжениям. Известия ВНИИГ, т. 53, 1955.
35. Белов А. В. К определению температурных напряжений в столбчатых массивах высоких плотин. Известия ВНИИГ, т. 66, 1960.
36. Б е р г О. Я. Некоторые физические обоснования теории прочности бетона. Теория расчета и конструирования железобетонных конструкций. Госстройиздат, 1959.
429
37. Берг О. Я. Прочность бетона и других материалов, имеющих различное сопротивление растяжению и сжатию в условиях сложных напряженных состояний. Исследование бетона и железобетонных конструкций транспортных сооружений. Трансжелдориздат, I960.
38 Берг О. Я. Физические основы теории прочности бетона и железобетона Госстройиздат, 1961.
39. Б е р н а л Д. Структура продуктов гидратации цемента. Третий международный конгресс по химии цемента Госстройиздат, 1958.
40. Б л и н к о в В. В Исследование деформаций бетона при чистом сдви-ie Известия ВНИИГ, т. 53, 1955.
41. Блинков В. В Исследование ползучести бетона при повторных длительно действующих нагрузках. Известия ВНИИГ, т. 60, 1958.
42 Б о р и ш а н с к и й М. С. Исследование работы внецентренно сжатых железобетонных элементов. «Проект и стандарт», № 6, 1936.
43. Буданов Н. А. Расчет железобетонных конструкций с учетом пол-3}честь бетона. Госстройиздат, 1955.
44 Будников П. Б.. Г у л и н о в а Л. Г. Повышение теплоты гидратации портландцемента в бетоне. «Цемент» № 11, 1935.
45 Б у ж е в и ч Г. А. Испарение воды из бетона. Технология и свойства бетона. Труды НИИЖБ, вып. 1, 1957.
46 Б у л г а к о в В. С. О влиянии масштаба на несущую способность и деформации железобетонных внецентренно сжатых элементов прямоугольного сечения Расчет железобетонных конструкций. Экспериментально-теоретические исследования по усовершенствованию расчета. Труды НИИЖБ. вып 23 Госстройиздат, 1961.
47 Б у т т Ю. М. Изучение скорости гидратации портландцемеитных минералов, ЖПХ. т. 22. № 3, 1949.
48 Б у ш к о в В А. Железобетонные конструкции, ч. 1. Госстройиздат. 1940
49 Васильев П. И. Связь между напряжениями и деформациями в бетоне при сжатии с учетом влияния времени. Известия ВНИИГ, т. 45, 1951.
50 Васильев П И Некоторые вопросы пластических деформаций бетона Известия ВНИИГ, т. 49, 1953.
51 Васильев П. И., 3 у б р н ц к а я М. А. Температурные напряжения от экзотермии цемента в блоках типа плиты. Известия ВНИИГ, т. 56, 1956.
52 Васильев П И. О влиянии расстояний между температурными швами на величину температурных напряжений в массивных бетонных плотинах Научные доклады высшей школы. «Строительство» № 2, 1958.
53 В а с и л ь е в П И К определению расстояний между температурными швами в бетонных плотинах. Известия ВНИИГ, т. 64. 1960.
54 Be й н и к А. И Основные закономерности процессов тепло- и массо-обмена в строительных ограждениях. Труды Всесоюзного совещания по интенсификации процессов и улучшению качества материалов прн сушке. Проф-издат, 1958
55. Вейник А. И., Шубин А. С. Влияние температурных и влажностных факторов на перенос влаги. Труды Всесоюзного совещания по интенсификации процессов и улучшению качества материалов при сушке. Проф-издат, 1958.
56 В и ш н е в е ц к и й Г. Д. Введение в техническую теорию деформаций набухания и усадки бетона. Труды ЛИСИ, вып. 26. Госстройиздат, 1957, и вып. 29. Госстройиздат, 1958.
57. Вишневецкий Г. Д Расчет температурных, прочностных и деформационных изменений в бетоне массивных сооружений. Научно-техническое совещание по изучению свойств бетона, определяющих его трещиностойкость в массивных гидротехнических сооружениях. Доклады. Госэнергоиздат, 1963.
58. ВласовО. Е., Еремеев Г. Г. Некоторые вопросы долговечности ограждающих конструкций Известия АСиА СССР, № 3, 1959.
59. В л а с о в О Е. Физические основы повышения долговечности конструкций. Известия АСиА СССР, № 2, 1962.
430
60. Волжеиский А. В., Снлаеиков Е. С. Деформации автоклавных мелкозернистых бетонов при изменении их влажности. «Бетой и железобетон» № 4, 1959.
61. Воронков Н. И. Научно-техническая конференция по бетону и железобетону. Тезисы докладов и сообщений. Госстройиздат УССР, 1956.
62. Гансен Т. К. Ползучесть и релаксация напряжений в бетоне. Гос-стройнздат, 1963.
63. Гвоздев А. А. Температурно-усадочные деформации в массивных бетонных блоках. Изв. АН СССР, ОТН № 4, 1953.
64. Гвоздев А. А. Ползучесть бетона и пути ее исследования. Исследование прочности, пластичности и ползучести строительных материалов. Стройнздат, 1955.
65. Гвоздев А. А. Температурно-усадочные напряжения в бетонных блоках и массивных сооружениях. Сб. трудов МИСИ, № 17. Госстройиздат, 1957.
66. Гвоздев А. А. Некоторые особенности деформирования бетона и теория ползучести. Ползучесть строительных материалов и конструкций. Стройнздат, 1964.
67. Гвоздев А. А., Нофаль М. Ш., Белобров И К Влияние сжатых полок тавровых и других сечений на деформации (прогибы) железобетонных элементов. Расчет и конструирование элементов железобетонных конструкций. Стройнздат, 1964.
68. Г е и н е в Г. А. К вопросу решения плоской задачи теории упругости методом аналогии с изгибом пластинки. «Строительная механика и расчет сооружений», № 3, 1963.
69. Гинзбург Ц. Г Определение коэффициента теплопроводности бетона. Изв. ВНИИГ, т. 47. 1952.
70. Г л у ж г е П. И. Усадка бетона. Пуццолановые цементы. Госстройиздат, 1936.
71. Го л ьд е н б л а т И. И. Введение в теорию ползучести строительных материалов. Госстройиздат, 1952.
72. Г о л ь д е и б л а т И. И., Николаенко Н. А. Теория ползучести строительных материалов и ее приложения. Госстройиздат, 1960.
73. Г о р я и и о в К. Э. Исследование дегидратации при нагревании для определения характера новообразований гидратированных минералов портландцемента, ДАН, т. 104, № 3, 1955.
74. Гришин М М., Орехов В. Г., К а м з и н Б. И. Исследование температурного режима и термонапряженного состояния блоков гидротехнических сооружений, бетонируемых в знмнее время с применением периферийного электрообогрева. Сб. трудов МИСИ, № 32, Госстройиздат, 1960.
75. Гутман С. Г. К решению плоской задачи термоупругости при уста новившемся тепловом режиме. Известия ВНИИГ, т. 45. 1951.
76. Гутман С. Г. Определение тепловых напряжений при гармонических колебаниях температуры. Известия ВНИИГ, т. 47, 1952
77. Дзюба К. И. Исследования термонапряженного состояния элемен тов гидротехнических сооружений, выполненные в НИСе Гидропроекта. Тру ды координационных совещаний по гидротехнике, вып IV. Совещание по вопросам термонапряженного состояния бетонных гидротехнических сооружений. Госэнергоиздат, 1962.
78. Дмитриев С. А., Калату ров Б. А. Расчет предварительна напряженных железобетонных конструкций. Госстройиздат, 1963.
79. Долговечность ограждающих и строительных конструкций (физические основы). Труды НИИСФ, под ред. О. Е. Власова. Госстоойиздат. 1963
80. Дубницкий В. И. Стационарный тепло- и массообмен в термо изоляционных покрытнях. Диссертация, ВТИ, 1956.
81. Дятловнцкий Л. И., Рабинович Л Б. Определение термо-упругнх напряжений в массивах с учетом наращивания массива Труды координационных совещаний по гидротехнике, вып IV. Совещание по вопросам термонапряженного состояния бетонных гидротехнических сооружений. Госэнергоиздат, 1962.
43i
82. Е р е м е и о к И. П. Влияние температуры на тепловыделение цемента, прочность и модуль упруго-мгновенных деформаций бетона. Труды координационных совещаний по гидротехнике, вып. IV. Совещание по вопросам термонапряженного состояния бетонных гидротехнических сооружений. Гос-эиергоиздат, 1962.
83 Задоян М. А. Упруго-пластическое состояние прямоугольных бетонных блоков при равномерном распределении температуры. Доклады АН Арм. ССР, т. 23. № 5, 1956.
84 Задоян М. А. Термонапряженное состояние блоков с учетом ползучести материала. Известия АН Арм. ССР, серия физ.-мат., ест. и техн, наук, т. 10, вып 5, 1957.
85. Запорожец И. Д. Основы теории тепловыделения в бетоне. Научно-техническое совещание по изучению свойств бетона, определяющих его трсщнностойкость в массивных гидротехнических сооружениях. Госэнер-гоиздат, 1963.
86. Иванов Ф. М.. Нефедова Е. Ф. Усадка бетона и методы ее измерения. Бетон в дорожном строительстве. Сб. трудов Союздорнии. Изд. автотранспортной литературы, 1958.
87. И л ь н н с к и й В. М. Проектирование ограждающих конструкций зданий с учетом фнзнко-климатических воздействий. Госстройиздат, 1955.
88. К а р а п е т я н К- С. Ползучесть бетона при высоких напряжениях Изв. АН Арм. ССР, серия физ мат., ест. и техн, наук, т. VI, № 2, 1953.
89. Карапетян К. С. Влияние размеров образца на усадку н ползучесть, Изв. АН Арм. ССР, серия физ.-мат., ест. и техн, наук, т. 9, вып. 1, 1956.
90. Карапетян К. С. Влияние масштабного фактора на ползучесть бетона при сжатии и растяжении. Докл. АН Арм. ССР, т. XXXVIII, № 3, 1963.
91. Карапетян К. С. Ползучесть бетона при кручении. Ползучесть строительных материалов и конструкций. Госстройиздат, 1964.
92. Карапетян К. С. Влияние анизотропии на ползучесть бетона при сжатии и растяжении в зависимости от величины напряжения. Доклады АН Арм. ССР, т 36, № 1, 1964.
93. Карс л оу X. С. Теория теплопроводности. Гостеориздат, 1947.
94. Катин Н. И. Исследование ползучести бетона при высоких напряжениях. Исследование свойств бетона и железобетонных конструкций. Труды НИИЖБ, вып. 4. Госстройиздат, 1959.
95. К в и р и к а д з е О. П. О зависимости между деформациями бетона и скоростью нагружения. Издательство АН Груз. ССР, Тбилиси, 1962.
96. К и н д В. А., О к о р о к о в С. Д., Вольфсон С. Л. Теплота твердения портландцементов различного химического состава, «Цемент» № 7, 1937.
97. Коган Л. С. Значение минералогического состава клинкера и роль добавок в специализацин цементов. Труды IV Всесоюзного совещания заводских лабораторий цементной промышленности. Госстройиздат, 1948.
98. Коган Л. С., Ру щук Г. М. Цементы для гидротехнического бетона. Труды Гипроцемента, вып XI, 1949.
99. К о р е н е в Б. Г. Стационарное температурное поле в неограниченной пластине, лежащей на сплошном однородном основании. Доклады АН СССР. т. 107, вып. 9, 1957.
100. Коренев Б. Г. Некоторые плоские задачи теории тепловых волн. Доклады АН СССР, т. 112, № 1, 1957.
101. Коренев Б. Г. Некоторые задачи теории упругости и теплопроводности. решаемые в Бесселевых функциях. Физ.-мат. изд., 1960.
102. Корсак Н. Г. Исследование прочности и упругих свойств бетона. Прочность, упругость н ползучесть бетона. Госстройиздат, 1941.
103 Лебедев Н. Н. Температурные напряжения в теории упругости. ОНТИ, 1937.
104. Л е р м и т Р. Проблемы технологии бетона. Госстройиздат, 1959.
105. Лукьянов В. С. Расчет температурного режима бетонных и каменных конструкций при зимнем производстве работ. Стройиздат, 1934.
106. Лукьянов В. С. Борьба с появлением температурных трещин в бетонных мостовых опорах. Трансжелдориздат, 1937.
432
107. Лыков А. В. Теория теплопроводности. Гостехтеориздат, 1952.
108. Лыков А. В. Явления переноса в капиллярно-пористых телах, Гостехтеориздат. М., 1954.
109. Лыков А. В. Тепло- н массообмен в процессах сушки. Госэнерго* издат. 1956.
110. М а л м е й с т е р А. К. Виброползучесть бетона. Сб «Вопросы ди* намикн и динамической прочности», вып 4, Рига, 1956
111. Малмейстер А. К. Упругость и неупругость бетона. Изд. АН Латв. ССР, 1957.
112. Малюга И. Свойства портландцемента. «Инженерный журнал» № 9, 1891.
113. Мальцов К. А. Вопросы трещинообразования бетонных армиро* ванных конструкций. Изв. ВНИИГ, т. 49, 1953
114. Мальцов К. А. Влияние водонасышеиия на прочность бетона. «Гидротехническое строительство», № 8, 1954.
115. Манукян М. М. Термонапряженное состояние массивных бетон* ных блоков с учетом ползучести. Изв. АН Арм. ССР, серия физ.-мат., ест. и техн, наук, т. IX, вып. 1, 1956.
116. Манукян М. М. Определение напряжений в некоторых железобетонных элементах с учетом ползучести и изменения модуля упруго-мгновенных деформаций. Изв. АН Арм. ССР, серия физ.-мат., ест. и техн, наук, т. XII, вып. 6, 1964.
117. Маслов Г. Н. Температурные напряжения и деформации бетонных массивов иа основах теории упругости. Известия ВНИИГ, т. 13, 1934.
118. Маслов Г. Н. Задача теории упругости о термоупругом равново* сии. Известия ВНИИГ, т. 23, 1938.
119. М а с л о в Г. Н. Элементарные статические расчеты сооружений иа температурные изменения. Известия НИИГ, т. 26, 1940
120. Маслов Г. Н. Термическое напряженное состояние бетонных массивов при учете ползучести бетона. Известия НИИГ, т 28, Госэнсргоиздат,
121. Майзе ль В. М. Температурная задача теории упругости Изд. АН УССР, Киев, 1951.
122. Мел ан Э., П а р к у с Г. Термоупругие напряжения, вызываемые стационарными температурными полями. Физ.-мат. изд, 1958.
123. Милованов А. Ф. Жаростойкий железобетон. Госстройиздат, 1963.
124. Миронов С. А. Расчет охлаждения бетона на морозе Стройиз-дат, 1935.
125. Миронов С. А. Температурный фактор в твердении бетона Госстройиздат, 1948.
126. Михайлов В. В. Элементы теории структуры бетона Госстрой издат. 1941.
127. Михайлов В. В. Предварительно напряженный железобетон. Госстройиздат, 1963
128. Москвин В. М., Каокии М. М. Деформации цементного камня при низких отрицательных температурах и методика их изучения Методика лабораторных исследований деформаций и прочности бетона, арматуры и же лезобетониых конструкций. Госстройиздат, 1962
129. Мещанский Н. А. Плотность и стойкость бетонов. Госстройиздат, 1951.
130. М о щ а н с к и й Н. А. Об изменении прочности бетона при его водо-насыщенин, «Гидротехническое строительство» № 10, 1956
131. Некрасов В. В. Изменение объема системы при твердении гидравлических вяжущих. Изд. АН СССР, ОТН, № 6, 1945.
132. Некрасов В. В. Кинетика гидратации цементов различных типов. ЖПХ, т. XXI, № 3, 1948.
133. Некрасов К. Д. Жароупорный бетон. Промстройиздат, 1957.
134. Ниле н де р Ю. А. Исследование деформаций и температурного режима в тел*, плотины Днепростроя. Госстройиздат, 1933.
433
135. Н плен дер Ю. А. (ред.) и коллектив авторов. Испытание Днепровской плотины. Госстройиздат, 1937.
136. Н и л е и д е р Ю. А. Поверхностная прочность бетона и связь ее с появлением трещин. Труды конференции по коррозии бетона. АН СССР, 1937.
137 Ниленд ер Ю. А. Расчет разрезки массивных бетонных сооружений. Труды IV Всесоюзной конференции по бетону и железобетонным конструкциям, ч. II. Госстройиздат, 1949.
138. Н и л е н д е р Ю. А. Монолитность массивной бетонной кладки, возводимой из отдельных блоков. Коррозия бетона и меры борьбы с ней. АН СССР, М., 1954.
139. Нормы и технические условия проектирования бетонных и железобетонных конструкций гидротехнических сооружений (СН 55—59). Госстрой-кздат, 1959.
140. Окороков С. Д. Синтез портландских минералов и изучение их роли в формировании некоторых свойств цемента. Труды ЛПИ, изд. МВ н ССО РСФСР, 1940.
141. Окороков С. Д., Запорожец И. Д., П арийский А. А. Прогноз возможного тепловыделения бетона при расчетах его термонапряженного состояния Научно-техническое совещание по изучению свойств бетона, определяющих его трещиностойкость в массивных гидротехнических сооружениях Госэнергоиздат, 1963.
142 Орехов В. Г. Расчет температурных напряжений в плоских конструкциях гидротехнических сооружений. Труды МИСИ. № 29. Госстройиздат, 1958.
143 Орехов В. Г. Исследование термонапряженного состояния бетонных и железобетонных конструкций гидротехнических сооружений. Труды координационных совещаний по гидротехнике, вып. IV. Совещание по вопросам термонапряженного состояния бетонных гидротехнических сооружений. Госэнергоиздат, 1962.
144 О стр и ко в М. С., Ростовцева И. В., и др. Влияние сил капиллярной контракции на механические свойства и структуру высыхающих тел «Коллоидный журнал», т 22, № 4, 1960.
145 Панарин Н. Я Температурные напряжения в бетоне с учетом ползучести Труды ЛИСИ, вып. 23. Госстройиздат, 1956.
146. Панарнн Н. Я. Некоторые вопросы расчета армированного и не-армированного бетона с учетом ползучести. Госстройиздат, 1957.
147. П а р к у с Г. Неустановившиеся температурные напряжения. Физ.-мат изд., 1963.
148. Поляков С. В. Ползучесть каменных и армокаменных конструкций Ползучесть строительных материалов и конструкций. Госстройиздат, 1964
149 Прокопович И. Е. К теории ползучести бетона. Научные доклады высшей школы «Строительство» № 4, 1958.
150. Прокопович И. Е. Приближенный метод определения температурных напряжений в массивных прямоугольных бетонных блоках. Труды координационных совещаний по гидротехнике, вып. IV. Совещание по вопросам термонапряженного состояния бетонных гидротехнических сооружений. Госэнергоиздат, 1962.
151. Прокопович И. Е. Влияние длительных процессов на напряженное н деформированное состояние сооружений. Госстройиздат, 1963.
152 П р о к о л о в и ч И. Е., У л и ц к и й И. И. О теориях ползучести бетона. Ползучесть строительных материалов и конструкций. Госстройиздат, 1964.
153 Путане А В. Усадка бетона при цикличных нагревании и охлаждении Исследования по бетону и железобетону. Труды института строительства и архитектуры АН Латв ССР, вып. VII, изд. АН Латв. ССР, 1963.
154 Р а б о т и о в Ю. Н. Равновесие упругой среды с последствием, П.М.М., т. XII. № 1, 1948.
155. Работ нов Ю. Н. Некоторые вопросы теории ползучести. Вестник МГУ, № 10, 1948.
434
156. Ребиндер П. А. Физико-химические исследования процессов деформации твердых тел Юбил. сб. АН СССР, посвященный 30-летию ВОСР, 1. 1947.
157. Ребиндер П. А. Физико-химическая механика. Изд. «Знание», М., 1958.
158. Рж ан иц ыи А. Р. Некоторые вопросы механики систем, деформирующихся во времени. Гостехтеориздат, 1949.
159. Ржаницын А. Р. Температурные напряжения, возникающие в бетонных плотинах от действия наружных температур. Исследования по строительной механике. Госстройиздат. 1954.
160. Ржаннцын А. Р. Температурно-влажностная задача ползучести Исследования по вопросам теории пластичности и прочности строительных конструкций Труды ЦНИИСК- Госстройиздат, 1958.
161. Ржаницын А. Р. Определение напряжений в тонком слое при сушке с учетом изменения характеристик ползучести материала. Труды Всесоюзного совещания по интенсификации процессов и улучшения качества материалов при сушке в основных отраслях промышленности и в сельском хозяйстве. Профиздат, 1958.
162. Ржаницын А. Р. Разработка основ общей теории ползучести. Исследование прочности, пластичности и ползучести строительных материалов. Госстройиздат, 1955.
163. Розовский М. И. Температурные напряжения при наличии последствия. Журнал техн. физ. АН СССР, т. 19, вып. 6, 1949
164. Розовский М. И. Полусимволический способ решения некоторых задач теории ползучести. Изв. АН Арм. СССР. Серия физ -мат, ест и техн, наук, т. IX, вып. 5, 1956.
165. Саталкин А. В. Ползучесть бетона. Прочность, упругость н ползучесть бетона. Сборник статей под ред Н. М. Беляева, Стройиздат, 1941.
166. Саталкин А. В. Деформативная способность бетона. Сборник ЛИИЖТ, вып. 46, Трансжелдориздат, 1954.
167. Саталкин А. В., Сенченко Б. А. Раннее нагружение бетона и железобетона в мостостроении. Автотрансиздат, 1956.
168. Сиверцев Г. Н. Пробужденный бетон. Гостехиздат Украины, 1950.
169. С ил а е н к о в Е. С. Долговечность крупноразмерных изделий из автоклавных ячеистых бетонов. Стройиздат, 1964.
170. С и л а е н к о в Е. С., Т и х о м и р о в Г. В. и др Влияние карбонизации автоклавных ячеистых бетонов на их долговечность. Вопросы лоно вечности ячеистых бетонов и изделий из них. Труды НИИ по строительству, Свердловск, 1962.
171. Скатынский В. И. Исследование ползучести и релаксации напряжений в силнкагном бетоне при сжатии. Ползучесть строительных материалов и конструкций. Стройиздат, 1964
172. Ск рам та ев Б. Г., Панфилова Л. И. Исследование явления вакуума в твердеющих цементах. Труды НИИЦемента, вып 2. Госстройиздат, 1949.
173. Столяров Я. В. Введение в теорию железобетон? Госстройиздат, 1941.
174. Строительные нормы и правила, честь II, раздел В, гл. 1. Бетонные и железобетонные конструкции. Нормы проектирования (СНиП П-В 162) Госстройиздат. 1962.
175. Строительные нормы и правила, часть II, раздел А, гл. С. Строительная климатология и геофизика. Основные положения проектирования (СНиП II-A.6-62). Госстройиздат, 1963.
176. Таль К. Э., Чистяков Е. А. Экспериментальное исследование влияния длительного воздействия нагрузки на несущую способность гибких железобетонных колонн. Методика лабораторных исследований деформации и прочности бетона, арматуры н железобетонных конструкций. Госстройнз дат, 1962.
435
177. Т ахта м ы шев С. Г. Лабораторные опыты по определению коэффициента температ>рного расширения бетона. Испытание Днепровской плотины. Госстройиздат, 1937.
178. Темнов И. И. Влияние на деформации ползучести размеров поперечного сечения бетонного призматического образца и формы эпюры напряжений. Изв АН Арм. ССР, серия физ.-мат наук, т. XIII, № 6, 1961.
179. Технические условия проектирования железобетонных, автодорожных и городских мостов и труб (СН 200—62). Госстройиздат, 1962.
180. Троицкий Е А. Влияние скорости нагружения на деформации бетона. Труды Казанского института инженеров коммунального строительства, вып. 5, Казань, 1938.
181. Улицкий И И. Ползучесть бетона. Гостехиздат УССР, 1948.
182. Улицкий И. И. Определение напряжений от усадки бетона в элементах гидротехнических сооружений. «Гидротехническое строительство» № 8, 1951.
183. Улицкий И. И. Напряженное состояние сечения железобетонных элементов, возникающее в результате усадки бетона. Сб. статей «Сборные железобетонные конструкции», вып. II. Госстройиздат УССР, 1957.
184. Улицкий И. И., ЧжанЧжун-Яо, Голышев А. Б. Расчет железобетонных конструкций с учетом длительных процессов. Госстройиздат УССР, 1960.
185. Улицкий И. И., Киреева С. В., Фа нети ль И. В. Потери предварительного напряжения от ползучести и усадки бетона в железобетонных конструкциях. Госстройиздат УССР, 1962.
186. Улицкий И И. Определение величины деформаций ползучести и усадки бетонов. Госстройиздат УССР, 1963.
187. Ф о к и н К Ф. Строительная теплотехника ограждающих частей зданий. Госстройиздат, 1954
188 Франчук А. У. Таблицы теплотехнических показателей строительных материалов. Госстройиздат, 1949.
189. Франчук А. У. Вопросы теории и расчета влажности ограждающих частей зданий. Стройиздат, 1957.
190 Франчук А. У. Исследования и методы расчета тепло- и массо-обмепа в пористых материалах ограждающих частей зданий. Труды Всесоюзного совещания по интенсификации процессов и улучшению качества материалов при сушке. Профиздат, 1958.
191. Фрайфельд С. Е. Собственные напряжения в железобетоне. Госстройиздат, 1941.
192. Фрайфельд С. Е. Об исходных предпосылках уравнений механического состояния реальных материалов. Труды ХИСИ, вып. 4, Харьков, 1955.
193. Фрайфельд С. Е. Основные вопросы теории деформаций бетона. Теория расчета и конструирования железобетонных конструкций. Госстройиздат, 1959.
194. Ф р а й ф е л ь д С. Е., К у з н е ц о в Ю. Д. Об учете ползучести при определении температурных напряжений в бетонных массивах. Совершенствование расчетов строительных конструкций. Госстройиздат УССР, 1964.
195. Фрейсннэ Е Переворот в технике бетона ОНТИ, 1938.
196. Фрид С. А. Расчет изменения температуры бетонных массивов под влиянием экзотермии цемента. Известия НИИГ, т. 41, 1949.
197. Ф р и д С. А. Температурные напряжения в бетонных и железобетонных конструкциях гидротехнических сооружений. Госэнергоиздат, 1959.
198. Харламов В. А. Исследование ползучести жароупорного бетона при высоких температурах. Исследования по жароупорным железобетонным и армокирпичным конструкциям. Труды НИИЖБ, вып. 6. Госстройиздат, 1959.
199. Цилосани 3 Н., Чикованн X. С. О водоудерживающей способности затвердевшего раствора и бетона. Труды Института строительного дела АН Грузинской ССР, вып. 8, 1960
200. Цилосани 3. Н. Усадка и ползучесть бетона. Изд. АН Грузин-ской ССР. 1963.
436
201. Ш ей к ин А. Е. К вопросу прочности, упругости и пластичности бетона. Строительная механика и мосты. Труды МИИТ, вып. 69. Трансжелдор-издат, 19-16.
202. Шей к ин А. Е., ГершманМ. И. Влияние минералогического состава цемента на усадку бетона. Труды НИИЦемента, вып. 2, Госстройиздат, 1949.
W
203. Ш е й к и н А. Е. О причинах непостоянства вида функции Rt = f )•
Труды Всесоюзной конференции по бетону и железобетонным конструкциям, ч. 111. Госстройиздат, 1949.
204. Ш е й к и и А. Е. Упруго-пластические свойства бетонов на портландцементах различного минералогического состава. Строительная механика и мосты. Труды МИИТ. Трансжелдориздат, 1950.
205. Ш е й к и н А. Е., Б а к с а к о в Н. С. Влияние минералогического состава портландцемента на ползучесть бетона при сжатии. «Строительная промышленность». № 9, 1955.
206. Шейнин А. Е. Ползучесть при повторных нагрузках н модуль деформации бетона. Исследования железобетонных и сварных мостовых конструкций. Труды МИИТ. Трансжелдориздат, 1956.
207. Шейк ин А. Е., Николаев В. Л. Об упруго-пластических свойствах бетона при растяжении. «Бетон и железобетон», № 9, 1959
208. Шкербелис К. К- Влияние вибраций на ползучесть железобетонных конструкций. Сб. «Вопросы динамики и динамической прочности», вып. 4, Рига, 1956
209. Щербаков Л. М. О связи молекулярного и фазового давления со степенью дисперсности. Ученые записки Кишиневского Государственного университета, т. 1, вып. 2 (физико-математический), Кишинев. 1949
210. Штейнберг В. М.. Прокопович И. Е, Гольдфарб И. В. Практический метод исследования температурного поля в геле массивных бетонных гидротехнических сооружений. Сб. трудов Одесского гидротехи. инет., вып. 5. Изд. Минист. культуры СССР, 1953.
211. Ш т е й н б е р г В. М. Некоторые вопросы метода расчета нестационарного температурного поля бетонных блоков. Труды координационных совещаний по гидротехнике, вып. IV. Совещание по вопросам термонапряженного состояния бетонных гидротехнических сооружений. Госстройиздат, 1962.
212. Яшин А. В. Ползучесть бетона в раннем возрасте. Исследование свойств бетона и железобетонных конструкций. Труды НИИЖБ, вып. 4, Госстройиздат, 1959
213. Alexander К. М., Wardlaw S. J. Possible Mechanism for Carbonation Shrinkage and Crazing, based on Study of this Layers of Hydrated Cement. Australian Journal of Applied Science, vol. 10, № 4. 1959.
214. Blanks R., Meissner H., Rawhouser C.. Cracking in mass Concrete, Journal of the American Concrete Institute, vol. 9. № 4, 1938
215. Boltzmann L. Zur Theone der elastischen Nachwirkung. Wiener. Ber., 10, 1874.
216. Carlson R. W. Drying Shrinkage as Affected by Many Factors. Proc, of the Amer. Soc. for Test. Mat., vol. 38, p. II., 1938
217. Considere А. Способность армированного бетона выдерживать значительные растяжения. Comptes Rendus, v. 140, Jan. 30, 1905, а также Le Genie Civil, v. 46, Feb. II, 1905.
218. Davis R E. Flow of Concrete under Sustained Compressive, stress. Proc. Amer. Concr Inst v. 24, 1928.
219. Davis R E., Davis H. E., Flow of Concrete under the Action of Sustained Loads, Journ. of the Amer. Concr. Inst, vol. 2, № 7, 1931.
220. Davis R. E., D a v i s H. E., Hamilton J S. Plastic Flow of Concrete under Sustained Stress. Proc. A. S T. M., vol. 34., 1934.
221. Davis R. E., Davis H. E., Brown E H., Plastic Flow and Volume Changes of Concrete. Proc. Amer. Soc. for Test. Mat., vol. 37., 1937.
222. Dischinger F. Elastische und plastische verformungen der Eisen-
437
betontragwerke und mbesondere der Bogenbrucken. Bauingenieur. Heft 33/34, 1937.
223. Duke С. M., Davis H- E. Some properties of Concrete Under Sustained Combined Stress. Am. Soc. for Test. Mat. proc., vol. 44, 1944.
224 D u t г о n R. Deformations lentes du Beton et du Beton — arme sous (action des Charges permanents. Annalas des Travaux pablics de Belgique, 1936, 1937.
225. Gehle г W. Hyppthesen und Grundlagen Гиг das Schwinden und Kriechen des Betons, Verlag Technik, Berlin, 1952.
226. G 1 a n v i 11 e W. H. Work of the building research Station on small movements in Concrete Congres de Liege, Beton Arme, 1930.
227. G 1 a n w i 11 e W. H. The Creep and Flow of Concrete under Load. Building Res., Studied in Reinforceed Concrete, part. III., Technic. Paper., № 12, 1930.
228. G 1 a n w i 11 e W. H. Creep of Concrete under Load. The Structural Engineering, London, № 2, 1933.
229. G 1 a n w i 11 e W. H. Thomas F. G., Further Investigations on the Creep or Flow of Concrete under Load. Studied in Reinforced Concrete, Part IV, Building Research., Technical Paper., № 21, London, 1939.
230. J о s c h i d a H. Uber das elastische Verhalten von Beton. Berlin, 1930.
231. Kalousek G. L. Fundamental Factors in the Drying Shrinkage of Concrete Block. Journal of the American Concrete Institute, Proc. vol. 51. vol. 26, № 3, 1954.
232 К г о о n e В., В 1 а к у F. A. Reaction between Carbon Dioxide gas and Mortar, Journ. of the Amer. Concr. Inst., vol. 31, № 6 (proc. vol. 56), 1959.
233. Lea F. M. The Chemistry of Concrete and Concrete, St. Marlins press. N. J. Rev. Ed, 1956.
234. Leber L, Biaky F. A Some Effects of Carbon Dicxide on Mortar and Concrete., Journ. of the Amer. Concr. Inst., proc. v. 53, vol. 28, № 3, 1956.
235. Lee C. R. Creep and Shrinkage in restrained Concrete. B. R. S. Note, No. E 208., March, 1950, а также Quarfieme Congres des Grand Barrages, New Dehh. 1951, Q. N. 15.
236 Me. Henry D. A New Aspect of Creep in Concrete und Its. Application to Design, Proc. Amer. Soc. for Test. Mat., vol. 43, 1937.
237. Meyers S. L. Volum changes in Cement mortar and Concrete., Concrete, vol. 43. № 8, 1935.
238. N e v i 11 A. Theories of Creep in Concrete, Am. Concr. Inst Journ., proc vol. 52, № 1, 1955.
239 Pickett D. Shrinkage Stresses in Concrete, Journal of the American Concrete Institute., vol. 17., N N. 3,4, 1946.
240. Powers T. C, Brownyard T. L. Studies of the physical Properties of Hardened Portland Cement Paste, Journal of the American Concrete Institute., vol. 18, N. N. 2, 3, 4, 5, 6, 1946, vol. 19, №. №. 1, 2, 1947.
241. Powers T. C. Cuses and Control of Volume Change, Journal of the Research and Development Laboratories, vol. 1, N. 1, 1929.
242. Powers T. C. Journal of Portland Cement Assoc, Res. and Dev. Lab, vol. 4, № 2. 1962.
243. Ross A. D. The Creep of Portland elast, furnace Cement Concrete, Journ. Inst. Civ. Eng., № 8., 1938.
244 Ross A D. Creep of Concrete Under variable Stress, Journ. of the Amer. Concr. Inst., vol. 29, № 9, 1958.
245. S c h a n к I. R. Plastic flow of Concrete Ohio University Engineering Experiment Station, Bulletin., №91, Sept., 1935.
246. Serafim J. L. Guerreiro M. Q., Influence of Temperature an the Greep of mass Concrete, Bulletin Rilem, 1960, № 6.
247. S p i n d e 1 M. Uber die Schwindung von Zement und Beton, Beton und Eisen, H. 15, 1936
248. The Experimental and Mathematical Analysis of Arch Dams with Special Reference to Dams by prof. D. Norman M. C. Allen M. A., Letitia Chitty
438
Ma., A. M. J. С. E., prof A. I. Sutton Pippard. The Institution of Civil Engineers, part. II, v. 5., May, 1956, № 3.
249. T h e u e r A. U. Effect of Temperature on the Stress-Deformation of Concrete, Journ. of Res. of the Nat. Bureau of St., vol. 18, No 2., February, 1937.
250. Tonindustrie — Zeitung. 1881, 1889
251. Verbech C. J. Carbonization of Hydrated Portland Cement., Am. Soc. for Testing Materials, Special Technical Pablication, № 205, 1958. P. C. A. Research Departament, Bull., 87.
252. Volterra V. Lecons sur les functions de lignes professeers a la Sorbonne en 1912, Paris, 1913.
253. Whitney C S. Plain and Reinforced Concrete Arches., Journ. Amer. Concr. Inst., № 7, 1932.
254. Woolson J H. Some remarkable tests indicating «Flow» of Concrete under pressure., Eng News., № 54, 1905.
СОДЕРЖАН ME
Предисловие..........................................................- 3
Глава 1. Некоторые вопросы теории теплопроводности бетона . . 5
§ 1.1. Теплопроводность. Основные уравнения теории теплопроводности бетона ............................................... б
§ 1.2 Граничные и начальные условия.......................... 8-
§ 1.3. Теплофизические свойства бетона......................... П
§ 14. Экзотермии бетона...................................... 16
§ 1.5. Уравнение теплопроводности при скорости экзотермии, зависящей от температуры процесса............................. 20
§ 1.6. Классический метод решения задачи теории теплопроводности при источниках тепла, зависящих от температуры 28
§ 1.7. Первая классическая задача теории теплопроводности при источниках тепла, зависящих от температуры. Одномерный тепловой поток в плите ................................... 29
§ 1.8. Вторая классическая задача теории теплопроводности при источниках тепла, зависящих от температуры. Одномерный тепловой поток в плите ................................... 34
§ 1.9. Упрощение задачи теории теплопроводности при источни-
ках тепла, зависящих от температуры. Метод автора . . 38
§ 1.10. Первая основная задача теории теплопроводности. Случай замкнутого решения........................................ 41
§ I 11. Первая основная задача теории теплопроводности. Обобщенный квазистационарный температурный режим прямоугольной призмы. Случай незамкнутого решения .... 44
§ I 12 Вторая основная задача теории теплопроводности при источниках тепла, зависящих от температуры. Одномерный тепловой поток в плите........................................ 46
§ 1.13. Вторая основная задача теории теплопроводности при источниках тепла, зависящих от температуры. Двухмерный тепловой поток в прямоугольной призме......................... 53
§ 1.14. Вторая основная задача теории теплопроводности при источниках тепла, зависящих от температуры. Тепловой поток в неограниченном цилиндре............................... 55
§ 1.15. Экспериментальная проверка теории.............. 56
§ 1.16. Пример расчета распределения температуры в массивной бетонной плите ............................................... 60
Глава II. Некоторые вопросы теории влагопроводности бетона ... 69
§ II.1. Влагопроводность. Основные уравнения теории влагопроводности бетона —
§ II.2. Граничные и начальное условия. Равновесная влажность
бетона........................................... 73
§ II.3. Влагофизические свойства бетона.............. 77
440
§ 11.4. Аналитическое выражение для скорости гидратации, зависящей от температуры процесса............................., 82
§ II.5. Уравнение влагопроводности при стоке влаги, зависящем от температуры. Упрощение и метод решения задачи теории влагопроводности........................................ 85
§ II.6. Первая основная задача теории влагопроводности. Случай замкнутого решения......................................... 88
§ 11.7. Первая основная задача теории влагопроводности. Обобщенный квазистацнонарный влажностный режим прямоугольной призмы. Случай незамкнутого решения .... 89
§ П.8. Вторая основная задача теории влагопроводности при стоке влаги, зависящем от температуры. Одномерный поток влаги в плите............................................ 90
§ II.9. Вторая основная задача теории влагопроводности при стоке влаги, зависящем от температуры. Двухмерный поток влаги в прямоугольной призме............................. 94
§ 11.10. Пример расчета распределения влажности в массивной бетонной плите ................................................ 96
Глава III. Температурные и влажностные деформации бетона . . 103
§ II 1.1. Температурные деформации бетона................. —
§ 111.2. Вода в бетоне.................................. 106
§ 111.3. Усадка бетона.................................. 111
§ 111.4. Набухание бетона............................... 121
§ II 1.5. Физические свойства бетона, связанные с его влажностными деформациями............................................. 125
§ II 1.6. Влияние длительного внешнего нагружения на режим высыхания и усадку бетона..................................... 128
§ II 1.7. Некоторые особенности усадки и набухания бетона, существенные для расчета влажностных напряжений . . . 131
Глава IV. Некоторые вопросы теории ползучести бстоиа............... 145
§ IV.L Ползучесть бетона................................ 147
§ IV.2. Релаксация напряжений в бетоне.................. 160
§ IV.3. Упруго-Miновенные деформации бетона............. >61
§ IV.4. Поперечные деформации бетона.................... 166
§ IV.5. Рабочие гипотезы современной линейной теории ползучести бетона.................................................. 1С8
§ 1V.6. Основные уравнения линейной теории ползучести бетона Г. Н. Маслова — Н. X. Арутюняна. Одномерная задача при наличии вынужденных деформаций . . ........ 173
§ IV.7. Физический смысл наследственных функций бетона L(t, т) и R(t, т)............................................. 178
§ IV.8. Общая трехмерная задача линейной теории упруго-ползучего тела при наличии вынужденных деформаций . . 187
§ IV.9. Некоторые общие замечания по поводу метода решения рассматриваемых задач линейной теории ползучести . . 192
§ IV. 10 О наследственных функциях теории ползучести бетона 201
§ IV.11. Об основных разновидностях современной теории ползучести бетона и наследственных функциях, фигурирующих в их уравнениях.......................................... 208
§ IV. 12 Новые аналитические выражения для наследственных функций теории ползучести бетона............................. 223
§ IV.13 Экспериментальные исследования областей применимости основных разновидностей теории ползучести бетона и проверка новых аналитических выражений для наследственных функций......................................... 23!
441
Глава V. Упруго-мгновенная задача теории упругости при наличии вынужденных деформаций. Общие уравнения и метод решения . 250
§ V.I. Общая трехмерная упруго-мгновенная задача теории упругости ........................................................... —
§ V.2. Плоская упруго-мгновенная задача теории упругости. Основные уравнения ......................................... 256
§ V.3. Плоская упруго-мгновенная задача. Метод решения . . 264
§ V.4. Повышение точности решений плоской упруго-мгновенной задачи................................................. 276
§ V.5. Одномерная упруго-мгновенная задача для бесконечного полупространства....................................... 279
§ V.6. Одномерная упруго-мгновенная задача для прямого бруса 280
Глава VI. Некоторые упруго-мгновенные задачи о температурных напряжениях . . ............................................ 283
§ VI. 1 Напряжения в бесконечном полупространстве при неравномерном изменении его температуры по глубине .... —
§ VI.2. Напряжения в прямом брусе при линейном распределении температуры вдоль его оси................................ 285
§ VI 3. Температурные напряжения в призматическом брусе со свободными гранями при неравномерном распределении температуры по его сечению................................... 286
§ VI.4. Напряжения в призматических прямоугольных брусьях при изменениях их температуры, равномерных по длине и неравномерных по высоте бруса.............................. 291
§ VI.5. Напряжения в плите при неравномерном изменении температуры по ее толщине....................................... 297
§ VI.6. Напряжения в длинном прямоугольном блоке, жестко защемленном по основанию при равномерном разогреве (торны блока закреплены от тангенциальных смещений) 299
§ VI.7. Напряжения в длинном прямоугольном блоке, жестко защемленном по основанию при равномерном разогреве (торцы блока свободны от напряжений)......................... 304
§ VI.8. Температурные напряжения в блоке, защемленном по основанию и имеющем свободные торцы, в общем случае его неравномерного разогрева............................. 312
§ VI 9. Некоторые замечания по поводу рассмотренных упругомгновенных задач............................................. 317
Глава VII. Учет ползучести при расчете напряжений в бетоне, вызываемых его вынужденными деформациями.................... 321
§ VII 1. Общие указания....................................... —
§ VII.2. Методика учета ползучести при расчете напряжений, вызываемых вынужденными деформациями........................... 324
§ VI 1.3. Случай стационарной вынужденной деформации .... 328
§ VI 1.4. Коэффициент приведения упругих напряжений в старом бетоне . , ................................................ 329
Глава VIII. Некоторые задачи о температурных и усадочных напряжениях в бетоне........................................................ 334
§ VIII.1. Некоторые одномерные задачи о температурных напряжениях в старом бетоне с учетом его ползучести . . • 337
§ V1II.2. Напряжения в бетонной плите от экзотермии при уче-
те изменений температуры наружного воздуха .... 341
442
§ VII 1.3. Напряжения о бетонных блоках прн их разогреве от экзотермии................................................. 347
§ VIII.4. Экспериментально-теоретические исследования температурных напряжений в бетоне................................. 349
§ VIII.5. Экспериментально-теоретические исследования усадочных напряжений в бетоне.................................... 364
Глава IX. Учет температурно-влажностных воздействий при расчете железобетонных конструкций.................................. 380
§ IX. 1. Общие методические указания....................... 381
§ IX.2. Расчет железобетонных конструкций на изменения их температуры и влажности.................................... 386
§ IX.3. Определение перемещений железобетонных конструкций при их расчете на изменения температуры и влажности 39)
§ IX.4. Расчет распределения температуры бетона по сечению элементов конструкций и выбор средней расчетной температуры и расчетного перепада температуры................ 395
§ IX.5. Расчет распределения влажности бетона по сечению элементов конструкций н выбор средней расчетной влажности и расчетного перепада влажности........................ 401
§ IX.6. Числовой пример расчета железобетонной статически неопределимой рамы на изменения температуры и влажности бетона................................................. 407
Приложения...................................................... 422
Литература . ................................................... 428
ОПЕЧАТКИ
<с сх 0.3 Ох Ci рока Напечатано Следует читать
34 Формула (Ы) Em Em
2*о *0
45 Формула (1.142) + Mm) sinamt/0I + Mm) Sh<»m %]
63 9-я сверху 627,597 — 627,597
63 10-я сверху Лг = — Az =
64 Табп. 14. 6-я графа, 5-я сверху 0,168 1,168
95 Формула (11.ЬЗ) в числите те cos2 Psl/rfy cos $sydy
225 Подпись к рис. 49, 3-я сверху ... по формуле (IV. 102)—сплошные линии и по формуле (IV. 133)—пунктирные ЛИППИ. ... по формуле (IV.133)—сплошные линии и по формуле (IV. 102)—пунктир- ные
254 Формула (V.19), 2-я снизу 1 у 1 1 у 1
I а 1 дх h ду 1
273 3-я сверху МО = -^7
314 Формула (VI. 128) fr=8 X А=1
326 Табл. 37, 2-я графа, 8-я снизу Ат Ат
60Ат{ — Д?2 60Дт? Дт?
343 6-я сверху Zq—толщина плиты 2z0—толщина плиты
348 417 Формула (VII1.28) 4-я сверку ау(/)|т] = ±1 1е = о 1 <М0 Й = ° h=±i
•10s-0,2 ] •10-0,2 ]