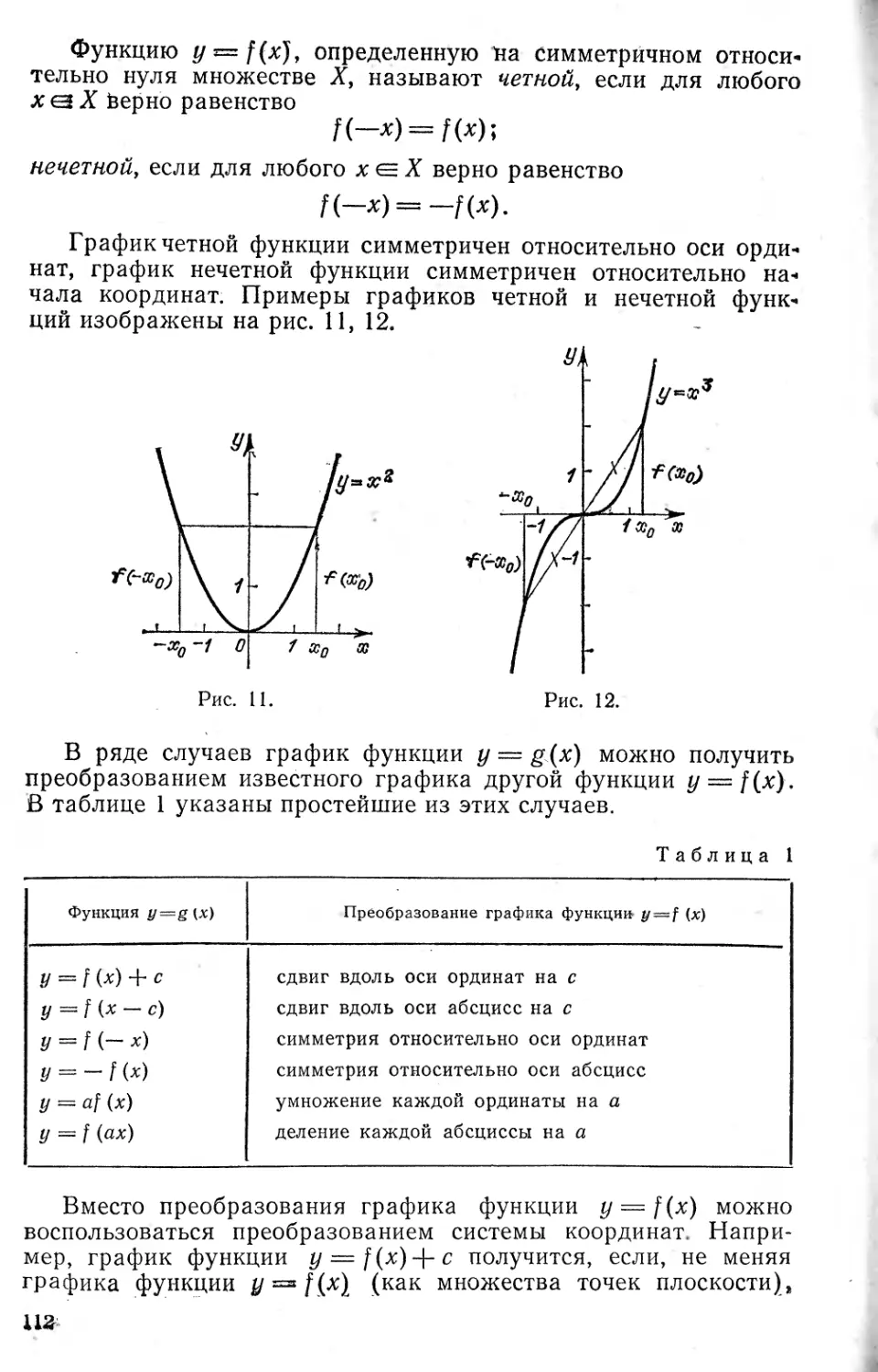
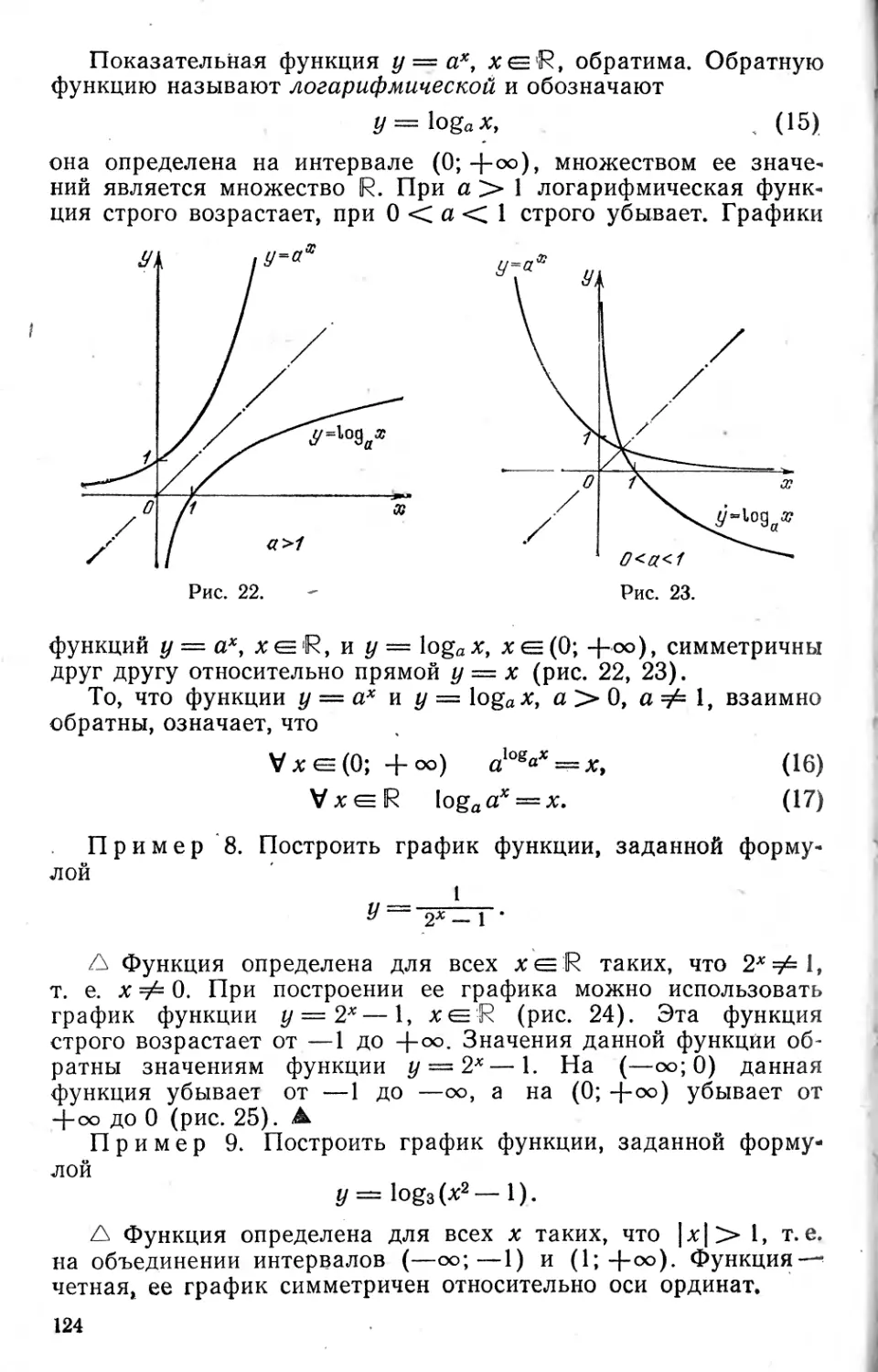
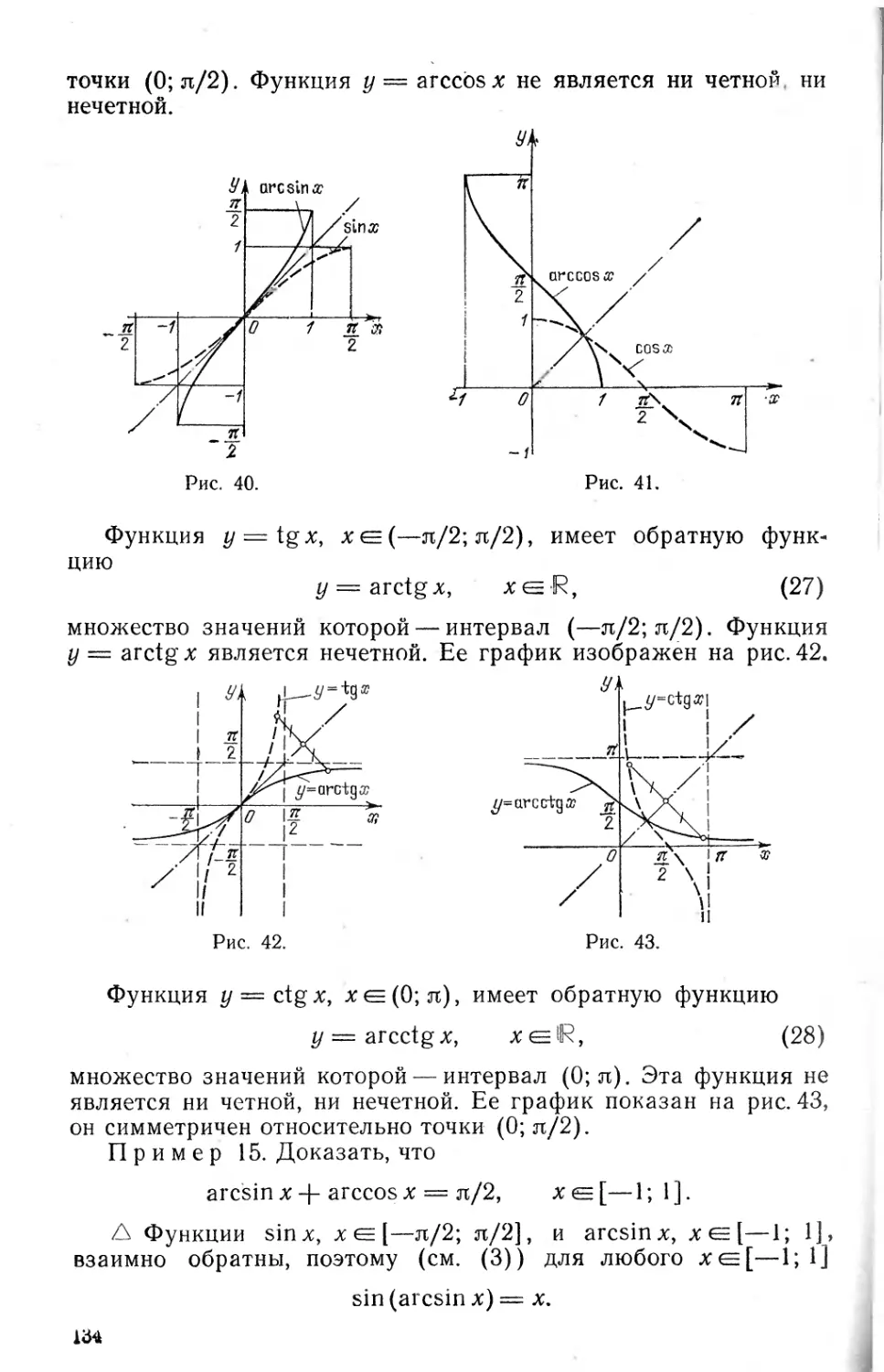
Author: Шабунин М.И. Кудрявцев Л.Д. Кутасов А.Д. Чехлов В.И.
Tags: анализ математика математический анализ сборник задач
Year: 1984
Text
Л. Д. КУДРЯВЦЕВ, А.Д. КУТАСОВ,
В.И. ЧЕХЛОВ, М.И. ШАБУНИН
СБОРНИК
ЗАДАЧ
по
МАТЕМАТИЧЕСКОМУ
АНАЛИЗУ
ПРЕДЕЛ
НЕПРЕРЫВНОСТЬ
ДИФФЕРЕНЦИРУЕМОСТЬ
Л. Д. КУДРЯВЦЕВ А. Д. КУТАСОВ
В. И. ЧЕХЛОВ, М. И. ШАБУНИН
СБОРНИК
ЗАДАЧ
по
МАТЕМАТИЧЕСКОМУ
АНАЛИЗУ
ПРЕДЕЛ
НЕПРЕРЫВНОСТЬ
ДИФФЕРЕНЦИРУЕМОСТЬ
Под редакцией Л. Д. КУДРЯВЦЕВА
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия для студентов
инженерно-технических специальностей высших учебных заведений.
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1984
22.16
С 23
УДК 517
Кудрявцев Л. Д., Кутасов А. Д.» Чехлов В. И., Шабунин М. И.
Сборник задач по математическому анализу. Предел. Непрерывность. Диффе-
ренцируемость: Учебное пособие/Под ред. Л. Д. Кудрявцева.— М.: Наука.
Главная редакция физико-математической литературы, 1984.— 592 с.
Использован большой набор оригинальных задач, предлагавшихся в те-
чение многих лет студентам Московского физико-технического института.
Много внимания уделено задачам, способствующим уяснению фундаменталь-
ных понятий.
Все задачи снабжены ответами, приводятся решения типичных примеров
и задач.
Для студентов университетов и втузов с повышенной программой по ма-
тематике.
Ил. 117.
Рецензенты:
кафедра высшей математики Московского энергетического института (за-
ведующий кафедрой доктор физико-математических наук профессор С. И. По-
хожие в),
доктор физико-математических наук профессор В. А. Ильин
Лев Дмитриевич Кудрявцев, Александр Дмитриевич Кутасов,
Валерий Иванович Чехлов, Михаил Иванович Шабунин
СБОРНИК ЗАДАЧ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Предел. Непрерывность. Дифференцируемость
Редактор А. Ф. Лапко
Техн, редактор G. Я. Шкляр Корректоры Н. Б. Румянцева и Е. В. Сидоркина
ИБ № 11649
Сдано в набор 21.11.83. Подписано к печати 05.11.84. Формат 60Х90’/1г„ Бумага книжно-
журнальная. Литературная гарнитура. Высокая печать. Усл. печ. л. 37. Усл. кр.-отт. 37,25.
Уч.-изд. л. 41,51. Тираж 50 000 экз. Заказ № 871. Цена 1 р. 60 к.
Издательство «Наука» Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Ленинградская типография № 2 головное предприятие ордена Трудового Красного Зна-
мени Ленинградского объединения «Техническая книга» им. Евгении Соколовой Союз-
полиграфпрома при Государственном комитете СССР по делам издательсть, поугиграфии
и книжной торговли. 198052, г. Ленинград, Л-52, Измайловский проспект, 29
1702050000-177
053(02)-84
© Издательство «Наука».
Главная редакция
физико-математической
литературы, 1984
ОГЛАВЛЕНИЕ
Предисловие........................................................ *
Глава I. Введение..................................................
§ 1. Множества. Комбинаторика..................................5
§ 2. Элементы логики. Метод математической индукции .... 20
§ 3. Действительные числа ... 36
§ 4. Прогрессии. Суммирование. Бином Ньютона. Числовые неравен-
ства ......................................................... 53
§ 5. Комплексные числа......................................70
§ 6. Многочлены. Алгебраические уравнения. Рациональные дроби 87
§ 7 Числовые функции. Последовательности..................105
Глава II. Предел и непрерывность функции....................... 181
§ 8. Предел последовательности........................... 181
§ 9. Предел функции........................................232
§ 10. Непрерывность функции -........................... . • 233
§ 11. Асимптоты и графики функций . . . . ... 290
§ 12. Равномерная непрерывность функции.......................312
Глава III. Производная и дифференциал.............................322
§ 13. Производная. Формулы и правила вычисления производных.
Дифференциал функции ... .... ................322
§ 14. Геометрический и физический * смысл производной .... 347
§ 15. Производные и дифференциалы высших порядков .... 356
Глава IV. Применение производных к исследованию функций . . . 370
§ 16. Теоремы о среднем для дифференцируемых функций .... 370
§ 17. Правило Лопиталя ........................376
§ 18 Формула Тейлора....................................... 382
§ 19. Вычисление пределов с помощью формулы Тейлора ... 401
§ 20. Исследование функций ... ...... 420
§ 21. Построение графиков.............. . . ..........443
§ 22. Задачи на нахождение наибольших и наименьших значений . . 460
§ 23. Численное решение уравнений........................... 465
§ 24. Вектор-функции. Кривые..................................487
Ответы.......................................................... 525
ПРЕДИСЛОВИЕ
Предлагаемый читателю «Сборник задач по математиче-
скому анализу» состоит из четырех глав.
Первая глава содержит материал, освоение которого имеет
целью подготовить читателя к решению задач по математиче-
скому анализу. Во второй главе представлены задачи, относя-
щиеся к таким понятиям, как предел и непрерывность функции.
В третьей и четвертой главах собраны задачи, связанные с по-
нятиями. производной и дифференциала и применением произ-
водных к исследованию функций.
При составлении сборника авторы опирались на многолет-
ний опыт преподавания курса математического анализа в Мо-
сковском физико-техническом институте. В сборнике содержится
большое число оригинальных задач, составленных преподавате-
лями кафедры высшей математики МФТИ и используемых в
работе со студентами. Значительная часть задач сборника под-
готовлена авторами. В сборник включены задачи из широкоиз-
вестных изданий и, в частности, из сборника задач по мате-
матическому анализу Б. П. Демидовича и сборника задач по
высшей математике Н. М. Гюнтера и Р. О. Кузьмина.
Каждый параграф сборника содержит теоретические сведе-
ния, примеры решения типовых задач и задачи для самостоя-
тельной работы. Задачи каждого параграфа сгруппированы по
темам и каждая группа задач расположена в порядке возраста-
ния трудности — от совершенно простых до достаточно сложных.
Большое внимание в сборнике уделено задачам, способ-
ствующим усвоению фундаментальных понятий математического
анализа. Большой набор задач, иллюстрирующих ту или иную
тему, дает возможность преподавателю использовать задачник
для работы в аудитории, для. домашних заданий и при состав-
лении контрольных работ.
Сборник задач предназначается в основном для вузов с рас-
ширенной программой по математике. Наличие большого
числа задач разной трудности дает возможность использо-
вать задачник как в университетах, так и в технических ву-
зах.
Авторы выражают глубокую благодарность коллективу ка-
федры высшей математики МФТИ, многолетняя плодотворная
работа которого в значительной степени способствовала появ-
лению этого сборника
ГЛАВА I
ВВЕДЕНИЕ
§ 1. Множества. Комбинаторика
1. Множества. Понятие множества и его элементов является
первичным понятием в математике. Множества обозначают
большими буквами какого-либо алфавита, обычно латинского;
элементы множества — малыми буквами. Для некоторых наибо-
леё важных множеств приняты стандартные обозначения. Так,
например, буквами N, Z, Q, R, С обозначают соответственно
множества натуральных, целых, рациональных, действительных
и комплексных чисел.
Если объект а является элементом множества А, то пишут
а е А или А а. Читают эти записи так: «а принадлежит мно-
жеству А» или «множество А содержит элемент а». Запись
а^А означает, что объект а не является элементом множе-
ства А. Например,
IeN, yG^Q, ji^R, V2 V~“2^IR-
Если каждый элемент множества А является элементом мно-
жества В, то пишут А с В или В zd А и говорят, что множество
А является подмножеством множества В. В этом случае гово-
рят также, что А содержится в В или что В содержит А. Из
определения подмножества следует, что Дс=Д, т. е. каждое
множество является своим подмножеством. Из определения сле-
дует также, что если A cz В и B<zzC, то A cz С. Примеры
включений:
N cz N, NczZazQczRcz:C.
Если существует элемент а е А такой, что а ф В, то множе-
ство А не является подмножеством множества В. В этом случае
пишут А ф В или В ф А.
Множества, состоящие из одних и тех же элементов, назы-
вают равными. Если множества А и В равны, то пишут А = В;
в противном случае пишут А В
Множества А и В равны тогда и только тогда, когда ис-
тинны включения A cz В и В cz А.
Для выделения подмножества М множества U часто исполь-
зуют какое-либо свойство р, присущее элементам множества М
и только им, — характеристическое свойство элементов множе-
ства М. В этом случае пишут
M = {x^U\p},
ь
что означает, что множество М состоит из тех и только тех эле-
ментов множества U, которые обладают свойством /?*).
Например, запись
R+ = {х <= R | х > 0}
означает, что R+ есть множество положительных действитель-
ных чисел.
Может случиться, что свойством р не обладает ни один эле-
мент множества U. Тогда подмножество {x^U\p} не содержит
элементов множества U и называется пустым подмножеством.
Например, подмножества
{х <= N |х + 2 = 1}, {х е Q|x =/= х}, {х е R |х2 + 1 =0}
являются пустыми подмножествами соответственно множества
натуральных, рациональных, действительных чисел. Пустое под-
множество обозначается специальным знаком 0 и считается
подмножеством любого множества.
Если М cz U и М =# 0, М #= U, то множество М называется
собственным подмножеством множества U. Подмножества 0 и
U множества U называются несобственными.
Пример 1. Указать все подмножества трехэлементного
множества {а, Ь, с}.
А Трехэлементное множество имеет несобственные подмно-
жества 0 и {а, Ь, с} и шесть собственных подмножеств: {«},
{fe}, {f}> {а, с}, {Ь, с}. Всего восемь подмножеств. А
2. Операции над множествами. Пусть А и В — произволь-
ные множества.
Множество, состоящее из всех тех и только тех элементов,
которые принадлежат хотя бы одному из множеств А и В, на-
зывается объединением множеств А и В и обозначается A (J В.
Множество, состоящее из всех тех и только тех элементов,
которые принадлежат как множеству Л, так и множеству В,
называется пересечением множеств А и В и обозначается A р В,
Например, если А ={1,2,3}, В — {2, 3, 4, 5}, то
A U В = {1, 2, 3, 4, 5}, А П В = {2, 3}.
Если A = {%g R|x > 1}, В = {%<= R |х < 2}, то
A (J В = R, А рВ ={хё R| 1 < х < 2}.
Если А П В = 0, то говорят, что множества Л и В не Пересе*
каются.
Операции объединения и пересечения обладают следующими
свойствами:
1) коммутативности
лив = вил, л рв = врл-,
*) Если рассматриваются только подмножества некоторого основного
множества Ut то указание х & U часто опускают и пишут М = {х | р).
6
2) ассоциативности
ли(вис) = <лив)ис, лп(впс) = (лпв)пс«,
3) дистрибутивности
(Див)пс = ипс)и(впс), (дп£)ис = иис)П(виси
4) идемпотентности
AJA = A, А{\А=А.
Если а е А и b В, то пару элементов а и Ь, записанную
в виде (а',Ь), называют упорядоченной парой, причем считают,
что пары (аг, Ь\) и (а2; &2) равны тогда и только тогда, когда
ах = а2 и bi = b2.
Множество, элементами которого являются все упорядочен-
ные пары (а; Ь), а^А, Ь<=В, называется прямым или декар-
товым произведением множеств А и В и обозначается А X В.
Например, если А ={1,2}, В = {2, 3}, то
ЛХВ = {(1; 2), (1; 3), (2; 2), (2; 3)},
ВХЛ = {(2; 1), (2; 2), (3; 1), (3; 2)}.
Прямое произведение не подчиняется коммутативному за-
кону. Равенство А\В=ВХА справедливо только в случае,
когда А = В. Произведение А X А называют декартовым квад-
ратом и обозначают А2. Например, декартов квадрат R2 =
— ‘R X R есть множество (%; у) всех декартовых координат то-
чек плоскости.
Множество, состоящее из всех элементов множества А, не
принадлежащих множеству В, называется разностью множеств А
и В и обозначается А\В.
Например, если А — {1, 2, 3}, В = {2, 3, 4, 5}, то
А\В = {1}, В\А ={4,5}.
Если А = {х eR |х > 1}, В = {х е R |х < 2}, то
А\В = {хё= R|x^ 2}, В\А ={xe= R.|xsC 1}.
Если A CZ В, то разность В\А называют дополнением множе-
ства А до множества В и обозначают Ав-
В тех случаях, когда рассматриваются только подмножества
некоторого основного множества U, дополнение множества М
до множества U называют просто дополнением М и вместо Ми
пишут просто М'.
Непосредственно из определения дополнения множества сле-
дуют равенства
M(JM' == и, М[\М' = 0, (MfY = м.
Для любых подмножеств А и В множества U справедливы
также следующие равенства, которые называют законами двой-
ственности или законами де Моргана'.
(A J В)' = A' f] В', (А П В)' = A' и В',
7
т. е. дополнение объединения двух множеств равно пересечению
их дополнений, а дополнение пересечения двух множеств равно
объединению их дополнений.
Пример 2. Доказать закон двойственности:
(Л пву = Л71]В7.
А Пусть х (Л П В)', тогда х ф A f] В и, следовательно,
хфА или хфВ, т. е. хеЛ7 или х В7, а это означает, что
хеЛ'ОВ7. Таким образом, доказано включение
(ЛПВ),с=Л,и^.
Пусть х е A' U В7, тогда хе Л' или хе В7 и, следовательно,
х ф А или х ф В, т. е. х ф A П В, а это означает, что х е
е(Л П В)7. Таким образом, доказано включение
Л7иВ7с=(Л Г)В)7.
Из включений (Л П В)' с Л7 U В' и Л7 U В7 cz (Л Г) В)7 следует,
что множества (Л ПВ)7 и Л7СВ7 состоят из одних и тех же эле-
ментов, т. е. равны. &
3. Эквивалентные и неэквивалентные множества. Говорят,
что между множествами Л и В установлено взаимно- однознач-
ное соответствие, если каждому элементу множества Л сопо-
ставлен один и только один элемент множества В, так что раз-
личным элементам множества Л сопоставлены различные эле-
менты множества В и каждый элемент множества В оказывает-
ся сопоставленным некоторому элементу множества Л.
Например, между множеством всех четных натуральных чи-
сел и множеством N можно установить взаимно однозначное
соответствие следующим образом:
2, 4, 6, 8, ..., 2п, ...
t t t t t
Y Y V V i
1, 2, 3, 4, ..., n, ...
Множества, между которыми можно установить взаимно од-
нозначное соответствие, называются эквивалентными. Если мно-
жества Л и В эквивалентны, то пишут Л — В; если они не экви-
валентны, то пишут Л В.
Отношение эквивалентности между множествами обладает
свойствами:
1) рефлексивности Л — Л;
2) симметричности: если А ~ В, то В — Л;
3) транзитивности: если Л — В и В ~ С, то Л — С.
Если А ~ В, то говорят, что множества Л и В имеют одина-
ковую мощность.
Если Л Ф В, но А ~ Bi cz В, то говорят, что множество А
имеет меньшую мощность, чем множество В.
Множество А Ф 0 называется конечным, если существует
такое число п е N, что
Л -{1,2,3, ..., п}.
8
в этом случае говорят, что множество А содержит п элемен-
тов или что множество А имеет мощность п.
Пустое множество 0 также считается конечным, его мощ-
ность принимается равной нулю.
Множество, не являющееся конечным, называется бесконеч-
ным-
Множество А называется счетным, если А ~ N. Говорят, что
счетное множество имеет счетную мощность. Если множество
конечно или счетно, то его называют не более чем счетным.
Множество называется несчетным, если оно имеет мощность,
большую, чем мощность множества N.
Теоремы Кантора:
1. Множество всех рациональных чисел счетно.
2. Множество всех действительных чисел несчетно.
Множество А называется множеством мощности континуума,
если А ~ R.
Пусть дано множество S = {s}, называемое множеством ин-
дексов, и каждому инде'ксу s сопоставлено множество As. Мно-
жество {/1s}, элементами которого являются множества
sg S, называют системой или семейством множеств. Понятия
объединения и пересечения двух множеств обобщаются на слу-
чай произвольной конечной или бесконечной системы множеств
следующим обр-азом.
Объединением системы множеств As, s е S, называется мно-
жество все,х элементов, принадлежащих хотя бы одному из мно-
жеств системы.
Пересечением системы множеств /4S, s е S, называется мно-
жество всех элементов, содержащихся в каждом множестве
системы.
Объединение и пересечение системы множеств As, s е S, обо-
значают
U А и П м
sе S seS
В частных случаях, когда система множеств конечна или
счетна, пишут
п п оо оо
и As, П a, nsN, или U л> П Л-
S=1 S=1 S=l S=1
Решить задачи 1.1—1.8, в которых А, В, С, D — произволь-
ные множества.
1.1. Даны множества А, В, С. С помощью операций объеди-
нения и пересечения записать множество, состоящее из элемен-
тов, принадлежащих: 1) всем трем множествам; 2) хотя бы од-
ному множеству; 3) по крайней мере двум из этих множеств.
1.2. Доказать, что равенства: 1) Д (J £ = 2) A Q В = А
верны тогда и только тогда, когда A cz В,
1.3. Доказать, что равенство (В\С) = (Д\В)и С верно
тогда и только тогда, когда A zd С.
9
1.4. Доказать равенства:
1) Л\(Л\В) = Л рв.
2) (Л\В)и(В\Л) = (ЛиВ)\(ЛрВ).
3) (л\в)\с = л\(вис).
4) (Л\В)ПС = (ЛПС)\(ВПС).
1.5. Доказать, что включение Л\В cz С верно тогда и только
тогда, когда A cz В U С.
1.6. Доказать включения:
1) Ли(В\С)=э(Л UB)\C.
2) (Л U Q\B cz (Л\В)и С.
1.7. Определить, в каком отношении (X cz У, X zz> У, X = У)
находятся множества X и У, если:
1) Х = Ли(В\С), У = (Л ив)\(лис).
2) Х = (ЛрВ)\С, У = (Л\С)П(В\С).
3) Х = Л\(ВиС), У = (Л\В)и(Л\С).
4) Х = (ЛХ^В)и(СХВ), У = (ЛиС)ХВ.
5) X = (4XB)U(CXD), У-(ЛХС)и(ВХ^).
1.8. Доказать, что если A cz С, В cz D, то
AXB = (AXD)(}(BXC).
1.9. Пусть А = {xeN|2<x^6}, В = {х N11 < х < 4}г
С = {х е N | х2 — 4 = 0}. Из каких элементов состоят множен
ства:
1) В U С; 2) ЛП5ПС; 3) A U В U С;
4) (Л П B)U (В U С); 5) ВХС; 6) СХВ?
1.10. Множества А и В составлены соответственно из элемент
тов а = 4п + 2, b = 3n, не N. Найти Л QВ.
1.11. Пусть множество Л содержит п
элементов, множество В — т элементов, а
пересечение Л f| В — k элементов. Найти
число элементов множества: 1) Л U В,
2) АХ В.
1.12. Пусть Л cz N и каждый элемент Л
есть число, кратное или 2, или 3, или 5.
Найти число элементов множества Л, если
среди них имеется: 70 чисел, кратных 2;
60 чисел, кратных 3; 80 чисел, кратных 5;
32 числа, кратные 6; 35 чисел, кратных 10;
38 чисел, кратных 15; 20 чисел, кратных 30.
1.13. Множества Л и В являются подмножествами множества
U (рис. 1). Заштриховать на рисунке следующие множества:
1) ЛИВ'; 2); Л'ПВ; 3) (ЛОВ)';
4) (ЛиВ')';5) HfW;6) И'ПВ)иИПВ').
ю
1.14. Пусть А и В — произвольные подмножества множества
U Доказать равенства:
1) (А\В)' — А’[)В.
2) (А ПВ')иИ'АЯ) = ЛиВ.
з) (див)П(Д'ив')= Див.
1.15. Пусть A cz U, В cz U. Найти множество X cz U, удовлет-
воряющее уравнению
(хид),и(^илл)==в.
1.16. Найти подмножества А и В множества U, если из-
вестно, что для любого множества X cz U верно равенство
Х(]А=ХЦВ.
1.17. Пусть Д5 cz U, s е S. Доказать:
1) ( U а¥= П X. 2) (П aY= U а',.
kssS / ssS \se=S J se=S
1.18. Дана система произвольных множеств Д5, seN.
п
1) Пусть Вп = U Л5, п е N. Доказать, что
s = l
оо оо
и Bs = U As.
s=l s = l
п
2) Пусть Вп = П А, п е N. Доказать, что
s = l
оо оо
П Bs= П А-
S = 1 S= 1
1.19. Пусть AsPi seN, — система произвольных мно-
жеств. Установить, верны ли включения:
оо / оо X оо / со \
1) и(ПлРЩП(иЛр).
$=1 \р=1 / Р=1 \$=1 /
оо z оо X оо / оо X
2) и ( П АрНП ( U Ар)-
s = l \р=1 / р = 1 \s = l /
1.20. Установить взаимно однозначное соответствие между
множествами А и В:
1) Д = Z, В = N.
2) А = {х е Z |х = k2, N}, В = N.
3) А == {x^R|0^x^l}, B = {x^R\a^x<^.b, b > a}.
4) A = R, I}.
11
1.21. Установить взаимно однозначное соответствие между
множеством всех точек интервала (0; 1) и множеством всех то-
чек отрезка [0; 1].
1.22. Доказать равномощность следующих множеств:
1) квадрата {(х; у) | |х| 1, |z/|^ 1} и круга {(х; 'у) |х2 +’
2) открытого круга {(х; у) ]х2 + У2 < 1} и всей плоскости
У);
3) открытого круга {(х; у) |х2 + У2 < 1} и замкнутого круга
{(*; У)\х2 + У2^ 1}.
1.23. Доказать, что множество является бесконечным тогда
и только тогда, когда оно эквивалентно некоторому своему соб-
ственному подмножеству.
1.24. Доказать, что если множество А—бесконечное, а мно-
жество В — счетное, то (Л J В) ~ А.
1.25. Доказать, что если Л\В ~ В\Л, то А ~ В.
1.26. Доказать, что если XczBczC и Л ~ С, то Л ~ В.
1.27. Доказать, что если А и В — счетные множества, то мно-
жество А X В счетно.
1.28. Доказать, что объединение не более чем счетной си-
стемы счетных множеств есть счетное множество.
1.29. Доказать счетность следующих множеств:
1) множества всех чисел вида 2\ k е N;
2) множества всех треугольников на плоскости, вершины
которых имеют рациональные координаты;
3) множества всех точек плоскости с рациональными коор-
динатами;
4) множества всех многочленов с рациональными коэффи-
циентами;
5) множества всех алгебраических чисел (число называется
алгебраическим, если оно является корнем многочлена с целыми
коэффициентами);
6) множества всех конечных подмножеств счетного множе-
ства.
1.30. Доказать, что если расстояние между любыми двумя
точками множества точек на прямой больше единицы, то это
множество не более чем счетно.
1.31. Доказать, что следующие множества имеют мощность
континуума:
1) множество всех точек непустого интервала (я; 6);
2) множество всех последовательностей, составленных из
цифр 0 и 1;
3) множество всех последовательностей действительных чи-
сел;
4) множество всех точек квадрата^
5) множество всех точек круга;
6) множество всех подмножеств счетного множества;
7) множество всех счетных подмножеств множества мощно*
сти континуума.
12
1.32. На плоскости построено множество попарно непересе-
каюшихся: 1) окружностей, 2) фигур, имеющих вид буквы Т,
3) фигур, имеющих вид буквы Г. Может ли это множество быть
несчетным?
1.33. Найти мощность множества всех подмножеств конеч-
ного множества, содержащего п элементов
1.34. Доказать, что для каждого множества множество всех
его подмножеств имеет мощность, большую, чем исходное мно-
жество.
1.35. Пусть А—несчетное множество, а В — не более чем
счетное. Доказать, что множества A J В й А\В имеют мощ-
ность множества А.
4. Упорядоченные множества. Множество называется у по- '
рядоченным, если для любых двух его элементов а и b установ-
лено отношение порядка а Ь или b а {а не превосходит b
или b не превосходит а), обладающее свойствами:
1) рефлексивности: а а, т. е. любой элемент не превосхо-
дит самого себя;
2) антисимметричности: если а Ь и Ъ а, то элементы
а и b совпадают;
3) транзитивности: если а b, b с, то а sg с.
Пустое множество считают упорядоченным. Множество мож-
но упорядочить различными способами. Например, в множестве
студентов группы отношение порядка (<Э можно установить
следующими двумя способами: студент а не превосходит сту-
дента &, т. е. а Ь, если 1) студент а ниже ростом студента
2) фамилия студента а в журнале группы стоит под боль-
шим номером, чем фамилия студента Ь. Устанавливая различ-
ными способами отношение порядка в одном и том же множе-
стве, получают различные упорядоченные множества.
Элементы конечных упорядоченных множеств обычно запи-
сывают в круглых скобках, располагая элемент а левее эле-
мента Ь, если а Ь. Например, запись А = (3, 2, 1), В — (2, 3, 1)
означает, что А и В — различные упорядоченные множества, в
отличие от записи А={3, 2, 1}, В = {2,3,1}, из которой сле-
дует, что А = В.
. Например, множество, содержащее три элемента а, b и с,
имеет 3 двухэлементных подмножества:
{а, Ь}, {а, с}, {Ь,с}
и 6 двухэлементных упорядоченных подмножеств:
(а, Ь), (6, а), (а, с), (с, а), (&, с), (с, Ь).
5. Размещения и перестановки. Пусть имеется множество,
содержащее п элементов. Каждое его упорядоченное подмноже-
ство, состоящее из k элементов, называется размещением из п
элементов по k элементов.
13
Число всех размещений из п элементов по k элементов обо-
значается Ап (читается: «число размещений из п по k» или
«А из п по £»; А — первая буква французского слова arrange-
ment, что означает размещение, приведение в порядок).
Число размещений находится по формуле
Ап = п(п-1)(п — 2) ... (n-k+l), k>0, (1)
т. е. число размещений из п элементов по k элементов равно
произведению k последовательных натуральных чисел от п до
п — k + 1 включительно.
Произведение всех натуральных чисел от 1 до п обозначают
символом п\ (читают: «эн факториал»), т. е.
п\ = 1-2-3 ... (п— 1)п.
Используя это обозначение, формулу (1) можно записать
в виде
<2)
причем, если условиться считать, что 0! = 1, то формула (2)
дает правильный результат и в случаях k = 0 и k = п.
. Размещения из п элементов по п элементов называются пе-
рестановками из п элементов.
Перестановки являются частным случаем размещений. Так
как каждая перестановка содержит все п элементов множества,
то различные перестановки отличаются друг от друга только
порядком элементов. Число перестановок из п элементов обо-
значают через Рп (Р — первая буква французского слова per-
mutation — перестановка).
Так как Рп = А”, то для числа перестановок справедлива
формула
Рп = п\. (3)
Из формулы (3) следует, что множество, содержащее п элемен-
тов, можно упорядочить п\ способами.
Пример 3. Группа студентов изучает 7 учебных дисцип-
лин. Сколькими способами можно составить расписание заня-
тий на понедельник, если на этот день недели запланированы
занятия по 4 дисциплинам?
А Различных способов составления расписания, очевидно,
столько, сколько существует четырехэлементных упорядоченных
подмножеств у семиэлементного множества. Следовательно, чис-
ло способов равно числу размещений из 7 элементов по 4 эле-
мента, т. е. равно Л?- По формуле (1), полагая в ней п = 7,
k = 4, находим
Л* = 7 - 6 • 5 4 = 840. Д
Пример 4. Сколько шестизначных чисел, кратных пяти,
можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе
цифры не повторяются?
14
А Для того чтобы число, составленное из заданных цифр,
делилось на 5, необходимо и достаточно, чтобы цифра 5 стояла
на последнем месте. Остальные пять цифр могут стоять на ос-
тавшихся пяти местах в любом порядке. Следовательно, иско-
мое число шестизначных чисел, кратных пяти, равно числу пе-
рестановок из пяти элементов, т. е. 5! = 5-4-3-2-1 = 120. ▲
Пример 5. Сколько различных перестановок можно обра-
зовать из букв слова «задача»?
А Образовать какую-либо перестановку из букв слова «за-
дача»— это значит на шесть занумерованных мест каким-ни-
будь образом поставить одну букву «з», одну букву «д», одну
букву «ч» и три буквы «а». Если буквы «з», «д» и «ч» как-то
поставлены, то остальные места заполняются буквами «а». Но
сколькими способами можно поставить три различные буквы
на шесть мест? Очевидно, что число способов равно числу всех
трехэлементных упорядоченных подмножеств шестиэлементного
множества, т. е. равно Лб = 6 • 5 • 4= 120.
Можно рассуждать и иначе. Если бы все шесть букв слова
были различны, то число перестановок было бы равно 6!. Но
буква «а» встречается в данном слове три раза, и перестановки
только этих трех букв «а» не дают новых способов расположе-
ния букв. Поэтому число перестановок букв слова «задача» бу-
дет не 6!, а в 3! раз меньше, т. е.
6! 6- 5-4- 3-2-1 „ - л
зГ =----ГУП-----= 6-5-4 = 120. а
6. Сочетания. Пусть имеется множество, состоящее из п эле-
ментов. Каждое его подмножество, содержащее k элементов,
называется сочетанием из п элементов по k элементов.
Число всех сочетаний из п элементов по k элементов обозна-
чается символом Сп (читается: «число сочетаний из п по k» или
«це из п по А»; С’—первая буква французского слова combina-
sion — сочетание).
Число сочетаний находится по формуле
<^ = Й<ГПЗГ' <4>
или по формуле
rk п (и — 1) (п. — 2) ... (п — &4-1)
Сп =-----------. (5)
Справедливы равенства
С* = С"Л (6)
C*i! = C*+1+C*, k<n. (7)
Пользуясь равенством (6), можно упрощать вычисление чи-
сел Сп в тех случаях, когда k > п/2, например,
с\1 = С?5 = = 455.
о • Z
15
Пример 6. Сколько экзаменационных комиссий, состоя-
щих из 5 членов, можно образовать из 10 преподавателей?
А Очевидно, столько, сколько существует пятиэлементных
подмножеств у десятиэлементного множества, т. е. число комис-
сий равно Cio. По формуле (4), полагая в ней п = 10, k = 5,
находим
^5 10! 10-9-8-7-6
Cl° 5|5! 2-3-4-5 “252, А
Пример 7. В чемпионате страны по футболу (высшая
лига) участвуют 18 команд, причем каждые две команды встре-
чаются между собой 2 раза. Сколько матчей играется в тече-
ние сезона? х
А В первом круге состоится столько матчей, сколько суще-
ствует двухэлементных подмножеств у множества, содержащего
18 элементов, т. е. их число равно С is. По формуле (5) нахо*
дйм
С?8= 1^=153.
Во втором круге играется столько же матчей, поэтому в те-
чение сезона состоится 306 встреч. А
Пример 8. Сколькими способами 2м элементов можно
разбить на пары?
Ответ на этот вопрос можно получить, используя формулы
для числа сочетаний и числа перестановок. Приведем другое
решение.
А Обозначим число разбиений на пары 2м элементов через
/?2я-
Выберем какой-нибудь элемент. С участием этого элемента
пару можно образовать 2м — 1 способами. Каждый раз после
образования одной пары будет оставаться 2м — 2 элемен-
тов, которые можно разбить на пары /?2n-2 способами. По-
этому /?2п = (2м — 1)Т?2м—2« Используя эту рекуррентную фор-
мулу, получаем /?2п= (2м — 1) /?2п-2= (2м — 1) (2м — 3)7?2лг_4= ...
... =(2м—1)(2м —3) ... 3-/?2 = (2м—1) (2м —3) ... 3-1.
Произведение всех натуральных чисел, не превосходящих м
и имеющих ту же четность, что и м, часто обозначают м!! (чи-
тается: «эн два факториал» или «эн двойной факториал»).
Таким образом, 2м элементов можно разбить на пары
(2м— 1)!1 способами. А
7. Случайные события и их вероятности. Рассмотрим опыт,
заключающийся в подбрасывании монеты. Этот опыт имеет два
исхода: либо монета упадет так, что сверху окажется герб, либо
она ляжет гербом вниз. Тот или иной исход опыта зависит от
многих причин, которые не поддаются учету, и заранее предска-
зать результат опыта нельзя. Событие, состоящее в том, что
«выпал герб», является примером случайного события. Другими
примерами случайных событий могут служить: «появление еди-
ницы» при бросании игральной кости (кубика из однородного
16
материала с гранями, занумерованными цифрами от единицы
до шести), выход из строя электролампы до определенного сро-
ка, несоответствие стандарту выбранного для контроля изделия.
Во всех этих случаях невозможно предсказать заранее, до окон-
чания опыта, произойдет или не произойдет соответствующее со-
бытие. Поэтому такие события и называют случайными.
В опыте с подбрасыванием монеты оба исхода равноправны,
до опыта нет никаких оснований предпочитать один исход дру-
гому. В таких случаях говорят, что оба исхода равновероятны,
а вероятность каждого из них равна 1/2. При подбрасывании
игральной кости имеется шесть исходов. Если кость однород-
ная и симметричная, то все исходы опыта одинаково возможны
или равновероятны. Вероятность каждого исхода равна 1/6.
Обобщением этих простых опытов будет опыт, в котором воз-
можно п равновероятных исходов u2, ..., ип, их называют
также элементарными событиями. В этом случае вероятность
каждого исхода принимается равной 1/п. Записывают это сле-
дующим образом:
P(iz1)=l/n, Р(^2)=1/п, ..., Р(ип) — \/п.
Первая из этих формул читается так: «вероятность события и\
равна \/п» (Р— первая буква английского слова probability —
вероятность).
Рассмотрим теперь опыт с п 'равновероятными исходами и
некоторое событие Д, которое происходит тогда, когда опыт окан-
чивается какими-то k исходами, и не происходит в том случае,
если имеет место один из остальных п — k исходов. Будем го-
ворить, что исходы, приводящие к событию А, благоприятствуют
ему. Вероятностью события Д, связанного с опытом с п равно-
вероятными исходами, называется отношение числа исходов,
благоприятствующих событию Д, к числу всех исходов, т. е.
P(A) = k/n, (8)
где k — число исходов, благоприятствующих событию Д. Ве-
роятность любого события А удовлетворяет неравенствам
0<Р(Д)< 1,
что непосредственно следует из формулы (8), так как очевидно,
что 0 С k п.
Пример 9. Опыт заключается в подбрасывании двух мо:
нет: медной и серебряной. Какова вероятность того, что хотя бы
на одной монете появится герб?
А Равновероятными исходами опыта считаются следующие:
Ui — герб появился на обеих монетах,
и2 — герб выпал только на медной монете,
из — герб выпал только на серебряной монете,
щ — герб не выпал ни на одной монете.
Благоприятствуют событию А (появлению герба хотя бы на
одной монете) исходы и\, U2 и w3. Полагая в формуле (8)
п = 4, k = 3, получаем Р (Д) = 3/4. А
17
Пример 10. Набирая номер телефона, абонент забыл две
последние цифры и, помня лишь, что эти цифры различны, на-
брал их наудачу. Какова вероятность того, что номер набран
правильно?
А Две последние цифры можно набрать числом способов,
равным числу упорядоченных двухэлементных подмножеств у
десятиэлементного множества (множества всех цифр). Это число
способов равно Л10. Следовательно, всего существует Д?о ис-
ходов. Благоприятствует событию А (цифры набраны верно)
только один исход. Поэтому Р (Л) = 1/Лю = 1/Ю • 9 = 1/90. А
Пример 11. Среди 100 электроламп 5 испорченных. Ка-
кова вероятность того, что выбранные наудачу 3 лампы ока-
жутся исправными?
А У множества, содержащего 100 элементов, существует С?оо
трехэлементных подмножеств. Поэтому 3 лампы из 100 можно
выбрать Cioo способами. Лампы выбираются наудачу. Это оз-
начает, что все эти способы выбора (все исходы) равнове-
роятны. Число благоприятных исходов — все три лампы оказа-
лись исправными — подсчитывается аналогично. Из 95 исправ-
ных ламп 3 лампы можно выбрать С95 способами, так как
именно столько существует трехэлементных подмножеств у
95-элементного множества. Полагая в формуле (8) п = С?оо,
k = С95, получаем
Р (А) = С|5/С?оо = foo'X'X °’856- А
1.36. Вычислить:
и . __. 2) .
^20+^20 61 (С7 + С?)
3) ---k<n- 4) C°+Ci + C*+ ... +Cl
(n-k)\Akn_\
1.37. Найти n, если:
1) 4^ = 24(L4*U 2) С"+з - = 15 (n + 1).
n-k
3) Cio > 2Cfo+1. 4) 4 (n — 2)!Л„+2 < 143 • n!
1.38. В группе 30 студентов. Сколькими способами можно
выделить двух человек для дежурства, если: 1) один из них
должен быть старшим, 2) старшего быть не должно?
1.39. На пять сотрудников выделены три путевки. Сколькими
способами их можно3 4 распределить, если: 1) все путевки раз-
личны, 2) все путевки одинаковы?
1.40. Сколькими способами можно расположить в ряд 5 бе-
лых и 4 черных шара так, чтобы черные шары не лежали ря*
18
дом? Рассмотреть два случая: 1) шары одного цвета неотли-
чимы Друг от друга;2) все шары разные. <
. 1.41. Сколько диагоналей имеет выпуклый /1-угольник?
1.42. Никакие три диагонали выпуклого десятиугольника не
пересекаются в одной точке. Определить число точек пересече-
ния диагоналей.
1.43. На первой из двух параллельных прямых лежат 15 то-
чек, на второй — 21. Сколько существует треугольников с вер-
шинами в этих точках?
1.44. Сколькими способами на шахматной доске можно рас-
ставить 8 ладьей одного цвета, чтобы они не били друг друга
и стояли только на черных клетках?
1.45. Из цифр 0, 1, 2, 3 составлены всевозможные четырех-
значные числа так, что в каждом числе нет одинаковых цифр.
Сколько получилось чисел? Сколько среди них четных чисел?
1.46. Сколько различных десятизначных чисел можно запи-
сать, используя цифры 1 и 2?
1.47. Сколько различных перестановок можно образовать из
букв следующих слов: 1) зебра, 2) баран, 3) водород, 4) абра-
кадабра?
1.48. Сколькими способами можно раздать 28 костей домино
четырем игрокам так, чтобы каждый получил 7 костей?
1.49. Хоккейная команда состоит из 2 вратарей, 7 защитни-
ков и 10 нападающих. Сколькими способами тренер может об-
разовать стартовую шестерку, состоящую из вратаря, двух за-
щитников и трех нападающих?
1.50. Сколько существует шестизначных чисел, все цифры
которых нечетны (1, 3, 5, 7, 9)?
1.51. Сколько делителей имеет число 462?
1.52. На полке стоят т книг в черных переплетах и п книг
в синих переплетах, причем все книги разные. Сколькими спо-
собами можно расставить книги так, чтобы книги в черных пе-
реплетах стояли рядом?
1.53. Сколькими способами можно упаковать 9 разных
книг в 5 бандеролей, если 4 бандероли должны содержать по
2 книги?
1.54. Сколькими способами 12 одинаковых монет можно раз-
ложить по пяти различным кошелькам так, чтобы ни один ко-
шелек не остался пустым?
1.55. Сейф запирается на замок, состоящий из пяти дисков,
на каждом из которых изображены цифры 0, 1, 2, ..., 9. За-
мок открывается, если на дисках набрана одна определенная
комбинация цифр. Хватит ли 10 дней на открытие сейфа, если
«рабочий день» продолжается 13 часов, а на набор одной ком-
бинации цифр уходит 5 секунд?
1.56. Среди всех целых чисел от 1 до 10" каких больше: тех,
Для записи которых используется цифра 9, или тех, которые
записываются без нее?
19
1.57. Некоторый алфавит состоит из шести букв, которые для
передачи по телеграфу кодированы так:
. * ,. . * ,. ? . *
при передаче одного слова не сделали промежутков, отделяю-
щих букву от буквы, так что получилась сплошная цепочка то-
чек и тире, содержащая 12 знаков. Сколькими способами можно
прочитать переданное слово?
1.58. Из урны, в которой находятся 3 белых, 4 черных, 5 крас-
ных шаров, наудачу вынимается один. Какова вероятность того,
что вынутый шар окажется: 1) белым, 2) черным, 3) желтым,
4) красным?
1.59. Бросаются две игральные кости. Какова вероятность
того, что сумма очков, выпавших на двух костях, окажется рав-
ной 8?
1.60. Экзаменационная программа содержит 40 вопросов. На
экзамене предлагается ответить на два из них. Студент подгото-
вил ответы на 30 вопросов.. Какова вероятность того, что на
экзамене ему предложат два вопроса, -на которые он подготовил
ответ?
1.61. В лотерее из 50 билетов 8 выигрышных. Какова вероят-
ность того, что среди первых пяти наугад выбранных билетов
два будут выигрышными?
1.62. Из десяти билетов выигрышными являются два. Опре-
делить вероятность того, что среди наудачу взятых пяти биле-
тов: 1) один выигрышный, 2) оба выигрышных.
1.63. При игре в «Спортлото» 6 номеров из 49 являются
«счастливыми». Участник игры указывает 6 номеров из 49. Ка-
кова вероятность угадать: 1) все 6 «счастливых» номеров,
2) 3 «счастливых» номера?
1.64. В лифт 8-этажного дома на первом этаже вошли 5 че-
ловек. Предположим, что каждый из них независимо друг от
друга и с равной вероятностью может выйти на любом этаже,
начиная со второго Найти вероятность того, что все пятеро
выйдут на разных этажах.
1.65. Первенство по баскетболу разыгрывают 18 команд,
среди которых 2 команды экстракласса. Для уменьшения общего
числа игр команды путем жеребьевки разбиваются на две рав-
ные группы. Какова вероятность того, что две команды экстра-
класса окажутся: 1) в разных подгруппах, 2) в одной подгруппе?
1.66. Доказать, что вероятность того, что у двенадцати слу-
чайно выбранных человек дни рождения приходятся на разные
месяцы, меньше 1/10 000.
§ 2. Элементы логики. Метод математической индукции
1. Высказывания. Операции над высказываниями. Под
высказыванием понимают всякое утверждение, о котором имеет
смысл говорить, что оно истинно или ложно. Из данных выска-
зываний при помощи так называемых логических связок, к ко-*
20
торым относятся частица «не», союзы «и», «или», слова
«если ..., то ...», «тогда и только тогда, когда ...», образуют-
ся новые высказывания.
Операция отрицания соответствует в обыденной речи частице
«не». Для каждого высказывания р можно образовать новое
высказывание р (читают: «р с чертой» или «не р»), которое
истинно, если р ложно, и, наоборот, ложно, * если р ис-
тинно. Высказывание р называют отрицанием высказывания р.
Например, для высказывания «последовательность {1/п} имеет
предел» отрицанием является высказывание «последователь-
ность {l/п} не имеет предела».
Высказывание, составленное из данных высказываний р и q
при помощи союза «и», называют конъюнкцией и обозначают
р /\ q (читают: «р и q»).
Конъюнкция р Л q считается истинным высказыванием в том
и только в том случае, когда оба высказывания р и q истинны.
Если высказывание образовано из высказываний р и q при
помощи союза «или», то его называют дизъюнкцией высказы-
ваний р и q и обозначают р V q (читают: «р или q»).
. _ Дизъюнкция р V q считается' истинным высказыванием тогда
и только тогда, когда истинно хотя бы одно из данных выска-
зываний.
Высказывание, образованное из данных высказываний р и q
при помощи слов «если то ...», называют импликацией и
обозначают p-^q (читают: «если р, то q»). Высказывание р на-
зывают при этом условием, а высказывание q — заключе-
нием.
Импликация p-^q считается ложным высказыванием только
в том случае, когда условие (высказывание р) истинно, а за-
ключение (высказывание q) ложно.
й Высказывание, образованное из данных высказываний р и q
при помощи слов «тогда и только тогда, когда...;», называют
эквиваленцией (или двойной импликацией) и обозначают р q.
Эквиваленция р •<-> q истинна в том и только в том случае,
когда оба высказывания р и q истинны или когда они оба
ложны.
Если истинным высказываниям сопоставлять букву Иу а
ложным — букву <77, то логические операции р, р A q, р\/ q,
p-*-q, р q можно определить формально при помощи сле-
дующих таблиц истинности:
/Р р
И л л И
р q P/\q
И И л л И л И л И л л л
р q pVq
И И И
И Л И
л И И
л л л
2Ь
р Q P~>q
И И И
И л л
л И И
л л И
р q P<—>q
И И л л И л И л И л л И
Новые высказывания могут быть образованы при помощи
нескольких логических операций, причем каждая из операций
может применяться несколько раз. Порядок, в котором должны
проводиться операции, указывают с помощью скобок.
Из таблицы истинности для импликации видно, что если
условие р и импликация p~>q истинны, то истинно и заклю-
чение q. В этом случае пишут р => q и говорят, что из р сле-
дует q. Это классическое правило вывода постоянно использует-
ся в математике.
Если из р следует q, а из q следует р, то высказывания р и
q называют равносильными. Равносильные высказывания соеди-
няют либо знаком <=>, либо знаком равенства, т. е. пишут либо
p<=>q, либо р = q.
При исследовании высказываний на равносильность в про-
стых случаях можно использовать таблицы истинности, так как
для равносильных высказываний, имеющих различную форму,
таблицы истинности совпадают. Например, используя таблицы
истинности для отрицания и импликации, легко построить таб-
лицу истинности для высказываний, имеющих форму q-+p\
р q q р q -> р
И И Л ' л И
И л И л л
л И л И И
л л И И И
Эта таблица совпадает с таблицей истинности для импликации
р-> q. Следовательно, высказывания р-><7 и q-^p равносильны,
т. е. р -> q <=> q~^P или p-^q = q~^P-
Таблица истинности, соответствующая высказыванию, обра-
зованному из п простых высказываний, содержит 2п строк. По-
этому обычно равносильность высказываний устанавливается
другим способом: некоторое количество основных равносильно-
стей (законов алгебры высказываний) проверяется на основа-
нии таблиц истинности, полученные равенства используются при
доказательстве других равенств точно так, как в элементарной
алгебре в тождественных преобразованиях используются алгеб-
22
раические законы: коммутативный, ассоциативный, дистрибутив-
ный и другие.
Основные законы алгебры высказываний-.
1. Коммутативность дизъюнкции:
pv <7 = qV р. (1>
2. Коммутативность конъюнкции:
р /\ q = qAp. (2)
3. Ассоциативность дизъюнкции:
р V (q V г) — (р V q) V г. (3)
4. Ассоциативность конъюнкции:
р rA (q А г) = (р A q) Лг. (4)
5. Первый дистрибутивный закон:
Р A(pV r) = (pAq)V(p Аг). (5)
6. Второй дистрибутивный закон:
pV(?Ar) = (pV ^) A(p Vr). (6)
7. Законы де Моргана:
pV q = p Aq, р Aq = p\/ q. (7)
8. Закон двойного отрицания:
р = р. (8)
9. Законы идемпотентности:
Р V р = р, рЛр = р. (9)
Важную роль в логике играют тождественно истинные и тож-
дественно ложные высказывания. Тождественно истинные вы-
сказывания истинны всегда, независимо от того, истинны или
ложны составляющие их высказывания. Например, высказыва-
ние pVp является тождественно истинным. Тождественно ис-
тинные высказывания будем обозначать буквой L
Тождественно ложные высказывания ложны всегда, т. е. не-
зависимо от истинности или ложности высказываний, которые
их составляют. Такие высказывания будем обозначать буквой /.
Например, рЛр='1, так как высказывание рЛр ложно неза-
висимо от того, истинно или ложно высказывание р.
Для тождественно истинных и тождественно ложных выска-
зываний при любом р верны следующие равенства:
р V p = i, р /\р = 1,
р V i = i, р f\i = p, (10)
p\j 1 = р, р Д I = 1, i = L
2Э
Законы (1) — (10) алгебры высказываний описывают свой-
ства трех операций: дизъюнкции, конъюнкции и отрицания. Им-
пликация и эквиваленция выражаются через дизъюнкцию, конъ-
юнкцию и отрицание с помощью следующих формул:
Р-*7 = Р V q,
Р*-+Я = (р hq) V (р A <?).
Пример L Доказать равносильность
p-+q = p A q-
(H)
(12)
(13)
А Применив равенство (11), получим
p ->q = p \j q.
Затем используем первый закон де Моргана (7) и закон двой-
ного отрицания (8):
р V q = p A q = P /\q-
Формула (13) дает правило построения отрицания для импли-
кации, часто применяемое в математических рассуждениях. А
Пример 2. Брауну, Джонсу и Смиту предъявлено обвине-
ние в соучастии в ограблении банка. Похитители скрылись на
поджидавшем их автомобиле. На следствии Браун показал, что
преступники были на синем «Бьюике», Джонс сказал, что это
был черный «Крайслер», а Смит утверждал, что это был «Форд
Мустанг» и ни в коем случае не синий. Стало известно, что,
желая запутать следствие, каждый из них указал правильно
либо только марку машины, либо только ее цвет. Какого цвета
был автомобиль и какой марки?
А При решении этой задачи для краткости будем опускать
знак конъюнкции, т. е. вместо р A q писать просто pq.
Рассмотрим высказывания:
р — машина синего цвета,
q — машина марки «Бьюик»,
г — машина черного цвета,
s — машина марки «Крайслер»,
t—машина марки «Форд Мустанг».
Из показаний Брауна, Джонса и Смита следует соответственно,
что высказывания pV q, rV s, p V t истинны. Следовательно,
.истинна конъюнкция этих трех высказываний:
(Р V q) (г Vs) (pV t).
Раскрыв скобки, получим дизъюнкцию восьми конъюнкций:
(prp) V (prt) V (psp) V (pst) V (qrp) V (qrt) V (qsp) V (qst).
Из условия следует, что все конъюнкции, кроме пятой, являются
ложными. Поэтому дизъюнкция может быть истинна только при
условии истинности высказывания qrp, а это означает, что пре-
ступники скрылись на черном «Бьюике». А
24
2. Предложения, зависящие от переменной (предикаты).
В математике и других науках наряду с высказываниями при-
ходится иметь дело с различными утверждениями (предложе-
ниями), зависящими от переменной, принадлежащей некото-
рому множеству. Такие предложения в логике называют преди-
катами Предложение (предикат) р(х), x^U, не является,,
вообще говоря, высказыванием. Предполагается, однако, что для
каждого фиксированного элемента xq^U предложение р(х0)
есть высказывание.
Множество U, на котором задано предложение р(х), можно
разбить на два подмножества. Одно содержит те и только те
элементы U, для которых р(х) истинно. Оно называется множе-
ством истинности предложения р(х). Другое подмножество со-
стоит из тех элементов [7, для которых р(х) ложно. Если пер-
вое из этих подмножеств обозначить буквой Р, то второе сле-
дует обозначить Р', так как оно является дополнением множе-
ства Р до множества Z7.
Например, для предложения х2— х < 0, xeR, множеством
истинности Р является интервал (0; 1), множеством Р'— объ-
единение промежутков (—оо; 0] и [1; +°°) (дополнение интер-
вала (0; 1) до всей числовой прямой).
Два предложения р(х) и q(x), заданные на одном и том же
множестве, называют равносильными, если их множества истин-
ности совпадают.
Например, два предложения (неравенства) х2 — 5х + 6 < О
и х4— 5х3 + 6х2< 0 равносильны на множестве R, так как мно-
жеством истинности каждого из них является интервал (2;3).
Для предложений, зависящих от переменной, как и для вы-
сказываний, вводятся логические операции.
Отрицанием предложения р(х), x^U, называется предло-
жение, определенное на том же множестве U и обращающееся
в истинное высказывание для тех и только тех значений х, для
которых р(х) ложно.
Рис. 3
Рис. 2.
Отрицание р(х) обозначается р(х). Если______Р — множество
истинности р(х), то множеством истинности р(х) будет Р . Н<*
рис. 2 схематически изображены множества U, Р и Р'.
25
Аналогично определяются и другие логические операции.
Например, импликацией р(х)-+ q(x) предложений р(х) и
q(x), определенных на множестве £7, называется предложение,
определенное на том же множестве U и обращающееся в
ложное высказывание для тех и только тех значений х, для
которых условие р(х) истинно и заключение q(x) ложно. На
рис. 3 заштриховано множество истинности импликации р(х)->
-+q(x) (Р и Q— множества истинности предложений р(х)
и q(x)).
3. Знаки общности и существования (кванторы). С предло-
жениями, зависящими от переменных, связаны два вида часто
встречающихся утверждений.
1. Предложение р(х), х^ U, обращается в истинное выска-
зывание для всех элементов множества CL
2. Предложение р(х), x^U, обращается в истинное выска-
зывание хотя бы для одного элемента множества U.
Эти утверждения принято записывать кратко, используя для
этого специальные знаки: знак общности V (перевернутая пер-
вая буква английского слова АП — все) и знак существования 3
(перевернутая первая буква английского слова Exists — суще-
ствует). В логике знаки V и 3 называют кванторами. Квантор
общности V соответствует словам «все», «всякий», «каждый»,
«любой»; квантор существования 3 — словам «хотя бы один»,
«найдется», «существует».
Используя знаки V и 3, утверждения 1 и 2 можно записать
следующим образом:
LVxp(x), х е U. 2. Зхр(х), х <= U.
Каждое из этих предложений либо истинно, < либо ложно
и, следовательно, является высказыванием.
Правила построения отрицания для высказывания, содер-
жащего кванторы, даются формулами
Vxp (х) = Зхр (х), Зхр (х) = Xfxp (%). (14)
Первая формула означает, что р(х) истинно не для всех х
тогда и только тогда, когда существует х, для которого р(х)
ложно. Вторая формула говорит, что не существует х, для ко-
торого р(х) истинно тогда и только тогда, когда р(х) ложно
для всех х.
Элемент Хо множества £7, для которого предложение
р(х) неверно, называется контрпримером для высказывания
Vxp(x).
Таким образом, чтобы убедиться в ложности высказывания
Vxp(x), достаточно найти (или, как еще говорят, построить)
один контрпример.
Предложение, определенное на множестве X X У (т. е. на
декартовом произведении множеств X и У), называют предло-
жением, зависящим от двух переменных, или двухместным пре-
дикатом и обозначают р(х;у), хеХ, у^У. Из такого предло-
26
жения с помощью кванторов V и 3 можно образовать восемь
высказываний.
1. VxVz/p(x; у).
3. Xfx3yp(x; у).
5. 3xVyp(x-, у).
7. ЗхЗур(х; у).
2. VyVxp(x; у).
4. ЗуУх р (х; у).
6. УуЗх р (х; у).
8. ЗуЗх р (х; у).
Высказывания 1 и 2, очевидно, равносильны так же, как и вы-
сказывания 7 и 8. Высказывания 3 и 4, а также 5 и 6 неравно-
сильны (см. задачи 2.21, 2.22). Поэтому говорят, что одноимен-
ные кванторы можно переставлять, а разноименные перестав-
лять нельзя.
4. Метод математической индукции. Во многих разделах ма«
тематики приходится доказывать истинность предложений р(х)г
определенных на множестве натуральных чисел, для всех зна-
чений переменной, т. е. истинность высказывания
Vn p(n), п N.
Часто это удается сделать методом математической индукции.
Этот метод основан на так называемом принципе математиче-
ской индукции (аксиоме индукции), который можно сформули-
ровать следующим образом. Предложение р(п) считается истин-
ным для всех натуральных значений переменной, если выпол-
нены следующие два условия:
1. Предложение р(п) истинно для п = 1.
2. Из предположения, что р(п) истинно для п = k (где k —
любое натуральное число), следует, что оно истинно и для сле-
дующего значения п = k + 1.
Под методом математической индукции понимают следую-
щий способ доказательства. Если требуется доказать истинность
предложения р(и) для всех натуральных значений п, то сначала
проверяют истинность высказывания р(1) и затем, допустив
истинность высказывания р(&), доказывают истинность выска-
зывания р(&+1). Если доказательство верно для каждого
натурального значения k, то в соответствии с принципом мате-
матической индукции предложение р(п) является истинным для
всех значений п.
ПримерЗ. Доказать равенство
р-]- 22 + 32 + ... +п2= »(»+ 1) (2»т 1)
п е N.
Л Это равенство представляет собой предложение р(п), за-
данное на множестве натуральных чисел. Докажем истинность
Р.(п) для всех значений п методом математической индукции.
1. Высказывание р(1) истинно, так как
1-2. (2- 1 + 1)
1 — • g ——.
27
2. Предположим, что p(k) истинно, т. е. справедливо равен-
ство
р + 22 _|_ . । fc2 . fe(fe + D(2fe + 1)
Прибавив к обеим частям равенства (& + I)2, получим
12 + 22+ ... + fe2 + (fe + I)2 — (fe + *e(2fe + ° + (^ + О2-
Преобразуем правую часть равенства следующим образом:
+ (^ + I)2 = А+1 (2^2 + 7k + 6)
= (k + 1) (k + 2) (26 + 3)
6
Следовательно,
12 + 22+ ... [ (k 1 I)2— (А + 1) ((^ + 1) + 1) (2 (А: + 1) + 1)
а это означает, что р(&+ 1) истинно. Таким образом, рассужде-
ние верно при любом fceN.
В силу принципа математической индукции исходное равен-
ство истинно. А
Пример 4. Доказать неравенство Бернулли
(1 + а)п 1 + сс > —1, n е N.
А 1. При п = 1 получаем истинное высказывание
1 + а 1 + а-
2. Предположим, что неравенство верно при п = А, т. е.
(1 + a)k 1 + ka.
Умножив обе части неравенства на 1 + а (это можно сделать,
так как а > —1), получим
(1 Ч-а)^1 >(1 +М (1 +а)^ 1 +(& + 1)а + &х2.
Учитывая, что ka2 0, приходим к неравенству
(1 +сс)*+1 > 1 +(/? + 1)сх.
Итак, предположив, что данное неравенство верно для п = ky
мы доказали, что оно верно и для п = &+1. Доказательство,
очевидно, остается справедливым для каждого значения k. Сле-
довательно, неравенство доказано. А
Пример 5. Доказать, что при каждом п е N число
5-23п~2 + 33n-i кратно 19.
Д 1. При п = 1 данное утверждение, очевидно, верно.
2. Предположим, что оно верно для п = fe, т. е. предполо-
жим, что 5-23/’~2 + З3*5-1 делится на 19. Тогда, так как
5,23(^+1)-2_|_ зШ+п-1 = 8.5.2ЗА5-2 + 27 • 33*-1 =
= 8(5 • 23&~2 + 33ft-‘) + 19 -З3*-1,
28
т0 утверждение верно и при п = &4-1. Действительно, первое
слагаемое правой части этого равенства делится на 19 в силу
индуктивного предположения; второе также делится на 19, так
как содержит множитель 19.
Оба условия принципа математической индукции выполнены.
Утверждение доказано. А
Пример 6. Доказать неравенство
/г + 1 + /г + 2 + * * ’
3n -J- 1
> 1,
е N.
Д 1. При п = 1 неравенство справедливо, так как
2 3 4 •
2. Предположим, что неравенство верно при п = k> т е.
—! l _1 . о _—!—_ > 1
k + 1 k + 2 36 + 1 1 *
Прибавим к обеим частям неравенства сумму трех дробей
. 1 +—1. +. I.
ЗА:+ 2 Т 3k + 3 3k + 4
и перенесем первое слагаемое левой части в правую часть не-
равенства. Тогда получим
Т+Т + ••• + 36 + 4 > 1 + ЗА: + 2 + ЗА- + 3 3£ + 4
1
k + 1
Правая часть этого неравенства больше единицы, так как
1 J--:___।____!__l —J_______!__=
т3£+ 2 ^36+ 3^36+ 4 £ + 1
= 1 J_________?_________\
(ЗА; + 2) (ЗА; + 3) (ЗА; + 4)
Следовательно, левая часть тем более больше единицы, т. е.
-----------ц .. -I-------!____> 1
(& + 1) + 1 ’ 3(k + 1) + 1
Последнее неравенство из исходного неравенства получается
при п = k 4- 1.
Итак, предположив истинность неравенства при п = ky мы
Доказали его истинность при n = k-]-l. Таким образом, мето-
дом математической индукции неравенство доказано. А
Пример 7. Пусть х2, ...» хп — произвольные положи-
тельные числа, причем %i%2 ... xn= 1. Доказать, что
+ %2 4“ • • • Н“ Хп П.
д 1. Если /7 = 1, то по условию Xi = 1 и, следовательно,
^ожно написать Xi 1, т. е. для п = 1 утверждение верно.
29
2. Предположим, что утверждение верно для п — k. Пусть
Xi, Xk+\ — произвольные положительные числа и
Xi%2 • • • XfoXfo+i — 1.
Могут представиться два случая: либо все эти числа равны
1, тогда их сумма равна £-|-1 и неравенство доказано, либо
среди этих чисел., есть хотя бы одно число, не равное единице,
и тогда обязательно есть по крайней мере еще одно число, не
равное единице, причем, если одно из них меньше единицы, то
другое больше единицы. Не ограничивая общности, можно счи-
тать, что xk > 1, a Xk+i < 1. Рассмотрим теперь k чисел
Х1, %2, •••, Xk-\, (xkxk+\).
Произведение их равно единице, и, следовательно, по индуктив-
ному предположению
Х1 + %2 + • • • 4“ Xk—1 4“ XkXk+\ k.
Прибавим к обеим частям последнего неравенства xk +
перенесем xkXk+\ направо и преобразуем правую часть неравен-
ства:
Х1 + Х2 + ... + Xk+\ k XkXk±\ 4“ Xk + Xk+\ —
— k + 1 4" xk (1 — *a>+i) 4~ xk+], — 1 =
= k 4- 1 4“ Xk (1 — Xk+\) —- (1 — Ajfe-и) --
= k 4-1 4- (1 “ Xk+i) (xk - 1) > k 4- 1.
Таким образом, из истинности утверждения при п = k выте-
кает его истинность при n = k-\-\. Утверждение доказано. Из
приведенного доказательства следует, что знак равенства в до-
казываемом соотношении имеет место тогда и только тогда,
когда == х2 = • • • = хп= 1. А
Пример 8. Доказать неравенство
+ Х2 + ... +хп П1—-------------—
——У Х\Х2 ... хп ,
где Xi, %2, хп — произвольные положительные числа.
А Это важное неравенство между средним арифметическим
и средним геометрическим п чисел является простым следствием
утверждения, доказанного в примере 7. В самом деле, пусть
Xi, х2, ..., хп — произвольные положительные числа.
Рассмотрим п чисел
х2 , . _ Хп
п _________ » п____________» • • » > п_________•
'х/х\Х2.-.Хп 'х/ххХ2...Хп у Х\Х2 . . . Хп
Очевидно, что все эти числа положительны и произведение их
равно единице. Следовательно, их сумма больше или равна п,
т. е.
Xi I Х2 || Хп „
~~~ri.......- ф - п ~1~ . . . ~1 п
'у/Х1Х2 . . . Хц '\/xiX2...Xn '\/х1Х2...Хп
80
откуда
*1 + *2 + - • + П /
п у МЛ2 • • • %п >
причем знак равенства имеет место тогда и только тогда, когда
= Х2 ==: -^3 • • • == Хп-
Иногда метод математической индукции применяется в не-
сколько видоизмененной форме. Чаще всего используются сле-
дующие две формулировки:
I. Предложение p(n), hgZ, истинно для всех целых зна-
чений п т (т— некоторое целое число), если выполнены
условия:
1: Предложение р(п) истинно для п = т.
2. Из предположения, что р(п) истинно для n = k (k — це-
лое, k^m), следует, что оно истинно для следующего значе-
ния п = k + 1.
II. Предложение p(n), neZ, истинно для всех п т
(т — некоторое целое число), если выполнены условия:
1. Предложение-^(п) истинно для п = т и п = т + 1.
2. Из предположения, что р(п) истинно для п = k и п =
«= k—1, следует (для любого k>m), что оно истинно для
/г = ^+1.
Формулировка I используется, например, при решении за-
дач 2.30, 2.36, формулировка II — при решении задачи 2.34.
2.1. Среди следующих предложений выделить те, которые
являются высказываниями, и установить (если это возможно),
истинны они или ложны:
1) Великий русский поэт А. С. Пушкин родился в 1799 году.
2) Анатолий Карпов — двенадцатый чемпион мира по шах-
матам.
3) Летайте самолетами Аэрофлота!
4 ) д/ 2 ge Q.
5) Для произвольных множеств А и В верно включение
AgzAUB.
6) Существуют внеземные цивилизации
7) 2СО + О2 = 2СО2.
8) Сумма углов треугольника равна 180°.
2.2. Даны два высказывания:
р —«число 3 является делителем числа 174»;
q — «идет дождь».
В чем заключаются высказывания:
1) р; 2) pV q\ 3) р Ар; 4) p-^q\ 5) p~^-q\ 6) р р?
Какие из этих высказываний истинны, если р истинно,
q ложно?
2.3. Составить таблицу истинности для высказываний, имею-
щих форму:
1) 5 = 2) S = (pA (^->p))Vp.
31
2.4. Доказать формулы (3) — (7).
2.5. Доказать формулы (11) и (12).
2.6. По мишени произведено три выстрела. Пусть pk— вы-
сказывание «мишень поражена fe-м выстрелом», k = 1, 2, 3.
Что означают следующие высказывания:
1) PiVp2Vp3; 2) Р1Лр2Лр3; 3) (piVp2)Ap3?
Какие из этих трех высказываний истинны, если истинно р3,
a pi и р2 ложны?
2.7. Какие из высказываний р, q, г должны быть истинны
и какие ложны, чтобы высказывание ((р V р) Л 7)“>г было ис-
тинным?
2.8. Упростить высказывания, имеющие форму:
1) (р V (р Л q)) V (р Л q). 2) (р Л q) V ((г V р) Л q)._
3) (г Л q) V (р Л q Л г) V (р Л q /\ г). 4) (р-><?) Л (г->р).
2.9. На вопрос, кто из трех студентов изучал логику,., был
получен правильный ответ: если изучал первый, то изучал
и третий, но неверно, что если изучал второй, то изучал
и третий. Кто изучал логику?
2.10. Виктор, Роман, Юрий, Сергей заняли на математиче-
ской олимпиаде первые четыре места. Когда их спросили о рас-
пределении мест, они дали три таких ответа:
1) Сергей — первый, Роман — второй;
2) Сергей — второй; Виктор — третий;
3) Юрий — второй, Виктор — четвертый.
Как распределились места, если в каждом из ответов только
одно утверждение истинно?
2.11. Определить, кто из четырех студентов сдал экзамен,
если известно, что:
1) если первый сдал, то и второй сдал;
2) если второй сдал, то третий сдал или первый не сдал;
3) если четвертый не сдал, то первый сдал, а третий не сдал;
4) если четвертый сдал, то и первый сдал.
2.12. Для полярной экспедиции из восьми претендентов А,
В, С, D, Е, F, G и Н надо отобрать шесть специалистов: био-
лога, гидролога, синоптика, радиста, механика и врача. Обя-
занности биолога могут выполнять Е и G, гидролога В и F,
синоптика F и G, радиста С и О, механика С и Н, врача Д
и D. Хотя некоторые претенденты владеют двумя специально-
стями, в экспедиции каждый сможет выполнять только одну
обязанность. Кого и кем следует взять в экспедицию, если F не
может ехать без В, D — без И и без С, С не может ехать одно-
временно с G, а А не может ехать вместе с В?
2.13. На множестве однозначных натуральных чисел даны
два предложения:
р(п): число 3 — делитель числа п;
q(л): п 6,
32
Найти множество истинности предложений:-
1) Р (п) V q (п); 2) р (п) Л q (п);
3) р(п) -><?(«); 4) р(п)-><?(п).
2.14. Какие из следующих утверждений являются высказы-
ваниями? Какие из высказываний истинны и какие ложны:
а) Сумма корней приведенного квадратного уравнения равна
свободному члену.
б) Сумма корней любого приведенного квадратного уравне-
ния равна свободному члену.
в) Существует приведенное квадратное уравнение, сумма
корней которого равна свободному члену?
2.15. На множестве всех натуральных чисел заданы три пред?
ложения:
р(п): число п2— 2 кратно?;
q (ri): число /г —2 кратно 7;
г (п): 4п2 — 360п + 8099 < 0.
При каких значениях п из данных трех предложений два ис-
тинны и одно ложно?
2.16. На множестве всех действительных чисел заданы три
предложения:
р (х): х — целое число;
q (х): х2 — Зх — целое отрицательное число;
г (х): х + — целое положительное число.
При каких значениях х ложно одно и только одно из этих трех
высказываний?
2.17. На множестве всех упорядоченных пар (т\п) целых
положительных чисел заданы предложения:
р (т, п): т + 1 делится на п;
q (т, п): т равно 2п + 5;
г (т, п): т + п делится на 3;
s (т, п): т-}-7п — простое число.
Найти все пары чисел для которых одно и только одно
из этих четырех высказываний ложно.
2.18. При каких значениях а система уравнений
( ах + У — Ь,
{ х2 — 4 z/2 = 1
имеет действительные решения при любых значениях
2 Л. Д. Кудрявцев и др. 33
2.19. Дана система уравнений
| Ьх — у = ас2,
( (b~-&)x + %by = c-\- 1,
где а, Ь, с — действительные числа. При каких значениях а при
любом b найдется такое с, при котором система имеет хотя
бы одно решение?
2.20. Даны две точки Л(0;9), В(3; 6) и система неравенств
{2% — у + а 0,
6х + Зу + 5а >0.
При каких значениях параметра а решением системы будут
координаты: 1) хотя бы одной точки отрезка АВ, 2) каждой
точки отрезка ЛВ?
2.21. Рассмотрим два определения легкой контроль-
ной.
1. Контрольная работа называется легкой, если каждую за-
дачу решил хотя бы один ученик.
2. Контрольная работа называется легкой, если хотя бы один
ученик решил все задачи.
1) Может ли контрольная быть легкой в смысле пер-
вого определения и трудной (не легкой) в смысле вто-
рого?
2) Может ли работа быть легкой в смысле второго определе-
ния и трудной в смысле первого?
2.22. Дано неравенство + При каких значениях
k истинны следующие предложения:
1) При любом / неравенство имеет хотя бы одно решение.
2) Существует /, при котором неравенство верно для всех х«
3) При любом I неравенство верно для всех х.
4) Существует /, при котором неравенство имеет хотя бы
одно решение.
2.23. Используя правила построения отрицания для выска-
зываний, содержащих кванторы (см. формулы (14)), сформули-
ровать отрицание следующих высказываний:
1) В некотором поезде, идущем из Москвы в Ленинград,
в каждом вагоне есть (существует) свободное место.
2) В каждом городе Швеции есть улица, на которой есть
дом, все окна которого выходят на юг.
2.24. Постройте контрпример для высказываний:
1) При каждом п е N число п2 + ^ + 41 является про-
стым.
2) Каждая функция, непрерывная в точке, имеет в этой точке
производную.
Методом математической индукции решить задачи 2.25—
2.40.
34
2.25. Доказать, что при каждом п е N верны равенства!
1) 1+3 + 5+ ... + (2п—1) = п2.
2) 1 -2 + 2-5 + ... + лг (Злг — 1) = лг2 (/г + 1).
3) 12 + 32+ ... +(2п- 1)2=
4) 1-2 + 2-3 + 3-4+ ... +(п-1)п = .
5) 13 * + 23 + З3+ ... + n3 = (-ra(n±^)2.
6) 1 • 22 + 2 • З2 + ... + (и - 1) п2 = - — - + 2) -•
7) —1— _i—!—1_ _|--------!----— —'1—.
1 -3 “ 3-5 ~ ~ (2/г — 1) (2/1 4- 1) 2/г + 1 •
1-5 5-9 + • • • + (4/1 — 3) (4п + 1) “ 4//+ 1 •
2.26. Доказать, что при любом п е N:
1) п(2п2— Зп+1) кратно 6.
2) 62п~2 + Зл+1 + З"-1 делится на 11.
3) lln+1 + 122п~1 делится нацело на 133.
4) и5 б)— п кратно 5.
2.27. Доказать, что при любом натуральном п >> 1 число
22П + 1 оканчивается цифрой 7.
2.28. Доказать справедливость следующих неравенств для
всех натуральных п > 1:
1) _L. А А . 2,1 ~1 < 1
2 4 6 2/г д/З/г + 1
9) _ 1 I 1 I
' /г + 1 ’ + 2 * ’ * ‘2/г 24 ’
3) < 1 Н---+ . . . Н------< 2 л]п.
* д/п
^)v<^l + '2“ + y+--- + —Г <
б)
2.29. Доказать, что при любом натуральном п > 2 верно не-
равенство
2пп\ < пп.
2*
35
2.30. При каких натуральных значениях п верны неравенства:
1) 3" > 2" + 7л; 2) 2” > л2 + 4л + 5;
3) 2" > пъ\ 4) п\ > 2"?
2.31. Доказать, что
3 + 33 + ... + 33 ... 3 = —--Ду" ~ 10 . п <= N
(левая часть равенства содержит п слагаемых).
2.32. Доказать равенство
дЛ + д/2+ ... + д/Х = 2 cos (п/2”+1), п е N
(в левой части содержится п корней).
2.33. Доказать равенство
arctg j + arctg у + ... + arctg = arctg , п <= N.
2.34. Последовательность {ап} задается рекуррентным соот-
ношением
ап = уan_i — а„_2 (л > I), «0 = 2, aj = y.
Найти п-й член последовательности.
2.35. Пусть х2, •••> хп — произвольные неотрицательные
числа, причем
+ х2 + • • • 4~ хп 1/2.
Доказать, что
(1__Х1)(1__Х2) _ (1-хп)> 1/2.
2.36. Доказать, что любую сумму денег, большую 7 копеек,
можно разменять только трехкопеечными и пятикопеечными
монетами.
2.37. На плоскости проведено п прямых, из которых никакие
две не параллельны и никакие три не проходят через одну
точку. На сколько частей разбивают плоскость эти прямые?
2.38. На сколько частей разделится сфера п плоскостями,
проходящими через центр, если никакие три плоскости не про-
ходят через один и тот же диаметр?
2.39. На плоскости произвольным образом проведено п пря-
мых. Доказать, что черной и белой красками можно так закра-
сить плоскость, что любые две части, имеющие общую сторону,
будут окрашены в разные цвета.
2.40. Доказать, что если р — простое число, п— натуральное,
то пР— п делится на р (теорема Ферма).
§ 3. Действительные числа
1. Рациональные и иррациональные числа. Действительным
числом называется бесконечная десятичная дробь. Для действи-
тельных чисел определены операции сложения и умножения,
36
подчиняющиеся коммутативному и ассоциативному законам
и связанные между собой дистрибутивным законом (подробнее
об этом см. ниже). Обратная к сложению операция называется
вычитанием, обратная к умножению — делением. Действитель-
ные числа можно сравнивать по величине. Множество действи-
тельных чисел обозначается через R.
Таким образом, всякое действительное число а согласно
определению записывается в виде бесконечной десятичной дроби
а = ±а0, ai а2 . •. , (1)
где ссо — неотрицательное целое число (т. е. а0 может принимать
значения 0, 1, 2, 3, ..., т, ...), а каждое из ап (п — 1, 2, ...) —-
одна из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Знак «+» в записи (1)'
обычно не пишется. В этом случае число а называют неотрица-
тельным: а 0 и пишут
а = а0, се 1 а2 ... ап ... (2)
’Число (2) называется абсолютной величиной числа (1) и обо-
значается через |а|. Таким образом,
| ±ao, aioc2 ... ап . ..| = a0, aia2 ... ап
Может случиться, что одно и то же действительное число
.допускает запись в виде двух различных десятичных дробей;
-в этом случае в одной из записей, начиная с некоторого места
(десятичного разряда) после запятой, будут стоять только одни
-нули, а в другой — одни девятки. Например,
1 = 1,000 ... 0 ... = 0,999 ... 9 ...
В дальнейшем в качестве записи действительных чисел будем
употреблять только бесконечные десятичные дроби (называе-
мые допустимыми), у которых нет такого десятичного разряда,
начиная с которого в записи числа стоит только цифра 9. При
этом соглашении каждое действительное число записывается
единственным образом в виде бесконечной десятичной дроби.
Если в десятичной записи (1) числа а, начиная с некоторого
места, стоят только одни нули:
а = ±ao,aia2 .. .an00 ... 0 ...,
wo обычно их не пишут:
а — zha0,aia2 ... ап (3)
и говорят, что число а записывается конечной десятичной
Дробью (3).
оДля неотрицательного числа а, записанного в виде допусти-
мой бесконечной десятичной дроби (2), конечная десятичная
Дробь
ап — ao,aia2 ... ап (4)
Называется его нижним десятичным приближением (или
37
десятичным приближением, с недостатком) порядка и, а число
ап = ao,<xia2 ... ап + 10~п (5)
— верхним десятичным приближением (или десятичным прибли-
жением с избытком) порядка п = 0, 1,2,...
Если же число а является отрицательным: а < 0, т. е. за-
писывается в виде допустимой десятичной дроби
а = —oco,tzia2 ... am ...,
где хотя бы одно из am (т = О, 1, 2, ...) не равно нулю, то
его нижнее ап и верхнее ап десятичные приближения порядка п
определяются равенствами
ап = — а0, — КГ", ап = — а0, .. ап. (6)
Таким образом, при любом а е R
О_п а
a fi 10 ,
^5 ^пЧ-1 > 1 •
Приближения конечными десятичными дробями (4), (5)
и (6) действительных чисел а R удобно использовать для
осуществления операций сложения, вычитания, умножения, де-
ления и сравнения действительных чисел.
Так, например, сумма а 4- b, aeR, fteR, является един-
ственным действительным числом, удовлетворяющим при всех
п = 0, 1,2,... неравенству
ап bn а b ап 4~ bn.
Произведение ab является единственным действительным
числом, удовлетворяющим при всех п = 0, 1,2,... неравенствам
апЬп ab дпЬп) если а 0, b 0,
a„b„ ab если а < 0,
anbn^ab ^anbn, если tz<0, b < 0.
Условие a < b равносильно тому, что существует такой но-
мер п, что ап < bn.
В § 1 уже отмечалось, что натуральные числа 1, 2, ... обо-
значаются через N, а целые 0, ±1, ±2, ... — через Z. Числа
вида
—, meZ, neZ, n=^0,
п
т
называются рациональными, а символ — , с помощью которого
38
они записываются, — рациональной дробью Одно и то же ра-
циональное число а может быть записано разными рациональ-
ными дробями: если
а = и а = ~, т, п, k, п^О, 1¥=0,
уо это возможно тогда и только тогда, когда Im — kn.
Множество всех рациональных чисел обозначается через Q.
Действительные числа, не являющиеся рациональными, назы-
ваются иррациональными. Множество всех иррациональных чи-
сел обозначается через [.
Бесконечная десятичная дробь называется периодической
•с периодом Pi ... рт и записывается в виде
a0,aia2 ... а/г(Р1Р2 ... Pm), (7)
если после некоторого десятичного разряда (его номер обозна-
чен п) группа цифр Piр2 ... Pm все время повторяется.
Беконечные десятичные периодические дроби и только они
являются рациональными действительными числами Отсюда
следует, что действительное число является иррациональным
тогда и только тогда, когда оно записывается непериодической
бесконечной десятичной дробью. Переход от записи рациональ-
ного числа рациональной дробью p/q, q<^'£, q О,
к его записи с помощью бесконечной периодической десятичной
дроби осуществляется делением «столбиком» числителя р на
знаменатель q. Переход от записи рационального числа в виде
(7) к его записи с помощью рациональной дроби производится
по формуле
гг г» ГУ п ( (\ R о \____а1а2 » • ♦ Рг • » » Pm а1а2 /о\
<ZQ,(XjCt2 • * • ^n(P 1Р2 • • • Pm) ^0 gg ggg g • w)
m раз n раз
В числителе дроби, находящейся в правой части равенства,
стоит разность чисел, стоящих после запятой в (7) соответ-
ственно до второго и до первого периода. В знаменателе стоит
число, запись которого начинается с цифры 9, взятой столько
раз, сколько имеется цифр в периоде, а затем следуют нули,
число которых равно числу цифр до периода. Применяя сфор-
мулированные правила, имеем, например,
4=0,(428571), 2,7(13) = 2 Z13^L = 2Z№=23g.
Между точками геометрической прямой и действительными
числами можно установить взаимно однозначное соответствие
такое, что если числу нуль соответствует точка О, единице —•
точка Е и вектор ОЕ принят на прямой за координатный орт,
то каждому числу поставлена в соответствие точка прямой
с абсциссой, равной этому числу. Поэтому множество действи-
тельных чисел называется также числовой прямой, или число-
39
вой осью, или действительной осью, сами действительные числа
называются точками числовой прямой, а например, вместо
«число х меньше числа у» говорят: «точка х числовой оси лежит
левее точки у».
Числовая прямая IR, дополненная двумя элементами, обо-
значаемыми Н-оо (плюс бесконечность) и —оо (минус беско-
нечность), такими, что для любого числа / gR по определению
считается
—сю <Z х <Z 4~°°,
называется расширенной числовой прямой R. Элементы -|-со
и —оо называют также бесконечно удаленными точками число-
вой прямой или бесконечными числами, в отличие от точек.
xeR, которые называют иногда конечными точками этой пря-
мой (соответственно конечными числами).
Для любой точки х0 е R интервал (х0— в; Хо+s), в > 0?
называется ее г-окрестностъю и обозначается £7(х0; в), т. е.
/7(х0; е)={х: |х — Хо|<в} (9)
(рис. 4). Для бесконечно удаленных точек 4-°° и —оо их е-окре-
, s; U(+ оо, е;
SC0 -*£ + £ — Е О Е
Рис. 4. Рис. 5.
стности 17(4-оо; в) и £7(—оо;е), е > О, определяются форму-
лами:
С7(4-°°; в) — {х: х>в}, /7(—оо;е)-Ч {х: х <—е} (10)
(рис. 5).
Иногда числовую прямую пополняют одним элементом, ко-
торый обозначают оо и называют бесконечностью. Бесконечность
без знака не связана отношением порядка с действительными
числами. Ее 8-окрестность 17(оо;в), в > 0, задается формулой
/7(оо;е)={х: |х|>е}. (И)
Бесконечность без знака также называют бесконечно удален-
ной точкой числовой прямой.
3.1. Записать рациональные дроби 2/3, 11/20, 3/14, —2/7 в
виде бесконечных десятичных дробей.
3.2. Записать периодические бесконечные десятичные дроби
0,125(0); 0,(3); 2,4(31); 0,2(9) в виде рациональных дробей.
3.3. Доказать, что число 0,121221222 122 ... 2 , иррацио-
п раз
нально.
40
3.4. Доказать, что Ig 2, log2 3— иррациональные числа.
3.5. Доказать, что числа <2, <3. <2/3, <2 4-<3— ирра-
циональные.
3.6. Может ли сумма двух иррациональных чисел быть ра-
циональным числом?
3.7. Доказать, что для любых рациональных чисел а и Ь та-
-ких, что а < 6, найдется иррациональное число с, удовлетво-
ряющее условию а < с < Ь.
3.8. Доказать, что для любых рациональных чисел р, р, г.
из которых хотя бы одно не равно нулю, число р + q ^3 +
4- г -у/2/3 — иррациональное.
3.9. Найти пять первых нижних и верхних десятичных при-
ближений чисел 3/10, 1/3, 11/9, —5/8.
3.10. Найти три нижних и верхних десятичных приближения
чисел <2, <5, <3-<2, <2-<3, <3 - <5 4-<7.
3.11. Соизмеримы ли отрезки, если отношение их длин вы-
ражается дробью 0,23(75)?
3.12. Сравнить следующие действительные числа:
I) 3,3 и 3,298. 2) 3,1416 и 3,14159. 3) 3,141592 и 22/7.
4) <3 4-2 и <2 4- <5. 5) <7 4- <10 и <3 4- <19.
3.13. Найти три первые значащие цифры в нижних и верхних
десятичных приближениях для следующих чисел:
1) 4+ <3. 2) <2 — 1,4. 3) <5-2|. 4) | <2.
О о о
5) <2 • <3. 6)-^.
3.14. Доказать, что у любых двух различных точек числовой
прямой существуют непересекающиеся окрестности.
3.15. Доказать, что у любых двух различных точек числовой
прямой, расширенной с помощью двух бесконечно удаленных
точек +00 и —00 или с помощью одной бесконечно удаленной
точки сю, существуют непересекающиеся окрестности.
3.16. Найти наибольшую с-окрестность точки х — 2, в которой
1) х1 2 - 5х 4- 4 < 0, 2) sin х > 0, 3) tgx < 0, 4) > 0.
2. Целые числа.
Пример 1. Доказать, что если aeZ, b е Z, b > 0, то су-
ществует и притом единственное представление числа а в виде
а — bq + ry O^r<Zb., q&Z, r^Z.
А Возьмем q^Z так, что bq а <6(7+!). Тогда 0*^3
— bq<by т. е. число г—а — bq удовлетворяет условиям
задачи.
Если а — bq\ + И, 0 г\ < Ь, то, вычитая из него почлен-
но равенство а = bq + г. получаем 0 = Ь(ср — + п — г и»
41
следовательно, rx — г кратно Ь. Поскольку | гх— r\<Zb, то это
возможно только тогда, когда г} = г и q} = q. А
3.17. Наибольший общий делитель натуральных чисел а и Ь
обозначается (а, Ь). Доказать, что если а = bq с, a, b, ceN,
q е Z, то (а,Ь) = (Ь, с).
3.18. Пусть ggN, b е N. Доказать, что существуют neN
и числа qi е Z (i =» 1, 2, ..., п), г/ е Z (/ = 1, 2, ..., п — 1)
такие, что
а = bqx + rb 0 < г! < &,
b = rxq2 + r2, 0<r2<rif
ri = >У7з + г3, 0 < г3 < г2,
(12)
гп_3 «= rn_2 qn^ + гп_ь 0 < < rrt_2,
и Ги-I является наибольшим общим делителем чисел а и Ь. (Та-
кой метод нахождения наибольшего общего делителя двух на-
туральных чисел называется алгоритмом Евклида.)
3.19. Доказать, что совокупность общих делителей двух на-
туральных чисел совпадает с совокупностью делителей их наи-
большего общего делителя.
Указание. Воспользоваться алгоритмом Евклида (12).
3.20. Доказать, что для любых натуральных чисел а, Ь и с
справедливо равенство (ас, Ьс) = (а, Ь)с.
Указание. Умножить равенства (12) на с.
Пример 2. Доказать, что если а и Ь— натуральные числа
и (а,Ь)==1 (такие числа называются взаимно простыми), то
для любого натурального с справедливо равенство (ас, Ь)=*
= (с,Ь).
А Покажем, что числа (ас, Ь) и (Ь, с) делятся друг на
друга, откуда сразу будет следовать, что они равны. Число Ь,
а следовательно, и число Ьс делятся на (ас, Ь). Поэтому число
(ас, Ь) является делителем чисел ас и Ьс, откуда согласно
задаче 3.19 вытекает, что (ас, Ь) является и делителем наиболь-
шего общего делителя (ас, Ьс) = с(а, Ь) — с чисел ас и Ьс. Та-
ким образом, (ас, Ь) является делителем чисел Ь и с, а потому
и делителем (Ь,с). Обратно, число (Ь, с) является делителем
чисел Ь и ас, следовательно, оно является делителем и их наи-
большего общего делителя (ас, Ь). Ж
Пример 3. Доказать, что если а, Ь и с — натуральные
числа, (а, b) = 1 и ас делится на Ь, то и с делится на Ь.
А Согласно примеру 2 имеем (ас, Ь) = (с, Ь), а поскольку
ас делится на Ь, то (ас, Ь)=Ь Таким образом, (с, Ь)=Ь, т. е.
число с делится на Ь. ▲
42
3.21. Доказать, что если каждое натуральное число а<^ ...
ап взаимно просто с каждым натуральным числом
то и произведение &i£2 ... ап взаимно просто с произ-
ведением b\b<2. ... Ьт.
3.22. Доказать, что если произведение нескольких неотрица-
тельных целых чисел делится на простое число р, то хотя бы
один из сомножителей также делится на р. (Натуральное число
называется простым, если оно не имеет целых положительных
делителей, кроме единицы и самого себя.)
3.23. Доказать, что всякое натуральное число, большее еди-
ницы, раскладывается на произведение простых сомножителей
и притом единственным способом, если отвлечься от порядка со-
множителей.
3.24. Доказать, что множество простых чисел бесконечно.
3.25. Доказать, что для любых двух натуральных чисел т
и п существуют такие целые числа р и q, что
pm + qn = (m, п).
В частности, если т и п — взаимно простые, то рт-{- qn= 1.
3.26. Доказать, что если £— иррациональное число, то мно-
жество дробных частей чисел вида ng, п е N, плотно на отрезке
[0; 1]. (Дробной частью действительного числа х называется
разность между этим числом и наибольшим целым числом, не
превосходящим х. Множество X cz [а; Ь] называется плотным на
отрезке [а; Ь], если в любой окрестности каждой точки этого
отрезка содержатся точки множества X.)
3.27. Доказать, что если натуральное число не является квад-
ратом натурддьного числа, то оно не может быть и квадратом
рационального числа.
Указание. Воспользоваться результатом задачи 3.23.
3. Аксиоматическая теория действительных чисел.
3.1. Аксиомы действительных чисел. Множеством действи-
тельных чисел называется множество, для элементов которого
выполняются следующие условия:
I . В множестве действительных чисел R определена бинар-
ная операция, называемая операцией сложения: любой упоря-
доченной паре действительных чисел а и b поставлено в соответ-
ствие число, обозначаемое а + Ь и называемое суммой чисел
а и Ь, При этом имеют место следующие свойства:
11 (коммутативный закон сложения). Для любых чисел а
и b выполняется равенство а + b = Ь +
12 (ассоциативный закон сложения). Для любых чисел а, b
и с выполняется равенство а + (Ь + с) = (а + Ь) + с.
1з . Существует такое число, обозначаемое 0, что для любого
числа а выполняется равенство а + 0 = а.
П- Для любого числа а существует такое число, называе-
мое противоположным к числу а и обозначаемое —а, что а +
+ (—а) = 0.
43
Число аЯ-(—b) называется разностью а — b чисел а и Ь.
II. В множестве действительных чисел определена бинарная
операция, называемая операцией умножения: любой упорядо-
ченной паре действительных чисел а и Ь поставлено в соответ-
ствие число, обозначаемое ab и называемое произведением чи-
сел а и Ь. При этом имеют место следующие свойства:
Hi (коммутативный закон умножения). Для любых чисел а-
и b выполняется равенство ab = Ьа.
П2 (ассоциативный закон умножения). Для любых чисел а>
b и с выполняется равенство a(bc) = (ab)c.
П3. Существует число, обозначаемое 1, такое, что для лю-
бого числа а выполняется равенство al — а,
П4. Для любого числа а 0 существует такое число, пазы-
Л ill
ваемое обратным к числу а и обозначаемое —, что а — = 1.
тт 1
Число а~ь называется частным от деления числа а на
число 6^0 и обозначается а/b или а : Ь,
III (дистрибутивный закон сложения относительно умноже-
ния). Для любых действительных чисел а, b и с справедливо
равенство (а + Ь) с — ас + Ьс.
IV. Для любого числа а определено одно и только одно из
соотношений a>Q (а больше нуля), а = 0 (а равно нулю)
и а < 0 (а меньше нуля). При этом, если а > 0 и b > 0, то
IVp я + &>0.
IV2. ab > 0.
Числа, большие нуля, называются положительными; числа,
меньшие нуля, — отрицательными. Если а — b > 0, то говорят,
что число а больше числа 6, и пишут а > b (или, что то же
самое, b меньше а и пишут: b < а).
Наличие сравнения «больше» или «меньше» для любой упо-
рядоченной пары различных действительных чисел называется
свойством упорядоченности множества действительных чисел.
V (непрерывность). Каковы бы ни были непустые множества
Ла R и В cz К, у которых для любых двух элементов а е А
и b е В выполняется неравенство а /?, существует такое
число а, что для всех а е А и всех Ь е В справедливо соотно-
шение а ос Ъ.
Для того чтобы пояснить аксиоматическое определение дей-
ствительных чисел, введем понятие поля. Если в некотором
множестве X, содержащем более одного элемента, определены
операции сложения и умножения, удовлетворяющие условиям
I—III (в формулировках этих условий термин «число» надо за-
менить на термин «элемент множества X»), то множество X
называется полем. Если, кроме того, выполняется условие IV,
то поле называется упорядоченным.
Пусть X и Y — упорядоченные поля и существует такое вза-
имно однозначное отображение (биекция) f; X~>Y поля X на
44
поле У, что для любых хе X и х' е X имеют место соотноше-
ния /(x + %z)= f(A') + f(xz), f(xx') = flx)f(x'), и если х < х',
то тогда упорядоченные поля X и У называются
изоморфными, а само отображение / — изоморфизмом (относи-
тельно сложения, умножения и упорядочения).
Если упорядоченное поле удовлетворяет условию V, то оно
называется непрерывным упорядоченным полем.
Теорема I. Два любых непрерывных упорядоченных поля
изоморфны.
Эта теорема показывает, что данное выше аксиоматическое
определение множества действительных чисел определяет это
множество однозначным образом с точностью до изоморфизма.
Множество бесконечных десятичных дробей является одной
из реализаций множества действительных чисел; примеры дру-
гих их реализаций будут даны в задачах 3.43 и 8.190.
В аксиоматической теории действительного числа для лю-
бого числа а число, обозначаемое |а| и определяемое по фор-
муле
( а, если а 7^ 0,
называется абсолютной величиной числа а или его модулем
(в случае реализации множества действительных чисел в виде
бесконечных десятичных дробей это определение совпадает
с приведенным выше в п. 1).
3.28. Исходя из свойств Ч—14 суммы, доказать следующие
утверждения:
1) Если а + b — с, то а — с — Ь.
2) Число, обладающее свойством нуля, единственно.
3) Число, противоположное данному, единственно.
4) Для любого числа а справедливо равенство а — а — 0.
5) Для любых чисел а и b справедливо равенство
—а — Ь — —(а 4~ Ь}.
6) Уравнение а -ф х = b имеет в R решение и притом един-
ственное: х = b — а.
7) Используя метод математической индукции, показать, что
если i1} /2, ...» in — перестановка чисел 1, 2, ..., /г, то
(... ((а^ + а/г) + а1я) + ... + ) + ain =
= (... ((«! + а2) + а3) + ... + ап_{) +
3.29. Исходя из свойств Hi—П4 произведения, доказать сле-
дующие утверждения:
1) Число, обладающее свойством единицы, единственно.
2) Число, обратное к данному отличному от нуля числу,
единственно.
45
3) Для любого числа а #= 0 справедливо равенство
1
а
4) Для любого числа а 0 справедливо равенство
5) Для любых чисел а 0 и 6 =И= 0 справедливо равенство
1 1 _ 1
a b ab '
6) Уравнение ах = b, а =^= 0f имеет в множестве действи-
тельных чисел решение и притом единственное:
7) Равенство
справедливо тогда и только тогда, когда ad — be.
8) Для любой дроби , b 0, и любого числа с =# О спра-
ведливо равенство
а __ ас
b Ьс
9) Справедлива формула (правило умножения дробей)
а с ас
b d bd
10) Обратным элементом дроби -у, а 0, b 0, является
' Ь а ь .
дробь — , т. е. -р — — 1.
r а ’ b а
11) Справедлива формула (правило деления дробей)
£: 4 = & с d ^0.
о d be
12) Если д’ь 12, .... in — перестановка чисел 1, 2, п, то
(• • • • • Чг-1)й‘п = Г • • ((сад)аз) •. • an-i)a:l.
3.30. Исходя из свойств 1—III сложения и умножения, до-
казать следующие утверждения:
1) Для любых чисел а, b и с имеет место равенство
а (Ь — с) — ab — ас.
2) Для любого числа а выполняется равенство аО = 0.
3) Если ab = 0, то по крайней мере один из сомножителей
а и b равен нулю.
46
4) Для любых чисел а и b имеет место равенство
(—а)Ь = —ab.
5) Справедлива формула (правило сложения дробей)
6) Справедлива формула
(ai + ... + а,г)Ь — а^Ь + ... + anb, meN.
7) Справедлива формула
па = а а, /2 ge N.
п раз
3.31. Исходя из свойств I—IV, доказать следующие утверж-
дения:
1) Если а > b и b Х> с, то а > с.
2) Если а > &, то для любого числа с справедливо нера-
венство а + с > Ь + с.
3) Для любых двух чисел а и b имеет место в точности одно
из трех соотношений а > Ь, а — Ь, а < Ь.
4) Если а < Ь, то —а > —Ь.
5) Если a<bnc^d, то а + с <_ b + d.
6) Если а < b и с d, то а — с <Zb — d.
7) Если а < b и с < 0, то ас > Ьс.
8) Справедливо неравенство 1 0.
3.32. Доказать утверждения:
1) Для любого числа а справедливы соотношения
|а|^0, |а| = |—а|, —|я|^а^|а|.
2) Для любых чисел а и b справедливы соотношения
|а’+6|^|а| + 1И> I Ы— |fe| | ^ | а — Ь\, |а&| — |а| |&|.
3.33. Доказать, что два множества, удовлетворяющие аксио-
мам I—V, изоморфны между собой.
3.34. Доказать, что множество допустимых бесконечных де-
сятичных дробей образует непрерывное упорядоченное поле,
т. е. удовлетворяет аксиомам I—V.
3.2. Сечения упорядоченных множеств. Множество X назы-
вается упорядоченным множеством, если для любых двух его
элементов а и b определено одно из трех отношений а < b
(а меньше b), а = b (а равно Ь) и а > b (а больше 6), при-
чем, если а < b и b < с, то а < с. Всякое подмножество упоря-
доченного множества упорядочено.
Примерами упорядоченных множеств являются множество
Действительных чисел и вообще любое упорядоченное поле.
47
Пара непустых подмножеств Л и В = Х\Л упорядоченного
множества X называется его сечением и обозначается Л|В,
если любой элемент из Л меньше любого элемента из В. Мно-
жество Л называется нижним классом, а множество В —
верхним.
Если X — упорядоченное множество и а е X, то множества
Л = {х: х ос}, В = {у: у > cz}, (14)
а также
Л = {х: х < ос}, В = {/у: у а} (15)
образуют сечения множества X. В обоих этих случаях говорят,
что сечение А\В производится элементом а, и пишут сс = Л|В.
Если два сечения Л11 Bi и Л2|В2 в упорядоченном множе-
стве X производятся элементами этого множества: Л1|В1 =
— Xi е X и Л2|В2 = х2еХ, то эти сечения называются раз-
ными, когда равны производящие их элементы: Vi — х2. Если
же хотя бы одно из сечений А[ | Bi и Л2|В2 не производится
элементом множества X, то эти сечения называются равными,
если Л1 — Л2.
Сечение А\В называется нулевым сечением упорядоченного
поля, если оно производится нулем: А\В = 0.
Если у ненулевого сечения Л|В упорядоченного поля мно-
жество Л содержит все отрицательные элементы, то сечение
Л|В называют сечением, большим нуля, и пишут Л|В>0.
Ненулевое сечение упорядоченного поля, которое не больше
нуля, называют сечением, меньшим нуля: А | 6 < 0.
3.35. Доказать, что если X = R или X — Q, то в случае се-
чения (14) в классе В нет наименьшего числа, а в случае се-
чения (15) в классе Л нет наибольшего.
3.36. Доказать, что в упорядоченном множестве элемент, про-
изводящий сечение, единствен.
3.37. Пусть В — множество всех таких положительных ра-
циональных чисел г, что г2 > 2 и Л — Q\S. Доказать, что
пара А, В образует сечение в множестве рациональных чисел
Q и что в классе Л нет наибольшего числа, а в классе В нет
наименьшего и, следовательно, не существует рационального
числа, производящего это сечение.
3.38. Доказать, что если в упорядоченном поле выполняются
аксиомы I—IV, то аксиома V имеет место тогда и только тогда,
когда каждое сечение рассматриваемого поля производится не-
которым его элементом.
В задачах 3.39—3.43 под сечением понимается сечение мно-
жества рациональных чисел.
3.39. Пусть Л11 Bi и Л2|В2— два сечения,
Л1 Л~ Л2 = {х = Х[ Л- ^2* -^i Aj, v2 Л2},
Bl + В2 = (х = Х1 Л" *^2« Bl, Х2 GE В2}.
48
Доказать, что существует и притом единственное сечение А\В
такое, что А + А2 cz А и Bi В2 с: В. Это сечение называется
суммой данных сечений и обозначается Ai | Bi + А21В2.
3.40. Доказать, что для любого сечения А\В существует ему
противоположное, т. е. такое сечение, обозначаемое —А | В, что
Л|В+(-/1|В) = 0.
3.41. Доказать, что если —А | В < 0, то А | В > 0.
3.42. Пусть А|В1 и А2\В2 — сечения, A|Bi>0, А21 В2 > 0,
/11/12 === Х]Х2, %1 ЕЕ А, Х2 ЕЕ А2},
BiB2 = {х = Х]Х2: х,еВ1, X2GB2}.
Доказать, что существует и притом единственное сечение А| В
такое, что 41Л2ее/1, BiB2czB (это сечение обозначается
А|В1-Л2|В2 и называется произведением данных сечений).
Абсолютная величина [ Л | В | сечения А\В определяется по
формуле
( Л1 В, если
। А 1В 1 = 1 л\ п
( — АI В, если
Л1 В>0,
Л| В <0.
Произведение произвольных сечений в
Л1|В1 и Л2|В2 определяется по формуле
о,
Л] | Bi * Л2 IВ2 —
I Л, IB! |.| Л2|В2 I,
-(I А{\В{ | • I л2| В2 I),
упорядоченных полях
если А | В, = 0 или
А (В2 = 0,
если А{ |Bt и Л21 В2
одного знака,
если A | В, и Л2]В2
разного знака.
3.43. Доказать, что множество сечений рациональных чисел
с введенными в нем сложением, умножением и упорядоченностью
является непрерывным упорядоченным полем, т. е. множеством
действительных чисел.
3.3. Рациональные степени. Пусть а е R и ne N. Число, по-
лучающееся от умножения числа а на себя п раз, называется
п-й степенью числа а и обозначается а\ По определению
а° — 1 и а~п—-^, а=А=0.
Пусть ge/, п N. Число бе К — такое, что Ьп — а
(если оно, конечно, существует), называется корнем п-й сте-
пени из числа а и обозначается г\/а или ах/п.
Если а 0, b — И & 0, то число b называется ариф-
метическим значением корня п-й степени из числа а. В даль-
нейшем под корнем из неотрицательного действительного числа
49
будем понимать арифметическое значение корня, если не ого-
ворено что-либо другое.
Пусть а е R, 0, г = т/п, т^'£, п е N, тогда по опре-
делению полагается
аг^^/ат.
3.44. Пусть а R, т Z, nsZ, причем если п О пли
т 0, то а =# 0. Доказать, что тогда:
1) атап == ат+п. 2) (ат)п = (ап)т.
3.45. Пусть celR, b е IR, а 0, b 0, neN, meN.
= 2)V«=n7^. 3)\O = VaW
4) л/1-Ж’ b>0' «(W-V?1.
3.46. Пусть a e R, b e R, a > 0, b > 0, reQ, r' e Q. До-
казать, что:
= 2)а/ = Д".
3) (</)" = </". 4) (ab)r = и’'br. 5) =
3.4. Верхняя и нижняя грани. Принцип вложенных отрез-
ков. Пусть X — подмножество расширенного множества действи-
тельных чисел: XczR. Элемент хо X называется наибольшим
(максимальным) элементом множества X и обозначается
тахХ, если для любого х <= X выполняется неравенство х х0.
Элемент х0^Х называется наименьшим (минимальным) эле-
ментом множества X и обозначается minX, если для всех
х е X имеет место неравенство х х0. Наибольший и наимень-
ший элементы данного множества, если они существуют, един-
ственны.
Множество X cz R называется ограниченным сверху (сни-
зу), если существует такое действительное число а е R, что
все х е X удовлетворяют неравенству х а (соответственно
х^а)\ число а в этом случае называется числом, ограничи-
вающим сверху (снизу) множество X. Множество, ограниченное
сверху и снизу, называется ограниченным множеством.
Наименьшее (наибольшее) из всех конечных или бесконеч-
ных чисел, ограничивающих сверху (снизу) множество X cz R,
называется верхней (нижней) гранью множества X и обозна-
чается sup X или sup {х} (соответственно inf X или inf {х}).
А' е А л е А
Б0
г
Если а — sup X (соответственно а — inf X), то
1) для всех х^Х выполняется неравенство х^а (соответ-
ственно х а);
2) для любого Р < а (соответственно для любого р > а)
существует такое х^Х, что х>р (соответственно х<(3).
Если а — конечное число, то условие 2) равносильно тому,
что для любого е > 0 существует такое хеХ, что х>а— е
(соответственно х < а + е).
Если верхняя (нижняя) грань множества является конечным
числом: аеК, то она называется конечной', в противном слу-
чае — бесконечной.
Верхняя и нижняя грани данного множества единственны.
Для неограниченного сверху множества X имеем sup X =-|-оо,
а для неограниченного снизу: inf X — —оо.
Теорема 2. Всякое ограниченное сверху (снизу) непустое
множество действительных чисел имеет конечную верхнюю
(нижнюю) грань.
Из теоремы 2 и аксиом I—V действительных чисел вытекает
так называемый принцип Архимеда: для любого положитель-
ного действительного числа а существует такое натуральное
число п, что п > а.
Множество отрезков {[аЛ; /teN, действительных чисел
(ап е R, bn g R) называется системой вложенных отрезков, если
для всех п имеет место включение
[ап+г, 6«+1]cz [ап; Ьп].
Теорема 3 (принцип вложенных отрезков). Любая система
вложенных отрезков действительных чисел имеет непустое пере-
сечение.
3.47. Доказать, что множество X cz R ограничено тогда
и только тогда, когда существует такое а, что для всех х^Х
выполняется неравенство |xj^ а.
3.48. Доказать ограниченность множества
3.49. Пусть X = {х: xzQ: х2 < 2}. Доказать, что множество
X не имеет ни наименьшего, ни наибольшего элемента. Найти
sup X и inf X..
3.50. Найти верхние и нижние грани множеств
Найти наибольшие и наименьшие элементы этих множеств, если
такие элементы существуют.
3.51. Пусть X cz R и —X — {х: —хеХ}. Доказать, что
sup (~Х) = —inf X, inf (—X) = —sup X.
51
3.52. Пусть Xk <= R (k = 1, 2, ..., п) и
E = < x: x = E xk, xk(= Xk, k = I, 2, .... n
k^\ ( /2 = 1
Доказать, что
sup X Xk = E supxft, inf E = E inf
/2 = 1 /2 = 1 /2 = 1 /2 = 1
3.53» Пусть Xc R, Ус R и
X — Y = {z: z — x — y, x e X, у e Y}.
Доказать, что sup (X — У) — sup X — inf У.
3.54. Доказать, что множество всех правильных рациональ-
ных дробей т/п, 0 < т < n, meN, ncN, не имеет ни наи-
меньшего, ни наибольшего элемента. Найти его верхнюю и ниж-
нюю грани.
3.55. Отрезком [а\ Ь] рациональных чисел называется мно-
жество
[a; = {х: a^x^b, b е Q, xeQ}.
Система {[сь; ficN, отрезков рациональных чисел на-
зывается вложенной, если для любого п выполняется включение
[я^-ьь сс[йг?;
Справедливо ли утверждение, что пересечение любой системы
вложенных отрезков рациональных чисел содержит по крайней
мере одно рациональное число?
3.56. Справедливо ли утверждение, что всякая система вло-
женных интервалов {(ап‘, Ьп)}, т. е. таких, что
(а«+1; bn±\) сс (^; bn)> п ge N,
имеет непустое пересечение?
3.57. Существует ли система вложенных интервалов, имею-
щая непустое пересечение?
3.58. Исходя из аксиом I—V действительных чисел дока-
зать, что для любого числа ае R, а > 0, существует такое
натуральное число п, что п > а (как отмечалось выше, это
свойство действительных чисел называется принципом Архи-
меда).
3.59. Доказать, что из принципа Архимеда следует, что для
любых двух чисел а е R и b ^'R, О <Z a <Z Ь, существует такое
п е N, что ап > Ь.
3.60. Пусть в упорядоченном поле X выполняется принцип
Архимеда, т. е для любого а е X, а > 0, существует такое
neN, что п Z> а. Тогда следующие три утверждения для
поля X равносильны:
1) . Поле X удовлетворяет аксиоме V.
52
2) Любая система вложенных отрезков поля X имеет не-
пустое пересечение.
3) Любое ограниченное сверху непустое подмножество поля
X имеет конечную верхнюю грань.
§ 4. Прогрессии. Суммирование. Бином Ньютона.
Числовые неравенства
1. Арифметическая и геометрическая прогрессии. Арифме-
тическая прогрессия — числовая последовательность {ап} такая,
что для всех n е Н
ап+х = ап + Ф (1)
где «1, d — заданные числа; d — разность арифметической про-
грессии.
Формулы для n-го члена и суммы Sn первых п членов ариф-
метической прогрессии:
ап — а\ + (п— l)d, (2)
О ____ ai+an ____ 2ax + d(n—l)
п 2 * ' 2 *
Свойства арифметической прогрессии:
= (4)
Gk + ^k+\ = ^ + (ini А=1,2, (5)
Геометрическая прогрессия — числовая последовательность
{Ьп} такая, что для всех ne N
&л4-1 == ЬпСр (6)
где &i, q — заданные числа, Ь\ 0, 0; q — знаменатель гео-
метрической прогрессии.
Формулы для я-го члена и суммы Sn первых п членов гео-
метрической прогрессии:
Ьп = bxqn-\ 7)
(8)
Свойства геометрической прогрессии:
bn = bn-fi,l+V (9)
bkbn-&4-1 Ь\ЬП) k = 1,2, ..., п. (Ю)
Если |?|< 1, то геометрическую прогрессию называют беско-
нечно убывающей, ее сумма S выражается формулой
5 = -Д-. (11)
1 — q 4 7
4.1. Доказать, что если положительные числа а, Ь, с яв-
ляются последовательными членами арифметической прогрессии,
5а
то числа
1 1 1
д/ 6 + д4? * Vс + д/а * д/а + д/b
также являются последовательными членами арифметической
прогрессии.
4.2. Доказать, что если положительные числа ах, а2, ап
являются последовательными членами арифметической про-
грессии, то
1।I 1 п— 1
д/си +Va2 д/а2 + У«з л/ап-х'х/ап а{ + д/ап
4.3. Пусть Sn — сумма первых п членов арифметической про-
грессии. Доказать, что:
1) 5,+3 = 35,+2 —35,+i+5,. 2) 53п = 3(52,г — 5,).
4.4. Доказать, что если последовательность {ап} является
арифметической прогрессией, то при любом п 3 и любом
k е N справедливо равенство
- сх++...+(_ i)"cx+I=о-
4.5. Пусть Sn — сумма первых п членов геометрической про-
гресии. Доказать, что
5, (5з, — S2n) — (S2n — Sn)* 1 2.
4.6. Доказать, что для любого числа а и для любого neN
выполняется равенство
(1+« + а2+ • •• +а"-1)(1 +а + а2+ ... +а"+1) =
= (1+« + а2+ ... +ап)2 — ап.
4.7. Найти следующие суммы:
1) 1 + 11 + 111+ ... +11 ... 1
(последнее слагаемое — я-значное число).
2)J- + — + — + + 2z. ~~ 1
2 ‘ 22 23 4 ‘ ‘ 2П ’
3) 1+2х + 3х2+ ... +(п+1)лА
4) хп + 2хлг~1 + ... + (/г — 1) х2 + пх.
4.8. Доказать, что последовательность {Ьп} отличных от нуля
чисел является геометрической прогрессией тогда и только
тогда, когда при каждом п 3 выполняется равенство
+ ... +62_!)(^ + ^+ ••• +^п) =
= (^1^2 + ^3 + • • • +
54
2. Суммирование. Пусть а2, . .., ап — заданные числа. Их
п
сумма а\ 4" а2 + • •. -\~ап обозначается X ak, т. е.
k~\
= + а2~У ••• + cin, (12)
k называется индексом суммирования.
Сумма не зависит от того, какой буквой обозначен индекс
суммирования, т. е.
k<=x i=x Р=1
Операция суммирования обладает свойством линейности, т. е.
для любых чисел аир имеет место равенство
Е (aak + х= а X ak + ₽ X bk.
/г=1 k=X k=X
Рассмотрим сумму, содержащую тп слагаемых aih где ин-
дексы i и / принимают значения от 1 до п и от 1 до т соответ-
ственно (1 i п, 1 j т). Эта сумма обозначается
п т
ЕЕ ац или У, aif
/=1/=1 1</ <п
1 < / < т
и называется двойной суммой. Имеет место равенство
п [.т т п
Ё Ё = Ё Ё «//•
/ = 1 /=| /=1 i = i
Задачу о вычислении сумм вида
sn=£f(k),
k=A
где f(x) — заданная функция, обычно рассматривают как задачу
о нахождении Sn как функции от п. Например, если f(k) =
ak+l — ak, где {ал}—заданная последовательность, то
п п
Sn = S f (^) S (^4-1 ak) ” ^2 — ^1+^3 — а2 + • • •
k—1 k=l
• • • ^п-Х 4“ ^п+1 ^п + 1 ^1>
т. е.
п
(^л+i ^п+Х ^х* (13)
55
Пример 1. Вычислить суммы:
zL k (k + 1) ’ 2) Zj k (k + 1) (k + 2) •
fe=l fe=1
A 1) Так как n = 4~~ TTT’ т0 п0 Ф°РмУле (13)
:одим
У —!—- = V ( А---------! V [_______1
ZL k (k 4- n Lt V k k 4- 1 ) /г 4- 1 *
/г = 1 /г = 1
2) Используя равенство
1 _ 1 ( (k 4- 2) — & А
k(k+ 1)(^4-2)“ 2 U(/?4- 1) (/г + 2) J
1(- ..............1_____
2к/г(/г+1) (/? + 1) (/г+ 2)
и формулу (13), получаем
п П
V________1 = 1 у < 1______________। \
Zak(k + l)(A’ + 2) 2Z_<U(/e+l) (/г 4- !)(/? +2)7
W fe=l
-1Г1— 1 А
2 к 2 (я+ 1) («+ 2) )’ А
П р и м е р 2. Вычислить сумму
S„ = I2 4- 22 + ... + п2.
А Рассмотрим тождество
(л-Р I)3 —х3 = 3х2 + Зх+1.
Полагая в этом тождестве х = 1, 2, ..., п и складывая почленно
получаемые равенства, находим
E((^ + D3-^) = 3 X
k = \ /г=1 = l
Так как
у & : О
/г-1
то, используя формулу (13), получаем
откуда
Итак,
(n+l)3_i=3Sn +|п(„ + 1) + П1
Sn = |(2П3 + Зп2 + п) == | п (п + 1) (2n + 1).
56
Пример 3. Вычислить сумму
/г
Sn W — X sin kx.
ы
А Рассмотрим равенство
п
Sn (х) • 2 sin — — У* 2 sin kx sin 4
/г=1
Так как
2 sin kx sin = cos (/г — Г-) х — cos (k + -i-) Л-
то по формуле (13) находим
Sn (х) • 2 sin = cos — cos I п + -н-) х = 2 sin —-— х sin -z- х,
Z \ Z / £ £
откуда
. П + 1 . П
sin —-— X sin — X Y
Sn (х) —-----------------» если sin =/= 0;
smy
если sin(x/2) = 0, то Sn(x) = 0. А
Пример 4. Последовательность {хл} задана формулой
хп = axn-i + Выразить через х\, а, b и п:
1) Хп, 2) Sn = X
k=i
А 1) Так как
хЛ = ахь-] + b, xk~\ — ахк-2 + b,
то
xk — xk^ = a (xk^x — xk^2) = a (xk_^2 — xk_3) =...== ak~' (x2 — xj
t, e.
Xfy — Xk~i = ak~2(x2 — Xi).
Полагая в этой формуле k = 2, 3, ... > п и складывая получае-
мые равенства, находим
Е (Xk — %fe-i) = (Х2 — Jfj) Е ak~2
k=>2 k^2
или
Хп - Xl = (х2 - jq) г1 = ((а- 1) х} + Ь) • t
откуда
п -1 . , ап~1 — 1 , .
хл = а Xi + ~V-i »
67
При а = I последовательность {хп} является арифметической
прогрессией с разностью Ь, и поэтому
Хп = Х1 +(п— 1)Ь.
2) Sn = х{ + Е xk = Xi + а £ Xk-i + (n — 1) b,
fe=2 fc=2
Sn = Xi + a (Sn — x„) + (n — l)b,
Sn (1 — a) = Xi — axn + (n— l)b =
an-\ — 1
= Xi — anXi — ab ----------F (ft — 1) b,
откуда
o (n — V) b . ab / n-1 Л I —1
-------Ft-----nr (ft —1)4--------t~xi> ft¥=l. A
n l—a 1 (a — I)2 v y * a — 1 1
Пример 5. Последовательность {xn} задана формулой
xn = (a + |3)л'/г-1 — a$Xn-2,
где оф =j^ 0. Выразить хп через х0, ос, (3 и п.
А Исходное равенство можно записать так:
Хп OCXfi—1 :: Р (%/г—1 (XXп—2) •
Обозначим уп = хп — ахп-\, тогда уп = $Уп-\, откуда уп =
— Р""1#!, т- е- хп— ахп-\ = $п~1У1 или
Хп = ОСХп-1 4- РЛ—1//ь
Полагая хп = рпг/г, получаем
a 1
^п 1 И •
Считая а =т^= р и используя результат предыдущего примера, на-
ходим
где z\ — %1/р, у\ = xi — ахо- Отсюда получаем
= Xi ---------a₽x0 —,
Если а — р, то хп = nan~lxi — хо(п — 1) ап. ▲
а Ф р.
п п
4.9. Вычислить двойную сумму £ У ft//> если:
4=1/=1
( 0, i j,
!) ^/ = ) 1 ; 2) ft/7 = ^
к 1» 1 !•
3) aij — i — j, 4) az/ = |i — /|.
58
4.10. Доказать, что для любых чисел а и b справедливы ра-
венства:
1) a'l+i — bn+1 = (а — b) £ bkan~k.
k^Q
2п
2) a2n+l + Z>2n+1 = (a + &) X ( - l)Wn~k.
k—0
4.11. Доказать тождество Лагранжа
\£=1 7 V-l 7 \fe = l 7
4.12. Пусть {а/г} и {bn}—заданные последовательности чи-
сел. Доказать:
m
1) Если то при любом neN справедливо ра-
венство {преобразование Абеля)
2Ej ^2 ctk+i) Bfo “i~ апВп,
k=\
а при любом п е N и при любом р е N выполняется равенство
п+р п+р
2Ej G'pbk ^2 ^л+i) в^ “F ®п+рВп+р ^п+\Вп*
k=n+\ /г=п+1
n+s
2) Если Ds= то для любого peN выполняется
/=п+1
равенство
п-Ьр р-1
2Ej ^2 (^/г+/ ^n+/+i) Bj -j- atl+pDр,
fe = n+l / = 1
4.13. Вычислить суммы:
п
Е (4/г-3)(4й+ 1) ‘
/г=1
п
Е (Зй —2)(3/г+ 1) '
/г=1
п
1
кд {2k — Г) {2k +1) {2k + 3) ’
fe=i
П 1 П 2
4) E /г(/г+ 1)(й + 2) (A + 3) • 5) E (2Л- 1)(2*+ 1) *
k=l k-i
4.14. Пусть {a,,} — арифметическая прогрессия, все члены и
разность d которой отличны от нуля. Доказать, что справедливы
59
равенства:
akak+l
«= I
1
лгс4-1
у______!_____= _L f-j____________’___
“ akak+iak+2 \ а1а2 апА-1ап+2
n
1________ 1 / 1 1
, ttA+A+2flU3 \a{a2a3 %+lan+2an+3
№i
4.15. Пусть
n
Sn(p)=Ykp, peN.
fe-1
1) Доказать формулу
L Cpm+isn(p) = (n + l)m+1 - (n + 1}.
И
2) Вычислить по этой формуле Srt(3), пользуясь тем, что
5 (1)-^ + 5 (2)~ п^п+ О (2п+ О
4.16. Доказать равенства:
1) £ (2fe-1)2 = CU1- 2) £ й.й1 = (п+1)1-1.
3) £(_1)^^==(_1)—Л(±ЕО.
/с«1
4) £fe(fe + 1)^ »<»+
/г = 1
5) £fe(fe + l)(fe + 2)= w(w+1)(ra + 2) (n + ^.
k-1
6) V ^4 _ ” + 1) (2n + 1) (3»г + Зм - 1) '
k=i
-7\ V1 I.S П2(п+ 1)2(2мг + 2«— 1)
7> L k =----------15-------•
ka\
60
4.17. Доказать равенства:
п • п + I / . п '
п sin —-— a cos и + у а
1) cos (х + ^а) —---------------------------й------------
fc=*o sin ~2
п sin п- а sin (к + ~ а'l
2) У sin (х + /га) -------------2-----------
Ьэ Sin —
а=#2л£, k e Z.
а^2л/г, k e Z.
4.18. Вычислить суммы:
п
1) У, sin (2/г — 1)
/г-1
п
3) X sin2£x.
л«=1
и
5) У, sin3£x.
• 2) У, cos(2& — 1)х.
ы
п
4) У cos2fex.
k=\
п
6) X COS3 kx.
/г=1
4.19. Последовательность {xn} задана формулой xn — axn-r^
4- bxn_2- Выразить xn через x0, x\ и /г, если:
1) a = 2, b = 3. 2) a — 3, b = —2. 3) a — a, b — 1 — a, a 2.
3. Бином Ньютона. Для любых чисел a, b и любого я е N
справедлива формула бинома Ньютона:
(а + Ь)п = С'\а + Спап~ ‘b + • • • + Cknan~kbk + ... + Cnnbn, (14)
где
С‘ = 1, а = {k=l 2.....п)
Слагаемые Cnan~kbk называют членами разложения (14), а чис-
ла Ск — коэффициентами разложения или биномиальными коэф-
фициентами. Коэффициенты разложения обладают следующими
свойствами:
Cfe ----k /^lk | /nfe- 1 _ /-i r*v
п = ^п ’ Cn + Crt =Cn+l- (10)
Полагая в формуле (14) а = b ~ х, получаем
(1 + Х)п = X CnXk. (16)
k = 0
Подставляя в равенство (16) х — 1 и х = —1, находим
Ес‘ = 2'1, Ё (- l)feC^ —0. (17)
61
П р и м е р 6. Вычислить сумму
£ <сх
_fe=O
А Рассмотрим тождество
(l+x)"(l+x)" = (l +*)2".
Приравнивая в этом тождестве коэффициенты при хп и исполь-
зуя формулу (16), получаем
/>Пх>0 1 х->П-“ г I । 1 _ z^n
СЛСД -j- С/г Cn-f- ... 4“ Cn <Un I ••• J CnUn 1X3 С2П.
n
Это равенство в силу (15) можно записать в виде 2 (Cnf = С 2^
о
Следовательно,
X (С*)2 = <Х (18) А
/г = 0
Пример 7. Вычислить сумму
А Используя равенства
1 pk ___ п (п — 1),., (п — k + I)
(k+\)kl ~
(п 4- 1) и (п — 1) ... (п 4- 1 — Л) __ Сц+\
(п 4" О 4- 1) • 4~ 1 э
получаем
п rk п+1
т+т Z С«+* А
/г-О Л== 1
4.20. Написать формулу бинома Ньютона:
1) (1+х)5. 2) (tz + fo)6.
3) U + t/)7. 4) (a-fe)8.
4.21. Найти член разложения > содержащий jA
4.22. Найти коэффициент многочлена:
1) (1 — х ф- х2)3 при л3.
2) (1 + 2х — Зх2)4 при х3 и лА
3) (1 + х2 — я3)9 при л8.
4) (1 + х2 + х3)7 при х11.
15
5) У (1 ф- x)fe при х3.
л=з
62
4.23. Вычислить следующие суммы:
1) 2(6+1)С*. 2)2(6-1)С^.
Ы /г«1
/г п
3)£сг“ 4)£сГ'-
/г-1 ы
т п
5) X (- № т < п. 6) £ (- 1)* (С£)8.
/г=0 &=»0
4.24. Доказать следующие равенства:
1) XfeC* = n2rt~l. 2) £(-1)^16С^ = 0.
/г-1
s tn
Q\ V* __ r>S V' yort /оП+1
£) /л —Ь/п+гг , ^n+k — bft+m+i.
fe=»0 fe=0
V2 c« _ 3 1 (nV'”1' C/t —
’ Zufe + i n +1 • °'Zu fe + i — «+1 •
к—Q k—1
4.25. Найти члены разложения, являющиеся целыми числами:
1) (V2 + V3 )5. 2) (V5 - V2 )8.
4.26. Найти наибольший коэффициент многочлена:
1 \ Г 1 £ 3 V Q4 / 1 . 2 уо
) V4 4 Х) ’ (з + 3 Х) ‘
4.27. Найти наибольший член разложения (1 + ^2)30.
4.28. Доказать формулы:
1) (а + Ь + с)2 — а2 + Ь2 + с2 + 2аЬ + 2Ьс + 2ас.
2) (а + b + с)3 — а3 + Ь3 + с3 + 3 (а2Ь + а2с + Ь2а +
+ Ь2с + с2а + с2Ь) + бабе.
3) (а + b + е)4 = а4 + Ь4 + е4 +
+ 4 (а3б + а3с + Ь3а + Ь3с + с3а + с3Ь) +
+ б (а2Ь2 + а2с2 + Ь2с2) + 12 {a2bc + b2ac + c2ab),
4.29. Доказать формулу
Uj + Х2 + . . . + хр) = ~kx\k2\ ... kp\ 1%22 • • • %рР»
+ ••• +^р=/г
где суммирование ведется по всем целым неотрицательным k[t
^2, .kp таким, что • + kp = п.
4. Числовые неравенства, Основные свойства неравенств:
1) если а > б, b > е, то а > с;
2) если а > б, то а + с > б + с при любом с;
63
3) если а > b, с > d, то а + с > b + d\
4) если а> b и с > 0, то ас > Ьс,
если а > Ь и с < 0, то ас < Ьс\
5) если a>b>0o>d>0, то ас > bd\
6) если а^6>0ис>^>0, то ~;
' de
7) если а > b 0, то ап > Ьп при любом не N;
8) если а > Ь, то а2п+1 > 62л+1 при любом ne N;
9) если а > 6^0, то "\/а > д/b при любом neN;
10) если а > Ь, то 2пЛ^/а > 2n+\/b при любом n&N.
Некоторые важные неравенства:
1) Для любых действительных чисел а и b выполняется не*
равенство
a2 + b2^2ab. (19)
2) Среднее арифметическое двух неотрицательных чисел не
меньше их среднего геометрического'.
(20)
Неравенство для среднего арифметического и среднего гео*
метрического справедливо для любых п неотрицательных чисел
а 1, a2i . -., ап, т. е.
Д'] + ^2 + • » + Дп П/ { q П
п z^'V ^1^2 • • • ®п* (21)
Равенство в (21) имеет место лишь при а\ — а2 = ... — ап.
Доказательство неравенства (21) дано в § 2 (пример 8).
3) Для любых действительных чисел ai, а2, ..., аП) b\yb2t ...
Ьп выполняется неравенство Коши — Буняковского
Равенство в (22) имеет место тогда и только тогда, когда су*
шествуют такие числа аир, что а2 + р2 =И= 0 и для всех k —
— 1, 2, ...» п выполняется равенство aak + fibk = 0.
Пример 8. Доказать, что для любых действительных чи*
сел а, by Су d справедливо неравенство
а4 + 64 + с4 + d4 ^abed.
А Используя неравенство (21), получаем
у (ал + Ьл + с4 + d4) \/a4b4c4d4 = | abed | abed,
откуда следует искомое неравенство. А
С4
Пр и м е р 9. Доказать неравенство Коши — Буняковскбго.
А Если ai = a'2= - • • = йп — 0, то в (22) имеет место ра-
венство. Пусть хотя бы одно из чисел а\, а2, ..., ап отлично от
нуля, тогда of + а2 + ... + а2 > 0. Рассмотрим квадратный
трехчлен относительно х:
й
ах2 + 2Ьх + с = X (akx + Ьк)2,
где
п п п
а = Е b = X акЬк, с = Е b2k.
Л=1 k k~\ k=l -
Так как {akx + bk)2 0, R (k = 1, 2, ..., и), то дискрими-
нант квадратного трехчлена ах2 + 2Ьх + с неположителен:
Ь2 ас. Следовательно,
/ п \2 / п \ / п \
Выясним, в каком случае в (22) имеет место равенство.
Пусть Ь2 = ас. Тогда, если а = 0, т. е. а\ = а2 = ... = ап — О,
то, положив а = 1, р = 0 (а2 + (З2 #= 0), получим
aak + Р&£ = 0 ’ (k — 1, 2, ..., п).
Пусть а Ф 0, тогда квадратный трехчлен ах2 + Ъх + с имеет
корень х0 (так как дискриминант трехчлена равен нулю), т. е.
- п
f. ах2 + Ьх0 + с = £ (afex0 + btf = 0.
Отсюда следует, что akXo + Ьк = 0 при k — 1, 2, ..., п. Поло-
жив а = х0, Р = 1, получаем аак + $Ьк = 0, где а2 + р2#=0
'(k= 1, 2, ..., п). ▲
Легко проверить, что при выполнении условий aak + $bk = 0
(k= 1, 2, ..., п) соотношение (22) превращается в равенство.
4.30. Доказать, что для любых действительных чисел а, b
справедливы неравенства:
1) а2 + &2> 2\аЬ\. 2) \а — й|>||а| —1&||. '
3) (a24-62)(a4 + &4)>(a3 + fe3)2.
4) а4 + й4 a3b 4- ab3.
4.31. Доказать, что для любых положительных чисел а, b
справедливы неравенства
2 а+Ь ГаГуЬ2
1 , 1 У аЬ^. 2 V 2
а + Ь
связывающие среднее гармоническое, среднее геометрическое,
среднее арифметическое и среднее квадратическое чисел а и Ь.
3 Л. Д. Кудрявцев и др. 65
4.32. Доказать, что для любых неотрицательных чисел а, Ь
справедливы неравенства:
1) ап + bn (а + b)n, п е N.
2) ап + bn > abn~k + ЬкаГк, п е= N, k <= N, k < n.
3) (a + b)n 2"-1 (an + bn), n N.
4.33. Доказать, что если | b | < | а | /2, то
I—^-1< —
I a — b I | а |
4.34. Доказать, -что для любых действительных чисел а, b
таких, что а2 + Ь2 — 1, выполняется неравенство | а + b | ^2.
4.35. Доказать, что для любых действительных чисел а, Ь, с
справедливы неравенства:
1) а2 4- Ь2 + с2 ab + Ьс + ас.
2) (а + Ь + сУ^З(а2 + Ь2 + с2).
3) Va2 + 62 + c2<la| + m + ld.
4) (а + b + с)2 ^3(ab + Ьс + ас).
5) (ab + Ьс 4- ас)2 3(а 4- b 4- с) abc.
6) (а 4- b — с)2 4- (Ь 4- с — а)2 4- (а 4- с — b)2 ab 4- Ьс 4- ас.
4.36. Доказать, что для любых положительных а, &, с спра-
ведливы неравенства:
Ьс . ас . ab .
О — + 1Г + — >а + Ь + с.
2) _L _|_ _L _i_ __L_ и—L_ j—L_,
а b с л/bc 'у/са 'y/ab
а3 + Z?3 4- с3 а + Ъ + с
а2 4- Ь2 + с2 3
4) 4 + - + ->3-
1 b с а
г-ч 2 , 2_____, 2 9
Ь-\‘с'с-\-а'~а-\-Ь^а-\-Ь-\-с'
PA а I Ь I с > А
b 4- с с 4- а а 4- b 2
4.37. Доказать, что для любых неотрицательных чисел а, 6, с
справедливы неравенства:
1) (а 4- Ь) (Ь 4- с) {с 4- а) 8 abc.
2) а3 4~ &3 4~ £3 ЗаЬс.
3) (а 4- b 4- £) 4“ Ьс 4- ас) 9аЬс.
4) (ab 4~ Ьс 4- ас)3 27 abc.
5) (а 4- b — с) (Ь 4- с — а) (с 4- а — b) abc.
66
6) (a + b + c)3 — 4 (a + b + c) (ab + be + ac) + 9abc > 0.
7) 3 (a3 + b3 + £3) (a + b + c) (ab + ac + be).
8) a4 + b4 + c4 abc(a + b + c).
4.38. Доказать, что для любого натурального п 3 выпол-
няются неравенства:
1) nn+1 > (п + 1)п.
2) (п\)2>пп.
4.39. Доказать, что для любого ne N справедливы неравен-
ства:
i »4T+^ + ... + i>|.2)(i+4)"<(>+a!"-
3) (2п)! < 2"“(»|)2. 4)£i<2.
fe=l
4.40. Доказать, что для любого натурального п 2 справед-
ливы неравенства:
1) 2 < (1 +-Y<3. ,2) 1 < д/«< 1 + -?=.
\ nJ л/п
з)
4.41. Доказать неравенство
У 1 _> 1.
“ vz? V п — k +1
fe = l
4.42. Пусть а > 0, п е N, k <= N, k п. Доказать, что
(l+a)rt> \+Cknak.
4.43. Доказать, что если х > 0, то справедливы неравенства
Г 1 + 2T7<Vr+r<i+^-.
4.44. Доказать, что если |х| < 1 и п N, п 2, то
(1 — х)п + (1 +*)” < 2\
4.45. Пусть а > 0, neN. Доказать, что
а + а2 + ... + а2п~х п (1 + а2п) — ап.
4.46. Пусть я>0, не N, me N, т ^п. Доказать, что
3*
67
4.47. Доказать, что если А — наименьшее, В — наибольшее
из чисел аь а2, ..., ап, то справедливо неравенство
д + #2 + »• • + Q/г < g
П •
4.48. Пусть Hi, а2, ..., ап — действительные числа, А — наи-
меньшее, а В — наибольшее из чисел |ai|, |а2[, |ап|. До-
казать, что _
л / ^ + ^ + ’ • • а
л < Л/-----------------< в.
4.49. Доказать, что для любых действительных чисел щ,
а2, ...» ап справедливо неравенство
(а(+а2+ ... + ап)2^п(а2 + а2 + ... +а2п).
4.50. Пусть аь а2, ..., ап — действительные числа, Ь2, ...
..., Ьп — положительные числа, М — наибольшая, а' т — наи-
меньшая из дробей 4~-, 4+ ..., Доказать, что
b\ U2 оп
41 4~ Ог + ••• + 4п
bi + bi + ... + bn
4.51. Доказать, что для любых действительных чисел аь
а2, а,п и Ь\, Ь2, ..., Ьп, удовлетворяющих условиям
п п
Е «1=Е ^=1
6=1 * /г-1 k
справедливо неравенство
п
Е akbk
*=i
<1.
4.52. Доказать, что для любых положительных чисел at,
а2, ..., ап справедливо неравенство
(01+02+ ••• +оп)(-^ + -^-+ ••• +^)>«2-
4.53. Доказать, что если ai, а2, ..., ап — положительные
числа такие, что aia2 ... ап = 1, то
(1+ai) (1+а2) ... (1+^)>2«.
4.54. Пусть щ > —1 (/=1,2, ..., п) и числа щ имеют один
и тот же знак. Доказать неравенство
(1 + а\) (1 Ч” Яг) (1 4“ Я/г) 1 + Щ + я2 + ... Ч"ЯЛ-
4.55. Пусть хь ..., аь а2, ..., ап — произвольные дей-.
•ствительные числа, а > 0. Доказать, что
S8
4.56. Доказать, что для любых положительных чисел &i,
а2, •.., ап справедливы неравенства
4~ Д2 + • • •
п
связывающие среднее гармоническое, среднее геометрическое,
среднее арифметическое и среднее квадратическое чисел
$2> • • • j Un*
4.57. Доказать, что если
... ап, 61 &2 ••• 6п,
то
fll 4~ ^2 + • « 4~ Дп + ^2 + • • • 4" 1 4~ ^362 4~
п п """ п
4.58. Пусть положительные числа аь а2, ..., ап являются
последовательными членами арифметической прогрессии. Дока«
зать, что
V«1«„ < • • • ап < ..
4.59. Доказать, что если А — наименьшее, В — наибольшее
из положительных чисел а,2> ..., то справедливы нера-
венства: •
1) А < V^i^2 • • - ап^В.
4.60. Доказать, что для любых действительных чисел ац
аъ ...» ant bi, Ьъ ...» bn справедливы неравенства:
69
4.61. Доказать, что если а\ 0, а2 О,
то
., ап 0 и ре N,
§ 5. Комплексные числа
1. Определение комплексных чисел. Свойства операций. Ком*
плексными числами называются выражения вида а 4- bi (а и
b — действительные числа, i — некоторый символ), для которых
следующим образом вводятся понятие равенства и операции
сложения и умножения:
а) два комплексных числа ai + ba и а2 + b2i равны тогда
и только тогда, когда а\ — а2 и Ь\ = Ь2\
б) суммой чисел а} + b\i и a2-\-b2i называется число
+ #2 + (Ь\ + b2) й,
в) произведением чисел ai + bit и а2 + b2i называется число
^1^2 — b\b2 4" (а 1Ь2 a2b\)i.
Таким образом, сложение и умножение комплексных чисел
производятся согласно формулам
+ b\i) + (а2 + b2t) — а\ 4“ а2 + (&i + b2) i, (1)
(ay + b{i) (а2 + b2i) = aiа2 — b\b2 + (&1&2 4“ chb\)i. (2)
Множество всех комплексных чисел обозначают С. Эле-
менты множества С (комплексные числа) часто обозначают од-
ной буквой, причем обычно используют для этого буквы 2, w,
иногда с индексами, например, zi, z2i wq. Равенство z = a-}-bi
означает, что комплексное число а 4~ bi обозначено буквой г.
Операции сложения (1) и умножения (2) обладают следую-
щими свойствами:
1. Коммутативности сложения
21 4“ 22 = 22 4“ 21.
2. Ассоциативности сложения
(21 4" 22) 4“ = 21 4“ (г2 4" 2з) .
3. Для любых комплексных чисел z\ и z2 существует комп-
лексное число z такое, что z\ 4- 2 = 22. Это число называется
разностью чисел z2 и zx и обозначается z2.~— 21. Разность комп-
лексных чисел z2—a2-\~b2i и Zi = ai 4~&U находится по фор-
муле
22 — 21 = (а2—ад)-\-(Ь2— bi)i. (3)
4. Коммутативности умножения
2122 = 2221.
70
5. Ассоциативности умножения
(Z1Z2)Z3 = Z1(Z2Z3).
6. Для любых комплексных чисел zi =+ 0 + О/ и z2 существует
число z такое, что Z\Z — z2. Это число называется частным
комплексных чисел z2 и z\ и обозначается или z2lz\. Де-
ление на комплексное йисло 0 + 0/, которое называется нулем,
невозможно. Частное z^/zx двух комплексных z2 = a2 + &2/ и
Z} — а\ + Ъ\1 при условии, что делитель отличен от нуля, может
быть найдено по формуле ,
^2 __ «1^2 + &1&2 I — a2bi .
a2 + b2 + a2l+b2 1' W
7. Дистрибутивности
£1 (^2 + г3) = zjz2 + Z1Z3.
Комплексное число вида a + 01 отождествляют с действи-
тельным числом а, т. е. считают, что а + 0-i = а. Например,
0 + 0-/ = 0, 1 + 0-/ = 1, — 1 + 0-/ = —1.
. Таким образом, множество действительных чисел является
подмножеством множества комплексных чисел, т. е. R cz С.
Числа 0 + bi называют чисто мнимыми и обозначают Ы. На-
пример, 0 — 21 = —2i, 0+1-/ = /. Действительное число а на-
зывается действительной частью комплексного числа а + bi.
Действительное число Ь называют мнимой частью комплексного
числа а 4- bi. Числа а Ы и а — Ы, т. е. числа, отличающиеся
только знаком мнимой части, называются сопряженными комп-
лексными числами Число, сопряженное числу г, обозначается
г.. Комплексное число i принято называть мнимой единицей.
Для мнимой единицы справедлива формула
i2 = -l. (5)
Формула (2) умножения комплексных чисел не нуждается в за-
поминании, так как она получается, если формально перемно-
жить двучлены <214-^1/ и п2 + &2/ по обычному правилу умно-
жения двучленов и затем в соответствии с формулой (5) заме-
нить i2 на —1.
Пример 1. Найти сумму и произведение комплексных чи-
сел
Si = —2 4- 3/, Z2 = 7 — 81.
А По формуле (1) находим
21 + z2 = (—2 + 7) + (3 —8)/= 5 —5/.
Произведение находим формальным перемножением двучле-
нов (—2 + 3/) и (7 — 8/):
ZiZ2 = (—2 4- 3Z) (7 — 8/) = —14+ 16/ + 21/ —24Z2 = 10 + 37/ а
71
1
Пример 2. Найти сумму и произведение сопряженных
комплексных чисел.
А Пусть z = х + yi, тогда z = х — yi.
Сумму находим по формуле (1):
zi + £2 = (х + yi) + (х — yi) = 2х.
Произведение находим по правилу умножения двучленов:
2122 = (X + yi) (х — yi) = х2 — xyi + xyi — y2i2 = x2 + у2.
Таким образом, сумма сопряженных чисел есть всегда число
действительное, а произведение — число действительное и, бо-
лее того, неотрицательное. А
Пример 3. Даны комплексные числа zx — —1 + 6/ и z2 =
= 2 + 5/. Найти разность г2 — 21 и частное Zz/zx.
А По формуле (3) находим
z2 — 21 =(2 + 5/) — (— 1 +Ы)= 3 — i.
Частное находим по формуле (4):
Z2 _ 2 + 5/ _ (- 1)-2 + 6-5 , (- 1)-5-2-6 28 _ 17
21“-1+6/" (_ i)2 + 62 (— 1)2 + 62 37 37 А
Пример 4. Выполнить действия'
3 + i
(1 + Z) (1 -20 •
А Перемножив числа, стоящие в знаменателе, получим
3 + i ____ 3 i ______ 3 z
2=== (1 + i) (1 - 2/) — "Т-2/+ /+ 2 — 3 —Z *
Далее можно воспользоваться формулой (4), но удобнее посту-
пить иначе. Умножим числитель и знаменатель дроби на число,
сопряженное знаменателю, тогда
(3 + /)(3 + /) _ 9 + 6/-1 _ 4 3 . .
2 (3 —/) (3 +/) 9+1 5Г51, А
5.1. Доказать свойства 1—7 операций сложения и умноже-
ния комплексных чисел.
5.2. Доказать формулу (5): /2 = — 1.
5.3. Найти сумму и произведение комплексных чисел zx и
z2, если:
1) zj — 4 + 5/, Z2 = 3 — 2/.
2) zx = 0,5 — 3,2/, Z2= 1,5 — 0,8/.
3) 2i = д/2 — V3 /, 22 — д/2 + V3 i-
5.4. Найти разность z2 — zi и частное z2/zi, если?
1) Zx = 3 + 4/, z2 = 0,4 — 0,2/.
2) zx = 1 — 2/, z2 = 0,6.
3) Zi = ^/5 — ц z2 = д/5 ” 2/.
72
5.5. Найти мнимую часть г, если:
1) z = (2-Z)3(2+lh). 2)
оч 5 + 21 3 — 4г 1
8)г = Т^5Г-Т+зГ“7
5.6. Выполнить действия:
1 + i J _ i 13 + 12г (1 +- 2г)2
-г^т+т+т- 4) -бГ-8 +-^+т~-
(1 +2г)2-(1 - г)8
’ (з + 2г)з - (2 + г)з '
5.7. Определить, при каких действительных значениях х и у
комплексные числа
Z! = у2 — 7у + 9xi и гг — —12 + 207 + x2i
равны.
5.8. Определить, при каких действительных значениях х и у
комплексные числа
zx = 8х2 — 20z9 и г2 = 9х2 — 4 + 1 Qyi3
являются сопряженными.
5.9. Решить уравнения:
1) (1 +2i)(z — z) + (4z — 3) (1 — iz)+ 1 + 7z = (K
2) г2 + г = 0.
5.10. Решить систему
( Zi + 2z2 = 1 + z,
( 3z{ + iz2 = 2 —- 3z.
5.11. Доказать равенства:
’ 1) Zl + z2 = Z1 + %2- 2) Zi — Z2 = z\ — ~Z2.
3) Z^2 = • ^2- 4) (zjz2) = zjz2l z2 o.
5) (zn} = (z}t\ neN.
2. Геометрическое изображение комплексных чисел. Модуль
и аргументы комплексного числа. Каждому комплексному числу
а-\-Ы может быть поставлена в соответствие точка М(а; Ь) ко-
ординатной плоскости и, наоборот, каждой точке М(а\Ь) пло-
скости — комплексное число а + bi. Установленное таким обра-
зом соответствие является взаимно однозначным. Оно дает воз-
можность рассматривать комплексные числа как точки коорди-
натной плоскости. Эту плоскость называют комплексной пло-
скостью. Ось абсцисс называют действительной осью (на ней
73
расположены точки, соответствующие действительным числам),
ось ординат — мнимой осью (на ней лежат точки, соответствую-
щие мнимым числам).
Часто комплексное число а + Ы удобно интерпретировать
как вектор ОМ (рис. 6). Каждому вектору плоскости с началом
в точке 0(0; 0) и с концом в точке М(сг, Ь) соответствует комп-
лексное число а + Ы и наоборот. Точке 0(0; 0) соответствует
нулевой вектор.
Соответствие, установленное между множеством комплекс-
ных чисел, с одной стороны, и множествами точек или векто-
ров плоскости, с другой стороны, позволяет комплексные числа
называть точками или векторами и говорить, например, о век-
торе а + bi или точке а + bi.
Изображение комплексных чисел векторами позволяет дать
простое геометрическое истолкование операциям над комплекс-
ными числами. Например, сумма комплексных чисел геометри-
чески может быть истолкована как вектор, равный сумме век-
торов, соответствующих слагаемым комплексным числам (рис. 7).
Модулем комплексного числа называется длина соответ-
ствующего этому числу вектора. Для модуля числа z исполь-
зуется обозначение |z|. Модуль комплексного числа z = а-{- Ы
может быть вычислен по формуле
I z | = 'х/а2 + Ь2 . (6)
Аргументом комплексного числа z=A=0 называется угол ме-
жду положительным направлением действительной оси и векто-
ром г, причем этот угол считается положительным, если отсчет
ведется против часовой стрелки, и отрицательным, если отсчет
производится по часовой стрелке. Для числа z = 0 аргумент не
определяется.
Аргумент комплексного числа, в отличие от модуля, опреде-
ляется неоднозначно. Например (рис. 8), аргументами числа
z = 1 + i являются следующие углы: <pi =-^, ср2 = -j —
74
— — л, ф3 — ~ - 2л = —~ ; вообще, каждый из углов qpfe = -^+
+ 2л&, где k — произвольное целое число
Любые два аргумента комплексного числа отличаются па
число, кратное 2л. Для обозначения множества всех аргументов
числа z = а + Ы используется символ
argz или arg(a + bi). Если речь идет о
каком-либо одном из аргументов, то его
обычно обозначают буквой ср.
Действительная и мнимая части
комплексного числа z = а + Ы выра-
жаются через его модуль |г] = г и аргу-
мент ф следующим образом (рис. 9):
а = г cos ф,
а • (7)
6 = г Sin (р. Рис 9
Таким образом, аргументы ф комплексного числа могут быть
найдены из системы уравнений
cos ф
sin ф
а
а2 + Ь2
b
'у/а2 + Ь2
(8)
Аргументы комплексного числа z = а + bi (а Ф 0) можно
найти и из уравнения
tgT = Z?/a, (9)
которое является следствием системы (8). Это уравнение не
равносильно системе (8), оно имеет больше решений, но отбор
нужных решений (аргументов комплексного числа) не пред-
ставляет труда, так как из алгебраической формы записи комп-
лексного числа всегда видно, в каком квадранте комплексной
плоскости оно. расположено.
Пример 5. Найти модули комплексных чисел
z{ — 2 — Z, z2 = 2 д/б + 5/, z3 — i.
А По формуле (6) находим
1^1 = 74+4 = 75, [г21 = 7(2 7б)2 + 52 =7.
75
Для вычисления модуля z3 нет необходимости использовать
формулу (6). Длина вектора z3 = I, очевидно, равна единице,
поэтому |z3|== 1. ▲
Пример 6. Найти аргументы комплексных чисел
Z] = —/, 22 = 1, 2з = —1 + I*.
. А Построив векторы zi, Z2, z3, находим один из аргументов
для каждого числа: <pi = —л/2, ф2 — 0, ф3 = Зл/4. Следова-
тельно,
arg^ — —+ 2л&, arg z2 = arg z3 — + 2л£,
где k — произвольное целое число. ▲
Пример 7. Найти аргументы комплексного числа г =
= -1 — д/З/.
А В данном случае а ==—1, 6=—V3« Система (8) имеет
вид
( cos ср = — 1/2,
1 sin ф — — V3/2.
Решив эту систему, найдем Ф& = -у + 2л&, k е Z. Следова-
тельно,
argz =-^-+ 2лй, k е Z. а
Пример 8. Найти аргументы комплексного числа г =»
= — д/3 Ч- /.
А Каждый из аргументов ф числа z =— '\/3 + i удовлет-
воряет уравнению
tg<p = —1/V3.
Из этого уравнения следует, что
Фй = — ~ + лй, k е Z.
Так как число z = — д/3 + i расположено во втором квадранте
комплексной плоскости, то его аргументами будут числа ф* при
нечетных значениях k. Следовательно,
arg(-7з + г) = -з + л(2n + 1) =-^ + 2лп, nsZ. д
5.12. На комплексной плоскости даны точки zi, Z2, z3, являю-
щиеся вершинами треугольника. Найти точку пересечения его
медиан.
5.13. В точках zb Z2, ...» zn комплексной плоскости рас-
положены материальные точки соответственно с массами mu
, т,п. Найти центр тяжести такой системы материальных
точек,
76
5.14. На комплексной плоскости даны точки zb z2, z3f яв-
ляющиеся тремя последовательными вершинами некоторого па-
раллелограмма. Найти четвертую вершину этого параллело-
грамма.
5.15. На комплексной плоскости даны точки zi = 6 + 8/,
22 = 4 — 3/. Найти комплексные числа, соответствующие точкам,
лежащим на биссектрисе угла, образованного векторами zi и z2.
5.16. Найти модуль комплексного числа z:
1) 2 = —4. 2) z =—I. 3) z = —5 —2д/б/.
4) z = 1 + cos (8л/7) + i sin (8л/7).
5.17. Решить уравнение:
1) z2 + 3|z| = 0. 2) z2 + 21 z | = 1.
3) z2 + |z|2 = 0. 4) z2 + z|z| + |z2| = 0.
5.18. Доказать равенства:
1) |ziz2| = |zi||z2|. 2) |zi/z2| = |zi|/|z2|, z2=#0.
5.19. Доказать неравенства
llzi|~|z2|]^|zi + z2|<|zi| + |z2|.
5.20. Доказать, что |zi— z2|, т. e. модуль разности комплекс-
ных чисел zi и г2, равен расстоянию между точками z\ и z2
комплексной плоскости.
5.21. Найти множество точек комплексной плоскости, задан-
ное условием:
1) |г+Г|=1. 2) 12 - i\<\z + /|.
3) |z + 2z-l]<2. 4) |z2 |2 + |z + 212 = 26.
5) |z — 2 | + 12 + 2 | = 26. 6) sin|2 | > 0.
7) lg| z — 10/1 < 1. 8) | z |2+ 3z + 3;z = 0.
5.22. Решить систему уравнений:
1) | z + 1 — i | = 13 + 2i — z| = | z + I |.
f|z+11 = 12 + 21, ( (l-z)z = (!+/)z,
t 132 + 9 1 = 152 + 10/1. 3) t 1z2 + 51/1 = 1.
5.23. Доказать, что система уравнений
| |z + 1 -d = V2,
I |z| = 3
He имеет решений.
5.24. Найти аргументы комплексного числа:
1) z = z. 2) z = —1. 3) z = 8. 4) z = 2 — 2Z.
б) z — sin(tt/9)— Zcos(jt/9). 6) z = 1 + cos(n/7) + /sin(jr/7).
77
5.25. Какое множество точек комплексной плоскости задает-
ся условием:
1) Один из аргументов числа z равен нулю.
2) Один из аргументов равен 5я/2.
3) Один из аргументов ф удовлетворяет неравенствам
2л < Ф < Зя.
4) Один из аргументов ф удовлетворяет неравенствам 0
ф < 2л?
5.26. Какое множество точек комплексной плоскости задает-
ся условием:
1) argz = (2k + 1)л;, k e Z.
2) n(8& + l)/4 < arg (г + f) < n(4& + l)/2, 6eeZ?
5.27. Среди комплексных чисел z, удовлетворяющих условию:
1) |z+l—f|=l, 2) | z + 3 — д/3/| найти число,
имеющее наименьший положительный аргумент.
5.28. Где находится точка г2, если точка z принадлежит пря-
мой Ims = 1?
5.29. Где находится точка z комплексной плоскости, если
точка г2 принадлежит мнимой оси?
5.30. Пусть г¥=±1. Доказать, что точка (z—1)/(г+0
принадлежит мнимой оси тогда и только тогда, когда точка z
принадлежит окружности радиуса R = 1 с центром в точке
z — 0.
. 5.31. Может ли точка z = 0 принадлежать какому-нибудь
многоугольнику, вершины которого находятся в точках
Zk = 1 + z + 22 + ... + Zk~\ I Z | < 1 ?
3. Тригонометрическая форма комплексного числа. Умноже-
ние и деление комплексных чисел, записанных в тригонометри-
ческой форме. Каждое комплексное число z — а-\-Ы, отличное
от нуля, может быть представлено в виде
z = г (cos ф + i sin ф),
где г — модуль числа, а ф — один (любой) из его аргументов.
Это представление комплексного числа называется тригономет-
рической формой комплексного числа. Запись числа в виде
z = а + Ы называют алгебраической формой комплексного
числа.
Для того чтобы перейти от алгебраической формы числа к
тригонометрической, достаточно найти модуль комплексного
числа и один из его аргументов.
Два комплексных числа, записанные в тригонометрической
форме
z\ = r\ (cos ф1 + i sin ф1) и г2 — r2 (cos ф2 + i sin ф2),
равны тогда и только тогда, когда
Г1 = Г2, Ф1 ф2 “Ь 2л&, k G— Z,
78
т. е. когда модули чисел равны, а аргументы отличаются на 2л&,
где k — некоторое целое число.
Запись комплексных чисел в тригонометрической форме ис-
пользуется при умножении и делении чисел. Пусть
= ri(cos<pi + Zsincpi) и г2 = r2(costp2 + Zsincp2)
— два числа, записанные в тригонометрической форме. Тогда
2^2 = Г1Г2 (cos (ф! + ф2) + i sin (<Р1 4- ф2)), (Ю)
-|1- = 1!-(С08(ф1 — ф ) 4-Z sin (Ф1 — ф2)). (11)
%2 ~2
Следовательно,
|ziz2| =/"1Г2, ' arg(zi22)= Ф1 4-<Р2 4-2л/г, ieZ,
arg А = ф1 _ ф2 4-2Л&, feeZ.
Таким образом, модуль произведения двух комплексных чи-
сел равен произведению модулей этих чисел, сумма аргументов
сомножителей является аргументом произведения; модуль ча-
стного двух комплексных чисел равен частному модулей этих
чисел, разность аргументов делимого и делителя является аргу-
ментом частного.
Пример 9. Записать числа zi ——1—/, z% =—2, zs = i
в тригонометрической форме.
а Так как ^^ = ^/2, a ф1 = — Зл/4, то
= д/2 (cos ( — Зл/4) + i sin ( — Зл/4)).
Модуль 22 равен 2, а одним из аргументов 22 является угол
ф2 = л, поэтому
z2 = 2 (cos л + i sin л).
Учитывая, что 123] = 1, а ср3 = л/2 —один из аргументов 23, по-
лучаем
23 = cos (л/2) + i sin (л/2). А
Пример 10. Записать числа
21 = 2соэ(7л/4) — 2i sin (л/4), 22 = —соз(л/17) + i зш(л/17)
в тригонометрической форме.
А Для записи чисел z\ и 22 в тригонометрической форме нет
необходимости предварительно находить их модули и аргументы
(хотя сделать это совсем не трудно). Воспользуемся тем, что
соз(7л/4) = cos (—л/4), а —sin (л/4) = sin (—л/4),
и сразу получим тригонометрическую форму для первого числа
21 = 2 (cos (—л/4) + i sin (—л/4)).
Аналогично, учитывая, что
л / л \ 16л
—- COS -уу = COS I Л-jyJ = COS -уу,
79
a
sin л/17 == sin(jt — л/17) = sin 16л/17,
получаем
Z2 = cos(16л/17) + i sin(16n/17). A
Пример 11. Найти произведение чисел
z{ — д/2(соэ (11л/4) + i sin (11л/4)) и z2==
= V$ (cos (Зл/8) + I sin (Зл/8)).
л Так как \zx\ = |z2|=VS» то (2t221 = 4.
Аргументом произведения Z\Z2 будет сумма
4- <р2 = 11л/4 4~ Зл/8 = 25л/8.
Следовательно,
2122 “ 4 (cos (25л/8) 4- i sin (25л/8)),
или
2i22 = 4(соз(9л/8)4- rsin(9tt/8)). А
Пример 12. Записать в тригонометрической форме комп-
лексное число
(cos (л/3) — i sin (л/3)) (V^ 4~ О
2 = -----------:--:------------♦
I — 1
А Число 2i =: cos(л/3) — /5ш(л/3) имеет модуль, равный 1р
и аргумент epi = —л/3; число 22 — -/3 4~ * имеет модуль 2 и
аргумент ф2 = л/6; число z3 — i—1 имеет модуль V^ и аргу-
мент фз = Зл/4. Поэтому
а аргумент
л । л Зл 11
ф = Ф1+ф2 — Фз = —у + у---4~ = ‘~’12’Я-
Следовательно,
^ = V2(C0S(—+ * sin ( ~~ угя)) • А
4. Возведение в степень. Степень комплексного числа z
с показателем ne N определяется формулой
Zn = ZZ ... 2,
в правой части которой содержится п множителей.
Пусть 2 = г (cos ф 4- i sin ф), тогда
(г (cos ф 4- i sin ф))п — rn(cos /гф + i sin шр), (12)
т. е. при возведении комплексного числа в степень с натураль-
ным показателем его модуль возводится в степень с тем же по-
казателем, а аргумент умножается на показатель степени.
80
Пример 13. Возвести в девятую степень комплексное число
z — V3 —- i-
А Модуль числа z равен 2, а одним из аргументов является
угол ф == —л/6, поэтому модуль числа г9 равен 29, а аргумент
числа z равен 9<р = —Зл/2. Следовательно,
(Уз _ г)9 = 29 (cos ( - Зл/2) + i sin ( - Зл/2)) = 5121. д
5. Извлечение корня. Число w называется корнем степени п
из числа z (обозначается д/г)> если wn — г.
Например, числа Wi — i и w2 = —i являются корнями сте-
пени 2 (квадратными корнями) из числа г — —1, так как
i2 = — 1 и (—02 = — 1.
Из определения вытекает, что каждое решение уравнения
wn — z является корнем степени п из числа г. Другими сло-
вами, для того чтобы извлечь корень степени п из числа г, до-
статочно решить уравнение wn = z.
Пусть z = r(cosq) + i sing?), тогда уравнение wn — z имеет
n решений (корней степени п из z), которые могут быть най-
дены по формуле
»» = V7(COs(i + ^) + isl„(5. + ^)). (13)
/г = 0, 1, 2, ..., и—1.
Из этой формулы видно, что все корни степени п из числа z
имеют один и тот же модуль д/г » но разные аргументы, отли-
чающиеся друг от друга слагаемым, кратным числу 2л/п. От-
сюда следует, что комплексные числа, являющиеся корнями сте-
пени п из комплексного числа z, соответствуют точкам комп-
лексной плоскости, расположенным в вершинах правильного
n-угольника, вписанного в окружность радиуса д/г с центром
в точке z = 0 (см. пример 14).
Заметим, что символ д/z не имеет однозначного смысла.
Поэтому, употребляя его, следует четко представлять себе, что
под этим символом подразумевается. Например, используя
запись V “ 1 > следует позаботиться о том, чтобы было ясно,
понимается ли под этим символом пара комплексных чисел I
и —i или одно, и если одно, то какое именно.
Пример 14. Найти все значения \/—16.
А Запишем число z ——16 в тригонометрической форме
z = —16 = 16(cos л + i sin я).
Согласно формуле (13) получаем
wA = 2(Cos(^H~£) + /sin(^ + vft))(/5=x0’ 2’ 3)-
81
Следовательно,
w0 = 2 (cos (л/4) + i sin (л/4)) = д/2 + * V2,
и>)=2 (cos (Зл/4) + i sin (Зл/4)) = — д/2 + i
w2 — 2 (cos (5л/4) + i sin (5л/4)) = — ^2 — 1^2,
w3 = 2 (cos (7л/4) + i sin (7л/4)) = ^2 — i д/2.
На рис. 10 изображены все четыре значения V— 16. Точки, со-
ответствующие числам wq, wi, W2, и>ъ, находятся в вершинах
Рис. 10.
Пример 15.
Уб + 12/ — Уб — 12/
Уб + 12/ + Уб — 12/
форме при условии,
части корней У5 +
квадрата, вписанного в окружность ра-
диуса 7? — 2 с центром в точке z = 0. А
Записать число
в алгебраической
что действительные
12/ и Уб —’ 12/ от-
рицательны.
А Для извлечения квадратного
корня из числа 5+12/ положим
Уб + 12/ — х + iy, тогда
5+12/ =-х2 + 2xyi — у2
и, следовательно, х и
у удовлетворяют системе уравнений
х2 — у2 == 5,
ху = 6.
Решив систему, получим два решения (3; 2) и (—3; —2). По
условию действительная часть Уб+12/ отрицательна, поэтому
У5 + 12/ = — 3 — 2/. Аналогично найдем У5 — 12/ == —- 3 + 2/.
Таким образом,
- 3 - 2/ - ( - 3 + 2/) _ 2 .
2 “ - 3 - 2/ + ( - 3 + 2/) 3 z* А
5.32. Представить комплексное число z в тригонометриче-
ской форме:
1) z = — Уз + /. 2) z »= — 1. 3) z = — cos ~~ — / sin
4) z = 1 + cos + / sin . 5) z = tg 1 — i.
82
5.33. Записать комплексное число z в алгебраической и в
тригонометрической формах:
.. _ i (cos (5л/3) + i sin (5л/3))
' Z cos (л/6) + i sin (л/6)
Z = cos (4n/3) — i sin (4л/3) ‘ 3) 2 = (i + Z)2 •
.к ____ — cos (5л/12) + i sin (5л/12)
' Z cos (13л/12) — i sin (13л/12)
( Я . . л \ ( 1 . Уз
.. _ lcosT-'sin3)U + l^~J
t>) z — .
5.34. Представить в тригонометрической форме комплексное
число z\
.. _ 5 (cos 100° + i sin 100°) i
1' Z ~ 3 (cos 40° — i sin 40°) ’
~ _ sin (2л/5) + i (1 — cos (2л/5))
2) Z — j — 1
5.35. При повороте на угол л/2 по часовой стрелке и удли-
нении в два раза вектор z\ — 2 + 5/ переходит в вектор г2.
Найти комплексное число, соответствующее вектору z2.
5.36. Вектор z = —2 4-3Z повернут на 180° и удлинен' в
1,5 раза. Найти комплексное число, соответствующее получив-
шемуся вектору.
5.37. Записать комплексное число z в алгебраической форме:
1) ri- — У)12- 2)~ z = (cos31° + i sin 31°) 10.
8) 2 = 1 р + Узг°у 4. (2iy _ = (1+09 I 4 )' " (-V2 +/V2)6 ’ (1- iY
5.38. Записать комплексное число z в тригонометрической
форме:
1) z=(V3-i)“”. 2)
3) z = > «eN- 4) z = (tg2 — i)\
5) z — (sin + i (1 + cos-^))5.
5.39. При каких целых значениях п справедливо равенство
(1 4-t)" = (1 — i)'!?
5.40. Найти все значения д/г. если:
1) z — — 1, п = 3. 2) z = 8i, п = 3. *
3) г = 1, /г = 5. 4) z = 1 + i, п = 8.
83
5.41. Решить уравнения:
1) г3 = 1 + i. 2) г4 + 1 = 0. 3) г5 = 1 + Уз/.
4) г6 + 64 = 0. 5) г2 = г3. 6) zn = г, п е N.
5.42. Пусть Ak (Л=1, 2, ..., п)— вершины правильного
n-угольника, вписанного в окружность единичного радиуса.
Найти:
1) |ЛИ2|2 + ИИз|2+ ... +|Д1ЛЛ|2.
2) ИИ21-1ЛИ31 ... |ДИп|.
6. Комплексная степень числа е. Операция возведения числа
е в комплексную степень z = х + yi определяется формулой
ег == ex(cos£/ + fsiny). (14)
Например,
eI+f — е (cos 1 + i sin 1),
ея//2 = cos (л/2) + * sin (л/2) = Z,
ея/ = cos л + i sin л = — 1.
Основные свойства комплексной степени числа ei
1) а) ez'+Z3 = ez'ez\ б) ez'-Z2 = ~,
т. е. для ег сохраняются обычные свойства степени.
2) Для действительных значений z == х + 0ч
ez = ex+Qi — ех,
т. е. комплексная степень числа е превращается в этом случае
в степень с действительным показателем.
3) Для любого комплексного числа z справедливо равенство
вг+2лп/ = ег, neZ, (15)
в частности, е2лпЛ = 1.
Из формулы (14) при г=ир, феР, получается важная
формула
е^ = cos ср + i sin ф, (16)
которая называется формулой Эйлера.
Каждое комплексное число г =/= 0 можно представить в виде
z = re\ (17)
где г — модуль числа z, а ф — один (любой) из его аргументов.
Это представление комплексного числа называется показатель-
ной формой комплексного числа. Для комплексных чисел, запи-
санных в показательной форме, формулы умножения, деления,
возведения в натуральную степень, извлечения корня прини-
84
мают следующий компактный вид:
а) если Zj = r1et4>‘ и z2 = r2ei<f2, то
(18>
___п gJ (<Р1~<Р2). (19)
Z2 г2 ’
б) если г = ге'4’, то
2л __ rneit«fy (20)
\lz = \lre^n nJ (k = 0, 1, 2, n- 1). (21)
Пример 16. Представить в показательной форме комп-
лексное число
Уз 1 ,
2 8 8 Z*
А Находим модуль числа
VI ; г 1
64 +’§4
и один из его аргументов
tgq) = — 1/д/зГ, <р = — л/6
'(так как г находится в четвертом квадранте). Следовательно,
г_2.е-‘«. А
Пример 17. Записать в показательной форме комплексное
число
____ ( — ]/~3 + 0 (cos (л/12) — i sin (эт/12))
2___1 — i *
А Каждое из чисел — Уз + Z, cos (л/12) — i sin (зт/12), 1— i
представим в показательной форме
— У 3~ + i = 2ё?5ш’/6,
cos (л/12) — i sin (л/12) — cos (— л/12) + I sin (— л/12) = е~пт2,
1 —/ = У2Ге"л£/4-
Используя формулы (18) и (19), получаем
ор5л//6 р~л i(-^--------------------5г+~>) / /
у___ е —л/9р vT 4 ) — л/9.р*п А
г~ ^е-пМ -\2.е . А
Пример 18. Представить в показательной форме комп-
лексное число z =(—1 + О5-
А Записываем в показательной форме основание степени
и применяем формулу (20):
(_ 1 + /)6 = (^2e3ni,J = 4 V^15""4 4 ^2e~nili. А
Пример 19. Записать все значения корня VV3 + * в по-
казательной форме.
Представляем число ^3 -j-z в показательной форме и
применяем формулу (21):
дД/З +/== V2e“/6 = V2e"Z(12ft+w24 (&=0, 1, 2, 3). д
5.43. Доказать свойства 1) — 3) комплексной степени числа е.
5.44. Пусть z = х + iy\ найти модуль и аргументы числа
5.45. Представить z в алгебраической форме:
о ; пх --f-JTZ+12ni 3i+7+3TtZ-~i
1) z — e2~l. 2) z = e 2 . 3) z = e 2 .
5.46. Представить в показательной форме комплексное число:
1) z = — д/12 —- 2z. 2) z — — cos (л/7) + i sin (л/7).
5.47. Записать в показательной и в алгебраической формах
комплексное число:
ni nl
1) z = 5е 4 • 0,2е6 (cos (5л/12) - г sin (5л/12)\
2) z = (4e"z/I2)
3) z==(V3 -z)6.
4) Z (cos 12° + i sin 12°)5 ’
5) Z =
<г~л;/3(1 +V3Z)7
i
5.48. Доказать формулу
(1 + cos a + z sin a)2n = (2cos yyVna, zieN, aeR.
5.49. Используя формулу (21), записать в показательной
форме все значения V2:
l)z = l, zz = 3. 2)z = —1, zz = 5.
3) z = — 4 + V48Z, n = 3. 4) z = — 1 - VTz, n = 4.
5.50. Найти суммы:
i) X e£ft4>.
/г-0
n
2) X sin Ф=т^2лр, peZ.
fe»i
n
3) У cos £qp, <р^=2лр, p e Z.
k =o
£6
§ 6. Многочлены. Алгебраические уравнения.
Рациональные дроби
1. Многочлены. Алгебраические уравнения. Многочленами
'{полиномами) относительно переменной z называются выраже-
ния вида
' anzn + an-xzn~x + ... + axz + aQi (1)
где n—неотрицательное целое число, ak (k = 0, 1, ..., п)—
некоторые числа.
Говорят, что многочлен (1) задан над множеством комп-
лексных чисел, если ak^ С, и над множеством действительных
чисел, если ak е R.
Числа ak называют коэффициентами многочлена; коэффи-
циент ао называют свободным членом, коэффициент ап — стар-
шим коэффициентом. Если ап— 1, то многочлен называют при-
веденным.
Если ап ф 0, то число п называется степенью многочлена.
Для сокращенной записи многочленов обычно используют
обозначения Р(г), Q(z), R{z), ..., если переменная z е С, и
Р(х), Q(x), R{x) и т. д., если переменная 2 = Если хо-
тят подчеркнуть, что многочлен P(z) имеет степень п, то пи-
шут Pn(z).
Многочлены P0(z) = a0, £о #= О, т. е. многочлены нулевой
степени, — это не равные нулю комплексные числа. Число О
также считают многочленом и называют его нулевым. Нулевой
многочлен — это единственный многочлен, который не имеет
степени.
Многочлены Pn{z) и Qm(z) считаются равными (пишут
Ptl(z) — Qm(z)), если равны их коэффициенты при одинаковых
степенях z. Для равенства многочленов, очевидно, необходимо
равенство их степеней.
Для многочленов определяются операции сложения и умно-
жения. Каждая из этих операций подчиняется коммутативному
и ассоциативному законам. Операции сложения и умножения
связаны между собой дистрибутивным законом.
Суммой Рn{z) + Qm(z) многочленов
Рп (?) = anzn + an_izn~l 4- ... + ajz + а0,
Qm (z) = bmzm 4- 4- ... 4- bxz 4- b0
называется многочлен, коэффициенты которого при каждой сте-
пени z равны сумме коэффициентов при этой степени z много-
членов Pn(z) И Qm(z).
Например, если Р5 (z) = z5 + 3iz3 —1 и Q3 (z) — iz3 + z + 1,
то
P5(z)+Q3(z)=z5 + 4zz3 + z.
.87
Сумма многочленов Pn(z) и Qm(z) есть многочлен, степень
которого не превосходит наибольшего из чисел п и т или не
существует.
Произведением Pn(z)Qtn(z) многочленов
Рп (z) = anzn + an_iZn~' + ... + atz + а0,
Qm (z) = bmzm + b^z™-1 + ... +blz + b0
называется многочлен
(2) = Cm+nZn^~m -J” • • • “I" CkZk -f* • • • C[Z “f* Co,
коэффициент Ck (0 k n + m) которого равен сумме всевоз-
можных произведений atbj, где i + / = k.
Для нахождения произведения многочленов Pn(z) и Qm(z)
достаточно каждый член akzk многочлена Pn(z) умножить на
каждый член biz1 многочлена Qm(z) и записать сумму всех не-
полученных произведений a,kbizk+l.
Например, если P4(z) —z4—1 и Q3(z) = 2z3 + z, то
Р4 (г) Q3 (z) = (г4 — 1) (2z3 + г) = 2z7 + z5 — 2z3 — z.
Если N(z)— нулевой многочлен, то для любого многочлена
P(z) по определению полагают
P(z) + W(z)=P(z), P(z)N(z) = N(z).
Разностью P(z)—Q(z) многочленов P(z) и Q(z) называется
многочлен Р(z) такой, что
P(z) = Q(z) + P(z).
Разность существует для любых двух многочленов и опре-
деляется однозначно.
Для любых двух многочленов Pn(z) и Qm(z) существуют
многочлены T’(z) и P(z) такие, что
Pn(z) = Qm(z)T(z) + R(z), (2)
причем либо степень R(z) меньше т, либо /?(г) = 0 (т. е.
R(z)—нулевой многочлен). Многочлены T(z) и R(z) опреде-
ляются однозначно; многочлен Г (г) называется частным, а мно-
гочлен R(z)— остатком от деления многочлена Pn(z) на мно-
гочлен Qm(z).
Если R(z) — 0, то говорят, что Pn(z) делится на Qm(z).
В этом случае Qm(z) называют делителем многочлена Pn(z).
Для определения частного и остатка от деления двух мно-
гочленов существуют разные способы. Чаще всего пользуются
«делением углом» или методом «неопределенных коэффициен-
тов»,
-88
Например, «деление углом» многочлена 2г4 — 5z3 + 2z на
многочлен z2— 1 проводится так:
, 2г4 — 5г3 + 2z \z2 — 1
______ ‘Zz2___ 2z2 — 5z + 2
~5z3 + 2z2 + 2z
— 5z3 -j- 5z
__ 2z2 — 3z
2z2 — 2
— 3^ + 2
Поэтому
2г4 — 5z3 + 2z = (z2 — 1) (2z2 — 5z + 2) + (-^3z + 2),
a*, e. многочлен T (z) = 2z2 — 5z + 2 является частным, a 7? (z) —
= —3z + 2 — остатком.
Для отыскания частного и-остатка от деления тех же мно-
гочленов методом «неопределенных коэффициентов» поступают
следующим образом. Так как первый многочлен имеет сте-
пень 4, а второй — степень 2, то частное ищут в виде T(z) =
= az2 + bz + с, а остаток — в виде /? (z) = b\z -}- С\. Записы-
вают равенство (2):
2г4 — 5z3 + 2z — (z2 — 1) (az2 + bz + с) + b\z + C\.
Если многочлены равны, то равны их коэффициенты при оди-
наковых степенях z, т. е. коэффициенты многочленов T(z) и
R(z) удовлетворяют системе уравнений
2 = а,
-5 = 6,
О = с — а,
2 = — b + bi9
О = — с 4-
Из системы находят а — 2, b — —5, с = 2, Ь\ — —3, С\ — 2.
Особый интерес представляет деление многочлена Pn(z) на
приведенный многочлен первой степени z — Zo. Равенство (2)
в этом случае принимает вид
Рп (г) = (z — z0) Тп-1 (-г) + ш0,
где Шо — некоторое комплексное число.
Если в этом равенстве положить z = z0, то получим
Pn(Zo) = Wo.
Число шо = Рп(^о) называют значением многочлена Pn(z)
при z = z0-
Таким образом, остаток от деления многочлена Pn(z) на
z — zQ равен значению многочлена Pn(z) при z = z0 (теорема
Безу).
Если шо = Pn(zo) = O, то многочлен Pn(z) делится на ли-
нейный двучлен z — 2о, т. е. z — z0 является делителем много-
члена Pn(z\.
8Э
Если значение многочлена Pn(z) при z — Zo равно нулю, т. е.
jP/i(zo) = O, то число z0 называют корнем многочлена Pn(z).
В этом случае говорят также, что число zQ является корнем
(или решением) уравнения
anzn + ... + axz 4- а0 = 0, #= 0. (3)
Уравнение (3) называют алгебраическим уравнением п-й сте-
пени. Решить уравнение (3) — это значит найти все его корни
или, что то же самое, найти все корни многочлена Pn(z).
Если многочлен Pn(z) делится на многочлен (г — Zo)kt
^eN, но не делится на многочлен (z— z0)fe+1, то корень zo
называют k-кратным корнем многочлена Pn(z) и ^-кратным
корнем уравнения (3). Однократный корень часто называют
простым корнем, ^-кратный корень при k > 1 называют крат-
ным. Многочлен
Рn(z) = tianz 4~ (ft — 1) ап-\Zn -j- ... 4~ 2a%z 4~
называется производной многочлена Pn(z). При определении
кратности корня многочлена часто используют следующее ут-
верждение: кратный корень многочлена Pn(z) является корнем
и многочлена
Алгебраическое уравнение нулевой степени, очевидно, кор-
ней не имеет.
Алгебраическое уравнение первой степени
az 4- b = 0
имеет один корень
z = —Ь/а.
Корни уравнения второй степени (корни квадратного урав-
нения)
az2 4- bz 4- с = 0
находятся по формуле
г=—W
Число D = Ь2 — 4ас называется дискриминантом квадратного’
уравнения, а под л/D понимается какое-либо значение корня.
Если D = 0, то квадратное уравнение имеет один двукратный
корень; если D =£ 0, то два простых корня.
Корни двучленного алгебраического уравнения
azn 4- ft = 0
находятся по формуле _____
z — ^J — blа. (5)
Если ft #= 0, то такое уравнение имеет п простых (однократных)
корней, которые могут быть найдены по формуле (13) § 5.
В общем случае не существует формул (подобных форму-
лам (4), (5)), позволяющих выразить корни алгебраического
90
уравнения через его коэффициенты. Отсутствие общего метода
решения .алгебраических уравнений не мешает, конечно, в част-
ных случаях использовать ту или иную специфику уравнения и
найти его корни. Тем более, что при решении многих задач тре-
буется найти не все корни уравнения, а только те, которые
принадлежат какому-либо множеству, например множеству
действительных чисел или множеству целых чисел. При реше-
нии уравнений с целыми коэффициентами часто оказывается
полезной следующая теорема.
Теорема. Целые корни алгебраического уравнения с це-
лыми коэффициентами являются делителями свободного члена.
Существование корней алгебраического уравнения устанав-
ливается основной теоремой алгебры комплексных чисел — тео-
ремой Гаусса.
Теорема. Алгебраическое уравнение степени п в множе-
стве комплексных чисел имеет п корней при условии, что каж-
дый /г-кратный корень считается k раз.
Из теоремы Гаусса следует, что каждый многочлен Pn{z)
допускает представление в виде
k k ki
Pn(z) = an(z —Zi) '(z—z2) 2 ...(z — zt) l, (6)
где zi, 22, zi — различные корни многочлена, a k\, Л2, ...
».., ki — их соответствующие кратности, причем
^2 “Г ♦ ’ • “Ь ki = м.
Каждый многочлен Р„(х) с действительными коэффициен-
тами допускает представление в виде
Рп (х) = ап(х — Xj)fe‘ ... (х — Xi)kl (х2 + Р\Х 4- qi)r'...
...(x2 + pmx + qm)rm, (7)
где Xi, Х2, ..., Xi — различные действительные корни многочле-
на; k2, ..., ki — их соответствующие кратности; pb ..
.. » Pm, qm — различные пары действительных чисел, удовлет-
воряющие неравенствам
р2-491 <0, .... p2m-4qm<0-,
И, Г2, ..., Гт — натуральные числа, причем
+ &2 + ••• + kl + 2(Г1 + Г 2 + ... + Гт) = fl.
Пример 1. Решить уравнение
22 + 32 + 3 = 0.
А По формуле (4) находим
~ — 3 ± Уч — 12 — 3 ± V —3 — 3 Уз з , . Уз
г -------=-------------==-----$----. = А
91
Пример 2. Решить уравнение
22 —(2 + г)г—1 + 71 = 0.
А По формуле для корней квадратного уравнения имеем
2 + i ± 7(2 + г)2 + 4 (1 - 7ТГ ,J2 + Z± V7-24Z
Z 2 2
Для определения какого-либо значения л/7 — 241 положим
V? — 24г = х + iy.
Тогда
7 — 24г — х2 + 2xyi — у2
и, следовательно, х и у удовлетворяют системе
х2 — у2 =. 7,
ху = — 12,
причем х и у — действительные числа. Система имеет решение
х = 4, у = —3. Поэтому
2 + I + 4 - 31 _ q .
Q О
Пример 3. Решить уравнение
г3 — 6г — 9 = 0.
А Рассматривая делители свободного члена, убеждаемся в
том, что только z = 3 является целым корнем уравнения. Де*
чим левую часть уравнения на г — 3:
_z3 — 6г — 9 | г — 3
г3 ~ З*2 г2 + Зг + 3
Зг2 — 6г — 9
~ Зг2 — 9г
Зг —9
” Зг — 9
0
Таким образом,
z6 — 6z — 9 = (z-З) (г2 + 3г + 3)
и, решая квадратное уравнение
г2 + 32 + 3 = 0,
получаем остальные корни. Итак,
о з . . Уз з . Уз
— 3, 22а= g ”т“ 2 * ^3 2 2 ’
Пример 4. Выяснить, существуют ли целые корни у уран-
нения
2г3 — 5г2 — 2г + 2 = 0.
92
А Целыми корнями уравнения могут быть только числа ±1,
'±2. Подстановка в уравнение показывает, что ни одно из этих
четырех чисел не удовлетворяет ему. Данное уравнение целых
корней не имеет. А
Пример 5. Решить уравнение
г5 — 2г4 — 13г3 + 26г2 + 36г — 72 = 0.
А Подвергая испытанию делители свободного члена, най-
дем, что 'г = ±2 суть корни уравнения. Разделив левую часть
уравнения на г2 — 4, придем к уравнению
г3 —2г2 —9г + 18= 0,
корнем которого является г = 2. Разделив левую часть полу-
ченного уравнения на г — 2, получим г2 — 9. Таким образом,
уравнение может быть выписано в виде
(г + 3) (г + 2) (г-2)2(г-3) = 0,
т. е. имеет три однократных (простых) корня г = —3, г = —2,
Z — 3 и один двукратный корень г = 2. А
Пример 6. Представить многочлен
Р(г) = г7 + г6 + 64г + 64
в виде произведения: а) линейных множителей, б) линейных и
квадратичных множителей с действительными коэффициентами.
Д Найдем все корни многочлена. Так как
г7 + г6 + 64г + 64 = (г + 1) (г6 + 64),
то z\ =—1, а для нахождения остальных корней нужно из-
влечь корень шестой степени из числа —64. По формуле (13)
§ 5 получаем
г$ == д/ 3 + Z, г3 = 'у/ 3 — Z, г4 = — д/3 + Z,
г5 = — г6 = 2Z, г7 = — 2Z.
Поэтому данный многочлен представим в виде произведения
семи линейных множителей:
P(2)'=(z + l)(z-V3-«)(z-V3 + 0(z + V3-0-
• (* + V3 + i) (Z - 2t) (z + 2/).
Перемножая попарно линейные двучлены, соответствующие
комплексно сопряженным корням, получаем разложение мно-
гочлена на множители с действительными коэффициентами:
Р (z) = (z + 1) (г2 - 2 V3z + 4) (z2 4- 2 V3z + 4) (z2 + 4).
93
Это разложение можно было получить и путем следующих пре-
образований:
z1 + z6 + 64г + 64 = (z + 1) (z6 + 64) =
= (г+ 1) (г2 + 4) (г4 — 4г2 + 16) =
= (г + 1) (г2 + 4) (г4 + 8г2 + 16 — 12г2) =
= (г+ 1)(г2 + 4)(г2 + 4-273г)(г2 + 4 + 2V32). д
Р (z)
2. Рациональные дроби. Выражение туг-г, где P(z) и
ч \z)
Q(z)—многочлены, причем Q(z)—ненулевой многочлен, назы-
вается рациональной дробью. Многочлен P(z) называют числи-
телем, многочлен Q(z)—знаменателем рациональной дроби.
Каждый многочлен Т (г) является, очевидно, рациональной
дробью (в этом случае Р (г) = Т (г), Q (г) = 1).
~ . Р (2) R (2)
Рациональные дроби и считаются равными,
если
P{z)S(z) = R(z)Q(z).
Отсюда следует, что две рациональные дроби с равными
знаменателями равны тогда и только тогда, когда равны числи-
тели дробей.
Суммой + рациональных дробей и
, Р (z) S (z) + Р (г) Q (z)
называется рациональная дробь —1---q » а их пр0"
Р(2) R(z) P(z)R(z)
изведением 777- Q ,\ — рациональная дробь 757 "Ге/ \ •
Ч \Z) О (2) Ч \Z) О (Z)
Разность и частное двух рациональных дробей определяют-
ся как результат операций, обратных по отношению к сложе-
нию и умножению.
Операции сложения и умножения рациональных дробей
коммутативны и ассоциативны; они связаны между собой ди-
стрибутивным законом.
. Р (2)
Рациональная дробь называется правильной, если
степень многочлена P(z) меньше степени многочлена Q(z).
Если степень многочлена P(z) больше или равна степени мно-
гочлена Q(z), то рациональная дробь 757-7 называется непра-
Ч. \Z)
вильной.
TZ * Р (*)
Каждую неправильную рациональную дробь можно
представить либо в виде многочлена, либо в виде суммы много-
члена и некоторой правильной рациональной дроби. В самом
деле, если Т(г) — частное и R (г)—остаток от деления много-
члена P(z) на многочлен Q(z), то верно равенство
р ----- (8)
Q (2) 1 + Q (2) ’
94
R (z)
где либо дробь -Q^y является правильной, либо /?(г) = 0.
Представление неправильной дроби в виде (8) называется
выделением целой части неправильной рациональной дроби.
«^6_, I J
Пример 7. Представить рациональную дробь —г3~ +1"—
в виде суммы многочлена и правильной дроби.
Л Разделив многочлен Р(г)==г6 — z2 + 1 на многочлен
Q(z) = z3+ 1» получим частное Т(г)==г3—1 и остаток /?(г) =
= —г2 + 2. Следовательно,
г6 — г2 + 1 = (г3 + 1) (г3 — 1) — г2 + 2,
откуда
г6 — z2 + 1 о , . 2 — z2
---Г-Н = Z — 1 Ч 3 Г Г • ▲
г3 + 1 1 г3 + 1 Л
3. Разложение правильной рациональной дроби в множестве
- r-r Р (г)
комплексных чисел на элементарные дроби. 11усть -п , . — пра-
Ч \2)
вильная рациональная дробь, и пусть разложение многочлена
Q(z) на линейные множители имеет вид (6).
Тогда существуют постоянные
/^(/=1,2,...,/; 6=1,2, kt),
при которых верно равенство
1 ki
= (9)
Q /Z1 (г~ г^к
Слагаемые (не равные нулю) правой части формулы (9) на-
зывают элементарными (простейшими) рациональными дро-
бями в множестве комплексных чисел. Правая часть формулы
(9) называется разложением рациональной дроби в сумму эле-
ментарных рациональных дробей. Коэффициенты разложения
определяются однозначно. Таким образом, каждая правильная
рациональная дробь в множестве комплексных чисел может
быть представлена, причем единственным образом, в виде сум-
мы элементарных рациональных дробей. Вид этой суммы пол-
ностью определяется тем, какие корни и какой кратности имеет
знаменатель рациональной дроби. Если корни знаменателя ра-
циональной дроби известны, то коэффициенты можно найти
разными способами. Чаще всего их находят методом «неопреде-
ленных коэффициентов».
Пример 8. Разложить рациональную дробь • в мно-
жестве комплексных чисел в сумму элементарных дробей
\ Знаменатель рациональной дроби имеет корни z\ — О,
22=—1, г3 = 1. Поэтому существуют постоянные Л, В, С
95
такие, что верно равенство
22+ 1 £ I в । С
Z3 ~ Z Z Z + 1 ’ 2 — 1 •
Для определения коэффициентов Л, В и С сложим дроби в
правой части равенства:
z2 + 1 ___ Л (22 — 1) Bz (2 - 1) + Cz (z + 1)
23 — 2 23 — 2
Рациональные дроби с равными знаменателями равны толь-
ко тогда, когда равны числители этих дробей. Поэтому
г2 + j =^(г2—1) + Вг(2~1)+Сг(г+1). (Ю)
Если два многочлена равны, то равны их значения при одина-
ковых значениях z. Полагая в равенстве (10) последовательно
z = 0, z = —1, 2=1, получим 1 = —Л, 2 = 2В, 2 = 2С, т. е.
Л = — 1, В = 1, С = 1. Искомое разложение имеет вид
23 — 2 2 ' 2 + 1 ' 2 — 1 А
2-4-3
Пример 9. Разложить рациональную дробь 2L j j (^2 4,1)"
в множестве комплексных чисел в сумму элементарных дробей.
А Знаменатель рациональной дроби имеет корни z\ = 1,
22 = /, 23 = —i. Поэтому искомое разложение имеет вид
2 Л । В . С
(2— 1)(22+1) 2—1 "Г 2 — / ‘ 2-Н’
Из этого равенства рациональных дробей следует равенство
многочленов
г + 3 = Л(г2+ 1) + B(z — 1) (z + i) + C(z- 1) (z-j).
Положив последовательно z равным 1, i и —i, получим
4 = 24, i + 3 = B(i —l)2i, — i + 3 = C(—i— 1)(—2i),
t. e.
4 = 2, B==-l+± C =
Итак,
— 1 +— — 1 ——
z + 3 2 2 2 . д
(z — 1) (z2 + 1) z — 1 ' z — i ' z + i
4. Разложение правильной рациональной дроби в множестве
« et т-г
действительных чисел на элементарные дроби. Пусть —
правильная рациональная дробь, Р(х) и Q(x)—многочлены
с действительными коэффициентами, причем разложение мно-
гочлена Q(x) на линейные и квадратичные множители имеет
вид (7),
96
Тогда существуют действительные постоянные
Л(?’ (/=1,2,...,/; k=\, 2, ...» ki),
M^hN? (/=1,2, .... tn; r=l, 2, ..., rt),
при которых верно равенство
= у у л/6) । у у п
Q(x) А А*, (х — Xj)k A-i (х2 + pjX + qj)k ‘
Слагаемые (не равные нулю) правой части формулы (11)
называют элементарными (простейшими) рациональными дро-
бями в множестве действительных чисел. Правая часть фор-
мулы (11) называется разложением рациональной дроби в
сумму элементарных рациональных дробей. Коэффициенты раз-
ложения определяются однозначно. Таким образом, каждая пра-
Р (х)
вильная рациональная дробь в множестве действитель-
ных чисел может быть представлена, причем единственным об-
разом, в виде суммы элементарных дробей. Подчеркнем, что вид
разложения (11) определяется тем, какие корни и какой крат-
ности имеет знаменатель рациональной дроби. Способы нахож-
дения коэффициентов разложения будут показаны на примерах.
Пример 10. Указать вид разложения в сумму элементар-
ных дробей в множестве действительных чисел для рацио-
нальных дробей:
1 \ х2 + х + 1 _________х7 + х3 — 13_______
' (х + I)2 (х — 2) * ' Xs + х7 + 2х6 + 2х5 + х4 + х3 *
Каждая из данных рациональных дробей является пра-
вильной, и поэтому искомые разложения существуют. Знамена-
тель первой дроби имеет простой корень х = 2 и двукратный
корень к ——1. Поэтому разложение для первой дроби имеет
вид
х2 + х + 1 _ Л'Л А(2} А^
(х+ I)2 (х-2) = 7=2 + х+ 1 + (х+ I)2 •
Знаменатель второй дроби разлагается на линейные и квадра-
тичные множители следующим образом:
х8 + х1 + 2х6 + 2х5 + х4 + х3 = (х + 1 Jx3 (х2 4- 1)2.
Поэтому разложение для второй дроби имеет вид
________х7 + х3 — 13_________
*8 + х7 + 2хв + 2х6 + х4 + х3
__ д’1’ 4П 42> д£> AfVWM1’ м^’х + М2*
X +1 X2 = х3 х2 + 1 •" (х2+1)2 • А
4 JL Д. Кудрявцев и др. 97
Пример 11. Разложить в множестве действительных чи-
сел на элементарные дроби:
1 ч________1 9ч х3 + 7х + 32
' 2 (х — 1) (х — 2) (х — 3)' х(х2 + 4)2 •
оч 2х + 1 .. х’ + З 6 + Зх3
°'х2(1 + х2)2' ^(х + 3)10»- (х2+1)(х2 + 4)’
Л 1) Знаменатель рациональной дроби имеет простые кор-
ни Xi = 1, х2 — 2, х3 = 3, поэтому искомое разложение записы-
вается в виде
1__________ At । Az . Аз
2 (х — 1)(х — 2)(х — 3) х—1 х — 2 х — 3‘
Из равенства рациональных дробей (по определению) сле-
дует равенство многочленов
1/2 = Д1(х — 2)(х — 3) + Д2(х—'1)(х — 3) +
+ Д3(х—1) (х —2). (12)
. Если многочлены равны, то равны их значения при одинако-
вых значениях х. Полагая в равенстве (12) последовательно
х = 1, х = 2, х = 3, находим 1/2 — 2Дь 1 /2 = —А2, 1 /2 = 2Д3,
т. е.
41 = 1/4, А2 = —1/2, Д3 —1/4.
Таким образом, искомым разложением является разложение
1 1/4 1/2 . 1/4
2 (х — 1)(х — 2)(х —3) х—1 х — 2 ' х — 3*
2) Знаменатель рациональной дроби уже разложен в произ-
ведение линейных и квадратичных множителей. Разложение
в сумму элементарных дробей в данном случае имеет следую-
щий вид:
х3 + 7х + 32 - А Вх + С . Dx + Е
х (х2 + 4)2 — х *" х2 + 4 + (х2 + 4)2 •
Из равенства рациональных дробей следует равенство мно-
гочленов
х3 + 7х + 32 = Д (х2 + 4)2 + (Вх + С) х (х2 + 4) -J- (Dx + Е) х.
Из равенства многочленов следует равенство их коэффи-
циентов при одинаковых степенях х. Приравняв коэффициенты
при одинаковых степенях, получим линейную систему уравне-
ний
о=д + в,
1=С,
0 = 8Д + 4В + О,
I 7 = 4С + Е,
132=16Д.
98
Решив эту систему, найдем А = 2, В — —2, С = 1, D ——8,
Е = 3. Следовательно,
х3 + 7х + 32 _ 2 2х — 1 8х — 3
х (х2 + 4)2 ~ х х2 + 4 (х2 4- 4)2 •
3) В данном случае можно получить искомое разложение,
не прибегая к методу «неопределенных коэффициентов». Пре-
образуем рациональную дробь следующим образом:
2х + 1 _/9у I п 1 + х2-х2 __
\2(1..+ х2)2 v Л ' х2 (1 + х2)2
_/2х 4- В Г —!___________1______-I- П 1+*2-*2 - 2£±L-
(1+х2)2; \х,х-г- I) ж2(1 +л.2) (1+х2)2—
/9.. ! 1 А 2х±1 ___ 2 1 2х + 1 2Х-+1
— 1+х27 (1+х2)2 Х^Х2 Х2+1 (х2+1)2*
Полученное разложение и является разложением данной
рациональной дроби в сумму элементарных дробей.
4) В этом случае, как и в предыдущем, искомое разложение
можно получить простыми преобразованиями. Положив х +
+ 3 = t, перепишем рациональную дробь следующим образом:
х3 + 3 _ (/-3)3 + 3 _ t3 — 9/2 + 27/ — 24 _
‘(Х 4-3)ioo “ /юо /юо
1 9 , 27 24 _ 1 9 । 27 24
& /W /08 + /98 /100 (х + 3)97 (X + З)98 + (х-Ь 3)" (х + 3)|00‘
Полученное разложение является искомым.
5) Разложение на элементарные дроби имеет вид
6-ЬЗх3 __ Ах + В . Cx + D
(х2+1)(х2+4) х2 + 1 + х2 + 4 •
Из равенства дробей следует равенство многочленов
6 + Зх3 = (Ах + В) (х2 + 4) + (Сх + D) (х2 + 1).
Полагая здесь последовательно х = i и х = 2/, получаем
Гб — 3i = 3(4/ + B),
(б — 24/= — 3 (2С/+ £)).
Из системы находим А — —1, В = 2, С = 4, D = —2. Следова-
тельно,
6 + Зх3 _ 2 — х 4х — 2
„ (х2 + 1) (х2 + 4) ~ X2 + 1 х2 + 4 • А
6.1. При каких значениях А, В, С, D равны многочлены
Р (z) = (Ах + В) (z2 - z + 1) + (С2 + D) (z2 + 3)
и
Q(z) = 2z3 + z2 + 5z + 1?
4*
99
6.2. Подобрать многочлены P(zj и Q(z)' наименьшей сте*
пени так, чтобы выполнялось равенство
(z4 — 2z3 — 4z2 + 6z + 1) Р (z) + (z3 — 5z — 3) Q (z) = z4.
6.3. При каких значениях А, В, C, D для многочленов
P(z) = z4+ Лг3 + Bz2 — 8z + 4 и Q (z) — z2-f~ Cz + О
справедливо равенство P(z) = Q2(z)?
6.4. Найти степень многочлена:
1) P(z) = z2(z4— 1) + (1 —z) (z5 + z4 + z3 + z2 + z 4- 1).
o\ Г) (г\ _ i (г — Zi) (z — z2) _ (z — z2) (z — z3) _ (z — z3) (z —Zi)
’ (z3 — zt) (z3 — Z2) (Zi — Z2) (Zi — Z3) (z2 —Z3) (z2 —Zi)’
Zi, Z2, z3 — попарно различные комплексные числа.
6.5. Найти частное T(z) и остаток R(z) от деления много-
члена Р(г) на многочлен Q(z):
1) P(z) = z3 + 5z2 — 7z — 3, Q(z) = z2 — 8z+ 16.
2) P(z) = z5 + 3z2 + 7iz—1, Q(z) = z —t.
3) P(z)=z5 — z3+ 1, Q(z) = (z — i)3.
4) P(z) = z2 — 1, Q(z) — 2z4 — 5z34-2z.
5) P(z) = z30—1, Q(z) = z54-1.
6.6. Определить, является ли многочлен Q(z) делителем
многочлена P(z):
1) P(z) = zI0° —3z24-2, Q(z)=z2—1.
2) P(z) = z100 —3z4-2, Q(z) = z2 — 1.
3) P(z) = 6z54- llz44-5z34-5z2 —z —6,.Q(z) = z2+ 1.
6.7. При каких значениях а и b многочлен Q(z) является
делителем многочлена Р (z):
1) Q(z) = (z — I)2, P(z) = az4 4- bz3 4- 1.
2) Q (z) — z2 — (1 4“ i) z 4- i, P (z) = z1982 4~ az 4- b.
3) Q(z) = z24- az + b, P(z)=z4 — 1?
6.8. При каких натуральных значениях пят (п т\ мно-
гочлен Q(z) является делителем многочлена P(z):
1) Q(z) = zm — ат, P(z) = zn — ап, а 0.
2) Q (z) = zm 4- ат, Р (z) = zn 4- ап, а=/= 0. °
3) Q(z) — zm 4- ат, P(z) = zn — an, а =/= 0.
4) Q(z) = z24-z4-1. P(z) = z3,l+I + z3m4-z2.
5) Q (z) = z4 4- z2 4-1. P (z) = z3rt+14- 23m + z5?
100
6.9. Найти многочлен наибольшей степени, являющийся де-
лителем многочленов Р (z) и Q(z):
1) P(z) = (z3—l)(z2 —2z + 1), Q(z) = (z2—I)3.
2) P(z) = z210 — l,Q(z) = z90 — 1.
3) p (Z) = z75 — z45 — z30 + 1, Q (z) = 75z74 — 45z44 — 30z29.
6.10. При делении многочлена P(z) на z—1 в остатке по-
лучается 3, а при делении на z —2 в остатке получается 4.
Найти остаток от деления P(z) на z2 — 3z + 2.
6.11. При делении многочлена P(z) на z — г в остатке полу-
чается i, а при делении на z + i в остатке получается 1 +1.
Найти остаток от деления P(z) на z2 + 1.
6.12. Найти остаток от деления многочлена P(z)=z1933—1
на многочлен Q (z) = (z2 + 1) (z2 + z + 1) •
6.13. Решить уравнения:
1) z2 —2z + 5 = 0. 2) z2 —2iz —5 = 0.
3) z2 —20z4-92 + 6/= 0. 4) z2—- 8z —3iz + 13 + 13/= 0.
5) (3 —i)z2 —(8 —i)z + 4 + 7t = 0.
6.14. Решить уравнения:
1) z4 — 30z2 +289 = 0. 2) z5 + z4 + z3 + z2 + z+1 =0.
3) )4 = Z. 4) (z - i) z (z + i) (z + 2i) = 24.
6.15. Найти корни уравнений, действительная часть котооых
отрицательна:
1) z6 —z3 —2 = 0. 2) z10 —z5 —992 = 0.
6.16. Доказать, что целые корни алгебраического уравнения
с целыми коэффициентами являются делителями свободного
члена.
6.17. Найти целые корни уравнений:
1) z3 + 2z2 + z + 2 = 0. 2) z3 — 6z24~15z — 14 = 0.
3) 2z3 —5z2 —2z —2 = 0.
4) 24 + 4гз _ 25z2 _ 16г 4. 84 = 0.
5) z6 —6z5+llz4 —z3—18z2 + 20z —8 = 0.
6.18. Доказать, что каждый рациональный корень алгебраи-
ческого уравнения с целыми коэффициентами представим в виде
р/<7, где р— некоторый делитель свободного члена, a q — неко-
торый делитель старшего коэффициента уравнения.
6.19. Найти рациональные корни уравнений:
1) 3z3 + z2 + z + 35 = 0. 2) 2z4 + 3z3 —46z2rh6z + 8 = 0.
101
6.20. Решить уравнения:
1) 2z3 + 12z2 + 13z +15 = 0.
2) z4 — 4z3 + 7z2 — 16z + 12 = 0.
3) z5 + 2z4 + 4z3 + 8z2 + 16z + 32 = 0.
4) z5 — 2z4 — 13z3 + 26z2 + 36z — 72 = 0.
6.21. Доказать, что если уравнение
anzn + t/n-iz"-1 + ... + oiz + a0 = 0
с действительными коэффициентами имеет корень zo, то число
Zo также является корнем этого уравнения.
6.22. Доказать, что если многочлен с действительными коэф-
фициентами имеет корень zo = а + Ы, то многочлен (z — а)2 +
+ Ь2 является его делителем.
6.28. Убедиться в том, что число Zo является корнем урав-
нения, и найти остальные корни:
.1) 3z4 —5z3 + 3z2 + 4г — 2 = 0, z0 = 1 + i.
2) z6 + z5 + 3z4 + 2г3 + 3z2 + z + 1 = 0, z0 = i.
6.24. Доказать, что каждый многочлен нечетной степени с
действительными коэффициентами имеет по крайней мере один
действительный корень.
6.25. При каких рациональных значениях а и b число
1 _]_ zy/2 является корнем уравнения
z5 + az3 + bz2 + 5z + 2 = 0?
Найти остальные корни уравнения при найденных значениях
а и Ь.
6.26. Найти общие корни уравнений:
1) z6 + 2z5 + 3z4 + 2z3 + 3z2 + 2z + 2 = 0,
z4 + 3z3 + 6z2 + 6z + 4 = 0.
2) z3 + 2z2 + 2z + 1 = 0,
zi982 + zioo+ 1==Oi
6.27. Определить кратность корня zo для уравнения:
1) 3z4 —4*z3+ 1 =0, z0= 1.
2) z5 —5z4 + 7z3 —2z2 + 4z —8 = 0, zo = 2.
' 3) z2n — nz”+1 + nz"-1 — 1=0, n > 1, Zo = 1.
6.28. При каких значениях а и b уравнение
. z5+10az3 + 5te-24 V3 = 0
имеет корень кратности 3?
102
6.29. Доказать, что уравнение
_п _п-I
^+тг=Т)г+- +-+!=+
не имеет кратных корней.
6.30. Найти многочлен Р(х) наименьшей степени, имеющий
корень х = 0 десятого порядка и такой, что многочлен Р(х)— 1
имеет корень х = 1 пятого порядка.
6.31. Найти приведенный многочлен наименьшей степени
с действительными коэффициентами, корнями которого яв-
ляются: 1) z\ — 3 и = 2 — г, 2) 2\ = i (корень кратности 2)
И 22 = —1 —ь
6.32. Найти приведенный многочлен наименьшей степени с
рациональными коэффициентами, корнем которого является
?о = V5 — V2.
6.33. Доказать, что корни zi, Z2, ..., zn уравнения
zn + On-iz"-1 4- ... + a^z + a0 — 0
связаны с .его коэффициентами формулами Виета:
-1 + z2 + г3 + ••• + гп =— ап-1>
zlz2 + zlz3+ ... +z„_1z„ = an_2,
ztz^34-ZiZ^t + ... 4-z„_2z„_lz„ = — an_3,
ZjZ2z3... z„ = (— l)"a0.
6.34. Уравнение 2z3 4~ oz2 4- bz 4- 12 = 0 имеет корни z\ = 1,
Zg = —2. Найти третий корень этого уравнения.
6.35. Пусть zi, Z2, гз — корни уравнения z3 — z2 — I =0. Со-
ставить уравнение, корнями которого были бы числа z2 4- z3,
Z3 4- г1> Z\ + z2-
• 6.36. При каких значениях с корни уравнения
z3 4* г2 4- 2z 4- с — 0
образуют геометрическую прогрессию? Найти корни при этом
условии.
; 6.37. Найти сумму квадратов и сумму кубов корней урав-
нения
8z4 — 5z24-2z4- 1 =0.
6.38. Найти сумму квадратов корней уравнения
z" 4- an-\zn~x 4- a„_2zn-2 4- ... 4- а0 = 0.
6.39. Найти сумму коэффициентов многочлена:
1) (4z — 5)'6. 2) (з V2z — -^)8-
<_ (4г2 —2z—- l)i3(5z2 —7)\
103
6.40. Представить многочлен в виде произведения линейных
множителей:
l)z3+l. 2)z3 — 6z2+ 112 — 6.
3) 6z4 — Hz3 — z2 — 4.
4) z5 — 4z4 — 6z3 + 16z2 + 29z + 12.
5) z3 + (1 — i) z2 + (1 — 2i) z — 1 — i.
6.41. Представить многочлен в виде произведения линейных
и квадратичных множителей с действительными коэффициен-
тами:
1) х44-4. 2) х6 + 27.
3) (х2 + х)2 + 4х2 + 4х— 12. 4) х2+(л?+1)2 + (х2 + х)2.
5) (х+ 1) (х + 3) (х + 5) (х+ 7)+ 15.
6) х4 —2х3 —27х2 — 44x4-7.
7) х7 4-х5 — х4 4- & — х2—1.
6.42. Существует ли многочлен, квадрат которого был бы
равен многочлену
zn + zn~l 4- ... 4-24-I?
6.43. Найти многочлен P(z) наименьшей степени, удовлетво-
ряющий условию:
1) Р(—3) = 13, Р(4) = 13, Р(5) = 21.
2) Р(—1) = 4, Р(0) = 3, Р(1)=0, Р(2)=7.
3) Р(— 1) = — 1, Р(1)==0, Р(3)= 1, Р(5) = 2.
6.44. Существует ли многочлен P(z) с целыми коэффициен-
тами, удовлетворяющий условиям Р(7)— 5 и Р(15) = 9?
6.45. Пусть zi, Z2, ..., zn, Zn+i—попарно различные числа.
Найти многочлен Pn(z), имеющий корни zi, Z2, .... zn и удов-
летворяющий УСЛОВИЮ P,i(Zn+l)= 1.
6.46. Пусть zi, Z2, ..., Zn, Zn+\ — произвольные попарно раз-
личные числа и Wi, W2, Шл+i — произвольные числа. До-
казать, что существует один и только один многочлен Pn(z)t
удовлетворяющий условиям
Pn(.Zk) = wk (k= 1, 2, ..., «4- 1).
6.47. Выделить целую часть рациональной функции:
., г3 + 3z2 + 5z + 7 ze - 7z4 + 8z3 - 7z + 7 -
z2 + 2 • > Z3+1
. z6 - z2 + 1 .. (z2 + I)10
°7 (z-1)3 • ’ z2 + 4 •
6.48. Указать вид разложения рациональной дроби на эле-
ментарные в множестве: а) комплексных чисел, б) действитель-.
104
ных чисел:
zi + 18г2 + 81’ 2(z + l)4 —32 ’ z6 + 2z3 + 1 ’
6.49. Разложить рациональную дробь на элементарные дроби
в множестве комплексных чисел:
4z2 - 2z + 1 ’ 2) z2 + (5 — 21) z + 5 — 51 *
3) +1 4)
г5 + z3 ’ > z4 - 1 ’
I 5) г« +1 • 6) zn-i ’
6.50. Разложить рациональную дробь на элементарные
дроби в множестве действительных чисел:
п х2 4-2x4-6_ 9х 6
Ч (х- 1)(х — 2) (х4) • X3 - 1 •
о\______ * + 4 - - 4) J*_____
х3 + 6х2+Нх + 6 * ' х2 —х5 *
п 5х2 4- 6х — 23 m 16х3 — 32х + 2
(х — 2) (х 4-I)2 (А: — I)3 ’ °'
2 Q\ __________1 ~ 3ft
х44-2х3 4- 2х2 4-2x4-1 * 7 X (х 4-1)2 (X2 4- X 4-1)2 *
§ 7. Числовые функции. Последовательности
1. Понятие числовой функции. Пусть дано числовое множе-
ство X cz R, и пусть каждому х^Х поставлено в соответствие
число г/eR, тогда говорят, что на множестве X определена
числовая функция. Правило, устанавливающее соответствие,
обозначают некоторым символом, например, f и пишут
y = f(x), xt=X.
В этой записи х называют аргументом или независимой пере-
менной, числа из множества X называют значениями аргумента,
множество X называют областью определения функции, его обо-
значают также D(f). Число у0) соответствующее значению аргу-
мента *х0, называют значением функции при х = х0 (или значе-
нием функции в точке х0) и обозначают f(%o) или f(x)|x==Xo.
Множество значений функции обозначают иногда E(f)>
Для указания функции используют иногда только символ,
которым обозначен закон соответствия, например, f.
Функции f и g называют равными, если D (f) *= D (g) и ра-
венство f (x) = g (x) верно для любого значения аргумента. Если
105
(1)
же это равенство верно лишь на множестве A cz D (f) f| D (g), то
функции fug называют равными на множестве А.
Например, функции у — ^х2, xeR (берется арифметиче-
ское значение корня), и у — х, xeR, равны на множестве
Л = [0; 4-оо), Если х < 0,то Vх2 =/= х- Указанная функция у —
— л]~х2, xeR, равна функции # = |х|, xsR, так как их об-
ласти определения совпадают и для любого хе R
( х при х > 0,
*у X2 = | X | = S -
I — х при х < 0.
Пусть заданы функции у = f(x) и z = F(y), и пусть область
значений функции f содержится в области определения функ-
ции F. Функцию
z = F(f(x)), xeD(f),
называют сложной функцией или композицией (суперпозицией)’
функций f и F и обозначают F о f.
Например, функция
z = д/1 — х2, хе[- 1; 1],
является композицией функций
У = 1 — х2, хе[- 1; 1], и z = ^/у, у [0; + °0)-
2. Элементарные функции. К основным элементарным функ-
циям относят постоянную, степенную, показательную, логариф-
мическую, тригонометрические и обратные тригонометрические
функции.
Элементарной функцией называют функцию, которая может
быть задана с помощью конечного числа арифметических опе-
раций и композиций из основных элементарных функций. На-
пример, элементарными являются функции:
линейная функция
y = ax + b, JteR,
здесь а, 6 е R, а =/= 0;
квадратичная функция
у = ах2 + Ьх + с, хе R,
здесь а, &, с R, а ф 0; функции
z = х2, хе[-1; 1], у — х sin(1/х), xeR, х =# 0,
и т. д.
Многочленом называют элементарную функцию вида
р (х) = апхп + an-ixrt-'1 + ... + ахх + aQ, х е R,
здесь ап, а,п-\, ..., «ь aoeR, neZ, п 0. Если ап =# 0, то
Р(х) называют многочленом n-й степени, обозначают его часто
100
Рп(х), а число n называют степенью многочлена. Если все
коэффициенты многочлена равны нулю, то его называют нуле-
вым многочленом. Имеет место теорема: два ненулевых много-
члена равны тогда и только тогда, когда их степени одинаковы
и коэффициенты при одинаковых степенях х совпадают.
Рациональной функцией называют элементарную функцию,
которая может быть задана в виде
где Р(х)— многочлен, Q(x)— ненулевой многочлен. Эта функ-
ция определена для всех значений х таких, что Q(x)#=0.
- Иррациональной функцией называют элементарную функ-
цию, которая не является рациональной и может быть задана
с помощью композиций конечного числа рациональных функ-
ций, степенных, функций с рациональными показателями и
арифметических действий. Примерами иррациональных функ-
ций являются функции
“ У — V1 “Я2, хе[- 1; 1], y — Kjx2— 1, xeR,
X — <\] X
Vx/з + 1
xgR.
Элементарные функции, не являющиеся рациональными или
иррациональными, называют трансцендентными. Показатель-
ная, логарифмическая, тригонометрические и обратные триго-
нометрические функции являются трансцендентными.
Под функцией, заданной формулой, понимают функцию, об-
ластью определения которой являются все значения аргумента,
для которых эта формула имеет смысл и результатом каждой
операции, указанной в формуле, является действительное число.
Пример 1. Найти область определения функции, задан-
ной формулой
з/ Х-1
л Значения х/х определены лишь при х^О. При х = 0
й х — 1 знаменатель х2 — -у/х равен нулю, поэтому следует счи-
тать, что х#=0, х=#1. Значения определены для любого
Действительного числа а, и при любом х > 0, х#= 1,
д» ______ I
а === —— действительное число. Поэтому областью опре-
х2 — V*
Деления рассматриваемой функции является множество всех
х>0, х=/=1. ▲
407
Найти области определения функций, заданных формулами
(7.1—7.2):
7.1. 1) г/ = —тт- 2) = 3) у = ~
' а x-f-l ' а х2 — 1 ' а х2 —6х + 8
.. (х 4- 2)2 1 ЙЧ *2
4) У — хз _ 4х • 5) У х 4-1 х | • 6) У 2 | х | — 3 ’
7\ 1*4-214-1 — 2х — 2х2
'' У I 2x4-2 I — 1
7.2. 1) = 2) у = 7^?. 3) y = V2zz7.
4) г/==У2 —х —х2. 5) //=-—1=. 6)
<1—X2 X
= 8)® = aW^2).
7.3. Найти линейную функцию у — ах ф- b и нарисовать ее
график, если:
1)Н1) = 0, z/(0) = —2. 2) z/( — 1) = 2, //(!) = —1.
3) г/(5) = 3, z/(-2)=l. 4) у(-1,5) =1,5, (2,5) = - 0,5.
5) «/Ui) = ^i, у(х2) = у2.
7.4. Найти квадратичную функцию f и нарисовать ее график,
если:
1) f(-1) = 0, f(0) = 5, f(6) = —7.
2) f(—2) = 2, f(l) = —1, f(3) = 7.
3) /(—6) = 7, f(—3) = —8, f(2) = 7.
4) f(xi) = yi, f(x2) = y2, f(x3) = y3, Xi^Xj, i,/ = 1,2,3.
7.5. Найти многочлен P(x) степени не выше трех, удовлет-
воряющий условиям:
1) р(-2)=1, Р(-1) = 6, Р(0) = 5, Р(1)=10.
2) Р(Х1) = у1, Р(х2) — у2, Р(х3) = уз, Р(х4) = у4, xt=£xh
i, j = 1, 2, 3, 4.
7.6. Найти многочлен Р(х) степени не выше п, удовлетво-
ряющий условиям
Р U1) = У1, Р (х2) = У2, .... р (хп) = уп, Р (Хл+1) = у п+1,
если Xi 5^ xj при i ф j (i, j — 1, 2, ..., п + 1). Такой многочлен
называют интерполяционным.
7.7. Найти области определения функций fi, f2, fi + /г, если
fi и f2 заданы формулами:
1) fl W = \/3 —X, f2(x) = Vх + 1 •
2) ли) = 71-л2, f2W=^27^T’
108
3) Мх) = V*—' V*—з, f2(x)=ig(x2—
4) Л(х) = т7===-. A>(x)==fgx.
V5x — x2
5) fi(x)==lg(16 —x2), f2(x) = t—"sinx*
6) fl (x) — X + -\/x — 1 , f2 (x) = X — Vx— 1 .
7.8. Найти области определения функций fa 1 /f, если f за-
дана формулой:
- 1) f(x) = x2 —х+1. 2) f(x) = |x| —2.
* 3) f(x) = lg(l —х2). 4) f('x) = x + Vr+2’.
5) f(x) = V2x+ 1 — 7x+T.
6) f(x) = 5x — 2X+1. 7) f(x) = 3 — 2cosx.
3) f (x) = V2 — 2 sin x- 9) f (*) = 1 — ctg x-
7.9. Найти /(3), f(a) + f(-a), f(b)-l, f(b-V),
M(p) , если:
1) f(x) == x/(x —2). 2) f(x) = (l+x)4-(l-x)\
7.10. Найти f(—4), /(—0,5), f(l), /(1984), если:
( 2 —|х| при —1 < х <
1) = ] 1 при X — 1
( 0 при х^2.
( 2х — | х | 2) f(x) — ^x+i ‘ при X > — 1, при х^ — 1.
7.11. Для функции
f (x) = 5xm + ax" + bx~m + 2x_ft,
xg‘R, x =#= 0, m, hgN,
найти а и b так, чтобы f(x) — f(l/x) для любого x =/= 0.
7.12. Найти f(a) + f(—а), если f(x)=x3 + 3x—1.
7.13. Найти f(l+b) — f(l — b), если f(x) = x4 — 2x2 + I.
7.14. Найти все значения а, при которых функция:
1) у = ах2 + (а + 3)х 4~ 4а, леК, имеет только положи-
тельные значения.
2) у —(а—1)х2+ (а + 1)х +а + 1, x&R, имеет только
отрицательные значения.
7.15. Найти + если У~л/х2 — ^ и
1) а > 1; 2) 0 < а < 1; 3) — 1 < а < 0; 4) а <, — 1.
109
7.16. Найти множество значений функции!
1) f(x) —2х —5, хе=[-2;2].
2) f(x) = |x- 1|, хе[0;5].
3) f(х) = х + signх, хеR.
4) f(x) = x2 + 2x— 3, xeR.
5) f (х) = — 2х2 + х + 1, xeR.
6) f(x) = 5- 12х —2х2, xs[—4; 1].
7) f(x) = x + y, хб=(0; + оо).
8) = х<=(—оо; 0).
9) хс;Р.
7.17. Найти множество значений функции, заданной фор-
мулой;
l)y = V*2+l- 2)у = д/х2—1. 3) # = Vx(4 —х).
4) */ = д/ 9Х%+ 1 ‘ 5) i/ = ax + -^, где а&>0.
6) у = ах + у, где ab < 0. 7) у = -^2+ 2* ~ 2 .
7.18. При таких а функция, заданная формулой
х3 + ах2 + 2х
У—27^1--------
на своей области определения совпадает с квадратичной функ-
цией?
7.19. При каких а и b функция
х3 + а*2 + Ьк + 2Ь
У ~ X2 + X + 1
является линейной?
7.20. Значения z/(0), #(1), у(2) квадратичной функции
у (к)—целые числа. Доказать, что при любом целом х значе-
ние у(х)—целое число.
7.21. Пусть Xi — нуль функции у = х2 + рх + q, х2— нуль
функции у = —х2 + рх + q. Доказать, что между Xi и х2 най-
дется нуль функции:
1) y = -jx2 + px + q. 2) y = ^x2 — px — q.
7.22. Найти композиции fog и gof и указать их области
определения для функций, заданных формулами:
1) f(x) = x2, g(x) = Vx. 2) f(x) = g(x) = v1 —
3) f(x) = 10x, g(x) = lgx. 4) f(x)==x5, g(x) = x + 5.
110
( х, х € [0; + оо), J 0, л' е [0; + оо),
5) f (х) | 0, XG (— оо; 0), & t X2, X е (— оо; 0).
6) f (х) = In х2, g (х) = sin х.
7.23. Написать формулы, задающие композиции:
l)lloVoW°yoZ, 2) Z°t/°WoV°U,
3)woyoyozou, 4) yoV°Z°U°W,
если и = sin х, v = log2 x, w — 1 + x, у = 1/x, z = Vx.
7.24. Доказать ассоциативность композиции, т. е. что
(f°g) oh = fo(goh).
7.25. Найти какую-либо функцию /, удовлетворяющую усло-
вию:
1) f(x-2)==-^-r, xeR, х^-1.
л т* 1
2) f (у) — х2 + 1, х е R, х 0.
3) f (тут)в^» — 1.
4) + xeR, х=#=0.
5) /(х2) = 1 — |х|3, xe=R.
7.26. Существует ли функция f(x), хе [0;+°°), удовлетво-
ряющая для любого xeR равенству f (х2) = 1 +х?
7.27. Пусть f(x) = —, g(x) = -====•• Найти:
ах + b 'у/а2 + х2
1) f.fof(x). 2) g-ogrog(x).
3) f ° f ° ... ° f (x) (n композиций).
4) g°go ... °g(x) (n композиций).
7.28. Пусть P(x)—многочлен и P(x) = 0 для всех х=/=0.
Доказать, что Р(0) — 0.
7.29. Доказать, что если многочлен равен нулю при любом
значении аргумента, то все его коэффициенты равны нулю.
3. График функции. Графиком функции у = f(x), x^D(f),
в прямоугольной системе координат Оху называют множество
всех точек плоскости с координатами (х; f(x)), x^D(f).
Не всякое множество точек координатной плоскости являет-
ся графиком функции. Для того чтобы данное множество было
графиком функции, необходимо и достаточно, чтобы каждая
прямая, параллельная оси ординат, пересекала это множество
не более чем в одной точке.
Hi
Функцию y = f(xj, определенную на симметричном относи-
тельно нуля множестве X, называют четной, если для любого
х сз X Нерно равенство
Ц-х) = Цх);
нечетной, если для любого № X верно равенство
График четной функции симметричен относительно оси орди-
нат, график нечетной функции симметричен относительно на-
чала координат. Примеры графиков четной и нечетной функ-
ций изображены на рис. 11, 12.
В ряде случаев график функции y = g(x) можно получить
преобразованием известного графика другой функции у — f (х).
В таблице 1 указаны простейшие из этих случаев.
Таблица 1
Функция y—g(X) Преобразование графика функции y = f (х)
+ । * 2 - -К н X - § «- Ч- 1 ‘ч" ч- II II II II II II £2} £2) ^2) сдвиг вдоль оси ординат на с сдвиг вдоль оси абсцисс на с симметрия относительно оси ординат симметрия относительно оси абсцисс умножение каждой ординаты на а деление каждой абсциссы на а
Вместо преобразования графика функции y = f(x) можно
воспользоваться преобразованием системы координат. Напри-
мер, график функции y = f(x)-\-c получится, если, не меняя
графика функции у = f (х) (как множества точек плоскости),
взять новую систему координат/сдвинутую на —с вдоль преж-
ней оси ординат, и т. д.
Пример 2. По известному графику функции у = х2
(рис. 11) построить график функции у — х2— 4х + 2, xeR.
А Поскольку у = х2 — 4х + 2 = (х — 2)2 — 2, искомый гра-
фик получается сдвигом параболы у = х2 (рис. 11) на 2 еди-
ницы вправо, а затем на 2 единицы вниз (рис. 13). Этот же ре-
зультат получится, если систему координат, в которой построена
парабола у = х2 (рис. 11), сдвинуть вверх на 2 единицы и влево
на 2 единицы, оставляя параболу неизменной.
Аналогично из графика параболы у — х2 можно получить
график квадратичной функции у = ах2 + 6х + с, записав ее
в виде
^ = ax2 + 6x + c = a(x + -^-)2 + (-аС~62-)- >
Характерными точками параболы у — ах2 + Ьх + с являются
вершина с координатами х0 ——Ь/2а, уо=(4ас— Ь2)/4а, точ-
ка (0; с) пересечения с осью ординат и точки пересечения
с осью абсцисс (если они есть).
Пример. 3. По известному графику функции у=1/х,
xeR, х#=0 (гипербола, рис. 14), построить график функции
» = . х ,xeR, х=И=1.
1 — X
А Имеем
X _ 1 + (х~1) _____1____1
У 1—X х — 1 х — 1
(2)
Симметрия относительно оси абсцисс гиперболы у=1/х дает
график функции у = — 1/х, х<^ R, х =/= 0 (рис. 14). Возьмем но-
вую систему координат, получающуюся из прежней в соответ-
ствии с (2) сдвигом влево вдоль оси абсцисс на единицу, а за-
тем сдвигом на единицу вверх по оси ординат (рис. 15), Кри-
вая, изображающая график функции у = —\/х, будет в новой
системе координат графиком функции # = х/(1 —х).
113
Пример 4. Построить график функции
У = Е(х), х eR (целая часть х),
где Е(х)—наибольшее целое число, не превосходящее х*).
А На каждом промежутке [п; п + 1), где п е Z, данная
функция постоянна и равна п. В соответствии с этим изобра-
Рис. 16.
жен ее график на рис. 16. Стрелка на графике указывает на то,
что точка в ее острие не принадлежит графику. ▲
7.30. Какие из указанных функций являются четными, ка-
кие нечетными, какие не являются ни четными, ни нечетными:
1) r/=.|x|, xgeR. 2) у = xeR.
Л -ф- 1
3) = 1’» 0- 4) ^==^-^4, хе(-1; 1).
( х4, х > 0,
6)!/ = 1Лх<0. 6)9-^. хе(-оо;1].
7) у — Iх + 11, хеR. 8) г/ = |х+1| + |х—1], хеR.
9) у — \ 10 — х| — 110 + х|, xeR?
7.31. Доказать, что произведение двух четных или двух не-
четных функций — функция четная, а произведение четной и не-
четной функций — функция нечетная.
7.32. Построить графики функций:
1) у — 2х2— 4х + 5. 2) у — 2х— х2— 2.
3) у — х2 — 2х + с, где а) с = 2; б) с = 1; в) с — 0; г) с = —3.
4) у — ^/х — 2 + х + — х .
) Иногда эту функцию обозначают у — [х].
414
7.33. В одной системе координат построить графики функ-
ций:
1) у = х; у = х2; у = х3; у = х*.
1 1 1
2) У = ^'< У = у==^-
3) у — х', у = х1/2; у — х113; y = xl,i.
.. 1 1 1
4) у = -; y — —i=\ y—~sj=-
к ух у х
Построить графики функций (7.34—7.37):
7.34. 1) у = ^4 — х2. 2) у = — V9 — х2.
2) у — 3—у^1—х2. 4) у — V2x — х2 — 1.
{1, х > О,
О, х = 0, (читается: «.сигнум икс'»).
— 1, х <0
7.36. 1) у = {х}, где {х} = х — Е(х) — дробная часть х.
2) t/ = E(l/x).
7.37. 1) 0 = |х—1|. 2) у = |* + 21. 3). 0 = |х.+ 1| +
гН * 11.
4) 0 = (|х4-11 — lx — 11)/2.
б) 0 = signx — (Iх4- 11 — |х — 11)/2.
6) у = sign х2. 7) у = sign (х2 — 1).
8) у = sign 9) 0 = sign (х3 — 4х).
7.38. Построить графики функций f(x), — f(x), f(—x),
>—f(—x), f(x)—3, f(x —3), если:
l)f(x) = 2x + 6. 2) f(x) = 4x-x2.
3) f (x) = 716^?. 4) f (x) = 1/x.
7.39. Построить графики функций:
1 \ 2X — 1 o\ 1 ox л \ X — 1
1 ) y = —~ • 2) 3) y — x_2- 4) y— x + 2 .
7.40. Построить графики функций f(x), |f(x)| и /(|х|),если:
1) f(x) = 3x-8. 2)/(x) = 3-2x. 3) f(x) = x2-x-2.
4)/(x) = 6x — x2 — 5. 5)f(x) = 7|I. 6)f(x) = ^±l_.
7.41. Продолжить функцию y = f(x), xe(0;a), на (—a;OJ
так, чтобы получившаяся на (—а; а) функция была: а) четной,
б) нечетной:
1) у — х, хе(0; 4- со). 2) у = х2, хs(0; + со).
3) У — л] х, хе(0; + со). 4) у — х-\-Ъ, хе(0; 4-со).
5) у — д/1 — х2, х е (0; 1). 6) у — х2 — 4х + 3, x s (0; + со).
7> хе(0; +оо)*
Задать продолжение формулой и построить график получив-
шейся функции.
7.42. Построить в одной системе координат графики функ-
ций f(x) и 1/f(х), если:
1) f(x)==3x —2. 2) f(x) = x2+l.
3)f(x) —х2—1. 4) f(x) = -§^.
7.43. Построить в одной системе координат графики функ-
ций fi, f2 и fi -j- f2, если:
1) fi(x) = x3, f2(x) = lx. 2) А(х) = х2, f2(x)x=-±.
3) ft (х) = х, f2 (х) = 4 • 4) f, (х) = х2, f2 (x) =
7.44. Построить в одной системе координат графики функ-
ций fi, f2 и fi — f2, если:
О fiW = V4 — х2, f2(x) = x2. 2) ft(x) = x, f2(x) = l/x.
3) fiU) = x3, f2(x) = 4x. 4) fi(x) = x3, f2(x) = l/x2.
4. Обратная функция. Пусть функция у = f (х), х е D (/),
такова, что для любых xb x2^D(f) из того, что Xi Ф х2, сле-
дует, что f(xi)=# f(x2). Тогда для каждого найдется
только одно значение x^D(f) такое, что f(x) = y.
Функцию, определенную на E(f) и сопоставляющую значе-
нию y^E(f) такое x^D(f), что f(x) = у, называют обратной
для функции f и обозначают f~l, т. е.
x = f~'(y), У^Е[Г)-
Согласно определению = E(f), E(f~1) = D(f), т. е. мно-
жества определения и значений исходной и обратной функций
меняются местами.
Функцию, имеющую обратную, называют обратимой.
Каждая прямая у = yOj где y0^E(f), пересекает график
обратимой функции в единственной точке (х0; у0), где f(x0) = f/o.
Обозначая, как обычно, аргумент обратной функции х, а
значение у, ее записывают в виде
y=J-lW, x&Dtf-1},
Из определения обратной функции следует, что
Vxe£(f) f(f->(x)) = x, (3)
VxeD(f) f~4f(x)) = x. (4)
График обратной функции y = f~l(x), xeDfJ-1), симметри-
чен графику функции у — f(x), x^D(f), относительно прямой
у = х. На рис. 17 изображены графики взаимно обратных функ-
ций у = х3 и У =X , X G R.
Пример 5. Доказать, что функция, заданная формулой
у — х2 — 4х + 2: (5)
а) на R необратима;
б) на (—оо; 2] обратима.
В случае б) построить график обратной функции.
А а) Уравнение
х2 — 4х + 2 = у о (6)
имеет решения
X] = 2 + д/^о + 2 и х2 = 2 — д/Уо + 2
для любого у0 —2. При у0 > —2 эти решения различны, т. е.
для у0 > —2 имеются два различных значения аргумента Х\ и
$2 такие, что у(хх) = у (х2) (каждая прямая у — у0, у0 > —2,
пересекает график функции в двух точках (см. рис. 13)). Зна-
чит, функция, определенная формулой (5) на всем R, необра-
тима.
б) Уравнение (6) для любого у0 —2 имеет лишь одно ре-
шение
x = 2-V^+"2 (7)
•из промежутка (—оо; 2]. Значит, функция, определенная фор-
мулой (5), на (—оо; 2] обратима. Графиком этой функции
является левая от прямой х = 2 часть параболы на рис. 18,
117
каждая прямая у — yQ, yQ —2, пересекает этот график только
в одной точке. Область значений данной функции — промежу-
ток [—2; + оо) — является областью определения обратной функ-
ции, которая согласно (7) задается формулой
у = 2 — л/х + 2. (8)
Чтобы получить график обратной функции, совершим сим-
метрию параболы у — х2— 4х + 2 (см. рис. 13) относительно
прямой у = х (рис. 18). Нижняя от прямой у ^2 часть полу-
чившейся параболы и будет графиком функции (8). Л
7.45. Доказать, что функции f и g взаимно обратны:
О/М-Нтт «<*>=гЬ-
2) f(x) — -^l -х», g(x) = Vl
7.46. Доказать, что график функции f симметричен относи-
тельно прямой у — XI
1) f (X) = 7 (а 0). 2) f (х) = л/2^.
7.47. Являются ли взаимно обратными функции, заданные
формулами:
1) У = ^~Т' & = Т=Т- 2) у=1 — ^7, у = (1—х)3.
3) г/ = 1 + Vx, у = (х — I)2. 4) г/ = V1 — х2, z/ = V1 — х2?
7.48. Среди функций указать обратимые:
1) z/ = 2x — 1. 2) у = \х\. 3) у=1/х3.
4) i/ = x2 + 2x — 3. 5) у — -у/х?. 6) у — л]х—1.
7) i/ = signx. 8) z/ = x2signx.
Обратные функции задать формулами и построить их гра-
фики.
7.49. 1) При каких а и b функция у = ах + b имеет обрат-
ную и совпадает с ней?
2) При каких aeR функция у = х“, х > 0, совпадает со
своей обратной?
5. Ограниченные и неограниченные функции. Функцию f на-
зывают ограниченной сверху на множестве XcD(f), если су-
ществует число С такое, что для любого хе А' верно неравен-
ство
f(x).^C4
118
Используя символы 3 и V, это определение записывают так:
3CVx((xeX)=>(f(x)=^C)). (9)
- Аналогично, функция f ограничена снизу на множестве
XaD(f}, если
3CVx((xeX)=>(f(x)>C)). (10)
Функцию, ограниченную и сверху и снизу на множестве X,
называют ограниченной на множестве X. Это определение рав-
носильно следующему: функция f ограничена на множестве
Xc.D(f), если существует число С >0 такое, что для любого
х^Х верно неравенство |f(x) С; короче,
3C>0Vx((xeX)=>(|f(x)|^C)). (11)
Если в этих определениях X = D (f), то функцию называют
соответственно ограниченной сверху, ограниченной снизу, огра-
ниченной.
Например, функция у—\/х, xsR, х#=0, ограниченна
сверху на множестве X = (—оо; 0), так как 1/х < 0 при х < 0,
т. е. (9) выполнено при С = 0. Эта же функция ограничена снизу
на (0; +оо), так как (10) выполнено при С — 0. Квадратичная
функция у — ах2 + bx -J- с, хе R, ограничена снизу при а > 0,
так как для любого хе R
ах2 4- &х + с = а (* + (12)
и, значит, ах2 + Ьх + с (4ас — Ь2)/4а, т. е. (10) выполнено
при С — (4ас — Ь2) /4а. При а < 0 квадратичная функция огра-
ничена сверху, так как из (12) следует, что для любого xe'R
выполнено неравенство v
ах2 4- Ьх + с (4ас — Ь2) /4а.
Пр и м е р 6. Доказать, что функция
у — * , , х е R,
а хг + 1 ’
ограничена.
—х Из неравенства для среднего геометрического и среднего
арифметического следует, что |х| ^(х2 4-1)/2. Отсюда имеем
| х I |х| < _1_
| х2 + 1 I х2 + 1 2
Для любого хе R, т. е. (11) выполнено при С — 1/2 и, значит,
Данная функция ограничена. А
Отрицание определения ограниченной функции (см. (11))
выглядит так: функция f неограничена, если для любого С > О
найдется xeD(/) такое, что |)(х)|>С; короче,
VOO 3x((xeZ)(f))=H|f(x)|>0)). (13)
Аналогично формулируются отрицания определений ограни-
ченной сверху (снизу) функции.
119
Пр и мер 7. Доказать, что функция
y = \Jx,\ xgR, х#=0, неограничена, и
построить ее график.
у_ j А Пусть С — произвольное положи-
'а2 тельное число. Неравенство 1/х2>С
L равносильно неравенству |х| < 1 / д/С
при х У= 0. Взяв, например, х = 1/(2 VQ
получим, что 1/х2 = 4С > С, а это со-
2 ^гласно (13) и означает, что данная функ-
ция неограничена.
Рис 1Q т- 11
График функции представлен на рис.
19. Он симметричен относительно оси
ординат, поскольку данная функция четная, и расположен выше
оси абсцисс, так как 1/х2 > 0 для любого х =/= 0. А
7.50. Доказать ограниченность функций:
1) г/ = х2 — х~ 1, хе[- 1; 5]. 2) г/ = - 10~. хе[0;5],
3) + 1 4) у = °' . л-eR.
5)z/ = -4=2-, 6)^3*; + 6*+10.
I x3 — 1 | ’ y Vo.lx4 + 1
7.51. Сформулировать и записать, используя символы В, V,
определения того, что функция: 1) неограничена сверху, 2) не-
ограничена снизу.
7.52. Доказать, что функция у=1/х, xeR, х#=0: 1) не-
ограничена сверху, 2) неограничена снизу.
7.53. Доказать, что функция у = —^2===-, яе(-1; 1), огра-
<1 — х2
ничена снизу и неограничена сверху.
7.54. Доказать, что квадратичная функция у = ах2 -f- bx + а
1) неограничена сверху при а > 0, 2) неограничена снизу при
а < 0.
- 7.55. Доказать, что 1) сумма, 2) произведение ограниченных
функций — ограниченная функция.
6. Верхняя и нижняя грани, наибольшее и наименьшее зна-
чения функции. Монотонные функции. Верхнюю (нижнюю)
грань множества всех значений функции г/ = f (х), xeD(f), на-
зывают верхней (нижней) гранью функции и обозначают
sup f, sup f(x) (inff, inff(x)).
Если в этом определении рассматривают значения функццц
лишь на множестве XczD(f), то говорят о верхней (нижней)
грани функции на множестве X и пишут
sup f, sup f (x) (inf f, inf f (x)).
X x<sX X xsX
120
• Значение f(x0), где х0 (= X cz D (f)\ функции называют наи-
большим (наименьшим) на множестве X, если для любого / е X
верно неравенство f(x) f(xQ) (соответственно f (х) f (х0)) •
В этом случае число f (х0) обозначают
max/, maxf(x) (соответственно minf, minf(x)).
X xgeX X хеХ
Если X — D(f), то говорят коротко о наибольшем (наимень-
шем) значении функции и обозначают его
maxf, maxf(x) (minf, minf(x)).
Наибольшее (наименьшее) значение функции называют
также максимальным (минимальным) значением.
Если существует maxf, то supf = maxf; если существует
ххх
minf, то inf f = minf.
х _ х х
- Из существования конечного sup f (inf f) не следует, вообще
X X
говоря, существование максимального (минимального) значения
функции. Например, функция, график ко-
торой изображен на рис. 20, не имеет ма-
ксимального значения, и в то же время
supf = 1.
Функцию f называют возрастающей
(неубывающей) на множестве XczD(f),
если для любых Xi,x2eX из неравен-
ства *1 < х2 следует неравенство f(xi)^
Cf(x2).
Это определение коротко записывают
так:
VxiVx2((x} е= X, х2 е X, Xi < х2)=> (f(Xi)^f(X2))).
Функцию f называют убывающей (невозрастающей) на мно-
жестве XczD(f), если для любых Xi,x2(=X из неравенства
*1 < х2 следует неравенство f (xi) f(x2)', короче,
VXiVx2((xi (= X, х2(=Х, Xi < x2)=>(f(Xi)^ f(x2))).
Если в этих определениях из неравенства Xi < х2 следует
строгое неравенство f(Xi) < f(x2) (соответственно f(Xi)>
l>f(x2)), то функцию называют строго возрастающей (соответ-
ственно строго убывающей) на множестве X.
Возрастающие и убывающие функции объединяют названием
монотонные, строго возрастающие и строго убывающие —
строго монотонные.
Если X — D(f), то указание на множество X опускают.
Примером строго возрастающей функции является функция
У = х3, х е R (см. рис. 12). Функция у = х2, х е R (см. рис. 11),
строго убывает на (—оо;0) и строго возрастает на (0}У-оо),
121
на всей своей области определения R она не является моно-
тонной.
7.56. Найти maxf, minf, если:
X X
1) f(x) = x2 —4х — 5, Х = [0; 5].
2) f(x) = — x2 + 5x-6, Х = [0; 4].
з) zw=7T2-’ х=[~10; -31-
4) fU) = 4^-. * = [-1; 3].
5) = x = [l-, 2].
6) f(x) = -^-, X —R.
7.57. Доказать, что если функция f знакопостоянна на мно-
жестве X, то
1 . с • 1 с
max-г = minf, min-7- = maxf.
xi х х г х
7.58. Доказать, что maxf и minf не существуют, если:
1) fW = -i7j-. xeR, х#=0.
2)f(x) = -^-. хе(-1; +оо). 3) f(x) = —7==== , xe=R.
7.59. Доказать, что существует minf, но не существует
max f, и найти min f, если: .
1) f(х) = х2 — Зх, xeR. 2) f(x) = x3 + -^-, хе(0; +оо).
3) /w= vrr?' *sR- 4) fw=-v5r’ хе|1; 2>-
7.60. Доказать, что существует maxf, но не существует
minf; найти maxf, если:
1) f(x) = 4x — х2 — 6, xsR.
2) f(x) = 2^F + J=, xg=(-8;0).
3) f(x) = j-qrp. xe=R. 4) f(x)= . xe[0; 1).
7.61. Найти supf, inff, а также maxf, minf, если послед-
xx xx
ние существуют:
1) /(Х)=^^-. Х = (0; +оо).
2) /(х) = ^-. ^ = (-00; 0).
122
3)f(x)=-^rr, J = R.
4) = X = {xe[-2; 3], x 2).
5) t{x) — x — E(x), X = R.
7.62. 1) Доказать, что если существует maxf, то
х
sup f = max f.
X X
2) Доказать, что если существует min f, то
x
inf f = minf.
X X
7.63. Доказать, что
inf (— f (x)) = — supf(x).
xeX x&X
7.64. Доказать, что квадратичная функция у — ах2 + Ьх + с:
I) при а>0 строго убывает на (—оо; —Ь/2а] и строго воз-
растает на [—6/2а;+°°); 2) при а<0 строго возрастает на
(—оо; — Ь/2а] и строго убывает на [—Ь/2а\ +оо).
7.65. Доказать, что функция у = х3 + * возрастает.
7.66. Доказать, что функция у = (1 — х2)/х убывает на лю-
бом интервале, не содержащем нуля.
7.67. Доказать, что функция у = (1 + х2)/%; 1) строго воз-
растает на (—оо; —1] и на [1; +°°); 2) строго убывает на
[—1; 0) и на (0; 1].
7.68. Найти наибольшие проме-
жутки, на которых функция у—х4— /7
— 2х2—2: 1) возрастает, 2) убывает.
7.69. 1) Доказать, что строго мо-
нотонная функция взаимно одно-
значна.
г 2) Привести пример взаимно од- '
позначной немонотонной функции.
7. Показательная и логарифми-
ческая функции. Пусть а — данное
положительное число, а #= 1. Пока-
зательная функция
у — ах (14) Рис. 21.
определена на R, множеством ее значений является интервал
W; +оо). При а > 1 функция строго возрастает, при 0 < а < 1
строгр убывает (рис. 21).
123
Показательная функция у — ах, xe R, обратима. Обратную
функцию называют логарифмической и обозначают
y=logax, ч (15)
она определена на интервале (0;+°°), множеством ее значе-
ний является множество R. При а > 1 логарифмическая функ-
ция строго возрастает, при 0 < а < 1 строго убывает. Графики
функций у = ах, xeR, и у = log^x, хе(0; 4-оо), симметричны
друг другу относительно прямой у = х (рис. 22, 23).
То, что функции у = ах и у = logax, а > 0, а ф 1, взаимно
обратны, означает, что
V хе(0; + оо) alogax = x, (16)
Vx^R logaa* = x. (17)
Пример 8. Построить график функции, заданной форму-
лой
1
У — 2х 1 •
А Функция определена для всех xeR таких, что 2Х=И=1,
т. е. х #= 0. При построении ее графика можно использовать
график функции у = 2х—1, xe:R (рис. 24). Эта функция
строго возрастает от —1 до J-°°- Значения данной функции об-
ратны значениям функции у = 2х—1. На (—оо; 0) данная
функция убывает от —1 до —оо, а на (0; +оо) убывает от
4-оо до 0 (рис. 25). ▲
Пример 9. Построить график функции, заданной форму-
лой
У = log3(x2— 1).
А Функция определена для всех х таких, что |х| > 1, т. е.
на объединении интервалов (—оо;—1) и (1; 4”°°)- Функция—*
четная, ее график симметричен относительно оси ординат.
124
Данная функция является композицией функций у = х2—1
(ее график показан на рис. 26) и логарифмической функции
# = log3x. На интервале (1; +оо) значения х2 —1 строго воз-
растают от 0 до +°°, поэтому значения log3(x2—1) строго
возрастают от —оо до 4~оо. График пересекает ось абсцисс при
х = д/2 и х =—д/2 (рис. 27). А
8. Гиперболические функции. Гиперболические синус и коси-
нус определены на R соответственно формулами
, ех — е~х ех + е-х /<Л.
shx =—2-----, chx==——------. (18)
Функция z/ = shx— нечетная, строго возрастающая. Функция
у = ch х — четная, строго убывающая на
растающая на [0; +°°)- Графики этих
функций изображены на рис. 28, 29.
Гиперболические тангенс и котан-
генс определены формулами
<l9>
cthx = -^-. (20)
sn X '
(—оо; 0] и строго воз-
Обе функции — нечетные, их графики
представлены на рис. 30, 31.
Функции y = shx и у = th х, x&R, обратимы, их обратные
функции обозначают соответственно
y = arshx, x&R (21)
(читают: ареасинус гиперболический),
y = arthx, xeR (22)
(читают: ареатангенс гиперболический).
Пример 10. Доказать, что функция, обратная для функ-
ции
y = chx, хе [0; 4-оо),
является элементарной, и построить ее график.
Л На [0; +оо) функция f/ = chx строго возрастает и по-
этому обратима. Областью определения обратной функции бу-
126
дет промежуток [1;Ц-оо), являющийся множеством значений
исходной функции. Для каждого у е [1; 4-°°) уравнение
ch х = у, т. е.
ех + е-х
---2--= У,
сводится к квадратному относительно ех уравнению
(е*)2 — 2уех + 1 =0.
Отсюда находим ех — у ± <\/ у2 — \, х =Лп(у ± ^У2 — 1 )• Усло-
вию х 0 удовлетворяет только решение
Таким образом, обратная функция зада-
ется формулой
у — In (х 4" -yjх2—1 ), хе [1; + °°)-
(23)
Видно, что эта функция получается с по-
мощью конечного числа арифметических
операций и композиций степенных и ло-
гарифмической функций, т. е. является
элементарной.
График обратной функции получаем симметрией относитель-
но прямой у = х графика функции w = chx, хеГ0;4-°°)
(рис. 32). А
7.70. Найти области определения функций:
2)y = V2^3^.
3) у = log2x2 и r/ = 2Iog2x.
' 4) У = log,5. 5) у = (1g (100 - х))-’.
6) l/ = lnx + ln(x— 1) и # = lnx(x— 1).
7) у = log3+JC (х2 — 1). 8) у = log3 logo.5 х.
г
7.71. Найти множество значений функций:
1)//=10-Л 2) 3)^ = 4* —2*4-1.
4) У = 1g (х2 4- Ю)- 5) у = log2 (4 — х4).
6) # = log3x4- logx3.
7.72. Какие из функций являются четными, какие нечет-
ными, какие не являются ни четными, ни нечетными:
1) у-х-2~х. 2) у = \\gx\. 3) у = \пе\ 4) =
5) у= 10*4-10-*. 6)г/ = ^-^.
127
7) у = thx — х. 8) # = ln(l—х2).
8) z/ = lncthx?
7.73. Доказать: х
1) sh (х + у) = sh х ch у + ch к sh у.
2) ch (х -f- У) = ch х ch у + sh х sh у.
3) sh (х — у) = sh х ch у — ch х sh у.
4) ch (х — у) — ch х ch у — sh х sh у.
5) sh х sh у — (ch (x у) — ch (x — y))/2.
6) ch x ch у — (ch (x + y) + ch (x — i/))/2.
7) sh x ch у = (sh (x + y) + sh (x — t/))/2.
7.74. Доказать ограниченно’сть функций:
1) y= Ю-Hl. 2) r/^0,3*’-1. 3) y = )g(2\_?)-.
4) y = log4(x2 +5) — log2(l +1 x I).
5) # = (lgx+ logx IO)"1.
7.75. Доказать неограниченность функций:
1) у = 0,4*, .reR. 2) z/ = logo,iX, xe(l; 4-o°).
3) y = xx, xe(0; + oo). 4) y = logx2, xg(1; + oo).
7.76. Доказать, что при a > 1:
1) sup a'lx — + oo, inf a1/x=l.
(0; 4-oo) (0; 4-°o)
2) sup inf a1/x = 0.
(—oo; 0) (— oo; 0)
7.77. Найти inf f, sup f, а также max f, min f, если они суще-
ствуют:
1) дх) = 2-1*+2|. 2) f(x) = (VF-l)1"*’.
3) f (x) = 1 - 2V«-n 4) f (x) = 8 - 2x+1 - 4*.
5) fU) = lg(x2 + x-2). 6) f(x) = logo,!(4x — 3 — x2).
7) f (x) = (log2 (2/x)) Iog2 8x.
7.78. Доказать, что функция у = 2!/* убывает на каждом
интервале, не содержащем нуля.
7.79. Доказать, что функция y = log3(x2— 2х) убывает на
(—оо; 0) и возрастает на (2; +оо).
7.80. Исследовать на монотонность функции!
1) у = (2/3)1/х. 2) у = $х\.
3) у = 21~х-2х-1. 4) f/ = lg(l+ х3 * 5).
5) t/ = logx10. '6) z/ = ln(4x — х2).
7) у = logo,5 •
128
Построить графики функций (7.81—7.82) :
7.81. 1) у = 3~1*+21. 2) у = 21/х.
3) у —2Х+1--1- 4) z/==log4|x+1 |.
5) у — 21ogi/3|x|. 6) «/ —I log0,5x | —-1.
7) jr=-lgx2. 8) y = log0,25*. 9) r/^8,oge(x-3).
7.82. 1) у ==(1,5)*’2) ^ = 2’*+'^.
3) у = log2 (х2 + х — 2). 4) у = log0>] (4х — 3 — х2).
5) у = log3 ((х + 2)/х). 6) у = logх. 3.
7.83. Функцию, заданную на (0; ф-оо), продолжить, задав
формулой, на (—оо;0]: а) четно, б) нечетно; построить график
получившейся функции:
1)у = -3-2х-’. 2)у=1—21gx.
3) z/=logx+2x. 4) y = th(x — 1).
7.84. Найти функцию, обратную данной функции, указать ее
область определения и построить ее график:
1) У = ^-к. 2) y^=l+lgU + 2).
3) г/ = аЛр}- 4)y = logx10.
5) у = 2Л-‘ —2~х. 6) z/ = !n(x —V^2- О-
7.85. Для указанной функции задать обратную функцию фор-
мулой и построить график:
1) r/ = chx, te(—оо; 0). 2) # = shx, xgR.
3) # = thx. xeR. 4) z/ = cthx, reR, x 0.
7.86. Доказать, что график функции у ~ 1п(1—ех) симмет-
ричен относительно прямой у = х.
9. Периодические функции. Тригонометрические функции.
Число Т У= 0 называют периодом функции f, если для любого
хе D(f) выполнено
x+TeD(f), x-T&D(f) и f(x+ T)=f(x).
Функцию, имеющую период, называют периодической.
Если Т—период функции, то для любого /isZ, п #= 0,
число пТ также является периодом этой функции.
График периодической с периодом Т функции при сдвиге
вдоль оси абсцисс на Т переходит в себя.
Тригонометрические'функции z/ = sinx и y — cosx— перио-
дические с наименьшим положительным периодом 2л, a y = tgx-
и y = ctgx — периодические с наименьшим положительным пе-
риодом л.
Ь Л. Д. Кудрявцев и др.
129
Функции z/ = sin х и r/ = cosx определены на R. Функция
У = tg х определена для всех х е R, х ¥= у + ям, ne Z. Функ-
ция у = ctgx определена для всех xeR, х #= лп, п е Z\
Графики функций r/ = sinx и r/-^tgx, наглядно показы-
вающие их свойства, изображены на рис. 33, 34.
Из формулы приведения
• ( .л
cos х = sin ! х + —
следует, что график функции y = cosx получается сдвигом
графика функции r/=sinx на л/2 влево по оси абсцисс
(рис. 35). Из формулы
Ctgx = — tg(x — у-)
вытекает, что график функции у = ctgx получается из графика
функции у = tgx сдвигом вправо на л/2 по оси абсцисс и-сим-
метрией относительно этой оси (рис. 36). Функции- r/ = sinx,
у = tg х, у = ctg х — нечетные, их графики симметричны отно-
сительно начала координат. Функция у = cosx— четная, ее гра-
фик симметричен .относительно оси ординат.
Пример 11. Построить график функции, заданной форму-
лой
у = cos2 х.
130
А Функция определена на R, является четной, периодиче-
ской с периодом л. Поскольку
cos2 х = (1 4“ cos 2х) /2,
ее график получается из графика функции у = cos х сжатием
вдвое вдоль оси Ох, сдвигом на единицу вверх по оси Оу и
сжатием вдвое вдоль оси Оу. В соответствии с этим изображен
график на рис. 37. А
Пример 12. Построить график функции, заданной фор-
мулой
1
и sin х
А Областью определения функции является множество всех
xe-R таких, что sinx=#0, т. е. х пп, n^Z. Функция — не-
четная, периодическая с периодом 2л. Построим график на ин-
тервале (0;л), затем продолжим его на (—л; 0) симметрично
относительно начала координат, а далее продолжим периоди-
чески с периодом 2л.
Если х е (0; л), то 0 < sin х < 1, и поэтому
1 ,
sin X
причем
1 1 I
11110 sin х sin х |л=л/2
= 1
131
Поскольку sin (у + ~ sin (у —- , график симметричен
относительно прямой х — л/2. При увеличении х от 0 до л/2
значения sin % строго возрастают от 0 до 1, поэтому значения
1 /sin х строго убывают от 4"°° Д° 1 (рис. 38).
Функции, заданные формулами
V sin х * cos х '
называют соответственно косеканс и секанс и обозначают
cosec х ~ -Д—, sec х = —-—. (24)
sin X COS X v '
Пример 13. Построить график функции у = xcosх, x^'R.
А Функция — нечетная, поэтому построим ее график при
х > О, а затем совершим симметрию относительно начала ко-
ординат. При построении графика будем руководствоваться
тем, что ординаты его точек получаются перемножением орди-
нат точек графиков функции у — х и у = cosx (рис. 39).
График проходит через начало координат, пересекает ось
Ох при х = -^- + лп, neZ (где cosx = 0). Поскольку —1
cos х 1, при х 0 имеем
—х х cos х х,
т. е. график лежит между прямыми у — х и у = —х. При
х = 2лп, n^Z (где cosx=l), график имеет общие точки
с прямой у — х, а при х = л + 2лп, n g Z (где cos х — —1), —•
общие точки с прямой у = —х.
Если 0 < х < 1, то 0 < х cos х < cos х и х cos х < х, т. е.
график лежит ниже графиков у = cosx и у = х. При х=1
гпафики у — х cos х и у = cos х пересекаются, при этом
132
у = cos 1 0,54. Если х>1, то |xcosx| > [cosx|, если
cos х т. е. точки графика y — x^QSx лежат дальше от оси
Ох, чем соответствующие точки графика у == cos х. В соответ-
ствии с этим, рассчитав и отметив несколько промежуточных
точек, изображаем график (рис. 39). Он представляет собой
кривую, колеблющуюся между прямыми у == х и у = —х. А
Пример 14. Доказать, что функция у = sin х2, х R, —•
непериодическая.
А Достаточно доказать, что функция не имеет положитель-
ного периода, так как если бы число Т < 0 было периодом, то
число —Т было бы положительным периодом. Доказательство
проведем методом от противного.
Допустим, что число Т >0 — период функции, т. е. для лю-
бого х е R
sin(x + Т)2 = sin %2.
При х = 0 отсюда следует, что sin Т2 = 0, т. е. Т2 = пп, а
Т = д/лп при некотором п е N. Если 0 < х < д/л > то sin х2 0,
а поскольку д/лп —период, то и sin (х + д/л/г )2 0. Если же
х = д/л,то sin (Vя + )2= sin (д/л )2 = 0. Значит, число
д/л + д/лгг является ближайшим справа к д/лп числом,
при котором sinx2 = 0. Отсюда следует, что д/л + д/лп
.<?д/л (n + 1), так как д/л (п -ф 1) > д/лп и sin (д/л (n + I))2 —
— 0. Но неравенство д/л + <д/л(п+1), равносильное
неравенству 1 д/п + 1 — д/и> неверно для любого п N,
так как
' д/п + 1 — Д/7Г — - -1----7= < 1.
v Vrc +1 + V
Значит, неверно и допущение о периодичности функции sinx2,
т. е., эта функция — непериодическая. А
10. Обратные тригонометрические функции. Периодическая
функция необратима; в частности, необратимы и тригонометри-
ческие функции. Но на некоторых подмножествах своей области
определения эти функции обратимы.
Функция sinx на отрезке [—л/2; л/2] имеет обратную, ко-
торую обозначают
z/=,arcsinx, xg[—1; 1]. (25)
Множеством значений этой функции является отрезок
[—л/2; л/2]. Ее график симметричен относительно прямой у = х
Графику функции у — sinx, хе [—л/2; л/2] (рис. 40). Функция
У ~ arcsin х является нечетной.
Функция у — cosх, хе[0;л], имеет обратную функцию
у = arccosx, х^[—1; 1], (26)
множество значений которой — отрезок [0;л], График этой
Функции представлен на рис. 41, он симметричен относительно
133
точки (0; л/2). Функция у = arccbsx не является ни четной ни
нечетной.
Функция z/ = tgx, хе(—л/2;л/2), имеет обратную функ-
цию
// = arctg?c, xeR, (27)
множество значений которой — интервал (—л/2; л/2). Функция
у—— arctgx является нечетной. Ее график изображен на рис. 42.
Функция r/ = ctgx, х^(0;л), имеет обратную функцию
r/ = arcctgx, xeR, (28)
множество значений которой — интервал (0; л). Эта функция не
является ни четной, ни нечетной. Ее график показан на рис. 43,
он симметричен относительно точки (0; л/2).
Пример 15. Доказать, что
arcsin х + arccos х = л/2, х е [— 1; 1 ].
Л Функции sinx, —л/2; л/2], и arcsin х, х ge [—1; 1],
взаимно обратны, поэтому (см. (3)) для любого /е[—1; 1]
sin (arcsin х) = х.
134
Отсюда и из формулы sin а = cos (у — а] следует, что
к — cos (у — arcsin х) , х<=| —1; 1|. (29)
функции cosf, /е[0; л], и arccos/, —1; 1], взаимно об-
ратны, поэтому (см. (4)) для любого t е [0; л]
arccos (cos t) — t.
В частности, это верно и для / = у—arcsin х, поскольку у —
— arcsinхе [0; л]. Отсюда и из формулы (29) получаем, что
arccos х = arccos (cos (у — arcsin х)) — у — arcsin х, т. е.
arcsinх + arccosх — л/2 для любого хе[—1; 1]. А
Пример 16. Построить графики функций, заданных фор-
мулами:
1) у = sin(arcsin х); 2) у — arcsin(sin х).
А 1) Эта функция определена на [—1; 1]. Функция sinx,
хе[—л/2; л/2], является обратной для функции arcsinх,
1; 1], поэтому (см. (3)) для любого хе[—1; 1] верно
равенство
sin (arcsin х) = х.
Отсюда следует, что у — х, хе[—1; 1], т. е. графиком данной
функции является отрезок прямой у — х (рис. 44).
2) Эта функция определена на R, периодична с периодом
2л, так как sin (х + 2л) — sin х и, значит,
arcsin (sin (х + 2л)) = arcsin (sin х).
Из того, что sin (у + а) = sin (у — а) для любого aeR,
следует, что
arcsin (sin (у + а)) = arcsin (sin (у — а)) ,
значит, график данной функции симметричен относительно пря-
мой х = л/2. Построим график на отрезке [—л/2; л/2], продол-
жим его симметрично относительно прямой х — л/2 на отрезок
135
[л/2; Зл/2], затем с отрезка [—л/2; Зл/2] продолжим перио-
дически с периодом 2л.
Функция arcsin л, хе[—I; 1], — обратная для функции
sinx, хе[—л/2; л/2], поэтому для любого хе[—л/2; л/2]
имеем
arcsin (sin х) = х.
Таким образом, на отрезке [—л/2; л/2] график данной функ-
ции совпадает с прямой у = х (рис. 45). Из симметрии графика
относительно прямой х=л/2 следует, что на отрезке [л/2; Зл/2]
он совпадает с прямой у — л — х, т. е.
arcsin(sinх) = л — х, хе[л/2; Зл/2].
На этом отрезке функция у — arcsinх, хе[—1; 1], не является
обратной для функции у = sinx. А
Пример 17. Построить график функции, заданной фор-
мулой
arctg
А Данная функция является композицией функций z — \/х2ч
xeR, х =/= 0, с множеством значений (0;+°°) и функции
у = arctg г, z R. Областью опреде-
ления данной функции являются все
значения х У= 0. Функция — четная, ее
график симметричен относительно оси
ординат.
Из свойств функций г = 1/х2 (ри<\
19) и у = arctg г (рис. 42) следует, что
при возрастании х от 0 до 4-°° значе-
ния 1/х2 убывают от 4-оо дб 0, а зна-
чения arctg(1/х2) убывают от л/2 до 0.
Рассчитав и отметив несколько промежуточных точек, рисуем
график (рис. 46). Точка (0; л/2) не входит в график. А.
7.87. Доказать, что функция
у = х — £(х), хе R,
— периодическая, и найти ее наименьший положительный пе-
риод.
7.88. Доказать, что функция Дирихле
( 1, если х — рациональное,
D(x)=d п
( 0, если х — иррациональное,
периодична и любое ненулевое рациональное число — ее пе-
риод, никакое же иррациональное число периодом не является.
7.89. Найти наименьший положительный период функции^
1) у = sin Зх.
3) У = tg (Зх 4- 5).
2) у = 6 cos (Злх/4).
4) у — sin2(x — 1).
136
5) у = I tg x + ctg 2x |. 6) у — sin x + cos 2x.
7) у = cos 2x cos 6%.
7.90. Доказать, что следующие функции непериодетчны:
1) z/=sin|x|. 2) у = cos (1/х).
3) у — cos х cos <у/3х
7.91. Доказать, что если функция y — f(x) периодична с пе-
риодом Т, то функция = + а =/= 0, периодична с пе-
риодом Т/а.
7.92. Найти область определения функции:
1) //== ct?-£-. 2) у — ^созх.
7 и sin (х/3) 7 v
3) у = (sin х — 2 sin2х)~3/4. 4) у = arccos (3 — х).
5) у — arcsin (0,5х — 1) + arccos (1 — 0,5х).
6) у — In cos х. 7) #=Vlnsinx.
7.93. Найти множество значений функции:
1) у = 1 — 21 cos х |. 2) у — sin х + sin [х + у) .
. л , л .х 1 + sin х
3) У = sm4x + cos4x. 4) у = sin.
5) у = arccos | x |. 6) z/ = л — | arctg x |.
2x
7) у = cos arcsinx. 8) у — arctg
Какие из функций являются четными, какие нечетными и ка-
кие не являются ни четными ни нечетными (7.94—7.95)1
7.94. 1) z/ = x+sinx. 2) у — х2 — cosx.
3) у = siii х tg х. 4) у = (1 — х2) cos х.
Б) у = (1 + cosx)ctg х. 6) у =- sin% .
7) у = cos (х + 1). 8) у = sin 5х + cos Зх.
7.95. 1) у — arcsin х2. 2) у = 2 arccos (— х).
3) у = arccos |х|. 4) у — | arctg х |.
5) у = arccos (cos х). 6) у = cos (arccos х).
7) у — arcsin х + arccos х.
7.96,. Доказать:
1) arccos (—х) = л — arccos х, |х|^1.
2) arctg х + arcctg х = л/2, х е R.
3) arcctg (—х) = л — arcctg х, х е R.
137
7.97. Используя неравенства
sin х < х < tg x, хе=(0:л/2),
доказать неравенства:
1) sinx^x, х^О. 2) | sin х ] | х |, xeR.
3) ctg x < 1/x, x e (0; л/2). *4) cos x < у— x, x e (0; л/2).
5) ctg x > -y — x, x e (0; л/2).
2
6) x < Я_- 2Х • x e= (0; л/2).
7) cos x > 1 —у, x e R.
8) sinx^x-----2“ , xe(0; + oo),
9) arcsin x > x, x e (0; 1).
10) | arctg x |^| x I, xeR.
7.98. Доказать ограниченность функции?
14 cos х 2 sin х
1) у — -г=---;—- . 2) у = , 2— .
’ v 1,5 — sin х ' v 1 + tg2 x
3) у = ctgx sin 2x. 4) # = cos2xsec (x—
5) # = —- sinx.
7.98. Доказать неограниченность функции:-
1) z/ = xsinx. 2) у =l/cosx.
_ sin x л\ 1
3) У o,5 + sin x ' arctg x
7.99. Найти sup f, inf f, а также max f и min f, если они су.
шествуют:
1) у — 4 sin2 х — 12 sin х + 5. 2) у = д/у — sin х .
3) z/= 1 i°ScJs7- 4) Z/= tg2 х + ctg2 х. 5) f/ = cosxtgx.
6) y — arctg (1/x). 7) у = arcctg | x |.
7.100. Исследовать на монотонность функцию:
1) t/=l/cosx, хе [—л; л], | х | л/2.
2) у= sin (1/х), х>2/(3л). 3) у = arctg U/x).
4) у == arccos | х |. 5) у — sin = .
6) у = cos 7) у = arctg х - х.
1W
Построить график функции (7.101—7.103):
7.101. 1) z/ = cos3x. 2) у = 2 sin (2х — 3).
3) y = tg^2x— + 4) у = sin х + -\/3 cosx.
6) у= sin | х |.
Б) У == I sin х |. 6) у = sin | х |.
7) z/ = sin2x. 8) у = cosx и у = ^1 — si
9) t/ = tgxctgx.
7.102. 1) y = secx. 2) у == sin (cos x). 3)y = Vsin.
4) у = 2COS x. 5) у — log2 sin x.
7.103. 1) у = arcsin (1 — x). 2) z/=arctg|x|.
3) у = arcctg(l/x). 4) у = cosarccos x.
5) у = arccos cos x. 6) у = x — arcsin (sin x).
8) у = cosx и у = <\/\— sin2x.
2) у == sin (cos x). 3) y = '\!sin x.
5) у — log2 sin x.
7.104. Функцию, заданную формулой при х > 0, продол-
жить, задав формулой, на значения х 0: а) четно, б) нечетно;
построить график получившейся функции:
1) У =1 + sinх. 2) # = ctgx. 3) у^=-===
-V I + tg2 х
4) у = arccos 2х. 5) у = arctg (х—1).
7.105. Выразить через элементарные функции обратные функ-
ции к заданным и построить их графики:
1) z/==sinx, xs[—Зл/2; —л/2]. 2) у = cosx, хе[—л; 0]
3) z/ = tgx, хе (л/2; Зл/2). 4) г/ —ctgx, хе (—л; 0).
5) i/ = 2sin3x, хе[л/6; л/2]. 6) у — 2 arcsin (х/2), | х | 2.
7) у = arcsin — х2, х <= [— 1; 0].
8) у — arcsin -у/\—х2, хе[0; 1].
9) у — arctg (1/х), х #= 0, xelR.
7.100. Доказать, что график функции
у = arccos (2 sin2 (х/2)), хе[0;л],
симметричен относительно прямой у = х.
11. Неявный способ задания функции. Функцию называют
заданной неявно уравнением F(x,у) — 0 (неявной функцией),
если каждое значение ее аргумента х и соответствующее ему
значение функции у являются решением данного уравнения
f(x,y) = 0.
Графиком уравнения F(x, у)= 0 в прямоугольной системе
координат хОу называют множество всех точек плоскости, ко-
ординаты (х; у) которых удовлетворяют этому уравнению.
139
График всякой функции, заданной неявно уравнением
F(x, У) = 0, содержится в графике этого уравнения.
Уравнение F(x,y) = 0 может задавать не одну, а множество
функций.
Иногда от неявного способа задания удается перейти к яв-
ному, т. е. задать функцию формулой y = f(x). Например,
Рис. 47.
Рис. 49.
функцию с неотрицательными значениями, заданную уравне-
нием х1 2 3 + у2 = 1, можно задать явно в виде у = '\/1—х2, xq
—1; 1]. График данного уравнения — единичная окруж-
ность, а график рассматриваемой функции — верхняя полуок-
ружность (рис. 47). Это же уравнение задает и другие функ-
ции, графики двух из них изображены на рис. 48, 49 сплошной
линией.
7.107. Доказать, что следующее уравнение задает функцию,
и построить ее график:
1) 1 =о. 2) -';~2х!;
У — х
4)
х2 + #2 ~ 6
= 0. 3) ----- = 0.
# — 8 V*/ + x
_ — а ~ У6 — q
-2 “U- °' lg2* + z/2 ‘
7.108. Изобразить графики уравнений:
1) \Х\ + \У\=1- 2) \х\ — \у\ = 2. 3)%4 *-z/4 = 0.
4) %2 —/у4 = 0. 5) х2 + у2 — 4z/ = 0. 6) у2 + 2 cos 2х = 2.
7) + у2 = 1 (эллипс). 8) х2 — у2 = х4.
7.109. Доказать, что график следующего уравнения является
объединением графиков нескольких функций y = f(x) или
х — g(y); построить графики этих функций:
1) | ^14-lx —2| = х. 2) |x + */l + l*-Z/l=l.
3) \у\ = logo,5*. 4) (% — | х |)2 + (у — | у |)2 = 4.
7.110. Построить график уравнения и показать, что он не
может быть получен объединением конечного числа графиков
функций:
1) 1 х 1 — х = | у | — у. 2) | у | = | у — sin х 1.
140
12. Функции, заданные параметрически. Пусть на множестве
Т заданы две функции x = (p(t) и y = ty(t). Множество всех
точек координатной плоскости с координатами (<р(/); ф(/))>
/ е 7, называют кривой, заданной параметрически.
Например, пара функций х == cos t, y = s\r\t, /е[0;2л],
задает параметрически единичную окружность.
Пример 18. Построить кривую
х = /2, у = /3, /е R.
X
А Функция х = i2 при t
является функция t =
^ = (7Г)3 = Е2
у — х3/2, х :> 0 (рис. 50). При t 0
/ = — д/х, Х^О, И у = (— V*)3 = ~ (*)3/2,
кривая совпадает с графиком функции у —
= —(х)3/2, х 0 (рис. 50).
Отметим, что данная кривая совпадает с
графиком уравнения х3 = у2, а также с гра-
фиком функции х = ?/2/3.
Пусть X и У— соответственно множества
значений функций x = q(t) и у= ф(/), опре-
деленных на Т. Для каждого t^T значению
х==ф(/) сопоставим значение г/ = -ф(/). При
этом может случиться, что значению хе А'
сопоставлено более чем одно значение у У
(см., например, рис. 50). Пусть.дано правило,
по которому из множества значений у, со-
поставленных указанным выше способом зна-
чению х, выбирается только одно значение.
Функции х = <р(0 и г/ = *ф(/), t^T, вместе
с этим правилом определяют функцию у =
= /(х), х^Х, которую называют заданной
О обратима, и обратной к ней
0. Поэтому при /^0 имеем
:, т. е. кривая совпадает с графиком функции
аналогично
имеем
параметрически.
Например, функции х = t2, у = t3, /eR, вместе с условием
у 0 задают параметрически функцию z/ = /(x), х 0, кото-
рую в данном случае можно задать и явно в виде у = х3/2,
х 0.
7.111 . Какие из данных точек А и В принадлежат кривой:
1) х = /2„ 1, y = f3_t. Л(0; о), 23(3; 3).
2) x=sin/+ 1, г/ = cos/ — 1; Л (0; — 1), В(1,6; —0,2).
3) х = 2 cos t — cos 2/, у = 2 sin t — sin 2/; A (3/2; -\/з); В (1; 2).
4) x = 2'sin/, у = 2,cos/; А (2; 2), В (0; 2я)?
7.112 ? Исключив параметр /, получить уравнение, график
которого совпадает с кривой; изобразить этот график:
141
1) x — t — 1, y — t2 — 2t + 2. 2) x = 2 — 3cost, у — 1 + 3 sin t.
3) x==2cos/, y = 3 sin/. 4) x —| ln/|, y= 1 + /3.
5) x = (/+l)2, y = (t-\)2.
7.113. Построить по точкам кривые:
1) x — t — sin t, у = 1 — cos t (циклоида).
2) x — cos31, у = sin3/ (астроида).
13. График функции в полярных координатах. Зафиксируем
на плоскости луч I с началом О (рис. 51). Паре чисел (<р;г),
где г > О, сопоставим точку М плоскости такую, что
а) |ОЛ1| = г;
б) угол поворота луча I до луча ОМ равен ср, причем, если
Ф > 0, то поворот совершается против часовой стрелки, а если
Ф < 0 — по часовой стрелке.
Всем парам (ф; 0) сопоставим точку О.
Таким образом, каждой паре чисел (ф;г), г 0, сопостав-
лена одна точка плоскости. Каждая точка плоскости, отличная
от О, оказывается сопостав-
ленной множеству пар
(ф + 2пп\ г), где п е Z,
г > 0. Эти пары чисел назы-
вают полярными координа-
тами точки.
Пусть дана функция г =
= /(ф), ф Ф, причем
Иф)^0. Графиком этой
функции в полярных коор-
динатах называют множе-
ство всех точек плоскости с
полярными координатами
(ф; Йф))-
Если луч I совпадает с
положительным лучом оси
Ох прямоугольной системы координат хОу (рис. 52), то коорди-
наты (х; у) и (ф; г) точки связаны формулами
х = г cos ф, У = г sin ф.
(30).
142
Пример 19. Построить график функции г = ф,ф^[0; +оо)
в полярных координатах.
С ростом ф растут и значения г, т. е. расстояние от точки
графика до центра О. Рассчитав и отметив на плоскости не-
сколько точек, рисуем график. Отметим, что каждый луч, со-
ставляющий с лучом I угол а (0 а < 2л), пересекает график
в бесконечном множестве точек вида (а + 2лл; а + 2л/г),
п^. 2, п^О (рис. 53).
График данной функции называют спиралью Архимеда. А
При построении графиков функций в полярных координатах
иногда бывает удобно перейти к прямоугольным координатам.
В свою очередь для некоторых функций их графики в прямо-
угольных координатах бывает проще построить, перейдя к по-
лярным координатам.
Пример 20. Построить в полярных координатах график
функции, заданной формулой
cos ф — sin ф
(31)
А Областью определения этой функции являются все те зна-
чения ф, для которых
cos ф — sin ф > 0.
(32)
Функция периодична с периодом 2л, поэтому достаточно рас-
смотреть лишь значения ф из промежутка
(—Зл/2; л/2), удовлетворяющие неравенству /
(32), т. е. фе(—Зл/4; л/4). Для таких ф
имеем г cos ф — rsinq) = 1, или, переходя к
прямоугольным координатам согласно (30),
х — у = 1, т. е. у = х — 1. График функции
у = х—1 есть прямая (рис. 54). Как дока-
зано, каждая точка графика функции (31) / 4
принадлежит этой прямой. Легко показать, /
что верно и обратное: каждая точка прямой
у==х-Ц1 принадлежит графику функции Рис. 54.
(31). Значит, графиком (31) является прямая у — х~ 1. А
7.114. Записать в полярных координатах уравнение и по-
строить график: 1) х + у + 1 = 0. 2) х2 + у2 — 2х, 3) 2ху —
= х2 — у2. 4) х = £/2--т.
7.115. Построить график функции в полярных координатах:
1) г = 1/ф (гиперболическая спираль). 2) г = е{[) (логарифмическая
спираль). 3) г = 8 sin (<р — -у). 4) г = -j -- -sin <p ‘
7.116. Построить график уравнения, перейдя к полярным ко-
ординатам:
1) (я2 + у2)2 = 2 (х2 — у2) (лемниската Бернулли).
2) у2 (1 — х) = х3 (циссоида).
Найти область определения функции (7.117—7.120):
7.117. 1) у = у/. 2) у = V3-5x-2x2.
3) # = х t 4) г/=д/х2 —|х|~^2.
5) г/ = ^3 + * +1/3-Х. 6) г/ = (8-2х —х2)-3/2.
7.118. 1Ц,.|В(1- + |). =
= 4) 9=л/1»8,-^ .
Л/ 1 . V 1
7) £ = logx+1(x2 — Зх + 2).
8) у = logx log0,5(y— 2 ). 9) i/ = lg(l,25‘“x' —0,40961+х).
Ю) z/==ln(l — lg(x2 —5х+16)).
7.119. i) у = -±Ц-. 2) у=Л/>* + С0!± .
7 COS 2% 7 * 9 V Sin X — COS X
3) £ = lg(16 —x2) + ctgx.
7.120. 1) у = arccos (0,5x — 1). 2) у — arccos x — arcsin (3 — x).
3) у = arclg • 4) у = arcsin —1
5) у — Varcsin x — arccos x. 6) у = arcsin (2 cos x).
7) z/ = tg (2 arccos x).
arcsin (0,5% — 1)
9) = - -====-
Vx2 — 3x 4- I
A / cos x — ~
id /У ЧГ.---А
V6 — 35x — 6x2
8) y — lg(l — 2arcctgx).
io)?= ,.
arcsin (2 — x)
12) z/ =------------------
arccos (2x 1)
Найти множество значений функции (7.121—7.122) :<
7.121. 1) у — X2 + э 2) у — 3 + Х2
3) У — -\/х2 + 2х + 2 . 4) у — д/8 — 2х — х2.
5) у = - 1 - х2. 6) у = 2x44x-5.
7) у = log3 (5 + 4х — х2).
8) z/ = logx2x. 9) у = y21og2x — log2x.
7. 122. 1) у = sin к — 5 cosx. 2) у = 1 — 2| sin 2х |.
__ 1 4~ cos х .. _ sin х — cos х
' U 1 — cos х * 'У sin х + cos х ’
5) у — д/lg sin х . 6) // = cos2x—sinx.
7) y = log2(cosx + sin2x). 8) у — cos (T arcsin x).
9) z/ = arcctg(sin x).
7.123. 1) Доказать, что для любого xeR:
а) £(х+ 1) = £(х)+ 1;
б) Е (х -f- п) = Е (х) 4- п, п е Z.
2) Найти множество значений функции х — £(х — 2).
7.124. Пусть f(x) — х4~6, g(x) = 6/(х 4-. 1). Найти все зна»
чения х, для которых:
I)
2)
3)
4)
f(x)4- g(x)
f(x) + g(x)
f(x)+ g [х)
f(x) + g(x)
= f(x)+g(x)-
= f(x) — g(x).
= \f(x) | + |g(x) |.
==lfW I — IsW I-
7.125. Используя арифметические операции и композиции
функций, выразить данную функцию через основные элементар-
ные функции:
1) У = ^(TW- 2) у = (у^т)2.
з) g = 4) g = ln2(l +ех).
5) //^coslgx2. 6) у = Vsin (arcctgx3).
7.126. Для функции f(x) = (x3—1)/%2: а) найти все значе-
ния а, для которых уравнение f(x) = f(a) имеет единственное
решение; б) найти наибольшее значение b такое, что для лю-
бого оо; 6) уравнение f(x)=f(a) имеет на интервале
(—oo;fe) единственное решение.
7.127. При каких значениях а область определения функции
f содержит область значений функции g, если:
1) fM = 'у/ а — х'' = X2 + 2X + 4а - 2 •
2) f (х) = 1g(х2 + a); g (х) = *2 + *~а •
3) f (х) = arcsin (2х — а); g (х) = log2 (2а 4- — а • 2х)?
7.128. В равнобедренной трапеции ABCD с основаниями
AD = 2, ВС = 1 и высотой h = 1 проведена прямая, перпен-
дикулярная основанию AD и пересекающая его в точке М,
Найти зависимость площади S отсеченной части с вершиной А
°т расстояния х = AM,
145
7.129. Около сферы радиуса г описан конус. Найти зависи-
мость объема V этого конуса от его высоты; указать область
определения получившейся функции.
7.130. Рассматриваются сечения правильного тетраэдра
ABCD, параллельные ребру АВ и высоте DO тетраэдра. Найти
зависимость площади S сечения от расстояния х между пло-
скостью сечения и ребром АВ, если высота грани тетраэдра
равна Ь. Найти наибольшее значение S.
7.131. Радиус окружности, описанной около равнобедрен-
ного треугольника, равен R. Найти зависимость радиуса впи-
санной окружности от угла а при вершине треугольника. Найти
наибольшее значение этого радиуса.
7.132. На бесконечную нить с началом О равномерно на
расстоянии I друг от друга нанизаны бусинки, первая из них
находится в точке О. Нить однородна с линейной плотностью
р, масса каждой бусинки равна т. Найти зависимость массы
участка ОМ нити от длины х = ОМ.
7.133. Два луча, угол между которыми равен 60°, имеют об-
щее начало. Из этого начала по одному из лучей вылетела ча-
стица со скоростью v а через час по другому лучу — вторая
частица со скоростью 3v. Найти зависимость расстояния между
частицами от времени движения первой частицы. На какое наи-
меньшее расстояние сблизятся частицы после вылета второй
из них?
7.134. Функция f(a) определена для всех a gR, при кото-
рых уравнение
(а2 —4а+ 9)\х — 11 = (9 — а2) |х|
имеет решение. Значение f(a) равно наибольшему при данном
а корню этого уравнения (если корень один, то f(a) равно
этому корню). Найти: 1) область определения функции f(a);
2) minf(a).
7.135. Область определения функции содержит т элемен-
тов, а область значений — п элементов. Доказать, что 1) п т;
2) для того чтобы функция была взаимно однозначной, необхо-
димо и достаточно, чтобы п = т.
7.136. Найти число всех
1) функций, определенных на множестве D из т элемен-
тов, со значениями из множества Е из п элементов;
2) взаимно однозначных функций, область определения и
множество значений которых содержат по п элементов.
7.137. Область определения функции f — счетное множество.
1) Доказать, что если функция f взаимно однозначна, то
и множество ее значений счетно.
2) Привести пример не взаимно однозначной функции ft
множество значений которой также счетно.
7.138. Какие из заданных функций обратимы;
1) у = 2-\-х — х2, % е [0,5;+°о).
2) у = х3 — х, хе R.
146
3) у = х4— 2х2— 8, xs[0;2],
4) у = —х|х|— 2x4-8, хей.
5) у — 1—sinx, хе[О;л].
6) f/ = tgx, х е (0; л), х #= л/2.
7) у = 9* — 3\ xeR.
8) у = arccos(|х|—1), хе[—1;2].
9) у — arcctg(x|x|), xeR?
7.139. Доказать, что функции f и g взаимно обратны:
2) f(x) = x24-l, хе(-oo;0]; g(x) = — Vx— 1, xe [1; -|- oo).
3) f(x) = -e(1-x’)/2, xe[0; 4-<x>);
g(x) = дЛ — 2In(—x), xe[—0)-
4) f (x) = In ** xe (0; 4- oo); g (x) = f (x).
6) f (x) — sin x, x e [л/2; Зл/2];
g(x) = л — arcsin x, x e [— 1; 1].
6) f(x) = tgx, xe[—л; 0], x^—л/2;
{arctgx — л, x > 0,
arctg x, x < 0.
Функции, обратные к заданным, выразить через элементар-
ные и построить их графики (7.140—7.142) t
7.140. 1) y — ^fx3, xe[0; 4“ °°)-
2) i > хе (— оо; 0], х#= — 1.
3) z/ = x|x|4-2x, xgR.
4) г/ = £ 15* , х, е R, х =£ 0, х 5.
5) у 1- ’ +°°)-
6) У = хе(0; 1].
7) t/ = x —д/х2—1> хе(—оо; —1].
8) у = Vx2 — 1 4~ X, ХЕ(-оо; — 1].
7.141. 1) у = 2х2~2х, хе(—оо; 1].
2) у = 1 - e{{~xW+x\ х е R, х^-1.
147
qx_____ox
3) у — --х х , X R.
3+2
5) у = loga (х + д/*2 + 1 )> х е R, а > 0, а ^=\.
7. 142. 1) y—smx, х е [5л/2; 7л/2].
2) у = 2 cos (х/2), хе [2л; 4л].
3) z/ = ctgx, хе(—л/2; л/2), х#=0.
4) у = sin2(х/2), хе [2л; Зл].
5) у — 1/cos х, х е [— л; 0], х #= — л/2.
6) z/ = arccos д/1 — х2, х е [0; 1].
7) у — arccos д/1 — х2, х е [— 1; 0].
8) у = arctg , xeR, х #= 1.
7.143. 1) Доказать, что функция у — х3+-^х обратима.
Построить в одной системе координат графики данной и об-
ратной функций. Найти точки пересечения этих графиков.
2) Доказать, что если п—нечетное натуральное число,
р > 0, q е R, то функция у = хп + рх + q обратима.
7.144. Доказать, что функция
// = ^х + Vх2 “ 1 +ZV/'х-~ ^х2 — 1
имеет обратную, и найти ее.
7.145. Пусть z/ = archx, х2>1,— обратная функция для
функции у = ch х, х 0. Доказать, что функция
' 2 ch (4- arch , х 1,
О /
<
2 cos fу arccos х^ , — 1 х < 1,
является обратной для функции у — (х3 — Зх)/2, х^= 1.
7.146. Найти функцию, обратную для функции
у = (х3 + Зх) /2, х е R.
7.147. Найти наибольший промежуток вида [а; +оо), на ко-
тором функция
1 1 о • % 1
у = 1 -Р 2 Sin -7—7
обратима, и найти на этом промежутке обратную функцию.
2х + 3
7.148. 1) Доказать, что функция у = --совпадает со
своей обратной.
148
2) При каких условиях на a, b, с, d функция у = сх'+~л
обратна самой себе?
7.149. Доказать, что график функции у = log^ p^xtry >
сф 5^—1, симметричен относительно прямой у = х.
7.150. Пусть а и Ь — такие числа, что область определения
функции у == In (а + Ьех) — непустое множество. При каких а
и b эта функция совпадает со своей обратной?
7.151. При каких а функция
у = (а—1)|х—l| + (a+l)|x+l| + x
обратима?
7.152. При каких а, b и с функция
у = arctg(а + b tgх) + с, хе (л/2; Зл/2),
совпадает со своей обратной?
7.153. При каких X обратима функция
у = (arcsinх)2 + К arccosх, хе[—1; 1]?
Задать обратную функцию формулой.
7.154. Доказать, что:
1) cos (2 arccos х) = 2х2 — 1, х е [— 1; 1].
2) sin (3 arcsin х) = Зх — 4х3, хе[—-1; 1].
3) tg(3 arctg х) = , хе₽, х2=Н=1/3.
4) 3 arccos х — arccos (Зх — 4х3) = л, хе [—1/2; 1/2].
5) arccos * ~ *2 = 21 arctgх |, xeR.
7.155. Найти все значения х, для которых верны равенства:
1) arccos д/1—х2 = arcsin х. 2) arccos V1—х2= — arcsin х.
- 3) arctg х = arcctg(l/x). 4) arctg х = arcctg(l/x) — л.
5) arctg-J-^7 = arctg х + ^-.
6) arctg = arctg x — .
Какие из функций являются четными, какие нечетными, ка-
.кие не являются ни четными, ни нечетными (7.156—7.159):
7.156. 1) у = 2х2—1. 2) у = — 5х3. 3)^=1— х3.
4) г/ == х5 — у. 5)z/ = Vl—x + Vl+^-
6) у = д/7^2+ Vr+~2. 7) у = 6х2 + 8 + (х — 2)3.
149
7.157. 1) у = 2* + 2--*'. 2) г/ —In
3*-3~* 1 + х
3) z/ = ch(x + shx). 4) t/ = th(x 4-chx).
5) у = In2 (Vх2 + 1 4- х).
6) у — cos х sh х + sin x ch x. 7) у — arsh (sh x).
S) # = th(arthx). 9) Z/ = |-^44’|?
7.158. 1) # = -S1"* . 2) у — sin x + 2x3.
3) y = tgx — cosx. 4) #=-• 5) # = (x — I)2 sin2x.
6) У = cos (x - -J-) 4- sin (x - -J-) .
7) r/=sintgx. 8) z/ = ctgcosx?
7.159. 1) # —arcsin x2. 2) у = 2 arccos (— x).
3) у = arccos | x |. 4) y = arccos x —
5) y — arcctg (ctgx). 6) # = ctg (arcctg x).
7) y= arcsin (arccos x). 8) f/ = sin(2x— arcctg x)?
7.160. Представить функцию f в виде суммы четной и не*
четной функций:
1) f(x) = (x4- I)3- 2)/(х) = ^.
3) f(x) = sin (х 4- 1). 4) f(x) = ^4-i- , |x| < 1.
7.161. Доказать, что всякая функция, определенная на сим-
метричном относительно начала координат множестве, предста-
вима в виде суммы четной и нечетной функций.
7.162. Представить функцию в виде суммы четной и нечет-
ной функций, если:
1)^ = |х—1|. 2)у = ах. 3) z/ = ln(l+^).
4) у= sin (х3 + х2). 5) r/ = tg(x —5). 6) у — arccos х.
7) =— arcctgх. 8) у = arctg (1 — х).
7.163. Функция f — ни четная, ни нечетная, функция g— чет-
ная, функция h — нечетная. Может ли сумма:
I) f + g быть: а) четной, б) нечетной.
2) f + h быть: а) четной, б) нечетной?
7.164. Функция f—ни четная, ни нечетная, функция g—•
четная, функция h — нечетная, и имеет смысл композиция лю-
150
бых двух из этих функций. Указать все композиции, являю-
щиеся: 1) четными, 2) нечетными функциями.
7.165. 1) Доказать, что функция, обратная к нечетной, — не-
четная функция.
2) Может ли функция, обратная к данной, быть четной?
Доказать ограниченность функции (7.166—7.168) :
7.166. 1) у — х д/*2 ““ 1» + оо).
2) ^дТ + 8-.t. 3) г/ = \/х4 + 2 - | х |.
4) у = |х^~г- 5> хе[0; 4)*
х4 — 1 2 — ух
6) У — —- +3/^ , х (= (— оо; — 1).
’ У x + J/x*
х7,'л - х2
7.167. 1) Z/ = 2sin\ 2) y = 2I/x, хе (-00; 0).
5) у = log* (1 + х), хе [2; + оо).
7.168. 1) z/ = tgxcos3x. 2) у = ctg*_TT • 3> я - 2х •
4) z/ = ctgx — |х|<-у’ х=^°-
7.169. Доказать, неограниченность функции:
1) у = х3— Зх. 2) г/ = х3/(х2—1), хе(—оо; —2].
4х 2Х
3) У = — > х<==(— °о; 0). 4) У = —, хе[1; + оо).
X А
5) z/ = 21/x, хе(0; + оо). 6) у = log*(1 + х), хе(1;2].
7) f/ = xsinx. 8) у = (cosx)/x.
ГУХ 1.1
9) У = ~ sin у.
7.170. Пусть Рт(х) и Qn(x)—многочлены степени т и п,_
т и, и ()л(х)=/=0 для любого xeR. Доказать, что функция
______________________________ Р т W
у~ QnM
ограничена.
7.171. Доказать, что любой многочлен степени не ниже пер-
вой — неограниченная функция.
7.172. Привести пример функции, определенной на отрезке и
неограниченной на нем.
7.173Л Привести пример функции, определенной на отрезке
и неограниченной в окрестности каждой точки этого отрезка.
151
7.174. Исследовать на монотонность и построить график
функции: *
i\ х—1 о, х + 2 1 — |х—1|
1) У — ~\-ПГТ • %) У — ~\-i--т- 3 У—-—г-T“i------г2-.
I х I + 1 и 1*1 — 3 7 и 1 +1 х |
Л\ I X — 1 | — I X + 1 | -ч х2 X2
4) У ~ | X — 1 I + I X + 1 г 5) # — х2 + I ' У — Х2 _ ! •
Исследовать на монотонность функции (7.175—7.176):
7.175. 1) z/ = Vx2-l. 2)i/ = A/2TT. 3) у =
Ух2 — 5 — 2
4) У — и/1 — х2. 5) у — 1 — Vх3 “ 1
6) г/ = -у4=Т- 7) У = V* —2 + V* + 2.
-ух2 — 8
8) у — ^х — 1 — 9) у = х — х2 — 1.
7. 176. 1) у = sin4 х + cos4 х, х е [0; л].
2 Sin X гм сл 1
2) У== 2 + sinx ’ ^е[°;2л].
3) у =с= tg х -|- ctg х, хе(0; л), х =/= л/2.
4) у = 0,3(*2-1>/х. 5) у = log2 (8х - х2).
6) z/ = ln(Vx2Tl+ х). 7) г/= 2 • 31-х — 9-Л.
8) z/ = 2Iog2(l + х2) — log2(l + х2).
7.177. Доказать, что функция
у = х — esinx, где 0<е^1,
строго возрастает.
7.178. Доказать, что функция у = х3 + х2: 1) возрастает на
^0; 4~оо); 2) немонотонна на [—1; 0].
7.179. Доказать, что функция
монотонна на любом интервале, содержащемся в ее области
определения.
7.180. Функция z/==f(x) монотонна. Доказать, что: 1) функ-
ция у = —f(x) монотонна; 2) если f(x)> 0 для любого xeD(f)t
то функция у = 1//(х) монотонна.
7.181. Доказать, что сумма возрастающих (убывающих) на
интервале (а\ Ь) функций — возрастает (убывает) на (а\ Ь).
7.182. Доказать, что композиция монотонных функций яв-
ляется монотонной функцией.
7.183. 1) Доказать, что функция, обратная к возрастающей
функции, является возрастающей.
2) Доказать, что функция, обратная к убывающей функцищ
является убывающей функцией.
152
7Л84. Сформулировать и записать, используя символы 3, V,.
утверждение: 1) функция не является возрастающей; 2) функ-
ция не является убывающей; 3) функция не является моно-
тонной.
7Л85. Привести пример двух возрастающих на интервале
(а\ Ь) функций, произведение которых 1) возрастающая на
(а; Ь) функция; 2) убывающая на (а; Ь) функция; 3) немоно-
тонная на (а; Ь) функция.
7.186. Привести пример функции, определенной на R, кото-
рая не является монотонной ни на одном интервале.
7Л87. Функцию f(x), x^(a\b), называют возрастающей
в точке х0^(а;6), если существует S > 0 такое, что
^f(xo) для всех х^(х0— 6, х0) и f(x)^f(x0) Для всех
хе(х0, Хо + 6).
Является ли монотонно возрастающей на (а; 6) функция,
возрастающая в каждой точке интервала 6)?
7Л88. Пусть х0 — решение уравнения
ах + Ьх — с,
и пусть либо 0 < а < 1 и 0 < b < 1, либо а > 1 и b > 1. До-
казать, что других решений это уравнение не имеет.
7.189. Пусть f, g и f — g—-возрастающие функции и f(x0) =
= g(xo). Доказать, что система
' f№ = g(y),
‘ f(y) = g(z),
- f(z) = g (х)
имеет единственное решение.
7.190. Пусть функции f и g определены на множестве X.
1) Пусть f(x)^g(x) для любого хеХ. Доказать, что
sup f > sup g, inf f inf g>
XX XX
2) Пусть sup f = + oo, infg#= — °0. Доказать, что
A' X
SUp(f+ £)=+ oo.
X
3) Пусть inf f = — oo, supg =£ + °0. Доказать, что
X X
inf (f + g)= —oo.
X
7.191. Пусть функция f—нечетная. Доказать, что
inf f = —sup f, sup f = — inf f.
x<0 x>0 x<0 x>£
7.192. Сформулировать и записать, используя символы 3,
утверждение: 1) число а не является верхней гранью функции;
2) число а не является нижней гранью функции.
7Л93. Найти minf, если:
х
153
l)f(x)=x + |. Z = (0;+oo).
2) Z(x) = ^T. X = (l; +oo).
3) ^x) = ^7 + ctg2x+L r=[?: fl’
4) f (x) — tg x + ctg 2x, X — (0; л/2).
7.194. Найти:
1) min(x —- 2 V* )• 2) max(3 tgx — tg2x).
(Os Л/2)
7.195. Найти maxf, если:
x
1) f(x) = 9x5 + ^-, X = (-oo;0).
2) = X = (0; +oo).
3) /(х) = хУГ=Л?> X = [-l; 1].
4) f (x) = logx (x + 1) + logx+1 x, X = (0: 1).
7.196. Найти max/, min/, если:
1) f(#) = e~lxi — e~2lxi. 2) f (x) = coszx + cos x + 3.
3) f (x) = sin2x — 4 sin x + 3. 4) f(x) = sin6# + cos6#.
5) f (x) = sin x sin 3x. 6) f (x) = cos (1 + sin x).
7) f (#) = sin (2cos#1). 8) f (#) = #2/(#« + 1).
9) /(#) = (#+l)/(#2 + 3).
7.197. Два тела двигаются по прямым по направлению к
их точке пересечения А. Скорости тел постоянны и равны
и и2, в начальный момент тела находятся от точки А на рас-
стояниях а и Ь соответственно. Угол между направлениями
движения тел равен а. Найти наименьшее расстояние между
телами.
7.198. В треугольник вписан прямоугольник так, что одна
его сторона лежит на одной стороне треугольника и две вер-
шины — на двух других сторонах треугольника. Найти наиболь-
шую возможную площадь прямоугольника, если площадь тре-
угольника равна S.
7.199. Угол в осевом сечении конуса равен 2а, радиус осно-
вания— R. Найти наибольшее значение площади сечения, про-
веденного через вершину конуса, если 1) 2а < л/2; 2) 2а > л/2.
7.200. Найти расстояние от параболы у = х2/4 до прямой
У = — х — 2.
7.201. Найти maxf, min Л если:
1) f (*) = logi/3(x2 + х - 2), Х=[3, 6].
154
2) f (x) = log9 (8x - xI 2 - 7), X = [2; 5].
3) f(x) = cos2x + sin x, Х = [л/3; л].
4) f (x) = (x2 + 4)/x, X = [l; 3].
5) = ^ = [“14; -7].
6) X = [—1,5; 1,5].
7.202. Сформулировать и записать, используя символы 3, V,
утверждение: 1) значение f(x0), Xq^X, не является наиболь-
шим; 2) значение /(х0), хоеХ, не является наименьшим зна-
чением функции на множестве X.
7.203. Найти min (% — V* + 3).
7.204. Найти maxf, min f, если:
1) 2) /(х) = V6^x + л/Г=^2.
7.205. Найти радиус основания и высоту цилиндра, вписан-
ного в сферу радиуса /?, если площадь боковой поверхности
цилиндра имеет наибольшее из возможных значение.
7.206. Найти радиус основания и высоту конуса, описанного
около сферы, если объем конуса имеет наименьшее значение
из возможных, а радиус сферы равен R.
7.207. Все ребра правильной треугольной призмы АВСАХВХС\
имеют длину а. Концы отрезка, параллельного плоскости АВВ^А^
лежат на диагоналях ВС} и СА^ боковых граней. Найти наимень-
шую длину такого отрезка.
7.208. Длина ребра куба ABCDAiB^CiDi равна а. Точки Е
и F — середины ребер ВВХ и CCi соответственно. Вершинами
треугольника служат точки пересечения плоскости, параллель-
ной основаниям куба, с прямыми ACi, СЕ, DF. Найти наимень-
шее значение площади такого треугольника.
7.209. Найти наименьшее значение суммы х2 + у2, если
х + 2у = 1.
7.210. Найти наибольшее значение, произведения ху, если:
1) х + 2у= 1- 2) х2 + Зу2 = 1.
7.211. Найти min f, если:
1) f(x) = (х — 1) (х — 2) (х — 3) (х — 4).
2) f (х) == (х — 1) (х — 2)(х — 5) (х — 6).
3) f(x) = (х — а) (х — Ь) (х — с)(х —/Z), где b — a = d — c.
I 4) /W = f(A'-irf. б) №)=(тМ-
k=\
7.212. Найти
min
[0; 1)
1
165
7.213. Доказать:
1) Графики функций у = f(x) и у = f(—x) симметричны от-
носительно оси ординат.
2) Графики функций у = f(x) и у = —f(x) симметричны от-
носительно оси абсцисс.
3) Графики функций y = f(x) и у = —/(—х) симметричны
относительно начала координат.
4) Графики функций y = f(x) и z/ = /-1(%) симметричны
относительно прямой у — х.
7.214. График функции g симметричен графику функции f
относительно прямой х = х0. Выразить значения функции g че-
рез значения функции f.
7.215. График функции g симметричен графику функции f
относительно прямой у — yQ. Выразить значения функции g че-
рез значения функции f.
7.216. График функции g симметричен графику функции f
относительно точки (хо\уо)> Выразить значения функции g че-
рез значения функции f.
7.217. По известному графику функции у = х2 построить
график функции и указать множества, на которых функция мо-
нотонна:
1) у = 2х2 — 8х + 4. 2) у = Зх - 4 - 2х2.
3) у = %2 — 31 х | — 7. 4) у = | 5 — 41 х | — х21.
7.218. Построить график функции (7.218—7.225):
1) у = \х - 1 | + | х-2 | - | х-3 |.
2) у = \х-2\ + \х\ + \х + 2\-3.
3) у = |х-2|х - 1||. 4) у = \2х — \х\ — 1 |.
5)г/=2^-(|х + а| — I х — а |), а > 0.
6) у = signх — -^(|х + а| — | х — а|), а > 0.
7.219. 1) г/ = 2(х + 2)3-3. 2) у = 1,2 + ^(1 -х)3.
3) z/ = x3 + x. 4)£/ = -|—-|* — *3-
5) (/ = 0,1 (1 —х)4—1. 6) у = 2--|(х + 2)4.
7.220. 1) # = V1 — 2х —2. 2) г/ = 3 —0,5 д/Зх —2.
3) (/ = 2^3F=6+ 1. 4) (/ = 2+ -|х.
5) у = (2х + 1)‘/4. 6) у = 3 - у(8х - 1)2/3.
7) (/ = 3-|х8/3. 8) z/ = (x-l)7/2-l.
156
7.221. 1) y==Vl3-x|. 2) у === дЛ) — 41 х j.
3)f/ = ^8-|х-1|. 4) г/ = =Vi х +1 р-1.
7.222. 1 \ it — J— — 9\ у — - — —. з) п = J—
^2% + 8 — I
1! — 3
V У— ' 2 V* + 1 ' 4 — 1 2 + 1 ’
7.223. 1) у — хI) 2 -j- 4 % — x2 — 4
Ч У х -ЧУ 2x
q\ и = 1 1 1 их 2x -v x2 4 — x2 ' °’ У x2 + 1 '
о; у х 4- 1 ' х — 1 ' V
и — - ! 7) у — 1 o> * X| IJ ^r— -
Ч У х2 + 2х + 3 ‘ 4 5 У х2 _ 9 • °) У X2 _ 2x — 8 *
7.224. l)f/ = ^T. 2)^/ = ^.
' v x2 + 1 7 y x2 — 2x + 2
7.225. 1) у = 'у/Ь + 4x — x2. 2) у = (дЛ — & + 0 sign x.
3) У = 2 - V8 - 2x - x2. 4) у = J_-.
Vl — X2
5) У = slgn(x~ Д. 6) y = x^lQ0 — x2. 7) y = x + Vl — x2.
ySx — X2
7.226. При каком соотношении между a, b, с, d график
функции у = +-~ получается сдвигом графика функции:
I) У = ~. 2)у = ^^, х,#=х2?
л л л 2
7.227. Найти центр симметрии графика функции:
1 \ х л\ ах + b z п
1) ----г* 2) У =-----с #= 0.
3) у = х3 — 6х2. 4) у — ах3 + Ьх2 + сх + d, а Ф 0.
7.228. Доказать, что графики функций у = х3 — За2х и
У = х3 — Зах2 получаются один из другого сдвигом.
7.229. Доказать, что функция у = х3 — За2х возрастает на
промежутках (—оо; —а] и [а; +оо) и убывает на [—а\ а\
(а >* 0). Построить график этой функции при а — 2.
7.230. Доказать, что функция у = х3 — ЗЬх2 (6 > 0) воз-
растает на (—оо; 0] и [26; +°°) и убывает на [0; 26]. Построить
график этой функции при 6=1.
Построить график функции (7.231—7.235):
7.231. 1) у = х3 — Зх2 + 2х. 2) у = х3 + 6х2.
7.232. 1) у = Е(\х\). 2) z/ = E(x2-l).
8)» = в(у). 4) г/ = (Е(х))2-2^(х)-1.
5) £/ = |х-Е(х)-0,5|. 6) у = (х — Е (х))2..
167
7. у = ±-Е(х). 8) i/«= (—1)В(,/х).
7.233. 1) у= 1 — 30,5х-1. 2) г/ = 4-21-3х + 2.
3) у = 10g3(0,5л + 2). 4) у = — -|log4(l — х).
5) у = З2"1 х+3'. 6) у. = 10,5х - 21.
7) # = 1g (3 — х)2. 8) z/ = log05| 1 — 2х | + 2.
9) У = I log21 х ||.
7.234. 1) t/ = 2|log2X|. 2) # = 21/х.
3) у = 3(1~х)/<1+х). 4) у = 0,5х2"х.
5) у = log1/3 (х2 — 8х) + 2. 6) у = 1g ^-3 .
9) у = In (V-v2 + 1 +х).
7.235. 1) // —Е(2Х). 2) у = 2ЕМ.
3) // = 2х-£ <х). 4) у = Е (log2х). 5) у = 1g (х - Е (х)).
7.236. Доказать, что данная функция — периодическая, и
найти ее наименьший положительный период:
1) у = х — аЕ (х/а), а е R, а =# 0.
2) г/ = £(2х + 5) —2х.
3) у — | sin (V2 х + 1)|. 4) у = sin 2х + sin23x.
5) у = sin 4х + 5 cos 6х. 6) у — 3 sin 4х + 2 tg 5х.
7) у = sin4x + cos4x. 8) у — tg(x + sin х).
9) у = sin (cos х). 10) z/ = cos(sinx).
11) у — sin3x + cos3x.
7.237. Доказать, что данная функция непериодична:
1) У = sin ^\х\. .
2) у = cosх + cosx -д/2 + • • • + cosxп , raeN, п^2.
3) у = sin х + sin д/2 х.
7.238. Доказать, что если отношение периодов периодических
функций fug является рациональным числом, то функции ’
f + g и fS периодичны.
7.239. Найти наименьший положительный период функции!
1) у = 8 sin (9х/8) + 2 cos (Зх/2).
2) у — sin (Зх/4) + sin (9х/8).
3) у == a sin (pxxfqi) + b cos (jt^/to). где py pa, qlt q2 e N,
Р\Уъ =7= PzQi-
158 .
4) у —a sin (pxx!qx} + b sin (p2x/^), где p{9 p2, q{9 <?2 e= N,
Pl?2 =# p2<71-
5) y = asin(pxx/qx) + btg(p2x/q2)9 где pi9 p2f q[9 <72gN,
Pl?2 P2?l*
7.240. При каких а и b (ab^O) функция у — ax — E(bx-[-c}
периодична и каков ее наименьший положительный период?
7.241. Привести примеры непериодических функций f и g
таких, что функции: 1) f + g, 2) f-g периодичны и имеют наи-
меньший положительный период.
7.242. Привести примеры периодической функции f и не-
периодической функции g таких, что функции: 1) f A-g9
2) f'g периодичны и имеют наименьший положительный пе-
риод.
7.243. Существует ли функция, для которой каждое ирра-
циональное число является периодом, а каждое рациональ-
ное — не является?
7.244. График функции y — f(x), xeR, симметричен отно-
сительно каждой из прямых х = а и х — Ь, а=/= Ь. Доказать,,
ЧТо y = f(x) — периодическая функция, и найти ее период.
7.245. График функции y = f(x), xe'R, симметричен отно-
сительно точки А (а; Ь) и прямой х — с (с=^а). Доказать, что
f(x)—периодическая функция, и найти ее период.
7.246. Доказать, что функция f является периодической, если
существует Т 0 такое, что для любого х е D (f) х+Тв
х—T<=D(f) и выполнено одно из условий:
1) f(x-X-T) = —f(x). 2) f(x + T’) = 7^-.
I 3)№+г>=та^т- 4>«* + п=т^та>-
Найти период функции f.
7.247. Пусть функция g обратна самой себе, и пусть опреде-
лена композиция g of. Пусть существует Т =+ 0 такое, что для
любого x^D(f) выполнены условия x-\-T^D(f), х—
^D(f) и Т) = g(f(x)). Доказать, что f — периодическая
функция, и найти ее период.
- Построить графики функций (7.248—7.249):
7.248. 1) у = 2 cos (2х +1). 2) у = ctg (у + - 1.
3) у — sinxctgх. 4) y = cosx + lcosx|.
5) z/ = [sin2x— cos2x|. 6) у = sin4 x + cos4 x.
2 .9 1—cos X
7.249. 1) у = , ----• 2) r/ = ctgx. 3) y = t-j—-
1+2 cos x J 1 + cos x
лх I . L . t-ч l 1 + sin X
4) y = l sinxtgx|. 5) -V = A/ l - sin x '
V * oiii Ле
159
7.250. Построить в одной системе координат графики функ*
ций:
1) z/=sinx и у = — Vl ““ cos2*«
2) у = cosх и #= 1/V1 + tg2*-
• tg x
3) Z/= SIH X И у — —7=^...o—
J * Vl+tg2x
o 1 — tg2 x
4) 11 = COS 2% И у —
J * 1 + tg2 X
Построить графики функций (7.251—7.253):
7.251. I) у = 0,51smx 1. 2) у = 2‘е*.
3) у = logo.s cos x. 4) у = log2 sin (7t/6) + sinx •
5) у = logcos x Sin x. 6) у = 1 + Vig cos 2jlx-
7.252. 1) у = cosx2. 2) y=sinx2. 3) у = cos (cos x).
4) у = sin (2 sin x). 5) у = sin (1/x). 6) у = tg (n/x2).
7) у = sin ! . 8) у = cos iog2 -J.
7.253. 1) y = x+sinx. 2) y = xsinx. 3) y = x2cosx.
4) y = e~*sinx. 5) у — x cos (1/x). 6) у = (2 sin 3x)/( 1 + x2).
7) у = cos22--. 8) y = — sin—. 9) у = (1 + cosx)cos4x.
ЭС X X
7.254. Построить график функции
f(x + 2/) + f(x-2Z),
где _
f 1 + cos x, | X | Л,
№)=={ 0, Ix | > л,
полагая: 1) / = 0; 2) t = л/6; 3) t — л/4; 4) / = л/3; 5) t — л/2.
Построить графики функций (7.255—7.258):
7.255. 1) у —3 arccos (х/2)+1. 2) у — arcctgl х |.
3) у = arcctgl х | — arctg|x|. 4) y = x + arctgx.
5) у — arcsin (1/x).
7.256. 1) у = arctg (tg x) и у = tg (arctg x).
2) у — arcctg (ctg x) и у = ctg(arcctgx).
3) у — arccos(sinx). 4) у — arccos(cosx) — x.
5) у — x — arctg(tg x). 6) у = xarcsin (sin x).
7) у = x arccos (cos x). 8) у = arctgx — arcctg(l/x).
9) у — arccos(cosx) — arcsin (sin x).
7.257. 1) = arccos Vl — %2-
2) у = 4 arcsin \/l — x2. 3) у = cos (2 arccos x).
4) у = sin (3 arcsin x). 5) у — tg (3 arctg x).
160
6) t/ = arctg 7) у = arccos -
7.258. 1) r/ = £'(sin x). 2) y — cosx— £(cosx).
3) у = arcsin (x —£(x)). 4) у — arccos x — E (arccos x).
7.259. Пусть max {f (x), g (x)} — наибольшее, a min {f(x), g(x)} —
наименьшее из двух чисел f(x) и g(x) при х е D(f)(]D(g). По-
строить график функции:
1) y = max{x2, Vlх ll- 2) У — тах{х3, 1/х).
3) z/ = max{sinx, cosx). 4) i/ = min{2*, 9/(1 + 2~*)}.
5) у — min {cos х, cos2x}. 6) у = min {log2x, logx2).
7.260. Построить график функции:
1) у = cos (3arccos х). 2) у — cos (4arccos х).
3) у — sin (2arccos х). 4) у = sin (3arccos х).
7.261. Доказать, что для любого п е N:
1) Функция Тп (х).= cos (n arccos х) совпадает на [—1; 1] с
полиномом степени п.
2) Функция sin (п arccos х) совпадает на [—1; 1] с функ-
цией вида дЛ—x2'Qn-iM> где Qn-i(x)— полином степени
5 п— 1.
7.262. Построить график уравнения:
1) г/2 = х2 + 4|х| + 4. 2) #2 + 4| z/+ х | —4х + 3 — 0.
3) £2-(5*-1)(г/-1) = 0.
5) lg(xz/-l) = lg((l-x)(l-f/)).
6) ll/l = log1/3||x + 2|-l |.
7) x^ + y2-x-3y = 0. 8) х2+х/2 = 2(|хЦ-|у|).
7.263. Доказать, что уравнение
V*/3 + ху — X Vy — х2 = 0
задает функцию, и построить ее график.
7.264. Доказать, что график уравнения
х3 + х2у + ху2 — х — у = 0
является объединением графиков трех функций; построить эти
графики.
7.265. Построить график уравнения:
1) | у | = cos х. 2) cos | х | + sin | у | = 0.
3) | sin x \y +1 cos x \y — 1.
4) | у — sin x + 1 | +1 У — sin x | = 1.
7.266. Найти значения /, соответствующие точке А кривой:
.1) 4(0; 0); х = /2-1, z/ = /3-/.
6 Л. Д. Кудрявцев и др. .161
2) Л(3; 2); х = /24-2/, i/ = /3+/.
3) Л (2; 2); x = 2tg/, у = 2 sin21 + sin 2/.
4) Л (—9; 0); x = 3 (2 cos t — cos 2t), у — 3 (2 sin t — sin 2/).
7.267. Какие из точек Л, В принадлежат кривой:
1) Л(5; 1), В(1; -1); x = 2 + 5cos/, r/ = 5sin/-3.
2) Л(—31; 3), 23(10; 8); х = /3 + /, y = t2 + 2t?
7.268. Задать кривую уравнением и построить ее:
1)х = 6/ —/2, г/ = 3/. 2)х = /3+1, y = t2.
3) х = cos t, у= sin 2t. 4) x = tg t, у = sin 2t 4- 2 cos 2t,
5) x = sin 3/, у = sin t.
7.269. Построить кривую:
2 + f2 t2 o. 1 t2
X 1 + t2 ’ 1 + t2 ’ 2) X j _ /2 • У 1 — /2 •
ПЧ t И1 .x I t | t
3)-x— 1 + |/|’ У— !+/• 4)x-~|l-f|’ У—
5) x = 3cos/, у = 4 sin/. 6) x = /2 — 2/, y = t2-\-2t.
7) x —cost, y — t-\-2s'mt. 8) x —2*-1, y — (t3 + l)/4.
7.270. Пострить график функции в полярных координатах!
1) 2) r~2|cos3<₽l-
3) Ф — г_2 i'• 4) ф == arcsin(г—1).
7.271. Пусть а — иррациональное число,
f(x)=ax — £(ах), xgZ.
Доказать, что:
1) f (х) < 1 для любого х е Z.
2) f Ui) — f (хг) = f(xi — x2), если f (Xi) — f (x2) > 0;
f Ui) — f (x2) = f (xi — x2) — 1, если f (xj) — f (x2) < 0.
3) Для любого e > 0 найдется число х е Z такое, что
0 < f (X) < 8.
7.272. Функцию f называют выпуклой вверх (вниз) на про-
межутке X, если для любых Xi,‘ х2 е X и любого ае[0; 1] вер-
но неравенство
f(axi +(1 — a)x2)> af(xi) + (l — a)f(x2)
(соответственно
f(axi +(1 —а)х2)^ af(xi) + (l —a)f(x2)).
График выпуклой вверх на отрезке [а; 6] функции лежит
не ниже прямой, проведенной через точки (a; f(a)), (Ь; f (/>))>
162
Доказать, что функция:
1) у — ах2 + Ьх + с выпукла вниз на R при а >0 и вы»
пукла вверх на R при а < 0.
2) у = ах выпукла вниз на R.
3) у — logoх выпукла вверх на (0; 4~оо) при а>1 и вы-
пукла вниз на (0; +оо). при 0 < а < 1.
4) у = sin х выпукла вверх на [0; л] и выпукла вниз на
[—л; 0].
7.273. Указать промежутки выпуклости вверх и выпуклости
вниз функции:
1)у = |х|. 2) у^х\ 3) у — 1/х. 4) у = ^~.
5) у — ch х. 6) t/ = shx. 7) z/ = lg|x|. 8) # = |lnx|.
7.274. Доказать, что если f и g — выпуклые вверх функции,
то и функция af 4~ ₽g> где а 0, р 0, также является вы-
пуклой вверх.
7.275. Доказать:
1) Функция, обратная к выпуклой вверх строго возрастаю-
щей функции, выпукла вниз.
2) Функция, обратная к выпуклой вверх строго убывающей
функции, выпукла вверх.
7.276. Указать промежутки выпуклости вверх и выпуклости
вниз функции:
1) у = tgх, х <= (—л/2; л/2). 2) z/ = cos2x, хе(0; 2л).
3) # = arcsinx, хе[—1; 1]. 4) # = arcctgx, xeR.
- 7.277. Функция f такова, что для любых Хь х2 Е R верно не-
равенство
/(Х1+а.)<|(/(Х1)+/(Х2)).
Доказать, что для любых хь х2, е R верно неравенство
f (*-+** + *з.) < | (f (Х1) + f (Х2) + f (д.з))>
7.278. Функция f выпукла вниз на R. Доказать, что для лю-
бых Xi, х2, ..., хп е R и любых аь а2, ..., ап, 0 а/ 1
(/ = 1, 2, ..., п), а] 4-ос2... 4-ап=1, верно неравенство
(неравенство Йенсена)
f(aixi4-a2x24- •••4-an*n)<aif(Xi)4-a2f(x2)4- ... +anf(xn).
7.279. Функция f(x) определена на R, и для любых Xi, х2е R
/(Х1)4-/(х2)==/(Х1 4-х2).
1) Доказать, что для всех рациональных х
/(*!=« ЯП-X
6*
163
2) Доказать, что если f неограничена в окрестности некото-
рой точки, то она неограничена в любой окрестности любой
точки.
7.280. Функция f с £>(/)У={0} такова, что для любых
a, f s R и любых хь х2 е D(f) выполнены условия
СХХ1 Р%2 €= D (/),
f(a%i + ₽х2) = af(xi)+ pf(x2).
Доказать, что D (f) = :R и для любого х g R
/(x) = f(l)x.
7.281. Для функции f существуют числа Т ф 0 и а такие, что
для любого х е D (/) имеет место
x+Te/)(f), х— T<=D(f)
и верно одно из равенств:
1) f(x+T) = f(x)+a, 2) f(x + T)=f(x)+ ах.
Доказать, что соответственно:
1) /(х) = ф(х) + у-Х,
2) /(х) = Ф(х) + ^г(х2-Гх),
где ф(х)— периодическая с периодом Т функция.
7.282. Для функции f существуют число Т #= 0 и много-
член Qn(x) степени п такие, что для любого x^D(f) имеет
место
x+Tf=D(f), x—T(=D(f)
и
f(x + T) = f(x) + Qn(x):
Доказать, что существует многочлен Pn+i (х) степени n + 1 та-
кой, что
f(x)= ф(х)4-Рл+1 (х),
где <р(х) — периодическая с периодом Т функция.
7.283. .Для функции f существуют числа Т =#= 0 и k > 0 та-
кие, что для любого xeD(/) имеет место
x+reD(f), x-TeD(f)
и
f(x + T) = ^(x).
Доказать, что существует число а > 0 такое, что
f(x) = а*<р(х),
где <р(х)— периодическая функция.
164
14. Последовательности. Функцию, областью определения
которой является множество N натуральных чисел, называют
последовательностью. Значения такой функции обозначают хп
(или Ьп и т. д.) и называют членами последовательности,
число п называют номером члена хЛ. Последовательность обо-
значают
{хп}, или хп, nsN, или Хп, П=1,2, ...
Другими словами, если каждому натуральному числу п сопо-
ставлено число хп, то говорят, что задана последователь-
ность {Хп}-
В качестве множества номеров может быть взято не только
множество натуральных чисел, но и какое-либо другое беско-
нечное подмножество целых чисел, например, множество чет-
ных натуральных чисел (тогда последовательность обозначают
{xzk}), множество неотрицательных целых чисел 0, 1, 2, ...
и т. д.
Множество значений последовательности может быть как ко-
нечным, так и бесконечным, например, множество значений по-
следовательности {(—1)"} состоит из двух чисел 1 и —1, мно-
жество значений последовательности {1/п} бесконечно. После-
довательность, множество значений которой состоит из одного
числа, называют стационарной.
Последовательность может быть задана с помощью фор-
мулы вида
xn = f(n), neN, (33)
выражающей хп через номер п, например,
xrt = 2rt, neN;
хп = п\, п^ N.
Такую формулу называют формулой общего члена последова-
тельности. Для задания последовательности используют и ре-
куррентные формулы, т. е. формулы, выражающие n-й член
последовательности через члены с меньшими номерами (пред-
шествующие члены). Так определяют арифметическую и гео-
метрическую прогрессии (§ 4). Другими примерами являются
последовательности
х{=а, xn+i — bxn_x + с, п^2,
х{= а, x2 = b, xn = (xn_l + хп_2)/2, /igN, п^З,
здесь а, Ь, с — заданные числа. Последовательность может
быть задана и другими способами, например, хп — h-я цифра в
-десятичной защиси числа л (т. е. Xi = 3, х2= 1, %з = 4 и т. д.).
Пример 21. Найти формулу общего члена для последова-
тельности:
1) Xi — 1, Xz — 1, Хп = хп-1 хл-2, п е N, п 3 (последо-
вательность Фибоначчи)!
165
2) xt=a, x2 — b, x„ = jc„_( —-|-x„_2, «gN, n^>3;
3) Xi = 0, X2 — 1, Xn — Xn-\ — Xn-2, n g N, n > 3.
Al). Найдем последовательность вида {X”), удовлетворяю*
щую условию хп = Хп-y + хл-2, n G N, п > 3 (здесь X =# 0 и
может быть, вообще говоря, и комплексным числом). После
подстановки хп = № получим уравнение X2 == X + 1 (его назы-
вают характеристическим уравнением), откудаХ! = (1 + Т5)/2,.
Х2 = (1—V^)/2. Каждая из последовательностей {х“} и {х"}
удовлетворяет условию хп = хп-\ + хп-2- Для любых чисел а
и р последовательность с общим членом хп = аЛ” + Р^2 также
удовлетворяет этому условию. Найдем аир так, чтобы
Х1 = (ХЛ1 -f- РЛ/2 ===: 1, = CtZi -f“ Р^2 = 1 \
получим
а 1 - • = 1_ о = ^-1 _______
Aj (Л1 — Л 2) д/5 Л<2 (Л] — Л2) ^5
Подставляя значения Ль Лг, а и р в формулу
находим формулу общего члена
Хп = 4” р^2>
neN,
последовательности, определяемой условиями 1).
2) Поступая, как и в случае 1), придем к характеристичен
скому уравнению 4Л2 — 4Л + 1 = 0, имеющему один двукрат-
ный корень Л = 1 /2. Последовательность {2~п} удовлетворяет
условию
•—- Хп_\ Xn__2i 3»
Другой такой последовательностью является, как легко прове-
рить, последовательность {и2-л}. Последовательности вида
{а2~Л + рп2-л} также удовлетворяют этому условию. Опреде-
лив а и р из условий
Xi = a-y+ Р--| = а, х2 = а4 + ₽ • 2 •= Ь,
получим
а — 4а — 46, р = 4Ъ — 2а.
Значит, формула общего члена последовательности, заданной
условиями 2), имеет вид
х„=(2а —26 + (26 —а)п)21-«, п е= |Ч.
3) В этом случае характеристическое уравнение X2 = X — I
имеет комплексные корни Xi = ein/a и Х2 = е_,я/3. Последова-
тельность, удовлетворяющую условиям 3), будем искать в виде
хп = ае<яп/3 + ре-‘яп/3 и из условий Xi — 0, х2 == 1 найдем, что
а-7?Ге ’Р“ ‘
166
Отсюда
*n = ^(el*^w *eN. А
i V3 - Уз 3
Последовательность, заданную рекуррентной формулой вида
хп = а{хп-1 + ^п-2 + ... +akxn-k, neN, n>&,
тде ab ak и k — заданные числа, k е N, называют возврат*
ной последовательностью порядка k.
Последовательность xrt, ne N, ограничена снизу, если су-
ществует число С такое, что для всех n е N верно неравен-
ство
Х/2 С.
Последовательность хЛ, neN, ограничена сверху, если су-
ществует число С такое, что для всех rzeN верно неравенство
хЛ С.
Последовательность хп. ne N, ограничена, если существуют
числа Ci и С2 такие, что для всех « е N верны неравенства
^-'2*
Это определение равносильно следующему: последовательность
хп, пе N, ограничена, если существует число С > 0 такое, что
для всех п е N верно неравенство |xrt| С. или, короче,
20 0 VheN: |хп|< С. (34J
Пример 22. Доказать, что последовательности:
2) хп — -^п, neN, где а> 1,
ограничены.
А 1) Поскольку
|(- 1)"п+ Ю|<|(— 1)"п|+ 10 = «+ 10, Vn2 + 1 > я
имеем
I v I— I(~ !)"«+ Ю| «4-Ю
’*nl~ V??+T п
т. е. (34) выполнено при С — 11.
2) Очевидно, для всех n е N
4>°-
1 + —<11,
п
Поскольку а— 1 > О, по неравенству Бернулли имеем для
рсех п е N:
an==(l 1)«>п(а—1),
167
откуда
- п 1
ап а — 1
Таким образом, для всех и верны неравенства
О
т. е. последовательность ограничена. А
Отрицание определения ограниченной последовательности
.выглядит так: последовательность хп, не N, неограничена, если
для любого С > 0 найдется я е N такое, что |хл| > С; короче,
VC>0 3nf=N: |х„|> С. (35>
Аналогично формулируются отрицания определений ограни-
ченной сверху (снизу) последовательности.
Пример 23. Доказать, что последовательности:
1) Xn = nCOS7in, neN;
100 —л3 м
2) Хп л2 — 10 ’ П
<неограничены.
Л I) Если п — 2k, то cos 2л& = 1 и х2л = 2k. Пусть С — про-
извольное положительное число. Возьмем четное число 2k, боль-
шее С (например, 2k = 2(Е(С) + 1)), тогда x2k> С, т. е. (35)
выполнено, и данная последовательность неограничена.
2) Из формулы общего члена имеем
100 ,1 100
л3 I _ л3
I п2 I и2
Если п 6, то
100 I , 100 1
га3 < 2 И 1 п3 > 2 ’
а 0 < 1 — < 1, поэтому
100 1
ti л3 _ 2 л
I хп I п пг~ > п ~ т •
1 -’Л2'
Для произвольного положительного числа С возьмем п > 2С
(например, п =[2С]+ 1), тогда |х„|> -у >С и, значит, дан-
ная последовательность неограничена. А
Последовательность хп, neN, называют возрастающей (не-
убывающей), начиная с номера по, если для любого л по»
п е N, верно неравенство хп-м хп.
16в ...
Последовательность хп, п N, называют убывающей (не-
возрастающей), начиная с номера По, если, для любого п п0>
л е N, верно неравенство xn+i хп.
Если в этих определениях верны соответственно неравенства
jCn+\ > хп или < хп, то последовательность называют соот-
ветственно строго возрастающей или строго убывающей, начи-
ная с номера по.
Возрастающую или убывающую, начиная с номера ио, по-
следовательность называют монотонной, начиная с номера и0
(строго возрастающую йли строго убывающую — строго моно-
тонной) .
Последовательность, возрастающую с номера По=1, назы-
вают возрастающей (аналогично, убывающей и т. д.).
Данное определение последовательности, возрастающей с но-
мера по» равносильно введенному ранее (п. 6) определению
функции, возрастающей на множестве натуральных п п0, а
именно: последовательность хп, п е N, возрастает, начиная с
номера по, если для любых п\, п2 N, п\ и0, и2 и0, из не-
равенства щ < п2 следует неравенство Аналогичная
равносильность имеет место и для убывающей, начиная с но-
мера по, последовательности и т. д?
Пример 24. Доказать, что последовательность
*п=4г’
строго убывает, начиная с некоторого номера.
А Рассмотрим отношение
хп+1 _ 5"+’п! _ 5
хп ~~ (л 4-1)15" п +1 •
Видно, что при п 5
^n+t 5^<
хп 6
в, значит, Xn+i <. Хп (так как хп > 0). Итак, данная последова-
тельность строго убывает, начиная с п = 5. А
Пример 25. Доказать, что последовательность
хп — ’ п
строго возрастает.
ZX Рассмотрим отношение
xn+i _ (n + 2)"+1 -п" _/п2 + 2пУ+1 n+ 1
- хп (п+1)',+‘(п4-1)'* V(« + D2/ ' и
_ (। _ 1 v+l Д+1
V («+1)27 * п *
Из неравенства Бернулли имеем для любого neN:
(I _ 1 y+l > 1 _ " + > = _д_
V («+1)‘/ («+0* п+1*
499
Поэтому для любого neN
\ *»+' •> « . »+ 1 _ |
Хп Я + 1 * Л ’
т. е. х„+1 >• хп, и, значит, данная последовательность строго»
возрастает. ▲
Пример 26. Доказать, что последовательность {хп}, где.
Xj = а, хп+\ = V6 + хп, ne N:
1) строго возрастает, если а = 0;
2) строго убывает, если а = 4.
А Для я е N имеем х2п+2 — 6 + xn+l, x2+t = 6 + хп, откуда
Хп+2 Хп+1 ~ Хп+1 Хп‘ (36)-
Доказательство проведем методом математической индукции,.
1) Если Xi = 0, то ха = > хР
Допустим, что неравенство xn+i > х„ верно для п е N.
Тогда из (36) следует, что х2п+2> х2п+х, и так как хп+2 > 0 и
Xn+i > 0, то верно неравенство хп+2 > хп+\. Значит, xn+i > хп.
для любого «е N, т. е. последовательность строго возрастает»
2) В этом случае Х! = 4, х2 = < xi- Как и выше, легко-
доказать, что для любого я е N из неравенства х„+1 < х„ сле-
дует неравенство хп+2 <. хп+ь Значит, x„+] < х„ для любого
п е N, т. е. в этом случае последовательность строго убывает. А.
Верхнюю (нижнюю) грань множества членов последователь-
ности {хп} называют верхней (нижней) гранью последователь*
ности и обозначают
sup{xn) .(inf{xn}).
Член хп. последовательности {хп} называют наибольшим
(наименьшим), если хпхп.(хпхПо) для любого п, и обозна-
чают его
max{xn} (min{x„)).
Наибольший (наименьший) член последовательности назы-
вают также максимальным (минимальным).
Если существует шах{хп} (min{x„}), то
sup{xn} = max{x„} (inf{x„} = min{x„}).
Из существования конечного sup{xn) (inf{x„}) не следует суще-
ствования тах{хл} (тт{хп}).
7.284. Какие из чисел а, b являются членами последователь-
ности {х„}, если:
1) а =1215, t>=12 555; x„ = 5-32n-3, hgN.
*$) а = 6, 6«8; х„ = Vn2 + 32n — rt, яеЧ’
3) й = 6, 6 = 11; хп = (и2+ П)/(п+ 1), neN.
4) а = 248, 6 = 2050; xn = 2" — п, neN?
J70
7.285. Для каких членов хп последовательности {(—3)3~2л}
’выполнено неравенство \хп\ > 0,001 ?
7.286. Указать какой-либо номер N такой, что для всех
*п N члены последовательности {хп} удовлетворяют задан-
ному неравенству:
= neN; |х„|<0,1.
2)x„=-J±|, neN;
3) xn= ne=N; | xn + 2| < 0,001.
4)x„ = VU5> «eN; |xre-l|<0,l.
5) xn = (log2n)/n, « e N; | xn | < 1/fe, g N.
Указание. Доказать и использовать неравенство
21/4-1 >i' fesN-
7.287. Найти наибольший член последовательности!
1) {21/(Зп2 - 14п - 17)}. 2) {п/(п2 + 9)}.
3) {2~" — 3 • 4~п}. 4) {«2/2п}.
7.288. Найти наименьший член последовательности!
- 1) {(2м —5)(2п—11)}. 2) {«+!}•
3) {logfn — 3 log3n}. 4) {1,4"/га}.
7.289. Пусть s(p) — сумма цифр натурального числа р (если
Р ^9, то $(р) = р).
1) Доказать, что если р 100, то s(p) < р/10.
2) Пусть XieN, xn+i == s (х„), neN. Доказать, что есть
•номер п0 такой, что все члены хп с номерами п по одина-
ковы.
3) Пусть Xi е N, Xn+i = s(s(x„)-f-xn), «eN, Найти Xi984,
•если: a) Xi = 1983; б) Xi кратно 9 и х2< 1985; в) Xi = 1984.
7.290. Является ли последовательность {pft} подпоследова-
тельностью последовательности {хп}, если:
1) хп—п, neN; a) Pfe=&24-1, AeN; б) yk=k2—4k+5, £eN.
2) хп—2п, neN; а) yk—2k, fteN; б) yk~2(k+(— l)ft), AeN.
3) xn = l/n, «eN; a) yk = 1/(A — cosnk), 6) yk —
— l/(3& — cos nk), &eN?
7.291. Пусть {xnk} — подпоследовательность последова-
тельности {xn}. Доказать, что k, k e N.
7.292. Привести пример последовательностей {xn} и {ук}
таких, что V&Bnfe? Ук—хПк, но {у^ не является подпоследо-
вательностью последовательности {хя}.
171
7.293. Привести пример последовательности {хп}, удовлет-
воряющей условию:
1) V/пЗя: хт=£ хп.
2) 3NVn^N: xn<xN.
3) BNftn. > JVj: xNt > xn и 3N£/n N2: xNa < x„.
4) 32VVn > NMtn >'n: xn < xm.
5) Vn3/n > n3k > n: xm<xn< Xk-
7.294. Указать формулу общего члена последовательности,,
первыми членами которой являются числа:
1) {8; 14; 20; 26; 32;
2) {—0,5; 1,5; —4,5; 13,5; —40,5;
3) {2; 3/2; 4/3; 5/4; 6/5;
4) {1; 3; 1; 3; Г,
5) {5; 7; 11; 19; 35;
6) {1; 2; 6; 24; 120;
7) {—2;—1/2;—4/3;—3/4;—6/5; ...}.
8) {0,3; 0,33; 0,333; 0,3333; 0,33333; ...}.
9) {1/2; 1/2; 3/8; 1/4; 5/32; ...}.
7.295. По известным трем членам Xi, Хг, xs последователь-
ности найти формулу общего члена в виде xn — f(n), где
j(x)— многочлен не выше второй степени.
7.296. Доказать, что если Xi = a',k
xn+1~(a/xn)llk, neN, то xn~a^~(~krn^k+iK
7.297. Пусть
х0=1, х{ = а, х„ = (а + 0)~” £ an~k^kxn_kxk,
й=0
ne N, л > 2,
где а, а, 0 — положительные числа. Найти формулу общего
члена этой последовательности и номер наибольшего члена.
7.298. 1) Найти общий член последовательности {хп}, если
Xi = а и хт+п = хт -|- хп + тп для любых т, п е. N.
2) Существует ли последовательность {х„} такая, что для
любых т, п <= N верно равенство хт+п — хт +хп + т + п?
7.299. Найти формулу общего члена последовательности, за*
данной рекуррентным способом (а, Ь, а, 0 — заданные числа);
1) Xi == 0, Хп+1 в (хп + 1)/(п + 1), и g N.
2) Xi=a, %„+,=(»+ 1)(х„4- 1), neN.
3) X]« 1/2, xn+i = 1/(2 — хп), пеМ.
4) Х1=ьа, х„+1 — ах„ + 02", а =#= 2, neN.
5) Xi «= 1/2, х„+1 = 2/(3 — х„),' п & N.
172
6) X[ = 0, x2=l, xn+2 = (3xn+l — xn)/2, neN.
7) Xi — a, x2 = b, xn+2 — xn+l + 2xn, n e= N.
7.300. Найти формулу общего члена для последовательно-
стей {хп} и {уп}> если Xi = Ь,
= (2хп -Н Уп)/3, уп+1 = (Хп + 2уп)/3, П е= N.
7.301. Последовательность {хп} задана рекуррентным спо-
собом: Xi = а, х2 = Ь, Хп+2 = pxn+i + qxn, meN; a, b, р, q —
заданные числа.
1) Доказать, что если уравнение X2 = pX-J-9 имеет различ-
ные корни Xi и Х,2, то общий член последовательности {хп}
имеет вид
„eN.
— Л1
2) Доказать, что если уравнение X2 = pZ + q имеет крат-
ный корень А, =# 0, то общий член последовательности [хп}
имеет вид
Хп — (2аК— b + п(Ь— ак))№-2, п N.
7.302. Последовательность {хп} задана рекуррентным спосо-
бом:
Xi = a, x2 = b, Хп+2 = pXn+i + qxn +г, meN;
a, b, р, q, г — заданные числа. Найти формулу общего члена>
если
1) уравнение X2 = pZ + q имеет различные корни и Х2;,
2) уравнение Z2 = рК + q имеет кратный корень Хо =/= 0.
7.303. Найти формулу общего члена последовательности^
заданной рекуррентным способом:
1) Х{ = Х2 == 1, Хп+2 === 0,5 (Хп+\ 4" Хп) + 1, п ее N.
2) Xi = х2 — 1, Хп+2 = Хп+1 + 2x^ + 2, п е N.
7.304. Найти формулу общего члена последовательносте
{хп}, если Xi =а > 0, xn+i — 1/(1 4-хл), n N.
7.806. Найти все значения aeR, для которых формулы.
Xi s=s a, Xn+i — Хп/(2 + хп), пе N, задают последовательность..
Найти формулу общего члена этой последовательности.
7.306. Пусть Xi = a, x«+i = хп/(4 — xn), п е N.
1) Показать, что если а^[3;4], то эти формулы задают
последовательность, и найти формулу ее общего члена.
2) Найти все значения а, при которых эти формулы не оп-
ределяют последовательность.
7.307. Найти формулу общего члена последовательности, за- *
данной рекуррентным способом (a, b.c.d — заданные числа) :
1) xi = a, Xn+i = Хп/(Ь + хл), neN.
2) xi — a, Xn+i — bxn/(c + dxn), пN.
173
7.308. Пусть Xi = р, ps N, Хл+i = Xn'+ 2", пе N. Доказать,
что существует подпоследовательность этой последовательности,
все члены которой делятся на 3.
7.309. Пусть
s«=2+4-+if+-“+-^> ««=
_ О _ 1_______1 ____________1
° 1-2-2! 2-3-3! (n-l)n-nl‘
Доказать, что
«n=S„ + ^f.
7.310. Доказать, что если {хп} и {#«}—ограниченные после-
довательности, то ограничены и последовательности
1) {Хп-уп}', 2) {ахп + Ру„}, a, peR.
7.311. Привести пример ограниченных последовательностей
{хп} и {уп}, Упх&О, neN, таких, что последовательность
{хп/уп} неограничена.
7.312. Последовательность {хп} ограничена, последователь-
ность {уп} удовлетворяет условию: существует С > 0 такое, что
для любого neN верно неравенство С. Доказать, что
последовательность {хп/уп} ограничена.
7.313. Последовательность {хя} неограничена. Доказать, что
она содержит подпоследовательность {xnjJ такую, что xn/t > k,
A eN, ИЛИ Xnk < — k, k<= N.
7.314. Доказать ограниченность последовательностей:
( 2л2- 1 ) ( 1 — п ) ( п + (— 1)" )
( 2 + п2 }’ 2) { Vn2 +1 }' 3) { 3/1—1
. ( п2 + 4п + 8 1 1 5n° + 6 1
1 («+1)2 J‘ ’ I (п4+ 1) (га2 — 2) ]'
7.315. Доказать неограниченность последовательностей:
1) {(-1)пп}. 2){n2 —n}. 3){(l-n)/V^}. 4) {п + (-!)"«}•
5) {п(“1)П}. 6) {(l-n)sin<IW/2)}. 7) {n3/(n2+l)}.
8) {(n-n4)/(n + 2)3}.
7.316. Пусть Pk и Qi — многочлены степеней k и I соответ-
ственно, Qz(n)#=0 для любого zieN. Доказать, что последо-
вательность {Рк(п)/Qi(n)}: 1) ограничена, если k Г, 2) не-
ограничена, если k > I.
7.317. Доказать ограниченность последовательностей:
п п
neN- 2) neN-
Л=1
n i
3) = j,
i=i /«i
174
7.318. Доказать, что если at — 1, а„+1 = (п + 1) (а„+ 1),
п
neN, то последовательность x„ = JJ (1 + ограничена* *).
fe=i ак
7-.319 . Доказать ограниченность последовательности {хп} и
найти sup{xn}> inf{xn}, если:
п п
1) хп. = + р , N. 2) хп — 4fe2_ j » п *= N.
fe=l й=1
n &+1 п
3) Хп == У , n <= N. 4) хп = Y-—, n е N.
k £l2
Доказать ограниченность последовательности (7.320—7.322) :
п
7.320. 1) хп = £ _ 2fe , neN.
k=i
п
2) xn — (a + _1)d) (a + fed) > 72 *= N-
&==1
n
(26 - 1) (2fc + 1) (2£ + 3) ’ neN.
k—\
4) neN-
fe=l
5) x„ = log2((l-^)(l--^)... (1-4-))’ rtsN> n>^
7.321. 1) 2) {------------k
) <. (n + 3)(V« +1) J
o\ { иУ»6 + 2n + V»3 + 2 ) «
6> ( 3n-2n2 J*
7.322. 1) {Vn2 + 1 — n}. 2) {Vn — 1 — Vn + 1}.
3) {«(V«4 + « —Vn4 —n)}- 4) {y/^n — n3 + ^9n + n3}.
5) {^ft3+1 — V«2—1}. 6) — Vn2— 1 J.
7.323. Доказать неограниченность последовательности:
1) {д/п4 + n3 + 1 —— га3 + 1}.
2) {д/n2 + (—l)”Vn3 — nJ-
n
*) JJ ck — произведение чисел Ci, cn.
17&
7.324. При каких р, q, 0 q < р, ограничена последователь-
ность:
1) {д/V 4- /г9 + 1 — д/V - n" + 1 }•
2) {иУ/гр — n9 + 1 — V«₽ + 1 }•
3) {д/п^ + an9 + 1 — д//гр + 6п9+ 1}, k e= N, k 2, a #= 6?
7.325. Доказать ограниченность последовательности:
1>{(‘ + 4)"}- 2) {W- 3) {(‘ + т)Т x>0-
7.326. 1) Доказать, что последовательность {(lnn)/n} огра-
ничена сверху числом In 2.
2) Найти sup {(In п)/п}.
7.327. Доказать ограниченность последовательности:
1 ( 2*+1 | 2) Г 52га+1 +2П |
' 3« _ 2 J' ' I 1 — 25ra J ’
3) { Sri } • 4) {tg (3п + 5) - ’g(« + !)}•
5) {In (V2TF+T - «) - In n}. 6) { ln(^ + g-^+1) } •
8) |rt|n2L±lj. 9) {In2(«+!)-In2nJ.
7.328. Доказать неограниченность последовательности:
l){5’-4“). 2){^4r}- 3)V»T.
S) (2"«. 6) (a"/»1}, |o|> 1, 7) {loB"+^.l) }•
7.329. Доказать ограниченность последовательности:
1) {n/X1}. 2) {n2/2n}. 3) {п^2п}, р е= R.
4) {nqn}, | q | < 1. 5) {npqn}, peR, | q | < 1.
7.330. Доказать:
1) Ограниченность последовательности .
xn — ^kqk, neN, |<?|<1.
2) Неограниченность последовательности
xn = ^kqn~k, nsN, <?eR, q 0.
Л-1
’) (2n)!! — 2-4-6 ... 2n; (2n—1)1! = 1-3-5 ... (2n—1).
J 76
7.331. Доказать, что последовательность {хп}—такая, что
х4 +1
*i = 2, xn+i — -^~, ne=N,
1) ограничена снизу числом 1/5; 2) ограничена сверху числом 2.
7.332. Доказать ограниченность последовательности:
1) Xl — a>0, Xn+i=-j(xn + -^)-
2) Xi=a, x2 = b, xn+2 = (xn+l + xn)/2.
7.333. Доказать неограниченность последовательности:
1) X{ = %2 == 1 j %ti+2 ===
2) — 4, %2 = 3, %n+2 = "~b
7.334. Доказать, что последовательность {xn}, где Xi — x? = 1,
xn+2 xn+i +, П g= N, ограничена.
7.335. Пусть {xn} — последовательность натуральных чисел
такая, что последовательность
Sn = —+ —+ ... +—, «gN,
п Xl х2 1 1 хп ’ ’
ограничена. Доказать, что последовательность
п
^ = П(1 + ^)’ nsN’
6=1
ограничена.
7.336. Доказать неограниченность последовательности
п
xn = £(-l)k+'k2, ne=N.
fc=l
. ft
_ 7.337. 1) Доказать, что если последовательность Sn — хп
k^\
ограничена, то ограничена и последовательность {хЛ}.
2) Верно ли, что если последовательность {хп} неограни-
п
чена, то неограничена и последовательность Sn = хп, tie. N?
fe-i
7.338. Доказать ограниченность последовательности:
1) {п (а1/п — 1)}, а > 0, а #= 1.
[ 4Vn-'l),- '4
з) {n“(V«- 0), « < и
177
Доказать, что данная последовательность монотонна, начи-
ная с некоторого номера (7.339—7.341):
7-339. 1){^г}- 2){^}-
( п? + 24 | ( п? | ~ J я2 |
I п +1 ) U2 - 3 J ‘ ' I п3 + 32 ) '
7.340. 1) {д/Зп-2}. 2) {Vn + 2-Vn+l}. 3) {^п3-1-п}.
4) {д/п2 + п — п]. 5) | —7== 1 • 6) |...Г. 3 |.
’ *v ’ ( V»2 + 7 J I д/«2 + 1 J
7.341. 1) {2П- ЮОп}. 2){3" —2”}. 3) {2"+1 — Зп"2}.
f 6n+1 —5"+1 1 f 4"~1 + 3n~I 1 ( 100" )
4> t 6n + 5n J • 4” + 3n J ‘ b' I nt J
7){v}‘ 8) {lg(n+l)-lgn}. 9) {In(n2 + 9n) — 2 Inn}.
7.342. Доказать, что последовательность {nqn}, 0<7<l,
монотонна, начиная с некоторого номера; указать этот номер.
7.343. При каких соотношениях между a, b, с, d последова-
{ап 4- b )
—г >, начиная с некоторого номера, будет;
cti a j
1) возрастающей, 2) убывающей?
7.344. Доказать, что последовательность
п
Хп = 1 ~ X 2й (2Й + 1) — 2 (n + 1)
k=\
монотонна.
7.345. Доказать, что последовательность
п
Хп== («4-1)1 X ‘
fe=i
возрастает и ограничена. Найти inf{x„}, sup{x„}.
7.346. Сформулировать, используя символы 3, V, утвержде-
ние:
1) Последовательность {хп} не является возрастающей.
2) Последовательность {%„} не является убывающей
7.347. Доказать, что данная последовательность немоно-
тонна:
1) {(-!)")• 2) (С"‘-гЬ
3){» + (-1)“}- 4) (sin,,}.
5) JCi=l, x„+i=
nsN.
178
I
7.349. Доказать, что если {хп}—монотонная последователь-
ность, то и последовательность (%i + х2 + • • • + хп)| моно-
тонна.
7.350. Доказать, что ' данная последовательность убывает,
начиная с некоторого номера:
1) {п/4п}. 2) {(Зп+ 1)2/Зл}. 3) {п3/2“}. 4) {п1'"}.
7.351. Доказать монотонность последовательности:
1) {п — 61gn}. 2)-{lgn —п}. 3) {(lgn)/n}.
7.352. Доказать, что последовательность;
» {(1 возрастает; 2) {(1 } убывает.
7.353. Доказать, что при любом х > 0:
1) Последовательность {о+т возрастает.
2) Последовательность {(1 +}> гДе Iе N, 1>х,
губывает.
7.354. Доказать, что при а ф 1, а > 0, последовательность:
1) | } 2) {п(1—о’7")} возрастает.
7.355. Доказать, что последовательность Х\ ——10, хп+1 =
X «4- 1
> neN, убывает, начиная с некоторого номера; ука-
зать, этот номер.
7.356. Пусть Xj = 3, хп+1 = 0,5х2 — 1, neN. Доказать, что
эта последовательность: 1) ограничена снизу, но неограничена
сверху; 2) возрастает.
' 7.357. Пусть х1 — 2, xn+i — 0,5х2 — 1, п е N,
1) Доказать, что эта последовательность ограничена.
1. 2) Доказать, что подпоследовательности {x2k} и {x2k_\}
Данной последовательности монотонны, начиная с некоторого
номера.
7.358. Доказать, что последовательность {хп}, где х1=4,
2 4-х2
хп+1 = neN, убывает.
7.359. Последовательности {хп} и {уп} заданы рекуррент-
ным способом: — а >* 0, у\ — b > 0,
хп+1=|(х„ + ^)’ ^п+1 = л/т(хп + ^)> «eN.
Доказать, что: 1) уп^хп, neN, п 2; 2) последовательность
|{хп} возрастает (п 2); 3) последовательность {</„} убывает
> 2); 4). |ум-1 -*«+11 |Ь ~ «IM
179
7.360. Доказать, что если Xi = а > 0, yi — b > 0,
•^п+1 '''/ХпУп* У п+1 (хЛ 4“ Уп\ ПЕ N,
то: 1) последовательность {хп} возрастает, а последовательность
{уп} убывает; 2) обе последовательности {хп} и {уп} ограничены;
3) \yn+i — xn+i\^\b — a\/2n.
7.361. Доказать, что любая последовательность содержит мо-
нотонную подпоследовательность.
7.362. Пусть С°а = 1, Са = Са"1 • - . п €= N, где а е= R.
Доказать^, что:
1) С^а(а~п
2) последовательности {С3/2}, {С1/2}, {С-1/2}, {C-i} ограничены;
3) последовательности {С--2}, {С-3,5} неограничены;
4) последовательность {Са} ограничена при ос —1;
5) последовательность {Са} неограничена при а<—1;
6) последовательность {| |} убывает (в широком смысле)
при a —1, начиная с некоторого номера;
7) последовательность {| Са |} возрастает (в широком
смысле) при а <—1, начиная с некоторого номера;
8) последовательность {(?«• q1} ограничена при а < — 1,
|<7|<1.
ГЛАВА II
ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§ 8. Предел последовательности
1. Понятие предела.
Определение 1. Число а называется пределом последо-
вательности {хп}, если для каждого 8 > О существует такое на-
туральное N, что для любого n^N верно неравенство
\хп — а\ < 8.
С помощью символов V и 3 определение 1 записывается
так: число а — предел последовательности {хп}, если
Vs > OBNVn N: {хп— а| < е.
Используя понятие окрестности точки, определение предела
можно сформулировать следующим образом: число а называет-
ся пределом последовательности {хп}, если для каждой окре-
стности числа а найдется номер, начиная с которого все члены
последовательности принадлежат этой окрестности.
г: Иными словами, какую бы окрестность числа а ни взять,
вне этой окрестности либо нет ни одного члена последователь-
ности, либо находится лишь конечное число ее членов.
В символической записи: число а — предел последователь-
ности {хл}, если
VU(a)3NVn^N: xn^U(a).
Теорема. Последовательность может иметь только один
предел.
Если а — предел последовательности {хп}, то пишут
lim хп =а.
' Последовательность, имеющую предел, называют сходя-
щейся.
Пример 1. Доказать, исходя из определения 1, что число 1
является пределом последовательности хп — п/(п-\-\) (п —
«== 1, 2, ...).
А Рассмотрим модуль разности
Возьмем произвольное число е > 0. Неравенство | хп — 11 < в
будет выполнено, если —гт <в, т. е. при п> 4— 1- В ка'
Л 1 ж Л
181
честве W возьмем какое-нибудь натуральное число, удовлет*
воряющее условию N > — 1, т. е. -jy< е *)^ Тогда для
всех n^N выполнены неравенства
I — 11 — 1 1
1 Хп
Это и означает, что 1 есть предел последовательности
{n/(n+ 1)}, т. е.
,im 7TT = t А
п->оо 1
Пример 2. Доказать, исходя из определения 1, что
lim (1/3)" = 0.
П->оо
Д Так как 3" > п для любого п 1, то
Ц1/3)" — 0|=1/3"<1/п.
Пусть е > 0, выберем натуральное N такое, что 1/N < в. Тогда
для любого n^N имеем
|(1/3)п — 0|< l/ns£ \/N <г.
Значит,
lim (1/3)" = 0. д
П->оо
Сформулируем отрицание определения 1: число а не яв* ।
ляется пределом последовательности {хп}, если существует та-
кое 8 > 0, что для любого натурального N найдется номер
N такой, что
| хп — а | е.
В символической записи: число а не является пределом по-
следовательности {хп}, если
Be > OVNB/i N: \хп — а| е.
На языке окрестностей: число а не является пределом после-
довательности {хл}, если существует окрестность числа а, вне
которой находится бесконечно много членов последователь-
ности.
Последовательность называют расходящейся, если никакое
число не является пределом этой последовательности, другими
словами, последовательность {хп} является расходящейся, если
для любого числа а существует такое е, что для каждого на-
турального N найдется п^ N такое, что
|хл — а\^и е,
или, короче,
УяЗв > 0VN3n \хп — а\^5 е.
*) Например, /V — £(1/е), где Е[а) — целая часть числа а.
182
Пример 3. Доказать, что последовательность |(— 1)п+~-^
расходится.
А Нужно доказать, что никакое число не является пределом,
данной последовательности.
Отметим на числовой прямой несколько членов последова-
тельности, например,
Xi = 0, х2 = 3/2, х3 — —2/3, х^ — 5/4, х5 = —4/5,
х6 = 7/6, Х12 = 13/12, Х13 = —12/13 (рис. 55).
Этот рисунок подсказывает, что расстояние между двумя сосед-
ними членами последовательности больше 1. Докажем, что это
О
7^2 Xz Z
*~7
Рис. 55.
действительно так для любых двух соседних членов. Из этих,
членов один имеет четный номер п = 2k и
~ 1 + ~2k > 1 ’
Соседний член имеет нечетный номер 2k + 1 (или 2k—1) и
Л2А+1 == I “Ь 2Й + 1 О ^ИЛИ %2fe—1 == I Н- 2^___ 1 О) '
Отсюда следует, что |хя— x„+I|> 1.
Для произвольного числа а возьмем окрестность единичной
длины — интервал (й~ у: а + у)' Любые соседние члены хп
и x„+i оба вместе не могут находиться в этой окрестности, так
как расстояние между ними больше 1. По крайней мере один
из этих членов будет лежать вне окрестности.
Таким образом, для любого числа а существует е= 1/2 та-
кое, что для любого натурального N найдется п, равное либо N>
либо N -j- 1, такое, что | хп — а | > 1 /2 = е. Это и означает, что
данная последовательность расходится. А
Теорема. Если последовательность имеет предел, то она
ограничена.
Ограниченность последовательности — необходимое условие
ее сходимости; т. е. если последовательность неограничена, то
она расходится.
Пример 4. Доказать, что последовательность {(п2 — 10) /nJ-
расходится.
А Докажем, что данная последовательность неограничена.
Имеем
10
хп = п~ —
183.
Пусть С — произвольное положительное число; Возьмем какое-
нибудь натуральное число по > С + 10, тогда хПо п0— 10 > С.
Это означает, что последовательность {(п2—Ю)/п} неограни-
чена, а поэтому расходится. А
Определение 2. Последовательность {хп} называется
бесконечно малой, если
lim хп = 0.
П->оо
Теорема. Если последовательность {хп}—бесконечно ма-
лая, а последовательность {уп} — ограниченная, то {хпуп}—бес-
конечно малая последовательность.
Теорема. Для того чтобы число а было пределом после-
довательности {хп}, необходимо и достаточно, чтобы для всех п
хп = а + ап,
где {ап}—бесконечно малая последовательность.
8.1. Для каждого данного в указать такое натуральное
что 1/м < в для всех п N, и заполнить таблицу
е 10 0,5 I 0,03 |з-10—4 7-10-10
1 1
8.2. Доказать, что lim хп — 0, указав для каждого е > 0 та-
П->оо
кое N, что для любого n^N верно неравенство | < е, если:
1) х„ = 1/п. 2) xn = aln (а — произвольное данное число).
3) х„ = (-1)”+1/п. 4) х„ = (2 4-(—!)")/«•
5) х„ = (1 +(-1)п)/л. 6) x„ = |sin-^-.
Отметить на числовой прямой (в случае 2) взять а — —1) пер-
вые шесть членов этих последовательностей. *
8.3. 1) Доказать, что для всех п е N
«+10 1
2п — 1 > 2 ‘
Найти все и g N, для которых
”+Ю J । с
где е равно: а) 1/6; б) 1/10; в) 1/2{2й + 1), feeN.
2) Доказать, что lim
8.4. 1) Для каждого данного е указать такое натуральное N,
что
2n — 1
п + 0,5
184
для всех п N, и заполнить таблицу
10 0,5 0,03 3-Ю-4 7- 10—’°
2/2 — 1
2) Доказать, что lim —= 2.
/1~»оо П “Г v,O
8.5. Доказать, что:
1) где b е R.
д->оо П
2)Д^гг=4- 3)„^2^т=<-
4) limfej==-1- 5) lim-^J_=l.
П->ОО 2 П п~>оо п
6) lim-4 — 0, где р>1.
п~>оо а
8.6. Пусть limxn = x, а последовательность {уп} такова,
П“>ОО
что существуют натуральные р и п0 такие, что уп — хп+р (или
уп = Хп-р) для любого п по. Доказать, что последователь-
ное! ь уп сходится и limz/n = x. Иными словами, изменение
П->оо
(в частности, отбрасывание или добавление) конечного числа
членов сходящейся последовательности оставляет ее сходя-
щейся к тому же пределу.
8.7. Для каждого данного 8 указать такое натуральное N,
что 1 / < е для любого п N, и заполнить таблицу
ю 1
0, 01
8.8. Доказать, что:
- 1) iim , 2 =0. 2) lim „ 1 ^ = 0.
n->oo 'у 2/2 — 1 п->оо 3/2 — 11
’* 3) lim 4_=0, гдейеМ
n->oo fc/fl
8.9. 1) Для каждого данного е указать такое N, что
< е
для любого и N, и заполнить таблицу
I0-2
е
10-4
185
2) Доказать, что lim —== = 1.
n->oo -yn2 + n
8.10. 1) Для последовательности {xn} заполнить таблицу
в
10
0,5 0,03 3-10-4 7- IO-10
N
указав для каждого данного в такое натуральное N, что |хя| < е
для любого n^N, если а) хп = (—0,5)"; б) хя=(0,99)".
2) Доказать, что
a) Iim(—0,5)" = 0; б) lim (0,99)" = 0.
n-»oo П->оо'
8.11. Доказать, что если |<?| < 1, то
lim <у" = 0.
П->оо
8.12. Доказать, что числд а не является пределом последо-
вательности {хп}, если:
1 \ /1 \fl 1 2 ~ COS ЗХЛ л
1) х„ — (—1) ; а =— 1. 2) х„=-^-.----------; а = 3
' " ' ' ’ ’ п 2 + cos яп
3) х„ = cos (лп/3); а = 1/2. 4) xn = 2t"I)”rt; а = 0.
8.13. Доказать, что последовательность {хя} расходится,
если:
1) хп=(— 1)". 2) х„ = п.
3) х„ = sin (лп/2). 4) х„ = Е ((-1)п/п).
5) х„ = sin п°. 6) х„ = cos .
8.14. Последовательность {хп} расходится, а последователь-
ность {уп} такова, что существуют натуральные р и такие,
что уп — хп+р (или уп = Хп-Р) для любого п п0. Доказать, что
последовательность {#„} расходится. Иными словами, измене-
ние (в частности, добавление или отбрасывание) конечного чис-
ла членов расходящейся последовательности оставляет ее рас-
ходящейся.
8.15. Доказать, что последовательность {хп} расходится1
если:
1) хп = (—1)пи. 2) хп = и<"-1Л
п2 — 2п 2 л. л/г
3) Хп п -р 1 * 4) %п П 4 •
5) х„ = (0,5)(<-1>л-1К
8.16. Доказать, что {хп}—бесконечно малая последователь-
ность, если:
1)х„ = -^-. 2) xn = ^t±. 3) х„ = 4.
186
4\ х . 2и + 1„- 5) х = ^-
, п (и+1)2"- °) Х" 7Й
8.17. Для того чтобы последовательность {хп} была бес*
конечно малой, необходимо и достаточно, чтобы последователь-
ность {|х„|) была бесконечно малой. Доказать.
2. Теоремы о пределах, связанные с арифметическими дейст*
виями.
1. Если существует lim хп, то для любого сс существует
П->оо
lim (ахп) — а lim хл.
П~>оо П->оо
2. Если существуют lim хп и lim уп, то
н->оо п-»оо
а) существует
lim (х„ + уп) = lim хп + lim уп-,
П->оо - П->оо
б) существует
lim (хпуп) = lim хп • lim уп-,
И->оо П-»оо п->оо
в) если к тому же уп Ф 0 и lim уп =/= 0, то существует
П->оо
lim хп
lim
П->оо Уп
Пример 5. Найти
.. 5п3 — Зп2
hm—т-ПТ-
lim уп '
Преобразуем формулу для общего члена к виду
5-J-
п
п3
Учитывая, что {1/п} и {1/п3}—бесконечно малые последо
вательности, и используя теоремы о пределах, получаем
5-А
п
lim
п->оо
lim
5
1
1
п3
8.18. Найти lim хп, если:
П-»со
2) х = ..3 + Р>5?.....
Хп 0,Зв+1 + 5*
3) хп —
п
3/t 2
187
4)
7)
п + 1 “и п + 2 ‘ 5)
(и + 5)? — я (» + 7)2
9)
19) хп
8)
|б 6) X -”3 + 27
I • о; — га4 _ 15~.
-1 Зп24-1
х" ~’ 2« 4-1 6n + 1 ’
12) хп
5 • 2п — 3 • 5n+l
100-2“ 4-2-5" *
п2
1
п
%п 1
лП+2 | q/l + 3
11) ^ = ' 2» + з»-
. (-l)».6»-5n+1
’ п 5"-(-l)n+1.6n+1 ’ п + 2
8.19. Известно, что хп =/= 1, lim хп — 1. Найти Нту„,
14) хп
если:
Хп — 1
лп 1
хп 2
2xn 1
хп~2 ’
хп + х,, — 2
3) Уп —-------:— • ип — 2—1 •
хп “ 1 хп ~ 1
8.20. Пусть ап — общий член, a Sn — сумма первых п
арифметической прогрессии с разностью d ф 0. Найти:
1) Ши % 2) lim^f (а„=#0).
п->оо п п-+<х> ап
п
8.21. Пусть ]<71 < 1, Sn — ^aqn. Доказать,
*=о
О Уп
2) Уп
• 4) уп
членов
что
гг->оо * Ч
8.22. Найти lim
если:
—
2 — п , п • 2 п
5 4-3"+*
п
2
1) х„ = 0,11 ... 1.
п
2) х1 = 0,4; %2 — 0,45;
= 0,45454; ...;№* = 0,4545
3) Xi = 0,2; х2 = 0,23;
= 0,23423; х6 = 0,234234; ..
8. 23. Доказать, что
п
Й(^ + 1) ==L
Л = 1
х3 = 0,454; х4 = 0,4545;
.. 45; ...
х3 = 0,234; х4 = 0,2342;
*5
3. Теоремы о пределах, связанные с неравенствами
1) Если lim хп — lim zn = a и для всех п, начиная
*5 ==*
неко-
с
188
тороГо, Хп уп zn, то lim уп — а (теорема о трех последо-
П->оо
вателъностях).
2. Если lim хп = а и для всех п, начиная с некоторого,
П->оо
хп Ь (или хп с), то а b (или а с),
3. Если lim хп > а (или lim хп < Ь), то для всех п, начиная
п->оо п->оо
с некоторого, хп > а (или хп < Ь).
Пример 6. Доказать, что lim (5п/пп) = 0.
П->оо
А Для всех 15 верно неравенство 5/п 1/3, поэтому
0<(5/п)”<(1/3)п
при п 15. Здесь слева и справа стоят члены последователь-
ности, имеющих пределом нуль. Значит, по теореме о трех по-
следовательностях и
lim (5/п)" = 0. д
* П->ОО ''
Пример 7. Пусть lim хп — 0 и хп — 1 для любого и;
П->оо
пусть р — натуральное число. Доказать, что
lim V1 + хп — 1.
П->,оо
А Если хп 0, то
1 С < (VT+T„)P = 1 + хп = 1 +1 хп |,
а если —1 Хп < 0, то
1 5^1 + хЛ (V1 + хп) ~ 1 4“ хп = 1 I хп |.
Объединяя эти результаты, для любого хп^—1 получаем
1 — \хп К VI +х„ < 1 + I х„ |.
Так как lim хп = 0, то lim | хп | — 0 и
• П->оо П->оо
lim (1 — |х„|)= lim (1 +|х„|)= 1.
П->оо П-»оо
Отсюда следует, что и
' р______
lim V1 + хп = Ь ▲
П~»оо
При мер 8. Найти lim(Vrt2 + n — «)•
п->оо
А Преобразуем формулу общего члена:
V^+^ - п = (V^^-2W^+F+«). _
______п_______________1_____
- 7^4^ + » " /{ + 1 + ! ‘
189
Поскольку lim (1/п) = 0, то
П->оо
lira (V»2 + « — n) =---------J===-----— 1. д
llmVl + l+1
П->оо V П
Пример 9. Пусть a > 1. Доказать, что
п
lim '\fa— 1.
П~>оо
П __
л Обозначим -у/a—1— an, тогдаа„>0и а = (1+ап)п^
nan (по неравенству Бернулли, § 2), 0 < ап ^а/п, для всех
п. Значит, lim ап = 0, а
П->оо
п —
lim Vй = 1нп (1.+а„) — 1. а
П->оо П->оо
п—
Пример 10. Доказать, что lim -у/п—1.
П->оо
Л Обозначим Vra—1=ал, тогда ап^0 и п = (1+<*„)";>
> геа2 при п 2 (см. § 4). Так как п— 1 н/2 при
п 2, то п п2а2/4, откуда получаем 0 =Са„ 2/д/п. След о»
вательно, lim ап = 0, а
/2->оо
П
lim л/п = lim (1 + art) = 1. д
гг->оо п-»оо
В следующих двух примерах дано сравнение скорости роста
трех возрастающих последовательностей {ап}> {п} и {Ioga^}j
где а > 1.
Пример 11. Пусть а > L Доказать, что
lim (п/ап) = 0.
П->оо
А Поскольку а — 1 > 0,
ап — (\ +а— 1)"> .п(а — 1)2^_1_(а_ 1)2дЛя всех n > 2S
Отсюда следует, что "
0 п/а11 4/п(а— I)2.
Так как
lim (4/n(a — I)2) = 0,
• П-»оо
то и
lim (п/ап) = 0. д
П->оо
Пример 12. Пусть а > 1. Доказать, что
limbfon=0.
П->оо
190
Для доказательства воспользуемся определением предела
и результатом предыдущего примера.
Пусть е > 0. На множестве натуральных чисел п неравен-
ство
lOga П о
п
равносильно неравенству п<(аЕ)п. Поскольку ае > 1, имеем
=0
lim
П-»<»
для всех n^N
поэтому существует натуральное N такое, что
п
т.. е. п < аеп. Отсюда следует, что для всех n N
q logg П
п
это и означает, что
Jim-fe
П->оо П
0. А
Таким образом, из трех последовательностей {ап}, {«},
{Iogan}, а > 1, первая возрастает существенно быстрее других,
а третья — медленнее других.
Пример 13. Доказать, что lim — 0.
П->оо
Если k 4, то 2/k 1/2, поэтому при п 4
2" _ 8 2 ... 2 4 _ 32
и< п! _ 1 • 2 3 ’ 4 ... /! ^ 3 I 2 J 3 V 2 7 •
Так как lim-^-(4-) =0, той ПтД- = 0. а
П-»оо 1 ' П->ОО т
8.24. Найти:
1) lim . 2) lim (—) (а — произвольное число).
П->оо X П / п->оо X п /
( 2п + зу
I п2 ) •
3) lim
п-»оо
4) ^lim (см. задачу 8.3).
5) lim
П->оо
П + 1
V«2 + 2/г
8.25. Найти lim хп, если:
П->оо
1)X„=V9+|- 2)
o\ .. . j/n + 0,25 _ n+1
3)Х«-Л/1^“Г- 4)x"“vWr-
J-X 1 1 , |_____1
Xn Vn2 + 1 + +
191
дч v _ У«2 + п -ч _ Уяг + 1 +У»
Хп~ «4-2 • ' п ^/Т^Гп + п •
8) хп — л]п2 — 1 — п — 1. 9) хп = л/п2 + п — ^п2 — п.
10) х„ = нУп3 + 2/г2 — п. 11) хп = -^ (^1 + 4 — 1 )•
8.26. Пусть 0 < a sg 1. Доказать, что
lim '\]а — 1.
П->оо
8.27. Найти limxn, если хп равно:
П->оо
3/г 2п, п2 rr-z
1) V8. 2) УбД 3) и/б. 4) V °~2 .
1 + УбдГ
П ______ п ___________ п __________
5) У2+У «У^- чУ^±|.
п __ п
8) V3n + 2n. 9) Уз-1 . 10) V8-1.
Уэ - 1 Уг - 1
11) 4,п+2Мп+1>
13'1 а'(п+р\ где
12) (1 + И")1'1"’1.
а > 0, р > 0.
8.28. Найти lim хп, если хп равно:
п->оо
п п 2п 4п __ п2
1) д/п2- 2) V3n- 3) Aj'ln. 4) Vft- 5) Vra-
7)-^±Д. 8)
1 + У2П зУ«2 + Узп
п _________
9) 73^2. 10) 7»3 + Зи. 11) V2ra2J+i+3
V ft т *
8.29. Доказать, что:
1) lim nqn = 0, где | q | < 1.
П->оо
м2 иЗ
2) lim 4г = 0. 3) lim 4- =0.
П->оо 0 п-^оо °
4) lim Аг = 0, где |а|> 1, Л — натуральное число.
П »ОО °
8.30. Найти lim хп, если хп равно:
П->оо
!) - +»ТГ • 2) Ч- 3) л/Зп + п-2".
п + 3n+1 1 + п • 1,1"
192
Vn2 + 4« c. /10 1
w + 5" * 5) Д/ n 1,2" •
8.31. Пусть 0 < a < 1. Доказать, что
lim =
n->oo n
8.32. Найти lim xn, если xn равно:
П->оо
n n 1g n 9, 5n + 1g n log2 (n + 3)
*' га2-Г ’ ra-3,5 ‘ ra—1,3 •
ЛХ logs (ft2 + 1) « П — Ign
4' n ’ °> log2(4«+l) •
8.33. Доказать, что для любого а
8.34. Найти lim хп, если хп равно:
П->оо
п <~2)” 2) 1 3) n'3"+1 4) 4П + "2-2”-!
' (п + 2)! ’ * 7 (0,3)"га! * ’ nl + 1 7 п4 + (п!)2
... 10“ +га! (-3)n,~” 2”/2 + (n + D!
7 2"+(«+!)! ’ 7 (га3)! * 7 «(З^ + га!)
4. Бесконечно большие последовательности.
Определение 3. Последовательность {хп} называют бес*
конечно большой, если для каждого е > 0 существует такое на-
туральное 7V, что для любогоn^N верно неравенство
| хп [ > е.
В этом случае пишут
lim хп = оо.
П->оо
Последовательность {хп} имеет пределом +°° (соответ-
ственно —оо), если для каждого е > 0 существует натуральное
N такое, что для любого л N верно неравенство хп > е (со-
ответственно хп < —е). Это записывают так:
lim хп — + оо (соответственно lim хп — — оо).
/1->оо Л->оо
Во всех этих случаях говорят, что последовательность имеет
бесконечный предел.
Ясно, что всякая .бесконечно большая последовательность яв-
ляется расходящейся в смысле определения 1.
Пр имер 14. Доказать, что lim Vn== + °°-
П-»оо
А Пусть е — произвольное положительное число, a N — та-
кое натуральное число что Л^> е2*}, Тогда для всех n^N
*) Например, N == Е(г2) + 1.
7 Л. Д, Кудрявцев и др.
193
верно неравенство Vn^ > в. Это и означает, что lim
n-> оо
==+ ОО. А
8.35. Доказать, что:
1) limn = + oo. 2) lim (5 — 0,5ft) = —-оо.
rt->oo n->oo
3) lim (—l)nn = oo. 4) lim an =.<», где |a| > L
П->оо ft->oo
5) lim -\/n — 100 — +'oo. 6) lim nlp = 4- oo, где p e N.
n->O0 n->oo
7) lim Ign = H-oo. 8) lim logan = 4-оо, где a > Г.
n-»OO n->oo
9) lim logan = — oo, где 0 < a < 1.
П->оо
8.36. Доказать, что для того, чтобы limxn= оо, необходимо
П->оо
и достаточно, чтобы lim | хп [ = + оо.
П->оо
8.37. Пусть lim уп — 4~оо (limуп = —оо) и для всех п,
П~>оо П->оо
начиная с некоторого, хп ^суп (соответственно хп^суп),
где с>0. Доказать, что limxn = 4“°° (соответственно
п->оо
lim хп = — оо).
П-»оо
8.38. Пусть lim уп = + °° и для всех ft, начиная с некого-
П~>оо
рого, |х„| суп, где с > 0. Доказать, что lim хп = оо.
' П->оо
8.39. Доказать, что:
1) limn2 = 4-°°- 2) lim лр = 4~ °°> где 1.
П->оо П->оо
3) lim (2я — 5)5= + оо. 4) lim (lgft)3 = + оо.
П->со П->оо
5) lim (loga ft)p = + оо, где a > 1, p 1.
rt->oo
6) lim (0,5 — (—l)"'V/,n)= oo.
W->oo
7) lim (—n)n = oo. 8) lim(4Vft — n) = —oo.
rt-»OO n->OO
8.40. 1) Пусть xn =# 0, lim xn — 0. Доказать, что
П-> oo
.. 1
lim — = oo.
П->оо
2) Пусть xn =# 0, lim xn — oo. Доказать, что
П->оо
lim — = 0.
П->оо
194
8.41. Доказать, что {хп}—бесконечно большая последова-
тельность, если хп равно:
( п \п п2 п\ .v 1 2
О (ю) • 2) п + 8' 3) 4" • «27’
<2—1 1 — <п
ЦП Пп
6) —. 7) —г, где |а|> 1, fteN.
п2 пк
8.42. 1) Пусть lim хп = + оо iiyn^c для всех п <= N. До>
П~>оо
казать, что lim (хп + уп) = + оо.
П->оо
2) Пусть lim хп = — оо и уп с для всех я е N.
П->оо
Доказать, что lim {хп 4- уп) — — оо.
П-> оо
8.43. 1) Пусть limxrt=a, где а — это +°° или —оо. До-
гг -> оо
казать, что:
а) Если для всех п, начиная с некоторого, уп с > 0, то
lim хпуп = а.
П->оо
б) Если для всех и, начиная с некоторого, уп с < 0, то
lim хпуп = —
П-> ОО
2) Пусть lim хп — оо и для всех п, начиная с некоторого,
П->оо
с > 0. Доказать, что lim хпуп = оо.
П->оо
8.44. Доказать, что:
1) lim Г— — п\ = — оо. 2) lim (Ign + 2 cos лм) = + оо.
П->оо П ' п->оо
3) Пт = + оо.
П->оо rL > 1
4) lim {an 4- Ь) = 4- 00 при а > О,
тг~> оо
lim {ап 4- Ь) — — оо при а < 0, b е R.
П->оо
5) lim na+WO =+ °°~ 6) ,im (V«2 — 1 — V«) = 4-oo.
n-»oo n b n->oo
7) lim ----- = -- oo.
n->oo (Vn2 — 1 — П)
8Л5. Записать с помощью символов V, 3 определение того,
что:
1) limxn = oo. 2) limxrt = + oo. 3) lim xn — — oo.
n->oo n-»oo n-»oo
8.46. Верны ли утверждения:
1) Всякая бесконечно большая последовательность неогра-
ничена.
7*
195
2) Всякая неограниченная последовательность является бес-
конечно большой?
8.47. Сформулировать в позитивной форме утверждения: по-
следовательность: 1) не стремится к оо; 2) не стремится к 4-оо;
3) не стремится к —оо.
8.48. Доказать, что последовательность {хп} неограничена*
но не стремится к оо, если:
1) Хп — п2 cos(пл/2). 2) хЛ = п(”1).
3) ^=-7-7----------777, neN,
7 п 1 + п sin (лп/2)
5. Теорема Больцано — Вейерштрасса. Частичный предел.
Теорема. Если limxrt = a, где а — число или одна из
п-> оо
бесконечностей +оо, —оо, то любая подпоследовательность
{хпЛ} последовательности {хп} имеет предел (конечный или бес-
конечный) и
lim хПь~а-
£->оо Л
Теорема Больцано — Вейерштрасса. Любая ог-
раниченная последовательность имеет сходящуюся подпоследо-
вательность.
Определение 4. Если ~ подпоследовательность
последовательности {хп} и lim хп.=а, где а — число или одна
k->OO
из бесконечностей +оо, —оо, то а называют частичным преде-
лом, последовательности {%п}.
Пример 15. Доказать, что всякая неограниченная после-
довательность имеет частичный предал, равный либо +оо, либо
•—оо.
А Неограниченная последовательность обязательно неогра-
ничена либо сверху, либо снизу.
Пусть последовательность {хп} неограничена снизу. Это оз-
начаем, что для любого 8 > 0 найдется член последовательности
хп такой, что хп < —8. Для 8 = 1 найдется член последователь-
ности такой, что хП} < 1, его и примем за первый член под-
последовательности. Среди конечного числа членов последова-
тельности с номерами от 1 до п\ имеется наименьший, его обо-
значим mi. Возьмем теперь 8 = 2. Из неограниченности по-
следовательности снизу следует, что найдется член хП2 такой,
что хП2 < — 2 и хп.2 < Последнее в силу выбора mi означает,
что п2 > пь Примем хП2 за второй член подпоследовательности.
Аналогично будем находить члены подпоследовательности хПз и
т. д.
Докажем, что этот процесс не оборвется. Допустим, что най-
ден член подпоследовательности Xnk, k 2, удовлетворяющий
неравенству Xnk< — k. Обозначим через гпь наименьший среди
196
членов последовательности от х\ до хПк. Возьмем e = £-f-L
В силу неограниченности снизу найдется член последователь-
ности такой, что xnk+1 <-—(£+ 1) и <т^ Из по-
следнего следует, что nk+\ > и, значит, Xnk+x можно при-
нять за (k + 1) -й член подпоследовательности.
Таким образом, существует подпоследовательность
такая, что xnk < — k для любого k и, значит,
lim хп, = — оо.
fe->oo к
Аналогично доказывается, что последовательность, неогра-
ниченная сверху, имеет подпоследовательность, пределом ко-
торой служит +°°-
Пусть L — множество всех частичных пределов последова-
тельности {хп} (наряду с числами L может содержать и +°°
и —оо). Для любой последовательности множество L непусто.
Верхним пределом последовательности {хп} называют sup L
и обозначают его lim хп, т. е. по определению
П->оо
lim xn = sup£;
П->оо
аналогично определяют нижний предел последовательности
lim хп — inf L.
П-><х>
Например, если хп = п, neN, то L ={-|-оо} и, следова-
тельно,
lim хп — lim хп — + оо.
Пример 16. Для последовательности
_ (3 cos (ли/2) — 1) п + 1
хп~ п
п <= N,
найти множество частичных пределов, lim хп, lim хп, а также
«->°° п->оо
sup{x„}, inf{x„}-
А При п — 4k имеем
и, значит, lim x4fe = 2, 2 < x4ft<2 + 4, причем х4 = 9/4. При
Л->оо *
п = 4k + 1 или п — 4k + 3 имеем
197
и, значит, — 1 < хп < 0, lim x4fe+i = lim x4ft+3 = — 1. При
k->OO k->oo
n — 4k + 2 имеем
—- 4n + 1 . , 1
=-------— = — 4 H-----,
" n n
значит, —4 < xn <_ 0, lim x4fe+2 = — 4.
n-> oo
Таким образом, числа 2, —1, —4 являются частичными пре-
делами данной последовательности. Рассмотренные четыре под-
последовательности {х4а}, {*4М-1}> {*4/е+2}> {^4/г+з} СОСТВВЛЯЮТ
вместе всю данную последовательность. Отсюда следует, что
других частичных пределов данная последовательность не имеет.
Очевидно,
lim хп = 2, lim хп — —- 4.
п”>0° д->оо
Из предыдущих рассмотрений следует также, что
sup{xn}=9/4, inf{x„}——4. А
8.49. Указать сходящуюся подпоследовательность последо-
вательности {хп}, если хп равно:
l)(-l)n. 2)sin(-^). 3)n(-J)". 4)n-5E(^).
8.50. Привести пример последовательности, не имеющей ни
одной сходящейся (к числу) подпоследовательности.
8.51. Привести пример неограниченной последовательности,
имеющей сходящуюся (к числу) подпоследовательность.
8.52. Доказать, что для того, чтобы а (число, -J-oo или —оо)
было частичным пределом последовательности, необходимо и
достаточно, чтобы в любой окрестности а содержалось беско-
нечно много членов этой последовательности.
8.53. Найти все частичные пределы последовательности {хп}>
если Хп равно:
Ч-JTT- 2>TTs- 3»тт£-
5) 3("1) п. 6) sin(ttn/4). 7) ncos(nn/2).
8.54. У последовательности {хп} подпоследовательность
Ы имеет пределом а, а подпоследовательность {х2/г-1} имеет
пределом b (а,Ь— числа или + °о, —°°)- Доказать, что только
а и b являются частичными пределами последовательности
{%«}.
8.55. Доказать, что всякая монотонная последовательность
имеет только один частичный предел.
8.56. Для последовательности {хп} найти множество частич-
ных пределов, lim хп, lim хп, если:
Г2->ос П->оо
1) Хп = cos (лп/3). 2) хп = (-.
198
3) хя = (1,5соз(2ля/3)Л 4){х„} = {1, -1.. А....А, -±,
2 99 1 2 10" — 1
102”«-» iOn • 10n><“> lon
8.57. Для последовательности {хп} найти Пт хп, Пт х„,
а также sup{xn}. inf{xn}, если хп равно:
п* 2 sin (ли/2) + 1 .. (( — 1)" — 1) л2 + п + 1
п + 1 • п
(1 + cos зтп) п 4- 1g п
lg 2п *
6. Фундаментальные последовательности. Критерий Коши.
Определение 5. Последовательность {хп} .называют
фундаментальной, если она удовлетворяет условию Коши*, для
каждого 8 > 0 существует такое натуральное число jV, что для
любого п N и любого N верно неравенство
Хп Хт I С.
Кратко это условие записывают так:
V8 > ОЭ/VVn NVm > N: jxn — хт| < е.
Условие Коши формулируют и таким образом: для каждого
8 > 0 существует такое натуральное число Af, что для любого
п N и для любого натурального р верно неравенство
| Хп+р хп | <С а.
Теорема (критерий Коши). Для того чтобы последова-
тельность имела конечный предел, необходимо и достаточно,
чтобы она была фундаментальной.
Пример. 17. Доказать, что последовательность
cos 1 . cos 2 . . cosn IK I
xn = —з---b-~32~+ ••• ne=N,
сходится.
Л Оценим модуль разности
COS (tl + 1) . , COS (tl + p) I
3П+1 "T* • • • I I
1 *п+р
1
3n+1
1 1
3«+p 3П+1
1
2 • 3n 3n *
' 3“ , I
‘-I
Пусть e — произвольное положительное число. Поскольку
lim (l/3n) = 0, для этого е существует N такое, что для любого
199
N верно неравенство 1/Зп<е. Значит, если п Л£, а
р— произвольное натуральное число, то
I хп+р хп I < <8*
Таким образом, условие Коши выполнено, и поэтому данная
последовательность сходится. Л
Из критерия Коши следует, что для того, чтобы последова-
тельность не имела конечного предела, необходимо и доста-
точно, чтобы она не удовлетворяла условию Коши, иначе го-
воря, удовлетворяла отрицанию условия Коши\ существует та-
кое е > 0, что для любого натурального N найдутся п N и
m N такие, что
|%п — Хт | 8’,
короче,
3eVN3n N3m N: ]хп — х,п^^ е.
Пример 18. Доказать, что последовательность
хп — 1 + у + у + ••• *+*V’
расходится.
А Оценим разность
1 . 1 , । 1 >
Хп+р хп n+l_'"n + 2‘i'”'‘'n + ps^
> — + -!-+ ... +—
^п + р п + Р п + р п + р'
Если здесь взять р = п, то получим
х2п— хп п/(п + п)= 1/2, п N.
Отсюда видно, что данная последовательность удовлетворяет
отрицанию условия Коши. А именно, при е = 1 /2 для любого
натурального N возьмем п = N, m = 2N, тогда будем иметь
| X2N — Xn | = X2N — Xn 1 /2.
Значит, данная последовательность не имеет конечного предела,,
т. е. расходится. А
8.58. Доказать, что последовательность {хл} фундаменталь*
на, если:
1) х„==-Г, neN. 2) хп = 3” + 2 , neN.
3) хп = 0,77 ... 7, п е N.
п цифр
4) xn = a-\-aq + ••• + где |<?|< 1, п е N.
. 1 1 11 1 1 1 ]
5) {хп} I 1, 1, 2 , 2’3’ 3 ’ ' п' «’•••}’
6) Xi = 1, хп = xn_i + (- 1)”~ 7«1 (П = 2, 3, ...).
200
8.59. Пусть aQ — целое неотрицательное число, {ап}—после-
довательность, члены которой — цифры. Рассмотрим последова-
тельность конечных десятичных дробей хп = ЯоЛЯг ... an, п N.
Доказать, что эта последовательность фундаментальна.
8.60. Доказать, что последовательность {хп} сходится, если
равно:
1 х sin а , sin 2а , sin За , . sin па
1) —2~- + -—22—F—23—h ••• +• 2h eeR.
2) IW- где |7| < 1, |a*|<C, k g= N.
/2 = 1
3) 1-^2Г+ ••• + лГ' 4) 1 • 2 — 2.3 + + n(n+ 1) •
8.61. Доказать, что фундаментальная последовательность
ограничена.
8.62. Доказать, что у фундаментальной последовательности
любая подпоследовательность фундаментальна.
8.63. Доказать, что для того, чтобы последовательность {хп}
•была фундаментальной, необходимо и достаточно, чтобы выпол-
нялось условие
Ve > OBTVVm > N: \хп~~ xN\<Z
8.64. Пользуясь отрицанием условия Коши, доказать, что по-
следовательность {хп) расходится, если хп равно:
1) 0,2(-1>%. 2) wcos^~1 . 3) (-1)"(1 + 1)".
. (-1)"Y ex ’ I 2 , ! n
4) (H-----—J • 5) 2^+ Ж+ + (»+lp ’
7. Монотонные последовательности Число e.
Теорема Вейерштрасса. Если последовательность
монотонна, начиная с некоторого номера, и ограничена, то эта
последовательность имеет конечный предел.
В частности, всякая монотонная ограниченная последова-
тельность имеет конечный предел.
Пример 19. Доказать, что последовательность
(2n+ 1)!! *)’
имеет предел, и найти его.
А Составим отношение
хп+1 _ (п + 1)! • (2п + 1)1! _ п +1
хп ~~ (2/1 + 3)!! -п! 2/г + 3 '
♦) (2n + 1 >!! — произведение всех нечетных чисел от 1 до 2n + 1 вклю-
чительно.
201
Поскольку (и + l)/(2n + 3)< 1/2 для любого п Т,
хп+х < 2”ХЛ<х/1. Значит, данная последовательность — убы-
вающая. Очевидно, для любого п 1 выполнены неравенства
О < хп хх — 1/3, т. е. последовательность ограничена. Отсюда
следует, что она сходится.
Обозначим с = lim хп. Последовательность {хЛ-н} является
к-»оо
подпоследовательностью данной последовательности, поэтому
lim x„+J = c. Переходя теперь к пределу в равенстве хп+1 —
п+ 1
= получаем
lim xn+i = lim у • Ит хп,
п-^со П->со I ° П->ОО
откуда с — ^-с, с = 0. Значит, lim хп — 0. д
2 П->оо
Пример 20. Доказать, что последовательность {хп}, где
Xi — 0, хп+1 — д/б + хп9 neN, имеет предел, и найти его.
А В примере 26, 1) § 7 было доказано, что данная последо-
вательность строго возрастает. Докажем ее ограниченность.
Очевидно, для любого п е N
И Х2<х2 + 1=6 + х„,
т. е.
^„-хЛ-6<0,
откуда хп < 3.
Таким образом, {хп}—ограниченная возрастающая после-
довательность и, значит, существует lim хп — с. Заметим, что
П->оо
с > 0.
Переходя к пределу в равенстве *2^ = 6 + хп и учитывая,
что lim хп+х—с, получаем с2 = б + с, откуда находим с = 3.
П-»ОО
Значит, lim хп = 3. д
ОО
Важным примером возрастающей последовательности яв-
ляется последовательность
Xn+i > хп, 2^xn<Z 3. Предел этой последовательности — ирра-
циональное число, его обозначают е, т. е.
lim Г1 + —} —е.
ЛЧ-ooV nJ
Заметим, что е == 2,718281828459045 ...
Пример 21. Доказать, что
lim (1 = ek, - где k е N, k 2.
202
z k \n
л Очевидно, ( 1 + —j >0, а из неравенства
следует, что
(> + 4У<(-+4Г<«‘-
Значит, данная последовательность ограничена.
Обозначим общий член последовательности через хп и рас-
смотрим отношение
( п(п + k+ 1) Ч"+‘ n + k
к (п + 1) (п + k) ) п •
Так как (n + 1) (n -f- k) = п (п + k + 1) + k, то
п (п -J- k + 1) _ (п 4~ 1) (fi “Ь Aj) — k __। k
(fl + 1) (n + k) ~ (n+l)(n + k) ~ ~ (n+l)(n + k)'
В силу неравенства Бернулли
к(» + £ + о V+1 = f > _ fe V+1 i _ = «
. (fl + 1) (n + k) ) \ (n + 1) (fl + k) ) n + k 'n + k'
Учитывая это, получаем
Xn+l ____ / n(n + k+ 1) \n+1 n+k n . n + k
Xn k (fl + 1) (fl + k) ) n n + k n
t. e. Xn+i > %n и, значит, {xn}—возрастающая последователь-
ность. Из доказанного следует, что существует lim хп.
Рассмотрим подпоследовательность = + Я) ”Р»
п = pk, р е N. Так как lim (1 _}_ -LV = е, то lim xpk — ek. Зна-
р-»оо \ Р ) п->оо
чит, и
lim хп = lim xpk = ек.
8.65. Доказать, что последовательность {хп} сходится, и
найти ее предел, если хп равно:
1) —
4 Юп
2)^-
О 8 11
3) Xj = 8, Х2 = у -у,
8 11
•* ” Хп~ 1 * 7
За + 5
Qn — 59
205
8.66. Доказать, что последовательность {хп} сходится, если
хп равно:
п (2п)!! - *) 9) 1+ —+ —4- 4- —
(2/1+1)!! 1 22 З3 ••• пп •
3) 1 + 22 + *32 + ••• + -^2“ •
8.67. Доказать, что последовательность {хп} имеет предел, и
найти его, если:
1) === 13, 4~ ^п*
2) Xj = д/'б, xn+i — \jbxni где k е N.
3) х{ — \/а, xn+i = %Jaxn, где k е N, а>0.
4) хЛ+1 = 4-хЛ — х2п\ а) х\ = 1/6; б) %i = l/2; в) Xi = 7/6.
о
5) — 1, Хп+\ = 1 + 1 /хп, neN. (Указание: рассмот»
реть подпоследовательности {x2k} и {x2k-1} •)
8.68. Доказать, что последовательность {(1 + } моно*
тонно убывает и
/ 1\п+1
lim ( 1 + —) = е.
л-»<хЛ «/
8.69. Найти lim хп, где хп равно:
/I—>оо
о (1 + ^ЬУ.
0(1 +Я"- =>(‘ + i)“- 6>(1-4)“-
8.70. Пусть {kn}—последовательность натуральных чисел»
lim kn = +<x>. Доказать, что
П->оо
8.71. Доказать, что
lim In (1 + т) =0.
n->oo 4 U Z
'(Указание: доказать, что In (1 +
8.72. Последовательность {хп} сходится, limxn = a. Дока*
П->оо
зать, что сходится и последовательность {|хЛ|} и lim|xn| —|а|.
*) (2/г)!! — произведение всех четных чисел от 2 до 2п включительно.
204
8.73. Привести пример расходящейся последовательности
'{хп}, для которой последовательность {|х«|} сходится.
8.74. Привести пример такой последовательности. {хп}, что
lim хп = 0 и из двух последовательностей {signxn},
«-><»
{(signxn)2}: 1) обе сходятся; 2) обе расходятся; 3) первая рас*
ходится, а вторая сходится.
8.75. Привести пример такой последовательности {хп}, что:
1) Хп > —1 для любого пе N, a lim хп — — 1.
п->сю
2) хп < 2 для любого n е N, a lim хп = 2.
3) хп "> 100 для п = 1, 2, .... 100, a lim хп = 0.
П->оо
4) lim хп = 5, и для любого N найдутся n^N и m~^N
такие, что хп <. 5, а хт > 5.
8.76. Привести пример таких последовательностей {хп} и
{уп}, что:
1) хп <. уп для любого neN, но lim хп = lim уп.
П->оо П->оо
2) хп > уп для п — 1, 2, .... 1000, но lim хп < lim уп.
гг->оо п-»оо
3) Xn/уп 1000 для любого neN, но lim xn = lim уп.
П->оо П->оо
8.77. Привести пример последовательностей {хп} и {уп}9
имеющих одно и то же множество значений и таких, что:
1) {хп} и {уп} сходятся, но lim хп =/= lim уп.
2) {хп} сходится, а {уп} расходится.
8.78. Последовательности {хп} и {уп} сходятся, и lim хп
п->оо
lim уп. Множества значений этих последовательностей со*
/2->оо
впадают. Доказать, что эти множества конечны.
8.79. Пусть lim хп = х, тп — inf {xk}, Мп= sup {xk}, neN.
П->оо k^n k^n
Доказать, что
lim m„= lim M„ — x.
П->°° П n-too
8.80. У последовательности {хл}ч подпоследовательности
{*2*} и {Xik-1} имеют один и тот же предел. Доказать, что и
сама последовательность сходится к этому пределу.
8.81. Последовательность {хп} такова, что limx2ft = a,
Л->оо
Птхгл--! — b, а Ф b. Доказать, что последовательность {x„} рас-
Л->оо
ходится.
8.82. Доказать, что последовательность {хл} расходится, если
хп равно:
1) loga (2+ (-!)«’), а > 0, а#=1.
. (-1)"га 2”+1-(-3)п
2) arcsin п + j . 3) (_2)« _|- •
го 5
8.83. Доказать, что последовательность;
п
1) х„ =-Г (—!)«-*&, nsN, сходится.
п
2) хп = ±£ (— l)k~l k, ftsN, расходится.
k=i
8.84. Доказать, что если neN, lim хп — а, то:
П->оо
1) lim д/хп — -у/а. 2) lim-\/xre = \/а, йеМ.
п->оо п->оо
П
8.85. Доказать, что lim — V ~ = 0.
п k
8.86. Доказать, что сходящаяся последовательность дости-
гает хотя бы одной из своих граней — верхней или нижней.
8.87. Привести пример последовательности {хп}, удовлетво-
ряющей условию
Ve XJBNVn^N: хп < 8
и такой, что 1) она не имеет предела; 2) она имеет предел. Мо-
жет ли этот предел быть равным 1?
8.88. Сформулировать на языке «е — N» отрицание того, что
{хи}—бесконечно малая последовательность, и записать его,
используя символы 3, V.
8.89. Является ли обязательно число а пределом последова-
тельности {хп}, если 1) существует такое натуральное число N,
что для любого е > 0 и для любого п N справедливо нера-
венство \хп — а]<е; 2) для любого е>0 существуют такие
натуральные числа N и N, что |хЛ— а \ < е?
8.90. Пусть Xn>0, neN, lim хп = 0. Доказать, что:
П->оо
1) VJV3rto > NVn > п0: хп < хПа.
2) VW3n0 5s A’Vn (1 п < п0): хп> х^.
8.91. Пусть К — множество всех сходящихся последователь-
ностей, а К\, Т<2, К& — множества всех последовательностей,
удовлетворяющих соответственно условиям;
1. 3e>03W3n>W: |х„|<е.
2. 3O03WVn^N: |х„|<е.
3. 3 е > 0 V N 3 п N: | х„ | < е.
4. Ve> 03Af3rt^Af: |х„|<е.
5. 3e>0V NVn^N: | хп | < е.
6. Ve> 03ATVn>2V: |х„|<в.
206
7. Ve > ОVЛг3TV: |x„|<8.
8. Ve>OV.VV/i>.V: |xn|<e.
1) Какие из следующих включений верны: а) Кб с Къ,
б) KtCzKt-, в) К7с=К2; г) К8сК; д) КсК8?
2) Для каких / = 1, 2, 8 верно включение К, с-К?
3) Какие из множеств К/ (/=1, 2, ..., 8) содержат как
сходящиеся, так и расходящиеся последовательности?
4) Какие из множеств Kj (/ = 1,2, ..., 8) содержат неогра-
ниченные последовательности?
5) Какому из условий 1—8 удовлетворяет любая последо-
вательность?
6) Какие из множеств К/ (/ = 1,2,..., 8) совпадают?
8.92. Доказать, что если последовательность {хп} удовлетво-
ряет условию
Ve > ОЗаЗЛ/Vn N: |хп— а|<е,
то {хп}—сходящаяся последовательность. Доказать, что верно
и обратное.
8.93. Доказать, что последовательность {хп} расходится
тогда и только тогда, когда
Зе > OVaVNSn N: \хп — а|^е
(сравните эту запись с определением расходящейся последова-
тельности, стр. 182).
8.94. Последовательность {yk} получена перестановкой чле-
нов последовательности {хп}, т. е. для любого п существует kn
такое, что хп — ykllj причем, если п\ =# п2, то knx kn2, и
обратно, для любого k существует такое п*, что t/£ = xnfe, при-
чем, если k\ =/= &2, то nkl Доказать, что:
1) Если Пт хп = а, то и lim у к —а-
П->оо &->оо
2) Если {хп} расходится, то и {ук} расходится.
8.95. Найти lim хп, если хп равно:
П->оо
«I п\ /г2 — 4 п sin п\
пп п* + п2 — 1 н V п + л] п + 1
4)-^- 5)±£(-1М 6) (^Г'И“+1>
Ч\ f ” + 1 >(1- -V^l/d-n) о\ f 2п — 1
7Ц я + 2 J • 8Ц 5п + 1 ) •
/ Зпг — п +1 \п3 */(1-я)
Ч 2/is * * + п + 1 )
Ю)
Vrt!
207
8.96. Пусть ап =И= 0 и lim =7, где qZ> I. Доказать, что
П->оо I ttn+l I
lim а„ =0.
П->оо
8.97. Найти:
ап
1) Нт ТГ~i---Г77—1------7T~i--FFT. О > 0.
п->оо (1 + fl) (1 + а2) ... (1 + ап) '
2) lim (-7 1 + -.J.. + • • • + -Д=-\
П->оо V Vn2 + 1 V^2 + 2 л/п2 4- tl)
8.98. Последовательность {хп} имеет конечный предел а. На
координатной плоскости проведены прямые ААп через точ-
ки А (ст, а2) и Ап(хп- Хп), п N. Пусть ап — абсцисса точки пе-
ресечения прямой ААп с осью Ох. Найти lim ап. *
П->оо
8.99. Найти lim хп, если хп равно:
П->оо
.) („+ 1)4_(П- 1)« (я2 + Зп + 4)3 _ (П2 + Зп _ 4)3
' (я2 + I)2 - (я2 - I)2 • ’ (я2 + 5я + 6)3 - (я2 + 5п - 6)3 • у
я2 я3 .. 3
3) . я + 1 я2 + 1 * П 3_____________3.1*
П П2 п3
-ч (2 + я)100 ~ ft100 — 200п" 1g2 10n '
' n98 — 10n2 4-1 * ' 1g2 ti
7\ ln (ft2 ~ ft + 1) o\ lg (n2 4-2n cos n 4- 1)
' In (n10 4- ft + 1) * 1 + lg (ft 4-1) *
8.100. Найти lim xn, если xn равно: n->oo £
2п + з~га 2-« - 3n * 2> J
an 3> 1+T .. an-.a-n , n 4) ———, a ¥= 0. a 4- ft n
8.101. В круг радиуса 7? вписан квадрат, в этот квадрат впи-
сан новый круг, в него новый квадрат и т. д. Пусть Si — пло- <
щадь первого (исходного) круга, S2 — площадь второго круга
и т. д., 04 — площадь первого квадрата, о2 — площадь второго
квадрата и т. д. Найти
lim (Si + S2 + ... +Srt), lim (04 + 02+ ... + crn).
n->oo n->oo
8.102. Найти:
l) (ттз + Тб + ♦ ‘ • + (2я- 1)(2«+ 1) ) •
208
2) lim -4= (-F=^—7=- + 7-^ 1 -1=- + • • • + -7=1-7=) .
3) ( 1 -^3 + “2^4 + • • • + n (n + 1) (n + 2) ) ’
8.103. Пусть {an}—арифметическая прогрессия с разностью
d ф 0. Найти:
1) lim ( ——J---—|- ... 4-------—) , если ап ф 0, п е N.
’ а2а3 anan+i J ’ п '
2) lim 1 f 1_________| 1______|_ -|______I \
П-»оо Vя ' Vs! 4" Ve2 "Va2 + 'у/<*п + Vа«+1 '
если ап > 0, м g N.
8.104. Пусть а — цифра, а =/= 0. Найти
lim 10~"(а + аа + ... + аа ... а).
П-^<х> \ —V— z
п знаков
8.105. Пусть pi, р2, .... p'k, аь П2, .... о* — положительные
числа. Существует ли
„ I Лп4-1 I । п ~п-М
4- р2^2 4- ... +Pkak -
11 m-----------------------— ?
п-»оо р{а{ 4- Р2а2 4- ... 4“ Pkak
Если существует, то найти этот предел.
8.106. Найти lim хп, если хп равно:
П->оо
1) V^TT- д/^Т. 2) ^гГ+Т —нУ/ГПГ.
.3) V(n + 2)(n+ 1) - д/п(п-1).
4) д/n3 * + n2 + 1984 - п.
5)n3/2(v^+r+-2V«). 6)^(^/1 + 4-“О-
' 8.107. При каких а последовательность
х„ = д/ап2 + Ьп + 2 — п, я е N,
имеет предел? Чему равен этот предел?
8.108. Найти:
1) lim (V(n + Oj) (n + o2) — n).
П->оо
2) lim (д/(n + Oi>(n + a2) (n + a3) — n).
П->оо
3) lim (V(n + ai) (n + a2) • • • (n + ap) —
П-»оо
8.109. Пусть xn = (n+l)« — n“, n e N. Доказать, что1
1) lim xn = 0 при0<а<;1.
П->оо
209
2) lim xn — + oo
8.110. Найти lim
П-»оо
1) —. 1 —r.
n (V«2 — i — /0
~ V4n2 — 1
V^2 4“ 3 — n
5) V”2 + i — n
V^3 + 1 ~ пл]п
8.111. Найти lim
при a > 1.
сп, если xn равно:
2) + 1 ~~n_ .
Vfl +1 — Vn
4\ Vn2 4~ 1 ~ Vft2 — 1
д/n2 + л — n — 1
6) 7
Vn 4-1 — V«
xn, если xn равно:
V^3 + ^ — л/ti
n 4- 2 4* 4-1
n2 + 3rt_2 9. 14-34-54- ... +(2/г-1)
1 + 2+ ... +n ’ z' n3
1-2 + 3- ... +(2n-l)-2n I2 + 22 + ... + n2
W /—o““i—Г • ^7 o
-уП2 + 1 ns
1-2 + 2-3+ ... +n(n+l)
' n3 ’ ,
-A l2 + 22+ ... 4-n2 n 7. l2 + 32+ ... +(2n-I)2
6) ------2-------y- 7) ----------3-------.
»)4((‘-+В!+(“+4У+-+(«+^1П-
8.112. Доказать, что последовательность
5«=SE+
/=1 /«I
имеет предел, и найти его.
8.113. Найти lim хп, если:
П->оо
(п+1)(п + 2))’
2) Л1 = 1, хЛ = (1-+)(1-^-)...(1-+),леЧп>2
8.114. Пусть хп =/= 1, п е N, lim хп = 1. Найти
П->ос
Нт ^+±L+ 7- +^~fe , k еN.
п->оо ^/1 *
8.115. Найти lim •
„->«> (2и)!!
8.116. Какие из утверждений верны:
1) Если а’->а2, то ап->а.
2) Если то ои-»о?
810
8.117. Привести примеры последовательностей {х„} и {уп}
таких, что lim хп — lim //„ = 0 и
П->оо
1) Пт = 0;
7 11.-
2) lim ~ =
П -> оо У П
3) lim — =4-оо; 4) lim— не существует.
/г->оо Уп п-^жУп
8.118. Известно, что lim хпуп — О. Следует ли отсюда, что
П-»оо
1) lim хп = lim —0;
П->оо п->оо
2) хотя бы одна из последовательностей {хп} или {уп} стре
мится к нулю?
8.119. Привести примеры расходящихся последовательно-
стей {%/г} и {уг}, для которых сходится последовательность:
1) {хп + Уп}; 2) {хпуп}; 3) {хп/уп}.
8.120. Последовательность {хп} сходится, а последователь-
ность {уп} расходится. Доказать, что при b =/= 0 последователь-
ность {ахп + Ьуп} расходится.
, 8.121. Последовательность {хп} сходится, и limx„ = x,
П~>оо
х #= 0, последовательность {уп} расходится. Доказать, что по-
следовательность {хпуп} не сходится.
8.122. Привести пример последовательностей {хп} и {</„}
таких, что {хп} сходится, {уп} расходится, a {хп«м} сходится.
, 8.123. Пусть lim хп=х, =/= О, ле N.
П->оо
1) Существует ли lim ?
лг->оо хп
2) Доказать, что если этот предел существует и равен qt то
1.
3) Может ли последовательность {x„+i/xn} быть неограни-
ченной?
8.124. Найти lim хп, если хп равно:
И->оо
I 1) 2)
п —
3) Va" 4- 6". а > О, Ь > 0. 4) Y8 ~ 1 .
VT6-1
3 7'16-4 78'4-1 3 5
5) п • О/ п п___•
(тт — 0 1 — 7в 1 — 7з2
п
7) , а>1, fe.meN.
л/ak — 1
211
8.125. Найти:
1)
2) lim (1-Jr)".
Г2-> oo У
3) lim(l+A.)Vn
п->оо V ft' Z
8.126. Доказать, что:
1) lim 2l/^n = 1. 2) limaI/^ = l, a > 0.
П->оо П->оо
8.127. Пусть lim x„ = 0, a > 0. Доказать, что lima*”=l.
П->оо n-»o©
8.128. Пусть pi, p2, .pk, ai, a2, .... ak — положительные
числа. Существует ли
п^л/p^i++ • • • +?
Если существует, то найти этот предел.
8.129. Найти lim х
П->оа
ЗП/~
I) уп.
з) Vn + a"
5) V«3 —Зп+ I.
7) V2"«2 + 2«- !•
если хп равно:
2) nplnk, р, k е N.
4)
6) ^7п2— I.
+ 2 - 3 1 3« /П4_2п + з
- ' п _ п _ • 10) Д/ п2+ 1 *
: — +2
"> ^RR+ww+2.
8.130. Доказать, что
аопр + ainp~‘ + ... + ар-1П + ар
bofl^ + + ... + bq—itl 4- bq
где р, q е N, а0/ь0 > 0.
8.131. Доказать, что если для любого п ё Nj
0 < хп bnp, k,p е N,
то
lim Vxn — Ь
П->оо
212
8.132. Доказать, чт® lim n1^" = 1.
П->оо
8.133. Доказать, что если limx„=+oo, хп > 0, neN, то,
П->оо
lim хпЧхп — 1.
Й->ОО
8.134. Найти:
п
8.135. Пусть |<?| < 1,
Sn = q + 2q2 + З?3 + ... + nqn, n е N.
Доказать, что существует lim Sn, и найти его.
П->оо
8.136. Найти
Пт 'g(5n2 + 3w+1) .
п-»оо -у/ п + 1
8.137. Доказать, что для любых а > О, а=И=1, а>0
lim-fe^o.
П-»оо П
8.138. Пусть lim хп = 4-оо и хп > 0, neN. Доказать, что
П->оо
для любого а > 0, а 1,
lim =
П-»оо ХП
8.139. Привести пример неограниченной последовательности^
не являющейся бесконечно большой.
8.140. Доказать, что любая подпоследовательность бесконеч-
но большой последовательности является бесконечно большой
последовательностью.
8.141. Сформулировать на языке «8 — N» отрицание того,
что {%п}—бесконечно большая последовательность, и записать,
его с помощью символов В, V.
8.142. Доказать, что:
1). lim -
2)
lim
П-»оо
п3 — 100
п2 + 100
+ ОО.
8.143. При каких а последовательность
_ п4 + 1 ап2
хп — пз _ 2 ~ 5/14-2 ’
п е N,
сходится к 1) +оо; 2) —оо; 3) конечному пределу?
8.144. При каких р и q из N последовательность
аопр 4- а\пр~1 4- • • • 4” ар—\П 4- яр _м
V* —— .- ——-- . ... ——- гь * I ч)«
п btflQ + b\nq~x + .. . + bq—\H + bq ’
где ao^=o, 6o¥=O, имеет: 1) конечный предел; 2) бесконечный
предел?
213.
8.145. Доказать, что:
1) lim '\fn\ =-f-oo. 2) lim 2^"-1 = 4- oo.
Н-><» n->oo
3) 'i«e."»+n = +»“>4Ч^,^=+“•
8.146. Доказать, что:
1) lim —7=—..a- — — 00.
n->oo Vn — Vrt + 1
2) lim Vra3(Vn + 1 ~ Vtt—\/n-l)=-oo.
n->OO
8.147. При каких а последовательность
xn — у/n2 + na — n, n e N,
сходится к 1) +°°; 2) конечному пределу? Во втором случае
найти этот предел.
8.148. Доказать, что lim хп = 4~ если хп равно:
П-»оо
1) (П + О (П + 2) . (2я — 1) 2п у—|
3) О+ О 0 + £Г
5) — (1 + л/2 + ... + V«)-
8.149. Пусть limx„ = oo, t/n#=0, neN, и для всех п, на-
П->оо
чина я с некоторого, |ул| С. Доказать, что
lim — = 00.
и->оо Уп
8.150. Пусть limx„ = x, где х — не равное нулю число,
П->оо
lim уп = о° (или +°°> —°°)- Доказать, что:
«П->оо
1) lim хпуп — оо (соответственно 4-°°> —°°) при х > 0.
П->оо
2) Итхпуп — оо (соответственно —оо, -f-оо) при х<0,
п->оо
8.151. Пусть limxra = oo. Верно ли:
П->оо
1) Если If/nKC, neN, то lim хпуп — оо.
2) Если уп^хп, neN, то lim уп — оо.
/2->сх>
3) Если lim уп = оо, то lim (х„ -f- уп) = оо?
П->оо П->о®
1214
8.152. 1) Пусть
lim хп = 4~ Hm уп — + °°
П-»оо П->оо
или
lim хп — — оо, Нт#л= — оо.
П->°° П->оо
Доказать, что
lim хпуп= + оо.
П->оо
2) Пусть
lim хп — 4- оо, Нт уп = — оо.
П->оо И-»со
Доказать, что
lim хпуп = — оо.
П->оо
8.153. Указать такие последовательности {хп} и что-
lim хп+ °о, lim уп — + оо
П->оо П->оо
И
1) Пт (х„ — уп)= +оо, 2) Нт (хп — уп)=\.
3) lim (хп — уп)= — оо.
П->оо
4) Последовательность {хп — уп} не имеет ни конечного, ни
бесконечного предела.
8.154. Указать такие последовательности {хп} и {уп}, что
lim хп = + оо, lim уп = + оо
П->оо »2->оо
И
1) lim -^- = 0. 2) lim -^-=1.
М->оо У П /?->оо Уп
3) lim — = 4-°°.
П->оо У Н
4) Последовательность {хп/уп} не имеет ни конечного, ни
бесконечного предела.
8.155. Указать такие последовательности {хп} и {«/„}, что
lim хп = 0, lim уп — ео
П~><х> П-*°о
И
1) lim х„г/„ = О. 2) limx„«/„=l. 3) \im хпуп = оо.
/2->оо П->оо П->оо
4) Последовательность {хпуп} не имеет ни конечного, ни бес-
конечного предела.
8.156. Доказать, что если lim хп = оо, то последовательность-
л п->оо
I У1 1.
If1» x*j неограничена.
21&
8.157. 1) Доказать, что если последовательности {хп} и
{уп} таковы, что
lim (| хп + уп I “ I *п ~ Уп I) = + °°>
Л->оо
ТО
lim | хп | = lim | уп | = lim хпуп = + оо.
rt->OO П~>ОО ГС~>ОО
2) Доказать, что верно и обратное утверждение.
8.158. 1) Пусть lim хп = + оо, тп = inf {xk}, п е N. Дока-
П->оо k^n
зать, что lim тп = + оо.
П->оо
2) Пусть lim хп — — оо, Мп — sup {х&}, я g N. Доказать,
п -> оо k^n
•что lim Мп = — оо.
П->оо
8.159. Привести пример расходящейся последовательности,
имеющей только один частичный предел.
8.160. Доказать, что последовательность сходится тогда и
только тогда, когда она ограничена и имеет один частичный
предел.
8.161. У последовательности {хп} подпоследовательности
{*2fe}> {xzk-1} и Ы сходятся. Доказать, что сходится и сама
последовательность.
8.162. Доказать, что всякая неограниченная последователь-
ность либо является бесконечно большой, либо имеет конечный
частичный предел.
8.163. Последовательности {xk} и {yk} таковы, что для лю-
бого k существует tik такое, что yk — xnk. Известно, что после-
довательность {хп} имеет предел. Следует ли отсюда, что и по-
следовательность {у^ имеет предел?
8.164. Для последовательности {хп} найти множество частич-
ных пределов, lim хп, lim хп, sup {хп}, inf {хп}, если хп равно:
П->оо П->оо
1) (cos (зш/2))п+1. 2) (1 + ( - 1)"п)/п.
3) ( _ rt)sln (яп/2). 4) 1 4- sin .
5) (»-(-lf)2ra+ L. 6) 7) 2<-»йп • п.
8) 4(„-2-3B(ifl))(«-3-3E(i=J-)).
8.165. Найти множество частичных пределов последователь-
ностей:
nfi 12 11221 2 1 2" +1 1
И р, 2 . 2 ’ 2 ’ 4’ 4’ 4’ 4’ 4 ’ ’ 2п’ ‘ 2п ’ ' ’ * J*
9\fi 1221221 2 12 2- I
1 *’ 2 ’ 2 ’ 2 ’ 4 ’ 4 ’ 4 ' 4 ’ ’ ' " 4 ’ ' ’ ‘' 2п’ 2п’ ’' ‘ ’ 2п ' * ' ’) *
:216
8.166. Последовательность {хЛ} такова, что
%! = 0, X2k — 1 > *2&+l = 1 + X2k> A G N.
Найти lim ^л> хп*
П->оо П->оо
8.167. Доказать, что если последовательность {хл} не дости-
гает своей: а) верхней грани Л4, то НтхЛ = Л1; б) нижней
П->ОО
грани т, то lim хп = т.
П->оо
8.168. Последовательность {хп} и число а таковы, что
Ve > ОВм: \хп — а| < в. -
Является ли число а частичным пределом последовательности
{хя>?
8.169. Доказать, что у любой последовательности есть моно*
тонная подпоследовательность.
8.170. Доказать, что для всякой последовательности {хп}
Пгпхп и lim хп являются ее частичными пределами.
П->°° П->оо
8.171. 1) Пусть последовательность {хп} ограничена снизу,
тп — inf {x/J. Доказать, что последовательность {тп} схо-
дится и
limmn = limxn.
П->оо И->оо
2) Пусть последовательность {хл} ограничена сверху,
Мп = sup {%Л}. Доказать, что последовательность {Л4Л} сходит*
k^n
ся и
lim Мп — lim хп.
8.172. Доказать, что множество частичных пределов после-
довательности замкнуто (см. задачу 10.94).
8.173. Пусть {хп} и {уп}—ограниченные последовательности.
Доказать, что
lim хп + lim lim (xn + #„).
П->оо П-»оо П-»оо
8.174. Доказать, что если последовательности {%„} и {«/„};
1) ограничены сверху, то
lim (х„ + t/„) < lim хп + lim уп;
П-+<х> П->оо
2) ограничены снизу, то
lim (хп + уп) > lim хп + Нт уп*\
П-><х> П-+<х> П->оо
♦) Считают, что (+°°) + (+°°) =. +°°» + (—°°i s—°°»
-
217
8.175. Пусть Хп > 0, не N. Доказать, что:
1) lim *”+l lim Vxn«
— Хп -----
П-><х> П~>оо
2) lim Vxn lim ~*n+1 •
П->оо П->оо . Xfl
8.176. Привести пример последовательности, у которой мно-
жество частичных пределов совпадает с множеством значений
последовательности и 1) конечно; 2) счетно.
8.177. Указать последовательность, множеством частичных
пределов которой является множество натуральных чисел.
8.178. Указать последовательность, частичными пределами
которой были бы: 1) все числа вида l/n, п е N; 2) все рацио-
нальные числа. Может ли множество частичных пределов по-
следовательности состоять только из этих чисел?
8.179. На плоскости даны несовпадающие точки Л, В, С. Точ-
ка Ai — середина отрезка СВ, точка Л2— середина отрезка ААЬ
Лз — середина СА2, ..., A2k — середина ЛЛ2^Ь A2k+\ — сере-
дина CA2k> ... Найти частичные пределы последовательности
точек {Л п}.
8.180. Построить последовательность, множеством частичных
пределов которой является отрезок [я; &].
8.181. Последовательность {хп} ограничена,
lim(xrt— *«4-1) = 0> а== хп, &=limxrt, а =# Ь.
Доказать, что любое число из отрезка [а; Ь] является частич-
ным пределом последовательности {хл}-
8.182. Последовательность {хп} такова, что x^i > хп — ап,
где ап > 0, limart = 0. Пусть а = lim xn, b= Нтхл. Дока-
п->оо п->оо гг->оо
зать, что любое су а^с ^Zb, является частичным пределом по-
следовательности {х4-
8.183. Пусть {х4 и {уп}—фундаментальные последователь-
ности. Доказать, что 1) {х„ + //4—фундаментальная последо-
вательность; 2) {хпуп}— фундаментальная последовательность;
3) если \уп\^с>Ъу neN, то {хп/уп}—фундаментальная по-
следовательность.
8.184. Две последовательности {хп} и {уп} называют эквива-
лентными и пишут {%4 ~ {Уп}, если
lim (xrt — уп) = 0.
П~>оо
Доказать, что 1) {хп} ~ {хп} (рефлексивность); 2) если
{хп\~{Уп}, то {уп} ~ {хп} (симметричность); 3) если {хп} ~
~ {f/я}, а т0 {хп} ~ {zn} (транзитивность).
8.185. Множество всех попарно эквивалентных последова-
тельностей называют классом эквивалентных последовательно-
стей.
218
Доказать, что любые два класса эквивалентных последова-
тельностей либо не пересекаются, либо совпадают.
8.186. Пусть А — класс эквивалентных последовательностей
и существует последовательность {хп}^ А такая, что limxn = x.
П-»оо
Доказать, что для любой последовательности {(/л}еД имеет
место Iimz/„ = x.
П->оо
Если существует {хп}^А такая, что limxn = 0, то класс А
называют нулевым.
8.187. Пусть А' и А" — классы эквивалентных последова-
тельностей, [х'| е Л', {х''| е А". Рассмотрим два класса экви-
валентных последовательностей: А' + А” — класс, содержащий
{хп "1“ хп}; — класс, содержащий {х'п х'^.
Доказать, что 1) класс Л' + ^// не зависит от выбора после-
довательностей {х'} е А' и [х'п] е А"; 2) если последова-
тельности, входящие в Л', и в Л", ограничены, то класс А'-А"
не зависит от выбора последовательностей {х'} е Л' и {х"} е Л".
8.188. Доказать, что множество всех классов эквивалентных
фундаментальных последовательностей рациональных чисел с
введенными в задаче 8.187 сложением А' -}-А" и умножением
Л'-Л" классов является полем.
8.189. Доказать, что если Л — ненулевой класс эквивалент-
ных фундаментальных последовательностей рациональных чи-
сел, то для любой последовательности {гп}еЛ существует та-
кой номер 7V, что все члены последовательности гп с номерами
n^N имеют один и тот же знак, причем этот знак не зависит
от выбора последовательности {гп}еЛ. Если этот знак —
«плюс», то по определению полагают Л > 0, а если — «минус»,
то А < 0.
8.190. Доказать, что множество всех классов эквивалентных
фундаментальных последовательностей рациональных чисел с
определенными сложением и умножением (задача 8.187) и
сравнением с нулем (задача 8.189) образует непрерывное упо-
рядоченное поле, т. е. поле действительных чисел.
8.191. Доказать, что последовательность {xnJ сходится, если
хп равно:
Ы * Ь 1
8.192. Доказать, что последовательность {хп} расходится,
если хп равно:
1) V((- l)n+1 - l)n+ 1- 2) cos n. 3) Е (-^-y-L) —-у-.
4) ——E (> PeN, pi>3. 5) sinn.
6) cos (an + b), где a, b <= R, a =£ 2kn, k e N. 7) tg n.
219
8.193. Пусть ln, п е N, — число натуральных чисел р, удов-
летворяющих неравенству
ЮОп + 1 ^Р2 1ОО(лг + 1).
Доказать, что последовательность {1п} расходится.
8.194. Пусть In, п е N, — число натуральных чисел р, удов-
летворяющих неравенству
nk + 1 р*+1 (п + 1) *,
где k — данное натуральное число. Доказать, что последователь-
ность {In} расходится.
8.195. Последовательность {хп} такова, что последователь-
ность < У, хп f сходится. Доказать, что lim хп = 0.
8.196. Последовательность {хЛ} монотонна, и limxrt = 0.
П->оо
Доказать, что последовательность
Sn = ХХ—Х2+ ... +(— l)n~lXn, men,
сходится.
8.197. Доказать, что монотонная ограниченная последова-
тельность фундаментальна.
8.198. Последовательность {хл} такова, что |хл+1 —
Сапу где 0<а< 1, Доказать, что последовательность
{хп} сходится.
8.199. Доказать, что для любого xe'R последовательность
sn=i+n +4 + rteN’
сходится.
8.200. Привести пример расходящейся последовательности
{хп} такой, что для любого ре N
lim | хп+р — хп | = 0.
П->оо
8.201. Последовательность {хп} не сходится. Доказать, что
существует последовательность натуральных чисел {рп} такая,
что последовательность {хп+Рп — хп} не стремится к 0.
8.202. Для последовательности {хп} обозначим
' Мп = sup {| xk — Xi |}.
Доказать: для того чтобы последовательность {хл} удовлетво-
ряла условию Коши, необходимо и достаточно, чтобы
lim Мп — 0.
П~>оо
8.203. Последовательность {хп} такова, что для всех п, на-
чиная с некоторого, 0 < xn±i < хп, и последовательность
220
xn f сходится. Доказать, что
limnx„ = O.
8.204. Пусть {рп}—последовательность натуральных чисел,
1 1 1
, %2 1 » Х3 . , • • • »
1 Pi + — Pi Ч------1—
Р2 „ । 1
р2 + —
Рз
хп =-------------—1----------, п G N.
р| + , И-------------
РгЧ-----------------*
. 1
Рп-i + —
Рп
Доказать, что {хп}—фундаментальная последовательность.
8.205. Доказать, что монотонная последовательность имеет
предел, если какая-либо ее подпоследовательность имеет пре-
дел.
8.206. Найти если хп равно:
П->оо
•)£“><>• 3)-^.
пп пп - А
4) --. 5) —— , а > 0.
' (л!)2 (п!)а
6) Ioga , а > 0, а ф 1.
8.207. Доказать, что последовательность {%„} сходится, если
Хп равно:
04+-^-+...+^. 2)i+4+j+...+^.
8.208. Пусть {рп}—последовательность натуральных чисел,
й пусть последовательность
S„ = - + -+...+-, neN,
п Pi Рг Рп
сходится. Доказать, что сходится и последовательность
<’"=(1 + a(1+j.):-(l + fj)'
221
8.209. Пусть хп > 0 для всех п и0. Доказать, что последо-
п
вательность Sn = У, xk, п N, имеет предел, конечный или бес-
k—1
конечный.
8.210. Последовательность {хп} ограничена,
Уп = max {xk}, zn = min {xk}, ne N.
k^n 1< k
Доказать, что последовательности {yn} и {zn} сходятся. Обяза-
тельно ли их пределы являются частичными пределами после-
довательности {хл}?
8.211. Пусть хп+1 хп, Уп+\ Уп, и N, и lim (хп —• уп) =0.
П->оо
Доказать, что последовательности {хп} и {«;„} сходятся и
limx'(l= lim уп.
П->ОО
8.212. Найти lim хп, если хп равно:
П-»оо
+ М^)"- 3)(£±2-)-,
д\ ( п?_+_п у / Па —п + 1 у
’ к п2 + 2я + 2 ) • °> к п2 + п + 1 ) •
8.213. Доказать, что для любого ne N:
+ "• 2) - -А < in(i + -) <-.
' \ п J ’ п п2 к П J п
8.214. Найти:
2) lim л In fl + --1).
8.215. Доказать, что для любого k е N
lim (1 + т~У = -Vе •
„_>оок knj v
8.216. Доказать, что для любого рационального числа г > 0
lim (1 + — )” —ег.
П->оок ' п )
8.217. Доказать, что для любого действительного числа
х > 0
Пт (1 + ±у = ех.
П^оо \ " Z
8.218. Доказать, что lim + = если 1) х =»
= —k, k е N; 2) х — —l/k, N; 3) x&R, x < 0.
222
8.219. Пусть Hm хп — 4- оо-, > 0. Доказать, что
lim (14--------------------------'j п = е.
\ XflJ
8.220. Найти:
/ 2п + 3 \«
V 2п - 1 J ’
1) lim
П->оо
2) lim
П->оо
р - 1 \П/2
\п+\) •
8.221. Пусть
Доказать, что:
I) limS„ = e.
п->оо
П
Х"-'+Е5Г' neN-
fc=-l
п + 2
пХ (п + I)2 ’
8.222. Доказать, что разность е — Sn, neN (Srt из задачи
8.221) , убывает с ростом п быстрее, че^ разность е —
8.223. Доказать, что
lim
П->оо
8.224. Доказать, что число е иррационально.
8.225. Пусть
п
°п = 3 — X /с (/: + 1) (й + 1)1 ’ « е N.
k — \
Доказать, что:
1) limc„=e.
П->оо
2) Разность оп — е убывает быстрее, чем разность е — Sn,
где Sn из задачи 8.221.
8.226. Доказать, что для любого ne N
е <
0+4УС + Й-
8.227. Доказать, что для всех и, начиная с некоторого n0,
верны неравенства
(п+1)ге . рп пп+1
п\ Ш •
' Найти по для левого и правого неравенств.
8.228. Последовательность {хп} такую, что Xi = at xn±i —
= qxn + d, n^N, называют-арифметико-геометрической про-
грессией co знаменателем q и разностью d. Доказать, что: 1) при
|^| <1 эта последовательность сходится, и найти ее предел;
2) при |?1> 1 и a^d/(\ — q)t эта последовательность расхо-
дится.
223
8.229. Пусть {хл}—арифметико-геометрическая прогрессия
со знаменателем q =# 1 и разностью d (см. задачу 8.228),
Sn = Xi + ... + хп, п е N.. Найти:
1) lim — . 2) lim(S„ — пхп).
П-> ОС Г1, п->оо
8.230. В треугольнике АВС{ проведена биссектриса С\С2,
в треугольнике АС^С2 проведена биссектриса С2С3, в треуголь-
нике АС2С3 — биссектриса С3С4 и т. д. Доказать, что последо-
вательность величин углов Сп+\СпА, п N, имеет предел, и
найти его, если угол ВАС равен а.
8.231. Вписанная в треугольник А\В\С\ окружность касается
его сторон BiCi, СИ] и AvB\ в точках Л2, В2у С2 соответственно,
вписанная в треугольник А2В2С2 окружность касается его сто-
рон В2С2, С2Л2, А2В2 в точках Д3, В3, С3 соответственно и т. д.
Найти предел последовательности величин углов ВпАпСп при
п—> оо.
8.232. В трапеции ABCD (AD || ВС) точки Bi и Ci — середины
диагоналей АС и BD, в трапеции AB^Crf) точки В2 и С2 —сере-
дины диагоналей АСХ и B\D и т. д. Найти lim | ВпСп|, если
|Л/)| — а в случаях: а) | AD | > | ВС |; б) |ЛР| < | £ С |.
8.233. Пусть а > 0, х{ = ^/а, xn+i = ^Ja + хп9 neN. Дока-
зать, что существует lim хп> и найти его.
П->оо
8.234. Исследовать на сходимость последовательность:
1) ^ = 0, хп+1=^±±, neN.
2) Xi = 1/2, xn+i = (1 — х„)2, ne N.
8.235. Пусть Xi = а, 0 < а < 1, xn+l = 1 + qx2n, ne N. При
каких q е [0; 1 ] последовательность {хп} сходится?
8.236. Пусть Xi > 0, хп+1 — , где а > 0, п е N.
Доказать, что существует lim хп, и найти его.
8.237. Пусть xt > 0, хп+1 = — (%хп + > n е N. Дока-
3 \ хп /
зать, что существует lim хп, и найти его.
П->оо ________
8.238. Пусть х{ = ^2, хп+1==^2 + п е N. Доказать,
что последовательность {хп} сходится.
8.239. Доказать сходимость и найти предел последователь-
ности:
1) 0<а< 1, хл+1 = 1 —
2) х1=а, 1, ял+1 — ।
224
8.240. Исследовать на сходимость последовательность
(п е N):
1) х,== — 3, х„+1 = 1+ —. 2)х1=—уу, xn+i=—2хп .
3) xi = i7« x-n+i==Tn~'2' xi = 7> xn+i=4 ——•
8.241. Пусть Xj > 0, х„+1 — — + b, ne N, где а > 0, b > 0.
Доказать, что последовательность {%«} сходится, и найти ее
предел.
а а х„
8.242. Пусть а е R, х{ = у, xn+i + -у. Найти все зна-
чения а, при которых последовательность {хп} сходится, и найти
ее предел.
8.243. 1) Пусть 0 < Xi < 1, хп+1 — хп(2— хл),леМ.
а) Доказать, что последовательность {хп} сходится и
lim хп — 1.
б) Исследовать последовательность {хл} на сходимость, если
Xi ^(0; 1).
2) Пусть 0<xi<l/a, хп+1 — хп(2 — ахп), neN, где
а > 0. Доказать, что последовательность {хп} сходится и
limxrt = 1/а.
П->оо
3) Пусть 0 < Xi < а, хл+1 — хп(а — xn), п е N. Доказать,
что
a) limx„ = a—1 приа>1;
П-»оо
б) limx„ = 0 при 0<а<1.
П->оо
8.244. Последовательности {хп} и {уп} удовлетворяют усло-
виям:
1) Xi = и > 0, t/\ = b > 0, xrt+i = (хп Уп)9 У«ч-i === л/9%пУп,9
neN.
2) Xi = ci > 0, у\ — b > 0, xn+i = -g- {хп + уп}, уп±\ = Л »
I Уп
п е N.
Доказать, что последовательности {хп} и {у«} сходятся и
limx„= li$n уп. В случае 2) найти этот предел.
8.245. При каких а и Ь из R сходится или расходится после-
довательность {хп}, если X] — а, Х2 — b и
1) Хп+2 2Хп+1 ”” Хп. 2) X„-f-2 — 4х«ц-1 Зх^.
3) Хп+2 = ’—2х«+1 Хп- 4) Хп+2 — Хп+1 “h 2Хп, nsN?
8.246. Пусть Xi = a, xn+i = хп/ (4 — xn), п е N. Доказать,
что последовательность {хп} имеет предел, и найти его, если:
1) 0 < а < 3. 2) 3,5 <« <4.
8 Л. Д. Кудрявцев и др.
225
8.247. Доказать сходимость последовательности и найти ее
предел,если:
1) Xj=4, x„+i = V6 + xn.
2) Х1 = 1, хп+1=н/б + х„.
3) X] = 3, xn+l = V12 + x„, ne М.
8.248. Доказать, что последовательность
х1 = а, х„+1= 2 + хге'’
имеет предел, и найти его, если:
1) а < 0. 2) а <—2. 3) —1 < а < 0.
8.249. Доказать, что последовательность
Xi — a, xrt+1 = I + — , n е N,
Хп
где b < —1/4, расходится.
8.250. Пусть
х^а, xn+l = x2n + 3xn+ 1, nsN.
Установить, имеет ли эта последовательность предел (конечный
или бесконечный), и найти его, если:
1) а = —5/4. 2) а = —3/4. 3) а = 4) а =—9/4.
8.251. Доказать, что существует limxn, и найти его, если
П->оо
%i = 2, xrt+1 = 2 — .
8.252. Доказать, что последовательность
%i=a, xn+I = 1 —neN,
сходится, и найти ее предел, если:
1) а >1/2. 2) а < 0. 3) 0 < а < 1/4.
8.253. Доказать, что если
Xj>0, xn+i=a(xn+ -Ц, ne= N,
\ Лп/
то:
1) limx„ = 4-0° при а^1.
П-»оо
2) limxrt = д/а/(1 — а) при 0<а<1.
П-»оо
8.254. Исследовать на сходимость последовательность
(neN):
1) х, = 9/10, х„+1 = 1/(2х„ —1).
2) Xi = 2, хга+1 == 6/(xn —1).
8.255. Пусть
xi = а> xn+i = х2п 4- (1 - 2р)х„ 4- р2, ns N.
226
Найти все значения аир, при которых последовательность
{Хп} СХОДИТСЯ.
8.256. Доказать, что последовательность
I xt=a, ne=N,
имеет предел, и найти его (a, b, с, d е R и таковы, что с ’+
0 для любого п е N, bd =И= 0, |6|=тЧс1> ad=^=b — с).
8.257. Доказать, что последовательность
хх—а, х„+1==1 +^г, «eN,
хп
0> Ь> —1/4, сходится; найти ее предел.
8.258. Пусть
Xi > 0, хп+1 =ахп + ^-, п <= N,
хп
где а > О, b > 0. Доказать, что существует конечный или бес-
конечный предел этой последовательности, и найти его.
8.259. Доказать, что существует единственная последователь-
ность {хп} такая, что Xi — 1, хп — xn+i + хп+2, хп > 0, zie N.
Доказать, что эта последовательность имеет предел, и найти его.
8.260. Последовательность хп такова, что
5
%п+2 "2“ " I -^1 :~ &>•
Как следует выбрать х2, чтобы эта последовательность сходи*
лась? Чему будет равен ее предел?
с 8.261. Доказать, что последовательность
= ••• +-^2zL’
где а >» 0, сходится.
8.262. 1) Пусть limxn —0. Доказать, что
П~>ОО
lim ± U] + х2 + ... + хп) = 0.
П->оо
2) Пусть lim хп — а. Доказать, что
lim -J- (Aq + х2 + ... + хп) = а.
П->оо п
3) Привести пример расходящейся последовательности {xn}t
для которой существует
lim 4-(*i + *2+ ... +х„).
П-»ОО П
8.263. Найти
8*
227
8.264. Последовательность {хп} такова, что lim (хп+1 —<х„) —
П ->оо
= а. Доказать, что lim — — а,
П->оо П
8.265. Пусть х„>0, neN, lim хп — а. Доказать, что
П->оо
lim —j-----;— --------j— = а.
П->оо _L_| !_ _L Ц-_
X| *2 Xn
8.266. Пусть
lim x„ = x, limz/„ = z/,
n->oo n->oo
где y=/=0 и y\ + уг + ... +t/n=/=0 для любого п <= N. Дока-
зать, что
!im X1t*2t tXra=v
п-»оо У' + Уч + • • • + Уп У
(здесь у — ЧИСЛО, X— ЧИСЛО, -|-оо ИЛИ —оо).
8.267. 1) Пусть limxn=l, хп > 0, п N. Доказать, что
М->оо
П _________
lim д/Л|Х2 • • • хп = !•
Г2->ОО
2) Пусть lim хп = х, х„>0, ne N, х#=0. Доказать, что
П->оо
И _________
lim Vxix2 ••• хп — х.
3) Привести пример расходящейся последовательности {%„},
для которой существует
г?_________
lim V%ix2 • • • хп*
П-^оо
8.268. Пусть хп > 0, п е N, и
Доказать, что
8.269. Найти:
lim Xn+1- = х.
П->оо ХП
П __
lim Vxn = x*
П->оо
п___ р _
1) lim 2) lim#.
t7->°° " П-»00 —
3) lim - V(n+ l)(n + 2) ... (2n) •
n-»oo n
ЛЧ ,• 4nn! C4 .. 3r,nl
4 Ilm 73nF 5) Ilm
228
8.270. (Теорема Штольца.) Пусть последовательность {хп}
-строго монотонна, начиная с некоторого номера, и lim хп — +<».
п->оо
Последовательность {уп} такова, что
lim Уп+1 ~Уп — а
П-><х> xtl+l ХП
Доказать, что и
Пи =а
П->оо Хп
(здесь а — число, +°°» —°° или оо).
8.271. Пусть {хп}—строго монотонная, начиная с некоторого
номера, последовательность, lim хп — 0. Пусть lim у„=0 и
п->оо гг->оо
[im - У»
П->оо Хп+1 ХП
Доказать, что и lim —— а, где а — число, +оо, —оо или оо.
п->оо ХП
8.272. Пусть реМ. Найти:
1) lim -Ьг(1р 4- 2Р + ... 4-пр).
П->ОО
8.273. Пусть
lim хп = а, lim yn = b.
П->оо П->оо
Доказать, что
ц + x2yra-i + ... + хп|у2 + хпу|
и->оо П
8.274. Функция f неограничена сверху (снизу) на множе-
стве X. Доказать, что существует последовательность {хп},
хп е X, п<= N, такая, что lim f(xn) = + оо (соответственно
П-»оо
Jim, f(xn) = — °°).
8.275. Доказать, что если функция неограничена на отрезке,
то существует точка этого отрезка, в каждой окрестности ко-
торой функция неограничена. Верно ли это утверждение для
интервала?
8.276. Пусть
Iimxn = 0, Sn = xI + x2+ ... +xrt, _neN.
П ->ОО
Может ли последовательность {Sn} иметь только два частич-
ных предела, если 1) хп — действительные числа; 2) хп — комп-
лексные числа?*
8.277. Последовательность {хп} такова, что для любого
^>1, k <= N, ее подпоследовательность {xPk} имеет предел.
229
равный 1. Следует ли отсюда, что и последовательность {хпУ
сходится к 1?
8.278. Доказать, что всякую ограниченную последователь-
ность можно разбить на счетное множество последовательно-
стей, имеющих один и тот же предел.
8.279. Пусть {хп} и {уп}—ограниченные последовательности
с общим множеством частичных пределов. Доказать, что най-
дется такая перестановка {гп} последовательности {уп} (см. за-
дачу 8.94), что
lim(xn — zn) = 0.
/2->оо
8.280. Дано счетное множество последовательностей
(£=1, 2, ...) таких, что х{£} > 0 для любых п, k е N и
lim х{^} — + оо для любого k е N. Доказать, что существует
П->ОО
последовательность {&л} такая, что
lim bn — Q и lim 4^ = 0 для любого k е N.
п->оо Г2->оо ХУп
8.281. Привести пример возрастающей ограниченной по-
следовательности {хп} такой, что последовательность
{(п + 1) (хл+1 — Хп)} неограничена.
8.282. 1) Последовательность {хп} ограничена. Доказать, что
последовательность {n(xn+i—хп)} не может иметь пределом
+ °°-
2) Привести пример сходящейся последовательности {хп}>
для которой
lim п(хп+1 — хп) = оо.
П-»оо
8.283. Доказать сходимость ограниченной сверху последова-
тельности, удовлетворяющей условию:
1) ЛтгЧ-1 %п "2п ’
2) Яп+1 > ft N.
3) — хп^ап, ft^N, где ап таковы, что последователь-
( п 'I
ность 1 £ ан сходится.
I )
8.284. Последовательность {хп} такова, что для любых
т, п е N
0 Хггг-\-п Хт “F Хп.
Доказать, что последовательность {хп/п} сходится.
8.285. Пусть {хп}—возрастающая неограниченная последо-
вательность, neN. Пусть Кп — число членов этой по-
230
•следовательности, не превосходящих n, п е N. Доказать, что
если существует один из пределов
lim — или lim — ,
П->оо п П->оо Хп
-го существует и другой и эти пределы равны.
8.286. {Признак Лейбница.) Последовательность {ап} та-
кова, что
lim (a„+i—а„) = 0,
П-»оо
| ^«+2 | | ап_\.\ ап |,
(Я/н-2 — ап+1) (ап+1 — ап)^0, n е N.
Доказать, что последовательность {ап} сходится.
8.287. Последовательность {хп} имеет ограниченную вариа-
цию, если ограничена последовательность
= |х2 — Х1| + |Хз — Х2|+ +|хп+1 — Х„|, «eN.
Доказать, что:
1) Монотонная ограниченная последовательность имеет ог-
раниченную вариацию.
2) Последовательность с ограниченной вариацией сходится. .
3) Для всякой последовательности с ограниченной вариа-
цией существуют возрастающие ограниченные последователь-
ности {tZ/г} и {Ьп} такие, что хп == ап — bn, п<= N.
8’288. Пусть хп #= 0, п & N,
lim —< 1.
П->0О ХП
Доказать, что
lim хп = 0.
П->оо
8.289. Пусть все члены последовательности {х^} различны,
Доказать, что множество подпоследовательностей последова-
тельности {хп} несчетно.
8.290. Пусть
lim ап = а, а > 0, ап > 0, п е N,
П->оо
и пусть lim bn = b, Доказать, что
П->оо
lim abn = ab.
n
8.291. Найти:
1) lim n(el/n — 1).
n->OO
2) lim C“, где = a(<^.~1) ••• <« — <«— 1»., aeR>
231
8.292. 1) Доказать, что последовательность
*п=1+4'+4‘+ ••• 1п/2, ле^>
имеет предел (его называют постоянной Эйлера).
2) Доказать, что
,,™(7+ттт+-
8.293. В треугольнике АВС проведены медианы AD, BE и
CF. На стороне АС взята точка Мо, М0У=А, Л40 #= С, и по ней
найдена на АС точка М\ следующим образом: проведены отрезки
[Л1оМ)] II [CF] (Noe=AB), затем [N0P0] || (AD) (PQ^BC) и, на-
конец, [Р0Л11] || (BE). Отправляясь от точки аналогично на-
ходится точка М2 и т. д. Доказать, что последовательность то-
чек {Л1Л} сходится, и найти ее предел.
8.294. Точка движется в круге равномерно и прямолинейно,
отскакивая от его границы по закону отражения. Центральный
угол, под которым видны две, первые точки встречи с границей
круга, равен 1 рад. Доказать, что в любом секторе будут на*
ходиться точки встречи с границей.
8.295. Доказать, что
lim n((n + 1)а — «а) = + оо, 0 < а.
п->оо
8.296. Найти:
1) lim-fel.
П->оо П
2) lim — |ln(Vn2+ 1—n)|₽.
/2->Оо П
П __ П __
oxi- (Va+V^)” л .л
3) hm ——, где а > О, Ъ > 0.
П->оо 2
8.297. Доказать, что из всякого бесконечного множества ин*
тервалов, объединение которых покрывает отрезок [а; 6], мож-
но выделить конечное подмножество интервалов, объединение
которых также покрывает [а; 6].
§ 9. Предел функции
1. Основные определения. Первое определение предела функ-
ции (определение Гейне). Пусть область определения функции
f(x) содержит интервал (а;Р), кроме, быть может, точки
хсе=(а; р).
Число а называется пределом функции f(x) в точке х0 (или
при х->х0), если для любой последовательности {хп}, &
е(а;Р), сходящейся к х0, последовательность {/(Хл)л
сходится к а.
232
Из определения следует, что функция не может иметь двух
разных пределов в одной точке. Из определения следует также,
что значения функции f(x) в точках х, лежащих вне некоторой
«окрестности точки х0, и значение функции f(x) в точке х0 не
влияют ни на существование, ни на величину предела функции
j(x) в точке х0.
Для того чтобы доказать, что функция f(x) не имеет пре-
дела в точке х0, достаточно указать какую-нибудь последова-
тельность Ж*")}, не имеющую предела, или указать две по-
следовательности {/(хп)} и {f (*„)}, имеющие разные пределы.
Второе определение предела функции (определение Коши).
Число а называется пределом функции f(x) в точке х0 (или
при х->х0), если для каждого числа 8>0 существует такое
число 6 > 0, что для всех х, удовлетворяющих условию 0 <
г<|х — х0|<б, выполняется неравенство |f (x)—а | < е.
Определение Коши и определение Гейне равносильны.
Если число а является пределом функции f(x) в точке Хо,
то пишут
lim f(x)=a или f(x)->a при х->х0.
х->х0
Используя логические символы, определение Коши можно
записать следующим образом:
lim f(x) = a<=>
X->Xt
<=> Vs > 0Э6 > OVx (0 < | X - x01 < 6 => | f(x) - a | < e). (1)
Утверждение lim f(x)=^a записывается так:
X->Xo
lim f (x) =/=
<=>3e> 0V6>03x(0 <|x-x0| <6 Alf(x) —a|>e). (2)
д-2 _ 16
Пример 1. Найти предел функции f (х) =в точке
х — 4.
А Воспользуемся первым определением предела функции в
точке. Будем рассматривать данную функцию в некоторой ок-
рестности точки х = 4, например, на интервале (3; 5). Возьмем
какую-либо последовательность хпе(3;5) таку1б, что хп #= 4 и
lim хп = 4. Тогда на основании теорем о пределах последова-
п->оо
тельностей имеем
Г г/ \ Г Xfl I* Х^ + 4
lim f(xn)= lim —-----------= lim --------
П-»оо n->oo'Xn — 4xn n->oo Xn
lim xn + 4
П->оо
lim xn
П-^оо
В силу произвольности выбранной последовательности хп, со-
гласно первому определению предела функции в точке
lim
Х~>4
X2 — 16
х2 — 4х
2. А
233
Пример 2. Доказать, что lim *2 |6 = 2, используя вто-
х->4- х
рое определение предела функции в точке.
А Рассмотрим функцию f (х) = *2 в некоторой окре-
стности точки х = 4, например, на интервале (2; 5).
Возьмем произвольное положительное число в и преобра-
зуем \f(x) — а | при х =# 4 следующим образом:
|^_2|=р±<_2|_^.
Учитывая, что хе (2; 5), получаем неравенство
I *2 16 _ о I ।х ~ 41
| х2 - 4х z I 44 2
из которого видно, что если взять 6 = 2в, то для всех хе(2; 5)
и удовлетворяющих неравенствам 0<|х — 4|<6 выполняется
неравенство
I х2- 16 п| 6
-2—-----2 < — = е.
I х2 — 4х I 2
Согласно второму определению предела число а = 2 являет-
X2 ' 16
ся пределом функции f (х) =-^23747 в точке х = 4. А
Пример 3. Доказать, что функция f (х) = зш(л/х) не
Имеет предела в точке х = 0.
А Возьмем две последовательности хп = 1/и и х' = 2/(4п + 1)г
сходящиеся к точке х = 0.
Рассмотрим соответствующие последовательности {f(xn)} и
значений функции. Так как последовательность f(xn) =
= sin пл сходится к нулю, а последовательность цх') =
= sin(n(4n + 1)/2) — к единице, то предел функции f(x) —
= sin(n/x) в точке х — 0 не существует. А
2. Теоремы о пределах.
Теорема о пределе суммы (разности) и про-
изведения двух функций. Если функции f(x) и g*(x)
имеют пределы в точке х0, то функции f(x)±g(x) и f(x)g(x)
также имеют пределы в точке хо, причем
lim (f (х) ± g (х)) = lim f (х) ± lim g (х), (3)
lim (f (х) g (х)) = (lim f (х)) (lim g (x)). (4)
X-»X0 X->X3 X->Xq
В частности, для любого числа С
lim (С7(х)) = С lim f(x). (5)
Х->Х' Х->Х0
Теорема о пределе частного. Если функции f(x)
и g(x\ имеют пределы в точке Хо и lim g-(x) 0, то функция
ЯМ
f(x)/g(x} также имеет предел в точке х0, причем
lim
х->Х0
fjx)
gw
lim f (x)
X->Xo
lim g(x) ’
X->Xn
(6)
Теорема о пределе композиции функций.
* Пусть существуют lim f (х) = a (f (х) =/= а при х #= х0) и
х-»х0
limgQ/); тогда в точке хо существует предел композиции
g°f=g(f(x))> причем
lim g (f (х)) = lim g (у). (7)
x->x0 у->а
Эта теорема позволяет вычислять пределы, переходя от пере-
менной х к новой переменной у — f(x).
В случае непрерывности функции g(y) в точке а равенство
(7) можно записать в виде формулы
Hm g (f (х)) = g (lim f (x)), (8)
X-»X0 X->Xo
из которой видно, что знак предела (lim) и знак функции (g),
если она непрерывна, можно переставлять.
3. Предел функции при х —> оо. Число а называется пределом
функции f(x) при %->ое, если для каждого числа е>0 суще-
ствует такое число б > О, что для всех х, удовлетворяющих усло-
вию |х| > 6, выполняется неравенство |/(х) — < в.
Если число а является пределом функции f(x) при х~>оо,
то пишут
lim f(x) = a.
Х->оо
Теоремы о пределах справедливы и для пределов функций
при Х-> оо.
4. Бесконечный предел. Говорят, что предел функции f(x) в
точке Хо равен бесконечности, и пишут
lim f (х) = оо,
Х-»Яо
если для каждого числа в > О существует такое число 6 > О,
что для всех х, удовлетворяющих условию 0 < |х — х01 < б,
выполняется неравенство |/(х) | > в.
Аналогично,
lim f (х) = оо,
Х->оо
если для каждого числа в > О существует такое число б > О,
что для всех х, удовлетворяющих условию |х| > б, выполняется
неравенство |/(х)|> 8.
Функция f(x) называется бесконечно большой при x->Xof
если
lim f (х) = оо.
235
Функция f(x) называется бесконечно малой при х->х0, если
lim f (х) = 0.
Х->ЛГ.
Аналогично определяются бесконечно большая и бесконечно
малая функции при х-> оо.
5. Свойства бесконечно малых и бесконечно больших
функций.
1. Сумма (разность) бесконечно малых функций есть функ-
ция бесконечно малая.
2. Если функция f(x) при х->х0— бесконечно малая, а
функция g(x) в некоторой окрестности точки х0 удовлетворяет
условию |g(x)|<C x=£xG, с — некоторое положительное чис-
ло, то произведение f(x)g(x) при х->х0 является бесконечно
малой функцией. Таким образом, произведение бесконечно ма-
лой функции на ограниченную функцию является бесконечно
малой функцией. В частности, произведение бесконечно малых
функций есть функция бесконечно малая.
3. Если функция f(x) при х->х0— бесконечно большая, а
функция g(x) в некоторой окрестности точки х0 удовлетворяет
условию | g (х) | > г, х Ф Хо, с — некоторое положительное чис-
ло, то произведение f(x)g(x) ПРИ х-^х^ является бесконечно
большой функцией. В частности, произведение бесконечно боль-
ших функций есть функция бесконечно большая.
4. Функция f(x), определенная и не равная нулю в некото-
рой окрестности точки хо, кроме, быть может, точки х0, является
бесконечно малой при х->х0 тогда и только тогда, когда функ-
ция l/f(x) при х->х0 является бесконечно большой.
Сумма (разность) и частное бесконечно больших функций
не обязательно являются бесконечно большими функциями. На-
пример, f(x)= 1/х и g(x) =—1/х при х->0 —бесконечно боль-
шие функции, но f(x) + g(x) при х->0 не является бесконечно
большой функцией.
При вычислении lim (f (х) ± g (*)) в случае, когда f(x) и
Х->Хо
g(x)—бесконечно большие при х—<-х0 функции, теорема о пре-
деле суммы (разности) функций непосредственно неприменима.
В таких случаях принято говорить, что сумма f(x)-|-g(x) или
разность f(x)— g(x) при х->х0 представляет собой неопреде-
ленность вида оо оо и оо — оо. Аналогично, говорят, что ча-
стное f(x)/g(x) представляет собой при х-+х0 неопределен-
ность вида если f(x) и g(x)— бесконечно большие при
х-*хо функции, и неопределенность вида если f(x) и g(x) —
бесконечно малые при х->х0 функции. Вычисление пределов в
этих случаях часто называют «раскрытием неопределенности».
Пример 4. Найти:
v2_л г2 — 4
1) у2 __ г — 2 * 2) %2 __ х _ 2 •
236
3) lim x’~4
лч .. х2 —- 4
-2-----------о • 4) lim —2---------------j;.
х2 __ х ___ 2 . X2 — X — 2
Л 1) Применяя теоремы о пределе разности (3) и произве-
дения (4), находим предел знаменателя
lim (х2 — х — 2) — (lim х) (lim х) — lim х — lim 2 — —2.
к->1 х->1 х->1 х->1 х—>1
Предел знаменателя не равен нулю, поэтому по теореме о
пределе частного (6) получаем
lim (х2 — 4)
х2 4 = х^\ = ~ 3 ^_ 3
х2 х •— 2 lim (х2 — х — 2) — 2 2
2) Здесь числитель и знаменатель стремятся к нулю:
lim(x2 —4) = 0 и lim(x2 —х —2) = 0,
Х->2
V z-r^
т. е. имеет место неопределенность вида —, Теорема о пре-
деле частного (6) непосредственно неприменима. Для «раскры-
тия неопределенности» преобразуем данную функцию. Разделив
числитель и знаменатель на х — 2, получим при х =И= 2 равен-
ство
х2 — 4 __ х 4- 2
х2 — х — 2 х 4* I *
Так как
найдем
lim (х + 1) =И= 0, то по теореме о пределе частного (6)'
х-»2
lim
х->2
х2 — 4
х2 — х — 2
lim
Х->2
lim(x + 2)
х + 2 х~>2 ___ 4
х 4- 1 Ит (х 4- 1) 3 ’
х-»2
3) Числитель и знаменатель при х->оо являются бесконеч-
но большими функциями. Поэтому теорема о пределе частного
(6) непосредственно неприменима. Разделим числитель и зна-
менатель на х2 и к полученной функции применим теорему о
пределе частного (6):
4) Данная функция представима в виде произведения двух
функций /(х) — 1/(х4~ 1) и g(x) = (x2 —4)/(х —2). Функция
f(x) = 1 /(х 4- 1) при х->-И является бесконечно большой,
функция g(x) = (x2 — 4)/(х — 2) в окрестности (—3/2; —1/2)
точки х = —1 удовлетворяет условию
I х2 — 4
|х-2
£
2 •
| =1 х + 2 j >
237
Следовательно, согласно свойству 3 произведение f(x)g(x) яв-
ляется бесконечно большой функцией, т. е.
Пример 5. Найти:
1) lim —-Л—-=, а > 0.
х-^-а -х/х — V а
2) ПтУ^+Н-2Ух-1
х-»5 х2 — 25
5 <
3) lim ^32 + *~- . 4) lim (Vx4 + 8х2 + 3 - д/х4 + х2).
Х->0 Х Х->оо
ГЛ 1) Здесь имеет место неопределенность вида Преоб-
разуем данную функцию, разложив ее числитель на множи-
тели:
х — а ___ {^Jx + д/д)
V* — д/a д/х — д/а
— д/х д/ а •
Теперь находим
lim = lim (Vх + д/а) = Нт д/х + "\!а •
х->а Д/Х —Д'а х->а х->а
Используя непрерывность функции д/х в точке .а (см. (8)), по-
лучаем ___
lim д/х = д/ Нт х = д/а
х->а х->а
и, следовательно,
lim = 2 д/а.
х->а ух — у а
2) Для «раскрытия неопределенности» вида ~ умножим и
разделим данную функцию на д/х4-П + 2д/х — 1. Тогда при
х =# 5 будем иметь
д/х Ч- И — 2 д/х — 1 __х + 11 — 4 (х •— 1)__
х2 - 25 “ (х2 - 25) (7хТи + 2 д/х - 1) “
___________3___________
— (X + 5) (V7+1T+ 2 VT=T)в
К полученной функции применима теорема о пределе частного
(6), поэтому
.. д/х Ч~ 11 —- 2 д/х — 1 ____________3_____________ = _3_
х2 — 25 — lim (х + 5) (д/х + 11 +2 д/Г=Т)
х->5
При вычислении последнего предела мы воспользовались непре-
рывностью функции д/х в точках х=16 и х = 4 (см. (8)).
238
3) Здесь удобно ввести новую переменную. Положим
у V32 ~Р х, тогда получим
V32 + х - 2 у-2 1 _ 1
ft * "-^2«/6-32 yi + 2г/3 + 4у* + 8у + 16 80 -
4) В этом случае имеет место неопределенность вида оо —оо.
Преобразуем данную функцию следующим образом:
л/х4 + 8х2 + 3 - д/х4 + -v2 =
7 + —
х4 + 8х2 + 3 - (х4 + х2) ~ х2
Так как
______±,(7+?)=7’
Jin л/1 +4+т‘=л/лц(1 +^+тг)=1>
lim а/1 lim (1 +-4-) = 1>
Л->оо V л V х->оо \> Л /
то ___________ __________
lim(-\/x4 + 8х2 + 3 — Ух4 + х2) = 7/2. д
Л->оо
6. Некоторые замечательные пределы. Вычисление пределов
во многих случаях производится с помощью двух важных фор-
мул:
= (9)
х->0 х
lim (1 +х)1/х = е. (10)
х->0
Часто используются также следующие формулы, являющиеся
следствием формулы (10):
lim 0+4)* = *’ <п)
X-»oo V Л /
lim 10^(1+-Х-- = -йГ7, а>0,а^1, (12)
lim - ~~ 1 — ina, а > 0. (13)
х->0 х
В частности, при а = е
lim ln(1 + x) =zl, (14)
х-»0 х
рх — 1
lim——- = 1. (15)
v-xCl Л
239
Пример 6. Найти:
sin ах . _ о, cos Зх — cos 7л:-
1) lim------, а ф 0. 2) lim------------5.
х-»0 х х->С х*
3) lim ar*g* . 4) lim ctg 2х • ctg (-£— x).
x->0 x x-*nf4 4 4 '
Л 1) Положив ax = у, согласно формуле (9) получим
sin ах f. sin ах «. sin у
lim---------= a lim —-— = a lim---------------— = a.
X->0 x x->0 ax t/-»0 У
2) Так как
cos Зх — cos 7x __q sin 5x sin 2x
x2 x * x
.. sin 5x _ sin 2x n
lim--------= 5, lim---------— 2
x-»0 x x->0 x
. (см. пункт 1)), то по теореме о пределе произведения (4)
находим
cos Зх — cos 7х ____2о
3) Перейдем
чим
lim
х->0
к новой переменной у = arctg х,
X2
тогда полу-
limirctgx=iim^_==lim cos£.
х-»о х у+п [%У у^.0 Sln У
У
Из непрерывности функции cos у в точке у = 0 следует, что
lim cos у—1. Согласно формуле (9) lim-^-^- = l. Поэтому
#->0 У
по теореме о пределе частного (6) получаем
lim cos у
lim = —
iim S!n-L
У i/->0 У
= 1.
4) Данная функция является произведением бесконечно ма-
лой при х-^л/4 функции ctg2x на бесконечно большую функ-
цию ctg(n/4 — х).
В таких случаях говорят, что имеет место неопределенность
вида О-оо. Для вычисления предела перейдем к новой пере-
менной у = л/4 — х:
lim ctg 2х • ctg ( j — x) = lim ctg (y — 2y\ ctg у =
Х->л/4 V 7 y->0 .
— lim sin cos У
V™ sin У ' cos2^ *
Так как lim
li.n^
siaM==2i a |im^JL = i, TO
y^,0cos2y
соз2д sin у у_^0 cos2y
240
Пример 7. Доказать формулы (а > 0, а Ф I):
1) lim loga= у!—. 2) lim ~ = Ina.
’ x->0 x ln« ' z->0 x
A 1) Запишем данную функцию в виде loga(I 4-x}i/x, В силу
непрерывности логарифмической функции (см. (8))
lim loga (1 + x)l/x = loga lim (1 + *)‘М>
x->0 x->0
и так как, согласно формуле (10), lim (1 + х)Х1х = е9 то
х->0
logaU^ 1
х-»о х &а Ы а
2) Для доказательства перейдем к новой переменной у =
==ax—1.
Тогда х = loga(l 4-У), и если х->0, то и у-^0; поэтому
.. ах — 1 «. у 1 ।
+ ° 11п,^» + »'=|п“- “
г/->о У
Пример 8, Найти:
1) lim (1 — 2x3)w. 2) lim (cos x)l,x\
х->0 x->0
4) lim (е1/х + ^)*.
Х->2 Х Z Х->оо л '
ГД 1) По определению показательно-степенной функции имеем
(1 — 2%3)1/х3 = ^1п(1“2х3))/%3.
Используя непрерывность экспоненты (см. (8)), запишем ра-
венство
Hm (In (1-2х3))/х3
lim(l — 2x3)1/JC’= ех“*°
х->0
Для вычисления последнего предела положим у — —2х3, тогда
(см. формулу (14)) получим
.. 1п(1—2х3) о|. In (1 + у) о
lim —1 = — 2 lim —1= — 2,
х^О Я3 у^.0 У
и, следовательно,
lim (1 — 2х3)|/х’= е-2.
Х->0
2) Используя определение показательно-степенной функции
я непрерывность экспоненты (см. (8)), имеем
lim (In cos х)/х2
lim (cos x)1/JC’ = ex^°
x->o
241
Для вычисления lim (In cos я)/х2 запишем равенство
X-+Q
In COS X In (1 + COS X — 1) COS X — 1
X2 COS X—1 X2
Так как
lim ln(l+cosx—1) = lim ln.(l+y) = !
x->o c°s x 1 z/->o У
cos x — 1 .. — 2 sin2 (x/2) 1 .. ( sin (х/2) \2 1
x->0 *2 x->0 * 2 x-»(A X/2 7 2
то по теореме о пределе произведения (4) получаем
Следовательно,
lim (cos x)lz*2 = е"1/2.
х->0
3) Представим данную функцию в виде разности двух функ-
ций:
2х — х2 2х — 22 — (х2 — 22) . 2Х~2 — 1 х2 — 4
х —2 х —2 х —2 х —2
Так как
оХ-2__1 пу__1
lim 4-----—1=4 lim--------1=4 In 2
Х->2 х 2 1/->0 У
(формула (13), а — 2),
|im = lim (* +2)=4>
х->2 х z х->2
то по теореме о пределе разности (3) получаем
lim------У = 4 In 2 —4.
Л'->2 х~2
4) Перейдем к новой переменной у = \/х:
lim (e'lx + — V — lim (еу + у)11у.
JC->OO \ X 7 y_>Q
По определению показательно-степенной функции и в силу не*
прерывности экспоненты (см. (8)) имеем
lim (in (еУ+у))/у
lim {еу + у)Х1у — еу^°
у^
Для вычисления lim(In(e-J + У))IУ воспользуемся равенством
1/->0
In {еУ 4- у) In (1 ч- — О е 4- j/ — 1
у еУ 4- у — 1 * у
242
. Положив t = еу 4- у — 1, получим
,^0 e’ + j-l '
Находим
г/->о У У >
По теореме о пределе произведения (4)
lim |»(еЛ±У).==2,
г/-»0 У
и, следовательно, искомый предел равен е2. А
7. Односторонние пределы. Пусть область определения функ-
ции f(x) содержит интервал (а; х0). Число а называется преде-
лом слева функции f(x) в точке xQ (или при х-+х0—0), если
для каждого числа е > 0 существует такое число 6 > 0, что для
всех х, удовлетворяющих неравенствам х0 — б < х < х0, выпол-
няется неравенство \f(x)— а|<е. Предел слева функции f(х)
в точке Хо ¥= 0 обозначают lim f(x) или f(xo — 0). Если
х-»хо-О
Xq = 0, то пишут lim f (х) или f(—0).
х->-0
Аналогично, в случае, когда область определения функции
f(x) содержит интервал (х0;₽), вводится понятие предела
справа. Предел справа обозначают так: lim f(x) или f(x0 + 0),
х->хо4-О
если х0 =И= 0, и lim f(x) или f (+0), если х0 = 0.
х->4-0
Функция f(x) имеет предел в точке х0 тогда и только тогда,
когда существуют предел слева и предел справа и они равны;
при этом
lim f (х) = f (х0 — 0) = f (х0 + 0).
х->х
Для функций, область определения которых содержит интер-
вал (а; +°°) или интервал (—оо; (3), вводятся понятия предела
при х->+°о и соответственно при х->—оо. Эти пределы обо-
значают lim f(x) и lim f(x).
Х->4*°° X-» —оо
Например, число а называют пределом функции f(x) при
если для каждого числа е > 0 существует такое число
£ > 0, что для всех х, удовлетворяющих неравенству х > б, вы-
полняется неравенство |f(x) — а|<е.
Для односторонних пределов справедливы теоремы о пре-
деле суммы (разности), произведения, частного и о пределе
композиции функций.
По аналогии с конечными односторонними пределами опре-
деляются и односторонние бесконечные пределы:
lim f(x) = oo, lim f(x) = —оо, limf(x) = +oo
X->Xq-0 X~*Xq 4-0 Л->-оо
Й т. Д.
243
Например, запись lim f(x)=—оо означает, что для каж-
Х->Ло+0
дого числа е существует такое число б > О, что для всех х, удо-
влетворяющих неравенствам Хо < х < х0 + S, выполняется не-
равенство f(x)< е.
Пример 9. Доказать формулы:
1) lim а1/х = 0, а>1. 2) lim arctg~=~.
х->-6 х-»+0 х 2 3 *
А 1) Возьмем в > 0 и для х < О решим неравенство
а]/х < 8. Если 8^1, то неравенство справедливо при всех
х < 0. Поэтому для каждого е 1 в качестве б можно взять
любое положительное число, например 6=1. Если 8<1, то,
логарифмируя обе части неравенства, получаем ^1пя<1п8г
откуда х> Таким образом, и для s< 1 существует б,
а именно б==----> 0, такое, что для всех х, удовлетворяю-
щих неравенствам —б < х < 0, выполняется неравенство
аг/х < 8. Следовательно, предел слева функция ai/x, а>1, в
точке х = 0 равен нулю.
2) Возьмем положительное число 8 и для х > 0 решим не-
равенство
| arctg у — у| < е. (16)
Если е л/2, то неравенство верно при всех х > 0. По-
этому в качестве б для всех 8 л/2 можно взять любое поло-
жительное число, например 6=1.
Если 8 < л/2; то, решая неравенство (16), получаем
у — arctg- < е, arctgy>j —е,
7>*g В~е)> х<^8>
т. е. для каждого е < л/2 в качестве 6 можно взять 6 = tge.
Таким образом, для каждого числа 8 > 0 существует такое
число 6, что для всех х, удовлетворяющих неравенствам
0 < х < б, выполняется неравенство | arctg ~ < е. Это
означает, что предел справа функции arctg (1/х) в точке х = 0
равен л/2. А
Пример 10. Найти:
.. Vx2+14 + x
hm . ;—
x-H-oq Д/х2— 2 + X
2)
.. д/х2+14 + х
lim — -'—.
х->~-оо д/х2— 2 ч- X
3) lim th (1/x). 4) lim th (1/x).
x->4-0 x->-0
244
Zs 1) Данная функция при х->4~оо является отношением
двух бесконечно больших функций (неопределенность вида
. Разделив числитель и знаменатель на х, получим
„т Дй+д.. ,1т л/1+.у + 1=1.
х-»4-оо ух2 — 2 + X х->+оо / 2
Л/ ^ +
2) При х-э—оо функции д/%24“14 + х и Vх2 — 2 4-х-
представляют собой неопределенность вида оо — оо. Для вы-
числения предела переходим к новой переменной t = —х:
lim
14+ х .. д/72 + 14 — Г
--= Iim v__----------- _
•2 + х f->4-oo — 2 — t
lim (V/2 + 14-z)(VF+14 + <)(V7~2 + z) =
-»+oo (V^ — 2 — Z) (Vz2 — 2 + 0 (V/2 +144-/)
= lim
= — 7<
— е
3)
1 е'/*_е-»/л j _ e-2/x
lim th—= lim -r-j---------тт7г= lim ---------577 = 1> так
c->+o x x^.+0 e4x + e-nx x-.+o 1 + e~2,x
lim e~2/x— lim evt = 0 (пример 9, 1)).
1 р^,х . P~Ux p2jx _ __ 1
4) lim th — = lim —rr---------rr = lim —5--------= — 1,
r-x_n X v_»_n e'lx 4- e llx v_>._n e2lx -I- 1
как..
так как lim e2/JC = 0 (пример 9,1)). ▲
x->—0
8. Сравнение функций. Символы O(f) и
называется ограниченной по сравнению с
х->х0, если существуют такой интервал
точку Хо, и такая постоянная С, что
|g(x) К СЩ*) I. хе=(а;р),
off). Функция g(x)
функцией f(x) при
(а; р), содержащий
х=/=х0.
Ограниченность g(x) по сравнению с f(x) при х->х0 кратко
записывают следующим образом:
^(х)=О(/(х)), х->х0. (17)
Эта запись читается так: «g(x) есть О большое от )(х) при х\,
стремящемся к х0».
Аналогично определяется смысл записи g(x) = O(f(x)) при
х^х0 — 0, х->Хо + О, Х->оо, х—>—оо, х->4~°°-
В частном случае, когда f(x)— 1,запись g(x)= О(1),х~>х0,
означает, что в некоторой окрестности точки х0, не содержащей
точки хо, функция g(x) ограничена.
245»
Если g(x) ограничена по сравнению с f(x), a f(x) ограни-
чена по сравнению с g(x) при х->х0, то g(x) и f(x) называются
функциями одного порядка при x-+xQ.
В этом случае пишут
gWX/W. х-+х0. (18)'
Теорема. Для того чтобы функции g(x) и f(x) были
функциями одного порядка при х-*~х0, достаточно, чтобы при
х-*-хо существовал конечный и не равный нулю предел отно-
шения этих функций.
Пример 11. Какие из следующих пар функций являются
функциями одного порядка при х->0:
1)
2)
3)
4)
f(x) = ex, g(x) — 100 х.
f(x)=13/x, g(x) = l/ln(l+x).
f(x) = x(24-sin(l/x)), g(x) — x.
f(x) — x2, g(x) — x?
1) Так как
lim414 = limioo±£== wo,
x->o I (x> x-»o ex
то ex X 100 -f- x, X -> 0.
2) Так как
.. f(x) .. 13 In (1 + x) 1o
lim ' 7-v = hm------- — 13,
X->0 ё W x-»0 x
TO 13/xX l/ln(l + x), x->0.
3) В этом случае
lim -Ц4- = lim (2 + sin —)
x-»o£(*) x^.ok. xj
не существует.
Тем не менее данные функции являются функциями одного
порядка. Действительно, так как
го неравенство
|Дх)|^С|£(х)|
выполняется при С —3 и, следовательно, функция f(x)=x
= х(2 + sin(l/x)) является ограниченной по сравнению с функ«
цией g(x) = х при х->0.
С другой стороны,
т. е. неравенство
|g(x)|^C|f(x)|
246
верно при С — 1 и, следовательно, функция g(x) = x является
ограниченной по сравнению с функцией f(x) = х(2 + sin(l/x))
при х—>0. Таким образом, х(2 + sin(l/x)) X х, х->0.
* 4) Данные функции не являются функциями одного порядка
при х->0, так как, какова бы ни была постоянная С, неравен-
ство
| х | С | х21, х #= 0,
очевидно, не выполняется ни в какой окрестности точки х = 0
и, следовательно, функция g(x) — x не является ограниченной
по сравнению с функцией f (х) — х2 при х->0. ▲
Если
g(x)X (х — х0)п, х—>х0, (19)
то функцию g(x) называют бесконечно малой порядка п при
х->х0.
Если
gWX (х-хо)"’ neN, х->х0,. (20)
то функцию g(x) называют бесконечно большой порядка п при
х->х0.
Например, функции
е/ ч 13 , х 1
f (х) = — и g (х) = -7—77-п—г
при х->0 (пример 11.2)) являются бесконечно большими 1-го
порядка, а функции f(x) = х(2 + sin(l/x)) и g(x) = x при
х->0— бесконечно малыми 1-го порядка (пример 11.3)).
Функция g(x) называется эквивалентной (асимптотически
равной) функции f(x) при х->х0, если на некотором интервале
(а; ₽), содержащем точку х0, существует такая функция <р(х),
что
g (х) = <р (х) f (х), хе(а;Р), х =/= х0 и lim<p(x)— 1. (21)
Х->Хо
Если g(x) эквивалентна f(x) при х->х0, то пишут
g(x) ~ f(x), х—>х0. (22)
Отношение эквивалентности функций:
1) рефлексивно, т. е. f(x) ~ f(x), х->х0;
2) симметрично, т. е. если g'(x)~f(x), х->х0, то f(х) ~
g(x), х->х0;
3) транзитивно, т. е. если g(x)~f(x) и f(x)~ h(x) при
х->х0, то g(x) ~ h(x) при х —>• х0.
Аналогично определяется эквивалентность функций в слу-
чаях X—>Хо — о, X—>Хо + О, X—>оо, Х->—оо, X—
Теорема. Для того чтобы функции f(x) и g(x) были экви-
валентны при х->х0, достаточно, чтобы предел их отношения
при х—>х0 был равен единице.
247
При х->0 справедливы следующие часто применяемые экви-
валентности:
х ~ sinx ~ tgx ~ arcsin х ~ arctg х ~ In (1 + х) ~ ех — 1. (23)
Пример 12. Какие из следующих пар функций являются
эквивалентными при х->0:
1) f(x) = ех; g(x) = 2х+ 1.
2) f(x) = Vx +Vх! g^ = ^x.
3) f (x) = ax— 1, a > 0, a =/= 1; g(x) = x.
4 ) f sin x, если x рационально,
(0, если х иррационально;
{х, если х рационально,
0, если х иррационально?
А 1) Так как Нт — lim —-j-?-- — 1, то ех ~ 2х -4- 1
х -> 0 / w х->0 е
при х->0.
2) Так как __
lim -Ц^г = Ит ==Птд/1 + Ух = 1,
х->0 Цх хч-О v
ТО л/х + Vх
3) Так как
V* при х->0.
Нт
х->0
f (*)
g (х)
= lim
х-> 0
ах — 1
In а,
х
то функции f(x) = ax—1 и g(x) = x при х->0 являются экви-
валентными только тогда, когда а = е.
4) В этом случае lim(f(x)/g(x)) не существует. Тем не ме-
х->0
нее данные функции при х->0 эквивалентны, так как при
х 7^ 0 существует функция ф(х), а именно ф(х) = (sinx)/x, та-
кая, что
g (х) = ф (х) f (х) и lim ф(х) = 1,
х->0
а это и означает, что g(x) ~ f (х), х->0. А
Функция g(x) называется бесконечно малой по сравнению
с функцией f(x) при х-^х0, если на некотором интервале (a; Р),
содержащем точку х0, существует такая функция ф(х), что
g (х) = ф (х) f (х), xe(a;p), х #= х0, limqp(x) = 0. (24)
X-+XQ
Из этого определения следует, что в случае, когда
f(x)=^=O, x^(a; Р), х=7^х0,
.248
функция g(x) будет бесконечно малой по сравнению с f(x)
при х->х0 тогда и только тогда, когда
Если g(x)—бесконечно малая по сравнению с f(x) при х->яс?
то пишут
g(x)= o(f(x)), хXg. (25)
Эту запись читают так: «g(x) есть о малое от f(x) при х, стре-
мящемся к х0».
Аналогично определяется смысл записи g(x) — o(f(х)) при
X—>Хо — 0, Х->Хо + О, X—>оо, X—> оо, Х->+°о.
В частном случае, когда f(x) = 1, запись g(x) = о(1),х-^х0>
означает, что функция g(x) является бесконечно малой при
х—>х0.
Если g(x)= o(f(x)), х->х0, где f(x) — бесконечно малая при
х->х0, то g(x) называют бесконечно малой более высокого по-
рядка по сравнению с f(x) при х->х0.
Пример 13. Доказать или опровергнуть утверждения:
1) sinx3 = o(x2), х->0. 2) x2 = o(sinx3), х->0.
3) 1+х==о(1/х), х->0.
4) x2D (х) = о (xD (х)), х->0,
где
{1, если х рационально,
О, если х иррационально.
•А 1) Утверждение верно, так как
.. sin х3 «. .. sin х3
hm----г- = hmx-hm-------g— = 0.
x->0 x x->0 x->0
j^2
Утверждение неверно, так как lim ——г =/= 0.
%-> оsin х
3) Утверждение верно, так как
lim * 1 =limx(x+ 1) = 0.
х->0 *>х х->0 4
4) Здесь функция f(x) = xD(x) обращается в нуль в точ-
ках, сколь угодно близких к точке х = 0. Поэтому воспользуемся
определением символа o(f). Так как существует функция <р(х),
а именно ф(х) = х, такая, что
g (%) = x2D (х) = <р (х) f (х) и lim<p(x) = 0,
л-»0
то x2D (х) = о (xD (х)), х->0, т. е. утверждение верно. А
При обращении с символом o(f), х->хо, полезно иметь
в виду следующие правила:
1) o(Cf) = o(f), С — постоянная.
244
2) o(f) + o(f) = o(f).
3) o(f)-o(g) = o(f • g).
4) o(o(f)) = o(f).
В силу этих соотношений левую часть каждого из этих ра-
венств можно заменить правой; заменять правую часть левой,
вообще говоря, нельзя.
Вычисление пределов функций во многих случаях сильно
упрощается, если использовать эквивалентность функций, пра-
вила обращения с символом o(f) и следующую теорему: g(x) ~
~ f(x), x-^xq, тогда и только тогда, когда
g(x)= f(x) + o(f(x)), х->х0;
При вычислении предела частного двух функций часто ока-
зывается полезной следующая теорема:
Если f(x)~fi(x) и g(x) ~ gi(x) при и если суще-
ствует lim - ffi-,
J х->хо Si М
то
fW р Л (х)
lim = lim
Х-»Хо & Х->ХЭ Si W
Пример 14. Вычислить:
. ч .. sin 2х + 2 arctg Зх + Зх2
1) lim . Z1 о—;—Ло-т—i-—•
7 x_>q In (1 + Зх + sin2x) + хех
3UX*(ln 0+ ?)-'"£)
2) lim
х->0
In COS X
tg х2
4) lim (1 + x2)ctg *.
x->0
A 1) При x->0 имеем
sin 2x ~ 2x, arctg 3x ~ 3x, xex ~ x.
Так как ln(l + w) ~ w при и—>-0, то
ln(l + 3x-|-sin2x) ~.3x4-sin2x ~ Зх при х->0.
Следовательно,
sin 2х = 2х + о (2х), arctg Зх = Зх + о (Зх),
In (1 + Зх + sin2x) — Зх + о (Зх), хех = х + о(х),
и поэтому
г sin 2х + 2 arctg Зх + Зх2
ln (1 + Зх + sin2 х) + хех
2х + о (2х) + 6х + 2 • о (Зх) + Зх2
Зх + о (Зх) + х + о (х)
8 + А«. 8 + limAM.
“ l*m Т' 1-—М"= -----7~\~ —'——-— = 2
х-»о 4* + о(х) х-»о «И 4 + Нт о (х)
X х->0 X
250
Здесь мы использовали соотношения о (2х) + 2 • о (Зх) + Зх2 —
= о (х) ио (Зх) 4- о (х) = о (х) при х -> 0.
Решение можно записать короче. Так как при х->0
sin 2х + 2 arctg Зх + Зх2 ~ 8х,
In (1 +3х + sin2 х) + хех ~ 4х,
то
,. sin 2х + 2 arctg Зх + Зх2 _____________«. 8х
In (1 + Зх + sin2 х) + хех 4х
2) Используя эквивалентности
2 In cos x = In (1 — sin2 x)--sin2 x ~ —x2,
tgx2 — x2 при x->0,
получим
.. In COS X
hm t 2--
x->0 X
1«. In (1 — sin2 x)
— lim -----г-?------
2x->0 Vх
1 -x2 + o(- X2) Ip 1 X2
— -и- hm-----0-4—гтг—- — -7Г bm ---------—
2 x->0 x2 + o(x2) 2 x_>0 o(x2)
2 ’
х2
3) lim x (in (1 + y) — lib4 = lim Л In (1+4
%_>+oo \ X Z 7 2 7 X->+oo X X
lim x
X-> + oo
(4+°(l))= llm (2+tF)-2-
\ X \ X / / x_^_j_oo X l/X /
4) lim(l + x2)c‘e * = e°,
где
In (1 + X2) .. X2 + o(X2)
a =Iim—fTT----==Ilm x + o(x) = llm
x-»0 4> X X->0 xO(X) X-»O
o(*2)
0.
x
Следовательно, искомый предел равен 1. А
9. Частичный предел функции. Число а называется частичным
пределом функции f(x) при х->х0, если существует последова-
тельность {хп}, хп =/= х0, такая, что хп-*х0 и limf (хп) = а.
П->оо
Аналогично определяются бесконечные и односторонние ча-
стичные пределы.
Наименьший и наибольший частичные пределы функции f(x)
при х—>хо называют нижним и верхним пределом функции и
обозначают lim f (х) и lim f (х).
Х-»Хо Х-»Хо
Пример 15. Найти все частичные пределы функции
f (х) — sin (1 /х) при х -> 0.
Л Если | а | < 1, то хп = a-jn + -> 0 и f (хп) = sin ->
т. е. каждое число а такое, что |а|=^ Ъ является частич-
ным пределом.
251
Из неравенства |sin(l/x) [I, х =£ 0, следует, что других
частичных пределов у функции нет. Поэтому lim f (х) = — 1 и
___ J
lim f(x') = 1. А
х-> и
9.1. Определить, при каких положительных значениях б из
неравенства 0 < |х — х0| < б следует неравенство |/(х)— а|<е,
если:
1) f(x) = x2; *о = 2; а = 4; е = 0,001.
г / . х2 — 4х + 3 о 1 ~ ,
2) f (%) х2 2х 3 * %®— —~2 ’ &— 0,01.
3) f(x)=sinx; х0 = л/2; а—\\ в = 0,01.
4) f(x) = signx; х0 = 0; а—\\ 8=1,5.
9.2. Определить, при каких положительных значениях 6 из
неравенства |х— 11 < б следует неравенство:
1) | lgx| < 2. 2) |lgx|<l.
3) I Igx | < 0,1. 4) | Igx| < 0,01.
9.3. Для каждого числа e > 0 найти такое число б > 0, при
котором из неравенств 0 < | х—11 < б следует неравенство
9.4. Для каждого числа 8 > 0 найти такое число б > 0, при
котором из неравенств 0<|х— 3|<б следует неравенство
9.5. При каких б из неравенства |х| > б следует неравенство
1/(1 + *2) <е, где е — некоторое положительное число?
9.6. При каких б из неравенства х < б следует неравенство
arctg х + л/2 < е, где е — некоторое положительное число? Чему
равен lim arctg %?
Х-> -оо
9.7. Доказать, что limf (х) не существует, если:
х->о
1) f(x) = arcctg(l/x). 2) f (x) = sign sin (1/x).
9.8. Доказать, что lim /(х)не существует, если:
X->4-oo
1) f(x) = cosx. 2)f(x) = x— E(x).
9.9. Пусть функции f(x) и g(x) не имеют предела в точке
х0. Следует ли отсюда, что f(x) + g(x) и f(x)g(x) также не
имеют предела в этой точке?
9.10. Доказать, что если для любой последовательности {хп},
сходящейся к точке Хо, последовательность {/(х„)} сходится, то
lim f(x) существует.
х->Хо
252
9.11. Доказать, что если из любой последовательности {хп},
сходящейся к точке х0, можно выделить подпоследовательность
(хпь}> для которой lim f (xnk) = а, то lim f (х) = а.
1 k' k-+<x> X->Xn
9.12. Доказать, что если функция f(x) в точке х0 имеет ко-
нечный предел, то f(x) = 0(1) при х->х0.
9.13. Доказать, что если функция f(x) удовлетворяет нера-
венству f(x)^C, xs(a;P), х =# х0 е (ос; р), С — постоянная, и
существует lim f (х), то справедливо неравенство
Х->Хо
lim f(x)^C.
Х->Хч
9.14. Доказать, что если функция f(x) в точке х0 имеет ко-
нечный положительный предел, равный числу а, то существует
такой интервал (а; р), содержащий точку х0, что
f(x)>a/2, хе(а;Р), х #= х0.
9.15. Доказать, что если на интервале (а;Р), содержащем
точку Хо, справедливы неравенства
gi (х) f (х) g2 (х), х #= х0,
и функции gi(x) и gz(x) в точке х0 имеют один и тот же конеч-
ный предел, равный а, то
lim f (х) = а.
Х->Х0
9.16. Сформулировать утверждения:
1) lim f(x) = a. 2) lim f(x) = oo.
X ->Xo—О X—»Xo+O
3) lim f(x)== + °°- 4) limf(x)= —oo.
X->-oo X-»oo
9.17. Используя логические символы, записать утверждения:
1) lim f(x) = Q. 2) limf(x) = 4,
X~> — 0 x->oo
3) lim f(x) = — oo. 4) lim f(x) — °o.
X-»14-0 X-> —oo
9.18. Используя логические символы, записать утверждения:
1) lim f (х) 0. 2) lim f (х) =И= 4.
Х->-0 х-»оо
3) lim f(x) —оо. 4) lim /(х) =/= оо.
Х->1+0 Х-> —ОО
9.19. Используя логические символы, записать утверждения:
1) Функция f(x) в точке х0 имеет конечный предел.
2) Функция f(x) не имеет конечного предела в точке х0.
Найти пределы функций (9.20—9.38):
.20, 1) lim--. 2) lim ——9—7.
Х-»2 ^-1 ’ Х^.1 *2-1
253
.. х24-4х — 5
3) lim—-т—:—
л \ 1 • х2 4~ 4х — 5
4) hm ,—
пт i\ г х7 + 5хб + 4х3
9.21. 1) lim 7 2x3
Х-> о л •
оч .. х4 — X3 4-X2 — Зх + 2
3) hm-----§---------гт2—
7 х3 — х2 — х + 1
1-^ 2х — 11 х — 21
2) lim—ъ—т—г-7Т“
%->7 х 9х + 14
,х .. х4 — 2х + 1
4) lim -7—~—~т.
7 х->1 х8-2х4- 1
_х X101 — 101x4-100
5) hm х2_2х4_.......
6)
lim (х2 4-2х)2 — 14 (х2 4-2х) — 15
х4 — 29х2 4- 100
7>!™(Т+Т
™ / х2 -4х + 6 ,
8) lim (
х->2 '
х — 4 \
““i к х2 — 5х 4- 4 "И Зх2 — 9х + 6 7 ’
9.22. 1) lim .^ + 5)s + (x4-6)b4-(x4-7P
X5 + б5
2) lim (*±.JH3-7x)2
(2Х-1Г
.. (1 4-X1'4-7х18)3
4) hm /i-4-x«po
. 2 +________________!______)
2х — х2 * х2 — Зх + 2 /
a)
5> ±.(4^-0
1
6) 1Тоо( 2x4-1
9.23. lim . Рп (*) = аохп + Qk (х) = Ьох^ + ...
. 4- — многочлены.
9.24. 1) lim х • - 1 n, k е N.
л->1 хл— 1 ’
хп+1 — хА+* + xk — пх 4- п — 1 * м
------------------------ "*eN-
„т niks
л->1 (x—1) (x2—l)...(x^~ 1) ’
4) limf—--------—t) M^N.
7х->Д1-х" 1-xV’
9.25. 1) lim -V% 72?2--
л->6 x °
2) lim
2)
x->o^l 4- x — 1
lim J___
x~>11 — Vх
4) lim 2Vx24-x+1-2-x ,
x->0 x
v Vo — x — 1
lim—-----7==r-.
x->5 3 — <4 4- x
6) lim
x->2
V7 4~— x2 — Vl 4- + >g2
2x — x2
264
7)
lim + * + x + 7
x->—8 ^15 + 2x + 1
5 7
B) lim^2*2 + 10x + 1 - v%2 + io* + 1
9.26. 1) lim
X -> OO
1 + 14x
2x 4- $x2
2) lim -j=.rl-ZLi-
X->oo Vx12 + 5x5 - 1
3)
.. д/4x2 4- V*3 + *4
lim ---........... —
X ->oo Vx2 4- 4
4)
V9x2 + 1 - - 1
lim -4 ---*----
X->oo Vx4+1-Vx4-1
5) lim yxi±6 + |xl_
^°°VF+2-|x|
6)
9.27. 1) lim (Vx2 — 1 — Vx2 + 1).
X->oo
'2) lim (V*4 + 2x2 — 1 — Vx4 — 2x2 — 1 ).
X->oo
8) lim (и/4х4 + 13x2 — 7 - 2x2).
X->oo
4) lim x3 + 3x2 + 4x — x3 — 3x2 + 4)»
X->oo
5) lim (-Vx2 + Vх2 + V%2 — V%2) •
X->co 7
6) lim x2 (Vх4 + x2-\/x4 + 1 — V2x4)-
X->oo
9.28. 1) lim n, k e N.
— i
2) lim Vg-±_x- Уд-zjL me N, a > 0.
x->0 X
8) limV.L+ax- Vi + »x
x->0 X
4) lim-------, n, feeN,
1 + axV 1 + bx — 1
255
5) lim(Vl + x2 + ^".--(V1+.x2-^ f n e N.
x->0 x
6) lim (-\/(l + %2)(2 + x2).. .(n + x2) — x2), n<=N.
x->oo
л лл tv i* sin 3x .. tg 4x
9.29. 1) lim----. 2) lim-^—.
x->o x ' X^osmx
3) limxctg5x. 4) lim-£f£-, 0 ¥= 0.
x->0 x->0 5111 Px
5) lim . fiS'n % 7 . 6) lim ( . 2 .----Л-1
' X-»0 Sln °X — Sin 7x ’ X-»0 ' sln 2* sm x sm2x )
4 sin + лЛ sin + 2x^ — 1
8) lim________k®______L______к®_______L_____
%->o sin x
cn lim tg(1 + x) tg(1 ~ tg*1
9.30. 1) lim
X-»l
sin 7лх
sin 2jxx
оч sin x
2) lim Tf-V
х~>л n x
3) lim x sin (n/x). 4)
X-»oo
r-\ I- 1 — tg2 x
5) lim 6.
Х-»Л/4 у 2 cos X — 1
lim x2(cos (1/x) — cos (3/x)).
X->oo
cos(£ - x)
6) lim—7=—--------
х->л/б V3 — 2 cos x
7) lim4T^7“2xtgx)*
x^K/2^COSX 7
_ 4 ,. 1 — cos x cos 2x cos 3x
8) —
tg2X
9.31. 1) lim —7=-----,
x-»o V2 —v 1 + cos x
.•„ л/Г+г" sin 3x — Vl — 4 sin 5x
j™--------------Eel---------------•
'у/cos 4x — cos 5x лд г * ~* cos x cos %x
1 - cos 3x ’ 4) tgx2
2)
3)
lim
x-»0
5)
lim
ysinx-Vsinx, 6) n ( _ sin
cos2 x ’ „ . „ ' v 1 v '
9.32. 1) lim
x->0
arcsin 2x
x
. .. tg 2x — 3 arcsin 4x
2) a sin 6x — 6 arctgZx
. X 1
л — 4 arctg -j-7;
3) lim-----------——
x->o x
256
4) lim arcsin x — 1 + arctg 2x
x J д/ j -j- arctg 3x — Vl — arc sin 4x
s-33- 4i (гтттГ
2) lim (Л
x->oo 4 л
x/(2x+l)
(2x4-1) '
4)±о(^ттГ
9.34. 1) lim -^-ГГ
x->io x m
2) Jim ln (1 + 3* + *;) + in (1 - 3x 4- *2)
’ х^Л *2
3) lim x log2 •
' X-»oo &Z 5 + *
In tg (-T + 4x)
5) lim-------4--------L,
Х->С л
7) lim 8)
x->l/4 Intgnx 1
9.35. 1) lim ffi-".1-.
X-»(i z 1
4) lim 1 + * ~ 1 ~ sin *
X->‘J In (1 4" x)
6) lim
x-»0
In cos 5x
In cos 4x
lim x2 In cos — .
X->oo X
2) lim х(з‘'* — 1).
X->oo
3) lim №(4,/x-4I/U+1)). 4) lim—-~e" .
X->oo x->0 *8 X
sin 5x _ sin x x2 1
5) lim—i9y<~- 6) lim —7-- -----.
x->o ln(14-2x) x->0 ^/14-sinx2— 1
9.36. 1) lim (*г + 1У • 2) lim(Vl + * — *)'*•
x->oo ' x 4 ' x-»0
3) lim(l+3*4)lslIrtc. 4) lim (1+ctgx)tg\
X-»0 x->n'2
5) lim (cos x)“1/x\ 6) lim (sinx)lg x.
x->0 х->я'2
7) lim (cos 6x)c,gI x. 8) lim (In (e 4- x))cts x.
x->0 X-»U
9) lim ( ^xir) 10) lim (cosx 4-arcig2x)''arctg
x->0 x^ “T 1 / x->0
t\ 1 \ 1 • sh x qk * • ch 2x 1 n\ 1 • iri ch 5x
9.37. 1) lim——. 2) lim- . 3) lim—-2—.
X->0 X X->0 C0S X 1 X->9 X
sh 3x _ sh X / rh 9 v \
4) lim------и—-----. 5) lim (x- —Inch л-). 6) lim (-j—)
x->0 In X x-»oo X->‘J x СП X /
9 Л. Д. Кудрявцев и др.
257
- /7^
9.38. 1) Hm а* a > 0.
x->a u л
2) lim , a > 0, b > 0, a=?= b.
,v->o ax — bx
3) Hm a > o, 6>0.
Х-»(Л 2 * 7
4) lim ( ^+1 + ^+1Y/X, a > 0, b > 0.
9.39. Найти a) f(—0); 6) /(+0):
1) f (x) = - — • 2) f (x) = arccos (x — 1).
3) f(x) = e~1/!: 4) f(x) = 2ctgJ£.
9.40. Найти a) f(xo— 0); 6) f(xo + O):
i f (x} - 2 (1 — x2) + 11 — x21 _ t
П / W— 3(1_X2)_|1_A.2| > л0 b
2) f (x) = sign cos x, x0 = n/2.
3) f (x) = arctg tg x, х0 = л/2.
4) = x + з'ьхз” ’ %o = 3.
9.41. Найти a) f(xg—0); 6) f(xo + O):
l)Hx) = T^w. X0 = -l.
2) f(x)==x + [x2], x0=10.
3) /(x)= lim x0=l.
П->оо 1 Л
4) f (x) = hm , x0 = 1.
9.42. Найти a) lim f (x); 6) lim f(x)s
1) f (x) »= arctg x. 2) /(x) = arcctgx. 3) f(x) = ex.
4) f(x)=arcsin^. 5) f(x)=(jL±^)*. 6) f(x)=(l +|4т)*-
7) f(x) = Vl 4-7x +x2- д/l - x + x2. 8) f(x) = -ln^ + 4JC)-.
9.43. Вычислить пределы:
1) lim (д/х2 4- 8x 4- 3 — + 4x 4- 3).
X->-oo
2) lim (x 4- a/) . 3) lim (2x — V4x2 — 7x 4- 4}
X-»-oo\ v X -1- 1 J x->+oo
$5S
4)
8)
lim arcsin (^x2 + x + x). 5) lim——Vcosx
1 4~ sin x — cos x A [/x «.
7-7—-----------7- . 7) lim
1 + sin 4x — cos 4x ) ’ y_>+c
r In (4 + 5e6X) p arccos (1 — x)
lim —-—---------- . 9) lim ---------7=------
x-»+oo In (1 + 2e3X) x->+0 Vx
Varccos x
10) lim
9.44. Какие из следующих функций являются бесконечно
малыми:
I) f (х) = —^з--”. , Х-+1.
1 — COS VX
4) f (-4 = , +2x : a) x
5) f (x) — sin In (x2 + 1) — sin In (x2 — 1), x
<• , , In (x2 — X + 1)
6) f (x) = -7—7-7-:-----Hr ,> X -> OO?
' 1 x 7 n (r4 4- r 4- I
— oo.
9.45. Какие из следующих функций являются бесконечно
большими:
I) f (Х) х3 __ 4х2 _[_ 4х х2 — Зг_|_9 > Х—>2.
2) f (х) — х(^/х2 + I — х); а) х -> + оо, б) х—^~ оо.
3) f(x) = ^=^==, х-ж/2.
V И — sin х)2
4) jF (х) — chx — sh %; а) х—>+©о, б) х—>—оо.
Б) Н-4 = (4ггт) ; а) *-> + оо, б) Х->—ОО.
6) f (,v) = (l - x)I/x!; а) х^ + о, б) х->-0?
9.46. При каких значениях аир функция f(x) является бес-
конечно малой:
Ч f (х) = +~TF — ах — Р> х-^оо.
2) f (х) = у/4х2 + х + I — их — р; а) х -> + оо, б) л- —> — оо.
3) f (х) = д/х2 — х3 — ах — р, х —> оо.
4) f (#) = ех^~[—ах — Р; а) х~>+ °°> б) х->~ ov.
9*
259
I
5) f (x) — (x + 4)e1/x — ax — 0; a) x-»oo, 6) x-> —0.
6) f (x) = ln(l 4-e3*) — ax — 0; a) x-> + oo, 6) x—> — oo.
7) /(x) = xarctgx— ax—0; a) x—6) x->—oo?
9.47. При каких значениях а и 0 функция f(x) является бес-
конечно малой при х—> + 0:
1) / (х) = х° sin (1/х13). 2) f (х) = ln (1 + *а) .
3) f (x) = xa arctg (1/хр). 4) f (х) — (1 — х“)х ?
9.48. Определить порядок п бесконечно малой функции при
х~>0:
1) / (х) = 3 sin2x2 —5х5. 2) /(х) = д/4 —- х4 + х2 — 2.
3) f (х) = 1 — х4 — cos х2. 4) f (х) — 2 sin х — tg 2х.
5) f (х) = sin (д/х2 + 9 — з). 6) f(x) = 2*'—1.
9.49. Определить порядок п бесконечно большой функции:
1) Н*) = !+4--2T2-> Х->О°-
2) / (х) = д/х4 + х + 1, х —* оо.
3) f (X) = .....7=г , х -> + оо.
V* + 2 — 2 V* + 1 + V*
4)
5) f (х) = ctg2 х3, ,r->0.
f / x 1 — cos x • д/cos 2x ~
6) f(x) =--------, x->0.
9.50. Установить, какие из следующих утверждений верны:
1) х2 = о(х) при а) х—>0, б) х—>оо.
2) х = о(х'2) при а) х —>0, б) х->оо.
3) дД2 + х — х = о (1) при а) х~>4-оо, б) х—>—оо.
4) In (1 + ех) = о(1) при а) х->+°°, б) х-^-оо.
9.51. Пусть х-*-0, /ieN, feeN, n^k. Показать, что:
1) о (хп) + о (xk) = о (xk).
2) о (хп) * о (xk) = о (xn+k),
9.52. Какие из следующих пар функций являются функциями
одного порядка:
1) f (х) = х3 — х2 — х + 1, g(x) = я3 — я; а) 1, б) х-> оэ.
260
2) И*) = $44. £(*) = y: *_>1, 6) x->oo.
Л- *p Z л
3) f (x) = д/х2 + 1 — Ух2 — 1, g (x) — l/x, X —> OO.
4) f (x) = д/х2 + 1 — x, g(x') = l/x; a) x-*+oo, 6) x-> — oo.
6) £^=!’ x^°°-
6) f (x) = X COS (l/x), g(x)==X, x->0?
9.53. Установить, какие из следующих утверждений верны
при х->
1) 100% + х sin х = О (х). 2) х = О (100% + х sin х).
3) х + х sin х = О (%). 4) х — О (х + х sin %).
5) д/Тг+Т-|х|==О(1/х). 6) 1/х = 0(д/?+Т-|х|).
9.54. Доказать:
1) О (0(f)) = 0(f). 2) о (0(f)) = о (f).
3) О (о (D) = о (f). 4) о (f) + О (f) = О (f).
5) o(f)-O(f) = o(f).
9.55. Пусть х->0, neN, 6eN, п > k. Показать, что:
1) О (хп) + О (xft) = О (xfe). 2) O(x")-O(xft)= О(х«+*).
9.56. Пусть х-> оо, nsN, k е N, п > k. Показать, что:
1) О(хп) + О(х*) = О(х«). 2) O(x«)-O(x*) = O(xn+k).
9.57. Определить, при каких значениях а и |3 функции f(x)
и g(x) = ах₽ эквивалентны:
I) f(х) — V 2х + л/х + Ух ; а) х—>Д0, б) х-> + °°.
2) f(x)== УТ — 2х — У1 — Зх, х->0.
3) f (х) = 2ех’ + (cos х — I)2 + х5 — 2, х -> 0.
4) f (х) = sin2 2х + arcsin2 х + 2 arctg х2, х->0.
5) f(x) = l—cos(l—cos(l/x)), X->oo.
6) f(x) = E(l/x), x—>oo.
9.58. Вычислить:
1)
2)
3)
arctg (2 — x) + sin (x — 2)2
x2 — 4
lim
X -»2
Urn Vi + W-1.
In COS X
10 _
lim x3 * cos x s*n3 x
x-»o 1 — 71 + x3
261
«. 2 sin л/*2 + Vх'3 + In (1 +
lim---------------, -—.
Y-» + n X + у X X
3__
.. Vx arcsin Vx (e7^x — 1)
x->+0 tg уx • In (1 + 3%)
.. (sin 2x — 2 tg x)2 + (1 — cos 2x)3
lim --------, -Л —r~6---------------
0 tg76x+sin6x
9.59. Пусть lim ф (/)==«, причем ф(/)у=а при t =/= tQ в пеко-
торой окрестности точки to. Доказать, что
1) если f(x) = o(g(x)) при х-+х0, то /(<₽(/)) = o(g(q?(/)))
при
2) если f(x) = O(g(x)) при х->х0, то /(ф(0) = О (g(cp (/)))
при to.
9.60. Найти lim f(x), a'o^IR. если
( 1/q при x=p/q, где р nq — взаимно простые целые числа,
[0 при х иррациональном.
9.61. Пусть lim f(x) = a и lim g(t) = xQ. Следует ли отсюда,
что lim f(g(t)) = a?
t —> to
9.62. Доказать, что если функция f(x), х ее (х0; +°°), огра-
ничена в каждом интервале (х0; Xi) и существует конечный
или бесконечный
lim (ft = o, 1, 2, ...),
Х-> + оо Х
9.63. Доказать, что не существует рациональной функции
R(x) с целыми коэффициентами такой, что для любого ра-
ционального числа г найдется целое число k такое, что R(k) = г.
9.64. Вычислить
/ 1 х/п\(\ 0\
.. \—х/п 1 ) \0 1/
hm lim -------------------•.
X -> о п -> со Х
9.65. Найти lim f (х) и limf(x), если:
х ® х -> 0
1) Mx) = eC0S(W>. 2) /U) = T.sin2T,
3) f (Ч = arcctgT. 4) f (х) = д/д - 1 - 1.
И/ у V Л Л-
262
9.66. Найти Hm f(x) и lim f(x), если:
X ->°° x ->oo
1) f (x) = cos2x + arctg %.
2) =
3) f (x) = (д/4х2 + x + 1-Щх2 — x + 1)(1 + cos 2x).
4) f(x) = (l + cos2x)1/cos4
9.67. Доказать, что lim (cos x + sin -yj2x) = 2.
§ 10. Непрерывность функции
1. Непрерывность функции в точке.
Определение 1. Функцию f, определенную в окрестности
точки Хо, называют непрерывной в точке х0, если
lim f(x) = f(x0).
X->Xn
Определению 1 равносильно следующее (на языке «8 — б»)
Определение 1'. Функция f, определенная в окрестности
точки хо, непрерывна в этой точке, если для каждого 8 > 0
существует такое б > 0, что для любого х ^ /)(/), удовлетворяю-
щего условию |х —х0|<б, верно неравенство \f (%) — f (х0) | <
< 8; короче,
V8>036 >0VxgeD(D (|х — x0|<6^|f(x)-f(x0)| < е).
Разность х — xq называют приращением аргумента и обо-
значают Ах, а разность f(x)— f(x0) называют приращением
функции, соответствующим данному приращению аргумента Ах,
и обозначают Ау, т. е.
Ах = х — хо, Аг/ = f (х0 + Л*) — f (*о) •
В этих обозначениях определение 1 имеет вид:
Определение Г'. Функцию f, определенную в окрестно-
сти точки хо, называют непрерывной в точке х0, если
lim Аг/ = 0.
Дх->0
Функцию f, определенную на промежутке (а;х0], называют
непрерывной слева в точке х0, если
lim f(x) = f(x0).
X ->Хо— 0
Функцию f, определенную на промежутке [х0;6), называют
непрерывной справа в точке х0, если
Hm f(x) = /(x0).
X Хо+0
263
Пример 1. Доказать, что функция Vх непрерывна в каж-
дой точке х0 > 0 и непрерывна справа в точке х0 — 0.
А Докажем непрерывность д/х в точке х0 > 0, пользуясь
определениелМ 1. Преобразуем и оценим модуль разности:
о< | Vх — V*ol
| х — х01 < | X —- Хо |
Vx + Vx0 Vx0
Так как lim | х — х0 | = 0, a 1/Vxo — постоянная, то
Х->Х)
Пт 1-^1 =0.
Х~>Хо 'у *0
Отсюда следует, что
lim | Vх — Vxol = 0.
х->Хо
и поэтому
lim Vx=r=Vxo-
Л->Хо
Значит, функция Vх непрерывна в каждой точке х0 > 0.
Докажем, что функция Vх непрерывна в точке х0 = 0
справа. Пусть 8 — произвольное положительное число. Неравен-
ство |д/х — 0| < е равносильно неравенству 0 х < 82. Возь-
мем б — 82, тогда из неравенства 0 х < б следует неравен-
ство Vх < 8- Значит, lim л]х = 0, и поэтому функция д/х не-
х-> + 0
прерывна справа в точке хо = 0. А
Пример 2. Доказать, что функция у = х4 непрерывна
в каждой точке х0 К.
А Воспользуемся определением 1". Для любой точки хо^‘К
и любого Ах имеем
/\у = (х0 Ах)4 — хо = 4х’бАх + бхо (Ах)2 + 4х0 (Ах)3 + (Ах)4.
Используя теоремы о пределе суммы и произведения функ-
ций, получаем
lim Az/ = lim (4х3Ах + 6х2 (Ах)2 + 4х0 (Ах)3 + (Ах)4) = 0,
Дх->0 Дх->0
следовательно, функция у = х4 непрерывна в каждой точке
хо е К. А
Пример 3. Указать такую границу б отклонений аргумента
/ от его значения /0, чтобы отклонение значения функции у =
— о/4 (о > 0) от значения z/o = a/o не превышало 8, т. е. чтобы
из неравенства \t— /0| < б следовало неравенство
|t/(0 —уо|< е. (1)
А Оценим модуль разности:
] У (t) — Уо I = С R — /о | < о I / — /о | (I /1 + t | /о | + 11 j /О + I /о I )♦
264
Рассмотрим только такие значения Z, для которых
|/-/о|<1. (2)’
Тогда р | < 1101 + 1, а так как р01 < ро | + 1, то
|z/P)-£/o|<4o(po|+l)3p-/o|.
Отсюда видно, что неравенство (1) будет верно, если на-
ряду с (2) будет выполняться неравенство
4а(р0|+ 1)3р — /0| < е,
т. е.
— । < 4a(|/0| + D3 •
Возьмем
6 = (4 + 8).0.(|/о|+ I)3 ’
тогда из неравенства \t— tQ | < б следуют неравенства (3), (2),
а значит, и (1). Величину б из (4) и можно принять за границу
допустимых отклонений аргумента. А
ЮЛ. Для функции f заполнить таблицу
Дх 0,9 0,5 0,1 0,01
&У
Ax — 0,9 — 0,5 — 0,1 — 0,01
Лу
указав для данного приращения Ах = х — 1 соответствующее
приращение функции A# = f(l+Ax)— f(l); построить график
функции f и указать па нем точки, соответствующие Ах = 0,5
и Ах = —0,5:
1) f (у) = 2х — 1. 2) f (х) = х2.
3)/(х) = дД- 4)/(х) = 1/х.
10.2. Для функции f(x) заполнить таблицу
8 2 0.5 0.01 0,001
б
указав для каждого данного значения е какое-либо значение 6
так, чтобы для любого хе D(f) из неравенства |х—11 < 6
следовало неравенство Р(х)— f (1) | < е:
1)/(х) = 2х-1. 2) f(x) = x2.
3) /(х)== Vx. 4) f(x)=l/x.
265
10.3. Для функции f заполнить таблицу, указав для каждого
значения х0 наибольшее значение бтах так, чтобы для любого
xeD(f) из неравенства |х— х0|<бтах следовало неравенство
|f(x)-f(x0)|<0>5:
1) f(x) = 2x — 1
2) f(x) = x*
х0 | 0,01 | 0,1 | 1 | 10
бщах
1/4
7/8 17/12 31/16
(2/2—1)/4/, /<=N
10.4. Функция 6(л'о), х0 > 0, определена следующим образом:
6(хо) есть наибольшее из всех чисел б таких, что для любого
x^D(f) из неравенства |х— х0|<;б следует неравенство
I/U) —fU'o) I < 1/2- Построить график б(х0), х0 > 0, если:
1)/(х)==1/х. 2)f(x) = VT
10.5. Доказать, что функция у{х) непрерывна в каждой точке
своей области определения, если:
1) z/ = 2x — 1. 2) у = х2. 3) г/ = д/х.
4) у = \[х. 5) у = ах-\-Ъ, а 0. 6) у = \х\.
7) у = х3. 8)у = ^х. 9)у=1/х2.
10.6. Доказать, пользуясь неравенством |sinх| |х|, непре-
рывность функции у в каждой точке области определения, если:
—sinx. 2) у = cosx. 3) у — sin {ах + Ь).
10.7. Сформулировать на языке «в — б» определение непре-
рывной 1) слева, 2) справа в точке хо функции и записать его,
используя символы 3, V.
10.8. 1) Доказать, что функция \/1 —х непрерывна в каждой
точке хо < 1 и непрерывна слева в точке х0 = 1.
2) Доказать, что функция х£(х) непрерывна справа в каж-
дой точке хо = п, neZ.
10.9. Доказать, пользуясь свойствами предела и результа-
тами задач 10.5—10.6, непрерывность функции у(х) в каждой
точке области определения, если:
0 У= • 2) = 3) г/= х2 + 2 sin х.
4) у — д/х sin 2х. 5) у = хп, п <= N. 6) у — l/xn, п N.
10.10. Доказать, пользуясь монотонностью функции у = ах,
х^ R, и тем, что lim а,п= 1 (см. § 8 пример 9 и задачу 8.26),
/г->оо
непрерывность в каждой точке х^ R функции
у — ах, х R.
10.11. Функция f определена в окрестности точки х0, кроме
самой точки xq. Доопределить функцию f, задав f(x0) так, чтобы
получившаяся функция была непрерывна в точке х0, если:
1) *0 = -!- 2) f(x)=^4-> х0=1.
3) f(x) = V1 + *~J.. , хо = О. 4) f (х)=-^, х0 = 0.
5) f(x) = xctgx, хо = 0. 6) у = 1 ~ , х0 = 0.
10.12. Сформулировать определение непрерывной в точке
функции, используя определение предела функции по Гейне
(т. е. на языке последовательностей).
10.13. Доказать, что если функция непрерывна в точке, то
она ограничена в некоторой окрестности этой точки.
10.14. Пусть функция f непрерывна в точке х0 и f(xo)y=O.
Доказать, что существуют число С > 0 и окрестность точки х0
такие, что для любого х из этой окрестности верно неравенство
10.15. Функция f непрерывна в точке хо, и в любой окрестно-
сти этой точки имеются как значения х, в которых функция
положительна, так и значения х, в которых функция отрица-
тельна. Найти f(x0).
10.16. Пусть функция определена в окрестности точки хо.
Сформулировать, используя символы 3, V, утверждение, что
функция не является непрерывной в точке хо.
10.17. Доказать, что функция f не является непрерывной
в точке хо; построить график этой функции, если:
1) f (*) = {
2) f W = {
х + 1, х > 0,
х2, х^0, хо = О.
1/х, х =^= 0,
0, х = 0, х0 == 0.
3) / (х) = sign (х + 1), Хо = — 1.
267
f w = {
l/x2, x 0,
1, x — 0, Xn — 0.
5) f (x) — E (x), x0 = 2.
2. Точки разрыва функции.
Определение 2. Пусть функция f определена в окрестно-
сти точки х0, кроме, быть может, самой точки х0. Точку х0 на-
зывают точкой разрыва функции f в следующих случаях:
1) функция f не определена в этой точке;
2) функция f определена в точке хо, но
а) не существует lim f (х),
X ->х-
б) существует lim f(x), но lim f(x)=£ f(x0).
Если существует lim f (x), но или f(x) не определена в точке
Х~>Лп
хо, или lim f (х) f (х0), то х0 называют точкой устранимого
х->хо
разрыва.
Если в точке разрыва хо существуют
lim f (х) = f (x0 — 0), ’5)
lim f (x) = f (x0 + 0), (6)
X-»Xo+O
to x0 называют точкой разрыва 1-го рода, а разность
Д/ (х0) = f (х0 + 0) - f (хо - 0) (7)
— скачком функции f в точке х0. Его обозначают также АД
Если в точке разрыва х0 не существует хотя бы один из
пределов lim f(x) или lim f(x), то х0 называют точкой
х->хо-О Л->Хо+О
разрыва 2-го рода.
Если х0 — точка разрыва функции, то эту функцию назы-
вают разрывной в точке хо.
Употребляются термины: непрерывная функция, разрывная
функция. Непрерывной функцией называется функция, непре-
рывная в каждой точке области определения (если функция
определена в конце промежутка, то имеется в виду непрерыв-
ность соответственно слева или справа). Разрывной функцией
называется функция, имеющая хотя бы одну точку разрыва
Пример 4. Найти точки разрыва функции, установить их
род, вычислить скачки в точках разрыва l-ro рода, построить
график:
1) z/ = (signx)2. 2) z/ = E(x). 3)
1) Из определения функции signx следует, что
( 1, х #= О,
(siEn.^ = |Oi
268
График этой функции изображен на рис, 56. Функция
^:=(signx)2 непрерывна во всех точках, кроме х = 0. В этой
же точке у{—0) = г/(+0) =И= z/(0). Значит
х = 0— точка устранимого разрыва.
2) Пусть « g Z. Если п — 1 х < п,то
Е(х) — п—1, а если п х <. пто
Е(х)—п. График показан на рис. 57. Если
х0 — нецелое число, то существует окре-
стность точки х0 (не содержащая целых Рис 56
чисел), в которой функция постоянна,
а потому и непрерывна в точке xq. Если же х$ — п— целое
число, то Е(п — 0) = п—1, E(n + 0) = n и, значит, хо = п —
точка разрыва l-ro рода, причем Д£(/?)= 1.
Рис. 57.
3) Функция # = (|х| — х)/х2 определена для всех xeR,
кроме х — 0. Следовательно, х = 0—точка разрыва этой функ-
ции. Так как
_ | х | — х _ ( % > 0,
У~ ~ ~ I — 2/х, х < 0,
то lim # = 0, lim z/ = 4-oo, это означает, что х — 0 — точ-
х->+0 х->-0
ка разрыва 2-го рода. График этой функции изображен на
рис. 58. _________
10.18. Найти точки разрыва функции, установить их род,
найти скачки функции в точках разрыва 1-го рода, построить
график функции:
( 1/(х - 1),
1) У= (* + 1)2>
х < О,
0<х<2,
. 1 — х,
2 < х.
2) 3) у == . -L- . 4) г/ = Ц—1
' и х 4- 2 J х2 — 4 х2 -— х
5) у = х — Е(х'). 6) у = х_'е(х-)-- 7) у = —
269
2 sign (1 •— x)
8) -?/ (sign (х + I))2 (х + 1 + (х — 1) sign х) •
9) '/= 1/cosx. 10) у — x/sin х.
10.19. Установить, существует или не существует значение а,
при котором функция f непрерывна в точке хо, если:
( х sin (1/х), х Ф О,
a,
х = 0, х0 = 0.
2) f (x) =
a,
3) f (Х) = {
COS X,
4) f(x) =
1),
х — — 1,
, х > 0,
х < 0,
xsjCO,
х > О,
x0= —1,
x0 = O.
х0 = 0.
10.20. Установить, существуют или не существуют значения
а и Ь, при которых функция f непрерывна на своей области
определения, если:
г U -1)3,
1) f(x) = < ax + b,
х^О,
0<х< 1,
х^ 1.
Ь, |х|>1.
X,
2) f(4 =
3) f(x) = 2
(х-1)2
X2- 1 ’
а,
Ь,
х cos (х/2)
sin х
а,
Ь,
X — 1.
x — 0.
Зя
2
4) / W = <
2
если функция
монотонна, то всякая ее
10.21. Доказать, что
точка разрыва является точкой разрыва 1-го рода.
10.22. Доказать, что функция
( 1, если х — рациональное число,
f (*) = ) А
tO, если х — иррациональное число,
разрывна в каждой точке.
270
10.23. Доказать, что функция
( х, если х — рациональное число,
1 (О, если х — иррациональное число,
непрерывна в точке х — 0 и разрывна в остальных точках.
3. Свойства функций, непрерывных в точке. Если функции /
и g непрерывны в точке хо, то в некоторой окрестности этой
точки определены функции cf (с — постоянное), f + g, fg и они
непрерывны в точке х0. Если, кроме того, g(xo)=AO, то в неко-
торой окрестности точки х0 определена функция f/g и она не-
прерывна в точке xq.
Если функция у = g(x) непрерывна в точке х0, а функция
f(y) непрерывна в точке go = g(x0), то в некоторой окрестности
точки л'с определена композиция f(g(x)) и она непрерывна
в точке Хо.
Из этих свойств следует, что знак предела можно перестав-
лять со знаком непрерывной функции, и следует также правило
замены переменной при вычислении предела (см. § 9).
10.24. Доказать непрерывность функции в каждой точке ее
области определения:
1) У ==3х5 + ~. 2) g = shx. 3) у = '\/х2 — 6х3.
4) У = z/= cos (х —— д/1 — х2 )•
6) 1/ — xe(sin
10.25. Исследовать на непрерывность функции f(g(x))
g(f(x)) в точках, где определены эти композиции, если:
1) f(x) = signx,
2) f(x) = signx,
3) f (х) = sign (х — 1),
4) f(x) = signx,
10.26. Доказать, что
точке функция.
10.27. Доказать, что функция
и
g- (х) = 1 + х2.
g (Х) = х3 — х.
g (х) = sign (х ф- 1).
g(x)= 1 ф-х —£(х).
многочлен — непрерывная в каждой
_ Р (х)
Q (х) ’
У
где Р и Q — ненулевые многочлены, непрерывна в каждой точке
хс, где Q(x0) 0.
10.28. 1) Функция f непрерывна в точке х0, а функция g
разрывна в точке х0. Доказать, что функция f + g разрывна
в этой точке.
271
2) Привести пример разрывных в точке хо функций f и g,
сумма которых: а) разрывна в точке хс; б) непрерывна в точке хп.
10.29. 1) Привести пример непрерывной в точке х0 функции
f и разрывной в точке х0 функции g, произведение которых:
а) разрывно в точке х0; б) непрерывно в точке х0.
2) Привести пример разрывных в точке х0 функций f и g,
произведение которых: а) разрывно в точке х0; б) непрерывно
в точке хо.
10.30. Привести пример непрерывных в точке х0 функций f
и g, частное f/g которых разрывно в точке хо.
10.31. Доказать правило замены переменной для пределов
непрерывных функций: пусть функция y — g(x) непрерывна
в точке хо, а функция f(y) непрерывна в точке уо = £(х0); тогда
lim /(cr(x))= lim f(y).
10.32. Доказать перестановочность знака предела и знака
непрерывной функции. Пусть для функции у = g(x) существует
предел lim g (х) = у0, а функция f(y) непрерывна в точке у0;
Х->Хо
тогда в некоторой окрестности точки хо, исключая, быть может,
саму эту точку, определена композиция f(g(x)) и существует
lim f (g (х)) = f (lim g (x)) = f (z/0).
X->X,. X->Xo
4. Свойства функций, непрерывных на отрезке. Функцию на-
зывают непрерывной на отрезке [a;fe], если она непрерывна
в каждой точке интервала (а; Ь) и непрерывна в точке а справа
и в точке b — слева.
Пусть функция определена и непрерывна на отрезке [а; Ь\.
Тогда эта функция
1) ограничена на [а;&];
2) достигает на [а; Ь] своих верхней и нижней граней, т. е.
существуют хц х2 е [а\ Ь] такие, что
f (х,) = sup f (х), f (х2) = inf f (х)
[я; b] [а; д]
(теоремы Вейерштрасса).
Пусть функция определена и непрерывна на отрезке [а; 6].
Тогда для любого числа С, заключенного между f(a) и f(b),
найдется точка такая, что f(^)—C (теорема о про-
межуточных значениях).
Пусть функция f определена, строго возрастает (убывает) и
непрерывна на отрезке [а;&]. Тогда она имеет обратную функ-
цию, которая определена, строго возрастает (убывает) и непре-
рывна на отрезке [f(a)\ f(fe)] (соответственно [f(b)\ /(а)]) (тео-
рема о непрерывности обратной функции).
Пусть функция f определена, строго возрастает (убывает)!
и непрерывна на интервале (я; 6), и пусть
с= lim / (х), d= lim f(x).
2 72
Тогда опа имеет обратную функцию, которая определена, строго
возрастает (убывает) и непрерывна на интервале (с; </) (соот-
ветственно (^; с)).
При этом, если а =—оо, то под пределом lim /(х) по-
Х->- оо + о
нимают lim f(x), а если b — +°о, то под пределом lim f (х)
Х->-оо Х-> + оо—О
— предел lim f (х).
X + ОО
5. Непрерывность функции, заданной параметрически. Пусть
функции ср(/) и ф(/) определены и непрерывны на интервале
(а; ₽) и функция ф(7) строго монотонна на (а;Р). Тогда си-
стема уравнений
х = ф(0, */ = Ф(0
определяет единственную и непрерывную функцию
у(х)= 1р(ф-'(х))
на интервале (а; Ь), где
а = lim ф(/), b = lim ф(/).
t —> и+О t —> (3 — fi
6. Непрерывность элементарных функций. Все основные эле-
ментарные функции: постоянная, показательная, логарифмиче-
ская, степенная, тригонометрические, обратные тригонометриче-
ские непрерывны на своих областях определения.
Пример 5. Пусть функция f определена и непрерывна на
отрезке inf f, М — sup f.Доказать, что для любого
сг,Ь\ \a\b\
С^[т\М] найдется g <= [а; Ь] такое, что f(g) — С.
/\ По первой теореме Вейерштрасса функция f ограничена
на [a; Ь], поэтому ее верхняя и нижняя грани — числа, и имеет
смысл говорить об отрезке [т;7И]3 По второй теореме Вейер-
штрасса существуют х{,х-> е [а\ Ь} такие, что f(xi) = m, f(x2) =
= М. Допустим, что х\ < х2. По теореме о промежуточных
значениях на отрезке [хг, х2] найдется число g такое, что
f(£) = С, Если Xi > х2, го теорему о промежуточных значениях
следует применить к отрезку [x2;xi]. Если же Xi = х2, го
т — М, a f — постоянная, и в этом случае утверждение оче-
видно. ▲
Пример 6. Пусть а>\, 6>1. Доказать, что уравнение
ау + Ьу = х (8)
задает единственную непрерывную функцию z/(x), определен-
ную на (0; Н~оо).
Л Функции ау и Ьу строго возрастают и непрерывны па R.
Значит, и их сумма строго возрастает и непрерывна на R.
Кроме того,
lim (ay-\-by) — Q, lim (ау + by) = + оо.
//->-оо Z/->4-oo
273
В силу этого по второй из указанных теорем о непрерывности
обратной функции существует функция, обратная к функции
ау _р уу> определенная, строго возрастающая и непре-
рывная на (0;+°о). Этот результат можно выразить и иначе:
уравнение (8) для любого х > 0 имеет
и притом единственное решение у, не-
прерывно зависящее от х и строго воз-
растающее с ростом х.
Пример 7. Доказать, что после-
довательность, заданная рекуррент-
ным способом:
Xi = 0, Л'/г+i = COS Хп, rt GE N,
А Очевидно, х2 и все
сходится и ее предел является реше-
нием уравнения х = cosx.
члены с большими номерами удовле-
творяют условию 0<xrt^l, /геМ, т. е. данная последова-
тельность ограничена (рис. 59). При п 3 преобразуем раз-
ность
х„,1 ~ x,i 1 = cos хп — cos х„__2 = — 2 sin .Ап.Т Л^.т2... sin
fL 1 IL 1 IL IL L i1
Поскольку
имеем
*П 4~ ХП — 2
2
1,
О
sin +/» Л > о, sign (sin Л” 2 ) = sign (%n _ х„_2).
Следовательно,
sign (.v„+1 — х„_() = — sign (хп — хп_2)
при п^З, а при п^4
sign (х„+)-х„_()=— (— sign х„_3)) = sign (хп_, — х„_3). (9)
Рассмотрим подпоследовательность {x2/e-i} с нечетными номе-
рами. Имеем
Хз = COS х2 = cos cos 0 = cos 1 > О,
т. е. Хз >rxi. Отсюда и из (9) по принципу математической
индукции следует, что {x2/?-i} —возрастающая последователь-
ность: х2/с+1 > x.‘2k-i, Для подпоследовательности с чет-
ными номерами {x2k} имеем
Х4 = cos Хз = cos cos 1 < 1,
т. е. х4 < х2; отсюда и из (9) заключаем, что {х2Д—убываю-
щая последовательность. Таким образом, подпоследовательности
{х2Л_1} и {х2/г} ограничены и монотонны, следовательно, они
сходятся. Обозначим
lim x2k_x = a, lim x2k — b.
k->OQ
274
Из равенства x<^k — cos х2*-ь в силу непрерывности
функции cos х следует, что
Z?= lim x2k = lim cos x2k_x = cos (lim x^_1) = cos<i,
fe->oo &->OO £->oo
я из равенства x2fe+i = cosx2/?, k e N, следует, что
a = lim cos x2k = cos ( lim x2k) = cos by
k->oo /г->оо
т. e.
b = cos a, a — cosb. (10)
Заметим, что поскольку 0 xn 1, n e N, то и 0 a 1,
Из соотношений (10) для разности а — b имеем
1 1 • а — b . а 4- b
а — Ь~ cos b — cos а = 2 sin —-— sm —.
Учитывая, что 0 (а + b)/2 1, а следовательно,
0 sin —-— sin 1
и что
получаем
| а — Ь | | а — b | - sin 1.
Это возможно лишь, когда |а — b | = 0, т. е. а = Ь. Итак, обе
подпоследовательности {x2aJ и {xzk_\} сходятся к одному и тому
же пределу ау значит, и вся последовательность {хп} сходится
к этому пределу. Из (10) и того, что а = Ьу вытекает, что этот
предел является решением уравнения а = cos а. А
10.33. Исходя из непрерывности показательной функции, до-
казать непрерывность гиперболических функций:
1) y==chx. 2) у = th х. 3) ^ = cthx.
10.34. Исходя из непрерывности показательной функции, до-
казать непрерывность логарифмической функции z/ = logax,
а >> 0, а #= 1.
10.35. Исходя из непрерывности тригонометрических функ-
ций, доказать непрерывность обратных тригонометрических
функций:
1) у = arcsin х. 2) у = arccos х, 3) у = arctg х. 4) у —
= arcctg х.
10.36. Исходя из непрерывности показательной функции, до-
казать непрерывность степенной функции у = х^ (х >0, р.е
e=R).
10.37. Доказать, что если # = f(x)— непрерывная функция,
то непрерывны и функции у = | f (х) |, у = f (|х|).
275
10.38. Пусть f — непрерывная на
Доказать, что функции
0>
( 0,
f~ W==={ f(x),
промежутке X функция.
если
если
если
если
f(x) > О,
f(x)>0,
f М < о,
непрерывны на промежутке X.
10.39. Привести пример функции, непрерывной на каждом из
промежутков Xi и Х2, но не являющейся непрерывной на мно-
жестве Х\ U ^2-
10.40. Привести пример непрерывной на интервале функции:
1) неограниченной на этом интервале; 2) ограниченной на этом
интервале, но не достигающей ни своей верхней, ни нижней
грани.
10.41. 1) Функция f определена и непрерывна на отрезке
[а;/?], и все ее значения положительны. Доказать, что суще-
ствует число ц>0 такое, что для любого
2) Привести пример функции f, непрерывной на интервале
(a;fe), принимающей лишь положительные значения и такой,
что для любого р > 0 найдется значение /'(%) < ц, х^(а\ Ь).
3) Привести пример функции f, определенной на отрезке
[а; Ь], принимающей лишь положительные значения и такой,
что для любого ц > 0 найдется значение функции ?(x)<Zia,
л (а; Ь).
10.42. Функция f непрерывна на интервале {а; Ь),
т = inf Д М = sup f.
(а; b) (а; Ь)
Доказать, что для любого z/e(m;7W) существует х^(а\Ь), та-
кое, что f(x) = у.
10.43. Доказать, что если функция определена и непрерывна
на отрезке, то множество ее значений — отрезок.
10.44. Привести пример разрывной функции, определенной
на отрезке и имеющей в качестве множества значений отрезок.
10.45. Привести пример непрерывной функции, которая при-
нимает значения, равные 1 и 3, но не принимает значения 2.
10.46. Пусть функция определена и монотонна на проме-
жутке и множество ее значений — промежуток. Доказать, чго
эта функция непрерывна.
10.47. Доказать, что уравнение х5 — Зх — 1: 1) имеет хотя бы
один корень на (1; 2); 2) имеет не менее трех корней на R.
10.48. 1) Доказать, что любой многочлен нечетной степени
имеет хотя бы один действительный корень.
2) Доказать, что если многочлен четной степени принимает
хотя бы одно значение, противоположное по знаку коэффи-
циенту старшего члена, то он имеет не менее двух дейсгвитель*
ных корней.
276
10.49. Доказать, что уравнение х = у— esini/, где 0<8^
1, задает одну непрерывную функцию у = f(x).
10.50. Доказать, что разрывная функция r/ = e,x|signx имеет
непрерывную обратную.
10.51. Доказать, что данная система уравнений определяет
непрерывную функцию у(х) или х(у); построить график этой
функции:
1) х = arctg/, z/ = yX_.
2) х = ch t, у — sh t.
3) x = ln(l +e-'), z/= In(1 +e').
10.52. Доказать, что система уравнений
х =
/2- 1
/2+ 1
2/
У 2t
определяет две непрерывные на R функции х(у) и четыре не-
прерывные на множестве {х: |х|^ 1} функции у(х).
10.53. Пусть функция f определена в окрестности точки xq.
Будет ли функция f непрерывной в точке х0> если:
1) Зе > O36 > 0ух (| х — х01 < б => | f (%) — f (х0) | < е).
2) уб> 03е> 0ух(|х —х0| < б => |/(х) — f(x0)| < е).
3) V8 > 036 > 0Vx( |f (х) - f (х0) | < 8=>| х - х01 < б).
4) V6 > Озе > 0yx( \f (х) - f (х0) | < е=>[ х - х0| < б).
5) 38 > 0V6 > 0ух ( I х — х0 ] < б => | f (х) — / (х0) | < 8)?
10.54. Функция f определена в окрестности точки Хо, и суще-
ствует последовательность {еп} такая, что еп >0, n е N,
Нт ъп — 0 и для каждого существует бЛ > 0 такое, что если
П-»оо
xefl(f) и |х— л'о|<бп, то |/(х)— f(x0) |< еп. Доказать, что
функция f непрерывна в точке Хо-
10.55. Функция f непрерывна в точке х0. Пусть
S (6) = sup f, s(6) = inf t.
(xP-6: Xo+6) Un-6; Xo+6)
Доказать, что lim (S (6) — s (6)) — 0.
10.56. Указать множество точек, в которых непрерывна функ-
ция, найти ее точки разрыва, установить их род, нарисовать
график функции:
х2 + 2,
х — 1,
х < 0,
х > 0.
2)
1 —- х3, х < 0,
(х — I)3, о х 2,
4 —х, 2 < х.
У =
3) у = |
— 1/х, х < 0,
5х — х1, х 0.
х :С — 1
4) // =
2/(х— 1), х> — 1.
277
{cosx, —л/2 x < л/4,
1, х = л/4,
х2 — л2/1б, л/4 < х л.
Найти точки разрыва функции, установить их род, доопре-
делить функцию по непрерывности в точках устранимого раз-
рыва (10.57—10.59):
10.57. 1) //= ~г~—2) у = —3—Л—г--
7 J х2 + х — 6 7 J х3 ~ Зх2 — 4х
О\ 1 Л\ 1 Ч- X
3) У = 1^==- 4) У= —— •
Vx3 — 1 1 + х3
1 1
X х+1 р. 2х — 1 1 — д/ х
°) У~ 1 1 ' • У ~• 2х2 + Зх — 2 • 7) У ~ - 1
X — 1 X
10.58. 1) У = -~^- 2) г/= (sin %) sin (1/х).
arcsin х cos (пх/2) sin Зх
3> У^-^Г- 4) g = • 5) У = -^.
10.59. I) у =Т^2Г. 2)^/==^. 3) z/ = lg(x2 + 3x).
4) # = lg(x—I)2. 5) у = 21'х. 6) y = ! । •
7) у = 3%/(l-%2). 8) у — 9) у = In In(1 + ^2)-
10.60. Найти точки разрыва функции, установить их род,
найти скачки в точках разрыва 1-го рода:
1) // = sign(x2— 2х— 3). 2) у = sign cosx. 3) z/ = (—1)£(Ч
4) У = (—1)£ (1/х). 5) у = arcsin (1/х). 6) у = arctg (1/х).
7) у = arcctg (1/х2). 8) у~—“г~лтт~г- 9) у = —.
7 J & \ / 7 arctg (1/х) 7 J arctg х
i ах __ 1 in— 3l/x +21/% 1 о\ — 1 1 1 + х
Ю) V— • 11) У — 3i/x_2i/x * I2) 1н 1 __ .
10.61. Доказать, что функция непрерывна в каждой точке
своей области определения:
1) у = sin (х — 1g (д/х — 1)). 2) г/ = х2 — 4 ctg х 2tg (Я/Х).
х~5/3 — COS V*
3) У = ------—
7 tg arcsin I х I
278
10.62. При каком значении а функция у(х) будет непре-
рывна, если:
1) У = \ ’ X L a, x = 0, n e N.
2) U = \ ( xctg2x, x ф 0, | x | < л/2, a, x = 0.
3) u = \ ( (л + 2x) tg x, —л < x < л/2, x^—л/2, [a, x = — л/2.
4) y = y (arcsin x) ctg x, x 0, [ ц, x = 0.
5) y = < ( cx — 1 , n i x 0, 1 X I x = 0, 0 < c.
6) y = < f ’in (1+2.Г)"’ X=^°’ I a, x = 0.
7) y = < ( sh x , n z i 9 , ъ x 0, । xlnx“, x 0, 8) y===\ a x-0 la, л: = 0. a’ x 9-
9) y = < r e x o, ( (1 + xY''x, x 0, ! _ io) z/ = < (a, x — 0. 7 J (a, x = 0?
10.63. Можно ли доопределить функцию в точке разрыва х&
так, чтобы она стала непрерывной в этой точке:
1) У = 4+т7Г хо = °- 2) г/ = 2’2',(1 Х>, х0=1.
Л | Л j
о\ 1 1 1 г\ я \ ^h (д/X — 1) .
3) У — *о = °- 4) у =--------, х0=1.
5) ^/ = 2-£<1/5 хо = 0?
10.64. Исследовать на непрерывность и построить график
функции /, если:
1) f(.r) = lim • 2) f(x) = lim ——.
/д->оо X -р * /;->оо 1 -j- X
3) f(x) = lim cos'1*. 4) f(x)= lim ————
/г->оо n->oo 1 + (2 Sin X)
5) /(*) = lim 6) f(.t)= lim
/1->оо n 4“ fl 1 -|“ xe
7) f (x) = lim Vl + x2n • 8) f (x) = lim (x arctg (n ctg ,v)).
П->оо П->оо
279
9)
f (x) =
lim
/_> 4 co
In (1 + ext)
In (1 + ef)
10) f(x) = lim (1 + x) th tx.
10.65. В каких точках непрерывна функция
( х1 2-— 1, х—иррациональное число,
У W 1 п з
< 0, х — рациональное число?
10.66. Пусть
( 0, х — иррациональное число,
У(х) I х = p/q, р е Z, 7 g N,
где p/q— несократимая дробь (эту функцию называют функ-
цией Римана). Доказать, что:
1) Эта функция непрерывна в каждой иррациональной точке.
2) Каждая рациональная точка является для данной функ-
ции точкой разрыва 1-го рода.
10.67. Исследовать на непрерывность функцию
( | х |, х — иррациональное число,
f W | 4- 1), х = p/q, р <= Z, q е N,
где p/q — несократимая дробь.
10.68. Исследовать на непрерывность композиции f ° g и g.°f,
если
/(х)=1~|х-1|,
( х, х — рациональное число,
g (х) = Л
ь < 2 — х, х — иррациональное число.
10.69. Функция f возрастает на отрезке [а; Ь] и разрывна
в точке х0^[а;6]. Функция g(x) монотонна на отрезке
1) Привести пример таких функций fug, что g(f(x)) непре-
рывна В Xq.
2) Доказать, что если g(x) строго монотонна в окрестности
точки f(xQ), то g(f(x)) разрывна в точке xQ.
10.70. Функция f непрерывна на отрезке [а;&]. Доказать,
что:
1) inf f= inf f. 2) sup f= sup f.
(a; b) [a; b] {a\ b) [a; b]
10.71. Функция f непрерывна на отрезке [a; 6]. Доказать,,
что функции т(х) и М(х) непрерывны на [а; Ь]:
1) m(x)=minf. 2) М(х) = max f.
[<?; х| |а; х\
10.72. Функция f непрерывна на промежутке [я; Ь), Дока-
зать, что функции т(х) и М(х) непрерывны на [а, Ь)}
1) m(x) = inf /. 2) /И(х)= sup/.
La; х) la; х)
*280
10.73. Функция f определена и ограничена на отрезке [cz; b}.
Доказать, что функции
т (х) — inf f и М (х) = sup /
'с; х) 1а; х)
непрерывны слева в каждой точке х е [а; Ь).
10.74. Пусть / и g— непрерывные на X функции. Доказать,
что функции М (х) и т(х) также непрерывны на X:
1) М(х)= max{f(x),g(x)}. 2) т(х) = min{/(x), g(x)}.
10.75. 1) Пусть f — непрерывная на X функция, a,
а < Ь. Доказать, что функция
f(a; b\ х) = s я,
если а f(x) Ь,
если f (х) < а,
если f (х) > Ь,
также непрерывна на X.
2) Пусть функция f определена на R. Доказать, что для
того, чтобы f была непрерывна на R, необходимо и достаточно,
чтобы для любого а > 0 функция f(—cz;cz;x), определенная
в 1), была непрерывна на R.
10.76. Функция f непрерывна на [cz; +°°), и существует ко-
нечный lim f(x). Доказать, что / ограничена на [а;+°°)-
Х->+°о
10.77. Функция f непрерывна на интервале (cz; b) (конечном
или бесконечном), и существуют конечные lim f (х) и limZ(x)..
х ->а х->Ь
Доказать, что функция f ограничена на (cz;fe).
10.78. 1) Доказать, что функция
I (Х+ 1)Li 'I 1 ’)5 : ф 0, |х|<2,
0, х = 0,
принимает все значения между f(—2) и /(2), но разрывна. По-
строить график этой функции.
2) Доказать, что функция
(sin (1/х), х =И= 0,
ZW — | x = Oj
принимает на любом отрезке [0; cz] все промежуточные значе-
ния между /(0) и f(cz), но не является непрерывной на [0; cz].
10.79. Функция f определена на отрезке [cz; &] и обладает
следующим свойством: для любых xi,x2e [cz;b] и для любого
числа С, лежащего между f(xi) и /(х2), существует точка
се (хь х2) такая, что f (%) = С.
1) Указать функцию, обладающую таким свойством, но не
являющуюся непрерывной на [cz; 6].
2) Доказать, что функция, обладающая указанным свой-
ством, не может иметь точек разрыва 1-го рода.
281
10.80. Доказать, что если функция определена и непрерывна
па промежутке, то множество ее значений — промежуток (т. е.
отрезок, или интервал, или полуинтервал).
10.81. Привести пример функции, непрерывной на интервале,
множеством значений которой является: 1) отрезок; 2) интер-
вал; 3) полуинтервал.
10.82. Пусть функция, определенная на отрезке [а;Ь], не-
прерывна и обратима. Доказать, что эта функция строго моно-
тонна па [а; Ь].
10.83. Доказать, что если функция определена и строго моно-
тонна на промежутке, то ее обратная функция непрерывна.
10.84. Привести пример функции f, непрерывной в точке х0,
имеющей обратную функцию, разрывную в точке у0 = Дл0).
10.85. Привести пример непрерывной, строго возрастающей
функции, обратная к которой разрывна.
10.86. Доказать, что ограниченная, выпуклая (см. за-
дачу 7.272) на интервале функция непрерывна па этом ин-
тервале.
10.87. Доказать, что данная система уравнений определяет
непрерывную функцию у(х) или х(у);
м Z - 1 * уг • t + 1 у-
2) х=-^(( — 4)е*, y = ^/t е*
t3 3) Л /2 + 1 ’ У /4 + 1 ’
10.88. Привести пример такой системы уравнений
Л-=ф(0, y =
в которой функции <р и ф необратимы, но которая определяет
единственную непрерывную функцию у(х).
10.89. Функция f непрерывна на интервале (я; 6). Доказать,
что для любых чисел Xi < х2 < ... < хп из (а; Ь) и любых
чисел
п
> 0, У аг = 1,
i-l
найдется число g, Xi хп, такое, что
i = l
10.90. Функция f определена на отрезке [а;Ь]. Для любого
отрезка [с; d], а < с < d < b, множество значений f(x), х
е [с; d], является отрезком. Следует ли отсюда непрерывность
функции f на \а\ ?
10.91. Функция f непрерывна и ограничена на интервале
(ц; +оо), и не имеет предела при х, стремящемся к -фоо.
282
Доказать, что найдется число а, для которого уравнение f (х) = а
имеет бесконечно много решений.
10.92. Функция f непрерывна на интервале (a; b), I = lim f (х),
х-> b
£ = lim f(x), L> l. Доказать, что для любого числа С, 1<.C<.L,
x-+b
уравнение
J * £ [ \ /^1
f(x) = С
в любой окрестности b имеет бесконечно много решений.
10.93. Функция f непрерывна и ограничена на промежутке
\а\ +оо). Доказать, что для любого числа Т найдется последо-
вательность {х/г} такая, что lim хп = + оо и
/г-> оо
lim (/ (хп -\-Т) — f (%„)) = 0.
ц-> ОО
10.94. Множество ДеК называют открытым, если каждая
точка из А имеет окрестность, принадлежащую Л. Точку х0 на-
зывают точкой прикосновения множества А, если в любой окре-
стности х0 имеется хотя бы одна точка из А. Множество назы-
вают замкнутым, если оно содержит все свои точки прикосно-
вения. Множество всех точек прикосновения множества А на-
зывают замыканием А и обозначают А.
Функция f непрерывна па отрезке [а; Ь], число С заключено
между f(a) и f(b), f(a) f(b). Доказать, что:
1) Каждое из множеств:
а), А = {х ^ (а; b): f (х) < С},
б) В = {х <= (а; &): f (х) > С}
открыто.
2) Множество {х^[а;&]: f(x)=C} имеет и наибольший
и наименьший элементы.
10.95. Пусть функция f непрерывна на R, AczE(f), f~i(A) =
= {х е R |f(x) е Л}. Доказать, что:
1) Если Л замкнуто, то и /-1(Л) замкнуто.
2) Если Л открыто, то и /-1(Л) открыто.
10.96. Множество В называют плотным в множестве А, если
замыкание В содержит Л, т. с. В zd Л. Пусть функция f непре-
рывна на X, множество Л плотно в X, f(X)—множество всех
значений функции f(x) при х^Х, f(A)—множество всех зна-
чений функции при х е Л. Доказать, что f(A) плотно в f(X).
10.97. 1) Существует ли непрерывное отображение: а) от-
резка на интервал; б) интервала на отрезок?
2) Построить взаимно однозначное отображение отрезка па
интервал.
10.98. 1) Доказать, что функция, определенная на R, не мо-
жет быть непрерывной во всех рациональных точках и разрыв-
ной во всех иррациональных.
283
2) Существует ли функция, непрерывная во всех рациональ-
ных точках отрезка [0: 1] и разрывная во всех его иррацио-
нальных точках?
10.99. Доказать, что уравнение х3— Зх2 + 6х—1 имеет един-
ственный корень; найти этот корень с точностью до 0,1.
10.100. Доказать, что уравнение х4 + Зх2 — х — 2 = 0 имеет
два (и не более) действительных корня.
10.101. Доказать, что уравнение
X a*x2ft+* + с = о,
где ак 0 (k = 0, 1, ..., п — 1), ап > 0, имеет лишь один дей-
ствительный корень.
10.102. Доказать, что уравнение хп = Рп-\(х), где Pn_i(x) —
многочлен (п—1)-й степени с положительными коэффициен-
тами, имеет единственный положительный корень.
10.103. Доказать, что:
1) Уравнение
-Ц- 4--4--------= °>
х — Л, х — л2 х — м
где а\ > 0, «2 > 0, > 0, М < Х2 < А3, имеет по одному дей-
ствительному корню в интервалах (Аг, А2) и (А2; А3).
2) Уравнение
где а}- > 0 (у = 1, 2, ..., п), Ai < А2 < ... < Ап, имеет по од-
ному действительному корню в интервалах (A,; A/+i) (/=1,
2, ..., п — 1).
10.104. Доказать, что уравнение имеет и притом единствен-
ное решение:
1) Х’2х = 1. 2) хех = 2.
3) х — еsinх + а, 0<е<1.
4) х2 arctg х = а, а 0.
10.105. Доказать, что уравнение x=asinx + &, где 0 <
< а < 1, b > 0, имеет по крайней мере один корень на
[0; а -|- Ь].
10.106. Доказать, что уравнение 10х”1 = х имеет только один
корень х0 ¥= 1.
10.107. Доказать, что уравнение 2х = 4х имеет по крайней
мере два действительных корня.
10.108. Доказать, что уравнение xsinx — 0,5 = 0 имеет бес-
конечно много решений.
10.109. 1) Доказать, что существует бесконечно много функ-
ций, определенных на (а; Ь) и удовлетворяющих уравнению
У2 — 1.
284
2) Пусть f — непрерывная и положительная на (а; Ь) функ-
ция. Доказать, что существует единственная непрерывная на
(а\Ь) функция = удовлетворяющая уравнению
r/2 = f(x)
,и условию, что ф (%о) > 0 в некоторой точке хое(а; Ь).
3) Сколько существует непрерывных на R функций, удовле-
творяющих уравнению у2 = (я2— I)2?
4) Сколько существует непрерывных на отрезке [0; п\, n^N,
функций, удовлетворяющих уравнению
у2 + 2у + cos2 лх = 0?
10.110. Доказать, что существует единственная непрерывная
функция у(х), удовлетворяющая уравнению
у = arcctg ху, xeR.
10.111. Найти все непрерывные на R функции f, удовлетво-
ряющие условию: для любого xeR верно равенство:
1) + 2) Щ) + №) = х.
3) f (ах) + f (Р%) = ах + bt оф Ф 0. 4) f (Зх) — f (2х) = х.
5) f (х2) + f (х) = х2 + х. 6) f (х2) — f (х) = х- — х.
10.112. Найти все непрерывные на R функции f такие, что
для любого хе R верно равенство
Af(ax) + Bf($x) = ах + 6,
где аа$АВ ф 0, Аа + В$ Ф 0, А + В ф 0.
10.113. При каких а существуют непрерывные на R функции
Д отличные от постоянной, такие, что для любого хе R:
1) f(x2 + a)=f(x). 2) f(ax2 + l) = f(x)?
10.114. При каких а, 6, с существует непрерывная на R функ-
ция f, отличная от постоянной, такая, что для любого хе R
f (ах2 + Ьх + с) = f (%)?
10.115. 1) Найти все непрерывные на R функции Д удовле-
творяющие для любых х,//ей равенству }(хфу) = f(x)-\-f(y).
2) Привести пример разрывной функции Д удовлетворяющей
для любых %, у е R равенству f (х + у) = f (х) f (у).
10.116. Найти все непрерывные на R функции, удовлетво-
ряющие для любых х, у е R равенству f(x ф у) — f(x) f (у).
10.117. Найти все непрерывные на (0;+°°) функции, удов-
летворяющие для любых х, у е(0; + °°) равенству:
I) = + 2) =
10.118. Найти все непрерывные на R функции, удовлетво-
ряющие для любых х, у е R равенству
1(хфу)Ф1(х-у)^21(х)1(у)
И условию: 1) f (х) 1. 2) f(x) 1.
285
10.119. Найти все непрерывные на R решения функциональ-
ного уравнения
J(x + /(x)) = f(x), xeeR.
10.120. Функция f определена и непрерывна на R, и для
любых х, у е R верно равенство
f (±тА)==4(^л')+^^-
Доказать, что f — линейная функция, т. е. существуют а и b
такие, что f(x) = ах + Ъ.
10.121. Доказать, что периодическая, непрерывная на всей
числовой оси функция, отличная от постоянной, имеет наимень-
ший положительный период. Привести пример периодической
функции, определенной на всей числовой оси и отличной от по-
стоянной, которая не имеет наименьшего положительного пе-
риода.
10.122. Пусть / и g—непрерывные, периодические с перио-
дом Т функции и lim (f (х) — g (х)) = 0. Доказать, что f — g,
10.123. Непрерывная функция / имеет два несоизмеримых
периода 1\ и Т2 (т. е. Т\/Т2 — иррациональное число). Доказать,
что f = const.
10.124. Построить непрерывные на R функции f и g такие,
что для любого 7>0 функции f(x-RT) и g(x) различны, но
для каждого 8 Z> 0 существует Тг > 0 такое, что для любого
х (= R верно неравенство
!/(% + Л) — g(x) I < е.
10.125. Пусть функция f непрерывна на [—1; 1] и |/(х) | <С 1,
[—1; 1]. Доказать, что функция
f (х) — cos (n arccos х), п N
(см. задачу 7.261) не менее п раз обращается в нуль на отрезке
1-1; Я-
10.126. Пусть Р(х) — 2п~1хп 4- а\хп~х ... R-ап. Доказать,
что найдется [—1: 1] такое, что |P(g) | 1.
10.127. Функция [ непрерывна на [0; 1], и f(0) = f(l) = 0.
Доказать, что существует непрерывная, выпуклая вверх (за-
дача 7.272) функция g такая, что g(0) = g(l) = 0 и g(x) f (х)
на [0; 1].
10.128. Функция f непрерывна и периодична с периодом Т.
Доказать, что есть такая точка хо, что
/ (*о+ -|-) =/(^о).
10.129. Функция f непрерывна, монотонна на [0; 1], и f(0) =
= 0, /(!)=!. Доказать, что если для некоторого neN при
любом х ее [0; 1 ]
fo/o. . _of(x) = X,
п раз
то и / (х) — х на [0; 1].
286
10.130. Пусть функция f непрерывна на [0; 1] и множество
ее значений содержится в [0;1]. Доказать, что существует
точка с е [0; 1] такая, что f(c)= с (всякое непрерывное отобра-
жение отрезка в себя имеет неподвижную точку).
10.131. Пусть f и g определены и непрерывны на отрезке
Ця; Ь] и f(a)<g(a) и f{b)>g(b). Доказать, что имеется
точка Ь) такая, что f(c) = g(c).
10.132. Функции f и g определены и непрерывны на [0; 1],
и jog — go f. Доказать, что существует точка се[0; 1] такая,
что f(c) = g\c).
10.133. Непрерывные функции f и g отображают отрезок
[[0; 1] на самого себя. Доказать, что существует точка се[0; 1]
такая, что f (g(c)) = g(f (с)).
10.134. Функция f непрерывна на R, и f(/(x)) = х для лю-
бого xeR. Доказать, что существует точка с, в которой
f(c)=C.
10.135. Привести пример функции: 1) непрерывной на интер-
вале (0; 1), 2) непрерывной на 1R, для которой уравнение
f(x) = х не имеет решений.
10.136. Функция f монотонна, непрерывна на [0; 1], и 0
^.f(x)^.! для любого х^[0;1]. Доказать, что для любого
(iiG [0; 1] последовательность — f , neN, сходится
к одному из решений уравнения f (х) — х.
10.137. Пусть функция f непрерывна на [а; 6], и пусть опре-
делена последовательность {хп} : хое[а;&], хп = f(xn-i), пеН
(т. е. для любого neN f(xn-i) е [а; Ь]). Доказать, что:
1) Если f возрастает, то {хп} — монотонная последователь-
ность и существует lim хп = с такой, что с — f(c).
гг-»оо
2) Если f убывает, то {x2k} и {х2/г—1} — монотонные подпо-
следовательности, имеющие пределы. Получить уравнения для
этих пределов.
10.138. Функция f строго возрастает, а функция g строго
убывает на [а; &], и Е (/) П £ (g) #= 0.
1) Доказать, что уравнение f(x) —g(x) имеет и притом
единственное решение.
2) Пусть хое[а;&] таково, что f(xo)e E(g), и для любого
neN уравнение g(xn) = f(x.?-i) имеет решение xfb т. е. опре-
делена последовательность {хп}. Доказать, что подпоследова-
тельности {x2/J и {x2k~1} сходятся, каждая к одному из реше-
ний уравнения g~l(f(x)) — f~l(g(x)).
10.139. Для последовательности {хД, заданной рекуррент-
ным способом: Xi = 1/2, xrt+i = f (хп), п ею N, где
6(2 — Зх)/5, х < - 1/6.
f(x) = < — Зх, |х|< 1/6,
I - (2 + Зх)/5, х > 1/6,
287
найти пределы подпоследовательностей {х^} и {x2£-i}. По-
строить график функции / и показать на рисунке построение
пяти первых членов последовательности.
Ш.140. Функция /, определенная на IR, удовлетворяет усло-
вию Липшица: существует k > 0 такое, что для любых Xi, X2^R
верно неравенство
—f(^) | А: |Xi — -х2|.
Доказать, что если k <Z 1, то существует и притом только одно
решение уравнения f (х) = х.
10.141. Множество значений функции f, определенной на
[а; Ь], содержится в [а; Ь]. Для любых х, у [а; Ь], х =# у, вер-
но неравенство
IfW—f(y) I < Ц — у\-
1) Доказать, что уравнение f(x) = x имеет и притом един-
ственное решение с.
2) Пусть Хо е [a; b], xn — f(Xn-i), hgN. Доказать, что:
а) последовательность {\хп— с|} убывает и имеет предел
lim | хп — с | — А;
/2->оо
б) существует подпоследовательность {xnAJ, сходящаяся к d,
равному либо с + А, либо с — А;
в) \f(d) — с| = А и А = 0, т. е. limxn = c.
П->оо
10.142. 1) Доказать, что уравнение tgx = a/x, а > 0, имеет
на каждом интервале (—у + лп), neN, одно ре-
шение.
2) Пусть Хп — решение уравнения tgx = a/x, а > 0, из ин-
тервала — у4-шг; у + лп^, л е N. Доказать, что
0 < хп — пп <-------..... , п N.
ли + V л2/?-2 + 4а
10.143. 1) Доказать, что уравнение
tgx = ах, а > 0,
имеет на каждом интервале^ —у + т; -у + яп) , ле N, одно
решение х«.
2) Пусть хп — решение уравнения tgx = ax, а > 0, из ин-
тервала —-у + лп, -у + шг), ncN. Доказать, что при всех
достаточно больших л g N
~ . л . . 2/а
0 < V + пп ~~ Хп <------------/7 ......-=7
z л , , ( л . V 4
- + ««+ + --
3) Найти lim (х„+1 — х„), где последовательность {л„} опре«
П->оо
делена в 1) и 2).
288
10.144. Для последовательности, заданной рекуррентным спо-
собом, доказать существование предела и найти его;
1) Xi е R, xn+l — sin хп, п е N.
2) х{ = 0, хп+1 ===== хп — sin хп + j, ne N.
3) Х|=-|, xn+l = xn + cosxn — rt<=N.
4) Xi <= R, xn+i = arctg xn, raeN.
5)Xi = 0, xn+l=xn — arctgxn + ~p neN.
6) Xi — 2, xn+l = 1 + In xn, n e N.
10.145. 1) Пусть limxre = oo. Доказать, что
Л->оо
lim (1 +^-Y"==e.
П->оо V '
2) Пусть lim xn = 0, xn ф 0. Доказать, что
lim (1 + = e.
П->оо
Q 10.146. Пусть tzi, a2, &i, b2 e R. Исследовать на сходимость по-?
следовательность
#2^ + Ь2 ) J
и найти ее предел, если он существует.
10.147. Используя непрерывность соответствующих функцищ
вычислить предел последовательности:
1) {П+'тг) ! где limx„=xe=R.
4 ™ J п->оо
2) | (cos + Л sin |, где х,Ле R.
3) {(Jk±A.)“}, гдс о>0’ 6>0-
4> {((‘ +1)(‘ +4)--- (' +¥•))“}•
МО+тЮ+^-О+Й}-
6) I COS-3- COS -g2- ... COS -^г j .
7) {sin2(л V«2 + »)}- 8) { п - } •
9) {п — ctg(l/n)}. 10) {(cos(x/Vn))"}.
10.148. Последовательности {an} и {&„} таковы, что 0<Jj
С ап < 1, lim ап = 1,0 < Ьп < л/2, cos bn — ап. Найти
10 л. Д. Кудрявцев и др.
289
§ 11. Асимптоты и графики функций
Использование понятия предела часто позволяет более точно
отразить свойства функции при построении ее графика. Перед
построением графика следует выяснить, имеет ли функция ле-
вые или правые пределы (конечные или бесконечные) в конце-
вых точках своей области определения и в точках разрыва. Если
функция имеет предел при х-+х0 (x->xo + O или — 0),
то иногда удается, используя метод выделения главной части,
установить «схожесть» ее графика в окрестности точки х0 с гра-
фиком более простой функции. Например, если lim f(x) = O
и если g (х) — главная часть функции при т. е.
fW = g(*) + o(gW), (1)
где lim g(x) = 0, то график функции f(x) «схож» с графиком
функции g(x) в окрестности ТОЧКИ Xq.
Если
lim f(x) = oo или lim f(x) = oo, (2)
х->хо-О я->хо+0
то прямую х = хо называют вертикальной асимптотой графика
функции f(x). Например, прямая х = 0 является вертикальной
асимптотой графиков функции 1/х (рис. 14 § 7) и 1пх, так как
lim(l/x) = oo и lim 1пх = —оо. График функции tgx имеет
х->0 х->+0
бесконечно много вертикальных асимптот, а именно, каждая
прямая х = у + лл, neZ, является асимптотой. Выделение
главной части бывает полезно и тогда, когда
lim f(x)“oo или lim f(x) = oo.
Если в этих случаях
f(x) = g(x)+’o(l)
при — 0 (или %->хо + О), то графцк функции f(x) «схож»
с графиком функции g(x).
Пример 1. Найти вертикальные асимптоты графика функ-
ции f и построить его, если:
1) f(x)=-7=^==.. 2) f(x)= 3)f(x) = 7^=b
VI — X2 V X
Д 1) Функция определена и непрерывна на интервале.
(—1; 1). Так как
lim —х2 = lim д/1—х2 = 0,
х->1-0 х->—1+0
ТО
lim = + оо и lim —7==^==== = оо,
Х + 1-OVl" X2 X-»~l+oVl~ х2
290
Следовательно, прямые х =—1 и х=1—вертикальные асим-
птоты графика.
Данная функция нечетная. Она строго возрастает на интер-
вале (0; 1). Действительно, если 0 < х < 1, то
fW-VS-V-ri?-!.
откуда и видно, что ори возрастании х от 0 до 1 функция
1/(1—х2), а вместе с ней и функция /(х) строго возрастают.
Отметим еще, что х/^/1 TF > х при х > 0. Для того чтобы
уточнить вид графика вблизи точки х =
= 0, выделим главную часть функции
при х->0. Так как
lim = lim — 1,
x->0 x x->0 Vi —x2
'TO f(x)/x = 1 +о(1)> откуда
f(x)=*x + o(x).
Это означает, что график данной функ-
ции вблизи х = 0 «похож» на график
функции g(x) = x (точки этих графиков,
соответствующие значению х, сближаются
по вертикали быстрее, чем х убывает).
График функции изображен на рис. 60.
2) Функция определена и непрерывна
Так как
на промежутке (0; 1].
lim Л/-—£ = + оо,
х->4-0 у X
то прямая х = 0 — вертикальная асимптота графика. Кроме
того,
/(х)= * . д/1 —X
Vx
И _____
lim -\J\ — х — 1.
Для разности f (х)---->=• имеем
поэтому
1 V1 — х — 1
Пс -у/ X
-^=±-7-^- = о<1),при х->0,
X
10*
291
Таким образом, функция 1/д/х является главной частью дан-
ной функции f(x) при х->-+0 и, более того, расстояние по вер-
тикали между точками графиков функций д/(1—х)/% и 1/д/х
стремится к нулю при х->+0. Как иногда говорят, график
функции 1/д/х является криволинейной асимптотой графика
данной
ство
функции (рис. 61). Используя равен-
и учитывая, что
получаем
lim -|=- = 1, при х-+-1 —О
Х->1 —О Vx
= 1 =1+0(1).
Vx
откуда
/ (х) = д/1 х + ° (V1 “ *)•
Рис. 61. Следовательно, график данной функции в ок-
рестности точки х=1 (х < 1) «схож»
с графиком более простой функции д/1—х (рис. 61). По-
скольку ____
f«=Vv-b
данная функция, очевидно, убывает на (0; 1].
3) Функция определена и непрерывна на промежутках
(—оо;—1] и [1;4-оо), значит, вертикальных асимптот ее гра-
фик не имеет. Функция четная. Рассмотрим ее на промежутке
(1; + оо). Здесь функция х4, а значит и функция д/х4 — 1,
строго возрастает. Используя формулу
f (X) = V(x+l)(x2+l)
и учитывая, что • ____________
lim V(x+1)(х2+1) =2,
' Х-»1+0
при х-> 1 + 0 получаем
f (х) = 77^1 (2 + о (1)) = 2 77^1 + о(7%- 1).
Следовательно, график данной функции в окрестности точки
х = 1 (х > 1) «схож» с графиком функции 2 7х — (рис. 62).
Кроме того, f(x) > 2 7* — 1 при х>1, т. е. при х->1+0
точки графика Данной функции приближаются сверху к гра-
фику функции у = 2 7х—!• Так как
292
что при х-^'-роо получаем
/(Х)_Х2 = Х2(д/ 1 -^г- 1) =
f(x) = x2±o(l).
откуда
При этом f(x)<Zx2, т. е. точки
ближаются к параболе у =
= х2 снизу (рис. 62). Л
Прямую у = kx + Ь на-
зывают асимптотой графи-
ка функции r/ = f(x),
^(^;4-до), при х->+оо,
если
lim (f (х) — (kx + &)) = 0.
#->4-00
(3)
Прямую у = kx + b на-
зывают асимптотой графика
функции y=f(x),- xg(—оо; а),
при х—*—оо, если
•lim (f (%) — (kx 4- b)) = 0.
Л->-оо
(4)
графика данной функции при-
Рис. 62.
Если й#=0, то асимптоту у = йх + & называют наклонной.
Если k — 0, то асимптоту у *=Ь называют горизонтальной.
Для того чтобы прямая у = kx + Ь была асимптотой гра-
фика функции y = f(x) при х-^+°° (ПРИ —°°)> необхо-
димо и достаточно, чтобы
1- f(x) .
lim ^-^- = k
Х->4-оо х
lim (f(x) — kx) — b
X-»4-oo
Г lim -Hi! _= /Л,
'X->-oo X '
( lim (f(x) — kx) = b).
(5)
(6)
В случае горизонтальной асимптоты (k = 0) вместо (5) и (6)
имеем: для того чтобы прямая у = b была горизонтальной
асимптотой графика функции у — f(x) при х->Д-оо (при
—оо), необходимо и достаточно, чтобы
lim f(x) = b ( lim f(x)=*b). (7)
X->4-oo X-> — oo
Примерами функций, графики которых имеют горизонталь-
ные асимптоты, являются функции arctg х и arcctg х (рис. 42
и 43 § 7). График функции arctg х имеет горизонтальную асймп?
тоту у = п/2 при х->4-оо и горизонтальную асимптоту у
=== —л/2 при х—^—оо.
293
Пример 2. Найти 'асимптоты графика функции f и по*
строить его, если:
'>№>=W' 2)fW = ^.
Л 1) Поскольку
lim
Х->°°
6(х2 — 4)
'зх2 + 5
= 2,
прямая у = 2 является горизонтальной асимптотой графика
и при и при —оо. Функция непрерывна на R, сле-
довательно, вертикаль*
ных асимптот ее гра-
фик не имеет. Данная
функция четная. Из ра-
венства
f(x) = 2 —
40
Зх2 + 8
следует, что на (0;.4-оо)
с ростом х значения
функции строго возрас-
тают. Из этого же ра-
венства видно, что точки графика функции приближаются при
х—>оо к прямой у = 2 снизу (f(x)<2 для любого xeR). При
х = 0 функция принимает наименьшее значение f (0) = —3. Для
того чтобы уточнить вид графика вблизи точки х = 0, предста-
вим функцию в виде
н . 3 (5х2 - (Зх2 + 8)) _ 15х2
/ W Зх2 8 Зх2 + 8 d
и воспользуемся тем, что при х->0
-dTT-4 + oW. “>» '>»• (8)
Последнее равенство доказывается легко:
х2_____х2 _______ах4 __________ах2 2
ах2 + b b Ъ (ах2 + b) b (ах2 + Ь) Х ’
।ах2 /у ах2 п г
и так как 1пт. ъ =* 0, то тх2 = о(х2), откуда
и следует (8).
Используя (8) при а — 3, b = 8, получаем равенство
f (х) == х2 — 3 + о (х2),
которое означает, что при х->0 график данной функции «схож»
с параболой у^~х2 — 3. График представлен на рис. 63.
294
2) Функция определена всюду, кроме точки х — 0. Поскольку
.. Vi + х2 I 1 • Vi + х2
11т _2 !--— +оо, 11Ш ——~ = —оо,
х->4-0 х х-»-0 х
прямая х = 0— вертикальная асимптота графика. Далее,
Пт Нт
X -> + оо Х X — ОО Х
поэтому у = 1 —горизонтальная асимптота при х->- 4-°°, а у =
g= —1 — горизонтальная асимптота, при х~*—оо. Поскольку
j^l+x2/x|> 1 при х =# О, точки графика при x-^-J-oo при-
ближаются сверху к прямой г/= 1, а при х->—оо—снизу
к прямой у — —1. Данная функция нечетная. Если х > О, то
Г ?W = V^+1-
поэтому с ростом х от 0 до 4“00 значения f(x) строго убывают
от +°о до 1. График функции показан на рис. 64. А.
Пример 3. Найти все асимптоты графика функции /(х)
и построить его, если:
I 1) 2>
3) fU) = 3 д/4- ’•
Д 1) Функция определена и непрерывна всюду, кроме х=1,
и
.. х2 — 2х . «. х2 — 2х
11Ш -----— — 4-00, 11Ш -----*- = — оо,
х->1-0 х 1 х->14-0 х 1
295
следовательно, график имеет только одну вертикальную асимп-
тоту X = 1. Поскольку
х2 — 2х 1 1
-----— = X — 1------г ,
X — 1 х — 1
(9)
прямая у — х—1 является, очевидно, наклонной асимптотой
графика и при и ПРИ —°°- При х>1 функции
х—1 и —1/(х—1) строго возрастают, значит, и их сумма,
т. е. данная функция, строго возрастает. Аналогично, при х < 1
данная функция строго возрастает. Из (9) видно, что при
х—>+°° точки графика приближаются к асимптоте снизу
(/(%)< х—1), а при х->—оо — сверху. График показан на
рис. 65.
2) Функция определена и непрерывна во всех точках, кроме
х = 0, и
г л/4х4 + 1 .
hm ^-- = + 00,
х->0 I х I
т. е. х = 0 — вертикальная асимптота графика. Выясним, есть
ли асимптоты при х->оо. Находим (см. формулы (5) и (6))
1
Д/4 +Д-*2 при Х->+оо.
f (х\_2х = 1 — 2x2 =------!------> О
Г(Х) - х (УЗх^ТТ + 2х2) U
при
X
Значит, у = 2х— наклонная асимптота графика при х->4-оо,
причем f(x)>2x, т. е. точки графика при х->4-оо прибли-
жаются к асимптоте сверху. Далее,
lim = Hm (— аД + -Д) = — 2,
—оо х —оо XV Л ✓
— У4х4 + 1 + 2х2
X
lim (/ (%) + 2х) — lim
Х->-оо Х-»-оо
lim —7------------7-_ . = 0.
->-00 х (2х2 + дМх4 + 1)
значит, у — —2х— наклонная асимптота при х~*—оо. Отме-
тим, что f(x)>—2х, т. е. точки графика при х->—оо прибли-
жаются к асимптоте у — —2х сверху. Теперь исследуем функ-
цию на монотонность. Поскольку
Н«> = У^ = У4*2+^>У2У4*!'^=2-
причем знак равенства имеет место лишь при 4х2 = 1 /х2, т. е.
при х=±1/У2, значение функции f(l/y2)==2 является
наименьшим на интервале (0;-}-оо), На интервале (0; 1/У2)
296
функция строго убывает, так как если 0 < xt < х2 < 1/д/2, т0
2 _ 2 Л 2 2__ 1
f2 (*2) —’ f2 (Xl) = 4 (Х2 — Х1) 2 2 — (Х2 — ХТ) < °"
Л1Л2
Аналогично доказывается, что на интервале (1/д/2; + оо)
функция строго возрастает. Функция четная. График ее изобра-
жен на рис. 66.
3) Функция определена и непрерывна при |х| 2, значит,
вертикальных асимптот не имеет. Функция четная, рассмотрим
ее при х 2. Здесь функция строго возрастает. Используя ра-
венство
f(x) = y V% + 2 V% — 2
и учитывая, что
Пт л/х + 2 = 2,
Х->2 ‘
при х->2 находим
f (х) = 3 V* —2 + о (Vx - 2),
т. е. график данной функции «схож» с графиком функции
у = 3 Vх ~ 2 (рис. 67). Находим последовательно пределы
(формулы (5) и (6))
!im lim i^=|,
X->-f-oo Л Х-» + оо л
lim (f (%) — — х) = — lim —7...-------= 0;
х-»4-оо \ 2 / 2 х->+°° д/х2 — 4 -р х
отсюда следует, чт<х график имеет наклонную асимптоту у —
= Зх/2 (рис. 67). График данной функции, изображенный на
297
рис. 67, является частью гиперболы, заданной уравнением
*2 У2 — у
другая часть гиперболы изображена на этом рисунке штрих-
пунктирной линией. А
При построении кривых, заданных параметрически, также
используется понятие асимптоты.
Прямую х = х0 называют вертикальной асимптотой кривой
x = x(t), y = y(t), (Ю)
если существует такое а (число, 4-°° или —оо), что
limx(/) = %0, lim у (f) = oo, /->a (11)
или lim x(t) = x0, lim y(f) — oo, (12)
t -> a-Y 0
или Jim x(/) = x0, lim y(t)==eo. (13)
Прямую у = b называют горизонтальной асимптотой кривой
х = х(/), у — y(t) при х->+°°» если существует такое а
(число, +оо или —оо), что
lim x(t) = + oo, i~>a lim y(t) = b, t->a (14)
или lim x(t) = oo, lim y(f) = b, (15)
i-+a-0 i-^a-0
или lim x(/) = + oo, i -> о 4-0 lim y(t) = b. t-^ £Z + 0 (16)
Прямую у = kx + b, k #= 0, называют наклонной асимпто-
той кривой x = x(t), y — y(t) при х->+°°, если существует
такое а (число, 4-оо или —оо), что
lim x(t) = + оо, limz/(/) = oo, (17)
Нт|^- = Л, (18)
lim(y(t)-kx(t)) = b, (19)
i -> а
или условия (17) —(19) выполнены при t-+a — 0,
или условия (17) — (19) выполнены при +
Аналогично даются определения асимптот при х-=>—оо,
П р и м е р 4. Найти все асимптоты кривой
t2 — 2/ V<4+ 1
х - t У-—г-
построить эту кривую.
298
'Л Функции x(t) и y(t) определены для всех значений t,
кроме t-О и t = l. Находим пределы этих функций при
оо, /->4-°°, а также левые и правые пределы в точках
у = 0и/=1:
1) lim х(/) =—оо,
/-> —оо
2) lim x(t) =—О,
/->-0
lim х (/.) — 4-0,
/->+0
3) lim x(t) = 4-00,
о
lim x(t) =—oo,
/->1+0
4) lim x(/) = 4-oo,
/->4-00
lim #(/) =—oo.
/-> —oo
lim y(t) = — oo;
/->—о
lim у (t) = +o°.
f->+0
lim y(t) = ^2 +0;
/->1-0
lim //(/) = + 0.
/->14-0
lim у (t) = + oo.
/->4-00
Из 2) следует, что прямая х = 0 — вертикальная асимптота
кривой, причем кривая при у-^>—оо приближается к асимптоте
• слева (х(/)<0); а при —
y\t-~+o справа (%(/)> 0) (рис. 68). Из 3) за-
\ ключаем, что прямая у = ^2— гори-
\ зонтальная асимптота кривой и при
\ х—^—оо, и при причем
Рис. 69.
Рис. 68.
в обоих случаях кривая приближается к асимптоте сверху
(рис. 69). В случаях 1) и 4) исследуем, имеет ли кривая на-
клонные асимптоты. Находим (см. (18) и (19))
Д±ооХ« /"Too ^(/-2)
lim (y(t)—х(0)
= lim
, .= lim ( , ,... * =——г4”Д—1=1.
t t-lj /->±ooM(V<44-1+<2) i—lJ
Следовательно, кривая имеет асимптоту у = х 4-1 и при -
—оо, и при х->4-о°. Так как
у (/) — X (t) — 1 =----------!-----1---......../,-------г- ,
t— i t (i/t* 4-1 4- /2)
299
то y(t)—x(t)—1->—0 при —оо (соответственно
—оо) и y(t)— x(t)—1-^+0 при t-+--\-oo (соответственно
х(0“>+°°)* Поэтому при х-+—оо кривая приближается
к асимптоте снизу, а при х->4-оо — сверху (рис. 70). Таким об-
разом, кривая имеет вертикальную асимптоту х = 0, горизон-
тальную асимптоту //—д/2 и наклонную асимптоту =
(и при х->+°°, и при х-*----оо). Изобразим в одной системе
координат графики данных функций х(/) и y(t). Первый из них
был построен в примере 3, 1) (рис. 65), второй строится так же>
как в примере 3, 2), отличие лишь в том, что данная функция
y(t) — нечетная. На рис. 71 первый график изображен сплошной
линией, второй — штрих-пунктирной. Используя оба эти гра-
фика и учитывая предыдущее исследование асимптот, можно
представить себе движение точки (%(£); //(/)), говоря языком
механики, в плоскости хОу при изменении t от —оо до +°°«
Проведем в плоскости хОу асимптоты прямые у = х + 1 и
у = ^1^л Рассмотрим три промежутка оси /: (—оо;0), (0; 1)^
!(1;+00)- При возрастании t от —оо до 0 значения x(t)
(рис. 71) строго возрастают от —оо до 0, значения y(t) сначала
возрастают от —оо, достигая максимума при t = —1 (z/(—1)=*
—д/2, *(—1) = —1,5), а затем убывают до —oo„ При
t—>—oo точка кривой (x(t) ',y(t)) приближается к асимптоте
у = % + 1 снизу (рис. 70), а при t-*—0 — к асимптоте х = 0
слева (рис. 68). Найдя несколько промежуточных точек, рисуем
эту часть кривой (рис. 72). На втором промежутке при возрас-
тании t от 0 до 1 значения x(t) возрастают от 0 до +оо, а зна*
чения y(t) убывают от 4-оо до д/2 (при t= 1 точка кривой не
определена, поэтому можно говорить лишь о пределах x(t) и y(t)
при /->1 ±0). Точка кривой движется в первом квадранте, пе-
реходя от асимптоты х = 0 (при /->+0) к асимптоте у =^2
(сверху) при —0. Наконец, при возрастании t от I до
'+оо значения x(t) возрастают от —оо до значения y(t)
300.
в § 21.
, что интер-
возрастают от л/2 до 4“О°. Эта часть кривой расположена
в 1-м и 2-м квадрантах, точка кривой движется, переходя от
асимптоты у—-л^2 (при Z->l+0) к асимптоте г/ = х-|-1
(сверху) при /->+оо. С учетом всего этого и изображена кри-
вая на рис. 72. Конечно, отдельные детали рисунка («плавность
или гладкость», поведение вблизи точки миксимума х — —1,5,
= —д/2 и т. д.) еще требуют обоснования. Оно может быть
дано методами дифференциального исчисления, и соответствую-
щие примеры будут рассмот]
валы (—оо; 0), (0; 1), (1;-
каждом из них определены
и непрерывны обе функции
х(/) и y(t), причем функ-
ция x(t) строго возрастает.
Поэтому для функции х =
= x(t) на интервале (—оо; 0)
существует непрерывная,
возрастающая обратная
функция t = /i (х), х
ее (—оо; 0), множеством
значений которой является
интервал (—оо; 0). Следова-
тельно, пара функций x(t),
y(t), —оо;0), задает
параметрически функцию
y = fi(x) =z/(/i(x)),
е(—оо;0). График этой
функции является частью
кривой, соответствующей
значениям /е(—оо; 0) (рис
‘fe (0; 1), определена непр
функция t = t2(x), хе(0;
.(0; 1). Пара функций-%(/), y(t), £g(0; 1), задает параметриче-
ски функцию у = /2(х) = у(/2(х)), xg(0;+oo), График этой
фуйкцйй — часть кривой, соответствующая £е(0;1) (рис. 72).
Для x = x(t), /е(1;-[-оо), есть обратная функция t = t3(x),
хеК, с множеством значений (1;+°°). Часть кривой прй
/е(1;4-оо) является графиком функции у = /з(х) = у(Мх))>
xeR (рис. 72). Указанные части кривой иногда называют её
Ветвями. Вместо участков монотонности функции x(t) бывает
удобно рассматривать участки монотонности функции y(t) и, со*
ответственно, заданные параметрически функции вида х = g(y).
Отметим, что построенная кривая имеет, как говорят, точку
самопересечения (точка А на рис. 72). Для нахождения точек
самопересечения нужно найти все решения системы
' х(и) — x(v),
‘ у(и) = У («)»
:. 72). Аналогично, для
ерывная, возрастающая
4-оо). с множеством
х = х(/),
обратная
значений
и > V,
301
относительно и и V. В данном случае эта система имеет един-
ственное решение и = (з + д/б )/2, v = (3 — д/5 )/2> яхточка
самопересечения имеет координаты х(и)=1, г/(и) = д/7.
В полярных координатах прямая, задаваемая уравнением
г = . / V , , d 0, (20)
sin (<р —Чро) ’
является асимптотой графика, функции г = г(<р), если выпол-
нены условия
lim г (<р) =-f-oo, (21)
ф“>фо
lim г (ф) sin (ф — фо) = (22)
Ф“>Фо
Эта прямая удалена
куляр, опущенный из
лучом угол, равный
от центра на расстояние |d|; перпенди-
центра на прямую, составляет с полярным
Фо+ 7 signd.
Если наряду с условием (21) вместо (22) выполнено условие
lim г (ф) sin (ф — фо) = 0, (23)
ф->фо
то асимптотой графика функции г = г(ф) является прямая, про-
ходящая через центр и содержащая луч ф = ф0.
Пример 5. Найти асимптоты графика функции
, ч 3 sin ср cos ср
Г (ф) =------------------з--у—
C0S3 ф + Sin3 ф
и построить этот график в полярных координатах.
Д Данная функция — периодическая с периодом 2л, по-
этому достаточно рассмотреть отрезок [—л/2; Зл/2] длины 2л.
Здесь функция определена для
фе[-л/2; л/4)0[0; л/2]и(Зл/4; л],
причем
lim г(ф) = +°° и lim г(ф) = +°°-
ф->——о г ф->—
Соответственно находим
.. / \ • / I Я\ 1- ЗС08ф81пф 1
lim г (ф) sin 1 ф 4— I — lim —7=-------------=-----7z=-,
л n k 47 л V2 (1 — cos <p sin q>) ^2
lim Ilm rW(_s|„^+i))=_L.
Ф1 > j 4-0 Ф4-0
Таким образом, при ф->—л/4 — 0 асимптотой является прямая
=______________________________1_____
V5" sin (ф + (л/4)) ’
302
3«rt i
а при <р->—+ 0— прямая
Поскольку sin (ф — (Зл/4) ) =—sin (ф + (л/4)), это одна_и та же
прямая. Строим ее: отрезок О А (рис. 73) длины 1/д/2 пово-
рачиваем на угол — j + y(—1)“ — и через получив-
шуюся точку Ai проводим
прямую перпендикулярно
OAi, она и является асимп-
тотой. Определим, как рас-
положена кривая отно-
сительно своей асимптоты.
При ф-> —0 имеем
({рис. 73)
| MQ ] = | г (<р) sin^cp -
з I_____________1______
д/2 I 1 — cos ф sin ф
Значит, |A1Q | < | PQ |, т. е. точки кривой находятся над асимпто-
той. Если срЗл/4 + 0, то
] 1VSI = Г (ф) sin (ф — -^) =
= Д71_________I____"R-Wl
V2 \ 1 —cos ф sin фу д/2\ 3) V2
поэтому | TVS | < |/?S| и здесь точки кривой расположены над
асимптотой. Из проведенных вычислений следует, что
—?—Y
2 — sin 2ф /
и видно, что | РМ | строго убывает при возрастании ср от —л/2
до —л/4. Аналогично устанавливаем, что | RN\ (рис. 73) строго
убывает при убывании (р от л до Зт&/4. Это и показано схема-
тично на рис. 73. Кривая проходит дважды через центр О, так
как г = 0 при ср — —л/2 и ср = л (т. е. О — точка самопересе-
чения кривой). Исследуем вид кривой вблизи точки О. Если
ср-э—л/2, то
cos ф = sin + ф) ~+ ф, ЬП1Ф~— 1;
803
поэтому СОЭ3ф "4“ sin3cp ~ —1 и
, v — 3 (л/2 + qp) o / л । \
Г (ф)-----= 3 + qpj .
Переходя к декартовым координатам, получаем
X = r(<p)COS<p~3(y + ф)2,
У = Г (ф) sin ф----------------з (у + ф),
откуда х ~ у2/3, т. е. при ф—>—л/2 кривая «сливается» с па-
раболой х = у213 (рис. 74). Аналогично, при ф->л имеем
sin ф = sin (л — ф) ~ л — ф, cos <р ~ — 1,
sin3 ф + cos3 ф ~ -1, г (ф) ~ 3 (л — ф),
откуда
х ~ —3 (л — ф), ~ 3 (л — ф)2 ~ х2/3,
т. е. график данной функции
у — х2/3 (рис. 74). Точно так
г = г(ф) «схож» с параболой
же найдем, что у ~ х2/3 при
Ф~>0 и х ~ у2/3 при ф->л/2. Оставшуюся часть графика
(Ф е [0; л/2]) строим по точкам (рис. 75). Отметим, что эта
часть, как и весь график, симметрична относительно прямой
ф = л/4, так как г (-j — ф) — г (ф), что равносильно равенству
г (j + а) =г *“ а)- Более обоснованное построение «петли»
ОАВА'О будет проведено далее с использованием понятия про-
изводной.
Построенная кривая носит -название «декартов лист», упо-
минание о ней впервые встречается в письмах Р. Декарта. В де-
картовых координатах эта кривая, как легко проверить, задается
уравнением х3 + у3 = Зху. &
При исследовании и построении кривой, заданной уравне-
нием F(x, у) — 0> иногда удается представить кривую или ее
30*-
часть как график функции y = f(x] (эта функция удовлетво-
ряет равенству ,F(%, f(x)) = 0) или как график функции г —
г (ср) в полярных координатах (эта функция удовлетворяет
равенству F (г (ср) cos ср, г (ср) sin ср) = 0). Иногда же бывает воз-
можным задать кривую параметрически. В этих случаях для
исследования и построения кривой можно применить указанные
метод выделения главной части и приемы нахождения асимптот
(пример 3, 3), пример 5).
Алгебраической кривой п-й степени называют кривую, кото-
рую в декартовой системе координат можно задать уравнением
вида
Y.aklxkyl =0, ' (24)
где сумма составлена по всем целым k и I таким, что
0 I n, k + I п, и имеется хотя бы одно ненулевое слагае-
мое, для которого k + I — п. Если прямая у = kx + b — асим-
птота алгебраической кривой, то коэффициенты k и b можно
найти следующим путем. Подставим в уравнение (24) у = kx+b
и в получившемся многочлене относительно х приравняем нулю
коэффициенты при двух старших степенях х, коэффициенты k
и / являются решениями этой системы из двух уравнений.
Если прямая х = Хо — вертикальная асимптота алгебраиче-
ской кривой, то Хо — корень многочлена относительно х, являю-
щегося коэффициентом при старшей степени у в уравнении
кривой.
Пр и м е р 6. Найти асимптоты кривой
х3 —Зх//2 = /?(х2 + у2), R > 0, х 0.
'Л Коэффициент при старшей степени у (т. е, при у2) равен
Зх’+7?. Следовательно, вертикальной асимптотой может быть
только прямая х = — R/3. Для нахождения наклонных асимптот
подставим в данное уравнение у = kx -\- b, получим
(3k2 — 1) х3 + (6kb + Rk2 + R)x2 + (3b2 + 2Rkb) x + Rb2 = 0
и, приравняв нулю коэффициенты при старших степенях х (т. е.
при х3 и х2), придем к системе
| 3k2- 1=0,
I 6^ + ^2 + /? = 0.
Эта система имеет два решения
k = ± 1/д/Т, Ъ = 4= 27?/3 VT.
Значит, только прямые
х 27? х . 27?
у — —==------i= И у =------Н------
7з зУз J уз зУз
могут быть наклонными асимптотами данной кривой. Все три
найденные прямые действительно являются асимптотами дан-
305
ной кривой. В этом легко убедиться, например, перейдя к по-
лярным координатам, тогда уравнение данной кривой примет вид
г = /?/созЗ<р.
Можно воспользоваться и заданием этой кривой с помощью
параметра t = у/х. Подставляя у = tx в уравнение кривой,
найдем, что
х-п 1 + *2 „_п *а + <2)
Л -* 1 — 3/2 ’ У 1—3/2 ’
эти функции задают исходную кривую. Рассмотренную кривую
называют трисектрисой Лоншама. Она может быть использо-
вана для деления угла на три равные части. ▲
Найти асимптоты графика функции у = у(х) (11.1—11.7),
если:
пл. 1)» = ^. 2)!z = -L_-J-_ + _L_.
3) ~ Сл2 — 8 — х* ' ~ I + Л2 '
х2 42х + 1 / х — 2
5) У — Х2 + 1 • 6) У — Д/ х + 2 •
7) у = л/ЯЙ - • 8) у = (2 - х)2/3 - (2 + х)2/3.
Л 1 \ I 1 пч I X2 X2 + 8х — 6
11.2. 1) у х 4~ -~2 . 2) у х 2 t 1 • 3) у —
Jv Л/ j 1 Л
у 2 у 2
4) „ = —5) ^===--4-—. 6) у
J и х + 4 3 v | х I + 1 1 v
rjx х3 оч х2 — 2х 4- 3
у~ (х+1)2* У— х + 2
m х3 — Зах2 + а3 ш\ х5
9) У ~~ х2 — 36х -ь 2&2 • 7 8 * 10) У~ X4 + 1
2х4 + х3 4~ 1
х3
11.3. 1) у = ^х2-А. 2) у — ^х2 + Ъх- 1.
3) у = '\/х3 — 6х. 4) у = иУ%3 + х2.
7) у — Vх4 + х3 — л/х4 — хэ.
8) У == л/х2 — 1 — х. 9) у — х + -у^Ах2 -ф 1.
11.4. 1) у=е~У\ 2) = 3) y«2"v<
лл 2Ж
4) !/= — •
__________1
хе 1*1
ех ~ 11.
5) у^=х2ех. в)у = еУх — х. 7)// = 1 —
8) у = 1 + xe2ix. 9) у = х2Ух\ 10) у = |
306
11) y — \x-\-2\e-llx.
11.5. 1) Z/==(l +1)*. 2)у=х(1-1)*. 3) y = thx.
4) y = cthx. 5) y = th2x. 6) у — xthx.
1 — e~x
7) у == 2x + cth x. 8) у = x i .
11.6. 1) у = logs (4 — x2). 2) у = logo.5 (2x2 — Зх+1).
3) у = 1g sin 2x. 4) у = x+
5) y = ln(l+ ex). 6) y==xlg (e + y).
1
11.7. 1) y = —3------2) y = cosec2x.
COS f X-g j
3) У = ^~- 4) y==x + -^p-. 5) y = xsin(l/x).
6) у — 2 4- cos(2/x). 7) у — arcctgx. 8) у = arctg(l/x).
X 1
9) у = arcsin (l/x2). 10) у = j + arccos . t
И) у == 2x — arctg(x/2). 12) y = xarcctgx.
13) у = x arctg x. 14) у = arccjW.
11.8. Найти асимптоты функции, обратной к функции f, если:
1) . X>-1. 2)f(x) = 7^r.
3) f (х)=1 -2-^х3 + Зх. 4) f(x) = thx.
5) f (%) = cth х. 6) f (х) = 2х + arctg х.
11.9. 1) Функция f определена на интервале (а;+оо). До-
казать, что для того, чтобы прямая у = kx + b была асимпто-
той графика функции f при необходимо и достаточно,
чтобы расстояние р(х) от точки (х;/(х)) до этой прямой стре-
милось к нулю при х~>+оо.
’ 2) Доказать, что в случае вертикальной асимптоты необхо-
димость предыдущего утверждения верна, а достаточность не-
верна.
11.10. Может ли график функции иметь две разные асим-
птоты при х->4~оо?
11.11. Используя метод выделения главной части, построить
график функции у — y(x)t если:
г3'2 /----а
1) y=~7f=~- 2) у = х ^4 —х^.
VI — к
307
3) у = д/х2 — x4. 4) z/ = -vW — x4. 5) t/ = z^/-T. *
‘'HM?' 8>»"V4-
9) у = x3/2 — 4x1/2.
11.12. Функция f определена в окрестности точки х0, и
f (%) = а (х — Хо) + о((х — х0)), а #= 0.
Доказать, что:
1) д//(л) = '\/а(х — х0) +о(У|х — х0|) при а(х — х0) 0,
т. е. графики функций V/W и 'у/а^х — х0) «сближаются» при
х->хо.
2) Если а > 0, то
(/(х))а = (а(х — х0))а + о(|х — х0|а)
при а(х — х0)>0, т. е. графики функций (f(x))a и (а(х — х0))°°
«сближаются» при х—>х0.
11.13. 1) Функция f определена в окрестности точки хо, и
f(x)= а(х — Хо) + о((х — хо)2), а =£ 0.
Доказать, что
f (х) а(х — х0) * 0 '
т. е. графики функций и “7—"—V «сближаются» при
/ \Х) С1 \Х — Xq)
Х->Хо.
2) Проверить, что функция f (х) = х + х4/3 удовлетворяет
условию
f (х) = х + о (х) при х -> 0,
но равенство
W==t + °(1) пРи х->0
неверно.
11.14. Доказать, что расстояние между точками (x;fi(x))
и (х; f2W) графиков функций fi и f2 стремится к нулю, если:
1) fl(х) = УX3 + Зх2, f2(x)= , Х^ОО.
2) fl (х) — Vх3 + t>x + с> fi (х) = Х3/2, X —> + оо.
3) fi М = л]х3 + ах2 + Ьх + с, f2 (х) — —, х оо.
\х — а
4) fi (*) = Vх6 + 2х4 + Ьх2 + с, f2 (х) — х3 + х, х —> + оо.
5) fi(x) = chx, f2 (х) = -~ех, х-»+ оо.
308
6) fi (x) — sh x, f2(x) = --^-e~x, x-> —oo.
7) fi (x) = ctg x, f2 (x) = 1/x, x -> 0.
8) f1(x) = -7X=, f2(x) = -=L=, x->l+0.
’ 71 v ' Vx2- 1 V2(x-1)
11 .15. Какие из функций f, g имеют асимптоту при x->4~.°°r
если: ___________________________________
1) f (х) = х + х, g (х) = х + д/ утт?
2) f (х) = In (ех • x'/Vx), g (х) = 1П _£1_.
Ql f Iy\ — (x+Qlnx + 1 „ zri _ '<* + 1) In X + X
о) / W — in x + I ’ s W in x + 1
4) f (x) = -\/x3 + x2, g (x) = д/х4 + bxf
11.16. Найти асимптоты функции
___ an+iXra^~* -J- nnxn 4~ Pn—i (x)
bnxn + bn—iXn 1 + Qn—2 (x)
при x->~oo, если neN, ti 2, tz„+i #= 0, bn =/= 0, an, bn-i — за-
данные числа, a P„_i(x) и Qn_2(x)—многочлены степени не
выше п — 1 и п — 2 соответственно.
11.17. Пусть Pk(x) = xk + aixk~l J- ... ak, Qi(x) = xl +
[-j- bixl~1 + ... + bi, neN, n 2. Определить, при каких
n /Pk (x)
Л/ QzW
k, I e N функция
имеет асимптоту при x->-f-oo,
и найти эту асимптоту.
11.18. Установить, сверху или снизу приближаются точки
графика функции у = у(х) к наклонной асимптоте при
х->4-°о и при х-^-оо, если; ‘
п ,,-.^+1 2) и== х*+1 „.^.(х+П8
t х х2 ' (х 2)2 '
X2 сч Vx4+ 1 „ x3 + 2sin x
4)y=|r+Ti- 5)у = —
Найти асимптоты графика функции и построить этот график
[(11.19—11.22):
,, ,ч 2 —4х2 х —1 х3
11.19. 1) у— ! __4л,2 . 2) у — х2_2х‘ 3) у—
.. (X —З)2 еч х3 с\ . 1 / X
4) 4х-Г- 5)^=Т+^- 6) ^==Л/‘х = 2--
7)z/ = Vn=^. 8) у = /Г4Ц=- 9) z/ = l- V4x2+1.
VI х2 — 11
10) у — д/х2 + 4х -f- 5 — 2. 11) у = -\/х3 — х2»
309
11.20. 1) 1/ = е1/(з+х)< 2) y = In (4 —xz).
3) У — । • 4) У ~ ^^х’-бх+т^-
5) у == In (1 + 2ex). 6) у = In cos x.
7) у = In arctg x. 8) y = el/s'nx.
11.21. 1) y — x+ S|rc*. 2) z/ = x2sin(l/x).
3) //— (x + I)2 sin (2/x). 4) г/= x + arctg x.
5) y — (x+ 1) arcctgx. 6) y = xarccos(l/x).
7) у =“ Зх + arctg 5x. 8) у = arctg (l/x) — x.
9) I/= x2 arctg (l/x).
11. 22. 1) V = 2) ? =
3)B=^.
,11.23. Найти асимптоты кривой:
3at y- _ 3aZ2 /7 0
x 1 +13 • У ~ 1 + /4 ’ Lt \J •
/ — 8 3
v ~.
x y t(t2 — 4)
Q\ at* y* at3 1 / - - zy >> Л
X~ 1 - /3 ’ у ~ i — t3 ’
Z3 V T—~ L t3 — 2t2
X t2 + i ’ V t2 + 1
5a/2 5a/3 1J r п 0
°; л 1 +15 ’ J ~ 1 +15 ’ (X \j 9
6)x = /3 + 3/4-l, y = t3 — 3/4-1.
7) х = /3 — Зл, у = t3 — 6 arctg/.
8) x = /-|-sin/, у —t-]-cost. 9) x — te*, y = te~f.
10) x = / In /, у — t In (/ 4- 1).
И) Х = ~П=Т> y = T=T‘ 12)x = /4-e-^, y = 2i+e-2t.
11.24. Найти асимптоты кривой и построить эту кривую:
.. 1 t 2/ t2
1) х—z , у— / + 1 • 2) х— l_f2, y—x_t2‘
3) x — acht, у — ftsh/. 4) x = 2cos/, у — tg2/.
5> Tik’ y = 6) X==-H=T> ^ = 7ZT‘
~ 2 + /2 /3 O4 /2 t
7) x ~ 1 4-12 ’ У ~ 1 4-t2 • 8) x “ t — 1 ’ У ~ t2 — 1 •
310
11.25. Найти асимптоты графиков функций, заданных в по-
лярных координатах:
=4 / 24 91 — 4 / 4
*' Г у sin 2ф (1 — sin 2ф) ’ ' Г у sin 4ф ’
2а sin2 ф 4 cos2 ф sin ф , , п ч
3) Г = — —г-г— • 4) г =--------—— (скифоида).
7 cos ф 7 cos 2ф 7
5) г = 3 cos2 Ф___. 6) г =___________sin2<?
7 cos3 ф + sin3 ф ’ 7 cos2 ф (cos ф — 2 sin ф)
11.26. Найти асимптоты графиков функций и построить эти.
графики в полярных координатах:
1)г==_£__. 2) г (жезл).
Ф-т
3) Ф = r> 1. 4) <р = 72^у, г>0.
5)r = 2tg<p. 6) r = -rz^v, р>0, е> 1.
7) r-~ l+e^coscp ’ Р>°> е>1-
10) г = —?—., а> 0. 11) г= . а. , а> 0.
созЗф УсозЗф
12) г— a th<p. , «>0.
7 ф — 1
13) г — 2R tg ф sin ф, R > 0 (циссоида).
14) г = со" ± a tg ф, а > 0 (строфоида).
СО5 2ф з/2созф
15) г = а----—. 16) г — л/—ткт- •
7 cos ф 7 V cos2 2ф
V2 sin 2<р 18. / tg 2<₽
17>Г= |cos2<p| • 18> Г-Л/--------------~-
11.27. Найти асимптоты кривой, заданной уравнением:
1) х2у2 + х — 2г/ = 0. 2) х2у2 + у = 1. .
3) (х — 1) (х — 2) у2 — х2. 4) х2у + ху2 = 1.
Б) у3 — х3 = 6х2. 6) у2 (а — х) = х2 (а + х), а> 0.
7) х3 — Зху2 = 2. 8) (х2 — I)3 — xV = 0.
9) х4 — z/4 = х2 — 2г/2. 10) ху (х — у) + х + у — 0.
11) ху (х 4- у) + х2 = 2у2. 12) (х2—1)г/2 = х2(х2 —4).
13) у3 - х3 + у - 2х = 0. 14) х4 = 4х2#.
811
15) х4 — 2х2у2 + у3 = 0.
16) (x+f)G2 ~4)+4а*2=0’ а>°- 17> xV=yx-
11. 28. Пусть 7И0 — фиксированная точка, а М — переменная
точка кривой второго порядка
ах2 + Ьху + су2 + dx + еу + f = 0.
Доказать, что координаты точки Л4 являются рациональными
функциями углового коэффициента прямой
11. 29. Найти асимптоты кривой и построить эту кривую;
= 2) (у + х+1)2 = х2 + 1.
3) 2х2 — Ьху + 2у2 + х + у — 3 = 0.
4) 4х2 + 9//2 = х2у2. 5) z/3 + x3 = 8.
6) #2(х2 + 1) — х2(х2 — 1). 7) #2(4 — х) — х3 (циссоида).
8) 4х4/3 __ умз = 1. 9) х2у2 у4 = 4х2.
10) ху (х2 — у2)1 +1=0. 11) (х2 — у2)2 + 4ху — 0.
12) (х2 + у2) (у — I)2 — у2 = 0 (конхоида).
§12. Равномерная непрерывность функции
Определение. Функцию f называют равномерно непре-
рывной на множестве X cz.D(f), если для любого 8 > 0 суще-
ствует такое б > 0, что для любых х', х" е X, удовлетворяющих
условию |хх— х"\ < б, верно неравенство
короче,
Vе > 036 > °VxZ X \jx" е X
(| Z - х" | < б => | f (%') - f (x"j | < 8). (1)
Пример 1. Доказать, что функция у = sinх равномерно
непрерывна на R.
А Пусть х', х” — произвольные числа; оценим модуль раз-
ности:
I sin х' — sin х" ] = 12 sin . cos х — | х' — х” 1, (2)
так как
Пусть 8 — произвольное положительное
б = е, тогда для любых xr е R, Ag R
|х'— х"| < б в силу (2) следует неравенство
число. Возьмем
из неравенства
| sin х' — sin х" 1 < б = е,
312
Таким образом, функция у = sin х равномерно непрерывна
на R.
Отрицание определения равномерной непрерывности функ-
ции f на множестве X выглядит так:
де > Оуб > 03*' Л^х" ge X
(I х' - х" | < б => | f (х') - f (х77) | > е). (3)
Пример 2. Доказать, что функция у — 1/х: 1) равномерно
непрерывна на любом промежутке [а;+оо), где а > 0; 2) не
является равномерно непрерывной на любом промежутке (0; а].
А 1) Пусть х7, х" ^[а\ +оо), а > 0; тогда
так как х7 а > 0, х” а > 0. Пусть е — произвольное поло-
жительное число; возьмем б = а28, тогда для любых х', х” ив.
[а; +<*>) из неравенства |xz — х"| <£ 6 следует, что
Это и означает равномерную непрерывность функции 1/х на
промежутке [а\ +°°), а >0.
2) Пусть х', х” е (0; а\, где а > 0. Из равенства
|_1____1_ I | xz - х" |
I х' х" I х'х"
I 1 1 I >
видно, что величина -р—-рг будет расти, если при сколь,
угодно малой, но фиксированной разнице \х7— х"\ приближать,
меньшее из чисел х7 или х" к нулю.
Возьмем х” — х'/2, тогда |х' — х"| = х'/2,
Так как 0 < х' < а, то
I Чтобы удовлетворить неравенствам х' < а и |х'— х//\== х7/2 <
< б, достаточно взять х' = ба/(б + а). Итак, возьмем & = а
и для произвольного положительного числа б возьмем х7
*= 6а/(б + а), х" = 6а/2(6 + а). Тогда
Iх ~х 1=27дТНГ<6- а |^-ТП>а = е-
Следовательно, функция у=\/х не является равномерно не-
прерывной на (0; а]. А
Теорема. Непрерывная на отрезке функция равномерна
непрерывна.
31&
Например, любой многочлен непрерывен на произвольно
взятом отрезке и, следовательно, равномерно непрерывен на
этом отрезке.
Справедлива более общая
Теорема (Г. Кантор). Функция, непрерывная на ком-
пакте, равномерно непрерывна.
Компакт в R — это ограниченное, замкнутое (ем. 10.94) мно-
жество.
Пример 3. Доказать, что функцияу — ^х равномерно не-
прерывна на [0; —|—оо),
Л Функция # = непрерывна на [0; +°о), в том числе
и на [0; 2]. Значит, по теореме Кантора, она равномерно непре-
рывна на [0; 2]. Докажем, что данная функция равномерно
непрерывна на [1;+°о). Пусть х', х" е [ 1; + °°); тогда
Для произвольного е > 0 возьмем 6 = 28, тогда для любых
х', х" e[Jj +°о)_из неравенства [х' — х'Д< б следует неравен-
ство | 'у/х' — х" | < 0,56 = 8. Значит, функция у = -у/х равно-
мерно непрерывна на [1; -[-оо). Докажем, что эта функция рав-
номерно непрерывна на всем промежутке [0;-|-оо). Пусть 8 —
произвольное положительное число. В силу равномерной непре-
рывности на [0; 2]
3 6i > OVx' <= [0; 2] Vx" е= [0; 2]
(| х' —- х" | < 6t =>| <у[х' — ^х"\ < 8), (4)
а в силу равномерной непрерывности на [1; 4-оо)
362>0Vx'g=[1; + оо] Vx" [1; + оо]
(|x'-x"|<S2=>| VP-V?7! < е). (5)
Возьмем за б наименьшее из трех чисел 61, 62 и 1, т. е. 8 =
= min {бг, б2; 1}. Тогда для любых xz, х" е [0; -]-оо) из нера-
венства |х'— xzz | < 6 будет, во-первых, следовать (так как
б< 1), что х' и х" оба принадлежат либо .[0; 2], либо [1; -(-оо),
а во-вторых, отсюда в силу либо (4), либо (5) будет следовать,
что | х' — л]х" | <8. Значит, функция у = <у/х равномерно не-
прерывна на [0; +°°) •
Пусть б — произвольное положительное число.
Модулем непрерывности функции f на множестве XczD(f)
называют
(о (6; f; X) = sup (f (х') - f (x"))> (6)
I x'- x" К 6
x'f=X, x" <=1X,
где верхняя грань берется по всем парам точек х' и х" из X,
расстояние между которыми не больше 6,
314
Этому определению равносильно следующее определение:
со (б; f; Х) = sup | f (х') - f (х") |, (7>
| х'— х" | < 6
xr е X, х" е X.
Модуль непрерывности для краткости обозначают также
0(6;f) или со (б), если ясно, о каких X и f идет речь.
Модуль цепрерывности для данного б может быть как чис-
лом, так и 4-°°. В этом смысле модуль непрерывности опреде-
лен для любого б > 0.
Теорема. Для того чтобы функция f была равномерно
непрерывна на множестве X, необходимо и достаточно, чтобы
для некоторого б0 > 0 ее модуль непрерывности со (б) был чис-
лом для каждого б е (0; б0) и чтобы
lim со (б) = 0.
6-^ +0
Пример 4. Найти на (0; +оо) модули непрерывности
функций и исследовать с их помощью заданные функции на
равномерную непрерывность:
1) У = ^х. 2) у = sin (1/х). (3)i/=l/V*-
Д 1) Пусть б > 0, х\ х" ^(0; +оо), \х'— хЛ,|^б. Положим
для определенности х' > х”, т. е. xf — х" + Дх, где 0 < Дх б.
Тогда при любом х” > 0 имеем
| л]х' — л]х” | = ^х" + Дх — ^х" < л]х” + б — ^х".
а
<X = '
так как -у/х" + 6 4- х" > д/б. Итак , | -yjx' — д/х"|^ при
|х'— х"|^б, значит, и
со(6) = sup I д/х'—V*" I •
I x'-x" I < 6
В то же время , при x' = x" -f- 6
lim (д/x" + 6 — д/x") = д/б,
x"->0
• поэтому co (6) д/б. Отсюда и из предыдущего следует, что
со (б) = д/б, б > 0. Поскольку
lim <о (б) = lim д/б =
б->4“0 6->+0
Функция у--\/х равномерно непрерывна на (0;+оо).
2) Пусть б > 0, х', х" е (0;+°°)> I*' — х"|^б. Очевидно,
| sin -±г — sin.-X. | < 2, х', х" ® (0; + оо),
значит,* и со (б)Х 2>
315
Рассмотрим точки
____________________J____ тт у" =____5____
n — (л/2) + 2лп « (л/2) + 2ля ’
где sin(l/x) равен соответственно —1 и 1. Поскольку
lim х'п — lim х"п = Ъ,
П->ОО n->OQ
найдется такое neN, что 0 < х'п< 6, 0 < х" <_ 6. Тогда
1<~<1<6. а
1'1 -1 Q
Sin —---Sin —7Г = 2.
хп _ хп
Значит, со(б)=2 для любого б > 0. Отсюда следует, что
lim (о (б) = 2 =/= 0,
б->+0
и поэтому функция y = sin(l/x) не является равномерно не-<
прерывной на (0; +°°)-
3) Пусть б > 0, х' > 0, х” = х' + б; тогда
1______1____ 1_________1_
х' 'х/х" 'у/х' V*' + 6 *
Так как
lim —i=- = + oo, lim — —Lr,
x'->+0 Vx' x'-»+oVx' + d 'X/d
TO
lim f—7=----7=L=r>| = + oo.
хч+okVx Vx' + dz
Следовательно,
/ 1 1 \ ,
sup (—=-----7=—= + oo,
x'>o\V* Vx +V
а поскольку
CO (6) > SUp (-7=--= " Y
X'>0\Vx Vx +6/
то и cd(6)=+oo для любого б > 0. Отсюда следует, что
функция 1/V* не является равномерно непрерывной на
(0; +оо). А
12.1. Доказать, что функция f равномерно непрерывна на
множестве Ху если:
1) f(x) = 2x-l, X = R. 2) f(x) = x2, Х = (—1; 1).
3) f (х) = ^х, X = [0; 2]. 4) f (х) sin х2, X = (-3; 3].
5) f(x) = x sin (1/х), Х = (0; л].
12 .2. Доказать, что функция не является равномерно непре-
рывной надмножестве X:
1) r/ = cos(l/x), Х = (0; 1). 2) z/==sinx2> X = R.
316
3) y = x2, X = R. 4) у = In х, X = (0; 1).
Исследовать функцию на равномерную непрерывность на
множестве X (12.3—12.4):
12 .3. 1) у = e~arcsinx, Х = [-1; 1].
2) у = arctg Х = [0; 10].
\ \ X2 + 1 + | Sin X I )
3) у = ^х, X = R. 4) у = ех, X = R.
5) y = ctgx, Х = (0; 1). 6) у = -^=-, Х = (-1; 1).
7) у — sin 'yjx, X = [1; + о°). У
( 1. — х2, — 1 <х<0,
8) у = { . . „ Х = [- 1; 1].
г (. 1 + х, 0 < х^ 1,
9) у = хsin(1/х), X = (0; Н-оо).
( х + 1, х^ О,
12. 4. 1) у = 1 _х X = R.
I е х, х > О,
2) у = (cos х) cos (л/х), Х = (0; 1).
3) у — S1" *-, X = (0; л). 4) у = х + sin х, X = R.
5) y = xcosx, X = R. 6) у = sin (1/х), X = [0,01; + оо).
7) у = п2 при 2п х 2п + 1, п е N, X — это объединение
всех отрезков [2n; 2п + 1], п е N.
8) У=-[^ЛГ, Х = (-л; 0)Щ0; л).
12.5. Функция f удовлетворяет на множестве X следующему
условию: существуют числа k > 0 и а > 0 такие, что для лю-
бых Xi и %2 из X верно неравенство
—f(*2) | < Л|Х1 — Х2|“
(при а = 1 это условие называют условием Липшица, при
а < 1 — условием Гёлъдера порядка а). Доказать, что функция,
удовлетворяющая этому условию, равномерно непрерывна на
множестве X.
12.6. Доказать, что если функция равномерно непрерывна на
промежутке, то она и непрерывна на этом промежутке.
12.7. Доказать, что если функция неограничена на ограни-
ченном интервале, то она не является равномерно непрерывной
на этом интервале.
12.8. 1) Привести пример функции, ограниченной и непре-
рывной на ограниченном интервале, но не являющейся равно-
мерно непрерывной на нем.
317
2) Привести пример функции, непрерывной на замкнутом
(см. 10.94) множестве и не являющейся равномерно непрерыв-
ной на нем.
12.9. 1) Доказать, что если функция f равномерно непре-
рывна на ограниченном множестве, то она ограничена на этом
множестве.
2) Привести пример функции, равномерно непрерывной па
множестве и неограниченной на этом множестве.
12.10. Нарисовать график модуля непрерывности со (6) функ-
ции f на множестве X, если:
1) f(x) = l-2x, X = R. 2) f(x) = \x\, X = R.
3) f(x) = x, X = [—-2; — 1]U[1; 2].
4) /W=2^(lx + «l-lx--al)> a>0, X = R.
5) f(x) = x3, X = [0; 1]. 6) f(x) — E(x), xe=R.
12.11. Найти модуль непрерывности функции/на множестве ‘
X и, используя его, установить равномерную непрерывность
функции, если:
1) /(х) = 2х —1, X = R.
2) f (х) = х2, X = [— а; а], а > 0.
3) f (х) = 1/х, X = [а; + оо), а > 0.
4) / (х) = cos х, X = R. 5) f (х) = In х, X = [l; + оо).
12.12. Доказать, что для любого 6 > 0
<о(б;/; Х)=+ОС,
если:
1) f(x) = x3, X = !R. 2) / (х) = 1/х2, X = (0; 1).
12.13. 1) Привести пример функции, модуль непрерывности
о (б) которой удовлетворяет условию со(+0)=8>0, где 8 —
данное число.
2) Привести пример неограниченной на промежутке функ-
ции, у которой модуль непрерывности со (6) на этом промежутке
удовлетворяет условию со(б)< +°° Для любого б > 0.
12.14. Пусть со(б)—модуль непрерывности функции f на
множестве X.
1) Доказать, что если 61 < б2, то co(6i) со(б2).
2) Доказать, что если f ограничена на X, то со(б)< +<ю для
любого б > 0.
3) Доказать, что если множество X ограничено, 'а функция
f неограничена на X, то со(б) = -фоо для любого б > 0.
4) Доказать, что если со(6о) — число для некоторого б0, то
и для каждого б, 0 < 6 <С бо, со (б)—число, т. е. со (б)—функция
на (0; до), и существует
lim со (д) = со (+ 0).
318
5) Доказать, что если X — промежуток, то для любых
& > 0, 62 > О
СО (61 + 62) со (61) + со (62) .
6) Доказать, что если X— промежуток и со(6о)=+оо для
некоторого 60, то со(6) = 4-сю для любого 6 >0.
7) Привести пример функции, у которой со (6) = 6 при
0 < 6 < 1; со (6) = +°° ПРИ 6^1.
12.15. Доказать, что для любого е > 0 существует 6 такое,
что для любых из неравенства |%i—х21 < 6 сле-
дует неравенство
|/(^i)-f(x2)|<co(+0) + e.
12.16. Доказать, что если функция f равномерно непрерывна
на множестве X, а У cz X, то f равномерно непрерывна и на
множестве У.
12.17. Функция f равномерно непрерывна на отрезках [а; Ь]
и [й;с]. Доказать, что она равномерно непрерывна и на от-
резке [а; с].
12.18. Привести пример функции, равномерно непрерывной
на отрезке [а; Ь\ и на полуинтервале (&; с] и не являющейся
равномерно непрерывной на отрезке [а; с].
12.19. Доказать, что если функции f и g равномерно не-
прерывны на множестве X, то для любых a,функция
а/ + ₽£ равномерно непрерывна на X.
12.20. 1) Доказать, что если функции f и g ограничены и
равномерно непрерывны на [а; +оо), то и их произведение
fg— равномерно непрерывная функция на [а; +оо).
2) Привести пример равномерно непрерывных на [cz; +оо)
функций, произведение которых не является равномерно непре-
рывной на [а; +оо) функцией.
3) Доказать, что если функции f и g равномерно непрерыв-
ны на ограниченном множестве, то их произведение fg — рав-
номерно непрерывная функция на этом множестве.
12.21. Доказать, что непрерывная периодическая функция
равномерно непрерывна.
12.22. Функция f равномерно непрерывна на [cz;+oo). До-
казать, что выполнено одно из трех условий: либо f(x) огра-
ничена на [а; +оо), либо lim f(x) = +oo, либо lim f(x) =
+ Х->4-оо
!= ---ОО.
12.23. Функция f непрерывна на [cz; +©о), и существует (ко-
нечный) lim f(x). Доказать, что f равномерно непрерывна на
Х->4-оо
[cz; +°°) •
12.24. Доказать, что ограниченная монотонная, непрерывная
на интервале функция равномерно непрерывна на этом интер-
вале (конечном или бесконечном).
12.25. Доказать, что для равномерной непрерывности функ-
ции f на ограниченном интервале (а>Ь) необходимо и доста-
819
хточно, чтобы функция была непрерывна на (а; Ь) и чтобы су-
ществовали пределы lim f(x) и lim f(x).
x->a+0 x^-b-0
12.26. Доказать, что для того, чтобы функцию f, определен-
ную и непрерывную на интервале (а;&), можно было продол-
жить как непрерывную функцию на отрезок [&;&], необходимо
и достаточно, чтобы функция f была равномерно непрерывна
на интервале (а; Ь).
12.27. Доказать, что если функция f равномерно непрерывна
на интервале (а; &), то ее можно продолжить как непрерывную
функцию на всю числовую прямую R, т. е. существует непре-
рывная функция F(x), определенная на R, такая, что F(x) =
— f(x) для любого хе (а; Ь).
12.28. Функция f равномерно непрерывна на !R. Доказать,
что существуют числа а 0, 6^0 такие, что |/(х) | а|х| + b
для любого xeR.
12.29. Непрерывная на отрезке [а; 6] функция f называется
кусочно линейной, если существует разбиение отрезка [а; Ь]
точками х0, Xi, ..., хп такое, что
О :— Xq Х\ ... Xi Хп—1 <'^ Хп — Ь,
и функция f линейна на каждом отрезке [xz_r, xj, £=1,2, ...
..., п (т. е. f (х) = щх + bi). Доказать, что всякая непрерывная
на отрезке [а; Ь] функция F может быть с любой точностью
аппроксимирована кусочно линейной функцией, т. е. для любого
е > 0 существует такая кусочно линейная функция f, что для
всех хе [а; Ь] верно неравенство
|/Д) — F(x) I < 8.
12.30. Для функции F подобрать кусочно линейную функ-
цию f. так, чтобы для всех х^[а; 6] было выполнено неравен-
ство |F(x) — f(x) | < 0,1:
1) F(x)=x2, [a; = 1; 1].
2) F(x)=l/x, [а; Ь] = [2/3;2].
12.31. Найти такую кусочно линейную на отрезке [0; 100]
функцию Д что для всех zg[0; 100] верно неравенство
|2-_/(х)|<1/4.
12.32. Функцию f, непрерывную на R, называют кусочно ли-
нейной на R, если существуют такие числа а и Ъ, а < Ь, что
функция f линейна на промежутках (—со» а], [6; +оо) и ку-
сочно линейна на [а;&]. Доказать, что, каково бы ни было
число е, не существует кусочно линейной на 'R функции f, для
которой | х2 — f (х) | < 1 для всех х е R;
320
12.33. Доказать, что всякая кусочно линейная функция мо-
жет быть задана формулой
п
f (х) = а + X 1 х — Xi |.
i = 0
12.34. Найти формулу, указанную в предыдущей задаче, для
кусочно линейной на отрезке функции f, если;
' х + 4, — 3 С х < : — 1,
I) = < 2 — х, — 1 < х < 1, *
. X, 1 X ;з.
< 2x4-3, — 2^Х = со,
1 3 — х,- 0 < X = С1>
2) /(x)=J х+ 1, 1 < X! сз,
1 4, 3<х = <5.
3) f(0)= 1, /(!)=-!, f(3) = 2, f(4) = —4, f(6) = 0,
где {0, 1,3,4, 6}— разбиение отрезка- [0; 6].
12.35. Доказать, что кусочно линейная на R функция рав-
номерно непрерывна на R.
12.36. Пусть
( sin (1/х), х #= 0, | х | =С 1/л,
= U х_0.
Доказать, что ни при каком а не существует кусочно линейной
на [—Д/ат; 1/тс] функции g такой, что ]/(%)— g(*)|<l/2 для
любого хе[—1/л; 1/л].
12.37. Сформулировать в позитивной форме утверждение, что
функция, определенная на отрезке, не может быть аппроксими-
рована с любой точностью кусочно линейной функцией.
12.38. Доказать, что если функция f определена, но разрыв-
на на отрезке [а; 6], то ее нельзя аппроксимировать с любой
точностью кусочно линейной функцией.
12.39. Доказать, что если функцию f на промежутке можно
аппроксимировать с любой точностью кусочно линейной-функ-
цией, то f равномерно непрерывна на этом промежутке.
12.40. Доказать, что если функцию f на промежутке [с* Д-оо)
можно аппроксимировать с любой степенью точности кусочно
линейной функцией, то f имеет асимптоту при х->Д-оо (функ-
ция кусочно линейна на [с; Д-оо), если она непрерывна на
[с; —|—оо), линейна на [d; Д-оо) при некотором d>c и кусочно
линейна на [с; d]).
п Л. Д. Кудрявцев и др.
ГЛАВА III
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
§ 13, Производная. Формулы и правила вычисления
производных. Дифференциал функции
1. Определение производной. Предел отношения
f (х0 + Ах) — f (х0)
Ах
при Ая->“0 называется производной функции f(x) в точке xOq
Этот предел обозначают одним из следующих символов:
Таким образом,
f'(x0)= lim Hx° + Ax)-f(xo) (l)
Av-хП АХ
Если в каждой точке х^(а\ Ь) существует
jim f (х + Ах) - f (х)
ДХ-»0
т. е. если производная f'(x) существует .для всех х^(а;Ь), то
функция f называется дифференцируемой на интервале (а;Ь)<
Вычисление производной называют дифференцированием.
Пример 1. Найти f(x0), вычислив lim -—°+ —
Дх->0
если: •«
1) f=lA2, ХО=1- 2) / = д/2 + х, хо = О.
3) f = 3|x+ 1 I, х0 = —2. 4) f = хо = О.
___1------1
.. .. (1-4-Дх)2
д 1) lim ->----д------
Дх->0
.. 2 -J- Ах q
==“д™о(1+^)2
.. — 2 Ах — Ах2
— д‘™0 Дх (1 + Дх)2
.. д/2 + Ах —д/2 1. Ах
111T1 —--1---------= 11Ш ---т- ,........г=7~~-----/=-•
дх->о Ах Дх-»о Ах (V2 + Ах + V2 ) 2^2
31—1+Ах | — 3 3 —ЗАх —3
—------х-------“ Ьт -------т------=
Ах дх~>0
322
л/ l\x2 1
4) lim —-----— lim -^=- = 00. Следовательно, данная
Дх->0 Ax Дх-»0 У Ax
функция при Xq = 0 производной не имеет. А
Пример 2. Найти f'(x), вычислив lim —HiL, если:
_ Дх->0
1) f = x^\/x. 2) f = 3*sinx.
А 1) Пусть х > 0; в противном случае предел, очевидно, не
существует. Выберем Ах так, чтобы выполнялось неравенство
| Ах| < х. Тогда
(х + Ах) Ух + Ах—-хУх _
Ах
Пт
Дх->0
(х + Ах)3 — х3
2)
_ |jm--------------7——
дх~>0 Ах ((х + Ах) Ух + Ах + хУх)
Зх2 + Зх Ах + Ах2 _ Зх2 3
о (х + Ах) Ух+Ах + хУх 2х Ух 2
Зх+Дх sin 2_ зх sin х
lim--------------------------—’
Дх->0
= lim
Ах
0.
3х sin х lira
„ г 1 • 3Лх (sin х cos Ах + cos х sin Ах) — sin х
= 3* hm ---------*-------------Т---------------------=
дх-»о ЛХ •.
3Лх cos Дх — 1 . 1- sin Дх
+ 3 COS X 11ГП —т---------=
Дх->0 Дл
= 3х (In 3 • sin х + cos х),
Ах
так как
Нт
Дх-»0
3AjccosAx —Пт
Ах Дх->0
.. sin Ах «
-1'
С3"-1 cos Дж + "У -
\ Ах ‘Ах 7
1- Лчл г 3Лх—1 о .. sin2(Ax/2) . о *
= lim cosAx- lim —г-------2 lim ---а—— = 1пЗ. А
Дх->0 Дх->0 &х Дх->0 &х
13.1. Вычислив lim ~ найти f' (х0):
1) / = х2, х0 —0,1. 2) f = 2 sin Зх, х0 = л/6.
3) f= 1 4- 1п2х, х0= 1. 4) / = х + ctg х, х0 = л/4.
13.2. Вычислив lim - ~ , найти f'(x). Указать
Дх->0 АХ
область существования производной:
• 1) f==x3H-2x. 2) f=\/x. 3) f = V-v* 4) f — x^/x.
5) f=l/(l +x2). 6) f = 2x+1. 7) f = lnx.
11*
323
8) f = sin2*. 9) f = ctgx + 2. 10) f — arcsin r.
11) f = arccos 3л:. 12) / = 7 arctg (л: + 1).
2. Правила вычисления производных, связанные с арифмети-
ческими действиями над функциями. Если функции fi, /2, ...» fn
имеют производные в некоторой точке, то функция
f — Cifl + ^2/2 + ... +cnfn (Cl, c2, ...» Cn — постоянные)
также имеет в этой точке производную, причем
. f' = cif'i + c2f2 + • • • + cJ'n- (2)
Если функции fi и f2 имеют производные в некоторой точке,
то и функция f = fif2 имеет производную в этой точке, причем
f' = fif'2 + f'if2- (3)
Если функции fi и /г имеют производные в некоторой точке
и f2 0 в ней, то функция f = fi/fz также имеет производную
в этой точке, причем
(4)
'2
Формулы для производных основных элементарных функций.
с' = 0, т = const. (5)
(%«)' = х > 0, aeR« (6)
Область существования производной может быть и шире.
Например, если а е N, то
= ах01-1, х е R. (71
Если а > 0 и а ф 1, то
(а*) ' = ах In а, xeR; (81
в частности,
(ех)' = ех, (9)1
Если а > 0 и а =# 1>до
(logax)'- , Л Ш U/ х > 0, (Ю)
(logjx 1)' = —Г 4 &а1 17 х In а , X =И= 0; (П)
в частности,
(In х)' = 1/х, х > 0, (12)
(In 1 х |)' — 1/х, х^=0. (13)
(sin х)' — cos х, xsR, (14)
(cos х)' — — sin х, XG R, (15)
(tgx)' 1 cos2 x 1 x^^(2n+l), «eZ, (16)
(ctgx)' 1 sin2 x * x лп, n^Z, (17)
(arcsin x)' = , , |X|< 1, Vl — X2 (18)
(arccos x)' = /-1— |x| < 1, Vl ~ X2 (19)
(arctg x)' = -1 + x2. xeR, * (20)
(arcctg x)' = 1 + x2 ’ X e R’ (21)
(sh x)' = ~ ch x, x e R, (22)
(ch x)z = = sh x, x g R, (23)
(thx)' = —Д—, xeR, ch2 x ’ (24)
(cth x)' = , 2 , X =И= 0e sh2 x ’ (25)
Пример 3. Вычислить производную функции
з/— ех
f = Vx arccos х + 2 log2x + —. xe(0; 1).
д f' — (^x arccos x)' 4- 2 (log2 x)' + (ex/x2)' =
= у/ x(arccos x)' + arccos x(-\/x)' + 2 - -R
x2 (ex)' — ex (x2)‘
y x , arccos x . 2 t (x — 2) ex
л/\ — x2 3 л!x2 x In 2 x3 ч
3л/
Вычислить производную функции y — \(x). Указать область
существования производной (13.3—13.38):
13.3. у — х3 + х2 + х + 1. 13.4. у = «х3 + 6х2 + сх + d.
13.5. у = 7х13 + 13х-7. 13.6. у = + е2.
13.7. у — + -А- + —j-. 13.8. у — -у/х-[-'\/х-\-\/х.
13.9. z/ = -|-x5 */3 + x-2 + -^. 13.10. у = х3^х2 + х7^'х.
13.11. у = х^ — x-Vs-. 13.12. у = cx + rf • с^°-
ч л ч л X2 — 5х + 6 ч о Ч л Vx
13.13. у= * —. 13.14. у — — .
а Х2-+ х + 7 2 + Vx2
13.15. i/ = 5xcosx. 13.16. y = (x4-l)tgx.
325
(xО
13.17. у = x2 ctg x + 2. 13.18. y = < x ’
I 1, x = 0.
13.19. у = ^~. 13.20. = .
tg X u COS X — sin X
13.21. у = arctg x + x + arcctg%. 13.22. y = x arcsin x,
13.23. и = arctg2x. 13.24. g = -arcc?s* .
’ arcsin x
13.25. у = In x3 * -1 . 13.26. у = (л/2/ + (Уб)"* ►
13.27. у — (x2 — 7x + 8) e*. 13.28. y = 2*ln|x|.
13.29. у = ёх log2 х. 13.30. у = log2x • In х • log3x.
13.31. y = logx2. 13.32. y = logx 2х.
13.33. у = ary x . 13.34. у = eax (a sin bx - b cos bx).
13.35. у = shx • chx. 13.36. y = sh2x— ch2x.
13.37. y=-^- 13.38. y = ^.
Вычислить производную функции y = f(x) в точке х0
(13.39—13.51):
13.39. у^=(х+ 1) (х + 2) (х + 3) (хф-4), х0 = —3,
13.40. у — (х — а)(х— Ь)(х — с), х0 — а.
13.41. У = узгу. х0 = а.
13.42. у = (1 4-ахь)(1 +bxa), х0=1.
13.43. у = х (х — 1) (х — 2)... (х — 1984) (х — 1985),
х0 = 0, х0 = 1985.
13.44. у = (2 — x2)cosx + 2х sinx, хо = О.
. „ sin X — X cos X л
13.45. у =--------—*—, х0 = -тг•
cos х + х sin х и 2
13.46. у = (ах + b) cos х -ф- (ex + d) sin х, х0 = 0.
13.47. у = arctg х • arccos х, хо = О.
13.48. у = log2xln2x, х0=1.
13.49. у = -^—, х0 = е.
и . in х и
13.50. у = х5е~х, %0 = 5.
13.51. у = xsh2%, х0=1.
3. Вычисление производной сложной функции. Если функция
У — f(x) имеет производную в точке х0, а функция z = g(y) —
в точке yo = f(xo),m сложная функция (композиция f и g)
z = ф.(х) = g(f(x)) также имеет производную в точке х0, при-
чем
ч' (Хо) = g' (Уо)Г (x0)t
(26)
326
Опуская аргумент и используя другое обозначение для произ-
водных, формулу (26) можно переписать в виде
dz dz dy
dx dy dx '
(27)
Правило вычисления производной сложной функции распро-
страняется на композицию любого конечного числа функций,
Например, для сложной функции вида г(у(х(^))), в случае диф-
ференцируемости функций х(0, £/(*),г(у) соответственно в точ-
ках /о, х0 = х(/0), */о = */(*о), в точке /0 имеет место равенство
dz________________________dz dy dx
~dt ~4y~dx~dF'
Пример 4. Вычислить производную функции z = In sin x
в точке Хо — л/3.
\ Функция z = ф (х) = In sin х является композицией двух
функций: y = f(x)= sinx и z = g(y) = In у. Функция f(x) =
= sinx в точке х0 = л/3 имеет производную, причем /'(л/3) =
— cos(л/3)= 1/2. Функция g(y) — In у в точке у о = sinxo =
— sin (л/3) = V 3/2 также имеет производную, причем gz(V3/2)=
— 2/д/з. По формуле (26) получаем
<р' (л/3) = g' (Va/2) f' (л/3) = (2/д/з) • (1/2) = 1/V3. А
Пример 5. Вычислить производную функции
Z = д/1 + *2> х R-
А Данная функция является композицией функций у = 1 + х2
в z — ^jy, причем
По формуле (27) получаем
dz 1 о х
— =------==- • 2х — ........ .
dx 7.^1 у V1 + х2
П р и м е р 6. Найти производные функций:
1) r/ = 2ctg2x, х =£ лй, k^Z.
2) у = In cos arctg sh 2x, xeR,
Л 1) Применив дважды правило дифференцирования слож-
ной функции, получим
у' = 2ctg2 х In 2 (ctg2 х)' = 2ctg2 х In 2 • 2 ctg х (ctg x)z.
Следовательно,
у'= -2\n2-2cte2-x-^-, x^=nk, k<=Z.
V sin2x ’
327
2) Применяем правило дифференцирования сложной функ-
ции четыре раза:
у' ==-----г—гд- (cos arctg sh 2x)' =
v cos arctg sh 2x v b 1
— sin arctg sh 2x z , - n
=--------г—гГо---(arctg sh 2x)' —
cos arctg sh 2x ° 7
«= — tg arctg sh 2x • t + ^22л.' (sh 2x)' =
sh 2x
1 + sh2 2x ch 2x '
Следовательно,
, 2 sh 2x ch 2x n . < n
# =-------— — — 2 th 2x,
u 1 + sh2 2x
Пример 7. Найти производную функции
t/ = ln^-l+ecosx’ ^^л(2«+1), neN.
'А Здесь выгодно предварительно упростить формулу, с по-
мощью которой задана функция:
у =А 1п ех — 4- In (1 + cos %) = 4 ~ i In (1 + cos х).
О О О О z
Дифференцируя, получаем
___ 1 1 (cos хУ _ 1 । 1 sinx _ I + tg (x/2)
У — 1 + cosx —1 + cosx ” 3 • A
Пример 8. Найти производную функции
У—- Х^=лп, neN.
ух4 sin7X
'А Здесь удобно рассмотреть функцию z = 1п]г/|. По фор-
муле дифференцирования сложной функции имеем
dz dz dy 1 dy
dx dy dx у dx ’
. T. e.
^Г-==У1Г- (29)
dx J dx \ r
Записав функцию z в виде
z = In | у | = In (1 + x2) — у ln I x 1 ““ In | sin x |,
продифференцируем ее:
dz 2x______4 у cos x
dx 1 + x2 3x sin x
dz
Подставив найденное выражение для в формулу (29), по-
лучим
dy __ 1 + х2 / 2х_____4 __со§ х \
dx ^x4sin7x \ 1 + х2 Зх sinx/
S28
Пр и м е р 9. Найти производную функции:
1) у = (2 + cos %)х, xelR. 2) z/==x2\ х > 0.
Al) По определению показательно-степенной функции
у — qx ln(2+cos х)
Дифференцируя, получаем
у = ех In (2+cos х) [п (2 + cos X))' =
_ ex In (2+cos x) ([n (2 -J- COS X) — X 2 *s ~ , XG R.
2) Так как у = e2X lax, то
У = e2*ln x (2х In x)' = e2*'« x 2х + 2х In 2 • In x)
= 2хx2* (у- + In 2 • I.o x), x > 0. д
Найти производные функций (13.52—13.152) j
13.52. у = (Зх—7)10.
13.53. z/ = ^U -х)-"-^(1 -хГ98 + -^(1 -X)-97.
13.54. у = (а + Ьх)а.
13.55. у — (0,4 cos (8х + 5) — 0,6 sin 0,8х)2.
13.56. у = —2—х — 4-sin (2х + 3).
13.57. у = (a cos х + b sin х)а.
13.58. y = Ae^k‘‘x sin (сох + а).
13.59. у = (д/х + -^)12. 13.60. у = V2x2+V^+T.
13.61. г/ = ^9 + 7 д/2х-
13.62. = 13.63. у=
13.64. У _|_ x4 ^/1 х4)
,,Vx3 + л/ха2 — х/х2а — Va3
л/а5 + V~ Vа4х — V*5
13.67. у = cos(l/x). 13.68. z/ = ctgx2 — уtg32x.
1 Q АО „ 1 — C0S <8х — 3j0
13.69. Z/= tg2-x”ctg^—
329
13.70.
13.72.
у = е~хт. 13.71. z/ = 2s,n2x
1 , X 1 , X
у = у arctg у — у arctg у.
13.73. у
sin2 х . cos2 х
1 + ctg х "1” 1 + tg x
13.74. t/ = Vl + tg(x2 + x-2).
13.75. y = 13.76. z/= In l,n (x/2).
VI + x
13.77. z/ = log3(2x + 3)2. 13.78. у = In | sin x |.
13.79. y=sinln|x|. 13.80. у = cos 1 - .
13.81. у = 3arctg (2x+n). 13.82. у = arcctg 2х.
13.83. t/= 10x/Iogs*. 13.84. z/ = —arctg 4*~5.
V3i V3i
1 v2 _ I
13.85. z/=—arctg .
y -у/2 s V2 x
13.86. у — Vchx. 13.87. y = arctg th x.
13.88. y=-thx +VLin 1 + Vg_thx
2 8 1 - V2 th x
13.89. у = sin cos2x • cos sin2x.
13.90. у = tg2x/(tgx2). 13.91. г/= In tg (x/2) — cosx- Intgx..
13.92. z/=y (sin Inx + cos Inx).
13.93. у = cos” x cos nx.
13.94. y- | In (1 + x2) - 1 In (1 + x4) -y^^ .
13.95. у — In (x2 + V*4 4“ О*
13.96. у = 2xln(2x+ д/4х2+ 1) — д/4х2+ 1.
13.97. у = sin (arcsin x). 13.98. у = cos (2 arccos x).
13.99. z/=s cos (3 arccos x).
13.100. z/ = arcsin s*n •
1
13.101. у = arccos —nr--.
x2n + 1
13.102. у = ♦
\ x + 2 7 (x + 2) (x 4- 3)
13.103. z/ = ^—-Inf ^ + хл/ДТ.
2л/б \V2 — x д/3 7
13.104. y^=-^lnf ----4-arctg-Д.
V2 V x + V2 ) д/з 7з
13.105. z/ = 2sinxi. 13.106. z/ = 3cos’\
830
A / l~X
13.107. 13.109. у — e’V i+% . 13.108. у = arctg tg2 x. у = log2 log3 log5 x- 13.110. t/= In in In x2.
13.111. z/=Vx2+l -ln(|+ д/l +^f).
13.112. ^==yln(V-*:7 + Vl + *7)-
13.113. z/=tg2x+lncos2x. 13.114. i/=ln(V2 cosx+ Vcos2x)«
13.115. ,3.116. g _ |n .
13.117. У = ' / 2X' — arCtS ~ 1 • д/е2 - 1
13.118. ch x2 1 j, x2 У ~~ sh2x2 — П Cth ~T •
13.119. t/=ln tg ^+'S*2* ) • 13.120. z/=arccos (sin x4—cosx4).
13.121. 1 । । sin4 x У sin4 x + 1 П sin4 x + 1
13.122. < Уз — V2 cos x V3 + V2 cos x
13.123. 1 . b 4- a cos x + Vb2 — a2 sin x у =± .....In . V^2 — a2 a + & cos x
13.124. У = |+V3’ arctg
13.125. у — arctg e*/2 In V + 1 •
13.126. sin a • sin x f/ = arcsin .
13.127. у = _L_ in 1+X _ ctg a • Inl+^i. v sin a 1 — x 0 1 — x cos a
13.128. у — In -\/x2 — 2x cos a + 1 + ctg a • arctg ~ Tina^”’ •
13.129. у = x2 a2 + x4 + a2 In (x2 + V^2 + *4X
13.130. xu i л/2~ i 1 + V2 th x У = th x 4- In v,- —. v 4 1 - V2 th x
13.131. « x2 + a .a , x2 У =ln / 4 ; ;2' + . arctg Vx4 + b2 b b
13.132. у = x -\Ja2 — x2 + a2 arcsin -j-jy.
13.133. у — x + ctg x • In (1 + sin x) — In tg (x/2).
13.134. у = x — In V1 + e2X -j- e~x arcctg e\
831
13.135. у = In 1 /*2== + Уз arctg -1 + ^Ух2 .
71 + Ух2 + Ух- Уз
. „ < ncs 1 / 7х4 + 1--1/2 X , VF X
13.136. z/ = ln л ~=^=------7=------arctg—/-. .
V 7x4 + 1 + 72 x s yX4 + !
13.137. у = In ~ 2/^ 1 +4 arctg (x + 1) — arctg (2x + 1).
13.138. у =...A..±..2.... - 4- In л/ —1)2 4- -A arctg-2*+ 1 ,
y x2-|-x+lr Vx4H173 g VT
13.139. у = 3 ~ sin * Vcos2x — 2 sinx + 2arcsin 1 + 3ln - .
2 72
13.140. y = ex arcsin y\J7/^7 + arctS “ 7®* •
13.141. y = xx. 13.142. r/ = x7/tax.
13.143. z/ = logx7. 13.144. z/= log2 x • logx e + log2 x • In 2.
13.145. у = x2/In x — 2xlog*eel+ln x + e1+2/logxe.
13.146. z/ = x< 13.147. z/ = x<
13.148. y = 2x\ 13.149. z/ = x<
13.150. y = \ sinx|c0S*. 13.151. y = (arcsin sin2x)arctg\
13.152. z/=(chx)<
Вычислить в указанных точках производные для следующих
функций (13.153—13.166):
1 —I— X. —
13.153. = х = 0, х=1.
13.154. у = (1 + х) 72+ х2 7з + х3, х = 0.
13.155. у = 2tg(1/x), х = 1/л.
13.156. у = 3 cos 2х — 7^ — sin 2х (sin х + cos х), х = л/6.
13.157. у = log1/2 (х — у У + log2 74х2 —4х+ 1, х = 0.
13.158. у — 71пх (1пх — logexx) 71nx + logxe + 2, х~е.
13.159. у = In (1 + sin2x) — 2 sin х • arctg sin х, х = л/2.
13.160. у — arcsin (2x/(l +x2)), x = 0, x = 2.
13.161. z/ = arcsin((l—x2)/(l+x2)), x = —1, x==l, x = 0.
13-182-« = 1п4т£4т + 2^агс'ет=7- *“L
, —- 5
13.163. у = Д/arctg 7C0S ln3x , x=l.
232
13.164. у = (ch x)sh x, x = 0.
13.165. у = (д/l +3X)'nx‘, x = l.
13.166. y — ((sin x)/x)x, x — n/2.
13.167. Решить уравнение y'(x) = 0, еслиг
1) у = х3 — 6х2 + 9х+ 12.
_ х2 + х — 6 ______1____
' U х2 — 1Ох + 25 ' У 1 + sin2 х
4) у — х(х — 1)2(х— 2)3. 5) у = е~^х~х 1/(1 4-х).
6) у — max (7х — 6х2, | х |3).
13.168. Пусть f(x), xeR, — всюду дифференцируемая функ-
ция. Найти у'(х), если:
1) = fW>0. 2) z/ = ln|f(x)|, /(х)=И=О.
3) у = f (х3). 4) у = f (arcsin f (х)), | f (х) | < 1.
' 13.169. Пусть f(x), xgR, и g(x), xeR, — всюду диффе-
ренцируемые функции. Найти у'(х), если:
1) у == Vf2(x)4-g2(x), f2W + S2 (*) > 0.
2) z/ = ln|-^-|, f(x)g(x) =4= 0.
3) # = f(sin2x) + g(cos2'x). 4) y = (f(x))sM, f(x)>0.
13.170. Пусть функции f// (1 i, j n) дифференцируемы
в некоторой точке. Доказать, что в этой точке справедливо ра-
венство
fll /12 • •• fin / fll fl2 • • • fll
fil fi2 ••• fin II fil f'i2 ••• f'i,
fnl fП2 ••• fnn fm fn2 ••• fn
13.171. С помощью формулы,
задаче, найти А'(%), если: 1
приведенной в предыдущей
1) А(*) =
1 2 3
х 1 2
X х 1
3) А (х) =
х 1 0
х2 2х 2
х3 Зх2 6х
13.172. Доказать или опровергнуть следующие утверждения:
1) Если функция имеет производную в некоторой точке, то
она непрерывна в этой точке.
2) Если функция непрерывна в некоторой точке, то она
имеет производную в этой точке.
333
13.173. При каких значениях а функция
{] х ]а sin (1/х), если х =# О,
О, если х — О,
в точке х — 0: 1) непрерывна; 2) имеет производную; 3) имеет
непрерывную производную?
13.174. При каких значениях а и [3 (Р > 0) функция
( | х |а sin (1/| х р), если х 0,
У 1 0, если х = 0,
в точке х = 0: 1) непрерывна; 2) имеет производную; 3) имеет
непрерывную производную?
13.175. Построить пример функции, имеющей производную
всюду, за исключением точек Xi, х2, ..., хп.
13.176. Определить значения аир, при которых следующие
функции а) всюду непрерывны, б)- всюду дифференцируемы:
3)^ =
ах+Р, если х<П, ( а + рх2,
х2, если х>1. f 1/| х |,
ах3 + рх, [ х | 2,
1 • 1 1,^0
— arcsin — , х > 2.
л х 1 1
если
если
1*|< 1,
I * I
2х — 2, если х^ 1,
4) У — ' а(х — 1)(х — 2)(х — р), если 1 < С х < 2,
— — 1 [ 2 если х^ ? 2.
13.177. Определить значения
iвсюду дифференцируемы:
аир, при которых функции
1) // = 1
2)> = {
(х + а) е~$х,
ах2 + Р* + 1,
аХ Р>
если х < О,
если х^О.
если х < О,
а cos х + р sin х,
если
х^О.
13.178. Определить значения аир, при которых функция
arctg ах,
р sign *4
если | X | 1,
если | х | > 1,
х — 1
2
имеет производную: 1) в точке х — 1, 2) в точке х——1,
13.179. Исследовать на дифференцируемость следующие
функции:
1) У=\хЧ*+ 1)2U + 2)|. 2) # = |sinx|.
3) У = х | х 4) у = | л — х | sin х.
334
5) у = arccos(cosx). 6) у = - ( х21 cos (л/х) 1, если ( х3, если :о,
1 е~1/х, если х> х #= 0, • о.
7) у = \ n п (0, если х — 0. ( х, если х — рациональное число,
3) У Q, если х — иррациональное число.
13.180. Вычислить значения производной для функции во
всех точках, где производная существует:
если
если
{х2,
2| х | — 1,
х — рациональное число,
х — иррациональное число,
если х — рациональное числом
если х — иррациональное число.
13.181. Верно ли утверждение: если 4Ункния имеет произ-
водную в точке, то она дифференцируема в некоторой окрест-
ности этой точки?
13.182. Доказать или опровергнуть следующие утверждения:
1) Если функция f имеет, а функция g не имеет производ-
ной в некоторой точке, то функция f + g не' имеет производной
в этой точке.
2) Если функции f и g-не имеют производной в некоторой
точке, то и функция f + g не имеет производной в этой точке.
3) Если функция f имеет, а функция g не имеет производной
в некоторой точке, то и функция fg не имеет производной
в этой точке.
4) Если функции f и g не имеют производной в некоторой
точке, то и функция fg не имеет производной в этой точке.
13.183. Привести пример функции f(x), для которой /'(хо)
и (f2(x0)Y не существуют, a (f3(%o))' существует.
13.184. Привести пример функции, не имеющей производной
ни в одной точке хеК, квадрат которой имеет производную
в каждой точке х е R.
13.185. Привести пример сложной функции f(g(x)), имею-
щей производную в точке х0 и такой, что:
1) f'(g(xo)) существует, g'(xo) не существует.
2) Г(£(*о)) не существует, g'(x0) существует.
3) f' (gWY и g'(xo) не существуют.
13.186. Доказать или опровергнуть следующие утверждения:
1) Если для дифференцируемых на интервале (а; Ь) функ-
ций f й g верно неравенство f < g, то f' g' на (а; Ь).
2) Если на интервале (а; Ь) верно неравенство < g', то
/< g «а (а; Ь).
.335
3) Если f(a)=g(a) и f'(x)<Zg'(x) на интервале (а;Ь)у то
f(x)<Cg(x) на (a; b).
13.187. Доказать или опровергнуть следующие утверждениям
1) Для того чтобы дифференцируемая функция у(х), хе
е(а;Ь), имела монотонную на интервале (а\Ь) производную,
необходимо, чтобы у(х) была монотонна на (а; Ь),
2) Для того чтобы дифференцируемая функция у(х), хе
е(а; Ь), имела монотонную на интервале (а\ Ь) производную,
достаточно, чтобы у(х) была монотонна на интервале (#;&).
•3) Для того чтобы дифференцируемая функция имела пе-
риодическую производную, необходимо, чтобы функция была
периодической.
4) Для того чтобы дифференцируемая функция имела пе-
риодическую производную, достаточно, чтобы функция была
периодической.
13.188. Доказать или опровергнуть следующие утверждения:
1) Для того чтобы производная дифференцируемой функции
была четной функцией, достаточно, чтобы функция была не-
четной.
2) Для того чтобы производная дифференцируемой функции
была четной функцией, необходимо, чтобы функция была не-
четной.
3) Для того чтобы производная дифференцируемой функции
была нечетной функцией, необходимо, чтобы функция была
четной.
4) Для того чтобы производная дифференцируемой функции
была нечетной функцией, достаточно, чтобы функция была
четной.
13.189. Верно ли утверждение: если функция f имеет произ-
водную в точке хо, то последовательность
{«(7(*о+4) — Ж))}
сходится? Верно ли обратное утверждение?
13.190. Верны ли следующие утверждения:
1) Если функция у(х) дифференцируема на интервале
(а; Ь) и lim у'(х) = оо, то lim у(х) = оо.
х->а+0 х->а+0
2) Если функция у(х) дифференцируема на интервале
Ь) и lim у(х) = оо, то lim г/(х) —оо.
х->а+0 х-»а-Н)
3) Если функция у(х) дифференцируема на интервале (а; 4-оо)
и lim у(х) существует, то существует и lim у'(х).
Х-> + оо
4) Если функция у(х) дифференцируема на интервале
Ya;‘4’°°) и существует lim у' (х), то существует конечный или
бесконечный lim у(х)?
^->4-00
336
4. Понятия бесконечной и односторонней производных. Если
+ В»>
то говорят, что функция f в точке х0 имеет бесконечную поло-
жительную производную. Аналогично, функция f в точке х0
имеет бесконечную отрицательную производную, если
lim FUo + Ax)-f(xo)
Дх->0
Односторонние пределы
lim f(xo + Ax)-f(xo) и Hm f(Xo + M-f(xo)
Дх->+0 ' • Дх-> —О k 7
называют соответственно правой и левой производными функ-
ции f в точке хо и обозначают f' (х0) и fl (*о)-
Для существования производной функции f в точке необхо-
димо и достаточно существование в этой точке правой и левой
производных и их равенство.
Функция f называется дифференцируемой на отрезке [а; р],
если она дифференцируема на интервале Ь) и существуют
конечные односторонние производные и
• Примерю. Доказать, что функции
9/_ ( 1/х, если х #= О,
1) f(*) = V*> 2) g’W = ’{ л ' л
7 ' 7 v 7 (0, если х = О,
в точке х — 0 имеют бесконечную положительную производную.
с//п\ .. f (Ах) — f (0) р ^Ах .. I .
д f (0>=4'1Т«—Ц—=А1;5»’1Г=^»да=+“-
2) g'(0)= lim - lim -<££ = Ilm = A
Дх-»0 Лх Дх-»0 Лх Дх->0ах
Пример 11. Найти f'+ (0) и f'_ (0), если
( е1/х, если х 0,
1) f (х) = I sin 2х 1, 2) = <
’ 'v ’ 1 ' ’ (.0, если х = 0.
, х с/ /гх\ 1- I sin 2Ах | .. sin 2Ах о
Л I fl(0)== lim J—-Г—1= hm Т- =2,
+ Дх^ + 0 Дх-^+О
//хх .. | sin 2Ах I .. sin 2Ах п
f'_(0)= hm <—L = - hm -д^- = -2.
Дх->-0 Дх-»-0
рЦ&Х / с\\ 1*
2) Г+(0)„ |,т Д_»+оо, /-(0) = ^™,^=». А
337
13.191. Найти правую и левую производные в указанных
точках для следующих функций:
1) f (х)~ I х|, х = 0.
2) /(х) = |х2 — 5x4-6 |, х = 2, х = 3.
3) / (х) = | 2* — 21, х = 1.
4) f (х) = xj sin пх, x — k, ft е Z.
5) f (х) = Vsin *2, х = ®, х = л/п.
6) f (х) = sinх| cosx14-cosx| sinхI, x = nk/2, keZ.'
7) f (x) = x| cos(n/x) I, x = 2/(26 4-1), 6 e Z.
8) f(x) = arccos(1/x), x = —1, x=l.
9) f (x) = arcsin sin x, x — (2k 4- l)n/2, k e Z.
13.192. Найти f'_ (0) и f'+ (0) для следующих функций:
f х, если х* СО,
1) f(x) = ] 1 д/х4 In х, если х : > 0.
Г 2х, если х < : о,
2) /(х)= •] 5 1 1п(1 4-V*7), если х^ sO.
Г 1 4~ е1/х, если X < :о“
3) f(x)=] 1 Vi + если х^ 5 0.
13.193. Найти правую и левую производные в точках раз*
рыва следующих функций:
TTTd -X2), если х #= 0,
1) f(x)= 1*1 если х — 0.
11,
2) f(x) — (1 — x2)signx.
1 f —Ц77 , если x y= 0,
з) /W = j 4) f(x)=j ; 1 + e'lx [ 0, если x = 0. [ arctg । j;--" , если r#= 1 1 л/2, если x — 1
5) /(х) = ^ f arctg (1/1 x |), если x ¥= 0. ( зт/2, если x = 0.
6) f(x) = - ( arctg (1/х), если x =Д 0, 1 — л/2, если x — 0.
338
13.194. Найта f+ (х0) nf_ (х0)для функции f (х)i = |х — х0|ф(х),
где ср(х)— заданная функция, непрерывная в точке Хо.
13.195. Привести пример функции, имеющей в точке разрыва
бесконечную отрицательную производную.
13.196. Привести пример функции, непрерывной в некоторой
точке и не имеющей в этой точке ни левой, ни правой произ-
водной.
5. Производная обратной функции. Пусть функция y = f(x)
непрерывна и строго монотонна в некоторой окрестности точки
*> df (х0) , п
х0, и пусть в этой точке существует производная 0;
тогда обратная функция в точке yo=f(xo) имеет производную,
которая может быть найдена по формуле
1* (33)
dy df ’
dx
Пример 12. Найти производную функции, обратной
к функции
у = хЦ-х\ x.elR,
Л Данная функция всюду непрерывна и строго монотонна,
ее производная = 1 + Зх2 не обращается в нуль ни в одной
точке, поэтому
а =_____!__ А
dy 1 + Зх2 * ж
Пример 13. Найти у'(х), если х = sh у.
Л Функция х = sh у непрерывна и строго монотонна при
всех t/eR. Производная x'^ch# не обращается в нуль ни
в одной точке. Следовательно,
1^, 1 = 1 = 1
V * хг (у) ch у V1 4* sh2 # V1 + х2
Функция t/(x), т. е. функция, обратная для гиперболиче-
ского синуса, обозначается arshx. Таким образом,
(arsh х)' =.7-4—; » R. д
V1 + X2
1 3.197. Найти производные обратных функций в указанных
точках:
1 \ I 1 с г\ h <1 COS X 1
1) У = * + g-x5, z/ = 0, «/ = -§-• 2) у — 2х------— ,^ = ——.
3) у = 0,1х + е°’1х, у=1. 4) у = 2х2 — х4, х> 1, у = 0.
5) у — 2х2 — х4, 0 < х < 1, у — 3/4.
839
13.198. Найти производные обратных функций. Указать об»
ласть их существования:
1) г/ = х + 1пх, х> 0.
2) z/ = x + ex.
j^2
3) у — -/ т 2 , х < 0. 4) у — ch х, х > 0.
1 ~Г' X
13.199. Найти производную функции, обратной для гипербо*
лического тангенса.
, 13.200. Дана функция z/ = x + sinx, xeR. В каких точках
обратная функция имеет бесконечную положительную произ*
водную?
6. Производная функции, заданной параметрически. Пусть
функции x = x(t) и y = y(t) определены в некоторой окрест-
ности точки to и параметрически задают в окрестности точки
xo = x(to) функцию y = f(x). Тогда, если x(t) и y(t) имеют
, dx (t0) , „ ,
в точке to производные и если —- у= 0, то функция у =
= f(x) в точке Хо также имеет производную, которая может
быть найдена по формуле
dy (/о)
df (х0) _ dt
dx dx (to)
~dt
Эту формулу обычно записывают короче:
У'х(хо)
Ut «о)
xt (/о)
(34)
Пример 14. Функция у — f (х) задана параметрически фор-
мулами
x = acos3t, у = b sin31, /е(0;л/2).
Найти у'х.
А Функции x(t) и y(f) дифференцируемы при всех t,
и x't~—За cos2/sin / =/= 0 на интервале (0;л/2). По фор-
муле (34) находим
y't 3b sin2 t cos t
x't — 3a cos2 t sin t
X
b
=-------tg t, t (0; n/2). A
a
Пример 15. Функция у = f(x) задана уравнением
г = а (1 + cos ср), ф е (0; 2л/3),
где г и ср — полярные координаты точки (х; у). Найти у*.
340
Перейдем к параметрическому заданию функции
х — г cos ф = а (1 + cos <p)cos ср,
у== г sin ф = а (1 + cos ф) sin ф
и воспользуемся формулой (34):
t Уф а (1 + cos ф) cos ф — a sin2(p
Ху а (1 + cos ф) sin ф + a cos ф sin (р
cos ф + cos 2ф _ cos (Зф/2) cos (ф/2) __
' sin ф + sin 2ф sin (Зф/2) cos (ф/2)
= — ctg(Зф/2), (ре(0; 2л/3). д
13.201. Найти у'х для функций у = у(х)> заданных парамет-
рически:
l)x=sin2/, z/ = cos2/, 0</<л/2.
2) х — е~1, y — t\ — оо < / < + °°.
3) х — a cos /, у =,Ъ sin /, 0 < t < зт.
4) x = achZ, у = b sh/, — оо < / < 0.
5) х = t2 + 6/ + 5, у = Р ~ 54 , 0 < t < + оо.
6) х = (/-1)2(/-2), у = (/-1)2(/-3), 5/3 <t< + оо.
7) х — a(t— sin0, z/ = a(l—cos/), —оо</<-|-оо.
8) х = In sin (t/2), z/ = lnsin/, 0 < t < n.
13.202. Найти x'y для функций x = x(y), заданных парамет-
рически:
1) x = / + 2/2 + /3, y = — 2 + 3/ —1\ 1</< + oo.
2) x = (/3 —2/2 + 3/ —4)^, y = (/3 —2/2 + 4/—4)^,
1 < / < + oo.,
3)x = ctg2/, y = 2cosf-, 0</<-2-.
13.203. Для функции y = y(x), заданной, параметрически:
x = 2/ + |/|, у — 5/2 + 4/1 /|, —oo < t < oo, вычислить произ-
водную в точке х = 0. Можно ли использовать при этом фор-
мулу (34)?
13.204. Найти у'х для функции у = у(х), заданной парамет-
рически:
( t, если t — рациональное число,
X — < у —t2.
( — /, если t — иррациональное число,
13.205. Вычислить у'(х$) для функций у = у(х), заданных
Уравнением г = г(ф), где г и ф — полярные координаты точки
lU; y)i
341
1) г = шр, 4л/3 < Ф < 2зт, х0 = 0.
2) г = е®, — зт/6 < ф < л/6, х0 = 1.
3) r — a^cos 2ф, 0 < ф < л/4, х0 = а д/б/4.
13.206. Для функции # = #(*), .заданной уравнением
z = a^\Jсоз2ф, 0^ф^л/4, вычислить у'+($) и у'_ (а).
7. Производная функции, заданной неявно. Если дифференци-
руемая на некотором интервале функция у — у(х) задана не-
явно уравнением F(x;z/) = 0, то ее производную у'(х) можно
найти из уравнения
9)-0. (35)
Пример 16. Пусть у = у(х), х<=(—а; а), — положитель-
пая функция, заданная неявно уравнением -^5--f--р-= 1.
Найти у'(х).
А Уравнение (35) в данном случае имеет вид
Дифференцируя, получим
Из этого уравнения находим
У'(х) = — xt=(—a; а), у>0.±
13.207. Найти у' для дифференцируемых функций y — y(x)t
заданных неявно следующими уравнениями:
1) У5 + У3 + У — х = 0. 2) у — х — е sin у, |е|<1.
3) у2 = 2рх, у> 0. 4)-J---^-=l, г/> 0.
5) (2а — х) у2 = х3, у < 0. 6) Vx + л] у = 2.
7) х2/3 + у2>* = а2/3, у > 0.
8) 5х2 + 9г/2 — ЗОх + 18г/+ 9 = 0, у<—1.
9) х2 — 4ху + 4г/2 + 4х — Зг/ — 7 = 0, х < 2у — 1.
13.208. Для дифференцируемых функций у — у(х), задан-
ных неявно, вычислить г/'(хо):
1) х2 + у2 — 6х+ Юг/ — 2 = 0, у > — 5, хо = О.
2) 6хг/4-8г/2—12х —26f/+11=0, у <2, х0= 11/12.
•342
3) еу + ху — е, у> 0, х0 — О.
4) ху + In у = 1, у < е2, х0 = О.
8. Дифференциал функции. Если приращение Дг/ функции
у -== f (х) в точке Хо представимо в виде
ку 1х=х0 = (хо)Д* + а (Д*) Д*, (36>
где Д(х0) не зависит от Дх и а(Дх)->0 при Дх->0, то функция
y = f(x) называется дифференцируемой в точке х0, а произвё-
дение Д(х0)Дх называется ее дифференциалом в точке х0 и обо-
значается df(xo) или dy\x~x.
Таким образом, если равенство (36) верно, то
dy\x=x=A(xo)\x. ' (37}
Дифференциалом dx независимой переменной х называется
ее приращение Дх, т. е. по определению полагают dx = Дх.
I , Для дифференцируемости функции в точке (т. е. для суще-
ствования дифференциала) необходимо и достаточно, чтобы
функция имела в этой точке конечную производную.
Дифференциал функции z/==f(x) в точке х0 выражается
через производную f'(x0) следующим образом:
df(x0) = f (x0)dx. (38)
-Эта формула позволяет вычислять дифференциалы функций,
J-если известны их производные.
Если функция г/ == f (х) дифференцируема в каждой точке
интервала (&;&)> то
dy = f'(x)dx (39)
для всех х е (а; 6).
Равенство (36) может быть записано в виде
у (хо + Дх) — У (хо) + dy (хо) + а (Дх) Дх.
Если Л/(хо)¥=О, то для приближенного вычисления значения
функции в точке х0 + Дх можно пользоваться формулой
у (х0 + Дх) ж у (х0) + dy (хо), (40)
так как абсолютная и относительная погрешности при таком
приближении как угодно малы при достаточно малом Дх.
Пример 17. Найти дифференциал функции у — х — Зх2’
в точке х — 2.
А 1-й способ. Найдем приращение функции в точке х=2:
Д^|х=2 = //(2 +Дх) —у(2) =
= 2 + Дх — 3 (2 + Дх)2 — 2 + 12 = — 11 Дх — ЗДх2.
Приращение функции представлено в виде (36); в данном слу-
чае оказалось, что А =—11 и а(Дх) = —ЗДх->0 при Дх—>0.
Следовательно,
dy\x=2 — —lldx.
343-
2-й способ. Вычислим производную функции в точке х=2:
у' (х) = 1 —6х, //'(2) = —11«
По формуле (38) находим
dy(2) = y'(2)dx = —\\dx. Д
Пример 18. Найти дифференциал функции у = ctgЗх.
А По формуле (39) находим
dy = у' (х) dx = — dx, х^~, k G= Z. д
Пример 19. Найти приближенное значение функции
у = д/х в точке х = 3,98.
А Положив в формуле (40) ~ д/х> х0 = 4, Дх = —0,02,
получим
7^98 « д/4 + -ф=- (- 0,02), 7^98 « 1,995. д
9. Свойства дифференциала.
1°. Для любых дифференцируемых функций и и v справед-
ливы равенства
d(au + (За) = a du + (3 dv, (41)
где а и (3 — произвольные постоянные,
d(uv) = и dv + а du, (42)'
,(и\ v du — и dv , Л /лпх
= —&—• v^°- <43>
2°. Формула для дифференциала dy = f'(x)dx справедлива
и в том случае, когда х является не независимой переменной,
а функцией. Это свойство называют свойством инвариантности
формы дифференциала.
П р и м е р 20. Вычислить дифференциал функции
у — х д/б4 — х2 + 64 arcsin (х/8).
А Используя свойства дифференциала, получаем
,dy = d(x д/б4 — х2) + d64 arcsin (х/8) =
= xd д/64 — х3 + V64 — х2 dx + 64tZ arcsin (х/8) —
= X -(<?4 ~-х2)- + 764 - х2 dx + 64 —=
2 764-х* V Г.
Л/ 1- 64
= - + 764 - х2 dx + 64 , ___ =
V64 — х2 V V64 — х2
= 2 д/64 — х2 dx, | х | < 8 • а
"344
Пример 21. Пусть и и v — дифференцируемые функции,
и их дифференциалы du и dv известны. Найти dy, если
у = arctg (u/v) + In ^Ju2 + v2.
&dy = d arctg (u/v) + —• d In (u2 + v2) =
d (u/v) । 1 d (u2 + a2) _ v du — и dv . и du v dv __
u2 ’ 2 w2 + u2 u2 + v2 * u2 + v2
1 + H2'
_ & ±i±du + (v— u) dv 2 । 2 „
И2 + V2 ' “
13.209. Найти Д(хо) и a (Ax) в формуле (36), если:
1)у = х3— 2х, Хо = 1. 2) у = х10, Хо = 0.
13.210. Найти разность между приращением и дифферен-
циалом функции у = (х— I)3.
13.211. При каких значениях х дифференциал функции у =
== соёхще эквивалентен при Дх-Ю ее приращению?
13.212. Какой порядок при Ax->0 имеет бесконечно малая
Ду — dy, если у = х3 — Зх?
13.213. Найти дифференциалы:
Г) d (е~х + In х). 2) d (^х + 2aJ~x + V* )•
3) d(2 V*3(3 In х — 2)). 4) d (arccos ex).
5) dln(VTT2’ sin x + -у/2 sin x — 1 ).
6) d (5 sh7 (x/35) + 7 sh5 (x/35)). 7) d (-^-cs!n/.- + In л/•
\ -yl — x2 V 1 + x J
' 8) d fin 1 V31”^- + 2 arctg Vsin • 9) d (x*2).
\ 1 — V sin x /
13.214. Найти дифференциалы в указанных точках!
? 1) d(l + ln^-), x = -l.
2) d arctg , Xi = 1/e, x2 = e.
я ((2x-l)3V2 + 3^\
7 d k (5x + 4)2^l —x J ’
4) d (^). x1 = 1(x2 = 2.
13.?15. В указанных точках найти дифференциалы функций
у = у(х), заданных неявными или параметрическими уравне-
ниями:
1) У3-У = ^2, ,(1;2).
345
2) х4 + z/4 —8х2 — 10z/2 + 16 = 0, (1;3).
3) z/5 + x4 = xz/2, (x0; y0). 4) x+z/lnz/ = 0, (x0; y0).
5) xy — '\j'xyi + 6=0, (2; 1). 6) x/^7-1) — 2y = 0, (4; 2).
7) 3sin^!_3x(y_ n) —1 = 0, (1; л).
8) 4xz/3 + In Vx/(x + z/)-= 0, (1; 0).
9) x = (/— 1)2(/— 2), y = (t- 1)2(Z —3), (4; 0).
10) x = e*lt, z/ = ((—l)2ef, (—2/д/е; 9/(4 Дё)).
13.216. В точке (0; а) найти дифференциал функции у ==
— у(х), заданной в полярной системе координат уравнением
г = а(\ + cos ср), 0 < <р < л.
13.217. Найти дифференциал функции у, считая известными
дифференциалы функций и и v:
1) y — u2v. 2) y = u2!v.
3) у = uv/(u2 + v2). 4) у = euv, 5) у — ^и2 + v2.
6) z/ = In tg (v/w). 7) y = u”.
13.218. Заменяя приращение функции дифференциалом, най-
ти приближенное значение функции у = у(х) в указанных
точках:
1) г/ = Дх, а) х = 65, б) х= 125,1324.
2)г/ = Дх, а) х = 90, б)х=15,8.
3) #=sinx, а) х = 29°, б) х = 359°.
4) y = tgx, х = 44°50/. 5) у — arcsin х, х —0,51.
6) у= arctg х, х=1,05. 7) у = lntgx, х = 47°15'.
8)^ = л/1т^’ х = 0’15-
13.219. Доказать, что для всех малых, по сравнению с хо,
значений Дх верна приближенная формула
п
Дх0+ Дх « ДД + Ах, х0 > 0. (44)
С помощью этой формулы приближенно вычислить:
1) Дб4+ 2) Д200; 3) Д243.45; 4) ДТООО.
13.220. Определить, насколько приблизительно увеличится
объем шара, если его радиус R = 15 см увеличить на 0,2 см. '
13.221. Определить приблизительно относительную погреш-
ность при вычислении поверхности сферы, если при определе-
нии ее радиуса относительная погрешность составила 1%..
346
13.222. Насколько приблизительно изменится (в процентах)
сила тока в проводнике, если его сопротивление увеличится
на 1 % ?
13.223. Насколько приблизительно следует изменить длину
маятника I =±= 20 см, чтобы период колебаний маятника увели-
чился на 0,05 с? Период Т определяется формулой? = 2u'y]llg.
§ 14. Геометрический и физический смысл производной
1. Геометрический смысл производной. Если функция
y = f(x) имеет производную в точке х0, то угловой коэффи-
циент касательной ТТ' (рис. 76) к графику функции в точке
M(xo;f(*o)) равен f(xo)« Следовательно, уравнение касатель-
ной в точке М (х0; Дх0)) имеет вид
у — f(x0) = f'(х0) (X — Хо). (1)
Если функция у = f(x) непре-
рывна в точке х0 и
lim fUo + y-f(xo) =
'ДХ->0
Рис. 76.
то касательная к графику функции в точке Al-(x0;f (х0)) имеет
уравнение х = хо. В этом случае график функции y = f(x)
в окрестности точки Хо имеет вид, схематически изображенный
йа рис. 77—80.
Прямая, проходящая через точку Л1(х0;/(х0)) перпендику-
лярно касательной, называется нормалью (прямая MN на
рис. 76).
Если f/(xo)#=0, то уравнение нормали записывается в виде
У — f (*о) = — (х- — х0). (2)
Если f'(xQ) = 0, то нормаль имеет уравнение х — Хо.
347
Пусть к графику функции y — f(x) в точке М проведены
касательная и нормаль (рис. 76), которые пересекают ось абс~
цисс соответственно в точках Т и N. В прямоугольном тре,
угольнике TMN катет ТМ называют отрезком касательной, ка,
тет NM — отрезком нормали. Отрезок ТМ\, где ЛЛ —проекция
точки М на ось абсцисс, называют подкасательной, отрезок
NMi — поднормалью. Длины этих четырех отрезков выра-
жаются через значения функции и ее производной в точке х0
следующим образом:
IТМ71+(П2, \nm|=|fIV1 +(П2. (3)
11^1 = 1^1, | NM! | = | ff |. (4)
Пусть графики функций y = fi(x) и у = f2(x) пересекаются
в точке М (рис. 81). За угол <р между графиками этих функ-
ций принимается величина угла, образованного касательными,
проведенными к графикам в точ-
ке М. Угол ф находится с помо-
щью формулы
tg<p =
1 + f'llz
о< т-
(5)
Если 1 + f[f2 = 0, то <р = л/2.
Если функция у = f(x) имеет
р 81 в точке х0 правую производную
f'+(xo)> то уравнение правой
касательной к графику функции y — f(x) в точке М(х0", f(xo)\
имеет вид
У ~ f (*о) = f'+ (хо) (* - *о). (6)
Аналогично записывается уравнение левой касательной:
348
Пример 1. Под какими углами синусоида у — sinx пере-
секает ось абсцисс?
• А Синусоида у — sinx пересекает ось абсцисс в точках
= Если х = 2л&, то yf (2nk) = cos 2nk — 1, т. е.
угловой коэффициент касательной к синусоиде равен единице.
Следовательно, в точках х = 2nk синусоида пересекает ось
абсцисс под углом 45°. Если х = (2£+ 1)л, то у'( (2^+1) л) = —L
Поэтому в точках х = (2Л -f- 1) эх синусоида пересекает ось абс-
цисс под углом 135°. А
Пример 2. Написать уравнения касательной и нормали
к графику функции у = 2х/(1 -J- х2) в точке с абсциссой
Х=л/2-
А Находим производную функции
У W — £ (1 + *2)2 — (1 + х2)2*
{Вычисляем значения функции и ее производной в точкех = ^2:
У (V2) = 2 д/2/3, у' ( V 2) = - 2/9.
Записываем уравнение касательной
К =
и уравнение нормали
Упрощая уравнения, получаем
2 8 л/%
у — — ----§— (уравнение касательной),
^ = -^-х---g— (уравнение нормали), А
Пример 3. Вычислить длину отрезка нормали к цепной
линии у = a ch(x/a) в каждой ее точке.
А Подставив значения данной функции и ее производной
у' = sh(x/a) в формулу для длины отрезка нормали, получим
INM | = | у 1 д/1 + (у')2 = a ch (х/d) д/1 + sh2 (х/а) — a ch2 (х/а). &
Пример 4. В точках пересечения эллипсов
Ai । Jd.— 1 Al . ^1=1
16 9 ъ 9 ‘ 16
Найти угол между ними.
'А Эллипсы расположены симметрично относительно коор-
динатных осей. Рассмотрим поэтому только первый квадрант
координатной плоскости. Решив систему
16 9 ъ
I 9 “ 16
т. е.
найдем точку пересечения эллипсов (12/5; 12/5). Из уравнения
первого эллипса получаем
-Гб+-Т=0’ т-е-
и, следовательно, у' (12/5) = —9/16. Аналогично, для второго
эллипса полупим у' (12/5) =—16/9. Формула (5) в данном
случае имеет вид
I (—9/16)— (— 16/9) | 1/5
tg ф I 1 + (—9/16)(— 16/9) I 286 *
Итак, эллипсы пересекаются в четырех точках под углом <р =
= arctg (175/288), т. е. под углом, равным приблизительно ЗГ#
14.1. Найти углы, под которыми график функции y — f(x\
пересекает ось абсцисс:
1) У — sin Зх. 2) f/ = tgx.
3) у = 1п|х|. 4) у = 1 — ех.
Ь) у = arctg ах, а > 0.
6) s=(x-W-W-3). 7)
8) х = (/— 1)2(/— 2), y = (t — 1)2(Z —3), 2</< + оо.
n. 3at 3at2 , . , . 1
9) X /з _|_ i > У /з _|_ j > 1 < t < 2 *
10) x2 + y2 + 2y — 9 = 0, y> — 1.
14.2. Найти точки, в которых касательные к графику функ-
ции y — f(x) параллельны оси абсцисс:
1) г/= 2х3 —Зх2—12х + 7.
2) z/= Зх4 + 4х3—12х2 —1.
3) у = 3х4 — 28х3 — 6х2 + 84х + 1.
4) у = cos 2х — 5 cos х. 5) у = (3 — х2) ех.
6) у = (2 — х)3/(х — З)2. 7) £/ = |лг — 5 | - (х — З)3.
8) х = /3/( 1 + /2), у = (t3- %2)/( 1 + /2).
9) х2 + 2у2 + 4х — 4z/ = 0, у>\.
14.3. Написать уравнение касательной к графику функции
у = f (%) в указанной точке:
1) у = ^5 — х2, х=1. 2) i/ = arctg2x, х = 0.
36 0
i л:2 — 2х + 1 п
3) у — In x2 + x + 1 , X — 0.
5) У — tfx — 1, х=1.
6) у = (х3 + 2х2)/(х — 1 )2, х = — 2.
7) у = | х — 11 • •vZx4-2, х = 6.
8) х2 + У1 — 2х + бу = 0, yZ>3, х = 0.
9) х = te*, у = (е~*, t > — 1, t —10 > — 1.
Ю) x — a(t— sin/), y = a(l—cos/), t=t(i=^=2nk, k<=Z.
14.4. Написать уравнение касательной к эллипсу= 1
в точке (х0; уо)
14.5. Найти точки пересечения касательных к эллипсам
х2 У2 _ 1
100 "г' &2
в точках с абсциссой х0 с осью абсцисс.
14.6. Найти угол между касательными к кривой
2х2 — 4ху + у2 — 2х + бу — 3 = 0,
проходящими через точку (3; 4).
14.7. Написать уравнение нормали к графику функции
у = f(%) в указанной точке:
1) z/ = cos2x — 2sinx/x = n.
2) у = arcctg(l/x), х=1. 3) у = х3/(2— х)2, х = 6.
4) у = х/'у/х + 1, х = — 3. 5) у2 = 2рх, у^О, х—х0.
6) x = e2<cos2/, y = e2tsin2t, 111 < л/4, / = л/6.
14.8. Написать уравнение нормали к эллипсу 3x2 + 2xz/ +
4* 2у2 4- Зх — 4у = 0 в точке (—2; 1).
14.9. Написать уравнение нормали к гиперболе
zL-vL— 1
а2 &2 ~~ 1
в точке (х0; уо)
14.10. Написать уравнение касательной и нормали к кривой
в точке М:
1) х3 + у2 + 2х — 6 = 0, М(—1;3).
2) 4х3 — Зху2 + 6х2 — бху — 8у2 + 9х 4- 14 = 0, М(—2;3).
3) г/4 ^-4х4—6x^ = 0, Л1(1;2) ,
4) 4- у^ _2ху = 0, М(1; 1),
5) (4 — х)у2 = х2, М(хо',уо)_,
351
6) (тУ + (fУ=2> п е N> М V-
7) х ==/2,//=/3,/И (4; 8).
8) x = /cos/, у — t sin/, Л1(лд/2/8; тц/2/8).
9) х =-•у/2 cos3/, У = V2 sin3/, М (1/2; 1/2).
10)х = -Ш, у = ^ + Л-, М(2; 2).
11) х = (2/ — I)//2, y = (3t2 — I)//3, Af(l; 2).
14.11. Определить, в каких точках и под каким углом пере-
секаются графики функций:
1) f 1 (х) = х — х3, f2 (х) — 5х.
2) Л (х) — д/ 2 sin х, /2 (х) — V 2 cos х'
3)/i(x) = x2, f2(x) = x3.
4) fi (Л) = 1/х, f2{x) = ^fx. 5) /, (х) = х3, /2 (х) = 1/х2.
6) Л(х) = 1пх, /2(х) = х2/(2е).
7) Л (х) = х2 — 4х-ф 4, /2 (х) = —х2 + 6х —- 4.
8) Л (х) = 4х2 + 2х — 8, /2(х) = х3 —х+10.
9) fi(x) = <р(х), f2(x) = (p(x)sin их, ф(х) —всюду дифферен-
цируемая функция.
14.12. Определить, в каких точках и под каким углом пере-
секаются кривые:
1) у = х2 и х = у2. 2) i/ = -|-x5 — -&х3 и xi==l,
3) у — ех12 и х = 2. 4) х2 + у2 = 5 и у2 — 4х.
5) у2 = 2х3 и 64х — 48//—11 — 0.
6) х3 у3 — ху — 7 = 0и// = х+1.
/3 /3-2/2 , . 5х А
7) х j р , у 1 <2 и у + In 8 0.
8) х = (1 +4)*’ +тУ+1 и У = х-
14.13. Доказать, что семейства парабол у2 = р2 — 2рх и у2 =
= 2qx + q2, р =7^= 0, q 0, образуют ортогональную сетку, т. е,
кривые этих семейств пересекаются под прямыми углами.
14.14. Доказать, что семейства гипербол
х2 — у2 _ а и Ху _
образуют ортогональную сетку.
14.15. Доказать, что семейство эллипсов
х=-7>- (а +4) cosZ> “4) sin/> < 2п>
352
и семейство гипербол
* = 4 0 + 4) cosa«
у=4 С ~ 4)sin а* ° < * <+°°
(а и а — постоянные, причем а > 0, а #= лй/2, AeZ), обра-
зуют ортогональную сетку.
14.16. Определить угол между левой и правой касательными
в точке М графика функции у = f(x):
1) г/ = |х|, М(0;0). 2) у = ^/х2, Л1 (0; 0).
8) у = arccos (cos х), М (я; л). 4) у — д/1 — е-3*2, М (0; 0).
5) у = V2*3 + 9х2, М (0; 0).
1 2х я-гЛ. л \
6) y = —i= arcsin------, All 1; —т=г|.
’ v V3 1 + x2 k 2 V3 7
7) x3 + y3 = 3x2, M(0; 0).
X рр TTW Y 0
vvi/lrl Л -f— V,
8) У = 1 + e,/x ’ М (0; 0).
о, если х = 0,
9)^А±^1,
10) x-/-TTP. M(0; 2)-
14.17. Вычислить в точке (1;2) параболы у2 = 4х длины
отрезков: 1) касательной, 2) нормали, 3) подкасательной,
4) поднормали.
14.18. Найти длину подкасательной графика функции у—ах,
а > 0, а =# 1, в каждой его точке.
14.19. Найти длины подкасательной и поднормали графика
функции у = ахп, пе N, а #= 0, в каждой его точке.
14.20. Найти длины подкасательной и поднормали: 1) пара-
болы у2 = 2рх\ 2) гиперболы х2 — у2 — а2.
ip
14.21. Доказать, что подкасательные эллипса — 1
и окружности х2 + у2 = а2 в точках с равными абсциссами равны,
14.22. Доказать, что в точках с равными абсциссами поднор-
мали графиков функций
y — f(x) и у^^/Р(х) + а2,
где f(x)— дифференцируемая функция, равны.
14.23. Найти длины подкасательной и поднормали для
кривых:
1) у2 = х3. 2) ху2 = 1.
12 Л. Д. Кудрявцев и др.
353
14.24. Найти длины отрезков касательной, нормали, подка-
сательной и поднормали у циклоиды
х = a(t — sin t)f у — а(1 —cos t)
в каждой ее точке, не лежащей на оси абсцисс.
14.25. Найти длины отрезков касательной и нормали у трак-
трисы
х = a (In tg(//2) + cos /), у — a sin/, 0</<л, а > 0.
14.26. Доказать, что у кривой
х = 2а(Insin/ — sin2/), у = a sin2/, 0 < t < л, а>0,
сумма длин подкасательной и поднормали постоянна и равна 2ав
14.27. Доказать, что если г = /(ф)— уравнение кривой в по-
лярной системе координат и со — угол, образованный касатель-
ной и полярным радиусом точки касания, то tgco = r/\r'|.
14.28. Найти угол между касательной и полярным радиусом
точки касания для следующих кривых:
' 1) Спирали Архимеда г = аср.
2) Гиперболической спирали г = а/у.
3) Логарифмической спирали г = аеь®.
4) Кардиоиды г — a (cos <р + 1) •
5) Дуги лемнискаты Бернулли r2=a2cos2cp, 0 ф < л/4.
14.29. Под каким углом пересекаются кривые г = ф и г —
— I /ф в точке (1; 1) ?
14.30. Доказать, что угол между касательной к спирали Ар-
химеда г = аф и полярным радиусом дочки касания при
ф—оо стремится к л/2.
14.31. Найти расстояние от полюса до произвольной каса-
тельной кривой г = аеь®.
14.32. Записать в декартовых и в полярных координатах
уравнение нормали к кардиоиде г=а(1-^со5ф) в точке с по-
лярным углом ф = л/6.
2. Физический смысл производной. Средней скоростью изме^
нения функции f(x) на отрезке [й; 6] называют отношение
b - а • к ’
Мгновенной скоростью или скоростью изменения в точке х
функции f(x) называется
Пт ^(х + АЛх)-^=Г(х). (9)
дх->о
Таким образом, производная есть скорость изменения функ-
ции. На интерпретации производной как величины мгновенной
364
скорости изменения функции основано применение прозводной
к изучению разнообразных физических явлений.
Пример 5. Высота h снаряда, вылетевшего с начальной
скоростью оо под углом а к горизонту, изменяется по закону
h = (fl0 sin a) t — ,
где t — время, g— ускорение силы тяжести. В какой момент
скорость изменения высоты снаряда над горизонтом равна
нулю?
А Вычисляем производную функции h(t):
h' (/) = Уо sin a — gt.
Следовательно, скорость изменения высоты снаряда над гори-
зонтом равна нулю при
, vG sin a
Пример 6. Количество электричества q (в кулонах), про-
текающее через поперечное сечение проводника, изменяется по
закону q = 3t2 Найти силу тока в конце пятой секунды.
А Сила тока i в момент времени t равна мгновенной скоро-
сти изменения количества электричества, протекающего через
поперечное сечение проводника. Поэтому i (t) = q'(t) = Gt + 2
и i(5) — 32, т. e. сила тока в конце пятой секунды равна 32 ам-
перам. ▲ _________
14.33. Поезд Москва — Тбилиси проходит весь путь в 2400 км
за 44 часа 14 минут. Определить среднюю скорость поезда.
14.34. Определить среднюю скорость изменения функции
у = sin (1/х) на отрезке [2/лс; 6/л].
14.35. Тело с массой т=1,5 движется прямолинейно по
закону $(/) = /2 + /+1. Найти кинетическую энергию тела че-
рез 5 с после начала движения (масса т задана в килограм-
мах, путь S — в метрах).
14.36. Точка движется по параболе у — 8х— х2 так, что ее
абсцисса изменяется по закону х = д/^ (х измеряется в мет-
рах, t — в секундах). Какова скорость изменения ординаты
точки через 9 с после начала движения?
14.37. Радиус шара возрастает равномерно со скоростью
5 см/с. Какова скорость изменения объема шара в момент,
когда его радиус становится равным 50 см?
14.38. Колесо вращается так, что угол поворота пропорцио-
нален квадрату времени. Первый оборот был сделан за 8 с.
Найти угловую скорость через 64 с после начала движения.
14.39. По оси абсцисс движутся две точки, имеющие законы
движения
100 + 5/ и х® /2/2.
С какой скоростью удаляются они друг от друга в момент
встречи (х измеряется в метрах, t — в секундах)?
12*
355
14.40. Паром подтягивается к берегу при помощи каната,
который наматывается на ворот со скоростью 3 м/мин. Опре-
делить скорость движения парома в тот момент, когда он нахо-
дится в 25 м от берега, если ворот расположен на берегу выше
поверхности воды на 4 м.
14.41. Закон движения материальной точки, брошенной под
углом а к горизонту с начальной скоростью и0, без учета со-
противления воздуха, имеет вид
о-
х — (vQ cos a)t, у — (t>o sin a) t — ,
где t — время, g— ускорение силы тяжести. Определить коор-
динаты вектора скорости и величину скорости.
14.42. Точка движется по спирали Архимеда г — ау так, что
угловая скорость вращения ее полярного радиуса постоянна
и равна 6° в секунду. Определить скорость удлинения поляр-
ного радиуса г, если а — 10 м.
14.43. Расстояние г спутника Земли от ее центра прибли-
женно может быть выражено формулой
2л (t — t0) е2 ( 4л (t — t0)
— 8 COS--^COS--------------°7— 1 j J ,
где t — время, a — большая полуось эллиптической орбиты,
е — ее эксцентриситет, Р — период обращения спутника, во-
время прохождения через перигей. Найти величину скорости
изменения расстояния г (так называемую радиальную скорость
спутника).
14.44. Количество тепла Q Дж, необходимого для нагревания
1 кг воды от 0°-С до f С, определяется формулой
Q = / + 2 И О-5/2 + 3 • 10-7/3.
Определить теплоемкость воды при t= 100° С.
14.45. Масса m(t) радиоактивного вещества изменяется по
закону
т —
где t — время, то — масса в момент времени f0, Т — период по-
лураспада. Доказать, что скорость распада радиоактивного ве-
щества пропорциональна количеству вещества. Найти коэффи-
циент пропорциональности.
§ 15. Производные и дифференциалы высших порядков
1. Производные высших порядков. Пусть функция f(x)
дифференцируема на интервале (a; ft). Производную f'(x) на-
зывают производной первого порядка или первой производной
функции /(х). Если первая производная f'(x) дифференцируема
на интервале (а;&), то ее производную называют второй про-
изводной или производной второго порядка функции f(x). Для
356
производной второго порядка приняты следующие обозначения:
Г(*)> R4 f"x, f">.
Аналогично определяется производная
_ dnf (%)
dxn
порядка fieN: если на интервале (а; Ь) существует производ-
ная порядка п—1, то ее первая производная называется про-
изводной порядка п, т. е*. по определению
^)(х) = (^-1)(х))/, zzgeN;
при этом под производной f(0)(x) нулевого порядка подразуме-
вается функция f(x).
Если s = s(f) — закон прямолинейного движения материаль-
ной точки, то s,z(/) есть ускорение этой точки в момент вре-
мени t. В этом заключается физический смысл второй произ-
водной.
Пример 1. Найти производную второго порядка функции
f (х) = In 11 + х|.
А Так как fz(x) = 1/(1 + х), то
Г (*) = (т-r-У = - 7,-V -<2-. Л
' v 7 \1 + х7 (1+х)2 “
Пример 2. Найти производную порядка п функции f(x) =
= 23х.
Л Так как
f (х) = 23х • 3 In 2,
Г (х) = (23х • 3 In 2)' = 23х • З2 In2 2,
f'" (х) = (23х • З2 In2 2)' = 23х • З3 In3 2,
то естественно предположить, что
(х) = 23х-3'Чп'г 2.
Докажем справедливость этой формулы методом матема-
тической индукции. При п = 1 формула верна. Предположим,
что она верна при п = k, т. е.
f(*)(x) = 23*-3*ln*2.
. Тогда
(%) == (23х • 3* In* 2)z = 23* • 3*+! In^1 2
и, следовательно, формула верна и при n — k-\-\. Отсюда вы-
текает ее справедливость при всех значениях п. А
При вычислении производных высших порядков часто ис-
пользуются следующие основные формулы:
(ах)(п) _ ах 1п п Ц)
357
б частности,
(gX) (n) _ ^2) (sin ax){n> — a1 sin (ax -ф-) , (3) (cos ax)’n) — an cos (ax + . (4)
((ах’+ = апа(а— 1).. .(а—n + 1) (ах + &)“-«. (5)
(I°gjxi)w= , (6) xn In a ’ v '
в частности, (inixiy^bjirl^-1)1. (7)
Если функции и(х) и v(x) имеют производные порядка п,
то функции au(x) + &v(x), где а и р — постоянные, и u(x)v(x)
также имеют производные порядка п, причем
(аи + ро)(га) = au(n) + po<n), (8)
п
(uv)w = X Сп и(п~ k)v{k\ (9>
fc=0
Последняя формула называется формулой Лейбница.
Пример 3. Найти производную порядка п функций:
1) f (х)== v~-4 • 2) fW = *2cos2x.
А 1) Представим данную функцию в виде (разложим на
элементарные дроби; см. § 6)
1 1 / 1____________1 \
х2 — 4 4 \х — 2 х + 2 ) ’
Согласно формуле (8) имеем
( 1 Уд)_1 ( 1 Yn) jl ( 1 Yn)
\ х2 — 4 ) 4 \х — 2) 4 \ х + 2 /
Положив в формуле (5) ос = —1, а — 1, b = ±2, получим
. = (—l)nn!-----Цтг-
(x±2)n+1
Следовательно,
/ 1 \(«) _ (—1)пп! / 1___________1 \
Vx2-4/ ~ 4 \(х-2)',+1 (х + 2)rt+1)'
358
2) Применим формулу Лейбница, положив в ней и =*
-= cos 2х, v = х2:
>(х2 cos 2х)(п) =
= СпХ2 (COS 2х)(ш + Сп (х2/ (cos 2х){п~ *’ + С~п (х2)" (cos 2х)(п-2).
Остальные слагаемые равны нулю, так как
(х2)(^ _ о ПрИ k>2.
.Для вычисления производных порядка и, п—1 и п — 2 функ-
ции cos 2х используем формулу (4):
(cos 2x)(n) — 2n cos ^2х + -ф-) ,
(cos 2х)(ге-1) = 2га~1 cos (2х + -° ) = 2"-1 sin (2х + ,
(cos 2х)<п~2) = 2n-2cos (2х + я(я2~~' 2) ) = — 2n~2 cos (2х + .
•Следовательно,
,(х2 cos 2x)w = 2" (х2 - я (га4~1)) cos (2х + +
+ 2ппх sin (2х + . А
Пример 4. Для функции f(x) = arctg х вычислить f(n)(0).
А Так как f'(x)= 1/(1 + х2), то
(1+х2)Г(х)=1.
Вычислим производные порядка п — 1 от обеих частей этого
равенства. Для вычисления производной от левой части приме-
ним формулу Лейбница, положив в ней u = f'(x), ц = 1-|-х2.
Получим
(1 +x2)f(«)(x) + 2(n—l)xf<”-1>(x)+ (n—1) (n —2)f<"-2)(x)=0,
•откуда при x — 0 найдем рекуррентное соотношение
f(«) (0) = — (п — 1) (п — 2) f<«-2) (0).
При четном п (п = 2k), поскольку (0) = 0, получаем
f(2« (0) = 0.
При нечетном п (п = 2й-|-1), поскольку f'(0)= 1, находим
^(2fe+i) (0) = _ (2/г) (2Й — 1) fk~ ° (0) = ...
... =(-1№)1П0)=(-1№)! ▲
Пример 5. Найти вторую производную функции, обратной
к функции
y — x^x^i zeR,
359
Л Данная функция всюду непрерывна и строго монотонна,,
ее производная у'х — 1 + 5х4 не обращается в нуль ни в одной
точке, поэтому
/ 1 1
X = —7“ =-------Г •
у ух 1 + 5х4
Дифференцируя это тождество по у, получим
/z _/ 1 V г______ — 20х3
Хуу ~ k 1 + 5х4 )х ‘ ху ~ (1 + 5х4)3 • А
Пример 6. Функция y — f(x) задана параметрически фор-
мулами
x—t— sin/, у = 1—cos/, /е(0;2л).
Найти у"х.
Л По формуле (34) § 13 находим
, y't sin i 2 sin (//2) cos (//2)
x't 1 — cos / 2 sin2 (//2)
t. e. y'x — ctg (//2). Дифференцируя обе части полученного равен-
ства по х, получим
у"х=(cfg w2»; • <=(ctg m't • 4-=
xt
_________i _ i *
2 sin2 (Z/2) 1 — ccs t 4 sin4 (t/2) ’
Пример 7. Пусть функция y = f(x) задана параметри-
чески формулами
x — x(t), y = y(t), t^(a;b),
и пусть x(t) и y(t) дважды дифференцируемы и %'(/)#= О при
/е(а; д). Найти у"х.
А По формуле (34) § 13 находим первую производную f'(x)i
Дифференцируя обе части этого равенства по х, получаем
т. е.
п" xiy"t-Vtx"t НО) А
-------7з • (1и,
xi
360
Пример 8. Пусть у = у(х), |х|>-'а,— положительная
•функция, заданная неявно уравнением
V2 _ 1
а2 Ь2 ~ *'•
Найти у"х.
А Для нахождения у'х воспользуемся уравнением (35) § 13,
которое в данном случае имеет вид
dx\a2 Ь2 ) и’
Дифференцируя, получаем
>-•(11)
Из этого уравнения находим У'х — ~^^ |х|>а!, {/>0. Диф-
ференцируя по х обе части равенства (11), найдем
Следовательно,
УXX у V a2 Vx) ) уха2 а4 у2 )
Ь4 / х2 у2\ Ь4 ~
— а2у3 Ка2 ~Ь2)~ а2у3 ’ У > U’ А
Пример 9. Определить, какого порядка производными об-
ладает в точке х — 0 функция у — |х|3.
А Если х =/= 0, то
( Зх2 при х > О,
У W | _ зх2 ПрИ х < о.
При х — 0 по определению производной находим
/(0) = Пт У(0 + Ах)-у(0) = 1^ = 0.
* ’ дх-*о Л* Дх_0 Дх
Таким образом, первая производная существует при всех х,
причем
у' (х) = 3x2sign х.
Аналогично, для второй производной получаем
( 6х при х > 0,
У U) | _ бх при х < 0,
^(0)= Нт ./<9 +(°) = Hm A^signAx =0>
Дх->0 Ах->0
Дх
т. е. вторая производная существует при всех х, причем
//"(х)=6|х|.
361
Функция |х| недифференцируема в точке х = 0. Следова-
тельно, данная функция у = |х|3 обладает в точке х — 0 про-
изводными до второго порядка включительно. А
2. Дифференциалы высших порядков. Пусть функция у =
= f(x) дифференцируема на интервале (а; Ь). Ее дифферен-
циал
dy = f'(x)dx, (12)
который называют также ее первым дифференциалом, зависит
от двух переменных х и dx. Пусть производная f'(x) также
дифференцируема на интервале (а; 6). Тогда при фиксирован-
ном dx дифференциал dy является функцией только х, для ко-
торой можно в свою очередь вычислить дифференциал, причем
в качестве приращения Дх независимой переменной х взять то
же самое приращение, которое было выбрано при нахождении
первого дифференциала функции f(x), т. е. dx. Вычисленный
при этом условии дифференциал от первого дифференциала
называется вторым дифференциалом или дифференциалом вто-
рого порядка функции y = f(x) и обозначается d2y или d2f.
Таким образом, по определению
d2y — d~(dy) = d (f' (x) dx) — (df' (x)) dx = (x) dx dx — f" (x) (dx)2,
или
d2y = (x) dx2. (13)
Аналогично, в случае, когда функция y — f(x) на интервале
Ь) имеет производную порядка п, определяется n-й диффе-
ренциал dny как первый дифференциал от (п—1)-го диффе-
ренциала при условии, что при вычислении первого дифферен-
циала в качестве приращения Дх берется то приращение dx,
которое выбиралось при вычислении (п—1)-го дифференциала.
Методом индукции для n-го дифференциала получается
формула
dny — f(fl} (*) dxn. (14)
Дифференциал и-го порядка независимой переменной х при
п > 1 по определению считается равным нулю, т. е.
dnx — 0 при п>\. (15)
Если для функций и(х) и v(x) дифференциалы dnu и dnv
существуют, то функции ош(х) + $v(x), где а и р— постоян-
ные, и и(х)ь(х) также имеют дифференциалы n-го порядка,
причем
dn (аи + р^) — adnu + $dnv, (16)
dn(uv)=~ X Cndn~ku-dkv. (17)
3 а м e ч а и и e.. Формула (13) и формула (14) при п > 1
справедливы только тогда, когда х является независимой пере*
?62
'менной. Для сложной функции у = y(x(t)) формула (13) обоб-
щается следующим образом:
d2y = d (dy) = d (y'x dx) = (dy'x) dx + y'xd (dx),
t. e.
d2y = У"* dx2 + y'xd2x. (18)
В случае, когда x — независимая переменная, d2x — 0 и фор-
мула (18) совпадает с формулой (13).
Пример 10. Найти второй дифференциал функции у—хе~\
•считая х независимой переменной.
Л I способ. По определению второго дифференциала на-
водим
<d2y — d (dy) — d(xde~x + e~xdx) = d(— xe~xdx + e~x dx) —
d (xe~x) dx + (de~x) dx — — (x de~x + e~x dx) dx — e~x dx2 =
= xe~x dx2 — e~x dx2 — e~x dx2 = (x — 2) e~x dx2.
II способ. Вычисляем вторую производную
у" = (хе~х)" = (е~х — xe~x)f — — е~х — е~х + хе~х = (х — 2) е~х
и по формуле (13) находим
d2y = (* — 2) e~~xdx2. А
Пример 11. Найти второй дифференциал функции у ==
= sinx2, считая х\ а) функцией некоторой независимой пере-
менной; б) независимой переменной.
Да) I способ. По определению второго дифференциала
имеем
d2y — d(d sin х2) = d (2x cos x2 dx) = (2x cos x2) d2x +
+ (d (2x cos x2)) dx = 2x cos x2d2x + (2 cos x2 — 4x2 sin x2) dx2.
II способ. Вычисляем первую и вторую производные дан-
ной функции по х:
у'х = 2х cos х2,
у"х = 2 cos х2 — 4х2 sin х2.
•Согласно формуле (18) получаем
d2y — (2cos х2 — 4х2 sin х2) dx2 + 2х cos x2d2x*
б) В этом случае d2x = 0 и, следовательно,
d2y = (2cos х2 — 4х2 sin х2) dx2. А
Пример 12. Найти d2y, если y = u[v и du, dv, d2u, d2v
известны,
363
А При решении используем свойства первого дифферен-
циала (формулы (41) — (43) § 13)
v2d (v du — и dv} — (v du — и dv) dv2
v4
v2 (vd2u + dv du — ud2v — du dv) — 2v (v du — и dv) dv
v4 =
= — d2u---d2v------ du dv + dv2. a
v V2. V2 1 ^3 A.
15.1. Найти производную второго порядка:
1) №=*2+13x+l 1. 2) у = 14-10% + -Tj-.
x(l+3Vl“*2) Л\ 2
з) у4) у = cos х-
5) У — sh2x + ch2x. 6) у = In (х + д/х2 + 0*
7) у = arctg (х + V*2 + 1 )• 8) у = arcctg -7=3/ ..
V2x — х2
f\ \ . x2 — 1
9) у = arcsinтг+Г-
4 ________________ 4 ________
im о i. Vx4-f-l , Vl+x4 + x
10) у = 2 arctg ----In v4- - —.
Vl + X4 — X
15.2. Найти вторую производную в указанной точке:
1) у = е^х, х = 4. 2) ----g----, * = 5.
3) (/ = —7==-, х = 0. 4) y — esin * cos (sin х), х = 0.
-yl — X2
5
15.3. Точка движется по закону s(t) = 2t2 + у/3 (s изме-
ряется в метрах, t — в секундах). Найти ее ускорение через 5с
после начала движения.
15.4. Доказать, что при движении тела по закону s(t) =
е= ае* + Ье~~* его ускорение численно равно пройденному пути.
15.5. Доказать, что при движении тела по закону $(/) = д//
его ускорение пропорционально кубу скорости.
t2 1
15.6. Одна точка движется по закону Sj (/) = /3 + — + t +
2
другая — по закону s2(/) = -^/3 + З/2 — 5/ (si, s2 измеряются
в метрах, t — в секундах). Найти ускорения точек в тот мо-
мент, когда их скорости равны.
15.7. Найти величину силы, действующей на точку с массой
т = 0,1, движущуюся по закону s(t) — t2 — 4t4 в момент вре-
мени t = 3 (m, s, t заданы в системе СИ).
364
15.8. По окружности радиуса 5 м движется точка с постоян-
ной угловой скоростью 2 рад/с. Найти величину ускорения
точки.
15.9. Найти второй дифференциал функции;
1) ^ = (х2 + %+ 2) # = 2х + ctg 2х.
3) # = x(coslnx+sinlnx). 4) у = хх.
15.10. Найти- второй дифференциал функции в указанной
точке:
1 \ х3 1 п\ Зх + 2 Л
— 3 —х2 ’ х~ • 2^— х2 — 2x4-5’ Х~ °*
3) у = Х'\/(х — 5)2, х = — 3. 4) # = arctg | j, х = 0.
15.11. Определить, удовлетворяет ли функция у = у(х) за-
данному уравнению:
1) у = A cos ах + В sin ах,
2) у = Аеах + Ве~ах,
3) у = (Л cos Зх + В sin Зх) е~х,
4) у==Аех А- Ве~х — -Ь,
5) у = 1 -f- cos ех + sin ех,
6) У = (х+ д/1 +х2)10,
7) у___в10 arcsin
8) у = cos (10 arccos х),
у" + а2у = 0.
у" — а2У = 0.
i/" + 2/+10z/ = 0.
У" ~У' + е2ху = 0.
(14-х2) у" 4- ху' — 100z/ = 0.
(1-х2) у" — ху' — 100г/ = 0.
(1 -х2)у" -ху' 4-100z/ = 0.
15.12. Найти у'', считая известными и', и'', v', v"i
1) У = (у 4- 2и)[и. 2) y — euv.
3) у — arctg (о/м). 4) у — In V“2 + v2-
15.13. Найти d2y, считая известными du, d2u, dv, d2vi
1) y = u(2A-v). 2) у = u\nv.
3) У = Vм2 + v2. 4) У = u°.
ti
15.14. Найти Для функций, заданных параметрически
уравнениями:
1) х = /2, у — t2, 2) X = J ^3 > у । । ^з •
3) x = lncos/, у = In cos 2/. 4) x = ncos/, у = b sin/.
5) x — (1 4- cos2/) sin /, у — sin2 / cos /.
6) x = / ch / — sh /, у = / sh / — ch t.
fit J. 1
7) x=-rT?, // = (/-1)Л 8) x = -^, y = tgt-t.
9) x=sinlog2/, y — tglog2/. 10) x = 2cos?/, z/ = 2sin<.
365
ti
15.15. Найти в заданной точкег
1) х = (/2+1)е<, ^==/2e2t. ц. 0)>
2г-/2 t2 tri ..
2) y^——. (0; 4).
3) x = ln(l + sin ф), у — ln(l — cos2cp); (In(3/2); In (1/2)).
4) x = ch/sin/ 4-sh/cos/, у = ch/cost — sh/sint; (0; 1).
d^~ X-
15.16. Найти для функций, заданных параметрически
уравнениями:
1) # = _ 2 + 3/— f3, ^ = / + 2/2 + /3.
2) x = lntg(//2), y = lntg/.
3) х = logs sin t, у — logs cos /.
4) x — arcsin tg^> у = Vcos2/«
15.17. Доказать, что функции у — у(х), заданные парамет-
рически, удовлетворяют заданным уравнениям:
1) x^t3 + t, t/ = |/44-|/2 + 1; у"(1+3/2) = 1.
2) x==e*cos/, # = e*sin/, —л/4</<л/4;
(x — y)2y" = 2(xy' — y).
3) x = sin /, у =^Ae^2 f + Be~^2 *, — л/2 < / < n/2,
А и В — произвольные постоянные; (1—х2)у"— ху' — 2у = 0.
4) х — ЗЛ/2 + In Bt, у — 2Л/3 + /, А и В — произвольные
положительные постоянные; (Зу — 2у') у" = у'2.
15.18. Найти для функций, - заданных параметрически
уравнениями:
1) x = acos/, у —a sin t, 2) x = ach/, z/ = ash/.
3) x = acos3/, y = asin3/.
4) x — a (/ — sin /), у = a (1 — cos /).
5) x = e~<cos/, z/==e_/sin/.
6) x = cos / — In ctg (//2), y = sin/.
dnu
15.19. Найти Для функций, заданных параметрически
уравнениями:
1) x=*acos2t, у sin2/. 2) x = cos/, у = cos nt, nsN.
3) x==/2 — / 4-1, r/==/24-/4~l- 4) x — y4_ j , у = •
15.20. Пусть для функции y==/U) известны f'(x), f"(x),
f'"(x). Найти вторую и третью производные обратной функции
л- = f-1 (у), предполагая, что они существуют.
366
15.21. Для функций у — у(х), заданных неявно, найти у":
1) х2 у2 = а2. 2) х2—у2 —а2.
3) ^ + ^ = 1- 4) г/2 = 2рх.
5) ex~v = х + у. 6) е2у — 2 In х — 1=0.
7) у — xtg In 7%2 + r/2 = 0. 8) y2 = ex>~v\
15.22. Найти d2y в точке (х0; у о) для функций у — у(х), за-
данных неявно:
1) х2 + 2ху + у2 - 4х + 2у - 2 = 0, (1; 1).
2) 21п(у — х) + sin ху = 0, (0; 1).
3) х3у + arcsin(у — х)=1, (1;1).
4) 3(у — х+ 1)+arctg(i//x) = О, (1;0).
15.23. Доказать, что функции у — у(х)9 заданные неявно,
удовлетворяют уравнениям:
1) у = Д1пу + х'+В, уу" = (у')2 — (у')3.
2) (Л + Вх) еу/х = х, х3у" = (ху' — у)2.
15.24. Найти z/(n)(x)' Для следующих функций:
1) у = Xs +' х + е3х. 2) у = аохп + ajx"-1 ап.
5) у = 1п(ах + Ь). 6) y = sin2x.
7) у = sin ах sin bx. 8) у =chaxchbx.
9) у = sin2x sin 2х. 10) у = sin4 х + cos4x.
11) J, = cos‘x. 12) U=j==-
13) X2- 4х - 12 14) У ~ 1 — х2 • = 2х2 + Зх — 2 ‘
15.25. Найти z/(n)(x) для следующих функций:
1) у = (х- 1)2*-1. 2) у = (2х — 1) 23х • 32х.
3) у — (3 — 2х)2 е2~3х. 4) у = xlog2(l — Зх).
5) г/ = 1п(х-1)2х. 6) y = xln|±y.
7) у == хIn(х2 — Зх + 2). 8) y = xcosx.
9) у = 2х cos2 (х/3). 10) у = (х2 + х) cos2 х.
15.26. Найти у(п)(х) для следующих функций:
1) у =..г^=. 2) у = /£= .
’ Vl — 5х V1 — 2х
3) у = еах cos (bx 4- с). 4) у = е2х sin 2х.
367
5) z/ — ch ax sin bx9
6) У = xn~xe{!x.
7) у — xn~x\nx. 8) у — arctgx.
15.27 . Вычислить в заданной точке производную указанного
порядка:
1) у = (2х— 7)2(3% + 7)3; a) n = 5, x — xQ; б) п = 6, х = х0.
[— у2
2) г/ = -ух; п=10, х—1. 3) у = 1 _х'; п = 8, х = 0.
4) у = *+1 ; п=13, х = -1
5) У — Vх2 + Зх3; п = 5, х=1.
6) г/= J..72L. п = 6, х = -1.
V2-3x
7) f/ = x2lnx; п=100, х—1.
8) у = (х2 — 2х) cos Зх; п =101, х=1.
9) у = х sin х cos 2х; п =100, х = л/2.
10) у — (х—sinx)2; и =16, х = л/4.
11) у — arctg2х; а) «=10, х = 0; б) «=11, х = 0.
15.28 . Вычислить в заданной точке дифференциал указанного
порядка:
1) </ = (х + 5)5; п — 3, х = 0.
2) У = (Зх —2)2 ’ п==10> х=1-
3) г/ = (Л/х2^й'+д/х^Т)2; п =16, х=1.
4) у = sin х sin 2х sin Зх; «=10, х = л/6.
5) z/ = (2x2+l)sh2x; n = 8, х = 0.
6) у = arcsin х; а) п=19, х = 0; б) « = 20, х = 0.
15.29 . Определить, какого порядка производными обладает
в точке х = 0 функция у = у(х), и вычислить в этой точке все
существующие производные:
f 1 — cos х, если х < 0,
1) #(Х) = 1 1 /1 I X п
( 1п(1+х)—х, если х^О.
( 2х cos х, если х < 0,
2) У(х) = ') - о
(. sm2x, если х^>0.
( shx — х, если х < 0,
3) — < п
(. х — sin х, если х 0.
368
5) z/(x) =
0,
0.
x — рациональное число,
x — иррациональное число,
если х =# 0,
если х = 0.
x = 0.
4
( shx, если х
4) г/(х) = < . .
7 1 sin х ch х, если х
х10, если
— х10, если
. х100 sin (1/х),
6) у (х) = | 0,
( е~ , если
, 7) f/(x) = < п
7 и 7 ( 0, если
15.30 . Пусть f (х) е С"-1 [0;+°о). Доказать, что существуют
числа ak (1 п) такие, что функция
п
X akf (~- kx), если х < 0,
<p(x) =
I fU),
если
o,
непрерывно дифференцируема на всей оси.
15.31 . Пусть функция ф(х) дифференцируема и удовлетво-
ряет условию ф'(х) = f(cp(x)), где f имеет производные всех
порядков. Доказать, что ф(х) также имеет производные всех
порядков.
15.32 . Доказать, что если существует, то
15.33 . Пусть
Рп,т(х) = -^г(1 — хт)п, т>0.
Найти Рп,т(1).
ГЛАВА IV
ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
§ 16. Теоремы о среднем для дифференцируемых функций
1. Теорема Ролля. Если функция f непрерывна на отрезке
{a;ft], имеет во всех его внутренних точках конечную или
определенного знака бесконечную производную и f(a) = f(b),
то существует такая точка Ее(а; Ь), что
Ш) = 0. (1)
Условие (1) означает, что в точке (£;/(£)) графика функ-
ции f касательная к нему горизонтальна (рис. 82). В условиях
теоремы Ролля среди точек g, удовлетворяющих условию (1),
всегда существует точка, в которой функция f имеет экстремум.
Рис. 82.
Рис. 83.
2. Теорема Лагранжа. Если функция f непрерывна на отрезке
(а; Ь] и имеет во всех его внутренних точках конечную или
определенного знака бесконечную производную, то существует
такая точка £е(а; &), что
f(b)-f(a) = f(|) (Ь — а).
(2)
Формула (2) называется формулой конечных приращений
Лагранжа. Ее геометрический смысл состоит в том, что
в условиях теоремы на графике функции f найдется точка
(£;/(£))> а < £ < в которой касательная к графику парал-
лельна хорде графика (рис. 83), соединяющей точки (a;f(«))
370
и Действительно, если формулу (2) переписать в виде
m
fW-f(g)
b — а
(3)
то ее левая часть равна тангенсу угла, образованного указан-
ной хордой с осью х, а правая — тангенсу угла, образованного
соответствующей касательной с той же осью.
Положив а — х, b — а = hf формулу (2) можно удобно запи-
сать в виде
f(x + h) — /(х) = Нх + 0Ж О<0<1. (4)
Следствие 1. Пусть функция f непрерывна на некотором
промежутке и дифференцируема во всех его точках, кроме
конечного их множества. Тогда, если производная функции f
равна нулю во всех точках, где производная существует, то
функция f постоянна на рассматриваемом промежутке.
Следствие^. Пусть функции fug непрерывны на неко-
тором промежутке и дифференцируемы во всех его точках,
кроме конечного их множества (вообще говоря, различного для
каждой из них). Если во всех точках, в которых одновременно
существуют производные f' и g\ они совпадают: f'(x) = g'(x),
то на всем рассматриваемом промежутке функции f и g отли-
чаются на постоянную:
f (*) — S W + G с — const.
Следствие 3. Пусть функция f непрерывна в некоторой
окрестности точки х0 и дифференцируема в проколотой окрест-
ности этой точки. Тогда, если существует конечный предел
lim f' (х) — А, то функция f дифференцируема в точке х0 и
Z(x0) = А.
3. Теорема Коши. Если функции х = ф(0 и у = ф (t) непре-
рывны на отрезке [a; fe] и имеют во всех его внутренних точках
конечные производные, причем ф'(0^0, а < t < b. то суще-
ствует такая точка 6), что
Ф W — Ф (а) _ фЛ (g)
ф(&)-ф(а) ф'(£) ’
Если ф(а) ф <р(6), то условие ф'(£)=#0 на (а; Ь) можно
заменить условием [ф'(/)]2 + [Ф'(012 > О, a<Zt<b.
Геометрический смысл теоремы Коши состоит з том, что на
параметрически заданной кривой х = ф(£), у — ф (t)y
существует точка (ф(£); ф(£)), а < g < 6, в которой касатель-
ная параллельна хорде, соединяющей начало (ф(а); ф^а)) и
конец (ф(6)| ф(Ь)) этой кривой. В самом деле, дроби и
ф (Ь) — ф (а) ~
Ф (6) — у Равны соответственно тангенсам углов, образован-
ных указанными касательной и хордой о осью х,
371
Пример. Доказать, что все корни многочленов Лежандра
<0-1, 2,...) (6)
действительные, простые и лежат на интервале (—1; 1).
А Рассмотрим многочлен Q2«(x) = (х2 — 1)п. Он имеет сте-
пень 2/г, и его корнями являются х\ =—1 и х2=1, причем
каждый корень имеет кратность п. Поэтому, если /г>1, то
производная Q'2n также имеет xi и Х2 своими корнями, но уже
кратности п~\. По теореме Ролля, у производной су-
ществует еще по крайней мере один корень х3, лежащий между
Xi и х2. Поскольку сумма кратностей всех корней многочлена
равна его степени, а степень многочлена Q'2n(x) равна 2п— 1, то
кратность корня х3 равна 1 и других корней, кроме хц х2 и х3,
у 'многочлена О2п(х) нет. Продолжая этот процесс, по индукции
получим, что производная Q(2"-1)(x) имеет п-\- 1 простых корней
Xi (1=1,2, ..., /г+1). Занумеруем их в порядке возрастания:
—1 = xi < х2 < ... < хп < Хп+у = 1. По теореме Ролля, на
каждом отрезке [х£; xz+i] (7 = 1, 2, ..., /г) лежит хотя бы один
корень производной многочлена Q2"~*1}(x), т- е- корень многочле-
на Лежандра, ибо
[QaT ° (х)]' = Q® (х) = 2пп1Рп (х).
Таким образом, многочлен Лежандра имеет на интервале
(—1; 1) п различных корней, а так как его степень равна /г, то
все они простые и других корней, действительных или комплекс-
ных, у него нет. ▲
16.1. Проверить справедливость теоремы Ролля для функции
х(х2—1) на отрезках [—1; 1] и [0;1].
16.2. На интервалах (—1; 1) и (1; 2) найти точки, в которых
касательная к графику функции f (х) = (х2 — 1) (х — 2) гори-
зонтальна.
16.3. На интервале (0; 1) найти такую точку g, что каса-
тельная к графику функции у = х3 в точке (g; g3) будет парал-
лельна хорде графика, соединяющей точки (0; 0) и (1; 1).
16.4. Доказать, что между двумя действительными корнями
многочлена с действительными коэффициентами имеется корень
его производной.
16.5. Доказать, что если функция f дифференцируема п раз
на отрезке [a; ft] и обращается на нем в нуль в п + 1 точках,
то существует такое g е (а; Ь), что (g) = 0.
16.6. Доказать, что если функция f дифференцируема п раз
на отрезке [a; b], а = Xi < х2< ... < xk — b, Xi е [а; 6], /г/ —
натуральные числа, щ + ... -\-nk = n—1 и f(//)(xz) = 0,
= 0, 1, ..., /г/ 1, f = 1, 2, ...,£, то на отрезке [а; Ь] суще-
ствует такая точка g, что (g) = 0.
372
16.7. Доказать, что корни производной многочлена
х (х — 1) (х — 2) (х — 3) (х — 4)
действительные, простые и лежат на интервалах (0; 1), (1;2)
(2;3), (3; 4).
16.8. Доказать, что все корни уравнения
(|+>у^(1 + ^-_0
' 1 7 dxn
действительные.
16.9. Доказать, что все корни уравнения
л dn - 1/х
v2/2p- 1/Х а е__ __ П
Х 3 dxn ~U
действительные.
16.10. Доказать, что все производные от многочлена с дей-
ствительными коэффициентами, имеющего только действитель-
ные корни, также могут иметь только действительные корни.
16.11. Доказать, что корни всех производных (порядка
т < 2п) многочленов Лежандра
р 1
\л) 2nnl dxn
действительные, простые и лежат в интервале (—1; 1)«
16.12. Доказать, что у многочленов Лагерра
Т , ч х dnxne~x
Ltl W = е dxn
все корни положительны.
16.13. Доказать, что у многочленов Чебышёва — Эрмита
Лпр~х^
все корни действительны и лежат в интервале
(— и/2п+ 1; д/2«+ О-
16.14. Применив теорему Лагранжа к функции 1/ха, дока-
зать, что при любом ne N и любом а > 0 справедливо нера-
венство
1 1 г 1_______11
na+1 a L (п — 1)а па J
16.15. Пользуясь теоремой Лагранжа, доказать неравенства:
1) n(b -—d)an~l < bn — ап < п(Ь — <а)Ьп~х при 0 < а < b, neN.
2)< In (1 + ^) < ^ при х>0.
3)е*>1+х при xeR. 4) ех > ех при х>1.
5) ха| lnx| < при 0<х<1, а>0.
373
16.16. Доказать, что при х^О справедливо равенство
л/ X -р 1 — л/ X =-------;
2 Vх + 0 (%)
где 1/4 0(х) < 1/2, причем lim 0 (%) = 1/4, lim 0(х)=1/2.
х 4- 0 х —4“ оо
16.17. Доказать: если функция f дифференцируема п раз при
х^О, f(O) = f'(O) = ... =/(n-D(0) = 0, a fW(x)>0 при
х > 0, то и f (х) > 0 при х > 0.
16.18. Доказать: если функции f и g дифференцируемы п раз
при х>0 и f(O) = g(O), f(O)=g'(O), ..., f(-i)(0) = ^-i)(0),
(х) > (х) при х > 0, то и f(x)> g(x) при х>0.
16.19. Доказать, что если функция f дифференцируема и не-
ограничена на конечном интервале (а;&), то ее производная
также неограничена на этом интервале.
16.20. Доказать, что если функция f дифференцируема на
конечном или бесконечном интервале (а; Ь) и существуют рав-
ные конечные или одного и того же знака бесконечные пределы
lim f(x) и lim f(x), то существует такая точка
X—^п-ЬО х-^Ь—0
что f' (g) = 0.
16.21. Пусть f(x)— f (0) = xf'(£(x)), 0 < g(x) < x. Доказать,
что если f(x) — % sin (In x) при x>0 и /(0) = 0, то функция
£(л) разрывна в сколь угодно малом интервале (0; е), е > 0.
16.22. Доказать, что если функция f дифференцируема при
х > а и lim f'(x) = O, то lim =0.
Х->4-оо Х-»4-оо х
16.23. Доказать, что если функция f дифференцируема при
х>а и lim Ч*) =0, то lim |/'(х)| = 0.
Х Х^+оа
16.J24 . Доказать, что если функция f дифференцируема на
отрезке [a; fe], ab > 0, то
где а < g < b.
16.25. Доказать, что если функция f удовлетворяет условиям
теоремы Ролля на’отрезке [а; Ь] и не является постоянной, то
на этом отрезке существуют такие точки gi и g2, что
rui)>o, mxo.
16.26. Доказать, что если функция f непрерывна на отрезке
[а;&], дифференцируема на интервале (а; &) и не является
линейной, то существует такая точка 6), что
1Г(Ю1> | 1 -
16.27. Доказать, что если функция f дважды дифференци-
руема на отрезке [а\ Ь] и f\(a) == = 0, то существует такая
374
точка g <='(а; b), что
1Г(Ю1>7Г^1Н^)-На)|.
16.28. Пусть функция f непрерывна в некоторой окрестности
точки- хо и дифференцируема в проколотой окрестности этой
.точки. Доказать, что если существуют пределы lim f'(х) и
х->хо-О
lim f'(%),причем они не равны между собой, то функция f
х->хо+0
недифференцируема в точке х0.
16.29. Доказать, что если функция f дифференцируема в не-
которой проколотой окрестности точки хо, непрерывна в самой
этой точке и существует конечный предел lim (х), то суще-
х-»х0
ствует и производная f'(xG), причем Д(х0) = Дт f'(x) (иначе
х->х0
говоря, доказать следствие 3 теоремы Лагранжа).
16.30. Доказать, что если функция f дифференцируема на
отрезке [1; 2], то существует такая точка |е(1; 2), что
16.31. Доказать, что если функция f дифференцируема на
отрезке [а; 6], причем f(a) = f(b), то существует такая точка
£е=(а;&), что f(a) — f ft) = | If' ft).
16.32. Пусть функция f непрерывно дифференцируема.на ин-
тервале (а; Ь) и ее производная монотонна на этом интервале.
f (х)
Доказать, что если /(х0) — 0, х0 е (а; 6), то lim \ = 0.
Х->Х0 1 W
16.33. Выяснить, будет ли всегда существовать такая точка
что f(g) = O, если функция f удовлетворяет всем
условиям теоремы Ролля, кроме одного из следующих: а) функ-
ция f непрерывна на отрезке [а\ 6]; б) функция f имеет во всех
точках интервала (сг, Ь) конечную или определенного знака
бесконечную производную; в) f(a)— f(b).
‘ 16.34. Являются ли условия теоремы Ролля необходимыми
и достаточными для того, чтобы существовала такая точка
ft), что fz(g) = 0?
16.35. Справедлива ли формула конечных приращений Ла-
гранжа на отрезке [—1; И для функции
( xsin(l/x), если х=?^0,
t 0, если х = 0?
16.36. Пусть функция f непрерывно дифференцируема на
интервале Верно ли, что для любого суще-
ствуют такие точки xj Ь) и х2е(а; 6), что
fft) = п ?
Л2
375
§17. Правило Лопиталя
Теорема (правило Лопиталя раскрытия неопределенно-
сти вида или Пусть функции f(x) и g(x):
а) дифференцируемы в окрестности точки а, за исключе-
нием, быть может, самой точки а, причем g'(x)^0 в этой
•окрестности;
б) функции f(x) и g(x) являются одновременно либо беско-
нечно малыми, либо бесконечно большими при
в) существует конечный
Г м
g' W
lim
х->а
Тогда существует
х->а S (•*)
firn.
х->а
Г(х)
е'(*) ‘
(1)
Если функции f(x) и g(x) дифференцируемы в точке а,
,f(a) = g(а) = 0, g'(а) 0, то
lim _ /' (д). (2)
В М g' (а)
Пример 1. Найти lim -х-з-----г.
ГД Применяя формулу (2), получаем
.. х5 — 1 .. 5х4 t
lim тп------г = llm —г — 1 • А
хч>|2х3-х-1 ^бх2-!
Теорема остается в силе при а — +'оо, а — —оо, а также
в случае одностороннего предела (х->а-ЬО, — 0) при
выполнении условий а)—в) соответственно на интервалах
(6;+°°)i (—°°;—б), (а; а + 6), (а — 6; а),6>0.
f' (х)
Если выполнены условия а), б), a lim -Л-г равен ‘4-оо или
х->а ё \Х)
f (х)
—оо, то Пт ; у также равен соответственно к+°° или —°°*
х->а ё \Х)
Пример 2. Найти lim * ~ а^—.
х~>0 X
'Л Раскрывая неопределенность вида по правилу Лопи-
таля, получаем
i_____1_
Й “ х™ ЗР - Й 3^ (I + х3) “ 3 • Л
Пример 3. Найти lim
Х-> + оо V X
-376
'Л Раскрывая неопределенность вида — по правилу Лопи-
таля, получаем
lim lim , = lim —=0. А
v->4-oo "у X х->4-оо 1/(2 Vх ) х->+©о *у X
Применяя правило Лопиталя, часто бывает выгодно предва-
рительно использовать асимптотические равенства вида
sin а ~ tg а ~ еа — 1 ~ In (1 + а) ~ sh а ~
~ tga ~ arctg а ~ arcsin а ~ а, (3)
где а = а(х)->0 при х-+а.
т-т . тт « 1- sinx — X COS X
Пример 4. Наити hm ----------—------.
х->0 s,n х
А Замечая, что sinx ~ х при х->0, по правилу Лопиталя на-
ходим
sin х — х cos х i. sin х — х cos x
lim------г-;----= lim —
X->0 sin x x-»0
.. cos x —- cos x 4- x sin x 1
= lim —
x~>0
X3
Зх2
.. sinx 1
Tlim ——- = -о-
° х->0 х °
Пример 5. Найти lim-
Х->0
А Замечая, что In(1 + х)
правило Лопиталя, получаем
sh2 х in (1 4- х)
tg х — х
~ х, shx ~ х при х->0 и применяя
X3
.. sh2 x In (1 + x) «.
hm ----;——'—- = hm T —
X-»0 tg*-* х-Я tg* —*
.. 3x2 .. Зх2 о n
= hm —;--------= hm —-2— cos2 x — 3. A
x+0___!__1 *->0sln2*
COS2 X
Иногда при вычислении пределов правило Лопиталя прихо-
дится применять несколько раз.,
р-г г? тт •’ 1- х10—10x4-9
Пример 6. Наити lim —=—=—/-г-.
г х->\ х5 ~ 5x4-4
А Применяя правило Лопиталя, снова получаем неопреде-
о
ленность вида — :
lim
х->1
х10- 10x4-9 _г 10х9— 10
х5 - 5х 4- 4 Л?! 5х4 - 5
Пользуясь еще раз правилом Лопиталя, находим
lim
х->1
10х9 — 10
5х4 — 5
= 2 Ит
х->1
х9 — 1
х4 — 1
О1. 9х8 9
2 '”1^=2-
Следовательно, искомый предел равен 9/2. А
ха
Пример 7. Найти lim где а > 0, Р>0.
х-»+оо ер
377
Пусть & = [а]Ч-1; тогда а — k<ZO. Применяя правило
Лопиталя k раз, получаем
аха 1
ха
Нт ТГ = lim -----------r7“ — • • •
->4-оо е* х->4-оо .
... = lim М—1>.-<°-/+1>^-=0.
х->4-оо
1па г
Пример 8. Найти lim —к— где а > О, |3 > 0.
Х->4-оо Х‘ *
1па X /а
А Пусть In X = /; тогда х = е* и lim —о— = lim —^ = 0
х->4-°° Хр /->4-00
(пример 7). А
Неопределенности вида 0*оо и оо — оо часто удается свести
к виду -Q- или — с помощью алгебраических преобразовании,
а затем применить привило Лопиталя.
Пример 9. Найти lim х In х.
4-0
А Преобразуя неопределенность вида О-оо к виду
и применяя правило Лопиталя, получаем
lim xlnx = lim •77^-= lim —тгт = lim (—х) = 0. а
х->4-0 х->4-0 1'х х->4-0 1/х х->4-0
Пример 10. Найти lim -Дт1/%2-
1 г х->0 х
А Полагая 1 /х2 = /, получаем
lim •'= lim ~ = Q. д
x->o x /->4-00 e
П p и м e p 11. Найти lim f——ctg2/).
x->0 V x '
rA Преобразуя неопределенность вида oo — 00 к виду
и используя асимптотическую формулу sin л—>х при х->0,
получаем
lim (Д- — ctg2х) = lim
х->0 ' х ' х->0
sin2 х — х2 cos2 х
х2 sin2 х
.. (sin x + x cos x) (sin x — x cos x) _
~~ X2 sin2 x
1. sin х-4-х cosx .. sin x — x cos x
— lim-----7------lim------3---.
x->0 x x->0 x
1. sin x + x cos x .. sin x , .. n
Так как lim--------------= lim------F lim cosx = 2, a
x->0 x x->0 x x->0
lim sin x(пример 4), то искомый предел равен 2/3. А
х->0 х о
378
При вычислении пределов функций вида <р (х) = (f (х)) е<х>
часто приходится раскрывать неопределенности вида 0°, оо°, 1°°.
Представляя функцию <р(х) в виде <p(x) = е^х~>,n можно све-
сти вычисление предела функции g-(x)lnf(*) к раскрытию не-
определенности вида 0-оо.
Пример 12. Найти lim Xх.
х->+0
д Так как хх = ехХах, a lim xlnx = 0 (пример 9), то
lim Xх = е° — 1. д
Пример 13. Найти lim (sinx)tg*.
х->л/2 ,
л Так как (sinx)ts% = etgxIn8inx = e(ln8inA:^ctg^, то, применяя,
правило Лопиталя, получаем
t. In sin х .. ctgx 1’ / • \ /л
,lm efrr х = ,lm - l/s'in^v " ,lm (—COSX- SIH x) = 0,
х->л/2 С1иx х->л/2 l/sin x х->л/2
а, следовательно, lim (sinx)tgx = e° = 1. д
Пример 14. Найти lim (x + д/х2 + 1 )1/In \
X-> + oo
А По правилу Лопиталя находим >
1__
lim Jnk+_vgH) = Hm .-V^+T
X->4-oo la x X-> + oo Vх
и поэтому lim (x +Vx2+ l)I/ln* = e. A
X->+°° ,
Найти пределы функций (17.1—17.75):
17.1. lim X->1 3x2 + 4x 2x2 + 3x — 7 -5 ’ 17.2. lim ,.1?-c?7 . x_>0 In cos 3x
17.3. lim X —>3 In (x2 — 2x2 — 5x 8) -3 • * - - .. ch 2x —• 1 17.4. hm § . x~>0 x
17.5. lim x->0 sin ax — sh ax — sin bx sh bx ’ a b>
17.6. lim xtt— I p ¥=0. In cos ax
В i ’ 17.7. lim —72
X->1 xp — 1 x->0
17.8. lim x~>a xc-q* ax - aa ’ a > < ), a 1.
17.9. lim
хй-а*
x-t-a xa — aa
17.10. lim ln ° ,-2x)—
x-»o tg2 x
379
arccos x
17.11. lim
In (1 + x)
17.12
lim
X->n/4
In tg x
ctg 2x
17.13. lim
X~> Л/6
4 sin2 x — 6 sin x + 1
3 sin2 x + 5 sin x — 4
17.14.
lim *5 - 3x2 4- 7x - 5
x4 - 5x 4- 4
Xх — 1
17.15. lim |n %
x->l
17.16. lim -V^.3
x-H Mx* - 1
17.17.
lim
X-»1+O <х24-х —2
17.18. lim
x-»l
x3 — 3x2 4- 7x — 5
x3 + 2x2 — 9x4-6 *
17.19.
.. Уз tg2 x — 1
х-^л/6 2 sin2 x 4- 5 sin x — 3
17.20.
.. cos (2m 4- l)x
x->n/2 cos(2n4-l)x ’
m e N, n e N.
17.21. lim
x->0
x arcsin x2
x cos x — sin x
17.22. lim
x->0
x — sin x
tg X — X
17.23. lim
x->0
(x + 1) In (1 + x) — x
ex — x — 1
f 1 + x o
In -----------2x
17.24. lim------^=4--------
X->0 x — sin X
.. (a 4- x)x — ax ~
17.25. hm v , a > 0.
x-»o x
17.26. lim
x->0
2 tg 3x — 6 tg x
3 arctg x — arctg 3x
«. x20 — 2x + 1 --i. tgx —x
17’27* X30 - 2x 4- 1 ’ 17,28, In3 (1 4- X) •
17.29. limsi" -4---. 17.30. lim------
x->o x arcsin x x_^0 arcsin x — In (1 + x)
17.31. lim [(x10 - lOx 4- 9)/(x - I)2].
ofl .. x50-50x4-49 17 O9 2x4 4- 3x3 - 4x2 - 9x - 4
17«32. hm %l00 _ 100x + g9 . 17.33. ^hm^ 3z< + 5л;3 + 3x2 + 3x + 2 •
17.34. iimaxa+2-gj;;2xa+1+x.
17.35. lim a(1,~*P awP(1~7*a) . «₽ 0-
x->i (1 - xa) (1 - x₽) 1
17.36. lim
17.38. lim — X -> — 1
17.39. lim T x->+0 lr
17.41. lim
x->-~+0
r — r 4- 1 esin x — px
-—17.37. lim Л—y- -
X — Xх sin X — X
:4 + x3 — 3x2 — 5x — 2
x4 + 2x3 — 2x —- 1
17.40. lim
n sin X
in (x — зт/2)
tgx
17.42
In sjn X
ctg X
1Jm Ml-C^x)
X-»+0 Intgx
380
17.43. lim
17.45. lim
3 + In x
2 — 3 In sin x
'у/x In In X
^2x + 3 Vln x
17.44. lim
17.46. lim
xa Inp x
eyx
xa In^
X
17.47. lim sin x • In ctg x. 17.48. lim x In (— arctg x').
17.49. lim xne~x\ 17.50. lim (л — 2 arctg Vх ) Vх •
X->4-oo X-»4-oo
17.51. lim х(л — 2arcsin (x/Vx2 + !))•
X->4-oo
17.52. lim x“ln₽(l/x), a > 0, P > 0.
x->4-0
17.53. lim (xx— l)hix. 17.54. lim xaax, a > 0, a 1.
X->+0 X-> + oo
17.55. lim(—3---------17.56. lim f—-------------—
x->0'sin% x) х-яА* arcsin x J
17-57- I7-58-
17-59-1™«( - “?) • 17 W>- “x“’ ln’*>-
17.62. Iimx,/(X-1). 17.63. lim f-arctg xV.
X->1 X->+oo ' /
17.64. lim (-^-arccosx') . 17.65. lim (cosx)l/JC'.
x->0 ' n ' x->0
17.66. lim (l+x),n\ 17.67. lim V .
x->+0 x->0 V e ’
1
17.68. lim (arcsin x)tg*. 17.69. limxinshJC.
x->+0 _ x->+0
17.70. lim (n —2x)cosa:. 17.71. lim x**-‘.
x->n/2—0 x->+0
17.72. lim (tgx)c0SX. 17.73. lim (3x2 + 3*)1/x.
X->Jl/2—0 X->+oo
17.74. lim | In x |2\ 17.75. lim (l/x)sln\
x->4-0 x->+0
17.76. Показать, что следующие пределы не могут быть вы-
числены по правилу Лопиталя, и найти эти пределы;
1) lim^M1/*). 2) lim -* + ^х
Х->0 sin X 7 х_>оо X —cosx
381
17.77. Выяснить, можно ли применить правило Лопиталя
для вычисления предела
|jm 2 4~ 2х 4~ sin 2%
(2х + sin 2х) esin х
Найти этот предел, если он существует.
17.78. Найти
Ит Н^ + Л) + /(а-Л)~2/(а)
л-»о 7,2
предполагая, что существует Г (а).
17.79. Найти
f {а + за) - 3/(0 + 2/i) + 3f(a + h)-f (а)
предполагая, что существует f,u(а).
17.80. Показать, что функция
( x^=Q,
= { 0, х = 0,
бесконечно дифференцируема на всей числовой прямой, и найти
f(*)(0), feeN.
17.81. Найти пределы функций:
.. । . ч .. In х- In (14-х)
1) lim Inx • 1п(1 —-х). 2) lim --------т=----
л->1-0 х->+0 УХ
. COS X — COS Зх + X3 cos (л/х)
3) hm------------j-------.
х->0 л
Г 14--1______L—1
.. I /1 . а \ * х(х4с) I
4) hm х I I 1 + — ) —- х I.
х->4-оо L4 х z J
§ 18. Формула Тейлора
Пусть функция f(x) определена в окрестности точки хс,
имеет в этой окрестности производные до (п—1)-го порядка
включительно, и пусть существует f(rt)(xo). Тогда
/(х) = /(Хо) + -^Ц^(х-хо) + -^^(х-хо)2+ ...
••• + ' ~ и*”)' (х ~ х°^п + ° ~ Хо)П) при Х-^-Хо,
или, короче,
/"5 X 1~Г'(х ~ Хо)к + °~ *о)п)> х->х0. (1)
*=о
Многочлен
(2>
л=о
389
называется многочленом Тейлора функции f(x) в точке Хо,
а функция
гДх) = f(x) —РДх) (3)
— остаточным членом п-го порядка формулы Тейлора,
Формула (1) называется формулой Тейлора п-го порядка
для функции f(x) в окрестности точки х0 с остаточным членом
в форме Пеано, ее называют также локальной формулой Тей-
лора,
Функция f(x), имеющая в точке ло производные до n-го по-
рядка включительно, единственным образом представляется
в виде
/(*) = £ ak(x — Xo)ft + о((х —х0)"), х->х0, (4)
fc=0
причем коэффициенты разложения (4) определяются форму-
лами
a^==J-r~' * = 0,1, (5)
Если Хо = 0, то формула (1) принимает вид
f(x) = f; ^P-xk + o(xn), X^Q, - , (6)
и называется формулой Маклорена,
Пусть функция Нх) имеет в окрестности точки — 0 про-
изводные всех порядков (бесконечно дифференцируема). Тогда:
а) если f — четная функция, то при любом п е
/(*)=£ х2к+° (х2п+1); (7>
fe=0
б) если f — нечетная функция, то при любом n s N
f(x) = £ х + °(х )• (8)
fc=O
Формулы Тейлора в окрестности точки х0 = 0 (формулы
Маклорена) для основных элементарных функций имеют вид:
*--i+*+4+... +4+°<*“)’
ИЛИ
п k
е*=Е ^г+о(х">;
fe=0
зПл = х + 4+4+ +'Йт)Г + <)<ж“+2>’
383
или
sh*=S7^^+°(*2'l+2); п°)
k=Q
chx_l + ^ + 4+ ...+1gr + ()(^«),
или
П 2k
chI=E on
Л=0
y3 5 /__i\n y2n+l
sinx = x — -3f + -5f + ••• + (2w 1)1 + о (x2n+2),
или
A v2*+i
sin X = У (— 1)* 1)t' + о(x2n+2); (12)
/2=0
cosx=1-4 + 4+ •+(-l)"-(gr + «U!-+').
ИЛИ
П 2k
cosx = y (-l)ft-|^- + 0(x2"+1); (13)
л=о
(l+x)« = l+ax + -^=-^x2+ ...
... +<х(а-1)--Л<х-(п-П) xn + o{xn)t
ИЛИ (l+x)a=f C^ft + o(x"), ft=0 (14)
где Cl=l, Ci _ «(a—1) ... (a —(ft — 1)) . « 9 . и част-
kl , /? 1, z, в
НОСТИ, fl
ттт=Х(-^^ + о(х")’ 1 “Г A X—J A=0 (15)
In (1 +x) ,2,-jy + oM; /2 = 0 -X ’ + 3 + ...+ ' +»(«"), (16)
или in <1+x)=+ о («"j, Л=1 (17)
In (1 -%) = -£ k +o(xn). A=1 (18)
384
Пр и мер 1. Разложить по формуле Маклорена до о(хп)
функцию
f (х) = sin (2х 4- -j-).
л Так как
/<*>(*) = 2*sin (2х + ^ + Л-£)
И
7<*)(0) = 2fe sin-J(2&4- 1),
то по формуле (6) получаем
sin (2-« + -?) = Х ^sin-J(2&4- l).xft4-o(y»). д
*=о
Если
/(*)=£ akxk + o(xn),
*=0
то
/ {Ьх) = £ bkakxh 4- о (хп).
fcx=0
Пример 2. Разложить по формуле Маклорена до о(хп)
функцию f(x), если:
1) Цх) = Лх+\ 2) f(x) = —
VI — X
3) f W = 2FR • 4> = In (5 - 4х).
А 1) Используя разложение (9) и равенство
е^х+2 =е2-е^х,
получаем
я~0
2} Так как
Vf=7=(1 + (-1)*>‘‘’
то, применяя формулу (14) при а = —1/2, находим
Т7т= = 1 +£ (-1)‘С*1/2х*4-о(х"),
где
(“К-? ~ ') ' (“2' *0 , 124-1)11
с-и“------------------й-----------------“<~1) “AT’-
13 Д. Кудрявцев а др.
$85
Следовательно,
п
^=='+X£S^-^ + o^- «•>
3) Используя равенство
2-'+з
и разложение (15), получаем
п
st>4£(-')‘(|P+.w
fe»0
т. е.
п ь
4) Из равенства
1п(5 — 4‘х) = 1п5 + In (1 — у
и формулы (18) следует, что
In (5 — 4х) = In 5 — £ -у (у)* xk + о (х"). а
*-1
Если
f(x) = E ак (х — х0)к + о ((х — х0)п), (20)
Л «о
g (х) = £ Ьк (х — х0)к + о ((х — х0)"), (21)
&=0
то
f (х) + g (х) = £ (ак + Ьк) (х - x0)ft + о ((х - х0)"), (22)
/г=0
f (х) g (х) = Д ск (х — x0)ft + о ((х — х0)"), (23)
k
где ск = Е арЪк_р.
Пример 3. Разложить по формуле Маклорена до о(хп)'|
функцию /(х), если:
1) f(x) = (x + 5)e4 2) f(x) = ln|±J.
. 3) f (x) = exln(l 4-х), n = 4.
386
Zs 1) Используя равенство f(x) = хе2х 4- 5е2* и формулу (9),
получаем
f (л) = х(£ + о (х"-1)) + 5 £ 4г + 0 =
\fc=0 / k=*Q
Так как
П-1 . . л. п
у» 2fexft+1
k~0 k^l
то
/«=5 + Ё(1й)Г + т> + -’<’") =
А=1
= 5+ £ ^-(k+ 10)xft + o(xn) =
Л»1
п ъ I
= £ 1kT(k+\0)xk + o(xn).
й=0
2) Из равенства
Hx) = ln| + ln(l +f)-ln(l -у)
и формул (17), (18) следует, что
П х Ь_1 х
f « = In f + X j (-jr + -4г—) + о (*“)
fe=l
3) Используя разложения (9) и (17), получаем
/(x)=(i+x+4+4+o(^)) («-4+4-4+o<*’>)=
=* + (-4+1)^+(у-| + т)^ +
+ Н+т-т + т)1' + »М=
= x + -5-*2 + -tx3 + °(*4)- ж
Z о
Пример 4. Разложить по формуле Маклорена до о(х")
функцию f(x) = cos% + W3* Какие значения может прини*
мать п?
Л Пусть g(x) = |x|3; тогда g(0) = £'(°) = &"(0) = 0» а
g'"(0) не существует (§ 15, пример 9). Поэтому разложения
g(x) по формуле Маклорена до о(х") при п = 1 и п = 2 имеют
13* 387
.вид соответственно
g(x) = o(x) и g(x) = o(x2),
а разложение функции g*(x) по формуле Маклорена до о(х3\
не существует. Используя разложение функции cosx по фор-
муле Маклорена до о(хп) при n = 1 и п — 2 (формула (13))*
получаем разложение f (х) при п = 1 и п = 2:
f(x)= 1 +о(х),
f(x) = l-^ + o(x2).
Разложение по формуле Маклорена функции f(x) до о(х3) не
существует. А
При разложении по формуле Тейлора рациональной дроби
эту дробь обычно представляют в виде суммы многочлена и эле*
ментарных дробей.
Пример 5. Разложить по формуле Маклорена до о(хп)
рациональную дробь
х2 + 5
х2 + х — 12 ’
А Так как f(x) не является правильной дробью, то, разде-
лив числитель на знаменатель, представим f(x) в виде
с z \ j 17 х ___* 1 3 » 2
7 W 1 -Г (д. + 4) _ 3) — 1 — Х4- 4 » 7~з *
Преобразуем f(x) так, чтобы можно было использовать разло
жения (15) и (16):
f(x) = l
Отсюда получаем
ИЛИ
f W—I+Z R3T --5И-) +° («") А
Пример 6. Разложить по формуле Маклорена до o(x2rt+I)
функцию
fW= х4_3х2_4-
А Представим f (х) в следующем виде:
~ (х2 - 4) (х2 + 1)I “ 5 ( х2 - 4 х2 + I
388
Заметим, что нет необходимости заменять дробь j- суммой
А В
элементарных дробей вида -----и —. Записав эту дробь
X — 2. X Z
в виде-------—-—2V" и используя разложения (15), (16), по-
4(‘-т)
лучаем
р, X 1 / 1 1 \_
/ W — 5 | z 1 +х2 )
к Ч1-—) J
П 9Ь
fe=0 4
При разложении по формуле Маклорена произведения три-
гонометрических функций часто бывает полезным представить
это произведение в виде суммы тригонометрических функций.
Пример 7. Разложить по формуле Маклорена до о(х2"+1)
функцию f(x), если:
1) f(х) = sin2 х cos2 х. 2) /(х) —cos3x.
л 1) Так как sin2xcos2x = -j sin22x = -g-(l—cos4x),
до, применяя формулу (13), получаем
sin2X COS2X = У - ---------Х2к + о (x2n+1).
ft-l
2) Используя равенство cos Зх = 4 cos3 х — 3 cos х, получаем
cos3x=^-cos3x4-j cosx -^^-(32ft-1+l)x2*+o(x2"+1).▲
ьо
Если функция f(x) представляется в виде f(x)=-|-—у-
и если известны разложения функций g и ft по формуле Тей-
лора в окрестности точки х = х0 до о((х — х0)п), т. е. известны
разложения
g (*) = Е bh (х — x0)ft + о ((х — х0)п),
/г-0
ft W = I ck (х — х0)к + о ((х — х0)п),
А»=0
причем cQ = h(xQ)^ 0, то для нахождения разложения по фор-»
муле Тейлора функции f можно применить метод неопределен-
ных коэффициентов, который состоит в следующем»
389
Пусть
f (х) = £ ak (x — x0)k + о ((x — x0)n)
4=0
— искомое разложение. Приравнивая коэффициенты при
(х — х0)\ где k = 0, 1, п, в левой и правой частях равен-
ства
( Е ak (х - x0)k + о ((х - Хо)")) ( Е ck(x — x0)ft + о ((х — х0)")) =
\/г=®0 ✓ \£=0 /
= Ё bk (X — X0)fe + о ((х — х0)"),
Л=0
получаем систему уравнений, из которой можно найти коэффи*
циенты а0, aif ..., ап.
Пример 8. Применяя метод неопределенных коэффициен-
тов, разложить по формуле Маклорена до о(х5) функцию tgx.
А Так как tgx — нечетная функция и tgx = x + o(x), то
tgx = х + а3х3 + а5хб + о(х6).
Используя формулу sinx = tgxcosx и разложения (12) и (13),
получаем
— (х 4- о,*3 + а.х'1 + о 0с6))( 1 — + X. + о («’)).
Приравнивая коэффициенты при х3 и х5, находим
1 1 . 1 1 а3 .
6 — 2 +йз’ 51 4! 2! + а5-
Из этой системы получаем а3 = 1/3, «5 = 2/15. Следовательно,
tgx=x+4+4x5+o(*6)- (24>
Заметим, что разложение (24) можно получить и по общей фор-
муле (6). Л
Пусть F(x) = f(<p(x)) — сложная функция, и пусть известны
разложения функций <р и f, т. е.
Ф (х) = Ё ck (х — x0)fe + о ((х — х0)"), (25)
ьо
/ (да) = Z О* (да — да0)* + о ((да — да0)"), (26)
jfe==0
где дао = ф(Хо). Тогда для нахождения коэффициентов
Ьк (й = 0, 1, .... п) разложения
F (х) = f (ф (х)) = £ bk (х — x0)k'+ о ((х — х0)")
Л=0
390
нужно в формулу (26) подставить w — <р(х), заменить функцию
ф(х) ее разложением (25), произвести соответствующие ариф-
метические действия, сохраняя при этом только члены вида
б/i (х — Хо)к, где k — 0, 1, ..., п. В частности, если
<р (х) = Ахт, т е N, . f (w) = £ akwk + о (wn),
TO
f (<p (x)) == f (Axm) = £ Akakxmk + о (xmn).
k-0
Например, из (15) и (19) следует, что
п
— 1 = У (-1)* х2к + о (х2"+>), (27)
1 Лг 1 J
fe«0
7==r = 1 + £ '-2W)H + ° (x2"+,)< (28)
V1 — x2 *-J 2Rkl
fe=»i
Пример 9. Разложить по формуле Маклорена до о (х3)
функцию е* 008*.
А Искомое разложение должно иметь вид
з
ех cos X _ £ akXk о (д.3).
k=0
Так как xcosx = х +о(х), (хcosх)к = хк + о(xft) при k = 1,
2, ..., то в формуле
где w — х cos х, нужно взять п = 3. При этом функции
ну* (k — i, 2, 3) следует разложить по формуле Маклорена
до о(х3). Используя разложение (13), получаем
W = XCOSX = X-----^r+o(x4), W2 — X2 + О (х3), W3 = X3 + о(х3)',
•Следовательно,
3 k 3
.gxcosx = + о(ш3) = ! + х + О(Х4) + 4-(х2 + О (X3)) +
/е=0
+ ^р(*3 + о(х3)) + о(х3)== 1 +х + уХ2 — ±х3 + о(х3). А
Пример 10. Разложить по формуле Маклорена до о(х6)
функцию
891
'Д Искомое разложение должно иметь вид
€
f(x) = X акхк + о(х6).
4-0
Поэтому функцию -j ^*8j — следует разложить по формуле
Маклорена до о(х4). Так как sinx = x-}-o(x), то в формуле
п.
А»0
где z = sin х, нужно взять п = 4.
Применяя формулу (12), получаем
z — sin х = х —+ ° (%4)» z2 = *2 %4 + ° (*4),
23 — х3 + о (х4), z4 — х4 + о (х4).
Следовательно,
__1_ = 1 _ (х—0 + (х2 - 1х<) -хз + X4 + о(х4) =
= 1 — X + X2 — -|-х3 + у X4 + о (х4)
и
f (х) = X2 — X3 + X4 — у X® + у X6 + о (х6).
Пусть известно разложение по формуле Тейлора в окре-
стности точки Хо до о((х — Хо)"). производной функции f, т е.
известно разложение
f(x) = Z Ьк(х — х0/ + о((х — х0)"), где Ьк = —.
А=0
Тогда существует /(л+1)(х0), и поэтому функцию /(х) можно
представить в виде
я+1
/ (х) = X ак (х — x0)ft ч- о ((х — ХоГ1) =
= f (*о) + S аА+1 (Х — *o/+I + О ((X — АГ0)"+1)г
А<=0
где
/(Л+1)(хо) _ /(Л+1)(хо) 1 _ bk
«A+i— (Л 4-1)! — k\ ‘hi А4-1’
Следовательно,
г П
/(X) = f (Хо) + X (X - x0)ft+1 + о «х - ХоГ1), (29)
А-0
где bk — коэффициенты ряда Тейлора функции 1'£х)л
392
по формуле Маклорена до
Пример 11. Разложить i
,о(х2п+1) функции: 1) arctg х; 2) arcsin х.
А 1) Так как
(arctg x)' = -77- = 2 (— l)k*2k + о (x2n+l)
fe=0
.(формула (27)), то по формуле (29) получаем
n 2&4-1
arctgx = £ (-i)fe A__ 4. O(x2n+2).
k=*0
Полагая в равенстве (30) n = 2, находим
4*3 ^5
arctg х = х — — + -7- 4- о (х6).
2) Используя разложение (28), получаем
п
(arcsin х)' = ^==- = 1 + £ (2^,°11 x2k + о (х2"+‘),
Л=«1
откуда по формуле (29) находим
arcsin х = х + У x2ft+1 + о (х2п+2).
Aj 2kkl (2k + 1) ’
(30)
(31)
(32)
1
в
окре-
Из формулы (32) при п — 2 получаем
arcsin х = х + ^х3 + -^-х5 + о(хе). д
Разложение функции f(x) по формуле Тейлора
стности точки Хо заменой х—х0 — t обычно сводят к разло-
жению функции g(t) — f(x0-f-t) по формуле Маклорена.
Пример 12. Разложить функцию
f(x)---------------------Зх + 3
(33)
V3— 2х — х2
окрестности точки х = —1 до
/2 \ “ 1/2
з/
-/
2
по формуле Тейлора в
*>((*+I)2")-
А Пусть х + 1 = /; тогда
f М = _ .... = _
7 7 V4— U+l)2 V4 — t2
Для получения разложения функции f(x) нужно разложить
•функцию §•(/) по формуле Маклорена до о(/2п).
Применяя формулу (14), находим
п-1 2k
g (0 = 41 + 71 2 Ск-1/2 (-1 )ft + о (t2rt),
393
ск ( i? ( 4~(Л~1}) _(2fe-Dit
С_1/2(-1) =(-1) ---------------------- = 2*й1 •
Следовательно,
« w=| i+Е <“*'+° «а"’-
fe=l
Заменяя t на х + 1, получаем
п-1
f (х) = | (X + 1) + X 3J^r (Х + 1)2ft+1 + ° ((х + 1)2П)- А
Пример 13. Разложить по формуле Тейлора в окрестности
точки х = 2 до о((х — 2)") функцию f(x)=ln(2x— х2 + 3).
А Так как 2х — х2 + 3 = (3 — х)(х+1), то, полагая
х — 2 = t, получаем
2х-х2 + 3 = (1 -/)(3 + 0 = 3(1 -0(1+у)-
Отсюда следует, что
f(x) = g(0 = ln3 + ln(l-0 + ln(l+4).
Разложив функцию g(t) по формуле Маклорена до o(tn\, полу-
чаем
8И«1пЗ-Хт + t
Следовательно,
п
f(x) = ln3 + £
- 9 +°((х -2П а
Если функция f(x) имеет в некоторой окрестности точки
Хо производные до («+1)-го порядка включительно, то для
любой точки х из этой окрестности найдется точка |, лежащая
между х и хо (х < g < хо или х0 <. g < х) и такая, что
/(*) = £ (X - x0)fe + ^>1()V' (X - x0)n+1. (34)
Формула (34) называется формулой Тейлора с остаточным чле-
ном
= (35)
в форме Лагранжа.
394
Разложить по формуле Маклорена до о(хп) функции
[(18.1-18.4): .
18.1. 1) е5*-1. 2) sin (2x4-3). 3) cos (у 4-2).
4)—. 5)6) ---Ь.-. 7) In (ex 4- 2).
1 — 2х Зх + 4 V1 + 4х
8) З2"*. 9)-^.
18.2. 1) (х — 1)ех12. 2) (х2 — х)е~х. 3)
4) (2х 4-1) л/Г^х. 5) (2х — 3) In (5х 4- 6).
... 1 4- 2х , 2 — Зх
6) 1П 1 - х • 7) 1п 3 + 2х •
8) In (х2 4- Зх 4- 2). 9) In (2 4- х - х2).
18.3. 1) (1 4- х2) In дЛ+*. 2) (х — О (х 4- In (1 4- х)).
3) (1—х)1п(1 4-х)—(14-х) 1п(1—х).
4) х^4 — 4х4-х2. 5) 3/. * — . 6) In—.
7 v 7 ^9 - 6х 4- х2 7 х2 - 5jc 4- 6
7) In(64- Их4-6x24-х3). 8) In (-2х-~25х + 2 )"*.
18-4. 1) (х+Л_2/. 2) ^1. 3)
>|\ х3 с\ 2х + 5 Зх—1
х — 1 • °’ х2 + 5х + 4 - °' х2 + х — 6 '
х2 4- 4х - 1 R. 1 — 2х2 Зх24-5х —5
'' х2 + 2х — 3 • °’ 2 + х — х2 ' У' х2 + х — 2 •
Разложить по формуле Маклорена до о(х2") функции
[(18.5—18.6):
18.5. 1) sh(x/2). 2) xch3x. 3) xsin22x. 4) xch2x.
5) sinxcos2x. 6) sin3x. 7) shxch2x. 8) sin3xcosx.
18.6. 1) X2 + ! • 2) 3x2 _ 4 . 3) 3a,4 + 10x2 4- 3 •
.. x2 4- 2 x . x2 — 1
4) x3 + x2 + x+l’ 5' 3 ln x2 — e '
6) (1 4- 2x) e~2x — (1 — 2x) e2x. 7) In (x 4- д/хМ7!).
Разложить по формуле Маклорена до o(x2n+1) функции
[(18.7—18.9):
18.7. 1) cos3x. 2) x2cos2x. 3) cos3xcos5x.
4) sin х sin Зх. 5) chxch3x. 6) shxsh5x.
18.8. 1) sh2x. 2) cos4x. 3) sin2 x cos4 x.
4) cos4 x sin4 x. 5) cos6 x 4- sin6 x. 6) sin8 x 4- cos8 x.
18.9. 1) 2 —x2 —x4' x4 — 8x2 4-15 * 3) x 'У/'
395
4) 1___________ 5) 1~V1+~JC'2
Vx2 4- 2 + V2 — x2 1 + Vl + x2
3 / 2 + x2 ,ч 1
Ь' 1П Л/ x4 — 3x2 + 2 ' ' 1 — x + x2 — x3 *
18.10. Разложить по формуле Маклорена до o(x3") функ-
ции:
________1_____ о) S*6 11 q\ _____1
’ 2x6 — 10x3 + 12 ' ’ x6 — x3 — 2 * ’ 1 + x + x2 •
18.11. Разложить по формуле Маклорена до o(x3"+1) функ-
ции: _______________________
1A * In л / e *3 q\ 5x3 4~ 28
4 (1 + X3)2 • ’ ШЛ/ 1 — ex3 • °7 14 + 5x3 — xe '
Разложить по формуле Тейлора в окрестности точки Хо до
о((х— Хо)") функции (18.12—18.16):
18.12. 1) 1/х, х0 = 2. 2) aJx., х0=1.
3) sin(2x —3), х0=1. 4) хе2*, х0 = — 1.
5) х2е-2*, х0 =— Е 6) (х2—ре2*, х0 = — 1.
7) sin (х + 1) sin (х + 2), х0 = — 1.
18.13. 1) in (2x4-1), х0=1/2. 2) log3 д/зх —, х0 = 3.
3) In (2 4- х — х2), х0 — 1. 4) In (х2 — 7х 4- 12), х0 — 1.
18.14. 1) in д/7х — 2 , х0 = 1.
2) In А/-^—, х0 = 3. 3) xln(2 — Зх + х2), х0 = -2.
-4) ln х0==2. 5) 4±Г1П*’ *о = Е •
6) In (5 -Ь 14х 4- 14х2 4- бх3 4- х4), х0 = —2.
„ 18.15. 1) х0 = 2. 2) *о = 2.
3) Т+7’ *0=1°. 4) 2х — 4 ’ Х°= ЦТ 5) х+ 1 ’ *0=1-
б) х — 2 ’ Х° 3- Z) х (2x4-7)’ Х° 1'
18Л6- 0 х^+10х + 25’ *о = -2- 2>
3> X *« = 3- 4)-^-, Л-2.
5> Х х5-.Л + в+5’ Л=1- 6) *((»- 1>3 ~ ')’ Ж«“2-
Разложить по формуле Тейлора в окрестности точки х0 ДО
о((х — Хо)2") функции (18.17—18.19):
18.17. 1) ех1+2х~\ х0 = —1.
2) (х 4- 3) е3*!+18*, х0 = —3.
396
3) (х 4- 2) In (2х2 + 8х + 11), х0 = —2.
4) (х — 5) 1п (26 — 10х + х2), х0 == 5.
18.18. 1) -z-L-t, x0=l. — x2 3) -т-Аг-Гя'- = 4> Vx2 — 4x 4- 8 5) <*+1)3_ x =-l ' Vx2 +2x + 2 ’ 0 2) -Z;: V.+ 1 X0 = -l. V^2 4- 2x 4- 2 x2 — 2x 4- 1 i ^x(2 -x) ’ X° U
18.19. 1) Х,’2Д5. x. = l. 3) x2 — 4x 4- 8 ’ x0 — 2. 3x2 — 6x4-6’ x0—!•
Разложить по формуле Тейлора в окрестности точки х0 до
о((х— Хо)2"+1) функции (18.20—18.23):
18.20. 1) е2*2+8*+3, х0 = —2. 2) е2*г~12\ х0 = 3.
3) 2*-х\ х0 = 1/2. 4) (х + 3) еы+вх+ь, Xq = _2,
5) (х+ 1)22*2+2\ х0 = — 1.
6) х(х — 2)2*2~2*-1, х0 = 1.
7) (Зх2 — 6x4-4) е*х‘~4х+5, х0=1.
18 .21. 1) sin2(x — l)cos(x — 1), х0 = 1.
оч . 9 з п
2) sin-g-xcos s-х, х0 = —.
3) (х4--^) (sinx 4- cosx), x0 — —
4) (x2 — 3tx)cos(x4-y), x0 = |.
5) ^ycosnx, Xo = -|.
18 .22. 1) log2 (3x2 — 24x 4-50), x0 —4.
2) (x 4- 2) In (2 — x2 — 2x), x0 = — 1.
3) ’oe» *« = >.
4) (x! + 4x + 2) In (—2x2 — 8x — 5), x„ = —2.
*8-23-11 x»=2-_________________________
2> .,F4. *»=2- 3> Vrh’ *>=’•
.1 ^x2 ___JL k'i a v_______________§
Vjc + V1 — x ’ ° 2 ' x2 — 3x + 2 * 0 2 ’
2x2-8x + 5
x2 — 4x + 3 ’ X°~
7) (*+l)2________ x--l
< (2x2 + 4x 4-1) (x2 4-2x 4-3) ' Л°"~ *
397
18.24. Разложить по формуле Тейлора в окрестности точки
Хо — 1 до о((х— Хо)3”) функцию 2х3~3х2+3х.
18.25. Разложить по формуле Тейлора в окрестности точки
Хо = 2 до о ((х — 2)2nt2) функцию
V х/(4 — х) — д/(4 —-х)/х.
18.26. Разложить по формуле Тейлора в окрестности точки
х0 = 2 до о((х — 2)3”+1) функцию
(х — 2)/-<(х — 4) (х2 — 2х + 4).
18.27. Разложить по формуле Тейлора в окрестности точки
х0= 1 до о((х— l)4^1) функцию
1 —у^2х — х2
1 — Vx2 — 2х +2
18.28. Разложить по формуле Тейлора в окрестности точки
хо до о ((х — Хо)4") функции:
1) sin (х2 — 2х + 3), х0=1. 2) cos (х2 — 4х + 3), х0 = 2.
3) sin (Зх2 + 6х + 4), х0 = — 1.
18.29. Разложить по формуле Тейлора в окрестности точки
Хо до о((х —Хо)4”+3) функции:
1) cos х2 — 4х + л), x0 = -j.
2) sin(-Jx2 — 2х+-|-л), x0 = -j.
3) x sin (x2 + 2 д/л x), x0 — —-yjn .
4) x sin (x2 + 2x + 2) cos (x2 + 2x), x0 = — 1.
18.30. Разложить по формуле Маклорена до o(x")' функции:
1) x3|x| + cos2x. 2) sin|x|3 -f- ex. 3) |x|2ft+1, AeN.
Число n выбрать наибольшим.
18.31. Найти f(ft)(0), если:
1) f(x) = e-x’> ^ = 6.
2) f (x) = 1/(1 + x + x2), k = 32.
3) f (x) = 1/(1 — x4), 6 = 60.
18.32. Пусть Pn(x)—многочлен степени не выше п. Дока-
зать, что
Л=0
18.33. Представить функцию /(х) в виде многочлена по сте-
пеням х — Хо, если:
1) f(x) = x3, х0=1.
2) f (х) = х4 + 8х3 4- 24х2 + 32х + 17, х0 = —2.
3) f (х) = 1 х ~}~ я2 + я3» хо ~ 1 • 4) f (х) = (х3 8)2, х0==2.
398
18.34. Пусть
/ W = 2 ak (x — x0)* + O ((x — x0)n).
Л««0
Доказать, что
f' (x) = X kak (x — x0)ft~1 + о ((x — x0)"- ’)•
л-i
18.35. Пусть
f (x0 + h) = f (x0) + X 7Г fw (*o) + -ЛГ + e/l>’
k=i
где 0<6< 1, и пусть существует f("+1) (Хо) =# 0. Доказать, что
lim 6 =—т-т
18.36. Разложить по формуле Маклорена до о(х2) функции:
1) eiex. 2) e^i+2x. 2) ch (sin х). 4) cos (sh (х/д/5 )).
5) (1—x + x2)3. 6) Incosx.
18.37. Разложить по формуле Маклорена до o(x3) функции:
1) 2) V1 + 2x-x2-^1-3x + x3.
3) —3xcos2x. 4) arctg (sin х). 5) esin*.
6)ln3(l-|). 7)(l+x),/x.
8) д/1 + 3 sin x. 9) In (1 + arcsin x).
18.38. Разложить по формуле Маклорена до o(x4) функции:
V)e^"x. 2) sin4cosx. 3) tg(sh3x).
4) sin (arctg x). 5) • 6) Vcos x.
7) ---. 8) —4—• 9) ex x.
7 arcsin x 7 arctg x 7
18.39. Разложить по формуле Маклорена до o(x5) функции:
1) (1 - 2x + Зх2 + 4x3)3. 2) In (1 + x + x2 + x3).
3) —. 4) ex^+*. 5)
7 COS X 7 7 X
6>. 7> ('+*)'“
18.40. Разложить по формуле Тейлора функцию f(x) в ок-
рестности точки хо до о ((х — х0)"):
1) f (х) = th х, Хо = 0, п = 6.
п, « . . 1 — 2х Ve + ex2 1 Л
2) / (х) = -7=--; - х0 = —, п = 9.
А/ — In (2х — х2 уе )
899
3) / (х) = (б —Vl - 10x4)cos2*’, *0 = 0, n = 9.
4) f(x) = (x2 —I)1973, x0 = l, n = 1973.
18.41. Найти такие числа А и В, чтобы при х->-0 были спра-
ведливы асимптотические равенства:
1) Л^-147 = -4х2-|х3 + о(х’).
2) sin х (Л + В cos х) = х + о (х4).
3) Aarcsinк + Вarctgх = + х3 — + х5 + о(х6).
4) ^х=4Н? + о(х6)-
18.42. С помощью формулы Тейлора (34) приближенно вы-
числить (с точностью до 10~3):
1) VT27. 2) д/83. 3) и/250. 4) Je. 5) sin 85°.
6) cos72°. 7) In 1,3. 8) arctg0,8.
18.43. Оценить с помощью формулы Тейлора (34) абсолют-
ную погрешность приближенных формул!
A хь
ьо
уЗ у5
2)sinx«x—ог + -гг. I*I<1.
ОI DI
^-4 4Ь*в
3) cosx~ 1—+ ip |x|<0,5.
4) tgx«x + -y-, |x|<0,l.
у 2 уЗ y4
5) ln(l+ x)^x-+- + +--+-, |x|<0,l.
Z О тс
6) « 1 +|~4 + 4’ 0<x<0,2.
18.44. Вычислить с помощью формулы Тейлора (34)’f
1) e с точностью до 107. 2) д/Ю c точностью до 10-3.
3) sin 1° с точностью до 10~6. 4) cos 5° с точностью до 10 5.
5) 730 с точностью до 10-4. 6) 1g 11 с точностью до 10~4.
18.45. Доказать, что для всех neN (п > 2) выполняется
равенство
е==1 + 1г+2Г+-”+'?н+И7’
где 0 < 0 < 1.
18.46. Доказать, что е — иррациональное число.
18.74. Пусть f(x)e= С<2> [0; 1], f(0)= f (1) = 0, и пусть суще-
ствует число М такое, что для всех х е (0; 1) выполняется не-
wo
равенство \f"(x) |^М. Доказать, что •
’ 1Г(х)|^М/2 при хе(0; 1).
18.48. Пусть функция f(x) дважды дифференцируема на R, .
и пусть АГ* = sup | /<*>(х) | < 4~oo (k — 0, 1, 2). Доказать, что
x e R
Mi 2MqM2>
§ 19. Вычисление пределов с помощью формулы Тейлора
Пусть требуется найти
lim
х->0 g (*)
где f(O) = g(O) = O. Предполагая, что функции fug можно
разложить по формуле Маклорена, ограничимся первыми отлич-
ными от нуля членами в разложении этих функций:
f (х) = ах" 4- о (х"), а #= О,
g (х) == Ьхт 4- о (xm), b =/= 0.
ахп + о (хп)_а_
x^Qbxn + o(xn) ~b'
Если т = и, то
.. f (x) «•
hm > 4- = hm
x->o в M
(1)
Если п > т, то
lim -Ц4 = 0:
x->o gM
(2)
если же т > п, то
lim = 00 •
Х-Ю g (X)
(3)
Пример 1. Найти
lim
х~>0
+ 2 tg х — ех + х2
arcsin х — sin х
А Функции, стоящие в числителе и знаменателе дроби, яв-
ляются бесконечно малыми при х->0.
Так как
V - 1*^ л
sin х = х----g- 4- о (х3),
arcsin х — х + -g- + о (х3), х -> О,
то разложение знаменателя дроби по формуле Маклорена имеет
.вид
arcsin х — sin х — -у 4- о (х3), х-*0.
Поэтому числитель дроби следует разложить по формуле Мак-
лорена до о(х3). Используя формулы
tg X = X 4--J- 4- о (x3),
401
получаем
Vl + 2tgx= 1 -F-(2tg x) — -|(2tgx)2 + -4(2tgx)3 + о(tg3x) =
y3 v2 y3 у2 К
=1+х + |-| + | + О(х3)=1+х-|+|? + О(Д
Учитывая, что
у* 2 у 3
^==1+х + Л_ + ^ + о(хЗ)1
находим разложение по формуле Маклорена числителя дроби
V1 + 2 tg х — ех + х2=-| х3 + ofx3), х->0.
м
Таким образом, дробь представляется в виде
4 х3 + о (х8)
А--------> *->0,
yd > »
4- + о (Xs)
о
откуда следует, что искомый предел равен 2. £
Пример 2. Найти
'Л Используя формулы
ln(H-x) = x-4 + 4 + °<*3)’
у2 у8
1П (1 - X) = -X - + О (X3),
находим разложение знаменателя дроби
In-!-~7 ~ 2х = 4х3 + о(х3), х->0.
Поэтому числитель дроби следует разложить до о(х3). Так как
Л9
arctg х — х —§~ + ° (х3),
то
earcig X == ! _|_ (х_ + +1 хз + о (Х3) =
у 2 у 3
= НИу-у + о(х3), Х^О.
Заметив, что
J — 1 + X + х2 + х3 + о (х3), х —» О,
получаем разложение числителя дроби
«arctg+ + ^-^0.
402
Таким образом, данную дробь можно записать в виде
7
х3 + о (х3)
О м
-5---------, Х-»0,
•о- X3 + О (х3)
о
откуда следует, что искомый предел равен —7/4. А
Пример 3. Найти
(. X X \ L хг
lim 1 V5-) Ла 2
х->о ch(sinx) —е '
ГА Используя разложения
X3
sin х — х —ё~ + ° (х3), х -> О,
ch/=i+4+-£-+on ^->о,
получаем
Ch(sinx)=l+4(x2-4)+^+ °(*4)^+4-4 + О<х4)’
х->0.
Учитывая, что
ex’/2=l+^- + ^-4-O(X4)t
находим разложение знаменателя дроби
ch(sinx) — ехг/2 =—j/ + o(?), х->0.
Числитель дроби следует разложить по формуле Маклорена
до о(х4). Так как
sh-^ = -^- + — (-£Й3 + о(х4) = -£=г + —^+о(х*), х->0,
V5 V5 3! k V5 7 7 V5 30 V5 7
•Cos/=l-4 + ir + o('4)» <-0.
ТО
“s (sh w)=1 - т (т+£)+т i+° (/)=
= 1 io 200 + 0 X -► 0.
Используя формулу
(l+0l/5=l + |'-i'2 + °('2)’
получаем
1/1-4+
f->0,
х-*0.
403
Итак,
cos (sh —7=-') — д/' 1 —— = x4 + о (x4), x -» О,
\ V5 7 r 2 200
и поэтому заданная дробь представляется в виде
200 х< + °(х<)
_^ + о(х<) ’
х—>0,
откуда следует, что искомый предел равен —3/50. ▲
Пример 4. Найти
in (х + V1 + X2) — X + 4- X3
1* «
А Так как thx— нечетная функция и th х — х -ф о(х) при
х->0, то
th х = х + а3х3 + о (х4).
Используя разложения
shx = x + -^- + o (х4),
chx= 1 +-^-4-о(х3)
и равенство
sh х — th х ch х,
получаем
х + + о(х4) = (х + а3х3 + о{х4)) (1 +-у-4-о (х3)).
Приравнивая коэффициенты при х3 в этом равенстве, находим
откуда а3 = —1/3 и, следовательно,
th х = х —у + о (х4), х — ihx — ^~ + o (х4).
Поэтому числитель дроби следует разложить до о(х3). Заме*
тим, что _____
(in (х + V1 + X2 ))' = 1/V1 4-х2,
где
1/VT+^ =l-j?+o(4
Поэтому (§ 18, формула (29))
Л 1л. (х 4-. V-1Н- х2) = х — Т х3 4- о (х4)
404
й числитель дроби есть о(х4). Таким образом, дробь представ-
ляется в виде
о (х4)
<5
откуда следует, что искомый предел равен нулю. Л
Формула Тейлора часто применяется для вычисления пре-
делов вида
lim (f(x))e(x\
Х-»Х0
где
f(x)>0, limf(x)=I, limg(x) —оо.
Рассмотрим сначала случай х0 = 0 и предположим, что-
функции f и g представляются в виде
f (х) — 1 + ахк + о (xft),
g(x) — l/(bx*4- о (хк)), х О,
где а =И= О, b 0, k е N. Так как
lim (1 + ахк + о (x*)),^ejt*+G <**)) = е,
я->0
Ит
х->о Ьхк + о (хк) b
ТО h ь
Нт (/(х))8<ж) — lim (I + axk + о (хк))'^Ьх +° <* — e°tb. (4),
л->0 л~>0 7
Если
_ 1 + axk -Ь о (хк)
/ W i । n Yk । n(Yk\ ’
1 -j- Cl\X -j- O \X J
. fe J / М при x->0,
bxK -|- о 1.x )
причем a =# 0, at =/= 0, b ^=6, k e N, to
lim (f (x))fi (JC) = e(o“Ol)/b. (5) •
x->0
Заметим, что для вычисления предела функции (f(x))g(x>
при х->0 можно предварительно найти цредел ее логарифма,
т. е.
lim g (х) In f (х),
x->0
разложив функции g(x) и lnf(x) по формуле Маклорена.
Пример 5. Найти
lim (cos (хех) — In (1 — х) — x)ctg х\
Л Так как
= %->0’
405-
то функцию
f(x)= cosfxe*)—ln(l — x) — x
следует разложить по формуле Маклорена до о(х3). Исполь-
зуя разложения
хе* = х + х2 + о (х2), х —> О,
cos t — 1 — -у + о (<3), 1-*0,
-1п(1-х) = х + ^- + 4- + о(х3), х->0,
получаем
/(х) = 1-|х3 + о(х3),
(f (х)Г‘-=(1 _2х3 + оСх3))1^0'0, х->0,
откуда следует, что искомый предел равен е~2/3. Ж
Пример 6. Найти
lim ( 2tg* \1/(1~cosx)
х->о \ х + sin x J
& Используя разложения
1 — COS X = ~ + О (X2), tg X = x + ^-^ + o (x3),
£ о
J^3
sinx = x----g-^-oCx3), x->0,
получаем
( 2 tg x \W-cosx) / 2x + 3-X3 + о (x3) \
\ x + sin x ) I „ x3 . , I
2x---g- + o(x3) J
1
x2
, X3 s ~+0(X!)
/l+^- + o(X2)\
= —--------------
V“-^-+o(x2) J
откуда следует, что искомый предел равен е^3 ( 12)) , т. е.
равен е5/6- А
Заметим, что если
f(x)=l +ахп + о(хп), g(x)= . Х-+0,
где а =/= О, b =^= 0, т, п е N и т #= п, то
lira (f (х))й (*’ = 1 при п > т; (6)
-ъ ft * 7
406
если т> пп т — п — четное число, то
, ч (4- со, ab > О,
оЬ<0. <7>
если же т> пи т — п — нечетное число, то lim (f (х))'! w не су-
x-> О
ществует.
Пример 7. Найти
Г . . . . 1 , . 42\l/U’(Vi+^-l))
hm I cos (sin х) + =- (arcsin ху I
х-*0 V z 7
А Используя разложения
cos/ = l — -у +-^ + о (/5), >0,
sinx = x—g-4-o(x4), arcsin х = х +— + о(х4),
д/1 + 2х = Г + x-f-о(х), х->0,
получаем
/ (х) = cos (sin х) + у (arcsin х)2 —
=i-4P-4)+4+IG2+-t)+°^>=
= 1 + 4 X4 + о (х4),
8 ~ х2 (V1 + 2х - 1) ~~ Xs + о (х3)
Следовательно, искомый предел
/ ч х 1/(х’+о (Xs))
lim (f (х))г< > = Нт (1 + 4-х4 + о(х4))) = 1. а
При вычислении предела с помощью формулы Тейлора в ко-
нечной точке Хо ф 0 следует положить t — х — х0 и свести за-
дачу к вычислению предела в точке t = 0. Случай х->оо
заменой х = \/t сводится к случаю t «= 0.
Если имеется неопределенность одного из видов 0-оо,
оо — со, ее следует привести к неопределенности вида .
Пример 8. Найти
lim(V3 — х+ In(x/2))1/s'n <х-2>,
Х-»2
А Полагая х — 2 — t, получаем
lim (V3 — х-Нп (x/2))1/sin'(x-2) = lim (Vl — / + In (1 + *
407
Так как
sin2f = /2 + o(/2), д/П=7=1 +
|"(| + 4)=т-т+»«!)
при /~>0, то
/ ---- z Кч1/8|П«Г / /2 чШЧчНП)
(Vl_/ + ln(l + £)) = (.1-4 + о(О)
откуда следует, что искомый предел равен е~!/4. Л
Пример. 9. Найти
lim x7/4(Vx+ 1 + Vх — 1 — 2 V%).
X->-f-oo
ГЛ Используя равенство a
\! x + 1 + Vх — — 2 д/х — х* */4(д/1 + у + д/1 —~ — 2^
и полагая 1/х = t, получаем
lim x7/4(Vx + 1 + VX-~1 —2д/х) =
= lim Д+/>'С.+ П-0''‘-г
/->4-0
Так как
(1+о,/4=1+4-^/2+о(/2).
то
(1+01/4 + (1 -0,/4-2 = -4/2 + о(А /-* + 0,
откуда следует, что искомый предел равен —3/16. Л
Пример 10. Найти
lim ( —-—г-----7----—:—).
х->0 \ sin х arctg х tg х arcsin x J
fA Используя разложения
j^3 уЗ
sin x — x —g- + о (x4), arctg x — x —3- + о (x*),
X3 X3
tgx = x + -g- + ° U4)» arcsin x = x + -g- + о (*4)»
получаем
____1________________1__ tg x arcsin x — sin x arctg x
sin x arctg x tg x arcsin x sin x arctg x tg x arcsin x
X4 + О (x4) Xi + о (x4)
• откуда следует, что искомый предел равен 1. ▲
-408
Найти пределы (19.1—19.18):
<Л . .... In (14-х) — х о, .. sh2x — 2shx
19.1. 1) hm—-Н-------. 2) hm-------а----.
х->0 Л л->0 х
3) lim —1-~-* . 4) lim —* J + 2 . 5) limch 3%+c°s3x~2
х->0 х х->0 х х-»0 х
6) Ит. 7) limyr+^4-Vm-2VT^ ,
х->0 х х->0 х
я) i;m arctg х — arcsin х
19.2. 1) lim-^—-
х->0 sm х - X
у arctg x ~~ arcs*n x
x™ tg x — sin x
2 arcsin x — arcsin 2x 4) lim 2je — '
*3 ’ x^° vm - vr^ ’
5)
lim
x->0
1 + x cos x дЛ 4- 2x ex — Vl + 2x
. /« i \1 • o) 11 m . ~
In (1 4“ x) — X x-»0 In COS X
7)
3 cos x 4* arcsin x 3 ^14- *
In (1 — x2
.. — x2 — x ctg x
-----TTiiTI-------
,9.3. ,) nm 2) lim .
x->0 x x-»0 x
(l + x)l/x-e[l-y) cos cos x)
3) lim----------2-^------— . 4) lim-----v . . 2 /•.
jk->o x x->o ®ln (sin x)
19.4. 1)
lim
x->0
2)
3)
4)
Б)
1- In (1 4-*3) —• 2 sin x + 2x cos x2
a------------яг?------------•
x Vl + sin x —i- in (1 4- x2) — x
lim------------7-3—-----------.
x-»o ‘83jc
esin X _ x2 _ x cos x
-------
esin x In COS X _ (1 _|_ 4x)'/. + x _ 3. X2
—————- sin —2———
1ЛК Ml- earclg x 4-In (1 — x) — 1
19.5. 1) hm----------. .
' x->o 2 —4/4 + Л3
409
Vl + х sin x -f~ In cos x — x
— X3 — 1
Vl + x sh x + In cos x — x
x-»o 1 — 1 — x3
lim
x->0
5
In (e2X + sin x) — 3 arcsin x + — x2
4) lim---------------==------------------2—
x->o ^8 + x3 — 2
5)
. (, . In (1 + X) \ , . . „
In I H---. v ~ I — tg (* — 2x2)
lim—S-------L.+ 5...Z------------
z->0 v4 + x3 — 2
1S.6. 1)
x->o sin x x
*yr+ sin x "f" In (1 — x)
tg x — sin x
2) lim^t?*3'-008*4
' x-»o tg*-*
3) lim
x->0
Vl — X In (1 + x) — *
4) lim--------;-------=---Ш-
x->o tg x — sin x
19.7. 1) Hm/^+Jnd-x)-!
x-»o arcsin x — sm x
2) iim VL+2..t^-g* + ^.
x->o arcsm x — sm x
3) Hm ln (t + *)cos x ~~ etg * + Vi + 2*2
' х^й x — sin x
Vl — sin x — In f 1 —£1 — 1
4) lim------;.
x-*o tg x — sm x
5) iim-gy-~x~chx •
7 sin x —arctg x
6) lim g^^+lnd-sinx)-!
x->o tg x — arctg x
^T+3^-esIn* + 4*2
arcsin x — tg x
+ 3x In (1 — x) + sin (sin x) + x2
lim------------;-------------------------
*.^0 tgx —arcsin x
19.8. 1) lim
x->0
gtg x ^/1 4. 2x — x (x + x2)
x — arctg x
2) lim
X-»0
In (1 +£-) — Vl + sin x + 1
sh x — arctg x
410
etg Iх® — Vl + sin x —~-
arccos x — arcctg x *
+ 3x 4- x2 + sin In (1 — x) — e~7x2P
4> 1™-------------------------------------------
.. Vl + sh 2x — cos x — x
' x-^o tg x — arctg sin x
6)
.. V2 — e2* — cos 2x + In (1 + x)
I i rn —-----------------:-----2------
0 sin x— arcsin tg x
xetg x — sin2x — x
x 4- x3 — tg x
19.9. 1) lim
x->0
2)
3)
4)
+ X3 “ X ctg X----- X2
1! d
x cos x — sin x
,. cos x — Vl — 2x — x
I'™ ,4, «-.-.• + ! •
Г sin x — In (sin x + Vl + x2)
tg x — x cos2 x
ex—i 1
e\ t- 6 1 — X
5) Itm—j-q—----------.,
In -----2sin x
tg (sin x) — In (x 4- + x2) — -qr-
6) S th (x-x’)-x
19.10.
1)
e2X — ch 2x — 2x
lim—.
tg 2x — 2sin x
2)
lim
x->0
In 4- x —~ x2) — sh x 4* у x2
sin 2x — 2x cos x
«. x2e2X 4- In (1 — x2)
hm-------5
_^0 X cosx—sin X
4) lim
x->0
arcsin x4-3 cos x — 3^14**
1 4- in (1 4- x) — ex
5)
«. x2ex — In (1 4- x2) — arcsin x3
lim-------------x sin X - x2--------------
Q " olll Л Л
6) lim
x-»0
el+tg X _ eVl+2x
sin -----4 In (1 — x)
/ о
ex _ yj + 2x + 2x2 o\ (!m tg sin x - x cos x
x + tg x - sin 2x * x ™ eX + ln( 1 - *) - 1
19.11. 1) hm Sinxchx-shx *
7)
411
.. tg х — In (х 4- Vl + х2)
sinx — x cos к
।. 2 In cos x 4- x sh x
sin (x2/2) — sh (x2/2) ’
j. ex* tg x —- x cos sin x
x->o in (1 4- x) — xV 1 — x
3) ||m <«•-In (H-.ln,)-!
x->o x cos x — sh x
6) Hm
x->0
arcsin x — xex*
x^J 1 — x2 — tg X
19.12.
1 \ 1 • Vl — 2x + eis x — 2
1) hm —\-------------!-----------s“
v -urt sm x x2
----------cosx-------
x 3
_____________________ 3
VCOS X — X in (1 -F x) + — tg X2 — 1
xex — arcsin x — x2
ox sh 2x + In (1 — sin x) — sin In (1 4- x)
(i_2x)-V2_^-x2
4) |jm U~ 2x)~l/2—(l+2x)~1/2—arctg 2x
7 x_>o e~x 4- In (1 + arcsin x) — 1
In Gsin *+ In (1 - X) + 4)
5) lim—---------------p---
x->0 in ch x--
lirn 7 arctg x-tgx..
7 x->o esh — (1 4- 2x)lt — x2
19 13 1) lim + *2 ~~ e* /3
inn ln {1 + 3x2) _ 3x2 COS x •
m I. In (Vl 4- x2 — x) 4- tg x
x (ch x — e )
Vln(e + x)-e^4-^-
3) x ch x — sin x *
.. esln x — Vl 4- x2 —- arcsin x
4) hm ----==— .
x-^o sh (x — x2) — InVl 4-2x
chV^+cosV^-2eX'/2
x->0 tg Vl -h^4 —tg Vl —
el+cos X _ e24- x2 _(_ .11 e2 Sjn x2
6) tn (1 + x2) — (arctg x)2 •
14 1) |im ln ('+ sin 2x) ~ 2x + 2x2
я-*0 4- tg —-arcsin x
Vl + sin x — 4-tg X + -5- X2 — 1
2) lim-----------/ . t;-..”--------.
x->0 ex — }/1 + 2x — X2
412
.. Vl + 2x eis x + 6x3 + x2
hm—1—11-----------——
x->0 In (1 + x) — arctg.x + ~
ch 2x —- (1 +3x)“I/3- x
lim—;-------—5--------
x">0 — x2 + In (1 4- tg x) — arcsin x
' ex^ x) — sh x — cos x
5) hm e , e---------------------•
x~>0 Vi + x + Vi ~ x — 2
.. X + Ch x - earcsfn x
6) hm----------.
x ->o tg x + V1 — 3x — 2cos x •+ 1
—к .. V2x + cos 2x — e*8 x 4- 2x2
' 2sin x — 2 In (1 4- x) — *2
.. sh sin x3 + sin sh x3
8) hm -----------------------
x“>0 — Vl — x 4- In (1 4* x) ~ x cosx
19.15. 1) lim
X->0
tg2 X — tg X2
^arcsin x___gSin x_____— x3
2)
lim
x->0
, sin x , . x *
ln-------p ch —7=r — 1
X_________Уз
sh x — In (x + Vl + x2)
3) lim
x->0
4) lim
3 arctg sin x — tg sh 3x
Vl 4" x sin x3 — x2 In 1----— x
sin Vl-t-x3 — sin 1
x->0 --------------
V1 — 2x In cos x — 1
ч л i л i \ i • e*2 •— Vl 4- 2x2
19.16. 1) hm---------A—--------
x->0 x
|jm ^ + ln(l-Smx)-t
Ve - X4 - 2
8) lim
x->0
In ^COS X 4-
e-x2/2 __ cos x
gx/(14-x) CQS e x) —• arctg x
4) lim
x->0
2
sin (xex) + sin (xe-x) — 2x — --- x9
19.17. 1) lim--------------------j----------1—
sin (x cos x) 4- x In (1 4- x2>) — x
2) lim--------------7=^---------<--------
x->0 V1 + *5—’1
413
7'-4—
3) x2 In (1 4- x) —• (tg x3 4) cos sh (x/2) *
In (cos x 4“ x sin x)-— ex
^-^l— Л+ 1 + ----------------Sin (X/2)— 1
1)
x">0 — arcsin 2x — 2 ch x2
x
In (Vl + 2x — tg x) + 4- arctg x2
lim- 2
x-»0
4) lim
x~>0
19.18.
2)
3)
xex* — sin x
iim Vr=^-<?-*4-x2V
4)
sin2 x — In ch2 x
In (1 4- x) 4- 4- sh x2 — x
lim —7=^---------.
х-»о VI 4-tg x — VI 4-sin x
19.19 . Найти числа aeR и n^N такие, чтобы существо
вал конечный предел
!. еах — cos х2
!'m-----р-------•
х->0 Л
Найти пределы (19.20—19.42):
19.20 . 1) lim(7Г+х — х)1/х- 2) lim (cosх)с‘в2*.
л->0
3) lim (ch x)1/sin2 х.
f cos x V/*2
4>Й(те) •
arcsin х \ Vx2
~Х )
/ ех* V*2
5<S;UF
19.21 . 1) lim(£^)w. 2) lim('"(Vl + >‘
3)S(^r- ^ЬВГ-
19.22 . 1) limf- . 2^-?-Д’"”.
x-»ok2(Vl 4-х- 1)7
2) lim f-^1 ~-y ~ ~ 3x Y *♦
*-><Л Inch* J
3) lim
x->0 x sm x )
4) lim ( 3* + cos 4x — cos 2x \ Vsin x
x->o \ In Vl + 3x — In Vl ~ 3x /
l/sin3X
X3
19.23 . 1) lim (1 + 6 *-sin x
x->0
19.24 . 1) lim (Vl + tg 2x + In (1 - x))v<
x->0
2) lim(tg(x/3) + 2 - ^r+x)ctg’x.
3) limf ch x-cosx y/x
x->0 к 2 V1 + 2x — 2^1 + 3x J
ctg' X
19.25. 1) lim
x-»o
„ f-Lsinx, 3/------- Xl/lnd+x»)
3) lirnU3 + ^1—tgx —1)
X~>0
4)'!s(t<' +*>'“+ тгГ
arctg x \ 1/x'
<»2 | *
ex-l-^J
3) iimpc°s*±n№
19.26. 1) lim (V1 + -
x-xA s
2) НтС + ^-УГ^Т'
x ->o ch x 1 /
3) ”™Cx-ln(l+xU '
19.27. 1) nmf(arcsin/)2-^Y/stn,JC
x->0\ sin2(x2/V3) )
f L ix \ctg'x
I arct£ 2"x2 ~X J
x sin (x2/6) / *
COS X
l/x*
/П Um ( *sinx y/«‘
4) 1™ t'gchg —gj
I Y \ I/sin' x
•ycos x
Vl + tg x2
Ux*
2) lim
x->0
3) итр2~ (arctg x)2xw
*->°l x2 sinx2 I
<5 /
3 arccos (1 -- 2x2) — 6x V**
4) lim f
x->0
xz
(9z>x^x2 — o \(sln x)fx*
Д—Л)
2x-x2 )
(VcosT \I/arcsinx’
xcos/-------A
Vl + x — — sh x J
3) limf-sh(x + sinx) rt8’*.
к sm x + arcsin x )
415
19.29 . 1)
х->(Л x In (e2 — xe2) J
2) 1 im ( arcs*n arcsin 3x — arctg x \ Vln cos 3x
' ,v->0 V X ) •
3) ]im ( sin <2x *3 4) ~~ sh (* + 2x8) \1/<21n Q+**)~ in2 d-ix))
x-»0 \ X )
4) ]im ( te &x 4- x3) - th (x + 2x8)
л->0 \ * J
19.30 . 1) lim(cos2x + -r^-_ jrY/X>.
2>1™»(^1 + 2х + л!’-^Тз)'Я'-
3) lim (-^2 + ln (* + ^*+1)) W.
4) Hm ( + sin In (1 4- x))’7*’.
19.31 . 1) lim (x — In (1 + x) 4- cos (хе~л ))'*’.
X->0
2) lim(<?sinjt — е2*-*!4-е*8л)1/х\
x-»0
8)lirn(i;4ln4±i-arclex)''""'”'.
4) limf-,____*•-»--------Yw.
x->0\Vl + x2 — In (1 + №)7
19 .32. 1) lim(-^8+Tx5 * — cosx2)I/arcslnx’«
x->0
2) lim (cos x — x 4- earc,e x — l)1^’ *,
jc->0
3) Hm (4x24- #1 4- 3 sin x 4- In (1 - x))’/sh’*.
4) lim (^1 - 3x cos 2x + 4x2 4- —x?
19.33. 1) lim(e‘sx4-ln(l — х))с‘8<
x->0
2) Uni (Vl 4- sinx — -jtgx4--g-x2)c’8.
3) lim (V1-2x4-3x2 4- x (1 — sh x))c,«! x.
J£-»0
4) lim (esin л + cos x — Vl 4- 2xY4e
19.34. 1) lim (In (1 — x) 4- ex «*> *>’/<«’ (Vi+a*-i)).
*->0
<16
2) lim (— arccos x + sin 2£.Y/(Vi+2*’ 0 .
3) lim (1 + th (xex) + ± in (1 - 2x)) */*’.
x->0 \ z J
19.35. 1) lim(earctgJC —-j-5—+ cosx + x2y/S,nX\
x~>0 V lx J
2) lim(l + 2arctg % ~ sh 2x)1/ln (I~x).
x-»0
i/ii? (i-|)
3) limpinx~4--xcosx)
x~>0 \ '
/ .---------- Y v/Q\ V(* In COS X)
19.36. 1) lim (Vl+ tgx-4
x-»0 ' о 7
/ -X . -------- l/(x (cos x-1))
2) + т ^ln V1 +— tg x)J
z , s/------5--xl/(tgX-X)
3) lim (ex x —x a/1 —- ~ x)
x-»(A V 2 j
/ ,---------- v2 \ l/(sh x—arctg x)
19.37. 1) lim ( Vl + 2 tg x +-5----sin x j
x->0 4 2 Z
2) lim (1 — sin x + arctg x)1/ish *~sin x}.
x->0
(.---------- y 4 l/(tg X- sh x)
l + VT^lnfl+x)--^-)
* -r X J
(1 X l/(tg x-sh x)
cos (sin x) + у arctg x2 + 4x3J
19.38. 1) lim(esin2x —2x —2x2)1/sinx’.
x-»0
2) lim (esin x + In (1 - x) + 4)•
3) lim ( -« + Sin x — In (x + Vl + X2) YZ*'
7 x->cV x ) •
19.39. 1) lim(l 4- sin x arcsin x — x2ex^'&m x»
x->0
2) lim(l + tgxarctgx — х2сЬ2х)1л1-со8д:)’.
x->0
3) lim (1 + th x In , - — 2x2 cos x2') ' .
x->o ' IX J
19.40. 1) lim (1 + shx In (x + Vl +*2) ~ x2cosx2)’/x’.
x->0
14 Л. Д. Кудрявцев и др.
417
z 1ч 1/sin
2) lim ( cos sin * + у arctg x2j
ch X + 2 COS X . X1 \ l/arctg x*
3 H 6(Ц-Х2) J
Ю/li П1- ( 2x 2 A^’-arctgx’)
19.41. 1) hm I . „ — x21
x->0 ' sin 2x 3 /
z /----—x (x+e)/arcsin x3
2) lim ( cos x + x2 л x + t)
x-^o\ v 4 7
o\ I- / 3/1—i—77— , . , 9\I/(arctg x—x cos x)
3) lim (V 1 + 3% — tg sin X + X2)
X->0
I- fi (i4-x2)1/x2-ecos^1/Wch2^?Z)
4) 1 im I 1 — -—5— ---------)
x->(A e /
ctgsx+'
19.42. 1) lim (cos (2xx2) + 2 arcsin (xe*) — 2x)
x->0
2) lim (1 + arcsin x3)eX/(x^°^-sinjc+tg4).
X-»0
19.43. Доказать, что
lim (— )*'* (arccos sh x + x)ctg x* — е-2'(3я).
x->0 4 31 '
Найти пределы (19.44—19.60):
19.44. l)-lim pln(1 +x)
' ^0' x
2 ^ct8 *
(x + 1) sh x )
f________6______________________4_________
/^0 \ In (1 + 3 sin2 x) In (2 — cos 2x)
19.45. 1) lim (chx)x2(tg(1/x,-arctg(1/4
X-> + oo
2) lim e-*2/3 f-|- In] ) ..
X->oo Z X 1 /
3) lim (
X->oo \
X4 4.X2_|_ J к X< Sin» (1/X)
X4 — X2 — 1 )
z /“5-- 1 _\X2+sin3x
19.46. I) lim ---------- + Tsin_2_)
Л->+ео\ X '4 Xj
, I X X2 arctg x
2) lim ( x In (I 4- x) — x In x + arctg -у- I
19.47 lim (sh x - In (x + д/l + *2))1/ln
x->4-0
19.48. lim (("y — x)tgx)tg*.
x-*-j-0
19.49., 1) lim (ex-l _lnx)'Asin(x-l)+cos(x-l)-x)
418
2) lim (esln(jc-1) — lnx)ctg’(x-1).
Y~>1
/ /— 1 \ l/(cos2x sin2(l-x))
3) lim I Vx — — In x )
x->l V /
19.50. 1) lim(x-lnx)1/(cos2xsin41-x)).
x-> 1
2) lim (2х-1 - Xх In 2)1/(sin (x-1)~cos C-xi+x),
3) lim (ln(x2-x)-ln(x-l) + e1-^)1/arcsin(x-’)S.
x —1 +0
-i .. ( 1 2 \l/sin(x-l)
19-5L
19.52. lim . e<X. 1),X-..Y4£-3__..
x—>1 ch (x — 1) — cos 2 (x — 1)
19.53. 1) lim
x-> 1
3 'у/ x — arcsin (x — 1) — 3 cos (x — 1)
ex-1 — 1 — In x
2)lim
1
2 Vx —- sin (x —• 1) — 2 cos (x — 1)
arctg (x — 1) — In x
19.54.
1) Hm
’ J£_>1 In (1 + In X)
<_„лх-2хг In ctg x-J-2x —
2) lim -----------• 3) lim ------—т—---------
7 „ COS x Л (1—tgx)3
x+l-
19.55.
.. x(l — x2)1'2— cosxln(l + x)
11 m —-------гЧ---------;----'------
„ , n In sin X — In X
19.56. 1) lim (-Д-----------Д—) . 2) lim (—J—
x->0 \ Sin x tgx ) x^.0 V arctg x
1____
arcsin x
3) lim f—------г—'I • 4) lim (-.— * /---------7 — ).
x->(A x xtgxy *.>0 \ (x+ l)shx x2 /•
19.57. 1) lim xfl — xln(l +—)).
X->oo x X / /
2) lim x((2e)1/x + e1/x-2).
X->OO
3) Jim (x31n(l +±)-x2 + f).
6 6
19.58.
.. Vx6 + x5 + Vx6 x5 — 2x
11171 ----------!----! —-------------------
x-»4-oo x ln (1 + x) — x In X — x sin (l/x)
19.59. 1) lim (e1/x (x2—x-\-2) — V%4 + %2+0*
X-»+°o
2) lim ((x3 — x2 +-j + 1) eI/x — Vх'2 ~+ 2
14* 41M
5 _____ 5_________
19 .60. 1) lim (V*5 + *4 ~ V*5 *“ *4)-
Х-> оо
2) lim ((х3 + х) sin —— \/х6 — Зх'1 +~П •
3) Hm (x2--J-(x3 + x+ I)ln (1 +4))-
4) lim ^+±(1 -^+!-ln^+A+L).
§ 20. Исследование функций
1. Условия возрастания и убывания функции. Для того что-
бы дифференцируемая на интервале (а; Ь) функция f(x) строго
возрастала на этом интервале, достаточно, чтобы производная
f'(х) была положительна всюду на (а; Ь), т. е.
f(x) > 0, хе(а; Ь).
Для того чтобы дифференцируемая на интервале (а; Ь)
функция f(x) возрастала (не убывала) на этом интервале, не-
обходимо и достаточно, чтобы производная f'(x) была неотри-
цательна всюду на (а; Ь), т. е.
f'(x)^O, x^(a;b).
Аналогично, достаточным условием строгого убывания диф-
ференцируемой функции f(x), хе(а;&), является условие
f(x)<0, хе(а;&);
необходимым и достаточным условием убывания — условие
f'(x)^O, хе(а;1>).
Пример 1. Найти интервалы возрастания и убывания
функции:
1) f(x) = x3-30x2 + 225x+ 1.
( l/е, если х < е,
2) f(x) = s ,, ..
- ’ 1 ' ’ ( (In х)/х, если х^е.
3) f (х) = cos (л/х).
'Л 1) Данная функция всюду дифференцируема, причем
f'(x) = Зх2 — 60х + 225 = 3 (х — 5) (х— 15).
Так как f'(x)>0 при хе(-<»;5) и хе(15;+оо) и /'(х)<0
при хе(5; 15), то на интервалах (—оо; 5) и (15; ф-оо) функция
строго возрастает, а на интервале (5; 15) строго убывает.
420
2) Функция дифференцируема на всей числовой прямой,
причем
z ( 0, если х < в,
f — 1пх)/х2, если
Так как f'(x)^O при всех х, то данная функция является не-
возрастающей на всей числовой оси. На интервале (—оо; е)
юна постоянна, на интервале (е; +©о) строго убывает.
3) Данная функция является четной, поэтому достаточно
найти интервалы монотонности при х > 0. Решая при х > 0
неравенство
rw=^sin^->0,
получаем
0 < п/х < л или 2nk < л/х < л + 2л6, N,
откуда
х> 1 или 1/(26 + 1)<х< 1/(26); 6c=N.
Таким образом, на интервалах (1; +°°) и (1/(26 + 1)1 1/(26)),
k N, функция строго возрастает. На интервалах
(1/(26); 1/(26—1)), 6eN, очевидно, справедливо неравенство
/'(х)<0, и поэтому на этих интервалах функция строго убы-
вает. Если х < 0, то, используя четность функции, получаем, что
на интервалах (—1/(26); —1/(26 — 1)), 6gN, функция строго
возрастает, а на интервалах (—оо;—1) и (—1/(26 + 1); —1/(26)),
6 е N, строго убывает.
Следует обратить внимание на то, что данная функция не
является монотонной ни в какой окрестности точки х = 0.
В любой окрестности этой точки содержится счетное множе:
ство интервалов возрастания и счетное множество интервалов
убывания данной функции. А
2. Экстремумы функции. Точка х0 называется точкой ло-
кального максимума функции /(£), если существует окрестность
точки Хо, для всех точек которой верно неравенство
Если для всех х =# х0 из некоторой окрестности точки хо
верно строгое неравенство
f(x)<f(xo),
то точка хо называется точкой строгого локального максимума
функции f(x).
Аналогично, если в некоторой окрестности точки х0 выпол-
няется неравенство
то точка х0 называется точкой локального минимума; если для *
всех х #= хо из некоторой окрестности точки х0 верно строгое
421
неравенство
f«>f(x0),
то точка %о называется точкой строгого локального минимума.
Для краткости слово «локальный» часто опускают и пишут
просто «точка минимума» или «точка строгого максимума».
Точки максимума и минимума функции называются точками
экстремума, а значения функции в этих точках — ее экстре-
мумами.
Например, для функций £/ = |х| и у=\—х2 точка х = 0
является точкой строгого экстремума, причем для первой функ-
ции— точкой строгого минимума, а для второй — точкой стро-
гого максимума. Для функции у — sign х каждая точка х О
является как точкой нестрогого максимума, так и точкой не-
строгого минимума. Функция f(х) = cos(jt/x) имеет счетное
множество точек строгого экстремума хп — \/п,
причем точки х2л, k е Z, k 0, являются точками максимума,
а точки x2/s+i, AeZ, — точками минимума. Экстремумы этой
функции равны
f(x„) = f(l/n) = (-!)«
Необходимые условия экстремума. Если точка
хо является точкой экстремума функции f(x), то либо f'(x0)= О,
либо f(x0) не существует.
Эти условия не являются достаточными. В самом деле, для
функции f(x) = x3 производная в точке х = 0 равна нулю,
а для функции
( х, если х < О,
gM I 2х, если х О,
производная в точке х = 0 не существует, но ни для f(x), ни
для g(x) точка х = 0, очевидно, не является точкой экстремума.
Точки, в которых функция определена, а производная функ-
ции равна нулю или не существует, называют критическими точ-
ками функции. Экстремумы функции следует искать среди ее
критических точек.
Достаточные условия строгого экстремума
(с использованием первой производной). Пусть функция f(x)
дифференцируема в некоторой окрестности точки х0, кроме,
быть может, самой точки х0, в которой, однако, функция Дх)
непрерывна. Тогда точка х0 является точкой строгого макси-
мума, если существует окрестность точки х0, в которой
f,(x)>0 при X < Хо и f/(x)<0 при X > х0. (1)
При выполнении условий (1) принято говорить, что произ-
водная функции при переходе через точку х0 меняет знак плюс
на знак минус.
Если же
f'(x)<0 при х<х0 и fz(x)>0 при х > Хо, (2)
422
т. е. если производная при переходе через точку х0 меня'ет
знак минус на плюс, то х0 — точка строгого минимума.
Условия строгого экстремума (с использованием
производных высших порядков). Пусть функция f(x) имеет
в точке Хо производные до порядка гг (neN) включительно.
Тогда, если
Г(^о) = Гио)= ... =^-1)Ы = 0, а ^(хо)=#О, (3)
то при четном п точка х0 является точкой строгого экстремума,
причем точкой максимума, если (хо) < О, и точкой мини-
мума, если f(n)(xo)>O; при нечетном п экстремума в точке хо
нет.
В частности, если
Г(хо) = О, а ГЫ¥=0,
то в точке Хо строгий максимум в случае f"(xo)<O и строгий
минимум в случае f" (х0) > 0.
Пример 2. Найти точки экстремума функции f(x) =
= (%+ V)e2x.
А Функция имеет производную при всех xgR, причем
f' (х) = е2х + (х + 1) 2е2х = (2х + 3) е2х.
Следовательно, у функции может быть только один экстремум
в точке х = —3/2. Так как f'(x) < 0 при х < —3/2 и f'(x) > 0
при х > —3/2, то точка х = —3/2 является точкой строгого
минимума. А
Пр и м е р 3. Найти экстремумы функции
f (х) = 2х3 — 15х2 + 36х — 14.
А Так как
f (х)= 6х2 —30х + 36 = 6(х —2) (х — 3),
то критические точки функции х = 2 и х = 3. Экстремумы мо-
гут быть только в этих точках. Так как при переходе через
точку х = 2 производная меняет знак плюс на знак минус, то
в этой точке функция имеет максимум. При переходе через
точку х = 3 производная меняет знак минус на плюс, поэтому
в точке х — 3 у функции минимум.
Тот же результат можно получить, используя вторую произ-
водную. Так как fzz(x)=12x— 30 и fzz(2)<0, a fzz(3)>0, то
в точке х = 2 функция имеет максимум, а в точке х = 3—
минимум.
Вычислив значения функции в точках х = 2 и х = 3, най-
дем экстремумы функции: максимум f(2) = 14 и минимум
/(3) = 13. А
Пример 4. Исследовать на экстремум функцию:
1W М = . 2) f (X) = ^(1-х)(х-2)*.
3) f (х) = ch х + cos х.
423
1) Функция определена и дифференцируема при всех
xeR, кроме точки х — —1. Вычисляем ее производную
( (х + I)2 3 (х + З)2 - (х + 3)3 2 (х + 1) _ (X + 3)2 (х - 3)
1 (х+ I)4 (х-ь I)3
и находим критические точки х — —3 и х — 3. Легко видеть,,
что существует окрестность точки х = —3, в которой f'(x)^O,
т. е. при переходе через точку х — —3 знак производной не
изменяется. Следовательно, эта критическая точка не является
точкой экстремума. В точке х = 3 функция имеет строгий ми-
нимум, так как существуют левая окрестность этой точки,,
в которой /'(xJcO, и правая окрестность этой точки, в которой
/,(х)>0. Вычисляя значение функции при х = 3, находим ми-
нимум:
f(3) = 63/42 = 13,5.
2) Функция определена и непрерывна при всех xeR. Вы*
числяем ее производную
г/ , ' == (1-х)2(х-2)^(х-2)2 = 4 - Зх
1 } 3^/(1 — х)2 (X — 2)4 3 ^(1 - х)2 (х - 2) ’
х Ф 1, х Ф 2.
В точках х=1, х = 2 производная не существует. Таким об*
разом, функция имеет три критические точки: х=1, х = 4/3,
х — 2. При переходе через точку х — 1 производная не меняет
знака, поэтому критическая точка х = 1 не является точкой
экстремума. При переходе, через точку х = 4/3 производная
меняет знак минус на плюс, поэтому в точке х = 4/3 функция
имеет минимум. При переходе через точку х = 2 производная
меняет знак плюс на минус, поэтому х = 2 — точка максимума.
Минимум функции равен f (4/3) = — ^4/2, а максимум равен
f(2) = °.
3) Функция дифференцируема при всех хек. Так как
(x)=shx — sinx и уравнение shx — sinx = 0 имеет только
одно решение, а именно х = 0, то экстремум может быть
только в точке х = 0. Вычисляем вторую производную
f" (х) — ch х — cos х.
Поскольку f/z (0) = 0, находим следующие производные в точке
х — 0:
f" (х) = sh х + sin х, f'" (0) = 0,
fIV (х) = ch хcos х, fIV(0) = 2.
Таким образом, первой не равной нулю оказалась производная
четного порядка. Следовательно, в точке х = 0 функция имеет
экстремум. Так как fIV(0)>0, то при х = 0 у функции мини-
мум, равный f (0) = 2. А
424
Пример 5. Исследовать на экстремум функцию t/ = f(x)t
заданную параметрически уравнениями
/з _ /з _ 2/2
х ~ t2 + 1 ’ У ~ t2 + 1 •
Д Функции x(t) и y(t) дифференцируемы при всех значе-
ниях параметра /, причем производная
(Z2 + 1) З/2 — 2Z4 _ t2 (t2 + 3)
Xt~ (*2+l)2 “ (/2+l)2
при t =# 0 положительна. Поэтому y'x при t ф 0 можно найти
по формуле y'x = y't[x'r Так как
, _ (t2 + 1) (З/2 - 4t) - 2t (t3 - 2t2) _t(t-l)(t2 + t + 4)
yi~ (*2+iL2 — (*2 + D2
Производная y'x равна нулю только при t— 1, поскольку f2+’
4“ t + 4 > 0 при всех t. Следовательно, у данной функции две
критические точки: х=1/2 (при t = 1) и х = 0 (при / = 0).
Если х принадлежит левой окрестности точки х — 0, то пара-
метр t принадлежит левой окрестности точки t = 0, где
у'х > 0. В некоторой правой окрестности точки х = 0 производ-
ная у' < 0. Поэтому в точке х = 0 функция имеет максимум,
равный f(0) = 0. Аналогично убеждаемся в том, что при пере-
ходе через точку х = 1/2, соответствующую значению t — 1,
производная у'х меняет знак минус на плюс. Таким образом,
в точке х=1/2 у функции минимум, равный f (1/2)—#(1) =
= —1/2. А
3. Наибольшее и наименьшее значения функции. Для функ-
ции, непрерывной на отрезке, существуют на этом отрезке
точка, в которой функция принимает наибольшее значение,
и точка, в которой функция принимает наименьшее значение
(теорема Вейерштрасса)-.
Пусть функция f(x) непрерывна на отрезке [а; 6] и имеет
на нем k локальных максимумов в точках хь х2, ..., х*. Тогда
наибольшее значение функции f (х) на отрезке [а; 6] равно
наибольшему из чисел:
/(«)> fM, f(x2), f(Xfe), f(b).
Аналогично, если фун: ия f(x) непрерывна на отрезке
[[а; Ь] и имеет на нем п локальных минимумов в точках
х%, .х', то ее наименьшее значение на этом отрезке
равно наименьшему из чисел:
f(«), f(x')...f(x'n), f(b).
425
I
Пример 6. Найти наибольшее и наименьшее значения
функции
f (х) = 2х3 — Зх2 — 36х — 8
на отрезке [—3; 6].
А Находим экстремумы функции. Вычисляем производную
/'(%) = 6х2 — 6х —36 = 6(х + 2) (х — 3).
Обе критические точки х = — 2 и х = 3 функции f(x) принад-
лежат отрезку [—3; 6]. Находим вторую производную f,,(x) =
= 12х — 6. Так как f" (—2) < О, a f"(3)>0, то в точке х — —2
максимум, а в точке х = 3 минимум. Вычисляем значения
функции в точках экстремума и в концах заданного отрезка:.
f(—3)=19, /(—2) = 36, Д3) = —89, f(6)=100.
Таким образом,
max f (%) = шах {19, 36, 100} = 100,
[-3; 6]
min /(х) = min {19, —89, 100} = —89. а
1-3;6]
Пр и мер 7. Найти наибольшее и наименьшее значения
функции
f(x) = (x —3)2^1
на отрезке [—1; 4].
А Так как f(x)Z^ 0 и f(3) = 0, то наименьшее значение дан-
ной функции равно нулю. Для определения наибольшего зна-
чения найдем локальные максимумы функции на интервале.
(—1; 4). Вычисляем производную
z 2 (х — 3) е~х — (х — 3)2е-* = (х — 3) (5 — х) е~х,
z если х < 0,
/ (х) = ч| 2(х-3)ех + (х — 3)2е* = (х-3)(х- 1)ех,
V если х > 0.
В точке х = 0 производная не существует. Критическими
точками являются точки х = 0, х = 1, х = 3. Все они принад-
лежат отрезку [—1; 4]. При переходе через точку х = 0 произ-
водная меняет знак минус на плюс, т. е. в этой точке минимум
функции. В точке х = 3, как уже было отмечено, функция
принимает наименьшее значение. При переходе через точку
х = 1 производная меняет знак плюс на минус, т. е. в точке
х — 1 у функции максимум. Вычисляем значения функции в
точке максимума и в концах заданного отрезка:
/(—!)== 1бе, f(l) = 4e, f(4) = e4.
Так как е4 > 16е > 4е, то наибольшее значение функции равно
е4. Итак,
min fU) = /(3) = 0, max f (x) = f (4) = e4. a
1-1; 4]
426
Пример 8. Доказать неравенство:
1) ех^1+х.
2) ха 1 + а In х, если х > 0, а > 0.
А 1) Рассмотрим функцию f(x) = ez—1—х. Исследуем ее
на экстремумы. Уравнение f,(x) = e*—1=0 имеет одно ре-
шение х = 0. Так как /"(х) = ех > 0, то в точке х = 0 мини-
мум, который является наименьшим значением функции. Сле-
довательно, для всех х верно неравенство f(x)^f(O), но
f (0) = 0, поэтому ех — 1 — х 0, т. е. ех 1 + х.
2) Рассмотрим функцию f(x) = xa—1—alnx. Исследуем
ее на экстремум. Производная
f' (х) = аха-1 —— = — (ха — 1)
X х
равна нулю только при х = 1. Так как а > 0, то f'(x) < 0 при
л?е(0;1) и fz(x)>0 при хе(1;+оо). Следовательно, в точке
х = 1 функция имеет мини-
мум, который одновременно
является наименьшим зна-
чением функции. Таким об-
разом, при всех х > 0 вер-
но неравенство f(x)^f(l),
но f(l) = 0, поэтому ха—
*—1 — alnx^O, т. е. ха
^2 1 —|— ос In X.
4. Условия выпуклости. Точки перегиба. Функция f(x) на-
зывается выпуклой вниз (или вогнутой вверх) на интервале
{а; Ь), если для любых точек Xi и х2 этого интервала и любых
чисел сс] 0 и а2 0 таких, что oci + oc2=l, верно нера-
венство
f (aiXi + а2х2) С arf (xj + a2f (х2).
(4)
Геометрический смысл выпуклости вниз функции f(x) на
интервале (а; Ь) заключается в том, что точки любой дуги гра-
фика функции расположены не выше хорды, стягивающей эту
дугу (рис. 84). Если функция выпукла вниз на некотором ин-
тервале, то ее график тоже называют выпуклым вниз.
Если при тех же условиях относительно Xi, х2, oti, а2 выпол-
няется неравенство
/(cziXi + а2х2)> a!f(xi) + a2f(x2), (5)
то функция f(x) называется выпуклой вверх (или вогнутой
вниз).
В том случае, когда при х\ ф х2 и а\ > 0, а2 > 0 неравен-
ства (4) или (5) являются строгими, функция f(x) называется
строго выпуклой вниз или соответственно строго выпуклой вверх
на интервале (а; Ь).
Например, функция f(x) = x2 строго выпукла вниз на всей
числовой оси.
427
Всякий интервал, на котором функция (строго) выпукла
вниз, называется интервалом (строгой) выпуклости вниз этой
функции; интервал, на котором функция (строго) выпукла
вверх, — интервалом (строгой) выпуклости вверх этой функции.
Например, для функции f(x) = x3 интервал (—оо;0)—интер-
вал строгой выпуклости вверх, а интервал (0;+°°) — интервал
строгой выпуклости вниз. Интервалы выпуклости вверх и ин-
тервалы выпуклости вниз называют интервалами выпуклости.
Условия выпуклости функции. Для того чтобы
функция f(x), дважды дифференцируемая на интервале (а; 6),.
была выпуклой вниз на этом интервале, необходимо и доста-
точно, чтобы вторая производная f"(x) была неотрицательна
на (a; fe), т. е.
Г(х)^0, хе(й;&). (6}
Условие
(х)>0, хе(д;6), (7)
является достаточным условием строгой выпуклости вниз функ-
ции f(x) на интервале (а; Ь).
Условие (7) не является необходимым. В самом деле, функ-
ция f(x) = x4 строго выпукла вниз на всей числовой прямой,
однако ее вторая производная f"(x)—12x2 равна нулю
в точке х = 0.
Аналогично, для функции f(x), имеющей на интервале
(а; Ь) вторую производную, необходимым и достаточным усло-
вием выпуклости вверх на этом интервале является условие
f"(x)^09 x^(a-,b), (8)
а достаточным условием строгой выпуклости вверх — условие-
f,,(x)<0, х^{а\Ь). (9)
Пусть функция f(x) определена в некоторой окрестности
точки х0, за исключением, быть может, самой точки хо. Если
существуют интервалы
(хо — б; хо) и (хо;хо + б), б > 0,
на одном из которых f(x) строго выпукла вниз, а на другом
строго выпукла вверх, то говорят, что при переходе через
точку Хо функция f(x) меняет направление выпуклости.
Пусть функция f(x) определена в некоторой окрестности
точки хо, непрерывна в точке х0 и имеет в этой точке конечную
или бесконечную производную. Тогда, если функция f(x) при
переходе через точку хо меняет направление выпуклости, то
точка Хо называется точкой перегиба функции f(x). В этом
случае точку (xo;f(xo)) называют точкой перегиба графика
функции Цх).
Если (x0;f(x0)) — точка перегиба графика функции f(x), то
график функции f(x) переходит с одной стороны касательной
428
к нему в этой точке на другую ее сторону. Заметим, что об-
ратное утверждение неверно (см. задачу 20.62).
На рис. 85 и 86 представлены график функции у = х3 и гра-
фик обратной ей функции z/ = ^x, для которых точка (0; 0)
является точкой перегиба. Функция у = ^/х в точке х = 0
имеет бесконечную производную.
Функция (рис. 87)
( 1/х, если х 0>
( 0, если х = 0,
при переходе через точку х = 0 меняет направление выпукло-
сти, в точке х = 0 имеет бесконечную производную, однако
точка х = 0 не является для нее точ-
кой перегиба, так как при х = 0 функ-
ция разрывна. Для функции у = ^\х\
точка х = 0 (рис. 88) не является точ-
кой перегиба, поскольку при переходе че-
рез точку х = 0 направление выпуклости
Ук
0
я
не меняется (это так называемая точка возврата) . При переходе
через точку х = 0 функция
( sinx, если х^О,
t х2> если х < 0»
429
меняет направление выпуклости, но точка х — 0 не является
для нее точкой перегиба (рис. 89), так как в этой точке
у функции нет ни конечной, ни бесконечной производной (это
так называемая угловая точка).
Необходимые условия существования точки
перегиба. Если точка хо является точкой перегиба функции
f (х), то либо f,z(x0) = 0, либо f/z(xo) не существует.
Эти условия не являются достаточными. В самом деле, для
функции f(x) = x4 вторая производная в точке х = 0 равна
нулю, а для функции
х3,
х2,
если
если
х> О,
х < О,
вторая производная в точке х = 0 не существует, но ни для
Дх), ни для g-(x) точка х = 0 не является точкой перегиба.
Точки перегиба функции следует искать среди критических
точек ее первой производной.
Достаточные условия существования точки
перегиба (с использованием второй производной). Пусть
функция Дх) дифференцируема в точке х0 и дважды диффе-
ренцируема в некоторой окрестности точки х0, кроме, быть мо-
жет, самой точки х0. Тогда точка х0 является точкой перегиба
функции Дх), если существует окрестность точки х0, в которой
либо
fzz(x)<0 при х < х0 и Д(х)>0 при х > х0, (10)
либо
Д(х)>0 при X < Хо и fzz(x)<0 при X > х0. (11)
В этом случае принято говорить, что при переходе через
точку Хо вторая производная меняет знак.
Условия существования точки перегиба (с ис-
пользованием производных высших порядков). Пусть функция
Дх) имеет в точке Хо производные до порядка п > 2 включи-
тельно, и пусть
f/(%o) = f,z,(xo)= ... = ^-1)(хо) = О, а Д*)(хо)#=О; (12)
тогда, если п — нечетное число, то х0 — точка перегиба; если
же п— четное число, то х0 не является точкой перегиба.
В частности, если
Г(хо) = О, а fzz,(xo)#=O, (13)
то хо — точка перегиба функции Дх).
Пример 9. Найти интервалы выпуклости и точки перегиба
функции:
1) f(x) = x4 — 6х2 —6х+1.
= 3)fw = -77r-
430
A 1) Так как f'(x) = 12х2—12 = 12(х2 —1), то Г(х)>0
при |х|> 1 и //,(х)<0 при |х| < 1. Следовательно, (—оо;—1)
и (1;+°о) — интервалы выпуклости вниз, а (—1; 1) — интервал
выпуклости вверх. При переходе через точки х = ±1, в кото-
рых вторая производная равна нулю, функция меняет направ-
ление выпуклости. Поэтому х=±1—точки перегиба функции.
В том, что точки х=±1 являются точками перегиба, можно
убедиться и другим способом, используя достаточное условие
(13). Действительно, /у/(±1) = 0, f"'(х) = 24х и fz/,(±l) =/= О,
т. е. условия (13) выполнены. Следовательно, х==±1—точки
перегиба функции.
2) Функция дифференцируема при всех xeR, кроме х— 1,
причем
f" (Х) = 2 *2 + 4х + 1 = 2 - <~2 ~ V3 »~ (~2 + V3 »
' ' ' (х — 1)5 (% _ 1)5
В точках х = — 2±д/3. вторая производная равна нулю, а в
точке х — 1 не существует. На интервалах
(— оо; —2 — УЗ), (—2 — V3; —2 + УЗ),
(-2 + УЗ; 1), (1;+оо)
вторая производная сохраняет знак. Следовательно, каждый из
этих интервалов — интервал выпуклости. На первом и третьем
интервалах /"(xJcO, значит, это интервалы выпуклости вверх;
на втором и четвертом интервалах f" (х) > 0, т. е. это интер-
валы выпуклости вниз. При переходе через точки % = — 2 ± д/3,
х — 1 функция меняет направление выпуклости. Но в точке
х = 1 функция не определена, поэтому х = 1 не является точ-
кой перегиба. Итак, функция имеет две точки перегиба:
х — 2 — д/ 3 и х = — 2 -f- д/3.
3) Функция определена на интервале (0; 4-оо) и дифферен-
цируема в каждой его точке, кроме точки х = 1. Вычислив вто-
рую производную, получим
хе(0;1),
4 х6 ух
= хе(1;+<х>).
4 х6 ух
Вторая производная равна нулю в точке х — 5 и не существует
в точке х= 1. Определяем интервалы, на которых f"(x) сохра-
няет знак:
J"(x)>0 при хе(0; 1),
при хе(1;5),
f" (х) > 0 при х е (5; 4- оо).
431
Следовательно, на интервалах (0; 1) и (5; 4-оо) функция вы-
пукла вниз, а на интервале (1; 5) выпукла вверх. При переходе
через точки х = 1 и х — 5 функция меняет направление выпук-
лости. Но в точке х = 1 у функции нет ни конечной, ни беско-
нечной производной. Поэтому точка х = 1 не является точкой
перегиба. Точка х = 5 является точкой перегиба, так как в ней
функция имеет конечную производную. А
Пример 10. Найти точки перегиба графика функции
у = и угловые коэффициенты касательных к графику
функции в его точках перегиба.
А Вычислим первую и вторую производные функции
' г \ // / \ 'х/ х {'х/х — 2) .у— А
!/W = T₽' » <*> = —55--------------; ’
В точке х — 0 функция непрерывна и имеет бесконечную про-
изводную. Вторая производная не существует при х = 0 и равна
нулю при х = 8. Следовательно, точки перегиба функции могут
быть только в точках х = 0 и х = 8. При переходе через эти
точки у"(х) меняет знак, и, следовательно, у(х) в этих точках
меняет направление выпуклости. Поэтому точки х — 0, х = 8
являются точками перегиба функции, а точки (0; 1) и (8; е2)—
точками перегиба графика функции. Касательная к графику
функции в точке (0; 1) вертикальна, так как z/'(0)=4-oo.
В точке перегиба (8; е2) угловой коэффициент касательной ра-
вен у' (8) = е2/12. А
Пример 11. Определить, является ли точка х = 0 точкой
перегиба функции
= — tgx+ sinx.
А Найдем вид главного члена разложения функции по фор-
муле Маклорена (6) § 18. Так как согласно формулам (12) и
(24) § 18
sinx = x — + + о(*6)> = + + -Yg-^ + oC*:6),
ТО
f (х) = с5х5 + о (х6), С5 =# 0.
Отсюда следует, что
^(O) = f"(O) = fIV(O) = O, а fv(0)#=0.
Таким образом, условия (12) выполнены, причем п = 5— не-
четное число. Следовательно, х = 0 — точка перегиба функ-
ции. А
Пример 12. Найти точки перегиба графика функции у —
х= f(x), заданной параметрически уравнениями
x=l+ctg/, */ = -^77. 0 < 1 < л. (14)
432
ГА Функции %(/) и y(t) при /е(О;л) дважды дифференци-
руемы, причем производная = —1/sin2/ отрицательна. По-
этому уравнениями (14) определяется дважды дифференцируе-
мая функция y — f(x)1 производные которой можно найти по
формулам
Так как
г__ cos t (2 sin21 + 1)
V* sin21
TO
y'x = cos t (2 sin21 + 1).
Вычисляем вторую производную функции y = f(x). Так как
= 3 cos 2/ sin t, то
у" — —- 3 sin31 cos 2/.
Вторая производная ухх равна нулю при t = л/4 и t = Зл/4.
При переходе через эти точки у"х меняет знак. Следовательно,
при этих значениях параметра t график функции у — f(x) имеет
точки перегиба. Значениям параметров t = л/4 и t — Зл/4 со-
ответствуют точки (2; 0) и (0; 0) графика функции. Таким об-
разом, график функции имеет две точки перегиба (0; 0) и
(2;0).А
Пример 13. Доказать неравенство
е(х+у}/2 е + X, 0 G R .
^2 ’
'Л Рассмотрим функцию f(x)=ex. Так как f" (%) — ех > 0,
то f(x) на всей числовой прямой выпукла вниз. По определе-
нию всюду выпуклой вниз функции для любых точек Xi и х2
числовой прямой и любых чисел oci 0, а2 0 таких, что
+ сс2 = 1, верно неравенство
f(oci%i + а2х2)^ aif(xi) + a2f(x2).
Если f(x) = ex, то это неравенство имеет вид
e«i%i+a2x2 cqe*1 -}- (х2£Х2‘
Положив %1 — х, х2 = у, <Х1 = а2 = 1/2, получаем
е(х+у)/2 + бУ .
Так как f"(x) = ex строго больше нуля, то функция f(x) = ex
строго выпукла вниз. Поэтому при х =# у получаем строгое не-
равенство
е(х+г/>/2 <- е* + ,eL д
433
Найти интервалы возрастания и убывания функции
(20.1—20.5):
20.1. 1) f = 4х3 — 21х2+ 18х + 7. 2) f = 8х3 — х4.
3) f = х5 - 5х4 4~ 5х3 — 1. 4) f = (х — 1)3(2х4-3)2.
20.2. 1) f = xe~3x. 2) f = exlx. 3) f = x!e~x2.
4) f = xae~x, x>0, a > 0. 5) f = x2—lOlnx.
6) f = x2lnx. 7) f = x/lnx. 8) f = 3t/(x~3).
9) f = arctg x — In x. 10) f = enx cos rex.
20.4. 1) f = и^х/(х4-50). 2) f = д/8х2 - x4.
3) f = д/2х3 + 9x2. 4) f = x V(x4- I)3.
5) f = x/^F=l. 6) f = (x 4- 1)
7»' = (1+тУ-
20.5. ,) . 2)f=4L£+^.
20.6. Найти интервалы возрастания и убывания для функции
у — f(x), заданной неявно уравнением:
1) х2у2 + У = 1 > У > 0. 2) xV — х — у, х > 0.
20.7. Найти интервалы возрастания и убывания для функ-
ции y = f(x), заданной параметрически уравнениями
е~г е* / \ 1
Л = У = ^~Г' t>l-
20.8. При каких значениях параметра а функция f(x) воз-
растает на всей числовой прямой:
1) f(x) — x3— ах. 2) / (х) = - ~ 1 х3 4~ (а—1)х24-2х.
3) f (х) — ах — sin х. 4) f (х) — ах 4- 3 sin х 4- 4 cos х.
5) f (х) — (8а — 7) х — а sin 6х — sin 5х.
6) /(х) = 4х 4--^-|-—In (х2 — х 4- 1) 4-arctg ?
20.9 . Доказать, что если функция / (х) непрерывна на интер-
вале (a; b) и f,(x)>0 всюду на (а;&), кроме конечного числа
точек, то f(x) строго возрастает на (а; Ь).
20.10 . Доказать, что для строгого возрастания функции f(x)
на некотором интервале необходимо и достаточно, чтобы для
434
любых точек Xi и х2 (xi < х2) этого интервала существовала
точка § е (хг, х2) такая, что f'(i) > 0.
20.11 . Пусть функция f(x) возрастает на интервале (а\Ь).
Следует ли из этого, что производная f'(x) также возрастает на
интервале (а; Ь) ?
20.12 . Функция f(x) называется возрастающей в точке хо,
если существует такое число б > 0, что f (х) < f(x0), если х<=
е(х0— б; хо), и f(x)> f(xo), если х<=(х0; х0 + б).
Доказать, что: 1) из возрастания функции f(x) в каждой
точке некоторого интервала следует возрастание f(x) на этом
интервале; 2) функция
{х + х2 sin (2/х), х #= 0,
0. х —0,
возрастает в точке х = 0, но не является возрастающей ни
в каком интервале, содержащем эту точку.
20.13 . Найти точки максимума и минимума функции:
1) //= х3 — 4х2. 2) z/ = x(x —3)2(х+I)3.
3) у = 2 sin х + cos 2х. 4) у = -3 _ 2л./_ % + 2 .
5) у = (х ~ 5) ех. 6) у = х2еХ1х.
7) У = (2х + 1) иУ(Г=Т2р. 8) у -
20.14 . Найти точку минимума функции
п
f(x)=X (х~ xk)2, xfe <= R, я е N.
20.15 . Найти многочлен наименьшей степени, имеющий
локальный максимум, равный 6, при х = 1 и локальный мини-
мум, равный 2, при х = 3.
( х2 + 1, х 0,
1 2, х = 0.
Найти максимумы и мимимумы функции (20.16—20.25):
20.16 . 1) z/ = x4 —8х2+12. 2) у =
з) //=4~2х3+4х2~б*+3-
4) у = х4 — 4х3 + 6х2 — 4х + 5.’
5) у = (х3 - 10) (х + 5)2. 6) у = (х + 2)2 (х — З)3.
20.17 . 1) У ——• 2) у = ~ 3) у=^~ V2 .
7 х2 —• X ' V X2 + 4 ' U X ~Ь 1
.. (2 — х)3 х3 + 2х2 х4
4) (3 — х)2 • У — (х—1)2- 6) (Х_|_ 1)3 •
20.18 . 1) у = sin х + 4- sin 2х, 2) у = sin3 х + cos3 х.
435
3) ^=2~Тсо1т- 4) у = х4~ sinx. 5) у = х — 2sin2x.
6) у=*х— 2 arctg х. 7) у = (х— 2)созлх—^-sinnx.
8) у — (x2 + 1) arctg x — -у x2 — x.
20.19. 1) y — (x — 1)4'. 2) y = (3 — x2)ex. 3) y = (x2 — 8)e~*.
4) y = x3e~ix. 5) y = x*e~x\ 6) у— {x\)5 e~x.
7) г/ = (х3 + Зх2 + 6х + 6)е-\ 8) у = (x + 2) е{'х.
20.20. у — л]x\nx. 2) у = --*- .
3) ^=1п(Р + 4хЗ + 30)~- 4) у = х2 — 4х — 1 — In (х2 — 4х + 4).
5) у = Incosx — cosx. 6) у = In(х2 + 1) — 2arctgх.
20.21. 1) z/ = x + д/З — х. 2) у = 'х/х3 — 2х2 + х.
3) У — 'у/х2 — х. 4) у — х^х — 1. 5) # = и^х2 — ^х2 — 1.
6) у = xl'y/х2 — 4. 7) у — ^(х — 2)2(х — 4)2.
8) у = ^(1 — х)(х —2)2. 9) у = ^(Зх - 2)2/(х - 1).
1-) У = 1 - и^(х + 1)2/(х + 2)2 .
20.22. \) у = Xх. 2) у=х1/х.
20.23. 1) у = \х — 5|(х — З)3. 2) г/ = тах{7х — 6х2, | х31
3) у = V1 Ч-2(х — 11/(6 +1 Зх - 21). 4) у = Ч/х2|2-х|.
5) z/ = |x- 1 |^х + 2. 6) у — |х2 — 1 |е!*>•
7) у = \х2 — 4|е_|л|. 8) у = е~1 Х~1 У(х 4- 1).
20.24. 1) у = sin (х + 1) — | cosх|, хе (0; л).
2) у — sin|х — 31 + cosх, хе (0; л).
оч .. 1 + 1 COS X I /п \
3) У = — ^—/= .--------• X е (0; л).
2 + cos х + -уЗ sin х
{х, х < 0,
х In х, х>0.
(14-Х, X < 0, ( 1 + х, х < 0^
2) = { (х^ л>0_ 3) г/(х) = | хХ2{пх, х>^
20.26 . Исследовать на экстремум функцию:
1) у = (х+ \)пе~х, neN.
2) y= (14-Х + 4+ ••• +^г)е^’
436
3) y = xk(\—x)n, k,neN.
4) у = aepx + be~px, a, b, p <=R.
20.27 . Исследовать на экстремум в точке х = а функцию
у = (х—а)пф(х), neN;
<р(х) непрерывна в точке х = а, и <р(а) =/= 0.
20.28 . Исследовать на экстремум функцию y = f(x), задан-
ную неявно уравнением:
1) х3 + у3 = Зх2. 2) ху = ху(у — х), |#|<|х|.
3) х4 — г/4 = х2 — 2t/2, i/>|x|.
4) (х2 — у2) (х — у) — 1, у>|х|.
20.29. Исследовать на экстремум функцию y = f(x), задан-
ную параметрически уравнениями:
</ = ^, />0,
2) х = In sin (t/2), у — In sin t. *
20.30. Доказать, что если в точке минимума существует пра-
вая производная, то она неотрицательна, а если существует
левая производная, то она неположительна.
20.31. Пусть функция f(x) определена на интервале (a; b)
и непрерывна в точке Хо се (а; Ь). Доказать, что если f(x) воз-
растает на интервале (а; х0) и убывает на интервале (х0;6), то
Хо является точкой максимума; если же f(x) убывает на интер-
вале (а; Хо) и возрастает на интервале (x0;ft), то хо — точка,
минимума.
20.32. Доказать, что функция
( х2 sin2 (1/х), х 0,
»*Но, .«-о,
в точке х — 0 имеет нестрогий минимум.
20.33. Доказать, что функция
( х2 (2 + cos (1/х)), х о,
/W = lo, х = 0,
имеет строгий минимум в точке х — 0, но ни в каком интервале-
,(—S; 0), 6 > 0, не является убывающей и ни в каком интервале
(0; 6), 6 > 0, не является возрастающей. -
20.34. Пусть
. Г |Х 1(2 +COS(1/х)), х =И= 0,
fW = lo, х = 0,
gW_|с~м''(!+“+). **<>.
I 0, х = 0.
437-
Доказать: . 9
1) f(0) не существует, g(n)(0) = 0, neN.
2) f(x) и g(x) в точке х = 0 имеют строгий минимум.
3) f(x) и g(x) ни в каком интервале (—б;0), 6 > 0, не
являются убывающими и ни в каком интервале (0;б), б > 0,
не являются возрастающими.
20.35. Пусть
( е~1/х\ х 0, ( xe~iIX\ х 0,
/W = to, х = 0, gW=(o, х = 0.
Доказать:
1) /<«>(0) = g(«>(0) = 0.
2) f(x) в точке х — 0 имеет строгий минимум, g(x) в точке
х — О*не имеет экстремума.
20.36. Пусть f(x) — четная, дважды непрерывно дифферен-
цируемая функция, причем /"(0)^=0. Доказать, что точка
х = 0 является точкой экстремума этой функции.
Найти наибольшее и наименьшее значения функции (20.37—
20.40):
20 .37.1) у = х3 — 6х2 + 9, ле|-1;2].
2) у = у х3 — 9х2 + 48х, х е [0; 9].
3) у = 2х3 + Зх2 — 120х + 100, х е (—4; 5].
4) у = х4 —8х2 + 3, хе[—1;2].
5) у = х5 — 5х4 + 5х3 + 1, х <= [—1; 2].
20.38. 1) у=^ + -^, хе(0; 1).
2) у- 1 + х-Й- xgto; И- з) у =
4) П-
20.39. 1) у = х — 2 Vх, хе[0;5].
2) у = х — 21пх, хе [3/2; е]. 3) z/ = xln(x/5), хе[1;5].
4) у = \ х2 + 2х — 3 | + 1,5 Inx, хе [1/2; 2].
5) z/ = (x — 3)el*+1’, хе[—-2; 4]. 6)у = хх, хе(0;1].
20.40. 1) у — 2 sin х + sin 2х, хе[0;Зл/2].
2) у = cos2 х + cos2 (-у + х^ — cos х cos (-у + х), х е R.
3) у = 4х + -у- + sin х, хе [л; 2л].
4) ?/ = 2 arctg х + arcsin t , xeR.
-438
Найти экстремумы функции y = f(x) на интервале (а;Ь),
а также ее наименьшее значение т и наибольшее значение М
на отрезке [а; 6] (20.41—20.43):
20.41. 1) у = (х — 3)2е'Ч а = — 1, 6 = 4.
2) у = (х — 3)3е|х+1>, а — — 2, 6 = 4.
3) у = е^ТП I, а = — 2, 6 = 1.
4) ,y = in(l + A/|%|(x+ 1)2), а = -2, 6 = 1.
5) у = arctg Vl х I (х— 1)2> а== — 1> 6 = 2.
6) у = arcctg Vх21 1—х1> а = — 1, 6 = 2.
( — х2, х «С 0,
20.42. 1) г/ = | 2ех1пх, х > 0, а = — 1, 6 = 2.
( 1 + Зх, х < 0,
V t (х)*2, х>0, а = — 1, 6 = 2.
•3)г/=-у~ + у, а=1, 6 = 3.
20.43. 1) г/ —cos(x+^-signx) + sin(x+-|-),а = —л, 6 = л..
2) у = sin (х — -у) — cos l^x-— sign x), a = — л, b = n.
3) y= sin |^x — y) — cos (X---3-signx), а = — л, 6 = л.
20.44. Найти номер п наибольшего члена последователь-
ности:
11){105» + 3В!-Я’}. 2){^г}. 3>{4^}.
( п2 ) Г п12 1 ( Я10 )
4) I п3 + 200 J • I ~ё^ J • 6) | уд* | •
Найти inf f и sup f (20.45—20.47):
20.45. f = y + x2, xe(0; I]. 2) f = lnx —x, xe(0; 4-00).
3) f== 2tgx — tg2x, xe(—л/2; л/2).
4) f = igx — Зх, хе [—л/4; л/2).
20.46. 1) f = (x2 + 4)e~x, х<=(0, + оо).
2) f = e-*2cosх2, хе= R. 3) f = у е~, хе (0; + оо).
4) / = хх, хе(0; 1/2].
20.47. 1) f = х + (у^2-)2. х е (3/2; 5).
439
2) f = (x+l)(^l)2, xe(3/2;6). 3) f=^+J *-21, xeR.
4) f = з x(=(a; +oo), aeR.
20.48. Найти интервалы выпуклости функции:
1) f — xa, а>1, х>0. 2) f = xa, 0<а<1, х>0.
3) f = ex. 4) / = 1пх. 5) f = х In х. 6) f = arctg x.
Найти интервалы выпуклости и точки перегиба функции
(20.49—20.50):
20.49. l) f = 2x4 —Зх2 + х—1. 2) f = х5 —10х2 + Зх.
3)f—5)/ = У^+3. .
7> ! = №~ 12*-
20.50. 1) f = cosx. 2) f = x+sinx. 3) f — e~x\
4) f = el/x. 5) / = -^-1п-уу. 6) f = xsinlnx.
7) f== arctg (1/х). 8) / = garctgx>
Найти точки перегиба функции (20.51—20.53):
20.51. 1) 7 = х4 —6х2 + 5х. 2) / = х4—12х3 + 48х2.
3) /== 2х4 + 2Х3 + Зх2 + Зх + 1- 4)/ = (х2—I)3.
20.52. 1) / = 4х2 + |. 2) f = —3) /=^Г2-^=4.
4) f = ^(l-x)(x-2)2. 5) / =
20.53. 1) f = (х2 + 1)е*. 2) f = x3e~ix. 3) / = х21пх»
4) / = 5) f = ecosx.
ух
Найти точки перегиба графика функции (20.54—20.56):
20.54. 1) f = 36x(x — I)3. 2) f = х + 36х2-2х3- х\
3) f = \+x2-X.. 4) f = -g--x4 + 8x3-32x2.
s 2х2 — х — 4 £ х4
°) / — х2 —4х + 4 * “ (х+ I)3 ’
20.55. 1) / = ^1 -х3. 2) / = ^х-^хЧЛ.
3) /==5 + ^(Т^5р. 4)f=z^/-l^l.
20.56. 1) f = e2x~x\ 2) f = xe-W2>2.
3) f = 2x2 + lnx. 4) f = e-2x sin2x.
-440
20.57. Найти точки перегиба функции fi
1) f = —е-^202, о > 0.
2) f= а=£0, ЬУ=0.
20.58. Исследовать на точки перегиба многочлены;
1) Ps (х) = axs + bx2 + ex + d, а ф 0.
2) P4 (x) = ax4 + 6x3 + ex2 + dx + e, a 0.
20.59. При каких значениях параметра а функция f = ех 4-
[4- ах3 имеет точки, перегиба?
20.60. Доказать, что график функции
У W “ х2+ 1
имеет три точки перегиба, лежащие на одной прямой.
20.61. Доказать, что точки перегиба графика функции
y(x) = xsinx лежат на кривой
у2 (4 4- х2) — 4х2.
20.62. Пусть
( х3 (2 4- cos (1/х2)), х ф 0,
/W = l О, Л = о.
Доказать, что:
1) График функции f(x) в точке (0; 0) имеет касательную.
2) График функции f(x) переходит с одной стороны каса-
тельной к нему в точке (0; 0) на другую ее сторону.
3) Точка (0; 0) не является точкой перегиба графика функ-
ции f(x).
20.63. 1) Может ли точка перегиба функции быть ее точкой
экстремума?
2) Может ли всюду выпуклая вниз (вверх) функция иметь
более одного экстремума?
20.64. Доказать, что у любой дважды дифференцируемой
функции:
1) Между двумя точками экстремума лежит хотя бы одна
точка перегиба.
2) Между точками перегиба функции может и не быть точек
экстремума.
20.65. Доказать, что:
1) Каждый многочлен нечетной степени, отличный от ли-
нейного, имеет хотя бы одну точку перегиба.
2) Каждый четный многочлен с положительными коэффи-
циентами не имеет точек перегиба.
20.66. Пусть f(x)—непрерывно дифференцируемая на интер-
вале (а; Ь) функция, и пусть для любых точек Xi, х? этого
441
интервала существует единственная точка с такая, что
/ (*2) — f (*1)________________
х2 — ХГ ' Л ’
Доказать, что f (х) не имеет точек перегиба.
20.67. Найти точки перегиба графика функции у — f(x), за-
данной параметрически уравнениями:
1) x = tel, y — te-t, t > 0.
/2 /3
2) *-т=Т' s-TZT- <>2-
V = у-**”*1 . 0<(<1.
. s _ /2 — 2/ — 5 _ f2 — 4t + 5 ’ .
x~ Z2+ Ю/+ 25 ’ /2 + 4/— 5’ />1-
20.68. Доказать, что если функции f(x) и g(x) удовлетво-
ряют условиям (х0) — gw (х0) (k — 0, 1, ..., п — 1) и
/(л)(х) > g<">(x), X > Хо, то f(x) > g(x) при X > х0.
Доказать неравенства (20.69—20.71):
20 .69.1) ех Rs ex, zeR.
2) х — +- < In (1 + х) < х, х > 0.
3) 1п(1 + х)>-^-г, х>0.
4) 1 — 2 In xs£C -Г, х > 0. 5) > 1 + In (1 + х).
6) ---—j=-, х > 0, х =/= 1.
х — 1 ух
20.70. 1) cos х 2^1—^-,x<=R. 2) chх1 +, zeR.
3) tgx>x + +-, 0 <х 4) arctg х^х, х^0.
о Л
г-\ ^2
5) sinx^ — х, — .
7 л 2
уЗ уЗ у5
6) X--g-< sin X < X--§-+-(20 •
7) sin х + tg х > 2х, 0 < х < л/2.
8) х — +- < arctgх < х—0<х^1.
( sin х \3^ гч я
9) (—— J >cosx, 0<|х|<^-.
20. 71 I) д/х— ^х — у, х^у^О.
2) х>0, y^Q, neN.
442
3) (ха + //а)1/а > (х& + х > О, у > О, О < а < р.
х — и х . х ~ у . . п
4)----------------— < In — <----—, Х> у > О.
' х у У
5)
X In X + у In у . х у
Т+~У > 1п—2~~
х > О,
У > о.
20.72. Доказать неравенство
ха — 1 а(х — 1), х > О, 0 < а < 1.
20.73. Доказать неравенство Юнга: если а > О, b > О,.
1 1 । 1 .
р > 1 и------— = 1, то
' р q
Р q
причем знак равенства имеет место только при а = Ь.
20.74. Доказать неравенство Гёльдера: если х/ 0, yi О
(/ = 1, 2, ..., и), р > 1 и 1 + -1 = 1,то
п / п \ 1/р / п \ 1/<?
(,?л) •
20.7,5 . Доказать неравенство Минковского: если
yt > 0 (f = 1, 2, ..., п), р > 1, то
/ П \1/р / п \VP / п Х1/Р
(,?, (*<+<) Ч?л) +С?л) '
§ 21. Построение графиков
При построении графика функции можно придерживаться,
например, следующей схемы:
1. Найти область определения функции. Проверить, является
ли функция четной, нечетной, периодической.
Найти точки пересечения графика с осями координат, про-
межутки, где значения функции положительны, отрицательны.
Найти точки разрыва функции.
2. Найти асимптоты графика (§ 11).
Найти односторонние пределы функции в граничных точках
области определения и в точках разрыва.
3. Сделать набросок графика, отразив на нем полученные
результаты.
4. Вычислить первую производную функции, найти экстре-
мумы и промежутки ее возрастания и убывания.
5. Вычислить вторую производную, найти точки перегиба
графика, промежутки выпуклости вверх или вниз.
6. Нарисовать график функции.
При решении конкретной задачи отдельные этапы этой схе-
мы могут быть расширены, другие же могут оказаться излиш-
ними или невыполнимыми. Например, если точки графика мо-
443
нотонно приближаются к асимптоте, то следует попытаться
выяснить, с какой стороны от этой асимптоты они расположены.
Это можно сделать методом выделения главной части или по
известному направлению выпуклости кривой. Метод выделения
главной части можно использовать и для уточнения рисунка
вблизи отдельных точек или при х->+°°, —°°- Часто бы-
вает нетрудно найти и нарисовать касательную к графику
в точках перегиба, в угловых точках и т. д.
Пример 1. Построить график функции
у = у (х3 + Зх2 — 9х — 3).
Л Данная функция определена и бесконечно дифференци-
руема на R, асимптот не имеет,
lim /7(х) = —оо, lim z/(x) = + oo.
Х->-оо Х->4-оо
График пересекает ось ординат в точке .(0; —3/4).
Найдем экстремумы функции. Вычисляем производную
/ = |(*2 + 2х-3)
и находим, что / > 0 при х<—3, у' < 0 при —3<х<1,
у' > 0 при х> 1. Значит, х = —3 — точка максимума, у(—3)==
= 6, а х = 1 —точка минимума, у (1) = —2.
Отметим найденные три точки графика и сделаем его на-
бросок (рис. 90, а)).
Вычислив вторую производную
найдем, что функция выпукла вверх при х < —1 (с/" < 0)
и выпукла вниз при х>—1 (^,/>0). В точке перегиба х —
=—1 вычисляем у(—1) = 2, у'(—1) = —3. Для более точного
изображения графика находим еще несколько значений функ-
444
дии (табл. 1). Наносим полученные точки на чертеж, проводим
касательную к графику в точке (—1;2) с угловым коэффициен-
том, равным —3, и рисуем график (рис. 90,6)). Из табл. 1 и гра-
фика видно, что корни данного многочлена нецелые, поэтому
Таблица 1
X — 5 — 4 — 3 — 2 — 1 0 1 2 3
уМ -2 17/4 6 19/4 2 -3/4 — 2 1/4 6
начинать исследование функции с нахождения корней было бы
нецелесообразно. А
Пример 2. Построить график функции
„ _ X3
4 (2 — х)2 ’
Функция определена при всех xeR, кроме х — 2. Гра-
фик ее пересекает оси координат в одной точке (0; 0). Функ-
Рис. 91.
Ция положительна при х > 0, х =# 2, и отрицательна при х<0.
Функция разрывна в точке х = 2, и поскольку lim у(х) = + оо,
х-> 2
прямая х — 2 — вертикальная асимптота графика. Из того.
445
что
нт-Ц^-—-р |im (yW —тл) = lim 4^2F’==1>
X-»oo л JC->oo v Z x-»oo \л
следует, что при x->oo график имеет наклонную асимптоту
y = T'v+ L
Отметив еще, что -^-х3 при х—>0, делаем предварительный
рисунок графика (рис. 91,а)).
Вычисляем первую производную
у' W
х2 (х — 6)
— 4 (х — 2)3
и находим единственную точку экстремума х = 6, которая яв-
ляется точкой минимума, z/(6) = 27/8. На интервалах (—оо;2)
и (6; +оо) функция возрастает, на интервале (2; 6). убывает.
В точке х — 0 касательная к графику горизонтальна, как
и было указано на рис. 91,а). Вычисляем вторую производную
Отсюда следует, что имеется только одна точка перегиба функ-
ции х = 0, причем у(0) = 0 и у'(0) = 0. При х<0 функция
выпукла вверх, поэтому ее график при х->—оо приближается
к асимптоте снизу. При 0 < х < 2 и при х > 2 функция вы-
пукла вниз. Отсюда следует, что при х->+°° график прибли-
жается к асимптоте сверху. Вычислив еще несколько точек
графика, на основе проведенного исследования делаем более
точный рисунок (рис. 91,6)). А
Пример 3. Построить график функции
= I)2.
А Функция определена и непрерывна на R. График пересе-
кает оси координат в точках (0; 0) и (—1; 0). Функция поло-
жительна при х>0 и отрицательна при х < 0, х^=—1. Так
как у(—1) = 0, то х =—1—точка максимума функции. Оче-
видно,
Иш ^/(х) = + ос, z/(x)~x5/3 при +
X —4- со
lim у(х) = — °°, г/(х)~х5/3 при х->—оо.
Х-> - оо
Легко также видеть, что
у(х)~х при х—>0,
# (х) ~ — (х + 1)2/3 при х—> — 1.
Делаем набросок графика: при «больших» значениях |х| он
«похож» на график степенной функции у = хБ/3, в окрестности
446
точки х = —1 —на график функции у — —(х + 1)2/3, а в окре-
стности точки х = 0 сближается с прямой у — х (рис. 92, а)).
Для уточнения рисунка найдем и исследуем производные
/ (*)
У"№
5 (х + 3/5)
3 (х + 1)1/3 ’
10 (х + 6/5)
“ 9 (х + 1)4/3 ’
(I)
(2)
Из (1) следует, что функция возрастает на интервалах
.(—оо;—1), (—3/5; +оо) и убывает на интервале (^-1;—3/5),
В точке х = —1 функция имеет максимум (//(—1) — 0), что
было отмечено выше, а в точке х = —3/5 — минимум, у(—3/5) =
= —-^-^20 — 0,3. В точке х — 0 график касается прямой
у — х, а в точке х = —1 касательная к графику вертикальна,
поскольку
lim //'(*) = + °°, Пш у'(х) = — сю.
Из (2) следует, что на интервале (—оо;—6/5) функция вы-
пукла вверх, а на интервалах (—6/5;—1) и (—1;+°°) вы-
пукла вниз. Точка х — —— точка перегиба функции,
Используя эти результаты и вычислив еще несколько точек
графика, делаем более точный рисунок (рис. 92,6)). А
Пример 4. Построить график функции
, х / х3 — 2х2
Преобразуем формулу к виду
447
Данная функция определена при х 2 и при х > 3, положи-
тельна при х #= О и х =# 2, #(0) = у (2) — 0. Так как
lim у (х) = +
х-»3+0
то х = 3 — вертикальная асимптота. При х->оо имеем
= |х|(1 - 4 + о(1/х)) (1 +£- + <> (1/х))-
= |х|(1+^ + о(1/х>);
отсюда при х—>+°° получаем
у(х) = х + ± + о (1),
а при х->—оо
У(х) = — Х — -^-Н-О (1).
„ , 1 I 1
Значит, у = х + уасимптота прих~>+оо, az/= —х—у —
асимптота при х->—оо. _____
Отметим еще, что у(х) ~ 2 д/2 ~~ * при х->2 — 0 и у (х)
~ д/2/3|х| при х->0 (д/2/3 0,8).
Первый эскиз графика дан на рис. 93,а).
Данная функция на своей области определения бесконечно
дифференцируема всюду, кроме х = 0 и х = 2. Вычисляем про-
изводные
..//.А— . Л--2 2х2- 11x4-12
У W — Д/ х _ з 2 (X — 2) (х — 3)
sign х,
(3)
„ / х /х —2 Их —24 .
У (х)—Д/ТЗТз 4 (х _ 2)2 (х - З)2 slgnx-
(4)
448
Из (3) находим, что при х = 3/2 функция имеет максимум,
.равный у (3/2) = д/3/2 0,9, а при х = 4 — минимум, у (4)—
= 5,7. При х->2— 0 касательная к графику стано-
вится вертцкальной, так как
-lim у'(х) = + °о.
х->2-0
Отметим еще, что
* lim г/'(х) =—д/2/3, lim у' (х) — V2/3 «= 0,8.
х х->-0 %->+0
Из (4) следует, что при х > 3 и при х < 0 функция выпукла
вниз, в частности, это означает, что график приближается
к асимптоте сверху- и при х-^Ц-оо и при х->—оо, При 0 <С
<х<2 функция выпукла вверх. График функции изображен
на рис. 93, б). А
Пример 5. Построить график функции
у(х) = ^-^-е-5^х\
А Функция определена при всех хе IR, х У= 0. График ее
пересекает ось абсцисс в точках (2; 0) , (—2; 0). Функция поло-
жительна на интервалах (—2;0), (2; + °°) и отрицательна на
интервалах (—сю;—2), (0;2).
В точке х = 0 функция разрывна, и
lim ^/(х) = + оо, lim z/(x) = — 0.
х->-0 х~>4-0
Отсюда следует, что х = 0 — вертикальная асимптота графика
при х->—0; при этом у(х)-> Н-оо.
Применяя формулу Тейлора для экспоненты, находим, что
5 47 I (1 \
= Х—-X------rz--Fol — I, X —ОО ,
3 18% 1 к х)
Отсюда следует, что график имеет; наклонную асимптоту
5
у — х— у и приближается к ней снизу при х->4~оо, а при
—оо — сверху. Предварительный эскиз графика показан на
рис., 94, а).
Вычисляем производные
Г <б>
Из (5) находим, что на интервалах (—оо;0) и (1;+оо) дан-
ная функция возрастает, а на интервале (0; 1) убывает. При
х =1 функция имеет минимум, г/(1) = — Зе~5/3 —0,6. Нахо-
дим еще, что
lim у' (х) — — lim -Д-в’5/3х = 0,
449
15 Л. Д. Кудрявцев и др.
т. е. при х->-'+0 касательная к графику становится горизон-
тальной.
Из (6) находим точки перегиба функции
1n 12-V97 nR „ .„12 + V97 л с
Xi — 10 0,5, Хо —— 10 ' а'7 ^>0
1 47< z 47
и вычисляем
r/(xi) « 0,2, у(х2) « 2,8.
На интервалах (—оо;0) и (хв х2) функция выпукла вниз, а на
Вычислив, как и обычно, еще несколько точек графика, ри-
суем его (рис. 94,6)). А
• При построении кривой, заданной параметрически, полезно
предварительно построить графики функций x(t) и y(t). Удобно
бывает разбить ось t на интервалы, на каждом из которых обе
функции x(t) и y(t) монотонны. На каждом таком интервале
эта пара функций определяет функцию у(х) или х(у), и здесь
можно использовать все ранее указанные приемы исследования
и построения графиков.
Пример 6. Построить кривую
t2 t3
х (0 = 4 (1 _ t) ’ У (0 = 8 (/ - 1У •
« А Строим графики функций x(f) и y(t), (рис. 95,а), 6)).
Укажем некоторые результаты исследования этих функций:
х = — (t + 1)/4 и t — 1 — асимптоты графика х(/), /=1 —
асимптота графика, у (t),
г _ / (2 — 0 , _ t2 (2/ - 3)
xt — 4 (i _ t)2 9 8 (/ - I)2 ’
f==0 —точка минимума функции x(/J, x(OJ — 0,
/==2—точка максимума функции x(/), x(2) — — 1,
t «= 3/2 — точка минимума функции у (/)> у (3/2) = 27/32.
450
Отметим дополнительно, что:
а) — -^-(£+1)> У~ (^2 +1 + 1) при /->—оо и при
f-^-4-оо; отсюда следует, что у ~ -g- (16х2 4~ 4x4- 1) при /->
—оо и при /->4-о°.
б) x~t2/4, у~— /3/8 при /->0, откуда следует, что х~
у213 при t-+0.
в) х ~ . t/~ 8(f_уу при г->1, откуда вытекает, что
у ~ —х/2 при 1.
Рассмотрим пять интервалов: (—оо;0), (0; 1), (1; 3/2)’,
(3/2; 2), (2;+оо). На первом интервале значения х и у убы-
вают от -}-оо до 0. Из а)
следует, что
асимптоту при Нахо-
z/~-L(16x24-4x+1)
При X4-00
(это здесь соответствует то-
му, что /->—оо), а из б)
следует, что
х ~ у2/3, или у ~ х3/2
при х->4“0
['(это соответствует тому, что
/->—0). По этим данным
и делаем набросок первой
части кривой (рис. 96).
На втором интервале
значения х возрастают от О
до 4-°°, а значения у убы-
вают от 0 до —оо. При этом
из б) и в) следует, что
х ~ у2/3, а у ~ —х312
при х->4~0,
й
у ~ —х/2 при х->4-00
(здесь это соответствует то-
му, что /-> 1 — 0). Выяс-
ним, имеет ли эта часть (го-
ворят также — ветвь) кривой
дим, что
]im
Л™ о* (О 2’
16*
461
Следовательно, прямая
’ X _|_±
Z о
— наклонная асимптота кривой. В соответствии с этими резуль-
татами изображена вторая часть кривой.
На интервале (1; 3/2) значения х возрастают от'—оо до
х(3/2) =—9/8, а значения у убывают от 4-°° до 27/32. Из в)
следует, что у ~ —х/2 при
—оо (это соответствует
тому, что Z->l+0)« Как
и в предыдущем случае,
устанавливаем, что
- У=--2-х+т
— асимптота этой части кри-
вой при х—ъ—оо (рис. 96).
На интервале (3/2; 2) зна-
чения х возрастают от—9/8
до —1, а значения у воз-
. растают от 27/32 до у (2) = 1.
На интервале (2; -j-oo) значения х убывают от —1 до —оо,
а значения у возрастают от 1 до +°°, причем согласно а)
у ~ -i-(16%2 + 4х + 1) при -ОО.
На рис. 96 указано, каким значениям / соответствует та или
иная часть кривой.
На каждом из рассмотренных интервалов функции x(t)
и y(t) определяют функцию у(х) (и функцию х(у)). Для уточ-
нения рисунка кривой обратимся к производным этой функции.
Находим
„ _ 4 (/ — 1)3 (/ — 3)
Ухх t (t — 2)3
при t^2. Рассматривая эти производные на вве-
денных интервалах, устанавливаем, что I часть кривой является
графиком возрастающей, выпуклой вниз функции (у'х > О,
у"к > 0), II часть — график убывающей, выпуклой вверх функ-
ции (у'х < О, у"х < 0), III часть — график убывающей, выпук-
лой вниз функции (*4 < 0, у"х > 0), IV часть—график воз-
растающей, выпуклой вниз функции (у'х > 0, z/''x > 0),
V часть — график-убывающей функции (у'х < 0). В последнем
случае кривая имеет точку перегиба при t = 3, х = х(3) =
= —9/8, .у — у(3) — 27/16. Кривая выпукла вверх при
^(—9/8;~1) ц выпукла ,>вниз при хе(—оо;—9/8),.
452
е - q
Отметим еще, что lim z/' = 0 и для первой и для второй
х -> 4*0
частей кривой (соответственно t-+—0, Z->+0)» кроме того,
и' I = (/ L = 0, т. е. касательные к кривой в начале ко-
1х=-9/8 4=3/2 * г
Ординат и в точке (—9/8; 27/32) горизонтальны. В точке (—1; 1)
касательная к кривой вертикальна,
так как lim у'х = lim у' = оо.
х->-1 /->2 .
С учетом этих новых сведений
делаем более точный рисунок кри-
вой (рис. 97).
Пример 7. Построить график
уравнения
х3 + у3 = Зху (декартов лист).
(7)
'Л В примере 5 § 11 (рис. 73—75)
уже было проведено предваритель- • Рис, 97.
ное исследование этой кривой, яв-
ляющейся в полярных координатах (х — г cos ф, у = г sin ф)
графиком функции
г 3 sin Ф cos Ф , ,
cos3 ф + sin3 ф ' i
Дополним это исследование, определив экстремумы и направ-
ления выпуклости и дав тем самым обоснование рис. 75..
Если cos ф = 0, то из (8) следует, что и г = 0, т. е. получаем
точку х = у = 0. При cos ф =/= 0, полагая t — 1§ф, придем к па-
раметрическому заданию кривой
• 3/ ~
р + 1' у
з/2
/3 +1 •
' Из (9) и из того, что
3(1-2Р)
t (<3 + 1)2
(9)
(Ю)
следует, что функция x(t) строго возрастает на (—оо;—1) от
0 до +°° и на (—1; 1/5/2) от — оо до ^4 и строго убывает
на (1/^2; + оо) от 4 до 0 (рис. 98). На каждом из этих
Интервалов функция x(t) имеет обратную, и, следовательно,
функции x(t) и y(t) определяют функцию у(х) при х^(0; -|-оо)
(I часть кривой, рис. 99), при х е(—• оо; 4) (II часть кривой)
и при х е (0; $4) (III часть). Находим
и
, _ 3/ (2 — Р)
“ (t3 + I)2
, /(2-/3)
1 - 2f3 ’
(ID
4&3
а также
„ _ 2 (! + <»)*
yxx 3(1 —2i3)3 ’
(12)
Из (И) и (12) следует, что ух<0 при —оо;—1), т. е.
у(х) убывает при возрастании х от 0 до +°° (I часть кривой),
а так как у"х > 0, то кривая выпукла вниз и, следовательно,
подходит к асимптоте сверху. При /е(—1; 1/^2) функция
Рис. 99.
у\х) имеет минимум при_ t — 0, т. е. х = 0; при возрастании х
от —оо до * 1<=]/^2 = '^4 значения у(х) сначала убывают от
И-00 Д° 0 (при х = 0), а затем возрастают от 0 до у |<=1/^2 =
= -^2. При этом у"х> 0, кривая выпукла вниз и при х->—оо
подходит к асимптоте сверху. Поскольку lim у' = +• оо и
1
«-♦-?=—о
^2 _
lira у'х =—оо, касательная к кривой в точке х = ^4,
-^2 _ _
у — 'х/ 2 (соответствует t = l/rf2) вертикальна.
На третьем интервале /е (1/^2; 4-оо) функция у(х) имеет
максимум при t = 2, а х \t^2 — ^/2. Этот максимум равен
У 1/=-<2= ^4.Поскольку Ухх<®, кривая выпукла вверх. Если
>х->+0, что соответствует тому, что /т*4-оо, то у'х-*--\-оо,
т. е. в точку (0; 0) кривая «входит» с вертикальной каса-
тельной.
Таким образом, получено полное обоснование рис. 99 и най-
дены две дополнительные точки 4; 2) и 2; д/ 4) с вер-
тикальной и горизонтальной касательными. А
21.1. Привести пример такой дифференцируемой функции
У = х <=Х01 -£оо), что:
464
1) Ее график имеет асимптоту при x-s-'Tp00- но Пт f'(x)
г Х->4-оо
не существует.
2) Ее график не имеет асимптоты при х->4-оо, но
lim f' (х) существует.
«->+<»
21.2. График функции t/ = f(x) имеет наклонную асимптоту
при х->+оо. Доказать, что если f"(x)>0 при х > х0, то гра-
фик приближается к этой асимптоте сверху, а если f"(x)<0,
то график приближается к асимптоте снизу.
Построить график функции (21.3—21.20):
21.3. 1) у = х3-Зх24~4. 2) у = -х34-4х-3.
3) # = (х-1)2(х4-2). 4) у = ^--Зх + 4.
5) у = х(х — I)3. 6) у = (х + 2)2(х-1)2.
7) у = (х - I)3 (х 4- I)2. 8) у = 32х2(х2 - I)3.
21 4 1) U —' -к2 + * ~ 1 2) и — + х — 2х2 _ 20х2
21Л* ЧУ ж2 —2x4-1’ (х — 2)2 * У — (х_ 1)S
. .. (х—I)2 х3 х3 —2х2 —х + 2
4) у = 4—пу. 5) у — ——г- 6) у -----------1— .
’ (х + I)3 ’ X— 1 X
71 „ — _L+_£L_ R1 5х2 + 42х + 77
У~ 1 + (х — 2)2 • >У х2 +7х+14 •
21.5.1)9-44- 2)9 —
4) = 5) у = х + ^_6) г/ = (х4-1)(^)2.
\Л 1) л л \Л — л/
21.6.1)1/ = ^^-. 2) У~~г~у~тт2' 3) y==3x4----V.
4)*=-(т±т)‘- =
7) 8)9 = -^.
21.7. 1) у = х4- д/х2 — 1. 2) г/ = х—д/х2 — 2х.
3) y^^ix + W+^ix^2- 4) z/ = ^(T+2)'2-V(^:r2)'2.
5) у == д/^Т“1 - 2 V7+T. 6) у = 4 V(2x4- 1)34- 4 д/Т.
21.8. 1) # = д/2х34~9х2. 2) г/==д/х2 —х3. 3) ^ = д/х3 —Зх.
4) у = х2д/х+Л. 5) у = х(х4- 1)3/2. 6) у = д/х4-4х3.
2,e-1> 2) 9= v?SW 3) s”vfe-
4)S=vszei. 6)!,=^t. в) 9=^4-.
455
Зх — 2 ox / (х + 6)2 п, .. /(х—1)2
7)!'“V3^T- «’“V-vrr- 9> *=4 л/
,лч / Зх2 — 4 . 1Ч /х2 2~
Ю)г/ = д/——. П) y=VV-^7-
12) г/ = 1д/-^-. 13) у = -Д=-- —.
3 V X —2 Vx^+ 1 2
21.10. 1) y — 'x/i—х3. 2) у = ^/х2(“&— х).
3) У = '\/х{х — I)2; 4) у — 'у/х3 — 4х.
5) у — х'\/(х — 5)2. 6) у =-( .'+ 1)3V(X — I)2.
7). у = (1 4- х) х2'3. 8) у = х3 (х —1 )2/3.
9) у = (х2 — 4)2/3. 10) у = (х2 + 8х + 12)2/3.
П) у = -\/х(3 — х)2 — х. 12) i/ = ^x2—\/х2 — 4.
D У=^- 2) у = -^Тт • 3)
7) „ Я) ^+1H
7) У X + 2 • °) У х2
21.12. 1) у = | х |V1 — х2. _ 2) у = х Vl х2 — 11.
3) у = 4 VHz.U. 4) у = VIЗх2-х3!.
5) у = (х + 1) Vl^H- 6) у = ’
7) у = (х2 - 1) V^M- 8) У =
9) у = | х L.V 1 + Зх. 10). у = V^2| 2 —х|.
21.13. 1) у = ех — х. 2) у = хе~2х. 3) у = х2е~х.
4) у = х3е~х. 5) у = (х2 — 2)е~2х.
6) у = (1 —- х) £3%+1. 7) у^=е1~х\
8) yz=e4x~x\ 9) у = хе~хЧ2.
Ю) у==(х2 + 2)е-Л 11) У = -^.
21.14 . 1)- у = еО-яМНх). 2) у==х2е'/х.
3) у = (х — 2)e~i,x. 4) у= - ~ 3 е'/х. 5) у = хе1^х2.
21.15 . 1) г/ = 1пх-х+1. 2) !/-= — . 3) у=-^.
X у X
456
. 4) # = x2lnx. 5) y = xln2x. 6) y — ^^-
7)!' = TF- 8) «“'"ItTtI + tTT- 9)9=^-2|„i.
21.16 . 1) у = cos x + у sin 2x. 2) у = sin x + sin 2x.
j
3) у = sin x — sin2x. 4) у — cosx — cos2x.
б) у = cos 3x + 3 cos x.
21.17. 1) у = sin x sin 3x. 2) y — cosxcos 2x.
- 3) y — sin x + у sin 2x + у sin 3x.
I '21-18- 9/-”4./— 3)<,-2x-tgx.
21.19. 1) y = -^—arctgx. 2) у—-------—.
3) i/ = xarctgx. 4) у = -у + 2 arcctg x. ”
5) z/ = -|-x —arccos^-. 6) у = arcsin t .
1 — x2 ox x 2x
7) у = arccos . 8) у = у — arccos - + .
21.20. 1) y = ecosx. 2) у — e~ arct& x. 3) y = sinx — In sinx.
4)y = x*. 5) y = (l+x)'lx. 6) // = (1+4)*.
21.21. Построить графики функций без исследования выпук-
лости:
1) у = хх/х. 2) 1/=~х (1 +-у) - *>0. 3) у = cos3х + sin3х.
4) у — sin 5х — 5 sin х. 5) у = -ySin ,'v—.
6) у = COS X + 4 COS 2х -ф 4 cos Зх. 7) z/ = 21nx — 5 arctg х.
8) У = е^1-хХ 9) у =
21.22. Построить графики функций y = f(x), заданных па-
раметрически уравнениями:
1)х = /3 + 3/+1, y = t3 — 3/+L-
2) х = /3 — Зл, y = t3 — 6arctg/.
_ t3 _ /з — 2i2
О} X— J +t2 , у — 1 _|_/2 -
4) x = tn sin (7/2), у = In sin /.
457
Б) х = t — sin t, tz = 1 — cos t (циклоида).
6) x = cos t + In tg (t/2), у — sin t (трактриса).
Построить кривые (21.23—21.25):
21.23. 1) x = t3 + 2t2 + t, у = - 2 + 3/ -t3.
2) x = (t — l)2(t — 2), /z = (t-l)2(t-3).
3) x- 1 .. t2 t2— 1
x t (t + 1) ’ y t • x = t _ 1 > У t *
5) _ (t+l)a x t t+1 y ~ t + ъ ’
7)x = ^±L. 21.24. 1M_£±«+1, s = о t3-54 ' “ 2t *
2) t* t* 1! i - 3)x- <2 u
л 1 - 2f ’ У 1 — 2t ' °7 л i + /з ’ y i + p •
4) X = /3_3/, MW Б) * t _ t2 » У “ t _ р •
6) 1 1 7) x — 1 и — -
Л /з _ /2 > y t2-t • x t — t5’ y 1 - z4 •
8) x = V2-pi^-, </ = V24tF-
21.25. l)x = e< — t, y = e2t — 2t. 2) х = 1е*, y — te~{.
3) x = (Z3 —2Z2 + 3t — 4)ef, // = (z3-2t2 + 4t-4)et.
4)x = 4> У = (1-1)2е\ 5)% = -^-, У=^у.
6) x = 2/ + ln|/-l|, iz = t + ln|t-l|.
7)x«=/lnt, y = ^~.
8) x = 2t2, у = ^--31п|—]-|.
sin / + cos / _ cos 2/
j X = &jn / > У sin t
1 A\ л» 4- OJt 2 COS 2/ 1
10)x = ctg2t, y = - .2-os/ .
11) x = 2 cos t — cos 2/, у = 2 sin t — sin 2t.
12) x = 2cos2t, y — 2 cos 3/.
13) x — sin 21, у = sin 3/.
14) x== cos Z +1 sin t, y= sint — /cost, Z^O
15) x = e* cost, // = ezsint.
458
Построить кривую (21.26—21.27):
21.26. 1) х3 — у»=1. 2) х4 + / = 1.
3) у2(1— х) = х2(1+х). 4) 3#2х = х3 — 2.
5) г/2 = 2х3 —х4. 6) у2 = 9 (х4 — х6).
7) t/2x2 = 4(x —1). 8) г/2(2 —х) = х3.
9) у2х4 = (х2— I)3. 10) ^2(х2— 1) = х4 —4х2.
11) (x-1)(j/2-4)=4x2.
21.27.1) (х-у+1)(х + у-1)= 1.
2) (х - 2у)2 + (4х + 2у}2 = 4. 3) x2z/2 + у = 1.
4) ху2 + х2у = 1. 5) ху (х — у) + х + у = 0.
6) х? 4- у3 = 6х2.
21.28. Кривую, данную как график уравнения, задать пара-
метрически и построить ее:
1) х4 — у4 = Ах2у. 2) (x+z/)3 = x#.
3) (х + г/)4 = х2 + у2. 4) х4 — 2х2у2 + у3 — 0.
л 5) х3 — у3 + 2х — у = 0. 6) (х2 — у2) (х — у) = 1.
7) х2/3 + у2'3 = 1. 8) х4/3 — у4'3 = 1.
21.29. Построить кривую, перейдя к полярным координатами
1) (х2 + у2)х = у. 2) (х2у2)2 = ху. 3) х4у4 = х2 у2.
4) х4 + у4 ==2ху. 5) х4—у4 = ху. 6) х4 — у4 — х2— 2у2.
7) (х2 + у2 — 2х)2 = х2 + у2. 8) (х2 + «/2 —х)2 = 4(х2+>2).
21.30. Построить кривую:
1) х4 + У* — 6z/3 + 8х2у — 0.
2) (х2 + у2)3 = 27х2у2. 3) х4 + 2г/3 = 4х2г/.
4) (х2 — у2) (х — у) = 4х2. 5) х2у2 + У4 = 4х2.
6) х3 + у3 = х2 + У2- 7) х2у2 — х3 — у3. 8) ху = ух,
21.31. Построить график функции в полярных координатах:
1) r = |sin2<p|. 2) г — cos3<p. 3) r = tg2<p.
4) Г УЖЗ?’
5) г = 2 + cos <р. 6) г = 1 + c°s (р. 7) г — 1 + 2 cos ф.
о
8)г = 1—2созф. 9)г = -^- — 1. 10) r = l 4~tg<j>.
459
л
§ 22. Задачи на нахождение наибольших
и наименьших значений
В прикладных задачах при нахождений наибольшего или
наименьшего значения дифференцируемой функции f(x) на от-
резке [а; или на интервале (а; Ь) уравнение f7(x) = 0 обычно
имеет единственное решение х0^(а;Ь), причем производная
f'/x) имеет один и тот же знак на интервале (а;х0) и противо-
положный знак на интервале (х0;Ь). В этом случае число f(xQ)
в является не только локальным экстре-
®мумом функции Д но и ее наиболь-
шим значением на интервале (а;Ь) или
отрезке 1а; Ь], если производная при
переходе через' точку х0 меняет знак
плюс на * минус, и наименьшим зна-
чением, если производная - при пере-
ходе через точку х0 меняет знак минус
на плюс.
Пример 1. Среди всех равнобед-
ренных треугольников, вписанных в дан-
Рис. 100. ный круг, найти треугольник с' наиболь-
шим периметром.
А Пусть треугольник АВС вписан в круг .радиуса /?, при-
чем АВ = ВС (рис. 100). Обозначим /ВАС —а. По теореме
синусов АВ = ВС = 2R sin а, АС = 27? sin (л — 2а) = 2R sin 2а,
поэтому периметр треугольника АВС равен
Р (а) = 2R (2sin а + sin 2а),
где 0 < а < л/2, откуда находим
Р' (а) = 4R (cos 2а + cos а) = 4R (2cos2 а + cos а — 1) =
= 4R (2cos а — 1) (cos а + 1) <
Уравнение Р'(а) = 0 имеет на интервале (0; л/2) единственное
решение а = л/3, причем Р,(а)>0 при ае(0;л/3) и P'(a)<j
<0 при ае(л/3;л/2). Следовательно, число Р(л/3) является
наибольшим значением функции Р(а) на интервале (0; л/2)«
Но если /.ВАС — а — л/3, то /ВСА = л/3 и, значит,
/АВС — л/3, т. е. АВС — равносторонний треугольник. Итак,
среди всех равнобедренных треугольников, вписанных в дан-
ный круг5 наибольший периметр имеет равносторонний тре-
угольник. А
Пример 2. Определить размеры закрытой коробки объема
v с квадратным основанием, на изготовление которой1 расхо-
дуется наименьшее количество материала.
, А Пусть х — сторона основания коробки, h — высота ко-
робки, S— ее полная поверхность. Тогда
S = 2х2 + 4xh, v = x2h3
460
откуда
и, следовательно,
S(x) = 2x2 + ~
'Уравнение S'(x) = 0 при х > О имеет единственное решение
= причем при переходе через точку xq функция S'(x)
меняет знак" минус на плюс. Следова-
тельно1 хо— точка минимума функции
S(x), а число S(x0) является наимень-
шим значением этой функции при х > 0.
. Из формулы v = x2h следует, что если
x — ^\/v9 то Л==^у. Таким образом, вы-
сота коробки должна быть равна сто-
- роне основания, т. е. коробка должна
быть кубом с ребром 'y/v. А
Пример 3. Найти радиус основа-
ния цилиндра наибольшего объема, впи-
санного в шар радиуса R.
А "Пусть г и h — радиус основания и высота цилиндра, впи-
санного в шар радиуса /?, и —объем цилиндра (рис. 10’1).
Тогда
откуда
V = лг2й, (Л/2) 2+ г2 = R2,
v = 2зтг2 R2 — г2, где 0 < г < R.
Обозначим t = г2, тогда
v — 2л/ д/7?2 — /,
0 < t < R2.
Рассмотрим функцию
^2 = 4^2 (#2 — ^
Так как v 0, то функция v(t) имеет на интервале (О;/?2) те
же точки экстремума, что и функция
v2/4n2 = t2(R2 — t) = f(t).
Найдем критические точки функции f (/), решая уравнение
- f'(t) — 2tR2 — 3/2 = 0.
Это уравнение имеет на интервале (0; 7?2) единственное реше-
ние to = 2/?2/3, причем точка /0 является точкой максимума
функции, а число /(/о)— наибольшим значением функции f(/)
на интервале (О;/?2). Следовательно, при г — = R д/^/З
функция v принимает наибольшее значение, т. е. радиус осно-
вания цилиндра, вписанного в шар радиуса R и имеющего наи-
больший объем, равен А
461
22.1. Среди всех прямоугольников, имеющих данную пло-
щадь S, найти прямоугольник: 1) с наименьшим периметром;
2) с наименьшей диагональю.
22.2. Найти наибольшую площадь прямоугольника, вписан^
ного в круг радиуса /?.
X2
22.3. Найти на гиперболе ---У2 = 1 точку, ближайшую
к точке (3; 0).
22.4. Найти на параболе у = х2 точку, ближайшую к точке
Л (2; 1/2).
22.5. Найти наибольшую площадь прямоугольника, две вер-
шины которого лежат на осях Ох и Оу прямоугольной системы
координат, третья — в точке (0; 0), а четвертая — на параболе
у==3 — х2.
22.6. Найти угловой коэффициент прямой, проходящей че-
рез точку А(1;2) и отсекающей от первого координатного угла
треугольник наименьшей площади.
22.7. Найти длину боковой стороны трапеции, имеющей
наименьший периметр среди всех равнобедренных трапеций
с заданной площадью S и углом а между боковой стороной
и нижним основанием.
22.8. Через точку А(2; 1/4) проводятся прямые, пересекаю-
щие положительные полуоси в точках В и С. Найти уравнение
той прямой, для которой отрезок ВС имеет наименьшую длину.
22.9. Найти острые углы прямоугольного треугольника,
имеющего наибольшую площадь среди всех треугольников,
у которых сумма длин однбго из катетов и гипотенузы по-
стоянна.
22.10. Найти наименьшую длину отрезка, который- Делит
равносторонний треугольник со стороной а на две равновели-
кие фигуры.
22.11. Определить углы треугольника АВС с наибольшей
площадью, если задана длина его основания ВС и известно,
что угол ВАС равен а.
22.12. Найти стороны прямоугольника наибольшей площади,
вписанного в эллипс
так, что стороны прямоугольника параллельны осям эллипса.
22.13. Вычислить наибольшую площадь трапеции, вписанной
в полукруг радиуса R так, что нижним основанием трапеции
служит диаметр полукруга.
22.14. Сечение тоннеля имеет форму прямоугольника, завер-
шенного полукругом. Определить радиус полукруга, при кото-
ром площадь сечения будет наибольшей, если периметр сече-
ния равен р.
22.15. Через какую точку эллипса
—+ -^== 1
а2 Ь2 *
462
следует провести касательную, чтобы площадь треугольника,
образованного этой касательной и положительными полуосями
Ох и Оу, была наименьшей?
22.16. Лист картона имеет форму прямоугольника со сторо-
нами а и Ь. Вырезая по углам этого прямоугольника квадраты
и сгибая выступающие части крестообразной фигуры, получим
открытую сверху коробку, высота которой равна стороне квад-
рата. Какой должна быть сторона квадрата, чтобы объем ко-
робки был наибольшим?
22.17. Из трех досок одинаковой ширины нужно сколотить
желоб. При каком угле наклона боковых стенок площадь попе-
речного сечения желоба будет наибольшей?
22.18. Найти высоту правильной треугольной призмы наи-
большего объема, вписанной в шар радиуса R.
22.19. Круг радиуса 7? разделен на два сегмента прямой /,
отстоящей от центра круга на расстояние h. Среди всех прямо-
угольников, вписанных в меньший из этих сегментов, найти пря-
моугольник с наибольшей площадью.
22.20. Найти наибольший объем цилиндра, периметр осевого
сечения которого равен а,
22.21. Вычислить наибольший объем цилиндра, полная по-
верхность которого равна S.
22.22. Консервная банка имеет цилиндрическую форму.
Найти наиболее выгодные размеры банки, т. е. определить от-
ношение диаметра основания к высоте цилиндра, имеющего при
заданной полной поверхности наибольший объем.
22.23. Каким должен быть котел, состоящий из цилиндра,
завершенного полусферами, со стенками заданной толщины, •
чтобы при данной вместимости v на него пошло наименьшее
количество материала?
22.24. Определить отношение радиуса основания к высоте
цилиндра, имеющего при данном объеме наименьшую полную
поверхность.
22.25. Найти наибольшую полную поверхность цилиндра,
вписанного в шар радиуса R.
22.26. Из всех цилиндров, вписанных в куб с ребром а так,
что ось каждого цилиндра совпадает с диагональю куба,
а окружности оснований касаются граней куба, найти цилиндр
наибольшего объема.
22.27. Найти высоту конуса наибольшего объема, вписанного
в шар радиуса 7?.
22.28. Найти высоту конуса наименьшего объема, описанного
около шара радиуса R.
22.29. В конус, радиус основания которого равен 7?, а вы-
сота Н, вписан цилиндр наибольшего объема. Найти радиус
основания и высоту этого цилиндра.
22.30. Из круглого листа жести вырезают сектор и сверты-
вают его в коническую воронку. Каким должен быть угол сек-
тора, чтобы воронка имела наибольший объем?
463
22.31. Найти наименьшую боковую поверхность конуса,
имеющего объем v.
22.32. Найти наибольший объем конуса с данной образую-
щей I.
22.33. Найти наименьший объем конуса, описанного около
полушара радиуса г (предполагается, что основания полушара
и конуса лежат в одной плоскости и концентричны).
22.34. Рассмотрим пучок прямых, проходящих через точку
М (а;Ь), где а > О, b > 0, и пересекающих положительные
полуоси Ох и Оу. Найти наименьшую длину отрезка PQ, где
Р и Q — точки пересечения прямой пучка с положительными
полуосями.
22.35. Камень брошен с заданной начальной скоростью под
углом а к горизонту. Пренебрегая сопротивлением воздуха,
определить, при каком а дальность полета камня будет наи-
большей.
22.36. Внутреннее сопротивление гальванического элемента
равно г. При каком внешнем сопротивлении мощность тока,
получаемого от этого элемента во внешней цепи, будет наи-
большей? -
22.37. В чашку, которая имеет форму полушара радиуса
7?, ойущен однородный стержень длиной /, где 2R < I 4/?.
Найти положение равновесия стержня.
22.38. К реке, ширина которой равна а, под прямым углом
построен канал шириной Ь. Найти наибольшую длину бревна,
которое можно провести из реки в этот канал.
22.39. Чтобы уменьшить трение жидкости о стенки канала,
площадь, смачиваемая водой, должна быть возможно меньшей.
Показать,что лучшей формой открытого прямоугольного ка-
нала с заданной площадью поперечного сечения является та-
кая, при которой ширина канала в 2 раза больше его высоты.
22.40. Из круглого бревна вытесывается балка с прямоуголь-
ным поперечным сечением. Считая, что прочность балки про-
порциональна ah2, где а — основание, h — высота прямоуголь-
ника, найти такое отношение h/a, при котором балка будет
иметь наибольшую прочность.
22.41. - Сосуд с вертикальной стенкой высоты h стоит на
горизонтальной плоскости. Из отверстия в стенке сосуда бьет
струя. Определить положение отверстия, при котором дальность
струи будет наибольшей, если скорость вытекающей жидкости
равна ^2§х, где х — глубина отверстия (закон Торричелли).
22.42. Завод А нужно соединить шоссейной дорогой с пря-
молинейной железной дорогой, на которой расположен поселок
В. Расстояние АС от завода до железной дороги равно а,
а расстояние ВС по железной дороге равно Ъ. Стоимость пере-
возок грузов по шоссе в k раз (&>1) выше стоимости пере-
возок по железной дороге. В какую точку D отрезка ВС нужно
провести шоссе от завода, чтобы стоимость перевозок грузов от
завода А к поселку Вбыла наименьшей? -
464
22.43. На какой высоте над центром круглого стола радиуса
R следует поместить электрическую лампочку, чтобы освещен-
ность края стола была наибольшей?
22.44. Светящаяся точка расположен-а на линии центров
двух шаров и лежит вне этих шаров. При каком положении све-
тящейся точки сумма площадей освещенных частей поверхно-
стей шаров будет наибольшей?
22.45. Груз, лежащий на горизонтальной плоскости Р,
нужно сдвинуть с‘ места силой, приложенной "к этому грузу.
Определить угол, образуемый этой силой с плоскостью Р9 при
котором величина силы будет наименьшей, если коэффициент
трения груза равен k.
22.46. Наблюдатель находится напротив картины, закреплен-
ной на вертикальной стене. Нижний край картины расположен
выше уровня глаз наблюдателя на а, верхний край — на Ь. На
каком расстоянии от стены должен стоять наблюдатель, чтобы
угол, под которым он видит картину, оказался наибольшим?
22.47. Точка Л(%о;#о) расположена внутри параболы у2 ==
— 2рх, р L> 0, точка В — на самой параболе, F — ее фокус. До-
казать, что длина ломаной ABF будет наименьшей, если отре-
зок АВ параллелен оси параболы, а угол FBA делится нор-
малью к параболе в точке В пополам (принцип параболического
зеркала).
22.48. Точки А и В расположены соответственно в верхней
и нижней полуплоскостях прямоугольной системы хОу. Частица
движется по ломаной АМВ, где М—точка оси Ох. Скорости дви-
жения частицы в верхней и нижней полуплоскостях соответ-
ственно равны Vi и у2. Доказать, что время движения частицы
sin а V! п „
будет наименьшим, если , где а, р—углы, образуемые
отрезками AM и ВМ с нормалью к оси Ох (в оптике эти углы
называют соответственно углом падения и углом отражения).
§ 23. Численное решение уравнений
Интервал, содержащий только один корень *) (одно реше-
ние) уравнения
f« = 0, (1)
называют интервалом изоляции этого корня. Отделить корни
уравнения — значит указать для каждого из них интервал изо-
ляции. Для отделения корней обычно используют следующие
утверждения.
Пусть функция f имеет значения разных знаков на концах
Отрезка* [а; Ь]у т. е. f (a) f (b) < 0. Тогда:
*) В этом параграфе всюду, если не оговорено иное, речь идет только
о действительных корнях уравнения.
485
1) Если f непрерывна на [а; 6], то уравнение (1) имеет на
интервале (а; Ь) по крайней мере один корень.
2) Если f непрерывна и строго монотонна на то
уравнение (1) имеет на интервале (а; Ь) один и только один
корень.
Пример 1. Определить число корней уравнения и отде-
лить эти корни:
1) 2х3 —8х+1=0. 2) ех~2 — х = 0.
Л 1) Обозначим f(x) = 2x3— 8x4“ Е Так как
/(—3) = — 29 < 0, f(0)=l>0, Д1) = —5<0, f(2)= 1 >0,
то данное уравнение имеет корень на каждом из интервалов
(—3;0), (0; 1), (1;2). Многочлен третьей степени имеет не
более трех корней, поэтому каждый из указанных интервалов
содержит только один корень, т. е. является интервалом изо-
ляции.
2) Рассмотрим функцию f(x) = ex~2— х. Данное уравнение
не имеет решений при х 0, так как f(x)>0 при х 0.
Наименьшее значение функция f принимает при х = 2
и f(2) =—1 <0. Поскольку /(0) = е-2>0 и поскольку функ-
ция f строго убывает на [0; 2] (так как f'(x) = ex~2—1<0
при 0гС%<2), данное уравнение имеет и притом только один
корень на (0; 2). За интервал изоляции для этого корня можно
принять меньший интервал (0; 1), так как f(l) = e~“1— 1 < 0.
При х>2 функция f строго возрастает, так как f'(x)>0
и, кроме того, f(3)=e — 3 < 0, a f(4)=e2 — 4 > 0. Отсюда
следует, что данное уравнение имеет корень на интервале (3; 4)
и притом только один. Итак, данное уравнение имеет два корня,
(0; 1) и (3; 4) — интервалы изоляции этих корней. А
По известному графику функции у — f(x) можно с той или
иной точностью указать его точки пересечения с осью абсцисс,
т. е. найти приближенные значения корней уравнения f(x) = O,
как говорят, решить уравнение графически.
Иногда бывает возможно представить уравнение f(x) = O
в таком виде g(x) = Л(х), где графики функций g и h построить
проще, чем график f. В этом случае приближенные значения
корней уравнения f(x) = O находят как абсциссы точек пере-
сечения графиков функций g и h.
П р и м е.р 2. Найти графически приближенное значение наи-
меньшего корня уравнения:
1) 2х3 — 8x4-1 =0. 2) ех~2 — х = 0.
/Л 1) Пользоваться графиком функции 2х3— 8х+1 не-
удобно, так как уже при х = —3 она имеет значение —29,
и пришлось бы брать слишком мелкий масштаб. Рассмотрим
функцию / (х) = у (2х3 — 8х 4" !)• Ее график изображен на
рис. 102 (при х = —~V3 и х —-j-V3 ~ 1>15 функция имеет
466
соответственно максимум и минимум), а в таблице приведено
Рис. 102.
несколько значений функции. Из рассмотрения рис. 102 видно,
что уравнение f(x) = O (равносильное данному) имеет три
' корня: « —2, х2 «0, х3 ~ 2. Таким образом, наименьшим
является корень Xi, приближенным значением для него можно
взять х* = — 2,1 (см. рис. 102).
• Используя свойства графика функции /, с помощью неслож-
ных вычислений найдем погрешность взятого приближенного
значения. В таблице содержатся координаты трех точек А, В, С
графика (рис. 103). При х < 0 функция у = f(x) выпукла вверх,
• поэтому часть АВ ее графика расположена левее отрезка АВ
(рис. 103). Отсюда следует, что если х[ — абсцисса точки пере-
сечения отрезка АВ с осью Ох, то х' > хь Уравнение прямой АВ
имеет вид
1+41
4 Т 16
'Подставляя сюда у — 0, находим х[ — —92/45.
Из выпуклости вверх функции при х < 0 следует также,
что корень Xi лежит правее точки пересечения прямой ВС
с осью Ох, т. е. если х" — абсцисса этой точки, то х" < хг
Составляем уравнение прямой ВС:
У 4 _ х+,2
2. __± “1+2
4 4
и, полагая у — 0, находим- х" = — 13/6. Итак,
—13/6 ^Х!^—92/45.
467
F
Приближенное значение х* = — 2,1 также удовлетворяет
этим неравенствам, поэтому
| х* — Xj | < max |х' — х*, х* — х") = 1/15.
2) Запишем уравнение в виде х = ех~2. Графики функций
у = х и у — ех~2 изображены на рис. 104. Видно, что уравне-
ние имеет два корня, за приближенное значение меньшего
корня Xi возьмем 0,2.
Пользуясь тем, что функция ех~2 возрастает и выпукла
вниз, можно легко оценить погрешность этого приближения.
Возьмем на графике точки Л(0; е~2) и ^(Ije-1)- Отрезок АВ
пересекает прямую у = х в точке, абсцисса х\ которой больше,
чем корень xi (рис. 105). В уравнение прямой АВ\
. подставляем// = х и находим
/ = -—Ц-г< 0,177.
1 е2 — е + 1 ’
Прямая, проведенная через точку А параллельно оси абс-
цисс, пересекает прямую у — х в точке, абсцисса х" = е~2
которой меньше корня Xi (рис. 105). Таким образом,
0,135 < -V < *1 < ~2 -ITT < 0,177.
’ е2 1 е2 — е 4- 1
- Оценим погрешность приближенного значения Xi ~ 0,2:
0,2 — xi < 0,2 — 0,135 = 0,065. -
Проведенные вычисления позволяют указать значительно луч-
шее приближенное значение
= "2 (Х1 + *1) = 2е2 (е2 — е + 1)
468
с погрешностью
| xi ~ xi I < У (xi ~ ХТ) = 2е2 (е2-е + 1) *> 0,021 ’
Округляя вычисления, возьмем окончательно х* = 0,156 с по-
грешностью округления 5 • 10-4 и с общей погрешностью
' | xt — 0,1561 < 0,021 + 0,0005 < 0,022. А
Метод деления пополам («половинного деления», «взятия
в вилку») используют для нахождения первого (часто гово-
рят— нулевого) приближения к корню уравнения, а также для
улучшения границ корня, т. е. для нахождения достаточно ма-
лого интервала изоляции.
Пусть f(x) непрерывна на отрезке [а*, Ь], (а;Ь)—интервал
изоляции корня g уравнения f(x) = Q, Определим знак f(c)
в середине с отрезка [а; ft] (если f(c) = O, то. корень % —с
найден), и пусть, [аг, fti] тот из отрезков [а; с], [<?;&.]» на кон-
цах которого функция f(x) имеет значения разных знаков. Ана-
логично выберем отрезок [а2;Ь2], вдвое меньший чем [ai;&i],
и т. д. В результате получим последовательность вложенных
отрезков {[an;-ftn]}, длина n-го отрезка равна (Ь — а)/2п, или
на каком-то шаге найдем корень g. Имеем
. lim ап= lim ft„ = g
П->оо П->оо
И
0<g-a„C(ft-a)/2", 0<ftn-g<(ft-a)/2". (2)
По этим формулам можно определить число шагов, достаточ-
ное для достижения заданной точности.
Метод итераций (метод последовательных приближений)
используют для нахождения приближенных значений корней
уравнения с большой точностью.
Пусть уравнение f(x) = G имеет на [а; 6] единственный ко-
рень g. Для этого уравнения подбирают равносильное ему на
[а; 6] уравнение-вида
х = ф(х) (ЗУ
и значение %o^[a;ft] так, чтобы была определена последо-
вательность
Хп = ф (Хп-1), П е N, (4)
и чтобы эта последовательность сходилась к корню g.
Достаточные условия сходимости процесса итераций та-
ковы*.
Пусть функция ср дифференцируема на [а; ft] и
|ф'(х) | k < 1, хе [a; ft]. (5)
Пусть xoe[a;ft] и хп = ф(хл_1)е [a; ft] для любого neN-
Тогда уравнение (3) имеет на [a; ft] единственный корень g и
lim хп = g.
П->оо
46$
Для существования последовательности (4) при условии (5)1
достаточно выбрать
х0 е + -у; Ь —, где d — b — а.
Для оценки погрешности метода итераций используют не-
равенства
h
- «eN, (6)
здесь и ниже k берется из условия (5). Для оценки числа п ите-
раций при заданной погрешности можно использовать формулу
1гп
Ц — ~х0|, neN. (7)
При заданной погрешности А процесс итераций продолжают
до получения оценки
' (8)
тогда заведомо | g — хп | Л-
Вычисление приближений хп обычно происходит с округле-
нием, и погрешность округления следует учитывать при нахож-
дении погрешности приближения.
В сходящемся итерационном процессе последовательность
]g— хп\ монотонно стремится к нулю.
Пусть функция ф удовлетворяет условию. (5) и ф'(х)^0 на
[a; Zb]; тогда последовательность (4) монотонно сходится к
корню g. Если же q/(x)^0 на [а; Ь], то одна из последователь-
ностей {X2k} и {x2k-1} возрастает, а другая убывает. В этом слу-
чае корень g лежит между двумя соседними членами последо-
вательности хп и Хп-н для каждого neN, следовательно, уста-
новившиеся десятичные знаки приближения хп принадлежат и
корню g.
При выборе уравнения (3) следует учитывать, что чем
меньше величина k из условия (5), тем меньше итераций тре-
буется для достижения заданной точности (как говорят, тем
быстрее сходится процесс итераций).
П ри,мер 3. 1) Указать сходящийся итерационный процесс
для вычисления наименьшего корня уравнения
2х3 — 8х+ 1 =0.
2) Найти с помощью итераций приближенное значение наи-
меньшего корня уравнения
х — 1пх— 2 = 0
с погрешностью не более чем 5-10*5.
А 1) В примере 2 был найден интервал (—13/6; —92/45)»
изоляции наименьшего корня g данного уравнения. На этом
интервале уравнение равносильно каждому из следующих
470
уравнений:
2х3 + 1 /X
х=-------i^- = 4Pl(x),
~ 8х —• 1 z ч
Х==—2х^~=='(РАх):
Для производных (p'k(x) (k — 1, 2, 3) на отрезке [-g-; — ^]
имеем оценки
|<р1М| = |^>4-4 = з>1,
1 + 4- —
| <₽2 (х) |= I | ( 1з у > 0>95,
Ясно, что для построения итерационного процесса следует вы-
брать третье уравнение x — Правая часть этого
уравнения удовлетворяет условию (5) с k — 0,32. Если в ка-
честве нулевого приближения взять полученное в примере 2
значение х0 = —2,1, то последовательность (4) будет опреде-
лена и будет сходиться к корню g.
2) Левая часть данного уравнения положительна при х =
— \/е2 и отрицательна при х=1. Производная левой части
отрицательна при 0 < х < 1, поэтому на интервале (0; 1) урав-
нение имеет и притом только один корень g, он и является наи-
меньшим. Данное уравнение, записанное в виде х==1пх + 2,
непригодно для построения итерационного процесса, так как
(In х + 2)' = 1/х > 1 при х е (0; 1). Преобразуем уравнение
к виду
х = ех~2. (9)
Здесь (ех~2)' = ех~2 е-1 < 1 при хе[0; 1], и, значит, для
уравнения (9) итерационный процесс будет сходиться. В при-
мере 2 были найдены приближенное значение наименьшего
корня х0 = 0,156 и его интервал изоляции (0,135; 0,177). На
этом интервале
(ех~2)'^ е-1’823 < 0,162 = k
(для вычислений в данном примере использована мини-ЭВМ
из серии «Электроника»). Вычисляем первое приближение
%1 = е^2 = 0,1581834...
Видно, что х0 < Итерационная последовательность хп —
^exn-i~2t является возрастающей, Округляя с недостат-
471
ком, примем Xi = 0,158183 и найдем согласно (7) число ите-
раций, требуемое для достижения заданной точности:
^^—(0,158183 —0,156) <5- 10-5,
0,162" С 1,919-10~2, 1,62"-10-”^ 1,919-Ю-2;
проверяя п = 2 и п = 3, находим, что п — 3. При этом п будем
иметь оценку согласно (7):
0<g —х3< 1,11-10~5. (10)?
Результаты вычислений приведены в таблице
п хп еХп~2
0 0,156 0,158183-
1 0,158183 ОД 58529
2 0,158529 0,158584
3 0,158584
Округляя еще раз по недостатку, можно взять х*= 0,15858
с погрешностью, заведомо не превышающей 2-10-5. Можно
также заметить, что из (10) следуют неравенства
0,158584 <g< 0,158596
(с учетом погрешности округления), поэтому выбор приближен-
ного значения х* = 0,15859 дает большую точность. А
Ряд итерационных формул для решения уравнения f(x) = O
получают из формулы Тейлора для функции f или функции, об-
ратной f.
Пусть функция f дифференцируема на [а\ &] и
0 < mi |f(x) Afb хе[а;.&]. (11)
Пусть g— корень уравнения f(x) = O на (а; Ь) (единственный
в .силу (11)); тогда при хе[а;&] имеем f (х) — f(g) -р;
+ Г (6 (*) )_(* — 5), откуда
£ = г (0(х)) ’ 62)
где 6(х) лежит между g и х. Выбрав х0^[а;6] и подставив
в (12) хп-\ вместо х, хп вместо g и какое-либо приближенное
выражение вместо fz(0(x)), получим итерационную формулу
вида (4).
Пусть в дополнение к указанному функция f дважды диф-
ференцируема на [а\ 6] и
0<т2^|Г(х)|^М2, х^[а;&], (13)
и пусть хо выбрано так, что
f_Uo)№o)>O. (14)
472
Подставляя в (12) f'(x) вместо приходим к фор-
муле
хп = хп_1 — . n6=N", (15)
определяющей последовательность {хп}, которая монотонно
сходится к корню g. Формула (15) описывает метод Ньютона
(йетод касательных).
Для оценки погрешности (без учета погрешности округле-
ния) в методе Ньютона используют формулы
neN, (16)
(17>
где ш\ удовлетворяет условию (11), а М2 — условию (13).
Если х0 выбрано так, что
-Й-^-^oKh (18)
то процесс итераций сходится быстро, а если Af2/2mi 1, то
число верных десятичных знаков на каждом шаге удваивается.
Заменяя в (12) f'(0(x)) на , придем к формуле
X — Хо
хп = хп-\ f (Хп-д — f (х0) ~~ Х°)’ (19)
или, что то же,
хп = хо~~ f (Xn_j) — f (x0) “ %°)’ neN, (20)
для -построения последовательности, монотонно сходящейся
К корню g. Формулы (19), (20) описывают метод хорд (метод
ложного положения). Оценку погрешности приближения по
методу хорд можно получить по формуле (16), а также по
формуле
IБ — К л!| ~ — |хп — хга_, I, neN. (21)
Упрощенный метод Ньютона применяют, когда производ-
ная /'(х) мало изменяется на отрезке [а;&]. В этом случае
в (12) заменяют Г(0(х))- на /'(хо), тогда формула
хп = хп_} nc=N, (22)
задает последовательность, сходящуюся к корню g. Погреш-
ность приближений можно определять по формулам (16), (21).
Комбинированный метод получается объединением метода
хорд и метода касательных. В силу (И) и (13) производные
f'(x) и Г(х) не меняют знаков на отрезке [а;&]; пусть для
определенности
Г(4>-0> №)>0. /23)
473
Выберем х' и х" из [а; 6] так, что f(x")<0, a /(*о)>О
(рис 106), тогда х" <g<x'. Последовательность {х'} зададим
по методу касательных, а последовательность {х"} — по ме-
тоду хорд:
пеЧ (24)
« -<-)• та
Тогда
lim х' = lim х" = g и х" < g < х', (26)
П->оо П-»оо " п
о<^~хп <х'п~ хп> nc=N. (27)
При вычислениях значения х" можно округлять с недостат-
ком, а значения л/—с избытком. Процесс прекращают, когда
правая часть в (21) будет меньше
заданной погрешности. За прибли-
женное значение корня часто при-
нимают (л/ + х")/2.
Аналогично строится последова-
тельность и при других сочетаниях
знаков f'(x) и f"(x). В каждом слу-
чае последовательность по
методу касательных строят от на-
чального значения x'Q9 удовлетво-
ряющего условию (14).
Рис. 106. Указанные итерационные после-
довательности, построенные на ос-
нове формулы (12), сходятся быстро, если производная f'(x)’
достаточно велика (см. (16), (17), (21)).
Отправляясь от формулы Тейлора с остаточным членом бо-
лее высокого порядка, чем первый, можно получать итерацион-
ные последовательности, сходящиеся более быстро, чем ука-
занные.
Порядком метода итераций называют число т такое, что для
итерационной последовательности, сходящейся к корню |, верна
оценка
|£-хл+1|^ С\1-хп\\ (28)
Метод Ньютона имеет порядок т — 2.
Пример 4. Найти наименьший корень уравнения 2х3 —
— 8%+ 1 — 0 с погрешностью, меньшей чем 5-10“5.
А В примере 2 был найден интервал (—13/6; —92/45) изо-
ляции наименьшего корня Для уменьшения этого интервала
воспользуемся комбинированным методом. Поскольку
f'(x)j=6x2 —8^> 16>0f а Г(4= 12х<:— 24<0,
474
итерационную последовательность по методу касательных по-
строим от начального приближения х' =— 13/6:
<=<-1 - J п е N> (29>
а для последовательности по методу хорд возьмем за началь-
ное приближение х" = — 92/45,
остальные ; члены последова-
тельности вычисляем, используя
(20), по формуле
(зо)
подставляя в (20) на каждом
этапе вместо х0 значение
(рис. 107). Вычисления прово-
дим, например, по схеме, указан-
ной в таблице
п 0 1 2
j: x'n 13^ 6 —-2,067034 — 2,059829 r
xn __92 45 — 2,058686 — 2,059786
f (xn) 217 108 — 0,127069
r (4) 121 6 17,635777
f (<) 0,265011 0,019292’
Pn 217 2178 — 0,007205
Qn — 0,664269 — 0,868189
xn xn 0,122222 0,008348
Здесь
___ f(xn) __ f (*n)
Рп~ i'q‘ /(0-/(4)'
(31)
475
Уже после второго этапа вычислений получаем, что
—2,05983 ё < —2,05978,
поэтому, полагая
х* = — ± (2,05983 + 2,05978) « — 2,05980,
получаем приближенное значение корня с погрешностью не бо-
лее чем 2,5-10-5. Л
23.1. Решить графически уравнение, указав для каждого
корня интервал изоляции, длина которого не превосходит 0,5:
1) х3 —6x4-2 = 0. 2)х4 — 4х —1=0. 3) х3 + 2х + 7,8 = 0.
4) х3 — 1,75x4-0,75 = 0. 5) 2х3 — х2 - х - 3 = 0.
6) х3 + х2 —5х—12 = 0. 7) х3 —0,2х2 —0,2х—1,2 = 0.
8) 0,Зх4 — 0,7х3 — 0,Зх2 — 2 = 0.
23.2. Решить графически уравнение, указав для каждого
корня интервал изоляции, длина которого не превосходит 0,1:
- 1) 2х3 + х+ 1 =0. 2) х4 — х — 1=0. 3) х + ех = 0.
4) х — sinx—1=0. 5) x = ctgx, хе (0; л).
6) х2 — cosx = 0. 7) 4х — 51пх = 5. 8) Xх = 10.
23.3. Доказать, что с помощью сдвига вдоль оси Ох или
сжатия (растяжения) вдоль оси Ох уравнение
аохп + а\хп~' + ... + ап-\х + ап = 0, «о =/= О',
можно привести к виду
botn + b2tn~2 + ... • + bn-it + bn = 0
или к виду
cozn -ф ciz"-1 4- ... 4- сп — 0,
где |с0| = |с„|.
23.4. Пусть коэффициенты многочлена
Р„ (х) = аохп 4- щх"-1 4- • • • 4- Qn-iX 4* «п, «о =# 0,
удовлетворяют равенствам at = an-t (i = 0, 1, .... п). Дока-
зать, что:
1) Если п нечетно, то х = —1—корень многочлена и коэф-
фициенты частного
Q„_i = boxn~' 4-6ixn-24- ... 4-6„_2х4-6„-i
от деления Рп(х) на х4-1 удовлетворяют равенствам 6, =
= bn-i-i (i = 0, 1, ..., п — 1).
2) Если п четно, то замена z = х 4- -у приводит уравнение
рп (х) = 0 к уравнению степени п/2 и к п/2 квадратным урав-
нениям.
476
3) Если п четно, то замена
х+1 у
х — 1 )
также приводит уравнение Рп(х) — 0 к уравнению степени п/2
и к п/2 квадратным уравнениям.
23.5а Пусть коэффициенты многочлена
Рп (х) = аохп + aixn~l + ... + ап_[Х + ап, aQ =/= О,
удовлетворяют равенствам сц — —an-i (/ = 0,1, ..., п). Дока-
зать, что:
1) Если п нечетно, то х = 1—корень многочлена, а если
п четно, то х = 1 и х = —1 — корни многочлена.
2) Коэффициенты частного
Qn-i (х) = bQxn-' + Ъ\Хп~2 + ... +Ьп-2х + ЬГ1_л
от деления Рп(х) на х—1 удовлетворяют равенствам bi =
= bn-x-i (i = 0, 1, ..., п — 1).
23 .6. Пусть функция f определена, дважды непрерывно диф-
ференцируема на R и f" не меняет знака на R. Доказать, что:
1) Уравнение f(x) = O не может иметь более двух действи-
тельных корней.
2) Если f(xo)f'(xQ) < 0, f (х0)Г(х0) <
имеет единственный корень в интервале
О, то уравнение f(x)=O
(Х°;
3) Если f(xo)=O, f (xQ)f"(x0) < 0, то уравнение f(x) = O
имеет по одному корню в интервалах (—оо;хо), (хо;
23 .7. 1) Пусть функция f непрерывна на [#;+оо), диффе-
ренцируема на (а;+°°), f(a)<0, f(x)^m>0 на (а;+°°)-
Доказать, что уравнение f(x) = O имеет, притом только один,
действительный корень на (а; 4~оо).
2) Привести пример, который показывал бы, что условие
«/'(х) т > 0 на (а; 4-°°)'» нельзя заменить условием
«Г(х) > О».
3) Доказать, что при условиях 1) корень уравнения принад-
/ f (а) 1
лежит промежутку I а; а — .
. 23.8. Корень g уравнения f(x) = O называют р-кратным
(peN), если f(x) = (x— g)^cp(x), где ф(£)¥=0. Однократный
корень называют простым.
1) Доказать, что если f дифференцируема в окрестности
р-кратиого (р 2) корня g уравнения /(х) = 0, то g является
(р— 1)-кратным корнем уравнения /'(х) = 0.
2) Доказать, что если а2 — 36 < 0, то уравнение
х3 + ах2 + Ьх + с = О
имеет один простой действительный корень.
477 •
23.9. Доказать, что уравнение
х2А+1 + ахх2к-х + a2x2k~'3+ + akx + ak+i==0,
где at 0 (i— 1, 2, ..., k — 1), а* > 0, имеет единственный,
причем простой, действительный корень.
23.10. Пусть R-(x)— наибольший общий делитель многочлена
Рп{х) и его производной Р'(х) (nsh). Доказать, что все корни
частного от деления Рп(х) на R(x) простые и совпадают с кор-
нями многочлена Рп (х).
23.11. Доказать, что если все корни многочлена
хп + а2хп~2 + а3хп~3 4- ... + йп-\х + ап
действительны, то а2 0.
23.12. Доказать, что многочлен
хп + а\хп~х + а2хп~2 + ... -Ь ап_\х — ап,
где at 0 (/=1, 2, ..., п—1), ап > 0, имеет только один
положительный корень, причем этот корень простой и не пре-
п ___________
восходит ^ап.
23.13. Доказать, что все корни производной многочлена
р4 (х) = (х + 1) (х — 1) (х — 2) (х — 3)
действительны, и найти их интервалы изоляции, длина которых
не более чем 0,5.
23.14. Доказать, что многочлен
aQxn + aixn~i+ ... +ап_1Х + ап, а0 Ф 0,
имеет по крайней мере один корень на интервале (0; 1), если
7^т + -^+ +^ + о. = 0.
23.15. Расположим по возрастанию номеров коэффициенты
многочлена
Рп (х) = а*хп 4- а\хп~х 4- ... 4- ап-\х 4- ап,
а0, ..., пропуская коэффициенты, равные нулю. Числом пере-
мен знака получившегося упорядоченного набора называют
число пар соседних элементов, имеющих разные знаки.
Доказать, что число положительных корней многочлена не
больше числа перемен знака в наборе его коэффициентов, не
равных нулю.
23.16. Доказать, что многочлен:
1) х5 — 2х4 -—X2 — 5 = 0 ..имеет и притом единственный дей-
ствительный корень; указать для этого корня интервал изоля-
ции, длина которого не более чем 0,1.
2) х6 4" 2х4 4"х — 3 = 0 имеет и притом только два действи-
тельных корня; указать для этих корней интервалы изоляции,
длина которых не более чем 0*1.
478
23.17. Доказать, что все корни уравнения
аохп 4- aixn~l + ... 4-cin-ix 4- ап = 0, ао#=О,
1) удовлетворяют неравенству
|gl < 1 _|_. .Afl
Hol ’
где
Mi = max{|ai|, |a2|, ..., |an|};
2) при an =/* 0 удовлетворяют неравенству
ш>(1 +тггт)_1-
X I ап I /
где
М2 = max{|tz0|, |ai|, .... |an-i|}.
23.18. Пусть в уравнении
aoxn + aixn-1+ ... + == О
€io>0, ak (6^1)— отрицательный коэффициент с наимень-
шим номером, А — наибольшая из абсолютных величин отри-
цательных* коэффициентов. Доказать, что все действительные
корни этого уравнения удовлетворяют неравенству
^<1 + лМ
(теорема Лагранжа).
23.19. Пусть для многочлена
Рп (х) = аохп + aix"-1 + ... + an-ix ап
существует такое число с > 0, что
Р<*>(с)>0 (6 = 0,1, ..., п),
и пусть ао > 0. Доказать, что все действительные корни этого
многочлена удовлетворяют неравенству | с (теорема Нью-
тона) .
23.20. Пусть многочлен Рп(х) представлен в виде
РДх) = <2(х) + Я(х),
где Q(x) содержит старший по степени член многочлена Рп(х)
с положительным коэффициентом и все члены с отрицатель-
ными коэффициентами, a R(x) содержит все остальные члены
Рп(х). Доказать, что если Q(c)>0 при некотором с >* 0, то
все действительные корни Рп(х) меньше с.
23.21. Доказать, что уравнение Р(х) = 0 не имеет отрица-
тельных корней, и, пользуясь результатами задач 23.17—23.20,
указать отрезок [а;Ь], 0<а<6, содержащий все положи-
тельные корни, если:
1) P(x) = 2x5-100x2 + 2x—L
2) Р(х) — х4 —35х3-Ь380х2 — 1350x^1000,
479
23.22. Указать отрезки [ar,6i], а\ <i b\ <. О, и [а2;Ь2], 0<
< а2 <. Ь.2, содержащие соответственно все отрицательные и все
положительные корни уравнения
Зх5 + 7х4 — 8х3 + 5х2 — 2х — 1 = 0.
Для положительных корней указать интервалы изоляции, дли-
ны которых не превосходят 0,5.
23.23. Доказать, что уравнение
х5 + х4 + х2+10х — 5 = 0
имеет ёдинственный корень, и указать интервал его изоляции,
длина которого не превосходит 0,1. .
23.24. 1) Доказать, что если 4р3 + 27</2>0, то уравнение
х3 + рх + q = 0, р, q ge R, имеет один действительный корень,
а если 4р3 + 27</2 < 0, то это уравнение имеет три действитель-
ных корня.
2) При каком условии на а, &, с все корни уравнения
х3 + ах2 + Ьх + с = 0
действительны?
23.25. При каком .условии на р и q все корни уравнения
х5 — 5рх2 + 5р2х + 2q — 0
действительны?
23.26. При каком условии на р и q все корни уравнения
хт + рхп + <7 = 0,
где т > п > 0, m, n е N, q =/= 0, р += 0, действительны?
23.27. 1) Доказать, что уравнение
x2n+i + HiX2"-1 + ... + апх — аОу (32)
где a/eR (i = 0, 1, ..., п), имеет хотя бы один корень в ин-
тервале (—2; 2), если | а0| <Z 2.
2) Доказать, что уравнение (32) имеет корень в интервале
(—2/; 21), где I = (| а0 |/2)1/(2п+1) (теорема Чебышева).
23.28. Указать в зависимости от значений а е R количество
действительных корней уравнения:
1) х4 — 4ах3 — 2 = 0. 2) 2х3 — Зах2 + 1 = 0.
23.29 Найти все значения ggR, при которых уравнение
имеет указанное число действительных корней:
1) 2х3 + 13х2 — 20х + а = 0, один корень.
2) Зх3 + 1,5х2— 12х + а = 0, один двукратный корень и один
простой.
3) Зх4 + 8х3 + а — 0, два простых корня.
4) 9х4 + 14х3— 15х2 + а = 0, четыре различных корня.
23.30. Доказать, что уравнение
... 2ех + х2+ 18х — 6 = 0
480
имеет единственный положительный корень; указать его ин-
тервал изоляции, длина которого не превосходит 0,2.
23.31. Указать в зависимости от значений а число корней
уравнений:
1) 1пх + ах = 0. 2) х!пх = а. 3) ех = ах2.
4) chx = ax. 5) cos3x sin х = а, х,<^ [0; л].
23.32. Указать все значения а е R, при которых уравнение
имеет указанное число действительных корней:
1) ех = а + х — х2, два различных корня.
2) х2 + х — In х + а — 0, один двукратный корень.
3) х2 — a In х, два различных корня.
4) 6arctgx— х3 + а — 0, три различных корня.
23.33. Дано уравнение
1пх— а — Ьх — 0.
1) Доказать, что это уравнение не может иметь более двух
корней.
2) Указать на координатной плоскости множества точек
(a;h), для которых число корней данного уравнения равно
0, 1, 2.
23.34. Дано уравнение
ех — а — Ьх3 = 0.
1) Доказать, что это уравнение не может иметь более четы-
рех корней.
2) Указать на координатной плоскости множества точек
(n;fe), для которых число корней уравнения равно 0, 1, 2, 3, 4.
23.35. Пусть а > 1. Доказать, что уравнение
ах = Ьх
1) имеет два действительных корня при b > eln а\
2) имеет один двукратный действительный корень при b —
= elna;
3) не имеет действительных корней при 0 b < eln а;
4) имеет один простой корень при b < 0.
23.36. Указать количество корней уравнения
хп = аех, не N,
в зависимости от а е R.
23.37. Отделить действительные корни уравнения, указав
интервалы изоляции, длины которых не превосходят единицы:
1)х3 + 2х — 7 = 0. 2) х3 —27х—17 = 0. '
3) х3 — 6х2 + 9х— 10 = 0. 4) х4-2х3 —5х2 + 2х + 2 = 0.
5) х4 — 4х3 — Зх + 23 = 0. 6) х4 + 6х3-2х2+ 1=0.
7) х5 - 10х3 + 6х + 1 = 0. 8) х5 + 5х3 — 7х + 2 = 0.
16 л. Д. Кудрявцев и др.
481
9) х5 + 7х3-5х + 11 =0.
10) х5 — 2х4 — бх3 + 19х2 — 17х + 1 = 0.
23.38. Отделить корни уравнения
Р2 । । £ _ 1
а2 + х ’ Ь2 + х ‘ с2 + х ’
где р, q, г, a, b, R, а2 > b2 > с2, pqr #= 0.
23.39. Отделить действительные корни уравнения, указав
для каждого корня интервал изоляции, длина которого не пре-
восходит 0,1:
1)х—sin2x = 0. 2) х = 4 cosx. 3) ех — х — ~ — 0.
4) 2х2 — ^+1 = 0. 5) х+1п(х + 2) = 0.
23.40. Методом деления пополам решить уравнение с ука-
занной погрешностью А:
1) / + *-10 = 0, Д=10-2.
2) х3 — 12х — 8 = 0, Д=10”2.
3) х3 + х2 — 5х — 12 = 0, Д = 1(Г2.
4) х4 + 2х3 + 6х2 — 1 = 0, Д = 10-3.
5) х4 — 2х3 + х — 1 = 0, Д = 10~3.
6) (х—I)2 — 2sinx = 0, Д=10-2.
7) ех = 2(1— х)2, Д = 10~2.
8) 10 (х — 1) = sinx, Д=10-3.
9) 101пх = х3 —3, Д=10-3.
Ю)х/=1, А=1(Г3.
23.41. Шар радиуса 1 м с удельной плотностью 0,75 пла-
вает в воде. Вычислить высоту выступающей из воды части
шара с погрешностью 0,05 мм.
23.42. Используя графики гипербол
ху ~ У + 1 и %2 — р2 = 1 .
и метод деления пополам, вычислить с погрешностью 0,01 ко-
ординаты точек пересечения этих гипербол.
23.43. 1) Привести пример уравнения f(x) = O с корнем g
и его приближенным значением х* так, чтобы были выполнены
неравенства fz(x) >0 и
|х* — g|> 103, |f(x*)|^ 10-3,
т е. удостовериться в том, что из «близости» f(x*) к нулю не
следует «близость» х* к корню g.
482
2) Привести пример уравнения f(x)*=O с корнем § и его
приближенным значением х* так, чтобы выполнялись неравен-
ства f' (х) > 0 и
|х* — || <10-3, | f (х*) | > 103,
т. е. удостовериться в том, что из «близости» приблщ^|рного
значения х* к корню g не следует «близость» f(x*) к нулю.
23.44. Уравнение
Зх4—16х3+192 = 0 (33)
при х > О равносильно каждому из следующих уравнений:
a) it —2д/>‘у'г ; б) №-j-^/-|(x4 + 64) ;
*)—?('-#)•. ^=4(4+4)-
1) Доказать, что уравнение (33) имеет два положительных
корня, и отделить их.
2) Указать из уравнений а)—г) то, для которого итерации
наиболее быстро сходятся к меньшему положительному корню
уравнения (33).
Вычислить этот корень с точностью до 10~3.
3) Выполнить для большего корня уравнения (33) задание,
аналогичное 2).
23.45. Методом итераций найти действительные корни урав-
нений с указанной погрешностью Д:
1)ха+х=1000, Д=10-4.
2) х3 —Зх2 + 8х+10 = 0, Д=10-5.
3) х5 + 5х + 1 = 0, Д = 10-5.
4) 10х = е-*, Д = 5- 10~4.
б) 4% = 8х, Д=10"5.
6) 4ех = 5(х+1), Д = 10~4.
7) х3 — 2х — 5 = 0, Д=10-1°. #
8) sinx = 2x —0,5, Д = 5-10“\
9) х — sinx = 0,25, Д=10~3.
23.46. 1) При каких а > 0 уравнение
х = ах
имеет решение?
2) При каких а сходится итерационная последовательность
xQ = a, хп — аХп~\
16* 433
23.47. Найти с четырьмя верными знаками после запятой:
1) Наименьший положительный корень уравнения
xsin%+ 1 =0.
2) Два положительных корня — наименьший и ближайший
к нему — уравнения
cos х ch х — 1.
23.48. Решить с погрешностью не более чем 10-4 уравнение
4х — 51пх = 5,
выбрав для каждого корня сходящийся итерационный процесс.
23.49. Решить методом хорд уравнение с указанной по-
грешностью Д:
1) х3 — 4х + 2 = 0, Д=10-3.
2) х4 + х— 1=0, Д=10~3.
3) х3 — 3,2х2 + 3,1х — 2,2 = 0, Д = 10~3.
4) 0,1 sin х = х + 2, Д=10-3.
5) cosx = x2, Д=10-3.
6) х3 — 5х+1=0, Д = 10~5.
23.50. Методом хорд и методом касательных решить урав-
нение с указанной погрешностью Д:
1) х2 = 13, Д=10~8.
2) 2х3 + 2х2 — 11х + 3 = 0, Д = 10~6.
3J х3 + х2 + 2х —3=0, Д = 5-10~5.
23.51. Методом касательных решить уравнение с указанной
погрешностью Д:
1) х3- 2х — 2 = 0, Д = 5-10~5.
2) х3 + х —3 = 0, Д = 5-10~5.
3) 2х3 —7х2 + х + 9 = 0, Д = 10-3.
4) х2 + -^- = Юх, Д=10-3. 5) х = cos х, Д= 10~6»
6) xlgx=l, Д=10-4. 7) х + е*=1, Д=10-5.
8)xthx=l, Д=10~6.
9) tg х = х, Д = 5-10~5 (наименьший положительный ко-
рень).
10) ctgx = --~-1-, Л=10~3 (найти только два положу
тельных корня — наименьший и ближайший к нему)*
484
23.52. Методом касательных вычислить отрицательный ко-
рень уравнения
х4 _ Зх2 + 75х — Ю ООО = О
с тремя верными знаками после запятой.
23.53. Найти с четырьмя верными знаками чисто мнимые
корни уравнения
z sin z + 1 == 0.
23.54. Решить уравнение
х3 J-1,1х2 + 0,9х — 1,4 = 0
1) методом деления пополам с точностью 5*10~3; 2) методом
хорд с точностью 5-10~4; 3) методом касательных с точностью
5-10-4.
23.55. К какому из корней уравнения х3— х = 0 сходится
последовательность, построенная по методу касательных, в за-
висимости от выбора начального приближения Хо^ R?
23.56. Доказать, что для уравнения д/lх 1sign х — 0 метод
касательных йе сходится.
23.57. Проверить, что для функции
последовательность, построенная по методу касательных, на-
чиная с Хо = 1, сходится к числу, не являющемуся корнем
уравнения f (х) == 0.
23.58. Используя метод касательных, построить итерацион-
ный процесс 2-го порядка для вычисления
23.59. Доказать, что если х0 > 0, х п+1 = (хп + , то
(34)
где т = т'т{хп, а/хп}.
23.60. Доказать, что если g— двукратный корень уравнения
/(х) = 0, то для его нахождения можно использовать итера-
ционный процесс
xn+i = xn-2-pg± (35)
(модифицированный метод Ньютона). Указать достаточные ус-
ловия сходимости последовательности {хп} к корню g.
23.61. Какую точность дает двукратное применение комби-
нированного метода при вычислении корня уравнения
х4 — х — 1 = 0,
начиная с интервала {1,22; 1,23)?
23.62. Решить уравнение
х3 —4,1х2 + 6,1х— 1,6 = 0
1) методом деления пополам с точностью 5-10“3; 2) методом
хорд с точностью 5-10-4; 3) методом касательных с точностью
5-10“4; 4) комбинированным методом с точностью 5-10~4.
23.63. Вычислить комбинированным методом наибольший
корень уравнения х5— х — 0,2 = 0 с точностью 10“4.
23.64. Вычислить комбинированным методом корни урав-
нения
х4 — Зх2 + 75х — 10 000 = 0
из интервалов (—11;—10) и (9; 10) с точностью 10“4.
23.65. Вычислить наименьший положительный корень урав-
нения
xsinx = 0,5
с точностью 10“6.
23.66. Решить комбинированным методом с указанной по-
грешностью А уравнение:
1) 2х2 — е1-х = 0, Д = 10~5.
2) 2 - х - 1g х = 0, Д = 10~\
23.67. Доказать, что метод Ньютона (метод касательных)
имеет второй порядок.
23.68. Доказать, что итерационная формула
хп + %ахп
— о 2 I
%хп "Р а
для решения уравнения х2 — а, а> 0, имеет третий порядок.
23.69. Используя разложение функции по- формуле Тейлора
до 2-го порядка, получить итерационную формулу для решения
уравнения f(x) = O и доказать, что она имеет третий порядок:
1) Xn+i =Хп----------. (36)
(Г (xn))2--^f(xn)f"(x„)
V _ Y f (хп) f2 (Хп) f"
Х^~Х” f'(xn) 2(f'(xn))*
(формула Чебышёва).
23.70. Доказать, что наименьший положительный корень £
уравнения
ctgx = X — х, % > 2,
удовлетворяет неравенству
£ <______2..-—
Л + д/Л2 - 4
23.71. Пусть {хп}—возрастающая последовательность по-
ложительных корней уравнения xsinx=l. Доказать, что при
п—у оо:
I) х„ = л/г + о(1). 2) хп == лп + + о (X) •
486
3) х„ = ЯП + -— -------------(1
’ п 1 пп пРп3 \
23.72. Пусть {хп}—возрастающая последовательность по-
ложительных корней уравнения
tg*=-nh^-
Доказать, что при оо
х„ = яп + (яи)2 + о .
23.73. Пусть {хп}—возрастающая последовательность поло-
жительных корней уравнения
tgx = х.
Доказать, что при п->оо:
1) Х„=-у +ЛП + О(1).
§ 24. Вектор-функции. Кривые
1. Вектор-функции скалярного аргумента. Если X — подмно-
жество множества действительных чисел (XczR) и каждому
значению t^X поставлен в соответствие вектор г(/) трехмер-
ного пространства /?3, то говорят, что на множестве X задана
вектор-функция (или векторная функция) г(/) скалярного ар-
гумента t.
Если в пространстве R3 фиксирована декартова система ко-
ординат х, у, 2, то задание вектор-функции r(/), t <= X, равно-
сильно заданию трех скалярных функций x(t), y(t), z(t) — ко-
ординат вектора r(f) (эти функции называются координат-
ными функциями вектор-функции г (/)):
r(0 = U(0; //(0; z(0)-
Если i, j, k — координатные орты, то
r(0 = x(0i+ «/(/) j + z(/)k. (1)
Если начало всех векторов г(/) помещено в начало коорди-
нат, то они называются радиус-векторами, а множество их кон-
цов — годографом вектор-функции г (/), t е X. Физический
смысл годографа вектор-функции r(t) состоит в том, что он
является траекторией движущейся точки, совпадающей с кон-
цом радиус-вектора г(/), причем за параметр t можно принять
время.
Если вектор-функция г(/) определена в некоторой проколо-
той окрестности точки /0, то вектор а называется пределом
487
функции г(/) в точке /о (или, что то же самое, при если?
для любого е > О существует такое 6 > 0, что для всех /, удов-
летворяющих условию
R— /о|<б, /У=/о, (2>
выполняется неравенство
|г(/)-а|<е. (3)
В этом случае пишут
lim г (0 = а или lim г(/) = а. (4)
Геометрически это означает, что вектор г(/) при t->to стре-
мится к вектору а как по величине, так и по направленик>
^рис. 108).
Условие (2)—(3) равносильно тому, что для любой после-
-Довательности tn^X, tn=£t0, пеМ, такой, что lim/n = /0,
П->оо
имеет место равенство
lim г(/„) = а. (5)
П->оо
Если a = (ai; а2- аз), то для того, чтобы a = lim г(/), необ-
2->/о
ходимо и достаточно, чтобы
lim х (0 — ait lim у (t) — а2,
t-^t$ t-^tb
Если
lim г(/) = о,
/ ->/о
то вектор-функция г(/) называется
t —> /0.
lim z (t) = а3. (6)
(7)
бесконечно малой при
488
Если функция г (/) определена в некоторой окрестности
ТОЧКИ Z0 И
lim г (Z) = г (Zo), (8)
/->/о
то функция r(Z) называется непрерывной в точке tQ.
Если существует предел
lim Г(О~/(М - (9)
то он называется производной вектор-функции r(Z) в точке tQ
в обозначается г'(/q) или-^-(/0).
Если
Ы = Z —Zo, Аг = r(Z) — r(Z0) = r(Z0 +AZ) —r(Z0)
(вектор Аг называется приращением вектор-функции r(Z) в
точке Zo), то (рис. 109)
г'(/0) == lim (10)
Д/->0 1X1
Вектор-функция r(Z) = (x(t); y(t); z(t)) имеет в точке Zo
производную тогда и только тогда, когда ее координатные функ-
ции имеют в этой точке производные, причем
r'(Zo) = (x'(Z0); / (Zo); z'(Z0)). (11)
Если годограф вектор-функции r(Z) является траекторией
движущейся точки, а за параметр Z принято время, то произ-
водная
является мгновенной скоростью в момент времени Z = Zo.
Прямая, проходящая через конец Мо вектора r(Z0) в направ-
лении вектора Аг (см. рис. 109), называется секущей годо-
графа, а ее предельное положение при AZ->0 — касательной
Аг
к годографу в точке Л1о. Если Аг =# о, то вектор -& при любом
-знаке приращения AZ #= 0 всегда направлен по секущей в сто-
рону возрастания параметра Z; поэтому, если производная
t'(Zo)=#o, то согласно (10) она направлена по касательной
к годографу в точке 7И0 в сторону возрастания параметра Z.
В этом случае уравнение касательной имеет вид
г = г (Zo) (Zo) —°° и <С Ч~°о, (12J
или в координатном виде
* = *o + *'(Zo)^ У = Уо + Уг (Zo) Щ z=zo + z' (Z0)w, (13)
— ОО < и < + ОО,
489
где г(/о) = (хо; Уо', zo). Отсюда следует, что
* х0 __ у — Уо z — z0
х' (/о) у' (to) z' (/р) •
(14)
Для того чтобы вектор-функция, определенная в окрестности
точки to, имела в этой точке производную, необходимо и доста-
точно, чтобы ее приращение Дг в этой точке было представимо
в виде
Дг = аД^ + е(Д/)Д/, (15)
где lim е(Д/) = о. Из равенства (15) следует, что
А/ —^0
а == г'(/0),
т. е. равенстйо (15) можно записать в виде
Дг = г'(/о) А/ + е(Д0 А/. (16)
Бесконечно малая при t-+t0 вектор-функция а(/) называется
бесконечно малой более высокого порядка, чем бесконечно ма-
лая при t-+t0 скалярная функция р(/), если существует бес-
конечно малая при t-^to вектор-функция e(Z) такая, что
a(t) = р(Ов(О-
В этом случае пишут
а(0 = о(₽(0), (17)
Используя это обозначение, равенство (16) можно записать
в виде
. дг = г'(/0)Д^ + о(Д/), Д/->0. (18)
Линейная по аргументу Д/ вектор-функция г'(/0)Д/ назы-
вается дифференциалом вектор-функции г(/) в точке /0 и обо-
значается dr или, более подробно, dr(tQ). Приращение аргу-
мента Д/ в этом случае часто обозначают dt, таким образом,
dr = г' (/о) dt. (19)
Если вектор-функция r(Z) имеет в точке t0 производную, то
говорят также, что она в этой точке дифференцируема.
Производные и дифференциалы высших порядков опреде-
ляются для вектор-функций индуктивным образом.
Производная г<л> порядка п является производной от произ-
водной порядка п — 1:
r(n)^(r(«-i)); Г(°) = г (п=.1, 2, ...). (20)
Дифференциал dnr(f) порядка п определяется как диффе-
ренциал по переменной t от дифференциала dn~Ar(t) =
_ г^-^ (t}dtn~x порядка п—1 при условии, что приращение
аргумента t при взятии нового дифференциала совпадает со
старым приращением аргумента, т. е.
dnr (/) = d(/) dtn~l) = r(n) (/) dtn. (21)
490
Из этой формулы следует, что
= («=1. 2, ...). (22)
Если вектор-функция r(t) имеет в точке /0 производные до
порядка п включительно, то в окрестности этой точки справед-
лива формула Тейлора с остаточным членом в форме Пеано:
г(/) = г(/о) + -£^-(/-/о)+ ••• + ^^(t-t0)n +
+ о((/-/о)п), Мо. (23)
Если годограф вектор-функции есть траектория движущейся
точки, а за параметр t взято время, то вторая производная
г"(/0) является ускорением точки в момент времени t0.
Если а и b — векторы, то через (а, Ь) обозначается скаляр-
ное, а через [а, Ь] — векторное произведение', скалярное произ-
ведение (а, а) иногда обозначается а2. Для трех векторов а, b
и с через (а, Ь, с) обозначается их смешанное произведение
(а, Ь, с) — ([а, Ь], с).
Для вектор-функций справедливы следующие правила диф-
ференцирования:
(гао+г^оу^гио+г'ах (24)
(f(0r(0)' = r(0r(0 + n0r'(0, (25)
( П (0, r2 (0)' = «(Д r2 (/)) + (г, (0, r2 (/)), (26)
[»j (/), r2 (/)]' = [r, (/), r2 (/)] + [г, (0, Г2 (/)]. (27)
Пример 1. Построить годограф вектор-функции
r(Z) = a cos ti + a sin t j + bt k, teR, (28)
написать уравнение его касательной в произвольной точке и до-
казать, что она образует постоянный угол с осью z.
Для любой точки (х; у; z) годографа вектор-функции (28)
имеем х = a cos t, у = a sin t, z = Ы, и потому при любом
feR выполняется равенство х2 + у2 = а2, т. е. все точки годо-
графа вектор-функции (28) лежат на цилиндре, направляющей
которого является окружность х2 + у2 = а2 в плоскости пере-
менных х, у, а образующая параллельна оси z. Если параметр t
интерпретировать как время, то при равномерном движении по
окружности проекции конца радиус-вектора (28) на плоскость
переменных х, у его проекция на ось переменной z будет дви-
гаться равномерно и прямолинейно со скоростью Ъ Иначе го-
воря, аппликата точки годографа вектор-функции (28) растет
пропорционально углу поворота ее проекции на плоскость х, у.
Поэтому искомый годограф будет иметь вид, изображенный на
рис. ПО, и он называется винтовой линией. Для уточнения изо-
491
бражения можно составить таблицу положений точек годографа
для отдельных значений /, например таблицу
Для нахождения касательных к винтовой линии найдем?
производную вектор-функции (28):
г' (/) = sin t i + a cos t j + b k.
Отсюда следует, что уравнение касательной к винтовой линии
имеет вид
X — Хо _ У — У q _ 2 — 2р
— a sin /0 a cos tQ b ’
а для косинуса угла ф, образованного касательной с осью zt
справедливо равенство
(г' (О, Ю ь
COS ф = --....,
| Г (0 1 V«2+^2
таким образом, угол ф постоянен, это означает, что винтовая
линия пересекает под одним и тем же углом все образующие
цилиндра х2 + у2 = а2, на котором она расположена. А
Пример 2. Доказать, что если
г^)(/о) = о (£ = 1, 2, п— 1), г^(/0)¥= о, (29)
то уравнение касательной к годографу в конце радиус-вектора
г (/о) имеет вид
г = г(п)(/о)/+ г(/0), —оо</<4-оо. (30)
А Из условия (29) следует, что в рассматриваемом случае
формула Тейлора для вектор-функции г(/) имеет вид
Дг = г (/о + ДО - Г (/0) = 4 г<"> (/о) дг + О (Д/п), Д/ -> 0.
Поэтому для всех достаточно малых А/ выполняется условие
дг =# о и> следовательно^ прямая, проходящая через концы ра*
492
диус-векторов r(Z0) и г(#оЧ-ЛО» однозначно определена. Век-
Дг ««
тор параллелен этой прямой, и существует предел
Поэтому при Д/->0 существует предел указанной секущей, т. е.
существует касательная к годографу в конце радиус-вектора
г (/о) и ее уравнение имеет вид (30). А
Пример 3. Доказать, что если го — г (to) ф о, существует
го = г' (/0), е(/) — единичный вектор в направлении вектора г(0
и е0 = е(/0), то существует e' = ez(/0) и
г0 = (е0, г0) е0 +11*о । е0. (31)
Каков механический смысл этой формулы?
А Ясно, что из непрерывности r(t) в точке t0 и условия
Го¥=о следует, что в некоторой окрестности точки to выполня-
ется неравенство г(/)#=о, поэтому в этой окрестности опреде-
лена функция
е (А =.£19
е 1' IГ(о | ’
причем, очевидно,
|е(0 | = 1. (32)
Поскольку г — | г | е и
<iri);.,.=(VP);.,.=J42-l --^1 =(е0.гЭ,
то из дифференцируемости в точке to вектор-функции r(t) сле-
дует дифференцируемость в этой точке скалярной функции
г (t)
|г(0 | и вектор-функции е (/) = . Поэтому
I г \Ч I
га = r' Со) = (Ir I e)U0 = (I г Г е + | г | ez) |<=/о = (е0, г') е0 + | г01 е',
т. е. равенство (31) доказано. Из (32) следует, что е2(/)=1.
Дифференцируя это равенство, получим (е(/0), е'(/0)) = 0, что
означает, что векторы ео = е(^0) и eQ==ez(/0) ортогональны.
Поэтому в случае, когда годограф вектор-функции г(/) является
траекторией движущейся точки, а параметр t есть время, ра-
венство (31) показывает, что движение этой точки в каждый
момент времени tG можно рассматривать как результат сложе-
ния двух движений: поступательного в направлении радиус-век-
тора Го и вращательного по окружности радиуса | г0 ], т. е. в на-
правлении, перпендикулярном вектору г0. Формула (31) дает
разложение мгновенной скорости vo = r6 на радиальную состав-
ляющую (е0, Гд)е0, представляющую собой проекцию скорости
Vo на направление радиус-вектора г0, и трансверсальную со-
ставляющую | г01 вд в направлении вектора е^, т. е. перпен-
дикулярно вектору е0, а следовательно, и вектору г0. А
493
Пр и мер 4. Пусть вектор-функция r(Z) определена и не
обращается в нуль в некоторой окрестности U точки /о, и пусть
<p(Z)—наименьший неотрицательный угол, выраженный в радиа-
цах, м^КДу векторами r(Z0) и r(Z), ZeC7, 0^ф(/)^л; тогда
Аф =3 ф(’/) —ф(/0) =*= (?(/) (ибо ф(/о)=О). Положим Ikt == t—tQ.
Предел
lim
At ->о
I Дф
kt
(33)
называется угловой скоростью вращения вецтор-функции r(Z)
в точкё /о и обозначается через со = co(Z0; г). Доказать, что если
г0 = г (/0) =7^ о и существует производная г' = г' (/0), то суще-
ствует и-угловая скорость вращения co = (o(Z0;r), причем
т= 11'»'?! I . (34)
Г0
Для случая |r(Z)| = const получить отсюда формулу
Каков ее механический смысл?
А В силу существования производной tg вектор-функция
r(t) непрерывна в точке Zo. Отсюда и из условия г0 =И= о следует,
что для всех достаточно малых приращений А/ выполняется
неравенство r(Z0 + А/) */= о, и потому определен угол Аф между
векторами r0 = r(Z0) и r(Z0 + AZ), причем
lim Аф = 0.
At ->0
Для вычисления предела (33) заменим бесконечно малую
при AZ->0 функцию Аф на эквивалентную ей функцию эшАф,
которую найдем из равенства
| [г (Zfl), г + AZ)] | = ] г (to) 11 r (Zo + AZ) 11 sin Лф |.
Таким образом, будем иметь
a — lim |А₽ | — Hm I sil?A<p I— Hm । tr r + A<)11 ==
ЙоЫ “И M I A™0 lr(/o)l|r(/o + AOI|A/|
= 4 lim IHlskHlo+JOLI (36)
fg Af->0 | kt I
(здесь снова была использована непрерывность вектор-функции
r(Z) в точке Zo: lim г (Zo + AZ) == г (Zo)). Далее, в силу дифферен-
д*->о
цируемости функции r(Z) в точке Zo имеем
г (/0 + kf) = г0 + г' А/ + 8 (AZ) kt,
где lim 8(А/) = о. Подставив это выражение в (36) и заметив,
At “^0
что [г0>г0]=о, a lim [r0, е(А/)] = о, получим формулу (34).
494
Если ]г(/)| = г — постоянная, то, дифференцируя равенство
г* — г2, будем иметь(г0, г')—0,т. е. |r011 г' | cos ф=0, где ф — угол
между векторами г0 и г'. Поскольку г0 о, то либо г' = о,
либо ф = л/2 и, следовательно, зтф = 1. В обоих случаях
|[ro> ro']| = |ro||<||sint| = ro|r'|.
Подставляя это выражение в (34), получим формулу (35)’.
В случае, когда годограф вектор-функции г(/) является траек-
торией движения точки, а параметр t — временем и, следова-
тельно, г' = v — скоростью движения, в силу (35) получим
v I. I.
<о=у, v — I V |, Г = I г |,
т. е. формулу, связывающую значения угловой скорости со и ли-
нейной v при движении точки по поверхности шара |г| — г —
= const.
Пример 5. Доказать, что если вектор-функция г(/) непре-
рывна на отрезке [а; Ь] и дифференцируема внутри него, то
существует такая точка | е (а; Ь), что
|r(6)-r(a)|<|r'(g)|(&-a). (37)
А Если г(а) = г(&), то равенство (37) верно при любом
выборе точки g^(&;6). Поэтому предположим, что г(а)^=
и обозначим через е единичный вектор в направлении
вектора г(&) — г (а). Тогда
| г (b) — г (а) I = (г (6) — г (а), е) = (г (&), е) — (г (а), е). (38)
Рассмотрим, скалярную функцию f (/) = (г(/), е). Она удовле-
творяет условиям теоремы Лагранжа о среднем значении, по-
этому существует такая точка §е(а; &), что f(b) — f(a) —
= f' (I) (b — a), т. e.
(r(&), e) —(r(a), e) = (r'(g), e) (b-a).
Отсюда, применив неравенство Коши для оценки правой части
этого равенства:
| (г'(Ю.е) |^|г'Ш | |e| = |r'(g) |
и воспользовавшись равенством (38), получим неравенство
(37). А
24.1. Построить годографы вектор-функций (—оо < t < + оо):
l)x = cos/, z/= sin/, z = l. 2)x = sin/, z/ = cos/, z — t2
3) x — 1, y = t, z — t2. 4) x — t, y — t2, z = t3.
5) x — a(t — sin/), y = a(l — cos/), z = 0, a > 0.
6) x = /2-2/ + 3, ,z/ = /2 — 2/+1, z = 0.
7)x = asin2/, y = bcos2t, z = t.
495
24.2. Доказать, что годограф вектор-функции
г = sin 2<р i 4- (1 — cos 2tp) j + 2cos ср k
лежит на сфере.
24.3. Доказать, что годограф вектор-функции
г = (а^2 + + <4)1 + (а^2 + b2t + с2) j + (аз/2 + b3t + е3) к
лежит в некоторой плоскости, и найти уравнение этой пло-
скости.
24.4. Доказать: если limr(f) = a, то lim|г(Z) | = |а|. Верно
t-^to
ли обратное утверждение?
24.5. Доказать, что вектор-функция
г (/) — t i + sin t j
является бесконечно малой при /->0.
24.6. Найти пределы вектор-функций:
1) г(0=т+7> Н------—1-------t----k ПРИ *_>0-
/jx sin t . , In (t/л) . . * ,
2) г(0 = 7тг^4 * * * 8+ я_/1+к ПРИ
24.7. Доказать, что для того, чтобы вектор-функция г(/)'
имела при предел, равный а, необходимо и достаточно,
чтобы ее можно было представить в виде
r(/) = а + а(/),
где а(^) — бесконечно малая при вектор-функция.
24.8. Доказать: если limr(/) = a и Кт/(/) = Л, то
t -> Zq t -> to
limf(/)r(/) = A,a.
24.9. Доказать: если lim tj (0 = a, limr2(0 —b и lim MO =
t->t„ i-»to
— c, to:
1) lim (MO + MO) = a + b.
2) lim (MO, r2(0) = (a, b).
t-> to
3) lim [г Д0. r2 (/)] = [a, b],
Г->Л
4) lim (г ДО. r2(0, M0) = (a, b, c).
t t o
24.10. Доказать, что если скалярные функции М(0, ^(0
и вектор-функции гД/), г2(/), г3(/) непрерывны в точке /0, то
в этой точке непрерывны и функции:
1) MOMO + MWO. 2) (гдо, г2(0)
3) [МО, г2(0]. 4) (гДО, МО. Гз(0).
5)|ГДОЬ
496
24.11. Найти производную вектор-функции г(/) и написать
уравнение касательной в произвольной точке ее годографа,
если:
1) г (/) = ti + Z2j + i3k. 2) г (t) — sin t i + cos t j — k.
3) r (/) = a sin2 co/ i 4~ b cos2 at j + t k.
24.12. Найти производные функций:
1) r2(0- 2) УгЧО? 3) [[r(/),r'(/)],r"(/)].
4) (r(/),r'(O,r"(/)).
24.13. Доказать, что если длина векторов г(/) постоянна
в окрестности точки /0 и существует производная г'(/0), то век-
торы г (/о) и г'(/о) ортогональны. Каков механический смысл
этого факта?
24.14. Доказать, что для того, чтобы во всех точках неко-
торого интервала векторы r(f) и г'(0 были ортогональны, не-
обходимо и достаточно, чтобы скалярная функция |г(/)| была
постоянной на этом интервале.
24.15. Доказать, что для того, чтобы дифференцируемая и не
обращающаяся в нуль на интервале (а; Ь) вектор-функция
г(/) имела постоянное направление (т. е. чтобы при любом
t^(a\b) вектор г(/) был коллинеарен, например, с вектором
r((& + 6)/2)), необходимо и достаточно, чтобы векторы г(/)
и г'(/) были коллинеарны.
24.16. Пусть вектор-функция r = r(f) имеет в точке про-
изводную. Будет ли дифференцируема в этой точке функция
|г(/)|? Верны ли в этой точке равенства |г,| = 1г|/ и (г> Н =
= |г||гГ?
24.17. Доказать, что если r — xi(x,y,z,£)i4-x2(x,f/,z,/)j-|-
Ч-х3 (х, у, г,/) к, где xi, х2, х3— непрерывно дифференцируемые
функции своих аргументов, а х, у, z — непрерывно дифферен-
цируемые функции от /, то
24.18. Построить годографы вектор-функции г(/) —
~ (a sin /, —a cos bt'2) и ее производной.
24.19. Пользуясь определением производной вектор-функции,
доказать формулы:
1) (rj + г2)'= + r2.
2) (fr)' = f'r + fr', f — скалярная функция.
3) (rp r2)' = «, r2) + (rp r').
4) [rn г2Г = [г;, r2] + [rp r2'].
5) (rp r2, r3)' = (r[, r2, r3) + (rp r', r3) + (rp r2, r;).
497
24.20. Доказать: если г = a cos <$t + b sin со/, где о, а и b —
постоянные, то:
[г’ 1г] = ЬЬ 2) + ®2г = °-
24.21. Доказать: если г = аею/ + Ье~®*, где <о, а и b — по-
стоянные, то
24.22. Доказать, что если вектор-функция г(/) дифференци-
руема в точке /о, то она и непрерывна в ней.
24.23. Пусть вектор-функция r(Z) удовлетворяет дифферен-
циальному уравнению г" = [г'? а], где а — постоянный вектор.
Выразить через а и г':
1) [rz,г"]2. 2) (г', г", г'").
24.24. Пусть для дважды дифференцируемой на отрезке
[а; Ь] вектор-функции г(/) во всех точках этого отрезка выпол-
няются условия
(r(Z),rz(/),r'z(/)) = O, [г(/),/(/)]#= о.
Доказать, что тогда годограф вектор-функции г(/) лежит на
некоторой плоскости.
24.25. Доказать, что если у дважды дифференцируемой на
отрезке [а\ 6] вектор-функции г(/) во всех точках этого отрезка
векторы г'(/) и г"(/) отличны от нуля и коллинеарны, то годо-
граф вектор-функции г(/) является отрезком прямой.
24.26. Доказать, что годографом вектор-функции г(/) =
= а + /Ь4-^2с, /еР, где а, b и с — постоянные векторы, при-
чем векторы b и с не коллинеарны, является парабола. Что
будет представлять из себя годограф, если векторы b и с кол-
линеарны?
24.27. Доказать, что годограф вектор-функции г(0 = а-^
+ cos t b + sin / с, 0 2л, где а, b и с — постоянные векторы,
причем векторы b и с не коллинеарны, является эллипсом.
24.28. Доказать, что траектория материальной точки, дви-
жущейся под действием центральной силы, является плоской.
24.29. Траектория движения точки задана в цилиндрических
координатах:
r(/) = (pcoscp; psintp; г),
где t — время, р(/), ф(/), z(t)—известные функции. Найти:
1) Косинус угла а между радиус-вектором движущейся
точки и вектором ее мгновенной скорости.
2) Величину ускорения в случае движения по цилиндру
р = ро.
498
24.30. Траектория движущейся точки задана в сферических
координатах:
r(Z) = (pcoscpcos0; р sin ср cos 0; psinO),
где t — время, р(0< ф(0» 0(0— известные функции. Найти ве-
личину мгновенной скорости.
24.31. Пусть т — масса точки, F=F(0— действующая на
нее сила, r = r(f) — закон движения точки, а = а(/) — ее уско-
рение, W — W (t)— кинетическая энергия (t — время, т — по-
стоянная). Из закона Ньютона F = та вывести формулу
dW = (F, dr).
24.32. При условиях предыдущей задачи доказать формулу
dN = М dt, где N — момент количества движения точки отно-
сительно произвольно выбранного начала координат О, М —
момент силы F относительно точки О. (Количеством движения
материальной точки называется вектор, равный произведению
ее массы на скорость. Если какой-либо вектор b приложен
к точке Р, то моментом вектора b относительно точки О назы-
вается вектор [ОР, Ь].)
24.33. Привести пример дифференцируемой вектор-функции
r(0, a^Zt^b, для которой не существует такой точки £<=
е [а; Ь], что г (b) — г (а) = г'(§) (Ь — а) (т. е. показать, что для
вектор-функций в этом смысле неверен аналог формулы конеч-
ных приращений Лагранжа).
24.34. Доказать, что для того, чтобы дифференцируемая на
интервале (а; Ь) вектор-функция г(/) была постоянной, т. е.
г(/) = с, а < t < ft, с — постоянный вектор, необходимо и до-
статочно, чтобы производная г'(/) тождественно равнялась
нулю на интервале (а;Ь).
2. Кривые на плоскости и в пространстве. Кривой (или, бо-
лее подробно, параметрически заданной кривой) называется
множество Г в пространстве Р3, заданное как непрерывный
образ некоторого отрезка [а; &], т. е.
где M(t)— непрерывное отображение. В этом случае пишут
Г = {M(t)\a^t^b}. (39)
Если в пространстве Р3 фиксирована декартова система ко-
ординат х, yf z, то задание отображения M(t) равносильно за-
данию таких трех функций
х(0, y(t), z(t), a^Zt^Zb, (40)
называемых координатными функциями отображения M(t), что
W) = (*(0;y(0!*(0)- (41)
Непрерывность отображения M(t) означает непрерывность
на отрезке [а;Ь] всех его координатных функций. Отображение
499
M(t) называется параметризацией или представлением кри~
вой Г; а отображение (40) при выполнении условия (41) — ее
координатным представлением. Переменная t называется пара-
метром на кривой Г.
Множество значений отображения M(t) в пространстве R3
называется носителем кривой Г. Если одна и та же точка носи-
теля кривой Г является при отображении Л4(/) образом двух
разных точек отрезка [а;Ь], то она называется точкой самопе-
ресечения (или кратной точкой) кривой. Обычно кривая и ее
носитель обозначаются одной и той же буквой, а часто носи-
тель кривой называется также кривой.
Например, когда говорят, что график уравнения F(x, г/) = 0
на плоскости или пересечение графиков уравнений F\ (х, у, z) =0,.
F2(x, у, z) — 0 в пространстве являются кривыми, то под этим
понимают, что эти множества являются носителями соответ-
ствующих кривых.
Если
/ = Ц^), ax^tx^ Ьх,
(42)
— строго монотонная непрерывная функция, то отображение
Л4(/(/0), пи < t} Ьх,
называется представлением той же самой кривой (39), а функ-
ция (42) — допустимым преобразованием параметра.
Таким образом, кривая является определенным классом не-
прерывных отображений отрезков в пространстве, связанных
допустимыми преобразованиями параметра.
Вектор-функция
г (/) = (х(/); y(t)\ z(t)), а t Ь,
(43)
называется векторным представлением кривой (39), причем пи-
шут
Г= {r(t);a^t^b}.
Таким образом, кривую Г можно задать в одном из трех
видов:
Г = {M(t)-,a<^t^b},
Г = {%(/), y(t), z(f)\ а t b},
Г= {r(t)-,a^t^b}.
Иногда под кривой понимается также и множество в про-
странстве, заданное как непрерывный образ любого промежутка
числовой оси (т. е. не обязательно отрезка, а возможно, интер-
вала или полуинтервала).
Всякая параметризация кривой порождает на ней опреде-
ленный порядок точек: если Г = {Л4(/); а t Ь}, то точка
Л4(/2) называется следующей за точкой Л4(/1), если t2 > 6.
Если на кривой задан порядок точек (для чего достаточно за-
фиксировать некоторую ее параметризацию), то она называется
500
ориентированной кривой. Для ориентированных кривых допу-
стимыми преобразованиями параметра являются только строго
возрастающие функции (42). Если Г = {Л1(/); а i 6}, то
ориентированная кривая, заданная представлением М (а + b—t),,
b, называется кривой, ориентированной противополож-
но заданной кривой Г.
Если координатные функции (40) отображения 7И(/)
(см. (41)) или, что то же самое, координатные функции вектор-
функции (43) дифференцируемы, либо непрерывно дифферен-
цируемы, либо дважды дифференцируемы и т. д., то кривая
'(39) называется соответственно дифференцируемой, либо не-
прерывно дифференцируемой, либо дважды дифференцируемой
и т. д. Для дифференцируемой (непрерывно дифференцируемой,
дважды дифференцируемой и т. д.) кривой допустимыми преоб-
разованиями параметра являются только дифференцируемые-
(соответственно непрерывно дифференцируемые, дважды диф-
ференцируемые и т. д.) преобразования параметра, у которых
производная не обращается в нуль.
Точка М (а) называется начальной, а точка М(Ь)— конеч-
ной точкой кривой (39). Если М(а) = М(Ь), то кривая (39) на-
зывается замкнутой.
Если кривая лежит в некоторой плоскости, то она назы-
вается плоской, а если она лежит на некоторой сфере, то —
сферической кривой. Если на плоскости, на которой лежит-
рассматриваемая плоская кривая, задана полярная система-
координат р, ср, то задание кривой уравнением р = р(ср), а^.
ср называется ее представлением в полярных коорди-
натах. Если воспользоваться формулами перехода от прямо-
угольных декартовых координат х, у к полярным: x = pcoscp,,
t/ = psincp, то из представления кривой в полярных координа-
тах можно получить ее параметрическое представление с пара-
метром <р:
х = р (ср) cos ср, у — р (ср) sin ср, а ср Ъ.
Если заданы две кривые
Г1 = {ЛНО; a^t^b} и Г2 — {М2(/); b^t^c},
причем Л<1(6) = М2(&), то кривая
где
Г — {M(t)\a^t^c},
если
U Ы2(/), если
называется объединением (суммой) кривых и Г2 и обозна-
чается через Г1 U Г2.
Пусть Г = {r(/); а t Ь} —дифференцируемая кривая и-
г'(^о)^о (или г(/0)= ... = г(п“1)(/0) = о, г(/г)(/0)#= о),
е [a; t], Тогда прямая, являющаяся касательной к годографу
501.
вектор-функции г(/) в конце радиус-вектора r(Z0), называется
и касательной к кривой Г. Так определенная касательная к кри-
вой не зависит от выбора параметризации кривой.
Вектор называется касательным вектором к кри-
вой Г, а его направление — положительным направлением на
касательной при фиксированной ее пара-
метризации; оно соответствует возраста-
нию параметра, поэтому вектор г' (/0)
называют также касательным вектором
ориентированной кривой Г.
Плоскость, проходящая через ко-
нец радиус-вектора г(/0) и перпендику-
лярная к касательной прямой, назы-
Рис. 111.
вается нормальной плоскостью (в соответствующей точке
кривой), а каждая прямая, проходящая через конец указанного
радиус-вектора и лежащая в нормальной плоскости, называется
нормалью.
Углом между ориентированными кривыми, пересекающимися
в некоторой точке, называется угол между их касательными
в этой точке.
Пусть
Г = {r(/); а t Ь} (44)
— кривая, T = — разбиение отрезка \а\ b]: а = tQ <
< и < ... < tn = &, Lx — ломаная с вершинами в концах ра-
диус-векторов r(/z) (I = 0, 1, ..., п) (рис. 111), от — ее длина:
Gx= Z |гЮ — Г
1=1
Величина
Sr =sup от,
т
где верхняя грань берется по возможным разбиениям т отрезка
[а; &], называется длиной кривой (44).
Если Sr < +°°, то кривая Г называется спрямляемой.
Теорема 1. Если кривая (44) непрерывно дифференци-
руема, то она спрямляема и ее длина Sr удовлетворяет нера-
венству
| г (&) — г (а) | Sr (b — a) max | г' (/) (45)
[а; Ь]
Теорема 2. Если кривая (44) непрерывно дифференци-
руема, то переменная длина дуги $, отсчитываемая от начала
кривой или соответственно от ее конца, является возрастающей,
соответственно убывающей, непрерывно дифференцируемой
функцией параметра t\ при этом
ds
dt
dr I ds I dr
-тс , соответственно -тт = ~ -тт
dt I dt I dt
(46)
502
Если г (/) = (%(/); у(/); z(f)), то
ds . /( dx X2 । / dy \2 । ( dz X2
^=±л/Ы) +Ш +Ьг) •
(47)
Когда параметром непрерывно дифференцируемой кривой
является переменная длина дуги $:
Г= {r(s);0<s<S}, r(s)=-(x(s);i/(s);Z(s)), (48)
то
|£Н-
т. е. вектор
является единичным касательным вектором к кривой (48). По-
этому, если cos a, cos р и cosy — направляющие косинусы по-'
ложительного направления касательной к кривой (48), т. е.
т = (cos а; cos Р; cos у),
то
dx dy п dz
= cosa, — = cosp, = cosy. (50)
ds ds r ds r 7
Если кривая является графиком функции y = f(x), а^
х ^.Ь, и переменная длина ее дуг s — s(x) отсчитывается от
начала графика (а\ f(a)), то
£-71+ (?'«)*•
Точка (x(tQ); y(to)-, z(tQ)) кривой (44) называется особощ
если г'(/о) = о; если же г,(/0)=#о, то — неособой.
У всякой непрерывно дифференцируемой кривой (44) без
особых точек существует ее представление r(s), 0 •$ 5,
в котором за параметр s взята переменная длина дуги этой
кривой.
Пример 6. Представить пересечение шара %2 + у2 + z2 =
— R2 и цилиндра х2 + у2 = Rx в виде параметрически задан-
ной кривой (точнее, носителя кривой).
А Из уравнения х2 + У2 — Rx следует, что 0 х R. По-
этому можно положить х — R sin2 t. Тогда
у2 = Rx — х2 — R2 sin21 cos2 /,
z2 = R2 — (%2 + y2) = R2 — Rx — R2 cos2 /,
и легко проверить, что кривая
х — R sin2 /, у = R sin t cos /,
z — R cos/, 0^С/=С2л, J (50
совпадает с пересечением сферы x2 + у2 + z2 — R2 и цилиндра
x2 4- у2 = Rx, причём точка (/?; 0; 0) получается при значениях
параметров / = л/2 и / = Зл/2, т. е. является точкой самопе-
503
Рис. 112.
ресечения. Кривая (51)' называ-
ется кривой Вивиани (рис. 112). А!
Пример 7. Найти касатель-
ные прямые и нормальные плос-
кости кривой z — х2 + у\ у — к.
А Примем переменную х за
параметр на данной кривой.
Тогда представление кривой бу-
дет иметь вид
г(х) = (х; х; 2х2).
Найдя отсюда касательный век-
тор г'(х) = (1; 1; 4х), получим, в
•силу формулы (14), уравнение касательной в точке {хо; х0; 2х^)
в виде
z — 2xq
Х-Хо^^-Хо^-^.
Поскольку вектор г'(х0) = (1; 1; 4х0) перпендикулярен нор-
мальной плоскости кривой в рассматриваемой точке, то урав-
нение этой плоскости имеет вид
(х — хо) + (у — х0) 4- 4х0 (г — 2х2) = О,
т. е.
х + У + 4x0z = 2х0 + 8x3.
Пример8. При каких а кривая
x = ea*cos/, y = eat sinf, 1
z = eatу — oo < t < 4~ oo, J
пересекает все образующие конуса х2 4- У2 — г2 под углом л/4?
А Простой подстановкой в уравнение конуса легко прове-
рить, что кривая (52) действительно лежит на нем. Если
?г(/)— вектор с координатами (52), то касательный вектор г'==
= г'(/) к кривой (52) имеет вид
г' (/) = (eat (a cos t — sin t); eat (a sin t 4- cos t); aeat),
.а вектор I = !(/), направленный по образующей конуса x2 4d
4~ г/2 = 22 в той же точке кривой (52), — вид
1(/) = (х; у\ х2 4- y2} = {eat cos/; ea/sinZ; eat}.
Поскольку
[r'(OI = eaf V2a2+1. 11(0\ = eat V2 ,
10 _
COS (Pl) = = -A2._.. (53).
Ir'IHI V2as+1
• 504
Поэтому, если угол между векторами г' и 1 равен л/4 или Зл/4,.
то из (53) получается уравнение
V2a2 +1 V2 ’
откуда а — ± 1/V2 • А
Пример 9. Найти длину дуги s(t) винтовой линии
х — a cos/, у— a sin/, z — bt, 0 ^ / < +°°, (54)
и получить параметризацию винтовой линии, когда за параметр
на ней принята переменная длина дуги.
А Поскольку для касательного вектора г'(/) винтовой линии
имеет место формула
г'(/) — (—а sin а cos Ь),
то, в силу формулы (46), для производной по параметру t дли-
ны дуги, отсчитываемой в сторону возрастания параметра, бу-
дем иметь
4 = 7^4^.
Если производная некоторой функции постоянна, то сама функ-
ция линейна, и так как в данном случае s(0) = 0, то
s (/) = / 'у/а2 + Ь2, /^0.
Подставляя /=—т=^=- в формулы (54), получим
у а2 + Ь2
s s
х — a cos / 2 . , 2 , У — а sm »
V^2 + ^2 V#2 + Ь2
__ bs
~ '\/а2 + Ь2 * А
24.35. Составить параметрическое уравнение развернутой
окружности, т. е. траектории конца туго натянутой нити, сматы-
вающейся с неподвижной круглой плоской катушки.
24.36. Прямая OL, не перпендикулярная оси Ozt равномерно
вращается вокруг нее с постоянной угловой скоростью со.
Точка М движется по прямой OL: 1) со скоростью, пропорцио-
нальной расстоянию ОМ подвижной точки М до точки О;
2) с постоянной скоростью. В первом случае точка М описы-
вает коническую спираль, а во втором — коническую винтовую
линию. Написать параметрические уравнения этих кривых.
24.37. Доказать, что уравнения
х = cos /, у = sin /, —л/2 t л/2,
и ______
х = д//(2-0, у = 0</<2,
являются параметризациями одной и той же кривой.
505
24.38. Доказать, что уравнения
х = a cos у = b sin t, —л < t < л,
и
^==6т^7?’ — °°<^< + оо>
являются параметризациями одной и той же кривой. Как точка
движется по этой кривой, когда параметр t растет от —сю до
4-00?
24.39. Показать, что кривая
х — eat cos t, у = eat sin t, z== eat
лежит на конусе z2 = x2 + У2-
24.40. Показать, что кривая
/ /2 ~ /3
х “ 1 -Н2 -Н4 ’ У ~ 1 + t2 + t4 ’ Z ~ 1 +12 + t4
является сферической кривой.
24.41. При каком условии на матрицу (ац) j = 1, 2, 3)
кривая
X = «пФ (0 + 012’1’ (0 + «13% (0 + &1,
У = «21Ф (0 + «22’1’ (0 + «23% (О + Ь2.
z = а31ф (/) + а32ч|) (/) + а33х (/) + Ь3
является плоской кривой?
24.42. Доказать, что проекция кривой Вивиани
х = R sin2 /, у = R sin t cos t, z = R cos t, 0 2л,
на плоскость переменных х и z является дугой параболы.
24.43. Найти проекцию кривой x = ezsin/, y = e/cos/,
z = /, —сю < t < 4-°О, на плоскость переменных х и у.
24.44. Доказать, что проекция винтовой линии
x=acosf, // = &sin^, z = bt, — сю < t <Z 4~oo,
на плоскость переменных у и z является синусоидой.
24.45. Доказать, что при переносе начала координат в точку
0\ — (0; 0; рб) и повороте осей абсцисс и ординат вокруг новой
оси аппликат на угол (3 представлению винтовой линии х =
= acos/, у = a sin /, z — bt можно придать вид Xi — a cos t\9
у\ — a sin Zi, zi = bt\. Это показывает, что винтовая линия спо~
собна скользить сама по себе.
24.46. Найти уравнение касательной к кривой:
1) х — е\ у = е~*, z—t2 при t = 1.
2) х = е* cos /, у — e* sin t, z — e1 при t — 0.
24.47. Составить уравнение касательной к кривой
х = а (/ — sin /), у — а (1 — cos /), z = 4а sin (//2)
при t = л/2. Какой угол образует эта касательная с осью Oz?
506
24.48. Найти уравнение касательной прямой и нормальной
плоскости кривой х = /4, у = /3, z = Z2 в произвольной ее точке.
24.49. Найти касательную к кривой Вивиани (см. 24.42), па-
раллельную плоскости у = 0.
24.50. В каких точках касательная к кривой х = 3/ — г3,
у == З/2, z = 3t + t3 параллельна плоскости Зх + у + z + 2 — 0?
24.51. Найти нормальную плоскость кривой z — х2 + у2,
у %, перпендикулярную прямой х = у = z.
24.52. Найти касательную к кривой x2 + f/2=10, y2-\-z2 —
5= 25 в точке (1; 3; 4).
24.53. Найти косинусы углов с осями координат у касатель-
ных к кривой х2 = 2az, у2 = 2bz.
24.54. К кривой у2 = 2рх, z2 = 2qx проведена касательная
в точке, в которой х = (р + q) /%. Найти длину отрезка этой
касательной от точки касания до плоскости х == 0.
24.55. Доказать, что нормальные плоскости кривой х =
= a cos /, у — a sin a sin /, z — a cos a sin t проходят через пря-
мую х = 0, z + у tg а — 0.
24.56. Доказать, что касательные к кривой х2 = Зу, 2ху —9z
образуют постоянный угол с некоторым определенным направ-
лением.
24.57. Координаты точек некоторой кривой удовлетворяют
соотношению
(х2 + У2 + z2 — a2) {dx2 -j- dy2 + dz2) — (xdx-{-ydy-\-z dz)2.
Доказать, что касательные к этой кривой касаются шара х2 -j-
н- У2 + Z2 = а2.
24.58. Доказать, что касательные к кривой
х — a (sin t + cos t), у = a (sin t — cos t), z = Ье~1
пересекают плоскость переменных х и у по окружности х2 +
4- у% = 4а2.
24.59. Написать уравнение касательной и нормальной пло-
скости кривой х = t, у = t2, z = в точке (1; 1; 1). Какая
кривая получится в пересечении касательных с плоскостью пе-
ременных х, у?
24.60. Найти уравнение нормальной плоскости в произволь-
ной точке кривой х2 + у2 ~ 1, у2 + z2 = 1 (у ±1).
24.61. Доказать, что все нормальные плоскости кривой Ви-
виани x = asin2£, у — a sin t cos t, z = acost проходят через
начало координат.
24.62. Доказать, что если все нормальные плоскости про-
странственной кривой проходят через фиксированную точку, то
кривая является сферической.
24.63. Доказать, что кривая х — е* cos /, у — ef sin /, z = el
пересекает все образующие конуса х2 Д- у2 = z2 под одним и тем
Же углом.
24.64. Доказать, что кривые пересечения цилиндров у2 +
d- Z2 = Ь2 с поверхностью ху = az пересекают все образующие
507
'этой поверхности, принадлежащие одной системе, под прямым
углом.
24.65. Доказать, что кривая х = a tg /, у — b cos t, z —
= о sin t лежит на поверхности параболоида и пересекает все
его образующие одной системы под прямым углом.
24.66. Кривая, называемая локсодромией, определяется урав-
нением
<P = «lntg(-J--y),
где 0 — широта, а ф— долгота точки на шаре. Доказать, что
она пересекает меридианы шара под углом а, тангенс которого
равен а.
Сформулируем определение стереографической проекции плоскости на ка-
сающуюся ее сферу. Пусть в пространстве /?3 фиксирована декартова прямо-
угольная система координат х, у, г и за-
дан шар радиуса а/2 с центром в точке
В = (0; 0; а/2) и, следовательно, касаю-
щийся плоскости переменных х и у
(рис. 113). Его уравнение имеет вид
х2 у2 z2 __ aZt (55)
Соединим прямой верхнюю точку
шара, т. е. точку А = (0; 0; а), с про-
извольно фиксированной точкой М ==»
= У\ 0) плоскости переменных хи у.
Тогда точка Mi = (хн ус в которой
эта прямая пересечет сферу (55), на-
зывается стереографической проекцией
точки М на сферу (55), а точка М —
стереографической проекцией точки сфе-
ры Mi на рассматриваемую плоскость.
Стереографическая проекция устанавли-
вает взаимно однозначное соответствие между точками плоскости и сферы
с выколотой точкой А. Координаты точек Л/ и Mi связаны соотношениям и5
.. __ а2У „ а(х2 + у2)
1 ~ х2 + у2 + а2 ’ У' х2 + у2 + а2 9 1 х2 + у2 + а2 ‘
(56)
24.67. Доказать, что стереографическая проекция дает кон*
формное • отображение, т. е. что кривые на плоскости пересе-
каются под тем же углом, что и их образы на сфере.
24.68. Доказать, что кривая р = ех<₽, расположенная на пло-
скости переменных х и у так, что полярная ось совпадает с по-
ложительной частью оси х, при стереографической проекции
(56) отображается на локсодромию.
24.69. Доказать, что окружности на шаре при стереографи-
ческой проекции переходят в окружности или прямые на пло-
скости.
24.70. Центральная проекция координатной плоскости пере-
менных х, у на полусферу х2 + у2 + z2 = 2az, 0 z < а, со-
508
стоит в следующем. Произвольно фиксированная точка М =
= (%; у\ 0) плоскости переменных х и у соединяется прямой
с центром указанной полусферы, т. е. с точкой Л = (О;0;а).
Точка Mi, в которой эта прямая пересекает полусферу, прини-
мается за изображение точки М на полусфере. Доказать, что
эта проекция не является конформным отображением, т. е. она
не сохраняет, вообще говоря, углы между кривыми.
24.71. Найти производную длины дуги по параметру для
следующих кривых:
1) Цепной линии у = ach(x/а),—а х а.
2) Эллипса х = a cos /, у = b sin /, 0 t 2л.
3) Гиперболы х — a ch t,у — b sh /, —оо < t < Д-оо.
4) Астроиды х — a cos31, у = a sin3 t, 0 t 2л.
5) Циклоиды х = аЦ — sin t), у — а (1 — cos t), —оо < / <;
>< Д-оо.
6) Винтовой линии х = a cos t. у — a sin t, z — ЬГ —оо <;
< t < +оо.
7) Кривой Вивиани х = R sin21, у = Rsint cos /, z = R cos ty
0 t 2л.
24.72. Пусть плоская кривая Г задана в полярных координа-
тах уравнением р==р(ф), где функция р(ф) непрерывно диф-
ференцируема на некотором отрезке [а; 6]. Доказать, что если
s = s(cp) есть длина дуги кривой Г, отсчитываемая от ее на-
чала, то _________________________________
#-V(£)’+*
24.73. Найти производную длины дуги для следующих кри-
вых, заданных в полярных координатах:
1) Архимедовой спирали р = aq.
2) Гиперболической спирали р = а/ф.
3) Логарифмической спирали р — аеь®, —оо < ф < Д-оо.
24.74. Доказать, что граница ограниченной выпуклой фигуры
на плоскости является спрямляемой кривой.
24.75. Доказать, что при объединении кривых их длины скла-
дываются: если Г = Г1 U Гг, то Sr= Sri+ Sr2.
3. Кривизна и кручение кривой. Пусть
Г= {r(s); (57)
дважды непрерывно дифференцируемая кривая, s — перемен- -
dv
ная длина ее дуги и т = т (s) = -----единичный касательный
вектор. Угловая скорость вращения (см. (33)) касательного
509
вектора т в данной точке кривой называется кривизной кривой
в этой точке и обозначается k = k(s), т. е. (см. (35))
fe(s) = w(s; r) = |-^-(s)|. (58)
Обратная величина к кривизне называется радиусом кри-
визны кривой в данной точке:
<59>
Если Л($о)=#О, soe[a; 6], то единичный вектор в направ-
dx
лении вектора (s0) (он перпендикулярен вектору t = t(s0))
называется главным нормальным вектором и обозначается
v = v(5o). Таким образом,
dr
= (60)
Прямая, проходящая через точку кривой параллельно вектору
v, называется главной нормалью.
Векторное произведение [т, v] называется бинормальным
вектором и обозначается через 0, т. е.
Р = [*,*]. (61)
Прямая, проходящая через точку кривой параллельно вектору
Р, называется бинормалью. Если кривая (57) трижды непре-
рывно дифференцируема, то производная бинормального век-
тора р коллинеарна с вектором v; множитель, на который надо
умножить вектор v, чтобы получился вектор обозначается
через —х:
Коэффициент x = x(s) называется кручением кривой в дан-
ной ее точке. Для производной справедлива формула
-^ = _йт + хр. (63)
Формулы (60), (62) и (63) называются формулами Френе.
Для кривой Г уравнения
k = k(s), x = x(s) (64)
(5 — переменная длина дуги на кривой Г, k — ее кривизна,
а х — кручение) называются натуральными уравнениями кри-
вой Тетраэдр с вершиной в точке кривой Г, ребра которого
имеют длину, равную единице, и направлены по векторам т, v
и р, называется сопровождающим трехгранником Френе.
Иногда, для краткости, сами векторы v и р называются соот-
ветственно главной нормалью и бинормалью.
510
Если кривая Г = {г (t); а t Ь} трижды непрерывно
дифференцируема (t — произвольный параметр), то в предпо-
ложении, что знаменатели написанных ниже дробей не обра-
щаются в нуль, имеют место следующие формулы:
„ _ [[г\гЧ И
|[[г',г"],г']| ’
(г', г", г"') _ (г', г", г"')
Х — fe2 I г' I6 I [г', г"] I2
или в координатном виде:
. _ V(/z" - z'z/'T + (z'x" - x'z")2 + (х'/' - /х")2
(x'2 + /2 + z'2)3/2
х' у' г'
х" у" z"
___________________х"' у"' z'"___________________
(y'z" — z'y")2 + (z'x" — x'z")2 + (x'y" y'x")2
(65)
(66)
(67)
(68)
(69)
(70)
(71)
Точки, в которых кривизна равна нулю, называются точ-
ками распрямления кривой, а точки, в которых равно нулю
кручение, — ее точками
уплощения.
Плоскость, проходящая
через данную точку кривой
параллельно касательной и
главной нормали (т. е. пер-
пендикулярно бинормали),
называется соприкасающей-
ся плоскостью. Плоскость,
параллельная главной нор-
мали и бинормали (т. е. ‘ ----i
перпендикулярная касатель- / s' Сплос^п^
ной), как уже отмечалось /
раньше, называется нор-
мальной плоскостью, а пло-
скость, параллельная каса- Рис. 114.
тельной и бинормали (т. е.
перпендикулярная главной нормали), — спрямляющей плоско-
стью (рис. 114).
Уравнение соприкасающейся плоскости в точке, в которой
кривизна не обращается в нуль, имеет вид
(г — Го, Го, Го) = 0.
(72)
511
Здесь го = г (tQ) = (х0; Уо', 2о) — радиус-вектор данной точки кри-
вой, го = г' (/о) = (хб; г/6; ^6), го = г" (/о) = (%о; #6'; 20), а г —
— (х\у\ г) — текущий радиус-вектор соприкасающейся плоско-
сти. В координатном виде уравнение (72) записывается сле-
дующим образом:
х — х0 у — у О Z — ZQ
/ Г г
хо Уо Ч
77 // 77
*о Уо *о
(73)
Бинормаль в точке (х0; Уъ, zo) перпендикулярна соприка-
сающейся плоскости, и потому ее уравнение имеет вид
Х~ Хо _____ у — Уо _____
7 7/ 7 77 Г 77 7 77 7 77 7 // * V ^7
УоЧ - ЧЧ — хоЧ хоУо “ УоЧ
Векторная запись уравнения нормальной плоскости выгля-
дит следующим образом:
(г — го, гб) = 0, (75)
а координатная —
(х — Хо) Хо + (у — у о) Уо + (г — го) z'Q = 0. (76)
Векторная запись уравнения спрямляющей плоскости имеет
вид
(Г — Го> [[го, Го], Го]) = 0. (77)
Если же за параметр на кривой взята переменная длина дуги,
то уравнение спрямляющей плоскости имеет более простой
вид:
(г“г<” -S-<so))=°> (78)
или в координатной записи:
(* — *о) («о) + (у — Уо) («о) + (г — z0) (s0) = 0. (79)
Точка, лежащая на главной нормали, к кривой на расстоя-
нии, равном радиусу кривизны R в направлении вектора глав-
ной нормали v, называется центром
кривизны кривой в данной ее точке
/\ (рис. 115). Если через р = р(/) обо-
/ I 4 значить радиус-вектор центра кри-
v(t)X R____________________визны кривой Г = {r(/); а t Ь},
/ / то
/ Р (0 = г (/) + /?(/)V (/). (80)
0^ Круг, лежащий в соприкасаю-
Рис. 115. щейся плоскости с центром в цент-
ре кривизны кривой в данной ее точ-
ке, радиус которого равен радиусу кривизны в этой точке, на-
зывается кругом кривизны кривой в рассматриваемой точке
кривой.
512
Кривая, для которой вектор-функция (80) является ее пред-
ставлением, называется эволютой кривой Г (коротко говорят,
что множество центров кривизны кривой образует ее эволюту).
Если кривая Г1 является эволютой кривой Г, то кривая Г назы-
вается эвольвентой кривой IY
* Уравнение эволюты кривой Г можно записать в виде
р (/) = !•(/)
1 s'r" — s"r'
k2 s'3
(81)
где если r(/) = (х(/); y(t)\ то
S' = |r'| = V?4F+7, s" = TO
•V*' +y'2 +z'2
Если кривая Г лежит в плоскости переменных х и
z = 0, а
1 _ I х'у" — х"у' I .
R (х'* + у'^ ’
у, ТО
(83)
если (g; т]) — ее центр кривизны, то
£ =» х — у'
•Ц = У + х'
,2 I /2
х +у
х'у" — х"у*
,2 . ,2
х' +у'
х'у" — х"у‘
(84)
Для случая, когда кривая Г является графиком функции
y — f(x), a^.x^b, формулы для ее кривизны k и координат
|, т) ее центра кривизны принимают вид
(85)
(86)
Пример 10. Найти сопровождающий трехгранник Френе
винтовой линии; вычислить ее кривизну и кручение.
/А В примере 9 этого параграфа было показано, что пред-
ставление винтовой линии, когда за параметр принята пере*
Генная длина дуги, имеет вид
S . S
х — a cos —===, у = a sin -7— ,
Va2 + b2 'у/а2 + Ь2
bs Л
Z — ... . 5^0.
Va2 + b2
17 Л. Д. Кудрявцев я др.
513=
Поэтому
__ f dx А_____
\ ds 9 ds 9 ds J
f a . s a s b
\ Va2 + ^2 Vcl2 + b2 у a2 + b2 V^2 + ^2 'x/a2 b2
dx f a s a . s
ds \ a2 + b2 a2 + b2 a2 + b2 д/a2 + b2 )
Отсюда
/г —|_gl| —- a
K I ds I a2 + b2 •
Кроме того, в силу первой формулы Френе (см. (60)) имеем
V = ( — cos --------; — sin ........ ; 0 )
\ Va2 + ^2 V^2 + ^2 J
и, следовательно,
Р = [Т, v] =
i j к
a . s a s b
= ^a2 + b2 'у/a2 + b2 <x/a2 + b2 д/а2 + b2 ^a2 + b2 =
5 $
— COS -7==- — sin — 0
л/a2 + b2 'у/a2 + b2
b . s . b s . . a <
'x/a2 + b2 \a2 + b2 <x/a2 + b2 \a2 + b2 J a2 + b2
Дифференцируя это равенство, получим
dp b s . . b . s b
ds a2 + b2 "X/a2 + b2 a2 + b2 a2 + b2 a2 + b2
Отсюда, согласно третьей формуле Френе, x = 6/(a2 + ^2).
Пример 11. Найти радиус кривизны и эволюту эллипса
Zs Запишем уравнение эллипса в параметрическом виде:
х — a cos /, у — b sin /, 0 t 2л.
Заметив, что х' — —a sin /, у' = b cos/, х" — —a cos/, у” =
= —b sin /, получим (см. (59), (83))
Р 1 _____ (a2 sin2 t ^b2 cos2 /)3/2 _ (a2 sin2 t b2 cos2 /)3^2
= T ab sin21 + ab cos2 / ab *
514
Отсюда, воспользовавшись формулами (84), получим уравне-
ние эволюты
, a2 sin21 + b2 cos21 a2 — b2 4 ,
t — a cos t — b cos t-------7-------=----------cos3 /,
ъ ab a
i . a2 sin21 + b2 cos21 b2 — a2 . o,
n — b sin t — a sin t-------r-------— —7— sin3/.
1 nh fr
ab
Таким образом, эволютой эллипса является астроида. А
Пример 12. Доказать, что при монотонном изменении ра-
диуса кривизны на некоторой части плоской кривой его прира-
щение равно соответствующему приращению длины дуги эво-
люты (т. е. длине пути, пройденного центром кривизны по эво-
люте) .
А Уравнение эволюты кривой Г= {г (s); 0 s S}, где s—
переменная длина дуги кривой Г, имеет вид
p(s) = r(s) + 7?(s)v(s).
Поэтому
dp __ t/г \dR dv
d s ds ' ds ' ds '
где
dr П dv ,
-d7=T’ /?^=-Ш = -т
(так как Rk~ 1). Таким образом, = откуда
CLS Uo w
Обозначим через о переменную длину дуги эволюты кривой Г,
отсчитываемой в направлении возрастания длины дуги s самой
кривой Г. Тогда
I dp I da
I ds j ds
(cm. (46)). Если, для определенности, на рассматриваемом уча-
dR
стке кривой Г ее радиус кривизны возрастает, т. е. О,
то из (87) следует, что
da __ dR
ds ds *
т. e. <r(s) = 7?(s) +с, где с — некоторая постоянная. Отсюда
сразу и получается, что для указанных значений параметра s
приращение длины дуги эволюты Aa = a(s + As)—a(s) со-
впадает с соответствующим приращением радиуса кривизны
АТ? — R (s + As) — Я (s), т. e. Ao — AT?. A
Пример 13. Если кручение кривой тождественно равно
нулю, то кривая плоская.
А Если у кривой Г = {г (s); 0 s S}, s — переменная
Длина дуги, ее кручение во всех точках равно нулю: х = 0, то
в силу третьей формулы Френе (см. (62)) имеем-^-=0, т. е.
17*
515
бинормаль 0 кривой Г является постоянным вектором. Обозна-
чим его через ро. Тогда для любой точки кривой Г будем иметь
(г, ₽о) = 0, или
(£<•).
откуда
^(r(s), ₽о) = О.
Следовательно, (г ($), 0О) = с, где с — некоторая постоянная.
Это означает, что концы всех радиус-векторов r(s) лежат на
плоскости (г, Ро) = с (здесь г — (х; у\ г)— текущий радиус-век-
тор точек плоскости, на которой лежит кривая Г). А
а) Плоские кривые.
. 24.76. Найти кривизну и радиус кривизны в произвольной
точке следующих кривых:
1) Параболы у = ах2.
2) Кубической параболы у = х3.
3) Синусоиды у = sin х.
4) Цепной линии у = a ch (х/а).
5) у = a In cos(х/а).
24.77 . Найти кривизну и центр кривизны в произвольной
точке следующих кривых^
j^2 <»2
1) Гиперболы —-^ — 1.
2) Полукубической параболы Зау2 — 2х3.
3) Астроиды х2/3 + У2/3 — а2/3.
24.78 . Найти кривизну кривых в произвольной точке:
1) Эллипса х = a cos t, у = Ь sin t, 111 л.
2) Гиперболы х = a ch t, у = b sh t, t е R.
3) Циклоиды x — a(t— sin/), y = a(\—cos/), /elR, .
24.79 . Найти эволюты кривых:
1) x — t2, у = t3.
2) Гиперболы x = a ch /, у = b sh t.
3) Циклоиды x — a(t — sin /), у = a (1 — cos/).
4) Эвольвенты круга x == a(t — sin/), у — a(sin/— /cos/)'.
24.80 . Найти наименьший радиус кривизны у параболы
У2 = 2рх.
24.81 . Найти наибольшую кривизну у кривых:
l)j/ = lnx. 2) y — aln (1 — 3) y — ach(x/a).
24.82 . Доказать, что радиус кривизны' параболы х2 = 2ру
равен /? = p/cos3a, где а — угол наклона касательной к оси
абсцисс.
24.83 . Пусть y = f(x) — дважды непрерывно дифференци-
руемая на отрезке [а; Ь] функция и а = а(х) — угол, образо-
ванный касательной к ее графику с осью Ох в точке (x;f(x)).
Доказать, что если k(x) — кривизна графика в этой точке, то
A(x) = |-g-|. a^x^.b (s — переменная длина дуги).
24.84 . Пусть Г — дважды дифференцируемая кривая без осо-
бых точек, лежащая на плоскости переменных х, у\ а — угол
наклона ее касательной в некоторой точке к оси х; k* =
($ —переменная длина дуги); R* = 1Д*; (g; т}) — координаты
центра кривизны в той же точке кривой Г. Доказать, что
g = х — R* sin а, т) = у + R* cos а,
а также что
р dy . dx
ъ da 1 1 da
24.85 . Доказать, что если р = р(ф)— представление дважды
непрерывно дифференцируемой кривой в полярных координа-
тах, то для ее кривизны имеет место формула
ь — lp2 + 2p'*-ppff|
k~ (р2 + р'’)3/* * <88)
24.86 . Найти радиусы кривизны кривых, заданных в поляр-
ных координатах:
1) Лемнискаты р2 = a2 cos 2<р.
2) Кардиоиды р = а (1 + cos <р).
3) р = a cos3 ф.
4) Спирали Архимеда р == аф. 4
5) Гиперболической спирали р — а/у.
6) Логарифмической спирали р — aeb<t.
24.87 . Что представляет собой эволюта окружности?
24.88 . Составить уравнение эволюты}
1) Трактриссы x = aln a — Ау...~ -^a2 — у2.
2) Логарифмической спирали р = ех<₽.
3) Кардиоиды р = a (1 + cos ф).
24.89 . Доказать, что эволюта циклоиды является также
циклоидой, отличающейся от данной только положением.
24.90 . Доказать, что эволютой кардиоиды Является также
кардиоида.
617
24.91 . Доказать, что эволютой астроиды является астроида,
подобная данной, с коэффициентом подобия 2, повернутая отно-
сительно данной на угол л/4.
24.92 . Найти условие для параметра а логарифмической
спирали р = са®, при выполнении которого ее эволюта совпа-
дает с самой спиралью.
24.93 . Доказать, что эволютами эпициклоиды
— (1 4~ Л) cos Kt — К cos (1 —f- Л) /,
-J = (1 + A) sin M — A sin (1 + A) t,
a> 0, Z > 0, — oo < t < + oo,
и гипоциклоиды
i = (l — A) cos А/+ A cos (A — 1)/,
£- = (1 — A) sin W + Л sin (A — 1) t,
a > 0, 0 < л < 1, —oo < t < +oo,
являются снова соответственно эпициклоида и гипоциклоида,
получающиеся из заданных с помощью поворота и преобразо-
вания подобия.
24.94 . Доказать, что для точек спирали Архимеда р = аср
при ф->+°° величина разности между длиной радиус-вектора
и радиусом кривизны стремится к нулю.
24.95 . Доказать, что в условиях задачи 24.94 центр кри-
визны перемещается по кривой, стремящейся к совпадению
с окружностью р = 1.
24.96 . Пусть р = р(ф), а ф р, — представление дважды
непрерывно дифференцируемой кривой в полярных координа-
тах, а = ос(ф) — угол наклона ее касательной в некоторой
точке М к полярной оси, a ip— угол, образованный этой каса-
тельной с продолжением радиус-вектора ОМ точки касания М.
Пусть прямая ON перпендикулярна прямой ОМ, прямая MN —
нормаль к заданной кривой в точке М, а С — центр кривизны
кривой в той же точке. Доказать, что
NC _ dip
CM dtp
24.97 . Доказать, что у кривых р" = ап cos rap, а > 0, поляр-
ная нормаль, т. е. отрезок нормали от точки кривой до точки
ее пересечения с полярной осью, в « + 1 раз больше радиуса
кривизны.
24.98 . Доказать, что у кривых р" = ап sin пф, а > 0, длина
части радиус-вектора, заключенной внутри круга кривизны,
равна 2р/(«4д О*
518
24.99 . Пусть г — длина радиус-вектора точки данной дважды
непрерывно дифференцируемой кривой, р — длина перпендику-
ляра, опущенного из начала координат на касательную в ука-
занной точке прямой, и R — радиус кривизны. Доказать, что
dr _ R
dp г
24.100 . Доказать, что на эллипсе существуют, вообще го-
воря, три таких точки, что круги кривизны к эллипсу в этих
точках проходят через данную точку эллипса.
24.101 . Доказать, что центры кривизны в точках спирали
Архимеда р = аср, лежащих на одном луче, расположены на
эллипсе, полуоси которого не зависят от выбора луча.
24.102 . Пусть некоторая точка дважды непрерывно диффе-
ренцируемой кривой принята за начало координат, положи-
тельно направленная касательная к кривой в этой точке — за
ось х, а ось у направлена от точки касания к центру кривизны.
Доказать, что в окрестности точки касания кривая имеет пред-
ставление
У 2 ✓
г/= 2^- + о(х2), х->0.
24.103 . Доказать, что если в точке Л1(/о) кривой Г =
= {Ai(£); а t Ь} радиус кривизны имеет максимум, то су-
ществует такая окрестность U точки to, что часть кривой, соот-
ветствующая значениям параметра t^U, лежит внутри круга
кривизны в точке 7И(/о).
24.104 . Доказать, что если в точке 7И(/0) кривой Г =
= {2И(0; a^t^Zb} радиус кривизны имеет минимум, то су-
ществует такая окрестность U точки /0, что часть кривой, соот-
ветствующая значениям параметра t^U, лежит вне круга
кривизны в точке М (to).
24.105 . Найти параболу, соединяющую начало координат
(0; 0) с точкой ЛГ(1;0) так, чтобы дуга параболы ОМ обра-
зовала вместе с нижней половиной окружности х2 + у2 = 1 кри-
вую с непрерывной касательной и непрерывной кривизной.
24.106 . Найти параболу с осью симметрии, параллельной
оси у, имеющую с синусоидой у — sinx в точке (л/2; 1) общие
касательную и кривизну.
24.107 . Доказать: если (g; ц) — координаты центра кривизны
дважды непрерывно дифференцируемой кривой x — x\t), у =
~ у (t), а t Ь, то
Г2 , /2 _ /2 , /2
X + у = g + ч
х'у" - х"у' g'-r)" - g'V ’
24.108 . Пользуясь свойствами эволюты, найти длины сле-
дующих кривых:
1) Одной дуги циклоиды x = a(t— sin/), у = а(1 — cos
0 2л.
2) Астроиды х2/3 Д- у2/3 = а2/3 между точками (а\ 0) и (0; а).
619
3) Кардиоиды р = а (1 + cos ф), 0 Ф 2л.
б) Пространственные кривые.
24.109. Написать уравнения соприкасающейся, нормальной
и спрямляющей плоскостей для произвольной точки следующих
кривых:
1) Винтовой линии x=acosf, t/ = asinf, z = bt.
2) х = t, у = t\ z = /3.
3) x = е\ у = z — t'\j<l.
4) x — cos t, у = sin t, z — e*.
5) y2 = xt x2 = z.
6) у = (fW, г = a<p(x) + b.
24.110. Найти уравнение главной нормали и бинормали
к кривым:
1) х = a cos t, у = a sin t, z = bt,
2) x — у2, z = x2.
3) x = /4/4, у = /3/3, z = /2/2.
24.111. Доказать, что главная нормаль винтовой линии х =
₽ a cos /, у з= a sin t, z = bt перпендикулярна оси z, а ее би-
нормаль образует с этой осью постоянный угол, косинус кото-
рого равен а/а2 + Ь2.
24.112. Доказать, что одна из биссектрис углов между каса-
тельной и бинормалью к кривой х = 3/, у = 3£2, z = 2/3 имеет
постоянное направление.
24.113. По главным нормалям (но в противоположную сто-
рону) винтовой, линии х = a cos /, у — a sin /, z = bt отклады-
ваются отрезки длиной /. Найти кривую, описываемую их
концами.
24.114. Доказать, что прямая, проведенная из произвольной
точки М кривой х = /, у = /2, z = /3 параллельно плоскости
z — 0 до пересечения с осью z, лежит в соприкасающейся пло-
скости кривой в точке М.
24.115. Написать уравнение соприкасающейся плоскости
кривой х = a cos /, у = b sin t, z — ef при t — 0.
24.116: Написать уравнение соприкасающейся плоскости
в точке (2; 1;2) кривой, являющейся пересечением сферы х2 +>
C|_^2_|_22_ g и гиперболического цилиндра х2 — у2 = 3.
24.117. Доказать, что если все соприкасающиеся плоскости
дважды непрерывно дифференцируемой кривой проходят через
фиксированную точку, то эта кривая плоская.
24.118. Найти векторы т, v и р кривой x==fsin/, у =
= t cos t, z — tef в начале координат.
24.119. Найти векторы т, v и р в произвольной точке кривой:
1) # = cos31, у = sin3 z == cos 2/.
520
2) x = a(t— sin/)', y = a(l—cost), z = 4acos(t/2).
24.120. Доказать, что кривизна кривой тождественно равна
нулю в том и только том случае, когда кривая является про-
межутком прямой.
24.121. Найти кривизну конической винтовой линии х =»,
я= t cos t, у = t sin t, z = at в начале координат,
24.122. Найти кривизны следующих кривых!
1) x — acht, y = asht, z — bt.
2) х — In cos t, # = lnsinf, z = t^2.
3) x — t — sin t, y=l — cos t, z = 4 sin (//2).
4) x — ei, у — е~*, Z’=t-\/2.
5) x — a ch t cos t, у=a ch t sin t, z = at.
cos t sin t fi «1 ,\
6) x===a‘chT’ ^ = a7hT’ z=a(/ —th/).
7) x2 = 2az, y2 = 2bz.
24.123. Найти кручение кривых:
1) x = etcost, y=^etsvat, z — e‘.
2) x = a ch t cos t, у — a ch t sin t, z = at.
3) y2 = x, x2 — z.
24.124. Найти кривизну и кручение кривых:
1) 2ау = х2, 6a2z = x3. 2) x — acht, y = asht, z — at.
3) x = 2abt, y — a2lnt, z — b2t2.
4)x = 3/— t3, y — 3t2, z = 3t + t3.
5) Кривой Вивиани x = R sin21, у — Rsint cos t, z =
e= R cos t; есть ли на кривой Вивиани точки распрямления
и точки уплощения?
24.125. Найти точки распрямления, точки уплощения и дуги,
на которых кручение сохраняет знак, для кривых:
1) х = t, у — sin t, z — sin 3t.
2) x = cos t, у — sin t, z— t3 — 9t.
24.126. Исходя из определения главной нормали v как еди-
ничного вектора в направлении вектора (т — единичный
касательный вектор, as — переменная длина дуги заданной
трижды непрерывно дифференцируемой кривой без особых то-
чек) и определения бинормали р = [т, v], доказать, что:
1) Производная бинормали коллинеарна с главной
нормалью.
521
2) Если “j- = kv, -т- — — xv, то
7 as as
dv
ds
— kT + x₽
'(иначе говоря, доказать формулы Френе).
24.127. Доказать, что для трижды непрерывно дифференци-
руемой кривой r={r(s); O^s^S}, s — переменная длина
дуги, выполняются соотношения
I ds3 j 1 1 \ ds ) ’
dr tZ2r \_______________п /_dr J3r \_____________________________у 2 ( d2r d3r\__________________h dk
ds1 ds2 J ’ \ds’ ds3J~ R ’ \ ds2 ’ ds3 .)~*ds-
24.128. В предположениях предыдущей задачи доказать, что»
/ dfb d2$ d3p\ 5 d k
\ ds ’ ds2 * ds3 ) К ds x ’
/ dx d2x d3x \___. 5 t/ %
\ ds ’ ds2 ’ ds3 ) ds k'
24.129. Доказать, что если в точке 7И0 кривизна k кривой Г
не равна нулю, то k равна кривизне проекции Г на ее сопри-
касающуюся плоскость в точке 7И0.
24.130. Доказать, что если все нормальные плоскости дважды
непрерывно дифференцируемой кривой без особых точек и
с кривизной, не обращающейся в нуль, параллельны постоян-
ному вектору, то эта кривая плоская.
24.131. Доказать, что у кривой х = ezsin/, у — efcos t*
z = е* каждое ребро сопровождающего трехгранника Френе об-
разует с осью z постоянный угол.
24.132. На бинормалях винтовой линии х = a cos t, у —
— asxnt, z = отложены отрезки одной и той же длины.
Найти уравнение кривой, образованной концами этих отрезков.
24.133. Кривая называется линией откоса, если касательные
к ней образуют постоянный угол с какой-либо прямой. Дока-
зать, что дважды непрерывно дифференцируемая кривая с не
равной нулю кривизной является линией откоса тогда и только-
тогда, когда выполняется одно из следующих условий:
1) все главные нормали параллельны некоторой плоскости;
2) все спрямляющие плоскости параллельны некоторой
прямой;
3) в случае трижды непрерывно дифференцируемой кривой
существует такая постоянная с > 0, что x(s)— ck(s)-t при
этом | с | = ctg ос, где а — угол, о котором шла речь при опре-
делении линии откоса.
522
24.134. При каком условии центр кривизны винтовой линии
ж = a cos t, у — a sin /, z = Ы лежит на том же цилиндре, что
и сама винтовая линия?
24.135. Доказать, что у кривой x = ach/cos/, у —
= a ch/sin/, z = at отрезки нормали от точки на кривой до
оси z равны обратной величине абсолютного значения кручения
кривой: 1/|х|.
24.136. Пусть Г = {/И (/); а t Ь} — дважды непрерывно
дифференцируемая кривая без особых точек /Ое[бг;6], /0+,
4- А/i е [а; &] и /о + Д/г [tx; 6]. Проведем через точки М(/о),
Л4(/о + Д/1) и 7И(/о + А^2) плоскость. Доказать, что если в точке
.Л1(/о) кривизна не равна нулю, то при A/i -> 0 и Д/2->0 эта
плоскость стремится (определите это понятие) к соприкасаю-
щейся плоскости в точке М(/о).
24.137. Пусть л — плоскость, проходящая через касательную
прямую в точке М (s0) дважды непрерывно дифференцируемой
кривой r={7W(s); O^s^S}, s— переменная длина дуги
кривой Г, s0 е [О, S] и d (As) — расстояние от точки M(s0 + As)
до плоскости л. Доказать, что плоскость л является соприка-
сающейся плоскостью кривой Г тогда и только тогда, когда
lim AS^L —
As->0 As2
0.
24.138. В предположениях задачи 24.136 проведем через те
же три точки М(/о), Л1(/о + A/i) и М (to + Д/г) окружность. До-
казать, что эта окружность при A/i-->0 и Л/2~>0 стремится
к окружности, являющейся границей круга кривизны в точке
M(t0) (эта окружность называется соприкасающейся окруж-
ностью в данной точке кривой).
24.139. Через четыре точки кривой можно провести сферу.
Если они стремятся к одной точке, то при соответствующих
условиях эта сфера стремится к некоторой предельной сфере,
называемой соприкасающейся сферой. Найти ее центр и ра-
диус.
24.140. Доказать, что вектор ускорения а движущейся ма-
териальной точки перпендикулярен бинормали траектории дви-
жения, и найти его разложение по касательному вектору и век-
тору главной нормали. Доказать, что
где v = | v |, v=-^p R — радиус кривизны траектории дви-
жения.
24.141. Доказать, что для трижды непрерывно дифференци-
руемой кривой Г = {М(s); 0 s S}, где s — переменная
длина дуги;
523
1) Справедлива формула
г (s 4- As) — г (s) =
= (As - | k2 (s) As3) т (s) 4- (| k (s) As2 + ~k' (s) As3)v (s) +
+ -g- k (s) x (s) As30 (s) 4- о (As3), As->0.
2) Если через £, rj, £ обозначить координаты точки в си-
стеме координат, задаваемой ортами t(s), v(s), ₽(s), то в окре-
стности точки кривой Л4($) проекция кривой на соприкасаю-
щуюся плоскость имеет вид
П=^(«)^4-о(П,
на нормальную плоскость —
Ч= V£2/3 + ° <£2/3)’ °’ * <s^0’
на спрямляющую плоскость —
? = 4^(s)x(s)g34-o(g3), S->0.
24.142. Доказать, что если на трижды непрерывно дифферен-
цируемой кривой Г= {г(s); 5 — переменная длина
дуги, параметр s рассматривать как время, то при его измене-
нии сопровождающий трехгранник Френе будет двигаться вдоль
кривой как твердое тело с угловой скоростью со = хт + &р. Тем
самым кривизна численно равна скорости вращения трехгран-
ника Френе вокруг бинормали (причем это вращение всегда
происходит от касательного вектора т к вектору главной нор-
мали v), а кручение — его скорости вращения вокруг каса-
тельной.
24.143. Доказать, что формулы Френе можно записать в виде
^^-===== [<о, т], = v], -^|-= [<*>,₽] (вектор «определен
в предыдущей задаче).
ОТВЕТЫ
Глава I. ВВЕДЕНИЕ
§ 1. Множества. Комбинаторика
1.1. 1) ДПВПС; 2) ^UBUC; 3) (А П В) U (В А С) U (С ГМ). 1.7. 1) Х=)У.
2) X = У. 3) X cz У. 4) X == Y. 5) X cz Y. 1.9. 1) {2, 3}. 2) 0. 3) {2, 3, 4, 5, 6}.
4) {2, 3}. 5) {(2; 2), (3; 2)}. 6) {(2; 2), (2; 3)}. 1.10. {12& - 6}, k е= N.
1.11. 1) — k. 2) n/n. 1.12. 125 элементов.
1.13.
1.15. X = В'. 1.16. A = U, В = 0.
1.19. 1) Да. 2) Нет.
1.20. 3) Можно, например, элементу х е А поставить в соответствие эле-
мент (Ь — а)х 4- а е В. 4) Можно, например, элементу х^В поставить в со-
X А
ответствие элемент * _ । -1 е А.
1.32. 1) Может, 2) не может, 3) может. 1.33. 2п. 1.36. 1) 1/256. 2) 15.
3) n(n+ 1). 4) 2Л. 1.37. 1) И. 2) 28. 3) {7, 8, 9). 4) {2, 3, 4}. f.38. 1) 870.
2) 435. 1.39. 1) 60. 2) 10. 1.40. 1) 15. 2) 43 200. 1.41. п (п — 3)/2. 1.42. 210.
1.43. 5355. 1.44. 576. 1.45. 18; 10. 1.46. 1024. 1.47. 1) 120. 2) 60. 3) 420. 4) 83 160.
1.48. 1.49. 5040. 1.50. 15 625. 1.51. 16. 1.52. (и + 1)1 лп! 1.53. 945. 1.54. 330.
1.55. Может не хватить. 1.56. Если п < 7, то чисел с цифрой 9 меньше;
если п 7, то чисел с цифрой 9 больше.
1.57. 233. 1.58. 1) 1/4. 2) 1/3. 3) 0. 4) 5/12. 1.59. 5/36. 1.60. 29/52
1.61. 164/1081. 1.62. 1) 5/9. 2) 2/9. 1.63. 1) I/C49. 2) Сб’С4з/С49- 1-64. 360/2401
1.65. 1) 9/17. 2) 8/17.
525
§ 2. Элементы логики. Метод математической индукции
2.1. Все предложения, кроме предложения 3), являются высказываниями-
Высказывания 1), 2), 5), 7) истинны, высказывание 4) ложно. В настоящее
время неизвестно, истинно или ложно высказывание 6). Высказывание 8) счи-
тается истинным в геометрии Евклида и ложным в геометрии Лобачевского.
2.2. 1) «174 не делится нацело на 3» ложно; 2) «число 3 является дели-
телем числа 174 или идет дождь» истинно; 3) «число 3 — делитель числа 174
и идет дождь» ложно; 4) «если 174 делится на 3, то идет дождь» ложно;
5) «если 174 не делится на 3, то идет дождь» истинно; 6) «174 делится на 3
тогда и только тогда, когда не идет дождь» истинно.
р и и л л
q и л и л
S и и и л
2) Высказывание s — тождественно
истинное.
2.6. 1) «Мишень поражена по крайней мере одним выстрелом», высказы-
вание истинно; 2) «все три выстрела попали в цель», высказывание ложно?
3) «из первых двух выстрелов хотя бы один неудачный, а третий удачный»,
высказывание истинно.
2.7. Данное высказывание является тождественно истинным, т. е. оно
истинно независимо от того, истинны или ложны высказывания р, qf г.
2.8. l)pV?- 2)p\/(q/\r). 3) г. 4) р Д q А г.
2.9. Только второй студент изучал логику.
- 2.10. Сергей, Юрий, Виктор, Роман.
2.11. Экзамен сдали все четыре студента.
2.12. В экспедицию следует взять Е— биологом, В — гидрологом, С — ра-
дистом, D — врачом, F — синоптиком, Н — механиком.
2.13. ' 1){1, 2, 3, 4, 5, 6, 9}. 2). {9}. 3) {1, 2, 3, 4, 5, 6, 9}. 4) {9}.
2.14. Второе и третье, причем второе ложно, а третье истинно.
2.15. п = 45. 2.16. 2, 2.17. (9; 2); (17; 6). 2.18. | а | < 1/2.
2.19. — 1/16<а<1/12. 2.20. 1) — 36/5 < а <9. 2) — 27/5 < а <0.
2.21. 1) Да, может. Такой контрольной будет, например, контрольная,,
в которой количество задач равно количеству учеников, причем первый уче-
ник решил только первую задачу, второй — только вторую, третий — только
третью и т. д. 2) Нет, не может. Из того, что существует ученик, решивший
все задачи, следует, что каждая задача решена хотя бы одним учеником
(например, тем, который решил все задачи). Замечание. Этот пример по-
казывает, что в высказывании Vx2pp(x; у} нельзя, вообще говоря, пере-
ставлять кванторы.
2.22. 1) & =# 0. 2) k = 0. 3) Таких значений k не существует. 4) k — лю-
бое число.
2.23. 1) В каждом поезде, идущем из Москвы в Ленинград, есть (суще-
ствует) вагон, в котором все месте заняты. 2) В Швеции существует город,
на любой улице которого в любом доме есть окно, не выходящее на юг.
2.24. 1) п — 41. 2) у = | х |, х = 0. 2.30. 1) п 4. 2) п > 7. 3) п = 1, м^Ю.
-4) п > 4. 2.34. а„ = 2" + 2~п. 2.37. - + + 1. 2.38. п2 — п + 2.
§ 3. Действительные числа
3.1. 0,(6); 0,55; 0,2(142857); —0,(285714).
32 _L- I- 2^1- X
• • 8 ’ 3 ’ 990 ’ 10 ’
3.9. 1) 0 и 1; 0,3 и 0,4; 0,30 и 0,31; 0,300 и 0,301; 0,3000 и 0,3001.
2) 0 и 1; 0,3 и 0,4; 0,33 и 0,34; 0,333 и 0,334; 0,3333 и 0,3334. 3) 1 и 2;
526
1,2 и 1,3; 1,22 и 1,23; 1,222 и 1,223; 1,2222 и 1,2223. 4) —1 и 0; —0,7 и —0,6!
—0,63 и —0,62; —0,626 и —0,625; —0,6251 и —0,6250.
3.10. 1) 1 и 2; 1,4 и 1,5; 1,41 и 1,42. 2) 2 и 3; 2,2 и 2,3: 2,23 и '2,24-
3) 0,3 и 0,4; 0,31 и 0,32; 0,317 и 0,318. 4) —0,4 и —0,3; —0,32 и — 0,3 Ь
—0,318 и —0,317. 5) 2 и 3; 2,1 и 2,2; 2,14 и 2,15.
ЗЛ1. Да. &12. О 3,3 > 3,298. 2) 3,1416 > 3.J4159. 3) 3,141592 < 22/7.
4) V3 + 2 > V2 + Уб. 5) УТ + У10 < Уз + У19.
3.13. 1) 2,06 и 2,07. 2) 0,0142 и 0,0143. 3) —0,0973 и —0,0972.
4) 0,471 и 0,472. 5) 2,44 и 2,45. 6) 0,534 и 0,535.
3.16. 1) U (2; 1)._2) U (2; л - 2)^3) U (2; (4 - л)/2). 4) U (2; 1).
3.49. supX = y2, infX =— У2. 3.50. 1 и + оо; 0 и 1; 0 и 3/2; 1/2 и 1.
3.54. sup {т/п, 0 < m < n, т е N, п е N} = 1,
inf {mln, 0 <т < п, т е N, п е N} = 0.
§ 4. Прогрессии. Суммирование. Бином Ньютона. Числовые неравенства
2> з-2±+з.
3) -.<» + „р„ х *
(п+1)(/г + 2)
-—!—~~ ПРИ * = !•
4) ^+2-g+l)/ + »< при
4.9. 1} 2) 3) 0. 4)
4 14 11 " 21 - 31 ”+ * 2) 3
' Зя + 1 ’ 4я + 1 ’ ’ 3(2я+ 1)(2п + 3) ’
.. J_________1________ ~ »(»+!)
’ 18 3 (п + 1) (п + 2) (я + 3) • ’ 2 (2я + 1) '
... „з е _ n2(«+D2
4.15. 2) Sn (3) — - .
4.18. 2) 3)
' sin х 2 sin х
п sin пх cos (п + 1) х
2 2 sin х
4)
б)
я , sin пх cos (я + 1)х
2 "Т” 2 sin х
Л . п + 1 . пх . 3(«+1) . Зпх
3 sin ——х sin ~2 sin " ' 2—Х Sin —2~"
л • Зх
4sm —
4sinT
3(«+1)х.3 о„п+1 пх
cos —1—-—-— sin — пх 3 cos —-—X sin
6) —2 ..............-+—^—х—.
4 sm ~2~ 4 sin —
,) + 3 (3,_, + (_|)Я)Л
2) хп = (2" - 1) X! - 2 (2П-1 - 1) х0.
3) хп= (а ~^ Xi — ((а — 1)”~1 — 1) х0 при а =4= 2;
Хп — nxi — (я — 1) Хо при а = 2.
527
4.20. 1) (1 + х)5 = 1 + 5х + 10х2 + 10х3 + 5x4 + x®. 2) (a + b)6 = a8 +
+ 6a56 + 15a4/»2 + 20a363 + 15a2/>4 + 6a65 + b8. 3) (x + y)7 = x7 + 7xey +
4- 21x5z/2 + 35x4y3 + 35x8y* + 21x2f/3 + 7xy6 + y7. 4) (a — b)8 = a3 — 8aTb +
+ 28a6 b2 — 56a563 + 70a464 — 56a365 + 28a2/»6 — Sab7 + b8.
4.21. C?6x3. 4.22. 1) —7. 2) -40; -74. 3) 36Cf + C£ = 378. 4)245. 5) Cf6>
4.23. 1) (n + 2) 2«-i. 2) (n — 2) 2«-l + 1. 3) 22«-l. 4) 22n-l. 5) (—
6) (— l)m C™m при n = 2/n; 0 при n = 2m + 1.
4.25. 1) 60. 2) 625; 7000; 7000; 1120; 16.
4.26. 1) -g-. 2) Cf0~. 4.27. C*g29.
§ 5. Комплексные числа
5.3. 1) 7 + 3i; 22 + 71. 2) 2-4/; -1,81-5,2/. 3) 2д/Г; 5.
5.4. 1) -2,6 - 4,2/; 0,016 - 0,088/. 2) - 0,4 + 2/; 0,12"+ 0,24/. 3) - /;
5.5. 1) 0. 2) -11/17. 3) 3.
О о
1Q QQ 99 К
5.6. 1) 0. 2) —21. 3) 0. 4) - — + — /. 5) -j^---^/. 5.7. (4; 3),
(5; 3), (4j_4), (5; 4). 5.8. (-2; -2), (2; -2). 5.9. 1) -1 - i. 2) 0. -1,
1 , л/З . cm y _i . „ _ . r 19 2?1+^г + ^з
— ± — I- 5.1U. Zi = 1 — I, Z2~t. 5.12. -----------.
5.13. ( У, /( У mk 'j. 5.14. z4 = z{ + z3 — z2. 5.15. t (7 + /),
\ft-i // U-i /
/ — произвольное положительное число. 5.16. 1) 4. 2) 1. 3) 7. 4) 2 sin (п/14).
5.17. 1) 0; 3/; -3/. 2) ^2 - 1; 1 — ^2 ; /; — /. 3) bi, b «= R. 4) c ± ^3 ci,
c — произвольное действительное неположительное число.
5.21. 1) Окружность радиуса R « 1 с центром в точке z = —1. 2) По-
луплоскость Im z > 0. 3) Круг (вместе с границей) радиуса R = 2 с центром
в точке 2=1 — 2i. 4) Окружность радиуса R = 3 с центром в точке z = 0.
5) Эллипс с фокусами в точках Zj = —2, Z2 = 2 и с большой полуосью
а = 13. 6) Система концентрических колец с центром в точке z = 0, содер-
жащая интервалы (2&л; 2&л + л), — целое, действительной оси. 7) Круг
радиуса Я=10 с центром в точке z=10i, за исключением центра круга и гра-
ничной окружности. 8) Окружность радиуса Я=3 с центром в точке z=—3.
5.22. 1) 4+4Z- 2) -4-2<- 3> 5“5Z; -5 + 5«’;
О О ^4
V26 —V26Z; — V26 + V26/.
5.24. 1) -5- + 2л&, k е Z. 2) л + 2л&, k е Z. 3) 2л£, k е Z.
4) —т* "Ь 2л&, k е Z. 5)------ л + 2л&, k е Z. 6) + 2л&, k е Z. >
4 1о 14
5.25. 1) Действительная положительная полуось z = х > 0. 2) Мнимая
полуось z = /г/, у > 0. 3) Полуплоскость Imz > 0. 4) Вся комплексная пло-
скость, за исключением точки z = 0
5.26. Действительная отрицательная полуось z = х, х < 0. 2) Угол (без
границы) с вершиной в точке z = —г, стороны которого проходят через точ-
ки 2=1 и z = 0, содержащий точку z = 1/2. 5.27. 1) Z. 2) —~ +
3 л^з
Ч------— /. 5.28. Точка z2 = х + iy принадлежит параболе х = —-------1. ,
5.29. Точка z=x+iy находится на кривой у = |х(.
528
5.32. 1)2 (cos (5л/6) + i sin (5л/6)). 2) cos n + i sin л.
3) cos (13л/12) + i sin (13л/12). 4) —2 cos (5л/9) (cos (14л/9) + i sin (14л/9))
5.33. 1) z = 1 =cosO + f sin 0. 2) z = — J- - ~~i = cos -^-4-Z sin %?.
& £ <5 о
3) z ===y (cos 0 + ^'sin 0). 4) 2 = ~------^~-Z = cos+ Z sin
5) z — — Z = cos (Зл/2) + Z sin (Зл/2).
5 ___
5.34. 1) -5- (cos 230°+« sin 230°). 2) V2 sin'(n/5) (cos (29n/20)+Z sin (29л/20)).
О
9
5.35. —10 + 4/. 5.36. 3 — — i.
1 a/T
5.37. 1) 1. 2) cos 50°+ Z sin 50°. 3) -гг — ~-i. 4) —2. 5) 2.
04 04
5.38. 1) 2100 (cos (4л/3) + Z sin (4л/3)). 2) 8 (cos (Зл/2) + I sin (Зл/2))-
3) 2 (cos 0 + i sin 0), если ti — четное, 2 (cos л + Z sin л), если ti — нечетное-
4) - (cos 8 + Z sin 8). 5) —32 cos5 (Зл/5) (cos (л/2) + i sin (л/2)).
5.39. n = 4k, k(=Z.
5.40. 1) y+ -1. 2) Vr+Z. -V3+Z, —2Z.
3) cos (2л£/5) + Z sin (2nA:/5) (k = 0, 1, 2, 3. 4).
4) V2 (cos n + Zsin - + -- л) (k =. 0, 1, 2, 3, 4, 5, 6, 7).
\ oz 0 6 /
5.41. 1) V2 (cos (л/12) + Z sin (л/12)), V2 (cos (Зл/4) + Z sin (Зл/4)),
e__ . . -y/2 V2 л/2
V2 (cos (17Л/12) + Z sin (17Л/12)). 2) 2L~ + ^lt _JV_ + JY—z>
s_
V2 V2 . V2 V2 .
2 2~ *’ 2 2 *'
s
(cos (7л/15) + Z sin (7л/15)),
5 — 5/— a—
V2 (cos (19л/15) + Z sin (19л/15)), у 2 (cos (5л/3) -f- Z sin (5л/3)). 4) y3 + Z, 2Zt
—2Z, — i* 5) 0; cos (2л&/5) + Z sin (2л£/5)
, 2л& , . . 2л&
6) Если n > 1, то z. = cos —г-г + i sin —r-т
« n4- 1 /2 4-1
(6 = 0, 1, 2, 3, 4).
3) ^2 (cos (Л/15) + Z sin (n/15)),
5 _
V2 (cos (13Л/15) + Z sin (13Л/15)).
(k = 0, 1, ..., n); если n == 1, то. уравнению удовлетворяет каждое действи-
тельное число.
5.42. 1) 2п. 2) п, 5.44. ех, у + 2л£ (k s Z). 5.45. 1) е2 cos 1 — ie2 sin 1.
2) i. 3) — e1 sin 3 + ie7 cos 3. 5.46. 1) 4е7я£/6. 2) е6л£/7.
5.47. 1) е2л/ = 1. 2) 8e-ni/4 = 4 УГ—4д/2 Z. 3) 64е<л = - 64.
4) е-лг/3 = у —Z 5) 27е3л//2 =-27Z.
5.49. 1) e2nkil3 (k — 0, 1, 2). ‘ 2) e^+OnZ/S = 0> j, 2, 3, 4).
3) 2е2(3*+1)л//9 (fe = 0, 1, 2). 4) 1/2 е<3*+2>яг/6 (й = 0, I, 2, 3).
529
5.5„. ,) 5) ".<<»+ w> SI„ („ф/2).
ei<₽ - 1 sin (<p/2)
^п((п+1)ф/2)со
sin (ф/2)
§ 6. Многочлены. Алгебраические уравнения.
Рациональные дроби
6.1. Л = Z) = О, В=1, С = 2. 6.2. P(z)=$z2 — 26г — 21,
Q (?) = —9г3 + 44г2 — 39г — 7. 6.3. А = 4, В = О, С = 2, D = — 2 или
А = —4, В = 8, С = —2, D = 2. 6.4. 1) 2. 2) Q (г) = 0 и, следовательно, не
имеет степени.
6.5. 1) 7(2) = г +13, 7? (г) = 81г-211. 2) Т (г) = г4 + iz* - г2 +
+ (3 - Z) г + 1 + 10/, R (г) = i - 11. 3) Т (г) = г2 + З/г - 7, R (г) = -13гг2-
- 18г + 1 + 7i. 4) Т(г) = 0, 7? (г) = г2 - 1. 5) Т (г) = z25 - z2° + г15 —
— г10 + г5 — 1, R (г) = 0.
6.6. 1) Является. 2) Не является. 3) Является.
6.7. 1) а = 3, b = — 4. 2) а = — 1 — Z, Ъ = Z. 3) а = 0, Ъ = — 1; а = 0,
b = 1; а — — 1— Z, b = Z; а =—1 + Z, b = —Z; а = 1 — i, b=^ — ii
а = 1 + Z, b = Z.
6.8. 1) п = km, k е N. 2) п = (2k + 1) m, k <= N. 3) n~2ktn,
4) n и m — произвольные натуральные числа. 5) n — четное, m — нечетноеw
6.9. 1) (z — I)3. 2) z30 — 1. 3) zls — 1. 6.10. z +2. 6.11. -i-z + 4-+ «.
6.12. z3 — 1.
6.13. 1) 1 + 2г; 1 - 2г. 2) 2 + i; -2 + i. 3) 13 - г; 7 + i. 4) 5 + г; 3 + 2г
6.14. 1) 4 + Z; —4 + Z; —4 — Z; 4 — Z. 2) cos (л/г/З) + Z sin (л&/3>
(k = 1, 2, 3, 4, 5). 3) — tg (лй/16) (k = 1, 9, 17. 25). 4) 2г: -3г; -
V15 i
2 2 *
Л/о"* __ a^2* _
6.15. 1) G-— (-1 +г д/з); — 1; 1 - 1 д/з ). 2) 2 (cos 144°-}-
Л £
5___ 5 ____________________________
+ Z sin 144°); 2 (cos 216° + Z sin 216°); -v 31 (cos 108° + Z sin 108°); — д/31;
5____
V31 (cos 252° + Z sin 252°).
6.16. Пусть г = k — целый корень уравнения
anzn + ап-1Хп-* + ... + п4г + aQ = 0
с целыми коэффициентами. Тогда
cink4 + an—tkn~~* + ... +&iAj + а0 = 0
и, следовательно,
Gq = ——k(Gnkn’~l +» . . + t?i).
Число ankn~} + ... + «j при сделанных предположениях, очевидно, целое»
значит ‘г — делитель числа а0.
6.17. 1) —2. 2) 2. 3) Целых корней уравнение не имеет. 4) —7j —2; 2; 3.
5) 2. 6.19. 1) —7/3. 2) 1/2; 4.
6.20. 1) -5; — -j + г; — ~ l- 2) 1; 3; 2Z: ~2i‘ 9) ~2; 1 + ^3 I',
—1 + Уз г; —1 — д/з" г; 1 — д/з" г. 4) —3; —2; 2; 3.
6.21. Указание Воспользоваться задачей 5.1 L
630
6.23. 1) 1 - i- (V13-0/6; - (У13 + 1)/б. 2) — Z; (-1 + Уз z)/2:
(-1 - Уз' i)/2.
6.25. а = — 6, 6 = —2; z2 = 1 — У2’, z3 = l',_ zt — — 1; z-a => — 2.
«.26. 1) —1 + Z; -1 - i. 2) — -j- + i; — у — 6.27. 1) 2. 2) 3. 3) 3.
6.28. a = — einkil5, b = 9 • e&nki/5, k = 0, 1, 2, 3, 4. 6.30. P (x) = 1 +
4- (x - I)5 £ Cl+4xft. 6.31. 1) z3 - 7z2 + 17z - 15. 2) (z2 + I)2 (z2 + 2z + 2).
6.32. z4 — 14z2 + 9. 6.34. 3. 6.35. z3 —2z2 + z+1 =0. 6.36. c = 8, z, == -2,
z2 = (1 + i У15)/2, z3 = (1 - i УТ5)/2. 6.37. 5/4, -3/4. 6.38. a2n_ i - 2a n_ 2.
6.39. 1) 1. 2) 1/16. 3) 16.
6.40. 1) U+l)(z--|-Z^)(z--l-+Z^). 2) (z-l)(z-2)(z-3).
3) 6 (z - 2) (z + (z - -1 - i (z -1 + i .
4) (z + I)3 (z - 3) (z - 4). 5) (z - Z)2 (z + 1 + Z).
6.41. 1) (x2 + 2x + 2) (x2 - 2x + 2). 2) (x2 + 3) (x2 + 3x + 3) (x2 - 3x + 3).
3) (x- 1) (x + 2) (x2 + x + 6). 4) (x2 + x+l)2. 5) (x + 2) (x + 6) (x —
— Уб + 4) (x + Уб +4). 6) (x — 7 + 3 ) (y — ----------) (x2 + 5x + 7).
7) (x - 1) (x2 - x + 1) (x2 + x + I)2.
2. 1
6.43. 1) z2 - z + 1. 2) 2z3 - z2 - 4z + 3. 3) - ±.
nz — Zb 3z + I
7 ' 6.47. 1) г + 3 + 7ТТ. 2) г.-7г + 7.
fc=l n+l *
9
3) гз+32Чб7+.0+ . 4) £ <-!>' +4>e- 4 yy.
/г=0
Л<2>
6.48. 1) a) z _ 3/ + (2_3z)2 + z + M + (z + 3Z)2 ’
MV’x + Л112’х + M2)
€) ^+9 + (x2 + 9)2 '
21 а) - Л‘ + —— +----------b----—----;
’ ’ z-1 z + 3 T z + 1 - 2Z T z + 1 + 2Z ’
A , В , Cx±D
O) x- 1 hx-f-3’t'x2 + 2x + 5-
4l) , Л<2> ( A^ f A^ r Л<’> ( Л<2>
3) a) z + i + {z + i)2 + z _ e^/3+(2 _ e№/3)2+ 2 _ e-w+^_e~i^
Л*1» X2' + <>x + m2)
л + 1 + (x + I)2 + x2 - x + 1 + (x2 - x + l)e ’
531
z — /4-2 z — i 4“ 3 ’ z + z* + z - i + z 4- i*
2_______2________2/ 2/
2—1 24-1 z — i z 4- i ’
n~ 1 1 fi2knifn
V2 z —1—Z -14-1 1-/ 1 + i A 6. V n
8 V2-I-1 2-14-/ 24-I-/ 24-I4-/A ' Lj z_e2kni/n*
bo
6.50. 1)
7 . 5 2 2x 4- 4
x — 2 ’ x — 4 ’ ' x—1 x2 4- x 4- 1 *
3/2 2 1/2 _3________1 t x-1
x 4-1 x 4- 2 r x 4- 3 * 7 x2 x - 1 r x2 4- x 4- 1
1 _ 4 3__________2__________1 1
x-1 (x — I)2 "* (x — I)3 x4-l (x4-l)2 + x-2*
127 66 129 62 1 , I x
x-2 (x-2)2 ф x4-2 (x 4-2)2’ x 4- 1 Ф(х4-1)2 х24-Г
1 7 3 6x 4- 2 Зх 4- 2
x x4-l (x4-D2 +x24-x4-l + (x24-jc4-1)2‘
50
1 1 V* 2x cos (4зтА?/101) — 2 cos (2jtZ?/ 101)
x— 1 Zu x2 — 2x cos (2Л&/101) 4- 1
k=^l
x -4- 2 cos (л/9) + x 4- 2 cos (7л/9) x 4- 2 cos (1 Зл/9) ‘
X — x2
5) -----7"
Xj — X2
§ 7. Числовые функции. Последовательности
7.1. l)x #= — !*). 2) x 1; x^=-l. 3) x 2; x =/= 4. 4) x 2.
x =/= 0; x ¥= 2. 5) x > 0. 6) x - 3/2; x =# 3/2. 7) x =?£= — 3/2; x — 1/2.
7.2. 1) R. 2) {0}. 3) x<2. 4) [-2; 1]. 5) (-1; 1). 6) (-oo; -1)U(1; + oo).
7) x - 3; x =/= 3. 8) {0} (J [2; + oo). 9) (0,5; 1) U (3; + oo). 7.3. 1) у = 2x - 2.
3 , 1 2x+ll .. 3 — 2x
2) У = - y x 4- у- 3) у =---------. 4) у =--------.
, X — Xi
^~‘x2 — x” У2*
7.4. ij 5 4- 4x - x2. 2) x2 - 2. 3) x2 4- 4x - 5.
(X — X2)(X — X3) , (X — Xj) (x — x3) ,
4> -----У' + (X2 _ X1) (X2 _ Хз) У2 +
(x — x2) (x — Хз) (x — x4)
___________________ __________________________ (x — X]) (x — x2)
(X! — Xt) (X! — ХЭ) ' (X2 — Xi) (X2 — X3) 4/2 ”Г (X3 — Xj) (xs — X2) "3"
7.5. 1) 2x3 + 3x2 + 5. 2) (x ~ Xa) ~ Хз) (x ~ - yt +
' (Xj - X2) (X! - X3) (X! — X4) '
(x — Xi) (x — Хз) (x — x<) (x — Xi) (x — x2) (x — x4)
’’ (x2 — Xi) (x2 — x3) (x2 — x4) У2 (хз — X)) (хз — X2) (Хз — x4) Уз
(X —Xi) (x —x2)(x —Хз) ,
r (x4 —X1)(X4 —x2)(x4 —x3)
n+1 n+1
J=1 fel, v i u
7.7. 1) (-oo; 3]; [-1; 4-oo); [—1; 3]. 2) [-1; 1]; {x €= R: x Ф 1/2},
{X€=[-1; 1]: x=/»l/2}. 3) [3; 4-oo); (-oo; 2) U (2; 4-oo); [3; 4- oo).
4) (0; 5); {xs R: x =/= л/2 4-лп, neZ}; (xe(0;5): x =/= л/2; x =/= Зл/2}’
♦) Такая краткая запись означает, что областью определения является
множество (xeR: х ф—1}.
532
5) (—4; 4); {xeR: и + л/2 4- 2лп, п е Z); {х <= ( —4; 4): х =* л/2}.
6) [1; +«>); П; +«>); [1; +<»)•
7.8. 1) R; R. 2) R; (xeR: х¥=2, х=з*—2). 3) (—1; 1); (хе(-1; 1): х=?*0}.
4) (-2; + оо); {хе 1-2; 4-оо): х=#-1). 5) [-1/2; + оо);
{хе [-1/2; +оо): х=5*0). 6) R; {xeR: 7) R; R.
8) R; {xeR: x =/= (—l)"-j 4-nezj. 9) {xeR: x =5* лп, neZ]-r
{xeR: x =#= ли, х^ + м, nezj. 7.9. 1) 3; 2a2/(a2 — 4); 2/(b — 2);
(b _ \)/(b - 3); 1/(1 - 2p); (p - 2)/p. 2) 240; 0; 8b3 4- 8b - 1; 86s - 24b2 4-
4-326-16; 8(p24-l)/p3; l/(8p (14-P2))- 7.10. 1) 1; 1; 1,5; 1; 0.
2) 1/8; 1; 0,5; 1; 1984. 7.11. a = 2, b = 5 при m =£ tv, aeR, b = a + 8 при
w = n. 7.12. —2. 7.13. 8b3. 7.14. 1) a > 1. 2) a<-l. 7.15. 1) a--L
2)1-a. 3) a —1. 4) 1-a. 7.16. 1) [-9; -1]. 2) [0; 4]. 3) (-oo; -1)Q
u {0} U (1; 4- oo). 4) [-4; 4- oo). 5) (- oo; 9/8[. 6) [- 9; 23]. 7) [2; 4- oo).
8) (-oo; -4]. 9) [0; 1). 7.17. 1) [1; + oo). 2) [0; 4-oo). 3) [0; 2].
4) fV^4-oo). 5) (-oo; -2 Vab]U[2 Va6; 4-oo). 6) R. 7) [-2; 2].
7.18. a = — 4,5. 7.19. a — b = — 1. 7.22. -1) f °g (x) = x, x >0; g°f (x) = | x |,
xeR. 2) fog(x) = g°f (x) = |x|, x e [— 1; 1]. 3) f<,g(x) = x, x > 0:
gof(x) — x, xeR. 4) Mg(x)=^f4 5)', xeR; g°f (x) = x5 4- 5, xeR.
5) f®g(x) = f °’, +<*2’ g°fW = 0, xeR. 6) f“g(x) = Insin2x_
x , x €= (— oo; uj;
neZ; g°f (x) = sin In x2t x 0. 7.23. 1) sin log2 +-~=^.
2) 1 3) 1 +------------7==~. 4) ----—L.:......... .
Vl + log2 sin x log2 Vsin x log2 Vsin (1 + x)
7.25. l)f(x)=—l,-. 2)/(х)=4-+Ь 3)/(x)—4)f(x) = x2-2..
5) f (x) = 1 - x3/2. 7.26. He существует. 7.27. 1) /»/»/ (x) =.
{xeR: ax + b^0, a (1 4- b) x 4- b2 0, a (1 4- b 4- b2) x 4- ba 0}.
2) g » g ° g(x)=~7=? , . * 2 , 2 • 3) Если T<>
Vfl6 + (a4 + a2+l)x2
fof® ... °f (x) =—hn '~\---9 |xeR: ay—~х + 6л=/=0, Aj = 1, 2,..., n|,
a 4--------~x + bn 1 }
о — 1 *•
а если b = 1, то/°/° ... °/(x) = * . , {xeR, akx 4- 1=5*0, fc=l,2.n}.
urvx " | ‘ 1
4) Если а2У=1, to go^ro ... o^(x)==-----—, а если a2 == К
то gog® ... °gW = —j ......- 7.30. 1) Четная; 2) нечетная; 3) ни четная,.
V1 + ПХ2
ни нечетная; 4) четная; 5) ни четная, ни нечетная; 6) ни четная, ни нечетная,
7) ни четная, ни нечетная; 8) четная; 9) нечетная. 7.41. 1) а) у == — х,
х е (— оо; 0), у (0) е R *); б) у == х, х е (— оо; 0]. 2) а) у = х2, хе (— оо; 0),
у (0) е R; б) у = — х2, хе (- оо; 0]. 3) а) у = V— х, х €= (— оо; 0), у (0) е R-
*) Здесь и далее в аналогичных примерах эта запись означает, что за
£/(0) можно взять любое действительное числа
533
>б) у — — V— х, х е (—- оо; 0]. 4) а) у — — х + 5, х е (— оо; 0), у (0) е R;
б) у = х — 5, х ^ (— оо; 0), у (0) = 0. 5) а) у~'\/\ — х1, хе(-1;0),
у (0) е R; б) у = —• V1 — х2, хе (-1; 0), у (0) =0. 6) а) у = х2 + 4х + 3,
х G (- оо; 0), у (0) €= R; б) у = —- х2 — 4х — 3, х <= (— оо; 0), у (0) = 0.
7) а) У = 777~ТГ’ х е °°: 0)> У(0) е R: б) У = Тл 1 гТ> х s (—°°; °)’
у (0) = о,
7.47. 1) Являются. 2) Являются. 3) Не являются. 4) Не являются.
7.48. I) Обратная функция у = (х + 1)/2. 2) Необратима. 3) Обратная
5 __________________________________________________________
функция у = х"1/3. 4) Необратима. 5) Обратная функция у = 6) Об-
ратная функция у — 1 + х2, х 0. 7) Необратима. 8) Обратная функция
у — Vl х | sign х.
7.49. 1) а = — 1, b gR или а = 1, b — 0. 2) а = ± 1.
7.51. 1) VC > 0 Зх е D (/) f (х) > С, 2) VC > 0 Зх g= D (f) f (х) < - С.
7.56. 1) max/ — 0 *), min/ = — 9. 2) max / = 1/4, min/ = — 6. 3) max / = 3,
min/ = 5/4. 4) max/=l, min f — — 5/13. __ 5) max f = 5, min f = 4.
6) max/ = 1/6, min/ = 0. 7.59. 1) —9/4. 2) 4 V2. 3) 0. 4) — 1/3. 7.60. 1) —2.
2) —2д/2. 3) 1. 4) 1. 7.61. 1) sup f = + 00; inf f == min f — 2. 2) sup / =
= max f = —2; inf f — — 00. 3) sup f = 1; inf f = min f = 0. 4) sup f — + 00;
in / = — 00. 5) sup/=l; inf f = min f = 0. 7.68. Возрастает на [—1; 0] и
{1 + oo), убывает на (— оо; —1] и [0; 1].
7.70. 1) (—оо; 0) U (0; 0,25) (J (0,25; + оо)?*2) (—оо; 0]. 3) (—оо; 0) (J (0; + оо);
(0; +оо). 4) (0; 1) U (U + <*>). 5) (-оо; 99) U (99; 100). 6) (1; + оо);
(-00; 0)U(l; +00). 7) (-3;-2)U(-2; - 1)U(1; +00). 8) (0: 1).
7.71. 1) (0; 1]. 2) (-00; 0)U(l; +00). 3) [3/4; +00). 4) [1; +00).
-5) (—00; 2]. 6) (—00; —2) U (2; + oo). 7.72. 1) Ни четная, ни нечетная
2) Ни четная, ни нечетная. 3) Нечетная. 4) Ни четная, ни нечетная. 5) Чет-
ная. 6) Нечетная. 7) Нечетная. 8) Четная. 9) Ни четная, ни нечетная.
7.77. 1) sup / = max / = 1, inf / = 0. 2) sup / = + 00, inf / = min / = V2 — 1.
3) sup / = 1, inf / = — 00. 4) sup / = 8, inf / = — co. 5) sup / = + 00,
inf / = — 00. 6) sup / = + 00, inf / = min / = 0. 7) sup / = max / = 4, inf / = — oo,
7.80. 1) Строго возрастает на (—oo; 0) и (0; -f-oo). 2) Строго убывает
на (—оо; 0], строго возрастает на [0; фоо). 3) Строго убывает на R.
4) Строго возрастает на (—1; +оо). 5) Строго убывает на (0; 1) и (1; 4-оо).
6) Строго возрастает на (0; 2], строго убывает на [2; 4). 7) Строго убывает
на (—оо; —1), строго убывает на (0; 4-оо).
7.83. 1) а) у = — 3-2-*-1, х е (— оо; 0), у (0) <= R * **); б) z/ = 3-2-x-1,
х <= (— оо; 0), у (0) = 0. 2) а) у == 1 — 2 1g (— х), х <= (— оо; 0), у (0) е R;
-б) у = — 1 + 2 Ig (— х), хе=(— оо; 0), у (0) = 0. 3) а) у = log2-x (~ х),
х е (— оо; 0), у (0) R; б) у = — log2-% (— х), х е= (— оо; 0), у (0) = 0.
4) а) у = — th(x+l), xg(-oo;0), у (0) s R; б) у = th (х + 1)?
х е (— оо; 0), у (0) = 0.
7.84. 1) у = logs (3/х), хе(0;+«>). 2) f/ = 10x-1 —2, х е R.
3) r/ = log2(x/(l— х)), х<=(0;1). 4) у = Ю1^, х е R, х =/= 0.
5) у = log2 (х + д/х24- 2), х е R. 6) у = ch х, х е (— оо; 0).
7.85. 1) у = In (х — Vx2 — 1). 2) у — In (х + Vx2 + 1). 3) у = — In
4) у= j-ln -* ‘ . 7.87. 1. 7.89. 1) 2л/3. 2) 8/3. 3) л/3. 4) л. 5) л/2.
6) 2л. 7) л/2.
* Там, где ясно, о каком множестве X идет речь, вместо max f написано
X
max /.
**) См. сноску на с. 533.
534
7.92. 1) х лл/2, п е Z. 2) xs[----------+ 2лп; ~7г + 2лл], neZ.
3) хе(2лл; -^г-+ 2лп) U (~^~ + 2ля; л + 2лп),ие2. 4) х е [2; 4].
5) хе [0; 4]. 6) х е= (— -у- + 2ли; у- + 2лп), neZ. 7) х = у + 2лп, n<z=Z.
7.93. 1) 1-1; 1]. 2) [- У£ Уз ]. 3) [1/2; 1]. 4) (- оо; 0] U [2; + со). 5) [0; л/2].
6) (л/2; л]. 7) [0; 1]. 8) [-л/4; л/4].
7.94. 1) Нечетная. 2) Чётная. 3) Четная. 4) Четная. 5) Нечетная.
6) Ни четная, ни нечетная. 7) Ни четная, ни нечетная. 8) Ни четная, ни не-
четная. 7.95. 1) Четная. 2) Ни четная, ни нечетная. 3) Четная. 4) Четная.
5) Четная. 6) Нечетная. 7) Четная. 7.99. 1) sup /=тах f=21, inf /—min f = — 3.
2) sup f = max f = V3/2? inf f = min f = 0. 3) sup/ = max / = 1/2, inf f = — oo.
4)sup/ = + °°, inf f — min/ = 2. 5)sup/ = l, inf / = — 1. 6) sup/ — л/2,
inf / = — л/2. 7) sup / = max / = л/2, inf f = 0.
7.100. 1) Строго убывает на [—л; — л/2) и (—л/2; 0], строго возрастает
на [0; л/2) и (л/2; л]. 2) Строго возрастает на [2/(Зл); 2/л], строго убывает
на [2/л; + оо). 3) Строго убывает на (— оо; 0) и (0; + оо). 4) Строго воз-
растает на [—1;0], строго убывает на [0; 1]. 5) Строго возрастает на R.
6) Строго возрастает на (— оо; 0], строго убывает на [0; + оо). 7) Строго
убывает на R. 7.104. 1) а) у = 1 — sin х, х < 0, у (0) е IR *); б) у = — 1 + sin х,
X < 0, У (0) = 0. 2) а) у = — ctg х, х < 0, у (0) е R; б) у = ctg х, х < 0, у (0) = 0.
3) а) у== л/. 2^» х<0> б) У = ; 2. > *<о,
, V1 + tg2 X V1 + tg2 X
у (0) — 0. 4) а) у — л — arccos 2х, х < 0, у (0) е R; б) у = arccos 2х — л, х < 0»
х/(0) == 0. 5) а) у = — arctg (х + 1), х < 0, у (0) (= R; б) у — arctg (х + 1),^
X < 0, у (0) = 0. 7.105. 1) у = — л — arcsin х. 2) у = — arccos х.
3) у == л + arctg х. 4) у = arcctgx — л. 5) у = (л — arcsin (х/2))/3.
6) у — 2 sin (х/2), х <= [— л; л]. 7) у = — cos х, х е [0; л/2]. 8) у — cos х,
X е [0: л/2]. 9) у ~ ctg х, х е (— л/2; л/2), х #= 0. 7.107. \)_у = 1/х, х =/= 0,
х =/= ± 1. 2) у — 2х2, х #= ± 2. 3) = V6 — х2, х — V2. 4) х = —- г/4/5,
y=£Q. 5) х = у2. 7.111. 1) А. 2) А и В..З) В. 4) Ни Л, ни В. 7.112. 1) г/ = х2+1.
-2) (х — 2)2 + (^ — I)2 = 9. 3) ^-+-^-=1. 4) Зх = | In (х/— 1)
5) 8 (х + у) = (х - у)2 + 16. 7.114. 1) г =-----Д-----5—. 2) г = 2 cos q>.
У 2 cos (<P + -^-)
3) <р = -| + ^(» = 0)1,2,3)иг = 0. 4)r=4s.J((p/2). 7.117. 1) [0; 6).
2) [—3; 0,5]. 3) х ± 1. 4) (-оо;-2] U [2; + оо). 5) [-3; 3]. 6) (-4; 2).
7.118. 1) R. 2) х е (—— + 2яп; 2лга) (J (2лп; -^- + 2ля), п е Z.
3) (-oo;0)U(l;3). 4)_(-оо; 1)Ц(2; +оо). 5) (—5; 8/5) U (8/5; 9/5).
6) (-оо; - V5- 1)U(-Уб - 1; —3)ll[2; + оо). 7) (-1; 0)1)(0; 1)U(2; + оо).
' 8) (0; 1) U (1; log2 (8/3)). 9) (-1;5). 10) (2; 3). 7.119. 1) х + лп,
х > n s Z. 2) + лп < х + лп, п е Z. 3) —4 < х < 4,
#=/=:£: Л, Х=И=0. __ __
- 7.120. 1) [0;4]. 2)0. 3) х ± 3. 4) [- (1 + Уб)/2; (1 - Уб)/г] (J
I) [(Уб’- 0/2; (Уб + 1)/г]. 5) [1/Уз- 1]. 6) -5- + лп<х<^- + лп, n^z.
О о
7) -К х < 1, х^± 1/^2. 8) (ctg 0.5;; + оо). 9) [0; (3 - Уб )/2) U 0+^; 4].
*) См. сноску на с. 533.
535
10) [1; 2). 11) (-6; -5л/3] и [-Л/З; 1/6). 12) (0; 1/2) U (1/2; 1).
7.121. 1) [- 1/3; 1/3]. 2) (-1; 1]. 3) [1; + оо)^4) [0; 3]. 5) {0}. 6) [2~9; + оо).
7) (- оо; 2]. 8) {1/2}. 9) [0; 1]. 7.122. 1) [- V26; У2б]. 2) [-1; 1]. 3) [0; + оо).
4) R. 5) {0}. 6) [-1; 5/4]. 7) (- 00; log2 (5/4)]. 8) [1/V2; 1]. 9) [л/4; Зл/4].
7.123. 2) [2; 3). 7.124. 1) [-4; -3] (J (-1; + оо)^ 2) {-6}.
-3) (_оо; -6]U(-1; +<»). 4) [—4; -3]. 7.126. а) а > 1/^4; б) b = - $2.
7.127. 1) а > 1. 2) а > 0, а < — 1. 3) 0 < а < 1/2. 7.128. S = х2, хе [0; 1/2],
.3 = (4х — 1)/4, х <= [1/2; 3/2], S = 1,5 — (2 - х)2, х <== [3/2; 2].
—r2 L2
7.129. V = -^5----т---Z-, h > 2г. 7.130. S = 4 л/2]3х (Ь — 2х), 0 < х < 6/3;
о П — ,
3 = V2/3(6 — *)2. 6/3 < Х<6; maxS = 62/V^ 7.131. 2R sin (а/2) (1—sin (а/2));
R/2. 7.132. рх 4- т (1 + Е (х//)). 7.133. S = vt, 0 < t < 1, S = v V7Z2 - 15Z + 9,
t > 1; min S = v. 7.134. 1) [-3; 3]. 2) (3 5)/4.
7.136. 1) nm. 2) nt.
7.138. Обратимы функции: 1), 4), 6), 9).
3) у = 1 — Vl — x, x < 0; у = — 14- Vl 4- x, x > 0. 4) у = (5x 4- 3)/(x — 1),
x =/= 1, x #= — 3/5. 5) у = x4* V*2— 1» *>1. 6) у = x — V*2 — b x>l.
7) у = (x2 + l)/2x, x 1. 8) у = (x2 4- l)/2x, -1 < x < 0.
7.141. 1) у = 1 - Vlog2 2x, x> 1/2. 2) у = (1 - In (1 - x))/( 1 + In (1 - x)),
x<l, x¥= l-e-L 3) ff = logi(5 * + -1 <x< 1. 4) y«0,51g-^ t
0 < x < 2. 5) у es 0,5 {ax ~ a~x\ x e R.
7.142. 1) у = 3л — arcsin x, xs[-l;l|. 2) у = 4л — 2 arccos (x/2)
x e [—2; 2], 3) у = arcctg x, x (= (0; + oo), у = arcctg x — л, x e (— oo; 0)’
4) у = 2л 4- 2 arcsin л/x = 2л + arccos (1— 2x), xe[0; 1]. 5) у = — arccos (1/x),
xe(— oo; — 1]U[1; +°°)- 6) # = sinx, хе[0;л/2]. 7) у = — sin x9
x e [0; л/2]. 8) # = tg(x —x g= (—л/2; — л/4) U (— л/4; л/2).
7.143. 1) (0; 0), (2/3; 2/3), (-2/3; —2/3). ______ _______________
7.144. у = (х3 - Зх)/2, | х |>2. 7.146. у = $ х+л/x^+i + ^х-V*2+l.'
х е R.
7.147. [-
7.148. 2) а + d
7.150. 6 =
. X 1 + arcsin 0,5 (x — 1) , . , ,
+ 00 L -----------------"лТ7-------xs -1; l + 2sin 1,
) v 1 — arcsin 0,5 (x — 1) 1 7
| а | + I с | =/= 0 или b = c = 0, а = J 0.
a > 0 или b = 1, <2 = 0. 7.151. — 0,5 < a < 0,5.
2 — л в
2 + я ;
0,
h
7.152. с = л, b =s — 1, aeR или с = л, 5 = 1, а = 0. 7.153. ] К | > л; если
—л, то у = sin 0,5 (Л 4- V^2 ~ 2Лл + 4х), х е + Ал; еслй
Л>л, то у = sin 0,5 (Л — V^2 ~ 2Лл 4- 4х), х е £-^-; ~j“4-Ajij.
7.155. 1) 0<х<1. 2) -1<х<0. 3) 0 < х. 4) х<0. 5) х < 1. 6) х > 1.
7.156. 1) Четная. 2) Нечетная. 3) Ни четная, ни нечетная. 4) Нечетная.
5) Четная. 6) Ни четная, ни нечетная. 7) Ни четная, ни нечетная. 8) Четная.
7.157. 1) Нечетная. 2) Нечетная. 3) Четная. 4) Ни четная, ни нечетная.
5) Четная 6) Нечетная. 7) Нечетная. 8) Нечетная. 9) Четная. 7.158. I) Чет-
ная. 2) Нечетная. 3) Ни четная, ни нечетная. 4) Четная. 5) Ни четная, ни
нечетная. 6) Нечетная. 7) Нечетная. 8) Четная. 7.159. 1) Четная. 2) Ни чет*
ная, ни нечетная. 3) Четная. 4) Нечетная. 5) Ни четная, ни нечетная. 6) Не-
счетная. 7) Ни четная, ни нечетная. 8) Четная.
7.160. 1) (Зх2 4-1) 4- (*3 4- Зх). 2) — 4- 3) cos х sin 1 4- sin х cos L
4) —2 1 ; +-2--T. 7.162. l)0,5(|x-l|+lx+l]) + 0,5(|x-ll)-|x+ll).
536
2) О,б(ах + а *) + 0,5 (ах — а~х). 3) In 2 ch 4) cos Xs sin х2-Ь
-f- sin х3 cos х2. 5) Не представима. 6) ~- + (~ arcsin х). 7)---- + arctg х.
8) 0,5 (arctg (1 — х) + arctg (1 + х)) + 0,5 (arctg (1 — х) — arctg (1 + х)) =
== arctg —---------------arctg — ——-------------.
Vx4 + 4 + х2 Vx4 + 4 — х2 + 2
7.163. 1) а) Нет; б) да. 2) а) Да; б) нет. 7.164. 1) f ° g, g ° A, h°g.
2) h ° h. 7.165. 2) Нет.
7.174. 1) Постоянная на (—оо; 0], строго возрастает на [0;-[-оо). 2) Стро-
го убывает на (—оо-; —3), (—3; 3), (3; 4-оо). 3) Строго возрастает на
|(—оо; 1], строго убывает на [1; -f-oo). 4) Строго возрастает на (—оо; —1] и
[1; +«>), строго убывает на [—1; 1]. 5) Строго убывает на (—оо; 0], строго
возрастает на „ [0; +оо). 6) Строго возрастает на (--оо, —1) и (—1; 0],
строго убывает на [0; 1) и (1; -|-оо).
7.175. 1) Убывает на (—оо; —1], возрастает на [1; +сю). 2) Возрастает
на [0; 1], убывает на [1; 2]. 3) Возрастаетна (—со; —3) и(—3; —VtT], убы-
вает на [л/5; 3) и (3; +°°)« 4) Возрастает на (—оо£ 0], убывает^ на
[0; Ч-оо). 5) Убывает на R. 6) Возрастает на(—оо;—2 V2 ) и (—2^2; о]г
убывает на [0; 2 л/2 ) и (2л/%\ + оо). 7) Возрастает на [2; 4-оо). 8) Возра-
стает на [1; +оо). 9) Возрастает на (—оо; —1], убывает на [1; 4-оо).
7.176. 1) Убывает на [0; л/4] и [л/2; Зл/4], возрастает на [л/4; л/2] и
[Зл/4; л]. 2) Убывает на [0; л/2] и [Зл/2; 2л], возрастает на [л/2; Зл/2].
3) Убывает на (0; л/4] и [Зл/4; л], возрастает на [л/4; л/2] и (л/2; Зл/4].
4) Убывает на (—оо; 0) и (0; Ч-оо). 5) Возрастает на (0; 4], убывает на
(4; 8). 6) Возрастает на R. 7) Возрастает на (—оо; —1], убывает на
—1; -|-оо). 8) Возрастает на (—оо; —1] и [0; 1], убывает на [—1; 0] и [1;
Ч-оо). 7.187. Является.
7.193. 1) 2^3. 2) 4. 3) 4. 4) 1. 7.194. 1) -1. 2) 9/4. 7.195. 1) -6.
2) 1/8. 3) 1/V2. 4) —2. 7.196. 1) max f = 1/4, min f = 0. 2) max/ = 5,
min/=11/4. 3) max/ = 8, min/ = 0. 4) max/=l, min/=1/4.
5) max / = 9/16, min / = —1. 6)max/=l, min/ = cos 2. 7) max/ = sin I,
min/ = —1. 8) max/=1/2, min/ = 0. 9) max/=1/2, min/ = —1/6.
7.197. Если "tl-cos a, to min S = J a2 + b2 — 2ab cos a, если
Ьщ + av2
avi + bv2 . о I fah — м)2 I sin a
bvi + av2 D2 __ 2vyv2 cos a
7.198. 0,5S. 7.199. 1) /?2ctga. 2) R2/(2 sin2 a). 7.200. l/V?.
7.201. 1) max f = — 1/lg 3; min / = — 1g 40/lg 3. 2) max f = 1; min / = 1g 5/lg 9.
3) max/ = 5/4; min/ = l. 4) max / = 5; min/ = 4. 5) max/ = — 18;
min / = — 20,5. 6) max/ = —1;_ min/ = —32/7. __ 7.203. —3,25.
7.204. 1) max/ = l; min_/ = —V2. 2) тах/ = 2д/2; min / =_2.
7.205. r = #1л/2, H = R л/2 . 7.206. r = R л/2 , Ji = 4/?. 7.207. а/л/Ъ .
7.208. 7a2/32. 7.209. 1/5. 7.210. 1) 1/8. 2) 1/2 Уз. 7.211. 1) —1. 2) —4.
n
3) — (ad — be)2/4 = -((b- a) (c - a))2/4. 4) ~ 1 £ «2. 5) 3. 7.212. 2.
Ы
7.214. g (x) = / (2x0 - x). 7.215. g (x) = 2yQ - / (x).
7.216. g (x) = 2y0 — / (2x0 — x).
7.217. 1). Убывает на (—oo; 2], возрастает на [2; +oo). 2) Возрастает на
(—оо; 3/4], убывает на [3/4; Ч-оо). 3) Убывает на (—оо; —3/2] и [0; 3/2],
возрастает на [—3/2; 0] и [3/2; 4-оо). 4) Убывает на (—оо; —1] и [0; 1]г
возрастает на [—1; 0] и [1; Ч-оо).
7.226. 1) с г/1 0, Ьс— ad = с2. 2) с=#0, Ьс— ad = с2(х2 — Xi).
7.227. 1) (1/2; 1/2). 2) (-d/c; ale). 3) (2; -16).
4) (—Ь/За; (2Ь3 — Vabc + 27a2d) /27а2).
537
7.236. 1) |а|. 2) 1/2. 3) n/VT. 4) л. 5) л. 6) л. 7) л/2. 8) 2л. 9) 2л.
10) л. 11) 2л.
7.239, 1) 16л/3. 2) 16л/3. 3) 2лп0 — = 2лт0где piqzlpzqi = nJmQ
Pi Р2
несократимая дробь. 4) 2лп0 — == 2лт0—, где pi^2/p2<7i — nJtnQ — несо-
Р1 Р2
кратимая дробь. 5) 2л/0 —= л£0 —» где p^q^pzqx — l0/k0 — несократимая
Pi Р2
дробь.
7.240. а = Ь, Т=1/|а|.
7.243. Нет. 7.244. 2|а — Ь\. 7.245. 4|а — с|. 7.246. 1) 2Т. 2) 27. 3) Если
ab #= —1, то период равен 27, если ab = —1, периодом является любое, не
равное нулю, число. 4) 37. 7.247. 27.
7.266. 1) / = ±1. 2) / = 1. 3) I = л(4п + 1)/4, neZ.4) t = л(2п+1),
neZ. 7.267. I) А. 2) В. 7.268. 1) х = 2у — 2) у=(х — 1)2/з.
3) у2 = 4х2(1 — х2). 4) у = 2(1 +х — х2)/(1 +х2). 5) х = 3у — 4у3.
7.273. 1) Выпукла вниз на R. 2) Выпукла вверх на (—оо; 0], выпукла
вниз на [0; 4-°°)- 3) Выпукла вверх на (—оо; 0), выпукла вниз на (0; Ч-°°).
4) Выпукла вниз на (—оо; —Г), выпукла вверх на (—1; Ч-00)- 5) Выпукла
вниз на R. 6) Выпукла вверх на (—оо; 0], выпукла вниз на [0; Ч"°°)- 7) Вы-
пукла вверх на (—оо; 0) и (0; 4-°°)- 8) Выпукла вниз на (0; 1], выпукла
вверх на [1; Ч-°°)« 7.276. 1) Выпукла вверх на (—л/2; 0], выпкула вниз на
[0; л/2). 2) Выпукла вверх на [0; л/4], [Зл/4; 5л/4], [7л/4; 2л], выпукла вниз
на [л/4; Зл/4], [5л/4; 7л/4]. 3) Выпукла вверх на [—1, 0], выпукла вниз на
[0; 1]. 4) Выпукла вверх на (—оо; 0], выпукла вниз на [0; +°°)-
7.284. 1) а. 2) Ь. 3) а, Ь. 4) а. 7.285. п 4. 7.286. 1) 6. 2) 200. 3) 12. 4) 5.
5) 8&2 —4&Ч-1- 7.287. 1) хв = 3. 2) х3 = 1/6. 3) х3 = 5/64. 4) х3 = 9/8.
7.288. 1) х4 = —9. 2)х2 = 4,5. 3) х5 = log2 5 — 3 log3 5. 4) х3 = 1,43/з.
7.289. 3) а) 6; б) 9; в) 5. 7.290. 1). а) Да; б) нет. 2) а) Да; б) нет-
3) а) Нет; б) да. 7.294. 1) х„ = 2 + 6/г. 2) хп = (-3)п/6. 3) х„ = («+1)/п-
4) х« = 2 + (—1)”. 5) х„ = 3 + 2га. 6) x„ = n!. 7)х„ = ((-1)п-«)/п-
В) = (1 - 10~")/3. 9) хп = я/2".
7.295. хп = -у- (п - 2) (п - 3) - х2 (п - 1) (п - 3) + (п - 1) (п - 2).
7.297. xn — an/nl; если 0 < а < 2, то шах{хп} = х1; если а 2>2, то
п— 1
тах{х„} = хЕ(а}. 7.298. 1) х„ = п (а + у (п — 1)). 7.299. 1) хп = -^^ы-
fe=i
। \ 2п~1___пп~1
а + > ТГ I- 3) х„ = п/(п + 1). 4) хп = да"-1 + 20 —--------—
Z—< й! / 2 — а
&=1 7
5) х„ = 6) х„ = 2 - 22-". 7) хп = ((а+6) 2"-1 + (5-2а) (-1)")/3.
7.300. хп = (а + b + (а — 6) • 31-п)/2; уп = (а + Ь - (а - Ъ) • 31-п)/2.
7.302. 1) Если р + q =/= 1, то
_ (Л2 (а + а) - b - а) А"-1 - (%! (а + а) — (6 - а)) А”-1 '
Xfl == Л А (X,
/V2 — М
где а = г/(р Ч- <7 ~ 1); если р Ч- q = 1, то
хл==а
г (п — 1
р-2
U'p—2) р-2
538
2) Если р ф 2, то хп == (2Х0 (а 4- а) — b — а + п (Ь + а — Л.о (а + а))) Л”-2 — а,
где а = — 4г/(р—2)2; если р = 2, то хп = а + (п — 1) (й — а) + г.
7.303. 1) х„ = (би - 1 — 8 (—0,5)п)/9. 2) хп = (2га+1 - 2 (-1)п)/з — 1.
7 чпд v - ~ ^}П~' + + 1)
Ха+ 1 + Л (Л - а) (- %2)п~1
где Л = (д/б — 1)/2-
7.305. аУ= — 2fe/(2ft—1), k <= N; хп = а/((а + 1) 2п~1 — а).
7.306. 1) хп = За/(а — (а — 3) 4га-1). 2) а = 3 • 4ft/(4fe - 1), k е N.
7.307. 1) Если b =/= 1, а =A — (й — 1) й^/(й6 — 1), fee N, то xn =
= a (b— \)/((a-\-b— 1)йга-1— a), n e N, n^2; если b = 1, a =/= — \/k,
feeN, то xn = a/(T + (и — 1) a), n e N. 2) Если b=/=c, ad=/=(c—b) ck/(bk—ck),
fe e N, to xn = a (b — c) bn~l/(adbn~l + (b — c — ad) c"-1), n e N, n^2;
если b = c, ad — й/fe, fe e N, то xn — аЬЦЬ + (n — 1) ad), neN, n^2.
7.319. 1) sup {xn} = 1, .inf {xn} = 1/2. 2) sup {xn} = 1/2, inf {xn} = 1/3.
3) sup{x„} = 1, inf{x„} = 1/2. 4) sup{x„}=2, inf{x„} = 1/2. 7.324. 1) p > 2q.
2) p> 1,57. 3) p>fe<?/(fe—1). 7.326. 2) (ln3)/3. 7.337. 2) Верно.
7.342. E(q/(l — q)) + 1. 7.343. 1) ad > be. 2) ad < be. 7.345. inf{x„) = 0,5,
sup{xn} = 1. 7.355. 6.
Глава II. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§ 8. Предел последовательности
8.1. У 1 3 34 3334 2-10s
8.2. 1) £(1/е) + Г 2) Е(|а|/е) + 1. 3) £(1/е) + 1. 4) £(3/е) + 1.
5) £(2/е)+ 1. 6) £(1/е)+ 1.
8.3. 1) а) п 33. б) п 54. в) п 21fe + 12.
8.4. 1) N 1 4 67 6667 3- ю8
8.7. 1) N 1 2 101 Ю4 4-1 1 *
8.9. 1) N 1 2 50 5000 •
8.18. 1) 5. 2) 0,6. 3) 1/3. 4) —1. 5) 1. 6) 0. 7) 1. 8) —1/6. 9) —1. 10) 0.
11) 27. 12) —15/2. 13) 1/6. 14) —0,5.
8.19. 1) —1. 2) 1/2. 3) 3. 4) —1/2. 8.20. 1) d/2. 2) l/2d. 8.22. 1) 1/9.
2) 5/11. 3) 26/111. 8.24. 1) 0. 2) 0. 3) 0. 4) 0. 5) 1. 8.25. 1) 3. 2) 1/2. 3) 1/2.
4) 1. 5) 1. 6) 0. 7) 1/2. 8) —1. 9) 1. 10) 2/3. 11) 1/3. 8.27. 1) 1. 2) 1. 3) 1.
4) —1/2. 5) 1. 6) 1. 7) 1. 8) 3. 9) 1/2. 10) 3. И) 4. 12) 11. 13) 1. 8.28. 1) 1.
2) 1. 3) 1. 4) 1. 5) 1. 6) 1. 7) 1. 8) 1/2. 9) 1. 10) 1. 11) 1. 8.30. 1) 1/3.
2) 0. 3) 3. 4) 4/5. 5) 1. 8.32. 1) 0. 2) 5. 3) 0. 4) 0. 5) 1/2. 8.34. 1) 0. 2) 0.
3) 0. 4) 0. 5) 0. 6) 0. 7) 1.
8.45. 1) Ve > 0 ЗЛ'Уп N \ хп \ > е. 2) Уе > 0 37VVn N хп> е.
3) Ve > 0 JNVn^N хп< — г. 8.46. 1) Верно. 2) Неверно.
8.47. 1) Зе > 0 У/уЗге> W I хп К е. 2) Зе > 0 VN3n > N хп < е.
3) Зе > 0 VN3n^>N хп> — е. 8.53. 1)0. 2) 4-оо. 3) — оо. 4)1, —1.
5) 0, 4-оо. 6) О, ±ь 7> °> ±о°-
539
8.56. 1) ±1/2, ±1; Hm xn = 1, lim xn = — l. 2) ±2; Hm xn» 2,
__________________________________ ri^o n~*°°
lim xn = —- 2. 3) 0, + oo; Hm xn = + °°> Hm xn = 0. 4) [0; 1],
л->оо n->oo n->oo
lim xn = 1, lim xn = 0.
n->oo
8.57. 1) lim xrt=l; Hm xn = 0; supxrt = l,5; infrrt= — !•;
__ "->°° H->oo _
2) lim xn = sup xn = 3; Hm xn = inf xn = — 3. 3) lim xn == sup xn = + oo;
П->оо n^o n-х»
lim xn = inf xn = — oo. 4) lim xn = 1; supxrt = 3/2; lim xn = inf xn = — oo.
П->оо П->оо H->oo
5) Hm xn ~ sup xn ~ + oo; lim = 1; inf xn = 0.
n->OO rt->oo
8.65. 1) 0. 2) 0. 3) 0. 8.67. 1) 4. 2) V5. *3) -\Ja. 4) a)_— в) 1/3.
5) (1+л/б)/2. 8.69. 1) e. 2) e. 3) e~'. 4) e2. 5) Ve- 6) e~l.
8.87. 2) He /может. 8.89. 1) Является. 2) He обязательно.
8.91. 1) а), г) — верны, б), в), д) — ложны. 2) j = 6, 8. 3) /Сь К2, Лз, Kt, Ks, Кт
4) /<i, Лз, /С4> К7. 5) 1. 6) /С2 == TCs. 8.95. 1)-5) и 8)—10) 0. 6)—7) 1.
8.97. 1) 0. 2) 1. 8.98. а/2. 8.99. 1) + оо. 2) 2/3. 3) —1. 4) —1. 5) 19800.
<3) 1. 7) 1/5. 8) 2. 9) pq(q-p)/2.
8.100. 1)0. 2) 1, если | а | > 1; 1/2, если а = 1; 0, если | а | < 1.
3) 0, если | а | 1; 1/2, если а — 1; не существует при а = — 1. 4) 1, если
| а | > 1; 0, если | а | = 1; —1, если | а | < 1. 8.101. 2л/?2, 47?2. 8.102. 1) 1/2.
2) 1/V^. 3) 1/4. 8.103. 1) l/atd. 2) \1л/Т. 8.104. 10а/81.
6.105. тах{ар а2, .... ak}. 8.106. 1) 0. 2) 0. 3) 2. 4) 1/3. 5) —1/4. 6) 1/3.
6.107. а = 1; Ь/2.
8.108. 1) (at + Яг)/2. 2) (Я1 Яг + Яз)/3. 3) (fli-f-Яг + ... + яр)//?.
8.110. 1) —2. 2) 0. 3) 1/6. 4) 0. 5) 4-oq. 6) —оо. 7) 0. 8.111. 1) 2. 2) 0.
3) —1. 4) 1/3. 5) 1/3. 6) 1/2. 7) 4/3. 8) а2 + а + 1/3. 8.112. 1/6. 8.113. 1) 1/3.
2) 1/2. 8.114. k(k+\)/2. 8.115. 0. 8.116. 1) Неверно. 2) Верно. 8.118. 1) Не
следует. 2) Не следует. 8.123. 1) Не обязательно. 3) Может. 8.124. 1) 3. 2) L
3) тах{я; Ь}. 4) 3/4. 5) 6. 6) —1. 7) m/k. 8.125. 1) 1. 2) 1. 3) 1.
8.128. max {Я1, а2, ..., ak}. 8.129. 1) 1. 2) 1. 3) 1. 4) 1. 5) 1. 6) 1. 7) 2.
8) 1. 9) —8. 10) 1. 11) 4. 8.134. 1) 0. 2) 0. 8.135. q/(l—q)2, 8.136. 0.
8.141. 3eV/V3n > N | xn | < e. 8.143. 1) a < 5. 2) a > 5. 3) a = 5.
8.144. 1) p q. 2) p :> q. 8.147. 1) a >• 1. 2) lim xn = 1/2 при a —
fl->oo
= 1, lim хЛ=0приа < 1.8.151. 1) Неверно. 2) Неверно. 3) Неверно. 8.163. Не
П->оо
следует.
8.164. 1)0, ±1; lim хп = 1, Hm хп = — 1, supxn=l, inf хп = — L
П->°о
2) ±1; lim xn = 1, lim xn = — 1, sup xn = 3/2, inf = — 1. 3) — oo; 0; 1;
_ П-»оо
lim xn = 1, lim xn == — oo, sup xn — 1, inf xn = — oo. 4) 0, ±д/з/2;
n->oo n_>OQ
lim Xn — 'y/sl^, lim xrt = —д/з/2, sup xn = (2 + V3 )/2, inf xn = — V3~/2.
n~>°° П->оо
5) 0, 2; lim xn = 2, lim xn = 0, sup xn = 2, inf xn = 0. 6) 1;
«-*°° ______________________________________________
lim xn = lim xn = 1, sup xn = inf xn = 1- 7) 0, + oo; Hm xn = + oo;
n->oo n->oo n->oo
lim. xn = 0, sup xn ~ + oo, inf xn = 0. 8) 0, 1; lim xn = 1, lim xn =»
n->oo n->°o n->OQ
sup xn = 1» inf xn = 0.
540
8.165. 1) [0; 1]. 2) [0; +«>) и +оо.
8.166. lim xrt = 2, lim xn = 1.
8.168. Является. 8.178. 2) He может. 8.179. Ms [ДС] и Ме[ЛС], где
1 2
ДМ = -±АС, AN——АС. 8.206. 1) 0. 2) 0. 3) 0. 4) 0. 5) 0, если а > 1;
О О
ч-°°. если а 1. 6) 4-°°, если а > 1; —оо, если 0 < а < 1.
8.210. Не обязательно. 8.212. 1) 1. 2) 1. 3) е3. 4) 1/е. 5) 1/е2
8.214. 1) Ч-оо, если а> 1; —оо, если а < 1. 2) 1. 8.220. 1) е2. 2) е-*1.
8.228. 1) d/(l — q).
8.229. 1) d/(l — q), если |?| < 1 или q == — 1; оо, если |^| > 1.
2) а-------f если | q | < 1; оо, если | q | 1.
8.230. (л —а)/3. 8.231. л/3. 8.232. а) и б) а/3. 8.233. (1 + У14-4а )/2.
8.234. 1) Сходится. 2) Расходится. _8.235. q «= [0; 1/4]. 8.236. Уо". 8.237. 5V
8.239. 1) (Уб — 1)/2. 2) (Уб — О/2- 8.240. 1) — 4) Сходится.
8.241. (b + Уб2 + 4а )/2. 8.242. 1 — У1 -- а при —3 < а 1; 4 при а == — 8.
8.243. 1) б) Сходится при Х[ =0, Xi е [Г, 2]; расходится при Xi < 0, хх > 2.
8.244. 2) л/ab .
8.245. 1) Сходится при а = Ь\ расходится при а =# 6. 2) Сходится при
<1 = Ь\ расходится при а =/= Ь. 3) Сходится при а = b = 0; расходится при
<1 #= 0 или 6 =/= 0. 4) Сходится при а = b = 0; расходится при а #= 0 или
6 0.
8.246. 1) 0. 2) 0. 8.247. 1) 3. 2) 2. 3) 4. 8.248. 1)—3) 0. 8.250. 1) -1.
2) +оо. 3) —1. 4) +оо. 8.251. 1. 8.252. 1)—3) 1/2. 8.254. 1) Сходится
к —1/2. 2) Сходится к —2. 8.255. Сходится к р, если O^Jp — а^1.
8.256. 0 при а — 0 или | b | < | с |; {b — c)/d при | b [ > | с |.
8.257. (1 + У1 4~ 46 )/2 при а #= (1 — У1 4~ 46 )/2 и а ¥= 0; а при
« = (1 — У1 4-46 )/2. 8.258. 4~ 00 при а^>1; Уб/(1 —а) при 0 < а < 1.
8.259. 0. 8.260. х2 = а (б —У4Г)/4, lim хп = 0. 8.263. 0. 8.269. 1) 1/е. 2) 0.
П->оо
3) 4/е. 4) 0. 5) 4-00. 8.272. 1) 1/(р 4~ 1)- 2) 1/2. 8.291. 1) 1. 2) 0 при
<х > — 1; оо при а < — 1; не существует при а — — 1. 8.293. lim Мп = М,
П->оо
Где AM = ~АС. 8.296. 1) оо при 0 при а > 1. 2) 0. 3) Уab.
о
§ 9. Предел функции
9. 1. 1) б <V4,001— 2 « 0,00025. 2) 6 <4/51. 3) б <-^ — arcsin 0,99 «0,14.
4) 6 не существует. 9.2. 1) б <0,99. 2) 6 <0,90. 3) б<1--4—«0,21.
V10
4) б < 1 — « 0,023. 9.3. б < е/3. 9.4. б < V9+T — 3. 9.5. Если е > 1,
Vio’ ________
то б — любое число; если е < 1, то 6^V(1 — е)/е. 9.6. Если е/>л, то
б — любое число; если е < л, то б < — ctg е; lim arctg х = — л/2.
Х->-оо
9. 9. Не следует.
9.17. 1) Ve > 0 36 > 0 Vx(—б < х < 0 => | f (х) | < е).
2) Ve > 0 36 > 0 Vx (| х | > б=> | f (х) - 4 | < е).
3) Ve36 > 0 Vx(l <х< 1 + б =►/(х) < е).
4) Ve > 0 36Vx (х < б => | f (х) | > е).
9.18. 1) Зе > О V6/5- 0 Эх (- б < х < О Д |f(x) | > 8).
2) 3e>0 V6>0 Эх(|х|>бДП (х)-4|>е).
541
3) НеУб >0 Эх (1 < x < 1 + б л f (х) > е).
4) Зе > 0 УбЗх (х < б Д / (х)< е).
9.19. 1) ЗаУе >0 36 > О Vx (0 < | х — х0 | < б => | f (х) — а | < е).
2) УаЭе > 0 Уб > 0 Зх (0 < | х - х0 | < б Д | f (х) - а | > е).
9.20. 1) 7/3. 2) 3. 3) 1. 4) оо. 9.21. 1) 2. 2) 17/5. 3) 2. 4) 1/3. 5) 5050.
6) 64/105. 7) 1. 8) — 1/2. 9) 1. 9.22. 1) 3. 2) 49/16. 3) 8. 4) 0. 5) 3. 6) —9/4.
9.23. О, если п < k\ а01Ь0, если п = k; оо, если п > k. 9.24. 1) n/k^
2) (п2 — 2fe + n)/2. 3) С* 4) (n — k)/2. 9.25. 1) 1/4. 2) 3. 3) 5/3. 4) 3/4?
5) 3. 6) V7/4. 7) 2. 8) 4/7. 9.26. 1) 7. 2) 5. 3) Уб. 4) 3. 5) -2. 6) 7/12.
9.27. 1) 0. 2) 2. 3) 13/4. 4) 2. 5) 1/2. 6) У2/8. 9.28. 1) k/n. 2) 2^1 па.
3) (ak — bn) Ink. 4) nkl(ka nb). 5) 2n. 6) (/г+ l)/2. 9.29. 1) 3. 2) 4. 3) 1/5.
4) a/0. 5) -1. 6) 1/2. 7) -9/128. 8) 3 У if. 9) tg4 1 - 1 = - (cos 2)/cos4.
9.30. 1) -7/2. 2) 1/2л. 3) л. 4) 4. 5) 4. 6) 1. 7) 2. 8) 14. 9.31. 1) 4У2.
2) 13/6. 3) 1/3. 4) 3/2. 5) 1/24. 6) 0. 9.32. 1) 2. 2) 10/37. 3) 2. 4) —2/21.
9.33. 1) 0. 2) 0. 3) He существует. 4) 1/e. 9.34. 1) 1/(10 In 10). 2) —7.
3) 5/ln 2. 4) —2/3. 5) 8. 6) 25/16. 7) 1. 8) — л2/2. 9.35. _1) (In 10)/ln 2.
2) ln3. 3) In 4. 4) 5. 5) 2. 6) 2. 7) 3/2. 9.36. 1) e3. 2) l/Уе. 3) e3. 4) e.
5) Уе. 6) 1/Уе. 7) e~18. 8) e1/e, 9) е/л. 10) Уе. 9.37. 1) 1. 2) —4.
3) 25/2. 4) 2. 5) In 2. 6) e3/2. 9.38. 1) aa° In a. 2) In (alb). 3) УУГ
4) aa/(a+fc)6b/(a+b). 939 a) 1; 6> Q_ 2) a> He существует; б) л. 3) a) 0;
6) 0. 4) a) 0; 6) + 00. 9.40. 1) a) 3/2; 6) 1/4. 2) a) 1; 6) —1. 3) a) л/2;
6) — л/2. 4) a) 0; 6) 1/3. 9.41. 1) a) 1; 6) +00. 2) a) 109; 6) 110. 3) a) 0;
6) 1. 4) a) 3; 6) 2. 9.42. 1) a) — л/2; б) л/2. 2) а) л; б) 0. 3) a) 0; б) + oo.
4) a) —л/2; б) He существует. 5) a) + 00; б) 0. 6) a) 1/e; 6) e. 7) a) —4;
6) 4. 8) a) 0; 6) In 4. 9.43. 1) —2. 2) -1/2. 3) 7/4. 4) - л/6. 5) 1/2. 6) 0.
7) 3. 8) 2. 9) -у/2. 10) 1/У2Л-. 9.44. 1); 2) a); 3); 4) a); 5). 9.45. 1); 2) 6);
3); 4) 6); 5) 6); 6) 6). 9.46. 1) a = 1, 0 = - 3. 2) a) a =- 2, 0 = 1/4.
6) a = - 2, 0 = — 1/4. 3) a = — 1, 0 = 1/3. 4) a) a = 1, 0 = 0; 6) a = 0 = 0.
5) a) a = 1, 0 = 5; 6) a = 0 = 0. 6) a) a = 3, 0 = 0; 6) a = 0 = 0.
7) a) a = л/2, 0 = - 1; 6) a = - л/2, 0 = - 1. 9.47. 1) a > 0, 0 - любое;
a 0, 0 < 0, a > 0. 2) a > 0. 3) a > 0, 0 — любое; a 0, 0 < 0, a > 0.
4) a + 0 > 0. 9.48. 1) n = 4. 2) n = 2. 3) n = 4. 4) n = 3. 5) и = 2. 6) n = 2.
9.49. 1) n = 3. 2) n = 2. 3) n = 2. 4) n= 1. 5) и = 6. 6) n = 3. 9.50. 1) a);
2) 6); 3) a)- 4) 6). 9.52. 1) 6); 2) a); 2) 6)^3); 4) a); 5). 9.53. 1), 2), 3), 5), 6).
9.57. 1) a) a=l, 0 = 1/8; б) а = Уг, 0 = 1/2. 2) a =1/2, 0 = 2.
3) a = 9/4, 0 = 4. 4) a = 7, 0 = 2. 5) a = 1/8, 0 = - 4. 6) a = 1, 0 = - 1.
9.58. 1) —1/4. 2) —1/2. 3) —2. 4) 2. 5) 7/3. 6) 12. 9.60. 0 9.61. He следует.
Рассмотреть при /->0 функцию где
{1/q при х — р/q, где р и q — взаимно простые
о
__ ( 1 при х #= О,
g ( ( 0 при х = 0.
9.64. ( -J ’ 9.65. 1)
9.66. 1) л; —л/2. 2) 3; —3. 3) 1; —1. 4) е; 2.
при х иррациональном,
е; 1/е. 2) + оо; 0. 3) л; 0. 4)
числа,
+ оо; —1/2.
§ 10. Непрерывность функции
10.1. 1)
Аг/ 1,8 1 0,2 0,02
— 1,8 — 1 — 0,2 — 0,02
542
Ду 2,61 1.25 0,21 0,0201
Ду — 0,99 — 0,75 — 0,19 — 0,0199
Ду*) 0,3784 0,2247 0,0488 0,0050
Ду — 0,6838 — 0,2929 — 0,0513 — 0,0050
Ду*) — 0,4737 - 0,(3) — 0,(09) — 0,(0099)
Ду 9 1 0.(1) 0,(01)
10.2. 1) 6 1 0,25 0,005 0,0005
б 0,732 0,224 0,0049 49 • 10-5
б 1 0,75 0,0199 1,999- 10-8
б 2/3 1/3 1/101 1/1001
10.3. 1)
бшах 0,25 0,25 0,25 0,25
бшах 1/2 1/4 1/6 1/8 1/2/
бтах 1/210 1/36 1/3 1 32/5
бгпах 1/4 1/2 3/4 11/36 3/4 7/4
10.4. 1) б (х0) = хЦ(2 + х0). 2) 6(xo) = Vxo + 4- при 0 < х0 < 1/4,
«(x0)=V^-l/4 при х0>1/4. 10.11. 1) f(-l) = -2. 2) f(l) = 3/2.
3) f(0) = 1/2. 4) f(0) = 1. 5) f(0) = 1. 6) ИО) = 1/2. 10.15. f(x0) = 0.
1018. 1) х = 0, Af(O) =2; х = 2, Д/(2) = —10. 2) х = —2, Д/(—2) = 2.
3) х ==—2, х — 2— точки разрыва II рода. 4) х = 0— точка разрыва
II рода; х = 1, Af (1) — —2. 5) хп = n, А/(п) = —1, п <= Z. 6) хп — п,
п eZ,— точки разрыва II рода. 7) х — 0, АЯ0) — 0; х = 1 —точка разрыва
II рода. 8) х =—1, А/(—1) = 0; х — 1, А/(1) =—2; х = 0— точка раз-
рыва II рода.9) хп = + лп, гге Z,—точки разрыва II рода. 10) х = 0,
Af(O) == 0, хп — лгс, п ф 0, n е Z,— точки разрыва II рода. 10.19. 1) а = 0.
2) а = 1/3. 3) Не существуем. 4) а = —1. 10.20. 1) 2, b = —1. 2) а — 1,
6 =—1. 3) Не существуют. 4) а = 1, Ъ == л/2. 10.25. 1) f°g непрерывна;
g ° f разрывна в точке х = 0. 2) f ° g разрывна в точках х = 0, х = ±1;
g°f непрерывна. 3) f ° g разрывна в точке х — —1; g°f разрывна в точке
х = 1. 4) f°g и g°f непрерывны. 10.51. 1) # = cos2x, хе(-л/2; л/2).
*) Указаны приближенные значения Дг/ с погрешностью не более 5 • 10~5.
543
2) х = Vl + У2 , £ e R. 3) у = —ln(l — e~x), x>0, или x = —In(1 — £-*),
у > 0,10.52. Xj (у) = — x2 (у) = V#2+ 1, У e= R, yx (x) = — y2 (x) == Vx2 — 1,
|x I > 1, уз (x) = — y4 (x) = V*2 — 1 sign x, |x| >1. 10.53. 1)—5) не будет
10.56. 1) {x e R; -x =# 0}, x — 0— точка разрыва I рода. 2) {x e R; x =# 0,
x =/= 2}, x = 0, x = 2 — точки разрыва I рода. 3) {xe R; x #= 0}, x = 0 —
точка разрыва II рода. 4) {x e R: x =# —1, x =# 1}, x = —1 —точка разры-
ва I рода; x = 1 —точка разрыва II рода. 5) {х е [—1; 4]; хУ= 1}, х=1 —
точка разрыва I рода. 6) {х е [—л/2; л]: х =й= л/4}, х = л/4 — точка разрыва
I рода. 10.57. 1) х = —3, х = 2 — точки разрыва II рода. 2) х — —1, х = 0,
х — 4 — точки разрыва II рода. 3) Точек разрыва нет. 4) х — —1 —точка
устранимого разрыва; [(—1) = 1/3. 5) х — —I—точка разрыва II рода,
х == 0, х — 1 —точки устранимого разрыва; f (0) — —1, f (1) = 0. 6) х=—2 —
точка разрыва II рода; х= 1/2 — точка устранимого разрыва; /(1/2) = 2/5.
7) х = 1 —точка устранимого разрыва; /(1) = —1/4. 10.58. 1) х = -~ + лп,
/ieZ,—точки разрыва II рода. 2) х = 0— точка устранимого разрыва;
/(0)=0. 3) х — От-точка устранимого разрыва; /(0)=1/2. 4) х = 0 —
точка разрыва II рода; х = 1—точка устранимого разрыва; /(1) =—л/2.
5) х = л/2 + лп, п е Z,— точки разрыва II рода; х = лп, п е Z,— точки
устранимого разрыва; /(лп) = (—1) *3/2. 10.59. 1) х = 0 — точка разрыва
II рода. 2) х = 1 —точка разрыва П рода. 3) Точек разрыва нет. 4) х = 1 —
точка разрыва II рода. 5) х = 0 — точка разрыва II рода. 6) х =0, х = 2 —
точки разрыва II рода; х=1—точка устранимого разрыва; /(1) = 0.
7) х =—1, х = 1—точки разрыва II рода. 8) х = 0 — точка устранимого
разрыва; /(0) = 0. 9) х = 0 — точка разрыва II рода. 10.60. 1) х =—1,
х = 3 — точки разрыва I рода; Д/(—1) = —2, Д/(3) = 2. 2) хп = —- + лп,
neZ,- точки разрыва I рода; Д/(хл) = 2(—l)"+i. 3) хп = п, п е Z, —
точки разрыва I рода: Д/(х„) = 2(—1)я. 4) х = 0 — точка разрыва II рода;
хп == 1/п, п(=2, — точки разрыва I рода; Д/(хл) = 2(—1)я“*. 5) Точек раз-
рыва нет. 6) х = 0 — точка разрыва I рода; Д/(0) = л. 7) х = 0 — точка
разрыва I рода; Д/(0) =0. 8) х = 0—точка разрыва I рода; Д/(0) = 4/л.
9) х = 0 —точка разрыва I рода; Д/(0) = 2. 10) х=1—точка разрыва
I рода; Д/(1) = — 1. 11) х = 0—точка разрыва I рода; Д/(0) = 2.
12) х = 0— точка разрыва I рода; Д/(0) =0. 10.62. 1) а = п. 2) а = 1/2.
3) а = —2. 4) а = 1. 5) а = 1пс. 6) а = 1/2. 7) а = 1. 8) а = 0. 9) а = 0.
10) а = е. 10.63. 1) Нельзя. 2) Нельзя. 3) #(0) = 0. 4) г/(1) = 1/4. 5) Нельзя.
10.64. 1) Область определения R, непрерывна на (—оо; —1), (—1; 1) и
(1; 4-°°); х — —1, х=1—точки разрыва I рода. 2) Область определения
х Ф—1, непрерывна на (—оо; —1), (—1; 1) и (1, +°°); х = —1, х = 1 —
точки разрыва I рода. 3) Область определения х =й=л + 2лп, n е Z, перио-
дична с периодом 2л, непрерывна на (2лп; л + 2лп) и (л + 2лп; 2л(n + 1)),
neZ; х = лп, пе Z, — точки разрыва I рода. 4) Область определения R,
( । л । \ \ 5л . \ гу
непрерывна на I—— 4-лп, — 4*лп I и 1-£- + лп; —k^nj, n е Z;
х = ± + пл, пе Z, - точки разрыва I рода. 5) Область определе-
ния R, непрерывна на (—оо; 0) и (0; +<»); х = 0 — точка разрыва I рода.
6) Область определения R, непрерывна на (—оо; 0) и (0; +°°); х = 0—
точка разрыва II рода. 7) Область определения R, непрерывна на R. 8) Об-
ласть определения х =/= лп, neZ, непрерывна на (лп; л/2 + лп); х = 0 —
точка устранимого разрыва, х = лп/2, п 0, п е Z, — точки разрыва I рода.
9) Область определения R, непрерывна на R. 10) Область определения R,
непрерывна на (—оо; 0) и (0; 4-со); х=0—точка разрыва I рода. 10.65. х=
= —1, х—1. 10.67. Непрерывна в каждой иррациональной точке, каждая ра-
циональная точка — точка устранимого разрыва. 10.68. f°g непрерывна на R;
g°f непрерывна в точке х = 1; разрывна й остальных точках. 10.99, 0,2.
544
10.109. 3) 8. 4) 2". 10.111. 1) f(x) =x. 2) f(x) = x/4. 3) Если ₽ Ф — a. to
., . a b
если P — —a, то решение существует только при а = 0 и
/ (х) = <р(х) +-J-,
где ф(х)—произвольная непрерывная, нечетная функция. 4) f(x)=x4-C,
СеР.5) f(x) = х. 6) f(x) - НС, CeR.
10.112. f (х) = -^х И- д _|_’В + Ф(*), гДе: если|а/Р| = 1 или|сс/р|<1
и | В/А | 1, то
Ф (х) = 0, хе R;
если | сх/р| < 1 и \В/А | < 1, то
Ф (х) = -^ф (In х), х > 0,
ф (х) == | х ф_ (In I х I), х < 0,
Ф (0) = 0,
где q = logja/p| | BjА |, и если ос/р > 0, то ф±(/) — произвольные непрерывные
на R функции, удовлетворяющие условию
ф± (О = •— ф± (/ 4- In (P/a)) sign АВ, t е R,
(периодичность при АВ <. 0, антипериодичность при АВ > 0), а если a/Р < 0,
то ф+(0—произвольная непрерывная на R, периодическая с периодом
2 In | 1 функция,
Ф_ (/) = -ф+ р + 1п
1 ) sign МВ).
При | a/р | > 1 в приведенном ответе следует поменять местами а и р, А и В.
10.113. 1) а > 1/4. 2) а > 1/4. 10.114. Если а Ф 0, то (Ь — I)2 < 4пс;
если а = 0, то b — 1. 10.115. 1) f(x) - ох, се R, хе R. 10.116. f(x) = еах,
aeR, и f(x)=O, xeR. 10.117. 1) f(x)=alnx. 2) f(x) = xa, a e R,
и /(x) = 0, xeR. 10.118. 1) f(x)=cosax, aeR, и f(x)=O, xeR.
2) f(x)=chax, oeR. 10.119. f(x)= const, xeR. 10.137. x=of(f(x)).
10.139. lim x9, = — 1, lim x9fc . = 1. 10.143. 3) л. 10.144. 1) 0. 2) л/6.
^_>oo 6-»oo
3) л/3. 4) 0. 5) 1. 6) 1. 10.146. 0, если at < a2\ если ftl —
4-oo, если «1 > a2. 10.147. 1) ex. 2) e^x. 3) 4) ek(k+\) a/2.
6) (sinx)/x при x #= 0; 1 при x = 0. 7) 1. 8) 0. 9) 0. 10) e~x^2. 10.148 V2-
§ 11. Асимптоты и графики функций
11.1. 1) х = 1, х = —1, у — 0. 2) х =0, х —- —1, х — —2, у —= 0.
3) х == —2, х = — д/2, х = л/2, х = 2, у =» 0. 4) у = 0. 5) у = 1.
6) х = —2, #=1.7) у = 0. 8) у = 0. 11.2. 1) х == 0, у = х. 2) у — х 4- 1.
3) х = 0, у = х 4- 8. 4) х — —4, # = х— 4. 5) у ——х—1, у = х—1.
6) х = 0, # = 2x4-1 7) х = —1, # = х—2. 8) х = —2, # = х — 4.
9) х ~ Ь, х = 2Ь, у = х — 3(а — Ь). 10) у = х. 11.3. 1) у = — х, у = х.
2) # = — х — 3/2; у = х 4- 3/2. 3) у = х. 4) # = х4-1/3. 5) х = 2,
у = —х—1, # = х4-1. 6) х = —4, у = х — 2. 7) # = х. 8) # = —2ху
У = 0. 9) у = —х, у = Зх. 11.4. 1) х — 0, у = 1. 2) у = 0. 3) у = 1.
4) х = 0, у = 0. 5) у э= 0. 6) х = 0, у = 1 — х. 7) # = 1 — х, # = 3 — х.
8) t - 0, # - 34-х 9) х = 0, у == х. 10) у = 1. 11) х =? 0, # =* —х —1,
18 л. Д. Кудрявцев и др, 545
V = *+ 1- Ч-5- 1) У = е. 2) y = 3) у = — 1, У~ 1. 4) х = 0.
У — —1, У = 1. 5) у = 1. 6) у = —х, у = х. 7) х = 0, у ~ 2х — 1,
у = 2х + 1. 8) у = —-х, у = х. 11.6. 1) х = —2, х = 2. 2) х == 1/2, х =- 1.
3) х — лм/2. п е Z. 4) х == 0, у = х. 5) у = 0, у = х. 6) х = —1/е,
У = к 1g е 4- (1g а)/е. 11.7. 1) х = (Зп ± 2)п/3, «е Z 2) х = ля/2, п е= Z.
3) х = 0, у — 0. 4) у = х. 5) у == 1. 6) у = 3. 7) у ~ л, у = 0. 8) у — 0.
9) у = 0. 10) г/=(х4-л)/2. 11) z/= (4x4-л)/2, У = (4х — л)/2.
12) у == лх 4- 1, у = 1. 13) у = — (лх± 2)/2, у == (лх — 2)/2. 14) х = 0м
у — 2/л. 11.8. 1) у = — 1, у = х~ 1. 2) у — х/2. 3) # = (1 — х)/2.
4) х = —1, х = L 5) х — —1, х = 1, у = 0. 6) у — (2х 4- л)/4,
у = (2х — л)/4.
11.10. Не может. 11.11. 1) Область определения 0^х< 1; у ~ х3/2 при
х -> 4- 0, у х/'х/х — х при х —> 1 — 0; х = 1 — асимптота. 2) Область опре-
деления |х| 2; начало координат — центр симметрии графика, у ~ 2х при
х->0, у~\^2~ х при х->20; максимум у = у (V^) =: 2- 3) Область
определения |х| 1; ось ординат — ось симметрии графика, у~х при
х->4~0, у ~ 'х/ 2'\/х — х при х->1—0; максимум у — у (1/V2)= 1/2.
4) Область определения |х| 3; ось ординат — ось симметрии графика,
4__ 4 _____
У~ V3x при х -> 4- 0, у ~ V54 Уз — х при х-^3 — 0; максимум
у == у (з/ д/‘2 ) = 3/V2. 5) Ось ординат — ось симметрии графика, у ~ х2/3 при
х->0; у = X— асимптота при х->-±оо. 6) Ось ординат — ось симметрии
4
графика, #~х/Уз при х->4-0; У~ 1 — асимптота при х->±оо. 7) Об-
ласть определения |х| > 1; начало координат — центр симметрии графика,
У ~ 1/(V 2Vx — 1) при х -> 1 4- 0; х — 1, х = —1, у — 1, у = —1 — асимпто-
ты графика. 8) Область определения х < 0, х 1, у ~ 1/V— х при х->—0,
у ~ 'х! х— 1 при х-> 1 -НО; х — 0 и у — 1 —асимптоты. 9) Область опреде-
ления х 0; у ~ — Ьл/х при х ->_+ 0, у х3^2 при х-> 4~°°, У ~ 2(х — 4)
при х—>-4; минимум у =— 1б/(з Уз) при х = 4/3 (для исследования можно
сделать замену x = ±cos2/, 0</<л/2). 11.15. 1) g(x). 2) f(x). 3) g(x).
4) f(x) и g(x). 11.16. у = (an+lx + a,,bn — an+lbn-i)bn. 11.17. у = 0 при
k < /, у == 1 при k = /, у — x 4- («1 — b[)ln при k = I 4- n. 11.18. 1) Сверху
при x-^-J-00. снизу при x->--------------oo. 2) Сверху и при х->-±оо и при х->-—оо.
3) Сверху при х->4-оо, снизу при х->—оо. 4) Сверху и при х->4-°° и при
х->—оо. 5) Сверху при х->4-°°, снизу при х~>—оо. 6) Снизу при х->4-°°»
сверху при х->—оо. 11.19. 1) Асимптоты х = ±1/2, у — 1; область опреде-
ления х=/=±1/2; ось симметрии — ось ординат; функция возрастает на
(0; 1/2) и (1/2; 4"°°)» У ~ 4х2 + 2 при х-+0, у ~ 1/(2(1 —2х)) при х-> 1/2.
2) Асимптоты х = 0, х = 2, у — 0; область определения х #= 0, х =# 2;
(1; 0)—центр симметрии, функция убывает на [1; 2), (2; 4-°°)’. У ~ 1 х
при х-> 1, у 1/(2(х — 2)) при х->2, у ~ 1/2х при х->0. 3) Асимптоты
х = 1, у — —1; область определения х 1; функция возрастает на (—оо; 1)
и (1; 4-°°); У при х->0, у ~ 1/(3(1—х)) при х-^Х. 4) Асимптоты х=1,
{/= (х — 5)/4; область определения х 1; (Г, —1)—центр симметрии;
функция убывает на (1; 3], возрастает на [3; ±оо); у 1/(х— 1) при х->- 1,
у ~ (х — 3)2/8 при х->-3, у ~ —2—(х 4- 1)2/8 при х-»--------1. 5) Асимптота
у = х; (0; 0) —центр симметрии; функция возрастает на IR, г/~х3 при х->0.
6) Асимптоты х = 2, у = 1; область определения х =# 2; функция убывает
на (—-оо; —2) и (—2; 4-°°); У — Vx/2 при х->0, у V2/(x — 2) при
х 2. 7) Асимптота у == —х; ось симметрии — прямая у = х; функция убы-
вает на R; ~ 1 —х3/3 при х->0, у Уз(1 — х) при х-> 1. 8) Асимптоты
х = 1, х = —1; у = х при х->4~°° и у == —х при х->—оо; область опре-
деления х =/= ±1; ось симметрии — ось ординат; функция возрастает на [0; I)
и [V2; + оо), убывает на (1; V2 ]; у ~ х2 при х->0, у ~ 1/V 2 | х — 11
646
при х -► I, у ~ 2 2 (х — V?) при х -> V2' Асимптоты у = 1 — 2х при
и у = 1 + 2х при х->—оо; ось симметрии — ось ординат; функция
убывает на [0; 4-°°); У ~—2х2 при х->0. 10) Асимптоты у == х при
х->-f-o° и у = —х — 4 при х->—оо; ось симметрии — прямая х = —2;
функция возрастает на [—2; 4“°°); у~—1 + (х + 2) 2/2 при х->—2.
11) Асимптота у = х—1/3; функция возрастает на (—оо; 0] и [2/3; 4-°°).
убывает на [0; 2/3]; # ~ — х2^3 при х->0, у ~ х — 1 прих->1, у~
^4 QZ—
~-----3---3V4(x—2/3)2/4при х-^2/3. 11.20. 1) Асимптоты х = —3,у == 1; об-
ласть определения х —3; функция убывает на (—оо; —3) и (—3; 4-°°).
2) Асимптоты х = —2 и х — 2; область определения ]х| <2; ось симмет-
рии— ось ординат; функция убывает на [0; 2), у ~ 1п 4 — х2/4 при х->0.
3) Асимптоты х = 0, у = 0, у = 1; функция убывает на (—оо; 0) и (0; 4-°°).
4) Асимптоты х = 3 — V3, x = 34“V3, у~ 0; область определения
|х— 3|>V2, x#=3±V3; ось симметрии—прямая х — 3; функция убы-
вает на (3 + V2; 3 + Уз ) и на (3 4- + °о). 5) Асимптоты у = 0 при
х-»—оо, у = х4-1п2 при х->4-°°; функция возрастает на R. 6) Асимптоты
х = л(1 -j-2n)/2, neZ; функция периодична с периодом 2л; функция опре-
делена на (—л/2; л/2); ось симметрии — ось ординат, функция убывает на
[0; л/2). 7) Асимптоты х = 0, у — In (л/2); область определения х > 0;
функция возрастает на (0; +<»). 8) Асимптоты х = лп, ncZ; функция пе-
риодична с периодом 2л; область определения х =# лп, п е Z; оси симмет-
[л \
---2~* И
11.21. 1) Асимптота у = х; область определения 2) Асимптота
у — х; область определения х =/= 0; центр симметрии — начало координат.
3) Асимптота у = 2х 4- 4; область определения х =/= 0. 4) Асимптоты
у — (2х — л)/2 при х —*-оо, у = (2x4-л)/2 при х->4"°°; функция возра-
стает на R; у ~ 2х при х->0. 5) Асимптоты у = лх 4- я 4* 1 при х->—оо,
у = 1 при х-> 4-°°- 6) Асимптота у = (лх — 2)/2 при х-*-—оо и х—>-+оо;
область определения |х| 1. 7) Асимптоты у — (6х —л)/2 при х-»—оо,
у — (6х4~я)/2 при х->4-оо; центр симметрии — начало координат, функция
возрастает на R. 8) Асимптота у = —х\ область определения х =0= 0, центр
симметрии — начало координат, функция убывает на (0; 4-°°)» У~ (я — 4х)/2
при х->-4~0 9) Асимптота у = х при х->-оо и х->4-°°; область определе-
ния х =/= 0, центр симметрии — начало координат; функция возрастает на
(—оо; 0) и (0; 4-°°); У ~ 0,5лх2 sign х при х->0. 11.22. 1) Асимптота
у = 0; область определения х<0, х 1. 2) Асимптоты у — 0, х—1; об-
ласть определения х #= 0, х =/= 1; у~ 1/(х—1) при х->0. 3) Асимптота
у == х. 4) Асимптота у = 0; ось симметрии — ось ординат.
11.23. 1) у — — х — а. 2) х = 2, у = 3(2х 4- 3)/40, у = — (2х + 1)/8.
3) у ——а, у — х 4- «/3. 4) у ~ х— 2. 5) у~—х 4- «• 6) Нет асимптот.
7) у — х 4- 6л при х -> —оо, у = х при х -> 4-°°- 8) Нет асимптот. 9) х = 0
при у-+—оо, у = 0 при х->4-°°- Ю) у = х 4- 1 при х->4-°°- П) У ==
= (x-f-2e)/2, при х->4-°°- 12) у — 2х при х-*-4“°°- 11.24. I) х"— ^1'
У = 0. 2) у =—(х4^_1)/2, у (х—1)/2. 3) у =—bx/а, у = bx/а при
х -> 4-оо. 4) х == — V2, х = V2. 5) х = —1, х = 1, у = х/2, у = —х/2.
6) х = 0, х = 1/2. 7) х == 1. 8) х = —1/2, у = 0, у = (2х — 3) /4.
11.25 1) (р = л^/4 (k = 0, 1, 2, 4, 5, 6). 2) ф = л^/4 (k == 0, 1, 2, 3, 4, 5,
6, 7). 3) г = 2а/созф. 4) г=— 1/^V2 sin^~-г=1/^ •
5) г з/^V2 sin ( ф 4- qp . б) г == — 1/(4 VTsin (ф — ф0)) , где
фо = arctg(l/2). 11.26. 1) г х= л/sin (ф — 2) ф = 0. 3) г ««= 1/81п(ф— 1).
18*
547
р
р
4) г= 1/sin ф. 5) г=±=2/созф, г=—2/cos ф. 6) г=———-------------------------------*-9
Д/е2 — 1 sin (ф — arccos (1/e))
•-------, ...-------------------------- 7) См 6). 8) г = 2/cos ф,
Ve2 — 1 sin (ф 4- arccos (1/e))
r x== —2/cos ф. 9) r = 1/sin ф, r == —1/sin ф, r = 1/cos ф, r == — 1/cos ф.
a a a
10) r =-------:, r—-----------------------------——, r —------n------. И) Ф =
O . < у о <3 COS ф
3 sin - ~ 1 ° — 1 ~ 1 1
3 sin
~ (л 4~ 2лЛ)/6, k — О, 1,2, .3, 4, 5. 12) г — sjn^y 12 уу 13) r ~ 2/?/cos ф.
14) г = 2«/cos ф. 15) ' = —o/cos ф. 16) ф == (л 4- 2лп)/4 (п = О, 1, 2, 3).
17) г — V2 /sin
(п = О, 1, 2, 3). _ _ , _ _
х ~ 1, х =_2. 4) у = О, х = О, у = —х. 5) у — х + 2. 6) х = а. 7) у = х/д/З,
у^= — х/д/3, х = 0. 8) у — х, у ~ —х. 9) у = х, у ~ —х. 10) у — О,
х = 0, у = х. 11) у = —1, х — 2, у — —х— 1. 12) х — 1, х = —1, у = х,
у = —х. 13) у = х. 14) у -•= х— 1, у = —х—1. 15) у « ~+~,У = —~ 4~
д/ 2 8 д/ 2
х 2а х . 2а л
——--------==, у —--== 4-------—, х ==------. 17) у = 1,
д/3 Зд/З д/3 Зд/З 3
11.29 . 1) -у = 4х/3, у =—4х/3. 2) у ~—1, //=—2х—1.
у — х 4- 1- 4) х == 3, х = —3, у — 2, у — —2. 5) у = —х'
6) у — х, у — —х. 7) х = 4. 8) у — 2 д/2х, у — — 2 д/2х. 9) у = 2, у ——2.
10) х = 0, у = 0, у = х, у — —х. 11) у = —х 4- 1, г/ х= —х —1. 12) у = 1.
ф —г ~ — л/2/sin ^ср---------------5-^. 18) ф = (л + 2яп)/4
11.27. 1) у = 0, х = 0. 2) у == О, х = 0. 3) у = ~1,
+4-1б) у—
8
х = 1, у = х.
3) у = 2х — 1,
§ 12. Равномерная непрерывность функций
12.3. Равномерно непрерывными являются функции; 1) 2), 3), 6), 7), 8), 9).
12.4. Равномерно непрерывными являются функции: 1), 3), 4), 6), 7).
12.10. 1) со(6) — 26. 2) со(6) = 6. 3) Если 0 < 6 1 или 2 6 4, то
ц>(6) == 6; если 1 < 6 < 2. то со (6) = 1; если б > 4, то о(6) = 4. 4) Если
О С 6 sC 2g, то о(6) == 6/g; если 2а <Z 6, то со(6) —2 5) со (6) ==
= 6(62 —36 4- 3). 6) w(6) = —Е(—6). 12.11. 1) со(6) = 26. 2) Если 6 а,
то со(6) = G2; если О < 6 < а, то со(6) ~ 6(2а — 6). 3) со(6) — 6/g(g 4~ 6).
4), Если 6 л; то. со(6) = 2; если 6 < л, то со(6) — 2sin(6/2). 5) со(6) —
= In (1 4-6). 12.30. 1) Например, у — —(9,1х 4- 3,1)/6, если —1 х —0,4;
у — 0,09, если |х|< 0,4; у = (9,1х — 3,1)/6, если 0,4 х 1. 2) Напри-
мер, у = 2,45— 1,5х, если 2/3 -С х 1, у — 1,45 — 0,5х, если 1 х 2.
12.31. Например, у — (8 — Зх)/8, если 0 х 2; у — (100 — х)/392, если
2< х 100. 12.34. 1) f(x) = -14-|x4-3|~|x4- П4-|х-1|. 2)/(х)—
= |+|х + 2|-||х| + |х - 1|-2|х_3]. 3) Их) = --у-+ 2-1 % - И-
--!2|х-3| + 4|х-4|.
Глава III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ.
§ 13. Производная. Формулы и правила вычисления производных.
Дифференциал функции
13 .1. 1) 0,2. 2) 0. 3) 1. 4) —1. 13.2. 1) Зх24-2х, xeR. 2) —1/х2, х=^0.
8) 1/(2 Vx ), х > 0. 4) ~ V*, х е К. 5) —2х/(1 4- х2)2, х е R. 6) 2х 1-1 In 2,
! и
548
7) Мк. к > 0. 8) 2 cos 2х, хе R. 9) — l!/sin2 х, x =/= nk, k Z,
10) , 1 -=-, |x| < 1. 11) —3/V 1 — 9x4 | x | < 1/3. 12) 7/(x2 + 2x + 2),
Vl — *
,tsR. 13.3. 3x24-2x+1, xe=R. 13.4. 3ax2 + 2bx + c, x e= R.
13.5. 91 (x12 — x-8), x=#0. 13.6. —ln3/x2, x#=0. 13.7. —2ax~3 — 36x-4 — 4ex~5.
X#=0. 13.8.—i—4------------4--------jl—, x > 0. 13.9.V^-2x-3-2x-2, x#=0.
2Vx_ 3V*2_
13.10. (1 Lx2 Vv + 22xe V x)/», x e R.
13.11.
13.13.
13.15.
V5 (x^5 4- x~^5 )/x, x > 0. 13.12. (ad —bc)/(cx 4- d)2, x?*= — d/c.
6V..+ 1V-.11.., xgR. 13.14. .....-Izife x>0.
(x2 4- x 4- 7)2 6 V * (2 4- V*2)
5 (cos x — x sin x), x e R. 13.16. tg x 4~ * "t "» x =/= -2- (2k 4- 1),
COS X 2
x2
k e Z. 13.17. 2x ctg x---------г-5—, x ¥= nk, k e Z.
sin2 X
13.18. если x o; y' (0) =0.
x2
13 19. c£s x___________.У*— , x > 0, x Ф nky eN.
2 x sin x sin2 x
13.20. 2 (cos x — sin x)“2, x — + я/?, k s Z. 13.21. 1. 13.22. arcsin x +
4- |x|<l 13.23.^^, xeR.
Vi - x2 . I 4- X2
13.24.---------7=5-------------, | x | < 1, x=/=0. 13.25. (3/x) 4-(3/x)2 4-(3/x)3,
2 Vl — x2 arcsin2 x
x > 0.
13.26. -'y- (V2T — (V5 )*, xeR. 13.27. (x2 —5x4- D ex, x <= R.
13/28. (in 2 • in I x I + —2х, x =# 0. 13.29. f log2 x 4---гЦт- e* x > 0.
\ X / К, X In 2 /
1 / In % log3 X , , , , In X log2 X \ n
13.30. — ----F Iog2 X Iog3 x -1--------j, x > 0.
13.31. i------7-------♦ X > 0, x 1. 13.32. - —------:, x > 0, x 1.
X in X log2 x In X ’ log2 JC
13.33. (—, -г--arcsin дЛ e~x, | x I < 1.
Wl-x2 /
13.34. (a2 + b2) eax sin bx, x ce R. 13.35. ch 2%, xsR. 13.36. 0.
13.37. 1 ~?.th-2 -. xeR. 13.38. ---------i----1- , x > 0. 13.39. 2.
cnz x x ctti X Cuz X
13.40. (a — b)(a — c). 13.41. l/(a — b). 13.42. ab (a 4- b 4- 2). 13.43. y' (0) =
= —1985!, /(1985) = 1985!. 13.44. 0. 13.45. 1. 13.46. a + d. 13.47. л/2.
13.48. 1. 13.49. e. 13.50. 0. 13.51. (3e2 4- e“2)/2. 13.52. 30 (3x — 7)9.
13.53. x2/(l — x)100. 13.54. ab (a 4- 6x)“_|.
13.55. —0,64 (2 cos (8% + 5) — 3 sin 0,8x) (2 sin (8x 4- 5) + 0,3 cos 0,8a>).
13.56. sin x sin (x + 3). 13.57. a (a cos x + b sin x)®"'1 (— a sin x 4- b cos x).
13.58. Ae~k2x (co cos (cox 4- «) — k2 sin (cox + «))•
,3.59. 1 у
X Vx к Vx /
.оел 1 4- 4 V*2 + I x
lo.Ov, ... ...... .Ц,,. z ' t -(Mr •
2 V2*2 4" V*2 + 1 *
549
13.61.
13.62.
13.63.
14
13_______________
65 V(2x)4 V(e + 7 V2v)'2
2x2 »/П
xe - 1 Л/ 1
ad — be
n (ax 4- b) (ex + d) ex -j- d
-2x/V(l 4- x4)3. 13.65. 0, x
1 . 13.68. —2 *
X \ sin2 X
Л « . 31 । 31 Jt
— fe, —+ — k, x -
1 — х3
13.64.
18.67. -L sin —.
X2
. л . л . JI , 31
13.71. 2 in 2 • cos 2x • 2si n2x.
5/(x4 + 13x2 + 36). 13.73. - cos 2x.
x4 — 1
0. 13.66.
. tg22x \
cos2 2x ) ‘
— 1/(4 д/х9), x =£ a,
13.69. —4 cos 8x,
13.70. — хе~ху2.
13.72.
13.74.
18.76.
13.81.
12 log^ (2x + 3)a
in 2 2x4-3
2x arctg x2 1
—= 13.76. —i - — , x > 2. 13.77.
V(14-x4)3 x In (x/2)
18.78. ctgx. 13.79. C0Sln|x| . 13.80. /"WM.
x (x loggx) In 2
2 In 3___narctg (2л+3)
1 -H2x + 3T)2
18.82. - У-2 . 13.83. —— ~ -‘° I0*'lo*>\ 18.84. l/(2x2 - 5x 4-7).
22x 4- 1 In x • log3x
13.85. (x24- l)/(x4 4- 1). 13.86. sh x/(2 Veh x). 13.87. l/ch2x. 13.88. 1/(1 — sh4 x).
13.89. — sin 2x • cos (cos 2x).
i er 2 X/1 1 \
13.90. 4 —---j- ( —:— ------;. 13.91. sin x • In tg x. 13.92. cos In x.
tg x2 \ sin 2x sin 2x2 J B
in~' x-sin («4- Dx. 13.94. 2x/((l 4-х2)2 (1 4-x4)). 13.95. 2x/Vx44-l.’
1. 13.98. 4x, |x| < 1. 13.99. 12x2 — 3.
13.101. -2n | x |n/(x (x2n 4- 1)).
13.103. 2/(2 —3x2). 13.104. 20/(x4 4-x2 — 6).
13.106. — (In 3) sin 2x • 3е08’*.
1
13.93. — И COS1
13.96. 2 In (2x 4- V^x2 4- 1). 13,97, 1, |x|
| x | < 1. 13.100. cos x/V2 4- cos 2x.
13.102. l/(x2 4-5x 4-6)2. ‘
18.105. 2 (in 2) x cos %2 • 2sin x\
13.107.------------1 - ^Vd-xWl+x)
(1 4-x) Vi -x2
13.108. ; Sln 2* , 13.109. -rr--—;-------—------
sin4 x 4- cos4 x (In 2) x In x In log5 x
13.110. 2/(x (in x2) in inx2), x > e. 13.111. Vx24- 1/x. 13.112.
13.113. 2 tg3 x. 13.114. — V2 sin x/Vcos 2x.
(Or I n „Vln (x!+x+l )
13.115. -----UX4-1)Q
2 (x2 4- x 4- 1) V'n (x2 4- x 4- 1)
13.117. — xe2W(e2x — l)3- 13.118. — 4x/sh3 x2. 13.119. cos x/cos sin x.
13.120. —4x3 (cos x4 4-sin x4)/Vsin 2x4. 13.121. 4 ctg x/(sin4 x 4- I)2-
13.122. 2 sin x/(3 — 2 cos2 x). 13.123. }](a 4- b cos x).
1 ex/2 — 1
13.124. (2 + ch x)/(l 4- 2 ch x). 13.125. у
sin a
1 — cos a • cos x
13.116. —1/cosx.
13.126. -I..S-08X-cosa
I cos x — cos a |
ЬБО
13.127. 2 sin a I V 1 z* 1
(1 — х2) (1 — х2 cos2 Y a) ’ 1 1 < ’• 2 13.130. . 1 — sh4 x
13.128. x2 — 2x cos a 4- 1 ’ 2 (a2 4- b2) x (x2 4- a) (x4 41 b2) ‘ in (1 4- sin x) sin2 x 13.129. 4x Va2 4- x4.
13.131. 13.133. 13.132. 2 V<22 — x2. 13.134. - .
2^x П1ЧЙ V8X- + 8
lo.l 45.---------г-. I a. I ou. -т--;—.
1 — X1 x4 1
1Я1Ч7 ______________5x2__________ x2 + 3x - 2
2x44-6x34-9x24-6x4-2 • ’ *°0, °’ (x- 1)(х24-х4- I)2 '
13.139. sln‘x:c°sx—. 13.140. ex arcsin V<?*/(I 4- e*).
Vcos2 x — 2 sin x
13.141. Xх (1 4- In x). 13.142. 0, x > 0, x 1. 13.143.----;-----?----.
X In X log7 X
18.144. l/x, x>0, x#=l. 13.145. 2e (x — e), x>0, x^l. 13.146. x1+*’(l 4- 21nx).
13.147. ex xe (-1- 4- In x). 13.148. (In 2) 2xX • xx (1 4- In x).
13.149. xx • xx~{ (x In2 x 4- x In x 4- 1).
13.150. | sin x |cos x (cos x • ctg x — sin x In | sin x |).
.r. / . .9 ,arct<7x/In arcsin sin2 X , sin 2x • arctg x \
13.151. (arcsin sin2 х)агс1{эЛ[-----------]----------------..... •- V
\ 1 4-x2 arcsin sin2 x Vl —sin4 x /
13.152. (ch x) e* • ex (In ch x + th x).
e__
13.153. y'(0) = 2, z/'(l) =—2.13.154. V72.13.155. —л2 In 2. 13.156. -2 V&
13.157. 2/1 n 2. 13.158. 2/e. 13.159. 0. 13.160. /(0) == 2, /(2) =
— —2/5. 13.161. y'(—1) = 1, */'(!) = —1, i/'(0) не существует. 13.162. 6.
13.163. 0. 13.164. 0. 13.165. 2 In 2. 13.166. — (л/2)^-31/2 (1 + In (л/2)).
13.167. 1) 1; 3. 2) 7/11. 3) лп/2, neZ. 4) 1; 2; (5±V13)/6. 5) 0. 6) 7/12.
13.168. 1) Hx)/(2 V/W). 2) f(x)/f(x). 3) 3x2/,(x3). 4) £ ^Гс^..(х))
V1 — F W
13 169 1) — • (x) f- (x) + g (x) g' (x> 2) g (x) (x) ~ L (x) g/ (x)
' n ",------------------—7 f(x) g (x)
-y (F (x) 4- g2 (*))"
3) sin 2x (/' (sin2 x) — g' (cos2 x)). 4) (gz (x) In f (x) 4- ) (f(x))sW.
13.171. 1) 6x — 3. 2) 3x2^30x—18. 3) 6x2. 13.173. 1) a > 0. 2) a > 1.
3) a > 2. 13.174. 1) a > 0, p произвольно. 2) a > 1, 0 произвольно.
3) a >> 1, P <Z a—1 13.176. 1) a) a + P=l; 6) a = 2, 0 =—1.
2) a) a+₽=l; 6) a = 3/2, P = —1/2. 3) a) 4cc 4-P == 1/12; 6) a =
==— (л + 2 'у/З )/96л, P = (Зл + 2 V3 )/24л. 4) a) a, p — произвольные числа;-
6) a = 5/2, 0 = 9/5.
13.177. 1) a = 1, p = 1/2, 2) a == p. 13.178. 1) a = 1, 0 = л/4. 2) a = 1,
p = (л —4)/4.
13.179. 1) Дифференцируема всюду, кроме точки х — —2. 2) Дифферен-
цируема всюду, кроме точек х = лЛ, k — целое. 3) Дифференцируема всюду.
4) Дифференцируема всюду. 5) Дифференцируема всюду, кроме точек
х = nk, k — целое. 6) Дифференцируема всюду. 7) Дифференцируема всюду,
кроме точек х = 2/(2^+ 1), k — целое. 8) Нигде не дифференцируема.
13.180. 1) Дифференцируема в точке х — 0: причем у'(0) — 0. 2) z/'(l) =
= 2, у'(—1)= —2. 13.181. Утверждение неверно. См., например задачу 13.179
7) и 8). 13.182. 1) Утверждение верно. 2) Неверно (контрпример: f — |х|,
g ~ —|х|, х = 0). 3) Неверно (контрпример: / 0, g — |х|, х = 0). 4) Не-
551
верно (контрпример: f =» |х|, g= |х|, к — 0). 13.187, 1) Утверждение не-
верно (контрпример: у ~ х2, х е(—1; 1)). 2) Неверно (контрпример:
у '== х -j- sin х, xeR). 3) Неверно (контрпример:- у == х, xgR). 4) Утвер-
ждение верно. 13.188. 1) Утверждение верно. 2) Неверно (контрпример:
у = х + 1). 3) Верно. 4) Верно. 13.189. Утверждение верно. Обратное утвер-
ждение неверно (контрпример: функция задачи 13.179, 8), х0 произвольно).
13.190. 1) Утверждение неверно (контрпример: у — дЛП х е (0; 1)). 2) Не-
верно ^контрпример: у “““Ь sin х е (0; 1)). 3) Неверно ^контрпример:
# ~ ~ + °°)^- 4) Неверно (контрпример: у = sin In х,
х €= (2; Ч-оо)).
13.191. l)f'+(0)=M, 4(0)==-1. 2) f'_ (2)-4 (3) = —- 1, 4(2)-
- 4 (3) = 1. 3) 4 (0 = ln f- (0 = ~ In 4. 4) f' (2k) - Ч-oo,
f' (2k — I) = — oo. 5) f'+ (0) = 1, f'_ (0) = — 1, f'_ (V«) = — oo. f'+ (Vn)
/ f / A:k I \ ,/ z z x
не существует. 6) (2n&) == f+ I----л J = f- ((2Z? + 1) n) —
= 4(—— л)=0. f'+(2nk)=C ( 4fe~ 1 л) =2, f'+ ((2k + 1) л) =
—2. '4wt)~ <“+»?
f+(lfeTr)==(2fe+l)T- 8) Г-(-0==Г+(1) = + ~. f+(-D и 4(0
cz ( 4- 1 A ( 2k 4-1 fz ( 4k 4-1
не существуют. 9) t_ I--— л 1 = /+ I--— л 1 = 1, t+ I -g— л I—
13.192. 1) f'_ (0) = 1. f'+ (0) = 0. 2) 4 (0) = 2, f+ (0) = 0. 3) f' (0) = 0.
13.193. 1) 4(0)=0, 4(0) = 4-oo. 2) 4(0) = 4-0°, 4(0) = +°o.
3) 4(0) = —°°, 4(0)=0. 4) 4 (0) = 0, 4(0) = -°°. 5) 4(0) = l,
4 (0) = -1.6) 4 (0) = - 1, 4 (°) = + °°-
13.194. 4 (x0) = — Ф (x0), 4 (xo) = Ф (xo)- 13.195. у = — sign x.
( x sin (1/х), если x=#0,
13.196. у = 1 '
( 0 если x = 0.
13.197. 1) x' (0) = 1, x' (6/5) — 1/2. 2) x' (—1/2) — 1/2. 3) xz (1) = 5.
4) x' (0) = - V2/8. 5) x' (-j) = V 2/2.
13.198. 1) x’(y) = x/(x+ 1), г/e R 2) x'Jy) = 1/(1 +y — x), R.
3) x'(y) = x3/(2y2), у e (0; 1). 4) x' (y) = il'y/y2 — 1, У s (1; + °°).
13.199. (arcthx)' = 1/(1 — x2), xs (—I; 1).
13.200. у = я(2Л 4- 1), k eZ.
13.201. 1) (/'= — 1, 0 < x < 1. 2) y'x = — St2e*. 3) i/z=-^-ctgt
4)^=^-ctht 5) y;=i-|+|. y'x=^r=i- 7) *4=С‘8Т’
2 cos t
X 2nkat y'x (2nka) не существует, k e Z. 8) yx = “fTRcosT
13.202. 1) x^ = 3 • 2)x' = l—^5-. 3) x'y= sins / (з + 4 cos2/) •
13.203. jf'(O)=O. 13.204. y'K = 2x. 13.205. 1) —2/(Зл). 2) 1. 3) 0.
^'52
,«»«. П (0)_ „1 («>_- ,8.207. ,, 5g; + ;y, + |. 2)
»A 4) *1, !,!>». 5> 0<,<2o. 6, ,--* . 0<x<4.
у а2у (2a-— x) x \ x
7) “ ~T ’ 1K1 < a' x ф °’ 8) 4 y+T’ 1 x ~ 31 < 3'
x < 3.
4y — 2x — 4
8y — 4x ~ 3 f
13.208. 1) 1/V3. 2) -24/41. 3) -l/e. 4) -e2.
a (Ax) = 3 Ax + Ax2. 2) 4 = 0, a (Ax) = Ax9. 13.210.
13.211. x — nk, k e—Z.
13.212. Второй, если x =/= 0; если x = 0, то третий.
13.209. 1) 4=1,
3 (x - 1) Ax2 + Ax3.
13.213. I) (±-e~Adx. 2} ^±^+^±±dx
/ 2 Vx (x + Vx )
3) 9 V* In x dx. 4)---- ---r- dx. 5) —-—-C-°-?-x -dx.
Vl-e2x V4 sin2 x-1
, 4 । o / x arcsin x
6) sh4 (x/35) ch3 (x/35) dx. 7) --dx.
(1 — x2) Vl — x2
8) ----2 r-r- dx. 9) xx’ (1 4- 2 In x) x dx
cos x Vsin x
13.214. 1) -~dx. 2) dx\ 0. 3) -^£-dx. 4) (2 + In 4) dx-, 0.
Л 6 “j-* 1 i
12 1 Уо- 4x„ yu
13.215. 1) ----dx. 2) — dx. 3) —f-----------------— dx. 4) ------------"---dx.
11 4 5t/0 2x0jz0 x0 — y0
5) -^-dx 6) ±-dx. 7) - 2n _ j” dx. 8)0. 9) 1 dx. 10)1^
ZU о О 111 о Z о
13.216. dx.
13.217. 1) и2 dv2uv du.
2) 2 — du-------у dv. 3)
V V2
u2 — v2 ( ^_ r v
(w2 [ v2}2 {u dv v du).
4)
7)
б)
2)
на
euv (u dv + v du).
и du + v dv
u2 -f- v2
Л. 2 udv — v du
6)--------------------------
sin (2v/u) u2
uv du + In и dv J .
13.218. 1) a) 4,0208, 6) 5,00177. 2) a)
—0,017. 4) 0,9942. 5) 0,512. 6) 0,810. 7)
5,85. 3) 3,001. 4) 1,9953. 13.220. 565 cm3.
1%. 13.223. Увеличить на 2,23 см.
3,083, 6) 1,9938. 3) a) 0,485.
0,079. 8) 0,925. 13.219. 1) 25,3.
13.221. 2%. 13.222. Уменьшится
§ 14. Геометрический и физический смысл производной
14.1. В точках х = 2nk/3 угол <р = arctg 3, в точках х = л(2& 4- 1)/3
угол ф = л — arctg 3. 2) л/4. 3) В точке х = 1 угол ф = л/4, в точке
х = —1 угол ф = Зл/4. 4) Зл/4. 5) arctg а. 6) В точках х = 1 и х = 2 угол
ф = 0, в точках х = 3 угол ф = arctg 8. 7) В точке х=1 угол ф =
= л — arctg (3/2), в точке х = — 2 угол ф = л — arctg (3/4). 8) arctg (1/2).
9) 0 10) В точке х =—3 угол ф = arctg 3, в точке х = 3 угол ф =
= Л — arctg 3. 14.2. 1) (—1; 14), (2; -13). 2) (0; —1); (1; —6); (—2; —33).
3) zi- _58); (1; 54); (7; —2106). 4) (лб; 1 -5 (-1)*), ke-Z. 5) (1; 2е),
(-3; -бе-3). 6) (2; 0), (5; -27/4). 7) (3; 0), (9/2; 27/16). 8) (1/2; —1/2),
9. (—2: 1 + Уз"). 14.3. 1) у = — у + у. 2) у = 2х. 3) у = —Зх. 4) у =
Зтг
л= —Зх + -^. 5) х=1. 6) 4х —9z/ + 8 = o. 7) 29х — 12г/ — 54 = 0.
553
8) х —Зр == 0. 9><1 -Уо)£-Ч-(1 + <o)eS + 2Zn = O. 10) у = (ctg (/0/2)) х 4-
+ 2а - а/е ctg (/,/2). 14.4.-^i- 4- = 1. 14.5. (ЮО/хо; 0). 14.6- у - arctg -I.
14.7. 1)
3
x~h2i/ — л — 2==0.
«= (х 4- 3).
2) 8х 4- 4у — 8 — л = 0. 3) х = 6.
5) V2pxc х + ру — л/2рхй (р 4- хс) = 0.
6) У~~ел13= — V3 ctg-^ (* — 4^3)-
14.8. 4х - 7 у + 15 = 0.
14.9. а2у0х 4- Ъ2хйу — хкуй (а2 4- Ь2} — 0.
14.10. 1) 5х 4- бу - 13 = 0; 6х - 5у 4- 21 = 0. 2) 9x4-2^4-12 = 0;
2х — 9g + 31 = 0. 3) 14х — 131/ 4- 12 = 0: 13х 4- }4у — 41=0.
х« (6 — хп)
4) х 4- У — 2 = 0, у = х. 5) у — i/c = —А----- >. (Х _ х ).
Уо
У — Уо — — -^7---^—(x — xt). 6) —+ ~ =2: ах — by = а1 — Ь2.
Ао(6~Ао) а ь
7) Зх — у - 4 = 0; х 4- 31/ — 28 = 0. 8) (л 4- 4) х 4- (л - 4) у — = 0;
4
(л — 4) х — (л 4- 4) у 4- л д/2 =0. 9) х 4- у — 1 — 0; х — у = 0.
10) 7х — 10g + 6 = 0; 10х + 7g — 34 = 0. 11) Зх — у - 1 = 0; х 4- Зу — 7 = 0.
14.11. 1) (0; 0), ф = arctg (2/3).
2) (-у + лЛ; (-1)*),
3) (0; 0), <р = 0; (1; 1), <р = arctg (1/7). 4) (1; 1), <р = arctg 3. 5) (1; 1), <р = л/4.
6) (Ve; 1/2), ф = 0. 7) (1; 1) и (4; 4), ф = arctg (6/7). 8) (3; 34), ф = 0;
(-2; 4). <р =• arctg (25/153). 9) (г* 4- Ф fa 4- у)), teZ, угол равен
нулю.
14.12. 1) (0;0), ф = л/2; (1: 1), ф = arctg (3/4). 2) (1; 5/9), ф = arctg (1/3).
3)(2;е), ф = arctg (2/е). 4) (1; ±2), ф = arctg 3. 5) (1/8;-1/16), ф = л/2.
6) (1; 2), ф = arctg (6/5). 7) (8/5; 0), ф = arctg (75/31). 8) (е; е), ф = л/2.
14.16. 1) л/2. 2) 0. 3) л/2. 4) л/3. 5) arctg (3/4). 6) 2л/3. 7) 0. 8) Зл/4.
9) л — 2 arctg (1/18). 10) 0. _
14.17. 1) 2V2. 2) 2V2- 3)2. 4)2. 14.18. 1/1п а. 14.19. |х|/«,
ла2|х|2,1_1. 14.20. 1) 2 | х |, р. 2) (х2 - «2)/| х |, | х |. 14.23. 1) 2х/3, Зх2/2,
х 0. 2) 2х, 1/(2х2).
14.24. 2а sin (//2) tg (Z/2), 2а sin (//2), 2а sin2(Z/2) tg (Z/2), a sin t.
14.25. a, a sin//1 cos / |. 14.28. 1) arctg qp. 2) arctg qp. 3) arctg (1/h).
4) | Л — qp | /2, 0 qp < л, л < qp < 2л. 5) --------2qp. 14.29. л/2.
мл. -«Л ш _ (1 + аУз)а
V1 + t)z 4 4 (cos qp — sin qp)
14.33. ^54,3 км/ч. 14.34. — л/8. 14.35. 90,75 Дж. 14.36. (1/3) м/с.
14.37. 0,05 м3/с. 14.38. 4л рал,/с. 14.39. 15 м/с. 14.40. л; 3 м/даин.
14.41, v = faQ cos a, vQ sin а — g/), I v | == — 2t’i5 g/ sin a -f .
14.42. л/3 м/с,
2лае . 2л (Z — tQ) ( 2л (t — /0) \
14.43. —p— sin ------I 2e cos--------------——1 I.
1. лл . Дж . . In 2
14.44. 1,013 -Tvy-. 14.45.----------.
1\ J
554
§15. Производные и дифференциалы высших порядков
1В.1. 1) 2. 2) 9702/х100. 3) Зх (1 — х2)-52. 4) — 2 cos 2х. 5) 4 ch 2х.
6) - х (х2 + 1)-3/2. 7) -х(1+х2)~2. 8) (х-1) (2х-х2)”3'2.
9) - 4xsignx/(l + х2)2, х^О. 10) 4х3 (1 + х«)-5/4. 15.2. 1) е2/32.
2) 625/1024. 3) 0. 4) 0. 15.3. 54 м/с2. 15.6. При t = 2 с: 13 м/с2 и 14 м/с2,
при / = 3 с: 19 м/с2 и 18 м/с2. 15.7. 43/7. 15.8. 20 м/с2.
15.9. 1) (х2 - Зх + 1) е~х dx2. 2) -8^-dx2. 3) - - sm-1,1 - dx2.
v ' sm2 2x x
4) (x (1 +<nx)2+ l)x*-ldx2. 15.10. 1) ^-dx2. 2) dx2. 3) — -f- dx2.
2 I ZD о
4) dx2.
15.11. 1) —4) удовлетворяет при произвольных Л и В; 5) не удовле-
творяет; 6) — 8) удовлетворяет.
t. u2v" — uvu" — 2uu'v' + 2v (и')2
15.1 z. 1) ----------------.
ил
2) (uv" 4- 2u'v' 4- vu" 4- (uv' 4- vu')2) euv.
(u2 4- v2) (uv" — vu") 4- 2uv (и')2 4- 2 (u2 — u2) u'v' — 2uv (v')2
3) (u2 4- v2)2
(u2 4- v2) (uu" + vv") 4~ (v2 — Ц2) (и')2 — 4шш/о/ 4~ (u2 — v2) (v')2
4) (u2 4- v2)2
15.13. 1) (v 4~ 2) d2u 4" 2 du dv 4- ud2v.
2) In vd2u 4- dudv + ~- d2v------dv2.
(u2 + v2) (ud2u 4~ vd2v) 4- (v du — и dv)2
(u2 4-1>2)3/2
3)
4) uv(— d2u + In ud2v + C’г-. * du2 + 2 <p ln » + 0
' V u и2 и
du dv 4- In2 и dv2
15.14. 1) —2/9/4. 2) у Q 3) - 8 cos2 //cos2 2t. 4) - b/(a2 sin3t).
5) l/(cos3 / (3 cos3 / — 1)). 6) — 1/(1 sh3/). 7) 2 (1 +/)3/(/e'). 8) cos3//sin/.
9) (3 sin log2/)/(cos5 log2/). 10) 23s,n4-1. 15.15. 1) 2. 2) 1/2. 3) -12. 4) -1/2.
15.16. 1) — 12 (/4-1) 1 (3/ + 1)“3. 2) — sin2/cos/. 3) — 2 in 5 COs2 *
sin2 t — cos 2t
sin3 2t cos/
3 cos t . 3 ch /
a2 sin5 t * a2 sh51 9 a'2 cos71 sin31
be2t (2 sin t — cos /) sin / (1 4~ 3 sin7 /)
4«2 sin7 (//2) * (sin / 4" cos Z)5
sin4 t *
4)
4)
2 д/cos 2t
15.18. 1)
cos (//2)
cos7 t
cos71 — 4 sin2 t
15.19. 1) y' = — b/a, y{n} = 0, n > 1. 2) y{n} =2n~’nL
3) У{п}= (~1)П l2"^n~ 3)l! - 4) ^ = 2x4-1, y" = 2, y'n’ = 0, n > 2.
(2/— I)2"-1
15.20. х" = -Г/(П3, x"’ = (3 (Г)2 - rrw)5- 15.21. 1) -a2!y2.
2) -a2!y\ 3) -/>4/(«V). 4) -p2!y2. 5) 4 (x + y)Kx + у + I)3.
6) - (3 + 2 In x)/(x2 (1 + 2 In x)2). 7) 2 (x2 + г/2)/(х - у)3-
2x2y (3y4 + 2 (3 - x4) y2 + 3 + 2x4)
’ (f/2+D3
1 1 3
15.22. I) ~-^dx2. 2) —~£dx2. 3) 0. 4) — dx2.
15.24. 1) y,n) = 3"e3x, n > 3; y"' — 6 + 27e3x; y" = 6x + ^eix:
y' = 3x2 + 1 + Зе3л. 2) a0 • nl. 3) 2 • «1/(1 - x)re+1.
4) (-I)"- 1 nlc"-1 (ad - be) (ex 4- d)-"’1.
Б55
5) (-!)"-•(«-l)lan/(ax+b)n. 6) - 2n"1 cos (lx + ^-).
7) у (a - b)n cos ((a - b) x + — 1 (a + 6)« cos ((a + b) x + 2EL
S) U{2k~1 ’ = у (« + b)2k~1 sh (a + b) x + (a - b)2k~1 sh (a - b) x;
У{2к> = 4- <a + b)2k ch (a + b) x + Y (a — b)2k ch (a — b) x.
Z* z
9) 2n~‘ sin (2x + -^-) +4"”1 sin ( 4x + 4r-Y
x Z у \ Z у
10) 4n 1 cos ( 4x + —.
11) 2rt_1 cos ( 2x 4- + 22"-3 cos ( 4x 4-
12) (2ra — 1)1! (1 — 2x)-(2rt+1*/2.
13) (-.V." ”!. (3 (x _ 6)-»-1 4- (x 4- 2)~"~ ‘).
14) rat((l - хГ'1-' 4-(—1)" (1 4-x)-"-1).
15) (—1)" nl(2" (2x — l)_n~1 + (x4-2)~'!-1).
15.25. 1) (ln"~ l2) 2*~1 ((in 2) (x — 1) 4- n).
2) (In 72)""1 72х ((In 72) (2x — I) 4- 2ra).
3) (—3)"~2 (36x2 — 12 (9 + 2ra) x 4- 81 4- 32ra 4- 4raz) e2~3*
4) (ra - 2)13"--(3* _ ft) (1 _ n > t
5) (-1)" 2 (ra - 2)! (x - n) (x - 1)“". n > 1.
6) (ra - 2)! ((Зга - x) (3 - x)~n + (-1)" (Зга 4- x) (3 4- x)-n), га > !.
7) (—1)" (га — 2)!((x — га) (x — 1)“" 4-(x — 2га) (x — 2)-fi), ra>l.
8) x cos f x 4- 4- n sin ^x 4 •
( ^\n~l ( ( 1 nn > 2 f2 . nra\\
9) Ы г81П1тх + “) + тхсоЧтх + ^-))’ n>l-
sin ^2x
n > 2.
15.26.1)——— 5x) (1 — 5x)-(2n+u/2, ra > 1.
2) (2ra — 5)11 (3x2 — 2nx 4" ra2 — ra) (1 — 2x)"(2n+1)/2, ra > 2.
10) 2" 3^(4x24-4x — ra2 4-ra) cos ^2x 4--^-J 4-2ra (2x 4-1)
3) Qax (a2 + b2)n/2 cos (bx + c + /2(p)> cos ф ~ а!л/a2, + b2, sin ф = bl^Ja2 + b2,
4) 2"- le2x (1 - 2n/2 cos ( 2x 4- •
5) (a2 4- h2)"'2 (ch ax cos (ra<p — s*n +
4- sh ax sin
cos <p = a/Va2 4- b2,
7) (ra — l)!/x.
sin <p = b/Va2 4-&2. 6) (-\)n x-n~lel,K.
8) (—1)" 1 (ra — 1)! (1 4-x2) "/2 sin (ra arcctg x).
15.27. 1) a) 12960; 6) 0. _2) --171I/28 * 10. 3) 8!. 4) —13!(2/3)*4.
5) _2~‘4-35-5-l9. 6) 336/(625-^5). 7) -2(97!). 8) I0109(3")sin 3.
9' ~~ (1 4-3100). 10) (16-^)V2. 11) a) 2»-32-7-37. 6) 0.
556
2711 а/2
16.28 . 1) 1500 dx*. 2) 194-10!39 dx™. 3) Лх16. 4) —27-1025 д/з dx™.
Б) 29-29dx8. 6) а) (17!!)2rfxie, б) 0.
15.29 . 1) у'— 0, £/"(0) не существует. 2) у' (0) — 2, у” (Ъ) = О, ^"'(О)
не существует. 3) у'(0) = 0, у"(0) = 0, у'"(0) = 1, £/(IV)(0) = 0, z/(v)(0) не
Существует. 4) у'(0) = 1, у"(0) =0, не существует. 5) #'(0) = О,
£/"(0)—не существует. 6) г/(п) (0) =0 для п 50, */(51)(0)—не cymecTBveT.
7) (0) = 0, п ее N. 15.33. (—
Глава IV. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ
ФУНКЦИЙ
§ 16. Теоремы о среднем для дифференцируемых функций
16.2. %], 2 = (2 ± )/3. 16.3. £=д/з/з. 16.23. Применить теорему Ко-
щи о среднем к функциям ffx)/x и 1/х. 16.29. Применить теорему Коши;
о среднем к функциям f(x) и 1/х.
§ 17. Правило Лопиталя
17.1. 10/7. 17.2. 1/9. 17.3. 6/7. 17.4. 2. 17.5. 1. 17.6. сс/р. 17.7. —а*12.
17.8. ааа~а~1/\па. 17.9. 1— In в. 17.10. —1/2. 17.11. —2/я. 17.12. —1.
17.13. —1/4. 17.14. —6. 17.15. 1 17.16. 15/4. 17.17. 0. 17.18. —2. 17.19. 16/105.
17.20. (—1)т-"(2//г +1)/(2и+ 1). 17.21. —3. 17.22. 1/2. 17.23. 1. 17.24. 4.
17.25. 1/а. 17.26. 2. 17.27. 9/14. 17.28. 1/3. 17.29. —4/3. 17.30. 0. 17.31. 45.
17.32. 49/198. 17.33. —1/6. 17.34. а(а+1)/2. 17.35. (а —0)/2. 17.36. 1/2.
17.37. 1. 17.38. 3/2. 17.39. 1. 17.40. 0. 17.41. 0. 17.42. 2. 17.43. —1/3.
17.44. О при у > 0 (а, Р —любые), при у = 0 (а < 0, р— любое; а = О,
Р < 0); Ч~оо при у С 0 (а, р — любые), при у = 0 (а >> 0, р — любое;
а = О, р > 0); 1 при а — р — у — 0.
17.45. 0. 17.46. О при а> I и при а = 1, Р > —1; 1 при а = 1, Р = —1;
-}-оо при а< 1 и при а = 1, р < —1. 17.47. 0. 17.48. —2/л. 17.49. 0. 17.50. 2.
17.51. 2. 17.52. 0. 17.53. 0. 17.54. О при 0 < а < 1 (а— любое), 4~оо при
«>1 (а —любое). 17.55. 0. 17.56. 0. 17.57. —1/3. 17.58. 1/2. 17.59. 1/3.
17.60. -|-оо. 17.61. (а—₽)/2. 17.62. е. 17.63. е~2/я. 17.64. <Г2я. 17.65. в-1'2.
17.66. 1. 17.67. е~1/2. 17.68. 1. 17.69. е. 17.70. 1. 17.71. 1.
17.72. 1. 17.73. 3. 17.74. 1. 17.75. 1. 17.76. 1) 0. 2) 1. 17.77. Правило Лопиталя
неприменимо, предел не существует. 17.78. /"(а). 17.79. f"'(a). 17.80. / <л) (0) =
« 0, k ее N . 17.81. 1) 0. 2) 0. 3) 4. 4) а.
§ 18. Формула Тейлора
Д 5* ь “ 2*sin^3 + ^J
18.1. 1) У —тг xk + о (хп). 2) У------------Д---------i
Z—/ е • к\ £—1 kl
Xk + о (xrl).
k-o
cos (2 + feTf)
2*6!
8)
n
xk + о (xn). 4) 2kxk + о (xn).
A:=0
б) У (-\)kXk + о (xn). 6) У(-1)й2^(2м 1)11 X* + о (Ю-
/.j Лк'т1 l—i Ki
/г=0 A=0
’> ,„2 + £<=y +
fe=l
557
в) + 9) £(*4-Пхй4-о(И-
k~o fc=O
n n
18.2. 1) -1 4- V J^Zll кк + о U«j. 2) - к + У (~V*fe xk + o (л;Я)
£i 2ftfe! £2с*-»»
n
3) 34-у (3 + k(k-l)2k-2)l^-xk + o(xn).
fe=i
, , 3 9 , A 3 (2k - 1) (2k — 5)!t k , , _v
4) 14---x----x2 — > —'-------xk 4- о (xn).
5) - 3 !„ в + (2 6 - A) , + £ (-,)* jS—tj •(!)'-> + « <•">.
/s=2
6) кк + о{хПу
k=i
7)
k^i
n
8)
/ 1\ft— 1
----(l+2~k)xk + o(xn).
«)
n
Ш24-У
„.3. .)|-^+ё,-‘>;6Лг1)
Xk + O(K%
О J 5 2 > V (-l)*(2fe- I) k , z
2) - 2x + - л" 4- У —k(k^ 1) X + ° (K}-
/г»3
n
3) 2^+Ут%2Цг((-1)^* + 1)х'г4-О(х'г).
/5 = 2
n --k
4)X(-Oft-*23 Ck-3lxk + o(xn).
/5 = 1
П J__
5) Ёз3 (-l)k~lCk-2'3xk+o(xn).
/5=1
6) ln|4-f^-1-)-^fe + rfe + 3~ft^ + o^).
Ы
7) ln6+^^-^-------(14-2-/i4-3_ft)jc'i4-oUft).
Й = 1
55d
^y 2eh((t+l)l„2) г + о1Л
R -f- 1
Ze=O
n
18.4. 1) £|((-1)^‘- 2-(й+1,)хй + о(х").
bo
2) -3+ У 5(—l)ft~l xk + o(xn).
fe=l
n b
o. 1 2 13 V ( 2 у k . . rt.
3) ____х___2Д-з) x* + o(x«).
fe=2
4) — У xk + о (xn). 5) У (— l)ft(l 4-4“(ft+1>) xft + о (xn).
&=3 fe=0
6) У (2(— 1)&3-Ift+I) — 2~{k+l)) xk + o(xn).
n
7) 4 + ^((-Dft3~u+1:- l)xfe + o(x").
k=l
8) l+y.(T.0fe+1-7-2^+,>xfe + o(xrt)
Z X .J о
fe=l
9)
18.5.
3)
n
У + У ((—0ft 2“(ft+l) — 1) xk + о (xrt).
r2fe+l <• 42ft
1 У-^ТГ-----------------+ o(x2rt). 2) V 3 x2ft+, + o(x2re).
Дз 22fe+1 (2fe + 1)! <2W
(_Ofe-l 24fe-l
(2k)l
5)
fe = L
У ЖГПГ <32ft+l - ° *2ft+1 + °
/ j z {Zr —f— 1
/г=0
k-l
o2fe- 1
w-^+1+oUn
6)
3( —l)fe /. o2fe\ 2fe+l । n(..2n\
4(2fe + 1)! u ’ + U ’
7)
.'2=0
32fe+l _ ! (
2u 2(2fe+ 1)! + 1 ’’
8)
( 0 o2fe—1 /1 2/г (-L f (
(2fc + i)T u 2 )x +o{x
/г=»0
n
18 .6. 1) 1 — x2 + X 2 (— 1) *2k + °
k^2
559
2) -X
k-1
3ft-'
4*
x2h + о (x2n).
3) £.<-')».1.(№ + 1)1,.з)>„ + |1Ьг„)
л=о
fe=o А=0
S) -7+ Zrsri«!‘+'+ »(>“).
/2=1
« X^F^4»(4>.
kt=s2
7)
х+У±7П\^-1)п x^ + o(x^
fa 2k (2k -J- 1) Z?J •
/2=0
<•—ч q2/j—3
2) x2+ £(-l)*-‘-^-_^ + o(^n
4»hJ \ Хп X IJ
/2 = 2
3) £ +42ft) x'2k+° (*2n+1)-
/2=0
4) £ ±zw~(1 ~22A) x2h t ° (х2п+Х}‘
/2=0
6) £ Т2ИГ + 1) *2ft + о U2rt+1).
\ЛК J I
/fe=0
" p2k A2k
O'
fe=0
Д 92'»-1
,e-8-" XW-a+"«
/2=1
2) 1+£—1 (1 -22A-2) x2k+° Ge"+1)-
/2 = 1
3) £ ~ (2Й)Г~ 0 - 22A+1 - Э2*) xlk + о U2"+1).
ы
660
4) 1 + J (- l)ft x2k + о (x2»+').
5)
3(— 1/ 42Л-1
2 (2k)l
x2k + o(x2rt+I).
„ / nfeA2(fc-l)
6) i+y —(7+4*~ *) *2k+° ^2"+')-
18.9. 1) У
ЬО
(__ 1)Л+1 2~ — 1
3
A=0
2) X 4 (3- <*+1) - 5- <*+>) x2k + о (x2«+').
ЬО
3> Z C- v'2 x2h + Z c- vs *2t+1 + ° ^+1)-
л=1 2 *=o 4
4)ZCV2’2l 2?<1 + (- l/)x2ft + o(x2n+1).
л=о
5) £ C*+1x2ft + O(x2n+').
Л=1
18.10. 1) У 4-(2-<*+0-3-<‘+»)x3‘ + OUn
A=0
2) -j- + У (2(- l)ft - 3 • 2~ <*+1>) X3J + o
k^l
3) £ x3k-П^ хзк+'+ о (x3n).
k^O л==о
18.11. 1) J (- !)*(*+ l)x3ft+1+o(x3n+1).
л=о
2) 4+Z ^x3A + o(x3«+‘).
k=l
3) £ ((-1)а2~*4У-*)х3* + о(л3"+1).
л«0
19 Л. Д. Кудрявцев и gj>4
561
18.12. 1) У* (х - 2)ft + о((х - 2)").
Z-J 2М-1
&»»0
2) X <ч/2(х- 1)й + о((х- 1)ге).
" 2fe sin (-^-—1)
3) У------------------ (х - l)ft + о ((х - I)«)
fe==O
4) - e~2 + У - (x + 1)* + о ((х + 1)«).
ы
Б) у ,( 1)ftfef- -2 + 3ft + 4) (х + l)ft + о ((x + l)n).
fc=O
n
6) у e-2 2 .(fe-5) (x + I)fe + о ((x + 1)").
Z—/ (к — 1)!
k=*\
7)
(«/2] £. 1 9b , i(n-l)/2|
У (-D^COSl.g2*--1, 2k . У -Sin 1 . (- l)ft 22*
L (2ft)l U+) + L (2ft+1)1 x
kal
x (X + 1)2Й+1 + о ((X + 1)").
n
18.13. 1) ln2 + yl(-l?-1(x-f)fc + o((*-l)re).
In (26/3) , у (~ l)ft"‘ ( 9 V (x _ 3}k , o ((x 3yn
2) 31n3”+ L (31n3)“l26j (* 3) +0<(* 3)h
fe«l
3) In 2 + У (~ Г...1. (X - l)ft + о ((X - !)«).
fe“l
n _b _b
4) in 6 - £ ------±3— (X - l)fe + 0 ((X - 1)«).
k—\
18.14. 1) -l^+У (-I)4"1 (Zy±^l^ + 0((x-l)'’)._
o / > \ О / OK
2) _^+2±^±2^(,_з)й + о((х-ЗП.
ы
3) - 2 In 12 + (in 12 + -0 (x + 2) —
i tYh? Cv2 + ^t) <’+2>'+“ «*+2)“>-
562
4) (ж — 2) + 22 (т + (х - 2? + О ((X - 2)«).
Ь2
Б) 3 + У ~ Dft + о ((х - 1)").
L-j к \к -f- 1)
Л=1
п [п/2]
6) “ 2 X (А '/г2)" + У (-D6-1 + 0(U + 2)")-
fe=i k=i
18.15. 1)3+£ (—l)fe (х — 2)ft + о ((х — 2)”).
2) £ (х - 2)fe + о ((х - 2)").
Л=2
П Л-1
3) 7 + £ таит - Wk + ° «* - ’°)")-
Л = 1
П U t.
Л»=1
п k
б) 2 + - (х - 1) + У (—l)fe-1 <Х-Г ?.L + О ((X - 1)«).
2 Z-r 2k
k— 2
п
6) з + £ (-1/ (х - 3)ft + о ((х - 3)п).
Л«2
7) Е (( з^---7ет)^+2>й+°^ + 2^
п k
18.16. 1) У (~1) -У ~ П (х + 2)ft + о ((х + 2)”).
2—। 3*
Л-2
2) 1 + Е (1 — 2~ft)(x—l)ft + o((x—1)").
Л-1
п
9) у+Е (3-^т)(х-3)" + о((х-3)П)-
п
б) у+^-(х- 1) +Е (1 +2-<ft+1))(x- Dfc + o((x- 1)п).
Л-2
п
6) _ 6 (X - 2) + 2 (-Dft ~ + °2(fe + ~ (X - 2)ft + о ((х - 2)").
*=2
19*
663
18.17. l) Ё '1Г(Н 1)2ft + °((x + 1)2Л)'
ЬО
k
2) У e"27 A- (x + 3)24+1 + о ((x + 3)2").
Ь9
n-l k-1 k
3) (x + 2) In 3 + У i"1!--2-...(X + 2)2ft+1 + о ((x + 2)2”).
3 k
4) У (— l)ft~1 ~ - + о ((x - 5)2re).
fc=l
n
18.18. 1) 1 + £ -<2* ~J} (x - 1)2Й + о ((x - I)2"),
ы 2 k]
n-1
2) (x + D + У (-0* (2,~У1! (X + l)2ft+1 + о ((X + I)2").
Ah—/ \£iK>) i I
Ы
n-l h
3) + у <-~»‘^-|)!' (I _,)№ + „((,_ in
2 22k+{(2k)U
4) (X -1)2 + У -1-i_4:7-- -<3fe -2>. (X - 1)2*+2+о ((X - I)2”),
“ 3%
n-2
5) (x + I)3 + У (~1} (2*~1)l! (x + l)2ft+3 + о ((x + I)2").
2 ki
«-1 k
18.19. 1) У (x _ i)2ft+l + 0 ((X - l)2n).
fe=0
n— 1
2) У (-Dft (x - l)2ft+1 + о ((x - l)2re).
/5 = 0
* i +г
k=0 fe=0
n -5 k
18.20. 1) У (x + 2)2ft + o((x + 2)2n+1).
l2n).
л-18п£
2? £ (x “ 3)2ft + 0 ((x - 3)2ft+ ’)•
k=>0
3)
n
s
^=•0
(,_ i) “+«((«-4/“"
664
4) £ ((х + 2)2* + (х + 2)2*+’) + о((х + 2)2п+‘).
ЬО
5) Е + ’)2ft + ° ((* + О2"*1),
ы
«> - 4+Е (lnXi~{k ~,n 2) (* -i)2fc+° (с* - i)2rt+i).
fe-1
7) ,- + у ,>>«>).
£_j ki
Ы
*
18.21. 1) У (~14(2feji3 (X ~ 1)26 + 0<(* “ 1>2n+‘).
fe=*0
, V (—О^З2* ( n\^ , ff nV*+i\
+ X 2(2fe)! (. б) +°(.v e) )•
л«о
А Л2 t V/ A\k( n* 1 Jt\2fc ff n\2rt+I\
4) 4 +X( ° k4(2*)l (2k-2)l)\.X 2) +°(.V 2) )‘
fe=»l
5) - , у (-»>--' f , <”*' V,, If.
b) 8 Zu 2 k(2^-1)! ф 4(2^+1)17 К + 2 J +
+<4D-
——— / 1 lr>k
• 18.22. 1) I + У - t - (x - 4)2ft + о ((x - 4)2"+1).
A— 1
2) ln3 + (x+l)ln3-y^^-yl£+^ + o((x+02^):
k^l
n+l 2fe-l
3> aEs-Zi^f’-+ "fc~
Ы
4) - 2 In 3 + fin 3 +4)(x + 2)2 Ч-V У ' (fe 4> (x+2)2ft+o((x+2)2>>+1).
\ 3 7 3 (k — 1)
18 .23. 1) У Ck_ 1/3 (x - 2)2ft+* + о ((x - 2)2rt+1).
л=о
S63
2) -4= + Ц=Г (х - 2) + У 124- У" ((X - 2)2ft + (х-2) 2*+1)_
V5 д/5 р V5 ю*Л;1 ' ’
К — 1
+ о((х —2)2п+1Х
п
3) 1 + (X - 1) + £ 11 ((X - I)2* + (X - 1)2*+ ‘) + 0((х-1)2«+1).
k=\ 2 k[
П~ 1 9Ь . 5
4) £с“+’г + <
fe=0
-2>Ч«ЧГ'+<4Г)-
Л=0
6) 3+£ (х — 2)2ft + о ((х — 2)2n+1).
/г=1
Е ~ т)(x+1)2ft+°((х+1)2"+1)-
k—\
п k
18^24. £ 2 ('^2) (х - I)3* + о ((х - l)3").
/г=0
п
18.25. (х - 2) + У (2^~-1)" (х - 2)24+1 + о((х - 2)2"+2).
feZi 2 ki
п (___1\k+lpk
18.26. £----- 3fe+1~1/3- (х - 2)3ft+1 + о ((x - 2)3"+‘).
л=о
n
k~2
+ О ((x — l)4rt+I).
,8-28-1} £ (722+cois)i2 (x - 1)4ft+2+E (~(£)in2(* - - d4")-
/г=0 /г=0
n-1 ь n ъ
2) £ уйМу-(x -2)4ft+2+E (~(2feY°s 1,1 (x ~2)4ft+°{(x - 2)4n>-
x k~0
1 n 1
k=Q fe=0
n ( _J^\4k+2
,8.». ,) £ +
/г=0
566
n f 1\k n /
fe-Э fc-0
4) s!|2.+ »»2(,+ 1) + £ (_l).__2±_(,+ ,)..+.+
fe«»O
+ £ (-l)ft+1 ^~П)~ <x + !)4Й+2 + о((x + 1)4п+3).
fe-0
18.30. 1) 1 - x2 + о (x3). 2) 1 + x 4- -у- + о (х2). 3) о (х26).
18.31. 1) —120. 2) 0. 3) 601.
18.33.1) 1+3(х—1)+3(х—1)2+(х—1)«. 2) 1 + (х + 2)4
3) 2(х + 1) —2(х + I)2 + (х + I)3. 4) 144(х —2)3 +144(х—2)3+'
+ 60(х — 2)4+ 12(х — 2)’+ (х — 2)«.
18.36 . 1) 1 + х + у х2 + о (х2). 2) е + ех + о (х2). 3) 1 + у х2 + о (х2).
4) 1 - + о (х2). 5) 1 - Зх + 6х2 + о (х2). 6)-^- + о(х2).
7
18.37 . 1) 1 — 2х + 2х2 + о (х3). 2) 2х + — х3 + о (х3). 3) 1 - х — х2 4-
О
+ |х3 + о (X3). 4) х - 4 Xs + о (Xs). 5) 1 + X + 4 X2 + О (х3). 6) —^-4-0(х3)
о Z 2 о
7) в — 4 X + 4^- X2 — X3 + О (х3). 8) 1 + X — х2 4- 4 X3 + о (х3).
«) х--^4-^4-о(х3).
18.38 . 1) е + ^х* + -^-Х' + о(Х"). 2) 1 - « 4-Ах2 -х3 4--^-х4 4-
о OU 2 О о
4-о(х4),. 3) Зх 4-х3 4-о (х4). 4) х — 4г 4"0 (х4)- 5) 1 -1 x 4.-L х2 -
z 42 2 12
1 у2 у4 у2 1 *7
--^х4 + о(х4). 6) 1-4— ^ + о(х4). 7) l-^-^ + o^).
S) 1 4- 4- х' + о(*4)- 9) 1 4- X2 4- 4- 4- О (X4).
о 40 о
18.39 . 1) 1 — 6х4-21х2 — 32х34- 15х4 4-66х6 4-о (х5). 2) х4--2-х24-
+ ‘ хз_ 3 х,4_ 1 х5 + о (л.6) 3) 1+ 1 Х2+ 5 х4 + о(х6) 4) 1+х +
О тг О 2 2Z±
1 1 11 2 1*2 уА
+ 4 Xi - 3 х3 “ 14 + 15 XS + ° б> - 1Г ~ W + ° (Х5)‘ 6) 1 + х2~
- хз 4- 41х* - 4гх&+°(х6)- 7>1+х2 - 4xs+4х4+4хб+° (*5)-
l^r о л о о
18.40 . 1) х-~х3 + — х5 + о (хб). 2) eV2 (х-~ е2л/ъ(х-----UY+
3 15 \ л]е) \ \е)
+ «‘V2“(* - | «• V? (л -+ ”((«-3> S +
— 10 In 5 • х6 4- -у- X8 4- О (х8). 4) 21973 (X - Г)1923 4- о ((х - I)1973).
18.41 . 1) А = 1, В = 1. 2) А = 4/3, В = —1/3. 3) 4 = 1, fi = —I.
4) А =—1/15, В =—2/5.
567
18.42 . 1) 5,027. 2) 3,019. 3) 3,017. 4) 1,396. 5) 0,996. 6) 0,309. 7) 0,262.
8) 0,675.
18.43 . 1) e/(n+ 1)!. 2) 1/7!. 3) 1/(2®S1). 4) 2-10-8. 5) 2-10-8. 6) 1,5-10-»-
18.44 . 1) 2,7182818. 2) 3,162. 3) 0,017452. 4) 0,99619. 5) 3,1072. 6) 1,0414.
§ 19. Вычисление пределов с помощью формулы Тейлора
19.1. 1) -1/2. 2) 1. 3) 1/2. 4) 1/24. 5) 27/4. 6) 1/2. 7) 4/3. 8) 0. 19.2. 1) -2
2) -1. 3) -1. 4) 8/15. 5) -1. 6) —2. 7) 7/6. 8) 0. 19.3. 1) -е/2
2) 1. 3) Не/24. 4) л/4. 19.4. 1) 3/2. 2) 4/3. 3) -1/8. 4) -Г/2. 5) -4
19.5. 1) 2. 2) 7/8. 3) 1/8. 4) 44. 5) 40/3. 19.6. 1) 0. 2) 3. 3) -11/12. 4) -13/12
19.7. 1) —1. 2) 2. 3) —4. 4) 1/8. 5) 3. 6) —1/4. 7) —10. 8) —1. 19.8. 1) —3
2) 1/8. 3) -1/6. 4) 5/2. 5) 7/5. 6) 11/4. 19.9. 1) 3/4. 2) -1. 3) 1/4. 4) 1/8
5) -1/6. 6) -1/8. 19.10. 1) 4/9. 2) -1. 3) -6. 4) 7/6. 5) -6. 6) 21е/20
7) 2/5. 8) —4. 19.11. 1) 7/4. 2) 3/2. 3) 3,2. 4) 13/15. 5) 4. 6) 1. 19.12. 1) 15/2
2) 3/4. 3) 3/7. 4) 23. 5) 9/2. 6) 5. 19.13. 1) 1/18. 2) -1. 3) 5/(12е3). 4) 1/7
5) —-^-соз21. 6) — Че2. 19.14. 1) —32/3. 2) 9/16. 3) 9. 4) 28/3. 5) —72/5
6) 1/4. 7) —1. 8) 24/7. 19.15. 1) 2. 2) 0. 3) —27/5. 4) у cos 1. 19.16. 1) I
2) 1/2. 3) 1/2. 4) 7/24. 19.17. 1) —7/5. 2) 7/45. 3) 1/12. 4) 72/5. 19.18. 1) 5е/8
2)1/7. 3)14/3. 4)4/3. 19.19. а =—1/2, п = 4. 19.20. 1) в~1/2. 2) е-1/2
3) е1^2. 4) е~5. 5) е”7^2. 6) Не существует. 19.21. 1) е1^6. 2) е-1^6. 3) е-1^3
4) е2/3. 19.22. 1) е|/4. 2) е7/3. 3) е-2/3. 4) е~2. 19.23. 1) е. 2) е-7/3. 3) е7/3
19.24. 1) е~1. 2) е1/9. 3) е-1/18. 4) е~1/6. 19.25. 1) е~}/2. 2) е2/3. 3) е“3'8
4) е"|/4. 19.26. 1) е~1/24. 2) е1/6. 3) е~Б/4. 4) е~3/4. 19.27. 1) е8/|Б. 2) е~3/1°
3) е“23/3°. 4) е9/2°. 19.28. 1) е-Б/6. 2) е~|/8. 3) е7/|2. 19.29. 1) е7/|2. 2) е~25''3
3) e-s/2. 4) е~‘. 19.30. 1) е6'2. 2)е33'31. 3) е~5/12. 4) е-1'12. 19.31. 1) е2'3
2) е2/е. 3) е2'3. 4) е’7». 19.32. 1) е1712. 2) е~1'е. 3) е’78. 4) е23'3. 19.33. 1) е176
2) е~3'13. 3) е. 4) в"172. 19.34. 1) е~^9. 2) в^<л'+4)7(3л’). 3) е-7/е 19.35. 1) е-7/.
2) е2. 3) е-‘. 19.36. 1) е-25781. 2) е-»73.- 3) е-77‘. 19.37. 1) е2. 2) е~1'2
3) е~13/‘. 4) е2‘. 19.38. 1) е~2. 2) е~3/‘. 3) е-*71®. 19.39. 1) е~3. 2) е~‘. 3) 1
19.40. 1) е172. 2) е5721. 3) е-‘78. 19.41. 1) eli'13. 2) ее. 3) е». 4) е7718
19.42. 1) е~3'2. 2) е. 19.44. 1) e~>. 2) 19.45. 1) е273. 2) е13780. 3) е2
19.46. 1) е~178. 2) вя/6. 19.47. 1) е3. 19.48. 1. 19.49. 1) е~2. 2) е. 3) е1/'8"5271’
19.50. 1) 2) Предел не существует. 3) е178. 19.51. e~i/3. 19.52. —1/6
19.53. 1) 7/6. 2) 3/2. 19.54. 1) — л. 2) —л. 3) 1/6. 19.55. —3. 19.56. 1) 0. 2) 0
3) 1/з. 4) —1/2. 19.57. 1) 1/2. 2) 2 + In 2. 3) 1/3. 19.58. 5/18. 19.59. 1) 1
2) 17/12. 19.60. 1) 2/5. 2) 11/6. 3) —4/3. 4) 1/2.
§ 20. Исследование функций
20.1. 1) (—оо; 1/2), (3; 4-°°)—интервалы возрастания, (1/2; 3)—интер-
вал убывания. 2) (—оо; 6)—интервал возрастания, (6; 4-оо)—интервал
убывания. 3) (—оо; 1), (3; 4-оо)—интервалы возрастания, (1; 3)—интервал
убывания. 4) (—оо.; —3/2), (—1/2; 4-оо) — интервалы возрастания,
(—3/2; —1/2) —интервал убывания.
20.2. 1) (—оо; 1/3)—интервал возрастания, (1/3; 4-оо)—интервал убы-
вания. 2) (—оо; 0), (0; 1)—интервалы убывания, (1; 4-оо)— интервал воз-
растания. 3) (—оо; —1), (0; 1)—интервалы возрастания, (—1; 0), (1; -f-oo) —
интервалы убывания. 4) (0; а)—интервал возрастания, (а; 4-оо) — интервал
убывания. 5) (О; д/5 ) — интервал убывания, (д/б ; + оо) интервал возраста-
ния. 6) (0; 1/V^)— интервал убывания, (1/д/е ; + °°)— интервал возраста-
ния. 7) (0; 1), (1; е)—интервалы убывания, (е; 4-°°)—интервал возраста-
ния. 8) (—оо; 3), (3; 4-о°) — интервалы убывания. 9) (0; 4-оо) — интервал
убывания.
668
10) ^2k — 2k + , keZ, — интервалы возрастания, ^2k 4- 2k + »
/г g Z, - интервалы убывания.
20.3. 1) (-oo; -2), (-2; — V2 ), (V2 ;4~ oo) — интервалы возрастания,
(—V2; —1), (—1; V2)— интервалы убывания 2) (—oo;—1), (—1; 0), (0; 1),
(1; 4-00) — интервалы убывания. 3)__(—оо; —3), (3; 4-оо)— интервалы убыва-
ния, (— 3; — V5"), (— V3 ; Уз ), (V3 з) — интервалы возрастания. 4) (—оо; 0),
(2; 4-°°) — интервалы убывания, (0; 2) — интервал возрастания
20.4. 1) (—оо; —50), (—50; 25)—интервалы возрастания, (25; 4-оо)—ин-
тервал убывания. 2) (—2V2; —2), (0; 2) — интервалы возрастания, (—2; 0),
(2; 2 V2 ) — интервалы убывания. 3) ; —з), ( 0; 4~°°) — интервалы воз-
растания, (—3; 0)—интервал убывания. 4) (—1; — 2/5)_—интервал убыва-
ния, (—2/5; 4-°°) —интервал возрастания. 5) (— °°£_— V3), (V3; 4- оо)—ин-
тервалы возрастания, (—V3’, —1), (—1; 1), (1; V3)- интервалы убывания.
6) (—оо; —1), (1; 4-°о)—интервалы возрастания. 7) (—оо; —1); (0; 4-°°) —
интервалы возрастания.
20.5. 1) (—2; 0)—интервал возрастания, (—оо; —2), (0; 4-оо)—интерва-
лы убывания. 2) 4- 2&л; 2/гл), k е Z,— интервалы возрастания,
+ 2kn; 4- 2^л^, k е Z, — интервалы убывания.
20.6. 1) (—оо; 0) —интервал возрастания, (0; 4-°°) —интервал убывания.
'2) (0; 1) —интервал возрастания, (1; 4-°°) —интервал убывания.
20.7. (—оо; —е~2)—интервал возрастания, (—е~2; 0)—интервал убы-
вания.
20.8. 1) а 0. 2) а^ — 3, а 1. 3) а > 1. 4) а > 5. 5) а > 6.
•6) —1 С « С 7.
20.11. Нет, не следует; контрпример f(x) — х 4- sin х, х s R.
20.13. 1) х — 0 — точка максимума, х — 8/3 — точка минимума.
2) х = (3 — V17 )/4 и х = 3 — точки минимума, х — (3 4- V^7 )/4 — точка
максимума. 3) х = (—1)Л-~ + nk — точки максимума, х = 4- nk — точки
минимума, k е Z. 4) х = (2 4" V7 )/3 — точка максимума, х = (2 — V7")/3 —
точка минимума. 5) х — 4 — точка минимума. 6) х = 1/2 — точка минимума.
7) х = 1 —точка максимума, х — 2 — точка минимума. 8) х = —5/4 — точка
максимума.
п
20.14. х = ~ У* xk. 20.15. х3 — 6х2 + 9х + 2.
fe-1
20.16. 1) Максимум у = 12 при х — 0, минимум у~—4 при х =* ±2.
2) Максимум у — 2 при х == 0. 3) Максимум у — 1 при х = 2, минимумы
у = 3/4 при х — 1 и х = 3. 4) Минимум у — 4 при х == 1. 5) Минимум
у = —324 при х — 1, максимум у = 0 при х =* —5. 6) Минимум у — —108
при х — 0, максимум у — 0 при х = —2.
20.17. 1) Максимум у = —4 при х = 1/2 2) Минимум у = —1/4 при
х — —2, максимум у — 1/4 при х «= 2. 3) Максимум у =* —8 при х — —3,
минимум у = 0 при х = 1. 4) Максимум у = —27/4 при х = 5. 5) Минимум
у — 0 при х = 0, минимум у = 32/3 при я =4, максимум у = 1/4 при
х = —1. 6) Минимум у — 0 при х_== 0, максимум у = —256/27 при х = —4.
3 л/3 л 3"А/3
20.18. 1) Минимумы у -----— при х = 2itk —f максимумы у ———
при х = 2nk 4- k s Z. 2) Максимумы у = 1 при к — 2nk и х — 2nk 4- ~тг»
о 2
2 бзт
, максимумы у ==-— при х = 2nk 4—минимумы у=—1 при х=2эт&4-я
569
3 л т/^
и х ~ 2nk + минимумы у = при х = 2nk + —, k е Z. 3) Макси-
V3 о 1 । 2л д/3 2 л
мумы у = —— при % = 2nH-v> минимумы у =--------— при х = 2nk----—,
о о 3 3
, п лх г\ г-\ л "4“ 6 д/З — 12
k е Z. 4) Экстремумов нет. 5) Максимумы у =-----!-----------р лЛ при
л
X = -ру + ^k, минимумы
1х
12
бл — б'х/З ’’-12 5л , , , _
у -----------j*g-----2- + л/г при х = -ц- + л&, kz=Z.
6) Максимум у = -^~-1 при х= — 1, минимум у = 1-при х = 1.
2
7) Минимумы у = —2п при х = 2 — 2п, минимумы у = 1 — 2п при х =
= 1 +2п, максимумы у = 2n — 1 при х = 3— 2п, максимумы у = 2п при
х = 2 + 2п, п е N. 8) Минимум у ~—1 при х = 1, максимум у = О
при х *= 0.
20.19. 1) Минимум у = — е2/3 при г = 2/3. 2) Минимум у = — 6е~8 при
х = —3, максимум у = 2е при х == 1. 3) Минимум у — —4е2 при х — —2,
максимум у = 8е~4 при х = 4. 4)_Максимум у = 27е~3/64 при х = 3/4.
5) Максимумы у = 4е~2 при х == ± д/2 . минимум у = 0 при х=0. 6) Мак-
симум у *= 55е~4 при х = 4. 7) Максимум # = 6 при х — 0. 8) Максимум
у = l/е при х = —1, минимум у = 4 Vе при х = 2.
20.20. 1) Минимум у = —2/е при х = е~2. 2) Минимум у = 0 при х — 1,
максимум у — 4е~2 при х = е2. 3) Максимум у — 1 /1п 3 при х = —3.
4) /Минимумы у = —4 при х = 1 и х = 3. 5) Максимумы у = —1 при
х = 2&л,7г eZ. 6) Минимум у = In 2 — л/2 при х — [.
20.21. 1) Максимум //=13/4 при х = 11/4, односторонний минимум
л/4
у = 3 при х = 3. 2) Минимум у = 0 при х = 1, максимум у = —— при
х = 1/3. 3) Минимум у = 0 при х = 0; максимум # = 4/27 при х = 8/27.
4) Минимум у = —3 ^2/8 при х_= 3/4. 5) Минимум у = 1_при х = 0. ма-
ксимумы # = V^ при x = ±V2/2. 6) Л4инимум # = д/з при x = 2V3,
максимум при х = —2V3. 7) Минимумы у = 0 при х = 2 и
х = 4, максимум у = 1 при х = 3. 8) Минимум у = — V^/З при х = 4/3.
максимум у = 0 при х = 2. 9) Минимум у = д/12 при х = 4/3, максимум
у — 0 при х — 2/3. 10) Максимум у = 1 при х = —1.
20.22. 1) Минимум у — е~1/е при х = 1/е. 2) Максимум у = е^е при
х = е.
20.23. 1) Максимум # = 27/16 при х = 9/2, минимум # = 0 при х = 5.
2) Максимум у = 49/24 при х — 7/12, минимум # — 0 при х = 0, минимум
# = 1 при х = 1. 3) Максимум у = \1л]~2\ при х — 1/3, максимум
у = 1/д/зЗ при х = 7/3, минимум у = 1/7 при х = 1. 4) Максимум
у е= 2 ^4/3 при х = 4/3, минимумы # = 0 при х = 0 и х = 2. 5) Максимум
# = 9д/б/8 при х~ —5/4, минимум у — 0 при х = 1. 6) Максимумы
# = 2 (д/2 — 1) 1 при х = ± (1 — д/2 ), минимумы у = 0 при х — ±1,
минимум у = 1 при х = 0. 7) Максимумы у = 2 (д/5 + Ое"1 при х-—
=± (1 + Vs), максимум у = 4 при х = 0, минимумы у = 0 при х = ±2.
8) Максимум # = 1/2 при х = 1, минимум у = 1/е при х = 0.
20.24. 1) Максимум у = cos 1 при х = л/2. 2) Максимум # =
= 2 sin ((л + 6) /4) при х = (6 — л) /4, минимум # = cos 3 при х = 3. 3) Ми-
нимум # = 2 —V3 при х = л/2.
20.25. 1) Д4аксимум # = 0 при х = 0, минимум у = — 1/е при_ х = 1/е.
•2) Максимум # = 1 при х = 0, минимум у = е“ 1/(3е) при х = 1/Ve* 3) Мак-
симум у при х = 1/е, минимум у = 1 при х = 1.
570
20.26. 1) Максимум у — ппе1~п при х — п—1, ne N; если п — четное,
“то минимум у — 0 при х — —1. 2) Если п — нечетное, то максимум у— \ при
х — 0; если п — четное, экстремумов нет. 3) Максимум у = kknnl(k +
при х ~ k/(k + п); если k — четное, то минимум у = 0 при х — 0; если п —
четное, то минимум у = 0 при х = 1. 4) Если ab > 0, а > 0, то минимум
у = 2 'yjab при х — In если ab > 0, а < 0, то максимум у — — 2 д/ab
1 । ь
при X ~ —— In —•
2р а
20.27. Если <р(а) >0 и п — четное, то минимум у = 0; если cp(d) < 0 и
и — четное, то максимум # = 0;_если п — нечетное, то экстремума нет.
20.28. 1) Максимум у = ^4 при х = 2, минимум у = () при х = 0.
2) Максимум у — V2 — 1 при х = —1, минимум у — 1 — д/2 при х—1.
3) Максимум у = V2 при х — 0, минимумы //—__V(2 + V3 )/2 при х =
— ± V2/2. 4) Минимум у = 3/^32 при х = — 1/^32.
20.29. 1) Минимум у = 4 при х — 1/2. 2) Максимум у = 0 при
х = —In 2/2.
20.37. 1) 9; —7. 2) 80; 0. 3) Наибольшее значение не существует; —204.
4) 3; —13. 5) 2; —10.
20.38. 1) Наибольшее значение не существует; 64; 2) 1; 3/5. 3) 2; 2/3.
4) 1; 2 УГ —2.
20.39. 1) 5 — 2 Уб; —1. 2)е —2; 2 —2 In 2. 3)0; — 5/е. 4) 54-1,5 In 2; 0.
5) е5; —е3 *. 6) 1; 1/е1/е.
20.40. 1) 3 Уз"/2; —2. 2) 3/4; 3/4. 3) 13л; 12л — 1. 4) л; —л.
20.41. 1) Минимум у = 0 при х = 3, минимум у = 9 при х = 0, макси-
мум у —~4е при х — 1; т = 0, М — е\ 2) Минимум у — —27е при х — 0,
максимум у — —65 при х — —1, т = —1_25е, М = е5. 3) Минимумы у = 1
при х — 0 и х = —1, максимум у = е2 V3/9 при х = —2/3; т — 1, М==е2.
4) Минимумы у — 0 при х — 0 и х — —1, максимум у — In ^1 +
при х = —1/3; т — 0, М — 1пЗ. 5) Минимумы у 0 при х = 0 и х = 1,
максимум у = arctg (2 д/з79) при х — 1/3; т = 0, М = arctg 2. .6) Минимум
у = arcctg (2\/з/9) при х = 2/3, максимумы у = л/2 при х = 0 и х= 1; т —
— arcctg 2, М = л/2. ,
20.42. 1) Минимум у — —2 при х = 1/е, максимум у — 0 при х = 0;
т — —2, М — 4е In 2. 2) Минимум у = е~1/(2е) при х — максимум
у = 1 при х = 0; т = —2; М — 16. 3) Минимум у = 2/V3 при х = д/з ; ми-
нимум у = 4/д/б при х = д/б", максимум у — 5/3 при х = 2; т — 2/д/з,
М = 2.
20.43. 1) Минимум у = —2 при х — —2л/3, максимум у — 3/2 при
V2
х = 0; т — —2, М = 3/2. 2) Минимум у == —1---— при х — 0, минимум
г— Л/Ъ
у = — д/2 при х = —л/2, максимумы у = 0 при хе (0; л); т = —-1---—>
М = 0. 3) Минимум у = — V2 при__х=—5л/12, минимум //=—2з!п(л/12)
х/з
при х == л/4, минимум у == — 1----— при х -= 0; т == — 1--------—, М ==
_ — 1
2
20.44. 1) п « 7. 2) п = 1985. 3) п = 10. 4) /г = 7. 5) п = 12. 6) п = 14.
Q
20.45. 1) + оо. 2) —оо;
V4
-1.
3) — оо; 1. 4) V2 ~ 3 arccos—+оо.
V3
571
20.46. 1) 0; 4. 2) — (У2/2) е’3^4; 1. 3) 0; 1/e. 4) l/ev*; 1.
20.47. 1) 5; ±oo. 2) 5/2; +<». 3) 0; Уз.
4) inf f =
3’
a ^0,
a2 + 1
a2 + 3 ’
0 < at
sup /= 1.
20.48. 1) Выпукла вниз. 2) Выпукла вверх. 3) Выпукла вниз. 4) Выпук-
ла вверх. 5) Выпукла вниз. 6) Выпукла вверх при х > 0, выпукла вниз при
х С 0.
20.49. 1) Выпукла вверх на интервале (—1/2; 1/2), выпукла вниз на ин-
тервалах (—оо; —1/2) и (1/2; 4-оо); точки перегиба х = ±1/2. 2) (—оо; 1) —
интервал выпуклости вверх, (1; ±оо) —интервал выпуклости вниз; точка пе-
региба х = 1. 3) (—оо; —1) и (1; ±оо)—интервалы выпуклости вверх,
(—1; 1)—интервал выпуклости вниз; точек перегиба нет. 4) (—оо; —6) и
(0; 6)—интервалы выпуклости вниз, (—6; 0) и (6; ±оо)—интервалы вы-
пуклости вверх; точки перегиба х = 0, х = ±6. 5) (—оо; —3) — интервал
выпуклости вниз, (—3; ±оо) — интервал выпуклости вверх; точка перегиба
х = —3. 6) (0; (2 ± Уз )/Уз ) — интервал выпуклости вверх, ((2 ± Уз )/УЗ;
+ оо) — интервал выпуклости вниз; точка перегиба х = (2 + УУ)/уЗ.
7) (—оо; — Уз) и (О; Уз) — интервалы выпуклости вниз, (—УЗ; О) и
(УЗ; + оо) — интервалы выпуклости вверх; точки перегиба х==0, х = ± Уз.
8) (—оо; —3), (—1; 0), (1; 3)—интервалы выпуклости вниз, (—3; —1),
(0; 1), (3; ±оо)—интервалы выпуклости вверх; точки перегиба х = 0,
х = ±3.
20.50. 1) (л(4Л + 1)/2; л(4& + 3)/2)—интервалы выпуклости вниз,
(л(4&±3)/2; л(4& ± 5)/2)—интервалы выпуклости вверх, точки перегиба
х = я (2k + 1)/2, k&Z. 2) (2&jt; (2£±1)л)—интервалы выпуклости вверх,
,((2/г±1)л; (2k + 2)л) —-_интервалы_выпуклости вниз; точки перегиба х=^л,
k е Z. 3) (— оо; — 1/У2) и (1/У2; ± оо) — интервалы выпуклости вниз,
— 1/У2; 1/У2 ) — интервал выпуклости вверх; точки перегиба х==±1/У2.
4) (—со; —1/2)—интервал выпуклости вверх, (—1/2; 0) и (0; +оо)—ин-
тервалы выпуклости вниз; точка ^перегиба х — —1/2. 5) (0; ЮеУг) — ин-
тервал выпуклости вверх, (10еУе; + оо) — интервал выпуклости вниз; точ-
ка перегиба х=10еУе. 6) еМ8Н-1)/4)__ интервалы выпукло-
сти вниз, (ел (8fe+1V4; еп <8^+5)/-4) _ интервалы выпуклости вверх; точки пере-
гиба х = е Л(4Л+1)/4, k е Z. 7) (—оо; 0)—интервал выпуклости вверх,
(0; Ч-оо)—интервал выпуклости вниз; точек перегиба нет. 8) (—оо; 1/2) —
интервал выпуклости вниз, (1/2; ±оо)—интервал выпуклости вверх; точка
перегиба х = 1/2.
20.51. 1) х = ±1. 2) х = 2, х = 4. 3) Точек перегиба нет. 4) х — ±1,
х — ± 1/Уб. _
20.52. 1) х = — У2/2. 2) х = — 2 ± Уз". 3) х = ±2. 4) х = 1. 5) х =_3.
20.53. 1) х = — 3, х = —1. 2) х =» 0, х = (3 ± Уз )/4. 3) х = \/е е .
4) х = е8^3. 5) х = 2kn ± arccos ((Уб — 1)/2), k е Z.
20.54. 1) (1; 0), (1/2; —9/4). 2) (—3; 294), (2; 114). 3) (1/Уз ; 23/18),
(— 1/У5-; 23/18). 4) (4; —1024/5). 5) (8/7; —31/9). 6) У графика функции
точек перегиба нет.
20Л5. 1) (0; 1), (1; 0). 2) (—1; —1), (0; —1). 3) (5; 5). 4) (У2; УГ).
20.56. 1) ((2 + У2 )/2; Уё), ((2 - У2 )/2; Уё).
572
2) (ft <». (Ув: 1д/4), (-ЛЛГ --1 д/4). 3) (1; l-,„2).
4) ((в4 + (_1Л„/12;22^_г-<“+'-»*>«)1 *eZ.
20.57. 1) x = ±or. 2) x — 0, № ± ft V3.
20.58. 1) Одна точка перегиба x == —ft/(За). 2) Если 3ft2 — 8ac>0, то две
точки перегиба х = (—3ft ± V$ft2 — 24аг)/12а; если 3ft2 — 8ас 0, то точек
перегиба нет.
20.59. а е со; —а е (0; + со). 20.63. 1) Не может. 2) Не мо-
жет. 20.67. 1) (УГеЛ УГе~^).2) (9/2; 27/2). 3) (5; 21/2). 4) (1/10; 1/4).
20.73. У к аз а н и е. Можно либо воспользоваться неравенством из за-
дачи 20.72, положив в нем х == a/ft, а = 1/р, р/(р — 1) == q, либо, пролога-
рифмировав неравенство Юнга, использовать выпуклость вверх функции 1пхв
20.74. Указание. В неравенстве Юнга (задача 20.73) положить
-У-
Ё у1
и просуммировать полученные неравенства по i от 1 до п.
20.75. У к а з а н и е. Применить неравенство Гёльдера (задача 20.74) к
суммам правой части тождества:
п п п
У (Xi + yi)p = У Xi (Xi + yi)p-1 + У У1 (Xi + yt)p~\
i *=1 i = 1 i = 1
§ 21. Построение графиков
21.3. 1) Точки пересечения с осями координат: (—1; 0), (2; 0), (0; 4);
минимум у — 0 при х = 2, максимум у — 4 при х = 0; точка перегиба (1; 2).
(2 Точки пересечения с осями координат: (1; 0), ((—1 ± V13)/2; О), (0; —3);
минимум у == — 16 V^/9 — 3 при х = —2 д/з/З, максимум г/= 16V3/9 — 3
при х = 2V3/3; точка перегиба (0; —3). 3) Точки пересечения с
осями координат: (1; 0), (—2; 0), (0; 2); минимум у = 0 при х= 1, макси-
мум у — 4 при х = —1; точка перегиба (0; 2). 4) Точки пересечения с осями
координат: (2; 0), (—4; 0), (0; 4); минимум у = 0 при х = 2, максимум
у = 8 при х = —2; точка перегиба (0; 4). 5) Точки пересечения с осями
координат: (0; 0), (1; 0); минимум у = —27/256 при х = 1/4; точки перегиба
(1/2; —1/16), (1; 0). 6) Точки пересечения с осями координат: (—2; 0), (Г, 0),
(0; 4); минимумы у — 0 при х ==—2 и х == 1, максимум у — 81/16 при
х = —1/2; точки перегиба (0; 4), (—1; 4). 7) Точки пересечения с осями
координат: (—1; 0), (1; 0), (0; —1); максимум I/= 0 при х ==—1, мини-
мум у — —864/3125 при х = —1/5; точки перегиба функции х = 1,
х = (V34 — 2)/10 ~0,4, х = —-(д/34 + 2)/10^ — 0,8. 8) График симметричен от-
носительно оси ординат; точки пересечения с осями координат: (0; 0),
(±1; 0); минимумы у = —27/8 при х = ±1/2, максимум у = 0 при х == 0;
точки перегиба функции _______________
х=±1, ± У(17 + У177)/56 яа ± 0,7,
х = ± У(17 —У177)/56 « ± 0,3.
21.4. 1) Область определения: вся числовая ось, кроме х — 1; точки пе-
ресечения с осями координат ((±Уб - 1)/2: о), (О; -1); асимптоты у = 1 и
573
< я = 1; минимум у == —5/4 при х — 1/3; тоцка перегиба (0; —1). 2) Область
определения: х =# 2; точки пересечения с осями координат: ((1 ± V33)/4; 0),
(0; 1); асимптоты у = —1 и х — 2; максимум у = 33/8 при х = 10/7; точка
перегиба (8/7; 31/9). 3) Область определения: х Ф 1; точка пересечения с
осями координат (0; 0); асимптоты у = 0 и .№ 1; максимум у = 0 при
х = 0, минимум у == —80/27 при х = —2; точка перегиба функции
х = — 2 ± Уз. 4) Область определения: х =/= —1; точки пересечения с осями
координат (1; 0), (0; 1); асимптоты # = 0 и х =—1; минимум у — Q при
х — 1, максимум у^2/27 при х==5; точки перегиба функции х = 5 ± 2 Уз.
5) область определения: х 1; точка пересечения с осями координат (0; 0);
асимптота х—1; максимум у === 27/4 при х = 3/2; точка перегиба (0; 0).
6) Область определения:- х Ф 0; точки пересечения с осями координат (2; 0),
(±1; 0); асимптота х = 0; минимум у & —0,3 при х ж 1,5; точка перегиба
функции х — — У2. 7) Точка-Пересечения с осью ординат (0; 0,2); асимпто-_
та у — 1; минимум у = 3 — 2 У2 при х = 1 — У$Г» максимум у — 3 + 2 У2
при №1 + 72; точки перегиба (— УЗ; 2~Уз), (Уз~; 2 + Уз), ч
(3; 5). 8) Точки пересечения с осями координат: (0; 5,5), ((—21±2 У14)/б; о)^
асимптота у = 5; минимум z = — 4 У? при х== — 1 — 2У2, максимум у ==»
®=4У2 при х = 2У2 —1; точки перегиба (—3; —2), (± У2Г 1 ± У21).
21.5. 1) Область определения: х ±1; график симметричен относительно
начала координат; точка пересече1шя с осями координат (0; 0); асимптоты
у = х, х — минимум у = 3 Уз /2 при х — Уз, максимум у — —3 Уз /2
при х — — Уз; точка перегиба (0; 0). 2) Область определения: х =# 2; точки
Пересечения с осями координат: (1; 0), (0; —1/4); минимум у —27/4 при
х — 4; асимптоты у = х + 1, х — 2; точка перегиба (1; 0). 3) Область опре- ’
деления: х^7\ точки пересечения с осями координат (5; 0), (0; —125/49);
асимптоты у — х— 1, х — 7; минимум у — 13,5 при х = 11; точка перегиба
(5; 0). 4) Область определения: х+= 1; точки пересечения с осями координат
(0; 0), (—2; 0); асимптоты у — х + 4, х = 1; минимумы у = 0 при х = 0 и
у — 32/3 при х — 4, максимум у — 1/4 при х =—1; точка перегиба
(—2/7; 16/189), 5) Область определения: х =/= 0; асимптоты у — х и х = 0;
минимум у = 19/4 при х == 2, максимумы у = 5 при х = 1 и у — —17/3 при
х » —3; точка перегиба (9/7, 929/189). 6) Область определения: х =И= 2; точки
Пересечения с осями координат (1; 0), (—1; 0), (0; 1/4); асимптоты t/=x4~3>
X — 2; максимум у — 1/4 при х = 0, минимумы у — 0 при х — 1 и у — 32/3
при х — 5; точка перегиба (5/7; 16/185).
21.6. 1) Область определения: _х — У2; точка пересечения с осями
(0; 0); асимптоты у =*= х, х = — У2 ; минимум у — 0 при х — 0; максимум
у — —8/3 при х = —2; течка перегиба (У4; бУ25 /з). 2) Область опреде-
ления: х =/=—1; точка пересечения с осями координат (0; 0)-; асимптоты
у — х— 3, х — —1; минимум у — 0 при х = 0, максимум у — —256/27 при
х — —4. 3) Область определения: х У= 0; график симметричен относительно
начала координат; точки пересечения с осями координат х — ± У2/Уз — 1~
0,4; асимптоты у — Зх, х — 0; точки перегиба (1; 8), (—1; —8); функция
возрастает всюду в области определения. 4) Область определения: х #= I;
точки пересечения с осями координат: (—1; 0), (0; 1); асимптоты t/=l,x=l; ‘
минимум у — 0 при х — —1; точка перегиба (—4; 81/625). 5) Область опре-
деления: х =# ±1; график симметричен относительно начала координат; точка
пересечения с осями координат (0; 0); асимптоты у == х, х — ±1; минимум
у — 25 Уб /16 при х = Уб, максимум у = — 25 Уб/16 при х — — Уб;
точка перегиба (0; 0). 6) Область определения: х =# 2; точки пересечения с
осями координат (1; 0), (0; —1/16); асимптоты у = х +^3, х = 2; минимум
у = 55/44 ПрИ х — g; точка перегиба (1; 0). 7) Область определения: х=£0;
точка пересечения с осью абсцисс (У8; б) ^*(1,52; 0); асимптота у = х; ми-
нимум у = —2,5 при х — —2. 8) Область определения: х^±1; график-
574
симметричен относительно начала координат; точка пересечения с осями ко-
ординат (0; 0); асимптота у — х; максимум у — — 5 д/5 /4 « — 1,87 при
4 4 __ 4
х = — д/б~ ~ — 1,49, минимум у = 5 д/5 « 1,87 при х = д/б" ~ 1,49; точка
перегиба (0; 0).
21.7. 1) Область определения: |х| 1; асимптоты у = 2х при х->±о°
и у =5= 0 при х->—оо; функция убывает при х —1 и возрастает при х 1;
выпукла вверх. 2) Область определения: х 0 и х 2; точка пересечения с
осями координат (0; 0); асимптоты у = 1 при х-^±оо и у = 2х— 1 при
х-> — оо; функция возрастает при х 0 и убывает при х 2; выпукла вниз.
3) Область определения R; симметрия относительно оси ординат; точка пере-
сечения с осью ординат (0; 2); минимумы у = 'у/А «1,6 при х = ±1, мак-
симум у = 2 при х = 0; функция выпукла вверх. 4) Область определения R ;
симметрия относительно начала координат; точка -Пересечения с осями ко-
ординат (0; 0);_асимптота у = 0; максимум у = Д^16 « 2,5 при х = 2, мини-
мум # == — ^16 « —- 2,5 при х = — 2; точка перегиба (0; 0). 5) Область
определения: х — 1; точки пересечения с осями координат (0; —1),
(2 ± д/7 • О):- минимум у = — д/2 при х = 1; функция выпукла вниз. 6) Об-
ласть определения: х 0; общая точка с осью ординат (0; 1/3); функция
строго возрастающая; точка перегиба х0 = (д/б + 1)/2 « 1,62, у (х0) ~ 8.
21.8. 1) Область определения: х^—9/2, точки пересечения с осями ко-
ординат (0; 0), (—9/2; 0); минимумы у == 0 при х == 0 и х =—9/2, макси-
мум у == 3 д/3 при х = —3; функция выпукла вниз при х>0 и выпукла
вверх при —9/2 < х < 0; угловая точка (0; 0). 2) Область определения:
х 1; точки пересечения с осями координат (0; 0) и (1; 0); максимум
у = 2/(3 д/з) « 0,38 при х = 2/3, минимумы у = 0 при х = 0 и х = 1;
(0; 0) — угловая точка; функция выпукла вниз .при х 0 и выпукла вверх
при 0 х 1. 3) Область определения: — V3^x^0 и_х^>д/3: точки
пересечения с осями (0; 0), (± д/3 ; 0); максимум у = д/2 при > х — —1;
точка перегиба функции х == -Д^З + 2 д/3 . 4) Область определения: х —1;
точки пересечения с осями координат (—1; 0) и (0; 0); минимумы у = 0 при
х — —1 и х == 0, максимум у = 16/(25 д/5) « 0,29 при х == —4/5; точка пере-
гиба функции х — (д/5 — 5)/5 « — 0,55, у = (б — 2 д/5 )/б д/5 «0,21. 5) Об-
ласть определения: х —1; минимум у ~ — 6 д/Тб/125 « — 0,19 при
х =—2/5; точка перегиба (—-4/5: — 4/(25 V5)). 6) Область определения:
х<0, х 4; точки пересечения с осями координат (0; 0) и (4; 0); асимп-
тоты у = х—1 при х->4-оо и у — 1—х при х —>—оо; функция убывает и
выпукла вверх при х 0, возрастает и выпукла вверх при х 4
21.9. 1) Область определения: R; точки пересечения с осями координат
(0; д/2) и (—2; 0); асимптоты у = —1 при х->—оо и у = 1 при x-^j"°°»
максимум у = д/3 при х = 1; точки перегиба (—0,5; 1) и (2; 2д/б/з).
2) Область определения: R; точки пересечения с осями координат (0; 2) и
(—8; 0); асимптоты: у — —1 при х->—оо и # = 1 при х->+оо; максимум
у = 2 при х = 0; точки перегиба функции Xj = — (1 ± д/зз)/2 « — 3,4 и х2=»
«= (д/33 — 1)/2 « 2,4, y(Xi) & 1,2, у(х2) « 1,9. 3) Область определения:
|х| > 2; симметрия относительно начала координат; асимптоты у = *8,
х = ±2; функция строго убывающая на интервалах (—оо; —2) и (2; 4-оо).
4) Область определения: |х| 1/2; симметрия относительно начала коорди-
нат; точки пересечения с осями (±1/2; 0); асимптоты у = 2 при х->+оо и
у = —2 при х —>—со; функция возрастающая. 5) Область определения:
х гС 0 и х 4; точки пересечения с осями координат (0; 0), (4; 0); асимп-
тоты у — —1 при х—>-±оо и г/= 1 при х->—оо; функция убывающая.
6) Область определения: |х| 1; симметрия относительно оси ординат; точки
пересечения с осями координат (±1; 0); асимптоты у = х/2 при х->±оо и
у »—х/2 при х->—оо; убывает на интервале £—оо; —1) и возрастает на
575
(1; 4“°°)- 7) область определения [х| "> 1; асимптоты: у == 3 при х->4-°°»
у == —3 при_х -> —оо, х ~ 1 при х -> 1 -|- 0, х = —1__ при х -> 1 — 0; мини-
мум у = Уб при х = 3/2; точка перегиба (2; 4/УЗ). 8) Область определе-
ния: |х| > 2; асимптоты у = 1 при х->оо, х =—2 и х = 2 (z/->-f-oo);
точка пересечения с осью абсцисс (—6; 0); минимум «/= 0 при х = —6;
функция выпукла вверх при х < —6 и выпукла вниз при —6 <. х <Z —2 и
2 С х. 9) Область определения: х Z> 0; асимптоты у = 0 при x->-f-oo, х — 0
(//—^+°о); минимум у = 0 при х = 1, максимум у = 8/(3 Уз) « 1,5 при
х = 3; точка перегиба функции х = 5, «/(5) « 1,4, на (0; 1) и (5; +°°) функ-
ция выпукла вниз. 10) Область определения: —- 2/Уз х < 0, х 2/УЗ;
асимптоты _у = 0 при х->-{-оо, х —0 (//->+«>); минимум у = 0 при
х = ± 2/Уз 1,2, максимум у — 1 при х = 2; точки перегиба Х\ —
= — 2дА 1 — 2 УТэ/з « — 1,0, х2 « 2 д/п + 2 УГэ/з « 3,0, у(х^ « 1,0,
у(х2) ж 0,9, функция выпукла вверх на (—2/УЗ; Xi) и (2/УЗ; х2).
11) Область определения: х < 0, х^н^2; точка пересечения с осью абсцисс
л = У2; асимптоты: у = Уз х/3 при х -> + оо, у = — Уз"х/3 при х->—оо,
х == 0 при х-+—0; минимум у — 1 при х = —1. 12) Область опреде-
ления: х С 0, х > 2; асимптоты у — —(х + 1)/3 при х->—оо, у = (х+ 1)/3
при х->4-оо, х = 2(у->+00)*, минимумы «/ = 0 при х=0 и г/==Уз при х = 3;
функция выпукла вверх при х<0 и х > 2. 13) Область определения: R;
точка (0; 0) —центр симметрии; асимптоты у — —(х + 8)/2 при х—> оо,
у — —(х— 8)/2 при х->+°°; точки пересечения с осями координат (0; 0),
(0; ± 3 УГ); минимум у = —- 3 Уз/2 при х = — Уз, максимум у == 3 Уз /2
при х = УЗ; точка перегиба (0; 0), на (0; +©о) функция выпукла вверх.
21.10. 1) Область определения R; точки пересечения с осями координат
(1; 0), (0; 1); асимптота у = —х; функция убывающая; точки перегиба
(1; 0), (0; 1). 2) Область определения R; точки пересечения с осями коорди-
нат (0; 0), (3; 0); асимптота у == 1—х; минимум у = 0 при х = 0, макси-
мум у = У4 ж 1,6 при х = 2; точка перегиба (3; 0). 3) Область определе-
ния R; точки пересечения с осями координат (0; 0), (1; 0); асимптота
у » х — 2/3; минимум у = 0 при х = 1, максимум // —У4/3«0,5 при
х = 1/3; точка перегиба (0; 0). 4) Область определения R; симметрия отно-
сительно начала координат; точки пересечения с осями (0; 0), (±2; 0); асимп-
тота у =^_х; минимум «/ = —-2У2/УЗ «—1,5 при х = 2/Уз, максимум
г/ = 2У2/Уз «1,5 при х = —2/УЗ; точки перегиба (0; 0), (±2; 0).
5) Область определения R; точки пересечения с осями_координат (0; 0).
(5; 0); минимум у = 0 при х = 5, максимум # = 3^4 «4,8 при х == 3;
точка перегиба (6; 6). 6) Область определения R; точки пересечения с
осями координат (—1; 0) (1; 0), (0; 1); минимум у~0 при х = 1, мак-
2436 3/ 2 7
симум у «= - Л / -ггт- « 2,2 при х = —; точки перегиба функции х = —1,
1 1 у 1X1 11
х == (7 + 3 Уз )/11 « 1,1, х == (7 — 3 Уз )/11 « 0,2. 7) Область определения: R;
точки пересечения с осями_координат (0; 0) и (—1; 0); минимум у = 0 при
х = 0, максимум у = 3 V20/25 « 0,3 при х = —2/5; точка перегиба функции
х = 1/5, «/(1/5) = 0,4, функция выпукла вверх на (—оо; 0) и (0; 1/5). 8) Об-
ласть определения: R; точки пересечения с осями координат (0; 0) и (1; 0)?
минимум у = 0 при х — 1, максимум у — 93 ^44/114«0,2 при х==9/11;
точки перегиба функции xi = 0, х2 = (27 — 3 У37 )/44 « 0,2, х3 = (27 4-
+ 3 У37 )/44 « 1,03, функция выпукла вверх на (—оо; 0), (х2; 1), (1; xs) .
9) Область определения R; ось ординат — ось симметрии; точки пересечения
с осями координат^ (±2; 0), (0; 2^2); минимумы «/= 0 при х = ±2,
максимум у —2^2 «2,5 при х = 0; точки перегиба функции х1 = —х2==
= — 2Уз^^(Х1) == у(х2) = 4, функция выпукла вверх на (х2; —2), (—2; 2)
576
и (2; х2). 10) Область определения: R; прямая х =—4 — ось симметрии;
точки пересечения с осями координат (—6; 0), (—2; 0), (0; 2^18); мини-
мумы у — 0 при х = —6, х = —2, максимум у = 2^2 2,5 при х — —4;
точки перегиба функции хь 2 = —4=р2Уз, y(xi) =у(х2) = 4, функция выпукла
вверх на (хг, —6), (—6; —2), (—2; х2). 11) Область определения R; асимптота
у ——2 при х->оо; точки пересечения с осями координат (0; 0), (3/2; 0);
минимум у = —3 при х = 3, максимум у = 1 при х == 1/3; точка перегиба
(0; 0), функция выпукла вверх на (0; 3), (3; +<»). 12) Область определения:
R; центр симметрии—(0; 0); асимптота у = 0 при_х->оо; точка пересече-
ния с осями координат (0; 0); минимум у = — ^4 ж — 1,6 при х = —1,
максимум у = 'х/ 4 ж 1,6 при х — 1; точка перегиба (0; 0), функция выпукла
вниз на (0; 1), (1; Ч-оо).
21.11. 1) Область определения: симметрия относительно начала
координат; точка пересеченное осями (0; 0); асимптоты х = ±1; минимум
у = V3/V2 « 1,4 при х = V3, максимум r/== — V3/V2 « — 1,4 при х =
= — V3; точки перегиба (0; 0), (3; 3/2), (—3; —3/2). 2) Область определения:
х —1; точка пересечения с осями координат (0; 0); асимптота х — —1;
минимум г/== 3 V2/2 1,9 при х = —3/2; точка перегиба (—3; 3^4/2).
3) Область определения: х ф 2; точка__пересечения с осями координат (0; 0);
асимптота х = 2; минимум f/—3/V2 «2,4 при х = 6; точка перегиба
(12; 12/V100 ). 4) Область определения: х =/=—1; точка пересечения с осями
координат^(0; 0); асимптота х = —1; минимум у = 0 при х = 0, максимум
у = — V4 « — 1,6 при х = —2; точки перегиба функциих = V3 — 2 — 0,3,
х = — V3 —2 « — 3,7. 5) Область определения: х =/= 1, точки пересече-
ния с осями координат (Q , (О; —V^), асимптота х = 1, минимум
у — V12 «2,3 при х = 4/3, максимум у = 0 при х = 2/3, точки перегиба
функции х = (4 ± V3)/3. 6) Область определения: х У=—2; точки пересече-
ния с осями координат (—1; 0), (О; l/V^); асимптоты у — 1, х = —2; ми-
нимум у = 0 при х = —1; точка перегиба (—7/6; 1/V25). 7) Область опре-
деления: х #=—2; асимптоты у = 0 при х->оо, х ==—2; точка пересечения
с осями координат (0; 0); минимум у = 0 р?ри х — 0, максимум y===V2/3
при х — 4; точки перегиба Xi = 4 — 3 V2 «— 0,2, х2 = 4 + 3 л] 2 « 8,2,
i/(xi) « 0,2, г/(х2) « 0,4, функция выпукла вверх на (—оо; —2), (хг, 0),
(0; х2). 8) Область определения: х 0; асимптоты у = 0 при х->оо, х — 0;
точка пересечения с осью абсцисс (—1; 0); минимум у =* 0 при х = —1,
максимум у — V16 /9 « 0,3 при х = — 4,5; точки перегиба xt —
- = (21 + 3V7)/14 л? — 2,1, х2 = — (21 — 3V7 )/14 « — 0,9, y(xi) & 0,2,
t/(x2) «0,1. функция выпукла вверх на (хг, —1), (—1; х2).
21.12. 1) Область определения: |х| 1; симметрия относительно оси
ординат; точки пересечения с осями (—1; 0),__(0; 0), (1; 0); минимум у — 0
при х = 0, максимумы у = 1/2 при х =» dz V2/2- 2) Область определения R;
симметрия относительно начала координат; точки пересечения с_ осями (0; 0),
(±1; 0); максимумы у =» 0 при х == —1 и у = 1/2 при х = V2 /2» минимумы’
# — 0 при х = 1 и у = —1/2 при х== —V2/2; точки перегиба (0; 0),
(V3/2 ; -уЗ/2 ), (— V3/2 ; — V3/2 ). 3) Область определения: х =/= 2; асимп-
тоты у «я 0 при х~>оо, х = 2; точки пересечения с осями координат (0; —2),
(1; 0); максимум г/ == 0 при х = 1, минимум у ==* —2 при х = 0; точки пере-
гиба функции Xi = —- х2 = — 2 V3/3, у (xi) = у (х?) = — д/2^3 « — 1,9,
функция выпукла вниз на (хг, 1), (1; х2), (2; 4-оо). 4) Область определе-
ния: R; точки пересечения с осями координат (0; 0), (3; 0); минимумы
у — 0 при х = 0 и х = 3, максимум у = 2 при х — 2; точка перегиба (4; 4),
на (—оо; 0) и (4; 4-оо) функция выпукла вниз, на (0; 3) и (3; 4)—вверх.
5) Область определения: R; точки пересечения с осями координат (—1; б),
577
(0; 1), (1; 0); максимум у = 3 & 1,3 при х = 0,5, минимум у ®= 0 пр»
х == 1; точки перегиба функции Xi = —1, х2 = (1— д/з")/2 & —0,4, х3 —
«= (1+д/з)/2 « 1,4, y(xi) =0, у(х2) ж 1,2, ,#(х3) & 2,2, функция выпукл»
вверх на (—оо; —»1), (х2; 1), (1; х3). 6) Область_определения: R; асимптота
у — 0; точка пересечения с осью ординат (0; д/з); максимумы у = Д^З при
х == 0 и у « д/2/4 при х = 3, минимум у = 1/3 при х = 2; точка перегиба
4
функции х0 = (9 + 4 д/з )/3 5,3, у (х0) = V3/4 0,3, функция выпукла
вниз на (—оо; 0), (0; 2), (х0; +°°). 7) Область определения R; точки пере-
24 /~6~
сечения с осями координат (±1; 0), (0; —1); минимум у ——А/-р-
ZO у о
« —1,1 при х — 1/5; точки перегиба (—1; 0), )• Об-
ласть определения: |х| 1; точки_пересечения с осями (±1; 0); асимптоты-
у = 0, х = 2; минимум #_= — д/з/б при х = —4; точки перегиба функции
л==2/д/з, х =— 4 —2д/з. 9) Область определения: R; точки пересечения
с осями координат (0; 0), (—1/3; 0); минимум у = 0 при х = 0, максимум
I/==^2/8 при х == —1/4; точки перегиба (—1/3; 0), (—1/2; 1 — 1/(4-^2 )).
10) Область определения: R; точки пересечения с осями (0; 0), (2; 0); асимп-
тоты у = х—2/3 при х->+оо, у =— х + 2/3 при х-э—оо; минимумы у = 0
при х —0 и х = 2, максимум у = 2^4/з при х = 4/3; функция выпукла
вверх.
21.13. 1) Асимптота у — —х при х->—оо; минимум у ===== 1 при х — 0;
функция выпукла вниз. 2) Точка пересечения с осями координат (0; 0);.
асимптота у = 0 при х->+°°> максимум у — 1/(2е)« 0,2 при х = 0,5; точка
перегиба (1; е~2). 3) Область определения: R; асимптота у = 0 прих->+оо;
точка пересечения с осями координат (0; 0); минимум у = 0 при х = 0,
максимум у = 4г-2 « 0,54 при х = 2; точки перегиба функции хх ~ д/з — 1,
= д/з +1, y(xi) & 0,3, у(х2) ~ 0,47, на (х4; х2) функция выпукла вверх.
4) Область определения: R; асимптота у == 0 при х—>+°о; точка пересече-
ния с осями координат (0; 0); максимум у === 27е~3 » 1,3 при х = 3; точки
перегиба функции xi = 3 — д/З, х2 = 3 + д/з, z/(xi) w 0,2, z/(x2) ~ 0,9, на
(хг, х2) функция выпукла вверх. 5) Точки пересечения с осями координат
(-V2; 0), (V2; О), (0; -2); асимптота у = 0 при х->4-°°, минимум
у = —е2 « —7,4 при х = —1, максимум у = 2е~4 » 0,04 при х = 2; точки
перегиба функции х = 1 — д/10/2 — 0,6 и х = 1 + V10 /2 2,6.6) Область
определения: R; асимптота у = 0 при'хн—оо; точки пересечения с осями
координат (0; е), (1; 0); максимум у — е3/3 « 6,7 при х == 2/3; точка пере-
гиба (—1/3; 4/3), на (—оо; —1/3) функция выпукла вниз. 7) График сим-
метричен относительно оси ординат; асимптота у — 0; максимум у — е при
х == 0; точки перегиба функции х = ± 1/д/2. 8) График симметричен относи-
тельно прямой х = 2; асимптота у == 0; максимум #*= е4 при х = 2; точки
перегиба функции х — 2 ± 1/V2. 9) График симметричен относительно начала
координат; асимптота у = 0; минимум у~-----------t=r ~ —0,6 при х = —1,
д/е
максимум у = 1/д/Г при х==1; точки перегиба функции х = ± V3«
10) График симметричен относительно оси ординат; асимптота у — 0; макси-
мум г/ ===== 2 при х = 0; точки перегиба (—1; 3/е), (1; 3/е). 11) Область опре-
деления: х = 1; асимптоты: х = 1 и у = 0 при х->4-оо; максимум у— 1 при
х = 0; функция выпукла вверх при х> 1 и выпукла вниз при х < 1.
21.14. 1) Область определения: х Ф—1; асимптоты: у — \/е и х = —1
при х —>— 1+0, у(—1 —0) == 0; точка перегиба (—2; е~3). 2) Область опре-
деления:^ =/= 0; асимптота х = 0 при х->+0, у(—0) = 0; минимум у = е2/4
при х = 1/2; функция выпукла вниз при х<0 и при х > 0. 3) Область опре-
578
деления: х #= 0; точка пересечения с осью абсцисс (2; 0);- асимптоты?
у~х — 3 и х = 0 при х->—0, #(4-0) = 0, #'(4-0) = 0; максимум
у = — 4 V7 при х = —2 и минимум у = —1/е при х — 1; точка перегиба
(2/5; — 8е~*5^2/б). 4) Область определения: х =£ 0; точки пересечения с осью
абсцисс (—3; 0) и (1; 0); асимптоты #==х4-3 и х = 0 при х-^4-0;
#(—0) = 0, #'(—0) — 0; максимум у = 4/е при х = —1; точка перегиба
функции'х——5 ± V^2. 5) Область определения: х#=0; начало коорди^
нат — центр симметрии; асимптоты^ х = 0, # = х при х-*-оо; максимум
ж — 2,3 при х = —V2, минимум у = ^2е при х = V2 ;
на (0; 4-оо) функция выпукла вниз.
21.15. 1) Область определения: х >> 0; асимптота х = 0 при х->-4-0;
максимум # = 0 при х — 1; функция выпукла вверх. 2) Область оиределе-
ния: х > 0; точка пересечения с осью абсцисс (1; 0); асимптоты у = 0 при
х-> 4-°° и х = 0 при х-^-4-0; максимум у = 1/е при х = е-; точка перегиба
^е3/2; 1,5е~3/2) 3) Область определения: х > 0; точка пересечения с осью
абсцисс (1; 0); асимптоты # = 0 и х = 0, максимум у — 2/е при х = е2;
точка перегиба (е8/3; 8е“4/3/3). 4) Область определения: х > 0; #(4"0) = 0,
#'(4-0) = 0; точка пересечения с осью абсцисс (1; 0); минимум # = —в In 2
при х = Уе; точка перегиба (е~3/2;—3/(2е8)). 5) Область определения:
х > 0; #(4-0) — 0,, #'(4-0) = 4-°°, максимум # = 4/е2 при х = 1/е2; мини-
мум у = 0 при х = 1; точка перегиба (1/е; 1/е). 6) Область определения;
X > 0; асимптоты х = 0 и у = 0; минимум у = 0 при х = 1, максимум
у == 4/е2 0,6 при х = е2 « 7,4; точки перегиба функции х = e(3±V5 )/2.
7) Область определения: х > 0, х #= 1; асимптота х = 1; #(4-0) = 0,
#'(4-0) =0; минимум # —е при х = е; точка перегиба (е2; е2/2). 8) Об-
ласть определения: х =Л ±1; асимптоты х = —1, х = 1, # = 0; точки пересе-
чения с осями координат (» 0,9; 0), (^1,2; 0), (0; 6); максимум у = 2—In 3
при х = 2; точки перегиба (0,5; 4 — 1пЗ), (3; 1,5 — In 2). 9) Область опре-
-деления: х >> 0; асимптота х = 0 (#->4-°°); минимум #=1 при х = 1;
функция выпукла вниз.
21.16. 1) Функция периодическая с периодом 2л; точки переселения с
осями координат (0; 1), (л/2^ 0), (Зл/2; 0); максимум # = зУз/4 при
х = л/6, минимум у = — 3 Уз/4 при х = 5л/6; точки перегиба (л/2; 0),
(л 4-arcsin(l/4); — 3 V15/16), (Зл/2; 0), (2л — arcsin(1/4); зУ15/1б).
2) Функция периодическая с периодом 2л; график симметричен относительно
начала координат; максимум # = 3 д/Т/4 при х = л/3, минимум # =
= 3 Уз/4 при х =—л/3; точки перегиба (—л; 0), (—л 4- arccos(1/4);
— 3V15/16), (0; 0), (л — arccos(1/4); 3 V15/1б), (л; 0). 3) Функция перио-
дическая с периодом 2л; #(0) = #.(л/2) — #(л) = 0; максимумы # = 1/4 при
3
х = л/6 и х = 5л/6, минимумы у = 0 при х = л/2 и у = —2 при х~~ л,
.14- V33 : 1 4- V33
Точки перегиба функции х = arcsin-------g---, х = л — arcsin-----g----р
, . Узз"—1 п • Узз — i лч
х = л 4- arcsin ——5, х = 2л — arcsin--------5--. 4) Функция периоди-
о о
ческая с периодом 2л; график симметричен относительно оси ординат;
у ^л — arccos = 0, максимумы # = 3/4 при х = ±л/3, минимумы
#=1/2 при х = 0 и # = —3/2 при х = ±л; точки перегиба функции
1 4- Узз , ( Узз“ — 14 _
х = ± arccos ——~, х = ± ( л — arccos ——5----I. 5) Функция перио-
о \ о 7
дическая с периодом 2л; х = 0 — ось симметрии, (л/2; 0) — центр симмет-
рии; на [0; л] максимум у = 4 при х = 0, минимум у = —4 при х = л; на
[0; л] точки перегиба функции Xi ==_arcsin (1/Уз ), х2 = л/2, х3 =
— л — arcsin (l/Уз ), # (xi) == — # (хз) ===8 Уб/9 « 2,2, #(х2)=0.
579
21.17. 1) Периодическая с периодом л функция; график симметричен
относительно оси ординат; */(0) = //(л/3) — у(—л/3) = 0, минимумы у = 0
при х — 0 и у——1 при х= ±л/2, максимумы t/=9/16 при x=±arccos(l/4);
я 1 У129 +1 , 1 ( У129 - 1 \
точки перегиба х — ± — arccos ——77----,х = ± -77( л — arccos ———-----L
г 2 16 2 \ 16 7
2) Периодическая с периодом 2л функция; график симметричен относительно
оси ординат: #(л/4) = у (л/2) = у_(Зл/4) = 0; на отрезке [0; л] максимумы
у—\ при_х = 0, у = 2/(зУб) при х = л-arcsin Уб/6, минимумы
2/(3 Уб ) при х = arcsin Уб/6, у =—1 при х == л; точки перегиба
(arccos 'Уу|-: ^2’ (я — arccos У13/18; —V13/18).
3) Периодическая с периодом 2л функция, график симметричен относительно
начала координат; */ (0) = у (л) — 0; _на отрезке [0; л] максимумы
у = (3 + 4 У2 )/б при х = л/4 и */ = У2—1/2 при х = Зл/4, минимум
у = Уз/4 при х — 2л/3; точки перегиба функции х = 0, х = л, х ~
. У 7 — 1 . У7 - 1
*= arcsin--------, х = л — arcsin —— ---.
21.18. 1) Область определения х =И= л/2 + л/г, zzeZ, периодическая с пе-
л
риодом 2л функция; асимптоты У=-^-\~л,п, п & Z; на интервале
(—л/2; Зл/2) максимум у — 1 при х — 0, минимум у = —1 при х — л;
функция убывает на интервалах (0; л/2) и (л/2; л), возрастает на интервалах
(—л/2; 0) и (л; Зл/2). 2) Периодическая с пергюдом л функция; асимптоты
х — л/г, /ieZ; точки перегиба (л/2 + л/г; 1/У2 ), п е Z: функция возра-
стает на интервале (0; л). 3) График симметричен относительно начала
координат; асимптоты х = л/2 +»л/г, п е Z ; максимум у = л/2 4- 2/гл — I
при х = л/4 + л/г, п е Z ; минимум у — Зл/2 + 2л/г + 1 при х — Зл/4 + л/г,
neZ; точки перегиба (л/г; 2л/г), не Z.
21.19. 1) График симметричен относительно начала координат; асимпто-
ты: у = (х—л)/2 при и у = (х + л)/2 при х->—оо; максимум
у — 1 при х~ (2 — л)/4, минимум у = —1 при х — (л — 2)/4; точка пере-
гиба (0; 0). 2) Область определения: R; асимптоты у = 1/л при х->—оо,
у == х при х->4-оо; точка пересечения с осью ординат (0; 2/л); функция
выпукла вниз. 3) Область определения: R; (0; 0) — центр симметрии; асимп-
тоты у — (лх + 2)/2 при х->----оо, у — (пх — 2)/2 при х->4-оо; точка пере-
гиба (0; 0), на (—оо; 0) функция выпукла вверх. 4) Область определения: R;
(0; л)—центр симметрии; асимптоты у = (х + 4л)/2 при х—>-—оо, у = х/2
при х-> Ч-оо; */(0) =л( у = 0 при х 12,2; максимум у = (10л — зУз)/б«4,4
при X = — Уз , минимум у = (2л + 3 Уз )/б AJ 1 ,9 при х == Уз ; точ-
ка перегиба (0; л), на (—оо; 0) функция выпукла вверх. 5) Область опре-
деления: |х| 1; (0; —л/2)— центр симметрии; асимптота у = (Зх — л)/2
при х->оо; максимум у = — (б Уз 4- 5л)/б ж — 4,4 при х = —2Уз/з,
минимум у — (бУз — л)/б«1,2 при х = 2 Уз/3; на (—оо; —1) функция вы-
пукла вверх. 6) Область определения: R; график симметричен относительно
начала координат; асимптота у — 0 максимум у — л/2 при х = 1, минимум
у =—л/2 при х ==—1; у'(1—0) = 1, */'(1-4-0)=—1; точка перегиба
:(0; 0). 7) Область определения: R; график симметричен относительно оси
ординат; асимптота у — л; функция возрастает при х > 0, //'(4-0) = 2.
8) Область определения: R; точки пересечения с осями координат (0; —л/2),
(хо, 0), где Хо_« 0,7; асимптота у = (х — л)/2; максимумы у = 1 при х = 1
и у = — (3 Уз 4~ 5л)/б при х = —_Уз, минимумы у — —1/2 — л при х — —I
и у = (3 Уз - л)/б. при х = УЗ; функция выпукла вверх на интервалах
(—оо; —1) и (0; 1), выпукла вниз на интервалах (—1; 0) и (1; 4-°°); точ-
ка перегиба (0; —л/2) ;//'(—1—0) =—1/2, у'(—1 + 0) = 3/2, */'(1—0) =•
= 3/2, /(1+0) =-1/2.
Б80
21.20. 1) Периодическая с периодом 2л функция, график симметричен
относительно оси ординат; максимум у = е при х = 0, минимум # == 1/е при
х «= л; точки перегиба функции х = arccos —- и х = 2л—arccos
2) Асимптоты: у = ея/2 при х->—оо, у = е~п/2 при х->4-оо; функция убы-
вает; (—1/2; earctg (1/2)) — точка перегиба. 3) Область определениях
2Лл < х < (2k 4- 1)л, k g Z, периодическая с периодом 2л; асимптоты
х = пл, Z; минимум у = 1 при х = л/2 4- 2лп, п е Z. 4) Область опре-
деления: х > 0; минимум у = (1/е)1^ « 0,69 при х = 1 /е; у (4-0) = 1; функ-
ция выпукла вниз. 5) Область определения: х >—1; х =/= 0; #(4-0) ==
= у(—0) = е; асимптоты х =—1, у «= 1; функция выпукла вниз. 6) Об-
ласть определения: х < — 1, х > 0, асимптоты у = е при х->оо, х =*
= —1(*/->4-°°); на (—оо; —1) функция выпукла вниз, на (0; 4-°°)—вверх.
21.21. 1) Область определения: х > 0; асимптота у = 1; максимум
у = е11е « 1,44 при х *= е\ #(4-0) = 0. 2) Асимптота у = е(х—1/2);
#(4-0) = 0. 3) Периодическая функция с периодом 2л; максимумы у =_1_
при х = 0 и х = л/2, у = — 1/V2 при х = 5л/4, минимумы у=\1^2
при х = л/4, у = —1 при х == л и х = Зл/2. 4) Функция периодическая с
периодом 2л; х = л/2--ось симметрии, (0; 0)—центр симметрии; на [0; л]
минимумы # = — 3 д/з при х = л/3 и х = 2л/3, максимум у = — 4 при
х = л/2. 5) Периодическая с периодом 2л функция; максимумы у — 1 при
х — л/2, у = 1/3 при х = Зл/2, минимумы у — 0 при х = 0, х = л. 6) Пе-
риодическая с периодом 2л функция, график симметричен относительно оси
ординат; максимумы у — 11/6 при х = 0, # = — 5/12 при х=2л/3, минимумы
у == —1/2 при х = л/2 и у = — 5/6 при х — л. 7) Область определения:
х > 0; асимптота х = 0; максимум # = —2 1п 2 — 5 arctg(1/2) при х == 1/2,
минимум # = 21п2 — 5 arctg 2 при х = 2. 8) Область определения: х ±1,
график симметричен относительно оси ординат; асимптоты х = —1 при
х —>—1 4- 0, х = 1 при * 1 — 0, у — 0; минимум у = е при х = 0, макси-
мум # = 1/(4 0,15 при х = ± 9) Область определения: х =£ 0,
х ф ±2; асимптоты х = 2, х == —2, у _== 1, х = 0 при х-> 4-0; #(—0) = 0;
минимум #«0,94 при х = —4— 2дЛ> &— 8,48, максимум #«—0,5 при
х ~ — 4 4- 2 0,48, функция возрастает на интервалах (— 4 — 2 ; _2),
(—2; 0), (0; — 4 4-2-Vs), убывает на интервалах (— оо, — 4— 2^/5),
(-4 4-2 V5 ; 2), (2; + оо).
21.22. 1) Область определения: R; максимум (—3; 3), минимум (5; —1);
точка перегиба (1; 1). 2) Область определения: R; асимптоты у = х,
# = х 4-6л; максимум (—Зл—1; Зл/2—1), минимум (—Зл4-1; 1—Зл/2);
точка перегиба (—Зл; 0). 3) Область определения: R; точки пересечения с
осями координат (0; 0), (8/5; 0); асимптота # = х — 2; максимум (0; 0), ми-
нимум (1/2; —1/2); выпуклость вниз. 4) Область определения: х < 0; асимп-
тоты у = х 4- In 2, х = 0; максимум (—In 2/2; 0); выпуклость вверх. 5) Об-
ласть определения: R; функция периодическая с периодом 2л; прямые х—лп,
п е Z, — оси симметрии; на [0; 2л) минимум # = 0 при х = 0, максимум
у = 2 при х = л; на (0; 2л) выпуклость вверх. 6) Область определения: R;
ось ординат — ось симметрии; асимптота у — 0 при х-^оо; максимум # = 1
при х == 0; функция выпукла вниз на (—оо; 0) и (0; 4-°°)-
t — со -1 -1/3 0 1 4- оо
X — оо 0 -4/27 0 4 + оо
У + «= — 4 — 80/27 — 2 0 — со
(0; -4) — точка возврата.
581
t — оо 1 5/3 2 7/3 3 4-00
X — оо 0 -4/27 0 16/27 4 4- оо
У — оо 0 — 16/27 — 1 — 32/27 0 4~ ОО
(0; 0) —точка возврата.
3) Асимптоты: у = х 4- 3, у = 0, х — 0.
t — оо -1-0 -1 + 0 - 1/2 — 0 + 0 1 + оо
X 4-0 + оо — оо — 4 — оо + ОО 1/2 + 0
У — оо -0 — 0 - 1/2 — оо + оо 4 + оо
4) Асимптоты: у = х— 1, у — 0, х = 0; точка самопересечения (—1; 1).
/ — оо — 0 + 0 1 —0 1 + 0 2 4- ОО
X — оо . —0 -0 — оо + о° 4 + оо
У — оо 4- оо — оо -0 + 0 3/2 4~ оо
5) Асимптоты: # = 1, у =1/2, х = —1/2.
t — оо — 2 — 0 — 24-0 -1 -0 + 0 1 4“ ОО
X — оо — 1/2 —0 -1/2+0 0 — оо 4- оо 4 4“ оо
У 1+0 + оо — оо 0 1/2—0 1/2 + 0 2/3 1—0
6) Асимптоты: у == 2, у — 2/3, х — 1, х = 4/3.
— оо — 2 — V5 -2-0 -24-0 -1—0 -1+0 0 -2+V5 1-0 1 + 0 4-00
X 1+0 « 1,1 Оо| Ф» 1 О 4 у+0 + оо — оо 0 «0,1 — оо 4~ оо 14-0
У —оо « -8,5 — оо + °о 24-0 2 — 0 1/2 «0,5 1-» т+» + <Х>
7) Асимптота у = х при х->оо; точки перегиба (приближенно)
(—2,4; 3,0), (2,2; 3,0), (3,2; 3,0).
t — оо — 1 то 4=0 1 4= 0 ^2 4=0 4- оо
X — оо — 2 — 0 "4“ оо 24-0 2^2 + ^4 — =F 0 « 2,1 =F0 4- ОО
У — оо то + 00 2±0 + 0 « 1,9 + 0 2 + °°
582
б 2(77/3 ^27/2)СИМПТ°Та Х ~ точка возврата (—-4/3, 27/2), точка пере-
t — оо — 3 — 0 + 0 + ОО
X 4~ оо 4 ~ 3 о 1 ю |оо о + ю |т + °°
У + ОО 27 2 4~ оо — оо + ОО
2) Асимптота у= (4х—1)/8, точка возврата (0; 0), точка перегиба
(—9/8; —27/16).
t ОО 0 1 2 ~° 1 Y + 0 2 4 1 + оо
X 4“ ОО 0 + ОО — оо 9 “ 8 - 1 — оо
У ОО 0 4~ ОО — оо 27 “ 32 — 1 — оо
3) Асимптота у = —х + 1/3, точка возврата (0; 0),
t .— оо -1-0 -1 + 0 0 ^2 4- оо
X — 0 — оо 4“ ОО 0 ^4~ 3 + 0
У 1+0 4“'00 '— оо 0 2 3 1 -0
4) Асимптоты: у — 1, х = 0, точка возврата (—2; 0), точка перегиба
(117/64; 49/9), при t = (— 3 ± д/21 )/4 точка самопересечения с координа-
тами х —1,1, у 2,4.
t — оо — 1 — 0 + 0 1 4- ОО
X — оо 2 + 0 ~ —0 — 2 4- оо
У 1 + 0 4 4- оо 4“ оо 0 1 —0
5) Асимптоты: у == (2х + 1)/4, у = х— 1, х — —1/2.
t — оо -1-0 -1+0 1 — 0 + 0 1 2 1 1 —0 1+0 4- оо
д/3
X -0 -|+0 1 — 2 —° « — 1,1 — оо 4“ оо 4 «4,1 4- ОО ОО — 0
У , + 0 4“ ОО — оо « —2,6 — оо 4“ ОО 8 3 «2,6 4“ ОО ОО — 0
6) Асимптота у = х 4~ 1, точка перегиба (—27/2; —9/2)
1 — оо -0 + 0 1/2 2/3 1-0 1+0 4- оо
X -0 — оо — оо -8 — 27/4 — оо оо + 0
У + 0 + оо — оо — 4 — 9/2 — оо + оо + 0
7) Кривая симметрична относительно оси ординат, асимптоты у =
== ±х — 5/4, у = 0.
t + 0 1/V5 1—0 1 + 0 + оо
X + оо 4 5V5/4 + оо — оо — 0
У + 0 1/4 4~ оо — оо — 1—0
8) Оси координат — оси симметрии; (0; 0)—точка перегиба.
X _ V3+i.T0 V2 - 1 то V2 — 0
-4±» - V2 + 0 д/з - — + 0 -0
У .L-о 2 ±0 -1+» — 0
21.25.
1) Асимптота у = 2х при
jc4-°°’» (1; О—точка воз-
врата.
t — оо то 4“ оо
X 4“ оо 1+0 4~* оо
У + оо 1+0 4- оо
2) Асимптоты #<= 0, х — 0; точ-
ки перегиба
(V2-е^\ л/2 е~
(-VfeV2-. _^e-V2)
t — оо -1 0 1 4- ОО
X — 0 -1/е 0 е + оо
У — оо — е 0 1/е + 0
3) (—4; 4) — точка перегиба.
t — ОО — 1 0 1 4” оо
X -0 — 10/е — 4 — 2е 4~ ОО
У -0 — 11/^ — 4 — в 4- оо
4) Асимптота у = 1, точка воз-
врата (е; 0), точка перегиба
t — оо — 1 -0 + 0 1 4- ОО
X -0 — 1/е — оо 4~ оо е 4“’ оо
У + 0 4/е 1 + 0 1—0 0 + °°
584
5) Асимптоты: у = е2х — 2е, у =
== 0, х — 0.
6) Асимптота у — х— 1 при
X —» со.
t — оо — 2 — 1—0 -1+0 0 ±оо
X — 0 — 1/е2 — оо +°о 1 + <50
У — оо — е2 — оо + 00 1 +0
t — оо 0 1/2 1—0 14-0 ±оо
X — оо 0 1 — In 2 — оо — оо + <5О
У — оо 0 у — In 2 — оо — оо 4-00
7) Асимптоты: у = 0, х = 0; точки перегиба (— V2 е ; — ^2 ё^2 )>
(V2 eV2. V2e-V9.
t + 0 1/е 1 е + °°
X -0 - 1/е 0 е + оо
У — оо — е 0 Ме + 0
7) та же кривая, что и в задаче 2)).
8) Асимптоты у = х/4, х = 2, угловая точка (0; 0).
t — оо -1-0 - 1+0 0 1 -0 1 + 0 2 + оо
X + оо 2 + 0 2-0 0 2-0 24-0 8 4~ оо
У ± оо — оо — оо 0 + оо + оо 2 4-31пЗ + оо
9) Кривая симметрична относительно оси абсцисс; асимптоты: у = х—1,
у = 1 —х\ точки самопересечения (0; 0), (2; 0).
t + 0 Л 4 л 2 Зл 4 л — 0 л 4- 0 5л Т Зл 2 7л 4 2л -0
X + оо 2 1 0 — оо ± оо 2 1 0 — со
У ± оо 0 - 1 0 + оо — оо 0 1 0 — оо
10) Кривая симметрична относительно осей координат; асимптоты
у = ±3х, у = ±1/2; точки самопересечения (± д/з/З; О), (0; ±
t + 0 л/6 л/4 л/2 — 0
X оо Уз/з 0 — оо
У 1-0 0 -V2/2 — оо
685
11) Ось абсцисс — ось симметрии; (1; 0) — точка возврата.
2_ — л-J-O — 2л/3 0 — л/3 Т 0 — 0
х -3±0 - 1/2 Т 0 3/2-0 1 + 0
У -0 - 3 V3/2 + 0 — V3/2 Т 0 — 0
12) Ось абсцисс — ось симметрии.
t — л 5л — 1Г Зя “V 2л ~"Г л ~ 2 л ~ 3 л ~ т л ~ 6 0
X 2 1 0 — 1 — 2 — 1 0 1 2
У -2 0 V2 2 0 — 2 — V2 0 2
13) Оси. __координат— оси симметрии; точки самопересечения
( ±1/2; ± 1/V2) (знаки произвольны).
t + 0 л g-TO л Т=Е0 Л -з то л 2-ТО
X + 0 д/з — то 1-0 Уз —2~±° ±0
У + 0 1-0 —L.±o V2 ± о - 1+0
14) Эта кривая — эвольвента единичной окружности; касательные парал-
лельны оси абсцисс в точках ((—1)п; лп(—1)п), касательные параллельны оси
ординат в точках ((—1)пл(1 ±2л)/2; (—1)°), n&Z.
15) Касательные параллельны оси абсцисс в точках с координатами
/ / ( 1) тг (4 fi — 1
хп = Уп~-------е 1 , касательное параллельны оси ординат в точ-
V2
п " ( — 1)Л тг(4п4-В/4
ках с координатами хп — уп = —1
21.26. 1) у =—х — ось симметрии; асимптота у == х; точки пересечения
с осями координат (0; —1), (1; 0), они же и точки перегиба. 2) Оси коорди-
нат и прямые у = ±х— оси симметрии; (±1; 0), (0; ±1)—точки пересече-
ния с осями координат; максимум х = 1 и минимум х = —1 при у = 0;
максимум у = 1 и минимум у =—1 при х = 0. 3) Ось асбцисс — ось сим-
метрии; асимптота х = 1; точки пересечения с осями координат (0; 0) и
(—1; 0); (0; 0)—точка самопересечения; минимум х =—1 при у = 0; ма-
ксимум у « 0,3 при х = (1 — д/б)/2 « 0,6. 4) Ось асбцисс—_ось симметрии;
асимптоты у = ±х; точка пересечения с осью абсцисс (^2; 0); минимум
х = ^2 при # = 0; минимум у = 1 при х =—1, максимум у ——1 при
х — 1. 5) Ось абсцисс —ось симметрии; (0; 0), (2; 0)—точки пересечения
с осями координат; (0; 0) —точка возврата; максимум х = 2 при у = 0, ми-
нимум х == 0 при у = 0; максимум у == 27/16 и минимум у = —27/16 при
х == 3/2; точки перегиба х » (3 — V^)/2 « 0,23 у « ±0,35. 6) Оси коорди-
нат— оси симметрии; (±1$ 0), (0; 0) — точки пересечения с осями координат;
(0; 0) — точка самопересечения; максимум х = 1 и минимум х = —1 при
у == 0; максимумы у « 2/V5"h минимумы у = — 2/д/з” при х == ± V2/3 ; точ.
ки перегиба (приближенно) £±0я52| ±0,70). 7) Ось абсцисс —ось симметрии;
586
асимптота у = 0 при х->Ч-оо; точка пересечения с осью абсцисс (1; 0);
максимум х = 1 при у — 0; максимум у — 1 и минимум у = —1 при х = 2;
точки перегиба х — (б + 2 V3 )/3 «3,15, г/== ± д/\/3~/2 « ± 0,93. 8) Ось
абсцисс—ось симметрии; асимптота х == 2; (0; 0) —точка возврата; минимум
х = 0 при у = 0. 9) Оси координат — оси симметрии; асимптоты у = ±х;
(±1; 0)—точки пересечения с осью абсцисс; минимум х=1 и максимум
х = —1 при у — 0. 10) Оси координат — оси симметрии; асимптоты у = ±х,
х = ±1; (0; 0), (±2; 0)—точки пересечения с осями координат; (0; 0)—
точка самопересечения; минимум к — 2 и максимум х = —2 при у — 0.
11) Ось абсцисс — ось симметрии; асимптоты у = ± (х + 2)/3 й х — 1; мак-
симум _х — —3 при у — 0; минимум у ж 2,54 и максимум у ж —2,54 при
х = д/3.
21.27. 1) Гипербола с осями х = 0 и у — 1 ис асимптотами у — 1 + х.
2) Эллипс с осями на прямых у = —2х и х = 2у. 3) Ось ординат — ось сим-
метрии; асимптоты х — 0, у — 0; (0; 1) —точка пересечения с осью ординат;
максимум у = 1 при х = 0; точки перегиба х = zh <\/V3/8 « ±0,47, у ®
— (б — 2 д/3 )/3 « 0,85. 4) Прямая у =_х — ось симметрии; асимптоты
х ~ 0, у — 0, у = —х; максимум х = — н^4 при у = — д/4 /2; максимум у ==
s= — дМ при х —— V^/2. 5) (0; 0)_—центр симметрии; асимптоты у = 0,
у = х, х = 0; минимумы у = 1 ± д/2 при х==1, максимумы у — —1 ± V2
при х = —1. 6) Асимптота у — 2 — х; (0; 0), (6; 0) —точки пересечения с
осями координат; (0; 0)—точка возврата; максимум у = 2д^4 при х — 4;
(6; 0) — точка перегиба.
21.28. 1) х —47/(1—/4), у = 4/2/(1 — /4) *); ось ординат — ось симмет-
рии; асимптоты у = ±х— 1; (0; 0) —точка самопересечения и точка возвра-
та; точки перегиба (± 6/V3 ; 2д/з). 2) х = (/—I)//3, у~ (/—I)2//3; пря-
мая у = х — ось симметрии; (0; 0)—точка самопересечения; максимум
х = 4/27 при у = 2/27; максимум у = 4/27 при х — 2/27.
3) х = t (j ± V^/2 — 1 ), У == t (1 Ve/2 — 1 ); прямые у = ±х — оси сим-
метрии; точки пересечения с осями координат: (0; 0), (0; ±1), (±1; 0);
(О’; 0) — изолированная^ точка;_ ближайшие к началу координат точки
(1/V2; 1/V2"), (~-l/V2; —1/V2); точки перегиба х == \/у = ± (V2 — 1),
х = 1/£ = ± (д/2 + 1). 4) х =/3/(1 — 2/2), у = t*l(1 — 2/2); ось ординат —
ось симметрии; асимптота у ~ — (4 V2 х + 1)/8; максимум х = —3 V3/(4V2)
и минимум х = 3 V3 (/4 V2) при у — —9/8; максимумы £ = —1 при х = ±1,
минимум у ~ при х = 0; точки перегиба (=Е 3 V3/5; — 9/5). 5) х =
== ± д/(/ — 2)/( 1 — /3), у = ± / V(* 2)/( 1 — /3); (0; 0) — центр симметрии;
асимптота у = х; три точки перегиба, (0; 0) одна из них. 6) х = (/2 + 1//)/2,
г/== (/2—1//)/2; прямая # = х—ось симметрии; асимптоты у = ±х; точки
пересечения с осями координат (0; 1), (1; 0); минимум х —З/д/32 при
у =—1/V32, минимум z/ = 3/V32 при х = —1/V32. 7) Астроида; х —
= cos3 /, у = sin3 /; оси координат и прямые у — ±х — оси симметрии;
(±1; 0), (0; ±1)—точки возврата. 8) х = ±ch3/2 /, у = sh3/2 /; оси абс-
цисс— оси симметрии; асимптоты у — ±х; максимум х — —1 и минимум
х — 1 при у — 0. ____
21.29. 1) г — Vtg ф ; (0; 0) — центр симметрии; ^асимптота х — 0; макси-
мум х = 1/V2 при z/==l/V2, минимум х = —1/V2 при у == —Xl'yJ'l: точки
4 _________________________________________________
перегиба: Xi = У\ = 0, х2 == —х3 = V3 V3 — 12/2 « 0,6, у2 ~ — уз —
4_________________
= д/24 V3 + 36 « 1,5. 2) Лемниската; г = Vsin 2qp /2; прямые у = ±х — оси
4
симметрии; (0; 0)—точка самопересечения; максимум х = V27/4 при у =
*) Указан один из возможных вариантов параметризации.
587
= Уз/4, минимум х — — V27/4 приу = — V3/4; максимумы г=\/л/2 при
Ф = л/4 и ф = 5л/4. _________
3) Бисквит; г == 2/ V3 + cos 4ф ; оси координат и прямые у == ±х — оси
симметрии; (0; 0)—изолированная точка; (±1; 0), (0; ±1)—точки пересе-
чения с осями координат; максимумы х == V(V2 +1)/2 ^1,1 и мини му м ы
X = — V(V2 + 1)/2 при у ~ ±. 1/V2 ; максимумы # == V(V2 + 1 )/2 и ми-
нимумы у == — (^2 + 1 )/2 при х = ± 1/V2; точки перегиба (приближен-
но) (=Ь1,05; ±0,35), (±0,35; ±1,05) (знаки произвольны).
4) г =* V2 sin 2ф/(2—зт22ф); прямые у = ±х— оси симметрии; максимум
8 _________ 8______________ 8 ____________________ 8 _______________
x = V27/16 при ^ == V3/10 , минимум х —— V27/16 при у ==— д/з/16 ;
8 _____ 8 ____________ 8 ____________________
максимум у — V27/16 при х = V3/10, минимум # = —д/27/16 при х ==
®—\/3/16 ; максимум r=V2 при ф=л/4 и ф = 5л/4. 5) г = д^£2ф/2; (0; 0)—
центр симметрии; асимптоты у =* ±х; (0; 0) — точка самопересечения; точки
перегиба (приближенно): xt = —Хз » 1,11, У\ ~ —Уз ~ 0,68, х% — —Хгк ж
ж —0,68, #2 = —f/4 « 1,11. 6) г = V(3 c°s 2ф — 1 )/2 со$2ф; оси координат —
оси симметрии; асимптоты у — ±х; (0; 0) — точка самопересечения; макси-
мум х =а 1 и минимум х ==—1 при у = 0; _максимум у — л]2 и минимум
У ~ — д/2 при х_= 0, максимумы у = (V3 — О/2 и у = —(V3 + 0/2 и
минимумы у = (V3 + 0/2 и у « — (V3 — 0/2 при х = ±1/д/2. 7) Улит-
ка Паскаля: r=2coscp±l; ось абсцисс — ось симметрии; (0; 0)—точка
самопересечения; (3; 0), (1; 0), (0; ±1)—точки пересечения с осями коор-
динат; максимумы х = 3 и х=1 при у = 0, минимумы х =—1/8 при
^ == ±д/15 /8 ± 0,48; максимум у « 1,76 и минимум у « —1,76 при
х = (15± V33 )/16« 1,3, максимум у « 0,37 и минимум уж—0,37 при
х = (15 —• V33 )/16 ж 0,58. 8) Улитка Паскаля: г = 2 ± cos ф, г = 0; ось абс-
цисс— ось симметрии; (0; 0)—изолированная точка; максимум х = 3 и ми-
нимум х = —1 при у — 0; максимум у ж 2,2 и минимум у ж —2,2 при
х = д/з/2 ж 0,87.
21.30 . 1) Ось ординат — ось симметрии; (0; 0)—точка самопересечения;
(0; 6) —точка пересечения с осью ординат; максимум г/ == 6 при х=0, мини-
мумы у — —2 при х = ± 2^2; имеются два максимума и два минимума х.
2) Четырехлепестник; оси координат и прямые у = ±х— оси симметрии;
(0; 0) —точка самопересечения; максимумы х — 2 и минимумы х = —2 при
у = ± V2; максимумы у = 2 и минимумы у = —2 при х = ± V2 ;
(0; 0) — точка перегиба. 3) Ось ординат — ось симметрии^ (0; 0) — точка
самопересечения; максимум х = V2/3 и минимум х = —д/2/3 при у — 1С/Э
максимумы у — 2 при х = ±2. 4) Асимптота у = 1 — х; (0; 0) —точка воз-
врата; (4; 0) — точка пересечения с осью абсцисс; максимум х = 27/8 при
у == —9/8; точка перегиба (27/4; 9/4). 5) Каппа; оси координат—оси симмет-
рии; асимптоты у = ±2; (0; 0) — точка самопересечения и перегиба. 6) Пря-
мая у = х — ось симметрии; асимптота у — (2—3х)/3; точки пересечения
с осями координат (Г, 0), (0; 1); (0; 0)—изолированная точка; максимум
х ж 1,1 при у — 2/3, минимум х = 1 при у — 0; максимум у ж 1,1__при
х = 2/3, минимум у = 1 при х — 0; точки перегиба (2 (3 =F V3)/9^
2(3 ± V3)/9)- 7) Прямая у = — х — ось симметрии; (0; 0) —_точка пере-
сечения с осями координат; минимум х = 3 д^2/2 при у — — 3^4/2; макси-
мум у = —3 \/2 /2 при х = 3^4/2; точки перегиба (з^(3т7±2;
—3-\/(3 ± V5 )/2 )’ приближенно (2,18; —4,13), (4,13; —2,18). 8) Прямая
у = х — ось симметрии; асимптоты у — 1, у == х, х = 1; точка самопересече-
ния (е; с).
21.31 . 1) Четырехлепестковая роза; оси координат и прямые t/=±x-r-
оси симметрии; точка самопересечения (0; 0); максимумы г=1 при
588
ф = п(1 ± 2&)/4, k = О, 1, 2, 3; при 0 < ф < -у- максимум х = 4 Уз /9 при
у = 2 Уб/9 (ф e arccos У2/3 ); максимум г/= 4 Уз/э При X = 2 Уб/9 (<р =
= arcsin У2/3). 2) Трехлепестковая роза; прямые у = 0, у = ± УЗх — оси
симметрии; (0; 0)—точка самопересечения; максимумы г=1 при ф = 0,
± 2л/3; максимум х=1 при у = 0 (ф —_0), минимумы х = — 9/16 при
у = ± 3 У15/16 « ± 0,73 (ф = ± arccos (— Уб А)); максимум у « 0,185 и
минимум у « —0,185 при х « 0,63, максимум у « 0,88 и минимум у » —0,88
при х = —0,44. 3) (0; 0) — центр симметрии, точка самопересечения и точка
перегиба; асимптоты у = ±х—1/УГ при Xj->-f-oo и у = ± х + 1/У2 при
х->—оо. 4) Прямые х = 0 и у = ±х^/3 — оси симметрии; асимптоты
у — 0, у = ±хУЗ; минимумы г == 1 при ф = л(1 + 4&)/6, k = 0, 1, 2;
минимум х « 0,83 и максимум х « —0,83 при у « 0,68; максимум у ж —1
при х = 0. 5) Кривая из задачи 21.29. 8) без изолированной точки (0; 0).
6) Кардиоида; ось абсцисс — ось симметрии; (0; 0)—точка возврата; (2; 0),
(0; ±1) —точки пересечения с осямд координат; максимум х = 2 при у — 0,
минимумы х — —1/4 пр_и у == ± Уз /4 (ф = ± 2л/3); максимум у = 3 У3 /4
и минимум # = —зУз/4 при х==3/4( ф = ±л/3). 7) Часть кривой из за-
дачи 21.29. 7). 8) Кривая, симметричная кривой 7) относительно оси ординат.
9) Ось абсцисс — ось симметрии; асимптота х — 2; минимум х = 1 при у — 0
(ф = 0). 10) (0; 0)—центр симметрии; асимптоты х ==_±1; точки пересече-
ния с осями координат (±1; 0), (0; 0); максимум х = У2 при у = У2, мини-
мум х = — У2 при у = — 'у/?-', максимум у « 0,23 при х ж —0,5, минимум
у « —0,23 при х ж 0,5; точки перегиба (0; 0) и (приближенно)
(±1,35; ±2,58).
§ 22. Задачи на нахождение наибольших и наименьших значений
22.1. 1) Квадрат со стороной <y/S. 2) Квадрат со стороной <y/S .
22.2. 2R2. 22.3. (2; 1), (2; — 1). 22.4. (1; 1). 22Л 2. 22.6. —2. 22.7. Vs/sina*.
22.8. 2х + 4у = 5^ 22.9. л/3 и л/6. 22.10. а)^2 • 22.11. (л —а)/2, (л — а)/2.
22.12. a V2, b У 2 . 22.13. R2 У57/4. 22.14. р/(л + 4). 22.15. (а/^2; b/^2\
22.16. (a + b — ^a2 — ab + b2)/Q. 22,17. л/3. 22.18. 27?/Уз. 22.19. Расстоя-
ние от центра круга до стороны прямоугольника, параллельной прямой Z,
равно (А +'Ув/?2 + А2 )/4. 22.20. лп3/216. 22.21. S3/2/(3 УблГ). 22.22. 1.
22.23. Котел должен иметь форму шара с внутренним радиусом У3у/(4л).
22.24. 1/2. 22.25^ л (Уб + 1)7?2. 22.26. Высота цилиндра ciIaJs, радиус его
основания а/Ъ. 22.27. 41?/3. 22.28. 47?. 22.29. Радиус _основания 27?/3, вы-
сота Н/3.22.30. 2л V2/3 .22.31. 37/6(ли2/2)1/3. 22.32. 2л/3 Уз/27. 22.33. лг3 Уз/2.
22.34. (п2/3 ± ^2/з)з/2_ 22.35. л/4. 22.36. г. 22.37. Угол наклона стержня к гори-,
зонту равен arccos ((/ + У/2 + 1287?2 )/167?). 22.38. (п2/3 + &2/3)3/2. 22.40. V2,
22.41. h/2. 22.42. BD = b-----т—а-—-, если b > a/Vfea — 1; BD = 0, если
д42 - 1
— 1. 22.43. /?/V2. 22.44. rf/rf = где rt и гг — расстояния от
светящейся точки до центров шаров с радиусами Ri и Т?2 соответственно.
22.45. arctg k. 22.46. Уab .
§ 23. Численное решение уравнений
23 .1. 1) (—3; —2,5)*), (0,5; 1), (2; 2,5). 2) (-.0,5; 0), (1; 1,5).
3) (—2; —1,5). 4) Xi = —1,5, х2 = 0,5, х3 = 1. 5) х == 1,5. 6) (2,5; 3).
7) (1; 1,5). 8) (-1,5; -1), (2,5; 3). 23.2. 1) (-0,6; -ч),5). 2) (1,2; 1,3).
*) Здесь и далее указан один, из возможных интервалов изоляции корня.
589
*3) :(—0,6; —0,5). 4) (1,9; 2). 5) (0,8; 0,9).. 6) (—0,9; -0,8), (0,8; 0,9).
7) (0,5; 0,6), (2,2; 2,3). 8) (2,5; 2,6). 23.13. (—0,5; 0), (1; 1,5), (2,5; 3)
23.16. 1) (2,3; 2,4). 2) (—1,1; —1), (0,9; 1). 23.21. 1) [0,5; 3,7]. 2) [0,74; 22].
23.22. [—11/3; —1/9], [0,27; 2,64]; (1; 1,5). 23.23. (0,4; 0,5). 23.24. 2) 4b3 4-
4- 27c2 4- 4a3c — a2b2 — 18abc < 0. 23.25. p5 > q2. 23.26. 4q < p2 при m =2,
n(= 1; 0 < 27q2 —4p3 при m = 3, n = 1; —4p36< 27 q <Z 0 или 0 < 27 q
< —4p3 при m = 3, /2 = 2; p < 0 и 0 < 4q p2 при tn = 4, n = 2; при
всех остальных тип при любых р и q уравнение будет иметь хотя бы один
комплексный корень. 23.28. 1) Два корня. 2) Один корень при а < 1, три
корня при 1, два корня, из которых один двукратный, при а == 1
23.29. 1) а <—175, а > 188/27. 2)^ а = 7,5, а = 104/9. 3) а < 16, а Ф 0.
4) 0 < а < 23/16. 23.30. (0; 0,2). 23.31. 1) Один корень при а < 0, два корня
при 0 < а < 1/е, один двукратный корень при а = 1/е, нет корней при
а > \/е. 2) Нет корней при а < —1/е, один двукратный корень при —1/е,
два корня при —1 /в < а < 0, один корень при а 0. 3) Нет корней при
& < 0, один корень при 0 < а < с2/4, один простой и один двукратный ко-
рень при а = е2/4, три корня при а > ег/4. 4) Нет корней при |а|< shxo «
» 1,5, один двукратный корень при |а| = sh Хо, два корня при |а| > sh х0,
где хо — положительный корень уравнения cth х « х. 5) Нет корней при
| а | > 3 Уз716, один двукратный корень при | а । = з Уз/16, два корня при
0 < | а | < 3 УЗ/16, три корня, из которых один трехкратный, .при а = 0.
23.32. 1) с>1. 2) а = — (3 + In 16)/4. 3) а > 2е. 4) |й|<Зл/2—1.
23.33. 2) Нет корней при b > е~'-а, один двукратный корень при Ь — е~1-а,
два корня при 0 < Ь < е-1-0, один корень при 6^0.
23.34. 2) Границей областей в плоскости (а; Ъ) служат • прямая
b = 0 и параметрически заданная кривая а = е* (3 — х) /3, b — е*/3х2.
23.36. Если п — четное число, то: один корень при а> (п/е)", два корня,
из которых один двукратный, при а = (п/е)п, три корня при 0 < а < (п]е)п,
один n-кратный корень при а = 0, нет- корней при а < 0; если п — нечет-
ное число, то: нет корней при а > (nle)n, один двукратный корень при
а — (п/е)", два корня при 0 < а < (л/е)", один n-кратный корень при
а — 0, один корень при а < 0. 23.37. 1) (1; 2). 2) (—5;—4), (—1; 0), (5; 6).
3) (4; 5). 4) (—2; -1), (-1; 0), (0; 1), (3; 4). 5) (2; 3), (3; 4).
6) (—7; —6), (—1; 0). 7) (—4; —3), (—1; —0,5), (—0,5; 0), (0; 1), (3; 4).
8) (—2; -1), (0; 0,5), (0,5; 1). 9) (—2; —1). 10)(—3; —2), (0; 1), (1; 2).
23.38. (—а2, —Ь2), (—Ь2- —с2), (—с2; +<»). 23.39. 1) (—1; —0,9), (0,9; 1).
2) (—3,6; —3,5), (—2,2; —2,1),. (1,2; 1,3). 3) (—0,9; — 0,8)Д (0,6; 0,7).
4) (_о,8; —0,7). 5) (—0,5; —0,4). 23.40. 1) х, = —1,86, х2 = 1,70.
2) Xi = —3,06, хг = —0,69, х3= 3,76. 3) х = 3,63. 4) х(= —0,435, х2= 0,381.
5) xi =—0,867, Хг = 1,867. 6) х, = 0,27, хг = 2,25. 7) х = 0,21. 8) х = 1,088.
О) Xi = 0,776, х2=2,223. 10) х=0,567. 23.41. 652,7 мм. 23.42. (—1,10; —0,48),
(1,71; 1,39). 23.44. 1) х, е(3; 3,1), х2<=(4,7; 4,8). 2) х, = 3,028. 3) х2 =4,728.
23.45. 1) х = 9,9667. 2) х = —0,88677. 3) х = —0,19994. 4) х = 0,091.
5) х = 0,15495. 6) х = —0,5283. 7) х = 2,0945514815. 8) х = 0,4816.
9) х = 1,172. 23.46. 1) а<е|/е. 2) е~е <й<е1/е- 23.47. 1) 3,4368. 2) х, =
= 4,7300; Хг = 7,8532. 23.48. х' = 0,5896, x„+i = e°’8*n-1;x" = 2,2805,
Xn+t = 1,25(1 + In xn). 23.49. 1) xt = —2,214, x2 = 0,539, x3 = 1,675.
2) X, = —1,221, x2 = 0,724. 3) 2,259. 4) x = —2,087. 5) Xi =.—x2 = —0,824.
6) xi =—2,33006, x2 = 0,20164, xs = 2,12842. 23.50.-, 1) x = ±3,60555127.
2) X! =—2,666667, x2 = 0,292893, x3 = 1,707107. 3) 0,84375. 23.51. 1) x =
= 1,76926. 2) x= 1,21341. 3) x, = —0,951, x2 = 1,756, x3 = 2,694.
4) xj = 0,472, x2 = 9,999. 5) x = 0,739087. 6) x = 2,5062. 7) x = —0,56715.
8) x= ±1,199678. 9) x = 4,49341. 10) x, = 2,081, x2 = 5;940. 23.52. x =?
= —10,261. 23.53. z= ±10,9320. 23.54.. 1) x = 0,675_ 2) x = 0.670a.
3) x = 0,6705. 23.55. Сходится к sign Хо, если |_x0 | > 1/Уз: сходится к 0,
если | х0 | < 1/Уб ; не сходится при | х0 | = 1/Уб ; при |хо| = 1/Уз" после-
довательность не определена; при 1/Уб < |х0| < 1/Уз, если последователь-
иость определена, то она сходится либо к -Н, либо к —1. 23.58. х/г+1
590
x — a sin2 gj/0
aco sin 2W0
ppz + zz‘
«= (Xn + a/x«)/2. 23.61. |g —x2] < 10-L 23.62. 1) x « 0,325. 2), 3), 4) x =*
«= 0,3295. 23.63. x « 1,0448. 23.64. Xi == —10,2610, x2 = 9,8860. 23.65. x =
= 0,740841. 23.66. 1) x « 0,78669. 2) x = 1,755581.
§ 24. Вектор — функции. Кривые
24.6. 1) i + j 4-k, 2) — i — j7n;«k. 24.11. 1) i + 2/j + 3/2k; x - tQ ==
= 0-$/(>0) = (z -*о)/(3Ф- 2> .cosZi — sin t j; (x — sin tQ )/cos to =>
!=x — (y — cos /0)/sin /0, z + 1 = 0.3) co sin 2w/(ai — &j) 4~ k;
У — Ь COS2 (dtp _
ba> sin 2co/o ~~ °*
24.12. 1) 2(r, r'). 2) (r, r')/Vr^ 3) [[r, г"], г"] + [[г, г'], r'"]. 4) (r, r', r'").
24.23. 1) (г')2[г/, а]2. 2) —(г', а) ГН ар.
24.29. 1) _ (Vp° + *2>
V(pz)g ч-(pq>z)a + (г^)3 Vp2 + Z2 У(р')2+(Рф')2+(£')2
2) I г" I = УрЖ)4 + (фТ1 + (Ж
24.30. | r'\ =» V(pz)2 4- Р2 [(О')2 + (ф' cos О)2]. 24.35. х = a (cos t 4- t sin t),
у = a(sin t — teas t). 24.36. 1) х = ае&(рсозф, у == aek^ sin (p, z = bek^.
2) x —at cost у == at sin/, z » bt. 24.41. (a^y)—вырожденная матрица.
24.43. р = £ф(/ = ф). 24.46. 1) (x — e)/e = (y —_e“l)/( — a~1) = (z — l)/2.
2) % = #4- 1 =s z. 24.47. x + a (4 — л)/2 = у == г/д/2 —• a; ф == л/4. 24.48. Если
/о ¥= 0, то (х - ф/(4^) = (г- <о)/(3<о) = (z - <о)/2. (* ~ ф +
3/0 + (z/-^)4-2(z- /2) я а если = 0, то х = J/ = 0 — касательная
прямая, z = 0 — нормальная плоскость.
24.49. х + (—l)w z V2 « (0,5 + (-l)n) R, %У — (~On R =» 0, ш, п = 0,1.
24.50. (—2; 12; 14), (—2; 3; —4). 24.51. 8(х + у + г) — 5 = 0.
24.52. х 4~ 3// = 10, Зр 4~ 4г = 25. 24.53. cosa==VWc> cos р — Vblс,
cos Y = V2z/с, с = *Ja + b + 2г . 24.54. (р 4- 7)/V2 . 24.59. (х — 1)/1 ==
х= (у — 1)/2 «= (г — 1)/3, х 4- 2р + Зг-6 = 0, парабола у == Зх2/4. 24.60. х/х0 —
— у/Уо + z/zQ « 1. XpypZo Ф 0. _______________ ________________________
24.71. 1) ch(x/a). 2) ''Ja2 sin2 t 4- b2 cos21. 3) \/a2 sh2/ 4- b2 ch2t.
4) 3a | sin 2/ |/2. 5).2a | cos (//2) |. 6) Va2 4- b2 . 7) R л/\ 4- sin2 /
24.73. 1) a Vl 4- Ф2 • 2) a Vl + Ф2 /ф2. 3) aeb* Vl 4- b2.
24.76. 1) & ==» fl-1 == 2 | a |/(1 4- 4a2x2)3/2 2) /? == /?-' = 6 | x |/(1 4- 9x4)3z2.
3) k == — = -—I S1‘n ' ~o/2 . 4) k = — = —---. 5) k = — = [ cos (x/a) |/a.
R (14-cos2x)3/2 R ch2(x/a) R
24.77. 1) k = 2”4&<4 2ЧЗД-” / 9 г06 2X3/2- % = xV/a'- 4 = ~y3c2/bi’
(b x2 4- а. У) (e“x2 — агг’
V3a2
—7o--- "iT »
x (2a 4" 5x)
g = — x (a + 3x)/a, = 2y (a + 2x)/x. 3) k = 1/3 a | xy |, g = x1^3 (3a2/3 —
— 2х2/3), t] = г/1/3 (a2/3 + 2х2/3). 4) k = |x + 2a| (a — x)2/a(2a2 — x2)3'2,
g = a(x3 — 2a3)/(x + 2a) (a — x)2, r] = 2ay(x + a)/x(x-j- 2a).
24.78. 1) a&/(a2 sin21 + b2 cos2 /)3/2.
2) ab/(a2 sh21 + b2 eh2 t)312. 3) l/(4a | sin (//2) |).
24.79. 1J g = — (9/2 + 2) P/2, r) = 4 (3/2 + 1) t/3. 2) g = — ± - ch31.1)=
a2 *I b^
---------у---sh3/. 3) | 5= na 4- a(t — sin /), t] s=s -—2a 4- a(l — cos /).
4) x2 4- #2 = cl2. _
24.80. p. 24.81. 1) 2/(3 Уз). 2) 2/a, a > 0. 3) l/a, a > 0.
591
24.86. 1)а2/3р. 2) -g-л | cos1. 3) a cos2<f> (1 + 8 sin2q>)3/2/(4 + 8 sin2 ф).
4) а(1 + <р2)3/2/(2 + ф2). 5) а (ф2 + 1)3/2/ф«. 6) р 71 + 62 •
24.88. 1) у == ach(x/a). 2) При том же полюсе и соответствующем пово-
роте оси: р — qpj = <р 4- л/2. 3) Кардиоида. 24.92. In а = ап^.
24.105. у = у/2 (х - 1 +V1 — х). 24.106. у = —х2/2 + пх/2 + 1 — л2/8.
24.108. 1) За. 2) За/2. 3) За. 24.109. 1) х sin t0 - у cos/0 + 4 z — a/о = 0;
О
х sin /0 — У cos to — z + -у- to = 0; х cos t0 + у sin t0 — a = 0. 2) 3/2x —
-3/oy + z-/o = O; x + 2t0y + 3t20z-t0(l + 2/g + 3/J) = 0; Z0(9/g + 2)x +
+ (9£a-l)y-3/0(2/^+l)z-/2(H^6/g + 3/^) = 0. 3) е~*°х - e*°y -
- V2_ z + 2/0 = 0; e*'x - e~hy + ^2 z + 2 (t0 + sh2/0) =0; x + у -
— V2 sh /oz + 2 (/0 sh tQ — ch t0) = 0. 4) (sin t0 — cos /0) x — (sin t0 + cos /0)y +
+ 2z — e*“ = 0; (cos to — sin /о) x + (cos to + sin tB) у + z — 2e<0 = 0;
(sin t0 + cos t0) x + (sin t0 — cos /0) у — е*° = 0. 5) 6y2 (x — x0) — 3yf (y — y0)~
— (z - ZO) = 0; 2y0(x - x0) + (y - y0) + 4y3 (z - zd) = 0; (1 - 32//q)(x - xu)-
- 2yu (12 yj + 1) (у — y0)+ 2y2 (8уо +з) (z — z0) = 0. 6) ay—z + b—0,
x + V \x0) у + aq>' (x0) z = Xo + (a2 + 1) ф (x0) ф' (x0) + abtp' (x0), (a2 + 1) X
X ф' (x0) X — у — az = (a2 + 1) ф' (x0) x0 — (a2 + 1) ф (x0) — ab.
24.110. 1) xy0 — ХоУ = 0, z = z0; xox + yoy = a2, a2 (x — x0) = byB (z — z0).
2) У~ Уо z — zo x —x0_ У~Уо__ ,
l-32y^ 2y0(12y^+l) 2y0 (8y2 + 3) ’ Gy2 8y3
x —Xp _ y —y0 Z — Zq , _ у — Уо _ z — Zo
} /§ + 2/0 l-/<5 /0(2/2+l)’ ° 2/0 t2
24.113. Винтовая линия: x= (a + l)cos t, у == (a 4-/) sin/, z = bt,
24.115. bx — ay 4- abz = 2ab. 24.116. 4x — у -j-z — 9 = 0.
24.118. т = (j + kVVT, v = (21 - j + k)/V6", ₽ = (i + j - kj/VT.
24.119. 1) T = (3 cos /1 — 3 sin /j 4- 4k)/5, v = sin /i 4~ cos /j,
p = _1_ (4 cos /1 — 4 sin /j —- 3k). 2) т = ( sin 4- i + cos 4" j — к Y
О Л \ Лл Л J
t . * • fl : i j 1 • I 11
v = cosyi — sinjb ₽ =-----------2“Ysin "2 i + cosyj +
24.121. 2/(l+a2). 24.122. 1) a[a2.+ b2ch 2/]1/2/[a2ch2/+ft2]3/2. 2) | sin2/|/V2 .
3) 0,25 Vl + sin2 (t/2). 4) V2/(x + y)2. 5) sh i/(a -у/2 ch2 t). 6) 2/(a ch t).
7) (a + fc)I/2/(a + b + 2z)3/2.
24.123. 1) e‘/3. 2) l/(ach2/). 3) — 12y/(64y« + 36y‘+ 1).
24.124. 1) k — и == a/(a + y)2. 2) k = x = l/(2a ch2 /). 3) k — —x =
= 2abU(a2 4- b2t2)2. 4) k = x = 1/(3(i2 4- I)2).
5) & = V5 4-3 sin2//(/? (1 4-sin2/)3/2), точек распрямления нет: x =
= 6 sin //(/?(5 4- 3 sin2 /)) , точки уплощения (0; 0; ±/?).
24.125. 1) Точки распрямления x =/гл; точки уплощения х = л/2 4~ птс
2) Точек распрямления нет; точки уплощения / ~±1. 24.132. Винтовая ли-
ния. 24.134. Шаг винта равен длине окружности цилиндра. 24.139. Центр
к I 1 dR I
лежит на бинормали на расстоянии —, где R — радиус кривизны.
I х as I 'ч
592
1р. 60к