Author: Нахин П.Дж.
Tags: анализ математический анализ функциональный анализ математика интегралы
ISBN: 978-5-97060-763-3
Year: 2020
Text
5
. {ft
Пол Дж. Нахин
Секреты
интересных интегралов
Paul J. Nahin
Inside Interesting
Integrals
(with an introduction to contour integration)
A Collection of Sneaky Tricks, Sly Substitutions,
and Numerous Other Stupendously Clever, Awesomely Wicked,
and Devilishly Seductive Maneuvers for Computing Nearly
200 Perplexing Definite Integrals From Physics, Engineering,
and Mathematics (Plus 60 Challenge Problems with Complete,
Detailed Solutions)
Springer
Пол Дж. Нахин
Секреты
интересных интегралов
(с введением в контурное интегрирование)
Коллекция ловких трюков, хитрых подстановок
и множество других невероятно искусных, удивительно озорных
и рискованных маневров для вычисления почти 200 дьявольски
запутанных определенных интегралов из физики, техники
и математики (плюс 60 сложных задач с полными,
подробными решениями)
* >,
Москва, 2020
УДК 517.37
ББК 22.161
Н12
Нахин П. Дж.
Н12 Секреты интересных интегралов / пер. с анг. Н. К. Смоленцева. - М.: ДМК
Пресс, 2020.-428 с: ил.
ISBN 978-5-97060-763-3
В книге приведена целая коллекция из почти 200 запутанных определенных
интегралов из физики, техники и математики, а также 60 задач с полными решениями. Если
вам что-то говорят имена Римана, Бернулли, Эйлера, Френеля, Дирихле, Фурье, Коши,
Фейнмана — эта книга точно для вас.
Издание доставит истинное удовольствие математикам, физикам, думающим
студентам, а также всем читателям, кто еще только планирует стать великим учёным!
УДК 517.37
ББК 22.161
Authorized Russian translation of the English edition of Inside Interesting Integrals ISBN
9781493912773 © 2015 Springer Science+Business Media New York.
This translation is published and sold by permission of Packt Publishing, which owns or
controls all rights to publish and sell the same.
Все права защищены. Любая часть этой книги не может быть воспроизведена в
какой бы то ни было форме и какими бы то ни было средствами без письменного разрешения
владельцев авторских прав.
ISBN 978-1-4939-1277-3 (анг.) © 2015 Springer Science+Business Media New York
ISBN 978-5-97060-763-3 (рус.) © Оформление, издание, перевод, ДМК Пресс, 2020
Бернгард Риман (1826-1866), немецкий математический гений,
интеграл которого является предметом этой книги
(AIP Emilio Segre Visual Archives, T. J. J. See Collection)
Эта книга посвящена всем, кто, прочитав следующую строку из
шпионского романа времен холодной войны Джона Ле Карра
1989 года «Русский дом», сразу узнает, что столкнулся с очень
интересным персонажем:
«Иногда он даже не следил за тем, на что смотрел,
но он мог наслаждаться весь день хорошей
страницей математики»,-
а также всем, кто понимает, насколько разочаровывает
сетование в книге Энтони Зи «Квантовая теория поля в двух словах»:
«Ах, если бы мы только могли взять интеграл... Но
мы не можем».
/
d(cabin)
cabin
Jex={f(u)}n
logjcabin} + С = houseboat
(3π1
J>·
cos
= ln{Ve}
"The integral of ζ squared dz
From one to the cube root of three
ALL times the cosine
Of three pi o'er nine
EquaLs the naturaL Log of the cube root of e"1.
Это три классические интегральные шутки,
любимые той любопытной группой людей,
которые, если бы им дали выбор между борьбой
с хорошей математической задачей или чем-то
еще, подумали бы, что решение очевидно.
1 «Интеграл от ζ в квадрате dz
От единицы до корня кубического из трех,
Умноженный на косинус
От три пи-на-девять,
Равен натуральному логарифму корня кубического из е»
Для поддержки теоретических расчетов, выполненных в этой
книге, предоставляются числовые «подтверждения» с
использованием нескольких команд интегрирования, доступных в
программных пакетах, разработанных Math Works, Inc. of Natick, MA.
В частности, MATLAB® 8.1 (Release 2013a) и пакет расширения
Symbolic Math Toolbox 5.10, оба пакета работают на ПК с
Windows 7. Эта версия MATLAB® сейчас несколько устарела, но все
команды, использованные в этой книге, работают с более
новыми версиями и, вероятно, будут работать в последующих версиях
еще несколько лет. MATLAB® является зарегистрированным
товарным знаком Math Works, Inc. Компания Math Works не
гарантирует точности текста в этой книге. Использование или
обсуждение MATLAB® и пакета расширения Symbolic Math Toolbox здесь
не означает одобрения или спонсорства компании Math Works,
конкретного педагогического подхода или конкретного
использования MATLAB® и пакета Symbolic Math Toolbox.
Содержание
Вступительное слово от издательства и
Предисловие 12
Глава 1. Введение 22
1.1. Интеграл Римана 22
1.2. Примеры риманова интегрирования 26
1.3. Интеграл Лебега 28
1.4. «Интересно» и «секреты» 31
1.5. Некоторые примеры трюков 33
1.6. Особенности 38
1.7. Интеграл Далцелла 43
1.8. Откуда берутся интегралы 46
1.9. Заключительные слова 60
1.10. Задачи для упражнений 61
Глава 2. «Легкие» интегралы 64
2.1. Шесть «легких» для разминки 64
2.2. Новый прием 68
2.3. Два старых трюка, плюс один новый 75
2.4. Еще один старый прием. Лог-синус Эйлера 84
2.5. Задачи для упражнений 90
Глава 3. Любимый трюк Фейнмана 92
3.1. Формула Лейбница 92
3.2. Удивительный интеграл 101
3.3. Интеграл Фруллани 103
3.4. Обратная сторона трюка Фейнмана 106
3.5. Сочетание двух приемов 115
3.6. Интеграл Улера и символьное интегрирование 118
3.7. Интеграл вероятности, новый взгляд 122
3.8. Интеграл Дини 125
3.9. Любимый прием Фейнмана решает физическое уравнение 128
3.10. Задачи и упражнения 130
Глава 4. Гамма- и бета-функции 134
4.1. Гамма-функция Эйлера 134
4.2. Интеграл Валлиса и бета-функция 136
4.3. Перестановка порядка интегрирования в двойном интеграле 147
4.4. Гамма-функция встречает физику 158
4.5. Задачи для решения 161
Глава 5. Использование степенных рядов для нахождения интегралов 164
5.1. Число Каталана 164
5.2. Степенные ряды для логарифмической функции 168
10 ♦ Содержание
5.3. Интегралы дзета-функции 176
5.4. Константа Эйлера и связанные с ней интегралы 181
5.5. Задачи и упражнения 195
Глава 6. Семь сложных интегралов 199
6.1. Интеграл Бернулли 199
6.2. Интеграл Ахмеда 201
6.3. Интеграл Коксетера 205
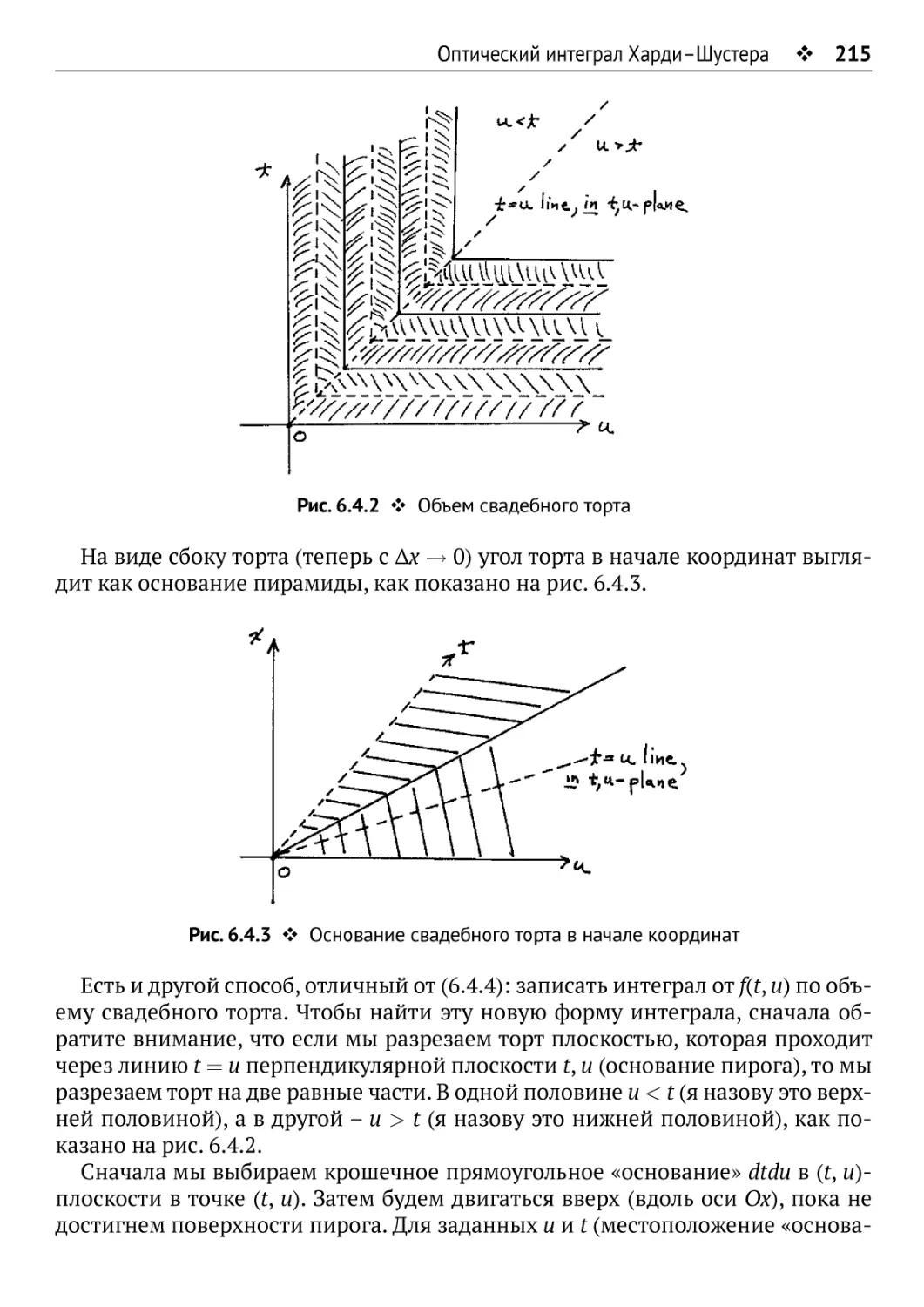
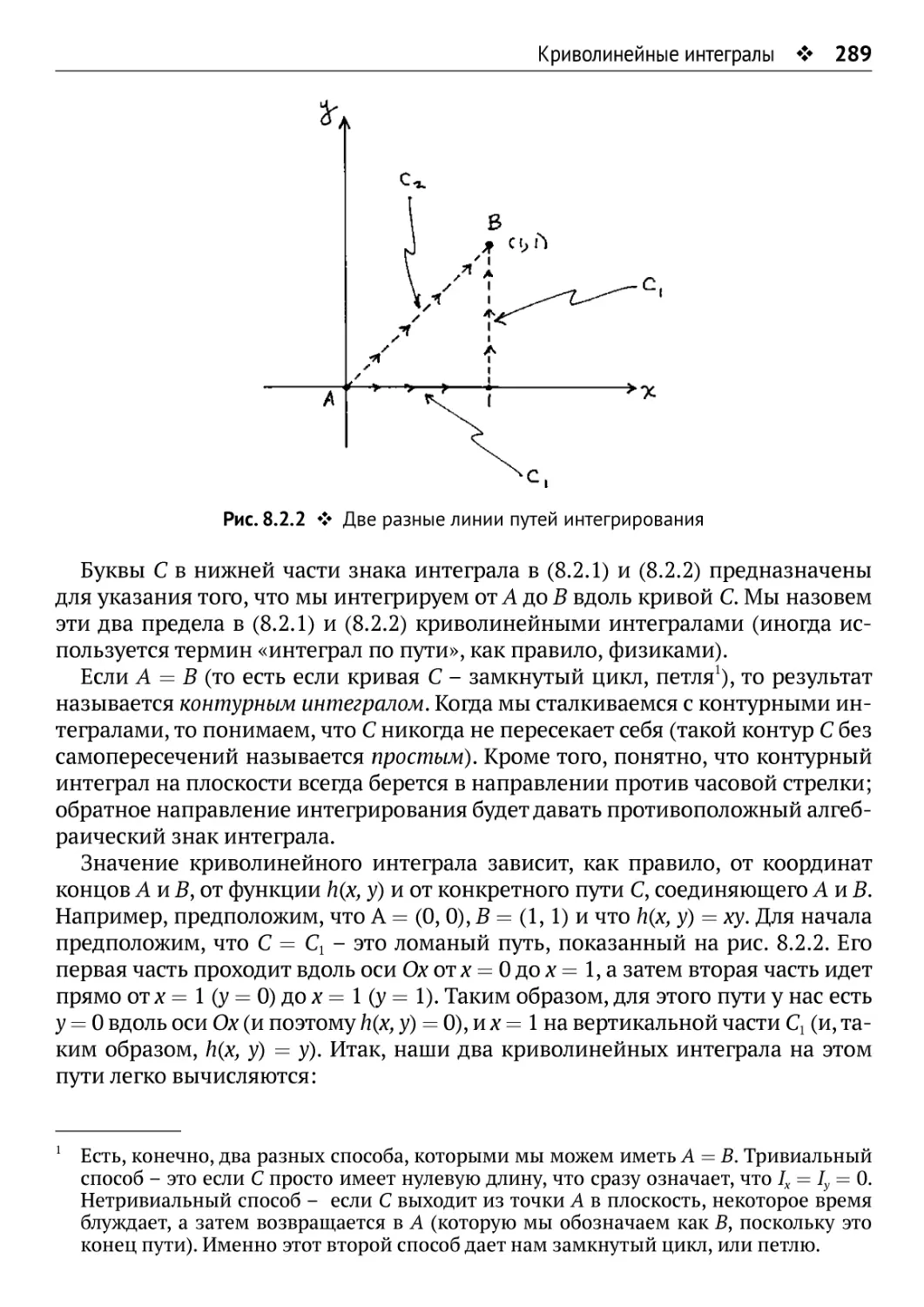
6.4. Оптический интеграл Харди-Шустера 212
6.5. Тройные интегралы Уотсона/Ван Пейпа 217
6.6. Эллиптические интегралы в физической задаче 223
6.7. Задачи и упражнения 229
Глава 7. Использование V-1 для нахождения интегралов 235
7.1. Формула Эйлера 235
7.2. Интегралы Френеля 236
7.3. ζ(3) и снова интегралы лог-синуса 240
7.4. ζ(2), наконец! 245
7.5. Опять интеграл вероятности 248
7.6. За пределами интеграла Дирихле 250
7.7. Дирихле встречает гамма-функцию 256
7.8. Преобразования Фурье и интегралы энергии 259
7.9. «Странные» интегралы из радиотехники 265
7.10. Причинность и интегралы преобразования Гильберта 275
7.11. Задачи и упражнения 283
Глава 8. Контурное интегрирование 287
8.1. Вступление 287
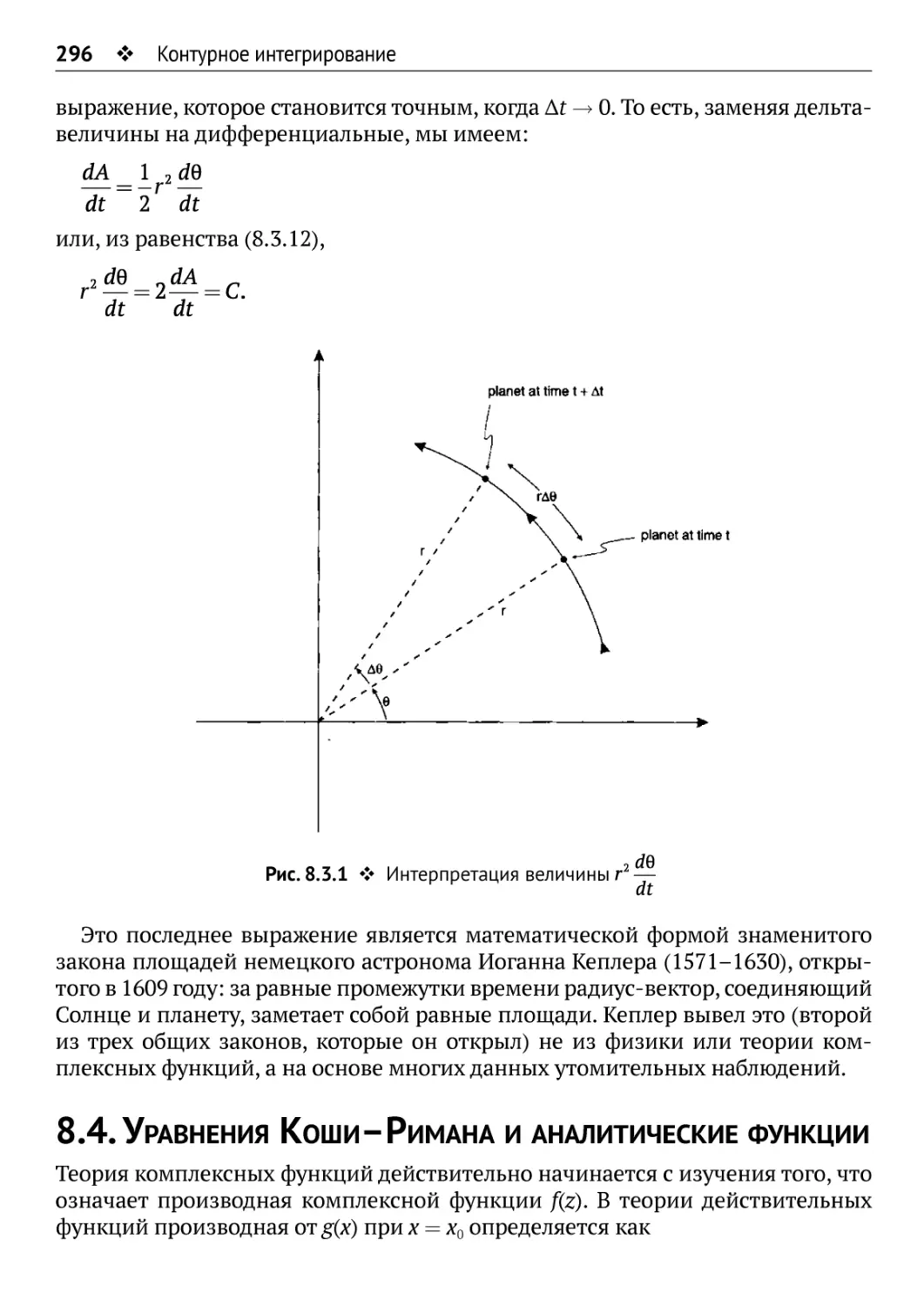
8.2. Криволинейные интегралы 287
8.3. Функции комплексной переменной 290
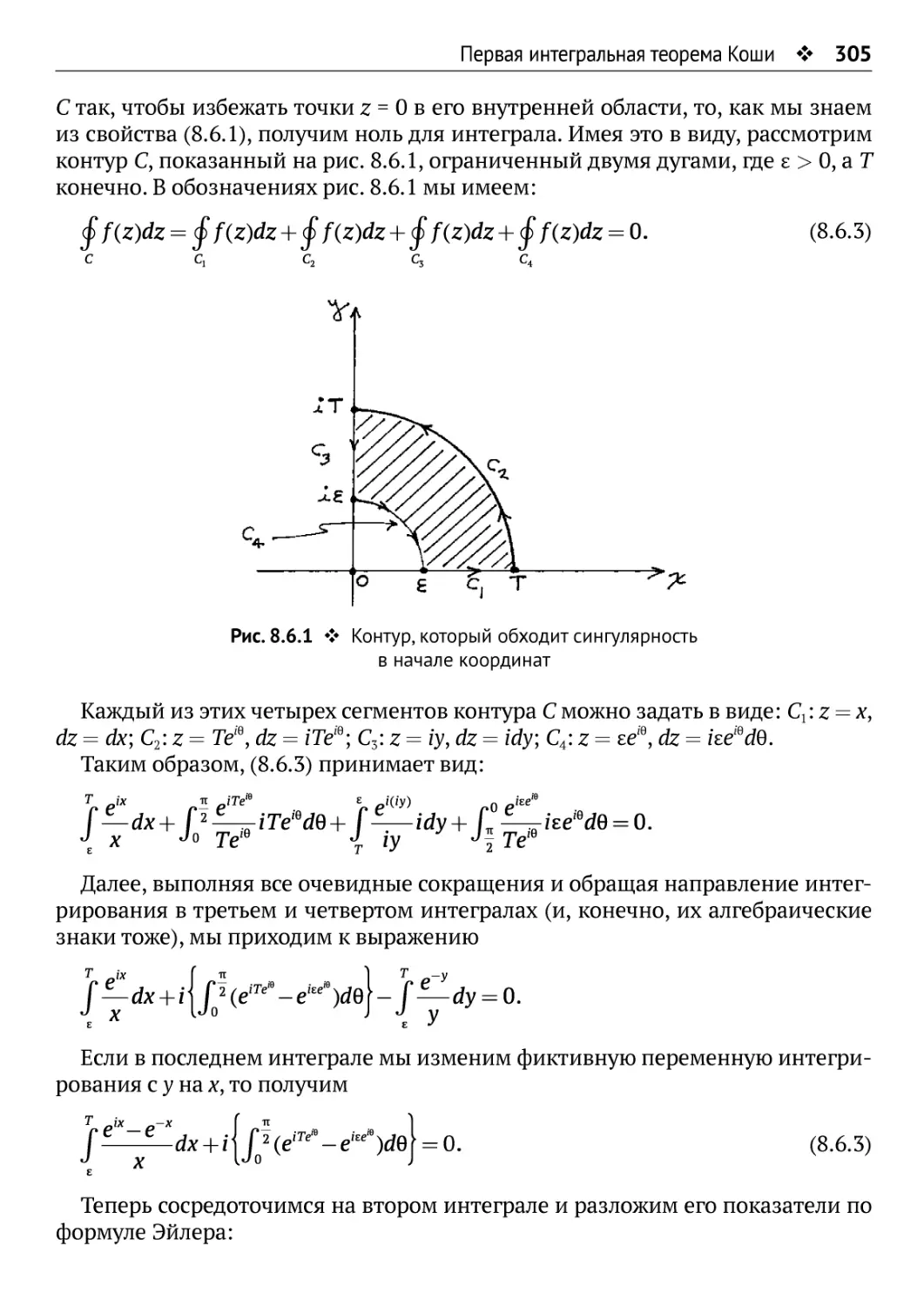
8.4. Уравнения Коши-Римана и аналитические функции 296
8.5. Интегральная теорема Грина 300
8.6. Первая интегральная теорема Коши 303
8.7. Вторая интегральная теорема Коши 316
8.8. Особенности и теорема о вычетах 330
8.9. Интегралы с многозначными подынтегральными функциями 338
8.10. Задачи и упражнения 346
Глава 9. Эпилог 349
9.1. Риман, простые числа и дзета-функция 349
9.2. Вывод функционального уравнения для ζ($) 359
9.3. Вопросы для упражнений 372
Решения задач и упражнений 375
Предметный указатель 426
Вступительное слово
от издательства
ОТЗЫВЫ И ПОЖЕЛАНИЯ
Мы всегда рады отзывам наших читателей. Расскажите нам, что вы думаете об
этой книге - что понравилось или, может быть, не понравилось. Отзывы важны
для нас, чтобы выпускать книги, которые будут для вас максимально полезны.
Вы можете написать отзыв на нашем сайте www.dmkpress.com, зайдя на
страницу книги и оставив комментарий в разделе «Отзывы и рецензии».
Также можно послать письмо главному редактору по адресу dmkpress@gmail.com;
при этом укажите название книги в теме письма.
Если вы являетесь экспертом в какой-либо области и заинтересованы в
написании новой книги, заполните форму на нашем сайте по адресу http://dmk-
press.com/authors/publish_book/ или напишите в издательство по адресу dmk-
press@gmail.com.
СПИСОК ОПЕЧАТОК
Хотя мы приняли все возможные меры для того, чтобы обеспечить высокое
качество наших текстов, ошибки все равно случаются. Если вы найдете ошибку
в одной из наших книг - возможно, ошибку в основном тексте или
программном коде, - мы будем очень благодарны, если вы сообщите нам о ней. Сделав
это, вы избавите других читателей от недопонимания и поможете нам
улучшить последующие издания этой книги.
Если вы найдете какие-либо ошибки в коде, пожалуйста, сообщите о них
главному редактору по адресу dmkpress@gmail.com, и мы исправим это в
следующих тиражах.
Нарушение авторских прав
Пиратство в интернете по-прежнему остается насущной проблемой.
Издательства «ДМК Пресс» и Springer очень серьезно относятся к вопросам защиты
авторских прав и лицензирования. Если вы столкнетесь в интернете с
незаконной публикацией какой-либо из наших книг, пожалуйста, пришлите нам
ссылку на интернет-ресурс, чтобы мы могли применить санкции.
Ссылку на подозрительные материалы можно прислать по адресу
электронной почты dmkpress@gmail.com.
Мы высоко ценим любую помощь по защите наших авторов, благодаря
которой мы можем предоставлять вам качественные материалы.
Предисловие
Инженерия - это как танцы; вы не изучаете это
в затемненном лекционном зале, просматривая
слайды: вы изучаете это, выходя на танцпол и
наступая на пальцы ног.
- Профессор Джек Олфорд (1920-2006),
соучредитель инженерной клиники в колледже Харви Мад-
да, который нанял автора в 1971 году в качестве
доцента. То же самое можно сказать и о
нахождении определенных интегралов
Чтобы по-настоящему оценить эту книгу, посвященную тайному искусству
вычисления определенных интегралов, необходимо (хотя, возможно,
недостаточно) быть человеком, который в жестокой битве один на один за первое
место в списке греховных удовольствий находит следующий вопрос более
привлекательным, чем чашка горячего кофе с сахарным пончиком:
без фактического вычисления χ показать, что
1 л 7 1
если χ + — = 1, из этого следует, что χ + — = 1.
χ χ
Хорошо, я знаю, что многие (но, я надеюсь, не вы) подумают, столкнувшись
с таким вопросом: какое земное значение может иметь такая задача? Ну,
насколько я знаю, никакое, но ее очарование (или нет) для вас обеспечивает
(я думаю) превосходное психологическое понимание того, стоит ли вам
тратить время и/или хорошие деньги на эту книгу. Если вы смущены, озадачены
или равнодушны (а может быть, все вместе), то я советую вам отложить эту
книгу и вместо этого поискать хороший детективный роман, последнюю
биографию Линкольна (кажется, каждый год появляется новая - что еще могло
остаться невысказанным?) или, возможно, вегетарианскую кулинарную книгу.
Но если ваша ручка уже вынута и на вашем столе накапливаются
нацарапанные страницы расчетов, то, черт возьми, вы - просто тот человек, для которого
я написал эту книгу. (Если после доблестных усилий вы все еще в тупике, но тем
не менее просто ощущаете необходимость посмотреть, как это сделать, или
если ваша ручка просто исписалась - решение задачи представлено в конце
книги.)
Точнее говоря, я написал для трех разных категорий читателей: (1)
студентов, изучающих физику/инженерию/математику; (2) профессоров, которые
ищут интересный материал для лекций, и (3) неакадемических
профессионалов, которым нужно «хорошее техническое чтение».
Есть две возможные проблемы, связанные с вычислением определенных
интегралов, которые мы должны рассмотреть сразу. Во-первых, действитель-
Предисловие ♦ 13
но ли математики делают подобные вещи? Разве простые вычисления - не
грязное дело (которое лучше всего делать вне поля зрения, в тени переулков,
чтобы не нанести непоправимого ущерба юным умам впечатлительных
юношей) покрытых жиром инженеров с дырявыми рукавами их рубашек или
придурковатых физиков в потрепанных штанах и с меловой пылью на носу? Разве
не в глубоком, чистом океане аналитических доказательств и теорем мы
находим настоящих математиков, плавающих, как могучие лоснящиеся тюлени?
Как инженер я сам нахожу это отношение немного элитарным, и поэтому мне
приятно отметить удовольствие от вычислений, которым наслаждались
многие великие математики, от Ньютона до наших дней.
Позвольте мне привести два примера. Во-первых, репутация величайшего
английского математика первой половины XX века Г. X. Харди (1877-1947)
частично опирается на его феноменальное умение находить определенные
интегралы. (Имя Харди часто упоминается в этой книге.) И во-вторых, герой этой
книги (Риман) сегодня известен (помимо своего интеграла) формулировкой
величайшей нерешенной проблемы математики, о которой я расскажу вам
гораздо больше в конце книги. Но после его смерти, когда его личные заметки по
этой самой проблеме были изучены, было обнаружено, что во всех глубоких
теоретических материалах заложено вычисление V2 до 38 знаков после запятой!
Мне кажется просто безумием жалоба, которую я иногда слышу, на то, что
нет конца определенным интегралам. (Но ведь это должно быть поводом для
радости!) Вы можете играть с интегралами, с верхним и нижним пределами
бесчисленным множеством способов1, но идет ворчание - какой смысл
вычислять определенные интегралы, поскольку вы не можете решить их все? Я
надеюсь, что изложения этой проблемы на словах достаточно, чтобы прояснить
ее смехотворный характер. Мы никогда не сможем найти все возможные
определенные интегралы, так зачем беспокоиться? Ну, а что дальше - вы не можете
сложить все возможные пары действительных чисел, так зачем беспокоиться
о том, чтобы научиться складывать? Как я уже сказал, это безумие!
Что делает вычисление конкретных интегралов в этой книге ценным, так
это не конкретные ответы, которые мы получим, а скорее уловки (извините,
методы), которые будем использовать для получения этих ответов; методы,
которые вы можете использовать при вычислении интегралов, с которыми вы
столкнетесь в будущем в своей работе. Многие из интегралов, которые я
покажу вам, действительно имеют важное применение в математической физике
и технике, но другие включены только потому, что на первый взгляд они
выглядят настолько чертовски крутыми, что испытываешь настоящий удар, когда
видишь, как они просто рушатся, когда на них нападают с правильным трюком.
Из всего вышесказанного вы, вероятно, поняли, что я написал эту книгу
в легкой манере (что означает «это не строгий учебник по математике»). Я не
В следующей главе вы увидите, что при соответствующем изменении переменной
мы можем преобразовать любой интеграл в интеграл от 0 до оо, или от 1 до оо, или от
О до 1. Так что все не так плохо, как я это представлял.
14 ♦ Предисловие
собираюсь сильно беспокоиться, например, о том, чтобы доказать
равномерную сходимость чего-либо, и если вы не знаете, что это значит, не
беспокойтесь об этом, потому что я тоже не буду беспокоиться об этом. Дело не в том,
что вопросы строгости не важны - они важны, - но не здесь для нас.
Когда, проделав длинную запутанную последовательность манипуляций,
чтобы получить то, что мы считаем значением некоторого определенного
интеграла, я просто запускаю замечательную команду quad численного
интегрирования MATLAB (quad - сокращение от quadrature, квадратура), и мы
вычисляем значение этого интеграла. Если наш теоретический ответ говорит, что
Vtt = 1.772453..., a quad говорит, что это равно 9.3, мы, конечно, будем
подозревать, что где-то во всех наших вычислениях мы, возможно, просто
лопухнулись! Однако если quad говорит, что это значение равно 1.77246, то это
достаточно хорошо для меня, и мы пойдем, довольные успехом и покрасневшие
от удовольствия, к следующей проблеме.
Сказав это, я был бы не совсем честен, если бы прямо сейчас не признал,
что такое счастье может быть бредовым. Рассмотрим, к примеру, следующий
контрпример к принятой философии этой книги. Предположим, вы
использовали пакет программного обеспечения, чтобы показать следующее:
сю
. .sin(4x)
cos(x) —-αχ
= 1.57079632679...,
сю
f cos(x)cos
о
оо
f cos(x)cos
sin(4x)
dx = l.57079632679..
cos
ix!sin(4x)
dx = l.57079632679.
и так далее, вплоть до
сю
fcos(x)
COS
Μ
—
u
COS
Μ
—
[з]
•COS
Μ
1 зо J
sin(4x)
dx = l. 57079632679....
Нужно быть слепым (а также полностью лишенным воображения), чтобы не
заподозрить сразу две вещи:
π
повторяющееся значение 1.57079... есть на самом деле —,
(1)
сю
Hcos
lsin(4x)dx = Tt
для всех п.
(2)
Это впечатляет! Но затем вы запускаете следующий случай с η = 31, и
компьютер возвращает ответ
Предисловие ♦ 15
°г (χ) (χ) (χ) (xlsin(4x)
fcos(x)cos - cos - .-cos — cos — —-dx = 1.57079632533....
о l2J l3J l30J l31J x
В этой книге я бы отбросил отклонение (обратите внимание на последние
три цифры!) как ошибку округления - и был бы неправ! Это не ошибка
округления, и, несмотря на весьма убедительные численные вычисления,
предполагаемое тождество «для всех и» просто не соответствует действительности. Это
«почти» верно, но в математике «почти» не считается1.
Это такая кошмарная вещь, которая заставляет математиков чувствовать себя
обязанными четко формулировать любые предположения, которые они
делают, и, если они действительно безупречны, показать, что эти предположения
обоснованы, прежде чем идти вперед к анализу. Я не буду здесь так стесняться
и, несмотря на предыдущий пример того, как плохо все может пойти не так,
буду предполагать почти все, что удобно на данный момент (если не считать
чего-то действительно абсурдного, например 1 + 1 = 3), откладывая момент
истины, когда мы «проверяем» теоретический результат с помощью MATLAB.
Истинный математик почувствовал бы стыд (возможно, даже подумав, что
наступило состояние морального вырождения), заняв такую бесцеремонную
позицию. Я, с другой стороны, буду невосприимчив к таким душераздирающим
сомнениям. Тем не менее имейте в виду, что мы будем рисковать.
Поэтому я снова признаю, что нарушение одного или нескольких условий,
установленных строгими выкладками, может привести к катастрофе.
Дополнительные юмористические примеры этого обескураживающего события
могут быть найдены в статье2 одного математика с чувством юмора. Эта статья
начинается с такой провокационной строки: «Просматривая таблицу
интегралов в унылый воскресный полдень [разве вы часто не делаете то же самое?],
некоторое время назад я наткнулся на четыре расходящихся
тригонометрических интеграла. Мне было интересно, как эти расходящиеся интегралы [с
неверными конечными значениями] оказались в респектабельной таблице».
Через пару предложений автор пишет: «У нас нет намерения опорочить ни
известного математика, который сделал первоначальную ошибку [заслуженно
известный французский гений Огюстен-Луи Коши (1789-1857), с которым вы
познакомитесь, когда мы доберемся до контурного интегрирования], ни
редакторов других прекрасных таблиц, в которых появляются интегралы. Мы все
совершаем ошибки и не собираемся ни на кого указывать пальцем...»
А если мы лопухнулись, ну и что? Никто не должен знать. Мы просто
спокойно соберем наши страницы с ошибками, разорвем их на части и бросим всё это
Информативное обсуждение увлекательной математики, стоящей за этими
вычислениями, см. в ст.: Лорд Ник. Забавная последовательность тригонометрических
интегралов // Математическая газета. 2007. Июль. С. 281-285. (Lord Nick. An Amusing
Sequence of Trigonometrical Integrals//The Mathematical Gazette. July 2007. P. 281-285).
Talvila Erik. Some Divergent Trigonometric Integrals // The American Mathematical
Monthly. May 2001. P. 432-436.
16 ♦ Предисловие
гнилое месиво в камин. Наши математические грехи будут только между нами
и Богом (который хорошо известен как прощающий).
Однако уход от компьютера не обязательно поможет. Вот конкретный
пример того, что я имею в виду под этим. В своем классическом жанре1 Мюррей
Шпигель (покойный профессор математики в Политехническом институте
Ренсселера) просит читателей показать, что
?1η(χ) . π!η(2)
что равно 1,088793.... Можно только догадываться, сколько студентов
боролись (и как долго), чтобы доказать это, поскольку данный ответ неверен. Позже
в этой книге, в (5.1.3), мы возьмем данный интеграл правильно, но
использование функции quad (недоступной Шпигелю в 1964 г.) быстро показывает, что
числовое значение на самом деле значительно больше 1,4603.... В конце этого
предисловия я покажу вам два примера (включая интеграл Шпигеля)
полезного использования функции quad.
Наше использование quad вызывает вопрос, почему, если мы всегда можем
вычислить значение любого определенного интеграла с тем количеством
десятичных цифр, которое мы хотим, мы вообще заботимся о поиске точных
выражений для этих интегралов? Это действительно философский вопрос, и я
думаю, что он относится к таинственной особенности математики, где, казалось
бы, несвязанные понятия могут оказаться тесно связанными. Выражения,
которые мы найдем для многих определенных интегралов, найденных в этой
книге, будут включать такие знакомые числа, как 1п(2) и π, и другие числа,
которые не так хорошо известны, как, например, постоянная Каталана
(обычно записываемая как G) по имени французского математика Эжена Каталана
(Eugene Catalan, 1814-1894).
Общая нить, соединяющая эти и другие числа, заключается в том, что все
они могут быть записаны как бесконечные ряды, которые, в свою очередь,
могут быть записаны как определенные интегралы:
1η(?)-ΐ4 + 5~ + |--|^-0.693147...
Ϊ^-Μ-Μ--)^^0·785398··
в = \-\ + ±-\ + \-...= \Щ<1х = 0.9159655...
I2 З2 52 72 92 J0 1 + х2
1 Spiegel Μ. R. Outline of Theory and Problems of Complex Variables with an Introduction
to Conformal Mapping and Its Applications. Schaum, 1964. P. 198 (problem 91).
[Шпигель Μ. P. Изложение теории и проблем комплексных переменных с введением в
конформные отображения и их приложения. Шаум, 1964. С. 198 (проблема 91).]
Предисловие ♦ 17
И конечно, на гораздо более глубоком уровне понимается, что известные
интегралы Френеля Г cos(x2)dx и £ sin(x2)dx не просто «довольно близки»
к 0,627, а точно равны -
В 2004 году два математика опубликовали замечательную книгу, очень
похожую по духу на эту, и я надеюсь, что мои бесцеремонные слова покажутся
ужасными только самым суровым пуристам. Книга «Неотразимые интегралы»
(Irresistible Integrals. Cambridge University Press) покойного Джорджа Бороса
и Виктора Молла из Университета Тулейна (George Boros, and Victor Moll, Tulane
University) не так охотно, как эта, обращается к дьявольской математике XVIII
века времен Эйлера, но я сильно подозреваю, что авторы часто искушались. Их
подзаголовок выдавал их: Символика, Анализ и Эксперименты [особенно
обратите внимание на это слово!] в вычислении интегралов. Будучи
математиками, они обладали большей силой воли, чем мой тщедушный инженер-электрик,
склонный к строгости, но время от времени даже они не могли полностью
подавить свое истинное удовольствие от нахождения определенных интегралов.
И затем три года спустя, в другой книге, соавтором которой является Молл,
мы находим философское утверждение, которое точно отражает мое
собственное (и этой книги): «Рассматривая интересное тождество, зарытое в длинной
и сложной статье по незнакомому предмету, что дало бы вам больше
уверенности в его правильности: посмотреть доказательство или численно
подтвердить, что оно верно с точностью до 10 000 знаков после запятой?»1 Эта книга
и «Неотразимые интегралы» - действительно интересные математические
книги.
Однако «Неотразимые интегралы» отличается от этой книги тем, что Бо-
рас и Молл писали для более подготовленной математически аудитории. Для
понимания данной книги достаточен уровень знаний, эквивалентный
уровню знаний по математике для младших и старших курсов математического
колледжа. Они также гораздо больше используют компьютерные вычисления
Mathematica, чем я MATLAB. С другой стороны, хотя я и предполагаю
гораздо меньшие знания у моих читателей, только то, что хороший студент знал
бы после первого года расширенного курса математического анализа (АР
calculus), плюс лишь небольшое знакомство с концепцией дифференциального
уравнения, но с одним БОЛЬШИМ исключением. А большое исключение - это
контурное интегрирование, которого Борас и Молл избегали в своей книге,
потому что «не все [математические специальности] (мы боимся, немногие)
изучают комплексный анализ».
Должен сказать, что это застало меня врасплох. Для современного бакалавра
математики не иметь курса комплексного анализа - это мне кажется шоки-
1 Петере А. К. Экспериментальная математика в действии. 2007. С. 4-5 (Peters А. К.
Experimental Mathematics in Action). Наши вычисления здесь с quad не будут до
10 000 знаков после запятой, но идея та же самая.
#
18 ♦ Предисловие
рующим. Будучи специалистом в области электротехники, 50 лет назад я
начал изучать комплексный анализ с помощью контурного интегрирования (на
математическом факультете Стэнфорда) в начале первого курса, используя
знаменитую книгу Р. В. Черчилля «Комплексные переменные и приложения»
(Churchill R. V. Complex Variables and Applications). (У меня до сих пор
сохранилась потрепанная, испачканная кофе копия.) Я думаю, что контурное
интегрирование - это слишком красивая и мощная теория, чтобы ее можно было
исключить из этой книги, но, признавая, что мой предполагаемый читатель
может не иметь предварительных знаний о комплексном анализе, все
интегралы, вычисленные в этой книге методами контурного интегрирования, собраны
в отдельной главе в конце книги. Кроме того, в эту главу я включил
«ускоренный мини-курс» в теоретический комплексный анализ, необходимый для
понимания техники (при условии что читатель уже сталкивался с комплексными
числами и действиями над ними).
«Неотразимые интегралы» содержат много прекрасных интегралов, но
значительная их часть представлена в основном как «наброски», а детали вывода
(часто представляющие существенные проблемы) оставлены на усмотрение
читателя. А в данной книге каждый интеграл получен полностью. Здесь даже
есть интегралы, которых нет в книге Бораса и Молла, такие как знаменитый
интеграл, впервые разобранный в 1697 году швейцарским математиком
Джоном Бернулли (1667-1748), интеграл, который настолько очаровал его, что он
назвал его «чудесные ряды» («series mirabilia», «marvelous series»):
[xxdx = l-\ + \-\ + lr — . = 0.78343...,
J0 22 33 44 S5
или его вариант
[xxdx = l + \ + \ + \ + ^-- = 1.29128....
J0 22 33 44 S5
В этой книге также получены столь же экзотические интегралы
.89648...
xxdx = l- — + ——- + —-... = 0.
I 32 S3 74 95
и
о
1
= 1-1-1 +1-1 -1-1 +1-1 —- = 0.65858.
fx^dx-
f2]
—
1з
2
+
f2l
—
[4j
3
—
f2l
—
L s J
4
+
f2l
—
6
Я не верю, что какой-либо из этих двух последних интегралов уже появлялся
в какой-нибудь книге.
Один знаменитый интеграл, который также отсутствует в «Неотразимых
интегралах», особенно интересен тем, что он, по-видимому (я немного это
объясню), обязан своим вычислением математику из университета Тулейна
(Tulane University), профессору Моллу (Victor Η. Moll). Тогдашний глава мате-
Предисловие ♦ 19
матического факультета Тулейна профессор Герберт Бьюкенен (1881-1974)
начал свою статью11936 года следующими словами: «Рассматривая проблему
исследования в квантовой механике, профессор Дж. С. Моррис из Принстонского
университета недавно столкнулся с интегралом
1/3
/;
Х А
-ах.
-1
Поскольку интеграл не поддается никаким обычным методам, профессор
Моррис попросил автора найти его [Джозеф Чандлер Моррис (1902-1970) был
выпускником Тулейна, он защитил свою кандидатскую диссертацию по
физике в Принстоне; позже он был главой физического факультета, а затем вице-
президентом в Тулейне]».
Профессор Бьюкенен показал, что интеграл равен бесконечному ряду, сумма
которого составляет 6,49..., и сразу после того, как он пришел к этому
значению, он написал: «Из других соображений [детали которых не упоминаются,
но которые, я предполагаю, были результатами либо численных расчетов, либо
даже, возможно, физических экспериментов, проведенных в Принстоне
Моррисом], интеграл должен иметь значение от 6,3 до 6,9. Таким образом, выше-
обеспечивает теоретическую проверку
упомянутое значение
6.4939... = —
15
экспериментальных результатов».
Итак, здесь мы имеем важный определенный интеграл, который,
по-видимому, «обнаружен» физиком и решен математиком. На самом деле, как вы
узнаете в главе 5, Бьюкенен был не первым, кто нашел этот интеграл; он был
вычислен Риманом в 1859 году, задолго до 1936 года. Тем не менее это хорошая
иллюстрация плодотворного сосуществования и позитивного взаимодействия
эксперимента и теории, и она полностью соответствует подходу, который я
использовал при написании данной книги.
Есть еще одно отличие этой книги от «Неотразимых интегралов», которое
отражает мое образование как инженера, а не профессионального математика. На
протяжении всей книги я старался привлечь к обсуждению множество
физических приложений из таких разных областей, как теория радио и теоретическая
механика. Однако во всех таких случаях математика играет центральную роль.
Так, например, когда поднимается тема эллиптических интегралов (в конце
главы 6), я делаю это в контексте известной проблемы физики. Происхождение
этой проблемы связано, однако, не с физиком, а с математиком XIX века.
Бьюкенен X. Е. Об одном интеграле, возникающем в квантовой механике //
Национальный математический журнал. 1936. Απρ. С. 247-248. (Buchanan Η. Ε. On a Certain
Integral Arising in Quantum Mechanics // National Mathematics Magazine. April 1936.
P. 247-248.) В своей книге «Электрическое одеяло миссис Перкинс» (Mrs. Perkins's
Electric Quilt), Принстон, 2009, с. 100-102, я рассматривал этот интеграл не так, как
Бьюкенен, и в главе 5 мы выведем его еще иным способом, как частный случай
формулы (5.3.4).
20 ♦ Предисловие
Позвольте мне закончить это предисловие на той же ноте, что и его начало.
Несмотря на всю математику, эта книга написана в духе «давайте
повеселимся». Точно такое же отношение было у Харди, когда в 1926 году он ответил на
просьбу о помощи молодого студента Тринити-колледжа в Кембридже. В тот
год, еще будучи подростком, X. С. М. Коксетер (1907-2003) предпринял
исследование различных четырехмерных форм. Его исследования привели его
(«путем геометрического рассмотрения и проверки графически») к нескольким
весьма впечатляющим определенным интегралам, таким как1
π/2
/cos"
0
COS*
l + 2cosx
,. 5π2
\dx = .
24
В письме в «Математическую газету» (Mathematical Gazette) он спросил,
может ли кто-нибудь из читателей журнала показать ему, как получить такой
интеграл (мы вычислим вышеупомянутый так называемый интеграл Коксетера
позже, в самом длинном выводе этой книги).
Коксетер стал одним из величайших геометров мира, и он писал
десятилетия спустя в предисловии к своей книге «Двенадцать геометрических очерков»
издания 1968 года: «я до сих пор помню трепет получения [решений от
Харди], когда я второй месяц учился на первом курсе в Кембридже». К решениям
Харди прилагалась записка, нацарапанная на полях: «я очень старался не
тратить время на ваши интегралы, но для меня вызов определенного интеграла
непреодолим»2.
Если вы разделяете увлечение Харди (и мое) определенными интегралами,
то эта книга для вас. Тем не менее, несмотря на мое восхищение почти
магическим талантом Харди к интегралам, я не думаю, что он всегда был прав.
Команда quad MATLAB говорит, что этот интеграл есть 2.0561677..., что очень хо-
5π2
рошо согласуется с = 2.0561675.... Синтаксис кода: quad(@(x)acos(cos(x)./(l+
24
2*cos(x))),0,pi/2).
Для интеграла, который я показал вам ранее, из книги Шпигеля, код quad (я
использовал 1е6 = 106для бесконечного верхнего предела): quad(@(x)log(l + χ) ./(1 + х.л2),0,1еб).
Большинство интегралов в этой книге являются одномерными, но для тех случаев,
когда мы столкнемся с интегралами более высокой размерности, есть функции dbl-
quad и triplequad, и компаньон MATLAB, пакет Symbolic Math Toolbox и его команда int
(от слова «integrate») могут сделать то же самое. Синтаксис для этих случаев объясню,
когда мы впервые столкнемся с многомерными интегралами.
Итак, мы видим, откуда Борас и Молл взяли название своей книги. Несколько лет
назад в своей книге Dr. Euler's Fabulous Formula (ПолДж. Нахин. Необыкновенная
формула доктора Эйлера. М.: ДМК Пресс, 2020) я привел еще один пример увлечения
Харди определенными интегралами: см. раздел 5.7 данной книги «Харди и Шустер
и их оптический интеграл», с. 263-274. Там я написал: «показать Харди на невзятый
определенный интеграл было очень похоже на размахивание красным флагом перед
быком». Позже в этой книге я покажу вам вывод «первых принципов»
оптического интеграла (гораздо более изощренный вывод Харди использует преобразования
Фурье).
Предисловие ♦ 21
Я пишу это почти кощунственное утверждение, потому что, помимо Бораса
и Молла, еще одним обильным источником интегралов является «Трактат об
интегральном исчислении», массивная двухтомная работа - почти 1900
страниц - английского педагога Джозефа Эдвардса (1854-1931).
Несмотря на то что в настоящее время все эти книги давно распроданы и не
переиздаются, оба тома имеются в интернете и доступны для бесплатного
скачивания. В апрельском обзоре Nature за 1922 год Харди почти с издевкой
совершенно ясно дал понять, что ему не нравятся работы Эдвардса («Книга
мистера Эдвардса может служить напоминанием о том, что начало
девятнадцатого века еще не умерло, и ее нельзя рассматривать как серьезный вклад
в анализ»). В конце, признав, что в книге есть что-то хорошее, Харди не
удержался и бросил Эдвардсу в утешение последнюю фразу: «короче говоря, книга
может быть полезна достаточно опытному преподавателю, при условии что
он постарается не допустить, чтобы она попала в руки его ученика». Ну, я не
согласен. Я нашел трактат Эдвардса потрясающим чтением, сундуком с
сокровищами, наполненным математическими драгоценными камнями.
Некоторые из них вы найдете в этой книге. Она включает также десятки
задач с подробными решениями в конце книги, если вы застряли.
Наслаждайтесь!
Дарем, Нью-Хэмпшир (Durham, NH) Пол Дж. Нахин (Paul J. Nahin)
Глава
ι
Введение
1.1. Интеграл Римана
Непосредственная цель этого вступительного раздела - рассмотреть вопрос
о том, сможете ли вы понять технические комментарии в книге. Говоря прямо,
знаете ли вы, что такое интеграл? Вы можете смело пропустить следующие
несколько абзацев, если это окажется «старой шляпой», но, возможно, для
некоторых это будет полезно. Изложение будет гораздо менее строго, чем хотелось
бы чистому математику, и я намерен просто определить терминологию.
Если у = f(x) - некоторая (любая) «достаточно хорошая» функция (если вы
сумеете ее рисовать, то для нас это и будет «достаточно хорошая»), то
определенный интеграл от функции f(x), где χ изменяется от χ = а до χ = Ь, - это
площадь (число, полностью определенное с помощью а, Ъ и f(x)) фигуры,
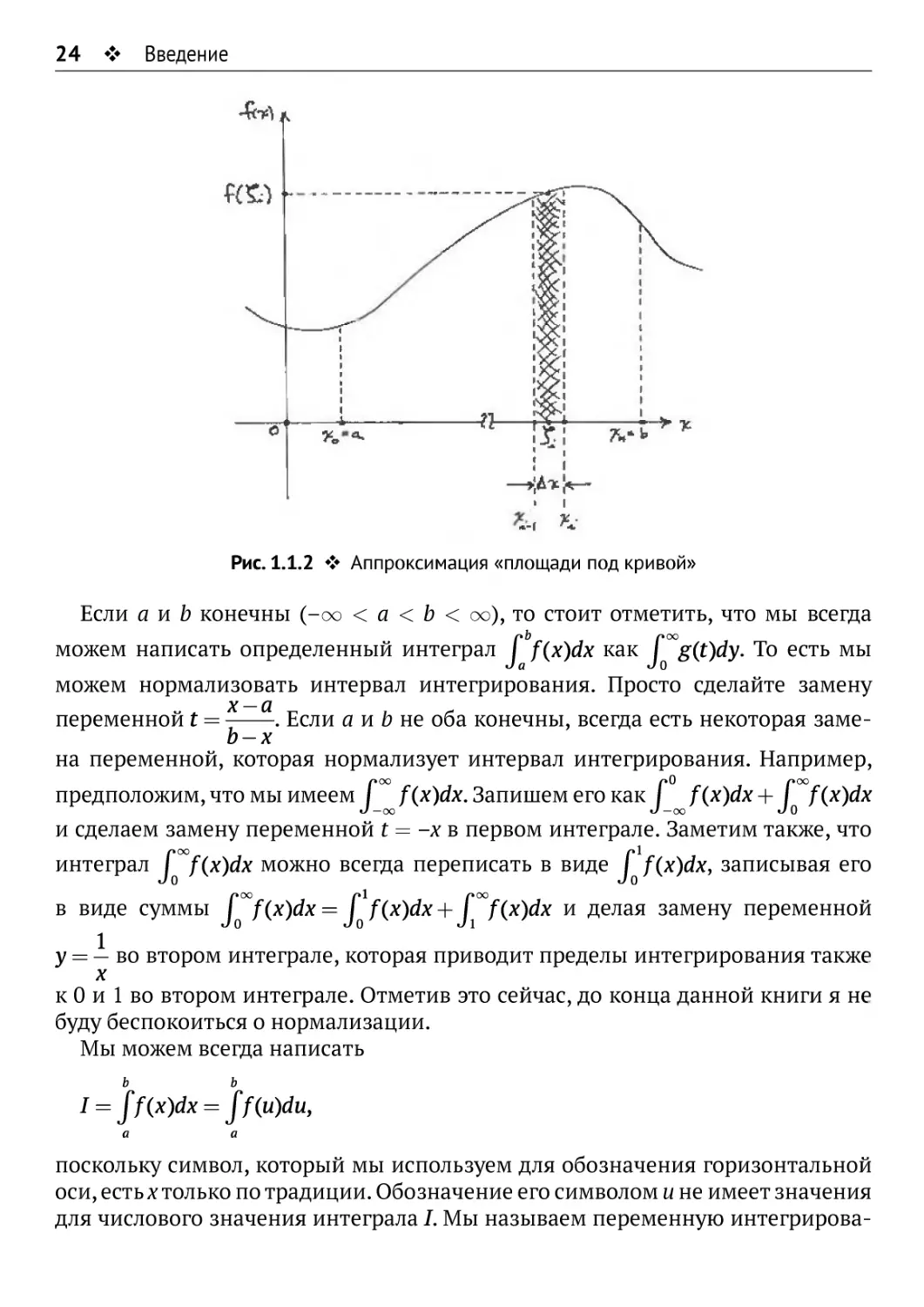
ограниченной функцией f(x) и осью Ох. Это, по сути, затененная область, показанная
на рис. 1.1.1. Вот почему вы часто увидите фразу «область под кривой» в этой
и других книгах по интегралам. (Мы будем иметь дело в основном с вещест-
венно-значными функциями в этой книге, но в конце будет довольно много
обсуждений, касающихся комплексных функций.) На рисунке я показал f(x),
пересекающую х-осъ при χ = с; площадь выше оси Ох (от χ = а до χ = с) - это
положительная площадь, в то время как площадь ниже оси Ох (от χ = с до χ = Ъ)
является отрицательной.
У*
Λ*)
-^х
Рис. 1.1.1 ♦ Определенный интеграл Римана
Интеграл Римана ♦ 23
Этот интеграл, называемый интегралом Римана, - в честь гениального
немецкого математика Бернгарда Римана (1826-1866) - мы записываем в мате-
f(x)dx, где удлиненное S (это знак интеграла!)
а
означает суммирование. Стоит взглянуть на то, как строится интеграл Римана,
потому что не все функции имеют интеграл Римана (это функции, которые
ведут себя «нехорошо»). Я покажу вам такую функцию в разделе 1.3. Идеи Римана
датируются 1854 годом.
Суммирование вступает в игру, потому что интеграл на самом деле является
предельным значением бесконечного числа членов в сумме. Вот как это
происходит. Чтобы вычислить площадь под кривой, представьте, что интервал
интегрирования по оси хот а до Ъ разделен на η подынтервалов, при этом z-й
подынтервал имеет длину Δχ,·. То есть если конечные точки подынтервалов - это
а = х0 < хх < х2 <... < хм < xt < ... < хп_х <хп = Ь,
тогда
Ахг = *;-*;_!, i= 1,2,..., п.
Если мы сделаем подынтервалы равной длины, то
xt = a + -(b-a),
η
откуда получаем
л л Ь~а
Δχ. = Δχ = .
η
Мы предполагаем на данный момент, что η - это некоторое конечное (но
«большое») целое число, что означает, что Ах является «малым».
Действительно, мы предполагаем, что Ах настолько мало, что Дх),
рассматриваемая на подынтервале, изменяется лишь незначительно на протяжении
всего подынтервала. Пусть ζ,- - любое значение переменной χ в интервале
*,·-ι < ζ/ < Xi- Теперь площадь, ограниченная f(x) над этим подынтервалом,
является просто площадью очень тонкого вертикального прямоугольника высоты
f(Q и горизонтальной ширины Ах, то есть площадью, равной f(QAx.
(Затененная вертикальная полоса на рис. 1.1.2.) Если мы сложим все эти прямоугольные
области от χ = а до χ = Ь, то получим очень хорошее приближение к общей
площади под кривой от от χ = а до χ = Ь, причем приближение становится
только лучше, когда η —> оо, и тогда Ах —> 0 (отдельные прямоугольные ленты
становятся тоньше и тоньше). То есть значение / интеграла задается так:
I = limjyut)bx= fbf(x)dx,
ι=1
где символ суммирования стал символом интеграла, а Ах стал
дифференциалом ах. Будем называть f(x) подынтегральным выражением, а а и Ъ - нижним
и верхним пределами интегрирования соответственно.
24 ♦ Введение
-frtf
KUU
5й· *■
-n-
"ГЦ
KA^l·
л**ь
->χ
Рис. 1.1.2 ♦ Аппроксимация «площади под кривой»
Если а и Ь конечны (-оо < а < b < оо), то стоит отметить, что мы всегда
J-»b poo
f(x)dx как / g(t)dy. To есть мы
можем нормализовать интервал интегрирования. Просто сделайте замену
переменной t = . Если а и Ъ не оба конечны, всегда есть некоторая заме-
Ъ-х
на переменной, которая нормализует интервал интегрирования. Например,
/ОО рО рОО
f(x)dx. Запишем его как I f(x)dx+ I f(x)dx
-оо J—оо JO
и сделаем замену переменной £ = -х в первом интеграле. Заметим также, что
J^oo nl
f(x)dx можно всегда переписать в виде / f(x)dx, записывая его
о J о
/»оо п\ роо
в виде суммы J f(x)dx = J f(x)dx + I f{x)dx и делая замену переменной
1
у = — во втором интеграле, которая приводит пределы интегрирования также
к 0 и 1 во втором интеграле. Отметив это сейчас, до конца данной книги я не
буду беспокоиться о нормализации.
Мы можем всегда написать
I = ff(x)dx = ff(u)du,
поскольку символ, который мы используем для обозначения горизонтальной
оси, есть столько по традиции. Обозначение его символом и не имеет значения
для числового значения интеграла /. Мы называем переменную интегрирова-
Интеграл Римана ♦ 25
ния фиктивной переменной интегрирования. Предположим, что мы
используем и в качестве фиктивной переменной, и заменим верхний предел в
интеграле переменной х, а нижний - минус бесконечностью. Теперь у нас больше нет
определенного интеграла с конкретным числовым значением, а есть функция
от х. То есть
F(x)=jf(u)duy
— оо
и наш первоначальный определенный интеграл задается формулой
ъ
I = F(b)-F(a) = ff(u)du.
а
Какова связь между F(x) и f(x)? Напомним, что из определения производной
мы имеем:
_ = 11ш = 11Ш -~mdu-J-J(u)du =
dx Δ*^° Αχ Δ*^° Αχ
/χ+Δχ
= mil—^ = ^—t- = f{x),
где равенства в последней строке выполняются, потому что f(x) по существу
является константой в интервале интегрирования длины Ах. Интегрирование
и дифференцирование - это взаимно обратные операции друг к другу.
Поскольку производная любой константы С равна нулю, мы записываем так
называемый неопределенный интеграл (интеграл без верхнего и нижнего
пределов) как
F(x) + C = ff(x)dx.
Таким образом, один из способов найти интегралы - просто найти функцию
F(x), которая при дифференцировании дает подынтегральное выражение f(x).
Это называется «поискать в таблице», и это отличный способ брать интегралы,
когда у вас есть таблица с нужным вам выражением.
Что вы делаете, когда такой записи нет? Вот тогда все становится
«интересным»! Вам нужно будет либо получить более обширную таблицу пар F(x) <r+ f(x),
либо создать F(x) для себя. Или, может быть, неохотно, но придется признать
тот факт, что, возможно, для конкретной функции Дх), которая у вас есть,
просто нет соответствующей функции F(x). Удивительно, однако, что в последнем
случае может случиться так, что хотя F(x) не существует, все же может
существовать вычислимое выражение для определенного интеграла для конкретных
значений пределов интегрирования. Например, не существует F(x) для f(x) = е~х\
и все, что мы можем написать для неопределенного интеграла, - это допущение
26 ♦ Введение
Je^dx
И все же (как будет показано позже в этой книге) мы можем написать
определенный интеграл
ОО -ι
о 2
Это все о том, как близко к чуду то, что вы получаете в математике.
Л"
■^тМ
Ни
с WUtt |Н 5 . wt>.
Рисунок использован с согласия Сидни Харриса,
ScienceCartoonsPLus.com
На рисунке: «Здесь происходит какое-то чудо...».
Под рисунком: «Спасибо, но вы должны быть
более аккуратными здесь, на втором шаге»
1.2. Примеры риманова интегрирования
Вот относительно небольшие вычисления, которые наглядно демонстрируют
пространственную интерпретацию интеграла Римана. Рассмотрим
совокупность всех точек (х, у), которые вместе образуют область R в л^у-плоскости, с
условием \х\ + |у| < 1, где -1 < χ < 1. Какова площадь этой области R? Решение
относительно у дает
Примеры риманова интегрирования ♦ 27
1у К 1 - М,
что является краткой версией двойного неравенства
-(1-W) = y2<y< 1-M=yi.
Рассмотрим отдельно случай χ > 0 и случай χ < 0.
Случай 1. Если χ > 0, тогда \х\ =х,и двойное неравенство принимает вид
-(1-х) = у2<у< 1-х = уи
и часть площади R для χ > 0 есть
f(y1-y2)dx = f((l-x) + a-x))dx = f(2-2x)dx =
0 0 0
= (2х-х2)\[ =2-1 = 1.
Случай 2. Если χ < 0, тогда \х\ = -х, и двойное неравенство принимает вид
-(1+х) = у2<у< 1+х = уи
и часть площади R для χ < 0 есть
0 0 0
-1 -1 -1
= (2х + х2)|° =2-1 = 1.
Так что площадь всей области R равна 2.
Обратите внимание, что мы сделали все расчеты, не заботясь о форме R. Но
как выглядит R? Если бы мы знали это, то, возможно, площадь была бы
очевидна (так и будет!). Для χ > 0 мы имеем неравенство
1у К 1 - М,
которое говорит, что одна сторона R есть
уа(х) = 1-х, х>0,
а другая сторона R есть
уь(*) = -(1-*) = -(1+*), х>0.
Для χ < 0 мы имеем
Μ + \у\ < 1,
или, поскольку |х| = -х для χ < 0,
|у|<1+*.
Тогда третья сторона R есть
ус(*) = 1+*, х<0,
28 ♦ Введение
а четвертая сторона R есть линия
у,(х) = -(1+х) = -!-*, *<0.
На рис. 1.2.1 показаны эти четыре стороны, и мы видим, что R - это
повернутый (на 45°) квадрат с центром в начале координат с длиной стороны V2. То есть
он имеет площадь, равную 2, как мы и рассчитали с помощью интеграла Римана.
Рис. 1.2.1 ♦ Область R - это затененный повернутый квадрат
1.3. Интеграл Лебега
Теперь, чтобы быть честным с инженерами, читающими это (и чтобы избежать
презрительного осуждения математиками, читающими это!), я должен взять
здесь тайм-аут и сказать вам, что интеграл Римана (и его интерпретация
площади) не является концом пути, когда речь идет об интегрировании. В 1902
году французский математик Анри Лебег (1875-1941) расширил интеграл
Римана, чтобы иметь возможность обрабатывать подынтегральные функции,
которые не очевидным способом ограничивают область. Такие функции есть;
вероятно, самой известной является та, которая была построена в 1829 году
немецким математиком Леженом Дирихле (1805-1859).
[1, если χ рационально
φ(χ) = \
[0, если χ иррационально
Попробуйте изобразить график функции φ(χ) - и я уверен, что вы не
сможете! В любом интервале конечной длины есть бесконечно много как
рациональных, так и иррациональных чисел, и функция Дирихле очень занята, дико
прыгая взад-вперед бесконечное число раз от 0 до 1, как лягушка под кофеи-
Интеграл Лебега ♦ 29
ном с высоким сахаром (то, что рациональные числа являются счетной
бесконечностью, а иррациональные числа - несчетной бесконечностью, - это два
замечательных положения в математике, оба известных благодаря немецкому
математику русского происхождения Георгу Кантору (1845-1918)). И если вы
даже не можете изобразить ее, то как вы можете говорить о функции Дирихле
как «ограничивающей область»? Никак, и функция Дирихле является
примером функции, которая не является интегрируемой в смысле Римана.
Вы можете подумать, что именно бесконечное число разрывных скачков
в пределах конечного интервала делает функцию φ(χ) не интегрируемой по
Риману, но на самом деле можно иметь аналогичную дико разрывную
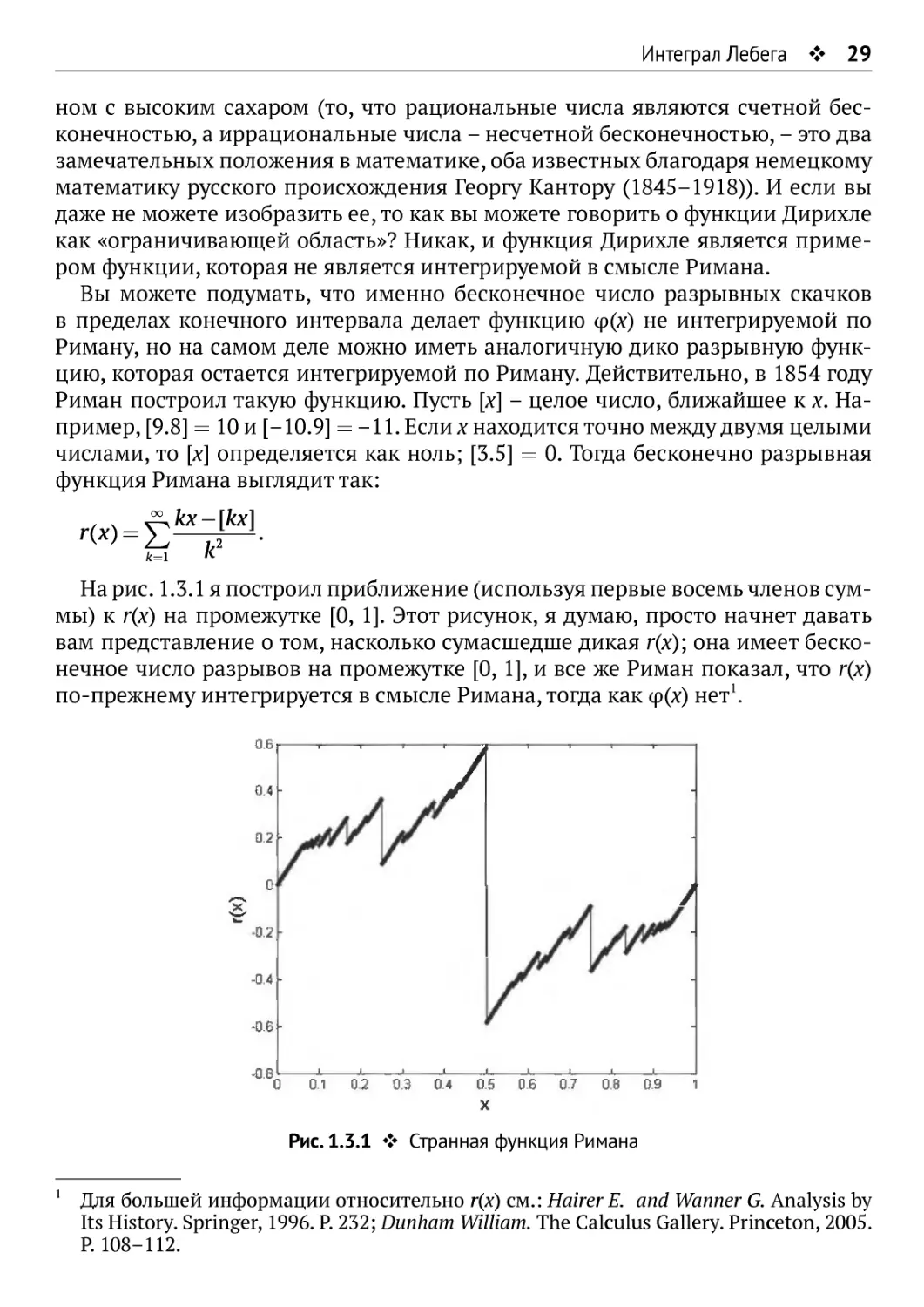
функцию, которая остается интегрируемой по Риману. Действительно, в 1854 году
Риман построил такую функцию. Пусть [х] - целое число, ближайшее к х.
Например, [9.8] = 10и [-10.9] = -11. Если χ находится точно между двумя целыми
числами, то [х] определяется как ноль; [3.5] = 0. Тогда бесконечно разрывная
функция Римана выглядит так:
fe=l
кх-[кх]
На рис. 1.3.1 я построил приближение (используя первые восемь членов
суммы) к г(х) на промежутке [0, 1]. Этот рисунок, я думаю, просто начнет давать
вам представление о том, насколько сумасшедше дикая г(х); она имеет
бесконечное число разрывов на промежутке [0, 1], и все же Риман показал, что г(х)
по-прежнему интегрируется в смысле Римана, тогда как φ(χ) нет1.
и.ь
0.4
Q.2
0
0.2
-0.4
-OR
Г^
-
г
J | J J, _J
ι 1 1 1 1 1
j
/
J
j
L k. i_ X L J
0 0.1 0 2 03 0.4 0.5 0.6 0.7 08 0.9 1
X
Рис. 1.3.1 ♦ Странная функция Римана
1 Для большей информации относительно г(х) см.: Hairer Ε. and Wanner G. Analysis by
Its History. Springer, 1996. P. 232; Dunham William. The Calculus Gallery. Princeton, 2005.
P. 108-112.
30 ♦ Введение
Однако функция Дирихле интегрируема в смысле Лебега. Вместо того чтобы
делить интервал интегрирования на подынтервалы, как в интеграле Римана,
интеграл Лебега делит интервал интегрирования на множества точек.
Центральным интеллектуальным вкладом Лебега было введение концепции меры
множества. Мерой подынтервала Римана была просто его длина. Интеграл
Римана, таким образом, является лишь частным случаем интеграла Лебега,
поскольку подынтервал является лишь одним конкретным способом
определения множества точек; но есть и другие способы. Когда существует интеграл
Римана, существует и интеграл Лебега, но обратное неверно. Когда оба
интеграла существуют, они равны.
Чтобы увидеть, как это работает, давайте вычислим интеграл Лебега φ(χ) на
промежутке [0, 1]. На этом интервале сначала сфокусируемся на всех
рациональных значениях х, имеющих конкретное целое число η в знаменателе
дроби т/п (по определению, это общая форма рационального числа). Для данного
и, которое мы выбрали, мы видим, что т может изменяться от 0 до и, то есть
существует η + 1 таких рациональных значений (точек) вдоль оси хот 0 до 1.
Теперь представьте себе каждую из этих точек вложенной в интервал длины —,
η
где ε - сколь угодно малое (но ненулевое) положительное число. Это означает,
что мы можем представить себе сколь угодно малый интервал ненулевой
длины. Общая длина всех η + 1 интервалов равна
1Ч ε ε ε
(и + l)—= —+ —.
η η η
Напомним, что это все было для конкретного п.
Теперь суммируем по всем возможным и, то есть пусть η пробегает от I до
бесконечности. Повторений, конечно, будет много, например η = 2 и т = I,
η = 26и т = 13 определяют одну и ту же точку. Таким образом, общая длина
всех интервалов, содержащих (охватывающих) все рациональные числа от 0 до
1,не более, чем
ОО 1 ОО 1
Как известно, обе суммы имеют конечные значения (первая - это, конечно,
знаменитый результат Эйлера π2/6, который будет получен в главе 7, а вторая
сумма явно еще меньше). Дело в том, что общая сумма в скобках имеет
некоторое конечное значение S, и поэтому общая длина всех интервалов,
охватывающих все рациональные числа от 0 до 1, не превышает ε£, и мы можем сделать
это число настолько маленьким, насколько захотим, просто выбирая все
меньшие значения для ε. Говорят, что лебегова мера множества всех рациональных
чисел от 0 до 1 равна нулю, и тогда в смысле Лебега мы имеем1:
Теперь промежуток [0, 1] разбивается всего на два подмножества. На одном из них
функция может достигать значения 1, но мера этого подмножества не превышает ε5,
на втором подмножестве функция равна нулю. Поэтому интегральная сумма не
превосходит eS и стремится к 0 при ε —> 0. - Прим. перев.
«Интересно» и «секреты» ♦ 31
1
§φ(χ)άχ = 0.
о
Теперь, подводя итог сказанному, я признаю красоту интеграла Лебега, но
и одновременно «скандальный» факт, что в этой книге я не собираюсь
беспокоиться об этом! В 1926 году президент математического общества (Англия)
строго заявил, что «быть серьезным математиком и не использовать интеграл
Лебега - это принять позицию старика в сельской деревне, который
отказывается путешествовать в поезде»1. С другой стороны, американский инженер-
электрик и ученый-компьютерщик Ричард Хэмминг (1915-1998)
несколько кавалеристски опроверг это, когда заявил (в обращении2 к математикам
в 1997 году!):
...на протяжении более 40лет я утверждал, что если бы полет самолета
зависел от того, была ли какая-то функция, возникшая в его конструкции,
интегрируема по Лебегу, а не по Риману, то я бы не летал в нем. А ты бы
полетел? Признает ли природа эту разницу? Я сомневаюсь! Вы можете,
конечно, выбирать, что вам угодно, в этом вопросе, но я заметил, что год
за годом интегрирование Лебега, да и вся теория меры, кажется, играет
все меньшую и меньшую роль в других областях математики, иные одной
из тех, которые просто используют математику [мой акцент].
Я думаю, что у Хэмминга более сильная позиция, и все интегралы, которые
вы увидите в этой книге, следует понимать как интегралы Римана.
Для математиков, у которых может возникнуть соблазн отклонить слова
Хэмминга фразой «Ну, что еще вы ожидаете от инженера!», позвольте мне
отметить, что за год до выступления Хэмминга один математик сказал, по сути,
то же самое в статье, которую Хэмминг наверняка читал. Признав, что
интеграл Лебега «стал "официальным" интегралом в математических
исследованиях», Роберт Бартл (1927-2003) затем заявил, что «пришло время отказаться от
интеграла Лебега как первого интеграла [акцент Бартл а]»3.
1.4. «Интересно» и «секреты»
Итак, что такое интересный интеграл и что значит говорить о том, что он
имеет «секреты»? Я полагаю, что честный ответ на «интересную» часть
примерно соответствует знаменитому комментарию судьи Верховного суда Поттера
1 Комментарий, сделанный после презентации статьи: Francis E. С. Modern Theories of
Integration//The Mathematical Gazette. March 1926. P. 72-77.
2 В статье Hamming's: Mathematics On a Distant Planet // The American Mathematical
Monthly. August-September 1998. P. 640-650.
3 См. отмеченную наградами статью Bartle's: Return to the Riemann Integral // The
American Mathematical Monthly. October 1996. P. 625-632. Он был профессором
математики в университете штата Иллинойс в течение многих лет, а затем в
университете Восточного Мичигана.
32 ♦ Введение
Стюарта 1964 года: на вопрос «Что такое порнография?» он признал, что это
трудно определить, «но я знаю это, когда вижу». То же самое и с интересным
интегралом!
В 1957 году летом на каникулах перед старшими классами средней школы
я купил копию второго издания знаменитого учебника Джорджа Б. Томаса
«Математический анализ и аналитическая геометрия» для занятий в летней
школе в местном колледже. Я до сих пор помню волнение, которое испытал,
когда, пролистывая страницы в первый раз, столкнулся (на стр. 369) со
следующим (Томас говорит, что это из «теории подъемной силы» аэродинамики):
ах = π.
ιΜι
Почему я, еще ребенок, не достигший и семнадцати лет, который еще
недавно строил модели самолетов из комплектов бальзового дерева и протекающих
тюбиков клея, нашел это «интересным»? Я не знал тогда - и я не уверен, что
знаю даже сейчас, - за исключением того, что это выглядит просто
«таинственным и экзотическим».
Теперь некоторые могут посмеяться над этим, но мне все равно - мне
кажется, что аэродинамический интеграл все еще выглядит таинственным и
экзотическим! Эта строка с формулой - такая же замечательная строка, как и все, что
вы найдете у Хемингуэя или Достоевского, но, в отличие от даже величайшей
фантастики, это строка, которую никто не мог просто выдумать. В конце
концов, какое отношение к π имеют все эти странные (для меня) вещи в левой
части знака равенства? Конечно, я знал даже в те давние времена, что они тесно
связаны с кругами, но я не видел никаких кругов слева. Интересно!
Такая эмоциональная реакция не ограничивается только математиками-
любителями; профессионалы могут быть охвачены той же эйфорией.
Например, в 1935 году в конце своего президентского обращения к Лондонскому
математическому обществу английский математик Г. Н. Уотсон (1886-1965)
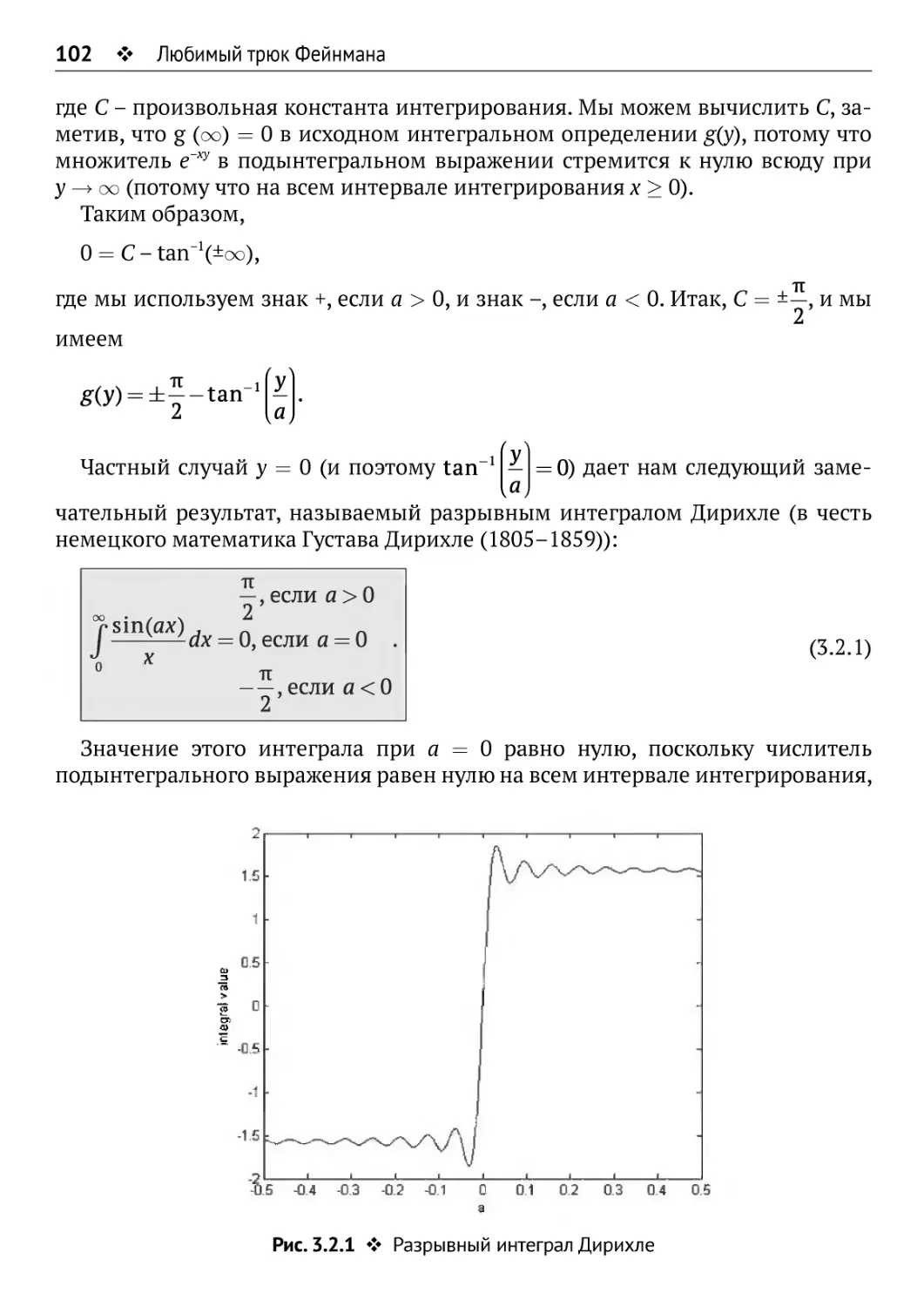
упомянул этот удивительный определенный интеграл:
? w sinhQix) 1 ^ е-2"("+1)"
•J sinh(3ux) eW3V3 ^(l + e-u)2(l + e-3u)2...(l + e-(2n+1)u)2'
Он заявил, что это дало ему «острые ощущения, неотличимые от острых
ощущений, которые я испытываю, когда вхожу в Новую Ризницу Капеллы
Медичи и вижу перед собой строгую красоту четырех статуй, представляющих
День, Ночь, Вечер и Рассвет, который Микеланджело поставил над могилами
Джулиано Медичи и Лоренцо Медичи».
Вот это да!
Хорошо, теперь что значит «секреты интегралов»? Я постараюсь ответить на
это примером. Предположим, я говорю вам, что
Некоторые примеры трюков ♦ 33
{ 1 + х2 8
Вы, вероятно, просто пожмете плечами и скажете (или, по крайней мере,
подумаете, если будете слишком вежливы, чтобы это сказать): «Хорошо. Откуда
ты это взял, из хорошей таблицы интегралов? Какую из них ты использовал?
Я тоже посмотрю, что там». И вы могли бы, но могли бы вы получить результат?
Вот что я имею в виду, говоря о «секретах» интегралов. Это искусство начинать
с интеграла по левую сторону от знака равенства и каким-то образом
вычислять выражение с правой стороны. (Мы найдем этот интеграл позже в книге,
см. (2.2.4).)
Я намеренно использую слово искусство. Нет теории для нахождения
определенных интегралов. Каждый новый интеграл - это совершенно новый
вызов, и каждый новый вызов почти всегда требует нового трюка или, по крайней
мере, одного или двух обращений к предыдущему трюку. Это вправду трюк.
Некоторые люди могут в ужасе отшатнуться, но настоящий аналитик просто
улыбается с предвкушением обещания праведной борьбы. И даже если
интеграл выигрывает на данный момент, оставляя аналитика в изнеможении
и с мучительной головной болью, аналитик знает, что всегда есть завтра, когда
можно попытаться снова.
1.5. Некоторые примеры трюков
Теперь, просто чтобы вы знали, о чем я говорю, когда использую слово «трюк»,
вот первый пример трюка в этой книге (остальная часть этой книги - по сути,
всего лишь один новый трюк за другим!). Что стоит в интеграле справа
V1/x+i
Этот интеграл почти наверняка выглядит довольно страшно почти всем
с первого взгляда; попытка найти функцию F(x), при дифференцировании
которой получается подынтегральное выражение, конечно, не кажется
многообещающей. Но на самом деле этот определенный интеграл может решить
даже первокурсник, если увидит хитрость! Поэкспериментируйте с этим
некоторое время, пока я прокладываю себе путь к потрясающему откровению
ответа, и посмотрим, сможете ли вы победить меня в этом.
Рассмотрим более простой интеграл
г COS* ,
Ι ι dxy
где d(x) - это любая функция отх, какая вам нравится. (Для исходного
интеграла d(x) = е(1/х).) Я наложу небольшое ограничение на d(x), но не сейчас. Если мы
напишем
34 ♦ Введение
, ч cos*
£(*) = -
с/(лг) + 1'
тогда мы приходим (конечно!) к интегралу
1
fg(x)dx.
Не важно, что представляет из себя g(x), мы всегда можем записать ее как
сумму четной функции ge(x) и нечетной функции g0(x). To есть
g(x)=ge(x)+g0(x).
Откуда мы знаем, что можем это сделать? Да потому, что мы можем всегда
записать, что такое ge(x) и g0(x). По определениям четной и нечетной функций
мы имеем:
<?(-*) = &(-*) + &(-*) = &(*) ~ g0(x),
и простая алгебраическая выкладка приводит нас к равенствам:
И
/ ч g(x)-g(~x)
g0(x)=by 2όν—^.
Теперь
1111
Jg(x)dx = Jge (x)dx + Jg0 (x)dx = Jge (x)dx,
-1 -1 -1 -1
потому что благодаря «симметрии» нечетной функции относительно χ = 0 мы
имеем (представьте себе «область под кривой»):
fgo(x)dx = 0.
-ι
Для нашего первоначального интеграла мы имеем:
, ч COS*
d(x) + l
и тогда
8М) = \
cosx cos(-x)
d(x) + l + d(-x) + l
или поскольку cos(-x) = -cos(x), то есть потому что косинус является четной
функцией:
Некоторые примеры трюков ♦ 35
&(*) =
COS*
1
1
COS*
или
ieW:
COS*
d(x) + l d(-x) + l]
2 + d(-x) + d(x)
d(-x) + l + d(x) + l
d(x)d(-x) + d(x) + d(-x) + l
d(x)d(-x) + d(x) + rf(-x) +1
Хорошо, предположим, что теперь мы наложили ограничение на d(x).
Предположим, что d(x) d(-x) = 1. Вы заметите, что это как раз тот случай, и для d(x)
в нашем исходном интеграле (d(x) = е(1/х)), потому что
d(x) d(-x):
: е(1/х)е(-1Д) :
1.
Итак, теперь вы должны увидеть, что числитель и знаменатель всего этого
хлама в скобках в правой части последнего выражения для ge(x) равны! То есть
все в скобках сводится к 1, и тогда
geW-
COSX
и наш страшный интеграл исчез, как воздушный шарик, уколотый булавкой:
/■COS(*) , fCOS(x) . lr . ч , lr . f 0ιΐ
sin(l)-sin(-l)
:sin(l) = 0.8414709...
Вот это трюк! Функция интегрирования quad MATLAB соглашается, вычисляя
значение 0,8414623. Синтаксис кода: quad(@(x)cos(x)./(exp(l./x) + 1), 1,1).
Это был довольно сложный прием, но иногда даже приемы довольно
низкого уровня могут привести к «хитрым» успехам. Например, каково значение
1П(АГ)
/
1
-dx
поо nl поо
Давайте начнем с очевидного равенства J = J + J .В первом интеграле
справа сделаем замену переменной t = 1/х (и тогда dx = -dt/t2). Тогда
rln(»). 'Mt]t ι .Λ r'nt,, r'uL find),,
В записи sin(l) имеется в виду, что это синус 1 радиана, равного
1 градус).
180°
= 57,3° (не
36 ♦ Введение
То есть, признавая, что t и χ являются всего лишь фиктивными переменны-
п\ поо
ми интегрирования, мы имеем / = — / .И поэтому мы немедленно получаем
наш результат (первоначально полученный Эйлером):
1п(х)
Jo 1 + АГ2
(1.5.1)
На самом деле это частный случай более общего интеграла
1п(х)
/
0Ь2+х2
dx.
Посмотрите, сможете ли вы вычислить этот интеграл (ваш ответ, конечно,
должен сводиться к нулю, когда Ъ = 1); если у вас возникнут проблемы, мы
найдем этот интеграл в следующей главе - в (2.1.3), где вы увидите, что знание
специального случая помогает (очень много!) и при выполнении общего случая.
В качестве третьего примера трюка позвольте мне показать вам пример,
демонстрирующий, насколько умными могут быть новички в интегральном
исчислении, когда надо вычислить значение определенного интеграла. Этот
трюк восходит к 1719 году, когда итальянский математик Джулио Фаньяно
ОО Ί
(1682-1766) вычислил Г— -. Конечно, сегодня даже первокурсник сразу
о <* +х
узнает неопределенный интеграл, равный tan"1^)1, и поэтому ответом будет
tan_1(oo) - tan_1(0) = π/2. Но хитроумный трюк Фаньяно требует не знания
неопределенного интеграла2, а только умения дифференцировать. Вот как это
сделал Фаньяно.
Представьте себе круг с радиусом г с центром в начале координатной
плоскости. Длина дуги L вдоль окружности этого круга, которая опирается на
центральный угол Θ, находится по формуле L = γΘ. Теперь предположим, что г = 1.
Тогда L = Θ, и тогда с t в качестве фиктивной переменной интегрирования
имеем:
В книге используется мало распространенное у нас обозначение tan_1(A:) для функции
arctg(x), и также обозначение функции тангенса у нас tg(x), а в книге tan(x). - Прим.
перев.
г 1
Я предполагаю, что когда вы видите / — -dx, то сразу определяете это как
J сг + х2
1 ( λ
—tan-1 — . Это один из немногих «фундаментальных» неопределенных интегралов,
а [а)
который, по моему предположению, вы видели ранее на первом курсе
математического анализа. Другие табличные интегралы: Г—dx = \n\x\, Jexdx = ex,
/yn+1 г dx _i г
xndx = -—, η * -1, Ι ι = sin" (χ) и / \n(x)dx = χ · 1η(χ) - χ.
п + l J Vl-x2 J
Некоторые примеры трюков ♦ 37
О
L = e = fdt.
Затем Фаньяно поиграл с этим очень простым подынтегральным
выражением (в самом деле, что может быть проще?!?), чтобы сделать его более сложным!
В частности:
1 1 1
L= [<°Ш&= Г ™^\ dt= Г «"'(О dtm
J0 1 J0 cos2(Q + sin2(0 J0 l + tan2(t)
cos2(t) cos2(t)
Затем замена переменной χ = tan(t) показывает:
dx
cos2(t)'
i ι+χ2
Тогда
ta„(e) ^
"o l + <
Предположим, что θ = π/2. Тогда tan (θ) = tan (π/2) = oo, и, конечно, длина L
составляет одну четвертую окружности круга и поэтому равна π/2, потому что
π/2 составляет одну четвертую от 2π, длины окружности круга с единичным
радиусом. Таким образом, моментально получаем:
π _°f dx
По тем же соображениям мы сразу имеем:
dx
π _ г ах
Тъ dx
π _ г ах
Ъ~1Т+х~
+ гг
Гъ,ъ dx
π _ г ах
Довольно умно!
38 ♦ Введение
1.6. Особенности
Трюки изящны, и открытие каждого нового похоже на острые ощущения,
которые вы получаете, когда копаетесь в коробке с изюмом (подумайте о
«рутинных» методах интегрирования, это тоже хорошо для вас, да, но скучно) и время
от времени натыкаетесь на арахис в шоколаде (подумайте, «фантастический
новый трюк»). Но нужно всегда быть начеку, чтобы не попасть в ловушку,
против которой, мы надеемся, функция quad из MATLAB будет нашей последней
защитой. Вот пример того, что я имею в виду, когда эта самая распространенная
операция - слепое подчинение стандартной формуле интегрирования - может
привести к катастрофе.
Предположим, что мы имеем интеграл I = / —. Подынтегральная функция
iif
f(x) = — всюду неотрицательна, поскольку она является квадратом вещест-
{х)
венного значения (от -1 до 1). Таким образом, из области интерпретации
интеграла Римана мы сразу узнаем, что / > 0. Однако из дифференциального
исчисления мы также знаем, что
dl
dx{
1
X
=
1
х1
и поэтому, интегрируя, имеем
/ =
1
г
X .
il
1
1
1
-1
=
1-1:
Это точно, минус 2, что, безусловно, меньше нуля. Что здесь происходит?
Проблема в том, что f(x) имеет разрыв при χ = 0, прямо в середине
интервала интегрирования. Этот интеграл называется несобственным, а х = 0
называется особенностью. Вы должны всегда быть внимательны к особенностям,
когда имеете дело с интегралами; всегда держитесь подальше от особенностей.
Особенности - это черные дыры интегралов; не попадайте в одну из них (не
интегрируйте через особенность). Вы обнаружите, что когда мы доберемся
до контурного интегрирования, это будет очень важно иметь в виду. Вот как
это сделать для нашего интеграла. Мы напишем / следующим образом, где ε -
сколь угодно малая положительная величина:
\άχ Λ. ~Ь άχ Λ. \άχ
1= \ — = hm / —- + hm I —.
Χ ε->οο J χΔ ε->οο J χΔ
Особенности ♦ 39
Тогда
/ = lim
ε—»οο
= lim
ε—>οο
--1
ν χ)
-ε
+ lim
ε—»οο
1-1
1-1-1+Ц
ε
ε
--]
{ χ)
= lim
ε—>οο
1
= lim
ε—»οο
ε
'2
[ε]
1
—ε
-2 = +οο.
' J_]
[-lj
+ lim
ε—»οο
1
[ 1
ί 4
{ ε)\
Этот интеграл (как мы и ожидали) положителен - на самом деле он
бесконечно положителен! Это, конечно, не отрицательно. Заметьте также, что наш
первый (неправильный) результат -2 теперь понятен - он прямо в правильном
ответе вместе с бесконечным вкладом сингулярности, который мы изначально
пропустили.
Теперь, чтобы увидеть, действительно ли вы поняли проблему с
вышеуказанным интегралом, рассмотрите следующий интеграл, который стал
известным в математической физике благодаря лауреату Нобелевской премии
Ричарду Фейнману (1918-1988): если а и Ь являются произвольными вещест-
венно-значными постоянными, то
г
1 А 1
[яаг + Ь(1-аг)]2 ab
(1.6.1)
Вы видите здесь проблему? Если а и Ь имеют противоположные
алгебраические знаки, то правая часть приведенной выше формулы отрицательна. Но
с левой стороны подынтегральное выражение всегда является чем-то в
квадрате, независимо от того, какими могут быть а и Ь, и поэтому подынтегральное
выражение никогда не бывает отрицательным. У нас, кажется, есть конфликт.
Что здесь происходит? Подсказка: спросите себя, есть ли у подынтегральной
функции особенность, и если да, где она находится1? (См. задачу Ъ в конце этой
главы.)
Прежде чем покинуть тему сингулярностей, я должен сказать вам, что
существуют и другие проблемы с бесконечностью, помимо разрывности
подынтегрального выражения, которые могут возникнуть при выполнении интегра-
f(x)dx? Интерпретация
-оо
интеграла Римана через площадь в этом случае может не сработать, даже если
f(x) - «хорошая» функция. Например, сколько площади находится под кривой
f(x) = sin(x), -оо < χ < оо? Поскольку sin(x) - нечетная функция, кажется, мы
должны утверждать, что всегда есть часть отрицательной области, которая отменяет
каждую часть положительной области, и поэтому мы хотели бы написать
1 Этот интеграл появился в известной работе Фейнмана: Space-Time Approach to
Quantum Electrodynamics//Physical Review. September 15,1949. P. 769-789. Некоторая
историческая дискуссия об интеграле содержится в моей книге Number-Crunching.
Princeton, 2011. P. xx-xxi.
40 ♦ Введение
оо
fsin(x)dx = 0.
Но что тогда с площадью под кривой f(x) = cos(x), -оо < χ < оо? Теперь у нас
есть четная функция (это просто сдвинутая синусоидальная функция!). Но мы
все еще можем использовать аргумент сокращения
отрицательных/положительных площадей области; итак, это правда, что
оо оо
fcos(x)dx = 2 fcos(x)dx = 0.
-оо 0
Следовательно, это правда, что
оо
fcos(x)dx = 0?
о
поо поо
Ответ - нет, не существует ни / sin(x)dx, ни / cos(x)dx. Мы можем, од-
J—оо J—оо
нако, написать то, что математики называют главным значением Коши
интеграла:
ОО Л
Jf(x)dx = limjf(x)dx,
интеграл, который равен нулю, если fix) нечетно. Этот подход, использующий
операцию симметричного ограничения области интегрирования, означает,
/оо
sin(x)dx действительно существует (оно
-оо
равно нулю), даже если интеграл не существует.
Однако если у нас есть подынтегральная функция Дх), такая что limx_+±00f(x) = 0
и стремится к нулю «достаточно быстро», что означает, например, быстрее,
1 , sin(x\
чем — (например, ^-), - тогда у нас нет этих концептуальных трудностей.
χ χ
Но даже этого недостаточно, чтобы полностью охватить все тонкие проблемы,
которые могут возникнуть в бесконечности. Это потому, что подынтегральное
выражение, такое как f(x) = cos (χ2), которое не стремится к нулю при χ —> ±°о,
имеет определенный интеграл по -оо < χ < оо (вы помните этот интеграл,
называемый интегралом Френеля, из предисловия). Это потому, что cos (л^)
колеблется все быстрее и быстрее между ±1, так как χ увеличивается в обоих
направлениях, и поэтому положительные и отрицательные области выше и ниже
оси χ по отдельности стремятся к нулю все быстрее и быстрее и, таким образом,
вносят все меньше и меньше в общую площадь под кривой (площадь, которая
является конечной).
Наш маленький трюк с «подкрадыванием» к сингулярности может быть
довольно мощным. Рассмотрим, например, интересный интеграл
dx
о*3-1'
оо
Особенности ♦ 41
Когда χ находится между 0 и 1, подынтегральное выражение является
отрицательным, тогда как при больших χ подынтегральное выражение
является положительным. Очевидно, что в точке χ = 1 имеется особенность, причем
подынтегральное выражение увеличивается до минус бесконечности, когда
χ приближается к 1 из значений, меньших 1, и уходит в плюс бесконечность,
когда χ приближается к 1 из значений, больших 1. Мы можем задаться
вопросом: возможно ли, чтобы эти два бесконечных разрыва (с противоположными
знаками) могли уничтожить друг друга? На самом деле они это делают, и
чтобы убедить вас в этом, я воспользуюсь уловкой «подкрасться», чтобы написать
наш интеграл как
l~f dx °f dx
а затем исследовать, что происходит, когда ε —> О!
В духе этой книги я впервые использую функцию quad из MATLAB для
экспериментального изучения того, что происходит при ε —> 0. В следующей таблице
я перечислил результат выполнения следующей команды MATLAB для
различных, уменьшающихся значений ε (сохраненных в векторе e(i)):
quad((a(x)l./(x.A3-l),0,l-ei)) + quad((a(x)l./(x.A3-l),l + ei),1000)
ε
0.1
0.01
0.001
0.0001
0.00001
0.000001
0.0000001
l~f dx °f dx
b3-i7+£*3-i
-0.53785
-0.59793
- 0.60393
- 0.60453
- 0.60459
- 0.60459
- 0.60459
Таким образом, из этой вычислительной работы может показаться, что
1-р— = -0.60459.
Хорошо, но что могло быть этим любопытным числом? Оказывается, мы
можем точно ответить на этот вопрос, потому что оказывается возможным
фактически найти неопределенный интеграл! Это потому, что мы можем написать
подынтегральное выражение как разложение на частные (простейшие) дроби:
1 _ 1 2х + 1 1
хъ -1 ~ 3(х-1) 6(х2 +х + 1) 2(х2 +х + 1)
или выделив полный квадрат в знаменателе последнего слагаемого:
42 ♦♦♦ Введение
1
1
2χ + ί
хъ-1 3(х-1) 6(х2+х + 1)
х + :.
1)
+-
Каждый из отдельных членов справа легко интегрируется:
/■
— = -1п(х-1)--1п(аг2+аг + 1)-
3 6
1 ^ _if2x + l)
г tan
-ι з ч ' б ' ' 7з
-{21п(х-1)-1п(а:2+а: + 1)}—^tan"1
I Я Г
f2x + l)
In
In
(χ -Ι)2
χ2 + ί + ί
x2-2x + l
-;=tan
λ/3
2χ + ί
S )
Χ + АГ + 1
^tan"1
л/3
ί л/з" Γ
f2x + l)
{ S J
Аргумент функции log ведет себя хорошо для всех χ в интервале
интегрирования, кроме х = -1, где мы получаем log(O), и поэтому давайте снова
воспользуемся хитростью, но на этот раз аналитически. То есть мы будем
интегрировать от 0 до 1 - ε и добавим его к интегралу от 1 + ε до оо. Потом мы положим
ε —> 0. Итак, заметив, что функция log обращается в ноль при χ = 0 и при χ = оо
(каждый случай дает log (1)), мы имеем:
Г—— = lim
Jnx3-1 ε-°
6
(1-ε)2-2(1-ε) + 1
(1-ε)2
Η—= tan~
л/3
(1-ε) + 1
(■—;=tan
л/3
2(1 - ε)+ 1)
л/3"
+
1
Ιλ/^J
+ lim
-^tan Чоо)—In
у1ъ б
(1 + ε)2-2(1 + ε) + 1
(1 + ε)2+(1 + ε) + 1
+
^
tan
2(1 +ε)+ 1
^
Логарифмические члены раскладываются так:
1
In
1-2ε + ε2-2 + 2ε + 1
1-2ε + ε2 + 1
1
1
In
1 + 2ε + ε2-2-2ε + 1
1 + 2ε + ε2 + 1 + ε + 1
6
ε2-3ε + 3
--1η
6
ε2 + 3ε + 3
6
■3ε + 3
ε2-3ε + 3
Интеграл Далцелла ♦ 43
Поскольку ε —> 0, то последнее логарифмическое выражение, очевидно,
исчезает. Члены с арктангенсом раскладываются так:
л/3
1[2-2ε + ΐ1 1+-ι
1 '-h-^tan
^
л
ι
т itan~1(oo)+itan~
!Γ2 + 2ε + ΐΊ
7з~
^tan"1
V3
ί3-2ε) 1 . j
Ч—=tan г
{ λ/3 j λ/3 1a/3J λ/3
1
1
π
1 . -ιί3 + 2ε)
Η—;=tan
V3
Ι >/з
и, поскольку ε —> 0, это все сводится к выражению:
J_
'S
tan
1
11 ч—^tan 1
[S\ S [&} S
1
1
π
+ -i=tarr1
= -^tarr1
π
j_
s
tan !
' \Л
Ш
π
Ш
7з[б 2
π π
3n/3 9
Итак, наконец:
(1.6.2)
что любопытно, это действительно есть 0,60459.
1.7. Интеграл Далцелла
Остальная часть этой книги содержит просто намного больше трюков,
некоторые даже более впечатляющие, чем тот, который я показал вам в разделе 1.5.
Но почему, спросят некоторые, мы должны изучать фокусы? В конце концов,
с современным компьютерным программным обеспечением даже, казалось
бы, невозможные интегралы могут быть вычислены гораздо быстрее, чем
может выполнить человек. Пожалуйста, поймите, я не говорю о численных
интеграторах, таких как quad MATLAB (хотя и не так быстро, но математики могли
делать такие вещи столетия назад!). Я говорю о символьных интеграторах,
таких как, например, интегратор от программного обеспечения символьного
Mathematica on-line (доступно бесплатно), которому требуется всего лишь доля
секунды для вычисления предыдущего неопределенного аэродинамического
интеграла из введения (раздел. 1.4):
44 ♦ Введение
Вы можете убедиться, что это действительно правильно, просто
дифференцируя правую сторону и наблюдая, как появляется подынтегральное
выражение в интеграле слева. И когда подставляем нижний и верхний пределы -1 и +1
соответственно, мы получаем π, как писал профессор Томас в своей книге.
Я был бы первым, кто признал бы, что использование автоматических
компьютерных интеграторов имеет множество преимуществ. Если бы мне
пришлось вычислять сложный интеграл как часть работы, за которую мне
платили, первое, что я бы сделал, - это обратился бы к Wolfram (хотя, я должен
сказать вам, Wolfram терпит неудачу на неопределенном интеграле Г ^-dx,
J d(x) + l
который мы решили для случая определенного интеграла с нашим
маленьким четно/нечетным трюком, - да, терпит неудачу, почти наверняка, так как
нет неопределенного интеграла). Это признание игнорирует удовольствие от
решения определенных интегралов, это такое же удовольствие, что у многих
людей, когда они разгадывают головоломки судоку. Борьба с головоломками
судоку или с интегралами - это битва умов с «противником» (правилами
математики), который не терпит обмана. Если вы преуспеете в любом из них, это
не удача - это умение.
Теперь, чтобы просто показать вам, что я серьезен, когда говорю, что
решение определенных интегралов может быть забавным, посмотрим на интеграл
*)4л
который впервые появился (в 1944 году) на страницах журнала лондонского
математического общества. Что в этом такого «забавного», спросите вы?
Посмотрите, что мы получаем, когда находим интеграл I. Перемножая числитель,
а затем делая деление результата на знаменатель, мы получаем
I = fix6 - 4xs + 5х4 - Ах2 + 4 -
1 + х2
dx,
что легко интегрируется и дает
гх4(1-аг)4
/= ι - ν- --/ dx
i i+*2
12,4,
= hi \-4-π.
7 3 3
Таким образом:
χ7 2χ6 5
7 3
Ахъ
+ 4x-tan_1(x)
г*4 α-*)4
1 + аг'
dx-
22
7 '
•π.
(1.7.1)
Интеграл Далцелла ♦ 45
Поскольку подынтегральное выражение неотрицательно, мы знаем, что
/ > 0, и поэтому мы имеем неожиданный (и я думаю, совершенно неожидан-
22
ный) результат, что — > π. То есть классическое приближенное значение к π -
это завышенная оценка1, факт, который нелегко установить иным образом.
Наши вычисления на самом деле дают нам больше информации, чем прос-
22
то — > π; мы также можем получить представление о том, насколько хорошо
22
приближение — к π. Если мы заменим знаменатель подынтегрального
выражения на 1, то определенно получим большее значение для интеграла, а если
заменим на 2, получим меньшее значение для интеграла. То есть:
Jo 2 { 1 + х2 7 {
или перемножая, интегрируя и подставляя пределы:
1
2
(_1_2 6_1 J.
5 3 + 7 2+9
1 22
< π<
1260 7
1.2 6__1 1
5 3 + 7 2+9
630
или умножив на -1 (что меняет направление неравенства):
1 22 1
<π <--
630 7 1260
или,наконец:
22 1 22 1
<π<
7 630 7 1260
Это показывает, что с точностью до пяти знаков после запятой 3.14127 < π
< 3.14206, что красиво и довольно жестко ограничивает π (= 3.14159...). Кто
станет отрицать, что это забавно?!
Автором статьи 1944 года, впервые опубликовавшей эту жемчужину, был
Д. П. Далцелл, любопытный парень, который в основном существует как
призрак в истории математики. Во всех современных ссылках на интеграл Дал-
целла ничего не говорится о самом человеке, хотя он написал ряд
математических работ высокого качества и имел отличную репутацию среди математиков.
Далцелл не помог своему делу из-за его привычки всегда использовать свои
инициалы. Фактически он был Дональдом Перси Далцеллом (1898-1988),
который в 1921 году окончил колледж Св. Иоанна в Кембридже по
специальности математика и механика. Он получил степень магистра в 1926 году, но он
не стал профессиональным математиком, а скорее дипломированным инже-
1 В некоторых штатах США «школьное значение» числа π равно 4. В данном случае
22/7 = 3,142857..., что, конечно, больше π = 3,14159... -Прим. перев.
46 ♦ Введение
нером (chartered engineer - термин, используемый в Англии для
профессионального инженера). В течение нескольких лет он работал в компании Standard
Telephones and Cables в Лондоне и получил два патента на электрические
кабели связи. Единственная известная его фотография - это фотография на
вебсайте MacTutor по математике (сделана на Коллоквиуме Эдинбургского
математического общества 1930 года в Сент-Эндрюсе).
1.8. Откуда берутся интегралы
Почти все обсуждения в этой книге проходят в форме «вот интеграл, как мы
можем его оценить?». Конечно, математики могут «составлять» интегралы просто
«из головы», но инженеры и физики обычно сталкиваются с интегралами,
возникающими в результате анализа физической проблемы. Поэтому я подумал,
что мне следует включить примеры такого рода происхождения интегралов
в дополнение к чистому воображению математиков. Тем не менее в каждом из
первых двух примеров в этом разделе я приложил усилия, чтобы сохранить
интерес и математиков; я выбрал физические проблемы, каждая из которых
порождает интеграл и которые являются математическими проблемами по сути;
оба эти примера взяты из теории вероятности. В качестве третьего примера
того, откуда происходят интересные интегралы, я выбрал проблему, с которой
впервые столкнулся, читая книгу «Неотразимые интегралы», о которой
упоминал в предисловии. Я думаю, что это прекрасно иллюстрирует, как
математикам также может понадобиться мотивация (как и физикам) для некоторых
«странных» интегралов, которые они вызывают в воображении!
Итак, для начала вот что я называю проблемой «круг в круге». Представьте
себе круг (назовем его Q), который имеет радиус а. Затем мы выбрали
случайным образом1 и независимо друг от друга три точки внутри этого круга. Эти три
точки, если они не коллинеарны, однозначно определяют другую окружность С2.
Она может быть или не быть полностью в Q. Какова вероятность того, что С2
лежит внутри Q полностью2?
Чтобы ответить на этот вопрос, представьте, что после выбора трех точек мы
нарисовали С2, как показано на рис. 1.8.1. Там я показал С2 полностью
лежащей внутри Си но это только потому, что я произвольно решил сделать это
таким образом и не показывать альтернативу. Без какой-либо потери общности
мы можем далее представить, что горизонтальная ось проходит через центр
1 «Случайным образом» имеет следующее значение. Если мы посмотрим на любой
крошечный участок области dA внутри Q, участок любой формы, то вероятность
того, что точка будет выбрана из этого участка, равна dA, деленному на площадь Q.
Мы говорим, что каждая из трех точек выбрана единообразно внутри Q.
2 Я думаю, что интуитивно почти очевидно то, что вероятность является масштабно-
инвариантной (одинаковой для любого значения а), но на случай, если для вас не
очевидно, я буду учитывать радиус Q в явном виде. В конце нашего анализа вы
увидите, что параметр масштабирования а исчезнет, подтверждая мое утверждение.
Откуда берутся интегралы ♦ 47
С2 (как показано), потому что мы всегда можем повернуть фигуру так, чтобы
сделать это. Пусть г - расстояние от центра С2 до центра Q, а радиус С2
принимается за х.
Рис. 1.8.1 ♦ Окружность внутри окружности
Теперь представьте себе тонкую круглую полосу шириной Ах, которая
охватывает окружность С2. Площадь этой полосы в первом приближении равна
2юсАх, и это приближение становится все лучше и лучше при Ах —> 0.
Вероятность того, чтобы точка, выбранная случайным образом из внутренней части
Q, находилась бы в этой полосе, является, следовательно, отношением
площади полосы к площади С2 (см. снова первую сноску на стр. 47):
ΙπχΑχ 2 д
— = — хАх.
ποτ α1
(Я прокомментирую это утверждение чуть позже.) Поскольку три точки,
которые определяют С2, все попадают в полосу (по определению!) и выбираются
независимо, то вероятность этого события равна:
-хАх\
8
1 {Ах}2 Ах ■■
8
хъАААх,
48 ♦ Введение
где ΔΛ = {Ах}2 - это элемент площади в прямоугольных координатах. (Я
подробно остановлюсь на этом утверждении чуть позже.) Теперь я буду писать
ΔΛ и Ах как dAndx соответственно.
Очевидно, что если χ = 0 (то есть если С2 - это вырожденная окружность,
которая на самом деле является точкой), мы видим, что С2 обязательно находится
внутри Q. Фактически, когда радиус χ увеличивается от 0, он может достигать
а - г, до того как С2 пройдет через Q. Таким образом, вероятность того, что
окружность С2, центрированная на конкретной линии (горизонтальной оси),
полностью находится в пределах Q, равна
8dAa~f ЪА ЫА
—— \ x5dx = ——
π6 J π6
2dA . ч4
—(«-г) .
В общем, конечно, центр С2 может попадать в любое место внутри Q с
любым значением г от 0 до случившегося, и поэтому нам нужно интегрировать
вышеуказанную дифференциальную вероятность (дифференциальную из-за
dA) по всей внутренней части Q. Это проще всего сделать, записав dA в
полярных координатах, как rdrdQ, и поэтому вероятность, которую мы ищем,
равна
2π я η η 2π \ а 1 А а
ff±(a-rYrdrdQ = ^f\f(a-rYrdr\dQ = ^f(a-r)4rdr,
00^ ^ 0 L 0 J ^0
поскольку θ-интеграл, очевидно, просто равен 2π (в подынтегральном
выражении нет θ-зависимости).
Оставшийся г-интеграл легко найти, сделав замену переменной и = а - г
(и, следовательно, du = -dr). Тогда:
и и и и
J (а - г)4 таг = Ju4 (a - и) (-dr) = afu4dr - Ju5dr =
= а
6
сг_
30'
Таким образом, вероятность того, что С2лежит полностью внутри Счесть
4π
а
30
4π
30^
2π
15
0.418879....
Обратите внимание, что радиус а окружности Q исчез, что
подтверждает мое предыдущее утверждение о том, что вероятность не зависит от
масштаба.
Ну ладно, все это хорошо, но есть одно НО - откуда мы действительно знаем,
что у одной из наших, по общему признанию, случайных манипуляций на этом
Откуда берутся интегралы ♦ 49
пути не было скрытого недостатка1? (Вроде, например, утверждения, что {Ах}2
является элементом площади в прямоугольных координатах, где в обычном
выражении dA = АхАу я заменил Ау на Ах. Или как насчет утверждения, что
случайно выбранная точка внутри Q находится в полосе Ах вокруг С2, поскольку
это предполагает, что С2 полностью внутри Q?) Интеграл, который мы
вычислили, не был технически сложным, но как мы узнаем, что пришли к
корректному интегралу? Это вопрос, часто стоящий перед техническим аналитиком,
может не иметь большого значения для чистого математика, который просто
ищет «интересный интеграл».
Когда мы «проверяем» интегралы, которые нам даны, то используем
функции численного интегрирования quad или int, но когда мы сталкиваемся с
вопросом о корректности, нам нужно сделать что-то другое. Мы по-прежнему
будем использовать компьютер, но теперь будем моделировать физический
процесс черчения круга С2, используя точки, выбранные случайным образом
внутри данного круга, Q. То есть наш компьютер «нарисует» много таких
случайных кругов С2 и буквально подсчитает долю из них, которые полностью
находятся внутри Q. Компьютерный код, который выполняет это, будет
разработан с помощью анализа, который является особым, отдельным и независимым
от математических аргументов, используемых для получения интеграла в
нашем теоретическом результате. Итак, вот как можно создать то, что физики
называют моделированием проблемы методом Монте-Карло, технику,
которую Эдварде в предкомпьютерные дни 1920-х годов мог представить только
в научной фантастике.
Для трех точек, не являющихся коллинеарными, ри р2 и р3, где рх = (х19 у^,
Pi = (*2> У ι) и Ръ = (*з> Уз)> мы построим две хорды: хорда а как рхр2 и хорда Ь
как р2ръ с центрами в точках
*1+*2 У1+У2
*2+*3 У2+У3
2 2
Уравнения этих двух хорд следующие:
уа = та(х-х1) + уи
а также
Уь = ть(х-х2)+у29
где таить- наклоны хорды а и хорды Ь соответственно. По сути,
У2-У1
х2 χλ
и
у5-у2
соответственно.
ти
1 Анализ, который я только что провел, - это анализ, приведенный на стр. 817-818
книги Эдвардса, о которой я упоминал в предисловии. Результат 2π/15 является
ответом, полученным Эдвардсом.
50 ♦ Введение
Центр С2 является точкой пересечения серединных перпендикуляров двух
хорд (пунктирные линии на рис. 1.8.1). Наклон линии, перпендикулярной
линии с наклоном т, является отрицательной обратной величиной т, и поэтому
уравнения серединных перпендикуляров - это
Ул =
и
Ув =
1
х,+х2
χ—! -
2
, У1+У2
2
1
Χη "Τ" Χ?
Χ
2 .
,У2+У3
2
Точка пересечения серединных перпендикуляров (центр С2) такова, что
Уа = Ув> и поэтому, приравнивая правые части и решая, для х-ординаты центра
мы имеем:
χ = ™дЩ(У1-Уъ) + тъ(Х1+Х2)-та(Х2+Хъ)
2(ть-та)
Значение ус, ординаты у центра, определяется путем подстановки хс в
любое из уравнений уА, ув. Наконец, расстояние от центра С2 до центра Q равно
ί
х2с+у]· Радиус С2 - это расстояние между центром С2 и любой из трех точек ри
р2 и ръ. Пока сумма этих двух расстояний не превышает 1, С2 находится внутри
Q. В противном случае С2 выходит за пределы Q.
Код MATLAB circle.η выполняет всю эту грубую числовую работу раз за
разом, в общей сложности миллион раз, отслеживая при этом, сколько раз С2
находится внутри Q. Многократный запуск кода circles.η давал оценки1
вероятности нахождения С2 внутри Q в интервале от 0,39992 до 0,400972. Сравнение
этого интервала с теоретическим результатом, который мы вычислили ранее,
0,418879, вызывает (во всяком случае, у меня) чувство беспокойства.
Миллион образцов - это много образцов, и все же у нас есть несоответствие между
теорией и «экспериментом», составляющее около 5 %. Нельзя сказать, что это
незначительная разница. Заметим, кроме того что интервал оценок кода не
включает теоретический результат, в то время как, как правило,
множественные компьютерные моделирования Монте-Карло почти всегда переплетаются
с теоретическим результатом, иногда переоценивая, а иногда недооценивая
теоретическое значение. Трудно смотреть на результаты моделирования и не
испытывать чувства, что фактическая вероятность того, что окружность С2 на-
2 2 2π 2
ходится внутри Си точно равна 0,4. То есть - = , а не — = . Но это
5 15/3 15 15/π
просто предположение с моей стороны.
Этот интервал оценок является результатом использования кода генератора
случайных чисел (с помощью команды rand) - каждый раз, когда мы запускаем код,
получаем новую оценку, которая (немного) отличается от оценок, произведенных
предыдущими запусками.
Откуда берутся интегралы ♦ 51
Почему нет лучшего согласования между теорией и экспериментом? Я не
знаю. Вероятно, есть небольшая ошибка в теоретическом анализе. Или,
возможно, я сделал ошибку в коде. Но это не важно для данной книги.
Единственное, что я хочу, - это показать на данном примере, как теоретический анализ
(с интегралом) и компьютер могут работать вместе. Что-то здесь не совсем так,
но я собираюсь оставить это на усмотрение инициативного читателя. Если этот
читатель - вы, пришлите мне свою работу, и я опубликую ее во втором издании
моей книги!
circles.η
% Created by P.J.Nahin (9/12/2012 for Inside Interesting Integrals.
% This code perforns sinulations of the 'circle in a circle' problen
% one million tines.
inside=0;
for loopl=l:1000000
for loop2=l:3
done=0;
while done==0
x=-l+2*rand;y=-l+2*rand;
if хЛ2+уЛ2<=1;
px(loop2)=x;py(loop2)=y;done=l;
end
end
end
na=(py(2)-py(l))/(px(2)-px(l));
nb=(py(3)-py(2))/(px(3)-px(2));
xc=na*nb*(py(l)-py(3))+nb*(px(l)+px(2))-na*(px(2)+px(3));
xc=xc/(2*(nb-na));
yc=(-l/na)*(xc-((px(l)+px(2))/2));
yc=yc+(py(l)+py(2))/2;
center=sqrt(xcA2+ycA2);
radius=sqrt((xc-px(l))A2+(yc-py(l))A2);
if center+radius<=l
inside=inside+l;
end
end
inside/loopl
А теперь давайте вернемся к июню 1827 года, когда шотландский ботаник
Роберт Броун (Robert Brown, 1773-1858) наблюдал (через однолинзовый
микроскоп, то есть увеличительное стекло, с увеличением, превышающим 300)
хаотическое движение крошечных зерен пыльцы растений, взвешенных в
каплях воды. Это движение ранее было замечено мимоходом и другими, но Броун
нашел время, чтобы опубликовать то, что он увидел, в статье в «Философском
журнале» за сентябрь 1828 года, и тем самым инициировал исследование того,
что происходит.
Немецкий физик Альберт Эйнштейн (1879-1955) в серии работ,
опубликованных между 1905 и 1908 годом, применил статистическую механику,
чтобы показать, что то, что сейчас называется броуновским движением, является
результатом случайной бомбардировки частиц молекулами суспензионной
52 ♦ Введение
среды. Действительно, броуновское движение рассматривается как сильное
макроскопическое экспериментальное свидетельство реальности молекул
(и также атомов).
На рис. 1.8.2 показано четыре типичных пути частиц, выполняющих
броуновское движение в двумерном случае1, и они довольно неустойчивы. В самом
деле, в начале 1920-х годов американский математик Норберт Винер (1894-
1964) провел глубокий анализ математики броуновского движения (Эйнштейн
объяснил физику), в частности изучив, что происходит в пределе, когда
частица непрерывно поражается молекулами (то есть последовательные попадания
молекул разделены исчезающе малыми временными интервалами). В этом
пределе броуновское движение становится тем, что математики называют,
несколько устрашающе, стохастическим случайным процессом Винера. Каждая
реализация такого процесса называется «случайным блужданием по Винеру»,
и такие реализации представляют собой непрерывные кривые, которые
настолько странны, что почти в каждой точке не могут иметь производную (то
есть иметь направление)!
■ и
10
5
0
А".::
5 ■ ' "i ''-
^■'ч
*v
-15
20
10
о
40
-10 *5 0
χ ι recti on
3 20
χ i recti on
30
-20
10
0
-10
-20
■%
-10 0 10
χ direct on
20
-10 0
χ direction
10
Рис. 1.8.2 ♦ Типичные траектории
двумерного броуновского движения (каждые 1000 шагов)
Представьте себе, что мы определили максимальное абсолютное значение хода,
которое будет нашим единичным расстоянием. Затем в одном измерении (назовем это
х) частица после каждого молекулярного удара перемещается на расстояние,
случайно выбранное из интервала от 1 до +1. Во втором, перпендикулярном направлении
(назовем это у) частица после каждого молекулярного удара перемещается на
расстояние, случайно выбранное из интервала от 1 до +1. На рис. 1.8.2 показан
объединенный результат этих двух независимых движений для четырех частиц, каждый для
1000 попаданий (эти четыре кривые получены моделированием MATLAB).
Откуда берутся интегралы ♦ 53
Теперь предположим, что в момент времени t = 0 мы помещаем частицу
в начало системы координат плоскости, а затем наблюдаем, как она выполняет
одномерное блуждание Винера по оси х. Где она будет через некоторое время
t > 0? Конечно, это всегда будет на оси х, но где? Поскольку блуждание
является случайным, лучшее, что мы можем сделать, - это найти вероятность того,
что частица будет где-то, и это было одно из первых, что Эйнштейн рассчитал
в 1905 году. Чтобы быть точным, давайте запишем W(x, t) как вероятность того,
что частица будет где-то в интервале (χ, χ + Ах) в момент времени t (W,
конечно, в честь Винера.) Предположим, что эта вероятность для очень коротких
интервалов линейна по Ах (т. е. повторяет длину интервала и, следовательно,
повторяет вероятность того, что частица находится там), итак:
W(x,t)=f(x,t)bx,
где f(x, t) называется функцией плотности вероятности блуждания Винера
(плотность, потому что мы умножаем ее на длину интервала Ах, чтобы
получить вероятность).
Эйнштейн с помощью гениальных физических аргументов (которые мы
можем здесь проигнорировать) показал, что f(x, t) является решением уравнения
в частных производных второго порядка
dt дх2'
где D - постоянная (D определяется рядом физических констант, таких как
масса частицы и температура, Эйнштейн вывел формулу для Д но для нас
достаточно просто написать D). Это дифференциальное уравнение на самом деле
известно в математической физике и называется уравнением
теплопроводности, или диффузии, поэтому D называется константой диффузии. В обычном
представлении этого уравнения функция решения - это температура в
твердом теле как функция местоположения и времени, но Эйнштейн показал, что
функция плотности вероятности для блуждания Винера удовлетворяет тому
же уравнению. Удивительно!
Это решение f(x, t) есть
e-x2/4Dt
f(x,t)
l4bDt'
что легко проверяется путем прямой подстановки, хотя формально оно
может быть получено с использованием только простых комбинаторных (то есть
чисто математических) аргументов1. Поскольку частица должна быть где-то
(я надеюсь, что это очевидно!), то должно быть верно, что если мы проинтег-
Если вам интересно узнать подробности такого вывода, то вы можете найти их
в моей книге «Электрическое одеяло миссис Перкинс», издательство Princeton
University Press 2009, с. 263-267. (Mrs. Perkins's Electric Quilt Princeton University Press
2009, pp. 263-267.)
54 ♦ Введение
рируем плотность вероятности по всей оси х, то должны получить
вероятность l.To есть
оо
ff(x,t)dx = l
для всех t > О1.
Из элементарной теории вероятностей мы знаем, что среднее значение χ
в любой момент времени t есть
оо
(х)= Jxf(x,t)dx = 0.
— оо
Это математически так, потому что f(x, t) четная, и поэтому
подынтегральная функция является нечетной функцией от х, а физически это так, поскольку
одномерное блуждание Винера эквивалентно тому, что частица с одинаковой
вероятностью будет двигаться в любом направлении в каждый момент
времени. И все же, как ясно показывает рис. 1.8.2, двумерное блуждание Винера имеет
тенденцию медленно мигрировать на некоторое абсолютное расстояние от
начала координат при увеличении t Мера этого отклонения - это среднее
значение квадратах (потому что отдельные горизонтальные (и вертикальные)
движения частицы, имеющие противоположные знаки, не имеют тенденцию взаимно
компенсировать друг друга). Итак, следуя Эйнштейну, давайте подсчитаем
ОО л ОО
<х2) = ΐχ4(χ,ι)άχ = —ϊ= fx2e-x2/4Dtdx,
t 2y/nDtt
или, поскольку подынтегральная функция является четной функцией οτχ,
-. оо
(x2)=^J=[x2e-x2/4Dtdx,
л/πθί J0
х2
делая очевидную замену переменной и = , мы имеем:
du
dx
2х
4Dt
и также
dx =
2Dt ,
du.
χ
2Dt
Χ
Или, поскольку χ = 2^/Dt^lu, мы имеем:
A 2Dt
dx =
2VDt
du
[yfU)
y/U
1 Для доказательства этого см. снова «Миссис Перкинс», стр. 282-283.
Откуда берутся интегралы ♦ 55
Тогда:
л ОО 1 а ОО
(х2)= -=L= {ADtueu4Dt^ = Dt-^= f^fueudu.
JnDt о vm νπ ο
На данный момент у нас фактически есть основной результат Эйнштейна,
что (х2) изменяется линейно относительно ί, потому что независимо от
значения мы знаем, что интеграл - это просто число. Однако для нас в этой книге
вычисление интеграла (который естественным образом появился в
физической проблеме) является сложной задачей. В главе 4 мы сделаем это
вычисление - см. (4.2.8) - и обнаружим, что значение интеграла составляет -νπ. Итак
л
(как и писал Эйнштейн), (х2) = 2DL
Мой третий пример, на этот раз из чистой математики, просто представьте,
что кто-то только что бросил вам вызов: покажите, что
оо [Х]
Г 2.£*х = -1 + 1п(л/2тг) = -0.08106...,
1 Х
где [х] обозначает дробную часть χ (например, {5.619} = 0,619 и {7} = 0). Боже
мой! Я слышу, как большинство читателей восклицает: как ты докажешь что-то
подобное?
Авторы книги «Неотразимые интегралы» (Irresistible Integrals) обрисовывают
в общих чертах его происхождение (см. их стр. 92-93), но пропускают очень
большой шаг, с небольшим намеком на то, как поступить. По крайней мере, не менее
интересным, чем сам вывод, является то, что интеграл был не просто «взят из
ниоткуда», но на самом деле является результатом предварительного анализа.
Прежде чем углубляться в детали вывода, полезно получить «физическое
ощущение» этого интеграла. На рис. 1.8.3 показан график подынтегрального
выражения на интервале 1 < χ < 20. Из этого графика видно, что
подынтегральное выражение начинается с отрицательной области в интервале 1 < χ < 1,5,
площадь которой затем частично компенсируется положительной площадью
при 1,5 < χ < 2, за которой следует отрицательная область при 2 < χ < 2,5,
которая затем почти компенсируется положительной площадью на 2,5 < χ < 3,
и т. д. Эти взаимные сокращения чередующихся площадей никогда не бывают
полными, но при χ —> оо компенсации площадей становятся все ближе к
некоторому итоговому значению, что физически объясняет, почему существует
интеграл (не обращается в бесконечность).
Поскольку отрицательные площади немного больше по величине, чем
положительные, то имеет смысл ожидать окончательного слегка отрицательного
значения для интеграла.
Мы можем численно проверить эти наблюдения с помощью функции quad на
интервале интегрирования на рис. 1.8.3. Таким образом, quad(@(x)(x-floor(x)-
0.5)./χ, 1,20) = 0,0769..., где floor(x) вычисляет наибольшее целое число, мень-
56 ♦ Введение
шее χ. Итак, floor(x) округляет χ вниз, и x-floor(x) = {χ}. Это довольно хорошо
согласуется с теоретическим результатом книги «Неотразимые интегралы».
■0.6
\Ш^
J ι ι L·
6 8 0
X
2 1 16 18 Ζ]
Рис. 1.8.3 ♦ Подынтегральное выражение непреодолимых интегралов
Мы начнем с известного результата в математике - асимптотической
формулы Стирлинга для и!:
л!~л/2тгл 2е~",
названной в честь шотландского математика Джеймса Стирлинга (1692-1770) -
хотя известно, что французский математик Абрахам де Муавр (1667-1754)
знал эквивалентную форму в то же время (или даже раньше) и опубликовал
ее в 1730 году. Факториалы очень быстро становятся довольно большими (мой
ручной калькулятор отказывает уже на 70!), и формула Стирлинга весьма
полезна для вычисления и! для больших п. Она называется асимптотической,
потому что хотя абсолютная ошибка в правой части при оценке левой части
стремится к бесконечности при η —> оо, относительная ошибка обращается в ноль
при η —> оо (именно поэтому вместо «=» используется «-»). То есть
lim
л—>оо
л!
2πΛ-"
= 1,
или альтернативно:
л!
lim-
л
ι
"+2,
■ = >/2π.
Откуда берутся интегралы ♦ 57
Забудьте пока это, потому что мы будем использовать это в конце нашего
вывода вышеуказанного интеграла. Итак, поехали.
Начнем с записи
1п{п!} = 1п{п(п - 1)(л - 2)... (3)(2)(1)} = 1п(л) + 1п(л - 1) + ... + 1п(2) + 1п(1),
или, поскольку 1п(1) = 0:
1п{п!} = £>(*).
fe=2
Далее, сначала отметим, что поскольку
jf={m«}i:=in(*)>
тогда
а затем дополнительно отметим, что
/f-£7f·
ι х /=ι / х
Поэтому
1п{п!} = Е
k-li+rdx
Все идет нормально. Однако именно в этот момент авторы «неотразимых
интегралов» пишут, что следующее, что нужно сделать, - это «перемена
порядка суммирования», а затем они сразу же пишут
Щп1]= flL^ldX)
где [χ] означает целую часть χ (например, [5.619] = 5).
Ясно, что
*=[*] + {*}·
Этот шаг «перемены» может показаться вам загадочным (так сначала было
для меня!), но вот как это увидеть. Выпишем члены внутренней суммы для
каждого значения /с, когда этот индекс меняется от 2 до π (внешняя сумма):
58 ♦ Введение
2 3
1 2
2 3 4
2 3 4
* = »:/ + /+/ + - + /·
2 3
Согласно записи, двойное суммирование складывает все эти интегралы по
горизонтали, строку за строкой. Обмен порядка сумм означает просто
сложение всех интегралов по вертикали, столбец за столбцом. Вы получите тот же
ответ в любом случае! Таким образом:
2>dx , *rdx , *cdx nrdx
1п{Я!} = (Я-1)Г™+(Я-2)Г™+(Я-3)Г™+-+Г™ =
J у J у J у J у
1 Л 2 Л 3 Л п-1 Л
2с{п-\), г(и-2), г(л-З), п}\,
= / - -dx+ / - -dx+ / - -dx + -~ + / -d*.
U у %) у U у %) у
Общая форма слагаемых в последней сумме, когда 1 < / < η - 1, есть
J+1/м ;ч 7+1
J. X J. Χ
потому что для интервала интегрирования/ <x<j+l мы имеем по
определению [х] = j. Таким образом:
in{nl}="r1zMdX}
J У
как и утверждается в «Неотразимых интегралах».
Теперь так как
[х]=х-{х],
то
п-[х] = п-(х-{х}) = п-х + {х}.
Откуда берутся интегралы ♦ 59
Поэтому
1η{π!}= ]η-χ + Μάχ= "fV-dx- "fdx+ Щах-
J у J у J J у
-м-
= п\п(п)-(п-1)+ Г—dx = nln(n)-n + l + -ln(n) + Г
J χ 2 J χ
-dx-
п + -
"М-
1п(>7)-и + 1 + Γ ^dx =
1 х
=ln
w
+ ln(e-") + l + J
-.м-i
-dx
=lnU"+2e-")+lnl
1+ / ^dx
= ln
Таким образом
{η 2e~ne 1
f{*}_2
f / ^
n\ = n 2e~ne 1
1+ / ^dx
ИЛИ
1
1+ / ^dx
e *
π!
-+U
η L e
или, если мы теперь допустим п^оои вспомним формулу Стирлинга,
получим:
7[х]~2
1+ / ^dx
J х п:—
е 1 = ν2π.
Поэтому
оо {Х}
1 + J ^dx = lnl^)j,
и как утверждали «Неотразимые интегралы»:
60 ♦ Введение
(1.8.1.)
Чтобы действительно убедиться, что вы поняли происхождение (1.8.1),
попробуйте свои силы в решении второй задачи главы 5 (когда вы туда
доберетесь).
1.9. Заключительные слова
Физик Ричард Фейнман пишет в известной по праву (и очень забавной)
подборке автобиографических очерков1:
Я научился брать интегралы различными методами, показанными в
книге, которую дал мне мой школьный учитель мистер Бадер.... она была для
младших или старших курсов колледжа. В ней были ряды Фурье, функции
Бесселя, детерминанты, эллиптические функции - все виды
замечательных вещей, о которых я ничего не знал. В этой книге было также
написано, как дифференцировать по параметру под знаком интеграла - это
определенная операция. Оказывается, в университетах этому не очень-
то учат, не подчеркивают. Но я понял, как использовать этот метод,
и я использовал этот проклятый инструмент снова и снова. Так что,
поскольку я был самоучкой и использовал эту книгу, у меня были особые
методы нахождения интегралов. В результате у парней из Массачусетского
технологического института или Принстона были проблемы с
некоторыми интегралами, потому что они пыталиисъ сделать это
стандартными методами, которые изучали в школе. Если бы это было контурное
интегрирование, они бы нашли его; если бы это было простое разложение
в ряд, они бы его нашли. Тогда я прихожу и пытаюсь дифференцировать
под знаком интеграла, и часто это работает. Так что я приобрел
отличную репутацию за интегралы только потому, что мой набор
инструментов отличался от всех остальных, а они перепробовали все свои
инструменты, прежде чем передать мне эту задачу.
Фейнман писал о своем опыте в конце 1930-х годов, тогда еще символьный
интегратор от Wolfram онлайн был просто научной фантастикой, и даже
гораздо менее доступной. И хотя он явно получал удовольствие от нахождения
интегралов, его знание «трюка», которого не знали другие, также приносило
реальную отдачу. Позже в той же книге он пишет2 о встрече с другим аналити-
1 В эссе под названием «A Different Box of Tools», in: Norton W. W. Surely You're Joking,
Mr. Feynman! 1985. P. 84-87.
2 В эссе «Los Alamos from Below», in: Surely You're Joking, Mr. Feynman! P. 107-136.
Задачи для упражнений ♦ 61
ком, который был поставлен в тупик интегралом, появившимся во время его
работы над проектом атомной бомбы в период Второй мировой войны.
Когда один из ребят объяснил [свою] проблему, я сказал: «Почему бы вам
не сделать это путем дифференцирования под знаком интеграла?»
Через полчаса он ее решил, а они работали над этим в течение трех недель.
Итак, я кое-что сделал, используя свой «другой набор инструментов».
Позже в этой книге я покажу вам многочисленные примеры
излюбленного трюка Фейнмана «дифференцировать под знаком интеграла» (который
можно проследить вплоть до Лейбница в конце XVII века), хотя кажется, что
окончательный вид, который мы используем сегодня, на самом деле
является развитием идей Лейбница. Мы также будем использовать другие приемы,
включающие более привычные операции замены переменной (как мы это
делали в интеграле «круг в круге» в предыдущем разделе), степенные ряды
и интегрирование по частям. И, как я обещал в предисловии, мы рассмотрим
и контурное интегрирование. На самом деле зачем ждать? Давайте начнем
прямо сейчас.
1.10. Задачи для упражнений
Однако, прежде чем перейти к следующей главе, представлю вам четыре
задачи для развлечения.
(С1.1). Используйте прием «подкрадываться к сингулярности», чтобы
вычислить
8г dx
Это несобственный интеграл из-за особенности в интервале
интегрирования при χ = 2, но он имеет решение. Повторите это для интеграла
ъг dx
и покажите, что, несмотря на особенность при х=1, этот интеграл также имеет
решение. Обратите внимание, что, в отличие от первого интеграла,
подынтегральное выражение всегда положительно (нет взаимного сокращения
отрицательной и положительной площадей). Тем не менее интеграл имеет решение.
(С1.2). Показать, что
62 ♦ Введение
существует, потому что существует конечная верхняя граница его значения.
В частности, показать, что этот интеграл1 меньше 4.
(С1.3). Каков ответ на интегральную головоломку Фейнмана в (1.6.1)? Начните
с вывода (1.6.1) и подумайте, насколько произвольными являются на самом
деле константы а и Ь.
(С 1.4). Для любой положительной постоянной с начните с подтверждения того,
что интеграл
I
-dx
о *
преобразуется путем замены переменной у = сх в интеграл
, — dy.
Ό У
Теперь если это так, то для любых двух положительных констант а и b может
показаться, что
1= [- —dx = f—dx- f—dx= Г—dy- f—dy = 0.
Jo x ox ox о У о У
Но, как мы увидим в главе 3, в формуле (3.3.3)
-Ъх (fo\
I
е — е
dx = ln
а
которое равно нулю только для частного случая а = Ь. Итак, есть загадка - что
не так с первым аргументом, утверждающим, что / равно нулю для любых
положительных значений а и Ь?
(С 1.5). Вот еще один пример интеграла, который появляется в реальной
ситуации, и того, как MATLAB легко с этим справляется. Это интеграл Меркатора,
названный в честь изобретателя Герхарда Меркатора (1512-1594),
родившегося там, где сегодня находится Бельгия, автора знаменитой карты Меркатора,
которая отображает сферическую поверхность Земли на плоской карте. Этот
интеграл Г 2 появляется как фактор «искажения», или «деформации»,
Jei COS(6)
при построении «плоской карты» (θλ и θ2 - крайние значения географических
широт на карте). Меркатор (который был картографом, а не математиком)
столкнулся с этим искажением в 1569 году, задолго до того, как были разра-
Для обсуждения того, как этот интеграл появляется в задаче физики, см. мою книгу:
Электрическое одеяло миссис Перкинс. Принстон, 2009 (Mrs. Perkins's Electric Quilt.
Princeton, 2009). С. 2-3 (а также стр. 4 о том, как приступить к контрольному вопросу,
но попробуйте его решить самостоятельно, прежде чем искать там решения).
Задачи для упражнений ♦ 63
ботаны методы аналитического интегрирования, и он был вынужден искать
этот интеграл другими способами (разве он не любил бы MATLAB!). Сегодня,
конечно, он просто использовал бы таблицу интегралов.
Каково значение интеграла Меркатора, если θλ = 0 и θ2 = π/3 (60°)? MATLAB
вычисляет так: quad(@(x)l./cos(x),0,pi/3) = 1.3169579... (если у вас есть
таблица интегралов под рукой, то вы должны найти, что теоретический ответ равен
ln(2+V3) = 1.31695789...).
Глава
2
«Легкие» интегралы
2.1. Шесть «легких» для разминки
Когда вы сталкиваетесь с определенным интегралом, вы всегда должны быть
начеку, чтобы не пропустить счастливой возможности того, что хотя бы один
интеграл может быть «интересным» (то есть трудным!), и возможно, он все же
уступит прямой лобовой атаке. Первые шесть интегралов в этой главе
относятся к этой категории. Если аиЬ- положительные постоянные, вычислите:
оо -.
Г -^dx, (2.1.a)
J0 (x + a)Vx-l
( ί\
х1
dx, (2.1.b)
оо
Л"
О
IP^dx, (2.1.0
оо -.
Г- -dx. (2.1.d)
Наконец, вычислите
ОО -ι
Г ^dx (2.1.e)
Для решениия первого интеграла (2.1.а) сделаем замену переменной
χ - 1 = £2, и тогда
— -2ί
Шесть «легких» для разминки ♦ 65
или
dx = 2tdt = 2y/x-ldt.
Поскольку
x=l+t\
то мы имеем
Г ' А = Г №-Ы' -2? ? .
J! (x + a)Vx^1 J0 (l + i2+fl)Vx^l J0(l + t2+a)
Мы немедленно узнаем этот последний интеграл как имеющий форму
dt
с2+е
dx-
tan
Φ
и поэтому
1
J! (х + а)л1х-1
что дает нам
dx = 2*
,tan !
л/β + Ι Wfl + lJ
2 2
tan_1(oo) =
π
л/β + Ι
л^+12'
/
1
t/X:
π
' (х + а)л/х-1 -s/α + Ι
(2.1.1)
ΊΙ
Для проверки: если α = 99, то мы получаем значение интеграла, равное — =
0.31415..., в то время как quad дает следующее: quad(@(x)l./((x+99).*sqrt(x-
1)),1,1е5) = 0.30784.... Обратите внимание, что верхний бесконечный предел
был заменен конечным (но «большим») числом 105.
Для решения (2.1.Ь) применим интегрирование по частям. То есть мы будем
использовать формулу
fudv = (uv)\^-fvdu,
где
„2Ϊ
1 + -
и dv = dx. Тогда ν = χ и
66 ♦ «Легкие» интегралы
Тогда
оо
Л»
1 + -
dX:
х\п
1 +
2\
Χ
dx
оо
■I*
la
1\(
x2+a2)
dX:
JQx2+a2
■2a2
-tan"1
a
V
:2atan '(oo)»
и поэтому
(2.1.2)
Для проверки пусть а = 10, тогда мы имеем значение интеграла, равное
31.415926, а функция quad говорит нам: quad(@(x)log(l+(100./x.A2)),0,1000) =
31.31593....
Для решения интеграла (2.1.с) пусть а: = Ι/t, и тогда dx-
1
dt. Наш интеграл
тогда принимает вид:
Щх)
In
ill
t
In
t2
rdt\
l^wdt=-U
ln(0
■dt.
Пусть s = bt (и тогда dt= — ds). Следовательно:
b
ln(t)
In
J>2t2+1 Jns2+1
m
ds =
Jns2+1 Jn52+1
В этих выкладках мы предполагаем, что limxln
«2 Ϊ
1 + -
= limxln
1 + -
= 0. Чтобы
убедиться, что эти два предположения верны, вспомните разложение в степенной
1 (Л \ 1 2 1 3 О2
ряд функции log, когда ρ ^0·Αη\ι~^~Ρ) = Ρ~^Ρ +^Ρ * Тогда прир = — (которое
► 0 при а: —► по) мы имеем χ In
«2 Ϊ
1+-
= х
а^_1
х2 2
^
^
X
~х 2х:
3+-,ко-
торое —► 0 при а: —► оо. С другой стороны, если х —► 0, мы имеем χ In
1 +
2Ϊ
λ* In
(^
xln(a2) - λΊη(λ-2) = xln(a2) - 2xln(x), и оба эти члена стремятся к нулю, так как χ
стремится к нулю (первый член очевиден, а во втором член χ исчезает быстрее, чем уходит
в бесконечность ln(x)).
Шесть «легких» для разминки ♦> 67
или поскольку первый интеграл в скобках равен нулю - мы показали это
в (1.5.1), тогда имеем:
1п(Ь)
°°г 1 . 1п(Ь).. -ι, Ч1|~
{^Vids= ъ {tan (s)}lo'
и таким образом:
1п(х) . π, ...
-T±-^dx = —ln(b).
x2+b2 2b
(2.1.3)
Заметим, что этот интеграл сводится к нулю (как это и должно быть) при Ь = 1.
ти
Для Ь = 2 наша формула говорит, что этот интеграл равен —1п(2) = 0.544396...,
л
и подтверждается MATLAB: quad(@(x)log(x)./(4+x.A2),0,10000) = 0.543365....
Для решения (2.1.d) все, что нам нужно, - это простая замена. Пусть и = еах
du ax j du du ч
(и поэтому — = е и, следовательно, ах = —^ = — ), мы тогда имеем:
dx
аеи
J0 l + efl* ·{ 1 + u^auJ a\ u(l + u) a\
1
J.
и 1 + и
= --ln
τ
2
или
OO -ι
f—
J 1 + e"
-dx =
ln(2)
(2.1.4)
Для a = π, например, значение этого интеграла есть 0.220635.
согласованность с quad(@(x)l./(l+exp(pi*x)),0,1000) = 0.220635....
Для решения (2.1.е) рассмотрим неопределенный интеграл
dx г x~mdx
, и мы имеем
Г ах — Г х
J у ι Yra J у1-
Отметим, что
d_
dx
и тогда
dx
-ln(AT1-m+l) =
m+l
(l-m)x1-m-
х1_и+1
(l-m)x~"
at1""1 +1
/
1
Х + АГ"
1-m
1п(лг1-т+1) + С,
где С - это произвольная константа интегрирования. Поэтому т = у/2, мы
имеем:
68 ♦ «Легкие» интегралы
ix + xS L-V2 ί V
или, поскольку 1 - V2 < 0 и поэтому lim^^x1 =0, немного элементарной
арифметики комплексных чисел дает нам наш ответ:
(2.1.5)
Выражение справа равно 1.5063322..., в то время как quad говорит, что
значение интеграла есть quad(@(x)l./(x+x.Asqrt(2)),sqrt(2),le5) = 1.48592....
Для решения (2.1.f) пусть t = ех, и поэтому — = ех, или dx = — = —. Тогда
dx ех t
ОО 1 , ОО
J cosh(x) J
dx
ex + e~
oo
dx
ex +e~
о t + _ l
t
OO -j
= 2/^T^ = 2tan-40|:=2
ίπ\
и поэтому
ОО
dx
cosh(x)
π.
(2.1.6)
MATLAB подтверждает результат: quad(@(x)l./cosh(x),-20,20) = 3.1415929.
2.2. Новый прием
Следующие четыре примера иллюстрируют часто применяемый мощный
прием для вычисления определенных интегралов, который заключается в
«переворачивании» направления «переменной интегрирования». То есть если χ
меняется от 0 до π, попробуйте изменить на у = π - χ. Это может показаться почти
тривиальным, но это часто работает! Имея в виду эту идею, давайте вычислим:
π/2
/
Λ
sin a:
о \lsinx -Ьл/cosx
xsinx
dx,
h
0 Х
π/2
+ COS Χ
sin χ
-dx,
SinAT + COSAT
-dx
(2.2.a)
(2.2.b)
(2.2.c)
Новый прием ♦ 69
fl*^dx.
x'+l
(2.2.d)
Для решения интеграла (2.2.а) сделаем подстановку χ = π/2- у. Тогда dx
-ау,и
'-I
sin
π
-У
π/2
sin
π
+ JCOS
π
i-dy) = J
4
cosy
[ Vcosy+^siny
dy.
Добавление этого выражения к исходному / (и изменение фиктивной
переменной интегрирования у обратно на х) дает:
π/Γ ylsinx + Vcosx . π/Γ2. π
J T^=—^=dx=Jdx = -,
ο vsinx+vcosx о ^
и тогда
л
sin л:
π/2
Г-
о yfshvx + yfcosx
dx-
π
4"
(2.2.1)
Это говорит о том, что интеграл равен 0.785398..., и функция численного
интегрирования quad это подтверждает: quad(@(x)sqrt(sin(x))./(sqrt(sin(x))+sqrt(c
os(x))),0,pi/2)= 0.785398....
Для решения интеграла (2.2.Ь) делаем подстановку χ = π - у (и тогда dx =
-dy). Следовательно:
/ = jfr-y),Infr-y)
t l + cos2(7i-y)
p(u-y){sin(u)cos(y)-cos(u)sin(y)|
: / —r T^dy'
о l + {cos(u)cos(y) + sin(u)sin(y)j
или
Un-y)sln(y) *r sin(y) dy_ г ysin(y) dy
J0 l + cos2(y) J0 l + cos2(y) J0 l + cos2(y)
Таким образом:
sin*
"/τ
'0 1 + cos χ
dx-I,
70 ♦ «Легкие» интегралы
или
/
π
= -[-
2-il
sin*
+ cos2x
-dx.
du
Теперь пусть и = cos(x), и тогда — = -sin(x) (то есть dx = -du/sin(x)). Таким
dx
образом:
rsinxi du ϊ_ π г du _ίιγ du
<|l + u2l sinxj" 2 \ 1 + u2 ~ 2 *_х\ + и
2 Jj 1 + u21 sin*
2
Итак
^{tan-1 u}L = litan-'CD-tarr'C-1)} = | j
π π
ΞΙ
4
ίϊ
xsin(x) ^π2
J0 l + cos'(x)
(2.2.2)
Это равно 2.4674... и согласуется с quad(@(x)(x.*si.n(x))./(l+(cos(x).A2)),0,pi)
= 2.4674....
Для решения интеграла (2.2.с) делаем подстановку χ = π/2- у. Тогда dx =
-с/у, и
71/2 sin
sin
π
-У
π
+ cos
π
-Л-dy).
Поскольку
(.
sin
π
2^
sin
V
cos
(у)-
COS
sin(y) = cos(y)
COS
π
2^
= cos
V
cos(y) + sin
rn\
sin(y) = sin(y),
мы имеем
π/2
с os2 (у)
{ cos(y) + sin(y)
dy.
Новый прием ♦ 71
И, изменяя фиктивную переменную интегрирования обратно на χ и
складывая интегралы, получаем:
π/2
1
2/ = ^sin2(y)W(y)rfy = г
J0 cos(y) + sin(y) J0 cos(y) + sin(y)
Теперь сделаем замену переменной:
dy.
z = tan
Тогда мы имеем
1
dz_ = 2 _
dx
2
cos
Yj
2
2
COS
Μ
2,
/ \ / \
2
cos'5
X
—
I'M
• 2
+ sirr
*
—
[^J
2
1
1 + tan2
X
2
1
~~ 2
1 + tan2
2)
ИЛИ
dz_
dx
.1 + z2
2
поэтому
dx =
2
1
1 + Z2
dz.
Из тригонометрических формул двойного угла мы можем написать:
sin(x) = 2sin
Υ
2d
cos
Υ
2,
и поэтому
sin(x) = 2sin
X
2d
COS
2,
sin
= 2
COS
X
J,
2J
cos2
x\
.2)
)
= 2 tan
X
k2,
1
l + t£
in2
(x
2.
2z
1 + Z2
72 ♦ «Легкие» интегралы
а также
cos(x) = cos2
Μ
—
2
4 '
. 2
-sin
ίχ)
—
2
v 7
2
= cos^
f*l
—
2
v 7
1-
• 2
sin
Ml
2
2
cos
x\
ы\
1 + tan2
tan2
X
2
1 + tan2
x\
1
1 + tan
2
x)
2)
1 + tan2
x)
2
1-tan2
2)
1 1_z2
1 1 + z2
Поэтому
"=/
о 2z | 1-z'
U + z2J
dz
Ό l+2z-r
1 + z' 1 + z'
If
dz
^
dz
'2-(z'-2z + l) J02-(z-l)'
Далее, раскладывая подынтегральное выражение на элементарные дроби,
мы имеем:
21-
2Л{
2V2J0
2
ι ι
Л
о
/
ι
-+-
1
λ/2-(ζ-1) λ/2+(ζ-1)
1 1
-+-
2^2
1 + λ/2-
dz
■1 + V2
dz
\dz —
\dz =
+ z
r az r az
l Z + V2-1 {z-l-
V2"
Обозначив u = z + V2-1b первом интеграле в скобках, мы получаем:
J0 ζ + λ/2-1 i_, u ^
In
ί V2" )
л/2-1
Полагая « = z-1-V2bo втором интеграле в скобках, мы получаем:
Jo Z-1-V2 _^ U ""^
ί Л )
ι+S
Новый прием
73
Тогда
21 =
ί -Ji ι+л/г)
или
■г_!тМ_Л= 1 ln(3+2V2).
J0 sin(x) + cos(x) 2v2
(2.2.3)
Значение этого интеграла есть 0.623225..., и MATLAB соглашается: quad(@(x)
sin(x).A2./(sin(x)+cos(x)),0,pi/2) = 0.623225....
Для решения интеграла (2.2.d) положим
* = tan(6) = ^,
cos(6)
и тогда
d, = cos\e) + sin2(e)
άθ cos2(9)
следовательно, мы имеем dx = {1 + tan2(0)}<i0, и наш интеграл принимает вид:
/= flny+1)d,=Tln(tan(92)+1){i+tan2(e)}rfe:
JQ x2+l JQ l + tan2(0)
π/4
= jln(tan(6) + l)da
Теперь сделаем замену переменной, которая «переворачивает» направле-
71
ние интегрирования, то есть и = θ (и тогда du = -dd). Поэтому
4
/=/ln
π/4
( (π ^
π
и
4
tan
1
π/4
(-du) = J In
tan
π
и
4
1
du,
или возвращаясь κ θ в качестве фиктивной переменной интегрирования:
π/4
= /!„
tan
2-е
4
+ 1 t/θ.
74 ♦ «Легкие» интегралы
Теперь напомним тождество
tan(ct)-tan(p)
tan(ct-p) =
l + tan(a)tan(p)
π
Если α = — и β = θ, мы имеем:
4
tan
tan
π
π
-θ
-tan(6)
1 + tan
( \
π
tan(6)
l-tan(6)
l + tan(6)'
и поэтому
π/4
/=/ln
о
π/4
l-tan(6)
+ 1 \de
π/4 Γ
-Η
l + tan(6)
π/4
Jln{2}d6- jln{l + tan(6)}da
+ tan(6)
\de =
о о
Но ведь последний интеграл есть I, и, следовательно,
4
или, наконец (и используя χ в качестве фиктивной переменной
интегрирования):
rln(x + l)dx = nr ln{1 + tan(x) }dx=*\n(2).
Jn *2+l i 8
(2.2.4)
Этот интеграл часто называют интегралом Серре, после того как
французский математик Жозеф Серре (1819-1885) решил его в 1844 году. Наш
результат говорит, что оба приведенных выше интеграла равны 0.27219826..., и quad
соглашается с этим: quad(@(x)log(tan(x)+l),0,pi/4) = 0.27219826... и quad(@(x)
log(x+l)./(x.A2+l) A1) = 0. 27219823....
Если мы сделаем замену переменной χ = —, то можем обобщить этот
резулfeci
тат следующим образом. Поскольку dx = —dt, то
а
Два старых трюка, плюс один новый
75
8 J0 *2+i { m2+1U J J0
αΓ1η(ί + α)-1η(α)
t2+a2
dt =
itan-μ
α Ια
= α
rln(i + a)
/1чг-Л-1п«"
;^«)Л_11п(а)[1ап-.(1)]
ln(t + a)., π
Ό t2+«2
dt-
ln(t + a)., π.
4a
1»W -./=^£i*-itoW
Таким образом,
ι
8a
ar ln£+a) Л = JLin(2) + ^_in(a) = ^ln(2)+pin(a),
^ln(a) = ^ln(2)+^:
0 ..' + aA Xa 4a 8a 8a
или, наконец, изменив фиктивную переменную интегрирования обратно на х,
получаем:
/—i ^ώ = —1η(2α2).
(2.2.5)
2.3. Два старых трюка, плюс один новый
Следующий интеграл с произвольно большим количеством различных
квадратичных сомножителей в знаменателе подынтегрального выражения на
первый взгляд может показаться невероятно трудным:
°r dx
{ (χ2 + α?)(*2 +α22)(χ2 +α2)...(χ2 +α2)'
где все αζ· ^ 0 и различны. Но это не так, и я вам сейчас покажу. Давайте сначала
запишем подынтегральное выражение в форме суммы элементарных дробей
(оглянемся на то, как мы получили интеграл (2.2.3)), как
1
- + -
- + -
(χ* +αί)(* +я2)(* + a5)-(* + 0 x +< x +< x + аъ
-+...+
*2+al
где все сг - некоторые константы1. Обратите внимание на любой из членов
справа, скажем, fc-й. Тогда, умножив обе части равенства на х2 + а\, мы имеем:
1 Это разложение на элементарные дроби имеет место в предположении, что все а(
различны. Если какое-либо из аг появляется несколько раз, то правильное частичное
разложение дроби подынтегрального выражения не такое, как я написал.
76 ♦ «Легкие» интегралы
х2+а2
(χ2 + а2)(х2 +α22)(χ2 +а2ъ)...(х2 +α„2)
Μχ2+αΙ) с2(х2+а2к)
х2+а2
- + -
х2+а2
+... + С .+...+
х2+а2 "
Теперь, если мы сократим коэффициент х2 + а\ в числителе и знаменателе
в левой части последнего равенства и подставим вместо χ конкретное
значение \аъ где \ = х/^4, то получаем1:
1 1
(-а2 + а2)(-а2к + а22)(-а2к + α32)...(-α2 + α2) ~ Цп.=1.^(а2 -α2) "^
где в выражении справа выживает только один член ск, так как все остальные
члены в разложении обращаются в ноль в их числителе. Итак, наше
разложение первоначальной дроби есть просто
1 к с
(χ2 +α2)(χ2 +α22)(χ2 + α32)...(χ2 + α2) fci*2 + α2'
и поэтому
/
dx
>0 {χ2 + α\)(χ2+α22)(χ2 +а2ъ)...(х2+а2п)
Κ σο
dx
X2+CL2
k 1
tan"1
к J
=Σ^
V
k=l"k
или,наконец,со всеми а,-,ф0:
dx
π
'0 (χ2 +α2)(χ2 +а22)(х2 +а2ъ)...(х2+а2п)
1 . .
где ск = — — и а,. * а;., если у * ι
еь
fc=l Mfc
rw«,2-«*2)
(2.3.1)
Например, предположим, что а2 = 1, я2
и а3 = 3. Это дает следующие значения с,:
4 и σ32
9. Тогда Й! = 1, я2
1
1
1
(4-9)(9-1) 24' 2 (1-4)(9-4)
1
15' Сз
1
(1-9X4-1)
J_
40'
Здесь есть два момента, которые необходимо прояснить. Во-первых, поскольку мы
работаем с тождеством, это должно быть верно для всех значений х, и я только что
выбрал самое удобное. Во-вторых, если вам мешает использование мнимого «а»,
просто запомните философский дух этой книги - все (ну, почти все) проходит, и мы
проверим наш результат, когда доберемся до конца!
Два старых трюка, плюс один новый ♦ 77
Тогда значение интеграла есть
1
Ϊ4
1
1 1
15 ,40
2 3
=
Л)
1
24
ι ι 1
1
30 120J
=
ίπ)
\ν
120
π
= — = 0.0261799...,
120
и quad подтверждает это в виде quad(@(x)l./((x-A2+l).*(x.A2+4).*(x.A2+9)),0,100)
= 0.02617989....
Вот еще один пример использования разложения рациональной дроби для
оценки интеграла. Здесь я найду
dx
I
[ x4+2x2cosh(2ct) + l
где α - это произвольная константа. Записав гиперболический косинус в
знаменателе подынтегрального выражения в экспоненциальной форме, мы
имеем:
х4 + 2х2 cosh(2ct) +1 = χ4 + 2х2
е2а+е~2а
Ь
= Х4 +χ262α +χ26-2α + j = (χ2 +62α)(χ2 ^^α^
Итак, мы можем записать подынтегральное выражение в следующей форме
правильной рациональной дроби (с константами А и В):
1 А В
х4 +2x2cosh(2ct) + l ~ (χ2 +е2а) (х2 +е~2а)'
Отсюда получаем выражение
(А + В)х2+Ае-2а + Ве2а=\,
которое, поскольку справа нет члена х2, сразу говорит нам, что А = -В. Тогда
-Бе-2а + Бе2а=1,
и константа В задается формулой
78 ♦ «Легкие» интегралы
Поэтому
J dx l
•J χ4 + 2χ2 cosh(2a) +1 ~ e2a - e~2a
1
e2a-e"2a
1
e2a-e~2a
°h dx J dx
ix2+e~2a JQx2+e2a
f ! t -if *1
—tan —
e"a U"a.
2 2j
oo
0
=
1
-—tan"1
ea
Kea\
π ea-e"a
2e2„_e-2„
IOO
lo
1
π ea — e~a π Ι π 2
2(ea+e~
x)(ea-e-a)
2
. (ea+e"a
)
2
ea+e-a'
или окончательно:
dx
π
a:4 + 2x2 cosh(2a) +1 2cosh(a)
(2.3.2)
Для a = 1, например, этот интеграл равен 0.5089806..., и quad дает почти то же
самое: quad(@(x)l./(x.A4+2*cosh(2)*x.A2+l),0,1000) = 0.5089809....
Обратимся к главе 1 (раздел 1.5). Я показал там, как «четность» или
«нечетность» подынтегрального выражения (если присутствует одно из этих двух
свойств) может оказать большую помощь в преобразовании «сложного»
интеграла в «легкий». Как более сложный пример этого давайте найдем значение
dx
I
[ x4+2x2cos(2ct) + l
где, как и прежде, α - это произвольная константа. Внешне это может
выглядеть очень похоже на интеграл, который мы только что закончили вычислять,
но, как вы скоро увидите, мы возьмем его совершенно по-другому.
π „ 1 , dy 1
Для начала мы сделаем замену переменной у = — (и тогда — = -, или
χ dx χ1
dx = -x\ dy = —rdy). Тогда
У
Два старых трюка, плюс один новый ♦♦♦ 79
1
dx
ι= Г ™ = Г >
{ Ar4+2Ar2cos(2a) + l ± 1 , „ 1
2dy
'0*4+2*2COs(2a) + l J l+2lcos(2a) + 1
y2dy
>0 y4+2y2cos(2a) + l
Если затем мы добавим две наши версии интеграла (самые левые и самые
правые интегралы в предыдущей строке, помня, что χ и у - просто фиктивные
переменные интегрирования), то мы имеем:
{\ + x2)dx
2/ = /
[ x4+2x2cos(2a) + l
или
1 ОО
(l + x2)dx
2 «J Ar4+2Ar2cos(2a) + l
И поскольку подынтегральное выражение четно, то мы пишем:
1 °°
(\ + x2)dx
4 JooAr4+2x2cos(2a) + l
Так как cos(2a) = 1-2 sin2(a), можно показать прямым вычислением, что
х4 + 2x2cos(2a) + 1 = [χ2 - 2xsin(a) + 1][х2 + 2xsin(a) + 1],
и тогда
(l + x2)dx
л СЮ
4 J [7
4 JJx2-2xsin(a) + l][x2 + 2xsin(a) + l]
Поскольку подынтегральное выражение является четным, то, включив в
числитель подынтегрального выражения нечетную функцию, такую как 2xsin(a),
мы не изменим значение интеграла, и поэтому
1 °г [x2-2xsin(a) + l]rfx
4 i0[λ:2-2λ:sin(a) + l][λ:2+2λ:sin(a) + l],
или
dx
Л J I
4Joo[x2 + 2Arsin(a) + l]
Или поскольку sin2(a) + cos2(a) = 1, то
80 ♦ «Легкие» интегралы
1 оо
A J
dx
л ОО
A J I
dx
4yTOx2+2*sin(a) + sin2(a) + cos2(a) 4yoo[x + sin(a)]2+cos2(a)"
Пусть u=x + sin(a), du = dx, и тогда
A OO
4/
du
__1
4^00ы2 + cos2 (a) 4
1
ί 1 ]
[cos(a)J
tan 1
ί u 11
cos(a)JJ
4cos(a)
и наконец:
[tan ^oc^-tan ^-oo)],
dx
f
J0 x4 + 2x2 cos(2a) +1 4cos(a)
(2.3.3)
Особые, интересные случаи имеют место для некоторых очевидных значе-
нии а. В частности, для a = — мы имеем:
J dx = °r x2dx = π72
{ χ4+1~*Ι х4+1~ 4
(2.3.4)
Поэтому эти два интеграла равны 1.11072..., для сравнения вычисляем
их в MATLAB, как quad(@(x)l./(x.A4+l),0,1000) = 1.11072... и quad(@(x)(x.A2)./
π
(χ.Λ4+1),0,10000) = 1.11062.... Для α = 30° (тоестьа = — ) мы имеем:
6
dx
г
J0x4+x2+l 2S
(2.3.5)
Это равно 0.906899..., и снова MATLAB соглашается: quad(@(x)l./(x.A4+x.
А2+1), 0,1000) = 0.9068993.... Для α = 60° (то есть α = — ) мы имеем:
dx
-|аг4-аг2+1 2
(2.3.6)
Это равно 1.570796..., и действительно, quad(@(x)l./(x.A4-x.A2+l),0,1000)
1.570796.... И наконец, для α = 0 мы имеем:
dx
π
Ό χ4 + 2x^+1 4
(2.3.7)
Это равно 0.785398..., и quad(@(x)l./(χ.Λ4+2*χ.Λ2+1),0,1000) = 0.785398.
Два старых трюка, плюс один новый ♦ 81
Вот новый трюк, использующий разностное уравнение для оценки класса
определенных интегралов, индексированных целочисленной переменной п.
А именно
/„(«)=/
f COS(fl6) - COS(HCX) .
UO.
cos(6)-cos(a)
где a - это константа и η - неотрицательное целое (η = 0, 1, 2, 3,...). Первые
два интеграла очевидны: /0(а) = 0 и ^(а) = π. Однако при η > 1 все становится
сложнее. То, что я буду делать дальше, будет совершенно понятно, когда мы
пройдем этот анализ шаг за шагом, но я понятия не имею, что мотивировало
человека, который первым сделал это. Тайна математического гения!
Если вы помните тригонометрическое тождество
cos{(n + 1)θ} + cos{(n - 1)θ} = 2cos(6)cos(ne),
тогда, возможно, вы подумали бы о том, чтобы взглянуть на величину/п+1(а) +
/η_ι(α), дабы увидеть, связана ли она каким-то «хорошим» способом с /„(а).
Итак, представляя, что мы вдохновлены именно этим, давайте посмотрим на
величину О = Ах1п+1(а) + Бх/П(а)+ Сх1п_г(а)у где А, В и С - постоянные, чтобы
увидеть, что мы получаем.
Тогда
о-/
A[cos{(n + l)Q}-cos{(n + l)a}] + B[cos(nQ)-cos(na)] +
+ С [cos{(n - 1)θ} - cos{(n - l)a}]
w θ.
0 cos(6)-cos(a)
Предположим, что мы теперь установили А = С= 1 и В = -2cos(a). Тогда
[cos{(n + l)6} + cos{(n-l)e}-2cos(a)cos(ne)]-
[cos{(n + l)a} + cos{(n - l)a} - 2cos(a)cos(na)]
o=/
da
0 cos(6)-cos(a)
Из нашего тригонометрического тождества второе слагаемое в числителе
исчезает, а первое слагаемое сводится к
j>2cos(e)cos(ne)-2cos(a)cos(ne) j>2cos(ne)[cos(e)-cos(a)]rf
^ J cos(6)-cos(a) J cos(6)-cos(a)
-2fcos(nQ)de--
sin(7?9)
0, η = 1,2,
To есть мы имеем следующее линейное разностное уравнение второго
порядка:
/п+1(а) - 2cos(a)/n(a) + /^(а) = 0, η = 1, 2, 3,...
с условиями /0(а) = 0 и ^(а) = π.
82 ♦ «Легкие» интегралы
Хорошо известно, что так называемое рекурсивное уравнение имеет
решения вида In = Се5П, где С и s - постоянные. Так,
Ces(n+1) - 2cos(a)Cesn + Ces^l) = О,
или, сокращая на общий множитель Cesn,
es-2cos(a) +e"s = 0,
или
e2s - 2cos(a)es +1 = 0.
Это квадратное уравнение на е5, поэтому
s 2cos(a)±V4cos2a-4 2cos(a) -cos2a
cos(a)±zsin(a),
2 2
где i = x/^4. Теперь из легендарной формулы Эйлера мы имеем е5 = е±ш и,
следовательно, s = ±/а. Это означает, что общее решение для /п(а) есть
/п(а) = С,ёпа + C2e~ina.
Поскольку /0(а) = 0, то Q + С2 = 0, или С2 = -Q. Также из /х(а) = π мы имеем
равенство
Схёа - Схе~1а = π = Cxi2un(a),
которое говорит, что
-Ί
/2sin(a)
Тогда
и С,
π
/2sin(a)
7η(«) = ^τ
π
π
2sin(a)
/2sin(na)|
i \
2sin(a)
или, наконец, используях в качестве фиктивной переменной интегрирования:
|»cos(Hx)-cos(Ha) , _ sin(fla)
J cos(x)-cos(a) sin(a)
(2.3.8)
π
Например, если п = 6 и α=—, то этот результат говорит, что наш
интеграл равен π
(
sin
6-
1 lj
/ \
.
sin
π
—
(llj
, что равно 11.03747399..., и функция интегрирования
quad это подтверждает, поскольку quad(@(x)(cos(6*x)cos(6*pi/ll))./(cos(x)-
cos(pi/ll)),0,pi) = 11.03747399....
Два старых трюка, плюс один новый ♦ 83
Вот последний, быстрый пример рекурсии, используемый для решения
целого класса интегралов:
оо
In = fx^e^dx, η = 0,1,2,3,...
о
Мы начинаем с наблюдения, что
А'-(х2"-^-"2) = (2n-l)x2"-V*2 -2х2пе-"\ η > 1.
dx
Интегрируя теперь обе части равенства:
ОО 1 ОО ОО
j—(x2n-le-x2)dx = (2n-l)fx2n-2e-x2dx-2fx2ne-x2dx.
о "* о о
оо ι
f±(x^e-*2)dx = (2n-l)In _,-21п.
Самый правый интеграл - это /„, а средний интеграл - /„_[. Таким образом:
d_
0dx
Теперь обратите внимание, что оставшийся интеграл (слева) является
просто интегралом производной, и его очень легко решить! Действительно,
Г—(х2"-^-"2 )dx = (χ2π-ν*2 )Γ = О,
J0 dx lo
поскольку x2n~le~^ = О при χ = О и при χ —> оо. Итак, у нас сразу же получилась
рекуррентность
_2η-1 _2η(2η-1)
Для первых нескольких значений η мы имеем:
/, =—?—/п,
1 (4)(1) °'
= (4КЗ) (4)(5)(2)
2 (4)(2) ' (4)(2)(4)(1) °'
7 = (6К5) 7 = (6)(5)(4)(5)(2) f
3 (4)(3) 2 (4)(3)(4)(2)(4)(1) °'
и теперь вы должны увидеть закономерность:
= (2п)!
" 4"п! °"
Это, конечно, хороший результат, но очевиден следующий вопрос: чему
равен 10? По факту
84 ♦ «Легкие» интегралы
оо -.
I0=fe-x2dx = -^,
и это мы еще не показали (пока). В следующей главе, как результат (3.1.4), я
покажу вам (используя новый прием), что
оо
je-"2/2dx = ^.
— оо
Если мы сделаем замену переменной у = хл/2 (и вспомним, что Г f(x)dx =
J —оо
J»oo
f(x)dx, если функция f(x) четная), тогда значение интеграла /0 получается
о
сразу:
Г 2п -*А (2л)!ill г
\ xlne x dx = -—— - Κ/π,
4пп\
(2.3.9)
Если η = 5, то это равенство говорит, что интеграл равен 26.171388..., в то
время как диас1(@(х)(х.л10).*ехр(-(х.л2)),0,10) = 26.1713896....
2.4. Еще один старый прием. Лог-синус Эйлера
В 1769 году Эйлер вычислил (для а = 1) значение интеграла (где а > 0)
π/2
fln{asin(x)}dx,
о
который равен
π/2
rin{acos(x)}dx.
о
Эти два интеграла равны, потому что подынтегральные выражения
принимают одинаковые значения на интервале интегрирования (sin(x) и cos(x)
являются зеркальными отображениями друг друга в этом интервале). В
течение многих лет в учебниках часто заявлялось, что это довольно сложные
интегралы, лучше всего решаемые с помощью мощных методов контурных
интегралов. Однако, как вы увидите из следующего анализа, это просто не
тот случай.
Итак, для начала заметим, что
π/2 л π/2
- r[ln{asin(x)} + ln{acos(x)}]dx = -
-i π/ δ -ι π/ δ
Ι = — r[ln{asin(x)} + ln{acos(x)}]dx = - rin{a2sin(x)cos(x)}dx.
о
Еще один старый прием. Лог-синус Эйлера ♦ 85
Поскольку sin(2x) = 2sin(x)cos(A'), мы имеем sin(x)cos(x) = sin(2x)/2, и поэтому
1 π/2 Ι
a-asin(2x)
л π/2
z о
π/2
1η(α) + 1η
+ ln(asin(2x))
dx
-ι π/ δ
:-1η(α)--1η(2) + -jln(asin(2x))dx.
В последнем интеграле пусть t = 2х (и тогда dx = dt/2). Тогда
1 π^ 1 π 11
- J ln(asm(2x))dx = - J*ln(asin(t))-dt = -/,
где последнее равенство следует, потому что (подумайте о том, как sin(t)
меняется в интервале от 0 до π)
π/2
J ln(asin(t))dt = -fln(asin(t))dt.
0 ^ 0
Таким образом,
J = -ln(a)--ln(2) + -J = -ln
4 v } 4 w 2 4
[я]
u
.
+-Λ
2
ИЛИ
1 π,
-/ = — In
2 4
V
и, наконец, для а > 0:
π/2 π/2
f ln{asin(x)}dx = f ln{acos(x)}dx = — In
V
(2.4.1)
Особый интерес представляет значение а = 1 (интеграл Эйлера), для кото-
ти
рого оба интеграла равны 1п(2) =-1.088793..., и a = 2, для которого оба
л
интеграла равны нулю. Мы можем проверить оба этих случая с quad: quad(@(x)
log(sin(x)),0,pi/2) = -1.0888035... и quad(@(x)log(cos(x)),0,pi/2) = -1.0888043...,
в то время как quad(@(x)log(2*sin(x)),0,pi/2) = -1.0459χ 10"5 и quad(@(x)log
(2*cos(x)),0,pi/2) = -1.1340xl0~5. Мы снова увидим этот логарифмический
интеграл Эйлера в главе 7.
Теперь, получив этот результат для а = 1, мы можем вычислить интересный
интеграл
π/2
/
In
sin(x)
\dx.
86 ♦ «Легкие» интегралы
Так как этот интеграл есть
Г lnsin(x)dx- [2ln{x}dx
π
21η(2)-[χ1η<χ)-Α·]|>
-flnO)-
-fln(2)-
71, 71 71
—In — —
2 [2j 2
It , /r»4 It ι • . It ι т»ч It
■-1η(2)--1η(π) + -1η(2) + -:
71 , . ч 71
-21η<™>+2·
и таким образом:
Г/21п
Jo
sin(x)
π.
\dx = -^[l-ln(n)].
(2.4.2)
Наш результат говорит, что интеграл равен 0.22734..., и функция quad
подтверждает: quad(@(x)log(si.n(x)./x),0,pi/2) = 0.22734....
Простым изменением переменной в интеграле лог-синуса Эйлера мы
можем получить еще один симпатичный результат. Поскольку sin2(0) = 1 - cos2(0),
то
sin2 (θ)
cos2 (θ)
tan2 (θ):
1
cos2 (θ)
-1,
и
tan2(0) + l:
1
cos2 (θ)
это говорит, что
1
In
[cos2(6)
То есть
ln{cos2(0)} = -21n{cos(e)} = ln{tan2(e) + l}.
ln{cos(9)} = —ln{tan2(9) + l}.
Наконец, в интеграле
π/2
Г ln{cos(x)}dx
Еще один старый прием. Лог-синус Эйлера ♦ 87
заменим фиктивную переменную интегрирования хна θ и напишем
π/2 π/2 Γ
Jln{cos(6)}de= J
о
или
π/2
-|ln{tan2(9) + l}
π.
ав = ~Щ2),
f ln{tan2(9) + 1}ίίθ = π 1η(2).
Теперь сделаем замену переменной χ = tan(6). Тогда
dx _ 1
de-cos2(9)'
и таким образом:
de = cos2(Q)dx =
1
tan2(6) + l
-dx =
x2 + l
-dx.
π
А поскольку at = 0, когда θ = 0,иаг = оо, когда Θ = — ,мы имеем:
°rln(x2+l) , , ,_
(2.4.3)
Таким образом, интеграл равен 2.177586..., и quad соглашается: quad(@(x)
1од(х.л2+1)./(х.л2+1),0,1еб) = 2.1775581.... Чтобы закончить это обсуждение,
вот небольшое вычисление для тренировки: написать Г —Ц -dx как
Jo АГ2+1
\ + \ > сделать замену переменной и=1/хв последнем интеграле и показать,
что это приводит к
(2.4.4)
Это равно 1.088793..., и MATLAB соглашается, потому что quad(@(x)log(x
+(1./х))./(х.Л2+1) ΑΙ) = 1.088799....
Замена и = 1/х- это уловка, о которой стоит помнить. Вот другое ее
использование для получения результата, который почти наверняка было бы гораздо
труднее получить в противном случае. Рассмотрим интеграл
fln(*-+l)
·£ χ2- bx + l
88 ♦ «Легкие» интегралы
где α ^ 0 и Ь - константы. Если мы положим и = 1/х (и в этом случае dx = —ψάν),
и
то имеем:
{*-Ъх + \ iA_bi + 1i и2 ) J01-
иа
и
1п(1 + ив)
{\-Ьи + и2 {\-
1п(м)
bu + u2
bu + u2
-du.
du
To есть
Jv2_bv_Li Jl-Ьх + х2 ·£ 1
1η(χ«+1)^_?1η(1 + χ«)^ „? ln(x)
v2- bx + 1
bx + x
-dx,
и поэтому мы сразу имеем:
ι-:
(Л А
1п(х)
Ьх + х2
-dx = 0.
(2.4.5)
Обратите внимание, что случай Ь = 0 в (2.4.5) сводит этот результат к (1.5.1),
1п(х)
/
Ό 1+^
dx = 0,
что мы также получаем, когда полагаем Ь = 1 в (2.1.3). Однако значение Ь не
может быть любым, и вам будет предложено больше узнать об этом в разделе
задач и упражнений.
Чтобы закончить главу, позвольте мне напомнить вам о простой технике,
с которой вы столкнулись еще в школьной алгебре, - это «выделение
полного квадрата». Это «уловка», о которой стоит помнить, когда мы сталкиваемся
с интегралом с квадратичным полиномом в знаменателе подынтегрального
выражения (но см. также задачу 2 для его использования в кубическом
знаменателе и посмотрите еще на последнее интегрирование раздела 1.6). Давайте
вычислим другой пример:
J0 1+Х + Х2
Мы начнем с переписывания знаменателя подынтегральной функции,
выделяя квадрат:
Х2 + Х + 1 = Х2 + Х-\ Ь
ί, 11
1
4
=
ί Л
* + d
2)
+-
Еще один старый прием. Лог-синус Эйлера ♦ 89
Поэтому
J 1j_vJ_vz J
dx
1+x + x2
"4
-/
+-
ι Υ2
-dx.
* + ;
+ -
Теперь замена переменной:
1
(и следовательно, dx = du). Тогда наш интеграл принимает вид:
du
ъ 1
2 U
du
и*+-
u*+-
u*+-
242 4 2 42
Первый интеграл справа есть
ы*+-
jj
du
w2 +
ί^Ι
^tan"1
л/з
и
I 2 J
"S
tan
2u
l^J
J2_
tan-1
π π
"з~"б
l^J
tan-1
l^J
2_
tan_1(V3)-tan_1
π
Зл/з"
Таким образом:
Jo 1+x + x2
VjMt*
zS
w+-
fj_)|
В интеграле справа заменим переменную и на
t = u2 + -.
Тогда dt = 2u du, и
Ji 2 , 3 Jit2u 2Ji t 2 W|1 2
2 u'+t
4
90 ♦ «Легкие» интегралы
Итак:
ϊ—
J 1 J_V_L Л
о
или
1+х + х2 Зл/з 2
(2.4.6)
который равен 0.35759..., и MATLAB соглашается, потому что quad(@(x)(l-x)./
(1+х+х. Л2),0,1) = 0.357593....
2.5. Задачи для упражнений
Все это было довольно просто, но вот некоторые задачи, которые, я думаю,
дадут вашему мозгу действительно хорошую тренировку. И все же, как и почти
все остальное в этой книге, если вы увидите хитрость, то они для вас
развернутся, как бабочка в покое.
(С2.1). Согласно «Трактату об интегральном исчислении» Эдвардса (см. конец
предисловия), на экзамене 1886 года в Кембриджском университете появился
следующий вопрос: показать, что
1п(*)
о лМх-х2
I
dx = 0.
У Эдвардса не было решения, и, учитывая, что мне потребовалось около 5
часов в течение 3 дней, чтобы доказать это (в моем тихом офисе, без давления),
мой трепет перед предполагаемым математическим уровнем некоторых
студентов Кембриджа XIX века неограничен. Посмотрим, сможете ли вы сделать
это быстрее, чем я (а если нет, то мое решение в конце книги). Быстрая
числовая проверка MATLAB должна убедить вас в правильности данного ответа:
quad(@(x)log(x)./sqrt(4*x-x.A2) A4) = 0.0000066.
г1 dx
(С2.2). Вычислить значение интеграла J —^—-. Подсказка: сначала подтвер-
X ~г 1
дите правильность разложения дроби
1
х3 + 1
1
х-2
1
■х + 1
, и в этом
случае
г1 dx I г1 dx 1 pi х-2 , _
/ — = -/ / — αχ. Первый интеграл справа поддастся
X —|— 1 «J X —г" 1 «J X X ~\~ 1
при очевидной замене переменной, а второй интеграл справа берется другой
Задачи для упражнений ♦ 91
заменой переменной, столь же очевидной, если сначала выделить квадрат
в знаменателе подынтегрального выражения. Ваш теоретический ответ
должен иметь числовое значение 0,8356488....
(С2.3). Вот относительно небольшая рекурсивная задача для вас.
Предположим, вы знаете значение
°°r dx
Ιχ4 + ι
+ .
π
Этот интеграл не особенно сложен - мы решили его в (2.3.4), получив —ί=.
Дело в том, что, зная это, вы также можете сразу узнать значение интеграла
dx
S:
■i (** + !>"
для всех целых т > 1 (и не только для т = 1). Покажите это, выводя рекурсию
°r dx _4m-l°r dx
J Cy4-U1Y"+1 ~ Am J l
J0(x4 + l)m+1 4m J0(x4 + l)m
Например:
dx (4)(2)-l? dx I'} dx
°f dx =(4)(2)-l?· dx = ТЪ dx
Ux4 + lf~ (4) (2) «J(x4 + 1)2"8-J(x4 + 1)2
J dx =(4)(1)-1°?- dx ^5J dx
•J(x4+1)2~ (4)(1) {x4 + \~4{ x4+l
Тогда:
dx f7l
8
\(Ъ)°°г dx
dx i2ll
32
* =^L = 0.72891.
2V2 64V2
•|(x4 + l)3
MATLAB соглашается: quad(@(x)l./((χ.Λ4+1).Λ3),0,1000) = 0.72891....
OO J
Подсказка: начните с Г— и интегрируйте по частям.
о \Х +1)
(С2.4). Для каких значений Ъ имеет смысл интеграл в (2.4.5)? Подсказка:
подумайте, где находятся какие-либо особенности подынтегрального выражения.
(С2.5). Покажите, что Г— dx = 2π. Подсказка: интегрируйте по частям,
о W*
Глава
з
Любимый трюк Фейнмана
3.1. Формула Лейбница
Отправная точка для трюка Фейнмана «дифференцирование под знаком
интеграла», упомянутого в конце главы 1, - это формула Лейбница. Если у нас
есть интеграл
На)
J(a) = ff(x,a)dx,
а(а)
где а - это так называемый параметр интеграла (не фиктивная переменная
интегрирования, которая здесь, конечно, х), то мы хотим вычислить производную
от I по а. Мы делаем это так, как вы ожидаете, исходя из самого определения
производной:
dl = lim/(a + Aa)-/(a)
da Δα^° Δα
Теперь, поскольку пределы интегрирования зависят (в общем случае) от а,
приращение Δα будет вызывать приращения Δα и а АЬ, и поэтому мы должны
написать:
b+Ab
Ι(α + Δα) - /(a) = Г /(*, α + Δα)άχ - ff(x, a)dx =
+Δα α
a b b+Ab\ b
J +J+ J \f(xya + Aa)dx-ff(xya)dx =
a+Aa a b ) a
b b+Ab
= r{f(x,a + Aa)-f(x,a)}dx+ f f(x,a + Aa)dx —
a b
a+Aa
- f f(x,a + Aa)dx.
Формула Лейбница ♦ 93
Поскольку Δα —> 0, мы имеем Δα —> 0 и ЛЬ —> 0, и тогда
ь
Ηπι{/(α + Δα)-/(α)} = lim Г{/(АГ,а + Ла)-/(АГ,а)}^АГ+/(Ь,а)ЛЬ-/(а,а)Ла,
Δα->0 Aa->0J
а
где два последних члена получаются такими, потому что при Δα —> 0 и ЛЬ —> О
значение переменной χ в интервале интегрирования практически не
отличается οτχ = α или χ = Ь соответственно. Таким образом:
ь
dl_
da
Umf(a + Aa)-f(a) = limJ_ г +Δα)_/(χ>α)}ώ
Δα—>0 Д(^ Δα—>0 Д(^ J
Δα*
u
Έ. r/1 ЧАЬ Έ. r/ 4Δα
+ hm/(b,a)— - im/(fl,a-,
Δα^Ο Да Δα^Ο Да
1
или перенося — внутрь интеграла (сам интеграл Римана определяется как
Δα
предел, поэтому то, что мы делаем, есть перемена порядка двух предельных
операций, что чистый математик хотел бы оправдать, но, как обычно в этой
книге, мы не будем беспокоиться об этом!):
— = I ^-dx + f(b,a)- /(a, a) —.
aa J да да да
(3.1.1)
Это полная формула Лейбница для дифференцирования интеграла,
включая случай, когда подынтегральное выражение и пределы являются
функциями параметра а. Если пределы не являются функциями параметра (например,
когда пределы являются константами), то последние два члена исчезают, и мы
просто дифференцируем (находим частную производную) подынтегральное
выражение под знаком интеграла по параметру α (не х).
Вот простой пример мощности формулы Лейбница. Мы уже неоднократно
использовали следующий элементарный результат:
/
1
Ό*2 + α2
dx =
- tan"1
а
V
π
2а'
Рассматривая а как параметр, дифференцирование сразу же дает нам новый
результат:
-2а 2π
I
>0{х2 + а2)2
dx
4а2
или же
I
1
И^ + оТ
-dx
π
4а>'
(3.1.2)
94 ♦ Любимый трюк Фейнмана
Можно, конечно, не останавливаться на достигнутом и продолжать
дифференцировать этот новый результат снова (а затем снова и снова), каждый раз
получая новый результат. Например, следующее дифференцирование дает
СЮ 1
Г L
Jo (*2+α
, 3π
-dx
2f 16α5
(3.1.3)
Для а = 1 это есть 0.58904..., и quad(@(x)l./((x.A2+l).A3),0,100) = 0.58904....
Более сложным примером использования формулы Лейбница является
нахождение
'dx.
Это знаменитый интеграл вероятностей1, называемый так потому, что он
появляется в теории случайных величин, описываемых гауссовыми (колоко-
лообразными) функциями плотности вероятности (о которых вам ничего не
нужно знать для этой книги). Поскольку этот интеграл имеет четную
подынтегральную функцию, мы можем вместо него изучить
ου χ
fe 2dx,
а затем просто удвоить результат.
Чтобы ввести параметр (£), по которому мы можем дифференцировать,
давайте определим функцию
*(*) =
Ге 2dx
о
итак, что нам нужно, так это
Обратите внимание, что параметр t и фиктивная переменная
интегрирования χ являются независимыми величинами.
Интеграл вероятностей чаще всего находится в учебниках с помощью приема
преобразования его в двойной интеграл в полярных координатах (см., например, мои
книги: Мнимая сказка: история числа уРл. Принстон, 2012. С. 177-178;
Электрическое одеяло миссис Перкинс. Принстон, 2009. С. 282-283) (An Imaginary Tale: the
story of ^Ί. Princeton, 2012. P. 177-178, and Mrs. Perkins's Electric Quilt. Princeton, 2009.
P. 282-283), а использование формулы Лейбница, которую я собираюсь показать вам
здесь, является редкостью. Это настолько важный интеграл, что в конце этой главы
мы вернемся к нему с дополнительным анализом.
Формула Лейбница ♦ 95
Дифференцируя g(t) по формуле Лейбница (обратите внимание, что
верхний предел интеграла является функцией параметра £, а подынтегральное
выражение и нижний предел - нет), получим
— = 2Je 2dx\e 2 J = 2Je 2 dx.
dt о о
Затем сделаем замену переменной у = x/t (когда χ изменялось от 0 до ί, у
будет варьироваться от 0 до 1). То есть χ = yt, и, следовательно, dx = t dy, и мы
имеем:
dg
dt
= f2te 2 dy = J2te 2 dy.
Теперь заметим, что подынтегральное выражение может быть записано как
(частная) производная следующим образом:
2ie 2 = —
dt
То есть1
(1+ГГ
2е 2
1 + Г
dt {dt
(l+y2)t2 "
2e 2
1 + У2 J
(i+yzr
dti 1
+yz
-dy.
И тогда, интегрируя, получаем:
(i+yz)tz
g(t) = -l]- -dy + C,
i 1 + y2
о 1 + У
где С - постоянная интегрирования. Мы можем найти С следующим образом.
Пусть t = 0. Тогда
Ί2
£(0) =
Ге 2dx
0,
и при t —> 0
(i+yV
ίτϊ^ίϊΤ^'^
4"
1 Причина, по которой мы вводим частную производную под интеграл, а полную
производную вне интеграла, состоит в том, что подынтегральное выражение является
функцией двух переменных (t и у), а сам интеграл - функцией только от t (мы
«проинтегрировали» у-зависимость).
96 ♦ Любимый трюк Фейнмана
171 71
— + С, следовательно, С = —, и поэтому
4) 2
(1+уУ
Теперь пусть t —> оо. Подынтегральная функция явно исчезает во всем интер-
71
вале интегрирования, и мы имеем g(oo) = —. Таким образом:
00 -— ίττ
fe~2dx = 2J- = -Jhi.
(3.1.4)
V2tt = 2.506628..., и quad подтверждает: quad(@(x)exp(-(x.A2)/2),-1000,1000) =
2.506628....
Мы можем снова использовать дифференцирование под знаком интеграла,
чтобы обобщить этот результат в оценке интеграла:
ου χ
I(t) = Jcos(tx)e~Ydx.
Из нашего последнего результата мы знаем, что 1(0) -
цируя по V.
dl(t)
4
Тогда, дифферен-
dt
= Г-xs'm(tx)e 2dx.
Мы можем сделать это интегрированием по частям; пусть и = s'm(tx)
и dv = -хе 2 dx. Тогда du = t cos (tx)dx и ν = е 2. Таким образом:
dl(t)
dt
sin(£x)e
- ftcos(tx)e 2dx.
Первое слагаемое в правой части исчезает как при верхнем, так и при
нижнем пределах, поэтому мы имеем элементарное дифференциальное
уравнение первого порядка
dm
dt
ου χ
-tJcos(tx)e~Ydx = -tl(t).
To есть переписывая:
dl(t)
i(t)
= -tdt,
Формула Лейбница ♦ 97
и легким интегрированием это дает
щщ)} = --+с,
где, как обычно, С - постоянная интегрирования. Поскольку 1(0) -
имеем С = in|j— |, и тогда
Ί2'
ТО МЫ
ln[I(t)}-ln\M = ln\l(t)M
или наконец:
— /π" —
Jcos(tx)e 2dx = J—e 2
(3.1.5)
Для t = 1, например, наш результат говорит, что интеграл равен
0.760173..., и quad(@(x)cos(x).*exp(-(x.A2)/2),0,1000) =0.760171....
Зная этот последний результат, вернемся к исходным пределам от -оо до оо,
мы можем написать:
Je 2cos(tx)dx = 2J-e 2 =^Ые 2.
—oo
Тогда, записав
oo_x2 oo_a:2 °° _^_
fe 2cos(s + tx)dx= fe 2cos(s)cos(tx)dx- fe 2sin(s)sin(tx)dx,
— oo —oo —oo
где я использовал тригонометрическое тождество для косинуса суммы, мы
имеем
оо χ2 оо χ2 оо χ2
Ге 2cos(s + £x)dx = cos(s) Ге 2cos(£x)dx-sin(s) Ге 2 sin(tx)dx.
— оо —оо —оо
Но поскольку последний интеграл справа равен нулю, так как его
подынтегральное выражение нечетно, мы имеем
оо х2 оо х2
[е 2cos(s + tx)dx = cos(s)[e 2cos(tx)dx,
— оо -оо
итак, наконец (используя наш результат (3.1.5)):
98 ♦ Любимый трюк Фейнмана
[е 2cos(s + tx)dx = j2ne 2cos(s).
(3.1.6)
Для t = s= 1 это равно 0.82144..., и quad(@(x)exp(-(x.A2)/2).*cos(l + χ),-10,10)
= 0.82144....
Прием оценки интеграла путем нахождения дифференциального
уравнения, для которого интеграл является решением, может использоваться для
определения значения следующего интеграла
'COS(flX)
ад=/!
2 ,2d*>
r + b2
где а и Ь положительны (а является параметром, а Ъ является константой). Если
мы будем интегрировать по частям, то напишем:
1
и-
тогда
du-
x2+b:
-у dv = cos(ax)dx,
2х
(х2 + Ь2)2
и поэтому
sin(ax)
dx, v =
sin(ax)
1(a)--
a(x2+b2)
+
2 °f xsinjax)
a{(x2 + b2fUX'
или, поскольку первый член справа исчезает как при верхней, так и при
нижней границе, мы имеем:
aJ0 (x2+b2)2
и поэтому, возможно, все выглядит так, как будто мы все ухудшаем! Как вы
скоро увидите, мы покажем, что это не так.
Последнее равенство умножаем на α и приходим к
xsin(ax)
al(a) = 2f-
-dx,
Jo(*2+b2)2
а затем дифференцируем по α, чтобы получить
dl(a)
da
+
1(a) = 2 J
χ2 cos(ax)
Ό (*2 + Ь2)2
dx.
Подынтегральное выражение может быть разложено на элементарные
дроби:
Формула Лейбница ♦ 99
χ2 cos(ax) _ cos(ax) b2 cos(ax)
(х2 + Ь2)2 "х2+Ь2 ~(х2+Ь2)2 '
Тогда
J0 (х2+Ь2)2 J0 х2+Ь2 J0 (x2+b2)2
и, поскольку первый интеграл справа есть 1(a), мы имеем:
dl(a) т/ ч пт/ ч nl2°r cos(ax) ,
a-^ + I(a) = 2I(a)-2b2 2 \'<fr»
da J0 (x2+b2)2
или
dl(a) т/ ч οϊ2°ρ cos(ax) .
da J0 (x2+b2)2
Дифференцируя это по переменной α, мы получаем
rf2/(g) dJ(fl) rf/(g)_ 27>xsin(ax)
* da2 + da da "2M (*Ч Ь2)2 **'
или
a^ = 2brrxsin(ax) χ
da2 J0 (x2+b2)2
Если вы вернетесь в начало последнего абзаца, то увидите, что мы уже
нашли интеграл в правой части:
°r xsin(ax) . а т. ч
и тогда
d2I(a) ηΊ2α т/ ч
а^У = 2Ь21(а)'
или, приводя в порядок, мы имеем следующее линейное дифференциальное
уравнение второго порядка для /(a):
^-Ь2/(а) = 0.
da2
Хорошо известно, что такие уравнения имеют экспоненциальные решения -
1(a) = Сека, где С и к - постоянные, а подстановка в дифференциальное
уравнение дает
Ск2ека - Ь2Сека = О,
100 ♦> Любимый трюк Фейнмана
и поэтому к2 -Ъ2 = О, или к = ±Ь. Таким образом, общее решение этого
дифференциального уравнения является суммой этих двух частных решений:
1(a) = С,еаЬ + С2е~аЬ = 0
Нам нужны два условия для 1(a), чтобы определить константы Сх и С2, и мы
можем получить их из наших двух различных выражений для 1(a): оригинала
Κα) = J
cos(ax)
dx
и выражения, которое мы получили путем интегрирования по частям:
2 °r xsin(ax)
dx.
Jo(*2+b2)2
Из первого мы видим, что
ου
К0) = J
1
Όχ4*
dx
tan !
π
а из второго видим, что lima^c 1(a) = 0. Тогда
π
Д0) = - = С1 + С2
Ι(οο) = 0,
которое говорит, что Q = 0. Тогда С2
ный результат:
π
2b
°fcos(ax) π b
,и мы имеем следующий замечатель-
(3.1.7)
π
открытый в 1810 году Лапласом. Если Ь = 1 и а = π, то интеграл равен —е
0.06788..., и quad(@(x)cos(pi*x)./(x.A2+l),0,lel0) = 0.06529.... Прежде чем
перейти к новым трюкам, позвольте мне заметить, что простым изменением
переменной мы зачастую можем получить некоторые впечатляющие результаты
из ранее полученных. Например, поскольку (как мы показали ранее в (3.1.4))
Je 2dx = j2^,
— оо
то из этого следует (с и = *V2), что
Удивительный интеграл ♦> 101
ОО л
о 2
Тогда, полагая ί = е~х\ мы имеем χ = ^—1η(ί) (а также dx =
Л
2хе~х
2xV
и поэтому
{ { -2Л 2^ОЛр1гйг) 2
которое говорит, что
;т>/тс,
1
ах
{ у]~\п(х)
νπ,
(3.1.8)
значение которого есть 1.77245... и согласуется с quad(@(x)l./sqrt(-log(x)),0,l)
= 1.77245....
3.2. Удивительный интеграл
Начнем с функции g(y), определенной как
^) = ^«1η(«0 у>0,
где а - некоторая константа (скоро обсудим а подробнее). Дифференцируя по
параметру у (обратите внимание, что χ - это фиктивная переменная
интегрирования):
dy I ду
-ху
sin(ax)
\dx=7-xe--S-^^dx,
Jn χ
или
di
dy о
fe~xvsm(ax)dx.
Если затем этот интеграл интегрировать дважды по частям, то легко
показать, что
dg = a
dy a2 + у2'
последнее уравнение легко интегрируется и дает
gCy^C-tarr1
102 ♦> Любимый трюк Фейнмана
где С - произвольная константа интегрирования. Мы можем вычислить С,
заметив, что g (оо) = 0 в исходном интегральном определении g(y), потому что
множитель е_Ау в подынтегральном выражении стремится к нулю всюду при
у —> оо (потому что на всем интервале интегрирования χ > 0).
Таким образом,
0 = С - tan_1(±oo),
где мы используем знак +, если а > 0, и знак -, если а < 0. Итак, С = ±—, и мы
имеем
π
S'(y) = ±^-tan-1
У
Частный случай у = 0 (и поэтому tan !
^У^
: 0) дает нам следующий
замечательный результат, называемый разрывным интегралом Дирихле (в честь
немецкого математика Густава Дирихле (1805-1859)):
π
, если а > 0
сю
sin(ax)
dx = 0, если а = 0
π
—,если а<0
2
(3.2.1)
Значение этого интеграла при а = 0 равно нулю, поскольку числитель
подынтегрального выражения равен нулю на всем интервале интегрирования,
5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0 5
Рис. 3.2.1 ♦ Разрывный интеграл Дирихле
Интеграл Фруллани ♦> 103
за исключением единственной точки χ = О, где подынтегральное выражение
имеет значение а. Эйлер между 1776 годом и своей кончиной в 1783 году вывел
частный случай для а = 1. График на рис. 3.2.1, сгенерированный с
использованием quad для оценки интеграла для 1000 значений а на интервале 0,5 < а < 0,5,
намекает на правильность наших вычислений, с наглядной иллюстрацией
крайне важного внезапного скачка от отрицательного к положительному
значению (колебания происходят из-за явления Гиббса, которое присуще любой
попытке представить разрывную функцию в виде конечной суммы синусоид
и последующего интегрирования с quad такой суммы - см. любую книгу о рядах
Фурье).
3.3. Интеграл Фруллани
В качестве еще одного примера дифференцирования под знаком интеграла
давайте подсчитаем
• tan-1 (αχ) - tan-1 (bx)
I(a,b)=ran (αχ,-™η (OX,dx.
J У
Заметим, что 1(а, а) = 0. Дифференцирование по а (с использованием
частной производной, поскольку/является функцией двух параметров аиЬ):
\dx =
1+flV
00 1 1 1
-/iT??'«»-;i»»-,(««)C-;t-.-(=o)-i.
Таким образом, интегрируя по а:
/(fl,b) = ^ln(fl) + C(b),
где Сф) - это произвольная функция (от Ь) интегрирования. Записывая Сф)
ти
в другом виде как — 1п(С(Ь)) - это более удобная константа! - мы имеем:
А
/(a,b) = -|ln(a) + ^ln(C(b)) = |ln(aC(b)).
Поскольку/(α, а) = 0, мы имеем аС(а) = 1, или С(а) = —.Аналогично Сф) = —,
а Ъ
и тогда
Ι χ 2 Ы
(3.3.1)
104 ♦ Любимый трюк Фейнмана
Если а = π и b = 1, например, то
оо
/
tRn-\Tzx)-tSLn-\x) άχ=πΙη(π) =1 ?98137
и в подтверждение quad(@(x)(atan(pi*x)-atan(x))./x,0,1000) = 1.797461....
Этот результат является частным случаем того, что называется интегралом
Фруллани, в честь итальянского математика Джулиано Фруллани (1795-1834),
который впервые написал об этом в письме к другу в 1821 году. Мы будем
использовать интеграл Фруллани позже в книге, и поэтому стоит сделать общий
вывод, который обычно не приводится в учебниках.
Вот один из способов сделать это, где мы предполагаем, что у нас есть
функция f(x), такая что существуют значения ДО) и Доо). Наш вывод начинается
с определения ί/как (где а - некоторая положительная постоянная):
h/a
"=/
f(ax)-f(0)
dx.
где h - некоторая положительная константа (сейчас h - конечная константа, но
чуть позже мы позволим h —> оо). Заменив а на Ь, мы могли бы написать
u = hJf(bx)-f(Q)dx.
(Чтобы увидеть, что эти два выражения для [/действительно равны, помните,
что а - это произвольная константа, и поэтому не имеет значения, пишем мы
а или Ь). Итак:
hff(™idx=u+mh/ndx
J у J у
hff^ldx=u+mhfidx.
J у J γ
Вычитая последнее уравнение из предыдущего:
-а Пах)
f(bx).
r.nmdx_nnmdx=m
JO χ JO χ
f'-dx- rb-dx\ = f(0)f«-dx
Jo χ Jo χ j А/ЛХ
/
/(0)1η
= /(0)ln<*C
(b)
a
Затем вычитая и добавляя Г ——-dx к начальной левой части этого по-
Jh/Ь ν
следнего равенства, мы имеем:
Интеграл Фруллани ♦> 105
-;/«»)
Л№)^ п/(Ь*Ь„, гЛЪх), (»
р1Ш-ах- р'-Ш-ах- K^dx+ Г/Д^Л = /(0)1п
Jo χ Jo χ JL· χ Jl Χ
или комбинируя второе и третье слагаемые слева:
-£/(«).
•ϊΜ
№).
X X и X
или
Jo x J£ X
(ь)
Теперь представьте, что h^oo. Тогда верхний предел на самом левом
интеграле —> оо, и обе границы на втором интеграле —> оо. Это означает, что ДЬх) —>
Доо) по всему интервалу интегрирования во втором интеграле, и тогда
ΛίΦχ)
dx
lim f~a^^-dx = Urnf(об) /> — = /(oo)limln
h—Kx>J- χ h—юо J- χ h—>oo
Ы
:/(00)1П
Все это означает, что наше последнее уравнение при h —> оо принимает вид:
оо
I
f(ax)-f{bx)
или,записывая In
лани):
dx + /(οο)1η
-In
V
= /(0)1η
, мы получаем наш результат (интеграл Фрул-
оо
f(ax)-f(bx)
dx = {f(oo)-f(0)}ln
V
(3.3.2)
Этот результат предполагает, как я уже говорил ранее, что Дат) таково, что оба
Доо) и ДО) существуют. Это имеет место в первом примере Дат) = tan'V). а также
все работает и для f(x) = е~х, так как тогда ДО) = 1 и Доо) = 0, и поэтому
°°-е-°*-е-ь*
Г-
dx = -ln
V
In
V
, α, Ь>0.
(3.3.3)
Но не каждая функция Дх) отвечает этому требованию. Например, можем ли
мы найти интеграл
'Cos(ax)-cos(bx)
I(a,b) = f-
-dx,
используя интеграл Фруллани? Нет, потому что здесь мы имеем f(x) = cos(x),
и, таким образом, в то время как ДО) = 1 существует, Доо) - нет (функция коси-
106 ♦ Любимый трюк Фейнмана
нуса колеблется бесконечно между -1 и +1 и не имеет предельного значения).
Однако мы можем вычислить
оо
I(t) = Je
cos(ax)-cos(bx)
[dx
и посмотрим, что получится, когда t —> 0. Я отложу выполнение этого
вычисления до следующего раздела, где сначала покажу вам еще один полезный прием
для вычисления интегралов, а затем мы будем использовать его для
нахождения 1(f). Интересно, что это как бы прием, «обратный» приему Фейнмана
дифференцирования под знаком интеграла.
3.4. Обратная сторона трюка Фейнмана
Я продемонстрирую этот новый прием, используя его для вычисления
значения
оо
I(a,b) = J
cos(ax)-cos(bx)
dx.
Мы можем написать подынтегральное выражение этого интеграла как
интеграл, потому что
cos(ax) -cos(bx) _ ар sin(xy)
b
= _rsmWdy
Это выполняется, поскольку данный интеграл (помните, что интегрирование
относится куй, таким образом, а: может рассматриваться как константа) есть
rsin(xy). Г/- . . . . 1
- / ^^dy = — / sin(xy)dy = -
cos(xy)
cos(ax)-cos(bx)
Таким образом:
со и
I(a,b) = -f\f
'Sin(xy)
dy
[dx.
Это может выглядеть как (огромный!) шаг назад, так как теперь у нас есть
двойной интеграл. Но есть одна вещь, которую вы можете сделать с двойными
интегралами и которую вы не сможете сделать с однократными
интегралами, - это перемена порядка интегрирования. Конечно, мы можем столкнуться
с возражениями, что мы не доказали, что это оправдано, но помните
философский подход, который мы используем: мы просто пойдем вперед и сделаем
все, что пожелаем, и не будем беспокоиться об этом, и только тогда, когда мы
все получим, мы «проверим» наш формальный ответ с помощью численного
интегрирования quad. Итак, меняем порядок:
Обратная сторона трюка Фейнмана ♦> 107
sin(xy)
Iia,b) = -f\f™W>.dx
dy.
Теперь напомним наш предыдущий результат - разрывный интеграл
Дирихле в (3.2.1).
оо
sin(cx)
dx-
π
2'
если о 0
0, если с = 0.
π
—, если с<0
2
Во внутреннем интеграле нашего двойного интеграла переменная у (взятая
как положительная) играет роль с, и поэтому
I(a,b) = -f±dy,
и вот так, у нас есть наш ответ:
ОО
cos(ax)-cos(bx)
dx-
π
(b-a).
(3.4.1)
Если, например, а = 0иЬ = 1,то
ОО -ι
■1-соадЛ = 1£=1_57079^)
и quad подтверждает: quad(@(x)(l-cos(x))./x.A2,0,1000) = 1.57073....
«Более» существенно, если а = V2 и b = V3, тогда наш результат говорит, что
интеграл равен — (V5 - V2) = 0.499257..., и снова quad подтверждает как quad(@(x)
(cos(sqrt(2)*x)-cos(sqrt(3)*x)). /χ. Л2,0,1000) = 0.498855....
Обратная сторона приема дифференцирования Фейнмана -
интегрирование интеграла по параметру: это полезный новый трюк, применимый во
многих интересных способах. Например, вспомним ранее полученный результат
ОО -ι
Je~x2dx = -y[n.
о 2
Делаем замену переменной χ = Ыа (и также ах = Vadt), тогда
ОО л
fe-at2yfadt = -^fH,
108 ♦> Любимый трюк Фейнмана
или
Vi
о 2>ДГ
Теперь интегрируем обе части этого равенства по переменной а, от ρ до q:
|[^*|ί.-|^Λ.ΐΛ|^-ΐΛ{ϊΛ)[-Λ(Λ-ν?).
Меняем порядок интегрирования в двойном интеграле:
ОО Ч Ι UU I
°^ е~рг -
η L
dt,
или,наконец:
(3.4.2)
Если ρ = 1 и q = 2, этот интеграл равен Vii(V2 - 1) = 0.73417..., и quad(@(x)(exp
(-(х.л2))-ехр(-2*(х.л2)))./х.л2,0,20) = 0.73416....
Как другой пример этой техники, предположим, вы столкнулись с оценкой
интеграла
{ ln(x)
Мы можем сделать это, заметив, что подынтегральное выражение может
быть записано как интеграл следующим образом:
и и
fx'dy = Jeyln{x)dy =
о о
Таким образом:
РУ1п(х)
ln(x)
fdx,
-aln(x)
-1 x°-1
ln(x) ln(x)
или после изменения порядка интегрирования:
1„α ι "ί1 1 * f уУ+! 11 ° 1
Г- dx = Π (Vdx[dy = И \\ dy= f dy,
i,y+]
Обратная сторона трюка Фейнмана ♦> 109
Делая очевидную замену переменной и = у + 1, мы имеем
)f^dx = ln(<
и, наконец, приходим к очень красивой формуле:
[-—-dx = ln(a + l), α>0.
(3.4.3)
Например, f'- dx = ln(2) = 0.693147...,ι
Jo ln(x)
1 2_i
f-—-dx = ln(3) = 1.098612...
Jo ln(x)
Соответственно, quad(@(x)(x-l)./log(x),0,l) = 0.693139..., и quad(@(x)(x.A2-
1)./ log(x),e,l) = 1.098604....
Из этого результата мы можем написать
ι
W-1
J λη(ν\ J ληίνλ J
ι „ь
X°-\
J0 1П(АГ)
и поэтому
ο lnW ο lnW
dx = ln(a + l)-ln(b + l),
K^d* = In
Jo ln(x)
fa + ll
lb + lj
(3.4.4)
Теперь, когда мы увидели, как работает интегрирование под знаком
интеграла, давайте вернемся к интегралу, который я не доделал в конце
предыдущего раздела,
[cos(ax)-cos(bx)l
I(t) = Je
dx.
Обратите внимание, что мы можем записать часть подынтегрального
выражения в скобках как интеграл:
cos(ax)-cos(bx)
υ
f sin(xs)ds.
Тогда
oo
I(t) = fe-tx\fsin(xs)ds
\dx,
110 ♦> Любимый трюк Фейнмана
или, изменив порядок интегрирования (обратите внимание, что поскольку мы
сначала будем интегрировать по х, то должны также внести экспоненциальный
множитель во внутренний интеграл), мы имеем:
υ ου
I(t) = f\fe-txsin(xs)dx
Ids.
Из стандартных таблиц интегралов находим:
e~tx{ssin(xs)-scos(xs)}
t2 + s2
Ге txsin(xs)dx
и тогда
fe_i*{ssin(xs)-scos(xs)}
m=f
t2+s2
ds= f-
2+s2
ds.
du.
Сделав замену переменной и = t2 + s2 (и также ds= —), получим:
2s
1(f) = /
t2+a
или,наконец
"fsdu I'fdu 1
f+a<U2S V.-
r au
In
t2+b2
t2 + a2
I(t) = fe
cos(ax)-cos(bx)
dx = In
t2 + b2
tz + az
(3.4.5)
Кроме того, при t —> 0 мы находим:
°rcos(ax)-cos(bx)dx = Jn
b
la)
(3.4.6)
Если й = 2 и α = 1, то интеграл равен 1п(2) = 0.693147..., что согласуется
с quad((@(x)(cos(x)-cos(2*x))./x,0,1000) = 0.6935.... Обратите внимание,что если
а или Ь равно нулю, интеграл обращается в бесконечность. То есть интеграл
l-cos(x)
dx
не существует.
Вернемся к использованию дифференцирования интеграла в задачах
вычисления интегралов, таких как
f{ln(x)}2dx,
Обратная сторона трюка Фейнмана ♦ 111
или
1
fy[x{ln(x)}2dx.
Уловка, которая позволяет выполнить эту работу, состоит в том, чтобы
ввести параметр (я назову его а), по которому мы можем дифференцировать, и
затем, если мы установим этот параметр равным конкретному значению, сведем
интеграл к одному из приведенных выше. Например, рассмотрим
1
I(a) = fxa{ln(x)}2dx,
который сводится к вышеуказанному первому интегралу, если а = 0, и ко
второму интегралу, если а = 1/2.
Итак, дифференцируя:
dl=d_
da da
feln(*fl){ln(x)}2dx = — [ealn(x){ln(x)}2dx
1 1
= Jealn(x)ln(x){ln(x)}2dx = fxa{ln(x)Ydx.
о о
Пока это может выглядеть так, как будто мы только усугубили ситуацию, -
и мы это сделали! Но это также должно дать вам подсказку о том, как
развернуть ситуацию в нашу сторону. Посмотрите, что случилось:
дифференцирование 1(a) вернуло нам тот же интеграл, за исключением того, что степень \п(х)
увеличилась на 1. Это должно подтолкнуть вас к пониманию того, что наш
исходный интеграл можно рассматривать как результат дифференцирования
интеграла Г ха \n(x)dx, при этом данный интеграл, в свою очередь, происходит
J о
отдифференцирования Г xadx, а этот интеграл легко решить.
Jo
То есть
[xaln(x)dx=— fxadx
Тогда
1 1 1 1
[xa{ln(x)}2dx = -=- fxa ln(x)dx
d \
da\
\ xa+1}
[a + l\
il
lo
d
~ da
1 N
a + 1,
(a + 1)2
da
(a+ir
2(a + l)
(й + 1)4'
112 ♦> Любимый трюк Фейнмана
или
1
[x"{ln(x)}2dx = —^.
Jo (я + 1)5
(3.4.7)
Итак, для а = О имеем:
J{ln(x)}2dx = 2,
О
и в согласии с quad(@(x16)log(x).A2,0,l) = 2.000009.... Для а = 1/2 мы име-
2 16
ем интеграл, равный - =— = 0.5925925...; в соответствии с quad(@(x)
sqrt(x).*log(x).A2Al) = 0.592585....
В качестве заключительных примеров этого раздела давайте посмотрим,
как вычислить интегралы
π
1(a) = fln{a-\-bcos(x)}dx9
о
где а > Ъ > 0, и
/(b)=fln{1+bcos(*V
Jo C0SW
где 0 < Ь < 1. Анализ будет состоять из двух этапов, причем первым этапом
будет оценка производной от 1(a) по а, то есть интеграл
f = j ' a,
da J0 a + bcos(x)
где а > Ь > 0. Для этого интеграла измените переменную на ζ = tan(x/2). Затем,
как показано в главе 2 (в анализе, приведшем к формуле (2.2.3)), мы
установили, что
cosW = TT7
и
dx = Tdz,
1 + z2
Обратная сторона трюка Фейнмана ♦> 113
так что
0 а + Ь
2 )
ί—τ—άχ= ί—цл \dz=2f
Jna + bcos(x) Jn . , 1-zl + z J„
U+z2J
dz
J0 a(l + z2)+b(l-z2)
2 J
1 + Z2
dz
{ (a + b) + z\a-b)
ί 2 )
2 f dz^
0 -^ + z2
a-b
a-b
1
o + b
a-b
rtan-1
ί z ]
/α + Ь
Wa-bJ
a2-b2
-tan !
α-Ь
α + Ь
Тогда1
J»TT 1
0 a + bcos(x
π
,,а>Ь.
(3.4.8)
Теперь для оценки наших двух интегралов начнем с /(а). Дифференцируя по
а, мы получаем из (3.4.8), что
1
-dx = -
(U__ г
da~{ a + bcos(Ar)^v~^/fl2_b2 "
Таким образом, интегрируя неопределенно относительно а:
Ι(α)= Γ rfq,
или из стандартных таблиц интегралов:
/(fl) = uln{a + Vfl2-b2} + C,
Интеграл в (3.4.8) встречается в статье: Dimeo R. Μ. Fourier Transform Solution to the
Semi-Infinite Resistance Ladder//American Journal of Physics. July 2000. P. 669-670, - где
контурное интегрирование на самом деле не нужно. Профессор Димео утверждает,
что контурное интегрирование «вполне соответствует возможностям специалиста
по физике», что согласуется с философской позицией, которой я придерживаюсь
в предисловии. Обратите внимание, что мы можем использовать (3.4.8) для решения
всех видов новых интегралов путем дифференцирования. Например, предположим,
J*71 1 ΊΤ
ах = . . Тогда, дифференцируя обе
0 a-cos(x)
\ dx= πα
[a-cos(x)]2 (α2-1)3/2'
5π 5π
что b --
стороны этого равенства относительно а, получим Г
Если, например, а = 5, этот новый интеграл равен
243/2 48>/б
проверить,мы видим,что quad(@(x)l./((5-cos(x)).A2),0,pi) = 0.1335989....
0.1335989.... Чтобы
114 ♦> Любимый трюк Фейнмана
где С- постоянная интегрирования. Мы находим С следующим образом: когда
Ъ = 0 в первоначальном интеграле, мы имеем
π
1(a) = fln(a)dx = nln(a),
о
и поэтому, приравнивая это значение к результату неопределенного
интегрирования (с Ъ = 0), мы имеем
π1η(2α) + С = п\п(а),
что говорит нам о том, что С = -π1η(2). Таким образом,
1(а) = п1п1а + л1а2 -ί?2}-π1η(2),
или
Если, например, а = 2 и Ъ = 1, наш интеграл равен π In
2 + λ/3
(3.4.9)
1.959759...,
и проверка: quad(@(x)log(2+cos(x)),0,pi) = 1.959759....
Обратимся, наконец, к интегралу/(b), в котором 0 < Ъ < 1.
Дифференцирование по Ьдает:
cos(x)
dl = U+bcos(x)dx= г 1 άχ
db JQ cos(x) JQ l + bcos(x)
Но из (3.4.8) имеем (при а = 1)
dl π
db Vl-Ь2 "
Таким образом, интегрируя неопределенно относительно Ь:
/(b) = usin-1(b) + C,
где С- постоянная интегрирования. Поскольку7(0) = 0 для исходного
интеграла, мы, наконец, получаем наш ответ:
rln(l + bcos(x)} , . _1/ΪΛ
I— ^^-dx^usin (Ь).
Jo cos(*)
Если, например, b = 1/3, то интеграл имеет значение π sin !
(3.4.10)
1.067629...,
и, проверяя, мы видим,что quad(@(x)log(l+(cos(x)/3))./cos(x),0,pi) = 1.06761....
Сочетание двух приемов ♦ 115
3.5. Сочетание двух приемов
В этом разделе мы объединим дифференцирование интеграла по параметру
с трюком рекурсии, который мы использовали в главе 2 (раздел 2.3), чтобы
решить целый класс интегралов. Здесь мы будем искать интегралы
π/2
W
1
dx, л = 1, 2, 5,...,
Ι {αcos x + bsin χ}'
где возьмем и α, и b в качестве параметров, по которым мы можем дифферен-
д/ д1„
цировать. Если вы вычислите —- и —-, то сможете увидеть, что
да дЪ
π/2
COS Χ
да J0 [α cos2 χ + bsin2 χ}
2 νΊ"+1
dx
EL=.n1f «в!* dx
db J0 {acos2x + bsin2x}"+1
Из этих двух результатов мы сразу имеем:
Ыа д1п *Г 1
да db { {acos2A: + bsin2A:}"+1 n+1
Или, если мы заменим η на η - 1, имеем рекурсию:
п-\
η—Ι ι п—1
да
аь
Из рекурсии в рамке мы видим, что первое значение и, которое мы можем
использовать в нем, - это η = 21, но только тогда, когда мы уже знаем 1г. Затем,
когда у нас есть /2, мы можем использовать его, чтобы найти /3, и т. д. Но сначала
нам нужно найти
1
1
π/2
'.-/
π/2
[ flcos x + bsinLx
dx=f
cos2x
a + btan2x
-dx.
αχ = без зависимости от а
о 2
или Ь. То есть —^ = —^ = 0, и рекурсия становится бесполезной, неопределенной:
да db
11=°-0.
1 о
116 ♦> Любимый трюк Фейнмана
dy
1
Заменяя переменную у = tan(x), мы имеем — = —, или dx = cos (x)dy,
dx cos χ
Тогда
ι
j = J^cos2 (X)dy = ff-^dy = M/tan-
Jo a + by2 bJ0 a+y2 bVia
У!--1
Mil
н
Ub}\\
yfab
tan Ч00))
или
π/2
'■-/
dX =
π
I α cos2 (χ)+ b sin2 (χ) 2л/ай
Для нахождения 1г мы сначала вычислим
Oil-
da
-2nS-a~V2
Л
4ab
f^
а
ab
(3.5.1)
дъ
-2n4a~h-vi
А
4ab
_Ь_
ab
Таким образом, используя рекурсию в рамке (незаштрихованную) для η = 2:
[ π )a + b
π
4ab
[/*
1-+1
\α 1
PI
-
life]
=
4afe
4ab'
ИЛИ
π/2
J
1
{ {acos (x) + fesin2(Ar)}2
-dAT =
π
\A4ab)
Ί 1)
(3.5.2)
Мы можем повторять этот процесс бесконечно (хотя алгебра быстро
становится все более неприятной!), и я позволю вам заполнить детали, чтобы
показать, что рекурсия (для п = Ъ) дает
π/2
W
1
{ [acos (x) + bsin (x)}
-dx =
π
[l&Jab)
[Ъ
21
2+b2+ab
(3.5.3)
Для проверки этого (а также результатов, которые мы получили ранее,
поскольку здесь также будет отображаться ошибка, сделанная ранее), положим
Сочетание двух приемов ♦> 117
4 75π
а = 1 и Ъ = 2, тогда L = —'-—=- = 0.65949.... Использование MATLAB напрямую
16л/2
для вычисления интеграла: диас1(@(х)1./((со5(х).Л2+2*51п(х).Л2).Л3),0,р1/2) =
0.65949....
В качестве последнего примера рекурсии рассмотрим обобщенную версию
интеграла, которая появилась в первом разделе этой главы, в (3.1.2) и (3.1.3):
,M'l^hrdx-
Ранее у нас был частный случай у = оо. Мы можем использовать рекурсию
в сочетании с интегрированием по частям, чтобы оценить этот более общий
интеграл. В формуле интегрирования по частям пусть
1
Ы~(х2 + а2Т
и dv = 1. Тогда очевидно, что ν = χ, и вы можете быстро убедиться, что
2х
du = -n-
Тогда
(х' + а'У
2\п+1
(х2 + а2)"
dx.
yr 2x2dx
+ П{(х2 + а2Г1'
или, поскольку 2х2 = 2(х2 + а2) - 2а2, мы имеем:
или
(у2 + а2)"
■ + п
2(x2 + a2)dx
i (χ2 + α2)"+1 '
I
■*I
dx
Ж+ят
- + 2«/п(у)-2па27п+1(у),
(у2 + а2)"
и вот, наконец, мы приходим к рекурсии:
'„+1(У) =
-+-
2п-1
2п а1 (у2 + а1)" 2па2
Ш-
(3.5.4)
Начнем рекурсию в (3.5.4) с интеграла
У ι ι
/i(y)= f— Jdx= -tan"1
J ν1 Λ- η1 Π
(χ^
χΔ + α
= -tan !
α
<УЛ
118 ♦ Любимый трюк Фейнмана
71
и поэтому для случая у = оо, /х(у) = —. Тогда, поскольку
2а
Ι^(00)=τ^ΙΛοο)'
мы имеем:
J2(oo) = JLjl(oo) = JL
А(°о) = —Л,(оо) =
>^'-4а2 2V /_16α5'
а это именно то, что мы вычисляли в (3.1.2) и (3.1.3) соответственно. И новый
результат, которого у нас не было раньше, - это
/4(00)=i^Wdx=67/3(00):
15π
96α7
В качестве проверки: если а = 1, то значение 14(оо) равно 0.490873..., и quad
(@(χ)1./((χ.Λ2+1).Λ4),0,100) = 0.490874....
3.6. Интеграл Улера и символьное интегрирование
В этой главе «дифференцирование под знаком интеграла» ассоциируется
с именем Фейнмана, но, конечно, эта техника применялась значительно
раньше. Как проясняют его собственные слова в конце главы 1, он выучил
данный метод по известному учебнику («Advanced Calculus» 1926 г. профессора
математики Массачусетского технологического института Фредерика Вудса
(1864-1950)), и этот метод был популярен среди математиков и физиков
задолго до того, как Фейнман вошел в историю. Например, в октябрьском
выпуске «Американского математического ежемесячного журнала» (The American
Mathematical Monthly) за 1914 год появилась небольшая проблема,
поставленная профессором физики Йельского университета по имени Гораций Скаддер
Упер (Horace Scudder Uhler1) (1872-1956). Там он спросил читателей, как они
будут вычислять двойной интеграл
а а+х -Су
I = f(a2-x2)xdxf—dy,
0 а-х У
Улер был пионером в героических вычислениях, тем более впечатляющих, что он
работал в то время, когда компьютеров еще не было. Его основным инструментом
был хороший набор логарифмических таблиц. Я описываю его вычисление 1921 года,
более 100 десятичных цифр, значения (ν—1) =е ^ в моей книге: An Imaginary Tale:
the story of уЁЛ. Принстон, 2010. С. 235-237.
Интеграл Улера и символьное интегрирование ♦ 119
который возник «в процессе решения некоторой физической проблемы».
Значения а и с являются положительными.
Упер действительно уже знал, как это сделать, - он даже включил
окончательный ответ, когда объявлял вызов, но ему было любопытно, как другие
могут подступиться к этому двойному интегралу. Решение от читателя было
опубликовано в декабрьском выпуске, а Упер наконец показал (в выпуске за
январь 1915 года, более чем за три года до рождения Фейнмана), как он это
сделал, - путем дифференцирования по параметру с. Вот что он написал:
«Продифференцируем / по параметру с, тогда
jt а а+х
%- = -f(a2-x2)xdxfe-*>dy,
"С 0 а-х
который можно найти сразу [я думаю, что это "сразу" просто немного вводит
в заблуждение, поскольку, даже используя стандартные таблицы
интегрирования, я нашел эту рутинную алгебру довольно противной], и тогда получается
-2ас
Теперь мы можем проинтегрировать обе части этого уравнения [для
условия, определяющего постоянную интегрирования, обратите внимание, что
/(оо) = 0, потому что подынтегральное выражение внутреннего у-интеграла
обращается в ноль при с —> оо], тогда [и затем Упер дает ответ]
dl 2а1
dc~ съ '
6а 6
~с4+с5
6а 6 2а2)
— + - + —
с с с
1
Ъа \{
— + -
с с
а + -
2с
(1
-е~2ас)
Мы можем сделать частичную проверку этого равенства следующим
образом. Например, для случая а = 1 и с = 1 формула Улера принимает вид:
1-3-
1-
(1-е-2)
-2 + ^(1-е-2):
0.16166179.
MATLAB (если он включает пакет Symbolic Math Toolbox) может численно
оценить (с двойной точностью) двойной интеграл Улера для выбранных
значений α и с, символы χ и у сначала объявляются как символьные переменные,
следующим образом:
syns χ у
double(int(int((l-xA2)*x*exp(-y)/y,y,l-x,l + χ),χ,0,1))
Компьютерный результат находится в полном согласии с формулой Улера.
0,16166179.... Причина, по которой формула Улера и интегрирование MATLAB
находятся в таком хорошем соответствии, заключается в том, что вложенные
команды int (для «интегрирования») фактически выполняют символьные
интегрирования, что приводит к точному ответу -5/2*ехр(-2)+1/2. Последняя
120 ♦ Любимый трюк Фейнмана
команда double просто преобразует этот точный символьный ответ в числовую
форму с двойной точностью.
Синтаксис использования вложенных команд int для символьного
нахождения нескольких интегралов теперь должен быть очевиден, но, для
уверенности, вот задачка. Возможно, вы помните, что в конце предисловия я упомянул
нечто, называемое «оптический интеграл Харди-Шустера». Мы рассмотрим
этот интеграл аналитически позже в книге, где, немного углубившись в анализ,
приведем его к виду тройного определенного интеграла:
\du
dx.
J\J\Jcos(t2-u2)dt
0 [ χ [ χ
Наш анализ покажет, что это, возможно, пугающее выражение равно
1 /π
2V2
2"
0.62665706.... Однако для того, чтобы Symbolic Math Toolbox оценил бы его, все,
что требуется, - это следующие две строки (где inf - символьное
представление для бесконечности):
syns χ t и
int(int(int(cos(tA2-uA2),t,x,inf),u,x,inf),x,0,inf)
Когда MATLAB возвращает ответ, он начинает с сообщения о том, что в
явном виде интеграл не может быть найден, но затем выводит довольно длинное
и загадочное выражение, которое он вызывает ans1 (ответ, от слова «answer»).
Если затем вы конвертируете эту переменную ans в числовую форму, исполняя
команду double(ans), вы получаете... (громкая барабанная дробь): 0.62665706....
Разве это не здорово?
До сих пор я использовал функцию quad из MATLAB для проверки
одномерных интегрирований, а теперь int для проверки многомерных
интегрирований. Но, конечно, int также может легко брать одномерные интегралы, если
пакет расширения Symbolic Math Toolbox установлен на вашем компьютере
вместе с MATLAB (функция quad входит в основную часть MATLAB и поэтому
всегда доступна). Чтобы увидеть использование int на одномерном интеграле,
вспомним наш результат (2.1.4):
„1-
-^ = ^.
Дифференцируя по параметру а, мы получаем:
(1 + ея*)2 а2
1 В современных версиях MATLAB ответ ans сразу получается в виде (2Λ(ΐ/2)*ρίΛ(ΐ/2))/4
без всяких оговорок и загадочных выражений. - Прим. перев.
Интеграл Улера и символьное интегрирование ♦> 121
Теперь изменим переменную на t = еах и, таким образом, х = — 1п(£). Это
а
A dt
означает, что ах = — и, следовательно,
at
Г-
J г
1ln(t)t
(1 + ί)2
dt]
at
ln(2)
a2 '
или после сокращений а и t и замены фиктивной переменной интегрирования
обратно нах:
?-^Λ = 1η(2).
(3.6.1)
Запустив Symbolic Math Toolbox, мы можем проверить этот результат,
написав команды
syns χ
int(log(x)/((l + x)A2),x,l,inf)
которые возвращают точный символьный результат:
ans = log(2).
Или, для другого одномерного примера, вспомните аэродинамический
интеграл из введения:
1
1Шах=п-
Symbolic Math Toolbox соглашается, выполняя команды
syns χ
nt(sqrt((l + х)/(1-х)),х,-1,1)
что дает точный символический результат:
ans = pi
в то время как quad(@(x)sqrt((l+x)./(l-x)),-l,l) = 3.14159789... (Фактическое
числовое значение числа pi составляет, конечно, 3,14159265....)
В качестве еще одного примера использования Symbolic Math Toolbox
вспомним вторую задачу из упражнений главы 1, где вам предложили показать, что
ОО -ι
Г . dx<4.
С помощью Symbolic Math Toolbox мы можем получить гораздо более точное
значение для этого интеграла:
syns χ
double(int(l/sqrt(xA3-l),l,inf)) = 2.42865
122 ♦ Любимый трюк Фейнмана
3.7. Интеграл вероятности, новый взгляд
В сноске 1 этой главы я обещал вам еще немного обсудить интеграл
вероятностей
оо _х^
Ге 2dx.
— оо
Для начала я выведу его снова, но другим способом (однако все же
использую дифференцирование под знаком интеграла). Пусть
оо
I = fe-*2dx,
и далее определим f(x) — if e t2dt\ ng(x) — J — dt.
-x2(l+r2)
Тогда
df
dx
= 2
Je-t2dt\e-x2^2e-^Je-t2dt
dg_ lc-2x0. + t2)e-^e)
ug_= с
Ну J
dx
1 + i2
dt = -2jxe-x4l+t2)dt =
-2xfe-x2e-xVdt = -2xe-"2 Je-x2'2dt.
Пусть и = tx (что значит du = xdt), и тогда dt — —.Получаем:
χ
dg
idU
df
^ = -2хе~*2 [е-2™ = -2е~*2 fe^du = -^
dx Jn χ Jn dx
Таким образом:
dx dx
или если С - константа, то мы имеем f(x) + g(x) = С.
В частности, ДО) +g(0) = С, но поскольку ДО) = 0 и поскольку
*0) = /i^A = tan"1(t)C=i»
π
мы получаем, что С = —. То есть f(x) + g(x) = π/4.
4
Интеграл вероятности, новый взгляд ♦ 123
Но это означает, что Доо) + g(oo) = —, и поскольку Доо) = I2 и g(oo) = 0 (потому
4
что подынтегральное выражение g(x) интеграла —> 0 при χ —> оо), то
/2 = *.
4
То есть
ОО -ι
1 = fe~**dx = -yfn,
о
или удваивая интервал интегрирования:
оо
Je~x2dx = л/π.
Теперь пусть χ = -= (и также dx = -η=). Тогда:
V2 V2
Ге *2dx = Je 2 -η= = л/π,
-оо -оо v^
или как мы и вывели в (3.1.4), с фиктивной переменной интегрирования,
замененной обратно нах:
оо χ
Je~Ydx = yfln.
Теперь, чтобы завершить обсуждение интеграла вероятности, давайте
выведем еще одно его обобщение, которое впервые сделал французский математик
Пьер-Симон Лаплас (1749-1827) 200 лет назад. То, что мы вычислим, является
интегралом
- ах - —
I = Je *2dx,
и, в частности, мы видим, что 21 сводится к интегралу вероятности для а = 1/2
иЬ = 0.
Для начала пусть t = лУа. Тогда dx = -η=, и поэтому
у/а
оо .г ab ι. 1 оо 2 аЬ л
1 = 1е-С^^='1е-1-^='12>
J у/а у/а о у/а
/а = /в «Ά.
0
где
124 ♦ Любимый трюк Фейнмана
Далее, положим
4аЬ
Тогда
dy =
dt
л,2
ab
или
dt
dy
И поскольку ab = y2t2, мы имеем:
о _^__
ab
00
Таким образом:
-dy
У )
оо
■dy.
_t2-—
ОО _ 2 _ ЯЬ ОО f2
2I2 = fe~ ~t2dt + Jabf?-^—dt,
или
2I*=F[ '
1
dt.
Теперь снова заменим переменную, на этот раз
s = t-^.
t
Тогда
ds
dt
= 1 + -
\/flfr
ί2
Λ = -
ds
ab
ab
Поскольку s2 = i2 — 2vab + -5-, мы имеем (заметим, что если s = -00, то ί = 0):
Интеграл Дини ♦ 125
l4ab
2i2= JVs2-2^
1 +
ds
1 +
ab
или
I.
Ijy,-^
-2yfab
ds-
oo
fes2ds,
и
oo
I2 = e-^b]e-*ds.
Теперь, поскольку I = —12, то
л/fl
°SL _Λν2_Α
/ = /e х2с/аг =
1 -l4ab
Га
oo
Je-j2c/s,
и поскольку
•ί 2
мы имеем красивый результат:
ОО
*4χ = -1-β-2^.
2\α
(3.7.1)
Для численной проверки этого результата положим а = Ь = 1, тогда ин-
л/тт
теграл равен —- = 0.11993777..., что согласуется с quad(@(x)exp(-((x.A2)+l./
(χ.Λ2))),0,10)= 0.119939....
3.8. Интеграл Дини
Чтобы завершить эту главу, давайте проработаем логарифмический интеграл
с важными приложениями в математической физике и технике, который
впервые был найден в 1878 году итальянским математиком Улиссом Дини (1845-
1918). Это интеграл
/(α)= fln(l-2acos(x) + ct2)dx,
где параметр α - любое действительное число. Обратите внимание, что
поскольку cos(x) принимает все свои значения от -1 до 1 при изменении χ от 0
126 ♦ Любимый трюк Фейнмана
до π, мы видим, что знак α несуществен, то есть 1(a) = 7(|а|). Поэтому я буду
обсуждать только два случая: 0<а<1иа>1.
Дифференцируя, мы имеем:
dl _ г -2cos(x) + 2a
Jo 1-2
π 1
da
2acos(x) + a2
1 π
dx = ±[
a
π ι η
a aJ 1
l-az
о
dx.
1 —
1-a2
l-2acos(x) + a2
[dx =
0 χ -2acos(x) + a
Затем делаем замену переменной ζ = tan(x/2), что означает, как мы показали
в главе 2 (см. вывод формулы (2.2.3)), что
•Л
COS(X):
\-zl
1 + z2
dx-
1 + z2
-dz.
Тогда
da a a^
1-a2
\-zL
0 l-2a^^ + a'
1 + z2
— a ) -
a -i 1-
( 2
[l + Z2
dz
-dz
a a J l + 22-2a(l-z2) + a2(l + z2)
что дает после небольших преобразований:
dl__n
da a
1-a
1 + a
dz
il-ol
[l + aj
+ Z*
Последний интеграл находится следующим образом:
= - U-2tan_1
dl
da
π
α
2
α
1-α
1 + α
1
1-α
1 + α
tan '
ί ζ 11
1-α
ιοο
Ιο
_ 1
α
fl + α )|
ζ
1-α
Если а>1,то1 + а>0и1-а<0, что означает, что
1 + α
1-α
< 0, и поэтому
tan-1
1 + α ^
ζ
[ΐ-α J
_ 1
α
π-
ιοο
0
-2
π
α
( W
π
aJJ
, и тогда
2π
α>1.
Интеграл Дини ♦ 127
Если 0<а<1,то1 + а>0и1-сс>0, что означает, что
π
= -\—, и тогда
α
1 + α
1-α
> 0, и поэтому
п1
dl
da
1 + <
-z
[l —α J
_ 1
α
π-
ιοο
= 4
0
■2
-ί
-\\ = 0, 0<α<1.
a J]
Теперь, поскольку
π
J(0) = Jln(l)dx = 0,
о
то интегрирование — = 0 при 0 < a < 1 дает следующий результат:
da
1(a) = 0, 0<а< 1.
тт г dl 2π i
Чтобы проинтегрировать — = —, α > 1, нам нужно получить конкретное
da a
значение /(a) для некоторого a > 1, дабы определить константу
интегрирования. Увы, нет очевидного значения а, которое приводит к «хорошему»
интегралу, который можно легко найти (как для 7(0))! К счастью, есть хитрый трюк,
который поможет нам справиться с этой трудностью. Вот что мы сделаем:
вначале выберем такое значение (обозначим его β), что 0 < β < 1, и такое, что
/(β) = Jln(l^cos(x) + β2)άχ = 0
по нашим предыдущим аргументам. Затем мы выберем для параметра а,
который будем использовать, значение, равное a = -, что, конечно, будет означать,
что a > l.To есть
Ιφ) = 0 = Ι
-1= fln[l-2-cos(x) + -VI
[a) J0 { a a )
π
a -2acos(x) + l
dx =
\dx =
II U
= Jln{a2-2acos(x) + l}dA:-Jln{a2}dA: =
о о
π π
= Jln{a2-2acos(x) + l}dA:-j21n(a)dA:,
128 ♦> Любимый трюк Фейнмана
который, напомним, равен нулю (посмотрите на начало этой математической
строки: 7(β) = 0 = J
Ίλ
). То есть когда α > 1, мы имеем
ΤΙ ΤΙ
Jln{ct2-2ctcos(x) + l}dx = J2ln{a}dx = 2π1η{α}
dl 2π
и на самом деле видим, что это действительно согласуется с — = — для α > 1.
da a
Итак, мы получили
[ 0, 0 < α < 1
[2π1η{α} α>1
7(α) =
а также 1(a) = 1(\а\). Самый простой способ написать все это компактно
следующий:
[ln{l-2acos(x) + a2}dx = °'a, K} .
{ π1η{α2}α2>1
(3.8.1)
Для проверки, пусть, например, а = -, тогда мы имеем quad(@(x)log((5/4)-
cos(x)),0,pi) = 1.127χ10~7 (довольно близко к нулю), и для α = 2 мы имеем
quad(@(x)log(5-4*cos(x)),0,pi) = 4.3551722..., в то время как7г1п(22) = 2π1η(2) =
4.3551721....
3.9. Любимый прием Фейнмана
решает физическое уравнение
В одной статье по физике, опубликованной1 несколько лет назад, классическая
проблема механики получила новый интересный подход. Детали этого
анализа здесь не важны, и, после того как вся пыль осела, после того как физика
была сделана, автор пришел к следующему уравнению, которое необходимо
решить:
φ
у2(ф) = у2(0) + 2{cos(c|>) - usin(c|>)} - 2\ifv2 (x)dx. (3.9.1)
о
В этом уравнении (3.9.1) μ - неотрицательная постоянная, и У2(0) также
является постоянной (это, конечно, значение У2(ф) при φ = 0). Цель состоит
в том, чтобы решить (3.9.1) относительно У2(ф) как функции от φ, μ и У2(0).
1 Klobus Waldemar. Motion On a Vertical Loop with Friction // American Journal of Physics.
September 2011. P. 913-918.
Любимый прием Фейнмана решает физическое уравнение ♦ 129
Как только он пришел к уравнению (3.9.1), автор написал: «[Это]
интегральное уравнение Вольтерра второго рода [по имени итальянского математика
Вито Вольтерра (1860-1940)], решение которого является простым». Он не
предоставил никаких подробностей решения; сославшись на краткое
приложение, где он привел общую формулу решения такого уравнения (в общем
случае интегральные уравнения могут быть трудными, потому что неизвестная
величина, которую нужно найти, появляется как внутри, так и вне интеграла),
он просто записал ответ. Использование этой формулы позволило «найти
решение прямо, хотя и с трудом». Фактически он был совершенно прав, назвав
решение «простым», ведь на самом деле ничего, что могло быть «трудоемким»
в решении уравнения (3.9.1), нет. То есть нет, если вы знаете, как
дифференцировать интеграл.
Итак, дифференцируя (3.9.1) по ф, используя (3.1.1), мы имеем
άΥ\φ)
άφ
= 2{-8Ш(ф)-ЦС08(ф)}-2цУ2(ф),
или, переставляя члены, имеем следующее дифференциальное уравнение
первого порядка относительно У2(ф):
^^ + 2цУ2(ф) = -2{8т(ф) + цсо8(ф)}. (3.9.2)
αφ
Теперь, умножая обе части (3.9.2) на е2цф, получаем:
*¥-Ш ew + 2цУ2(ф)е2цф = -2{δίη(φ) + цсоз(ф)}е2цф.
αφ
Это полезно, потому что теперь левая часть выражается как полная
производная следующим образом:
^-{У2(ф)е2цф} = -2{81п(ф) + цсо8(ф)}е2цф (3.9.3.)
αφ
Этот последний шаг, по сути, представляет собой применение метода, с
интегрирующим множителем (е2цф - это множитель). Этот метод обычно
преподается в курсе дифференциальных уравнений.
И наш следующий шаг - интегрирование (3.9.3) от 0 до ф:
f—{V2(x)e2»x}dx = -2f{sin(x) + ]icos(x)}e2]lxdx.
о "* о
Левая часть:
J-f{V2(x)e2]lx}dx = Jd{V2(x)e2]lx} = {V2 (x)e2]lx£ = У2(ф)е2цф - V2(0),
о "* о
и поэтому
130 ♦ Любимый трюк Фейнмана
У2(ф)е2цф = V2(0)-2f{sin(x) + ]icos(x)}e2]lxdx,
или
ψ
У2(ф) = е-2цфУ2(0)-2е-2цф f{sin(x) + ]icos(x)}e2]lxdx. (3.9.4)
о
Оба интеграла в правой части (3.9.4) легко берутся (либо по частям, либо
просто можно посмотреть их в таблице интегралов), и если вы немного
поработаете с деталями (которые я предоставляю вам), то получите:
У\ф) = е
_ ρ-2μφ
у2(0)+2(2^2-1)
1 + 4μ2
2 ™ „,
1 + 4μ2
[3μβΐη(φ) + (V - 1)соз(ф)]. (3.9.4)
Это действительно то решение, которое дано автором упомянутой статьи по
физике, и поэтому у нас есть еще одна история успеха для «любимой уловки
Фейнмана».
3.10. Задачи и упражнения
(С3.1). Рассмотреть а как параметр и вычислить
J0 b2+x2
где а и Ь положительны. Если вы посмотрите на формулу (2.4.3), то увидите, что
там - обобщение этого интеграла для частного случая а = Ь = 1. То есть ваш
ответ для приведенного выше интеграла должен сводиться к π1η(2), если а = Ь=1.
(С3.2). Вычислить главное значение Коши интеграла
cos(ax)
r-^dx, a>0,b>0.
Подсказка: сделайте разложение дроби, затем соответствующую замену
переменной (это должно быть очевидно), а затем, наконец, вспомните интеграл
Дирихле.
(СЗ.З). В (3.1.7) мы нашли, что
7>cos(flx) π яЬ
J *ЧЬ2 2Ь6 '
Объедините этот результат с результатом из предыдущей задачи, чтобы
вычислить интеграл
Задачи и упражнения ♦ 131
Lb4-x4
(С3.4). Показать, что значение принципа Коши
оо .
^AU1dx = -cos(ab).
Опять же, не забудьте про интеграл Дирихле.
(С3.5). Поскольку мы так много используем интеграл Дирихле, то вот еще один
взгляд на него. Предположим, что а и Ь являются действительными числами,
причем Ь > 0, но а может иметь любой знак. Показать это равенство:
f cos(ax)
sin(bx)
dx-
π Μι
—, если \a\<b
О, если |а|>Ь.
π Μι
—, если \a\ = b
4 ' '
(С3.6). Я несколько раз упоминал в книге интеграл «теории подъемной силы»
и говорил, что его значение равно π. MATLAB согласен с этим, и
действительно, я показал вам неопределенный результат интегрирования в главе 1
(раздел 1.7), что вы можете подтвердить путем дифференцирования. Посмотрим,
сможете ли вы напрямую получить конкретный случай / J dx = π. Под-
Jl V 1-х
сказка: попробуйте заменить переменную χ
двойного угла.
cos(2u) и вспомните тождества
(С3.7). Вот классическая головоломка с двойными интегралами, над которой
вы можете подумать (поскольку мы затронули двойные интегралы в
разделе 3.6). Стандартная уловка, чтобы примерить двойные интегралы, как я
обсуждал в разделе 3.4, состоит в том, чтобы изменить порядок интегрирования.
Порядок интегрирования не должен менять значение, но, возможно, может
облегчить поиск результата. То есть предположение состоит в следующем:
и \ и и ι и
f\ff(x,y)dx\dy = f\ff(x,y)dy
[dx.
«Обычно» это так и есть, если f(x, у) - это функция, про которую математики
говорят «хорошо себя ведет». Но это не всегда так. Если, например, а = с = О
(-у
и
Ь = d = 1 и f(x,y)-
-, то равенство не выполняется. Каждый из двух
(* + У)
повторных интегралов действительно существует, но они не равны. Покажите,
132 ♦ Любимый трюк Фейнмана
что это так, путем прямого вычисления каждого двойного интеграла. Есть ли
идеи, почему они не равны?
(С3.8). Покажите, что
ОО -ι .
fxe~x2~xdx = —v^Ve
J 2
— оо
и что
j 4
— оо
Подсказка: рассмотрите I(a,b)= I e~ax+bxdx, выделите полный квадрат
J — оо
в показателе степени, сделайте очевидную замену переменной и
вспомните (3.7.1). Затем дифференцируем 1(а, Ъ) по а и Ъ и в каждом случае полагаем
а = 1 и Ъ = 1.
1-
для а > 0, т > 0 (позже,
(C3.9). При условии что / ^——dx = —
Jq х(х2 + а2) 2{ а
в главе 8 (в задаче 8.2), вам будет предложено получить этот результат, исполь
зуя криволинейные интегралы), продифференцировать по параметру α и та
sin(mx)
*(х2 + а2)
π
ким образом найти Г ^—^-dx. Подсказка: если т = а = 1, тогда ваш ре-
Jo x(x2 + a2)2
зультат должен свестись к
А
1-А
2е
0.70400..., что подтверждает и MATLAB:
quad(@(x)sin(x)./(x.*((x.A2+l).A2)), 0,1000) = 0.70400....
(СЗ. 10). Несмотря на энтузиазм Фейнмана в отношении техник
дифференцирования интегралов по параметру, он, безусловно, использовал и другие методы;
его знаменитая статья 1949 года (см. примечание 7 в главе 1), например, полна
криволинейных интегралов. И все же даже там он вернулся к своему
любимому трюку. Напомним его интеграл — = Г . В примечании в кон-
ab Jb[ax + b(\-x)}
це своей статьи от 1949 года Фейнман показал, как из этого интеграла можно
1 г1 xdx
легко получить дополнительные тождества, такие как —— = \ -.
Продифференцируйте его исходный интеграл по переменной а и
подтвердите этот второй интеграл. (Хотя это хорошее упражнение - и вы должны это
сделать, - оно такое легкое, что я не потрудился включить решение в конце
книги.)
(C3.ll). Как я уже говорил, интегральные уравнения могут быть очень
сложными для решения. Вот еще одно, которое немного сложнее, чем (3.9.1), но тем не
менее его можно решить, используя только математику на уровне этой книги.
Задачи и упражнения ♦ 133
А именно для р(0) = 1 решить
р(х)ф(х) = f"p(u)du
в зависимости от заданной функции ф(х) и, таким образом, показать, что
1η{ρ(χ)} = 1η{φ(0)}-1η{φ(χ)}- )-£-
Эта проблема встречается в моей книге по теории вероятностей: Будете ли
вы живы через десять лет? Принстон, 2014 (Will You Be Alive Ten Years From
Now? Princeton, 2014), и вы можете найти решение там на стр. 170-172.
Глава
4
Гамма- и бета-функции
4.1. Гамма-функция Эйлера
В двух заметках, написанных в 1729 году и выпущенных в 1730 году, великий
Эйлер создал то, что сегодня называется гамма-функцией Г(п) и определяется
в учебниках интегралом
оо
T(n) = fe-xxn-1dxy n>0.
о
Это современное определение (эквивалентное определению Эйлера)
относится к 1809 году и принадлежит французскому математику Адриен-Мари Ле-
жандру (1752-1833). Для η = 1 нетрудно понять, что
оо
Г(1) = /е-*& = {-е-*}|" = 1.
0
Тогда, используя интегрирование по частям в интеграле
оо
T(n + l) = fe-*xndx9
о
где мы определяем и = хп и dv = e~xdx (и тогда du = nxn~ldx и dv = -е-*), мы
получаем
оо оо
Г(л +1) = {-хпе~х }ζ + fexnxnldx = nfexxnldx.
о о
То есть мы имеем так называемое функциональное уравнение для гамма-
функции:
Г(п + 1) = иГ(п). (4.1.2)
Тогда, в частности, для положительных чисел п:
Г(2) = 1·Γ(1) = 1-1 = 1,
Γ(3) = 2·Γ(2) = 2·1 = 2,
Гамма-функция Эйлера ♦ 135
Г(4)
Г(5)
З-Г(З)
4·Γ(4)
3-2:
4-6:
6,
24
и т. д. В общем, вы можете видеть, что для положительных целых значений η
Т(п + 1) = л! Или эквивалентно:
Г(п) = (л-1)!, п> 1. (4.1.3)
Гамма-функция тесно связана с функцией факториала (и эта связь
фактически была первоначальной мотивацией интереса Эйлера к Г(«)).
Важность функционального уравнения (4.1.2) состоит в том, что оно
позволяет распространять гамма-функцию на все действительные числа, а не только
на натуральные числа. Например, если мы подставим η — — в (4.1.2), то полу-
Позже в этой главе мы вычислим,
им
1
2
Г
1
2
4-
= -!г
2
гс, и тог
1
2
да w
, и тогда Г
[ы получас
1
2
;м, ч
f
[то Г
2Г
'
.2;
1]
2
-2νπ. Мы можем использовать
эту же технику для расширения значений Г(п) для положительных η (которые
определяются интегралом в (4.1.1)) на все отрицательные числа.
Гамма-функция также может быть расширена и на комплексные аргументы. Когда мы
дойдем до главы 8, я покажу вам, как Риман делал то же самое для дзета-функции
(будет определена в следующей главе). Функциональное уравнение Римана
для дзета-функции расширяет (или продолжает) определение дзета-функции
для комплексных чисел с вещественной частью, большей 1, на всю
комплексную плоскость. Это, в свою очередь, привело к величайшей нерешенной
проблеме в современной математике. Захватывающие вещи! Но это на потом.
Уравнение (4.1.3) интересно еще и тем, что оно показывает, почему 0! = 1,
в отличие от первоначальной реакции большинства учащихся 0! = 0, когда они
впервые сталкиваются с факториальной функцией. Действительно,
подстановка η = 1 в (4.1.3) дает
1 = Г(1) = (1 - 1)! = О!
Гамма-функция встречается во многих приложениях- от чистой математики
до эзотерической физики и до практических инженерных задач. Как и в случае
с другими полезными функциями (такими как тригонометрические функции),
значения Г(п) были тщательно вычислены и сведены в таблицу. MATLAB даже
имеет специальную команду с именем (не удивляйтесь) gamma.
В качестве примера ее появления в математике давайте оценим интеграл
ах.
136 ♦> Гамма- и бета-функции
Делаем замену переменной у = хъ (что означает χ = у1/3), и тогда
dx = ^ = %,
Зу3
Таким образом:
ОО ОО 1 -ι ОО 2
JexZdx =Jey-^j = -Jeyy~4y.
Зу3
2 1
Это выглядит точно также, как (4.1.1) с η — 1 = —, поэтому η = -, и мы имеем
ОО -ι
Или, используя (4.1.2),
1 ..
-I
3
[1]
з
= г
[4]
з
получаем
Г°° V3 ■.
I e~xdx = T
Jo
f-l
13 J
(4.1.4)
Функция gamma MATLAB дает тот же результат, что и функция
интегрирования quad: gamma(4/3) = 0.8929795... и quad(@(x)exp(x.A3),0,10) = 0.8929799....
4.2. Интеграл Валлиса и бета-функция
Примерно в 1650 году английский математик Джон Валлис (John Wallis) изучил
интеграл
1
I(n) = f(x-x2)ndx,
который он мог непосредственно вычислить для малых целочисленных
значений п. Например,
l(0) = fdx = l,
о
ι
I(l) = f(x-x2)dx-
1 2 1 з
-χ2 --хъ
2 3
2 2~б'
Интеграл Валлиса и бета-функция ♦ 137
/(2)= f(x-x2)2dx = [(х2 -2хъ +х4)ах = \-хъ --х4 +-х5
Jo о 13 2 5
_l_l i_10_15 A-J_
~3 2 + 5~30 30 + 30 ~ 30
и т. д. Из этого короткого списка чисел Валлис как-то угадал (!) общий
результат для 1(п). Ты можешь? В этом разделе мы выведем формулу 1(п), но
посмотрим, сможете ли вы продублировать умение Валлиса до того, как мы закончим
формальный вывод.
Начнем с определения бета-функции:
B(m,n) = Jxm-\l-x)n-1dx> m>0,n>0.
(4.2.1)
Я покажу вам, что бета-функция тесно связана с гамма-функцией. Заменив
переменную в (4.1.1) на χ = у2 (и поэтому dx = 2ydy), мы имеем
оо оо
Г(л) = Jey2y2n-22ydy = 2fey2y2nldy.
Мы получим другое равенство, если заменить η на т, а фиктивную
переменную интегрирования у - на фиктивную переменную интегрирования х, и тогда
оо
Г(!И) = 2fex2x2mldx. (4.2.2)
о
Таким образом:
оо оо оо оо
Т(т)Т(п) = 4je-"2x2m-1dxje-yyn-ldy = 4ffe-(x2+y2)x2m-ly2n-ldxdy.
0 0 0 0
Этот двойной интеграл выглядит довольно ужасно, но хитрость, которая
ставит его на колени, заключается в переходе от декартовых координат к
полярным координатам. То есть мы напишем г2 = х2 + у2, где χ = rcos(6) и у = rsin(6),
и тогда элемент площади dxdy преобразуется в rdrdQ.
Когда мы интегрируем двойной интеграл по области 0 < х, у < μ, то
интегрируем по всему первому квадранту плоскости, что эквивалентно
интегрированию в области 0<г<ци0<6< π/2. Итак:
I оо
Г(т)Г(п) = 4 J Je-r2{rcose}2m-1{rsine}2"-1rdrc/e,
или
Г(т)Г(п) =
2je-rV2(m+")-1dr
2jcos2m-19sin2"-10de
(4.2.3)
138 ♦ Гамма- и бета-функции
Давайте теперь по очереди рассмотрим каждый из интегралов в квадратных
скобках справа в (4.2.3). Во-первых, если вы сравните
оо
2je-r2r2im+n)-1dr
с (4.2.2), то увидите, что они одинаковы, если мы подставим χ вместо гит
вместо (т + п). Делая эти замены, первая квадратная скобка в (4.2.3) становится
равной
оо
2je-r2r2(m+n)1dr = T(m + ri).
о
Таким образом,
Т(т)Т(п) = Т(т + п)
ι
2jcos2mlesin2nlede
(4.2.4)
Далее, для приведения к бета-функции (4.2.1), сделаем замену переменной
χ = cos2(6) (и тогда ах = 2sin(6)cos(6)d6), что приводит также к тому, что 1 -х =
sin2(6). Поэтому
1 О
в(!и,л) = Jxml(i- x)mldx = -2f cos2m-2esm2n-2QsmQcosedey
или
В(т,п) = 2jcos2mlQsm2nlQdey
что совпадает с интегралом в квадратных скобках (4.2.4). Следовательно,
Г(т)Г(и) = Г(т + п)В(т, и),
или, переписывая, мы получаем очень важный результат, который связывает
гамма- и бета-функции вместе:
В(т,п)= ) v J (4.2.5)
Г(ш + η)
Теперь мы можем записать ответ к интегралу Валлиса почти сразу. Просто
заметьте, что
I(n)= f(x-x2)ndx= Гхп(1-х)п^ = В(У7 + 1^ + 1)=Г(П + 1)Г(П + 1),
•J Jo Г(2п + 2)
или используя (4.1.3):
Интеграл Валлиса и бета-функция ♦> 139
т=
Итак,
п\п\
(л!)2
(2л+ 1)! (2п + 1)!
ι
7(л) = j(x-x2)ndx =
(η!)2
(2η+ 1)!
(4.2.6)
Если вы оглянетесь назад на начало этого раздела, то для первых нескольких
значений /(и), которые мы (Валлис) вычислили путем прямого
интегрирования, вы увидите, что (4.2.6) дает те же результаты. Однако при «больших»
значениях η прямая оценка интеграла становится довольно противной, в то время
как правая часть (4.2.6) легко вычисляется. Например, если η = 7, мы имеем
(7!)2
f(x-x2)7dx = ^- = 1.94,
JK f ία
.xlO"
что сходится с вычислением bMATLAB: ςυθοΙ(@(χ)(χ-χ.Λ2).Λ7,0,1) = 1.93...χ 1СГ5.
Один весьма полезный результат получается непосредственно из (4.2.6) для
случая и = 1/2. Это, конечно, нецелое значение, в то время как мы до сих пор
(по крайней мере, неявно) принимали и за положительное целое число. Однако
в соответствии с духом этой книги давайте просто спокойно проигнорируем
этот момент и посмотрим, куда это нас приведет. Для η = 1/2 равенство (4.2.6)
приводит к утверждению
я>
ХЧХ:
N
U',
2!
2
1
~2
\1А
Альтернативно, мы можем непосредственно оценить интеграл слева,
используя интерпретацию площади интеграла Римана, следующим образом.
Интеграл - это площадь под кривой (и выше оси х), заданной уравнением
у(х) = л]х-х2 при изменениихот χ = 0 до χ = 1.
Эту кривую, вероятно, будет легче узнать, если мы напишем ее как у2 = χ - χ2,
или χ2 - χ + у2 = 0, или, выделяя полный квадрат, как
ίι'2
21
' 1
χ —
■\2
+ У =
То есть кривая - это просто окружность с радиусом 1/2 и центром на оси Ох
в точке χ = 1/2. Площадь, соответствующая нашему интегралу, является
плоти
щадью верхней половины круга, то есть равна —. Таким образом:
8
140 ♦> Гамма- и бета-функции
π
8'
или
ill
-νπ.
(4.2.7)
Имеет ли (4.2.7) «смысл»? Да, и вот одна из проверок. Напомним (4.1.3):
Г(л) = (л-1)!,
3 3 3
тогда при η = - это дает -!, и поэтому, положив η = - в (4.1.1) и используя
(4.2.7), мы приходим к формуле
ОО -ι
[е~х\[хах = -лрк.
(4.2.8)
Это значение равно 0.886226..., и MATLAB дает то же самое: quad(@(x)
exp(x).*sqrt(x),0,100) = 0.8862228.
Мы можем использовать (4.2.8), чтобы установить еще один интересный
интеграл:
1
0
Сделаем замену переменной у = -ln(x). Тогда
У _ „-ln(x) _ „Щх-1) _ „1п(1/х) _
е> _ е-«ч*у _ е
= е"
1
и поскольку
dy__j._
мы имеем
dx = -^.
-е\
Таким образом:
J4-^)dx = J4y \-Щ- =JVye-ydy.
Интеграл Валлиса и бета-функция ♦> 141
Но этот последний интеграл равен (4.2.8), и, следовательно,
ι ^
Jyj-\n(x)dx = -л/π.
(4.2.9)
MATLAB подтверждает результат, поскольку quad(@(x)sqrt(log(x)),0,l) =
0.88623.... (Интересно сравнить (4.2.9) с (3.1.8).)
В результате нашей работы в этой главе мы можем даже говорить об
отрицательных факториалах; предположим, например, η = - в (4.1.3), тогда получаем
(л\ ( γ\
2
Из (4.1.1), полагая η = -, мы имеем
(V
2,
= J-rzdx>
интеграл, который мы можем найти, используя (3.7.1). Поэтому если мы
положим а = 1 и Ь = 0, то мы имеем
ОО л
ds
Если мы теперь заменим переменную на s=χ2 и, следовательно, — = 2х = 2\[s,
dx
dx = —1=. Это дает нам
24s
ОО ОО 1 л
[e~*2dx= fe~s—= = ->/ϊτ,
или, заменяя фиктивную переменную интегрирования s обратно на х,
Γ—=άχ = 4π.
о V*
(4.2.10)
Это значение равно 1.77245... и совпадаете результатом процедуры MATLAB:
quad(@(x)exp(-x)./sqrt(x),0,10) = 1.772448.
Таким образом,
ί -ί\ ( л\
! = Vir.
(4.2.11)
142 ♦ Гамма- и бета-функции
Другой способ получить (4.2.11) - это использовать (4.2.4). Там, считая
т = п = 1/2, мы имеем
= Γ(1)π,
,2,
Г
1
,2,
= Г(1)
2[4Θ
Jo
= Г(1)
2
πϊ
2)
или, поскольку Г(1) = 1,
АЛ w
и опять
UJ
Гамма- и бета-функции вместе позволяют нам вычислять некоторые
совершенно неприятные интегралы. Например, несмотря на то что само
подынтегральное выражение выглядит довольно просто, интеграл
f^sin(x)dx
кажется неуязвимым для атаки любым из приемов, которые мы разбирали
до сих пор, но посмотрите, что происходит, когда мы меняем переменную
и = sin2(x). Тогда
du
dx-
2sin(x)cos(x)'
sin(x) = u2,
и еще
cos(x) = 7l-sin2(x) = (1 - и)2,
тогда мы имеем:
2 1 4 1 г _1 _1 1
f^sin(x)dx = Г—^ -du = - fu 4(l-u) 2du = -
0 ° 2u*(l-uj* 2 ° 2
В
4'2
Из (4.2.5) получается (интеграл справа стоит, потому что в интервале
интегрирования синус и косинус принимают одинаковые значения) следующее
равенство:
Интеграл Валлиса и бета-функция ♦> 143
fyls'm(x)dx =
2Г
= fyjcos(x)dx.
(4.2.12)
Функция gamma MATLAB показывает, что это значение равно gamma(3/4)*
ganna(l/2)/(2*ganna(5/4.)) = 1.19814... и совпадает со значением quad-функции
quad(@(x)sqrt(sin(x)),0,pi/2) = 1.19813.
Та же самая замена работает для интеграла
1
Jo
Ах,
^sin^cosi*)
который превращается в
du
2 о Г ι iV2 -
\Ы2(1-Ы)2/
или используя (4.2.11)
ι 1 3 3 Л (Л Л\
2-1 2 4 2
(I)
4
2Г
ΊΪ'
X
dx
0 ^/sin^cos^)
(4.2.13)
Функция gamma MATLAB показывает, что это значение равно (датта(1/4)л2)/
(2*sqrt(pi)) = 3.708149... и совпадает со значением quad-функции quad(@(x)l./
sqrt(sin(x).*cos(x)) Api/2) = 3.708170.
В качестве другого примера мы можем использовать (4.2.13) и формулу
двойного угла из тригонометрии для записи
Г2'11
dx г? dx
Г2
Jo
yJsin(x)cos(x)
Г2
Jo
sin(2x)
2л/тг
Сделаем замену переменной и = 2х и, таким образом, dx = du/2, и тогда
Γ2ΐ ι Ι
du л/2 _ г? du
I.
2J-sin(u)
-т®^
jsin(u) 2л/тт
144 ♦> Гамма- и бета-функции
или
Jo
du
ί 1
Vsin(u) [л/2 J 2л/тг
^
ill
Или наконец (интеграл справа выполняется тоже, потому что на интервале
интегрирования синус и косинус принимают одинаковые значения):
(4.2.14)
Функция gamma MATLAB показывает, что это значение равно (датта(1/4)Л2)/
(2*sqrt(2*pi)) = 2.62205..., функция quad дает тот же результат quad(@(x)l./
sqrt(sin(x)) Api/2) = 2.62205....
Наконец, в определении (4.2.1) бета-функции сделаем замену переменной:
* = -^,
1 + У
и тогда
1-х = 1-- "
1+У 1+У
ах
1
dy (1 + У)2'
и тогда
dy
dx-
(1+У)2
Таким образом,
B(m,n) = J
U+yJ
U+yJ
dy
= Г_У.
(1 + у)2 ·£ (1 + у)
dy.
Теперь, полагая п = 1 -т, мы получаем:
оо д.т-1
Г^—dy = B(myl-m) = T(m)T(l-m),
Jn 1 + У
(4.2.15)
где второе равенство следует из (4.2.5), потому что Г(1) = 1. Позже, в главе 8
(в формуле (8.7.9)) мы покажем с помощью криволинейных интегралов, что
Интеграл Валлиса и бета-функция ♦ 145
00 IF™-1 ^
J0 1 + У sin(mir)
и поэтому
Г(1Я)Г(1-1Я) = (4.2.16)
sin(ftm)
- это знаменитая формула отражения для гамма-функции, открытая Эйлером
в 1771 году.
Эта формула отражения будет очень полезна для нас, когда мы доберемся
до главы 9 (эпилог). Там я покажу вам главное достижение Римана, его
вывод функционального уравнения для дзета-функции (дзета-функция будет
представлена в следующей главе), в которой (4.2.16) будет играть центральную
роль. Там будет еще один дополнительный результат, который мы можем
получить прямо сейчас с помощью бета-функции. Начнем с (4.2.5):
Г(т + п) (1И + Л-1)!
из чего следует, что
В(!Я + 1,л + 1) = ———.
V J (1И + Л + 1)!
Итак, полагая т = n=z, мы имеем
Из определения В-функции (4.2.1):
1
B(z + l,z + l) = fxz(l-x)zdx,
и тогда
zlzl
(2z + l)!
= Jxz(l-x)zdx.
Теперь сделаем замену переменной х = (и также 1 — х = ), чтобы
получить
zlzl
(2z + l)!
или, поскольку подынтегральная функция четная,
146 ♦ Гамма- и бета-функции
zlzl
(2z + l)!
= 2"1ζ/(1 -s2)zds.
du
Сделаем вторую замену переменной, и = s2, и также ds = —-j=, чтобы прийти
*/£'
к выражению
ζ\ζ\
du
(^^■"i(1-u,^=2"""'i<1-")'"""*,iu·
По формуле (4.2.1) последний интеграл равен
В
-,Ζ + 1
Γ(ζ + 1)
ί 1.1
2
!ζ!
~ί
ι
Ζ + 2
!
и поэтому, ссылаясь на формулу (4.2.11), мы имеем:
ζ\ζ\ _2-ΐζ-ι *!^
(2ζ + 1)!
чк
Сокращая на ζ! с каждой стороны, а затем перемножая крестом, мы
получаем
zL + ^\ = 2-2z-1^(2z + l)\,
(4.2.17)
и поскольку
1
1
1)
2z + l)
1)
2
и также
(2z+l)! = (2z+l)(2z)!,
мы можем альтернативно написать
.ί !]
Ζ4 Ζ
Г 2,
! = 2"2zVi(2z)!.
(4.2.18)
Формулы (4.2.17) и (4.2.18) являются вариациями того, что математики
обычно называют формулой дублирования Лежандра. Мы будем использовать
(4.2.18), в частности, в главе 9.
Перестановка порядка интегрирования в двойном интеграле ♦ 147
4.3. Перестановка порядка интегрирования
в двойном интеграле
В главе 3 (раздел 3.4) я обсуждал, как изменение порядка интегрирования
в двойном интеграле может быть полезной техникой, которую можно иметь
в своем багаже трюков. В этом разделе я покажу вам еще несколько примеров
этого трюка, в котором появится гамма-функция. Наша отправная точка - это
двойной интеграл
оо оо
JJsin(bx)yp-1e-xydxdy.
Если мы утверждаем, что значение этого интеграла не зависит от порядка
интегрирования, то можем написать
оо оо оо оо
Jsin(bx) \jyp~le-xydy \dx = Jyp-1\Jsin(bx)e-xydx
\dy.
(4.3.1)
Обратите внимание на правую часть (4.3.1). Для внутреннего х-интеграла
имеем
оо
fsin(bx)e~xydx =
Ъ2+у2'
результат вы можете получить либо путем интегрирования по частям, либо
найти, используя еще один прием, который я покажу вам в главе 7, в
формуле (7.1.2). Сейчас, однако, вы можете просто принять это. Тогда правая часть
(4.3.1) вычисляется как
Ь л__ Л Ур~
/^sb*-»/-
Ъ1+у
О U2
,2 Ϊ
1 + ^
*-i/
ι" ур-
1 +
-dy.
Теперь сделаем замену переменной
и тогда dy = b dt, что означает, что правая часть (4.3.1) есть:
If (lb)"-1
J l + ί2 Jn 1 + ί
dt.
Как я покажу вам в главе 8, когда мы доберемся до криволинейных
интегралов, мы найдем в (8.7.8), что
148 ♦> Гамма- и бета-функции
π
fJ^dx = ^^l
0 sm\(m + l) — \
(m + 1)-
Итак, если мы положим п = 2ит =р - Ι,το имеем:
π
ос^ -р-1
Ό 1 + ^
dt = -
sin
ρπ
Таким образом, правая часть (4.3.1) есть
Ьр1п
ρπ
sin
Затем перенесите ваше внимание на левую часть (4.3.1). Для внутреннего
у-интеграла сделайте замену переменной и = ху (конечно, в этот момент мы
рассматриваем χ как константу). Тогда du=x dy, и поэтому
оо °°/. \Р-1 ι . ι оо
о о νΛ/ Λ Λ о
Последний интеграл является просто определением Г(р) в (4.1.1), и поэтому
оо ■<
/ур-1е-^у = 4г(р)·
О Х
Таким образом, мы непосредственно видим, что левая часть (4.3.1) есть
'Sin(bx)
Г(Р)^
-dx.
Приравнивая два наших результата для каждой стороны (4.3.1), мы имеем
(дляО<р <2):
rsin(to)
{ X"
Ы-'п
2r(p)sin
ρπ
Τ
(4.3.2)
Этот результат воспроизводит интеграл Дирихле, если b = 1 и ρ = 1 (это,
конечно, хорошо!), но реальная ценность (4.3.2) состоит в том, что его можно
использовать в интеграле, который до сих пор бы останавливал нас холодно:
Перестановка порядка интегрирования в двойном интеграле ♦ 149
оо
sinix")
dx-
Например, если q = 3, что это
sin(x3)
/
-dx-
Обратите внимание, что в этом случае уже не так:
UU I
л
sin(x)
dx,
что мы и покажем позже в главе 7, в (7.6.2).
Начнем с очевидного шага, с замены переменной на и = xq. Затем
du _
~dx~
и тогда
qx
Уч
■ί-1.
■■q— =
qu
dx = du.
qu
Таким образом:
Js-^dx=J™
J V4 J I;
(u)\ul,q
du
qu
1 °rsin(M)
;/
ίο u
2-1/q
du.
Последний интеграл имеет вид (4.3.2), где Ь = 1, ρ = 2 - l/q, и тогда
сю
sin(x«)
dx-
π
Поскольку
sini
2-1
2qT
= sin
(
2-
,
1]
—
ij
sin]
(
2-
{
1]
—
ij
π
—
2j
π-
π
2^J
sin(u)cos
π
-cos(Tr)sin
π
—
Ы
= sin
ίπ)
Ы
мы имеем:
■sin(*q)
ρ
dx-
π
2<?Г
2 —
ij
sin
π
(4.3.3)
150 ♦ Гамма- и бета-функции
Этот результат в (4.3.3) формально является ответом на наш вопрос, но мы
можем немного его упростить. Ниже приведено краткое описание свойств
гамма-функции, где из-за функционального уравнения (4.1.2) ζ теперь
представляет собой любое действительное число, а не просто положительное целое
число:
(a) Γ(ζ) = (ζ-1)!;
(b) Γ(ζ+1) = ζ!;
ζ'
(c) (ζ-1)! = — (альтернативно,ζ! =ζ(ζ- 1)!);
(ά)Γ(ζ)Γ(1-ζ) = -
π
sin(uz)
Из(Ь)
Ml
мы может написать Г
! —
Μ
[--
{ я,
|
Ml
=
fi-ll
! И тогда из (с):
Таким образом, (4.3.3) дает
siniAr")
dx = -
π
2?
Ч)
I 4J
sin
π
I2~4j
или
сю
sin(xq)
dx-
2(q-
-i)
π
1
!sin
π
(4.3.4)
Далее, из (а), (Ь) и (d) мы имеем:
Γ(ζ)Γ(1-ζ) = ^^- = (ζ-1)!(-ζ)! =
Sin(uZ)
и следовательно,
(-г)! = -г-: ·
zlsin(uz)
Записывая 1/q вместо ζ, получаем:
π
ζ(ζ-1)!(-ζ)! z\(-z)\
_1
I _
Ύ
W
4
!sin
π
9 J
(4.3.5)
Перестановка порядка интегрирования в двойном интеграле ♦> 151
Подставляя (4.3.5) в (4.3.4), мы получаем:
sin(x«)
/
-dx-
или
π
π
2(q-l) 4 sin
1
!sin
π
( \
π
Ы
1]
я)
!sin
π
—
(л \ ( \
2(q-
-i)
W
sin
JL
'ιϊ
!2sin
π
Ы
2cos
π
Ы
2(q-l)
sin
1
π
ii]
k
1
|
' 1
cos
,2<?J
(4.3.6)
Из (с), которое говорит, что ζ! = ζ(ζ - 1)!, мы можем написать
[1]
и.
1
, 1
я
Μ
[я 1
1
f'-ll
[я 1
! = Г
ί1)
,?J
q q
где последнее равенство следует из (а). Используя это в (4.3.6), мы наконец
получили наш ответ:
(4.3.7)
Если, например, q = 3, (4.3.7) дает выражение
J у*
ill
2
-cos
'π
Γ
[1]
3)
2
ш
12
4
Ί1
и вычисления в MATLAB совпадают: sqrt(3)*gamma(l/3)/4 = 1.16001... и quad(@(x)
sin(x.A3). /χ. Λ3,0,10000) = 1.15928-с хорошей точностью.
Прием перемены порядка интегрирования настолько полезен, что давайте
используем его снова для вычисления интеграла
152 ♦ Гамма- и бета-функции
оо
cos(bx)
dx,
что является очевидной вариацией формулы (4.3.2). Начнем с интеграла
оо оо
JJcos(bx)yp-1e-xydxdy,
о о
а затем, как и прежде, предположим, что значение двойного интеграла не
зависит от порядка интегрирования. То есть
ОО I ОО I ОО ОО
fcos(bx)\fyp-1e-'vdy\dx =fyp-1\fcos(bx)e-xydx
dy.
(4.3.8)
Сосредоточим наше внимание на правой части (4.3.8). Мы имеем, для
внутреннего, х-интеграл (при интегрировании по частям):
[cos(bx)e~xydx =
ь2+/
Тогда правая часть (4.3.8) есть
оо оо ρ л оо ρ
b2
0
о 1 + J
Теперь сделаем замену переменной t = y/b, и тогда dy = bdt, и правая часть
(4.3.8) принимает вид:
b2j0 1 + t2 J0 1 + t2
Снова, как и прежде, мы теперь используем результат, который будет
получен позже в формуле (8.7.8):
оо т
i 1 + x"
π/η
0 i + x" sin{(m + l>it/n}
Тогда, если п = 2ит = р, мы имеем:
π/2 π/2
I 1 + t"
0 x , . sin{(p + l)u/2} οο8{ρπ/2}
Следовательно, правая часть равенства (4.3.8) есть
2cos{pn/2]
Перестановка порядка интегрирования в двойном интеграле ♦> 153
Затем перенесем внимание на левую часть (4.3.8). Что касается внутреннего,
у-интеграла, вы помните, что мы уже получили его как
ОО л
Следовательно, левая часть равенства (4.3.8) есть
»cos(bx)
вд/!
'-dx.
Приравнивая эти два выражения для сторон равенства (4.3.8), мы имеем
°rcos(bx) Ьр-'п
J yP ί
2r(p)cos
ρπ
, 0<ρ<1.
(4.3.9)
С этими результатами еще многое можно сделать. Например, если мы
напишем (4.3.2) с фиктивной переменной интегрирования и, а не х, то
/
sin(bu)
du
bpln
2T(p)sin{pn/2}'
и если мы положим ρ = 1 —, то получим
к
Js^du-
Ъ кп
или
P*m<Mdu
Теперь пусть и = хк, и тогда
*t = kxk~\
dx
и еще
du = к—dx = k—rdx.
154 ♦> Гамма- и бета-функции
Таким образом,
p*B@udu= p™^k»dx=k7sin(bxb)dXt
J 11 J И λ J
и поэтому
оо
fsin(bxk)dx
π
2kbkT
1)
sini
π π
Из формулы отражения (4.2.16) для гамма-функции
получаем:
1-4
1)
π
sin
ι
fil
—
UJ
π
sin
πΐ
l*J
Jsin(bxk)dx
Тогда, поскольку
sini
мы можем записать:
Г
2W
1
Ч\
sin
η
π
π
Γ
Γ
1'
2
2sin{4
kb*sin
π
."2
cos]
π
~2k
π ]
2feJ
[π
—
[2
π
2k \
= sin
π
—
L 2 J
cos
π
—
[2k\
-cos
π
—
L 2 J
sin
π
—
[2k\
= cos
π 1
—
[2k\
uo
fsin(bxk)dx =
(i)sinfe
, b>0,fc>l.
kb~k
(4.3.10)
Например, если b = 1 и к = 3, тогда интеграл (4.3.10) принимает значение:
оо
Jsin(x3)dx
fil
—
,3
sin
π
—
6
3
lr
г
2
ill
—
3
3
1 ..
■ — —Г
6
1
з
: 0.446489...
Перестановка порядка интегрирования в двойном интеграле ♦> 155
Если в формуле (4.3.9) в качестве фиктивной переменной интегрирования
мы используем и, а не х, то
UP-K
•J up 2T(p)cos{pn/2}'
Как и прежде, пусть ρ = 1— (и еще и = хк), и мы получаем (пропуская не-
к
сколько шагов)
к fcos(bxk)dx = —-, г
0 2Г 1-|
Ъ къ
и тогда
Jcos(bxk)dx = г
cos
π
π π
I~2k
2kbkT
ί, ι]
1 —
{ fcj
cos]
π
—
[2
π 1
2k\
Поскольку
[π
[2~~
π
"2k
= cos
π
2~
cos
π
2k
+ sin
π
2~
sin
π
= sin
π |
2kJ
cos
и, как и раньше,
1-
1]
к
1
fl]
А
rt
sin
π
I
2Γ
[1]
A
sin
π
π
Ж
cos
π Ι
2k\
мы имеем:
\ cos(bx)dx
fi]
—
UJ
COS
π 1
—
[2k\
bkk
, b>0,fc>l.
(4.3.11)
Если b = 1 и fc = 3, тогда интеграл (4.3.11) принимает значение:
1^
fcos(x3)dx
fi]
—
UJ
cos
π
Le> J
I
Г Ί Ί
—
isj
1
3 3 2V3
oo oo
Отметим, что jcos(x3)dx^ Jsin(x3)dx.
=0.77334.
156 ♦> Гамма- и бета-функции
Под конец представляем еще один пример приема перемены порядка
интегрирования. Напомним нашу более раннюю отправную точку в выводе
формулы (4.3.9):
оо
fcos(bx)e~xydx
ь2+у2
Если мы проинтегрируем обе части по у от 0 до с > 0, то имеем:
Π f cos(bx)e~xydxldy = Г
иттг*'
οίο J Job+r
или, меняя порядок интегрирования слева,
оо ί С 1 С
/cos(bx) JWydx = f-^^dy.
о [о J о"~'~У
Ясно,что
fe-*>dy =
χ
1-е"
■ = 2у,
Теперь в интеграле справа в (4.3.12) положим и = Ь2 + у2, и тогда
или
dy:
2у'
Тогда
с Ь2 + с2 , лЪ2+с2 , 1
J Ь2 _l л,2 ^ J ,ι 9л/ 9 J π 9 V "■
Ь2+с2 1
J0b2 + y
u2y 2
In
b2 + c2
Таким образом, из (4.3.12) получаем
°г 1 - е_с* 1
1 cos(bx)dx = -ln
«J x 2
V + c2'
ь2
•
(4.3.12)
(4.3.13)
Это очевидно верно при с = О (нулевые значения слева и справа (4.3.13)).
Если Ъ = с = 1, тогда (4.3.13) говорит, что
Г1 е cos(bx)dx = -ln(2) = 0.3465...,
J у 9
Перестановка порядка интегрирования в двойном интеграле ♦> 157
и MATLAB «соглашается», так как quad(@(x)(l-exp(-x)).*cos(x)./x,0,500)
0.3456....
Запишем (4.3.13) дважды, сначала полагая с = г и Ъ = р, мы имеем:
1-е
Г cos(px)dx = -
= Iln
ί 2 2\
lp2 + r2]
{ Ρ )
и затем снова при с = s и Ь = q:
оо
• 1 - e~sx 1
cos(qx)dx = -In
Χ Λ
<q2+s2
{ <Г )
0
или
Тогда мы получаем:
°г 1 - e~sx °г 1 - е~гх 1
I cos(qx)dx- \ cos(px)dx =-ln
J, х J. х 2
ί <?2 ,
1,
—In
2
У+r2)
. p2 J
°pcos(qAr)-cos(px)^ | °pe racos(px)-e sxcos(qx)d^ =
J У J У
In
In
q2
P2+r2
ί Ρ2 J
-ilnl
2 I
|qLt£l.£l
(У+г2 q2J
-In
<?2+s2
[p2+r2J
+2-
I?2 J
f„2 . „2 ^ ( „\
q +s
[p2+r2)
+ ln
Но так как первый интеграл в начале последнего равенства равен In
гласно (3.4.6), то мы имеем результат:
ы
Ы
со-
/
e-r'cos(pA:) - e-sxcos(qx) ^ = 1^
(q2+s2'
(Р2+г2)
(4.3.14)
Например, если г = q = 0 и ρ = s = 1, то (4.3.14) сводится к
cos(Ar)-e"*
/
-dx = 0,
это результат, который мы снова получим в главе 8, в (8.6.4), совершенно иным
образом с использованием контурного интегрирования.
158 ♦ Гамма- и бета-функции
4.4. Гамма-функция встречает физику
В главе 1 (раздел 1.8) я показал вам несколько примеров интегралов,
возникающих в физических задачах, и, поскольку мы сейчас находимся примерно
на половине этой книги, я думаю, что настало время для другой такой
иллюстрации. В следующем анализе вы увидите, как проявляются гамма-функции
в задаче, связанной с движением точечной массы под воздействием силового
поля обратной зависимости (необязательно ограниченного обратной
квадратичной зависимостью закона гравитации). В частности, представьте себе
точечную массу т, находящуюся в состоянии покоя в точке у = а в силовом
поле величины —-, где /сир являются положительными постоянными. Поле
р+1 " г
направлено прямо вниз по оси у к началу координат. (Гравитационное силовое
поле является частным случаем, когда ρ = 1, но наш анализ будет справедлив
для любого ρ > 0. Для случая ρ = 0 см. задачу 7.) Наша проблема проста в
изложении. Материальная точка начинает двигаться в момент времени t = 0, и
поэтому, конечно, она начинает ускоряться вниз по оси у к началу координат. За
какое время t = Τ масса достигнет начала координат?
У мистера Ньютона есть наблюдение «сила равна ускорению массы», или
в математике1:
dt2
Если мы обозначим скорость массы ν, то
dy
dt
dt ~ dt2'
которое говорит (используя удивительно полезное правило
дифференцирования сложной функции), что
dv (dv)
F = m— = т\ —
dt [dy
(dy)
dt
dv
= mv—.
dy
Ньютон на самом деле говорил не это (так называемый второй закон движения), но
гораздо глубже: «сила - это скорость изменения импульса». Если масса не
изменяется со временем (как в нашей задаче), то с вышеизложенным все в порядке, но если вы
хотите изучать физику ракет (масса ракеты уменьшается, когда она сжигает топливо
и выбрасывает продукты сгорания), то должны использовать то, что на самом деле
сказал Ньютон.
Гамма-функция варечает физику ♦ 159
Итак,
к
„Р+1
dv
= mv—,
dy
(4.4.1)
мы используем знак минус, потому что силовое поле действует в
отрицательном направлении, вниз по оси у в направлении начала координат. Это
дифференциальное уравнение легко интегрируется, поскольку переменные
разделяются:
kdy
ту
Р+1
= vdv.
Теперь, интегрируя неопределенно,
1
-λ
2
или
т
Г
dy_
„Р+1
т
fy-^dy-
к]
т
-Р
+ С--
тру"
■ + С,
2 2к
v2 = г + С,
тру"
где С - это неопределенная константа интегрирования. Используя начальное
значение ν = 0 при у = а, мы видим, что
2к
С =
трар
Итак,
2к
2к
тру" mpav
Таким образом:
2к_
тр
I 1_
{ур а"
{df
dt
2к_
тр
1 1
[У
или, решая1 относительно дифференциала dt,
dy
п~
ьр
1
а"
= ±,
= ±,
Обратите внимание, что знак dt написан с неоднозначностью ±. Я делаю это, потому
что на данный момент не ясно (по крайней мере, для меня!), какую из двух
возможностей, исходящих из операции с квадратным корнем, следует использовать. Однако
физически мы знаем, что Τ > 0, и в конечном итоге будем использовать это условие
для принятия решения.
160 ♦ Гамма- и бета-функции
Интегрируем по переменной t от 0 до Τ левую часть равенства (что означает,
что мы интегрируем по у от α до 0 правую часть):
(άΐ = Τ = ±α^\Ηΐ
dy
2к
-1
Замена переменной и = у/а (и тогда dy = a du) дает равенство
_, ^ р/2 \щ> г а , ^ (| 1+1 Ш °г ир/2 ,
Τ = ±ар/ . —- \ , du = ±а[2> .М- / , du,
или, используя знак минус, чтобы сделать Τ > 0 (см. последнюю сноску),
Теперь пусть
и тогда
dx Ό_λ рир рх
— =рир 1 = ^^ = ^т,
du и -
или
du = —dx.
рх
Таким образом,
Т = а[
) г X2
2к{ VT^
рх
dx = a
I 2k (p)
VP 2
Γ
ifr:
Ί+ι
1
IPJ
1 1 1
J>~5(1-a:)~5c/a:.
Этот последний интеграл имеет вид интеграла бета-функции в (4.2.1), где
1 1
т-\
Ρ 2
Задачи для решения ♦ 161
п-1 = --
То есть
т
1 1
1
п = -.
2
Итак,
\1
Τ = ώ2
И
т
В
\2кр
и так как из (4.2.5)
[р
ι ι ι)
[р + 2'2
В
(1 1 1
р + 2'2
ill
2
1 1
νπ
IP
- + 1
+ 1
наконец-то мы получили ответ:
Т = а[
КМ
?ηπ
2fcp
Г
Г
\ 111
Ip JJ
ρ>0.
(4.4.2)
Заключительное наблюдение. Материальная точка приходит в начало
координат с бесконечной скоростью, потому что поле становится сколь угодно
большим, когда материальная точка приближается к у = 0. Это означает, что
на положительной оси у есть некоторая точка, где скорость точечной массы
превышает скорость света, но известно со времен специальной теории
относительности Эйнштейна, что это невозможно. Это хороший учебный текст по
математике/физике для новичков в классической физике, но он не является
релятивистски правильным.
4.5. Задачи для решения
(С4.1). Найти
I(n) = J{l-yfxjdx,
162 ♦ Гамма- и бета-функции
и, в частности, используя общее решение, покажите, что
/(9) = )(l-^)9dx = ^.
о JJ
(С4.2). Доказать, что
fxm\n"(x)dx = (-1)" ^—г.
Мы будем использовать этот результат позже, в главе 6, для некоторых
действительно впечатляющих, исторически важных интегралов.
(С4.3). Покажите, что интеграл от хауъ по треугольной области, определенной
а\Ь\
осями координат и линией х + у=\, равен , где аиЬ-
неотрицательные константы.
roosin(x)
(С4.4). Используя (4.3.2), вычислить / —-^-ах и, применяя (4.3.9), вычислить
J0 у/Х
fooCOS(Ar) .
/ —ι=^-αχ. Это известные интегралы, которые мы позже повторно полу-
J0 у/Х
чим совершенно другим способом в (7.5.2). Кроме того, используйте (4.3.10)
и (4.3.11) для вычисления / sin(x )ах и / cos(x )ах. Это также известные
интегралы, и мы повторно получим их позже совершенно другим путем в (7.2.1)
поо „ поо „ поо „
и (7.2.2). Отметим, что / cos(x )dx^ J sin(x )ах, но / cos(x )ах равен
f°°sm(x2)dx.
(С4.5). Примените прием изменения порядка интегрирования, который мы
,ач лъ r°°sin(bx) _сх , п .
использовали для получения (4.3.13), для вычисления / —-е αχ φ > 0,
JO χ
с > 0). Подсказка: начните с интеграла, который мы использовали в начале
sin(bx)e~xydx = — -, а затем интегрируйте обе части от-
0 Ъ + у
носительно у от с до бесконечности. Отметим, что этот результат есть
обобщение интеграла Дирихле в (3.2.1), к которому он сходится при с —> 0.
(С4.6). Вычислите интеграл I ь~т^х в теРминах Г-функций, где а, Ь и с -
(1-\-х )
постоянные, такие что а > -1, b > 0 и be > а + 1, и используйте полученную
формулу для вычисления интеграла Г -dx. Подсказка: сделайте замену
переменной у = хь и затем используйте интегральную форму от нуля до бес-
Задачи для решения ♦ 163
конечности для бета-функции, которую мы получили непосредственно перед
(4.2.15): В(1И,л) = / —^ dy.
v J v ' ' Jo (l + y)m+n y
(C4.7). Обратите внимание, что Τ в (4.4.2) не определено для случая ρ = О
(случая силового поля обратной зависимости первого порядка). Посмотрите,
сможете ли вы найти Τ для случая ρ = 0. Подсказка: установите ρ = 0 в (4.4.1)
и затем проинтегрируйте. Вы найдете (3.1.8) весьма полезным для вычисления
интеграла, с которым столкнетесь.
(С4.8). Как ведет себя гамма-функция при отрицательных целых числах?
Подсказка: используйте формулу отражения (4.2.16).
r°°sin(x2)
(С4.9). Показать, что J —-^-ах
π
^
4Г
sin
3π
и что
Jo
>cos(x )
dx
π
41'
fsl
UJ
COS
ί3π)
—
l8 J
Чтобы «проверить» эти результаты, вычислим значения правых частей
равенств pi/(4*gamma(3/4)*sin(3*pi/8)) = 0.69373... и pi/(4*gamma(3/4)*cos(3*pi/8))
= 1.67481... соответственно, а сами интегралы вычисляются так (используя
Symbolic Toolbox, после определения χ как символьной переменной): double
(int(sin(xA2)/sqrt(x),0,inf)) = 0.69373... и double(int(cos(xA2)/sqrt(x),0,inf)) =
1.67481....
Подсказка: в (4.3.2) и в (4.3.9) положите Ь = 1 и сделайте подстановку χ = у2.
Глава
5
Использование степенных
рядов для нахождения
интегралов
5.1. Число Каталана
Чтобы начать эту главу, приведем очень простую иллюстрацию техники
степенных рядов для вычисления интегралов, в данном случае дающую нам то,
что называется числом Каталана (упоминаемым в предисловии) и
записывается как G = 0,9159655.... Разложения tarf *(*) в степенной ряд для \х\ < 1 - это
наша отправная точка, и ее можно описать следующим образом. Основная
идея состоит в том, чтобы написать
/1-^Tdy = tan-1(y)r =tan"1(x).
Jo 1 + У l0
Тогда, после деления столбиком числителя на знаменатель
подынтегрального выражения, мы имеем:
X
tan"1 (а:) = /(1-У2 + у4 -у6 +У8 -
0
3 5 7
X X X
= χ-Ύ+Ύ-Τ+->
так что
tan-1(x) , χ2 χ4 χβ
χ Ъ 5 7
...)dy =
( 3 5
У 3 5
Λ,7 Λ.9 1
_у_+у__...
7 9 J
Число Каталана ♦> 165
и поэтому, интегрируя почленно, мы имеем:
ill
ftan~lw^
J у
хъ xs χ7
J__J_ J__J_
l2 32+52 72+'"
То есть
J Υ
(5.1.1)
Проверяем наши вычисления с quad(@(x)atan(x)./x,0,l) = 0.9159656....
Мы можем использовать степенные ряды, чтобы показать, что совершенно
другой интеграл также равен G. В частности, давайте взглянем на следующий
интеграл (упомянутый в предисловии):
1п(х)
-dx.
{ х2+1
Мы можем написать «нижнюю часть» подынтегрального выражения как
1
χ2+ί х>
1
ί 11
X
1
~х2
1
1 1
АГ2" + Х4 X6
+■■■
где бесконечный сомножитель в скобках получается из деления столбиком.
Таким образом:
<χ2+ι JA
Щх) 1п(х) 1п(х)
dx.
X X X
Мы видим, что все интегралы справа имеют один общий вид
1п(х).
/
- dx, к четное целое > 2,
такой интеграл легко берется по частям. Полагаем и = ln(x) - и тогда
dx
1
что дает du = —, и далее полагаем dv = —dx, следовательно, ν
, тогда мы имеем
du_^
dx χ'
x~k+1 =
-fc + 1
1
1-fc
' 1 ]
y-1
166 ♦> Использование степенных рядов для нахождения интегралов
I
ln(x)
dx
ln(x)( 1 )
fe-1
χ
fe-1
+ -
—?f—1
dx 1 °f dx
χ fe
-fe + 1
1
(k-l)V
Итак
«{ х2+1
ln(x) , 1
1 1
■+-
ο (fc-D2
1 1 1
(2-1)2 (4-1)2 ' (6-1)2 "' Ι2 32+52 ""'
или
ln(*)
', АГ2+1
dx = G.
(5.1.2)
Кроме того, quad(@(x)log(x)./(χ.Л2+1),1,1еб) =0.91595196....
Мы можем объединить этот результат с более ранним, чтобы сейчас
вычислить
оо
1п(аг + 1)
dx,
i *2+i
который можно записать как
J0 Χ2+ί ·{ X2+l
π.
Мы уже нашли первый интеграл в нашем результате (2.2.4) равным — 1п(2)
о
и поэтому имеем
•ln(x + l)
In
1 +
1)
rlnfx + l), π. /0. 7*ln(x + l), π η. \ у χ
\ „ 'dx = -ln(2)+ \ \ 'dx = -ln(2)+ —ι ν '
dx--
1Щ +
1
= ^Щ2) + У-Щах+]-^>ах.
8 \ χ2+1 { χ2+1
В этой формуле первый интеграл справа есть в формуле (5.1.2), и поэтому
lnll + i
J0 x2+l 8 J x2+l
Число Каталана ♦ 167
а в оставшемся интеграле справа сделаем замену переменной и = 1/х (и тогда
du 1 , 2, du. _
-— = —-, что дает dx = -χdu = —-). Тогда
dx χ2 и2
1Ы1 + -1 о ΙηίΐΗ-1^
ШЧ+тШ=Ш^
но это снова в точности (2.2.4)! Таким образом:
Г-
>1П^^="1п(2) + С + ^1п(2),
* +1
или наконец:
8
8
(5.1.3)
Это равно 1.46036..., в то время как quad(@(x)log(x+l)./(x.A2+l),0,le6) =
1.46034839....
Возвращаясь к основной теме этой главы, в качестве нашего последнего
примера использования степенных рядов в этом разделе рассмотрим интеграл
0sin(9)
-άβ,
J0 a + bcos2(9)
где а > b > 0. Затем, раскладывая подынтегральную функцию как степенной
ряд, получаем:
/ = -Jesin(9)
й о
l-|-|cos2(9) +
а
cos4(9)-
cos6(9)-
de=
Jesin(6)(ie- - Jesin(e)cos2(6)de+ - Jesin(e)cos4(e)de-··
Мы видим, что интегралы справа имеют следующий общий вид, для η = 0,
1,2,...:
τι
Jesin(e)cos2n(e)de.
Такой интеграл легко берется по частям (полагая и = θ и dv = sin(6)cos2(6)
сЮ), получаем:
168 ♦> Использование степенных рядов для нахождения интегралов
Jesin(e)cos2n(e)de =
ecos2n+1(e)
2и + 1
2л + Н 2л + 1'
потому что это ясно из симметрии (обратите внимание, что 2п + 1 нечетно для
всех и), что
Jcos2n+1(e)de = o.
о
Таким образом:
π
1
(и\ л(и\
+-
π να
у1Е libylb)
4а Ъ\а4а
π
'ьГ
а
1
~7
+ -
Ь
+ -
(Ь*
1
+■
а
a2Ja~
l(b'S)
аъ4а
+ ·
( ι ^/2 ι ( ι ^/2
+ ··
или если мы вспомним разложение tan г(х) в степенной ряд из начала этого
раздела и положим χ =
'ъГ
, то увидим, что
(5.1.4)
Например, если а = I и Ь = 3, то
Г *sin(*> dx = -^tan-Чл/^) = 1.899406...,
J0 a + bcos2(x) V3
ВТО время какquad(@(x)x.*sin(x)./((l+3*cos(x).A2)),0,pi) = 1.8994058....
5.2. Степенные ряды для логарифмической функции
Используя, по сути, тот же подход, который мы применяли для изучения числа
Каталана, мы можем оценить
rln(l + x)
dx.
Сначала получим разложение в степенной ряд для \п(х + 1), при \х\ < 1,
записывая
Степенные ряды для логарифмической функции ♦ 169
dy
/т^- = 1п(1 + у)|*=1п(1 + х) = /(1-у + у2 -у3 +-)dy-
η *■ ~~Т~ У η
У У У
^ 2 3 4
или
х2 хъ х4
1п(1 + х) = х-у + у- — + -, |х|<1.
(Вы можете вспомнить, что я ранее цитировал этот ряд (без вывода) в сноске
в главе 2.)
Тогда
rln(l + x)
о
1
/
dx =
1
/
0
(
=
X
χ χ2 хъ
+·
X X X
dx-
_ J_ J__J_
22+32 42+·
В 1734 году Эйлер показал, что1
^ ι , ι ι ι
U к2 22 Ъ2 А2
π
~6
что является суммой обратных квадратов всех положительных чисел. Если мы
напишем только сумму обратных квадратов всех четных положительных
чисел, то получим:
2
1
S(W
4tik2 24'
Таким образом, сумма обратных квадратов всех нечетных натуральных
чисел должна быть равна
2
^2 ^2
π π
π
6 24 8
Я упоминал эту сумму ранее, во введении (раздел 1.3). Позже в этой книге, в главе 7,
я покажу вам прекрасный способ - конечно, используя интегралы! - получить этот
знаменитый и очень важный результат. Однако покажу вам не тот способ, каким
Эйлер сделал это. Способ, который я покажу, обладает явным достоинством того, чтобы
быть совершенно корректным, в то время как оригинальный подход Эйлера (хотя
и гениальный - подробности см. в моей книге «Воображаемая сказка» (An Imaginary
Tale. Принстон, 2010. С. 148-149) вызывает некоторые серьезные опасения.
170 ♦> Использование степенных рядов для нахождения интегралов
Если вы посмотрите на результат, который мы получили для нашего
интеграла, вы увидите, что это сумма квадратов обратных значений всех
нечетных целых минус сумма квадратов обратных величин четных целых (то есть
^2 ^2
π π
π
8 24 12
), и тогда
χ 12
(5.2.1)
Это равно 0.822467..., и quad подтверждает: quad(@(x)log(l+x)./x,0,l) =
0.822467.... Следующий интеграл является тривиальной модификацией
(я предлагаю вам показать это! - см. также задачу 7 в разделе 5.5):
/•Ιη(Ι-χ)
/
dx-
π
~6~
(5.2.2)
Это значение есть 1.644934..., и quad снова подтверждает: quad(@(x)log(l+
χ)./χ,0,1) = 1.64494....
Хорошо, а что можно сделать с этим интегралом:
ίίι+*12Ί
1-х
\dx = ?
Вы, конечно, подозреваете, что ответ такой: использовать степенные ряды!
Для начала напишем
"1 + АГ' \dx = 2f-{ln(l + x)-(l-x)}dx.
Ί>
1-х
Ранее мы выписали разложение в степенной ряд для 1п(1 + х), и поэтому
можем сразу получить разложение для 1п(1 - х), просто заменив χ на -х. Наш
интеграл становится таким:
44
i х\
х2 хъ х4
X 1
2 3 4
2 4 4
_ _х__?__х__
~Χ~Ύ~Ύ~Ύ~'"
dx =
ρ 1 ( 1 1 ^
= 2 Г—|2х + 2-аг3+2-лг5+...
i x\ 3 5
1 ( 1 1 )
dx = 4 f\l + -x2 +-х4 +...\dx =
4\х + ^хъ+^х5+.
fill Ί
1 1 h...
U2 з2 s2 J
= 4
fir2
8
или наконец:
Степенные ряды для логарифмической функции ♦ 171
Это значение равно 4.934802..., и quad подтверждает: quad(@(x)log(((l+x)./(1-
х)).Л2)./ х,0,1)= 4.934815....
Мы можем смешивать тригонометрические и логарифмические функции,
используя идею степенных рядов для оценки интеграла неприятного вида,
таких как
π/2
Г cot(x)ln(sec(x))dx.
о
Пусть t = cos(X). Тогда — = -sin(x),илиdx = .Таким образом:
dx sin(x)
π π -ι
f 2cot(X)ln(sec(x))dx = Γ2 In
Jo Jo \v\r\(y\
1
cos(x)
tan(x)
-|^-r^ln{cos(x)}
Jx sin(x)
\dx--
dt
sin(*)J
= - J^^lnicosix)^ = -J-L-lnWt.
{ sin2(x) J0 1-i2
На всем интервале интегрирования мы можем написать:
—^ = t(l + t2 + t4 + t6 + ...),
что вполне очевидно. То есть
t
:t + i3+i5 + t? + .
ι е Σί
1 — t л=0
Тогда наш интеграл есть
2п+1
-/
fVn+1 fln(t)A,
или, предполагая, что мы можем изменить порядок интегрирования и
суммирования1, имеем:
/»— оо Г 1
J 2cot(x)ln(sec(x))dx = -^\jt2n+1ln(t)dt
п=0 [ о
Мы можем взять этот последний интеграл по частям. Пусть и = 1п(£) и dv
f2n+2
t2n+1dt. Тогда — = 1 и du = -dt v = —
dt t t 2n + 2
Итак:
Эта перемена порядка операций является примером шага, на котором математик
будет чувствовать себя обязанным сначала показать равномерную сходимость, прежде
чем продолжать. Я же, с другой стороны, с полным отсутствием стыда буду просто
плыть вперед и делать перемену, а затем, как только у меня будет «ответ», спрошу
у quad, что он «думает».
172 ♦> Использование степенных рядов для нахождения интегралов
Jt2n+1ln(t)dt =
2п + 2
ln(t)
1
2п + 2
м.2п+2
-I
о о
1
1 +2п+2 fi\
2п + 2
2п + 2
dt
= 1—1[t2n+1dt =
9n_u9 J
2п + 2
(2n + 2f
Таким образом,
^ 001 1 ОО 1 -| СХЭ -■ -|
[icot(x)\n(sec(x))dx = Y -— = -V—— = ~у^- = -
^2
π
или
2 ^2
/ТС
cot(x)ln{sec(x)}dx = —
24
(5.2.4)
Это значение равно 0.4112335..., и quad подтверждает: quad(@(x)cot(x).*log
(sec(x)),0,pi/2)= 0.411230.
Еще один пример интегрирования степенными рядами с использованием
логарифмических функций. Давайте посмотрим, что мы можем сделать с
интегралом
1
Jln(l + x)ln(l-x)dx
о
Если вы немного на это посмотрите, то сможете убедить себя в том, что с
помощью симметрии подынтегрального выражения относительно χ = 0 мы
можем написать
1 ι 1
Jln(l + x)ln(l - x)dx = - Jln(l + x)ln(l - x)dx.
(Или, если хотите, измените переменную и = -х и обратите внимание, что ин-
ln(l -u)n(l + u)du. Подынтегральная функция не из-
10 0 111
менилась. Итак, f = fy поэтому f+f=f = 2j, как и утверждалось.) Теперь
0-1 -10-10
АГ + 1
сделаем замену переменной у = (и dx = 2dy). Поскольку χ = 2у- 1,то 1 +х =
2у и 1 - χ = 1 - (2у - 1) = 2 - 2у, все это говорит, что
Степенные ряды для логарифмической функции ♦ 173
1 г
J ln(l + х) 1п(1 - x)dx = - J ln(2y) ln(2 - 2y)2dy = J ln(2y)ln{2(l - y) }dy =
0 ^ 0 0
1
= J[ln(2) + ln(y)] [ln(2) + ln(l - y)]dy =
0
1
= J[{ln(2)}2 + ln(2){ln(y) + ln(l - y)} + ln(y)ln(l - y)]dy =
j ln(y)dy + /ΐη(1 - y)dy + jln(y)ln(l - y)dy.
= {ln(2)}2+ln(2)
Так как
1 1
/ln(y)dy = /ln(l-y)dy,
0 0
что очевидно «сразу» либо путем замены переменной и = 1 - у в одном из
интегралов, то мы имеем после замены фиктивной переменной интегрирования
обратно нах:
1 1 1
J ln(l + х) 1п(1 - x)dx = {1п(2)}2 + 2 ln(2) J ln(x)dx + J ln(*)ln(l - x)dx.
0 0 0
Поскольку
Jln(x)dx = {xln(x)-x}\1o = -ly
0
мы имеем:
1 1
J ln(l + χ) ln(l - x)dx = {ln(2)}2 - 2 ln(2) + J ln(x)ln(l - x)dx,
о о
и все, что нам осталось сделать, - это интеграл справа. Для нахождения
интеграла
Jln(x)ln(l-x)dx
мы будем использовать разложение в степенной ряд функции 1п(1 -х). Как
показано ранее:
1п(1-*) = -х-
х2 хъ х4
2 Ъ
·, *<1,
и тогда мы имеем:
1
Л г
Г1п(л:)1п(1-л:)с/а: = -£)- fxkln(x)dx.
k=lk 0
о
174 ♦> Использование степенных рядов для нахождения интегралов
Если вы посмотрите на наши выкладки, которые приведены к формуле (5.2.4),
то увидите, что интеграл справа мы уже вычисляли. Там мы показали, что
1 ι
ft2n+1ln(t)dt = ^—j-,
{ (2и + 2)2'
и поэтому сразу получаем (заменяя 2п + 1 на к) следующий результат:
1
Jtkln(t)dt:
1
(к + 1)2
Следовательно:
Jln(x)ln(i-x)dx = ^2
1
fcife(fc+i)2 и
(л \ (
fe=l
= Σ
1
1
1
l*+ij
k(k+l) (k+lf
1
,111
1+~+^ + T+···
2 3 4
(fc + 1)2
(1 1 1 ^
2+3+i+-
-Σ
1
= 1-
Итак, окончательно
il 1
1
~т ~> _т ~> . τ ~> ' ''
= 1-
<π2
6
fei(fc+i)2
2
= 2-^
2
Jln(l + x)ln(l-x)dx = {ln(2)}2-21n(2) + 2- —
(5.2.5)
Это значение равно 0.550775... и согласуется с quad(@(x)log(l+x).*log(l-x),
0,1) = 0.55078....
Я закончу данный раздел вычислением интеграла
который найдет важное применение позже в книге. Хитрость здесь в том,
чтобы сделать замену переменной χ = е~у, что эквивалентно у = -1п(лг). Таким
образом, dy — —dxvidx = -xdy = -e~ydy. Итак:
χ
)^рах = )-^{-е-Чу} = ]У\1-е^ + е^-е^ + ...)е-ЧУ =
ο λ + χ ^ 1 + е 2y J0
oo
= Jy2(e"}'-e-3y + e-5y-e-7)' + -)c/y.
Степенные ряды для логарифмической функции ♦> 175
Из стандартных таблиц интегралов (или интегрированием по частям)
оо
fy2e°4y.
еауЬ_2у 2)
* 2
а а
■>о,
потому что а < О, как в каждом члене нашего подынтегрального бесконечного
ряда выше. Таким образом:
{\n(x)f
dx = 2
J__J_ J__J_
l3 33+53 73+*
но известно1, что этот знакочередующийся ряд равен —. Итак:
i 1 + a:2
3
16'
(5.2.6)
Это значение равно 1.9378922..., и используя quad для проверки: quad(@(x)
1од(х).Л2./(1+х.Л2),0,1) = 1.9379....
Есть два дополнительных комментария, которые мы можем сделать об этом
интеграле. Первый:
>{1п(х)}
J0 1 + х2 J0 1 + х
2 8
Я предлагаю вам заполнить детали (просто обратите внимание, что
оо 1 оо
Г = Г+ Г, а затем сделайте замену переменной у = 1/х во втором интеграле).
О 0 1
Во-вторых, посмотрим, что мы получим, когда рассмотрим, казалось бы,
несвязанный интеграл
π/2
J[ln{tan(6)}]2de,
если сделаем замену переменной χ = tan(G). Так как
rfx_cos2(e)-r-sin2(e)
de~ cos2 (θ)
мы имеем:
1
= l + tan2(6),
rfe =
dx
1
l + tan2(6) 1 + x
-dx,
1 См. мою книгу: Dr. Euler's Fabulous Formula. Princeton, 2011. P. 149 - для вывода этого
результата с использованием рядов Фурье.
176 ♦> Использование степенных рядов для нахождения интегралов
и тогда
π/2
{ln«}2
о о 1_hA
Таким образом:
π/2 з
Jf[ln{tan(0)}fde = ^-.
О "
(5.2.7)
Это значение равно 3.8757845..., и quad подтверждает: quad(@(x)log(tan(x)).
Λ2,0,ρϊ/2) = 3.8758.... Мы будем использовать данный результат в главе 7, когда
наконец вычислим сумму Эйлера взаимных целых квадратов.
5.3. Интегралы дзета-функции
В предыдущем разделе я упомянул открытие Эйлера
На самом деле это частный случай того, что называется дзета-функцией Ри-
мана:
оо 1
fe=l К·
где s - комплексное число с действительной частью, большей 1, чтобы
гарантировать сходимость1 ряда. Сумма Эйлера соответствует значению s = 2, но на
самом деле метод нахождения ζ(2) - произносится как дзета-два - работает для
π4 π6
всех положительных, даже целочисленных значений s; ζ(4) = —, ζ(6) = ,
ζ(8) = и ζ(10) = . Вообще, l(s) = —π5, где тип- целые, если
SW 9450 SV ' 119750400 SV ' η
s - четное целое число. Однако метод Эйлера не подходит для всех
положительных нечетных целочисленных значений s, и никому не удалось в течение
почти 300 лет после открытия Эйлером ζ(2) найти формулу, которая дает t,(s)
даже для одного нечетного значения s.
Математики, конечно, могут вычислить числовое значение t,(s) для любых s
с максимально возможной точностью. Например, ζ(3) = 1.2020..., и значения
этих точек теперь известны как минимум до ста миллиардов (!) десятичных
знаков. Но та формула, которую хотят математики, и открытие ее для ζ(3) было
бы событием открытия сверхновой в мире математики.
Для s = 1 ζ(1) - это просто гармонический ряд, который, как было известно за много
веков до Эйлера, расходится.
Интегралы дзета-функции ♦> 177
По иронии судьбы, легко написать ^(s) для любого целого значения s,
четного или нечетного, в виде двойного интеграла. Чтобы увидеть это, запишем
хауа
разложение в степенной ряд для
1—ху
, где а (пока) является константой:
-^— = хауа{1 + ху + (ху)2+(ху)ъ+(ху)4+(ху)5 +···}, \ху <1.
1 - ху ' '
Затем, используя это в качестве подынтегрального выражения двойного
интеграла, мы имеем:
λ- λ~ χαγ
о о — *У
JJ ^— dxdy = fxa J{ya + xya+1 + x2ya+2 + хъуа+ъ + - - - }dy
Г\ Г\ * /*.У Q I П
-/
α+1 α+2 а+Ъ уа+4
^-— + х^—— + х2^—— + хъ^-— + ·
α + 1 α + 2 a + 3 a + 4
,α+3
№ =
Л:
-+
xa+1 xa+2
- +
+ Г + ·
α + 1 α + 2 a + 3 a + 4
[dx =
Lfa+2
fl+4
- + -
- + -
-+-
(а + 1У (α + 2)2 (a + 3Y (α + 4)2
- + ·
1 1
-+-
1 1
■ + -. T7T + -
(α + 1)2 (α + 2)2 (α + З)2 (a + 4)2
и поэтому
(5.3.1)
Теперь если мы положим а = 0, то формула (5.3.1), очевидно, сводится к
о о х АУ п=\п
но на самом деле мы можем сделать гораздо больше с формулой (5.3.1), чем
просто ζ(2). Вот как это происходит. Вспоминая любимый трюк Фейнмана по
дифференцированию под знаком интеграла, давайте дифференцируем (5.3.1)
по параметру а (который вначале был константой, но теперь будем
рассматривать а как параметр). Тогда правая часть дает нам выражение
ι
-2V ·
ti(n + af
Для левой части мы сначала напишем
ха уа — (ху)а — е1п{(*у)0} = еа1п(ху)
178 ♦> Использование степенных рядов для нахождения интегралов
и поэтому дифференцирование интеграла дает
daJnJn 1-ху -Н 1
1г1г1п(ху)ея1п(дгу)
■ху
dxdy.
ху
о о - "*У
Тогда
Ή 1-xy ti(n + fl)s
Теперь дифференцируем снова и получаем
' ' {ln(*y)}V-> dxdy = (_2)(_3)£. I
\3 *
\4 '
оо - ХУ " Ί^Λη + αγ
Продолжая дифференцировать, легко увидеть закономерность:
"lln^)1*"*e""",«y=(-2)(-3)...<-IS-i))f;. '
II
1-АГу
U(n + a)s
Итак, записывая снова еащху) в виде (ху)", мы имеем для s > 2:
^WM*"^,,.,^^. ι
II
1-АГу
£^(И + й)5
(5.3.2)
Или для особенно интересного случая а = 0:
(5.3.3)
Например, для s = 5 легко вычислить ζ(5) непосредственно из
определения дзета-функции как суммы и получить 1.0369277..., в то время как правая
часть (5.3.3) находится с помощью следующего кода MATLAB Symbolic Toolbox
(factor = -1/24 есть
(~1)ь
(4)!
) и будет равна 1,0369277.,
syns χ у
factor^ -1/24;
int(int(log(x*y)A3/(l-x*y),x,0,l),y,0,l)*factor
Чтобы закончить этот раздел, я сейчас покажу вам прекрасный результат,
который связывает гамма-функцию из главы 4 с дзета-функцией. Из формулы
(4.1.1) вы помните, что
r(s) = fe-'x^dx.
Интегралы дзета-функции ♦> 179
Итак, начнем с интеграла
оо
fe^x^dx, k>0,
о
и сделаем замену переменной и = кх, которая дает
{ { UJ к к*{ к>
Тогда, суммируя обе части равенства, мы имеем:
оо °о оо Г/оЛ оо 1
Σ fe-V-to = Σττ2 = Γ(*)Σΐ7 = TW(s).
fc=l о fe=l " k=l K-
Далее, предполагая, что мы можем поменять порядок суммирования и
интегрирования, мы имеем:
оо оо
О к=1
Сумма в подынтегральном выражении представляет собой сумму членов
геометрической прогрессии, которая легко вычисляется как
оо 1
и поэтому у нас сразу же получается удивительная формула
оо с-1
f-—dx = r(sK(s),
Jn е*-1
(5.3.4)
которая была открыта в 1859 году не кем-нибудь, а самим Риманом, героем
этой книги. Например, для s
формула (5.3.4) говорит, что
π4
этой книги. Например, для s = 4 - напоминаем результат Эйлера ζ(4) = —
/-^-(ίχ = Γ(4)ζ(4) = (3!)
n С 1
π4^
π
90
15'
и вы вспоминаете и этот интеграл, и его значение из предисловия (см. в нем
примечание 6). Это теоретическое значение равно 6,493939... и согласуется
cMATLAB, так как quad(@(x)(x.A3)./(exp(x)-l),0,100) = 6.493939....
С небольшой предварительной подготовкой мы можем использовать тот же
подход, чтобы получить интересный вариант формулы (5.3.4), а именно
180 ♦ Использование степенных рядов для нахождения интегралов
Для нашего подхода определим две функции
1111
vs =
1
Is
1
2s +3
1 1
s 4s
+ ·
' * J
и тогда
111 1
7(s) = U-\ 1 1 \-... = и-\
•>W s 2s 4s 6s » r
[1 1 1
|ls+2s+3s+'"
= us +
Тогда
4, = ζ(*)
i-l
2s
•
Кроме того:
vs =
111
1S+3S+5S+"'
-
1 1
2S+4S+"'
1
1 1 1
1S+2S+3S +
Итак, используя (5.3.5):
ν, = ζ(5)
i-l
2s
-1ζ(5) = ζ(5)
i-1
2SJ
•
Таким образом:
ν5 = ζ(5)[1-5'η.
Но, заметив, что
fe=l К·
мы имеем
оо /
-л
-1
- = ζ(
s)[l-2
l-s
]■
-m-
(5.3.5)
-ζ(«).
(5.3.6)
(5.3.7)
Вот теперь мы можем взять наш интеграл! Начнем с интеграла
/(-l^e-^x^dx,
о
снова сделаем замену переменной и = кх, а затем повторим то, что сделали
при выводе (5.3.4). Все пройдет точно так же, как и раньше, за исключением
того, что вы получите одну сумму, которая даст (5.3.7), а другая Σ™=1(- \)k~le~kx
Константа Эйлера и связанные с ней интегралы ♦> 181
вместо Σ7=ιβ кХ' ^ем не менее это сУмма членов геометрической прогрессии,
которая легко находится:
е~х _ 1
1 + е* ~е* + Г
Окончательный результат:
Τ^-^ = [1-2ΐ5]Γ(5)ζ(5), s>l.
i ех+1
(5.3.8)
Например, для s = 4 эта формула говорит, что
оо 3 /-\ л
Г-—-ί/χ = [1-2-3]Γ(4)ζ(4) =
Jn е*+1
— = 5.68219...,
15
и MATLAB подтверждает, поскольку quad(@(x)(x.A3)./(exp(x)+l),0,100) = 5.68219....
Кстати, обратите внимание, что для s = 1 формула (5.3.8) дает
неопределенное значение для интеграла:
ОО л
f^—dx = \l-2l~lnmi) = (0)(1)(оо) =?,
+
потому что ζ(1) - это расходящийся гармонический ряд. И это несмотря на то,
что интеграл явно существует, так как подынтегральное выражение всегда
конечно и очень быстро стремится к нулю, когда χ стремится к бесконечности.
Эта неопределенность, разумеется, и объясняет, почему существует
ограничение s > 1. Итак, каково значение интеграла для s = 1? Мы уже ответили на это,
вернувшись к нашему результату (2.1.4), где показали, что
?->-*=ад.
J0efl*+1 a
Для s = 1 в формуле (5.3.8) мы полагаем а = 1 в (2.1.4), и тогда наш интеграл
равен 1п(2).
5.4. Константа Эйлера и связанные с ней интегралы
С XIII века известно, что гармонический ряд расходится. То есть
п 1
lim у*— = НтЯ(п) = оо.
п—>оо 7^ Ь п—>оо
fc=l ,v
Расходимость довольно медленная, частичная сумма Н(п) растет только как
логарифм от и, и поэтому вполне разумно предположить, что разница между
Н(п) и log(n) = 1п(п) может не расходиться. Фактически предел этой разности
182 ♦ Использование степенных рядов для нахождения интегралов
известен в математике как константа Эйлера (или просто как гамма,
обозначается как γ)1. То есть γ = Нт^^и), где
У(л) = Й-1п(л).
fe=i К
Я думаю, что вовсе не очевидно, что это выражение имеет предел при η —> оо,
но, используя интерпретацию интеграла Римана в виде площади, легко
установить, что предел существует и что он находится где-то в интервале от 0 до 1.
Вот как это можно сделать.
Поскольку
у(л) = 1 + - + - + - + — 1п(л),
2 3 η
то
γ(η + 1)-γ(η) =
,11 11
1 + _ + _ + ... + _ + --
2 3 η пч-1
1
л + 1
-ln(fi) —1п(п + 1) =
-1п(л + 1)
1 - + Ш
1 1 1 1 I / Ч
1 + 2 + 3 + - + й"1п(П)
п + 1
п + 1
или
γ(η + 1)-γ(η) = - + ln
п + 1
1 —
п + 1)
Ясно,что In
n + lj
:1П
1-
π + 1
< 0, так как это логарифм числа, меньшего 1.
Но на самом деле мы можем сказать гораздо больше, чем просто это.
Вспоминая степенной ряд для 1п(1 + х), который мы установили в начале раз-
дела 5.2, и полагая χ = , мы получаем:
In
1 —
1
п + 1)
1
п + 1'
1
1
п + 1 2(п + 1)2 3(п + 1)3
Технически сложное, но вполне читаемое изложение темы «все о γ» на уровне этой
книги - в книге «Гамма» Джулиана Хавила, изд-во Princeton University Press, 2003
(Julian Havil's Gamma). Эту константу также иногда называют константой Эйлера-Мас-
керони, чтобы отметить некоторое признание итальянцу математику Лоренцо Мас-
керони (17S0-1800), который в 1790 году вычислил γ до 32 десятичных знаков (но,
увы, не без ошибок). Отмечу, что γ была рассчитана машиной буквально до
миллиардов десятичных знаков, причем первые несколько цифр были 0,5772156649.... В
отличие от π или е, которые, как известно, иррациональны (фактически трансцендентны),
рациональность (или нет) числа γ неизвестна. На планете нет математика, который не
верит, что γ иррациональна, но нет никаких известных доказательств этой веры.
Константа Эйлера и связанные с ней интегралы ♦ 183
Это говорит о том, что In
Ί- '
n + lj
является более отрицательным, чем —
л + Г
и тогда γ(π + 1) - γ(π) < 0.
То есть γ(π) монотонно убывает с ростом и, и фактически, поскольку γ(1) =
1 - 1п(1) = 1, мы установили, что γ(π) монотонно убывает от значения 1 при
увеличении п.
Далее заметим, что
/dt , /Jt4in rdt rdt г dt
-=mi=jT+jT+...+j-,
1 12 η—1
Теперь
,+}dt 1
ίτ<7·
из-за того что функция l/ί монотонно убывает на интервале интегрирования,
и принимая подынтегральное выражение равным его наибольшему значению
в этом интервале, получаем оценку сверху интеграла. Таким образом:
1п(л)<1 + - + - + -» + -
2 3 л-1
и тогда
0<1 + - + - + .-. + --1п(л).
2 3 л-1
Прибавим — к обеим частям этого неравенства
л
-<1 + - + - + - + г + — 1п(л) = у(л),
η 2 3 л-1 л
а это в сочетании с нашим первым результатом говорит, что
0<-<У(л)<1.
л
Итак, мы показали, что γ(π) находится (для всех η > 1) в интервале от 0 до 1
и что с ростом η значение γ(π) неуклонно уменьшается от 1, никогда не
достигая 0. Таким образом, γ(π) должен приближаться к предельному значению при
η —> оо. Но что это за предельное значение?
На рис. 5.4.1 показан полулогарифмический график зависимости γ(π) =
Н(п) - 1п(л) при изменении η в интервале 1 до 10 000, и, по-видимому, предел γ
существует (с приблизительным значением 0,57) и сходимость довольно
быстрая. Такой график, конечно, не является доказательством того, что предел γ
существует (мы это уже установили), но он полностью соответствует духу данной
184 ♦> Использование степенных рядов для нахождения интегралов
книги. Добавив γ в наш каталог констант, объединив такие рабочие лошадки,
как е, π, 1η(2) и G, мы теперь можем найти некоторые новые, очень интересные
интегралы.
0.95
0.9
^0.85
о °·8
— 075
=П 0.7
0.65
0.6
η ее
■\ ■*
\
\ "1
\ 4
^^^-^
10°
10'
ю2
η
10Г
10
Рис. 5.4.1 ♦> Постоянная Эйлера как предел
Я начну с того, что покажу вам, как написать Н(п) в виде интеграла, а затем
мы будем преобразовывать этот интеграл в форму, которая также будет
выражать γ как интеграл. В интеграле
сделаем замену переменной и = 1 - χ (dx = -du) и получим
Vl-a-x)"
1-й"
Jn X J, l-U J
*(l-u)(l + u + u2 + иъ +··· + ^_1)
1-й
du
= J{l + u + u2+u3 -{ \-unl}du
1 2 1 3 1 4 1
u + -u + -uъ + — u -\ \--i
2 3 4 η
, 111 1 TT, ч
= 1 + 2 + 3 + 4+- + η=Η(η)·
Затем заменим переменную в нашем исходном интеграле (интеграле,
который мы теперь знаем, что это Н(п)) на и = пх (и поэтому dx = — du) и напишем:
η
Константа Эйлера и связанные с ней интегралы ♦ 185
du
.1-
/-
π
-du + J-
1-1
c/u =
,ι-ι-
Wm Μ* л
/ —* }-du + I / ^ >-
-du
-du.
= г Ι ") du+ln(n)_ [L^l
J и J и
0 и. л и.
Таким образом, мы имеем:
ι 1-
γ(η) = Η(η)-1η(η)= Г—*—^-du- Π—^
■du.
Полагая η —> оо и вспоминая определение е" как
eu = lim
1 + ^
Л
мы приходим к формуле
1-1 р-и сю -и
y = limy(n)= Г du- Г—du.
П^ОС Q U ϋχ U
(5.4.1)
Это любопытное выражение в (5.4.1) для числа γ чрезвычайно важно - вот
почему я поместил его в рамку, - и я покажу вам некоторые его применения
в нижеследующих вычислениях. А пока проверим это равенство с помощью
quad, quad(@(x)(l-exp(-x))./x,0,l)-quad(@(x)exp (-χ)./х, 1,10) = 0.577219....
Для начала рассмотрим интеграл
оо
fe~xln(x)dx,
о
который мы можем записать как
оо 1 оо
fe-xln(x)dx = fe-xln(x)dx + §е~хЩх)ах. (5.4.2)
186 ♦ Использование степенных рядов для нахождения интегралов
Предупреждение! Обратите особое внимание на наш следующий шаг, там
мы увидим, что
e-* = --f(e-*-l).
ах
Это, конечно, верно, но почему (и вам наверняка интересно) мы пытаемся
написать простое выражение слева в более сложной форме справа? Ответ
заключается в том, что мы собираемся взять первый интеграл справа в (5.4.2) по
частям, и без этого трюка в обозначении все пойдет не так (когда мы закончим,
вы должны попробовать сделать это все заново, но уже без этого трюка
переобозначения).
Итак, продолжая, мы имеем для первого интеграла справа
-f-f(e-x-l)ln(x)dx,
о "*
который становится, если мы положим
и = \п(х)
и
dv = — (e~x-\)dx
αχ
(итогдас/и = -с/хи v = e~x - 1):
χ
Je~xln(x)dx = -J-^-(e-x-l)ln(x)dx = -{ln(x)[e"x- l]}f - J^^dx
0 0 "* { 0 X
Jo x
Второй интеграл справа в (5.4.2) мы также интегрируем по частям, теперь
полагая и = \п(х) и dv = e~"dv, и тогда
ОО ОО л ОО л
Ге-х1п(Аг)с/л: = {-е-,[1п(Аг)}Г+ [е~х-ах= (е~х-dx.
J lO J y J у
1 1 Л 1 Л
Таким образом:
оо 1 ι р-х оо -ι
fe~xln(x)dx = - Г dx+ fe~x-dx.
О О Л 1 Л
Согласно формуле (5.4.1) правая часть равна γ (помните, я говорил вам, что
равнство (5.4.1) будет важно!), и поэтому мы видим, что
Константа Эйлера и связанные с ней интегралы ♦> 187
Ге xln(x)dx = -γ.
(5.4.3)
Проверка этого с помощьюMATLAB:quad(@(x)exp(-x).*log(x),0,10)= -0.57733....
Иногда, особенно при чтении продвинутой математической книги, вы
натолкнетесь на комментарий, в котором говорится, что равенство (5.4.3) можно
установить, дифференцируя интегральное определение гамма-функции Γ(ζ),
а затем задав ζ = 1. Если вы пишете
Λζ-Ι)ΐη(χ) .
е*1п(х)е-1п(х)
х" - = е"чл ' = е
то нетрудно продифференцировать
Γ(ζ) = Jexxzldx
и получить
dr(z)
T'(z) = fe-xln(x)xz-1dx,
и тогда
оо
r'(l) = fexln(x)dx.
о
Но это говорит нам, что Г'(1) = -γ ?????
Авторы таких книг предполагают, что их читатели знакомы с тем, что
математики называют дигамма-функцией, которая определяется равенством1:
Γ(ζ) ζ U
1
(1
г r + z
Подстановка в это равенство ζ = 1 дает (поскольку Г(1) = 0! = 1)
Γ'(ζ) = -1-γ + Σ
1
(1_
г r + lj
1-γ+
1)
2 3
или
Г'(1)
-у,
rf(z)
Я не буду продолжать вывод , но если вам интересно, вы можете найти хорошее
Γ(ζ)
представление этого вопроса в книге Гавила (Havil, см. сноску на стр. 182). Мы будем
использовать дигамма-функцию в окончательных вычислениях данной главы,
вывод (5.4.11). См. также задачу 5.10.
188 ♦> Использование степенных рядов для нахождения интегралов
как утверждалось, и мы получаем (5.4.3).
Хорошо, давайте теперь рассмотрим интересный интеграл
1
fln{-ln(x)}dx.
о
Сделаем очевидную замену переменной и = -ln(x) и, дополняя процедуру
интегрирования деталями, получаем равенство
1 оо
Jln{-ln(x)}dx = Jeu ln(u)dx,
о о
которое совпадает с (5.4.3). Тогда
fln{-ln(x)}dx = -y.
(5.4.4)
Проверяем с MATLAB: quad(@(x)log(-log(x)),0,l) = -0.57721....
Другая драматическая иллюстрация мощности равенства (5.4.1), что
исходит от математика начала XX века Рамануджана (будет обсуждаться более
подробно в главе 9), который оценил набитый экспонентами интеграл
оо
I = f{eaeX + eaeX-l}dxy
о
где α - любая положительная константа. Заметив, что подынтегральная
функция является четной функцией, он начал с удвоения интервала
интегрирования и записи этого интеграла в виде:
оо
21= f{e-ae* + e-ae'-l}dx
и последующей замены переменной на и = е* (и поэтому dx = —). Таким об-
У
разом:
21
+ е "-1
о м
Затем он разбил этот интеграл на сумму двух интегралов:
Константа Эйлера и связанные с ней интегралы ♦ 189
1
21= Га
Jo
е~аи+е »-1
*+Л
>e~au+e "-1
du.
и и
После этого он разбил каждый из этих двух интегралов еще на два:
>е и -1
27= /fl du + /fl du+ L du+ L du =
Jo и Jo и J- и J- и
1-е
J'-i — e , r°°e , J f-e j fo°i —e
fl du + L du\ + ] \a—du- L
0 и J- и \ \Jo и J- и
-e u
1-е "
du
Теперь для двух интегралов в первой паре фигурных скобок сделаем замену
переменной χ = аи (и поэтому du = —dx), а для двух интегралов во второй паре
α
сх
фигурных скобок сделаем замену переменной χ = а/и (и поэтому du = —-dx).
χ
Затем
1-е-
rl-e-'fl.l ге-х[1,1 аге~х α,ϊ иг1-е
21 = - \-dxU —\-dxU /——-dx\- /
Jn х α S х [a J a { χ2 I J а
—Tdx
χ2
a
a
1 ι p-x oo -χ σο -χ α -ι -χ
= -f dx+ f—dx+ f—dx- Г dx.
J у J Υ J Υ J Υ
0 Λ 1 Л а2 О Л
Поскольку первые два интеграла справа равны -γ согласно (5.4.1), то
*J γ J γ J γ
α2 Λ 0 Λ О Л
или объединяя первый и последний интегралы справа:
2/ = -γ + Ι —dx- / —.
*J γ J γ
Продолжая:
2/ = -γ +
Ι —dx+ Ι —dx
ο χ ιχ
г dx /· dx
или объединяя первый и третий интегралы справа:
lrdx
2/ = -γ +
= -Υ +
/ —dx + / dx
J Υ J Υ
+
rax
Ix
[ + 1П(АГ)Г
190 ♦> Использование степенных рядов для нахождения интегралов
Два интеграла в последней паре фигурных скобок, опять по формуле (5.4.1),
равны -γ, и поэтому
2/=-2γ-1η(α2).
Таким образом, наконец, мы имеем интеграл Рамануджана
ОС
" + ε-Μ"'-1}ίίλ: = -γ-1η(α).
(5.4.5)
Для проверки этого равенства положим a = 1, тогда интеграл будет равен
-γ, а при a = 2 интеграл равен -γ - 1п(2) = -1.270362..., и эти значения
согласуются с вычислениями MATLAB: quad(@(x)(exp(-exp(x))+exp(-exp(-x))-l),0,100) =
-0.577216... и quad(@(x)(exp(-2*exp(x))+exp(-2*exp(-x))-l),0,100) = -1.270357....
В качестве еще одного примера применения формулы (5.4.1) рассмотрим
следующий загадочно выглядящий интеграл:
ι-!**-**<*.
J у
где а и Ь являются положительными константами. Этот интеграл «выглядит»
как интеграл Фруллани (см. снова главу 3), но это не так. Это намного глубже.
Без нашего столь же загадочного равенства (5.4.1), я думаю, было бы
невозможно добиться прогресса с этим интегралом. Вот как это можно сделать.
- е-х° - e~xb J °°r е~ха - е'^ J °°r ^ - е~(*°)Р J Ъ
\ ах= \ ах= \ ах, р = —.
о * о * о * а
Пусть
и=ха,
и поэтому
, du
dx = г.
αχ""1
Тогда
Константа Эйлера и связанные с ней интегралы ♦> 191
"-е-*-е
Г — и — С
J ν J ν
π Л π л
"Ρ ( du ) 1
ax"
1 J
-du-
ao u
>e"-l
eu-\
Jn U Jn U
du
1 „-«
e"-l
>e"-l
1 л-"р
e" -1
>e"-l
Г du+ Г du- f du- f
Jn u J u Jn u J, u
du
1 _ p~u °° p~u p~u _ 1 °° p~u
-f du+ f—din-] Г du+ f du
η u J u I \Jn u ^ u
-Ύ-]
f- du+ f-—du\
Jn u I u \
где снова в игру вступает равенство (5.4.1).
Затем в двух интегралах справа в предыдущей строке сделаем замену
переменной
У = ир,
и поэтому
dy
du =
puy
Тогда
1
1
1
Г du+ Г dui = -J Г dy + Г—dy
i u J u ρ К У J у
и мы имеем (где еще раз используется (5.4.1)):
1
I
ах = —
χ а
1
-Y—
Ρ
ге-"-1 . се-"
- Ι du+ Ι —du
J 11 J 11
-γ—{-γ}
= γ
= Y
Ь α
или наконец:
^е-*°-е-'^ g-b
•{χ ab
(5.4.6)
192 ♦ Использование степенных рядов для нахождения интегралов
Для проверки этого равенства положим а = 2 и Ь = 1. Тогда (5.4.6) говорит,
что
1
Г —άχ = ^Ύ,
или эквивалентно:
-dx = γ.
И MATLAB фактически соглашается: 2*quad(@(x)(exp(-(x.A2))-exp(-x))./x,
0,100) = 0.5772153....
Наш результат в (5.4.1) настолько полезен, что я думаю, что было бы полезно
увидеть его развитие альтернативным, совершенно другим способом. Мы
начнем с результата (3.3.3) из предыдущей главы, где показали, что
In
(b)
™e-™_e-b*
I
dx.
В частности, если мы установим а = 1 и Ь = £, то имеем
ОО —У — tX
ln(t)= f- —dx.
J У
(5.4.7)
Далее, для любого натурального числа η мы имеем:
ОО
fe^dx--
1
Итак, суммируя по всем η от 1 до Ν, получаем:
ЛГ 1 ЛГ оо оо I
N
ΣΧ
\dx.
п=\ 0 0
Это легко вычисляемая сумма членов геометрической прогрессии:
\^е-ПХ = - .
^ 1 ρ'*
л=1 1~е
Тогда:
м
п=\ п о Х
-(iV+l)v
-dx.
(5.4.8)
Теперь напомним определение γ из начала этого раздела:
Константа Эйлера и связанные с ней интегралы ♦ 193
γ= lim
N 1
χ;--ΐη(ΛΓ).
ζ—■* и
Подставив (5.4.7) и (5.4.8) в выражение справа, получим:
'= lim Г
-(N+l)x
1-е*
dx,
так что
^ р — А ^ ρ — Л ^ ρ — Λ α ρ — Л ^ ρ — Л
γ= Γ — dx- f—dx = f —dx-\ f—dx+ f—dx
J0 1-е x J0 χ J0 1-е * [J0 χ ^ χ
π ι -χ гп ds _x , ds
В первом интеграле справа положим s = I - е . Тогда — = е и dx = ^—.
dx e *
Поэтому:
/!
ί ds ) г е~* °г е~х г 1 г е~* °г е~*
/ —dx- / —dx = / -ds- / —dx- I —dx,
и у и ν «^ с «-'ν *J ν
О Л 1 Л 0 ^ О Л 1 Л
ИЛИ
γ= Г dx- Г—dx,
о * Iх
а это в точности есть (5.4.1).
Равенство (5.4.1) - это не единственный инструмент, который у нас есть для
работы с числом γ, и чтобы проиллюстрировать это, давайте возьмем
экзотический интеграл
оо
Je-*2ln(x)dx
о
в качестве последнего вычисления в данной главе. Это будет вычисление,
которое потребует от нас вспомнить любимый трюк Фейнмана
дифференцирования под знаком интеграла из главы 3, а также степенной ряд для функции
логарифма, который мы использовали ранее в этой главе. Нас ожидает
(возможно) удивительное появление числа γ в ответе. Начнем с класса интегралов,
занумерованных по параметру т:
1{т) = fxme-x2dx.
о
Дифференцируем по т:
dl(m) _ d γ^^-*^ = A- Te>"^e-*2dx = Ьп(х)етЩх)е-х2ах,
ι J (jrn J J
(5.4.9)
dm dm'
194 ♦ Использование степенных рядов для нахождения интегралов
так что
dl(m)
dm
: fxmln(x)e-x2dx.
Это говорит нам о том, что интеграл, который мы собрались изучить,
соответствует случаю производной при т = 0, то есть
Je~x2ln(x)dx--
dl_
dm
(5.4.10)
Далее, возвращаясь к (5.4.9), сделаем замену переменной t = χ2 (и тогда
a dt dt ч τ,
dx = — = —j=). Тогда:
2х 2Vt
rlt I °° ml
t αι _ί r^tT2dL
{ 2^ г{
Вспоминая (4.1.1), мы видим, что этот последний интеграл является гамма-
функцией Г(и) для случая η — 1 = (для η = ). Таким образом:
I{m) = h:
(т + 1)
итак, из (5.4.10):
ОО -ι I
fe-x'ln(x)dx = ±\
(т + 1)
dm
(5.4.11)
Чтобы продифференцировать гамма-функцию, вспомните
дигамма-функцию, упоминаемую ранее в этом разделе, откуда мы имеем
Л ι 11
γ'(ζ) = ^ = γ(ζ)
dz
1
-у+Σ
г r + z
гр 1И + 1
Тогда при ζ = —ζ— мы имеем:
dT
d\
(m + 1
{ 2
m + 1)
2 J
dT
2
m + 1
2
dm
dT
— 2
m + 1
2
dm
= T
m + 1]
2 J
m +
A г—Л
(1
r r + m + l
2 )
Константа Эйлера и связанные с ней интегралы ♦> 195
То есть для случая т = 0:
(т + 1)
dm
-2-Υ + Σ
(1
1
г 1
Г + 2)
^
-2-Υ + Σ
(2
2г 2г + 1)
и поэтому, подставляя это в (5.4.11), мы имеем:
Ге"х21п(х)^х = — 7π
J A
-2-Y + 2J2
1
ίι
[2r 2r + lj
(5.4.12)
Теперь сосредоточимся на суммировании:
Σ
ι
ίι
[2r 2r + lj
\
=
fi 11
[2 3j
+
Μ Я
[4 5j
+
fi Л
[6 7)
+·
Вспоминая степенной ряд для ln(l + χ), который мы получили в начале
раздела 5.2, мы видим, что
1η(2) = 1-2 + 3-4- + 5-·='
и поэтому
111111 л , /оч
1 - + 1— = 1-1п(2),
2 3 4 5 6 7 '
что означает
°ΜΊ 1 ^
Σ
[2r 2r + l)
= 1-1п(2).
Подставляя это в (5.4.12), мы имеем
Je-x2ln{x)dx = jyR[-2-y + 2{l-ln(2)}],
о 4
и, наконец, у нас есть красивый результат:
ОО -ι
fe-"2 ln(x)dx = - - 4π [γ + 2 ln(2)].
(5.4.13)
Это значение равно 0.8700577... и согласуется с результатом MATLAB: quad(@
(х)ехр(-(х.Л2)).*1од(х),0,10) = 0.87006....
196 ♦> Использование степенных рядов для нахождения интегралов
5.5. Задачи и упражнения
(С5.1). Рассмотрим следующий класс определенных интегралов:
VI-
п 1 Л
где тип- положительные целые числа. 1(т,п) существует для всех таких тип,
поскольку подынтегральная функция везде конечна на интервале
интегрирования1.
Сделайте разложение в степенной ряд подынтегральной функции, а затем
проинтегрируйте поэлементно, чтобы получить бесконечную сумму, которую
можно легко оценить с помощью простой компьютерной программы (без
использования программы quad MATLAB или любой другой подобной мощной
программы!). Если у вас есть доступ к компьютеру, напишите код для оценки
1(т,п) при заданных значениях тип. Проверьте свой код, посмотрев, дает ли
он правильные ответы для тех случаев, которые легко сделать вручную
(очевидно, 1(п, п) = 1 для всех ή). Например:
1 -j _ 2 1
1(2,1) = J ^-?- dx = J(l + x)dx =
1 2
-χ2
2
1.5
/(1,2)= f^-dx= f—dx= Γ—dx = ln(2) = 0.6931.
J0 1-х2 J0 1 + x J u
Затем, используя свой код, вычислите значения 7(5,7) и 7(7,5) с верными, по
крайней мере шестью первыми, десятичными знаками.
(С5.2). Показать, что
ШЛ=1_Т.
где {х} - это дробная часть х. Чтобы дать вам уверенность, что это правильно,
MATLAB вычисляет интеграл как quad(@(x)(x-floor(x))./x.A2,1,100) = 0.41861...,
где 1 - γ = 0.42278.... Подсказка: вам может быть полезно оглянуться на главу 1
и посмотреть вывод (1.8.1).
(С5.3). Если вы действительно понимаете хитрость, связанную с интегралами
1 При верхнем пределе интеграл становится неопределенным, но мы можем
использовать правило Лопиталя для вычисления вполне приличного предела
lim
\-хт
-ι 1-
lim
-гюС
-пхп
т
η
Задачи и упражнения ♦> 197
с дробными частями в подынтегральном выражении, то должны показать, что
великого противника великого Эйлера ζ(3) можно записать в виде довольно
интересного интеграла
«*>-§-*?£*·
Для уверенности, что это правильно, вспомните, что значение ζ(3) есть
1.20205..., в то время как MATLAB вычисляет как 1.5-3*quad(@(x)(x-floor(x))./
х.Л4,1,100) = 1.202018....
(С5.4). Можно показать (используя технику контурного интегрирования,
которую мы обсудим в главе 8), что Г —dx = 1 , а > 0.
Jo (χ + α){1η2(χ) + π2} \-α 1η(α)'
Каждый член справа уходит в бесконечность, когда а = 1, и поэтому не сразу
видно, каково значение интеграла, когда а = 1. Однако странно, что
подынтегральное выражение ведет себя спокойно а = 1, и MATLAB не испытывает
никаких проблем при а = 1: quad(@(x)l./((x+l).*(log(x).A2+piA2)),0,lel7) = 0.474....
Используя разложение в степенной ряд для 1п(1 + х) при -1 < χ < 1, показать, что
фактическое значение интеграла при а = 1 есть 1/2. (Обратите внимание, что
1 1
1η(α)
это отдельные бесконечности противоположного направления
1-й
при а —> 1, либо слева, либо справа, и поэтому априори правдоподобно, что их
сумма может быть конечной.)
(С5.5). Для случая s = 2 равенство (5.3.7) говорит, что
ζ(2) =
1
2
1 -(-Ι)'"1 1
-2"!έί к* j_
1111
I2 22+32 42+'"
1
2
•
1
ι2"
1 1
-22+32"
1
"42
Но по первоначальному определению Эйлера мы знаем, что
1111
22 З2 42
"■^ γ ' о2 ' ,χΐ ' λ2
Таким образом, должно быть верно, что
1 1 1
1
I2 22+32 42+'
1 1 1
1
12+22+32+42+'
Начиная с выражения слева, покажите, что оно действительно равно
выражению справа.
198 ♦ Использование степенных рядов для нахождения интегралов
(С5.6). Показать, что
о х
Подсказка: попробуйте изменить переменную 1 -х = е~\ а затем вспомните
(5.3.4).
(С5.7). Показать, что Г '* άχ = Γ(ρ + 1)Ζ,(ρ + 1),ρ > 0. Отметим, что слу-
Jo 1-х
чай ρ = 1 говорит, что ζ(2)= Γ1" n(*) dx = ]^ = 1.644954..., и MATLAB под-
Jo 1-х 6
тверждает: quad(@(x)-log(x)./(l-x),0,l) = 1.64494.... Подсказка: сделайте
соответствующую замену переменной в (5.3.4). Также обратите внимание, что если
вы сделаете замену переменной и = 1 - х, то результат для ρ = 1 даст другой
вывод (5.2.2). Вы должны подтвердить это.
J A nl 1
/ dxdy =
о J о 1 — ху
= ζ(2).
Покажите, что это частный случай η = 2 более общего интегрирования по
п-мерному единичному гиперкубу. То есть покажите, что
111 j
J/Ji_xx eV*2-tfV
η η η Α ΛιΛη· · · Λ„
= «π).
(С5.9). Показать, что Г In
e* + l
1
dx = —
(C5.10). Показать, что f°°e xln2(x)dx = y2-\ . MATLAB согласен с этим,
Jo 6
2 π2
поскольку γ Η равно 1.978111..., и quad(@(x)exp(-x).*(log(x).A2),0,100) =
6
1.97812....
J»oo
xme~xdx, а затем подумайте, как
о
выразить 1(т) через вторую производную гамма-функции. Чтобы провести
соответствующие дифференцирования, вам необходимо принять двойную дозу
дигамма-функции.
Jul — е~х — е х
dx. Это особенно
0 χ
полезное выражение для γ, потому что на всем конечном интервале
интегрирования подынтегральное выражение конечно. MATLAB вычисляет этот
интеграл как quad(@(x)(l-exp(-x)-exp(-l./x))./x, 0,1) = 0.577215....
Глава
β
Семь сложных интегралов
6.1. Интеграл Бернулли
Как я уже упоминал в предисловии, в 1697 году Иоганн Бернулли нашел
экзотически выглядящий интеграл
1
fxxdx.
о
Как это может быть сделано? А как насчет других подобных интегралов, на
которые может вдохновлять интеграл Бернулли, например:
Jxxdxy
о
и
Jxx2dx,
о
и
JV*dx,
и... ну, вы поняли! В этом разделе я покажу вам единый способ выполнения
всех этих вычислений. Начнем с тождества
χεχα _ е\п{хсх°) _ есхаЩх)
где а и с являются константами. Тогда поскольку разложение экспоненты в
степенной ряд есть
то, подставляя у = сха1п(х), мы имеем:
200 ♦> Семь сложных интегралов
хсха = \+сха\п(х) +—c2x2flln2(x) + —съхЪа\ъъ(х)-
2!
3!
и тогда
1 11 1 1 1 1
Вы можете найти все интегралы в (6.1.1), если выполнили задачу, которую
я поставил вам в конце главы 4. Вывод формулы:
[хт In" (x)dx = (-1)" ^—.
Если вы этого не сделали (или застряли), то сейчас самое время взглянуть
на решения задач и упражнений в конце книги. Все интегралы в (6.1.1) имеют
такой вид, с разными значениями тип1.
Используя этот общий результат для каждого из интегралов в правой части
формулы (6.1.1), приходим к равенству
1
fxcx"dx =
Ιο
или
1
Jxcx°dx = l-
с с^
(а + 1)2+2!
с с
- + -
[ 2!
1(2а + 1)3
с5
3!
3!
.(За + 1)4
с4
+ 4!
4! ]
(4a + l)5J
-+-
0 (а + 1)2 ' (2а + 1)3 (За + 1)4 ' (4а + 1)5
Итак, при а = с = 1 мы имеем интеграл Бернулли:
/■
,1111
ххах = 1—5" + ^-—г Η—г
22 33 44 55
(6.1.2)
(6.1.3)
Легко написать небольшую программу для суммирования правой части;
используя первые десять слагаемых, мы получаем 0,78343..., и, соответственно,
quad(@(x)x.Ax,0,l) = 0.78343....
Если с=1иа = 1,то формула (6.1.2) дает нам
1
_1 _1 J_ λ
22+33+44+55
χ-χάχ = 1 + — + — + — + -τ-\-
(6.1.4)
1 Это не тот способ, которым Бернулли получил свое оригинальное решение, а
современный. Нахождение интеграла Г xmlnn(x)dx, которое я даю в решениях, использует
гамма-функцию, которая была еще в будущем во времена Бернулли. Бернулли
использовал повторное интегрирование по частям, что на самом деле прекрасно.
Отсутствие специализированного инструмента не останавливает гения!
Интеграл Ахмеда ♦> 201
Суммирование первых десяти слагаемых справа дает 1,29128..., а интеграл
получается KaKquad(@(x)x.A(-x),0,l) = 1.29128....Кстати,поскольку (6.1.4)
можно записать в виде
V ι °° ι
хх hkk
I
то его иногда называют фантазией второгодника, потому что хотя сходные
формы с каждой стороны равенства «выглядят слишком хорошо, чтобы быть
правдой», это верное утверждение.
Если с = 1 и а = 2, то (6.1.2) дает нам формулу
1
1 1 1
1
З2 S3 74 95
(6.1.5)
Суммирование первых шести слагаемых справа дает 0,896488..., и MATLAB
соглашается с этим: диас1(@(х)х.Л(х.Л2),0,1) = 0.896487....
Если с = 1 и а = -, то (6.1.2) принимает вид:
А
ι
Jxrxdx = l-
1 1
- +
1 1
+-
о
или
(3/2)2 (4/S)3 (S/2)4 (6/2)
fxr*dx =
Ιο
'2^
,3;
2
+
(Ι)'-
5,
4
+
.б]
(6.1.6)
Суммирование первых десяти слагаемых справа дает 0,658582..., и MATLAB
соглашается: quad(@(x)x.Asqrt(x),0,l) = 0.658586....
6.2. Интеграл Ахмеда
В этом разделе мы найдем интеграл Ахмеда, названный в честь индийского
специалиста по математической физике Зафара Ахмеда, который предложил
его в 2002 году. Интересно, что мы будем использовать его в следующем
разделе, чтобы вывести интеграл Кокстера, о котором я упоминал в предисловии.
Интеграл Ахмеда - это
{ (l + x2)V2 + x2
(6.2.1)
и его можно взять, используя любимую уловку Фейнмана, заключающуюся
в дифференцировании под знаком интеграла. То есть мы начнем с «и-парамет-
ризованной» версии (6.2.1):
202 ♦ Семь сложных интегралов
т, ч rtair^ii^ + x2) ,
Ι(μ)= \ ν , 'dx,
Jo (1 + х2)л/2 + х2
(6.2.2)
а затем продифференцируем его по переменной и. Тогда 1(1) является
интегралом Ахмеда.
Обратите внимание, что если и —> оо, то аргумент арктангенса также —> оо
π
для всех* > 0, и тогда, поскольку tan !(оо) = —, мы имеем:
dx
π г ах
i(oo) — — \ ,
2 о (1 + аг2)л/2 + х
(6.2.3)
Этот интеграл в (6.2.3) легко взять, если вспомнить стандартную формулу
дифференцирования
-ftan-\f(x))= I
dx 1+fW
(#1
dx
Если мы используем эту формулу для вычисления
d+ -ιί * )
—tan . _ ,
dx [λ/2 + λγ2 J
тогда вы должны подтвердить, что
—tan
dx
1
t л/2 + at2 J (1 + аг2)л/2 + аг2 '
что совпадает с подынтегральной функцией в интеграле (6.2.3). То есть
7(оо) = — Г—tan !
2\άχ
{<&+*)
Л:
π
tan λ
[λ/2 + α:2 J
tan"1
IV^J
-tan^O)
^
или
/(00) = —.
V ' 12
Теперь дифференцируем (6.2.2) снова по и, используя
-ftan-'(/W)= *
du 1 + Г(и)
[*f\
du
с f(u) = щ2 + χ2. После некоторых преобразований получаем:
Интеграл Ахмеда ♦ 203
dl
-Ι-,
dx
du JQ(l + x2)(l + 2it2 + u2x2)
Раскладываем на элементарные дроби подынтегральную функцию:
di__ \ l
du~{(\ + u2)
1
или
1
dl
du (ί + u2)
1 + x2 l + 2u2+u2x2
dx
dx,
Ϊ—-Ϊ-
{ 1 + x2 i l + 2«2
+ XA
Эти два последних интеграла имеют вид:
Г—
-dx-
1
tan !
αΔ+χΔ
а
χ
[а)
и таким образом, находя эти интегралы, мы имеем:
ill
dl
1
du (1 + и2)
или же
tan_1(Ar)-
и
.tan !
Vl + 2u2 [Vl + 2u2J
хи
1
dl
du (1 + и2)
π
4 Vl + 2i/2
tan"1
[Vl + 2t/2 J
(6.2.4)
Далее интегрируем обе части (6.2.4) от 1 до оо относительно и. Слева мы
получаем
>dl
Jj-du = fdI = I(oo)-I0),
± du
а справа:
nf 1 , f и ^ -if м Ι
— / -du- \ . tan
А\\ + и2 \ (l + u2)Vl + 2u2 Ul + 2u2J
dw.
Первый интеграл очевиден:
ОО 1
π г 1
4^ 1 + и:
, du = -[tan_1(oo)-tan_1(l)] = -
+ и 4 4
π π
2~~4
π
16'
204 ♦ Семь сложных интегралов
Поэтому
2 оо
/(оо)-/(1) = —- Г >
16 J, (1 + m2)V1
+ 2и2
.tan
Ul + 2u2J
du.
(6.2.5)
Этот последний интеграл выглядит довольно ужасно, но внешность
обманчива. Интеграл берется даже без хныканья, если мы сделаем замену
переменной ί = — (а также du=—-dt) следующим образом:
00 ι.
г ч
ι (1 + и2)л/1 + 2ы:
-tan"1
г
( \
и
Vl + 2u2,
du
Теперь вспомним тождество
tan_1(s) + tan_1
1
S
π
~ 2
)
0
' Η)
1
^^=tan"1
1
ι -
=/ t-n=tan~1
0(t2+1)V^±l
ί
1 J Г
= Г . tan"1
o(t2+l)Vi2+2 (
1
1
t
Vt2+2
ι 1
A =
it.
которое сразу становится очевидным, если вы нарисуете прямоугольный
треугольник с катетами длиной 1 и s и вспомните, что два острых угла в сумме
дают —. Это говорит, что
tan !
1
= tan
2
и тогда мы можем написать
'(л/РТг),
/
1
,tan_1
1
;o(t2+lWt2+2
Формула (6.2.5) принимает вид
dt
*=ff
dt
{Vi2 + 2 J 2 J (i2 + i)A/t2 + 2 J0 (ti + i)A/t2 + 2
dt.
/(oo)-/(!) =
2 1
π π
/
16 2 J (f + l)Jt2+2 J0 (t2 + l)Vt2+2
dt + J-tan-'(^2)dt>
Интеграл Коксетера ♦> 205
и теперь вы должны увидеть, что произошли две чудесные вещи. Во-первых,
если вы посмотрите на (6.2.3), то увидите, что первый интеграл справа - это
7(оо). Во-вторых, самый правый интеграл из (6.2.1) - это просто 1(1), то есть
интеграл Ахмеда! Итак:
π
Доо)-/(1) = —-/(оо) + /(1),
16
и тогда
π
2/(оо)-^ = 2/(1),
или наконец:
Щ) = 1(оо)-
2 2 2
71 71 71
32 12 32
и мы имеем ответ:
(6.2.6)
Это значение равно 0.51404189..., что подтверждает MATLAB: quad(@(x)
atan(sqrt(2 +x.A2))./((l+x.A2).*sqrt(2+x.A2)),0,l) = 0.51404188....
6.3. Интеграл Коксетера
В этом разделе мы будем решать интеграл Коксетера. В предисловии я
рассказывал, как юный X. С. М. Коксетер обратился за помощью и как ответил
великий Харди. Я не знаю деталей того, что Харди отправил Коксетеру, и поэтому
здесь я покажу вам вывод, который использует равенство (6.2.6). Интеграл,
который мы собираемся оценить, следующий:
π/2
I
COS
cos(x)
l + 2cos(x)
\dx,
(6.3.1)
и это будет довольно долгий путь; приготовьтесь к самому длинному выводу
в данной книге. Я постарался сделать каждый шаг кристально ясным, но тем
не менее выражаясь бессмертными словами Бетт Дэвис в ее фильме 1950 года
«Все о Еве»: «Пристегни ремни, это будет ухабистая ночь».
Чтобы начать наш анализ, мы приведем (6.3.1) к другой форме. Из
тригонометрии формула двойного угла для косинуса говорит, что для любого Θ:
cos(26) = 2cos2(e)-l.
(6.3.2)
206 ♦ Семь сложных интегралов
Если мы напишем и = cos(6), и поэтому θ = cos \u) - тогда (6.3.2) говорит, что
cos(26) = 2u2-l,
из чего сразу следует, что
cos_1(2u2 - 1) = cos_1{26} = 2Θ = 2cos_1(u).
Таким образом, поскольку и - это произвольная переменная (как и Θ), мы
можем написать
cos_1(2e2 - 1) = 2cos"1(e).
Далее, записав α = 2Θ2 - 1, что означает θ =
что
(6.3.3)
1 + а
, мы из (6.3.3) получаем,
cos !(a) = 2cos !
1 + a
Оглядываясь назад, на (6.3.1), давайте напишем:
cos(x)
a =
l + 2cos(x)'
и тогда мы имеем:
cos
cos(x)
[l + 2cos(x)J
1 + :
cos(x)
ο _ι L l + 2cos(x)
= 2cos \\ ^^
= 2cos !
l + 3cos(x)
2 + 4cos(x)
. (6.3.4)
Теперь, если применим теорему Пифагора к прямоугольному треугольнику,
/l + 3cos(x)
косинус острого угла которого равен, ^—^-, мы увидим, что тангенс это-
V2 + 4cos(x)
, l + cos(x)
го же угла равен л \-—= ^-. То есть
cos
cos(x)
l + 2cos(x)J
l + 3cos(x)
tan \
l + cos(x)
l + 3cos(x)
и поэтому интеграл Кокстера/в (6.3.1) принимает вид:
π/2
π/2 Γ Г
/=itan_I ν
l + cos(x)
ll + 3cos(x)
dx.
(6.3.5)
Сделаем замену переменной χ = 2у (и, следовательно, dx = 2dy), которая
преобразует (6.3.5) в интеграл:
Интеграл Коксетера ♦ 207
π/4
/ = 4jtan1
l + cos(2y)
l + 3cos(2y)
dy.
Снова используя (6.3.2), а затем применив немного алгебраических
упрощений, получим:
l + cos(2y)
cos(y)
l + 3cos(2y) ^2-3 sin2 (у)
π/4
/ = 4/
tan
cos(y)
V2-3sin2(y)
dy.
(6.3.6)
Теперь отложим (6.3.6) на некоторое время и обратим внимание на
следующий интеграл (может показаться, что это не имеет отношения к интегралу/, но
будьте терпеливы, и вы скоро увидите его актуальность):
) . ' . *
°1 +
cos" (у)
[2-3sin2(y)
имеет вид:
Ыу * 4| ТТТ*=¥1ШпЛЬ< - £«»«--'»».
0 ht'
ь2 +
cos(y)
V2-3sin2(y)
Тогда
1
/
1
cos (у)
dt = V2-5sin2(y)tanl
cos(y)
cos(y)
[V2-3sin2(y)J
[2-3sin2(y)j
Таким образом, подынтегральное выражение в (6.3.6) имеет вид:
tan !
cos(y)
V2-3sin2(y)
cos(y)
1
г_
V2-3sin2(y)J0l
+
1
cos2 (у) Ι
[2-3sin2(y)|
-dt,
208 ♦ Семь сложных интегралов
и поэтому (6.3.6) является собственно двойным интегралом:
тс/4
*f
cos(y)
о V2-3sin2(y)
/
1
°1 +
cos2(y)
2-3sin2(y)
-dt
dy.
Вот это да! Это выглядит так, как будто мы сделали (намного) хуже. Что ж,
держитесь, потому что интегралы будут еще хуже, прежде чем они
поправятся, - они станут (намного) лучше, хотя и ненадолго.
Продолжая, мы имеем:
— 1
Jo Jo
4cos(y){2-3sin2(y)}
V2-3sin2(y){2-3sin2(y) + i2cos2(y)}
dtdy =
= p'4 r1 4cos(y)V2-3sin2(y)
Jo Jo2-3sin2(y) + i2-i2sin2(y)
или
dy
J = YJ.4cos(yW2-5,i^)0_
•H(t2+2)-(t2 + 3)sin2(y)
Затем делаем замену переменной sin(y)
cos(w)
-ё
(6.3.8)
sin(w) в (6.3.8), и тогда
I
π
dw. Мы имеем w = 0, когда у = 0, а когда у = —, то sin
cos(y) 4
ί 11 ^
—, что означает w = —. Итак:
2 3
и поэтому sin(w)
(I)
Л'
ш
π/31 4cos(y)J2-3-sin2(w) , ч
JoJo(i2+2)-(t2+3)|sin2(w) cos(y)
I-
-dtcos(w)dw
Л-
_ "j? j. 4^/2-2[1-cos2(w)]
о o(t*+2)-(t2+3)-[l-cos2(w)]
_п/г /» 4V2cos(w)V2cos(w) 1
о о (t2+2)-(i2+3)-[l-cos2(w)] ^
и после некоторых простых алгебраических преобразований, которые я
предлагаю выполнить вам, мы приходим к интегралу
Интеграл Коксетера ♦ 209
1 = 1 j2 8V!C0S2W2 dtdw. (6.3.9)
J0J0 t2 + (2t2+6)cos2(w)
Наш следующий шаг - это еще одна замена переменной s = tan(w). Таким
^ , ч sin(w)
>ν.οο^η. ο^τ,η^^^^Λ,Λ- , мы имеем
υυραουιι
ds _
dw
и тогда
1 + S2
fl, llVJ\^I\yjJlOI\y UC
cos2(w) + sin2
cos2(w)
dw = cos2(w)ds
= l + tan2(w) =
мы имеем
1
1 + s2
И
dw =
= cos2(w)
ds
ILLyVV J
cos(w)
(w)_ 1
cos2(w)'
. Поскольку
1
cos2(w),
1 + s2
Поэтому, так как s = 0, если w = 0, и s = л/Ъ, когда w = —, мы имеем:
Λι 8^ΪΤ? ,. ds ί'Γ 8S
J0J0t2 + (2t2 + 6)^_ 1 + s2 J/0t2(l + s2)2+(2t2 + 6)(l + s2)
-dtds,
i + s' "0"o r(i + s"r+(2r + b)(i+s-;
1 + s2
или, после нескольких еще более простых алгебраических преобразований,
которые вы можете сделать самостоятельно, приходим к выражению
1 = Г Г πτ—5 dtds- (6-ЗЛ0)
J0J0 (l + s2)(t2s2 + 3t2+6)
Клоун Красти из мультфильма-комедии Симпсона любит кричать, когда он
расстроен: «Это когда-нибудь закончится?» И ответ здесь: «Пока нет». Итак,
отважно пашем дальше и теперь сделаем разложение подынтегрального
выражения в (6.3.10) на элементарные дроби. То есть если мы напишем
1 А В
- + -
(l + s2)(t2s2 + 3t2 + 6) 1 + s2 t2s2 + 3t2 + 6'
тогда легко проверить, что
210 ♦ Семь сложных интегралов
А = ^—, В = - 1
2ί2 + 6
2t2 + 6
и тогда
■Л ι
I = Jf8S
1
2ί2 + 6 2ί2 + 6
1 + s2 tV + 3t2 + 6
dtds,
что после небольших алгебраических преобразований (и изменения порядка
интегрирования) может быть записано как
' = )#
i_ds_jf ds
I 1 + s2 Ι
о s2 + 3 + 4
ί2
dt.
(6.3.11)
Первый внутренний интеграл справа совсем простой:
{tan-1(s)}|f = tan-1(N/3) = |.
Второй внутренний интеграл почти столь же прост, поскольку он равен
I-
ds
1
s2 +
3 + -
tan
3 + -
SyJF+2
tan
st
(ylbyJFTi)
s
SJF+i
tan
{yjf+2j
Тогда
it2+3
π
3 JbJf+2
tan-1
4>/3π г dt
J0e+(Sf J0
Wt2+2j
(i2+3)Vi2+2
Λ:
tan-1
[Vt2+2j
dt-
4yfcn
s
tan !
о о
tan"1
LV3 JJ|0 J0 (t2+3)Vi2+2 Wt2 -1-2 J
dt,
или,поскольку
473π
v^
tan"1
IS)
4πχ _■
= —tan
3
^J
4π<
3
9
Интеграл Коксетера ♦ 211
мы имеем
, 2π2
4/
tan !
(t2+3)Vt2+2 [л/t2 +2
Л.
(6.3.12)
Теперь мы находимся на финишной прямой, так как можем найти интеграл
в (6.3.12) по частям. Чтобы увидеть это, положим
u = tan !
л/t2 + 2 J
dv-
=dt.
(t2 + 3)Vt2 + 2
Затем, помня, как дифференцировать арктангенс; это мы обсуждали в
начале этого раздела, мы имеем
du _ 1
*"(t2+l)>/? + 2'
И легко убедиться, что
v = tan_1(Vt2+2),
просто продифференцировать это ν и увидеть, что мы вернем dv, указанное
выше. Итак, подставляя все это в формулу интегрирования по частям, мы имеем:
9
9
tan
tan !
Ut2+2j
tan"1 (Vi2+2)
/
tan_1(Vi2+2)
(t2+l)Vi2+2
Л
Ufc
2tc2
9
2π2 2π2
tan-\S)-J
о
tan-1 (Vt2+2)
tan"1(Vt2+2)
W
Γ
J ' (i2+l)Vt2+2
tan"'(Vt2+2)
(t2+lb/t2+2
(i2+l)Vt2+2
Λ =
dt
\dt,
212 ♦> Семь сложных интегралов
и поэтому
'-*Л
tan
l(Vt42)
(t2 +
l)Vt2+2
di.
Теперь оглянемся на (6.2.6) - наш результат для интеграла Ахмеда. Это точно
вышеупомянутый интеграл. Интеграл Коксетера в четыре раза больше
интеграла Ахмеда, и наконец (!):
π/2
COS
cos(x)
l + 2cos(x)
Α 5π'
[dx = .
24
(6.3.13)
Вот это да! Какой вывод! Но правильно ли это? MATLAB говорит, что наш
теоретический ответ 2.05616758... соответствует численному: quad(@(x)acos
(cos(x)./(l+2*cos(x)))A Pi/2) = 2.0561677....
6.4. Оптический интеграл Харди-Шустера
В 1925 году английский физик немецкого происхождения Артур Шустер (1851-
1934) опубликовал статью по теории света. В этой статье он столкнулся с
интригующим интегралом
r = f{C\x) + S\X)}dx,
(6.4.1)
где С(х) и S(x) сами являются интегралами (называемыми интегралами
Френеля, и мы увидим их снова в следующей главе для частного случая χ = 0):
ου ои
С(х) = fcos(t2)dt, S(x) = fsin(t2)dt.
На самом деле поскольку в конечном итоге нам, чтобы найти /, понадобится
знать только одно из этих двух конкретных значений - S(0) (мы выведем его
в следующей главе как результат (7.2.2)), а сейчас вот его значение:
оо ■* \
S(0) = jsin(t2)dt = -^.
(6.4.2)
Шустер не смог найти /, но написал, что со стороны физики для проблемы,
которую он изучал, было бы достаточно, чтобы интеграл / имел определенное
значение. Увы, он не мог показать, что интеграл / имеет значение, и именно
здесь он оставил вопрос.
Статья Шустера вскоре привлекла внимание великого Харди, который затем
(вы удивлены, и если да, почему?) быстро вычислил / (подтверждая гипотезу
Шустера), используя два разных подхода. В одном из них применялась сложная
Оптический интеграл Харди-Шустера ♦ 213
теория преобразования Фурье1, но в этом разделе я покажу вам
альтернативный вывод на уровне «математического анализа первокурсника», в котором
свободно используется физическая интерпретация интеграла Римана. Он
основан на идее, которую сам Харди набросал в своем другом подходе.
Из определений С(х) и S(x) мы можем написать:
оо оо оо оо
С\х) = Jcos(t2)dt fcos(u2)du = f f cos(t2)cos(u2)dtdu
X X XX
И
оо оо оо оо
S2(x) = Jsin(t2)dtjsin(u2)du = J Jsin(t2)sin(u2)dtdu.
Χ Χ XX
Тогда
оо оо
С2 (х) + S2 (at) = ff{cos(t2) cos(m2 ) + sin(i2) sin(u2 )}dtdu.
X X
Из тригонометрии мы имеем тождество
cos(fl-b) = cos(fl)cos(b) + sin(a)sinb(y),
и оно немедленно дает, что
оо оо
C2(x) + S2(x) = ffcos(t2-u2 )dtdu.
χ χ
Из формулы (6.4.1) мы имеем:
ии ι ии ии
J = f\ffcos(t2-u2)dtdu
\dx.
(6.4.3)
(На этом этапе вам следует взглянуть на раздел 3.6, где я показал, как
использовать MATLAB Symbolic Math Toolbox для численной оценки этого тройного
интеграла.)
Давайте теперь обозначим f(t, и) = cos(£2 - ι/2), и тогда (6.4.3) принимает вид
ОО I ОО ОО
I = f\fff(t,u)dtdu
\dx.
(6.4.4)
Можно выразить словами то, что говорит равенство (6.4.4), следующим
образом. Внешний интеграл (по х) означает, что «начиная с χ = 0 вычисля-
Подробное обсуждение решения интеграла Шустера и преобразования Харди см.
в моей книге: «Необыкновенная формула доктора Эйлера» (Dr. Euler's Fabulous
Formula). Princeton, 2006. С. 263-274.
214 ♦ Семь сложных интегралов
ем \ J J f(t,u)dtdu>Ax. Затем увеличиваем χ на Ах до χ = Ах и вычисляем
\ I I f(tyu)dtdu>Ax. Потом увеличиваем χ на Ах до χ = 2Ax и вычисляем
\ I I f(t,u)dtdu >Δχ. И т. д. И наконец, складываем все эти значения».
[ J 2Δχ J 2Δχ J
Мы можем переформулировать эту математическую интерпретацию
равенства (6.4.4) как физическую, взяв эти три переменные х, t и и на осях
трехмерной декартовой системы координат, как показано на рис. 6.4.1, где оси χ и и
находятся в плоскости страницы, а ось t перпендикулярна странице
(положительная ось t направлена в страницу).
У- I
^1С Ои4-о fM*4)
>*
Рис. 6.4.1 ♦ Система координат
Каждый из отдельных интегралов в нашей сумме - это просто интеграл от
функции f(t, и) по объему бесконечной «плиты» толщиной Ах, где угол
«нижней» плиты1 начинается в начале координат (t = 0,u = 0). Углы последующих
плит, лежащие над нижней плитой, постепенно сдвигаются вверх (вдоль оси
х) и от начала координат вдоль линии t = и. Итак, если вы представляете себя
в космосе, зависаете над плоскостью ί, и и смотрите вниз по оси х, то вы
увидите рис. 6.4.2. То есть объем, который мы интегрируем в f(t, и), выглядит как
слоеный свадебный торт! Ступени, образованные слоями, имеют высоту и
глубину Ах. (Для плотника, строящего лестницу, это будут значения подступенка
и шага ступеней соответственно.)
/= Jf(t,u)dV, (6.4.5)
торт
где dV- дифференциальный элемент объема свадебного торта.
Поскольку объем, по которому мы интегрируем, имеет бесконечную протяженность
как в направлении £, так и в направлении и, то угол в начале координат является
единственным углом нижней плиты.
Оптический интеграл Харди-Шустера ♦ 215
χΝ
т
т
it
r'v
u.<jt*
/
U>>h
-£*u. Ifnt.^ ί»ι *i;t^p!avie.
|^<vv\vu\vv\vi\uu^_
& !Х^ЧЧ^\\\\\\\\\\
w///?"/7777/f/7/ //<"
^u.
Рис. 6.4.2 ♦ Объем свадебного торта
На виде сбоку торта (теперь с Δχ —> 0) угол торта в начале координат
выглядит как основание пирамиды, как показано на рис. 6.4.3.
Рис. 6.4.3 ♦ Основание свадебного торта в начале координат
Есть и другой способ, отличный от (6.4.4): записать интеграл от f(t9 и) по
объему свадебного торта. Чтобы найти эту новую форму интеграла, сначала
обратите внимание, что если мы разрезаем торт плоскостью, которая проходит
через линию t = и перпендикулярной плоскости £, и (основание пирога), то мы
разрезаем торт на две равные части. В одной половине и < t (я назову это
верхней половиной), а в другой - и > t (я назову это нижней половиной), как
показано на рис. 6.4.2.
Сначала мы выбираем крошечное прямоугольное «основание» dtdu в (£, и)-
плоскости в точке (£, и). Затем будем двигаться вверх (вдоль оси Ох), пока не
достигнем поверхности пирога. Для заданных и и t (местоположение «основа-
216 ♦ Семь сложных интегралов
ния») это происходит на высоте χ = min(£, и). Если основание находится в
нижней половине, то min(£, и) = £, и если основание находится в верхней половине,
то min(£, и) = и. В любом случае, дифференциальный объем этого
вертикального цилиндра в свадебном торте определяется как
dV-
min(t,i/)
Idx
[dtdu
иdtdu, u<t(верхняяполовина)
t dtdu, u>t (нижняя половина)"
(6.4.6)
Для и > t (нижняя половина) мы имеем изменение переменой и в диапазоне
от 0 до 1, а переменной t - в диапазоне от 0 до и. Таким образом, для случая
и > t интеграл в (6.4.5) есть
'lower
ου и
-f\ftf(t,U)dt
\du.
Для и < t (верхняя половина) мы имеем изменение переменой t в диапазоне
от 0 до 1, а переменной и - в диапазоне от 0 до £. Таким образом, для случая
и < t интеграл в (6.4.5) есть
/upper = J\Juf(t,U)dU
\dt.
Тогда
Οϋ I U Ι О) 1
/ = /lower + /upper = //*/(*> U)dt \dU + ί\Η{ί> ")d"
\dt =
OO U OO It
J\Jtcos(t2-u2)dt idu + f\fucos(t2-u2)du
[dt.
Эти два последних интеграла, очевидно, равны, так как если мы поменяем
местами фиктивные переменные t и и в одном интеграле, то получим другой
интеграл. Таким образом:
сю ι
J = 2f\fucos(t2-u2)du
[dt.
Внутренний интеграл может быть проинтегрирован непосредственно:
fucos(t2-u2)du
-sin(t2-u2)
2 v '
^sin(t2),
и поэтому
OO л OO
/ = 2 J-sin(i2)di = fsin(t2)dt,
Тройные интегралы Уотсона/Ван Пейпа ♦> 217
что есть в точности 5(0). То есть
ОО [ ОО ОО л \
Г \ffcos(e-u2)dtdu \dx = ±Jl·
π ν ν Δ\ Δ
(6.4.7)
Это равно 0,626657..., и, как показано в разделе 3.6, Symbol Math Toolbox
вычисляет такое же значение.
6.5. Тройные интегралы Уотсона/Ван Пейпа
В 1939 году английский математик Джордж Н.Уотсон (1886-1965) опубликовал
элегантную статью1, в которой он показал, как найти следующие три
интеграла:
dudvdw
л π π π
11 0 0 0х
л π π π
'■=iftf
cos(u)cos(v)cos(w)
dudvdw
π ο ο ο 3-cos(v)cos(w)-cos(u)cos(w)-cos(u)cos(v)
Λ π π π
dudvdw
π ο ο ο 3-cos(u)-cos(v)-cos(w)
Эти три интеграла не были взяты из воздуха, скорее всего, все они появились
в статье2, опубликованной в прошлом году У. Ф. Ван Пейпом, учеником
известного голландского физика X. А. Крамерса (1894-1952). Ван Пейп смог найти 119
но не /2 и не /3. По-видимому, Крамере был достаточно очарован этими
интегралами, и он отправил их британскому физику Ральфу Фаулеру (1889-1944),
который, вероятно, также был озадачен и передал их в руки - кому же еще? -
Г. X. Харди, знаменитому убийце определенных интегралов.
В этот момент дело становится интересным не только математикам. Как
писал Уотсон в начале своей статьи, «проблема стала общеизвестной сначала
в Кембридже [логове Харди], затем в Оксфорде, откуда она без труда
совершила путешествие в Бирмингем [Уотсон работал на факультете в Бирмингем-
Watson G. N. Three Triple Integrals // Quarterly Journal of Mathematics. 1939. P. 266-276.
Peype van W. F. Zur Theorie der Magnetischen Anisotropic Kubischer Kristalle Beim Ab-
soluten Nullpunkt (Теория магнитных анизотропных кубических кристаллов при
абсолютном нуле) // Physica. June 1938. P. 465-482. То есть Ван Пейп изучал магнитное
поведение некоторых кубических кристаллических решетчатых структур при очень
низких температурах (низкие значения близки к абсолютному нулю). Интегралы
Уотсона/Ван Пейпа появляются не только в физике замороженных магнитных
кристаллов, но и в чистой математике случайных блужданий. Вы можете найти полное
обсуждение истории и математики интегралов в статье И. Дж. Цукера: 70+ лет
интегралов Уотсона // Журнал статистической физики (Zucker I. /. 70+ Years of the Watson
Integrals//Journal of Statistical Physics). 2011. Нояб. С. 591-612.
218 ♦ Семь сложных интегралов
ском университете]». Возможно, я придаю этому слишком большое значение,
но я подозреваю, что это был один из тех редких случаев, когда Харди не смог
найти определенный интеграл, и Уотсон был только рад (не очень тонко)
намекнуть на это, когда он начал представлять свои решения. Бирмингем был
мелкой сошкой по сравнению с Кембриджем, и я думаю, что здесь было мало
личного дружелюбия.
Анализ Уотсона интегралов Ilf I2 и 1Ъ довольно искусный. Уотсон писал, что 1г
и 12 «легко выражаются в терминах гамма-функций, аргументы которых
являются простыми дробями», но он не смог сделать это для 1Ъ. Он подозревал, что 1Ъ
требует использования эллиптических интегралов1, математических существ,
о которых я расскажу чуть подробнее в следующем разделе. В этом убеждении
Уотсон был неправ. На самом деле:
ill
4
4π3
ЪГ
214π4
1.393203929.
: 0.448220394.
' \
24
Г
(51
[ 24 J
Г
'7'
24
Г
1Г
124)
16л/бтг3
0.505462019.
Чтобы дать вам возможность почувствовать «вкус» того, что сделал Уотсон,
я проведу вас через вывод производной от 1Х. Перед началом, однако,
обратите внимание, что все три интеграла являются объемными интегралами по
1
и Jl-k2sin2(Q) явля-
Интегралы с подынтегральными выражениями -
jl-k2sm\Q)
ются эллиптическими интегралами первого и второго рода соответственно
(существует и третья форма). Подобные интегралы встречаются во многих важных
физических задачах, таких как теория нелинейного маятника. В качестве другого примера
итальянский математический физик Галилео Галилей (1564-1642) изучил так
называемую проблему «минимального времени спуска», которая включает в себя
эллиптический интеграл первого рода, и его нахождение озадачивало математиков на
протяжении более столетия. В конце концов, французский математик Адриан Мари
Лежандр (1752-1833) показал, что причиной трудности было то, что такие
интегралы являются совершенно новыми функциями, отличающимися от всех других
известных функций. Вы можете найти больше информации о проблеме Галилея и об
эллиптическом интеграле, с которым она связана, в моей книге: Когда наименьшее
является лучшим (When Least is Best). Принстон, 2007. С. 200-210 и 347-351. Хорошее
обсуждение нелинейного маятника и численная оценка его эллиптического
интеграла содержится в работе: Чжэн Т. Ф. и др. Обучение нелинейному маятнику//Учитель
физики. 1994. Апр. С. 248-251 (Zheng et al. Т. F. Teaching the Nonlinear Pendulum // The
Physics Teacher).
Тройные интегралы Уотсона/Ван Пейпа ♦ 219
трехмерному кубу с длиной ребра π, нормализованными по объему этого куба.
Я буду игнорировать нормализацию π3, пока мы не дойдем до конца анализа.
Начнем с замены переменных
tan
1
y = tan
(1 1
-ν
2
tan
(1 1
-w
2
которые преобразуют интегрирования от 0 до π по переменным и, ν и w в 1г
в интегралы от 0 до оо по переменным х, у и ζ соответственно. Тогда поскольку
и = 2tan-1(X),
то
du
dx 1 + x2'
или
2
du
dx.
\ + хА
Аналогично:
dv =
1 + У
-dy
dw-
1 + z2
-dz.
Кроме того, из формулы половинного угла для тангенса мы имеем
tan
ίι 1
-и
2
= ll-cos(M) =χ
\l + cos(u)
И, решая это относительно cos(u), получаем:
COS(M) = -.
1 + АГ2
Аналогично:
1-У2
C0S(V) = ^T
1 + У
гпя(
'W4! -
_1-^2
1 + z2
220 ♦ Семь сложных интегралов
Подставляя эти результаты для дифференциалов и косинусов в интеграл 1Х
(помните, мы временно игнорируем нормализующий множитель π3), мы
имеем:
dudvdw
г г г auavaw _ о Г Г Г
о о о l-cos(w)cos(v)cos(w) J I JQ
(
dx )(
u+*2A
fl-x2
[l + x2
dy )f
i+y2Ji
lii-y2
J[i+y2
dz )
l + z2\
)fi-22)
J[l + z
2
■411:
dxdydz
iii(l + x2)(l + y2)(l + z2)-(l-x2)(l-y2)(l-z2)'
который после перемножения и приведения подобных в знаменателе
сводится к
оо оо оо
*ш-
dxdydz
•Ό "Ό "Ό *2 + y2 + z2 + x2yV
Обратите внимание, что это объемный интеграл по всему положительному
октанту (х > 0, у > 0, ζ > 0) в трехмерном пространстве.
Затем снова заменим переменные следующим образом:
χ = rsin(6)cos(6), χ = rsin(6)sin(cp), x = rcos(6),
физически это просто переход к сферическим координатам от прямоугольных
координат в нашем последнем интеграле1. Чтобы продолжить физическое
интегрирование по всему положительному октанту в трехмерном пространстве,
мы видим, что наш тройной интеграл с дифференциалами dr, dQ и άφ должен
ти ти
находиться в интервалах от 0 до оо, от 0 до — и от 0 до — соответственно. Диф-
А А
ференциальный элемент объема в прямоугольных координатах {dxdydz)
становится элементом объема r2sin(6)dcpd6dr в сферических координатах. Таким
образом, в этой новой системе координат интеграл 1Х принимает вид:
π/2 π/2 οο
r2sin(6)d(pdedr
28Ϊη2(θ)οο82(φ) + Γ28ΐη2(θ)8Ϊη2(φ) + Γ2οο82(θ) +
+ г6 8ΐη2(θ)οο82(φ)8ΐη2(θ)8ΐη2(φ)οο82(θ)
= Λ2 %2 °η sin(9)^d9dr
ο ^ ^ 1 +г4sin4(θ)cos2(θ)sin2(φ)cos2(φ)'
или при явно указанном порядке интегрирования:
1 В этих обозначениях угол φ измеряется от положительной оси а:, а θ измеряется от
положительной оси ζ. Некоторые авторы применяют другие соглашения, но,
конечно, если быть последовательным от начала до конца, все получается одинаково при
любых соглашениях. В конце концов, символы - это просто чернила.
Тройные интегралы Уотсона/Ван Пейпа ♦ 221
π/2 π/2 Γ оо
■4Ι\Ι\Ιττ?
Π Π Π х \ *
sin(6)
-dr
dQ
о [о ю - + r4sin4(e)cos2(6)sin2((p)cos;'((p)
Теперь определите переменную
ψ = 2φ.
Тогда формула двойного угла для синуса говорит, что
sin(cp)cos((p) = -sin(2cp).
Следовательно:
sin2(cp)cos2((p) = — sin2(2cp) = —sin2(i|j).
4 4
Поскольку
d(p = -di|j,
[dcp.
наш интеграл тогда становится таким:
π
0
π/2
А
0
/
sin(6)
-dr
о l + -r4sin4(e)cos2(6)sin2(i|;)
4
de
ίίψ.
На первый взгляд может показаться, что ситуация граничит с отчаянием, но,
как гласит старая пословица, «видимость может быть обманчивой»; на самом
деле мы почти закончили. Во-первых, самое внешнее интегрирование (отно-
π
сительно ψ) симметрично по ψ относительно ψ = —. То есть как говорит Уотсон
в своей статье:
1 }
π/2
<<-/(...)ίίψ=/(...)ίίψ»,
что, конечно, является результатом появления ψ в подынтегральном
выражении только как sin2(i|/). Таким образом, наш интеграл становится таким:
π/2
/
sin(6)
о l + -r4sin4(0)cos2(6)sin2(i|;)
dr
άθ
ίίψ.
Во-вторых, Уотсон использует тот факт, что самое внутреннее (то есть
первое) интегрирование (по отношению г) выполняется при фиксированных θ
и ψ. То есть при замене переменной
222 ♦ Семь сложных интегралов
t = rsin(6)J-cos(6)sin(i|;)
переменная t на самом деле является функцией только от г, а не от г, θ и ψ. Итак,
делая эту замену, мы имеем
dt
dr-
sin(6)J-cos(6)sin(i|;)
t4 = -r4sin4(6)cos2(e)sin2(i|j),
4
что преобразует наш интеграл следующим образом:
π/2
/-
sin(6)
-dt
0 Sin(6\/-COS(e)sin(l|;)(l + t4)
ίίθ
ίίψ =
π/2
472/
π/2 οο
{ Vcos(9)Vsin(t)(l + i4)
Λ
Ш
c/ψ,
страшно выглядящий объект, который - внезапно и с невероятной радостью
для аналитика1 - разбивается на произведение трех одномерных интегралов,
каждый из которых мы уже сделали! То есть мы имеем
ооо l-cos(u)cos(v)cos(w) ~ { (1 + t4) -J 7cos(e) i φ
t/ψ
5ΪΠ(ψ)
n-Ji
Первый интеграл (no ί) по формуле (2.3.4) равен , а каждый из интег
ралов по θ и ψ по формуле (4.2.14) равен
m
4
2л/2й
Таким образом, вспоминая
нормализующий множитель π , мы имеем:
π3
4 J
/
Г2
fiV
4J
г2
12V
4J
1 Могу только представить, что сказал Уотсон своему коту, когда дошел до этой точки
в своей работе. Возможно, слова были примерно такими: «клянусь Юпитером, Лорд
Пушок, я сделал это! Расколол эту чертову штуковину, как тогда, когда этот яйцего-
ловый Шалтай-Болтай свалился со стены!»
Эллиптические интегралы в физической задаче ♦> 223
и тогда
л π π π
,L (\ (\ (\ *■
dudvdw
Γ4
ill
4
cos(u)cos(v)cos(w) 4π
(6.5.1)
Этот ответ дается в статье ван Пейпа без вывода.
Если мы попытаемся (как делали ранее с оптическим интегралом Харди-
Шустера) проверить (6.5.1) с помощью MATLAB Symbolic Toolbox, написав код:
syns и vw
int(int(int(l/(lcos(u)*cos(v)*cos(w)),w,0,pi),v,0,pi),u,0,pi)/(piA3)
тогда нас постигает неудача! MATLAB просто переходит в бесконечный цикл.
Но еще не все потеряно, поскольку мы можем использовать числовую
квадратурную команду MATLAB triplequad. Она делает для тройных интегралов то же,
что и quad делает для одномерных интегралов (для двойных интегралов тоже
есть dblquad, которая работает так же, как triplequad). Для этой нашей проблемы
синтаксис такой:
integrnd = @(u,v,w) l./(lcos(u).*cos(v).*cos(w));
triplequad(integrnd, 0.001, pi, 0.001, pi, 0.001, pi)/(piA3)
который дает ответ: 1.3879..., в довольно хорошем согласии с теоретическим
результатом, который я дал вам ранее для 1Х. (Обратите внимание, что
пределы интегрирования начинаются с чуть большего, чем ноль, поскольку когда
и = ν = w = 0, подынтегральное выражение обращается в бесконечность.)
6.6. Эллиптические интегралы в физической задаче
Чтобы закончить эту главу, я немного подробнее остановлюсь на теме
эллиптических интегралов, которые были упомянуты мимоходом в предыдущем
разделе (см. снова примечание 6). В частности:
F(fe,cp) = j f/ (6.6.1)
Jo Vl-k sin2((p')
φ .
E(k,(p) = ^\-k\m\(p')dq>' (6.6.2)
о
являются эллиптическими интегралами первого и второго рода соответствен-
но, где 0 < к < 1 (постоянная к называется модулем). Когда φ < —, эти интегра-
лы называются неполными, а когда φ = —, интегралы называются полными. За
исключением двух частных случаев к = 0 и к = 1, F(k, φ) и Е(к, φ) не выражают-
224 ♦ Семь сложных интегралов
ся через какие-либо элементарные функции, которые мы обычно используем
(тригонометрические, экспоненциальные, алгебраические и т.д.).
Вы можете подумать, что для появления F или Ε потребуется сложная
физическая ситуация, но это не так. Сейчас я покажу вам, казалось бы, простую
физическую проблему, которая тем не менее будет включать эллиптические
интегралы (на самом деле как Е, так и F). Проблема становится еще более
интересной, поскольку она появилась в учебниках уже более века назад, но до
1989 года регулярно анализировалась неправильно1.
На рис. 6.6.1 показана идеально гибкая, нерастягиваемая (то есть не
растягивающаяся, как трос) веревка с постоянной массовой плотностью μ на единицу
длины. Веревка имеет длину L, причем один конец (левый) постоянно
прикреплен к потолку. Другой конец также временно удерживается на потолке,
пока в момент времени t = 0 этот конец не освободится. Освобожденная часть
веревки затем, конечно, начинает падать (на рисунке показана ситуация после
того, как падающий конец опустился на расстояние х), пока в момент времени
t = Τ веревка не свисает прямо вниз. Наш вопрос прост: чему равно Т?
ι
Рис. 6.6.1 ♦ Падающая веревка
Одно из предположений, которое мы сделаем, отвечая на этот вопрос,
заключается в том, что падающая веревка сохраняет энергию, а это означает,
что в игре нет механизмов рассеивания энергии (таких как внутренние потери
тепла при трении в веревке, вызванные распрямлением в нижней части
изгиба). Во все времена сумма потенциальной и кинетической энергий веревки
будет постоянной. Когда мы закончим с нашим анализом, то обнаружим, что
результат для Τ имеет очень удивительный аспект.
Центр масс левой стороны веревки равен
ifi+χΊ
L + x
а центр масс правой стороны веревки равен х + -
2
l(L-x)
ниже потолка,
L + Ъх
от потолка.
1 См.: Calkin Μ. G., and March R. H. The Dynamics of a Falling Chain (Динамика падающей
цепи)//American Journal of Physics. February 1989. P. 154-157.
Эллиптические интегралы в физической задаче ♦ 225
Итак, взяв за ноль потенциальную энергию (Р.Е.) у потолка, Р.Е. веревки, когда
высвобожденный конец веревки опустился на х, определяется как (где g -
ускорение силы тяжести)
Р.Е..
L + x
8-
(L-x)
8-
L + Ъх
что приводится (после небольших преобразований) к
Р.Е.
1
Vgtf + lxL-x1].
(6.6.3)
Кинетическая энергия (К.Е.) веревки - это К.Е. нисходящей правой
стороны веревки, являющейся единственной частью веревки, которая движется.
Так как К.Е. массы т = μ
1
[L-
движущеися со скоростью ν =
dx
"dt
, составляет
την, мы имеем следующее выражение для К.Е. веревки:
K.E. = ^(L-x)
(dx)
~di
(6.6.4)
1
Из (6.6.3) начальная (при χ = 0) Р.Е. равна -—\igl}. Кроме того, так как веревка
4
начинает падать из состояния покоя, начальная К.Е. - это ноль. Таким обра
зом, полная начальная энергия веревки равна
энергии, это полная энергия веревки для всех ί > 0. Итак:
1 Г2
—yLgu, и, по закону сохранения
4
4
(dx)
dt
-\vg[L2 + 2xL- x2] = - KgL\
4 4
что приводится к
1
(L-x)
dx)
dt
1
g(2L-x)x.
(6.6.5)
Обратите внимание, что μ сократилось, и поэтому наш анализ справедлив
для любой веревки с произвольной (постоянной) плотностью массы.
Решая (6.6.5) относительно дифференциала dt, получаем
dt-
или
g(2L-x)x'
4gdt
(2L-x)x'
(6.6.6)
226 ♦ Семь сложных интегралов
Если мы проинтегрируем обе части (6.6.6), где время меняется от 0 до £,
а расстояние спуска падающего конца веревки варьируется от 0 до х, то имеем
(я изменил фиктивные переменные интегрирования t на t! и хна х', чтобы мы
могли сохранить t и χ в качестве наших конечных переменных) тогда:
L-x
[^={Ш^=^- (6·6·7)
Теперь χ изменяется от 0 (при t = 0) до L (при t=T). Итак, если мы определим
переменную φ как
8ΐη(φ):
ίτ
тогда φ изменяется от 0 до —. Поскольку χ = 1Бт2(ф), давайте теперь изменим
л
переменную в (6.6.7) на х' = Lsin2^'), и тогда
dx'
— = 2Lsin(<|/)cos(<|/),
αφ
или
dx! = 2181П(ф/)С08(ф/)^ф/.
Кроме того, с помощью небольших алгебраических преобразований можно
показать, что
L-x' соз(ф')
(2L - х')х' VLsin^Vl + cos2^)'
Таким образом, (6.6.7) принимает вид:
tVs= *f-= С°8.(ф/) 2Lsin(^)cos^W,
о л/Ь sin(c|/)Vl + cos2(φ")
или после нескольких сокращений и перестановок:
^ = V2f,COs2^ d«,
21 J0 7l + cos2(^)
8
ΊΙ
и наконец, так как t=T, когда φ = —:
cos2 (φ')
/2L Jo Vl + cos2(^)
Is
dtf. (6.6.8)
Эллиптические интегралы в физической задаче ♦ 227
Вы, несомненно, задаетесь вопросом: «почему левая часть (6.6.8) в такой
любопытной форме?» Чтобы понять причину этого, предположим, что вы
бросили точечную массу в момент времени t = 0 и при χ = 0. Сколько времени
потребуется, чтобы эта точечная масса упала на расстояние L? Из физики
первокурсника мы знаем, что масса упадет на расстояние Igt2 за время t и, следо-
2
вательно, -gt2 = L или t = I—, что и является тем любопытным знаменателем
2 V S
ίϊΕ
в левой части (6.6.8). Таким образом, если Τ > —,το есть если падение каната
ν ε
занимает больше времени, чем время свободного падения точечной массы, то
правая часть (6.6.8) будет больше 1, но если веревка падает быстрее, чем
точечная масса, тогда правая часть (6.6.8) будет меньше 1. Наконец, если веревка
падает с ускорением силы тяжести (как и точечная масса), тогда правая сторона
(6.6.8) будет ровно 1. Итак, что это?
Для нас это простой вопрос, на который MATLAB может ответить, и на самом
деле веревка падает (!) быстрее, чем масса точки, потому что sqrt(2)*quad(@(x)
(cos(x).A2)./sqrt((l+cos(x).A2)),0,pi/2) = 0.847213.... Это значительное
отклонение от 1 (то есть это не ошибка округления), и веревка падает более чем на
15 % быстрее, чем масса точки. Вы удивлены? Если нет, то почему? В конце
концов, как я упоминал, точечная масса падает с ускорением силы тяжести,
и поэтому, чтобы веревка била точечную массу, она должна упасть «быстрее,
чем под действием силы тяжести»! Как это может быть1?
В этот момент инженер или физик, вероятно (после покачивания головой
в веселом удивлении), начнет искать физическую причину этого любопытного
результата. Математик2, однако, скорее всего, сначала задался бы вопросом:
1 Причина в том, что падающая часть веревки движется под влиянием не только одной
гравитации, но и ненулевого натяжения в ней, которое объединяется с гравитацией
при притягивании веревки вниз. Дальнейшее рассмотрение этого вопроса уведет нас
слишком далеко от темы книги, но если интересно, все это изложено в статье,
приведенной в примечании 9. Прогноз «быстрее, чем гравитация» был экспериментально
подтвержден, косвенно, в примечании 9, через измерения натяжения, сделанные во
время фактических падений. В 1997 году было опубликовано прямое
фотографическое свидетельство, и сегодня в интернете можно найти видеоролики на YouTube, где
четко видно, что падает «быстрее, чем под действием гравитации».
2 Математиков эта проблема и связанные с ней проблемы интересуют не меньше, чем
физиков. Действительно, изучение падающих веревок и цепей было начато
британским математиком Артуром Кэли (1821-1895): см. его заметку: О классе
динамических проблем // Труды Лондонского Королевского общества. 1857. С. 506-511 (On
a Class of Dynamical Problems // Proceedings of the Royal Society of London), - которая
начинается словами: «Есть класс динамических проблем, которые, насколько мне
известно, не рассматривались в общем виде». Это, конечно, не тот случай, когда
проблема Кэли, в частности, все еще вызывает споры о том, когда энергия сохраняется
(и не сохраняется): см. Чун ва Вонг и Косукэ Ясуи. Падающие цепи // Американский
физический журнал. 2006. Июнь. С. 490-496 (Chun Wa Wong and Kosuke Yasui. Falling
Chains //American Journal of Physics). Взгляните также на проблему 6.4.
228 ♦ Семь сложных интегралов
а какому хорошему математическому выражению равно это любопытное
число 0.847213...? Ответ, как и следовало ожидать из названия этого раздела, -
эллиптические интегралы. И вот почему.
Начиная с интеграла в правой части уравнения непосредственно перед
(6.6.8) - множитель V2 мы добавим в конце, - мы имеем:
г:**-/-
sin2(c|/)
Jo 71 + соз2(ф') i Vl + cos2^') J0 ν2-8ΐη2(φ') i yj2-sm2(<i>')
ί/φ' =
= 1}J I 1 d*—fiJ Ι ι άφ>
V2 » ^1-|5т2(ф') V2 » |-|8ΐη2(φ')
и тогда, вспоминая (6.6.1):
cos2^ «*</ * f
V2
о л/Г+со^Сф7)
№ф]
J_ У sir
sin2 (φ')
,ίίφ'.
(6.6.9)
sin2 (φ')
Теперь рассмотрим интеграл в правой части (6.6.9).
1
/
81П2(ф')
1
0 |1-^8Ш2(ф')
Φ 1-^8ΐη2(φ') Φ -1 + |8ΪΠ2(φ')
ά$ = ]-ΓΛ d<V+J ι ^άφ' =
° λ|ΐ-^8ΐη2(φ')
0 |1-|81П2(ф')
= Πΐ--8Ϊη2(φ')£ίφ'-/
ί/φ'
3 >
8ΪΠ2(φ')
^1-|5ϊη2(φ') 2 ° ^1-|5ίη2(φ')
,ίίφ'.
Таким образом, используя (6.6.2) и (6.6.1) снова, мы имеем:
/
δΐη2(φ')
0 ^sinV)
с/ф' = £
ί 1
,Φ
{λΙΪ' J i>/2' J
1
,Φ
z о
sin2 (φ')
l-^sinV)
*dtf,
или
ф- sin2 (φ')
If sir
:d<tf=F
81П2(ф')
,Φ
[S'l [S'l
,,φ
To есть мы имеем интересное тождество
J Sin (Ф) άφ> = 2Ρ
0 ^1-^81П2(ф')
4γ.φ
-2£
u/2'η ""ΐ,/2'η
4γ.φ
0<φ<-.
_Ψ_2
(6.6.10)
Задачи и упражнения ♦ 229
Используя (6.6.10) в (6.6.9), мы имеем
о sjl + cosW) л/2
l^**J
J_
л/2
2F
,,φ
-2£
,Φ
1
Ιλ/2
-λ/2
1Л'Ф]
U/2'Ч Ιλ/2'Ί
л/Ы-^ф,
lV2 J
и поэтому у нас есть второе интересное тождество
1
Ιλ/2'Ί л/2 U/2'Ч
1
,Ф
, 0<ф<
π
(6.6.11)
Подставляя этот результат в (6.6.8) и добавляя множитель, включив V2 перед
ТТч
интегралом, мы приходим к равенству (для φ = —):
А
■ 2Е
1 π
Ιλ/2'2] |,V2' 2j
1 π
(6.6.12)
Соответствует равенству (6.6.12) результат MATLAB в 0,847213...? Да, потому
что быстрый просмотр в математических таблицах значений полных
эллиптических интегралов первого и второго рода показывает, что
Ιλ/2'2]
= 1.8540746...
ι-ί- =1-3506438....
U/2 2 J
Таким образом, правая часть (6.6.12) численно равна
2(1.3506438...) - (1.8540746...) = 0.847213...,
и поэтому (6.6.12) и MATLAB находятся в отличном согласии.
6.7. Задачи и упражнения
Чтобы закончить эту главу о сложных интегралах, кажется уместным
предложить вам некоторые сложные интегралы.
(С6.1). Оглянитесь на раздел 6.3, где мы оценили то, что я назвал интегралом
Коксетера. Но это был не единственный интеграл Коксетера. На самом деле
(как вы помните из предисловия) Коксетер был озадачен рядом интегралов,
которые Харди решил. Итак, вот еще один из оригинальных интегралов
Коксетера, чтобы вы могли попробовать свои силы:
230 ♦ Семь сложных интегралов
π/2
COS
1
l + 2cos(x)
[dx.
Когда это передается MATLAB, то мы получаем quad(@(x)acos(l./(l+2*cos(x))),
θ,pi/2) = 1.64493..., что позволяет нам предположить (после чтения
раздела 5.3), что это есть точное эйлерово значение ζ(2):
π
Ваша задача здесь
доказать, что это действительно так. Подсказка: на самом деле это не так уж
сложно - по крайней мере, так не должно быть после прочтения раздела 6.3, -
и интеграл даст результат, используя тот же подход, который мы использовали
там в тексте.
(С6.2). Когда мы доберемся до главы 8 по контурному интегрированию, то
найдем интеграл Г — dx, где (чтобы гарантировать, что интеграл
существует) тип- неотрицательные целые числа, такие что η - т > 2. Для част-
J*°° χ τι/η
αχ = ,п>Ъ.
0 х" + 1 sm(2n/n) ~
Если мы оценим правую часть для первых нескольких допустимых значений
и, то получим:
η
3
4
5
6
7
Значение интеграла
1.2091995
0.7853981
0.6606532
0.6045997
0.5740354
поо
Теперь рассмотрим интеграл / ——
л —г" л
dx
+ ···+* + !
,п>Ъ. Если мы
используем функцию quad из MATLAB для численной оценки этого интеграла для
тех же значений и, то получаем:
η
3
4
5
6
7
Значение интеграла
1.2091992
0.7853988
0.6606537
0.6046002
0.5740356
Эти численные результаты убедительно показывают, что эти два
интеграла могут быть равны. Вы можете изучить данный вопрос напрямую, «просто»
Задачи и упражнения ♦ 231
находя второй интеграл (но это может быть не так «просто»!). Другая
возможность состоит в том, чтобы сначала записать разность двух подынтегральных
χ 1
выражений fix) = , а затем (каким-то образом) по-
хп + 1 хп~1 + хп~2 -\ h χ +1
J^oo
f(x)dx = 0. Посмотрите, сможете ли вы сделать это.
о
(С6.3). Вот проблема, напоминающая «мечту второгодника» (6.1.4).
Существует значение с, 0 < с < 1, такое что J cxdx = J^^c*. Вычислите это значение с
с точностью не менее 13 десятичных знаков, и, для этого значения, каково
будет общее значение интеграла и суммы? Подсказка: для начала заметим, что,
поскольку с находится между 0 и 1, то должно быть некоторое λ > 0, такое что
с = е~\ (λ = 0 дает с = 1, а λ = оо дает с = 0.) Этот нотационный трюк
облегчает оценку как интеграла, так и суммы. Затем сравните ваши выражения для
интеграла и суммы, чтобы получить трансцендентное уравнение для λ,
уравнение, которое может быть решено численно с использованием любого числа
известных алгоритмов (мое предложение: посмотрите любую книгу по
численному анализу и найдите обсуждение алгоритма бинарного деления (binary
chop)), чтобы найти с необходимой точности.
(С6.4). Я упомянул «проблему Кэли» в тексте, но не предоставил никаких
подробностей. Задача состоит в том, чтобы вычислить, как равномерно
соединенная цепочка с массовой плотностью (μ), изначально находящаяся у края стола,
падает со стола, скользя без трения по краю. Если χ - длина цепи, висящей над
краем в момент времени £, то задача состоит в том, чтобы найти
дифференциальное уравнение движения (включающее χ и £), а затем решить (то есть
проинтегрировать) его относительно χ как функции L В своей книге «Механика»
1943 года немецкий физик Арнольд Зоммерфельд (1868-1951) без
каких-либо выводов заявил, что уравнение движения есть —(хх) = хх + х2 = gx (где g -
dt
ускорение силы тяжести). Здесь точки обозначают (по Ньютону) производные
. dx .. d2x
х = — их = —-
dt dt2
dx)2
dtj
и он сказал, что «его интегрирование довольно сложно». Очень искусный
вывод уравнения Зоммерфельда можно найти в статье Дэвида Кейффера:
Падающая цепь и потеря энергии //Американский журнал физики. 2001. Март.
С. 385-386. (Keiffer David. The Falling Chain and Energy Loss //American Journal of
Physics). Кейффер не ссылался на Зоммерфельда, а скорее основал свой вывод
на прямом анализе того, как цепочка соскальзывает со стола, звено за звеном.
Кейффер дал интересный поворот проблемы, преобразовав ее в определение
и χ = -γγ- В более наглядных обозначениях Лейбница для производных
уравнение движения Зоммерфельда имеет вид —
dt
dx)
xTt
2„ (,' ч2
d2x
dt2
gx,
232 ♦ Семь сложных интегралов
скорости падающей цепи как функции не времени, а, скорее, как функции
длины цепи, которая уже соскользнула со стола (то есть х). Обозначая скорость v(x),
d(v2) 2 2 0
его уравнение движения имеет вид —-—- = —ν + 2g.
dx x
(a) Показать, что уравнение Кейффера и уравнение Зоммерфельда - это
одно и то же.
(b) Заметив, что уравнение Кейффера является дифференциальным
уравнением первого порядка от ν2, использовать тот же подход, который
мы использовали в главе 3 (раздел 3.9), для интегрирования уравнения
Кейффера, чтобы найти ν2. Подсказка: рассмотреть возможность
использования х2 в качестве интегрирующего множителя.
(c) Показать, что цепь падает с постоянным ускорением g (это был главный
результат Кэли).
(d) Используйте результат из (Ь), чтобы вычислить Г, время полного со-
скользывания со стола цепи длины L.
Теперь, чтобы быть честным, я должен сказать вам, что хотя все ваши
расчеты в ответ на вышеупомянутые вопросы представляют собой
хорошую, твердую математику, в последние годы было много споров о том,
является ли это хорошей физикой! Анализ Кэли, Зоммерфельда и Кейффера
включает нарушение закона сохранения энергии, когда цепь
соскальзывает со стола. Это на самом деле довольно легко показать.
Первоначально потенциальная энергия (Р.Е.) и кинетическая энергия (К.Е.) обе равны
нулю (столешница является нашим нулевым опорным уровнем для Р.Е.,
и цепь изначально находится в состоянии покоя), и поэтому начальная
полная энергия равна нулю. Когда цепь только что полностью соскольз-
\2gL
нула со стола, ее скорость равна Л-9—, результат, который вы уже должны
были встретить в своих предыдущих рассуждениях. Итак, ее К.Е. составля-
1 T2gL gL2 TT L
ет -(μι/) = μ . Центр масс цепи находится на — ниже столешницы,
А О О А
L zC
поэтому ее Р.Е. составляет -\iLg — =-\ι-—. Таким образом, при завер-
А А
σ]} σ]}
шении падения его полная энергия равна μ- μ-— < 0. Энергия была
D А
потеряна во время падения. (Это головоломка сама по себе, поскольку,
как отмечалось, скольжение не имеет трения. Итак, как же рассеивается
энергия? Собственно говоря, именно этот вопрос и побудил Кейффера
написать статью.) В последние годы другие физики утверждали, что
падающая цепь Кэли действительно сохраняет энергию. Итак, для вашего
последнего вопроса здесь:
(e) Предполагая сохранение энергии, покажите, что цепочка падает с
постоянным ускорением -g(a не —g как у Кэли).
Задачи и упражнения ♦ 233
(С6.5). Эта задача включает в себя совершенно другое появление интегралов
в еще одной физической проблеме. (См.: ДжеймсМ. Супли и ФрэнкВ. Шмидт.
Брахистохрона в центральном силовом поле [fames M. Supplee and Frank W. Schmidt.
Brachistochrone in a Central Force Field //American Journal of Physics. May 1991.
P. 402 and 467].) Представьте себе крошечный шарик массой т с проволокой,
продетой через отверстие в нем, позволяющей шарику скользить без трения
по проволоке.
Провод лежит полностью в горизонтальной плоскости, одним концом (в
полярных координатах г и Θ) в точке
Я π
; а другой конец на горизонтальной оси
в точке (R, 0).
Единственная сила, действующая на шарик, - это обратная квадрату
расстояния гравитационная сила, обусловленная точечной массой М,
расположенной в начале координат. То есть шарик скользит по проволоке, потому что
он испытывает радиальную силу притяжения F=G——, где G - универсальная
гравитационная постоянная. Шарик имеет начальную скорость J2 . Какую
функцию формы γ(Θ) должен иметь провод, чтобы минимизировать время при
π ι
скольжении шарика из точки (R, 0 ) в точку
s
? Для ответа на этот вопрос
выполните в деталях следующие шаги.
(a) Покажите, что начальная потенциальная энергия (Р.Е.) шарика равна
GMm /ТГ ^ ч GMm
, а начальная кинетическая энергия (К.Е.) шарика , и по-
R R
этому полная начальная энергия равна нулю. Подсказка: начальная Р.Е.
является энергией, необходимой для переноса массы m из
бесконечности вдоль положительной горизонтальной оси к положению г = R,
которая определяется как Г Fdr. Эта энергия отрицательна, потому что
J оо
гравитация притягивающая.
(b) Если Т- общее время прохождения шарика от одного положения к
другому, то Τ = fdt = Г—, где ν - мгновенная скорость шарика, a ds -
дифференциал длины пути вдоль провода. В полярных координатах (ds)2 =
l(~dr)2
(drf + (rdQ)2 и, таким образом, ds = ddj\ — + г2. Используя закон сохра-
\{dQ)
нения энергии (К.Е. + Р.Е. = 0 всегда, потому что нет трения), покажите,
234 ♦ Семь сложных интегралов
(с) Минимизация Т- это проблема не для обычного начального
дифференциального исчисления, где мы пытаемся найти значение переменной,
которая дает экстремумы некоторой функции. Наша проблема здесь
состоит в том, чтобы найти функцию, которая минимизирует интеграл для
Т. Это проблема из области, что называется вариационным исчислением,
и фундаментальным результатом данного предмета является уравнение
Эйлера-Лагранжа: если мы записываем подынтегральное выражение
жг гъ—τ / dr дк d (дк)
Т-интеграла в виде К = ^гг +г , где г =—, тогда
дг'
0.
ίίθ7 ~~~~" dr dQ{
Этот результат имеется в любой книге по вариационному исчислению
(или см. мою книгу: Когда наименьшее лучше (When Least Is Best). Прин-
стон, 2004; 2007. С. 233-238). Эйлер знал это к 1736 году, но вывод,
который я даю в упомянутой книге, является теперь стандартным,
полученным французско-итальянским математическим физиком Жозефом
Луи Лагранжем (1736-1813) в письме, тогда еще подростка (!) Лагранжа,
написанном Эйлеру в 1755 г. Используйте уравнение Эйлера-Лагранжа,
чтобы показать, что искомая функция γ(Θ) удовлетворяет дифференци-
d2r
альному уравнению 5г/2 + Зг2 " ' " "
:2г'г",вдег" =
dtf
(d) Сделайте замену переменной и = — и покажите, что дифференциаль-
г
2^2, , du π
ное уравнение в (с) принимает вид и +1 = -и , где и =—. Подсказка:
3 d6
начните с записи дифференциального уравнения в (с) в виде Зг/2 + Зг2 =
2г'г" - 2г/2.
(e) Дифференциальное уравнение в (d) есть -сЮ = -,
2 1 + ir
которое вы
можете легко проинтегрировать неопределенно, чтобы показать, что
(3 )
^ , где Q - произвольная постоянная.
u = tan
-θ+ς
\dr
(f) Результат в пункте (е) говорит, что =tan
(Ъ
2в + С'
, для этого
выражения вы можете найти неопределенный интеграл и показать, что
г = С, cos273
-θ+ς
(g) Используйте координаты концов провода для оценки констант Q и С2,
получая, таким образом, γ(Θ) = ^- г, кривую, называемую
V2
COS
брахистохроной, от греч. brachistos (самое короткое) и chronos (время).
Обратите внимание, что это не самая короткая кривая по длине, которая,
конечно, будет отрезком прямой линии.
Глава
7
Использование
для нахождения интегралов
7.1. Формула Эйлера
Использование мнимой единицы i = V^4 для вычисления интегралов хорошо
иллюстрируется следующим легким примером. Давайте применим /, чтобы
найти
dx
f—
1)
Делая разложение подынтегрального выражения на элементарные дроби,
мы можем написать:
I
dx
\ х(х'+1)
оо
I
±__\. \__
χ 2(x-i) 2(x + i)
1
dx
1п(а:)-1п
№
In
[Jx+i)
ln(x)--ln(x-i)--ln(x + i)
In
V(x-i)(x + i)
In
V?
1
ln(l)-ln
Ш
= 1пШ) = -ln(2) = 0.34657.
Проверка с quad: quad(@(x)l./(χ.*(χ.Λ2+1)), 1,1000) = 0.34657....
Это хорошо, да, но полезность комплексных величин в выполнении
определенных интегралов действительно станет ясной, когда мы перейдем к
следующей главе, посвященной контурному интегрированию. Однако ценность
комплексных чисел можно сразу оценить на «более низком» уровне, не дожидаясь
контурных интегралов, и все, что нам действительно нужно для начала, - это
знаменитое тождество Эйлера:
eibx = cos(bx) + fsin(to), (7.1.1)
236 ♦> Использование лРл для нахождения интегралов
где Ъ - любая действительная величина. Я принимаю (7.1.1) как известное, но
если вы хотите изучить его подробнее, как математически, так и исторически,
то можете найти это в двух моих предыдущих книгах1.
Очень простая и все же довольно интересная демонстрация тождества
Эйлера может быть найдена в проблеме вычисления интеграла
оо
fe~xysm(bx)dx.
Обычно это делается по частям в элементарном математическом анализе,
но использование уРл проще. Поскольку
e~lbx = cos(bx) - is'm(bx),
gibx _ g-ibx
то из этого следует, что
sin(bx) = -
Тогда
2ί
e~xysm(bx) =
и поэтому
e~x(y-ib) _ g-x(y+ib)
2ί
оо -ι oq
Je-xysm(bx)dx = Λ J{e-*(y-,b) - e
-x(y+ib)
2/·
J_
2i
}dx
2/
-x(y-ib)
-x(y+ib)
-(y-ib) -(y + ib)
1
1
y-ib y + ib
2i
y + ib-y + ib
v2 + b2
lib
2i(y2 + b2)'
и тогда
оо
fsin(bx)e~xydx
у2+ь2
(7.1.2)
7.2. Интегралы Френеля
Что ж, эти последние вычисления были, конечно, интересными, но, чтобы
действительно продемонстрировать вам силу тождества Эйлера, я сейчас покажу
вам, как использовать его для получения двух известных определенных
интегралов, названных в честь французского ученого Августина Жана Френеля
«Мнимая сказка: история о V^T» (An Imaginary Tale: the story ofyf^I) и
«Необыкновенная формула доктора Эйлера» (Dr. Euler's Fabulous Formula), опубликованные
издательством Princeton University Press (оба в нескольких изданиях).
Интегралы Френеля ♦ 237
(1788-1827). Имеется небольшая ирония в том факте, что, несмотря на
название, на самом деле значения этих интегралов:
оо оо
fcos(x2)d*M fsin(x2)dx-
впервые нашел Эйлер в 1781 году - еще до рождения Френеля! - используя
подход, отличный от того, что я собираюсь показать вам1. (Мы использовали
значение второго интеграла в разделе 6.4 при обсуждении оптического
интеграла Харди-Шустера.)
Мы начнем с интеграла
ад=
1„ eix2(t2+l)
о I о L "τ" х
(Я вскоре объясню, откуда появилось это довольно любопытное выражение G(x).)
Попутно обратите внимание, что
G(0) = 0 + /)^- = /tan-1(l) = /j)
что будет важно для нас через несколько шагов с этого момента.
Дифференцируем G(x) по х:
dG(x)
dx
J J t 4-1
о J ο ι -r ι
2e"2 feit2dt -2χ]βϊχψβϊχ2άί = 2e*]eedt - 2xe"' Je'^dt.
В последнем интеграле заменим переменную на и = tx (и, следовательно,
du = xdt или, dt = du/x). Затем
dG(x)
dx
du
■■ 2eix'feit2dt - 2хе"2 Je'"2 — = 2е'у Jefdt - Jeh
ldu
= 0.
То есть G(x) имеет нулевую скорость изменения относительно χ для всех х.
Следовательно, G(x) является константой, и поскольку G(0) = г —, то G(x) = i —.
4 4
Данный результат объясняет происхождение этого удивительно «странного»
интеграла G(x); он был специально создан, чтобы иметь свойство нулевой
производной!
1 Эйлер использовал гамма-функцию (еще одно его творение, которое вы помните из
главы 4) в своем анализе 1781 года, и вы можете увидеть, как он находил интегралы
Френеля, в моей книге «Мнимая сказка» (An Imaginary Tale), стр. 175-180. Как и
следовало ожидать от Эйлера, это потрясающе умно.
238 ♦> Использование лРл для нахождения интегралов
Теперь при χ —> оо мы имеем
ix\tA+\)
lim f—7 dt = 0
утверждение, которое я обосную в конце этого раздела (но посмотрите,
сможете ли вы сделать это самостоятельно, прежде чем я доберусь до конца раздела).
А пока просто примите это. Тогда:
G(oo) = \jeit2dt\ = \fcos(t2)dt + ifsm(t2)dt
[о J L о о
Запишем это так:
G(oo) = (А + /Б)2,
где А и В - это интегралы Френеля:
оо оо
А = fcos(t2)dt и В = fsin(t2)dt.
71
Тогда, поскольку G(oo) = f — (вспомните, что G(x) не меняется при изменении
4
х, и поэтому G(oo) = G(0)), мы имеем:
(А + /Б)2 = i - = А2 + Ϊ2АВ - В2,
4
и теперь, приравнивая действительные и мнимые части с обеих сторон
последнего равенства, мы имеем А2 -В2 = 0 (что означает А = В) и 2АВ = —. Итак,
4
2А = —, и неожиданно мы закончили
А = Б) у нас есть интегралы Френеля:
А = J— = -,/— = 0.6266..., и (поскольку
и
jfcos(x2)dx = ^
Jsin(x2)d* = i^b.
(7.2.1)
(7.2.2)
Проверка: quad(@(x)sin(x.A2),0,30) = 0.6255... и quad(@(x)cos(x.A2),0,35)
1 ίτ^
0.6235..., оба достаточно близки к - J—. И поскольку
Интегралы Френеля ♦> 239
feix2dx= fcos(x2)dx + i fsin(x2)dx,
0 0 О
у нас есть интересный интеграл
(7.2.3)
Чтобы закончить это обсуждение, я действительно должен обосновать свое
предыдущее утверждение, что
1 ix\t2+l)
Чтобы показать это, используем тождество Эйлера в записи:
1 _ix2(t2+l)
Г£^Д=Г«"С»С + ВД dt+if
sin(x2(t2+l))
t2+l
at.
Поскольку
cos(Ar2(t2 + l)) = cos(Ar2i2 + Ar2) = cos(A:2i2)cos(A:2)-sin(A:2i2)sin(A:2)
sin(Ar2(t2 + l)) = sin(Ar2i2 + Ar2) = sin(A:2i2)cos(A:2) + cos(A:2i2)sin(A:2),
и так как при х —► оо, множители cos(x2) и sir^x2) остаются ограниченными ±1,
наше утверждение будет доказано, если мы сможем показать, что
А = 0.
,. fsin^t2) , ,. /.cos(*2t2)
Рассмотрим первый интеграл и сделаем замену переменной и = £2. Тогда
— = 2tndt = —du, или, поскольку t = Vu, мы имеем dt = —i=du. Итак:
2л/и
dt
2t
\s[n2(x42)dt= [^Шл = 1 rsin(A>Ai< fsinf"V
■£ t2 + l J0 ii + l Ua/mJ 2^0(u + 1)^ j0 ^
где неравенство следует как из отбрасывания множителя -, так и из замены
знаменателя в подынтегральном выражении на меньшую величину. Обратите
внимание, что подынтегральная функция самого правого интеграла является
синусоидой с амплитудным демпфированием, с каждым новым
полупериодом, ограничивающая все меньшую область (с чередующимися знаками).
Площади полупериодов образуют члены монотонно убывающего
знакопеременного ряда, а общая площадь полупериодов является значением интеграла.
240 ♦ Использование лРл для нахождения интегралов
Теперь вспомним прекрасный результат численного анализа, который
говорит, что любая частичная сумма такого ряда, содержащего более одного
слагаемого, меньше первого слагаемого1. Поскольку нули функции sin(x2i0
встречаются при х2и = ππ, то первые два нуля в интервале интегрирования (начало
и конец первого полупериода) находятся в точках и = 0ии = — соответствен-
х
но, и поэтому, заменяя sin(x2i0 на его наибольшее значение 1, мы имеем еще
более сильное неравенство:
\sm{x2t2) . π/χη 1 . п( Γψ/χ2 2^
и поэтому, поскольку любая частичная сумма наших знакочередующихся
рядов явно никогда не бывает отрицательной, мы имеем:
limf»i°(^)dt = lim^ = 0.
*^°<Ч £+1 х^°° х
Тривиальная модификация приведенных выше аргументов показывает, что
Цт^оз(х¥)
что и требовалось.
7.3. ζ(3) И СНОВА ИНТЕГРАЛЫ ЛОГ-СИНУСА
Вы помните из главы 5 (раздел 5.3) увлечение Эйлера дзета-функцией
оо 1
ζ(5) = Χ^Τ7· Он нашел явные формулы для t,(s) для любого положительного чет-
fe=i fc
ного целого значения s, но не мог сделать то же самое для нечетных значений
s, хотя посвятил поиску огромное количество времени и энергии. В 1772 году
он подошел очень близко к решению, когда заявил:
J\ln{sin(x)}dx = ^(3)-^ln(2).
Ключом к пониманию того, как такой невероятный результат может быть
обнаружен, как вы могли ожидать из предыдущих разделов этой главы,
является личность Эйлера. Вот как это происходит.
Вы можете найти доказательство этого факта (которое требует только элементарной
алгебры) практически в любом учебнике по математическому анализу для
начинающих. Посмотрите в разделе условной сходимости знакочередующихся рядов или
что-то в этом роде. Например, в моей старой копии Томаса «Математический анализ
и аналитическая геометрия», о которой я упоминал во введении (глава 1, раздел 1.4),
этот факт находится на стр. 614-615.
ζ(3) и снова интегралы лог-синуса ♦ 241
Определим функцию S(y) как
5(у) = 1 + е/у + е/2у + е/5у + · · · + е/иу,
где m - некоторое конечное целое число. Это выглядит как геометрический
ряд, и поэтому, используя стандартный трюк для суммирования таких рядов,
умножим на общий коэффициент егу, который соединяет любые два смежных
члена. Тогда:
e*S(y) = ёу + е/2у + е/5у + · · · + е/иу + е/(и+1)у,
и поэтому
eiyS(y)-S(y) = ei(m+1)y-l.
Решая относительно S(y), получаем:
5(у) =
0i(m+l)y
-1
0i(m+l)y
-1
еТ^_е
COS
-1
ίί ι]
.Ν)
e
У
2 U 2 - е 2j
"Ч-isinJ
ί ι]
Г + 2.
/2 sin
У
-co
[у
2
^^
\
у'
2
+ isin
[у)
,2,
/2sin
Теперь, оглядываясь на первоначальное определение S(y), мы видим, что
оно также может быть записано как
т т
S(y) = l + 5>os(ny) + z£sin(ny).
Итак, приравнивая мнимые части наших двух альтернативных выражений
для S(y), мы имеем:
^sin(ny).
В этот момент удобно заменить переменную на у = 2£, и тогда
cos{(2m + l)t}
cos]
И
2
sin
/ \
У
2J
У
cos
ι ^
у)
1 (.Л
2sin
\У
2
sin(t)
+ cot(0 = 2^sin(2nt)·
π
Теперь интегрируем это выражение почленно от £ = χ до £ = — и получаем:
pC0S«2m + 1)tW ft cot(t)A = 2£psin(2nt)dt.
sin(t)
242 ♦ Использование лРл для нахождения интегралов
Интеграл справа от знака равенства легко взять:
π
psin(2nt)dt
cos(2nt)
2п
-cos(mi:) + cos(2Hx) _ cos(2nx)-(-l)n
2n
2n
Последний интеграл слева от знака равенства такой же легкий:
J2cot(i)rfi = [ln{sin(0}]L2 =ln
Тогда:
sin
-ln{sin(x)} = -ln{sin(x)}.
r^cos{(2m + l)t} , ι r - , ч1 ^cos(2nx) А(-1)я
"Ι „ч sdt-ln{sm(x)} = J2 — Σ^^~·
Jx sin(t) l^i η ςί η
Напомним, что в начале раздела 5.2 у нас был степенной ряд
у^ уЗ у4
ι /■* ч Л Л Л
ina+x)=x-y+y-T+-,
из которого прих= 1 следует
п=1 И
1п(2) = -£<
Итак, если мы допустим, что т —> оо в приведенном выше уравнении в
рамке, то мы имеем
r rf cos{(2m + l)t} , ι г · / м ^cos(2nx) , . /оч
-hm Ι 2 - — dt-ln{sin(x)} = V - + 1η(2).
m^ocJx Sin(t) ~^ Π
Поскольку предел интеграла слева равен нулю1, мы приходим к равенству:
ln{sin(x)} = -^ - ^-ln(2).
п=\ "
Следующий шаг (не вполне очевидный!) - сначала умножить на х, а затем
интегрировать от 0 до —. То есть написать:
Это утверждение следует из почти интуитивно очевидной леммы Римана-Ле-
бега, которая гласит: если f(t) абсолютно интегрируема на отрезке от а до Ь, то
lim ff(t)cos(mt)dt = 0. В нашем случае f(t) = , которая абсолютно интегрируе-
m-ooJ Sin(t)
Ίΐ
ма на интервале 0 < а: < t < —, так как на этом интервале \f(t)\ < оо. Вы можете найти
доказательство леммы (это несложно) в книге: Толстое Георгий П. Ряды Фурье/перев.
с рус. Ричарда А. Сильвермана. Dover, 1976. С. 70-71.
ζ(3) и снова интегралы лог-синуса ♦ 243
π оо -ι ττ ττ
J2 x\n{sin(x)}dx = -J2~f2 xcos(2nx)dx-\n(2)J2 xdx ■-
n=\ "
= -JT-pxcos(2nx)dx-—ln(2).
Чтобы взять интеграл справа, используйте интегрирование по частям,
с и = χ и dv = cos(2Hx)dA\ К этому времени вы должны уже считать это
привычным делом, и поэтому я позволю вам заполнить детали, чтобы показать, что
π
f2xcos(2nx)dx =
Тогда
π
Г2 xln{sin(x)}dx =
-
1
In2'
[ о,
1
2
если п нечетно
если п четно
Г
L, η нечетно у.Ъ
8
ln(2).
Мы уже почти закончили. Осталось только отметить, что
ΣΟΟ
п=1,п
1111
, η четно yJb
Λ·ζ >^ . ·ζ l^ ^·ζ ~>
1
- + -
1
- + -
1
ij_ J_ J_
l5+25+35+'"
(2·1)3 (2·2)3 (2-3)3
1 °° 1 1
-+...=
И поскольку
Σοο
η=\,η
мы имеем:
1
, η нечетно ~3
+Τ°°,
, η четно yJ>
= «3),
Ζ—/η=1, η нечетно у.Ъ ^ν ' Ζ—/π=1,π четно у.Ъ Ά / Я Я
8
8
Таким образом, как и заявлял Эйлер:
Jxln{sin(x)}dx = ^a3)-yln(2).
(7.3.1)
7 π2
Правая часть (7.3.1) имеет вид —(1.2020S...) 1п(2) = 0.32923..., а интег-
16 8
рал слева равен quad(@(x)x.*log(sin(x)),0,pi/2) = 0.32923....
Как я уже упоминал в главе 2 (раздел 2.4), много лет назад в учебниках
часто утверждали, что лог-синусный интеграл Эйлера лучше всего оставить для
мощного контурного интегрирования. Тем не менее, как вы видели в этой
книге, классические приемы тоже довольно хороши. Теперь я вам покажу, что даже
244 ♦ Использование лРл для нахождения интегралов
если мы «поднимем ставку» до лог-синусных интегралов с квадратом
подынтегрального выражения, то все равно можем многое сделать. В частности, пусть
π π
/, = j4n2{asin(6)}c/0 = j4n2{acos(e)}de
π
I2= pln{asin(e)}ln{acos(6)}de,
J 0
где а - положительная постоянная. Эти интегралы были найдены не Эйлером,
а скорее благодаря почти забытому английскому математику Джозефу Вол-
стенхолму (Joseph Wolstenholme, 1829-1891). Вот как это можно сделать.
π π
p[ln{asin(G)} + ln{acos(6)}]2 de = j4n2{a2sin(6)cos(e)}de =
π π π
= J2ln2{asin(e)}de + JIln2{acos(6)}t/e + 2jIln{asin(e)}ln{flcos(e)}de =
= 2/1 + 2/2.
Но поскольку
π π
pln2{a2sin(Q)cos(e)}dQ = pin2
sin(29)
то
2/, + 2/2 = /0*ln2
2 sin(20)
de= Ρ
Jo
Ш,
ln{asin(29)}-ln
dQ-
= Pln2{asin(26)}d0-21n - Pln{asin(26)}de + ln2 - Πάθ,
JO Q JO Q JO
Обозначим φ = 2Θ. Тогда, поскольку dQ = -άφ, мы имеем:
1 г
π/2
J2 ln2{asin(2e)}de = -fln2{asm($)}d($> = J 1п2{сшп(ф)}с/ф =119
и по равенству (2.4.1):
π/2
2 12
f2ln{asin(26)}de = - f 1η{α8ΐη(φ)}<ίφ = f ln{asin(<|>)}d<|>=-ln
Jo 2J0 J0 1
Поэтому:
2/1 + 2/2=/1-21nj
π
In
-In2
ζ(2), наконец! ♦ 245
ΊΙ,
- -In
+ -ln2
2 Ί
или
/1 + 2/2 = -21nj-
Также имеем:
π π π
j2[ln{asin(e)}-ln{flcos(e)}]2de = ^1η2{α8ΐη(θ)}ίίθ + ^1η2{αοο8(θ)}ίίθ-
τι τι
-2pln{asin(e)}ln{acos(e)}de = 2I1-2I2 = pin2
= /Jln2{tan(6)}de=^
по формуле (5.2.7). Итак, у нас есть пара уравнений:
asin(9)
flcos(9)
d6 =
/! + 2/2=-21η
1-1=^
1 2 16'
2
α
— 1η
2
α
2,
π, 2
+ -1η2
2
'2]
aj
которые легко решаются и дают
π/2 π/2 3
rin2{asin(0)}d9= f ln2{acos(0)}d9 = —+ -
о о 24 6
In2·
2]
-21n
π/2
Γ ln{asin(6)}ln{acos(e)}d6 = -
0 6
In2
2
a.
-21n|-
u
-}ln
l]
Й
1 π5
| 48'
2
a
Hfl
(7.3.2)
(7.3.3)
π
Например, если а = 2, то это равно —— = 0.645964..., и MATLAB подтверж-
48
дает в виде quad(@(x)log(2*sin(x)).*log(2*cos(x)),0,pi/2) = 0.645979..., а для
а = 1 равенство (7.3.3) сводится к значению —In2{2} = 0.108729..., и quad(@
2 48
(x)log(sin(x)).*log(cos(x)) Api/2) = 0.10873....
7.4. ζ(2), наконец!
Гораздо более впечатляющей демонстрацией использования тождества
Эйлера является вывод, который я вам давно обещал, - значение, впервые вычис-
π
ленное Эйлером. Мы уже использовали этот результат
перь я выведу его так, как вы наверняка не видели раньше.
много раз, но те-
246 ♦ Использование ν^ϊ для нахождения интегралов
Вспомним еще раз разложение степенного ряда из главы 5 (раздел 5.2) для
ln(l+z):
ζ2 ζ5 ζ4
но теперь я беру ζ как комплексную переменную, а не просто вещественное
значение, как в главе 5, где я написал χ вместо ζ1. Если мы напишем ζ = ае1в, где
α и θ действительные, то
„2„/2θ Λ3„/3Θ
1п(1 + ае'е) = ае/е-
- + -
- + ·■·,
2 3 4
или раскладывая каждый член по тождеству Эйлера и собирая вместе
вещественные и мнимые части:
ln(l + fle/e) = flcos(e)--a2cos(2e) + -fl3cos(3e)--fl4cos(4e)+· · +
Δ Ο τ:
+1
asin(e)--fl2sin(2e) + -fl3sin(3e)--fl4sin(4e)-
4
2 v ' 3
Теперь 1 + aelB = 1 + acos(6) + zasin(6) - комплексная величина с модулем
и углом в комплексной плоскости (относительно положительной
действительной оси)2, и поэтому мы можем записать ее как
1 + aeie = V{1 + α cos(6)}2 + α2 sin2 (θ) е/ф =
= Vl + 2acos(e) + fl2cos2(e) + fl2sin2(e) ei(p = Vl + 2acos(e) + a2e/(p.
Тогда
ln(l + аеш) = In {Vl + 2acos(6) + a2} + /φ,
или приравнивая действительные части:
2
или
1ln{l + 2acos(e) + fl2} = flcos(e)--fl2cos(2e) + -fl3cos(3e)--fl4cos(4e)-
ln{l + 2acos(6) + a2} = 2
Arcos(e)--a2cos(2e) + -fl3cos(3e)--fl4cos(4e) + -
1 Откуда мы знаем, что можем это сделать? Это нетривиальный вопрос, и математик
по праву хотел бы его энергично исследовать. Но помните наш философский
подход - мы просто делаем предположение, что все в порядке, посмотрим, к чему это
нас приведет, а затем проверим ответы, которые мы в конечном итоге получим с
помощью quad.
Угол определяется формулой φ = tan l
книге не потребуется.
asin(cp)
l + acos((p)
но нам на самом деле в этой
ζ(2), наконец! ♦ 247
Итак, если мы напишем а = -х, то имеем
ln{l-2xcos(6) + a2} = -2
и тогда
ln2{l-2xcos(6) + x2} =
= 4
Arcos(e) + -a2cos(2e) + -fl3cos(3e) + -fl4cos(4e) + ·
xcos(e) + -x2cos(2e) + -x3cos(3e) + -x4cos(4e) + ···
J.
4
= 4
у4 у6
x2cos2(6) +—cos2(26) +—cos2)3e) + ···
22 3
+ ·
плюс
все члены попарных произведений вида cos(m6)cos(n6), при шфп.
Интегралы этих членов для разных попарных произведений легко взять, так
как
1 }
fcos(mQ)cos(nG)dG = -f[cos{(m-n)G} + cos{(m + n)Q}]d&
Эти интегралы легко взять, потому что интеграл от косинуса с ненулевым
аргументом (помните, гпфп) дает синус, и поэтому между заданными
пределами каждый из интегралов перекрестного произведения равен нулю. Итак:
Jln2{l-2xcos(0) + Ar2}de =
π 4 π 6 π
x2Jcos2(6)de +—Jcos2(26)de +—Jcos2(3e)de + ···
0 Δ 0 ^ 0
Из таблицы интегралов мы имеем:
θ sin(2fce)
2+ 4k
Jcos2(k6)de =
о
и тогда
π
Jln2{l-2xcos(9) + A:2}de = 4
π
2'
о
ИЛИ
2 х4 хв
х+¥+¥
1 г
2π
jfln2{l-2xcos(e) + x2}de = ^ + ^ + ^ + ··
248 ♦ Использование лРл для нахождения интегралов
Поскольку cos(6) изменяется от +1 до -1 на интервале интегрирования, мы
можем изменить знак в подынтегральном выражении, не меняя значение
интеграла, чтобы получить
2π·
Теперь, полагая χ = 1, мы имеем:
1 π
1 г
2тг
-/ln2{2 + 2cos(e)}de = l + l + l + ... = «2).
Мы приближаемся к завершению!
Если мы сможем найти интеграл справа, то получим знаменитый результат
Эйлера. Итак, продолжаем, формула двойного угла из тригонометрии говорит,
что cos(2a) = 2cos2(a) - 1, и тогда
«2>=-LjV
2cos2
ίθ)
2
de=— fin
= J-f41n2
2ni
2cos
ίθ)
2
\dQ = -fln2
n2
r
2cos
l'l
ν /J j
2cos
CD | CN
άθ.
- de =
Теперь пусть a = -, и тогда άθ = 2da. Следовательно:
ζ(2) = - pln2{2cos(a)}2da = - pln2{2cos(a)}t/a.
ТС ТС
Из формулы (7.3.2), при а = 2, мы видим, что
3
24'
/o4n2{2cos(a)}da = b.,
и тогда
ζ(2) =
π
π
з Ί
24
π
что и показал Эйлер (совершенно по-другому).
7.5. Опять интеграл вероятности
Ранее я показал, как некоторые из наших приемов можно объединить, чтобы
действительно придать потрясающую силу для особенно сложных интегралов.
Здесь я сделаю это снова, но теперь можно добавить к ним тождество Эйлера.
Во-первых, позвольте мне напомнить о формуле (3.7.1), где если мы установим
а = 1 и Ъ = 0, то получим
Опять интеграл вероятности ♦ 249
оо -.
(7.5.1)
Теперь заменим переменную χ = i/VE, где ζ - положительная величина. Тогда
ах = y/zdu, и поэтому
ОО ОО л
fex2dx = jeu2z4zdu = -л/π,
о
или
х-х?^*1
λ/ζ л/π о
Следующий шаг - это центральный трюк: умножим обе части на elz,
проинтегрируем по ζ от а до Ъ (где Ь > а > 0), а затем изменим порядок интегрирования
в полученном двойном интеграле справа. Когда мы делаем это, то приходим к
υ ιζ υ ι г) ии г) ии о
« VZ Jfl [VuJo J νπ-Jlfl
Внутренний интеграл легко берется:
№.
jez(iu2)dz-
9ζ(ί-*)
l-U
eb(i-u2)_ ea(i-u2)
Далее, предположим, что Ъ —> оо и α —> 0. Тогда первая экспонента в правой
части —> 0, а вторая экспонента —> 1. То есть1
i i-u2
и тогда (помня, что i2 = -1) мы имеем:
2 °г 1 , 2
» е*
■i + ir
re j zri, zr -z - и . δ ri-\-u
I ~^dz = —1= \ -—vdu = —= I -—- :——аи = -= I
J0Vz Jnii-u2 ^J0(i-u2)(-i-u2) V^J0l + iz
du.
Или если мы используем тождество Эйлера в z-интеграле и приравняем
вещественную и мнимую части, получим следующую пару уравнений:
cos(z) ,
о VZ νπ
ОО
/
г J и2
du
1 Математики захотят проверить, что ограничивающие операции Ь^ооиа^Ои
перестановка порядка интегрирования в двойной интеграл допустимы, но опять же
помните нашу руководящую философию в этой книге: просто сделайте это и
проверьте с помощью quad в конце.
250 ♦ Использование лРл для нахождения интегралов
J. -Jz ΛΊ 1+u4
Ранее в формуле (2.3.4) мы показали, что каждый из этих двух ιζ-интегралов
тгл/2
равен , и поэтому мы сразу получаем прекрасные результаты (где я снова
4
вернулся к фиктивной переменной интегрированиях):
J^dx=7s-^dx=R
i Ji { Ji V2
(7.5.2)
То есть оба интеграла численно равны 1.253314..., и мы проверяем этот
вывод с MATLAB: quad(@(x)cos(x)./sqrt(x),0,1000) =1.279... и quad(@(x)sin(x)./
sqrt(x),0,1000) = 1.235.... Эти числовые оценки функции quad не так хороши,
как многие из предыдущих проверок, которые мы сделали, и это потому, что
подынтегральные функции действительно не так малы даже при χ = 1000
(у/х не является быстрорастущим знаменателем, а числители не уменьшаются,
а просто бесконечно колеблются между ±1). Я скажу немного больше по этому
вопросу в главе 8.
7.6. За пределами интеграла Дирихле
Оглядываясь на интеграл Дирихле, который мы вывели в (3.2.1),
>sin(ax) _π
/ ^^dx = -, α>0,
•i x 2
οο
/
0
вам может прийти в голову спросить, чему равен интеграл
\sm(x)]2dx = ?
о I х I
На этот вопрос легко ответить, если вспомнить (3.4.1):
•cos(ax)-cos(bx) , π
~χ* *~~2
rcosiax)—costox) , π.,
J У2 'Ф = -(Ь-а).
о
Когда α = 0 и Ь = 2, мы имеем:
°rl-cos(2x),
J—^π^* = π>
о Λ
и поскольку 1 - cos(2x) = 2sin2(x), мы немедленно получаем ответ:
За пределами интеграла Дирихле ♦ 251
1М*-т
(7.6.1)
Это равно 1.57079..., и MATLAB подтверждает: quad(@(x)(sin(x)./x).A2,0,1000)
= 1.57056....
Хорошо, это было не очень сложно, и поэтому следующий очевидный
вопрос - спросить, чему равен интеграл
: ?
Ι ν I
На него немного сложнее ответить, но, конечно, не так уж и невозможно. Ин-
dx
тегрирование по частям делает необходимую работу. Пусть и = sin3^) и dv = —,
лг
■■ 3sin2(x)cos(A:) и ν = -. Таким образом:
№saf*-,
и поэтому
isin(A:)
/
dx
3
dx
sin (x)
2x2
2x2
3 fSin2(x)cos(x) _ 5 °psin2(x)cos(x) .
+u
dx
Снова интегрируем по частям: и = sin2(x)cos(x) и dv = —. Тогда ν
χζ
du
J.
χ
и — = 2sin(x)cos2(x) - sin3(x) = 2sin(x)[l - sin2(x)] - sin3(x) = 2sin(x) - 3sin3(x). Ta-
ким образом:
I
sin(x)
dx = -
2
sin2(x)cos(A:)
oo
sin(x)
dx-
;/
ο Ό
3
^2sin(x)-5sin3(x)dv
9 °rsm\x)^_Jn) 9°rsm\x)
4 *
-dx = 3
LP
ч *
-dx.
Поскольку
OO · ^ / \ OO
jsm0c)dx = j
3 1
— sin(x)—sin(3x)
-dx-
3fSin(x). 1 °psin(3x)
;/
4Jo *
-dx— / —-—-dx-
4-J x
4 2 4
'π^
π
4'
тогда
sin(x)
dx = 3
π
12π 9π
~8 8"'
252 ♦ Использование лРл для нахождения интегралов
или
оо
/
sin
(*)Г
dx-
3π
8 '
(7.6.2)
Это значение равно 1.1780972..., и проверка MATLAB подтверждает: quad(@
(x)(sin(x). /χ). Λ3,0,1000) = 1.178086....
оо
Продолжать в том же духе - чему равен, например, интеграл Г
sin(x)
\dxl-
это скоро окажется обременительным. Попытайтесь! Однако при более
систематическом подходе мы можем получить дополнительные интригующие
результаты с некоторым (небольшим) мучением. Мы начинаем с тождества
Эйлера и запишем:
ζ = elx = cos(x) + ίsin(x), ί = ν-1.
Тогда для любого целого т > 0:
zm = ешх = cos(mx) + zsin(mA')
— = z~m = e-
zm
и тогда
' = cos(mx) — isin(mx),
zm —- = /2sin(^A:).
В частности, для πι = 1
ζ — = /2sin(A:).
ζ
Поэтому
{/2sin(A:)}
-ИГ-
или раскладывая по биномиальной формуле (где вы вспомните обозначение
а!
V
{а-Ъ)\Ъ\
):
2п-1
{tfsinW}2"-1 = Σ
r=0
i2n-ll
г
( j."
ζ
2η-1
r=0
Г2П-Ц
Γ
Когда индекс суммирования г пробегает от г = 0 до г = 2п - 1, он принимает
2п значений. Половина из них имеет значения отг = 0дог=п-1 (для которых
За пределами интеграла Дирихле ♦ 253
показатель степени переменной ζ больше нуля), а другая половина (от г = η до
г = 2п - 1) дает те же показатели, но с отрицательными знаками. Итак,
учитывая симметричность биномиальных коэффициентов, мы можем написать:
{Пвт(х)}2"-1 =Σ(-1)Γ
г=0
Но
212-1
Г
(2п-1)-2г
1
(2п-1)-2г
_(2п-1)-2г _
1
*Г'"х'"" —^127 = i2 sin{(2n - 2r - ОД,
и тогда
{i2sin(*)}2^ = f>l)r
(2п-1)
г
2isin{(2n - 2г - 1)*} = f2и"122n_1 sin(x)2""1.
Здесь z2n_1 = z"(-l)n_1, и поэтому1
ί(- ΙΓ^2"-1 sin(x)2"-1 = ]П(- l)r
r=0
ИЛИ
2л-1
г
2isin{(2n-2r-l)*},
/_1чп-1 n-1
2n-l
2sin{(2«-2r-l)A:}.
(7.6.3)
Разделив обе части (7.6.3) над" и интегрируя от 0до оо, получим:
>sin(x)
(-1)'
П-1 л-1
/™^* = ^В-1>'
f2n-ll
г
If
sin{(2H-2r-l)x}
dx.
В интеграле справа заменим переменную на у = (2п - 2г - 1)*, и тогда
°°rsm{(2n-2r-l)x}dx= r
о х
sin(y)
о L·
dy
2n-2r-l
с»
У 2"
2n-2r-l
Таким образом:
η л Ζ r=n
i2n-ll
г
Мы можем упростить это выражение, вспомнив следующее комбинаторное
тождество, которое вы можете подтвердить, раскладывая обе стороны
равенства:
Л2п _.(Р)п _.(-!)" _.
Чтобы убедиться в этом, напишем i = ii = z— = i^—^— = i
(-1) (-1)
К-IT
254 ♦ Использование лРл для нахождения интегралов
V
kfe
=
s-1
fe-1
+
5-1]
,k \
Вот как этот результат поможет нам. Рассмотрим знакопеременную сумму
B-D'
fc=0
5
[к\
S
[о\
У
[lj
+
У
ί2]
( \
5
[з]
-\Л+-н-^т
( \
5
m
Первое слагаемое справа равно 1, а каждое из оставшихся слагаемых
раскладываем по нашему комбинаторному тождеству. Тогда мы имеем:
B-D'
fc=0
5
1
( л\
[5-1]
О
+(-1Г
+
( л\
5-1
{ 1 )
I 5-1 I
m-i
+
+
[5-1]
|5-1|
m
+
is-ΙΪ
2
is-И
2
+
|5-1|
3
+···+
Поскольку
is-И
О
1 и второе слагаемое в каждой квадратной скобке
сокращается с первым слагаемым в следующей квадратной скобке, мы видим, что
остается только последнее слагаемое в последней квадратной скобке. То есть
fc=0
5
= (-1)"
( л\
|5-1|
m
Тогда, при m = n-l,k = rns = 2n-l, мы имеем:
2n-i , 1ЧИ-1 (2п-2)
I
О
sin(*r-^(-^
χ 22"-1
п-1
или, поскольку (-1)" (-1)" =(-1)" = 1, мы получаем красивый результат:
сю
sin2""1 (χ)
άχτι
f2«-2l
п-1
(7.6.4)
Для η = 5, например, это говорит:
sin(x)
/sin^.
х
dx-
35π
256
=0.42951.
и проверкаMATLAB соответствует: quad(@(x)(sin(x).A9)./χ,0,1000) = 0.4292....
Теперь, оглядываясь на равенство (7.6.3) и умножая его на cos(x):
.(2η-ί\
г
(-1)'
п-1 п-1
sin^-'cosW = Ц-^-£(-1)'
sin{(2n—2r - l)x}cos(x),
За пределами интеграла Дирихле ♦ 255
вспоминая, что sin(a)cos(P) = -[sin(a + β) + sin(a - β)], мы имеем:
(2η-ί)
"sin{2(n - r)x} + sin{2(n - г - l)x}].
Тогда:
sin(x)2n-1cos(X)
0
oo
I
dX:
(-1)"^ гГ2и-Ц
z r=0
OO
sin{2(n-r)A:}
sin{2(n-r-l)A:}
dx
π
Для каждого значения г от 0 до η - 1 первый интеграл справа равен — - это
из интеграла Дирихле. Для каждого значения г от 0 до η - 1, за исключением г =
η - 1 (где аргумент функции синуса равен нулю), второй интеграл справа также
имеет значение —. Для г = η - 1 второй интеграл равен нулю. Итак, если мы
«допустим», что случаи г = п - 1 для второго интеграла также дает —, то можем
написать следующее (где последний член исправляет наше «допущение»!):
оо
sin(x)2n_1cos(x)
dx-
(-1)'
n-1 n-1
-"B-Dr
(2n-l)
r
π
i2n-ll
n-1
Теперь, как и прежде,
п-1
D-Dr
г=0
так что
(2л-11
г
= (-1)"
2п-2
п-1
оо
sinW-cosWdx=(-^
X 22„-1
π
ί2η-2) π
п-1
ί2ιι-2]
π-lj
(2п-Ц
п-1
π
2^
π
2*"
2η-1
η-1
ί2η-2)
η-1
ί2η-ΐ)
η-1
Или, поскольку
(2η-2)
η-1
ί2η-ί|
η-1
(2η-21
η-1
как вы можете легко проверить, разложив биномиальные коэффициенты, мы
имеем:
256 ♦ Использование лРл для нахождения интегралов
°°rsm2n-\x)cos(x)dx= π (2п-2\
Ι χ Χ~ 22ηη\ η-ί
χ 22ηη
Для η = 2, например:
Ι
χ
(7.6.5)
/гл
= — = 0.196382.
16
°psin(x)3cos(x) , _ π
о * *_2*2ч ,
И проверка MATLAB говорит: quad(@(x)(sin(x).A3).*cos(x)./x,0,1000) =
0.196382....
Чтобы закончить этот раздел, заметим, что
о Л
ах
можно интегрировать по частям следующим образом. Пусть и = sin2"^) и dv = —.
χ2
Тогда ν = — и — = 2nsin2n~1(x)cos(A'), и мы имеем:
a: dx
su?Mdx =
г Sin
sin2" (x)
о * о
оо _· 2п-1/
X
и вот теперь, учитывая (7.6.5), мы видим, что
π {2η-2}
п-1
J0 x2 22nn(n-lJ
г)2п-1
Таким образом, учитывая равенство (7.6.4), мы получаем интересный
результат:
W^x) _ W-'(x). _ _jr_
J" Υ2 Μ']' V2 aX-72n-l
(2п-2
η-ί
(7.6.6)
Например, если η = 19, то (7.6.6) показывает:
оо _· 38
sin38(x)
я^*=/
Sin57(*by- π
χ 237
36
18
0.20744.
иМАТЬАВ соглашается: quad(@(x)(sin(x).A38)./(χ.Λ2),0,1000) = 0.20628...Hquad(@
(x)(sin(x).A37)./x,0,1000) = 0.208078....
7.7. Дирихле встречает гамма-функцию
В этом предпоследнем разделе главы мы продолжим последовательность
вычислений, которую начали в предыдущем разделе, - нахождение интегралов
Дирихле встречает гамма-функцию ♦ 257
СЮ
/■
sin(x)
dx.
которые мы уже сделали для случаев η = 1, 2 и 3. Выполнение случая η = 4
становится сложной задачей, если только мы не увидим новый трюк. Это то, что
я покажу вам сейчас.
Мы начнем с интеграла (скоро вы увидите, почему)
сю
$uq-le-xudu.
Если мы изменим переменную на у = хи, то дифференцирование по у (считая
χ положительной «постоянной») дает
du = —dy.
χ
Тогда
[ич-1е-шаи = [ \Ц e~y-dy= Г*— е~Чу = — fy^e^dy.
J J у γ J л/Ч л/О. J
о о \л J л о л л о
Этот последний интеграл должен выглядеть знакомым - это
гамма-функция, определенная в (4.1.1), равная Y(q) = (q - 1)! Таким образом:
— = —!— (uq-le-mdu,
χ" (q-iY.J0
и поэтому
Ι χ' (q-DH Η
dx,
или изменив порядок интегрирования (это должно напомнить вам о том, что
мы делали в разделе 4.3):
оо'р^ч л оо Гею
J x" (q-DH Η
du.
Внутренний х-интеграл легко взять с помощью интегрирования по частям,
дважды. Я позволю вам заполнить детали, а результат будет такой:
сю
fe-xusinp(x)dx:
P(P-1)
P2+«2jo
сю
Je-xusinp-2(x)dx.
258 ♦ Использование лРл для нахождения интегралов
Предположим, что ρ четно (> 2). Затем мы можем повторять
интегрирование по частям, снова и снова, каждый раз уменьшая степень функции синуса
в подынтегральном выражении на 2, пока не уменьшим эту степень до нуля,
получая в конце интеграл
оо
Je xudx =
о
И тогда
оо
fe-xusmp(x)dx =
I
и
<1"
lp2+u2][(p-2f + u2]...[22 + u2]
ρ - четное.
Аналогично для нечетного р, за исключением того, что мы прекращаем
интегрирование, когда получаем степень функции синуса первой степени:
OU
Je-*"sinp(A:)iix =
)!
[р2 + и'][(р-2У + и']...[Г + и<]
Итак, у нас есть центральные результаты:
, р — нечетное.
sinp(x)
dx
, оо
— f
и
q-2
(i-l)!J0[iii+2i][iii+4i]...[iii+pi]
du, ρ —четное,
(7.7.1)
rsinpWdv= Ρ! Γ
{q-\)\W+lW + *\-A* + PA\
du, ρ-нечетное.
Чтобы ответить на вопрос, чему равен интеграл
оо
/
sin(x)
dx = ?,
(7.7.2)
который мы задали (но не ответили) сразу после (7.6.2), мы имеем ρ = q = 4
(и, следовательно, ρ четно), и тогда формула (7.7.1) говорит нам, что
sin(x)
Ъ1->0[и<+2'][и<+4<]
ου
du = 4f
[u2+4][u2+16]
-du.
Преобразования Фурье и интегралы энергии ♦ 259
Делая разложение на элементарные дроби, мы имеем:
1 4
/
sin(x)
dx = 4
I^""+I
и2 +16
-du
1, -if"
-tan Ί-
2 2
+ :
16
tan"1
2 4 2
= —tan_1(oo) +—tan_1(oo) = -tan_1(oo) =
3
или же
DO
/
sin(x)
[ dx
π
(7.7.3)
Это значение равно 1.047197..., и MATLAB соглашается: quad(@(x)(sin(x).
/χ).Λ4,0,1000) =1.0472....
Из всех этих расчетов вы можете подумать, что наши интегралы всегда
окажутся рациональным числами, умноженными на π. Это, однако, не
соответствует действительности. Например, предположим, что ρ = 3 и q = 2. Тогда мы
получим результат совершенно другой природы. Используя (7.7.2), потому что
ρ нечетно, имеем:
сю
/
sin3(x)
dx
3! ^ и
и{[и2+12][
-du = 6
W+У]
|ln(u2+l)-|ln(u2+32)
1 1
оо ΙΑ oo XX
[-%— du+ f^-^du
-In
0
2 . ·. \
u'+l
и2+Ъ2
-In
ln(32),
или наконец:
/
sin5(x)dA, = 5ln(5)
(7.7.4)
Это равно 0.8239592..., а проверка MATLAB дает quad(@(x)(sin(x).A3)./
(χ.Λ2),0,1000)= 0.82387....
7.8. Преобразования Фурье и интегралы энергии
В этом разделе мы вернемся к первой части и использованию там тождества
Эйлера. Здесь я покажу вам новую уловку, которая иллюстрирует некоторые
260 ♦ Использование лРл для нахождения интегралов
физические соображения, хорошо известные электротехникам и физикам,
которая позволяет нам получить некоторые очень интересные интегралы.
При изучении электронных схем обработки информации передача
импульсных сигналов во времени лежит в основе работы таких схем. Итак, начнем с
самого простого временного сигнала, одиночного импульса, конечного как по
амплитуде, так и по длительности. Например, пусть
[1 a<t<b
fit)-
(7.8.1)
0 при остальных t
где а и Ь являются положительными константами. (Для
инженеров-электронщиков конкретное время t = 0 просто для удобства соответствует
какому-нибудь особенно интересному событию, например «когда мы включили питание
в цепях» или «когда мы начали обращать внимание на выходной сигнал».)
Сигнал f(t) может быть, например, импульсом напряжения единичной
амплитуды и длительности Ъ - а (где, конечно, Ь> а). Если этот импульс напряжения
представляет собой, например, падение напряжения на резисторе, то
мгновенная мощность сигнала f(t) пропорциональна f2(t), что является прямым
следствием закона Ома для резисторов, закона, знакомого всем школьникам
старших классов из физики1. Поскольку энергия - это интеграл по времени от
мощности, то энергия этого сигнала f(t), обозначаемая как Wf, равна (так как
f\t) = 1)
оо Ъ
Wf = ff\t)dt = Jdt = b-a. (7.8.2)
—оо а
Все эти комментарии, по общему признанию, являются «инженерными»
по своему происхождению, но на самом деле, учитывая (7.8.1), даже чистый
математик, если его спросить об энергии f(t) в (7.8.1), также сразу напишет
(7.8.2). Физическая терминология силы и энергии была принята
математиками. Теперь дальнейшие размышления о проблеме энергии временного
сигнала приводят к понятию так называемого энергетического спектра этого
сигнала. Временной сигнал можно рассматривать как совокупность многих
(возможно, бесконечно многих) синусоидальных компонент разных
амплитуд и частот (обычно записываемых как ω = 2πν, где ν в циклах в секунду
или герцах, а ω в радианах в секунду). Энергетический спектр функции f(t)
представляет собой описание того, как полная энергия ^распределяется по
частотным компонентам функции f(t). Чтобы получить представление о том,
куда мы движемся с этим, предположим, что у нас имеется энергетический
спектр сигнала f(t), который я обозначу как £;(ω). Если мы проинтегрируем
Sf(u>) по всем ω, то должны получить полную энергию f(t), то есть Wf. Это
значит, используя (7.8.2):
1 Я напоминаю это только для полноты. Если закон Ома вас не интересует, это
нормально.
Преобразования Фурье и интегралы энергии ♦ 261
сю сю
Wf = J f\t)dt = J Sf(u>)du> = b-a, (7.8.3)
—oo —oo
и именно это равенство двух интегралов может дать нам некоторые вполне
«интересные интегралы». Итак, это наша непосредственная задача. Как
рассчитать энергетический спектр для данного временного сигнала? Ответ - это
преобразование Фурье.
Одним из замечательных результатов из так называемой теории Фурье
(в честь французского математика Жозефа Фурье (1768-1830)) является так
называемое преобразование Фурье. Если мы обозначим G(o)) преобразованием
Фурье произвольного временного сигнала g(t), то
оо
G(u) = fg(t)e-"°tdt. (7.8.4)
— оо
Мы можем восстановить g(t) из G(o)), взяв другой интеграл, называемый
обратным преобразованием:
л ОО
#(t) = —/С(оо)е'^о). (7.8.5)
—оо
Вместе g(t) и G(o)) образуют то, что мы называем парой1 преобразования
Фурье, обычно записываемой как
g(t) ~ ОД.
В общем случае функция G(o)) будет комплексной с действительными и
мнимыми частями β(ω) и Χ(ω) соответственно. То есть G(o)) = β(ω) + ίΧ(ω). Если
g(t) является действительной функцией времени (как, разумеется, все сигналы
в любой электронной схеме, которые действительно могут быть построены),
то G(o)) будет обладать некоторыми особыми свойствами. В частности,
функция β(ω) будет четной, а Χ(ω) будет нечетной. β(-ω) = β(ω) и Χ(-ω) = -Χ(ω).
Если в дополнение к вещественности g(t) обладает определенными
свойствами симметрии, то G(o)) будет обладать дополнительными соответствующими
специальными свойствами. Например, если g(t) четная (как cos(o)t)), то G(o))
будет действительной, а если g(t) нечетная (как sin(o)t)), то G(o)) будет мнимой:
Χ(ω) = 0 и β(ω) = 0 соответственно. Все эти утверждения легко
устанавливаются простым выписыванием интеграла преобразования Фурье с
использованием тождества Эйлера и рассмотрением подынтегральных выражений
интегралов β(ω) и Χ(ω) (эти утверждения настолько легко проверить, что на самом
деле они не появляются на уровне задач и упражнений, но вы должны быть
уверены, что сможете их решить).
1 Откуда берутся эти определяющие интегралы в паре Фурье, объясняется в любой
хорошей книге о рядах и/или преобразованиях Фурье. Или об инженерных трактовках
в том же духе, что и в этой книге, см. д-р Эйлер (примечание 1), с. 200-204.
262 ♦ Использование лРл для нахождения интегралов
Что делает операции (7.8.4) и (7.8.5) столь невероятно полезными для нас
в этой книге - это то, что называется теоремой Рэлея, в честь английского
математического физика Джона Уильяма Струтта (1842-1919), который получил
Нобелевскую премию по физике 1904 года и сегодня более известен как лорд
Рэлей (Lord Rayleigh). Он говорит нам, как рассчитать энергетический спектр
функции g(t) (и, конечно, функции f(t), которая является просто конкретным
выражением g(t)). Теорема Рэлея довольно легко выводится, что создает
любопытную загадку в истории математики, почему она не появлялась в печати до
относительно недавней даты 1889 года.
Мы начнем с записи
оо ои
Wg=fg2(t)dt=fg(t)g(t)dt
и затем заменим один из сомножителей g(t) во втором интеграле по формуле
обратного преобразования из (7.8.5). Так,
ОО Г л ОО
Wg=fg(t) — jG(o))e'wdco
at.
Поменяем порядок интегрирования:
ОО л Г ОО
Wg=f-G(a»\fg(ty»<dt
[άω.
Поскольку g(t) является действительной функцией времени - как бы
выглядел комплексный импульс напряжения на экране осциллографа?! - то
внутренний t-интеграл справа является сопряженным к G(o)), потому что интеграл
выглядит так же, как (7.8.4), за исключением того, что в экспоненте +/ вместо
-/. То есть
fg(t)eio"dt=G\o>),
так что
°° 1 ОО ι f~,s ч |2
W= Г—G(o>)G*(a>)da>= [Ι^^-άω.
8 J 2π J 2π
Или если теперь мы специально определим g(t) = f(t), то теорема Рэлея об
энергии есть
ОО ι τ-γ ч |2 ОО
Wf = fL^-doi = Jf\t)dt, F(oo) = Λ(ω) + ίΧ(ω),
— οο —οο
и поэтому энергетический спектр функции/(ί) в (7.8.1) равен, согласно (7.8.3),
5;(ω):
|F(co)|2
2π
- οο < ω < οο.
Преобразования Фурье и интегралы энергии ♦ 263
Для всех вещественных ДО |F(a))|2 = β2(ω) + Χ2(ω) будет четной функцией,
поскольку обе β2(ω) и Χ2(ω) четные.
Преобразование Фурье функции ДО, определенной формулой (7.8.1), есть
оо υ
F(o>) = Jf(t)e-i0"dt = je-i0"dt ■■
-ζω
_—ioib _—ίωα _—ίωα _—ioib
-ζω ζω
и поэтому энергетический спектр Дг) имеет вид:
^/(ω)=' η \ '■ (7.8.6)
2πω
Подставляя (7.8.6) в (7.8.3), мы получим:
1 °л Ιβ"ίωα - e~i<ub\2
— f- τ—-du = b-a. (7.8.7)
2nJ ω2
— oo
Теперь временно забудем всю упомянутую мной физику, то есть отложим
пока все эти дела о функциях времени и энергии, распределенных по частоте,
и просто воспринимайте (7.8.7) как чисто математическое утверждение.
Чтобы быть абсолютно уверенным, что мы сейчас думаем «чисто математически»,
давайте изменим фиктивную переменную интегрирования с ω на х, чтобы
написать
— Г- ^^dx = b-a, b>a. (7.8.8)
2*L x
Рассмотрим пока числитель подынтегрального выражения в (7.8.8):
используя тождество Эйлера, мы имеем
|е ^а — е г^ь|2^ |{cosC«at) — fsin(«A:)} — {cos(bAr) — ιsin(bA:)}|2 ^
= \{cos(ax) - cos(bx)} - i{sin(ax) - sin(bx)}| =
= {cos(ax)-cos(bA:)}2 + {sin(aA:)-sin(bA:)}2 =
которое, если вы перемножите и сгруппируете члены, принимает вид:
= 2[l-{cos(aA:)cos(bA:) + sin(flA:)sin(bA:)}].
Подставляя это в формулу (7.8.8), мы приходим к
1 7* l-{cos(fl^)cos(b^) + sin(fl^)sin(b^)} , , ,
— / —- — —'- — ——dx = b-a, b>a,
71 no *
— oo
или в слегка преобразованном виде (скоро вы увидите, почему):
°rl-cos(ax)cos(bx) , °r sin(ax)sin(bx) , п ч , ,-опч
\ ^^ —-dx- J —'——-—-dx = n(b-a), b>a. (7.8.9)
264 ♦ Использование лРл для нахождения интегралов
А теперь оглянемся на формулу (3.4.1), которую мы можем использовать для
записи этого интеграла (при частном случае содержащихся там параметров,
положив а равным нулю, а Ъ - единицей):
l-cos(u) , π
fl-C°2SWdu
J ц1
о и* 2'
или поскольку подынтегральное выражение четно:
I-cos(h)
J 1Г
Далее сделаем замену переменной в (7.8.10) на и = (а + Ь)х, и тогда
°г l — cos(ax + bx), 14J
Joo (« + Ь)2Х2
или используя тригонометрическое тождество для cos(ax + Ьх):
°°r l-[cos(ax)cos(bA:)-sin(aA:)sin(bA:)l
/ —- = 1-dx = (a + b)n,
rl-cos(ax)cos(bx) . r sm(ax)sin(bx) . I4 /««-их
J ^—^ -—-dx+ J -—-2—-—-dx = n(a + b). (7.8.11)
η r sin(aA:)sin(bA:) , Ι4 /Ί ч η ,
2J ^—^—^—^χ = π(α + &)-π(&-α) = 2πα, b>a,
и мы получаем, в слегка преобразованной форме:
l-cos(ax)cos(bA:) , °r sin(ax)sin(bA:)
-2 dX+J -2
-iaj —ОО
В заключение вычтем (7.8.9) из (7.8.11), чтобы получить
sin(aA:)sin(bA:)
или наконец:
sin(ax)sin(bA:)
Конечно, по симметрии подынтегрального выражения мы могли бы
одинаково правильно написать
°r sin(ax)sin(bA:) , , ,
J —-——2—-—-dx = nb, a>b.
-оо Х
Оба эти утверждения могут быть записаны как одно в виде:
г sm(ax)sm(bx) , Ί
Ι —'——-—-άχ = πα, b>a.
r sin(ax)sin(bA:) , . , , ч
I ——2—-—-dx = nmm(a,b).
(7.8.12)
В частном случае, если а = Ь, (7.8.12) сводится к следующему:
«Странные» интегралы из радиотехники ♦ 265
sin2 (αχ)
dx = πα,
а это, при а = 1, просто формула (7.6.1) (см. также задачу 7.5).
7.9. «Странные» интегралы из радиотехники
В этом разделе я покажу вам довольно интересные (почти странные)
интегралы, возникающие в теории радио (хотя я ограничусь в обсуждении чистой
математикой, и ни один транзистор, конденсатор или антенна не появятся).
Начнем с напоминания интеграла Дирихле из (3.2.1):
^sin(ta>)da) =
π
2'
0,
π
если
если
если
£>0
t = o,
£<0
(7.9.1)
2'
где я заменил параметры а и χ в (3.2.1) параметрами £ и ω соответственно.
Поскольку подынтегральное выражение в (7.9.1) является четным, мы можем
удвоить интеграл, интегрируя от -оо до оо. Таким образом:
/
sin(ta))
άω
ω
π, если £ > 0
0, если £ = 0.
—π, если £ < 0
(7.9.2)
В радиотехническом анализе установлено, что сигнал времени, равный -1
для отрицательного времени и +1 для положительного времени, очень полезен
(вы скоро поймете, почему). Ему дается специальное имя signum - пишется как
sgn(£) - за его свойства быть функцией знака (не путать с функцией синуса!).
Итак, (7.9.2) можно записать в виде:
/
sin(£a))
ω
da) = 7isgn(£).
Обратите внимание, что, используя тождество Эйлера, мы можем написать:
"cos(ta>), , .°psin(£a))
/t , г СОБ(ГШ) , . г
ω J ω J
ω
-da),
и поскольку первый интеграл справа исчезает, так как его подынтегральное
выражение нечетное, мы имеем:
Г άω = msgn(£).
J ω
(7.9.3)
266 ♦ Использование лРл для нахождения интегралов
Еще один временной сигнал, который радиоинженеры считают полезным,
тесно связанный с sgn(t), - это так называемая единичная ступенька, сигнал
равен нулю для отрицательного времени и +1 для положительного времени.
Обозначив его как u(t), мы можем связать u(t) и sgn(t) следующим образом:
т = ! + *&&. (7.9.4)
Эта единичная ступенька является константой для всех £, за исключением
t = 0, где он мгновенно переходит с 0 на 1, когда t переходит от
отрицательного состояния к положительному. Этот скачок происходит за нулевое время,
и поэтому «производная» от u(t) бесконечна при t = 0 и равна нулю для всех
t φ 0. Долгое время математики не считали производную от u(t) достойной
функцией, но тем не менее английский физик Пол Дирак (1902-1984) показал, что
работа с такой штукой, называемой импульсной функцией и записываемой как
δ(£), действительно может быть весьма полезной1. Дирак формально написал
6(t) = ^n(t),
at
и поэтому, формально дифференцируя (7.9.4), мы имеем:
rl + sgn(t)l
*>=ί
i^WPXTO.
Теперь, если (как обычно в этой книге) мы смело предположим, что можем
дифференцировать под знаком интеграла в (7.9.3), то
-f f^—dw = -=-{msgn(t)} = m-f{sgn(t)}= [=^—άω = ϊ [ειωΐάω.
dtJ ω dt dt J ω J
— oo — oo — oo
To есть
OO J
/eiMtdW = u-{sgn(t)}. (7.9.5)
Хотя Дирак получил в 1933 году Нобелевскую премию по физике, он был Лукасов-
ским профессором математики в Кембриджском университете (англ. Lucasian
Professor of Mathematics - именная профессура в Кембриджском университете. Одна из
самых престижных академических должностей в мире). Его физическое понимание
такой странной вещи, как бесконечная производная, было подкреплено (по его
собственному признанию) его бакалаврской подготовкой в области электротехники:
он закончил ее с отличием в университете Бристоля в 1921 году. Дирак был явно
«человеком на все времена»! Математика импульсов была поставлена на прочную
теоретическую основу с тех пор, как Дирак интуитивно использовал ее в квантовой
механике. Центральной фигурой в этом великом достижении, как правило,
считается французский математик Лоран Шварц (1915-2002), который опубликовал две
книги по теории распределений (1950, 1951). За эту работу Шварц получил медаль
Филдса 1950 года, часто называемую «Нобелевской премией по математике».
«Странные» интегралы из радиотехники ♦ 267
Из дифференцирования (7.9.4) мы имеем:
и тогда
^{sgn(t)} = 25(f).
Подставляя это в (7.9.5), получаем:
(7.9.6)
Это утверждение в (7.9.6) удивительно, потому что интеграл просто не
существует, если мы попытаемся его реально найти, поскольку emt даже не имеет
предела при χ\ω\ —> оо. При изменении ω и действительная, и мнимая части
emt просто колеблются при всех £, кроме нуля. Единственный способ понять
смысл (7.9.6), как это сделал Дирак, - интерпретировать интеграл слева как
набор напечатанных закорючек, обозначающих то же самое понятие, что и
напечатанные закорючки справа (для которых, по крайней мере, есть физическое
ощущение). Каждый раз, когда мы сталкиваемся с интегральными
закорючками, мы просто заменяем их закорючками «2πδ(ΐ)>>. Как вы вскоре увидите,
импульсы могут возникать с аргументами, более сложными, чем просто «£»,
общее правило состоит в том, что импульс уходит в бесконечность, когда его
аргумент исчезает. Так, например, δ(£ - £0) равно нулю для всех t φ t0 и
бесконечности при t = £0.
С помощью (7.9.3) и (7.9.6) мы теперь можем найти преобразования Фурье
2
sgn(£), δ(£) и u(t). Я утверждаю, что для sgn(£) его преобразование равно —. Что-
ζω
2
бы увидеть это, подставим — в интеграл обратного преобразования (7.8.5) для
ζω
получения
ΐωΐ
1 °° О 1 °° л
2π J ζω πζ J ω
—οο — οο
и затем вспомним (7.9.3), в котором говорится, что интеграл справа равен
msgn(£). To есть
1 °г еш 1
— / άω = —msgn(£) = sgn(£).
πζ J ω πζ
—οο
Итак, у нас есть пара преобразований
sgn(t)<-^- (7.9.7)
ζω
268 ♦ Использование у/-1 для нахождения интегралов
Энергетический спектр sgn(i) представляет функция
Sf(a>) =
2'2
ζω
— оо <ω<οο,
2π πω2
и поэтому, если мы проинтегрируем этот спектр по всем ω, получим
бесконечность. То есть sgn(t) - это сигнал с бесконечной энергией (что очевидно с
самого начала для сигнала, абсолютная величина которого равна 1 за все время),
явный признак того, что его фактически невозможно сгенерировать!
Далее я утверждаю, что преобразование Фурье δ(£) равно 1, и снова вы
можете увидеть это, поместив 1 в интеграл обратного преобразования (7.8.5), чтобы
получить
л ОО л ОО
— fleiMtdco = — [ешаш,
2πJ 2nJ
— oo —oo
и затем вспоминаем формулу (7.9.6), которая говорит, что интеграл справа
равен 2πδ(£). Итак, у нас есть пара преобразований
δ(ΐ) <-► 1. (7.9.8)
Энергетический спектр δ(£), одинаковый при всех ω, или, как иногда
говорят радиоинженеры, δ(£) имеет плоский спектр1. Из теоремы Рэлея мы видим,
что δ(£), как и sgn(i), является сигналом бесконечной энергии, и поэтому его
фактически невозможно сгенерировать. В отличие от сигнала sgn(i), эта
бесконечность не очевидна из временного поведения импульса (какое свойство
доминирует, бесконечное значение в один момент времени или тот факт, что
это всего лишь один момент времени?). Этот энергетический спектр дает нам
ответ.
Теперь, каково преобразование единичной ступеньки, u(t)? Из (7.9.4) мы
можем записать преобразование u(t) как сумму преобразований - и -sgn(t). To
есть, используя (7.9.7), мы имеем
00 1 1
u(t)++ [-ε-'ω1άί +—. (7.9.9)
J 2 /ω
— oo
«Все», что нам нужно сделать, - это выяснить, что такое интеграл справа
в (7.9.9), и для этого позвольте мне показать вам аккуратный трюк с
обозначениями. Посмотрите на (7.9.6). Поскольку это равенство, оно остается равен-
По аналогии с белым светом, в котором присутствуют равномерно все оптические
частоты (цвета), такое распределение энергии также нередко называют белым
спектром. Чтобы продолжить эту терминологию, говорят, что сигналы с энергетическими
спектрами, которые не являются плоскими (не белыми), имеют розовый (или
цветной) спектр. Кто сказал, что радиоинженеры не романтические души?!
«Странные» интегралы из радиотехники ♦ 269
ством, если мы выполняем одинаковые операции с обеих сторон. Итак, слева
заменим каждый ω на £, а каждый £ на ω, и справа сделаем то же самое. Тогда:
оо
JeIt0)d£ = 27i6(o)),
(7.9.10)
где δ(ω) - импульс в ω-области. Так же, как δ(£), который равен нулю для всех
£ φ 0 и бесконечен при £ = 0, так и δ(ω) равен нулю для всех ω φ 0 и бесконечен
при ω = 0. То есть вся бесконечная энергия сигнала, постоянная во все время,
не должна иметь энергии на любой ненулевой частоте, потому что в
противном случае сигнал не был бы постоянным, а скорее имел бы изменяющуюся во
времени составляющую.
Далее, изменим переменную в (7.9.10) на и = -£ (dt = -du). Тогда
оо —оо оо
feiMdt= JeiM(-u)(-ifa)= Je^du.
—оо оо —оо
То есть
оо
2πδ(ω)= fe-iaudii,
— оо
или если мы заменим фиктивную переменную интегрирования и обратно на V.
/ε-'ωίίίί = 2πδ(ω).| (7911)
Обратите внимание, из (7.9.10) и (7.9.11), что мы показали, следует:
оо оо
fe,0,tdt = 2πδ(ω) = $e-atdt.
—оо —оо
То есть δ(-ω) = δ(ω), и поэтому импульсная функция математически четна.
В любом случае интеграл справа в формуле (7.9.9) преобразования Фурье равен
πδ(ω), и теперь мы имеем пару
ΐ/(£)^πδ(ω) + —, (7.9.12)
ζω
и, конечно же, подобно sgn(£) и δ(£), функция u(t) является сигналом
бесконечной энергии.
Мы можем расширить физический смысл δ(ω), вычислив преобразование
Фурье чистого синусоидального сигнала cos(a)0£), -оо < t < оо. По определению,
это преобразование есть
оо оо ϊω0ΐ _|_ p-iu>0t -ι оо л оо
Jcos(a>0t)e-iwidt = J -—^—е~шй1 = - fe-'^-^dt + - fe-'^^dt.
270 ♦ Использование лРл для нахождения интегралов
Вспоминая (7.9.11), мы видим, что первый интеграл справа равен 2πδ(ω - ω0),
а второй интеграл справа 2πδ(ω + ω0). Итак, у нас есть пара
cos(a)0£) <-► πδ(ω - ω0) + πδ(ω + ω0). (7.9.13)
Поскольку импульс «возникает», когда его аргумент равен нулю, мы видим,
что вся (бесконечная) энергия чистого синусоидального временного сигнала
cos(o)0£) одинаково сконцентрирована на двух частотах1 ω = ±ω0.
Есть еще одно последнее свойство импульсной функции, которое важно
установить. Возвращаясь к формальному определению Дирака импульса как
производной от ступеньки, то есть
W) = ■%;№},
at
если мы формально проинтегрируем это равенство, получим:
fd(y)dy = J |-My)}dy = Jd[u(y)\dy = iiGoL, = n(t)-n(-oo),
— oo —oo У — oo
или, поскольку н(-оо) = 0,
[1, £>0
J8(y)dy = u(t)--
0, £<0
To есть хотя импульс имеет нулевую длительность, он тем не менее
«настолько бесконечен», что ограничивает единицу площади! Это невозможно
оправдать в рамках математики XIX века, поэтому математики так долго
отвергали импульс как абсолютную бессмыслицу (однако инженеры-электрики
и физики не имели с ним особых проблем, так как импульс решил многие из
их «реальных» проблем) - еще до работы Лорана Шварца.
Одним из интуитивно понятных способов «понять» этот результат
(мнение, распространенное среди физиков и радиоинженеров), является восприя-
1 ε ε
тие импульса как очень узкого импульса высоты - для — < £ < — (где ε ^ 0)
ε 2 2
и с нулевой высотой для всех остальных £. (Обратите внимание, что это
делает импульс четным, как и должно быть по нашим выводам после получения
(7.9.11).) Таким образом, этот импульс всегда ограничивает единицу площади,
даже если мы допустим ε —> 0. Теперь предположим, что ф(£) - любая функция,
В преобразовании есть две частоты из-за двух экспонент в интеграле
преобразования, каждая из которых представляет вращающийся вектор в комплексной
плоскости. Один вращается против часовой стрелки на частоте +ω0 (делая мгновенный
угол ω0£ с действительной осью), а другой вращается по часовой стрелке с
частотой -ω0 (делая мгновенный угол -ω0£ с действительной осью). Мнимые компоненты
этих двух векторов всегда сокращаются, в то время как действительные
компоненты складываются вдоль действительной оси, чтобы создать действительный сигнал
cos(a)0£).
«Странные» интегралы из радиотехники ♦ 271
ε ε
непрерывная при £ = 0. Тогда в пределах малого интервала — < £ < - функция
ф(£) не может сильно измениться и, таким образом, является практически
постоянной на протяжении всего этого интервала (приближение становится еще
лучше, если мы примем ε —> 0) со значением ф(0), и тогда можно написать:
оо ε л л
fWmt)dt =f\-№dt =φ(0)-ε = φ(0).
— оо 2
В более общем случае, если функция ф(£) непрерывна при £ = а, то
^(£-α)φ(£)<ί£ = φ(α).
(7.9.14)
Интеграл (7.9.14) часто называют свойством выборки импульса.
Теперь, чтобы закончить этот раздел, я приведу три простых теоретических
результата из теории преобразований Фурье. Мы найдем все три очень
полезными в следующем разделе. Для начала мы можем использовать тот же
нотационный прием, который использовали для получения (7.9.10), чтобы вывести
так называемую теорему двойственности. Предположим, у нас есть пара
преобразований g(t) <r+ G(o)). Тогда из интеграла обратного преобразования (7.8.5)
имеем:
л ОО
2π_
или, заменив £ на -£ в обеих частях равенства (что оставляет равенство
равенством), получим:
л ОО
2n_w
Затем, снова используя наш трюк со сменой символов (так что это метод!),
заменим £ на ω, а ω на £ - и получим:
л ОО
g(-cy>) = — jG(t)e-^dt,
—оо
или же
оо
2π#(-ω)= jG(t)e-'t<0dt.
— оо
То есть
если g{t) <-► G(co),
то G(£) <-► 2π£(-ω).
(7.9.15)
272 ♦ Использование лРл для нахождения интегралов
Наш второй результат, называемый теоремой масштабирования времени/
частоты, начинается с заданной пары преобразований f(t) <-» F(o)). Затем мы
спрашиваем: что будет в результате преобразования f(at), где а -
положительная постоянная? Ответ - это, конечно, интеграл
оо
ff(at)e-it(udt,
который, если мы заменим переменную на и = at (at = —), станет
а
ОО Μ J,, 1 OO
j те-^=l-J те
J a aJ
— OO —OO
To есть
если fit) <-> F(
1
mf(at) <-> —F
a
ω),
ω
a
•
4 du =
a
V
(7.9.16)
И наконец, если даны две временные функции g(t) и m(t) с
преобразованиями Фурье G(o)) и F(o)) соответственно, что представляет собой преобразование
Фурье функции m(t)g(t)? По определению, это преобразование есть
ОО ОО Г Λ ОО
fm(t)g(t)e-it(udt = Jm(t)\— JG(u)eiutdu
2π<
*dt,
где g(t) было записано в форме интеграла обратного преобразования Фурье
(я использовал и в качестве фиктивной переменной интегрирования во
внутреннем интеграле, а не ω, чтобы избежать путаницы с внешней ω). Продолжая,
если мы изменим порядок интегрирования, мы получим преобразование m(t)
g(t) как
00-| Г ОО 1 -| ОО Г ОО
f—G(u)\ fm(t)eiute-itu>dt\du = — [G(u)\ fm(t)e-'(u>-u)tdt
J 9тг J 9тг J «J
2π
2π
\du,
или, поскольку внутренний интеграл равен просто Μ(ω - и), имеем пару
преобразований Фурье
л ОО
m(t)g(t) <-> — [G(u)M(u> - u)du.
Этт J
2π
(7.9.17)
Интеграл справа в (7.9.17) встречается в математической физике так
часто, что имеет собственное имя: интеграл свертки, кратко записываемый как
«Странные» интегралы из радиотехники ♦ 273
0(ω)*Μ(ω)1. Поскольку нам все равно, какую функцию времени мы
называем m(t), а какую g(t), фактически свертка коммутативна, и поэтому m(t)g(t) <-»
—G(a>)*M(a>) = — Μ(ω)*σ(ω).
2π 2π
Мы будем использовать (7.9.17) в следующем разделе как чисто
математический результат, но, чтобы закончить этот раздел, вам может быть интересно
узнать, что именно поэтому радио и работает. И вот почему. Представьте, что
Алиса и Боб говорят в микрофон на радиостанциях А и В соответственно.
Поскольку звуки, создаваемые обоими, генерируются посредством одного и того
же физического процесса (вибрирующие голосовые связки человека), то
энергии двух голосовых сигналов будут концентрироваться, по существу, на одних
и тех же частотах, обычно от нескольких десятков герц до нескольких тысяч
герц. То есть частотный интервал, занимаемый электрическими сигналами,
создаваемыми на проводах, выходящих из микрофона Алисы, совпадает с
частотным интервалом, занимаемым электрическими сигналами,
создаваемыми на проводах, выходящих из микрофона Боба. Этот общий интервал частот
определяет так называемый спектр основной полосы частот, центрированный
на ω = 0.
Применение электрического сигнала основной полосы частот от микрофона
непосредственно к антенне не приведет к эффективному излучению энергии
в пространство, так как уравнения Максвелла для электромагнитного поля
говорят нам, что для эффективной связи антенны с пространством необходимо,
чтобы физический размер антенны был сопоставим с длиной волны
излучения (если вы не инженер-электрик или физик, просто поверьте мне на слово).
Например, на частоте основной полосы частот 1 кГц длина волны
электромагнитного излучения составляет один миллион футов, что довольно много.
Чтобы получить антенну разумного размера, нам нужно уменьшить длину волны,
то есть увеличить частоту.
То, что делается в коммерческом радиовещательном AM (амплитудно-мо-
дулированном) радио для достижения этой цели, заключается в том, чтобы
сдвинуть спектр основной полосы сигнала микрофона вверх примерно между
500 кГц и 1500 кГц, так называемый АМ-радиодиапазон. (Каждая
радиостанция США получает лицензию от Федеральной комиссии по связи (FCC), которая
дает ей разрешение выполнять сдвиг частоты вверх на величину, которую не
может использовать никакая другая станция в том же географическом районе.)
Например, при 1000 кГц длина волны в тысячу раз короче, чем при 1 кГц, то
1 Осторожно: символ * обозначает комплексное сопряжение при использовании его
в качестве верхнего индекса, как это было сделано в разделе 7.8 при обсуждении
энергетического спектра, и символ * обозначает свертку, когда используется в
строке. Уравнение (7.9.16) называется интегралом частотной свертки, чтобы отличить его
от двойника, интеграла временной свертки, который говорит m(t)*g(t) <-> G(a>)M(a>).
Мы не будем использовать эту пару в дальнейшем, но теперь вы сможете найти ее
просто для себя. Попытайтесь!
274 ♦ Использование лРл для нахождения интегралов
есть 1000 футов. Если антенна станции построена на четверть длины волны,
например, тогда у нее будет антенна высотой 250 футов, что примерно
соответствует тому, что вы увидите, когда в следующий раз проедете мимо
передатчика вашей местной радиостанции AM.
Итак, предположим, что на станции А сигнал основной полосы частот Алисы
сдвинут вверх на 900 кГц, а на станции В сигнал основной полосы частот Боба
сдвинут вверх на 1100 кГц. Затем радиослушатель выбирает, какой сигнал
прослушивать, используя надстраиваемый фильтр с центром либо в 900 кГц, либо
в 1100 кГц (в АМ-радио полоса пропускания такого фильтра составляет 10 кГц,
и знание того, как проектировать такой фильтр, является частью набора
навыков радиоинженеров). Обратите внимание, что радио использует сдвиг
частоты вверх по двум причинам: (1) для перемещения энергии основной полосы
до так называемой «радиочастоты» для достижения эффективного излучения
энергии и (2) для разделения энергий основной полосы нескольких
радиостанций с использованием различной частоты сдвига вверх на каждой станции.
В приемнике нам нужен окончательный сдвиг частоты вниз, чтобы поместить
энергию выбранного сигнала станции обратно на частоты основной полосы,
на которые реагируют наши уши.
Выполнение этих сдвигов частоты как вверх, так и вниз так же просто, как
и умножение1. Вот как (7.9.17) работает с повышением частоты передатчика.
Пусть Μ(ω) - преобразование Фурье микрофонного сигнала Алисы или Боба.
Затем, вспоминая (7.9.13), преобразование для cos(a)0£), (7.9.17) говорит нам,
что преобразование m(£)cos(a)0£) есть
ч ОО
Μ(ω) * [πδ(ω — ω0) + πδ(ω + ω0)] = — Γ [πδ(η — ω0) + πδ(ι/ + ω0)] Μ(ω - u)du =
—οο
-J ΟΟ
= - Γδ(ι/-ω0)Μ(ω-ι/)ίίι/ +
— οο
л ΟΟ
+ - Γδ(ι/ + ω0)Μ(ω-ι/)ίίι/,
— οο
и, помня (7.9.14), свойство выборки импульса, преобразование m(£)cos(a)0£)
равно - Μ(ω - ω0) + - Μ(ω + ω0). То есть в то время как энергетический спектр
m(t) центрирован на ω = 0, энергетический спектр m(£)cos(o)0£) центрирован
на частоте ω = ±ω0. Энергетический спектр основной полосы частот
исходного сигнала m(t) теперь соответствует дополнительному значению cos(o)0£)
(живописно называемому радиоинженерами несущей частотой) и эффективно
1 Если честно, умножать на радиочастоты нелегко. Чтобы узнать, как радиоинженеры
выполняют умножение без фактического умножения, см. книгу: Д-р Эйлер (Dr. Euler).
С. 295-297, 302-305 или мою книгу: Наука о радио (The Science of Radio). Springer,
2001. С. 233-249.
Причинность и интегралы преобразования Гильберта ♦ 275
излучается в пространство с помощью физически «короткой» антенны. При
использовании в радио соотношение (7.9.17) называется гетеродинной
теоремой1.
7.10. Причинность и интегралы преобразования
Гильберта
Вспомним, что в разделе 7.8 я сделал следующие утверждения об общей паре
преобразований^*:) <-» G(o)): в общем случае G(o)) будет комплексной, с
действительной и мнимой частями β(ω) и Χ(ω) соответственно. То есть G(o)) = R(cu) +
ίΧ(ω). Если g(t) является действительной функцией времени (как, впрочем,
и все сигналы в любой электронной схеме, которые могут быть построены), то
G(o)) будет обладать некоторыми особыми свойствами. В частности, β(ω) будет
четным, а Χ(ω) - нечетным: R(-cu) = R(cu) и Χ(-ω) = -Χ(ω). Если в
дополнение к вещественности функция g(t) имеет определенные свойства симметрии,
то G(o)) будет иметь дополнительные соответствующие специальные
свойства. Например, если g(t) четная (как и cos(a)t)), то G(o)) будет действительной,
а если g(t) нечетная (как sin(a)t)), то функция G(o)) будет чисто мнимой: Χ(ω) = 0
и β(ω) = 0 соответственно.
Если мы теперь наложим еще больше ограничений на g(t), то, как и
следовало ожидать, будет еще больше ограничений на R(cu) и Χ(ω). Одним из
ограничений, которое является фундаментальным для реального мира, является
причинность. Чтобы понять, что это значит, предположим, у нас есть то, что
инженеры-электронщики называют «черным ящиком» со входом и выходом.
(Термин «черный ящик» означает, что мы не знаем деталей схемы внутри
коробки и, действительно, нам все равно, что там.) Все, что мы знаем, - это то, что
если мы подадим входной сигнал, начинающийся в момент времени t = 0, то,
каким бы ни был выходной сигнал, он должен быть нулевым при t < 0. То есть,
до того как мы подали сигнал на вход, не должно быть никакого выхода. В
противном случае у нас есть то, что называется упреждающим выходом, что
является деликатным названием для машины времени! Итак, вот наш вопрос. Если
g(t) является выходным сигналом, вещественным и нулевым для всех t < 0,
что еще мы можем сказать о его преобразовании Фурье G(o)) = R(cu) + ζΧ(ω)?
Чтобы начать наш анализ, запишем g(t) как сумму четной и нечетной
функций времени, то есть
1 Математика всего этого была, конечно, известна задолго до изобретения АМ-радио,
но название данной теоремы принадлежит американскому инженеру-электрику
Реджинальду Фессендену (1866-1932), который в 1901 году запатентовал идею
умножения для использования в радиосвязи. Слово «гетеродин» происходит от греч. heteros
(для внешнего) и dynamic (для силы). Фессенден считал сигнал cos(o)0t) «внешней
силой», генерируемой самой схемой радиоприемника для окончательного понижения
частоты принимаемого сигнала до основной полосы частот (действительно,
радиотехники называют эту часть радиоприемника AM контуром местного гетеродина).
276 ♦ Использование лРл для нахождения интегралов
g(t)=ge(t)+g0(t), (7.10.1)
где, по определению,
ge(-t)=ge(t),g0(-t) = -g0(t).
То, что действительно мы можем представить g(t) таким образом, проще
всего показывается простой демонстрацией того, что такое ge(t) и g0(t) (мы
сделали это еще в главе 1, но здесь это снова). Из (7.10.1) мы можем написать
g(-t)=ge(-t)+go(-t)=ge(t)-g0(t), (7.10.2)
И, складывая (7.10.1) и (7.10.2), мы получаем:
ge(t) = ^[g(t) + g(-t)]y (7.10.3)
И, вычитая (7.10.2) из (7.10.1), получаем:
g0(t) = \[g(t)-g(-t)]· (7·10·4)
Итак, (7.10.1) всегда можно написать.
Поскольку сигнал g(t) является причинно-следственным (и тогда по
определению g(t) = 0 при ί < 0), из (7.10.3) и (7.10.4) имеем:
, если t > 0,
g0<t) = \g<t)
ge(t)=^g(-t)
λ , если t < 0.
g0(t) = ~g(-t)
To есть
ge(t)=go(t), t>0,
&(t) = -go(t), t<0,
и тогда
&(i)=&(i)sgn(t). (7.10.5)
Аналогичным образом мы также можем написать:
&(9=&(t)sgn(t). (7.10.6)
Теперь, согласно (7.10.1), мы можем написать:
G(co) = Ge(co) + G„(co),
Причинность и интегралы преобразования Гильберта ♦ 277
и поскольку функция ge(t) четная, мы знаем, что функция Ge(a)) чисто
вещественная, в то время как#0(£) нечетна, и мы знаем, что G0(o)) чисто мнимая. Таким
образом,
Ge(a)) = Д(о))
и
σ0(ω) = ϊΧ(ω).
Теперь вспомним пару преобразований из (7.9.7):
2
sgn(t)<->—.
ζω
Из (7.10.5) и теоремы о частотной свертке (7.9.17) имеем:
G>) = ^-G0(a))*-,
2π ζω
и тогда, используя (7.10.7) и (7.10.8),
Д(о)) = — /Χ(ω) * — = - ίΧ(ω) * —.
2π ζω π ζω
Также из (7.10.6) и теоремы о частотной свертке имеем:
G„(co) =
2π /ω
и тогда, используя (7.10.7) и (7.10.8),
/Х(со) = ^-Д(со)=Д,
2π /ω
или
Χ(ω) =
•-Λ(ω)*—.
π /ω
(7.10.7)
(7.10.8)
(7.10.9)
(7.10.10)
Записав свертки (7.10.9) и (7.10.10) через интегралы, приходим к
следующему:
1 °г Х(и)
π J ω-ы
1 °г R(u)
π J ω —и
du.
(7.10.11)
Эти два уравнения показывают, что β(ω) и Χ(ω) определяют друг друга для
причинно-следственного сигнала. Интегралы, связывающие ^(ω) Μΐ(ω), назы-
278 ♦ Использование лРл для нахождения интегралов
ваются преобразованиями Гильберта1, имя, введенное нашим старым другом
в этой книге Г. X. Харди. Харди впервые опубликовал преобразование на
английском языке в 1909 году, но когда он позже узнал, что немецкий математик
Давид Гильберт (1862-1943) знал об этих формулах с 1904 года, Харди начал
называть их преобразованиями Гильберта. Но и Гильберт не был первым, так
как они появились десятилетиями ранее в докторской диссертации 1873 года
русского математика Юлиана-Карла Васильевича Сохоцкого (1842-1927).
Обратите внимание, что преобразование Гильберта не меняет область, как
и преобразование Фурье. То есть в (7.9.11) преобразование Гильберта
находится в одной и той же области (ω) с обеих сторон уравнений. Можно также взять
преобразование Гильберта функции времени2 x(t) и получить новую функцию
времени, которую мы обозначим как x(t):
ф) = ±- 7^-du. (7.10.12)
π J t-u
— oo
Например, если x(t) - любая постоянная функция времени (назовем ее к),
то ее преобразование Гильберта равно нулю. Чтобы показать это, я
воспользуюсь нашим старым приемом для обработки сингулярности подынтегральной
функции при и = L То есть
π J t — u π
— oo
Меняя переменную в обоих интегралах справа на s = t - и (ds = -du),
получаем:
1 Их также иногда называют соотношениями Крамерса-Кронига в честь голландского
физика Хендрика Крамерса (мы встречались с ним в разделе 6.5 при обсуждении
тройных интегралов Уотсона/Ван Пейпа) и американского физика Ральфа Кронига
(1904-1995), который столкнулся с (7.10.11) при изучении спектров рентгеновских
лучей, рассеянных атомными решеточными структурами кристаллов. См. задачу 7.9
для альтернативного способа написания (7.10.11).
2 Комбинируя временной сигнал x(t) с его преобразованием Гильберта для
образования комплексного сигнала z(t) = x(t) + ix(t)y вы получаете то, что родившийся
в Венгрии инженер-электрик Деннис Габор (1900-1979) - он получил Нобелевскую
премию по физике 1971 года - назвал аналитическим сигналом, который
представляет большой интерес для инженеров, изучающих однополосное радио (SSB).
Чтобы увидеть, как аналитические сигналы встречаются в теории радио SSB, см. книгу:
Д-р Эйлер. С. 309-323.
du
du
г аи г аи
J t-u J t-u
Причинность и интегралы преобразования Гильберта ♦> 279
'~Τί ds)
s
f—di/+ Γ—du
J s J s
du
log^0>r_ ln(s)|; +ln(5)|-
= - log^0,r_ [1η(ί + Τ) - 1η(ε) + 1η(-ε) - 1η(ί - Γ)] =
log^0>r^
In
In
t + T)
ε J
(t+r
fin
ε
\{τ~-
t-
у
-t)
ε Υ
Γ J|
и тогда, заметив, что ε сокращаются:
x(t) = -logT^o
π
In
(t + T)
T-t
= -ln(l) = 0.
π
Это дает нам интересное равенство
] — -
t-u
(7.10.13)
Чтобы закончить данный раздел, позвольте мне провести вас через анализ
конкретного причинно-временного сигнала, который закончится открытием
еще одного интересного интеграла. Для начала вспомним преобразование
Фурье функции ДО в (7.8.1):
F(co) =
для
fit)--
p-iu>a p-iu>b
ζω
1, a<t<b
0, при остальных t
Предположим, что мы установили а = — и Ъ = -. Тогда у нас получается сиг-
нал, который достаточно важен в радиотехнике, чтобы иметь собственное имя
(оно называется гейт-функцией) и собственный символ π(ΐ). То есть
280 ♦ Использование у/-1 для нахождения интегралов
π(ί) =
1,
-I<t<i
2 2
(7.10.14)
[О, при остальных t
Преобразование Фурье функции π(ί) есть
2/ sin
Π(ω) =
/ Ν
(λ)
2
sin
( \
ω
—
l2j
ζω
ζω
ω
-οο<ω<οο.
(7.10.15)
Из теоремы двойственности (7.9.15) мы имеем, используя (7.10.14) и (7.10.15),
пару1
П(£) <-> 2τπτ(-ω),
и тогда
sin
2ππ(—ω) = 2ππ(ω),
(7.10.16)
потому что π(ω) является четной функцией. Далее, применяя теорему
масштабирования времени/частоты (7.9.16) при а = 2, соотношение (7.10.16) говорит:
sin(t)
<-> тш
Поскольку гейт-функция равна 1 на интервале, где ее аргумент меняется от
1 1/ 1 со 1
_-до - (этот интервал есть — < — < -, или -1 < ω < 1), мы имеем:
Zi Zi Ак Ак 2ι
sin(t)
π, -1 < ω < 1
0, при остальных t
(7.10.17)
Теперь временной сигнал в (7.10.17) не является причинно-следственным
сигналом, поскольку он существует для всех ί, но мы можем использовать его
для создания причинно-следственного сигнала (ноль при t < 0), умножив его
на функцию ступеньки. То есть
Осторожно: обратите внимание на двойное использование символа «π» - только для
числа и снова для имени гейт-функции. Однако путаницы никогда не будет, потому
что гейт-функция всегда будет обозначаться с аргументом, а если просто π - это число.
Причинность и интегралы преобразования Гильберта ♦ 281
является причинно-следственной функцией времени. Как мы показали в
начале этого раздела, мы всегда можем записать любую причинно-следственную
функцию времени в виде суммы четной функции и нечетной функции, где
- л, 1 /*л - sin(t)
четной функцией является —g(t), которая для нашей задачи здесь есть —.
А АС
Напомним также, что мы показали, что действительная часть G((o) полностью
связана с этой четной функцией времени. Так,
sin(t)
2t
•Д(а>).
Оглядываясь назад на (7.10.17), мы видим, что
sin(t)
It
sin(t)
Д(а>) =
π
2'
-1<ω<1
0, при остальных t
Итак, из (7.10.11) мы можем найти Χ(ω), мнимую часть G((o), как
(7.10.18)
πJω-ι/ 2J,u>-u
Найти этот интеграл не так просто, как может показаться на первый взгляд.
Это потому, что при и = ω есть особенность. Если |ω| > 1, эта особенность не
находится в интервале интегрирования, и мы можем действовать очевидным
образом. Заменим переменную на s = ω - ι/, и, таким образом, ds = -du. Тогда:
*<»>~;7trM/
=-1п(5)г;=-1п
2 Ιω+1 2
ίω-1)
[ω + lj
|ω|>1.
Для |ω| > 1 аргумент логарифмической функции положительный, и все в
порядке. Однако для случая |ω| < 1 аргумент отрицательный, и функция log дает
мнимый результат, что нехорошо. Причина этой трудности заключается в том,
что когда |ω| < 1, особенность находится в интервале интегрирования.
Исправление заключается в использовании нашего хитрого трюка. В
пределе, при ε —> 0, мы пишем:
Χ(ω) = -
_1
"2
_1
~ 2
du
Г_аи_+г
J /,\ — 11 J
ω-u
i^C+^C1
du
ω —
ιω—1
и
—
1
"2
1
2
Η
Щ
ω+1 V 3 )
ω + lj
-ь
η
т
-ε J
=
In
ω + 1
+ 1η
(λ ^l
1-ω
282 ♦ Использование лРл для нахождения интегралов
или, сокращая ε еще до того, как мы положим ε —> 0:
|ω|<1.
л (л \
ν. Ι. 1-ω
Χ(ω) = -1η
2 [ω + lj
Мы можем объединить оба случая, |ω|>1π|ω|<1, одновременно, записав
так:
Χ(ω) = -1η
V } 2
1-ω
ω + 1
-οο<ω<οο.
(7.10.19)
Теперь из теоремы Рэлея об энергии и (7.10.7) можно записать:
ОО л ОО
— оо —оо
а из теоремы Рэлея об энергии и формулы (7.10.8) мы можем написать:
ОО л ОО
fg20(t)dt = — fx2(o>)do>.
—оо —оо
Из (7.10.5) или (7.10.6) мы видим, что интегралы по времени (левые части
этих формул) явно равны, и поэтому должны быть равны и частотные
интегралы. То есть для причинно-следственного сигнала:
оо оо
fR2((3})d(3}=fx2((3})d(u.
— оо —оо
Поскольку соотношение (7.10.18) говорит
оо 12 2
— оо —1
тогда, используя (7.10.19) в интеграле Χ(ω), мы имеем:
2'
ОО л
J 2
— оо
J-»oo \ poo
= — ι , мы получили красивый результат:
0 9 J —оо
Γΐη2
Jo
1-х
1 + Х
dx = π2.
(7.10.20)
Это значение равно 9.8696..., и MATLAB соглашается: quad(@(x)log(abs((x-l)./
(х+ 1))).л2,0,10000) = 9.8692....
Задачи и упражнения ♦ 283
7.11. Задачи и упражнения
(С7.1). Чему равно значение интеграла
isin(A:)l"
/
dx
о ι х
для η = 5,6 и 7?
(С7.2). Используйте тождество Эйлера, чтобы показать, что если
оо оо
F(x) = J Jsin(£2 - и2)dtdu,
χ χ
toF(X) тождественно равна нулю (то естьДх) = 0 для всех*). Подсказка:
вспомните раздел 6.4, где обсуждается оптический интеграл Харди-Шустера, там мы
использовали тригонометрическую формулу для cos(a - Ь), чтобы установить,
что если С(х) и S(x) являются косинусными и синусными интегралами Френе-
ля соответственно, тогда С\х) + S\x) = J J cos(t2 - u2)dtdu. Начните сейчас
poo . 2
с J elt dt = C(x) + iS(x) и посмотрите, куда это вас приведет. (В какой-то
момент подумайте о том, чтобы взять сопряжение.) Это (я думаю) неочевидный
результат, и просто для того, чтобы дать вам уверенность в его правильности,
в следующей таблице показано, что пакет символьных вычислений MATLAB
Symbolic Math Toolbox численно находит значения F(x) для различных
произвольно выбранных значений х, используя код
syns t и
int(int(sin(tA2-uA2),t,x,inf),u,x,inf)
Числовое значение χ подставлялось во вторую строку перед каждым
выполнением.
X
-7
-2
0
1
5
29
F(x)
-1χ1(Γ33-ζ3.03χ1(Γ34
0
0
-Ι.όχΙΟ"34
-9* ΙΟ"36
-2χ1(Γ37
(С7.3). В недавней работе1 по физике встретились интегралы вида
dx
I
JT-
IX
1 Carl Bender, et a\. Observation of PT phase transitions in a simple mechanical system //
American Journal of Physics. March 2013. P. 173-179.
284 ♦ Использование лРл для нахождения интегралов
Авторы без доказательства утверждают, что этот интеграл существует.
Показать, что это утверждение - на самом деле правда. Подсказка: использовать
теорему из математического анализа, которая говорит, что
IX) IX)
Jf(x)dx\<J\f(x)\dx,
которая, используя интерпретацию интеграла Римана как площади, должна
быть для вас очевидна для случая, когда функция f(x) является вещественной.
Используя контурные интегралы в комплексной плоскости (см. главу 8), эту
теорему можно распространить на случай, когда Дх) является комплексной.
(С7.4). Вспомните интеграл, с которым мы работали в первой главе (п. 1.8),
-м-1
Г -dx = -l + ln(V2Tij, а также интегралы второй и третьей задач гла-
Jl χ
poo (χ)
вы 5: \ ^-dx = 1 — γ, где {х} - дробная часть числа χ и γ - постоянная Эйлера,
и ζ(5) = ^—= — 3 f ^-dx. Посмотрите, можете ли вы применить тот же
к=\ К 2 1 X
трюк, который мы использовали там, чтобы показать, что
№ = 1-1
Ji хъ 12'
тг2
теперь, когда мы формально вычислили ζ(2) = — (в разделе 7.4). MATLAB мо-
6
π2
жет дать вам уверенность, что это правильно, так как 1 = 0.177532..., в то
время какquad(@(x)(xfloor(x))./x.A3,1,100) = 0.177279....
(С7.5). Выведите более общий вид равенства (7.6.1), дифференцируя
"•sin2 (αχ)
т/ ч Г Sin {UX) ,
χ
относительно параметра а. То есть покажите, что 1(a) = —\а\9 и поэтому (7.6.1)
является частным случаем, когда а=\.
(С7.6). Посмотрите результаты в (4.3.10) и (4.3.11) и покажите, как интегралы
Френеля сразу вытекают из них.
(С7.7). Применить теорему Рэлея к временному сигналу
\е~а\ 0<t<m
[ 0, при остальных t
где а и m оба - положительные константы. Подсказка: вы должны обнаружить,
что повторно вывели (3.1.7) способом, сильно отличающимся от метода,
используемого в главе 3.
Задачи и упражнения ♦ 285
(С7.8). Найти преобразования Фурье следующих временных сигналов:
(а)ф;
(Ь)
t2+i
(с) >+/έ?
(A)E,(ty.
ου -и
f—du,
Ч и
t>0
О, t<0
Подсказка: для (а) вы можете найти полезным (3.1.7), для (Ь) не забудьте
любимый трюк Фейнмана (о дифференцировании интегралов), а для (с)
вспомните (7.9.3) и (7.9.14). (Преобразование Фурье комплексного сигнала времени
в (с) лежит в основе радио SSB.) И наконец, для (d) сделайте замену
переменной х = —, запишите интеграл преобразования Фурье (который, конечно, будет
двойным интегралом), а затем измените порядок интегрирования. (Возможно,
таинственно выглядящий E^t) является экспоненциально-интегральной
функцией, он встречается во многих передовых приложениях техники и физики.
Например, в исследовании длительного свободного падения через атмосферу
с переменной плотностью с квадратичной силой сопротивления см. мою
книгу: Электрическое одеяло миссис Перкинс и другие интригующие истории
математической физики. Princeton University Press, 2009. С. 70-78. (Mrs. Perkins's
Electric Quilt and other intriguing stories of mathematical physics)).
(C7.9). Из первого интеграла преобразования Гильберта в (7.10.11) мы видим,
„, ч г~ Х(и) , г о χ(μ) , Гоо χ(μ) , _
что можем записать π.Κ(ω) = / —±^-du = \ —^-аи+ I —^-аи. Если x(t)
J-oom — u J-°°o)-i/ Jo ω —и
вещественное, то β(-ω) = β(ω) и Χ(-ω) = -Χ(ω), и поэтому, если мы сделаем
замену переменной s = -и в первом интеграле справа, получим
π*(ω)= r^)(-ds)+ rmdu=-rmds+ rmdu=
Jo ω + s Jo ω-u Jo ω + s Jo ω-u
1 1
lu
X(u)\ \du= f X(u) 2 2du
0 [ω-u ω+ι/ Jo ω-u
To есть альтернативная форма для первого интеграла преобразования
Гильберта в (7.10.11) есть #(ω) = 2 /π Γ du. Используйте этот же подход, что-
Jo ω - и
бы найти альтернативную форму для второго интеграла преобразования
Гильберта в (7.10.11), который дает выражение Χ(ω) как интеграл οτβ(ω) для случая
вещественного сигнала x(t).
286 ♦ Использование лРл для нахождения интегралов
(С7.10). Предположим, что x(t), y(t) и h(t) являются временными сигналами, так
что выполняются следующие три условия:
(a) x(t) имеет конечную энергию;
x(u)h(t-u)du;
-оо
/оо
|й(0|Л<оо.
-оо
Покажите, что у(£) имеет конечную энергию. Подсказка: используйте
преобразования Фурье, теорему Рэлея об энергии и посмотрите на подсказку для
(С7.3).
(C7.ll). Вычислить преобразования Гильберта функций cos(a)0£) и sin(a)0£).
Подсказка: используйте тождество Эйлера в определенном интеграле для
преобразования Гильберта временного сигнала, вы также можете обнаружить, что
полезно вспомнить (7.9.3).
Глава
Контурное интегрирование
8.1. Вступление
В этой предпоследней главе книги я предлагаю вам очень быструю,
сокращенную, «ускоренную» презентацию самых основ теории комплексных функций
и применения этой теории к одной из жемчужин математики: контурному
интегрированию - и ее использованию при нахождении определенных
интегралов. В начале этой главы я буду предполагать, что вы знакомы с комплексными
числами и с операциями над ними. Я, конечно, уже делал это в главе 7 и
поэтому думаю, что не ошибаюсь, предполагая это. Первые несколько разделов
заложат теоретическую основу, а затем, совершенно неожиданно, вы увидите, как
все они собираются вместе, чтобы дать нам красивую и мощную технику
контурного интегрирования. Каждый из этих предварительных разделов не очень
сложен, но каждый абсолютно необходим для понимания. Не пропустите их!
В соответствии с духом этой книги изложение теории в значительной
степени опирается на интуитивные, правдоподобные аргументы, и хотя я не
думаю, что делаю что-то дико возмутительное, хотя надо признать, будут случаи,
когда профессиональные математики могут почувствовать легкие уколы.
(Математики - это довольно сложная группа, и они выживут!) Здесь уместно
процитировать математика Джона Сталкера (John Stalker из Тринити-колледжа,
Дублин), который однажды написал: «В математике, как и в жизни,
добродетель не всегда вознаграждается и порок не всегда наказывается [мой курсив]»1.
Как всегда, я буду чувствовать себя оправданным, когда после ряда
манипуляций численные расчеты MATLAB будут соответствовать любому
теоретическому результату, который мы только что получили.
8.2. Криволинейные интегралы
Представьте себе две точки, А и Б, в двумерной плоскости хОу. Далее
представьте, что А и В являются двумя конечными точками кривой С на
плоскости, как показано на рис. 8.2.1. Точка А является начальной, а В - конечной
1 В своей книге: Комплексный анализ: основы классической теории функций. Birkhaus-
ег, 1998. С. 120 (Complex Analysis: Fundamentals of the Classical Theory of Functions).
288 ♦ Контурное интегрирование
точкой. Теперь предположим, что мы делим С на π частей (или дуг), причем
fe-я дуга имеет длину Ask (где к принимает значения от 1 до п). Каждая из этих
дуг разбиения Ask имеет проекцию на ось Ох, которую мы будем обозначать
Ахк. Таким же образом мы обозначим Аук проекцию Ask на ось Оу. Опять же, см.
рис. 8.2.1. Наконец, мы будем считать, что если η —> оо, то Ask —> 0, это означает,
что Ахк -^Ои Аук —> 0 для каждого к (т. е. точки, которые делят С на π дуг,
распределены, условно говоря, «равномерно» вдоль С).
Далее, предположим, что у нас есть некоторая функция h(x, у), которая
определена в каждой точке (х, у) кривой С. Если мы сформируем две суммы
^пк=1Кхк9ук)Ахк и Y?k=lKxkiyk)Ayki где (хъ ук) - произвольная точка на дуге Asb
тогда запишем предельные значения этих сумм в виде1:
Umfb(xk,yk)Axk =fh(x,y)dx = Ix (8.2.1)
' к=\
Ит^Ъ(хк9ук)Аук = fh(x,y)dy-
fc=l С
(8.2.2)
h
*>l
Δ3Κ
^
>/τ Ι
^""A! ! I !
Г *ь
4'
«u
Рис. 8.2.1 ♦ Кривая на плоскости и ее проекции на оси χ и у
В соответствии с нестрогим подходом, который я использую в этой книге, я просто
предположу, что эти два предела существуют, и тогда мы посмотрим, куда нас
приведет данное предположение. В конечном счете мы придем к новому способу
нахождения определенных интегралов (контурное интегрирование), а затем проверим наше
предположение, посмотрев, согласуются ли наши теоретические расчеты с прямыми
числовыми оценками MATLAB.
Криволинейные интегралы ♦ 289
Рис. 8.2.2 ♦ Две разные линии путей интегрирования
Буквы С в нижней части знака интеграла в (8.2.1) и (8.2.2) предназначены
для указания того, что мы интегрируем от А до Б вдоль кривой С. Мы назовем
эти два предела в (8.2.1) и (8.2.2) криволинейными интегралами (иногда
используется термин «интеграл по пути», как правило, физиками).
Если А = В (то есть если кривая С - замкнутый цикл, петля1), то результат
называется контурным интегралом. Когда мы сталкиваемся с контурными
интегралами, то понимаем, что С никогда не пересекает себя (такой контур С без
самопересечений называется простым). Кроме того, понятно, что контурный
интеграл на плоскости всегда берется в направлении против часовой стрелки;
обратное направление интегрирования будет давать противоположный
алгебраический знак интеграла.
Значение криволинейного интеграла зависит, как правило, от координат
концов А и Б, от функции h(x, у) и от конкретного пути С, соединяющего А и Б.
Например, предположим, что А = (0, 0), В = (1,1) и что h(x, у) = ху. Для начала
предположим, что С = Q - это ломаный путь, показанный на рис. 8.2.2. Его
первая часть проходит вдоль оси Οχούχ = 0 до χ = 1, а затем вторая часть идет
прямо от χ = 1 (у = 0) до χ = 1 (у = 1). Таким образом, для этого пути у нас есть
у = 0 вдоль оси Ох (и поэтому h(x, у) = 0), и χ = 1 на вертикальной части Q (и,
таким образом, h(x, у) = у). Итак, наши два криволинейных интеграла на этом
пути легко вычисляются:
Есть, конечно, два разных способа, которыми мы можем иметь А = В. Тривиальный
способ - это если С просто имеет нулевую длину, что сразу означает, что 1Х = 1У = 0.
Нетривиальный способ - если С выходит из точки А в плоскость, некоторое время
блуждает, а затем возвращается в А (которую мы обозначаем как Б, поскольку это
конец пути). Именно этот второй способ дает нам замкнутый цикл, или петлю.
290 ♦ Контурное интегрирование
1 1
Ιχ = Jh(x,y)dx = fodx + fydx = 0 + 0 = 0
и ι
: jh{x, y)dy = J0dy + fydy = 0
+
(1
I
2'
С другой стороны, на пути С2 мы имеем у = χ от А до В, и поэтому h(x, y) = x2
(или, что то же самое, у2). Итак, на этом пути криволинейные интегралы равны:
Ix = fh(x,y)dx = fx2dx =
(1
Iy = Jh(x,y)dy = fy2dy =
il з
-у
3
Ясно, что значения криволинейных интегралов 1Х, 1У зависят от пути, и для
данного пути линейные интегралы 1Х, 1У могут быть или не быть равными. Мы
можем объединить криволинейные интегралы 1Х и 1У, чтобы записать
криволинейный интеграл вдоль кривой С в комплексной форме, как 1С = 1х + Пу, и по-
г 1 . 1 .1
этому 1С =г-,вто время как/с =- + г—.
Оглядываясь на предыдущий раздел, обратите внимание, что на рис. 8.2.2
мы могли бы записать неломаный линейный сегментАВ какz = x+ iy или как
у = χ, ζ = χ + ix = χ (1 + 0 и также dz = (1 + f) dx. Тогда, поскольку h(x, у) =
h(x, χ) = χ2, мы имеем:
Ic=$x\l + i)dx = {l + i)
(I
1 .1
з+гз'
что то же самое, как мы вычислили ранее.
Сейчас мы отложим эти соображения и перейдем от обсуждения в этой
книге функций вещественной переменной к функциям комплексной переменной.
Вскоре, однако, вы увидите, как это расширенное представление функций
«вернется» - как и должно! - к интегралам по замкнутым контурам, и то, что
мы сделали в этом разделе, окажется наиболее полезным.
8.3. Функции комплексной переменной
Я буду записывать комплексную переменную ζ в виде:
z = x + iy, (8.3.1)
Функции комплексной переменной ♦ 291
где χ и у - действительные числа, каждое из которых изменяется в течение
двукратно бесконечного интервала от -оо до +оо, a i = уГЛ. Мы будем
геометрически интерпретировать ζ как точку в бесконечной двумерной плоскости
(называемой комплексной плоскостью), где χ изменяется по горизонтальной
оси, а у - по вертикальной оси. И мы будем записывать комплексную функцию
комплексной переменной ζ как
f(z) = f(x + iy) = и(х, у) + ίν(χ, у), (8.3.2)
где и и ν - вещественные функции двух вещественных переменных χ и у.
Например, если
f(z)=z2 = (x + iy)2 = x2-y2 + /2лу,
тогда в этом случае и = х2 - у2 + /2лу и ν = 2лу. Говорят, что, применяя
переменные х, у мы работаем в прямоугольных (или декартовых) координатах.
Часто удобно работать в полярных координатах, что означает, что мы
записываем комплексную переменную ζ в виде:
z = re\ (8.3.3)
где гиб являются действительными: г - это радиальное расстояние от
начала системы координат комплексной плоскости до точки ζ (и, следовательно,
О < г < оо), а θ - это угол радиус-вектора (длины г), измеренный от
положительного направления горизонтальной оси Ох против часовой стрелки до радиус-
вектора точки ζ (и поэтому мы обычно принимаем 0 < θ <2π). Обратите
внимание, однако, что θ не определяется однозначно, так как мы можем добавить
(или вычесть) любое кратное 2π κ θ и по-прежнему говорить об одной и той же
точке ζ в комплексной плоскости.
По легендарной формуле Эйлера (оглянемся на главу 7) мы получаем из
(8.3.3), что
ζ = r{cos(6) + /sin(6)}. (8.3.4)
Например, если f(z) = ζ2, то
f(z) = (re*)2 = r'icoste) + fsin(8)}2,
или, раскрывая скобки в последнем равенстве,
rV29 = r^cos^e) + /sin(26)} = r2{cos2(6) - sin2(6) + /2cos(6)sin(e)}.
Поскольку действительная и мнимая части выражений в последнем
равенстве должны быть отдельно равны, мы заключаем, что cos(26) = cos2(6) - sin2(6),
а также sin(26) = 2cos(6)sin(6). Эти две формулы являются известными
формулами двойного угла из тригонометрии, и поэтому у нас уже есть хорошая ил-
292 ♦ Контурное интегрирование
люстрация мощной способности комплексных функций выполнять полезную
для нас работу1.
Я закончу данный раздел еще двумя впечатляющими демонстрациями этой
силы. Во-первых, интеграл
2π
Jecos(0)d6,
о
вычисление которого, я абсолютно в этом уверен, вы никогда не видели
«обычными» методами интегрирования для новичков. Мы сделаем это здесь
(используя полярную форму комплексного числа ζ) с использованием контурного
интегрирования в комплексной плоскости. Если ζ = еге, что означает, что ζ
находится на единичной окружности (г = 1) с центром в начале координат, то мы
можем написать:
cos(6) = -
v J 2
1)
z + -
z
потому что — = e ιθ и формула Эйлера говорит, что это cos(6) - /sin(6). Теперь
ζ
рассмотрим комплексную функцию
№ = - ,
ζ
которую мы будем интегрировать против часовой стрелки один раз по
единичной окружности. То есть мы вычислим
/
е1Н)
dz,
с *·
где С - единичная окружность ζ = е1в. (Круг на знаке интеграла просто
подчеркивает, что мы работаем с интегралом по замкнутому контуру.)
Причина появления ζ в знаменателе подынтегрального выражения
заключается в том, что dz = ielQdQ, и нам нужно ζ = е1в в знаменателе, чтобы сократить
е1в в dz. Итак,
2{Ζ+~ζ] 2π cos(0) 2π
§- dz = J^-^ieiedQ = /Jecos(0)da (8.3.5)
с % о € 0
ι
Если бы вместо этого мы начали с функции f(z) = ί = (re'ef - r^cos^) + zsin(9)}3, то
могли бы довольно легко получить формулы для тройного угла, что не так легко
получить с помощью других средств (просто взгляните в любой учебник по
тригонометрии средней школы).
Функции комплексной переменной ♦ 293
То есть контурный интеграл слева в (8.3.5) - это наш интеграл, который мы
еще умножаем на /. Чтобы непосредственно вычислить контурный интеграл,
мы начнем с разложения экспоненты в крайнем левом интеграле в степенной
ряд. То есть
Л ζ)
1
[1
[2
ill
ζ + -\
ζ)
Используя биномиальную формулу
1.
-*-#S5
1
Z^2"n!
1
Z + -
z
dz.
z+-
1
= Σ
fe=0
V
1 "
fe=olKJ Ζ k=o
2fe
мы имеем:
jhi
с Ζ c Ζ η=ο λ П!
UTn\
1
2—")η η Ι
η=0 Δ П!
Σ
§'■
2Μάζ
ι
\dz-
Теперь сконцентрируемся на этом последнем интеграле, где мы заменим ζ
на е'в, a dz на ie'ed&:
Δ\1 Δ\1
§ζ2Μάζ = Jiey^-He^dQ = ijeK2kn)QdQ =
2πζ, если 2к — п = 0
О, если 2к-п^0'
Это замечательно! Каждый из этих интегралов справа обращается в ноль,
когда η и к пробегают свои значения, за исключением тех случаев, когда к = п/2.
Это имеет глубокое значение, так как тогда к может быть целым числом (что,
конечно, так и есть), только если η четно. Для всех нечетных значений η
интегралы равны нулю, а в случаях η четные тоже равны нулю, если к ^ -. Мы
л
можем включить все интегралы, которые не обращаются в ноль, с помощью
простого трюка записи η = 2т, где т = 0,1, 2, 3,..., и поэтому мы имеем:
JK
§-^**=Т,-.
ι
"021т(2т\)
(2т)
т
2πϊ = 2πίΣ
1
(2m!)
t2ln(2m\)\m\m\
= 2π/Σ-
1
'021т (ml)1
Из (8.3.5) мы можем теперь написать:
2πΐγ , =ifecosmdQ,
tO22m(ml)2 i
294 ♦ Контурное интегрирование
или, сокращая ι, мы имеем ответ:
2π
Jecos(e)de = 27i£;-
1
JQ2lm(m\y
(8.3.6)
Слагаемые ряда справа очень быстро убывают, поэтому ряд быстро сходит
ся. Используя только первые четыре члена, сумма равна 2π Ц 1 1
= 7.95488, и MATLAB соглашается: quad(@(x)exp(cos(x)),0,2*pi) = 7.95492....
А теперь финальная демонстрация в этом разделе (это из физики)
удивительной полезности комплексных функций. Представьте точечную массу т,
движущуюся в плоскости вдоль пути, заданного геометрической формой
(8.3.3):
z(t) = r(t)el\t),
(8.3.7)
где теперь ζ, г и θ специально обозначены как функции времени (£). (Значение
каждой из этих переменных определено в начале данного раздела.) Движение
точки т обусловлено исключительно силой, действующей вдоль линии,
соединяющей массу с источником силы. Классический пример этой ситуации -
Земля («точечная» масса), движущаяся под воздействием гравитационного поля
Солнца (которое мы будем считать источником координатной системы хОу).
Сила притяжения на Земле, конечно, всегда направлена радиально к Солнцу.
Если мы напишем величину силы, действующей на т как Дг,6), то
знаменитый второй закон движения Ньютона («сила - это масса, умноженная на
ускорение») говорит:
f(r9Q)eiQ=m
dh
dt2'
(8.3.8)
Из (8.3.7) мы имеем:
dz
dt
dr ίθ . dQ и
—elQ+ir—eI(
dt dt
и тогда
d2Z
d2r
dt2 dt2
,e dr.dB .
e,e + —-1 —- + ί
dt dt
drdB ,e
e
dtdt
dt2
——e"+ r^re^+r—i — e"1
dt dt
или
dh
dt2
dt2
dt
eie + i
Zdtdt6
+ r
dt2
(8.3.9)
Используя (8.3.9) в (8.3.8) и сокращая на е (что никогда не равно нулю), мы
приходим к выражению
Функции комплексной переменной ♦ 295
f(r,B) =
dV
dt2
(dr_"2
dt
+ ι
dt dt dt2
Приравнивание действительных и мнимых частей этого последнего
выражения дает нам известные дифференциальные уравнения движения в
радиальном силовом поле:
f(r,Q)
dV
dt2
dr]
dt
(8.3.10)
drdQ ю d2Q
Ldtdte +rdt2
0.
(8.3.11)
Интересно, что результат в (8.3.11) был неявно известен задолго до Ньютона.
Только математика говорит нам, что
d
dt
\ ,del
г —
dt
= 2r
idrl
[dt]
de 2 d2e
hr^- = r
dt dt2
2
(dr)
[dtj
de d2e
\-r—T
dt dt2
и поскольку выражение в квадратных скобках равно нулю по (8.3.11), мы
имеем:
d_
dt
de
dt
= 0.
Таким образом, интегрирование дает нам
Г dt9
(8.3.12)
где С является константой. Этот результат имеет исторически важную
физическую интерпретацию в теории движения планет.
Посмотрите на рис. 8.3.1, где показано местоположение планеты в моменты
времени t и t + At, когда Солнце находится в начале нашей системы
координат. Мы предполагаем, что At настолько мало, что угловое изменение ΔΘ угла
вектора радиуса также очень мало и что длина вектора радиуса остается
практически неизменной. Тогда площадь между двумя пунктирными линиями, по
существу, равна площади равнобедренного треугольника с площадью ΔΛ,
которая находится как
Δ А = - основания на высоту « -(гА6)г = -γ2ΔΘ,
деление на At дает нам
ΔΑ Ι 2ΔΘ
At 2 At
296 ♦ Контурное интегрирование
выражение, которое становится точным, когда At —> 0. То есть, заменяя дельта-
величины на дифференциальные, мы имеем:
dA_l 2dQ
dt ~2Г dt
или, из равенства (8.3.12),
dt dt
planet at time t + At
planet at lime t
Рис. 8.3.1
Интерпретация величины г
dQ
dt
Это последнее выражение является математической формой знаменитого
закона площадей немецкого астронома Иоганна Кеплера (1571-1630),
открытого в 1609 году: за равные промежутки времени радиус-вектор, соединяющий
Солнце и планету, заметает собой равные площади. Кеплер вывел это (второй
из трех общих законов, которые он открыл) не из физики или теории
комплексных функций, а на основе многих данных утомительных наблюдений.
8.4.Уравнения Коши-Римана и аналитические функции
Теория комплексных функций действительно начинается с изучения того, что
означает производная комплексной функции Дг). В теории действительных
функций производная от#(х) при х = х0 определяется как
Уравнения Коши-Римана и аналитические функции ♦ 297
dx
х=хп
.. g(x0+Ax)-g(x0) ,
: hm ^ °- = g'(x0).
Мы делаем почти то же самое с комплексной функцией. Действительно,
формальное определение производной комплексной функции f(z) при ζ = ζ0
имеет вид:
dz
= limf(Zo+A*)-/(Z0) = f
ζ=« Δ-° Δζ
Стремление к нулю Δζ = Ах + /Ау, однако, не так просто, как в случае с
вещественной переменной. В этом более простом случае, где мы обозначаем Ах —> О
для вычисления g'(x0), Ax должно стремиться к нулю только вдоль одномерной
вещественной оси. То есть Ах может уменьшаться до нуля всего двумя
способами: либо слева οταό, либо справа ούχ0. Но в комплексном случае мы должны
принять во внимание, что поскольку z0 является точкой в комплексной
двумерной плоскости, то Δζ может приближаться к нулю бесконечным
множеством способов (слева от ζ0, справа от ζ0, снизу ζ0, сверху ζ0 или, действительно,
с любого направления компаса). Итак, как же Δζ^ О?
Математики считают, что лучшим определением для производной
является определение, наиболее свободное от условий, и поэтому их ответ на наш
вопрос такой: нужно, чтобы f'(z0) была одинаковой независимо от того, как
Δζ —> 0. Чтобы это было так, как вы можете догадываться, нужно чем-то за это
заплатить. Если f=u + fv, то плата за производную, которая не зависит от
точного характера того, как Δζ —> 0, состоит в том, что функции и и ν не могут быть
просто любыми функциями от χ и у, а скорее должны удовлетворять
определенным условиям. Если эти условия выполняются при ζ = ζ0 и во всех точках
области (или окрестности - этот термин также используется), окружающей ζ0,
то мы говорим, что f(z) является аналитической функцией в этой области (не
путать с аналитическим сигналом из теории радио, с которым мы столкнулись
в предыдущей главе).
Эти условия аналитичности функции f(z) называются уравнениями Коши-
Римана (C-R), которые на самом деле довольно легко сформулировать: при
z = z0 должны выполняться два равенства:
^ = ^ (8.4.1)
дх ду
*Н = -^. (8.4.2)
ду дх
298 ♦ Контурное интегрирование
Например, предположим, что f(z) = ζ. То есть fix, y)=x + iy = и(х, у) + i v(x, у),
следовательно, и(х, у) = χ и ν(χ, у) = у. Тогда:
^ = 1, ^ = 0, * = 0, ^ = 1,
а* <9у а* <9у
и мы видим, что уравнения C-R выполняются. Действительно, поскольку
уравнения C-R не зависят от ζ (от ζ0), то f(z) = ζ является аналитическим по всей
конечной1 комплексной плоскости. В качестве контрпримера функции Дг),
которая нигде не является аналитической, рассмотрим функцию f(z) = z = x-i,
где ζ - сопряженное к ζ. Тогда
ди_ ди_п ду__п ^1-_л
0* 0у 0* 0у
и условие (8.4.1) никогда не выполняется.
При не очень жестких требованиях уравнения C-R являются
необходимыми и достаточными условиями аналитичности функции f(z), и я отсылаю вас
к любому хорошему тексту, посвященному теории комплексных функций,
чтобы доказать это2. Однако показать, что уравнения C-R необходимы,
совсем не сложно. Поскольку Δζ = Ах + /Ау, то свойство Δζ^ 0 требует, чтобы оба
Ах^ 0 и Ау^ 0. То есть говорить о производной функции f(z) при z = z0 означает
вычислить
п )= Um /(*о + А*,Уо+АУ)-Я*о,Уо).
и/ ах-о,ау-о Ax + iAy
Теперь среди бесконечности способов, какими и Ах, и Ау могут исчезать,
давайте рассмотрим только два. Сначала предположим, что Ау = 0 и,
следовательно, Δζ = Ах. То есть ζ приближается к ζ0 параллельно оси Ох. Во втором
случае предположим, что Ах = 0 и, следовательно, Δζ = iAy. To есть ζ
приближается к ζ0 параллельно оси Оу. Если ^(Ζο) определяется единственным образом,
независимо от того, как Δζ —> 0, то эти два частных случая должны давать
одинаковый результат. В первом случае мы имеем:
Слово «конечное» важно: функция f(z) = ζ уходит в бесконечность при |ζ| —> оо, и
поэтому нельзя сказать, что она является аналитической в бесконечности. Фактически
в теории комплексных функций существует теорема, в которой говорится, что
единственными функциями, которые являются аналитическими на всей комплексной
плоскости и даже в бесконечности, являются константы. В этом случае все четыре
частные производные в уравнениях C-R тождественно равны нулю.
См., например: Бак Джозеф и Нъюман Дональд Дм. Комплексный анализ. 3-е изд.
Springer, 2010. С. 35-40 (Bak Joseph, and Newman Donald J. Complex Analysis (3rd ed.)).
Хотя только одних уравнений C-R недостаточно для доказательства аналитичности,
но если частные производные в них непрерывны, то мы имеем достаточность.
Уравнения Коши-Римана и аналитические функции ♦ 299
п )= Ит f(*o+A*,y0)-f(Wo) =
= ИтМ^о+А^Уо) + г'у(^0+А^У0)}-Мх0>У0) + /У(х0>У0)} =
Δχ^Ο ДХ
= ИтМ^о+А^У0)-Ц(Хо>У0)} + /{У(х0+Ах>у0)-У(х0>у0)} =
Δχ^Ο ДХ
aw .βν
= И— ·
дх дх
А во втором случае имеем:
f'(z0)= lim Я*о»Уо+АУ)-/(*о,Уо) =
U Az=iAy->0 /Ду
= lim {u(*0>y° +Ay) + *'v(*o>yo + АУ)}-{ц(х0>у0) + /у(х0,у0)} =
Δχ^Ο /Ду
= lim {u(*0>y° + АУ)-^о>Уо)} + *М*о>Уо + Ау)-у(х0,у0)} =
Δχ^Ο /Ду
_1ди ду^_ду__.ди
~idy ay~ay z<9y'
Приравнивание действительных и мнимых частей этих двух выражений для
f'(Zo) дает уравнения C-R в условиях (8.4.1) и (8.4.2).
Аналитические функции, несомненно, представляют собой довольно
специфическое подмножество всех возможных комплексных функций, но они
включают достаточно широкие классы функций, такие как:
(1) каждый многочлен от ζ является аналитической функцией;
(2) сумма и произведение двух аналитических функций аналитичны;
(3) частное двух аналитических функций является аналитическим, за
исключением тех значений, в которых функция знаменателя равна нулю;
(4) аналитическая функция от аналитической функции является
аналитической.
Таким образом, из (1) следует, что f(z) = ζ2 и f(z) = e\ обе являются
аналитическими, поскольку в первом случае f(z) является полиномом, а во втором -
поскольку экспонента может быть разложена в степенной ряд. Из (2) следует,
что f(z) = zV аналитична, а из (3) следует, что f(z) = ez/(z2 + 1) аналитична, за
исключением точек ζ = ζ, которые называются1 особенностями f(z), потому что
при этих значениях ζ функция f(z) обращается в бесконечность. И наконец, из
(4) следует, что f(z) = eeZ является аналитической.
1 Если функция f(z) аналитична всюду в некоторой области, за исключением
конечного числа особенностей, математики говорят, что f(z) мероморфна в этой области,
и я говорю вам это просто, чтобы вас не парализовало от страха, когда вы столкнетесь
с этим термином.
300 ♦ Контурное интегрирование
8.5. Интегральная теорема Грина
В этом разделе мы продолжим наше начальное обсуждение
криволинейных интегралов, чтобы получить то, что называется теоремой Грина1.
Предположим, что замкнутый путь (контур) С охватывает область R комплексной
плоскости, как показано на рис. 8.5.1. Далее мы предположим, что есть две
действительные функции действительных переменных хиу, Р(х, у) и 0(х, у),
определенные в каждой точке вдоль Сив области R (внутри Q. Тогда теорема
Грина говорит, что
§{P{x,y)dx + 0{x,y)dy}= Ш
дО дР
дх ду
\dxdy.
(8.5.1)
Рис. 8.5.1 ♦ Контур С и его внутренность R
Круг на интеграле по кривой С в левой части (8.5.1) призван подчеркнуть,
что С является замкнутым, несамопересекающимся путем (простая кривая,
пройденная в против часовой стрелки, как упомянуто в разделе 8.2). R
называется односвязной областью, что означает, что каждая замкнутая кривая в R
охватывает только точки области R. Если область не односвязна, то она
называется многосвязной. Примером является односвязная область, в которой
вырезано отверстие. Точки «в отверстии» считаются внешними для С.
Теорема Грина связывает контурный интеграл по контуру С с двойным
интегралом по области R. Для контура, показанного на рис. 8.5.1, довольно
очевидно, где находится область внутри С, но через некоторое время мы
столкнемся с контурами, где это не так очевидно. Вот простой низкоуровневый
способ всегда правильно определять область внутри С. Когда вы идете по С
Интересную историю этой теоремы, названной в честь английского математика
Джорджа Грина (1793-1841), см. в моей книге: Мнимая сказка (An Imaginary Tale).
Принстон, 2010. С. 204-205.
Интегральная теорема Грина ♦ 301
против часовой стрелки, то ваша левая рука будет внутри, а ваша правая рука -
снаружи С.
У'
3ι
А'
L
>
j
Ί
* С> -
'V/VY/\
' С|
t 4
'. У
Ί
Рис. 8.5.2
Область R - прямоугольник
Доказать теорему Грина нетрудно, или, по крайней мере, нетрудно, если мы
сделаем некоторые очень упрощающие предположения. Эти предположения
на самом деле не требуются, но их удаление усложняет доказательство. Для
начала наше первое предположение состоит в том, что R представляет собой
прямоугольник, ориентированный параллельно осям χ и у, как показано на
рис. 8.5.2. (Я нарисовал путь полностью в первом квадранте, но то, как я его
нарисовал, для последующего не имеет значения.) Длина линии,
ограничивающей R, равна С=СХ + С2 + СА + С4, что просто означает, что С имеет четыре
стороны. Когда мы закончим с этой специальной областью R, я приведу несколько
общепризнанных доводов (но, я надеюсь, и правдоподобных), чтобы убедить
вас, что гораздо более сложные формы для R тоже подойдут.
Начиная с члена ff- — dxdy в правой части теоремы Грина, мы имеем:
jr/-f**~/l
ду
dx = -f{P(x,yi)-P(x,y0)}dx-.
Л1 Л0
: JP(x, y0 )dx + JP(x, у, )dx = fP(x, y)dx + fP(x, y)dx.
Обратите внимание, что в последних двух интегралах я отбросил индексы
у переменных у0 и уи которые были включены в предшествующие интегралы.
Я могу сделать это, потому что индексы изначально были там, чтобы различать
интегрирование по нижнему краю (у0) или по верхнему краю (уг) области R,
302 ♦ Контурное интегрирование
а теперь в двух последних интегралах под ними написаны Q (нижний край)
и С3 (верхний край), под соответствующими знаками интегралов.
Заметим также, что равенство Г * — dy = Р(х,у.) — Р(х,уп) предполагает от-
JyQ ду
дР
сутствие разрывов у —,то есть частная производная непрерывна.
ду
Аналогичные интегралы по χ можно записать и для двух других сторон (С2
и С4), и, поскольку они являются вертикальными отрезками, мы знаем, что
везде вдоль них их = 0. То есть
Л1
fP(x,y)dx = JP(x,y)dx = 0
ло
fP(x,y)dx = fP(x,y)dx = 0.
Поскольку эти интегралы равны нулю, мы можем формально добавить их
к нашим интегралам по Q и С3, ничего не меняя. Итак:
// - ^ dxdy = fP(x, y)dx + fP(x, y)dx + fP(x, y)dx + fP(x, y)dx = fp(x, y)dx.
r ОУ q q q q c
Л* дО
-^dxdy в теореме
R дх
Грина и заметите, что dy = 0 вдоль горизонтальных сторон Q и С3, то должны
легко увидеть, что
ff^dxdy = §Q(x9y)dx,
дх
и это завершает доказательство теоремы Грина для нашего красиво
ориентированного прямоугольника на рис. 8.5.2. На самом деле, однако, это
доказательство довольно легко распространяется на другие гораздо более сложные
формы области R.
Например, на рис. 8.5.3 вы видите, как полукруглый диск может быть
построен из множества очень тонких прямоугольников - чем они тоньше, тем
их больше, да, но это нормально; сделайте их все тоньше, чем тончайшая
прозрачная почтовая бумага, если хотите - чем тоньше, тем лучше они
приближаются к полудиску. Если граничный край полудиска обозначен через С и если
периметры (сумма всех четырех сторон) отдельных прямоугольников
обозначены через Q, С2, С3,..., то
(f [Pdx + dy}=(f) [Pdx + dy} + (f [Pdx + dy} + (f [Pdx + dy}
+ ■
Первая интегральная теорема Коши ♦ 303
потому что те стороны отдельных прямоугольников, которые параллельны оси
Ох, пройдены дважды, по одному разу по часовой стрелке и против часовой
стрелки, и поэтому их вклад в различные линейные интегралы в правой части
вышеприведенного уравнения сокращается. Единственным исключением
после этих сокращений остается самый нижний горизонтальный край полудиска.
V
ί
А / /
/г
ί : с
<■
•^\
<' \
V *
г *
?*
Рис. 8.5.3 ♦ Создание полудиска
из множества тонких прямоугольников
Кроме того, интегралы вдоль отдельных вертикальных краев тонких
прямоугольников не сокращаются, и если прямоугольники очень тонкие, то
объединение вертикальных краев является частью окружности полудиска. Таким
образом, после интегрирования по всем прямоугольникам нам остается только
интегрирование по нижней части полудиска и окружности. Вы можете видеть,
что, используя ту же самую базовую идею, мы можем строить очень сложные
фигуры из надлежащим образом расположенных прямоугольников, и
поскольку теорема Грина работает для каждого прямоугольника, то она работает
для всех их вместе, поэтому теорема Грина работает для составленной из них
(и возможно, довольно сложной) области R.
8.6. Первая интегральная теорема Коши1
Хорошо, чтобы дойти до этого момента, потребовалось некоторое время, но
скоро станет ясно, что оно того стоило. Наш основной результат легко
сформулировать: если f(z) аналитична всюду на и внутри контура С, то
1 По общему соглашению теорема в этом разделе названа в честь Коши, который
опубликовал ее в 1814 году, но в письме от декабря 1811 года, написанном великим
Карлом Фридрихом Гауссом (1777-1855) его коллеге немецкому математику Фридриху
Вильгельму Бесселю (1784-1846), он приводит (без доказательства) теорему, которую
мы докажем здесь. В математике, увы для Гаусса (как будто ему действительно
нужно еще что-то добавить к своим достижениям), приоритет идет первому, кто
опубликовал результат.
304 ♦ Контурное интегрирование
§f(z)dz = 0. (8.6.1)
С
Чтобы показать это, вспомним (8.3.1) и (8.3.2). То есть, с учетом Дг) = и(х, у) +
iv(x, у) и dz = dx + idy, мы имеем:
£>f(z)dz = £(u + iv)(dx + idy)= £(udx + iudy + ivdx-vdy),
ее с
или
(f) f(z)dz = §\udx -vdy) + i(f)(vdx + udy). (8.6.2)
с с с
Теперь, по теореме Грина каждый из двух контурных интегралов справа
равен нулю. Чтобы увидеть это, рассмотрим первый интеграл в правой части
(8.6.2) и оглянемся на (8.5.1). Мы видим, что в нашем случае Р(х, у) = и(х, у)
и 0(х, у) = -v(x, у), и поэтому частные производные в правой части (8.5.1) будут
следующими:
dQ__dy_ дР__д\±
дх~ дх' <9у~<9у'
Уравнение Коши-Римана (8.4.2), которое выполняется здесь, потому что мы
предполагаем, что f(z) является аналитической, говорит, что подынтегральная
функция двойного интеграла в теореме Грина
дО дР _ dv ди_ dv ( ду)
дх ду дх ду дх
дх
:0.
Для второго интеграла в правой части (8.6.2) имеем Р(х, у) = у(х, у) и 0(х, у) =
и(х,у).Итщв.
Щ_ди. дР__ду_
дх~дх' ау~ау'
и другое уравнение Коши-Римана (8.4.1) говорит, что подынтегральное
выражение двойного интеграла в теореме Грина равно
дО дРди ду _ду ду _
дх ду ~ дх 9у ~ 9у ду ~ '
потому что снова Дг) является аналитической. Итак, равенство (8.6.1) доказано.
Нельзя отрицать, что свойство (8.6.1) выглядит довольно мягко. Но оно
обладает огромной силой. Например, рассмотрим случай
/(*) =
elz
когда функция f(z) является аналитической всюду, кроме ζ = 0, потому что там
f(z) обращается в бесконечность. Итак, если мы интегрируем f(z) по любому
Первая интегральная теорема Коши ♦ 305
С так, чтобы избежать точки ζ = 0 в его внутренней области, то, как мы знаем
из свойства (8.6.1), получим ноль для интеграла. Имея это в виду, рассмотрим
контур С, показанный на рис. 8.6.1, ограниченный двумя дугами, где ε > 0, а Т
конечно. В обозначениях рис. 8.6.1 мы имеем:
f f(z)dz = § f(z)dz + § f(z)dz + § f(z)dz + § f(z)dz = 0.
(8.6.3)
Рис. 8.6.1 ♦ Контур, который обходит сингулярность
в начале координат
Каждый из этих четырех сегментов контура С можно задать в виде: Q: ζ = χ,
dz = dx; C2: ζ = Тё\ dz = iTeiQ; C3: ζ = /у, dz = idy; Q: ζ = гё\ dz = ieeiQdQ.
Таким образом, (8.6.3) принимает вид:
\ x J° Те* { /у *" Jf Те*
Далее, выполняя все очевидные сокращения и обращая направление
интегрирования в третьем и четвертом интегралах (и, конечно, их алгебраические
знаки тоже), мы приходим к выражению
Т oix ί — 1 Т р~у
Если в последнем интеграле мы изменим фиктивную переменную
интегрирования с у на х, то получим
}^х+1уу'-^}=0.
(8.6.3)
Теперь сосредоточимся на втором интеграле и разложим его показатели по
формуле Эйлера:
306 ♦ Контурное интегрирование
eiTe*-e"
. _iT{cos(0)+isin(0)} _ _i£{cos(0)+isin(0)} .
. _-rsin(0) _iTcos(0) _ _-Esin(0)-i£cos(0)
Если теперь Т^ооие^О, тогда первый член стремится к нулю, потому что
π
lim7 ^e rsin(e) = 0 для любого 0 < θ < —, в то время как второе слагаемое стре-
π
мится к 1, потому что lim£^0e εδΐη(θ) = Нт£^0е'
Z£COS(9)
е = 1 для любого 0 < θ <
Таким образом, (8.6.3) при Τ ^ оо и ε —> 0 принимает вид:
°°е1Х-е-
I
-dx + i\
l:^de
= о,
или, снова используя формулу Эйлера,
fCOS(x) + zsin(x)-e*^ π
J у 1 '
о
ИЛИ
I
cos(x)-e
-dx + z/ ^
sin(x) л.. ,π
-dx = i-
0 0
Приравнивая мнимые части, мы имеем формулу
/
зЭД^я
2'
которую уже получили в (3.2.1) - и, конечно, приятно видеть, что наше
контурное интегрирование согласуется, в то время как приравнивание реальных
частей дает:
cos(x)-e
-dx = 0.
(8.6.4)
MATLABтоже согласен: quad(@(x)(cos(x)-exp(-x))./x,0,1000) = 0.000826...,что,
конечно, не совсем ноль, но довольно мало. Вы можете вспомнить этот
интеграл как частный случай (4.3.14), полученный с использованием «нормальных»
методов.
Вы можете видеть, что контурное интегрирование в комплексной плоско-
/»оо
сти способно находить несобственные вещественные интегралы, такие как J
, зависящие от правильного выбора контура С. Вначале С охватывает ко-
-оо
нечную область плоскости, где часть контура С лежит на действительной оси.
Затем, когда мы позволим контуру С расшириться так, чтобы часть действи-
Первая интегральная теорема Коши ♦ 307
тельной оси растягивалась в пределах от -оо до оо или от 0 до оо, другие части
контура С приводят к интегралам, которые в некотором смысле «легко найти».
Вычисление (8.6.4) было довольно впечатляющим примером этого
процесса, но вот еще одно применение первой интегральной теоремы Коши, которое,
как мне кажется, превосходит первое. Предположим, что а, Ъ и с - любые
действительные числа (а ^ 0), такие что Ь2 > Аас. Вопрос: каково значение
интеграла
^ах2-\-Ьх-\-с
Я думаю, вы будете удивлены ответом. Вот как это можно вычислить.
Начинаем с контурного интеграла
£f(z)dz=£—— dz,
Jc Jc az+bz + c
где мы замечаем, что подынтегральное выражение имеет две особенности,
которые находятся на действительной оси, как показано на рис. 8.6.2. Это из-
за заданного условия Ь2 > Аас, которое говорит, что знаменатель обращается
в ноль при двух действительных значениях (вспомните формулу корней
квадратного трехчлена!)χΊ = Vb2 -Аас их, = 1 Vb2 -Aac.
F F f 2 2a 2a l 2a 2a
Равенство b2 = Aac - это случай, когда два действительных корня слились
в один.
На рис. 8.6.2 я показал, что особенности находятся на отрицательной
действительной оси, но они могут быть и на положительной действительной оси -
то, где они находятся, зависит от знаков а и Ь. Однако что действительно имеет
значение, так это то, что особенности находятся на действительной оси. Это
означает, что когда мы выбираем контур С, мы должны расположить его
вещественную ось так, чтобы избежать этих особенностей; как вы помните, мы
заключили большое соглашение по этому вопросу в главе 1, когда там
обсуждался трюк «подкрадываться к особенности». С контурным интегрированием
мы не столько «подкрадываемся» к особенности, сколько «крутимся вокруг
и избегаем» ее, что мы делаем с С2 и С4 - частями контура С, показанными на
рис. 8.6.2 (и оглядываемся на рис. 8.6.1 тоже с его С4, исключающим
особенность при ζ = 0). Эти круговые колебания (называемые вырезами) таковы, что
они сохраняют особенности во внешнем пространстве к контуру С. У
каждого выреза есть радиус ε, который мы в конечном итоге сведем до нуля, взяв
предел при ε —> 0.
Итак, вот что мы имеем с контуром С= Сг + С2 + Съ + С4 + С5 + С6. На Q, С3, С5:
z = x,dz= dx; hslC2:z = x2 + εε'θ, dz = ieelQdQ, π > θ > 0; на С4: ζ = хг + ге1в, dz = ieelQdQ,
π > θ > 0; на Q: ζ = Тё\ dz = iTeiedQ, 0 < θ < π.
308 ♦ Контурное интегрирование
*'
I cz ^
--Τ/Ϊ \ > X,
с, сз
t
^^?
">*
Рис. 8.6.2 ♦ Обход особенностей с круглыми вырезами
Первая интегральная теорема Коши говорит:
§f(z)dz = \
§ f(z)dz + § f(z)dz + § f(z)dz I + Ы f(z)dz + ^ /(z)cfe + § f(z)dz
Когда мы наконец полагаем Τ —> оо и ε —> 0, тогда первые три
криволинейных интеграла объединятся, чтобы дать нам реальный интеграл, к которому
мы стремимся. Следовательно, значение этого интеграла будет равно
φ f{z)dz + § f(z)dz + § f(z)dz
Давайте теперь посчитаем каждый из этих трех криволинейных интегралов.
Для С2:
§f(z)dz = ]
ieeiedQ
а(х2 + гет у + Ъ(х2 + εβ'θ) + с
0 iWde
■/
{ а{х22 + 2χ2εε'β + г2ет) + Ь(х2 + εείβ) + с
0 iWde
I
{ ах\ + Ьх2 + с + (2ах2Ее/е + czeV20 + &εβ'θ)
Поскольку ал^ + Ъх2 + с = 0, x2 является нулем знаменателя (по определению
х2), и так как ε2 —> 0 быстрее, чем ε —> 0, то для очень малых ε имеем:
Πην -4- Μρρ'θ J ί
de
J (2αχ2 + Ъ)ге1* J0 (2αχ2 + Ь)
-πζ-
1
2αχ7 + Ь
Первая интегральная теорема Коши ♦ 309
Таким же образом
lim £ f(z)dz = —πί
И наконец,
§f{z)dz = ]
2ax1+b
iTeiedQ
аТ2ет+ЬТе*+с
и так как подынтегральное выражение исчезает как 1/Тпри Τ ^ оо, то
lim(ff(z)dz = 0.
с6
Тогда
оо
dx
ах2 +Ъх + с
Поскольку
2ах2 + Ь = 2а
πζ
1 1
- + -
2ax1+b 2ax2+b\
+ b = -Vb2-4ac
2a 2a
2ax1 + b = 2a
1 Vb2-4ac
2a 2a
+ b = \lb2-4ac,
мы видим, что эти две особенности взаимно компенсируют друг друга, и
поэтому мы получаем следующий интересный результат:
dx
ах2 +bx + c
= 0, a^0,b2>4ac
(8.6.5)
для всех возможных значений а,Ьис. Это, я думаю, совсем не очевидно! (В
задаче 8.5 вам предлагают найти интеграл, обобщающий этот результат.)
Естественный вопрос, который сейчас наверняка приходит на ум: а что
будет, если Ь2 < 4ас? Если это так, особенности функции f(z) больше не находятся
на вещественной оси, поскольку корни имеют ненулевые мнимые части. Мы
вернемся к этому вопросу в следующем разделе, где обнаружим, что интеграл
в (8.6.5) больше не равен нулю при этом новом условии.
Вырезы контура вокруг сингулярностей являются настолько полезным
инструментом, что их применение требует еще одного примера. Итак, что я буду
делать дальше - это использовать вырезы для получения результата, который
было бы чрезвычайно трудно получить другими способами: значение
310 ♦ Контурное интегрирование
оо ах
Г dx, 0<а<1.
J 1-е*
Чтобы оценить этот интеграл, мы изучим контурный интеграл
£ -dz,
(8.6.6)
используя любопытный контур С, показанный на рис. 8.6.3.
Рис. 8.6.3 ♦ Любопытный контур
Причины выбора именно этого контура С (похожего на кусок сыра, который
погрызли мыши), вероятно, требуют некоторого объяснения. Части
действительной оси (Q и С3), возможно, очевидны, поскольку в конечном итоге мы
будем считать, что Τ —> оо, и эти части С (где ζ = χ) дадут нам интеграл, к которому
мы стремимся. Таким образом, сумма интегралов Q и С3 равна
Г с™ а Г еах л
\ dx+ \ dx.
J 1-е* J 1-е*
Полукруглый отступ (С2) с радиусом ε (который мы в конечном итоге будем
считать —> 0) вокруг начала координат также, вероятно, очевиден, поскольку
ζ = 0 является особенностью подынтегрального выражения, и, как вы
можете видеть, я пытаюсь установить все до использования первой интегральной
теоремы Коши (которая требует, чтобы контур С не содержал особенностей).
Именно другие части С, две вертикальные стороны (С4 и С8) и две стороны,
параллельные реальной оси (С5 и С7), вероятно, являются теми, которые
озадачивают вас прямо сейчас.
Первая интегральная теорема Коши ♦ 311
Так как я пытаюсь избежать каких-либо особенностей, вы можете понять,
почему я не использую наш предыдущий подход, включающий полукруглую
дугу от Τ на положительной вещественной оси обратно в -Г на отрицательной
вещественной оси - дуге, которая затем расширяется до бесконечности при
Τ —> оо. Это не сработает, потому что подынтегральное выражение имеет
бесконечное число особенностей на мнимой оси, распределенных вверх и вниз
с интервалами 2π/ (поскольку тождество Эйлера говорит нам, что 1 - ez = 0
имеет решения ζ = 2nik для любого целого числа к). Полукруглая дуга в конечном
итоге будет заключать в себе бесконечное число особенностей!
Есть и другая проблема. Особенность к = 0 - это та, которую мы уже обошли
на действительной оси, но почему (вы можете спросить) мы намеренно
движемся прямо к особенности для к = 1 (при 2π/ на мнимой оси)? Разве контур С
на рис. 8.6.3 просто не напрашивается на неприятности? Да, в конечном
итоге мы обходим эту особенность другим полукруглым вырезом, но почему бы
просто не взять верхний сегмент контура С ниже сингулярности к = 1 и
полностью и автоматически избежать особенность таким образом? Ну, поверьте
мне - на это есть причина, которая скоро будет раскрыта.
Поскольку мы договорились, что внутри контура С не должно быть никаких
особенностей, то по первой интегральной теореме Коши имеем:
if,
:dz = 0,
к=0~Ск 1_е*
или поскольку ζ = хна Q и С3, то
-ε αχ Τ πχ
—Τ ε С2 С4 С5 С6 С7 С8
Скоро, конечно, мы будем считать, что Т^ооие^Ов этих интегралах.
Давайте теперь посмотрим на те, что справа, более подробно, начиная с С4.
На С4 мы имеем ζ = Т+ /у, где 0 < у < 2π. Поэтому подынтегральное
выражение интеграла по С4 есть
eaz ea(T+iy) £αΊ ^
1-е* 1_е<г+'з» i_eVy
Поскольку Τ —> оо, мы видим, что величина числителя увеличивается как еаТ
(\ешу\ = 1), а величина знаменателя увеличивается как ет. Таким образом,
величина подынтегрального выражения ведет себя как е(а~1)Т при Τ —> оо, что
означает, что при 0 < а < 1 подынтегральное выражение стремится к нулю, и поэтому
мы заключаем, что интеграл С4 обращается в ноль при Τ —> оо. Точно так же на
С8 имеем ζ = -Т+ /у, где 2π > у > 0. Подынтегральное выражение в интеграле
С8 есть
eaz ea(-T+iy) e~aT giay
1_е<-г+'у> l-e-Vy
312 ♦ Контурное интегрирование
Поскольку Τ —> оо, мы видим, что величина числителя стремится к нулю
как е~аТ (так как а положительно) (|егау| = 1), а величина знаменателя
стремится к 1. То есть величина подынтегрального выражения ведет себя как е~аТ при
Τ —> оо, и тогда подынтегральное выражение интеграла по С8 также стремится
к нулю при Τ ^ оо.
Далее, давайте посмотрим на интегралы С5 и С7. Будьте бдительны! Именно
здесь вы поймете, почему сдвиг контура С прямо к сингулярности на мнимой
оси в точке 2π/ является хорошей идеей, хотя мы собираемся избегать этого
«в самый последний момент» (так сказать) с помощью полукруглого выреза С6.
На интегралах С5 и С7 имеем ζ = χ + 2π/ и, следовательно, dz = dx (как на
интегралах Q и С3). Подробно выписав интегралы по С5 и С7, получим:
ρα(χ+2πι)
I ^ах+ I ^ах = I ^ах + I ^ах,
_2πι
-ее
,2πί
или, поскольку e"lt = 1 (это критическое наблюдение!), мы имеем сумму
интегралов С5 и С7 в следующем виде:
τ
gj /-» gj
-dx\
-e
Jl-ex JTl-t
Обратите внимание, что с точностью до постоянного множителя е2™' это
сумма интегралов по Q и С3. У нас получилось такое упрощение только
потому, что мы направили верхний сегмент С прямо по особенности 2πί. Все это
означает, что теперь мы можем записать (8.6.7) в следующем виде (потому что,
не забывайте, интегралы по С4 и С8 исчезают при Τ^ оо):
(1-е2ш)
Ι «αχ -ε αχ
J λ—ΡΧ J Λ—ΡΧ \ J J '
л. с _т j. с г г
(8.6.8)
На С2 мы имеем ζ = гёе для π > θ > 0, и поэтому dz = ize'edQ. Тогда
s-ff-,
Г.. w 1 — С
:zWU
Вспоминая разложение экспоненты в степенной ряд и оставляя только
члены, где ε в первой степени (поскольку все члены более высокого порядка
стремятся к нулю даже быстрее, чем ε), мы имеем:
1 - βεβ'Θ«1 - [1 + εβϊθ] = -εβιθ.
Точно так же
еа*е"п1 + агею,
и тогда
о
lim f = lim Г
ε->0 J ε->0 J
Ι + αεε*
-ιεε
md
-εε
Φ*'
πι.
Первая интегральная теорема Коши ♦ 313
На С6мы имеем ζ = 2π/ + ге1в для 0 > θ > - π, и поэтому dz = ieelQdQ. Тогда
-π а(1т+гев) -π aim aeem
f = f- riEe*de= f ,e ϊεβ^θ,
J J ι -2πΐ+εε'θ J ι _εε'θ
c6 о 1 — e о 1 — e
или, когда мы полагаем ε —> О,
J = fe«a«'J-l—ee»^ = -iea2ni JdQ = me"
„aim
-EC
Q- 0 cc 0
Подставляя эти два результата для интегралов С2 и С6 в (8.6.8), получим
efl* . πζ' + ζπβ"2™' .l + efl2lri .efl7II[e-fl7II+efl7rI] .2cos(au)
dx = —— = m^—. = πζ—^—: A = m —-,
_e* i_e2™ e2nai-l eam[eam-eam] 2isin(an)
ь
или
St.
-dx = , 0<fl<l.
tan(au)
(8.6.9)
Обязательно обратите внимание на то, что значение интеграла в (8.6.9)
целиком исходит из исчезающе малых полукруглых путей вокруг двух
особенностей. Сингулярности и интегрирование по дуге «нулевой» длины вокруг них
имеют значение! Если а = гЛ, то интеграл равен π, и MATLAB согласен, потому
что (используя наш старый трюк «подкрадываться» к сингулярности при х = 0)
quad((a(x)exp(x/4)./(l-exp(x)),-1000,-0.0001) + quad((a(x)exp(x/4)./(l-exp (x)),0.0001,1000)
= 3.14154....
Прежде чем покинуть этот раздел, я должен сказать вам, что не каждое
использование первой интегральной теоремы Коши является вычислением
значения интеграла в замкнутой форме (т. е. в виде формулы). Другое весьма
отличное и очень изящное приложение - это преобразование интеграла,
который трудно точно вычислить численно, в другой эквивалентный интеграл,
который намного легче вычислить численно. Два примера этого:
I(a)=°fS^ldx = limTrS^ldx
J0 x + a г-ooJ x + a
где а - положительная постоянная. Эти два интеграла не имеют значений
в замкнутой форме, и каждый должен быть численно оценен для каждого
нового значения а.
314 ♦ Контурное интегрирование
Точно сделать это, используя обычные методы численного интегрирования,
нелегко, по тем же причинам, которые я привел в предыдущей главе, когда мы
получили формулу (7.5.2). То есть подынтегральные выражения - как 1(a), так
и J(a) - действительно не так уж малы даже для «больших» Г, поскольку
знаменатели увеличиваются медленно, а числители на самом деле не уменьшаются
вообще, а просто бесконечно колеблются между ±1. Численное нахождение
интеграла 1(a), например, в виде quad(@(x)cos(x)./(x+a),0,T) с указанными
числовыми значениями аиТие работает должным образом. Например, если а = 1,
то для четырех случаев Τ =5,10, 50 и 100 мы получаем:
Τ
5
10
50
100
Д1)
0.18366...
0.30130...
0.33786...
0.33828...
Вычисленные значения 1(1) не являются стабильными более, чем на пару
десятичных знаков, даже для Τ = 100. Аналогичная таблица для J(l):
Τ
5
10
50
100
/(1)
0.59977...
0.70087...
0.60264...
0.61296...
Эти значения для /(1) еще более нестабильны, чем для 1(1).
Теперь я покажу вам, как можно использовать первую интегральную
теорему, чтобы получить действительно превосходную числовую точность, даже
с «небольшим» значением Т. Что мы сделаем, так это рассмотрим контурный
интеграл
£ dz,
Jcz + a
где С = Ci+ C2+ Съ есть первый квадрант кругового контура, показанного на
рис. 8.6.4. Подынтегральная функция имеет единственную особенность на
отрицательной вещественной оси при ζ = а < 0, которая лежит вне С. Таким
образом, мы сразу знаем из первой теоремы, что для этого С
£-?—dz = 0. (8.6.10)
Первая интегральная теорема Коши ♦ 315
Рис. 8.6.4 ♦ Контур, исключающий особенность/ζ
Для этих трех частей С = Сх + С2 + Съ мы имеем: на Q: ζ = χ и dz = dx,
О < χ < Τ; на С2: ζ = Тё\ dz = iTeiedQ, 0 < θ < -; на С3: ζ = /у, dz = idy,T>y > 0.
Итак, выходя из начала координат и обходя контур С в направлении против
часовой стрелки, интеграл (8.6.10) принимает вид:
f-^dx + Г2— 1Теюйв+ Г—^—zdy = 0,
J0 х + а Jo TelQ-\-a JT iy + a
или
τ
i x + a Jn iy + a J°
Тею+а
Наш следующий шаг - посмотреть, что происходит, когда мы положим
Τ —> оо. Используя формулу Эйлера, мы имеем
JTem
. _iT{cos(0)+/sin(0)} -!Tsin(0) iTcos(0)
и поэтому
e'TeVe Г
Ге'Ча
. e-rsin(0)eiTcos(0) /Θ -/(-/β + α)
(TelQ + a)(Te~lQ + a)
-rsin(0) iTcos(0) T+aTe
Г+аГ(е'Че-,е) + А
и тогда
lim
Г—>оо
e'Te ею
Ге*+а
lim|e
-rsin(9) iTcos(9)
T2+aTe№
Т2+аТ(е,в+е-в) + а2
= lim|e-rsin(9)| = 01.
Поскольку \el
'iTcom\ = 1 и lim
T2+aTeiQ
Т2+аТ(е* + е~") + а2
316 ♦ Контурное интегрирование
Таким образом, при Τ —> оо мы приходим к равенству:
Jn x + a Jn iy + a
: +
То есть
о 1У + С
°pcos(y) + isin(y)dy= °г_
-ί * + α π О":
ie y(-iy + fl)
ОО
ye y + iae
f+a2
-dy,
о - - - о (iy + a)(-iy + a) 0
или приравнивая действительные и мнимые части и заменяя фиктивную
переменную интегрирования с у на х:
>cos(x)
т/ ч г cos(x) , г хе
1(a) = I —f-^dx= I -—-
i x + a i χ1 +α
dx
'Sin(x)
Jn x + a Jn xL + a
dx.
Эти новые интегралы справа для 1(a) и J(a) имеют подынтегральные
выражения, которые быстро уменьшаются при увеличении χ от нуля.
Вычисляя снова Да) и/(а), используя эти альтернативные интегралы справа,
мы получаем следующие новые таблицы:
Τ
5
10
50
100
/(1)
0.342260...
0.343373...
0.343378...
0.343378...
Τ
5
10
50
100
/(1)
0.621256...
0.621449...
0.621450...
0.621450...
Из этих таблиц вы можете видеть значительно улучшенную численную
производительность наших расчетов, и теперь мы можем с уверенностью сказать,
что
оо
/
cos(x)
х + 1
sin(x)
dx = 0.34337.
I х + 1
dx = 0.62145.
(8.6.11)
8.7. Вторая интегральная теорема Коши
Бывает так, что при попытке применить первую интегральную теорему Коши
мы можем обнаружить, что невозможно построить полезный контур С так,
Вторая интегральная теорема Коши ♦ 317
чтобы его часть лежала вдоль действительной оси, но при этом не имела
особенности внутри. Интеграл (8.6.5) для случая Ь2 < Аас является примером такой
ситуации, а в этом разделе я покажу вам и другие примеры. Наличие
особенностей внутри С означает, что первая интегральная теорема Коши больше не
может применяться. Стремление «избежать» этой неприятности приводит нас
ко второй интегральной теореме Коши. Если f(z) аналитична всюду как внутри,
так и на С, то если z0 находится внутри С:
i^-dz = 2nif(z0). (8.7.1)
/
Последовательное дифференцирование по переменной z0 под знаком
интеграла может показать, что существуют все производные функции f(z) (мы
будем использовать это наблюдение в следующем разделе) и они имеют вид:
Гад=^|^гИ=2"№л
и+1
где z0 - любая точка внутри С, a f{n) обозначает п-ю производную функции f.
Хотя функция f(z) сама по себе не имеет особенностей (потому что она
аналитическая) внутри С, подынтегральное выражение (8.7.1) имеет особенность
первого порядка1 при ζ = ζ0. Теперь, прежде чем я докажу формулу (8.7.1),
позвольте мне показать вам хорошее ее применение, так что вы поверите, что
вам стоит потратить время и усилия, чтобы понять доказательство. Что мы
сделаем, так это оценим следующий контурный интеграл:
§
-dz,
где С - контур, показанный на рис. 8.7.1, а а и Ъ - положительные константы.
Когда мы почти закончим, будем считать, что Τ —> оо, и вы увидите, что мы
получили известный результат (который мы уже сделали фактически в (3.1.7)),
с той разницей, что использование второй интегральной теоремы Коши будет
легче для вывода! Вдоль части действительной оси С мы имеем ζ = χ, а вдоль
полукруглой дуги ζ = Те1в (dz = zTel9d6), где θ = 0 при χ = Τ и θ = π при χ = -Т.
Итак:
iaz Τ iax π ία(Τβ«)
Особенность в (8.7.1) называется первого порядка, потому что она появляется в пер-
№
U-z0)2
вой степени. Соответственно, —'^ ' имеет особенность второго порядка и т. д.
Я расскажу гораздо больше об особенностях высших порядков в следующем разделе.
318 ♦ Контурное интегрирование
Τ ic
Рис. 8.7.1 ♦ Контур, охватывающий одну особенность
первого порядка
Подынтегральное выражение в интеграле по контуру можно разложить
в виде:
1
1
b2+z2 (z + ib){z-ib) i2b[(z-ib) (z + ib)\
и поэтому мы имеем:
J_
ilb
eia(Te®)
eiaz ιαζ ι tax π ш(Ге-)
Поскольку подынтегральное выражение второго контурного интеграла в
левой части аналитично всюду внутри С - действительно, у подынтегрального
выражения есть особенность, но она находится в точке ζ = -ib вне С, как
показано на рис. 8.7.1, - тогда мы знаем из первой интегральной теоремы Коши,
что второй контурный интеграл в левой части равен нулю. И как только Т> b
(помните, в конце концов мы будем использовать Τ —> оо), то особенность для
оставшегося контурного интеграла слева будет внутри контура С, при ζ = ib.
Таким образом:
—f
ilb* z-ib
ζ J- ριαχ π
oiW)
b2+x2
-iTeiede.
Подынтегральное выражение в контурном интеграле слева выглядит точно
так же, как f(z)/(z - z0), где f(z) = e'az и z0 = ib. Вторая интегральная теорема Коши
говорит нам, что если Г > Ъ, то контурный интеграл равен 2π//(ζ0), и поэтому
левая часть последнего равенства:
1
—2ти'е'а(№)
ilb
^e-°b.
b
Вторая интегральная теорема Коши ♦ 319
То есть
eia(TeB)
Теперь, если, наконец, Τ —> оо, то, приняв те же аргументы, что и в
отношении криволинейного интеграла вдоль дуги окружности в предыдущем разделе,
мы увидим, что второй интеграл слева обращается в ноль как 1/Г. Используя
формулу Эйлера, мы имеем:
Г С" d _ π „ _ °f cosjax) °f sin(ax)
Приравнивая мнимые части, мы приходим к равенству
sin(aA:)
/
Ь2+х2
dx = 0,
что, безусловно, неудивительно, поскольку подынтегральная функция
является нечетной функцией от х. Приравнивание вещественных частей дает нам
гораздо более интересный интеграл:
cosiax) , π _
i2 2dx = Te
b2+x2 b
Однако я не поместил этот результат в рамку, поскольку мы уже вывели его
с использованием «рутинных» методов - см. (3.1.7). Мы также сделали это,
применяяя концепцию энергетического спектра временного сигнала, в
задаче 7.7 (вы справились с этой задачей, верно?). Как я уже говорил ранее, приятно
видеть, что контурное интегрирование согласуется с предыдущим анализом.
Хорошо, а как посмотреть, что стоит за второй интегральной теоремой
Коши? Доказательство красиво и элегантно. На рис. 8.7.2 я нарисовал контур С
и внутри его обозначил точку z0. Кроме того, я нарисовал окружность С* с
центром в z0 и с радиусом р, достаточно малым, чтобы С* полностью лежала внутри
С. Теперь представьте, что с некоторой произвольной точки (назовем ее А) мы
начинаем путешествовать вдоль С в положительном (против часовой стрелки)
направлении, пока не достигнем точки а, после чего движемся внутрь к
точке Ъ на С*. Достигнув точки Ь, мы движемся по часовой стрелке (то есть в
отрицательном направлении) вдоль С*, пока не вернемся в точку Ь. Затем мы
возвращаемся к контуру С по тому же пути, по которому шли внутрь, пока не
вернемся в точку а. Потом продолжим движение по С в направлении против
часовой стрелки, пока не вернемся к нашей исходной точке А.
Вот первое из двух критически важных замечаний о том, что мы только что
сделали. На всем пути, которым мы следовали, кольцевая область между С и С*
всегда была слева от нас. То есть этот путь является границей области,
которая не содержит точку z0. Таким образом, в той кольцевой области, из которой
320 ♦ Контурное интегрирование
точка z = z0 была исключена по построению, функция f(z)/(z - z0) всюду анали-
тична. Таким образом, по первой интегральной теореме Коши, поскольку ζ =
ζ0 находится вне С, мы имеем:
§
/W
C,ab,-C\baZ Z0
dz = 0.
(8.7.2)
Рис. 8.7.2 ♦ Простая кривая С (окружающая точку z0),
соединенная с внутренней окружностью С* поперечным разрезом ab
Мы написали -С* в описании пути контура интегрирования из-за того, что
обошли С* в отрицательном направлении.
А вот второе из двух наших принципиально важных замечаний. Два
прохода по ab-соединению между С и С* (математики называют это двустороннее
соединение поперечным разрезом) происходят в противоположных
направлениях и поэтому взаимно сокращаются. Это означает, что мы можем написать
(8.7.2) как
№
f(z)
J у 7 J 7 7 J
С,-С
Ζ-Ζ,
ζ-ζη
ζ-ζη
άζ.
(8.7.3)
Причина знака минус перед контурным интегралом С* в крайнем правом
интеграле (8.7.3), опять же потому, что мы обошли С* в отрицательном
направлении. Однако два крайних правых интеграла в (8.7.3) берутся в
положительном направлении, и поэтому знак минус был вынесен из дескриптора пути -С*
внизу знака интеграла на место перед самим интегралом.
Теперь, когда С - произвольная простая кривая, охватывающая ζ0, пусть С* -
окружность с радиусом ρ с центром в ζ0. Таким образом, на С* мы можем
записать ζ = ζ0 + реге (что означает άζ = fpe'ed6), и, следовательно, при изменении
θ от 0 до 2π в нашем одном полном обходе вокруг С* (8.7.3) принимает вид:
Вторая интегральная теорема Коши ♦ 321
§l®-ta = fJ®-*c = /М±^Лй = ψ(Ζο +ре.)Л.
с ζ ζ0 с* ζ ζ0 0 ре 0
Если крайний левый интеграл должен иметь значение, то, чем бы оно ни
было, оно не должно зависеть от р. В конце концов, интеграл слева не имеет р!
Таким образом, самый правый интеграл также не должен зависеть от р, даже
если в нем есть р. Это означает, что мы должны иметь возможность
использовать любое значение р, которое пожелаем. Итак, давайте используем то
значение для р, которое нам удобно.
В частности, используем очень маленькое значение, действительно такое
маленькое, чтобы сделать разницу между Дг) и f(z0) для всех ζ на С* настолько
малой, насколько нам нужно. Мы можем сделать это, потому что f(z)
предполагается аналитической, и поэтому имеет производную всюду внутри С (в том
числе и при ζ = ζ0), и поэтому, безусловно, непрерывна. Таким образом, когда
ρ —> 0, мы можем считать, что f(z) —> f(z0) по всей линии С*, и таким образом:
^I^Ldz = ijf(Zo)dQm
Наконец, вынося константу f(z0) за знак интеграла, мы имеем:
f-^-dz = if(Z0)fdQ = 2πί/(Ζο),
с Ζ Ζ0 0
что представляет равенство (8.7.1), и наше доказательство второй
интегральной теоремы Коши закончено.
Теперь мы можем взять интеграл в (8.6.5) для случая Ь2 < 4ас. То есть теперь
мы изучим контурный интеграл
dz
, a^Oyb < 4ac.
az +bz + c
Подынтегральное выражение этого интеграла имеет две особенности, ни
одна из которых не расположена на вещественной оси. Поскольку Ь2 < 4ас, эти
особенности являются комплексными и задаются формулами:
χη = f — ы4ас-Ь2
2 2а 2а
χλ = \-i—\l4ac-b2.
1 2а 2а
На рис. 8.7.3 я показал, что эти особые точки имеют отрицательные
действительные части, но они могут быть и положительными, в зависимости от знаков
а и Ь. Это в действительности не имеет значения, однако что имеет значение,
322 ♦ Контурное интегрирование
так это то, что для контура С, нарисованного на рисунке, только одна из особых
точек находится внутри С (произвольно выбранной какг^, в то время как
другая особенность (z2) находится снаружи С.
Рис. 8.7.3 ♦ Контур,
заключающий одну из двух особенностей
Запишем подынтегральное выражение как разложение на частные дроби:
а . а
1 _1
az2+bz + c a
Тогда
л в
ζ-ζλ ζ-ζ2
ι
yj4ac-b2 yJAac-b2
ζ-ζΛ
Z-Zn
Jc az +bz + c aJ
-ι
(л n
с ζ ζλ a c ζ ζ2
Второй интеграл справа равен нулю по первой интегральной теореме Коши
(особенность z2 не заключена в Q, и поэтому
dz . 1
§
= —ι-
caz2+bz + c *yl4ac-b
:£ dz.
J 7—7
2 u Z — Z
c Α, Α,χ
Из второй интегральной теоремы Коши, которую мы только что доказали
(при Дг) = 1), мы имеем:
Вторая интегральная теорема Коши ♦ 323
£ dz = 2ni,
J 7— 7
с Ζ Ζχ
и тогда
dz 2π
§
caz2+bz + c yJAac-b2 '
Но криволинейный интеграл вдоль С выражается формулой
г dx j- iTe* dQ
_Г„Л -г^-г. 9 а(Ге1е)2+Ь(Геш) + с
и θ-интеграл явно исчезает, подобно 1/Тпри Τ ^ оо. Таким образом:
dx 2π
/—а—: = ι a^0,b2<4ac.
(8.7.4)
Например, если а = 5,b = 7 ис=Ъ (заметим, что Ь = 49 < 4ас = 4(5)(3) = 60),
2π
то (8.7.4) говорит, что наш интеграл равен — = 1.89445..., и MATLAB
подтверждает: quad(@(x)l./(5*x.A2+7*x+3),-le5,le5) = 1.894449...
Для впечатляющей иллюстрации первой и второй теорем я сейчас буду
использовать их для вычисления целого класса интегралов:
оо т
{х"+1
где тип- любые неотрицательные целые числа, такие что (чтобы
гарантировать, что интеграл существует) п-т>2. Мы изучим контурный интеграл
£z"+l
dz (8.7.5)
с соответствующим образом выбранным контуром С. Подынтегральное
выражение в (8.7.5) имеет η особенностей первого порядка с η корнями п-й степени
из -1. Эти особые точки равномерно распределены вдоль единичного круга
в комплексной плоскости. Поскольку формула Эйлера говорит нам, что
-1 = е/(1+2/с)тт
для любого целого числа к, то эти особые точки расположены в точках
zk=(-l)»=e[ п ] , * = 0,1,2,...,л-1.
Конечно, для остальных значений к эти же η точек просто повторяются.
Теперь давайте сконцентрируем наше внимание только на одной из этих особых
точек, той, для которой к = 0. Мы выберем контур С так, чтобы заключить толь-
324 ♦ Контурное интегрирование
ко эту особенность, при ζ = z0 = e ", как показано на рис. 8.7.4. Центральный
2π г π
угол клина равен —, а особенность равна половине этого угла, —.
η η
Рис. 8.7.4 ♦ Контур в форме кусочка торта,
заключающий в себе одну из η особенностей
Поскольку мы обходим контур С, чтобы взять интеграл в (8.7.5), то описания
трех частей контура таковы: на Q: ζ = χ, dz = dxy 0 < χ < Τ; на С2: ζ = Теш (dz ■-
2π „ №( -2π
= re n \c
iTelQdQ), 0 < θ < —; на C3: ζ
η
dz = e "^г/,Т>г>0.Итак:
—2
% zn +1 { x" +1 J0 (Ге*)" +1 { r"e'2n +1
2π
η (те1<> γ,
142π
i(m+l)—
2π
Теперь ясно, что при Τ —> оо θ-интеграл стремится к нулю, поскольку m + 1
< п. Также
V 1Ч2"*
τ ™ '(и+i)—
-dr = e
·/ гп+\
2π Τ
" f——dr = e
гЧ1
ί(ι»+1)- Ρ Xm .
n \ dx.
Итак, при Τ —> оо
£ζ"+1 Jnx"+1
1-е
/(m+l)
2π
Вторая интегральная теорема Коши ♦ 325
Или, поскольку
i(m+l)-
1-е
мы имеем:
Так как
/(1И+1)-
-2zsinj
-i(m+l)-
i(m+l)-
-2zsinJ
(m + 1)
π
/(m+1)-
(m + 1)
π
/(m+1)
dx.
(8.7.6)
Zn+l = l\(Z-zk),
мы можем записать подынтегральное выражение контурного интеграла
в (8.7.5) в виде разложения на элементарные дроби:
Nn
+ -
ΝΛ
- + -
Νη
ζ"+1 ζ-ζ0 ζ-ζλ ζ-ζ:
. + ... + -
Λί„
ζ-ζ».
где числа N являются константами. Интегрируя это расширение почленно, мы
получаем:
dz
iWxdz = 4
с % Ζ0
так как первая интегральная теорема Коши говорит, что все остальные
интегралы равны нулю, потому что по построению контур С не охватывает
особенности Ζι, ζ2, ..., ζ„_ι· Единственная особенность, которую контур С заключает
в себе, - это ζ0. Вторая интегральная теорема Коши в (8.7.1), при f(z) = 1,
говорит, что интеграл справа равен 2πί, и поэтому (8.7.6) принимает вид:
-2/sinj
(т + 1)-
/(m+1)- ρ AT , 0 ._.
\е п \ άχ = 2πιΝη.
(8.7.7)
Наш следующий (и последний) шаг - это найти N0. Чтобы сделать это,
умножим разложение дроби подынтегрального выражения в (8.7.5) на ζ - ζ0, тогда
получим:
(z-z0)zm_ = jv | (z-z^N, | (z-z0)N2 | | (z-z^N^
zn+l
ζ-ζΛ
Ζ-Ζη
ζ-ζ„
'"Ι *- *-2 *- *Ίι-1
а затем пусть ζ —> ζ0. Это приводит к тому, что все члены справа после первого
исчезают, и поэтому
iVn=lim(Z Zq)Z"
0 —о z"+l
lim
zm+1-z0zm
z"+l
326 ♦ Контурное интегрирование
Итак, чтобы устранить эту неопределенность, мы будем использовать
правило Лопиталя:
Nn
Hm(^ + l)zm-^z0zm"1 _ ттГ+тГ-тт^тГ-1 _ ζ.
m-\ ,y m-n+1
0
z^z0
nz
z^z0
nz
или подставляя z0 = e ":
.π, 1ч .пт . .π
ι—(m-n+l) ι m+i—
ζη e η η e'le
ΐπ _ Ι η
η η η η
Подставив этот результат в (8.7.7), получаем:
.(m+l)
°r Xm
2πζ
dx-
n
-2/sinJ
— \e
/
-dx-
i(m+l)-
и поэтому у нас есть замечательный результат
sinj(w + l)
, n-m>2.
(8.7.8)
Вы можете увидеть, что при т = 0 и п = 4 это выражение воспроизводит наш
результат в (2.3.4). При т = 0 и п = 3, (8.7.8) дает результат
π
π
sin
?}
Υ = 2π
2
1.209199...,
mMATLAB подтверждает: quad(@(x)l./(χ.Λ3+1),0,1000) = 1.209199....
Результат (8.7.8) можно представить как минимум в трех альтернативных
формах, которые обычно встречаются в математической литературе. Сначала
определим ί = χ", и тогда
— = пхп \
ах
что означает
dt
dx
пх
dt
п—1
rKty
Вторая интегральная теорема Коши ♦ 327
Тогда (8.7.8) дает
(t)"
at
[n(t)» J
π
sin
ИЛИ
m-n+1
m+1
f (0 "
-dt
π
(0"
sin](w? + l)
π
Jn t + 1
-Λ.
Теперь пусть
w + 1
fl = ,
что дает нам
оо а-1
Г dx = , 0<α<1
·£ x + l sin(cm)
Например, если а = гЛ, то
ах
π
л£(* + 1) siJ
sin
= π,
(8.7.9)
иМАТЬАВ подтверждает: quad(@(x)l./(sqrt(x).*(x+l)),0,lel0) = 3.141546....
Другой способ переформулировать (8.7.8) - это начать с (8.7.9) и положить
t = \п(х), и тогда
dx a: ec
Таким образом, левая часть равенства (8.7.9) принимает вид (потому что
χ = 0 означает t = -оо):
°° gt(fl-l)
оо е«
J 1 + е* J l + ec
dt.
1 Ограничения на α обусловлены тем, что, во-первых, поскольку η - т>2, то m + 1 <
и - 1, и поэтому α < 1. Кроме того, подынтегральное выражение в (8.7.9) ведет себя
ха
как Xя"1, которое интегрируется к функции —, а это выражение обращается в беско-
а
нечность в нижнем пределе интегрирования, если а < 0. Поэтому О < а.
328 ♦ Контурное интегрирование
Поэтому
1 + е*
-dx =
π
sin(6m)'
0<α<1.
Например, если 1/3, то интеграл равен
π
π 2π
(8.7.10)
: 3.62759.
sin(<n/3) д/з ^3
2
и MATLAB подтверждает этот результат: quad(@(x)exp(x/3)./(l+exp(x)),-100,100)
= 3.62760.... Интересно сравнить (8.7.10) с (8.6.9).
И в заключение сделаем в (8.7.9) замену переменной:
1
и = -,
χ
и тогда
dx
du
и2'
Поэтому
( du)
г χ , г\и аи\ г
о Л + х оо £_|_i ^ " J о
di/
fl + ul
ι/
(IIя-1 )И2
du
1 + u
и
и тогда
dx
π
J (l + x)xa sin(an)
0<α<1.
(8.7.11)
В конце этого раздела я приведу пример использования второй
интегральной теоремы Коши в задаче, где появляется несколько особенностей первого
порядка. Для произвольной положительной константы а мы вычислим
значение интеграла
2π
/
de
ι + sin2e
Мы можем справиться с несколькими особенностями, просто используя
общую идею, приведенную ранее в этом разделе. То есть когда мы проходим по
контуру С, просто движемся внутрь по разрезу до первой особенности, а затем
обходим ее по крошечному кругу радиуса ρ и потом возвращаемся назад по
разрезу к контуру С. Затем, после того как мы проходим дальше по С, делаем
то же самое с новым разрезом ко второй особенности. И так далее, для всех
Вторая интегральная теорема Коши ♦ 329
остальных особенностей. («Крошечный» означает выбор достаточно малого
радиуса р, чтобы окружности около особенностей не пересекались между
собой и всегда были бы внутри С.) Для каждой особенности мы выберем
значение 2πζ/(ζ0), если подынтегральное выражение контурного интеграла, который
f(z)
мы изучаем, имеет вид .
z-z0
Итак, какой контурный интеграл мы будем изучать? На единичном круге
С мы имеем:
z = e'e=cos(e) + zsin(e), - = e"'e = cos(e)-zsin(e), (8.7.12)
ζ
и тогда
dz = ieiede = izdQ,
а также
1
sin(6) = z-4 =
z2-l
2/ 2zz
Тогда
shrt= (Z2"1)2
4z2 '
и поэтому контурный интеграл, который мы будем изучать, имеет вид:
dz
£ Щ T = 4i<£— —5 dz. (8.7.13)
ίπ (^2-1)2 lz4-z\2 + 4a) + l
4ζ2
Подынтегральное выражение явно имеет четыре особенности первого
порядка, все они расположены на вещественной оси в точках:
z = >/h, H = (l + 2a) + 2Va(a + l),
а также
z = ylu, ii = (l + 2fl)-2>/fl(fl + l)-
Из проверки видно, что для первой пары особенностей \z\ > 1, и поэтому оба
корня лежат вне С, в то время как для второй пары \z\ < 1, и поэтому оба корня
лежат внутри С. В частности, давайте запишем zx и z2 как внутренние
особенности, где
330 ♦ Контурное интегрирование
Z2 = ->/(l + 2fl)-2>/fl(fl + l) = -z19
a z3 и z4 как внешние особенности, где
ζ4 = ->/(1 + 2α) + 2Λ/α(α + 1) = -ζ.
Подынтегральное выражение в контурном интеграле справа в (8.7.13)
принимает вид:
ζ ζ
(ζ-ζ1)(ζ-ζ2)(ζ-ζ3)(ζ-ζ4) ~ (ζ-ζιΧζ-ζ2)(ζ-ζ^)(ζ + ζ5) ~
ζ
"(ζ-ζλ)(ζ-ζ2)(ζ2-ζΙ)
Теперь, из второй интегральной теоремы Коши, контурный интеграл равен
2πί
(ζ-ζ2)(ζ2-ζξ)
(z-Zl)(z2-z23)
Я оставляю вам проверить алгебру (которая на самом деле не является
ужасной, если вы будете аккуратны), показывающую, что каждый из двух членов
в квадратных скобках равен , Таким образом:
8^0(0 + 1)
г zcte , _ πζ
|ζ4-Ζ2(2 + 4α) + 1 Ζ~~2^φΤΤ)'
и, умножая на 4/, получаем из (8.7.13):
dQ 2n
I
[ a + sin2(6) yja(a + l)
, α>0.
(8.7.14)
Если а = 3, то интеграл равен 31.81379936..., и MATLAB подтверждает,
поскольку quad(@(x)l./(3+(sin(x).A2)),0,2*pi.) = 1.81379936....
8.8. Особенности и теорема о вычетах
В этом разделе мы выведем замечательную теорему о вычетах, которая сводит
кажущийся поразительно сложным определенный интеграл к такому, который
просто имеет «обычный» статус. Мы начнем с функции Дг), аналитической
Особенности и теорема о вычетах ♦ 331
всюду в некоторой области R в комплексной плоскости, за исключением точки
ζ = ζ0, которая является особенностью порядка т > 1. То есть
fW-j^. (8.8Л)
где g(z) аналитична на всей области R. Поскольку g(z) аналитична, мы знаем,
что она «ведет себя хорошо», что является выражением математического
условия «все производные g(z) существуют». (Оглянитесь на (8.7.1) и последующий
комментарий.) Это означает, что g(z) имеет разложение в ряд Тейлора
относительно ζ = ζ0, и поэтому мы можем написать:
g(z) = с0 + c,(z - z0) + c2(z - Zo)2 + c,(z - ζ0Ϋ +.... (8.8.2)
Подстановка (8.8.2) в (8.8.1) дает:
или как обычно пишут:
оо оо Ъ\
f(Z) = J2an(z-zJ+Z-^—;> (8-8-3)
п=0 п=0 \Z Zq)
где во второй сумме все Ъп = 0 при п> т.
Разложение функции Дг) в окрестности особой точки в ряд вида (8.8.3),
включающий как положительные, так и отрицательные степени (ζ - ζ0), называется
рядом Лорана функции Дг), названным так в честь французского математика
Пьера Альфонса Лорана (1813-1854), который исследовал его в 1843 году. (В
книгах, посвященных комплексному анализу, гораздо более подробно, чем
здесь, показано, что разложение в ряд Лорана единственно.) Мы можем найти
формулы для коэффициентов апиЬпв разложении (8.8.3) следующим образом.
Начнем с наблюдения, что если к - любое целое число (отрицательное, нулевое
или положительное) и если С - окружность радиуса ρ с центром в ζ0 (что
означает, что на С мы имеем ζ = ζ0 + реге), то
§{z-zjdz = fpkeikeieiedQ = i9k+1 JV(fe+1)0de = ipk+1 ^ = $— {e/(fe+1)0}|
ei(*+i)e
При условии что k^-l9 это последнее выражение равно 0. Если к = -1, наше
выражение становится неопределенностью —. Чтобы обойти это, для к = -1
просто сделаем дополнительно пару действий и напишем:
2π ι 2π
§{z-z0Y1dz = f—^ie№dQ= ifdQ = 2iri.
332 ♦ Контурное интегрирование
То есть для любого целого числа к
О, к-1
(f)(z-z0)kdz-
п . , v (8.8.4)
2πζ, к = -1
Итак, чтобы найти конкретный α-коэффициент (скажем, aj)f просто
разделим (8.8.3) на (ζ - ζ0))+1 и проинтегрируем почленно. Все интегралы исчезнут
вследствие (8.8.4), за единственным исключением:
-ζ
То есть
<£ '{Z).,dz = £—— dz = 2π/α,..
i(z-z0)'+1 {z-z0
А чтобы найти конкретный Ь-коэффициент (скажем, bj), просто умножим
(8.8.3) на (ζ - ζ0);_1 и проинтегрируем почленно. Все интегралы исчезнут
вследствие (8.8.4), за единственным исключением:
§f(z)(z-zQ)hldz = §bj(z-zQTldz = §—i—dz = 2nibr
с с с Z~ z0
То есть
«i-Siftt^*· >~W <8'8·6)
Одно из настоящих чудес контурного интегрирования состоит в том, что
из потенциально бесконечного числа коэффициентов, заданных формулами
(8.8.5) и (8.8.6), только один из них будет для нас интересен. Этот избранный
коэффициент есть Ъъ и вот почему. Если мы установим/ = 1 в (8.8.6), то1
ff(z)dz = 2mbi, (8.8.7)
с
что почти (с точностью до 2πζ) является конечной целью наших расчетов для
нахождения интеграла
§f{z)dz.
С
Но, конечно, мы не берем интеграл, чтобы найти Ьх (если бы мы могли
напрямую найти интеграл, кому интересно значение Ь^!), а скорее наоборот, мы
Контур С в (8.8.7) был окружностью радиуса ρ с центром в этой точке ζ0, но на самом
деле, используя идею поперечного разреза на рис. 8.7.2, мы можем считать контур С
любым контуром, обходящим ζ0, так что f(z) всюду аналитична на контуре С и внутри
его (кроме, конечно, z0).
Особенности и теорема о вычетах ♦ 333
вычисляем Ъх другими способами, отличными от интегрирования, а затем
используем этот результат в (8.8.7) для нахождения интеграла. Значение Ъх
называется вычетом функции f(z) в особенности ζ = ζ0.
Что означает «другие способы, отличные от интегрирования»?
Оказывается, совсем не сложно заполучить Ъх. Предположим (как мы это делали в
начале данного раздела), что f(z) имеет особенность порядка т. То есть выпишем
(8.8.3) чуть более подробно:
/(z) = - + a1(z-z0) + fl0+—^ + -—*—2- + - +
(ζ-ζ0Υ (ζ-ΖοΓ
Тогда умножение на (z - z0)m дает:
(ζ - ζ0)Ύ(ζ) = ... + αλ(ζ - ΖοΓ1 + α0(ζ - z0)m + bx(z - zQ)m~l + b2(z - zQ)m~2 + ... + bm.
Далее дифференцируем по ζ всего πι-Ι раз. Это дает три эффекта: (1) все
члены с α-коэффициентами будут сохранять коэффициент (ζ - ζ0) по меньшей мере
до первой степени; (2) член Ъх будет умножен на (т-1)!, но не будет иметь
множителя (ζ - Ζο) и (3) все остальные члены с Ь-коэффициентом будут
продифференцированы до нуля. Таким образом, если ζ —> ζ0, то члены с α-коэффициентами
исчезнут, и мы останемся только с (т-Х)\Ъх. Следовательно:
&ι=ΓΛτ7Ηιη^Γί(ζ-ζοΓΑζ)},
(m-iy.z^zodz
(8.8.8)
где z0 - особенность m-ro порядка функции f(z). Это настолько важный
результат, что я показываю (8.8.8) в рамке.
Для особенности первого порядка (т = 1) формула в (8.8.8) сводится при
corf™ 1
глашении -— = 1, если т = 1, к следующей:
bl=lim(z-z0)/U)·
z^>zQ
Как более общий вариант возьмем f(z) в виде:
Κζ)
где, как и прежде, функция g(z) аналитична в особенности z = z0 (которая тогда,
конечно, является нулем первого порядка h(z)). To есть
h(z0) = 0.
Тогда
lim(z-z0)/(z) = lim(z-z0)f^ = lim(z-z0)- *(z)
h(z) ~*v 0/ft(z)-ft(z0)'
334 ♦ Контурное интегрирование
где знаменатель в крайнем правом выражении равен h(z) = h(z) - h(z0), потому
что h(z0) = 0. Итак:
lim(z-z0)/(z) = -
g(z)
dz
КЦ
Z=ZQ
To есть вычет для особенности первого порядка в точке ζ = ζ0 в
подынтегральном выражении f(z) можно вычислить как
Ь,
_ g(Zp)
1 h\zQ)
(8.8.9)
Я покажу вам пример использования (8.8.9) в следующем разделе этой главы.
Иногда вы можете применять другие «хитрости» для нахождения вычета
сингулярности. Вот тот, который непосредственно использует ряд Лорана, не
требуя никакого дифференцирования вообще. Давайте подсчитаем
2π
fcosk(Q)dQ
о
для четного целого числа к. (Интеграл, конечно, равен нулю для нечетного
целого числа /с, потому что косинус симметричен относительно оси θ в интервале
от 0 до 2π и поэтому ограничивает нулевую область.) Снова используя (8.7.12)
на единичной окружности C(z = еге), мы имеем:
COS(6):
z2+l
2z
ndz = izdQ. Итак, давайте изучим контурный интеграл
\к * + , 2 . 14fe
J\ 77 \ 17 i7kJ
iz ilk
dz.
(8.8.10)
Здесь мы имеем особенность при ζ = 0 порядка т = к+ 1. Это значит, что
может быть много дифференцирований при использовании формулы (8.8.8),
если к - большое число!
Более подходящий способ получить вычет этой особенности высокого
порядка состоит в том, чтобы использовать формулу бинома Ньютона для
разложения подынтегрального выражения как
(z2+l)fe
1 к
Ζ /=ο
2у/1\*-;'
(ГУО)'
к
Έ
72}-к-1
что является разложением в ряд по отрицательным и положительным
степеням ζ вблизи особой точки в нуле. Так и должно быть, это есть разложение
Лорана подынтегрального выражения (помните, что такие разложения един-
Особенности и теорема о вычетах ♦ 335
ственны), из которого мы можем буквально взять вычет (коэффициент при ζ ι).
Полагая 2/ - к - 1 = -1, мы находим, что /= —, и поэтому вычет есть
{ к )
fc!
к\
к/2
Тогда
(Ζ2+1/
(k/2)!(fc/2)! [(fc/2)!]2
/
yfe+l
dz = 2ni-
k\
[(k/2)!]2
и из формулы (8.8.10) получаем:
(8.8.11)
Например, если к = 18,то интеграл равен 1.16534603, и MATLAB соглашается,
потому что quad(@(x)cos(x).A18,0,2*pi) = 1.165347....
Давайте теперь разберем еще один пример, используя (8.8.8). В формуле (3.4.8)
мы вывели результат (где аиЬ- положительные постоянные, причем а > Ъ)
/
1
C/θ:
π
I a + bcos(0) Va2-b2'
который эквивалентен следующему:
I
1
de =
2π
a + bcos(6) 4a>~tf9
потому что cos(6) от π до 2π просто повторяет те же значения, что и от 0 до
π. Теперь предположим, что мы взяли а = 1иЬ = к<1. Тогда формула (3.4.8)
говорит нам:
2π
Г—-
_de = _j5=> u<l.
cos(6) д/ГЗр
Этот результат может побудить нас «поднять ставку» и задаться вопросом
о значении
2π
1
-de=?
i {l + fecos(9)r
Если мы примем, что С - это единичный круг с центром в начале координат,
то на контуре С, как и в предыдущем разделе, мы имеем ζ = еге, и,
следовательно, из тождества Эйлера мы можем записать:
336 ♦ Контурное интегрирование
cos(6) = -
f 1
z + -
z,
I
_Z2+l
2z
•
Итак, на С мы имеем
1
l + kcos(6)
и поэтому
1
{l + kcos(6)}2
1 2z
1 + fc
( 2 *λ
Z2+l
2z
2z + fcz2+fc
=
'41
Л2)
z2
z2+^z + l
l к
2 '
Так же, как и прежде:
dz = ieiedQ = izdQ
iz
Все это говорит о том, что мы рассматриваем контурный интеграл
§
_4_
к2)(
dz l
2 2
/ζ ι
_4_
fc2
ί
ζ2+?ζ+1
V2
dz.
Мы видим, что подынтегральная функция имеет две особенности, и каждая
из них второго порядка. То есть т = 2 и особенности в точках
I
Z = 2
--± --4
k Vfc2
i±Vi-fc2
Поскольку /с < I, то особенность
Ζ ΖΠ1 "
находится вне С, в то время как особенность в точке
-1 + VI^F
% ~ ^02 — "
находится внутри контура С. Таким образом, ζ02 - это единственная
особенность, для которой нам нужно вычислить вычет, как указано в (8.8.8).
Особенности и теорема о вычетах ♦ 337
Итак, при т = 2 этот вычет есть
h = lim -
Поскольку
(*-*02)2-
(z-z02f
.2 . 2.
.2 . 2.
z'+-z + l
: (£ ^02) ,_ _ v2/_ _ 42
z'+-z + l
(z-^rU-^,2)
£H ;
Y2'
мы имеем выражение
dz
(*-*ο2):
.2 . 2
z'+-z + l
dz
z +
ι+VT^e
которое, после небольших алгебраических преобразований, которые я
оставляю выполнить вам, сводится к
-Z +
i+VI^F
2 Η ;—
з ·
_ι+Λ/ΙΓ^
Теперь, наконец, мы положим ζ=ζ02 = и получаем:
Ь,=
1-7Г^)ё | ι+λ/ϊ^"
i-i+VTF i+VTFf 8(1-fe) 4(1"k)
Тогда
+
ζ , η . к
-dz = 2m
>2чЗ/2 '
nik2
Ίζ2+?ζ + 1
V2
4(l-k2)3/2 2(l-fe2)3/2'
338 ♦> Контурное интегрирование
и поэтому
1 1Г 4 1 π/fc2
I
-άθ = -
0 {l + kcos(9)}2 " /
То есть
2(1-к2)3/2'
1 ,„ 2π
Г 1 dQ = ζπ
■J {l + kcos(9)}2 (l-k2)3/2'
(8.8.12)
Например, если к = -, то наш результат есть 9.67359..., что подтверждает
MATLAB, поскольку quad(@(x)l./(l+O.5*cos(x)).A2,0,2*pi) =9.67359....
Чтобы закончить этот раздел, я сейчас официально обобщу то, что мы делали
на протяжении всего этого: если f(z) аналитична на контуре С и внутри его, за
исключением N особенностей, и если Rj является вычетом ;-й особенности, то
ff(z)dz = 2ni£Rr
/=1
(8.8.13)
Это знаменитая теорема о вычетах. Для каждой особенности мы берем ее
вклад в интеграл как вычет в этой особенности, умноженный на 2πί, когда
вычет находится в соответствии с формулой (8.8.8) или (8.8.9), если т = 1,
используя свое значение т для каждой особенности. Вот так! В следующем (и
последнем) разделе этой главы я покажу вам пример применения формулы (8.8.13)
к интегралу, который имеет еще одно дополнительное усложнение, с которым
мы еще не сталкивались.
8.9. Интегралы с многозначными
подынтегральными функциями
Вся удивительная сила контурного интегрирования проистекает из теорем,
которые говорят нам, что происходит, когда мы обходим один раз по замкнутому
пути в комплексной плоскости. Теоремы применимы только для замкнутых
путей. Я подчеркиваю этот момент - особенно слово «замкнутых», - потому
что есть тонкий способ, когда замкнутость может потерпеть неудачу, настолько
тонкий, что его слишком легко пропустить. Признание проблемы, а затем
понимание способа ее решения приводит к важным концепциям ветвей разрезов
и точек ветвления в комплексной плоскости.
Существует множество примеров того, как могут возникать ложные
замкнутые пути, но классический включает в себя интегралы, содержащие
логарифмическую функцию. Записывая комплексную переменную, как мы это делали
в (8.3.3), как ζ = гё\ мы имеем log(z) = ln(z) = 1п(гей) = 1п(г) + /Θ, 0 < θ < 2π.
Внимательно обратите внимание на знак < слева от Θ, но справа там строгий знак
Интегралы с многозначными подынтегральными функциями ♦ 339
неравенства <. Как было указано в разделе 8.3, параметр θ определяется не
однозначно, поскольку мы можем сложить (или вычесть) любое кратное 2π с Θ,
и, по-видимому, все это будет относиться к одной и той же физической точке ζ
в комплексной плоскости. То есть нам действительно нужно записать log(z) =
1п(г) + ί(θ±2πη), 0 < θ < 2π, η = 0, 1, 2,....
Говорят, что логарифмическая функция многозначна, поскольку мы
бесконечно зацикливаемся вокруг начала координат. Математическая
проблема, с которой мы сталкиваемся при этой более полной формулировке
логарифмической функции, состоит в том, что она не является непрерывной на
любом пути, который пересекает положительную действительную ось! Вот
почему.
Рассмотрим точку ζ = ζ0 на положительной вещественной оси. В этой
точке г = х0 и θ = 0. Но мнимая часть log(z) не является непрерывной функцией
ζ в точке х0, потому что ее значение во всех бесконечно малых окрестностях
«чуть ниже» положительной вещественной оси в точке х0 и сколь угодно близко
к 2π, а не 0. Важнейшим следствием этого нарушения непрерывности
является то, что производная логарифма log(z) не существует, когда мы пересекаем
положительную вещественную ось, что означает, что аналитичность тоже не
срабатывает. А это значит, что все наши замечательные интегральные теоремы
находятся за окном!
Геометрически то, что происходит, когда мы двигаемся по замкнутому
круговому пути (начиная с х0, а затем обходя вокруг начала координат),
заключается в том, что мы не возвращаемся в начальную точку х0. Скорее, мы
пересекаем положительную вещественную ось и входим в новую ветвь log-функции.
Ежедневный пример этого происходит, когда вы двигаетесь по спиральной
дорожке в многоуровневом гараже в поисках места для парковки и
переходите от одного уровня (ветви) к следующему уровню (другой ветви) гаража. Ваш
спиральный путь «выглядит замкнутым» для наблюдателя на крыше, который
смотрит вниз (точно так же, как вы смотрите вниз на математический лист,
когда рисуете то, что кажется замкнутым контуром в плоской комплексной
плоскости), но траектория пути к вашей парковке в гараже не замкнута. И
конечно, это не «замкнутый» контур. Без сомнения, это не проблема для вашего
автомобиля, но это кажется фатальной проблемой для наших интегральных
теорем.
Или, возможно, нет. Помните старую поговорку: «если ваша голова болит
от того, что вы бьетесь ею о стену, то перестаньте стучать головой по стене!»
У нас такая же ситуация. «Если пересечение положительной вещественной
оси разрушает интегральные теоремы, тогда не пересекайте положительную
действительную ось». Что нам нужно сделать здесь, при построении контура,
включающего логарифмическую функцию, - так это просто избежать
пересечения положительной вещественной оси. Мы отмечаем положительную
вещественную ось от начала координат до плюс бесконечности как так
называемый разрез ветвей (конечные точки разреза, χ = 0 и χ = +оо, называются
340 ♦ Контурное интегрирование
точками ветвления), а затем будем избегать пересечения с этой линией. Любой
контур, который мы нарисуем, удовлетворяя этому ограничению, абсолютно
гарантированно будет замкнутым (то есть всегда будет оставаться на одной
ветви), и, следовательно, наши интегральные теоремы остаются в силе.
Другой часто встречающейся многозначной функцией, которая
представляет ту же проблему, является дробная степень zp = гре1рв, где -1 < ρ < 1, и, как
и прежде, мы считаем, что 0 < θ < 2π. Предположим, например, что у нас есть
функция VE, и поэтому ρ = -. Любая точка на положительной вещественной
оси имеет θ = 0, но в очень малой окрестности «чуть ниже» этой оси полярный
угол точки ζ сколь угодно близок к 2π, поэтому полярный угол λ/ζ равен — = π.
То есть на положительной вещественной оси значение функции в точке равно
Vr, тогда как сколь угодно малое смещение точки вниз в четвертый квадрант
дает значение функции Vrem = -Vr. Значение функции не является
непрерывным на положительной вещественной оси. Решение для работы с функцией
zp опять же состоит в том, чтобы определить положительную действительную
ось как разрез ветвей и избегать использования контура С, который пересекает
этот разрез.
Тот факт, что я взял 0 < θ < 2π, является причиной того, что разрез ветвей
проходит вдоль положительной вещественной оси. Если бы вместо этого я взял
-π < θ < π, мы бы столкнулись с проблемой нарушения непрерывности,
когда пересекали бы отрицательную часть вещественной оси, и в этом случае мы
просто делали бы отрицательную вещественную ось разрезом ветвей и
избегали бы ее пересечения с любым контуром С. В обоих случаях ζ = 0 будет точкой
ветвления. Действительно, в примерах, которые я здесь обсуждал, мы могли
выбрать любое направление, которое пожелаем, просто начиная с точки ζ = 0,
нарисовать прямую оттуда до бесконечности и назвать это нашим разрезом.
Давайте посмотрим, как это все работает. Для последних вычислений
данной главы, используя эти идеи, я найду
Τ 1ПУ ήχ, а>0,Ъ>0, (8.9.1)
J0(x + a)2+b2
где aub - постоянные. Мы уже сделали два особых случая интеграла (8.9.1).
В формуле (1.5.1) для а = 0 и Ъ = 1 мы нашли, что
и в (2.1.3) мы немного обобщили это на случай произвольного Ь:
l^dx=^> ь>°-
J0 χ2 + b2 2b
Интегралы с многозначными подынтегральными функциями ♦ 341
Теперь мы позволим также параметру а в формуле (8.9.1) иметь любое
неотрицательное значение. Контур С, который мы будем использовать, показан
на рис. 8.9.1, и, как вы заметили, избегает пересечения разреза ветви
(положительной действительной оси), а также обхода точки ветвления в начале
координат. Это гарантирует, что С полностью лежит на одной ветви
логарифмической функции, и поэтому контур С действительно замкнутый.
b*-*.ncV\ cu-i*
Рис. 8.9.1 ♦ Замкнутый контур,
позволяющий избежать пересечения разреза ветви
Контур С состоит из четырех частей, ρ и R - радиусы малого (С4) и большого
(С2) круглых участков соответственно, а ε - маленький положительный угол: на
Q: ζ = гё\ dz = ekdr, ρ < г < Я; на С2: ζ = Reie, dz = iReiedQ, ε < θ < 2π - ε; на С3: ζ =
rei(2n-£\ dz = ei(2n-£)dr, R> r> p; на Q: ζ = pe/e, dz = ίρβ^θ, 2π - ε > θ > ε.
Потом мы будем считать, что р^О, β^οοπε^Ο.
Обратите внимание, что для части С3 я избегал упрощения множителя ег(2тт_£)
для ζ и dz. То есть я не поддался искушению написать ег(2тт_£) = ег2тте~г£ = е~г£
(заменив el2n на 1 из тождества Эйлера). Это было бы ошибкой, потому что тогда
мы бы работали с отрицательным углом -ε и попали бы на новую ветвь
логарифмической функции (при использовании метафоры парковки - на уровень
ниже уровня входа). Работа с е~1г привела бы к тому, что С не был бы замкнутым
контуром, и это обрекало бы наш анализ на провал.
Наше подынтегральное выражение будет таким:
№ =
{ln(z)}2
(z + af+b2
(8.9.2)
342 ♦ Контурное интегрирование
и вы почти наверняка задаетесь вопросом: почему числитель имеет квадрат
ln(z)? Почему не просто ln(z)? Быстрый ответ состоит в том, что интегралы по
Q и С3 находятся в противоположных направлениях при ε —> 0 и поэтому
сокращались бы, если бы мы просто использовали ln(z). Это не «неправильно»,
но это не даст нам того, к чему мы стремимся. Использование 1η2(ζ) позволяет
избежать сокращения, и я укажу на это, когда наш анализ дойдет до того места,
где в противном случае произойдет сокращение.
Подынтегральная функция имеет три особенности: одна в точке ζ = 0, где
числитель уходит в бесконечность, и две в ζ = -a±ib, где знаменатель
обращается в ноль. Только последние две особенности находятся внутри контура С,
так как ρ и ε оба стремятся к нулю, a R уходит в бесконечность, и каждая
особенность имеет первый порядок. Из теоремы о вычетах (8.8.13) имеем:
где i?! - вычет особенности в точке ζ = а + ib, a R2 - вычет в точке ζ = а - \Ъ. Как
мы показали в (8.8.9), вычет особенности первого порядка при ζ = ζ0 в
подынтегральной функции
Κζ)
задается формулой
g(z0)
h'(z0)'
В нашей задаче
g(z) = {\n(z)f
§№■■
и
h(z) = (ζ + α)2 + b\
Поскольку
ft'(z0) = -f-ft(z)|
dz
= 2(z + a)
ι Ζ—Z0
Z=ZQ
так как
2(-fl + ib + a) = 2ib
и
2(-fl - ib + fl) = -2/b,
мы имеем:
= {1п(-а + /Ь)}2
1 ilb
Интегралы с многозначными подынтегральными функциями ♦ 343
*2
{ln(-g-zb)}2
-ilb
Поскольку а и Ъ оба неотрицательны, особенность -а + ib находится во
втором квадранте, а особенность -а - ib - в третьем. В полярной форме
особенность из второго квадранта имеет вид:
π π-tan -
-а + /Ь = л/я2+Ь2е'
а особенность из третьего квадранта имеет вид:
. j"J тг^+ЪП—1\ II
-a-ib = ja2 + Ь2е'
Поэтому
{ln№
+ b2e
lnUa2+b2) + i
π-tan 1
ib)
a
ilb
ilb
R.
|ln№
2 , 1,2
+ b2e'
н π+tan
lnfVa2+b2) + z
π + tan l
ib]
a
-ilb -ilb
Теперь умножаем на 2π/ и складываем вычеты:
2πζ'(β1+β2) = 2πζ
ln(Va2+b2) + z-
1 ΐ2
π-tan г
b
а ι су
Ι2
In
V^+Fj + z
π + tan l
ilb
2тп
i'2b
ln(Va2+b2) + z
21niVfl2+b2)z|
π-tan x
π-tan
ln(Va2+b2) + z
π-tan"1
π + tan"1
-21n
V^+F)z{
π + tan l
^zlniVfl'+b'jtan"1
π-tan г
π2-2πΐ3η-1
tan"1
+
4nt3LX\ г
π2+2πΐ3η λ
4zlnfVfl2+b2)tan-1
tan"1
ib)l
a
b
a
4π
tan1
π-ζ1η(να2+^)).
344 ♦ Контурное интегрирование
Итак, для функции f(z) вида (8.9.2) и контура С, как на рис. 8.9.1, мы имеем:
(Ь\\
ff(z)--
4 π _!
—tan
b
π-ilnUa2 +b2) = <£+£+£+£.
(8.9.3)
Основываясь на предыдущем опыте, мы ожидаем, что наш конечный
результат будет получен из интегралов по Q и С3, потому что предполагаем
перейти к пределам по переменным ρ, ε и R (к значениям 0, 0 и оо
соответственно), и ожидаем, что интегралы по С2 и С4 будут равны нулю. Чтобы убедиться,
что это действительно так, давайте сначала найдем эти интегралы по С2 и С4.
Для интеграла С2 имеем:
2π-ε
*-/
(1п(Дею))2
(Де'Ча)2+Ь2
[iReie]dQ.
Теперь, когда i? —> +оо, рассмотрим выражение в крайних левых квадратных
скобках в подынтегральном выражении. Числитель уходит в бесконечность как
\n2(R) для любого заданного θ в интервале интегрирования, а знаменатель - как
ln2R
R2. То есть крайние левые квадратные скобки ведут себя как ——. Выражение
R
в самых правых квадратных скобках растет как R. Таким образом,
подынтегральная функция ведет себя как
1п2(Д) 1п2(Д)
и поэтому интеграл по С2 ведет себя как
о 1п2(Я)
R
>и1? —> оо. Теперь
,· η 1η2(Φ
1ιηι2π ^^ =
оо
.оо
что, конечно, неопределенно, и поэтому давайте воспользуемся правилом Ло-
питаля:
Iim2iri^ = lim2ir^
In2 (Я)
R
dr
R
2тгНт21п(Д)^
Таким образом, наше ожидание исчезновения интеграла по С2 оправдано.
Обращаясь к интегралу по С4, мы имеем:
Интегралы с многозначными подынтегральными функциями ♦ 345
f= Г .2 a №е"ЦЙ.
? 2li(pe'e+a)2 + b2]LP
При ρ —> 0 выражение в крайних левых квадратных скобках в
подынтегральном выражении ведет себя как
1п2р
, тогда как выражение в крайних правых
а2+Ь2
квадратных скобках ведет себя как р. Итак, интеграл С4 ведет себя как
9 1Д2Р
2π?τρ-ρ
при ρ —► 0. Теперь
ι- η 1П'Р
1ιηι2π ——^гр:
2π
р^О
а2+Ъ2 р-о
limpln2p.
1
Положим ι/= -. Тогда при ρ —> 0 мы имеем и —> оо и получаем
limpln2p = lim-ln21
р^О'
lim
In2 (ι/)
ι/
предел, который мы только что вычислили (в интегральном анализе С2) и
который равен нулю. Таким образом, наше ожидание исчезновения интеграла С4
также оправдано.
Обращаясь наконец к интегралам Q и С3, мы имеем:
" {1п(ге'·)]2 ,,. , {■ (1п(ге,0->)]!
М=/
(reiE + a)2+b2
ehdr + f
7 (rei(2.-e)+a)2+b:
_ei(2u-E)dr =
fr {1η(Γ) + ίε}2 & "r{ln(r) + i(2TC-E)}2 ,(2l_e)d
•J (reh + a)2 + b2 «{ (re/(2u-£) + a)2 + b2
или, при ρ ^ 0, R—>οοΗε—>0,
,2/
{ { J(r + fl)2+b2 •/(re^+itf+b2
=°pln2(r)-{ln(r) + /2u}2 rfr= ^-/4π1η(Γ) + 4π2 ^
{ (r+af+b2 i (r + af+b2
(r+aY+V ·>0 (r + aY
(Обратите внимание, что члены 1п2(г) сокращаются в этих последних
вычислениях, оставляя только 1п(г) в конечном выражении.) Подставляя эти результаты
в (8.9.3), мы имеем:
346 ♦ Контурное интегрирование
dr
4π2 Γ -—-y-/4u Г
J0(r + af+b2
4π2
-tan
£(r + a)2+b2
ifb) .4ir. _!
— -ι—tan
α b
<b"
a
In
(T^+F).
Приравнивая вещественные части, получаем:
'-1
а]
О
dx 1
—— = -tan
(х + а)2+Ь2 Ь
что не должно быть сюрпризом. Приравнивание мнимых частей - вот что дает
нам приз:
1 1η(ί°,^*4**η-'
J0(x + af+b2 b
fl^
υ
β)
ln(Va2+b2).
(8.9.4)
Это равенство сводится к нашим более ранним результатам для конкретных
значений а и Ь. Чтобы увидеть (8.9.4) в действии, если и а и Ь равны 1
(например), то
1, ^f и2=^Ш) = 0.272198...,
J0 (x + af+Ъ2 4
и MATLAB подтверждает, поскольку quad(@(x)log(x)./((x+l)-A2+l),0,le5)
0.27206....
8.10. Задачи и упражнения
(С8.1). Предположим, что функция f(z) аналитична всюду в некоторой области
R в комплексной плоскости с нулем m-го порядка при ζ = z0. To есть f(z) = g(z)
(ζ - z0)m, где g(z) аналитичен всюду в R. Пусть С - любой простой замкнутый
положительно ориентированный контур в области R, который окружает z0.
Объясните, почему
2πΐ? f(z)
т.
(С8.2). Ранее, в задаче С3.9, я попросил вас согласиться с этим равенством:
°° sin(mx) . _ π
х(х2+а2) 1
1-е"
для а > 0 и т > 0. Здесь вы должны получить этот
Г
результат с помощью контурного интегрирования. Подсказка: обратите вни-
поо \ поо
мание на то, что подынтегральное выражение четное, поэтому / = - / . Ис-
Задачи и упражнения ♦ 347
пользуйте f(z) --
—, найдите, где находятся особенности (это должно
ζ(ζ2 + α2)
помочь вам построить соответствующий контур для интегрирования), а затем,
в какой-то момент, подумайте о взятии мнимой части.
(С8.3). Выведите следующие формулы для интегралов:
d6
(b)J cosW
2π
2acos(6) + a2 ί-α2
2 tu2dx = le~bcos
, 0<α<1;
sin(x)
(x + ay+b
cos(x)
/ ч Г Siri
)2+Ь2
-dx--
-е bsin(a), α>0, Ь>0;
г cos(jg , _ π
(С) £(х2+а2)(х2+Ь2) Х~а2-Ь2
оо
(d)/
Ъ
, а>Ь>0;
cos(ax)
π
4b1
dx = -^{\ + ab)e-ab, a>0,b>0.
М2+ъ2?
В пункте (а) используйте подход из раздела 8.3 для преобразования
интеграла в контурный интеграл вокруг единичного круга. В (Ь), (с) и (d) используйте
контур как на рис. 8.7.1.
·* п(1-к)
(С8.4). Используя контур на рис. 8.9.1, покажите, что / — ах
(X +1)
4cos
(кп
-1 < к < 3. Прежде чем делать какие-либо вычисления, объясните
ограничения на к. Подсказка: используйте f(z) -
(обратите внимание, что
(Z2+1)2
особенности при ζ = ±ζ обе являются второго порядка, и запишите zk в виде:
COS
(mb)
сю
(С8.5). Покажите, что Г
cos(mx)
ах2 +Ьх + с
dx-
2а
sin
[m4b2
-2π-
-Аас
2а
4b2-\ac
-, когда
(С8.6). Покажите, что J
Ь2 > 4ас. Обратите внимание, что этот результат содержит (8.6.5) как частный
случай т = 0.
> хр π 1
dx = (2p-l) —,-1<р<1.Дляр = -
(* + 1)(* + 2) sin(pn) 2
этот интеграл равен (V2 - 1)π = 1.30129..., и MATLAB подтверждает это
значение как quad(@(x)sqrt(x)./((x+l).*(x+2))Ale7) = 1.300.... Используйте контур
на рис. 8.9.1.
(С8.7). В своей превосходной книге 1935 года «Введение в теорию функций
комплексной переменной» Эдвард Копсон (1901-1980), который был
профессором математики в университете Сент-Эндрюс в Шотландии, написал: «Опреде-
348 ♦ Контурное интегрирование
ленный интеграл, который может быть найден методом вычетов Коши, всегда
можно найти другими способами, хотя, как правило, не так просто». Вот
пример того, что имел в виду Копсон, интеграл, приписываемый самому великому
Коши. Его легко взять контурным интегрованием, но в противном случае (я ду-
_ . r-ecos(x)sin{sin(x)} , π, 1Λ
маю) было бы чертовски сложно: показать, что / ^-^ах = —(е — 1).
Результат MATLAB соответствует Коши, поскольку интеграл равен 2.69907...
иquad(@(x)exp(cos(x)).*sin(si.n(x))./x,0,1000) = 2.6978....Подсказка: вспомните,
как мы вывели формулу (8.6.4), в частности контур на рис. 8.6.1, и попытайтесь
построить правильную f(z) для интегрирования по этому контуру.
(С8.8). Вот пример интеграла, который сам Копсон поставил в качестве задачи
в конце главы и который должен быть найден путем контурного
интегрирования и вычетов, но который на самом деле легче сделать с помощью матема-
оо у2 π
тического анализа для первокурсников. Показать, что Г — —dx = —-,
J-~ (χ2+α2)3 8α3
a > 0. Две особенности в подынтегральном выражении - каждая третьего
порядка, и хотя это не очень сложное вычисление (вы должны это сделать), здесь
есть более простой и более общий подход. Вы должны заполнить недостающие
детали.
лЛ
Х°° χ
— ^-ах, где а ф Ь, сделайте разло-
°°(xz -\-az)(xz+bz)
жение на простейшие дроби и получите в результате два простых
интеграла.
Хоо χ2
2 Т~2^Х-
(с) Наконец, используйте любимый трюк Фейнмана с
дифференцированием интеграла, чтобы получить ответ Копсона.
Обратите внимание, что теперь вы можете продолжать дифференцировать
лЛ
— —αχ для любого η > 3.
-~(х2+а2)и
Глава
Эпилог
9.1. РИМАН, ПРОСТЫЕ ЧИСЛА И ДЗЕТА-ФУНКЦИЯ
Начиная с фотографии на фронтисписе, вся эта книга, посвященная
нахождению римановых определенных интегралов, была непрерывной одой гению
Бернхарда Римана. Он умер слишком рано от туберкулеза, в возрасте 39 лет.
И все же, хотя он только достиг полной силы своего интеллекта, когда
покинул этот мир, вы можете оценить, как много раз его имя появлялось здесь,
насколько продуктивным он был. Он оставил нам много блестящих
результатов, но также оставил мир математики с его величайшей нерешенной
проблемой - проблемой, которую часто называют святым Граалем математики. Это
настолько сложная и таинственная проблема, что многие математики всерьез
допускают, что ее невозможно решить. И она изобилует интересными
интегралами!
Это знаменитая (по крайней мере, в мире математики) гипотеза Римана
(RH)1. Хотя Риман сформулировал ее в 1859 году, все усилия величайших
математических умов в мире (включая его самого), усилия либо доказать, либо
опровергнуть до сих пор были напрасными. И спустя сорок лет после
опубликования этой гипотезы и так как она все еще не была решена, великий
немецкий математик Давид Гильберт (мы обсуждали его преобразование еще
в главе 7) решил добавить некоторый стимул. В 1900 году на Втором
Международном конгрессе математиков в Париже он выступил с известным докладом
под названием «Математические проблемы». В ходе этого доклада он обсудил
ряд проблем, которые, по его мнению, представляют собой потенциально
плодотворные направления для будущих исследований. Эти проблемы включали,
например, трансцендентную природу (или нет) числа 2 , последнюю теорему
Ферма (FLT) и RH, в убывающем порядке сложности (по оценке Гильберта).
1 Гипотеза Римана утверждает, что все нетривиальные нули дзета-функции имеют
1
действительную часть, равную -, то есть являются комплексными числами,
расположенными на прямой Re(s) = -. - Прим. перев.
350 ♦ Эпилог
Все проблемы Гильберта стали известны в одночасье, и решение одной из
них приводило к мгновенной известности среди других математиков.
Однако собственная оценка Гильбертом сложности его проблем была немного
сомнительной, так как проблема 2 была решена к 1930 году (это число
трансцендентное, a FLT была установлена к середине 1990-х годов. RH, однако, хотя
и считалась «самой легкой» из трех, оказалась самой трудной. Гильберт в
конце концов пришел к пониманию этого. Хорошо известная в математических
кругах история гласит, что однажды он заметил, что если он проснется после
500 лет сна, то задаст первый вопрос: «Была ли доказана гипотеза Римана?»
Ответа на этот вопрос до сих пор нет, и поэтому спустя столетие после
знаменитого доклада Гильберта в Париже Институт математики Клея в Кембридже,
штат Массачусетс, предложил в 2000 году семь так называемых «призов
тысячелетия», каждый из которых будет стоить миллион долларов, тому, кто ее
решит. RH - одна из тех элитных проблем, и, когда я пишу эту книгу в 2014 году,
миллион долларов для ее решения остается невостребованным.
Гипотеза Римана (RH) важна не только потому, что не решена; в
математике существует множество теорем, которые математики считают правильными
и которые основаны на предполагаемой истинности RH. Если RH когда-нибудь
окажется ложной, существующие доказательства всех этих теорем рухнут, и их
придется пересмотреть и найти новые доказательства (надеюсь). Глубоко
обсуждать RH выходит далеко за пределы уровня этой книги, но поскольку она
включает в себя комплексные числа и функции, носит имя Римана, изобилует
интегралами и не решена, она тем не менее кажется подходящей темой, на
которой можно закончить эту книгу.
Наша история начинается, как и многие увлекательные истории в
математике, с удивительного результата Эйлера. В 1748 году он показал, что если s
вещественно и больше 1 и если мы напишем дзета-функцию (снова см. раздел 5.3)
ТО
ζ(*)=
Пм
_1_
(9.1.2)
где р] - j-e простое число (рх = 2, р2 = 3, ръ = 5, р4 = 7 и т. д.). То есть Эйлер
показал, что существует тесная, удивительная связь между ζφ, непрерывной
функцией от s, и простыми числами, которые как целые числа являются самим
смыслом разрывности1.
1 Вывести (9.1.2) не трудно, а просто «чертовски» хитро; вы можете найти
доказательство в любой хорошей книге по теории чисел. Или посмотрите мою книгу: Мнимая
сказка: история V^T. Принстон, 2010. С. 150-152.
Риман, простые числа и дзета-функция ♦ 351
Риман пришел к дзета-функции из-за связи этого результата Эйлера с
простыми числами (он назвал это «отправной точкой»), надеясь, что изучение t,(s)
поможет ему в поиске формулы для функции тг(Х), определяемой как число
простых чисел, не больших χ. π(χ) - это мера распределения простых чисел сре-
ίιϊ
ди целых чисел. Должно быть очевидно, что π - = 0, что тг(2) = 1 и что π(6) = 3,
но, возможно, не совсем очевидно, что π(1018) = 24,739,954,287,740,860. Когда
Риман начинал свои исследования по распределению простых чисел, одним
из известных приближений к тг(Х) был так называемый логарифмический
интеграл, записываемый как
И(х) = /-^, (9.1.3)
2 ln(u)
что на самом деле является довольно хорошим приближением1. Например:
π(1,000) =168 = 0 94 }
Н(100,000) 178
π(100,000) = 9,592
Η(ΙΟΟ,ΟΟΟ) 9,630
π(ΙΟΟ,ΟΟΟ,ΟΟΟ) _ 5,761,455
Η(ΙΟΟ,ΟΟΟ,ΟΟΟ) ~~ 5,762,209
π(1,000,000,000) 50,847,478
0.999...,
= 0.9999..
Π(Ι,ΟΟΟ,ΟΟΟ,ΟΟΟ) 50,849,235
В письме 1849 года великий немецкий математик К. Ф. Гаусс, который
подписал докторскую диссертацию Римана 1851 года с пылким одобрением,
утверждал, что знал об этом поведении Н(лг) с 1791 или 1792 года, когда ему было
всего 14 лет. С тем, что известно о гении Гаусса, нет сомнений, что это правда!
Численные расчеты, подобные приведенным выше, сразу позволяют
предположить
lim^ = l,
*->°° \\{х)
что является утверждением того, что математики называют теоремой о
простых числах.
Хотя это наводит на размышления, такие численные расчеты, конечно,
ничего не доказывают, и на самом деле только в 1896 году математические
доказательства теоремы о простых числах были одновременно и независимо от-
Современный вариант с небольшим изменением Щх) = Г h 1.045..., которое,
J2 Щи)
например, для а: = 1000 MATLAB вычисляет так: quad(@(x)l./log(x),2,1000)+1.045 =
177.6.
352 ♦ Эпилог
крыты Шарлем-Жозефом де ла Валле-Пуссеном (1866-1962) в Бельгии и Жаком
Адамаром (1865-1963) во Франции. Каждый использовал очень продвинутые
методы из теории комплексных функций, применяемые к дзета-функции. Это
был поиск (с использованием дзета-функции), аналогичный тому, что Риман
проводил в 1859 году, за годы до рождения Валле-Пуссена или Адамара.
Увлечение Римана распределением простых чисел легко понять. Простые
числа обладают многочисленными свойствами, которые, хотя их легко
сформулировать, почти парадоксальны. Например, со времен Евклида известно,
что число простых чисел бесконечно, и тем не менее если взглянуть на
список последовательных простых чисел от 2 до очень высоких значений, то
становится очевидным, что в среднем они встречаются все реже. Я подчеркиваю
«в среднем», потому что время от времени встречаются последовательные
нечетные целые числа (каждое простое число, кроме 2, конечно, нечетное),
которые оба являются простыми числами. Такая пара образует двойное простое
число-близнец. Неизвестно, бесконечно ли число простых чисел-близнецов.
Математики верят в это, но не могут доказать.
Если образовать сумму обратных величин всех натуральных чисел, то мы
получим гармонический ряд, который, конечно, расходится. То есть ζ(1) = оо.
Если исключить все члены в этой сумме, кроме обратных величин простых
чисел, то сумма все равно расходится, что почти всегда удивляет, когда его
впервые демонстрируют. (Это также доказывает, в отличие от доказательства
Евклида, что простых чисел бесконечно много.) В 1919 году норвежский
математик Вигго Брун (1885-1975) показал, что если затем исключить из суммы
все слагаемые, кроме обратных величин двойных простых чисел-близнецов,
то сумма конечна. В действительности сумма не очень большая. Это значение,
называемое постоянной Бруна, равно
М 1]
-+^
[Ъ 5J
+
fi 11
^+-
[5 7J
+
fi Η
—ι—
Ul 13j
+
f ι il
—ι—
[17 19j
Однако конечное значение постоянной Бруна не исключает бесконечного
числа простых чисел-близнецов, и поэтому этот вопрос остается открытым.
Вот еще один пример любопытного распределения простых чисел: для
любого а > 1 всегда есть хотя бы одно простое число между а и 2а. И тем не менее для
любого а > 1 всегда есть отрезок, по крайней мере, из а - 1 последовательных
целых чисел, не содержащий простых чисел! Это правда независимо от того,
насколько большим может быть а. Первое утверждение принадлежит
французскому математику Жозефу Бертрану (1822-1900), чья гипотеза о нем в 1845 году
была доказана (это не «легкое» доказательство) русским математиком П. Л. Че-
бышевым (1821-1894) в 1850 году. Для второго утверждения просто обратите
внимание, что каждое из последовательных чисел а\ + 2, а\ + 3, а\ + 4,..., а\ + а
делится, и поэтому ни одно из них не является простым.
В 1837 году Дирихле установил действительно замечательный результат (это
тот самый Дирихле, которого мы впервые встретили в главе 1): если а и Ь явля-
Риман, простые числа и дзета-функция ♦ 353
ются взаимно простыми положительными целыми числами (это означает, что
их наибольший общий множитель равен 1), то арифметическая прогрессия а,
а + Ь, а + 2Ь, а + ЗЬ,... содержит бесконечное число простых чисел. Эта
простая теорема сразу же дает нам не очень очевидный вывод о том, что
существует бесконечно много простых чисел, заканчивающихся на 999 (как и 1,999,
100,999 и 1,000,999). Это потому, что все числа в прогрессии (не все из которых
являются простыми), образованные из а = 999 и Ъ = 1000 (которые имеют
только коэффициент 1), заканчиваются в 999.
Имея в виду подобные примеры, теперь должно быть легко понять, что имел
в виду математик Пал Эрдёш (Erdos Pal, 1913-1996), когда он лихо (по
крайней мере, в мире математики) заявил: «пройдет еще миллион лет, прежде чем
мы поймем простые числа». Как может математик, включая Римана, не
восхищаться простыми числами1, имеющими такие свойства, как описано выше?
Чтобы начать свою работу, Риман сразу же занялся техническим вопросом,
касающимся самого определения ζφ, приведенного в (9.1.1), а именно сумма
сходится только в том случае, если s > 1. В более общем случае, если мы
продолжим переменную s в определении Эйлера дзета-функции от вещественной
до комплексной (то есть s = σ + it), то ζφ, как указано в (9.1.1), имеет смысл,
только если σ > 1. Риман, однако, хотел иметь возможность обращаться с t,(s)
как определенной всюду в комплексной плоскости, или, как он выразился, он
хотел получить формулу для ζφ, «которая подходит для Bcexs». Такая формула
должна давать те же значения для ζφ, как и (9.1.1), когда σ > 1, но она также
должна давать разумные значения для ζ(Ξ) даже при σ < 1. Риман с
невероятным успехом нашел, как это сделать.
Он сделал это, обнаружив то, что называется функциональным уравнением
дзета-функции, и, просто немного предвосхищая события, вот это уравнение
(мы выведем его в следующем разделе):
ζ(5) = 2(2π),-18Ϊη
US
Γ(1-5)ζ(1-5). (9.1.4)
Функциональное уравнение Римана считается одной из жемчужин
математики. Вот как это работает. Что мы имеем:
ζ(5) = ί(5)ζ(1 -s), F(s) = 2(2π)5~1 sin
^
r(l-s).
F(s) - это корректно определенная функция для всех σ. Итак, если у нас есть
s с σ > 1, мы будем использовать (9.1.1) для вычисления ζφ, но если σ < 0, мы
будем использовать (9.1.4) (вместе с (9.1.1) для вычисления ζ(1 - s), потому что
действительная часть 1 - s будет > 1, если σ < 0).
Английский математик А. Э. Ингхэм (А. Е. Ingham, 1900-1967) открывает свою книгу
«Распределение простых чисел» (Distribution of the Primes. Cambridge University Press,
1932) комментарием «Проблема на самом пороге математики [курсив мой] - это
вопрос распределения простых чисел среди целых чисел».
354 ♦ Эпилог
Конечно, остается вопрос вычисления ζ(5) для случая 0 < σ < 1, где s
находится в так называемой критической полосе (вертикальная полоса шириной
1, простирающаяся от -zoo до +/оо). Функциональное уравнение нам сейчас не
помогает, потому что если s находится в критической полосе, то и 1 - s там же.
Однако на самом деле это проблема, которую мы уже решили, как вы можете
увидеть, посмотрев на (5.3.7), где мы показали
-Ι)*"1
Σ
(-
[l-2lsK(s).
Так, например, прямо в середине критической полосы, на действительной
1
оси, мы имеем s = -, и тогда
Σ
(-1)*-
к1/2
1-2 2\ζ
Поэтому
ζ
1
1-л/2
-1- —
i_ _ι ι_
ν/2 л/3 л/4
J_ J \_
л/2 л/з л/4
Если мы возьмем миллион первых слагаемых - хорошо известная даже
первокурсникам теорема говорит нам, что частичные суммы
знакочередующегося ряда (с монотонно убывающими членами) сходятся, а максимальная
ошибка, которую мы совершаем, меньше, чем первый член остатка, которым мы
пренебрегаем, и поэтому наша ошибка для такой суммы должна быть меньше
мы получаем
Ί)
1СГ3,
ζ
ί-1.459147.
Известно, что фактическое значение есть
ζ
1.460354.
Это, очевидно, не очень эффективный способ (миллион членов!?) для
вычисления ζ
ΊΪ
но суть здесь в том, что (5.3.7) является правильным.
В случая чисто вещественного s, как у Эйлера, графики на рис. 9.1.1
показывают обычное поведение ζ(5). При s > 1 значение ζφ плавно уменьшается от
+оо до 1 при увеличении s от 1, в то время как при s < 0 функция ζφ колеблется,
в конечном итоге снижаясь до -оо, когда s приближается к 1 слева.
Риман, простые числа и дзета-функция
355
На рис. 9.1.1 показано, что ζ(0) = -0.5, а в следующем разделе я объясню вам,
как показать, что ζ(0) = —, используя функциональное уравнение. Также об-
ратите внимание, что рис. 9.1.1 подсказывает нам, что ζφ = 0 для
отрицательного целого четного числа s, это еще один вывод, подтверждаемый
функциональным уравнением.
ф)ч%.
\\ i
\J
^^с^
S
0.01
о
-0.01
-0,02
-0.03
-8
о
-0.5
•1
-1.5
1 -0.5
ФУ
ι ·
ЧЪ. S
^ χ
\\ ■·■
-4
S
ФУ
\/S. S
-Ч^"
О
S
Рис. 9.1.1 ♦ Дзета-функция для действительных s
05
Чтобы сделать это последнее наблюдение кристально ясным, положим
s = -2л, где η = 0,1,2, 3,.... Тогда (9.1.4) принимает вид:
ζ(-2π)
2ππ-(3π+1)
Г(1 + 2π)8ίη(ππ)ζ(1 + 2ή) = 0,
потому что все сомножители справа в первом равенстве конечны для всех п,
включая s'm(nn), который, конечно, равен нулю для всех целых чисел п.
Однако мы должны исключить случай η = 0, потому что тогда ζ(1 + 2п) =
ζ(1) = оо, и этой бесконечности достаточно, чтобы подавить ноль sin(0). Мы
знаем это потому, что, как указано выше и как будет показано в следующем
разделе, ζ(0) φ 0, а точнее ζ(0) = —. Когда значение s дает ζφ = 0, мы называем
ζ*
это значение s нулем дзета-функции. Таким образом, все четные
отрицательные целые числа являются нулями ζφ, а поскольку их так легко «вычислить»,
их называют тривиальными нулями ζφ. Однако есть и другие нули ζφ, кото-
356 ♦ Эпилог
рые не так легко вычислить1, и они находятся в комплексной плоскости, о чем
и говорит гипотеза RH.
Вот что правильно считал Риман относительно нетривиальных нулей (даже
если он не смог доказать все это в 1859 году):
1) их бесконечно много;
2) все они комплексные (вида σ + it, t φ 0);
3) все находятся в критической полосе (0 < σ < 1);
4) они встречаются парами, симметрично смещенными вокруг
вертикальной линии σ = - (называемой критической линией), то есть если
- - ε + it - это ноль, то нулем будет и - + ε + it для некоторого ε в интервале
5) они симметричны относительно действительной оси (t = 0), то есть если
σ + it- ноль, то и σ - it - ноль (нули появляются в виде сопряженных пар).
RH теперь легко сформулировать: ε = 0. То есть все комплексные нули
находятся на критической линии и поэтому имеют действительную часть -. Точнее,
Риман предположил, что «очень вероятно [мой акцент], что все [комплексные
нули находятся на критической линии]». С 1859 года все, кто пытался доказать
RH, потерпели неудачу, включая Римана, который написал: «Конечно, хотелось
бы [доказательства]; между тем я временно отложил поиск [доказательства]
после некоторых мимолетных тщетных попыток, поскольку это кажется
ненужным для [нахождения формулы для тг(х)]».
С 1859 года были получены некоторые впечатляющие частичные
результаты. В 1914 году датчанин Харальд Бор (1887-1951) и немец Эдмунд Ландау
(1877-1938) показали, что все нули, кроме бесконечно малой доли
комплексных нулей, сколь угодно близки к критической линии (то есть они находят-
1 1
ся в «сколь угодно тонкой» вертикальной полосе --ε<σ<- + ε для любого
ε > 0). В том же году Харди доказал, что бесконечное число комплексных нулей
находится на критической линии (но это не доказывает, что все комплексные
1 Методы, используемые для вычисления нетривиальных нулей, далеки от
«очевидных» и выходят за рамки этой книги. Если вам интересно узнать, как выполняются
такие вычисления, я могу порекомендовать следующие четыре книги:
1) Эдварде X. М. Дзета-функция Римана (Edwards Η. Μ. Riemann's Zeta Function).
Academic Press, 1974;
2) Титчмарш Э. С. Теория дзета-функции Римана. 2-е изд., перераб. Д. Р. Хит-
Брауном (Titchmarsh Ε. С. The Theory of the Riemann Zeta-Function. 2nd ed., revised
by D. R. Heath-Brown). Oxford Science Publications, 1986;
3) Ивич Ллександар. Дзета-функция Римана (Ivic Aleksandar. The Riemann
Zeta-Function). John Wiley & Sons, 1985;
4) Гипотеза Римана (Peter Borwein et al., редакторы). Springer, 2008.
Риман, простые числа и дзета-функция
357
нули находятся на критической линии). В 1942 году норвежцем Атле Селбергом
(1917-2007) было показано, что (неопределенная) дробная доля нулей
находится на критической линии. В 1974 году американцем Норманом Левинсоном
(1912-1975) было показано, что доля Сельберга выше, чем -, а затем в 1989 году
2
американец Дж. Б. Конри показал, что эта доля больше, чем -.
Существует также то, что на первый взгляд представляет собой весьма
существенную вычислительную поддержку истинности RH. С тех пор как Риман
сам вычислил местоположения первых трех комплексных нулей1, за последние
несколько десятилетий это достижение значительно превзошло все ожидания.
В 2004 году было показано, что первые 1013 (да, тентриллион!) нулей находятся
на критической линии. Поскольку даже один ноль вне критической линии -
это достаточно для опровержения RH, это выглядит довольно внушительно, но
математики, честно говоря, не впечатлены. Как написал Ивич в своей книге
(см. примечание 4): «Несомненно, числовые данные будут продолжать
накапливаться, но теория чисел, к сожалению, является одной из отраслей
математики, где вычислительные данные не имеют большого значения».
05 1 1.5 2 25
Magnitude of ζ(1/2 + i t)
Рис. 9.1.2 ♦ Первые шесть нетривиальных нулей ζ - + /t
Из-за свойств симметрии местоположений комплексных нулей нужно только
рассмотреть случай t > 0. Значение t для нуля называется высотой нуля, и нули
упорядочиваются по возрастанию t (первые шесть нулей показаны на рис. 9.1.2, где
ноль возникает в каждом месте, где
ψ*
касается вертикальной оси t). Высоты
первых шести нулей составляют 14,134725,21,022040,25,010856,30,424878,32,935057
и 37,586176. В дополнение к первым 1013 нулям еще миллиарды нулей на высотах,
порядка 1024, также были подтверждены как лежащие на критической линии.
358 ♦ Эпилог
На самом деле в математике существует множество исторических
примеров, когда первоначальные огромные вычислительные «доказательства»
вызывали гипотезы, которые впоследствии оказались ложными. Особенно
известный пример касается значений π(Χ) и \i(x). Для всех значений х, для
которых известны π(Χ) и Н(х), π(χ)< \i(x). Кроме того, разница между этими двумя
увеличивается с увеличением х, а для «большого» χ разница значительна; для
χ = 1018, например, d(x) = \i(x) - π(χ) & 22.000.000. На основании этих
впечатляющих численных «доказательств» долгое время считалось, что d(x) > 0 для всех
х. Гаусс верил в это (как и Риман) всю свою жизнь. Но это неправда.
В 1912 году друг и соратник Харди, Дж. Э. Литтлвуд (1885-1977), доказал,
что существует некоторое значение х, для которого d(x) < 0. Два года спустя
он расширил свое доказательство, чтобы показать, что при увеличении χ знак
d(x) бесконечно меняется назад и вперед. Значение х, при котором
происходит первое изменение знака d(x), неизвестно, кроме того что оно очень
велико. В 1933 году Стэнли Скьюз из Южной Африки (Stanley Skewes, 1899-1988)
получил колоссально большую верхнюю границу для значения этого первого
х: е6' «1010 . Оно стало известным (по крайней мере, в мире математики) как
первое число Скьюза. В своем выводе Скьюз предполагал истинность RH, но
в 1955 году он отбросил это предположение, чтобы вычислить новую верхнюю
границу для первого х, при котором d(x) меняет знак: это второе число Скьюза,
10юоо
равное 10 , и это, конечно, намного больше, чем первое. В 2000 году
верхняя граница была снижена до 1,39х 10316. Все эти цифры намного превосходят
все, что может быть численно получено на компьютере, и число комплексных
нулей, которые были вычислены на критической линии, является ничтожно
малым, по сравнению с ними.
Вполне возможно, что первый комплексный нуль вне критической линии
(таким образом, опровергающий RH) может не появиться до тех пор, пока не
будет достигнута значительно большая высота, чем это было исследовано до
сих пор.
Некоторые математики были явно не в восторге от RH. Литтлвуд, в
частности, был довольно резким, написав: «Я считаю ее [RH] ложной. Доказательств
ее нет... Не следует верить в то, чему нет доказательств... Я обсуждал этот
вопрос с несколькими людьми, которые знают проблему в отношении
электронных вычислений; все они согласны с тем, что шансы нахождения нуля вне
линии в расчетах за всю жизнь составляют миллионы против одного. Похоже,
мы никогда не узнаем»1.
Немного более приглушенной (но, возможно, не слишком) является позиция
американского математика X. М. Эдвардса (1936 г. р.), который написал в своей
классической книге о дзета-функции (см. примечание 4): «Риман основал свою
1 Из эссе Литтлвуда «Гипотеза Римана» в кн.: Ученые размышляют: антология
частично испеченных идей (The Riemann Hypothesis in: The Scientist Speculates: An
Anthology of Partly-Baked Ideas (I. J. Good, editor). Basic Books, 1962).
Вывод функционального уравнения для ζφ ♦ 359
гипотезу на отсутствии понимания... которое не доступно нам и сегодня...
и наоборот, если бы он знал некоторые факты, которые были обнаружены с тех
пор, он вполне мог бы передумать... если не работает какая-то основная
причина, которая ускользала от математиков в течение 110 лет [155 лет на момент,
как я пишу эту книгу в 2014 году], случайные [комплексные нули]
[критической] линии вполне возможны... Прозрение Римана было колоссальным, но не
сверхъестественным, и то, что казалось ему "вероятным" в 1859 году, сегодня
может показаться менее вероятным».
9.2. Вывод функционального уравнения для ζ(5)
Вывод функционального уравнения для ζφ, который появляется в
известной работе Римана 1859 года, включает в себя контурный интеграл, в котором
участвует разрез ветви. Однако мы уже рассмотрели пример этого, и поэтому
здесь я покажу вам другой вывод (также благодаря Риману), широко
использующий результаты, которые мы уже получили в книге.
Мы начнем с интеграла
оо
Jxmleaxdxy m>l,a>0,
о
и сделаем замену переменной и = ах (и, следовательно, dx = —). Таким об-
а
разом,
оо оо / ,ЛШ_* J,, 1 °°
fx™-ie-°*dx = Г ρ е"" — = — [и^е-Чи.
I 1\а\ а ат1
0 0 V" / ** ** 0
Самый правый интеграл, согласно (4.1.1), есть Г(т), и тогда
0
а"
(9.2.1)
Теперь если мы положим
m-l = -s-l
2
1
m = -s
2
а = π π,
тогда формула (9.2.1) принимает вид:
оо 1
2S ρ-η"πχ
Ρ
dx =
ίι 1
2 )
(πΊι)
ίΐ 1
-S
2 ,
(9.2.2)
360 ♦ Эпилог
Тогда, суммируя (9.2.2) по всем положительным целым числам п, получим
1
2S
£jVS~e-"4ix = £^A
п=\ о
"-1 π* У
или меняя порядок суммирования и интегрирования слева:
оо 1
ι. (Х \
1
ι. (Х \
fx*S~ jy-^dx = π~^Γ\-s £4 = π"^Γ
0 n=l V^ Jn=l"
В этот момент Риман определил функцию
ζ(*)·
ф(х) = ^е-"21
(9.2.3)
(9.2.4)
и затем использовал тождество
оо 1 оо
n=-oo VΧ η=-οο
(9.2.5)
Левая часть (9.2.5) имеет вид (потому что п2 > 0 для η как отрицательных, так
и положительных):
— 1 оо оо оо
£ е-"1™ +1 + ^V"2™ = jy-"1™ +1 + jy-"2™ = 2ψ(χ) +1.
η=1 η=1 η=1
Правая часть (9.2.5) (по той же причине):
й
1 °° 7 1
1 у^ е-п2я/х _ _J_
4х п=-оо 4х
2ψ
+ 1
Тогда
2ψ(*) + 1 = -=
2ψ
ill
+ι
или выражая ψ(χ):
1 В моей книге: «Необыкновенная формула доктора Эйлера» (Dr. Euler's Fabulous
Formula). Princeton, 2011. С. 246-253, - вы найдете вывод этого тождества Ση?— е " =
J—^2°° е~пп/а. Если вы напишите α = π*, то (9.2.5) сразу же получится. Вывод
в книге о докторе Эйлере объединяет теорию Фурье с тем, что математики называют
формулой суммирования Пуассона, и все это может звучать впечатляюще экзотично.
Но на самом деле все это не более чем на уровне заключительных глав
математического анализа первокурсников. Если вы можете прочитать эту книгу, то можете легко
разобрать вывод (9.2.5) в «Необыкновенной формуле доктора Эйлера».
Вывод функционального уравнения для ζφ ♦ 361
ψ(Χ):
ι .ill
Ψ
^
+-
1 1
:£e-2'
2jx~ 2 ^ί
Теперь подстановка (9.2.4) в (9.2.3) дает нам
1. (л \ оо 1.
(9.2.6)
π 2 Γ
-s
2
ζ(5) = |^-1ψ(χ)(ίΧ)
или разбивая этот интеграл на две части:
_1
π 2V
1 )
-s
2
1 1
ζ(5) = jx2' 1\\i(x)dx + jx^ 1\\i(x)dx.
(9.2.7)
Используя (9.2.6) в первом интеграле справа в (9.2.7), получаем:
π 2 Γ
(ι 1
ζ(*) = /*
о
1
1 l·-
о
1 1
1
,х)
1
"2
+
1 1
24х~ 2
со 1 ,
/—s—1
χ2 ф(л:)ск:
1)
— \dx+ [χ2* 2ψ - dx+ Γα:2' i|/(*)d*.
2 J. χ «ί
Первый интеграл справа легко берется (для s > 1):
^х = - fx2 2dx— fx2 dx = -
7 J 7 J 7
ι l
ι ι
24x 2
4 2-0
1 1
ι ι
-s —
\2 2)
,1
0
1
2
( \
1
1
[2 )
1
2
ί l }
1 1
— s —
12 2)
1
2
ί*1
1
— s
[2 )
1 1
1
Тогда
π 2 Γ
1
ζ(*) =
1
s(s-l)
s -1 s s(s -1)
1 1. 3 ί л \ оо 1
fx2 2ψ — \dx+ fx2 \\j(x)dx.
Далее в первом интеграле справа в (9.2.8) сделаем замену переменной и
(9.2.8)
1
(и, таким образом, dx = —-). Тогда
и1
1 1.s_3 ( л \ 1
fx2 2ψ — \dx= Г
1)25 2
ψ(ϊ!)
du
и2
со -| оо 1 1
= Г——γ\\ί(η)άιι= fx 2 2\\j(x)dx,
362 ♦ Эпилог
и поэтому (9.2.8) принимает вид:
π
1
2sr
1
ζ(*)=
1
s(s-l)+ 1
f\X 2S 2+Х2* Jl|/(*)d*·
(9.2.9)
Хорошо! - могли бы вы воскликнуть на этом этапе, когда смотрите на
интеграл в (9.2.9), - и что нам теперь делать? Возможно, вам даже захочется
повторить слова, которые Оливер Харди часто обращал к Стэну Лорелу, после того
как два комика из старого кинофильма наткнулись на один из их идиотских
джемов: «Посмотри, во что ты нас втянул на этот раз!»
На самом деле, однако, не все так бестолково, и все, что нам нужно сделать, -
это заметить, как и Риман, что правая часть (9.2.9) не изменится, если мы
заменим каждое вхождение s на 1 - s. Попробуйте и посмотрите. Но это означает,
что мы можем сделать то же самое в левой части (9.2.9), потому что, в конце
концов, (9.2.9) является равенством. То есть должно быть верно, что
-Wl-s). (9.2.10)
π
ι
"2sr
1
ζ(5):
π
2(1-5)Γ
1
Теперь мы почти закончили, осталось всего несколько «рутинных» шагов,
чтобы получить вид функционального уравнения для ζ(5), которое я дал вам
в (9.1.4). Выражая ζφ из (9.2.10), имеем
Л-
?(*) =
π
1
yW-s).
(9.2.11)
Теперь вспомним равенство (4.2.18), одну из форм формулы дублирования
Лежандра:
z!
! = 2-2ζπ2(2ζ)!,
или, выражая через гамма-функцию,
Γ(ζ + 1)Γ
1)
Ζ + 2
= 2""π2Γ(2ζ + 1).
(9.2.12)
Если мы напишем 2ζ + 1 = 1 - s, тогда ζ
1)
■ + 1
s
'2 + 2
:2su2r(l-s) = T
1-
,и(9.2.12) принимает вид:
Вывод функционального уравнения для ζφ ♦ 363
или
(1-s) 2s^r(l-s)
1--
Из формулы (4.2.16) отражения для гамма-функции:
π
Г(7Л)Г(1-7Л) = —
s'm(mn)
или, при т ■■
(9.2.13)
и это дает нам
π
sin
ns
Τ
1-*
k 2,
Γ
У
2
π
sin
ns^
Τ,
Теперь, подставляя (9.2.14) в (9.2.13),
1-*
ч 2.
2
sn
2Г(1
-5)
π
Г
Υ
2
sin
ns^
τ,
= 25π 2Γ
1 ^ \ /" \
sin
Γ(1-5),
или
г
(
1
г
s
2
:25π ^sin
(ns"
r(l-s).
Подставляя (9.2.15) в (9.2.11), мы приходим к
Γ(1-5)ζ(1-5),
ζ(5) = π* 225π 2sin
fns"
или наконец:
ζ(5) = 2(2Tt)s_1sin
'ns"
Γ(1-5)ζ(1-5),
(9.2.14)
(9.2.15)
(9.2.16)
364 ♦ Эпилог
это функциональное уравнение, которое я дал вам ранее в (9.1.14).
В качестве простого «теста» (9.2.16) предположим, что s = -. Тогда
ζ
'V
: 2(2π) 2sin
( \
π
φ
из которого следует, что только мы сократим на ζ
то
φ
в каждой части равенства ,
1 =
1
Ш
Η·
Это правильно? Да, потому что правая часть есть
Итак, (9.2.16) согласуется при s
1
В качестве примера того, как работает (9.2.16), давайте используем его для
вычисления ζ(-1). Таким образом, положим s = -1:
ζ(-1) = 2(2Tt)-2sin
Γ(2)ζ(2).
Поскольку Г(2) = l,sin
ζ(-1) = —(-1)—= -—.
* ^ 4π2^ 'б 12
π
■1Μζ(2) = — ,το
Ο
Этот результат является основанием для одного из самых интересных
рассказов в истории математики, в котором снова выступает Дж. Харди.
В конце января 1913 года Харди получил первое из нескольких загадочных
писем из Индии. Написанные тогда еще неизвестным
математиком-самоучкой Сринивасой Рамануджаном (1887-1920), который работал в Мадрасе
скромным клерком, эти письма были мольбами к всемирно известному Харди
посмотреть некоторые из его работ. Многое в них было озадачивающим, но не
более того:
Мы знаем, что можем сделать это, потому что, как показано в предыдущем разделе,
й = -1.4...,0.
Вывод функционального уравнения для ζφ ♦ 365
1 + 2 + 3 + 4 + - = --^.
12
Большинство профессиональных математиков просто выбросили бы это
в мусорное ведро и отвергли бы клерка как жалкого сумасшедшего. Гений Хар-
ди состоял в том, что он этого не сделал, но вместо этого вскоре понял смысл
суммы Рамануджана. Что имел в виду клерк (но плохо выразился), можно
понять, записав сумму как
л η ч л 1111 1111
1 + 2 + 3 + 4 + -. = т + т + т + т + - = - + - + - + - + -,
12 3 4
что формально есть ζ(-1). Откуда Рамануджан взял —, я не знаю, но, как мы
только что показали, используя (9.2.16), ζ(-1) = . Рамануджан обнаружил
специальный случай продолженной дзета-функции еще до того, как услышал
оРимане!..
После смерти Рамануджана Харди заметил (в своем некрологе 1921 года,
который появился в трудах лондонского математического общества, а также
в Трудах Королевского общества (Proceedings of the Royal Society)), что
математические знания его друга имели некоторые заметные пробелы. «[Он]
самостоятельно нашел функциональное уравнение дзета-функции», но «он
никогда не слышал о... теореме Коши», «в действительности он имел, но смутное,
представление о том, что такое функция комплексной переменной», и «ему
невозможно было представить, как идти по жизни, предполагая, что все нули
дзета-функции вещественны». Харди позже, с небольшим преувеличением,
сказал, что Рамануджан был его величайшим открытием1.
Я буду использовать формулу (9.2.16) для более важного вычисления значения
ζ(0), предпоследнего вычисления в этой книге. Если мы сделаем что-то грубое,
просто вставив s = 0 в (9.2.16), то мы быстро увидим, что ничего не добьемся:
ζ(0) = 2(2π)-18ίη(0)Γ(1)ζ(1) = ????,
потому что ноль sin(O) и бесконечность ζ(1) воюют друг с другом. Кто победит?
Чтобы выяснить это, нам нужно быть намного более аккуратными в наших
расчетах. Как ни странно вам это покажется, но мы получим наш ответ, изучив
случай с s = 1 (а не s = 0), что я просто попрошу вас принять на веру, когда мы
начнем.
Вы можете прочитать больше об удивительной жизни Рамануджана в биографии:
Канигел Роберт. Человек, который знал бесконечность: жизнь гения Рамануджана.
Сыновья Чарльза Скрибнера, 1991 (Kanigel Robert The Man Who Knew Infinity: A Life
of the Genius Ramanujan. Charles Scribner's Sons, 1991).
366 ♦ Эпилог
Оглядываясь назад на формулу (9.2.9), мы имеем:
1
ζ(*) =
π
ίΐ )
- + -
s(s-l) π 2 ΓΙ-s
ν ) ι2
ι °° J _IS_A is_i \
^"- f\X 2$ 2 +λ:2' Jl|j(*)d*.
2SP 1 I 1
Если мы положим s —> 1, тогда видим, что правая часть действительно
стремится к бесконечности (как и должно быть, потому что ζ(1) = оо), строго из-за
одного первого слагаемого справа, поскольку интеграл, очевидно, сходится1.
Ί1
На самом деле, так как lim π 2 Γ
s->l
-^ = -= = 1, t,(s) раздувается как —-
при s —> 1. Запомните этот момент - он окажется ключом к нашему решению.
Теперь из (9.2.16) мы имеем:
гсги)5-1 sin
us
Г(1-5)
Из формулы отражения для гамма-функции мы имеем:
Г(5)Г(1-5)= π
sin^s)
π
и тогда
Г(1-5) = -
T(s)sm(ns)
это говорит нам, что
W-s)--
ζ(*)
2(2π)5_1 sin
π5
Τ
π
r(s)sin(sii)
Γ(5)5ίη(π5)ζ(5)
2π(2π),_1 sin1
Я использую это слово, потому что во всем интервале интегрирования
подынтегральное выражение очевидно конечно и стремится к нулю очень быстро при
а: —> оо. Действительно, подынтегральное выражение исчезает даже быстрее, чем
экспоненциально, при а: —> оо, что можно показать, используя (9.2.4) для записи и оцен-
ки1|/(х)=£7=1е-"2га = е-
+ е 2та + е Зта + ..., это геометрическая
-ух> 0, где правая
прогрессия, легко суммируемая для получения оценки ψ(χ) < -
е™ - Г
часть ведет себя как е ™ при «больших» х. При s = 1 подынтегральное выражение ве-
ψ(χ) е~™
дет себя (при «больших» х) как 3/^ 1/2 « —=.
Вывод функционального уравнения для ζφ ♦ 367
Поскольку sin(us) = 2 cos
ns
sin
us
τ
мы приходим к
(9.2.17)
альтернативной форме функционального уравнения для дзета-функции. Это
форма, которую мы будем использовать, чтобы применить ее при s —> 1, что
дает ζ(0) слева.
Итак, из (9.2.17) мы имеем:
T(s)cos
lim ζ(1 — s) = ζ(0) = lim
s-»l - "
US
№
Г(1)
—limcos
^ π(2π)5
π5|
limcos
ns
ζ(*)=
ζ(*),
или
COS
^
ζ(0) =
-lim-
π s-l 5-1
(9.2.18)
где я использовал наш предыдущий вывод (что я сказал вам вспомнить,
помните?): t,(s) ведет себя как —- как при s —> 1. Этот предел в (9.2.18) есть не-
0
s-1
определенность типа —, поэтому мы используем правило Лопиталя для его
вычисления
d
«0) = Ilim*J
cos
ϊ~7"
ns)
~2~J
- = —lim-
π *-*
π .
- — sin
2
1
us]
ч 2 J
ds
{5-1}
ζ(0) =
и, наконец, у нас есть ответ:
_1
2'
Чтобы закончить наши вычисления конкретных значений ζ($), позвольте
мне теперь показать вам прекрасный способ вычисления ζ(2), - что мы уже
сделали в главе 7, - это также дает нам одновременно все другие значения ζ(2η)
для л > 1. Что делает этот расчет вдвойне интересным, так это то, что весь ана-
368 ♦ Эпилог
лиз находится на уровне только начальных разделов математического
анализа. Начнем с нахождения разложения в степенной ряд для tan(X) при χ ж О, то
есть так называемого ряда Тейлора.
Почему мы начинаем с этого, конечно, совсем не очевидно, но следуйте за
мной некоторое время, и вы увидите, что все это будет иметь смысл. Итак, что
мы сделаем, так напишем
tan(x) = Yj:kxk = c0 + схх + с2х2 + съхъ + · ■ ·,
fc=0
а затем найдем коэффициенты с. Это стандартная часть математического
анализа для начинающих, и я собираюсь предположить, что большинство
читателей видело это раньше и может пропустить. Однако если это было давно, вот
краткий обзор. Если вы подставите χ = 0 в ряд, то сразу получите tan(O) = 0 = с0.
Чтобы найти с19 сначала продифференцируйте ряд по х, а затем подставьте
χ = 0. То есть
sin(x)
—{tan(*)} = —
ах ах [cos(X)
и теперь, подставляя χ = 0
1
1
cos2(x)
= q+2c2A: + 3c3A:2+···,
cos2(0)
= l = q.
Чтобы найти с2, снова дифференцируем, а затем подставляем χ = 0 (должно
получиться, что с2 = 0), и так далее для всех остальных с. Если будете аккуратны
с арифметикой, то должны получить
* , ч 1 з 2 5 17 7 62 , 1382
tan(x) = *H—х3Н х5+- ~7
^9+:
хп+·
3 15 315 2835 155925
ну а когда вы перестаете вычислять коэффициенты, зависит только от вашей
выносливости!
Далее мы будем использовать этот результат, чтобы получить степенной ряд
для cot(X), написав
1 1
cot(x) =
tan(x)
, 1 з , 2 5 17 7 , 62 9 , 1382 π ,
χ + -χ Η χ Η χ Η χ Η χ11 +··
3 15 315 2835 155925
1
α:1
1
1 + ^2+" "4
2 4 17 6
— χ4 Η -χ +·
15 315
Затем, если вы тщательно выполните длинное деление, указанное дробью
внутри фигурных скобок, то должны получить
Вывод функционального уравнения для ζφ ♦ 369
cot(x) =
ι-Ιχ2
з
1 4
—χ
45
945
или
w ч 1 λ 1 з 2 5
cot(x) = χ χ χ -·
χ Ъ 45 945
(9.2.19)
Хорошо, пока отложим это равенство (9.2.19).
Далее рассмотрим следующее удивительное тождество: для любого
действительного нецелого значения а:
cos(at):
sin(a7i:)
π
ι °° (—\\п
-+2«Е^ЛС0^)
(9.2.20)
Это выглядит довольно эффектно, но на самом деле (9.2.20) быстро
выводится с помощью простого, рутинного разложения в ряд Фурье функции cos(at)1,
которое является повторением одного периода, -π < t < π, и продолженного
бесконечно далеко в обоих направлениях вдоль оси £2. (Теперь вы можете
видеть, почему α не может быть целым числом, - если бы оно было целым, то
член η = α в сумме был бы бесконечностью.)
Если мы положим t = π в формуле (9.2.20), то получаем:
cos(au) =
silvan)
π
- + 2«E-nCos(mt)
a n=i ос — η
или поскольку cos(mr) = (-1)п и (-1)п(-1)п = [(-1)2]п = 1,то
cos(aTi) 1
—- = cot(aii) = —
sin (απ) π
Тогда
+ 2«Σ"
1
t/ ч 1 απ ~ 2
cot(au) = — +—Σ — 2
απ π2 ^α.-η~
= ^+Σ;
2(απ)
απ ^ί(απ)2-π2π2'
Если мы определим х = απ, то получим еще один ряд для cot(x):
1 А 2х
cot(*) = - + £
χ ^
п^х2-п2п2
(9.2.21)
Это разложение cos(at) только на интервале -π < t < π. - Прим. перев.
2 Все детали вывода (9.2.20) можно найти на стр. 154-155 моей книги «Доктор Эйлер».
370 ♦ Эпилог
Из (9.2.21) следует, что
l-xcot(x) = -^2
v2 „2 2 L·^ „ϊ-l ν2
η=ι χ —η τι η=ι η π — χ
Σ-
2χ2
2χ2 " 1 |
τ2 2_-^ „2 J
π
и=1
Π
π2π2
_ 2χ2 " 1
_ ^-2 Ζ-/ „2
π и=1 л
, χ2 χ4
1 + ^^ +
^2^2
Π4ΤΤ4
+
+ ·
или
l-*cot(*):
2χ2
1 2χ
1 2хь
2-^ ^2 """ „4 Ζ-/ „4 """ „6 Ζ-/ <b ~"~
π" и=1л π η=1η
А из (9.2.19) следует, что
11 2
l-xcot(x) = -x2H χ4 Η χβ +·
w 3 45 945
π
(9.2.22)
(9.2.23)
Приравнивая коэффициенты при равных степенях χ в равенствах (9.2.22)
и (9.2.23), получаем:
π и=1л 5
π4 tin4 45'
2 " 1 _ 2
^t^~945
и так далее. Это дает нам:
т-\
Τ
ζ(4) =
ζ(6) =
45
2
945
π
A \
π
Τ9
~905
π
.6 ϊ
π
945
и так далее. Это не так, как нашел Эйлер ζ(2π), но, поверьте мне, ему бы
понравился такой подход!
Один из открытых вопросов о дзета-функции касается значений (2п + 1),
η > 1. Все эти значения, даже самое первое ζ(3), известны только
посредством прямой численной оценки его определяющего бесконечного ряда.
Конечно, нет известных формул, включающих степени π, как для для ζ(2π).
Почему существует такое резкое различие между четными и нечетными ар-
Вывод функционального уравнения для ζφ ♦ 371
гументами дзета-функции - это одна из глубоких загадок математики,
которая озадачивала величайших математиков мира от Эйлера до наших дней.
Теперь несколько заключительных комментариев. Все, что я рассказал вам
здесь о дзета-функции и RH, - это лишь малая часть того, что известно. И все
же RH остается сегодня огромной темной тайной, ее разрешение спрятано где-
то в казалось бы очень длинном (возможно, бесконечном) извилистом туннеле,
и впереди не видно даже проблеска света, чтобы намекнуть, что этому есть
конец. Риман по праву славится многими вещами в математической физике1, но
немало иронии в том, что самым известным из всех его созданий является
головоломка, которая (до сих пор) противостояла всем попыткам величайших
математиков мира разгадать ее. Однако все эти мощные усилия не прошли даром.
Одним из современников Исаака Ньютона был Роджер Коте (Roger Cotes,
1682-1716), который был профессором в Кембридже в возрасте 26 лет и
редактором второго издания шедевра Ньютона «Начала» (Philosophiae Naturalis
Principia Mathematica), работы, которая произвела революцию в физике. Его
смерть от сильной лихорадки за месяц до его 34-го дня рождения - даже
моложе, чем были Риман и Клиффорд в годы их смерти, - оборвала по-настоящему
многообещающую научную жизнь. Сообщалось, что после смерти Котса сам
Ньютон сказал о нем: «Если бы он жил, мы могли бы узнать что-нибудь
особенное». Однако никто никогда не говорил этого о Римане, потому что мир
многому научился у него еще до того, как он покинул эту жизнь.
Данная книга начинается с рассказа, в котором участвует Г. X. Харди, и
только для симметрии позвольте мне закончить еще одним. Харди был очарован
RH всю свою трудовую жизнь и никогда не упускал шанс поразгадывать ее. Вот
одна известная история, которая забавно отражает то, насколько глубоко RH
зацепила его. После завершения визита с другом-математиком в Копенгаген,
1 Когда Риман представил свою докторскую диссертацию («Основы общей теории
функций комплексной переменной») Гауссу, этот великий человек объявил ее
«прозорливой», «творческой», «красивой» и работой, которая «намного превосходит»
стандарты таких работ. Однако, чтобы иметь право преподавать, Риман должен был
прочитать пробную лекцию перед аудиторией старших профессоров (включая
Гаусса), и Гаусс попросил, чтобы она была на основе геометрии. Это было сделано Рима-
ном в июне 1854 года, и, по словам математика из Калифорнийского
технологического института Эрика Темпла Белла, в его знаменитой книге «Люди математики»
(Eric Temple Bell, «Men of Mathematics») он «произвел революцию в
дифференциальной геометрии и подготовил почву для геометризованной физики [сегодняшнего
дня]». Белл имел в виду более позднее описание Эйнштейном гравитации как
проявления искривленного пространства-времени, идеи, которая могла бы прийти Ри-
ману в голову, если бы жил дольше. После смерти Римана британский математик
Уильям Кингдон Клиффорд (1845-1879) перевел лекцию Римана на английский язык
и был, пожалуй, единственным живым человеком, который действительно ценил
то, что сделал Риман. Сам Клиффорд в короткой, загадочной записке, написанной
в 1876 году («О космической теории материи»), за три года до рождения Эйнштейна,
был близок к идеям теории гравитации Эйнштейна. К сожалению, Клиффорд тоже
умер молодым от той же болезни, которая убила Римана.
372 ♦ Эпилог
Дания, Харди собирался вернуться в Англию. Он должен был путешествовать
на корабле по дикому и бурному Северному морю. Надеясь избежать
возможного крушения, Харди быстро, незадолго до посадки, написал и отправил по
почте открытку своему другу, в которой говорилось: «У меня есть
доказательство гипотезы Римана!» Позже Харди сказал, благополучно добравшись до
Англии, что он был уверен, что Бог не позволит ему умереть с ложной славой,
когда его будут помнить за то, чего он на самом деле не достиг. Стоит отметить,
что Харди был искренним атеистом во всех других аспектах своей жизни.
По какому-то невероятному совпадению я пишу эти последние слова этой
книги на британском круизном корабле «Королева Елизавета», возвращаясь из
отпуска в Норвегии. «Королева Елизавета» базируется в Саутгемптоне, Англия,
и мое путешествие туда привело меня через Северное море и прямо мимо
Копенгагена. Итак, вот я сижу, через 100 лет после Харди, опираясь ногами на
перила балкона моей каюты, и пишу о его маленькой шутке, возможно, именно
там, где он плавал столетие назад. Так или иначе, я думаю, что призрак Харди
совсем не удивлен, когда он заглядывает мне через плечо, что тайна RH все еще
не разгадана, и, возможно, если заглянуть в будущее, она все еще останется
загадкой и 100 лет спустя.
Однако для математиков это такая же большая приманка, как для Индианы
Джонса древний магический артефакт, спрятанный в огромном древнем
хранилище, и поэтому охота славно продолжается!
9.3. Вопросы для упражнений
Поскольку эта глава посвящена нерешенной проблеме RH, я решил быть
больше философом, чем аналитиком при постановке этих задач. Итак, вместо задач
вот три вопроса для размышления.
(С9.1). Пусть рп обозначает п-е простое число. рх = 2, р2 = Ъ и т. д. Предположим,
что мы определили qn как первое простое число, большее ΡιΡ2···Ρπ + 1> а затем
вычислим qn - (ΡιΡ2···Ρπ)· Если мы сделаем это для первых семи значений п, то
получим следующую таблицу:
η
1
2
3
4
5
6
7
ΡιΡ2...Ρη
2
6
30
210
2,310
30,030
510,510
рхр2—рп + 1
3
7
31
211
2,311
30,031
510,511
Qn
5
11
37
223
2,333
30,047
510,529
<Ζη-(ΡιΡ2...Ρη)
3
5
7
13
23
17
19
Вопросы для упражнений ♦ 373
Глядя на крайний правый столбец таблицы, насколько хорошо он вам
подсказывает гипотезу? Можете ли вы доказать свою гипотезу? Подобные вопросы
о простых числах, которые так легко приготовить и которые так трудно
доказать, очаровали Римана в 1859 году и продолжают очаровывать нас и сегодня.
Например, гипотеза простых чисел-близнецов, о которой я упоминал в
разделе 9.1, послужила причиной для недавнего (2013 г.) волнения в мире
математики. Это было связано с доказательством того, что существует бесконечное
количество простых чисел-близнецов, разделенных пробелами не более 600.
Долгий путь от первоначальной гипотезы с пробелом 2, да, но все же...
(С9.2). Хотя численные расчеты, как правило, не доказывают теоремы (но они
вполне могут опровергнуть гипотезу путем нахождения контрпримера), они
могут быть весьма полезны, предлагая возможность, заслуживающую
дальнейшего изучения. Например, поскольку на рис. 9.1.1 показано, что для ε >
0 Ηηιε^0ζ(1 - s) = -оо и Ηηιε^0ζ(1 + s) = +oo, то, по крайней мере, возможно, что
Ηηιε^0{ζ(1 — s) + ζ(1 + s)} может быть конечным. На самом деле MATLAB легко
использовать для вычисления следующей таблицы:
ε
0.1
0.01
0.001
0.0001
{ζ(1-5) + ζ(1+5)}/2
0.577167222774279
0.577215180384336
0.577215660056368
0.577215664853611
Из этих расчетов следует, что Ηηιε^0{ζ(1 - s) + ζ(1 + s)}/2 = 0,57721566.... Это
говорит о том, что предел является известной константой? Можете ли вы
доказать свою гипотезу?
(С9.3). Два студента, специализирующиеся по математике, Салли и Сэм,
обсуждают RH в целом и, в частности, мнение некоторых математиков о том, что
причина, по которой никто не решил вопрос, даже после 150 лет интенсивных
попыток, заключается просто в том, что он неразрешим. Салли говорит, что
хотя это вполне может быть правдой, но также верно, что никто никогда не
сможет доказать, что RH неразрешима. Когда Сэм спрашивает, почему нет, Салли
отвечает: «Если можно было бы показать, что RH неразрешима, это означало
бы, что никто и никогда не сможет найти комплексный ноль вне критической
линии, даже случайно, независимо от того, как долго они искали. Даже если
10
бы они могли искать нули со скоростью 1010 за наносекунду, независимо от
того, как высоко бы вы поднялись по экспоненциальной стопке из десятков.
Это потому, что если бы нашли такой ноль, то доказали бы, что RH ложна.
А это противоречит первоначальной предпосылке о неразрешимости
проблемы. В свою очередь, это означало бы, что нет нуля вне критической линии
и, значит, что RH была решена и она истинна. Это тоже противоречие. Единст-
374 ♦ Эпилог
венный выход из этой трясины - сделать вывод, что таких доказательств не
существует».
Сэм обдумывает это и, наконец, отвечает: «Ну, я не совсем уверен во всем
этом. Есть бесконечно много комплексных нулей, и поэтому независимо от
того, сколько из них вы можете проверить каждую наносекунду, все равно
потребуется бесконечное время, чтобы проверить их все. Таким образом, вы
никогда не закончите, а противоречие не возникнет, пока вы не закончите».
Что вы думаете о каждом из этих аргументов?
Пока вы обдумываете слова Сэма и Салли, мы подходим к КОНЦУ, и ваш
автор уезжает в математический закат, как «аризонский рейнджер с большой
пушкой на бедре» в той старой, но все еще великой балладе вестерна покойного
Марти Роббинса. Эта книга дала вам много боеприпасов для вашего большого
интегрального пистолета, поэтому, прощаясь, я просто желаю вам успеха
(когда вы в следующий раз сразитесь с новым «преступным интегралом»). А
поскольку вырос в 1950-х годах в Южной Калифорнии, всего в 100 милях к северу
от мексиканской границы, прощаюсь вот так:
Прощай, мой друг, иди с Богом.
Воспроизводится с разрешения Toon Vectors (Остин, Техас)
Решения задач и упражнений
Предисловие
ι 7
Поскольку χ + — = 1, то умножение на χ дает χ + 1 = χ, или, перегруппируя,
χ
х2 = χ - 1. Умножаем на χ снова, хъ = х2 - х, или, заменяя наше выражение для х2,
хъ = х- 1 -х = -1. Возведение в квадрат этого выражения даетх6 = 1, а затем,
умножая на х, мы получаем х1 = х. Итак, заменив хна х1 в исходном χ + — = 1, мы
χ
7 1 1
получаем χ + — = 1, и все готово.
Глава 1
(С 1.1). Заменим переменную на и = χ - 2 (и du = dx), что дает нам
8r dx _erdu _.. rdu erdu
■J x-2 Λ и ε^° Κ, и Ч и
= lim
ε^Ο
in(U)i:;+in(u)i;
= lim [1η(-ε) - ln(- 2) + ln(6) - 1η(ε)] = lim
In
+ ln
(6)
ε
lim
ε^Ο
In
ε Κ 6
2
:1П(3).
To есть
Jo (*-l>
Ό (χ-!)
+ lim Г
ε^Ο J
1+ε
dx
(x-1)
2/3
В обоих интегралах справа заменим переменную на и = χ - 1 (и du = dx).
Тогда
dx
3
I-
0 (χ-Ι)3
lim
ε^Ο
du
/au r
du
~~2~
= lim
ε^Ο
ЗыЧ
^ '
+ ЗиЧ
-ι ν J
2]
ε 1
= 31ίηι{(-ε)3-(-1)3+(2)3-(ε)5} = 311 + 25}.
376 ♦ Решения задач и упражнений
(С1.2). Пишем
dx
I
/
dx
<
оо
dx
оо
dx
ι у1хъ -1 ι Vx-Wx2+x + l ι Vx-lVx2^ i Wx-1 '
где неравенство выполняется, потому что в интеграле непосредственно перед
крайним правым я заменил знаменатель в подынтегральном выражении на
меньшую величину. Теперь заменим переменную на и = χ - 1 в последнем
интеграле. Так,
оо
dx
<
du
/аи г
di/
ί Vx3-1 о (и +1)Vw J0 и3/2 + и
.1/2 :
или, записав последний интеграл как сумму двух интегралов, мы имеем:
dx г du °r du
I
[ ν^τ
<
/
>0иъ,2 + ит
+
I
\ иъ,2 + ит
Мы сделаем неравенство еще сильнее, заменив знаменатели
подынтегральных выражений в правой части меньшими величинами, и поэтому
(C1.3). В интеграле Фейнмана J
1 =2 + 2 = 4.
и = ax + b(l -χ) wdx =
IUd"]
и2 [a-b
du
a-b
ι ί ιΥ
и
[ax + b(l-x)]
, и тогда интеграл принимает вид:
- сделаем замену переменной
а-Ь
а-Ь
Ъ а
а-Ь _ 1
(а - b)ab ab'
точно так же, как утверждал Фейнман. Все это имеет смысл, если
подынтегральное выражение не обратится в бесконечность где-то внутри интервала
интегрирования (то есть пока нет такого х, что ах + Ь(1 - х) = 0 в интервале
О < χ < 1. Теперь величина ах + Ь(1 - х) равна нулю, когда χ = , и поэтому
Ъ-а
мы требуем либо < 0 (назовем это условие 1), либо > 1 (назовем это
b-α Ь-а
условие 2). Для условия 1 мы можем написать для некоторого положительного
числа /с, = -к. Или Ь = -Ьк + ак и, умножая это на a, ab = -abk + а2к. Решая
Ь-а
относительно ab, мы имеем ab = -.Поскольку к положительно (и, очевидно,
1 -\- К
такое же а2), то мы заключаем, что ab > 0.
Решения задач и упражнений ♦ 377
Для условия 2 мы можем записать для некоторого числа /с, большего
единицы, = к. Или Ь = Ьк-аки,умножая это на а, ab = аЪк- а2к. Решая относи-
Ъ-а
а2к
тельно ab, мы имеем ab = . Поскольку fe> 1, то заключаем, что ab > 0.
То есть для обоих условий (условий, обеспечивающих, чтобы
подынтегральное выражение не обратилось в бесконечность где-то внутри интервала
интегрирования) мы заключаем, что ab > 0. То есть а и Ь должны иметь один и тот же
алгебраический знак, и это устраняет загадку интеграла Фейнмана.
J-»oo Р_ /»оо Р_ У
dx в / —dy при помощи замены пере-
0 χ ° у
менной у = сх (предполагая о 0). Поскольку х = —, мы имеем dx = -dy, и тог-
с с
_с1
да Г°° dx= Г°° -dy = Г°°—dy. Это формально хорошо, но на самом
с
деле это просто упражнение в манипуляции символами. Это сделано
потому, что ключом к этой головоломке является понимание того, что интеграл
оо е~у , .
— dy не существует!
0 у
Вот как это увидеть. Для любого заданного конечного значения верхнего
—dy — oo. Это потому,
0 У
что для 0 < у < δ мы имеем:
J—dy > f—dy = e~s {ln(y)}|; = оо.
о У о У
Таким образом, когда мы пишем
оо -ах р-Ъх оо -яаг оо р-Ъх оо -у оо -у
Г dx= Г dx- Г dx= Г—dy- Г—dy,
о х ох о х о У о У
на самом деле мы вычитаем бесконечное число из другого бесконечного числа,
и результат не определен. Для определения результата требуется более
глубокий анализ, как это сделано в главе 3. Проблема вычитания одной
бесконечности из другой получила интересную трактовку в коротком
научно-фантастическом рассказе Стэнли Винбаума «Край бесконечности» (The Brink of Infinity)
(1902-1935), который вышел посмертно в декабрьском номере журнала
«Захватывающие истории чудес» (Thrilling Wonder Stories) (переиздан в сборнике
Винбаума «Марсианская Одиссея и другие научно-фантастические рассказы»
(A Martian Odyssey and Other Science Fiction Tales. Hyperion Press, 1974). Человек,
f
Jo
378 ♦ Решения задач и упражнений
получивший ужасную травму в результате неудачного эксперимента,
обвиняет математика, который неправильно провел предварительный анализ. Мстя
математикам вообще, он заманивает одного к себе домой. Держа ученого под
дулом пистолета, он говорит, что его застрелит, если тот не ответит правильно
на следующий вопрос: преступник задумал математическое выражение, а
математик должен выяснить, что это за выражение, задавая ему не более десяти
вопросов. Один из вопросов математика - «Чему равно это выражение?», а
ответ - «что угодно». И это как раз то, что конец истории открывает читателю, -
преступник думает о «оо - оо».
Глава 2
(С2.1). В интеграле Г ^ dx = О сделаем замену переменной у = —. Тогда
Jo Я Αχ-χ2 4
χ = 4у и dx = 4dy. Этот интеграл принимает вид
Г, lnW 4с*уЛ1п^ + 1п^
Jo Vl6y-16y2 J0 λ/У-У2 о λ/УлА-У о λ/УлА-У
В обоих из этих двух последних интегралов сделаем замену переменной на
у = sin (θ), это означает, что когда у = 0, мы имеем θ = 0, а когда у = 1, то θ = —.
л
dv
Также -4- = 2sin(0)cos(0), и тогда
Г dy /.f 2sin(9)cos(9)d9 = 2 r\sin(9)cos(9)de = 2 rf de = π
о л/Ул/ь1^ Jo Vsin2(6)Vl-sin2(e) Jo sin(9)cos(9) J°
f^=dy= ρ i"(sin2(9)) 25ίη(θ)(:05(θ),θ;
о л/Ул/1-У Jo Vsin2(9)Vl-sin2(9)
π
: 4 J4n(sin(6))de = 4
fln(2)
-2π1η(2),
где я использовал логарифмический интеграл Эйлера, который мы вывели
в (2.4.1). Итак, мы имеем:
f-^dx = wf-b+fbMay = 1η(4)π-2π1η(2) =
J0 л14х-х2 JQ VyVi-y о Vyvi-y
= 1η(22)π - 2π1η(2) = 2π1η(2) - 2π1η(2) = О,
и мы сделали эту задачу.
Решения задач и упражнений ♦ 379
r»i dx ί г1 dx 1 г1 х-2
,пг> г,ч дуг Г1 «* 1 fi OX I fi Χ-Δ , _
(С2.2). Мы начнем с разложения / — = -ι / — ах. В пер-
вом интеграле справа пусть и = χ + 1 (dx = du). Тогда
lV dx 1 г Αι 1
3*
Во втором интеграле пишем (следуя подсказке):
Л_^=1^« = 1 |2=ι
3b2-x+l 3-J ..2 ..,1,3 3-i
0 x-x-\ h-
4 4
о I 1
X
2
v*
\2
dx.
Далее, пусть и=х- — (и тогда dx = du), и мы получаем:
I г *-2 dY ι π 2 du ι И if dx_I ρ «fa
З^-х-Н^З-Ц, Ш2 3J^2 №Г 2J^2 №
IT + — Μ + — И + —
Первый интеграл справа равен нулю, так как подынтегральное выражение
нечетно, а границы интегрирования симметричны относительно нуля, и
поэтому
If Г2 dx
■1-А
du
' 2
и2 +
IS
\2
-^tan"1
л/3
(Ы
Ш
J_
_2_
"V3~
jtan l
( Λ
π
fe
,%/3,
-tan"1
π
3^2
'-—1
, S)
1 l J
Г ^1
2tan_1
ii)
[S]
Итак,
r dx 11 /Пч π
/7ΤΊ-1η<2)+53·
o-' +
или
380 ♦ Решения задач и упражнений
Это выражение равно 0.8356488..., и MATLAB согласен: quad(@(x)l./(x.
Л3+1)А1) = 0.8356488....
(С2.3). Определим интеграл 1(т
■ч#
dx
+ 1)"
который затем мы
интегрируем по частям. То есть в стандартных обозначениях ludv = ι/ν- jvdu,
положим dv = ахи и
dx
1 т du
—-А . Тогда ν = χ и -—
(х4+1)т dx
-Am
(х4 + 1)"
, и мы получаем
/
0(x4+i)m (x4+iy
Теперь пишем:
°г х
+ Ат I — Tdx.
У ν4 _L 1 1
Г—л rdx= Г— Tdx- Г— Tdx
{ (χ4 + l)ffl+1 J (χ4 + l)ffl+1 { (χ4 + l)ffl+1
oo
dx
oo
Итак:
Οϋ
dx
(x4+lf
= Am
{(x* + l)m iix' + iy
OO J„. OO л
r ax r 1
\m+l
dx.
J0(x4+l)m J0(x4+l)
m+1
dx
или переставляя члены:
4m f д * tdx = 4mf-^ f—^ = (4m-l)f
dx
>0(χ*+\γ
Таким образом,
OO л
Am f— Tdx ■
и мы закончили.
4m-1
OO
dx
Am J0 (x4+lf
(C2.4). Знаменатель подынтегральной функции равен нулю при значениях,
заданных формулой χ = . Если -2 < Ь < 2, то оба этих значения
являются комплексными, поэтому находятся не на действительной оси; это
означает, что знаменатель никогда не равен нулю в интервале интегрирования.
А если Ъ < -2, то оба значения χ < 0, что опять же означает, что знаменатель
никогда не исчезает в интервале интегрирования.
Таким образом, интеграл в (2.4.5) существует, только если Ь < 2. MATLAB
соглашается, так как эксперименты с quad показывают, что случайный выбор
Решения задач и упражнений ♦ 381
для Ь, величины меньше 2, всегда дает значения для интеграла, которые либо
равны нулю, либо чертовски близки к нулю, в то время как любое значение
Ъ > 2 приводит к тому, что MATLAB отвечает 'NaN' (не числовое значение),
с точки зрения MATLAB интеграл не существует.
(С2.5). В интеграле Г— ._ dx положим и = 1п(1 + х) и dv = ^r-z-. Тогда
J0 χ4χ *'
dx 2
du = и ν = —=, и поэтому
1 + Х yfc
ln(l + x)d;g= 2ln(l + x)
о х4х 4х
/
0 JoVxl + x j0(1 + x)Va:
Затем сделаем замену переменной t = у/х, и поэтому χ = t2 ndx= 2tdt. Таким
образом:
°°r dx ^2°r ltdt ^Л dt
= 4tair1(t)P=4
π
= 2π.
Глава 3
(C3.1). Начнем с интеграла 1(a) = Г—Ц ^dx и, дифференцируя его по па
J hl Л- yz
раметру α, получаем:
оо
■/
2ах2
dl
da J0(l + a2x2)(b2 + x2)
оо
dx = J
1 Ъ2 + х2
А
l + a2x2+tf
-W/Υ У1,
[dx,
так что Ab2 + Αχ2 + В + BaV = x\A + Ba2) + Ab2 + В = lax2. Тогда A + Ba2 = 2a
2a „ 2ab2
и Ab + В = 0. Решая относительно An В, мы имеем А -
Таким образом
__2а
da~
\-а2Ъ2
иВ-
\-а2Ъ2
dl = 2a J dx 2ab2 J dx
\-a2b2{\ + a2x2 \-a2b2{b2+x2
2/a °r dx
0
■ 2 °o
_ Δ/α r ax 2ab °r dx
a''
l-a2b2J0b2+x2
—"--(a)tan '(™)L -q ^тч
\-a2b2 l0 \-aLbL
tan
2ab
l-a2b2 l-a2b2
= *2
2
1-ab
l-a2b2
= π-
V
1
1 + ab
382 ♦ Решения задач и упражнений
Итак, — = π , и поэтому I = π Г da. Положим и = 1 + ab, так что
da \-\-ab J \-\-ab
du 1 ~й(*и
—da = -di/.ТогдаI = π Γ-— = —1п(1/) + С,где С- константа интегрирования.
da b J и Ъ
Из самого определения 1(a) мы знаем, что 7(0) = 0, что говорит о том, что
С = 0. И наконец:
1п(1 + аУ) 1п(1 + аЬ)
ЬЧх2 Ь ·
(С3.2). Пишем
cos(ax)
1
2b
ф-х)ф + х)
cos(ax)dx | °rcos(ax)
•j (X> I
[dx = — fcos(ax)\
1 1
b+x b-x
\dx-
B первом интеграле положим u = b+x (так что du = dx), а во втором
интеграле положим и = Ь-х (такчто du = -dx). Тогда
оо
cos(ax)
Ь2-х
1
2 -»* 2Ь
2Ь
cos(au-ab)
cos(au-ab)
—оо
di/+ Г
оо
оо
du+ [
cos(ab-au)
cos(ab-au)
(-du)
du
cos(ax) , _1 °rcos(au-ab)
- 'dx = — \
hl — vl h J
du.
Теперь, так как cos(x - у) = cos(x)cos(y) + sin(x)sin(y), то
°rcos(^x)dx=i °r cos(au)cos(ab) du | 1 °rsm(au)sm(ab) du =
J b2-x2 Ь^ и Ь^ и
cos(ab) °r cos(au) , sin(ab) °r sin(au)
I
. -du-\ —- / —-—-du.
b J и b J и
—оо —оо
Первый интеграл имеет главное значение Коши, равное нулю, поскольку
—- - нечетная функция. При а > 0 второй интеграл есть от интеграла Ди-
и
рихле. Итак:
оо
/
cos (ax)
άχ = π
sin(ab)
Решения задач и упражнений ♦ 383
,гл- гч π г°° costax) , π _ah ,
(СЗ.З). Поскольку / v 'dx = —e , а так как подынтегральная функ-
J-oo ь2_х2 2b
oocos(ax)dx=ne_ab
b2-x2 2b
u2 ( 2
Тогда
-oo bZ+XZ
cos(ax)
cos(ax) , π _ab sin(ab)
>dx ъ
+ π-
b
oo
Γ cos(ax)
■ + :
[b2 + x2 b2
= 2b2 Τ COS(ax)
— с
и мы сразу получаем наш результат:
Ы*
b4-x4
оо
cos(ax), _ Tt{e ab + sin(ab)}
b4-x4
2b3
(С3.4). Обратите внимание, что так как подынтегральная функция является
четной функцией, мы можем написать:
°rxsm(ax) , 17" · / ч
J^T^d*=?J*sin(ax)
х2-Ь
1
-Jxsin(ax)
— oo I
1 °° I
-fxsin(ax)\
(x-b)(x + b)
1
(Ь-Х)(Ь + Х)
1 1
- + -
\dx =
\dx--
\dx-
4b
b + x b-x
xsin(ax)^ ( 7" xsin(ax)
b-x
. <?X + / ■
b + x J
dx
В первом интеграле заменим переменную на и = Ъ + х, а во втором интеграле
на и = b - χ. Затем
384 ♦ Решения задач и упражнений
xsin(ax)
х2-Ь2
dx--
4b
J_
4b
(u-b)sin(au-ab)
(u-b)sin(au-ab)
— OO
OO
du + f
(b-u)sin(ab-au)
(u-b)sm(au-ab)
(-du)
du
=--f
Ah J
1 <r2(u-b)sin(au-ab)
4b
J_
2b
du =
OO OO
f sin(ai/ - ab)di/ - b f
sin(ai/-ab)
du
В первом интеграле заменим переменную на s = аи - ab. Тогда
ОО ■( ОО
Г sin(ai/ - ab)di/ = — Г sin(s)ds,
который имеет равное нулю главное значение Коши. Таким образом:
°rxsin(ax) , _ 1 °r sin(au-ab)
J У2_Ь2 аХ-\] ~
-Αι,
или поскольку sin(a - β) = sin(a)cos(P) - cos(a)sin(P):
хът(ах) , 1 °r sin(au)cos(ab) — cos(au)sm(ab)
oo .
r-
e-b2
-dx-
du
I
cos(ab) Γ—-—-du-sin(ab) f —-du
J и J и
Первый интеграл, как интеграл Дирихле, равен π, а второй интеграл равен
нулю, поскольку подынтегральная функция является нечетной функцией.
Таким образом:
/
xsin(ax) , π , 1Ч
dx = —cos(ab).
2 v '
к2-Ь2
(C3.5). Начнем с напоминания тригонометрического тождества cos(ax)sin(to) =
-[sin{(b - а)х] + sin{(b + а)х}]. Поскольку косинус является четной функцией,
то cos(ax) = cos(№), и поэтому cos(ax)sin(bx) = -[sin{(b - \а\)х] + sin{(b + \а\)х}],
и тогда
sin(bx) _Пsin{(b-\а\)х] , 1 °rsin{(b + \а\)х]
\ cos(ax) —-dx = - I
]-dx.
Решения задач и упражнений ♦ 385
Из (3.2.1) мы имеем:
π
sin(cx)
dx = \
если о О
О, если с = 0,
—, если с<0
так что:
(1) если \а\ < Ь, то Ъ - \а\ > 0 и Ь + \а\ > 0, и тогда
fcos(ax)
sin(bx)dx=l
1 \
π
,~2
1
+ 2
π
Ϊ,
π
(2) если |α| > b, то Ъ - \а\ < О и Ь + |а| > 0, и тогда
fcos(ax)
sin(bx)dx=l
ί π]
I 2
1
+ -
2
ίπ)
2
(3) если |α| = Ь, то Ь - |α| = 0 и Ь + \а\ > 0, и тогда
/ cos(ax)-
^ϊιφΟ 1 1
χ 2W 2
π
di/
(C3.6). Начнем с подсказки, и пусть χ = cos(2u). Тогда — = -2sin(2i/), и поэтому
dx
(вспоминая тождество двойного угла) dx = -2s'm(2u)du = -4sin(i/)cos(i/). Таким
образом:
f^dx = hP^{-4sin(U)cos(u)dM} =
JJll-x Jn \l-cos(2i/)
= 4?,in(u)cosWJ1 + cos(2,lW
•i Vl-cos(2u)
-cos(2i/)
Далее, вспоминая тождества 1 + cos(2u) = 2cos2(u) и 1 - cos(2u) = 2sin2(u), мы
имеем:
№
π/2
0
ri /l + x ,
поэтому / J dx = π.
11
- + -cos(2i/)
2 2 V У
2 sin2 (и)
di/ = 4
1 1 · ,o ч
-i/ +—sin(2i/)
2 4 v У
4
π,
386 ♦ Решения задач и упражнений
J»l Г п\ X — V
0 lJo (* + у)3
рале. Тогда dx= dtu
{(χ+yf i t3 Jy t2 yjy
\dy положим t = χ + у во внутреннем интег-
dt
1+У
-2y
2t2
1+У
il 1 1
ly i+yj
+ У
1
1
(1 + y)2 y2
после небольших алгебраических преобразований это сводится к -
(1 + УГ
Итак,
1
{ К (*+у)3 1 {
'г dy
Jo (1 + У)
dt
Пусть ί = 1 + у, и этот интеграл становится -/-=- =
Ч«'
1_
'2'
То есть
о I о \л
х-У
+уу
dx
dy--
Если вы повторите это для интеграла
1 1
II
х-у
Jo (х + УУ
dy
1
\άχ,το получите +-. Несовпадение результатов вызвано тем, что
подынтегральное выражение уходит в бесконечность, когда мы приближаемся
к нижнему левому углу (х = у = 0) области интегрирования. Не забывайте урок
главы 1 - остерегайтесь взрывающихся подынтегральных выражений!
оо /
(С3.8). Из равенства (3.7.1) мы знаем, что (при Ь = 0) Je~ax2dx = J—. Теперь,
-оо
следуя подсказке, рассмотрим
оо оо оо _Jx2_b J оо _аЬ_Ьх+_Ь2 Ь2]
feax2+bxdx= fe(ax2bx)dx= fe [ a]dx=Je[ a 4fl2 4fl2W =
00 #_ -flx-Af #_ 00 _а\х_±Г
Je4ae [ 2aidx = e4aJe [ 2ai dx.
Далее делаем замену переменной у = χ . Тогда
2а
e4aJe [ 2aidx = e4a fe-ay2dy=e4a2J-,
Решения задач и упражнений ♦ 387
и таким образом:
оо
1(а, Ъ) = Je-ax4bxdx = еТа А-
Дифференцирование относительно Ъ дает нам
д!
дЬ
= $хе
-axz+bx
dx =
2b £ /ί b £ /π
4α
, =—e
α Ια
Подстановкая=1иЬ = -1 показывает Γ xe *2 xdx = —νπε4 = —vWe :
J-°° 2 2
-1.137937.... MATLAB соглашается: quad(@(x)x.*exp(-x.A2-x),-10,10)
-1.137938....
Если мы продифференцируем относительно а, то получим
да
оо
2e-ax+bxdx--
£
4Ь
2 V-
16α2
π b
2 b2
b^
+ e4a
λ/τι
-α 2νπ
Ι α 4α2 2α3/2
X°° 2 -х2-аг j /— 1 7 νπ 7
^x e αχ = \Ιπ — e +—^~e '-
1.7069068.... MATLAB соглашается: quad(@(x)x.A2.*exp(-x.A2-x),-10,10) =1.706907..
(C3.9). Следуя подсказке, дифференцирование дает
/
sin(mA:)
-2a
0
Итак,
(χ2 + α2)2
[dx =
π
a2(me-am)-(l-e-am)2a
I
>0x(x2 + a2)2
dx-
π
a2(me-am)-(l-e-am)2a
-2a5
которое после небольших алгебраических преобразований принимает вид:
sin(mA:)
>0х(х2 + а2)2
оо
I
dx-
π
2α7
2 + та
Глава 4
1 Jf -ι
(С4.1). Замена переменной и = 4х = х2, — = —1=, что означает dx = 2у/х du
dx 2Vx
2udu. Тогда
388 ♦> Решения задач и упражнений
1 . п 1 1
Дм) = J{l-yfx) dx = j(\-u)n2udu = 2Ju(l-u)"du = 2В(2,л+ 1) =
2Γ(2)Γ(η + 1) = 2 1!η!
Γ(π + 3) (π+ 2)!'
или наконец:
7(и)= f{l-^)"dx = .
Jo (п + 1)(п + 2)
(C4.2). Делаем замену переменной и = -\п(х). Поскольку \п(х) = -и, тогда
χ = е~и, и поэтому dx = -e~udu. Таким образом:
1 0 оо
fxmln\x)dx = fe-um(-u)n(-e-udu) = (-1)" funeHm+1)du.
Снова делаем замену переменной t = (т + 1)и и du ■-
dt
т + 1
. Таким образом,
1 ОО
fxmln"(x)dx = (-!)"/
т + 1
(-1)"
dt
т + 1 (т + 1)"
оо
-ft"e-'dt.
Из (4.1.1) мы имеем r(q)= / tq !e 'dt, и поэтому наш интеграл соответству
*J О
г°° -t j (— 1)
ет случаю π = д - 1, то есть q = η + 1, и поэтому I t e at —
по формуле (4.1.3), Г(п + 1) = л! и, таким образом,
, Г(л + 1).Но
(1Я + 1)И+1
1
fxmlnn(x)dx
(-1)"п!
(m + l)"+1
(С4.3). Запишем двойной интеграл по треугольной области R как
JJxaybdxdy = JV jy*dy [dx = /χ"
,.»+!
Ь + 1
[dx-
b +
- [xa(l-x)b+1
1J„
dx.
Из определяющего интеграла для бета-функции, В(т,п)= fxm~1(l — x)n~1dx,
о
мы имеем: т-\ = α и /ι - 1 =Ь+ 1. И m = 1 + аип = Ь + 2. Таким образом:
rrxydxdy = S(l+a,b + 2)_ Г(1+а)Г(Ь + 2) _ а!(Ь+1)! _ а!Ь!
R
Ь + 1 (Ь+1)Г(а + Ь+3) (Ь+1)(а + Ь + 2)! (а+Ь + 2)!-
Решения задач и упражнений ♦ 389
(С4.4).Просто положите Ь = 1ир = -в формуле (4.3.2),чтобы получить
sin(x)
о V*
I
dx
π _ π _ /π
Сделайте то же самое в (4.3.9), чтобы получить
оо
cos(x)
~4Г
dx = -
2Г
1
12J
π _ π _ /π
cos 2νπ-ί=
poo Γ poo Ί poo fj
(C4.5). I j I e"xysin(bA:)dA: Wy = / — -dy, и тогда, меняя порядок интег-
е 'sin
рирования в левой части,
оо I оо Ι υυ
Jsin(bx)j Je^dy \dx = bf
о
или
dy
b2+y2
= b
tan"1
У
оо
fsm(bx)\
dx = tan 1(oo) — tSLn l
"-tan"1
2
Но, поскольку tan l
= ^-tan-1
- если вы этого не видите, нарисуйте
очевидный прямоугольный треугольник, - мы имеем
°г е~сх
I sin(bx)—
dx = tan
[с
обобщение интеграла Дирихле (3.2.1), к которому он сводится при с —> 0. Если
Ъ = с= 1,мы имеем
•sin(x) _x
rsmwe_xdx = tan_1(1) = π = 0 78536
1 х 4
MATLAB соглашается: quad(@(x)(sin(x)./x).*exp(-x),0,20) = 0.78539....
роо χ
(С4.6). Следуя подсказке, сделаем замену хлЬ = у в интеграле J ь~7"х
(1 + Х )
Тогда -^- = Ь*ь_1 = Ь— = Ь-^- = Ьу1_1/Ь, или dx = —^—. Таким образом:
dx а: у1/0 , i-f
' Ьу ъ
390 ♦ Решения задач и упражнений
оо а/Ъ
ya/bdy _ 1 f у
If У"
Jo(l + ^)c o(1 + y)cby4 bJo(! + y)C bJ(l + y)c
Ут-1
.эти имеет вид иста-функции n\jn,ti)= ι ~^dy, гДе m
Ут-1
dy). Итак:
О (1_|_ууя+" "
1 + α
fl + fl)
f * „ dx = ^£
(1 + α 1 + α)
b
ί ι+fll
с —
о (! + **)'
Например, если а = Ъ, b = 2 и с = 4, то/
№(с)
оо χ"
fi+з)
(1 + х2)4
-dx = -
4
2Г(4)
Г(2)Г(2) 1!1! 1
0.0833333.... MATLAB соглашается: quad(@(x)(x.A3)./
2Г(4) 1(3!) 12
((1+х.Л2).Л4), 0,100) = 0.083334....
(С4.7). Записываем выражение (4.4.2) для закона обратной зависимости силы
к dv ι dy ,
первой степени — = mv —, которое разделяется на —к— = mvdv и интегриру-
у dy у
ется с помощью неопределенного интеграла, -kln(y) + ln(C) = -mv2, где С - это
произвольная (положительная) константа. Поскольку ν = 0 при у = а, то мы
имеем -Ип(а) + ln(Q = 0. Таким образом, ln(Q = kln(a). Тогда
-kln(y) + kln(a) = -mv2 =-m
'dy
dt
kin
То есть
(dy)
dt
2k, (
—In
m
a
[У)
Решая это уравнение относительно dt, получаем
т dy
dt = ±J^-^, и поэтому fdt = T = ±J^f
m ro dy
dy = adu. Тогда
a
Ы
2k J°
Положим u-
In
УУ)
Решения задач и упражнений ♦ 391
Т = ±А
и
adu
In
(1)
и
■■±аА
du
и
J
2к{ yl-Щи)9
m г1 du
или, используя знак минус, чтобы иметь Τ > О, Τ = aj— Г , Из (3.1.8)
этот интеграл равен Vtt, и таким образом Τ = ах
тс
(С4.8). Формула отражения для гамма-функции гласит: Г(1-т) = .
r(m)sin(mTu)
Для m > 1 мы имеем 1 - m < 0, и поэтому слева от формулы отражения имеем
гамма-функцию с отрицательным аргументом. Справа оба Г(т) и π
являются положительными величинами, в то время как sin(mu) проходит через ноль
для каждого целого значения т. Таким образом, когда т увеличивается от 2,
1 - т уменьшается от -1. В каждом новом отрицательном целом числе гамма-
функция уходит в бесконечность в обоих направлениях, поскольку знак sin(mn)
становится положительным или отрицательным, при периодическом
прохождении через ноль по мере увеличения т.
Глава 5
(С5.1). Подынтегральное выражение есть
1-х"
1-х"
(1-*и,)(1+*п+*2я+*3я + ···),
и поэтому
I(m,n) = f(l-xm)
о
оо
= Σ
fc=0
к=0
,кп
„*л+1
Лп+т+\
dx = Σ JV" -**и+те}Л*=
fr=oo
1
kn + l кп + т + 1
оо
Σ]
fc=0
1
1
кп + 1 кп + т + 1
1
~ kn + m + 1-kn-l ~
^(£и + 1)(Ь + т + 1) ^(£и + 1)(£и + т + 1)
Для заданных значений тип это последнее суммирование легко
закодировать как накопление суммы внутри цикла, что является почти тривиальной
ситуацией кодирования для любого современного языка. Код MATLAB с именем
ср5.т делает это для случая т = 9, η = 11:
392 ♦ Решения задач и упражнений
ср5.п
n=9; n=ll; s=0; k=0;
while l>0
fl=k*n+l; f2=fl+n; k=k+l;
s=s+l/(fl*f2); n*s)
end
Поскольку l всегда больше 0, то код ср5.т застрял в бесконечном цикле
while, и я просто позволил коду работать, в то время как наблюдал за
последовательными значениями потока суммирования на экране моего компьютера,
пока не увидел, что шестая десятичная цифра больше не меняется (и затем
я позволил коду работать еще 15 или 20 секунд). Я наконец остановил код с
помощью Ctrl+C. Конечно, это не слишком элегантно, но полностью
соответствует довольно простому философскому подходу, который я использовал в этой
книге. Результаты: 7(9,11) = 0.972662 и /(11, 9) = 1.030656.
(С5.2). Начнем с интеграла J —= — =*_~ь* Поскольку Г —
V / 1 *^
-kdx_
^2~
Σ к r>+L "Χ
. л \ —-, то мы можем написать
1=1 J> х2
т
к=\ ι *
k=ij=i j X
Έ
ι)
" 1
k=\ K
η 1
Теперь вспомните из начала раздела 5.4, что у(и) = у\ —1п(и), где
к~1к
η 1
γ = lim^^n) есть константа Эйлера, и, таким образом, J^k=1- = у(и) + 1п(и),
κ.
откуда следует, что ΣΊ=ι Σ =ι j ~Ύ = η~ Υ(π)~~ ^η(η) · Выписывая двойное
суммирование, член за членом, мы имеем:
к= 1: ничего;
Jl χ2
„ r2dx c^dx
к=Ъ: — + / —;
Jl χ2 J2 χ2
λ r2dx r3dx
fc=4:/^+I^+j
r4dx
i^
\dx \dx 4rdx "rdx
Решения задач и упражнений ♦ 393
Сложив эти члены по вертикали, мы получим двойную сумму:
(„_4f + (n-2>ff+<n-3)j-§ + ... + <.>jf =
ι Л г* Л. ι? Л ι Λ
/'
(n-l)dx 3r(n-2)dx 4r(n-3)dx
- +
/
+
Г-
- + ·■· +
"rdx
J —= л-у(л)-1п(л).
;+ι (η - j)dx
Поскольку интервал ин-
Общая форма этих интегралов есть I
тегрирования есть / < χ < j + 1, то мы имеем, по определению, [х] = j. Таким
r ri+i(n-[x])dx
образом, / -—Ч^-— и
J> xL
n-y(n)-ln(n)= f—\-^dx.
Или поскольку {χ} = χ - [χ] и [χ] = χ - {χ}, το η - [χ] = η - [χ - {χ}] = η - χ + {χ}.
Таким образом:
1)
η-γ(η)-1η(η) = J ^-L-Ldx = nJ ~^dx-J — + J 4^άχ =
[ln{x}]|"+J^dx = nfl--|-ln(«) + J^dx =
λ x { η) λ χ
= п-\-\п(п) + ]Щйх,
1 Χ
или Γ ^ίίλ: = 1-γ(π). Наконец, если η —> оо, то получим:
Jl a:
(С5.3). Для вычисления ζ(3) все идет примерно так же. Начиная с Г —
Jl χ
ч+idx ί 1 )
Зх3
k3
, мы имеем:
η 1 С
*=1 1
1 —
1) 1
1.
= з»-з?,(3),
где 1ΪΓη„_00ζη(3) = ζ(3). Записав двойное суммирование поэлементно, как мы это
делали в (С5.2), а затем выполняя трюк «сложения по вертикали», вы теперь
сможете показать, что
394 ♦ Решения задач и упражнений
3 3 ϋΛ χ4 Ι χ4 Jx xs Jx χ4
+ / ^-άχ = η
1
Ъх
1
{ 2х2)
1 1
3 Ъп\
1111 "г{х\, 1 1_,_.
Ч W 7 7п2 J у4 Ч ·7^ν /
1_ 1_
2 2n2J
+
г Μ
ι а:
3 Ъп1 2 2nz Jx χ4 3 3
rn\x\ 11 11 г°°М 1 1
Итак, / ^-dx = --{ --^„(3),или, при η -> оо, / ^-dx = ζ(3).
'Ji χ4 2 Зи2 2и2 3SnW ' Р ,Ji χ4 2 3SW
Таким образом:
ζ(3) =
3
2
•Μ,
■Ψ3*.
_J_
1
или, ис-
(С5.4). Пусть а = 1 + χ при χ « 0. Тогда 1 — , ,
\-а 1η(α) -χ 1п(1 + а:)
пользуя разложение в степенной ряд функции 1п(1 + х), приведенное в начале
раздела 5.2, для 1 < χ < 1 мы имеем
1 1
- + - = hm
\-а 1η(α) *-><ч
-χ
- + -
1
X X X
х—;г + ^ г + ·
2 3 4
= lim
АГ^О J
lim
х^О
1
— + -
—χ
■1 +
1-* + *^ + -
2 3 4
1
χ χ2 хъ
+·
Л\т.\
х^О
(С5.5). Мы начнем с равенства 2
1 1 1
1
Л2 22 ?2 /I2
= 2
-1 + 1 + -
Jl _L _L
l2+32+52+'"
Jl _L Jl
22+42+62+···
Г 2' 3' 4Z
Две суммы в фигурных скобках являются суммами
нечетных слагаемых в ζ(2) и четных слагаемых в ζ(2) соответственно. Теперь
рассмотрим сумму четных членов:
1 1
1
22+42+62"·
1
-+-
1
-+-
1
(2Лу (2·2)2 (2·3)2
1
—
4
1 1 1
—ι 1—
l2 22 З2
1
ζ(2).
Решения задач и упражнений ♦ 395
3
Это означает, что сумма нечетных членов есть — ζ(2). Итак, наше первона-
4
чальное выражение есть 2
Ιζ(2)-1ζ(2)
4 4
= ζ(2), как должно быть показано.
-ι In2 (1-х)
(С5.6). В интеграле / — -ах следуйте подсказке и замените переменную
JO χ
dx
1 - χ = е \ Тогда = -е \ или dx = e ldt. Теперь, когда х = 0, мы имеем t = О,
dt
а когда χ = 1, то t = оо. Так:
Wn^l-x), _rln2(e^)„_, °°- *2
Jn χ Ι 1-е"' -ί 1-е"1 J„e'-1
at.
Из (5.3.4) мы видим, что это есть r(sX(s) для s = 3. То есть
rln2(l-x).
О
Г1П(1 *^* = Γ(3)ζ(3) = 2!ζ(3) = 2ζ(3).
%, a:
dx
ИР
poo χΓ poo Λ j
Γ(ρ + 1)ζ(ρ + 1). Продолжаем: / dx = / — αχ. Пусть ι/ = е \ следо-
jo е* _i jo ех(1 — е х)
вательно, е* = -. Кроме того, 1п(и) = -х, или χ = -1п(и). Наконец, — = -е~х = -и
и dx
ndx = .Итак:
и
°г[-1п(и)Г( du)_ \{-\n(u)Y ^
г хИ dx= H-inwr au\ н-inw
(1-й)
ι/
Таким образом:
r{-ln(x)}'
0
/»ώ = Γ(Ρ + 1)ζ(Ρ+1).
TO
(C5.8). Поскольку -Ι_ = ΐ + ρ + ρ>+··· = ΣΓ=οΡ*' -- ι_χΛ...χη
ΣΧ, (*,*,...*„)*, и тогда
396 ♦ Решения задач и упражнений
111 j
η η η χ 12 ' ' ' П
//· · · jD*i*2 · · · χη f d*id*2 -dXn
οο ο &=ο
οο 1 1 1
fe=o ο ο ο
Теперь:
111 11 1
JJ..JxkX2...xkdx1dx2...dxn=Jx1kdxJx2kdx2...Jxnkdxn
0
k + l\
il
0
0
ί ν fe+M
k + lj
il
0
ί ν fe+M
[fc + lj
1
(k + l)"
Таким образом:
г г г 1 °° 1 1
/ /... / dxAxn...dxn = V* = —
JoJo J0l-^2-^ έί(* + 1)" 1"
/»oo
(C5.9). В интеграле / In
Jo
1 + е-
1-е-
1111
+ —+ —+ —+... = ζ(π).
2" 3" 4"
di/
dx пусть ι/ = е \ и поэтому — = -и, что озна-
dx
чает dx =
di/
Таким образом:
оо
1 + е"
1-е*
d,= flni—!--)=i1lnil + Ul
1 + ι/
dl/:
rl
f-{ln(l + M)-ln(l-M)}dii =
=Jl\
J U
о u '
1 \ A
и и их
и 1 h-
2 3 4
2u + 2 — + 2^+..
3 5
1
du = 2f
и2 и3 и4
, и2 и4
1+Т+Т+"
\du
иъ us
w + -—+ —- + ■
9 25
(J. J_ J_
l! + 32+52+'
2 "I
du =
= π2_
4 '
Решения задач и упражнений ♦ 397
dl
J'*00 ul
xme~xdx. Тогда — =
0 dm
Г°°1п(х)ет1п(х)е-Х^итакже -^Ц-= П1п\х)етЩх)ехах. Таким образом:
Jo dm2 Jo
оо
Jln2(x)e-*dx:
d2/
dm2
Обратите внимание, что 1(т) является гамма-функцией Г(п) для η - 1 = m, то
есть π = m + 1. Так что /(т) = Г(т + 1) и
оо
Je~xln\x)dx-
dni'
-Г(т + 1)
Теперь дигамма-функция говорит, что
dr(Z)
dz
■ = Г(г)
1 ^2,(1 1 )
---υ+Σ
Ζ r=l
и тогда, для z=m+ 1,
dr(m + l)_dr(m + l)
d(w? +1) dm
Опять дифференцируя
I/ г + zj
Г(ш + 1)
m +
ϊ-γ+Σ
1 г=1
Π ι
d2r(m + l) dr(m + l)
dm2
dm
1
m +
+ Γ(/η + 1)
ϊ-γ+Σ
1 r=l
1
1
1
(/ r + m + lj
00 1
■+Σ;
r r + m + 1
+
Итак, поскольку Г(1)=1
dT(m + l)
dm
= Г(1)
ι-γ+Σ
(m + 1)2 fri(r + m + l)2
'1 1_ϊ
r r + 1
= -ι-γ +
1)
1--
2
+
12 3 Γ
•· = -1-γ + 1 = -γ
398 ♦ Решения задач и упражнений
d2r(m + l)
dm2
= -γ
т=0
-1-
= γ+γ -
00 /
-γ+Σ
r=l V
γ
Γ
d ^
1--
l 2
+
1 ]
"r + lj
+ Γ(1)
[ι ι) 1
[2 ъ\
+···
+
ι+Σ
ι
i(r+irj
11 ~2 °°~
= γ+γ2-γ+ι+^-+-7+··· = γ2 + ζ(2) = γ2+^= Ге-х1п2(х)Л.
22 3 6 J0
Γι 1 _ е-и Гоо е_и 1
(C5.ll). Из (5.4.1) γ= / du- \ —du. Во втором интеграле пусть t = -
Jo и Jl и и
и, следовательно, du = ——dt. Тогда:
/t*-/t-f*Ht*
Итак:
γ= Γ du- Г — di/,
J и J и
о u ом
или, как должно быть показано,
1г\-еи-е«
г= I du.
i и
Глава 6
(С6.1). Следуйте тому же пути, который описан в разделе 6.3.
(Сб.2). Следуя подсказке, рассмотрим функцию
/(*) =
1
*и + 1 х"-Ч/"Ч...+ х + 1
Путем прямого умножения можно подтвердить, что хп - 1 = (х - 1)(хп 1 +
хп~2 + ... + * + 1), и тогда
Решения задач и упражнений ♦ 399
/(*) =
χ 1 _ χ х-1
х"+1 хп-\ ~х"+1 хп-\
х-1
2х 1
- + -
*и+1 хп-1
+
*"-1
х2"-1 х"-1
Затем выберите значение переменной а, так что 0 < а < 1. Тогда
in ixn-\ ix2n-\
dx.
2 dy n j dy
Во втором интеграле справа в поле пусть у = χ , так что — = 2х, или ах = —}
dx 2x
и тогда
lxln-\ Jnv"-12x J„v"-1
о - * о У
Таким образом:
о о Л х о -У х
или, так как а2 < а (поскольку α < 1), мы можем написать:
jyw*-jh£j.
Затем вернемся к первой формуле в рамке и заменим пределы интегрирова-
ния от Ь до бесконечности, где Ъ > 1. То есть / f(x)dx= ι / — dx.
Jb Jb yn 1 Jb ·ν1η 1
Во втором интеграле справа в поле пусть у = х2 (как раньше), и тогда
dx
dy
dx
[f(x)dx=[^-[^=f^-
V ixn-\ lvn-l ixn-\
так как b2 > b (поскольку b > 1). Теперь в интеграле справа в поле пусть у:
dy
1
так что -j- = —τ = _У , или dx = —γ. Таким образом:
dy
dx x2 ' у2
400 ♦ Решения задач и упражнений
dy
1 1
Ί*"-ΐ Ιν\_λ Ь-Г {i-/
•^ ъ ь2
и мы имеем
1 χη-2
Jf(X)dx = fbJL^dx
i Jul-x
Таким образом, сложив два результата во второй и третьей формулах в
рамках, мы получим:
а оо α ι 1 и-2
Jf(X)dX+Jf(X)dx = f^+Rf^d**
0 Ь а2 К L b2 L K
ИЛИ
а оо α ι ^ и-2
jf(X)dX+jf(X)dX=S^-Sijrr^·
0 Ь α2 Λ Х Ь2 Λ J
Пусть Ъ = - (поскольку а < 1, то Ь > 1, как мы и предполагали), и тогда
а оо α j α и-2 α 1 _ ν"-2
0 1/α я2 Λ Χ α2 Λ Χ α2 Λ Χ
ИЛИ
α οο α 1 _ γ"-2
0 1/α α2 Χ Λ
Наш последний шаг - это позволить а^\. Обратите внимание, что
подынтегральное выражение в интеграле справа является непрерывной функцией,
которая всегда имеет конечное значение, даже когда х = 1, по правилу Лопи-
1 — хп~2 —(п — 2)хпЪ п — 2
таля: lim = lim— —— = . Таким образом, интеграл всегда су-
х->1 1-х" х->1 -ηχη ι η
ществует. Итак, при а —> 1 мы имеем:
Vi-*"-2
ff(x)dx + ff(x)dx = -J—A__dx = о = ff(x)dx,
г\ 1 -ι ■!■ л η
0 1
и мы решили задачу.
Решения задач и упражнений ♦ 401
(С6.3). Следуя подсказке, запишем: Г cxdx= Г (е x)xdx = Γ е ^dx
еЛ-1 1-е
е_Ах
-λ
Также X^cfe = Х^е-^, что, конечно, есть просто сумма гео-
-λ λ
метрической прогрессии, легко суммируемая с использованием стандартного
приема (который, я полагаю, вы знаете - если вам нужно напоминание, посмот-
ех
рите в любом учебнике по алгебре средней школы), и эта сумма равна —.
1-е
1 - е~х е~х
Итак, = —, которое после небольших элементарных
алгебраических преобразований принимает вид: е2Х - (2 + Х)ех + 1 = ДА) = 0. Обратите
внимание, что хотя ДО) = 0, это не означает, что λ = 0 является решением
задачи. Это потому, что тогда с = е~х = 1, и это с, очевидно, не удовлетворяет
уравнению Г cxdx = ^2^_гск. Теперь заметим, что Д1) = е2 - Ъе + 1 = 0.23 > 0
ill
и что /1 - = е - 2.5л/е +1 = -0.4 < 0. Итак, ДА) = 0 для некоторого λ в интервале
- < λ < 1. Мы можем получить интервалы все лучше и лучше (то есть все коро-
л
че и короче), в которых λ лежит, используя простой в программировании
метод «бисекции». То есть мы начинаем с определения двух переменных, lower
и upper, и устанавливаем для них начальные границы по λ как 0,5 и 1
соответственно. Затем мы устанавливаем переменной lambda значение Vi{lower +
upper). Если [(lambda) > 0, то устанавливаем upper = lambda, а если [(lambda) < 0,
то устанавливаем lower = lambda. Каждый раз, когда делаем этот цикл
операций, мы уменьшаем наполовину интервал, в котором лежит решение λ (если
в какой-то момент [(lambda) = 0, то, конечно, мы немедленно заканчиваем).
Таким образом, выполняя 100 таких циклов (производимых в одно мгновение
на современном компьютере), мы уменьшаем начальный интервал длины Vi
в 2100 раз, и поэтому и lower и upper сойдутся друг к другу настолько, что
прижмут lambda к решению λ намного ближе, чем 13 требуемых десятичных знаков
после запятой. Результат (см. следующий код срб.т): λ = 0,9308211936517...,
и тогда с = е~х = 0.3942298383683.... Общее значение интеграла и суммы
составляет 0,65079....
срб.п
lower=0.5; иррег=1;
for loop=l:100
lanbda=(lower+upper)/2;
tern=esp(lambda);
f=ternA2-(2-lanbda)*tern+l;
if f<0
lower=lanbda;
else
402 ♦ Решения задач и упражнений
upper=lanbda;
end
end
c=exp(lanbda)
(C6.4)
(а) Воспользовавшись наводящим на размышления характером
дифференциальной нотации Лейбница, на которую я намекал в постанов-
, , „ d dx d . d
ке задачи, напишите дифференциальный оператор — = = х—.
dt dt dx dx
. Итак, заменяя оператор
Таким образом, —(х2) = 2х— = 2Jx—1-х
dx dx [[ dx
χ— в фигурных скобках на эквивалентный оператор —, мы имеем
dx dt
d dx x d χ
—(χ2) = 2 — = 2χ. Таким образом, (χ2) = — 2χ = χχ, и теперь, начи-
dx dt 2dx 2
ная с уравнения Зоммерфельда хх + χ2 = gx, мы можем переписать его
как (х2) + х2 = gx, или —(х2) + — x2 = 2g, или поскольку χ2 = ν2, мы
2 dx dx χ
приходим к — (ν2) = — v2 + 2g, которое является уравнением Кейффера.
dx χ
(b) Следуя подсказке, умножьте уравнение Кейффера на х2, чтобы
получить х2 — (v2) + 2xv2 = 2gx\ Тогда —(x2v2) = 2gx2, или, интегрируя,
dx dx
х А х х 1
J—7(x'2v'2)dx'= J2gx'2dx', и поэтому Jd(x'2v'2) = 2g-x3 = x2v2. Таким
2 2 {dx
образом, ν =-gx
dx
— ι, и теперь —
dt) v dt
(с) Из (b):
cfrc
dt2
dx
1
{2yfx)
dt
/2~~ ί 1 Ι /Г" г 2 1 1
dx
(d) Из (b): ^= = J-gdt,n,следовательно,/-^ = -^ [dt = TJ-g = (2x1/2)\
л/х V3 0Va:V30 \3
I% \έ\ τ
2λ/Ϊ. Таким образом, Τ = 2>/Z J— = Ι—.
(e) Когда длина х цепи (с массой \хх) скользит по краю, это движение со ско-
ростью ν = —, и поэтому его кинетическая энергия (К.Е.) есть -μχ\—- .
dt 2 [at)
Центр масс находится на —х ниже столешницы, и поэтому его потенци-
1 1 ?
альная энергия (Р.Е.) есть -\ixg-x = —\xgx. Предполагая, что закон сохра-
Решения задач и упражнений ♦ 403
1 (dx)
нения энергии говорит К.Е. + Р.Е. = 0, получаем -μχ
dt
1
[igx2 = 0,
или
d2x
(dx)
at
—— = gx. Таким образом, —
χ dt
gylx,u ускорение цепи есть
dt2
Глава 7
=4Ϊ
1
{ι4χ)
dx г- ί 1 ] /— г- 1
(С7.1). Для случая π = 5 мы имеем нечетное ρ и поэтому используем (7.7.2) для
записи (при р = q = 5):
ι5
/
sin(x)
dx
-Г-
I/
dl/:
4!^0 (u2+l2)(u2+32)(u2+52)
OO 4 OO π OO >o
f-= irdu+ f— ^du+ f—
J0u2+12 J0u2+32 J0w2+52
du
Таким образом, мы имеем
А[и2 + 9][и2 + 25] + В[и2 + 1][и4 + 25] + С[и2 + 1][и2 + 9] = и4.
Перемножая, мы приходим к уравнению
А[и4 + 34и2 + 225] + В[и4 + 26и2 + 25] + С[и4 + 10и2 + 9] = и4.
Тогда, приравнивая коэффициенты при одинаковых степенях, получаем три
алгебраических уравнения для А, В и С, которые должны выполняться
одновременно:
А + В + С=1,
ЪАА + 26Б + ЮС = 0,
225А + 25Б + 9С=1.
Эта система легко решается следующим образом с использованием
определителей (правило Крамера, которое вы можете найти в любой хорошей книге
по алгебре). Во-первых, определитель системы есть
D =
1 1 1
34 26 10
225 25 9
404 ♦ Решения задач и упражнений
который раскладывается так:
D-
26 10|
25 9
34 10|
225 9
+
34 2б|
225 25
= (234-250)-(306-2250) + (850-5850) =
= -16 + 1944-5000 = -3072.
Таким образом, значения А, Б и С есть:
1 1 1
0 26 10
0 25 9
26 10
25 9
16
16
В-
D
1 1
34 0
225 0
1
10
9
-3072 -3072 3072'
34 10
225 9
D
1944
-3072 -3072
и С находится из первого уравнения: С
3072-16 + 1944 5000
1944
3072'
: 1 - А
В = 1
16 1944
+-
3072 3072
сю
/
3072
sin(x)
dx = S
_ π
~2~
_ π
~~2
3072'
16
. Итак:
3072
80
'V
1
tan Ч00)-
1944
3072
tan 1(oo) +
5000
ill
5
9720ίΐ11
3072 3072
+-
25000 IT
3072
3072
80-3240 + 5000
tan '(oo)
3072
1840
3072
920
3072
π,
или,наконец,
Для случая η = 6 мы имеем четное ρ и поэтому используем (7.7.1) для записи
(при p = q = 6):
Решения задач и упражнений ♦ 405
со
/
sin(x)
/■ ■ ОО
6
-du
5!->(и2+22)(и2+42)(и2+62)"
ОО >. ОО о ОО ςι
f^~^dU+ Ϊ 2 „dU+ f-
-du
J0if+4 J0u2+16 J0u2+36
и тогда A[u2 + Щ[и2 + 36] + В[и2 + 4][и4 + 36] + С[и2 + 4][и2 + 16] = и4, и поэтому
А[и4 + 52и2 + 576] + В[и4 + 40и2 + 144] + С[и4 + 20и2 + 64] = и4, и тогда
А + В + С=\,
52Л + 40В + 20С = 0,
576А + 144В + 64С=1.
Определитель системы есть
1 1 1 I
52 40 20 =-7680,
|576 144 64|
и таким образом
D-
1 1
0 40
0 144
1
20
64
D
520
7680
, С
1
52
576
1 1
40 0
144 0
D
15552
7680 '
и В находится из первого уравнения: В = 1 - А - С
8192
[sin(x)
[ X
6
dx = 6
320
7680
-tan Ч00)-
8192
7680
7680
tan_1(oo) +
Итак:
15552(1'
7680
tan ^oo)
и после всего лишь тривиальной (но немного утомительной) арифметики:
Для случая п = 1 мы имеем нечетное ρ и поэтому используем (7.7.2) для
записи (при ρ = q = 7):
Ί7
/
sin(x)
[ dx
11 г
и
6!^0 (и2 + l2)(u2 + 32)(u2 + 52)(u2 + 72)
-di/ =
= 7
оо д °° D °° f~* °° ΓΊ
f^ ^dU+ [—2 rtdU+ [~2 rtdU+ f~2 ^2~dU
Jnu2+12 JnH2+32 Jnu2+52 JnH2+72
406 ♦ Решения задач и упражнений
И теперь вы видите, что мы будем работать с определителями 4><4, что
становится действительно утомительным на страницах этой книги, и поэтому
я оставляю вам разобраться с обычной арифметикой, чтобы прийти к формуле
sin(x)
5,887
[ dx = —- π.
23,040
Это равно 0.8027151..., и MATLA.B соглашается: quad(@(x)(sin(x)./χ).Л7,0Д00)
= 0.802710....
J*oo . 2 poo n poo п
elt dt = I cos(t2)dt + i \ sin(t2)dt = C(x) + iS(x).
X J X J X
Тогда He-*dt = f °°cos(t2)dt - i f °°sin(t2)dt = C(x) - iS(x) = Ге^аи. (На-
Jx Jx Jx Jx
помним, что tuu- фиктивные переменные.) Итак, [С(х) + iS(x)][C(x) - iS(x)} =
J"»00 . 2 pOO . 2 ^
e dt I e~m du, и таким образом:
X J X
οο οο οο οο οο οο
C\x) + S\x) = Jfe^-^dtdu = ffcos(t2-u2)dtdu + iffsin(t2-u2)dtdu.
χ χ
Поскольку С (χ) + S (χ) - вещественная функция, то ее мнимая часть должна
быть равна нулю, т. е. Г°° f °°sin(£2 — u2)dtdu = 0 для любого χ, и мы закончили.
Jx Jx
(С7.3). Для начала напишем 1 — 1ХЪ = \Jl + x6elQ, где θ помещает этот
комплексный вектор в четвертый квадрант, если χ > 0, и первый квадрант, если χ < 0.
Поскольку |ег9| = 1 для любого Θ, то конкретное значение θ на самом деле не
имеет значения, когда мы вычисляем абсолютное значение выражения 1 - 1хъ
как vl + х6 - Таким образом,
1
1-/У
1
1
1
|l-zx3|
^7 (1+*6)
6\1/2
, и поэтому
^
IX
1
(1 + х6)
■6\1/4
. Итак:
ίτ^ί-^-Γ-'/-
dx
,^
ιχ
э(1 + х6)4 ° (1 + х6)4
потому что подынтегральное выражение в среднем интеграле является
четным. Теперь
dx
dx
dx
с αχ ρ αχ ρ
Ι τ = / γ+Ι
0 (1 + χ6)4 0 (1 + χ6)4 1 (1 + Χ6)4
Решения задач и упражнений ♦ 407
Поскольку Г + М, где Μ - некоторое конечное число, потому что
° (1 + хвУ
подынтегральная функция конечна на всем интервале интегрирования,
и замечая, что 1 + χ > χ , мы можем написать / < Μ + /
И
noil + х6)4
скольку
(1 \1°°
—) г°° dx г°
-2х 2/^ =2, то / -<М + 2, и поэтому /
dx
(1 + х6)4
λ/Ϊ^Ι
IX
существует.
kdx
(С7.4). Начнем с интеграла /*—=- = У^_! Г —,
Jl χ* J-^j-lJj χ.
2x2
k2
Тогда
•dx
η k-li+}
Σ/?=ΣΣ/?=Σ
dx " 1L 1 )
*=ι ι
ί2
1-
1
(l-S(n)),
π Ι π2
где S(n) = У""" —г. (Напомним, что lirn S(ri) = —.) Записав двойное сумми-
рование поэлементно, как мы это делали в (С5.2), и затем выполняя трюк
«сложения по вертикали», теперь вы сможете показать, что
5-IS(n)= rn-*+mm=
! w Ji χ3 2 2n
2 2
To есть / ^-/dx = l—S(«) , и тогда, полагая « —> oo, мы имеем
Jl хл 2 2n
/;Mdx = l-i5(oo),
Jl a: 2
или,наконец:
Ji x3 12
sin (αχ)
(C7.5). Начнем с дифференцирования интеграла 1(a) = J \—-dx по
параметру а. Тогда
da
Г
Jo
2xsin(aA:)cos(aA:)
άχ=Γ
Jo
°o2sin(6ZA:)cos(aA:)
dx. Вспоми-
• / ч / ч 1 · /η ч dl r°° sin(2ax) , π
ная тождество sin(ax)cos(ax) = -sin(2<xv), мы имеем — = / -dx = ±—
2 da Jo x 2
согласно (3.2.1), где знак справа зависит от знака а (+, если а > 0, и -, если α < 0)
408 ♦ Решения задач и упражнений
Затем берем неопределенный интеграл, fdl = ±[—da, или 1(a) = ±— + С, где
J J 2 2
С - неопределенная константа. Поскольку 1(0) = 0, то С = 0, и тогда
(С7.6). Если вы положите Ь = 1ик = 2в формулах (4.3.10) и (4.3.11), то
интегралы Френеля следуют немедленно.
(С7.7). Следуя подсказке, преобразование Фурье для f(t) имеет вид (я позволю
вам заполнить детали простого интегрирования)
„, ч l-emacos(mcu)+ ie~mflsin(?wa>)
Доз) = -,
fl + ίω
и поэтому
|Ρ(ω)Ι= ?w ·
Интеграл по времени для энергии f(t) равен Г f2(t)dt= \ e 2atdt =
J -оо «/ 0
1-е"
2а '
в то время как частотный интеграл для энергии есть
Γ°°Ι^(ω)Γ^ 1 г°° 1 + е~2та - 2е~та cos(ma))
^-°° 2π 2π^-°° α2+ω2
Приравнивая эти два интеграла, а затем выполняя некоторые простые
алгебраические действия (где я также изменил фиктивную переменную интег-
ч г°° cos(mcx>) , π _та _ч
рирования ω нах), получаем / —^—^αω = -е .Выузнаете это как (3.1.7),
J-°° ω +fl a
где в этом результате я написал т вместо аиа вместо Ь, и интервал
интегрирования (четного подынтегрального выражения) составляет от -оо до оо, а не от 0
до оо (это учитывается как 2 в знаменателе справа в (3.1.7)).
(С7.8)
, ^ Г°° 1 -i<*t^ r00 cos(a>t) ,,. .r°°sin(a)£), _
(а) / — е dt= ι —г-^—-at —ι! —^—-dt. Последний интеграл
J-oot2+1 J^ t2+j J^ t2+j
обращается в ноль, поскольку подынтегральная функция нечетная. Те-
перь / — е at = 2 I —^—-dt, а последний интеграл при Ь = 1
J-°°r+l Jo £+1
и a = ω в (3.1.7) равен — е ω. Таким образом, для ω > 0 преобразование
а
Решения задач и упражнений ♦ 409
есть пе ω. Поскольку временной сигнал четный, мы имеем чисто
вещественное преобразование, и мы знаем, что оно четно. Таким образом, при
ω < 0 это преобразование есть пе ω. Тогда для всех ω — <-> пе
£2+1
/оо
f(t)e~l(utdt,
-оо
то — = Г -itf(t)e-i(utdt. Поэтому Г tf(t)ei(utdt = --— = i — . Тог-
άω J-°° J-°° i άω άω
dF
да если f(t) <-► ί(ω), то tf(t) <-► i—. Теперь, как показано в (а), при ω > 0
άω
преобразование — есть πβ~ω, и поэтому преобразование —г—- есть
ζ— (πβ"ω) = -ίπε"ω. Поскольку функция времени в данном случае нечет-
da)
ная, то мы имеем чисто мнимое преобразование, которое, как известно,
нечетно. То есть при ω < 0 это преобразование должно быть ζπεω. Тогда,
для всех ω, мы пишем —г <-> — me_0)sgn(a)).
-ΐωΐ
(c) Г \-8(t) + i—\е-ша1 = -Гте-ша1 + ^-Г^— at. Из (7.9.14)
следует, что первый интеграл справа равен 1. А из (7.9.3) мы имеем
1 dt = msgn(-a)). Итак, это преобразование есть
J -оо £
-Н {msgn(-a))} = sgn(-ω).
2 2π 5 V И 2 2 5 V J
Поскольку sgn(X) = 1, если χ > 0, и -1, если χ < 0, то это преобразование
есть (-1) = - + - = 1 при ω > 0 и (+1) = = 0при ω < 0. Но
2 2vy22 2 2vy22
это в точности есть функция ιζ(ω) - ступенька в ω-области. Итак:
Ιδ(0 + ί-±-~Η(ω).
2 2π£
(d) Следуя подсказке, пусть χ = -, xt = ι/, и тогда diz = tax. Таким образом,
poo g poo £ poo £
R(t) = / —du = ι tdx = ι dx для t > 0 и ноль при остальных
' Jf ιζ Jl xt Jl χ
значениях. Итак, преобразование Фурье есть
410 ♦ Решения задач и упражнений
оо * оо
Г ϊ—dx\е-шаг= Г- fe^x+Uu)tdt\dx = Г-
о L ι J iALo J ιΛ
= г ϊ ^=-?ί1 ^—1
·{ x(x + i(u) ί'ω^ (χ ΛΓ + ί со J
= Λ[1η(χ)-1η(χ + ΐω)Γ = ^-
U.\ L J|l ΪΛΛ
(χ-Ηω)Ε
(x + ζω)
dx =
' χ ^
[χ + ίω)
1
1η
То есть
poo e
·" и
du<
ζω
1η(1 + ζω)
ζω
1 + ζω
1η(1 + ζω)
ζω
(C7.9). Второй интеграл преобразования Гильберта в (7.10.11) есть
πΧ(ω) = - {Ш-йи = - (Ш-du- №
J ω-u J ω-u Jn ω-u
du.
Если в первом интеграле в правой части этого равенства мы сделаем замену
переменной s = -ι/, то получим
πΧ(ω) = - Г —-—- d(-s) - Г°° —— du = (когда x(t) вещественно)
Jo° ω + s Jo ω-ιζ
1 1
+ -
ω — и ω + ιζ
du
2ω r°° R(u)
ω2-и2
du.
Jo ω + s Jo ω-ιζ Jo
Jo ω -zr
и, таким образом, когда x(t) вещественно, то Χ(ω) = Г
1 Г°° I |2
(С7.10). По теореме Рэлея энергия x(t) есть — / \Χ(ω)\ άω, и, поскольку энер-
Х°° ι |2
Χ(ω) da) < оо. А также поскольку
-оо' '
y(t) = x(t) * hit), мы имеем Υ(ω) = Х(а>)Я(ц>). (См. примечание 14 в главе 7.)
Таким образом, |Υ(ω)| = |Χ(ω)Η(ω)| = |Χ(ω)||Η(ω)|, и тогда |Υ(ω)|2 = |Χ(ω)|2|Ή(ω)|2.
1 Г°° ι |2 1 Ρ°° ι ι2 ι ι2
Из этого мы заключаем: (В) — / \Υ(ω)\ da) = — / Χ(ω) Η(ω) do). Нако-
нец, Я(со) = Г h(t)e-i0itdt, и тогда |Я(со)| = I Г h^e'^dtl < Г |ft(t)e-i<ot|dt. (См.
*J — оо I I \*J — оо | «/— оо
подсказку к задаче С7.3.) Продолжаем: |Я(а>)| < f°° |h(t)||e"/Cut|dt= f°° |/z(t)|dt,
1 ' J—оо J— оо
Решения задач и упражнений ♦ 411
поскольку \e~llut\ = 1. Этот последний интеграл дан нам как конечный, и поэтому
|Η(ω)|< оо, то есть |Η(ω)|2 < оо. Это означает, что |Η(ω)|2 имеет максимальное
значение, которое мы будем обозначать М. Подставляя это в (В), мы имеем:
ι оо л оо Λ/f °°
— Г |7(ω)|2ίίω = — Г |Χ(ω)|2Μίίω = — Г |Χ(ω)|2ίίω.
2πJ 2πJ 2πJ
—оо —оо —оо
Из (А) мы знаем, что этот последний интеграл конечен, и поэтому
1 Г00 ι |2
— / \Υ(ω)\ αω < оо. Но этот интеграл является энергией y(t), и поэтому энер-
гия y(t) конечна.
1 poo cos(a>„tt 1 гоо e'4t+е"'Чс
(С7.11).Дляш0>0:х(0 = - Г K—^du = —\ -—— du.Пустьs = t-и,
πΛ-οο t — U 2nJ-°° t — u
du = -ds. Тогда
x{t) = —/ ds-\ / ds = / ds-\ / ds.
2uJo° s 2nJoc s 2π Jo° s 2π Jo° s
/оо £ poo С u
αω = msgn(t), тогда / αs = zπsgn(ω0) = m,
оо ω J-οο 5
поскольку ω0 > 0 и sgn(пoлoжиτeльнoгo аргумента) = +1. Также
Гоо е-'45
/ ds = msgn(-a)0) = -m,
J-oo 5
поскольку ω0 > 0 и sgn(oτpицaτeльнoгo аргумента) = -1. Итак,
x(t) = — [-me'4t + me-ia*] = —[e'4t - e'4t] = —2isin(a>0t) = sin(a>0t),
2π 2π 2π
это преобразование Гильберта функции cos(a)0t). Если вы снова сделаете все это
для преобразования Гильберта sin(a)0£), вы должны обнаружить, что это
преобразование равно -cos(a)0£).
Глава 8
(С8.1). Поскольку Дг) = g(z)(z - zQ)m, то
Jf(z) 1 g(z)(z-z0)m
= £^-dz + £^dz = m<£^ + <£^dz.
Jc z-z0 Jc g(z) Jc z-z0 Jc g(z)
Теперь первый интеграл равен 2π/ по (8.7.1), а второй интеграл равен нулю
по (8.6.1), потому что g{z) аналитична, что означает аналитичность g'{z), а так-
412 ♦ Решения задач и упражнений
g'(z)
же и ^—^ и без нулей внутри С (по заданному условию задачи). Таким обра-
зом, (£-—dz = 2nim, и задача решена.
т
(С8.2). Так как мы собираемся работать с f(z) = -2 ^-, то видим, что
должны рассмотреть три особенности первого порядка: ζ = О, ζ = -ia и ζ = ia. Это
говорит о контуре С, показанном на рис. С8, где в конечном итоге мы будем
полагать ε —> 0 и R —> оо.
*-*
Рис.С8 ♦ Контур для задачи С8.2
Первые две особенности всегда будут вне С, а третья, поскольку^ —> оо, будет
внутри С (напомним, что а > 0).
Теперь J f{z)dz = J +J +J +J . Ha Q и С3 мы имеем ζ = χ и dz = dv. Таким
образом, / + / = I —dx + /
x(x2 + a2)
r e
^-dx, или, при ε ^ 0 и i? ^ оо,
x(xz + az)
f + Г = f - —dx. На С2 мы имеем ζ = ге1в. -π < θ < 0, dz = ίεειθί/θ. Таким
>x(x2 + a2)
„/шее*
образом, Г = Г — —/Ее'е^е,или, πρπε^Ο, Γ =-/f -=- = -/-=-.
На С4 мы имеем ζ = Reie, 0 < θ < π, dz = iRelQdQ. Таким образом,
ί = Γ
Jc4 Jo
nimRe*
Rem(R2elW + a2)
—iReiedB = ir
a2) Jo
. г* е
tmRe"
R2em + a2
άθ.
Решения задач и упражнений ♦ 413
Абсолютное значение подынтегральной функции ведет себя при R —> оо как
—=-, потому что абсолютное значение числителя равно 1 для всех R и Θ. Таким
R2
образом, при R —> оо интеграл ведет себя как —, что стремится к нулю при
R
J» /»оо β , . ТС Ρ
= / —αχ — ί —. Но мы знаем, что / = 2тс/ (вычет осо-
бенности ζ = ία). Этот вычет равен
r,imia
lim(z-ia) = = —.
z^ia z(z-ia)(z + ia) ia(2ia) 2a
Итак, f°° г —dx-Ί—- = 2πί
J-°°x(A:2 + a2) a2
2a2
a2
. И тогда
-— -dx = i — -i—_ = i_(i-e mfl).
°°x(x2 + az) a1 a1 a1
Используя тождество Эйлера в числителе подынтегрального выражения,
получаем:
^х{х2 + а2) ^х{х2 + а2) а2
Приравнивая реальные части этого последнего уравнения, мы получаем
гоо COS(^X) ,
/ ^—it ax — 0, что неудивительно, так как подынтегральное выражение
J-°°x(x2 + a2)
нечетно. Более интересным является результат уравнивания мнимых частей:
poo sin(mx) , тс /л _та. г°° 1 Гоо
/ —г^——ах = —(\-е ),или,поскольку / =-/ .мыимеем:
J-°°x(x2 + a2) a2 Jo 2Jo°
что раньше мы просто предполагали.
(С8.3)
dz
(а) Записывая ζ = е1в (и тогда d6 = ^) на единичной окружности С,
ιζ
z-\-z_1 г
мы имеем cos(6) = . Теперь рассмотрим / f(z)dz с функцией
2 Jc
f(z) = ί—ϊ . Тогда
414 ♦ Решения задач и упражнений
η -1-
άθ
2acos(0) + a:
= /
C1_2ai±^L+a2
fdzl
iz
=LJ-
С 72_
dz
~α4ϊ
Z + l
a2+l
±,
Есть две особенности первого порядка в точках ζ =
α2+1
-4
которые после небольших преобразований сводятся κζ=απζ=—. Так
а
как 0 < a < 1, первая находится внутри С, а вторая - за пределами С. Так,
/ = 2π/ (вычет в ζ = α). Из (8.8.9) этот вычет есть
J<V-*±±z+i
ι
1
dz
z2-^z + l
2z-
a2 + l
a
2a-
a2 + l
a
a2-l
Итак,
η -1-
de
2acos(6) + <r a
= -2πζ^—- = - -, 0<a<l.
a -l l-<r
Если, например, a
2'
то мы имеем
0
de
2π 8π
--cos(9) l-j 3
4 4
8.37758..., и MATLAB подтверждает, поскольку quad(@(x)l./(l.25-
cos(x)),0,2*pi) = 8.37758....
eiz
то есть рассмотрим контурный интеграл
(b) Пусть f(z)-
L
\z + a)2+tf'
-dz, где С показан на рис. 8.7.1. Подынтегральное выра-
c(z + a)2+b2
жение имеет две особенности (каждая первого порядка) при ζ = -a±ib.
Поскольку а и Ь оба положительны, то внутри С находится только осо-
r eiz
бенность ζ = -а + ib. Таким образом, / - -dz = 2πί (вычет
Jc(z + a)2+b2
в ζ = -а + /Ь). На вещественной оси ζ = χ, dz = dx, а на дуге
полуокружности ζ = Теге, dz = iTelBdQ, 0 < θ < π. Итак, на полукруглой дуге мы имеем
Г * ί -zTe'ed6. Абсолютное значение числителя есть Τ для всех
J° (Ге'Ча)2 + Ь2
Θ, и при Τ —> оо абсолютное значение знаменателя ведет себя как —.
Решения задач и упражнений ♦ 415
Т2~Т
Итак, интеграл ведет себя как π— = — —► 0 при Τ —> оо. Таким образом:
ι -dz = lim I -dx = 2πί (вычет в ζ = —a + ib) =
Jc(z + a)2+b2 ^^JT(x + af+b2
oo ix
= f i 7Vdx·
Теперь, вычет в точке ζ = -а + ib равен
piz i(-a+ib)
lim (z-(-a + ib)) = =
*->-*+» [Z - (-a _|_ ib)] [z - (-a - ib)] -a + ib + a + ib
_ e-iae~b _ e-bcos(a) - fe"bsin(fl)
ilb ~ ilb
и поэтому
Г ϊ 7Vdx = 2lii
e cos(a) - ie sin(a)
ilb
Раскладывая числитель интеграла по тождеству Эйлера и приравнивая
вещественные части, мы получаем
cos(x) π _b
f+b2
sin(*) λ„_ π,
г coj
приравнивая мнимые части, получаем / V^—-dx = —е sin(a).
J— (x + af+b2 b
Если а = 1и b= 1, например, эти два интеграла равны 0.6244... и -0.97251...
соответственно, и MATLAB соглашается, поскольку quad(@(x)cos(x)./
((х+1).Л2+1),-1000,1000) = 0.6245... и quad(@(x)sin(x)./((x+l).A2+l),-1000,
1000) = -0.9697....
eiz
(с) Пусть f(z) = — — —, то есть рассмотрим контурный интеграл
г eiz
I —η η η ч-dz, где контур С показан на рис. 8.7.1. Подынтеграль-
Jc(z2 + a2)(z2+b2)
ное выражение имеет четыре особенности в точках ζ = ±ш и ζ = ±/Ь, но
поскольку а и Ь оба положительны, то внутри С находятся только
особенности ζ = ±ш и ζ = ±/Ь. Таким образом:
г e'z
/ —η η η ч-dz = 2πί (вычет в ζ = +ia плюс вычет в ζ = +ib).
J(z2 + a2)(z2+b2)
Эти вычеты есть: в точке ζ = /α
416 ♦ Решения задач и упражнений
eiz ei(ia)
lim(z-ia) =
z^ia (ζ - ia)(z + ia)(z - ib)(z + ib) i2a(ia - ib)(ia + ib)
■ = !-
-i2a(a-b)(a + b) 2a(a2-b2)
и в точке ζ = ib
lim(z-ib)
J№
z^ib
(z - ia)(z + ia)(z - ib)(z + ib) (ib - ia)(ib + ia)\2b
-i2b(b-a)(b + a) 2b(b2-a2)
На дуге полуокружности ζ = Те1в, dz = zTel9d6, 0 < θ < π. Поэтому на этой
полукруглой дуге мы имеем интеграл
Г-
Jo t
JTe"
который при Τ —> оо ведет себя как
π
(Тле™+ал)(Т*еш+1?)
0. Итак, все, что мы оставили, -
это часть контура С, которая лежит вдоль действительной оси, что дает
нам
оо
/
(х2 + а2)(х2 + Ъ2)
dx = 2πζ
- + ζ-
= -2π
2a(a2-b2) 2b(b2-a2)
- + -
2a(a2-b2) 2b(b2-a2)
■ π
b(a2-b2) a(a2-b2)
sin(x)
/cos(x) , . r sin(x
(x2 + a2)(x2 + b2) J (x2 + a2)(x
-2 + b2)
— LXJ —LXJ
Приравнивание вещественных частей дает нам наш ответ:
+ Ь2)
-dx.
I
cos(x)
π
-dx-
(xl + al){xl + bl) al-bl
b a
n(2e — Ϊ)
Если a = 2 и b = 1, это сводится к —- - = 0.31438... и согласуется с ре-
бе2
зультатом MATLAB: quad(@(x)cos(x)./((x.A2+l).*(x.A2+4)),-1000,1000) =
0.31436....
Решения задач и упражнений ♦ 417
(d) Пусть f(z)--
—, то есть рассмотрим контурный интеграл
-dz> где контур С показан на рис. 8.7.1. Подынтегральное
Г—-
Jc(z2 + b2)2
выражение имеет две особенности второго порядка в точках ζ = Mb, но
поскольку b положительно, то внутри С находится только особенность
с eiaz
ζ = Mb. Таким образом, | — —^ dz = 2π/ (вычет в ζ = ib). Мы вычисля-
Jc(z2+b2)2
ем этот вычет по формуле (8.8.8) следующим образом, используя т = 2:
г d ι
hm—\
z^ib dZ
{z-ibf
2ч2
(г2+Г)
d_
dz
(z + ib)2
(z+ibfiae™ - e,az2(z + ib)
z=ib
(z + ib)4
z=ib
что приводится (после небольших алгебраических преобразований)
Л + ab _аЪ m
к выражению -ι ^ е . Тогда
/
(z2+b2)2
4b5
dz = 2π/
A + ab ab\
π
2ЪЪ
(1 + аЪ)ё
-ah
На дуге полуокружности мы имеем: ζ = Те1в, dz = iTeiedQ, 0 < θ < π,
поэтому на этой полукруглой дуге подынтегральное выражение имеет
eiTeie
вид —г-— ^-iriTe1 с абсолютным значением, которое ведет себя как
(Г2е|29+Ь2)2
Г 1 π
-—- = —=- при Τ —> оо. Поэтому интеграл ведет себя как —-, что стремится
к нулю при Τ —> оо. Тогда, поскольку на вещественной оси ζ = χ, то мы
имеем в пределе при Τ^ оо:
26 2 2 А = -^ (1 + ab)e"ab.
(х2 + Ь2) 2Ьъ
Приравнивание реальных частей (после использования тождества
Эйлера в числителе подынтегрального выражения) дает нам результат:
Г.
оо cos(ax) . π _
7 9 9 <?* = —-(1 + дЬ)е
(х2 + Ь2)2 4Ь3
ab
или
рею 1 рею
, поскольку / = — / , так
как подынтегральное выражение четно, мы имеем наш результат:
iax
~ аЪ
Г
JO
π
2ч2
0 (*2+Ь2)
civ = —- (1 + аЪ)е~а\ Если а
4ЪЪ
π
Ь = 1, это равно — = 0.57786
и согласуется с результатом MATLAB: quad(@(x)cos(x)./((x.A2+l).A2),0,
1000) = 0.57786....
418 ♦ Решения задач и упражнений
ь
роо χ
(С8.4). В интеграле / — -ах подынтегральная функция для больших χ
Jo (*2 + 1)2
хк 1
ведет себя как — = —т—г. Чтобы интеграл расходился при χ —> оо, мы долж-
х4 х4~к
ны иметь показатель степени 4 - к > 1, или Ъ > к, или к < 3. Для малых χ
\_
-к
подынтегральная функция ведет себя как хк = —г. Для того чтобы интеграл
χ
не расходился при χ —> оо, мы должны иметь показатель степени -к < 1, или
fc> -1, или -1 < к. Таким образом, -1 < к < Ъ. Теперь, следуя подсказке, давайте
efcln(z)
рассмотрим интеграл / f(z)dz, где С - контур на рис. 8.9.1, a f(z) = —= =-.
Jc (Г + lr
Этот интеграл имеет две особенности второго порядка, в точках ζ = ±ζ, и обе
будут внутри С, когда мы будем считать, что R —> оо и оба числа ε и ρ —> 0. На С2
ζ = i?e*e, dz = iRelBdQ, и мы видим, что абсолютное значение подынтегрального
выражения ведет себя как —- при R —> оо. То есть интеграл на С2 будет обра-
щаться в ноль, когда R —> оо. На C4z = реге, dz = fpe'ed6, и мы видим, что
абсолютное значение подынтегрального выражения ведет себя как ρ при ρ —> 0. То есть
интеграл на С4 будет обращаться в ноль, когда ρ —> 0. Таким образом, все, что
нам осталось вычислить, - это Г + Г . На Q ζ = гег£, dz = eIEdr, а на С3 ζ = гег(2тт_£),
dz = e/(2"£)dr. Итак:
R лИп(л?|е) Ρ лИп(«|(211-е))
q c3 Jp(rV2' + l)2 i(rV2<2lM>+l)2
или, поскольку ε —> 0,
Я Ип(г) Ρ Μ1ηΓ+/2π}
ί+ ί= Γ"! 2аГ+ f—2 Tar·
i i pC- +i) i c-2+i)2
Если теперь ρ —> 0 и i? —> оо, мы имеем:
- еЫ(г») оо т^^апк <» * y2i*
/ + / = / —η 2аГ~ / 2 2~dr= / 2 г-d/" =
q { oC-2+l)2 о (r +1) о (r +1)
~J0 (r2+l)2 Г~1 (r2+l)2 r"-J (r2+l)2
Теперь
°Ve™*[_2/sin(TTk)]
Λτ, 4j Г' с —ZJSin(UK) , „ . ,
/ f(z)dz — I 4 ;r——dr — 2тп (вычет в ζ —-ι плюс вычет в ζ = +ι).
с о С-2+1)2
Решения задач и упражнений ♦ 419
Поскольку f(z) = ζ г- и так как для особенностей второго по-
(z+02U-02
рядка в точке ζ = ζ0 мы имеем из формулы (8.8.8) выражение для вычета как
d 2
lim — {(ζ - z0 )f(z)}, то для z0 = -i вычет Rx есть
z^z0 dZ
Я = lim —
z-^-i dZ
U + iT
(z+f)2(z-/)2
r d
■■ lim —
z-^-i dZ
;42 ьЛ-\ Л
{Ζ-if
k-l / :\kr
= lim
z^-i
(z - 0 fa;*"1 - z* 2(z - i) (-2i"r fc(-0 - H) 2(—2f)
или Л
(г-О4
-4fc(-t)*~x+(-i)*4i
16
_-fc(-/)*_1+/(-/)*
(-20'
Μ
. Если вы повторите это для другого вычета, R2> то
обнаружите, что
Д9 =lim—
(г-'Т
(ζ+/)2(ζ-02
lim—
ζ->ί dz
(ζ+02
-kitf^-iiif
Итак:
Rl + R2 = Λ[(-ΐ)*-ι + (i)*-i] + i[(_i)*_ (i)*] =
H)fc , (0fc
-ζ ζ
+ |[(-0*-(0*] =
^[(-0*-(0*]+{[Н)*-(0*] =
Αι 4
!(i-fc)[(-i)*-(ok].
4
π
.к i
"Z4 + 4
[(-i)k-(/)*] =
\* /;\kΊ
Таким образом, 2πζ"(Α1 + fl2) = (1 - k)[(-z) - (f)* ], и тогда
oo „kJnk
ι
0
ИЛИ
(Г + 1Г 2
°£ rfe dr_u(l-fc)[(-i)fc-(i)fc]
■J(r2 + 1)2 4i'sin(ufc)eilt,c
420 ♦ Решения задач и упражнений
.3π
Поскольку —ί = е 2 и ζ = е 2, мы имеем:
С—0fc—CO =e 2-e 2=emfelel 2 J-el2
= e^\ef2j_e-
ι*4
2jr = efl*2isin
&π
Таким образом:
ink r
оо к
1^
n(l-k)emK2ism
-dr-
кп)
и0(г' + \у 4/sin(irk)ei,rii
ί Ictt. 1
или, поскольку sin(iifc) = 2sin
ir(l-fc)·
2
sin
> 2 J
sin(ufe) J
COS
(kn)
, то, изменяя фиктивную перемен-
Г х
ную интегрирования г на х9 мы получаем / —
о(^ +1)
dx = π^ , \,-l<fe<3.
4cos
'*теГ
MATLAB соглашается, поскольку если к = —, то
оо /
J0(x2 + 1)2
π
π
π72
8cos
ΊΟ
'^
= 0.55536...,
и quad(@(x)sqrt(x)./(χ.Λ2+1).Λ2,0,1000) = 0.55535..., а если к = -,το
оо χ
poo
Jo ^
1/3
π
2+1)2
<&:
π
π
4cos
fTi) Jb Зл/3
6 —
2
: 0.60459...,
идиасК@(х)(х.Л(1/3))./(х.Л2+1).Л2, 0,1000) = 0.60459....
(C8.5). Рассмотрим интеграл Г f(z)dz, где /(ζ) =
αζ -\-bz-\-c
, где m > 0,
b > Aac и С - контур на рис. 8.6.2. Как и при выводе (8.6.5), есть две
особенности на вещественной оси в точкаххг и х2, как показано на рис. 8.6.2. Значения хг
и х2 приведены в тексте. Анализ здесь проходит так же, как и в тексте, с учетом
изменения вида f(z). Таким образом, три интеграла по Q, С3 и С5 будут
объединяться (когда мы положим е^ОиТ^ оо), чтобы дать нам интеграл, к ко-
Решения задач и упражнений ♦ 421
торому мы стремимся, и его значение будет] Г f{z)dz + Г f{z)dz + \ f(z)dz\.
Итак, давайте вычислим каждый из этих трех линейных интегралов. Для С2:
ff(z)dz = f-
eim(X2+£e»)i£eto
; а(х2 + ее'У + Ь(х2 + гет) + с
-άθ-
I
eimx*eimEe iee
/θ
Jn а(х% + 2х2гет + глеи*) + Ь(х2+гею) + с
ζεβζ1
-dQ-
0 pimx2 Jmzem ;„ JQ
ι
ττάβ.
Jn (ax2 + bx2 + с) + (2αχ2εβζϋ + αζλζιλ* + feezb)
Поскольку <xv22 + bx2 + с = 0, так как x2 - это ноль знаменателя, и поскольку
ε2 —> 0 быстрее, чем ε —> 0, тогда для «малых» ε мы имеем:
lim [f(z)dz = lim Г
»*='/
0 e/nuf2
2αχ9 + Ь
de =
-πι-
e""*2
2αχ9 + b
exmxl
Таким же образом:
Ит ff(z)dz = -ni-
ε^Ο-! 2щ + Ь
Так же, как и прежде, Jf(z)dz = 0. Таким образом:
I
cos(mx) + ζ sin(mAr)
ax2 + bx + c
с/а: = πζ
20^ + b 2ax2 + Ь
Теперь 2axx + b = Vb2 - 4шг и 20^ + Ь = -л/Ь2 - Aac, и тогда
°р cos(mx) + i sm(mx)
ах2 +bx + c
-dx = ni
emxi
e 2
Vb2 -Aac 4b2 -Aac
= i
W~-
(eim*i-eimxi) =
Aac
π
Ί*
Aac
г (cosim^) + ζ sm{mx{) - cos(mx2) - i sin(mx2)),
или, приравнивая вещественные части равенства,
/
COS(mx)
ax2 + bx-\-c
dx =
π
^
Aac
τ (sin(mx2) - sm{mx^j).
422 ♦ Решения задач и упражнений
Используя тригонометрическое тождество
sin(A) - sin(B) = 2 cos
А + Б
sin
(А-В)
мы имеем:
cos(mx)
/
αχ -\-bx-\-c
dx-
π
V^
Aac
π
4ъ2
Aac
π
2 cos
2 cos
mx2 +mxx
sin
mx2 - mx1
№
-Aac
2 cos
mb
la
(mb)
2a
sin
sin
--Vb2-4ac
m\b2 - Aac
2a
(C8.6). Следуя подсказке и используя рис. 8.9.1, мы видим, что внутри
контура С находятся две особенности первого порядка (когда мы положим ε —> О,
ρ —> 0 и i? —> оо), одна - в точке ζ = -1 = em и другая - в точке ζ = -2 = 2em.
Вычет особенности первого порядка в точке ζ = ζ0 функции f(z):
g(z0)
Kz)
есть
Для функции f(z) --
мы имеем g(z) = zf и h(z) = (ζ + 1)(ζ + 2),
й'(*о) " (ζ + ΐχζ + 2)
и тогда ft'(z) = (ζ + 1) + (ζ + 2) = 2z + 3. Таким образом, вычет в точке -1 есть
,ιπ\Ρ
(ет)
о™Р
2(-1) + 3 -2 + 3
Таким образом,
е р, а вычет в точке -2 есть
(2е"7
,ζπχρ
2ретр
2(-2) + 3 -4 + 3
-2ре/тгр.
J + J + J + J = 2uze^(l-2P).
Теперь
Jc~ Jo
(reiby
J£\P
, Jc, J«
(Γ6ί(2π-ε))Ρ
'с, J ρ (re,£ + l)(re,E + 2) Jc3 J* (ге'(2тс-£) + l)(rei(2lt-£) + 2)
и тогда поскольку ε —> 0, ρ —> 0 и i? —> оо, то
е/(2тс-£)с/г,
ΓΡ(1_6ί2πΡ)
0(r + l)(r + 2)
f+ГЛ " *-? rV2" ^Г^" '*■
q c3 ο (Γ + ^ + 2) ο (r + ^ + 2) - (r +1)(r ■ "
Далее:
2π-ε . dJQ\P
(i?effi+l)(i?e/e + 2)
Решения задач и упражнений ♦ 423
Поскольку при R —> оо числитель подынтегрального выражения стремится
к бесконечности как Rp+1 для любого θ в пределах интегрирования, в то время
как знаменатель стремится к бесконечности как R2, подынтегральное выра-
dp+i ι 2π
жение ведет себя как —— = Rp~x = —;—. Интеграл по С2 ведет себя как —;—.
R2 R1-? R1-?
При ρ < 1 Г —> 0, так как R —> оо. Точно так же.
Jc2
Далее, \ = \ —^-^-—^ zpez0d6. Теперь при ρ —> 0 числитель
Jc4 J2u-s(pele + 1)(pele+2) ^ ^ н
подынтегрального выражения ведет себя как рр+1, в то время как знаменатель -
как число 2, тогда интеграл по С2 ведет себя как πρρ+1, что, очевидно, —> 0 при
ρ —> 0, когда ρ > -1. Итак, мы имеем Г + Г =0, что означает
I. I J„(r + D(r + 2)
ИЛИ
Р ^_о„;^(1-2")_0„; е™"(1-2")
-dx = 2πζ ^-=—- = 2πζ
·} (аг + 1)(х + 2) 1 - βί2ρπ е™р (ε-ίρπ - е/рт)
= 2ГО^Ь^ = я-^1), -1<р<1.
-2isin(pii) sin(p7i:)
(С8.7). Следуя подсказке, мы будем использовать контур на рис. 8.6.1 для вы-
eiz
числения £ dz= f + [ + f + f = 0, потому что единственная
особенно £ JCX JC2 JCZ JC4
ность подынтегрального выражения (в начале координат) находится вне
контура С. Итак:
Т eix π e,7feffl ε ei(iy) n β/εβ*
f-^d*+ Γ2±_ϊΤβ^θ+ f—idy+ f * /εΛ = 0
J λ: Jo Γβιθ j zy j- ε6/θ
To есть
JJL-te+iffer dQ-fli—dy-ifie'· άθ = 0.
В последнем интеграле, когда мы положим ε —> 0, будем иметь ее —> е, и
тогда интеграл будет —е. Во втором интеграле
424 ♦ Решения задач и упражнений
JTem iT[cos(e)+/sin(e)] iTcos(e)-Tsin(e)
ее =ее =ее =е
eTsm(Q)
и когда Т^ О, подынтегральное выражение стремится к е° = 1, и тогда интеграл
тс
равен —. Таким образом, при ε —> 0 и Τ —> оо
л
Т Pix
/е , .π .π
dx + z 1 — e = 0.
a: 2 2
μ
Итак:
00 ecos(*)+isin(*) оо е"* π π π
/ άχ- Ι dy=i—e-i— = i—(e-1),
1 x I V 2 2 2ν У
J χ J ν 2
ο ο ^
и
^ecosW[cos{sinW} + isin{sin(x)}]rfv je ^, = 1-π
J γ J л/ 9
О " Ο ^
или, приравнивая мнимые части, мы имеем результат Коши:
JeC0SWsi^WU = ^(e-l).
о * 2
(С8.8). Следуя подсказке, напишем
оо 2 оо * оо ρ
f -*—5—ϊ—ъ-(Ьс= Г-*—^+ Г-*—5-d*>
оо (* + * X* + Ь2) ^ а:2 + а2 ^ а:2 + Ь2
и тогда
χ2 Δ °г Ах2 + АЪ2 + Вх2 + Ва2
г χ , _ г лх -\- ло -\- ΰχ -\- ΰα ,
_00(х2 + а2)(х2^-Ь2) Х~ ^ (х2 + а2)(х2 + Ь2)
Это означает, что А + В = 1 и АЬ2 + Во2 = 0. Эти два уравнения легко решаются
и даютА = — иБ = — г-.Итак:
а1 -Ъ1 а1- Ъ1
Решения задач и упражнений ♦ 425
/
2 сю
-dx
а г 1
_гЛ J v2 ,
u2 oo
(x2 + a2)(x2 + b2) a2 -b2 ^ x2 +a2 a2 -b2 ^ x2 +b2
dx
a
a2-b2
a
^tan"1
a
2 l2
a2-b
-tan"1
b
V
b π
π -π =
а2-Ь2 а2-Ь2 " α + Ь
°r x2 π
Теперь пусть b —> α. Тогда I — ^rdx = —. Наконец, дифференцируя
Ax* + a*Y
по а:
°r -2x2(x2 + a2)2a __]™__ π_
i (х2 + я2)4 ~ 4a2" 2a2"
poo χ 7t
Таким образом, / — -—dx = —-. Для а = 1 это равно 0.392699...,
>(*2 + a2)3
8a
nquad(@(x)(x.A2)./((x.A2+l).A3),-100,100) = 0.392699....
Предметный указатель
Адамар, Жак, 352
Бартл, Роберт, 31
Бернулли, Джон, 199
Бертран, Жозеф, 352
Бета-функция Эйлера, 137
Борас, Джордж, 17
Бор, Харальд, 356
Броун, Роберт, 51
Брун, Вигго, 352
Бьюкенен, Герберт, 19
Валле-Пуссен, Шарль-Жозеф, 352
Валлис, Джон, 136
ВанПейп,У.Ф.,217
Винер, Норберт, 52
Вычет комплексной функции, 333
Гамма-функция Эйлера, 134
Гильберт, Давид, 349
Гипотеза Римана, 349, 356
Далцелл, Д. П.,45
Дзета-функция, 176, 240, 350
ζ(2), 176,245,370
ζ(3), 176,240
ζ(4), 370
функциональное
уравнение, 353, 359
Дигамма-функция, 187
Дини, Улисс, 125
Дирихле, Густав, 102
Дирихле, Лежен, 28
Доля Сельберга, 357
Интеграл
Ахмеда, 201, 212
Бернулли, 199
Валлиса, 136
вероятностей, 122, 248
Далцелла, 44
Дини, 125
Дирихле, 102, 250
Коксетера,205,212
Лебега, 30
логарифмический, 351
лог-синус Эйлера, 84
Рамануджана, 190
Римана, 23
Улера, 118
Уотсон/Ван-Пейпа, 217
Френеля, 237
Фруллани, 104,105
Харди-Шустера, 212
Интегральная теорема Коши
вторая,317
первая, 303
Каталан, Эжен, 16
Квадратура MATLAB quad, 14
Коксетер, X. С. М., 20, 205
Константа Эйлера, 182
Контурные интегралы, 289
Коши, Огюстен-Луи Г. X., 15
Коши-Римана уравнения, 297
Криволинейные интегралы, 288
Ландау, Эдмунд, 356
Лаплас, Пьер-Симон, 123
Лебег, Анри, 28
Левинсон, Норман, 357
Лежандр, Адриен-Мари, 134
Литтлвуд, Дж. Э., 358
Лоран, Пьер Альфонс, 331
Молл, Виктор, 17
Моррис, Джозеф Чандлер, 19
Муавр, Абрахам, де, 56
Предметный указатель ♦ 427
Неотразимые интегралы, книга, 17
Особенность комплексной
функции,331
Преобразование Фурье, 261
Приемы интегрирования
дифференцирование интеграла
по параметру, 92
изменение направления
интегрирования, 68
по частям, 65
разложение дроби
на простейшие, 75
рекурсия, 81
Проблемы Гильберта, 350
Простые числа, 351
Разложение дроби на частные
(простейшие), 41
Разложения рациональной
дроби, 75
Рамануджан, Сриниваса, 364
Риман, Бернгард, 23
Ряд Лорана, 331
Селберг, Атле, 357
Серре, Жозеф, 74
Струтт, Джон Уильям, 262
Теорема о вычетах, 338
Теорема о простых числах, 351
Теорема Рэлея, 262
Улер, Гораций Скаддер, 118
Уотсон,Г.Н.,217
Уравнения Коши-Римана, 297
Фиктивная переменная
интегрирования, 25
Формула Грина, 300
Формула дублирования Лежандра, 146
Формула Эйлера, 235, 291
Френель, Августин Жан, 237
Фруллани, Джулиано, 104
Функция
аналитическая, 297
Гамма Эйлера, 257
«дельта» Дирака, 266
дигамма, 187
Дирихле, 28,107
комплексной переменной, 291
Римана, 29
Фурье, Жозеф, 261
Харди, Г.Х, 13, 356, 364, 371
Хэмминг, Ричард, 31
Чебышев,П.Л.,352
Число Каталана, 164
Число Скьюза, 358
Шустер, Артур, 212
Эдварде, Джозефа, 21
Эдварде, Х.М., 358
Энергетический спектр сигнала, 260
Книги издательства «ДМК Пресс» можно заказать
в торгово-издательском холдинге «Планета Альянс» наложенным платежом,
выслав открытку или письмо по почтовому адресу:
115487, г. Москва, 2-й Нагатинский пр-д, д. 6А.
При оформлении заказа следует указать адрес (полностью),
по которому должны быть высланы книги;
фамилию, имя и отчество получателя.
Желательно также указать свой телефон и электронный адрес.
Эти книги вы можете заказать и в интернет-магазине: www.a-planeta.ru.
Оптовые закупки: тел. (499) 782-38-89.
Электронный адрес: books@alians-kniga.ru.
Пол Дж. Нахин
Секреты интересных интегралов
Главный редактор Мовчан Д. А.
dmkpress@gmaiLcom
Перевод Смоленцев К К.
Корректор Синяева Г. И.
Верстка Чаянова А. А.
Дизайн обложки Мовчан А. Г.
Формат 70x100 1/16.
Гарнитура «РТ Serif». Печать офсетная.
Усл. печ. л. 34,78. Тираж 200 экз.
Веб-сайт издательства: www.dmkpress.com
ПИ IСЛ
эеш. э? Ίο,
ис; опг )т
но д^.ает ^ь 'HbiNi
Ί ОТ----!, KO"Opi
;ij )лу1
λ/ожете /спогэзоьа-
и ej/ что
. /ле, уоье, .j ии,
издание достав it l· " нн< э "довоюет
им юн
великие. учёнь.У:
■ иг,
' О l·
1 I'l·
—
чи
ахо>\_.^.ше <^нкре .jx 1/ jrpa ^j, -
ы пол'-им, г г ко ρ е^ метогы, кот' сые
1Я ? ΟΓΙ ВЫ
'j· .дих1Л7еграгов.
\п, )nyj icj
а км!., а τσ : для с :.
тика ν фи?/сам, ; ι,-
roj rule )у<!' ι
ляг
он и[)( . хх лек л о
университете ^ью Ге упшира. Нап/еал свь:^е 2С книг ^о ма ■
viaii/ и с 1ке, убл Pre -" Sf
,wrms -pkir.c и Ρ yjtor;. 3 2C ixvu юлу /,л n.
-ечдлера Дэв/.са за выдас-.иесг дос^/хения в пеиэгчых
дан' ю ι Шс ).
• wdrnkcess-cor"
К"< «[алак^/ка»
\s@c "■ :s-knigi
www-дмк.рф
ISBN 978-5-97060-763-3
9n785970M607633M>