ВЫСШЕЕ ОБРАЗОВАНИЕ серия основана в 1 996 г.
Министерство образования Российской Федерации Новосибирский государственный технический университет
С.В. СУДОПЛАТОВ, Е.В. ОВЧИННИКОВА
ЭЛЕМЕНТЫ ДИСКРЕТНОЙ МАТЕМАТИКИ
УЧЕБНИК
Рекомендовано
Министерством образования Российской Федерации в качестве учебника для студентов высших технических учебных заведений
Москва	Новосибирск
ИНФРА __________НСТУ-.. .-т.-
|>2002
УДК 519.1(075.8)
ББК 22.176я73
С89
Рецензенты: кафедра прикладной математики и кибернетики Сибирского государственного университета телекоммуникаций и информатики,
Е.А. Палютин — д-р физ.-мат. наук, проф.;
В.М. Зыбарев — канд. техн, наук, доц.'1
Судоплатов С.В., Овчинникова Е.В.
С89 Элементы дискретной математики: Учебник. — М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002. — 280 с. — (Серия «Высшее образование»).
ISBN 5-16-000957-4 (ИНФРА-М)
ISBN 5-7782-0332-2 (НГТУ)
В книге излагаются основы теории множеств, алгебраических систем, компьютерной арифметики, теории графов, комбинаторики, алгебры логики, формальных исчислений, которые образуют курс дискретной математики.
Для студентов технических вузов, изучающих дискретную математику. Может служить справочным пособием по дискретной математике.
УДК 519.1(075.8)
ББК 22.176я73
ISBN 5-16-000957-4 (ИНФРА-М)
ISBN 5-7782-0332-2 (НГТУ)
© Судоплатов С.В., Овчинникова Е.В., 2002
ОГЛАВЛЕНИЕ
Предисловие	6
Введение	8
Г л а в а 1. Элементы теории	множеств	10
§1.1.	Множества	и основные операции над ними	10
§ 1.2.	Отношения. Функции. Взаимно однозначные соответствия ............................ .	.	........ 16
§ 1.3.	Натуральные числа. Принцип математической индукции 23
§ 1.4.	Мощность множества. Конечные и бесконечные множества . . .	.............................. 26
§ 1.5.	Матрица бинарного отношения. Специальные бинарные отношения	...	...	.31
§ 1.6.	Отношения эквивалентности и разбиения. Фактор-мно-жества	.	34
§ 1.7.	Отношения порядка ....	. . . .	.	37
§ 1.8.	Аксиомы теории множеств	43
§ 1.9.	Задачи и упражнения .	45
Г л а в а 2. Алгебраические системы	48
§ 2.1.	Определения и примеры	48
§ 2.2.	Морфизмы .	51
§ 2.3.	Подсистемы................. .	.	53
§ 2.4.	Конгруэнции. Фактор-алгебры. Теорема о гомоморфизме 56
§ 2.5.	Декартовы произведения алгебр. Теорема Биркгофа 58
§ 2.6.	Решетки и булевы алгебры ................. .	.	59
§ 2.7.	Идеалы и фильтры булевой алгебры	64
§ 2.8.	Алгебры отношений и реляционные алгебры	65
§ 2.9.	Задачи и упражнения .	.	69
Г л а в а 3. Числовые системы	71
§ 3.1.	Бесконечные числовые системы	71
§ 3.2.	Системы счисления	.............. 77
§ 3.3.	Компьютерная алгебра и численный анализ	82
§ 3.4.	Списочное представление чисел .	84
§ 3.5.	Делимость в кольце целых чисел	87
§ 3.6.	Разложение целых чисел на множители	90
§ 3.7.	Целые числа по модулю т...................... 92
§ 3.8.	Линейные уравнения по модулю т. Китайская теорема об остатках...................................   .	96
§ 3.9.	Точные вычисления, использующие модулярную арифметику ............................................ 99
§ 3.10.	Задачи и упражнения........................ 107
3
Г л а в a 4. Элементы теории графов	108
§ 4.1.	Виды и способы задания графов	....... 108
§ 4.2.	Подграфы и части графа. Операции над графами . .	114
§ 4.3.	Маршруты. Достижимость. Связность .	.	. .	119
§ 4.4.	Расстояние в графах	. .	124
§ 4.5.	Нахождение кратчайших маршрутов .	126
§ 4.6.	Степени вершин	130
 § 4.7. Обходы графов	. .	131
§ 4.8.	Остовы графов.................. .	.	.	134
§ 4.9.	Обходы графа по глубине и ширине. Решение задачи коммивояжера ...................................... 137
§ 4.10.	Упорядоченные и бинарные	деревья	.	  144
§ 4.11.	Фундаментальные циклы...........	146
§ 4.12.	Разрезы . .	... 148
§ 4.13.	Векторные пространства,	связанные	с графами	150
§ 4.14.	Раскраски графов .	.	.	153
§ 4.15.	Планарные графы .	. .	154
§ 4.16.	Задачи и упражнения.	...	157
Глав а 5. Комбинаторика	159
§ 5.1.	Перестановки и подстановки .	. . . .	159
§ 5.2.	Размещения и сочетания .	.	. .	162
§ 5.3.	Размещения и сочетания с повторением	. .	163
§ 5.4.	Разбиения ...	...	. .	164
§ 5.5.	Метод включений и исключений	. .	166
§ 5.6.	Рекуррентные соотношения. Возвратные последовательности	...	...	167
§ 5.7.	Задачи и упражнения .	.	, .	170
Г л а в а 6. Алгебра логики	172
§ 6.1.	Формулы алгебры логики	172
§ 6.2.	Функции алгебры логики	.	175
§ 6.3.	Эквивалентность формул	. .	.........178
§ 6.4.	Дизъюнктивные и конъюнктивные нормальные формы 180
§ 6.5.	Двухэлементная булева алгебра. Фактор-апгебра алгебры формул . .	.	.	...	185
§ 6.6.	Минимизация булевых функций в классе ДНФ .	186
§ 6.7.	Карты Карно . .	.................... 189
§ 6.8.	Принцип двойственности для булевых функций	192
§ 6.9.	Полные системы булевых функций .	193
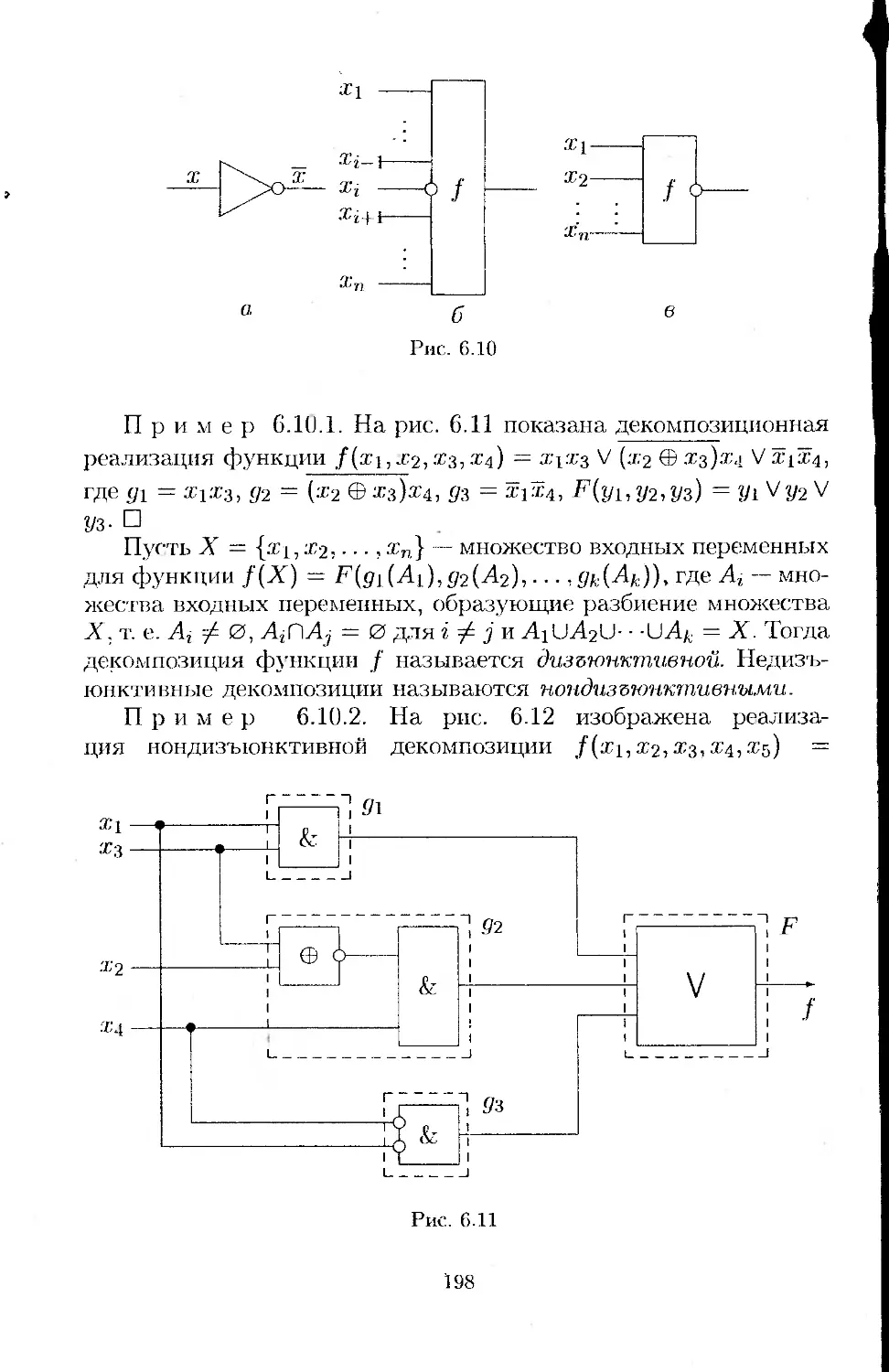
§6.10.	Функциональная декомпозиция	197
§ 6.11.	Логические сети .	. .	203
§ 6.12.	Задачи и упражнения .	210
Г л а в а 7. Формальные исчисления	212
§ 7.1.	Определение формального исчисления .	212
§ 7.2.	Исчисление высказываний......................213
§ 7.3.	Алгоритмы проверки общезначимости и противоречивости в ИВ..........................................216
4
§ 7.4.	Формулы сигнатуры Е. Истинность формулы на алгебраической системе............................. 222
§ 7.5.	Исчисление предикатов сигнатуры Е .	.	226
§ 7.6.	Эквивалентность формул ИГР. Пренексные нормальные формы .............. .'. .	227
§ 7.7.	Метод резолюций в ИГР'...................229
§ 7.8.	Задачи и упражнения .	.	..............238
Список литературы	241
Приложение. Варианты типового расчета	243
Предметный указатель	270
ПРЕДИСЛОВИЕ
Книга предназначена для студентов младших курсов технических вузов, изучающих дискретную математику, и написана на основе учебного пособия Судоплатов С. В., Овчинникова Е. В. Дискретная математика: Учеб, пособие. Новосибирск: Изд-во НГТУ. 1994. Материал составлен в соответствии с рабочими программами курсов дискретной математики, читаемых в НГТУ. Для более полного понимания излагаемого в настоящем учебнике материала желательно знакомство читателя с основами линейной алгебры, например, по книге: Ивлева А. М., Прилуц-кая И. И., Черных И. Д. Линейная алгебра. Аналитическая геометрия: Учеб, пособие. -- Новосибирск: Изд-во НГТУ, 2000.
Учебник включает семь разделов: основы теории множеств, алгебраические системы, числовые системы, теория графов, комбинаторика, алгебра логики, формальные исчисления. Взаимосвязь разделов приведена на. следующей схеме:
3
б
6
Для углубленного изучения материала в конце книги приводится список литературы, а также электронных материалов, доступных через систему Интернет. Для удобства поиска используемых терминов дан предметный указатель. Кроме того, в качестве приложения приведен типовой расчет по дискретной математике для самостоятельного выполнения студентами семестрового задания на основе материала, излагаемого в книге. Перед решением задач типового расчета полезно прорешать задачи и упражнения, помещенные в конце соответствующих разделов.
Рассматриваемые в учебнике понятия и утверждения, как правило, иллюстрируются примерами и пояснениями. Отмечаются прикладные аспекты изучаемого материала.
Знак □, используемый в тексте, означает конец рассуждения или его отсутствие. Знак читается “положим по определению”, “обозначим” или “имеет вид”, знак <=> - “тогда и только тогда”, знак => — “если ..., то ...” знак V “для любого”, знак 3 - “существует”.
Создание книги стало возможным с появлением в Новосибирском государственном техническом университете кафедры алгебры и математической логики, основанной профессором А. Г. Пи-нусом в 1992 г. На разных этапах подготовки настоящей книги авторы получали от него большую помощь и поддержку. Много полезных предложений и замечаний сделал доцент кафедры вычислительной техники НГТУ В. М. Зыбарев. Этим коллегам авторы выражают свою искреннюю благодарность.
Авторы благодарны И. Д. Черных, который взял на себя труд по детальному прочтению рукописи, устранению неточностей и компьютерному набору учебника.
ВВЕДЕНИЕ
Дискретная (или прерывная) математика представляет собой область математики, в которой изучаются свойства структур конечного характера, а также бесконечных структур, предполагающих скачкообразность происходящих в них процессов или отделимость составляющих их элементов. В отличие от дискретной математики классическая математика занимается преимущественно изучением свойств структур непрерывного характера. Деление математики па классическую и дискретную достаточно условно, поскольку, с одной стороны, происходит взаимопроникновение возникающих идей и методов, а с другой — средства дискретной математики используются для изучения непрерывных моделей и наоборот.
Бурное развитие дискретной математики обусловлено прогрессом компьютерной техники, необходимостью создания средств обработки и передачи информации, а также представления различных моделей на компьютерах, являющихся по своей природе конечными структурами.
Укажем основные цели, преследуемые в учебнике при рассмотрении основных разделов дискретной математики.
В первой главе рассматривается понятие множества, вводятся операции над множествами и перечисляются основные свойства этих операций. Определяется понятие отношения на множестве, указываются свойства отношений, различные виды отношений. Дается аксиоматика теории множеств, позволяющая, с одной стороны, избегать появления известных парадоксов, а с другой - получать содержательные результаты, покрывающие практические потребности.
Во второй главе приводится центральное понятие курса — понятие алгебраической системы, а также различных видов ал
8
гебраических систем, связей между алгебраическими системами, основные операции над ними.
Третья глава посвящена различным возможностям представления чисел и работы с числовыми системами, включая компьютерную арифметику. Приводятся способы точного вычисления арифметических выражений в рамках конечных систем, преимущества и недостатки компьютерных вычислений.
В четвертой главе излагаются основы теории графов. Приводятся основные виды и способы задания графов, операции над графами, их числовые характеристики, алгоритмы, используемые для решения практических задач, связанных с графами.
В пятой главе рассматриваются основные комбинаторные конфигурации и формулы.
Шестая глава посвящена изучению алгебры логики. Здесь приводятся понятия формулы и функции алгебры логики, алгоритмы минимизации функций алгебры логики, критерий полноты системы булевых функций, приложения алгебры логики.
В седьмой главе приведены основные формальные исчисления: исчисление высказываний и исчисление предикатов. Даны алгоритмы проверки общезначимости и противоречивости в исчислении высказываний, а также метод резолюций в исчислении предикатов, используемый при построении .языков логического программирования.
Глава 1
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
§ 1.1. Множества и основные операции над ними
Понятия множества и элемента множества относятся к понятиям, нс определимым явно, таким, как, например, точка и прямая. Это связано с тем, что некоторые понятия в математике должны быть исходными, служить теми “кирпичиками”, из которых складывается общая теория. Мы определяем только, как соотносятся эти исходные понятия, не говоря о природе рассматриваемых объектов.
По;; множеством М понимается совокупность некоторых объектов, которые будут называться элементами множества М. Тот факт, что х является элементом множества М, будем обозначать через х G М (читается “,т принадлежит 7П”), а если х не является элементом множества М, то будем писать х М (читается “т не принадлежит М”).
Заметим, что элементы множества сами могут являться множествами. Например, множество групп студентов состоит из элементов (групп), которые, в свою очередь, состоят из студентов.
Множество можно задать перечислением принадлежащих ему элементов или указанием свойств, которым элементы множества должны удовлетворять. Если xi,x2,... ,хп — все элементы множества Л1, то будем писать М = {.Т1,Ж2,..., хТ1}. Пусть имеется свойство Р, которым могут обладать или не обладать элементы некоторого множества А. Тогда множество М, состоящее из всех элементов множества А, обладающих свойством Р, будет обозначаться через {х 6 А | х обладает свойством Р}, а также {х | х обладает свойством Р}, {ж | Р(.т)} или {.т}р(х), когда из контекста ясно, о-каком множестве А идет речь.
10
Мы будем использовать следующие обозначения для числовых множеств: N или ш — множество натуральных чисел, Z — множество целых чисел, Q - множество рациональных чисел, R - множество вещественных чисел. С — множество комплексных чисел.
Пример 1.1.1. Множество М арабских цифр можно задать двояко: перечислением М = {0,1,2,..., 9} или посредством свойства М — {.г | х — арабская цифра}.
При м е р 1.1.2. Множество нечетных чисел {±1, ±3, ±5, ...} можно определить как {.г | х — 2к + 1 для некоторого к G Z}. □
Способ задания множества с помощью свойств таит некоторые опасности, поскольку “неправильно” заданные свойства могут привести к противоречию. Приведем один из наиболее типичных теоретико-множественных парадоксов — парадокс Рассела. Рассмотрим множество всех множеств, которые не являются своими собственными элементами: К {М | М М}. Спросим теперь, является ли множество К своим элементом? Если К G К, го должно выполняться свойство, задающее множество К, т. е. К К, что приводит к противоречию. Если же К JC, то, поскольку выполняется свойство, задающее К, приходим к тому, что К G К, а это противоречит предположению. Таким образом, нс всякое свойство приводит к осмысленному заданию множества. В конце настоящей главы мы рассмотрим систему аксиом теории множеств, исключающую подобные парадоксы.
Множество А называется подмножеством множества В (обозначается А С В), если все элементы множества А принадлежат В:
АСВ^ \/х(х G А=>х G В).
Другими словами, это означает справедливость следующего утверждения: для любого элемента х, если х G А, то х G В. Если А С В, го будем также говорить, что множество А содержится в В, илт имеется включение множества. А в В. Множества А и В назыв потея равными или совпадающими (обозначается А = В), если < пи состоят из одних и тех же элементов, т. е. если A Q В и В С /1. Таким образом, чтобы доказать равенство множеств, требуется остановить два включения.
П р и к ер 1.1.3. Справедливы следующие включения: N С Z, Z С Q, Q С R, R С С.
11
П р и м е р 1.1.4. Покажем, что множества Mi {ж | sins = 1} и М2 {ж | х = + 2/гтг, к G Z} совпадают.
Если х G Mi, то х является решением уравнения sin ж = 1. Но это значит, что ж можно представить в виде ж = ^ + 2ктг и поэтому s'G М2- Таким образом, Mi С М2. Если же ж G М2, т. е. ж = | + 2Аиг, то sin ж = 1, т. е. М2 С Mi- Следовательно, М\ — М'2- П
Запись А с В или A Q В означает, что А С В и А В (А не равно В), и в этом случае будем говорить, что А строго включено в В, или является собственным подмножеством, В. Так, включения из примера 1.1.3 являются строгими.
Заметим, что X С X; если X С У и У С Z, то X С Z; если X С У и У С X, то X = У.
Не следует смешивать отношение принадлежности G и отношение включения С. Хотя О G {0} и {0} G {{0}}, неверно, что О G {{()}}, поскольку единственным элементом множества {{0}} является {()}.
Совокупность всех подмножеств множества А называется его булатом или множеством-степенью и обозначается через Р(А) или 2Л. Таким образом, Р(А) {2?|В С А}.
Мы будем предполагать, что существует множество, не содержащее ни одного элемента, которое называется пустым и обозначается через 0. Ясно, что 0 С А для любого множества А.
П р и м е р 1.1.5. Если А = {1,2,3}, то Р(А) = {0, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, А}. □
Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсальным или универсумом и обозначается через U. Рассмотрим операции на булеане P(U). Если А, В G В(В), то пересечение АГ\В и объединение AUB множеств А и В определяются равенствами А П В {ж | ж G А и ж G В}, AU B {ж | ж G А или ж G В}. Пересечение множеств А и В называется также их произведением и обозначается А - В, а объединение — суммой: А + В. Множество А\/? ?= Л-Вс* {ж|ж G А и ж В} называется разностью множеств А и В, множество А® В (А \ В) U (В \ А) — кольцевой суммой или симметрической разностью множеств А и В, множество A~V\A — дополнением множества А в U (см. рис. 1.1, на котором изображены так называемые диаграммы Эйлера. — Венна, наглядно поясняющие соотношения между множествами).
П р и м е р 1.1.6. Докажем, что А \ В = А А В.
12
AuB .
Рис. 1.1
A\B
Сначала установим, что А \В С А Г'В. Пусть х — произвольный элемент А \ В. Тогда по определению разности множеств имеем х 6 А и х ф В, отсюда х G А и х G В, значит, х G А П В. Теперь покажем, что А'Г\ В С А \ В. Если х G А П В, то х G А и х G В, поэтому х G А и х В, значит, х G А \ В. На основании включений А\В С АПВ и АПВ С А\В делаем вывод, что А\ В = АГ\ В. □
Аналогично примеру 1.1.6 устанавливаются следующие основные свойства операций пересечения, объединения и дополнения:
1.	Ассоциативность операций U и Г):
A U (В U С) = (A U В) U С, А П (В П С) = (А П В) П С.
2.	Коммутативность операций U и С:
A U В = В U А, АП В = В П А.
3.	Законы идемпотентности
AUA = A, АпА = А.
4.	Законы дистрибутивности
A U (В П С) = (A U В) П (A U С),
13
А А (В U С) = (Л А В) U (А А С).
5.	Законы поглощения
Ли (Л А В) = А, ЛА (AU В) = А.
6.	Законы де Моргана
алТв = Л П В, ЛГЁВ = л и в.
7.	Законы нуля и единицы: положим 0^0, 1 В, тогда
Л U 0 = Л, Л А 0 = 0, Л U 1 = 1, Л А 1 = Л,
Л U Л = 1, Л А Л = 0.
8.	Закон двойного отрицания
А = А.
Отметим, что на основании примера 1Л.6 операция \ выражается через операции Пи .По закону де Моргана и закону двойного отрицания справедливо соотношение ЛиВ = Л А В, т. е. операция U также выражается через операции Г) и . По определению операция ф тоже выражается через А и . Таким образом, любая из определенных операций над множествами выражается через операции Гi и
Пересечение и объединение могут быть определены для любого множества множеств А,-, где индексы i пробегают множество 1. Пересечение А{Лг | i £ 1} и объединение U {Л,; | г £ 1} задаются равенствами
А {Лг | i £ 7}	{.?; | х £ Ai для всех i £ 1},
U {Л7 | г £ 1}	{.г: | х £ Л7 для некоторого г £ I}.
Вместо А{Лг | г £ 1} и U {Лг | i £ /} часто пишут соответственно А А-t и U Л,;, а иногда просто АЛг:, иЛг, если из контекста
ясно, какое множество I имеется в виду. Если I = {1,2, то используются записи
Л1 П А? П  •  Г1 А„ и Лг U Лг U • • • U Ап, а также А Лг и и Л,;.
i—l г=1
14
Множество [Аг | i Е /} непустых подмножеств множества А называется покрытием множества. А, если А = U Д. Покры-iei
тие называется разбиением, если A.j C\Aj = 0 при г j. Другими словами, множество {A, | i G 1} непустых подмножеств множества А является его разбиением, если каждый элемент х G А принадлежит в точности одному из подмножеств А,, каждое из которых не является пустым.
Предложение 1.1.1. Следующие условия эквивалентны:
J_) А С В; 2) АП Б = А; 3) А С В = В; Jt) А \ В = 0; 5)A0B = U.
Д о к а з а т е л ь с т в о. 1 => 2. Так как А П В С А, то достаточно показать, что А С В влечет А С А П В. Но если х G А, то по условию х G В, и, следовательно, х G А Г) В.
2	=> 3. Так как А И В = А, то A U В = (А И В) U В. По закону поглощения и закону коммутативности имеем (А И В) И В = В. Тогда A U В = В.
3	=> 4. Предположим, что AUB = В. Так как А\В = АС\В. то по закону де Моргана, закону ассоциативности, закону коммутативности и законам нуля и единицы имеем А\В = А И (A U В) = А П (А П В) = (А П А) П В = О П В = 0.
4	=> 5. Предположим, что А \ В — 0, т. е. А П В = 0. Тогда АГ)В = 0 — 1. По закону де Моргана и закону двойного отрицания получаем U = 1 =_А П В = A U В = AU В.
5	=> 1. Предположим, что АиВ = U и нс выполняется условие А С В, т.—С. найдется элемент х такой, что х G А и х В. Тогда х А и. значит, х A U В, а это противоречит равенству A U В = U. □
Упорядоченную последовательность из п элементов хг, х-ц, ..., хп будем обозначать через (.т,, ,Г2,..., хп) или х^, ..., ,гп). Здесь круглые или угловые скобки используются для того, чтобы указать на порядок, в котором записаны элементы. Будем называть такую последовательность упорядоченным набором. длины п, кортежем, длины п или просто п-кой. Элемент .r.i называется i-й координатой кортежа {х\,х?,... ,хп). В теории множеств кортежи кодируются с помощью операции взятия множества по двум элементам в соответствии со следующими правилами: ( }	0, (tj) xi,	{{.Т]}, {.1],х^}},
(.Т1, .Т2   - , Жп+1)	, Я'2  • • , ••ьу), Хп+] )•
15
Заметим, что две n-ки х = (жх,ж2,...,жл) и у = (ух, У2, • • •, уп) равны (ж — у) тогда и только тогда, когда жд = у\, х? = у%,
• • •; ХП — Уп-
Пример 1.1.7. Пары (1,2) и (2,1) не совпадают, хотя множества {1,2} и {2,1} равны. □
Декартовым, (прямым) произведением множеств Ai, А?, ..., Ап называется множество {(жх,жг, - -  ,жл) | жх G Alt х-2 G А%,  •., п
хп G Ап), обозначаемое через А] х А^ х • •  х Ап или А{. Если г=1
Ai = А2 = • • • = Ап — А, то множество. Ai х А2 х • •  х Ап назы-
вается /7-й декартовой степенью множества, А и обозначается Ап. Положим по определению А0 {0}.
П р и м е р 1.1.8. Пусть А = {1,2}, В = {3,4}. Тогда А х В = {(1,3), (1,4), (2,3), (2,4)}, В х А = {(3,1), (3, 2), (4,1), (4, 2)}, А х А = {(1,1), (1,2), (2,1), (2,2)}.
П р и м е р 1.1.9. (шахматная доска). Рассмотрим два множества А = {а, 6, с, d, е, f, g, h} и В = {1, 2, 3, 4, 5, 6, 7, 8}. Тогда множеству пар (ж, у) G
А х В соответствует множество клеток шахматной доски.
Пример 1.1.10. Множество [О, I]2 равно множеству {(а, Ь)|
0 о 1,0^6^!}, которому соответствует множество точек
на плоскости, имеющих неотрицательные координаты, не превосходящие единицы (рис. 1.2).
§ 1.2. Отношения. Функции. Взаимно однозначные соответствия
Часто при решении задач необходимо выбирать элементы, связанные некоторым соотношением. Примерами таких связей между элементами могут служить функциональные зависимости или отношение “меньше либо равно”.
п-мест.ным отношением, или ?i,-местным. предикатом Р на множествах Ад, Аг,..., Ап называется любое подмножество прямого произведения Ах х Аг х... х А„. Другими словами, элементы жх,Ж2,... ,хп (где жх G Ах,...,Жп G Ап) связаны соотношением Р (обозначается Р(жх,жг,... ,жп)) тогда и только тогда, когда (жх,ж2,    ,ж„) G Р.
16
При п = 1 отношение Р является подмножеством множества Ai и называется унарным отношением или свойством.
Наиболее часто встречаются двухместные отношения (п = 2). В этом случае они называются бинарными отношениями или соответствиями. Таким образом, соответствием Р между множествами А и В является подмножество множества А х В. Если Р С А х В и (ж, у) G Р, то пишут также х Р у.
Отношение Р С А" называется п-местным отношением, {предикатом) на, множестве А.
Пример 1.2.1. Если А = {2,3,4,5,6,7,8}, то бинарное отношение Р = {(х,у) | х,у € А, х делит у и х 3} можно записать в виде Р — {(2,2), (2,4), (2,6), (2,8), (3,3), (3,6)}.
Пример 1.2.2. Рассмотрим отношение Р — {(ж, у) | ж, у G К, х С у} па множестве R Тогда запись х Ру означает, что х ф у, и в качестве имени (обозначения) этого отношения можно взять сам символ ф.
П р и м е р 1.2.3 (ход ладьи). Рассмотрим множество шахматных клеток S = А х В из примера 1.1.9. Определим бинарное отношение С на множестве S по следующему правилу: (ct,C2) € С тогда и только тогда, когда ei,C2 6 S и ладья может пройти с клетки cj на клетку сэ одним ходом на пустой доске (напомним, что ладья за один ход может изменить либо горизонтальную координату, либо вертикальную, но не обе координаты одновременно). Нетрудно заметить, что С = {(с[,С2) | а = (•*>•] ,*1),с2 = («2,^),«1,«2 G A,f.i,t2 е В, И (si = з2 И И ф f2) ИЛИ (si 52 и Н = f2)}- □
Бинарные отношения Р С А х В иногда удобно изображать графически. Рассмотрим два таких представления. Начертим па-
I 14 I -I L I-2 3 4 5 6 7 8
х
Рис. 1.3
17
ру взаимно перпендикулярных осей (Ох горизонтальная ось, Оу вертикальная ось), на каждой оси отметим точки, представляющие элементы множеств А и В соответственно. Отметив на плоскости точки с координатами (х, у) такие, что (х, у) Е Р, получаем множество, соответствующее отношению Р. На рис. 1.3 показано множество точек, соответствующих отношению из примера 1.2.1.
Другой способ состоит в том, что элементы х £ А и у £ В, связанные, отношением Р, соединяются стрелками.
П р и м е р 1.2.4. На рис. 1.4 графически показаны отношение Р] = {(«, 2), (Ь, 1), (с, 2)} между множествами А = {а,Ь,с} иВ- {1,2,3}, а также отношение Рг = {(aib),(b,b), (с,а)} на множестве А. □
Для любого множества А определим тождественное отношение id/ ?=± {(ж,.-г) | х £ А} и универсальное отношение Uд А2. Отношение 1с1д называется также диагональю, a Ua ~ полным отношением.
Пусть Г — некоторое бинарное отношение. Областью определения отношения Р называется множество
Ар ?=± {х | (х, у) £ Р для некоторого у},
областью значений отношения Р — множество
Рр {У \ (ж,у) & Р для некоторого х].
18
Обратным к Р отношением называется множество
Р~[ — {(У,ж) I (®,У) G Р}-
Образом множества X относительно предиката Р называется множество
Р(Х) {у | (х,у) G Р для некоторого х G X}, прообразом множества X относительно Р — множество Р"1(Х) или, другими словами, образ множества X относительно предиката Р''.
Пример 1.2.5. Для отношения Р из примера 1.2.1 и множества X = {3} имеем 6р = {2,3}, рр — {2,3,4,6,8}, Р”1 = {(2,2), (4,2), (6,2), (8, 2), (3,3), (6,3)}, Р(Х) = {3,6}, Р'ДХ) = {3}. □
Произведением бинарных отношений Р± С Ах В и Р2 С В х С или композицией Pi и Р2 называется множество PioP2 = {(ж, у) | х G А, у € С, и найдется элемент z G В такой, что (.t,z) G Pi и (z,y) G Р2} (рис. 1.5). В дальнейшем произведение Pi о Р2 будем также обозначать через Р1Р2.
Предложение 1.2.1. Для любых бинарных отношений Р, Q, В. выполняются следуюгцие свойства:
1)	(Р”1)-1 = р
2)	(Р °	= Q~l ° Р~1;
3)	(Р о Q) о Д = Р о (Q о Р.) (ассоциативностъ композиции).
Д о к а з а т с л ь с т в о. 1. По определению обратного отношения условие (.т,у) G Р равносильно условию (у, .г) G Р"1,
19
что в свою очередь выполняется тогда и только тогда, когда (ж,у) £ (Р-1)-1- Следовательно, Р = (Р-1)-1.
2. Предположим, что (ж, у) G (Роф)-1. Тогда (у, ж) G P°Q, и, следовательно, (у, z) Е Р и (z,x) Е Q для некоторого элемента z. Значит, (ж, z) G Q-1, (z,у) Е Р~х и (ж, у) Е Q~1oP~1. Включение Q~l о Pl С (Р о Q)-1 доказывается аналогично.
3. Пусть (ж, у) G (PoQ)oP. Тогда для некоторых и их имеем (ж, u) Е Р, (u,v) Е Q, (v,y) G R. Таким образом, (щ у) Е Q о R и (ж, у) Е Р о (Q о Л). Включение Р о (Q о Я) С (Р о Q) о Я доказывается аналогично. □
Ассоциативность композиции позволяет обозначать композицию (Р о Q) о Я — Р о (Q о Я.) через PQR. По этой же причине однозначно определена композиция п предикатов (Pi,...,Pn). Отмстим, что существуют предикаты Р и Q, для которых не выполняется закон коммутативности Р о Q — Q о Р (приведите примеры таких предикатов).
Отношение / С А х В называется функцией или отображением из множества А в множество В, если = A, pj С В и из (ж, yi) Е f, {х,уф) Е f следует yi = у2. Если вместо б/ = А выполняется Sf С А, то f называется частичной функцией. Функция f из А в В обозначается через f : А —> В или А Л В. Если (ж, у) Е f, то пишем у = /(ж) (у — значение функции f при значении аргумента х) или f : ж >-> у (функция f ставит в соответствие элементу ж элемент у).
Пример 1.2.6. Отношение {(1,2), (2,3), (3,2)} — функция, отношение {(1,2), (1,3), (2,3)} не является функцией, а отношение {(ж,ж2 — 2ж + 3) | ж Е R} — функция, которая обычно обозначается через у = ж2 — 2ж + 3.
Тождественное отношение 1<1д = {(ж,ж) | ж Е А} является функцией idyi  А А, для которой Мд (ж) = ж для всех ж Е А. Другими примерами функций являются проекции : А х В -> А и тг.^’В : А х В -> В, которые задаются по следующим правилам: я(1,В((а,Ь)) а, ((а,Ь)) Ь. □
Функция f называется разнозначной, инъективной {инъекцией) или 1-1-функцией, если отношение Д1 является частичной функцией, т. е. для любых элементов Ж1.Ж2 Е 6f из жд х-2 сиедуе'г /(ж1) 7^ /(жг)- Если / — инъекция, то будем писать / : А В.
20
Рис. 1.6
Функция f : А —> В называется функцией А на В или сюръективной функцией (сюръекцией), если pj = В. Если f — сюръекция, то будем писать f : А В.
Функция f называется взаимно однозначным соответствием между множествами А и В или биективной функцией (биекцией), если f разнозначное отображение А на В. Таким образом, функция является биекцией, если она инъективна и сюръективна. Если f биекция между А и В, то будем писать f : А <-> В. Биекция f : А <-> А называется подстановкой мно-э/сества А. Простейшим примером подстановки является функция Й1д.
Прим е р L2.7. На рис. 1.6 графически показаны функции f, : [0, 1] —> [0,1] , i € {1,2,3,4}. Функция /1 сюръективна, ио не инъективна, функция /2 инъективна, но не сюръективна, функция /3 биективна и является подстановкой, а функция fa не инъективна и не сюръективна.
П р и м е р 1.2.8. Рассмотрим три функции : R —> R, i = 1,2,3:
1)	функция = ё* инъективна, но не сюръективна;
2)	функция fa(х) = х  sin х сюръективна, пене инъективна;
3)	функция ,/з(.т) -2.7: — 1 биективна.
П р и м е р 1.2.9. Биекцией между множеством натуральных чисел N = {0,1,2,...} и множеством целых чисел Z = {0,±1, ±2,...} является функция f : N —> Z, для которой
/(п) -
т, <
— 771,
если 77, = 2777 — 1, если 71 = 2771.
21
Предложение 1.2.2. 1. Если f : А —> В, </ : В -» С, то fog-.A-^C.
2. Если f : А —> В, то 1с1д ° f = f, f ° ide = /
3. Если f-.A^B,g-.B^C,mofog:A^B.
f. Если f и g — разнозначные отображения, то fog -- разнозначное отображение.
5. Если : А <-> В, д : В <-> С, то f о д : А О С.
С>. Если f : А <-> В, то f1 : В <-> A, f о f~l = id/. f 1 о f = idc.
Д о к а з а т е л ь ств о. Утверждения 1 и 2 очевидны.
3. Достаточно доказать, что для любого с G С найдется элемент а Е А такой, что f о д(а) = с. Поскольку д — сюръекция, найдется элемент b Е В, для которого д(Ь) = с. а. так как f — сюръекция, существует искомый элемент а, Е А такой, что /(а.) = Ь. Следовательно, f о д : А С.
4. Предположим противное, т. е. найдутся элементы Ж|,.'Г2, у такие, что .гд 7^ х2, (xi,y) Е f о д и (х2,у) Е f о д. В силу равнозначности f имеем /(.Т|) -у4 f(x2). Отсюда в силу равнозначности д получаем ,д(/(т1)) -f д(/(х2)), а это противоречит предположению q(/(.Ti)) = у = g(J(x2)).
Доказательство пн. 5 и 6 оставляется читателю в качестве упражнения. □
Если f отображение и Л' С бу, то множество {/(.т)|т Е X} называется образом множества X при отображении f и обозначается через /(А), а отображение /П (А' х pf) называется ограничением, f на X и обозначается через f\x-
Функция J : N —> В называется последовательностью. Ес можно представить в виде /(0), /(1), /(2),... , f(n),... пли /щ, Ь\, ..., Ьп,..., где bn — f(n), п Е N.
Множество всех функций из Ав В обозначается через ВЛ: Вл {/|/ : А -> В}. Функция f : Ап -> В называется п-местной функцией из А в В. Если у - значение п-местной функции / при значении аргумента (яд, х2,..., хп), то пишем у — f(xi, х2,..., Хп). Функция f : Ап —> А называется п-.мес.тной алгебраической операцией на множестве .1. При п. = 1 операция f называется унарной, при п = 2 — бинарной. При п -- 0 операция f : Л° —> А есть {(0,о)} для некоторого а Е А. Часто 0-местную операцию {(0,а)} на А будем называть константой па А и отождествлять с элементом а.
Пример 1.2.10. Операция сложения вещественных чисел
22
является двухместной, т. е. бинарной операцией + : К2 —> R, которая паре чисел (о, Л) ставит в соответствие число а + b по обычному правилу: + (а, Ь) = а + Ь. Любой выделенный элемент множества R, например \/2, является 0-местной операцией, т. е. константой на R. □
Очевидно, что n-местная операция на множестве А является (п + 1)-местным отношением на том же множестве А.
§ 1.3.	Натуральные числа.
Принцип математической индукции
Рассмотрим два подхода к заданию множества натуральных чисел. Первый подход — конструктивный — позволяет представлять натуральные числа в виде объектов, построенных из пустого множества. Второй подход — аксиоматический. Согласно этому подходу натуральные числа образуют множество, удовлетворяющее некоторому набору свойств (аксиом), и при этом природа элементов множества не важна. Таким образом, с одной стороны, указывается множество натуральных чисел, а с другой стороны — все существенные (определяющие) свойстве! этого множества.
Положим по определению 0	0,1	{0} = {0}, 2
{0,1} = {0, {0}},  - п = {0,1,..., п — 1}, ... Множества, обозначаемые 0, 1, 2, ..., называются натуральными числами. Объединив эти множества, получаем множество всех натуральных чисел {0,1,2,..., п,...}, обозначаемое через ш.
В силу обозначений предыдущего параграфа, если А = п = {0,1,...,п - 1}, В = 2 = {0,1}, то 2'4.— ВА = {/|/ : п -> {0,1}}. Это обозначение согласуется с тем, что в множестве ВА имеется ровно 2п функций. Действительно, поскольку функция f на аргументе-г G п может принимать одно из двух значений 0 или 1 и таких элементов i ровно п, то всего имеется 2-2-.. .-2 = 2" различных функций.
Аналогично имеем 2Ш = {/ | / : ш —> {0,1}} — множество, состоящее из всех последовательностей нулей и единиц.
Как уже отмечалось, второй подход к определению множества натуральных чисел является аксиоматическим. Мы рассмотрим аксиоматику Дедекинда — Пеано.
Пусть имеется некоторое множество N, в котором выбран
23
элемент, обозначаемый через 0, и функция, которая произвольному элементу п Е N ставит в соответствие элемент п! G N, называемый непосредственно следующим (элемент п' играет роль числа п + 1). Таким образом, с помощью функции п п' можно однозначно найти элементы О', О", О'" и т. д. (элемент 0^’^ играет роль числа п). Множество N называется множеством натуральных чисел, если система N = (УМ, 0, ') удовлетворяет следующим аксиомам:
1)	для любого т 0 найдется п G N такой, что п' = т;
2)	для любых т,п Е N, если т' = п', то т = п;
3)	п' 0 для любого п Е 7V;
4)	(аксиома математической индукции) для любого свойства Р (унарного отношения на множестве N), если Р выполняется на элементе 0 (т. е. 0 обладает свойством Р), и для любого п Е N из"выполнимости Р на элементе п следует выполнимость Р на элементе п', то свойство Р выполняется на любом элементе п Е N.
Последняя аксиома является наиболее содержательной, она символически записывается следующим образом:
VP((P(0),Vn(P(n) => Р(п')) => VnP(n)},
а также
Р(0), Vn(P(n) => Р(п + 1))	0 G Р, \/п(п е Р => (п + 1) Е Р)
VnP(n)	ШШ	P = N
Итак, утверждение “для любого п Е N выполняется Р(п)” считается доказанным, если установлены базис индукции (доказано Р(0)) и индукционный шаг (доказано, что для любого n Е N справедливо Р(п + 1) в предположении, что выполняется Р(п)). В этом состоит принцип математической индукции.
Принцип математической индукции позволяет также давать индукционные определения, т. е. определения понятий Р(п) для всех натуральных чисел п, построенные по следующей схеме:
1) задается значение Р(0),
2) задается правило получения значения Р(п. -I- 1) по числу п и значению Р(п).
Определим по индукции операции сложения а + b и умножения а  b на натуральных числах. Положим а + 0 а (базис индукции). Если известно значение а + п, то а 4- п' (а + п)'
24
(индукционный шаг). Аналогично а • 0	0. Если задано а  п, то
а. • п' (а. • п) + а.
Используя операцию сложения, можно ввести отношение С на множестве натуральных чисел: а Ь <=> Зс(а + с = Ь).
Определим по индукции функцию п! (п-факториал): 0!	1,
(п + 1)! ;= п!  (п + 1).
Пример 1.3.1. Докажем по индукции неравенство Бернулли: (1 + а)п 1 + ап для всех п G N п а > — 1, a. G R.
При п = 0 неравенство имеет вид (1 + а)0	1 + а  0 и оно
справедливо, т. е. базис индукции выполняется. Установим справедливость индукционного шага. Предположим, что
(1 +а)"	1 +<ш,	(1.1)
и покажем, что
(1 + o)n+1	1 +а(п + 1).	(1.2)
Умножим обе части неравенства (1.1) на положительное число 1 + а. Тогда (1 + а)”(1 + а) > (1 + <ш)(1 + а), т. е.
(1 + а)"+1	1 + а + ап + а2п.	(1.3)
Поскольку о2 0, имеем
1 + а. + ап + а2п 1 + а. + ап = 1 + а(п + 1).	(1-4)
Из неравенств (1.3) и (1.4) получаем неравенство (1.2). На основании принципа математической индукции заключаем, что (1 + о.)'!	1 + ап для всех п & N. □
Иногда удается установить только выполнение F(fc) для некоторого к > 0 и свойство Р(п) => Р(п + 1) для всех п к. Тогда по принципу математической индукции свойство Р выполняется для всех п к:
Р(к), Vn^k (Р(п) => Р(п + 1)) Vn к Р(п)
Другой эквивалентной формой принципа математической индукции является принцип полной индукции:
25
если для всякого п G N из предположения, что Р(к} верно при любом натуральном к < п. следует, что Р(к) верно также при к = п, то Р(п) верно при любом натуральном п:
Vn((Vfc < п Р(А:)) =>Р(п)) \/п Р(п)
Эта форма используется в том случае, когда для доказательства выполнимости P(n + 1) необходимо использовать выполнимость свойства Р не только на элементе п, но и на некоторых предыдущих элементах.
§ 1.4.	Мощность множества. Конечные и бесконечные множества
Понятие мощности возникает при сравнении множеств по числу элементов.
Множества А и В называются эквивалентными (обозначается А ~ В), если существует биекция f : А о В.
Отметим, что для любых множеств А, В, С выполняются следующие свойства:
1)	А ~ А (поскольку idzi : А <-> А);
2)	если А ~ В, то В ~ А (так как из f : А о В следует f 1 : В О А):
3)	если А ~ В и В ~ С, то А ~ С (так как из f : А о В, д : В о С следует’ f о д : А <-> С).
Мощностью множества А называется класс всех множеств, эквивалентных множеству А (обозначается |А|). Эквивалентные множества А и В называются равномощными: |А| = |В|. Если А ~ п для некоторого п G щ т. е. А имеет ровно п элементов, то множество А называется конечным,. В таком случае пишут: |А| = п. Таким образом, мощностью конечного множества является число его элементов.
Множество, не являющееся конечным, называется бесконечным,. Если А ~ щ то множество А называется счетным: |А| = и. Если А ~ 2Ш, то множество А называется континуальным или континуум,ом: |А| = 2Ш.
На мощность множества А можно смотреть и как на новый объект, называемый кардинальным числом или кардиналом. В качестве примеров кардиналов можно взять любое натуральное число п, а также и, 2Ш, 22“ и т. д. Эти числа можно рассматривать как имена, обозначающие соответствующие мощности.
26
Кардинальным числом конечного множества служит число его элементов.
Существование биекции между двумя эквивалентными множествами позволяет переносить изучение свойств с одного множества на другое, когда природа элементов не важна. Например, если |А! — п. то с элементами множества А можно работать как с числами 0,1,2,... , и — 1, которые являются элементами множества п.
Говорят, что мощность множества А не превосходит мощности множества В: |А| < |В|, если А эквивалентно некоторому подмножеству множества В. Мощность множества А меньше мощности множества В: |А| < |В|, если |А|	|В| и |А|	|В|.
Теорема 1.4.1 (теоремаКантора — Бернштейна). Если |А| |В| и |В|	|А|, то |А| = |В|.
Д о к а з а т е л ь с т в о. Пусть f : А —> В, g : В —> А — разнозначные отображения, Aq — A, Ai — у(В) и An+2 = (/°<7)(А„). Индукцией по п легко доказать, что A„+J С An, n G ш. Пусть D = П А^ и Mi = Аг \ Aj+i- Очевидно, что /Д — ( U Мг) U В к(Дд	к<д(Ра>
и Mi Г\ Mj = 0 при i j. Так как / о g разнозначно отображает Mi на Mi+-2 для любого г G ш, то отображение h : А -> А, определенное следующим образом:
{а,	если а G ( U Мь-щ) О В,
(/° <?)(«), если a G U M2l,
является разнозначным отображением А на А, = ( U MpUD.
Так как |В| = |Aj|, то |В| .= |А(. □
Следствие 1.4.2 (теорема о сравнении множеств). Для любых множеств А и В существует одна и только одна из следующих возможностей: |А| — |В|, |А| < |В|, |В| < |А|.
Определим на кардинальных числах операции сложения, умножения и возведения в степень. Если |А| = ст, |В| = /3, то сс + fl |А U В|, где А П В = 0; а • fl |А х В|; |АВ|. В случаях, когда ст,/3 G ц>, введенные таким образом операции совпадают с обычными операциями на натуральных числах. Для конечных кардиналов справедливы следующие три правила, используемые в комбинаторике.
27
Правило суммы. Если |А| — т, |В| = п, то |А U В\ — т + п — |А П В|, и |А U В| = т + п в том и только том случае, когда АПВ = 0.
Правило произведения. Если |А| = т. |В| = п, то
|А х В| — т  п.
Правило степени. Если |А| = т, |В| = п, то |АВ| = тп.
Следующее утверждение показывает, что операции па бесконечных кардиналах могут иметь “необычные” свойства.
Предложение 1.4.3. са2 ~ щ.
Доказательство. По определению множество са2 = ш х ш равно {(m, z?,)|m, п G и}. На координатной плоскости изобразим точки с натуральными координатами (т, п) (рис. L7).
Очевидно, что все эти точки расположены в первой четверти. Для доказательства утверждения требуется установить биекцию между множеством натуральных чисел и полученными точками, т. е. перенумеровать точки. Нумеруем точки “по диагонали”: 0 ь-> (0,0), 1	(0,1), 2	(1,0),
3 ь-> (0,2), 4 ь-> (1,1), 5 ь-> (2,0), 6	(0,3), 7	(1,2) и
т. д. Так как указанная ну-
рис J 7	мерация разнозначна и каж-
дая пара натуральных чисел имеет натуральный номер, то это отображение осуществляет взаимно однозначное соответствие w вы2. □
Упражнение. 1. Используя принцип математической индукции, показать, что а>п ~ и для любого п £ а> \ {0}.
2. Используя установленный в примере 1.2.9 факт, что Z ~ щ доказать эквивалентности са + са ~ со и Z” ~ со.
Предложение 1.4.4. w ~ U шп.
nQw
Доказательство. Так как для любого п G са существует биекция fn : ш <-> и", то достаточно установить, что найдется биекция </? : ш О ( U {(п, к) | к Е сД) U {0}, т. е. IjCziCcj
28
р : w о {(n, fc) | n, к G w, n 1} U {0}. Биекция ip легко строится с помощью биекции ip : ш w2 из предложения 1.4.3.: </?(0) = 0, />(ш + 1) — (n + 1, к), где ip(m) — (п, к), т G ш. □
Предложение 1.4.5. |Q| — ш.
Доказательство. Поскольку множество рациональных чисел Q состоит из дробей вида где т G Z, п G ш \ {0}, его можно представить в виде множества пар (т,п). Так как множество таких пар содержится в Z2, a |Z2| = ш, то |Q| < ш. С другой стороны, очевидно, множество Q бесконечно, т. е. |Q| ш. По теореме Кантора — Бернштейна заключаем, что |Q| = ш. □
Теорема 1.4.6. (ТДИ)] = 2^1 для любого множества U.
Доказательство. Очевидно, что любом)' подмножеству А С U взаимно однозначно ставится в соответствие индикаторная функция f G 2(, для которой
/(®) =
0,
1,
если х А, если х G А,
т. е. V(U) ~ 2и. Осталось заметить, что 2Н;1 = |2г/|. □
Теорема 1.4.7 (теорема Кантора). Выполняется |В| < 2^'^ для любого множества U.
Доказательство. В силу теоремы 1.4.6. достаточно доказать, что |П| < |Р(17)|. Так как отображение f : U —> Р(С7), действующее по правилу f(x) = {ж}, является разнозначным, то |(/| < |7’(С7)|. Предположим, что |77| — |P(t7)|. Тогда существует биекция ip : U о P(U). Рассмотрим множество К = {ж G U | х f(x)}. Поскольку f — биекция и К С U, т. е. К 6 P(U), то существует к 6 U такое, что f(k) = К. Если к € К, то из определения К получаем к f(k) = К. Если же к К, то к f(k) и, следовательно, должно выполняться к € К. Полученное противоречие показывает, что биекции / существовать не может. □
Предложение 1.4.8. Если |А| >ш и |В| то |А\В| = |А|.
Доказательство. Так как |В| < ы, то |А ПВ| ш. Рассмотрим множество С со следующими условиями: А 0 В С С С А, |С \ (А П В)| — Такое множество С существует, поскольку по условию имеем |А \ В| > ш. Так как С — (С\ (А П В))и(АпВ), то |С| = ш и существует биекция f : С\(АОВ) е-> С. Искомая биекция : А \ В <-> А строится по следующим прави
29
лам: <Дт) = х, если х G А \ С, = /'(ж), если х G С \ В. □
Предложение 1.4.9. 2Ш ~ 10ь; ~ оЛ.
Доказательство. Поскольку неравенства 2Ш Д 10ш Д <лш очевидны, достаточно доказать неравенство Д 2Ш, т. е. существование функции <р :	—-ч- 2Ш, которая кодирует все-
возможные последовательности натуральных чисел с помощью последовательностей, состоящих из нулей и единиц. Для последовательности f G определим последовательность </?(/) € 2Ш по следующим правилам:
1,1,..., 1,0,1,1,..., 1,0,..., 1,1,..., 1,0,...
/(0) раз /(1) раз	f(n) раз
Очевидно, что если Д /2 (Д, Д G то <ДД) <ДД). □
Предложение 1.4.10.	[0,1].
Доказательство. Равенство мощностей отрезка Ц = [0,1] и интервала /2 = (0,1) обеспечивается биекцией ip : Д <-> /2, задаваемой по следующему правилу:
если ж ^4 0,т /	\ {0},
если х = 0, если х = 1, если х = п > 1.
В свою очередь, биекция Д(.т) ~ tg(7r(-T— ^)) (рис. 1.8) определяет эквивалентность интервала /2 и множества К. Следовательно, [0,1]. □
Предложение 1.4.11. Множество вещественных чисел К контш суальч ю.
Доказательство. В силу предложений 1.4.9. и 1.4.10. достаточно установить, что 10ш ~ [0,1]. Рассмотрим множество X = {/ G 10ш|/(7п) Д 9 для некоторого т € <д и существует к 6 ш такое, что /(п) = 9 для всех п > к}. Так как множество 10ш \ X взаимно однозначно соотвествует множеству бесконечных десятичных дробей, задающих числа из [0,1], то по теореме Кантора и предложению 1.4.8. остается показать, что множество X счетно. Нетрудно заметить, что множество X эквивалентно множеству U и>п, поскольку каждая функция f G X однознач-
TlEbJ
но определяется кортежем цифр (/(0),..., f(k)), где f(k) 49 и
30
Рис. 1.8
/(n) = 9 для всех п > к. Теперь из предложения 1.4.4. получаем X ~ U ш’1 ~ щ т. е. |А' | = ш. □
§ 1.5.	Матрица бинарного отношения.
Специальные бинарные отношения
Рассмотрим два конечных множества А = {<ц,	, ат}.
В —	.. • ,bn} и бинарное отношение Р С А х В. Определим
матрицу [Р] = (р?/) размера m х и бинарного отношения Р по следующему правилу:
PlJ = о, ч
если (аг ,bj) Е Р, если (ai,bj) Р.
Полученная матрица содержит полную информацию о связях между элементами и позволяет представлять эту информацию на компьютере. Заметим, что любая матрица, состоящая из нулей и единиц, является матрицей некоторого бинарного отношения.
П р и м е р 1.5.1. Матрица бинарного отношения Р С А2,
31
A = {1,2,3}, заданного на рис. 1.9, имеет вид
/ ! 1 i \ [F] = I 0 0 1 .
\ 1 0 0 /
Отметим основные свойства матриц бинарных отношений.
1.	Если F, Q С А х В, [Р] = (рч), [Q] = (<?„), то [F U Q] = (Pij + ft?) и [Р П Q] = (pij  qij), где сложение осуществляется по правилам 0 + 0^0, l + l^l + O^O + l^l, а умножение — обычным образом. Итак, [Р U Q] = [F] + [Q], а матрица [F П Q] получается перемножением соответствующих элементов из [F] и [Q]:[FnQ] = [P]*[QL
Пример 1.5.2. Пусть [Р] = (о ? i )> [Q] = (о о 1) “ матрицы отношений Р и Q.
Тогда
Гп,,Л1 Гп1 . FZM	Л 0	1\	/0	1	1\	/1	1	1\
[F U Q] - [F] + [Q] - х	1J	+ (^о	0	1/ ~ (б	1	1J	’
ГгЯ FZM Л 0 1\	/0 1 1\	/0 0 1\ „
[Р П Q] - [F] * [<5] - х * (^0 о 1J ~ (^0 0 iy  П
2.	Если F С А х В, Q С В х С, то [F о Q] = [Р] • [Q], где умножение матриц [F] и [Q] производился по обычному правилу умножения матриц, но произведение и сумма элементов из [F] и [Q] — по определенным в п. 1 правилам.
32
П р и м е р 1.5.3. Если [F] = (J } р ), [Q] = (1 о), то
/О 1 (А I 1
[poQl= I о • 1 °
\ / \ 1 1
3.	Матрица обратного отношения Р 1 равна транспонированной матрице отношения Р: [F“l] = [F]1.
4.	Если Р С Q, [F] = (у^), [Q] = (тд?), то pij qij.
5.	Матрица тождественного отношения icl.i единична:
/1 0	0\
О 1    о
\0 0 ••• 1/
Пусть Р — бинарное отношение на множестве А:РСА2. От-
ношение Р называется рефлексивным, если (ж, ж) G Р для всех
А
х G А, т. е. iclx С Р, [F] =
Отношение F назы-
\ * '1/
вается симм,етричным, если для любых х,у G А из (ж, у) Е Р следует (у. ж) G F, т. е. F”1 = F. или [F]1 = [F]. Отношение F называется антисимметричным, если из (ж, у) € F и (у, ж) € F следует, что ж = у, т. е. F П F-1 С icl.y. На языке матриц это означает, что в матрице [Р П F”1] = [F] * [F]1 все элементы вне главной диагонали являются нулевыми. Отношение F называется транзитивным, если из (ж, у) G F и (у, г) G F следует (ж, z) G F, т. е. F о F С F.
Отметим, что антисимметричность не совпадает с несимметричностью. Действительно, отношение F — {(1,2), (2,3), (3,2)} на множестве А = {1,2,3} не симметрично (так как (1,2) G F, а (2.1) F) и не антисимметрично (поскольку 2	3, но (2,3) G F
и (3,2) G F). Тождественное отношение icL| является одновре
менно симметричным и антисимметричным.
П р и м е р 1.5.4. Проверим, какими свойствами обладает отношение F С А2, А = {1.2,3}, изображенное па рис. 1.10. Составим матрицу отношения F: [F] = ( о 1 I). Так как в матрице
2 Зак. Na 4872 Судоплатов
33
[F] на главной диагонали имеются нулевые элементы, отношение Р не рефлексивно. Несимметричность матрицы [F] означает, что отношение Р не симметрично. Для проверки антисимметрично-
Поскольку в полученной матрице все элементы, стоящие вне главной диагонали, нулевые, отношение Р антисимметрично. Так как [PoF] = [Р] (проверьте!), то РоР С Р, т. е. Р является
транзитивным отношением.
3	При м е р 1.5.5. Отношение < =
{(ж, у) | х, у G Q и х < у} на множестве /	рациональных чисел Q не рефлексив-
/	но, не симметрично, антисимметрично
/	и транзитивно.
/	 Пример I.5.G. Рассмотрим отно-
1 Рис. 1.10	шение Р = {(х.у) | х,у G Z и х-у < 1}
на множестве целых чисел Z.
Так как х — х = 0 < 1 для любого х Е Z, отношение Р рефлексивно. Поскольку (2,4) G Р, а (4,2) ф Р, отношение Р не симметрично. Заметим, что если х — у < 1 и у — х < 1, то х = у, так как из х у следует |т — у\ 1. Таким образом, отношение Р антисимметрично. Предположим теперь, что (ж, у), (у, z) G Р. т. е. х — у < 1 и у — z < 1. Имеем х < у и у < z, тогда ж < z, значит, ж — z < 1, т. е. (ж,г) G Р. Следовательно, отношение F
транзитивно.
§ 1.6.	Отношения эквивалентности и разбиения.
Фактор-множества
Отношение F называется отношением эквивалентности (эквивалентностью), если Р рефлексивно, симметрично и транзитивно. Эквивалентности часто обозначают символами Е и ~ (тильда): хЕу, х ~ у.
П р и м е р 1.6.1. 1. Отношение равенства х = у является эквивалентностью на любом множестве А, так как оно рефлексивно (х = ж), симметрично (ж = у => у = ж) и транзитивно (х = у, у = z => х = z).
34
2.	Отношение подобия на множестве треугольников есть отношение эквивалентности.
3.	На любом множестве P(U) отношение равномощности |А| — | £>| является отношением эквивалентности (см. § 1.4).
4.	Отношение принадлежности к одной студенческой группе на множестве студентов НГТУ отношение эквивалентности.
5.	Рассмотрим множество М программ, вычисляющих некоторые функции. Отношение Е = {(ж, у) | программы х и у вычисляют одну и ту же функцию} является эквивалентностью. □
Пусть Е эквивалентность на множестве А. Классом эквивалентности элемента х Е А называется множество Е(х) = {у | хЕ у}. Классы эквивалентности Е будут также называться Е-классами. Множество А/Е = {1?(ж)|ж Е А} называется фактормножеством множества А по отношению Е.
П р и м е р 1.6.2. Г.Для отношения равенства = на множестве А каждый =-класс состоит только из одного элемента: = (.т) = {ж} для .любого х Е А. Таким образом, фактор-множество А/~ имеет вид {{ж} | х Е А} и, следовательно, биективно множеству А.
2. Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы. Фактор-множество множества студентов НГТУ по этому отношению эквивалетности представляет собой множество студенческих групп НГТУ.
Предложение 1.6.1. Множество А/Е является разбиением множества А. Обратно, если 76 = {АД - некоторое, разбиение множества А, то можно задать соответствующее ему отношение эквивалентности Е по следующему правилу:
хЕу х,у Е А., для некоторого i.
Доказательство. Пусть Е — отношение эквивалентности на множестве А, А/Е фактор-множество множества А по Е. Так как в силу рефлексивности отношения Е выполнимо х Е Е(х) для любого х Е А. то каждое множество из А/Е непусто и U Н(•'.:) = А. Чтобы установить, что А/Е — разбиение хЕ-4
множества А, осталось показать, что если Е(х) А Е(у) Д 0, то Д(.т) = Д(у).
Пусть z Е Е(х) Г)Е(у) и и Е Е(х), т. е. (ж, z), (y,z), (х,и) Е Е. Так как отношение Е симметрично, (г. ж) Е Е. Тогда из транзитивности отношения Е следует {у, и) Е Е, г. е. и Е Е(у). Таким
2*
35
образом, Е(х) С Е(у). Включение Е(у) С Е(х) доказывается аналогично.
Предположим, что Е — отношение на множестве А. соответствующее разбиению 7Z = {А}- Рефлексивность и симметричность Е очевидны. Пусть теперь а: Е у и yEz. Тогда ж,?/ G А, у, z G Av где Ai. Aj G 11. Поскольку у G А,- и у G Aj, то А = А-Следовательно, x.z G Л, и xEz. □
Таким образом, существует биекция между множеством всех отношений эквивалентности на множестве А и множеством всех разбиений множества А.
В любом классе Е(.т) эквивалентности Е каждый элемент у G Е(х) связан отношением Е с любым элементом z G Е(х). Поэтому если Е — эквивалентность на конечном множестве А, А/Е = {Е(.Г1),.... Е(:г„)}, E(.tJ = {Ь\,...,Ьгт.}. i = 1,...,п и множество А перенумеровано в следующем порядке: b{...., Ь* ,Ь^,..., Ь„, ,.... 6'1,   • . т0 матрица [Е] имеет блочно-диагональный вид:
где блоки 1 состоял из единиц, а остальные элементы равны 0.
Если же множество А перенумеровано произвольным образом: А = {ai,... ,а„}. Е — отношение эквивалентности па А. то матрица [Е] = (егу) приводится к блочно-диагональному виду некоторыми одновременными перестановками строк и столбцов.
Элементы и a.j эквивалентны по отношению Е тогда и только тогда, когда г-я и j-я строки (а также столбцы) матрицы [Е] совпадают. Класс эквивалентности Е(щ) состоит из элементов aJt ДЛЯ КОТОРЫХ Cij = 1.
П р и м е р 1.6.3. Рассмотрим множество А = {1. 2, 3, 4, 5} с разбиением 71 = {{1.3,5}, {2.4}}. задающим отношение эквивалентности Е с двумя Е-классамп {1.3.5} и {2,4}. Матрица [Е]
36
(1 0 1 О 1 \ 010101 „ 10 10 1 .По этой матрице легко определить, что 10 10 1/
класс 15(3) равен {1,3,5}, так как в 3-п строке только в;л, е.33 и с-35 равны 1.
П р и м е р 1.6.4. Рассмотрим геометрическое векторное пространство £3 и множество направленных отрезков в нем. Направленные отрезки и А9В2 называются эквивалентными: A[Bi ~ A‘iB'2, если они имеют одинаковые длину и направление. Отношение ~ - это отношение эквивалентности. Вектором (геометрическим вектором,) it в £3 называется класс эквивалентности направленных отрезков it = ~ (А$) для некоторого Л/5). Фактор-множество множества направленных отрезков по отношению ~ образует множество векторов пространства £3.
§ 1.7. Отношения порядка
Отношение эквивалентности является обобщением отношения равенства: эквивалентные элементы считаются “равными”. Обобщением обычного отношения < служат отношения порядка.
Отношение Р С Аг называется предпорядком или квазипорядком, если Р рефлексивно и транзитивно.
П р и м е р 1.7.1. Отношение Р = {(1,1), (2,2), (3,3), (1, 2), (2, 1), (2,3), (1,3)} на множестве {1,2,3} является Чредпоряд ком (рис. 1.11). □
Отметим, что симметричный предпоря-док является отношением эквивалентности.
Отношение Р С А2 называется частич- XI/ ним порядком,, если Р рефлексивно, трап-	//	х,
зитивно и антисимметрично. Таким обра- <Лг—-----------~ЧЗ~)
зом, частичный порядок - это антисимметричный предпорядок. Частичный порядок Рис. 1.11 обычно обозначается символом ф. а обратное ему отношение — символом Отношение У также является частичным порядком и называется двойственным порядку ф Используя отношение ф определим отношение <, называемое строгим порядком, по следующему правилу: ;с < у <=> х у и х у. Заметим, что отношение строгого порядка нс является частичным порядком, гак как не выполняется условие рефлексивности (неверно, что х < х).
37
Пример 1.7.2. Частичным порядком является обычное отношение на множестве N. Действительно, это отношение рефлексивно (а:	х), транзитивно (х бу, у г => ж z) и
антисимметрично (а; у, у х => х = у).
Пример 1.7.3. Отношение, изобра-Q___________Q женное на рис. 1.12, является частичным по-
а	b рядком, а отношение из примера 1.7.1 — нет.
При м е р 1.7.4. Отношение включения V	С на булеане P(U) образует частичный по-
с	рядок. □
Рис. 1.12	Заметим, что в примерах 1.7.3 и 1.7.4 име-
ются элементы ж и у, про которые нельзя сказать, что ж у или у < х (например, при а = х, у — с из примера 1.7.3). Такие элементы пазываютя несравнимыми. Частичный порядок Л2 называется линейным порядком, если любые два элемента ж и у из множества А сравнимы, т. е. х у или у а; (линейным является частичный порядок из примера 1.7.2).
Непустое множество А, на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно) упорядоченным множеством (сокращенно ч.у.м. или л.у.м.).
П р и м е р 1.7.5. Пары (ш, $С), ([0,1], ^) с обычными отношениями < образуют линейно упорядоченные множества. □
Пусть (Л, <) — частично упорядоченное множество. Определим на множестве А2 отношение П условием (ai, &г) П (аг, Ьг) «1 $ а.2 и bi < b-2- Отношение П есть отношение частичного порядка. Оно называется отношением Парето. Пара (Л2,П) образует частично, но не линейно упорядоченное множество, если |Л|>1.
Элемент a G А частично упорядоченного множества 21 = (А, ^) называется максимальным (минимальным), если для всех х G А из а. < а; (х. < «) следует х = а. Элемент а Е А называется наибольшим (наименьшим.), если х а (а С х) для всех х Е А. Наибольший (наименьший) элемент ч.у.м. 21 (если он существует) обозначается через шах 21 (min 21). Наибольший элемент часто называют единицей, а наименьший — нулем множества 21. Заметим, что всякий наибольший элемент является максимальным. а всякий наименьший элемент — минимальным. Обратное утверждение, вообще говоря, неверно (см. пример 1.7.6). Всякое конечное ч.у.м. содержит как максимальные, так и минимальные элементы.
38
П р и мер 1.7.6. Ч.у.м. ({1,2,3},^), изображенное на рис. 1.13, имеет наибольший элемент 2, минимальные элементы 1, 3, но не имеет' наименьшего элемента.
q,	П р и м е р 1.7.7. Л.у.м. ([0,1), име-
ет наименьший элемент 0, но не имеет наи-'ДИЭ большего элемента. □
Пусть 21 = (Л,	-- ч.у.м., В — под-
множество А. Элемент a G А называется верхней (нижней) гранью множестве! В, ис' . если b а (а ф Ь) для всех b G В.
П р и м е р 1.7.8. Рассмотрим ч.у.м. (1R, и интервал В = [0,1]. Тогда любое число х 1 является верхней гранью В, а любое число х 0 — нижней гранью В. □
Элемент а € А называется точной верхней гранью (супремумом) множества В (обозначается sup В), если а, — наименьшая из верхних граней множества В. Элемент a. G А называется точной нижней гранью (инфимумом) множества В (обозначается inf В), если а — набольшая из нижних граней множества В.
В примере 1.7.8 имеем sup В = 1. inf В = 0.
Линейный порядок на множестве А называется полным, если каждое непустое подмножество множества А имеет наименьший элемент. Пара (А, ^), в которой отношение является полным порядком на множестве А, называется вполне упорядоченным множеством (сокращенно в.у.м.).
П р и м е р 1.7.9. Пара (ю, <() является в.у.м., в то время как пара ([0,1],^) — нет, поскольку, например, полуоткрытый интервал (1/2,1], являющийся подмножеством [0,1], не содержит наименьшего элемента. □
Определим отношение, на котором основано упорядочение слов в словарях.
Рассмотрим непустое множество символов X = (х, у, z, ...}, называемое алфавитном. Конечные наборы написанных друг за другом символов из X называются словами (например, х, у, ху, ух, zxx, xyyz и т. д.). Элемент Х{ слова хгх? ... хп называется его i-й координатой. Число п называется длиной слова хрх? ...хп. Множество слов алфавита X обозначим через W (X). При этом будем считать, что W(X) содержит слово Л, не имеющее символов и называемое пустым словом. Длина пустого слова Л по определению равна нулю. Заметим, что каждое слово хрх?    хп из W(X) взаимно однозначно соответствует упорядоченному на
39
бору (з,'1,з,'2; • -. ,хи) из Хп. Следовательно, множество ГУ(Х) биективно множеству U Хп, и, значит, бесконечно.
71 (Щ
Пусть - отношение порядка на множестве X. Определим на множестве ИДУ) отношение лексикографического порядка С по следующему правилу: хух2 . •  хт £у\У2    Уп <=> (т п и х = у для всех 1 i т), или (существует г т такое, что x-i < yi, и для всех j < г выполняется х7 = у
Утверждение 1.7.1. Если {X,	- л.у.м., то (W(X), £) -
л.у.м.	'
Д о к а з а т е л ь с т в о. Рефлексивность и транзитивность отношения £ очевидны. Для проверки антисимметричности предположим, что Х\Х2.  .Хт£у\У1-  - Уп И УуУ2-.- уп£х\х2  -хт. Так как отношение антисимметрично, не существует i такого, что x-i yi и x,j — у3 для всех j < i. Тогда по определению отношения £ получаем т п, п т, т. е. т = п, и х\х2    хт = У\У2    Уп- Покажем теперь, что любые два слова X = .щ.'лу • •  хт и У = У1У2    Уп сравнимы. Пусть i — максимальный индекс, такой, что Xj — y.j для всех j < i. Если ;с, < yi или i = т + 1 п, то X £Y. Если yi < хг или i = п + 1 т, то У £Х. Если же указанные случаи не выполняются, то т = п = г — 1 и X = У. □
Как показывает следующий пример, если |Х|	2, система
(W(X),£) не является в.у.м.
Пример 1.7.10. Рассмотрим в.у.м. (X, ^), где X = {0,1}.
{(0,0), (0,1), (1,1)}. Бесконечное множество, состоящее из слов 1,01,001,...,00... 01,..., не имеет наименьшего элемента но отношению £. Следовательно, система (ИДУ), У) не является в.у.м. □
Обозначим через 1ЕДХ) множество слов алфавита X. длина которых не превосходит п, через £,, — ограничение отношения £ на множество 1УДХ): £„	£ Г) (ИД(Х))2.
Утверждение 1.7.2. Если {X,	- в.у.м., то (ИД(Х),
£п) - в.у.м. для любого п Е uj.
Д о к а з а т е л ь с т во. В силу утверждения 1.7.1. достаточно показать, что любое непустое подмножество У множества Wn(X) имеет наименьший элемент по отношению £п. Если Л G У, то Л является наименьшим элементом. Предположим теперь, что Л У. Рассмотрим множество У] С У. состоящее из слов, у которых первая координата является наименьшей среди первых
40
координат слов из У. Если У1 содержит слово длины 1, то оно будет наименьшим элементом множества У. В противном случае рассмотрим множество У2 С У1; состоящее из слов, у которых вторая координата является наименьшей среди вторых координат слов из Ур Если У2 содержит слово длины 2, то оно будет наименьшим элементом множества У. В противном случае аналогично определим множество Уз и будем продолжать построение множеств У/с до тех пор, пока в У}. не найдется слова длины к, которое: будет наименьшим элементом множества У. По определению множества ЖП(Х) такое слово определится не более, чем за п шагов. □
П р и м е р 1.7.11. Рассмотрим множество букв русского алфавита, которое обозначим через А. Определим на А полный порядок в соответствии с обычным упорядочением букв по алфавиту. Пусть п — натуральное число, ограничивающее длину слов, употребляемых в русском языке, например, ??, = 1000. Отношение Сп на множестве 11’„ (/1) определяет упорядочение слов, по которому составляются словари. □
Рассмотрим частично упорядоченное множество (Л, С) - Говорят, что элемент у покрывает элемент х, если х С У и не существует такого элемента z, что х < z < у. Если множество А конечно, частично упорядоченное множество (Л, можно представить в виде схемы, в которой каждый элемент изобра
жается точкой на плоскости, и если у покрывает ж, то точки х и у соединяют отрезком, причем точку, соответствующую х, располагают ниже у. Такие схемы называются диаграммами Хассе. На рис. 1.14 показаны две диаграммы Хассе. Вторая диаграмма соответствует линейно упорядоченному множеству.
При м е р 1.7.12. 1. Рассмотрим частично упорядоченное множество (Р(А),С), где А = {1,2.3}. Множество Р(Л) содержит восемь элементов: {0, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}. {1,2,3}}. На рис. 1.15а изображена диаграмма Хассе, соответствующая (Р(А),С).
2. Пусть /1 = {1, 2, 3, 5, 6, 10, 15, 30}. Рассмотрим отношение частичного порядка < на множестве А, задаваемое по правилу: х < у <=> у делится на х. Диаграмма Хассе для ч.у.м. (Л, изображена на рис. 1.156.
а б
Рис. 1.14
41
Рис. 1.15
3. На рис. 1.15в изображена диаграмма Хассе линейно упорядоченного множества ({0,1,2,3,4, 5,6, 7}, с обычным отношением порядка на множестве натуральных чисел, не превосходящих семи. □
Заметим, что диаграммы Хассе первых двух отношений совпадают. Это означает, что эти частично упорядоченные множества имеют одинаковую структуру, причем отличную от структуры третьего ч.у.м.. хотя оно тоже содержит восемь элементов. Формально такая общность структуры определяется понятием изоморфизма.
Пусть 21 = {А, <2(), 93 = {В,	— частично упорядоченные
множества. Отображение f : А —> В называется изоморфизмом частично упорядоченных множеств 21 и *3, если выполняются следующие условия:
— f — биекция между множествами А и В;
- для любых «1,0.2 G Л, «1 ^21 «2 тогда и только тогда, когда /(«1) ^<8 f(«2)-
Если существует изоморфизм между 21 и 93, то частично упорядоченные множества 21 и $ называются изоморфными и этот факт обозначается через 21 — 93.
Теорема 1.7.3. Всякое частично упорядоченное множество 21 = (Л, изоморфно некоторой системе подмножеств множества А. частично упорядоченной отношением, включения.
42
Доказательство. Для каждого элемента a G А рассмотрим множество So = {.т G А|.т С а}. Тогда Sa С А и Y = {бДо, G А} — совокупность всех таких подмножеств. Докажем, что ч.у.м. 21 изоморфно ч.у.м. (У, С). Рассмотрим отображение : А —> Y такое, что Да) = Sa. Отображение инъективно. Действительно, если S(! = Sb, то а € St, и b G Sn, значит, а b и b а, откуда но антисимметричности отношения получаем а = Ь. Отображение сюръективно, так как у любого подмножества Sa есть прообраз а. Докажем, что сохраняет отношение частичного порядка. Предположим, что a Eh. Тогда из х X а. в силу транзитивности отношения X следует х X Ь. и, значит, Sa Q Si,. Напротив, если Sn С Si„ то, поскольку a G Sa. имеем a. G Sb, откуда а. X Ь. □
Пусть 21 = (А, ^) — ч.у.м., а — элемент множества А. Открытым {замкнутым,} начальным, сегментом множества 21 называется множество О {а, 21)	{.т 6 А|.т < а} (соответственно
О [а, 21] = {х Е А|т < а}), в котором определено отношение Д, являющееся ограничением отношения X из 21: Д Ь-2 тогда и только тогда, когда by /ъ в 21.
Теорема 1.7.4. Если 21 и Д — в.у.м., то 21 изоморфно некоторому начальному сегменту множества Д или Ъ изоморфно некоторому начальному сег.м.енту множества 21.
§ 1.8.	Аксиомы теории множеств
Сейчас у нас имеются все средства, чтобы сформулировать систему аксиом теории множеств ZFC. в рамках которой можно изложить все общепринятые в современной математике способы рассуждений и нс проходит ни один из известных теоретикомножественных парадоксов. Эта система позволяет строить все математические объекты исходя из пустого множества. Представим ^систему аксиом, Цермело — Френкеля (ZF).
1.	Аксиома существования пустого .множества'.
Существует пустое множество 0.
2.	Аксиом,а сугцес.твования пары.'.
Если существуют множества а и Ь, то существует множество {«,&}•
3.	Аксиома суммы:
Если существует множество X. то существует множество UX {Да G b для некоторого b G X}.
43
4.	Аксиома, бесконечности:
Существует множество ш ?=ь {0.1,... ,п....}. где 0^0, п + 1 ;=± П. U {п}.
5.	Аксиома множества всех подмножеств:
Если существует множество А, то существует множество
Р(А) - {В|В С А}.
6.	Аксиома замены:
Если Р(.т, у) — некоторое условие на множества ж, у, такое, что для любого множества х существует не более одного множества у, удовлетворяющего Р(х,у), то для любого множества а существует м ножсство
{Ь\Р(с,Ъ) для некоторого с G н,}.
7.	Аксиом,а. экстенсиональности:
Два множества, имеющие одинаковые элементы, равны, т. е. любое множество определяется своими элементами:
А = В Vt (ж G А х G В).
8.	Аксиома регулярности:
Всякое непустое множество х имеет элемент а 6 х, для которого
а П х = 0.
Из аксиомы регулярности следует, что каждое множество получается на некотором таге “регулярного процесса” образования множества всех подмножеств, начинающегося с 0 и подобного построению натуральных чисел из пустого множества по аксиоме бесконечности. Это означает, что любой элемент любого множества является множеством, сконструированным из пустого множества.
Покажем, как аксиоматика ZF позволяет определять теоретике- множествен и ы с о и ераци и.
П р и м е р 1.8.1. 1. Определим множество A U В, исходя из множеств А и В. По аксиоме существования пары образуется множество {А, В}. С помощью аксиомы суммы получаем множество U{А, В}, которое по определению совпадает с множеством A U В.
44
2. Пересечение АпВ множеств А и В определяется по аксиоме замены с помощью следующего свойства Р(я,у): х = у и х G А. Имеем множество {Ь|Р(с, Ь) и с Е В} = {6|с = b и с Е А и с Е В} = {с|с Е А и с Е В} = А П В.
3. Покажем, что из аксиом 5 и б следует существование множества А2 = {(a,b)\a,b Е А} для любого множества А. Так как (а, 6) = {{а}, {а, 6}}. то А2 С Р(Р(А)). Пусть свойство Р(т;,у) означает, что существуют такие а.Ъ Е А, что х = {{а}, {а, Ь}} и у = х. Тогда множество А~ равно {Ь|Р(с, b),c Е Р(Р(А})} и по аксиоме 6 оно существует. □
Система аксиом ZFC образуется из ZF добавлением одной из следующих двух эквивалентных аксиом, которые, с одной ('тороны, являются наименее “очевидными”, а с другой — наиболее содержательными.
1. Аксиома выбора. Для любого непустого множества А существует такое отображение у : Р(А) \ {0} —> А, что <р(Лг) Е X для всех X С А. X 0.
2. Принцип полного упорядочения. Для любого непустого множества А существует бинарное отношение на А, для которого (А,	— вполне упорядоченное множество.
В системе ZFC справедлив принцип трансфинитной индукции, являющийся обобщением принципа полной индукции: если {А,	- вполне упорядоченное множество, Р(.?;)  некото-
рое свойство, то справедливость свойства Р(ж) на всех элементах х Е А следует из того, что для любого z Е А выполнимость свойства В на элементах у. где у < г, влечет выполнимость Р(г):
Vj; Р(.г)
§ 1.9.	Задачи и упражнения
1.	Доказать, что {0} А 0.
2.	Доказать, что {{0,1}, {0,2}} А {О, В 2}.
3.	Доказать, что (A U 6) = А П В.
4.	Построить пример множеств А и В таких, что А х В В х А.
5.	Пусть [0,1], [0,2] — отрезки на числовой прямой. Дать геометрическую интерпретацию множеств [0,1] х [0,2], [0,1]2, [0,2]3.
45
6.	Изобразить отношения F = {(а. 1). (о, 2), (Ь, 2), (5.3), (с, 1), (с,4)} и Q =	(2, Д), (3, а)}. Найти 6q, pq и Р о Q.
7.	Для отношений Р = {(.г, у) G К2 = у2} и Q = {(ж,у) G К? \х-у > 0} найти Р о Q, Q о Р, Р о Р и F-1.
8.	Пусть Д и В - конечные множества мощности т и п соответственно. Найти:
а) число бинарных отношений между элементами множеств Д и В; б) число функций из Д в В: в) число инъекций из А в В; г) число биекций из Д в В.
9.	Доказать следующие эквивалентности:
а) А х В ~ В х Д; б) (Д х B'f ~ Ас х Вс.
10.	Доказать, что:
а)	если Д — конечное множество, В — подмножество множества Д, то множество В конечно;
б)	если Hi..... Д„ конечные множества, то множества Д1 U ... U Д„ и Д| х ... х Д„ конечны.
11.	Доказать, что если Д — счетное множество, В — конечное множество, то множество Д \ В счетно.
12.	Доказать, что если множества Д.,, i е а> счетны, то множество U Д, счетно.
13.	Доказать, что если Д - счетное множество, то множество U Ап n&d всех конечных последовательностей, составленных из элементов множества Д, счетно.
14.	Доказать, что множество всех многочленов от одной переменной с рациональными коэффициентами счетно.
15.	Доказать, что множества точек отрезка и квадрата эквивалентны.
1G. Построить бинарное отношение:
а)	рефлексивное, симметричное, не транзитивное;
б)	не рефлексивное, антисимметричное, не транзитивное;
в)	рефлексивное, не симметричное, транзитивное.
17.	Пусть С - множество всех прямых на плоскости. Являются ли эквивалентностями следующие отношения;
а)	отношение параллельности двух прямых;
б)	отношение перпендикулярности двух прямых?
46
IS.	Доказать, что отношение {((xi.^). (?/i,?/з)) | Jj + у2 = х% + '</1} является отношением эквивалентности на множестве IR2. Определить классы этой эквивалентности.
19.	Доказать, что отношение {(«, Ь) | (а — Ь) — рациональное число} является отношением эквивалентности на множестве вещественных чисел.
20.	Пусть на множестве ы определено отношение задаваемое сле-
дующим правилом:
т п <=> т делит п.
Считая, что 0 делит 0, показать, что — частичный порядок. Для произвольных натуральных чисел т и п найти inf{m, п} и sup{m, п) относительно указанного порядка.
21.	Для обычных отношений и < на множестве си показать, что <о<^<,^о< = <и^о^ = ю2.
22.	Построить пример ч.у.м. с единственным минимальным элементом, но без наименьшего.
2.3	. Рассмотрим на множестве К2 отношение Парето л
(.'ЩЛ/1) 7г(.т2,?/2) ад х2 и щ у2-
Для точек Д(«1,«2) и В(Ь1,Ь2) найти множество нижних и верхних граней множества {Д. В}. Чему равен inf{.4, В} и snp{ Л, В}?
24.	Построить линейный порядок на множестве комплексных чисел.
25.	Составить матрицу отношения полного порядка, при котором нумерация элементов ведется: а) по возрастанию отношения; б) по его убыванию.
Глава 2
АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
§ 2.1. Определения и примеры
- Часто объектом изучения в математике и ее приложениях служит множество вместе с определенной на нем структурой. Читателю уже известны поля, формирующие основу обычной арифметики, линейные пространства, обеспечивающие связь геометрических объектов с операциями над числами, множества с введенными на них бинарными отношениями. Все эти структуры образуют алгебраические системы, представляющие собой некоторые миры с определеными в них законами. Перейдем к точному определению алгебраической системы.
Рассмотрим непустое множество А. В § 1.2 было введено понятие n-местной операции на множестве A: f : А’1 —> А. Отметим, что, поскольку операция / является функцией, для любого набора (.Т1,..., хп) & Ап результат применения операции /(.гл,..., хп) однозначно определен. Так как область значений операции f лежит в множестве А, то будем говорить, что операция f замкнута на множестве А.
Сигнатурой или .языком S называется, совокупность предикатных и функциональных символов с указанием их местности. 0-местный функциональный символ называется константным символом или просто константой. Если о — функциональный или предикатный символ, то его местность обозначается через п-местные предикатные и функциональные символы часто будем обозначать соответственно через и Если в рассматриваемой сигнатуре используются стандартные символы, такие, например, как + для операции сложения, С для отношения порядка, | для отношения делимости, 0 для константного
48
символа и другие, то мы просто пишем Е = Е = {X, +, -,0}, Е - { + , |,6,1} и т.д.
Алгебраической системой 21 = (А, Е) сигнатуры Е называется непустое множество А, где каждому n-местпому предикатному (функциональному) символу из Е поставлен в соответствие п-местный предикат (соответственно операция), определенный на множестве А. Множество А называется носителем или универсумом алгебраической системы (А, Е). Предикаты и функции, соответствующие сим'волам из Е, называются их интерпретациями. Обозначать интерпретации будем теми же буквами, что и соответствующие символы сигнатуры. Заметим, что интерпретацией любого константного символа является некоторый элемент (константа) из А.
Алгебраические системы в дальнейшем будут обозначаться готическими буквами 21,	... (возможно, с индексами), а их но-
сители — соответствующими латинскими буквами А, В,... (с соответствующими индексами). Иногда мы будем отождествлять носитель с алгебраичесской системой.
Мощностью алгебраической системы 21 называется мощность ее носителя А. В дальнейшем будем часто опускать слово “алгебраическая” и называть 21 системой или структурой.
Сигнатура Е называется функциональной (предикатной), если опа не содержит предикатных (функциональных) символов. Система 21 называется алгеброй (моделью), если ее сигнатура функциональна (предикатна).
П р и м е р 2.1.1. 1. Набор (ш, +, ) является алгеброй с двумя двухместными операциями.
2.	Набор (ш, ^,+.Z.0,1) является системой с бинарным отношением (р(^) = 2), двухместными операциями +, • (//(+) = р(-) — 2), одноместной операцией ' : п г-> п +1 (р(') = 1) и двумя пуль-местными операциями (константами) 0, 1 (//.(()) = ц(1) = 0).
3.	Набор (Z,\/2) не образует алгебру, поскольку деление не является операцией на множестве Z (например, 2 : 3	Z), а
элемент \/2 не принадлежит Z.
4.	Набор (P(U), U, С, —, 0,1) с двухместными операциями U, П, одноместной операцией — : А н-> А, константами 0 = 0 и 1 = U является алгеброй, называемой алгеброй Кантора.
5.	Алгеброй является любое кольцо.
6.	Пара. ({f(x)\f : К -> R}, ^) (где - операция диффе-
49
ренцнрования) не является алгебой, поскольку не всякая функция дифференцируема, но если рассмотреть множество А = {/(•t)|/(.t) дифференцируема бесконечное число раз}, то отображение дифференцирования : f i-> является операцией на А и пара (А, образует алгебру. □
Заметим, что частичную операцию f, отображающую Ап в А, можно рассматривать как (п + 1)-местное отношение {(xi,;r2.  • •	. ,хп) 6 Ап и у = /(хг,... ,:?:„)}. Поэтому
в последнем примере пару ({./(-т)|/ : Ж —> R},	можно считать
алгебраической системой, если рассматривать 4- как бинарное отношение {(f,g)\g = ^}.
Алгебра 21 сигнатуры Е = {/}. где /?(/) = 2, называется группоидом. Единственная здесь операция f обычно обозначается символом •: 21 = (А,-). Если А — конечное множество, действия операции можно задать квадратной таблицей, в которой для каждой пары (щ.д.,) G Л2 записан результат действия ау). Такая таблица называется таблицей Кэли группоида 21. Группоид 21 называется полугруппой, если  — ассоциативная операция, т. е. для всех элементов x,y,z G А верно х  (у • z) = (х  у) • z. Полугруппа 21 называется моноидом, если существует элемент <?>G А, называемый единицей, такой, что e-х = х - е — х для всех х G А. Полугруппы и моноиды имеют особое значение в теории языков при обработке слов.
П р и м е р 2.1.2. Пусть 17(A) — множество слов алфавита X. Определим па Н,Г(А) операцию конкатенации ~ следующим образом: если а,/3 G И-Г(Х), то = а/3, т. е.. результатом является слово, полученное соединением слов а и /3 (например, x.yz'zx = xyzzx). Операция ~ ассоциативна, т. е. для любых слов о,/'Ey верно (а"/3)"у = «"(/Гу). Следовательно, система (И/’(ЛГ).') является полугруппой. Так как для всех о G ИЛ(А) верно Л*а = <у\\ = о, где Л — пустое слово, то Л удовлетворяет свойству единицы. Таким образом, система (JV(A’)/) является моноидом. □
Моноид 21 = (А. •) называется группой, если для любого элемента.?; 6 А существует элемент ж-1 G А, называемый обратным к х, такой, что х  х] = х~}  х = е. Группа 21 называется коммутативной или абелевой, если х  у = у  х, для всех х,у Е А.
Пример 2.1.3. 1. Если (/<,+,-) - кольцо, то (К. +) -абелева группа.
50
2. Система (GLn(jFC), ), где GLn(K) = {-4Ц — матрица порядка п над полем К, и det Л 0} является группой, которая некоммутативна при п 2.
§2.2. Морфизмы
Пусть даны алгебраические системы 21 = (A, Е), ® = (В, Е). Отображение </? : А —> В называется гомоморфизмом системы 21 в систему 93, если выполняются следующие условия:
1) для любого функционального символа G Е, соответствующих функций /а и f<s в системах 21 и 93 и любых o,i, а?,..., ап G А выполняется
^(/21(01, а2, • • , ап)) =	<^(02), •  •, Н°п)):
2) для любого предикатного символа Р^ G Е, соответствующих предикатов Р% и Р<% в системах 21 и 93 и любых oi, о,2, •  , а.п G А выполняется
(oj, о2, • • , о?г) G Лл => (</?(oi),</?(o2),.   ,^(оп)) G Р%.
Если р : А —> В — гомоморфизм, то будем его обозначать через р : 21 —> 93.
При гомоморфизме сохраняются действия операций и отношения. Это позволяет переносить изучение свойств с одной системы на другую.
П р и м е р 2.2.1. Рассмотрим системы 21 = (Z,+. «Д и 93 = (Z2, +, С), где в системе 93 сложение задается по правилу
(О]. bi) + (о2, b2) = (oi + о2, bi + b2),
а отношение порядка
(oi, bl) (о,2, ь2) Ф>О| <; О.2 и bl ь2.
Отображение tp : Z —> Z2, при котором </?(о.) = (о, 0), является гомоморфизмом. Действительно, для любых a, b € Z имеем
<До + Ь) = (а + Ь, 0) = (о, 0) + (Ь, 0) = <До) + <р(Ь),
и если а Ь, то (а, 0)	(Ь, 0), т. е. <До) <р(Ь). □
51
Гомоморфизм р : 21 —> 23. являющийся инъекцией, называется мономорфизмом. Гомоморфизм у? : 21 —> 23, являющийся сюръекцией, называется эпиморфизмом, и при этом система 23 называется гомоморфным образом системы 21. Гомоморфизм р : 21 -> 21 называется эндоморфизмом. Сюръективный мономорфизм р : 21 -э 23. для которого <д-1 — гомоморфизм, называется изоморфизмом 21 на 23 и обозначается через </? : 21^.23. Если существует изоморфизм </? : 21 С} 23. то системы 21 и 23 называются изоморфными и обозначается это так: 21 ~ 23. Изоморфизм . р : 21Д} 21 называется автоморфизмом системы 21. Заметим, что, поскольку изоморфизм р : 21 23 является биекцией А О В, изоморфные системы равномощны.
Утверждение 2.2.1. 1. icl.i : 21 су 21;
2. если р : 21 су. 23, то </?_| : 23 су 21;
,У. ('.ели р : 2li 2li и ф : 21-г су 21з, то р о ф : 211 су 21з.
Таким образом, отношение изоморфизма ~ является эквивалентностью на любом множестве алгебраических систем (отметим, что класс всех алгебраических систем не является множеством, поскольку не существует множества всех множеств). Это означает, что отношение изоморфизма разбивает множества алгебраических систем на классы эквивалентности, в каждом из которых содержатся системы, имеющие “одинаковое устройство”. Это дает возможность переносить изучение свойств с одной системы на другую, изоморфную ей. Так, используя факт изоморфизма геометрического векторного пространства пространству с трок, работу с геометрическими объектами можно свести к действиям с наборами чисел, что позволяет применять компьютеры.
П р 11 м е р 2.2.2. 1. Рассмотрим множество векторов геометрического векторного пространства с операциями сложения векторов п умножения векторов па вещественные числа. Получим с истему 21 = (Ед, Г, {А-)ле®.) бесконечной сигнатуры, где одноместные функции А- ставят в соответствие вектору а вектор Ха. Рассмотрим также систему 23 = (R3,+, {A-}yGHi), носитель которой состоит из троек вещественных чисел (ж, у, z), + - двухместная операция покоординатного сложения троек, а функция А- операция умножения троек на число А для всех вещественных чисел А. Системы 21 и 23 являются линейными пространствами над полем R. Отображение <д, ставящее в соответствие вектору (7. G E.-i его координатную строку (.т, у, z) в некотором фикси
52
рованном базисе щ. сДёз, является биекцией (<д : Е3 о К3), при которой сохраняются действия операции: 'рДа ~t Ь) = ip(a) + ip(b) и <д(А • о) = А  <д(<7). Таким образом, — изоморфизм линейных пространств 21 и 93. и, следовательно, изучение геометрических векторов можно свести к изучению троек чисел и наоборот.
2.	Рассмотрим два равномощных алфавита А”, X' и алгебры 21 = (ТУ(Х),'), 93 = (T-F(A’Z), ") (см. пример 2.1.2). Покажем, что 21 ~ 93. Так как 1А"| = |Л"'|, то существует биекция <д : X о X'. Построим по ней биекцию -ф : W(X) о W(А'), при которой слову о G И’(Х) ставится в соответствие слово ft Е ИДА'), получающееся заменой каждого символа х в слове а на символ <д(./:). Построенная биекция -ф дает искомый изоморфизм 21 на 93, поскольку ^(одЪ?) = Ф(оцУгф(а^ для любых «1,0-2 Е ИДА).
3.	Для заданного множества U система (P(U), П.-U, 0,1) изоморфна системе (P(U), U, П, 1,0) с биекцией <д : А А. Действительно. по законам де Моргана <д(£? П С) = В Г С = BUC = <д(В) и <д(С) и <д(В U С) = B1JC_= В П С = <д(В) П <д((7) для любых В, С Е P(U). Кроме того. 0 = 1, 1 = 0.
4.	Рассмотрим группы 21 = ((0, оо),-), 93 = (R,+) и отображение <д : (0. сю) -> R по правилу <д(.т) = logp(x) для некоторого фиксированного р Е (0, оо), р у/ 1. Отображение <д является изоморфизмом систем 21 и 93, называемым логарифмом (по основанию р). Это позволяет производить умножение положительных чисел при помощи сложения вещественных чисел на основании тождества
а  b = <д_1(<д(а) + <д(Ь)),
которое получается из равенства <д(а  6) = <р(а) + <д(6) применением отображения <д~ 1 к обеим частям.
§ 2.3. Подсистемы
Алгебраическая система 21 — (A, S) называется подсистем,ой системы 93 -(/ЛУЗ) (обозначается через 21 С 93), если выполняются следующие условия:
а)	А С В:
б)	для любого функционального символа /(") Е Е. соответствующих функций fft и и любых элементов щ, п2.....п„ Е А
выполняется равенство /<x(«j,... ,ап) = ДДщ,..., ап). т. е. интерпретации символа f действуют одинаково па элементах из А:
53
в)	для любого предикатного символа Р^ G Е, соответствующих предикатов Вд и Рщ справедливо равенство Р<д = Рщ А А", т. е. предикат Рц содержит в точности те кортежи отношения Рщ, которые состоят из элементов множества А.
Есин Е — функциональная (предикатная) сигнатура, то подсистема 21 алгебры (модели) 93 называется подалгеброй [подмоделью).
Пример 2.3.1. 1. Если V — подпространство линейного пространства V, то V — подсистема (подалгебра) системы V.
2.	Если Е = {Р^}, 93 = (В, Е) — система, 0 А С В, то 21 = (А, Е) является подсистемой системы 93 тогда и только тогда, когда Рц = Р<$ А Ап.
Теорема 2.3.1. Если 93 — алгебраическая система, X С В, X 0, то существует единственная подсистема 93 (X) С 93 с носителем. В(Х), такая, что X С В(Х) и 93(Х) С 21 для любой подсистемы 21 С 93, для, которой X С А.
Доказательство.В качестве В(Х) рассмотрим пересечение носителей А всех подсистем 21 С 93, содержащих X. Так как X С В(Х), то В(Х) / 0. Единственность подсистемы 93(Х) очевидна. □
Подсистема 93 (X) из теоремы 2.3.1. называется подсистемой, порожденной множеством X в 93. Она является наименьшей подсистемой системы 93, содержащей множество X.
П р и м е р 2.3.2. Напомним, что если V — линейное пространство, S — некоторое непустое множество векторов пространства V, то линейная оболочка £(5) множества S в V состоит из всевозможных линейных комбинаций векторов из S. Алгебра £(Р) является подалгеброй пространства V, порожденной множеством S. □
Для описания устройства подсистемы 93(X) определим индукцией по построению понятие терма сигнатуры Е:
1)	переменные и константные символы из Е суть термы;
2)	если / G Е — 71-местный функциональный символ, Н, t-2,.. - ,tn — термы, то . ,tTl) — терм;
3)	никаких термов, кроме построенных по пп. 1, 2, нет.
Таким образом, термом является любое функциональное выражение, составленное с помощью сигнатурных функциональных символов.
Множество всех термов сигнатуры Е обозначается через Т(Е).
54
Пример 2.3.3. 1. Термами сигнатуры Е = {+, , ^,0} будут, например, 0, ж, х + у, z  (х + z) + 0 • у, а х + у (0 + z) • х термом не является.
2. Если Е — {f,g,h} — функциональная сигнатура, где м(/) = 3’ /*(.?) = 1, /ДМ = 2, ТО выражения Л,(/(ад, х2, ж3),р(®2)), 5(/(^(ж1,Ж2),Жь3(3:2)) — термы, a h(x,i,/(ад.жз)) не образует терма.
3. В сигнатуре Е = {отец^\ Иван^} терм отец(отец(Иван)) можно проинтерпретировать как “дедушка Ивана”. □
Пусть t(xi,x2,    тХь) — терм из Т(Е), все переменные которого содержатся среди ад, х2,..., ж*.; 21 = {А, Е) — алгебраическая система. Значение терма t при значениях а.[, а2,..., «д G А переменных яд, х2,... ,Хк (i(o,i, а2,..., о,/-)) определяется по индукции:
1)	если t есть переменная х;. (константный символ с), то значение t есть (с);
2)	если терм t есть /(<1,.. -, in)> а значения	суть
Ь\,..., Ьп, то значение терма t есть f(bi,..., bn).
Теорема 2.3.2. Если 93 = (В, Е) - алгебраическая система, 0 X С В, то носитель подсистемы 93(A) равен {/(сд,.. ап) | t G Т(Е), ох,..., ап G X}.
Доказательство. Индукцией по числу шагов построения терма t получаем, что если t(xj,..., хп) G Т(Е) и сд....,ап G X, то t(ai,... ,ап) G X для любой подсистемы 21 С 93, содержащей X. Поэтому достаточно показать, что множество Y = {t(ai,... ,a.n)\t G Т(Е),сц,...,ап G X} замкнуто относительно операций системы 93. Пусть /(m) G Т(Е),	G Т(Е),
bi = ti(ai,... ,ап) G Y, i —	Тогда /(&],...,bm) G Y,
поскольку /(fi,..., tm) G Т(Е). □
Таким образом, носитель подсистемы 93(Х) состоит из всех элементов, которые получаются при подстановке элементов из X в термы.
П р и м е р 2.3.4. 1. Найдем носитель подсистемы 93(A) системы 93 = (Q\{0}, •) для множества X = {|}. Так как сигнатура Е системы 93 есть {•}, то Т(Е) = {тд, х\  х2, (ад • х2)  х%, ад • (х2  x-i),...}. По теореме 2.3.2. получаем В(Х) = {|. |-  } =
2.	Если ® = (Q \ {0},-,:), X = {|}, то, поскольку по сравнению с предыдущим примером сигнатура дополняется опера
55
цией деления х : у, множество В (А) содержит также числа ± : 2тл = 2m~n; т.п > 1, т. е. С = {271|n G Z} С В(А). Так как множество С замкнуто относительно операций умножения и деления, т. е. {С, S) является подсистемой системы и содержит множество X, то В (А) С С. Следовательно, В (А) = С.
3.	Найдем носитель подсистемы 93(A) системы 93 = (С, +, г) для множества А = {—2,2}. Так как все термы из Т(Е) являются переменными, константой г или образуются из переменных и константы ?' с помощью операции сложения, то каждый элемент из В (А) получается подстановкой элементов из А в некоторый терм х\ + Ж2 + • - - + хт + i + i	i. Следовательно,
В(А) = {2т + ni | пг G G w}. □
§ 2.4.	Конгруэнции. Фактор-алгебры.
Теорема о гомоморфизме
Конгруэнцией на алгебре 21 = (А, Е) называется такое отношение эквивалентности в С А2, при котором для любого nGw, любого 77-местного символа f G S (напомним, что сигнатура алгебры состоит только из функциональных символов), произвольных наборов (а,1, о.2, -  , a.n), (bi, b^, . -. Ьп) € А", если гц в Ь1; «20Ь2,... ,апОЬп, то /(cjba2,...,Gn)0f(bi,b2, Ап)-
Это означает, что все операции согласованы с отношением эквивалентности в. Например, для операции сложения это выглядит так: для любых элементов х,у G А, любых a G в(х), Ъ Е в (у) элемент о. + b принадлежит классу в(х + у).
Рассмотрим фактор-множество множества А по конгруэнции в: А/в = {0(.т;)|.т G А}. Определим на этом множестве алгебру сигнатуры S. Константе с алгебры А поставим в соответствие элемент'0(c), который в A/в будет интерпретировать константный символ с. Если f 7г-местный символ из Е, то зададим на множестве A/в действие функции f по правилу
/(0(х1),...,0(.тп))^0(/(.т1,...,Ж.„)).
Убедимся, что для любых ад,..., хп G А это определение корректно, т. е. не зависит от выбора представителей классов эквивалентности. Действительно, если в(хг) — в(у,). г = 1,2,..., п, то xiOyi, откуда в силу свойства конгруэнции имеем f (ад ,..., хп) в
  -,Уп), т- е- 6>(/(ж1,... ,®п)) = в(/(у},... ,y„)j.
Получившаяся алгебра 21/0	(А/0, Е) называется фактор-
алгеброй алгебры 21 по конгруэнции в.
56
Очевидно, что отображение А —> А/0, при котором элементу х Е А ставится в соответствие класс в(х), является эпиморфизмом алгебры 21 на фактор-алгебру 2*1/6*. Этот эпиморфизм называется естественным гомоморфизмом.
Если у? : 21 —> 93 гомоморфизм алгебр, то множество Кег <р {(а, н')|<д(«) = <р(а')} оказывается конгруэнцией на алгебре 21 и называется ядром гомоморфизма <д.
Докажем теорему, согласно которой гомоморфный образ алгебры изоморфен фактор-алгебре по ядру гомоморфизма.
Теорема 2.4.1 (теорема о гомоморфизме). Если <р : 21 —> 93 — эпиморфизм, ф : 21 —> 21/Кег<р — естественный гомоморфизм, то существует изоморфизм х : 93^21/Кег<р такой, что V>°X = ^
Доказательство. Положим х(Ь) = ф(а), где а Е А выбрано так, что b = <р(а). Если b = то (о,, о/) G Кегср, откуда ф(а) = Следовательно, отображение у определено корректно. Равенство <р о у = ф очевидно. Из него вытекает, что х — сюръекция. Непосредственно проверяется, что х ~ гомоморфизм. Если у(Ь) = х(Ь'), то ф(а) = ф(а'), где b = <д(а), Ь' = <д(о/). Отсюда (a, a') Е Кегср, следовательно, b = Ъ', что доказывает взаимную однозначность отображения у. Так как сигнатура функциональна, из существования функции х 1 11 того, что х ~~ гомоморфизм, следует, что х является изоморфизмом. □
Отображения <р, ф и х из теоремы 2.4.1 можно представить диаграммой, показанной на рис. 2.1.
57
§ 2.5.	Декартовы произведения алгебр. Теорема Биркгофа
Пусть A,, i Е I, — семейство множеств. Декартовым произведением, множеств A;, i G I, называется множество
П А {./Д' : / и А, где /(г) G Д для всех ?}. ~	iEl
lEl
Отметим, что если I = {1,2, ...,п} — конечное множество индексов, декартово произведение П А — {f\f : I -> U Aj, где /(1) G А1,..., /(n) G АД можно взаимно однозначно рассматри-71
вать как множество П А = {(/(1),../(п))|У : I -> U Ai, где •z=i	.	г=1
/(1) G Ai,...,/(n) G АД. Таким образом данное определение согласуется с введенным ранее определением декартова произведения конечного числа множеств.
Пусть 21,; = (А,,Е), i Е I, — некоторые алгебры сигнатуры Е. Декартовым, произведением алгебр 21-,, i Е I, называется алгебра П А = (П в которой функциональные символы iei iei
рМ е Е интерпретируются по следующему правилу: для любых функций /п G П А полагаем Т(/1, ...,/„) ^ /, где /(г) = «е/
Тц, (/] (г),. - -, /эт(г)) для любого i Е I. Если I — {1,2,..., п}, то декартово произведение алгебр f] 21,- будем как и для множеств icJ обозначать через 211 х 21г х  х 21п.
Пример 2.5.1. Для алгебр 2lj = (Ai, +Д, 21а = (Аг,+2) операция + декартова произведения 211 х 21г = (Ai х Аг, +) задается соотношением (ах,аг) + (пфа'г) — (а1 +1 Д,а2 +2 ^г)- □
Пусть НДг — термы сигнатуры S. Запись t\ к, t? называется тождеством сигнатуры Е. Эта запись означает, что любые значения, вычисленные по терму Н, совпадают с соответствующими значениями, вычисленными по терму £г-
Пример 2.5.2. Если ti = х + у, б2 = у + х — термы сигнатуры Е = {+}, то тождество х + у » у + х означает, что для символа + выполняется закон коммутативности. □
Класс Я алгебр сигнатуры Е называется многообразием, если существует множество тождеств Т = {£{ « t32\j Е J} сигнатуры
58
Е такое, что алгебра сигнатуры Е принадлежит классу Я тогда и только тогда, когда в ней выполняются все тождества из множества Т.
Пример 2.5.3. Множеством тождеств {ж  {у • z) я? (а:  у)  z, х  е ~ х, е  х ~ .г} сигнатуры Е =	определяется
многообразие, состоящее из всех моноидов.
Теорема 2.5.1 (теорема Биркгофа). Непустой класс алгебр Л сигнатуры Е тогда, и только тогда является многообразием, когда, 5? замкнут относительно подалгебр, факгпор-алгебр и декартовых произведений, т. е. класс Я вместе с каждой алгеброй содержит любую ее подалгебу, фактор-алгебру, а также вместе с любым семейством алгебр содержит их декартово произведение.
§ 2.6.	Решетки и булевы алгебры
Следующей нашей целью является определение и изучение понятия булевой алгебры, но сначала рассмотрим более обшее понятие — понятие решетки.
Решеткой называется ч.у.м. 21 = (А, ^), в котором каждая пара элементов имеет супремум и ипфимум. Для заданных элементов х,у G А элемент inf{rr,y} называется пересечением элементов х и у (обозначается ж Л у), a sup{.T,y} называется объединением элементов х и у (обозначается х V у).
Заметим, что если в системе 21 введены операции Л и V, то отношение можно по этим операциям восстановить следующим образом: х у О х Л у = х, а также х ^у х\/ у = у.
Наименьший (наибольший) элемент решетки, если он существует, называется нулем (единицей). Обозначаются эти элементы соответственно через 0 и 1. В конечных решетках всегда имеются нуль и единица.
Пример 2.6.1. 1. Любое конечное линейно упорядоченное множество является решеткой.
2. Рассмотрим ч.у.м. 21 = ({a, b, с, d, е}, ^), в котором а < Ь, а. < с, а < d, b < е, с < е, d < е, а элементы b, с, d попарно несравнимы. Система 21 образует решетку, показанную на рис. 2.2. В этой решетке а = 0, е = 1.
3. Если |А| > 1, то ч.у.м. (A, idx) не является решеткой, поскольку для любых различных элементов х и у не определены
59
операции inf{.r. у} и sup{.-r, у} по отношению idj. □
(J	Определим решетку подсистем системы 
ж.	23 = (В, Е), содержащих непустое множество
/	X С В. Рассмотрим множество Lffi) {21 |
5 К "с >d 21 =	® и %- — п зададим на нем
\	/ частичный порядок С по следующему пра-
/ виду: 2li 21.2	<11 С 212- Пара (£(23),^)
*	образует решетку подсистем. В этой решетке
для любых систем 21] = (Ai, Е), 212 = (А>, Е)
- из £{23) пересечение 21] Л21г есть подсистема (Ai П Л-2, Е), а объединение 2li V 2(2 - подсистема, порожденная множеством Ai U А?: 23 (Ai U А-/).
П р и м е р 2.6.2. Рассмотрим линейное пространство F и множество £(У) подпространств пространства 1Л. Система (£(У), <), где Vj С V'2 Bi — подпространство Р£ образует решетку подпространств, в которой У1Л1-2 = У1Ср2, Vi W2 = -^(ИиРг)- □
Пусть 21 = (Л, Е) — алгебра, Con 21 {did - конгруэнция на 21}. На множестве конгруэнций Сон 21 зададим отношение по следующему правилу: d( С do <=> для любых элементов a, b G Л из условия a di b вытекает а, 02 Ъ. Это означает, что каждый d2-K.nacc состоит из di-классов. Система (Сои 21, У) образует решетку конгруэнций. В этой решетке пересечение (Ц АО? конгруэнций di и О2 удовлетворяет следующему условию: для любых a, b G А тогда и только тогда a (di Л Ь, когда а в] Ь и а О? Ь. Объединение di V О2 конгруэнции d] и d2 определяется следующим отношением: для любых a, b £ А тогда и только тогда a (d, V (р) b, когда существуют такие ci, С2,.. -, с„ £ А, что щ = а, сп = Ь, и справедливо С, di Cl+ I ИЛИ Ci 6'2 Cj+1 для любого 2 = 1,... ,П — 1.
Решетка конгруэнций имеет нулевую конгруэнцию Од = {(а, а)|а € А} и единичную конгруэнцию 1д = А2.
Решетка 21 = (А, У) называется дистрибутивной, если она подчиняется дистрибутивным законам
х V (у Az) = (ж V у) Л (х V z), х Л (у V z) = (х Л у) V (л: Л г) для всех х, у, z G А.
Не все решетки являются дистрибутивными. Решетка Мз, изображенная на рис. 2.2. не дистрибутивна, поскольку b Л (cl V с) = b Л е ~ Ь, тогда как (Ь Л d) V (b Л с) = aVa= а. Недистрибутивной является также решетка Рь, изображенная на рис. 2.3.
60
Рис. 2.3
Теорема 2.6.1. Решетка 21 = (Л, Л) дистрибутивна тогда, и только тогда, когда 21 не имеет подрешеток, изоморфных или Р5.
Дистрибутивная решетка 21 == (Л, называется булевой алгеброй, если 21 имеет нуль 0, единицу 1, 0 0 1 и для любого элемента х G Л найдется элемент х (называемый дополнением элемента х) такой, что х\/х = 1 и х. А х = 0.
Предложение 2.6.2. Если 21 — булева, алгебра, то для любого элемента х дополнение х единственно.
Д о к а з а т е л ь с т в о. Предположим, что элемент х имеет два дополнения у и z. т. е. х V у = 1, х А у = 0, х V z — 1, х A z = 0. Используя законы дистрибутивности, получаем, что элементы у V z и у f\ z также являются дополнениями к ж, т. е. х V (у V z) = 1, х /\(yVz) =0, хУ (у/\z) = 1, х А (у A z) = 0. При этом из у / z следует, что 0 < y!\z <yVz < 1. Отсюда получаем, что подрешетка решетки 21 с носителем {0, у /\z,y\/ z, х, 1} образует решетку Гф что противоречит дистрибутивности решетки 21. Таким образом, двух различных дополнений элемента х не существует. □
Таким образом, булеву алгебру можно представить в виде алгебры 53 = (В. A, V, ,0,1) с двумя двухместными операциями пересечения А и объединения V, одноместной операцией дополнения (ж х) и двумя константами 0 и 1.
П р и м е р 2.6.3. 1. Если на множестве {0,1} задать линейный порядок с. условием 0 < 1, то получим двухэлементную булеву алгебру ({0,1}, A, V,, 0,1).
2.	Рассмотрим множество А = {0, а, Ь, 1} и зададим частичный порядок на А следующим образом: 0 < а, 0 < b, а, < 1.
61
о
Рис. 2.4
b < 1, а элементы а и b несравнимы (рис. 2.4). Система (Л, <) является булевой алгеброй, в которой а = b, b — а.
3.	Алгебра Кантора (7?(С7),С, U, ,0,(7) является булевой алгеброй. □
Оказывается, что основные свойства операций О, U, из § 1.1 выполняются в любой булевой алгебре.
Теорема 2.6.3. Если 23 = (B,A,V, ,0,1) — булева алгебра, то в 23 вътолняются следующие законы для любых x,y,z G В:
1)	ассоциативность операций V и А:
х V (у V z) = (ж V у) V z, х А (у A z) = (ж А у) A z;
2)	коммутативность операций V иА:
х V у = у V х, х А у = у А х;
3)	законы идемпотентности
х V х = х, х А х = х;
4)	законы дистрибутивности
ж V (у A z) = (ж V у) А (ж V z),
х А (у V z) = (ж А у) V (ж A z);
5)	законы поглощения
хМ (ж А у) = х, х А (ж V у) = х:
6)	законы де Моргана
х V у = хАу, х А у — х\/у-,
7)	законы нуля и единицы
ж V 0 — ж, ж А 0 = 0, ж V 1 = 1, ж А 1 = ж, ж V ж = 1, ж А ж = 0, 0 1;
8)	закон двойного отрицания
ж = ж. □
62
В следующей теореме описываются все конечные булевы алгебры с точностью до изоморфизма.
Теорема 2.6.4 (теорема Стоуна). Любая конечная булева алгебра изоморфна некоторой алгебре Кантора.
Так как для любого множества U мощность множества P(U) равна 21е* ।, то из теоремы Стоуна вытекает
Следствие 2.6.5. Любые две булевы алгебры, имеющие одинаковое число элементов, изоморфны. Число элементов конечной булевой алгебры равно 2п для. некоторого n g ш\ {0}.
Таким образом, конечная булева алгебра определяется однозначно с точностью до изоморфизма числом своих элементов.
Аналогично примеру 2.2.2 булевы алгебры (В, Л, V, , 0, 1) и (B,V, Л, ,1,0) изоморфны посредством изоморфизма : В —> В, в котором <д(.г) = х. На этом основан следующий
принцип двойственности для булевых алгебр: если в справедливом утверждении о булевых алгебрах, касающемся отношения и операций V, Л, , 0. 1, всюду заменить на V — на Л, Л - на V. 0 --- на 1, 1 — на 0, то получится также справедливое утверждение. Образованное таким образом утверждение называется двойственным к исходному.
При м е р 2.6.4. Закон де Моргана х f\y = х V у является двойственным по отношению к закону де Моргана хЧ у = x,f\y, а закон х Л х = 0 — к закону х V х = 1. □
Остановимся на связи булевых алгебр с кольцами. Кольцо (/?,+, ) называется булевым, если о2 = а. для всех a. G R.
Предложение 2.6.6. Булево кольцо коммутативно, и а. + а = 0 для. всех элементов а Е R.
Д о к а з а т е л ь с т в о. Во-первых, а + а = (о, + а)2 = о2 + а2 + а2 + а2 = а + а + а. + а, откуда а + а = 0, т. е. а = —а. Во-вторых, а + Ь — (« + Ь)2 = а2 + ab+Ьа. + Ь2 = a + b+ab+ba. Отсюда а.Ь + Ьа. = 0. Тогда ab = а,Ь + (Ьа + Ьа) = (ab + Ьа) + Ьа = Ьа. □
Напомним, что единицей кольца R называется такой элемент е, что а • е = е  а, — а для всех а Е R.
Пусть 23 — (В, Л, V, , 0,1) — булева алгебра. Определим операции кольцевых сложения и умножения на 23 по следующим правилам: х ф у (х Л у) V (ж Л у), xQ у х Л у для всех х, у Е В. Операция ф соответствует кольцевой сумме множеств, операция Q — пересечению множеств (см. § 1.1).
63
Теорема 2.6.7. Система (B,®,Q) образует булево кольцо с единицей 1.
Имея булево кольцо с единицей (В,®,®), можно однозначно восстановить операции Л, V, по следующим правилам: х. Л у — х Q у, х V у — х ф у ф (ж ® у), х = 1 ф х.
§2.7. Идеалы и фильтры булевой алгебры
Пусть 53 = {В, Л, V, ,0,1)— булева алгебра. Множество I С В называется идеалом, если выполняются следующие условия:
1) из а.,Ь G I следует а V b G /;
2) если b 6 I, a Е В и а Ь, то a G I.
Таким образом, идеалы замкнуты относительно операции V и взятия элементов, не превосходящих данного элемента идеала. Заметим, что если I 0, то 0 G I.
Идеал I называется главным., если существует элемент с Е I такой, что 1 = {о, G В | а. «С с}.
Пример 2.7.1. 1. Рассмотрим алгебру Кантора (Р(U), П,и, ,0,1) и выберем произвольное подмножество С С U. Тогда множество I = {Я|И С С} образует главный идеал.
Действительно, если А, В € I, то А, В С С, отсюда AUB С С и, следовательно, A U В G I. Если же В С С и А С В, то по транзитивности отношения С имеем А С С, т. е. А € I.
2. Если множество U бесконечно, то в алгебре Кантора идеат конечных множеств I — {А | А С U, А — конечное множество} является неглавным, поскольку для любого множества С Е I найдется элемент х EU \С. т. е. {.г} Г) С = 0, а {х} G I. □
Понятие фильтра является двойственным к понятию идеага.
Множество F С В называется фильтром, если выполняются следующие условия:
1) из a, b G F следует а Л b Е F;
2) если b G F, a G В и b а, то а Е F.
Фильтр F называется главным, если найдется элемент с Е F такой, что F — {а Е В\а с}.
П р и м с р 2.7.2. 1. В алгебре Кантора P(U) для любого С С U множество F = {Л|И Е P(U) и A D С} является главным фильтром.
2. Пусть U — бесконечное множество. Подмножество А С U называется коконечным, если множество А конечно. В алгебре Кантора P(U) фильтр F = {M|vl С U, А коконечное
64
множество} является неглавным. Фильтр F называется фильтром Фреше на множестве U.
Теорема 2.7.1. Если 93 — конечная булева алгебра, то в 93 все идеалы и фильтры являются главными.
Если I — идеал булевой алгебры 93, то множество I = {а|о G 1} является фильтром, называемым двойственным к идеалу I.
Теорема 2.7.2. Отображение : I н> I являет,ся биекцией .между множеством идеалов и множеством фильтров булевой алгебры.
Отметим связь идеалов и фильтров булевой алгебры с ее конгруэнциями.
Теорема 2.7.3. Пусть I — идеал булевой алгебры *8, I 0, В. Тогда бинарное отношение (/), определяемое по правилу а(1)Ь <=> вфЬ G I, является конгруэнцией булевой алгебры 93. Обратно, если имеется неединичная конгруэнция в булевой алгебры 93, то класс эквивалентности 0(0) есть идеал, а 0(1) — фильтр булевой алгебры 93.
Таким образом, существуют, с одной стороны, биекция между множеством идеалов и множеством конгруэнций алгебры 93, а, с другой стороны, по теореме 2.7.2. — биекция между множеством фильтров и множеством конгруэнций булевой алгебры 93.
§ 2.8. Алгебры отношений и реляционные алгебры
Важным классом алгебраических систем являются алгебры отношений и их расширения — реляционные алгебры.
Рассмотрим алгебру отношений, носителем которой является множество отношений 93 = {Pi, Р2,..., Рт,...}, а сигнатура Е состоит из символов частичных двухместных операций объединения U, пересечения Г), разности \ и декартова произведения х отношений.
Отношения Р{ и Pj называются совместимыми, если Рг, Pj С Л" для некоторого множества А и числа п € ш.
Объединением Pi U Pj двух совместимых отношений Pi и Pj называется множество всех кортежей, каждый из которых принадлежит хотя бы одному из этих отношений: Р, U Pj — {X | X G Pt или X 6 Pj}. Пересечением Pi О Р7 двух совместимых отношений Pi и Pj называется множество всех кортежей, при
3 Зак. № 4872 Судоплатов
65
надлежащих как отношению Pj, так и отношению Pj: Pi Г) Pj -{X | X G Pi и X G Pj}. Разностью Pi \ Pj двух совместимых отношений Pi и Pj называется множество всех кортежей, принадлежащих отношению Pi и не принадлежащих отношению Рр P, \Pj = {X \ X EPiii Х$ Pj}.
Пример 2.8.1. Если Р = {(a,b,d),(b,c,e)}, Q — {(a,b, rf), (b,d, e)}, to PUQ = {(a, b,d}, (b, c, e), (b/d. e)}, PnQ = {(a, b. d)}, P\Q = {(h,ce)}.U
Декартовым произведением Pi x Pj двух отношений Pj и Pj называется множество всех кортежей z таких, что z —- конкатенация кортежей х G Pi и у G Pj: z = аГу, где х~ у = (тц ..., xr, yi,..., ys}, если х = (xi,..., тг), у = (yi,...,ys). Итак, Pj х Pj = {х'у | х е Pi, у g Pj}-
Пример 2.8.2. Если Р = {(a,b), (b,c}}, Q = {(Ь, с, о), (с, а, а)}, то P*Q = {(а, Ь. Ь, с, а), (а, Ь, с, а, а), (Ь, с, Ь, с, а}, (Ь, с. с, а, а)}. □	'	-
Алгебры отношений находят применение при формализации реальных объектов. Рассмотрим, как используется алгебра отношений при создании информационного обеспечения — разработке реляционной базы данных. Основой построения реляционной базы данных является двумерная таблица, каждый г-й столбец которой соответствует г-му домену (если ?г-местное отношение Rti содержится в D\ х D-j х ... Dn, то г-м доменом отношения Р.п, где г = 1,... ,?г, называется множество Dj), строка — кортежу значений доменов, находящихся в отношении Rn.
Пример 2.8.3. Рассмотрим 4-местное отношение Р4 (расписание экзаменов) (табл. 2.1).
Отношение Р4 является подмножеством декартова произведения Di х D? х D3 х D4, и поэтому каждое из множеств Di является доменом:
Таблица 2.1
R4	Т>1	D-i	D3	Т>4
1	А-1	Информатика	10 января	Ауд. 320
2	А-2	Физика	10 января	Ауд. 324
3	.4-2	Анализ	15 января	Ауд. 324
4	.4-1	Физика	16 января	Ауд. 320
5	.4-1	Анализ	21 января	Ауд. 324
6	.4-2	Информатика	21 января	Ауд. 320
66
— домен Di (группа) содержит значения Л-1, Л-2: D\ = {Л — 1,Л —2};
— домен D-2 (дисциплина) D2 = {Информатика, Физика, Анализ};
— домен Рз (дата) —	— {10 янв., 15 янв., 16 янв., 21 янв.};
— домен D,i (аудитория) — Р4 = {Ауд. 320, Ауд. 324}.
Порядок столбцов в таблице фиксирован, строки в общем случае могут располагаться произвольно. Цифры первого столбца 1,2,... ,6 являются идентификаторами отношения Т?4. □
Итак, каждому отношению можно поставить в соответствие таблицу.
Для преобразования отношений определим реляционную алгебру. Носитель реляционной алгебры представляет собой множество отношений 9Я, а набор операций кроме введенных операций U, П, \, х включает специальные операции над отношениями: выбор, проекцию и соединение.
Операция выбора представляет собой процедуру построения “горизонтального” подмножества отношения, т. е. подмножества кортежей, обладающих заданным свойством.
П р и мер 2.8.4. С помощью операции выбора построим из отношения (расписание экзаменов), отношение R\ (расписание экзаменов по физике). Результатом операции выбора являются строки, в которых домен D? представлен значением “Физика”, это 2-я и 4-я строки (табл. 2.2). □
Результатом операции проекции отношения Rn С А] х Л2 х -•xAnHaAZ),A.(2,...,Ajm,rfle {H,...,im} С {1,2,...	< ik
при j < к, называется множество	{(аг1,(ц2,   . , o,Zm) |
(аь а2... .,an)eRn} .Например,^" {(цКсц, а2, •  , М е Rn}-
Операция проекции определяет построение “вертикального” подмножества отношения, т. е. из кортежей удаляются координаты, соответствующие невыделенным доменам.
П р и м е р 2.8.5. Проекция тт^ отношения Т?4 из примера 2.8.3 определяет множество пар, каждая из которых содержит название дисциплины и дату (табл. 2.3). □
Т аб лица 2.2
R'i	Pi	d2	Рз	Р4
2	А-2	Физика	10 января	Ауд. 324
4	А-1	Физика	16 января	Ауд. 320
3*
67
Таблица 2.3
«4 ^2,3	d2	Рз
1	Информатика	10 января
2	Физика	10 января
3	Анализ	15 января
4	Физика	16 января
5	Анализ	21 января
6	Информатика	21 января
Таблица 2.4
Й4	Р1	Р2	Рз	Р4
1	А-1	Информатика	10 января	Ауд. 320
2	А-2	Физика	10 января	Ауд. 324
Операция соединения по двум таблицам, имеющим общий домен, позволяет построить одну таблицу, каждая строка которой образуется соединением двух строк исходных таблиц. Из заданных таблиц берут строки, содержащие одно и то же значение общего домена; общему домену ставится в соответствие один столбец.
П р и мер 2.8.6. Найдем по двум заданным таблицам (табл. 2.4, 2.5) результат соединения по домену Di (табл. 2.6). □
В примере 2.8.6 кортежи соединяются по условию равенства соответствующих координат: соединяются кортежи а = (сц,..., (Ч,...,ап) и b = (bi,... ,Ьг,... ,bn), когда аг = bi. В зависимости от практических потребностей можно определять соединения по другим правилам, например соединять кортежи а и Ь, когда аг < Ь{.
Таблица 2.5
R'i	Pi	d2	Рз	Р4
1	А-2	Анализ	15 января	Ауд. 324
2	А-1	Физика	16 января	Ауд. 320
Таблица 2.6
Ry	Di	D-2	Рз	Di		Рз	D'i
1	А-1	Информатика	10 янв.	Ауд.320	Физика	16 янв.	Ауд.320
2	А-2	Физика	10 янв.	Ауд.324	Анализ	15 янв.	Ауд.324
68
§2.9. Задачи и упражнения
1.	Установить, образуют ли алгебры следующие системы:
a) (w, +, -)' б) (Z,:, •), в) (К,	1 - 2г).
2.	Обозначим через Т множество функций, действующих на множестве А. Образует ли система (.У, о): а) полугруппу, б) моноид, в) группу?
3.	Построить изоморфизм систем ({1,2,3,4}, {(1,3), (1,4), (2,4), (3,2)}) и {{a,b,c,d}, {(b,a), (c,b), (c,d),	Построить все
го.моморфные образы указанных систем.
4.	Построить всевозможные попарно неизоморфные группы с двухэлементным носителем.
5.	Рассмотрим алгебру 21 — ({а, 6, c,d}, •), определенную следующей таблицей Кэли:
	а	b	с	d
а	а	а	ь	а
ъ	с	d	а	b
с	а	с	d	d
d	d	а	d	a
Имеет ли алгебра 21 подалгебр)' с носителем: а) {а,Ь, с}; б) {а}; в) {а, d}?
6.	Являются ли термами сигнатуры S = {/^\ <?(2\	} следующие
а) /(.9(ж,т/)); б) g(f(x),h(x,y,z)); в) f(g(x), h(x,y,z))7
7.	Указать алгоритм построения всех термов сигнатуры У от переменной х, если: а) У = {У^} и б) S = {</2)}-
8.	Построить подсистему *В(А’), порожденную данным множеством X:
а) <В = (К, ^Г), X = {2}; б) ® = (ш, +), X = {2,3};
в) ® = (С,-), X = {г}; г) ® = (С,-, 2), X = {г}.
9.	Рассмотрим алгебру 21 = ({a, b, с, d, е}, ), определенную следующей таблицей Кэли:
а b с d d с
с а Ъ b а е
а Ь
с а а d b а е а b
d е b е b е а с b d е с
69
Какое из следующих разбиений образует конгруэнцию на алгебре 21:
а) {{а,Ь,с}, {d,e}}; б) {а, Ь}, {с, d}, {е}}?
Построить фактор-алгебру алгебры 21 по найденной конгруэнции.
10.	Доказать, что любое л.у.м. является решеткой.
11.	Доказать, что в решетке максимальный элемент является наибольшим, а минимальный — наименьшим.
12.	Построить пример решетки с наибольшим элементом, но без наименьшего.
13.	Построить булеву алгебру подмножеств трехэлементного (четырехэлементного) множества.
14.	Для терма .г V (у Л z) булевой алгебры найти соответствующий терм в булевом кольце.
Глава 3
ЧИСЛОВЫЕ СИСТЕМЫ
§3.1. Бесконечные числовые системы
1. Системы Дедекинда — Пеано. Как отмечалось в § 1.3, множество натуральных чисел можно определять двояко: 1) исходя из 0 последовательно выражать натуральные числа, как множества, состоящие из предыдущих натуральных чисел; 2) задавать алгебраическую систему N = (N, 0, удовлетворяющую системе аксиом Дедекинда — Пеано. В дальнейшем мы будем рассматривать второй подход и называть такие системы системами Дедекинда — Пеано.
Теорема 3.1.1 (теорема Дедекинда — Пеано). Любые две системы Дедекинда — Пеано изоморфны.
В § 1.3 показано, что по индукции в системе N однозначно определимы двухместные операции сложения и умножения. В дальнейшем через N будем обозначать систему Дедекинда — Пе-. ано с этими операциями: (7V, 0, ',+, •).
2. Кольцо целых чисел. Определим с помощью системы N кольцо целых чисел Z = (Z,+,•). Рассмотрим множество № = {(а, 5)|а, b G N} и зададим отношение ~ по следующему» правилу:
(«, Ь) ~ (с, а + d = b 4- с.
Положим
(а, Ь) + (с, d) (а + с, b + d),
(а,Ь)  (c,d) (а  с + Ь • d, а • d + Ь • с).
71
Лемма 3.1.2. Отношение ~ является конгруэнцией на алгебре (№, +, }.
Доказательство. Покажем сначала, что ~ является отношением эквивалентности. Действительно, ~ рефлексивно, так как из а + а = а + а следует (а, а) ~ (а, а). Из симметричности отношения равенства и (a, b) ~ (с, d) следует (с, d) ~ (а, 6), т. е. отношение ~ симметрично. Установим теперь, что отношение ~ транзитивно.
Предположим, что (ai,6i) ~ (02,62) и (02,62) ~ (03,63). Тогда по определению выполняются равенства a.] + b? = а? + Ь\ и а? + 63 = 03 + 62- Складывая равенства, имеем 01+62 + 02 + 63 = 02 + 61 + 03 + 62, отсюда О| + 63 = оз + 6], т. е. (01,61) ~ (03,63). Таким образом, ~ — отношение эквивалентности.
Докажем, что отношение ~ согласовано с операциями + и . Предположим (01,61) ~ (02,62) и (ci.di) ~ (буД-з). Необходимо доказать:
1) (oi,6i) + (с1,ф) ~ (о2,6г) + (c2,d2),
2) (01,61) • (ci,di) ~ (о2,6г) • (с2,с/2).
Для доказательства 1 нужно установить, что (01 +ci,6i + Ф) ~ (02+02,62+6/2), т. е. (oi+ci) + (62 + d2) = (o2+c2) + (6i+di). По условию имеем
О1 + 62 = о2 + 61 и Cl + d2 = с2 + di.	(3.1)
Тогда (oi + 62) + (ci + б/2) = (02 + 61) + (с2 + Ф), откуда получаем искомое равенство.
Для доказательства 2 покажем, что (oici +6rdi, oidi +61С1) ~ (o2C2 + 62б/2, O26/2 + 62C2), т. e. (01С1+61ф) + (02б/2+б2С2) = (o2C2 + 626/2) + (oidi + 61 ci). Умножая поочередно первое равенство из (3.1) на ci, di, С2, с/2, получаем
oiCi + 62С1 = 02С1 + 6ici, bidi + a^di = 01Ф + 626/1,
OiC2 + 62С2 = О2С2 + 6LC2, 6|б/2 + О2^2 = О1б/2 + &2б/2-
Аналогично, умножая поочередно второе равенство из (3.1) на oi, 61, 02, 62, имеем
OiCi + O16/2 — О]С2 + О1б/1, 61 С] +616/2 — 61С2 + b\d],
0-2С1 + O26/2 = О2С2 + О2б/1, 62С1 + 626/2 = 62С2 + &2б/1-
72
Складывая эти четыре равенства, после приведения подобных и деления пополам получаем искомое равенство. □
В дальнейшем носитель алгебры N будет также обозначаться через N. Определим фактор-алгебру 21 = (№/ ~, +, •).
Лемма 3.1.3. Алгебра 21 является коммутативным ассоциативным кольцом, с единицей.
Доказательство. Проверка законов ассоциативности, коммутативности и дистрибутивности для операций сложения и умножения осуществяется непосредственно. Нулевым элементом в 21 является класс ~ (0,0), единичным элементом - ~ (1,0). Для произвольного элемента а =~ (а, Ь) противоположный элемент —а равен ~(6, а). □
Множество №/~ разобьем на три части: 1) {Д (а, Ь) | а > Ь}, 2) {~ (а, Ь) | а = Ь}, 3) {~ (а, Ь) | а < Ь}. В первом случае класс ~ (а, Ь) содержит пару (А;, 0), где а = b + к. Такие классы можно интерпретировать как положительные натуральные числа к = ~ (к, 0). Второе множество содержит всего один класс, который играет роль нуля в 21: 0 = ~ (0,0). Каждый класс ~ (а, Ь) из третьего множества содержит пару (0, к), где b = а + к. Эти классы интерпретируются как отрицательные числа: —к (ОД). Введенные обозначения позволяют рассматривать алгебру 21 как кольцо целых чисел ({...,—п,...,—2,—1,0,1,2,... ,п, которое в дальнейшем будем обозначать через (Z, +, •) или просто Z. При этом ~-классы будем называть целыми числами.
3. Поле рациональных чисел. Рассмотрим множество Z х (1!\{0}). Пару (т, п) из этого множества можно представить в виде дроби (Д Если рассматривать дроби как рациональные числа, то некоторые из них считаются равными, например | и |, хотя записываются они по-разному. Чтобы отождествить эти записи, определим отношение эквивалентности ~ следующим образом:
(mi,ni) ~ (m2,n2) <=> mi • n2 = тп2  Пр
Классы эквивалентности по отношению ~ называются рациональными числами, а множество всех классов эквивалентности образует .множество рациональных чисел Q = (Z х (К\ {0})) /~.
Рассмотрим алгебру 23 = (Z х (N \ {0}), +, •), в которой опе
73
рации сложения и умножения определены так:
(mi, п.]) + (m2, n2)	(mi • n2 + т2  щ, щ • п2),
(mi, nJ • (m2,n2) ;=± (тг  т2,п\  п2)
для любых (mi,nj, (m2,n2) Е Zx(N\{0}). Эти операции можно представлять и виде сложения и умножения дробей. Проверим, что отношение ~ согласовано с операциями алгебры
Лемма 3-1.4. Отношение ~ является конгруэнцией на алгебре 53.
Доказательство. Пусть (mi, nJ, (m2,n2), (mJ nJ, (mJ nJ — пары из Zx(N \ {0}) с условиями
(mi,nJ ~ (mJ nJ и (m2,n2) ~ (mJ nJ. (3.2)
Требуется доказать, что:
a)	((mi, nJ + (m2,n2)) ~ ((mJnJ + (mJnJ),
6)	((mi,nJ  (m2,n2)) ~ ((mJnJ • (mJnJ).
Для проверки свойства а имеем
(mi,nJ + (m2,n2) = (mi • n2 + m2 • nbni • n2),
(mJ nJ + (mJ nJ = (nJ  n'2 + m2  nJ n\  n'2).
Нужно установить, что
(mi  n2 + m2 • nJ • (n'x *, n J = (т'г • n2 + m2  nJ • (ni • n2). (3.3)
Зная из (3.2), что
mi  n'i = m\  nj и m2 • n2 = m2  n2,	(3-4)
имеем
(mi-n2 +m2-nJ • (njnj = (пц-n2)  (njnj + (m2-nJ • (njnj =
= (-mi • nJ • (n2 • nJ + (m2  nJ  (ni  nJ = {по условию 3.4} =
= (n?/j  nJ  (n2 • nJ + (m2  n2) • (ni  nJ =
= (mjnjjni-n2)+(mjnj(ni-n2) = ((mjnj + (mjnj)-(ni-n2), и тем самым равенство (3.3) установлено.
74
Проверка свойства б проводится аналогично и оставляется читателю в качестве упражнения. □
Таким образом,'отношение ~ — конгруэнция, и фактор-алгебра ®/ ~ образует множество рациональных чисел Q с обычными операциями сложения и умножения: ®/ ~= (Q,+,•). В полученной алгебре выполняются все аксиомы поля. Нулевым рациональным числом является класс ~ (0,1), единицей — класс ~ (1,1), числом, противоположным числу ~(т, п) является число — (~(т, п))	~ (—т, п), обратным ненулевому числу ~(m,n) —
число (~ (т,тг))-1	~ (±n, ±tti), где знак плюс берется при
771 > 0 И минус — при 771 < 0.
4.	Поле действительных чисел. Последовательность рациональных чисел называется фундаментальной, если для любого рационального числа е > 0 существует такое по, что |т?) — х(.\ < е для всех р и у, больших 77-0- Фундаментальные последовательности (.тп)пеш и (уп)П£ы называются эквивалентными: (хп) ~ (Уп), если для любого рационального числа е > 0 существует такое по, что |жр — yj < е для всех р и q, больших по- Классы эквивалентности фундаментальных последовательностей; ~ (тп) называются действительными или вещественными числами. Таким образом множество R действигпельны.х чисел является фактор-множеством X/где X — {(.гп) | (хп) — фундаментальная последовательность}.
На множестве R определим основные арифметические операции. Для этого рассмотрим алгебру X = (X, +, •) со следующими операциями; (хп) ± (уп) ?=± (хп ± уп), (хп)  (уп) (хп -уп). Легко проверяется, что отношение ~ является конгруэнцией алгебры X. Фактор-алгебра Х/~ образует множество действительных чисел с обычными операциями сложения и умножения. В алгебре (R, +, -) выполняются все аксиомы поля. Нулевым элементом является класс ~ (0); единицей — класс ~ (1); противоположным классу ~ (,гп) является класс —(~ (хп))	(—хп); обратным
ненулевому классу ~ (тп), где (,гп) является последовательностью без нулевых элементов, — класс (~(жп)) 1 ?=± ~ ((т,,) '1).
Отметим, что каждый класс ~ (хп) содержит единственную последовательность (х'п), такую, что х'п = ±(щ.10А + щ..] Ю^1 + •   + ojlO1 + аоЮ° + а-110-1 ± а_210~2 + • • • + о_п10“"), где а.{ £ {0,1,..., 9} и не существует п с условием о_7; = 9 при i > п. Поэтому для обозначения действительных чисел используются
75
следующие записи, называемые {бесконечными) десятичными дробям,и:
zizCL^CLk — 1 • •  О] GQ.G—1G—2 • • •	п •  
Каждая фундаментальная последовательность {хп) может иметь или не иметь предел в множестве рациональных чисел. В первом случае любая последовательность из класса ~ {хп) сходится к одному и тому же рациональному числу q, и поэтому такие классы удобно называть рациональными числами. Во втором случае, когда предела в Q не существует, класс ~ {хп) называется иррациональным числом.
Десятичная дробь N.ay&i .. ,ап ..., где N £ Z, называется периодической, если существуют такие натуральные числа р, q, что Gfe+p = Qfc для всех k > q. Для обозначения периодической дроби используется запись N.aya^    a,q{aq+iaq+2    aq+p), где совокупность цифр gq+1oq+2  • • aq+p называется периодом дроби.
Предложение 3.1.5. Бесконечная десятичная дробь тогда и только тогда является рациональным числом, когда она периодична.
Поскольку для любого конечного алфавита А множество слов W(A) счетно, а множество действительных чисел континуально, справедливо следующее предложение.
Предложение 3.1.6. Не существует конечного алфавита, при помощи слов которого можно обозначить все действительные числа.
5.	Поле комплексных чисел. Множество С комплексных чисел строится из множества действительных чисел по правилу С = R2. Операции сложения и умножения определяются по следующим правилам: (ai,6i) + (02,62)	(«1 + 02,61 + Ъф).
(01Д1) • (а2,62) (aiG2 -6162,0162 + 0261). Алгебра (С,+,-) удовлетворяет всем аксиомам поля.
Естественным .образом определяются мономорфизмы, позволяющие вложить алгебру (N, +, •) в алгебру (Z,+, •), алгебру (Z, + , •) — в алгебру (Q, +, •), алгебру (Q, +, •) — в алгебру (R, +, ), алгебру (R, +,•) — в алгебру (С, +,•). Поэтому с точностью до изоморфизма можно считать, что каждая из этих алгебр является подалгеброй каждой из последующих алгебр и имеют место включения NcZcQcKcC.
76
Приведенные конструкции позволяют проследить процесс образования числовых систем с помощью основных теоретико-множественных операций, исходя из пустого множества.
§3.2. Системы счисления
1.	Позиционные системы счисления. В современных компьютерах любая информация представляется в виде двоичных кодов, т. е. упорядоченных наборов двух различных символов, которые обычно обозначаются через 0 и 1. В связи с этим часто приходится использовать системы счисления, отличные от привычной десятичной системы счисления. При этом в основном используются позиционные системы счисления, которые строятся по тем же принципам, что и десятичная система.
Как показано в § 3.1, запись произвольного действительного числа х (х 0) в десятичной системе представляет собой перечисление всех коэффициентов разложения числа х по степеням числа 10:	i • • - сцпо-0—1°—2 • • • о—п   
На этих же принципах основаны и другие позиционные системы счисления с любым целым числом Р (Р > 1), которое называется основанием счисления. В каждой из этих систем используется Р различных символов, называемых цифрами, для обозначения некоторых различных натуральных чисел, называемых базисными. В дальнейшем в качестве базисных принимаются целые числа от 0 до Р — 1.
Запись произвольного числа х в системе счисления с основанием Р также определяется разложением этого числа х по последовательным степеням числа Р: bkPk + bfc_iPfc-1 + ... + biP1 + 1)qP° + Ь-^Р-1 + /лцР2 + • • •, где каждый коэффициент bi является одним из базисных чисел и обознается одной цифрой. Аналогично записи в десятичной системе число х в Р-ичной системе изображается последовательностью своих коэффициентов с разделением целой и дробной частей с помощью точки: х = bkbk^ ... Ь0-Ь-1Ь-2 • • 
Для указания используемой системы счисления будем основание системы (в ее десятичной записи) приводить в качестве нижнего индекса у записи числа, например 758ц;.
Арифметические операции над числами в любой Р-ичной системе выполняются по тем же правилам, что и в десятичной, поскольку все они основываются на правилах выполнения опе
77
раций над соответствующими многочленами. При этом используются таблицы сложения и умножения, которые имеют место в системе счисления с данным основанием.
2.	Двоичная система. При Р = 2 для записи чисел используются всего две цифры: 0 и'1.
П р и м е р 3.2.1. 23ю = 1-24+0-23 + 1-22+1-21+1-2° = 101112. || = 1-2~‘ + 1  2"2 + 1 • 2-3 + 0  2~4 + 1 • 2“5 =0.11101-2 □
Полезно запомнить запись в двоичной системе первых шестнадцати натуральных чисел:
0	1	2	3	4	5	6	7
0	1	10	и	100	101	ПО	111
8	9	10	11	12	13	14	15
1000	1001	1010	1011	1100	1101	1110	1111
При выполнении арифметических операций над числами в двоичной системе используются следующие таблицы сложения и умножения:
0 + 0 = 0, 0+1 = 1, 1 + 0 = 1, 1 + 1 = 10;
0-0 = 0, 0-1 = 0, 1-0 = 0, 1-1 = 1.
Поскольку в этой системе для изображения чисел берутся только две цифры, для построения компьютера можно использовать элементы, имеющие лишь два различных устойчивых состояния, одно из которых соответствует цифре 0, а другое — цифре 1. При этом алгебраическая система с носителем, состоящим из двоичных кодов, изоморфна соответствующей алгебраической системе, элементы которой имеют десятичную запись.
3.	Восьмеричная система. В восьмеричной системе счисления используются цифры 0,1, 2, 3,4,5,6.7. Запись числа основывается на его разложении по степеням чиста восемь с указанными коэффициентами.
П р и м е р 3.2.2. 21510 = 192 + 16 + 7 = 3 • 83 + 2 • 81 + 7 • 8° = 3278, 30.2510 = 3  81 + 6 • 8° + 2  8"1 = 36.28.
4. Шестнадцатеричная система. В этой системе для
записи базисных чисел от нуля до пятнадцати используются следующие символы (цифры): от 0 до 9 — те же самые арабские
78
цифры, а для следующих чисел — от десяти до пятнадцати — символы а, Ь, с. d. е, f.
П р и м е р 3.2.3. ае.81б = 10-16 + 14 + 8/16 = 160 + 14 + 0.5 = 174.510.
5. Смешанные системы счисления. В некоторых случаях числа, заданные в системе счисления с основанием Р, приходится изображать с помощью цифр системы с основанием Q (Q < Р). Такая необходимость возникает, например, когда в память машины, способной воспринимать только двоичные цирфы, нужно ввести десятичные числа для их последующей переработки. В таких случаях используют смешанные системы счисления, в которых каждый коэффициент разложения числа по степеням Р записывается в Q-ичной системе. Такая смешанная система называется Q-P-ичной. При этом для записи каждого из упомянутых выше коэффициентов используется одно и то же количество Q-ичных разрядов, минимально необходимое для записи любого из допустимых коэффициентов.
П р и м е р 3.2.4. Представим число 8903щ в смешанной двоично-десятичной системе. Поскольку 8щ = ЮООг, 9щ = IOOI2, Зю =00112, имеем 890310 = 100010010000 00112-ю • □
Отметим, что запись в двоично-десятичной системе отличается от записи данного числа в двоичной системе счисления. Например, 890310 = 100010110001112, что отличается от записи этого же числа в смешанной двоично-десятичной системе.
.Особый интерес представляет случай, когда Р = Q (I £ ш). При этом запись любого числа в смешанной Q-P-ичной системе совпадает с записью этого числа в Q-ичной системе.
Пример 3.2.5. Если Р = 8, Q = 2 (8 = 23), то 2763s = 0101111100112-8 =010Ц11100112. □
Таким образом, запись числа в Р-ичной системе счисления в случае Р = Q1 является просто сокращенной записью изображения этого же числа в Q-ичной системе: для такой сокращенной записи Q-ичные цифры в изображении числа объединяются вправо и влево от точки в группы по I разрядов (дополняя, в случае необходимости, нужное количество нулей справа и слева), и каждое число, представленное в Q-ичной системе этой группой разрядов, записывается одной Р-ичной цифрой.
П р и м е р 3.2.6.
1011011011.1110112 = 001011011011.111011002 =
= 0010 1101 1011.1110 11002-16 = 2с?Реп16. □
79
6. Перевод чисел из одной системы счисления в другую. В связи с использованием различных систем счисления возникает необходимость перевода чисел из одной системы в другую. Задача перевода состоит в следующем. Пусть известна запись числа х в системе счисления с основанием Р: х = (p„pn_i ... Р0Р-1Р-2 • • -P-k)pj где Pi — цифры Р-ичной системы. Требуется найти запись числа х в системе счисления с основанием Q: х = (ll-mSlm-l   • Q0-9-19-2 • • •	W Qi — цифры Q-ИЧНОЙ СИ-
стемы. При этом можно ограничиться рассмотрением положительных чисел, поскольку перевод любого числа сводится к переводу его абсолютной величины с последующим приписыванием соответствующего знака.
Для определенности будем считать, что в процессе перевода должны использоваться только средства Р-ичной арифметики. В связи с этим необходимо рассмотреть перевод из Q-ичной системы в Р-ичную (Q —> Р) и из Р-ичной в Q-ичную (Р —> Q).
Перевод Q —> Р. Если известна запись числа х в Q-ичной системе х =	   </о-</-1</-2  •  перевод в Р-ичную
систему сводится к вычислению значения многочлена
х = qmQm + qm-iQm 1 +  •  +qo+q-iQ l + q~2Q 2 + --- + q-iQ l,
что следует из правил записи числа х в Q-ичной системе.
Пример 3.2.7. Переведем число х = Ьа.8к> в десятичную систему средствами десятичной арифметики. Здесь Q = 16, Р = 10. Имеем
х = 11 • 16 + 10 4- 8 • 16”1 = 186.510. □
Перевод Р —> Q. Рассмотрим перевод целых чисел и правильных дробей. В общем случае перевод любого числа сводится к независимому переводу его целой и дробной частей.
Перевод целых чисел. Пусть дана запись целого числа N в системе счисления с основанием Р. Поскольку N — целое число, его запись в Q-ичной системе будет иметь вид N = (цьЦкл   -Qo)q, где Qj (0 Qi < Q) — искомые цифры Q-ичной системы. Эта запись является сокращенной записью многочлена N = qkQk + qk-iQkX +  •  + Qo-
Для определения qo разделим обе части последнего равенства на Q: N/Q = qkQk~l 4- • • • + qi 4-Qo/Q- Приравнивая между собой
80
целые и дробные части в левой и правой частях (учитывая, что qi < Q), получим, что до есть остаток от деления N на Q.
Целочисленное частное от деления N на Q обозначим через N\. Тогда 2V1 = qkQk~l + - - - + <71- Поскольку N± есть целое число, к нему можно применить тот же прием для определения значения qi, которое равно остатку от деления на Q. Полученное при этом частное обозначим через AQ, и т. д. Этот процесс заканчивается, когда очередное частное окажется равным нулю. Для окончательной записи числа N в Q-ичной системе нужно в соответствующем порядке записать коэффициенты дг, изображая каждый из них одной Q-ичной цифрой.
Пример 3.2.8. 1. Переведем десятичное число N = 23 в двоичную систему средствами десятичной арифметики (Р = 10, Q = 2):
23/2 = 11 + 1/2, до = 1, М = 11,
11/2 = 5 + 1/2, щ = 1, N2 = 5,
5/2 = 2 + 1/2, q2 = 1,	=	2,
2/2 = 1 + 0/2, q3 = 0, W4 = l,
1/2 = 0 + 1/2, q4 = 1, Л% = 0.
Поскольку числа нуль и единица в каждой из этих систем обозначаются цифрами 0 и 1, то в процессе деления сразу получены искомые двоичные цифры: N — 101112.
2. Переведем число N = 175ю в шестнадцатеричную систему: 175/16 = 10 + 15/16, д0 = 15, М = 10, 10/16 = 0 + 10/16, щ = 10, А2 = 0.
Таким образом, N = 10 • 161 + 15 • 16°. Число 10 соответствует шестнадцатеричной цифре а, число 15 — цифре f, следовательно, N = а/16-
Перевод дробных чисел. Пусть требуется перевести в Р-ичную систему правильную дробь х (0 х < 1), заданную в ее Р-ичной записи: х = O.p_ip_2 .. -P-к- Запись этого числа в Q-ичной системе будет иметь вид х = O.q_iq_2 ... q_m .... Значит, х = <7-1Q-1 + <7—2Q—2 + • • • + q-mQ~m + ..., где % — коэффициенты Q-ичного разложения, подлежащие определению. Нетрудно убедиться, что эти коэффициенты можно получить путем последовательного умножения на Q сначала исходного числа х, а затем дробной части очередного полученного произведения. Этот процесс. продолжается до тех пор, пока дробная часть очередного произведения не окажется равной нулю либо не будет достигнута требуемая точность изображения числа х в Q-ичной системе.
81
П р и м е р 3.2.9. Перевод числа х = 0.1ю в двоичную систему приводит к такой последовательности действий:
0.1 	2 = 0.2,	g-i	= 0, дробная часть =	0.2,
0.2 •	2 = 0.4,	Q-2	= 0, дробная часть=	0.4,
0.4 	2 = 0.8,	д-з	= 0, дробная часть =	0.8,
0.8 	2 = 1.6,	q-4	= 1, дробная часть —	0.6,
0.6 •	2 = 1.2,	<7-5	= 1. дробная часть =	0.2,
Очевидно, что дальше результаты будут повторяться, и поэтому х = (0.0001100110011.. .)г = 0.0(0011)2-
§3.3. Компьютерная алгебра и численный анализ
Термин компьютерная алгебра объясняется способностью компьютеров манипулировать математическими выражениями, заданными символьно, а не численно. Системы компьютерной алгебры освобождают от рутинной работы, связанной с численными ошибками (усечение и округление).
Прежде чем рассматривать точную арифметику, реализуемую в системах компьютерной алгебры, отметим неотъемлемые недостатки численных расчетов с использованием компьютеров. Компьютер — это машина, с конечной памятью, состоящей из слов конечной длины алфавита {0,1}. Элементы компьютерного слова называются битами. Обычно длина компьютерного слова составляет 16 или 32 бита, при этом максимальное целое число, которое можно разместить в слове (в двоичной системе счисления), составляет 216 — 1 или 232 — 1, что соответствует пятизначным или десятизначным числам в десятичной системе счисления.
При выполнении численных расчетов на компьютере обычно возникает проблема представления бесконечного множества вещественных чисел в конечной памяти. Наиболее' распространенным способом решения этой проблемы в численном анализе является приближение (округление) вещественных чисел с использованием конечного множества с плавающей точкой. Множество F чисел с плавающей точкой характеризуется основанием счисления Р, точностью t и областью значений экспоненты где параметры P,t,L,U зависят от компьютера. Каждое число f Е F представляется в виде
< = . 
'	\Р^Р2	Р'1'
82
где целые числа di, i — 1,2,... ,t, удовлетворяют неравенствам О ф Р — 1, L е J7. Если di j- 0, число / G F называется нормализованным числом, с плавающей точкой.
Отметим, что при использовании чисел с плавающей точкой или целых чисел, помещающихся в одном компьютерном слове, арифметические операции выполняются очень быстро, поскольку они производятся не программным обеспечением, а электронными схемами компьютера.
Нетрудно подсчитать, что множество F содержит 2(Р—1)/>г | ([/ — L + 1) + 1 нормализованных чисел с плавающей точкой (включая нуль). Эти числа размещены на числовой прямой равномерно не на всей области значений, а только между последовательными степенями Р.
Пример 3.3.1. На рис. 3.1 изображено 33-элементное множество нормализованных чисел с параметрами Р = 2, t — 3, L = -1, U = 2. □
Приведенный пример показывает, что сумма (или произведение) данных чисел и /г из F может не принадлежать F и должна быть приближена ближайшим числом с плавающей точкой. Разность между истинным и приближенным значениями суммы (или) произведения является ошибкой округления. Отметим также, что частичные операции сложения и умножения в F не удовлетворяют законам ассоциативности и дистрибутивности. Например, в 33-элементном множестве F справедливо 5/4+(3/8+3/8) = 2, где 5/4, 3/8, 2 G F. Однако (5/44-3/8)4-3/8 / 2, поскольку в F не определена сумма (5/4+3/8) и это выражение должно быть приближено в F либо числом 3/2, либо числом 7/4. Ошибки округления могут возникать и при работе с целыми числами, например, при вычислении произведения двух s-значных чисел на компьютере, который не может обрабатывать числа, содержащие больше я цифр.
Таким образом, в численном анализе нужно тщательно оце-
-Ч--I-I-Ы I I IIII III I IIIIIIHW-H—I-1—+-
_Q1 -3	—2	-1 _1_1 0 1 1	1	2	3 31
°2	2442	°2
Рис. 3.1
83
кивать ошибки округления, возникающие при работе любого алгоритма. Это указывает на необходимость построения и использования программных систем, способных обрабатывать выражения в символьном виде и производить безошибочные вычисления. Опишем два подхода к построению таких систем, первый из которых использует списочное представление чисел, а второй — многомодульную арифметику.
§ 3.4.	Списочное представление чисел
1.	Списки и базисные операции над списками. Определим по индукции понятие списка над множеством S:
1)	любой элемент a G S является списком над множеством S';
2)	если ai,...,ап — списки над множеством S, п 0, то (ai,..., «„) — список над множеством S';
3)	никаких списков над множеством S, кроме построенных по пп. 1 и 2, нет.
Список, соответствующий п = 0 в п. 2, называется пустым и обозначается так же, как и пустое слово, через Л. По определению каждое слово непустого алфавита S является списком над S.
Определим основные операции над списками. Если а = («1,..., а,п) — список, то длина(а) 1(a) тг; первый(а) тгДа) = гц; последний(а) яп(а) — ап; хвост(а) тг2,...,п(а) — (а-2,...,а-п')- развернутый(а)	= (ап,... ,ai); если
b = (b],...,bk) — список, то присоединение^, а) ?=± Ь'а = (bl,..., bk, «i,..., ап), отсоединение^,^ а)	а.
2.	Списочное представление целых и рациональных чисел. Как уже отмечалось, компьютерное представление целых чисел ограничено длиной машинного слова. Для расширения возможностей такого представления и выполнения точных арифметических действий можно использовать задание целых чисел в виде списков. При этом, однако, необходимо разработать специальное программное обеспечение, позволяющее выполнять арифметические операции над списками.
Пусть Р — такое основание счисления, что Р — 1 — наибольшее значение, хранимое в компьютерном слове. Рассмотрим два типа целых чисел. Если — (Р — 1) <С т Р — 1, то целое число т называется коротким. Остальные целые числа называются длинными. Длинные числа т представляются в виде списка
84
т = (то,rn,i,..., пц), к 1, где /щ — короткие целые числа (|?7ii| + Р — 1), являющиеся коэффициентами в выражении fc
т. = 22 mi ' и имеющие тот же знак, что и число т. При г=0
хранении числа т в виде списка информацию о знаке будем записывать только в тк.
Пример 3.4.1. Предположим, что Р — 103, т. е. компьютерное слово может содержать только три десятичные цифры. Представление числа т = +23456789 в виде списка выглядит следующим образом: m = (789,456,+23). □
Рациональные числа г = представляются списками г = (т.п), где т, п — списки, представляющие целые числа т и п.
3.	Классические алгоритмы целочисленной арифметики. Рассмотрим классические алгоритмы выполнения арифметических операций с длинными целыми числами. Пусть т =
fc	I
^2 ггц-Рг и п = 22 ni'Pl ~ длинные целые числа, m = (то, mi,...
г=0	г=0
тк), п = (по,П1,... .щ) — соответствующие списки. При сложении списков тип последовательно складываются (с использованием встроенной в компьютер операции сложения) короткие целые числа, находящиеся в соответствующих координатах списков, и при сложении координат учитываются переносы от меньших разрядов к большим аналогично сложению десятичных чисел. Полученный список s называется суммой списков m и n: m + п. Точно так же, используя школьные алгоритмы целочисленного умножения, поразрядным перемножением коротких целых чисел с переносом от меньших разрядов к большим определяется произведение списков m и n: m  п.
Предложение 3.4.1. Алгебра {%, +, •) изоморфна алгебре (3,+г))	3 ~ множество списков, задающих целые числа.
При делении т на п ищутся целые числа q и г, обладающие свойством делимости с остатком: т = nq+ г, 0 + г < п. Для определения операции деления со списками достаточно описать случай, когда п ф т < Рп. Общий случай сводится к этому случаю аналогично тому, как к нему сводится общий случай деления столбиком.
85
Пример 3.4.2 При делении 1234 на 23 сначала делится 123 (начальное число т) на 23 (число п): 123 = 23-5 + 8, затем 84 (новое число т) делится на 23: 84 = 23-3 + 15. Таким образом, имеем 1234 = (23  5 + 8) • 10 + 4 = 23 - 50 + 84 = 23 • 50 + 23  3 +15 = 23  53 + 15. □
Наиболее очевидный подход к решению состоит в угадывании частного q по наиболее значимым цифрам чисел т и п. Полученное таким путем частное называется пробным частным и обозначается через qt. Согласно нашим предположениям, т = то + ... + тщ.  Рк, п = по + ... + П/.-1  Pk l. п т < Рп. Обозначим через [ж] целую часть числа ж, т.е. наибольшее целое число, не превосходящее числа х. Положим
<7/
'Р- 1,
* Гт^Р+тд.-! 1
если тк — nk~i,
если тк < пк~1.
П р и м е р 3.4.3. Обозначим истинное частное через д. Тогда при Р = 10 имеем:
— если т = 600, п = 69, то т? = ni, а следовательно, qt — 9, в этом случае q = 8;
— если 77?. = 480, п = 59, то qt = [48/5] = 9, в этом случае 9 = 8;
— если т = 200, п = 29, то т? = nj. поэтому qt = 9, в этом случае q = 6. □
Отметим, что во всех случаях qt слишком велико, однако при п = 69 угаданное значение не гак плохо, как при п = 29. Величина такого отклонения объясняется следующей теоремой.
Теорема 3.4.2. Если целые числа, qt и q являются пробным, частным и частным соответственно при делении т на, п, то Qt Q- Более того, если	Р/2, то qt — 2 < q < qt, т.е. qt
равно либо q, либо q + 1, либо q + 2.
Доказательство. 1Ь qn т, используя неравенство 77?.о + ... + 7пк-2РК~2 < Р/С~1, получаем, что дпк-1Рк~} < (1 + тк ] + ткР)Рк~}.. следовательно, qnk~t < +-ткР, где q Р — 1. Тогда из определения qt очевидно следует, что qt д.
Предположим теперь, что п Р/2. В этом случае достаточно показать, что (%—2)п С тп. Используя неравенство 77q+. . .+тг/с-2’ рк-‘2 < рк~Л_ получаем (qt — 2)тг < (qt~2)(п/с_] }1 )7;>А ! = (qtn\ + (/// 2  2?../ |	! < (mfcP + 7Hfc_1)Pfc~1 +(qt-2-2nk^Pk-1
86
по определению qt- Поскольку nr-! Р/2 и qt ф Р — 1, имеем
Qt — 2 — 2пд;_1 < О,
(mfcF + ?7ifc_1)Pfc-1 + (<7t-2-2nfc_i)Pfc“1 ф (ткР+ тк^)Рк^
(ткР + т,к_1)Рк~1 + mfc_2Pfc“2 4-Ь m0 = m,
что и требовалось доказать. □
Чтобы добиться выполнения условия, что старшая цифра делителя больше либо равна Р/2, нужно домножить т и п на 2е, где 2е — наибольшая степень 2, для которой 2е • п < Рк+1. Затем делим 2е  т на 2е • п.
Пример 3.4.4. Рассмотрим Р — 10, т = 200, п = 29. Вычислим наибольшее число е, для которого 2е  29 < 1000. Получаем е = 5 и 2е т = 32-200 = 6400, 2е  п = 32-29 = 928. Имеем qt = [64/9] = 7, что отличается от истинного частного q = 6 на единицу. □
После нахождения пробного частного qt достаточно выбрать истинное частное среди чисел qt, qt — 1, qt — 2.
§ 3.5.	Делимость в кольце целых чисел
Будем говорить, что ненулевое целое число а делит целое число b или а является делителем b (записывается а\Ь), если существует такое целое число с, что b = а  с. Например, ±7|28, так как 28 = 7-4 и 28 = (—7) • (—4). Для любого ненулевого числа а имеем а|0, ±1|а и ±«|а. Понятие делителя будет очень важным в нашем изложении теории целых чисел.
Одно из основных свойств целых чисел — свойство делимости или евклидовости.
Теорема 3.5.1 (свойство евклидовости). Для любого а и любого ненулевого b существуют единственные (целые) частное q и остаток г такие, utno а, = b • q + г, 0 С г < |Ь|.
Доказательство. Рассмотрим множество целых чисел вида a—kb, где k € Z. Выберем в этом множестве наименьшее неотрицательное число (такое число существует, поскольку система (о, ф) является вполне упорядоченным множеством). Обозначим это число через г, а через q соответствующее значение к. По определению имеем г = о. — qb 0. Для доказательства единственности допустим, что а = bqi 4- щ, 0 ф и < |Ь|, щ г.
87
Пусть для определенности г\ < г, так что 0 < г — щ < |Ь|; тогда г — уд = (щ — q)b и Ь|(г — уд), что противоречит неравенствам О < г -?д < |Ь|. □
Пусть а, b — целые числа, не равные нулю. Целое число d > О называется наибольшим общим делителем чисел а и b при выполнении следующих условий:
1)	d|a и d\b;
2)	если с|о, и с|6, то c|d.
Наибольший общий делитель чисел а и b обозначается через (а, Ь) или НОД(а, Ь). Единственность НОД следует из условия 2 и того, что он положителен. Например, (12,30) = (12,-30) = (—12,30) = (—12,-30) = 6. Наибольший общий делитель двух ненулевых целых чисел всегда существует.
Теорема 3.5.2. Если целые числа а и b не равны нулю, то существуют целые числа х и у такие, что (a,b) = ах + by.
Доказательство. Пусть d — наименьшее положительное целое число вида ах+by, например, d = axo+byo (такое число существует в силу полной упорядоченности множества (од $С)). Очевидно, что d > 0 и d удовлетворяет условию 2 из определения НОД. От противного докажем, что d удовлетворяет также условию 1. Допустим, что условие 1 не выполняется, и предположим для определенности, что d не делит Ь. Тогда b = dq+r, 0 < г < d, следовательно, г = b — dq — b— (axo + byo)q = а(—qxg) +Ь(1 — qyo), что противоречит минимальности d. □
Числа х и у, указанные в теореме, определяются неоднозначно. Например, 6 = (12,-30) = 12 • 3 + (-30)  1 = 12 • (-2) + (-30) • (-1)-
Пользуясь понятием НОД, можно охарактеризовать целые решения линейных уравнений от двух переменных (ах + by — с), которые называются линейными диофантовыми уравнениями.
Теорема 3.5.3. Пусть ах + by = с линейное диофантово уравнение, а,Ь 0, d — (a,b). Тогда
1) уравнение разрешимо относительно х и у тогда и только тогда, когда d,\c;
2) если (ту, уф) — -частное решение, то общее решение имеет вид (я?о — п(Ь/д),у$ + n(a/d)), п 6 Z.
Доказательство. 1. Предположим, что хиу - целые числа, такие, что ах + by = с. Так как d\a и d\b, то d\c. Предположим теперь, что d\c, т. е. с = dk для некоторого целого к. По
88
теореме 3.5.2. существуют целые числа s, t такие, что d — as + bt. Умножая это равенство на к, получаем с — dk = n,(sfc) + 6(tfc), откуда следует, что х = як и у = tk удовлетворяют уравнению ах + by = с.
Доказательство пункта 2 оставляется- читателю в качестве упражнения. □
Пример 3.5.1. Уравнение 12 т; — ЗОу = 84 разрешимо, поскольку (12,-30) = 6|84. Частным решением является пара (ж, у) = (2,-2), а общее решение имеет вид ж = 2 + 5п, у = —2 + 2п. □
Два целых числа а и Ь называются взаимно простыми, если (а, Ь) = 1. По теореме 3.5.3. это эквивалентно существованию целых чисел s и t таких, что as + bt = 1.
Теорема 3.5.4. Пусть а, b — ненулевые целые числа, d, — (а,Е). Тогда числа a/d, и b/d. взаимно просты.
Пусть а,Ь- целые числа, не равные нулю. Целое число т > О называется наименьшим, общим, кратным чисел а, и b при выполнении следующих условий:
1) о.|?п и Ь\гп;
2) если о.|с и Ь|с, то ?п|с.
Наименьшее общее кратное чисел а. и b обозначается через [а, Ь] или НОК(а, Ь). Единственность НОК следует из условия 2 и положительности т.
Теорема 3.5.5. Если а, b — ненулевые целые числа, то существует их НОК и справедливо равенство [«, 6] = |о,6|/(а. Ь).
Теперь изложим классический алгоритм, Евклида вычисления НОД двух целых чисел. Ключевым в этом алгоритме является следующий факт: если а = bq+r и d делит а, и Ь, то d\r = a—bq. Поскольку это верно для любого делителя, это справедливо и для d =НОД(а, 6), а значит, НОД(о, Ь) =НОД(6, г). Кроме того, НОД(о.,0) = |о[ для всякого а. Условимся также считать, что НОД(0,0)=0.
Итак, если заданы целое число а и ненулевое целое число Ь, выполняем последовательность делений:
пусть од = йи ai = b, тогда
«о = «191 + «2	(0 < «2 < |«1|),
«1 = «292 + «3	(о < «3 < «2),
89
O'k—I — (^k—lQk—A 4" dk (0 < dk <	1)>
o-fc-i = akqk + 0.
Указанный процесс рано или поздно останавливается, так как остатки а,; образуют строго убывающую последовательность неотрицательных целых чисел и ак = (од,0) = ... — (оцоД —
Пример 3.5.2. Проиллюстрируем работу алгоритма Евклида для чисел а = 342 и b = 612.
Имеем (342,612) = (612,342) = (342,270) = (270,72) = (72,54) = (54,18) = (18,0). Таким образом, НОД(а, Ь) = 18.
§3.6.	Разложение целых чисел на множители
Целое число а 0, ±1 называется неразложимым, если все его делители тривиальны, т.е. равны ±1 и ±а. Например, неразложимы числа 13 и —7. Целое число о^0,±1 называется разложимым или составным, если у него имеются нетривиальные делители, т. е. оно может быть записано в виде а = Ьс, где b и с не равны ±1 и ±а. Например, 276 = 12-23 — составное число. Делители также называются сомножителями. Если сомножители b и с разложимы, то они также могут быть записаны как произведения нетривиальных сомножителей и т. д. Этот процесс рано или поздно обрывается, поскольку не существует бесконечной строго убывающей последовательности положительных целых чисел.
Теорема 3.6.1 (существование неприводимого разложения). Любое целое число а 0, ±1 может быть записано как ± произведение конечного числа положительных неразложимых целых чисел, т.е. а. =	 ...  иг, где щ > 1, i = 1,..., г, — неразло-
жимые числа.
Пример 3.6.1. 1008 = 2- 2- 2- 2- 3- 3-7. □
Целое число р > 1 называется простым, если для любых а, b из p\ab следует р|а или р\Ь.
Предложение 3.6.2. Целое число р > 1 тогда и только тогда является простым, когда оно неразложимо.
Следующая теорема называется основной теоремой арифметики.
Теорема 3.6.3 (единственность неприводимого разложения). Всякое целое число а 0, ±1 может быть записано как ± яро-
90
изведение простых чисел единственным способом с точностью до порядка сомножителей.
Доказательство. Предположим, что положительное целое число а имеет два неприводимых разложения: а = щ ... <(т = vi vs, где Uj, — простые числа. Имеем «i|vi  ... • vs и, так как щ просто, для некоторого Д. Поскольку Vj1 не имеет нетривиальных делителей, ?zi = vn. Продолжая процесс, получаем, что и% делит произведение оставшихся сомножителей Vj и, следовательно, и^ = 'И?2 для некоторого Д и т- д- В конце концов получим, что г = s и после некоторого переупорядочива-ния щ — Vi для всех i. □
П р и м е р 3.6.2. Покажем, что существует коммутативное кольцо, для которого не выполняется теорема о единственности неприводимого разложения. Рассмотрим множество всех положительных четных чисел 2Z+	{2А:|/с G Z и А: > 0} с обычными
операциями сложения и умножения: (2Z+,+, ). В этой алгебре число 8 является разложимым, поскольку 8 = 2  4, а число 14 — неразложимым, поскольку оно не является произведением двух или более чисел из 2Z+. Число 840 имеет два неприводимых разложения: 840 = 2 • 14 • 30 = 6 • 10  14. □
Из основной теоремы арифметики следует однозначность (с точностью до порядка сомножителей) разложения произвольного целого числа а Д 0, ±1 в произведение степеней простых чисел:
а = ±pVP22 •  'Pk1-
где рг — различные простые числа, е,; — натуральные числа.
Имея такие разложения, легко находить НОД и НОК целых чисел: если а = ip®1 р?2 ...  pekk, Ь = р^р?2 ...  pkk, ei, fi 0, то
НОД(аД)	_ рпйп{еА.,Л.};
НОК(щ Ь) = ^х{ы,Л}ртах{е2,/2} ^{ekJk}
Теорема 3.6.4. Множество простых чисел бесконечно.
Доказательство. Предположим противное. Пусть существует лишь конечное число простых чисел рьрг, •  • ,Рт- Рассмотрим число п — р\  р2    рт + 1, которое либо является простым, и тогда оно будет новым простым числом, либо имеет простой сомножитель р. Если р является одним из перечисленных простых чисел рд то р делит произведение pi - рг      рт и,
91
поскольку р делит п — • р2  -.  • Pm + К оно делит также и разность этих чисел, т.е. единицу, что невозможно. Следовательно, р является новым простым числом, т. е. имеет место противоречие с предположением конечности множества простых чисел. □
Опишем алгоритм нахождения всех простых чисел, не превосходящих заданного целого числа, с помощью решета Эратосфена. Запишем по порядку все целые числа от 2 До п. Затем вычеркнем все четные числа, кроме 2, поскольку они делятся на 2 и потому не являются простыми. После этого вычеркнем все числа, кратные 3, и т. д. После г-го прохода будут вычеркнуты все числа, которые делятся на первые г простых чисел /ц,..., /д. Первое число х > Pi, которое останется невычеркнутым, будет (г + 1)-м простым числом. Затем будут вычеркнуты все числа, кратные Pi. Процесс вычеркивания заканчивается при р^ > у/п, так как у любого составного числа п есть простой делитель у/п.
П р и м е р 3.6.3. Найдем все простые числа 60. В исходный список включим нечетные числа больше 2:
2	3	5	7	9	11	13	15	17	19
21	23	27	29	31	33	37	39
41	43	45	47	49	51	53	55	57	59.
Числа, кратные 3, Js З2, подчеркнуты одной чертой, кратные 5,	52 — двумя, кратные 7,	72 — тремя. Для следующего
простого числа 11 выполняется неравенство И2 > 60, поэтому все неподчеркнутые числа являются простыми 60. □
Приведенный алгоритм достаточно трудоемок и может использоваться для нахождения сравнительно небольшого числа простых чисел. Более эффективные методы можно найти в специальной литературе, например в книге А. Акритаса [1]. Из этой книги заимствован дальнейший материал настоящей главы.
§ 3.7.	Целые числа по модулю т
Рассмотрим кольцо целых чисел (Z,+,-). Зафиксируем целое число т > 1 и зададим отношение эквивалентности =ш на множестве Z по следующему правилу:
b =ТП а b — а = т  q для некоторого q 6 Z.
Класс эквивалентности элемента а — это множество {а.4-'т-с;|су 6
92
Z} = {..., —3m + «, -2m + a, — m + a,a,m + a, 2m + a, 3m + a,...}, которое обозначается через a + mZ или просто a.
П p и_м e p 3.7.1. Если m = 5, то 0 = {..., -10. —5, 0, 5, 10, ...}, 1 = {..., —9, —4, 1, 6, 11, ...} и т.д. Таким образом, множество Z разбивается на непересекающиеся подмножества 0,1,2, 3,4, и фактор-множество есть Z/=5= {0,1,2,3,4}. Заметим, что, хотя каждый класс эквивалентности содержит бесконечно много элементов, множество классов эквивалентности содержит всего пять элементов. □
В общем случае множество Z/ =т= {0,1,... ,т — 1} содержит т элементов.
Вместо записи Ь =т а будем также использовать запись b = а (mod m), которая читается “Ь равно а по модулю т” или “6 сравнимо с а по модулю т”. Множество Z/ =гп обозначается также через Zm и называется множеством вычетов или множеством целых чисел по модулю т.
Доказательство следующего утверждения оставляется читателю в качестве упражнения.
Лемма 3.7.1. Отношение =т является конгруэнцией на алгебре +,
Из этой леммы следует, что на множестве ZTO можно корректно определить операции сложения и умножения по правилам: а + b а + Ь, а  b а  Ь. В получающейся таким образом алгебре (Zm, +, •) выполняются все аксиомы коммутативного кольца с единицей. Например, нулевым элементом является класс 0, единицей — 1, противоположным по отношению к а элементом — элемент —а т — а. Кольцо (Zm, +, ) называется кольцом вычетов по модулю т.
Арифметика целых чисел по модулю т может рассматриваться как арифметика остатков или модулярная арифметика. Полная система остатков по модулю т состоит из т целых чисел, по одному представителю из каждого класса эквивалентности. Чаще всего используются следующие две системы: система неотрицательных остатков по модулю т, состоящая из чисел 0,1, 2,... , т — 1, и система наименьших по абсолютной величине остатков, или симметричная система остатков, состоящая из чисел 0, ±1, ±2, ..., ±(т—1)/2 для нечетного т. В дальнейшем мы будем часто отождествлять классы с соответствующими остатками, а арифметические операции + и  выполнять по следующим правилам: суммой а + b остатков а и b называется остаток от
93
деления числа а + b на тп, произведением а  b остатков а и b называется остаток от деления числа а • b на т.
Теорема 3.7.2. Тогда и только тогда элемент а кольца имеет обратный (т. е. элемент, о,-1 такой, что а 	= 1),
когда (а,т) = 1.
Доказательство. По теореме 3.5.3. уравнение ах + ту = 1 разрешимо тогда и только тогда, когда (а,т) = 1, а это равносильно существованию элемента х, для которого остаток от деления числа ах на т равняется единице. Этот элемент х является представителем класса, который при умножении на класс, соответствующий остатку а, дает единицу, т. е. является обратным. □
Теорема 3.7.3. Кольцо вычетов {Zm, +, •) тогда и только тогда является полем, когда т — простое число.
Доказательство. По теореме 3.7.2. если т — простое число, то в все ненулевые элементы обратимы, следовательно, (Zm,+,•) является полем. С другой стороны, если число т нс является простым, то (Zm, + , ) не поле. Действительно, если т = а. • Ь, 1 < а < т, 1 < b < т, то уравнение ах + ту = 1 неразрешимо, поскольку (а,т) = а\ 1. □
При м е р 3.7.2. Кольцо Д, является полем. Все его ненулевые элементы 1,2,3,4 обратимы (обратные элементы — это 1,3, 2 и 4 соответственно). Кольцо Zg полем не является, поскольку не существует 21. □
По теореме 3.7.3. для любого простого числар алгебра (Zp, +. •) образует конечное поле. В отличие от полей Q R, С в этом поле сложением единицы р раз получается нуль: 1+1+---+1 = 0. Наименьшее количество таких слагаемых называется характеристикой поля и обозначается через chai’. Поле, в котором сумма любого количества, единиц не равна нулю, называется полем характеристики нуль. Таким образом, char(Q) =char(R) =char(C) = О, char(Zp) = р.
Опишем два алгоритма нахождения обратных элементов в поле (Z,„,+.-).
1. Использование алгоритма Евклида. Пусть а 6	-
ненулевой элемент. Так как (а, т) = 1, по алгоритму Евклида выполняются следующие соотношения:
94
т = aqi + 74, о. = riQi 4- г2, 7'1 = ’’292 + т'з,
О < т-i < |а|, О < 7'2 < Г1, О < Т'з < г2,
T-fc-2 = rk-lQq-1 + Гк, Гк-1 = rkqk + 1-
о < Гк < rk~i,
С помощью последней формулы выражаем число 1 через гк и rk_p. 1 = rk~i — rkqk. Затем с помощью полученного выражения и предпоследней формулы алгоритма Евклида выражаем число 1 через гЛ-_] и rk_2- 1 = rk^-rkqk = rfc_t - (rk_2 - rk^qk^i)qk = 7fc-i(l + qk-iqk) + rk_2(—qk). Продолжая процесс, на последнем шаге получим выражение числа 1 через а и ?n: 1 = ах + ту. Искомый класс а-1 есть класс, содержащий число х, поскольку ах = 1( mod m).
Пример 3.7.3. Найдем число а-1 при а = 9, т = 23. По алгоритму Евклида имеем 23 = 9 - 2 + 5, 9 = 5 -1 + 4, 5 = 4 -1 + 1. Тогда 1 = 51-4-1 = 5 —(9 —5-1) = 5-2-91 = (23-9-2)-2-9-1 = (—5)-9+23-2. Следовательно, класс а-1 содержит число —5. При рассмотрении симметричной системы остатков это число берется в качестве числа 9-1. Если же рассматривается неотрицательная система остатков, в качестве числа 9-1 нужно взять —5 + т = —5 + 23 = 18. Таким образом, 91 = 18 (mod 23).
2. Использование малой теоремы Ферма. Следующий способ нахождения обратного числа основан на малой теореме Ферма.
Теорема 3.7.4 (малая теорема Ферма). Если т — простое число и а — произвольное целое число, не делящееся на т, то ат~~г = 1 (mod m).
Из соотношения а • o,m-2 = nm-1 = 1 (mod т) получаем
Следствие 3.7.5. Если т — простое число, то в кольце 7ст-выполняется равенство а~1 = ат~2 * *.
П р и м е р 3.7.4. Если а = 2, т = 5, то 2-1 = 25~2 (mod 5) = 8 (mod 5) = 3 (mod 5). Тогда 2-1 = 3. □
Следующий метод, называемым бинарным, позволяет более эффективно использовать малую теорему Ферма, поскольку с его помощью ускоряется процесс возведения данного числа в
95
степень. Этот метод работает следующим образом. Предположим, требуется вычислить число ак. Запишем к в двоичной системе счисления, опустив нули перед первой значащей цифрой:
п— 1
к = 52 кг2г. Заменим каждую цифру 1 на пару букв SMa и каж-г=0
дую цифру 0 на букву S; после этого вычеркнем пару букв SMa слева. Получившаяся последовательность букв представляет собой правило для вычисления ак, если интерпретировать S как “ возвести в квадрат, и взять остаток по модулю т", а Ма как “ умножить на а и взять остаток по модулю т”.
Пример 3.7.5. В 2ц для нахождения 4-1 (mod 11) нужно вычислить 49, причем двоичное представление 9 равно 1001. Образуем последовательность SM4SSSM4 и, вычеркнув левые SM4, получим последовательность SSSM4, которая означает “возвести в квадрат, возвести в квадрат, возвести в квадрат и умножить на 4”, выполняя все эти операции по модулю И: 49 = ((42)2)2  4. Проводя последовательно вычисления в йц, получим 42 = 5, 44 = 52 = 3, 49 = (44)2 • 4 = (З2) • 4 = 9 • 4 = 3. Следовательно, 4"1 = 3 (mod И), т. е. 4~1 = 3 в 2ц. □
§ 3.8.	Линейные уравнения по модулю т.
Китайская теорема об остатках
Теорема 3.8.1. Уравнение ах = b (mod т) тогда и только тогда имеет решение, когда (а, т)|6. Если решение существует, то оно единственно по модулю m/d, где d = (а,т), и уравнение имеет d решений по модулю т.
Доказательство. Целое число х удовлетворяет уравнению ах = b (mod m) тогда и только тогда, когда существует целое число у такое, что ах + 'ту = Ь. По теореме 3.5.3. уравнение ах + ту — b разрешимо тогда и только тогда, когда (a, m)|b. Для доказательства второй части теоремы предположим, что х удовлетворяет условию ах = b (mod m), и пусть z сравнимо с х по модулю m/d. Тогда z = х + w(m/d) для некоторого w 6 Z, az = ах + aw(m/d) = ах + mw(a/d) = ах = b (mod т). Таким образом, az = b (mod т). Напротив, если ах = az = b (mod m), то ах — az = b — b = 0 (mod т), и, значит, т[а(х — z). Тогда m/d делит х — z, и, следовательно, х = z (mod т/d'). □
П р и м е р 3.8.1. Найдем решение уравнения 270а? = 36 (mod 342). По алгоритму Евклида получим (—5) • 270 + 4  342 =
96
18 = (270,342) и 18|36. По теореме 3.8.1. существует единственное решение данного уравнения по модулю 19 = 342/18. Для нахождения этого решения умножим равенство (—5)-270 +4-342 = 18 на 2 = 36/18 и получим (—10) -270Н-8- 342 = 36, откуда следует, что (—10) — одно из решений уравнения по модулю 342. Так как 9 = —10 (mod 19), то 9 — единственное решение по модулю 19. Общее решение уравнения представляется в виде х = 9 + 19/с. □ Частным случаем теоремы 3.8.1. является
Следствие 3.8.2. Уравнение ах = 1 (mod m) тогда и только тогда имеет решение, когда (а,т) = 1. Решение о,(mod m) единственно по модулю т и является обратным к а элементом по .модулю т.
П р и м е р 3.8.2. Уравнение 2х = 1 (mod 26) не имеет решений, поскольку (2,26) = 2. □
Рассмотрим теперь задачу решения системы линейных уравнении по модулю некоторого числа т. При этом возникает изоморфизм кольца Za/ и декартова произведения колец Zmi, Zm.2, ... ,Zmk. где М = тртъ   -iriki	— 1, i j. Прежде чем
формулировать изоморфизм в общем случае, рассмотрим
Пример 3.8.3. Кольцо Хб изоморфно декартову произведению колец Z2 и Z3: Za = Z2XZ3, М — 6,	= 2, m2 — 3. Шести
элементам кольца соответствуют пары (0,0), (0,1), (0,2), (1,0), (1,1), (1,2). Арифметическим операциям в Z(, соответствуют операции над парами, выполняемые покоординатно: (яд, ту) + (?/1,Уг) = (жх + г/1,х2 + уг), Си,т2)  (У1,'</2) = (ж1  Ш,Ж2  Уг)-Например, (0,2) • (1,2) = (0,1), где умножение 0 • 1 выполняется по модулю 2, а умножение 2  2 — по модулю 3.
Теорема 3.8.3 ( китайская теорема об остатках). Пусть ту,, т.2,    ,'т^ — попарно взаимно простые целые числа, больше 1, М = тргп^ -.. гщ. Тогда существует единственное неотрицательное. решение по модулю М следующей систем,ы. уравнений:
х = ai (mod тД, х = а.-2 (mod m2). . -., х = щ (mod шД.
Отображение, которое каждому целому числу х /0 х М — 1/ ставит в соответствие строку (04,02,... , о./Д, где х = (mod m) (i — 1,2, является изоморфизмом кольца на , х х ... 2^77,^.
Доказательство. Нужно найти число х (0 х
М — 1), удовлетворяющее всем сравнениям х = а.{ (mod шД,
4 Зак. № 4872 Судоплатов
97
i = 1,2,. Будем решать уравнения по два одновременно. Рассмотрим сначала первые два сравнения. Первое сравнение ж = ai (mod mi) справедливо для всякого х вида х = сц + rn^q, q Е Z. Для нахождения q подставим значение х во второе сравнение х = а,(mod m2). Имеем х = ax+m\q = az (mod m2). откуда q = (mi)-1(«2 — <?i) (mod m2). Таким образом, q — (тО'^аг — a J + rmj для некоторого г. Подставив значение q в выражение х = О] + miQ, получим, что решение х первых двух уравнений представляется в виде х = ащ + r(mim2) для некоторого г. Теперь первые два сравнения можно заменить на одно сравнение х = «12 (mod трт.Д. Применим описанную выше процедуру к сравнению ж = ащ (mod тдт2) и сравнению, которое первоначально было третьим, и будем повторять этот процесс, пока не найдем число ж, удовлетворяющее всем сравнениям.
Для доказательства единственности предположим, что существует х! (О < ж' < М — 1) такой, что ж' = щ (mod mJ для любого г. Тогда ж — х' = 0 (mod mJ для всех г, откуда следует, что mJ (ж — ж') для любого i. Тогда М|(ж — ж') и, поскольку |ж - ж'| < М, х = ж'. □
П р и м е р 3.8.4. Решим систему уравнений
ж = 1 (mod 2), ж = 2 (mod 5), ж = 5 (mod 7).
Из первого уравнения следует, что ж — 1 + 2q. Чтобы вычислить q, подставим ж во второе уравнение: 1 + 2q = 2 (mod 5) пли 2q = (2 — 1) (mod 5). Так как 2-1 = 3 (mod 5), то q = 2—1 (2 — 1) (mod 5) = 3 (mod 5) или q = 3 4- 5г для некоторого г. Следовательно, решением первых двух уравнений является х = 1 + 2(3 + 5г) = 7 + 5г, т. е. ж = 7 (mod 2-5).
Осталось решить систему двух уравнений ж = 7 (mod 2 - 5) п ж = 5 (mod 7). Имеем ж = 7 + 2  5</ = 5 (mod 7) или 2  5g = (5 - 7) = —2 = 5 (mod 7). Так как 10-1 = З1 = 5 (mod 7), то <7 = 5-5 (mod 7) = 4 (mod 7) или q = 4 + 7г для некоторого г. Следовательно, решением трех уравнений является число ж = 7 + 2 • 5(4 + 7г) или ж = 47 (mod 2-5-7).
Отметим, что 47 = 1 + 3 • (2) + 4• (2  5), где коэффициенты 3 и 4 являются значениями q. Отметим также, что при изоморфизме Z2-5-7 = Д х Д х Д число 47 соответствует данной тройке (1,2,5). □
В общем случае решение системы к уравнений
ж = «1 (mod m J, ж = н2 (mod m2),..., ж = ад. (mod т^)
98
представляется в виде
ж = 41 + qi  (mJ + 43 • (77117712) + ... + 4i:  (777,1 • m2  ...  тк),
где 0 4г <	|, 41 - остаток от деления ау на ту.
Опишем применение китайского алгоритма к задаче о безопасном хранении ключа. Пусть К Е Z — ключ, который необходимо сохранить. При этом требуется, чтобы любые L человек из тех к (к > L), которые получили информацию о ключе, могли бы вместе восстановить ключ, ио ни одна группа из L — 1 человек пли менее не могла этого сделать.
Для решения этой задачи выберем множество целых чисел {р, dy,dz,... ,dk} такое, что
1)	р > К-
2)	dy <d2< ... < dk,
3)	числа р.dy,d2,..., dk попарно взаимно просты,
4)	dy  d2 • •  •  dk > р • dk~L+2 ' ^fc-L-t-з ’  •  • dk-
Пункт 4 означает, что произведение L наименьших чисел di больше, чем произведение р и L — 1 наибольших чисел di. Положим D dy  d2      dk. Тогда D/p больше, чем произведение любых L — 1 чисел di. Выберем теперь целое число г Е [0, (D/p) — 1] так, чтобы число К' = К + г -р попало в интервал [D/p, D — 1]. Между разными людьми распределяются числа Ki = К1 (mod dz), i = 1,2, ...,к.
П р и м е р 3.8.5. Предположим, что требуется закодировать ключ К = 5 и при этом L — 2. к = 3, р = 7, ф = 11. d2 = 13, d-.i = 17. Имеем D = ф -d2 = 11-13 = 143 > 119 = 7-17 = pd3, как и требуется. Выберем число г Е [0, (143/7) — 1] = [0,19] так, что К' = К + г-р Е [D/p,D — 1], т.е. 5 + 7г 6 [20,142]. Возьмем, напр-мер. т = 3, тогда К' = 26. Распределяемые числа равны Ку = 26 (mod 11) = 4, К2 = 26 (mod 13) = 0, К3 = 26 (mod 17) = 9. По .любым двум из этих чисел можно восстановить К. Например, для Ку и A3 имеем К' = 4 (mod 11), К' = 9 (mod 17). Используя китайский алгоритм, находим АГ' = 26, откуда К = К' — г -р = 5.
§3.9. Точные вычисления, использующие модулярную арифметику
Используя результаты предыдущих параграфов, опишем способ выполнения точных арифметических действий с (большими)
4*
99
целыми числами, при котором целые числа представляются в виде кортежей остатков от деления данных чисел на попарно взаимно простые модули, а выполнение арифметических операций сводится к выполнению соответствующих операции над остатками.
Рассмотрим сначала случай одного модуля. Пусть дано выражение /(ti,Х2,. • -, ж/,.), являющееся гермом сигнатуры Е = {-Д2\ —-(2\ (()	и требуется вычислить (оценить) зна-
чение /('М’г2,   • Д/i); где ЙДг,    ЛЛ, € Тривиальный подход состоит в непосредственном вычислении значения терма. Однако промежуточные результаты могут не быть целыми числами (например, 1/3 = 0.333... = 0.(3)), и отбрасывание цифр пли округление может привести к неточности окончательного результата. Во избежание этого сопоставим вычислению значения	•   -’i-h) над Z соответствующее вычисление значения
f(i\, «2, •  , i'h) в поле Z,,( по обходному пути, показанному на рис. 3.2.
Вместо вычисления /(й Дг, •  , над Z мы сначала получаем эквивалентное выражение fin = /(zj.z^,... ,i'h) над Z,n для некоторого простого т, где z' = z;- (mod т), j = 1,2,..., h. Затем вычисляем выражение fm над Z,n и получаем эквивалентный результат resm, где res„, = res (mod rn). В заключение отображаем resm обратно в множество целых чисел.
Отмстим, что отношение res = res,(l (mod rn) не определяет однозначно окончательный результат res. Например, условие х = 7 (mod 13) означает, что х может быть равным 7, 20 и т. д.; однако если мы знаем, что 0 < х < 13, то х может быть равным только 7. Для того чтобы однозначно определить res, нужно иметь априорную оценку его величины. Эта оценка, используется в качестве модуля т, и все операции выполняются в кольце
Z ___________
Выражение (/) I Вычисление
I над Z
Результат (res) <—
Эквивалентное выражение (fm) i Вычисление над
Эквивалентный результат (res,,,)
Рис. 3.2
100
7Lm. Если имеется оценка на величину res, то ищем наименьшее неотрицательное решение уравнения res = resm (mod m). Если же мы имеем оценку на |res|, то ищем наименьшее по абсолютной величине решение.
Сложности с данным методом возникают при выполнении операции деления. Как уже отмечалось, в случае, когда р — простое число, кольцо (Z,+,-) является конечным нолем. Поскольку обратный элемент к любому ненулевому элементу всегда существует, деление по модулю р определяется следующим образом:
~ (mod р) = а  (If1 (modp)) (modp),
где 1г] (mod р) — элемент, обратный к элементу b по модулю р, который будет также обозначаться просто через Ь-1. Частное двух целых чисел в также является целым числом, даже если b не делит а в Z.
Пример 3.9.Е 3/4 (mod 11) = 3 • 41 (mod 11) = 3 - 3 (mod 11) = 9. Таким образом, 3/4 = 9 (mod 11). Число, полученное в этом примере и рассматриваемое как промежуточный результат, имеет смысл для дальнейших вычислений, поскольку (3/4) • 4 (mod 11) = 9 • 4 (mod 11) = 3 (mod 11). □
Предположим теперь, что модуль р ограничивает окончательный результат res. Если res не является целым числом, принадлежащим Zp, то resp res, и для того чтобы получить последнее число, требуется дополнительная информация (которую мы проиллюстрируем ниже двумя примерами). Если res лежит в Zp,'to resp = res. Таким образом, арифметика одного модуля может быть использована для выполнения последовательности точных арифметических операций над целыми числами в Zp, даже если эта последовательность включает операции деления. Трудности могут возникнуть лишь при интерпретации результатов.
Если вычисляемое выражение может быть положительным или отрицательным, необходимо использовать симметричную систему с носителем {—(р — 1)/2,..., — 2, — 1,0,1, 2, ..., (р — 1)/2}, которая изоморфна неотрицательной системе с носителем {0,1,... ,р — 1}. Изоморфизм между этими системами осуществляется по формуле
А:,
А: + р,
<р(А;) = <
если О Е к < (р — 1)/2, если — (р — 1)/2	А; < 0.
101
Рис. 3.3
II р и мер 3.9.2. На рис. 3.3 показано отображение при р = 11.
Уравнение х = 17 (mod 11) имеет наименьшее неотрицательное решение х = 6 и наименьшее по абсолютной величине решение х = —5. □
При выполнении арифметических операций удобно сначала отобразить данные в неотрицательное множество, выполнить в нем все операции, а затем отобразить обратно в симметричное множество.
II р и м е р 3.9.3. Выполним точные арифметические операции в Zu для вычисления х = 1/3 — 4/3. В этом примере априорная информация состоит в том, что результат ищется в симметричном множестве. Имеем х (mod 11) = (1/3 + (—4)/3) (mod 11) = (1/3 + 7/3) (mod 11) = (1 • З”1 + 7 • З"1) (mod 11) = (1-4+ 7-4) (mod 11) = 32 (mod 11). Отображая результат обратно в симметричное множество, получаем правильный ответ х = — 1. В приведенном примере resp = res, поскольку с самого начала известно, что res лежит в симметричном множестве для Хц.
Пример 3.9.4. Вычислим х = 1/2 — 2/3, пользуясь той же априорной информацией, что и в предыдущем примере. Имеем х (mod 11) = (1/2 + (—2)/3) (mod 11) = (1/2 + 9/3) (mod 11) = (пг^+э-з-1) (mod 11) = (1-6+9-4) (mod 11) = 42 (mod 11) = 9. Если мы отобразим результат в симметричное множество, то получим неправильный ответ: х = — 2. Поэтому требуется допол-
102
нительиая информация о том, что мы ищем рациональное число х (mod 11) = (ti/b) (mod 11), где b =НОК(2, 3). Тогда а = xb (mod 11) = 9-6 (mod 11) = 10 (mod 11) = —1. Следовательно, х — (—1)/6, что является правильным ответом. □
Перейдем теперь к арифметике нескольких модулей. Использование арифметики нескольких модулей является естественным решением проблемы компьютерного представления и работы с большими целыми числами, с которой мы сталкиваемся в арифметике одного модуля: как мы видели, модуль т должен быть достаточно большим, чтобы результат res определялся однозначно по его остатку resm (m > res). Поэтому при работе с большим т мы используем несколько модулей, кодирующих целые числа х (0 х С т — 1) в соответствии с китайской теоремой об остатках.
Для вычисления заданного выражения /(й, «2, • • • Д/,.), зависящего от целочисленных аргументов ?4,г’2,---,Д, сначала вычисляем fmk(iik,i2k, • • • Д/д), где ijk — остаток от деления ij на (j = 1,2, ...,h, к = 1,2, ...,п) для коротких модулей гп)~. При условии, что выражения fmk определены над йп1л., вычисляем их над и получаем эквивалентные результаты resTO/., к — 1,2,... ,п. В завершение, пользуясь китайским алгоритмом, получаем окончательный результат res. Модули выбираются таким образом, чтобы т\  т?  тп > res. Если дана положительная оценка на res, то ищется наименьшее неотрицательное решение системы уравнений по китайскому алгоритму, если же оценивается |res|, то ищется наименьшее по абсолютной величине решение. На рис. 3.4 представлена диаграмма, иллюстрирующая приведенный алгоритм.
Рассмотрим более подробно арифметику нескольких модулей. Описанные в § 3.2 системы счисления являются линейными,
Выражение (/)
i Вычисление над Z
Результат (res) 4----
Эквивалентное выражение (/,,ч.) I Вычисление 1 над
Эквивалентный результат (resmi.)
Рис. 3.4
103
позиционными и весовыми. Это означает, что всем позициям соответствуют веса, зависящие от одного основания Р: Р°, Р\ Р2 и т. д. Вместо этого многомодульная система счисления использует взаимно простые позиционные основания, mi, т?,..., тп. Это позволяет однозначно представлять mi • m2 • ... • тп различных чисел х в виде вектора остатков [гц, 0.2,..., ап\ относительно вектора оснований (3 = [mi,m2,...,mn], где х = щ (mod ‘ini), г — 1, 2,... ,п. Как и в случае одного модуля, мы можем определить наименьшую неотрицательную числовую систему (которую будем называть стандартным набором остатков) и при условии, что все модули нечетные, наименьшую по абсолютной величине числовую систему или симметричную систему остатков относительно данного вектора оснований /3. Если [а 1,а,2, . • ,ап] ~ стандартный набор остатков числа х относительно вектора оснований /3 = ['mi, m2,..., mn], то запишем
х (mod /3) = [01,02-.. -, оп].
Пример 3.9.5. Если п = 3, mi = 3, m2 = 5, m3 = 7, то в этой системе с помощью остатков можно представить 3-5-7 = 105 различных чисел. Вектор [2,3,1] однозначно определяет десятичное число 8 в неотрицательной системе остатков относительно вектора оснований /3 = [3,5,7]. В симметричной системе число 8 представляется вектором [—1,—2,1]. Имеем 8 (mod/3) = [2,3,1]. □
Из китайской теоремы об остатках вытекает
Теорема 3.9.1. Два целых числа гц и П2 имеют одинаковые стандартные наборы, ост,ат,ков относительно век7пора оснований (3 = [?П1,т2,    , т,г] 'тогда и только тогда, когда щ = п? (mod mi m2 ... тп).
И р и м е р 3.9.6. Рассмотрим вектор оснований /3 — [3,5.7]. Так как 9 = 114 (mod 3-5-7), то 9 (mod /3) = [0,4,2] = 114 (mod /3). □
Из теоремы 3.9.1. следует существование биекции между множествами Zaj ;=± {k (mod /3)|А? € Z} и Zm, где М =	 .-тпп.
Более того, из китайской теоремы об остатках следует
Теорема 3.9.2. Алгебры (Ду, +. •) и (Z,w, +, •) являются изоморфными конечными коммутативными кольцами.
Следовательно, многомодульная арифметика эквивалентна арифметике по модулю М.
104
Главное преимущество многомодульной числовой системы состоит в отсутствии переносов при выполнении операций сложения и умножения. Арифметика замкнута в каждой позиции, т. е. арифметические действия выполняются покоординатно. Поэтому сложение и умножение длинных целых чисел можно выполнять так же быстро, как и коротких чисел.
Для выполнения деления определим элемент К1 (mod />), обратный к элементу b = [/ц, 62,..., Ьп] по модулю вектора оснований /3 = [mi, т-2,... ,тп], следующим образом:
5-1(mod /в) — [^(mod mi), b? 1 (mod m2),..., 5~1(modmn)].
Теперь, если a = [a-i, a2,   ., an], то
(mod /3) = a • b~] (mod/3) = [ax • bf1 (mod mJ,
a2 • 52' (mod m2), -.., an • b~l (mod mn)].
Как и в случае одного модуля, если b не делит а при соответствующей интерпретации в кольце целых чисел, то результат не может быть проинтерпретирован без дополнительной информации. Однако он допустим в качестве промежуточного результата.
Основная трудность при работе с многомодульными числовыми системами заключается в сравнении величины целых чисел. Конечно, можно использовать симметричную систему остатков, вычесть из одного числа другое и затем определить знак разности. К сожалению, проблема этим не решается, поскольку остатки в симметричной системе не несут информации о знаке числа. Один из способов определения знака числа х состоит в обратном преобразовании к обычному виду, что разрушает саму идею многомодульной арифметики. Задача определения знака числа может быть решена гораздо лучшим способом с помощью преобразования числа х к так называемому представлению со смешанными основаниями. При этом преобразовании выполняем только операции многомодульной арифметики. Все выполняемые действия по вычислению знака основаны на представлении числа х по китайскому алгоритму в виде
х = щ 4- q2 • mi + дз • mi  т2 + ... + qn • тг • m2 -... - mn_x, (3.5) где О С q-i: < |mj, Qi — остаток от деления х на Ш]. Коэффициент qn называется старшим членом, числа х. В этой форме знак числа х совпадает со знаком его старшего члена.
105
Отметим, что в форме со смешанными основаниями мы име-п
ем х = ^2 Qi ’ Mi, W Mi = тут-} ... тг_х и М\ = 1; частные г=1
Mi/Mj-i различны для различных позиций г. Если mi = т-2 = ... — тп = Р, то получим представление с фиксированным основанием Р — представление в Р-ичной системе счисления.
При определении знака удобно, чтобы последний модуль тп в векторе оснований был равен 2, поскольку нужно знать, в какой половине множества возможных чисел лежит результат (если qn = 0, то х 0; если qn = 1, то х < 0). Например, на рис. 3.3 числа 0,1,..., 5 образуют нижнюю половину множества возможных чисел, соответствующую значению qn = 0, а числа 6,7,..,, 10 — верхнюю половину, соответствующую значению Qn — 1-
Предположим теперь, что нам дано представление х = [аь«2, ... , ап] относительно вектора оснований (3 = [mi,m.2, - . ,тп] и требуется определить знак числа х. Нам нужно преобразовать число х к форме (3.5) и определить знак старшего члена. Для этого необходимо найти цифры Qi, дг, содержащиеся в (3.5).
Очевидно, что из (3.5) вытекает х = q\ (mod mi), следовательно, Qi = ар Мы получили первую цифру. Далее возьмем разность х — qi (вычитая гд из каждого остатка, представляющего х). Имеем x—qi = q2-mi+q3-m1-m2+-  +qn-mi-m2-..
Первая цифра (в смешанном представлении) числа х — qi равна нулю, следовательно, первые цифры всех последующих чисел можно не рассматривать. Будем считать, таким образом, что длина вектора х — равна п — 1. Затем найдем (mi)-1 (mod Д), где (Зг = [ж,2,..., 2], и вычислим (многомодульное) произведение (;Г —Ql)(mi)-1, ДЛЯ ТОГО чтобы получить вторую цифру Q2- Будем продолжать этот процесс до тех пор, пока не вычислим значение Qn G {0,1}, которое является индикатором знака числа х.
П р и м е р 3.9.7. Определим знак числа х = [4,2,0,1] с вектором оснований /3 = [7,5,3,2]. Очевидно, что qi = 4, и х' = х — 4 = [0,3,2,1] или, как было объяснено выше, х! = [3,2,1], поскольку вектор оснований можно сократить до вектора Д = [5,3,2]. Для того чтобы получить вторую цифру вычислим (mi)-1 (mod Д) = 7-1 (mod Д) = [3, 1,1]. Умножив х' на этот элемент, получим х'  т-\ = [4,2,1]. Следовательно, q2 = 4, тогда, вычитая из последнего модулярного выражения, полу
106
чим х" = [0,1.1] или х" --- [1,1] для /Зг = [3,2]. Далее вычисляем (m2)"1 (mod Д) — 5-1 (mod Д.) = [2,1] и, умножая х" на этот элемент, получаем [2,1]; поэтому = 2. Вычитая д3 из последнего модулярного выражения, получаем х"' = [0,1], или х'" = 1 для /Зг — [2]. В заключение вычисляем (m3)-1 (mod /Зг) = З-1 (mod (Зг) — [1] и, умножая х'" на этот элемент, получаем [1], откуда. следует, что <74 = 1. Поэтому х является отрицательным числом. Действительно, ж = 4 + 4- 7 + 2- 7- 5 + 1- 7- 5- 3 = 207 (mod 7 • 5 • 3  2) = 207 (mod 210) = —3.
§ 3.10.	Задачи и упражнения
1.	С помощью алгоритма Евклида найти наибольший общий делитель чисел:
а) 6188 и 4709; б) 81719, 52003, 33649 и 30107.
2.	Составить таблицу простых чисел, меньших 130.
3.	Найти неприводимое разложение числа 82798848.
4.	Найти все целые решения уравнения:
а) 5х + 3;// = 1; б) 47.т - 111?; = 89.
5.	Решить сравнение:
а) 256ж ее 179 (mod 337); б) Ilk = 75 (mod 321).
6.	Составить таблицы Кэли для операций сложения и умножения в кольце Z2 х Z3.
7.	Решить систему сравнений:
а)	х = 4 (mod 5), х ~ 6 (mod 7), х = 9 (mod 11):
б)	х = 2 (mod 3), х = 4 (mod 5), х = 7 (mod 11), х = 3 (mod 13), х = 6 (mod 17).
8.	Используя многомодульную арифметик}' с вектором оснований /3 = [3,5,7]. вычислить а + Ь, а - Ь, а  b и Ь-1 (mod 0). где а = 9, 5 = 23.
9.	Относительно вектора оснований 3 — [3,5,7] найти многомодульные представления чисел 127, —127, 537 и —537 для симметричной системы остатков и системы наименьших неотрицательных остатков.
10.	Найти знак числа х = [6,3,1,1] с вектором оснований /3 = [7,5,3,2].
11.	Используя многомодульную арифметику с вектором оснований
0 — [3,5,7], вычислить 3L _ 1.
Глава 4
ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
§4.1. Виды и способы задания графов
Во многих прикладных задачах изучаются системы связей между различными объектами. Объекты называются вершинами и отмечаются точками, а связи между вершинами называются дугами и отмечаются стрелками между соответствующими точками (рис. 4.1).
2	Такие системы и образуют
графы. Граф может изображать /	\.	сеть улиц в городе: вершины гра-
/	/7	фа ~ перекрестки, а дуги — ули-
/ /	цы с разрешенным направлени-
/ /	ем движения (улицы могут быть
с односторонним и двусторонним
4	движением). В виде графов мож-
Рис 4 1	но представить блок-схемы про-
грамм (вершины — блоки, а дуги — разрешенные переходы от одного блока к другому), электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. Перейдем к точным определениям.
Графом называется алгебраическая система G = (M.R), где R двухместный предикатный символ. Элементы носителя М называются вершинами графа G, а элементы бинарного отношения R С ЛГ2 — дугами. Таким образом, дугами являются пары вершин (a, b) 6 R. При этом дуга (о, Ь) называется исходящей из вершины а и заходящей в вершину Ь.
Изображение графа G = (М, R) получается путем распо-
108
ложеппя различных точек на плоскости для каждой вершины " Е М, причем если (a, b) 6 R, то проводится стрелка (дуга) из вершины а, к вершине Ь.
Пример 4.1.1. Изображение графа G с множеством вершин М = {1,2,3,4} и множеством дут R = {(1,1), (1, 2), (2,3), (3, 4), (4,3), (4,1)} представлено иа рис. 4.1. □
При задании графа для нас не имеет значе-нпя природа связи между вершинами а и Ь, важ-но только т'О, что связь существует и информация / / / о связях содержится во множестве дуг R. Однако /	/
часто возникают ситуации, при которых такой ин-формации оказывается недостаточно, например, в а случаях, когда имеется несколько дуг, исходящих Рис. 4.2 из вершины а и заходящих в вершину Ь, такие дуги называются кратными (рис. 4.2). Тогда используется понятие мультиграфа.
Мулътиграфом G называется тройка (Л/, U, Р), в которой А/ — множество вершин, U — множество дуг, а Р С М х U х М — трехместный предикат, называемый инцидентором и представляемый следующим образом: (а, и, b) G Р тогда и только тогда, когда дуга и исходит из вершины а и заходит в вершину Ь. Отметим, что любой граф можно представить в виде мультиграфа.
Граф G = (M,R) называется ориентированным {орграфом), если найдется дуга («, b) Е R. такая, что (b, а,) R. Если же отношение R. симметрично, т. е. из (a, b) Е R следует (b, a) G R, то граф G называется неориентированным (неорграфом). Если одновременно пары (а, Ь) и (Ь, а) принадлежат R (рис. 4.3а), то информацию об этих дугах можно представить множеством [а, Ь] — {(а, Ь), (6, а)}, называемым ребром, которое соединяет вершины а и Ь. При этом вершины а и b называваются концами ребра [а, Ь]. Ребра изображаются линиями (без стрелок), соединяющими вершины (рис. 4.36).
Рис. 4.3
109
Если в мультиграфе вместо дуг рассматриваются ребра, то мультиграф также называется неориентированным. Отметим, что если в орграфе G = (М, R) к каждой дуге (а, b) G R добавить пару (5, а), то в результате образуется неорграф, который будем
называть соответствуют,им данному орграфу G и обозначать через F(G).
2	Пример 4.1.2. Орграфу G,
/	изображенному на рис. 4.1, соот-
/ уз	ветствует неорграф F(G). изобра-
। /	/	жснный на рис. 4.4. □
Губ	/	Введенные в § 2.2 понятия
/	морфизмов алгебраических си-
стем для графов представляются следующим образом. Пусть G =
Рж- 4 4	(М,Д), G' = (M'.R1) - графы.
Тогда отображение <р : М -» М' является гомоморфизмом, если для любых вершин a,b G М из (a, b) G R следует (99(a), 99(b)) G R'. Биекция <р : М о М' является изоморфизмом графов, если
(a,b) G До (99(a),<^(Ь)) G R'.
Пример 4.1.3. Рассмотрим граф G, состоящий из множества вершин {1,2,3,4} и множества дуг {[1.2], (1,3), (2,4), (3,2), [3,4], (4,1)} (рис. 4.5a). Граф G' = ({а,5, с}, {[а, £>], (а, с), (£>, Ь), [Ь, с]}) является гомоморфным образом графа G при гомоморфизме 99, в котором 90(1) = а, 99(2) = Ь, 99(3) = с, 99(4) = b (рис. 4.56). Граф G", показанный на рис. 4.5е, изоморфен графу G посредством изоморфизма чр, при котором ф(Х) = а,
Рис. 4.5
110
V>(2) = b, = c, ^(4) = d. Отображение у : {1,2,3,4} {1,2,3,4}, при котором y(l) = 2, y(2) = 1, y(3) = 4, y(4) = 3, является автоморфизмом графа G. □
Информация о структуре графа может быть задана матрицей бинарного отношения. Пусть G = (M,R) — граф, в котором множество вершин имеет п элементов: М = {aj.o.2, .... нп}. Матрицей смежности Ас; = (Ajj) графа G называется матрица порядка п. определенная следующим образом:
1, если (a.;, a.j) Е В., О, если (a.i,oy) $ В.
Если A;j = 1, то вершина a.j называется последователем вершины аг, а а; — предшественником iij. Вершины а; и a-j называются смежными, если Л17 = 1 или Ар = 1.
Если G — мультиграф, то в матрице смежности Ас; элемент
A.jj по определению равен числу дуг, исходящих из вершины а; п заходящих в вершину a.j (i,j Е {1,... ,п}).
П р и м е р 4.1.4. Граф G, изображенный на рис. 4.6. имеет матри-
цу смежности
А(; =	/1	1	0	0	0\ 0	0	10	0 0	0	0	1	0 0 0 110 \0	о	0	0	о)	. □
Отметим, что если G — пеорграф, то матрица смежности Ас; симметрична, г. е. не меняется при транспонировании: А^ = Ас;-
Петлей в графе G называется дуга, соединяющая вершину саму с собой. Если G - граф без петель, то в матрице смежности Ас; по главной диагонали стоят нулевые элементы:
111
Пусть G\ — {Mi,Ri), G-2 = (M^Rz) — графы, в которых Mi = {«],.. -, а,,}. М2 = {bi,..., bn}. Если ip — изоморфизм графов Gi и Gt, действующий по правилу ~ bi, i = 1,..., п, то матрицы смежности Ас, и Ag2 совпадают. В общем случае справедлива
Теорема 4.1.1. Графы изоморфны тогда и только тогда, когда их .матрицы смежности получаются друг из друга одновременными перестановками строк и столбцов (т.е. одновре-менно с перестановкой l-й и j-й строк переставляются i-й и j-й столбцы).
Согласно этой теореме по матрице смежности граф восстанавливается однозначно с точностью до изоморфизма.
В мультиграфе G = (М, U, Р) дуга и Е U называется инцидентной вершине а. Е М, если {а, и, b) Е Р или (Ь, и. a) Е Р для некоторого b Е М. Если М = {oi,... ,ат}, U = {'щ,..., w„}, то .матрицей инцидентности Вс = {Bij} мультиграфа G называется матрица размера т х п, определяемая по следующему правилу:
Рис. 4.7
если дуга Uj исходит из вершины если дуга Uj заходит в вершину а, и Uj не является петлей;
в противном атучае.
Пример 4.1.5. Мультиграф G, изображенный на рис. 4.7, имеет матрицу инцидентности
/—1—10 о о о \ BG = I	1	11	1-1	1	.
\	0	0 0	-1	1	-1	/
Мультиграфы G = {M,U,P} и G' — {M',U',P'} называются изоморфными, если существуют биекции : М <-> М' и ф : U <-> U1 такие, что {а, и, b) Е Р тогда и только тогда, когда G Р'.
Аналогично теореме 4.1.1. справедлива
Теорема 4.1.2. Мультиграфы G и G' изом.орфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга некоторыми перестановкам,и строк и столбцов.
112
Омск щ
681
«2 Новосибирск
а4 Павлодар
Рис. 4.8
оз Кемерово
Во многих задачах требуется дополнительная информация о вершинах и ребрах, например, о расстоянии между населенными пунктами в случае, когда граф представляет собой сеть дорог, или о времени прохождения сигнала от одного узла связи к другому и т. д. В таких задачах используются взвешенные графы.
Пусть Sm-, Sr — множества меток. Пометкой или распределением, меток графа G = {М, R) называется пара функций f : М -> Sm {распределение меток вершин), g : R Sr {распределение меток дуг). Четверка {М, R, f,g) называется взвешенным или помеченным графом. Для вершины о. G М элемент f{a) называется весом, вершины а, а для дуги и Е R. элемент д{и) — весом, дуги и. Часто бывают помеченными только вершины (в этом случае g =const.) или дуги (в этом случае / —const).
П ример 4.1.6. Пусть М = {01,02,03,04}, R, — {[01,02], [0.2,03], [01,04], [0.2,04]}, f : М —1 С, где С — множество городов, g : R -> а>, /(01) =Омск, /(0,2) = Новосибирск, /(0.3) = Кемерово, /(о4) = Павлодар, </([oi,a2]) = 681, {/([02,0.3]) = 274, {/([0.1,04]) = 413, {/([02,0.4]) = 589. Помеченный граф {M,R,f,g) изображен на рис. 4.8 и представляет собой схему автомобильных дорог с указанием их протяженности. □
Информацию о весах дуг во взвешенном графе можно представлять в виде матрицы весов W = {'Wij), где wij — вес дуги (о,;,о7), если дуга (ог,о;/) существует, а для несуществующих дуг веса обычно помечают нулем или знаком оо в зависимости от приложений. В примере 4.1.6 матрица весов имеет вид
	/ 0	681	оо	413
W =	' 681	0	274	589
	оо	274	0	оо
	U13	589	оо	0
113
Если граф G = (М, 7?.) является разреженным, т. е. число дуг |7?| достаточно мало по сравнению с числом вершин \М\, то более эффективным, чем с помощью матрицы смежности, является представление дуг графа посредством списка дуг. Этот список задается двумя наборами т = (иц,m2,   •,п?,|д|) и п = (П1,П2,... ,П|я|), где (ат.,а.П1) — i-я дуга графа G.
П р и м е р 4.1.7. Орграф, изображенный на рис. 4.6, представляется следующим списком дуг: т = (1,1,2,3,4,4), п = (1,2,3,4,3,4). Для представления рассматриваемого графа матрицей смежности требуется 52 = 25 элементов, а списком дуг — только 6-2 — 12 элементов. □
Другим представлением графа, удобным при работе с графами, в которых удаляются или добавляются вершины, является структура смежности, получаемая составлением для каждой вершины а списка номеров ее последователей, т. е. номеров вершин Ъ, для которых имеется дуга (а, 1>).
Пример 4.1.8. Орграф, изображенный на рис. 4.6, представляется следующей структурой смежности:
Вершины	Списки последователей
1:	1,	2
2:	3
3:	4
4:	3,	4
5:
§ 4.2. Подграфы и части графа. Операции над графами
Граф G' = (М1, R') называется подграфом графа G = если М' С М и R' — R Г\ (М1)2. Граф G' называется частью графа G, если М' С М и R.' С RD (М')2.
П р и м е р 4.2.1. Граф G' ~ ({1, 2, 3}, {[1,2], (1, 3), [2, 3]}) (рис. 4.96) является подграфом графа G = ({1,2,3,4}. {[1,2], (1,3), [1,4], [2.3], [3,4]}) (рис. 4.9а), аграф G" = ({1,2,3}, {[1,2]’ (3,2)}) (рис. 4.9в) частью графа G. □
Рассмотрим некоторые основные операции, производимые над графами.
Операцией добавления к графу G = (М, R) вершины а. образуется граф (М U {а},/?.). Операция добавления дуги (а,Ь) к
114
2
2
2
Рис. 4.9
графу G состоит в образовании графа {М U {a,b},B. U {(«,&)})• Под операцией удаления дуги (о., Ь) из Графа G понимается операция, заключающаяся в удалении пары (о, Ь) из множества дут /?., в результате получается граф {M,R \ {(о., b)}). Операция удаления вершины а из графа G заключается в удалении вершины а, вместе с инцидентными ей дугами:
(М \ {«}, В \ {(6, с)\Ь = а или с = а,}).
Операция отождествления вершин а, и b графа G = (М, В.) состоит в удалении из графа G вершин а. и b и присоединении новой вершины а1, дуг (а.1,с), если (о, с) G R или (6,с) G R, и дуг (с, о/), если (с, u) G В или (с, Ь) € R'.
((М \ {«,7»}) U {(/}, (R \ {(c,d)|c = а или d = а, или с = Ь,
или d = b})U {(Ф,с)|(а, с) G R, или (6, с) G В}0
U{(c, о.')|(с, а) G R, или (с, Ь) G В.}).
Говорят, что построенный граф получается из графа G отождествлением вершин а и Ь. В случае, когда а и b соединены дугой. операцию отождествления вершин а и b называют стягиванием дуги (а,Ь).
П р и м е р 4.2.2. Из графа G. показанного на рис. 4.10, добавлением вершины 5 образуется граф бц, добавлением дуги (3,1) — граф 6*2, удалением дуги (3,2) — граф G3, удалением вершины 2 — граф 64, отождествлением вершин 1 и 4 — граф G%, стягиванием дуги (2,3) — граф G(,. □
Дополнением, графа без петель G = {М, В.) называется граф G= (M,M2\(RUidM))-
115
Рис. 4.10
II р и и с р 4.2.3. Дополнением графа G, изображенного на рис. 4.10, является граф G, показанный на рис. 4.11. □
Пусть G} = (Mi.Ri), G‘2 —	- графы. Объединением,
Gi U G-2 графов G] и G? называется граф (Лф U M'2,Ri U R^). Если Mi П 0, то пересечением. G] П G<2 графов Gi и G2 называется граф (М\ Г.М2,Н\ Кольцевой суммой Gi ©G2 графов Gi и G2 называется граф {M1UM2, R1&R2), где Д,1фД,2 = (1?! \ R2) и (Д2 \ Д2).
При м е р 4.2.4. Для графов
2	з	Gi = <{«l,«2,»-з}- {[«1,«г]. (о2,а3)})
•	•	и Gi =	({01-02,04}, {(oi,o2),
/	(04,0.])}) (рис. 4.12) найдем GiUG2,
\у	Gi П G2, Gi ф G2. По определению
имеем Gi U G2 = ({04,02,0.3,04}, /	\	{[01,02], (о2,о3), (o4,oi)}), Gi П
.	.	G'2 = ({ai,a2}, {(ai,o2)}), Gi ф
G'2	=	({01,02,0.3,04}, {(0.2,04),
РиС-411	(О2, 0.3), (04,0!)}). □
Соединением Gi +G2 графов Gi и G2 называется граф (ЛДи М2. 7?i U R2 U {[о., 6] |о £ Mi ,b G М2, а. Ъ}).
П р и м е р 4.2.5. Для графов Gj и G2, показанных на
рис. 4.13а. соединением G\ + G2 является граф, представленный на рис. 4.136. □
Произведением Gi х G2 графов Gi и G2 называется граф (Лф х Л/2,Д), в котором ((04,61), (о2, b2)) G R, тогда и только тогда, когда 04 = о.2 и (61,62) £ /?2, или Ь\ = 62 и (ai,a2) € Ri-
П р и м е р 4.2.6. На рис. 4.14 изображено произведение Gi х G2 графов G, = ({1,2}, {(1,1), (2,1)}) и G2 = ({о, 6, с}, {[о, 6], (6, с)}). □
116
«2
02
Рис. 4.12
02	04	а5
О1	Оз	02
а
Рис. 4.13
(1,о) (1,Ь) (1,с)
(2,о) (2, Ь) (2, с)
Рис. 4.14
117
(1,0,1)
(1,1,1)
(0,1)	(1,1)
------------О
(0,0)	(1,0)
Рис. 4.15
Неорграф без петель называется полным, если его любые две различные вершины смежны. Полный граф, имеющий п вершин, обозначается через Кп.
С помощью операции произведения определим по индукции важный класс графов, называемых п-мерными кубами (п-куба-ми). Рассмотрим граф К^, вершины которого обозначим 0 и 1. n-мерный куб, или тг-куб Qn, определяется по следующим правилам: Qo — граф без петель, состоящий из одной вершины, Qi К%, Qn К'2 х Qn-\, п > 1. Вершинами n-мерного куба Qn являются всевозможные п-кп, состоящие из нулей и единиц (всего таких наборов 2”), а ребра задаются по следующему
правилу: вершины смежны тогда и только тогда, когда соответствующие кортежи различаются ровно одной координатой. На рис. 4.15 показаны двумерный Q2 и трехмерный Q3 кубы.
Композицией G] [6’2] графов 6д и 6’2 называется граф (Л41 х Мг,1?), в ко
Рис. 4.16
тором ((о],Ь]), (02,^2)) € R тогда и только тогда, когда выполняется одно из следующих условий:
1) (01,02) G 7?г,
2) Gq = G.2 и (Ь1,62) G R'2-
Пример 4.2.7. Композицией 6'1(62] графов 6’1 и G'2, рассмотренных в примере 4.2.6, является граф, изображенный на рис. 4.16, а композицией 6'2 [6’l] — граф, представленный
на рис. 4.17. □
Неформально композиция 6 [[6’2] означает, что каждая вер-
118
шина а графа Gi заменяется на изоморфную копию Ga. графа G2, а затем, если (01,02) € Ri, то между любыми вершинами bi из Gai и Ь‘2 из GU2 проводится дуга (bi, Ьг).
§ 4.3. Маршруты. Достижимость. Связность
Пусть G = {М, R) — граф. Последовательность
О1, О1, 02, 02,  • • , Qn~t~l	(^’1)
где ai, 02, -.., on+i € М,    ,ип £ R, называется маршрутом, соединяющим вершины ai и an+i ((ai,ап+1)-маршрутом), если щ = (oijOi+i), i = 1,2,... ,п (рис. 4.18).
Очевидно, что маршрут (4.1) можно задать последовательностью oi,...,o„.+i его вершин, а также последовательностью «1, •  • ,ип дуг. Число п дуг в маршруте (4.1) называется его длиной.
Пусть G — неорграф. Маршрут (4.1) называется цепью, если все ребра [ai, 02], -.., [о„, on+i] различны, и простой цепью, если все его вершины кроме, возможно, первой и последней, различны. Маршрут (4.1) называется циклическим, если 01 = an+i. Циклическая цепь называется циклом., а циклическая простая
On
Оп+1
Рис. 4.18
119
Рис. 4.20
цепь - простым циклом.. Неорграф без циклов называется ациклическим. Минимальная из длин циклов неорграфа называется его обхватом,.
П р и м е р 4.3.1. Рассмотрим граф, изображенный на рис. 4.19. В нем наборы (1,2), (1,2,4,7), (3,4, 5,6) являются простыми цепями; (1,2,4, 7,8,4) — цепь, не являющаяся простой; (1,2, 4, 7,8,4, 2) — маршрут, не являющийся цепью; (1,2, 4. 7,8.4,1) — цикл, не являющийся простым; (1,2,4,1) — простой цикл. Обхват этого графа равен 3. □
Пусть G — граф, возможно, ориентированный. Маршрут (4.1) называется путем, если все его дуги различны. Путь (4.1) называется контуром., если oj = «п-1-1- Граф, не имеющий контуров, называется бесконтурным. Вершина Ъ называется достижимой из вершины а, если существует (а, Ь)-путь.
П р и м е р 4.3.2. Граф, изображенный на рис. 4.20, имеет > контур (1,2,3). Вершина 5 достижима из любой другой вершины, а из вершины 5 не достижима ни одна из вершин. □
Неорграф называется связным., если любые две его несовпадающие вершины соединены маршрутом. Граф G называется связным, если соответствующий ему неорграф F(G) тоже является связным. Граф G называется сильно связным,, если для каждой пары различных вершин а и b существуют (a, Ь)-маршрут и (/), о,)-маршрут. Аналогично определяются понятия связности и сильной связности для мультиграфов.
П р и м е р 4.3.3. Граф, показанный на рис. 4.19, является связным, орграф, представленный на рис. 4.20, — связным, но не сильно связным, а граф, изображенный на рис. 4.21, не является связным. □
Заметим, что любой связный неорграф является сильно связным.
Всякий максимальный по включению (сильно) связный подграф данного графа называется его {сильной) связной компонентой или {сильной) компонентой связности.
120
Граф, показанный на рис. 4.21, имеет две компоненты связности с множеством вершин {1,2,3,4} и {5,6,7}. Граф, представленный на рис. 4.20, имеет три сильные компоненты, задаваемые множествами вершин {1,2,3}, {4} и {5}.
Теорема 4.3.1. Любой грцф представляется в виде объединения непересекающихся связных (сильных) компонент. Разложение графа на связные (сильные) компоненты определяетя однозначно.
Таким образом, множества вершин связных компонент, а также сильных компонент образуют разбиение множества вершин графа, а число c(G) связных компонент графа G определяется однозначно.
Следующая теорема позволяет по матрице смежности Ас; исследовать маршруты данного графа G.
Теорема 4.3.2. Если Ас; — матрица см,ежности графа G, то (i,j)-u элемент матрицы Aq = Aq • ...  Ас есть число (а,г, k раз
aj)-маршрутов длины к.
Следствие 4.3.3. 1. В графе G мощности п тогда и только тогда, существует, (щ,а,-^-маршрут, (а,;	а7), когда (i,j)-u
элемент матрицы Ас; + Aq + ... + Aq не равен нулю.
2. В графе G мощности п тогда, и только тогда существует, цикл, содержащий вершину а,;, когда. (г,г)-й элемент матрицы Ас; + А), + ... + Aq не равен нулю.
П р и м е р 4.3.4. Определим с помощью матрицы смежности существование (1, 3)-маршрута в графе G, изображенном на рис. 4.22. В матрице
121
2
3
1
4
Рис. 4.22
/О О 0 1\ 10 11] 0 10 0
\1 1 о о/
(1,3)-элемент равен 0, т. е. (1,3)-маршрутов длины 1 нет. В матрице
О	0	1\	/О	О	0	1\	/1
0111011]	1
1	0	0	0	1	0	0	~	1
1	О	0/	\1	1	О	О/	\1
1	о 0\
2	0 1]
0 11
О 1 2/
(1,3)-элемент также равен 0. В матрице
— -^G ’ &G —
(1 1 0 0\
12 0 1]
10 11
10 12/
/ООО 1 0 1 О 1 О \1 1 О
1\	/10	1	2\
1 ]	_	3 1	2	3 ]
О	“	12	0	1
О/	\2 3	О	1/
(1, 3)-элемент равен 1, т. е. существует один (1,3)-маршрут длины 3. Из рис. 4.22 видно, что этот маршрут определяется набором вершин (1,4,2,3). Эту последовательность можно найти на основе перемножения матрицы смежности: элемент (1,3) матрицы Aq получается при перемножении элемента (1,2) матрицы Aq и элемента (2,3) матрицы Ag', в свою очередь элемент (1,2) матрицы Aq образуется при перемножении элемента (1,4) матрицы Ag на элемент (4,2) матрицы Ас/, следовательно, двигаясь от 1 к 3 за три шага, получаем маршрут (1,4,2,3). '
В матрице А(, элемент (4,2) равен 3, т. е. существует 3 (4,2)-маршрута длины 3: (4,1,4,2), (4,2,4,2), (4,2,3,2). □
Образуем из матрицы (Ь^) = Е + Ag + A'g 4--1- A'q матрицу
122
С = (cjj) порядка п по следующему правилу:
1, если Вц О, 3	0, если bij = 0.
Матрица С называется матрицей связности, если G — неорграф. и матрицей достижим,ости, если G — орграф. В графе G тогда и только тогда существует (a,j, ал)-маршрут (г j), когда Cij = 1. Таким образом, в матрице С содержится информация о существовании связей между различными элементами графа посредством маршрутов. Если G — связный неорграф, то все элементы матрицы связности С равны единице. В общем случае матрица связности неорграфа является матрицей отношения эквивалентности, соответствующего разбиению множества вершин графа на компоненты связности.
Определим следующим образом матрицу контрдостижимости Q — (qij)-
, 1, если вершина щ достижима из вершины 0 — в противном случае, к
Нетрудно заметить, что если С — матрица достижимости, то Q = СТ.
Матрицы достижимости и контрдостижимости С — (cij) и Q — можно использовать для нахождения сильных компонент графа. Рассмотрим матрицу S — С * Q, где операция * означает поэлементное произведение матриц С и Q: sij = сц  qtj (см. § 1.5). Элемент Sij матрицы S равен 1 тогда и только тогда, когда вершины щ и aj взаимно достижимы, т. е. аг достижима из a,j и a,j достижима из аг. Таким образом, матрица S является матрицей следующего отношения эквивалентности Е:
выполнимо аг Е aj тогда и только тогда, когда и aj находятся в одной сильной компоненте.
Следовательно, сильная компонента, содержащая вершину aj, состоит из элементов av для которых Sij — 1.
Пример 4.3.5. Матрицы достижимости С и контрдости-
123
жимости Q графа, изображенного на рис. 4.20, имеют вид
1
1
0
\0
1 1 1
1 1 1
1 1 1
0 О 1
ООО
/1
1
1
1
V
1 1 0 0\ 110 0
110 0 1110 1111/
S = C*Q =
/1 1
1 о
\0
1 1 0 0\ 110 0
110 0 0 0 10 0 0 0 1/
По 2-й строке матрицы S находим, что сильная компонента, содержащая вершину 2, состоит из вершин {1,2,3}.
§ 4.4.	Расстояние в графах
Пусть G = (M,R) - связный неорграф, а, b — две его несовпадающие вершины. Длина кратчайшего (а, Ь)-маршрута называется расстоянием между вершинами а и b и обозначается через р(а, 6). Положим р(а, а) 0. Очевидно, что введенное таким образом расстояние удовлетворяет следующим аксиомам метрики:
—	р(а, Ь) > 0;
—	р(а, Ь) = 0 <=> я, = Ь;
—	р(Ь, а) — р(а, Ь) (симметричность);
—	р(а, Ь) р(а, с) + р(с, Ь) (неравенство треугольника).
Если М — {<21,0,2,... ,ап}, то матрица Р = (ул?), в которой Pij = p(a,i,a.j), называется матрицей расстояний. Заметим, что Р1 = Р, т. е. матрица Р симметрична.
Для фиксированной вершины а величина е(а) тах{р(а, Ь) | b £ М} называется эксцентриситет,ом. вершины а. Таким образом, эксцентриситет вершины равен расстоянию от данной вершины до наиболее удаленной от нее. Если Р — матрица расстояний, то эксцентриситет е(о,г) равен наибольшему из чисел, стоящих в г-й строке.
Максимальный среди всех эксцентриситетов вершин называется диаметром графа G и обозначается через d(G): d(G)
124
max{e(a) | a E M}. Вершина а, называется периферийной, если e(a) = d(G).
П р и м с р 4.4.1. Найдем диаметр графа G, изображенного
па рис. 4.23. Матрица расстояний Р имеет вид
/О 1 3 1 2\
10 2 11
3 2 0 2 1
112 0 1
\2 1 1 1 0/
отсюда е(1) = 3, е(2) = 2, е(3) = 3, е(4) = 2, е(5) = 2 и, следовательно, d(CT) = 3. Вершины 1 и 3 являются периферийными. □
Минимальный из эксцентриситетов графа G
Рис. -1.23 называется его
радиусом и обозначается через r(G): r(G) min{e(a) | a G М}. Вершина а называется центральной, если e(a) = r(G). Множество всех центральных вершин графа называется его центром.
П р и м е р 4.4.2. 1. Радиус графа, показанного на рис. 4.23, равен 2, а его центром является множество {2.4,5}.
2. В полном графе Кп все различные вершины смежны, и поэтому d[Kn) — r(Kn) = 1. □
Задача нахождения центральных вершин возникает в прак
тической деятельности людей. Пусть, например, граф представляет собой сеть дорог, т. е. вершины соответствуют населенным пунктам, а ребра дорогам между ними. Требуется оптимально разместить больницы, пункты обслуживания и т. п. В подобных ситуациях оптимизация заключается в минимизации
расстояния от места обслуживания до наиболее? удаленного населенного пункта. Следовательно, местами размещения должны быть центральные вершины графа. Реальные задачи отличаются от этой идеальной тем, что приходится учитывать и другие об
стоятельства — расстояния между населенными пунктами, стоимость, время проезда и т. д. Для учета этих параметров используются взвешенные графы.
Пусть G =	(М, В.) взвешенный граф, в ко тором
вес каждой дуги (а, Ь) есть некоторое вещественное число ц(а,Ь). Весом .маршрута (д, а-2,  -., ап, an+i называется число п
р = ^2 p(a?;, ffli+i). Взвешенным расстоянием (м-расстояиием) ?=1
125
pw(a,b) между вершинами а, и b называется минимальный из весов (о, 0-маршрутов. (а, 0-Маршрут, вес которого равен расстоянию ри.(а, 0, называется кратчайшим (а, 0-маршрутом во взвешенном графе G. Взвешенным эксцентриситетом ew(a) вершины а называется число max{pw(a, 0 I b G М}. Взвешенной центральной вершиной графа G называется вершина а, для которой е„,(а) = min{ew(0 | b Е М}. Взвешенный эксцентриситет центральной вершины называется взвешенным радиусом графа G и обозначается через rw(G).
П р и м е р 4.4.3. Во взвешенном графе G, показанном на рис. 4.8, центральной вершиной является вершина “Новосибирск”, а г,„ (G) = 681. □
§4.5. Нахождение кратчайших маршрутов
Пусть G = {M,R) — взвешенный граф, имеющий п вершин и матрицу весов W = (w^), Wij Е R. Опишем некоторые методы нахождения взвешенного расстояния от фиксированной вершины a.i Е М (называемой источником) до всех вершин графа G.
Мы будем предполагать, что в G отсутствуют контуры с отрицательным весом, поскольку, двигаясь по такому контуру достаточное количество раз, можно получить маршрут, имеющий вес, меньший любого заведомо взятого числа, и тем самым задача нахождения расстояния становится бессмысленной.
Определим алгоритм Форда — Беллма-на. Зададим строку = (d^'\d^\..., Wkj полагая cZ-^ = 0. d^ = w^, i j. В этой строке б/j1' (J г) есть вес wtj дуги °k (a.,, a.j), если (щ,а7) существует, и d^ оо, если (аг,а7)	В.. Теперь определим строку Г)(2) _ /,1(2) 1(2)	>(2)ч пппягяя я(2) _
«Д/}*:=!,...,«• Нетрудно заметить, что clj2^ — мини
мальный из весов (аг,а7)-маршрутов, состоящих не более чем из двух дуг (рис. 4.24).
Продолжая процесс, на шаге s определим строку = 4s), ..., d„^), полагая d^ min{(Zjs-1\ +wAj}fc=lv.„n. Искомая строка w-расстояний получается при s = п — 1: d\™	=
Рис. 4.24
miiifi/1), fZ?) +
126
/>u>(at,aj). Действительно, на этом шаге из весов всех (at,a?-)-маршрутов. содержащих не более ??, — 1 дуг, выбирается наименьший, а каждый маршрут более чем с n - I дугами содержит контур, добавление которого к маршруту не уменьшает w-расстояния. так как мы предположили отсутствие контуров отрицательного веса. Работу алгоритма можно завершить на шаге;
если = £>(fc+1).
П р и м е р 4.5.1. Продемонстрируем работу алгоритма Форда — Веллмана па примере взвешенного графа, показанного на рис. 4.25, с матрицей весов
	/° оо	1 0	3	3	3\ 8
W =	ос	оо	0	1	-5
	оо	ОС	2	0	оо
	\оо	оо	оо	4	0 J
В качестве источника выберем вершину 1. Тогда — (0,1,оо, .эо;3), D& = (0,1,4,4,3),	=
(О, 1,4,4,-1),	= (0, 1,4,3,
— 1). Таким образом, pw(l, 1) = О, рш(1,2) = 1, pw(l,3) '= 4, р,Д1,4) =3, pt„(l,5) = -1. О
Отметим, что, зная расстояние от источника сц до всех
остальных вершин графа, можно найти и сами кратчайшие (щ, н7)-маршруты. Действительно, пусть а^, bi,	Ьт, а3
кратчайший (щ, «^-маршрут. Тогда по строке	вершина
Ьг = а/Г1 находится из соотношения pw((ii,aj) = РыД^а,^) +Wf-i:i. вершина Ьг.\ =	— из соотношения 07,4) = Pw{ai-,ak>} +
wk.2kj и т. д.
П р и м е р 4.5.2. В примере 4.5.1 кратчайший (1,4)-марш-рут определяется следующим образом: pw(l,4) = 3 = —1 + 4 = pu;(1.5)+w5,|, тогда br = 5; pw(l, 5) = -1 = 4-5 = Pw(l,3)+w35, откуда ф । = 3; pw(l. 3) = 4=1 + 3 = гщд + W23- следовательно.
= l>2 = 3, br-tt = bi = 2. Таким образом, кратчайший (1,4)-маршрут задается последовательностью вершин (1,2,3, 5,4). О
Алгоритм Де.йкстры является более эффективным, чем алгоритм Форда — Веллмана, но используется только для взвешенных графов, в которых веса всех дуг неотрицательны.
127
Итак, пусть G — (M.R) — взвешенный граф, W = (wtj) — матрица весов графа G, где wij 0; а,: — выделенный источник. Зададим строку = (d^\ d^\ -  , (In полагая, как и в алгоритме Форда — Веллмана, d^ = 0. d^ = Wij, г j. Обозначим через Т\ множество вершив М\ {а,;}. Предположим, что па шаге я уже определены строка = (d[s\ ..., d^) и множество вершин Ts. Выберем теперь вершину' а3 G Ts так, что d^ = mm{d^|o,/L. G Т,}. Положим Д+| Ts \ {а/}, . ,d^+1)), где d^+^ =	+ wjk},
если ak e Ts+i, и d^+l>> — d^\ если сц. $ Ts+i- На шаге s = n — 1 образуется строка £>(’'“ l) w-расстояний между вершиной (ц и остальными вершинами графа: d^1	= pw(a,i,aj).
Отметим, что для реализации алгоритма Форда — Веллмана требуется порядка п3 операций, тогда как в алгоритме Дейкстры необходимо выполнить порядка п2 операций.
Рис. 4.26
При м е р 4.5.3. Рассмотрим взвешенный граф G с матрицей весов
	/0	1	оо	ОС'	оо	оо\
	оо	0	5	2	оо	7
	оо	оо	0	ОО	оо	1
W =	2	ОС'	1	0	4	оо
	оо	оо	оо	3	0	оо
	\оо	оо	оо	оо	1	о/
и источником 1 (рис. 4.26).
Тогда по алгоритму Дейкстры Д = {2, 3,4,5.6}, l/1) = (0,1,оо, оо,оо, оо), Т-2 = {3,4, 5.6},	— (0,1.6,3, оо, оо), Д =
{3.5.6}, 7>31 = (0,1,4,3, 7,8), Т4 = {5,6},	= (0,1, 4,3,7,5),
Д = (5}_ £>(5) = (0,1,4,3,6,5) (в Z/s) подчеркнута величина
<1^, для которой Ts-+i = Ts \ {«/}) Таким образом. pw(l, 1) = 0. рн;(1,2) - 1, /лД1,3) = 4, Pw(l,4) = 3. pw(l,5) = 6. р,„(1,6) = 5. □
Опишем теперь алгоритм нахождения кратчайших маршрутов в бесконтуриом графе. Так же, как и в алгоритме Дейкстры,
128
для выполнения этого алгоритма необходимо порядка п2 опе-
раций.
Прежде всего заметим, что в конечном бесконтурном графе G = (M.R.) вершины можно перенумеровать так, что каждая дуга будет иметь вид (a,i,a,j), где i < j. Действительно, в конечном бесконтурном графе всегда существует вершина а, в которую не заходит ни одна дуга. Обозначим эту вершину через а,] и рассмотрим граф Gi, полученный из G удалением вершины аг. Граф G|
также является бесконтурным и, следовательно, содержит вершину а', в которую не заходит ни одна дуга графа Gj. Вершину а! обозначим через а2, а граф, полученный из G, удалением вершины а2 — через G2. Продолжая процесс, получим в результате искомую нумерацию ai, a2, ..., a„, вершин графа G.
П р и м е р 4.5.4. На рис. 4.27 приведен пример нумерации вершин бесконтурного взвешенного графа, при которой из (ai,aj) € R следует г < j (в скобках указаны веса взвешенных
ДУГ)- О
Предположим, что в бесконтурном графе G = ({ai,..., an},R) для произвольной дуги (aj,a7) выполняется условие i < j. Заметим, что при такой нумерации все элементы матрицы весов, стоящие под главной диагональю, равны оо. Найдем расстояние от ai до всех вершин графа. Рассмотрим строку
4U,  • • ,4/4 W 4X) = 0;	=
wi?-; j 2. Если на шаге s строка Рб') =	44 • • •, 44 опре
£)(«+!)
делена,
положим
min{4’), djf1
+ wkj}, для к < j и (щ,аД G R, j = 1,...,и.
Данный алгоритм является аналогом алгоритма Форда Велл-
мана, учитывающим бесконтурность графа G, и при s = п — 1 получаем dj” = pw(ai,a.j).
5 Зак. № 4872 Судоплатов
129
П р и м е р 4.5.5. Для графа G (рис. 4.27) имеем
	/°	1	ОС’	2	оо	ОС	1	оо\
	ОС'	0	-2	ОС’	7	ОС’	ОС	оо
	оо	ОС	0	ОС	ОС’	10	ОС	ОС’
	оо	ОС’	ОС’	0	—5	ОС’	ОС’	оо
И7 =	оо	оо	оо	ОС	0	6	ос-	1
	оо	оо	оо	оо	оо	0	оо	ОС
	оо	ос-	ОС’	ОС'	ОС'	ОС	0	3
	\ос	ос	оо	ОО	ОС'	ОС'	оо	0/
= (0,1,оо,2,оо, оо,1,оо),	= (0,1, —1, 2, —3, се, 1,4),
D(3) = (0,1,-1,2,-3,3,1,-2) = DG) = Д(5) = £)(б) = £>(7) п
Отметим, что если в приведенных алгоритмах ос заменить на —ос, min — на max, то получим алгоритмы, которые позволяют в графах, не имеющих контуров положительных весов, находить маршруты наибольшей длины.
§4.6. Степени вершин
Степенью или валентностью вершины а неорграфа G называется число ребер, инцидентных вершине а, т. е. число ребер, концом которых является вершина а (при этом петли считаются дважды). Если G — орграф, то степени его вершин определяются как степени вершин в соответствующем неорграфе F(G). Аналогично вводится понятие степени вершины в мультиграфах. Степень вершины а, будем обозначать через degG а, или просто deg а. Вершина степени 0 называется изолированной, вершина степени 1 — концевой или висячей.
П р п м е р 4.6.1. Вершины графа G, изображенного на рис. 4.28, имеют следующие валентности: deg 1 = deg 2 = deg3 = 1 (т. е. 1, 2, 3 — висячие вершины), deg4 = 5, deg5 = 0 (т. е. 5 — изолированная вершина).
1
2	3
Рис. 4.28
130
Рассмотрим сумму степеней всех вершин графа. Поскольку каждое ребро входит в эту сумму дважды, справедливо
Утверждение 4.6.1 (лемма о рукопожатиях). Сумма степеней всех вершин графа является четным числом и равна удвоенному числу ребер.
Пусть G — бесконтурный орграф. Полустепенъю исхода deg+ а вершины а называется число дуг, исходящих из а. Полустепенъю захода deg' а. вершины а. называется число дуг, которые заходят в вершину а.. Справедливо соотношение deg о — deg+ о + deg- о.
В примере 4.5.4 имеем deg 2 = 3, deg+ 2 = 2, deg- 2 = 1.
§ 4.7. Обходы графов
Опишем одну из задач, положивших начало теории графов, — задачу о кенигсбергских мостах. На рис. 4.29 схематично изображена карта г. Кенигсберга в XVIII в. Город был расположен на берегах и двух островах реки Преголи. Острова между собой и с берегами были связаны семью мостами. Возник вопрос: можно ли, выйдя из дома, вернуться обратно, пройдя по каждому мосту ровно один раз?
Неориентированный мультиграф G, представляющий задачу, показан на рис. 4.30. Вершины х^, х^ соответствуют берегам реки, Х2, X'i — островам, ребра мультиграфа — мостам. Следовательно, на языке теории графов задача формулируется следую
Рис. 4.30
5*
131
щим образом: существует ли в мультиграфе цикл, содержащий все ребра данного мультиграфа?
Выдающимся математиком и механиком Л. Эйлером сформулирован и доказан критерий того, что связный неориентированный мультиграф имеет цикл, содержащий все ребра данного мультиграфа. Цикл, содержащий все ребра мультиграфа, называется эйлеровым, и мулътиграф, в котором имеется эйлеров цикл, также называется эйлеровым.
Теорема 4.7.1. Связный неориентированный мулътиграф тогда и только тогда является эйлеровым, когда степень каждой из его вершин — четное число.
Мультиграф, изображенный на рис. 4.30, не содержит эйлеров цикл, поскольку в нем есть вершины, имеющие нечетную степень; более того, все вершины имеют нечетную степень.
Опишем алгоритм построения эйлерова цикла в эйлеровом мультиграфе. Этот алгоритм задается следующими правилами.
1.	Выбрать произвольно некоторую вершину а.
2.	Выбрать произвольно некоторое ребро и, инцидентное а, и присвоить ему номер 1 (назовем это ребро пройденным).
3.	Каждое пройденное ребро вычеркнуть и присвоить ему номер, на единицу больший номера предыдущего вычеркнутого ребра.
4.	Находясь в вершине х, не выбирать ребро, соединяющее х с а, если имеется возможность иного выбора.
5.	Находясь в вершине х, не выбирать ребро, которое является перешейком (т.е. ребром, при удалении которого граф, образованный невычеркнуты-ми ребрами, распадается на две компоненты связности, каждая из которых имеет хотя бы по одному ребру).
6.	После того как в графе будут за
нумерованы все ребра, образуется эйлеров цикл, причем порядок нумерации соответствует последовательности обхода ребер.
Пример 4.7.1. Найдем эйлеров цикл в эйлеровом графе, изображенном на рис. 4.31. После выбора вершины а и прохождения ребер 1 и 2 имеются три возможности выбора: ребра 3, 6 или 7. Так как ребро 7 является перешейком, выбираем следующее ребро из оставшихся, например 3. Далее обходим оставшиеся ребра и получаем эйлеров цикл 1, 2, 3, 4, 5, 6, 7, 8. □
Рис. 4.31
132
Будем говорить, что набор ребер но непересекающихся цепей покрывает граф G, если каждое ребро графа G входит в одну из этих цепей. Пусть связный граф G содержит к вершин нечетной степени. По лемме о рукопожатиях число к четно. Рассмотрим граф G', полученный добавлением к G новой вершины а и ребер, соединяющих а со всеми вершинами графа G нечетной степени. Поскольку степени всех вершин графа G' четны, G' содержит эйлеров цикл. Если удалить из этого цикла все ребра, инцидентные вершине а, то получится не более к/2 цепей, содержащих все ребра графа G, т. е. покрывающих G. С другой стороны, граф, являющийся объединением г реберно непересекающихся цепей, имеет не более 2г вершин нечетной степени. Поэтому граф G нельзя покрыть цепями, число которых меньше к/2. Тем самым доказана
Теорема 4.7.2. Если связный граф содержит к вершин нечетной степени, то минимальное число покрывающих его реберно непересекающихся цепей равно к/2.
В частности, при к = 2 граф имеет цепь, которая соединяет вершины нечетной степени и содержит все ребра графа. Цепь, содержащая все ребра графа, называется эйлеровой.
Мы рассмотрели обходы ребер графа. Следующей нашей целью является изучение обходов вершин графа.
Граф называется гамильтоновым, если в нем имеется простой цикл, содержащий каждую вершину этого графа. Сам такой цикл также называется гамильтоновым. Гамильтоновой называется и простая цепь, содержащая все вершины графа. Очевидно, что любой граф, ребра которого образуют простой цикл, является гамильтоновым, а граф, показанный на рис. 4.31, — негамильтоновым.
Несмотря на схожесть задач о нахождении эйлеровых и гамильтоновых циклов, решение последней значительно сложнее. Известны следующие достаточные условия существования гамильтоновых циклов в связном неорграфе G без петель, имеющем п 3 вершин:
Теорема 4.7.3. Если для любых двух различных несмежных вершин о и b графа G выполняется условие deg а + deg 6 п, то существует гамильтонов цикл.
133
Следствие 4.7.4. Если для любой вершины а графа, G выполнено условие deg а п/2, то существует гамильтонов цикл.
С задачей нахождения гамильтонова цикла связана задача коммивояжера. Район, который должен посетить бродячий торговец, содержит некоторое количество городов, расстояния между которыми известны. Требуется найти маршрут, проходящий через все пункты по одному разу и возвращающийся в исходный город. Если таких маршрутов много, требуется найти кратчайший из них.
Математическая постановка задачи выглядит так: требуется найти гамильтонов цикл минимального веса. Решение этой проблемы рассмотрим в § 4.9, а здесь отметим некоторые практические задачи, сводящиеся к задаче коммивояжера.
1.	Пусть граф задает сеть коммуникаций между фиксированными центрами. Необходимо построить маршрут, обеспечивающий посещение всех центров ровно по одному разу.
2.	Имеется станок с числовым программным управлением, который высверливает отверстия в печатных платах по заданной программе. Составляя граф, в котором вершины соответствуют требуемым отверстиям, получаем задачу нахождения обхода вершин, такого, что суммарное время, затраченное на него, было бы минимальным.
§ 4.8. Остовы графов
Деревом называется связный неорграф, не содержаций циклов. Любой неорграф без циклов называется ациклическим графом или лесом. Таким образом компонентами связности любого леса являются деревья.
На рис. 4.32 изображен лес, состоящий из двух деревьев.
Теорема 4.8.1. Для неорграфа G без петель содержащего п вершин следующие условия эквивалентны:
134
1)	G — дерево;
2)	G — связный граф, содержащий п — 1 ребро;
3)	G - ациклический граф), содержащий п — 1 ребро;
4)	любые две несовпадающие вершины графы G соединяет единственная простая цепи;
5)	G ациклический граф), такой, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
Пусть G = (Л/, В.) — неорграф. Часть G' = {М1, В1) графа G называется остовом или каркасом, графа G, если М = М' и G' — лес, который на любой связной компоненте графа G образует дерево. Таким образом, если G — связный граф, то остов G' является деревом, которое будем называть остовным деревом графа G.
Понятие остова для орграфа G определяется как часть G' графа G, для которой F(G') является остовом графа F(G). Аналогично вводится понятие остовного дерева для связного орграфа G.
Очевидно, что в каждом графе существует остов: разрушая в каждой связной компоненте циклы, т. е. удаляя лишние ребра, получаем остов.
Пример 4.8.1. В качестве остова графа G, изображенного на рис. 4.33, можно взять лес с ребрами 2, 3, 4, 6, 7 (вообще говоря, остов определяется неоднозночно). □
Из теоремы 4.8.1. вытекает
Следствие 4.8.2. Число ребер произвольного неорграфы, G, которые необходимо удалить для. получения остова, не зависит от. последовательности их удаления и равно т — п + с, где т — число ребер, п — число вершин, с — число компонент связности графы, G.
Доказательство. Действительно, если г-я компонен-
135
та связности Cf графа G содержит щ вершин, то по теореме 4.8.1. соответствующее дерево /<•, остова содержи! щ — 1 ребро. Следовательно, для получения Ki из компоненты С; нужно удалить чщ — (н, — 1) ребер, где тг число ребер в Сд Суммируя удаляемые ребра по всем компонентам связности и замечая, С	с
что 52 mi = т-, 52 ni = п- получаем, что необходимо удалить i=l	г=1
с
52 (ч'Ч — ni + 1) = m — п + с ребер. □ i=i
Число m(G) = т — п + с называется цикломатическим числом или циклическим. рангом графа G. Число v*(G) = п. — с называется koi циклическим рангом или корангом. Таким образом, v*(G) есть число ребер, входящих в любой остов графа G, и z/(G) + z/*(G) = т.
Очевидны следующие два следствия.
Следствие 4.8.3. Неорграф G является лесом, тогда и только тогда, когда v(G) = 0.
Следствие 4.8.4. Неорграф G имеет единственный цикл, тогда и только тогда., когда v(G} = 1.
Опишем алгоритм нахождения остова минимального веса во взвешенном графе. Эта задача возникает при проектировании линий электропередач, дорог и т. п.. когда требуется заданные центры (вершины) соединить некоторой системой каналов связи (ребер) так. чтобы любые два центра были связаны либо непосредственно соединяющим их каналом (ребром), либо через другие центры и каналы, т. е. цепью, и чтобы общая длина (или, например, стоимость) каналов связи была минимальной. Искомая сеть будет остовом минимального веса полного графа.
Алгоритм, решающий задачу нахождения остова минимального веса во взвешенном графе G = {М, R), заключается в следующем.
1. Строим грае]) 7|, состоящий из множества вершин М и единственного ребра щ, которое имеет минимальный вес.
2. Если граф Т, уже построен и i < п—с, где п = \М|, с = c(G), то строим грае]) Т,+\, добавляя к множеству ребе]) графа 7} ребро «г+1, имеющее минимальный вес среди ребер, не входящих в Тг и не составляющих циклов с ребрами из TL.
Приведенный алгоритм, в частности, позволяет находить остов
136
2
1
Рис. 4.34
в невзвешенном графе, положив ш(-щ) = 1 для всех ребер щ Е R.
П р и м е р 4.8.2. На рис. 4.34 показан остов минимального веса взвешенного графа. Вес остова равен 9. □
Рис. 4.35
§ 4.9. Обходы графа по глубине и ширине. Решение задачи коммивояжера
При решении прикладных задач часто возникает необходимость обхода вершин графа, связанная с поиском вершин, удовлетворяющих определенным свойствам. Пусть G = {М, R) — связный неориентированный граф, Т - некото
рый остов графа G. а — некоторая фиксированная вершина, называемая корнем дерева Т. Разместим вершины из М по этажам таким образом, чтобы корень а находился в верхнем этаже, смежные с ним вершины занимали этаж на единицу ниже, смежные с отмеченными вершинами — еще на единицу ниже и т. д. (рис. 4.35). Таким образом, получаем е(а) +1 этажей, где е(а) — эксцентриситет вершины а.
Опишем обход графа по глубине.
При таком обходе после очередной рассмотренной вершины выбирается смежная с ней вершина следующего этажа. Если очередная рассмотренная вершина висячая и се достижение не дает желаемого решения задачи, то возвращаемся до ближайшей вершины степени 3 и просматриваем вершины другого, еще не пройденного маршрута в таком же порядке и т. д.
137
1
Рис. 4.36
Рис. 4.37
На рис. 4.36 показана очередность обхода вершин по глубине графа, изображенного на рис. 4.35.
При обходе графа по ширине просмотр вершин дерева ведется по этажам, переход к вершинам следующего этажа производится только после просмотра всех вершин данного этажа. На рис. 4.37 показан порядок обхода по ширине графа, изображенного на рис. 4.35.
Очевидно, что при обходе
всех вершин оба подхода: поиск в глубину и поиск по ширине — эквивалентны. Если же достаточно найти одну вершину с определенным свойством, то целесообразность применения поиска решения по глубине или по ширине определяется структурой дерева. Если дерево является достаточно широким, а висячие вершины расположены на сравнительно близких этажах, то целесообразно вести поиск по глубине. Для глубоких узких деревьев, когда висячие вершины могут встретиться на различных этажах и их разброс по этажам достаточно велик, предпочтение отдается поиску по ширине.
Отметим, что при компьютерной реализации обходов по глубине и ширине целесообразно использовать задание дерева структурой смежности вершин.
Часто при решении задач их разбивают на несколько более простых задач, которые, в свою очередь, разбиваются на более простые подзадачи и так до тех нор, пока не появляются подзадачи, поддающиеся непосредственному решению. Та-
138
Д(1,1) Л(1,2)-А(1,П1)
Рис. 4.38
Д(2,П1,1)- - А(2,щ,п2П1)
кое разбиение задач можно представить в виде дерева следующим образом. Если задача А разбивается на подзадачи >4(1,1), А(1,2), ..., А(1,П1), подзадача Д(1Д) — на подзадачи А(2,г, 1), ..., А(2, и т. д., то получается дерево, изображенное на рис. 4.38.
Для решения задач используются обходы таких деревьев с поиском по глубине или ширине. Опишем данный подход на примере решения задачи коммивояжера методом ветвей и границ.
Пусть W = (wij) — матрица весов графа G = (M,R), не имеющего петель, где М = {1,2,	Для простоты будем счи-
тать, что все веса Wij неотрицательны. Найдем нижнюю оценку весов гамильтоновых циклов. Для этого в матрице, весов найдем минимальные числа каждой строки: Wikl, W2k2,  , и)пкп. Очевидно, что вес произвольного гамильтонова цикла не меньше wifcj + U!2k2 Ч-F wnk„  Преобразуем матрицу весов, вычитая
из каждой строки соответствующее число . Получаем матрицу H/V = (w^), где = Wjj — Wiki- В ней найдем минимальные числа каждого столбца: w/j, w,v2, ..., дф п, и преобразуем ее, вычитая из каждого столбца соответствующее число
W* -- (w*A, где w*- = w.Y; — w,v... Для любого гамильтонова пик-ла X справедлива оценка веса w(X) цикла X: w(X) Э Л, где h = Wlkl + W2k2 + •   + wnkn + x + w^2 + ...+ w^n.
Обозначим через (бц,а2,..., a*;){bi, 62, • • • ,bt} множество гамильтоновых циклов, в которых первые к вершин «ц, а2,..ак, а (А:+1)-я вершина ak+i не принадлежит множеству {£ц, 62,..., bt}.
139
(.l-ki,kki.kkkj0
Рис. 4.39
Используя введенные обозначения, можем разбить нашу задачу
на две подзадачи, поделив множество гамильтоновых циклов на множества (1, fci)0 и (l){A;i} (рис. 4.39).
При рассмотрении множества (1, Ад )0 отождествим в графе G вершины 1 и kj (обозначим новую вершину через х) и получим граф G' с множеством вершин {.?;, 2,..., ki — 1, /д + 1,..., п} и
матрицей	весов / оо W21	Wkr2	Wk^ OO	W23		
ж =	Wfci + l,l	wAa-i,2 w*ki — 1,3	••• Wfcl + 1,2 '<Г'*Т1 + 1,3		
	\ <1	ъ	Jn2	w*n3 Wfcl,/cj+l 'U,2,fei-1	W2,fci + 1	   wkn \
			00	«Vl.fcx+l ••• Ч+1ЛХ-1	°°	” wG+l,n	
<л1+1	•••	00	/
Для графа G1 найдем нижнюю оценку h' весов гамильтоновых циклов аналогично тому, как найдены оценки h. Тогда нижняя оценка h] весов гамильтоновых циклов множества (l,A.j)0-
равна h + Л/.
140
При рассмотрении множества (1){Л]} в матрице весов W* элемент заменяется на ос и по полученной матрице W находится нижняя оценка h" весов гамильтоновых циклов графа с матрицей весов W". Тогда нижняя оценка Л.2 весов гамильтоновых циклов множества (1){ki} равна Л + Л".
Каждая из подзадач разбивается на свои подзадачи, и этот процесс с оцениванием весов гамильтоновых циклов продолжается до тех пор, пока не отыщется самая низкая из оценок, являющаяся весом некоторого гамильтонова цикла, который и будет иметь минимальный вес.
При рассмотрении подзадач целесообразно вести поиск в глубину, при котором на каждом следующем этаже выбирается та подзадача, которая имеет меньшую нижнюю оценку.
П р и м е р 4.9.1. Рассмотрим граф с матрицей весов
1 /оо		13	7	5	2	9\
2	8	оо	4	7	5	оо
ТТЛ 3	8	4	оо	3	6	2
W = 4	5	8	1	оо	0	1
5	оо	6	1	4	оо	9
6	\ю	0	8	3	7	оо/
(2 \ 4 1
q I, где 2 = ад15, 4 = W23>
1 / о/
2 = W36, 0 = W45, 1 = W53, 0 = W62-
Вычитая соответствующие числа из каждой строки, получим матрицу
/оо	11	5	3	0	7\
4	оо	0	3	1	оо
v	_	6	2	оо	1	4	О
W	~	5	8	1	оо	0	1	’
оо	5	0	3	оо	8
ЦО	0	оо	3	7	ос;
После нахождения наименьших значений по столбцам (4,0, 0,1,0,0) и вычитания из каждого столбца матрицы Wv соответствующего
141
Рис. 4.40
числа wi..j образуется матрица
/оо	11	5	2	0	7\
0	оо	0	2	1	оо
rrz*	2	2	оо	0	4	0
И =	1	8	1	оо	0	1
оо	5	0	2	оо	8
\ 6	0оо2	7	ооу
Суммируя элементы и w^j, получаем нижнюю оценку h = 14.
Так как ццз = min{wij|i = 1,...,п}, то множество гамильтоновых циклов разобьем на два множества (1,5)0 и (1){5} (рис. 4.40).
При рассмотрении множества (1,5)0 получаем матрицу весов
W = 2
3
4
6
х	2	3	4	6
/оо	5	0	2	8	\
0	оо	0	2	ос
2	2 оо 0	0
1	8	1	оо	1
\6	0	8	2 оо/
графа G', образованного отождествлением
вершин 1 и 5 графа
142
G. Минимальные элементы строк матрицы W' образуют столбец
			/оо 5	0	2 оо>	
	0		0 оо 0	2 оо	
	0	, поэтому (IV')4, =	2	2 оо 0	0	5
	1		0 7 0 оо 0	
	W		\6	0	8	2 ооУ	
а минимальные элементы столбцов матрицы (IV')v образуют ну-				
левую строку, и значит, (Ж')* = (H’')v. Таким образом, оценка h,\ будет равна h + h! = 14 + 1 = 15.
Рассматривая множество (1){5}. мы должны в матрице IV* заменить элемент wj5 = 0 на оо. Тогда оценка Л,2 будет h + h! — 14 + 2 = 16.
Поскольку /ц < /г2, выбираем множество (1.5)0 и соответствующую матрицу весов (IT')*. Теперь в силу того, что (ш*)жз = О, разобьем множество гамильтоновых циклов из множества (1,5)0 на множества (1,5,3)0 и (1, 5){3} (рис. 4.40). Рассматривая случай (1,5,3)0, получаем матрицу весов
х	2	4	6
х	/оо	2	0	0 \
W" =2	10	оо	2	оо)
4	0	7	оо	0
6	\ 6	0	2	оо/
графа G", образованного отождествлением вершин х и 3 графа G'. Оценка 71 ij равна 15, а (IV")* = W". При рассмотрении множества (1,5){3} в матрице (IV')* заменяем элемент (w')23 = 0 на оо и получаем оценку /л 12 = h\ + 2 = 17.
Так как /гп < Л12, выберем множество (1,5,3)0 с матрицей весов (IV")* = W". Поскольку (IV")*4 = 0. рассмотрим множества циклов (1,5,3,4)0 и (1,5,3){4}. Для оценивания весов в множестве (1,5, 3,4)0 отождествим вершины х и 4 в графе G" и получим граф G'" с матрицей весов
	X	2	6
IV'" = *	( ОС	7	0
2	1 0	оо	оо
6	\6	0	оо
143
Очевидно, что Лщ = Ли = 15, а (ТУ'7')* = W"'. Рассматривая случай (1, 5,3){4}. заменяем в матрице (W")* элемент (ы',')*л — О на оо и получаем оценку Лиг = Лц +2=17.
Так как Лц1 < Лц2, то переходим к рассмотрению множества (1,5, 3.4)0, состоящего из двух гамильтоновых циклов (1,5,3,4, 2.6,1) и (1, 5,3,4,6. 2,1). Первый из этих циклов будет иметь вес оо, поскольку (РР"')26 = оо, а вес второго цикла 15, что соответствует оценке Лщ = 15. Поскольку оценки Лг, Л12 и Лцг больше Л] и , соответствующие множества не содержат гамильтонова цикла веса, меньшего 15, и поэтому цикл (1,5,3,4,6,2,1) является гамильтоновым циклом минимального веса.
§ 4.10.	Упорядоченные и бинарные деревья
Определим по индукции понятие упорядоченного дерева:
1)	пустое множество и список (о), где а, -- некоторый элемент, является упорядоченным деревом;
2)	если Т[, Т'2;... ,Тп — непустые упорядоченные деревья, а — некоторый новый элемент, то список Т = (а,,Т,Т'2,    ,Тп) образует упорядоченное дерево. При этом элемент а называется корнем. упорядоченного дерева Т;
3)	любое упорядоченное дерево строится в соответствии с пн. 1 и 2.
Ес	ли Т1,Т-2,... ,Тп — упорядоченные деревья, то список (Ti, Т'2,. • • ,Тп) называется упорядоченным лесом,.
Для заданного упорядоченного дерева Т определим множество S(T) его упорядоченных поддеревьев:
-	если Т = 0, то S(T) = 0;
-	если Т — (а), то S(T) = {(а)};
-	если Т = (а, Т , Т2.Тп). то S’(T) = 5(71) U ... U S(Tn) U
{П
Непустое упорядоченное дерево Т может интерпретироваться в виде системы пронумерованных непустых множеств, каждое из которых взаимно однозначно соответствует упорядоченному поддереву из S(T) так, что:
1) если Т' — поддерево упорядоченного дерева Т", Т' ,Т" G S(T), то для соответствующих множеств X' и X" выполняется включение X' С Х"\
2) если Т' не является поддеревом упорядоченного дерева Т", Т',Т" G S(T), соответствующие множества не пересекаются.
144
Рис. 4.41
Рис. 4.42
Пример 4.10.1. Упорядоченному дереву
(1,(2, (4), (5)), (3, (6, (8), (9)), (7)))
соответствует система множеств, изображенная на рис. 4.41. □
Упорядоченное дерево может также интерпретироваться в
виде так называемого уступчатого списка, который используется в оглавлениях. На рис. 4.42 представлен уступчатый список,
соответствующий упорядоченному списку из примера 4.10.1.
Согласно следующему тезису любая схема, в которой заданы определенные приоритеты между элементами, может рассматриваться как некоторое упорядоченное дерево.
Тезис. Любая иерархическая классификационная схема интерпретируется некоторым упорядоченным, деревом,.
Например, в виде упорядочен
Рис. 4.43
ного дерева представляется любой терм. На рис. 4.43 изображено упорядоченное дерево, соответствующее терму t = а — b • (с : d + е : /).
Частным случаем упорядоченного дерева является бинарное дерево. Определение понятия бинарного дерева повторяет определение для упорядоченного дерева с ограничением п G {0.1,2} в п. 2. При этом для бинарного дерева Т —	,Тф), бинар-
145
ное поддерево Т| называется левым поддеревом ., а Т2 ~ правым поддеревом.
Бинарные деревья имеют более простое устройство, чем упорядоченные, и вместе с тем любой упорядоченный лес взаимно однозначно соответствует некоторому бинарному дереву.
Опишем алгоритм преобразования упорядоченного леса Т = (7[, Т2, •  • ,Тп) в бинарное дерево В(Т).
1. Если п = О, В(Т) — 0.
2. Если п > 0, то корнем бинарного дерева В(Т) является корень упорядоченного дерева 7ф левое поддерево дерева В(Т) — бинарное дерево В(Тп, Т12,..., Т1т), где Ц = ((ai),711,712, • • •, 7im). правое поддерево дерева В(Т) — бинарное дерево В(Т2,..., Тп).
На рис 4.446 представлено бинарное дерево, соответствующее упорядоченному лесу (ТЦТг), изображенному на рис 4.44а.
§ 4.11. Фундаментальные циклы
Пусть G — (М, R) — неорграф, имеющий п вершин, m ребер и с компонент связности, Т — остов графа G. В § 4.8 отмечалось, что Т имеет i/*(G) = п — с ребер щ,... ,ип-с, которые будем называть ветвями остова Т. Оставшиеся тп — п 4- с ребер vi, v2,..., vm-n+c, не входящие в Т, будем называть хордами остова Т. Согласно теореме 4.8.1., п. 5, если к лесу Т добавить произвольную хорду vi, то в полученном графе найдется ровно один цикл, который обозначим через Ci. Цикл Сг состоит из хорды Vi и некоторых ветвей остова Т, которые принадлежат единственной простой цепи, соединяющей вершины хорды иг. Цикл Ci называется фундаментальным циклом, графа G относительно хорды Vi остова Т. Множество {Cj,..., Cm_n+c} всех фун-. даментальных циклов относительно хорд остова Т называется фундаментальным .множеством, циклов графа G относительно
146
остова Т. Отметим, что мощность фундаментального множества циклов равна дипломатическому числу 12(G) = m — п 4- с.
Обозначим через (wi, W2,  • •, wm) последовательность (щ, v2, ...,vm_n+c,ui,u2,...,un_c) всех ребер графа G. Тогда фундаментальному циклу Ci соответствует вектор а = (ац,..., сч-/п), определенный по следующему правилу:
Щу — <
1, если Wj G Ci, О, если Wj $ С{.
Теперь фундаментальное множество циклов можно задать с помощью матрицы фундаментальных циклов, строки которой являются векторами ai,a2,... ,a^Gy.
С
/ Он	012	Ojm
021	022	а2т
\°//(G),l	Op(G),2	•	av(G),m
Так как каждый фундаментальный цикл Ci содержит ровно одну хорду, а именно Vi, то матрица С имеет вид
0 °l,p(G)+l	•  •	а1т \
fj _	a2,v(G)+l	  	а2т
\0	1 ap(G),p(G)-!-l ••• av(G)m/
Таким образом, С = (C1IC2), где С'| рядка 12(G).
Пример 441.1. Найдем матрицу фундаментальных циклов графа G, изображенного на рис. 4.45. Так как 12(G) = 8 — 6 + 1 = 3, то для получения остова удаляем из графа три ребра. Сопоставим этим ребрам номера 1, 2, 3.
Ребрам, входящим в остов, по-
— единичная матрица по-
ставим в соответствие номера 4, 5, 6, 7, 8. Легко видеть, что фундаментальный цикл С], соответствующий хорде 1, состоит
147
из ребер 1, 4, 6, цикл С? -- из ребер 2, 6, 7, цикл Сз — из ребер 3, 6. 7, 8. Поэтому матрица фундаментальных циклов С имеет вид
Ci с2 Сз
1 2 3
10 0
0 1 0
0 0 1
4 5 6 7 8
1 0 1 О (А
0 0 110
0 0 111/
§ 4.12. Разрезы
Понятие разреза играет важную роль при изучении вопросов, связанных с отделением одного множества вершин графа от другого. Такие задачи возникают, например, при изучении потоков в сетях (сетью называется связный орграф G = (М, R) без петель: потоком в сети G называется функция tp : R —> Z, которая ставит в соответствие дуге некоторое число — вес дуги). В этих задачах фундаментальную роль играет изучение поперечных сечений сети (т. е. множеств дуг, которые соединяют вершины двух непересекающихся множеств вершин) и нахождение ограничен
ного поперечного сечения, которое является самым узким местом. Эти узкие места определяют пропускную способность системы в целом.
Пусть G = (Л/,/?.) — неорграф 9JI = {Mi,M?} — разбиение множества М. Разрезом графа G (по разбиению 9JI) называется множество всех ребер, соединяющих вершины из Mi с вершинами из М-2 (рис. 4.46). Отметим, что в связном графе любой
разрез непуст.
Mi Разрез М?
Рис. 4.46
Непустой разрез К неорграфа G называется простым, разрезом или коциклом, если любое непустое собственное подмножество К' С К не является разрезом ни по какому разбиению. Другими словами, из К нельзя удалить ни одно ребро с тем, чтобы полученное множество было непустым разрезом.
Теорема 4.12.1. В конечном неорграфе G = (M,R), имеющем с компонент связности, множество ребер К тогда и только тогда является коциклом., когда граф (М, R \ К} имеет. (с + 1) компонент связности.
148
Понятия остова и коцикла являются противоположными в том смысле, что остову соответствует минимальное множество ребер, которые связывают посредством маршрутов все вершины связного графа, а коцикл состоит из минимального множества ребер, отделяющих некоторые вершины связного графа от остальных.
Следующие две почти очевидные теоремы дают информацию о связи остовов с разрезами, а также циклов с разрезами.
Теорема 4.12.2. В связном неорграфе остовное дерево имеет по крайней мере одно общее ребро с любым, из разрезов графа.
Теорема 4.12.3. В связном неорграфе любой цикл имеет с любым разрезом четное число общих ребер.
В условиях предыдущего параграфа рассмотрим неор-граф G с остовом Т. Снова пусть «1, и%, ..., ип_с — ветви остова Т. Удаляя из остова Т произвольную ветвь щ, получаем лес с (с + 1) компонентами связности, т. е. каждое ре
бро щ является разрезом остова Т по некоторому разбиению {Mi, М2} (рис. 4.47). В графе G могут найтись еще какие-то ребра v^, fj2, ..., Vi7 (являющиеся хордами Т), которые соединяют вершины из Mi и Му. Множество Кг — образует простой разрез, который называется фундаментальным разрезом графа G относительно ветви щ остова Т. Множество {А',, К‘2,   , Кп-С} всех фундаментальных разрезов графа G называется фундаментальным множеством коциклов графа G относительно остова Т. Отметим, что мощность фундаментального множества коциклов не зависит от выбора остова Т и равна корангу v*(G) = п — с.
Аналогично фундаментальным циклам фундаментальному разрезу К, ставится в соответствие вектор 6, = (Ьц,..., bim), определяемый по правилу
1, если Wj £
О, если Wj Кг.
Фундаментальное множество коциклов задается мащрицей фун-
149
даментал‘ьных разрезов К, строки которой являются векторами Ф,b2;  bp*(G):
< 6ц	...	6jm	\
К ___ Ьц	  	Ь'2т
\^p*(G),l	• • •
Поскольку каждый фундаментальный разрез Ki содержит ровно одну ветвь, а именно щ, матрица К имеет вид
/ &U	^l,c-(G)	1
к _	Ь21	Ъ2уу>(G)
VV(G),1	V(G),p»(G)	0	1/
Таким образом, К = (КА\К2), где К2 — единичная матрица порядка m*(G). Отметим, что если С — (С^Сг) — соответствующая матрица фундаментальных циклов, то К\ = CJ.
П р и м ер 4.12.1. Найдем матрицу фундаментальных разрезов графа G =	изображенного на рис. 4.45. Поскольку
;/* (G) = б — 1 = 5, имеется пять фундаментальных разрезов. Ребру 4 соответствует коцикл = {1,4}, так как при удалении ребра 4 из остова Т множество вершин М разбивается на две части: {«] } и М \ {<24 }, а ребра 1 и 4 образуют разрез по разбиению {{ai},М \ {а}}. Аналогично ребру 5 соответствует коцикл К2 = {5}, ребру 6 — коцикл Кз — {1,2, 3,6}, ребру 7 — коцикл /ф = {2,3,7}, ребру 8 — коцикл = {3,8}. Следовательно, матрица фундаментальных разрезов имеет вид
	1	2	3	4	5	6	7	8
К,	Л	0	0	1	0	0	0	°\
К3	0 1	0 1	0 1	0 0	1 0	0 1	0 0	0 0
	0	1	1	0	0	0	1	0
К5	\0	0	1	0	0	0	0	1/
§ 4.13. Векторные пространства, связанные с графами
Рассмотрим алгебраическую систему Z2 = ({0,1},©,©) с двухместными операциями кольцевого сложения © и умноже
150
ния 0, задаваемыми следующими правилами: О ф О = 1 ф 1 = О, 1 Ф О = О Ф 1 = 1, 000=001=100= О, 10 1 = 1. Система Z2 является булевым кольцом (см. § 2.6) и., более того, образует поле.
Пусть G = (Л/, /?.) — связный неорграф, имеющий п вершин и т ребер - - - , ит. Произвольному множеству ребер А С R поставим в соответствие вектор а = («1, «.2,  • •, ат), положив
1, если щ £ А, 1 I 0, если щ 0 А.
Каждому множеству ребер соответствует' единственный вектор, состоящий из нулей и единиц, а для любого набора (01,0,2,.... ат) нулей и единиц найдется единственное множество ребер, соответствующее этому набору. Таким образом, существует биекция между булеаном множества ребер R и множеством всех наборов длины т, состоящих из нулей и единиц: P(R) о {0.1}т. Пусть о = (aj,..., ат) и Ь = (Ьц ..., Ьт) — наборы (векторы) из {0,1}"'. Определим сложение векторов с помощью соотношения а ф b = («1 ф bi,..., ат Ф 6,„) по правилам, определенным в иоле Z2. Кроме этого, определим произведение векторов на элементы А € {0,1}, положив А © а = (А 0 ai,..., А 0 ат). Множество векторов {0,1}т с операциями сложения ф и умножения 0 на элементы поля Z2 образует линейное пространство над полем Z2. Это пространство обозначим через ЦД^Э).
Отметим, что сложение ф векторов а, и b соответствует кольцевой сумме множеств ребер А и В, представляемых этими векторами. Действительно, равенство а,{ ф bi = 1 выполняется тогда и только тогда, когда «, = 1,^ = 0 (т.- е. G А \ В) или сч = 0, Ь} = 1 (т. е. иг G В\А). Следовательно, сумме «ф b соответствует множество (Л \ В) U (В \ Л) = А ф В.
Внутреннее произведение векторов а = («1,0.2, - - -, о.т) и Ъ = (bi, Ь^,Ьт) определяется соотношением (а, 6) =	0 bi ф а-2 0
Ъ2 Ф •  • Ф ат Ф Ьт. Равенство (а, Ь) = 0 означает, что четное число произведений a.iQbi равно 1. Для таких произведений а.г — 1, Ь, = 1 и, следовательно, соответствующие векторам а и b множества ребер А и В имеют четное число общих ребер.
Множество ребер А называется границей (кограницей'), если А есть объединение множеств ребер некоторых циклов (коциклов), из которых любые два множества не имеют общих ребер.
151
Нетрудно заметить, что кольцевая сумма А] ф А? границ (кограниц) Л] и А2 также является границей (кограницей). Следовательно, множества 1ф = {«| вектор а соответствует некоторой границе} и Уц — {н| вектор а соответствует некоторой когранице} образуют линейные подпространства пространства (^2) -
Теорема 4.13.1. 1. Если {Ст, С%,   , Ст-п+1} — фундаментальное множество циклов графа. G, то множество = -   >om_n+i} векторов, соответ,ствующих фундаментам н ы и. циклам, образует базис подпространства границ 1'г.
2. Если {Ki,K-2,... ,/Ci-i} ~ фундаментальное множество коциклов графю, G, то .множество = {^1? Ь2, •  • , Ьп-1} векторов, соответ,ствующих фундаментальным разрезам,, образует. базис подпрост,ранства кограниц У/<.
Следствие 4.13.2. 1. Размерност,ь dim И’ подпространства границ 1’г равна цикломат,ическо му числу /y(G), а размерность diinV/< подпространства кограниц У к равна корангу v*(G).
2. Любой цикл (коцикл) в графе можно представить в виде кольцевой суммы некоторых фундаментальных циклов (разрезов).
Два подпространства Ц и У^ векторного пространства VTO(Z2) называются ортогональными (I) _Ll/2), если для любых векторов a Е 4ц и b 6 У2 их внутреннее произведение (а, Ь) равно 0.
Заметим, что по теореме 4.12.3. любой цикл С с любым разрезом К имеет четное число общих ребер, т. е. для соответствующих векторов а и b их внутреннее произведение (а, Ь) равно пулю. В частности, для любых векторов щ 6 Щд и bj € 'В/< справедливо (а,Ь) = 0. Так как множества и образуют базисы подпространств 1ф и 1Д<, то 1гРУк-
Отмстим также, что при умножении матрицы фундаментальных циклов С на транспонированную матрицу фундаментальных разрезов КТ в поле Z2 строка щ умножается на столбец 1ц по правилу внутреннего произведения и (аг,Ь7) = 0. Это означает, что С ® А’1 = 0, а также К © Ст = 0.
У п р а ж н е н и е. Проверить, что для матриц С и К из примеров 4.11.1 и 4.12.1 справедливо С ® А’1 = 0.
152
§ 4.14. Раскраски графов
Пусть G — {M,R) — неограф без петель. Раскраской (вершин) графа G называется такое задание цветов вершинам G, что если [а, Ь] — ребро, то вершины а, и b имеют различные цвета. Хроматическим числом \(G) графа G называется минимальное число цветов, требующееся для раскраски G.
П р и м е р 4.14.1. Так как в полном графе Кп любые две различные вершины связаны ребром, то х(Кн) = п. □
Многие практические задачи сводятся к построению раскрасок графов.
П р и м е р 4.14.2. 1. Рассмотрим задачу составления расписания. Предположим, что нужно прочесть несколько лекций за кратчайшее время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно (например, их читает один и тот же лектор). Построим граф G, вершины которого биективно соответствуют лекциям и две вершины смежны тогда и только тогда, когда соответствующие им лекции нельзя читать одновременно. Очевидно, что любая раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам одного цвета, могут читаться одновременно. Напротив, любое допустимое расписание определяет раскраску графа G. Оптимальные расписания соответствуют раскраскам с минимальным числом цветов, а число часов, необходимое для прочтения всех лекций, равно %(G).
2. Рассмотрим граф G, вершины которого — страны, а ребра соединяют страны, имеющие общую границу. Числу y(G) соответствует наименьшее число красок, необходимых для раскраски карты так, чтобы никакие две соседние страны не были окрашены в один цвет. □
Существуют и практические задачи, связанные с. раскраской ребер в мультиграфе.
Раскраска ребер в мультиграфе G может быть определена с помощью раскраски вершин так называемого реберного мультиграфа L(G). Для произвольного неориентированного мультиграфа G =	реберным мультиграфом L(G) называется
тройка (U, М., Р'}, где Р' С UxMxU, и выполняется (и, a, v) G Р' тогда и только тогда, когда в мультиграфе G вершина а является концом ребер и и и. Раскраской ребер мультиграфа G называется раскраска вершин мультиграфа L(G).
153
П р п м е р 4.14.3. Проводится монтаж аппаратуры. Чтобы нс перепутать проводники, необходимо их окрасить таким образом, чтобы два проводника, идущие к одной плате, имели разные цвета. В этом случае вершинами являются платы, а ребрами — проводники. □
Неорграф G называется дихроматическим, если y(G) = 2. Неорграф G = (М. 7?) называется двудольным, если множество всех ребер графа G образует разрез графа G. т. е. для некоторого разбиения множества вершин	концы любого ребра
принадлежат разным частям разбиения.
Теорема 4.14.1. Пусть G — неорграф без петель, имеющий хотя бы одно ребро. Тогда следующие условия эквивалентны.
1)	G - бихроматический граф);
2)	G двудольный граф;
3)	G не содержит циклов нечетной длины.
Следствие 4.14.2. Если G — лес, то y(G) ф 2.
Оценим хроматическое число графа G через его параметры. Обозначим через deg(G) максимальную степень вершин графа G.
Теорема 4.14.3. Для любого неорграфа G без петель выполняется неравенство y(G) ф deg(G) + 1.
Рассмотрим простой алгоритм построения раскраски, который во многих случаях приводит к раскраскам, близким к минимальным.
Алгоритм последовательной раскраски.
1. Произвольная вершина щ графа G принимает цвет 1.
2. Если вершины (ц,...,а{ раскрашены I цветами 1, 2, ..., I. I ф i, то новой произвольно взятой вершине припишем минимальный цвет, не использованный при раскраске вершин из множества {a.j | p(a?+i,a7) = 1, j < i}. □
Для некоторых классов графов последовательная раскраска является минимальной. В общем случае это не так.
§ 4.15. Планарные графы
Неорграф G называется планарным, если его можно изобразить на плоскости так. что никакие два ребра не будут иметь общих точек, кроме, может быть, общего конца этих ребер. Такое изображение графа на плоскости называется плоским. Таким
154
образом, если граф имеет плоское изображение, то он является
планарным.
П р и м е р 4.15.1. Граф К4 (рис. 4.48а) планарен, поскольку может быть изображен, как показано на рис. 4.486. □
Граф, описанный в примере
4.14.2, п. 2, является планарным. Также планарным является граф, вершины которого — отверстия печатной платы, а ребра — провод-
ники печатной платы, соединяющие а	б
отверстия.
Рассмотрим операцию подразбиения ребра в графе G = После подразбиения ребра [а, Ь] G R получается граф G' = (М',Я'), где М' = М U {ab}, R' = (R \ {[а, Ь]}) U {[а, ab], [аб, />]}, т. е. ребро [а, Ь] заменяется на (а, 6)-цепь длины два. Два графа называются гомеоморфными, если их можно получить из одного графа с помощью последовательности подразбиений ребер.
Не всякий неорграф является планарным. Критерий планар
ности описывает
Теорема 4.15.1 (теорема Понтрягина — Куратовского). Граф) G планарен тогда и только тогда, когда G не содержит подграфа, гомеоморфного или К$,з (рис. 4-49).
Эквивалентная форма критерия планарности описана в следующей теореме.
Теорема 4.15.2. Тогда и только тогда неорграф) G планарен, когда G не содержит подграфов, стягиваемых (т.е. получаемых последовательностью отождествлений вершин, связанных ребрами) к графу К& или К33 (рис. 4-49)
Вместе с тем трехмерного евклидова пространства оказыва
Рис. 4.49
155
ется достаточно для изображения любого конечного и счетного графа без пересечения дуг вне их концов.
Теорема 4.15.3. Любой граф, состоящий не более чем из 2й’ вершин, может, быть изображен в пространстве R3 без пересечения, дуг вне их концов.
Доказательство. Пусть G = (А/, Z?) — граф, для которого \М\	2Ы. Тогда имеем |7?.| ф 2й. Расположим все точки
графа G на некоторой прямой I и каждой дуге из R разнозначно сопоставим плоскость, содержащую прямую I. Искомое изображение графа G получается после проведения всех дуг в соответствующих плоскостях. □
Известна оценка хроматического числа планарных графов.
Теорема 4.15.4 (теорема о четырех красках). Если G — планарный граф), то y(G) ^4.
При исследовании принципиальной электрической схемы радиоэлектронного устройства с точки зрения возможности ее реализации с помощью печатного монтажа или монтажа на слоях микросхемы конструктору важно знать ответ на следующие вопросы: 1) является ли граф, соответствующий рассматриваемой принципиальной схеме, планарным? 2) если граф планарен, то как получить его изображение без пересечения ребер? На первый вопрос, принципиальный ответ дает теорема Понтрягина — Кура-товского, а методы получения плоских изображений планарных графов можно найти в книге Б. Н. Деньдобренко, А. С. Малина [8].
Если граф G непланарен, то для его геометрической реализации удаляют отдельные ребра (переносят на другую плоскость). Минимальное число ребер, которое необходимо удалить из графа для получения его плоского изображения, называется числом планарности графа G. При вынесении этих ребер на вторую плоскость получают часть графа, которая также может оказаться неплоской. Тогда вновь решают задачу вынесения отдельных ребер па следующую плоскость и т. д. Минимальное число плоскостей т, при котором граф G разбивается на плоские части G\, Gi, ..., Gm (разбиение ведется по множеству ребер), называется толщиной графа G.
Таким образом, толщина планарного графа равна 1.
Пример 4.15.2. Каждый из графов К$ и Кзд имеет толщину 2.
156
§ 4.16. Задачи и упражнения
1. Представить граф (рис. 4.50) в аналитической и матричной фор-
мах, списком дуг и структурой смежности.
2.	Составить матрицу инцидентности для мультиграфа, изображенного на рис. 4.51.
3.	Найти все неизоморфные подграфы и части графа Л'з-
4.	Представить в геометрической и матричной формах графы Gi UG->, Gi Пбг,
Gi Ф G-з (рис. 4.52).
5.	Для графов Gj и G2 из предыдущей задачи найти Gi х G2, Gi[G2] и G2[Gi].
6.	С помощью матрицы смежности графа (рис. 4.53) найти его
матрицы достижимости, контрдостижимости и сильных компонент.
7.	Найти матрицу расстояний, диаметр, радиус, центральные и периферийные вершины графа, изображенного на рис. 4.54.
8.	Найти все кратчайшие маршруты из вершины 2 для взвешенного графа (рис. 4.55).
9.	Доказать, что в любом конечном бесконтурном графе существуют вершины с нулевой степенью исхода и с нулевой степенью захода
10.	Проверить на эйлеровость и найти минимальное множество покрывающих цепей:
а) графа 7Д; б) графа, изображенного на рис. 4.56.
Рис. 4.51	Рис. 4.52
5	(4)	4
Рис. 4.56
Рис. 4.54	Рис. 4.55
157
Рис. 4.59
1
Рис. 4.61
Рис. 4.60
11.	Построить все неизоморфные трех-, четырех- и пятивершинные деревья.
12.	Найти остов минимального веса взвешенного графа (рис. 4.57).
13.	Найти упорядоченный лес, соответствующий бинарному дереву, изображенному на рис. 4.58.
14.	Найти матрицы фундаментальных циклов и фундаментальных разрезов графа (рис. 4.59).
15.	Найти хроматическое число графа (рис. 4.60).
16.	Найти толщину графа (рис. 4.61).
Глава 5
КОМБИНАТОРИКА
Комбинаторика — раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Поэтому целями комбинаторного анализа являются изучение комбинаторных конфигураций, алгоритмов их построения, оптимизация таких алгоритмов, а также решение задач перечисления. Простейшими примерами комбинаторных конфигураций являются перестановки, размещения, сочетания и разбиения. При подсчете комбинаторных конфигураций используются правила суммы, произведения и степени, сформулированные в § 1.4.
§ 5.1. Перестановки и подстановки
Пусть дано множество М — {«,, а^,.. •, ап}. Перестановкой элементов множества М называется любой кортеж (аг1,щ2,..., о.,;п), состоящий из п различных элементов множества М.
Перестановки отличаются друг от друга только порядком входящих в них элементов. Покажем, что число Р„ всех перестановок множества М равно п!. Действительно, на первое место в кортеже можно подставить любой из п элементов, на второе место - любой из п — 1 оставшихся и т. д. Для последнего места остается единственный элемент. Поэтому получаем всего п(п — 1)(п — 2)... 2 • 1 = п! перестановок.
П р и м ер 5.1.1. 1. Расставить на полке 10 книг можно Рю = 10! = 3628 800 различными способами.
159
2. Список студентов группы, состоящей из 25 человек, можно составить Р25 = 25! способами. □
Напомним, что биекция ст : М О М называется подстановкой множества М. Пусть ст — подстановка множества М = {1.2, ...,п}. Тогда ст(А') = Sfc, где 1	п, к = 1,2, ...,п,
{si, «2,..., s„} = {1,2,...,п}, и поэтому подстановку ст можно представить в виде матрицы, состоящей из двух строк:
fl 2 ... п
-ч2	• sn
Ясно, что если в матрице [ст] переставить столбцы, то полученная матрица будет также определять подстановку ст. Множество всех подстановок множества {1,2,... ,п} обозначается через Sn. Для подстановок ст, т 6 можно определить произведение ст  т как произведение двух функций. Зная матрицы подстановок
2 «2
п sn
и [т], переставив столбцы матрицы [т] так. чтобы ее первая строка совпала со второй строкой матрицы [ст]:
•Я «2
Н t2
получаем
г i/i 2 ••• пA /si s2 	_ (1 2
^2 - •  Sn J уН О • • • In J уН 1'2  • • In у
Пример 5.1.2. Если [Д = (2 i 4 3), И = (з 1 4 2)’ т0 [сгт] =
/ 1 2 3 41/2 14 3\_ /12 3 41
! 2 ы 3 м 1 з 2 4 / " \ 1 з 2 4 1-
Теорема 5.1.1. Алгебра {Sn. ) .является группой. При п 3 она некоммутативна.
Доказательство. Операция - ассоциативна как операция произведения функций. Легко проверяется, что существует единичная подстановка е с матрицей [Д = ([ 2 „) и для любой подстановки ст с матрицей [ст] = (Д ;• Д) существует обратная подстановка ст-1, соответствующая матрице (	®22 Sn У
160
Если п 3, то рассмотрим подстановки а и т с матрицами
Имеем [ат] = (И ? 1;;; ”), [та] = (И 2 4 :" "), т. е. ат та.
Таким образом, группа (Sn,-) некоммутативна. □
Группа (Sn. ) называется симметрической группой степени п. Число элементов этой группы |Sn| равно Рп = п!.
Подстановка а называется циклом длины г, если матрицу [а] перестановкой столбцов можно привести к виду
S1
82
S2 S3
S3 5'4
sr— I Sr -Sr+l
Sr Si Sr-|-1
Sn
Sn
Очевидно, что в этом случае а задает биекцию, в которой si ь-> S2, S2 >-> S3, ..., sr i-> si, а остальные элементы неподвижны. Описанный цикл а обозначается через (si S2 •  • sr).
Пример 5.1.3. Подстановка с матрицей (156432) является циклом (2536), а подстановка с матрицей ({ 111 6 з) Циклом не является, так как из нее можно выделить два цикла (1 4) и (2563). □
Циклы (si S2 -.. sr) и (Ц Ц  • • tp) называются независимыми, если {si,s2,..., sr} П {Ц, t2, ..., tp} = 0.
Теорема 5.1.2. Каждую подст,ановку можно однозначно (с точностью до порядка сомножителей) представить в виде произведения независимых циклов.
’В примере 5.1.3 имеем (156432) = (2 53 6), а (452163) = (14)(2 5 6 3).
Двухэлементный цикл (г J) называется транспозицией. При транспозиции г-й и j-й элементы меняются местами, а остальные сохраняют свое положение.
Теорема 5.1.3. Каждая, подстановка есть произведение транспозиций.
Доказательство. По теореме 5.1.2. достаточно установить, что любой цикл (si S2 •   sr) можно представить в виде произведения транспозиций, но легко проверяется, что (si s2  - - sr) = (si s2)(si s3)... (si sr). □
Пример 5.1.4. (1234) = (12)(13)(14).
6 Зак. № 4872 Судоплатов
161
§5.2. Размещения и сочетания
Пусть М — множество, состоящее из п элементов, т ф п. Размещением из п элементов по т или упорядоченной (п,т)-выборкой, называется любой кортеж (аг1,<^2,... ,aZm), состоящий из т попарно различных элементов множества М. Размещение можно рассматривать как разнозначную функцию f : {1,2,..., m] —> М, для которой /(j) =	.
Пример 5.2.1. Для множества М = {а, Ь, с} пары (а,Ь) и (6. а) являются размещениями из 3 по 2, тройка (а. с, Ь) — размещением из 3 по 3, а тройка (Ь, а, Ь) размещения не образует. □
Число размещений из п по т обозначается через А™ или Р(п, т). Покажем, что
77 ’
= 7---------Й = п^п - 1)  • • (n - m + !)
(71 — 771)!
(напомним, что 0! = 1). Действительно, размещение т элементов можно представить как заполнение некоторых т позиций элементами множества М. При этом первую позицию можно заполнить п различными способами. После того как 1-я позиция заполнена, элемент для заполнения 2-й позиции можно выбрать (?i — 1) способами. Если продолжить этот процесс, то после заполнения позиций с 1-й по (тт1 — 1)-ю будем иметь (п — т + 1) способов заполнения последней, тп-й позиции. Перемножая эти числа, получаем формулу (5.1).
Пример 5.2.2. Из десяти различных книг произвольным образом берутся и ставятся на полку одна за другой 3 книги. Имеется А^о вариантов расстановок, где А^о = -Ур = 10  9  8 = 720. □
Сочетанием из п элементов по т или неупорядоченной (п, т)-выборкой называется любое подмножество множества М. состоящее из 771 элементов.
Пример 5.2.3. Если М = {а,Ь, с}, то {а, Ь}. {а, с}, {Ь, с} — все сочетания из 3 по 2. □
Число сочетаний из ?i по тп обозначается через С™, или С(п, 77l).
Если объединить размещения из п элементов по т, состоящие из одних и тех же элементов (не учитывая порядка их расположения), в классы эквивалентности, то можно установить биекцию <р между сочетаниями и полученными классами
162
по следующему правилу: <р({аг1,щ2,...,щга}) {(Ьъ Ь2, ..., М | {bi, b2, • • -,Ьт} = {ац, щ2,..., щт}}. Так как из каждого сочетания С можно получить .тп! размещений (упорядочивая элементы из множества С ml способами по числу перестановок множества (7), то каждый класс эквивалентности содержит ml размещений и, значит, А™ = ml  С™, т. е. (7™ = Таким образом,
п (п — m)!ml
Пример 5.2.4. Из десяти чисел четыре можно выбрать С10 =	= ~4Г10' = т/зТ = 210 способами. □
Число С™ обладает следующими свойствами:
1) 67™ =
^с^ + с^ = с^-
3) (a+b)n = 52 С^гатЬп~т для любых a, b G R, п G ш (бином ,	m=0
Ньютона).
В силу последнего свойства числа (7™ называются биномиальными коэффициентами.
п
Пример 5.2.5. Из свойства 3 следует, что 271 = 52 С™.
771=0
Действительно, 2n = (1 + I)’1 = 52 С'™!™!"-™ = 52 &n-тп=0	т=0
§	5.3. Размещения и сочетания с повторением
Размещением с повторением, из п элементов по т или упо-рядоченной (п,т)-выборкой с возвращениями называется любой кортеж (щ,... ,а.т) элементов множества М, для которого \М\ = п.
Поскольку в кортеж (щ, а2,..., о.то) на каждое место может претендовать любой из п элементов множества М, число размещений с повторениями Р(п,т) равно п  п  ..,  п = пт-.
т раз
Р(п, т) = пт.
Пример 5.3.1. Из цифр 1, 2, 3, 4 можно составить Р(4,3) = 43 = 64 трехзначных числа. □
б*
163
Определим отношение эквивалентности на множестве размещений с повторениями из п по тп: (oi, 02, • • , ат) ~ (61,62, ..., Ьт) -ФФ для любого с G М число элементов ai, равных с, совпадает с числом элементов bi, равных с.
Сочетанием с повторением из п элементов по т или неупорядоченной {п,т)-выборкой с возвращениями называется любой класс эквивалентности по отношению ~ множества размещений с повторениями из п элементов по т. Другими словами, сочетания с повторениями суть множества, которые состоят из элементов, выбранных т раз из множества М, причем один и тот же элемент допускается выбирать повторно.
Число сочетаний с повторениями из п элементов по т обозначается через С{п, т) и вычисляется по формуле
С{п,т) = C™+m_i
(п + т — 1)! т!(п — 1)!
Пример 5.3.2. Число различных бросаний двух одинаковых кубиков равно С(6,2) = С? = 21.
§	5.4. Разбиения
Пусть М — множество мощности п, {Mi, М2,..., М^} — разбиение множества М на к подмножеств, \Мг\ = тщ, mi + m2 + • • • + mjt == п. Кортеж {Mi,..., М^) называется упорядоченным разбиением множества М.
Если к = 2, то упорядоченное разбиение множества М на два подмножества, имеющие соответственно mi и m2 элементов, определяется сочетанием (без повторений) из п элементов по т.\ или из п по m2 {m2 = п — mi). Следовательно, число разбиений R{mi,m2) равно биномиальному коэффициенту С'™1 = С™2. Таким образом, tv.	п'
ТП1!(п —7711)!	7711! 7722!
В общем случае число R{mi,m2, .. ,т^) упорядоченных разбиений {Mi, М2,   , М^), для которых |Мг| = mi, равно тр.тр.' mk’-’ а число R{nik) упорядоченных разбиений на к подмножеств вычисляется по формуле
R{n,k) —	T?(7771,7772,   • ,777/t).
mi +... +т.).—п, mi >0
R{mi, 7772) =
164
Числа R(mi, m2,..., тк) называются полиномиальными коэффициентами, поскольку для всех ai, «2,..., ak G R справедливо соотношение
(«1 + 02 +  • • + Ofc)”
nl
7711+ ...+ТП)е=П, пц>0
то71аГ2 mi!... ттц!
ak
Пример 5.4.1. В студенческой группе, состоящей из 25 человек, при выборе старосты за выдвинутую кандидатуру проголосовали 12 человек, против — 10, воздержались — 3. Сколькими способами могло быть проведено такое голосование?
Пусть М — множество студентов в группе, М] — множество студентов, проголосовавших за выдвинутую кандидатуру, М2 — множество студентов, проголосовавших против, М3 — множество студентов, воздержавшихся от голосования. Тогда |М| = 25, \Мг\ = 12, IM2I = 10, |1Из| = 3, (М1,Мг,Мз) — упорядоченное разбиение множества М. Искомое число /?.(12,10,3) равно = 1487285800. □
Число j?(mi,m2,. -. , m^) разбиений исходного множества М на к подмножеств Mi, М2,  .., Мк, = пц, неупорядоченных между собой, вычисляется по формуле
R(mi
mi!... mfc!(l!)TO1 ... (n!)mfe ’
а число всех возможных разбиений множества М на к подмножеств, неупорядоченных между собой, равно
R(mi,... ,тк).
7711+ ... +mt=n, 777., > 0
Пример 5.4.2. Сколькими способами из группы в 25 человек можно сформировать 5 коалиций по 5 человек?
Пусть X — множество людей в группе, тг- — число коалиций по i человек, где г = 1,..., 25. Тогда по условиям задачи \М\ = 25, /ns = 5, mi — 0, г G {1,2, ...,25} \ {5}, и, следовательно, искомое число будет равно R(0,0,0,0,5,0,.., , 0) — тдр’гуг — ^уув 
165
§5.5	. Метод включений и исключений
Пусть множество А имеет N элементов и п одноместных отношений (свойств) Pi, Р2,Рп. Каждый из N элементов может обладать или не обладать любым из этих свойств. Обозначим через число элементов, обладающих свойствами Ри,... ,Pik и, может быть, некоторыми другими. Тогда число 7V(0) элементов, не обладающих ни одним из свойств Pi, Р2,..., Рп, определяется по следующей формуле, называемой формулой включений и исключений'.
N(0) = Sq - Si + S2 - ... + (-l)nSn, (5.2)
где So = N-, Sk =	52	fc = 1,2,...,n.
1^11 <... <1^71
Пример 5.5.1. Пусть колода состоит из п карт, пронумерованных числами 1,2,... ,п. Сколькими способами можно расположить карты в колоде так, чтобы ни для одного i (1 i С п) карта с номером i не занимала i-e место?
Имеется п свойств F, в виде “г-я карта занимает в колоде i-e место”. Число всевозможных расположений карт в колоде равно п!. Число расположений, при которых карта с номером ij занимает место ij (j = 1,..., fc), равно (n — А:)!. Тогда So = nl,
Sk= £ Ntx.^=Ckn(n-k)\ = ^.
Используя формулу (5.2), получаем, что число TV (0) расположений, при которых ни одно из свойств Pi не выполнено, равно
71	71	1
£(-1)^ = п|£(-1)‘д.П . к=0	к=0
Обобщая формулу (5.2), получаем формулу, позволяющую вычислить число N(r) элементов, обладающих ровно г свойствами (1 С г п):
71—Г
N(r) = £(-i)fcc;+fcsr+fc.	(5.3)
к=0
166
В § 3.4 мы определили функцию [ж] для вещественных чисел х как наибольшее целое число, не превосходящее х. Для положительных целых чисел а и b значение функции [-] равно количеству чисел из множества {1,2,, Ь}, которые делятся на а, т. е. кратных а.
Пример 5.5.2. Сколько положительных чисел от 1 до 500 делятся ровно на одно из чисел 3, 5 или 7?
Обозначим свойства делимости на 3, 5 и 7 соответственно через Fi, Р2 и Р3. Тогда для N = 500 имеем Nx = [^] = 166, N2 =	= 100,	= [^] = 71. Так как TV12 — число общих
кратных для чисел 3 и 5, наименьшее общее кратное которых равно 15, то N\2 совпадает с количеством чисел, которые делятся на 15, т. е. N\2 = [^] = 33. Аналогично N\3 = [^р] = 23, N23 = [^у] = 14, М23 =	= 4. По формуле (5.3) находим
3-1
искомое число чисел Л7(1) = ^2 (~l)fcC'i+fc,$'i+fc = (~l^C'i'Si + к~0
(-iyc^s2 + (-1)2С3% = (М +N2 + N3) - 2(N12 + Мз + n23) + ЗМ23 = 166 + 100 + 71 - 2(33 + 23 + 14) + 3 • 4 = 209.
§5.6	. Рекуррентные соотношения.
Возвратные последовательности
Рекуррентным соотношением, рекуррентным, уравнением или рекуррентной формулой называется соотношение вида an+k = F(n, ап, an+i,... ,an+k-i), которое позволяет вычислять все члены последовательности «о, щ, а2, ..., если заданы ее первые к членов.
Пример 5.6.1. 1. Формула = ап + d задает арифметическую прогрессию.
2.	Формула «„+1 = q • ап определяет геометрическую прогрессию.
3.	Формула ап+2 = ап+\+ап задает последовательность -чисел Фибоначчи. □
В случае, когда рекуррентное соотношение линейно и однородно, т. е. выполняется соотношение вида
С^п+к “Ь Р1 ^п+к — 1 + . .  + Рк^п — 0	(6-4)
(р = const), последовательность qq, щ, а2, ... называется воз
167
вратной. Многочлен
Fo(s) = хк + p1xk~1 Н--h pk	(5.5)
называется характеристическим для возвратной последовательности {ап}. Корни многочлена Ра(х) называются характеристическими.
Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением.
Описание общего решения соотношения (5.4) имеет аналоги с описанием решения обыкновенного дифференциального уравнения с постоянными коэффициентами.
Теорема 5.6.1. 1. Пусть Л — корень характеристического многочлена (5.5). Тогда последовательность {cAn}, где с — произвольная константа, удовлетворяет соотношению (5-4)-
2. Если Ai, А2, ..., А/;. — простые корни характеристического многочлена (5.5), то общее решение рекуррентного соотношения (5.4) имеет вид ап = щА" + С2А2 + . - - + щА£, где щ, с%,   ск — произвольные константы.
3. Если Xi — корень кратности r,t (i = 1,..., .s j характеристического многочлена (5.5), то общее решение рекуррент-S
ного соотношения (5-4) имеет вид ап = 52 (сц + с^п + ... + г=1
с^пг’-1)А", гдё cij произвольные константы.
Зная обшее решение рекуррентного уравнения (5.4), по начальным условиям oq, ai, ..., Qfc-i можно найти неопределенные постоянные ctJ и тем самым получить решение уравнения (5.4) с данными начальными условиями.
Пример 5.6.2. Найти последовательность {<+}, удовлетворяющую рекуррентном}' соотношению ап+2 — 4an+i + За.п = О и начальным условиям ai = 10, 02 = 16.
Корнями характеристического многочлена Ра(х) = х2 — 4х+3 являются числа xi = 1 и х% — 3. Следовательно, по теореме 5.6.1. общее решение имеет вид ап — щ + С2З". Используя начальные условия, получаем систему
С] + Зс2 = 10,
С] + 9с2 = 16,
решая которую, находим q = 7 и С2 = 1. Таким образом, ап = 7 + 3". □
168
Рассмотрим неоднородное линейное рекуррентное уравнение
ап+к + PiOm+k-1 + ... + ркап = f(n), п = 0,1,...	(5.6)
Пусть {!)„} — общее решение однородного уравнения (5.4), а {с„} — 'частное (конкретное) решение неоднородного уравнения (5.6). Тогда последовательность {Ьп + сп} образует общее решение уравнения (5.6), и тем самым справедлива
Теорема 5.6.2. Общее решение неоднородного линейного рекуррентного уравнения представляется в виде суммы общего решения соответствующего однородного линейного рекуррентного уравнения и некоторого частного решения неоднородного уравнения.
Таким образом, в силу теоремы 5.6.1. задача нахождения общего решения рекуррентного уравнения (5.6) сводится к нахождению некоторого частного решения.
В отдельных случаях имеются общие рецепты нахождения частного решения.
Если /(п) = /Зп (где (3 не является характеристическим корнем), то, подставляя ап = с(Зп в (5.6), получаем c([3k + pi(3k~l + • • - + Рк) • (Зп = (Зп и отсюда с  Pa(b) = 1, т. е. частное решение можно задать фррмулой ап = улру • (Зп.
Пусть /(п) — многочлен степени г от переменной п, и число 1 не является характеристическим корнем. Тогда Ра(1) = 1 + Pi + • • • + Рк 0 и частное решение следуют искать в ви-Г
де ап = 52 <кпг. Подставляя многочлены в формулу (5.6), по-г=0
лучаем 52 <к(п +	+ Pi 52 ^г(п + & - 1)г + ... +	52 ^пг =
г=0	г=0	г=0
52 di((n + ky +p1(n+k-iy + .. .+ркпг) =	di(ginl +...) = f(n).
i-0	i=o
Сравнивая коэффициенты в левой и правой частях последнего равенства, получаем соотношения для чисел di, позволяющие эти числа определить.
Пример 5.6.3. Найти решение уравнения
р ^zz+i Т 2^71 — п +1	(5.7)
с начальным условием «0 = 1.
169
Рассмотрим характеристический многочлен Ра(х) = х + 2. Так как PQ(1) — 3	0 и правая часть /(п) уравнения (5.6) равна
п + 1, то частное решение будем искать в виде сп = do + di • п. Подставляя сп в уравнение (5.7), получаем (do+d1(n+l))+2(d0 + di -n) = (3d() + di) + 3di -n = 1 + n. Приравнивая коэффициенты в левой и правой частях последнего равенства, получаем систему
3do + di = 1, ’ 3dj = 1,
откуда находим do = |, di = |. Таким образом, частное решение уравнения (5.7) имеет вид сп = | По теореме 5.6.1. общее решение однородного уравнения + 2щ, = 0 задается формулой ЬГ1= с • (—2)", и по теореме 5.6.2. получаем общее решение уравнения (5.7): ап = | + ‘^п + с  (—2)п. Из начального условия «0 = 1 находим | + с = 1, т. е. с=|. Таким образом,
= I + 5п +
I
§ 5.7.	Задачи и упражнения
1.	Группе из пяти сотрудников выделено три путевки. Сколько существует способов распределения путевок, если:
а) все путевки различны; б) все путевки одинаковы?
2.	Крокодил имеет 68 зубов. Доказать, что среди 1617 крокодилов может не оказаться двух с одним и тем же набором'зубов.
3.	Сколько различных десятизначных чисел можно написать, используя цифры 0, 1 и 2?
4.	Алфавит X состоит из двух символов. Сколько существует слов алфавита А, длины которых не превосходят 4?
5.	Автомобильные номера данного региона состоят из трех цифр (всего 10 цифр) и трех букв алфавита X — {А, В, С, D, Е, Н, К, М, О, Р, Т, X, Y}. Сколько автомобилей может быть занумеровано различными номерами?
6.	Во взводе 3 сержанта и 30 солдат. Сколько существует способов выделения одного сержанта и трех солдат для патрулирования?
7.	Сколько различных перестановок образуется из следующих слов: а) зебра; б) баран; в) водород; г) абракадабра?
170
8.	Сколько положительных чисел от 20 до 1000 делятся ровно на одно из чисел 7, 11 или 13?
9.	Найти решение уравнения пп+2 —4n„+i + 4а„ = 3" с начальными условиями «о = 5, ai = 7.
10.	Найти общее решение уравнения ап+2 + 4ап+1 + 4а,, = п2 - Зп +1.
Глава 6
АЛГЕБРА ЛОГИКИ
§6.1. Формулы алгебры логики
Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.
В качестве примеров высказываний приведем предложения “НГТУ — крупнейший вуз Новосибирска” и “Снег зеленый”. Первое высказывание является истинным, а второе — ложным.
Поставим в соответствие высказыванию Р логическую переменную х, которая принимает значение 1, если Р истинно, и О, если Р ложно.
Если имеется несколько высказываний, то из них можно образовать различные новые высказывания. При этом исходные высказывания называются простыми, а вновь образованные -сложными. Соответственно из логических переменных можно составлять различные конструкции, которые образуют формулы алгебры логики.
Итак, пусть {.т, | i е 1} - некоторое множество логических переменных. Определим по индукции понятие формулы алгебры логики.'.
1)	любая логическая переменная является формулой (называемой атомарной):
2)	если <р и ф — формулы, то выражения -^>, (ср/\ф), (tp'Vip), (<р —> -ф), фр о ф) являются формулами;
3)	никаких других формул, кроме построенных по пп. 1 и 2, нет.
Если формула <р построена из логических переменных, лежащих в множестве {a?i, х^,   , хп}, то будем писать (p(xi,	, хп).
172
Символы -i, Л, V, —>, о, использованные в определении, называются логическими операциями или связками и читаются со-отвественно: отрицание, конъюнкция, дизъюнкция, импликация и эквивалентность.
Введенные в п. 2 формулы следующим образом интерпретируются в русском языке: — “не </?”, (<р Л -0) — ‘V и V’”> V V;) — “9? или V3”, (<Р Ф) ~ “если (р, то ф", (<р ф) — “9? тогда и только тогда, -когда ф”.
Вместо -к/? часто пишут 7р, вместо (99 Л ф) — (9?&-0), (99 • -0) или (узт/О-
Действия логических операций задаются таблицами истинности, каждой строке которых взаимно однозначно сопоставляется набор значений переменных, составляющих формулу, и соответствующее этому набору значение полученной формулы:
		ф	(9?Л-0)	(9?V^)	(9? -> ф)	(9? о ф)
	-49?	0	0	0	0 .	1	1
0	1	0	1	0	1	1	0
1	0	1	0	0	1	0	0
	1	1	1	1	1	1
Приведенные таблицы истинности называются также интерпретациями логических операций и составляют семантику формул (т. е. придание смысла формулам) в отличие от синтаксиса формул (т. е. формальных законов их построения, данных в определении формулы).
Исходя из таблиц истинности для логических операций, можно строить таблицы истинности для произвольных формул.
Пример 6.1.1. Построить таблицу истинности для формулы 97 = ((ж —> у) Л ((у -> z) -> ж)).
Будем строить таблицу истинности последовательно в соответствии с шагами построения формулы <р:
X	У	Z	(ж -> у)	(у -» г)	((у -	э г) -> ж)	93
0	0	0	1	0		1	1
0	0	1	1	1		1	1
0	1	0	1	1		1	1
0	1	1	1	1		1	1
1	0	0	0	0		1	0
1	0	1	0	1		0	0
1	1	0	1	1		0	0
1	1	1	1	1		0	0
173
Легко заметить, что таблица истинности для 9? совпадает с таблицей истинности для х. В дальнейшем выяснится причина этого совпадения. □
Расширим понятие формулы, введя новые, не менее важные логические операции:
— (^IV-1 2) — штрих Шеффера или антиконъюнкция, по определению (<д|^;)	-’(99 л ^);
— (93 | 'ф') — стрелка Пирса или ант.идизъюнкция, по определению (99 j. V>)	_|(99 v V’)>
— (99©V;) — кольцевая сумма, логическое сложение или сложение по модулю 2, по определению (99 ф V’)	~,(93 * * * * *	V0-
Составим, исходя из определений, таблицы истинности для этих трех операций:
93	ф	(¥#)	(W Ф)	(9?©^)
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	0	0	0
Как видно из примера 6.1.1, даже при составлении несложных формул возникает обилие скобок. Чтобы избежать этого, в алгебре логики, так же как и в арифметике, приняты некоторые соглашения относительно расстановки скобок. Перечислим эти
1. Внешние скобки не пишутся. Например, вместо высказывания ((tVj/) —> z) пишется (х V у) —> z.
2. На множестве {—1, A, V,	|, I
, ф} вводится транзитивное отношение
< “быть более сильным” и отношение эквивалентности ~ “быть равносильным” по правилам, показанным на рис. 6.1.
Согласно этим отношениям недоста-
ющие скобки в формуле расставляют-
ся последовательно, начиная с наиболее сильных связок и кончая наиболее сла-
быми, а для равносильных связок расстановка скобок выполняется слева направо.
П р имер 6.1.2. В формуле х А у V z скобки расставляются
соглашения.
Рис. 6.1
174
следующим образом: ((х Л у) V z): в формуле х\/у z -> и — ({х V у) О (z -> ?/,)), в формуле х ф у о z -> и V v Л w J, х\у -((ж ф у) -Н- (z -> (u V (((v Aw) j. ж)|у))). □
Отметим, что, например, в формуле х -> (у -» z) скобки убирать нельзя, поскольку в силу наших соглашений формуле х —> у —> z соответствует формула (ж —> у) —> z.
§ 6.2.	Функции алгебры логики
В предыдущем параграфе мы выяснили, что семантически формулы полностью характеризуются таблицами истинности. При этом можно забыть о синтаксической структуре самих формул и иметь дело с таблицами истинности. Таким образом, мы приходим к понятию функции алгебры логики, которое и будет исследоваться в дальнейшем.
Функцией алгебры логики (ФАЛ) от п переменных Ж1,ж2, ..., ж„ называется любая функция f : {0,1}п —> {0,1}, т. е. функция, которая произвольному набору (<5i, <^2,   -, дп) нулей и
единиц ставит в соответствие значение /(<51,^2, • • , Ф<) G {0,1}.
Функции алгебры логики называются также булевыми функциями, двоичными функциями и переключательными функ-
Булевой функцией описываются преобразования некоторым устройством входных сигналов в выходные. Предположим, что устройство, показанное на рис. 6.2, имеет п входов дц, жг, .хп, на которые может подаваться или не подаваться ток, и один выход, на который ток подается или не подается в за-
висимости от подачи тока на входы. При этом значение переменной x.i = 1 интерпретируется как поступление тока на ?’-й вход, а жг = 0 как непоступление тока. Значение /(<51, <$2,  • • , <5П) равно 1, если при Ж1 =	..., хп = 6п ток на выход проходит, и
 • • ,$п) = 0, если ток не проходит.
Например, операции конъюнкции хЛу соответствует устройство с двумя входами и одним выходом. При этом значение выхода равно 1, тогда и только тогда, когда оба значения входов равны 1 (рис. 6.3).
Ж1---
Ж 2--
/(ж1,ж2...,жп)
П---
Рис. 6.2
циями.
Рис. 6,3
175
Булева функция f (a?i, а?2,.. -, хп) полностью определяется своей таблицей истинности'.
	•т2	^3		хп—1	хп	/(ж1,ж2,-	• * 5	)
0	0	0		0	0	/(0,0,...	,0,0)
0	0	0		0	1	/(0,0,...	,0,1)
1	1	1		1	0	/(1,1,...	,1,0)
1	1	1		1	1	/(1,1,...	,1,1)
В каждой строке таблицы вначале задается набор значений переменных (<5i, 62,. • •, <5„), а затем — значение функции на этом наборе.
Если булева функция f и формула р имеют одну и ту же таблицу истинности, то будем говорить, что формула р представляет функцию f.
Булева функция также однозначно задается перечислением всех наборов, на которых она принимает значение 0, либо перечислением всех наборов, на которых она принимает значение 1.
Пример 6.2.1 (голосование). Рассмотрим устройство, фиксирующее принятие некоторой резолюции “комитетом трех”. Каждый член комитета при одобрении резолюции нажимает свою кнопку. Если большинство членов согласны, то резолюция принимается. Это фиксируется регистрирующим прибором. Таким образом, устройство реализует функцию f(x,y,z), таблица истинности которой имеет вид
X	0	0	0	0	1	1	1	1
У	0	0	1	1	0	0	1	1
Z	0	1	0	1	0	1	0	1
f(x,y,z)	0	0	0	1	0	1	1	1
Полученную функцию f можно также задать следующей системой равенств: /(О,0,0) = /(0,0,1) = /(0,1.0) = /(1,0,0) = 0. □
Вектором значений булевой функции f(xi,X2,.   ,хп) называется упорядоченный набор всех значений функции /, при котором значения упорядочены по лексикографическому порядку множества аргументов {0,1}”.
В примере 6.2.1 вектором значений булевой функции f(x, y,z) является набор (00010111).
Отметим, что поскольку всего имеется 2” наборов ^<5i,..., 6п) нулей и единиц (|{0,1}”| = 2”), существует ровно 22 булевых
176
ООО 001 010 011 100 101 ПО 111
Рис. 6.4
функций	., хп) от п переменных: |{/|/ : {0,1}7' ->
{0,1}}| = |{0,1}|1{°’11п1 = 22" (см. операции над кардиналами в § 1.4).
Таким образом, имеется, например, 16 булевых функций от двух переменных, 256 — от трех и т. д.
Наборы (Ф, <*>2,   , <*>„) нулей и единиц можно представить в виде вершин n-мерных кубов (см. § 4.2) или в виде вершин 2-дерева (рис. 6.4), каждая вершина которого представляет собой некоторый набор (<5i, 62, • • •, 8п) нулей и единиц или пустое слово Л. При этом с вершиной (<*>i, S2, . •, <5n_-i, бп), п 2, смежны вершины (5i,52,...,5ri_i), (Ji,^2,	0), (<5i,<52,...,<5„-i,1),
с вершиной <51 — Л, (<5i, 0) и (<5i, 1), с вершиной Л -- 0 и 1. На каждом этаже изображенного 2-дерева располагаются всевозможные наборы (<$1, <*>2,..., <5П) нулей и единиц фиксированной длины п.
Функция /(®i, ®2,..., хп) называется суперпозицией функций g(yi, • • • ,Ут) и hi(x!,x2,... ,хп), ..., hm(x1,x2,.. - ,хп), если
/(®1, .. .,хп) = g(h1(x1,.. .,хп),..., hm(xi,.. .,хп)).
Пример 6.2.2. Функция /, соответствующая формуле зцжгФжгжзФтдац, есть суперпозиция функции д, представляемой формулой yi ф у2 Ф уз, и функций hi, h2, Фз, соответствующих формулам Т1Т2, Т2®3, ®4Ж1- О
Булева функция f(xi,x,2,... ,хп), принимающая значение 1 (соответственно 0) на всех наборах нулей и единиц: f(xy,x2,..., х-п) = 1 (соответственно /(®i, х2,..., хп) = 0), называется константой 1 (константой 0).
Опишем булеву алгебру функций алгебры логики от п переменных. В качестве носителя рассмотрим множество Вп = {/ | f : {0,1}” -> {0,1}}. Отношение ф на множестве Вп определим по следующему правилу: /1^/2^ fi(X) /г(А')
177
для любого набора значений X = (<5i,..., ф,). Пересечением f Л д функций f и д называется такая функция h. что h{X) = miii{/(X), g(X)} на любом наборе значений X = (йх,..., ёп). Объединением fVg функций fug называется такая функция h, что h{X) = max{/(X), д{Х)} на любом наборе X. Дополнение f функции f определяется следующим образом:
О, если f{X) =i 1, 1, если /(X) = 0.
В качестве 0 рассмотрим функцию, являющуюся константой 0, а в качестве 1 возьмем константу 1. Система = {Вп, Л, V, , 0,1) образует булеву алгебру функций алгебры логики от п переменных {алгебру булевых функций).
§ 6.3.	Эквивалентность формул
Как показано в примере 6.1.1, различные формулы могут иметь одинаковые таблицы истинности. Так возникает понятие эквивалентности формул.
Формулы tp(xi,... ,хп) и ф{х±,... ,хп) называются эквивалентными (99 ~ ф), если совпадают их таблицы истинности, т. е. совпадают представляемые этими формулами функции ... ,ж„) и /^(жх,... ,хп).
П ример 6.3.1. Построив таблицы истинности формул ж —> у и у —> ж, убеждаемся, что (ж —> у) ~ {у -> ж). □
Легко видеть, что отношение ~ является отношением эквивалентности, т. е. оно рефлексивно (99 ~ 99), симметрично (99 ~ ф => ф ~ р>) и транзитивно (99 ~ ф, ф ~ х ~ у)-
Отметим основные эквивалентности между формулами:
1)	((99 Л ф) Л х) ~ (99 Л {ф Л у)), ((99 V ф) V х) ~ (<£ V {ф V у)) {ассоциативность Л и V);
2)	(99 Л ф) ~ {ф Л 99), (99 V ф) ~ {ф V 99) {коммутативность Л и V);
3)	(99 Л 99) ~ 99, (99 V 99) ~ 99 {идемпотентность Л и V);
4)	(\oA(^Vy)) ~ {{<рбф) V (99Лу)), (v’V(V’Ay)) ~ ((^V^A (99 V у)) {законы дистрибутивности)'.
5)	(99 Л {ip V ф)) ~ 99, (99 V {р Л ф)) ~ {законы поглощения)-,
6)	-<{р>/\ф) ~ -ыр\/-Д>, -1{<р\/ф) ~ -199Л-|?/’ {законы де Моргана)-, 7)	~ 99 {закон двойного отрицания)-.
178
8)	<р —> -ф ~ ->р> V ф;
9)	99 <-> 0 ~ ((99 —> ф) Л {ф -> 99) ~ (-199 V ф) Л (->0 V 99);
10)	(99 V ->99'0) ~ (99 V 0), (-199 V 990) ~ (-199 V 0);
11)	99(~199 V 0) ~ 990, -'99(99 V 0) ~ -'990.
Формула р{х\,х^,   , хп) называется выполнимой {опровержимой), если существует такой набор значений переменных, при котором формула принимает значение 1 (соответственно 0).
Пример 6.3.2. Формула х /\у является одновременно выполнимой и опровержимой, поскольку 0л0 = 0, а 1 Л 1 = 1. □
Формула 99(3?!,..., хп) называется тождественно истинной, общезначимой или тавтологией {тождественно ложной или противоречием.), если эта формула принимает значение 1 (соответственно 0) при всех наборах значений переменных, т. е. функция f является константой 1 (константой 0).
Пример 6.3.3. Формула х\/х является тождественно истинной, а формула ж Л ж — тождественно ложной:
X	ж V ж	ж Л ж
0	1	0
1	1	0
Если 99 — тождественно истинная формула, то будем писать |= 99. В противном случае пишем 99. Таким образом, |= х V х, У= х Л у, и х Л х.
Очевидным является следующее
Замечание 6.3.1. 1) Формула 99 тождественно ложна тогда и только тогда, когда -><р тождественно истинна f|= ~«р);
2) Формула 99 опровержима тогда и только тогда, когда она не является тождественно истинной р>);
3) Формула ip выполнима тогда и только тогда, когда она не является тождесгпвенно ложной.
Отметим, что тождественно истинные (соответственно тождественно ложные) формулы образуют класс эквивалентности по отношению
Предложение 6.3.2. Если формула р>\ тождественно истинна, — тождественно ложна, то для любых формул 99 и 0 справедливы следующие эквивалентности:
99Л99Х ~ 99; 99Л990 ~ 99О; <pV<pi ~ p>i; 99V уд ~ р>; {рФ -> 99) ~ pi; (99 —> 99 V 0) ~ 99Х; 99 Ф ~ 990; 99 Ф 991 ~ 0; 99 Ф 990 ~ 99.
179
§ 6.4. Дизъюнктивные и конъюнктивные нормальные формы
Если х — логическая переменная, 6 Е {0,1}, то выражение
г
х х, если <5 = 1, х = _
х, если <5 = 0
называется литерой. Литеры х и х называются контрарными.
Элементарной конъюнкцией или конъюнктом называется конъюнкция литер. Элементарной дизъюнкцией или дизъюнктом называется дизъюнкция литер.
Пример 6.4.1. Формулы х\/у\/гих\/у\/хУх — дизъюнкты, формулы Т1Х2Т3 и ГГ1Т2Т1 — конъюнкты, а х является одновременно и дизъюнктом, и конъюнктом. □
Дизъюнкция конъюнктов называется дизъюнктивной нормальной формой (ДНФ); конъюнкция дизъюнктов называется конъюнктивной нормальной формой (КНФ).
Пр и м е р 6.4.2. Формула xyV yz — ДНФ, формула (х V z V у)(х V z)y — КНФ, а формула ху является одновременно КНФ и ДНФ.
Теорема 6.4.1. 1. Любая формула эквивалентна некоторой ДНФ.
2. Любая формула эквивалентна некоторой КНФ.
Опишем алгоритм приведения формулы к ДНФ.
1.	Выражаем все логические цперации, участвующие в построении формулы, через дизъюнкции, конъюнкции и отрицания, используя эквивалентности (<д -> ф) ~ (~><д V ф), (<д о ф) ~ (~чр V ф) Л (~>ф V <д) и определения операций |, J. и ф.
2.	Используя законы де Моргана, переносим все отрицания к переменным и сокращаем двойные отрицания по правилу -1-1Х ~ х.
3.	Используя закон дистрибутивности (<д А (ф V у)) ~ ((<д Л ф) V (<д Л у)), преобразуем формулу так, чтобы все конъюнкции выполнялись раньше дизъюнкций.
В результате применения пн. 1-3 получается ДНФ данной формулы.
Пример 6.4.3. Приведем к ДНФ формулу
<д = ((ж -> у) | Ду -> z)).
180
Выразим логические операции —> и J. через Л, V и р ~ ((ж V у) J. ~>(у Vz) ~ —,((ж V у) V ->(у V г)). В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания: <р ~ (-Дж Vy)	V z)) ~ (ж Лу) Л (у Vz) ~ (ж Л у) Л (у V z).
Используя закон дистрибутивности, приводим формулу к ДНФ: <р ~ (х Л у Л у) V (ж Л у Л z). □
Приведение формулы к КНФ производится аналогично приведению ее к ДНФ, только вместо и. 3 применяется
3'. Используя закон дистрибутивности (99 V ('0 Л х)) ~ ((</? V 0) Л (99 V х)), преобразуем формулу так, чтобы все дизъюнкции выполнялись раньше, чем конъюнкции.
И р и м е р 6.4.4. Приведем к КНФ формулу = (х -> у) Л ((г/ -> z) -> ж).
Преобразуем формулу 99 к формуле, не содержащей —>: tp ~ (ж V у) Л (-Ду -> z) V ж) ~ (х V у) Л (-i(y V z) V ж). В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания: ip ~ (х V у) Л ((у Az) \/ж) ~ (ж V у) Л ((у Az) \/ж). По закону дистрибутивности получаем, что формула <р эквивалентна формуле (ж V у) Л (ж V у) Л (ж V z), являющейся КНФ.
Упростим полученную формулу: (ж V у) Л (ж V у) Л (ж V z) (2)	(3)
(ж V (у Л у)) Л (ж V z) ~ ж Л (ж V z) ~ ж (для преобразования (1) использовался закон дистрибутивности, для (2) — эквивалентность 4 предложения 6.3.2., для (3) — закон цогдощения). Таким образом, формула <р из примера 6.1.1 эквивалентными преобразованиями приводится к формуле ж (являющейся одновременно ДНФ и КНФ формулы 99). □
Любая булева функция может иметь бесконечно много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).
Пусть (ж1,...,жп) — набор логических переменных, Д = (Д,..., <5И) — набор нулей и единиц. Конституентой единицы набора Д называется конъюнкт КДД,..., ёп) = хрхр... Xj”. Конституентой нуля набора Д называется дизъюнкт К°№, ...,6п) = жГй1 V ж*-*52 V ... V х1^.
Отметим, что КДД,62, • • •, <5И) = 1 (K°(6i Д2, • • • ,дп) = 0) тогда и только тогда, когда .тц = ф, Ж2 = Ф, ..хп = ёп.
Совершенной ДНФ называется дизъюнкция некоторых кон-
181
ституент единицы, среди которых нет одинаковых, а совершенной КНФ называется конъюнкция некоторых конституент нуля, среди которых нет одинаковых. Таким образом, СДНФ (СКНФ) .есть ДНФ (КНФ), в которой в каждый конъюнкт (дизъюнкт) каждая переменная Xi из набора {дц,...,хп} входит ровно один раз, причем входит либо сама ж,, либо ее отрицание хг.
Пример 6.4.5. Формула Ж1Ж2Х3 есть конституента единицы К1 (1,0,1), формулаx\ly\Tz, есть конституента нуля К°(0,0,1), формула ацж2жз v 24Я2Ж3 ~ СДНФ, формула (х V у V z) Л (ж V у V z) Л (ж V у V z) — СКНФ, а формула ацжг^з V Т1Ж2Ж3 V не является СДНФ. □
Для решения задачи нахождения СДНФ и СКНФ, эквивалентных исходной формуле ip, предварйтельно рассмотрим разложения булевой функции f(xi,X2,   , хп) по к переменным (для определенности по жх, ж2,   жД — разложения Шеннона.
Теорема 6.4.2 (первая теорема Шеннона).
Любая булева функция f(xi,X2,---,xn) представима в виде разложения Шеннона:
f(xl,X2,...,Xk,Xk+1,...,Xn) =
/
= V Слх^)/(д1,б2,...,бк,хк+1,...,хп).
’	г=1
по всем наборам («51,-А)
Доказательство. Прежде всего заметим, что х?’ = 1 x,i = Подставим произвольно вместо первых к переменных их значения: хг = <^,ж2 = хк = ёк. Тогда левая часть доказываемой формулы равна /(й( Д2, •  •,	 ,%„) Пра-
вая часть представляет собой дизъюнкцию 2к конъюнкций вида ж^ж22 • • • x6kf(t>i, fo,. - • ,бк,xk+i,..., х.п), которые этой подстановкой разбиваются на два класса. К первому классу относится конъюнкция, у которой набор (<^i Дг, • • • Да) совпадает с набором (^Д2*,...ДД:
(^Ч^/2  •. (<^/(<5^,  • •	• • • ,*„) =
= 1 • 1  ...  1 -	Д2*,..., 6*к, хк+х, ..., хп) =
= Ж,^,...,^,^+1,...,ж„).
182
Эта конъюнкция равна левой части формулы. Ко второму классу относится 2к — 1 конъюнкций, у каждой из которых хотя бы в одной переменной Xi, г 6 {1,2, ...,&} выполнимо условие 6* ф ёг- Следовательно, каждая из них равна нулю. Используя закон aVO = а, получаем, что левая и правая части формул равны при любой подстановке переменных xi, х2,  - -, хп. □
В силу принципа двойственности для булевых алгебр справедлива
Теорема 6.4.3 (вторая теорема Шейнона). Любая булева функция f(xi,X2,..., хп) представима-е виде разложения Шеннона:
,3?2> • • •,	, • • • > %п) =
= Л (V,	Vf(^^2,---,dk,Xk+l,...,Xn)).
по всем наборам (<51, -А)
В предельном случае, когда к — п, для булевой функции /(ж1, а?2, • • •, хп), не равной нулю, получаем ее представление в виде совершенной ДНФ:
У(®1,®2,...,Жп) = V (,Л аф)-*	г—1
по всем наборам
(Й1,Й2,...,<5П), на которых
/(<51,...Л)=1
Аналогично для булевой функции /(®i, х2,   , хп), не равной единице, получаем ее представление в виде совершенной КНФ:
f(xi,x2,...,xn)= Д (V ' '	г=1
. по всем наборам
’	Лп),
на которых /(<51,...,<5п)=О
Приведенные формулы позволяют сформулировать следующую теорему.
Теорема 6.4.4 (о функциональной полноте). Для любой булевой функции f найдется формула представляющая функцию f. Если f 0, то существует представляющая ее формула tp, находящаяся в СДНФ:
<Р= V
Д<51,...,<5„)=1
183
и такое представление единственно с точностью до порядка следования конституент единицы. Если f 1, то существует представляющая, ее формула (р, находящаяся, в СКИФ: <р = и такое представление, единственно с Ж,....<5п)=о
точностью до порядка следования, конституент. нуля.
II р и м е р 6‘.4.6. Найти СДНФ и СКНФ функции f(x,y, z), заданной следующей таблицей истинности:
X	0	0	0	0	1	1	1	1
У	0	0	1	1	0	0	1	1
Z	0	1	0	1	0	1	0	1
f(x,y,z)	1	0	0	1	0	1	0	1
По теореме о функциональной полноте СДНФ имеет вид p>i = xyz М xyz \/ xyz V xyz, а СКНФ — <дг = (х V у V /)(т V у V z)(x V у V z) (х V у V z). □
Итак, для нахождения СДНФ и СКНФ исходной формулы <р составляется ее таблица истинности, а затем по ней строится требуемая совершенная нормальная форма.
В примере 6.4.6, имея, скажем, СДНФ для функции /, можно составить ее таблицу истинности и по ней найти СКНФ <Д2-Описанный способ нахождения СДНФ и СКНФ по таблице истинности бывает часто более трудоемким, чем следующий алгоритм.
Для нахождения СДНФ данную формулу приводим сначала к ДНФ, а затем преобразовываем ее конъюнкты в конституенты единицы с помощью следующих действий:
а)	если в конъюнкт входит некоторая переменная вместе со своим отрицанием, то мы удаляем этот конъюнкт из ДНФ;
б)	если в конъюнкт одна и та же литера xs входит несколько раз, то удаляем все литеры xs, кроме одной;
в)	если в некоторый конъюнкт х^1 ... xSk не входит переменная у, то этот конъюнкт заменяем на эквивалентную формулу гф ... xkk Л (у V у) и, применяя закон дистрибутивности, приводим полученную формулу к ДНФ; если недостающих переменных несколько, то для каждой из них к конъюнкту добавляем соответствующую формулу вида (у V у);
г)	если в полученной ДНФ имеется несколько одинаковых конституент единицы, то оставляем только одну из них. В результате получается СДНФ.
184
Пример 6.4.7. Найдем СДНФ для ДНФ <д = хх V х V yzy. Имеем ^x\/yz ~ (хфу V у) yz{x Vs)) ~ (ху\/ ху\/ xyz\/xyz} ~ (xy(zVz)\/xy(z\/z)\/xyzVxyz) ~ (xyz\/xyz\/xyz\/xyzVxyzVxyz) ~ (xyz V xyz V xyz V xyz V xyz). □
Описание алгоритма приведения КНФ к СКНФ аналогично вышеизложенному описанию алгоритма приведения ДНФ к СДНФ и оставляется читателю в качестве упражнения.
.§ 6.5. Двухэлементная булева алгебра.
Фактор-алгебра алгебры формул
Рассмотрим множество Bq — {0,1} и определим на нем операции Л, V, согласно таблицам истинности формул х Л у, xV у, х. Тогда система 23 о = (Bq, Л, V, ,0,1) является двухэлементной булевой алгеброй (см. пример 2.6.3, п. 1). Формулы алгебры логики, содержащие лишь логические операции Л, V, , являются термами в 23 о. По теореме о функциональной полноте в булевой алгебре 23о с помощью терма можно задать любую булеву функцию.
Обозначим через Ф„ множество всех формул алгебры логики с переменными из множества {xi, Х2,    ,хп}. На множестве Ф,, определены двухместные операции конъюнкции и дизъюнкции — Л: (<д, ф) t-э Л ф, V: (<д, ф) V ф — и одноместная операция отрицания :	<д. Выделим на множестве Фп две
константы х Л х и х V х. Тем самым получается алгебра формул Вп = (Ф„, Л, V, , х Л s, х V х). Нетрудно заметить, что отношение ~ эквивалентности формул является конгруэнцией на алгебре Вп, и поэтому можно задать фактор-алгебру Вп/~. На фактормножестве Ф„/ ~ операции Л, V и определяются следующим образом: ~ (<д)Л	(ф) =~ (<д Л ф), ~ (tp)V ~ (ф)	(</? V ф),
-|~(<д) =~(_,<д). На множестве Фп/~ выделяются две константы: 0 =~ (т?'Л ж) и 1 =~ (х V х). Полученная система (Фп/ ~ ,A,V,-, 0,1) является фактор-алгеброй 7?п/~.
Теорема 6.5.1. Фактор-алгебра Вп/ ~ изоморфна алгебре булевых функций 23п.
Доказательство. Искомый изоморфизм £: Вп/ ~ су. 23,, определяется по следующему правилу: классу эквивалентности ~ (<Д сопоставляется функция fv, имеющая таблицу истинности произвольной формулы из множества ^(<д). Посколь
185
ку разным классам эквивалентности соответствуют различные таблицы истинности, отображение £ инъективно, а так как для любой булевой функции f из Вп найдется формула <р 6 Фп, представляющая функцию /, то отображение £ сюръективно. Сохранение операций Л, V, , 0, 1 при отображении £ проверяется непосредственно. □
По теореме о функциональной полноте каждой функции f g Вп, не являющейся константой 0, соответствует некоторая СД-НФ ф, принадлежащая классу ~ (<Д = £-1(/) формул, представляющих функцию f. Возникает задача нахождения в классе ~ (</?) дизъюнктивной нормальной формы, имеющей наиболее простое строение.
§ 6.6.	Минимизация булевых функций в классе ДЙФ
Каждая формула имеет конечное число вхождений переменных. Под вхождением переменной понимается место, которое переменная занимает в формуле. Задача заключается в том, чтобы для данной булевой функции f найти ДНФ, представляющую эту функцию и имеющую наименьшее число вхождений переменных.
Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза.
Пример 6.6.1. Формула Т2®з^4 — элементарное произведение, а формула	элементарным произведением не
является. □
Формула Х2,  • •, Хп) называется импликантой формулы ^(®i,Х2,   ,хп), если <р — элементарное произведение и (р Л ф ~ <р, т. е. для соответствующих формулам р и.Ф функций Д и Д справедливо неравенство Д Д. Формула . - ,а?п) называется импликантой функции /, если р — /импликанта совершенной ДНФ, представляющей функцию /. Импликанта ...,хп) = х^х^---х^ формулы ф называется простой, если после отбрасывания любой литеры из <р не получается формула, являющаяся импликантой формулы ф.
Пример 6.6.2. Найдем все импликанты и простые импли-канты для формулы <р(х,у) = х —> у. Всего имеется 8 элементарных произведений с переменными х и у. Ниже приведены их таблицы истинности:
186
X О О 1 1
У_ о
1
о
1
<Р = х -+у
1
1
О
1
ху 1 О о о
ху о
1 о о
ху О О
1
О
ху О О о
1
х___у
1 1
1 О
О 1 о о
х
О' о
1
1
У ' о ’
1
о
1
г
Из таблиц истинности заключаем, что формулы ху, ху, ху, х, у — все импликанты формулы <р, а из этих импликаит простыми являются формулы х и у (формула ху, например, не является простой импликантой, поскольку отбрасывая литеру у, получаем импликанту х). □
Дизъюнкция всех простых импликант данной формулы (функции) называется сокращенной ДНФ.
Теорема 6.6.1. Любая булева функция, не являющаяся константой 0, представима в виде сокращенной ДНФ.
В примере 6.6.2 функция, соответствующая формуле х —> у, представима формулой ж V у, которая является ее сокращенной ДНФ.
Сокращенная ДНФ может содержать лишние импликанты, удаление которых не меняет таблицы истинности. Если из сокращенной ДНФ удалить все лишние импликанты, то получается ДНФ, называемая тупиковой.
Заметим, что представление функции в виде тупиковой ДНФ в общем случае неоднозначно.
Выбор из всех тупиковых форм формы с наименьшим числом вхождений переменных дает минимальную ДНФ (МНДФ).
Рассмотрим метод,Квайна для нахождения МДНФ, представляющей данную булеву функцию. Определим следующие три операции:
—	операция полного склеивания — <р • х V  х ~ <р(т V ж) ~ <р;
—	операция неполного склеивания
• х V  х ~ tp(x Vx)Vtp-xV<p-x~<p\/ipx\/ ipx;
— операция элементарного поглощения — <р • xs V ~ <р, 8е {о, 1}.-
Теорема 6.6.2 (теорема Квайна). Если исходя из совершенной ДНФ функции произвести все возможные операции неполного склеивания, а затем элементарного поглощения, то в результате получится сокращенная ДНФ, т. е. дизъюнкция, всех простых импликант.
187
Пример 6.6.3. Пусть функция /(ж, г/, z) задана совершенной ДНФ tp = xyz\Jxyz V xyz V xyz\/ xyz. Тогда, производя в два этапа все возможные операции неполного склеивания, а затем элементарного поглощения, имеем
tp ~ xy(z V z) V yz(x V ж) V yz(x V х) V xz(y V у)V
\/xy(z V z) V xyz V xyz V xyz V xyz V xyz ~
~ xy V yz V yz V xz V xy\]
Vxyz V xyz M xyz V xyz V xyz ~
~ y(x V x) V y(z V z) V xy V yzV yz V xz V xy\l
\Jxyz V xyz \J xyz V xyz V xyz ~
~ у V xy V yz V yz V xz V xyV
\Jxyz V xyz V xyz M xyz V xyz ~ у V xz.
Таким образом, сокращенной ДНФ функции / является формула у V xz. □
На практике при выполнении операций неполного склеивания на каждом этапе можно не писать члены, участвующие в этих операциях, а писать только результаты всевозможных полных склеиваний и конъюнкты, не участвующие ни в каком склеивании.
Пример 6.6.4. Пусть функция /(а?, у, z) задана совершенной ДНФ <р = xyz V xyz V xyz V xyz. Тогда, производя операции склеивания, а затем элементарного поглощения, имеем <р ~ х y(z \/z) V yz(x Vx)V xz(y V у) ~ xy V yzV xz. □
Для получения минимальной ДНФ из сокращенной ДНФ используется матрица Квайна, которая строится следующим образом. В заголовках столбцов таблицы записываются конституенты единицы совершенной ДНФ, а в заголовках строк — простые им-пликанты из полученной сокращенной ДНФ. В таблице звездочками отмечаются те пересечения строк и столбцов, для которых конъюнкт, стоящий в заголовке строки, входит в конституенту единицы, являющейся заголовком столбца.
Для примера 6.6.4 матрица Квайна имеет вид
188
Импликанты	Конституенты единицы			
	xyz	xyz	xyz	xyz
ху yz xz	*	* *	* *	*
В тупиковую ДНФ выбирается минимальное число простых импликант, дизъюнкция которых сохраняет все конституенты единицы, т. е. каждый столбец матрицы Квайна содержит звездочку, стоящую на пересечении со строкой, соответствующей одной из выбранных импликант. В качестве минимальной ДНФ выбирается тупиковая, имеющая наименьшее число вхождений переменных.
В примере 6.6.4 по матрице Квайна находим, что минимальная ДНФ заданной функции есть х у V xz.
В силу принципа двойственности для булевых алгебр все приведенные понятия и рассуждения очевидным образом можно преобразовать для нахождения минимальных конъюнктивных нормальных форм (МКНФ).
§6.7.	Карты Карно
Другой способ получения простых импликант формул с малым числом переменных (и, значит, нахождения с помощью матрицы Квайна минимальной ДНФ) основан на использовании так называемых карт Карно.
Карта Карно для п переменных служит эффективным средством иллюстративного представления n-куба. Она содержит 2'"' ячеек, каждая из которых соответствует одной из 2П возможных комбинаций значений п логических переменных Ж1, а?2, хп. Карта строится в виде матрицы размера 2п~к на 2к так, что ее столбцы соответствуют значениям переменных xi, ..., х^, строки — значениям переменных 2>+i,..., хп, а соседние ячейки (как по вертикали, так и по горизонтали) отличаются только значением одной переменной (рис. 6.5).
На рис^ 6.6 приведены карты Карно для функций трех и четырех переменных соответственно. В этих картах все ячейки, отмеченные скобкой Xi (по строке и столбцу), представляют входные комбинации err, — 1, а в неотмеченных строках и столбцах ячейки соответствуют комбинациям с з?г = О (см. рис. 6.6а, на котором разными способами изображена одна и та
189
же карта). Например, на рис. 6.6а ячейка а соответствует набору 001 значений переменных xi, Х2, ®з- Отметим, что для каждой функции может быть построено несколько различных карт. На рис. 6.65 изображены две карты Карно для функции четырех переменных. Первая карта соответствует разбиению переменных {{а?1,ж2}, {t3,t4}}, а вторая — {{a?i}, {т2,ж3,х4}}.
У каждой вершины n-куба есть ровно п смежных с ней вершин, т. е. вершин, отличающихся от нее только одной координатой. Поскольку в карте Карно каждая ячейка может иметь не более четырех ячеек, соседних по строке или столбцу, для представления точек, отличающихся только на одну координату,
	
	d
	е
	
	
	f
	9
	
а	б
Рис. 6.6
190
Ж1
Ж2
Рис. 6.7
необходимо использовать и более удаленные ячейки. Например, точки b и с на рис. 6.66 отличаются только значением переменной жз, т. е. являются смежными.
Булева функция может быть представлена на карте Карно выделением 1-ячеек (т. е. ячеек, в которых функция принимает значение, равное 1). Подразумевается, что необозначенные ячейки соответствуют 0-точкам.
На рис. 6.7 изображена кар
та, представляющая булеву функцию f(x,y,z), рдя которой /(0,0,0) = /(1,1.0) = /(1,1,1) = /(1,0,1) = О, /(0,1,0) = /(1,0,0) = /(0,0,1) =/(0,1,1) = 1.
Для построения импликант берутся всевозможные наборы 1-ячеек, образующих вершины некоторого fc-куба (т. е. 2к точек таких, что пары соседних отличаются ровно одной координатой). Совпадающие координаты образуют набор (ф,..., ф-л), и требуемая импликанта имеет вид х^ ...	, где Xj — переменная,
соответствующая значению ф.
. Пример 6.7.1. Точки b и с на рис. 6.66 лежат в 1-кубе, который определяет конъюнкт Ж1Ж2Ж4. Точки {d, е, f,g} образуют 2-куб, представляющий импликанту Ж1Ж4. □
Определение простых импликант функции сводится к нахождению всех /..-кубов, которые не содержатся в кубах более высокого порядка.
Пример 6.7.2. Простые импликанты для карты Карно, приведенной на рис. 6.7, равны Ж1Ж2, Ж1Ж2Ж3, Ж1Ж3.
П р и м е р 6.7.3. На рис. 6.8 показана карта Карно, простые импликанты которой имеют вид Ж2Ж3Ж4, лцжгжз, Ж1Ж3Ж4, Ж1Ж2Ж4, Ж2Ж3Ж4, Ж1Ж2Ж4, Т1Ж3. Заметим, что импликанты Ж1Ж2Т3, З/Ж2.Т3, Ж1Ж3Ж4 и Ж1Ж3Ж4 не являются простыми, так как образуемые ими 1-кубы содержатся в 2-кубе х\хз. □
После нахождения простых импликант задача построения минимальной ДНФ сводится к изучению матрицы Квайна, как показано в § 6.6. При наглядном размещении простых импликант в карте Карно удается непосредственно находить минимальную ДНФ, выбирая те простые импликанты. которые покрывают все единицы и имеют наименьшее возможное число вхождений пе-
191
ременных. Так, минимальной ДНФ для функции, изображенной на рис. 6.8, является формула Л2Ж3Ж4 V Ж1Ж3Л4 V Л1Ж2Л4 V ацлз-
§6.8.	Принцип двойственности для булевых функций
В § 2.6 мы говорили о двойственности в классе булевых алгебр, которая проявляется в том, что на множестве В со структурой булевой алгебры 23 можно ввести структуру двойственной алгебры 23+, в которой роль операции Л играет V, роль операции V — Л, а в качестве нуля (единицы) используется 1 (соответственно 0). При этом между алгебрами 23 и 23+ имеется изоморфизм : х i-> х. В этом параграфе мы рассмотрим соответствие булевых функций при изоморфизме <р.
Функция /+(.Т1,... , хп) называется двойственной по отношению к функции /(л1,... , лп), если f+(xi,... ,хп) = f(xi,... ,хп).
Двойственная функция получается из исходной при замене значений всех переменных, а также значений функции на противоположные, т. е. в таблице истинности нужно заменить 0 на 1, а 1 на 0.
Пример 6.8.1. Двойственной к функции х Л у является функция, соответствующая формуле -i(zA^), т. е. -у-\х\/у) или х V у: (л Л у)+ = х V у. Аналогично (х V у)+ = х Лу, (л)+ = х. □
192
Принцип двойственности. Если
то
.. ,т?1) = ,<7(/11(ж],... ,.-с„),... ,hm(xi,... ,.гп)),
Таким образом, функция, двойственная суперпозиции функций, есть соответствующая суперпозиция двойственных функций.
Принцип двойственности удобен при нахождении двойственных функций, представленных формулами, содержащими лишь конъюнкции, дизъюнкции и отрицания. В .этом случае в исходной формуле конъюнкции заменяются на дизъюнкции, а дизъюнкции - на конъюнкции. Таким образом, ДНФ соответствует КНФ, КНФ ДНФ, СДНФ СКНФ, СКНФ СДНФ.
П р и м е р 6.8.2. (xy\/xz\/xyz) + — (rz;Vу)/\(xVz)A(TVy\/z). □
Отметим, что если формула </? эквивалентна формуле ф: ~ ф, то р+ ~ ф+.
Функция /(ж] ,..., хп) называется самодвойственной, если жп) = /(.'Щ,...,.^,).
П р и м е р 6.8.3. Покажем, что формула = ху V xz- V yz задает самодвойственную функцию.
С этой целью убедимся, что на всех противоположных наборах значений переменных (ф,ф,ф) и (1 — Д,1 — Ф,1 — Ф) формула принимает противоположные значения.. Действительно, составив таблицу истинности
X	0	0	0	0	1	1	1	1
У	0	0	1	1	0	0	1	1
Z	0	1	0	1	0	1	0	1 ’
	0	0	0	1	0	1	1	1
получаем <Д0,0,0) = <Д1,1,1), <Д0,0,1) = </?( 1,1,0), <Д 0,1,0) ~ 97(1.0,1). ДО, 1.1) = <Д1.0,0).
§ 6.9.	Полные системы булевых функций
Как мы уже знаем из теоремы о функциональной полноте, любая булева функция представима в виде формулы, содержащей лишь операции A, V, т. е. в виде терма сигнатуры {A. V.->}. В этом параграфе будет дано описание сигнатур, позволяющих получать любые булевы функции.
7 Зак. Ns 4872 Судоплатов
193
Система булевых функций Т = {/ь/2........./„} называется
полной. если любая булева функция представима в виде терма сигнатуры {/1./2....Jn}> т. е. в виде суперпозиций функции
из .Т.
Из сказанного выше ясно, что система {Л, V, -i} является полной. Ответ на вопрос о полноте произвольной системы /С дает теорема Поста, формулируемая ниже.
Введем определение классов Поста.
1.	Класс Ро это класс булевых функций, сохраняющих нули, т. е. функций /’(.ci,...,.ту,), для которых /'(0,0.0) = 0: Fo =
{/ | ./'(0,0,... ,0) = 0}.
2.	Класс Г\ это класс булевых функций, сохраняющих единицу, т. е. функции f(x.[.г,п).	для которых /(1,1,.... 1) = 1:
3.	Класс S это класс самодвойственных функций: S = {/ | f - самодвойственная функция}.
4.	Класс Л/ - это класс монотонных функций. Булева функция /(лд...., называется монотонной, если для любых наборов пулен и единиц (од....,а„) и (/Зр... ,/Зп) из условий од < /31. ...,	/3,( следует /(од......ап) f(/3l..../Зп).	Таким обра-
зом, М = {f | f — монотонная функция}.
5.	Класс £ - эго класс линейных функций. Булева функция /(:гд,....хп) называется линейной, если в булевом кольце ({0,1}. ф, Э) функция / представима в виде /(тд...хп) — сд ф
C1X[ ф С-2Х-2 Ф . . . Ф С.„ХГ1. где Со, Cl, С.2, . . ., С,, 6 {0-1}.
Коэффициенты со, гд, .... с,( линейной функции определяются из следующих соотношении:
с0 = /(0.0...О),соФсд -/(1,0......0),
Со Ф г-2 = f(().1.0)...Со е с„ = /(0. 0...0,1),
т.е.	со = /(О.О...0),
ci =с0Ф/(1.0......0)....с„ - со®/(0.0.........1).	(6.1)
Таким образом, проверка линейности сводится к нахождению коэффициентов с,- но формулам (6.1) и сопоставлению таблиц истинности данной формулы /(:гд,... .хп) и полученной формулы Со © С] .ГД ф ... ф спх„.
П р и м е р 6.9.1. Проверим, является ли линейной функция х V у. Имеем со = 0 V 0 = 0, сд = 0 © (1 V 0) = 1, с-2 = 0 ф (0 V 1) — 1. Таким образом, со Ф с,\х © с2у = х ф у. Сопоставляя
194
таблицы истинности формул х V у и х ф у, убеждаемся, что они нс совпадают. Вывод: функция х V у нелинейна. □
Линейность функции можно также определить с помощью следующей теоремы.
Теорема 6.9.1 (теорема Жегалкипа). Всякая булева функция f(xi,... ,.т„) представима полиномом Жегалкипа, т.е. в виде f (xi,..., хп) = ф Xii-i'i-i    Xih Ф с, где в каждом наборе (ч,-а)
(«1, -.. ,tfc) все ij различны, а суммирование ведется по некоторому .множеству таких несовпадающих наборов. Представление булевой функции в виде полинома Жегалкипа единственно с точностью до порядка слагаемых.
Полином Жегалкипа называется нелинейным, (линейным), если он (не) содержит произведения переменных.
Таким образом, линейность булевой функции-равносильна линейности соответствующего полинома Жегалкипа.
Для получения полинома Жегалкипа булевой функции, находящейся в СДНФ, используются аксиомы булевой алгебры, аксиомы булева кольца ({0,1},ф, ©) и равенства, выражающие операции Л, V и -п через операции этого булева кольца: х V у = х ф у ф ху, х(у ф z) — ху ф xz, х — х ф 1, х ф 0 = х, х ф х = 1, хх = 0 и т.д.
Пример 6.9.2. Определим линейность функции f(x,y, z) = xyz V xyz V xyz.
Имеем f(x, у, z) = ((xyz ф xyz ф xyzxyz) V xyz = (xyz ф xyz) V xyz = xyz ф xyz ф xyz ф (xyz ф xyz)xyz = xyz ф xyz ф xyz ф 0 = ifz(y ф у) ф xyz = xz  1 ф xyz — (x ф l)z ф x(y ф l)(z Ф 1) = xz(&l.-zf&xyz(Bxz(Bxy(Bx = x®z®xy®xyz. Полученный полином Жеталкина является нелинейным, и, следовательно, функция f также нелинейна. □
Заметим, что если в эквивалентности </? V ф ~ </? ф ф ф </?  ф формулы </? и ф являются различными конституентами единицы, то их произведение ip  ф равно 0, и тогда р> V ф ~ </? ф ф. Следовательно, для получения полинома Жегалкина из СДНФ можно сразу заменить V на ф.
Отметим, что каждый класс Поста замкнут относительно операций замены переменных и суперпозиции, т. е. с помощью этих операций из функций, принадлежащих данному классу, можно получить только функции из этого же класса.
7*
195
П р и м е р 6.9.3. Определим, к каким классам Поста относится булева функция f(x,y) — х\у.
Так как /(0,0) = 1, а/(1,1) = 0, то f(x,y) Ро и f(x,y) $ Pi. Поскольку /(1,0)	/(0,1), то f(x,,y) S. Так как /(0,0) >
/(1,1), то /(ж, у) М. Полином Жегалина для функции /(ж, у) = ху имеет вид 1 ф жу в силу равенства х = 1 ф х. Поэтом у данная функция нелинейна. Таким образом, можно составить следующую таблицу
Функция	Классы				
	По	А	S	М	£
х\у	Нет	Нет	Нет	Пет	Нет
Теорема 6.9.2 (теорема Поста). Система Р булевых функций тогда и только тогда является полной, когда для каждого из классов Рц, Pi, S, М, £ в системе Р найдется функция, не принадлежащая этому классу.
В силу теоремы Поста функция х\у образует полную систему, т. е. с помощью штриха Шеффера можно получить любую булеву функцию. В частности, х ~ ж|ж, х Л у ~ -п-фт Л у) ~ ~фж|у) ~ (Ф)К-Ф)-
Система булевых функций называется базисом, если она полна, а удаление любой функции из этой системы делает ее неполной.
Теорема 6.9.3. Каждый, базис содержит, не более -четырех булевых функций.
Доказательство. Предположим, что существует базис р, состоящий более чем из четырех функций. По теореме Поста тогда получаем, что Р состоит ровно из пяти функций, каждая из которых не принадлежит ровно одному классу Поста. Пусть / — функция из Р, не принадлежащая классу Ро- Тогда, с одной стороны, /(0,0,..., 0) = 1, а, с другой — из / € Pi следует, что /(1,1,..., 1) = 1. Это означает, что / не является самодвойственной функцией, что противоречит предположению. □
Пример 6.9.4. Следующие системы булевых функций являются базисами: {Л,-}, {V, —},	{/}, {|}, {<->,V,0},
{ф,Л,<->}. □
196
Широкий набор базисов открывает большие возможности при решении задач минимизации схем устройств дискретного действия, поскольку из базисных схем с помощью суперпозиций можно составить схему, соответствующую любой булевой функции.
§ 6.10.	Функциональная декомпозиция
1.	Определение и примеры. Булева функция f(xi,.. хп) называется разложимой, если она может быть представлена в виде суперпозиции функций gi, 92 ,> 9k (к < п) и F, каждая из которых имеет менее п переменных: /(®i,Х2,  •., жп) = F(gi,...При этом функция f может быть реализована с помощью устройств, соответствующих функциям ,91, 92, . - , 9к и F, как показано на рис. 6.9. Разложение функции / в виде суперпозиции 91, 92, ..., 9fc и F называется декомпозицией функции /, а соответствующая схема, показанная на рис. 6.9, — декомпозиционной реализацией функции /.
В дальнейшем будем использовать следующие обозначения логических устройств. Устройство, соответствующее функции х, будем называть инвертором и обозначать, как показано на рис. 6.10 а, устройство, соответствующе функции /(т1,...	   ,хп), обозначим, как показа-
но на рис. 6.106, а устройство, соответствующее функции f (ti,.T2, .  • ,хп), — на рис. б.Юе.
Рис. 6.9
197
Рис. 6.10
П р и мер 6.10.1. На рис. 6.11 показана декомпозиционная реализация функции /(яд, Ж2, Жз, Х4) — жджз V (ж2 Фжз)ж4 \/Ж1Ж4, где </1 = Ж1.Т3, <72 = (ж2 Ф ж3)ж4, д3 = Ж1Т4, F(y!,y2,у3) = yi V у2 V Уз- □
Пусть X = {Ж1,а?2, - - -, хп} —- множество входных переменных для функции f(X) = F(gi (Ai), <72(^2), - • •, ЫА)). где Аг — множества входных переменных, образующие разбиение множества X, т. е. А{ 0, AiC\Aj = 0 для г ф j и AiUA2U- • -0А^ = X. Тогда декомпозиция функции f называется дизъюнктивной. Недизъюнктивные декомпозиции называются нондизъюнктивними.
Пример 6.10.2. На рис. 6.12 изображена реализация нондизъюнктивной декомпозиции /(ж1, а?2, жз, Т5)	=
Рис. 6.11
198
Рис. 6.12
^’01(;';Ьз;2;^з)-.92(жз,:Г4,Ж5))- Здесь множества Ai = {г’ь^^з} и Аг = {хз,Х4,х$} не образуют разбиение множества X = {жь Ж2,Жз,Ж4,.'Г5}, поскольку Ai П А‘2 ± 0.
2.	Простая дизъюнктивная декомпозиция. Дизъюнктивная декомпозиция функции /(ж,. ж2,..., х„) вида /(жц.... ту) = F(y(A[), А2) называется простой.
П р и м е р 6.10.3. На рис. 6.13 изображена реализация простое! дизъюнктивной декомпозиции Дж]. х-г, х-.}, 2:4, .7:5) = ТДДа.ц, T2,.T3).T4,Z5). □
Чтобы определить свойства булевых функций, которые позволяют получать простые дизъюнктивные, декомпозиции в виде F(g(Ai .)> Аг), рассмотрим карту Карно функции / (рис. 6.14), где строки соответствуют переменным множества А2, а столбцы — переменным множества А; (например, на рис. 6.6а изображена карта Карно с А] = {.-z;i..t2} и А2 = {-т,з}). Построенная таким образом карта Карно называется карпюй декомпозиции для пары (А,а2).
Рис. 6.13
Рис. 6.14
199
Xl
X-2
Рис. 6.15
Теорема 6.10.1. Булева функция f(xi,X2,---,xn) тогда и только тогда 'имеет простую дизъюнктивную декомпозицию в (форме f(X) = F(g(Ai), А?), когда карта, декомпозиции функции f для пары (А], А-ф) содержит не более двух различных столбцов.
П р и м е р 6.10.4. Рассмотрим карту декомпозиции функции /(#i, .ту, xz, Т4, ж-,), показанную на рис. 6.15. Так как имеются только два различных столбца, то существует простая дизъюнктивная декомпозиция функции f в форме f = F(g(xi, ж2, жз), Ж4, S5). Для нахождения функции g(xt, ж2, %з) выберем строку карты, в ячейках которой содержатся как нули, так и единицы, например 4-ю строку (рис. 6.16). По выбранной строке составим функцию g с соответствующей таблицей истинности, показанной на рис. 6.17: g — Ж]Ж2жз V Ж]Ж2Жз V Ж]Ж2ж3.
1	0	0	0	1	1	0
।_______________________________1
ж2
Рис. 6.16
200
Ж1	0	0	0	0	1	1	1	1
х2	0	О	1	1	О	О	1	1
S3 0 10 10 10 1 д	1	0	0	0	1	1	0	0
Рис. 6.17
Приведя полученную формулу к минимальной ДНФ, получаем д = S1Z2S3 V х\х2. Теперь для нахождения функции F заме-
тим, что по выбору строки карты декомпозиции имеем <7 = 0 для столбца (1110)т и у = 1 для столбца (1 00 1)т. Таким образом, мы получаем карту Карно функции F от переменных д,Х4,х$ в виде, изображенном на рис. 6.18. По карте Карно находим минимальную ДНФ функции F(<7, S4, Т5) = дх$ \/х^х^ V дх^. □
Если все столбцы карты декомпозиции идентичны, то функция не зависит от переменных множества Ai и декомпозиция является тривиальной. Если карта содержит два различных столбца, но комбинации цифр в них содержат либо все нули, либо все единицы, то функция не зависит от переменных множества А2.
9
1 1
|0 1
Рис. 6.18
3.	Сложные дизъюнктивные декомпозиции. Дизъюнктивная декомпозиция, не являющаяся простой, называется сложной. Рассмотрим два вида сложных декомпозиций: итеративную и множественную.
Итеративная функциональная декомпозиция представлена в следующей общей форме:
/(X) = F(<7m(...</3C<72(.gi(A1),A2),A3),...,Am)	(6.2)
и основана на повторении простой дизъюнктивной декомпозиции по переменным Ац А2. .... А,„.
Множественная функциональная декомпозиция имеет вид
/(X) =F(51(A1)„92(A2),...,<7ni(Am)).	(6.3)
Связь между сложными и простыми дизъюнктивными декомпозициями дается следующими теоремами.
201
Теорема 6.10.2. Для данной булевой функции f(X) тогда и только тогда существует итеративная дизъюнктивная, декомпозиция, вида, (6.2), когда, существует, простая дизъюнктивная декомпозиция вида
J (^) = (gm (-41, А‘2,....	А,„),
простая, дизъюнктивная, деком,позиция функции у'т
9 т	Fm—1 (От—1(41, 42. •   , 4m_2), Ат_[),
простая, дизъюнктивная декомпозиция функции д'т_ц и т. д. до т = 1. При этом F = Fm. gm = Fm^, дт^ = Fm.,2, , Я2 = F, gi = д\
Теорема 6.10.3. Для. данной булевой функции f(X) тогда
а только тогда, существует .множественная дизъюнктивная декомпозиция вида (6.3). когда, существуют 'простые дизъюнктивные декомпозиции вида.
f(X) = Fl(g1(Al).A2.A3,...,Am)„
/GV) = ^(/72(42),Л1,Аз,..-,4т),
./ (^0 — Fm(gm(Л,„), 4i, А2, .... Am_i).
П р и м е р 6.10.5. Пусть f = Х1Х2Х3Х4 V ж-]Ж2Ж3Ж4 V Т3.Т4 V Ж1Ж2:Г.1 V Ж1Э?2®4-
Из карты декомпозиции, показанной на рис. 6.19а, получим простую дизъюнктивную декомпозицию f: f = F(g\ («1, х,2. -т3). хД где <7i = x-i V Х\Х2 V х.\Х2 и F = <7iT.j V 9\Х\.
Теперь рассмотрим функцию <71. Из карты, приведенной на рис. 6.195. получим простую дизъюнктивную декомпозицию ду = Т1(<72('Г1,.'Г2),.гз). где <72 = Т1.Т2 \/х,Д,2 и Fl = д2 V э:3.
Ж2 б
202
Эти две простые дизъюнктивные декомпозиции дают вместе итеративную дизъюнктивную декомпозицию f = F ( Fl (с/2 (х 1, Х‘>), ,т3), т4).
П р и м е р 6.10.6. Пусть / — xix2x3 V .тДг.тц V xix2x3 V Ж1Я2Ж4- Карта декомпозиции, показанная на рис. 6.20, имеет две различные строки и два различных столбца и, следовательно, дает следующие две декомпозиции функции f:
f = Fi(gi (жца^дз,^),
где 91(.Т1,.т2) = Vxis2. П1(д1.ж3,ж4) = giх3 V51 т4,
f = F2(g2(.x3,x^,xi,X2),
где д2 = х3 V ж4, F2 = g2xix2 V <72^2-В соответствии с теоремой 6.10.3. существует множественная дизъюнктивная дскомпозция / = Н(<71(.Т1ДС2),.92(ж3, ж4)).
Для нахождения функции F составим ее таблицу истинности, определяемую всевозможными комбинациями значений gi и д2 и соответствующими 71 значениями функции /:
х4
Рис. 6.20
<Л(.Т1,.Т2)	.?2(-ТЗ,Ж4)	F
0	0	0
0	1	0
1	0	0
1	1	1
Из таблицы истинности находим, что F — д\  д2-
§ 6.11.	Логические сети
1.	Определение и реализация булевых функций. Мультиграф G = (M,U,R), в котором выделено к вершин (полюсов), называется к-полюсной сетью. Сеть G, задаваемая неориентированным мультиграфом с к полюсами, в которой каждое ребро помечено буквой из алфавита X = {т.}.Х2,... ,xn,xi,x2,-  ,хп}, называется к-полюсной контактной схемой.
На рис. 6.21 приведен пример контактной схемы с двумя полюсами С1] И (1,(1.
203
(А:-+1)-полюсная схема, в которой один полюс выделен (он называется входным), а остальные полюса (выходные) равноправны, называется (1, к)-полюсником. Таким образом, если в приведенной на рис. 6.21 двухполюсной схеме рассматривать, например, полюс о.1 как входной, а полюс at, как выходной, то получаем (1,1)-полюсник.
Ребра контактной схемы называются контактами. Контакт, соответствующий логической переменной Xi, называется замыкающим и обозначается через 0 I \_0. Замыкающий контакт пропускает ток при х^ = 1. Контакт, соответствующий литере л,, называется размыкающим и обозначается как	Через него
ток проходит при Xi = 0. Таким образом, значение 1 интерпретируется как состояние переключателя “ток проходит”, а 0 — “ток не проходит”. Функции Xi Л Xj соответствует последовательное соединение контактов 0 I ILJI L^,, а функции T,i V Xj — параллельное соединение контактов —f—'I—I—.
Нетрудно заметить, что схеме, показанной на рис. 6.21, соответствует электрическая схема, приведенная на рис. 6.22, а так-
Рис. 6.22
204
же схема контактов, изображенная на рис. 6.23. На последнем рисунке показаны контакты, зависящие от значений переменных Х[, х-2, хз, а также схема соединений контактов.
Пусть а, Ь — полюса контактной схемы Е, [а, 6] — некоторая цепь из а в Ь, — конъюнкция литер, приписанных ребрам цепи [а, Ь]. Функция	определяемая формулой /ОДХ) =
V ^[а.ф в которой дизъюнкция берется по всем простым це-[“>&]
пям схемы, соединяющим полюса а, и Ь, называется функцией проводимости между полюсами а и b схемы Е. Говорят, что функция д(Х) реализуется (1, к)-пол,юсником, если существует такой выходной полюс Ъг, что /а,ь,(Х) — д(Х), где а — входной полюс. (1,1)-полюсники называются эквивалентными, если они реализуют одну и ту же булеву функцию. Сложностью (1,1)-полюсника называется число контактов. (1,1)-полюсник, имеющий наименьшую сложность среди эквивалентных ему схем, называется минимальным. Сложность минимального (1, ^-полюс-пика, реализующего функцию /. называется сложностью функции f в классе (1,1)-полюсников и обозначается через
Заметим, что задача нахождения минимального (1,1)-полюс-пика среди эквивалентных данному (1,1)-полюснику Е равносильна нахождению среди функций, реализуемых схемой Е, функции, имеющей наименьшее число вхождений переменных. Действительно, функцию, реализуемую (1,1)-полюсником, нетрудно представить в виде формулы, которая строится из литер в соот-
205
—x-i-----x3—
|---<«—x2-----x3 —< >-
—x} —.7,'2—Л3—
Рис. 6.24
встствпп с контактной схемой и имеет ровно столько вхождений переменных, сколько контактов имеет схема. Например, изображенной па рис. 6.23 схеме соответствует булева функция
/(11,12,13) = (.Ti V ж2) • ((xi V л2)  хз V .т3) V х^хз- (6.4)
Таким образом, задана нахождения минимального (1,1)-
полюснпка сводится к минимизации соответствующей булевой
функции.
Эффективное уменьшение числа контактов достигается с по-
мощью нахождения минимальной ДНФ булевой функции.
Найдем минимальную ДНФ функции (6.4), реализуемой схе-
мой рис. 6.22. Придавая логическим переменным х\, х2, х3 всевозможные значения, по схеме или формуле (6.4) получаем та-
блицу истинности:
Х1
Х2
13 f
0	0	0	0	1	1	1
0	0	1	1	0	0	1
0 10 10 10
10 10 10 0
1
1
1
1
но которой определим совершенную ДНФ: Т1Т21з V ДтД.з V Т|Ж23?з V х 1X2X3. Используя один из методов нахождения минимальной ДНФ, получаем формулу V ж2ж3 V Ж1.7;2.тз, эквивалентную формуле (6.4) и соответствующую схеме, состоящей из семи контактов (рис. 6.24а).
Отметим, что схема, изображенная на рис. 6.24а, допускает упрощение, соответствующее формуле (дц V т2)т3 V i]i2i3. которое приведено на рис. 6.246 и является минимальной схемой. Сложность минимальной схемы равна 6: L^(f) = 6.
2. Схемы из функциональных элементов. Ориентированная бесконтурная сеть, в которой полюса делятся на входные (входы) и выходные (выходы), называется схемой из функ-ционалъных элементов. Входные полюса помечаются символа-
206
мн переменных, а каждая вершина, отличная от входного полюса, некоторым функциональным символом. При этом должны выполняться следующие условия:
если « входной полюс, то полустепень захода вершины а равна, нулю: deg-(а) = 0:
- если вершина а не является полюсом и помечена '/«-местным функциональным символом /. то deg (а) = п, и дуги, входящие в а, перенумерованы от 1 до п.
Функционалънъ/м элементом называется всякий подмультиграф схемы, состоящий из невходного полюса а. помеченного соответствующим символом f. и вершины, из которых исходят дуги в вершину а.
П р и м е р 6.11.1. На рис. 6.25о представлена схема из функциональных элементов. Здесь входные символы помечены символами переменных тц, .7:2, Т3, -> одноместный функциональный символ, соответствующий операции отрицания; & двухместный символ, соответствующий операции конъюнкции. /3 некоторый двухместный символ, /], /2- /1 некоторые трехместные символы. Вершины, помеченные символами /|, /3 и /.4, являются выходными полюсами. Им соответствуют термы: ./'1 (X1. Х-2, .Г 3 ) h	- /1 (® 1, «2, *3 ) ), /-1 ( /з С*! *2, fl (т I, Х2, Ж3), J>i),
^з,	•тз)./1(т;4,;Г2,жз),.'Гз)). На рис. 6.256 изображен
функциональный элемент, определяемый вершиной, помеченной символом /4. Ему соответствует устройство, показанное на рис. 6.25g. □
Рис. 6.25
В примере 6.11.1 продемонстрировано, что каждый вывод схемы порождает некоторый герм.
Говорят, что функция / реализуется схемой S, если существует такой выход а схемы S, что функция fu, соответствующая терму выхода а, эквивалента функции f.
Схемы из функциональных элементов с одним выходом, у которых входные полюса помечены символами ад, х2, .хп, а-вершины, отличные от входных полюсов, — символами V, &, называются Хп-функциональнымг1 схемам,и. Сложностью схемы из функциональных элементов называется число ее вершин, отличных от входных полюсов, ^^-функциональная схема S, реализующая функцию /, называется .минимальной, если всякая другая ^^-функциональная схема, реализующая f, имеет сложность, не меньшую, чем сложность схемы X. Сложность минимальной схемы, реализующей функцию /, называется сложностью функции / в классе схем из функциональных элементов и обозначается через L(f).
П р и м е р 6.11.2. Сложность функции f = (Эд V £2)^3 V Х1Х2Х3 совпадает со сложностью .^-функциональной схемы, изображенной па рис. 6.26, и равна 8: L(f) — 8.
3. Мультиплексоры. Мультиплексором. 2т каналов (MUX2'») называется схема с т + 2т входами уг, у2, , ут-, Z\, Z'2, ..., Z2m и ОДНИМ ВЫХОДОМ д. В которой при 1/1 = bl, ..., Ут ~ Ът выход д принимает значение д =	где
J(bi,...,bm) = 2°bi+2lb2 + -- + 2m~1bm.
На рис. 6.27 показан мультиплексор MUXg.
П р и мер 6.11.3. Если т = 3, yi = 1. у2 = 0, уз = 1, то 9 = zJ(i.o,i)+i = zc>- О
208
Z\ z2
—У1
---У-2
---УЗ
9 zJ(yi,y2,ys)+l
Рис. 6.27
С помощью мультиплексора MUX2™, придавая переменным zi, z2, ..z2»i постоянные значения, можно реализовать любую булеву функцию /(?Ц, ?/2, • • • , Ут)-
4. Программируемые логические матрицы.
Рассмотрим схему, состоящую из
Р входов Z1, ..., zp и q выходов щ, ____Решетка ______
gq (рис. 6.28), в которой значе- _ элементов _ ния выходов определяются матри- 2	' 2
цей соединений (ср,), 1 i р,	&
1 h q, cih G {0,1} по следу-
ющим правилам: g^ — (zi V •	:	1	:
(z2Vc2/l)... (zpVCp/J. Таким образом,
9h = ziizi-2   • ziri где (’iyh — ci-2h = z _ ______g
 • • = irh = a остальные сг/, рав-
ны 0. Полученная схема называется	,, с „„
решеткой с р входами и q выходами
элементов которая определяется матрицей соединений (сцг).
Программируемой логической матрицей (ПЛМ) называется изображенная па рис. 6.29 схема, получающаяся соединением решетки А с 2п входами и к выходами, определяемой матрицей соединений (а.ц,), и решетки В с. к входами и т выходами, определяемой матрицей соединений (bhj).
Опишем преобразования, которые происходят при прохождении через ПЛМ значений переменных .щ, .т2, ..., хп. Поскольку к каждому входу ж7- присоединен инвертор х2, на 2п входов решетки А подаются значения переменных xi, xi, т2, ®2, .... хп,
209
хп. После прохождения решетки Л /i-й выход принимает значение функции (.1'1 V флХтд V а2/?)... V a2n-i,h)(xn V а2ПуЬ), а последующей операции инвертирования соответствует функция
V «i/,)(«i V а2/г)    (^я V a2n-\,h)^n V «2п,/>)-
Полученные к значений (1 < h ф А;) подаются на входы решетки В, после прохождения которой на выходе j образуется значение функции
к
Д ((.'И V	V «2/7.) •   Un V а2п-1./,)(Т V «2«,Л.) V bhj)-
/7=1
В заключение после инвертирования по законам де Моргана на выходе j получаем значе-к
ние функции fj = V bhj /7=1
(ац V «1/,)(т1 V а2/()---(;ГП V O2n—l.h)(®n a2n.Ji)' j —	Функции fj
соответствует дизъюнкция конъюнктов (определяемых формулами (т] V«i/,.) (т.Ц V «2Л) •  • (^'П V ^2п—1,/|) (Т„ V а2п,л)) таких, что
Рис. 6.29
Таким образом, при соответствующем выборе матриц («,/,) и (bhj) можно одновременно реализовать т произвольных ДНФ. содержащих не более к различных конъюнктов переменных от Т1, х2. .... х„.
§ 6.12.	Задачи и упражнения
1.	Составить таблицу истинности формулы х Ф у —> z V .г|у Л х.
2.	Доказать тождественную истинность формулы
210
и
Рис. 6.30
и
Рис. 6.31
3.	Доказать эквивалентность
х Л (х V z) Л (у V z) ~ (х Л у) V (ж Л z).
4.	Привести к ДНФ. КНФ. СДНФ и СКНФ формулу
(т Л (у V z)) -> (ж Л у) V Z.
5.	Используя метод Квайна и карты Карно, найти МДНФ и МКНФ формулы
xyz V xyz V xyz V xyz V xyz.
6.	Найти СДНФ и МДНФ по карте Карно, изображенной на рис. 6.30.
7.	Найти СКНФ и МКНФ по карте Карно, изображенной на рис. 6.31.
8.	Найти полином Жегалкина для булевой функции f, заданной вектором значений (1011 0100). Определить, каким классам Поста принадлежит функция /.
9.	Проверить с помощью теоремы Поста полноту следующих систем булевых функций:
а) {—>, ->}; б) {<->, Ф}: в) {ф}; г) {Л, ->}. Какие из указанных систем образуют базис?
Г л а в а 7
ФОРМАЛЬНЫЕ ИСЧИСЛЕНИЯ
§7.1	. Определение формального исчисления
Введем общее понятие формального исчисления. Будем говорить, что формальное исчисление I определено, если выполняются следующие четыре условия:
1.	Имеется некоторое множество А символов — алфавит исчисления I.
Конечные последовательности символов называются словами пли выражениям,и исчисления I. Обозначим через S множество всех слов алфавита исчисления I.
2.	Задано подмножество Г Q S, называемое .множеством (формул исчисления I. Элементы множества У называются формулами.
3.	Выделено множество Ах С У формул, называемых аксиомами исчисления I.
4.	Имеется конечное множество 91 отношений R\, R%, .., Rn между формулами, называемых правилами вывода, причем если
, </?т, <£>) G R-t, то р называется непосредственным, следствием. (формул </?i, ..., рт по правилу Ri.
Итак, исчисление I есть четверка (А, У, Ах, 91).
Выводом, в исчислении 1 называется последовательность формул </д,	•  • , Рп такая, что для любого i (1 < г п) формула
р., есть либо аксиома исчисления I. либо непосредственное следствие каких-либо предыдущих формул.
Формула р называется теоремой исчисления I, выводимой в I или доказуемой в I, если существует вывод ру, ..., рп, р, который называется выводом, (формулы р или доказательством теоремы р.
212
Вообще говоря, может не существовать алгоритма, с помощью которого для произвольной формулы через конечное число шагов можно определить, является ли выводимой в исчислении I или нет. Если такой алгоритм существует, то исчисление называется разрешимым. Исчисление называется непротиворечивым., если не все его формулы доказуемы.
§	7.2. Исчисление высказываний
Используя понятие формального исчисления, определим исчисление высказываний (ИВ).
Алфавит ИВ состоит из букв А, В, Q, R, Р и других, возможно с индексами (которые называются пропозициональными переменными'), логических символов (связок) Л, V, —а также вспо.м.огателъных символов (, ).
Множество формул ИВ определяется индуктивно:
а)	все пропозициональные переменные являются формулами ИВ;
б)	если <р, ф — формулы ИВ, то -кр, (<рЛ0), (</?V0), (<р —> ф) — формулы ИВ;
в)	выражение является формулой ИВ тогда и только тогда, когда что может быть установлено с помощью пунктов “а” и “б”.
Таким образом, любая формула ИВ строится из пропозициональных переменных с помощью связок	Л, V, —>.
В дальнейшем при записи формул будем опускать некоторые скобки, используя те же соглашения, что и в предыдущей главе.
Аксиомами ИВ являются следующие формулы для любых формул ф, %:
1)	(0-></?);
2)	(<р -> ф) ((<р -> (ф -> %)) -> (<р -> х));
3)	(<р А ф) -> <р;
4)	(<£> А ф) -> ф-
5)	& -> Ф) -> ((</? -> х) -> (<р (ф Л х)));
6)	(<р V фф
7)	-> (0 V <р);
8)	(<р -> х) ((0 -> х) ((у? v 0) -> х));
9)	(<д -> 0)	((<д -» -.0) -> ~><р);
10)	—> <д.
Указанные формулы называются схемами аксиом ИВ. При подстановке конкретных формул в какую-либо схему получается частный случай схемы аксиом..
213
Единственным правилом вывода в ИВ является правило заключения (modus ponens): если <д и <д —> 'ф — выводимые формулы, то ф - - также выводимая формула. Символически это записывается так:
У, У Ф
Ф
Например, если высказывания А Л В и А Л В —> (Л —> С) выводимы, то высказывание А —> С также выводимо согласно правилу заключения.
Говорится, что формула <д выводима, из формул <дх, ..., <дт (обозначается <Д1, ..., <рт Г <д), сочи существует последовательность формул V’l,   Фк, V-, в которой любая формула либо является аксиомой, либо принадлежит списку формул (Дх, ..., <д,;1, называемых гипотезами. либо получается из предыдущих по правилу вывода. Выводимость формулы <д из 0 (Г <д) равносильна тому, что <д — теорема ИВ.
Пример 7.2.1. Покажем, что формула у <д выводима в ИВ. Для этого построим вывод данной формулы:
1)	в схеме аксиом 2 ф заменим на <д <д, х ~ Т- Получаем аксиому (<д	(<д -> <д)) —> ((<д -> ((<д -> <д)	<д)	(<д -> <д));
2)	в схеме аксиом 1 ф заменим на <д. Получаем <д	(<д —> <д);
3)	из 1 и 2 по modus ponens заключаем (<д	((<д	<д) —*
<д)) -> (<д -> <д);
4)	в схеме аксиом 1 заменяем ф на <д <д. Получаем <д —> ((<р -> <д) -> ед):
5)	из пи. 3 и 4 по правилу вывода справедливо Г <д -ч- <д. □
Предложение 7.2.1. 1. Если ipi,... ,<рп,(р,ф — формулы ИВ, Г = {<Д1,..., <д7|.}, Г I- -ф, то Г, <д Г ф (можно увеличивать число гипотез).
2.	Тогда и только тогда (Дх,...,<д„ Г <д, когда <дх Л.. -Л<дп Г <д (сведение м,ножест,ва гипотез к одной гипотезе).
Теорема 7.2.2. (теорема о дедукции) Если Г, <д Г ф. то Г Г <д —> ф, где Г — набор некоторых формул <дх, • •<рп.
Следствие 7.2.3. Тогда и. только тогда <дх,..., <д„ Н <д, когда.
Ь- (<дх (<д2	(^„-1 -> (<дп -> <д)) • •  ))•	(7.1)
Дока з а т е л ь с т в о. Пусть <д1;..., <д„ Г <д. Тогда, применяя теорему о дедукции, имеем <дх,..., <ди-х Г —> <д. Аналогично <дх,..., <Дп-2 В <дп-1 (<дп —> <д) и т. д. Продолжая процесс
214
необходимое число раз, получаем F -э (<д2 -» ... —> (<^n-i (<Рп 93)) •••))• Для доказательства достаточности предположим, что F ф, где ф = срг -> (<^2	• -з- (w-i (фп </>))  •
Воспользуемся предложением 7.2.1., п. 1: у?] F ф. По правилу заключения получаем y>i F <д2 -> ... -> (<^п-1 (фп -> </>))- Далее через п шагов имеем </ц, <д2,  • • , <рп F <р. □
Таким образом, благодаря следствию 7.2.3. проверка выводимости формулы у? из формул ip\. р>2- .., срп сводится к проверке доказуемости формулы <р\ -> (<д2 —> (<дз —> • • 	(<Ап-1 —> (<А» —>
В § 6.1 определялось понятие истинности формулы алгебры логики. В исчислении высказываний таблицы истинности формул определяются точно так же. Напомним, что формула <д(Р[. . ,.,Р„) называется тождественно истинной (обозначается |= </?), если значение формулы ср равно единице при любых наборах значений пропозициональных переменных.
Следующая теорема сводит проверку доказуемости фомулы к проверке ее тождественной истинности.
Теорема 7.2.4 (о полноте). Формула. ср доказуема, тогда и только тогда, когда ср тождественно истинна:
F ср <->F ср.
Таким образом, для того чтобы установить, доказуема ли формула, достаточно составить ее таблицу истинности. Как известно. существует эффективный алгоритм построения таблицы истинности, и, значит. ПВ разрешимо.
П р и м е р 7.2.2. Докажем, что Р F Р. По теореме о дедукции это равносильно тому,'что F (Р —> Р). В свою очередь, по теореме о полноте, достаточно доказать, что |= (Р Р). Составляя таблицу истинности для формулы Р Р, убеждаемся, что Р -> Р тождественно истинна и, следовательно, доказуема. □
Если ср F ф и ф F ср, то будем писать ср = ф. Полученное отношение = является отношением эквивалентности на множестве всех формул ИВ.
Обозначим через ср < > ф формулу (ср —> ф) А (ф —> ср). Заметим, что ср = ф равносильно выводимости формулы ср о ф и это по теореме о полноте равносильно эквивалентности формул ср и ф, что означает совпадение таблиц истинности формул ср и ф. Таким образом, отношение эквивалентности ~ (см. § 6.3) и отношение эквивалентности = совпадают: ср ~ ф 4А ср = ф.
215
П j) и м е р 7.2.3. Так как <р Л ф ~ ~,(“V v 'Д/О. то у? Л ^> = ~i(_v v _,V’)-
Замечание 7.2.5. Пусть Ф — множество формул ИВ с переменными из .множества J. Рассмотрим алгебру = (ф. Л, V, -1. хЛ~>х, x\/-ix), где х - некоторая фиксированная, переменная,. Тогда, фактор-алгебра = является булевой алгеброй, называемой алгеброй Линденбаума для. ИВ.
Теорема 7.2.6 (о непротиворечивости). Исчисление ИВ непротиворечиво.
Д о к а з а т е л ь ст в о. По теореме о полноте любая формула, не являющаяся тождественно истинной, не доказуема в ИВ. Например, такой формулой является формула х Л ->«. □
Множество формул Г называется противоречивым, если Г Е а: Л -!.•£. Если Г - противоречивое множество формул, будем обозначать этол факт через Г Е.
Утверждение 7.2.7. Формула <д выводима из множества (формул. Г тогда и. только тогда. когда множество Г U — противоречиво: Г Е <р Г U {-^} Е.
Схема аксиом называется независимой в исчислении. если хотя бы один ее частный случай не доказуем в исчислении без этой схемы.
Теорема 7.2.8. Схемы аксиом ИВ независимы.
§ 7.3. Алгоритмы проверки общезначимости и противоречивости в ИВ
1.	Алгоритм Квайна. Напомним, что формула от пропозициональных переменных А\. А%......А^ является тожде-
ственно истинной или (что то же самое) доказуемой, если булева функция jA : {0.1}А' —> {0.1}, соответствующая формуле <д. тождественно равна 1. Для проверки значений функции fv используется так называемое семантическое дерево, т. е. бинарное корневое дерево, удовлетворяющее следующим условиям:
— каждое ребро помечено литерой Аг};
-литеры, выходящие из одной вершины, контрарны: Ai, ~<Ар, ребра соответствуют литере одной и той же пропозициональной переменной Аг тогда и только тогда, когда они находятся на одинаковом расстоянии от корня (рис. 7.1).
216
Рис. 7.1
Семантическое дерево имеет 2А: висячих вершин и для проверки общезначимости необходимо пройти 21' маршрутов от корпя до этих вершин.
Алгоритм Квайна позволяет проходить не. все семантическое дерево, а только его часть. Он состоит в том, что пропозициональным переменным А,. упорядоченным в набор (Ai, Аг,..., А*), последовательно придаются значения 0 и 1 и анализируются таблицы истинности формул, содержащих меньшее число переменных.
П р и мер 7.3.1. Проверить общезначимость формулы
= (((А Л В) -> С) Л (А -> В)) -> (А -> С).
Упорядочим пропозициональные переменные (А, В. С). Придадим первой переменной А значение / (А) = 1. Тогда формула преобразуется следующим образом: (((1Л .В) -> С')Л(1 —> В)) -> (1 —> С) ~ ((В —> С) Л В) —> С. В полученной формуле переменной В придадим значение f(B) = 1. Тогда преобразованная формула примет вид ((1 —> С)Л1) С ~ С -> С, т. е. будет общезначимой. В случае f(B) = 0 имеем ((0 —> С) АО)	С ~ 0 —> С. что
217
также общезначимо. Рассмотрим теперь случай f(A) = 0. Имеем у?((),В,С) = (((ОЛВ) •-> С)Л(0 -> В)) -> (о'-> С) ~1Л1->1~1.
Таким образом, все возможные случаи приводят к тождественно истинным формулам. Следовательно, формула <д тождественно истинна. На рис. 7.2а изображено семантическое дерево, соответствующее формуле <д. а на рис. 7.26 показана часть семантического дерева, которая фактически использовалась для проверки общезначимости.
2.	Алгоритм редукции решает ту же задачу проверки общезначимости формулы, но используется в том случае, когда в формуле содержится достаточно много импликаций. Идея алгоритма состоит в попытке нахождения значений пропозициональных переменных формулы <д, при которых значение функции fv равно 0. на основе того, что импликация является ложной в том и только в том случае, когда посылка истинна, а заключение ложно.
П р и м е р 7.3.2. Проверить тождественную истинность формулы = ((.4 Л В) -> С) -> (А --э (В С)). ~
Предположим, что формула ложна при некотором наборе значений переменных А. В. С. Тогда истинностная функция / по этим значениям переменных дает следующие значения формул: /((А Л В) -> С) = 1. /(А —> (В -» С)) = 0. Тогда из второго равенства получаем /(А) = 1, /(В —> С) = 0, откуда имеем f(B) = 1. /(С) = 0. Однако при этих значениях справедливо /((А Л В) —> С) = 0. Получили противоречие. Таким образом, формула тождественно истинна.
218
3.	_ Метод резолюций в ИВ. Пусть Dx — D{ V A, D-> — В2 V А — дизъюнкты. Дизъюнкт D\ \J D'2 называется резольвентой дизъюнктов D\ и D2 но литере А и обозначается через гейд(В1,В2). Резольвентой дизъюнктов Di и В2 называется резольвента по некоторой литере и обозначается через гез(7Д, £)2), res(A, А) 0. Если дизъюнкты D\ и В2 не содержат контрарных литер, то резольвент у них не существует.
П р и м с р 7.3.3. Если_£>1 — А V В V С, D2 = А V В V D, то res..i(Z)i,P2) = В V С V В V D, геев(£)1, В>2) = А V С V А V D, resc(Di,D2) не существует.
Утверждение 7.3.1. Если res(Z?i,В2) существует. то Dy. P2Eres(Bl,B2).
Пусть S = {Di, D2,..., Dm} — множество дизъюнктов. Последовательность формул </?i, <д2, .... рп называется резолютивным выводом из S, если для каждой формулы <д,- (i = 1,...,п) выполняется одно из условий:
— Pi ё S-
-- существуют J, к < г такие, что р^ = ies(pj,pk)-
Теорема 7.3.2 (о полноте метода резолюций). Множество дизъюнктов S противоречиво в том и только в том случае, когда существует резолютивный вывод из S, заканчивающийся 0.
Отметим, что метод резолюций можно использовать для проверки выводимости формулы р из данного множества формул pi,... ,рп. Действительно, условие pi,...,pn Е р равносильно условию pi,... ,рп, -ур Е, что в свою очередь равносильно условию чр Е, где чр = pi Л ... Л рп Л ~>р- Приведем формулу чр к КНФ: -ф = Di Л Р2 Л ... Л Dm, тогда чр Е <4- Di Л £>2 Л ... Л Dm Е <=> Di,D2,...,Dт Е. Таким образом, задача проверки выводимости р\,..., рп Е р сводится к проверке противоречивости множества дизъюнктов S' = {1Д, 1?2,..., Dm}, что равносильно существованию резолютивного вывода 0 из S.
Пример 7.3.4. Проверить методом резолюций соотношение А н- (В -» С), CD Е, F -> DE Е А -> (В -> F).
Согласно утверждению 7.2.7. надо проверить на противоречивость множество формул S' = {А (В -> С), CD —> E,F-> DE, А (В —> F)}. Приведем все формулы из S к КНФ: S (AVBVC, CD \ГЕ, F \J_DE, -А V V F} ~ {А V В V С, С V D V B,(F VB)(F VB),ABF}.
219
Таким образом, получаем множество дизъюнктов S" = {Л V B\/C,C\/D\/E,F\/D,F\/E,A,B, F}. Построим резолютивный вывод из заканчивающийся 0:
1)	resx(A V В V С, А) = В V С;
2)	resB(BV С, В) = С- __
3)	resv(C VDVE,FVD)=C\/EVF;
4)	resE(C V_EV F,FV Е) = Cv F;
5)	resc(GCVF) =F-
6)	res(F, F) = 0. □
Отметим, что метод резолюций достаточен для обнаружения возможной выполнимости данного множества дизъюнктов S. Для этого включим в множество S все дизъюнкты, получающиеся при резолютивных выводах из S. Из теоремы о полноте метода резолюций вытекает
Следствие 7.3.3. Если множество дизъюнктов S содержит резольвенты всех своих элементов, то S выполнимо тогда и только тогда, когда 0 S'.
Двойственным к правилу резолюций является правило согласия. Пусть К\ = К\ А А, К‘2 = К} А А — конъюнкты. Положим fes4(ki, F2) — К{ A К'2, res(A, А) 1.
Пусть S = {К\, К-2,..., К,,,} — множество конъюнктов. Последовательность формул <Д1, <Д21    , Рп называется выводом из S по правилу согласия, если для каждой формулы (i — I,... ,п) выполняется одно из условий:
~ pi G S;	__
— существуют j, k < i такие, что pi = fes(<^j, pi}-
Теорема 7.3.4. Множество конъюнктов S = {К\,К-2, ..., Кт} общезначимо (т.е. выполняется |= К\ V К-2 V.. .V Кт) тогда, и только тогда, когда существует вывод из S по правилу согласия, заканчивающийся символом 1.
4. Метод резолюций для хорновских дизъюнктов. В общем случае метод резолюций неэффективен, так как количество переборов, которые необходимо сделать для получения ответа. экспоненциально зависит от количества информации (числа дизъюнктов и переменных), содержащейся в множестве дизъюнктов. Однако для некоторых классов дизъюнктов, к которым относится класс хорновских дизъюнктов, метод резолюций эффективен.
220
Дизъюнкт D называется хорновским, если он содержит не более одной позитивной литеры.
Пример 7.3.5._Х.орновскими дизъюнктами^являются следующие дизъюнкты: А V В V С V D, А V В V Q, А, В. □_ _ В общем случае хорновские дизъюнкты имеют вид Aj V ... V Ап V В, (что эквивалентно формуле (Aj Л ... Л А„) —> В) или Ах V ... V Ап. Хорновский дизъюнкт вида Aj V • •  V А„ V В называется точным. При этом переменные Aj,..., Ап называются фактами, а переменная В - целью. Хорновский дизъюнкт вида Aj V ... V Ап называется негативным,. Дизъюнкт D = В называется унитарным позитивным дизъюнктом.
Если S — множество хорновских дизъюнктов, то невыполнимость множества S проверяется следующим образом. Выбираем в S унитарный позитивный дизъюнкт Р и дизъюнкт D из S, содержащий Р. После этого заменяем S на (В \ {£)}) U {res(B, В)} и продолжаем процесс до тех пор, пока S не будет содержать О или не найдется дизъюнктов Р и D указанного вида. Если- на заключительном шаге множество дизъюнктов будет содержать О, то исходное множество S противоречиво, в противном случае S непротиворечиво.
П р и м е р 7.3.6. Проверить на протаворечиво£гь_мнржестао дизъюнктов S = {F V 7? V Т, Q, R, Т V Р V R, Т V Q, Р V Q V R.}.
Для доказательства противоречивости запишем дизъюнкты из S в таблицу и применим описанный алгоритм, записывая результат каждого следующего шага в таблицу. Литеры, использующиеся на данном шаге, будем подчеркивать.
Номер шага	FV RVT	Q	R	TV F V R	TVQ	PVQVR
1	PvRvT	Q	R	TV PVR	T	PVR
2	PvT	Q	R	TVP	T	P
3	Р	Q	R	TVP	T	P
4						d
На шаге 4 получаем 0, являющийся резолютивным выводом из S. Следовательно, множество S невыполнимо. □
221
§ 7.4.	Формулы сигнатуры Е. Истинность формулы на алгебраической системе
Большинство определений этого параграфа будут индуктивными. Обозначим через 7(E) множество всех термов некоторой фиксированной сигнатуры Е (определение см. в § 2.3).
Введем понятие атомарной формулы сигнатуры Е:
1)	если t], t-2 Е 7(E), то = t‘2 — атомарная формула;
2)	если Р^ £ Е — предикатный символ, ii, <2; • • tn G 7(E), то P(ti, t-2,. • ,/п) ~ атомарная формула;
3)	никаких атомарных формул, кроме построенных по пп. 1, 2, нет.
Формула сигнатуры Е определяется следующим образом:
1)	атомарная формула есть формула;
2)	если р. ф — формулы, то ->р, (у? Л ф), (у V ф), (у —> ф), \Jx.p. Зхр — формулы;
3)	никаких формул, кроме построенных по пп. 1, 2, нет.
Символы V, Я, использованные в определении, называются соответственно квант,ором всеобщности и квантором существования и читаются “для любого” и “существует”. Все соглашения относительно расстановок скобок, принятые в § 6.1, остаются в силе и для формул логики предикатов. Кроме того, вместо записей V.ti ... \/хп р и Зад ... Зхп р будем использовать записи Vx’i,..., хп р и ,..., хп р.
Определим подформулы формулы у сигнатуры Е:
1)	если у — атомарная формула, то р - ее единственная подформула;
2)	если р имеет вид , или V.r рг, или Вт pi, то подформула формулы р — это либо р, либо подформула формулы pi;
3)	если р имеет вид pi Л р^, или pi V р-2, или сщ -> р^. то подформула формулы р — это либо р, либо подформула формулы р\, либо подформула формулы рр.
4)	никаких подформул формулы р. кроме построенных по пп. 1, 2, 3, нет.
Пример 7.4.1. Пусть Е = {F^2\P^}, р = \/х(Эу(х = F(z,y)) V P(z\) -- формула сигнатуры Е. Тогда \/х(Эу(х = F(z,y)) V P(z)), Зу(х = F(z,y)) V P(z), By (х = F(z,y)), x = F(z,y)), P(z) — все подформулы формулы p. □
Говорят, что вхождение переменной х в формулу р связано в р, если оно находится в терме или предикате подформулы фор-
222
мулы ip вида Vt-i/i или Эх ч/r, в противном случае это вхождение называется свободным в ip. Переменная х называется свободной (связанной), если некоторое вхождение х в р свободно (связано).
П р п м е р 7.4.2. Пусть S =	Рассмотрим фор-
мулы:
Р1(х):
РАх,у) -дУхАСт): ^(А(т,у) -э А(*)).
Переменная х в первой формуле является свободной, во второй —-и свободной, и связанной, в третьей - связанной; переменная у во всех формулах свободна. □
Предложением или замкнутой формулой сигнатуры И называется формула сигнатуры S, не имеющая свободных переменных.
II р и м е р 7.4.3. Формула V.T, у (,т + у = у + х) является предложением сигнатуры {+}. □
Запись <д(.7д,... ,з;„) будет означать, что все свободные переменные формулы р содержатся в множестве {.'/j, ...	.
Дадим индуктивное определение истинности формулы <д(т;х, ... ,хп) сигнатуры S на элементах o.i,... ,ап G А в алгебраической системе 21 = {A, Е) (запись 21 |=~- <Дах,... ,пп) будет означать, что формула р истинна на элементах гц,..., ап G А в системе 2().
1)	21 |= й(«ь •   ,«•«) ~	. ,ап), где йИд G 'Г(Е),
значения термов tl: t2 в системе 21 на элементах о.х,...,о„ G А совпадают:
2)	21 |=.Р(й(о1-.----Щ|),...,й.(о1,...,ал,)), где Рдд G Е. й, ..., й: 6 TfE), (й(«1,   • ,а«),   ; й(а1,  •  ,а71)> 6 А
3)	21 |= 0(u1,...,a,t) Л x(ai,... ,a„) <=> 21 |= -i/4ax;..., ап) и 211= х(«ь- • ,««);
4)	21 (= </’ («х,..., аТ1) V х(пх...., ап) 4=> 21 Д ф(а},..., ап) или 21 |= х(«1....«п);
5)	21 ф ААч......ап) -> х(о.].... , о,„) если 21 |= ^(о.х,...,
о.,,), то 21 |= х(«ь- • •:«„);
6)	21 |= -ч/'(<11 • , ап) <=> неверно, что 21 |= '0(°-1,   -, «„);
7)	21 f= Vx '(/'(.т, о.х,.... а„) <=> 21 |= Ф{а., о.х,..., «„) для любого а £ А‘.
8)	21 |= З.т ф(з:, ах, •  , «п.) <=> 21 (= A(a, о.|,..., ап) для некоторого о G А.
Если не выполняется 2( (= <д(а[,... ,о.„), то будем говорить,
223
что формула <р(щ,..., u„) ложна в системе 21, и писать 21 </?(«!,..
П р и м е р 7.4.4. 1. Записать формулу <р(.-г), истинную в (ш, +, ) тогда и только тогда, когда х четно.
2. Записать формулу ср'(х, у, z), истинную в (ш,+,•) тогда и только тогда, когда z - наименьшее общее кратное чисел ж и у.
1. <р(.т) ;= Зу (х = у + у).
2. cp'(x,y,z) ф(х,у,г) /\x(x,y,z), где формула ф “говорит” о том, что z делится на х и на у, а формула у “говорит” о том, что z делит все общие кратные х и у, т. е. является наименьшим из всех общих кратных:
ф 3u, V (г = и - X Л 2 = V • у),
X Vw (Эи, v (w = и  х Aw = v • у) —> Зиц (и; = wj • 2)).
Итак, ср'(х,у, z) = 3u,v(z = и  х A z = и • у) Л Vw (Эи, v (w = и  х A w — v  у) —> 3wi’(w = гщ  2)). □
Формула <р(.гд,..., хп) сигнатуры Е называется тождественно истинной или общезначимой, если для любой алгебраической системы 21 = (A, S), любого кортежа элементов (ui,..., ага) G А" выполнимо 21 |= </?(«!, •   ,ап). Если — тождественно истинное предложение, то пишем (= ср.
Формула <р(.Т1,..., хп) называется выполнимой в системе 21, если 21 <p(ui,..., ап) для некоторых Gi,..., а.п G А.
П р и м е р 7.4.5. 1. Формула х = х общезначима, поскольку7 21 |= а = а для любой системы 21 = [A. S) и любого элемента а Е А.
2. Формула ср Vrc, у (х • у = у • х) выполнима, но не тождественно истинна, так как (Z, •) |= ср, а	, у <р, где
МДХ)  множество матриц порядка 2 с элементами из Z.
3. Определим выполнимость формулы ср(у) ->Эж (Р(ж) Л Q(.t, у)) в системе 21 = ({1,2}, Р, Q), где Р = {1}, Q = {(1,1), (1,2)} Составим таблицу истинности предикатов Р и Q:
Р(1)
1
F(2) Q(l,l)
О 1
Q(l,2) Q(2,l)
1 О
Q(2,2) О
где Р(«) = 1 <=> 21 }= Р(о), Q(a.,6) = 1 <=> 21 (= Q(a.,b). По таблице истинности предикатов Р и Q составляем таблицу истинности формулы Р(х) A Q(x,y)-.
224
X т
1
2 2
У
1
2
1
2
Р(ж) Л Q(x, у)
1
1
О
О
из которой следует, что 21 |= 3,т (Р(х) Л Q(x, 1)), поскольку 2( |= F(l) Л Q(l,l), а также 21 Эх (Р(.т) Л Q(x, 2)), так как 21 Р(1) Л Q(l,2). Таким образом, 21 )= —кд>(1) и 21 )= т- е-21	</?(!) и 21	9^(2). Следовательно, формула </? не выполнима
в системе 21. □
Теорема 7.4.1. Если f — изоморфизм системы на систему Дтд, •  • л) формула сигнатуры системы 21, то для любых а.] ,..., а.п G А свойство 21 |= <p(o.i,.... о,п) эквивалентно свойству 23 )=	),..., /(ап)).
Множество формул Г сигнатуры Е с множеством свободных переменных X называется выполнимым, если существует система ОТ = (М, S), элементы ах G М для каждого х 6 X такие, что для любой формулы <р(т1,... ,хп) G Г выполнимо ОТ |= <р(аХ1,, аХп). Система ОТ называется моделью множества формул Г, и этот факт обозначается через ОТ |= Г. Множество формул Г называется локально выполнимым, если любое конечное подмножество Го множества Г выполнимо.
Теорема 7.4.2 (теорема Мальцева о компактности). Каждое локально выполним.ое множество Г формул, сигнатуры Е выполнимо.
Следствие 7.4.3. Если для любого п G со множество формул. Г сигнатуры Е имеет модель мощности п, то Г имеет бесконечную м,одел,ъ.
Доказательство. Рассмотрим множество Г = Ги {Э.т1,...,;г;п(-.(.т1 = .т2) Л = тз) Л ... Л= .т„)) I п G ш}. По предположению для любого п (= со множество Г U {ЭЖ1, . . . ,Хп (~|(.Т1 = Ж2) Л -|(.Т1 = ж3) Л ... Л	= Sn))} вы-
полнимо. Значит, множество Г7 локально выполнимо. По теореме компактности получаем выполнимость множества Г'. Но Г' может иметь только бесконечные модели. Следовательно, найдется бесконечная модель ОТ множества Г', которая, в частности, является моделью для Г. □
8 Зак. № 4872 Судоплатов
225
§ 7.5.	Исчисление предикатов сигнатуры £
Зафиксируем некоторую произвольную сигнатуру Е и определим исчисление предикатов сигнатуры £ (ИПЕ).
Формулами ИГР' будут формулы сигнатуры Е.
Примем следующие соглашения. Пусть xi,...,хп — переменные, t\, . . . , tn — термы сигнатуры £ и <д —• формула сигнатуры S. Запись ((д)ц1’" будет обозначать результат подстановки термов t},..., tn вместо всех свободных вхождений в <р переменных Х[,... ,.т„ соответственно, причем, если в тексте встречается запись (<д)ц1г"^'1, то предполагается, что для всех i =	ни
одно свободное вхождение в <д переменной -лу не входит в подформулу вида Уудц или Эу<Д1, где у — переменная, входящая в ti-
Аксиомами ИГ!" являются аксиомы вида 1-10 ИВ (см. § 7.2), а также аксиомы
И) \/.т<д	(<д)£;
' 12) (</>)t -> З.т <д;
13)	х = .т;
14)	х = у-> ((<д)* -> (<д)*).
Формулы 1—14 называются схемами аксиом ИП5'.
Правила вывода ИП^:
<д, <д->У> 2)	-» У
1р ' 1р -Ч-^ХЛр'	Зх (Д —> ip’
где в правилах 2 и 3 переменная х не входит свободно в ip. Понятие доказательства в ИПЕ определяется аналогично понятию доказательства в ИВ.
В исчислении предикатов ИГР' справедлива
Теорема 7.5.1 (о дедукции). Если ГU {<д,ip} — множество формул ИП\ то из Г, <д В ip следует Г В <д —> ip.
Таким образом, как и в исчислении высказываний, проверка выводимости дд,..., <дп В <д в ИП£ сводится к проверке доказуемости формулы (<Д1 —> (<Д —> . . . —> (<Дп —> (д) . . .)).
В ИП" справедлив аналог теоремы о полноте в исчислении высказываний:
Теорема 7.5.2 (теорема Геделя о полноте). Формула <д исчисления ИП^ доказуема тогда и только тогда, когда <д тождественно истинна.
226
Таким образом, проверка доказуемости формулы сводится к проверке ее тождественной истинности. Однако в отличие от ИВ в общем случае не существует алгоритма распознавания доказуемости формул ИИ , т. е. ИПЕ неразрешимо. Тем не менее если в формуле “записать”, что каждая переменная может принимать конечное число значений, то перебором всех возможных систем можно установить, является ли формула тождественно истинной или нет. В § 7.7 описан метод резолюций в ИП52, который, как и метод резолюций в ИВ, позволяет определять невыполнимость формул.
§ 7.6. Эквивалентность формул ИП£. Пренексные нормальные формы
Формулы р и чр сигнатуры S называются эквивалентными (</? = чр), если </? Н чр и чр Н р.
Из теоремы о дедукции и теоремы Геделя о полноте вытекает
Утверждение .7.6.1. Следующие условия эквивалентны: a) р = чр;
б) Г (р О чр);
в) Н (т1 #
Утверждение 7.6.2. В ИГт выполнимы все эквивалентности ИВ, а также следующие эквивалентности, в которых предполагается, что переменная, х не входит свободно в формулу чр, а переменная у не входит в формулу р:
а)	-|Эж р = Ух -<р,
в) За: (р V чр) = За: рУ чр, д) За; (р Л чр) = За; р Л чр, ж) Ух р = У у (р)*,
б)	->Ух р = За: ->р, г) Ух (рУ чр) = Ух рУ чр е) Ух (р Лчр) = Ух. р /\чр з)3хр = Зу(р)р/.
И р и м е р 7.6.1. Рассмотрим форму-	2
лы За; Уу Р(х, у) и Уу За: Р(х, у). Легко ви- X.
деть, что За; Уу Р(х, у) Н Уу За: Р(х, у), по-
скольку из 21 |= Зх.УуР(х, у) следует 21 |=
У у Р(а, у) для некоторого a. G А, а значит,
21 |= УуЗх Р(х,у). Однако УуЗх Р(х,у)	Pll( ' 3
ЗхУу Р(х,у), так как, например, в графе 21 = {А, Р) = ({1,2,3}, {(1,2), (2,3), (3,1)}) (рис. 7.3) выполнимо 21 |= Уу Зх Р(х,у), но 21 За; У у Р(х, у).
8*
227
Замечание 7.6.3. В ИП^ справедливо утверждение, аналогичное замечанию 1.2.5.. Если Ф — множество формул сигнатуры, £ с переменными из множества J, то фактор-алгебра Е/ = алгебры Е — (Ф, Л, V, ж Л -<х, х V ->ж) является булевой алгеброй.
Теорема 7.6.4 (теорема о замене). Если формула р получается из формулы ф заменой некоторого вхождения подформулы ф' на (формулу <р', эквивалентную ф' (уф = ф'), то tp = ф.
Формула ip сигнатуры Е называется бескванторной, если она не содержит кванторов. Говорят, что бескванторная формула у> находится в дизъюнктивной (конъюнктивной) нормальной форме, если она получается из некоторой формулы ф исчисления ИВ, находящейся в ДНФ (КНФ) заменой всех пропозициональных переменных х\,...,хп на некоторые атомарные формулы </?1,..., <рп сигнатуры Е соответственно.
Говорят, что формула у> сигнатуры S находится в пренексной нормальной форме (ПНФ), если она имеет вид QiX-i ...Qnxn^, где Qi, 1 С г п, — кванторы, а ф - бескванторная формула, находящаяся в ДНФ.
Теорема 7.6.5. Для любой формулы tp сигнатуры Е существует. формула ф сигнатуры. Е, находящаяся в ПНФ и эквивалентная формуле tp.
Для приведения формулы <д к ПНФ используются эквивалентности, описанные в утверждении 7.6.2., а также эквивалентность (<д —> ф) = (-чр V ф). Сначала формула преобразуется в эквивалентную ей формулу tp', не содержащую символа импика-ции; затем формула tp' последовательным вынесением кванторов (при этом, если необходимо, переименовываются связанные переменные) приводится к виду QjXi ... Qnxn tp", где Qi G {3, V}, 1 <С г п, tp" — бескванторная формула, и, наконец, формула <д" приводится к ДНФ, как показано в § 6.4.
Пример 7.6.2. Привести к пренексной нормальной форме, считая формулы tp и ф атомарными, формулу у Зж Vy <д(ж, у) —> Зж \/уф(х,у).
Избавившись от импликации, получаем у = ->(3.ж Mytp(x, y))V Зж Vy ф(х, у). Используя пп. а, б утверждения 7.6.2. и теорему о замене, получаем у = УхЭу ~чр(х,у) V Эх\/уф(х,у). Так как в формуле ЗжУу ф(х, у) переменные ж, у являются связанными, то по пп. в, г утверждения 7.6.2. имеем у = Уж Зу (-><д(ж, у) V
228
Э.-г Vy	Пусть и, v — некоторые новые переменные. Тогда
по пунктам ж, з утверждения 7.6.2. получаем х = V.t By (-кДж, y)V 3wV-cV’(u,t;)), откуда х = VxByBuVv (~кр(х,у) V ^(п,?;)). Формула ~ыр(х,у) V ’ф(и,х) находится в ДНФ, а значит, формула Vrr ЗуЗи Vw (—у) \/ip(u,vY) находится в ПНФ.
§ 7.7. Метод резолюций в ИП£
Подстановкой сигнатуры, Е называется конечное множество вида (ti/xi,... ,tn/xn}, где Ф ~ терм сигнатуры И, отличный от х-i (1 г п), все переменные .гц,... ,хп различны. Подстановка, которая не содержит элементов, называется пустой й обозначается через г.
Мы будем использовать греческие буквы для записи подстановок.
П р и мер 7.7.1. Множества {Fi(z)/x, y/z}, {с^/х, F2{y)/y, Ft(F2(c2)) / z} — подстановки сигнатуры И = {Fp\ F^^Ci^}. □
Пусть 9 — {tx/xx,... ,tn/xn} — подстановка сигнатуры Е, W -- множество формул (термов) сигнатуры Е. Тогда W9 — множество формул (термов) сигнатуры И, полученных из формул (термов) множества W заменой в них одновременно всех вхождений Xi (1 i п) на термы ф (1 г ф. п).
Если W = {Ф} или W = {t}, где Ф — формула, t — терм сигнатуры Е, то вместо {Фи {tбудем писать Ф6 и tO соответственно.
Пример 7.7.2. Пусть 6 = {cx/x,F{c2)/y1y/z} — подстановка сигнатуры Е =	с2,F^\F^}, t = Fx(x,y,z),
Ф F(.t) = Fi(.t,ci,z). Тогда t,9 = Fi(cx,F(c2),y), Ф0 = F(cj) = Fi (ct,ci,i/). □
Пусть 9 = {ti/xi,... ,tn/xu} и A = {qi/yi, -  -,qmlym} - подстановки сигнатуры E,/1; ..., tn, </i, ..., q.nl G T(E). Тогда композиция подстановок 9 и А фо А) есть подстановка, которая получается из множества {Д Х/х\,..., tnX/xn, q\ /у\,.... qm/Ут} вычеркиванием всех элементов фХ/х-р для которых tjX — Xj, и всех элементов qi/yi, таких, что ус G {t’i, ... ,хп}.
П р и м е р 7.7.3. Пусть 9 = {t\/x\, t^/x?} = {F(y)/x, z/y}, = {qi/yi,q2/y2,q3/y3} = {ci/x,c2/y,y/z} - подстановки сигнатуры E = {ci,c2,F(^}. Тогда {ttA/.TiД2А/ж2,qi/yi, qi/y2, q:i/y3} = {F(c2)lx,yly,cxlx,C2ly,ylz}. Так как t2X = у, то у/у должно быть вычеркнуто. Так как х,у G {.т,у}, то с^/х.,
229
Ci)у также должны быть вычеркнуты. Таким образом, во А = {F(c2)/x,y/z}. □
Упражнение. Доказать: 1) ассоциативность композиции подстановок, т. е. (0оА)оц = #о(Аоц) для любых подстановок 9, А, р; 2) 0 о е = е о в для любой подстановки 0. □
Подстановка 0 сигнатуры У называется унификатором для множества {Ф1,..., Фа } формул сигнатуры Е, если Ф1$ = ... = ФдД Множество формул {Ф1,...,Фа} сигнатуры Е называется унифицируемым, если для него существует унификатор сигнатуры У.
П р и м е р 7.7.4. Множество {P(ci,y), Р(х, F(c2))} формул сигнатуры Е = {щ, с2, Р^, F^)} унифицируемо, так как подстановка 0 — {ci/x,F(cz)/y} является его унификатором. □
Унификатор ст для множества {Ф1,..., Фа} формул сигнатуры Е называется наиболее общим унификатором (НОУ), если для каждого унификатора 0 сигнатуры Е этого множества существует подстановка А сигнатуры Е такая, что 0 = о о А.
Пусть W = {Ф1,...,Фа} — непустое множество атомарных формул сигнатуры Е. Множеством рассогласований в W называется множество термов {<х,..., Д}, где t, входит в Фг и начинается с символа (который есть либо сигнатурный символ, либо переменная), стоящего на первой слева позиции в Фг, на которой не для всех формул Фр ..., Фа находится один и тот же символ.
Пример 7.7.5. Пусть W = {Р(х, F(y, z)), Р(х, с), Р(х, F(y, Fi(z))) — множество формул сигнатуры Е = {Р^2\ F^, Fp^}. Во всех трех формулах первые четыре символа Р(х, совпадают, а на пятом месте в первой и второй формулах стоят разные символы: F, с. Таким образом, множество рассогласований в W — {F(y,z),c,F(y,Fi(z))}. □
Алгоритм унификации предназначен для распознавания того, является ли данное конечное непустое множество атомарных формул унифицируемым, и нахождения НОУ для этого множества в случае его унифицируемости.
Пусть W — конечное непустое множество атомарных формул. Алгоритм унификации для множества W:
Шаг 1. Полагаем к = О, И а = Ш, ста = £
Шаг 2. Если Wk — одноэлементное множество, то остановка: ста ~~ НОУ для W. В противном случае найдем множество Dk рассогласований для Wk-
230
Шаг 3. Если существуют хк, tk G Dk, tk G 7(S) такие, чтс xk — переменная, не входящая в tk, то перейти к шагу 4. В противном случае остановка: множество W не унифицируемо.
Шаг 4. Полагаем <Tfc+1 = ст о {tk/xk} и W*+1 = Wk{tk/xk} (заметим, что Wk+i = Wok+i).
Шаг 5. Присвоить к значение к + 1 и перейти к шагу 2.
Теорема 7.7.1. Если W — конечное непустое унифицируемое множество атомарных формул, то алгоритм унификации будет всегда кончать работу на шаге 2 и последняя подстановка ак будет НОУ для W.
Пример 7.7.6. Найти НОУ для W = {Р(с.т, F2(Fi(y))), P(z.F2(z),F2(u))}.
1.	к = 0, Ио = W, сто = е.
2.	Так как W - неодноэлементное множество, то Щ) не является НОУ для W. Множество рассогласований для Ио: Ос, — {c,z}.
3.	В £>о существует переменная тд = z, которая не встречается в терме to = с. Поэтому переходим к шагу 4.
4.	Полагаем оу = од о {c/z} = е о {c/z} = {c/z}. Ну = Ho{c/z} = {F(c,T,F2(F1(y))),F(c.F2(c).F2M)}.
5.	к = 1.
6.	Wi — неодноэлементное множество. Множество рассогласований для W\: Di = {.t,F2(c)}.
7.	Из Di найдем, что ту = х, Н = F2(c).
8.	Полагаем о-2 = оу о {F2(c)/t}, И2 = И]{F2(c)/j:} = {Р(с. F2{c), F2{F}(y))). Р(с,F2(c), F2{u))}.
9.	к = 2.
10.	W — неодноэлементное множество. Множество рассогласований для И2: О2 — {Fi(y),u}.
11.	Из D2 найдем, что .т2 = и., t2 — Fi(y).
12.	Полагаем оу = о2 о {Fj(у)/и} = {c/z, F2(c)/x,F\ (у)/и}. Из = W2{FA(y)/u} = {Р(с, F2(c), F^F^y))), F(c, F2(c). ^(FK?/)))} = {F(c,F2(c),F2(F1(y)))}.
13.	Из — одноэлементное множество. Поэтому 03 = {c/z, F2(c)/t,Fi (у)/?;,} — НОУ для W.
П р и м е р 7.7.7. Определить, унифицируемо ли множество H = {F(F1(c),F2(x)).F(y,y)}.
1.	к = 0, Ио = W, оо = е.
2.	Ио -- неодноэлементное множество. Множество рассогласований для Ио: Dq = {Fi(с),у}.
231
3.	Из Do найдем, что x,q = у, t0 ~ Fife).
4.	сп = сто ° {Fi(c)/y} = {F^c)/?/}, WL = {P(Fi(c),F2(x)). Р(М(о),Г,(С))}.
5.	к = 1.
6.	Wi — неодноэлемептное множество. Множество рассогласований для W'p Di = {F2(x), Fi (с)}.
7.	В Di нет элемента, который был бы переменной. Поэтому W не унифицируемо. □
Литерой сигнатуры Е называется атомарная формула или отрицание атомарной формулы сигнатуры Е. Дизъюнкт,ом сигнатуры £ называется литера сигнатуры £ или дизъюнкция литер сигнатуры И.
Примеры дизъюнктов сигнатуры И = {Р^\ F^, F^, с}: F(Fi(a;)), -ъР(ВД), P(F\(x)) V->(F\(x) = F2(x,y)), РДДР(ж), г)) V ->P(F2(x,y)) Мх = с.
Пусть Ф — дизъюнкт сигнатуры Е вида ф\ V • • • V фн V у или -тф} V • • • V -apn V у, где ф1 — атомарные формулы сигнатуры Е (1 i <; ?/,). Предположим, что множество формул {ф],... ,фп} имеет НОУ ст. Тогда ф1сг V усг или соответственно -apicr V уст называется склейкой Ф. Полученную формулу в дальнейшем будем обозначать через Ф<т.
П р и м е р 7.7.8. Пусть Ф = Р(х) V P(Ffy)) V ->Р2(х). Формулы Р(х) и P(F(y)) имеют НОУ а = {F(y)/.-r}. Следовательно. Фст = F(F(y)) V -nF2(F(y)) -- склейка Ф. □
Пусть Ф], Ф‘2 — два дизъюнкта, не имеющих общих переменных, Li, L'2 = L2 — литеры в Ф[ и Ф2 соответственно. Если 1ф и ~^L2 имеют НОУ ст, то дизъюнкт, получаемый из дизъюнкта Ф|<т V Ф2<т вычеркиванием L\<r и Б2ст, называется бинарной резольвентой Ф1 и Ф2, а литеры L\ и L2 называются отрезаемыми литерами. Если Фхсг = Lj и Фг<т = Б2, то полагаем бинарную резольвенту Фг и Ф2 равной 0.
Если Ф] и Ф2 имеют общие переменные, то. заменив в формуле Фг эти общие переменные на переменные, не встречающиеся в Ф1 и Фг, получим формулу Ф2, которая не имеет общих переменных с формулой Фг- Бинарной резольвентой формул Ф, и Фг называется бинарная резольвента формул Ф[ и Ф2.
П р и мер 7.7.9. Найти бинарную резольвенту формул Ф1 Pifx) V РДх) и Ф2 -^Pi(c) V РДх).
Заменив переменную х в Фг нау. получим Ф2 = -iFi(c)VFj(y). Выбираем Li — Рфх), L2 — ~Fi(c). Так как ~<L2 = L'2 = Fi(c), то
232
L\ и L'2 имеют НОУ а — {с/т}. Бинарная резольвента формул Ф1 и Ф'2 получается из Фгсг V Ф2сг ~ Fi(c) V Р2(с) V ~iF](с) V Р3(у) вычеркиванием А (с) и ~<Р\(с). Следовательно, Р2(с) V Рз(у) — бинарная резольвента Ф] и Ф2, a Pi(x) и -тР| (с) — отрезаемые литеры. □
Резольвентой дизъюнктов Ф] и Ф2 (гев(Ф1,Ф2)) является одна из следующих бинарных резольвент:
—	бинарная резольвента Ф] и Ф2;
—	бинарная резольвента склейки Ф] и Ф2;
—	бинарная резольвента Ф4 и склейки Ф2;
—	бинарная резольвента склепки Ф4 и склейки Ф2.
Пример 7.7.10. Найти геь(Ф[,Ф2). где Ф1 = F(a:)VF(F(y))V Р1(^ (у)). Ф2 = -F(F(F1(c1))) V Р2(с2).
Склейка Ф1 есть Ф) = Ф1{Р(у)/.т} = F(F(y)) V Pi(Fi(y)). Бинарная резольвента Ф'( и Ф2 есть Fi(F(F1(ci))) V F2(c2). Следовательно, гс8(Ф1,Ф2) = Fi(F(Fi(ci))) V Р2(с2). □
Пусть S — множество дизъюнктов. Резолютивный вывод Ф из S есть такая конечная последовательность Ф i, ..., Фа дизъюнктов, что Фа = Ф и каждый дизъюнкт Фг или принадлежит S, или является резольвентой дизъюнктов, предшествующих Ф,.
Универсальным замыканием, формулы Ф(я1, - - -, хп) называется предложение V.7.4 ... V.T,, Ф(®1,..., хп).
Теорема 7.7.2 (о полноте метода резолюций). Если S — множество дизъюнктов, то множество универсальных замыканий формул из S невыполнимо тогда и только тогда, когда существует резолютивный вывод 0 из S.
Пример 7.7.11. Доказать невыполнимость множества формул W = {Ф1,...,Ф6}, где Ф1 = Fj(c].F(c2),F(c3)), Ф2 = P2(ci), Ф3 = Pi(x,x,F(x)), Ф4 = ->Fi(.T,y, z) VFi(jxz), Ф5 = -Р2(т) V ~iPx(y, z,и) V ->Fi(;r, и) V P3(;i;, у) V Р3(ж, z), Ф6 = ^F3(ci, c3).
Построим резолютивный вывод 0 из W:
Ф7 = ге8(Ф2,Фг>) = ген(Ф2, Ф.г,{г/у}) = ->Pi(z, z, и) V ->F3(ci, и) V Р3(с1,г);
Ф8 = гев(Ф3,Ф7) = ^Рз(щ.Р(хУ) V F3(ci..t);
Ф9 = гев(Фб,Ф8) = ”,Р3(с1, F(c3));
Ф10 = геб(Ф4,Ф9) = -^Рфсцу^^з));
Фц = гея(Ф|, Ф1П) = 0.
Пример 7.7.12. Выполнимо- ли множество предложений {Ф1,Ф2}? Если выполнимо, построить систему, на которой пред
233
ложения Ф1, Ф2 истинны:
ф] 3yVxz((P1(.T,z) -> (Р2(ж) Л Р3(у))) Л А(у)),
ф2 — V.T ((Р4(ж) -> ->Р3(ж)) Л Зу Pt (ж, у)).
Пользуясь эквивалентностями из утверждения 7.6.2., приведем формулы Ф1, Ф2 К виду QixQzyQsZ ф, где Q), Q2, Q3 — кванторы. ф — конъюнкция дизъюнктов:
Ф1 = 3yV.-rz((-1Pi(a.-,z) V Р2(ж)) Л (^РДж, z) V Р3(у)) Л Р^у)), Ф2 = Vt Зу ((-,Р4(.т) V ->Рз(.т)) Л РДж, у)).
Выполнимость множества формул {Ф],Ф2} сигнатуры Е = {Рр\ Р2Х\ Р;р\ Р}1)} равносильна выполнимости множества фор-
{MxZ (-1Р1 (ж, z) V P2(x)),\/xz (-1Р1 (ж, z) V Рз(с)),
Р1(ф, V.T ЬР4(ж) V -.Р3(ж)),УжР1(ж, Р(ж))}	(7.2)
сигнатуры Е' = Е U {с, F^}. Действительно, пусть множество формул {Ф1,Ф2} выполнимо. Тогда существует алгебраическая система 21 = {А, Е) и элемент с’ Е А, для которых 21 |= Vx z {->Р\(х, z) V Р2(ж)) Л Уж z (->Pi(x, z) V Р3(с')) А ,Р^с') и 21 |= Уж (~>Р4(ж) V -ВД)-
Кроме того, для .любого а Е А найдется элемент в А, который обозначим через G(a), такой, что 21 |= РДа, G(a)’), т. е. 21 [= \/.т РДт, G(t)). Тогда в системе 21' = (Л,Е'), где с' является интерпретацией с Е Е', G — интерпретацией Р £ Е', истинны формулы из (7.2).
Напротив, если все формулы из (7.2) истинны в системе 21' = (Л. Е'), то формулы Ф1, Ф2 будут, очевидно, истинны и в системе 21=(А,Е).
Исследуем множество дизъюнктов
{-РДж.Д V P2(t),~1Pi(.t,z) V Р3(с), Р4(с),-1Р4(ж) V -пРз(ж),
РДж,Р(ж))}	(7.3)
па выполнимость с помощью метода резолюций: res(->Pi(.z:, z) \J Р3(с), РДж, Р(ж))) = Р3(с), res(P3(c).-.P4(T) V -Рз(т)) = ->Р4(с), res(->P4(c),P4(c)) = 0.
234
Построили резолютивный вывод нуля. Следовательно, множество дизъюнктов (7.3) невыполнимо. Тогда и множество предложений (7.2) невыполнимо, что равносильно невыполнимости множества предложений {Ф1,Ф2}.
Пример 7.7.13. Выполнимо ли множество предложений {Ф1,Ф21Фз}? Если выполнимо, построить систему, на которой эти предложения истинны:
Ф1 ЭаДРДж) Л Vy(P2(y)Р3(.т,у))),
ф2 — Vs (Pi(ж) -> Vy (Р4(у) -» ~.Р3(ж, у))),
Ф3 Vs (Р2(ж) -> ->Р4(я)).
Приведем формулы Ф], Ф2, Фз к виду QixQzip, где Qi,Q2 — кванторы, -ф — конъюнкция дизъюнктов:
Ф1 = 3sVy(Pi(s) Л (~>Р2(у) V Р3(х,у)),
Ф2 = Vs у (-iPi(s) V “Pi (у) V ->Р3(.т,у)),
Ф3 = V.v; (-iP2(.t) V -ДД^)).
Так же, как в примере 7.7.12, строим множество дизъюнктов: {Р1(с),-'Р2(у) V P3(c,y),->Pi(s) V ~>Р4(у) V ~>Рз(х,у),
-P2(s)V-P4(s)}.	(7.4)
Исследуем это множество на выполнимость с помощью метода резолюций:
res(Pi(c),-iPi(s) V ~'Р4(у) V -пР3(ж,у)) = ->Р4(у) V ~1Р3(с,у),
res(-P2(y) VP3(c,y),-.P4(y) V-.P3(c,y)) =-тР2(у) V--P4(y). (7.5)
Других резольвент для множества (7.4) нет, поэтому резолютивный вывод 0 из (7.4) не существует. Рассмотрим множество, составленное из констант, входящих в формулу (7.4), т. е. {с}. Определим на множестве {с} предикаты Pi, Р2, Р3, Р4 так, чтобы множество формул из (7.4) и (7.5) выполнялось на системе ({с}; Pi, Р2, Р3, Р4). Из (7.5) следует, что необходимо потребовать либо с Р4, либо (с, с) Р3 и с Р2. Положим с £ Р4, (с, с) Р3, с Р2. Из (7.4) следует, что необходимо потребовать cEl], Таким образом, на системе ({с}; Pi, Р2, Р3, Р4, с) выполняются все формулы из (7.4); более того, на ней истинны все формулы из (7.4) с навешанными на них кванторами всеобщности по переменным х, у, что равносильно истинности формул Ф1, Ф2, Ф3 на системе ({с}; Pi, Р2, Р3).
235
П р и м е р 7.7.14. Выполнимо ли множество предложений Ф2}? Если выполнимо, построить систему, на которой эти предложения истинны:
Ф1 ЭмУтЭгУу (F3(z) Л ((F2(z,z) Л -’Pi(u)) V ~’((F3(y) ~>
Ф2 V.T (Зу Р2{х,у) -> ~‘Рз(х)).
Преобразуем формулы Ф1 и Ф2:
Фх = ЗиУхЗг\/у(Р3(уР) Л (P2(x,z) V ~-F3(y) V Fj(y)) Л ->Pi(u)), Ф2 = Vt у (-iF2(.t, у) V ->F3(.r)).
Исследуем множество дизъюнктов
{Fi(F(.r)), F2(.r, F(.-r)) V ^Рз(у) V F] (y), -А(с),
-’Р2(х,у) V-ад}	(7.6)
на выполнимость:
res(-F1(c),F2(.T,F(3;))V-F3(y)VF1(y)) = F2(a;, F(s))V-F3(c), rcs(F2(.?;, F(s)) V ->F3(c), ^F2(.t, у) V ~>F3(.t)) = -тР3(с), rcs(F2(s,F(T:)) V -тР3(у) V А(у), -.F2(a-,y) V ~^3(ж)) =
-'F3(y) VFt(y),
rcs(-'F3(y) V F] (y), F3(F(®))) = Ft(F(.T)),
res(~>F2(.r, у) V ->F3(.t), F3(F(s))) = -lP2(F(.t), y).	(7.7)
Таким образом, резолютивного вывода 0 из множества (7.6) не существует. Построим алгебраическую систему 21 = {A; F3, F2, Р3,Р,с), в которой будут истинны формулы (7.6) и (7.7) с навешанными на них кванторами всеобщности по переменным х, у. Ясно, что с G А. Так как 21 |= V.t(->F3(c) Л F3(F(.t)), то F(c) с. Пусть А = {с, с'}. Положим F(c) т=± с'. Так как 21 [= V.7:/ 3(F(.7:)), то необходимо, чтобы F(c') — с! и с! G F3. Из (7.7) следует, что с $ F3. Поскольку 21 |= Уху (Fi(F(.t)) V -,F2(F(x),y)), полагаем с' G Fi, (с', с) F2, (с'-.Р) i Р-2- Предикаты А и Р2 доопределяются произвольно. Таким образом, в системе ({с,с'};Fi,F2, F3) такой, что с' G Ft. (с', с), (с', с')	F2, с F3, с' G Р3, истинны
фор.мулы Ф[ и Ф2. □
Следующий пример показывает, как формализуются предложения и методом резолюций эффективно доказываются теоремы при переходе к соответствующим формализациям.
П р и м е р 7.7.15. Установить, что из посылки “Студенты суть граждане” следует заключение “Голоса студентов суть голоса граждан”.
236
Пусть S(x},C(x} и У(ж, у) означают “ж — студент’’, “ж — гражданин'’ и “ж есть голос у” соответственно. Тогда посылка и заключение запишутся следующим образом:
Vy(S(y) С*(у))	(посылка),
Vt (Ey(S(y) Л У(ж, у)) -> 3z(C(z) Л У(х,г))) (заключение). Формула, соответствующая посылке, эквивалентна дизъюнкту -S(y) V С(у). Так как
-Л/.ж(Зу(£(у) Л К(ж,у)) -> Bz(C(z) Л У (ж,г))) =
= -Mx^y(^S(y) V -У(ж,у)) V 3z(C(z) Л У(ж,г))) =
= -’УжУуЭд(-15(у) V ->У(ж,у) V (C(z) Л V(.t,z))) =
= 3.?;EyVz(S(y) Л К(ж,у) Л (-<C(z) V ->У(ж, z))),
имеем три дизъюнкта, определяющие отрицание заключения:
S(b), V(a, b), -iC(z) V	z).
Доказательство заканчивается следующим образом: res(^(y)vC(y),S(b)) = C(b),
res(C'(b), -'C(z) V ->V(tz, г)) = ->V(a, b),
res(K(a,b),^K(a,b)) = 0. □
. Приведенный метод резолюций служит основой языков логического программирования, главным отличием которых от “процедурных” языков является то, что программа не указывает, как что-либо следует делать для решения задачи, а описывает некоторые элементы и связи между ними (модель определенной сигнатуры) и ставит цель, т.е. задает вопрос об этой системе (на формальном языке это означает проверить истинность предложения на данной системе или найти элемент, удовлетворяющий заданной формуле). При этом компьютер самостоятельно ищет стратегию для решения поставленных вопросов.
Например, рассмотрим отношения отец(Х, У) |Х является отцом для У] и родитем>(У, Z) [У является родителем для Z], На языке Пролог программа, по которой выдается ответ на вопрос “Кто является дедушкой Ивана?” выглядит так: dedyuiKa(X,Z) : — отец(Х.У'), родителъ(У\ Z)
7 — дедушка (А'. Иван).
237
§ 7.8.	Задачи и упражнения
1.	Доказать выводимость в ИВ:
а)	(ф -> ФУ (Ф -> х) ь (95 -> х);
б)	(<р -> (ф -4 у)) н (Ф х));
в)	(<р -4 (Ф -4 у)) Р ((95 Л ф) -4 у);
г)	(<р -> ф) в ((95 л х) -> (Ф л х));
д)	(<Р -> Ф) Ь ((<Р V у)-4 (ф V у)):
е)	-.95 В (95 -4 ф).
2.	Выводимы ли в ИВ следующие формулы:
а)	((А V В) -4 (А Л С’)); б) (((А -4 В) -4 В) -4 А);
в)	(((А 4 В) 4 В) 4 В); г) (->(А V -А) -4 (А V ->А));
д)	(А -4 ->(А -> -А)); е) ((А -4 В) (В -4 А))?
3.	С помощью алгоритма Квайна и алгоритма редукции доказать тождественную истинность аксиом ИВ.
4.	С помощью алгоритма Квайна и алгоритма редукции проверить общезначимость следующих формул:
а)	((А -4 В) -4 (В -4 А));
б)	((А V В) -4 ((-.А Л В) V (-.В Л А))).
5.	Методом резолюций проверить следующие соотношения:
а)	(А V С), (С -4 В), (В -4 А) В (А -4 (В -4 С));
б)	((A VC) 4 В), (С -4 (А V В)), (ВС -4 (А V В)) I- (В -4 С).
6.	Проверить на_противоречивость множество хорновских дизъюнктов {AV В V С \/ D, В, AV В V С, С, В V D}.
7.	Состоялся розыгрыш футбольного кубка между командами “Пламя”. “Рекорд”, “Стрела” и “Трактор”. Было высказано три прогноза: победит “Пламя” или “Рекорд”; не победит “Пламя”; не победит ни “Рекорд”, ни “Трактор”. Известно, что подтвердился только один прогноз. Какая команда выиграла кубок?
8.	Пусть /В), д^1,	— функциональные, а	~ преди-
катные символы. Являются ли формулами следующие слова:
a)	P(f (х)) Л Vx -^Q(g(y, z), х, h(z, у, х));
б)	P(Q(x,p(x,y),/i(x,?/,x)));
в)	/г(х,р(х,1/),/(.г))?
9.	Выписать все подформулы формулы:
a) Q(x,g(x,y),h(x,y,z)y, б) (Vx-'P(x) -4 (VzP(x)AQ(t, у, z))).
238
10.	Перечислить свободные и связанные вхождения в следующих формулах:
а)	Зя: (F(x, у) V ->Уу Q(x, у));
б)	b\/xP(x,y)^Q(f(x,y))).
11.	Написать предложение, истинное в системе (ш; •) и ложное в системе (Z; •).
12.	Определим на множестве людей следующие отношения: отец(.т, у) — х является отцом для у, мать(.г, у) — х является матерью для у, муж(.т,у) — х является мужем для у, жена(.т, у) — х является женой для у, м(х) — х имеет мужской пол, ж(.т) — х имеет женский пол. В сигнатуре указанных отношений описать следующие отношения:
а)	брат(.т, у) — х является братом для у,
б)	сестра(.т, у) — х является сестрой для у,
в)	сын(.т,у) — х является сыном для у.
г)	дочь(я:, у) — х является дочерью для 1/,
д)	племянник^?, у) — х является сыном брата или сестры для у, е) племянница(.т, у) — х является дочерью брата или сестры Для у,
ж) зять(х, у) — х является мужем дочери или сестры для у.
з) невестка(.т, у) — х является женой сына или брата для у.
13.	Доказать выполнимость формулы
Vt Vi/3z (Р(.т, z) A P(z,y) А ->(х = z) А ->($ = у)).
14.	Доказать тождественную истинность формулы
V.7; (<д(.т) —> -ч/Я1))	_’(3т<д(.т) AV.tv(.t)).
15.	Привести к ПНФ формулу
(-'(V.rV?/ Р(х,у) -> \/х\/у R(x, у)) V VzVy Р(х,у)).
16.	Построить все попарные композиции F о Oj подстановок F — {Fi(y)/x,F2(x,z)/y,ci/z},e-2 = {F2(Fi(t),//)/t, Fi(cy)/y, Fi(z)/z}, #з = {Р2(щ)/.г, c-i/y, x/z] и в,у = {y/x,z/y,xlz} сигнатуры E = {c^c^F^F^}.
17.	Определить, унифицируемо ли множество И’. В случае унифицируемости найти наиболее общий унификатор:
а)	Н7 = {Р(с,я:),Р(с,с)};
б)	ТГ = {F(c,.T,F(.r)),P(c,?y,?/)};
в)	W = {F(u,Fi(x,y)) =x,F(y,z) = х, F(u, Fj(c, z)) = .т}.
239
18.	Определить, имеют ли склейки следующие дизъюнкты. Если да, построить их:
a)	F1(.7:)VF2(j/)VF1(F(.t));
б)	Ffr) = F2(y) V F(F2(c)) = F2(y) V F(z) = F2(z).
19.	Найти все возможные резольвенты следующих пар дизъюнктов: a) -F(ж) V Р2(ж,Ci), F (с2) V F2(c2,cj);
б)	-пЛ(ж) VF2(x,x), -F2(c,F(c));
в)	F:(ж) = F2(j/, щ) V F (ж), -F(F(?/)) = z V -F(F(у)).
20.	Проверить невыполнимость следующих множеств формул:
a)	{-F (-''О V F(.t) = ж, F (F(c)) V ->у = ж};
б)	{F(C1),-F2(.v) V F3(c1j2/),-F(.t) V -F4(y) V -Е3(ж,У), F2(c2), F(q)}-
21.	Установить, выполнимо ли множество предложений {Ф1,...,Ф„}. Если множество выполнимо, построить для него модель:
а)	ф, - -V;r(F(z) -> Чу(Р(у) -> ((С(ж) -> -<2(?/)) W^F^))));
б)	<F ^±y.ryy(Pi(x,y) -> Е2(ж,у)), ф, — V.tV?/(F2(.7:,j/) -> Ез(ж,у)), Ф3 3.t3?/F(.t,?/);
в)	Ф] \/ж((Е1(ж)Л-Е2(ж)) -> Зу (Р3(х,у) ЛР4(у))),
Ф2 Зж(Е5(ж) Л F(x) ЛУу(Рз(х,у) -> F5(i/))),
Ф3 \/ж(Е5(ж) -> -F2(.t)).
СПИСОК ЛИТЕРАТУРЫ
[1]	Акритас А. Основы компьютерной алгебры с приложениями. — М.: Мир, 1994. (Гл. З)1.
[2]	Басакер Р., Саати Т. Кончные графы и сети. — М.: Наука, 1974. (Гл. 4).
[3]	Белов В. В. и др. Теория графов. — М.: Высш, школа, 1976. (Гл. 4).
[4]	Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. — М.: Наука, 1977. (Гл. 4 - 6).
[5]	Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по курсу дискретной математики. — М.: Наука, 1992. (Гл. 4 - 6).
[6]	Гиндикин С. Г. Алгебра логики в задачах. — М.: Наука, 1972. (Гл. 6, 7).
[7]	Горбатов В. А. Фундаментальные основы дискретной математики. — М.: Физматлит, 2000. (Гл. 1, 2, 4, 6, 7).
[8]	Деньдобренко Б. Н., Малика А. С. Автоматизация конструирования РЭА. - М.: Высш, школа, 1980. (Гл. 4).
[9]	Ершов Ю. Л., Палютин Е. А. Математическая логика. — М.: Наука, 1987. (Гл. 1, 2, 6, 7).
[10]	Кнут Д. Искусство программирования для ЭВМ. Т. 13.	М.: Мир,
1977. (Гл. 4).
[11]	Кристофидес Н. Теория графов: алгоритмический подход. — М.: Мир, 1978. (Гл. 4).
[12]	Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. — М.: Энергия, 1980. (Гл. 1, 2, 4, 6, 7).
[13]	Кук Д., Бейз Г. Компьютерная математика. — М.: Наука, 1990. (Гл. 1-4).
[14]	Курейчик В. М. Математическое обеспечение конструкторского и технологического проектирования с применением САПР. — М.: Радио и связь, 1990. (Гл. 4).
[15]	Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. — М.: Наука, 1984. (Гл. 1, 2, 6, 7).
[16]	Лекции по теории графов/ В. А. Емеличев, О. И. Мельников, В. И. Сарванов, Р. И. Тышкевич. — М.: Наука, 1990. (Гл. 4).
[17]	Липский В. Комбинаторика для программистов. — М.: Мир, 1988. (Гл. 4, 5).
[18]	Логический подход к искусственному интеллекту/ А. Тейз, П. Грибо-мон, Ж. Луи и др. — М.: Мир, 1990. (Гл. 4, 7).
’В скобках указаны номера глав настоящего учебника, при изучении которых эта литература может оказаться полезной.
241
[19]	Мендельсон Э. Введение в математическую логику. — М.: Наука, 1984. (Гл. 1. 2, 7).
[20]	Нефедов В. Н., Осипова В. А. Курс дискретной математики. — М.: Изд-во МАИ, 1992. (Гл. 1, 2, 4 - 7).
[21]	Новиков Ф. А. Дискретная математика для программистов. — СПб: Питер, 2001. (Гл. 1, 2, 4 - 7).
[22]	Общая алгебра. / О. В. Мельников, В. Н. Ремесленников, В. А. Ро-маньков и др./ Под ред. Л. А. Скорнякова. Т. 1, 2 — М.: Наука, 1990. (Гл. 1, 2).
[23]	Оре О. Теория графов. — М.: Наука, 1980. (Гл. 4).
[24]	Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы: теория и практика. — М.: Мир, 1980. (Гл. 4, 5).
[25]	Свами М., Тхуласираман К. Графы, сети и алгоритмы. — М.: Мир, 1984. (Гл. 4).
[26]	Столл Р. Множества. Логика. Аксиоматические теории. — М.: Просвещение, 1968. (Гл. 1. 2, 6, 7).
[27]	Фридман А., Менон П. Теория и проектирование переключательных схем. — М.: Мир, 1978. (Гл. 6).
[28]	Фудзисава Т., Касами Т. Математика для радиоинженеров. —- М.: Радио и связь, 1984. (Гл. 1,2,4 6).
[29]	Харари Ф. Теория графов. — М.: Мир, 1973. (Гл. 4).
[30]	Холл М. Комбинаторика. — М.: Мир, 1970. (Гл. 5).
[31]	Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. — М.: Наука, 1983. (Гл. 6, 7).
[32]	Шенфилд Дж. Математическая логика. — М.: Наука. 1975. (Гл. 1, 2, 6, 7).
[33]	Яблонский С.В. Введение в дискретную матаматику. — М.: Наука, 1986. (Гл. 4, 6).
Список адресов электронной литературы
1.	http://catalog.unior.ru/resinfо.phtml?ReslD=474
2.	http://abs.vvsu.ru/Books/Diskr_za/default.asp
3.	http://mirea.boom.ru/diskret.html
4.	http://www.mail.ru/~k805/html/di skra.htm
5.	http://rk-cmb.chat.ru/algo/ln_dm_01.htm
6.	http://uuu.isu.ru/~slava/do/disc/curshome.htm
Приложение
Варианты типового расчета
Условия задач
1.	Докажите тождества, используя только определения операций над множествами.
2.	Докажите утверждение.
3.	Докажите методом математической индукции.
4.	А = {а, Ь, с}, В = {1,2,3,4}, Pr С А х В, Р2 С В2. Изобразите Pi, Р2 графически. Найдите [(Pi о Р2)-1]. Проверьте с помощью матрицы [Р2], является ли отношение Р2 рефлексивным, симметричным, антисимметричным, транзитивным?
5.	Найдите область определения, область значений отношения Р. Является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным?
6.	Является ли алгеброй следующий набор 93 = (В; S)?
7.	Постройте подсистему 23(X), если...
8.	Используя многомодульную арифметику с вектором оснований /3, вычислить а. + Ь, а — Ь, 3 • а, 17-1 (mod /3), 2/13 — 5/19. Каков знак числа х?
9.	Даны графы Gi и G2- Найдите Gi U G2, Gi П G2, G\ Ф G2, Gi x G2. Для графа Gi U G2 найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
10.	Найдите матрицы фундаментальных циклов, фундаментальных разрезов, радиус и диаметр, минимальное множество покрывающих цепей графа G. Является ли изображенный граф эйлеровым? Является ли изображенный граф планарным?
11.	Составьте таблицы истинности формул.
243
12.	Проверьте двумя способами, будут ли эквивалентны следующие формулы...
а)	составлением таблиц истинности;
б)	приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований.
13.	С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкипа.
14.	Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции f(x,y,z) двумя способами:
а) методом Квайна; б) с помощью карт Карно.
Каким классам Поста принадлежит эта функция?
15.	С помощью карт Карно найдите сокращенную, все тупиковые и минимальные ДНФ, КНФ булевой функции /(.г'1,.т2, Ж4), заданной вектором своих значений.
16.	Является ли полной система функций? Образует ли она базис?
17.	С помощью алгебры логики проверьте истинность соотношения для любых множеств А, В, С. Если соотношение неверно, постройте контрпример.
18.	С помощью алгебры логики докажите тождества из задания 1.
244
Вариант 1
1.	А Г) (В U С) = (А П В) и(Л П С), А х (В U С) = (А х В) U (Л х С).
2.	|Л|	|В|	|Л\В| = |Л|.
3.	7Т' — 1 кратно 6 для всех п > 1.
4.	В] = {(о, 1),(а,2),(/;,3),(с,2),(с,3),(с,4)}, Р2 = {(1,1), (2,1), (2,2), (2,3), (2,4), (3,3), (4,4)}-
5.	Р С R2, (ж, у) G Р ж2 + у2 = 1.
6.	(cv;+,0).
7.	® = (Z;+,-), X = {-5,4}
8.	/3 = [5,7,11,2], а. = 34, b = 58, ж = [2,5,1,1].
11.	(ж V у) Ф- (у / ж), ж|у) -> (z ф жу).
12.	ж -> (у ф г) и (ж -> у) ф (ж -> z).
13.	(ж V у) (z ф ж).
14.	/(0,1,0) = /(1,0,0) = /(1,0,1) =0.
15.	(1101 1101 ООП ООП).
16.	3 = {х V у,ж ф у}.
17.	(А U В) \ (С П Л) = (В \ С) \ (Л U С).
245
Вариант 2
1.	A U (В П С) = (A U В) Г) (A U С), (A U В) х С = (А х С) U (В х С).
2.	Cd ~Ь СО — со.
3.	п3 + 11и кратно 6 для всех п € со.
4.	Р1 = {(а,1),(а,2),(а,3),(а,4),(Ь,3),(с,2)}, Р2 = {(1,1), (1,4), (2,2), (2,3), (3,3), (3,2), (4,1), (4,4)}.
5.	Р С R2, (х,у) е Р О х • у > 1.
6.	(Q\Z; +,-,:).
7.	® = (Z;+,-), X = {-5}.
8.	/3 = [3,7,11,2], а = 32, b = 74, х = [1,4,7,0].
11.	(ж о у) V (у J. ж), ((.ж -> y)\z)®xy.
12.	ж|(у -> z) и (ж|у) -> (ж|г).
13.	(ж Vy) -> (гфж).
14.	/(0,1,1) = /(1,0,0) =/(1,1,0) =0.
15.	(1111 1100 1011 1011).
16.	3 = {ж у, ж Л у}.
17.	(A U В) \ (С П В) = (А \ С) U (А \ В).
246
Вариант 3
1.	АПВ = (A UP),
А х (В \ С) = (А х В) \ (А х С).
2.	[0,1] U [2,3] ~ [0,1].
3.	1-4 + 2- 7 + 3-10 + -- -+ n(3n + 1) = n(n + I)2.
4.	Pi = {(а, 1), (а, 2), (а, 4), (с, 3), (с, 2), {с, 4)}, Р2 = {(2,1), (3,1), (3,2), (4,1), (4,3)}.
5.	Р С IS2, (ж,у) g Р <=> у = |яг|.
6.	(R; •,:,—!).
7.	53 = (Z;+,-), X = {-3,4}.
8.	р = [7,11,5,2], а = 24, b = 67, х = [5,2,1,1].
11.	(.г V ?;) О (у } ж), ((ж|у) z) ®ху.
12.	ж Л (у ф z) и (ж Л у) ф (ж Л z).
13.	(ж V у) —> (z ф ж).
14.	/(0,0,0) = /(0,0,1) = /(1,0,1) = /(1,1,1) = 1.
15.	(1110 0101 ООН 0101).
16.	3 = {ж -н у,ж|?/}.
17.	(АиС)\(ВПА) = (А\В)\(АПС).
247
Вариант 4
1.	A\(BUC) = (А\ В) Г\ (А\С), Ах (В ПС) = (Ах В) П (Ах С).
2.	2Ш + 2й = 2В.
3.	10’1 — 1 кратно 9 для всех п Е ш.
4.	Pi - {<«, 1>, <«,2>,<Ь,2), <6,4>, <с,3), <с,2>}, Р2 = {(1,1), (1,2), (2,2), (3,3), (4,3), (4,4)}.
5.	Р С Ж2, (х, у) ЕР & х2 + х = у2 + у.
6.	<IR; У",
7.	Я8 = <^;+,-), X = {4,10}.
8.	ft = [7,11.3,2], а. = 46, b = 38, х = [4,5,2,0].
И. (,т <-> у) V (у х), ((ж -> y)|z) ф ху.
12.	.г, А (у Ф z) и (ж А у) ф (ж A z).
13.	(.т V у) -> (z о х).
14.	/(0,0,1) = /(1,1,1) = /(1,1,0) =0.
15.	(1101 ООП 1101 ООП).
16.	3 = {жфу,ж Vy}.
17.	(АПВ)и(А\С) = А\(ВОС).
248
Вариант 5
1.	(AUB)\C = (A\C)U(B\C), (А П В) х С = (Ах С) П (В х С).
2.	[а, 6] ~ К.
3.	1-2 + 2- 3 + 3- 4 + ... + п(п + ]) = »(»+У(»+2)
4.	А = {(«, 1), (а, 4), (6,2), (6,3), (с, 1), (с, 4)}, Р2 = {(1,1), (1,4), (2,1), (3,4), (4,3), (4,1)}.
5.	век2, (х, :</) G р Ф? х -у
6.	(Q; у/” :)-
7.	® = (w;+,-.3), X = {2,5}.
8.	(1 = [11, 7, 3,2], а = 67, 6 = 79, х = [6,5,1,0].
11	(•'• V у) -> (у ® ж), ((:/;	y)|z) | ху.
12.	х Л (у —> z) и (х Л у) —> (х Л z).
13.	(.7; V у) —> (z х).
14.	./(0,0,0) = f(l, 1,1) = /(1,1,0) = 0.
15.	(1100 1011 1111 1011).
16.	3 = {7г —> у, х Л у}.
17.	(А \ В) U (А \ С) = А \ (В U С).
249
Вариант 6
1.	(4UB) = (АПВ), (АГ\(В) х (CQD) = (АхС)П(В х В).
2.	|Z х Q| = iv.
9	_1 | 1 I 1 L J -А  — —S— °- 1-2 2-3 ~ 3-4 ~ ~ п(п+1) п+1 •
4.	Рг = {(а, 1), (а, 2), (а, 4), (Ь, 1), (Ь, 4), (с, 3)}, Р2 = {(1,1), (2,4), (2,1), (3,3), (4,2), (4,1)}.
5.	Р С R2, (ж, у) е Р <=> х + у = -2.
6.	(Z;+, —, —2).
7.	® = (R \ {0};1), X = {2}.
8.	/3 = [11,5,7,2], а = 58, b = 37, х = [7,2,1,0].
11-	(х ф у) о (?/|ж), ((х J. у) о z) V ху.
12.	х Л (у <-> z) и (х Л у) (х Л z).
13.	(х\у) ф (z -> х).
14.	/(0,0,1) = /(0,1,1) = /(1,1.0) - /(1,1,1) = 1-
15.	(0101 0101 1110 ООП).
16.	3 = {ж о у,ж|у}.
17.	(А \ В) П (А \ С) = А \ (В П С).
250
Вариант 7
1.	(А \ (В П С) = (А \ В) U (А \ С), (А\В)хС = (АхС)\(ВхС).
2.	[0,1] ~ [0,1).
3-	(1 - |)(1 - i)(i -	 (1 - £) = W Для п > *
4.	Рх = {{а, 1), (Ь, 3), (b, 1), (Ь, 4), (с, 3), (с, 2)}, Р2 = {(1,3), (1,4), (2,2), (3,3), (4,3), (4,4)}.
5.	Р С R2, (ж, у) 6 Р О ж2 + у1 — 4.
6.	(cu;:,—1).
7.	® = (R2;+,-), Х = {(1,2),(0,1)}.
8.	(3 = [5,3,11,2], а = 44, b = 59, х = [3,2,7,1].
11-	(ж v У) Ну -г), ((х|у) <-> z) ф ху.
12.	х Л (y|z) и (ж Л у)|(ж Л г).
13.	(z ->ж) о (?/|ж).
14.	/(0,0,0) - /(1,0,1) = /(1,1,1) = 0.
15.	(000 ООП 1101 1101).
16.	Д = {ж ф у, х\/у}.
17.	(А ф В) \ (А ф С) = А \ (В Ф С).-
251
Вариант 8
1.	лив = лпв, ССО=>ЛхССВх D.
2-	[0,1] ~ (0,1].
3.	I2 + 22-F З2 +    + n2 = п(п+1^2п—.
4.	Л = {(а, 1), (Ь, 3), (с, 1), (с, 4), (с,3), (с, 2)}, Р2 = {(1,1), (1,2), (1,4), (2,1), (2,2), (2,3) (3,3), (3,2), (3,4), (4,3), (4,4), (4,1)}.
5.	Р С R2. (х,у) G Р у < х - 1.
6.	(R\ £:+,•).
7.	»-(Q;-4),X = {3}.
8.	/1 = [3,11, 7,2], а = 21, Ъ = 77, х = [2,8,3,1].
И. (.-г Ф у) -> (?/ / х), ((х\у) Vz)<^xy.
12.	х V (у -> z) и (:r V у) -> (;r V z).
13.	(х\у) ф (z —> х).
14.	/(1,0,1) = /(0,1,0) = /(1,1,1) = 0.
15.	(1011 1011 1100 1111).
1G. 3 = {;к -> У-.^ л у}.
17. (А \ В) Ф (Л \ С) = А ф (В \ С\
252
Вариант 9
1.	(Л П В) \ С = (А \ С) П (В \ С), (А х В) U (С х £>) С (A U С) х (В U £>).
2.	ш2 ~ w’.
3-	2! + з; + • • • + “тп- = 1 — ТП Аля п 2.
4.	В, = {(а, 1), (а, 2), (а, 4), (Ь, 3), {с, 1), (с,4)}, Р2 = {(1.3), (1,2), (2,3), (3,2), (3,4), (4,1)}.
5.	РСК2, (;т?, у) G F я2 — у.
6.	(Q;+,-,:,|).
7.	® = (Z;+,-), X = {-2,16}.
8.	Р = [5, И, 7,2], а = 53, b = 88, х = [4,9, 3,0].
11.	х о (у -> (у 4 .-с)), ((?г|у) V z) ф ху.
12.	а: V (у|г) и (ж V у)|(,7; V z).
13.	(z -> .7.) О (х|у).
14.	/(1,0,0) =/(1,1,0) = /(0,1,1) = /(0,1,0) = 1.
15.	(0101 ООН 0101 1110).
16.	3 = {ж о у,ж|у}.
17.	(A U В) ф (A U С) = A U (В ф С).
253
Вариант 10
1.	A U (А П В) = А П (A U В) = А, (AUB)x (Си В) = (AxC)U(BxC)U(AxP)U(B х В).
2.	ш + п = ы.
3.	1-2 + 2- 5 + 3- 8 + ... + n(3n - 1) = n2(n + 1).
4.	Рх = {(а, 3), (а, 2), (5,2), (5, 3), (с, 1), (с, 4)}, Р2 = {(1,1),(1,2),(2,2),(3,3),(4,1),(4,4)}.
5.	Р С R2, (ж, у) € Р <=> х2 у.
6.	<R\{0};+,:)-
7.	® = <Q+,-), Х = {2,|}.
8.	/3 = [5,11,3,2], а = 48, b = 35, х = [2,5,1,1].
11.	х J, (у -> (у|х)), X ф (у V Z о ху).
12.	х V (у <-х z) и (x V у) <-> (х V z).
13.	(z -> х) ф (х\у).
14.	/(0,1,1) = /(1,0,0) = /(1,0,1) = 0.
15.	(000 1101 ООП 1100).
16.	3 = {я7Фу,х Vy}.
17.	(А \ В) ф (А \ С) = А П (В Ф С).
254
Вариант 11
1.	(А\В)\С = A\(BUC),
А С С, В С D => А х В = (Л х D) П (С х В).
2.	ш2 ~ Z.
3.	п3 + 5п кратно 6 для всех п Е iv.
4.	Л = {(а, 2), (а.4), (6,3), (с, 1), (с,2)},
Р2 = {(1,1), (1,3), (2,4), (3,1), (3,4), (4,3), (4,2}}-
5.	Р С Z2, (ж, у) Е Р х2 + у2 = 1.
6-	(Q; У”,-,-Ю).
7.	<В = (Z3;+,-), X = {(0,1,1), (0,0,1)}.
8.	V = [7, 5, И, 2], а = 54, b = 76, х = [4, 3,2,0].
11.	х ее (у —> (у ф ж)), ж|(у V z | ху).
12.	X ф (?/ ЕЕ z) И (ж ф у) ЕЕ (ж ф Z).
13.	((ж г у) ^2) Фу.
14.	/(0,0.1) =/(1.0.0) = /(1,1,0) = 0.
15.	(1011 1111 1011 1100).
16.	з = {ж Л у, ж -> у}.
17.	(А\В)и(Л\С) = А\(В®С).
255
Вариант 12
1. А\(В\С) = (А\ В) U (ЛПС),
U'2 \ (А х В) = (Л х В) U (В х В).
2.	ш2 ~ Z2.
3.	4П - 1 кратно 3 для всех п > 0.
4.	В( = {(ft,l),(ft,3),(c,l),(c,2),(c,3),(c,4)},
В2 = {(1,1), (2,2), (2,3), (2,4), (3,2), (3,3), (3,4), (4,2), (4,3), (4,4)}-
5.	ВС Z2, (ж, у) G В <=> х + у кратно 3.
G. (w; +,-,:)•
7. <В = (Q,+,-), X = {|}.
8. /3 = [3,11,5,2], а = 61, ft = 42, х = [1,7,2,0].
Q
9. Gp
(j4 зО
10.	G-.
11.	x -> (y|(y Ф ж)), X (у V z I жу).
12.	ж Ф (у -> г) и (ж ® у) -> (ж ф г).
13-	((ж|у) -> г) ® у.
14.	/(0,0,1) = /(0,1,1) = /(1,1,1) =0.
15.	(000 1110 0101 0101).
16.	3 = {ж|у,ж о у}.
17.	(Л\В)и(В\С) = (ЛиС)\В.
256
Вариант 13
1.	Аи(В\С) = (АиВ)\(С\А); А,В^0, (А х В) и (В х А) = (С х D) => А = В = С = D.
2.	(0,1] ~ [0,+оо).
3.	4” + 15п — 1 кратно 9 для всех натуральных п.
4.	Pj = {(g, 1), (о, 2), (о, 4), (6,2), (/>, 4), (с, 3)}, Р2 = {(1,1), (2,2), (2,4), (3,3), (4,4), (4,2)}.
5.	Р С Z2, (ж, у) 6 Р <=} х — у кратно 2.
6.	№
7.	ф = (w;4-,-), X = {2}.
8.	= [7,11,3,2], а = 73, b = 36, ж = [6,7,1,0].
11.	х 1 (у -4 (у V ж)), ж|(у О Z ф жу).
12.	ж ф (y|z) и (ж ф у)|(ж Ф z).
13.	((ж 1 у) -> z) фу.
14.	/(0,0,0) = /(0,0,1) = /(1,1,0) = 0.
15.	(000 ООП 1100 1111).
16.	3 — {жфу,ж\/у}.
17.	(А П В) ф (В U С) = (А \ В) ф С.
9 Зак. № 4872 Судоплатов
257
Вариант 14
1.	А П (В \ С) = (Л П В) \ (Л П С), (Л х В) U (С х D) С (Ли С) х (В U В).
2.	2“' + iv = 2Ш.
3.	11"+1 + 122"-1 кратно 133 для всех п > 0.
4.	Pj = {(а, 2),(а,3),(а,4),(с, 3),(с, 1),(с,4)}, Р2 = {(1,4), (2,3), (2,1), (3,4), (4, 2)}.
5.	В С Z2, (а;,у)ЕР^ 2.Г = Зу.
G. (Q;+,-,y/2).
7. <В = (R; У,2), X = {!}.
8. /1 = [3,5.11,2], а = 43. b = 87, х = [2,4,7,1].
11.	х ф (у -> (у О а;)), х J, (у V z\xy).
12.	х J, (у < -> z) и (j; J. у) <-> (.т J, z).
13.	((а: у) -> Р) о у.
14.	/(0.0,0) = /(0.1.0) = /(1,1,1) = 0.
15.	(1100 0101 ООН ООП).
16.	з = {а; А у, а.- -> у}.
17.	(Л U В) \ (Л U С) - Л \ (В U С).
258
Вариант 15
1.	ЛпВ = АиВ, _	__
и2 \ (С X D) = (С xU)U(U X D).
2.	2ш+п = 2“.
3.	9"+1 - 8n — 9 кратно 16 для всех п 0.
4.	А = {(а, 1), (а, 2), (6,3), (6,4), (с, 3), (с,4)}, Р2 = {(1,1), (1,4), (2,1), (2,2), (2,4), (3,3)}.
5.	Р С Z2, (ж, у) Е Р <=> х + у нечетно.
6.	(R+; у/~,:, •), где R+ = {х Е R | х > 0}.
7-	«В = (Q\{0}; :),* = {£, £}•
8.	(3 = [5,11,3,2], а = 58, b = 32, х = [3,5,1,0].
П- (а-’ 4- У)|(?/ V яг), (я о у) ф (z -> ху).
12.	т|(у ф z) и (з;|у) ф (x^z).
13.	((.т 1 у) ~^z)^ у.
14.	/(0,0,0) =/(0,0,1) =/(1,0,0) =/(1,1,0) = 1.
15.	(0010 0111 1010 1101).
16.	3 = {х Vy,x -н- у}.
17.	(Л\В)и(В\С') = (А\В)иС.
9*
259
Вариант 16
1.	(А П В) U (Л П В) = (Л U В) П (A U В) = А;
(A U В) х (С U В) = (Л х С) U (В х С) U (Л х В) U (В х В).
2.	|Z2| =
3.	п(2п2 — Зп + 1) кратно 6 для всех натуральных п.
4.	Pi = {(а, 2), (а, 3), (а,4), (6,1), (&, 2), (6,4)}, Р2 = {(1,1), (1,3), (1,4), (2,2), (2,3), (3,2), (3, 3), (4,3), (4,4)}.
5.	Р С Z2, (ж, у} е Р <=> х — у четно.
6.	(Q+; +, •, -1), где Q+ = {ж G Q|t > 0}.
7.	53 = (Z; X = {3,4}.
8.	= [7,11,5,2], а = 73, Ъ = 48, х = [2,8,3,1].
11.	(х\у) -> (у ф ж), (ж Л у) V (z о ж J, у).
12.	ж -> (y|z) и (ж ->• у)|(ж -> z).
13.	((ж | у) z) ф у.
14.	/(1,0,1) =/(0,1,1) -/(0,1,0) — 0.
15.	(000 1111 ООП 1100).
16.	J = {ж фу,ж Vy}.
17.	(Л \ В) U (Л П С) = Л \ (В U С).
260
Вариант 17
1. (Л\В)\С=(Л\С)\(В\С); АСВ, CQD^AxCCBxD.
2. ш  п = си.
9 1 I 1 | 1 I	I_____I____ __ _П 
°- 1-3	3-5	5-7 1	r (2n—1)(2п+1) - 2//+1 ’
4.	Pj ={(а.,3),(Ь,4),(6,3),(5,1),(Ь,2),(с,2)}, Р2 = {(1,1), (1,3), (2,4), (3,1), (3,3), (4,2)}.
5.	Р С Z2, (х',у) € Р <4* 5х = 2у.
6.	(Z~; +, -), где 7LT = {.г G Z | .т < ()}.
7.	*В = (R3; х), X = {(1,0,0), (0,0,1)}, х операция векторного произведения.
8.	(3 = [11,7,3,2], а = 57, b = 81, ж = [5,4, 2,0].
И. (з; V у) -+ (у J. .г-), (;г|у) <-> (z © ту).
12.	:/: -+ (у <+ z) и (.7; —> у) ++^.7: -> z).
13.	(,7;Vy)	(z++y).
14.	/(1,0,0) = /(0,1,1) = /(0,1,0) = 0.
15.	(0101 ООП 1100 ООП).
16.	3 = {т Лу,х -+ у}.
17.	(Л © В) \ (В П С) = А ф (В \ С).
261
Вариант 18
1.	Лф(ВфС') = (ЛфВ)фС, (А\В)хС = (АхС)\(ВхС).
2.	|Л х.В| = |В х Л|.
3.	п5 — п кратно 5 для всех натуральных п.
4.	Рг = {(а, 3), (Ь, 4), (Ь, 3), (с, 1), (с, 2), (с, 4)}, Р2 = {(1,2), (1,3), (1,4), (2,3), (4,3), (4,2)}.
5.	ВС Z2, (ж, у) е Р^ х = -у.
6.	(Z-; +, •), где Z~ = {ж G Z | х < 0}.
7.	© = (Z;+,-), X = {-2,7}.
8.	/3 = [7,5,11,2], а = 48, b = 63, х = [3.2,6,1].
И. (ж V у) 1 (у -4 ж), (ж Ф у) -> (г|жу).
12.	ж V (у Ф г) и (ж V у) Ф (ж V г).
13-	(ж|у) ф (z -> у).
14.	/(0,0,1) = /(0,1,1) = /(1,0,0) =/(1,0,1) = 1.
15.	(0111 1101 0010 1010).
16.	3 = {® 4- у,х <-> у}.
17.	(Л U В) \ (Л U С) = А ф (В U С).
262
Вариант 19
1.	А П В = (AUB) П А.
(А П В) х (С П D) = (А х С) П (В х В).
2.	|Z х ст| = и.
3.	62м-1 + 1 кратно 7 для всех 1.
4.	Ру = {(«. 1), (6, 2), (6,3), (с, 1), (с, 3), (с, 4)}, Р2 = {(1,1), (1,2), (1,3), (2,2), (2,3), (3,3), (3,4), (4,1), (4,4)}-
5.	В С Z2, (а:, у) G Р х ф 1 = у.
6.	({A eM„(Z)|detA^0};+,-).
7.	® = (R:i;+), X = {(1,2,3),(-1.0,0)}.
8.	/3 = [7, 3,11, 2]. а = 37, b = 74, х = [4,1,5,0].
11.	(.т © у)\(у |./;), (а: о у) (г V .ту).
12.	.7,- {. (у © z) И (.Т | у) ф (.7,- J. z).
13.	((.т I у) -> г) о .т.
14.	/(1,0,0) =/(0,0.1) = /(0,1,1) = 0.
15.	(1111 1100 ООН ООН).
16.	3 = {т ф у,.7; V у).
17.	(А П В) © (A U С) = А ф (В U С).
263
Вариант 20
1.	А П (В ф С) = (Л Г) В) ф (А П С), (АПВ) хС = (ЛхС)п(Вх С).
2.	Множества точек двух окружностей эквивалентны.
3.	13 + 23 + 33 + ...+п3 = ^1И.
4.	А = {<«, 2>, («, 4>, <«,, 3>, (с, 1), (с,2), <с, 3>}, Р2 = {(1,1), (1.4), (2,3), (3,3), (4,1), (4,3), (4,4)}.
5.	Р С Z2, {х, у) Е Р & у} х - 2.
6.	({Л G«| det А/0}; •,(_}_}))•
7.	© = <Q\{0};-,:), Х = {-5}.
8.	/3 = [5,11,7,2], а. = 63, b = 35, х = [3,4,2,0].
11.	(х Л у) -Н- (у 4- х), (х —> y)|(z Ф х XI у).
12.	х <-> (у Ф z) и (ж у) Ф (а;	z).
13.	(х V у) -> (z ж).
14.	/(0,0.1) =/(0,1,1) =/(1,1,0) =0.
15.	(000 ООП 0101 1100).
16.	3 = {ж -4- у,хЛу}.
17.	(Л \ В) \ (Л П С) = Л \ (В U С).
264
Вариант 21
1.	Аф(АфВ) = в,
А х (В ПС) = (А х В) П (А х С).
2.	(А х В)с - Ас х Вс.
3.	8” — 1 кратно 7 для всех натуральных п 1.
4.	В, = {<а.2>, <а,4>, <6,1), <В,2>, <6,4), <с,2>, <с,4)}, ^2 = {<1,1>, <2,2>, <2,4>, <3,3>, <4,4), (3,2>, <1,3>, <4,1>}.
5.	В С (Z+)2, (Ж,у) £ В НОД(а;,у) 1, где Z+ = {.-г G Z | z > 0}.
6.	(С \	у/*).
7.	S3 = (С+,-,1), X = {2г}.
8.	/3 = [3,11. 7, 2], а = 84, b = 26, х = [1, 7,5,1].
и. (х 4- (у ® (у -> :r;)), х V (y|z ф .ту).
12.	х -> (у | z) и (т; -> у) | (т —> z).
13.	((.т <-> y)|z) Ф у.
14.	f(0,0,0) =/(0,0,1) = /(1,0.0) = /(1,1,0) =0.
15.	(1110 1001 0111 0001).
16.	J = {л / у, X <-> у}.
17.	(А ® В) П (А Ф С) = А \ (В П С}.
265
Вариант 22
1.	AUB = АфВФ (АП В),
А х (В \ С) = (А х В) \ (А х С).
2.	(Ав)с ~ АВхС.
3.	I'2 + З2 + 52 + ... + (2n - I)'2 = "<2'--Ц№±!1.
4.	Pi = {(Ь. 1), (а, 3), (о, 4), (с, 2), (с, 4), (Ь, 4)}, Г2 = {(1. 1), (2,3), (2,2), (2,4), (3,3), (3,4), (4,2), (4.4)}.
5.	В С (Z+)2, (х, у) 6 х у-
б.	(ZL; ~h, ’,1	?<)•
7.	<В = (С;-), А" = {е*1}.
8.	/4 = [7,11,3,2], а = 65, 5 = 89, х = [6,7,2,0].
11.	х\(у Ф (у V х)), х -> (у J. (z <-> ту)).
12.	х j. (y\z) и (т J. у)|(т } z).
13.	((т ]- у) -> (z о у).
14.	/(0,1,1) = /(1.0.0) = /(1,0,1) = 1.
15.	(0001 ООП 1100 1110).
16.	3 = {х®у,х Vy}.
17.	(A U В) ф (А П С) = А ф (В \ С).
266
Вариант 23
1.	А \ В = А е (Л Р В), (Л U В) X с = (Л X С) U (В X С).
2.	Множества точек двух квадратов эквивалентны.
3.	4" + 6п - 1 кратно 9 для всех натуральных п > 0.
4-	А = {(«, 3), (а, 2), (а, 4>, <Ь, 1 >, (с, 2), (с, 4), (с, 3)}, Р2 = {(1,1), (2,2), (2,1), (3,3), (4,4), (4,3), (1,4), (2,4), (3,2), (3,4)}-
5.	Р С (Z+)2, (я?, у) Е Р <=> ж2 = у, где Z+ = {я? G Z | х > 0}.
6.	(С \ {0};+, •).
7.	93 = (С;+,-), X = {2г}.
8.	/3 = [11,3,5,2], а = 43, b = 67, х = [4,2,3,1].
11.	х ф (у —> (у о я;)), х 1 (y|(z V ту)).
12.	х о (y|z) и (я; <-» у)|(т о z).
13.	((ж j. у) -> z) о у.
14.	f(0,0,l)=f(l,0,0) = /(l,l,0) = l.
15.	(000 1100 ООН 0101).
16.	3 = {х Лу.х -> у}.
17.	(A U В) \ (В П С) = (Л \ В) U (Л \ С).
267
Вариант 24
1.	A\JB = (А©В) U (АПВ), А х (ВиС) = (А х В) U (А х С).
2.	|<^| =^.
з.	|-£ + f- £ + -- - +	= Н2 + Hrl3t4
4.	Ft = {(Ь,2),(а.,3),(Ь, 1),(Ь,4),(с, 1),(с,2),(с,4)},
Bi - {(1,1), (1,2), (1,4), (2,2), (2,4), (3,3), (3,2), (3,4), (4,4)}-
5.	Р С (Z+)2, (х,у) ЕР&Р 3 у, где Z+ = {х G Z | х > 0}.
С. (C\R+,-; у/’-2-i).
7. ® = (С;-), X = {Зг}-
8. /3 = [7,3,11,2], а = 31, b = 78, х = [6,1, 7,0].
11.	(;/; V у) -> (у © х), х | (у о (z j. ху)).
12.	х -> (у О z) и (.7; —> у) О (х —> z).
13.	х V у —> (z <-> у).
14.	/(0,1,1) =/(0,1,0) = /(1,0,0) = /(1,0,1) = 0.
15.	(1010 0010 1101 0111).
16.	3 = {aU У,х <-> у}.
17.	(A\B)U(C\B) = (BUC)\ А.
268
Вариант 25
1.	AUB = АПВ\
ACC, В CD => Ax В = (Ax D) П (С x В).
2.	ABu6' ~ Ar x Ac, если В П С = 0.
3.	n7 — п кратно 7 для всех п > 0.
4.	Рх = {(а, 2), (а, 3), (о.,4), (Ь, 3), (с, 1), (с,4)}, F2 = {(1,1), (2,3), (2,2), (3,4), (1,4), (2,4), (4,2)}.
5.	Р С (Z+)2, (rz:,y) G Р <=> х1 > у, где TLA ~ {:г G Z | х > 0}.
6.	(С \ К;+,-,:).
7.	«В = (С; +, г), X = R.
8. (3 = [5,7,11,2], а = 43, b = 74, х = [3,2,5,1].
11.	х <-> (у Л (у —> а:)), х V (у ф (z | з;|у)).
12.	х —> (у j. z) и (х —> у) | (х -> z).
13.	((ж у) -> z)|y.
14.	/(0,1,1) = /(0,1,0) =/(1,0,1) =/(1,1,1) = 1.
15.	(000 1101 0010 1100).
16.	3 = {х V у,х о у}.
17.	А\(В\С) = (А\В)\С.
предметный указатель
(1,1)-полюспик, 204
минимальный, 205
(1, &)-полюсник, 204
(«1, a„+i )-мартрут, 119
Е-класс, 35
А:-полюспая
контактная схема, 203
сеть, 203
л-ка, 15
71-куб, 118
n-мерный куб, 118
71-местная
алгебраическая операция, 22
функция, 22
71-местное отношение, 16
т?,-местный предикат, 16
«'-расстояние, 125
1-1-функция, 20
1-ячейка, 191
Автоморфизм, 52
Аксиома
бесконечности, 44
выбора, 45
замены,44
исчисления, 212
математической индукции, 24
множества всех подмножеств, 44
регулярности, 44
суммы, 43
существовав и я
пары, 43
пустого множества, 43
экстенсиональности, 44
Аксиомы
ИПЕ, 226
Дедекинда — Пеано, 23
ИВ, 213
Цермело — Френкеля, 43
метрики,124
Алгебра, 49
Кантора, 49
Линденбаума, 216
булева, 61
булевых функций, 178
компьютерная, 82
отношений, 65
реляционная, 67
Алгебраическая система, 49
Алгоритм
Дейкстры, 127
Евклида, 89
Квайна, 217
Форда - Веллмана, 126
последовательной раскраски, 154
редукции,218
унификации, 230
Алфавит, 39
ИВ, 213
исчисления, 212
Аптидизъюпкция, 174
Антиконъюнкция, 174
Аргумент, 20
Арифметика
модулярная, 93
остатков, 93
Ассоциативность, 13, 62, 178
композиции, 19
Атомарная формула, 172
Базис, 196
индукции, 24
Биекция, 21
Бином Ньютона, 163
Бит, 82
270
Булеан, 12
Булева
алгебра, 61
функция, 175
Булево кольцо, 63
Валентность вершины, 130
Вектор, 37
значении булевой функции, 176
оснований,104
остатков, 104
Вершина, 108
висячая, 130
графа, 108
достижимая, 120
изолированная, 130
концевая. 130
периферийная, 125
центральная, 125
взвешенная, 126
Вершины
взаимно достижимые, 123
смежные, 11 1
Вес
вершины. 113
дуги. 113
маршрута, 125
Ве твь остова. 146
Включение множества, 11
Восьмеричная система, 78
Вхождение переменной. 186
свободное, 223
связанное. 222
Выборка
неупорядоченная, 162
с возврапучшямп, 164
упорядоченная, 162
с возвращениями, 163 Вывод
в исчислении /, 212
по правилу согласия, 220
резолютивный, 219, 233
формулы, 212
Выражение исчисления, 212
Высказывание. 172
простое, 172
сложное. 172
Гипотеза, 214
Гомоморфизм, 51
естественныи, 57
Граница. 151
Грань
верхняя, 39 нижняя, 39 точная
верхняя, 39
нижняя, 39
Граф, 108
ациклический, 134 бесконтурпый, 120 бихроматический. 154 взвешенный, 113 гамильтонов, 133 двудольный, 154 неориентированный, 109 ориентированный. 109 планарный, 154 полный, 118
получаемый отождествлением вершин, 115
помеченный, 113 разреженный, 114 связный, 120 сильно связный, 120 Графы
гомеоморфные. 155
изоморфные, 112
Группа, 50
абелева. 50
коммутативная, 50 симметрическая, 161 Группоид,50
Двоичная система. 78
Декар това степень множества, 16 Декартово произведение
алгебр, 58
множеств, 16. 58
отношений, 66
Декомпозиция
дизъюнктивная сложная. 201
функции. 197
дизъюнктивная. 198 попдизъюнктпвная, 198 простая, 199
271
функциональная итеративная, 201 множественная. 201
Делитель, 87
наибольший общий, 88
Дерево, 134 бинарное, 145 остовиос, 135 семантическое, 216 упорядоченное, 144
Диагональ, 18 Диаграмма
Хассе, 41
Эйлера -- Вонна, 12
Диаметр графа, 124
Дизъюнкт, 180
сигнатуры X, 232
унитарный позитивный, 221 хорновский,221 негативный, 221 точный, 221
Дизъюнктивная нормальная форма, 180 минимальная, 187 совершенная, 181 сокращенная, 187 тупиковая, 187
Дизъюнкция, 173 элементарная, 180
Дистрибутивность, 13 Длина маршрута, 119 слова, 39
Доказательство теоремы, 212 Домен, 66
Дополнение
графа, 115 множества, 12 функции, 178 элемента, 61
Дробь десятичная, 76
Дуга, 108
графа, 108
заходящая в вершину. 108 инцидентная вершине, 112 исходящая из вершины, 108
Дуги кратные, 109
Единица моноида, 50 решетки. 59 частично упорядоченного множества, 38
Задача коммивояжера, 134, 139 нахождения остова минимального веса, 136
о безопасном хранении ключа, 99
о кенигсбергских мостах, 131 Закон
двойного отрицания, 14, 62, 178 де Моргана. 14, 62, 178 дистрибутивности, 13, 62, 178 идемпотентности, 13, 62 нуля и единицы, 14, 62 поглощения, 14, 62, 178
Замыкание формулы универсальное, 233
Значение
терма, 55
функции, 20
Идеал, 64
главный, 64
Идемпотентность, 13, 178
Изображение графа, 108
плоское, 154
Изоморфизм, 52 частично упорядоченных множеств, 42
Изоморфные
системы, 52
частично упорядоченные множества, 42
Импликанта
простая, 186
формулы, 186
функции, 186
Импликация, 173
Инвертор, 197
Индукционный шаг, 24
Интерпретация, 49, 173
Инфимум. 39
Инцидентор, 109
Инъекция, 20
272
Истинность формулы сигнатуры
Е, 223
Источник, 126
Исчисление
высказываний, 213
непротиворечивое, 213
предикатов сигнатуры Е, 226
разрешимое, 213
формальное, 212
Кардинал, 26
Каркас графа, 135
Карта
Карно, 189
декомпозиции, 199
Квазипорядок, 37
Квантор
всеобщности, 222
существования, 222
Класс
функций
линейных, 194
монотонных, 194
самодвойственных, 194
сохраняющих единицу, 194
сохраняющих нуль, 194
эквивалентности, 35
Классы Поста, 194
Кограница, 151
Код двоичный, 77
Кольцевая сумма
графов, 116
формул, 174
Кольцо
булево, 63
вычетов по модулю т, 93
целых чисел, 71, 73
Комбинаторика, 159
Коммутативность, 13, 62, 178
Композиция
графов, 118
отношений, 19
Компонента
связности, 120
сильной,120
сильная, 120
Компьютерная алгебра, 82
Конгруэнция, 56 единичная, 60 нулевая, 60
Конец ребра, 109
Конкатенация, 50
Константа, 22, 48, 49
0, 177
1, 177
Константный символ, 48
Конституента
единицы, 181
нуля, 181
Контакт, 204
замыкающий, 204 размыкающий, 204
Континуум,26
Контур, 120
Конфигурация комбинаторная, 159
Конъюнкт, 180
Конъюнктивная нормальная форма, 180 совершенная, 182
Конъюнкция, 173 элементарная, 180
Координата, 15
слова, 39
Кораиг, 136
Корень
дерева, 137 упорядоченного, 144 характеристический, 168
Кортеж, 15
Коцикл, 148
Коэффициент биномиальный, 163 полиномиальный, 165
Лемма о рукопожатиях, 131
Лес, 134
упорядоченный, 144
Литера, 180
отрезаемая, 232
сигнатуры Е, 232
Литеры контрарные, 180
Маршрут, 119
кратчайший, 126 циклический, 119
273
Математик;!
непрерывная, 8 прерывная, 8 Матрица
Квайна. 188
бинарного отношения. 31 весов, 113 достижимости, 123 инцидентности. 112 коптрдостижимости, 123 программируемая логическая, 209
расстояний, 124 связности.123 смежности, 111 соединений, 209 фундаментальных разрезов, 150 циклов, 147
Метод
Квайна, 187 бинарный, 95 резолюций в ИВ, 218 ДЛЯ хорновских ДИЗ'ЫОПК-тов, 220
Многообразие, 58
Многочлен характеристический, 168 Множества
равномощные, 26 равные, 11 совпадающие. 11 эквивалет ппыс, 26 Множество, 10 бесконечное, 26 континуальное., 26 счетное, 26
дщлоне упорядоченное, 39 вычетов., 93 действительных чисел, 75 коконечное. 64 комплексных чисел. 76 конечное, 26
коциклов фундаментальное. 149
-линейно упорядоченное, 38 натуральных чисел, 23, 24 пустое. 12 рассогласований, 230 рапипалытых чисел, 73
строго включенное, 12 универсальное, 12 формул ПБ, 213 формул исчисления, 212 формул противоречивое, 216 формул сигнатуры Е выполнимое, 225 локально выполнимое, 225 унифицируемое. 230
фундаментальных циклов, 146 целых чисел. 73
по модулю т„ 93
Частично упорядоченное, 38
Множество-степень, 12
Модель, 49
множества формул, 225
Моноид, 50
Мономорфизм, 52 Мощность
алгебраической системы, 49 множества. 26
Мультпграф. 109
реберный, 153 смешанный. 110 эйлеров, 132
Мультиграфы изоморфные, 112 Мультиплексор. 208
Набор
длины п, 15 остатков стандартный, 104
цепей, покрывающих граф. 133
Наибольший общий делитель. 88
Наименьшее общее кратное. 89
Неорграф, 109
аци кл ичсс к и й. 120 связный. 120
соответствующий данному орграфу, НО
Неравенство
Бернулли, 25
треугольника, 124
Нормальная форма дизъюнктивная, 180 митптмальпая, 187 сокращенная, 187 тупиковая, 187 конъюнктивная, 180
274
Носитель алгебраической системы, 49
Нуль
решетки,59
частично упорядоченного множества, 38
Область
значения, 18
определения,18
Образ
гомоморфный, 52
множества, 19, 22
Обратное отношение, 19
Обхват графа, 120
Обход графа
по глубине, 137
по ширине, 138
Объединение
графов, 116
конгруэнций, 60
отношений, 65
функций, 178
элементов решетки, 59
Объединение множеств, 12
Ограничение отображения, 22
Операция
/i-местная, 22
ассоциативная, 50
бинарная, 22
возведения в степень, 27
выбора, 67
добавления
вершины, 114
дуги, 114
кольцевого сложения, 63
кольцевого умножения, 63
конкатенации, 50
логическая, 173
отождествления вершин, 115
подразбиения ребра, 155
проекции, 67
сложения, 24, 27
соединения, 68
стягивания дуги, 115
удаления
вершины, 115
дуги, 115
умножения, 24, 27
унарная, 22
Определение индукционное, 24
Орграф, 109
Ортогональные подпространства, 152
Основание счисления, 77
Остаток, 87
Остов графа, 135
Отношение, 16
7)-местнос, 16
Парето, 38
антисимметричное, 33
бинарное, 17
па множестве, 17
обратное, 19
полное, 18 рефлексивное, 33 симметричное, 33 тождественное, 18 транзитивное, 33 унарное, 17 универсальное, 18 эквивалентности, 34
Отношения совместимые, 65
Отображение, 20
Отрицание, 173
Перевод
дробных чисел, 81
целых чисел, 80
Переменная
логическая, 172
свободная, 223
связанная, 223
Переменные пропозициональные,
213
Пересечение графов, 116 конгруэнций, 60 множеств, 12 отношений, 65 функций, 178 элементов решетки, 59
Перестановка, 159
Перешеек, 132
Период дроби, 76
Петля, 111
Плоское изображение графа, 154
Поглощение, 14
Подалгебра, 54
275
Подграф, 114
Поддерево
левое, 146
правое, 146
упорядоченное, 144
Подм! тожество, 11 собственное, 12
Подмодель, 54
Подпространства ортогональные, 152
Подсистема. 53
порожденная множеством, 54
Подстановка
множества, 21, 160
пустая, 229
сигнатуры £, 229
Подформула, 222
Покры тие множес тва, 15
Поле, действительных чисел, 75 комплексных чисел, 76 конечное, 94 рациональных чисел, 73 характеристики нуль, 94
Полином Жегалкпна, 195 линейный,195 пели ценный .195
Полное отношение, 18
Полугруппа, 50
Полустепень
захода, 131
исхода, 131
Полюс, 203 входной, 204 выходной, 204
Пометка, 113
Порядок
двойственный, 37 лексикографический, 40 линейный, 38 полный, 39
строгий,37
частичный, 37
Последователь, 114 вершины, 111
Последовате льность, 22
возвратная, 168 фундаментальная, 75
Поток в сети, 148
Правила вывода ИПЕ, 226
Правило
вывода, 212
вывода в ИВ, 214
заключения, 214
произведения, 28
согласия, 220
степени. 28
суммы, 28
Предикат, 16
па множестве. 17
Предложение сигнат уры £. 223
Предпорядок. 37
Предс гваление со смешанными основаниями, 105
Предшественник вершины, 111
Принцип
двойственности
/тля булевых алгебр, 63
для булевых функций, 193
математической индукции, 24
полного упорядочения, 45
полной индукции, 25
трапсфинитной индукции, 45
Програмируемая логическая матрица, 209
Проекция, 20 Произведение;
алгебр, 58
бинарных отношений, 19
векторов внутреннее, 151
графов, 116
множеств, 12
декартово, 16, 58
прямое. 16
остатков, 94
отношений декартово, 66
списков, 85
элементарное, 186
Прообраз множества, 19
Противоречие, 179
Путь. 120
Радиус
взвешенный, 126
графа, 125
Разбиение
множества, 15
упорядоченное, 164
276
Разложение Шеннона, 182
Размещение. 162
с повторением, 1G3 Разность
множеств, 12
симметри1 [некая, 12
отношений, 66
Разрез графа, 148
простой, 148
фундаментальный. 149
Ранг
коц11 кл и  теский ,136
циклический, 136
Раскраска
вершин графа, 153
ребер мультпрафа. 153
Распределение меток, 113
вершин, 113
дуг. ИЗ
Расстояние, 124
взвешенное, 125
Реализация декомпозиционная, 197 Резольвента
бинарная, 232
дизъюнктов, 219, 233
Решение
общее. 168
частное, 169
Решетка, 59
дистрибутивная, 60
копгруэппий,60
подсистем, 60
элемен тов fc, 209
Решето Эратосфена, 92
Свойство, 17
делимости, 87
евклидовостп, 87
Связка, 173
Сегмент начальный
замкнутый, 43
открытый, 43
Сеть, 148
А-полюсная. 203
Сигнатура, 48
предикатная, 49
функциональная, 49
Символ
вспомогательный. 213
логический, 213
Система, 49
Дедекинда - Пеано, 71 аксиом
ZFC, 45
независимая, 216 алгебраическая, 49 булевых функций
полная, 194 остатков
наименьших по абсолютной величине, 93
неотрицательных, 93
полная, 93
симметричная, 93, 104 счисления
восьмеричная, 78
двоичная. 78
позиционная, 77
смешанная, 79
шестнадцатеричная, 78 числовая
наименьшая неотрицательная, 104
наименьшая по абсолютной величине, 104
Системы
изоморфные, 52 Склейка, 232
Следствие формулы непосредственное, 212
Слово, 39
исчисления, 212
пустое, 39
Сложение
логическое, 174
по модулю 2, 174 Сложность
(1,1)-по.шосника, 205
булевой функции, 205
схемы из функциопальых элементов, 208
функции,208
Смешанная система счисления, 79 Соединение
графов, 116 контактов
параллельное, 204
последовательное. 204
Сомножитель, 90
277
Соответствие, 17
взаимно однозначное. 21
Соотношение рекуррентное, 167
Сочетание, 162
с повторением,164
Список
дуг, 114
над множеством, 84
пустой. 84
уступчатый, 145
Степень вершины, 130
Стрелка Пирса, 174
Структура, 49
смежности, 114
Сумма.
кольцевая, 174
множеств, 12
кольцевая, 12
остатков. 93
списков, 85
Суперпозиция функций, 177
Супремум,39
Схема
Л'п-фупкнциопальпая, 208 минимальная, 208
аксиом ПП, 213
из функциональных элементов, ' 206
контактов, 205
электрическая, 204
Схемы аксиом ИП'ф 226
Сюръекция, 21
Таблица
Кэли, 50
истинности, 173, 176
Тавтология, 179
Теорема
Биркгофа, 59
Геделя о полноте, 226
Дедекинда - Пеано. 71
Жегалкипа. 195
Кантора, 29
Кантора. Бернтштепна, 27
Квайна, 188
Мальцева о компактности. 225
Понтрягина — Куратовского, 155
Поста, 196
Стоуна, 63
Ферма малая, 95
Шеннона
вторая,183
первая,182
арифметики основная, 90
исчисления, 212
о гомоморфизме, 57
о дедукции, 214, 226
о единственности неприводимого разложения, 90
о замене. 228
о непротиворечивости, 216
о полноте, 215
метода резолюций, 219, 233
о сравнении множеств, 27
о существовании неприводимо-
го разложения, 90
о функциональной полноте, 183
о четырех красках, 156
об остатках китайская, 97
Терм сигнатуры Е, 54
Тождественное отношение, 18
Тождество сигнатуры У, 58
Толщина графа, 156
Транспозиция, 161
Универсальное отношение, 18
Универсум, 12
алгебраической системы. 49
Унификатор, 230
наиболее общий, 230
Уравнение
линейное диофантово, 88
рекуррентное, 167
линейное неоднородное, 169
У гверждение двойственное. 63
Факт, 221
Фактор-алгебра, 56
Фактор-множество, 35
Факториал. 25
Фильтр, 64
Фреше, 65
главный, 64
двойственный к идеалу. 65
Форма нормальная
дизъюнктивная, 180
совершенная, 181
278
конъюнктивная, 180 совершенная, 182 Формула
ИПЕ, 226
алгебры логики, 172
атомарная, 172 выполнимая, 179 общезначимая, 179 опровержимая, 179 представляющая функцию, 176
тождественно истинная. 179
тождественно ложная, 179 бескванторная, 228
находящаяся в дизъюнктивной НОрмаЛЫКЙ! форме. 228
находящаяся в конъюнктивной нормальной форме, 228
включений и исключений, 166 выводимая
в исчислении, 212
из формул, 214
доказуемая в исчислении, 212 исчисления, 212 рекуррентная, 167 сигнатуры Е, 222
атомарная, 222
выполнимая в системе, 224
замкнутая, 223
истинная,223
ложная, 224
находящаяся в пренексной нормальной форме, 228
общезначимая, 224
тождественно истинная. 224
Формулы
сигнатуры Е эквивалентные, 227 эквивалентные, 178
Функция, 20
/(.-местная. 22
алгебры логики, 175
биективная, 21
булева. 175
двоичная, 175
двойственная, 192 индикаторная, 29 инъективная, 20
линейная, 194 монотонная, 194 на, 21 переключательная, 175 проводимости. 205 разложимая, 197 разнозначная, 20 реализуемая
(1, Л)-нолюснпком, 205 схемой, 208
самодвойственная, 193 сохраняющая
единицу, 194
пуль, 194 сюръективная, 21 частичная, 20
Характеристика поля, 94
Хорда, 146
Целая часть числа, 86
Цель, 221
Центр графа. 125
Цени покрывающие, 133
Цепь, 119
гамильтонова, 133
простая. 119.
эйлерова, 133
Цикл. 119. 161
гамильтонов, 133
простой, 120
фундаментальный, 146 эйлеров, 132
Цифра, 77
Частичная функция, 20
Частичный порядок, 37
Частное, 87
пробное. 86
Часть
графа, 114
числа целая. 86
Числа
Фибоначчи. 167
взаимно простые, 89
Число
базисное, 77
вещественное, 75
действительное. 75
279
иррациональное, 76 кардинальное, 26 комплексное, 76 натуральное. 23 перестановок, 159 планарности графа, 156 разбиений, 164
упорядоченных, 164 размещений, 162
с повторениями, 163 рациональное. 73, 76 с плавающей точкой. 82
11 о р м ал изова и ное, 83 сочетаний, 162
с повторениями, 164 хроматическое. 153 целое, 73
длинное, 84 короткое, 84 неразложимое, 90 простое, 90 разложимое, 90 составное, 90
ци климатическое, 136
Ijieii числа старший, 105
Шестнадцатеричная система, 78
Штрих Шеффера, 174
Эквивалентность, 34, 173 Эквивалентные
(1,1)-полюсники, 205
Эксцентриситет вершины, 124
взвешенный, 126
Элемент, 10
максимальный, 38
минимальный,38
наибольший, 38
наименьший, 38
непосредственно следующий, 24
обратный. 50
покрывающий, 41
функциональный, 207
Элементы несравнимые, 38
Эндоморфизм, 52
Эпиморфизм, 52
Ядро гомоморфизма, 57
Язык, 48
Учебное издание
Сергей Владимирович Судоплатов, Елена Викторовна Овчинникова
ЭЛЕМЕНТЫ ДИСКРЕТНОЙ МАТЕМАТИКИ
Учебник
Редактор Т.П. Петроченко
Технический редактор Т.Е. Телятникова
Корректор И.Е. Семенова
Компьютерная верстка И.Д. Черных Оформление серии Е.А. Доний
ЛР № 070824 от 21.01.93
Подписано в печать 10.12.2001. Формат 60x90/16.
Усл. печ. л. 18,0. Печать офсетная.
Тираж 6000 экз. Цена договорная.
Заказ №4872.
Издательский Дом «ИНФРА-М» 127214 Москва, Дмитровское шоссе, 107
Тел.: (095) 485-74-00; 485-70-63. Факс: (095) 485-53-18
Робофакс: (095) 485-54-44
E-mail: boo ks@ i n fra - m. ru h 11 p:// w w w. i n fra - m. ru
Лицензия ИД 04303 от 20.03.01. Издательство НГТУ.
630092, г. Новосибирск, пр-т Карла Маркса, д. 20
Отпечатано в полном соответствии с качеством предоставленных диапозитивов в Тульской типографии.
300600, г. Тула, пр. Ленина, 109.
ISBN 5-1Ь-000Ч57-Ч
9
785160
009575