I
1
1
еяа ./7
	У«У—У ,У«У—V У'У—у 'у.у—.уУ«у—,у.__у.у—V— \7
/N.» /Ч—/\Р/Ч • «Л.—А.—А. • .Л. — А. /\ • /\—/\ /\ • А—А А • /Ч—А А
II
X
i
А
II
X
• •
X
X
•	•
X
•	*
X
I!
X
•	*
X
i
X
4
X
X
I I
] I
ii,
Б. Н РАШЕВСКИ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
19 8 0
f	I I
1	1 I
i	АТК К	i
i	__^ ____ _^ i->_^ _^ _____________________________________________ ___ ___,___,__. ___ ____ ___ _,_, ___ ___ ___, „__ ___, __, __, ___, ___,..__ ___ _,__ I
A
!
X
a»
X
x
A
A
I
X
X
X
A
X
X
• *
I
X
« •
X
i
A
X
X
	у. \/z^\y	у. v —-у-—У. у	у у: у	v	У»у—У—У
	 /Ч * /Ч•"—"/^Ч /Ч * /Ч *""*' /Ч /Ч * /Ч ""•" /Ч ' "/\ * /Ч *~~ /*• /\ • /\, *<Ач /Ч

ГОСУДАРСТВЕННОЕ ИЗД ТЕТЬСТВО
МОСКВА — ЛЕНИНГРАД
УЧЕБНЫЕ ПОСОБИЯ ПО МАТЕЛ Т КЕ
ПОВЫШЕННОГО ТИП
1Я ШКОЛ
I концентр
Берг М. Ф. Знаменский М ., П
ский И Ф., Хвостов Н. П
Рабочая книга по мате, ат ке
ронца. Для 5-го года ооуче в
Стр. 200. Ц. 70 к Для 6-го тс
ской школе. Стр. 212. Ц 83
ния в городской школе. Стр.
Березанская Е. С. (Ред.) 'ате т
для 5-го года обучения. Сост
Т Н. Крупенькин, Р А. Качнин.
Ц I р. Для 6-го года обучен
виц, Т. Н. Крупенькин В Э
таблица. Ц. 1 D. 15
Щ
Г.Н. Слуд-
н. и.
\. М Во-
о школе,
в город-
го обуче-
Ц
книга
Попов,
1 табл.
. О. Гур-
272+
Грацианский И. И. Рабоча
для 5-го года обучени С
Лебединцев К. Ф. Сборник з
иий по курсу алгебры. я
образования. Ч. I. Стр. 1 2. Ц
те итике
1
г упражне
с ы и само-
МАТЕМАТИЧЕСКИЕ ЗАДАЧ С рн к упражнений
по математике ля 5 го го о чения. Под ред
В. С. Давыдова С. Н Жа	. Г. Коломейцева
и С. А. Рыкунова. Стр. 1 5 Ц.
Перельман Я. И. Новы з ачн! к по геометрии.
(Концентрический.) ^ля 5-го 6-го и 7-го годов обу-
обучения. Стр. 216. Ц. 80 к.
ПРОДАЖА ВО ВСЕХ ОТДЕЛЕНИЯ
ГАЗИНАХ ГОСИЗДАТА

К. Н. РАШЕВСКИЙ
КРАТКИЙ КУРС
РИ МЕТИКI
ИЗДАНИЕ ЧЕТВЕРТОЕ
Научно-технической еенцией
Государственною ученого совета
допущена как руководство
длп подготовки в вузы
—65 тысяча
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
МОСКВА * 1930 * ЛЕНИНГРАД
WIOUV 1

Отпечатано е типографии Госиздатл
гКРАСНЫЙ ПРОЛЕТАРИЙ*.
Москеа, Краснопролетарская, 16,
ш количестве 20000 экз.
Главлит № А—68685
Газ у—13 М 37426
Зак. № 534
п. а.

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ.
Предлагаемое пособие по арифметике предназначается для лиц,
окончивших школу, но нуждающихся в повторительном прохождении
курса, а также в систематизации знаний, полученных в школе.
Второе издание дополнено построением плана, диаграмм и график;
кроме того в нем сделаны следующие изменения: добавлены особые
случаи действий (§ 39); более подробно изложено летосчисление (§ 50);
в задачах и примерах всюду введены метрические меры; приведен
другой способ решения задач на время (§ 54); определение площадей
и объемов (§ 57) пояснено чертежами; теория простых дробей изло-
изложена более наглядно; приведены другие таблицы перевода русских
мер в метрические и обратно (§110); выпущены тройное и цеп-
цепное правила- и приведен другой, более легкий способ вычисления
процентов.

I. ПЕРВОНАЧАЛЬНЫЕ ПОНЯТИЯ.
1. Определения. Когда мы хотим узнать, сколько предметов
находится где-нибудь, мы должны их сосчитать.
Каждый отдельный предмет, каждое отдельное явление при
счете называется единицей.
Результат счета единиц называется целым числом или про-
просто числом.
Одна единица называется также числом.
Число, при котором есть название (наименование) тех единиц
от счета которых оно получилось, называется именованным,
а если нет, то — отвлеченным.
Ряд чисел: один, два, три, четыре, пять, шесть и т. д. назы-
называется натуральным рядом чисел; этот ряд бесконечен, так как,
прибавив к последнему числу единицу, получим новое число.
Наука, изучающая свойства чисел и действия над нимиу назы-
называется арифметикой.
Часть арифметики, которая учит немногими словами выражать
всевозможные чиола, называется словесным счислением (словесной
нумерацией).
Часть арифметики, которая учит немногими письменными
знаками обозначать всевозможные числа, называется письменным
счислением (письменной нумерацией).
Знаки, употребляемые для обозначения чисел, называются
цифрами1). Их всего десять: 1, 2, 3, 4, 5, б, 7, 8, 9, 0; первые
девять цифр называются значащими) последняя цифра нуль озна-
означает отсутствие числа.
Число, обозначенное одной цифрой, называется однозначным,
двумя цифрами — двузначным, несколькими цифрами — много-
многозначным.
*) Нужно иметь в вгцу, что гщфра и число не одно п то же: цифра только
письменный, знак; число может быть обозначено не одной, а несколькими циф-
цифрами, может быть выражено словами.
— 5

Число, состоящее из единиц только одного какого-нибудь
разряда, называется разрядным числом, например: 40, 300,
5000 и т. д.
2. Таблица счисления
4-й класс — мил-
миллиарды
12-й разряд
Сотни
миллиардов
11-й разряд
Десятки
миллиардов
10-й разряд
Единицы
миллиардов
3-й класс — мил-
миллионы
9-й разряд
Сотни
миллионов
8-й разряд
Десятки
миллионов
7-й разряд
Единицы
миллионов
2-й класс—тысячи
и:
'0
се
&.
*s
i
Сотни
тысяч
5-й разряд
5 а*
1—1
— «•»
з 3
4 й разряд
Единицы
тысяч
1-й класс — про-
простые единицы
3-й разряд
Сотни
2-й разряд
Десятки
1-й разряд
Единицы
3. Римское счисление. Римляне для обозначения чисел упо-
употребляли семь знаков:
I, У, X, L, С, D М,
которые означают соответственно следующие чпсча: 1, 5, 10, 50Л
100, 500, 1000. Если написано несколько цифр рядом, то значе-
значения их складываются, за исключением обозначений: IV, IX, XL,
ХС, CD, ?M, в которых значение левой цифры отнимается от
значения правой; таким образом написанные обозначения будут*
выражать следующие числа: 4, 9, 40, 90, 400, 900. Числа: 7, 18,
74, 150, 322, 1554, 1883 по римской системе пишутся так:
VII, XVIII, LXXIV, CL, CCCXXII, MDLIV, MDCCCLXXXIII.
Числа 3000, 5000, 25000 пишутся так: Шга, Vm, XXVwl где т
означает mille — тысяча.
И. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ.
4г. Определения. Составление по данным числам нового числа
называется арифметическим действием.
Возьмем, например, число 7. Присчитаем к нему единицу»
получим новое число 8. Отсчитаем от 7 единицу, получим новое,
число 6.
1) Это счисление называется десятичным, потому что в нем десять единиц
одного разряда составляют единицу следующего высшего разряда.
— 6 —

Таким образом мы из двух данных чисел 7 и 1 составили
два новых числа: 8 и 6, т. е, произвели арифметические дей-
действия.
Присчитывание к числу единицы называется простым счетом,
отсчитывание от числа единицы называется обратным счетом.
Если действие производится над двумя числами, то оно на-
называется простым; если данных чисел более двух, то действие
называется сложным.
Основных арифметических действий четыре: сложение, вычи-
вычитание, умножение и деление.
СЛОЖЕНИЕ.
5.	Определения. Сложить два или несколько чисел — значит со-
составить новое число, содержащее в себе столько единиц, сколько
их находится в данных числах.
Возьмем, например, два числа 5 и 3 и присчитаем к первому
числу все единицы второго: пять да один шесть, шесть да
один семь, семь да один восемь. Таким образом из двух данных
чисел 5 и 3 мы получили новое число 8, содержащее в себе пять
единиц первого числа и три единицы второго, т. е. столько единиц,
сколько их было в обоих числах. Следовательно, произведенное
нами действие было сложение. Таким образом можно дать другое
определение сложения:
Сложить два числа—значит к первому присчит'ать столько
единиц, сколько их находится во втором.
Так как, складывая 5 и 3, мы получаем число, большее 5
на 3 единицы, то вместо того, чтобы говорить: «сложить 5 и 3»,
можно сказать иначе: «увеличить 5 на 3 единицы», «к 5 при-
прибавить 3», «к 5 приложить 3»; все эти выражения означают
одно и то же.
Те числа, которые складываются, называются слагаемыми.
То число, которое получается от сложения, называется
суммой.
6.	Свойство суммы. Сумма не меняется от перестановки сла-
слагаемых. Действительно, при перестановке слагаемых число еди-
единиц, заключающихся в каждом из них, не изменится, а сле-
следовательно, и число единиц, заключающихся в сумме, тоже не
изменится. Таким образом
	 7

7.	Таблица сложения. Чтобы уметь быстро складывать всякие
числа, нужно запомнить следующую таблицу:
2 + 2 = 4	3 + 3 = 6	4 + 4 = 8	5 + 5 = 10
2 + 3 = 5	3 + 4 = 7	4 + 5 = 9	5 + 6 = 11
2 + 4 = 6	3 + 5 = 8	4 + 6 = 10	5 + 7 = 12
2 + 5 = 7	3 + 6 = 9	4 + 7 = 11	5 + 8 = 13
2 + 6 = 8	3 + 7 = 10	4 + 8 = 12	5 + 9 = 14
2 + 7 = 9	3 + 8 = 11	4 + 9 = 13
2 + 8 = 10	3 + 9 = 12
2 + 9 = 11
6 + 6 = 12	7 + 7 = 14 8 + 8=16 9 + 9 = 18
6+7 = 13	7 + 8 = 15 8 + 9 = 17
6 + 8 = 14	7 + 9 = 16
6 + 9 = 15
8.	Постановка наименований. Так как складывать можно
только одноименные числа, то слагаемые всегда имеют одно и
то же наименование; сумма будет одноименна со слагаемыми.
Например:	_о_ л
sit T)VO
*"Ь 183 руб.
420 руб.
9.	Применение сложения. Сложение применяется:
I. Когда требуется найти число, зная все его части
II. Когда нужно данное число увеличить на несколько еди-
единиц (несколькими единицами), т. е. увеличить на другое число.
ВЫЧИТАНИЕ.
10.	Определения. Вычесть — значит по сумме и одному сла-
слагаемому найти другое слагаемое.
Таким образом вычесть из 8 5 — значит по сумме 8 и одному
слагаемому 5 найти другое неизвестное слагаемое, т. е. найти
такое число, которое, будучи сложено с 5, дало бы 8. Приба-
Прибавляя к 5 различные числа, найдем, что таким числом будет 3,
потому что 5 + 3 = 8.
По сумме 8 и одному слагаемому 5 можно найти неизвестное
слагаемое еще другим способом. Так как сумма содержит
столько единиц, сколько их находится во всех слагаемых, то,
отняв последовательно от 8 все единицы слагаемого 5, очевидно,
получим единицы неизвестного слагаемого, каковых будет 3.
Таким образом можно дать другое определение вычитания:
— 8 —

Вычесть — значит от большего числа отнять столько единиц,
сколько их заключается в меньшем.
Из сказанного видно, что при вычитании большее число умень^
шается на столько единиц, сколько их заключается в меньшем,
То число, из которого вычитают, называется уменьшаемым.
То число, которое вычитают, называется вычитаемым»
То число, которое получается от вычитания, называется остат-
ком или разностью.
11.	Применение вычитания. Вычитание применяется:
I.	Когда по целому и одной его части нужно найти другую часть.
II.	Когда нужно данное число уменьшить на несколько еди-
единиц (несколькими единицами), т. е. уменьшить на другое число.
III. Когда нужно узнать, на сколько одно число больше или
меньше другого.
12.	Сложение и вычитание называются обратными действиями,
так как при сложении даются слагаемые и отыскивается их
сумма, а при вычитании, наоборот, дается сумма и одно слагае-
слагаемое, а отыскивается другое.
13.	Постановка наименований. Вычитать также можно только
одноименные числа; поэтому уменьшаемое, вычитаемое и раз-
разность будут иметь одно и то же наименование, например:
_ 237 руб.
183 руб.
14. Примеры на вычитание
4000338
3230535
54
:
руб.
200000
18217
769803	181783
УМНОЖЕНИЕ.
15. Определения. Умножить — значит повторить одно число
слагаемым столько раз, сколько в другом находится единиц.
Например, умножить 5 на 3 — значит повторить 5 слагаемым
3 раза; таким образом имеем:
Отсюда видно, что умножение на целое число есть не что
иное, как сложение равных слагаемых.
4) При вычитании значение цифры с точкой считается на единицу мень-
меньшим, а каждый нуль с точкой — за 9.

То число, которое умножают, называется множимым.
То число, на которое умножают, называется множителем.
То число, которое получается от умножения, называется
произведением.
Из определения умножения следует, что произведение есть
не что иное, как сумма равных слагаемых.
Множимое и множитель называются также производителями
или сомножителями.
При умножении на целое число данное число увеличивается
в несколько раз.
Действительно, умножая 5 на 3, мы к 5 единицам приба-
прибавляем 5 единиц да еще 5 единиц; таким образом вместо 5 единиц
будем иметь 3 раза по 5 единиц, т. е. увеличим 5 в три раза.
16.	Главное свойство произведения. Произведение не меняется от
перестановки производителей. Докажем, например, что 5X3=3X5.
\	Умножить 5 на 3—значит 5 повторить слагаемым 3 раза. Заменив 5
суммою 5 единиц и сложив их в вертикальном порядке, получим:
( 5=1+1+1+1+1
5X3= {+5=1 + 1 + 1 + 1 + 1
, 5=1+1+1+1+1
3+3+3+3+3=3X5
17.	Особые случаи умножения. I. Если один из производителей
(или оба) равен нулю, то произведение равно нулю. Например,
требуется умножить 0 на 25; это значит, что н\ ль нужно повто-
повторить слагаемым 25 раз; очевидно, получится 0. Точно так же,
умножив 25 на О, т. е. ни разу не взяв 25 слагаемым, получим 0.
Таким образом:
U
25 X 0 = 0.
П. Число от умножения на единицу не меняется. Например,
умножив 25 на 1, т. е. взяв 25 слагаемым один раа, получим,
очевидно, 25; таким образом
25X1 = 25
Так как произведение не меняется от перестановки производите-
лей'Т0Н	1X25 = 25.
Таким образом, если один из производителей равен единице,
то произведение равно другому производителю.
18. Таблица умножения. Для умножения однозначного числа
на однозначное нет правила. Умножение однозначных чисел про-
— Ю —

изводят посредством сложения, повторяя одно число слагаемым
столько раз, сколько в другом единиц. Таким образом составляют
так называемую таблицу умножения, заключающую в себе все
произведения однозначных чисел. Чтобы уметь быстро умножать
какие угодно числа, нужно все эти произведения запомнить.
2Х
2Х
2Х
2Х
2Х
2Х
2Х
6Х
6Х
6Х
6Х
2= 4
3= 6
4= 8
5 = 10
6 = 12
7 = 14
8 = 16
6 = 36
7 = 42
8 = 48
9 = 54
3X3= 9
3X4 = 12
3X5 = 15
3X6 = 18
3 X 7 = 21
3X8 = 24
3X9 = 27
•
7X8 = 56
7X9 = 63
4Х
4Х
4Х
4Х
4Х
4-Х
8Х
8Х
4 = 16
5 = 20
6 = 24
7 = 28
8 = 32
9 = 36
8 = 64
9 = 72
5
5
5
5
5
9
X
X
X
X
X
X
5 = 25
6 = 30
7 = 35
8 = 40
9 = 45
9 = 81
1
2
3
4
5
6
7
8
9
2
4
6
8
10
12
14
16
18
3
6
9
12
15
18
21
24
27
4
8
12
16
20
24
28
32
36
5
10
15
20
25
30
35
40
45
6
12
18
24
30
36
42
48
54
7
14
21
28
35
42 .
49
56
63
8
16
24
32
40
48
56
64
72
9
18
27
36
45
54
63
72
81
4) Таблица умножения в таком виде называется пифагоровой, по имени
греческого философа Пифагора, родившегося на острове Самосе в VI веке
до начала нашего летосчисления.

19.	Правило. Чтобы умножить число на 10,100,1000 и т. д.,
нужно приписать к нему справа столько нулей, сколько их нахо-
находится во множителе.
Действительно, при умножении числа на 10 каждая единица
множимого повторяется слагаемым 10 раз; значит, в произведе-
произведении вместо каждой единицы множимого получится один десяток,
а всего столько десятков, сколько единиц во множимом.
При умножении на 100 вместо каждой единицы множимого
получается одна сотня; следовательно, в произведении получится
столько сотен, сколько единиц во множимом, и т. д. Следова-
Следовательно:
237 X Ю = 237 десятков = 2370
237 X ЮО = 237 сотен == 23700
20.	Правило. Чтобы перемножить числа, оканчивающиеся
нулями, нужно перемножить только значащие цифры и к про-
произведению приписать справа столько нулей, сколько их находится
во множимом и множителе вместе1), например:
12	12400
X 2400	Х420
48 •	248
24	496
28800	5208000
21. Определения. Произведением нескольких чисел называется
тот результат, который получится, если умножить первое число
на второе, полученный результат на третье и так далее. Таким
образом произведение чисел: 2, 5, 3, 4 есть результат, который
получится, если 2 умножить на 5, полученное произведение 10
на 3 и это новое произведение 30 на 4.
Обозначается это действие так:
2X5X3X4=120
и читается: 2, умноженное на 5, умноженное на 3, умноженное
на 4, равняется 120.
*) Примечание. Это правило выражено неточно: нулями может оканчи-
оканчиваться не число, а только его обозначение; перемножать цифры нельзя, потому что
цифры не числа, а знаки; точно так же не к произведению приписываются
нули, а к цифрам, обозначающим это произведение, и не столько нулей, сколько
их находится во „множимом" и „множителе", а сколько их находится в обозначе-
обозначениях множимого и множителя. Однако, для краткости мы и далее будем
употреблять такие неправильные выражения, условившись понимать их указан-
указанным образом.
— 12 -

Произведение одинаковых множителей называется степенью,
например произведение 2X2X2X2X2 называется пятой сте-
степенью двух и обозначается таким образом: 25. Число 5 назы-
называется показателем степени.
2-я степень числа называется квадратом, 3-я— кубом.
22.	Применение умножения. Умножение применяется, когда
нужно данное число увеличить в несколько раз
23.	Примеры на умножение:
547
•
X 2003
1641
1094
1095641
247
Х423
741 или
494
988
247 X 423
741
494 ИЛИ
988
104481
247 X 423
2961
1692
846
104481
104481
24. Постановка наименований. Множимое может быть имено-
именованным и отвлеченным.
Множитель есть всегда число отвлеченное, так как показы-
показывает только, сколько раз множимое нужно повторить слагаемым:
умножить, например, 5 на 7 рублей нельзя, так как такое умно-
умножение не имеет смысла
Произведение, будучи составлено из множимого, (*удет, оче-
очевидно, одноименно с ним.
Задача. Метр материи стоит 4руб. Сколько будет стоить
354 метра.
Для решения задачи нужно 4 рубля умножить на 354. Запись
такая:
354 *)
4DV6 4 руб.X 354
УУ или -ff-	—
4 руб. X 354-=1416 руб. или А УУ или ff
*J	*3	1416 руб.	1416 руб.
ДЕЛЕНИЕ.
25. Определения. Разделить — значит по произведению и одному
производителю найти другой производитель.
Таким образом, разделить 15 на 3—значит найти такое число,
которое, будучи умножено на 3, даст 15. Таким числом будет 5,
*) Нужно заметить, что здесь множимое не 354, а 4 руб., поставлено же
оно под множителем только для удобства; вообще при умножении нужно ясно
сознавать, какое из двух чисел множимое; нужно правильно говорить, что на
что умножаем, правильно ставить наименования, писать же множимое и мно-
множитель можно, где угодно.
— 13 —

потому что, умножив 5 на 3, получим 15. Очевидно, что б есть
третья часть 15, так как она в 3 раза меньше 15-; следо-
следовательно, мы разделили 15 на 3 равные части и нашли величину
3-й части; поэтому можно сказать, что:
1)	деление есть действие, посредством которого одно число
делится на столько равных частей, сколько в другом содержится
единиц, и определяется величина каждого части.
Из сказанного также вытекает, что разделить на целое число —
значит уменьшить в несколько раз. .
Вместо того, чтобы рассматривать число 15 состоящим из
3 частей, из которых каждая равна 5, можно рассматривать 15
состоящим из 5 частей, из которых каждая равна 3, потому что
3, умноженное на 5, тоже равно 15; следовательно, разделив 15
на 3, мы узнали, сколько раз 3 содержится в 15; таким
образом:
2)	деление есть действие, посредством которого узнается, сколько
раз одно число содержится в другом.
Последние два определения (на части и по содержанию)
заключаются в первом общем определении деления, из которого
видно, что деление есть действие, обратное \множению.
То число, которое делят, называется делимым.
То число, на которое делят, называется делителем.
То число, которое получается от деления, называется частным.
Для обозначения деления употребляются три знака: (:), (—Л
и (|_).
Например, деление 24 на 8 можно обозначить таким образом:
24
24:8, ИЛИ—, ИЛИ 24 8
о	_____
26. Деление с остатком. Разделяя одно число на другое, мы
не всегда можем найти такое число, произведение которого на
делитель равно делимому. Пусть требуется разделить 30 на 8.
Пробуя умножать 8 на 1, 2, 3, 4..., мы замечаем, что ни одно
из произведений не равно 30. Следовательно, 30 нельзя разделить
на 8. В таких случаях условились делить не все делимое, а только
наибольшую его часть, какая только может разделиться на де-
делитель. В данном примере наибольшая часть делимого, которая
может разделиться на 8, будет 24, другая же часть 6 не разде-
разделится. Разделив 24 на 8, получим число 3, которое и называется
целым частным. Неразделенная же часть 6 называется остатком.
Очевидно, что остаток всегда будет меньше делителя, иначе его
можно было бы разделить на делитель.
— 14 —

27. Особые случаи деления: I. Если делитель единица, то
частное равно делимому. Например, 5:1 = 5, потому что 5X1 = 5.
II. Если делимое равно делителю, то частное равно единице.
Например, 5:5 = 1, потому что 1X5 = 5.
III. Деление однозначного числа да однозначное производится
при помощи таблицы умножения.
IV. При делении какого-нибудь числа на 10, 100, 1000 и т. д.
надо в нем зачеркнуть справа столько цифр, сколько нулей в де-
делителе; оставшиеся не зачеркнутыми цифры представляют собою
частное, а зачеркнутые — остаток, например:
3748 [ 10	37?8 I 100	3748 I 1000
8 374
48 37
748
28. При делении многозначных чисел нужно обратить внима-
внимание на следующее:
I. Если делитель однозначное- число, то для нахождения
первой цифры частного нужно одну или две г^ифры1) делимого
разделить на делитель.
П. Если делитель многозначное число и вторая его гщфра
слева меньше 5, то нужно разделить одну или две левые цифры
делимого на левую цифру делителя и результат проверить,
умножив его на делитель и вычтя полученное произведение из
делимого.
III Если вторая цифра слева в делителе 5 или больше 5, то
надо разделить одну или две левые цифры делимого на левую
цифру делителя, увеличенную единицей, и результат про-
проверить.
IV. Если9 по снесении к остатку гщфры делимого, получится
число, меньшее делителя, то в частном ставят нуль 2) и только
после этого сносят к остатку следующую цифру делимого.
Примеры на деление:
1)
34258
3258
1678
1629
49
543
63
32500
25
75
75
25
1300
3)
1050245
105
_ 0245
245
35
30007
О
О
*) Здесь слово цифра употребляется для краткости вместо слов, число обо-
обозначенное цифрой.
*) Очень часто учащиеся забывают это и делают ошибку.
— 15 —

29.	Применение деления. Деление применяется в следующих
случаях:
I.	Когда до произведению и одному производителю нужно
отыскать другой производитель.
II.	а) Когда нужно данное число разделить на несколько
равных частей;
b)	когда нужно найти одну из равных частей данного числа;
c)	когда данное число нужно уменьшить в несколько раз
Так, например, деля данное число на 5, мы в то же время
находим его пятую часть и уменьшаем его в 5 раз.
III.	Когда нужно узнать, сколько раз одно число содержится
в другом.
30.	Постановка наименований. Для правильной постановки
наименований нужно различать два случая деления. При делении
на части делитель будет всегда число отвлеченное; делимое
может быть именованным и отвлеченным; частное, будучи в
этом случае частью г) делимого, будет одноименно с ним.
Задача 1. Ученик из 15 листов бумаги сделал 5тетрадей.
Сколько листов бумаги пошло на каждую тетрадь?
Для решения нужно 15 листов разделить на 5; запись такая:
	15 листов | 5
15 3 листа или 15 листов : 5 = 3 листа
О
В случае деления по содержанию частное будет всегда число
отвлеченное, так как показывает, сколько раз делитель со-
содержится в делимом. Делитель же и делимое могут быть отвле-
отвлеченными или именованными, но будут непременно одноименны
друг с другом.
Задача 2. Ученик из 15 листов бумаги сделал тетради,
употребив на каждую по 3 листа. Сколько тетрадей вышло?
Для решения задачи нужно 15 листов разделить на Элиста,
потому что тетрадей будет столько, сколько раз 3 листа содер-
содержится в 15 листах.
Запись:
15 листов |3 диета или 15 листов :3 листа = 5 (тетрадей)
"~15	5
О	5 тетрадей
*) Частное происходит от слова часть,
— 16 —

Частное 5 в этом случае будет число отвлеченное, показы-
показывающее, сколько раз 3 листа содержатся в 15 листах, но по
смыслу задачи оно должно означать также число тетрадей;
поэтому мы или переписываем его второй раз с наименованием,
или ставим наименование в скобках.
ЗАВИСИМОСТЬ МЕЖДУ ЧИСЛАМИ ВО ВСЕХ ЧЕТЫРЕХ
ДЕЙСТВИЯХ.
31.	Из определения действий вытекает:
I. Одно слагаемое равно сумме без другого слагаемого.
II.	а) Уменьшаемое равно вычитаемому плюс разность.
Ъ) Вычитаемое равно уменьшаемому минус разность.
III.	Один производитель равен произведению, разделенному на
другой производитель.
IV.	Делимое равно делителю, умноженному на частное, плюс
остаток.
В случае деления без остатка:
1)	делимое равно делителю, умноженному на частное
2)	делитель равен делимому, разделенному на частное.
ПОВЕРКА ДЕЙСТВИИ.
32,	Зшя свойства действий и зависимость между данными и
искомыми числами, можно легко каждое действие поверить или
тем же самым действием, или обратным ему.
Поверка сложения. Так как сумма не меняется от переста-
перестановки слагаемых, то, чтобы поверить сложение сложением,
нужно сложить слагаемые в другом порядке, и если полу-
получится прежняя сумма, то можно думать, что сложение сде-
сделано верно.
Чтобы поверить сложение вычитанием, нужно из суммы
вычесть одно слагаемое, и если получится другое слагаемое,
то можно думать, что сложение сделано верно.
Если имеем несколько слагаемых, то, отняв от общей суммы
часть слагаемых, должны, в случае верности действия, полу-
получить сумму остальных.	\
Поверка вычитания. Чтобы поверить вычитание вычита-
вычитанием, нужно из уменьшаемого вычесть разность, и если по-
получится вычитаемое, то можно думать, что вычитание сделано
верно.
2 Рашевский. Краткий курс арифм.	— 17 —

Чтобы поверить вычитание сложением, нужно к вычитаемому
прибавить разность, и если получится уменьшаемое, то можно
думать, что вычитание сделано верно.
Поверка умножения. Так как произведение не меняется от
перестановки производителей, то, чтобы поверить умножение
умножением, нужно перемножить производители в другом по-
порядке, и если получится прежнее произведение, то можно ду-
думать, что умножение сделано верно.
Чтобы поверить умножение делением, нужно произведение
разделить на один производитель, и если получится другой
производитель, то можно думать, что умножение сделано верно.
Поверка деления. Чтобы поверить деление делением, нужно
из делимого вычесть остаток и разделить полученную разность
на частное, и если получится делитель, то можно думать,
что деление сделано верно.
Чтобы поверить деление умножением, нужно делитель умно-
умножить на частное (прибавить остаток, если он есть), и если
получится делимое, то можно думать, что деление сделано
верно.
АРИФМЕТИЧЕСКОЕ ВЫРАЖЕНИЕ И СКОБКИ.
33. При решении задач бывает полезно раньше совершения
действия указать, какие действия и в каком порядке нэдо выпол-
выполнить над данными числами, чтобы получить ответ. Для этой
цели употребляются скобки.
Например, чтобы показать, что для решения какой-нибудь
задачи нужно сначала сложить 13 и 15 и полученную сумму
вычесть из 40, пишут так:
40 —A3+15)
Скобки, стоящие после знака минуса, показывают, что из 40
нужно вычесть не 13, а всю сумму:
13 + 15
Соединение чисел различными знаками называется арифмети-
арифметическим выражением.
Иногда приходится употреблять скобки различной формы,
чтобы отличить их одни от других; например, такое арифмети-
арифметическое выражение:
30 4-{ 100 — [25 — E-f 6)]}
— 18 —

означает, что нужно сначала сложить 5 и 6, полученную сумму
11 вычесть из 25, полученную разность 14 вычесть из 100, а эту
разность сложить с 30; получим окончательно 116. Скобки бы-
бывают: круглые (), прямые или квадратные [] и фигурные { }.
При вычислении арифметического выражения нужно сначала
целать такие действия, которые бы избавляли его от внутренних
скобок, потом от следующих за ними и т. д.; поэтому в нашем
примере мы сначала избавились от круглых скобок, потом от
прямых и, наконец, от фигурных. Когда в арифметическом выра-
выражении нет никаких скобок, то сначала делают все умножения
и деления, а потом уже сложения и вычитания *). Так, например,
в выражении:
+ 3X4 — 6
мы должны сначала 2 умножить на 5, 3 умножить на 4 и 6 раз-
разделить на 3, а потом уже сложить 10 и 12 и из полученной
суммы вычесть 2; результат будет 20.
ИЗМЕНЕНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ Я
ЧАСТНОГО.
34.	Изменение суммы. 1. Если к одному из слагаемых приба-
прибавим (или отнимем) несколько единиц, то и в сумме прибавится
(или отнимется) столько же единиц.
2. Если к одному слагаемому прибавим несколько единиц,
а от другого отнимем столько же единиц, то сумма не изме-
изменится.
35.	Изменение разности. 1. Если к уменьшаемому прибавим
(или отнимем) несколько единиц, то и к разности прибавится
(или отнимется) столько же единиц.
2.	Если к вычитаемому прибавим (или отнимем) несколько
единиц, то от разности отнимется (или прибавится) столько же
единиц.
3.	Если к уменьшаемому и вычитаемому прибавим (или
отнимем) одно и то же число, то разность не изменится.
36.	Изменение произведения. 1. Если один из производителей
умножим (или разделим) на какое-нибудь число, то и произве-
произведение умножится (или разделится) на то же число.
») Знаки умножения и деления теснее связывают числа, чем знак + и
поэтому произведение и частное в скобки не заключаются.
2»	— 19 -

2. Если один из производителей умножим на какое-нибудь
число, а другой разделим на то же число, то произведение не
изменится.
37,	Изменение частного. (В случае деления без остатка.) 1. Если
делимое умножим (или разделим) на какое-нибудь число, то част-
частное умножится (или разделится) на то же число.
2.	Если делитель умножим (шпг разделим) на какое-нибудь
число, то частное разделится (или умножится) на то же число.
3.	Если делимое и делитель умножим или разделим на одно
и то же число, то частное не изменится.
СВОЙСТВА ДЕЙСТВИЙ.
38.	1. Чтобы прибавить сумму, нужно прибавить одно сла-
слагаемое за другим, например:
2. Чтобы отнять сумму, нужно отнять одно слагаемое за дру-
другим, например:
16 —E + 7) = 1б —5 —7
3.	Чтобы прибавить разность, нужно прибавить уменьшаемое
и вычесть вычитаемое, например:
— 5
4.	Чтобы отнять разность, нужно прибавить вычитаемое и
вычесть уменьшаемое, например:
16 — G — 5) = 16-f 5 — 7
5. Чтобы умножить или разделить сумму или разность двух
чисел, нужно умножить или разделить каждое из этих чисел,
например:
E-f 2)-3 = 5-3 4-2-3; (8 + 6):2 = 8:2 + 6:2
E —2)-3 = 5-3 —2-3; (8 — 6):2 = 8:2 —6:2
6. Чтобы умножить или разделить на произведение нужно
умножить или разделить на первый производитель, полученный
результат на второй и т. д., например:
6 X B X 3 X 5) = [F X 2) X 3] Х5 = [12 X 3] X 5 = 36 X 5 = 180;
48:
— 20

Чтобы умножить или разделить произведение на какое-нибудь
число, нужно умножить или разделить на это число один какой-
нибудь производитель, например;
DX6 ХЗ):2 = 4Х F:2) X 3 = 4X3X3 =
9
39. Особые случаи действий, 1. При сложении и вычитании
часто дает хорошие результаты способ округления чисел, например:
542 + 297 = E42 + 300) — 3 = 842 — 3 = 839 ;
542 — 297 = E42 — 300) + 3 = 242 + 3 = 245
2.	Деление на 5 и на 25. Пусть требуется разделить 85 на 5.
Рассуждаем так: в 1 десятке 5 содержится 2 раза, а в 8 десят-
десятках будет содержаться 16 раз, да еще в 5 будет содержаться
1 раз; следовательно, 85:5 = 17.
Чтобы разделить 1275 на 25, рассуждаем так: в 1 сетне 25 со-
содержится 4 раза, в 12 сотнях будет содержаться 48 раз, да еще
в 75 содержится 3 раза, следовательно, всего 51 раз.
3.	Умножение числа, оканчивающегося 5, на самого себя,
т. е. другими словами — возведение его в квадрат; например
умножим 25 на 25.
3-2J5-5;	25-25 = 625 Пишем 25; отделяем одну цифру от
6 25	другой вертикальной чертой; правую
4	• 3 | 5 • 5;	35 • 35 = 1225 цифру умножаем всегда на 5, а левую
5	• 415 • 5;	45 • 45 = 2025 на цифру1), увеличенную на единицу,
и т. д.
4.	Умножение на 9, 99, 999 и т.. д.
127 • 999 = 1261873	В первом случае вместо 127 берем 126 и
43- 99= 421 57	затем каждую цифру этого числа вычи-
54- 99= 531 46	таем из 9; получим 873; всего 126873.
и т. д.
Ш. ИМЕНОВАННЫЕ ЧИСЛА,
40, Определения, Все то, что может увеличиваться и умень-
уменьшаться и может быть разделено на части, называется величи-
величиной, например длина, ширина, вышина, время, вес, температура
и т. д. Каждая величина имеет бесчисленное множество значений,
например длина может быть равна: 1см, 2см, Зсм и т. д.
4) Слово цифра здесь употребляется для краткости вместо: число, обозначен
ное цифрой.
- 21 —

Две величины называются однородными, если одна из них мо-
может составлять часть другой.
Измерить величину1)—значит узнать, сколько раз в ней содер-
шсится другая однородная величина (или какая-нибудь ее часть).
Та величина, которой измеряют другую, называется единицей.
Единицы, принятые всеми и утвержденные государством^ на-
называются мерами, например сантиметр, километр, килограмм
и т. д.
В результате измерения величины получается или одно
именованное число, называемое простым, например 7 килограм-
килограммов, или несколько именованных чисел, например 2 килограмма
3 грамма, совокупность которых называется составным имено-
именованным числом.
МЕТРИЧЕСКИЕ МЕРЫ 2).
41. Меры веса.
Тонна =1000 килограммов = 61 пуду (приблизительно).
1 килограмм = 1000 граммов = 2 фунтам 42 золотникам.
1 грамм = 1000 миллиграммов.
42. Меры длины.
Километр = 1000 метров (немного менее вррсты).
1 декаметр =10 метрам.
1 метр = 10 дециметрам = 100 сантиметрам.
1 дециметр = 10 сантиметрам.
1 сантиметр = 10 миллиметрам.
43. Меры поверхностей, или квадратные меры.
1 кв. километр = 100 гектарам.
1 гектар = 100 арам (немного менее десятины).
1 ар = 100 кв. метрам.
1 кв. метр = 10000 кв. сантиметров = 2 кв. аршинам (при-
(приблизительно),
1 кв. сантиметр = 100 кв. миллиметрам.
*) Для удобства употребляем слово „величина" в двух смыслах: понимая под
этим словом как величину в собственном смысле, так и значение (размер) ве-
величины.
*) См. § 108.
— 22 —

44. Меры объемов, или кубические меры.
1 куб. метр1) = 1000 куб. дециметров.
1 куб. дециметр = 1000 куб. сантиметров.'
1 куб. сантиметр = 1000 куб. миллиметров.
45, Меры сыпучих тел и жидкостей.
1 лптр = 1 куб. дециметру.
1 гектолитр = 100 литрам.
1 литр = 10 децилитрам (в ведре приблизительно 12 литров).
46. Меры бумаги.
Стопа = 20 дестям.
Десть = 10 тетрадям.
Тетрадь = 5 листам.
47, Деньги.
Цена предметов определяется металлическими и бумажными
деньгами. Металлические деньги обыкновенно бывают золотые,
серебряные и медные; они называются монетами. Золотые мо-
монеты: 10 рублей и 5 рублей.
Серебряные монеты.
Рубль = 100 коп.
Полтинник = 50 коп.
Двугривенный = 20 коп.
Пятиалтынный = 15 коп.
Гривенник = 10 коп.
Медные и бронзовые монеты.
5, 3, 2, 1 и полкопейки.
Бумажные деньги называются банковыми, или казначейскими
билетами; они бывают разной ценности.
48. Меры времени.
Век, или столетие = 100 годам.
Год простой = 365 дням (суткам).
Год високосный = 366 дням.
Год =12 месяцам.
Кубический метр называется стером.
- 23 —

Месяц = 30 суткам1).
Неделя=7 суткам-
Су тки = 24 часам.
Час = 60 минутам.
Минута = 60 секундам.
49. Летосчисление. Солнечный, или тропический год, т. е.
время, протекающее от одного весеннего равноденствия до сле-
следующего, содержит 365 дней 5 час. 48 мин. 46 сек. В течение
этого времени Земля совершает почти полный оборот около
Солнца. В гражданском летосчислении для удобства условились
считать три года подряд в 365 дней, а четвертый в 366 дней.
Год в 365 дней называется простым, а год в 366 дней — висо-
високосным. Високосным будет каждый год, число которого делится
без остатка на 4. Наше прежнее летосчисление называется юли-
юлианским (или старым стилем) по имени римского императора
Юлия Цезаря, установившего его еще в 45 г. до нашей эры.
Так как в юлианском летосчислении год считается равным
365 — суток вместо 365 суток 5 час. 48 мин. 46 сек., то юлиан-
юлианский календарь каждый год отстает от солнечного на 11 мин.
14 сек. и, как легко высчитать, через каждые 128 лет отстает
приблизительно на одни сутки. В 325 г. нашей эры на Никейском
соборе юлианский календарь был принят христианской церковью
и была исправлена накопившаяся к тому времени ошибка.
В 1582 г. папа Григорий XIII ввел новое летосчисление, полу-
получившею название григорианского, иди нового стиля. Он приказал
исправить накопившуюся к этому времени ошибку (почти
в 10 дней), именно, вместо 5 октября считать сразу 15 октября,
а во избежание ошибок в дальнейшем, из годов, числа которых
оканчиваются двумя нулями и, следовательно, делятся на 4,
считать високосными только те% у которых первые две цифры
обозначают число, делящееся на 4. Таким образом 1700 год по
юлианскому летосчислению был високосным, а по григорианскому
нет. Остальные високосные года будут одинаковы в обоих лето-
счислениях. В настоящее время разница между старым и новым
стилем составляет 13 суток (разница увеличивалась на одни
*) Январь, март, май, июль, августь, октябрь и декабрь — 31 день; февраль
в простом году — 28 дней, февраль в високосном году — 29 дней; апрель, июнь,
сентябрь, ноябрь — 30 дней. Месяц принимается в 30 дней, когда не требуется
определить число и название месяца.
- 24 —

сутки в i700-x, 1800-х и 1900-х годах). Новое Летосчисление также
делает ошибку, которая составит разницу в одни сутки через
3300 лет. В СССР новый стиль введен после революции (декрет
от 8 февраля 1918 г.).
50.	Обозначения метрических мер. Сокращенные наименования
метрических мер принято писать без точки, например:
метр	—м	ар —а
дециметр	—дм	гектар —га
сантиметр	—см	литр —л
миллиметр — мм	гектолитр — гл
километр	—км	грамм — г
кв. метр	—кв. м или м2	килограмм — кг
куб. метр	—куб. м или м3
51.	Обращение крупных мер в мелкие.
Пример. Обратить 17 км 243 м в метры.
В одном километре 1000 м;
в 17 км будет	1000 мХ 17 = 17000 м;
В 17 км 243 м будет 17000 м + 243 м = 17243 М
Замечание. Легко видеть, что для решения этого примера
достаточно в составном именованном числе 17 км 243 м выпус-
выпустить наименование км и написать просто: 17243 м
Точно так же: 43 м 27 см — 4327 см.
43 руб. 27 КОП. = 4327 КОП.
52.	Обращение мелких мер в крупные.
Пример. Обратить 3725 м в километры.
В 3725 м будет столько километров, сколько раз 1000 м со-
содержится в 3725 м.
Поэтому имеем:	.
3725
3000
725
3725
м
м
М —
| 1000
3
Зкм
3 км
м
725 М
Замечание. Легко видеть, что для решения этого примера
достаточно в числе 3725 м поставить буквы км между циф-
цифрами 3 и 7.
Точно так же:
2757 <ш = 27 м 57 см
2ЛЫ КОП. =27 руб. 57 коп.

53.	Сложение и вычитание составных именованных чисел
Примеры.
1) 2 м 47 см	2) 2 руб. 47 КОП.
-f- 3 м 58 см	+ 3 РУб- 58 КОП,
5 jm 72 см	5 руб. 72 коп.
11 м 77 б\м	11 руб. 77 коп.
3) 4 м 05 сш	4) 4 руб. 05 коп.
2 м 08 см	2 руб. 08 коп.
1 м 97 см	1 руб. 97 коп.
Замечание. Сложение и вычитание метров и сантиметров
очень удобно делать на русских счетах, если принять косточки,
означающие рубли, за метры, а косточки, означающие копейки,
за сантиметры.
54.	Задачи на вычисление времени.
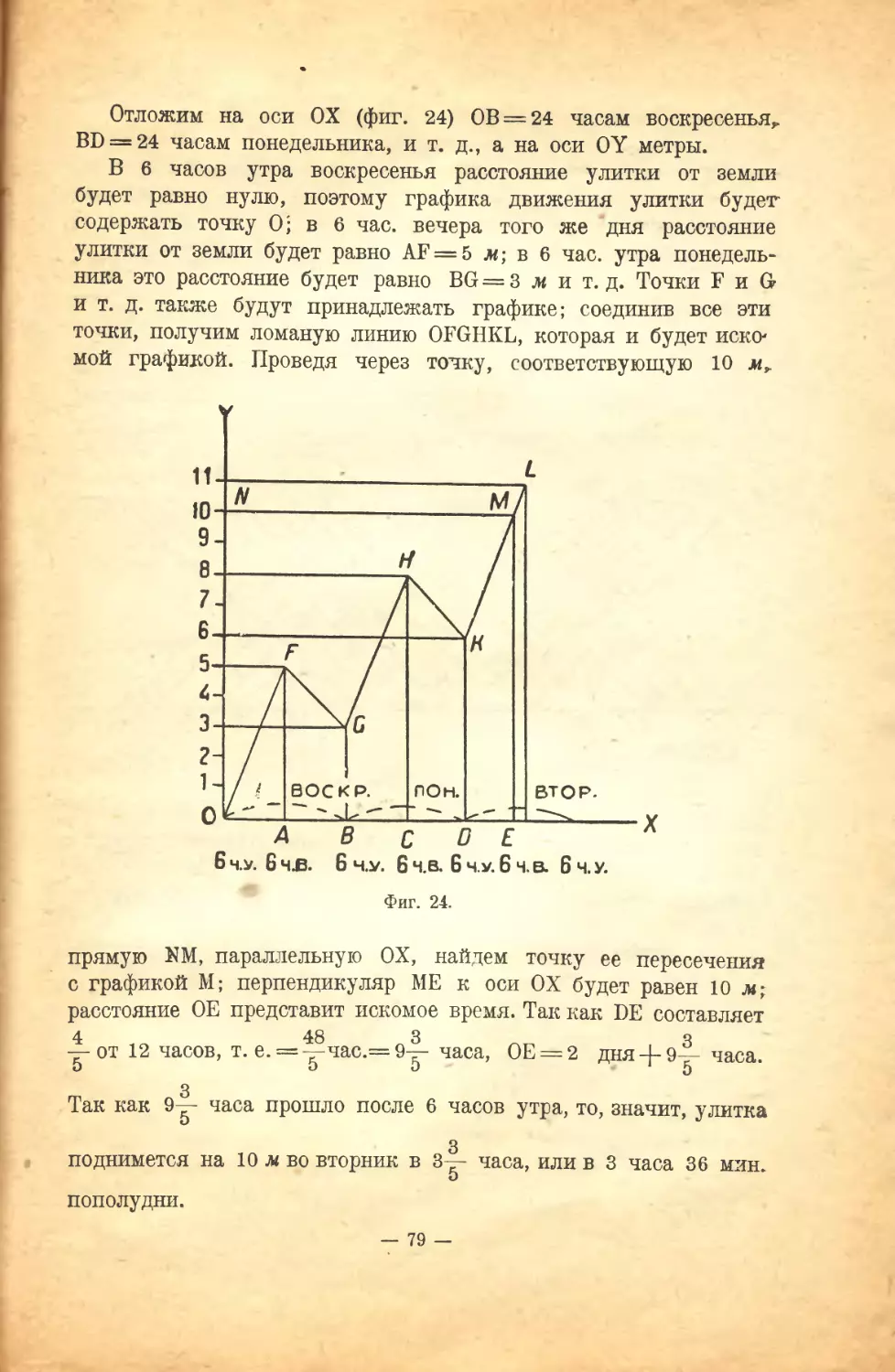
Задача 1. Некоторое событие случилось 10 апреля. Когда
исполнится 35 дней с момента этого события?
Решение. Условимся обозначать месяцы римскими v циф-
цифрами :
январь, февраль, март, апрель, май, июнь, июль, август,
I	II	III IV	V VI VII VIII
сентябрь, октябрь, ноябрь, декабрь;
IX	X	XI XII
число месяца и год будем обозначать индусскими цифрами.
Тогда
IV 10
~ 35
IV 45
V 15,
т. е. искомый момент наступит 45 апреля; но в апреле 30 дней;
следовательно, искомый момент наступит 15 мая D5 — 30 = 15).
Задача 2. Некоторое событие случилось 10 апреля. Другое
событие было на 35 дней ранее. Когда оно произошло?
Решение.
31
W
—
III
26
10
35
6

Так как из 10 дней апреля нельзя вычесть 35 дней, то к этим
10 дням прибавляем ?1 день предыдущего месяца, т. е. марта;
из полученного числа 41 вычитаем 35. Найдем, что событие
произошло 6 марта.
Задача 3 Известный математик Якоби, родившийся в Гер-
Германии 10 декабря 1804 г., прожил 46 лет и 70 дней. Когда он
умер!
Решение.
, 1804 XII 10
' 46 70
1850	XII 80
1851	I 49 (80 — 31 = 49)
1851 II 18D9 — 31 = 18),
т. е. Якоби умер 18 февраля 1851 года.
Задача 4. Мих. Бас. Ломоносов умер 4 апреля 1765 г., имея
от рождения 53 года 7 месяцев 10 дней. Когда он родился?
Решение.
31
_1765	IV 4
52	VII 10
1712 VIII 25,
т. е. Ломоносов родился 25 августа 1712 г.
Задача 5 Путешественник отправился 15 декабря 1903 г.
в 20 час. 45 мин. *) и вернулся обратно 5 марта 1904 г. в 2 час.
15 мин. Сколько времени он пробыл в дороге?
Решение.
1904
1903
Ш
XII
II
B9)
•
5
15
18
B4)
2
20
5
час.
час.
час.
F0 мин.)
15 мин. 2)
45 мин.
30 мин.
Следовательно, он пробыл в дороге 2 месяца 18 дней 5 час.
30 мин.
4) За начало суток принимается 12 час. ночи.
2) Чтобы вычесть 15 дней из 5 дней, придется от високосного 1904 года
занять II месяц, т. е. февраль, который будет содержать в этом случае
29 дней.
— 27 —

55* Умножение составных именованных чисел.
Пример. 3 кг 305 г умножить на 5.
Первый способ. 3 кг 305 г
Х5
15 кг 1525 г = 16 кг 525 г
Другой способ. 3 кг 305 г = 3305 г
3305 г
Х5
16525 г =16 кг 525 г
56, Деление составных именованных чисел. При делении
составных именованных чисел встречаются два случая: 1) деление
именованного числа па отвлеченное и 2) деление именованного
числа на именованное.
Пример 1. 53 км	375 м разделить на 5
53 км	375 м = 53375 м
_53375 М	| 5
5	10675 м = 10 км 675 м
33
30
_37
35
_25
25
0
Пример 2. Разделить 94 м 28 см на 23 м 57 см.
Имеем:
94 м 28 см = 9428 см _9428 СМ \ 2357 см
23 м 57 cjk = 2357 CM ~9428	4
ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ.
57. Четыреуголъник, изображенный на фигуре I, называется
прямоугольником. Каждый из углов прямоугольника называется
прямым.
Прямоугольник, у которого все стороны равны, называется
квадратом (фиг. 2).
Величина части плоскости, ограниченной сторонами прямо
угольника, называется его площадью,
— 28 -

Площадь квадрата, сторона которого равна сантиметру, назы-
называется квадратным сантиметром.
Площадь квадрата, сторона которого равна метру, называется
квадратным метром, и т. д.
Из рассмотрения фиг. 3 вытекает
Правило. Чтобы определить площадь (прямоугольника), нужно
умножить длину на ширину1), например площадь фигуры 3 рав-
равняется 3X4 кв. метрам = 12 кв. метрам. Из этого правила сле-
следует :
Чтобы определить длину, нужно площадь разделить на ширину.
Чтобы определить ширину, нужно площадь разделить на длину.
Задача 1. Определить площадь прямоугольника, длина кото-
которого 2 дм 5 см у а ширина 9 см.
Для решения задачи нужно выразить длину и ширину в ме-
мерах одного и того же наименования, например в сантиметрах,
и полученные числа перемножить.
2 дм 5 ом = 25 см
25 X 9 = 225 {кв. см)
4 К8.М
i	i
I	I
кем.
I
1
	1
1
1
~ - т -
1
¦ r
r
1
1
I
- — -
Зм
4x3 /кв.м/
Фиг. 1.
Фиг. 2.
Фиг. 3.
Ответ. 225 кв. см.
Задача 2. Площадь прямоугольника равнг 512 кв. см. Длина
64 см. Найти ширину.
Решение.
512:64 = 8 (см)
Ответ. Ширина равна 8 см
*) Примечание. Для краткости правило ыыражено неверно; длину нельзя
умножить на ширину, так как умножить можно только на отвлеченное число;
стедовало бы сказать: перемножить числа, выражающие длину и ширину в мерах
одного и того же наименования; полученное произведение будет выражать пло-
площадь в соответственных квадратных мерах.
2) Наименование ставим в скобках, потому что 225 отвлеченное число, так
как получилорь от перемножения отвлеченных чисел и лишь по смыслу задачи
оно дошно означать число квадратных сантиметров, заключающихся в площади
прямоуппьника.

58. Предмет, ограниченный шестью прямоугольниками (напри-
(например,, кирпич), называется прямоугольным параллелепипедом
(фиг. 4).
Параллелепипед (фиг. 5), у которого длина, ширина и высота
равны между собою, называется кубом.
Величина части пространства, занимаемой каким-нибудь
предметом, называется объемом последнего.
Объем куба, у которого длина, ширина и высота равны одному
метру, называется кубическим метром.
Объем куба, у которого длина, ширина и высота равны одному
дециметру, называется кубическим дециметром и т. д.
Из рассмотрения фиг. 6 вытекает следующее
Правило. Чтобы определить объем (прямоугольного паралле-
параллелепипеда), нужно перемножить длину, ширину и высоту а).
м-
У
Фиг. 4.
Фиг. 5.
w	q
Фиг. 6.
Задача 1. Определить объем ящика, длина которого 3 дм,
ширина 2 дм 5 см, вышина 1дм 6 см
Решение.
3 дм = 30 см
2 дм 5 см = 25 см
1 дм 6 см = 16 см
30-25-16 = 12000 (куб. см) = 12 куб. дм = 12 литрам.
Задача 2. Объем помещения 600 куб. м, длина 12 м, ширина
10 м. Определить высоту.
Для определения высоты нужно объем разделить на произ-
произведение длины и ширины.
1) 12ХЮ==120; 2) 600:120 =
Ответ. 5 м.
i) Примечание. Правильнее было бы сказать: перемножить числа, вы-
выражающие длину, ширину и высоту в мерах одного наименования. Полученное
произведение будет выражать объем в соответственных кубических мерах.
- 30

IV. ПРИЗНАКИ ДЕЛИМОСТИ.
59.	Определение. Если одно число делится без остатка на
е, то первое называется кратным второго, а второе — точ-
точны делителем первого.
Например, 10 есть кратное 5, а 5 будет точным делителем 10,
тому что 10 делится на 5 без остатка. Если число является
ратным или делителем нескольких чисел, то оно называется
т кратным или общим делителем.
Числа, кратные 3, называются четными, например: 2, 4, G, 8,
10 и т. д.
60,	Вывод признаков делимости основан на следующих
истинах:
Если каждое слагаемое делится г) на какое-нибудь число, то
сумма разделится на это число.
Если одно из двух слагаемых делится, а другое не делится на
какое-нибудь число, то сумма не разделится на это число.
1.	На 10, 100, 1000 и т. д. делятся те числа, которые2)
оканчиваются соответственно одним нулем, двумя нулями, тремя
нулями и т. д., потому что такие числа состоят или из одних
десятков, или из одних сотен и т. д.
2.	На 2 делятся те числа, которые оканчиваются нулем или
четной цифрой. В самом деле, всякое число можно рас-
рассматривать как сумму двух слагаемых, из которых первое со-
содержит все десятки данного числа, а второе — его единицы. Первое
слагаемое, как состоящее из одних десятков, всегда разделится
на 2, потому что каждый десяток делится на 2; следовательно,
делимость данного числа будет зависеть исключительно от де-
делимости второго слагаемого, т. е. единиц данного числа. Напри-
Например 546 = 540 + 6 разделится на 2, потому что оба слагаемые
540 и 6 делятся на 2.
3.	На 5 делятся те числа, которые оканчиваются 0 или 5.
Этот признак выводится так же, как и предыдущий.
4.	На 4 делятся те числа, которые оканчиваются двумя ну-
нулями или у которых две последние цифры обозначают число,
делящееся на 4.
Действительно, рассматривая какое-нибудь число, например
5712, как сумму двух слагаемых 5700 и 12, мы замечаем, что
Под словом „делится" мы будем разуметь: „делится без остатка".
Правильнее было бы сказать: обозначения когорых оканчиваются и т. д.
— 31 —

первое из них всегда разделится на 4 как состоящее из одних
сотен; следовательно, для делимости данного числа необходима
делимость числа, обозначенного двумя последними цифрами,
т. е. 12. Так как 12 делится на 4, то и 5712 тоже разделится.
Так же выводится признак делимости на 25.
5.	На 25 делятся те числа, которые оканчиваются 00, 25,
50 или 75.
6.	На 8 делятся те числа, которые оканчиваются тремя
нулями или у которых три последние гщфры обозначают число,
делящееся на 8.
Всякое число, оканчивающееся тремя нулями, как состоящее
из одних тысяч, будет делиться на 8, потому что 1000:8 = 125.
Рассматривая какое-нибудь число, например 37216, как
сумму двух слагаемых 37000 и 216, замечаем, что делимость его
зависит от делимости 216, т. е. числа, обозначенного тремя
последними цифрами.
7.	На 125 делятся те числа, которые оканчиваются тремя
нулями или у которых три последние цифры обозначают число,
делящееся на 125. Вывод этого признака подобен предыдущему.
8.	На 9 делятся те числа, сумма цифр1) которых делится на 9.
Докажем, что, например, число 2637 разделится на 9. Каждая
тысяча при делении на 9 дает в частном 111 ив остатке 1,
следовательно, две тысячи дадут в частном 222 и в остатке 2;
поэтому
2000 = 9 X 222 + 2 2)
Каждая сотня при делении на 9 дает в частном 11 и в
Остатке 1, следовательно, 6 сотен при делении на 9 дадут в
частном 66 и в остатке 6; поэтому
600 = 9X66
Точно так же
30 = 9X3
Число 2637 можно представить в виде такой суммы:
2637 = 2000 + 600 +30+ 7 = 9Х 222+ 2 + 9X66+ 6 + 9X3
= 9X222+9X66
*) Так как цифры суть знаки, то их складывать нельзя; поэтому выражение
„сумма цифр" неправильно; следовало бы сказать: „сумма чисел, обозначенных
цифрами данного числа"*
Делимое равно делителю, умноженному на частное, плюс остаток.
— 32 —

Слагаемые, составляющие число 2637, можно разбить на 2
группы, как показан© горизонтальными скобками. Каждое сла-
слагаемое первой группы всегда на 9 разделится; следовательно,
делимость числа 2637 зависит от того, разделится ли на 9 сумма
слагаемых второй группы, т. е. сумма цифр данного числа;
в данном случае эта сумма B + 6 + 3 + 7), равная 18, на 9 де-
чится, следовательно, и число 2637 на 9 разделится.
9. На 3 делятся те числа, сумма цифр которых делится на S.
Разложив по предыдущему какое-нибудь число, например
2637, на слагаемые:
2637 = 9X222 + 9X66 + 9X3
замечаем, что делимость числа 2637 на 3 зависит от делимости
суммы цифр этого числа на 3; и так как сумма B + 6 + 3 + 7==
= 18) на 3 делится, то и 2637 на 3 разделится.
10. На 6 делятся те числа, которые делятся на 2 и на 3.
На 12 делятся те числа, которые делятся па 3 и па 4.
На 15 делятся те числа, которые делятся па 3 и па 5.
На 18 делятся те числа, которые делятся па 2 и на 9 и т. д.
У. ПРОСТЫЕ ДРОБИ, ПРЕОБРАЗОВАНИЯ И ДЕЙ-
ДЕЙСТВИЯ НАД НИМИ.
61. Если разделим единицу на несколько равных частей, то
каждая такая часть называется долей. Изобразим единицу ли-
линией АВ (фиг. 7),
4 ^ --За	_ ?	В
Фиг. 7.
которая представляет собою дециметр; тогда линия АС будет
равна'3 сантиметрам или, иначе, трем десятым дециметра; число
три десятых называется дробью.
Дробью называется число, выраоюающее одну или несколько
равных долей единицы.
Дробь устно и письменно выражается двумя целыми чи-
числами; в письме эти числа отделяются друг от друга горизон-
3
та~1ьной черточкой, например АС=—-дм.
3 Рашевокий, Краткий курс арифм. — 33 -*¦

Верхнее число казываё^ся Числителем, нижнее —
дем, а оба вместе — членами дроби.
Знаменатель показывает, на "сколько равных частей разделена
единигщ, а числитель — сколько таких частей взято.
Если разделить поровну 3 яблока между 4 лицами, то каж-
каждое лицо получит по три четверти яблока (по одной четверти
от каждого яблока), т. е. по — яблока. Отсюда следует, что
дробь есть такоюе частное от деления двух чисел, когда одно
число не делится на другое. Таким образом, черточка дроби есть
3
не что иное, как знак деления; поэтому можно написать — или
о
3:5, что будет означать одно и то же; прочесть число — тоже
можно двояким способом: гри пятых или три, деленное на пять.
Целое число с дробью называется смешанным числом, напри*
Л 3
мер, 2—.
Та дробь, которая меньше единицы, называется правильной
3
например —-.
Та дробь, которая больше единицы или равна ей, называется
неправильной. Таковы будут дроби —; —.
о о
62. Правило. Чтооы обратить смешанное число в неправиль-
неправильную дробь, нужно целое число умножить на знаменатель, при-
прибавить числитель и подписать тот оюе знаменатель, напри-
3 4X8 + 3 35
мер: 4 —=ч	5-1— = -5"» так как в единице восьмых долей 8,
о	о	о
в четырех единицах их будет 32, да у нас еще имеется 3 вось-
восьмых, следовательно, всего будет 35 восьмых.
63. Правило. Чтобы обратить неправильную дробь в целое или
смешанное число, нужно числитель разделить на знаменатель.
Частное покажет число единиц, а остаток — число оставшихся
долей, например:
7
165
14
25
"1
7
23
- 34

Действительно, в единице 7 седьмых; следовательно, сколько
раз 7 седьмых содержится в 165 седьмых, столько и будет
единиц.
Это преобразование неправильной дроби называется исключе-
исключением целого числа из неправильной дроби.
64. Сравнение дробей. Из двух дробей с одинаковыми знаме-
знаменателями та больше, у которой числитель больше.
Например, — больше —, потому что доли в обеих дробях
о	о
одинаковы, но в первой дроби их больше, чем во второй. Если
изобразим единицу линией АВ (фиг. 8) и разделим ее на 8 до-
3	5
тей, то дробь — изобразится линией АС, а дробь — линией
о	о
AM; легко видеть, что AM больше АС.
I у	I	о
Фиг. 8.	Фиг. 9.
Из двух дробей с одинаковыми числителями та больше, у ко-
которой знаменатель меньше.
3	3
Например, — больше —, потому что число долей в обеих
дробях одинаково, но в первой дроби доли крупнее, чем во
второй (четвертые доли крупнее восьмых). Так как каждая чет-
четвертая доля больше восьмой доли в два раза, то и дробь —
будет больше дроби — в два раза. В справедливости всего ска-
сказанного легко также убедиться из рассмотрения фигуры 9.
Сравнивая между собою различные дроби с одинаковыми
числителями или с одинаковыми знаменателями, можно вывести.
65. Правило. Чтобы увеличить дробь в несколько раз, нужно
или числитель увеличить, или знаменатель уменьшить во
столько же раз; а чтобы уменьшить дробь, нужно или числитель
уменьшить, или знаменатель увеличить.
68. Главное свойство дроби. Величина дроби не изменится,
если числитель и знаменатель ее умножить или разделить на
одно и то же число, потому что, умножая, например, числитель
на какое-нибудь число, мы увеличиваем дробь в несколько раз,
о*	«¦— 3d —

а умножая на то же число знаменатель, уменьшаем дробь во
столько же раз.
К тому же выводу можно притти, рассматривая, например,
фиг. 10 (-- = -
А	\ л.
67. Сокращение дробей. Определение. Сократить дробь— зна-
значит представить ее в более простом виде, не изменяя ее величины.
Правило. Чтобы сократить дробь, нужно числитель и зна-
знаменатель ее разделить на одно и то оке число.
3	5	15
„	45^ 15W 3	45~ 3
Например: _ = — = *-, или —=т
E8. Выражение дробей в других долях. Задача 1. Выра-
Выразить — в восьмых до тх.
4
Изобразив единицу линией (фиг. 10), разделим ее на 8 рав-
^ -8 —
		-JL-
Фиг. 10.	Фиг. 11.
ных частей; найдя —линии, увидим, что она содержит —; та-
4	Q
s	12
ким образом, — = —.
Задача 2. Выразить— в двенадцатых долях.
Так как в единице двенадцатых долей 12, то в — их будет 3,
т. е-" = ^' То же самое можно усмотреть из чертежа (фиг, 11),
Задача 3 Выразить— в шестнадцатых долях.
Так как в единице шестнадцатых долей 16, то в — их будет 4,
т. е. —=~ (фиг. 12).
Замечание. Легко видеть, что — можно выразить только в
таких долях, знаменатель которых делится без остатка на 4;
выразить же — в 10-х, 15-х, 18-х долях нельзя.
— 36 —

Задача 4. Выразить— и — в одинаковых долях.
На основании предыдущего эти дроби можно выразить в 12-х,
12 3 9
24-х, 36-х долях. Выразив в двенадцатых, получим: — = —, —= —
(фиг. 13).
69, Выражение дробей в одинаковых долях называется при-
приведением дробей к общему знаменателю. В предыдущем примере
общий знаменатель 12 делится без остатка на знаменателей
6 и 4; следовательно, он будет их общим кратным (при этом
наименьшим). Легко видеть, что данные дроби мы могли бы
выразить в одинаковых долях, умножив числитель и знаменатель
первой дроби на 2 A2:6 = 2), а второй дроби на 3 A2:4 = 3).
Назвав числа (в данном случае 2 и 3), получаемые от деления
общего знаменателя на знаменатель каждой дроби, дополнитель-
дополнительными множителями, можем высказать следующее
1 1 1 1 1 1 1 1 1 1 1 1 Rm'i^	7 = 12	^=!z_
16	Г м f j I | I I | I i 1
Фиг. 12	Фиг. 13
Правило. Для приведения дробей к одному знаменателю
нужно:
1)	найти общее наименьшее кратное знаменателей] оно и
будет общим знаменателем;
2)	найти дополнительный множитель каждой дроби, деля об-
общий знаменатель на знаменатель этой дроби;
3)	умножить числитель каждой дроби на соответствующий
дополнительный множитель и подписать общий знаменатель.
70, Замечание. Таким образом выражать дроби в одина-
одинаковых долях можно и по соображению, и по правилу. Рекомен-
Рекомендуется сначала научиться приводить дроби к одному знамена-
знаменателю по соображению, а потом уже по правилу, причем надб
брать дроби с небольшими числителями и знаменателями, так
как только такие дроби встречаются в жизненном обиходе; что
же касается техников, инженеров и т. д., то они в своих вычи-
вычислениях пользуются не простыми дробями, а десятичными —
ввиду их громадных преимуществ. Таким образом простые
дроби с большими числителями и здаменателями никому ™
нужны.	. •. „.
37 —

71. Пример 1. Привести к общему знаменателю дроби: —
Общее наименьшее кратное знаменателей равно 10, потому
что делится на 10 и на 5;
дополнительный множитель для первой дроби равен 10:10 = 1
„	»	„ второй „	„ 10:5 =2,
поэтому получим:
10~10; 5 ХО
1
Пример 2. Привести к одному знаменателю дроби: —,
,
Общее наименьшее кратное знаменателей равно 60
дополнительный множитель для 1 -й	дроби = 60:6 = 10;
„ 2-й	„ = 60:4=15;
3-Й	„ =60:5 =
следовательно:
10	15	12
1~ 10 3W 45 2^	24
6 60' 4 60' 5 60
72. Сложение дробей. Определение. Сложение есть действие,
посредством которого из нескольких чисел составляют новое число,
содержащее в себе столько единиц и столько частей единицы,
сколько их находится во всех данных числах; поэтому сумма
3	2
2	\~ 5 — будет содержать столько единиц и столько одиннад-
одиннадцатых долей, сколько их находится в обоих слагаемых, т. е. 7 еди-
единиц и 5 одиннадцатых долей. Следовательно:
i) Чтобы найти общее наименьшее кратное знаменателей, нужно самый
большой знаменатель (в данном случае 6) помножить на 19 2* 3, 4 я т. до
В§ ВРлучиш Ш>до, делящееся на все знаменатели,
- 38 -

73, Правило. Чтобы сложиыь дроби, нуоюно привести их
к одному знаменателю, сложить числители и подписать тот же
знаменатель. Если при дробях будут целые числа, то нужно
отдельно сложить целые, числа, отдельно дроби, и первую сумму
стожить со второй.
4	3
тт	, 2 I 3~ 8
Пример!. _+
4 12
6	2
9
12
5
3
17
12
24
зсМ
5
12
I14 1
30 ~г
25!)
30 ~
Пример 2. 8T + l- + 4T = 8- + l + 4 =8
30	10
:• Вычитание дробей. Правило. Чтобы вычесть дробь из
дроби, нужно их привести к одному знаменателю; из числителя
уменьшаемой дроби вычесть числитель вычитаемой и подписать
тот же знаменатель, например:
3	2
_L _ JL1- ?! _ 12—!!
8~12~~24 24~4
п	11	5
Сложив разность — с вычитаемым —, получим уменьшаемое
7
—, что и доказывает справедливость высказанного правила.
о
Если при дробях будут целые числа, то нужно отдельно
вычесть дроби, отдельно целые числа и полученные результаты
сложить; если вычесть дробь из дроби окажется невозможным,
то нужно в уменьшаемом занять единицу и раздробить ее
в соответствующие доли, например:
з = 73 = 4
35 35 35 %5 * 35
75, Умножение дробей. Определение. Умножить какое-нибудь
число на дробь—значит найти часть этого числа, выражаемую
данной дробью.
4) Нужно непременно писать второй раз целые числа, что очень часто уча-
учащиеся забывают.
— 39 -

v к Ц	3	2
Например, умиооюить — на	значит найти— от —;
7	5	5	/
12	2
— от — будет в 5 раз меньше —-, следовательно (§ 65),
о	/	7
1	2'2
от — =
5	7 35
3
¦j- будут в 3 раза больше* следовательно,
Таким обра;
_?._ 6
°Т Т~35
2 3 6 2X3
7 'N 5 35 5X7
Отсюда можно вывести
76. Правило. Чтобы умнооюить дробь на дробь, нужно умно-
умножить числитель на числитель, знаменатель на знаменатель и
первое произведение разделить на второе.
Если один из производителей будет целое число, то нужно
его представить в виде дроби со знаменателем 1 и поступать
по предыдущему. Чтобы перемножить смешанные числа, нужно
предварительно обратить их в неправильные дроби.
Примеры:
1 7X1 7	7
Х 2-ЗХ 2- 6
11 1 Х11~Т><ТГ~П
523Х5
2-
77, Сокращение при умножении дробей. Никогда не следует
сразу перемножать числители и знаменатели дробей, а нужно
сделать предварительно сокращение, например:
24 w 42 Si X *2 3X3 9 ,4
35'" 16 SSX^K 5X1 5	5
5 4
1
— 40 —

78. Чтобы перемножить несколько дробей, нужно перемно-
перемножить числители, перемножить знаменатели и первое произведе-
произведение разделить на второе, например:
1 З1)
Б 3
35 42 2435 ХЙХЙ 1X3X3 9	4
ХХ	~5	5
5 X	5	5
2 5^
1	1
79, Следует заметить, что при умножении на правильную
дробь произведение будет меньше множимого, а при умножении
на неправильную—больше, например:
2
ю згахз2хз_ в
2
8-ЦХ8_2Х8_16_
~
Ъ 1 Л 5	Х
1
80,	Так как перемножение дробей сводится к перемножению
их числителей и знаменателей, т. е. целых чисел, то произведение
дробей обладает теми же свойствами, как и произведение целых
чисел: оно не меняется от перестановки производителей и т. д.
81.	Деление дробей. Правило. Чтобы разделить дробь па дробь,
нужно числитель первой дроби умножить на знаменатель второй,
а знаменатель первой на числитель второй и первое произве-
произведение разделить на второе, например:
А • 4 _ЗХ5_15
8 " 5 ~8Х4~~32
Чтобы убедиться в справедливости высказанного правила,
15	4
нужно полученное частное — умножить на делитель — и по-
ой	О
смотреть, получится ли делимое — • Имеем;
15 4_1%Х* 3
Х 5~~
32^ 5 тх* в
		8 1
Примечание. Следует запомнить, что каждое верхнее число можно сокра-
сокращать с каждым нижним, но нельзя сокращать верхнее с верхним, нижнее с нижним.
- 41 -

82. Если при делении дробей встретятся целые или смешан-
смешанные числа, то нужно их обратить в неправильные дроби и по-
поступать по предыдущему, например:
15.ОС_15 .25_15Х1_ЗХ1 3
8	8 1 8 X 2S 8X5 40
5
41)
«л 9р.21_28.21_8»Х5 4X5 20 2
3
7	2
_2_ J_ 35 .45_SSX22_7X2_14 5
11 22 11 2 11X4^ 1Х9"~9~ 9
83, Определение. Если разделим единицу на какое-нибудь
число, то полученное число называется обратным по отношению
я первому, например — есть число обратное 7; — есть число обрат-
7	о
ное -- и т. д. Легко видеть, что произведение обратных чисел равно 1.
о
84:, Общее правило деления. Чтобы разделить одно число на
другое, нужно делимое умножить на число, обратное делителю.
В справедливости этого правила легко убедиться на следую-
следующих примерах:
1)
2)
3
8
3
8
15
8
15
8
4: _
5
х ±-
" 9^ —
У-i-
Х25~
ЗХ»
8X4
3X5
8X4
15 25
"8 : 1 =
3
IS XI
"8X2S
5
15
32
15
~32
3
IS
8)
3
8
X
О
X
X
1
IS
5
1
5
3X1
8X5
3
ТО
_ 3
~40
4) Примечание. Прежде, чем на самом деле производить умножение
нужно непременно сделать сокращения.
— 42 —

85. Рассматривая различные случаи деления, легко заметить,
что частное, полученное от деления на правильную дробь, будет
огьше делимого, а от деления на неправильную — меньше, на-
например :
25
1) 100:* 10Q
1
5
2) 100 ¦ 2° 100 - П -Ш Х Ц - 55 - 55
2) 100. - — 100 Х^- ш —1—ЬЬ
НАХОЖДЕНИЕ ЧАСТИ ОТ ЧИСЛА И ЧИСЛА ПО ЕГО ЧАСТИ.
4
86. Задача 1. Найти — от 17.
5
Из определения умножения на дробь (§ 75) вытекает, что
4	4
для нахождения — от 17 нужно 17 умножить на — Следова-
о	о
тельно:
4 17Х468	3
-i ОТ 1? 17
5 °Т 1717Х 5	5	5ld 5
4
Задача 2. — неизвестного числа равняется 17. Найти это
4	4
По предыдущему — числа все равно, что —, умноженное
D	О
на это число. Поэтому, обозначив неизвестное число через х,
получим:
— х —17
5	'
или
Таким образом, нахождение числа по его части делается
посредством деления.
*) Производитель равен произведению, разделенному на другой произво-
производитель.
— 43-

ДЕЙСТВИЯ С ДРОБНЫМИ ИМЕНОВАННЫМИ ЧИСЛАМИ,
87. Задача 1. Килограмм чая стоит 3 рубля. Сколько стоят
5	о
— килограмма?
8
Первое решение.
1 кг стоит 3 руб.;
— кг будет стоить в 8 раз меньше, т. е. — руб.;
о	8
кг будут стоит в 5 раз больше, т. е.
8
3 к ку „ 3X5 * 15 Л	7
— руб. Х5 = —— руб.=— руб. = 1— руб.
Второе решение.
5
То же самое получим, если умножим 3 руб на —
8
Следовательно, другой способ решения будет:
. = 1т руб.
Задача 2. — метра материи стоят 2 руб Сколько стоит
1 метр?
Первое решение.
—	м стоят 2 руб.
1	2
—	м будет стоить в 3 раза меньше, т. е. 2 руб.: з = — ру%я.
1 л«, содержащий в себе 4 четверти, будет стоить в 4 раза
2	8	?
больше, т. е. — руб. Х4 = — руб. = 2-у рубля.
о	о	о
Второе решение.
Q
То же самое получим, если 2 руб. разделим на —
Следовательно, другой способ решения будет:
2 РУб-: Т = 2 РУ0-Хт=ГчГ5 РУб-=^- РУб- = 2-Б- РУб-
88. Замечание. Рассматривая вторые способы решения
этих двух задач, легко заметить, что с дробями нужно произ-
— 44 —

одить те же самые действия, как если бы вместо дробей были
целые числа. Поэтому, когда учащийся затрудняется решить
задачу с дробями, он должен мысленно поставить вместо дробей
целые числа и сообразить, какие действия он стал бы тогда
делать; те же самые действия он должен делать и с дюобями.
VI. ДЕСЯТИЧНЫЕ ДРОБИ.
89. Определение. Дробь, у которой знаменатель есть 10, 100,
1000 и т. д.у называется десятичной дробью или десятичным
числом, например:
45 35 ш 207
100 ; 1000 ; 1000
Десятичные дроби принято писать без знаменателя таким
образом: сначала пишут целое число, ставят запятую, после
запятой пишут десятые доли, потом сотые и т д. *), например:
<
351 =0,035
1000
207
1000
1,207
Цифры, которые стоят справа после запятой называются
десятичными знаками.
Из предыдущего видно, что всякая десятичная дробь имеет
столько десятичных знаков, сколько нулей в ее знаменателе 2)
99. Чтение десятичных дробей. Всякую десятичную дробь
можно прочесть тремя способами.
Например, дробь 3,46 можно прочесть,
во-первых: 3 целых и 45 сотых,
45
потому что 3,45 = 3-—;
во-вторых: 3 целых, 4 десятых и 5 сотых,
45	4 5
потому что 3,45 = 3 —= 3 + - + —;
*) Если целсго числа или каких-нибудь долей нет, то ставят О
2) Лучше сказать: „в обозначении знаменателя".
— 45 —

в-третьих: 345 сотых,
п лк	45 345
потому что з,45 = з — =~
91.	Правило. Чтобы обратить десятичную дробь в простую,
нужно написать ее числитель и подписать подразумеваемый зна-
знаменатель, например:
47
О 047 = ——
'	1000
92.	Главпое свойство десятичной дроби. Величина десятичной
дроби не изменится, если справа или слева приписать или за-
зачеркнуть сколько угодно нулей, например:
2,3 = 2,300 = 002,3,
потому что
2,3 == ^ То*
002,3 = 2^
(Приписывая нули к десятичной дроби справа, мы числитель
и знаменатель ее увеличиваем в одно и то же число раз.)
На этом свойстве десятичной дроби основано сокращение
дробей и приведение их к одному знаменателю.
93.	Правило. Чтобы сократить десятичную дробь, нужно за-
зачеркнуть нули, находящиеся справа *), так как от этоге величина
дроби не изменится, а вид ее сделается проще, например:
0,50000 = 0,5 2)
94.	Правило. Чтобы привести десятичные дроби к одному зна-
знаменателю, нужно уравнять число десятичных знаков нулями, так
Но отнюдь не нули, находящиеся внутри ее обозначения, как, например,
в дроби 2,3005 нельзя зачеркнуть два нуля, потому что 2,3005 не рав-
равняется 2,35.
з) 0,5 будет несократимая десятичная дробь, но сократимая обыкновенная:
A—JL
10 "~ 2
_ 46 —

как от этого величина дробей не изменится, а знаменатели их
сделаются одинаковыми. Например:
1,2 =1,20000
4,47 =4,47000
0,00247 = 0,00247
95. Сравнение десятичных дробей. Из двух десятичных дробей
та больше, у которой целое число больше; если целые числа
одинаковы, то та дробь больше, у которой десятых долей больше;
есш число десятых одинаково, то та дробь больше, у которой
сотых долей больше, и т. д.
Например, 2,37 больше 2,3675, так как число целых и десятых
в обеих дробях одинаково, но сотых в первой дроби на одну
75	75
больше, чем во второй, хотя во второй есть еще	, но
1	1	100
меньше _ таккак—=
96. Правило. Чтобы умножить или разделить десятичную
дробь на 10, 100, 1000 и т. д., нуоюно перенести запятую вправо
или влево через столько гщфр, сколько пулей во множителе или
делителе1). Например:
43,72 X 10 = 437,2
43,72 : 10 = 4,372
0,03 X Ю000 = 00300,0 = 300
0,03 : 10000 = 0,000003
Действительно, от умножения на 10 единица каждого раз-
разряда дает единицу следующего высшего разряда, а от де-
деления на 10 дает единицу следующего нилпего разряда; пере-
перенося соответственным образом запятую, мы этого как раз и
достигнем.
97. Сложение п вычитание десятичных дробей. В десятич-
десятичных дробях, как и в целых числах, каждая цифра выражает
единицы в десять раз большие единиц, стоящих справа,
а потому сложение и вычитание десятичных дробей произво-
производится совершенно так же, как и сложение и вычитание целых
чисел.
Если при перенесении запятой цифр нехватит, то нужно ставить нули,
так как от этого величина десятичной дроби ие изменится.
47 ~

Правило. Чтобы сложить или вычесть десятичные дроби,
нужно подписать их одну под другой так, чтобы целые числа
приходились под гьелыми, десятые доли под десятыми, сотые под
сотыми и т. д.; затем складывать или вычитать их, как целые
числа, и в полученном результате поставить запятую на преж-
прежнем месте.
Например:	. .
3,271	_ 1,123
0,005	0,741
2,935	(у
6,211
Если десятичные дроби имеют рашые знаменатели, то можно
их привести к одному знаменателю, а можно и не приводить,
например:
0,05	0,0500
-|- 2,2356
3,5	11ЛИ	3,5000
5,7856	5,7856
98. Умножение десятичных дробей. Правило. Чтобы перемно-
оюить десятичные дроби, нужно перемножить их, как целые
числа, не обращая внимания па запятые, и в полученном произ-
произведении отделить занятою столько десятичных знаков, сколько
их было во множимом и множителе. Например:
1) 2,13	2) 0,0005
Xl,2	X80
426	0,0400 = 0,04
213
2,556
Действительно, отбрасывая (пример 1) мысленно запятую во
множимом, мы умножаем его на 100; отбрасывая запятую во
множителе, умножаем его на 10; следовательно, произведение
умножится на 1000; чтобы получить истинное произведение,
нужно полученный результат 2556 разделить на 1000. Получим
2,556.
99. Деление десятичных дробей. Правило 1. Чтобы разделить
десятичную дробь на г^елое число, нужно поступать, как при
делении целых чисел, т. е. разделить сначала целое число, потом
десятые доли, затем сотые и т. д.
--48 -

При
8,37
5
со о
со со
37
"5
20
20
0
меры:
5
1,674
¦
0,37
35
20
20
0
5
0,074
13
10
30
30
0
5
2,6
2,00
200
0
| 25
0,08
Правило 2. Чтобы разделить на десятичную дробь, нужно
делителе зачеркнуть запятую, а делимое умножить на такое
ело, на какое мы умножили делитель, зачеркнув в нем запятую,
затем поступать, как щи делении на целое число.
Примеры:
1)
3,75:2,5 = 1,5
37,5 | 25
25 1,5
125
125
0
3) 0,18:0,008 = 22,5
180 | 8
16 22,5
20
40
40
2) 0,02:1,25 = 0,016
2
0
200
125
750
750
0
4) 3:0,5
30
30
0
125
0,016
= 6
5
6
о
Зачеркивая запятую в делителе (пример 1), мы умножаем
ечитель на 10; поэтому, чтобы частное осталось без перемены,
делимое должны умножить на 10, т. е. перенести в нем запя-
тлю вправо через одну цифру.
Замечание. При делении десятичных дробей может иногда
поучиться бесконечное частное.
|* щевский. Краткий юре арифм,	—
-та»

о,
9,3
7
23
21
20
93
1
1
:0,7
7
,328. .
100.	Приближенное частпое. При делении десятичных дробей
часто берут не все частное, а только целое число и несколько
десятичных знаков.
Деля, например, 0,93 на 0,7 и найдя второй
десятичный знак, мы можем прекратить деле-
деление, приняв за частное 1,32 или 1,33. Ошибка
в этом случае будет меньше 0,01, так как
истинное частное больше 1,32, но меньше 1,33,
разность же между этими числами равна 0,01.
Числа 1,32 и 1,33 называются приближенными
60	частными с точностью до --г-- • Вообще найти
~~—	.11 1
4 . значение числа с точностью до —» —-—» ——
и т. д. — значит найти такое значение, которое отличалось бы
1 1 1
от истинного меньше, чем на —, —-, —— и т. д.
Чтобы судить о том, какое из двух приближенных частных
1,32 и 1,33 ближе подходит к истинному, нужно вычислить
следующий десятичный знак и посмотреть, будет ли он больше,
равен или меньше 5, и после этого его отбросить, соблюдая
следующее правило:
101.	Правило. Если отбрасываемая гщфра есть 5 гели больше 5,
то предыдущую нужно увеличить единицей; а если меньше 5, то
увеличивать не нужно.
Так как 8 больше 5, то частное 1,33 будет ближе к истин-
истинному, чем частное 1,32.
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ.
102.	Сложение. Положим, что требуется сложить несколько
приближенных слагаемых, взятых с точностью до 0,01 с недо-
недостатком.
3,67	В полученной сумме 16,32 отбросим последнюю
2,38	цифру, а предпоследнюю увеличим на 1; результат 16,4
0,51	будет представлять значение суммы с точностью до 0,1.
1.13	Так нужно поступать, когда число слагаемых не бо-
0,47	лее 11; в этом случае (когда слагаемые взяты с точ-
8,16	ностыо до 0,01 с недостатком) полученная сумма будет
16,32	отличаться от точдой менее, чем на 11 сотых; от-
16,4	бросив в результате последнюю цифру, уменьшим

}мму не более, как на 9 сотых; следовательно, сумма будет отли-
отличаться от точной менее, чем на 11 -\-9 сотых, т. е. менее,чем на
20 сотых или 2 десятых; после увеличения цифры десятых на 1
наша сумма будет отличаться от точной менее, чем на 1 десятую.
Вычитание. Пусть даны два числа 4,7 и 3,5 с точностью
	4,7 до 0,1 с недостатком. Произведя вычитание, получим
3,5 результат 1,2 с точностью до 0,1.
1,2
103. Сокращенное умножение. Пусть требуется перемножить
числа 2,35 и 4,1, взятые соответственно с точностью до 0,01
и до 0,1.
Множитель (число с меньшим числом цифр) подписывают слева
под множимым в обратном порядке. Записывают
X '4 только тот результат, который получился от умножения
—	 на цифру множителя той цифры множимого, которая
стоит над ней^или левее, например, 5 X 4 = 20; этот резуль-
результат не записываем, так как 5 стоит правее 4; 2 держим
Л.	Л
6 в уме; 3X4= 12; 12-]-2 =14; 4 пишем, 1 держим в уме;
4 = 8; 8 + 1 = 9; пишем 9. Далее 5X1 = 5; этот результат
ie записываем и в уме ничего не держим (если бы получили
не о, а число, большее 5, то в уме держали бы 1); 3X1 = 3,
1 записываем и в уме ничего не держим, так как 3<5;
Х1 = 2; этот результат записываем. Складывая, получаем 9G.
ак как единицы множителя D) стоят под десятыми долями
ножимого C), то 96 будет означать десятые доли; если бы
-щипцы множителя стояли под сотыми долями множимого, то
эчученный результат (96) означал бы сотые доли и т. д.
101. Сокращенное деление. Пусть требуется разделить 3,547
2,838. Начнем деление обыкновенным способом. Получим
3517 12838 в частном *> и так как целых больше не будет,
— *>838 9до ставим после 1 запятую. К остатку 709 сносить
—— ' нуль не следует так как неизвестно какая цифра
нуль не следует, так как неизвестно, какая цифра
стоит справа от 7. Остаток 709 делим не на 2838,
а на 283; получим 2 десятых. Умножаем 8X2 =
= 16; этот результат не записываем, так как де-
114	лили только на 283; в уме держим 2, так как 16
_27	ближе к 20, чем к 10; далее умножаем 3 X 2 = 6;
_25	6_j- 2 = 8; 8 записываем и т. д. Потом второй оста-
2	ток 141 делим на 28; третий остаток 27 делим на 2.
\ченное частное 1,249 будет содержать три десятичных знака,
оторые мы можем ручаться.
— 51 —

Примеры^
1) 2,838X1,249 = 3,545
2,838
" 9,421
2838
568
114
25
3,545
3) 412X0,069 — 28,4
4,12
9,6
247
37
28,4
5) 28,4:412 = 0,069
28,4 [ 412
247 0,069
37
~~ 37
2) 14,92X^,17 =
14,92
71,3
448
15
10
47,3
4) 47,29:3,17 = 14,92
4729 | 317
317 14,92
1559
1268
291
285
в
0
0
105. Обращение простых дробей в десятичные. Так как про-
простая дробь есть не что иное, как частное от деления числителя
на знаменатель, то для обращения ее в десятичную выводим
следующее правило.
Правило. Чтобы обратить простую дробь в десятичную, нужно
числитель разделить на знаменатель по десятичному способу.
Примеры:
—=0,0875
80
17,0 | 25	7,00 1 80
. 0,68	640_ о,О875
^600
200	560
400
О
52-

S) — = 0,2727...	4) — = 0,833,
11	6
3,0 11	5,0 6
0,2727...	48 0,833...
_80	_20
77	18
_30	_20
~22	18
_80	2
77
3
Первые две дроби обратились в конечные десятичные дроби,
вторые — в бесконечные.
1 6. Определение. Бесконечная десятичная дробь, у которой
иги несколько десятичных знаков постоянно повторяются,
ется периодической, например: 0,2727... или 0,833...
ело, обозначенное повторяющимися цифрами, называется
ом, например, в предыдущих дробях периодами будут
: 27 И 3.
ги период начинается сейчас о/се после запятой, то перио*
я дробь называется чистой, как например: 0,2727...
и период начинается через одну или несколько цифр после
Г, то периодическая дробь называется смешанной, как
ер: 0,8333...
риодические дроби пишутся еще иначе:
0,2727... =0,B7)
0,833..* =0,8C)
. Теорема *). Бесконечная десятичная дробь, получающаяся
цения простой^ будет непременно периодической.
ащение простой дроби в десятичную делается посредством
я\ при делении же число различных остатков ограни*
к как каждый остаток меньше делителя; таким обра-
ц бесконечном делении через некоторое время остатки
повторяться, а следовательно, должны повторяться
ы частного, так как каждая цифра частного зависит
Г называется истина, которую требуется доказать.

МЕТРИЧЕСКАЯ СИСТЕМА МЕР.
108.	С метрической системой читатель уже знаком (§§ 41—45).
Теперь, после знакомства с дробями, можно сообщить некоторые
дополнительные сведения.
Основная единица этой системы — метр — представляет собою
1 qqqoooq часть четверти парижского меридиана 2). Метр рав-
равняется приблизительно 1,41 аршина или 1 - арш. без 1 - вершков;
3
1 кв. метр приблизительно 2 кв. аршинам, а 1 куб. метр 2- куб.
аршина. В науке употребляется еще мелкая мера микрон =
= 0,000001 метра.
109.	Единица веса — грамм — представляет собою вес \ кубиче-
кубического сантиметра чистой воды при d° Цельсия.
Килограмм равен приблизительно 2- фунтам.
Гектар	„	9	— десятины.
110.	Метрические монетные единицы 2).
Франк (серебряная монета весом в 5 граммов).
Сантим = 0,01 франка.
Су = 5 сантимам.
111.	Употребление таблиц.
Пример 1. Обратить 25 верст в километры.
В таблицах находим: 2 версты = 2,134 км, следовательно:
20 верст = 21,34 км
из таблиц: 5 верст = 5,33 км
25 верст = 26,67 км
Пример 2. Обратить 34 фунта в килограммы.
В таблицах находим: .3 фунта = 1,229 кг; следовательно:
30 фунтов = 12 29 кг
из таблиц: 4 фунта = 1,638 кг
34 фунта =13,928 кг
Так как все человеческие измерения приближенны вследствие несовер*
шенства инструментов и чувств, то, разумеется, и та длина, которую мы назы-
называем метром, не можег в точности равняться 0,0000001 четверти меридиана; она
отличается от нее приблизительно на толщину человеческого волоса
а) Употребляются во Франции.
— 54 —

112. Таблицы перевода русских мер в метрические.
рсты
1
2
3
4
5
6
7
8
9
ймы
1
2
3
4
5
6
8
9
т ны
1
2
3
4
5
6
9
км
1
¦
3
6
-
•
Километры
1,0668
2,134
3,200
4,267
5,334
6,401
7,468
8,534
9,601
Сантиметры
2,540
. 5,08
7,62
10,16
12,70
15,24
17,78
20,32
22,86
Гектары
1,093
2,19
3,28
4,37
5,46
6,56
7,65
8,74
9,83
Литры
26,239
52,48
78,72
104,95
131,19
157,43
183,67
209,91
—
Сажени
г
1
2
3
4
5
6
7
8
9
Кв. футы
1
2
3
4
5
6
7
8
9
Куб. футы
1
2
3
4
5
6
7
8
9
Пуды
1
2
3
4
5
6
7
8
9
Метры
2,1336
4,267
6,401
8,534
10,668
12,802
14,935
17,069
19,202
Кв. метры
0,0929
0,186
0,279
0,372
0,465
0,557
0,650
0,743
0,836
Куб. метры
0,0283
0,057
0,085
0,113
0,142
0,170
0,198
0,227
0,255
Килограммы
16,3805
32,761
49,141
65,522
81,902
98,283
114,663
131,044
147,424
Аршины
1
2
3
4
5
6
7
8
9
Кв. саж.
1
2
3
4
5
G
7
8
9
Куб. саж.
1
2
3
4
5
fi
7
8
9
Фунты
1
1
2
3
4
5
6
7
8
9
Метры
0,7112
1,422
2,134
2,845
3,556
4,267
4,978
5,690
6,401
Кв. метры
4,552
9,10
13,66
18,21
22,76
27,31
31,87
36,42
40,97
Куб. метры
9,7127
19,425
29,138
38,851
48,563
58,276
67,989
77,701
81,414
Килограммы
0,4095
0,819
1,229
1,638
2,048
2,457
.2,867
3,276
3,086
- 55

113. Преимущества метрической системы. Метрическая си-
система, введенная впервые во Франции, во время революции
1789 г., имеет громадные преимущества перед другими систе-
системами. Главное ее преимущество заключается в том, что все ее
единичные отношения равняются одному и тому же числу 10,
являющемуся также основанием нашей нумерации. Вследствие
этого все вычисления с метрическими мерами необыкновенно
упрощаются. Так, для обращения одних метрических мер в другие
достаточно перенести запятую вправо или влево через несколько
цифр, например:
0,33 км = 330 метрам
1033 г =1,033 кг
Так как в метрической системе меры объема и веса связаны
между собою, то часто бывает легко определить объем какого-
нибудь предмета по его весу и обратно. Например, зная, что неко-
некоторое количество воды весит 40 г, мы сразу можем сказать, что
объем этого количества воды равен 40 куб. см; если же кусок
железа весит 40 г, то можем сказать, что его объем равен приб-
приблизительно 5 куб. см, так как железо приблизительно в 8 раз
тяжелее воды. Третье преимущество метрической системы со-
состоит в том, что она теперь распространена почти во всех
цивилизованных странах (за исключением тех, которые говорят
на английском языке).
Названия мер образуются из названия основной меры с по-
помощью приставок:
деци = 0,1	дека = 10
санти = 0,01	гскто = 100
дшлли = 0,001	кило = 1000
мириа = 10000
Некоторые меры не вошли в употребление, как, например,
гектометр A00 м), мириаметр A0000 м) и т. д.
УП. О ДЕЛИТЕЛЯХ И КРАТНОМ %
. Числа абсолютно-простые п составные. Определение.
То число, которое делится только па единицу и па самою себя,
*) Эта глава можзт быть выпущена без ущерба для дальнейшего прохож*
д§ддя курса.

ется аосолютно-простым или первоначальным; например,
ча:
1, 2, 3, 5, 7, 11, L3, 17, 19, 23, 29, 31 и Т. Д.
лт абсолютно-простыми; все остальные числа:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22 И Т. Д.
аются составными у потому что могут быть составлены из
оначальных чисел; например,
6 = 2-3; 12=2-2-3; 10=2-5 и Т. Д.
П рвоначальных чисел бесчисленное множество.
. Эратосфеново решето 1).
3
IS
т
Si
63
т
ILL
Ш
135
4
16
28
4Н
Ш
84
18
88
1Ш
118
ш
1S8
5
17
29
41
53
6S
77
89
101
113
ш
137
8
18
30
42
84
66
78
9ft
1»8
114
128
138
7
19
43
SS
67
79
91
103
US
127
139
8
2ft
32
44
S6
88
8ft
92
Ш
118
128
14ft
9
21
33
1%
$7
69
81
93
iftS
117
129
141
10
22
34
48
S8
78
82
94
Ш
118
13ft
142
11
23
3S
47
59
71
83
95
107
119
131
143
12
24
38
48
6ft
72
84
98
Ift8
12ft
132
144
13
2S
37
49
61
73
8$
97
Ш
121
183
14S
Ч обы составить таблицу первоначальных чисел, нужно, на-
в натуральные числа, зачеркнуть каждое второе число
2, каждое третье после 3, каждое пятое после 5 и т. д.
аолица первоначальных чисел помещена в конце книги.
0. Разложение чисел на первоначальные множители. Чтобы
шпь данное число на первоначальные множители, нужно
v ть его на 2, полученное частное опять на 2 и т. д.,
можно; потом на 5, 5, 7 и на другие первоначальные
по порядку) затем представить его в виде произведения
чисел 2).
«) Эратосфен ¦—греческий ученый B76—193 гг. до нашей эры).
) Не нужно забывать, что одним из первоначальных множителей
1.
- 57

Примера»
13
13 13
60
60
30
15
5
I
1
2
2
3
5
6336
6336
3168
1584
792
396
198
99
33
11
1
1
2
2
2
2
2
2
3
3
11
2868
2868
1434
717
239
1
1
2
2
3
239
13 = 1X13
60 = 1X2X2X3X5
6336 =1X2X2X2X2X2X2X3X3X11
2868 = 1X2X2X3X239
Первоначальные множители называются также делителями.
117. Общий наибольший делитель. Правило. Чтобы найти
общий наиболыаип делитель нескольких чисел, нуоюно разложить
их на первоначальные множители, выписать все общие множи-
множители и перемножить их.
Пример. Найти общий наибольший делитель чисел: 180,
48, 96.
180
90
45
15
5
1
2
2
3
3
5
48
24
12
6
3
1
2
2
2
2
3
96
48
24
12
6
3
2
2
2
2
2
3
Общий н. д. =
118. Правило. Чтобы найти обгций наибольший делитель двух
чисел по способу последовательного деления, нужно большее число
разделить на меньшее, меньшее на первый остаток, первый оста-
остаток на второй, второй на третий и т. д., пока в остатке не
получится 0. Тогда последний делитель и будет общим наиболь*
шим делителем.
Пример. Найти общий наибольший делитель чисел: 101
И 351.

Первая запись-
частные
остатки
3
351
39
2
104
26
1
39
13
2
26
0
13
Вторая запись:
39
6
13
104
78
26
1
351
312
39
2
104
3
26
~26 2
О
Общий н. д. = 13
119. Правило. Чтобы найти общий наибольший делитель
ольких чисел по способу последовательного деления, нужно
чала найти общий наибольший делитель меоюду двумя какими-
удь числами, потом между найденным общим наибольшим
i телем и третьим числом и т. д.
Пример. Найти общий наибольший делитель чисел: 572,
и 182. -
156
156
0
208
156
52
3
572
416
156
1
208
2
52
52
182
156
26
2
52
3
О
Оощин н. д. = 21>
120. Числа взаимно-простые. Если два числа, кроме единицы,
ого общего делителя не имеют, то они называются взаимно-
остыми или первыми между собою, например: 8 и 25; 7 и 15;
3 и т. д. "
Таким образом общий наибольший делитель взаимно-п^остыоо
г будет 1,
- 59 -

Очевидно, что все абсолютно-простые числа будут в то же
время взаимно-простыми, так как, делясь только на единицу
и на самих себя, они других общих делителей, кроме единицы,
иметь не могут, например: 7 и 13; 5 и 2; 11 и 19 и т. д.
121. Правило. Чтобы найти общее наименьшее кратное не*
скольких чисел, нужно разложить их на первоначальные множи-
множители, выписать множители одного числа, приписать к ним
недостающие из других чисел и перемножить их.
Пример. Найти общее наименьшее кратное чисел 24, 150
и 336.
24
12
6
3
1
2
2
2
3
150
75
25
5
1
2
3
о
а*
О
33G
168
84
42
21
7
1
2
2
Общее наименьшее кратное =
=2X2X2X3X5X5X2X7
ПН. ПРОПОРЦИЯ. РЕШЕНИЕ ЗАДАЧ НА ПРО-
ПРОПОРЦИОНАЛЬНЫЕ ВЕЛИЧИНЫ.
122. Отношение и пропорция. Определение. Частное двух чисел
называется их отношением 2). Например: отношение 10 к 5 равно 2;
отношение 30 к 50 равно —. Очевидно, что отношение показы-
о
вает, во сколько раз одно число больше другого или какую часть
его составляет; так, например, 10 больше 5 в два раза; 30 соста-
3
вляет — от 50. Отношение чисел 10 и 5 записывается таким
о
образом:
В этом случае число 10 называется предыдущим членом, 5—
последующим и 2—знаменателем отношения. Очевидно, что между
Так как произведение не меняется от перестановки множителей, то
лучше перемножать их не по порядку, а так, как удобнее в каждом данном
случае; здесь, например, удобнее сначала умножить 2 на 5, еще раз 2 на 5
и полученное произведение 100 умножить на произведение остальных множи-
множителей.
а) Это отношение называется кратным в отличие от разности двух чисел,
которая иногда называется разностным отношением, как, например: 10—5,

этими тремя числами существует такая же зависимость, как
между делимым, делителем и частным, поэтому предыдущий
член равен последующему, умнооюенному на знаменатель] отноше-
отношение не изменится, если предыдущий и последующий члены умно-
умножить или разделить на одно и то owe число, и т. д.
123. Определение. Равенство двух отношений называется
пропорцией. Например:
10:5 = 6:3 или 10 =4"
О
Числа L0 и 3 называются крайними членами пропорции, а
5 и 6 — средними. Из определения пропорции вытекает, что члены
ее можно заменять другими, наблюдая только за тем, чтобы
отношения оставались равными. Поэтому можно умножить или
разделить на одно и то же число оба члена одного или обоих
отношений; оба предыдущих, оба последующих и т. д.
124. Главное свойство пропорции. Произведение крайних членов
равно произведению средних. Действительно, рассматривая различ-
различные пропорции, мы замечаем:
10:5= 6:3; 10X3 = 5X6;
9X4 = 3X12 и т. д.
Отсюда следует, что:
крайний член равен произведению средних, разделенному на
другой крайний;
средний член равен произведению крайних, разделенному на
другой средний. Например, из пропорции 10:5=.6:3 имеем:
5Х6 ЮХЗ
5
Зная главное свойство пропорции, легко определить ее неиз-
неизвестный член; например, из пропорции я$:8 = 6:3 получим:
') Эта пропорция называется кратной в отличие от разностной пропорции,
которая представляет собою равенство двух разностных отношений, как, на-
например:
10 — 5 = 20 — 15

125.	В пропорции можно переставить: 1) средине члены,
2) крайние члены, 3) крайние па место средних и обратно.
Например:
Ю: 5 = 6: 3
Ю: 6 = 5: 3
3: 5 = 6:10
5:10 = 3: 6
Все эти четыре пропорции верны, так как в каждой из них
произведение крайних равно произведению средних.
126.	Определение. Сумма чисел, разделенная на их число, на-
называется средним арифметическим этих чисел. Например, средним
арифметическим чисел 2, 3 и 7 будет
2 + 3 + 7 12
——— ш ш ШЩ	.41 ^^^Т	. .—	' ' /1
3	3
127.	Пропорциональные величины. Определения. 1) Если
с увеличением (или уменьшением) одной величины в несколько
раз другая величина во столько же раз увеличивается (или умень-
уменьшается), то такие две величины называются прямо-пропор-
прямо-пропорциональными; например: количество товара и его стоимость.
2) Если же с увеличением одной величины в несколько раз
другая величина во столько же раз уменьшается, и наоборот, то
такие две величины называются обратно-пропорционадьными;
например: число работников и число часов, которое требуется
для окончания определенной работы.
ПРОЦЕНТНЫЕ ВЫЧИСЛЕНИЯ.
128.	Определение. Одним процентом называется — - часть
какой-нибудь величины, двумя процентами —— части, тремя
процентами —— и т. д.1).
Слово „процент" обозначается знаком %•
Так как 1% от ЮО каких-нибудь единиц равняется 1; 2%
равняются 2; 3% равняются 3, и т. д., то следующие 4 предло
жения бутут означать одно и то же:
1) получено 7% прибыли;
*) Слово процент взято с лашнсксго: pro centum —за сщо%
- G2

2)	с каждых 100 ру . получили 1 руб. прибыли;
3)	с каждого рубля получили 7 коп. прибыли;
7
4)	полученная прибыль составляет —— капитала
Задача 1-го типа. Найти 5% от
Решение. 1%=305:100 = 3,05
Задача 2-го типа. 2°/0 от неизвестного числа состав ъяют
6,1. Лапти это число.
Решение. 2% —М
1%== 6,1:2 = 3,05
100 % = 3,05 X ЮО = 305
Задача 3-го типа. Найти процентное отношение 6,1
к 305, т е. узнать, сколько процентов 6,1 составляют от 305.
Решение. Первый способ:
1% = 3,05
6,1:3,05 = 2
Ответ: 2%-
Второй способ:
6,1
305
= 0,02 = 2 °/,
Замечание, b некоторых случаях задачи 1-го типа удобнее
решать другим способом.
Пусть, например, требуется найти 4% от 225.
Имеем: 4% = ^4
25
Поэтому не мешает запомнить, что 50%=-^
75%=-f; ю%--jo и т.д.
139. Определения. Процентами, в коммерческом смысле, пазы-
вается прибыль или убыток, получаемый с 100 руб. в 1 год.
Число процентов называется процентной таксою*
63

Йри§ыль, получаемая со всего капитала, называется процен!:-
пыми деньгами1).
Капитал, отданный на проценты (иначе в рост), называется
начальным капиталом.
Начальный капитал, сложенный с прибылью, называется
наращенным капиталом.
Если капитал находится в обороте несколько лет, и прибыль
начисляется не только на первоначальный капитал, но и на
прибыль, полученную в предыдущие года, то проценты назы-
называются сложными; в противном же случае — простыми.
При вычислении процентов принято считать в году 360 дней,
а в месяце — 30 дней.
130. Задача 1. Капитал 2400 руб. отдан в рост на 5 месяцев
по 6°/0. Определить прибыль и наращенный капитал.
Решение. 1% от 2400 руб.= 24 руб.
6% „ 2400 „ =24 руб.Х 6 = 144 руб.; следо-
следовательно, прибыль в 1 год = 144 руб.
„	В 1 Мес.= 144 руб.: 12 =12 руб.
„ в 5 мес.= 12 руб.Х 5 = 60 руб.
Сложив начальный капитал 2400 руб. с прибылью 60 руб.,
получим наращенный капитал 2460 руб.
Задача 2. Какой капитал, будучи отдан в рост по 7%>
принесет через 4 месяца 15 руб. прибыли?
В 1 год прибыли получится 15 руб. хз = 45 руб.;
7% = 45 руб.	_45 |_7
<уо = 45 руб.:7 = 6,43 руб.	42 6,428 = 6,43
100 % = 6,43 руб. X 100 = 643 руб. _ 30
Ответ. 643 руб.	28
А6
4
Задача 3. По сколько процентов нужно отдать в рост ка-
капитал 2400руб., чтобы через 4 месягщ получить 48 руб. прибыли?
Прибыли в год получится 48 руб. X 3 = 144 руб.
1% от 2400 руб.= 24 руб.
*) Таким образом проценты и процентные деньги — не одно и то же,
— 64 —

Сколько раз 24 руб. содержатся в 144 руб., столько и будет
процентов; поэтому получим:
144 руб.:24 руб.= 6. Ответ: 6%-
Задача 4. На сколько времени нужно отдать капитал
2400 руб. в рост по 6°/0У чтобы получишь 48 руб. прибыли?
Из задачи 1 мы уже знаем, что 6%. т е. годовая прибыль,
с 2400 руб. равны 144 руб.; в 1 месяц прибыли получится
144 руб.: 12 = 12 руб.; чтобы узнать, через сколько месяцев
получится 48 руб. прибыли, нужно 48 руб. разделить на 12 руб.
Имеем:
48 руб.: 12 руб.= 4 (мес).
Задача 5. Какой капитал, отданный в рост по 6°/0, обра-
обратится через 4 месяца в 2448 руб?
Определим сначала, во что обратятся 100 руб. через 4 месяца.
Со 100 руб. в 4 месяца прибыли получится — руб. = 2 руб.;
о
следовательно, 100 руб. через 4 месяца обратятся в 102 руб.
Таким образом имеем: *
в 102 руб. в 4 мес. обращаются 100 руб.;
в 1 руб. в 4 мес. обратится сумма, в 102 раза меньшая,
100
т. е. — руб.;
в 2448 руб. в 4 мес. обратится сумма, в 2448 раз бблыная,
100-2448 Л ^А^
т. е. 	——- руб. = 2400 руб.
УЧЕТ ВЕКСЕЛЕЙ.
131. Положим, что кто-нибудь занял 8500 руб. по 8% на
1 год. Тогда через год он должен будет уплатить 8500 руб. и
еще 680 руб.1) процентных денег, всего 9180 руб.
Обыкновенно должник (дебитор) в этом случае выдает
кредитору2) письменное обязательство, написанное на гербовой
бумаге по установленной форме, такого рода:
*) io/e от 8500 руб. = 85 руб.; 8% от 8500 руб. = 85 руб. X 8 = 680 руб,
2) Кредитором называют того, кто дает деньги взаймы.
5 Рашевский. Краткий курс арифм.	— 65 —

Москва, 18 марта 1928 г.
Вексель на 9180 руб. зол.
Тринадцатого марта тысяча девятьсот двадцать девятого года
по сему векселю повинен (такой-то) заплатить в г. Москве
(такому-то) или кому он прикажет девять тысяч сто восемь-
восемьдесят рублей золотом.
Подпись.
Это обязательство называется векселем. В векселе не пишутся
ни сумма, занятая в действительности, ни проценты, по которым
сделан заем, а только обозначаются срок платежа и подлежащая
уплате сумма, которая называется вексельной суммой или валю-
валютой векселя. Положим теперь, что должник (векселедатель)
захотел бы уплатить свой долг не через год, как было условлено,
а через 9 месяцев, т. е. за 3 месяца до срока. Тогда, очевидно,
процентные деньги, которые могли бы нарасти за эти 3 месяца
с 8500 руб., т. е. 170 руб.1), он платить не должен; их следует
вычесть из валюты, и должник вместо 9180 руб. должен за-
заплатить кредитору только 9010 руб. Сумма (в данном случае
170 руб.), вычитаемая из валюты, когда по векселю платят до
срока, называется учетом (вычетом) или дисконтом. Таким
образом в нашем примере 9180 руб. будет валютой, 170 руб.
учетом, 9010 руб. — уплатой; очевидно, что
валюта — учет = уплате
9180 р.—170 р.= 9010 р.
Должник почти никогда не платит по векселю до срока;
поэтому, когда владельцу векселя (векселедержателю) понадо-
понадобятся деньги раньше срока, то он продает вексель третьему
лицу или банку. Покупателю, понятно, нет никакого расчет*
платить, как в нашем случае, за вексель 9010 руб., потому что,
пустив эти деньги в оборот по 8 %> он через 3 месяца имел бы
9190,2 руб.2), с должника же он получит через 3 месяца только
9180 руб. Следовательно, чтобы не потерпеть убытка, покупатель
векселя должен заплатить меньшую сумму, т. е. учет (скидка
в пользу покупателя) должен быть больше.
*) В 12 мес процентных денег получается 680 руб* В 1 мес. получится
с	о	680-3 . ЛпГк *
руб., а в 3 мес. —j^— руб. = 170 руб.
») 1«/о от 9010 руб. = 90,1 руб.; 8% от 9010 руб. = 90,1 руб. X 8 = 720,8 руб.;
прибыль за 3 мес. = 720,8 руб.: 4 = 180,2 руб.; 9010 руб. + 180,2 руб. = 9190,2 руб.
— 66 -

Условились делать скидку в пользу покупателя векселя еще
больше — в вознаграждение за тот риск, которому он подвергается,
так как не всегда можно получить с должника деньги. Размер
учета представляет собою процентные деньги за время, остающееся
до срока, с валюты векселя. Такого рода учет называется коммерчес-
коммерческим. Определим коммерческий учет для предыдущей задачи.
Так как со 100 руб. в 3 мес. получается 2 руб. прибыли, то
2
с 1 руб. получится -— руб., а с 9180 руб. прибыли получится
2X9180 . 1836 , 1ООС , D
руб. = —— руб. = 183,6 руб. Вот эту прибыль и
100 rj	10
условились учитывать в пользу покупателя векселя и назвали
ее учетом. Таким образом при коммерческом учете покупатель
векселя заплатит за него меньше, именно: 8996,4 руб., так как
9180 руб.— 183,6 руб. = 8996,4 руб.
Замечание. Относительно коммерческого учета нужно за-
заметить следующее. Обыкновенно в действительности занимаю-
занимающему выдается не вся просимая им сумма, а с нее скидываются
процентные деньги за все время займа; должник же должен воз-
возвратить всю сумму сполна. Таким образом в нашем случае должник
получил бы не 8500 руб., а только 7820 руб., так как 680 руб.
процентных денег с него удержали бы вперед, но зато через
год он должен был бы уплатить не 9180 руб., а 8500 руб.
Таким образом при коммерческом учете валюта представляет
собою занятую в действительности сумму, а не наращенный
процентными деньгами долг.
Точно так же в действительности число процентов, по кото-
которому совершается учет, определяется по взаимному соглашению
и часто отличается от того числа процентов, по которому был
первоначально написан вексель.
Задачи на учет векселей могут быть 5 типов: 1) определение
учета и уплаты, 2) определение учетных процентов, 3) опреде-
определение срока векселя, 4) определение валюты по данному учету
и 5) определение валюты по уплате.
132. Задача. Определить валюту векселя, если коммеюческий
учет с него по .?% за 108 дней до срока составляет 22lj2 руб.
45	5
Решение. Учет в 1 день составит	руб.=—- руб.
2 /\ \\)о	4
5 УС 360
Учет в 360 дней „ —^-— руб. = 75 руб.
5*	— 67 —

6% от неизвестной валюты = 75 руб.
75
1% »	»	» =-g-py6.= 12,5 руб.
100% „	„	= 1250 руб.
Следовательно, валюта векселя равна 1250 руб.
ПРОПОРЦИОНАЛЬНОЕ ДЕЛЕНИЕ.
133. Задача. Число 30 разделишь на три части пропорцио-
пропорционально числам: 2, 3 и 5, т. е. разложить его на такие три сла-
слагаемые, которые бы относились между собою, как 2:3:5.
Обозначив искомые слагаемые римскими цифрами I, II и
Ш, имеем:
1:11:111 = 2:3:5.
Положим, что первое слагаемое содержит 2 каких-нибудь
части, тогда второе слагаемое будет содержать таких частей 3
третье 5, а все три слагаемые, т. е. число 30, будут содержать
таких частей 2 + 3 + 5 = 10; следовательно, каждая такая часть
будет равна
— = 3. Поэтому получим:
Замечание. Отношение 2:3:5 называется сложным. Если
члены сложного отношения дробные, то, приведя их к одному
знаменателю и умножив на него, заменим отношение дробных
чисел отношением целых.
134. Задача. Число 66разделить на такие три части, чтобы
перзая относилась ко второй, как 3:2, а вторая к третьей,
как 5:4.
Первый способ. Так как отношение не изменится, если
оба члена его умножим на одно и то же число, то умножим оба
члена первого отношения на 5, а оба члена второго на 2;
получим:
— 68 —

так как 15 + 10+8 = 33, то
30: п
Второй с особ. Имеем:
I: 11 = 3:2
П:Ш = 5:4.
Положим, что первая часть (I) равна 3, тогда вторая часть (П)
будет равна 2, а третья часть (III) определится из пропорции:
2:111 = 5:4,
ттт 2X4 8 «
которая даст:	III =—-— = ~гщ Поэтому
1:11:111 = 3:2:4-
О
Помножив все члены полученного сложного отношения на 5,
получим:
1:11:111=15:10:8;
далее задача решается по предыдущему.
135. Задача. Число 62 разделить на три части обратно-
пропорционально числам: 2, 3, и 5, т. е. разложить его на три
части, которые относились бы между собою, как
'5
Имеем:
т тт ттт 111 15 10 б
1:11:111 ==-2:з:5- = :
15 + 10 + 6 = 31; следовательно:
136. Задача. Три артели рабочих получили вместе 250 руб.
Первая артель состояла из 10 человек и работала 3 дня\ вторая
состояла из 7 человек и работала 5 дней; третья состояла из
15 человек и работала 4 дня. Сколько получила каждая артель^
— 69 —

Очевидно, что в этом случае плата пропорциональна числу
рабочих и числу рабочих дней. Следовательно, 250 руб. нужно
разделить пропорционально: 1) 10:7:15 и 2) 3:5:4. Рассуждаем
таким образом:
Если первая артель будет работать не 3 дня, а 1 день, то,
чтобы получить ту же самую плату, она должна будет иметь
рабочих втрое больше, т. е. 10X3 = 30 рабочих; если вторая
артель будет работать 1 день, то, чтобы получить ту же самую
плату, она должна будет иметь в 5 раз больше рабочих, т. е.
7X5 = 35 рабочих; третья артель при тех же условиях должна
будет иметь 15X4=60 рабочих.
Поэтому 250 руб. нужно разделить пропорционально числам
30, 35 и 60. Таким образом имеем:
1:11:111 = 30:35:60 = 6:7:12;
7+12 = 25;
= 120 руб.
ЗАДАЧИ НА СМЕШЕНИЕ.
137, Определение. Число частей (весовых) чистого металла,
приходящееся в метрической системе на 1000 частей сплава, на-
называется пробой1).
Отсюда следует, что пробой называется число граммов чи-
чистого металла, находящееся в 1 килограмме сплава.
Определение. Число частей (весовых) чистого спирта, прихо-
приходящееся на 100 частей вина, называется градусами.
Таким образом 90-градусный 2) спирт содержит 90 частей
истого спирта и 10 частей воды.
Очевидно, градусы то же, что и проценты.
Из чистого золота и серебра не делают вещей, так как они были бы
непрочны. К золоту обыкновенно прибавляют серебро, а к серебру — медь.
Эта примесь называется лигатурой. В прежних русских мерах пробой называли
число частей чистого металла, приходящееся на 96 частей сплава, или число
золотников чистого металла, находящееся в 1 фунте сплава.
2) „90 градусов" обозначается: 90°.
— 70 -

138. Задача. Сплавлено А кг серебра 800-й пробы и 6 кг
серебра 900-й пробы. Какой пробы получится сплав?
В 4 кг сер. 800-й пробы содерж. 800 гХ4 = 3200 г чист. сер.
„ 6„ „ 900-й „	„ 900гХ6 = 5400г „ „
В 10 кг сплава содержится	8600 г чист. сер.
» 1 » v	п 8600 г: 10 = 860 г	» »
Следовательно, сплав будет 860-й пробы.
139. Задача. Смешано 6 ведер спирта в 90°, 3ведра спирта
€ 80° и одно ведро воды. Сколько градусов будет содержать смесь?
В 6 в. спир. в 90° буд. чист. спир. 90 X 6 сотых в., т. е. 540 сотых в.
У)
v
„
«
80
„
„
„
„
80X3
„
„
„
„
„
240
О
В 10 ведрах смеси чистого спирта будет 780 сотых ведра
„ 1 ведре „	„	„ „ 78 „
Следовательно, смесь будет содержать 78 градусов.
140. Задача. Из трех сортов товара ценою в 90, 80 и 60 коп.
килограмм требуется составить 46 кг смеси ценою в 65 коп.
килограмм1).
Запись.
90 коп.
80 коп.
60 коп.
65 коп.
— 25 коп.
15 коп.
-{- 5 коп.
— 1 коп. — кг
— 1 коп. — кг
15
1 коп. — кг
— 1 коп.
кг
— 1 коп. — кг
15
2
-f- 2 коп. — кг
Объяснение. Если будем продавать каждый сорт по цене
смеси, то
продав 1 кг первого сорта, полечим 25 коп. убытку;
продав 1 кг второго сорта, получим 15 коп. убытку;
продав 1 кг третьего сорта, получим 5 коп. прибыли
1 коп. убытка полечится от продажи —кг 1-го сорта
1 коп. убытка
1 коп. прибыли
V
— кг 2-го
15
-—кг 3-го „
*) Когда дается более двух смешиваемых сортов, то задача делается
неопределенной, т. е. допускает бесчисленное множество решений, потому чтв
прибыль с убытком тогда можно уравнивать разнообразными способами.
71 —

Продав — кг первого сорта, — кг второго и — кг третьего, по
лучим 2 коп. убытку и 2 коп. прибыли, т. е. не получим ни
прибыли ни убытку. Поэтому количества смешиваемых сортов
должны относиться между собою, как
112
•	•
25' 15" "б"
Следовательно:
=^:^г:-|- = 3:5:30; 3
25 15 5
5 4-30 = 38.
46 X 3
12
46 X 5
Ш=
46X30
38
19
кг
IX. ЧЕРЧЕНИЕ ПЛАНОВ, ДИАГРАММ И
ГРАФИК.
. План. Снять план с какой-нибудь фигуры — значит
начертить на бумаге в уменьшенном виде подобную ей фигуру.
Пусть требуется начертить план квартиры по следующим данным:
Длина
Ширина
Сто-
Столовая
3 Чъм
3 м
Спаль-
Спальня
4 м
4 м
Каби-
Кабинет
3«|а.я
2 м
Кухня
4 м
2*/а-*
Шита
2 м
1 м
Убор-
Уборная
2 л«
1 м
Пе-
ред-
редняя
3 1/а .М
1 Vi м
Окно
1 м
Дверь
1 м
Стена
Условимся 1 метр изображать на плане 1 сантиметром; тогда
все линии на плане будут в 100 раз меньше настоящих (фиг. 14);
число 1/100 будет называться в этом случае численным масшта-
масштабом, в. линия, разделенная на сантиметры, линейным масштабом.
Н2. Диаграммы. Диаграммой называется графическое изобра-
изображение именованных чисел. Числа можно изображать линиями,
прямоугольниками, секторами кругов и т. д.
Пусть требуется построить диаграмму населения СССР.
— 72 —

По данным переписи 1920 г. в СССР имелось 110 миллионов:
крестьян, 5 миллионов рабочих и 16 миллионов остального насе-
ления. Если условимся каждый миллион изображать линией
СПАЛЬНЯ
У
/
кухня
СТОЛОВАЯ
5
4-
МЕТРЫ
МАСШТА6
Фиг. 14.
длиною в 1 мм, то данные числа изобразятся линиями (фиг. 15)-
получим линейную диаграмму. Если данные числа будем иэо-
КРЕСТЬЯНЕ ИОмлн,
™ш	1	\.
16
ПАН.
111 i 11 itiJ i.
ОСТАЛЬНОЕ НАСЕЛЕНИЕ
МАИ
РАБОЧИЕ
Фиг. 15.
бражать не линиями, а прямоугольниками той же высоты с оди-
одинаковым основанием, то получим прямоугольную диаграмму
(фиг. 16).
— 73 —

14:3. Процентные диаграммы. Найдем процентное отношение
числа крестьян, рабочих и т. д. к общему числу всех жителей.
Все население СССР равно 131 миллиону A10 + 16 + 5); 1%
ют 131 = 1,31; 16:1,31 = 12,2=12; 5:1,31 = 3,8 ==4.
I
i КРЕСТЬЯНЕ
МО млн.
116млк| } ОСТАЛЬНОЕ НАСЕЛЕНИЕ
РАБОЧИЕ
Фиг. 16.
Таким образом населения,
за исключением рабочих и кре-
крестьян, будет 12%,
рабочих 4%; тех и
других 16%; вы-
вычитая 16% из 100%»
згайдем, что крестьян будет 84%.
Изобразим все население прямоугольником (фиг. 17)
с основанием 1 см и высотой 10 ом = 100 мм; тогда
число рабочих изобразится прямоугольником с высотой
4 мм; число остального населения — прямоугольником
высотой 12 мм; число крестьян — прямоугольником
с высотой 84 мм. Нетруд-
Нетрудно также построить диа-
диаграмму, изобразив все
население квадратом, со-
состоящим из 100 малень-
маленьких квадратиков. Тогда
1 1
1 1
1 1
1
1 1
1
1
J_
1
" ~Г
1 1
1
1
1
1
1
1
Г|
1
" 1
1
1
1
1 1
1 1
¦" 1"
--L-4-
- L-L
1 г
1 •
КРЕСТЬЯ
1 1
1 1
1 1
• 1
1 1
I i
i
i
•
i
i
i
НЕ
|
1
1
1
1
!
1 1
1 1
1 1
1 1
|_ i
| '
\ J
1
1 ,
1
- 1- J
1
ОСТАЛЬНОЕ НАСЕЛЕНИЕ
\г%
1
1
1
~ т -
1
1
1
•
1
1
РАБО-
ш
I
ОС
и
о
ш
Q.
Рабо-
Рабочие
Фиг. 18.
Фиг. 19.
Фиг. 17.
число крестьян изобразится площадью, состоящей из 84 ква-
квадратиков, число рабочих — 4 квадратиками, и т. д. (фиг. 18).
141. Круговая диаграмма. Если в круге провести несколько
радиусов, то они разделят круг на части, называемые секторами.
Вот этими-то секторами и изображаются данные числа. Для по-
построения угла секторов лучше всего пользоваться транспор-
пиром (фиг. 19).
— 74 —

Узнаем, сколько градусов будут содержать углы секторов,
изображающих числа рабочих, крестьян и т. д. Так как вся
окружность имеет 360°, то 10/0=3,6°;
4% = 3,6° X 4 = 14,4°=14°; 12% =
= 3,6° X 12 = 43,2°== 43°; для кре-
крестьян получим: 14°+43° = 57°;
360°—57° = 303°. Отложив посред-
посредством транспортира углы в 14°
и 43° получим круговую диаграм-
диаграмму (фиг. 20).
Замечание. Прямоугольные
и квадратные диаграммы лучше
всего чертить на клетчатой бумаге,
причем надо сообразоваться с чис-
числом клеток, имеющимся на листе.
Положим что в нашем распоря-
распоряжении имеется только 30 клеток. Берем наибольшее число,
2
например, 110 м. Вычисляем: 110:30 = 3—; следовательно, одной
2
клетке должно соответствовать 3— миллиона. Для удобства
о
принимаем 1 клетку равной 4 миллионам
Фиг. 20.
ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ЗАДАЧ.
145, Функция. Если при решении какого-нибудь вопроса зна-
значение величины не меняется, то она называется постоянной,
в противном же случае—переменной. Пусть, например, мы
имеем ряд наблюдений над температурой воздуха:
Полдень
1 час.
2 „
3 „
4 *
5 а
6 ..
22°
23°
23,5°
23°
22,5°
21°
18°
7 час.
8 „
9 »
ю „
полночь
15°
14°
13,5°
13°
12,5°
12°
Здесь температура и время — величины переменные, причем
каждому значению времени соответствует вполне определенное
— 75 —

значение температуры; другими словами, температура зависит
от времени; в этом случае в математике говорят, что темпера-
температура есть функция времени; слово функция заменяет слово
зависит и обозначает зависимую переменную величину; время
в данном случая будет называться переменной независимой или
аргументом.
Относительно обеих переменных величин можно сказать, что
они находятся в функциональной зависимости между собою.
146. Графика. Проведем прямую АХ (фиг. 21); отметим на ней
равноотстоящие точки А, В, С, D, Е,... и будем изображать
промежутки времени в 1 час, 2 часа, 3 часа... соответственно
отрезками АВ, AC, AD... Температуру, имевшую место в полдень
часы 12 I 2 3
ПОЛДЕНЬ
5 6 7 8 9 10 II 12
ПОЛНОЧЬ
Фиг. 21.
и равную 22°, изобразим перпендикуляром ААГ, восставленным
к прямой АХ в точке А и равным 22 каким-нибудь отрезкам;
температуру, имевшую место в 1 час дня и равную 23°, изобразим
перпендикуляром ВВГ, восставленным в точке В и равным 23
таким же отрезкам и т. д. Соединив концы этих перпендику-
перпендикуляров отрезками, получим линию (в данном случае ломаную), кото-
которая называется графикой функции (в данном случае темпера-
температуры).
14:7, Задача 1. Поезд движется со скоростью 30 км в час.
1) Какое расстояние он пройдет в 2-^ часа? 2) Во сколько вре-
времени он пройдет 45 км?
Здесь время и расстояние, проходимое поездом, величины
переменные, а скорость величина постоянная, причем рас*
стояние является функцией времени. Чтобы построить гра-
— 76 —

фику 1), будем давать времени различные значения: 1 час, 2 часа,
3 часа и т. д.;тогда расстояние, пройденное поездом, будет рав-
равняться соответственно 30 км, 60 км, 90 км и т. д. Возьмем прямую
ОХ (фиг. 22) и отложим на ней отрезки ОА = АВ = ВС = ...
Пусть ОА изображает промежуток времени, равный 1 часу,
тогда ОВ будет изображать 2 часа, ОС — 3 часа и т. д. Расстоя-
Расстояния, равные 30 км, 60 км, 90 км и т. д., изобразим соответ-
соответственно перпендикулярами АК,
этих перпендикуляров, получим
линию ОМ, которая будет гра-
графикой движения поезда.
Из чертежа можно усмотреть,
что эта графика будет представ-
представлять собою прямую линию.
Найдем на линии ОХ отрезок
СМ и т. д. Соединив концы
Y
OD, изображающий 2— часа;
Li
в точке D восставляем перпен-
перпендикуляр до пересечения с ОМ
в точке Е; через Е проводим
прямую EF, параллельную ОХ
до пересечения с ОУ в точке F.
Искомое расстояние
км.
90
75
60
45
30
F Е
L
S В
к/
/
с
/
В
м
/
D
/
С
ЧАСЫ 1
\% 2
Фиг. 22.
Откладываем на линии ОУ отрезок OS, изображающий 45 км,
проводим SR, параллельную ОХ, и RQ, перпендикулярную к ОХ.
Измерив длину OQ, найдем, что OQ= 1— часа.
Нахождение промежуточных значений носит название интер-
интерполяции.
Задача 2. Начертить графику движения почтовых поездов
между Москвой и Раненбурюм в 1924 г. по следующим данным:
Км
108
254
332
Москва. . . .
Кашира . . .
Павелец . . .
Раненбург . .
Прих.
23.52
6.23
10.24
Отх.
19.30
0.12
6.53
Прих.
10
5.05
22.12
Отх.
5.30
22.47
18.43
Для построения графики рекомендуется пользоваться клетчатой бумагой.
— 77 —

По горизонтальной линии будем откладывать часы, изображая
каждый час линией, равной 0,5 см, а по вертикальной линии
километры, изображая каждые 30 км линией, равной 1 см. Из
полученной графики (фиг. 23) видно, что встреча поездов произой-
произойдет в 2 час. 37 мин. в 155 км от Москвы.
км
ззг раненбург
300
270- -
254 + ПАВЕЛЕЦ
240
7
210
180
155
150- "
120--
1084- КАШИРА
90
60
30 +
МОСКВА
1 <\ 1 I 1 1 1 1 Ч 1 1 1 1 1 Ml
18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 Ю ЧАСЫ
Фиг. 23.
Задача 3 2). Улитка поднимается в воскресенье в б час.
утра на дерево; впродолжение дня, т. е. до 6 час. вечера, она
поднимается на 5 м, но ночью опускается на 2 м. В какое время
она поднимется на 10 м?
*) Задачи 3-я и 4-я принадлежат Эдуарду Люкасу (Lucas).
— 78 —

Отложим на оси ОХ (фиг. 24) ОБ = 24 часам воскресенья^
BD = 24 часам понедельника, и т. д., а на оси OY метры.
В 6 часов утра воскресенья расстояние улитки от земли
будет равно нулю, поэтому графика движения улитки будет
содержать точку О; в 6 час. вечера того же дня расстояние
улитки от земли будет равно AF = 5 м; в 6 час. утра понедель-
понедельника это расстояние будет равно BG = 3 м и т.д. Точки F и G
и т. д. также будут принадлежать графике; соединив все эти
точки, получим ломаную линию OFGHKL, которая и будет иско*
мой графикой. Проведя через точку, соответствующую 10 м,.
6 чу. 6 чв. 6 чу. 6 ч.в. 6 ч.у. 6 ч. а 6 ч. у.
Фиг. 24.
прямую ИМ, параллельную ОХ, найдем точку ее пересечения
с графикой М; перпендикуляр ME к оси ОХ будет равен Юм;
расстояние ОЕ представит искомое время. Так как DE составляет
— от 12 часов, т. е. =—час.= 9— часа, ОЕ = 2 дня-{-9— часа.
5	о	о	о
3
Так как 9— часа прошло после 6 часов утра, то, значит, улитка
5
3
поднимется на 10 м во вторник в 3— часа, или в 3 часа 36 мин.
пополудни
— 79 —

Задача 4. Ежедневно в полдень из Америки в Европу от-
травляется пароход и в то же самое время пароход топ же ком-
-пании отправляется из Европы в Америку. Переезд в том и дру-
другом направлении совершается ровно в 7 дней. Сколько встретит
пароход, отправляющийся сегодня в полдень из Европы, на
своем пути пароходов той же компании, совершаюгцих обратный
рейс?
Отложим на оси ОХ (фиг. 25) отрезки, изображающие дни,
¦а на оси OY отрезок OF, изображающий расстояние от Европы до
Америки; следовательно, равные отрезки ОА, АВ, ВС и т. д.
45удут представлять собою каждый — всего пути, т. е. расстоя-
расстояние, проходимое пароходом в один день; поэтому ОК будет гра-
АМЕРИКА
К
I	3
ЕВРОПА
II
13 IS 17 19 21
Фиг. 25.
фика движения одного из пароходов. Построив все графики и
найдя точки пересечения графики парохода, вышедшего из
Европы 7-го числа, со всеми остальными, получим, что этот
пароход встретит всего 15 судов: 13 пароходов в море,
кроме того, в момент отплытия 1 пароход, прибывающий
в Европу, и в момент прибытия 1 пароход, отправляющийся
из Америки.
Задача 5. Еастрюля емкостью в 3 стакана стоит 37 коп.,
а 6 стаканов 53 коп. и в 13 стаканов 73 коп. Сколько стоят
кастрюли в 5 стаканов и в 14: стаканов?
Будем откладывать по оси ОХ (фиг. 26) отрезки, изображаю-
изображающие число стаканов, а по оси 0Y отрезки, изображающие их
стоимость в копейках. На основании условия задачи найдем
точки А, В и С.
ч
— R0 —

Приложим к ним гибкую линейку и проведем линию ABDCE,
которая и будет графикой стоимости кастрюль в зависимости
от их емкости.
Y
На основании этой
графики найдем, что ка-
кастрюля в 8 стаканов
стоит 60 коп., а кастрюля
в 14 стаканов 80 коп.
Решение первого вопроса
называется, как мы уже
знаем, интерполяцией так
как точка D находит-
находится между данными точ-
точками В и С; решение
второго вопроса назы-
называется экстраполяцгьещ
так как искомая точка Е
не находится между дан-
данными точками А В и С*
Интерполяция дает до-
довольно правильное при-
приближенное значениеиско-
мой величины; экстра-
экстраполяция же не всегда
может быть удачной.
Упражнения. 1) На-
чертигь графику для перевода футов в метры по следующим
данным:
1	фут. = 0,3 м	4 фут. = 1,2 м
2	фут. =0,6 м	5 фут. = 1,5 м
3	фут. = 0,9 м	6 фут. == 1,8 м
2) Начертить графику температуры больного воспалением
легких по следующим данным.
80	У г
0
м и i 1 1 i
1Л N CD
Фиг. 26.
Д^нь
болезни
1
2
3
4
5
>тро
37°
39,6°
39,2°
39°
39,6°
Вечер
40°
4',4°
40°
39,8°
40,2°
День
болезни
• 6
7
8
9
10
Утро
39,4°
39°
35,8°
36,2°
36,4°
Вечер
40,2°
37,8°
36°
36,6°
37,0°
6 Рашевский. Краткий курс арифы.

3)	Начертить графику возрастания населения России с 1850 г.
по 1900 г.
1850	г. . . .67 млн. чел. 1880 г. ... ЮЭ млн. чел.
1851	г. ... 68 » »	1890 г. ... 119 » »
1860 г. ... 76 » » 1897 г. ... 126 » »
1870 г.. -.85 » »	1900 г.. . . 135 » »
4)	Начертить графику движения поездов между Ленинградом
и Москвой в 1936 г. по следующим данным:
Ленинград . .
Любань . . .
М. Вишера . .
Бологое . . .
Лихославль .
Тверь ....
Клин ....
Москва . . .
Километры
83
162
320
442
484
561
651
Курьерский
прибывает
11.09
12.34
15.27
17.30
18.14
19.39
21.20
отходит
9.45
11.17
12.42
15.35
17.37
18.22
19.47
Пассажирский
прибывает
14.31
16.49
21.31
0.55
1.51
3.58
6.30
отходит
12.30
14.41
16.59
21.43
0.59
2.01
4.08
Москва . . .
Клин ....
Тверь ....
Лихославль .
Бологое . . .
М. Вишера . .
Любань . . .
Ленинград
Километры
89
166
208
330
488
567
651
Курьерский
прибывает
10.34
11.57
12.41
14.54
17.38
19.02
20.30
отходит
8.49
10.44
12.05
12.48
15.02
17.46
19.10
Пассажирский
прибывает
13.32
15.32
16.52
20.20
1.23
4.07
6.40
отходит
11
13.42
15.44
16.57
20.50
1.33
4.17
5) Начертить графику изменения мировой добычи золота по
следующим данным в миллионах фунтов стерлингов:
1913	г. ... 94,7 1916 г. ... 93,5 1919 г. ... 75,2
1914	г. • . . 90,7 1917 г. ... 86,3 1920 г. ... 60,5
1915	г. ... 96,4 1918 г. ... 79,0 1921 г. ... 69,0
— 82 —

ТАБЛИЦА ПЕРВОНАЧАЛЬНЫХ ЧИСЕЛ.
2
3
5
7
U
13
17
19
23
29
31
37
41
43
47
53
59
61
67
7L
73
79
83
89
97
101
103
107
109
113
127
131
137
139
149
151
157
163
167
173
179
181
191
193
197
Ш
211
223
227
229
233
239
241
251
257
263
269
271
277
281
283
293
307
311
313
317
331
337
347
349
353
359
367
373
379
383
389
397
401
409
419
421
431
433
439
443
449
457
461
463
467
479
487
491
499
503
509
521
523
541
547
557
563
569
571
577
587
593
599
601
607
613
617
619
631
641
643
647
653
659
661
673
677
683
691
701
709
719
727
733
739
743
751
757
761
769
773
787
797
409
811
821
823
827
829
839
853
857
859
863
877
881
883
887
907
911
919
929
937
941
947
953
967
971
977
983
991
997
1009
1013
1019
1021
1031
1033
1039
1049
1051
L061
L063
1069
1087
1091
1093
1097
1103
1109
1117
1123
1129
1151
1153
1163
1171
1181
1187
1193
1201
1213
1217
1229
1223
1231
1237
1249
1259
1277
1279
1283
1289
1291
1297
1301
1303
1307
1319
1321
1327
1361
1367
1373
1381
1399
1409
1423
1427
1429
1433
1439
1447
1451
1453
1459
1471
1481
1483
1487
1489
1493
1499
1511
1523
1531
1543
1549
1553
1559
1567
1571
1579
1583
1597
1601
1607
1609
1613
1619
1621
1627
1637
1657
1663
1667
1669
1693
1697
1699
1709
1721
1723
1733
1741
1747
1753
1759
1777
1783
1787
1789
1801
1811
1823
1831
1847
1861
1867
1871
1873
1877
1879
1889
1901
1907
1913
1931
1933
1949
1951
1973
1979
1987
1993
1997
1999
2003
2011
2017
2027
2029
2039
2053
2063
2069
2081
2083
2087
83 —

2089
2099
2111
2113
2129
2131
2137
2141
2143
2153
2161
2179
2203
2207
2213
2221
2237
2239
2243
2251
2267
2269
2273
2281
2287
2293
2297
2309
2311
2333
2339
2341
2347
2351
2357
2371
2377
2381
2383
2389
2393
2399
2411
2417
2423
2437
2441
2447
2459
2467
2473
2477
2503
2521
2531
2539
2543
2549
2551
2557
2579
2591
2593
2609
2617
2621
2633
2647
2657
2659
2663
2671
2677
2683
2687
2689
2693
2699
2707
2711
2713
2719
2729
2731
2741
2749
2753
2767
2777
2789
2791
2797
2801
2803
2819
2833
2837
2843
2851
2857
2861
2879
2887
2897
2903
2909
2917
2927
2939
2953
2957
2963
2969
2971
2999
3001
зон
3019
3023
3037
3041
3049
3061
3067
3079
3083
3089
3109
3119
3121
3137
3163
3167
3169
3181
3187
3191 ,
3203
3209
3217
3221
3229
3251
3253
3257
3259
3271
3299
3301
3307
3313
3319
3323
3329
3331
3343
3347
3359
3361
3371
3373
3389
3391
3407
3413
3433
3449
3457
3461
3463
3467
3469
3491
3499
3511
3517
3527
3529
3533
3539
3541
3547
3557
3559
3571
3581
2583
3593
3607
3613
3617
3623
3631
3637
3643
3659
3671
3673
3677
3691
3697
3701
3709
3719
3727
3733
3739
3761
3767
3769
3779
3793
3797
3803
3821
3823
3833
3847
3851
3853
3863
3877
3881
3889
3907
3911
3917
3919
3923
3929
3931
3943
3947
3967
3989
4001
4003
4007
4013
4019
4021
4027
4043
4051
4057
4073
4079
4091
4093
4099
4111
4127
4129
4133
4139
4153
4157
4159
4177
4201
4211
4217
4219
4229
4231
4241
4243
4253
4259
4261
4271
4273
4283
4289
4297
4327
4337
4339
4349
4357
4363
4373
4391
4397
4409
4421
4423
4441
4447
4451
4457
4463
4481
4483
4493
4507
4513
4517
4519
4523
4547
4549
4561
4567
4583
4591
4597
4603
4621
4637
4639
4643
4649
4651
4657
84

4663
4673
4679
4691
4703
4721
4723
4729
4733
4751
4759
4783
4787
4789
4793
4799
4801
4813
4817
4831
•
861
4871
4877
4889
4903
4909
4919
4931
4933
4937
4sm
4951
4957
4967
4969
4973
4987
4993
4999
5003
5009
5011
5021
5023
5039
5051
5059
5077
5081
5087
5099
5101
5107
5113
5119
5147
5153
5167
5171
5179
5189
5197
5209
5227
5231
5233
5237
5261
5273
5279
4
5281
5297
5303
5309
5323
5333
5347
5351
5381
5387
5393
5599
5407
5413
5417
5419
5431
5437
5441
5443
5449
5471
5477
5479
5483
5501
5503
5507
5519
5521
5527
5531
5557
5563
5569
5573
5581
5591
5623
5639
5641
5647
5651
5653
5657
5659
5669
5683
5689
5693
5701
5711
5717
5737
5741
5743
5749
5779
5783
5791
5801
5807
5813
5821
5827
5839
5843
5849
5851
5857
5861
5867
5869
5879
5881
5897
5903
5923
5927
5939
5953
5981
5987
6007
6011
6029
6037
6043
6047
6053
6067
6073
6079
6089
6091
6101
6113
6121
6131
6133
6143
6151
6163
6173
6197
6199
6203
6211
6217
6221

ОГЛАВЛЕНИЕ.
Стр.
Предисловие ко второуу изданию	....,•		3
I. Первоначальные понятия		5
II. Арифметические депствич	,		6
Сложение целых чисел		7
Вычитание целых чисел		8
Умножение целых чисел	,		9
Деление целых чисел		13
Зависимость между числами во всех: четырех действиях•: . ...	17
Поверка действий		—
Арифметическое выражение и скобки		18
Изменение суммы, разности, произведения и частного		19
Свойства действий		20
III.	Именованные числа		21
Метрические меры 		22
Определение площадеГ! и объемов		28
IV.	Признаки делимости		31
V.	Простые дроби, преобразования и действия над ними		33
Нахождение части от числа и числа по его части		43
Действия с дробными именованными числами		44
VI.	Десятичные дроби	 		45
Приближенные вычисления		50
Метрическая система мер		54
VII, О делителях и кратном		56
VIII. Пропорция. Решение задач на пропорциональные величины ...	60
Процентные вычисления	*		62
Учет векселей		65
Пропорциональное деление		68
Задачи на смешение		70
IX. Черчение планов, диаграмм п график		72
Графический способ решения задач		75
Таблица первоначальных чисел		83

ввг
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
МОСКВА — ЛЕНИНГРАД
РАБОЧАЯ ШКОЛЬНАЯ БИБЛИОТЕКА
СЕРИЯ ПО МАТЕМАТИКЕ
под общей редакцией А. М. ВОРОНЦА
н. и. идельсон
МЕХАНИЗАЦИЯ СЧЕТА
Стр. 128.	 					Ц. 90 к.
Н. И. ИОВЛЕВ
ВВЕДЕНИЕ В ЭЛЕМЕНТАРНУЮ ГЕОМЕТРИЮ
И ТРИГОНОМЕТРИЮ ЛОБАЧЕВСКОГО
Стр. 67.Ц.
Н. Г. КУВЫРКИН
ПРАКТИКА ГРАФИЧЕСКИХ ВЫЧИСЛЕНИЙ
Элементы номографии
Стр. 69 + 4 листа чертежей.
Ц. 50 к.
Стр. 36.
П. П. ОВСЯНИКОВ
НУЛЬ
Очерк его происхождения и его значения
в современной системе счисления
Ц. 25 к.
Г. Н. ПОПОВ
КАК ПРИМЕНЯЛАСЬ И ПРИМЕНЯЕТСЯ
ТРИГОНОМЕТРИЯ НА ПРАКТИКЕ
Стр. 64.
Ц. 40 к.
Г. Н. ПОПОВ
ПАМЯТНИКИ МАТЕМАТИЧЕСКОЙ СТАРИНЫ
В ЗАДАЧАХ
Стр. 59+1 карта.	Ц. 50 к.
И. И. ЧИСТЯКОВ
ЧИСЛОВЫЕ СУЕВЕРИЯ
Стр. 46.
Ц. 35 к.
ч	Н. И. ЩЕТИНИН
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
Стр. 64.
Ц. 30 к.
ПРОДАЖА ВО ВСЕХ ОТДЕЛЕНИЯХ И МАГАЗИНАХ ГОСИЗДАТА
¦к.

ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
МОСКВА — ЛЕНИНГРАД
УЧЕБНЫЕ ПОСОБИЯ ПО МАТЕМАТИКЕ ДЛЯ ШКОЛ
ПОВЫШЕННОГО ТИПА
II концентр
и для подготовки в Вузы
Берг М Ф., Знаменский М. А. Попов Г Н. Слуд-
ский И. Ф., Хвостов Н. П. и Щетинин Н. И.
Рабочая книга по математике. Составлена в соответ-
соответствии с программами Гусса. 1927 г. Под редакцией
А. М. Воронца. Для 8-го года обучения в городской
школе. Стр. 200. Ц. 80 к. Для 9-го года обучения в
городской школе. Стр. 232. Ц. 90 к
Брадис В. Четырехзначные математические таолицы
с готовыми поправками дтя школьного употребле-
употребления и технических расчетов. Стр. 42. Ц. 45 к.
Державин С. С. Учебник математики для 8-го года
обучения. Стр. 238. Ц. 1 р. 40 к.
Добровольский В. В. Краткий курс математики для
поступающих в техникумы. Составлена по программе
приемных требований по математике и графлке
Стр. 338. Ц. 3 р. 25 к.
Киселев А. Систематический курс арифметики. Посо-
Пособие для поступающих в вузы и техникумы и для I
самообразования Стр. 176. Ц. 70 к,
Киселев А. Элементарная геометрия. Стр. 346
Ц. 1 р. 40 к.
Киселев А. Элементы алгебры и анализа. Ч. I. Эле-
Элементы алгебры. С приложением четырехзначных таб-
таблиц квадратных корней, логарифмов и антилогарифмов.
Стр. 314. Ц. 1 р 65 к.
Ч. II. Элементы анализа и некоторые дополнительные
статьи алгебры Стр. 163. Ц. 90 к.
Киселев А. Задачи и упражнения к „Элементам алгебры .
Дополнено ответами на все задачи и упражнения.
Стр. 145. Ц. 70 к.
ПРОДАЖА ВО ВСЕХ ОТДЕЛЕНИЯХ И МАГАЗИНАХ ГОСИЗДАТА

ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
МОСКВА — ЛЕНИНГРАД
УЧЕБНЫЕ ПОСОБИЯ ПО МАТЕМАТИКЕ ДЛЯ ШКОЛ
ПОВЫШЕННОГО ТИПА
И концентр
и для подготовки 8 вузы
Лебединцев К. Ф. Руководство алгебры. Ч. I. Стр. 144-f-
+ 4 таблицы. Ц. 70 к. Ч. II. Стр. 208 + 5 таблиц. Ц. 1 р.
Лебединцев К. Ф. Сборник задач и других упражнений
по курсу алгебры. Для трудовой школы и самообразова-
самообразования. Ч L Стр 142. Ц. 55 к Ч. II
Пржевадьский Е Пятизначные таблицы логарифмов чи-
чисел и тригонометрических величин С прибавлением
логарифмов Гаусса, квадратов чисел квадратных и куби-
кубических корней из чисел и некоторых других таблиц
Стр. 201. Ц. в переплете 85 к.
Рашевский К, Элементарная алгебра. Стр. 246. Ц. 1 р
Л- *
Рашевский К. Систематический курс геометрии и методы
решения задач на построе ие. Стр 253. Ц. 1р. 10 к
Рашевский К Тригонометрия. Пособие для поступающих
в вузы, составленное по программе Наркомпроса РСФСР
1928 г. Стр. 88. Ц 50 к.
Рыбкин Н Сборник геометрических задач на вычисление
Ч. 1. Планиметрия Стр. 128. Ц. 50 к. Ч. II Стереометрия.
Стр. 96. Ц 45 к.
Рыбкин Н. Учебник прямолинейной тригонометрии со
брание задач. Стр. 175. Ц. 60 к.	-
Шапошников Н А и Вальцев Н К. Сборник алгебра- j
ических задач Ч. I Стр. 200. Ц. 80 к Ч. II. Стр 158.
Ц. 55 к.
Шмулевич П., инж. Прямолинейная тригонометрия и ее
приложение. Стр. 332. Ц. 1 р. 70 к
Шмулевич П., инж Сборник задач по алгебре и арифме
тике. Пособие для самостоятельной подготовки в Вузы
Стр. 320. Ц 2 р.
ПРОДАЖА ВО ВСЕХ ОТДЕЛЕНИЯХ И МАГАЗИНАХ ГОСИЗДАТА