А.А. Болотов, С. Б.Гашков
А. Б. Фролов
ЭЛЕМЕНТАРНОЕ
ВВЕДЕНИЕ
В ЭЛЛИПТИЧЕСКУЮ
КРИПТОГРАФИЮ
Протоколы криптографии
на эллиптических кривых
МОСКВА
URSS
ББК 32.81
УДК 512.8
Болотов Анатолий Александрович,
Гашков Сергей Борисович,
Фролов Александр Борисович
Элементарное введение в эллиптическую криптографию: Протоколы криптогра-
фии на эллиптических кривых. — М.: КомКнига, 2006. — 280 с.
ISBN 5-484-00444-6
Настоящая книга содержит описание и сравнительный анализ алгоритмов
на эллиптических кривых. Изучаются протоколы эллиптической криптографии,
имеющие аналоги — протоколы на основе алгебраических свойств мультиплика-
тивной группы конечного поля и протоколы, для которых таких аналогов нет —
протоколы, основанные на спаривании Вейля и Тейта. В связи с этим описаны
алгоритмы спаривания Вейля и Тейта и их модификации. Изложение теории
сопровождается большим числом примеров и упражнений.
Предназначено для студентов, преподавателей вузов и специалистов в об-
ласти защиты информации, прикладной математики, вычислительной техники
и информатики. Издание представляет интерес для лиц, связанных с кодирова-
нием и передачей информации и цифровой техникой, а также специалистов по
прикладной математике, интересующихся компьютерной алгеброй.
Издательство «КомКнига». 117312, г. Москва, пр-т 60-летия Октября, 9.
Подписано к печати 03.05.2006 г. Формат 60x90/16. Печ. л. 17. Зак. № 553.
Отпечатано в ООО «ЛЕНАНД». 117312, г. Москва, пр-т 60-летия Октября, д. ПА, стр. 11.
ISBN 5-484-00444-6	© КомКнига, 2006
НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
“р“1 E-mail: URSS@URSS.ru
Хх Каталог изданий в Интернете:
W http://URSS.ru
J Тел./факс: 7 (095) 135-42-16
URSS Тел ./факс: 7 (095) 135-42-46
3811 ID 35177
91785484 004447 >
Оглавление
Предисловие....................................................... 7
Глава 1. Алгоритмы на эллиптических кривых........................ 9
1.1.	Алгоритм сложения и удвоения точек........................... 9
1.1.1.	Общая схема алгоритма сложения........................ 9
1.1.2.	Частные формулы для сложения и	удвоения............... 11
1.1.3.	Алгоритмы сложения и удвоения точек эллиптических
кривых....................................................... 17
1.2.	Эллиптические кривые над GF(2n)............................. 17
1.2.1.	Суперсингулярные кривые.............................. 20
1.2.2.	Несуперсингулярные кривые............................ 25
1.2.3.	Стандарты о выборе кривых для реализации криптосистем
на эллиптических кривых..................................... 27
1.3.	Скалярное умножение на суперсингулярных	кривых............. 31
1.3.1.	Вычисление к • Р методом аддитивных цепочек ......... 32
1.3.2.	Использование проективных координат.................. 35
1.3.3.	Метод Монтгомери..................................... 37
1.4.	Скалярное умножение на несуперсингулярных кривых............ 39
1.4.1.	Метод Монтгомери для несуперсингулярных кривых....... 40
1.4.2.	Метод Монтгомери в проективных координатах .......... 42
1.4.3.	Метод Лопеса—Дахаба использования проективных
координат................................................... 43
1.4.4.	Алгоритм скалярного умножения, использующий операцию
«ополовинивания»............................................ 45
1.5.	Скалярное умножение на аномальных кривых.................... 54
1.5.1.	Свойства кривых Коблица.............................. 54
1.5.2.	Использование модулярной редукции.................... 64
1.6.	Вычисление дискретного логарифма............................ 72
1.6.1.	Проблема дискретного логарифмирования................ 72
1.6.2.	Алгоритм «большой шаг — малый шаг»................... 72
1.6.3.	Алгоритм для групп составных порядков................ 74
Глава 2. Протоколы на эллиптических кривых....................... 76
2.1.	Выбор точки и размещение данных ............................ 76
2.1.1.	Введение............................................. 76
2.1.2.	Решение квадратных уравнений ........................ 76
2.1.3.	Выбор точки эллиптической кривой..................... 81
4
Оглавление
2.1.4.	Размещение данных на эллиптической кривой.......... 82
2.1.5.	Определение порядка точки эллиптической кривой
и нахождение образующего элемента группы точек
эллиптической кривой......................................  83
2.2.	Распределение ключей...................................... 83
2.2.1.	Введение........................................... 83
2.2.2.	Распределение ключей для классической криптосистемы
(протокол Диффи—Хеллмана) ................................. 85
2.2.3.	Распределение ключей для классической криптосистемы
(протокол Месси—Омуры)..................................... 86
2.2.4.	Протокол распределения ключей Менезеса—Кью—Венстоуна
(MQV-протокол)............................................. 90
2.3.	Криптосистемы Эль-Гамаля.................................. 93
2.4.	Протоколы цифровой подписи................................ 96
2.4.1.	Электронная цифровая подпись....................... 96
2.4.2.	Обобщенная схема электронной	подписи Эль-Гамаля.... 98
2.4.3.	Электронная подпись Эль-Гамаля с возвратом сообщения —
схема Nyberg—Rueppel.......................................102
2.5.	Передача с забыванием.....................................105
2.5.1.	Введение...........................................105
2.5.2.	Схема некоторых протоколов передачи с забыванием...106
2.5.3.	Некоторые частные случаи передачи с забыванием.....109
2.5.4.	Передача комбинации к из п сообщений с забыванием...112
2.5.5.	Применение передачи к из п сообщений с забыванием...115
Глава 3. Криптосистемы на основе спариваний....................120
3.1.	Билинейная проблема Диффи—Хеллмана........................120
3.1.1.	Однораундовый протокол генерации общего секретного
ключа между тремя участниками..............................122
3.1.2.	Короткая цифровая подпись, основанная на спаривании.122
3.1.3.	Криптосистема с публичным индивидуальным ключом.....123
3.2.	Спаривание Андре Вейля на эллиптических кривых............124
3.2.1.	Дивизоры...........................................125
3.2.2.	Явное определение спаривания	Вейля.................128
3.2.3.	Функции на гиперэллиптических кривых...............130
3.3.	Алгоритм вычисления спариваний Вейля и Тейта .............136
3.3.1.	Усовершенствования алгоритма	Миллера...............139
3.4.	Спаривание Тейта..........................................143
3.4.1.	Применение спариваний для логарифмирования
в эллиптических кривых.....................................145
3.4.2.	Кривые, удобные для спаривания ....................146
3.4.3.	Искажающее отображение.............................148
3.4.4.	Удобные для спаривания кривые с множителем безопасности
fc<2...................................................... 152
Оглавление
5
3.4.5.	Удобные для спаривания поля........................153
3.5.	Кривые над полями характеристики три.....................154
3.5.1.	Устранение делений.................................155
3.6.	О больших значениях параметра безопасности...............160
3.6.1.	Скалярное умножение точек кривой над полем большой
характеристики........................................... 162
3.6.2.	Ускорение алгоритма Миллера для больших к..........163
3.6.3.	Итерированное удвоение в якобиевых координатах.....164
3.6.4.	Комбинирование с другими методами................  164
3.6.5.	Использование аддитивных цепочек с двойной базой ..166
3.7.	Алгоритм Дуурсма—Ли......................................168
3.7.1.	Алгоритм Дуурсма—Ли над полями характеристики два..174
3.8.	Некоторые алгоритмы арифметики конечных полей ...........176
3.8.1.	Извлечение квадратных корней в полях характеристики
большей двух..............................................176
3.8.2.	Извлечение корней р-й степени в полях характеристики р . . . . 177
3.8.3.	Один метод компактной записи точек суперсингулярных
кривых....................................................180
3.8.4.	Арифметика в полях характеристики большей двух.....182
3.9.	О реализации алгоритма Дуурсма—Ли........................188
3.9.1.	Использование нормального базиса в поле G..........189
3.9.2.	Умножение в поле К методом	Карацубы................190
3.9.3.	Умножение в поле К методом	Тоома...................191
3.9.4.	Возведение в степень р в поле	К ...................192
Приложение А. Алгоритмы с двоичными матрицами.................196
А.1. Представление векторов и матрицы ........................196
А.2. Умножение матрицы на вектор..............................197
А.З. Алгоритм GAUS-MATRIX-TRIAN ..............................199
А.4. Алгоритм проверки невырожденности матрицы................201
А. 5. Приведение матрицы к диагональному	виду.................202
А.6. Обращение матрицы........................................204
А.7. Умножение вектор-строки на матрицу.......................206
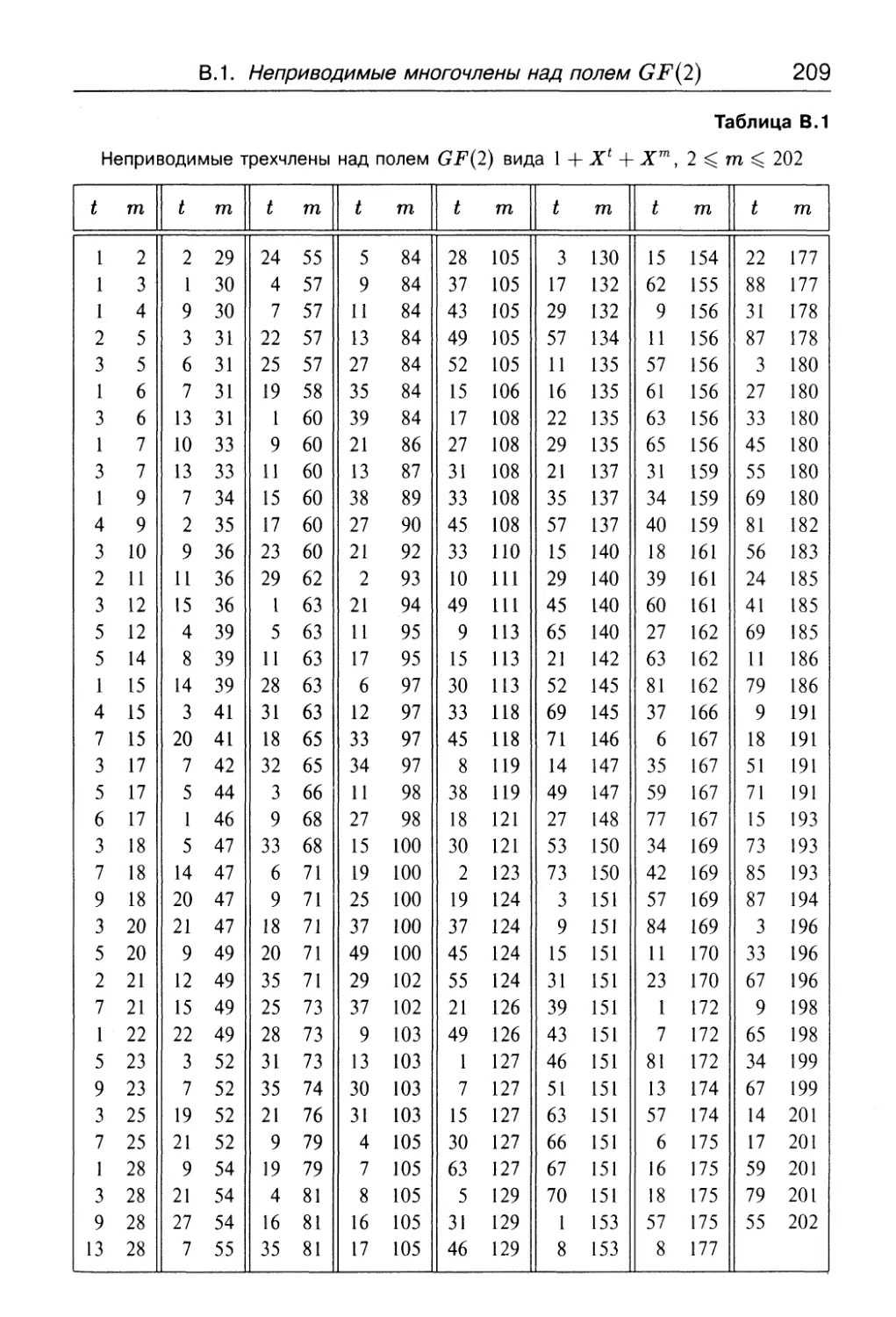
Приложение В. Таблицы неприводимых многочленов................208
В.1.	Неприводимые многочлены над полем GF(2) .................208
В.	1.1. Неприводимые трехчлены степени п, 2 < п < 2000 . 208
В.	1.2. Неприводимые трехчлены вида 1 + хп~1 + хп степени п,
2 <: п < 34 353 ......................................... 221
В.	1.3. Неприводимые пятичлены степени п, 8 < п < 290 .. 222
В.2.	Неприводимые трехчлены над полем GF(3)...................223
6	Оглавление
Приложение С. Таблицы ОНБ...................................226
С.1. ОНБ размерности п, 2 п 30 ..........................   226
С.2. ОНБ размерности п, 30 < п < 1013 ......................230
С.З. Возможные размерности ОНБ п, 998 < п < 10 000 ........ 251
Приложение D. Примеры исполнения MQV-протокола..............260
Литература................................................. 264
Предметный указатель........................................269
Односторонние улицы — это то, чем занимается крип-
тография с открытым ключом. Вот один из очень типичных
примеров. Устройство, являющееся ловушкой для ловли ры-
бы в северных странах. Рыбе очень легко забраться в клетку.
Форма входа ведет рыбу внутрь — здесь в качестве приман-
ки может находиться маленькая рыбка. С другой стороны,
рыбе очень трудно найти путь назад, хотя в принципе бег-
ство возможно. Легальный пользователь, то есть рыбак,
берет рыбу через отверстие в верхней части клетки.
А. Саломаа.
Криптография с открытым ключом.
Предисловие
Настоящее издание публикуется параллельно с книгой «Элементар-
ное введение в эллиптическую криптографию: Алгебраические и алго-
ритмические основы» (М.: URSS, 2006) [4], которая является сходной по
тематике. Поэтому ссылки на нее в тексте помечены как первая книга.
Первая глава данной книги посвящена базовым алгоритмам для
операций в группе точек эллиптических кривых. Такими операциями яв-
ляются основная операция сложения, операция умножения на константу,
равную характеристике поля, и основная криптографическая операция —
умножение точки на произвольную константу, аддитивный аналог опера-
ции возведения в степень элемента мультипликативной группы. Анали-
зируются условия безопасного применения этих операций, в связи с чем
приводятся рекомендации стандартов по выбору эллиптических кривых.
Приводится и алгоритм дискретного логарифмирования в группе точек
эллиптической кривой.
Во второй главе описаны примитивные операции — взятие точ-
ки эллиптической кривой и размещение данных в точке кривой. Здесь
формируется представление о реализации на эллиптических кривых ря-
да известных криптографических протоколов (распределения ключей для
классической криптосистемы, цифровой подписи, передачи с забывани-
ем), допускающих также реализацию с использованием мультипликатив-
ной группы конечного поля.
Третья глава отражает последние достижения в области криптографи-
ческих приложений эллиптических кривых. В ней рассматриваются так
называемые спаривания Вейля и Тейта и основанные на них криптосисте-
мы с новыми интересными свойствами, которые не удается реализовать,
используя только арифметику конечного поля.
В Приложении помещены таблицы неприводимых многочленов и не-
которые громоздкие примеры.
8
Предисловие
Для удобства пользования в конце книги приведен предметный ука-
затель, где ссылки на первую книгу [4] помечены символом I после номера
страницы.
Приведен также список цитируемых источников.
Теоремы, следствия, леммы, утверждения, примеры и упражнения
нумеруются по главам и разделам, например, «Теорема 3.2.1» есть первая
теорема второго раздела третьей главы; а уравнения (или алгебраические
выражения), таблицы и рисунки имеют сплошную нумерацию внутри
главы, и номер раздела в их обозначениях отсутствует.
В издании отражен опыт авторов преподавания математических
основ криптологии и криптографических методов обеспечения инфор-
мационной безопасности в Московском государственном университете,
Московском энергетическом институте, факультете защиты информации
Российского государственного гуманитарного университета, на кафедре
информационной безопасности Российского государственного социаль-
ного университета и даже в физико-математической школе-интернате
при МГУ.
При подготовке примеров использована библиотека алгоритмов
криптографии эллиптических кривых и «визуализирующий» ее алгебраи-
ческий процессор, разработанные под руководством авторов студентами
МЭИ П. И. Артемьевой, В. С. Гамовым, Я. Ю. Грачевым, А. Б. Дроздовым,
Ал. И. Мамонтовым и Е. В. Шестаковым при выполнении дипломных про-
ектов и магистерских диссертаций, и другие программы, разработанные
под руководством авторов студентами МГУ и МЭИ.
В заключение авторы выражают благодарность за замечания О. Н. Ва-
силенко и Д. В. Матюхину, прочитавшим рукопись, студентам МЭИ
и МГУ, заметившим ряд неточностей и осуществившим эксперименталь-
ную проверку описаний алгоритмов и числовых параметров, приведенных
в книге. Также мы благодарны заведующему кафедрой информационной
безопасности РГСУ профессору А. В. Бабашу и доценту РГГУ Э. А. При-
менко за поддержку настоящего издания. Мы с благодарностью примем
замечания наших читателей.
Глава 1
Алгоритмы на эллиптических кривых
...Недостаточно защитить себя законами, нужно
защитить себя математикой. Шифрование слишком
важно, чтобы оставить его только правительствам.
Брюс Шнайер. Прикладная криптография.
Триумф, 2002
1.1.	Алгоритм сложения и удвоения точек
1.1.1.	Общая схема алгоритма сложения
В соответствии с определением операции сложения в группе точек
эллиптической кривой общая схема алгоритма сложения точек Pi —
(a?i, 2/1) и Pi = (ж2, У2) представляется в виде алгоритма 1.1.1 на рис. 1.1.
Алгоритм 1.1.1
ВХОД: Коэффициенты эллиптической кривой,
точки Р[ = (ж1} у\) (или PY = О) и Р2 = (®2, Ут) (или Р2 = О).
ВЫХОД: Р = Р{ + Р2.
Вычислить: если Р\ — О, то Р = Р2,
если Р2 = О, то Р = Р[,
если Р2 = -Pi, то Р — О,
если Х\ Ф х2, то Р = -(ж3, у3),
иначе Р = 2Р, = -(ж3, у3).
Вернуть Р
Рис. 1.1. Общая схема алгоритма сложения и удвоения точек
эллиптической кривой
Координаты точек ~(хз,уз) вычисляются по формулам, вытекаю-
щим из определения (2.2.2) на с. 91 в первой книге [4] (в зависимости
от вида эллиптической кривой и условия различия или совпадения точек)
по общим правилам, описанным ниже. Далее эти формулы выведены:
—	для эллиптических кривых над полем F характеристики, большей 3,
это формулы (1.9) и (1.10);
—	для эллиптических кривых над полем характеристики 3 — формулы
(1.17) и (1.18);
10	Глава 1. Алгоритмы на эллиптических кривых
—	для несуперсингулярных эллиптических кривых над полем характе-
ристики 2 — формулы (1.24) и (1.25);
—	для суперсингулярных эллиптических кривых над полем характери-
стики 2 — формулы (1.31) и (1.32).
Эти формулы использованы в алгоритмах 1.1.2, 1.1.3, 1.1.4 и 1.1.5
в разд. 1.1.3, которые детализируют приведенную общую схему с учетом
типа кривой и характеристики поля, над которым она определяется.
Точка О имеет определенный идентификатор, например, она может
быть представлена парой (А, А), где А — пустая строка. Элемент О
никогда не используется в качестве входных данных и не возникает как
значение выходных данных при исполнении двух последних строк схемы
алгоритма. Поэтому изучаемые ниже формулы, определяющие операции
для этих случаев, не имеют смысла, если один или оба аргумента являются
точкой О.
Алгоритм включает случай удвоения точки (последняя строка ал-
горитма), когда слагаемые одинаковы, но не взаимно противоположны.
Некоторые кривые имеют «само-противоположные» точки (такие, что
Р = -Р), к таким точкам правило удвоения не применимо, но в этом
случае алгоритм заканчивает работу, не доходя до последней строки.
Детализируя построения, лежащие в основе определения суммы двух
точек, в принципе, можно построить формулы, выражающие координаты
точки (жз, у3) = ~(жз, уз) через координаты хз, У\, уз для суперсингу-
лярной или несуперсингулярной кривой любой характеристики, но эти
формулы окажутся громоздкими и неудобными для реализации. В то же
время в приложениях используется, как правило, кривая определенного
вида над полем известной характеристики. Формулы для кривых, описы-
ваемых уравнениями частного вида, определяемого характеристикой поля
и типом кривой, оказываются более компактными. Вывод таких формул
осуществляется по общим правилам, конкретизирующим упомянутые по-
строения, лежащие в основе определения суммы двух точек.
Эти правила следующие. Сначала следует вычислить координаты
точки R = (жз, уз). Для этого нужно привести уравнение кривой к виду
F(X, У) — 0 и выполнить следующие действия:
А. Если точки Pi = (xi, у\) и Рз = (хз, уз) разные, то принять Л =	,
/3 — У1 - Хх\\ подставить XX 4- /3 вместо У в Р(Х, У) и привести
F(X, XX 4- /3) = 0 к виду
Х~ + уХ2 + aX + b = 0, y,a,b&F,
И вычислить
Жз = -7 - Ж1 - Х2; Уз = У\ + A(s3 - ж,).
(1-1)
1.1. Алгоритм сложения и удвоения точек	11
Б. Если точки одинаковые, Р\ =	= Р = (ж, у), то по формальным
правилам дифференцирования получить выражение
mri	dF(X,Y)/dX
{	'	dF{X,Y)/dY’
по этому выражению при X = х, Y = у вычислить элемент А' =
Х(х, у) поля F; вычислить fl = у\— A'xj; подставить XX + fl вместо
Y в F(X, Y) и привести уравнение F(X XX 4- fl) = 0 к виду
Т3 + 7'Т2 + аХ + & = О, -y',a,b€F;
ВЫЧИСЛИТЬ
Жз = -7-22:; у3 = у{ + A'(s3 - Sj).	(1.2)
Далее с учетом равенства
-Р — (ж, -а\Х - а3 - у)	(1.3)
вычислить -R = ~(х3,Уз) = (х3,у3), где у = —а^х - а3 — у при
соответствующих уравнению кривой коэффициентах и а3, т. е.
получить результат сложения или удвоения. Окончательные форму-
лы получают конкретизацией полученных выражений (1.1) и (1.2)
с учетом уравнения эллиптической кривой. Выражение для у' можно
получить из 7 просто заменой константы А константой А'.
1.1.2.	Частные формулы для сложения и удвоения
Сложение и удвоение точек кривой
над полем большой характеристики
Уравнение эллиптической кривой в этом случае (характеристика поля
больше 3) приводится к виду (2.13) (см. с. 85 в первой книге [4])
У2 = Т3 + аТ + Ь, a,b, eF, char F £ 2,3.	(1.4)
с ненулевым дискриминантом (2.14) (см. с. 86 в первой книге [4]) правой
части этого уравнения.
В соответствии с формулой (1.3) для данного частного случая кривой
(ai = а3 = 0) противоположной к точке Р = (ж, у) О является точка
-Р = (х, -у).
Коэффициент 7 в формуле (1.1) в этом случае есть -А2, где
х _ У2 ~ У\
А —	,
Я?2 — Х\
а коэффициент 7' в формуле (1.2) есть -(А')2, где
. /Зж2 + а\
^У
12
Глава 1. Алгоритмы на эллиптических кривых
В случае Р Ф Q это позволяет получить выражение для хз и затем
для уз и, наконец, для уз и, тем самым, вычислить сумму P + Q = (хз, уз):
х3 = А2 - 21 - х2; у3 = у3 + Х(х3- Xi),
,	У2~У\
Уз = -Уз = -У1 + I ----—
у 2/2 X ।
(1-5)
(1-6)
(®1 - х3).
В случае Р = Q выражения для Хз и уз и координаты точки, соответству-
ющей сумме Р + Q = (жз, уз) = 2Р, т. е. удвоенной точки Р, получаются
через координаты х, у точки Р = (х, у) следующим образом:
х3 = (А')2 - 2х; у3 = у + А'(х3 - х);	(1.7)
Уз = ~У + А'(х - х3).	(1.8)
Окончательно для эллиптической кривой над полем характеристики,
большей 3, получаем (используя (1.5) и (1.6), (1.7) и (1.8)):
А. При Р\ = (х\,ух) / Р2 = (®2, Уз)
Pi + Р2 = -R = (х3, —уз) = (х3, -ух + А^, - хз», (1.9)
где
\	У2-У1	.2
А—----------, хз = А - Х\ - #2.
X 2 X ।
Б. При Р\ = Pi ~ Р — (ж, у)
2Р = —R = (жз, -уз) = (хз, -у + А'(ж - 2?з)),	(1.10)
где
Упражнение 1.1.1. Пусть Р = (0,0) — точка на эллиптической кривой
У2 + У = Х3-Х\	(1.11)
Найти 2Р = Р -|- Р и ЗР = Р + 2Р.
Указание. Преобразуем уравнение (1.11) в уравнение вида (2.13) (см. с. 85 в первой
книге [4]) путем замены переменных У ->У- 1/2, X 4Х + 1/3. Получим
На этой кривой точка Р становится точкой Q — (-1/3,1/2). Используя (1.10),
получим 2Q — (2/3, -1/2). Затем из (1.9) мы имеем 3Q = 2Q + Q = (2/3,1/2).
Заметим, что 3Q = -(2Q), и следовательно Q является точкой порядка 5, т. е.
5Q = О. Возвращаясь к исходной кривой, имеем 2Р = (1, -1), ЗР = (1,0) — -2Р.
1.1. Алгоритм сложения и удвоения точек	13
Сложение и удвоение точек кривой над полем характеристики три
В этом случае без ограничения общности мы можем полагать, что
в уравнении (2.10) (см. с. 84 в первой книге [4]) эллиптической кривой
общего вида а\ = аз = 0, а коэффициент а2 не обязательно равен 0,
и вместо этого уравнения следует использовать уравнение (2.12) (см. с. 85
в первой книге [4]), т. е.
У2 = X3 + а2Х2 + а4Х + а6, а(ЕР.	(1.12)
Согласно (1.3) противоположная к точке Р = (х,у) У О точка -Р =
(х, у) = (х, -у). В рассматриваемом случае F(X Y) = Y2 - X3 - а2Х2 -
а^Х - Аб — 0- Для сложения разных точек Pi = (жь ух) и Р2 =. (ж2, Уз)
используем уравнение
F(X. XX + /3) = (XX + р)2 -X3 - а2Х2 - а4Х - а6 = 0,
. У2 - У\ а .
А=---------, Р = у\Хх\.
Х2 X ।
Отсюда получим (как коэффициент при X2 после приведения к полино-
миальному виду) константу 7 = -(А2 - а2), и выражения для хз, уз и уз,
определяющие координаты точки Pi + Р2 = (жз, уз):
х3 — -у - Х[ - х2 = X2 - а2 - Х\ - ж2;	(1.13)
Уз = У1 + А(ж3 - Ж1), уз = -?/1 + А(Ж1 - ж3).	(1.14)
Для удвоения точки Р = (ж, у) вычислим
,	, За:2 + 2а2х + а4
X = X (х, у) =----------------,
2у
и, используя 7' = -((А')2 — а2) (в выражении для 7 заменили А на А'),
получим координаты точки 2Р:
х3 = -7' - 2х = ((А')2 - а2) - 2х,	(1-15)
Уз = У + А'(а:з - х), у3 =-у + Х'(х - х3).	(1.16)
Учитывая, что характеристика поля равна 3, выражение для А' можно
упростить:
Зж — 2а2ж Ад а2х Ад
”2?/	у '
Окончательно для эллиптической кривой над полем характеристики 3
получаем (используя (1.13) и (1.14), (1.15) и (1.16)):
А. При Р{ = (жь 2/1) 7^ Р2 = (^2, У1У-
Pi+P2 = -R = (жз, -уз) = (ж3, -2/1 4- A(xi - жз)),	(1.17)
14	Глава 1. Алгоритмы на эллиптических кривых
где
х У2~У\	М2 х
А =--------, Хз = (А - А2) ~ Х\~ Ж2.
Х2~Х\
Б. При Р\ = Pi = Р = (ж, у):
2P = -R = (х3, -уз) = (хз, -у + Л'(яг - хз)),	(1.18)
где
, d2X — Ад	//\/\2	\
А =--------, хз = ((А ) - а2) - 2ж.
У
Сложение и удвоение точек несуперсингулярных кривых
над полем характеристики два
Как отмечено в гл. 2 в первой книге [4], эллиптическая кривая над
полем характеристики два в несуперсингулярном случае имеет уравнение
F(X, У) = Y2 + XY + X3 + а2Х2 + а6 = 0.	(1.19)
Точка кривой -(х,у) = (х, у), противоположная относительно точки
кривой (ж, у) в этом случае определятся в соответствии с выражением (1.3)
как (ж, х + у).
Для сложения разных точек Р\ — (х\,у\) и Р2 = (ж2, ?/2) используем
уравнение
F(X, ХХ + /3) = (XX + /З)2 + Х(ХХ + /Э)+Х3 + а2Х2 + а6 = О,
где
л У2 - У\ д	х
А =--------; ^ = ух-Хх{.
Х2 ~ Х\
Откуда получим (как коэффициент при X2 после приведения к поли-
номиальному виду) константу 7 = -А2 4- А 4- а2 и выражения для хз, уз
и уз, определяющие координаты точки R = -(Pi 4-Р2) = (#з> Уз) и суммы
Р\ +Р2 = (х3,уз):
Хз = -у 4- Х1 4- х2 = (А2 4- А 4- а2) + хх + ж2,	(1.20)
2/з = 2/1 + А(жз + хх), уз = х3 + ух+ Х(х3 + Zj).	(1.21)
Для удвоения точки Р = (х, у) вычислим
V \ х2 + у , у
X = X (х, у) =-----— х Н—,
х	х
и, используя 7' = (А')2 + А'4-а2, получим выражения для Хз, уз и уз, опре-
деляющие координаты точки R = -2Р и удвоенной точки 2Р = (хз, уз):
хз=у+2х = (А')2 + А' + а2, у3 = у + А'(ж3 + х) = у 4- Х\х + х3), (1.22)
1.1. Алгоритм сложения и удвоения точек
15
2/з = -Ь х/4-А'(ж3 4-ж) = -ЬуН-А'(а: Н-ж3) = ж2 Н-(Д'+ 1)ж3.	(1.23)
Окончательно для несуперсингулярной эллиптической кривой над
полем характеристики два получаем (используя (1.20) и (1121), (1.22)
и (1.23)):
А. При Р\ = (жь 1/1) / Р2 = (ж2,2/2):
Pl +Р1 = (жз.жз + j/i -4-А(ж3 4-Ж])),	(1.24)
где
Л —---------, х% — (Л) 4- А 4- о>2 4~ Х[ 4- х2.
Х2 - Ж1
Б. При Р\ = Р2 = Р = (ж, у):
2Р = (ж3, х2 4- (А' + 1)ж3),	(1.25)
где
Л = х 4—,	х3 = (А )2 4- (А ) 4- &2-
х
Пример 1.1.1. Группа точек эллиптической кривой над полем GF(22), порожда-
емом корнем многочлена 1 4- X 4- X1 над GT(2), Y2 4- XY = X3 4- X2 4- 1 кроме
точки О включает точки ((0,0), (1,0)), ((1, 0), (0, 1)), ((1, 0), (1, 1)), ((0, 1), (1, 0)),
((0, 1), (1,1)), ((1,1), (1,0)), ((1,1)(0, 1)). Здесь (1,0), (0,0) суть единица и нуль
поля, (0,1) = х, (1, 1) = 1 + ж, где х — корень указанного многочлена. В данном
случае ((0,0), (1,0)) — «самообратная» точка.	f
Вычислим
2Р = 2((1,0), (0, 1)) = (х3, у3) =
= ((А )2 3“ А а2> 2-2 4 (А 4 1)хз) ~
= ((1, I)2 4 (1, 1) 4 (1, 0), (1, О)2 4 ((1, 1) + (1,0))хз) =
= ((0, 1) 4 (1, 1) 4 (1,0), (1,0) 4 (0, 1)х3) = ((0,0), (1,0)),
так как А' = (1, 0) 4	= (1, 1).
Проверим, что 2Р + (-Р) = Р, где Р = ((1,0), (0, 1)), -Р = ((1, 0), (1, 1):
2Р + (-Р) = ((0,0),(1,0)) + ((1,0),(1,1)) =
— (А 4А4в24^1 4®2,®з+ 1/1 + А(хз4Х|)) =
= ((1,1)4(0,1)4(1,0)4(0,0)4(1,0),Жз+(1,0)4 (0,1)((0,0) + Хз)) =
= ((1,0),(1,0)4(1,0)4(0,1)((0,0) + (1,0))) = ((1,0),(0,1)) = Р,
так как
а=;|,о;+j1-1-}=/Ц=<°’ о-(йог*=(о> о- (i.o)=(о, о.
(0,0) 4 (1,0)	(1,0)	'	’ v	v '
16
Глава 1. Алгоритмы на эллиптических кривых
Сложение и удвоение точек суперсингулярных кривых
над полем характеристики два
Если положить fli = <12 = 0 в общем уравнении эллиптической
кривой (2.10) в первой книге [4] и аз ф 0, то получим уравнение
У2 + а3У = X3 + а4Х + а6, аг. е F.	(1.26)
В этом случае F(X,Y) = Y2 + а3У + X2 + а4Х + ag и согласно (1.3)
противоположной к точке Р = (х, у) О будет точка -Р = (х, у + аз).
Для сложения разных точек Хх, у\ и х2, у2 используем уравнение
F(X, XX+ р) = (XX + р)2 + а3(ХХ + р) + X2 + а4Х + а6 = 0,
где
Уз и уз,
и суммы
А = ——р ~ Ух - Аж] = ?/1 + Ажь
Ж 2 Ж ।
Отсюда после приведения к полиномиальному виду получим (как ко-
эффициент при X2) константу у — А2 и выражения для жз,
определяющие координаты точки R — -(Pi 4- Р2) = (хз,у3)
Рх+Рз = (хз,уз)\
Хз = у + Ж! + Хз = А2 + Ж1 4- ж2,
уз = А(Ж1 4- жз) 4- у\, уз = А(ж! 4- х3) 4- ух 4- а3.
(1.27)
(1.28)
Для получения координат удвоенной точки 2Р = 2(ж, у) рассмотрим
выражение
ж2 4- а>4
а3
2*/4-а3
Используем у1 = (Л')2 (в выражение для у подставили А' вместо А)
и получим выражения для жз, уз и уз, определяющие координаты точки
R — -2Р и удвоенной точки 2Р = (жз, уз):
хз = у 4- 2х = у = А/2;	(1-29)
уз = А'(ж 4- хз) + у; Уз — А'(ж 4- ж3) + у + а3.	(1.30)
Окончательно для суперсингулярной эллиптической кривой над по-
лем характеристики два получаем (используя (1.25) и (1.26), (1.27) и (1.28))
А. При Рх = (х\, ух) ^Р2 = (х2, уз):
Рх+Р2 = (ж3, Уз) = (ж3, А(Ж1 4- ж3) 4- ух + а3),	(1.31)
где
х У\ +У2	х2 ,
Л —---------, ж3 — А -Ь х%.
XI + х2
1.2. Эллиптические кривые над GF(2n)‘
17
Б. При Р] = Pi = Р = (х, у):
2Р = -R = (х3, у3) = (ж3> Х'(х + х3) + у + а3),	(1.32)
где
х3 = А'2.
х, ж2 + а4
Л —	:
При аз = й4 = 1 имеем 2Р = (ж4 4- 1, х4 4- у4).
Упражнение 1.1.2. Докажите, что при а3 = а4 = а6 = 1 точка 2Р = (ж44-1, х4+у4).
Указание. Формула для первой координаты следует из свойства возведения по-
линомов в степень, равную характеристике поля, формула второй координаты
получается с учетом частного вида уравнения кривой, которое при подстановке
координат х и у точки Р имеет вид у2 4- у = х3 4- х 4- а6.
Пример 1.1.2. Группа точек эллиптической кривой У2 4- Y = X3 4- X над GF(2)
кроме точки О содержит точки (0,0), (0,1), (1, 0), (1, 1). Для Р = (0, 0) вычислим
-Р = (0, 1) и 2Р = 2(0, 0) - (04+1, 04+04) = (1, 0). Проверим, что 2P-h(-P) = Р.
Действительно,
(1, 0) 4- (0, 1) = (А2 + Х\ 4- ^2, Л(Я1 4- ж3) 4- У[ 4- 1) =
= (1 4- 1 4- 0,1(0 4- (1 4- 1 + 0)) 4- 0 4- 1) = (0,0),
так как
,	0+1	1	.
А = ---= - = 1 • 1 1 = 1 • 1 = 1.
0+1	1
1.1.3. Алгоритмы сложения и удвоения точек
эллиптических кривых
Приведем алгоритмы сложения и удвоения, конкретизирующие об-
щую схему на рис. 1.1 с учетом особенностей эллиптической кривой.
Алгоритм 1.1.2 сложения и удвоения для эллиптических кривых над
полем большой характеристики см. на рис. 1.2.
Алгоритм 1.1.3 сложения и удвоения для эллиптических кривых над
полем характеристики три см. на рис. 1.3.
Алгоритм 1.1.4 сложения и удвоения для несуперсингулярных эллип-
тических кривых над полем характеристики два см. на рис. 1.4.
Алгоритм 1.1.5 сложения и удвоения для суперсингулярных эллипти-
ческих кривых над полем характеристики два см. на рис. 1.5.
Обратим внимание, что при исполнении любого из этих алгоритмов
наиболее трудоемкая операция в арифметике конечного поля — мульти-
пликативное обращение — выполняется однократно.
1.2. Эллиптические кривые над GF(2n)
В криптографии используются и кривые над полями нечетной харак-
теристики, но чаще все же находят применение кривые над полем GF(2n)
18
Глава 1. Алгоритмы на эллиптических кривых
Алгоритм 1.1.2
ВХОД: Коэффициент а эллиптической кривой (1.4),
точки Р[ = (жь у{) (или Р[ = О) и Р2 = (^2> У1) (или Р2 = О).
ВЫХОД: Р = Pj + Р2.
	Если Р\ = О, то вернуть Р — Р2, если Р2 = О, то вернуть Р = Рь если Р2 = -Рь то вернуть Р = О, если £1 £ ж2, то вычислить А =	х3 = Л2 - Х\ - ж2, вернуть Р = (ж3, ~у\ + Л(Ж1 - ж3)), иначе принять х = Х\, у = j/b вычислить А = ^2у^’ Хз ~ Л2 ~ ?х’ вернуть (ж3, -у + Х(х - х3)).
Рис. 1.2.	Алгоритм сложения и удвоения для эллиптических кривых над полем большой характеристики
Алгоритм 1.1.3
ВХОД: Коэффициенты а2, а4 эллиптической кривой (1.12),
точки Pt = (жЬ х/1) (или Pi = О) и Р2 = (ж2, yz) (или Р2 = О).
ВЫХОД: Р = Р, + Р2.
	Если Pi = С?, то вернуть Р = Р2, если Р2 = О, то вернуть Р — Рь если Р2 = -Рь то вернуть Р = О, если Х\ ж2, то вычислить А =	, Жз = А2 - а2 - Xi - ж2, вернуть Р = (ж3, -j/i 4- А(Ж1 - ж3)), иначе принять ж = жь у = г/ь вычислить А = g2?~Q4, жз = А2 - а2 - 2ж; вернуть (ж3, -у 4- А(ж - ж3)).
Рис. 1.3.	Алгоритм сложения и удвоения для эллиптических кривых над полем характеристики 3
в связи с большим удобством таких полей для программной и схемной
реализации.
Рассмотрим пример кривой над полем GF(24).
Пример 1.2.1. Выберем в поле 6rF(24) стандартный базис, порождаемый кор-
нем х неприводимого многочлена 1 4- X 4- X4. Элементы поля представляем
в виде векторов их представлений в этом базисе в порядке возрастания степеней
его элементов. При этом генератор х базиса представляется вектором (0, 1,0,0),
единица поля представляется вектором (1,0,0,0).
1.2. Эллиптические кривые над GF(2П)
19
Алгоритм 1.1.4
ВХОД: Коэффициент а2 эллиптической кривой (1.19),
точки Pj = (я?!, у\) (или Pi = О) и Р2 = («2, Уг) (или Р2 — О).
ВЫХОД: Р = Pj + Р2.
Если Р{ = О, то вернуть Р = Р2,
если Р2 — О, то вернуть Р = Рь
если Р2 = -Р}, то вернуть Р = О,
если Xi ж2, то
вычислить Л =	, х3 = Л2 + А 4- a2 4- Ж1 4- х2,
вернуть Р = (ж3, ж3 4- У\ 4- А(ж3 4- «1)),
иначе принять х — х^ у — ух,
вычислить Л = х 4- , х3 = А2 4- А 4- а2;
вернуть (ж3, ж2 4- (А 4- 1)жз).
Рис. 1.4. Алгоритм сложения и удвоения для несуперсингулярных эллиптических
кривых над полем характеристики 2
Алгоритм 1.1.5
ВХОД: Коэффициенты а3, о4 эллиптической кривой (1.26),
точки Pi = (жь yi) (или Pj = О) и Р2 = (ж2, у2) (или Р2 = О).
ВЫХОД: Р =	4- Р2.
Если Д = О, то вернуть Р — Р2,
если Р2 = О, то вернуть Р == Рь
если Р2 = -Р1? то вернуть Р = О,
если Ж1 ж2, то
вычислить А = Хз — А2 4- хх 4- ж2,
вернуть Р = (Жз> А(Ж1 4- ж3) + у{ + а3),
иначе принять ж = Ж1, у = у^,
вычислить А = *1, Жз = А2,
а3 ’ J ’
вернуть Р = ((ж3) А(ж 4- ж3) 4- у 4- а3).
Рис. 1.5. Алгоритм сложения и удвоения для суперсингулярных эллиптических
кривых над полем характеристики два
Упражнение 1.2.1. Проверьте, что ж является Примитивным элементом поля, кото-
рый далее обозначаем 7. Составьте таблицу его Степеней 1 — 70, 7 = у1,72,..., 714.
Пример 1.2.2. Рассмотрим несуперсингулярную кривую У2+АГУ—Х34-74АГ24-1.
Проверим, что точка (73,713) лежит на кривой. Для этого достаточно проверить
равенство
7« + 737l3=79+7V + l,
очевидно, равносильное равенству 711 +7 = 79 + 710 4~ 1, которое легко проверить
с помощью таблицы степеней.
20
Глава 1. Алгоритмы на эллиптических кривых
Упражнение 1.2.2. Проверьте, что эта кривая содержит 15 конечных точек:
(73,713). (75,7"). (76,714), (?,713), fr'W), (712,712),
(1.76),	(73,78), (7W), (76Л), (79,7'°), (7‘°Л), ft'2-0), (0,1).
1.2.1.	Суперсингулярные кривые
Основное удобство суперсингулярных эллиптических кривых в том,
что для них легко вычислить порядок, в то время, как вычисление поряд-
ка несуперсингулярной кривой вызывает трудности. Суперсингулярные
кривые особенно удобны для создания с минимальными усилиями са-
модельной ЕСС-криптосистемы. Для их использования можно обойтись
без сложного алгоритма вычисления порядка кривой. Все необходимые
сведения можно найти в этом разделе.
Произвольная суперсингулярная кривая над полем характеристики
два, как уже отмечалось, изоморфна кривой с уравнением
У2 + а3У = X3 + а4Х + а6, а{еСР(2п), а3/= 0.
Заменой переменных X = a^X, Y = a^Y его можно свести к виду
У2 + У = а2Х3 + а4Х + а6, а- е GF(2n), а2 / 0.
Так как при нечетном п в поле GF(2n) из любого элемента извлекается
однозначно кубический корень, то заменой X = (а'2)~^3Х последнее
уравнение можно свести к виду
У2 + У = X3 + а4Т + а6, a, G GF(2").
Упражнение 1.2.3. Докажите это.
Указание. Достаточно доказать существование кубического корня. Воспользуемся
существованием примитивного элемента. При нечетном п имеет место равенство
2"- 1 = 3k -F 1, поэтому при m не кратном 3 согласно теореме Ферма
п? _	тт?-(-ЗА'-|-1	т+6А:4-2 _ 3Z
a = a = а = a .
Единственность вытекает из того, что уравнение X3 = 1 имеет единственный
корень.
Дальнейшее упрощение уравнения данной кривой можно получить
заменой переменных Y = Y + kX -Vl, X = X 4- к2, если выбрать к, I так,
чтобы
к4 + к + a4 е GF(2), I2 +1 + к6 + а4к2 + а6 G GF(2).
Тогда уравнение примет вид У2 + У = X3 + аХ + b, a,b € GF(2).
Упражнение 1.2.4. Проверьте это.
Указание. Для доказательства существования такой замены используем понятие
следа. След элемента у € GF(2n) в поле GF(2) определяется формулой
tr (у) = у + у1 + у4 + I/8 + ... + у1" ',
согласно тождеству Фробениуса линеен, удовлетворяет тождеству (tr (?/))2 =
tr (t/2) = tr (у) и всегда T(t/) е GF(2).
1.2. Эллиптические кривые над GF(2n)
21
Упражнение 1.2.5. Докажите, что уравнение У2 4-У = а разрешимо в поле GF(2n)
тогда и только тогда, когда tr(a) = 0. При нечетном п его решение у можно
найти в виде
у — a 4- fl4 4- а16 4- а64 4-... 4- а2
Второе решение получается прибавлением единицы.
Указание. В силу линейности tr (а) = tr (у2 4- у) = tr (у2) 4- tr (у) — 0. Согласно
тождествам Фробениуса и Ферма
у — л 4~ о> 4" о, 4~tt 4~ • • • 4- л — о 4~ й 4~ о 4~ fl 4~ fl 4~ • • • 4~ fl ,
откуда у2 4- у = о 4- (а 4- о2 4- а4 4- а8 4- ... 4- а2” 1) — а 4- tr (а) = а. Подробнее
о решении квадратных уравнений в этом поле см. разд. 2.1.
Упражнение 1.2.6. Докажите, что уравнение У4 4-У = а разрешимо в поле GF(2n)
тогда и только тогда, когда tr (а) = 0.
Указание. Необходимость доказывается так же, как и выше, если заметить, что
tr (я/4) = tr (у2) = tr (?/). Для доказательства достаточности вначале решим урав-
нение X2 4- X = а и выберем то его решение х, у которого tr (ж) = 0 (если
tr (ж) = 1, то tr (х 4- 1) = tr (ж) 4- tr (1) = 0, так как при нечетном п, очевидно,
tr (1) = 1). Потом решим уравнение У 4- У2 = х (найдем его корень у) и получим
а = у + у1 + (у + у2)2 = у + у4.
Упражнение 1.2.7. Докажите, что при нечетном п для любого a Е GF(2n) су-
ществуют у € GF(2n) такое, что у2 4- у 4- о € GF(2) и такое z € GF(2n), что
z4 + z + a€ GF(2).
Указание. Так как tr (а) = а при a € GF(2), то в случае tr (а) = 1, очевидно,
tr (а 4- 1) = tr (а) 4- tr (1) = 0. Теперь уже можно найти такое к, что к4 4- к 4- о4 €
GF(2), а потом такое I, что I2 4-1 4- к6 + а4к2 4- о6 6 GF(2).
Очевидно, что кривые У2 + Y = X},Y2 + Y = X3 4- 1 изоморфны.
Упражнение 1.2.8. Проверьте, что У = У 4- X, I = Т t I — изоморфизм.
В силу этого изоморфизма при нечетном п имеется три класса
неизоморфных суперсингулярных эллиптических кривых (согласно [70]
при четном п имеется 7 классов), стандартными представителями которых
являются кривые
E1:Y2+Y = Xi,
E2:Y2 +Y = X3 + X,
Е3 :Y2+ Y = X3 + X + \.
При нечетном п число точек для первой кривой равно 2П 4- 1 и 2П ±
л/2п+1 4-1 для второй и третьей (знак 4- или - выбирается в зависимости
от кривой и от сравнения п по модулю 8) (см. табл. 1.1).
Указанные значения легко вычисляются с использованием теоремы
Хассе—Вейля.
Отметим, что группы этих кривых при нечетном п являются цикли-
ческими.
22
Глава 1. Алгоритмы на эллиптических кривых
Таблица 1.1
Порядок групп кривых Е2 и Е3
Кривая	п	Порядок группы
у2 + у = X3	нечетное	2П 4- 1
у1 + у = х3 + х	n = l,7(mod 8)	2n -f- 1 4- 2^п+1)/2
у2 + у = х3 + х	n = 3,5(mod 8)	2П _|_ 1 _ 2^п+Й/2
у2 4- у = х3 4- X 4- 1	n = l,7(mod 8)	2ге 1 — 2^п+Й/2
у2 4- у = х3 4- х 4- 1	п = 3,5 (mod 8)	2П -р 1 -р 2(п+Й/2
Пример 1.2.3. Найдем порядок группы эллиптической кривой в случае Е2. Рас-
сматривая Е2 над полем GF(2), имеем на ней точки (0,0), (0, 1), (1,0), (1, 1)
и еще нулевой элемент О — всего пять элементов циклической группы. Таким
образом, g = 2, N = 5, t = -2, и мы находим корни квадратного уравнения
х2 4- 2х + 2 = 0 в стандартной декартовой форме a — -1 + i и Д = -1 - г или
в тригонометрической форме
г (	Зтг	Зтг \
а — v2 I cos-------1- г sin — ,
\	4	4 J
5тг	5тг \
cos------И г sin — .
4	4 /

По теореме Хассе—Вейля получим
z ч _ п ( Зтгп . Зтгп\ п ( 5тш . 5тгп
N(n) = 2 + 1 - 27 cos-----h г sin-- ) — 27 I cos---Ь г sin ——
\	4	4 / у 4	4
п	Зттп
= 2n+1 - 2-2^ cos----,
4
поскольку
5тг	/ Зтг\	Зтг
sin — = sin------= - sin —.
4	\ 4 7	4
Для cos — имеем cos	, если n = l(mod8) или п = 7(mod 8),
cos	, если n = 3(mod 8) или n = 5(mod 8)
(напомним, что п — нечетное). Окончательно получаем
N(п) = 2П 4- л/2п+1 4- 1, если п=1 или 7(mod8),
N(ri) — 2n - л/2п+1 + 1, если п = 3 или 5(mod8).
Тот факт, что порядок кривой Y2 +Y = X3 при нечетном п равен
2П 4- 1, можно доказать и без теоремы Хассе—Вейля.
Упражнение 1.2.9. Докажите это.
Указание. Уравнение У2 4- Y = а разрешимо только при tr (а) = 0 и имеет 2
различных корня. Ровно половина элементов поля GF(2n) имеет нулевой след
(так как tr(x) = 0 о tr (ж + 1) = 1). При нечетном п каждый элемент поля
имеет единственный кубический корень. Также элементарно можно доказать, что
1.2. Эллиптические кривые над GF(2n)
23
Таблица 1.2
Порядки кривых над полем GF(2n)
п	Кривая	Порядок группы
173		5- 13625405957 • Р42
173	Ез	7152893721041• Р40
191	Ег	3 • Р58
191	е2	5 • 3821 • 89618875387061 • Р40
191		25212001-5972216269-Р41
239	е2	5- 77852679293 -Р61
239	Е3	Р72
251	Е,	3-238451-Р70
323	Ез	137 - 953 - 525313 - Р87
порядок суперсингулярных кривых нечетен, а несуперсингулярных кривых —
четен.
Упражнение 1.2.10. Докажите это.
Указание. У несуперсингулярных кривых существует точка порядка два вида (0, у).
Поэтому по теореме Лагранжа порядок таких кривых четен. В суперсингулярной
кривой пары противоположных элементов имеют вид (ж, у), (х, у 4- 1) и их
элементы всегда различны, значит число конечных точек у нее четно.
Особый интерес будут представлять такие степени п, для которых
соответствующий порядок группы E(F) при разложении на простые
множители содержит большое простое число (большое простое с N
цифрами в десятичном представлении будем записывать как PN).
В таблице 1.2 приведены некоторые конкретные значения, которые
можно использовать для реализации.
Другим достоинством суперсингулярных кривых является простота
формул сложения для них, и особенно формул удвоения. Заметим, что
при сложении точек все же выполняется одна инверсия, которая является
самой трудоемкой операцией в арифметике конечного поля.
Отмеченное удобство использования суперсингулярных эллиптиче-
ских кривых не может скомпенсировать их главный недостаток: для таких
кривых известно [71] сведение задачи вычисления дискретного логарифма
к аналогичной задаче для конечных полей с повышением размерности
поля в некоторую константу к раз, зависящую от класса кривой. Это све-
24
Глава 1. Алгоритмы на эллиптических кривых
дение выполняется вероятностным полиномиальным относительно log2 q
алгоритмом, где q — порядок поля F.
Так, для суперсингулярной эллиптической кривой Е\, заданной над
полем порядка q, задача вычисления дискретного логарифма в группе этой
эллиптической кривой сводится к соответствующей задаче вычисления
в том же поле порядка q, так как к — 1. Значит, использование этой
кривой не более надежно, чем использование обычной криптосистемы
в том же поле. Для кривых Е2 и Е^ такое сведение в случае нечетного п
приводит уже к полям порядка q\ Но четное п использовать нельзя, так
как в этом случае константа к — 1.
Для полей GF(2n) известны специальные алгоритмы вычисле-
ния дискретных логарифмов (алгоритм Купершмита [37] сложности
exp {1,35п1//3(1п п)2/3})> тем не менее они остаются практически неосу-
ществимыми для полей размерности 800 и более. Это оправдывает ис-
пользование на практике кривых Е^ иЕ3.
Еще одна приятная особенность суперсингулярных кривых заклю-
чается в возможности быстрого вычисления у-координаты точки такой
кривой по х-координате путем решения квадратного уравнения в по-
ле GF(2n).
Этот прием, предложенный в [70], позволяет уменьшить объем ин-
формации, которой приходится обмениваться сторонам при выполнении
криптографических протоколов. Вместо того, чтобы пересылать обе ко-
ординаты точки кривой, можно послать только х координату и один бит,
с помощью которого можно из двух точек (ж, у) и (ж, у + 1) данной кривой
выбрать одну. Но для этого нужно уметь быстро вычислять у, т. е. решать
квадратное уравнение У2 4- Y = f(x) в поле GF(2n). Вычисление f(x)
для любой из указанных выше кривых требует только одного умножения,
одного возведения в квадрат и, может быть, сложения. Сложение делается
очень быстро в любом базисе, а для ускорения возведения в квадрат выби-
раем нормальный базис, если возможно, низкой сложности. Для решения
квадратного уравнения У2 4- У = а применяем полученную в упр. 1.2.5
формулу
у — a 4- а4 4- а16 4- а64 4-... 4- а2 .
Это можно делать при нечетном п. В случае четного п квадратное урав-
нение тоже решить можно, оно в нормальном базисе сводится к решению
системы линейных уравнений над полем GF(2), которая решается быст-
ро, но такой простой явной формулы уже не получается. Заметим, что
второе решение у 4- 1 получается из первого заменой всех битов на про-
тивоположные, так как 1 в нормальном базисе имеет только единичные
координаты. Вычисление у по х в нормальном базисе тем самым вы-
полняется с линейной сложностью как при программной, так и при
схемной реализации, причем в случае последней еще и с малой глубиной,
не большей log2 п 4- 1. Как решать квадратные уравнения в стандартном
1.2. Эллиптические кривые над GF(2п)
25
базисе подробно описано в разд. 1.4.4 и 2.1. Для несуперсингулярных
кривых пришлось бы решать уравнение Y2 +Yx = /(ж), которое заменой
Y = xZ сводится к уравнению Z2 + Z = /(ж)/ж2, но при этом при-
шлось бы выполнить дополнительно деление и умножение.
1.2.2.	Несуперсингулярные кривые
Несуперсингулярная эллиптическая кривая над полем GF(2n) имеет
уравнение
Y2 + XY = X3 + а2Х2 + а6.
Замена переменной Y = Y + кХ, где к2 4- к + а2 = а'2 переводит эту
кривую в кривую
У2 + XY = X3 + а2Х2 + а6.
Так как согласно упр. 1.2.5 уравнение к2 + к + а2 = а'2 разрешимо тогда и
только тогда, когда tr (<^2) = tr (а^), то кривые, связанные таким соотно-
шением, изоморфны. Можно доказать, что это условие и необходимо для
изоморфизма. В случае нечетного п можно далее считать, что й2 € GF(2).
Мы уже видели (см. разд. 1.1), что формулы сложения для таких
кривых чуть менее удобны для вычислений, а формулы удвоения —
существенно менее удобны, чем такие же формулы для суперсингулярных
кривых. Для несуперсингулярной кривой формула вычисления обратной
точки тоже чуть сложнее: -Р = -(ж, у) = (х, у + х).
Несуперсингулярные эллиптические кривые представляют больший
интерес с криптографической точки зрения, по сравнению с суперсингу-
лярными. Желательность их использования стала ясной после появления
работы [71] и со временем была закреплена во всех существующих крип-
тографических стандартах. Причина в том, что для несуперсингулярных
кривых проблема логарифмирования в них представляется более трудной,
чем для суперсингулярных. Однако для обеспечения максимальной без-
опасности необходимо соблюдать осторожность в выборе коэффициентов.
Например, коэффициент не должен быть нулевым. Эти кривые надо
выбирать так, чтобы их порядок не был гладким числом, иначе будет
возможной атака, основанная на алгоритме Полларда и даже на алгорит-
ме Нечаева—Полига—Хеллмана—Зильбера (об алгоритмах дискретного
логарифмирования см., например, [5] и разд. 1.6).
В следующих примерах указаны некоторые такие кривые.
Пример 1.2.4. Кривая
X2 + XY = X3 + X2 + 1
над полем GF(2163) имеет порядок
2 х 5846 00654 93236 11672 81474 17535 98448 34832 91185 74063.
Пример 1.2.5. Кривая Y2 + XY = X3 + 1 над полем GF(2131) имеет порядок
4 х 6805 64733 84187 69269 32320 12949 34099 85129.
26
Глава 1. Алгоритмы на эллиптических кривых
Среди несуперсингулярных кривых для практической реализации можно
брать кривые
Е\ : Y2 + XY = X3 + X2 + 1
или семейство кривых
Е2 :Y2+XY = Х3 + Х2+7,
где 73 = 7 -h 1, 7 6 GF(2n).
Так, группа точек кривой Ei над полем GF(2163) имеет порядок
2 • Р49, а группа точек кривой Е2 над GF(2177) имеет порядок 10 • F53.
Отметим также, что группы точек кривой Е\ имеют порядки с большим
простым числом и для случаев п — 283, 311, 331, 347 и 359.
Другие примеры кривых пригодных для практической реализации
можно найти в известных криптографических стандартах (см. следующий
раздел).
Во всех этих примерах кривые рассматриваются над полями простой
размерности. Действительно, для предотвращения гладкости порядка кри-
вой желательно ее брать над полями простой размерности, так как они
не содержат нетривиальных подполей, и потому группа кривой не содер-
жит в качестве подгруппы группу той же кривой, рассматриваемой над
подполем. Но если коэффициенты уравнения кривой не принадлежат ни-
какому подполю, то и у кривых, рассматриваемых над полями составной
размерности, порядок может быть гладким. Например, в IPS ЕС протоко-
лах [50] использовалась кривая с уравнением
Y2 +XY = X3 + {3,
где
/3 = ш18 + ш'7 + ш16 + Ш13 + ш12 + ш9 + ш8 + ш7 + OJ3 + ш2 + ы + 1,
а ш155 + шЬ2 + 1 = 0. Ее группа над полем GF(2155) имеет порядок
12 • 3 80599 38472 15893 01615 54638 26195 38626 63974 36443.
Вопрос о надежности кривых над полями составной размерности явля-
ется предметом дискуссии, так как некоторые современные алгоритмы
быстрее работают именно в таких полях. Но рассмотрение этого вопроса
в [94] применительно к данной кривой привело к оценке времени для
логарифмирования в ней порядка 1010 лет на сети из 80 машин Spares.
Отметим, что указанная кривая в ранних работах по реализации
криптосистем часто использовалась, так как в ее поле существует удоб-
ный стандартный базис, соответствующий трехчлену X155 4- X62 + 1=0,
в котором можно эффективно реализовать арифметику [87].
Другой подход к реализации этой арифметики основан на выполне-
нии операций по модулю неприводимого трехчлена на подполе GF(25).
Умножение и деление в подполе можно затабулировать и хранить в памя-
ти машины. С целью экономии памяти можно таблицу деления заменить
1.2. Эллиптические кривые над GF(2П)
27
на таблицу инвертирования, которая имеет меньшие размеры. Можно
и таблицу умножения заменить на таблицы логарифмов и антилогариф-
мов в этом подполе (тогда умножение и деление заменяется на сложение-
вычитание по модулю 25 - 1). Таблицы эти столь малы, что их можно
разместить непосредственно в программе.
Говорят, что неизоморфные кривые над полем GF(2n)
Y2 + XY = X3+a,X2 + b, Y2+XY = X3 + a2X2 + b
являются скручиванием друг друга, если tr (ai) tr (а2)-
Аналогом утверждения о скрученных кривых из упр. 2.3.6 в разд. 2.3
в первой книге [4] для кривых характеристики два является
Теорема 1.2.1. Сумма порядков двух скрученных кривых равна 2n+1 4- 2.
Доказательство. Можно без ограничения общности считать, что
а\ = 0, tr(a2) = Г При х = 0 оба уравнения имеют по одной точке
(о, Л), так как в поле GF(2n) квадратный корень всегда существует
и определен однозначно.
Упражнение 1.2.11. Докажите это.
При х 0 только одно из этих двух уравнений имеет корни, причем
два разных у и у 4- х. Действительно, если бы существовали х 0, у, z
такие, что
у2 + ху = ж3 4- Ь, z2 + xz = х3 + о>2Х2 4- Ъ,
то выполнялись бы равенства
OqX2 = z2 4- у2 4- xz 4- ху — {у 4- г)2 4- х(у 4- z),
откуда
/ y + z\2 y + z
a2 — I ---- ) H------,
\ X ) X
что противоречит неразрешимости уравнения и2 4- и = а при tr (а) = 1.
Поэтому общее число конечных точек у обеих кривых равно 2n+1.	
1.2.3.	Стандарты о выборе кривых для реализации
криптосистем на эллиптических кривых
Алгоритм цифровой подписи с использованием эллиптических кри-
вых (ECDSA) принят и описан в различных стандартах. Среди них ANSI
Х9.62, FIPS 186-2 (NIST), IEEE 1363-2000 [54], ISO/IEC 14888-3 [55],
ISO/IEC 15946-3 [56], SEC-1 [90], SEC-2 [91] и др.
Далее мы опишем основные рекомендации стандарта ANSI Х9.62
ECDSA, следуя статье [53].
К эллиптическим кривым предъявляются следующие требования.
28
Глава 1. Алгоритмы на эллиптических кривых
1	Кривые рассматриваются или над простыми полями (порядок q
которых равен простому числу р), или над полями характеристики
два (у которых q = 2W).
2	. Для представления элементов поля используется либо стандартный
базис, порождаемый трехчленом или пятичленом, либо гауссов нор-
мальный базис (ГНБ).
3	Кривая Е задается выбором двух элементов a, b поля GF{q). В случае
р > 2 она имеет вид У2 = X3 4- аХ + Ь, а в случае р = 2 вид
У2 4- XY = X3 4- аХ2 4- Ь. Таким образом, стандарт рекомендует
только несуперсингулярные кривые.
4	На кривой выбирается точка (xG,yG), xG,yG Е GF(q) простого по-
рядка n > 2160, n > 4y/q, и вычисляется кофактор h = \E(GF(q))\/n.
В качестве кривых можно и удобно выбирать в случае р = 2 кривые,
у которых а,Ь равны 0,1, но стандарт рекомендует все же случайные
кривые, т. е. кривые со случайно выбранными а, Ь.
При этом рекомендуется использовать следующие алгоритмы генера-
ции случайных кривых.
Алгоритмы генерации случайных кривых
I.	Случай q~P- Положить t = [log2Р\ , s~ L(^“ 0/160 J, v = t- 160-5.
Выбрать произвольную строчку битов («зерно», из которого вырастает
кривая) seedE длиной д 160 бит, и положить z, равным числу,
двоичная запись которого совпадает с seedE.
2.	Применить к seedE стандартную хэш-функцию SHA\ [72], вычис-
лить ^-битовую строку Н = SHA^seedE). Выбирая в Н v самых
правых битов, получить строку Со длиной v битов.
3.	Заменить в cq самый левый бит на 0, получить при этом строку Wq.
4	Для i от 1 до 5 выполнить следующее:
4.1.	Положить строку 5г равной ^-битной строке, являющейся дво-
ичной записью числа z 4- i mod 29.
4.2.	Вычислить «/-битовую строку Wi = SHA}(sj).
5. Положить битовую строку W равной конкатенации (произведению)
битовых строк Wj, i = 0,..., 5, т. е. W = И^о • • • W$.
Положить г равным целому числу с двоичной записью W. Выполне-
ние пункта 3 гарантирует, что г < р.
7. Если г = 0 или 4г + 27 = 0(modp), то вернуться к шагу 1.
8. Выбрать ненулевые a, b Е GF(p) так, чтобы rb2 = a3(modp). Напри-
мер, можно взять а = Ь = г.
д Полученная кривая есть Е : Y2 = X3 4- аХ 4- Ъ.
1.2. Эллиптические кривые над GF(2n)
29
Заметим, что условие невырожденности кривой 4d34-2762 O(modp)
гарантировано выполняется, так как при b 0, г = а3/Ь2 modp удовле-
творяет условиям г 0,4г 4- 27 O(modp). Имеется только две попарно
неизоморфные кривые с одним и тем же г; эти кривые являются скру-
ченными, и сумма их порядков равна 2 4- 2р; кривые с разными г
неизоморфны друг другу. На шаге 8 поэтому есть по существу только еще
одна возможность выбора а, Ь, кроме явно указанной.
II. Случай q=2m. Положить, как и выше, s=[(f-1)/16OJ, v=t- 160-s.
1.	Выбрать произвольную строчку битов seedE длиной g 160 бит,
и положить z, равным числу, двоичная запись которого совпадает
с seedE.
2.	Вычислить g-битовую строку Н = SHA^seedE). Выбирая в Н v
самых правых битов, получить строку &о длиной v битов.
3.	Заменяя в Ь$ самый левый бит на 0, получить строку Wq.
4.	Для i от 1 до s выполнить следующее:
4.1.	Положить строку Si равной (/-битной строке, являющейся дво-
ичной записью числа z 4- i mod 29.
4.2.	Вычислить g-битовую строку bi — SHAi(si).
5.	Вычислить битовую строку b = &о ‘ • • bs и положить b равным соот-
ветствующему элементу поля GF(q).
6.	Если b — 0, то вернуться к шагу 1.
7.	Выбрать произвольный а Е GF(q).
8.	Полученная кривая есть Е : Y2 4- XY = X3 4- аХ2 4- Ъ.
Две такие кривые Ei : Y2 4- XY = X3 4- агХ2 4- bi изоморфны, если
Ь\ = &2,tr(ai) = tr(d2), где
tr (d) = d 4- d + d 4~d 4~ • * • 4~ d E GF(2}.
Поэтому на шаге 7 есть только две существенно разные возможности,
например достаточно выбрать а = 0 или а = 7, tr (7) = 1.
Генерация криптографически надежных параметров кривых. Стандартом
рекомендуется определенный алгоритм генерации надежных параметров
кривых.
1.	Выбрать случайную кривую E(GF(q)) алгоритмом, указанным выше.
2. Вычислить ее порядок N = \E(GF(q))|.
3.	Проверить, делится ли N на ранее выбранное простое n (n > 2160,
п > 4д/д). Если нет, то перейти к шагу 1.
4.	Проверить, что п не делит ни одно из чисел qk - 1, k = 1,..., 20.
Если нет, то перейти к шагу 1.
5.	Проверить, что n q. Если нет, то перейти к шагу 1.
30
Глава 1. Алгоритмы на эллиптических кривых
6.	Выбрать произвольную точку G' е E(GF(q)) и положить G — (N/n^G1.
Повторять, пока не получится G О.
Шаг 3 необходим для того, чтобы кривая содержала точку G поряд-
ка п. Так как согласно теореме Хассе (y/q- I)2 < \E(GF(q))\ <	О2,
то условие n > 4^/q означает, что п2 не делит \E(GF(q))\ и поэтому
кривая не содержит подгрупп порядка п2, значит подгруппа порядка п
на ней только одна. Так как I)2 - (y/q~ I)2 = 4y/q < n, то существует
единственное h такое, что
(VQ- О2 nh (y/q+ I)2.
Точка G О, построенная в шаге 6, имеет, очевидно, порядок п.
Согласно [67] случайную кривую с подходящими криптографически-
ми свойствами над полем GF(2m) при тп примерно 200 можно с помощью
варианта SEA алгоритма сгенерировать за несколько часов.
Известен также другой метод генерации криптографически подходя-
щих кривых— метод СМ — комплексного умножения. Над полем GF(p)
его усовершенствования известны как метод Эткина—Морейна [76], а над
полем GF(2m) — как метод Лея—Циммера [66]. Подробное его описание
имеется в IEEE 1363-2000 [54].
Пусть E(GF(q)) кривая порядка N. Пусть известно разложение
4q - (q + 1 - N)2 = DV2,
где D свободно от квадратов. Тогда кривая Е обладает комплексным
умножением на D.
СМ метод вначале находит D и порядок N = nh, где п — простое
число, и далее проверяет, что q п и п не делит числа qk - 1, к =
1,... , 20. Потом вычисляются коэффициенты кривой. При малых D СМ
метод существенно быстрее алгоритма Шуфа, но при больших D его
эффективность сильно снижается.
Стандарты для кривых Коблица. Кривыми Коблица называются несу-
персингулярные кривые с коэффициентами 0, 1. Естественно только их
привести в качестве примеров кривых, рекомендованных стандартами.
Мы сделаем это только для случая q = 2т. В этом случае NIST ре-
комендует 5 кривых в полях размерностей т — 163,233,283,409,571.
Коэффициенты кривой обозначаются а, Ь, порядок кривой равен nh, где
п — простое число, образующий элемент подгруппы порядка п обозна-
чается {хв,уо), где хв,ус — элементы поля GF(2m), которые задаются
двоичным вектором координат в данном базисе. Младшие координаты
записываются справа, причем для краткости 32-битные блоки представ-
ляются в виде восьми шестнадцатиричных цифр 0, 1,..., 9, a, Ь, с, d, е, f.
Стандарт рекомендует два базиса — гауссов нормальный базис, который
однозначно определяется заданием параметра к, и стандартный полино-
миальный базис, который однозначно определяется своим неприводимым
1.3. Скалярное умножение на суперсингулярных кривых
31
многочленом. В качестве таких многочленов выбирается трехчлен, а если
неприводимого трехчлена не существует, то пятичлен, причем из множе-
ства таких пятичленов 1 + xd{ + xdl 4- xdy + хт выбирается тот, который
имеет минимальный показатель степени d3 > d2 > di. Далее приводятся
ддя примера две стандартные кривые.
Примечание. Префиксы «Ож :» предшествуют шестнадцатеричной записи (см.
выше), а префиксы «1ж :» — шестнадцатеричному полиномиальному представле-
нию (см. Приложение D) элементов поля.
Кривая К-163.
т 163 a 1 b 1
п 5846006549323611672814741753598448348329118574063;
h Ож 2 Гауссов нормальный базис, к — 4;
xG Ож :056796353caa46825/ea2d37136a450da0c2a4541;
1ж :1454a2c0ad054a63173d2ae/52864aac35369765;
yG Ож :23567c67100506899066ac3d9dec76a835591ed&2;
1ж :2Mel95538a67ced9d3ca&6099860500176c76532.
Полиномиальный базис с неприводимым многочленом
fix) = 1 + X3 + X6 + X1 + Л'163;
xG Ож :2/el3c053766cllacaa07d793de4e6d5e5c94eee8;
1ж :8eee49c5e5d6e4ed397d70aacal 1с667350с31е/2;
yG Ож :289070/605d38//58321/2e800536d538ccdaa3d9;
1ж :9d3aadcc835d635008e2/12385//83d506/070982;
Кривая К-233.
т 233 a 0 b 1 h 4
п 3450873173395281893717377931138512760570940988862252126328087024741343;
Гауссов нормальный базис, к = 2;
xG Ож :Qfde76d9dcd26e643ac26f 1ао901 aa 129784671 /c072262d05614d65063;
1ж :36056d41650d262270c/176487921aal09aal/62ca346e62dcd9d67ed/;
yG Ож :0643e317633155c9e04476a8020a3c43177450ee036d633501434cac978;
1ж :879cac434105336d630ee05477134c3a0208a67440e9c551336713e346.
Полиномиальный базис с неприводимым многочленом
f(X) = 1 +Т74 + ^233;
xG Ож :172326a853a7e731a/129/22//4149563a419c266/50a4c9d6ee/ad6126;
1ж :6216da/ee6d9c4a05/662c914a3659414//22/921/al37e7a358a623271;
yG Ож :ld6537(/ece81967/70/555a67c427a8cd9&/18ae&9&56e0cll056/ae6a3;
1ж :3a6ea/65011c0e65696ea81/69dc8a724c76a555/07/76918eced7356dl.
1.3. Скалярное умножение
на суперсингулярных кривых
Алгоритмы умножения точки Р эллиптической кривой на числовую
константу к (кратко — алгоритмы вычисления к • Р), они же — алго-
ритмы скалярного умножения точки, являются основными в арифметике
эллиптических кривых. В случае эллиптических кривых особенно удобно
использовать уравновешенные систем счисления (имеющие отрицатель-
ные цифры).
32
Глава 1. Алгоритмы на эллиптических кривых
Алгоритмической особенностью суперсингулярных эллиптических
кривых является то, что удвоение точки для таких кривых выполняется су-
щественно быстрее умножения, а при использовании нормальных базисов
в поле — почти бесплатно. Поэтому при оценке сложности алгоритмов,
основанных на аддитивных цепочках [7, 8], можно учитывать только
операции сложения, не являющиеся удвоениями (как и в алгоритмах
возведения в степень в нормальных базисах конечных полей). Используя
описываемые ниже алгоритмы, по-возможности минимизирующие чис-
ло «неудваивающих» шагов в аддитивных цепочках, можно существенно
ускорить вычисления в случае, когда точка Р не известна заранее.
Если же Р известна заранее и у нас достаточно памяти для хра-
нения предварительно вычисленной таблицы, то надо применять другие
алгоритмы, но в них использование суперсингулярных кривых не дает
существенного выигрыша.
1.3.1. Вычисление к • Р методом аддитивных цепочек
Чтобы вычислить точку к • Р, разложим к в системе счисления
по основанию 2Ш, используя отрицательные цифры, получим
[n/m\
к = ai2m\
i=0
вычислим и запомним все кратные агР (достаточно вычислить все не-
четные кратные Р, ЗР,..., (2W~1 - 1)Р с помощью поочередных удвоений
и прибавлений Р, или даже только Р, ЗР,..., (2т~2 * * * * * * * - 1)Р, если исполь-
зовать разложение с отрицательными цифрами ±1, ±3,..., ±(2Ш“2 - 1)),
а потом вычисляем кР по схеме Горнера
кР = (... (as^2m + а5_2)2ш + ... + fli)2w) + а0)Р -
= (... (a's_12m+/'~l + as_2)2m+h~2 + ... + a'l)2m+'1) + a'o2lo)P,
используя s — [n/m\ сложений-вычитаний с уже вычисленными точками
и столько же умножений на 2т+/ при подходящем I.
В общем случае оценка сложности имеет вид
2m~\A + D)+ — +nD,
т
где А и D — сложности сложения-вычитания и удвоения точек соот-
ветственно. Выбирая т = [log2 n - log2 log2 n - log2 log2 log2 n\ получаем
оценку сложности nK + Mn/m + o((Af + K)n/m).
Если к известно заранее (случай фиксированной экспоненты), эту
оценку иногда можно улучшить, увеличивая т, но при этом более ак-
куратно вычисляя точки агР, которых при удачном выборе т может
оказаться гораздо меньше, чем 2т. Можно написать программу с различ-
ными эвристиками для выбора т с минимизацией количества различных
1.3. Скалярное умножение на суперсингулярных кривых
33
чисел ai, причем за счет сдвига можно всегда считать, что двоичные
записи чисел аг всегда начинаются с единицы.
Приведем еще один способ вычисления кР, который можно при-
менять, если число к известно заранее. Если различных среди чисел в;
имеется ровно d, то разбивая все числа аг на группы одинаковых, можно
представить кР в виде
d	d
^а^2™Р = ^2тк>а^Р,
j=\	ieMj	j=\
откуда получаем, применяя схему Горнера, что сложность вычисления кР
оценивается сверху как dA + nD плюс сложность вычисления системы
всех различных точек агР, плюс сумма сложностей вычисления точек bjPj.
Далее проводим минимизацию по параметру т. Сложность вычисления
каждой из точек bjPj вычисляется рекурсивно, также рекурсивно вычис-
ляется сложность вычисления системы точек агР, если разложить числа
о,-., bj по схеме Горнера с одним и тем же параметром т.
На практике наиболее важен случай п порядка 200, тогда т можно
выбирать 6,7,8 в худшем случае. Если же точка Р выбирается заранее
(алгоритм с фиксированной базой), все ее кратные Р, ЗР,..., (2т-1 — 1)Р
можно заранее занести в память, и указанная выше проблема минимиза-
ции исчезает, тогда т можно выбрать порядка 16 (чтобы запоминаемые
точки уместились в быструю кэш-память).
Ускорения вычислений можно также достичь, выбирая к (если это
будет в нашей власти) с числом единиц в диапазоне 40-60. Для этого
годится такой простой алгоритм. Число к разложим в двоичной системе:
А: = ^аг2г, аг Е {0, 1}, т = ]log2(fc + 1)[.
i=0
Пусть г’1,	~ индексы единичных компонент в наборе во, ai,
•.., о>гп—1, Ч < ^2 < • • • < it • Тогда
кР = (^2 а^р= ($2 2*0р = "22liiR
' г=0	'	у — 1	j = l
По алгоритму 1.1.5 операция удвоения точки Р = (х, у) выполняется
по формуле 2Р = (ж4 4-1, ж4 + у4) и поэтому сводится к четырехкратному
возведению в квадрат в конечном поле. Используя п раз эту форму-
лу, можно получить 2ПР. Далее найдем последовательность Aj = 2^Р,
i = 1, 2,..., t по следующей схеме
А1=2г'1Р,	= 2^"гл1А>_1, ;=2,3,...,/.
34
Глава 1. Алгоритмы на эллиптических кривых
Сложив все точки Aj, j = 1, 2,..., t, получим искомое произведение кР.
Этот алгоритм использует не более t - 1 операций сложения точек,
но требует запоминания последовательно вычисляемых точек Д. От не-
обходимости запоминания этих точек можно избавиться, если применить
схему Горнера.
Пример 1.3.1. Пусть в поле GP(24) выбран стандартный базис с базисным
многочленом f(X) = 1 4- X + X4 и требуется вычислить ЮР, если Р = (xQ, уо) =
(1 4- х 4- ж3, 1 4- ж) . Имеем следующее разложение числа 10 в двоичной системе
счисления 10 = 23 4- 21 = 10102. Поэтому t = 2, ij = 1, i2 = 3. Обозначим через
(a?i, yi) координаты точки Ai = 2Р. Тогда, используя формулы удвоения, получаем
'4" 1 = (1 4- ж 4- ж3)4 4- 1 = ж2 4- ж3,
2/i = Xq 4- I 4- 2/о =	4- ж3 + (ж + 1)4 = х 4- х2 4- х3.
Найдем координаты (ж2, у2) точки А2 = 22А}. Для этого вычисляем
Ж1 = ж4 + 1 = 1 4- я 4- £3, 2/1 — Ж{ 4- 2/1 = х3 4- х 4- 1 4- х3 4- 1 = ж,
откуда
ж2 = ж'/ 4- 1 = (ж3 4- 1)2 4- 1 — ж2 4- ж3, j/2 = ж2 4- 2/i4 = 1 4- ж 4- 4-ж2ж3.
Таким образом, ЮР = А{ 4- А2 = (ж2 4- ж3, ж 4- ж2 4- ж3) 4- (ж2 4- ж3,1 4- ж 4- ж2 4- ж3).
Следуя правилам сложения точек, получаем ЮР = О, так как точки Ai и А2
имеют равные абсциссы, но разные ординаты.
Вычисление 2nP, n 1, можно выполнить быстрее, чем п-кратно
повторяя операцию усвоения, а именно по формулам
f / 22’”	22'”	22п \	/
\х	4-1, х 4-2/	если n=l(mod4),
(21-п	'у2'п	\	,
х ,у +1),	если n = 2(mod4),
z-r =
(а2 п	22 п 22 п .
х	+1,ж	4-2/ +0’ если ^ = 3(mod4),
, л2’п а2 п v
Дж , у ),	если n = 0(mod 4).
Эти формулы легко доказать по индукции. Действительно, база индукции
вытекает из следующих формул:
2'Р = 2Р= (?‘ + !,/+/) = (Z' + 1, Z' + /"),
22Р = 2-2'Р= (ж4’,/ + 1) = (ж2”,/2 + 1),
23Р = 2 • 22Р = (Z + 1, Z + / + 1) = (я2” + 1, a:2’'3 + /'3 + 1),
24Р = 2-23Р= (Z,/) = (Z4,/4).
1.3. Скалярное умножение на суперсингулярных кривых
35
Выполним шаг индукции. Пусть
/2-’ (ж		л2 п	о2 п ч + 1,а;2 + у2 ),	если	п ~ l(mod 4),
	(Y"	,/” + 1),	если	п = 2 (mod 4),
2пР = <	_,.п			
	/2 (ж	+ 1, ж2*” + у2'" + 1),	если	п ~ 3(mod 4),
	/ 22” 1 \Х	1	22п\ >у ),	если	п ~ 0(mod 4).
Тогда применяя формулу удвоения, получим
' ( 72(п+1)	^2-(п+1)	^2-(п+1)ч
(х 4-1, ж +2/	), если (п + 1) = l(mod 4)
\х ,у +0’	если (п +1) = 2(mod4),
, о2-(п+1)	э2-(пЧ-1)	э2-(п+1) ч	'
(ж2	4-1, ж2 4- у 4-1), если (п 4-1) = 3(mod 4),
Дж ,у ) = (ж ,?/	), если (п4-1) = 0(mod4).
Возведение в степени равные степеням двойки почти бесплатно выпол-
няется в нормальном базисе. При использовании стандартного базиса для
этой операции можно при малых показателях степени выполнять повтор-
ное возведение в квадрат, а при больших показателях степени применять
алгоритм из [3].
1.3.2. Использование проективных координат
Если время выполнения операции инвертирования в данном поле
в пять и более раз больше времени умножения, то ускорения в вы-
числении к • Р можно добиться почти полностью исключив операцию
инвертирования за счет увеличения в 4,5 раза общего числа умножений,
переходя к проективным координатам. До этого момента мы избегали ими
пользоваться, но час настал.
Заметим, что путем подстановки X = X/Z, Y — Y/Z в уравнения,
задающие эллиптические кривые Е\, и Е^ мы приходим к следующим
однородными уравнениями относительно X, К и К:
Ei : Y2Z + YY2 = X3,
Е2 : Y2Z + YZ2 = X3 + XZ2,
Е3 : Y2Z + YZ2 = X3 + XZ2 + Z3.
Наряду с обычными (аффинными) координатами мы можем теперь рас-
сматривать проективные координаты — ненулевые тройки из К3. Проек-
тивные координаты (X, У, У) и (X', У', Z') считаются эквивалентными,
если для некоторого ненулевого t из К9 выполняется X' = tX, Y' — tY,
Zl — tZ. Класс эквивалентности, порожденный тройкой (X, У, Z) обо-
36
Глава 1. Алгоритмы на эллиптических кривых
значаем (X : Y : Z) Множество всех классов эквивалентности для
данной тройки и называем ее проективными координатами. Геометри-
чески (двумерное) проективное пространство можно представлять себе
как множество прямых в обычном трехмерном пространстве, проходящих
через начало координат.
Теперь эллиптическую кривую можно рассматривать на проективной
плоскости как множество проективных точек, удовлетворяющих соот-
ветствующему однородному уравнению. Заметим, что единственной про-
ективной точкой с нулевой z координатой, лежащей на эллиптической
кривой, будет точка (0:1:0), которая соответствует бесконечно удален-
ной точке О. Для остальных точек кривой (X : Y : Z) ~ (X/Z *.Y/Z *. 1),
так что проективная точка (X : Y : Z) однозначно соответствует аффин-
ной точке (X/Z, Y/Z). Мы хотим теперь получить формулы для сложения
проективных точек Р и Q.
Пусть Р = (Xi : У1 : 1) € Е{) (таким образом, одна точка у нас
фактически задана обычными координатами) и Q = (Х2 : Y2 : Z2) Е Ei.
Предположим, что Р, Q О и P/Q (нас интересует основной случай
в сложении точек). Для точки R = Р 4- Q, R = (Х'3 : У3' : 1) мы можем
использовать формулы сложения в аффинном случае, после применения
которых, учитывая что X; = X2/Z2, Y{ = Y2/Z2 получим
. а2	Х2	.	а (а2 Х2\
т'=	+х1 +	-^,	y' = i	+ y1 +	- - + -П
и	ZZ2	и у и~ Z2 J
где а = Y\Z2 + Y2, b = X[Z2 4- X2. Полагая
Z3 = b3Z2, X3 = X3Z3, Y3 = Y3Z3,
находим R = (Хз: Уз : Z$) , где
T3 = a26Z2 + &4, Y3 = (l + Yt)Z3 + a3Z2 + ab2X2, Z3 = b3Z2.
Отсюда ясно, что, не считая сложений и возведений в степень, нам
для сложения точек в проективных координатах необходимо выполнить
9 умножений (в аффинных координатах только 2), но зато ни одного
деления. Умножения можно производить в следующем порядке:
YiZ2, XtZ2, bZ2, Z3 = b2(bZ2), a2(bZ2), (l+y,)Z3,
a2Z2, b2X2, a3Z2 + ab2X2 = a(a2Z2 + b2X2).
Рассмотрим теперь случай удвоения точек. Так как в обычных координатах
оно выполняется по формуле 2Р = (ж4 4- 1, ж4 4- у4), то в проективных
координатах оно выполняется по формуле 2Р = (X4 4- Z4, (X + У)4, Z4)
и требует только 6 возведений в квадрат. l
l) В отличие от аффинных проективные координаты обозначаются прописными буквами.
1.3. Скалярное умножение на суперсингулярных кривых
37
Используя формулу 22пР — (ж Л/" + 1) или формулу 22пР =
(ж24п, У2^) в аффинных координатах, в зависимости от четности п, можно
эти формулы аналогичным образом переписать в проективных координа-
тах. Поэтому многократное последовательное удвоение и в проективных
координатах можно выполнить быстрее, чем простым повторным удво-
ением, если использовать какой-нибудь быстрый алгоритм возведения
в степень 2к. Кроме того, в любом случае экономятся операции сложения.
При вычислении кР можно, используя любой вариант бинарного
метода, последовательно удваивать точки, а затем складывать некото-
рые из них, накапливая результат в Q. Но можно использовать также
и 2^-арный метод, запоминая точки Р, ЗР, 5Р,..., (2^-1 - 1)Р в обыч-
ных координатах. Окончательный результат, полученный в проективных
координатах, преобразуем в аффинные делением на z$ в самом конце
вычисления. Операция деления, Очевидно, выполняется только два раза.
1.3.3. Метод Монтгомери
Это метод вычисления точки к • Р с использованием минимальной
дополнительной памяти (минимального числа регистров), предложенный
в [75]. В данном случае не следует искать сходства с методом Монтгомери
ускорения модулярного возведения в степень. Он является некоторой
модификацией обычного бинарного метода, в котором к представляется
в двоичном виде к - (ki-i... £9)2 й последовательно вычисляются точки
данной кривой mzP, где тг =	. fc/_t-)2. Но в отличие от бинарного
метода вместо рекурсии
( 2РИ если kj = О,
1	(	— Д если kj — 1-
применяется рекурсия
( 2РЬ	если	к};= 0^	ГР2+Р1,	если	kj=O,
1	(Р1+Р2,	если	к} = 1,	t 2Р2,	если	kj; = 1,
которая программно реализуется с помощью цикла при начальных уста-
новках Pi = Р, Р2 = 2Р. По индукции легко проверяется, что инвариантом
цикла является соотношение Р2 = Р] + Р, и на i шаге Pi = mzP. Этот
алгоритм кажется более медленным, чем обычный бинарный, но в работе
П. Монтгомери [75] замечено, что на каждом шаге цикла при вычисле-
нии новых значений ж-координат точек Рг можно использовать старые
значения тоже только ж-координат, и ж-координату точки Р, не меня-
ющуюся во время цикла. Действительно, на каждом шаге цикла произ-
водятся вычисления Q2 := Q2 + Qi, Q\ := 2Qi, где {Qi,Qj} = {Рг,Ру}
и согласно правилам сложения и удвоения для суперсингулярных кривых
У2 + у = ж3 + ж(+1) новые ж-координаты точек Q\ = (жь 3/1), Q2 — (ж2, у2)
38
Глава 1. Алгоритмы на эллиптических кривых
получают значения
соответственно.
Если, например, для новых точек выполнено равенство Р = Q2 - Q\,
то, учитывая что -Q\ = (жь у^ 4-1), имеем
откуда новая координата ж2 принимает значение
1
х + 7------
(Ж1 4-ж2)2
В случае Р — Q\ - Q2 получается точно такая же формула. Поэтому
вычисление новых значений ж-координат Х\ и ж2 можно выполнять
по следующим формулам
с помощью одного инвертирования, трех возведений в квадрат и двух
сложений (в случае схемной реализации фактически одного сложения).
Что касается ^/-координат, то они в цикле вообще не вычисляются. Только
после того как вычислены точки Р\ — kP, Р2 = (к 4- 1)Р вычисляется
у-координата у\ точки кР = Р\ с помощью формул сложения Р2 = Р\ +Р
_ ( У\ + У \ t
ж2 — | I 4- Ж| 4- ж,
\Ж1 4- ж/
из которых следует, что
®2(Х1 + ж)2 = (у\ + у)2 + (Х1 + ж)3,
у2 + у2 = (si + ж)2(ж1 + х2 + х) = (ж2 + ж2)(ж1 + х2 + ж) =
= ж3 4- ж3 + х2х2 + Ж2Ж1 + ж (ж3 + х2),
а так как в силу принадлежности точек данной кривой
2	3	2	3
У1 + У1 +Ж! 4-Ж] = у 4- У 4- Ж 4-ж,
У\ +у = Ж|Ж2 4-ж2Ж] +ж(ж1 +ж2) +я?4-Ж] = Ж)(ж4-ж2)4- (ж^4- 1)(ж4-Ж1).
Поэтому для для вычисления у^ достаточно сделать два умножения,
два возведения в квадрат и пять сложений (в случае схемной реали-
зации фактически четыре). В случае программной реализации кроме
1.4. Скалярное умножение на несуперсингулярных кривых
39
регистров для хранения ж, y,Xi,X2 нужны еще два вспомогательных
регистра. Они используются только при вычислении щ в конце ра-
боты программы. Если пренебречь сложностью выполнения сложения
и возведения в квадрат, то программная сложность скалярного умноже-
ния на суперсингулярной кривой методом Монтгомери оценивается как
L(k) = [log2 A;jZ(I(n)) + 2Z(M(n))), где Z(I(n)), Z(M(n)) — сложность
инвертирования и умножения в поле GF(2n). Эта оценка лучше, чем
оценка сложности бинарного метода в худшем случае, но она может
быть хуже, в случае когда к имеет малое число vz(k) единиц в двоичной
записи. В сравнении с оценкой худшего случая при использовании би-
нарного метода с применением уравновешенной двоичной системы метод
Монтгомери, вероятно, проигрывает, если время инвертирования сильно
превосходит время умножения в поле. Но зато он использует меньше
пересылок во время работы, что отчасти компенсирует большее число
операций в цикле. Заметим, что для реализации разных вариантов бинар-
ного метода нужно не менее семи регистров.
В случае схемной реализации сложность универсальной схемы воз-
ведения в степень и для разных вариантов бинарного метода не Зависит
от i^k. В этом случае метод Монтгомери всегда превосходит простой би-
нарный метод. Глубина схемы для скалярного умножения к Р со входами
(к,х,у), х = (®i,... ,хп), у = (t/b... ,уп), k =	,ко),
оценивается сверху как
l(k)(D(I(n)) + 4) + Р(М(п)) + 4,
где	— глубина инвертирования и умножения в поле
GF(2n). Эта оценка также лучше оценки глубины схемы, построенной
простым бинарным методом. Но оценка глубины для бинарного уравно-
вешенного метода имеет вид l(k)(D(I(n)) + 2Р(М(п)) 4- 6)/2 + 1 и при
п 16 будет меньше. При автоматной реализации схема Монтгомери
будет иметь меньшую сложность, но работать медленнее.
Упражнение 1.3.1. Попробуйте применить метод Монтгомери при выборе проек-
тивных координат.
1.4. Скалярное умножение
на несуперсингулярных кривых
Описанные выше алгоритмы для суперсингулярных кривых можно
применять и для несуперсингулярных кривых, заменив лишь правила
удвоения и сложения точек. Но эти правила чуть сложнее, и работать
соответствующие алгоритмы будут медленнее. А так как в несуперсин-
гулярном случае удвоение делается лишь чуть медленнее сложения, то
алгоритмы, минимизирующие число сложений, не будут давать суще-
ственного ускорения. Поэтому в этом случае возникает необходимость
модернизации старых алгоритмов и создания новых.
40
Глава 1. Алгоритмы на эллиптических кривых
1.4.1. Метод Монтгомери для несуперсингулярных кривых
Это метод был развит в работе латиноамериканских криптографов
Лопеса и Дахаба [69]. Идея такая же, как и в суперсингулярном случае.
Рассматриваем произвольную кривую У2 4- XY = X3 4- аХ2 4- Ъ. Также
на каждом шаге цикла производим вычисления Q2 = Qi + Qi, Q\ — 2Q1,
где Qi = Qj 4- P, i / j, и согласно правилам сложения и удвоения
для несуперсингулярных кривых новые ж-координаты 24 и ж2 точек
Q\ — (24, 3/2) и Qz = (24, У1) вычисляются по формулам
(1.33)
04 4- 2*2 J Xj 4” 2*2
(1-34)
соответственно. (При 24 = 0 в результате удвоения получается бесконечно
удаленная точка.)
Упражнение 1.4.1. Выведите формулу (1.33) из стандартного правила удвоения
х3 = а2 4- а 4- а, где а — х\ -I-
Указание. у] 4- уi®i = х\ 4- ах2 4- Ъ.
Заметим, что формулу (1.34) можно переписать в виде, не содержащем
коэффициент а:
Х2У\ + iClS/2 + ^14 + 2^4
(24 +2J2)2
Упражнение 1.4.2. Проверьте это.
Указание, у} 4- 2424 4- у2 4- у2х2 4-	4- х\ = а(х\ 4- х\) = а(хх 4- ж2)2.
Если, например, для новых точек выполнено равенство Р = Q2 ~	,
то, учитывая что -Q\ = (04,2/1 4- Х\), имеем
24(24 +2/1) 4-242/2 4-242^ 4- х2х\
(®1 + хгу
откуда новое значение ж-координаты х2 вычисляется по формуле
Упражнение 1.4.3. Проверьте это.
Указание. х2хх = х2 4- 04(04 4- 04).
Поэтому вычисление новых значений х\ и 24 ж-координат точек Q\
и Q2 можно выполнять по формулам
Э Ъ	)
Х[ 4~ —т, х 4~ t 4" t, t =
1.4. Скалярное умножение на несуперсингулярных кривых
41
с помощью одного инвертирования, одного деления; одного умножения
на константу Ь (для кривых Коблица она равна 1 и это умножение
исчезает), двух возведений в квадрат и четырех сложений; //-координаты
в цикле не вычисляются, а находятся после его окончания, когда Pi =
kP, Pi = (fc-hl)P Вычисляется //-координата //i точки кР = Р\ с помощью
формул сложения Р2 = Р\ 4- Р
которые, согласно упражнению, переписываются в виде
4- х)2 == xyi 4- Х\у 4- Ж1Ж2 4- хх\,
а потом в виде
xyi = Xi(x\ 4-х)2 4-Х\у 4-Ж1Ж2 4-хх\ = ж2ж2 4- х^х2 4-хуу 4-Ж1Ж2 4-хх\ =
= Х\ (x\xi + xxx + x2 4-//2) 4-ж2ж2 =
= х\ [х\Xi 4-Х\х 4-х2 4-ХХ14-х2 4-у) 4- x(x\Xi 4-Х\Х4-xxi + у) + ху =
^(ж-4ж1)((ж + ж1)(ж4-ж2) + ж2 + //) +ху,
откуда имеем у{ — (х4-Ж1)((ж+Ж1)(ж+ж2)+а;24-//)/ж4-//. Для вычисления у\
нужен еще один вспомогательный регистр s, с помощью которого у\
вычисляется следующим образом:
з = ж + а:1, у{=х + х2, yi=yis, у\=ух+у, t = x2,
У\ — 3/1 +t, 3/i=yis, 3/1 = —,	3/1 =3/1+3/-
X
Для этого используется 5 сложений, одно возведение в квадрат, 2 умно-
жения и одно деление. Еще одно возведение в квадрат и сложение
используется при инициализации цикла с помощью равенств
2 и
Х\ = x,xi = х 4—г-
х1
Сложность скалярного умножения точек на несуперсингулярной кривой
методом Монтгомери оценивается как
L(k) = 2 Llog2 fc](Z(l(n)) 4- 2Z(A(n)) + ОДп)) + £(M(n))) +
+ 2Z(M(n)) 4- Z(/(n)) 4- 6Р(Д(п)) 4- 2Z(5(n)),
где Z(A(n)), £(S(n)) — сложность возведения в квадрат и сложения в поле
GF(2n). Глубина схемы для скалярного умножения k Р с входами
(к,х,у), х = (xi,... ,хп), у = (т/i,... ,уп), k = (ki-i,...,ko),
оценивается сверху как
3(fc)(Z>(l(n)) + D(M(n)) + 4) + 2(P(M(n)) + D(I(n))) + 2.
42
Глава 1. Алгоритмы на эллиптических кривых
1.4.2. Метод Монтгомери в проективных координатах
В этом случае х-координаты точек Р, представляются как XifZi.
Тогда вычисление ж-координаты точки 2Р: производится по формулам
X Xf + bZ} /ХЛ2 / Zi\2 2 ъ
Z ~ zfxj ~\Zi) +b\xJ ~Xi + x] ’
где
X = X- + bZ-, z = Z2X2.
Вычисление ж-координаты точки Р\ + Р2 производится по формулам
Ху	X\Z2X2Z\	%%	, S1S2
Zy	(X1Z2 + X2Z1)2	/	%Д2	(ii-ii)2’
V Zi Z2)
где
Xy = xZy + (XlZ2)(X2Zl), Zy = (XxZ2 +X2Zx)2.
Вычисление удвоения данной точки можно организовать с помощью
одного вспомогательного регистра Т\ следующим образом:
Т] .-y/b = br'1; Х:=Х2; Z := Z2; Tt := ZT\, Z :=ZX,
Т\-.= Т2, Х-.= Х2, Х:=Х+Тх.
Упражнение 1.4.4. Проверьте это.
В вычислении используется 4 возведения в квадрат, одно сложение
и 2 умножения (одно из них на константу, равную единице для кри-
вых Коблица).
Вычисление суммы двух точек можно организовать с помощью одного
вспомогательного регистра Т\:
Xx-.= XxZ2, Zx:=ZxX2, Тх:=Ххгх, гх:=гх+хх, ZX:=Z2,
XI:=Zlx, XI:=XI+TI.
При этом используется одно возведение в квадрат, 2 сложения и 4 умно-
жения.
Вычисление аффинных координат (ж|, у\) результата кР, где Р =
(х9у), проводится после окончания цикла по его проективным коорди-
натам (Xi : Y\ : Z\) следующим образом:
= V-; 2/1 = [х + X!)((X] + xZ{)(X2 + xZ2) + (яг2 + y))(xZxZ2y{ + у.
1.4. Скалярное умножение на несуперсингулярных кривых
43
Эти вычисления можно организовать с помощью двух вспомогатель-
ных регистров Т[, Т2:
Т\ — ZiZ2; Z\ — Z\X', Z\ — Z\ 4~ Xjj Z2 — Z2x\ Xi = Z2X\\
Z2 = Z2 X2; Z2 = Z2Z\', T2 = x2, T2 = T2 4- ?/; T2 = T2T\\
1
T2=T2+y; Tx=Txx- T{ = —; T2=T2TX- X2 = XxTx-
У2 = X2 4~	^2 ~ ^2-^2>	%2 ~ ^2 4~ У'
Упражнение 1.4.5. Проверьте это.
В вычислении используется одно инвертирование, одно возведение
в квадрат, 6 сложений и 10 умножений.
Сложность скалярного умножения на несуперсингулярной кривой
методом Монтгомери в проективных координатах оценивается как
L(k) = Llog2 fcj (3Z(A(n)) 4- 5Z(S(n)) + 6Z(M(n))) +
+ 12Z(M(n)) + b(I(n)) + 7Z(A(n)) + 6Z(S(n)),
где £(A(n)), Z(5(n)) — сложность возведения в квадрат и сложения в поле
GF(2n). Глубина схемы для скалярного умножения к • Р с входами
(к,х,у), X = (Ж],..., хп), у = (yi,... ,Уп), k = (ki-i,...,k0),
оценивается сверху как
/(fc)(22)(M(n)) + 3) + 5Р(М(п)) 4- ВДп)) + 2.
1.4.3. Метод Лопеса—Дахаба использования
проективных координат
С целью уменьшения числа операций при применении проективных
координат в [68] было предложено сопоставлять координатам (X : Y : Z)
аффинную точку (X/Z,Y/Z2). Тогда в этих проективных координатах
кривая Y2 + XY = X3 + аХ2 4- Ь представляется в виде
У2 + XYZ = X3Z + aT2Z2 + bZ4.
Упражнение 1.4.6. Проверьте это.
Указание. Сделайте подстановку X := X/Z, Y := Y/Z2 и умножьте на Z4.
Бесконечно удаленной точке соответствует точка (1 : 0 : 0). Обратной
для точки (X : Y : Z) является точка (X : XZ + Y : Z), так как ее
аффинные координаты (X/Z, (XZ 4- У)//2) = (Х/Z, X/Z + Г/Z2) =
(ж, х 4- у), где (ж,?/) = (Х/7,У/72) — аффинные координаты точки
(X : Y : Z). Удвоение точки 2(ж, у) = (жь у\) в аффинных координатах
выполняется по следующим правилам
Ж1 = а2 4- а 4- а, у{ = у 4- ш(ж + ж^ = ж2 4- (а 4- 1)жь
44
Глава 1. Алгоритмы на эллиптических кривых
где
У
a = х Н—.
х
Выше уже проверялось, что первое равенство можно переписать в виде
_ 2 .	&
X1 — X Я- .
X2
Упражнение 1.4.7. Проверьте, что удвоение точки 2(Х : Y : Z) = (Xi : Yi : Z\)
в рассматриваемых проективных координатах можно выполнить по следующему
правилу:
Zi = X2Z2, Xj = X4 + bZ4, Yx = bZ4Zx + Xx(aZx + Y2 + bZ4).
Указание. Положим x = X/Z,y = Y/Z1, тогда
Xi	2	Ki	bZ*	f	У2	bZ*\
xx = — =x+x 6, 2/i = ~2 =~^r+xlla+ — +	1,
Z/j	Zfj	Zj\	\	£j\	/
bZ4 Y2 Y X bZ2 .	,
~z^~x2z2 + Tz + 'z+a~^^x b~x +Xl’
У2	bZ4 Y	X	у
a+~ + — = — + — = x+~= a.
Z\	Zx	X Z	Z	X
Сложение точек в проективных координатах задается слишком слож-
ными формулами.
Упражнение 1.4.8. Получите эти формулы с использованием 14 операций умно-
жения.
Однако, если одна из точек задана аффинными координатами, то,
как и в суперсингулярном случае, формулы упрощаются.
Упражнение 1.4.9. Проверьте, что сложение точек (Xj : У1 : Zt) -Ь (Х2 : У2 : 1) =
(Хз : Уз : Z3) в смешанных координатах может быть выполнено по следующему
правилу:
A=Y2Zi+Y, B=X2Zl+Xt, C=ZXB, D=B2(C+aZ2), Z3=C2, E=AC,
x3=a2+d+e, f=x3+x2z3, G=(X2+Y2)Z23, Y3=(E+Z3)F+G.
Указание. Положим X| = X\/Z\,y\ = YJZ], x2 = X2,y2 = Y2, тогда
X3 A2+D + E A2 + AC + B2(C + aZ2') A2 A B2 (BZA2
X}~ z3~ c2 ~ c2 ~c2 + c+c+\c)a'
A = Y2Z2 + Yx = y2+yi BZt = ]
C	X2Z2 -I- XxZx x2 ~t~ Xi C
B2 _ X2Z2 + X2 _ X2 + x2 _ (Х2 + Ж|)2 _	_
C	X2Z2 + XxZi	X2 + xx X2 + xx 2 + Xl X2 + Xi’
1.4. Скалярное умножение на несуперсингулярных кривых
45
откуда имеем
2?3 = А -р 3?2 Н- Ж1 + CL, А — --,
2?2 4"
_ К _ (Хз + X2Z3)(AC + Z3) + (Х2 + Y2)Z23 _
Уз zl	z2
= (у+Х2)(1Г + 1)+Х2 + У2 =
\ z3 / \ z3 /
/4	\
= (х3 + Х2) ( — + 1 ) + х2 + у2 = А(х3 + Х2) + Хз + у2.
у С-	/
Таким образом, смешанное проективно-аффинное сложение точек
выполняется с помощью 9 умножений (одно из них умножение на кон-
станту а, обычно равную 0 или 1), 9 сложений и 5 возведений в квадрат.
Удвоение требует 5 умножений (одно из них умножение на константу а,
и одно из них умножение на константу Ь), 4 операции сложения и 5
возведений в квадрат.
Как и в случае суперсингулярных кривых, этот метод можно соче-
тать с любой версией метода аддитивных цепочек, в которой строятся
линейные цепочки. Вычисляемые в начале работы алгоритма и хранимые
далее «малые» кратные точки Р можно сразу вычислять в аффинных
координатах, так как при вычислении в проективных координатах все
равно потом результат придется переводить в аффинные координаты,
затрачивая по два деления на запоминаемую точку. При вычислении же
в аффинных координатах на каждую новую точку, как правило, требуется
только одно инвертирование.
Если аддитивная цепочка для числа к содержит v(k) удвоений и t(k)
сложений, то сложность соответствующего ей вычисления, если прене-
бречь сложностью сложений и возведений в квадрат, а также сложностью
перевода в аффинные координаты, равна L(k) = 4v(k) + 8^(fc), а в случае
кривых Коблица (когда b = 1) L(k) = 3v(k) + &£(&). Поэтому в сравнении
с суперсингулярным случаем сложность больше и минимизация числа об-
щих сложений точек дает меньший эффект. При использовании обычного
бинарного метода или бинарного метода с уравновешенной двоичной
системой указанный метод проигрывает описанному выше методу Монт-
гомери, но при использовании 2^-арных методов при к 4 начинает его
превосходить (за счет использования памяти, конечно).
1.4.4. Алгоритм скалярного умножения,
использующий операцию «ополовинивания»
Этот алгоритм был предложен независимо Кнудсеном [59] и Шрепе-
лем [88]. Он основан на том, что операция вычисления «половины» точки
может быть выполнена быстрее ее удвоения, и в бинарном алгоритме (на-
зываемом иногда алгоритм «удвоения-сложения») можно заменить удвое-
ние ополовиниванием . Так мы назовем операцию нахождения по точке Р
46
Глава 1. Алгоритмы на эллиптических кривых
такой точки Q, что 2Q = Р. Можно эту точку обозначить |Р. Если п —
порядок точки Р, то, очевидно, |Р = ^Р при нечетном п.
Но такой способ ополовинивания пригоден не всегда и неэффекти-
вен.
Эффективный способ основан на обращении операции удвоения.
Действительно, если 2Q = 2{u, v) = Р = (ж, у), то
х = А + А + а, у = и 4- ж(А -Fl), А = и 4-
и
Для решения этой системы относительно и, v сначала находим А из урав-
нения А24- А = х4-а, потом и1 = з/4-я(А+1), извлекая корень, находим и,
а потом v = Хи + и2. При этом используется 4 сложения (одно из них про-
сто прибавление 1), 2 умножения, одно возведение в квадрат, а вместо де-
ления — извлечение квадратного корня и решение квадратного уравнения.
Далее мы покажем, что эти операции можно делать быстрее инверти-
рования. Но вначале объясним, как вместо операции удвоения применять
операцию ополовинивания. Кратко напомним, как работает 2ад-арный
алгоритм вычисления к • Р.
Представляем к в виде
где \ki\ 2w“l. Это представление можно получить из обычного 2W-пред-
ставления с цифрами 0, 1,..., 2W - 1, заменяя по очереди каждую цифру
на равную ей по модулю 2W из интервала -2W-1,..., 2W-1 - 1 и прибавляя,
если надо, единицу к следующей цифре. Далее можно, изменяя Ц, сделать
так, чтобы все цифры стали нечетными. Для удобства используем запись
вида
t
к = '£/к^’ <^10g2fc+l,
г=0
полагая в добавленных слагаемых ki = 0.
Потом вычисляем и запоминаем точки Рг = гР, где i = 1, 3,...,
2W~* - 1. Полагаем Q = О — нулевому элементу группы (бесконечно
удаленной точке). Далее в цикле с обратным порядком изменения пара-
метра i от I - 1 до 0 выполняются следующие операции: если ki = 0, то
Q — 2Q, если ki > 0, то Q = Q 4- Р*., если ki < 0, то Q = Q - Р*,.
Использования ополовинивания обосновывается следующими лем-
мами.
Лемма 1.4.1. Пусть для нечетного п дано описанное выше представление
t
2*~1к mod п =	к\2\ t — [log2 nJ 4- 1.
г=0
1.4. Скалярное умножение на несуперсингулярных кривых 47
Тогда
t-i
2k't +	= k mod n,
2=0
дробь a/2l понимается как единственное Число Ъ в интервале от 0 до п— 1,
такое> что 21Ь = a mod п. Кроме того, очевидно, k't = 0, 1.
Доказательство. Заметим, что
a b a + b	s / а \ а	a s a
“7 + ту = ...ту.. mod n, 2	— = mod n, -v2 = -7— mod n.
yi 2i 2*	\ 2 J 2l~s	2	2+8
Тогда деля обе части равенства
t
2*-1fc mod n = ki2l, t = [log2 nJ 4~ 1
2=0
на 2l~1, получаем требуемое равенство.	
Лемма 1.4.2. Пусть порядок Р нечетной число п. Тогда
\~tP = ^Р |((а + Ъ)Р) = ](аР) + 1-(ЬР).
Доказа тельсгво.
a ( о	\ о
^У+\Р = у2 2Ш 1110(1 у =
2(](аР) +	= 2( '-(аР)} + 2(= аР + ЬР = (а + Ъ)Р,
у 2	2 J	у 2	J	у 2	у
1 у ч 1 z ч а + Ь _
-(аР) + -(ЬР) = — Р.	
Пусть ТП{ = &о/2г-Ь . . + &•, г = 0,1,.... Очевидно, mt-\-y2k't = kn\odn.
Тогда согласно лемме тг+1Р = |(тгР)+Д:'+1Р. Поэтому кР можно вычис-
лить следующим алгоритмом, аналогичным вышеописанному Вычисляем
и запоминаем Д = iP, i = 1,3, ... ,2w~l - 1. Полагаем Q = О. Далее
в цикле с прямым порядком изменения параметра i от 0 до t - 1 выпол-
няются следующие операции: Q — если кг > 0, то Q = Q + Р^-, если
кг < 0, то Q — Q - Pfct . После окончания цикла Вычисляем Q = Q + 2Р,
если k't = 1 и возвращаем Q в качестве результата.
Но этот алгоритм непригоден для применения проективных коорди-
нат. Аккумулирующая результат точка Q в случае их применения должна
быть записана в проективных координатах» однако тогда не применим
указанный выше способ ополовинивания* ДЛЯ применения проективных
координат удобен другой алгоритм, являющийся аналогом алгоритма [33].
48
Глава 1. Алгоритмы на эллиптических кривых
В этом алгоритме вначале инициализируются точки фг=О, i =1,3,
...	- 1, потом полагаем Qj = 2Р, если k't = 1, и в цикле с обратным
изменением параметра от t - 1 до 0 делаются следующие процедуры:
если к- > 0, то Qk>. = Qk< 4- Р,
если к\ < 0, то Q_k>. = Q_k^ - Р,
и потом всегда Р = Р/2. После завершения цикла каждая точка Qj будет
равна
После окончания работы цикла вычисляем
2W~2 —1
Q —	(2г + 1)<?2г+1 •
2=0
Упражнение 1.4.10. Проверьте, что Q = кР.
Заметим, что количество операций ополовинивания равно t = log2 n4-
0(1), причем часто эти операции выполняются блоками идущих подряд
операций, а количество операций прибавления или вычитания Р будет
не больше t/w 4- 0(1).
Сумму Q можно вычислять следующим образом:
Л = Q21+1, Л=Л + <?2/-1, •••, Л = Л-i + Qi,
Q = 2 (Л) 4~ • •. 4- Л-1) + Л> I = 2W 2 — 1.
Для этого требуется 21 = 2W-1 — 2 сложений и одно удвоение.
Упражнение 1.4.11. Проверьте это.
В случае применения проективных координат в этом алгоритме точ-
ки Qj задаются проективными, а точка Р — аффинными координатами.
В конце работы все точки складываются не в смешанных, а целиком
в проективных координатах. Это медленнее, чем в смешанных координа-
тах, но этих последних операций не более 2W-1 - 2 т. е. не более 14, так
как в реальных вычислениях обычно w 5. Можно, однако, для этих
вычислений перейти к аффинным координатам.
Для быстрого выполнения ополовинивания нам надо уметь быстро
быстро вычислять след, извлекать квадратные корни и решать уравнения
вида А2 4- А = a 4- х. В разд. 1.2.1 мы уже видели, что и то и другое очень
быстро делается в нормальном базисе. В случае нечетного п для решения
квадратного уравнения там была даже дана явная формула. Но быстрое
умножение в нормальных базисах удается выполнять не для всех раз-
мерностей п. Поэтому далее будет рассматриваться также случай выбора
в поле стандартного базиса. Но вначале рассмотрим вопрос о выборе
корня квадратного уравнения.
1.4. Скалярное умножение на несуперсингулярных кривых 49
Выбор корня квадратного уравнения. Для разрешимости квадратного урав-
нения необходимо и достаточно, чтобы след tr (х 4- а) = 0. Так как
д(ж + а) — tr(&) + tr(a) = 0, то из разрешимости уравнения следует
что tr (ж) = tr (а). Это верно для любой точки (ж, у) нечетного порядка,
потому что для любой такой точки ополовинивание существует. Согласно
стандарту NIST выбираются кривые, у которых tr (а) = 1. Далее мы пред-
полагаем, что выбрана такая кривая.
Уравнение Л2 + А = a -F х имеет два корня. Как выбрать нужный
нам корень? Так как он удовлетворяет еще условию и2 = у + х(Х + 1),
и точка (u, v) — половина точки (х,у), тоже имеет нечетный порядок,
то tr (у + х(Х -hl)) = tr (u2) = tr (и) = tr (a) = 1. В то же время согласно
линейности следа tr (у 4- жА)) = tr (у + ж(А -h 1)) + tr (ж) = 1 -h tr (ж) = 0.
Поэтому для проверки, что А именно нужный нам корень, достаточно
вычислить t — у 4- жА и проверить, что tr (у 4- жА)) = 0. Если это верно,
то вычисляем и — \/t + х, в противном случае вместо А надо брать А + 1,
значит, в качестве и нужно брать и = \/t. После этого находим v = Au4-и2.
Но если нам аффинные координаты половинной точки сразу не нужны,
так как после ее вычисления мы опять будем ополовинивать полученную
точку, то вместо v можно использовать А(и) = и 4- v/u, не вычисляя v.
Далее нам понадобится t = v -h иХ', где А' корень уравнения с правой
частью и 4- а, но t можно вычислить по формуле
(и \
и -4 и 4— ) 4- иХ' — и (и 4- X' 4- А(и)),
не зная v. Таким образом можно экономить вычисления при многократ-
ном повторном ополовинивании, что делает перспективным использова-
ние алгоритмов, основанных на аддитивных цепочках с малым числом
сложений. На одно ополовинивание в среднем будет расходоваться одно
умножение и два сложения, не считая извлечений корней и решения
уравнений.
Вычисление следа. Этот вопрос уже рассматривался в первой главе в общем
случае. Здесь мы его рассмотрим применительно к полю GF(2n). След
в нормальном базисе очень легко вычисляется по формуле
tr (ciQi 4- ... 4- cnan) = ci+ ... + Cn,
так как после каждого возведения в квадрат координаты вектора (ci,..., сп)
циклически сдвигаются, и след оказывается равен
(ci 4-... 4- cn)(ai + ... 4- an) = Ci + ... + сп.
Далее будем рассматривать вычисления в случае выбора в поле стан-
дартного базиса. Вычисление следа согласно его определению требует п
возведений в квадрат и n-1 сложение. В стандартном базисе это довольно
дорого. Лучше воспользоваться свойством линейности
tr (со -h <4Ж + ... + сп_1Жп-1) = с0 tr (1) + ... 4- cn_i tr (жп-1),
50
Глава 1. Алгоритмы на эллиптических кривых
предварительно вычислив и запомнив tr (жг) 6 GF(2). Фактически можно
вычислять след как линейный функционал. Часто многие из его коэффи-
циентов равны нулю.
Пример 1.4.1. Выберем в поле <7F(2163) базис с неприводимым пятичленом
1 4- X3 4- X6 4- х1 4- X163. Тогда tr (хг) — 1 только для i = 0,157. Поэтому
tr (со 4- С{Х 4-... 4~ cn-[Xn l) = Cq 4- с^.
Это еще проще, чем в нормальном базисе.
Решение квадратного уравнения. Рассматриваем случай использования
стандартного базиса. Пусть п нечетно. Назовем полуследом функцию
Н(Х) = X + X* + X16 + ... + Х2"~'.
Очевидно, это линейный оператор над полем GF(2), т. е. Н(Х 4-У) =
H(X) + H(Y).
Лемма 1.4.3. Н(с) — это решение уравнения Х2+Х — c4-tr (с), и Н (с) =
Н(с2) 4- с 4- tr (с) для любого с Е GF(2n).
Доказательство. Очевидно, согласно тождествам Фробениуса и Ферма
Я(с2) + Я(с) = Я(с)2 + Я(с) = (с2 + с8 + с32 + ... + с2’"2 + с) +
+ (с +с4 + с16 + ... + с2 ') = с + tr (с).
Так как нас интересуют уравнения X2 4- X = с, tr (с) = 0, то одним из его
решений является Н(с).
Способ вычисления полуследа на основе тождества линейности
Я(со + с,х + .+ Сп^х"-') = СоЯ(1) + ... + сп^Н(хп~1>),
очевидно, в п раз менее эффективен, чем аналогичный способ вычисления
следа. Так как полуслед — это линейный оператор, то несколько ускорить
его вычисление можно с помощью алгоритма «четырех русских».
Но прежде, чем это делать, можно уменьшить вдвое объем исполь-
зуемой памяти и вдвое длину вектора, на который будет умножаться
матрица, а значит и вдвое сложность вычисления. Правда, при этом будет
вычисляться не всегда точно полуслед, иногда к нему будет прибавляться
единица. Но так как нас интересует полуслед как формула для решения
квадратного уравнения, то этот факт не будет иметь значения.
Идея состоит в том, чтобы использовать равенство
Н(ж2г) = Н(хг) 4- хг + tr (жг)
и заранее табулировать только Н(х2г+[), i — 0, 1,.... Применяя индукцию,
можно получить формулу
Я (ж2’1) = Я(ж’) + ж2'’1’ + ... + ж2‘ + ж* + j tr (ж’).	
1.4. Скалярное умножение на несуперсингулярных кривых
51
Упражнение 1.4.12. Проверьте это.
Указание, tr(ж2) = tr(x).
Для вычисления полуследа тогда можно использовать формулу
Н(со + Cix + ... + Cn-jz"-1) = соЯ(1) + • •  +	-
= СоН( 1) 4- (ci 4- с2 4- с4 4- .. .)Н(х) 4-
4- (сз 4- Сб 4- С\2 4-.. >)Н(ж3) 4-... 4- Cn-iH(хп 2) 4-
+ (с2 4- с4 + с8 + .. .)ж 4- (с4 4- с8 4-.. .)ж2 +
4" (сб 4" Cj2 4" • • .)ж3 4-... 4" Сп-гХ^п 4-1,
где t € GF(2), г = 1, если п =. 3(mod4), г = 3, если n = l(mod4).
Упражнение 1.4.13. Проверьте это.
Указание. Примените предыдущее упражнение. В слагаемом t аккумулируются
следы tr (хг).
Таким образом, вычисление полуследа можно выполнить по формуле
Я(со + с,х + ... + Cn-js”’1) = С0Н(х) + С3Н(х3) + ... + Сп_2Н(хп~2) +
+ 3[Х + ... + s^-ij/ix^ ^2 +1, t € GF(2).
Обозначим s и С вектора длины п, дополненные нулями для тех
индексов, которые не входят в формулу.
Эти вектора можно вычислить более просто, чем непосредственно
по приведенной выше формуле, а именно можно в сумме
Со^О + .-. + Сп^Я^-1)
избавляться от четных слагаемых, применяя формулу
c2iH(а?) = с2;Я(а?) + c2ix' + c2i tr (xl)
по очереди, начиная со старших индексов. Если в начале положить
вектора s, С равными нулю, то указанная процедура их вычисления
заключается в выполнении в цикле с обратным порядком изменения
параметра i от (п - 1)/2 до 1 присваиваний
Cf = ф C2i, Si — Si ф
После окончания работы цикла получаются в точности те вектора, которые
нам нужны.
Упражнение 1.4.14. Проверьте, хотя нам это не понадобится, что
t = so tr (1) 4- Si tr (ж) 4-... 4- sn-i tr (zn-1).
52
Глава 1. Алгоритмы на эллиптических кривых
Если указанным способом построить схему в базисе ф, реализующую
линейное преобразование вектора с в вектора С, s то ее сложность будет
равна п — 1, а глубина [log2(n - 1)1 - 1. Выходы этой схемы надо подать
на входы схемы в том же базисе, реализующей линейное преобразование
(п - 1)/2 + 1-мерного вектора в n-мерный вектор.
Вместо формулы
Н(xVi) = Н(х') + ж2"'”1* + ... + x2i + х'' + j tr (ж*)
можно использовать формулу
Н(х2>') = H(xsr(x)) = H(xs+bl) + ... + H(xs+b') + H(xs),
где порождающий рассматриваемый базис неприводимый многочлен
f(x) = xn+r(x), г(ж) = xbl + ...H-aA-h 1, и п4-5 = 2Н, 0 s < п. Поэтому
вместо запоминания Н(х23г) можно запоминать H(xs+bi), i =
иЯ(ж5).
Упражнение 1.4.15. Докажите эту формулу.
Указание.
= xn+s = x\f(x) 4- г(ж)) = xsr(x) — xs+bl 4- ... 4- xs+b} 4- xs.
Если bi = degr < n/2 (а так обычно и бывает), то для любого г,
п/2 < i < n - deg г,
Я(^г) = Н (ж2г) + хг + tr (хг) = Н (г(х)х2г~т>) + хг + tr (х1) =
= H(xs+b>) + ... + H(xs+b') + H(xs) + я? + tr (?), s = 2г - m.
Так как s 4- deg г < i, эту редукцию можно применять для исключения не-
четных слагаемых Н(х1) при n/2 < i < n-deg г. После этого исключаются
все четные слагаемые. Этим экономится еще память, и соответственно
уменьшается число слагаемых до n/4 4- degr + 0(1) в формуле для вы-
числения
H(cq 4- CiX 4-... + cn_iXn~l) = s(x) 4- СгЯ(жг).
i
Заметим, что сложность схемы исключения нечетных слагаемых оценива-
ется сверху как (Z 4- 2)(n/2 - deg г)/2, а глубина — как log2((n/2 - deg г) х
+ 2»+ 0(1).
Пример 1.4.2. В качестве примера вновь рассмотрим неприводимый пятичлен
1 4- X3 4- X6 + X1 + Т163. Тогда исключение нечетных слагаемых с номерами
155 - 2г, i = 0,..., 36 выполняется с помощью формулы
Я(х155’2г) - Я(я31°-4г) + я155’* 44 tr (я155’21) -
= Я^147-4^163) +zl55-2t +tr (x155-2i) =
= z'55'2* + Я(ж|47-4‘'(ж7 + z6 + х3 + 1)).
1.4. Скалярное умножение на несуперсингулярных кривых
53
Сложность соответствующей схемы равна 5-37 = 185. Потом, применяя схему
сложности 162, исключаем все четные слагаемые. После этого остается построить
схему для (44, 163) линейного преобразования.
Однако число входов у подобной схемы можно и еще уменьшить. Так, еще
до применения второй схемы, можно для i = 0,..., 5 применять формулу
Я(х51-2') = Н(х102-4<) + ж51-2' + tr (ж51'2’) =
= Я (ж204-8-) + ж102’41 + ж51-21' + tr (ж102’4') + tr (ж51-и) =
= Я(ж41~8'ж163) + ж102"4'+ ж51-2'=
= Я(ж41~8'(ж7 + ж6 + ж3 + 1)) + ж102-41' + ж51-2*' =
= Я(ж48-8‘) + Я(ж47-8') + Я(ж44~8‘) + Я(ж4|-8‘) + ж'02’* + ж51-2£.
Сложность этой схемы 30. Если после ее применения применить схему слож-
ности 162 для исключения всех четных слагаемых, число оставшихся слагаемых
уменьшится до 38. Действуя так дальше, можно оставить только 21 слагаемое.
К оставшейся схеме можно применить алгоритм «четырех русских». Какой из мно-
гих возникающих вариантов предпочтительнее, зависит от того, схему мы строим
или пишем программу, от особенностей используемых компьютеров и т. д. Такие
вопросы приходится решать экспериментально.
В [43] утверждается, что время работы алгоритма равно примерно 2/3
времени умножения.
Вычисление квадратных корней. Очевидный метод извлечения квадратных
корней в поле GF(2n) основан на тождестве Ферма (ж2” ) = х и сводит
задачу к п - 1 возведению в квадрат.
Более эффективный метод основан на свойстве линейности квадрат-
ного корня
Разделяя четные и нечетные слагаемые, имеем
(п-1)/2	(п-3)/2
Г	( 2п-1\2г	/ 2п-1\2«+1
уС	C2i \Х j у C2i-j-iyX )
г=0	г=0
(п-1)/2	(п-3)/2	*	(п-1)/2	(п-3)/2
—	“Ь	^2г + 1*^ % = C2iX + \/х	C2i-\-\X •
i—Q	i=0	i=0	i—0
Поэтому извлечение корня сводится к сложению и умножению на зара-
нее вычисленный элемент у/х, причем второй сомножитель имеет степень
(п - 3)/2. Схемная сложность получается примерно вдвое меньше слож-
ности обычного умножения в поле. То же самое верно и для программной
сложности. Заметим еще, что вычисление векторов коэффициентов обоих
54
Глава 1. Алгоритмы на эллиптических кривых
многочленов можно ускорить, применяя заранее вычисленные таблицы
для аналогичных преобразований машинных слов.
Если используемый неприводимый многочлен есть трехчлен f(X) =
Xn + Xk + 1, и п нечетно, то у/х можно выразить явно. А именно, если
к нечетно, то 1 = Xn + Xk(modf(X)), откуда
_ т(п+1)/2 , „(*+1)/2
Если же к четно, то Хп = Хк + 1 (mod/(X)), откуда
у/Х = x~{n~i)/2(xk/2 + 1) mod f(X).
Для вычисления X~s mod f можно пользоваться равенствами X-t =
Xk-t + Xm-t mod	к
Пример 1.4.3. Пусть/(X) = Х233+Х74+1. Тогда л/Х = Х-11б(Х37+1) mod/(X).
Так как X"74 = 1 + X159, Х~42 = X32 + X19', то
X'116 = (1 + X159) (X32 + X191) = X32 + X117 + X191 mod /(X),
V® = (X32 + X1'7 + X191) (X37 + 1) mod /(X).
После раскрытия скобок получается шестичлен.
Таким образом, в приведенном примере сложность извлечения квад-
ратного корня будет приблизительно в шесть раз больше сложности сло-
жения и, очевидно, будет мала по сравнению со сложностью умножения.
Поэтому средняя сложность ополовинивания приблизительно вдвое мень-
ше сложности умножения (при использовании нормальных базисов при-
близительно равна сложности умножения). Если для вычисления кР при-
менять описанный выше метод с использованием проективных координат,
то его сложность приблизительно равна 2 log2 fc + (8 log2 k)/w+ 14(2W—1 -2)
умножений. На практике обычно к < 2300, w 5.
1.5. Скалярное умножение на аномальных кривых
Аномальными бинарными кривыми называются кривые Eq : У2 +
XY = X3 + 1, Еу : У2 + XY = X3 + X2 + 1. Они были предложены
в [62] и иногда называются кривыми Коблица. Дальнейшее изложение
основано на [95]. Некоторые усовершенствования алгоритмов [95], ориен-
тированные на вычисление точек вида к\Р -h fc2Q (подобные вычисления
встречаются в алгоритмах электронной подписи), были предложены в [35],
но они остались за рамками дальнейшего нашего изложения.
1.5.1. Свойства кривых Коблица
Легко проверить, что число точек в кривой Ea(GF(2)) = 3 - р,
а = 0,1, р = (-1)1-а. При четном п эти кривые изоморфны, а при
нечетном п они являются скручиванием друг друга.
1.5. Скалярное умножение на аномальных кривых
55
Согласно теореме Хассе число точек на кривой Ea(GF(2n)) равно
N(n) = 2п + 1 - ап - рп,
где а и 0 — корни квадратного уравнения X2 - tX 4- 2 = 0, в котором
коэффициент t = q 4- 1 - N(l) = 3 - Ea(GF(2)) = p. Корни уравнения
12±1 + 2 = 0в случае a = 1
o 1±гУ7
a,0 = —
а в случае a = 0
т. e. отличаются только знаком.
Известно, что последовательность Vn = an 4- 0п удовлетворяет рекур-
рентному соотношению Уп+1 - pVn 4- 2Vn_i = 0. Иногда такие последо-
вательности называются последовательностями Люка.
Упражнение 1.5.1. Проверьте это.
Так как Vq = 2, Vi = a 4- /3 р, то эту последовательность можно
вычислять с помощью указанного рекуррентного соотношения. Однако
иногда проще это делать, пользуясь явной формулой. Например, при
a = 1 применяя формулу Муавра имеем
Упражнение 1.5.2. Проверьте, что при нечетных п последовательности Vn для
а = 0,1 противоположны друг другу, а при четных п совпадают.
Так как группа Ea(GF(2)) является подгруппой Ea(GF(2n)), то поря-
док последней N(n) = 2п 4-1 - Vn кратен 1) = 3 - д. Для практического
использования надо выбирать кривые у которых г = N(ri)/N(l) — про-
стое число. Далее это мы будем предполагать.
Группы обеих кривых Коблица — циклические. Действительно, у кри-
вой Е\ порядок равен удвоенному простому, и она циклическая как про-
изведение циклических групп взаимно простых порядков.
Упражнение 1.5.3. Докажите это.
У кривой Eq подгруппа Eq(GF(2)) четвертого порядка циклическая,
так как 2(1,0) = (1,1), а в нециклической группе четвертого порядка все
ненулевые элементы имеют порядок 2.
Поэтому согласно предыдущему упражнению группа EQ(GF(2n)) то-
же циклическая.
Поэтому в группе Ea(GF(2n)) имеется циклическая подгруппа по-
рядка г.
Упражнение 1.5.4. Докажите это.
Ее назовем главной подгруппой.
56
Глава 1. Алгоритмы на эллиптических кривых
Упражнение 1.5.5. Точка Р принадлежит главной подгруппе тогда и только тогда,
когда Р = N(l)Q.
Указание. Воспользуйтесь свойствами циклических групп.
Есть более явный критерий принадлежности точки (ж, у) главной
подгруппе.
Упражнение 1.5.6. Точка (ж, у) принадлежит главной подгруппе кривой тогда
и только тогда, когда tr (ж) = 1.
Упражнение 1.5.7. Точка (х, у) принадлежит главной подгруппе кривой Eq тогда
и только тогда, когда tr (ж) = 0 и tr (у) = tr (Лж), где Л2 + А = ж.
Первое равенство вытекает из более общего факта.
Упражнение 1.5.8. Точка (ж, у) кривой Y2+YX = Х3+аХ2+Ь является удвоением
другой точки тогда и только тогда, когда tr (ж) = tr (а).
Указание. Согласно правилу удвоения ж = А2 4- А 4- а, откуда
tr (ж) — tr (A2) -h tr (А) + tr (а) = tr (а).
Обратно, пусть tr (ж) = tr(а), тогда tr(а 4- ж) = 0, значит А2 4- А = а 4- х при
некотором А. Возьмем Ж1 такое, что ж (А 4- 1) 4- ж? = у. Тогда ж2 (А2 4- 1) 4- х\ = у2,
ж2(А 4- 1) 4- ж?ж = ух, значит
у1 + ху = (А2 4- А)ж2 4- Ж1 4- ж?ж — (а 4- ж)ж2 4- х\ 4- ж?ж,
откуда 4- ж?ж = Ь. Положим у^ = Аж} 4- ж?. Тогда
г/2 = А2ж? 4-	= (А 4- ж 4- а)ж? 4- х*,
и Ж1?/1 = Аж2 4- х3, откуда
У1 + x^f = (А + ж 4- а)х2 4- ж? 4- Аж? 4- х\ =
= (ж? 4- аж?) + жж? 4- ж? = ж? 4- аж? 4- Ь.
Второе тоже вытекает из более общего факта.
Упражнение 1.5.9. Точка (ж, у) кривой Y2+YX = Х3+аХ2+Ь, tr (а) = 0, является
учетверением другой точки тогда и только тогда, когда tr (ж) = 0 tr (у) = tr (Аж),
где А2 4- А = х 4- а.
Указание. Пусть (ж, у) = 4(х\,у{), (х2,у2) = 2(ж1,х/1). Тогда tr (ж) = tr (ж2) = 0.
Пусть А = ж2 4- Уг/х2, тогда у = Ж2 4- (А 4- 1)ж, А2 4- А = ж 4- а. Так как tr (ж?) =
tr (ж2) = 0, то tr (у) = tr (Аж). Обратно, пусть tr (ж) = 0, tr (у) = tr (Аж), А2 4- А =
ж 4- а. Из tr (ж) = 0 следует, что (ж, у) = 2(ж2, у2) для некоторой точки (ж2, у2).
Из формулы удвоения следует, что А = ж2+у2/х2, у = ж2 4* (А 4- 1)ж, А2 4-А = ж 4-а.
Тогда у 4- Аж = ж2 4- ж, значит
0 = tr (у) + tr (Аж) = tr (у 4- А) = tr (ж? 4- ж) =
= tr (ж) 4- tr (ж?) = tr (ж?) = tr (ж2).
Поэтому (ж2, у2) = 2(жь yi).
1.5. Скалярное умножение на аномальных кривых
57
Эндоморфизм Фробениуса. Очевидно, что, если (ж, у) € Ea(GF(2n)), то
(Х2,у2) е Ea(GF(2n)).
Это отображение называется эндоморфизмом Фробениуса.
Упражнение 1.5.10. Проверьте это.
Указание. Обе части возведите в квадрат, пользуясь тождеством Фробениуса.
Рассмотрим на группе Ea(GF(2n)), отображение Фробениуса т:
(х,у)	(х2,у2У
Упражнение 1.5.11. Проверьте, что r(Pt 4- Pi) = T(Pi) 4- т(Р2).
Указание. Рассмотрите случаи Р[ = Р2 и / Р2 и обе части возведите в квадрат.
Отображения с таким свойством называют эндоморфизмами кривой.
Эндоморфизмы кривой можно складывать по формуле (/i + Л)(р) =
/1(Р) 4- fi(P) и умножать по формуле (/i * fi)\P) = fcCfiiP))- Кроме
эндоморфизма Фробениуса есть еще два тривиальных примера эндомор-
физмов — нулевой и тождественный эндоморфизмы.
Упражнение 1.5.12. Проверьте, что сумма и произведение эндоморфизмов явля-
ются эндоморфизмами. Множество всех эндоморфизмов данной кривой образует
кольцо.
Упражнение 1.5.13. Проверьте, что тп — тождественный эндоморфизм кривой
E(GF(2n)).
Известно, что т2 4- 2 = рт, т. е. для любой Р т(т(Р)) 4- 2Р = рт(Р).
Короткое доказательство этого тождества требует знания теории эллип-
тических кривых. Поэтому мы выполним прямую проверку. Сделаем ее
в случае а = 0, т. е. кривой Y2 4- XY = X3 4- 1. Тогда р = -1. Пусть Р
имеет координаты (х,у). Тогда, очевидно,
т(Р) = (а:2, у2), р.т(Р) = (х2,х2 + у2), т2(Р) = (а:4 ,/),
и согласно правилу сложения
2(ж, у) = (х2 4- ж"2,	4- ж^ (х 4- ж2 4- ж-2) 4- ж2 + ж-2 + у^ ,
при ж = 0, очевидно, у = 1 и 2(ж, у) = О — бесконечно удаленная точка.
Нам надо проверить тождество (ж4,т/4) 4-2(ж, у) = (ж2, ж2 4-?/2). При
ж = 0 оно очевидно, так как и слева и справа получается точка (0, 1).
Далее предполагаем, что ж 0. Сначала рассмотрим случай ж4 = ж2 4-ж”2.
Так как ж6 4- ж4 4- 1 = (ж3 4- ж2 4- 1) , то тогда ж3 4- ж2 4- 1 = 0,
\~+ ж) (ж 4- ж2 4- ж'2) 4- ж2 4- ж-2 + у = ( - 4- ж ) (ж 4- ж4) 4- ж4 4- у =
= ух2 + х2 + х5 +х4 = (ух + а:3 + 1)а:2 + х6 + 1 =
= у2х2 + х6 + 1- (ух + х3 + 1)2 = у4,
58
Глава 1. Алгоритмы на эллиптических кривых
значит (ж4, у4) =2(х,у),и для сложения надо применять формулы удво-
ения. Этот случай возможен только при п кратном трем, так как корни
уравнения х3 + х2 4-1 = 0 лежат в поле GjF(23) и порождают его, а оно со-
держится в поле GF(2n) только при указанном условии. В этом случае до-
статочно рассмотреть удвоение трех точек кривой (GF (23)), что можно
сделать непосредственным вычислением, которое мы оставляем читателю.
В случае же а?4 я2 + х~2 надо применять формулы сложения.
Сделаем вначале проверку для ж-координат. Надо проверить тождество
Л2 4- Л + х4 + х2 + х~2 = ж2, где
_ у4 4- (у/х 4- ж) (ж 4- х2 4- х~2} + х2 4- х~2 4- у
х4 4- х2 4- х~2
Заменяя у4 на 4- х3 4- 1)2 = у2х2 4- Xе 4- 1 = ух3 4- х5 4- х2 4- х6 4- 1,
имеем
ух3 4- х5 4- х2 4- х6 4-1 + (у + х2) (1 4- х + ж“3) 4- х2 4- х~2 4- у
Л=	ж4 + х2 + х~2	=
у(х 4- х3 4- х~3) 4- х5 + х6 4-1 4- я2(1 4- х 4- ж-3) 4- х~2
х4 4- х2 4- х~2
у х5 4- х6 4-1 + х2 4- х3 4- х~* * * * * * * * х 4- х~2
х	х4 4- х2 4- х~2
у х1 4- ж8 4- х2 4- х4 4- Xs 4- х 4- 1 у у
— —।-----------------------------— —1_ х 4- х 4~ 1 •
х	хь 4- ж4 4-1	х
Подставляя Л = у/х 4- х2 4- х 4-1, имеем далее
Л2 4- Л 4- х4 4- х~2 = ^г4--4-ж4 + ж24-14-ж24-ж4-1-Ьж44- х~2 =
х2 х
^ + *+1 + х-> = ^ + *х + х' + х=а.
X1 X	X2
и равенство х-координат доказано.
Для проверки равенства у-координат, используя доказанное тожде-
ство, достаточно проверить тождество
Л(я4 + ж2) 4- х2 + у4 = х1 4- у2.
Подставляя Х = у/х + х2 + х + \ и заменяя у4 на ух3 4- х5 + х2 + х6 4-1,
имеем
Л(ж4 4- ж2) 4- у4 =	+ х2 4- х 4-(ж4 4- х2) 4- ух3 4- х5 + х2 4- хв 4-1 =
= (х2 4- х 4- 1) (ж4 4- ж2) 4- ух 4- х5 + х2 4- хв 4-1 =
= ух 4- х3 4-1 = У2,
что и требовалось доказать.
1.5. Скалярное умножение на аномальных кривых
59
Кольцо эндоморфизмов и комплексное умножение. Рассмотрим подкольцо
кольца эндоморфизмов кривой l?e(GF(2n)), порожденное эндоморфиз-
мом Фробениуса.
Упражнение 1.5.14. Проверьте, что оно состоит из эндоморфизмов вида
1	+ • • • + О(Ь
где ai — целые числа, 2/ = / + /, 3/ = f 4- f 4- f, и так далее, (-/)(Р) =
Далее оно обозначается через Z[t]. Представление его элементов
в виде многочленов от т с целыми коэффициентами неоднозначно.
Например, согласно доказанному тождеству эндоморфизм т2 - рт 4- 2
нулевой. Рассмотрим написанное выше уравнение в поле комплексных
чисел и обозначим также через т его корень
р 4~ yj —"1
2	’
Сопоставим каждому эндоморфизму из кольца Z[r] комплексное число
1 4- ... 4- во-
Множество всех таких чисел также обозначим Z[r]. Говорят, что кривые
Еа обладают комплексным умножением на т.
Упражнение 1.5.15. Проверьте что это множество является подкольцом поля ком-
плексных чисел, а указанное выше отображение — гомоморфизмом колец (т. е. со-
храняет кольцевые операции). Пользуясь тождеством т2 - рт 4- 2 = 0, проверьте,
что кольцо Z\r] состоит только из элементов вида а 4- Ьт, где а, b — целые числа,
и запись в таком виде однозначна.
Назовем нормой N(a) элемента этого кольца число аа, где а —
число, сопряженное к а.
Упражнение 1.5.16. Проверьте, что N(a 4- Ьт) = (а 4- Ът)(а 4- Ьт) = а2 4- раЬ 4- 2Ь2.
В частности, N(t) = 2, N(r - 1) = 3 - р = N(l).
Указание, тт = 2,т + т = р.
Упражнение 1.5.17. Проверьте, что для а, ft G Z[t] N (aft) = N (a)N (ft), N(a/ft) =
N(a)/N(ft) (мультипликативность нормы).
Указание, aft = aft, l/a = (1 /a).
Упражнение 1.5.18. Проверьте, что для a € Z\r\ y/N(a) = совпадает с мо-
дулем комплексного числа a. Поэтому справедливо неравенство треугольника
\/N(a + /?)	y/N&) + у/щр).
Упражнение 1.5.19. Проверьте, что N(rn - 1) = |Fa(GF(2n))| = N(n).
Указание.
N(Tn - 1) = (тп - l)(fn - 1) = (тт)п + 1 - тп - тп =
= 2n + l-Vn = \Ea(GF(2n))\.
Упражнение 1.5.20. Проверьте, что 7У((тп - 1)/(т - 1)) = Л^п)/^!).
60
Глава 1. Алгоритмы на эллиптических кривых
Евклидовость и факториальность кольца Я[т]. В кольце Z[t] можно
выполнять деление с остатком в том смысле, что для любых его эле-
ментов a, fl 0 найдутся элементы S,p € Z[t], такие, что а =	4- р,
N(p) < 7У(/3). Далее это будет доказано. Кольца с таким свойством назы-
вают евклидовыми. Элемент р называется остатком, а элемент 6 частным.
Вообще говоря, они могут быть определены неоднозначно. Если остаток
равен нулю, то частное называется делителем. Наибольшим общим делите-
лем двух элементов кольца называется такой их общий делитель, который
делится без остатка на любой другой общий делитель. Наибольший общий
делитель определен неоднозначно, а с точностью умножения на обрати-
мый элемент кольца.
В любом евклидовом кольце с помощью алгоритма Евклида можно
найти наибольший общий делитель любых его элементов а, fl и предста-
вить его в виде xa+yfl, где х, у тоже элементы этого кольца. Доказывается
это точно так же, как для кольца целых чисел.
Упражнение 1.5.21. Докажите это для кольца Z\r] без использования алгоритма
Евклида.
Указание. Пусть д = ха 4- у fl /= 0 — элемент с минимальной нормой среди всех
элементов такого вида. Тогда а и fl делятся на 6 без остатка, в противном случае
остаток р — а - ду — а(1 - 2:7) - fly^ имел бы меньшую норму. Если другой
общий делитель a, fl, то он делит ха 4- у fl = 5.
Упражнение 1.5.22. Докажите, что в кольце Z[r] наибольший общий делитель
является наибольшим по норме среди всех общих делителей и определен с точ-
ностью до смены знака.
Указание. Примените свойство мультипликативности нормы и предыдущие уп-
ражнения.
Элемент кольца (коммутативного, с единицей, без делителей нуля)
называется простым, если его нельзя представить в виде произведения
необратимых элементов кольца. Элемент называется необратимым, если
он не имеет обратного элемента в этом кольце. Очевидно, что кольцо 7[т]
коммутативно, имеет единицу и не имеет делителей нуля, так как лежит
в поле.
Упражнение 1.5.23. Проверьте, что в кольце Z[r] обратимы только ±1, и других
элементов с единичной нормой в нем нет.
Указание. Из мультипликативности нормы следует, что, если элемент обратим, то
его норма равна 1. Очевидно,
0	о / Н>Ъ\2	7 b2 7Ь2
N(ц 4~ &т) = a 4~ pab 4" 2& — I а 4~	} 4—~	~
Поэтому N(a 4- br) = 1 тогда и только тогда, когда b = 0, a = ±1.
Упражнение 1.5.24. Проверьте, что, если у элемента норма — простое число, то
элемент — простой. В частности, т — простой элемент и простые целые числа
являются простыми элементами кольца Z[r].
Указание. Примените мультипликативность нормы и предыдущее упражнение.
1.5. Скалярное умножение на аномальных кривых
61
Упражнение 1.5.25. Докажите, что любой необратимый ненулевой элемент можно
представить в виде произведения простых элементов.
Единственность такого представления не для всех таких колец имеет
место, но ее можно доказать для евклидовых колец.
Упражнение 1.5.26. Докажите для евклидовых колец, что, если ab делится на про-
стой элемент р, то а или b делится на р.
Указание. Пусть а не делится на р. Тогда наибольший общий делитель аир равен
±1, так как р простой элемент. Поэтому для некоторых ж, у имеем ах +ру = 1.
Отсюда b = abx + pyb кратно р, так как ab и pby делятся на р.
Упражнение 1.5.27. Докажите для евклидовых колец, что, если а^ . ..ап делится
на простой элемент р, то хотя бы один из аг делится на р.
Указание. Примените индукцию и предыдущее упражнение.
Упражнение 1.5.28. Докажите для евклидовых колец, что разложение на простые
множители определено однозначно (с точностью до перестановки сомножителей
и домножения на обратимые элементы).
Указание. Так же, как и в случае кольца целых чисел, примените индукцию
по числу простых сомножителей и предыдущее упражнение.
Кольца с единственностью разложения на простые элементы назы-
ваются факториальными.
Минимальные уравновешенные т-адические коды. Представление произ-
вольного элемента кольца Z\r} в виде аттт 4-... 4- ао, где аг = 0, ± 1,
назовем уравновешенным т -адическим кодом. Уравновешенный т-адиче-
ский код назовем минимальным, если = 0 при любом г.
Пример 1.5.1. Число 9 имеет минимальный т-адический код (1, 0,-1, 0,0,1),
так как 9 = т5 - т3 4- 1.
Упражнение 1.5.29. Проверьте это прямым вычислением.
т-адические коды для натуральных чисел позволяют умножать ска-
лярно на эти числа точки кривой Еа, не используя операцию удвоения
точек, а используя только сложение.
Пример 1.5.2. Если Р = (ж, у), то согласно формулам Фробениуса
9Р = (х32,у32) - (x\ys) + (х,у).
Пренебрегая сложностью возведения в квадрат, получаем оценку сложности
скалярного умножения на 9 в виде L(9)	2(Р(1) 4-2Р(М)), где
сложность инвертирования и умножения в данном поле. Применяя формулы
9Р = т3 (т2Р - Р) 4- Р, можно воспользоваться проективными координатами
и получить оценку Z(9) < 16Р(М) 4- L(I) 4- 2L(M).
Если же воспользоваться двоичным кодом 9 = 23 4-1, то 9Р = 2(2(2Р)) 4- Р,
откуда имеем Z(9)	4(Z(Z) 4- 2Р(М)). Используя проективные координаты,
получаем, с учетом возвращения к аффинным координатам
Z(9) < 3(4Z(M)) + 8Z(M) 4- L(I) 4- 2Р(М).
62
Глава 1. Алгоритмы на эллиптических кривых
Упражнение 1.5.30. Попробуйте улучшить эту оценку методом Монтгомери и ме-
тодом использования ополовинивания вместо удвоения.
Справедлива
Теорема 1.5.1. Любой элемент кольца Z\r\ имеет единственный мини-
мальный код.
Доказательство основано на следующей лемме:
Лемма 1.5.1. Элемент Cq 4- суг 6 £[т] делится на г тогда и только
тогда, когда Со четно, и делится на т2 тогда и только тогда, когда
со = 2ci(mod 4). Всегда справедливо только одно из утверждений', а делится
на т, а = ±l(mod т2).
Упражнение 1.5.31. Докажите лемму.
Указание. Если Со+^т = r(d0+diT), то согласно тождеству Фробениуса с04-С1Т =
-2di 4- (d0 4- pd\)T, откуда с0 = —2d\. Обратно, если с0 четно, то
Со 4- Ci т	/ХСО + 2С1 Со
— .
т	2	2
Вместо деления на т2 делим на рт - 2. Тогда
с0 4- с{т = (do 4- d{T)(pr - 2) = -2(d0 4- pd{) 4- (pdQ - di)r.
Учитывая p — ±1, имеем c0 = 2ci mod 4. Обратно,
Co 4- C[T (1 4- 2p)c0 4- 2pCi c0 - 2c{
~r^~ =------------4-------+
Если co четно, то a = Со + с^т делится на т, если с0 нечетно, то с0± 1 = 2cY mod 4,
значит, a ± 1 делится на т2.
Из последнего утверждения леммы следует, что два минимальных
кода для одного элемента из 7[т] имеют одинаковые самые правые
цифры.
Упражнение 1.5.32. Проверьте это.
Отсюда, применяя индукцию, выводим единственность минималь-
ного кода.
Упражнение 1.5.33. Проведите это рассуждение более подробно.
Существование минимального кода для Со 4- С{Т вытекает из следую-
щего алгоритма его построения. Положим tq = cq, = Ci, i = 0. Пока
го 0 или и / 0, в цикле делаем следующие операции: если г0 нечетно,
то щ — 2 — (г0 - 2т \ mod 4), г о = го - щ иначе щ = 0 (вычисление оче-
редной цифры щ = 0, ±1); потом i = i 4- 1, r0 = и -4- prQ/2, r\ — -r0/2
(деление г о 4- Г\Т на т).
После окончания работы цикла в массиве (щ_\,... ,щ) будет записан
минимальный код.
Упражнение 1.5.34. Проверьте это.
1.5. Скалярное умножение на аномальных кривых
63
Определение минимального т-адического кода совершенно анало-
гично определению минимального 2-адического кода и между ними мож-
но установить взаимно-однозначное соответствие. Известно, что плот-
ность ±1 в минимальном 2-адическом коде в среднем асимптотически
равна 1/3. Поэтому то же верно и для т-адического кода. Однако дли-
на т-адического кода для числа п асимптотически вдвое больше, чем
у 2-адического кода, так как эта длина I для произвольного a G Z[r]
оценивается как
log2 N(a) - 0,55 < I < log2 + 3,52,
a log2 7V(n) = 21og2n.
Доказательство этих неравенств основано на следующих утверждени-
ях, которые мы формулируем в виде упражнений.
Обозначим JVmax(Z) наибольшую, а через 7Vmin(0 наименьшую норму
элементов Z[r] с минимальным кодом длины I.
Упражнение 1.5.35. Проверьте, что для любого I 2Nmax(l) 7Vmax((Z + 0)-
Указание. Если а элемент с минимальным кодом длины I и нормой NmaK(l), то
N(ат) = 2N(а) и его минимальный код имеет длину I + 1.
Упражнение 1.5.36. Проверьте, что наибольшая норма элементов Z[t] с мини-
мальным кодом длины не более I равна 7Vmax(0-
Указание. Примените предыдущее упражнение.
Упражнение 1.5.37. Докажите, что при с > к
у/nZJc) 2k,2yjNmm(c-k) + y/N^k),
^min(c) 2k/1y/Nmin(c-k)- y/N^ik).
Указание. Пусть 7 имеет код (ис_ь..., u0), N(y) = Nm(c), где Nm = Nmm
или jVmin, и р имеет код (ufc_b..., щ), тогда N(p) 7Vmax(fc), 7 =
7Vmin(c - k) N(8) 2Vmax(c - к), и из неравенства треугольника имеем
0V(7) 2к/2у/тЦд) 4- y/N(p), ^(7) 2k/2^N(i) - у/1Цр).
Положим для краткости Mi = -У2_/7Утах(/).
Упражнение 1.5.38. Выведите из предыдущего упражнения, что при с > к
Мс Мс_к + 2{с-к)/2Мк.
Упражнение 1.5.39. Докажите для положительных d, q
Mdq < Md
1 _ 2~d<i/2	1 - 2-d/2'
Указание. Из предыдущего упражнения следует, что M^^d - Mkd 2~kd/2Md;
просуммируйте эти неравенства и примените формулу суммирования геометриче-
ской прогрессии.
64
Глава 1. Алгоритмы на эллиптических кривых
Упражнение 1.5.40. Докажите, что для I > d
_ 2-d/2 ’	< pd/2 _ р2 •
Указание. Пусть (k - l)d < I kd; примените предыдущее упражнение.
Упражнение 1.5.41. Докажите, что для I > 2d
NmM > ^Nmin(d) -	 2‘-d.
Указание. Примените предыдущие упражнения.
Из предыдущих упражнений следует, что, если а имеет минимальный
уравновешенный т-адический код длины I > 2d, то
( Гм 7л\ Nmax(d)\ Id	^max(^)
^V^min(d) -	-2	< N(a) < (2<j/2 _ 1)2 • 2 .
Применяя это неравенство при d = 15 и вычисляя, что Nmax(15) = 47 324,
^min(15) = 2 996, имеем при I > 30
1,399 • 2 • 21-4 < 7V(a) < 0,731 • 2;+1,
откуда log2 N(a) - 0,55 < I < log2 jV(a) 4- 3,52. В [95] показано, что эти
оценки близки к точным.
Используя их, получаем, что кР можно вычислить, сделав в среднем
(2/3) log2 к сложений со сложностью ((2/3) log2 + 2L(M)) без ис-
пользования проективных координат и со сложностью
((2/3) log2 &)(8L(M)) + L(I) + 2Z(M)
с использованием проективных координат. В стандартном алгоритме
с применением двоичного кода среднее число используемых сложе-
ний точек кривой вдвое меньше, но зато используется log2 к удвоений,
и общая сложность без использования проективных координат равна
(4/3 log2 &)(£(!) 4-2Z(M)), а с использованием проективных координат
она равна
((4 + 8/3) log2 k)L(M) + Z(I) + 2Z(M).
Преимущество указанного метода еще более возрастает, если перед
построением минимального уравновешенного кода выполнить модуляр-
ную редукцию, которая уменьшает в два раза длину кода.
1.5.2. Использование модулярной редукции
Эквивалентность т-адических разложений. Будем говорить, что у,р 6 7[т]
эквивалентны, если эндоморфизмы 7(Р), р(Р) совпадают на данной кри-
вой Ea(GF(2n)).
Лемма 1.5.2. Если у = р mod тп - 1, то у и р эквивалентны.
1.5. Скалярное умножение на аномальных кривых	65
Доказательство. Так как согласно одному из упражнений тп — тож-
дественный эндоморфизм, то (тп - 1)Р = О для любой точки Р данной
кривой. Если в кольце Z[r] у = р mod тп - 1, то 7 = р + 6(тп - 1), значит
7(Р) = р(Р) + <5(гп - 1)(Р) = р(Р) + <5(0) = />(Р) + О = р(Р).
Положим 6 — (тп - 1)/(т - 1). Было ранее проверено, что N(6) =
г == \Ea(GF(2n))\/h, h — 3 - р, и г — порядок главной подгруппы. 
Лемма 1.5.3. Если Р точка главной подгруппы, то 6(Р) = О.
Доказательство. Из упражнений следует, что Р = hQ, (тп - 1)Q = О.
Поэтому <5((т - 1)Q) = (тп - 1)Q = О. Положим эндоморфизм т - 1 =
-1 4- р - т, тогда т - 1(т - 1) = 1 - р 4- рт - г2 = 3 - р = h,
О = (r“)(d((r - 1)Q)) = 5(т^Т(т - 1)Q) =	= J(P).	
Из леммы следует
Теорема 1.5.2. Если Р принадлежит главной подгруппе группы Ea(GF(2n)),
и р = у mod 6, то эндоморфизмы р и у совпадают на главной подгруппе.
Доказательство. Если в кольце Z[r] у = ртодд, то 7 = р 4- д/3,
значит
7(Р) = р(Р) + /3(<5(Р)) = р(Р) + /3(0) = />(Р) + 0 = р(Р).	
Пользуясь теоремой 1.5.1 для вычисления кР в случае Р, принад-
лежащего главной подгруппе, сначала можно найти р Е Z\r\ такой, что
р = kvaodqd, а потом для него вычислить минимальный т-адический
код и вычислить р(Р), пользуясь этим кодом. Для нахождения р можно
применить алгоритм деления, так как в качестве р можно взять остаток
от деления к на 6. Тогда N(p) < N(d) = г. Далее мы покажем, что
на самом деле даже N(p) 4N(S)/7 = 4т/7. Так как г = \Ea(GF(2n))\/h,
h = 3-p = 3-(-l)1"e = 22"а, Ea(GF(2n)) = 2n + l-Vn = 2n+O(2°/2), то
Поэтому для длины I минимального т-кода для р имеем неравенство
I < log2 N(p) + 3,52 < п 4- a 4- 0,8,
а так как I — целое, то I п 4- а, а = 0,1.
Можно доказать, что среднее число ненулевых цифр в минимальном
т-коде для р — fcmodJ асимптотически равно 1/3. Поэтому число сло-
жений точек при вычислении кР при к — О(т) будет вдвое меньше, чем
было раньше.
Далее будет доказана евклидовость этого кольца и предложен алго-
ритм деления, для которого оценка нормы остатка через норму делителя
имеет вид N(p) 4N(d)/7.
66
Глава 1. Алгоритмы на эллиптических кривых
Пчелиные соты и округление до целых точек. Определим на плоскости
(Ло, А}) выпуклый центрально-симметричный шестиугольник U системой
неравенств
— 1 2Ло + рХ\ <1,
—2 Ло 4- 4/zAj < 2,
—2 Лд — 3/1Л) < 2.
Очевидно, U является пересечением трех полос, каждая из которых
ограничена параллельными прямыми. Для каждой целой точки £ этой
плоскости обозначим шестиугольник, полученный из U параллель-
ным переносом на вектор Центром U(£) будет точка %.
Упражнение 1.5.42. Проверьте, что система {U(£), £ € Z2} состоит из попарно
непересекающихся шестиугольников, объединение которых покрывает всю плос-
кость.
Указание. Каждый из шестиугольников решетки имеет 6 соседей, каждые два
соседа имеют одну общую сторону.
Упражнение 1.5.43. Докажите, что для любой точки Л Е U 7V(A)	4/7.
Указание. Рассмотрите эллипс Ад 4- рХ^Х[ 4- 2Aj = 4/7, состоящий из точек с нор-
мой не большей 4/7 и проверьте, что он проходит через вершины С7, и поэтому его
содержит в силу выпуклости. Например, одна из вершин является точкой пересе-
чения прямых 2Л0 4- pXi = 1, Ао 4-4дЛ! = 2, т. е. точкой (2/7, З/7/z) — (2/7, ±3/7),
лежащей на эллипсе, так как 4/494-6/494-18/49 = 4/7. В силу симметрии остается
проверить еще две вершины.
Упражнение 1.5.44. Докажите, что для любой точки Л Е U и любого £	0, £ Е Z[t]
N(X)<N(X + O-
Указание. Проверьте, что N(А)<7V(A± 1) тогда и только тогда, когда 12Ао4-дA11 < 1,
N(X) < N(X±r) тогда и только тогда, когда |4Ai 4-/хА0| < 2, N(X) < N(X±t) тогда
и только тогда, когда \рАо - 3А!| < 2, где т — (p-iVl)/! = -т + р. Так как А € U,
то выполнены все три условия, поэтому неравенство доказано для £ = ±1, ±т, ±т.
Для остальных ненулевых £ € Z[r] N(£)	4, а так как N(X) 4/7, то согласно
неравенству треугольника
yfrfW ± < 2 - ± у/Й(£) - yGv(A) < yjN(X + ().
Для произвольной точки А обозначим к = Round (А) такую целую
точку, что А Е U(k) и определим ( := ((A)) = X - к. Очевидно, £ Е U,
поэтому 4/7, и для любого a Е Z[r] N(£) < N(£ 4- а).
Определим Round (А) для действительных чисел равенством
Round (А) = [А+ 1/2J,
тогда, очевидно, ((A))	1/2.
Для комплексных чисел А = (Ai, А2) вычислить Round (А) можно
следующим алгоритмом.
1.5. Скалярное умножение на аномальных кривых
67
Положим fi = Round (Аг), щ = Xi - fi, hi = 0, i = 1, 2.
Положим т/ = 2т/о + p^h •
Если ту 1,
то
если т/о ~ 3/17/1 < -1, то hi = р, иначе ho = 1
иначе
если т/о + 4/ZT/1	2, то hi = р
Если т/ < -1,
то
если т/о - З/17/i	-1, то hi = р, иначе До = -1
иначе
если т/о 4- 4/17/1 < -2, то Д1 = -р.
На выходе алгоритм выдает дг = Л 4- , г = 1, 2.
Упражнение 1.5.45. Убедитесь в правильности алгоритма.
Деление с остатком в кольце Z[r]. Пусть делимое 7 = со 4- CiT Е Z[t],
делитель 8 = d0 4- diT € Z[t], частное к = qo 4- q^r € Z[r], остаток р —
го + г1т € Z\r\ таковы, что 7 = к,8 + р, и мы хотим минимизировать N(p)-
Положим А = 7/J, тогда
7J _ 7J _ gp+gir
~ 86 ~ N(8) ~ N ’
Положим к = Round 4- ^т). Тогда р = у - кб, и алгоритм деления
выглядит следующим образом.
Положим
до = Codo 4- pc^di 4- 2cidi, gi = Cido — c^di, N = do 4- pdodi 4- 2di,
Xi=gi/N, г = 1,2, (go Л1) = Round (Ao, Ai),
ro = Co — doqo 4- 2diqi, Ti = Ci — diqo — doqi — pdiqi.
Упражнение 1.5.46. Проверьте правильность алгоритма.
Так как р = у - к8 = (А - к)8 — (А - Round (А))(5 = ((А))(5 = ((7/J)) J,
то ВД = jV(((A))<5) = tf(((A))W) ±N(6).
Далее этот остаток р обозначаем 7 mod 8.
Вычисление редуцированного т-адического кода. Для этого надо вычислить
k mod (5, где 8 = do 4- dir = (тп - 1)/(т - 1), N(6) = г, а потом вычислить
минимальный т-адический код. Для выполнения деления с остатком
применяем предыдущий алгоритм к 7 = к. Тогда	So = do 4- pdi,
si = -di.
Для вычисления целых чисел Si воспользуемся второй последова-
тельностью Люка, определяемой рекуррентными соотношениями
Uo = O, Ui = l, Ui+i = pUi - 2Ui-i, г>0.
68
Глава 1. Алгоритмы на эллиптических кривых
Упражнение 1.5.47. Докажите по индукции, что Ui целые нечетные числа.
Упражнение 1.5.48. Докажите по индукции, что Ui = (тг - т)/у/-7.
Упражнение 1.5.49. Докажите по индукции, что тг = tyr - 2Ui-i, i > 0.
Упражнение 1.5.50. Докажите, что U? — ригиг~\ + 2U^_{ = 2г-1, i > 0.
Указание. Предыдущее тождество умножьте на сопряженное.
Так как при переходе к сопряженным числам имеем
do + dXT = (fn - l)/(f - 1),
то, складывая с равенством
do + dir = (тп - 1)/(т - 1),
находим, складывая дроби, что
2do 4- pd\ —
UnT-2Un.{-\ Unr-2Un^-\
т - 1	f - 1
(4-д)СГп + (4-2м)^-1 + 2-д
Вычитая равенства, имеем
£7пт - 2^-! - 1	^7-2^,!-1 _ v^7(-t7n + 2CTn 1 + l)
откуда
Un - 2^| - 1
З-Д
значит
2so — 2do 4~ 2pd\ —
(4 - ц)Цп + (4 - 2д)[Гп! + 2 - д д(-С7п + 2LZn, + 1) _
3 — д	З-д
_ (4-2/z)rn4-4CZn 14-2 _2(2-/i)l7n4-2£7n-1 + l
3 - р	3 — р
Упражнение 1.5.51. Проверьте, что $г = (-1)г(1 - pUn+3-a-i)/(3 - д), г = 0,1.
Указание. При a = 0
Ui+l = pUi - 2Ui-{ = -Ui - 2Ui-{ = (U^ 4- 2Ui_2) - 2U^ = -U^ 4- 2^_2.
Вычисление tq 4- ryr = femod (rn - 1)/(т - 1) выполняется следую-
щим алгоритмом.
Положим do = so 4- psx, Xi = Sik/r, (qo, q\) = Round (Ao, Ai), тогда
го = k - doqo - 2s\qi, — s^qo - $o<7i.
1.5. Скалярное умножение на аномальных кривых
69
Оконный т-адический метод. Этот метод в определенном смысле ана-
логичен оконному 2-адическому методу, и также является обобщением
обычного т-адического метода на случай окна произвольной длины к.
В случае отсутствия ограничений на память, этот метод ускоряет скаляр-
ное умножение на несуперсингулярных кривых при подходящем выборе
ширины окна. Основан он на следующей теореме:
Теорема 1.5.3. Для любого натурального w и любого элемента кольца Z\r}
существует единственное его представление в виде
аттГП + ... + ^0?
где аг — 0, ±1, ±3,..., ±2W-1 - 1, и среди любых w подряд идущих коэффи-
циентов максимум один ненулевой.
Для доказательства понадобятся следующие определение и лемма.
Определим число tm так, что tm = 2Um-iU^ mod2w. Так как Um
нечетно, то Um 1 mod 2W существует и однозначно определено, значит tm
тоже определено однозначно, четно, но не кратно 4. Из упр. 1.5.50 следует,
что
- ptm + 2 = 0 mod 2m.
Упражнение 1.5.52. Проверьте это.
Таким образом, tm удовлетворяет по модулю 2г тому же уравнению,
что и число г в поле комплексных чисел. Поэтому соответствие т —> tm
можно естественным образом продолжить до отображения
Фт : UQ + U1T -> Uo + u\tm
кольца Z[t] в кольцо Z^ вычетов по модулю 2т.
Будем говорить, что элемент uq + U\T нечетен, если uq нечетно; эле-
мент uq + U[tm mod 2т нечетен, если Uq нечетно. Аналогично определяем
понятие четности.
Упражнение 1.5.53. Проверьте, что это отображение является гомоморфизмом
колец, т. е. сумму переводит в сумму и произведение — в произведение (а также
нуль — в нуль и единицу — в единицу). Проверьте, что нечетные элементы оно
переводит в нечетные, а четные — в четные
Следующая лемма обобщает лемму 1.5.1.
Лемма 1.5.4. фт{а) = 0 тогда и только тогда, когда a Е Z\r\ делится
нацело в этом кольце на тт.
Доказательство. Так как фт(т) = tm = 2 mod 4, то по индукции мож-
но проверить, что фт(т^) = 27 mod 2^+1. Значит, фт(тт) = 0 mod 2т,
поэтому
Фт(о) = Фт(/3гт) = фт(/3)фт(тт) = 0 mod 2m.
Для доказательства в другую сторону предположим, что a = /3rJ , j < т,
0 = uq + U[T, uq Ф 0, тогда можно считать, ЧТО Uq 6 Z[t] есть остаток
70
Глава 1. Алгоритмы на эллиптических кривых
от деления /3 на т, поэтому 0 < N(uq) < N(t) = 2, значит N(uq) = 1,
поэтому uq = ±1, откуда следует нечетность 0т(Д) = uq 4- фт(и\)Фт(т) и
Фт(а) = Фт(Рт3) = фт(Р)фт(т3) = 23 mod 2J+1 /= 0 mod 2m.	
Из леммы следует, что при отображении фт нечетные классы вычетов
в кольце Z\t\ по модулю тт переходят в нечетные классы вычетов
в кольце Z^, а четные — в четные, причем равные по модулю тт
элементы имеют одинаковые образы при этом отображении.
Упражнение 1.5.54. Докажите это.
Указание. Если два разных по модулю тт элемента из Z[r] переходят в один эле-
мент Z2m, то их разность согласно лемме должна делиться на тт, что невозможно.
Доказательство единственности разложения в теореме можно прове-
сти индукцией по его длине. База индукции очевидна. Для обоснования
шага индукции заметим, что любой нечетный элемент кольца Z[r] по мо-
дулю rw равен только одному из чисел ±1,±3,...,±2W-1 - 1. Поэтому
в разложении нечетного элемента
а = аттТП + • • • + а0
ао 7^ 0, поэтому аг = 0, i — 1,..., w - 1, значит a = Uq mod rw, равный
одному из чисел ±1, ±3,..., ±2W-1 - 1, определен однозначно. По пред-
положению индукции (а - (1q)/tw имеет единственное разложение
4~ ... ”h
Значит, разложение нечетного элемента а определено однозначно. В раз-
ложении четного элемента
Л —	4- •.. 4“ flo
а0 всегда должно быть четным, следовательно, по условию теоремы
нулем, и определяется также однозначно. Остальные коэффициенты также
однозначно определяются из разложения
a/т = аттт~1 4- ... 4- аь
Доказательство существования разложения проводится индукцией,
а само разложение строится следующими алгоритмом.
Пусть а = Uq 4- щт, иг; 6 Z. Вначале список S коэффициентов раз-
ложения, в котором в конце работы алгоритма появятся коэффициенты
ат,... ,uq, пуст. Если uq четно, то, то записываем clq = 0 в этот список
и заменяем элемент а на элемент а/т = puq/2 + щ - tuq/2, т. е. делаем
присваивания uq = щ 4- PUq/2, ux = -uq/2. Если же Uq нечетно, то
вычисляем ф-ш(а) — Uq 4- U\tw € Z^w, находим равный ему по модулю 2W
элемент и в списке ±1, ±3,..., ±2W-1 - 1, вычисляем а = а - и, делая
присваивание Uq = uq - и, заносим и в список коэффициентов на оче-
редное место, замечаем, что теперь а согласно лемме будет кратно rw,
и повторяем (не менее чем w раз подряд) указанную выше процедуру
деления четного элемента на г, пока не получится нечетный элемент или
щ не окажется равным нулю, на чем работа алгоритма заканчивается.
1.5. Скалярное умножение на аномальных кривых	71
Алгоритм Солинаса скалярного умножения на кривых Коблица. Известно
[95], что средняя доля ненулевых коэффициентов в разложении с шири-
ной окна w асимптотически равна l/(w +1). Поэтому общая оценка числа
сложений точек кривой Ea(GF(2m)) для выполнения скалярного умно-
жения равна 2W~2 — 1 + т/(w + 1) и требуется запоминание 2W~2 4- 2 точек.
Алгоритм заключается в следующем. Берется точка Р из главной
подгруппы. При вычислении точки кР можно предполагать, что к г/2,
где г — порядок главной подгруппы, иначе вместо Р можно взять —Р,
тогда кР = (г - к)(-Р). Далее вычисляем ко 4- к^т = к mod д, где 6 =
(тт - 1)/(т — 1). Потом строим для ко 4- к\т разложение
апт 4-... 4- йо»	4- й 4- 2, flj = O,dtl,i3,...,i2	— 1.
Потом с помощью этого разложения вычисляем
кР = (ко 4- к{т)Р = (аптп + ... 4- й0)Р
аналогично тому, как это делалось в случае использования 2-адического
разложения, но при этом удвоение (или ополовинивание) точек заме-
няется на гораздо более быструю операцию возведения в квадрат обеих
координат точки. При этом точки Р, ЗР,..., 2W-1 - 1 вычисляются, как
обычно, заранее и запоминаются. Если точка Р заранее известна, то
2W~2 - 2 предварительных сложений можно не учитывать в окончательной
оценке сложности.
Для ускорения вычисления к mod 6 в описанном выше алгоритме
деления с остатком можно заменить целочисленное деление на норму
N{6) = г = (2т 4- 1 - Vm)/(3 4- р), асимптотически близкую к степе-
ни двойки, приближенным выполнением этой операции, использующим
только целочисленные умножения. А именно, вместо точного вычисле-
ния Xi = SjTi/г оно находится с точностью С бит с помощью следующей
процедуры:
j'i = Vmh'i, I'i = Round	J :=
Вероятность того, что полученный с использованием этой процедуры
деления остаток р1 не совпадает с остатком р стандартной процедуры де-
ления, не превосходит 2-с+5. Но при это длина т-адического разложения,
построенного с помощью этой приближенной процедуры, не превосходит
m 4- а 4- 3, где а = 0, 1 — номер используемой кривой, т. е. не более чем
на 3 больше стандартной оценки. Все эти утверждения доказаны в [95].
72
Глава 1. Алгоритмы на эллиптических кривых
1.6.	Вычисление дискретного логарифма
1.6.1.	Проблема дискретного логарифмирования
Пусть G = (G; •) — конечная мультипликативная группа, а и a —
элементы группы G, п есть порядок элемента а. Натуральное число х
называется дискретным логарифмом элемента а при основании а, если
ах = а, 0 < х п.
Проблема дискретного логарифмирования заключается в том, что не-
обходимо найти дискретный логарифм х данного элемента а = ах при
основании а.
В аддитивной интерпретации рассматривается аддитивная группа G
с элементами А и Р, при известном порядке N элемента Р. Натуральное
число к, 0 < к < N, называется дискретным логарифмом элемента А при
основании F, если
к * Р = А.
Все известные алгоритмы для решения этих проблем (при подходя-
ще выбранных группе G и элементе а (или Р)) для мультипликативной
группы конечного поля или группы точек эллиптической кривой суб-
экспоненциальны, т. е. число выполняемых ими операций оценивается
как 2log п, где С > 0 — некоторая константа, ап — порядок группы. Для
некоторых групп даже порядка 2200 - 2300 сложность дискретного логариф-
мирования слишком велика для современной (и ожидаемой в ближайшем
будущем) вычислительной техники, и на этом факте основана значитель-
ная часть криптографии с открытым ключом. Изложение этих алгоритмов
не входит в наши планы, и интересующегося ими читателя мы вынужде-
ны отослать к списку литературы в конце книги. Однако, для того чтобы
читатель прочувствовал трудность этой проблемы, мы приведем два са-
мых простых для понимания (но, к сожалению, довольно медленных)
алгоритма дискретного логарифмирования.
Все алгоритмы дискретного логарифмирования можно представить
как в мультипликативной, так и в аддитивной интерпретации. Учитывая
специфику книги, далее в качестве группы берем аддитивную группу —
группу точек эллиптической кривой.
1.6.2.	Алгоритм «большой шаг — малый шаг»
Этот алгоритм был независимо открыт Д. Шенксом, опубликовавшим
его, по-видимому, в 1969 г. (и которому, вероятно, принадлежит и его
довольно удачное название) и А. О. Гельфондом, опубликовавшим его
в 1962 г. в закрытой печати. Мы даем его изложение, следуя книге [13],
но в аддитивной записи. Для этого понадобится следующая
Теорема 1.6.1. Пусть п,г — натуральные числа, г2 п. Для любого
целого х можно указать целые числа s и t такие, что
х = sr 4- f(mod n);	0 < s < г, 0 < t < г.
1.6. Вычисление дискретного логарифма
73
Доказательство. Можно предполагать, что 0 < х < п. Полагаем
I х I
s = I - I , t = х - sr.
Lr J
Имеем
X n
r r
С другой стороны,
OOC - <5+1,
r
поэтому
sr x < sr + r,
или
0^x-sr = t<r.	
Лемма 1.6.1 (Аддитивная интерпретация леммы 1.2.1 первой книги [4]),
[13]. Для вычисления кратного п*т, где т — элемент некоторого кольца,
ап - натуральное число, достаточно выполнить не более 2 |_log2 nJ операций
сложения.
Для доказательства достаточно применить бинарный метод построения
аддитивных цепочек.
Теорема 1.6.2 (А. О. Гельфонд). Пусть G = (G; +) — конечная группа
точек эллиптической кривой, А и Р — элементы этой группы, N —
порядок элемента Р,
к*Р = А.	(1.35)
Тогда число к можно найти, выполнив не более, чем 2(\/N + log2jV) — 1
операций сложения в группе G.
Доказательство. Полагаем г = [VNJ + 1. Рассмотрим ряды
О * Р = О, 1 * Р, 2 * Р, ..., (г — 1) * Р,
А, А + (Ь(-г))*Р, Л + (2-(-г))*Р, ..., А + ((г- 1)(—г)) *Р
Если уравнение (1.35) разрешимо относительно А;, то по теореме 1.6.1
(учитывая, что г2 п2) представим к в виде
к = t + 5 • r(mod N), 0 t < г.
Так как N есть порядок элемента Р, то к * Р = (sr + t) * Р = А в том
и только том случае, когда
t * Р = А + (-sr) * Р,
т. е. когда найдется элемент второго ряда, совпадающий с некоторым
элементом первого ряда.
При вычислении элементов первого ряда потребуется выполнить
не более г-2 сложений в группе G. Для вычисления (~r*P) — (N-r)*P
74
Глава 1. Алгоритмы на эллиптических кривых
в силу леммы 1.6.1 потребуется выполнить не более 21og27V умножений.
Не более чем г - 1 сложений потребуется для вычисления всех членов
второго ряда.
Таким образом, общее число операций умножения для решения
уравнения (1) не превосходит
2г - 3 4- 2 log2 n 2(Vn 4- log2 n) - 1.	
Пример 1.6.1. Выберем несуперсингулярную кривую У2 4- XY = X3 + X2 4-1 над
полем 6rF(25) = б?Р(2)(Л), где Л — корень неприводимого многочлена 1+Х2+Х5,
и базовую точку Р = (00101, ЮНО) этой кривой. Непосредственной проверкой
убедимся, что порядок N этой точки равен 22. Пусть А = к * Р = (01101,00101).
Вычислим константу к.
Определим г = LvC/V j + 1 = 5, -г = N - г = 22 - 5= 17 и вычислим
Р' = (-г) * р = 17 ♦ (00101, ЮНО) = (10111,01100).
Вычисляя ряды
0 * Р = О, 1*Р, 2 * Р, 3 * Р, 4 * Р
и
А, А + 1-Р', А + 2-Р', А + З-Р', А + 4-Р',
получим
0*Р = О,	А = (01101,00101),
1 * Р = (00101,	10110),	А +	1 • Р'	= (00010,11101),
2*Р = (OHIO,	10010),	А +	2-Р'	= (01100,00001),
3 * Р = (01101,01000),	А +	3 • Р'	= (01010,00011),
4*Р = (01010,00011),	А +	4-Р'	= (00101,10011).
Видим, что элемент £*Р — 4*Р = (01010,00011) первого ряда совпадает с эле-
ментом
А + s • 17 * Р = (01010,00011) = А + 3 • 17 * Р = (01010,00011)
второго ряда. Значит, к = sr + £ = 3- 5 + 4= 19. Действительно, 19 * Р =
(01101,00101) = А. При вычислении элементов двух указанных рядов выполнено
6 операций сложения и при вычислении точки 17 * Р = 24 * Р + Р выполнено
4 операции сложения (три удвоения при вычислении 24 * Р и одно сложение).
Всего выполнено 10 операций сложения. Верхняя оценка по теореме 1.6.2 есть
2(VN + Jog2jV) - 1 = 2(>/22) + log2 22) - 1 < 2(5 + 5) - 1 = 19.
1.6.3.	Алгоритм для групп составных порядков
Следующий алгоритм (а также некоторое его обобщение) был от-
крыт В. И. Нечаевым и опубликован 1965 г. в закрытой печати. В 1977 г.
основанный на близкой идее алгоритм, применимый ко всем группам,
порядки которых имеют достаточно малые простые делители, был опуб-
ликован Полигом и Хеллманом и независимо Зильбером.
Теорема 1.6.3 (В. И. Нечаев). Пусть G = (G; +) — конечная группа
(можно считать, что это группа точек эллиптической кривой), А и Р —
1.6. Вычисление дискретного логарифма
75
элементы этой группы, N — порядок элемента Р; к * Р = А. И пусть,
кроме того, число N — составное:
N = Г1 • Г2,	1 < Г1 < N, 1 < Г2 < N
Тогда дискретный логарифм элемента А по основанию Р можно вычислить,
выполнив не более чем
2(</п +	+ 6 log2 Г1Г2 + log2 Г1 - 1
операций сложения в группе G.
Доказательство. Заметим, что любое целое число х, 0 х < п, од-
нозначно представляется в виде:
к — Г2 • /1 + ТПь 1\, ТП\ е Z, 0 Ц < ГЬ 0 mi < Г2.
Равенство к * Р = А можно записать в виде
(г2 • li 4- mi) * Р = А.	(1.36)
Умножим обе части этого равенства на число п и с учетом того, что
п = Г1 • Г2 и N * Р = О, получим
(ri • mi) * Р = Ti * А.
Обозначив Pi = п*Р, Л1 = г-1*А, получим более удобное представление
последнего равенства:
mi * Pi =
Легко проверить, что порядок точки Pi равен г2- По теореме 1.6.2
mi как дискретный логарифм Ai по основанию Pi можно вычислить
выполнив не более чем 2(v/r7+log2 Г2) -1 операций сложения в группе G.
Прибавляя (-mi) * Р к обеим частям равенства (1.36), получим
Zi * Р2 = А2,
где Р2 = г2 * Р, А2 = А + (-mi) * Р
Аналогично предыдущему, Ц можно вычислить при помощи не бо-
лее чем за 2(л/г[ + log 2rj) - 1 операций сложения в группе G. Далее
Pi, Ai, Р2, А2 вычисляются соответственно не более чем за
21og2ri, 21og2ri, 21og2r2, 1 + 2 log21
операций сложения в группе G.	
Упражнение 1.6.1. Вычислите дискретный логарифм из примера 1.6.1, использую
для упрощения вычислений разложение порядка N точки Р, и подсчитайте
количество операций сложения в группе точек эллиптической кривой.
Глава 2
Протоколы на эллиптических кривых
Есть два вида криптографии: криптография, которая
помешает вашей младшей сестре читать ваши файлы,
и криптография, которая помешает читать ваши файлы
правительствам крупных стран.
Bruce Schneier. Applied cryptography, 1996
2.1. Выбор точки и размещение данных
2.1.1. Введение
Использование группы точек эллиптической кривой в криптографии
связано с выбором определенных ее точек. При этом в зависимЯо-
сти от криптографической задачи выбирают точку случайно или точку,
координаты которой отражают данные, помещаемые на кривую. Так,
значение координаты х может содержать как часть бинарного вектора
подпоследовательность х', значение координаты у при этом определя-
ется по уравнению кривой. Последнее связано с решением квадратного
уравнения определенного вида. Мы рассмотрим методы решения квад-
ратных уравнений, возникающих при вычислении координаты у точки
эллиптической кривой. Затем мы рассмотрим метод помещения данных
в эллиптическую кривую.
2.1.2. Решение квадратных уравнений
Этот вопрос уже обсуждался в разд. 1.2.1 и 1.4.4.
Рассмотрим еще один поход к его решению [83].
Суперсингулярный случай. Рассмотрим квадратное уравнение
Y2 + Y — a,	(2.1)
где а — элемент поля GF(2n), такой, что tr(a) = 0. (Если tr(a) = 1, то
уравнение не имеет решения, как показано в разд. 1.2.1).
Нетрудно видеть, что, если у — корень этого уравнения, то у + 1 —
второй его корень, так как у2 + у = у (у + 1).
Решение у как элемент поля GF(2n) можно представить в полино-
миальном базисе в виде вектора (t/o, 2/ь • • •, Уп-2, Уп-i), а также в виде
2.1. Выбор точки и размещение данных
77
многочлена — произведения этого вектора коэффициентов на покомпо-
нентное произведение единичной матрицы Т\ и вектора степеней корня А
неприводимого многочлена :
		( 1	0 ...	0	0		( 1	
У = (Уо.Уь--	•,Уп-2,Уп-1)	0	1 ...	0	0		А	.	(2.2)
		0	0 ...	1	0		дП-2	
								
		\ 0	0 ...	0	1 /		к А"-1 )	
Это матричное представление эквивалентно полиномиальному представ-
лению
У — Уо •	+ У1 • А1 4- ... 4- уг - Хг 4-... 4- уп-2 • Хп 2 + уп_\ • Хп \
Полиномиальное представление элемента у2, согласно тождеству Фробе-
ниуса имеет вид:
З/2 = ?/о-(А0)2 + 2/1-(А1)2 + ...
где sz = (st;o> stji,..., Si,n-i) ~ векторные представления элементов Х2г
поля GF(2n), i = 0,1,..., п - 1.
В свою очередь, уравнение (2.3) можно (после выполнения матричных
умножений и приведения подобных членов) представить в виде
У2 = Уо * О) • А0 4- У\ • Ci • Л1 + ... + уг * Cj * Хг 4-... 4- уп-2 • Сп-2 • Хп 2+
4- Уп-1 • Сп-1 • А” \
п-1
где С: = £	.
>0
Здесь и ниже матрица умножается на вектор-столбец (А0, А1,..., Ап 1)т покомпо-
нентно, в результате получается матрица размеров п х п.
78	Глава 2. Протоколы на эллиптических кривых
Эквивалентное этому векторному виду матричное представление у2
выглядит следующим образом:
у1 = (уо,У1,  ,Уп-2,2/п-1)х
	/	1	0	0	...	° X		/ 1	
	0	0	1	...	0		А	
X				• (2-4)
				
	^п-2,0	$п-2,1	•••	Sn-2,n-2	^n-2,n-l		А"-2	
	\ ^п-1,0	$п-1,1	£п-1,п-2	/		\ А”-' )	
Как видим, г-я строка матрицы Т\ представляет собой вектор полино-
миального представления элемента Аг поля GF(2n), тогда как г-я строка
матрицы Т2 представляет в полиномиальном базисе элемент Л2г это-
го поля.
Сумму + Т2 матриц и Т2 в представлениях (2.2) и (2.4) обозна-
чим Т. Тогда уравнение (2.1) можно записать в матричной форме
У  Т = ff = (а0, <71.ап-1).	(2.5)
Первая строка матрицы Т оказывается нулевой, но последующие
п - 1 строк соответствуют ровно п - 1 переменным уо, у^9..., уп_\. Этим
строкам соответствует матричное уравнение с п - 1 неизвестными:
(У1,... ,yn-2,yn-l) X
	/	0 0	0 1	0 1	0 \ 0			/ 1 А		
X									= а.
	^п-2,0 \ ^п-1,0	।	। st	е со со	... 1 + Sn-2,n-2 • • •	$п-1,п~2	^п-2,п-\ 1	8п-1,п-1	/		Ап~2 \ А”’1	/	
(2.6)
Переменная у$ не участвует в этом уравнении и может иметь любое
из значений 0, 1, что отражает неопределенность решения квадратного
уравнения (если при выборе уо = 0 получается решение у, то при выборе
?/о=1 получилось бы решение у + 1).
Заметим, что при работе с суперсингулярной эллиптической кривой
Y2 + Y = X3 + X + 1
или
Y2 + Y = X3 + X
уравнение (2.1) возникает при подстановке в правую часть уравнения
элемента х поля, над которым она определена. При подстановке разных
элементов х матрица Т вычисляются только один раз для заданного
неприводимого многочлена.
2.1. Выбор точки и размещение данных
79
Пример 2.1.1. Рассмотрим суперсингулярную эллиптическую кривую Y2 4- Y =
X3 4- X 4- 1 над полем GJ?(24) — <7F(2)(A), где А есть корень неприводимого
многочлена 1 + X 4- X4.
Выберем элемент х = (х0, Х[, х2, х3) = (1,0, 0,0). Вычислим ст(х) = 1 4-
х 4- х3 = (1,0,0,0). Как видим, tr (а) — tr (1, 0, 0, 0) = (1, 0, 0, 0) 4- (1, 0, 0, 0) 4-
(1,0,0, 0)4-(1,0, 0, 0) — 0.
Квадратное уравнение (2.1) принимает вид Y2 4- Y = (1,0,0,0). В данном
случае матрицы Т\ и Т2 следующие:
/	1	0	0	0	\
0	10	0
0	0	10
\	О	О	О	1	/
/	1	0	0 0	\
0	0	10
110 0
\	О	О	1 1	/
Матрица Т = Т\ 4- Т2 имеет вид
/ О О О О \
0 110
1110
\ О О 1 о /
Уравнение (2.6) в матричной форме имеет вид
(2/о,?/1,?/2Лз)
О
О
1
О
О 0 0 \
110
110
0 10/
i 1= (1,0,0,0).
Л I
\ А3 /
После упрощения имеем матричное уравнение:
/	0	1	1	0	\
(г/i. г/2, уз)	I	1	1	1	о	I
\	0	0	1	0	/
Умножая матрицу на вектор, получим
/О А А2	О X
(1/1,1/2, Из) 1 А А2 0	=(1,0,0,0).
\ О	О А2	0 /
Умножая вектор на матрицу, получаем (у-,, (г/|+г/2)А, (?/1+з/2+1/з)А2, 0) = (1,0,0,0).
Приравнивая коэффициенты, получаем систему уравнений
1/2 = 1,
< У\ + 1/2 = О,
,1/1+1/2+1/з=0.
Решая ее, получим 1/2 = 1, l/i = 1, 1/з = 0. Таким образом, имеем два решения
Уравнения (0,1,1,0) и (1,1, 1,0).
80
Глава 2. Протоколы на эллиптических кривых
Алгоритм 2.1.1
ВХОД: Уравнение (2.1) над GF(2n), n = 2k 4- 1.
ВЫХОД: Решения у, у 4- 1 уравнения (2.1).
1.	Вычислить t = tr (а) = а 4- а2 + ... + а2 — след элемента а.
2.	Если t 0, вернуть «решений нет».
2|.
3.	Вычислить у = а +	•
Рис. 2.1. Алгоритм решения квадратного уравнения (2.1) над GF(2n)
при нечетном п
Как упоминалось в разд. 1.2.1, для решения квадратного уравне-
ния (2.1) над полем GF(2n) при нечетном п, можно использовать алго-
ритм 2.1.1.
Действительно, при любом у след левой части уравнения равен нулю,
так как tr (у) = tr (j/2). Поэтому, если решение существует, то след правой
части также нулевой. Если вычислить
i=l
а затем взять s — у+у2, то получится s tr (ет)Н-(т = а, так как след элемента
а, как проверено в п. 2 алгоритма, равен нулю. Значит, у2 4- у — а.
Пример 2.1.2. При п — 5 у = а 4- а4 4- <т16, у2 = сг2 4- а8 4~ а32,
У 4- у1 = (т + а4 4- а16 4- а2 4- а8 4- а32 = а 4- а4 4- а16 4- а2 + а8 4- а =
= а 4- <т2 4- а4 4- а8 4- а16 4- (т tr (а) 4- (т = а.
Например, если базис в поле соответствует многочлену р(х) = 1 4- X2 4- X5
и а = ж4, то
tr (а) = х4 4-	4- ж16 4- ж32 4- ж64 = 0, у = ж4 4- ж16 + ж64 = 1 4- ж 4- ж2 4- ж3;
у2 = ж8 4- ж32 4- ж128 = 1 4- ж 4- ж2 4- ж3 4- ж4, у 4- у2 — ж4.
Несуперсингулярный случай. Рассмотрим квадратное уравнение
Y2 + xY + /(ж) = 0,	(2.7)
получающееся при переносе в левую часть правой части f(X) уравнения
несуперсингулярной эллиптической кривой и подстановке X = х. Поло-
жим Y = xZ и получим уравнение
zV + x'Z + f(x) = 0.
При х 0 оно эквивалентно уравнению
Z2 + Z + <7 = о,	(2.8)
где сг = /(ж) • х~2.
2.1. Выбор точки и размещение данных
81
Это уравнение (относительно Z) можно решить методами, описан-
ными выше для уравнения (2.1). Далее решение z можно преобразовать
в решение у = zx уравнения (2.6). Заметим, что в этом случае (ж, х + у)
также является решением этого уравнения.
2.1.3. Выбор точки эллиптической кривой
Суперсингулярный случай. Приведем два вероятностных алгоритма выбора
точки эллиптической кривой (алгоритмы 2.1.2 и 2.1.3).
Алгоритм 2.1.2
ВХОД: Уравнение У2 = f(X) суперсингулярной эллиптической кривой
над GF(2n).
ВЫХОД: Точка (ж, у), удовлетворяющая уравнению кривой.
0. Инициализация:
в соответствии с (2.2), (2.3) вычислить матрицу Т
1.	Выбрать случайно ненулевой элемент х поля GF(2n).
2.	Вычислить a = f(x).	n l
3.	Вычислить след tr (а) элемента a: t = tr (а) = 52 °"2 •
4.	Если t = 1, то перейти к п. 1.	г~
5.	Решить уравнение (2.1).
6.	Вернуть (ж, у).
Рис. 2.2. Вероятностный алгоритм выбора точки
суперсингулярной эллиптической кривой
Алгоритм 2.1.3
ВХОД: Уравнение суперсингулярной эллиптической кривой над GF(2n),
п = 2k -h 1
ВЫХОД: Точка (ж, у), удовлетворяющая (2.1).
1.	Выбрать случайно ненулевой элемент ж поля GF(2n).
2.	Вычислить а = /(ж).
3.	Применить алгоритм 2.1.1.
Если решение у существует, то вернуть (ж, у).
4.	Перейти к п. 1.
Рис. 2.3. Вероятностный алгоритм выбора точки суперсингулярной эллиптической
кривой над GF(2n) при нечетном п
Алгоритм 2.1.3 на рис. 2.3, использующий алгоритм 2.1.1, применяется
при нечетной степени расширения поля.
82
Глава 2. Протоколы на эллиптических кривых
Алгоритм 2.1.4
ВХОД: Уравнение Y2 + XY = /(ж), где f(x) — значение правой части
уравнения (2.7) при X = х.
ВЫХОД: Точка (ж, у), удовлетворяющая (2.7).
0. Инициализациия. По (2.2), (2.3) вычислить матрицу Т = Т\ + Т2-
1.	Выбрать случайно ненулевой элемент х поля GF(2n).
2.	Вычислить a = /(ж) • ж“2.
3.	Вычислить след элемента a: t = tr (а) = а2 -
4.	Если t — 1, то перейти к п. 1.	г~
5.	Решить уравнение у • Т = а. Если решения нет, перейти к п.1. '
6.	Вычислить у = ух.
7.	Вернуть (ж, у).
Рис. 2.4. Вероятностный алгоритм выбора точки
несуперсингулярной эллиптической кривой
Алгоритм 2.1.5
ВХОД: Уравнение У2 4- XY = /(ж), где f(x) — значение правой части
уравнения (2.7) при X — х.
ВЫХОД: Точка (х,у), удовлетворяющая (2.7).
1.	Выбрать случайно ненулевой элемент х поля GF(2n).
2.	Вычислить а — f(x) • ж-2.
3.	Применить алгоритм 2.1.1.
Если решение у существует, то вернуть (ж, ху).
4.	Перейти к п. Ь
Рис. 2.5. Вероятностный алгоритм выбора точки несуперсингулярной
эллиптической кривой над GF(2n) при нечетном п
Несуперсингулярный случай. Вероятностные алгоритмы выбора точки не-
суперсингулярной эллиптической кривой незначительно отличаются ал-
горитмов суперсингулярного случая.
На рис. 2.4 приведен один их таких алгоритмов — алгоритм 2.1.4.
При нечетной степени расширения поля применяется более простой
алгоритм 2.1.5 (рис. 2.5), использующий алгоритм 2.1.1.
2.1.4.	Размещение данных на эллиптической кривой
Заметим, что данные, которые можно разместить в некоторой точке
эллиптической кривой, должны состоять из несколько меньшего чис-
ла бит, чем элемент конечного поля, над которым строится кривая.
Несколько бит должны оставаться неопределенными, чтобы обеспечить
возможность попадания на кривую. Алгоритмы размещения данных на эл-
2.2. Распределение ключей
83
Алгоритм 2.1.6
ВХОД: Точка (ж, у) эллиптической кривой,
факторизация порядка кривой п = р\' • р22 .. .pekk,
где р^ i = 1,..., к, суть простые числа.
ВЫХОД: Порядок t элемента (х, у).
1.	Присвоить t n.
2.	Для i от 1 до к выполнять:
2.1.	Присвоить t t/p*'.
2.2.	Вычислить (х, у) <- t • (х, у).
2.3.	Пока (ж, у) Ф О выполнять (х, у) pi • (ж, у)
и присваивать t t • pt
3.	Вернуть t.
Рис. 2.6. Алгоритм определения порядка точки эллиптической кривой
липтической кривой аналогичны алгоритмам выбора точки эллиптической
кривой. Их отличие состоит в том, что выбирается не произвольная точка,
а точка (ж, у) такая, что часть вектора х фиксирована и соответствует
размещаемым данным. В разд. 1.2 были указаны некоторые кривые, при-
годные для использования в криптосистеме. Методы выбора кривых даны
в стандарте IEEE Pl363.
Пример 2.1.3. Пусть требуется разместить данные d = (di,d2) = (1,0) на эл-
липтической кривой из Примера 2.1.1. Прежде всего выберем элемент ж =
(ж0, Жь Ж2, ж3) такой, что (ж0, xj —	d2) и tr (<т) = 0. Элементы ж0 и Ж1 заданы,
а ж2 и ж3 подбираются, так чтобы tr (0, 1, ж2, ж3) — 0, а остальные варианты
для ж2 и Жз можно не рассматривать. Данные d можно разместить в точке
(ж, у) = ((0,1, 0,0), (0,1,1, 0)) или в точке ((0,1, 0,0), (0, 1, 1, 1)), используя ре-
шения у, у 4-1 квадратного уравнения из примера 2.1.1.
2.1.5.	Определение порядка точки эллиптической кривой
и нахождение образующего элемента группы точек
эллиптической кривой
Алгоритм определения порядка точки эллиптической кривой при
известной факторизации порядка п группы приведен на рис. 2.6.
Вероятностный алгоритм поиска образующего элемента группы точек
эллиптической кривой дан на рис. 2.7.
2.2.	Распределение ключей
2.2.1.	Введение
Рассмотрим ряд протоколов, криптографическая стойкость которых
основана на трудности решения проблемы дискретного логарифма (DLP)
и проблемы Диффи—Хеллмана (DHP). Проблема дискретного логарифма
84
Глава 2. Протоколы на эллиптических кривых
Алгоритм 2.1.7
ВХОД: Уравнение эллиптической кривой,
факторизация порядка кривой п — р*1 • р? ... pekk,
где Pi, i = 1,..., к, суть простые числа.
ВЫХОД: Образующий элемент a = (х, у) группы точек
эллиптической кривой.
1.	Выбрать случайную точку a = (х, у) эллиптической кривой.
2.	Для i от 1 до к выполнять:
2.1.	Вычислить /3 = (n/Pi) • а.
2.2.	Если /3 = О, то перейти к п. 1.
3.	Вернуть а.
Рис. 2.7. Вероятностный алгоритм поиска образующего элемента группы точек
эллиптической кривой
возникает в каждом случае, когда задана некоторая, циклическая группа,
известна степень у = дх некоторого ее элемента (если группа мультипли-
кативная) или кратное у = х * д (в аддитивной группе) и требуется найти
значение показателя степени или коэффициент кратности х (дискретный
логарифм элемента у по основанию д).
В одних случаях, например для аддитивной группы, заданной на
множестве Zp вычетов по модулю простого числа р, DLP легко решает-
ся с использованием алгоритма, подобного алгоритму Евклида, в других
случаях, например, для мультипликативной группы конечного поля, не-
известны полиномиальные по сложности алгоритмы для этой проблемы
(для произвольных полей).
Для группы точек эллиптической кривой проблема дискретного ло-
гарифма заключается в определении числа к по известным точке Р
данной эллиптической кривой и точке Q = кР. Сложность этой пробле-
мы не меньше сложности DLP для поля, над которым определена кривая.
Для эллиптических кривых неизвестны полиномиальные по сложности
алгоритмы решения DLP, но для суперсингулярных известен алгоритм
сведения этой проблемы к DLP некоторого расширения невысокой сте-
пени поля, над которым определена кривая.
Классическая проблема Диффи—Хеллмана формулируется примени-
тельно к мультипликативной группе конечного поля. Она заключается в
вычислении элемента аху по элементам а, ах и ау. Не известно, возмож-
но ли ее решение без предварительного вычисления индексов х и у, т. е.
минуя проблему дискретного логарифма. Применительно к циклической
подгруппе группы точек эллиптической кривой эта проблема заключается
в том, чтобы при известных точке Р Е E(F) и двух ее кратных кдР и
крР найти точку кдквР. Также неизвестно, можно ли это сделать без
предварительного вычисления констант к а и кв, т. е. не решая DLP для
2.2. Распределение ключей
85
эллиптических кривых. Не доказана и гипотеза об эквивалентности DLP
и DHP для эллиптических кривых.
2.2.2.	Распределение ключей для классической криптосистемы
(протокол Диффи—Хеллмана)
Заметим, что в качестве ключа классической криптосистемы можно
использовать неизвестную посторонним (секретную) случайную точку
(х, у) 7^ О группы точек эллиптической кривой E(F), если условиться,
как конвертировать ее в натуральное число, например, одну из координат,
скажем, х считать двоичной записью натурального числа.
Для получения такой секретной точки на двух терминалах открытого
канала связи можно использовать модификацию протокола Диффи-
Хеллмана 2).
Допустим, что Е — эллиптическая кривая и Р — предварительно
согласованная и опубликованная точка этой кривой. Абонент А выбирает,
сохраняя в секрете случайное число к а (секретный ключ Л), вычисля-
ет координаты точки клР (свою «половинку» ключа) и пересылает их
абоненту В. Аналогично В выбирает секретный ключ кв, вычисляет и пе-
ресылает абоненту А «половинку» квР ключа. Общим ключом является
точка Р = клквР- А вычисляет ее, умножая на свой секретный ключ к а
на «половинку» ключа, вычисленную В, а В вычисляет эту же точку,
умножая сообщение, поступившее от А, на свой секретный ключ кв-
Ввиду того что группа точек эллиптической кривой абелева, результат
не зависит от порядка вычисления и, следовательно, А и В имеют ко-
ординаты секретной точки3) кА(квР) = кв(кАР) = кАквР — (х,у) и
могут использовать х в качестве ключа симметричной криптосистемы
(при условии достаточности длины этой двоичной записи, что зависит от
порядка поля, над которым построена эллиптическая кривая, и при усло-
вии, что секретные ключи кА и кв были выбраны как случайные или как
криптографически стойкие псевдослучайные числа). Теперь А и В имеют
одинаковые копии искомой секретной точки эллиптической кривой.
Проблема, стоящая перед посторонним наблюдателем, имеющим
намерение узнать секретный ключ, заключается в вычислении кАквР по
Классическая версия этого протокола основана на проблеме Диффи—Хеллмана для
группы Zp. Абоненты А и В, предварительно по открытому каналу обуславливают ис-
пользовании большого простого числа р и образующего элемента а мультипликативной
группы Zp. Для совместной выработки секретной точки они выбирают независимо друг от
Друга секретные числа х € Zp и у Е Zp, вычисляют «половинки» ах и ау и обмениваются
ими по открытому каналу. После этого каждый из них вычисляет секретный ключ, возводя
полученную «половинку» ключа в свою секретную степень: (ах)у = аху, (ау)х = аух = аху.
3) Предполагается, что полученная точка не есть О. Вероятность получить О при боль-
шом порядке поля F чрезвычайно мала, но, тем не менее, для логической завершенности
следует осуществлять проверку и предусматривать возврат на этап выбора секретных ключей
И кв.
86
Глава 2. Протоколы на эллиптических кривых
известным Р, кАР, квР, но при неизвестных к а, к в , это и есть проблема
Диффи—Хеллмана для эллиптических кривых.
Пример 2.2.1. Как указано на с. 26, эллиптическая кривая
У2 + XY = X3 + X2 + 1
над полем GF(2163) имеет порядок 2 х Р49. Выберем неприводимый многочлен
1 + X + X2 + X4 s + х163
и возьмем точку этой эллиптической кривой
Р = (d42149e09429d/4563ecl816488c92de89/93a9&2,
ccdl8d6cc3042c4cl7a213506345c80965acld476).	(2.9)
Проверим, что ее порядок не равен 2:
2Р - (ccdl8d6cc3042c4cl7a213506345c809b5acld476,
835a2/56688d6a249&4M2a7550a4375e531d8a37) О.
Значит, ее порядок равен порядку 2 х Р49 группы или числу Р49, и ее можно
использовать для построения ключа.
Пусть к а = 12, к в = 123 (реально могут быть большие числа). Тогда
кАР — 12Р = (W9776&&e87a8&1024be2e415952/527eee928b43,
c67a28ed76137e756c37654/186a716/64e5ac546).
123Р —(a5684e246044/cl26e9832d!7513387e474290547,
56864137/09/5/79a8a650/e44cd/41d8e68ae2c6).
kBkAP = kAkBP = (12 xl23)P = (bb7356cecel3c71919534S7Sbcb6f3aSS7d613c92i
f661ffdfelbaScblb2ad!7b655Qc65aa6d4f07f41).
В качестве ключа симметричной системы используется код (или его часть)
х = &&7856cecel3c719195348786c66/3a887d613c92.
Заметим, что для выполнения этого протокола точное знание порядка эл-
липтической кривой не потребовалось.
2.2.3.	Распределение ключей для классической криптосистемы
(протокол Месси—Омуры)
Протокола Месси—Омуры позволяет передать сообщение от або-
нента А абоненту В по открытому каналу связи без предварительной
передачи какой бы то ни было ключевой информации.
4) Здесь и ниже в примерах применяется так называемый полиномиальный шестнадца-
теричный код, описанный в Приложении D.
2.2. Распределение ключей
87
Мультипликативный вариант. Первоначально данный протокол был опи-
сан применительно к мультипликативной группе Z*, где р — простое
чйсло, как аналог передачи секрета с помощью ящиков, запираемых на
один или два замка: абонент А запирает ящик с письмом своим ключом
и пересылает ящик абоненту В, который запирает ящик своим ключом
и отправляет его к А. Последний снимает свой замок и возвращает ящик
к В, который снимает свой замок. Вместо механических замков або-
ненты (два или более) могут использовать электронные, т. е. хранимые
в компьютерной памяти ключи. Для их организации они выбирают как
системный параметр большое простое число р. Затем абоненты А, и В
выбирают случайные числа ел и е#, взаимно простые с р -1, и вычисляют
числа dA и dB, обратные по модулю — р— 1 ( р — функция Эйлера)
к выбранным ранее числам:
еА -dA = l(mod92(p)), ев • dB = l(mod <р(р)).
Пары чисел (eAi dA), (eBi dB), представляют собой секретные ключи
абонентов.
Отметим, что для т такого, что 0 < т < р справедливо равенство
meA'dA _ т modp,
так как
me*d* = m^+i =	• т = т
(первый сомножитель равен 1 по теореме Эйлера).
Аналогично,
meB-dB _ т mO(jp
Пусть абоненту А необходимо послать сообщение т, 0 < т < р,
абоненту В (более длинные сообщения разбиваются на блоки). Абонент А
шифрует сообщение своим первым ключом, т. е. находит
mi = теА modp, 0 < т\ < р,
и пересылает т\ к абоненту В. Этот абонент «навешивает» свой первый
замок на это сообщение и вычисляет
m? = гп[в modp = теА'ев modp, 0 <	< р,
а потом пересылает w к Л. Тот снимает свой первый замок с помощью
второго секретного ключа, вычисляя
772з = mdA modp = meA'eB'dA modp, 0 < ttz3 < р.
Это сообщение пересылается абоненту В, который снимает свой
первый замок с помощью своего второго секретного ключа dB:
rri4 = mdB modp = mdB'€A'eB'dA modp = m.
Таким образом, абоненту В доставлено секретное сообщение т
от абонента А.
88
Глава 2. Протоколы на эллиптических кривых
Аддитивный вариант. Эллиптическая кривая имеет свойство приводить
константы, на которые умножаются ее точки, по модулю ее порядка.
Пусть Е — эллиптическая кривая порядка N, е — целое, 1 < е < N,
взаимно простое с N. Используя алгоритм инвертирования, найдем
d = e-1(mod^.	(2.10)
По определению сравнимости по модулю имеем е • d = jN + 1.
Поэтому для любой точки Р эллиптической кривой Е порядка N
(е • d)P = (j • N + 1)F = (j • N)P + P = jO + P = O + P = P,
т. e. выполняется тождество
(ed)P = P	(2.11)
Используя e и d из (2.10), и любую точку Р эллиптической кривой,
можно вычислить Q — еР, R = dQ. Очевидно, что R = Р.
В варианте протокола, использующего алгебру эллиптической кри-
вой, системными параметрами являются уравнение эллиптической кри-
вой Е и поле F, над которым она построена (поле задается неприводимым
многочленом). Этими параметрами определена группа E(F) точек эллип-
тической кривой и ее порядок, который также публикуется как систем-
ный параметр (хотя он, может быть, и вычислен по уравнению кривой
и полю F). Согласно этому протоколу после согласования системных
параметров абонент А выбирает как ключ шифрования число са , взаим-
но простое с порядком N эллиптической кривой, и вычисляет по (2.10)
обратное к число dA — ключ расшифрования. Аналогично, абонент В
выбирает число ев и ,вычисляет d#, т. е. создает свои ключи.
Абонент А помещает свое сообщение m в некоторую точку высокого
порядка М эллиптической кривой и, умножая ее на свое секретное
значение €а , получает точку
Pi = еАМ.
Эту точку А посылает абоненту В.
Тот вычисляет
Р2 = евР\,
и посылает результат абоненту А, который снимает свой «замок», вычис-
ляя
Рз =
и возвращает полученную точку абоненту В.
Последнему остается только расшифровать сообщение, зашифрован-
ное на его ключе шифрования, т. е. умножить полученную от А точку
на свой секретный ключ расшифрования и найти
М = dBP3.
2.2. Распределение ключей
89
Действительно, с учетом коммутативности и ассоциативности опера-
ции группы
dBPy =	= (dB • dA • ев)Р\ —
— (dB • dA • ев • са)М = (ев • dB) • (е^ • dA)M = М.
Сообщение т, «вложенное» в точку М, может быть использовано
в качестве ключа симметричной криптосистемы.
Заметим, что в данном случае не требуется опубликования никакой
информации о параметрах протокола, кроме самой эллиптической кривой.
Платой за это является необходимость трехкратной передачи по открытым
каналам.
Пример 2.2.2. Используем ту же несуперсингулярную эллиптическую кривую Е,
что и в примере предыдущего раздела. Ее порядок есть
N = 11692013098647223345629483507196896696658237148126.
Пусть абоненты А и В выбрали следующие секретные числа в качестве ключей
шифрования и расшифрования
еА = 12345,
dA = е~А mod Л = 4365207644525318136898038840394531946123759823063;
ев = 54321,
dB = е~в mod .У = 1999357700950535845392247423617974142877678335615.
Для передачи секретного сообщения
т = ///ade98d33M0/769a3a051175127d25
абоненту В абонент А размещает его в точке эллиптической кривой
М = (///ade98d33&dO/769a3aO51175127d25736c&6/l,
2b7058d9da/42aa3568009218668a896e01c75765).	(2.12)
Порядок использованной для передачи сообщения точки М = N/2	2, что легко
проверить, зная разложение порядка кривой. Следовательно, эту точку можно
использовать для безопасной передачи сообщения.
Затем он шифрует эту точку и пересылает результат
Р' = еАМ = (/0597/3/50c3e68d62097270d96074519142e31al,
e2247c04c6el9&6a72&7//43d50d211e8859e8ae)
абоненту В. Последний шифрует его своим ключом и возвращает результат
р2 = евР{ = 5de3478ae081e943a8/4d832b/24ae033&&18e2/,
327ca0c97d3c7730al69e9665/c5309e93/55adM)
абоненту А, который осуществляет первичное расшифрование (снимает свой
«замок») и осуществляет повторную пересылку результата
р3 = dAP2 = edl6730159652a21ec576557a0969cd8ed565dl82,
ea8//3da8d7258d892006ee358960c4M46c463el)
90
Глава 2. Протоколы на эллиптических кривых
абоненту В. Последний завершает расшифрование своим ключом, получая точку
Р4 — djjPi, — М.
2.2.4.	Протокол распределения ключей
Менезеса—Кью—Венстоуна (MQV-протокол)
Рассмотренные в Разделах 2.2.2 и 2.2.3 протоколы обладают тем
недостатком, что некоторое третье лицо С может взять на себя функции
посредника в передаче сообщений между двумя абонентами и завладеть
при этом их секретом.
Действительно, если Ап В взаимодействуют, например, по протоколу
Диффи—Хеллмана, то посторонний наблюдатель С, перехватив передачу
открытого ключа кдР абонента А, передаст абоненту В свой открытый
ключ ксР, абонент В передаст С свой открытый ключ квР, после чего В
и С будут иметь общий закрытый ключ
(кс-кв)Р	(2.13)
Далее, если С передаст свой открытый ключ также абоненту А, то С
и А будут иметь общий секретный ключ (к а • кс)Р (А вычислит этот
ключ, используя кс • Р вместо квР).
Однако при хорошо замаскированных действиях С легальные або-
ненты А и В не будут знать, что имеется посредник, который, получая
сообщение одного абонента, способен его расшифровать и вновь зашиф-
ровать с использованием другого закрытого ключа.
Для предотвращения таких действий активного криптоаналитика
необходима аутентификация (авторизация) этих кратковременных клю-
чей клР и квР (ключей одноразового использования), для чего исполь-
зуются публикуемые долговременные ключи и dBP (ключи многора-
зового использования). При этом протокол организуется таким образом,
что кратковременный открытый ключ связывается с долговременным
и поэтому третье лицо, не имеющее долговременного ключа (не заре-
гистрированное на сервере, где такие ключи хранятся), не сможет стать
посредником коммуникаций между двумя абонентами.
Использование кратковременного ключа обеспечивает невозмож-
ность использования раскрытого при одной из передач секрета для рас-
крытия секрета, вырабатываемого при последующих передачах.
Очевидно, что
кР = (к mod N)P
Поэтому вычисление константы к можно осуществлять как в модульной
арифметике кольца так и в кольце Z.
Соответственно, возможны две эквивалентные модификации прото-
кола.
В первой используются модульная арифметика целых чисел, вторая
основана на циклическом свойстве подгруппы точек эллиптической кри-
вой.
2.2. Распределение ключей
91
В случае использования модульной арифметики над такими числами
могут выполняться операции сложения и умножения по модулю N по-
рядка эллиптической кривой, в случае использования арифметики эллип-
тической кривой на такие числа могут умножаться точки эллиптической
кривой (тогда цикличность определяется порядком подгруппы точек эл-
липтической кривой и знание порядка эллиптической кривой или этой
подгруппы для выполнения операций не требуется).
Во всех случаях абоненты А и В располагают точкой Р эллиптиче-
ской кривой порядка N, над которой и осуществляются все вычисления.
Кроме того, они знают долговременные и кратковременные ключи друг
друга: открытые ключи абонента В
Qb — dBP = (ав, RB = kBP = (хв,Ув) известны абоненту А, а открытые ключи абонента А	(2-14)
Qa — ^аР = (^л> ЪА), RA = kAP = (ха,Уа)	(2-15)
известны абоненту В.
Рассмотрим описание и обоснование протокола с использованием
как модульной арифметики, так и циклического свойства эллиптической
кривой.
Протоколом предусматривается три этапа, симметрично выполняе-
мых каждой из сторон.
На первом этапе А и В вычисляют соответственно числа
sа = (к а + xAaAdA) mod N,
(2.16)
Зв = (кв + хвавйв) m°d N
(при этом они используют свои секретные данные А:л,^л и кв,(1в со-
ответственно, а также интерпретируемые как числа координаты точек
эллиптической кривой).
На втором этапе они вычисляют точки эллиптической кривой
и А = RB + Xb(o>bQb\	_
Ub = Ra + xa(^aQa)’
Здесь также используются конвертируемые в числовой формат коорди-
наты точек эллиптической кривой. На третьем этапе А и В вычисляют
общую для них точку эллиптической кривой
W = sAUA = sBUB. .	(2.18)
92
Глава 2. Протоколы на эллиптических кривых
Действительно, в соответствии с использованными обозначениями (2.14)-
(2.15) получим на стороне А:
sAUA = (kA + xAaAdA) mod N(RB 4- xBaBQB) =
= (kA 4- xAaAdA) mod N(kBP 4- xBaBdBP) =
= (kA 4- xAaAdA) mod N(kB 4- xBaBdB)P =
= (kA + xAaAdA)(kB 4- xBaBdB)P
Аналогично получим для стороны В:
sBUB = (kB 4- xBaBdB) mod N(RA 4- xAaAQA) =
= (кв 4- xBaBdB) mod N(kAP 4- ждадб/дР) =
= (kB 4- xBaBdB) n\odN(kA 4- xAaAdA)P =
= (kB 4- xBaBdB)(kA + xAaAdA)P.
Как видим, в рассмотренной интерпретации протокола модульная число-
вая арифметика сочетается с арифметикой эллиптической кривой: точ-
ка W вычисляется абонентом А, в конечном итоге, по формуле
W = ЦкА 4- xAaAdA) mod N)UA,	(2.19)
где используется точка UA, вычисляемая по формуле (2.17). Абонент В
получает точку W аналогично.
В варианте, не использующем модульную арифметику, та же точка W
получается абонентом А по следующему алгоритму:
1.	Вычислить точку UA по формуле (2.17).
2.	Вычислить точку W по формуле
W = кАиА + xA(aA(dAUAy).
Легко видеть, что с учетом модульного свойства умножения точки
на константу эта формула эквивалентна формуле (2.19).
Действия абонента В аналогичны.
По окончании исполнения протокола А и В располагают секрет-
ной точкой W эллиптической кривой, координаты которой могут быть
использованы для построения бинарного кода секретного ключа симмет-
ричной системы.
Пример 2.2.3. Рассмотрим реализацию протокола с использованием той же эл-
липтической кривой, что и в примере 2.2.1 и той же точки Р в качестве системного
параметра. Порядок кривой есть
N = 11692013098647223345629483507196896696658237148126
(при исполнении протокола порядок N в явном виде не используется).
Вычисления представлены в Приложении D на с. 260 в табл. D.I.
Пусть абоненты А и В выбрали числа
dA = 345, dB = 4567
2.3. Криптосистемы Эль-Гамаля
93
и зарегистрировали на сервере свои долговременные ключи (см. табл. D.l) QA =
345Р = (aA, bA), QB = 4567P. Пусть выбраны числа кА = 12 и кв = 123 и вычис-
лены кратковременные ключи RA = кАР = 12Р = (хА, yA),RB = квР = 123Р =
(хв,ув), которыми абоненты обменялись. Они получили также долговременные
ключи друг друга с сервера.
Затем они вычисляют W вторым из описанных выше способов.
В таблице D.2 на с. 262 дан пример исполнения протокола с теми же ключами,
но с использованием эллиптической кривой над полем малого порядка.
2.3.	Криптосистемы Эль-Гамаля
Элементы рассмотренного протокола Диффи—Хеллмана с использо-
ванием эллиптических кривых можно усмотреть в варианте криптосисте-
мы Эль-Гамаля5) применительно к группе точек эллиптической кривой.
Допустим, что множество сообщений представляется точками эллип-
тической кривой Е («вложено» в эту кривую условленным способом,
например, как это описано в Разделе 2.1.4, для упрощения дальнейше-
го изложения будем считать, что передаваемым сообщением является
некоторая точка М эллиптической кривой, которая для сообщения m
выбирается известным способом и из которой нужная форма сообще-
ния m также просто получается).
Пусть абонент В намерен переслать абоненту А секретное сообще-
ние т. Для этого можно построить криптосистему Эль-Гамаля на основе
алгебраических свойств эллиптической кривой. В качестве внешних пара-
метров выбираются эллиптическая кривая Е и точка Р высокого порядка
из группы точек E(F).
Абонент А выбирает секретный ключ кА 6 Z*N, вычисляет и объявляет
свой открытый ключ (Е, P,Y), где Y = кАР.
5) Классический вариант криптосистемы Эль-Гамаля формулируется применительно
к группе Zp. Внешними параметрами криптосистемы являются простое число р, и образу-
ющий элемент а мультипликативной группы Zp. Секретным ключом абонента А является
выбираемый им вычет a € Zp, его открытым ключом объявляется тройка (р, a, аа modp).
Абонент В для передачи абоненту А секретного сообщения т Е Zp:
1) получает авторизованную копию открытого ключа (р, а, /3);
2) выбирает случайное число г Е Zp (рандомизатор);
3) вычисляет сеансовый ключ д = (3r mod р;
4) вычисляет криптограмму с = (сь с^) = (оГ, т  д) mod р;
5) отправляет криптограмму с абоненту А.
Для расшифрования криптограммы абонент А, используя свой секретный ключ а,
1) вычисляет rf mod р (получает в результате аг'а);
2) инвертирует результат п. 1 и умножает полученный вычет на С2 по модулю р, получая
при этом сообщение т :
оГг а • С2 mod р = а~г'а • т • aa’r mod р = оГга • оГа • т mod р = 1 • т = т.
94
Глава 2. Протоколы на эллиптических кривых
Абонент В для передачи абоненту А секретного сообщения m
1)	получает авторизованную копию открытого ключа (Е, N, Р, У);
2)	«вкладывает» сообщение m в точку М G E(F);
3)	выбирает случайное число т 6 Z*N (рандомизатор);
4)	вычисляет сеансовый ключ Д = rY;
5)	вычисляет криптограмму С — (Cj, С2) — (гР, М 4- Д);
6)	отправляет криптограмму С абоненту А.
Для расшифрования криптограммы абонент А, используя свой сек-
ретный ключ ,
1) вычисляет (получает в результате &дгР);
2) обращает результат п. 1 и складывает полученную точку -кдгР с точ-
кой С2, получая при этом точку М:
-кАгР + М + Д = М + гкАР - кАтР — М.
Криптоаналитику известны открытый ключ (Р, Р, Y) и криптограм-
ма (Ci,C2), таким образом для получения точки М ему необходимо
вычислить точку кдтР. Для этого ему придется решить задачу Диффи—
Хеллмана для эллиптической кривой: найти эту точку по известным
точкам гР и Y = кАР, либо ему придется решать задачи дискретно-
го логарифмирования, вычисляя секретный ключ кА и рандомизатор г
по точкам кдР, гР и Р известной ему эллиптической кривой Е и извест-
ному ему порядку точки Р.
Отметим также, что как и в классическом варианте криптосисте-
мы Эль-Гамаля, повторное использование рандомизатора г недопустимо.
Действительно, если криптоаналитику удалось расшифровать одну крип-
тограмму (СЬС2) или узнать точку М иным способом, то он легко
получит и другие сообщения, зашифрованные с тем же рандомизатором.
Пусть (СЬС^) криптограмма, полученная с тем же рандомизатором г,
что и криптограмма (Ci,C2). Первые точки в этих парах одинаковые,
а вторые связаны соотношением
С2 = С2-М + М'.
Поэтому М' = С2 - С2 + М и второе сообщение найдено.
Пример 2.3.1. Используем эллиптическую кривую и точку Р (см. (2.9) из при-
мера 2.2.1. В разд. 1.2.2 указан порядок группы точек для этой кривой над
полем GP(2163). Определим порядок точки Р, используя разложение
2 х 5846006549323611672814741753598448348329118574063
порядка кривой. Получим
N = 5846006549323611672814741753598448348329118574063,
(так как 2Р (9, а 5846006549323611672814741753598448348329118574063Р = О.)
Допустимы сообщения длиной до 159 бит.
2.3. Криптосистемы Эль-Гамаля
95
Пусть сообщение
m = 7//ac32319a7/c/a8be7edd7634d0&15a/2ec.
Вложим его в эллиптическую кривую, получим, например, точку6)
М = (7//ac32319a7/c/a8be7edd7634d0bl5a/2eca465,
bee7/e/7&/8683/5ae5e6/eMal458d81c774906).
Пусть, как и в примере 2.2.1, кА — 12, тогда Y = кАР возьмем из этого
примера (точка (2.2.1)). Пусть рандомизатор г — 123, тогда первую точку С\ —
123Р криптограммы С также возьмем из примера 2.2.1 (точка (2.2.1)).
Y = кАР= 12Р = (М9776ЬЬе87а8М024&е2е415952/527еее928ИЗ,
C67a28ed7&137e756c37654/186a716/64e5ac546).
Вычислим сеансовый ключ
А = tY = 123У = (W7856cecel3c71919534878bcb6/3a887d613c92,
/661//d/el&a8cblb2adl7&6550c65aa6d4/07/41).
Вычислим вторую точку криптограммы
С2 - М 4- А - (ddl8e5099e285430d67e8611al802137d56569c67,
/99de0e/9c/4975/79c82&el312ba5a2ee5/2c947).
Для расшифрования умножим первую точку криптограммы на секретный ключ
a = кА, получим
(а • r)P = (&&7856cecel3c71919534878&cb6/3a887d613c92,
/661//d/elba8cMd2adl7&6550c65aa6d4/07/41).
Обращая полученную точку, получим
-(a-r)P = (&&7856cecel3c71919534878&c66/3a887d613c92,
4dl9a9112/a94ba8a&/e5/cee96a9602ea99143d3).
Складывая результат обращения со второй точкой криптограммы, получим точ-
ку М:
-(а • г)Р 4-М +А = (7//ac32319a7/c/a8&e7edd7634d0&15a/2eca465,
6ee7/e/76/8683/5ae5e6/e&lal458d81c774906).
Как видим, результат расшифрования оказался правильным (это есть точка М).
Из нее извлекается сообщение
тп = 7 //ac3231 9a7/c/a8 be7edd76 34d0615a flee
заранее согласованной длины.
6) Точка выбирается случайно из нескольких возможных вариантов.
96
Глава 2. Протоколы на эллиптических кривых
2.4. Протоколы цифровой подписи
2.4.1.	Электронная цифровая подпись
Электронная цифровая подпись {Digital signature) под сообщением т
представляет собой некоторый цифровой код Sign (т, к, г), зависящий
от этого сообщения, ключа подписи к и, возможно, рандомизатора (случай-
ного кода) г. Обозначим М, K,R,S — множества возможных сообщений,
ключей подписи, рандомизаторов и значений цифровой подписи. Тогда
цифровую подпись можно рассматривать как отображение
Sign (М, К, R) : М х К х R S.
При фиксированных т Е М и г 6 R и при фиксированных т Е М
и к 6 К отображения Sign (т, К, г) -> S и Sign (m, к, R) являются инъ-
екциями, а отображение Sign (М, fc, г) —> S сюръективно. Однако и этому
отображению можно придать свойство инъективности, если рассматривать
отображения Sign (М, К, R) вида Sign (Л(М), К, R), где h(M) : М -> Н —
хеш-функция7) отображающая множество М сообщений в множество Н
кодов фиксированной длины, и цифровую подпись формировать как зна-
чение отображения Sign (Н, К, R).
В этом случае подпись рассматривается как подпись под парой
(m, h(m)), которую иногда называют сообщением, подготовленным к под-
писи. Множество Ms таких пар обладает рядом важных в криптографи-
ческом отношении свойств
1.	Мощность множества Н много меньше мощности множества Ms'-
\Н\ <С |AfxjET| = [Ms| (мощность области определения хеш-функции
много больше мощности области ее значений).
Хэш-функция (подробнее см., напр. [2, 16]) — это легко вычисляемая функция
h : X —> Y, X Е {0, 1}*, Y Е {0,1}п, предназначенная для «сжатия» произвольного двоич-
ного сообщения х 6 X в некоторую битовую комбинацию у Е Y фиксированной длины п,
называемую «сверткой». (Число п есть длина блока, который, как правило, соответствует
нескольким машинным словам). В криптографии используют только хеш-функции, кото-
рые обладают определенными свойствами, обеспечивающими безопасность использующих
их протоколов. Такими свойствами являются
1) однонаправленность — высокая вычислительная сложность нахождения сообщения х
с заданным значением h свертки (т.е. такого ж, что h(x) = h);
2) устойчивость хеш-функции к нахождению второго прообраза — сообщения х' с тем же
значением свертки h(x') — h(x), которое получено для заданного сообщения х ;
3) устойчивость к коллизиям — высокая вычислительная сложность нахождения пары
сообщений х и х' с одинаковым значением свертки (т. е. сообщений, для которых
h(x) = h(x')).
Здесь и ниже под высокой вычислительной сложностью понимается отсутствие соот-
ветствующих полиномиальных алгоритмов.
8) Поскольку множество Ms, по существу, является графиком хеш-функции h, то
перечисляемые его свойства соответствуют ее свойствам.
2.4. Протоколы цифровой подписи
97
2.	Каждый элемент h множества Н имеет большое число прообразов:
\Н\	|lmm-1(/z)| = \{m : (m, h) E Л<$}|.
3.	Легко получить элемент этого множества с заданной первой коорди-
натой тп, для этого надо вычислить значение h(m) первой коорди-
наты по алгоритму вычисления значения хеш-функции. Тем самым
легко проверить, принадлежит ли данная пара элементов
m € М, h € Н множеству Ms- В то же время вычисление первой
координаты элемента этого множества по заданной второй коорди-
нате практически невозможно вследствие свойства односторонности
хеш-функции 9>.
4.	При заданном элементе (m, h(m)) Е Ms практически невозмож-
но подобрать элемент (m', Д(т')) = (m* 1, h(m)) Е Ms, тп1 / т, т. е.
элемент, отличающийся от заданного только первой координатой (по-
добрать второе значение т' аргумента хеш функции при котором она
получает то же значение, что и при заданном значении т аргумента).
5.	Практически невозможно подобрать два произвольных элемента
(тп, h) и (m', h) б одинаковыми значениями второй координаты
(два сообщения т и т' с одним и тем же значением хеш-функции
h(m) =
Цифровая подпись сообщения h(m) на ключе подписи к допускает
проверку с использованием опубликованного ключа проверки к', алгебра-
ически связанного с к.
Проверка основана на вычислении предиката P(S, Kf) проверки, где
К1 — множество ключей проверки. Цифровая подпись s удостоверяется
с использованием ключа проверки к', если
Р(з, к') = 1.
Односторонние функции f определяются в классе функций fn : Sn -> Sm, т = m(n),
где m(n) — некоторый полином.
Функция называется честной [6], если существует полином q(n), такой, что n^q(m(n)).
Это означает, что такая функция не слишком сильно «сжимает» входные значения. Честная
функция f называется односторонней, если
1) Существует полиномиальный алгоритм (алгоритм, исполняющий не более Р(п) эле-
ментарных операций при вычислении значения функции, Р(п) есть некоторый поли-
ном), вычисляющий ее значение f(x) при любом х. Ниже для сокращения подобное
условие мы будем формулировать так: «/(ж) легко вычислить для всякого х», а если
такой алгоритм не существует, будем говорить «практически невозможно вычислить».
2) Для любого вероятностного алгоритма А и случайно выбранной строки х Er Sn
и любого полинома р(п) вероятность
Pr{f(A(f(x))) = f(x)} <
98	Глава 2. Протоколы на эллиптических кривых
Предикат проверки цифровой подписи с возвратом сообщения10) опи-
сывается как
P(s, V) = {((mz, Ь!(гпУ) е Ms},
где т1 проверяемое сообщение, a h'(m) — хеш-значение подписанного
сообщения, извлеченное из цифровой подписи з на заданном ключе
проверки к', к' 6 К1.
Отображение Sign (М, К, R) обладает рядом свойств, гарантирующих
возможность и достоверность подтверждения подлинности подписи и, тем
самым, гарантирующих невозможность отказа от авторства подписавшим
документ, как и невозможность вскрытия ключа подписи.
1.	Односторонность отображения
Sign (7i(m), К, R) :
по значению отображения s = Sign (Д(т), к, г), такого, что Р(з, к'),
практически невозможно (при известных h(m) и к') узнать ключ к.
2.	Для заданного сообщения т и известного значения цифровой под-
писи з = Sign к, г), P(s,k') — 1, практически невозможно
подобрать другое (фальсифицированное) сообщение т! с тем же зна-
чением Sign к, г) = s цифровой подписи. То есть невозможно
подделать подпись под сообщением.
3.	Практически невозможно найти два произвольных сообщения т
и т' с одинаковым значением подписи з, таким, что Р(з, к') = 1, т. е.
удовлетворяющих предикат проверки на заданном ключе проверки к'.
То есть невозможно подменить подписанное сообщение.
4.	Не зная ключ подписи, практически невозможно найти произвольное
сообщение т и правильное значение цифровой подписи под ним.
То есть невозможно создать подписанное сообщение.
Эти свойства обеспечиваются использованием криптографически
стойкой хеш-функции, обладающей перечисленными выше свойствами,
а также биективных преобразований, соответствующих трудным алгебра-
ическим проблемам.
2.4.2.	Обобщенная схема электронной подписи Эль-Гамаля
Эта схема работает в любой абелевой группе с трудной проблемой
дискретного логарифма. Это могут быть мультипликативная группа лю-
бого поля Галуа, группа точек несуперсингулярной эллиптической кривой
или подгруппы высокого порядка этих групп. Ввиду того что обозначения
мультипликативной и аддитивной степени различаются, удобнее дать два
варианта описания протокола.
10^ Основана на возможности извлечения «отпечатка» h(m) сообщения т из цифровой
подписи Sign (m, k, г).
2.4. Протоколы цифровой подписи
99
Обобщенная подпись Эль-Гамаля в мультипликативной группе. Публикуе-
мыми системными параметрами являются описание группы (или под-
группы) G (характеристика поля, неприводимый многочлен (в случае
использования расширения поля), образующий элемент а, порядок N
группы).
Ключ подписи выбирается как целое число к, 0 < к < N.
Публикуемый ключ проверки вычисляется как элемент /3 = ак.
Цифровой подписью под документом m является пара (с, d), где
с = аг — случайный элемент группы G, определяемый случайным выбо-
ром рандомизатора г, 0 < г < N - 1,
d =	- kh(c)) mod N
— число, вычисляемое с использованием ключа подписи к, того же
рандомизатора г и значений h(m) хеш-функции от сообщения m и h(c)
от соответствующего рандомизатору случайного элемента с группы G
(код описания этого случайного элемента рассматривается как значение
аргумента хеш-функции).
Предикат проверки цифровой подписи (с, d) под документом т,
полученной на ключе подписи к, описывается следующим образом:
ceG, 0 < d < N — 1, /3h(c)cd = ah(m).	(2.20)
Если подпись вычислена абонентом, владеющим секретным клю-
чом к, то данный предикат выполняется. Действительно, в этом случае
d = r-1(/z(m) - &/z(c))(mod TV).
Умножив обе части сравнения на г, получим
rd = h(m) - fc/i(c)(mod TV),
что эквивалентно сравнению
Д(т) = kh(c) + rd(mod TV).
Отсюда следует
а^(т) = aWi(c)+rd _ (^ak^h(c)(^ary — ph^cd
Если же ключ подписи другой, то предикат имеет значение 0.
Заметим, что генерация подписи требует вычислений как в группе G,
так и в группе Zn, в то же время проверка подписи связана с вычислениями
только в группе G.
Чтобы подделать подпись под сообщением т', злоумышленник вы-
нужден взять случайное число г и вычислить с — аг с тем, чтобы затем
определить d — г-1(Д(т') - kh(c)) modN. Для этого надо, зная /3 = ак,
найти ключ подписи к, т. е. найти дискретный логарифм от /3 по осно-
ванию а, что практически невозможно. Остается выбирать d наугад
с вероятностью успеха 1/N.
100
Глава 2. Протоколы на эллиптических кривых
Если же он подделает подпись под сообщением т' тп каким-
то другим способом (т. е. возьмет некоторое число г, вычислит с — ar
и затем каким-то образом найдет d так, что при подстановке Д(т') вме-
сто h(m) будет выполняться предикат проверки (2.20)), то этим способом
он сможет решать задачи дискретного логарифмирования в соответству-
ющей мультипликативной группе: он сможет вычислить ключ подписи
k =	- rd)h(c)~l. Таким образом, проблема подделки подписи
столь же сложна, как и проблема дискретного логарифма в этой группе.
Число г должно уничтожаться сразу после вычисления подписи,
так как по этому числу (если оно станет известно злоумышленнику)
и значению подписи (с, d) под известным сообщением тп вычисляется
секретный ключ:
к — (h(rn) - rd)h(c)~l mod TV
Это же возможно в случае повторного использования числа г, так как
в этом случае оно с большой вероятностью вычисляется. Действительно,
пусть с использованием одного и того же числа г получены две подписи
(ci, di) и (с2, ^)5 Ci = С2 = ar = с под сообщениями тп^ и m2- При этом
di = r-1{/i(mi) - kh(c)} modN, d2 = ^1{^(m2) - kh(c)} modN.
Тогда
(di - d2)r = (/i(mi) - h(m2))(mod TV).
При di 7^ d2 получаем r = (di - d2)-1(fo(mi) - Njnz)) mod TV, теперь
можно вычислить к, как описано выше.
В алгоритме подписи используется не само сообщение, а значение
хеш-функции от него. Иначе возможен подбор сообщения с известным
значением подписи (т. е. не выполняется четвертое свойство цифровой
подписи). Например, можно выбрать случайные числа i,j, 1 < i < TV,
1 < j < N, (j, TV) = 1, и положить
с = a1 ft —	; d = -/i(c)j-1 mod N.
Тогда пара (c, d) является подписью под сообщением
тп = di mod N =	mod TV,
так как
\a a v — a pJ — c.
Действительно,
{ama~kh^)d 1	—
=	_ aiakj _ ^i+kj =
Теперь можно получить ama~kh^ = cd, откуда следует подтверждение
подписи (напоминаем, что aa = Д):
р у ’с ~ a .
2.4. Протоколы цифровой подписи
101
В предикате проверки подписи предусматривается проверка, что
с Е G. Если эту проверку не делать, то в некоторых случаях, например,
при построении протокола на основе группы Z* (порядка N = р - 1)
злоумышленник может подписать выбираемое им сообщение т', ес-
ли располагает подписанным на секретном ключе к сообщением т.
Пусть (с, d) — подпись под сообщением т. Допустим, что существует
m-1 mod(p- 1). Тогда можно вычислить и = т' -т~{. Затем по китайской
теореме об остатках можно вычислить d' = dumodN и d, такие, что
с = cw(mod N) и с = c(mod N + 1).
Пара (c^d') является подписью под сообщением т', которая подтвер-
ждается предикатом проверки подписи и сообщение т' будет принято,
если указанная проверка игнорируется [72].
Обобщенная подпись Эль-Гамаля в аддитивной группе. Рассматриваемая
схема наиболее удачно может быть реализована при использовании в ка-
честве группы G группы точек эллиптической кривой над конечным
полем. Проблема дискретного логарифма в этой группе гораздо сложнее,
чем в мультипликативной группе конечного поля F. Поэтому может быть
выбрано меньшее q, чем в случае реализации в группе F*.
В случае использования группы точек эллиптической кривой си-
стемными параметрами являются уравнение эллиптической кривой Е,
описание поля F и точка Р кривой известного большого порядка N —
образующий элемент подгруппы G С E(F) группы точек эллиптической
кривой. Публикуемым ключом проверки к' является точка Q = кР эллип-
тической кривой. Цифровая подпись (с, d) = (R, d), где с = R = гР —
случайная точка, элемент группы G, определяется случайным выбором
рандомизатора г, 0 < г < N - 1,
d =	- kh(R)) mod N
— число, вычисляемое с использованием ключа подписи к, того же
рандомизатора г и значений h(m) хеш-функции от сообщения т и h(R)
от соответствующей рандомизатору случайной точки R = (х, у) группы G
(конкатенация х\\у координат х и у этой точки рассматривается как
значение аргумента хеш-функции).
Предикат проверки цифровой подписи на документе т, полученной
на ключе подписи к, описывается следующим образом:
REG, 0<d<7V-l, h(c)Q + dR = h(m)P (2.21)
Если генерация подписи требует вычислений как в группе E(F),
так и в группе Zn, то проверка подписи связана с вычислениями только
в группе E(F).
Алгебраически и криптографически эквивалентным рассмотренному
варианту цифровой подписи является вариант, отличающийся тем, что
102
Глава 2. Протоколы на эллиптических кривых
вместо точки с = R эллиптической кривой в качестве первого элемента
цифровой подписи берется число с — h(R), хеш-значение от этой точки.
При вычислении второго числа подписи не производится умножение
на число г-1:
d = h(m) - kh(R).
Соответственно упрощается и предикат проверки подписи:
0<$<7V-l, 0<d<TV-l, cQ + dP = h(m)P.
В данном случае алгоритм получения подписи использует только операции
модульной арифметики, а алгоритм проверки — только операции группы
точек эллиптической кривой.
Последний вариант подписи используется в алгоритме ECDSA, при-
меняемом в американском стандарте электронной подписи [61].
2.4.3.	Электронная подпись Эль-Гамаля
с возвратом сообщения — схема Nyberg—Rueppel
Проверки цифровой подписи с возвратом сообщения основана на воз-
можности извлечения «отпечатка» h(m) сообщения т из цифровой под-
писи s — Sign (m, к, г), полученной на ключе подписи к при рандомиза-
торе г, и состоит в проверке условия
h'(m) = h(m),
где т' сообщение, подпись под которым проверяется, а h'(m) — хеш-
значение подписанного сообщения, извлеченное из цифровой подписи s
на заданном ключе проверки к’, к1 Е К’.
Пусть E(F) группа точек эллиптической кривой, Р — базовая точка
открытого ключа, N — порядок этой точки, к — секретный ключ подпи-
сывающего документ участника. Открытым ключом последнего является
точка
Q - кР	(2.22)
Пусть е = h(m) — значение хеш-функции h для документа т.
Алгоритм генерации подписи следующий.
1. Взять случайное число г, 0 < г < N, такое, что ж-компонента точки
R = rP = (х, у)	(2.23)
не равна 0.
2. Используя х-компоненту точки R как целое число, вычислить
с — (х -h е) mod TV,	(2.24)
d = (г - кс) mod N	(2.25)
Если с = 0 или d — 0, то вернуться к шагу 1.
Пара (с, d) является подписью для документа т, такого, что h(m) — е.
Для проверки, что /i(m) является корректным хеш-значением, вы-
полняются следующие действия.
2.4. Протоколы цифровой подписи	103
1.	Проверить, что 1 < с < N - 1, 1 < d < N - 1.
2.	Вычислить
R' = dP + cQ.	(2.26)
3.	Интерпретируя а:-компоненту точки R' как двоичную запись целого
числа, вычислить
е = (с - х) mod п.	(2.27)
4.	Если полученное значение е1 совпадает с хеш-значением
вычисленным для полученного сообщения т1, то последнее удосто-
веряется.
Поясним этот протокол следующим примером (при заведомо малых
значениях параметров).
Пример 2.4.1. Выберем несуперсингулярную кривую У2 -hXY = X3 4-X2 +1 над
полем GF(25) = GF(2)(A), где А — корень неприводимого многочлена 1+JT2+X5,
и базовую точку Р = (00101,10110) этой кривой. Непосредственной проверкой
убедимся, что порядок N этой точки равен 22. Пусть значение хеш-функции
сообщения т есть е = h(m) = (1011) = 13 и). Допустим, что секретным ключом
является двоичный код к — (111) = 7, тогда открытым ключом является точка
Q = кР = 7(00101, ЮНО) = (10011, 10111).
Для получения подписи сначала базовая точка Р умножается на случайно выби-
раемый рандомизатор г, пусть г = 5, и получается точка
R = 5P = (10111, ПОП);
ж-компонента (10111) = 29 этой точки R также является случайным числом.
Прибавление по формуле (2.24) этой точки к хеш-значению е = h(m) = 13
по модулю N = 22 (порядка точки Р) эффективно маскирует это хеш-значение,
в результате получается первое число кода цифровой подписи
с — (х 4- е) mod N = 29 4- 13 mod 22 = 20.
Второе число d кода цифровой подписи получается по (2.25) с использованием
секретного ключа к:
d — (г - кс) mod N = (5 - 7 • 20) mod 22 = 19.
Цифровая подпись под значением е — h(m) на ключе подписи к = 7 есть пара
чисел (с, d) = (20,19).
Этап проверки подписи по (2.26) позволяет восстановить точку R и, следом,
по (2.27) получить замаскированное хеш-значение е : если подпись корректна, то
получится R! — R:
R! = dP 4- cQ = dP 4- скР = (d + ck)P — (r - ck 4- ck)P = rP = R.
В нашем примере
R' = dP + cQ = 19(00101, 1011) 4-20(10011, 10111) = (10111, 11011) = R.
Используя ж-координату ж' = (10111 = 29) точки R, восстановим хеш-значение
е = с - х = 20 - 29 mod 22 = 13.
ll) Элементы двоичных кодов располагаются в порядке возрастания степеней или весовых
эквивалентов.
104	Глава 2. Протоколы на эллиптических кривых
Если это восстановленное значение е' совпадает с хеш-значени-
ем вычисленным по полученному сообщению т', то можно счи-
тать, что последнее мог подписать только обладатель секретного ключа к
и что ни сообщение, ни его хеш-значение не было изменено активным
криптоаналитиком или вследствие ошибок при передаче или хранении.
Заметим, что при проверке подписи операции умножения модульной
арифметики не используются.
В российском стандарте цифровой подписи с возвратом сообщения
используется другая схема генерации и проверки подписи.
Цифровой подписью под сообщением т со значением хеш-функции
е = h(m) на ключе подписи к является пара чисел (с, d), где с есть
отличное от нуля число, определяемое х-координатой точки R — гР,
а число d вычисляется как
d — (хк + re) mod N.
Для проверки цифровой подписи восстанавливают точку R, исполь-
зуя операции арифметики эллиптической кривой и модульной арифме-
тики:
R! =ziP + z2Q,	(2.28)
где
Z\ — dv mod N, z2 = -cv mod N
при у — e~x mod N.
В этом случае на этапе проверки цифровой подписи приходит-
ся выполнять операции умножения и мультипликативного обращения
в группе Z*N. Порядок N базовой точки Р в данном случае есть простое
число.
Пример 2.4.2. Возьмем базовую точку Р = (0001,11111) той же кривой, что
и в предыдущем примере, и образуем цифровую подпись под сообщением т с
хеш-значением е ~ h(m) = 2 (то же, что и в предыдущем примере, но приведенное
по модулю N = 11) на том же ключе подписи к = 7 и с тем же рандомизатором
г = 5. Порядок N точки Р есть простое число 11.
Точка ключа проверки есть Q = кР = 7(0001, 11111) = (ОНИ, 10101). «Точка
возврата» есть R = rP = 5(0001, 11111) = (0101,01001).
Первое число цифровой подписи с = (0101)2 = (Ю)ю.
Второе число цифровой подписи d = (ск + re) mod ТУ = (10-7 + 5- 2) mod 11 = 3.
Цифровая подпись есть пара чисел (с, d) — (10, 3).
Для проверки цифровой подписи вычислим
у — е-1 mod ТУ = 2-1 mod 11=6, Z\ = dy mod ТУ = 3 • 6 mod 11 = 7,
z2 = —су mod ТУ = -10 • 6 mod 11=6.
Восстанавливаемая точка возврата вычисляется в соответствии с (2.28):
R! = z{P + z2Q = 7(0001, 11110 + 6(01111, 10101) =
= (01111, 10101) + (11001, 10101) = (0101,01001) = « у).
Как видим, х1 = с.
2.5. Передача с забыванием
105
2.5.	Передача с забыванием
В этом разделе рассматриваются приложения эллиптических кри-
вых к построению протоколов передачи сообщений с забыванием, когда
отправитель уверен, что адресатом получено только к или не более к
сообщений из направленных ему п сообщений, п > к, а адресат уве-
рен, что отправитель не знает, какие именно сообщения получены, или
когда отправитель уверен, что отправленное им сообщение получено
с вероятностью не более к/п. Схемы основаны на трудности проблем
Диффи—Хеллмана и дискретного логарифмирования в группе точек эл-
липтической кривой.
2.5.1.	Введение
Передачей комбинации к из п сообщений с забыванием называется
общение между двумя участниками А и Б по следующим правилам.
1.	Участник А передает участнику В п сообщений тп\, m2,..., тп,
из которых В читает только нужные ему к, к < п, сообщений
(предполагается, что получателю известны имена т^, m2,..., тп,
этих сообщений, по которым он осуществляет свой выбор).
2.	Участник А не знает, какие именно сообщения прочитал В.
3.	Оба участника уверены, что условия 1 и 2 выполнены.
Если передаются п + к, к < п, сообщений, из которых сообщения
mn+i,... ,тп+к являются тривиальными случайными кодами, на несу-
щими информации, то имеет место передача с забыванием не более к
сообщений. В этом случае правило 2 заменяется следующим.
2'. Участник А не знает, какие именно I, I к, сообщений прочитал В
и прочитал ли он хотя бы одно сообщение.
Участник В имеет возможность сообщить участнику А, что он про-
читал не более t, t к, сообщений из числа mi,..., тп, вернув ему к -1
тривиальных сообщений из числа mn+i,..., тп+к.
Передача комбинации к из п сообщений с забыванием может приме-
няться, например, при продаже секретов [14], когда знание, какие именно
секреты приобретены покупателем, неприемлемо для него и, кроме того,
является новым секретом (секретом покупателя), который может прода-
ваться отдельно. Тогда уточнение числа t может потребоваться, например,
для обоснования размера оплаты участником В услуги участника А. Ино-
гда участнику В выгоднее перечислить большую сумму, чем раскрыть точ-
ное количество полученных сообщений. Информация, что В осведомлен
о всех темах, предлагаемых А, также может быть секретом участника В.
По правилу 2, с точки зрения отправителя, вероятность доставки
в процессе передачи с забыванием данной комбинации, содержащей к
из п переданных сообщений равна
. Это означает, что вероятность
106
Глава 2. Протоколы на эллиптических кривых
того, что при этом оказалось принятым (в составе некоторой комбинации)
конкретное сообщение из п переданных равна k/n.
Упражнение 2.5.1. Докажите это.
Таким образом условие передачи комбинаций к из п сообщений
достаточно для передачи одного из этих п сообщений с вероятно-
стью р — к/n. Поэтому протокол передачи с забыванием к из п со-
общений можно преобразовать в протокол дробной (с вероятностью к/п)
передачи данного сообщения. Но, видимо, не всякий протокол дробной
передачи с вероятностью р — к/n содержит ключевую информацию, до-
статочную для его преобразования в протокол передачи к из п сообщений.
Понятие передачи с забыванием {oblivious transfer) введено М. Ра-
биным в связи с изучением проблемы разделения секрета [81]. Другие
аспекты этой проблемы обсуждаются в [6].
Большое разнообразие протоколов передачи с забыванием представ-
лено в работах, цитированных в [26]. Первый неинтерактивный протокол
передачи с забыванием, т. е. протокол, не требующий после инициали-
зации в процессе передачи никакой информации от получателя, был
предложен в работе [25], что позволило на основе таких протоколов стро-
ить неинтерактивные протоколы доказательства с нулевым разглашением
секрета [84, 85].
Некоторые протоколы передачи с забыванием анализируются в кни-
гах [11, 14], неинтерактивные протоколы доказательства с нулевым раз-
глашением описаны в [11].
В этом разделе изучается общая схема, лежащая в основе многих не-
интерактивных протоколов передачи с забыванием. Основываясь на этой
схеме, мы приводим унифицированное описание ряда протоколов неин-
терактивной передачи с забыванием. Рассматриваемые протоколы могут
быть построены на основе ключевой информации систем дробной пере-
дачи с забыванием, описанных, например в [26] (см. также разд. 2.5.5).
В заключение рассматриваются некоторые применения протоколов это-
го типа.
Для конкретности и унификации изложения общая схема и протоко-
лы даются на основе алгебраических свойств группы точек эллиптической
кривой. В качестве криптосистемы для шифрования передаваемых сооб-
щений используется криптосистема Эль-Гамаля (в аддитивном исполне-
нии с использованием операций группы точек эллиптической кривой).
2.5.2.	Схема некоторых протоколов передачи с забыванием
Многие неинтерактивные протоколы передачи комбинации сообще-
ний с забыванием можно рассмотреть в рамках следующей общей схемы.
Взаимодействуют отправитель сообщений А и получатель сообще-
ний В. Вычисления производятся в подгруппе G группы точек эллипти-
ческой кривой с трудной проблемой дискретного логарифма. Предполага-
ется, что в такой подгруппе проблема Диффи—Хеллмана также является
2.5. Передача с забыванием	107
трудной. Параметры этой кривой и образующий элемент Р этой подгруп-
пы являются системными параметрами схемы передачи с забыванием.
Протокол передачи комбинации сообщений включает три этапа.
На этапе инициализации устанавливаются системные параметры, фор-
мируется открытый ключ зашифрования Ку получателя сообщений, соот-
ветствующий секретный ключ расшифрования КР и параметры предиката
проверки правильности открытого ключа Ку.
Открытый ключ Ку формируется на основе ключевой информации —
вектора
(Vi,...,K),	(2.29)
где Vi = Ку{ — Х\Р, ... , Vk = Kyk = xkP являются открытыми ключами
(ключами зашифрования) для криптосистем Эль-Гамаля, и получателю
известны соответствующие секретные ключи
Kpt = Xi, Kpk = xk	(2.30)
расшифрования.
Остальные элементы Г&+1,..., Vn для отправителя имеют вид откры-
тых ключей (являются элементами подгруппы), но для них у получателя
нет ключей расшифрования. Назовем их «пустыми» открытыми ключами.
Отправитель не может определить, является ли любой предъявленный ему
код открытым ключом некоторой используемой криптосистемы или нет.
Открытый ключ Ку получателя представляет собой набор
(У1...,У„) = (УИ1)...,У,(п)),	(2.31)
где тг есть некоторая перестановка на множестве индексов {1, 2,... , п},
являющаяся секретом получателя.
Секретный ключ КР получателя включает в себя секретные клю-
чи (2.30) и подстановку тг.
Подстановка тг выбирается получателем таким образом, чтобы индек-
сы имен ji, i = 1,... к, нужных ему к сообщений оказались на первых к
местах, а индексы i = 1,..., к либо сохранили свои позиции (если ji = г),
либо переместились в позицию , т. е. тг(г) = , 7r(j\) = i, i = 1,..., к.
Параметры U9 W],..., Ws предиката проверки также являются эле-
ментами подгруппы G. Предикат проверки зависит от элементов (2.29)
открытого ключа и при заданных параметрах выполняется только в случае
правильного построения последнего, т. е. если он содержит только к от-
крытых ключей криптосистемы, для которых получатель располагает сек-
ретными ключами расшифрования. Некорректное построение открытого
ключа должно противоречить практической невозможности вычисления
дискретного логарифма или решения проблемы Диффи—Хеллмана. Па-
раметр U является любым элементом с неизвестным обоим участникам
дискретным логарифмом по основанию Р. Участники могут его вырабо-
тать, например, путем исполнения протоколов, рассмотренных в разд. 2.2,
108
Глава 2. Протоколы на эллиптических кривых
или же получить его от доверенного центра Т. Остальные параметры
в некоторых протоколах могут отсутствовать.
На этапе авторизации и проверки открытого ключа ключ Ку публику-
ется и по авторизованному каналу доставляется отправителю А, который
осуществляет его проверку, вычисляя значение предиката проверки. Па-
раметр U имеется как у отправителя, так и у получателя. Остальные
параметры предиката проверки (если они имеются) публикуются и до-
ставляются отправителю А в том же порядке, что и открытый ключ.
На этапе коммуникации отправитель А шифрует сообщения т^...,тп,
используя истинные или «пустые» открытые ключи криптосистемы, и от-
правляет набор криптограмм
(с,,..., cn) =	, Е^(тп)) = (Еу^т^,Еу,м(тп))
получателю.
Получатель В расшифровывает криптограммы ..., и полу-
чает набор нужных ему сообщений (из множества {mi,..., тп} передан-
ных):
^7г( 1) ~ ^Крх (с?г( 1)) = DXi (Сте(j)) ,	. . . ,	m^.) = D^pk (c?r(A;)) = DXk ) •
Вместо традиционного алгоритма зашифрования и расшифрования
удобно использовать шифрование наложением маски, которая вычисля-
ется из шифра единичного элемента подгруппы G.
Например, если используется криптосистема Эль-Гамаля с открытым
ключом Y — хР и секретным ключом х, вместо криптограммы (C*i, Сз) =
(гР, М(т) + rY) точки М(т), содержащей сообщение т, можно вычис-
лить криптограмму (C^CS = (кР, т ф ^(kY)), где ij) — инъективное
отображение G —> {0, l}*', Г Z, где I есть максимальная длина бинар-
ного сообщения т. Расшифрование такой криптограммы осуществляется
следующим образом: т — Сз Ф ф(хС\) = тф ip(rY) ф ^(гУ). Как видим,
используются элементы криптограммы (гР, (9+гУ) = (гР, rY) единицы О
подгруппы G, получаемые на открытом ключе зашифрования У с исполь-
зованием случайного сеансового ключа к. Инъективное отображение
можно получить, например, как конкатенацию х\\у двоичных кодов ко-
ординат точки rY — (ж, у). В этом случае I' = 2t, где t = flog2 |РЦ, |Р| —
порядок поля Р, над которым определена эллиптическая кривая. Сообще-
ния т, как правило, являются ключами некоторой симметричной крипто-
системы, и их длина невелика. Для зашифрования более длинных сообще-
ний их можно развить на блоки длины не более I'. Выбор I < позволит
устранить взаимную зависимость разрядов маски, так как реально будет
использоваться только код х, отображение при этом остается инъектив-
ным. Но при таком выборе длины сообщения можно использовать неинъ-
ективное отображение ф : G —> {0, 1}* такое, что ty((x,y)) — х. Каждая
точка из {0, имеет при этом не более двух прообразов. Рассмотренный
2.5. Передача с забыванием	109
прием позволяет избежать размещение сообщения т на эллиптической
кривой и упрощает вычисления при зашифровании и расшифровании.
Аналогичная схема может быть описана и для мультипликативного
варианта протоколов (в ней вместо подгруппы аддитивной группы то-
чек эллиптической кривой используется подгруппа мультипликативной
группы поля, операции сложения точек кривой заменяются операциями
умножения элементов мультипликативной группы, а операции умножения
точки не константу — операциями возведения элемента мультипликатив-
ной группы в степень). Читатель может рассматриваемые ниже протоколы
переформулировать в терминах мультипликативной группы.
2.5.3.	Некоторые частные случаи передачи с забыванием
Частный случай к — п - 1. Рассмотрим один протокол передачи комби-
нации к из п сообщений с забыванием и убедимся, что в общем случае он
безопасен лишь в предположении пассивного мошенничества участников
(т. е. при соблюдении ими протокола), а в предположении активного мо-
шенничества он безопасен лишь при к = 1 или к = п - 1. Используются
обозначения из описания общей схемы из предыдущего разд. 2.5.2.
1.	Получатель В
а)	выбирает секретный ключ (жь ж2> • • •, тг) и числа Xj, k<j^n
так, чтобы выполнялось условие Q<Xj<N, (xj 4-... 4- хп) mod TV = 0,
где N — порядок подгруппы G, тг(г) = ji, i = 1,...к, где ji —
индексы имен fhji нужных ему сообщений;
б)	вычисляет Vi = XiP, j = 1,... ,к и V^U+x^P, гЕ{1,.. .,n}\{z*i,.. .,im}
и пересылает к А открытый ключ (Vi,..., Vn) =	• • •, ^тг(п)) •
Предикат проверки открытого ключа выражается равенством
V + v2 + ... + Vn - (n - k)U.	(2.32)
n
Заметим, что 52	= (n - k)U. Допустим, что В знает дискрет-
г=1
ный логарифм ki от некоторого элемента V: = U + XiP. Тогда он
знает дискретный логарифм ki - Xi mod N от U. Действительно,
U = (ki - Xi)P. Таким образом, В не известен дискретный логарифм
ни одного из элементов Vi = U 4- жгР, i = к 4- 1,..., п.
2.	Отправитель А при значении ИСТИНА предиката (2.32) выбирает
п разных чисел 0 < у\,..., уп < N - 1, вычисляет и посылает к В
набор криптограмм
=	ф	••• ’ (.Упр> mn.® V’G/nK))),
где ТП\,..., тп — сообщения, имена т\,..., тп которых были до-
ведены до сведения В до начала исполнения протокола.
110
Глава 2. Протоколы на эллиптических кривых
3.	Получатель В вычисляет = С2 ф ipfxijC-.') = С2. ф ^(ж^л/^.Р) =
С2 4-	= Cl + ip(yijVi) = mir Он не может вычислить
С2 4- ^уМ), i £ {ii,..., z\}, так как он знает только х'Р = U + XiP
и угР и, чтобы узнать (не зная ни х', ни yi) уМ = х’у^Р, ему
необходимо решить проблему Диффи—Хеллмана для группы точек
эллиптической кривой.
После проверки предиката (2.32) отправитель А уверен, что по-
лучатель В действует, не зная дискретного логарифма от U. С другой
стороны, сохраняя в секрете секретный ключ, В уверен, что А не может
различить, какими из п элементов открытого ключа являются элементы
Vii, VJ-2, • • •, Vik ’ соответствующие его выбору, т. е. условия 1-3 передачи
комбинации сообщений с забыванием выполнены.
Если к < п-1, протокол 4 не препятствует активному мошенничеству
покупателя. Действительно, отправитель А не заметит, что получатель В
выбрал секретный ключ
(xi,X2,...	ij G {1, ••• ,n}, i =	— 1,
0 < хг < q - 1, i = 1,... , n - 1,
вычислил Vij = жг.Р, j = 1,..., n - 1 и Vn = xnP 4- (n - k)U, где xn =
-(#i 4-. • .4-£n-i mod TV), и переслал к А открытый ключ (Vb ... Vn)9 соот-
ветствующий выбору им n— 1 (вместо разрешенных к < n-1) сообщений.
При к = п - 1 такой трюк окажется невозможным, т. е. протокол 4
является протоколом передачи комбинации п - 1 из п сообщений с забы-
ванием. При п — 2 этот протокол защищен от активного мошенничества,
являясь аналогом известного протокола передачи одного из двух сообще-
ний с забыванием [11,14,25,26], использующим эллиптические кривые.
Пример 2.5.1. Рассмотрим пример исполнения протокола передачи одного из
двух сообщений с забыванием, используя для наглядности поле малого порядка.
Выберемнесуперсингулярнуюкривую У2+ХУ — Х34-АГ24-1 надполем <7Р(2)(А),
где А — корень неприводимого многочлена 1 4- X2 4- X5, и базовую точку
Р — (00101,10110) этой кривой. Непосредственной проверкой убедимся, что
порядок N этой точки равен 22.
Рассмотрим возможную реализацию протокола передачи с забыванием с ука-
занными системными параметрами. Пусть отправитель А объявил получателю В
имена fhi и т2 Двух подготовленных к передаче сообщений ТП[ = (10001),
тп2 = (11100) длиной п = 5.
Допустим, что отправитель А и получатель В по протоколу Диффи-
Хеллмана выработали точку U = (10011, 10111).
Дискретный логарифм к этой точки по основанию Р участникам неизвестен
(это условно, так как при малом порядке кривой дискретный логарифм легко
находится перебором, в данном случае он равен 7).
Получатель и отправитель взаимодействуют следующим образом.
1.	Пусть получатель В выбрал ключ (ж, г) = (19,1) (это соответствует его
желанию получить сообщение с именем ) и вычислил
2.5. Передача с забыванием
111
Vi = Vt = хР = 19(00101,10110) = (01101,00101),
V^i = V2 = U -хР = (10011,10111) + (01101,01000) = (01111, НОЮ).
Он посылает отправителю А открытый ключ
(Vt,V2) =((01101,00101), (01111,11010)).
2.	Отправитель А выбирает два числа yi = 5, у2 = 16.
Он вычисляет набор из двух криптограмм
((С(, Cf), (d С22)) = ((ViP,	(У1Р, rn2 + tl>(y2V2))) =
= ((5(00101,10110), (10001) ©^(5(01101,00101))),
(16(00101, ЮНО), (11100)©^-(16(01111, НОЮ)))) =
= (((10111,11011), (10001) ©^(10011,10111)),
((11001,00111), (11100) ©^(11001,1111))) =
= (((10111, ПОИ), (10001) Ф (10011)),
((11001,00111), (11100) ©(11001))) =
= (((10111,11011), (00010)), ((11001,00111), (00101))).
Этот набор он посылает получателю В.
3.	Получатель В вычисляет
mi = ml	= 00010 + ^(19(10111, 11011)) =
= 00010 +^((10011, 10111)) = 00010+ 10011 = 10001.
Частный случай k = 1, п 2. Протокол передачи одного из п сообщений
можно построить на основе ключевой информации протокола дробной
(с вероятностью 1/п) передачи с забыванием, описанного применитель-
но к подгруппе простого порядка мультипликативной группы конечного
поля в [26].
Системными параметрами являются подгруппа G группы точек эл-
липтической кривой, имеющая простой порядок р, и образующий эле-
мент Р этой подгруппы. Отправитель А и получатель В вырабатывают
или получают от доверенного центра элемент U подгруппы G таким
образом, что дискретный логарифм этого элемента по основанию образу-
ющего элемента Р этой группы им неизвестен.
Получатель А выбирает случайный элемент х е Zp и элемент i е
{0,1,...,п - 1} (г есть индекс имени сообщения, которое он намерен
получить). Он вычисляет свой открытый ключ
(2.33)
где Vi = хР, Vj — хР + (j - i)U, j / i.
Предикат проверки открытого ключа представляется формулой
V j(Vj = V1 + (j - \)U).	(2.34)
112
Глава 2. Протоколы на эллиптических кривых
Нетрудно проверить, что В знает дискретный логарифм только одно-
го из элементов открытого ключа, знание дискретных логарифмов Xi и Xj
двух элементов Vi = хгР и Vj = XjP, 0 < i < j < р, эквивалентно зна-
нию дискретного логарифма элемента U. Действительно, поскольку Vj =
Vi + (j - i)U, можно получить (j - i)U = Vj -Vi — XjP - XiP = (xj - Xi)P.
Отсюда U = (xj - Xi)(j - i)~xP. Здесь j - i ненулевой элемент поля Zp.
В данном случае ключевая информация (2.29) есть вектор
(Vi, v2,..., Vi^, Vi, Vi+1,..., Vn) = (Vi, V2,..., Vi-i, Vi, vi+l, ...,vn),
а подстановка тг есть (1,г).
Секретным ключом получателя является пара (х, тг).
Открытый ключ (2.33) публикуется и доставляется отправителю А
по авторизованному каналу.
Отправитель А при значении ИСТИНА предиката 2.34 выбирает п
разных чисел 0 < у^,... ,yn < р - 1, вычисляет и посылает к В набор
криптограмм
((Cl,C(),..., (С‘,С?)) - (yiP,mi^(yiVi)),...,(ynP,mn®^(ynVn)),
где ТП[,... , mn — сообщения, имена fh\,..., mn которых были доведены
до сведения В до начала исполнения протокола.
Получатель В вычисляет
Ci ®ij)(xiCl') = Ci ® i/)(xiyiP) = с/ + -ф(уЖ) = тщ.
В не может вычислить С? 4- ^(yjVj), j i, так как он знает только
х'Р — U + XjP и угР,ЛА, чтобы узнать (не зная ни ж7, ни yi) yjVj — x'yiP,
ему необходимо решить проблему Диффи—Хеллмана для группы точек
эллиптической кривой.
После проверки предиката (2.34) отправитель А может проверить,
что получатель В действует, не зная дискретного логарифма от U. С дру-
гой стороны, сохраняя в секрете ключ (ж, тг), получатель В уверен, что А
не может различить, каким из п элементов является элемент Vi, соответ-
ствующий его выбору, т. е. условия 1-3 передачи комбинации сообщений
с забыванием выполнены.
Обратим внимание, что при п = 2 этот протокол совпадает с протоко-
лом передачи п - 1 из п сообщений с забыванием, рассмотренным выше.
2.5.4. Передача комбинации к из п сообщений с забыванием
Сведение к частным случаям. Передачу комбинации к из п сообщений
с забыванием можно осуществить, например, А;-кратным применением
протокола передачи одного из п сообщений с забыванием. При каждом
исполнении получатель «заказывает» и получает нужное ему сообщение.
Объем передаваемой информации возрастает при этом в к раз.
2.5. Передача с забыванием
113
Полиномиальная схема Беллара—Райвеста. Аддитивный вариант. В рабо-
те [26] применительно к мультипликативной группе простого порядка
описан протокол дробной (с вероятностью к/п) передачи с забыванием.
Покажем, как на основе ключевой информации, используемой в этом
протоколе, построить протокол передачи к из п сообщений с забыва-
нием. Мы опишем это с использованием подгруппы простого порядка
группы точек эллиптической кривой с трудными проблемами дискретного
логарифма и Диффи—Хеллмана.
Такие подгруппы имеются, например, в группах точек эллиптических
кривых Коблица, рассмотренных в разд. 1.5.1.
Схема передачи к из п сообщений с забыванием, к < п, основана
на сложности проблемы дискретного логарифма в подгруппе G большого
простого порядка р группы точек эллиптической кривой Е определенного
вида. Поскольку подгруппа G имеет простой порядок, все ее элементы,
отличные от О, являются образующими. Пусть Р — случайно выбранный
генератор подгруппы, тогда G = {iP : i 6 Zp}. Важно, что множество Zp
индексов является полем. Пусть U 6 G — элемент с неизвестным дискрет-
ным логарифмом logp U. Положим сц = 1 € Zp. Выберем п различных
элементов ... ап из Zp \ {«о}- Для простоты, будем считать, что это
элементы 2, 3,..., п + 1.
Параметры эллиптической кривой Е, значения к,п,р,Р, а также
«1,..., ап являются системными параметрами и общеизвестны.
Следуя оригинальной статье [26], первоначально поясним идею схе-
мы (учитывая специфику рассматриваемой подгруппы). Получатель В
формирует открытый ключ
7Ь...,К,ЖО,...,Ж,,	(2.35)
состоящий из п + к -h 1 точек кривой из подгруппы G. Последние к + 1
элементов являются параметрами предиката проверки и предназначены
для проверки отправителем А правильности построения открытого ключа.
Пусть Xi = logp Vi, i — 1,... , n. Ключ (2.35) должен быть сформи-
рован таким образом, что
1.	Получатель В знает случайные к элементов множества {xi,..., хп}.
2.	Существует многочлен /(ж) = /0 + f\x + • • • + fk%k € Zp[x] степени к
такой, что
2.1.	Для всех i — 1,..., п справедливо равенство Xi = f(&i)-
2.2.	Получатель В не знает многочлена /.
3.	Отправитель А может проверить свойство 2.
Получателю предоставляется возможность выбрать элементы Жо,
..., Wk таким образом, чтобы коэффициенты многочлена были дис-
кретными логарифмами этих элементов: /г- = logp Wi, i — 0,
114	Глава 2. Протоколы на эллиптических кривых
но оставались неизвестными ему. Более того, эти элементы должны удо-
влетворять условию
Жо + Wi + ... + Wk = U,	(2.36)
откуда следует, что В не может знать все коэффициенты, и следовательно,
не может знать f (это знание противоречило бы незнанию дискретного
логарифма элемента U). Условие 2.1 может быть проверено методом,
используемым в протоколах проверяемого разделения секрета [6].
Получатель В начинает построение открытого ключа (2.35) выбором
случайных к элементов х^,..., Xik и вычислением элементов
У^=х^Р, ..., Vik=xikP
Затем способом, описанным ниже, он вычисляет элементы ГИо,..., Wk.
Наконец, используя вычисленные элементы открытого ключа, он вычис-
ляет оставшиеся п - к элементов таким образом, чтобы их дискретные
логарифмы не были ему известны.
Элементы Wo,..., Wk получатель В вычисляет по формулам
к
Wi = /3ifiu + 52 д Д, i = о,... ,к,
где /3ij суть элементы (к + 1) х (к + 1) матрицы (Д;), получаемой обра-
щением матрицы Вандермонда, где i,1 — 0,..., к, — Оо
Тем самым он в неявной форме определяет многочлен /(ж) = /о + /1 ж 4-
... + fkxk 6 Zp[x] степени к такой, что fa = logP(JFz) (но В не знает
Недостающие элементы открытого ключа вычисляются по формулам
_ к
Vi = 53 Для всех Т i £ bb • >
)=0
Безопасность описанной схемы основана на следующих утверждени-
ях [26].
Утверждение 2.5.1. Определим в арифметике поля Zp матричное уравнение
Оо, А/ = (Д,>) (logp и, xit,..., Xik)T, (2.37)
и пусть /(ж) = /о + /1^ Ч- •.. + fkXk € Zp[x]. Тогда
для всех j, j = 0,..., к, logP Wj = fa,	(2.38)
для всех i, i = \,...,n, logP Vi = f(oti),	(2.39)
fo + fix + ... + fkxk: = logpK	(2.40)
Заметим, что из (2.38) следует Wj = faP и поэтому из (2.40) получа-
ется, что Wo + Wi + ... 4- Wk — U.
2.5. Передача с забыванием
115
Следующее утверждение обосновывает достаточность следующей
процедуры верификации открытого ключа Vi,..., Vn, Wq, ..., Wk отпра-
вителем A.
1.	Проверяется состав ключа, т. е., уточняется, что он содержит п
элементов группы G, дополненные еще к + 1 ее элементами.
2.	Проверяется, что U = Wq + ... 4- Wk,
3.	Проверяется, что для всех г, i = 1,..., п, выполняется условие
к
Утверждение 2.5.2. Пусть процедура верификации открытого ключа за-
вершилась успешно и пусть многочлен /0 + /1# + • • • + fkxk £ Zp[z] определен
посредством Wq, ..., Wk. Тогда выполняются условия (2.38, 2.39) и (2.40).
Безопасность схемы для получателя В обосновывается следующим
утверждением [26].
Утверждение 2.5.3. Пусть генерация открытого ключа (Vj,... , Vn,Wo,
..., Wk) осуществляется по описанной выше процедуре. Тогда вероятностное
распределение на пространстве открытых ключей будет таким же, как
и при генерации открытого ключа по следующему алгоритму'.
(1)	выбрать fo,..., fk € Zp случайно с соблюдением условия /о + • • • + Л =
logp U,
(2)	принять f(x) = /о + f\X + ... + fkxk Е Zp[x],
(3)	для г = 1,..., п принять Vi = f(pti)P,
(4)	для j = 0, ... k принять Wj = fjP,
(5)	вернуть (У1?..., Уп, Жо,. •. ,Wk).
Упражнение 2.5.2. Опишите рассмотренные выше в данном разделе конкретные
схемы и протоколы применительно к подгруппе простого порядка мультиплика-
тивной группы конечного поля.
2.5.5. Применение передачи к из п сообщений с забыванием
Электронная жеребьевка. Частные протоколы передачи одного из двух
сообщений с забыванием можно использовать для построения протокола
электронной жеребьевки. Участники А и В договариваются (с помо-
щью доверенного центра) о трактовке бинарного результата жеребьевки
и осуществляют протокол передачи с забыванием сообщений mj и m2,
7771 / m2, от участника А к участнику В. При этом эти сообщения имеют
одинаковые значения S — S(mi) = S(rri2) некоторого булева предиката S.
Значение S фиксирует выбор участника А. Сообщения гп\ и m2 преда-
ются участником А по протоколу передачи одного из них с забыванием
участнику В. Заметим, что к моменту получения единственного сообще-
ния от А участник В уже не может изменить выбранного им в процессе
116
Глава 2. Протоколы на эллиптических кривых
исполнения протокола значения бита 2 - i. Для определения результата
жеребьевки участник В возвращает участнику А полученное им сооб-
щение mi, тем самым он сообщает ему значение случайно выбранного
параметра г: участник А узнает это значение, сравнив полученное от В
сообщение тг с mi и m2. Результатом жеребьевки является бит S® (2-г).
Этот результат вычисляет каждый участник. Заключительной пересылкой
участнику В чисел у\ и у-) участник А должен подтвердить, что сообще-
ниям mi и m2 различны и им соответствуют одинаковые значения булева
предиката. Тогда участник В может вычислить m^-i.
Неинтерактивное доказательство с нулевым разглашением секрета12\ При-
менение передачи одного из двух сообщений с забыванием в протоколах
доказательства с нулевым разглашением секрета рассматривается в [11].
Приведем пример неинтерактивного доказательства знания дискрет-
ного логарифма х точки Y = хР эллиптической кривой по основанию Р.
Пусть проверяющий В знает параметры эллиптической кривой, осно-
вание Р и точку Y. Доказывающий А должен убедить проверяющего В
(с вероятностью 1 — 2“г), что он знает дискретный логарифм х точки Y
по основанию Р, не разглашая ни одного бита информации об х.
Пусть доказывающий А располагает последовательностью
(v'.y,2), .... (гДС), .... (уДуг2)
из г открытых ключей, полученных из центра Т, который на предвари-
тельном этапе принял ее от проверяющего В.
Доказывающий А посылает проверяющему В
(Гь • • •, Yt,... , Yr) - (eiP,..., егР,... , erP),
последовательность точек эллиптической кривой, где ег, < q, i =
1,..., n, — случайные натуральные числа, выбираемые им. После этого
доказывающий А пересылает проверяющему последовательность пар со-
общений
(jEfy (е,), Еу2 (е, + х)),...,	(е,), Eyi(ej + ж)),..., (Eyj (ег),Еу?(ег + х)).
Проверяющий располагает последовательностью секретных ключей,
позволяющей ему прочитать по одному сообщению, из каждой пары
полученных криптограмм, т. е. поучить последовательность сообщений
mi,..., mi,... ,mr, каждое из которых должно принадлежать множе-
ству {ег, х 4- Ci}. Более того, сообщение mz = если перестановка тгг
Свойство нулевого разглашения заключается в том, что проверяющий не получает
никакой информации о знании («секрете») доказывающего, например, о факторизации
числа п, а в следующем примере — о знании дискретного логарифма от элемента группы
большого порядка. Это свойство доказывается построением моделирующей машины, которая
без знания секрета выступает столь же успешно, как и доказывающий, поскольку ей известно,
какое из сообщений получает В в процессе передачи с забыванием. О доказательствах
с нулевым разглашением см. также [6].
2.5. Передача с забыванием
117
в г-м секретном ключе проверяющего тождественная, иначе тг• = х + ег .
Это возможно только в случае, когда доказывающий знает х. Это свой-
ство последовательности принятых сообщений проверяющий В может
верифицировать, убедившись, что каждое полученное им сообщение удо-
влетворяет предикату
( Y + Yi, если перестановка тгг есть транспозиция,
ТПгР = <
t Yi, если перестановка 7гг тождественная.
Протоколы голосования. Протоколы голосования наряду с другими долж-
ны удовлетворять следующим условиям [14]:
1)	возможность голосования предоставляется только законным (персо-
нально зарегистрированным) избирателям;
2)	бюллетени избирателей сохраняются в тайне;
3)	каждый избиратель не может использовать свой голос более одно-
го раза;
4)	каждый избиратель имеет возможность проверки правильности учета
его голоса в итогах голосования.
Условия 2, 4 будут выполнены, если все бюллетени будут опублико-
ваны с заменой явных идентификаторов избирателей секретными произ-
вольно выбираемыми каждым избирателем кодами. Для этого каждому
из к избирателей предоставляется возможность передачи от доверенного
центра Т одного из п, п к, временных удостоверений с забыва-
нием (в центре не знают, какое именно временное удостоверение взял
данный избиратель). Список имен временных удостоверений wt\,... , тг
публикуется и избиратель выбирает одно из них и выбором соответ-
ствующей транспозиции формирует из заранее выработанной ключевой
информации свой открытый ключ. Центр Т после проверки правильности
открытого ключа избирателя посылает ему на этом ключе полный список
временных удостоверений, из которого избиратель извлекает единствен-
ное удостоверение с выбранным им ранее именем. После отправления
зашифрованного списка избирателю его явный идентификатор удаляется
из списка законных избирателей.
Список временных удостоверений передается центром Т другому
доверенному центру С, осуществляющему прием бюллетеней и опубли-
кование итогов голосования.
Избиратель выбирает свой секретный идентификатор 5г , обозначе-
ние Vi своего голоса (например, имя выбранного кандидата) и посылает
центру С тройку (тг, зг-, Центр С проверяет, есть ли временное удо-
стоверение в списке, полученном от центра Т, вычеркивает его из этого
списка и помещает секретный идентификатор 5?- в список Ri голосов, от-
данных за кандидата Vj. Пересылка информации от избирателя в центр С
на должна раскрывать связь между тг и идентификатором избирателя.
118
Глава 2. Протоколы на эллиптических кривых
Дробная передача с забыванием. Дробной с вероятностью к/п передачей
сообщения с забыванием (fractional oblivious transfer) называется общение
между двумя участниками по следующим правилам [26].
1.	Участник А передает участнику В единственное сообщение тп, при
этом получатель В может прочитать его с вероятностью к/п.
2.	Участник А не знает, прочитал ли В посланное ему сообщение тп.
3.	Оба участника уверены, что условия 1 и 2 выполнены.
Как отмечено в [26], такая передача позволила бы в законодательном
порядке контролировать определенную часть секретной переписки, осу-
ществляемой по секретному симметричному каналу. В протоколе передачи
секретного ключа s симметричного канала связи между абонентами А и В
сети предусматривается дробная с вероятностью к/п передача с забывани-
ем этого ключа контролирующему центру Т, который имеет возможность
пассивно перехватывать информацию, передаваемую по открытому кана-
лу от абонента А к абоненту В. При этом абонент В имеет возможность
расшифровать криптограмму и получить ключ, как и последующую пе-
редаваемую на этом ключе информацию с вероятностью 100 %, в то
время, как вероятность овладения ключом и последующей информацией
центром Т равна к/п. Такие протоколы называются протоколами «полу-
прозрачной криптографии» (translucent cryptography). В отличие от схемы
забывающей передачи комбинации сообщений с забыванием, переста-
новка % при выборе открытого ключа выбирается случайно, а передача
открытого ключа отправителю сообщений и его верификация осуществ-
ляется на этапе инициализации. Детали этого протокола см. в [26].
Рассмотренные выше протоколы передачи к из п сообщений можно
приспособить для передачи одного сообщения с вероятностью р = к/п.
Пусть при формировании открытого ключа (2.31) центр Т выбирает слу-
чайную подстановку тг. Отправитель А направляет центру Т п сообщений
тп\,..., тщ,... тпп, где сообщение тпг есть сообщение, которое центр при-
мет с вероятностью к/п, а остальные п— 1 сообщений представлены одним
и тем же тривиальным кодом (например, вектором из нулей). Индекс i
при этом отправитель выбирает случайно. Для этого отправитель шифрует
этот набор сообщений на открытом ключе ЕКз центра и посылает ему
набор криптограмм
(Еу^тщ),...	... ,Eyn(m„)).	(2.41)
Центр Т сможет расшифровать к из них. Если среди полученных
после расшифрования окажется сообщение, отличное от тривиального
кода, то оно и есть сообщение тг. Вероятность этого события есть к/п.
Отметим, что на одном и том же открытом ключе можно одно-
временно контролировать п отправителей секретного ключа, каждого —
с вероятностью к/п и некоторую группу из к отправителей — с вероят-
ностью 1.
2.5. Передача с забыванием
119
Если же отправитель единственный, то протокол дробной переда-
чи можно упростить, действительно, передачу тривиальных сообщений
можно упразднить и предавать единственную криптограмму Ек3. из на-
бора (2.41), сопровождая ее передачей индекса i.
Такой протокол дробной передачи с забывание включает три этапа.
1.	Инициализация.
2.	Передача открытого ключа отправителю и его проверки им.
3.	Выбор отправителем случайного кода Vi открытого ключа и зашиф-
рование сообщения тп с использованием этого кода в качестве откры-
того ключа. Пересылка индекса i и сообщения EVi(m) получателю.
4.	Вычисление получателем сообщения m расшифрованием сообщения
Ек3. (т), если Vi является открытым ключом получателя.
Важной особенность взвешенной передачи с забыванием является
возможность ее неинтерактивной реализации и возможность многократ-
ного использования открытого ключа получателя. Действительно, откры-
тый ключ получателя может быть доставлен отправителю на этапе после
инициализации и затем многократно использоваться. После инициализа-
ции зашифрованные сообщения передаются от отправителя к получателю
и в обратном направлении никакие сообщения не передаются.
Таким образом, описанные в этом разделе методы получения клю-
чевой информации для передачи комбинации сообщений с забыванием
формируют и ключевую информацию для протокола дробной (с вероятно-
стью к/n) передачи на основе эллиптических кривых. Последние можно
было бы получить и непосредственно путем аддитивной интерпретации
их мультипликативных вариантов, использованных нами для построения
протоколов передачи комбинации сообщений с забыванием.
Глава 3
Криптосистемы на основе спариваний
Великая держава — это страна, которая имеет
ядерное оружие, космические ракеты и криптографию.
Дэвид Кан. Взломщики кодов.
Центрполиграф, 2000
В 2000 г. в работе Антуана Жу [52] предложено использовать спари-
вание Вейля для создания новых типов криптосистем, не получающихся
путем переноса на эллиптические кривые криптосистем, построенных
на основе труднорешаемости проблемы дискретного логарифмирования
в конечных полях. Это вызвало всплеск работ в этой области, который
продолжается до сих пор. Построены новые криптосистемы, имеющие хо-
рошие свойства, которыми не обладали криптосистемы, известные ранее.
Развитие методов их программной и аппаратной реализации, интенсивно
осуществляемое в настоящее время многими группами исследователей,
вероятно, скоро приведет к включению этих криптосистем в известные
криптографические стандарты.
Настоящая глава посвящена краткому изложению некоторых полу-
ченных в этой области результатов. В связи с тем, что используемая в них
техника требует более глубокого проникновения в теорию эллиптических
кривых, эта глава труднее для чтения, чем предыдущие разделы книги,
а стремление к краткости привело к тому, что местами изложение стало
конспективным, так как подробное изложение соответствующих разделов
теории требует специальной монографии.
3.1.	Билинейная проблема Диффи—Хеллмана
Пусть Gi — аддитивная группа порядка N, который в описываемых
далее приложениях будет выбираться простым числом, и Р — произ-
вольный образующий этой группы. Для операции возведения в степень п
в этой группе используем далее обозначение пР = Р 4-... 4- Р скалярно-
п
го произведения элемента группы на натуральное число. Это обозначение
в случае необходимости можно распространить и на произвольные целые
числа с помощью равенств (0)Р = О, (-п)Р = -(пР).
Пусть G2 — мультипликативная группа порядка N, и е : G} х G\ —>
G2 — невырожденное билинейное отображение, называемое спариванием.
3.1. Билинейная проблема Диффи—Хеллмана
121
Билинейность по определению означает выполнение следующих тождеств
е(5, + S2, Т) = e(S\,T)e(S2, Т),
e(S,Ti+T2) = e(S,Ti)e(S,T2),
а невырожденность означает, что еГ(Р, Р) 7^ 1. Если для вычисления спари-
вания известен быстрый алгоритм, то его можно применять для создания
криптосистем. Стойкость этих криптосистем основывается на трудноре-
шаемости следующей билинейной проблемы Диффи—Хеллмана (английская
аббревиатура BDHP): по данным Р,аР,ЬР,сР е C?i, где а, Ь, с — нату-
ральные числа, вычислить ?(Р, Р)аЬс.
Труднорешаемость BDHP влечет за собой труднорешаемость обыч-
ной проблемы Диффи—Хеллмана (DHP) и проблемы дискретного лога-
рифмирования (DLP) в обеих группах Gi. Но справедливость обратного
утверждения не установлена.
Покажем, что, если DLP в одной из групп Gi легкорешаема, то
и BDHP легкорешаема, что ведет к противоречию. Сначала заметим, что
справедливо следующее утверждение.
Упражнение 3.1.1. е(Р, аР) = е(Р, Р)а = е(аР, Р).
Если DLP в группе G\ легкорешаема, то по четверке (Р, аР, ЬР, cP)
легко найти а, Ъ, с, а потом легко вычислить последовательно abc, е(Р, Р),
е(Р,Р)аЬс. Если DLP в группе Gz легкорешаема, то вычислив вначале
е(Р, Р) и е(Р, аР) = е(Р, P)tt, с помощью дискретного логарифмирования
в группе Gz легко найти а, и аналогично Ь, с, а потом, так же как и выше,
легко вычислить е(Р, р)аЬс.
Покажем, что, если DHP в одной из групп Gi легкорешаема, то
и BDHP легкорешаема. Если DHP в группе легкорешаема, то по чет-
верке (Р, аР, ЬР, cP) легко найти аЪР а потом и е(аЬР, cP) = ?(Р, Р)аЬс
Если DHP в группе Gz легкорешаема, то вычислив вначале е(сР, Р),
е(сР,аР) = е(сР,Р)а, е(сР,ЬР) = е(сР, Р)\ легко найти е(сР, Р)аЬ =
(е(Р,РУ)аЬ ~е(Р,Р)аЬс.
Интересно, что распознающий вариант проблемы Диффи—Хеллмана
(DDHP) для группы Gj, который заключается в том, что по данным
Р, аР, ЬР, cP определить, верно ли, что cP = аЪР, легко решается
следующим образом (при условии существования эффективного алго-
ритма для вычисления спаривания): вычисляем а — е(Р,сР) = е(Р,Р)с
и /3 = е(аР, ЬР) = е(Р, Р)аЬ и замечаем, что
cP = аЬР <=> с = ab mod N о а = /3,
так как обе группы Gi — циклические равного порядка N.
Таким неологизмом мы для краткости заменяем словосочетание, означающее высо-
кую сложность алгоритма, решающего данную задачу. Подобные неологизмы далее будут
использоваться без особых оговорок.
122
Глава 3. Криптосистемы на основе спариваний
Примеры эффективно вычислимых спариваний с труднорешаемой
проблемой BDHP указать непросто, и это будет сделано далее без пол-
ного обоснования. Но вначале рассмотрим некоторые новые интересные
криптосистемы, основанные на спаривании. В изложении их мы исполь-
зуем работу [46].
3.1.1.	Однораундовый протокол генерации общего секретного
ключа между тремя участниками
Применяя последовательно три раза обычный протокол создания
общего секретного ключа Диффи—Хеллмана, можно создать общий сек-
ретный ключ и для трех участников, но процедура его генерации состоит
из двух раундов обмена ключами. В работе [52] был предложен для этой
цели однораундовый протокол, основанный на эффективном спаривании
'е : G\xGi -> G2 с труднорешаемой BDHP. В этом протоколе три участника
А, В, С случайно выбирают секретные числа а, b,cE[l,N-l], где N —
порядок групп Gi. Участник А вычисляет Рд = аР, где Р — (несекретная)
образующая группы G\, и посылает этот элемент остальным сторонам про-
токола. Одновременно с ним остальные стороны поступают аналогичным
образом. По окончании этого единственного раунда ключевого обмена у А
будут в наличии элементы Рв = ЪР, Pc = cP и число а, поэтому он сможет
быстро вычислить общий ключ К — е(Р,Р)аЬс как е(ЬР, сР)а. Стороны
В, С поступают аналогично. Пассивный перехватчик, имея публичные
ключи Р, Ра, Рв, Рс, должен будет для нахождения К решать BDHP.
В работе [40] описанный протокол обобщен на случай п-раундового
протокола для Зп участников.
3.1.2.	Короткая цифровая подпись, основанная на спаривании
В обычных алгоритмах, например DSA [72], цифровая подпись со-
стоит из двух элементов группы, используемой в алгоритме. В рабо-
те [32] Бонэ, Линн и Шахам предложили следующий алгоритм корот-
кой цифровой подписи BLS, основанный на эффективном спаривании
е : G\ х Gi -> G2 с труднорешаемой BDHP. Подписывающий А выби-
рает секретный ключ — случайное число х 6 [1,7V— 1] и вычисляет
публичный ключ Q = хР. Сообщение тп вначале хешируется одним
из стандартных алгоритмов криптографического хеширования с целью
уменьшения длины сообщения, если она чрезмерна, а потом полученное
бинарное слово с помощью публичного алгоритма превращается в нену-
левой элемент М = Н(т) группы G\. BLS-подписью для сообщения т
является S — хМ — единственный элемент группы G]. Каждый, кто
имеет аутентичную копию публичного ключа Q, может проверить не-
фальсифицированность подписи S', вычислив М — Н(т), и сравнив
е(Р, S) с e(Q, М). Если действительно S = хМ, то
е(Р, S) = е(Р, М)х - фР, М) - e(Q, М).
3.1. Билинейная проблема Диффи—Хеллмана
123
Если S / хМ, то е(Р,5) 7^ е(Р, М)х = e(Q,M), так как е(Р,М) / 1
порождает группу С2. Поэтому злоумышленник для подделки подписи
должен уметь вычислить S = хМ, зная лишь Р, Q = хР, М. Так как
М = уР при некотором у Е [1, N-1], то вычисление S = хМ = хуР есть
в точности DHP для группы G\. Если выбрано эффективно вычислимое
спаривание с труднорешаемой DHP для группы G], то BLS-подпись
надежна.
3.1.3.	Криптосистема с публичным индивидуальным ключом
Идея такой криптосистемы была предложена в 1984 г. А. Шамиром,
а осуществлена в 2001 г. Боне и Фрэнклином [31]. Она заключается
в такой организации дела, чтобы появилась возможность использовать
имя пользователя в качестве публичного ключа. Предложенная в [31]
криптосистема выглядит следующим образом. Пусть е : G\ х G\ —> Gi —
эффективно вычисляемое спаривание с труднорешаемой BDHP и трудно
решаемой DHP для группы G\. Пусть также Н — криптографическое
хеширование, отображающее строку битов во множество ненулевых эле-
ментов группы Gi, порождаемой элементом Р. Многостороннюю секрет-
ную переписку организует специальный центр, которому доверяют все ее
участники. Этот центр выбирает случайное число s Е [1, N - 1], где N —
порядок группы G[, и вычисляет публичный ключ Q = sP. Аутентич-
ные копии этого ключа рассылаются всем переписывающимся сторонам.
Каждому участнику А высылается также его частный ключ dA = sQa,
Qa = H(IDa), где ID a — строка битов, содержащая открытую инфор-
мацию, идентифицирующую А.
Заметим, что выслать частный ключ dA участнику А может только
этот доверенный центр (и тем самым исключается «атака посредника»),
так как для вычисления ключа dA по открытой информации (Р, Q,Qa)
нужно решать DHP в группе G]. Действительно, Qa = тР при некотором
т Е [1, N - 1], и (Р, Q, Qa) — (Р, зР, тР) — случайная тройка Диффи-
Хеллмана, по которой надо вычислить dA = sQa = smP.
Участник В шифрует сообщение m Е С2 для А следующим обра-
зом. Случайно выбирается n Е [1,7V - 1], вычисляется QA = H(IDA),
первая (неинформативная) часть криптограммы Cj = пР, и вторая (ин-
формативная) часть криптограммы С2 = m*e(QA, Q)n, где * — операция
в мультипликативной группе G2. Шифртекст (Сь С2) отсылается А. Рас-
шифрование основано на применении тождества
e(dA, G) - e(sQA, пР) = e(QA, nP)s = e(QA, P)sn =
= e(QA,sP)n = e(QA,Q)n
и выполняется следующим образом: m=C2*(c(<2^5Q)n)-1C2*(e(d4,Ci))-1 •
Атакующему для получения т на основе открытой информации (Р, Qa,
Q, Ci) надо вычислить c(Qa, Q)n (если т вычислено, то легко вычислить
124	Глава 3. Криптосистемы на основе спариваний
и ^(Qa, Q)n — С2 * m”1; обратное также очевидно). Но для этого ему надо
решить BDHP для случайной четверки (F, mP, sP, пР), так как Qa — тР,
Q = sP, Сх = пР, Q)n = е(Р9 P)nsm.
Использованию в криптографии групп, в которых DDHP легкоре-
шаема, a DHP труднорешаема, посвящено уже много работ, см., напри-
мер, [77].
Известны еще довольно много криптосистем, основанных на спари-
вании, например, [49,80,93].
3.2.	Спаривание Андре Вейля
на эллиптических кривых
Пусть Е — эллиптическая кривая над полем К = GF(q) ин —
число, взаимно простое с характеристикой поля. Обозначим К алгебра-
ическое замыкание этого поля. Рассмотрим кривую Е(К). Точку Р этой
кривой назовем точкой кручения порядка п (или просто n-кручения), если
пР — Р + ... + Р = О в группе точек кривой. Множество точек п-кру-
п
чения кривой Е(К) обозначим Р[п]. Несложно проверить, что Р[п]
замкнута относительно сложения точек и поэтому образует подгруппу
в группе кривой Е(К).
Известна (см. [92]) весьма нетривиальная теорема о том, что группа
Е[п] изоморфна прямой сумме двух циклических групп порядка п, короче,
Е[п] = Zn®Zn. Прямая сумма двух аддитивных групп G®H определяется
как множество всех упорядоченных пар (g, h), д € G, h е Н, на котором
операция сложения определяется покомпонентно, т. е. (^ь hi) 4- (^2, ^2) =
(#1 4- #2,^1 + ^2)- Нетрудно проверить, что прямая сумма двух групп
тоже будет группой с нулевым элементом (0,0) и порядком, равным
произведению порядков слагаемых. В частности, порядок Р[п] равен п2.
Если порядки слагаемых циклических групп взаимно просты, то и их
сумма будет циклической группой, но в рассматриваемом случае это
не так, и группа Е[п] не циклическая, так как порядок каждого ее
элемента равен п (но она содержит циклические подгруппы порядка п).
Обозначим рп С X* подгруппу всех корней n-й степени из единицы.
На самом деле эта подгруппа содержится уже в конечном подполе GF(qk)
поля К, где к — мультипликативный порядок числа q по модулю п,
т. е. наименьшее такое к, что qk - 1 кратно п, ине содержится в полях
меньшего порядка. Действительно, если в поле GF(qm) есть элемент х,
такой, что хп = 1, то его мультипликативная группа, имеющая поря-
док qm - 1, содержит подгруппу порядка п, состоящую из элементов
{1, х, х2,... , и по теореме Лагранжа о подгруппах qm - 1 делится
на п, откуда т к. В тоже время в поле GF{qk) в качестве х можно вы-
3.2. Спаривание Андре Вейля на эллиптических кривых
125
брать	где g — примитивный элемент поля, тогда xn = gqk~x = 1,
g группа корней n-й степени из единицы есть {1, х, х\..., жп-1}.
Спаривание Вейля2) — это отображение
еп : Е[п] х Е[п] -> рп С GF(qk)*,
удовлетворяющее следующим условиям (см., например, [92], параграф
III.8):
(1)	билинейность:
+ S2, Т) = en(S\, T)en(S2, Т), en(S, Г\ + Т2) = en(S, Т})еп{8, Т2);
(2)	невырожденность: для любой конечной точки Р Е Е[п] (т. е. Р О)
гомоморфизм Т -> еп(Р, Т) из группы Е[п] в группу рп не равен тож-
дественно единице, т. е. найдется Q Е Е[п], такая, что en(P, Q) 1;
(3)	альтернированность: всегда еп(Р, Р) = 1.
Заметим сразу, что из (3) следует тождество еп(Р, Q) ~ en(Q,P)-1
в силу вытекающего из (1) тождества
en(S + T,S + T) = en(S, Т)еп(Т9 S)en(S, S)en(T, T).
Заметим, что свойство (3) препятствует непосредственному применению
спаривания Вейля в описанных выше протоколах. Но эту трудность
удается обходить. Далее мы еще вернемся к спариванию Вейля. Но перед
этим необходимо познакомиться с понятием дивизора на кривой.
3.2.1.	Дивизоры
Группа Div (Е) дивизоров кривой Е(К) по определению состоит
из дивизоров — формальных сумм вида
л = £>р(р)
Р^Е
точек Р кривой Е, взятых с целочисленными кратностями Пр, со-
держащих лишь конечное число слагаемых с ненулевыми кратностями
(слагаемые с нулевыми кратностями в сумме обычно опускаются). Ко-
нечное множество точек Р, для которых Пр 0, называется носителем
дивизора D и обозначается supp (D). Очевидно,
D= £ пР(Р).
PGsupp (D)
Если supp (D) = 0, то дивизор называется нулевым и обозначатся 0.
Андре Вейль, так же как и Герман Вейль — из крупнейших математиков XX в. Но они
Не родственники и даже родились в разных странах.
126
Глава 3. Криптосистемы на основе спариваний
Операции сложения-вычитания в этой группе определяются поком-
понентно, например, если
а = 52 мп р = 52 mP(p),
PEE	PEE
TO
Dx ± D2 = (nP ± mp)(P), supp (Dj ± D2) C supp (Pi) U supp (D2).
PEE
Проверка выполнения аксиом группы осуществляется непосредственно.
Очевидно, что группа дивизоров коммутативна.
Степенью дивизора D —	^2 пр(Р) называется число
PEsupp (D)
deg (D) = 52 Пр'
PEsupp (D)
Множество DivQ(E) дивизоров нулевой степени, очевидно, образует под-
группу группы всех дивизоров.
Для произвольной ненулевой рациональной функции f над кривой Е
и произвольной точки Р этой кривой можно определить целое число
ordp(/), называемое порядком этой функции в точке Р. Тогда дивизором
функции f называется
div (/) = 52 °rdp(f)(py
pee
Такие дивизоры называются главными.
Определение понятия рациональной функции / над кривой Е и ее
порядка в заданной точке непросто и будет дано позднее. Пока чи-
тателю предлагается ограничится следующей грубой аналогией: пусть
f(X) — g(X)/h(X) — обычная ненулевая рациональная функция над
прямой (т. е. над полем К), или частное двух взаимно простых многочле-
нов, тогда для любой точки ordp(/) = ordp(^) - ordp(/z), где для любого
многочлена д(Х) порядок ordp(^) равен кратности точки Р как корня
этого многочлена. В частности, если точка Р не является корнем ни д,
ни h, то /(Р)	0, ordp(/) = 0. Если Р является корнем д, но не является
корнем h, то /(Р) = 0, ordp(/) > 0. Такую точку называем нулем функ-
ции f порядка ordp(/) > 0. Если Р является корнем h, но не является
корнем /, то 1//(Р) = 0, ordp(/) < 0. Тогда по определению полага-
ем /(Р) = оо и такую точку называем полюсом функции f порядка
- ordp(/) > 0. Для бесконечно-удаленной точки Р = О данной прямой
определим ordp(/) = deg (h) - deg(g), где через deg обозначена степень
многочлена. Если deg (д) < deg(/z), то значение f в точке Р = О опре-
делим нулем, если deg (д) > deg (Д), то значение / в точке Р = О опре-
делим равным оо, а если deg (д) = deg (Д), то значение / в точке Р — О
3.2. Спаривание Андре Вейля на эллиптических кривых
127
определим равным отношению старшего коэффициента g к старшему
коэффициенту h. Заметим, что в случае поля действительных чисел это
определение совпадает с обычным пределом дроби g(X)/h(X) при X,
стремящемся к бесконечности. Согласно данным определениям порядок
в нуле функции всегда положителен, порядок в полюсе — отрицателен,
а порядок во всех остальных точках равен нулю. Число нулей и полюсов
у любой функции конечно. Легко видеть, что, если поле К = К (т. е. К ал-
гебраически замкнуто, как например поле комплексных чисел), то сумма
порядков всех особых точек функции (т. е. всех нулей и полюсов, включая
бесконечно-удаленную точку) равна нулю, так как сумма порядков всех
нулей функции f равна сумме кратностей всех корней многочлена д, т. е.
deg (д), сумма порядков всех полюсов функции f равна сумме кратностей
всех корней многочлена h, т. е. deg(h), а порядок функции f в беско-
нечности равен deg(/i) - deg(<?). Очевидно также, что множество всех
рациональных функций на прямой образует поле. Определяя для любой
ненулевой рациональной функции дивизор так же, как и в случае эллип-
тической кривой, получаем отображение из мультипликативной группы
этого поля в группу главных дивизоров. Легко проверить (рассматривая
отдельно бесконечно-удаленную точку и общие особые точки у обеих
функций), что это отображение удовлетворяет тождествам
div (/1/2) = div (/1) 4- div (/2), div (/1//2) = div (Л) - div (/2)
(для проверки последнего тождества надо еще проверить, что при со-
кращении дроби ее дивизор не меняется), т. е. это отображение является
гомоморфизмом. Поэтому множество главных дивизоров образует под-
группу в группе DivQ(E).
Все сказанное выше справедливо и для дивизоров на эллиптиче-
ских (и гиперэллиптических) кривых, но доказываются эти утверждения
гораздо сложнее. Известна для эллиптических кривых также теорема
(теорема о группе главных дивизоров), характеризующая группу главных
дивизоров кривой как группу всех дивизоров D нулевой степени, удовле-
творяющую условию
12 прр = °’
РЕЕ
где О — нулевой элемент группы кривой, т. е. ее бесконечно удаленная
точка.
На группе Div\E) вводится отношение эквивалентности D\ ~ Р2
тогда и только тогда, когда D\ - D2 главней дивизор (это определение
можно ввести и для гиперэллиптических кривых). Если ~ D2, то
можно сказать, что дивизоры Di сравнимы по модулю группы главных
дивизоров. Относительно введенного отношения группа DivQ(E) разби-
вается на классы эквивалентности. На множестве этих классов можно
определить операцию сложения подобно тому, как это делается с клас-
сами вычетов по модулю в группе целых чисел. При этом получится
128
Глава 3. Криптосистемы на основе спариваний
группа, которая на алгебраическом языке называется фактор-группой
группы DivQ(E) по подгруппе главных дивизоров. В случае гиперэл-
липтических кривых С полученная группа называется группой классов
дивизоров или группой Пикара Pic°K(C). Иногда ее называют также яко-
бианом кривой С и обозначают J(C). Если поле К конечно, то эта
группа конечна (что не очевидно), и именно ее используют при постро-
ении криптосистем, основанных на гиперэллиптических кривых. Мы,
однако, не будем здесь касаться этой темы ввиду ее сложности. В случае
эллиптических кривчых группа Пикара изоморфна группе точек эллипти-
ческой кривой (группой Пуанкаре), в чем несложно убедится, используя
указанную выше характеризацию группы главных дивизоров эллиптиче-
ской кривой. Сказанное означает, что на эллиптической кривой любой
дивизор D нулевой степени эквивалентен дивизору (F) — (О), где Р —
некоторая точка кривой. При этом Р =	пр'Р1.
Р'€ suppD
3.2.2.	Явное определение спаривания Вейля
Дальнейшее изложение основывается на [28,73].
Пусть Е(К) эллиптическая кривая над алгебраическим замыканием
поля К = GF(q) и f — ненулевая рациональная функция над ней. Тогда
<>iv (/) = 52 °rdH/)CP), 52 °rdH/) = о, 52 °rdH/)-p = о.
PEE	PEE	PEE
Пусть D — пр(Р) ~ произвольный дивизор с носителем, не пересе-
рее
кающимся (в конечных точках) с supp (div (/)). Определим
fw = п рр)пр-
pee
Это определение корректно, так как если rip 0, то Р Е supp (Z>), значит
Р supp (div (/)), т. е. f(P) 0, f(P) оо. В частности, имеем, что
f(D) Е К*. Очевидно также, что /(Pj ТР2) — /(^i)/(^2), /(Pi -Р2) =
если носитель div (/) не пересекается (в конечных точках)
с носителями Dj.
Пусть Р, Q Е Р[п]. Выберем Dp ~ (Р) - (О), Dq ~ (Q) - (О) с по-
парно непересекающимися носителями, тогда согласно теореме о группе
главных дивизоров существует ненулевая рациональная функция fP та-
кая, что div (fP) = nDp ~ n(P) - п(О), ведь nP - nO — О, n - n = 0.
По аналогичной причине существует ненулевая рациональная функция /q
такая, что div (Jq) = tiDq ~ n(Q) - п(О). Тогда можно определить спари-
вание Вейля следующим образом:
en(P, Q) =
fp(PQ
fqiPp)
(3.1)
3.2. Спаривание Андре Вейля на эллиптических кривых
129
Отсюда следует, что, если RQE Е(К), то en(P, Q) € К. Для вычисле-
ния fP(DQ) согласно определению достаточно научиться вычислять fp(R)
для любой точки R Е supp (Dq). После этого для вычисления /p(Dq) до-
статочно конечного числа операций умножения и деления в поле К.
На самом деле вместо бесконечного поля К можно использовать конеч-
ное поле GF(qk), являющееся расширением поля К = GF(q), таким,
что E[n] С E(GF(qk)), т. е. группа n-кручения содержится в кривой Е
над полем GF(qk). Необходимые и достаточные условия этого в общем
случае были даны в [86]. Однако они сложны и неудобны для применения.
Для наиболее интересного с прикладной точки зрения случая удобные
условия были даны в [21]: в случае п, не делящего q - 1, значение к
равно мультипликативному порядку q по модулю п. Выше было пока-
зано, что это условие является также необходимым и достаточным для
того, чтобы поле GF(qk) содержало примитивный корень n-й степени
из единицы. Указанное значение к называют множителем секретности
(или безопасности) или MOV (Menezes—Okamoto—Vanstone) степенью.
Виктор Миллер в 1986 г. предложил для вычисления спаривания
Вейля следующую идею. Выберем случайную точку R на кривой Е(К)
и возьмем дивизор Dp = (Р + R) - (R). Очевидно, он имеет нулевую
степень, и Dp ~ (Р) - (О), так как
DP - (Р) 4- (О) = (Р + R) - (R) - (Р) + (О)
и Р -Е R - R — Р, таким образом, по теореме о главных дивизорах
Dp - (Р) + (О) есть главный дивизор.
Для каждого натурального к существует согласно теореме ненулевая
рациональная функция Д такая, что
div (fm) = т(Р + R) - m(R) - (тР) 4- (О),
потому что степень этого дивизора, очевидно, нулевая, и
т(Р 4- R) - mR - тР + О — О.
Тогда fn = fp, потому что в силу пР = О
div (fn) = п(Р 4- R) - n(R) - (nP) 4- (О) - п(Р 4- R) - n(R) = nDp
Аналогично определяется и Д>, если взять Dq — (Q + S) — (S). Выбирая
подходящим образом R, S, можно считать, что Dq и Dr имеют непере-
секающиеся носители.
Если не позаботиться заранее о том, чтобы носители не пересекались,
то в редких случаях возможно появление нулевого знаменателя, тогда
следует выбрать другие точки R и Q.
Билинейность указанной функции (3.1) по обоим аргументам сле-
дует из определения, если выбрать Ds}, Ds2, Dp так, чтобы их носители
не пересекались и аналогичным образом поступить с DTl, Dp, Ds. До-
казательство остальных свойств спаривания Вейля можно найти в [92]
130
Глава 3. Криптосистемы на основе спариваний
и [73]. Прежде чем продолжить описание алгоритма Миллера, полезно
познакомиться с точными определениями понятий рациональной функ-
ции на кривой и ее порядка в данной точке кривой.
3.2.3.	Функции на гиперэллиптических кривых
Эти определения удобно дать сразу в более общей ситуации, а именно
для гиперэллиптических кривых. Наше изложение будет следовать [15]
и [60].
Уравнением гиперэллиптической кривой рода g над произвольным по-
лем К назовем уравнение С : Y2 + Yh(X) — f(X), где h(X) Е Х[Х] —
многочлен с коэффициентами из поля К степени не больше g, a f(X) Е
if[X] — многочлен с коэффициентами из поля К степени не больше
2д 4- 1 с единичным старшим коэффициентом, такие, что в алгебраиче-
ском замыкании К неразрешима система из двух уравнений 2Y — -Л(Х),
h'(X)Y = f'(X), в которой символ ' означает производную многочлена.
Для произвольного расширения F поля К обозначаем C(F) множество
всех точек (х,у), х,у Е F, плоскости F х F, удовлетворяющих уравне-
нию С, и назовем его кривой над полем F. Условие о неразрешимости
системы уравнений означает, что на кривой в поле К отсутствуют особые
точки, т. е. точки, в которых обращаются в нуль обе частные производные
многочлена У2 + Yh(X) - f(X). В случае д = 1 получаем определение эл-
липтической кривой. Легко проверить, что, если h(X) = 0 и характеристи-
ка поля не равна двум, то у гиперэллиптической кривой многочлен f(X)
не имеет кратных корней в поле К, а если h(X) = 0 и характеристика поля
равна двум, то такой кривой без особых точек не существует. Если характе-
ристика поля не равна двум, то заменой переменных гиперэллиптическую
кривую Y2 + Yh(X) = f(X) можно преобразовать в кривую с h(X) = 0.
Очевидно, что, если два полинома f(X, Y) и д(Х, У) с коэффи-
циентами над полем К сравнимы по модулю многочлена с(Х, У) =
У2 + Уh(X) - / W, т. е. /(X У) -д(Х, У)_ = с(Х У )Д(Х К), где h(X, У) -
полином с-Коэффициентами над полем К, то их значения во всех точках
кривой С(К) совпадают. Поэтому, если мы представим произвольный по-
лином /(X Y) Е Х[Х, У] как полином от переменной У, коэффициенты
которого являются полиномами из К[X], точно также представим много-
член У2 + Yh(X) - f(X) как квадратный трехчлен от У, и поделим первый
из них на второй с остатком с помощью схемы Горнера, то получим, что
/(X К) = с(Х К)Д(Х Y) + r(X Y),
r(X Y) = а(Х) + &(Х)У, а(Х), Ь(Х) Е К[Х],
и r(X,Y) = /(X У) mod с(Х X) совпадает с f(X,X) на кривой С(К).
Значит, верно_и обратное, а именно, если два многочлена совпадают
на кривой С(К) (и даже на кривой С (К)), то они сравнимы по модулю
с(Х,Х), так как в противном случае на кривой совпадают два разных
3.2. Спаривание Андре Вейля на эллиптических кривых
131
многочлена первой степени от X, а это возможно, лишь когда она совпа-
дает с прямой, что противоречит определению.
Поэтому, если мы хотим определить понятие полиномиальной функ-
ции на кривой С, то естественно в качестве него взять класс эквивалент-
ности многочленов кольца K[X,Y] по модулю с(Х, У). На множестве всех
этих классов эквивалентности можно естественным образом (как, напри-
мер, при определении кольца вычетов по модулю целого числа) определить
операции сложения и умножения, относительно которых оно образует
кольцо, обозначаемое К[С] = К[Х, У]/(с(Х У)), и называемое кольцом
полиномиальных функций на кривой. Аналогично можно определить
кольцо 2Г[С] = К[Х, У]/(с(Х, У)), называемое координатным кольцом,
которое, очевидно, является подкольцом в If [С], и кольцо F[C] для любо-
го расширения F С К поля К. Так как в каждом классе эквивалентности
содержится единственный элемент вида a(X)+b(X)Y, а(Х), Ь(Х} Е К[Х],
то элементы кольца F[C] можно просто отождествить с многочленами
вида a(X) 4- b(X)Y, а(Х), b(X) Е F[X]. Операции сложения-вычитания
над этими многочленами определяются, очевидно, равенством
а^Х) + &1(Х)У ± а2(Х) 44 b2(X)Y = а^Х) ± а2(Х) + (^(Х) ± Ь2(Т))У.
Операция умножения представляет из себя умножение по модулю с(Х, У).
Обычное умножение выполняется, очевидно, следующим образом (для
краткости переменную X опускаем)
(ai 4- b\Y)(a2 4- b2Y) = aia2 4- (&1&2 Т" b2a\)Y 4- b\b2Y\
а после приведения по модулю с(Х, У) (т. е. деления на с(Х, У) с остат-
ком), окончательно имеем
(а, + &,У)(а2 + b2Y) = aia2 + (М2 + b2<h)Y + btb2Y2 - ЬхЬ2с(Х, Y) =
= axa2 4- (&ia2 4- b2a})Y - bib2(Yh - /) =
= fli<z2 4- b\b2f -j- (&i<22 4- b2d\ — b\b2hyY.
Хотя умножение в кольце F[C] похоже на умножение в поле комплексных
чисел, полем это кольцо не является, но оно будет областью целостности,
т. е. в нем отсутствуют делители нуля.
Упражнение 3.2.1. Докажите это утверждение.
Указание. В кольце F[A^] нет делителей нуля, поэтому, если a{a2 4- bib2f = О,
&ia2 4-	“ b[b2h = 0, то или аг = 0, bj = 0, г 7^ j, что ведет к противоречию,
так как тогда а;Ьг = 0 и поэтому ak 4- bkY = 0 при некотором к, или, в силу
равенства a{a2 = -b]b2f, имеем degai 4- dega2 — deg&i 4- deg&2 4- 2p 4- 1, откуда
deg (5lfl2)4-deg (b2d\) — 2(deg b\ -4deg b2) + 2g +1, значит без ограничения общности
deg(M2) (deg 4- deg&2) 4- g 4- 1 > deg (6^), поэтому deg(&ia2 4- b2a{) >
deg + deg b2+g = deg (bib2h), что противоречит равенству b[d2+b2di-b{b2h — 0.
132
Глава 3. Криптосистемы на основе спариваний
Можно было бы вывести предыдущее утверждение из следующего
далее упражнения и теоремы об однозначном разложении на неприводи-
мые множители в кольце F[X, У], но она доказывается более сложно, чем
в кольце F[X] (из-за невозможности воспользоваться алгоритмом Евкли-
да), и за этим доказательством мы вынуждены отослать интересующегося
читателя к учебникам алгебры, например [9].
Упражнение 3.2.2. Докажите, что c(X,Y) неприводим, т. е. не разлагается на не-
приводимые множители в кольце К[Х, У].
Указание. Если с(Х, У) = (а(Х) 4-У)(Ь(Х) Н-У), то a + b = h, ab = -f, значит без
ограничения общности deg а >	> д Ь, тогда deg (a + b) д+ 1 > д + deg h.
Следуя аналогии с комплексными числами, введем понятие нормы
в кольце Р[С]. Для элемента г = a 4- bY положим f = a - b(h 4- У)
(а не г = a — bY, как можно было бы ожидать, потому что, если у —
корень уравнения с(Х, У) = У2 4- Yh - f = 0, то согласно Виету второй
его корень есть -У ~ h) и определим норму
N(r) — rr — (a 4- bY)(a - bh - bY) =
= a(a - bh) - b2f + (b(a - bh) - ab + b2h)Y = a(a - bh) - b2f.
Очевидно, что N(r) E JF’fJT], N(f) = N(r) и
7У(Г1Г2) = Г1Г2Г1Г2 = Г1ПГ2Г2 = 7\Г(г1)7У(г2).
Определим степень полиномиальной функции r = a(X) + b(X)Y Elf [С]
как обычную степень многочлена N(r) Е Тогда очевидно, что
deg (г) = deg (г) и
deg (Г1Г2) = deg (N(r}r2)) = deg (N(rO) 4- deg (N(r2))
= deg (74) 4- deg (r2).
Упражнение 3.2.3. Докажите, что deg (a(X) 4- b(X)Y) = max{2 deg (a), 2 deg (b) +
2g 4- l}. При этом надо считать, что степень нулевого многочлен равна по опре-
делению минус бесконечности.
Указание. Если ab / 0, deg (bh) > deg (а), то
deg (abh) < 2 deg (bh) < 2 deg (b) + 2g < deg b2 f.
Область целостности F[C] можно погрузить в поле F(C) с помощью
известной конструкции поля частных (см. о поле частных, например, [9]).
По определению элементами поля F(C) являются формальные рацио-
нальные функции R, т. е. дроби г\/г2, где Е F[C], г2 0, точнее,
классы эквивалентности таких дробей относительно естественного от-
ношения эквивалентности Т\1т2 ~ Г3/Г4 тогда и только тогда, когда
Г]Г4 = г2г3. Арифметические операции над такими дробями определяют-
ся точно так же, как и в школе. Операции над классами эквивалентно-
сти определяются, как обычно, выбором произвольных представителей
3.2. Спаривание Андре Вейля на эллиптических кривых 133
в этих классах, применением операции к этим представителям, и заменой
результата операции на содержащий его класс эквивалентности. Легко
проверить корректность этого определения, т. е. независимость результата
операции от выбора представителей из данных операндов. Также легко
проверяется, что множество классов эквивалентности относительно вве-
денных операций образует поле, которое и обозначается F(C). Очевидно,
F[C] является подкольцом этого поля. Элементы поля ITfC] называются
рациональными функциями на кривой С.
Определим значение рациональной функции R € F(C) в любой конеч-
ной точке Р кривой C(F) равенством R(P) = ri(P)/r2(P), где тДт^
П Е Р[С] — любой представитель класса Р, такой, что г2(Р)	0.
Очевидно, это определение в случае существования хотя бы одного та-
кого представителя корректно, так как указанное отношение не зависит
от выбранного представителя. Если же ни одного такого представителя
не существует, то значение R(P) полагается равным оо, а точка Р назы-
вается полюсом функции R.
Можно определить значение рациональной функции R = ri/r2
и в точке О следующим образом:
(1)	если	deg	(и)	< deg (г2), то	Р((9) = 0;
(2)	если	deg	(и)	> deg (г2), то	R(O) = оо;
(3)	если	deg	(и)	= deg (г2), то	R(O) равно	отношению старших коэффи-
циентов многочленов гг .
Упражнение 3.2.4. Проверьте корректность этого определения.
Указание. Если г{/г2 — тз/г^ гг = аг: + Ьгу, i = 1,..., 4, то ах/а2 =
Ь\/Ь2 = Ъ^з/Ь^.
Справедлива следующая теорема, доказательство которой можно най-
ти, например в [15].
Теорема 3.2.1 (об униформизующем параметре). Для любой точки Р
гиперэллиптической кривой С существует обращающаяся в Р в нуль раци-
ональная функция U 6 К {С) (униформизующий параметр), такая, что для
каждой ненулевой полиномиальной функции G Е if [С] найдется не зависи-
мое от выбора функции U целое число d и рациональная функция S Е К (С),
для которых G = UdS, S(P) / 0, оо.
Число d называется порядком полиномиальной функции G в точке Р
и обозначается ordP(G).
Упражнение 3.2.5. Докажите, что ordP(GiG2) = ordP(Gi) + ordP(G2). Если
ordp(Gi) ordp(G2), то
ordp(Gi + G2) = min{ordp(Gi), ordP(G2)}.
Если ordp(Gi) = ordp(G2), G\ -G2, to
ordp(Gj + G2) ordp(Gz)}.
Указание. Прямое вычисление и применение предыдущей теоремы.
134	Глава 3. Криптосистемы на основе спариваний
В [60] дано эквивалентное, но более удобное определение степени
полиномиальной функции G = а(Х)4-6(Х)У на кривой С : Y2+Yh(X) =
/(X) в точке Р = (u, v):
(1) если точка Р конечна, и г — кратность корня и у наибольшего
общего делителя Ь(Х)) (возможно, г = 0), a s кратность
корня и у
( G \	2
И 7V-----v = ао(«о - boh) - bQf,
a,>{X)~W^T о( ) = (Т^Г
или нуль, если Qq(u) 4- bQ(u)v 0, то ordp(G') = 2r + s в случае
2v 4- h(u) — 0 и ordp(G) — г 4- s в противном случае;
(2) если Р = О, то
ordp(G) = - deg (G) = - max{2 deg (а), 2 deg (Ь) 4- 2д 4- 1}.
Упражнение 3.2.6. Пусть ненулевая полиномиальная функция G = а(Х) 4- Ь(Х)У
на кривой С : У2 4- УД(Х) = f(X) имеет нуль в точке Р — (и, v) Ф Р =
(и,—v - h(u)) и и не является общим корнем многочленов а(Х),Ь(Х). Тогда
функция G = а(Х) - b(X)(Y 4- h(X)) не имеет нуля в точке Р и функция
G — (X - и)к S, где S Е К (С) не имеет в точке Р ни нуля, ни полюса, a к —
кратность корня и у нормы N(G).
Указание. Если G(P) = 0, то а(и) 4- b(u)v = 0 = а(и) - b(u)(v Т h(u)), откуда
b(u)(2v 4- h(u)) = 0, следовательно Ь(и) = 0, а потому и а(и) = 0, что ведет
к противоречию. Так как G = N(G)/G = (X - u)kd(u)/G, то S = d(u)/G Е К (С),
S(P) £ 0, 5(Р) О, так как G(P) 0.
Следующее утверждения можно доказать и не пользуясь теоремой
об униформизующем параметре.
Упражнение 3.2.7. Пусть G = а(Х) + b(X}Y — ненулевая полиномиальная функ-
ция на кривой С : У2 4- Yh(X) = f(X), и точка Р — (и, v) Р = (и, -v - h(u)).
Тогда G представима в виде (2Г -u)kS, где S Е К (С) не имеет в точке Р ни нуля,
ни полюса, при этом обязательно к — ordp(G).
Указание. Если G(P) / 0, то к = ordp(G) = 0 и единственность к очевидна. Если
G(P) = 0, то пусть г > 0 — кратность корня и у многочлена (а(Х), b(X) nG/(X-
и)г = ац(Х)+Ьо(Х)У. Тогда, если функция а0(А')4-60(2Г)У не имеет нуля в точке Р,
то к = ordp(G) согласно определению порядка, G = (X - и)к(ао(Х) 4- bo(X)Y)
и все доказано. В противном случае, применяя к а0(Х) + bQ(X)Y предыдущее
упражнение, имеем ao(^) + ^o(^)^ = (X -u)kS, где S Е К(С) не имеет в точке Р
ни нуля, ни полюса, а к — кратность корня и у нормы N(a$(X) 4- 60(2Г)У). Тогда
G = (X - u)k+rS, k + r = ordp(G).
Пользуясь предыдущим упражнением, можно без применения теоре-
мы 3.2.1 проверить, что ordp(Gi<?2) = ordp(^i) + ordp^)-
3.2. Спаривание Андре Вейля на эллиптических кривых 135
Упражнение 3.2.8. Сделайте это.
Указание. Если Р = О или Р = Р, то все вытекает из определения порядка
и равенств deg(G?iG?2) = deg (Gj) 4- deg (G2), N(G{G2) = N(Gl)N(G2). Если
p P, то примените предыдущее упражнение.
Определим теперь порядок произвольной рациональной функции
R = G/H Е К(С), G,H Е К[С] равенством
ordp(7?) = ordp(G) - ordp(^).
Упражнение 3.2.9. Докажите корректносчть этого определения, т. е. независимость
от выбора представления R = G/H.
Указание. Если R — G/H — GJHx, то GH{ = G\H, и согласно предыдущему
упражнению ordp(G) + ordp(Ki) = ordp(Gi) 4- ordp(EG).
Упражнение 3.2.10. Докажите, что для произвольной полиномиальной функции G
J2 ordp(G) = 0.
Рес(к)
Указание. Достаточно проверить, что сумма порядков всех нулей функции G
равна обычной степени многочлена N(G). Над алгебраически замкнутым полем
сумма кратностей всех его корней равна его степени. Если и — корень кратности г
у (а(Х), Ь(Х)) (возможно, что г = 0), то ао(^) + ^о(^)^ и й0(Х) - bQ(X)(v + h(X))
не могут иметь общий корень и при условии 2v 4- h(u) ф 0, поэтому у одной
из точек Р = (и, v), Р = (и, -v - h(u)) порядок будет равен г 4- з, а у другой — г,
и их сумма 2r + s будет равна кратности корня и у многочлена N(G). Если же
2v 4- h(u) = 0, то Р = Р и порядок этой точки равен 2г 4- s — кратности
корня и. Если и — произвольный корень многочлена N(G)9 и г — его кратность
у (а(Х), Ь(Х)), то кратность корня и у многочлена N(G) равна сумме порядков
точек Р = (ц, v), Р = (и, -v - h(u)).
Упражнение 3.2.11. Докажите, что для произвольной рациональной функции G
ordp(G) = 0.
РЕС(К)
Указание. Примените предыдущее упражнение.
Теперь подобно тому, как это было сделано выше, можно дать все
соответствующие определения, касающиеся дивизоров на гиперэллипти-
ческих кривых. Например, для произвольной рациональной функции R
ее дивизор определяется как
div (В) = ordP(^)P,
PEC
при этом, очевидно, выполняются тождества
div — У^ ordpCRi^)^ = y^(ordp(#i) + ordp(J?,2))F =
Pec	pec
= УУ ordP(R\)P 4- У2 ordP(E2)F = div (R^) 4- div (jR2)
pec	pec
и div (Ri/Rz) = div (R^) - div (#2).
136
Глава 3. Криптосистемы на основе спариваний
Очевидно, что ненулевая константа имеет нулевой дивизор и обратно,
нулевой дивизор может быть только у константы. Поэтому, если div (Д) =
div (/2), то /1 = /2 с точностью до постоянного множителя.
Упражнение 3.2.12. Если для ненулевой полиномиальной функции div (G) =
52 ordP(G)P, то div (G) = 52 ordP(G)P
pec	тес
Указание. Проверьте, что ordp(G) — ordP(G).
3.3.	Алгоритм вычисления спариваний Вейля и Тейта
Здесь и далее E(F) — гиперэллиптическая кривая Е : Y2 + h(X)Y =
f(X) над полем F, К С F С К. Пусть Р = (a,b), Q = (c,d) —
точки этой кривой. Как известно, они лежат на одной прямой с точкой
-(P+Q) = (а, /3). Пусть gPQ = ХХ+l+Y, где XX+Y+l = 0 — уравнение
этой прямой. Очевидно, А = ~(d - b)/(c - а), I = -Ь - Ла, если Р Q.
В случае Р — Q линейная функция gpQ тоже вычисляется стандартным
образом, так как она имеет нули в точках Р, -2Р. Аналогично определим
функцию др = X - а 6 Р[Р], соответствующую прямой, проходящей
через точки Р, Р = (а, -Ь - /г(а)) = -Р и О.
Упражнение 3.3.1. Докажите, что N(gPq) = —(X — а)(Х — b)(X — a), N(gP) =
(Х — а)2.
Указание. Согласно формуле N(gPQ) — N(u + У) — u(u - h) - f есть кубический
многочлен со старшим коэффициентом минус единица, a N(gP) = N(X - a) =
(X - а)2. Так как N(G) = GG, a G = gPQ имеет нули в точках Р, Q, ~(Р + Q), то
N(G) тоже имеет нули в этих точках, значит этот кубический многочлен имеет
корни а, Ь, а (возможно кратные), но он всегда равен -(X - а)(Х - Ь)(Х - а).
Упражнение 3.3.2. Докажите, что div (gPq) = (Р) + (Q) + (-(Р + Q)) - 3(0),
div(jP) = (P) + (-P)-2(O).
Указание. Согласно определению степени deg(^p^) = deg (АХ ф I + У) = 3,
deg(^P) = deg(X-a) = 2, поэтому согласно определению порядка в О ся(\одР$ = -3,
ordo дР = -2. Так как для gPQ = XX + I + У = а(Х) + 6(Х)У, очевидно,
(а(Х), Ь(Х)) = 1, то при вычислении порядка нулей Р, Q, -(Р + Q) имеем г — О,
s = 1,2 (в случае кратности корня а), поэтому в любом случае
div (gPQ) = (Р) + (Q) + (-(Р + Q)) - 3(0).
При вычислении порядков нулей Р, -Р для функции дР = X - а имеем г = 1,
5 = 0, значит оба нуля первого порядка.
Выберем случайную точку R на кривой Е(К) и возьмем дивизор
Dp = (Р + R) - (Р). Вспомним, что выше была определена последова-
тельность рациональных функций Д Е F(E) такая, что
div (Д) = k(P + R) - k(R) - (kP) + (О).
Заметим, что ее можно определить этой формулой и при отрицательных к.
В основе алгоритма Миллера лежит следующая
3.3. Алгоритм вычисления спариваний Вейля и Тейта 137
Теорема 3.3.1 (формула Миллера). Для любых ki
fkx+k2 = fklfk29kiP,k2p/9(ki+k2)P-
Кроме того, Д = 1, Д = 9p,r/9р+я-
Для доказательства заметим, что согласно упр. 3.3.1, 3.3.2
div fee) = (р) + (Q) + (-(Р + Q)) - 3(0),
div (<?р) = (Р) + (—Р) - 2(0).
Учитывая div (Д) — к(Р + R) - к(К) - (кР) 4- (О), имеем
div (fki+k2) ~ div (А.) - div (Д2) =
= (*! + к2)(Р + Я) - (fej + *2)(Я) - ((fci + к2)Р) -kl(P + R) +
+ fcj(P) + (k{P) - k2(P + R) + k2(R) + (fc2P) - (O) =
= (fcjP) + (fc2P) - ((fcj + fc2)P) - (O) =
= (fc!P) + (fc2P) + (-(fcj + k2)P) - 3(0) -
- (((ft! + fc2)P) + (-(fcj + fc2)P) - 2(0) =
= div (gklp,k2p) ~ div (g(kl+k2)p),
следовательно, согласно свойству мультипликативности дивизоров раци-
ональных функций,
j. / *	\ л- (fkxfk29k\P,k2p\
div(A,+<t,) = div ------------- ,
\ д<к,+к2)р j
откуда fkx+k2 = 1кЛк2дкхр,к2р/д{кх+к2}р- Остается заметить, что div(/0) = О
div(A) = (P + P)-(P)-(P) + (O) =
= ((-(Р + Я)) + (Я) + (Р) - 3(0)) - ((Р + R) +
+ (-(Р + Я))-2(О)) =
= div (gRR) - div (gP+R),
div (/_,) = -(P + R) + (Я) - (-P) + (O) =
= -((P) + (-P) - 2(0)) + (-(P + R) + (Я) + (P) - (O)) =
= - div (gP) - div(/,) =
= div (gP+R) - div (gPyR) - div (gP).
Алгоритм Миллера почти без изменений применим и для вычисления спа-
ривания Тейта (иногда называемого спариванием Тейта—Лихтенбаума),
о котором пойдет речь в разд. 3.4. Для этого немного изменяется определе-
ние последовательности Д, а именно рассматривается последовательность
такая, что
div (А) = к(р + R) - (к(Р + Я)) -(к- 1)(О).
138
Глава 3. Криптосистемы на основе спариваний
Легко видеть, что справа стоит главный дивизор, так как его степень
равна нулю и
(Р + Д) + ...+ (Р4-Д) + - к(Р + R) = О.
к
поэтому согласно теореме о группе главных дивизоров такая рациональная
функция существует. Очевидно, что div (/о) = div (/^ = 0, поэтому /о =
Л = 1.
Упражнение 3.3.3. Проверьте, что рекуррентная формула Миллера при этом не из-
меняется.
Упражнение 3.3.4. Проверьте, что формула fkl+k2 = fk,fk29k,p.k2p/9(kl+k2)p при
к\ = к, к2 = -к превращается в формулу 1 == fkf-k9kP-
Алгоритм Миллера вычисления функции fn весьма похож на бинар-
ный алгоритм для построения аддитивных цепочек.
Алгоритм Миллера
Число п записывается в двоичном виде как
t
п =	ь,е{0,1}, &t = i.
Пусть S,P € E(F). Входом алгоритма является пара (n, S), а выходом—
значение fn(S) € F Для выполнимости алгоритма Миллера нужно выпол-
нение условия S Р, 2Р,..., пР, которое далее предполагается по умол-
чанию.
На шаге инициализации полагаем f — Z — Р.
Далее в цикле с убывающим параметром j от t - 1 до 0 с единичным
шагом повторяем:
f — f2^Z > Z — 2Z (шаг удвоения);
если b} = 1, то
f = Z-=Z + P
Возвращаемое значение равно fn(S) 6 F.
В алгоритме параллельно вычисляется аддитивная цепочка точек Z
вида кР, вычисляются значения функций gz,p(S), gz+p(S) € F, и вы-
числяется аддитивная цепочка значений fk(S) 6 F. Значение ==
(X - XQ)(xs,ys) = xs ~ xq , где хм,Ум ~ координаты точки М, так
как gQ(X, Y) = Х - xq — вертикальная прямая, проходящая через точки
Q, -Q, О. Так как др^(Х, Y) = XX +1 + Y, где Л = ~(yQ - yp)/(xQ ~ хрЪ
I — -уР - Ххр, то значение дрр(х$, ys) —	+1 + ys- В случае Р — Q
3.3. Алгоритм вычисления спариваний Вейля и Тейта
139
так вычислять нельзя, нужно вычислить точку -2Р, и проводить прямую
через нее и точку Р. Значение f\(S) вычисляется заранее.
Очевидно, что вариант алгоритма Миллера можно построить по лю-
бой аддитивной цепочке, вычисляющей число п, если запоминать про-
межуточные результаты. Число умножений и делений в поле F при
вычислении «коэффициентов» , ^7^ будет по порядку равно дли-
не цепочки, число остальных умножений по порядку такое же, а число
возведений в квадрат равно числу удвоений в в аддитивной цепочке.
Кроме этого, надо учесть сложность вычисления цепочки точек Z. Окон-
чательная оценка по порядку, очевидно, равна O(log2 п) числу операций
в в поле F = GF(qk), если К = GF(q).
3.3.1.	Усовершенствования алгоритма Миллера
Этому вопросу, важному как для ускорения работы основанных
на спаривании протоколов, так и для ускорения работы известного алго-
ритма MOV дискретного логарифмирования на кривых (правда, нужного
не для реализации криптосистем, а для их взлома) посвящено много
работ. В этом разделе мы рассмотрим некоторые усовершенствования,
пригодные в общем случае.
Заметим, что все описанные ранее методы построения аддитивных
цепочек порождают соответствующие модификации алгоритма Миллера.
Далее мы рассмотрим некоторые специальные методы ускорения алго-
ритма Миллера.
Дальнейшее изложение основывается на [28] и будет конспективным.
Мы опишем только два из предложенных в этой работе методов.
Справедливы следующие полезные в дальнейшем тождества. Пусть
Q € Р[п] — такая точка кривой E(F), что nQ — О, и пусть S
Q,2Q,...,nQ.
Упражнение 3.3.5. Докажите тождества:
9q,q(S) =	1	1
9q(S)92q($)	9q,q(~S)	9оя($У
9(k+l)Q,kQ(S)	_ _ 9kQ(S) _ _ 9kQ(S)
9(k+l)Q(S)9(2k+l)Q(S)	9(k+\)Q,kQ(~S)	9(k+\)Q,kQ(S) ’
9q,q(S)9iq,q(S) _ _9q,qY>)9q(S) _ _9Q,Q(S)gQ(S)
92Q(S)g3Q(S)	92Q,q(~^)	92q,q(S)
Указание. Проверьте, что gpq(S) = gpQ(S), gp,o(S) = gp(S). Используя предыду-
щее упражнение, имеем
9q,q($)	9q,q(s)9q,q(-S) =
g2Q(S)g2Q(S) - g2Q(S)g2Q(S)gQ,Q(-S)
=	N(gQ,Q(S))	=	1
(xs - xq)2(xs - x1Q)gQ,Q(-S) дд,д(-3)'
140
Глава 3. Криптосистемы на основе спариваний
Аналогично
9{k+V>Q,kQ(S)
9(k^i)Q,kQ(S)g^+i)Q!kQ(-S)
9{k+\)Q(S)g^k+\)Q(S)	g{k+^Q(S)g^k+\)Q(S)g^+^Q^Q(~S)
N(9(k+i)Q,kQ(S)) _ 9kQ(S)
(XS X(k+\)Q)2(XS X(2k+\)Q)9(k + \)Q,kQ( S) 9Q,q( 8)
9q,q(S)92q,q(S) = gQyQ (S)g2QyQ (S)g2QyQ(-S)
92Q (S)g3Q (S) g2Q (S)g3Q (S)g2QyQ(-S)
N(gi)Q,Q(S))gQyQ(S) _ gQ(S)gQyQ(S)
(XS - x2q)2(xS - x3q)92q,q(-S)	92Q,q(-S)
Из алгоритма Миллера выводится следующая точная формула (в ней для краткости
опущена подстановка S вовсе функции):
где t = [log2nj, Щ = |n/22J, &»-i = ni-i ~ 2ni> если = 0 тогда д2щр,ь{^р =
д2щр,о — 92щр ~ 9щ_хр- Без ограничения общности полагаем до = 1.
Упражнение 3.3.6. Докажите эту формулу.
Указание. Проверьте, что
n = Y^bi2\ €{0,1},
и примените индукцию по п. Для выполнения шага индукции возьмите формулу
для fni и воспользуйтесь тем, что
Упражнение 3.3.7. Проверьте, что произведение двух подряд идущих сомножите-
лей в предыдущей формуле можно преобразовать следующим образом:
I \	7 \9щ-хр,щ_хр
Указание. Примените упр. 3.3.5.
Ьг_1 — &1-2 — 1,
bi-l — 1, &г-2 — 0,
Ьг_1 — 0 — bj-2.
— 0,	— 1,
3.3. Алгоритм вычисления спариваний Вейля и Тейта
141
Заметим, что при вычислении fn можно опускать постоянные муль-
типликативные множители, так как div (с/) = div (/) для ненулевого
элемента поля F, и улучшенный алгоритм Миллера теперь выглядит так.
Ускоренный алгоритм Миллера
Число п записывается в четверичном виде как
t
n = Y^’bi 6 {0,1,2,3}, qt^0.
i=Q
Пусть S,P е E(F). Входом алгоритма является пара (n, S'), а выходом—
значение £ F
На шаге инициализации полагаем f = Z — Р; если qt = 2 то
выполняем присваивания
.2 9p,p(s) ,
92p(S) ’
Z = 2P;
в противном случае
з9р,р(8)9р(8)
92р,р(-8)
Z = ЗР
Далее в цикле с убывающим параметром j от t - 1 до 0 с единичным
шагом повторяем:
если qj = 0, то
.4 9z,z(8)
92z,2z(S) ’
Z = 4Z;
если qj = 1, то
- _ у /с\у4 9z,z(8)91Z,p(S)
)J 9^p(S)92Z,2z(-SY
Z := 4Z + P;
если qj = 2, то
f   f y4	9Z,z(8)g2z,p{8)	_ ..p
f - fdS> f Z-4Z + 2P'
если q} = 3, to
у _ у /m3 y4 9z,z(S)92ZJ>(8)94Z+2P,p(S)	.	7	7 р
92z(8)g2z^-p,2z^p(-S)g4z-h3p(8)'
Возвращаемое значение равно fn(S) € F.
Для кривых над полями характеристики три более удобен тернарный
вариант алгоритма Миллера, основанный на следующих тождествах.
142
Глава 3. Криптосистемы на основе спариваний
Упражнение 3.3.8. Докажите тождество
/зк — fk9kP,kP9lkP,kp/{92kP93kp)-
Указание. Примените тождество
fki+k2 = fkifk}9k1p,k2p/9(kl+k2)p
при = k2 = к и при k{ = 2k,k2 = k.
Упражнение 3.3.9. Докажите тождество
f _	,3 9q,q9q
J3k — ~Jk ------ ,
92Q,Q
где черта над Qiq^q есть знак операции сопряжения в кольце полиномиальных
функций.	i
Тернарный вариант алгоритма Миллера
Число п записывается в троичном виде как
b' £ {0, 1, 2}, ^0.
2=0
Пусть S,P 6 E(F). Входом алгоритма является пара (n, S), а выходом—
значение fn(S) € F.
На шаге инициализации полагаем f = Z — P; если qt = 2, to
выполняем присваивания
/ =	u = z = 2P.
92p(S)
Далее в цикле с убывающим параметром j от t - 1 до 0 с единичным
шагом повторяем:
,39z,z(S)gz(S)
92z,z(~S)
Z — 3Z;
если qj = 1, то
/ =
9z+p(S)
Z:=Z + P;
если q3; = 2, то
z := z + и.
gZ,2P(S)
J TgZ + 2P(Sy
Возвращаемое значение равно fn(S) Е F
Ускорение вычислений здесь достигается за счет того, что возведение
в куб в поле характеристики три делается существенно быстрее умноже-
ния. Подробнее об организации арифметики в таких полях будет сказано
далее.
3.4. Спаривание Тейта
143
Заметим, что g^z,z = 9-3z,z, так как эта линейная функция однознач-
но соответствует прямой, проходящей через точки 2Z, Z, а эта прямая
совпадает с прямой, проходящей через точки -3Z, Z согласно определе-
нию сложения точек на кривой. Поэтому для вычисления коэффициентов
линейной функции g2z,z достаточно знать координаты точек Z и 3Z,
и точку 2Z вычислять не надо. Поэтому последовательность вычисляемых
в этом алгоритме точек Z совпадет с последовательностью точек адди-
тивной цепочки, вычисляющей пР тернарным методом.
В разд. 3.5 будет показано, что операция утроения точки для суперсин-
гулярных кривых над полями характеристики три делается существенно
быстрее, чем операции сложения и удвоения. Некоторое ускорение тер-
нарного алгоритма в применении к таким кривым будет описано там же.
Отметим, что в некоторых приложениях при вычислении спаривания
первый аргумент Р можно считать фиксированным. Это позволяет зара-
нее вычислить и запомнить коэффициенты линейный функций ди,9иу,
которые зависят только от точки Р. Если же эта точка не фиксирова-
на, то некоторого ускорения алгоритма Миллера можно достичь за счет
любого из методов, ускоряющих вычисление аддитивной цепочки точек,
кратных Р, возникающей при работе алгоритма Миллера.
В частности, если есть возможность, простое число п выбирают так,
чтобы его запись в двоичной системе с использованием отрицательных
цифр содержала небольшое количество единиц, т. е. оно являлось ал-
гебраической суммой небольшого числа степеней двойки. Такие числа
называют простыми числами Солинаса.
3.4.	Спаривание Тейта
Это спаривание играет в эллиптической криптографии ту же роль,
что и спаривание Вейля, но иногда оно удобнее для применения, хотя
его формальное определение несколько сложнее. Дальнейшее изложение
следует [46]. Спаривание Тейта для гиперэллиптической кривой С (К)
определяется как билинейное невырожденное отображение
(•, -)п : Рг4(С)[п] х Pic°K(C)/nPic°K(C) -> К*/(К*)п,
где PicQK(C) группа классов нулевых дивизоров кривой С над полем К
(если кривая С — эллиптическая, то PicQK(C) — это просто группа точек
этой кривой), Ргс^(С)[п] — ее подгруппа, состоящая из дивизоров D,
таких что nD ~ 0 (в случае эллиптической кривой это подгруппа п-точек
кручения), nPicQK(C) — это подгруппа, состоящая из всех дивизоров
вида nD, где D 6 PicQK(C) (в случае эллиптической кривой это подгруппа,
состоящая из всех точек вида nP, Р е	PicQK(C)/n PicQK(C) —
фактор-группа, К* — мультипликативная группа поля К, (К*)п —
ее подгруппа, состоящая из п-х степеней, К*/(К*)п — фактор-группа
144
Глава 3. Криптосистемы на основе спариваний
(ее элементами являются классы эквивалентности отношения X ~ Y О
XjY — zn, z 6 К, обозначаемого также X = X mod Можно
считать, что значения отображения (Z>i,P2)n лежат в ТС, но при этом
его билинейность означает, что всегда выполнены сравнения
(Di + D'i, D2)n =	D2)n{D,1, D2)n mod(K*)n,
(D^D2 + D2)n 3= (Dx, D2)n(D{, D2)n mod (7T)n,
а невырожденность означает, что для любого ненулевого Dy Е PicQK(С*)[п]
существует D2 Е Ргс^(С) такой, что {D^ D2)n l(mod (if*)n). Без дока-
зательства сообщаем (см., например, [42]), что спаривание Тейта коррект-
но определено и выражается явной формулой (D\,D2)n —	где
такая функция на кривой С (К), что div (/р.) = nD\ (она существует,
так как nD\ 0 по модулю подгруппы главных дивизоров) и дивизор D2
выбран так, что его носитель не пересекается с носителем div (/) (суще-
ствование такого дивизора D2 можно доказать), а /рДТ^), как и ранее,
равна по определению
ПШ', где Р2 = ^>Р(Р).
РЕС	РЕС
Впрочем, билинейность по переменной D2 следует из тождества fD1 (D2 +
D2) — 7z>i(^2)/z>i(^2)’ очевидно, верного при условии, что supp (div(/pj))
не пересекается с supp (D2 4- D2)’ т-е- из условия
Р Е supp (D2 + D2) О /dJJP) °0-
Также очевидно, что, если D2 - D2 = nD, то /рДТ^) =
X Е К*, т.е. fDi(D2)'= fD}(D2) mod (К*)п. Чтобы избежать указанной
неоднозначности, используется не (Di,D2)n, a (Di,D2)n , где К =
GF(q). Действительно, тогда
/о, (^2)(9“1)/п =	= fa(D'2).
Билинейность по переменной D\ следует из тождества /р1+р; = /d^d'^
а это тождество следует из тождества div (fi(S)f2) = div (/i(S)) + div (f2).
Укажем без доказательства связь между спариваниями Тейта и Вейля.
Пусть Е(К) — эллиптическая кривая над полем К = GF(q) такая, что
T?[n] С Е(К) (т. е. все точки n-кручения кривой Е(К) лежат на кри-
вой Е(К)), и пусть п3 не делит порядок кривой Е(К) (из предыдущего
условия следует, что п2 делит порядок кривой Е(К)). Из этих условий
следует, что группа Е(К)/пЕ(К) изоморфна группе Е[п] (т. е. в каждом
классе эквивалентности группы Е(К) по подгруппе пЕ(К) лежит одна
точка n-кручения). Тогда для любых P,QE J£[n] справедливо
e„(P,Q) = 7|^mod(^)n.
3.4. Спаривание Тейта
145
Выше уже было показано, как вычислить спаривания Вейля и Тейта,
затратив O(logn) операций в поле К.
В криптографических приложениях обычно используется спаривание
Тейта в следующем виде:
en : £(GF(g))[n] х E(GF(qk))[тг] GF(qk)*,
где en(P, Q) =	дивизор Dq ~ (Q) - (О), дивизор div (/Р) =
n(P) - n((9), fp — рациональная функция на E(GF(q) (т. е. с ко-
эффициентами из GF(q\). Свойства билинейности и невырожденности
для нее принимают следующий вид: для любых Р, Р\,Р2 Е E(GF(q)),
Q, Qi, Q2 Е E(GF{qk)) справедливо
en(Pi + Р2, Q) = en(P},Q)en(P2, Q),
en(P, Qi НН Qz) = en(P, Qi)en(P, (?2);
если en(P, Q) = 1 для любого Q 6 E(GF(qk)), то Р — О.
3.4.1.	Применение спариваний
для логарифмирования в эллиптических кривых
Впервые такая возможность было продемонстрирована в [71], как уже
упоминалось выше. Сейчас появляется возможность дать более подроб-
ные разъяснения, как это делается, на некоторых конкретных примерах.
Допустим, что E(GF(q)) — эллиптическая кривая порядка dn, где п —
большое простое, не равное характеристике поля GF(q), a d — малое
(в сравнении с п) число. Пусть Р Е E(GF(q)) — точка порядка п,
и Q Е (Р), т. е. Q = кР, к < п. Задача дискретного логарифмирования
состоит в вычислении logP Q — к.
Пусть к — такое минимальное число, что qk - 1 делится на п.
Спаривание Вейля или Тейта при К — GF(qk) может быть использовано
для вложения циклической группы (Р), порожденной точкой Р, в муль-
типликативную группу поля GF(qk). Поэтому к называют иногда также
степенью вложения (Р).
Пусть е — спаривание Вейля или редуцированное спаривание Тейта,
определенное выше. Тогда атака (называемая MOV-атакой) на проблему
DLP для кривой E(GF(q)) проводится следующим образом. Выбираем
случайную точку R Е E(GF(qk)), такую, что е(Р R) 1. Существова-
ние такой точки гарантируется свойством невырожденности спаривания.
Для спаривания Вейля можно выбрать R Е E(GF(q))[n]. Согласно [21]
С E(GF(qk))), как уже отмечалось выше. Согласно свойству
билинейности, отображение R —> e(S, R) есть вложение (изоморфное
отображение) группы (Р) в группу GF(qk)*. Вычисляя a = e(P,R),
/3 — e(Q,R) получаем, в силу e(Q,P) = е(кР, R) = е(Р, R)k = ak, что
logp Q = к = logQ Д, т. е. ECDLP (DLP для эллиптических кривых) сво-
дится к DLP в конечном поле GF(qk). Для большинства эллиптических
146
Глава 3. Криптосистемы на основе спариваний
кривых над GF(q) параметр к близок к п, т. е. велик, и описанная ата-
ка не имеет практического значения. Но для суперсингулярных кривых
к 6, и поэтому для них, согласно известным результатам о DLP, ECDLP
решается в субэкспоненциальное время.
Пример 3.4.1. Рассмотрим конкретный пример эллиптической кривой Е : Y2 4-
Y = X3 4- X 4- 1 над полем К = GF(Zn) при нечетном п. Так как при n = 1
порядок кривой Е(К) равен 1, то по теореме Хассе—Вейля порядок этой кривой
равен q 4- 1 - \/Zq при n = l,7(mod 8), и равен q 4- 1 4- y/Zq при n = 3,5(mod 8).
Согласно теореме [86] о структуре групп суперсингулярных кривых группа этой
кривой циклическая. Так как
94 - 1 = (9 - 0(9 + 0(? + 1 - УМ (? + 1 + г/2?)>
то степень вложения к — 4. Действительно, если порядок кривой Е(К) равен nd,
п — большое простое, то п делит q4 - 1, но не делит q - 1 и q2 - 1, так как иначе
п делило бы q ± 1 (ведь (q - 1, q 4- 1) = 1), а так как п делит q 4- 1 ± y/Zq, то п
делило бы y/Zq ± 2 или y/Zq, что противоречит малости d. Спаривания Вейля
и Тейта сводят ECDLP для кривой Е(К) к DLP в поле GLF(g4).
В работе [42] MOV-атака была расширена и были найдены новые
криптографически слабые кривые с помощью спаривания Тейта, но мы
не будем углубляться в подобные вопросы.
3.4.2.	Кривые, удобные для спаривания
Для реализации описанных выше протоколов нужно подбирать спе-
циальные кривые. Здесь мы не будем рассматривать применения спарива-
ния Тейта к кривым рода больше 1, а ограничимся только эллиптическими
кривыми. При выборе таких кривых нужно обеспечить выполнение двух
условий:
(1)	порядок кривой должен делится на большое простое число п (для то-
го, чтобы DLP в подгруппе порядка п данной кривой была устойчива
к р-атаке Полларда и другим подобным атакам);
(2)	параметр к, такой, что п делит qk - 1 и не делит qk' - 1 при к' < к,
должен быть достаточно большим, чтобы DLP в группе GF(qk)*
выдерживала известные атаки, но в тоже время он должен быть
достаточно малым, чтобы арифметику в GF(qk) можно было бы
эффективно реализовать.
MNT-кривые. Примеры несуперсингулярных кривых, удобных для спа-
ривания, были предложены в работе [74]. Для этих кривых к — 3,4,6.
В семействе MNT-кривых порядок поля выбирается равным q(l), а по-
рядок кривой — равным n(Z) = q{l) 4- 1 - t(l),	2д/^(7). Тогда
параметр к должен быть таким, что n(Z) будет делителем Ф^,. (<?(/)), где
Фд,.(Х) — &-й полином деления круга (см. о них гл. 1), и не будет делите-
лем (q(l)k - 1)/Фа,. (</(/)), следовательно, не будет делителем (q(l)k/s - 1),
3.4. Спаривание Тейта
147
где s — делитель А именно, параметры MNT-кривых выбираются
следующим образом:
к = 3,	q(l) = 12Z2 - 1,	Z(Z) =	-1 ±6Z,	n(l) = 12Z2±6Z+ 1,
к = 4,	g(Z) = Z2 + Z + l,	Z(Z) =	-1,1 +1,	n(Z) = Z2 + 2Z + 2, Z2 + 1,
к = 6,	g(Z) = 4Z2 + l,	<(Z) =	-1 + 21,	n(Z) = 42±2Z+ 1.
Предполагается, что это семейство кривых бесконечно.
Построение MNT-кривых использует теорию кривых с комплексным
умножением. Согласно этой теории (см., например, [29]), если для D =
3(mod 4) существуют такие целые t, у, что р = (t2+Dy2)/4 — простое чис-
ло, тогда можно построить со сложностью O(D2(logQ)3 над полем GF(p)
эллиптическую кривую с р + 1 - t точками, где t — след этой кривой.
Представление о том, как это делается, можно получить по рабо-
те [78]. Кривые ищутся в виде Y2 = X3 - ЗХ + b над полем GF(p).
Выбирается р = 4Z2 + 1, t = 1 ± 21. Тогда из равенства р — (t2 -4 Dy2)/4
при х = 6Z=p 1 имеем х2 - 3Dy2 — -8, где D — дискриминант кривой, т. е.
максимальный свободный от квадратов делитель числа 4р - t2. Так как
квадрат нечетного числа по модулю 8 равен единице, то D = 3(mod 8).
Кроме того, очевидно, -8 должно быть квадратом по модулю 3D. Ищутся
решения в пределах D 3 • 109, 50	|ж|	300. Для быстрого решения
уравнения Пелля используется модификация алгоритма [82]. После нахо-
ждения дискриминанта D и простого р используется программа М. Скотта
[89]. Для больших D,p используется программа Андреаса Энге. В [78]
приведен список построенных MNT-кривых. Простейшая из них — кри-
вая Y2 = X3 - 3X + Ъ над полем GF(p),
р = 8C72P321£484A1419B22F914CB43C112B76Z>7AE5,
b = 299CE2\9B7B0\34SFC2B5Q07B6AB\EE1005676F7
с простым порядком
8C72D321E48AA1419B23B6B2E4A85A073822640F
(в шестнадцатеричной записи). При это множитель безопасности к = 6
и поле GF(p6) можно рассматривать как расширение поля GF(p), полу-
ченное присоединением корня неприводимого многочлена X6 4- X2 + 3.
Удобные для спаривания суперсингулярные кривые. Интересно, что в ка-
честве кривых, удобных для спаривания, во многих работах предлагается
использовать суперсингулярные кривые. Например, в [22] рассматрива-
ются с этой целью кривые
Elfi:Y2 =Т3 + (1-Ь)Х + b, be {0,1}
над полем GF(p), где р = 2(mod 3) при b = 1 и р = 3(mod 4) при b = 0,
имеющие порядок р 4- 1 и множитель безопасности к = 2, кривые
Е2Л:У2+У = X3 + X + b, b€ {0,1}
148
Глава 3. Криптосистемы на основе спариваний
над полем GF(2m) при нечетном т, имеющие порядок 2т 4- 1 ±
и множитель безопасности к = 4, и кривые
Е3,ь: Y2 = X3 - Х + Ь, 6 €{-1,1}
над полем GF(3m) при при т = ±l(mod 12) или т = ±6(mod 12),
имеющие порядок Зт 4-1 ± з(™+1)/2 и МНожитель безопасности к = 6.
Более точно, согласно упр. 2.3.3, 2.3.4, порядок кривой Е^ равен
Зт 4- 1 4- 3(т+1)/2 при т = ±l(mod 12) и равен Зт 4- 1 - 3^+1^2 при
т = ±5(mod 12), а порядок кривой Ез-i равен Зт + 1 - 3^т+1^2 при
т = ±l(mod 12) и равен Зт 4-14-3^т+1^2 при т = ±5(mod 12), и порядок
каждой из этих кривых делит 36/ - 1, значит множитель безопасности
не больше 6. Последнее утверждение очевидно, так как 36/ - 1 делится на
з4' + З2' + 1 = (з2' + 1)2 - З2' = (з2' + 1 - з')(з2' + 1 + з'),
а З2' + 1 - 3' = (3' + 1 - 3<'+')/2) (3' + 1 + 3<'+1>/2).
Упражнение 3.4.1. Докажите, что порядок кривой Е3уЪ не делит Зкт - 1, к < 6.
Указание. Достаточно доказать это для к = 1,2,3. Если бы он делил Зт - 1,
то делил бы и 3<т+1>/2 ± 2, что невозможно. Если бы он делил 32т - 1, то де-
лил бы и 32т - 1 - (32т 4- I - Зт) = Зт - 2, а значит делил бы и 3(т+1)/2 -|- 1
или 3<т+1)/2 - 3, что невозможно. Если бы он делил З3т - 1, то делил бы
и З3т - 1 - (32т 4- 1 - 3m)(3w 4- 1) = -2, что невозможно.
Утверждение о порядках кривых Е^ доказано в упр. 2.3.7 и 2.3.8
в первой книге [4].
Более точные утверждения о порядках кривых Е^ь были приведены
в примере 1.2.3.
Упражнение 3.4.2. Докажите что множитель безопасности для этих кривых ра-
вен 2.
3.4.3.	Искажающее отображение
Для использования спаривания в описанных выше протоколах необ-
ходимо, чтобы спаривались одинаковые группы, а спаривание Тейта виде:
е„ : #(GP(g))[n] х P(GP(g*))[n] GF(qk)*,
где к — соответствующий п множитель безопасности, не всегда удовле-
творяет этому условию. Спаривание Вейля удовлетворяет ему, однако для
него не выполнено условие невырожденности в форме еп(Р, Р) / 1. Это
затруднение было преодолено с помощью так называемого искажающе-
го отображения, предложенного в [97]. Так называют эндоморфизм
кривой E(GF(q)) на кривую E(GF(qkY) (т. е. отображение, сохраняющее
операцию сложения точек), такой, что (Р, ф(Р))п 1. Тогда можно рас-
смотреть спаривание
е(Р,3) = (Р,^(С)^’1)/п,
3.4. Спаривание Тейта
149
которое, кроме свойства билинейности (вытекающего из билинейности
спаривания (•, -)п и свойств эндоморфизма), может оказаться невырож-
денным в точке Р. Доказательство невырожденности спаривания, постро-
енного с помощью искажающего отображения, основывается на следую-
щей лемме.
Лемма 3.4.1. Пусть E(GF(q)) — эллиптическая кривая с порядком, крат-
ным простому числу п, такому, что qk - 1 кратно п, a qk - 1 не кратно п
при любом к' < к. Известно, что группа E(GF(qk))[n] точек порядка п
представима в виде (Р) 4- (Q), где P,Q — точки, порождающие ее цик-
лические подгруппы порядка п, такие, что (Р) П (Q) = {(9}. Тогда, если
en(P,P)=l,mo en(P,Q)^l.
Доказательство. Если еп(Р, Q) = 1, тогда согласно условиям леммы
и свойству билинейности имеем тождество
еп(Р, aP + bQ) = еп(Р Р)аеп(Р, Q)b = 1,
противоречащее невырожденности спаривания еп.	
Следуя [46] и [32], приведем примеры эллиптических кривых и ис-
кажающих отображений.
Пример 3.4.2. Пусть Е — Е^ь : У2 = X3 4- (1 - b)X 4- b, b Е {0, 1} — кривая над
GF(p), р = 3(mod4), р = 2(mod 3). Порядок этой кривой равен р 4- 1 и она су-
персингулярная. Пусть п — большой простой делитель р 4-1. Выберем i Е GF(p2)
такой что г2 = -1 (согласно критерию Эйлера в поле GF(p) при р = 3(mod4)
такого элемента нет, а в поле GF(p2) любое квадратное уравнение с коэффи-
циентами из GF(p) разрешимо). Рассмотрим отображение i/)(X,Y) = (-X,iY).
Очевидно, что оно точки кривой E(GF(p2)) переводит в точки той же кривой,
причем, если Р Е E(GF(p)), то не принадлежит E(GF(p)). Очевидно, что
^2(Р) = -Р, значит ip2 = -1. Непосредственно проверяется, что отображение
сохраняет сложение точек, т. е. сумму точек переводит в сумму (и поэтому является
автоморфизмом кривой E(GF(p2)) и эндоморфизмом кривой E(GF(p)) на кри-
вую E(GF(p2))). Очевидно, что степень вложения к — 2, так как (р - 1,п) <
(р-1,р4-1) = 2. На самом деле (р - 1, п) — 1 потому, что простое п > 2.
Известно (но не очевидно), что группа E(GF(p2))[n] изоморфна
прямому произведению группы E(GF(p))[n] на себя. Если Р = (х,у) Е
E(GF(p)) — точка порядка п, то у / 0, так как п > 2 (точки (х, 0) имеют
порядок два). Согласно свойствам спаривания Вейля еп(Р, Р) Е GF(p),
и в то же время еп(Р, Р)п = 1. Так как (n, р - 1) = 1, то это означает, что
еп(Р, Р) = 1. Но 'ф(Р) Е E(GF(p2)) \ E(GF(p)) имеет порядок п (в силу
того, что ф — автоморфизм), 'ф(Р) не принадлежит группе (Р), поэтому
{Р, 'ф(Р)} образуют базис в группе E(GF(p2))[n]. Применяя лемму, имеем,
чтоеп(Р,Р) = еп(Р,^(Р))^1.
Упражнение 3.4.3. Докажите, что сохраняет сложение точек.
Указание. Делая подстановку (X, У) -> (-Х, iX) в формулы сложения и удвоения
точек кривой, проверьте, что Л умножается на -г, Л2 умножается на -1, поэтому
«з меняет знак, а у;, умножается на i.
150
Глава 3. Криптосистемы на основе спариваний
Пример 3.4.3. Пусть Е — E3fb : Y2 = X3 — X 4- b, Ъ € {—1, 1} — кривая над
GF(3m), (m, 6) = 1. Нам уже известно, что она суперсингулярная и ее порядок
равен Зт 4- 1 ± з(™+0/2, а МНожитель безопасности к = 6. Отметим (хотя это нам
и не понадобится), что эти кривые при разных b являются скрученными друг
к другу.
Упражнение 3.4.4. Проверьте, что порядок кривой делит число 33m 4-1.
Указание. Примените при А — 3<m-1V2 тождество
1 + 27Л6 = (1 + ЗЛ2) (1 - ЗА 4- ЗЛ2) (1 + ЗЛ 4- ЗА2).
Пример 3.4.4. Построим для этой кривой искажающий эндоморфизм в кривую
Я(67?(36™)). Выберем i Е GF(9)\GF(3) так, чтобы г2 = -1 и a € GF(21)\GF(3)
так, чтобы a3 - a - Ь = 0 (такой элемент существует, так как в кубиче-
ском расширении разрешимо любое кубическое уравнение с коэффициентами
из GF(3), и он, очевидно, не принадлежит полю GF(3)). Тогда отображение
ф : (Т,К) -> (а - X, iY) является автоморфизмом кривой над любым по-
лем, содержащим GF(36), таким, что = -1. Поэтому, как и выше, если
Р 6 E(GF(3m)) имеет порядок, больший двух, то ф(Р) Е E(GF{36m))\E(GF(3m))
иеп{Р,Р) = еп(Р,ф(Р))^^
Упражнение 3.4.5. Докажите, что ф переводит кривую E(GF(36m)) в себя и со-
храняет сложение точек.
Указание. Проверьте, что при подстановке (а — X, iY) в уравнение Е3,ь вместо
(X, Y) обе его части меняют знак. Воспользуйтесь тождествами (а - с)3 = а3 - с3,
2а = —а и равенством а3 — а = Ъ. Делая ту же подстановку в формулы сложения
и удвоения точек кривой, проверьте, что Л = 1/ух и А — (у2 - ?/1)/(ж2 - Ж1)
умножается на -г, А2 умножается на -1, поэтому ж3 = А2 - хх - х2 превращается
в а - ж3,	- ж3 меняет знак, поэтому у3 = A(xi - х3) - у{ умножается на г.
Пример 3.4.5. Пусть Е2,ъ '.Y2-\-Y = X3 4- X 4- 6, 6 Е {0, 1} — суперсингулярная
кривая над полем GF(2m) при нечетном т, имеющая порядок 2т 4- 1 ± 2<т+1^2
и множитель безопасности к = 4. Отметим, что как и в предыдущем примере, эти
кривые при разных b являются скрученными друг к другу.
Упражнение 3.4.6. Проверьте, что порядок кривой делит число 22т 4- 1.
Указание. Примените при Л = 2<т-1^2 тождество
1 + 4Л4 - (1 - 2Л + 2Л2) (1 + 2Л 4- 2Л2).
Построим для этой кривой искажающий эндоморфизм ф в кривую
£(GF(24m)). Выберем sEGF(4)\GF(2), тогда ? = $, и tt GF(16)\GF(4)
так, чтобы t2 -4 t = s3 4- s2 (такой элемент существует, так как в квадра-
тичном расширении разрешимо любое квадратное уравнение с коэффи-
циентами из GjF(4), и он, очевидно, не принадлежит полю GF(4).) Тогда
отображение : (X, Y) —> (X 4- s2, Y 4- sX 4-1) является автоморфизмом
кривой над любым полем, содержащим GF(24), таким, что ф2 = -1.
Поэтому, как и выше, если Р е E(GF(3m)) имеет порядок, больший двух,
то ф(Р) Е E(GF(24m))\E(GF(2m)) и en(P,P) = еп(Р,ф(Р)) £ 1.
3.4. Спаривание Тейта
151
Упражнение 3.4.7. Докажите, что ip переводит кривую E(GF(34m)) в себя и со-
храняет сложение точек.
Указание. Проверьте, что при подстановке (s2 4- X, X 4- sX 4- t) в уравнение
Ег,ь вместо (X,Y) левая часть увеличивается на $2JT2 4- t2 4- sX 4-1, а правая
часть - на s24s64 X2s2 4- Xs4 = s2 4- s3 4- X2s2 4- Xs. Делая ту же подстановку
в формулы сложения и удвоения точек кривой, проверьте, что X = (у2-у\)/(х2-х{)
увеличивается на $, А2 увеличивается на s2, поэтому х3 = Л2-Ж1 -х2 превращается
в s2 4- ж3, значит Х\ - х3 не меняется, поэтому у3 = А(^1 - х3) - у{ увеличивается
на $(24 - ж3) 4- $®i 4-1 = sx3 -it.
Пример 3.4.6. Этот пример относится к несуперсингулярным кривым. Пусть
порядок кривой Е над полем GF{q) делится на большое простое число п. Пусть
на кривой выбрана подгруппа точек порядка п и соответствующий множитель
безопасности к < п. Пусть Р Е E(GF(qk)) такова, что en(P, Р) = 1. Обозначим тг
автоморфизм Фробениуса 7Г : (X, У) -> (Xя,Yq) кривой E(GF(qk)) и тгг его
степень, т. е. автоморфизм тгг : (X, У) -> (Xя ,Yq ), i = 0, 1,..., к - 1. Очевидно,
7г° = лк — тождественный автоморфизм. Возводя обе части уравнения кривой
в степень q и используя тождество Фробениуса, легко проверить, что автоморфизм
Фробениуса (и любая его степень) действительно переводит кривую E(GF(qk))
в себя. Также проверяется, что он сохраняет операцию сложения точек, так как
при возведении координат суммируемых точек в q-ю степень в ту же степень
возводится А и поэтому также координаты суммы точек.
Определим отображение Тг след точки
Тг(Р) = 52?(Р).
г-0
Здесь под сложением понимается сложение точек кривой, а не покоорди-
натное сложение. Заметим, что Tr(P) Е E{GF{q)). Действительно,
к	к-1
тг(Тг (Р)) = £ ?(Р) = 52 7Г!(Р) = Тг (Р),
г—1	г—О
поэтому координаты точки Tr (Р) при возведении в степень q не меняют-
ся, значит они принадлежат полю GF(q). Непосредственно проверяется,
что отображение след есть гомоморфизм группы E(GF(qk)) (т. е. сохра-
няет операцию сложения), поэтому пТг(Р) = Тг(пР) — Тг((9) = оо,
значит порядок точки Тг(Р) делит число п, поэтому он равен п, если
Тг(Р) = О. Если {Р, Тг(Р)} — базис в E(GF(qk))[n], тогда, как и выше
еп(Р, Тг(Р)) 1. Известно [30], что {Р, Тг(Р)} — базис тогда и только
тогда, когда тг(Р) = АР, А = 0, 1,..., п - 1. Если п делит порядок кривой
E(GF(q)), то последнее равенство возможно лишь при А = 1, q, причем
А = 1 возможно лишь при Р Е E(GF(q))[n]. В качестве искажающе-
го отображения можно использовать и само отображение Фробениуса,
но для реализации след удобнее.
152	Глава 3. Криптосистемы на основе спариваний
Указанный метод построения искажающего отображения годится
и для суперсингулярных кривых, но описанные выше отображения удоб-
нее. В [97] доказана следующая общая теорема:
Теорема 3.4.1. Пусть Е — кривая над GF(q), п — простое, Е[п] С
E(GF(qk)), Р Е ^[n], еп(Р, Р) — 1. Если Е суперсингулярна, то суще-
ствует искажающее отображение ф, такое, что еп(Р,ф(РУ) 1. Если Е
несуперсингулярна и тг(Р) ХР, Л = 0, 1,..., п — 1, то существует иска-
жающее отображение ф, такое, что еп(Р, ф(Р)) / 1.
В [47] дан алгоритм построения искажающих отображений для всех
суперсингулярных кривых.
3.4.4.	Удобные для спаривания кривые с множителем
безопасности к 2
Такие кривые рассматривались в [64]. В случае к = 1 примером таких
кривых является кривая У2 = X3 - X над полем GF(p) при р = А2 4- 1,
А = 0(mod4). Если же А = 2(mod4), то берется кривая У2 = X3 - 4Х.
Справедлива следующая
Теорема 3.4.2. Группа точек этой кривой изоморфна группе Za ® Zа-
Искажающим отображением является г/тч (X, У) —> (-X,AY). Если Р —
произвольная точка простого порядка п на этой кривой, то п делит А
и группа Е*[п] порождается точками Р и ф(Р).
Ее мы также приводим без доказательства.
Приведем также без обоснования пример конкретных значений
А, п, р для использования спаривания Вейля на кривых этого семей-
ства.
Пример 3.4.7. В качестве простого п можно взять 2256 - 2174 4- 1, а в качестве
A = nh,h = 21345. Тогда р = А2 + 1 = 23202 - 23121 + 23038 + 22947 - 22865 4- 22690 4- 1 -
простое.
Порядок поля очень велик и для уменьшения сложность операций
в нем специально выбираются простые числа Солинаса. Приведение
по модулю таких чисел выполняется несколько быстрее, чем для случайно
выбранных простых чисел. Но практическая пригодность таких кривых
вызывает сомнения.
Для случая к = 2 в работе [64] предлагается кривая У2 = X3 - ЗХ над
полем GF(p), р = nh-\, h кратно 4, но не кратно 3. Если же h кратно 12,
то кроме указанной кривой можно взять еще кривую У2 = X3 - 1.
Справедлива
Теорема 3.4.3. Порядок этой кривой равен р 4- 1 = nh, она суперсингу-
лярна и множитель безопасности к = 2. В случае У2 = X3 — ЗХ иска-
жающим отображением является ф : (X У) —> (-Х, iY), где i2 = -1,
i Е GF(p2), а в случае У2 = X3 - 1 искажающим отображением явля-
ется : (ХУ) -> (ДУ), где j2 = 1, j Е GF(p2) \ GF(p). Если Р -
3.4. Спаривание Тейта
153
произвольная точка простого порядка п на этой кривой, то группа ^[п]
порождается точками Р и 'ф(Р).
Приведем также без обоснования пример конкретного выбора пара-
метров для использования этой теоремы.
Пример 3.4.8. В качестве простого п можно взять 2160 4- 23 - 1, а в качестве
h — 2360. Тогда р = nh - 1 = 2520 4- 2363 - 2360 - 1 — простое. Этот выбор параметров
обеспечивает 80-битную надежность. Для 128-битного уровня надежности можно
взять п = 2256 4- 2225 - 1 , а в качестве h ~ 21326. Тогда р — nh - 1 = 21582 4- 21551 -
21326 _ ।
3.4.5.	Удобные для спаривания поля
Во встречающихся в литературе примерах обычно к < 32 и имеет вид
к — 2гЗЛ В [64] рекомендуется также выбирать р = l(mod 12) (в случае
j = 0 достаточно р = 1 (mod 4)) и для реализации арифметики в поле
GF(pk) пользоваться следующей теоремой:
Теорема 3.4.4. Пусть /3 Е GF(p) не является ни квадратом, ни кубом {по-
следнее условие нужно только при j >0). Тогда полином Хк — /3 неприводим
над GF(p).
За доказательством отсылаем читателя к [12].
Для реализации умножения в поле GF(pk), где к = 2г37, в [64]
предлагается представить его в виде башни кубических и квадратных
расширений и на каждом этаже этой башни выполнять умножение, ис-
пользуя метод Карацубы для квадратичных расширений, который сводит
умножение в очередном этаже башни к трем умножениям в предшеству-
ющем этаже, а также метод Тоома для кубических расширений, который
сводит умножение в очередном этаже башни к пяти умножениям в пред-
шествующем этаже (а также к большому числу сложений и умножений
на элементы простого подполя GF{p)). При достаточно большом числе р
в сравнении с к сложность умножения может быть оценена асимптоти-
чески как У57 умножений в поле GF(p). Мы предоставляем читателю
самому восстановить детали этого алгоритма, взяв описание алгоритма
А. Л. Тоома из 2-го тома «Искусства программирования» Д. Кнута.
Впрочем, более простой для понимания алгоритм можно полу-
чить, если просто перемножать многочлены степени меньшей к над
полем GF(p) (используя для этого комбинацию методов Карацубы и То-
ома), а потом выполнить приведение по модулю неприводимого много-
члена Хк - {3, которое сводится к к - 1 вычитанию в поле GF(p) и к - 1
умножению на {3 в том же поле (заметим еще, что в качестве Д можно
выбрать довольно малое число, так как вероятность не быть ни кубом
ни квадратом в этом поле приблизительно равна одной третьей, а умно-
жать на малые числа проще, чем на большие).
154
Глава 3. Криптосистемы на основе спариваний
3.5.	Кривые над полями характеристики три
Идея использовать поля характеристики три, как уже отмечалось,
была предложена в [22]. Конкретно, там рассматривались кривая
E3fi : Y2 = X3 - X + Ь, &е{-1,1}
над полем GF(3m) при нечетном т. В частности, предлагалось исполь-
зовать т = 97.
Правило сложения точек для этой кривой можно представить в сле-
дующем виде.
Если Pi = (xi,yi), Pt =4 -Р2, Р3 = Pt+P2 = (х3,у3), то А = 1/^
при Xi = х2, и А = (у2 - yi)/(x2 - Xi) при Ж] х2, и х3 = А2 - (х\ + х2),
Уз = У1 + Уз - А3.
Упражнение 3.5.1. Докажите это правило.
Указание. 2 = -1 по модулю 3.
В работе [22] сделано интересное наблюдение, что утроение точки
на кривой можно выполнить столь же быстро, как и удвоение
точки на суперсингулярных кривых над полями четной характеристики.
А именно, если Р = (ж, у), и ЗР = (ж', у'), то х' = (ж3)3 - Ь, у' = -Q/3)3.
Упражнение 3.5.2. Докажите это правило.
Это правило позволяет утраивать точки кривой Ез^ над полем
GF(3m) со сложностью О(т), так как возведение в куб при использовании
стандартного базиса с неприводимым многочленом малого веса над по-
лем GF(3) выполняется, очевидно, со сложностью О(т), поскольку воз-
ведение в куб троичного многочлена согласно тождеству Фробениуса мож-
но выполнить со сложностью О(т), а приведение по модулю многочлена
малого веса выполнятся со сложностью О(т) аналогично случаю характе-
ристики два. В нормальных же базисах возведение в куб и вовсе бесплатно.
Правда, умножение в них не так легко, но для него тоже можно применить
оптимальные нормальные базисы, подобно случаю характеристики два.
Благодаря отмеченному факту, для ускорения скалярного умножения
точек на кривой Ез,ъ лучше использовать не бинарный, а тернарный метод,
использующий разложение скалярного множителя п в троичной системе,
причем удобно применять, как и в двоичном случае, уравновешенную
троичную систему, в которой используются в качестве цифр нули и плюс-
минус единицы.
Другой подход к ускорению скалярного умножения для этой кри-
вой был указан в [63]. Он основан на использовании проективных
координат со следующим правилом сложения точек в смешанных ко-
ординатах (данным в [22]): если Pi = (Xi,YbZi), Р^ = (X^Y^i),
то Р3 = Р] ч- Р2 = (Хз, Уз, Z3) можно вычислить следующим образом
3.5. Кривые над полями характеристики три
155
за 9 умножений:
A = X2Z\—X\, B = Y2Zy-Y\, С = А3, D = С - ZXB2,
Х3 =Х\С- AD, Y3 = BD -У|С, Z3 = ZXC.
Упражнение 3.5.3. Докажите это правило.
Указание. Оно содержит 9 умножений потому, что возведение в куб делается
со сложностью почти такой же, как и сложение в этом поле.
Как и двоичном случае, переход к обычным координатам выполня-
ется в конце вычислений по формуле Р — (X/Z, Y/Z) — (жз, ?/з), поэтому
указанный метод требует только две операции деления в самом конце
вычислений. Заметим, что утроение точки Р — (X, Y, Z) в смешанных
координатах можно выполнить по формуле
Z = (z3)3, X = (т3)3 - bZ, Y = - (у3)3.
Действительно, переходя к обычным координатам, имеем известные фор-
мулы утроения
3\ 3
Поэтому использование проективных координат можно совместить с ис-
пользованием уравновешенной троичной системы.
3.5.1.	Устранение делений
В алгоритме Миллера, примененном к вычислению спаривания Тейта
en : E(GF(q))[n] х £(GF(/))[n] -* GF(qky,
для суперсингулярных кривых Eij, i — 1, 2, 3, где к — соответствующий п
множитель безопасности, можно устранить деления, как было показано
в [22] и [39]. Обоснование этого основано на следующих утверждениях.
Упражнение 3.5.4. Докажите для каждой из кривых ЕгЬ что q - 1 делит (qk - 1)/п.
Указание. Пусть N — порядок кривой. Очевидно, п делит N. Выше (упр. 3.4.4,
3.4.6) для всех этих кривых было показано, что N делит число qk?2 4- 1. Поэтому
и п его делит. Значит - 1 делит (qk - 1)/п.
Упражнение 3.5.5. Докажите для каждой из кривых Ег,ь, i = 1, 2, 3 и произволь-
ной рациональной функции f над этой кривой над полем GF(qkl2) и любого
дивизора Q над тем же полем такого, что div (/) и Q имеют непересекаюшиеся
в конечных точках носители, справедливо, что /(Q)^ ~l^n — 1.
Указание. Очевидно, f(Q) € GF(qkl2y, поэтому /(Q)9^2-1 = 1. Согласно упр. 3.5.4
qk/2 - 1 делит (qk - 1)/п. Значит, /(Q)(^-1)/n = 1.
Упражнение 3.5.6. Докажите для каждой из кривых Eiyb, i = 1, 2, 3, что en(P, Q) =
fp(Q)^k-^/n npnQ^O.
Указание. Используя теорему 3.2.1, можно выбрать рациональную функцию U,
для которой порядок в точке О равен единице, а точка Р не является ни нулем,
156
Глава 3. Криптосистемы на основе спариваний
ни полюсом. Тогда дивизоры Q — (С?) + div (U) и Q - (О) эквиваленты и носитель
Q - (О) + div (£7) не содержит точки Р и О. Поэтому fp(Q - (О) + div (U))
корректно определено и fp(Q- (О) + div (U)yqk~l^n — fp(Qyqk~[^n.
Из этих упражнений следует, что при умножении fp(Q) на любой
множитель из GF(q)* функция /p(Q)^"1^" не меняется. Поэтому далее
мы будем опускать постоянные множители (для спаривания Вейля такое
свойство не имеет места).
Покажем теперь, что при вычислении спаривания Тейта en(P, V’(Q))
с искажающим отображением для указанных кривых с помощью би-
нарного или тернарного вариантов алгоритма Миллера все знаменатели
вида gu^iQY) (и соответственно операции деления) можно опустить. При
этом алгоритмы принимают следующий вид.
Бинарный алгоритм Миллера
Число п записывается в двоичном виде как
t
n = ^/qi2t, bj G {0,1}, qt^0.
i=0
Далее, S ~ ^(Q).
На шаге инициализации полагаем f = Z — P.
Далее в цикле с убывающим параметром j от t - 1 до 0 с единичным
шагом повторяем:
f — f29z,z(S); Z = 2Z (шаг удвоения);
если ; = 1, то
f = fi(S)fgz,P(S)-, Z := Z + P
Возвращаемое значение равно fn(S).
Разумеется, такие же изменения можно внести и в другие варианты
бинарного алгоритма.
Тернарный алгоритм Миллера
Число п записывается в троичном виде как
t
п = 52 ft3!, ь, е {0,1,2}, 9(/о.
г=0
На шаге инициализации полагаем f — Z — Р; если qt = 2 то
выполняем присваивания
f = f2gp,p(S); U = Z = 2P.
Далее в цикле с убывающим параметром j от t - 1 до 0 с единичным
шагом повторяем:
f = f39z,Z(S)92Z,Z(S)-, Z = 3Z-,
3.5. Кривые над полями характеристики три
157
если q3; = 1, то
f = fi(S)fgz,P(Sy, Z:=Z + P',
если qj = 2, то
f = f2fgz,2p(sy, z-.= z + u
Возвращаемое значение равно
Для обоснования возможности удаления gui^KQ)) достаточно про-
верить, что gu(tf(Q))(qk~]^n — 1- Так точки U являются всегда кратными
точки Р с координатами из GF(q), то они тоже имеют координаты
из GF(q), поэтому gu(X, Y) = X 4- с, с 6 GF{q). Рассмотрим теперь три
случая, соответствующие трем кривым Eifb.
Случай г = 1, т. е. q = р > 3. Тогда gu^tQ)) = -х - с, х, с Е GF(p),
так как при Q = (х,у) V’(Q) = (~хЛу), 2'2 = -1. Тогда gu(^(Q))p —
-хр - ср = -х - с = ди(*Ф(С})) согласно тождеству Фробениуса, откуда
ди(зК<2))р~{ = 1- Так как (qk - 1)/N = (р2 - l)/N = р - 1, п делит
порядок кривой N = р + 1, то (qk - 1)/п делится на р - 1, значит
9uW.Q))(qt~i)/n = 1-
Случай i = 2, т. е. q — 2m, m нечетно. Тогда gu(rf(Q)) = х + s2 + с,
х,сЕ GF(q), s 6 GF(q4), так как при Q = (х, у)
= (х + s2, у + sx 4- f), s4 = s, t2 4-1 = s6 4- s2,	s, t e GF(q4).
Индукцией no t легко проверяется, что s4< = s, значит sq2 = s22m = s,
откуда (s2)q = s2. Поэтому в силу тождества Фробениуса
9u(^(Q))q = xq2 + (s2)q +cq2 = x + s2 + c = guMQ)),
так как в силу малой теоремы Ферма xq — х, xq2 = xq — х, cq — с,
cq2 = cq = с. Значит, gu^(Q))q2~] = 1- Так как (qk - 1)/7V = (q4 - 1)/2V =
(q+1 ±	- i), n делит порядок кривой N = q 4- 1 qp y/2q, to
(qk ~ l)/n Делится на q2 - 1, значит	= 1-
Случай i = 3, т. e. q = 3W, m нечетно. Тогда	~ x - c,
x, c € GF(q), rl = rb + b, rb E GF(q6), так как при Q = (ж, у)
^(Q) = (~х + rb, iy), г2 = — 1, г C GF(q6).
Индукцией no t покажем, что = rb + (t mod 3)6. База (t = 1) очевидна.
Шаг индукции обосновывается равенством
rb +1 = (гГ)3 = (rb + (t mod З)03 = rl + (t mod 3)3b3 =
= rl 4- (t mod 3)3b = rl + (t mod 3)& =
= rb 4- b 4- (t mod 3)b = rb 4- (t 4- 1 mod 3)b,
158
Глава 3. Криптосистемы на основе спариваний
в проверке которого надо учитывать тождество Фробениуса для харак-
теристики три и малую теорему Ферма для поля GF(3). Аналогично
проверяется, что xqt = х, cqt = с. Поэтому
gut'iKQ))^ = rf -xq3 -cq3 =rb-x-c = gut'iKQ)),
так как rq = rfm = rb 4- (3mmod3)& = rb. Отсюда gu('&(Q))qi~1 = 1,
а так как (qk - 1)/N = (q6 - 1)/N = (q4- 1 ± \/3q)(q + 1)(<73 - 1), n делит
порядок кривой N — q 4- 1 =p y/lq, to (qk - l)/n делится на q2 - 1, значит
guWQ)){qk-1)/n = ^
Заключительное экспоненцирование. Дополнительные возможности уско-
рить вычисление спаривания Тейта дает заключительная операция возве-
дения в степень (qk - 1)/п. Вместо прямолинейного применения любого
метода, основанного на построении аддитивных цепочек, можно при-
менить следующий более быстрый алгоритм, учитывающий специфику
используемых кривых. Каждый из трех случаев рассматриваем отдельно.
Случай i = 1, т. е. q — р > 3. Вспомним, что в этом случае
р = 2(mod 3) и р = 3(mod 4) и порядок кривой N = р 4- 1 делится на п.
Используемое в вычислениях поле GF(p2) представляется как поле, состо-
ящее из элементов u+iv, u,v Е GF(p), i2 = -1 (аналог поля комплексных
чисел). Экспонента Тейта равна z = (р2 - 1)/п = (р- 1)((р+ 1)/тг), поэто-
му для вычисления s = wz вначале вычисляем t =	= u + iv, тогда
в силу тождества Фробениуса, равенства р = 3(mod 4) и малой теоремы
Ферма имеем
tp (u + iv)p (up-ivp) (u-iv)
~~ ~ t ~
i2uv
u2 + v2'
s = wz требует только 0(1)
операций в поле GF(p).
Случай г = 2, т. е. q = 2m, тп нечетно. Тогда, как уже проверялось,
N = q 4- 1 =р л/lq, и экспонента Тейта равна z = (qk - l)/n = (q4 - l)/n =
(q 4- 1 ± \/2q)(q2 — l)N/n, поэтому для вычисления s = wz вначале
вычисляем u = wN^n, t = uq • u • а потом s = tql/t. Так как N/n
мало, то вычисление и требует только 0(1) умножений в поле OF(g4).
Остальные возведения в степени есть возведения в степени вида 21,
и в нормальном базисе в поле четной характеристики они делаются
почти бесплатно, в стандартном базисе с трехчленным или пятичленным
минимальным базисным многочленом сложность всех этих операций
равна 0(т2), и даже меньше [3].
t t	t
u - iv (u — iv)2 u2 - v2
u 4- iv u2 4- v2 u2 4- v2
Так как N/n = (p+\)/n мало, то вычисление
3.5. Кривые над полями характеристики три
159
Кроме операций возведения в степень, нужно еще два умножения
и одно деление в поле GF(q4). Эти операции также выполняются со слож-
ностью О(т2) и асимптотически даже меньше.
Случай i = 3, т. е. q = 3m, т нечетно. Тогда, как уже проверялось,
N — q + 1	и экспонента Тейта равна {qk - 1)/N — (q6 - l)/N =
(q+l± 0?)(<7 + 1)(<73 “ 1 поэтому для вычисления s — wz вначале
вычисляем u = wN^n, t = uq • u • и±у^, а потом h = tqi/t, s = hq - h. Так
как N/n мало, то вычисление и требует только 0(1) умножений в по-
ле GF(qe). Остальные возведения в степени есть возведения в степени
вида З1, и в нормальном базисе поля характеристики три они делаются
почти бесплатно, в стандартном базисе с трехчленным минимальным ба-
зисным многочленом сложность всех этих операций равна 0(т2). Кроме
операций возведения в степень, нужно еще три умножения и одно деление
в поле GF(qe). Эти операции также выполняются со сложностью 0(т2)
и асимптотически даже меньше (об организации арифметики в полях
характеристики три будет сказано далее).
Устранение делений в случае использования MNT-кривых. Эти кривые удоб-
но использовать в вариантах основанных на спаривании криптосистем,
которые не используют искажающих отображений, например [31], [44].
В таких системах спаривание имеет вид еп(Р, Q), Р 6 E(GF(q)), Q 6
E(GF(qk)), где en(P, Q) / 1. В MNT-критерии, как уже отмечалось,
порядок кривой N делит Ф&(#), но не делит (qk — 1)/Фд;(^), где Фд_.
есть k-и круговой полином. Благодаря этому свойству справедливы
аналоги упр. 3.5.4 и 3.5.5. Поэтому и описанная выше детерминист-
ская версия алгоритма Миллера тоже работает в случае MNT-кривых.
В случае четного к часто можно подобрать точку Q = (ж, у) так,
чтобы х € GF(c[kl2),y £ GF(qk/2). Тогда gu(Q) = ж + с е GF(qk/2),
так как с 6 GF(q). Поэтому gu(Q)qk/ = gu(Q), gu(Q)qk 2~} = L зна-
чит gu(Q)(q = 1, потому что qk^2 - 1 делит (qk — l)/n, так как
(^/2	1)
делится на п. Действительно, п делит N и, следовательно,
делит Ф&(<?), а так как N не делит (qk - 1)/Ф^(^), то простое п не делит
(qk ~ 0/(<?) и поэтому не делит qk^2 -1, следовательно оно должно делить
(дЛ72 + 1). Таким образом, для таких MNT-кривых тоже можно устранить
деление. Покажем, как можно выбрать точку Q = (ж, у) так, чтобы
х е GF{qk/2),y GF(qk!2). Для этого выберем неприводимый трехчлен
вида /(X) = Хк +Х2 -he, сЕ GF(q). Тогда трехчлен g(X) = Хк/2 + Х + с
тоже неприводим, иначе f(X) = д(Х2) был бы приводимым. Представим
поле GF(qk) как кольцо многочленов с операциями по модулю f(X).
Очевидно, что его подмножество, состоящее из многочленов с четны-
ми степенями, будет замкнуто относительно операций по модулю f(X)
и поэтому образует подполе, изоморфное GF(qkf2). Легко проверить,
что изоморфизм осуществляется заменой каждого одночлена вида сцХ21
160
Глава 3. Криптосистемы на основе спариваний
на одночлен аг-Хг. Можно показать, что точку Q = (х, у) можно выбрать
с х, состоящим только из четных степеней, т. е. х Е GF(qk^2) и у, состо-
ящим только из нечетных степеней, следовательно у GF(qkP).
3.6.	О больших значениях параметра безопасности
Оптимизации алгоритмов вычисления спаривания Тейта посвящено
много работ. Выше были изложены результаты некоторых из них, в кото-
рых рассматривались специальные частные случаи, в которых возможно
ускорение стандартного алгоритма Миллера. Здесь, следуя [57], будет
кратко рассмотрен общий случай для характеристики р > 3.
Пусть кривая Е: Y2 = Х3+аХ+Ь. Вспомним, что модифицированное
спаривание Тейта вычисляется по следующей формуле
\ jp(b) J
где q — порядок поля, над которым рассматривается кривая, к —
параметр безопасности, точки Р Е E(GF(q)), Q, S Е JE(GF(qk)), причем
пР = О, рациональная функция fp над кривой E(GF(qkf) с дивизором
div(/p) = П(Р) ~ п(О), а точка S выбирается произвольным случайным
образом так, чтобы Q + S, S не содержались в носителе дивизора div (fp).
Выше приводился алгоритм Миллера для вычисления fp. Приведем его
в виде, удобном для вычисления (fp(Q + S)/fp(Sf).
Вариант алгоритма Миллера
Число п записывается в двоичном виде как
t
г=0
bi € {0, 1}, qt 0.
На вход алгоритма подается n, Q, S Е E(GF(qk)).
На шаге инициализации полагаем f = 1; R = Р.
Далее в цикле с убывающим параметром j от t - 1 до 0 с единичным
шагом повторяем:
.	-29r,r(Q + s)92r(S) D nD /	\
f = f -—R = 2R (шаг удвоения);
9r,r(S)92r(Q + S)
если bj = 1, to
Д:=л+Р
9r,p(S)9r+p(Q + S)
Возвращаемое значение равно f.
3.6. О больших значениях параметра безопасности
161
По сравнению с раздельным вычислением fp(Q 4- 5), fp(S) в этом
алгоритме экономятся операции /2 и	Но если его выполнять пря-
молинейно, потребуется много дорогостоящих операций деления. Однако
их можно исключить, оставив лишь одно деление в конце алгоритма,
если представлять на каждом шаге функцию f в виде дроби, и каждую
из операций выполнять отдельно для числителя, отдельно для знаме-
нателя. Тогда работа алгоритма будет заключаться в последовательном
выполнении следующих операций.
Сложение точек и вычисление секущей
Для точек Р = (ж1,^/1), R — (^2,2/2), их сумма R + Р = (хз,Уз)
вычисляется следующим образом:
х У1~У1	\2	х/ х
Л =--------, х3 = А - Ж1 - х2, уз = Л(ж2 - х3) - у2.
Х\ — х2
Секущая и: д^р(Х,У) равна
и = (Y - у2) - Х(Хх - х2) = (Y - уО - А(Х - х{).
Удвоение точки и вычисление касательной
Для точки R = (х2,у2) удвоенная точка 2R = (х3,у3) вычисляется
следующим образом:
Зж| + а 2
А = —------, х3 = А - 2ж2, у3 = А(ж2 - х3) - у2.
Касательная и: д^я(Х, У) равна и = (У — j/з) — Х(Х - х?).
Вычисление вертикали
Для точки R = (х3, у3) вертикаль v\ дя(Х, X) равна v = X - х3.
Вычисление квадрата числителя
Ni = Nl_}Ui, г > 1, N0=l.
Вычисление квадрата знаменателя
Di = Di_iVi, i >1, Dq = 1.
Для оптимизации вычисления последовательности точек Z, сле-
дуя [36], используются якобиевые координаты (X,Y,Z), связанные с де-
картовыми координатами равенствами х = Х/Z2, у — Y/Z\
162
Глава 3. Криптосистемы на основе спариваний
3.6.1.	Скалярное умножение точек кривой
над полем большой характеристики
В якобиевых координатах кривая Е: Y2 — X3 + aX + b представляется
в виде Ej\ Y2 — X3 + aXZ4 4- bZ6, в котором любые две точки (X, У, Z)
и (А2Х, А3У, AZ), А^О, считаются равными. Точка (1,1,0) отождеств-
ляется с точкой О. Тогда операции удвоения и сложения точек в этих
координатах могут быть выполнены без операции деления следующим
образом.
Сложение в смешанных координатах
ВХОД: Р{ = (Х1г Yi, Zi), Р2 = (Х2, Y2, 1), Р, / ±Р2.
ВЫХОД: Р3 = Р\ + Р2 = (Х3, У3, Z3).
Вычисление суммы точек:
Ai = X2Zi- X2 = Y2zl, А3 = Al -Xi, А4 = А2-Уь
Х3 = -Х33-2ХхХ} + Х}- У3 = -У1А3 + А4(Х!А3-Х3); Z3 = ZiX}.
Вычисление секущей и вертикали:
<Д>|Л = Z3(y - Y2) - А4(Х - Х2), дРз = zlx - Х3.
В операции сложения точек используется 8 умножений и 3 операции
возведения в квадрат.
Удвоение
ВХОД: Р = (Хх, Yi,Zi}£(\, 1,0.).
ВЫХОД: 2Р = (Х3, У3, Z3).
Вычисление удвоения точки:
Ai = ЗХ2 + А2 = 4Х1У,2; Х4 = А2 - 2А2;
У4 = А1(А2-Х4)-8У14; Z4 = 2У,Х1.
Вычисление касательной и вертикали:
дрР = (Z3zly - 2У2) - Ai(Z2X - X,), д2Р = Z23X - Х3.
В операции удвоения используется 4 умножения и 6 операций возведения
в квадрат, причем одна из операций умножения есть умножение на кон-
станту а, поэтому при малых а она сводится к нескольким операциям
сложения и поэтому ее сложностью можно пренебречь. Все операции,
напомним, проводятся в поле GF(q). Отметим, что в отличие от полей
характеристики два операция возведения в квадрат лишь ненамного про-
ще общей операции умножения (примерно восемьдесят процентов от ее
сложности).
Упражнение 3.6.1. Проверьте сформулированные выше утверждения.
3.6. О больших значениях параметра безопасности 163
3.6.2.	Ускорение алгоритма Миллера для больших к
В работе [57] отмечено, что сложность описанных выше операций
уменьшится, если применить следующий прием Чудновских: добавить
к тройке координат (X, Y, Z) еще четвертую (зависимую от них) коорди-
нату Z2. Тогда сложность удвоения и сложения точек не изменится, так
как дополнительная операция возведения в квадрат для вычисления Zj
компенсируется тем, что мы имеем уже данный элемент Zj. Но при
вычислении коэффициентов секущей (касательной) и вертикали одна
операция возведения в квадрат экономится, так как мы уже имеем Z2 как
координату.
В [57] предложен также еще один прием, названный прямым вы-
числением. Он заключается в том, чтобы не вычислять по отдельности
на каждом шаге значения gP.P.(Q 4- 5), <?2Pt(£), <?/>•,р{ (5% 92pSQ + £)
(или значения gPi,P\Q + S), gPi+P](S), gPi^(S), gPt+Pl(Q + S)), а сра-
зу вычислить нужные в дальнейшем произведения gPi,Pi(Q 4- S'^p/S')
и «^рДЗ^рДФ + S). Если обозначить коэффициенты линейных функ-
ций gPi,Pi(X, Y), g2Pi(X, Y) через a, b, c,d,e, то, очевидно,
9Pi,Pi(Q 4- S') = qxq^s 4- byQ+s 4- c, <?2Pt(£) = dxs + e,
9Pi,pt(S) = cbxs + bys + c, g2Pi(Q + S) = dxQ+s + e,
откуда имеем
9p^pXQ + S)g2Pi(S) = (axQ+s + byQPS + c)(dxs 4- e) =
= ad(xQPsXs) 4- bd(yQ+sxs) 4-
4-	aexQPs 4- beyQPs 4- cdxq+s 4- ce,
9PiJ\(S)g2PSQ + S') = {axs + bys 4- c)(dxQ+s + e) =
= ad(xQ+sXs) + bd(ysXQ+s) +
+ aexs 4- beys 4- cdxQPS 4- ce.
Поэтому вычисление указанных произведений можно выполнить, сделав 6
умножений в поле GF(q) для вычисления коэффициентов и 9 умножений
коэффициентов из поля GF(q) на элемент поля GF(qk), что в итоге
по сложности равносильно 8& + 6 умножениям в поле GF(q) (сложностью
сложений пренебрегаем). После того как оба произведения вычислены,
остается сделать два умножения в поле GF{qk) для вычисления очередного
значения
При удачном выборе простого числа п большая часть операций
в алгоритме Миллера будут операциями удвоения, и многие из них
будут встречаться несколько раз подряд. Для вычисления итерированного
удвоения 2WP в якобиевых координатах в [51] предложен следующий
алгоритм, более быстрый, чем повторное удвоение.
164
Глава 3. Криптосистемы на основе спариваний
3.6.3.	Итерированное удвоение в якобиевых координатах
Пусть Pi = 2'Р = (Xi, Yi, Zi),i = 0,..., w.
ВХОД: P = (Xo, Yo, Zo), VP £ О, i = 0,... ,w - 1.
ВЫХОД: Pw = VP = (Xw, Yw, Zw).
W0 = aZ^; Mo = 3X(j + Wo, So = 4X0Y02; Xl=M02-2S0;
Y, = M0(S0 - Xi) - 8K04; Zi = 2Y0Z0.
для i = 1,... ,w - 1 {Ж,-= 2(8У/_]); Mi = 3X2 + Wi, S(s=4X,Y2;
Xi+i = M2 - 2Si- Yi+i=Mi(Si-Xl+i)-^- Zi+{ =2YiZi}.
Упражнение 3.6.2. Докажите правильность указанного алгоритма и проверьте, что
он содержит 4w умножений и 4w + 2 операций возведения в квадрат.
Указание. Докажите по индукции, что Wi = aZf и заметьте, что Y* в вычислениях
можно использовать дважды.
Чтобы дополнить этот алгоритм до подпрограммы вычисления ите-
рированного удвоения в алгоритме Миллера, надо еще вычислить коэф-
фициенты линейных многочленов
gPi.P.(X,Y) = (ZiZ2_iY - 2Y2_t) - Mi-i^X - Х^),
gPi(X,Y) = Z2X - Xi, i = 1,... ,w - 1.
Упражнение 3.6.3. Докажите правильность указанного алгоритма и проверьте, что
он требует три умножения и одно возведение в квадрат.
Указание. уже было найдено при вычислении коэффициентов дР. {.
3.6.4.	Комбинирование с другими методами
В [45] было предложено выбирать случайную точку S в E(GF(q)),
а не в E(GF(qk)).
Выбор S € E(GF(q)). Его надо осуществлять так, чтобы точки
±5, ±(Q + S) не совпадали с точками, кратными Р, принадлежащими
аддитивной цепочке, строящейся в процессе работы алгоритма вычисле-
ния fP(Q + S)/fP(S)).
Действительно, при выполнении алгоритма необходимо, чтобы зна-
менатели дробей
9r,p(Q + S)gR+p(S)
9r,p(S)9r+p(Q + S)
были отличны от нуля. А так как секущая (касательная) u : gRp(X,Y)
проходит через точки R,P, и вертикаль v : gR+p(X, Y) проходит через
точку R 4- Р, то для того, чтобы точки S, Q + S не были нулями функций
и, v нужно, чтобы точки 5, Q + S не совпадали с точками R, Р, -(R + Р)
(потому что, кроме точек R,P на секущей и : gR,p(X, Y) лежит еще
только одна точка кривой, а именно -(R + Р)) и не совпадали с точ-
кой R + Р (потому что на вертикали v : gR^P(X, У) лежат только две
3.6. О больших значениях параметра безопасности
165
точки кривой, а именно ±(7? 4- Р)). Количество точек в порождаемой
алгоритмом аддитивной цепочке по порядку равно log п = О (к log q), по-
этому вероятность совпадения точек ±5,	4- 5) с данными О(к log q)
точками кривой E(GF(qkY) при случайном выборе S из q(\ +о(1)) то-
чек кривой E(GF(q)) равна приблизительно <?(& log <?)/(? и поэтому при
больших q и ограниченных к пренебрежимо мала. Поэтому уже после
одной попытки с высокой вероятностью такую точку S можно найти.
Проверку выполнения указанных условий можно совместить непосред-
ственно с вычислением. В случае его провала просто делаем еще одну
попытку. Заметим, что то же самое справедливо и при выборе S на кривой
E(GF(qk), только в этом случае вероятность провала меньше.
При указанном выборе S вычисление gR^p(S) и gR,p(S) проводится
в поле GF(q) и требует только три умножения (так как коэффициенты
этих функций уже вычислены). Поэтому вместо указанного выше приема,
названного прямым вычислением, можно вычислять на каждом шаге
алгоритма отдельно числители и знаменатели по формулам
М = Ni_{gRj>(Q 4- S)^+p(S);
Dt = Di-igRj>(S)gR+p(Q 4- 5),
в которых используются только два умножения в поле GF(qk) и два
умножения элементов подпол я GF(q) на элементы поля GF(qk) (что эк-
вивалентно по сложности 2к умножениям в поле GF(q)), не считая
операций, используемых при вычислении gRj>(Q 4- 5), gR+p(Q 4- S).
Упражнение 3.6.4. Проверьте, что указанный метод имеет меньшую сложность,
чем метод прямого вычисления. Проверьте, что он также уменьшает сложность
итерированного удвоения.
Еще некоторого дополнительного ускорения можно добиться в сле-
дующем случае.
Случай, когда q - 1 не кратно п
В этом случае, как отмечалось выше, q - 1 делит (qk — 1)/п, потому
что п — простое число, поэтому ~x^n = 1 при a € GF(q)*. Следова-
тельно, при выборе S Е E(GF(q)) имеем
gR+P(sf-^n = l=gRAsf-')/n,
поэтому после заключительного возведения в степень (qk - 1)/п при
вычислении спаривания Тейта сомножители gR+p(S), gR,p(S) не будут
оказывать влияния на значение en(P, Q), поэтому их можно просто
не вычислять, заменив их формально на единицу. Это еще несколько
уменьшает сложность его вычисления.
Еще дополнительного ускорения можно достичь в случае суперсин-
гулярных кривых.
166
Глава 3. Криптосистемы на основе спариваний
Приложение к суперсингулярным кривым
Рассмотрим случай кривой Е : У2 — X3 4- аХ над полем GF(p),
р = 3(mod4). Вспомним, что тогда к = 2 и искажающее отображение
Ф : (ж, у) (-ж, iy), х е GF(p), iy Е GF(p2), i2 = -1.
Условие, что п не делит р- 1, уже проверялось выше. Вместо en(P, Q) вы-
числяем еп(Р, Ф(ф)). Можно выбрать Q = (ж, у) так, чтобы х,у Е GF(p),
например Q = Р. Тогда Ф(ф) Р, еп(Р, Ф(ф)) 7^ 1 и обе координаты Q + S
тоже принадлежит GF(p). Поэтому ж-координата Ф(<? 4- S) принадле-
жит GF(p) и, следовательно, ^р+р(Ф(<2 4- S)) Е GF(p). Значит, благодаря
равенству gP+R(&(Q -h S))^ ~^n = 1, значение gP+R($(Q + S)) можно
не вычислять, формально заменив на единицу, так как оно не влияет
на значение
Далее, ^р,,р.(Ф((2 + S)) = ly$(Q+s) + h, l,h Е GF(p), так как все ко-
эффициенты рассматриваемых линейных функций принадлежат GF(p),
и ж-координата Ф(ф 4- S) тоже. Поэтому вычисление gPi,Pj(&(Q 4- S))
требует 2 умножения в поле GF(p).
Умножение в поле GF(p2) методом Карацубы сводится к трем умно-
жениям в поле GF(p)\
(а 4- Ы)(с 4- di) = (ас — bd) 4- i(ad 4- be) =
= (ас - bd) 4- i((a 4- b)(c 4- d) - ac- bd).
Очевидно, что возведение в квадрат в поле GF(p2) требует только двух
умножений в поле GF(p) \
(а 4- Ы)2 = а2 — Ь2 4- 2abi = (а - Ь)(а 4- Ь) 4- 2abi.
Для заключительного возведения в степень (р2 - 1)/п можно восполь-
зоваться приемами, описанными в разд. 3.5.1, и описанный здесь метод
можно применять вместо метода из раздела 3.5.1.
3.6.5.	Использование аддитивных цепочек с двойной базой
В [38] предложено для вычисления скалярного умножения точки
кривой на число использовать аддитивные 2-3-цепочки. Так называет-
ся последовательность натуральных чисел Ку, Kn+\ = 2u3vKn 4-
Е {-!,}• Если k = Кт, то т называется длиной такой цепочки,
и тогда
т
fc =
i=\
где последовательности bi, ti нестрого убывают до нуля.
3.6. О больших значениях параметра безопасности
167
Известна теорема [96], из которой следует, что для некоторой кон-
станты С между пип- n/(log2 п)с можно найти число вида 2a3b. Для
построения короткой 2-3-цепочки можно применить очевидный жадный
алгоритм: находим число вида 2а36 ближайшее к числу к, повторяем этот
шаг для числа \к - 2а3&| и т.д, пока не получим число в точности вида 2а3&.
Этот алгоритм очевидным образом модифицируется так, чтобы получить
цепочку, в которой все = 1.
Упражнение 3.6.5. Докажите, пользуясь теоремой [96], что длина кратчайшей 2-
3-цепочки для к равна O(log fc)/(log log к), если не требовать монотонности
последовательностей Ьг, ti.
Указанный жадный алгоритм легко модифицировать так, чтобы он
давал цепочку с монотонными последовательностями: на каждом шаге
надо требовать выполнение условия bi < fy-j, ti < ^_j. При этом, одна-
ко, не гарантируется оценка длины О (log к)/(log log к), но практически
алгоритм дает короткие цепочки.
Для вычисления кР рекуррентно вычисляем = 2Ui3ViPi + s^P,
щ = bi~bi+\, Vi — ti~ti+\. Это вычисление выполняется путем ^-кратно-
го утроения, потом -кратного удвоения точки Pi, а потом прибавления
точки ±Р. Иногда бывает удобно часть удвоений заменить на вдвое
меньшее число операций учетверения, если воспользоваться быстрыми
алгоритмами, указанными в [34,41], сложность которых указана в следу-
ющей таблице:
Операция	Простое поле	Бинарное поле
P + Q	l[i]+l[s]+2[m]	l[i]+l[s]+2[m]
2Р	l[i]+2[s]+2[m]	l[i]+l[s]+2[m]
2P + Q	1 [i]+2[s]+9[m]	1 [i]+2[s]+9[m]
ЗР	l[i]+4[s]+7[m]	l[i]+4[s]+7[m]
УР + Q	2[i]+4[s]+9[m]	2[i]+2[s]+9[m]
4Р	l[i]+9[s]+9[m]	l[i]+5[s]+8[m]
4P + Q	2[i]+4[s]+l l[m]	2[i]+6[s]+10[m]
В этой таблице указано число инвертирований [г], число возведений
в квадрат [s] и число умножений [т] для каждой из операций, выполня-
емых в аффинных координатах. Из нее видно, например, что учетверение
выгоднее двух удвоений, и утроение выгоднее удвоения и сложения, если
инвертирование существенно медленнее умножения.
Заметим, хотя это и не отмечается в [38], что особенно удобно
использование 2-3-цепочек для суперсингулярной кривой Е^ъ над полем
168
Глава 3. Криптосистемы на основе спариваний
характеристики три, хотя его превосходство над тернарным методом в этой
ситуации, видимо, незначительно.
Отметим еще, что можно модифицировать алгоритм Миллера для
вычисления спаривания на основе использования 2-3-цепочек, и его
особенно удобно будет применять для кривых над полем характеристики
три, при этом возникающая последовательность точек, кратных Р тоже
будет вычисляться с использованием 2-3-цепочек.
3.7.	Алгоритм Дуурсма—Ли
В работе [39] алгоритм из [22] был усовершенствован и перенесен
на гиперэллиптические кривые Сь 'Y2 = Хр - X + b, b = ±1, определен-
ные над полем F = GF(pn), где п и 2р взаимно просты и р = 3(mod4).
Эти кривые рассматриваются также над расширениями поля F, а именно
над F = GF(pPn) и К = GF(p2pn). Рассматриваемые кривые являются
прямыми обобщениями эллиптических кривых Е^. В [39] доказано сле-
дующее утверждение, обобщающее известный нам частный случай при
р = 3, которое мы приводим без доказательства.
Лемма 3.7.1. Для любой точки V = (а,0) кривой Съ(К) дивизор
является главным. Функция
hv —/Зр - (otp - X + bf+1)/2
имеет дивизор div (hy) = p(V) + (V') - (р + где
V' = (с/ +2Ь,/Зр2).
Пусть r±(F) — группа классов дивизоров нулевой степени кривой C±i(F).
Тогда
|Г+(К)|(Г-(Г)| =
В частности, порядок любой из этих групп нечетен и делит ррп 4- 1.
Из леммы следует, что дивизор V - (О) эквивалентен дивизору
-p(V - О). Если с целью краткости писать вместо V - О просто V,
то последнее утверждение записывается как V = -pV. Оно является
обобщением утверждения из упр. 3.5.2. Из него следует, что pV — -V =
(ар + 2b, -f5p ), так как дивизоры -(у -О) и ((-V) - О) эквивалентны,
потому что дивизор (V - О) + ((-V) - О) = V + (-V) - 20 = div (gv),
где gv — линейная функция х - X, отвечающая вертикальной прямой,
проходящей через точку V = (ж, у) (и -V = (х, -у)).
Таким же образом, как упр. 3.5.5, доказывается
3.7. Алгоритм Дуурсма—Ли
169
Лемма 3.7.2. Для каждой из кривых Сь(Р) и произвольной рациональной
функции f над этой кривой над полем F и любого дивизора Q над тем же
полем такого, что div (/) и Q имеют непересекающиеся в конечных точках
носители, справедливо, что
KQf-' = I.
Используя предыдущую лемму, подобно упр. 3.5.6, доказывается
Лемма 3.7.3. Для каждой из кривых Cb(F) и точки Р О
е„([Р - 0], [Q - 0]) = /p(Q)p"+1 е К*
для любой точки Q / Р, О, где div (fP) = (рРп 4- 1)(Р - О).
Роль п в обеих леммах играет рРп 4- 1. Отличие этой леммы от ис-
пользованного выше в алгоритме [22] утверждения в том, что вместо
div (Zp) = п(Р ~ О) используется div (/р) = (ррп + 1)(Р - О). Это позво-
ляет сразу уменьшить число итераций в алгоритме [22] при р = 3, так как
число п' = ррп 4- 1 имеет всего лишь 2 единицы в р-ичной записи. Чтобы
явно описать алгоритм, понадобится следующее определение.
Пусть р Е GF(pP) С F = GF(pPn) — корень многочлена Хр -X 4-26,
и пусть а Е GF(p2) С К = GF(p2pn) — корень многочлена X2 + 1. Как
известно, Хр - X + 2Ь неприводим над полем GF(p), поэтому все его
корни лежат в поле GF(pP), не могут лежать ни в одном его собственном
подполе. Существование элемента а в поле GP(p2) и отсутствие его
в поле GF(p) было показано в разделе об искажающих отображениях; так
как он вместе с под полем GF(p) порождает поле GF(p2), то он не может
принадлежать также полю F, не содержащему <7Р(р2). Определим иска-
жающее отображение
Ф : С(.Р)	С{К), Ф(Х, У) = (р - X, aY),
очевидным образом обобщающее рассматриваемое ранее при р — 3.
С помощью него определяем (как и в случае р = 3) билинейное невы-
рожденное отображение
С(К) X С(К) -+ К*, (Р, Q) ->
Действительно, в силу тождества Фробениуса и выбора р и а выполняются
тождества
(aY)2 = -Y2 = -Хр + х — b = (р - Х)р — (р - X) + Ь.
Простейшая форма алгоритма Дуурсма—Ли (Duursma—Lee) выглядит
следующим образом.
Алгоритм Дуурсма—Ли
Пусть даны точки Р Е C(F), Q Е F х К, а = ррп -h 1. Положим
div (Ду) = p(V) 4- (-рУ) - (р 4- 1)((9) (явная формула для функции hv
170
Глава 3. Криптосистемы на основе спариваний
была дана выше, как и определение для ±pV) и div (/n) = п(Р) - (пР) -
(п — 1)((9). Тогда значение fa(Q) вычисляется следующим образом.
Вначале инициализируем V = Р, a = 1.
Потом в цикле по г от 1 до рп выполняем подстановки
g = hv(Q); a = pa; V=pV; f = fpg.
В конце цикла получаем f = fa(Q).
Возведение в степень выполняется отдельно в самом конце алгоритма.
Для краткости далее используем обозначение вместо хр'.
Упражнение 3.7.1. Обоснуйте этот алгоритм и докажите, что
Ш) = IW1HQ))(₽re’i>-
i=l
Указание. Докажите по индукции равенство для дивизоров
-/n((9) = tfnQ) - (С?) + div(/a(Q)).
Далее этот алгоритм будет усовершенствован.
Упражнение 3.7.2. Проверьте, что
(±1/г) = ±1,	= х, х^ = хр,	= x{l+j}, (х ± у)^ — (ж^ ± у^).
Если х е GF(p), то ж(1) = х, а если х € GF(pm), то ж(г+т> = х^.
Указание. Примените тождество Фробениуса.
Упражнение 3.7.3. Докажите, что для V = (а, Д) 6 С(Р)
(а(й) + 2гЬ,(-)^<2,)).
Указание. Примените индукцию. База (г = 1) была доказана в лемме 3.7,1. Шаг
индукции:
pi+lV = ptfV) = p(a(2i) + 2г&, (-1)гД(2°) =
= ((a(2°)2 + (2гЬ)(2) 4- 2b, ((-)г)(2) (Д(2г))(2)) =
= (а(2г+2) + (2г6) + 2Ь, (-)гД(2г+2)) - (а(2г'+2) 4- (2г + 26), (-)1>(2,ч’2)).
Упражнение 3.7.4. Докажите, что (-1)>_1(/рп_» — a.
Указание. Так как р = 3(mod4), то pk = (-l)A:mod4 и	=
a(-1),+1 ? a = -{/(у.
Упражнение 3.7.5. Докажите, что р(;) = р - 2jb.
Указание. Примените индукцию. База (j = l) равносильна равенству рР — р-\-2Ь =
0. Шаг индукции:
р(>+» =	0) = (р _ 2Я(1) =pw_ (2>6) 0) =
= р - 2b - 2jb = р - 2{j + 1)6.
Первая из формул следующей теоремы содержится в [39].
3.7. Алгоритм Дуурсма—Ли	171
Теорема 3.7.1. Для Р — Q — е C(F)
/р(Ф((?)) = П (-/3(,Vn+1-<)<7 - (aw +?п+1-° -р+Ь)^2),
г=1
п
2=1
Доказательство. Из предыдущего алгоритма видно, что
/pW)) = ri(V>p(0(Q)))<pn_')-
2 = 1
Положим
р-1	р-1
а = П^-рМЗ)))^"’0- в« = n(w*(Ww‘lw-
;=0	>=0
тогда
/р(ф(<?)) = П = П(в«)(п-°-
2 = 1	2 = 1
Из упр. 3.7.3, 3.7.2 следует, что
pi+nj-lp = ^a(2i-2+2jn) + 2(. + jn _ 1)&J (_1)i+„J-l/3(2i-2+2;n)-) =
= (a(2i~2) 4- 2(i + jn - l)b,
Так как
Ф(<Э) = (х - р, ay), hv(Q) = (yr)(1) - ((Жу)(1) - х + 6)(p+l)/2,
то отсюда с помощью упр. 3.7.2 имеем
hp.+ni-ip(</>(Q)) =	-
— (а(2’-1) + 2(г + jn — 1)6 — (р — х) + &)^+1^2.
Еще раз применяя упр. 3.7.2, получаем, что
р-1
А =	=
j=0
р-1
= П((-1)<+п>-1^-|)(<72/)((р-2)п-‘) - Aj),
Aitj =	+ 2(г + jn - 1)6 -	+ 6)<?+
172
Глава 3. Криптосистемы на основе спариваний
и, применяя упр. 3.7.5, 3.7.4, 3.7.2, имеем
Р-1
Л, =	+ 2(г + jn - l)b -
j=o
-{р- 2((р - j)n - г)Ь - ж(п-1>) + б)^4"1^2)
= (^‘’)2/(п-Оа - (а(<-1) - р - а/”-0) - Ъ)^12/ =
= fi^y(n+'-i}ap - (а(,) - р(1) -	- б)^1’72 =
=	- (aw - р - а:<п+1-^) + b)(p+v,l\
так как <тр = —а, р^ + Ъ = р — Ъ. Аналогично,
р-1
Bi = n(V+--pW(?)))((P’^1)n) =
J=o
р-1
= n«-1)i+n>“1^2,'“1)(^)<(p“J'’1)n) - ВгД,
j=0
Biyj = (a(2i-» + 2(i + jn - 1)6 -	+ b^+'»\
откуда
p-i
Bi = П((-1)‘"п/3<й’1)у<т- (a(2<-1) +2(i + jn- 1)6-
- (p((p-j-1M-x) + 6)(p+l)/2)
p-1
= n((-1),-n^-1)2/a-BtJ),
Bij = (с/2г-1) + 2(г + jn - l)b -(p- 2(p - j - l)nb - x) + &)^+l)/2,
следовательно
Bi = ((-1)г'-п/3(й“ V - (a(2,'_,) + (2(i - n) - 1)6 - p + a:)(^’+1)/2),’
=	- (a(2!) + (2(i - n) - 1)6 - p(1’ + x^+"12
= (-l)^2*^0^ - (o<2° + (2(i - n) + 1)6 - p + ж0*)^072.
Отсюда следует последнее равенство теоремы.	
Заметим, что из теоремы вытекает симметричность модифицирован-
ного спаривания Тейта: /р(Ф(ф)) = /^(Ф(Р)).
Из доказанной теоремы следует, что указанный выше алгоритм
Дуурсма—Ли можно ускорить двумя способами (последний из которых
при р = 3 был указан в [65]).
3.7. Алгоритм Дуурсма—Ли
173
Ускоренный алгоритм Дуурсма—Ли
Пусть даны точки Р — (а, /3) 6 C(F), Q = (р - х, ay) Е F х К,
(х,у) е C(F), где a2 - -1, рР - р + 2Ъ = О, F = GF(pn), F = GF(pPn),
К = GF(p2pn), и пусть а = рРп + 1.
Положим div (fn) = п(Р) - (пР) - (п - 1)0. Тогда значение fa(Q)
вычисляется следующим образом.
В цикле по i от 1 до п выполняем подстановки
а = с/; /3 = /Зр; g — (-(Зуа -(а + х-р + 6)^+1)/2);
f = fg', х = х1/р; у = у1/р.
В конце цикла получаем f = fa(Q)-
Возведение в степень выполняется отдельно в самом конце алгоритма.
Заметим, что длина цикла уменьшилась в р раз по сравнению с пер-
воначальной версией алгоритма, но в алгоритме появилась операция
извлечения корня p-и степени в поле GF(pn).
Упражнение 3.7.6. Докажите, что эта операция однозначно определена на всем
поле, и является линейным преобразованием поля, обратным преобразованию
Фробениуса.
Указание. Эта операция выражается формулой
х1/р = хрП~'.
Упражнение 3.7.7. Обоснуйте правильность алгоритма.
Указание. Согласно первой формуле теоремы
л((?) = П(-/3,0г/(п+1-1')<7 - (а<0 + ж(п+,-° - р + б)^0'2).
1=1
Алгоритм Дуурсма—Ли без извлечения корней
Пусть даны точки Р = (а,/3) 6 C(F), Q — (р - х, ay) е F х К,
(х,у) € C(F), где a2 = -1, рР -р + 2Ь = О, F = GF(pn), F = GF(ppn),
К = GF(p2pn), и пусть а = рРп 4-1.
Положим div(/n) = п(Р) - (пР) - (п - 1)0. Тогда значение fa(Q)
вычисляется следующим образом.
В начале выполняется инициализация
f = 1; х = хр, У = УР\ d = -(2п - 1)Ь.
В цикле по i от 1 до п выполняем подстановки
а = (ар)р', (3 = g = (/Зуа - (а + х + b - р)^+1^2);
f = fg'> у = -у; d = d + 2b
В конце цикла получаем f = fa(Q)-
Возведение в степень выполняется отдельно в самом конце алгоритма.
174
Глава 3. Криптосистемы на основе спариваний
Упражнение 3.7.8. Обоснуйте правильность алгоритма.
Указание.	n п
f«(Q) = П П В.<П~° = (' '' Ш    Вп-1УВп,
В, =	- (a(i) + а/”*1-0 - р + Ь)°’+1)/2).
В указанной версии алгоритма появляются в цикле три новые опера-
ции возведения в степень р (преобразования Фробениуса), причем одна
из них в поле К, вместо двух обратных к ним операций извлечения кор-
ня. При использовании нормальных базисов в полях F, К и те и другие
почти бесплатны, но второй алгоритм выглядит более медленным. При
использовании стандартных базисов извлечение корня более медленная
операция, чем возведение в степень, поэтому предпочтительнее выглядит
второй алгоритм, но все зависит от соотношения скоростей выполнения
этих операций. Этот вопрос мы рассмотрим далее.
3.7.1.	Алгоритм Дуурсма—Ли над полями характеристики два
В работе [65] описан аналог алгоритма Дуурсма—Ли для суперсингу-
лярных кривых -Ё?2,& : У2 У У — X3 + X b, b = ± над полями GF(2m),
m нечетно. Напомним, что искажающее отображение для этих кривых
имеет вид:
Ф(ХУ) = (X +s2,Y + sX + t),
где s2 + s + 1 = О, s € GF(22), t2 + t + s = 0, i 6 GF(24). Результаты [65]
мы изложим кратко и без доказательств.
Справедливы следующие леммы.
Лемма 3.7.4. Пусть Р = (а,Д) Е E2,b(F), F = GF(2m). Тогда 2*Р =
+ i - 1,	+ 1(о№} 4- бг-, где ei = 0 при i = 0, l(mod 4),	= 1 при
г = 2, 3(mod4);
Лемма 3.7.5. Справедливы равенства', s + 1 при нечетном j,	= s
при четном j,	= t, £6М’+1) = t + s, = t + 1,	= £ s j;
Лемма 3.7.6. Пусть P = (a,/3), Q = (x,y) E E2fb(F), F = GF(2m)
и рациональная функция gp такова, что
2(P)-(2P)-(C?) = div0P)
(уравнение касательной к точке Р). Тогда
g2-p($(Q)) =	+ £(i-l) + y(~i} + s(a(’'~0 + ®Н)) +1 + ъ.
3.7. Алгоритм Дуурсма—Ли
175
Теорема 3.7.2. Спаривание Тейта можно вычислить по формулам
т
/р(Ф(<?)) = И (Лн+1) + 4’ + ?/-г+1) + s2 (a(i) +	+t2 + b),
i=l
m
/р(Ф(<Э)) = Ца^, где
г = 1
Ai =	+ 4° + т/1* + з® (а<2’> + 4>) ++ b.
Алгоритм Дуурсма—Ли в характеристике два
ВХОД: Р = (а,/3), Q = (х,у).
ВЫХОД: С = /р(Ф(<?)).
Вначале инициализируем С — 1.
Потом в цикле по i от 1 до т выполняем следующие присваивания:
а = а2; (3 =/З2; z = a + x; w = z + ах +/3 + у + b;
С = C(w + zt + (z 4- 1)£2); x =	у = y^m~^.
Алгоритм Дуурсма—Ли в характеристике два
без извлечения квадратных корней
ВХОД: Р = (а,/3), Q = (x,y).
ВЫХОД: С = fp($(Q)Y
Вначале инициализируем
С = 1; и = ж2; v = у2.
Потом в цикле по i от 1 до т выполняем следующие присваивания:
а — a4; (3 = /З4;
A(t) = a(v 3-1) + и +/3 + у 3-b + —у— + (« 4- v)t 4- (а 4- v 4- l)f2;
С — С2 • A(t); и = и 4- v 4- 1; v = v 4- 1.
Конец цикла и алгоритма.
Заметим, что умножение произвольного элемента Со 4-	4- cyt1 4- c^t3
поля GF(24m) на элемент вида w + zt + (z+ l)f2 обычным алгоритмом при
использовании базиса {1, t, t2, t3}, t4 4- t + 1 =0, требует 12 умножений
в подполе GF(2m), а при использовании метода Карацубы — только 6
умножений. Например, можно воспользоваться следующей схемой:
О) = сог^ + (с2 + с3)(г+ 1) + с3;
с3 = (с1 4-c2 + c3)w4-(ci +c2)(w + z+ 1) + с2;
с'] =cow + (c] +c2 + c3)w4-(co + c2 + c3)(w4-^+ l)4-c3(z+ 1) + со4-с3;
с2 = соw -h (ci 4- с2 + с3)w 4- (со + с2 4-с3)(w + z +1) 4- (ci + с2)(w 4-z +1) + Cj.
176
Глава 3. Криптосистемы на основе спариваний
Количество используемых сложений при этом равно 17. Использова-
ние оптимального нормального базиса {7,71 2,74 * * *,78,716}, где 7 = t\
t = 7 + 73, дает схему с чуть большим числом сложений, но более регу-
лярного вида.
Дальнейшее развитие идей работы [39], данное в работах [23,24,48]
и др., мы вынуждены оставить за рамками книги.
3.8. Некоторые алгоритмы арифметики
конечных полей
3.8.1.	Извлечение квадратных корней
в полях характеристики большей двух
Как уже отмечалось в случае полей характеристики два, в стандарт-
ных протоколах для эллиптических кривых и в протоколах, основанных
на спаривании, можно в два раза сократить пересылаемую информацию,
если представлять точку кривой не как пару (х,у), а как пару (ж, а),
где a — один бит, указывающий, какой из двух квадратных корней урав-
нения кривой Y2 — f(X) выбирается в качестве значения у. Но чтобы
восстановить точку (х, у) по такой информации, нужно уметь быстро вы-
числять квадратные корни в поле, над которым рассматривается кривая.
Как это делать для полей характеристики два, объяснялось в разд. 1.4.4.
Для произвольных простых полей также известны быстрые алгоритмы.
Но эти алгоритмы не так быстры, как в поле характеристики два. В [22]
предложен следующий алгоритм извлечения квадратного корня в по-
ле GF(pn) при р = 3(mod 4) и нечетном п = 2к 4-1. Число
^ = ^(1+р(р-1)ЕИ)>
'	?=0	'
поэтому
,/7 _ n(Pm + l)/4 _ ( (_\(Р+1)/4
у Ct — (X	— I I GL	1	U/j
Упражнение 3.8.1. Докажите эти тождества.
Указание.
1 - u + u2 - ... + u2k = 1 + (u2 - u) (1 + u2 + ... + u2k~2).
Возведение в степени p(p - 1) и (p+ l)/4 бинарным методом выпол-
няется с помощью O(logp) умножений в поле GF(pn).
Возведение в степень (р2к — 1)/(р2 - 1) можно представить в ви-
де аддитивной цепочки с операциями умножения на р. Тогда можно
показать, что возведение в эту степень можно выполнить с помощью
не более чем 2к операций возведения в степень р и 1*(к) операций умно-
жения, где Г (к) — длина кратчайшей линейной аддитивной цепочки
3.8. Некоторые алгоритмы арифметики конечных полей
177
для числа к. Так как сложность всех операций возведения в степень р
оценивается как O(kpnM(logp)) при использовании стандартного ба-
зиса с неприводимым многочленом малого веса, a Z*(fc) = O(logAj),
то оценка сложности возведения в степень (р2к - 1) / (р2 - 1) равна
O(pn2M(logp) + log nM(n)M(logр)), где М(п) — сложность умножения
многочленов степени п, которая оценивается как O(nlog23) при исполь-
зовании метода Карацубы. При малых р оценка сложности возведения
в степень (р2к — 1)/(р2 — 1) равна О(п2). Оценка сложности извлечения
квадратного корня остается такой же.
Известен способ извлечения квадратных корней в поле GF(p) при
любом р, имеющий сложность <9(logpM(logp)) при условии что в этом
поле известен элемент, не являющийся квадратом. Этот способ, ускольз-
нувший от внимания авторов [22], без каких-либо изменений переносится
на случай произвольного поля GF(pn). При его обосновании возникает
лишь единственное затруднение, связанное с необходимостью доказать,
что в формуле бинома (а 4- &)^+1 в поле GF(q) не равны нулю только два
первых и два последних коэффициента. Это уже не так очевидно, как в слу-
чае q = р, но становится очевидным и для q = рк, если применить к вы-
числению промежуточных биномиальных коэффициентов формулу Люка
(см., например, [8]). Сложность этого способа равна <?(log qM(log q)) =
О(nM(ri) logpM(logp)) при условии что в этом поле известен элемент,
не являющийся квадратом. Указанный элемент можно найти один раз для
данного поля, поэтому сложность его вычисления можно не учитывать.
Если известен быстрый алгоритм проверки, является ли элемент поля
квадратом, то после к попыток такой элемент может быть найден с вероят-
ностью, близкой к 2~к, так как в поле ненулевых квадратов и неквадратов
равное количество. В поле GF(p) известен такой алгоритм сложности
О(М(logp) log logp, основанный на комбинации алгоритма Кронекера
вычисления символа Лежандра с модификацией Лемера—Шенхаге алго-
ритма Евклида. В произвольном конечном поле вместо закона взаимности
Гаусса надо использовать закон взаимности Дедекинда (см. [18]). В [17]
показано, что тестирование квадратности в поле GF(pn) можно выпол-
нить со сложностью O(M(n)M(logp) logn.
3.8.2.	Извлечение корней р-й степени в полях характеристики р
В случае р = 2 этот вопрос уже рассматривался выше в связи
с методом «ополовинивания». В общем случае его актуальность связана
с использованием указанной операции в одном из вариантов алгоритма
Дуурсма—Ли.
Выше уже приводилась явная формула для этой операции (обратного
преобразования Фробениуса) в поле GF(pn): Xх !р — ХрП . Из нее следует,
что при использовании нормального базиса программная сложность этой
операции почти такая же, как и прямого преобразования Фробениуса
178
Глава 3. Криптосистемы на основе спариваний
и меньше даже сложности сложения в этом поле. В случае же схемной
реализации эта сложность равна нулю.
При использовании стандартных базисов вопрос не так прост. Один
из подходов к его решению состоит в переходе к подходящему нормаль-
ному базису, решению задачи в нем, и обратном переходе. Сложность
каждого перехода, очевидно, равна сложности умножения матрицы пере-
хода на вектор. В соответствующих разделах книги было показано, что,
применяя алгоритм «четырех русских», это можно сделать с битовой слож-
ностью O(n2 / logn), где константа в знаке О зависит от р (но при этом
расходуется примерно такой же объем памяти). Для конкретных базисов
указанная оценка сложности может быть существенно меньше, например
для стандартных базисов, соответствующим оптимальным нормальным
базисам, эта оценка не выше O(nlogn), причем большой расход памяти
не требуется.
Другой подход основан на вычислении хрП с помощью O(logn)
операций модулярной суперпозиции, также рассматривавшихся в соот-
ветствующих разделах нашей книги, где была получена оценка сложности
такой операции
О(п(ш+1)/2),
где 0} — экспонента матричного умножения. Практического значения
при вычислении корней из произвольных элементов поля этот метод
не имеет, так как при п порядка нескольких сотен этот метод медленнее
указанного выше.
Практически приемлемым является предварительное вычисление
всех корней p-и степени из всех элементов базиса (их хранение требует
памяти объема О(п2)) и последующее вычисление обратного преобразо-
вания Фробениуса как линейного преобразования с помощью умноже-
ния предварительно вычисленной матрицы на вектор координат данного
элемента. Для этого умножения можно применить уже упоминавшийся
алгоритм «четырех русских», который нужно использовать только один
раз. Для конкретных базисов указанная матрица может иметь простую
структуру, и сложность умножения на нее может оказаться существенно
меньше указанной выше оценки.
Если минимальный многочлен базиса содержит мало членов, то пре-
образование Фробениуса можно вычислить с помощью обычного школь-
ного алгоритма деления со сложностью О(рп), поэтому обратное преоб-
разование можно вычислить со сложностью не выше О(рп2), не расходуя
лишней памяти.
Известен также метод, сводящий вычисление обратного преобразо-
вания Фробениуса к (р - 1) умножениям в поле GF(pn) на конкретные
заранее вычисленные элементы. Он основан на представлении произ-
вольного элемента этого поля
х = xq + x^a ... -h xn-Xan~\ Xi € GF(p), i — 0,..., n - 1,
3.8. Некоторые алгоритмы арифметики конечных полей
179
в виде
ч Xq 4- X4- . . . + Хр-\О? ,
Xj = Xj +x]+pap + Xj+2Pa2p + ..., j = 0,...,р-1
и использовании тождества
xl/p = Xl0/p + x[,pa'/p + ... + x/p1(a1/p)p-‘ =
= Уо + У1Я1/Р + • • • + Ур-1(а1/р)р"1,
Yj = Xj + Xj+pa + Xj+2Pa2 + ..., j = O,...,p-\.
Упражнение 3.8.2. Докажите эти тождества.
Указание. (X + Y)'/p = x'lp + Y'/p, (XY)1/p = X'lpYl/p, при x G GF(p) x'lp = x,
поэтому = Yj.
Так как вычисление Yj выполняется «бесплатно», то при использо-
вании базиса с минимальным многочленом, состоящим не более чем
из пяти членов, извлечь корень р-й степени можно не более чем
за (р - 1)М(п) + О(рп) операций в поле GF(p), где М(п) — сложность
умножения многочленов степени меньшей п. В общем случае оценка
возрастает асимптотически в три раза. Конечно, сложность предваритель-
ного вычисления а^р,не учитывается и все рп координат
этих элементов запоминаются. Если используемая память ограничена,
то можно запомнить только а^р, но тогда оценка сложности возрастает
асимптотически в два раза.
Заметим, что в умножениях Yj на (а1^)-7 первый сомножитель, рас-
сматриваемый как многочлен, имеет степень не больше п/р 4-1, поэтому
сложность каждого из этих умножений можно оценить асимптотически
как рМ(п/р), и окончательную оценку сложности получить асимптоти-
чески в виде (р - 1)рМ(п/р) (при использовании базиса с минимальным
многочленом, состоящим не более чем из пяти членов). При исполь-
зовании школьного алгоритма умножения полученная оценка при этом
улучшается приблизительно в р раз.
Упражнение 3.8.3. Докажите эти утверждения.
Если многочлены, представляющие а^р,... ,(а^р)р~1, содержат мало
членов, то указанная оценка сложности понижается вплоть до линейной.
Так будет, например, в случае, когда минимальный многочлен базиса
имеет вид
Xn + aXk + b, п = к mod р 0(mod р)
(частный случай р — 3 рассмотрен в [23]). Действительно, пусть п =
r(modp), г > 0, г < р.
Упражнение 3.8.4. Докажите, что при п = kmodp = O(modp) многочлен приво-
дим.
180	Глава 3. Криптосистемы на основе спариваний
Так как an 4- aak = -b, то an+p~r 4- aak+p~r = -bap~r, откуда,
извлекая корень, имеем a(n+p~r^p + aa^k+p~r^p = -ba^~r^p, так как n-r,
к-r делятся на р, значит, a^~r^p — -b~xa^p~r^p-ab~xa^p~r^p. Чтобы
вычислить произвольный элемент aslp, 0 < з < р, надо найти q < р такое,
что з = -rq modp и взять
as/p _	_ а^-1 a(k+p-r)/pya~[q(p~r)/p\
Так как q р - 1, то при возведении в степень q не возникают слагаемые
со степенями, большими (п/р 4- 1)(р -1) = п4-р-1- ть/р. Поэтому
при п р2 все показатели степени будут меньше п, значит приведение
по модулю минимального базисного многочлена не понадобится. Так как
все показатели степени не меньше q(k 4-р — г)/р > \_q(p - г)/р\, то при
делении на а^~г^р^ показатели степени во всех слагаемых остаются
положительными. Следовательно, число слагаемых в выражении
(-b-1a(n+p“r)/p - ab~la^k+p~r^p)qa_^(p-r)/pj
согласно формуле бинома не превосходит q 4- 1 р. Поэтому в разложе-
нии ots/р в данном базисе число ненулевых координат не больше р.
Упражнение 3.8.5. Докажите, что общее количество ненулевых координат в эле-
ментах аз/р, 0 < s < р, не больше (р 4- 2)(р - 1)/2.
Указание. Когда з пробегает все значения 0 < s < р, соответствующие числа q
пробегают те же значения. Следовательно, для выполнения всех умножений
на а1/р, ..., (а1/р)р-1 требуется не более (р 4- 2)(р - 1)п операций в поле GF(p).
Поэтому в рассматриваемом случае можно извлечь корень р-й степени не более
чем за (р 4- 2)(р - 1)п 4- О(рп) операций в поле GF(p).
3.8.3.	Один метод компактной записи точек
суперсингулярных кривых
Можно представлять точку кривой Е : Y2 = X3 - X 4- b не как пару
(ж, у), а как тройку (р, ai,a2), где (^1,02) — пара битов, указывающая
какой из трех корней кубического уравнения у2 = X3 - X 4- b выбирается
в качестве значения х. Заметим, что уравнение X3 - X = с, как известно,
разрешимо тогда и только тогда, когда след элемента с € GF(3n) равен
нулю, так как tr (ж3) = tr (ж)3 = tr (ж), и tr (ж3 - ж) = tr (ж3) - tr (ж) = 0.
Если оно разрешимо, то второй и третий корни выражаются через первый
по формуле ж8- = Ж1 4- г - 1, г = 2, 3, так как при а е GF(3)
(ж] 4- а)3 - (Ж1 4- а) = ж3 - Ж} 4- а3 - а = ж3 - Ж1 = с.
Чтобы отделить корни друг от друга, достаточно указать координату, соот-
ветствующую свободному члену при использовании стандартного базиса,
или вообще любую координату при использовании нормального базиса
(так как в нем прибавление элемента a Е GF(3) сводится к простому
или двукратному прибавлению этого элемента ко всем координатам, ибо
сумма элементов нормального базиса равна ненулевому элементу GF(3).)
3.8. Некоторые алгоритмы арифметики конечных полей
181
Чтобы восстановить точку (ж, у) по такой информации, нужно уметь
быстро решать в поле GF(3n) уравнения вида X3 - X = с. Эти уравнения
фактически являются линейными, так как отображение X —> X3 - X
является линейным оператором. Поэтому их можно решить быстрее, чем
извлекать квадратные корни в этом поле, что по сложности сравнимо
с инвертированием. Особенно легко решаются такие уравнения в нор-
мальном базисе, так как возведение в куб в нем сводится к циклическому
сдвигу координат
(Ж], . . . , Жп) >• (жп, Ж1, . . . , Жп-1),
и эквивалентная линейная система уравнений записывается в виде
Хп ~	— Ci, Ж] — Ж 2 = С2, . . • Xn—j Хп = Сп,
откуда имеем
Ж2 = Ж] — С2, Жз = Ж1 — С2 — Сз, . . . ,
Жп—1 = Ж1 — С2 ... — Cn—\, Xn = Х\ 4“ С1,
Ci + ... 4- cn = tr (с) = 0.
Очевидно, битовая сложность решения этой системы равна О(п). Очевид-
но, что с такой же по порядку сложностью можно извлекать и кубические
корни в поле GF(3n). Как получить более аккуратную оценку, будет ясно
из следующих далее разделов.
Решать уравнение вида X3 - X = с в стандартном базисе более
сложно. Так как уравнение сводится к линейной системе, и она разре-
шима только при tr(c) = 0, а множество таких элементов с образует
в поле GF(3n) (п - 1)-мерное подпространство (замкнутость относитель-
но сложения следует из линейности следа, а размерность определяется
из того факта, что число решений уравнения Зп-1-й степени tr (у) = с
не превосходит Зп-1, а значит и точно равна Зп-1, так как сумма коли-
честв корней в у всех трех уравнений равна Зп, потому что след любого
элемента равен 0, 1 или 2), то построив какой-нибудь базис ..., vn_i
в этом пространстве и вычислив заранее какие-нибудь корни х3 — Xi= Vi,
можно для любого v = C\V\ 4- ... 4- cn^\Vn-\,Ci е {0,1,2} найти один
корень уравнения X3 - X — v в виде ж = С[Х\ 4-... 4- сп_ 1ЖП_i. Применяя
алгоритм «четырех русских», можно показать, что вычисление корня ж
выполняется с битовой сложностью O(n2/ logn).
Упражнение 3.8.6. Восполните пробелы в проведенных рассуждениях.
Разумеется, при удачном выборе стандартного базиса, сложность ре-
шения уравнения X3 - X = v может быть и меньше. Действительно,
вместо того, чтобы решать данную систему в стандартном базисе, мож-
но свести ее к подходящему нормальному базису, выполнив линейную
замену переменных, связывающую эти базисы. Применяя алгоритм «че-
тырех русских», можно показать, что эта замена выполняется с битовой
182
Глава 3. Криптосистемы на основе спариваний
сложностью O(n2 / logn). Поэтому оценка битовой сложности решения
рассматриваемого кубического уравнения не выше O(n2/logn). На са-
мом деле для конкретных базисов она может быть существенно меньше,
например для стандартных базисов, соответствующим оптимальным нор-
мальным базисам, можно показать, что оценка не выше O(nlogn).
Все, сказанное выше, справедливо и для уравнений вида X3 + Х = с.
Уравнения X3 ± X — с сводятся друг к другу заменой X = iX, i 6 GF(32),
г2 = -1, поэтому в поле GF(3n) при четном п они решаются с одинаковой
сложностью.
Упражнение 3.8.7. Докажите, что в поле GF(32n) при нечетном п уравнение
X3 ± X = с = a + Ы, a,b € GF(3n), равносильно системе независимых уравнений
X3 ± X = a, У3 т У = ~Ъ в поле GF(3n).
Упражнение 3.8.8. Докажите, что в поле GF(3n) при нечетном п уравнение
X3 4- X = с всегда имеет единственное решение, и тем самым линейное отоб-
ражение X -> X3 + X имеет обратное отображение, которое тоже линейно.
Докажите, что, если х — корень уравнения X3 4- X = с, то ж ± 1 — корень
уравнения X3 + X = с =F 1. Докажите, что при с — у -h tr (у) корень х3 + х = с
равен у + у9 4- г/81 + •.. 4- г/3" . Докажите, что при n 2(mod 3) и с = у 4- tr (у)
справедливо, что tr (у) = tr (с)/(п 4- 1), у = с - tr (с)/(п 4- 1). Пусть n = 2(mod 3).
Докажите, что с = у 4- tr (у) - tr (с) при у = с 4- tr (с) и уравнение X3 4- X = с
имеет корень у 4- у9 4- ум 4- ... 4- узП + tr (с).
При использовании алгоритма Дуурсма—Ли для сжатия точек кривой
надо решать уравнение Хр - X = с в поле характеристики р. Для этого
уравнения справедливо все, сказанное выше.
Упражнение 3.8.9. Проверьте это.
3.8.4.	Арифметика в полях характеристики большей двух
Частично этот вопрос нами уже рассматривался ранее, но здесь
уместно кое-что вспомнить. Организация арифметики в простых полях
сводится к обычному сложению и умножению, а также к делению с остат-
ком на порядок поля р. Известно, что последняя операция может быть
сведена к умножению на число q, такое, что 22^log2^ — pq + г, 0 < г < р
(см., например, [8]). Поэтому сложность умножения в поле GF(p) асимп-
тотически не больше ЗМ(log2 р). Для простых чисел специального вида,
например чисел вида 2П ± а, где а не слишком велико, эту оценку можно
улучшить асимптотически до М (log2 р).
На практике для произвольных р в программных вычислениях ука-
занный способ не используется, так он требует применения быстрых алго-
ритмов умножения, а даже метод Карацубы для чисел с несколькими сот-
нями двоичных цифр не эффективен по сравнению с обычным школьным
алгоритмом, если его применять в системе счисления с основанием 2т,
где т равно разрядности используемого компьютера. Для деления в этой
3.8. Некоторые алгоритмы арифметики конечных полей
183
системе счисления используется обычный школьный алгоритм, модифи-
цированный как описано во втором томе Кнута. Для простых указанного
выше вида (псевдопростых Мерсенна) очевидная модификация школь-
ного алгоритма работает еще быстрее. Подобную модификацию можно
указать и для уже упоминавшихся простых чисел Солинаса (имеющих ма-
ло ненулевых цифр в двоичной записи с использованием минус единиц).
Для инвертирования в поле GF(p) можно использовать расширенный
алгоритм Евклида, который имеет оценку сложности O(logp)2 (см., на-
пример, [10]), а в модификации Шенхаге—Лемера имеет даже оценку
О(М(log р) log logp). Можно также использовать формулу а"1 = ар~2
и метод Монтгомери вместе с каким-нибудь методом построения адди-
тивных цепочек. Оценка сложности в этом случае равна C(M(logp) log р),
а для чисел специального вида, например простых Солинаса с малым
число единиц в двоичной записи, или псевдопростых Мерсенна, она
уменьшается, но не существенно.
Сложение в поле GF(pn) сводится к покомпонентному сложению
векторов по модулю р, и выполняется со сложностью O(nlog2p). Умно-
жение сводится к обычному умножению р-ичных многочленов степени
меньшей п и делению полученного результата с остатком на неприво-
димый многочлен, соответствующий выбранному стандартному базису.
Для удобства деления этот многочлен выбирается с минимальным числом
ненулевых членов. Экспериментально установлено, что это число не пре-
вышает 4 в случае р > 2. Тогда сложность приведения по модулю такого
многочлена равна O(nM(logp)), а сложность умножения в поле GF(pn)
асимптотически равна ЗМ(n)M(log р).
Арифметика в полях характеристики три. Вопросы организации арифме-
тики в этих полях обсуждались в работах [27,45, 58, 79].
В первых двух из них указан пригодный и для схемной реализации
алгоритм сложения векторов по модулю три. Числа 0, 1, 2 представляются
в двоичном виде как (0, 0), (0, 1), (1,0) соответственно. Сложение чисел
(«1, ао), (&ь Ьо) по модулю три выполняется по следующим формулам
t = (ai V до) Ф («о v &i), ci = (&о V &о) Ф t, Со = (ai V М Ф t-
Упражнение 3.8.10. Докажите эти формулы.
Указание. Если Vbi = 0, то аоФ&о = i = с0, Ci = aQbo. Если а^&Ь^ = 1, то t = 0,
Со = 1, Cj = 0. Если ai — 1, b[ = 0, то t = -ia0 — 1, cQ = aQ = Q, Ci = (o0 V d0) ® 1-
Если представить троичный вектор А = ((ai,i, ai,o),.. •, (an,i, ап,о))
в виде двух двоичных векторов А] = (а^,..., апд), Ао = (&i,o, • • •, fln.o)
той же длины, и аналогично представить троичный вектор В виде упоря-
доченной пары двоичных векторов (В], Bq), то, учитывая параллельность
сложения по модулю три компонент троичных векторов, получаем, что
троичный вектор С, являющийся их суммой по модулю три, представля-
ется в виде пары (Ci, Со), такой, что
Т = (Ai V Bq) ф (Aq У В[), Ci — (До V Bq) Ф Т, Cq = (Д1 V В\) ф Т,
184
Глава 3. Криптосистемы на основе спариваний
логические операции выполняются покомпонентно уже над векто-
рами. Поэтому операция векторного сложения по модулю три сводится
к 5 логическим векторным операциям и сложность ее программной реа-
лизации равна 5|’n/w‘|, где w — разрядность используемого компьютера
(обычно w = 32 или 64). Операция смены знака и операция умножения
на двойку по модулю три эквивалентны в силу равенств
2(ai, ao) = — («ь ^о) — (ao, &1),
из которых следуют векторные равенства
2А = 2(АЬ Ао) = -А = -(Аь Ао) = (40,
которые показывают, что смена знака и умножение на 2 выполняют-
ся простой перестановкой векторов (и поэтому бесплатны при схемной
реализации). Значит, операция вычитания имеет практически ту же слож-
ность, что и сложение.
Для выполнения умножения удобно выбрать базис с трехчленным
неприводимым полиномом (двучленный полином неприводим только для
степени два.) Очевидно, что трехчлены вида Xn 4- Хт 4- 1 приводи-
мы, так как имеют корень 1. Таблицы неприводимых трехчленов вида
Хп 4- Хт 4- 2, Хп 4- 2Хт + 1, Хп 4- 2Хт 4- 2, заимствованные из [27]
приведены в Приложении В.2 на с. 223.
Арифметика в полях большой характеристики. В [19, 20] в качестве полей,
удобных для программной реализации в криптографических приложени-
ях, предлагались поля GF(pn) с небольшими значениями пир, где р
есть псевдопростое число Мерсенна, т. е. простое число вида р = 2П - с,
log2 с п/2, а в качестве порождающего базис многочлена берется дву-
член вида Хт - ш. В этом случае операции арифметики в поле GF(p)
реализуются просто и быстро, так как требует всего нескольких машинных
операций. В случае псевдопростых Мерсенна с длиной близкой к машин-
ному слову приведение по модулю сводится к сложению или вычитанию
и умножению на малое число, например, по формуле
232a 4- b mod (232 4- с) =b - ca mod (232 4- с).
Так как умножение довольно медленная операция, в случае с с малым
числом двоичных единиц его выгоднее заменить на сложение и сдвиг
битов. Например, при р = 231 - 19 потребуется два сложения и два сдвига.
Приведение по модулю двучлена Хт - ш выполняется всего лишь
с помощью т-1 сложений и т-1 умножений на о; в поле GF(p). Особен-
но просто эта операция производится при ш = 2, так как такое умножение
сводится к сдвигу битов. Чуть сложнее эта операция делается для п ви-
да 2к ± 2т, так как кроме сдвига битов требуется еще одно сложение.
Поиск неприводимых двучленов облегчается следующей теоремой из [12].
Двучлен Хт - а} неприводим над полем GF(p) тогда и только тогда,
когда каждый простой делитель т делит е, но не делит (р - 1)/е, где е —
3.8. Некоторые алгоритмы арифметики конечных полей
185
порядок элемента ш, и m кратно 4. Например, при р — 261 - 1 в случае,
если р = l(mod 4).
Упражнение 3.8.11. Выведите из этой теоремы, что, если ш — примитивный
элемент в поле GF(p), и тп делит р - 1, то Xm - ш неприводим над полем GF(p).
В частности, X2 - ш неприводим для любого примитивного элемента.
В [20] в качестве простых особенно рекомендуются максимальные
числа вида р — 2n ± 1 (простые Мерсенна и Ферма), умещающиеся в пре-
делах машинного слова, так как для таких полей арифметика реализуется
особенно просто, потому что приведение по модулю и в случае умно-
жения сводится к сложению или вычитанию, а в случае сложения —
к инкременции или декременции.
Но 2 не является примитивным элементом по этим модулям, и в слу-
чае простых Ферма многочлен Хт - 2 всегда приводим, а в случае простых
Мерсенна многочлен Хт - 2 будет неприводимым, только если каждый
простой делитель т делит п, но не делит (р - 1)/п, и т не кратно 4.
Например, при р = 261 - 1 в качестве т годится только минимум 61.
Поэтому в качестве неприводимого двучлена в [20] предложен X3 - 37.
Там утверждается, что в поле <7F((261 - 1)3) арифметика работает в два
раза быстрее, чем в поле GF(2155 согласно [87].
Упражнение 3.8.12. Выведите из предыдущего упражнения, что для числа Ферма
р = 22 4- 1 двучлен Хт — 3 неприводим тогда и только тогда, когда т = 2l, I 2к.
Поэтому возможно также, что быстрая реализация может быть сде-
лана для р = 216 4- 1 и многочлена X16 - 3.
В [20] дано более развернутое изложение, чем в [19], в частности
вычислены таблицы с параметрами рекомендуемых расширений, назван-
ных там оптимальными. Однако в программе их вычисляющей имеется
не замеченная авторами ошибка в проверке условий приведенной выше
теоремы, и она дает иногда неправильные результаты, попавшие в таб-
лицы. Так, для чисел Ферма 28 4- 1 и 216 4- 1 неправильно утверждается
неприводимость в соответствующих полях многочленов вида X2” - 2.
На самом деле они приводимы, так как, очевидно, 2 является квадратич-
ным вычетом в этих полях и данные многочлены приводимы как разности
квадратов. Двойка является квадратичным вычетом в силу критерия Эйле-
ра и того факта, что ее порядок в этих полях делит 32, а значит, и (р - 1)/2
тоже, поэтому 2^-1^2 = l(modp).
Упражнение 3.8.13. Проверьте это.
Инвертирование в поле GF(pn') в [20] сводится к инвертированию
в поле GF(p) с помощью формулы
где у =	Е GF(p), а вычисление у и х^рП 1-1)/(р-0 сводится
к операциям возведения в степени р1 и A(n- l)4-^(n-1) - 1 умножениям.
186
Глава 3. Криптосистемы на основе спариваний
Так, например, при п = 8 проводятся следующие вычисления
_7	/	4_. ч я3 _3_,	4.	2
ХР-1 =(хр-1^ ХР-1 , ХР-1 — (хр+ху хр+\
pi _ 1	✓ р7_д \ р
х Р-1 = {хР4г^Р X, у = \Х Р-1 ) X,
требующие 4 полных умножения и одно умножение, в котором вычисля-
ется только одна координата, а также 5 операций возведения в степени рк.
Возведение в степень рк в поле GF(pn) сводится к возведению в эту сте-
пень одночленов, а оно выполняется по формуле
(хг)р = wsxe mod xn - cu, e = pkimodn, s=(pki-e)/n,
поэтому возведение в степень рк требует п - 1 умножений в поле GF(p).
В [20] не отмечено, что в случае составных п вычисления можно выпол-
нить быстрее, например следующим образом. Заметим, что Z\ = хр х €
GF(p4), так как zp — z\ , и zz = zp zi E GF(p2), так как zp =^2, тогда
pS-l p4-i p2-l	p8-i	2	4	p8-p
ZPZ2 = XP*-1^1 p~{ = X P-1 = y6GF(p), ZPZP XP = X P-1 ,
потому что
» »2 n4	» »2	p
ZjZ\ XPX = z\ — zlzl — У-
В этом вычислении использовались только 3 возведения в степени рк,
причем одно в поле GjF(p8), одно в поле GF(p4), и одно в поле GF(p2),
а также 5 умножений, из которых одно в поле GF(p8), но его результат
принадлежит подполю	GF(p4), одно	в поле	GF(p4), но	его результат
принадлежит подполю	GF(p2), одно	в поле	GF(p2), но	его результат
принадлежит подполю	GF(p), еще в	одном	умножении	элемент под-
поля GF(p4) умножается на элемент подполя GF(p2), и полученный
элемент zpzp подполя GF(p4) умножается на элемент поля GF(p%). Так
как вместе с двучленом Xs - ио неприводимыми над полем GF(p) являют-
ся двучлены X4 - ио, X2 - ио, и если a Е GF(p%) корень двучлена X* - ио,
то а2 будет корнем двучлена X4 - ио, значит a2 Е GF(p4), и а4 Е GF(p2)
будет корнем двучлена X2 - ш, поэтому базисом подполя GF(p4) будет
«подбазис» {1, а2, а4, а6} базиса {1, а,..., а7} поля GF(p8), а базисом
под поля GF(p2) будет «подбазис» {1,а4}. Значит для нахождения ко-
ординат в подполях нужно просто взять соответствующие координаты
в поле, игнорируя нули; так как при стандартном умножении в этих
базисах формулы для разных координат не имеют общих переменных, то,
например, сложность умножения в поле GF(p8) с результатом из под-
поля GF(p4) будет вдвое меньше сложности общего умножения, так как
формулы, дающие нулевые координаты можно не вычислять. Для умно-
жения и возведения в степени в подполе естественно использовать только
3.8. Некоторые алгоритмы арифметики конечных полей
187
координаты, соответствующие его базису, игнорируя остальные нулевые
координаты, поэтому эти операции фактически можно выполнять, как
внутренние операции этого подполя. Аналогичное утверждение верно для
умножения на элемент подполя, точнее умножение на элемент подполя
сводится к двум умножениям в этом подполе.
Если через M(GF(q)) обозначить сложность умножения в рассмат-
риваемых базисах данных полей, то общая оценка сложности инвертиро-
вания будет
M(GF(ps)) M(GF(p4))	M(GF(p2))
2	+	2	+	2
4- 2M(GF(p4)) + 2M(GF(p2')) + (7 + 3 4- QM(GF(p)) =
,	, 8чч 3M(GF(p4)) M(GF(v2Q ,	, ..
= M(GF(p8)) +------> 	” + 10Af(GF(p)).
Так как операция умножения в поле GF(p) медленнее сложения, то для
умножения многочленов над полем GF(p) в [20] предлагается уменьшать
количество операций умножения с помощью введения п(п - 1)/2 произ-
ведений вида (аг 4- a,j)(bi 4- bj). Из них с помощью еще п произведений
вида агЬг можно вычислить все суммы вида
CLibj 4~ CLjbi — (^Q>i 4“ ttj^(bi 4” by) 4“ ^ibi 4~ CLjbj.
Мультипликативная сложность основанного на применении этих тож-
деств алгоритма умножения многочленов степени п - 1 равна п(п -4 1)/2.
Эта идея похожа на использованную нами выше идею ускорения умно-
жения в нормальных базисах. Но в отличие от нормальных базисов
указанный алгоритм дает выигрыш только в мультипликативной сложно-
сти, и существенно проигрывает стандартному алгоритму в аддитивной
сложности. Тем не менее, рекуррентное применение этого алгоритма при
некоторых значениях п улучшает оценки, получаемые непосредственным
применением метода Карацубы. Например, для умножения квадратных
трехчленов рекуррентное применение метода Карацубы требует 7 умно-
жений, а предложенная в [20] схема требует 6 умножений и 13 сложений.
Заметим, однако, что выше нами использовалась еще лучшая схема, име-
ющая только 12 сложений. Эта схема выглядит следующим образом:
4-	(ZjX 4- (12*£ (b() Ь\Х Ь2& ) = Cq CjX С2Х 4“ CyX 4” C4,
Co = flo&O, c4 — ^2^2, C1 — (^0 + al)(^0 + bl) + (^obo 4~ fllbi),
c2 = (^obo + fllbi) 4- (во + ^2)(bo 4" b2) 4- <2-2?>25
c3 — (&i 4- ^2)(bi 4- b2) 4- fljbi 4- fl2b2-
Применяя ее в методе Карацубы, получаем схему для умножения много-
членов пятой степени лучшую по числу сложений, чем схема [20]. Обе
эти схемы можно использовать для ускорения операций в поле GF(p6)
методом, подобным приведенному выше.
188
Глава 3. Криптосистемы на основе спариваний
Поля малой характеристики, как мы уже видели, в последнее вре-
мя получили приложения в криптосистемах, основанных на спарива-
нии. Наиболее перспективными представляются поля характеристики
три. В [58] подробно описана организация арифметики в таких полях,
ориентированная применение алгоритма Дуурсма—Ли при р = 3. Мы
здесь рассмотрим этот вопрос в общем случае.
3.9. О реализации алгоритма Дуурсма—Ли
Вопрос о вычислении преобразования Фробениуса и обратного к нему
уже был рассмотрен выше. Рассмотрим вопрос об организации арифмети-
ки в полях GF(pn) и GF(p2pn). Так как в алгоритме Дуурсма—Ли в послед-
нем поле приходится выполнять операции д — (j3ya — (ot-]-x+b-
и f = fpg. Естественно, как и в [58] при р = 3, выбрать в поле
К = GF(jp2pn} над подполем F = GF(pn) базис, являющийся про-
изведением базиса {1,6т} поля GF(p2) над подполем GF(p) и бази-
са {1, р,..., рР'1} поля GF(pP) над подполем GF(p). Минимальный
многочлен первого базиса есть X2 4- 1, а второго — Хр — X 4- 2Ь. Произ-
ведением этих базисов является базис
В = {1, ст} х {1, р,...,	= {1, р,..., р?'1, а, ар,..., арр~1},
являющийся как базисом поля GF(p2p>) над подполем GF(p), так и ба-
зисом поля К = GF(p2pny над под пол ем F = GF(pn) при (n, 2р) = 1.
Произвольный элемент поля К разлагается по этому базису следующим
образом:
р-i	р-1
х = 52 XiPl+а 52 Zp+ip’,
г=0	i=Q
где Xi е F. Элементы
р-i	р-1
JTo — Xip и Х\ = Xp+ip
г=0	г=0
принадлежат подполю F = GF(pPn) и х — Х$ 4- аХ\. Можно представить
элемент жив виде
р-i
х =	+xP+ia)p\
i=0
где элементы ж, 4- хр^а Е G = GF(p2n).
Упражнение 3.9.1. Докажите сформулированные утверждения.
Разлагая указанным способом элемент д— (j3ya-(a+x+b-рУр+W2) ,
получаем, что д = д\ 4- д2а, где д\ = -(а 4- х 4- b - р)(Р+0/2 е F, д2 =
3.9. О реализации алгоритма Дуурсма—Ли
189
fly € F С F. У элемента р2 в базисе {1,р,... ,рр-1} поля F максимум
одна ненулевая координата. Так как а + ж + беТ^тоиз формулы бинома
видно, что элемент дх представим в виде
(р+1)/2
51 = У uiP\ W(p+1)/2=±1,
г—О
и вообще
(a + x + b-p)s =	и5 = ±1,
г=0
Поэтому при вычислении каждая операция умножения в поле F сво-
дится к обычному умножению многочленов. Если обозначить сложность
умножения многочленов степени I над полем F через М(1), то приме-
няя для возведения в степень кратчайшую аддитивную цепочку, можно
найти д\ со сложностью Ц(р 4- 1)/2)М((р 4- 1 )/2), а на самом деле даже
О(М((р 4- 1)/2)), так как вычисление (а 4- х 4- b - р)2* повторным возве-
дением в квадрат имеет сложность <?(М(25)).
Умножение fg можно рассматривать как умножение в базисе {1,р,
...,рр-1} над подполем G, а умножение в поле G можно проводить
в базисе {1, а}, и оно, как известно, сводится к трем умножениям
в подполе F и пяти сложениям:
(а + ba)(c 4- da) = (ас - bd) + a(ad 4- be) —
= (ас - bd) 4- а((а 4- b)(c 4- d) - ac- bd).
3.9.1.	Использование нормального базиса в поле G
Покажем, что число сложений-вычитаний по модулю р можно умень-
шить до четырех и двух удвоений, если воспользоваться вместо бази-
са {1, а} нормальным базисом {7,7Р}, где 7 = 1 4- а.
Упражнение 3.9.2. Докажите, что
tr (7) = у 4- 7Р — 2 = N(y) = 77Р, 72 — 2а = ~72р, 7 - ур = 2а,
(07 -|- &7Р)(с7 4- dyp) — (ас - bd)(y - ур) 4- (ad 4- be)(7 4- ур) =
— ((а 4- Ь)(с 4- d) - 2bd)y 4- ((а 4- b)(c 4- d) - 2ас)ур.
Указание. ур = 1 4- ap — 1 - а, 7 - ур = 2а.
Заметим, что умножение на два по модулю р сводится к приведению
по этому модулю, так как удвоение в схемной реализации выполняется
бесплатно. Приведение по модулю р при вычислении (а 4- Ь)(с 4- d) - 2bd
можно выполнить один раз, после умножения и вычитания.
Заметим еще, что при р — 3 удвоение сводится к смене знака, значит,
кроме трех умножений требуется дополнительно только четыре сложения-
вычитания.
190	Глава 3. Криптосистемы на основе спариваний
Отметим также, что возведение в степень р в указанном базис^
сводится к перестановке координат, а возведение в степень р в базису
{1, сг} требует еще и смены знака. Умножение произвольного элемента
на элемент подполя F сводится к двум умножениям в поле F, как
и в случае базиса {1, а}. Умножение произвольного элемента на элемент
вида а(7 - ур) = 2аа сводится к двум умножениям в поле F, как
и в случае базиса {1, сг} (при условии выполнения предварительных
удвоений со сменой знака).
Упражнение 3.9.3. Возведение в квадрат выполняется по формуле
(ау + &7Р)2 = ((а 4 Ь)(а - Ь) 4- 2а07 + (-(а 4- b)(a - b) + 2аЬ)ур
и требует двух умножений, четырех сложений-вычитаний и одного удвоения.
Эта операция лишь немногим сложнее, чем в стандартном базисе,
но она далее не будет использоваться.
3.9.2.	Умножение в поле К методом Карацубы
Умножение в базисе {1, р,..., рр~1} над подполем G сводится к обыч-
ному умножению многочленов степени не выше р - 1 над полем G и при-
ведению полученного многочлена
rfo "Г d\X 4-... 4- dip-zX^
по модулю Хр - X 4- 2Ь.
Упражнение 3.9.4. Проверьте, что приведение по модулю выполняется по форму-
лам
Ср—1 dp_ 1 4" б^2р—2, Ср-2 dp_2	2Ь(^2р—2 4" ^2р-3,
Ср-з — dp-3 2bd2p—2 4" d2p—4,	• • •, Ci — d[ 2bdp^.[ -Ь dp, Cq = d$ 2bdp.
Так как b = ±1, эти формулы содержат 2р - 2 сложения-вычитания
и р — 2 удвоения.
Для умножения многочленов можно применять вместо школьного
алгоритма любой алгоритм, уменьшающий число умножений коэффици-
ентов, например метод Карацубы.
Заметим, что при вычислении fg, где д = (j3ya-(a+x+b-р)(р+^2),
в алгоритме Дуурсма—Ли можно заметить, что Ру € F, поэтому запись
руа в базисе В имеет максимум одну ненулевую координату, а именно
координату хр, а запись элемента (а 4- х 4- Ъ - р)^+1)/2 может иметь
ненулевыми только координаты xq,... ,Х(р^)/2 € F, причем последняя
координата равна ±1. Поэтому
9 = 9о + 9\р + • • • +
9o^G, gi^F, i > 0,	^(р+1)/2 = ±1.
Упражнение 3.9.5. Проверьте это утверждение.
3.9. О реализации алгоритма Дуурсма—Ли
191
Учитывая особый вид коэффициентов д, можно заметить, что при
применении школьного алгоритма число умножений в поле G уменьша-
ется до р((р + 1)/2), причем р((р ~ 1)/2) из них являются умножениями
вида F х G, и чуть меньшего числа сложений в том же поле. Учи-
тывая сделанные выше замечания об умножении в поле G, получаем
(немного завышенную) оценку сложности умножения f на д в виде
р(р + 2)M(F) + р(р 4- 12)A(F), где M(F), A(F) — сложность умножения
и сложения-вычитания в поле F — GF(pn).
Упражнение 3.9.6. Проверьте это утверждение.
Использование метода Карацубы позволяет уменьшить число умно-
жений в поле F. Например, используя указанные в [58] формулы для
умножения при р = Зир3-р-1— О
(do 4- о>\р +	(b0 4- Ъ\Р 4- ^2р2) — с0 4- С\р 4- cip\
Со = flo^O + (а2 4" а1)(^2 + ^1) “ а2^2 ~ O1&1,
Ci = (do + di)(bo 4" bi) 4- (d2 4- di)(&2 4- bi) 4" di bi — dobo,
c2 — (fl2 4- do)(b2 4- bo) 4- di&i — dobo,
можно оценить сложность умножения fg как 13M(F) 4- ЗЗЛ(^).
Упражнение 3.9.7. Проверьте это утверждение.
Указание. Умножение а2Ь2 сводится к смене знака, так как у д координата
а2 = ±1, умножения (а2 4- di)(b2 4- &i), сцЬ[ являются умножениями типа k х G,
разность di&i - dobo вычисляется один раз и применяется трижды.
3.9.3.	Умножение в поле К методом Тоома
Покажем, что в общем случае число умножений в поле G можно
уменьшить до 2р - 1 с сохранением числа сложений О(р2). Для этого
используем идею Тоома: вычисление коэффициентов у произведения
многочленов
fi(X)f2(X) = (а0 + <цХ ... + ар_1-Х’р-1) (Ьо + ЬхХ + ... ЬР^ХР~1) =
= со + ClX ... + с2р_2Х2р’2 = f(X)
можно выполнить, вычислив /Да)/2(d) = f(d) в (2р— 1)-м элементе поля
GF(p2) С G с помощью интерполяционной формулы. В качестве узлов ин-
терполяции удобно выбрать все элементы поля GF(p) и еще элементы aa,
a Е GF(p)*. Тогда значения /z(d) можно вычислить с помощью р - 1-го
сложения в поле G пр умножений в этом поле на элементы вида а или crd,
где d е GF(p). Общая сложность этих вычислений оценивается как
(2р - 5)((4р - А)пА(р) 4- 4рпМ(р)) 4- (24р - 16)пА(р),
где А(р), М(р) — сложность сложения и умножения по модулю р, (в том
числе и тогда, когда вместо элементов а и aa берутся элементы d(7±7p)
в случае выбора базиса {7,7Р}•)•
Упражнение 3.9.8. Проверьте это утверждение.
192
Глава 3. Криптосистемы на основе спариваний
Вычисление значений /1(а)/2(^) = /(а) выполняется со сложностью
(2р - l)M(G) = (2р - 1)(3M(F) + 54(F))
и даже с чуть меньшей при выборе базиса {у,ур}> Фундаментальные
многочлены интерполяции Ц(Х), г; = 1,..., 2р - 1, вычисляются заранее.
При этом коэффициенты многочленов Ц(Х), i = 1,...,р принадлежат
подполю GF(p), а у остальных — подполю GF(p2). Многочлен f (т. е. его
коэффициенты) восстанавливается по интерполяционной формуле
2р-1
f(X) = £ f(ai)li(X).
i=l
Для этого используется (2р - 1)р умножений элементов поля G на эле-
менты подполя GF(p) и (2р - 1)(р - 1) умножений элементов поля G
на элементы подполя GF(p2) и (2р- 2)(2р- 1) сложений в поле G. Общая
сложность этих операций оценивается как
(2р- 1)р2пМ(р)4-(2р- 1)(р- 1)п(ЗМ(р)+44(р))4-(2р-2)(2р- 1)2п4(р) =
= (1 tip2 -11р+3)пМ (р) 4- (6р - 3) (2р - 2)пА(р).
Упражнение 3.9.9. Проверьте это утверждение.
Окончательно имеем оценку сложности умножения в поле К
(6р - 3)M(F) + (18р2 - 21р + 3)пМ(р) + (20р2 - 12р + 5)пА(р) =
(6р - 3)M(F) + O(p2n log р log log р log log logp).
Упражнение 3.9.10. Проверьте это утверждение.
В частности, при р '= 3 оценка сложности умножения в поле К равна
15M(F) + О(п)
с небольшой константой в знаке О(п), которую можно вычислить явно.
Осталось оценить сложность вычисления возведения в степень р
в поле К.
3.9.4.	Возведение в степень р в поле К
Задача возведения в степень р элемента х — (d- 0,..., dp_\), di € G,
i — 0,..., n - 1, сводится к возведению в степень р многочлена
f (X) = do + d\X + ... + dp^Xp~l
по модулю Хр - X + 2b. Очевидно,
f(X)p = dp + dpXp + ... + dp_16pT(p-1)p.
Для приведения по модулю Хр - X 4- 2Ъ выполняем деление в столбик.
Можно проверить, что в результате получится многочлен
Cq И- С\Х 4- ... 4- Ср-\ХР ,
3.9. О реализации алгоритма Дуурсма—Ли
193
где
^ = (-2Ь)^+1 ^+^+(-2&)2<+2 (г + 2) +... + (-2Ь)₽-,-г^_1	,
г=0,.. .р-1.
Таким образом, хр = (со, ci,..., cn_i).
Упражнение 3.9.11. Проверьте это утверждение.
Указание. Примените индукцию.
Как известно, (р^) — (-1)1 modp, поэтому
a = (-2d)d?+I (г + ’) + (-2Ь)Х2 (г 22) + • • •+
г — 0,... р - 1.
Систему всех биномиальных коэффициентов по модулю р можно заранее
с помощью тождества Паскаля вычислить за р(р - 1)/2 сложений по мо-
дулю р. Количество сложений в поле G, требующихся для вычисления
всех Ci по данным df, можно оценить как О(р2 logp).
Упражнение 3.9.12. Проверьте это утверждение.
Указание. Примените аддитивные цепочки.
Поэтому для вычисления возведения в степень р в поле К достаточно
2р таких же операций в поле F и О(р2 logp) сложений в этом же поле.
Возведение в степень р в поле F можно выполнить за <?(рп) опера-
ций в поле GF(p). Поэтому битовая сложность возведения в степень р
в поле К оценивается как O(p2nlog2p).
Заключительная операция в алгоритме Дуурсма—Ли — это возведе-
ние в степень рР - 1 в поле К. Она, очевидно, сводится к р-кратному
возведению в степень р и последующему делению на основание. Деление
сводится к инвертированию и умножению. В [65] было замечено, что для
проверки цифровой подписи не надо вычислять полностью указанную
степень, так как для сравнения двух значений спаривания Тейта хрР~х
и урР~х достаточно сравнить х^у и урРх и тем самым избежать деления.
Для инвертирования представим элемент х Е К в виде ay 4- byp,
где а, b € F, что делается бесплатно, и вычислим обратный элемент
по формулам
_j (by 4- ayp)2 (a 4- b)2 ~ 2a2)y 4- ((a 4- b)2 - 2b2)yp
(ay 4- byp)(by 4- ayp)	2(a2 + b2)
(a 4- b)2 - 2a2) (a 4- b)2 - 2b2 p
=	2(a2 + &2) 7 + 2(a2 + &2) 7 '
Упражнение 3.9.13. Докажите эти формулы.
194
Глава 3. Криптосистемы на основе спариваний
Инвертирование согласно этим формулам сводится к трем возве-
дениям в квадрат, двум умножениям, одному инвертированию, четырем
сложениям-вычитаниям и двум удвоениям в поле F. В случае р = 3 удво-
ения исчезают.
Использование базиса {1, ст} заменяет в двух используемых сложени-
ях вычитаниях одно из слагаемых на единицу, что делает их фактически
тривиальным. Однако формулы в базисе {7, ур} инвариантны относитель-
но перестановки a, b и это иногда бывает удобно в схемной реализации.
Инвертирование в поле F можно также свести к инвертированию
в поле F и зависящему от р количеству сложений-вычитаний и умноже-
ний в поле F. Например, при р — 3, b = -1 согласно [58] инвертирование
можно выполнить по формулам
(ао +	= Со 4- С1Р 4- с2р2,
aQ + а2 ~ аоа2 ~ fli(fli + ai) -aoai +	а\-а^а2~а\
Со	7	5 Cj	~	, С 2	~	,
д	од
д = (do — <12)^0 4" (^1 ~ С’0)а1 4- (ао — &1 4" (12)С-2-
Упражнение 3.9.14. Докажите эти формулы.
Согласно им, инвертирование в поле F = GF(33n) требует 3 воз-
ведения в квадрат, 12 умножений, 12 сложений-вычитаний и одно ин-
вертирование в поле F = GF(3n). Можно одно из умножений заменить
на более простую операцию возведения в куб.
Упражнение 3.9.15. Проверьте эти утверждения.
Формулам инвертирования и умножения можно придать вид, сим-
метричный относительно циклической перестановки координат, если
воспользоваться оптимальным нормальным базисом {£, £3, £9}, £ = р2,
р = £3 - £9. В этом базисе умножение выполняется по формулам
(doC 4-	4- й2^9) (&о£ +	4" &2^9) — со£ 4- Ci£3 4-	,
— [-г, 2 - г] 4- [1 - г, 2 — г] — (2 — г) + (1 - г),
где операции с индексами выполняются по модулю 3 и для краткости
используются обозначения (j) = dj&j, [г, j] = (d, 4- b$)(dj + bj). Инверти-
рование выполняется по формулам
(do£ 4- di£3 4- d2^9)	— со£ 4~ Cj£3 4- С2^9,
(do 4- di)2 — d](do 4- d2)	(di 4- d2)2 — d2(do 4- di)
41 =-------------s----• C| =------------6-------------•
(do 4- d2)2 — do(di 4- d2)
d — (do 4- dj 4- 02) — dodjd2 — dQdj — djd2 — d2dQ.
Упражнение 3.9.16. Докажите эти формулы.
3.9. О реализации алгоритма Дуурсма—Ли	195
Если в формуле для 6 представить вычитаемое в виде ao^i(^o + <*1) +
а2(а? + и раскрыть скобки в числителях, то для инвертирования
понадобится 3 возведения в квадрат, 8 умножений, одно возведение в куб,
инвертирование и 14 сложений-вычитаний в поле F.
Упражнение 3.9.17. Проверьте эти утверждения.
Заметим, что использование в поле К произведения оптимальных
нормальных базисов
W}x{u\£9}
позволяет выполнять в нем операцию возведения в куб без использова-
ния сложений. Поэтому применение этого базиса в схемной реализации
алгоритма Дуурсма—Ли позволяет практически при той же сложности
схемы уменьшить ее глубину. Заметим еще, что использование в поле К
оптимального нормального базиса первого типа
{С С3, С9, С27, С81, С243, С7 = 1}
приводит к некоторому увеличению сложности, но уменьшению глубины
за счет уменьшения глубины умножения.
Приложение А
Алгоритмы с двоичными матрицами
А.1. Представление векторов и матрицы
Двоичные векторы v = (щ,..., Vj,..., vm) длины тп будем представ-
лять как (1, тп)-бинарные матрицы
V = (mn ... mij ... тп1т) = (vl...vj... vm).	(A.l)
Матрицы (A.l) удобно представлять (lx п)-таблицами R(V)
(ti...tn),	(A.2)
n = Ру"], элементами которых являются целые неотрицательные числа1),
меньшие 25.
Элементы таблицы интерпретируются как 25-ричные цифры, число-
вые эквиваленты которых можно представлять в любой, например, в дво-
ичной или десятичной системе счисления. Их можно интерпретировать
также как многочлены степени менее s. Двоичные представления элемен-
тов t\j,... ,tik таблицы (А. 2) получаются путем разбиения строки матрицы
А.1 на отрезки длины s справа налево. Если последний «отрезок» t\n ока-
зывается неполным, то он пополняется младшими нулями до длины s.
Аналогично разбиением на отрезки длины s снизу вверх вектор-
столбец vT = (vi,... ,Vj,..., vm)T можно представить (n, 1) таблицей
C(V), которая получается транспонированием таблицы R(V).
Рассматривая строки двоичной к х тп матрицы М как матрицы вида
(А.1), будем представлять матрицу М таблицей Т = Е(М),
/	tn	• • •	t\n \
ji _	^21	^22	•• •	tin
\ tkl	tk2	• • •	tkn /
с к строками и n — |"™1 столбцами.
Аналогичная «упаковка» по столбцам приводит к ([ , тп) -таблице
С(М). Элементы tij таблиц R(M) и С(М) — целые неотрицательные чис-
ла, меньшие 2s, интерпретируются как 2s -ричные цифры.
Параметр s определяется длиной машинного слова (целого типа данных) или иного
адресуемого блока данных.
A. 2. Умножение матрицы на вектор
197
Заметим, что при переходе к таблицам, элементами которых явля-
ются числа типа unsigned long, количество столбцов или строк исходной
матрицы сокращается в 32 раза.
Пример А. 1.1. Пусть тп — к = 5 и з = 4, тогда п = 2. Рассмотрим бинарную
матрицу
/1 1 0 1 IX
10 10 1
0 0 110 .
1110 0
\0 0 1 1 1/
Имеем п = [у] =	—2, поэтому таблица R(M) имеет два столбца, а таблица
С(М) — две строки:
	/1 их
	1 5
R(M) =	0 6
	1 12
	\0	7/
1 1
10 2
0 1 1
15 5 9
Обозначим
Я(М)(г, j, t) = M(i,m - (n - j + l)s 4-1
t-й бинарный элемент элемента tij таблицы R(M) и
С(М)(г', /, t') — M(k-(n-i' + 1)5 +t', jf)
t'-й бинарный элемент элемента ti>j> таблицы C(M). Очевидно, что при
тп ~ к таблицы R(M) и С(М) удовлетворяют тождествам
С(М)(г',/,0=Д(М)(г,;Д),
где i = т-(п-г'4-1)5-И', j = n-q', t = s-m + j’-q’ при q' =
г' = п - q, j' = m - (n - j 4- 1)5 4-1, t' — s - m 4- i - q при q' =	,
позволяющим преобразовать таблицу R(M) в таблицу С(М) или таблицу
С(М) в таблицу R(M), минуя их преобразование в бинарную квадратную
матрицу М.
А.2. Умножение матрицы на вектор
Умножение двоичной к х m-матрицы М, представленной таблицей
R(M), на двоичный вектор-столбец v из тп компонент, представленный
таблицей C(v), можно выполнить следующим образом.
1.	Умножить (к, п)-таблицу R(M) на (п, 1)-таблицу C(v) по правилам
умножения матриц:
198
Приложение А. Алгоритмы с двоичными матрицами
/ £ц	£12	...	tin
£21	£22	•• •	t2n
\ tkl	tk2	• • •	tkn /
где сложение и умножение являются логическими (поразрядными).
Например, 10 • 12 + 9 • 11 = 1.
2.	Из вектора-столбца V получим бинарный вектор-столбец V" высоты к,
(v{\
V" =
где V- — результат суммирования по модулю 2 двоичных разрядов
п
числа ^2 tjivi •
i=\
3.	Результат R(Mxv) умножения матрицы М на вектор-столбец v пред-
ставляется таблицей C(V").
Вектор V"T представим таблицей CV", которая и и есть результат
умножения матрицы М на вектор-столбец v. Транспонируем вектор V",
сопоставим полученному вектору новый вектор с ]fc/s[ компонентами,
элементами которого являются целые неотрицательные числа не большие
Is — 1. Полученный вектор снова транспонируем. Новый вектор-столбец
является результатом умножения Т на V.
Пример А.2.1. Пусть, как и в предыдущем примере, m = =	= умножим
(к, тп) -матрицу М из этого примера на вектор-столбец (1,0, 1,0, 1)г, используя
их табличные представления.
/ 1 • 1 -Ь 11 - 5 \
1-1+ 5-5
0-1+ 6-5
1-1 + 12-5
\0- 1+ 7-5/
4
4
5
откуда V” = (0, 1, 1, 0, 0)г. Таким образом, R(M х v) =
При умножении к х п-таблицы на п-вектор используется кп логиче-
ских умножений, к(п - 1) логических сложений, зк выделений разрядов
А.З. Алгоритм GAUS-MATRIX-TRIAN
199
и бинарных сложений, а также О(к) операций при переходе от вектора
V" к результату умножения. При умножении же бинарной таблицы на би-
нарный вектор пришлось бы выполнить O(snk) операций.
А.З. Алгоритм GAUS-MATRIX-TRIAN
Опишем алгоритм Гаусса (GAUS-MATRIX-TRIAN) приведения мат-
рицы М, представленной в виде таблицы Т = R(M) (см. с. 196) к тре-
угольному виду. Пусть задана таблица Т = R(M), а также пустая таблица
Т\, Все строки таблицы Т считаем активными. После окончания рабо-
ты алгоритма матрица М' из нулей и единиц, соответствующая таблице
Т\ = R(Ml) доставляет треугольный вид матрицы М.
Пусть активны строки с номерами г’о, г’о 4-1,..., к. Среди чисел в ак-
тивных строках первого столбца а выберем наибольшее (среди многочле-
нов в активных строках первого столбца выберем многочлен Хг(1 + д(Х))
при наименьшем г). Пусть, например, это будет число (многочлен) tji,
j г‘о- Если tji = 0, то удаляем из Т первый столбец и добавляем
этот столбец в таблицу Т\ справа. Далее снова рассматриваем элементы
первого столбца уже полученной матрицы.
В противном случае определяем такое целое неотрицательное число г,
что 2Г tj\ < 2r+l. Если ^01 < 2Г, то к строке с номером г’о таблицы Т
прибавляем (в логическом смысле) строку с номером j.
Используемая операция прибавления одной строки таблицы к другой
есть операция сложения многочленов или поразрядного сложения двоич-
ных чисел.
Далее для каждого г, г = io + 1, г'о + 2,..., fc в случае tn 2r (deg^i = г),
г’-ю строку матрицы Г, заменяем логической суммой i-й и г’о-й строк,
г'о-ю строку таблицы Т далее считаем неактивной.
С полученной таблицей Т далее проделываем описанные выше дей-
ствия, начиная с поиска активной строки с наибольшим первым слева
элементом и т.д. до тех пор, пока в таблице Т не останется элементов
или не останется активных строк. Если в таблице Т не осталось активных
строк, но она не пуста, то приписываем ее справа к таблице Т\.
После этого работа алгоритма GAUS-MATRIX-TRIAN заканчивается.
Пример А.З. 1. Пусть s = 4 и
8
11
4
\ 10
15 3\
10 4
2 6
13 1
3 2/
Третья строка таблицы Т имеет наибольший первый элемент (11), 23	11 < 24
и г = 3. Так как 7 < 2Г, то к первой строчке таблицы Т прибавляем (в логическом
200
Приложение А. Алгоритмы с двоичными матрицами
смысле) третью. Получим новую таблицу
	/!2 8	13 10	Л 4
т =	11	2	6
	4	13	1
	\ 10	3	2/
Так как первые элементы второй, третьей и пятой строк полученной таблицы не
меньше 23 = 8, то к этим строкам прибавляем первую строку. Получим
4
7
4
\ 6
Т =
13 5\
7 1
15 3
13 1
14 7/
Первую строчку полученной таблицы далее считаем неактивной, а таблица
Ti остается пустой.
В полученной матрице Т наибольший первый справа элемент среди активных
строк — в третьей строке. Имеют место неравенства 22	7 < 23. Поэтому г = 2.
Так как 4	22, то вторую строку не меняем, а ко всем строкам, начиная с третьей
прибавляем вторую строку. Получаем новую таблицу Т,
4
3
0
\ 2
Т =
13 5\
7 1
8 2
10 0
9 6/
Вторую строку таблицы Т далее считаем неактивной. Таблица остается пока
пустой.
В полученной таблице Т среди активных строк, имеющих наибольший пер-
вый элемент — третья и 21^3<22,г = 2. Прибавляя эту строку к пятой, получим
		13	5\
	4	7	1
Т =	3	8	2
	0	10	0
	\ 1	1	4/
Третью строку таблицы Т далее считаем неактивной. Таблица Т[ по-прежнему
остается пустой.
На следующем шаге к четвертой строчке таблицы Т прибавляется пятая,
а после этого к пятой строке прибавляется новая четвертая. Получается
	4	13 7	5\ 1
Т =	3	8	2
	1	11	4
	\ 0	10	0/
Таблица снова остается пустой, а четвертая строка становится неактивной.
A.4. Алгоритм проверки невырожденности матрицы
201
Единственная оставшаяся активной строка таблицы Т имеет первый элемент
равный нулю. Поэтому переносим первый столбец из Т в . Получаем
Далее, так как в Т осталась единственная активная строка, правый элемент
которой не равен нулю, то таблица Т не изменяется, пятая строка становится
неактивной, В таблице Т не осталось активных строк. Поэтому приписываем
эту таблицу к Т\ справа. Получаем
/12
4
3
1
\ 0
13 5\
7 1
8 2
11 4
10 0/
Алгоритм заканчивает работу. Таблица Т\ — результат приведения Т к треуголь-
ному виду.
При приведении таблицы Ten строками и п столбцами к треуголь-
ному виду по приведенному выше алгоритму GAUS-MATRIX-TRIAN
используется:
1)	не более чем fc2]fc/s[ операций логического сложения s-разрядных
чисел;
2)	не более чем к2 операций сравнения при определении наибольших
элементов в столбцах;
3)	не более чем к2 операций деления на 2 при определении чисел г;
4)	не более чем к2 сравнений правых элементов в строках с числами 2Г
при определении необходимости складывать строки;
5)	не более чем к операций удаления столбцов, а также добавления
столбцов и придания неактивного статуса строкам;
6)	не более чем Зк операций с компонентами вектора V.
Всего операций не более A:2]k/s[ 4- Зк2 4- 6к. Поэтому при s = 32, к & 200
алгоритм GAUS-MATRIX-TRIAN дает существенный выигрыш по вре-
мени.
А.4. Алгоритм проверки невырожденности матрицы
Пусть матрица М представлена в виде таблицы Т = R(M), опи-
санной в разд. А.1. а — результат обработки таблицы Т алгоритмом
GAUS-MATRIX-TRIAN. Элемент таблицы Г], находящийся в г-й строке
и j-м столбце обозначим Пусть таблице Т\ соответствует квадратная
202
Приложение А. Алгоритмы с двоичными матрицами
матрица М' = (rriij) из нулей и единиц — результат приведения матри-
цы М к треугольному виду.
Опишем, как по таблице Т1 проверить, является ли матрица М,
невырожденной. Для этого будем работать с s -разрядными числами (эле-
ментами таблицы Т[). Для каждого г, i = 1, 2,..., к рассмотрим строку
таблицы Т\ с номером г. Пусть j = ]	[ — номер столбца (считая
справа), в котором должен находиться бит, равный тпц. Через г, обозна-
чим число к - i + 1 - (j - l)s. Если число Ц — [tij/2Г’-1] делится на 2,
то тц = 0 и матрица М вырождена. Если для каждого г, г = 1, 2,..., к,
число Ц не делится на 2, то матрица М невырождена.
Пример А.4.1. Пусть з = 2, к = 5 и результатом работы алгоритма GAUS-MATRIX-
TRIAN является таблица Т[,
Матрица М' из нулей и единиц, которая соответствует таблице Т\, имеет вид
М' =
о
\о
1 о о
1 0 1
0 1 о
0 0 1
ООО
1
1/
1
1
Имеем п = 3. Для первой строки таблицы выполнено: j = 3, п = 1, Ц = 1.
Число Ц не делится на 2. Далее проверяем, что 12, h, к не делятся на 2. Таким
образом, таблица Т\ соответствует невырожденной матрице из нулей и единиц.
Нетрудно видеть, что проверку невырожденности таблицы Т\, ал-
горитм NONSIGN-MATRIX выполняет за O(fc) действий, т. е. в случае
применения алгоритма GAUS-MATRIX-TRIAN проверка невырожденно-
сти матрицы М, заданной таблицей Т выполняется за O(k2]k/s[+3k2+6k)
действий.
А.5. Приведение матрицы к диагональному виду
Пусть далее матрица М невырождена. Представив ее в виде таблицы
Т = R(M) (см. разд. А.1) приведем ее к треугольной матрице ЛГ, по-
лучив представление Т\ — R(M() по алгоритму GAUS-MATRIX-TRIAN
(см. разд. А.2). Приведем матрицу М1, а следовательно и матрицу М
к диагональному виду. Для этого преобразуем таблицу следующим об-
разом. Пусть индекс i пробегает последовательность к, к - 1,..., 3, 2. Для
каждого i положим j = ] — *+1 [, гг; = к - i +1 - (j - l)s. Пусть i' пробегает
значения i + 1, i + 2,..., к. Положим j — [t^j/2Г*-1]. Если не делится
А.5. Приведение матрицы к диагональному виду
203
на 2, то элемент не равен нулю и нужно к строке таблицы Т, имеющей
номер i‘ прибавить (в логическом смысле) строку с номером г.
Интерпретируя строки таблицы Т\ = R(M') как многочлены, эти же
преобразования можно описать более просто:
для i = к, 2
для j = i + 1, 1
если deg tj = deg ti, то заменить ti = ti +1j.
Пусть выполнены все указанные действия. Тогда полученная таблица
?2 соответствует бинарной единичной к х к матрице Е,
/1 о ... 0\
\0 О ... 1/
являющейся результатом приведения исходной бинарной матрицы М
к треугольному виду.
Пример А.5.1. Пусть, как и в предыдущем примере, s = 2, к = 5 и
3
1
3
Так как последний элемент всех строчек (на пятую строку можно не смотреть)
не делится на 2 (каждая строка, кроме пятой представляет многочлен степени 5),
то к каждой строке (кроме пятой) прибавляем пятую строку. Получаем
Далее, последний элемент в первой и третьей строках таблицы Т\ делится
на 4 (вторая строка представляет многочлен степени четыре), поэтому четвертую
строку прибавляем (в логическом смысле) только ко второй. Получаем таблицу ,Т\,
Далее, предпоследний элемент первой и второй строк делится на 2, поэтому,
не меняя таблицу Т\, переходим к рассмотрению ее второй строки. Предпоследний
204
Приложение А. Алгоритмы с двоичными матрицами
элемент первой строки не делится на 4. Поэтому к первой строке прибавляем вто-
рую. Получаем
о
о
о

О
2
1
О
О
о
о
2
Полученная таблица Т{ соответствует диагональному виду матрицы М'.
Нетрудно видеть, что приведение матрицы М' к диагональному виду
алгоритм GAUS-MATRIX-DIAGON выполняет за О(п2) действий, так как
прибавляемая строка содержит ровно один ненулевой элемент.
А.6. Обращение матрицы
Рассмотрим таблицу Т, представляющую бинарную квадратную к х к
матрицу М, как это описано в разд. А. 1.
т =	f in hi	in • • hi • •	iin • hn	
	к ikl	ikl • •	• ikn /	
Обозначим через Е единичную к х к матрицу,				
	/1	0 0 .	.. 0\	
	0	1 0 .	.. 0	
Е =	0	0 1 .	.. 0	
	\o	0 0 .	.. 1/	
Ей соответствует таблица	i'll	f'12	.	•  ^ln	
Е' =	i'll	i'n •	• • 4	
	yt'kx	i'kl •	•• ikn ,	/
с элементами из Е[.
Применим алгоритм GAUS-MATRIX-TRIAN к таблице Т. При этом,
если в процессе работы алгоритма некоторая строка таблицы Т при-
бавляется к другой ее строке, то ту же самую операцию производим
с таблицей Е1.
Если матрица, соответствующая таблице Т, оказалась невырожден-
ной, и таблица — результат применения к Т алгоритма GAUS-
MATRIX-TRIAN, то применим к Т\ алгоритм GAUS-MATRIX-DIAGON.
A.6. Обращение матрицы
205
При этом опять, если в процессе работы алгоритма некоторая строка
таблицы Т\ прибавляется к другой ее строке, то ту же самую операцию
производим с таблицей, полученной из Е'.
После приведения таблицы Т\ к диагональному виду результат преоб-
разования таблицы Е’ соответствует матрице обратной к рассматриваемой
к х к матрице.
Пример А.6.1. Пусть к = 5, s = 2 и
Имеем
0 0\
2 0
1 0
0 2
о 1/
После обработки первой строки таблицы Т получим
Z1		2				0	
	0	2	1		0	2	0
т =	0	2	2	, Е' =	1	1	0
	0	1	1		0	0	2
	\0	3	2/		\1	0	1/
После обработки второй строки:
	/1 2 0\		/i 0 0\
	0 2 1		0 2 0
т =	0 0 3	, Е’ =	1 3 0
	0 1 1		0 0 2
	\0 1 3/		\1 2 1/
После прибавления четвертой строки к третьей и обработки третьей строки:
	/! 2 0\		/! 0 0\
	0 2 1		0 2 0
т =	0 1 2	, Е' =	1 3 2
	0 0 3		1 3 0
	\0 0 1)		\0 1 3/
Таким образом, таблица Т уже имеет треугольный вид и далее применяем
к ней алгоритм GAUS - MATRIX-DI AGON. После обработки пятой строки таблицы
206
Приложение А. Алгоритмы с двоичными матрицами
Т получаем:
	2		/1 0
	0 2 0		0 3 3
т =	0 1 2	, Е' =	1 3 2
	0 0 2		1 3 0
	\0 0 1/		\0 1 3/
После обработки четвертой строки:
	/1 2 0\		Zi 0 0\
	0 2 0		0 3 3
т =	0 1 0	, & =	0 1 1
	0 0 2		1 2 3
	\0 0 1/		\0 1 3/
После обработки третьей строки ничего не изменяется, а после обработки второй
получаем
Z1		0	0\			3	3\
	0	2	0		0	3	3
т =	0	1	0	, Е' =	0	1	1
	0	0	2		1	2	3
	\0	0	1/		\о	1	3/
Полученная таблица Е' соответствует бинарной матрице
	/1	1	1	1	
	0	1	1	1	1
м~1 =	0	0	1	0	1
	1	1	0	1	1
	\о	0	1	1	1/
которая является обратной к исходной:
	/1	1	0	0	
	0	1	0	0	1
м =	1	0	0	1	0
	0	0	1	0	1
	\1	0	1	1	0/
А.7. Умножение вектор-строки на матрицу
Пусть требуется умножить бинарный вектор-строку v длины тп
на (тп, fc)-матрицу М. Представим вектор v таблицей R(v) = (tj), а матри-
цу М — таблицей С(М) = (tij). Представление R(v х М) произведения
вектора-строки v на матрицу М можно получит следующим образом.
А.7. Умножение вектор-строки на матрицу
207
1.	Умножить (1, п)-таблицу R(v) на (п, А;)-таблицу С(М) по правилам
умножения матриц:
V' = (*1 «2 • • • in) х
(п	п
г=1	г=1
( til	t\2	• • •	t\k	\
h\	^22	•••	hk
\ ^n\	^n2	• • •	Ink	/
где сложение и умножение являются логическими (поразрядными).
2.	Из вектора-строки V получим бинарный вектор-строку У" длины к,
V"=(y[ У2' ... У/),
где V- — результат суммирования по модулю 2 двоичных разрядов
п
числа 52 tjivi-
1=1
3.	Результат R(v х М) умножения вектор-строки v на матрицу М пред-
ставляется таблицей R(V").
Пример А. 7.1. Пусть, как и в предыдущем примере, т = А: = 5и$ = 4, умножим
вектор-строку (1,0,1,0, 1), на (5, 5)-матрицу М из примера АЛЛ, используя их
табличные представления.
тг/ / , с х /11	0
г=" 5)Х(,0 2 15
1
5 9/
= (1-1+5-10 1-1 + 5-2 1-0 + 5-15 1-1 + 5-5 1-1 + 5-9) =
= (0001 0001 1010 0000),
откуда V" — (1, 1, 0,1,0)г Таким образом, R(y х М) = ( 1 10).
Приложение В
Таблицы неприводимых многочленов
В.1.	Неприводимые многочлены над полем GF(2)
В.1.1.	Неприводимые трехчлены степени п, 2 п 2000
В таблицах, сгенерированных программами из магистерской диссер-
тации П. И. Артемьевой (МЭИ), ВЛ, В.2, В.З, В.4, В.5, В.6, В.7, В.8, В.9,
В. 10, ВЛ1, ВЛ2 и ВЛЗ представлены неприводимые трехчлены над полем
GF(2) степени от 2 до 1999. Из двух различных взаимно возвратных мно-
гочленов в таблице представлен многочлен с меньшей степенью второго
члена.
В.1. Неприводимые многочлены над полем GF(2)
209
Таблица В.1
Неприводимые трехчлены над полем GF(2) вида 1 4- X1 + Хт, 2 т 202
t	т	t	т	t	т	t	т	t	т	t	т	t	т	t	т
1	2	2	29	24	55	5	84	28	105	3	130	15	154	22	177
1	3	1	30	4	57	9	84	37	105	17	132	62	155	88	177
1	4	9	30	7	57	11	84	43	105	29	132	9	156	31	178
2	5	3	31	22	57	13	84	49	105	57	134	11	156	87	178
3	5	6	31	25	57	27	84	52	105	11	135	57	156	3	180
1	6	7	31	19	58	35	84	15	106	16	135	61	156	27	180
3	6	13	31	1	60	39	84	17	108	22	135	63	156	33	180
1	7	10	33	9	60	21	86	27	108	29	135	65	156	45	180
3	7	13	33	И	60	13	87	31	108	21	137	31	159	55	180
1	9	7	34	15	60	38	89	33	108	35	137	34	159	69	180
4	9	2	35	17	60	27	90	45	108	57	137	40	159	81	182
3	10	9	36	23	60	21	92	33	ПО	15	140	18	161	56	183
2	11	11	36	29	62	2	93	10	111	29	140	39	161	24	185
3	12	15	36	1	63	21	94	49	111	45	140	60	161	41	185
5	12	4	39	5	63	11	95	9	113	65	140	27	162	69	185
5	14	8	39	11	63	17	95	15	113	21	142	63	162	11	186
1	15	14	39	28	63	6	97	30	113	52	145	81	162	79	186
4	15	3	41	31	63	12	97	33	118	69	145	37	166	9	191
7	15	20	41	18	65	33	97	45	118	71	146	6	167	18	191
3	17	7	42	32	65	34	97	8	119	14	147	35	167	51	191
5	17	5	44	3	66	11	98	38	119	49	147	59	167	71	191
6	17	1	46	9	68	27	98	18	121	27	148	77	167	15	193
3	18	5	47	33	68	15	100	30	121	53	150	34	169	73	193
7	18	14	47	6	71	19	100	2	123	73	150	42	169	85	193
9	18	20	47	9	71	25	100	19	124	3	151	57	169	87	194
3	20	21	47	18	71	37	100	37	124	9	151	84	169	3	196
5	20	9	49	20	71	49	100	45	124	15	151	11	170	33	196
2	21	12	49	35	71	29	102	55	124	31	151	23	170	67	196
7	21	15	49	25	73	37	102	21	126	39	151	1	172	9	198
1	22	22	49	28	73	9	103	49	126	43	151	7	172	65	198
5	23	3	52	31	73	13	103	1	127	46	151	81	172	34	199
9	23	7	52	35	74	30	103	7	127	51	151	13	174	67	199
3	25	19	52	21	76	31	103	15	127	63	151	57	174	14	201
7	25	21	52	9	79	4	105	30	127	66	151	6	175	17	201
1	28	9	54	19	79	7	105	63	127	67	151	16	175	59	201
3	28	21	54	4	81	8	105	5	129	70	151	18	175	79	201
9	28	27	54	16	81	16	105	31	129	1	153	57	175	55	202
13	28	7	55	35	81	17	105	46	129	8	153	8	177		
210
Приложение В. Таблицы неприводимых многочленов
Таблица В.2
Неприводимые трехчлены над полем GF(2) вида 1 + X1 + Хт, 204 т 382
t	т	t	т	t	т	t	т	t	т	t	т	t	т
27	204	88	225	82	255	91	276	142	295	81	324	138	353
99	204	97	225	12	257	5	278	147	295	93	324	143	353
43	207	109	225	41	257	5	279	5	297	99	324	153	353
6	209	113	228	48	257	10	279	83	297	135	324	173	353
8	209	26	231	51	257	38	279	103	297	149	324	99	354
14	209	34	231	65	257	40	279	122	297	34	327	135	354
45	209	91	231	71	258	41	279	137	297	152	327	57	358
47	209	74	233	83	258	59	279	5	300	50	329	68	359
50	209	31	234	15	260	73	279	7	300	54	329	117	359
62	209	103	234	35	260	76	279	45	300	99	330	63	362
7	210	5	236	95	260	80	279	55	300	89	332	107	362
105	212	73	238	105	260	125	279	57	300	123	332	9	364
73	214	117	238	93	263	93	281	73	300	2	333	67	364
23	215	36	239	42	265	99	281	75	300	55	337	29	366
51	215	81	239	127	265	35	282	91	300	57	337	21	367
63	215	70	241	47	266	43	282	111	300	135	337	171	367
77	215	95	242	25	268	63	282	147	300	139	337	91	369
101	215	111	244	61	268	53	284	41	302	147	337	НО	369
45	217	82	247	53	270	99	284	1	303	45	340	139	370
64	217	102	247	81	270	119	284	102	305	165	340	183	370
66	217	35	249	133 ,	270	141	284	15	308	125	342	111	372
82	217	86	249	58	271	69	286	93	310	133	342	135	372
85	217	103	250	70	271	73	286	79	313	75	343	165	372
11	218	15	252	23	273	71	287	121	313	135	343	16	375
15	218	27	252	28	273	116	287	15	314	138	343	64	375
71	218	33	252	53	273	125	287	63	316	159	343	149	375
83	218	39	252	55	273	21	289	135	316	22	345	182	375
99	218	53	252	56	273	36	289	45	318	37	345	41	377
7	220	59	252	67	273	84	289	36	319	106	345	75	377
33	220	67	252	88	273	37	292	52	319	63	346	43	378
49	220	77	252	92	273	97	292	129	319	103	348	63	378
33	223	81	252	98	273	33	294	31	321	53	350	107	378
34	223	105	252	ПО	273	49	294	41	321	34	351	147	378
64	223	109	252	113	273	61	294	56	321	55	351	47	380
70	223	117	252	67	274	81	294	76	321	79	351	63	380
91	223	46	253	99	274	48	295	82	321	116	351	105	380
32	225	52	255	135	274	112	295	155	321	134	351	81	382
74	225	56	255	63	276	123	295	67	322	69	353		
В.1. Неприводимые многочлены над полем GF(2)
211
Таблица В.З
Неприводимые трехчлены над полем GF(2) вида 1 + Xf 4- Хт, 383 т 560
t	т	t	ТП	t	т	t	т	t	т	t	т	t	т
		189	404	118	433	93	463	81	486	31	511	261	534
		141	406	153	433	168	463	189	486	160	511	94	537
90	383	157	406	165	436	214	463	243	486	202	511	195	538
108	383	71	407	65	438	31	465	94	487	216	511	9	540
135	383	105	407	49	439	59	465	127	487	26	513	11	540
6	385	87	409	133	439	103	465	83	489	85	513	81	540
24	385	147	412	145	439	124	465	219	490	175	513	99	540
51	385	13	414	156	439	158	465	7	492	242	513	113	540
54	385	53	414	171	439	217	465	17	494	67	514	135	540
111	385	102	415	7	441	27	468	137	494	103	514	155	540
142	385	163	415	31	441	33	468	76	495	211	516	165	540
159	385	107	417	35	441	143	468	89	495	91	516	179	540
83	386	113	417	127	441	171	468	118	495	33	518	191	540
159	388	155	417	196	441	183	468	226	495	45	518	207	540
9	390	199	418	212	441	189	468	78	497	ИЗ	518	211	540
49	390	7	420	217	441	195	468	216	497	79	519	16	543
89	390	45	420	81	444	9	470	228	497	32	521	28	543
28	391	65	420	105	446	149	470	155	498	48	521 .	58	543
31	391	77	420	153	446	177	470	27	500	158	521	203	543
7	393	87	420	73	447	1	471	75	500	168	521	235	543
62	393	127	420	83	447	119	471	95	500	39	522	122	545
91	393	135	420	134	449	127	471	125	500	171	522	193	550
135	394	161	420	167	449	200	473	185	500	259	522	135	551
25	396	195	420	47	450	191	474	243	500	167	524	240	551
51	396	149	422	79	450	215	474	245	500	195	524	39	553
87	396	177	422	159	450	9	476	3	503	97	526	57	553
109	396	25	423	38	455	15	476	26	503	47	527	94	553
169	396	12	425	62	455	129	476	248	503	123	527	99	553
175	396	21	425	74	455	141	476	156	505	147	527	109	553
26	399	42	425	16	457	121	478	174	505	152	527	255	553
49	399	66	425	61	457	104	479	23	506	198	527	258	553
86	399	111	425	123	457	105	479	95	506	239	527	153	556
109	399	191	425	210	457	122	479	135	506	42	529	273	556
154	399	63	426	217	457	158	479	9	508	114	529	73	558
181	399	105	428	226	457	224	479	109	508	157	529	34	559
152	401	120	431	203	458	138	481	69	510	1	532	70	559
170	401	200	431	19	460	201	481	197	510	37	532	148	559
171	402	33	433	61	460	231	481	10	511	81	532	210	559
65	404	61	433	73	462	105	484	15	511	161	534		
212
Приложение В. Таблицы неприводимых многочленов
Таблица В.4
Неприводимые трехчлены над полем GF(2) вида 1 + X1 4- Хт, 561 т 734
t	т	t	т	t	m	t	т	t	т	t	т	t	т
71	561	253	588	93	620	287	641	297	662	336	689	203	714
109	561	93	590	95	620	119	642	107	663	79	690	259	714
155	561	86	593	185	620	249	646	257	663	299	692	183	716
163	564	108	593	297	622	5	647	275	663	311	692	257	716
153	566	119	593	68	623	150	647	307	663	169	694	275	716
273	566	177	593	87	623	215	647	33	665	177	695	165	718
28	567	19	594	128	623	312	647	53	665	212	695	150	719
112	567	27	594	185	623	37	649	144	665	267	697	174	719
143	567	35	594	230	623	73	649	192	665	310	697	257	719
245	567	195	594	251	623	171	649	269	665	215	698	299	719
275	567	273	596	296	623	310	649	317	665	311	698	314	719
77	569	30	599	311	623	321	649	147	668	75	700	9	721
210	569	210	599	133	625	3	650	153	670	145	700	159	721
67	570	201	601	156	625	14	651	273	670	225	700	256	721
143	570	202	601	251	626	93	652	15	671	325	700	270	721
13	574	215	602	223	628	97	652	201	671	37	702	283	721
146	575	105	604	289	628	33	654	243	671	93	702	328	721
258	575	165	606	307	631	45	654	28	673	309	702	231	722
25	577	105	607	101	633	213	654	183	673	317	702	207	724
27	577	147	607	292	633	249	654	252	673	17	705	5	726
231	577	273	607	39'	634	88	655	259	673	19	705	241	726
237	580	31	609	315	634	192	655	300	673	68	705	180	727
85	582	91	609	217	636	38	657	31	676	79	705	217	727
261	582	128	609	269	636	73	657	241	676	161	705	357	727
130	583	181	609	311	636	92	657	277	676	194	705	58	729
88	585	233	609	315	636	148	657	66	679	266	705	253	729
121	585	127	610	16	639	292	657	216	679	328	705	147	730
151	585	81	612	88	639	55	658	171	682	331	705	343	732
157	585	157	612	95	639	163	658	243	682	15	708		
232	585	297	612	179	639	11	660	209	684	287	708		
256	585	45	614	224	639	21	660	197	686	301	708		
35	588	177	614	233	639	99	660	13	687	335	708		
77	588	211	615	295	639	121	660	133	687	92	711		
91	588	232	615	305	639	145	660	274	687	319	711		
99	588	238	615	11	641	253	660	14	689	41	713		
151	588	200	617	36	641	21	662	87	689	297	713		
201	588	295	618	45	641	141	662	179	689	23	714		
245	588	9	620	95	641	269	662	207	689	151	714		
В.1. Неприводимые многочлены над полем GF(2)
213
Таблица В.5
Неприводимые трехчлены над полем GF(2) вида 1 + X1 4- Хт, 735 < т 899
t	т	t	т	t	т	t	т	t	т	t	т	t	т
44	735	18	751	121	772	217	801	17	822	139	850	11	879
49	735	187	751	185	774	325	801	201	822	159	852	80	879
89	735	310	751	249	774	75	804	297	822	297	852	91	879
112	735	158	753	93	775	183	804	405	822	357	852	121	879
119	735	19	754	217	775	295	804	9	823	29	855	190	879
196	735	147	754	367	775	21	806	91	823	142	855	238	879
259	735	45	756	29	777	141	806	280	823	146	855	78	881
262	735	81	756	70	777	7	807	357	823	151	855	84	881
299	735	99	756	302	777	308	807	38	825	254	855	236	881
301	735	117	756	343	777	403	807	255	826	377	855	392	881
343	735	119	756	375	778	15	809	189	828	379	855	99	882
364	735	159	756	13	780	92	809	205	828	119	857	147	882
5	737	201	756	45	780	137	809	49	831	215	857	183	882
303	737	217	756	143	780	210	809	322	831	221	857	243	882
347	738	231	756	221	780	233	809	149	833	258	857	343	882
135	740	243	756	285	780	159	810	159	833	270	857	173	884
153	740	315	756	299	780	243	810	195	833	402	857	147	887
287	740	349	756	301	780	247	810	215	833	207	858	317	887
317	740	351	756	305	780	299	810	339	833	219	858	336	887
85	742	233	758	315	780	399	810	15	834	35	860	127	889
225	742	357	758	329	782	29	812	61	838	405	860	169	889
90	743	98	759	68	783	87	812	54	839	14	861	310	889
144	743	109	759	71	783	125	812	314	839	349	862	312	889
146	743	230	759	103	783	167	812	327	839	1	865	381	889
209	743	251	759	202	783	183	812	144	841	9	865	183	890
210	743	299	759	92	785	237	812	309	841	228	865	31	892
239	743	3	761	191	785	261	812	47	842	379	865	173	894
279	743	33	761	212	785	377	812	105	844	417	865	413	894
326	743	84	761	219	785	21	814	2	845	75	866	12	895
258	745	138	761	30	791	145	814	105	846	215	866	113	897
333	745	83	762	108	791	333	815	129	846	145	868	382	897
336	745	115	762	251	791	336	815	189	846	241	868	207	898
342	745	168	767	253	793	339	815	136	847	285	868		
351	746	254	767	143	794	52	817	153	847	301	870		
19	748	120	769	263	794	187	817	276	847	378	871		
31	748	216	769	53	798	355	817	393	847	352	873		
133	748	322	769	141	798	119	818	253	849	149	876		
309	750	7	772	25	799	123	820	111	850	291	876		
214
Приложение В. Таблицы неприводимых многочленов
Таблица В.6
Неприводимые трехчлены над полем GF(2) вида 1 + X1 + Хт, 900 т < 1084
t	т	t	т	t	т	t	т	t	т	t	т	t	т
1	900	141	919	187	945	404	969	65	996	399	1026	291	1052
15	900	274	919	191	945	446	969	369	996	119	1028	357	1052
21	900	336	919	203	945	7	972	101	998	203	1028	105	1054
79	900	390	919	229	945	115	972	417	998	98	1029	24	1055
135	900	221	921	189	948	153	972	477	998	343	1029	243	1055
165	900	340	921	405	948	155	972	59	999	93	1030	198	1057
171	900	364	921	461	948	243	972	17	1001	68	1031	331	1057
219	900	455	921	260	951	279	972	54	1001	116	1031	438	1057
225	900	31	924	290	951	297	972	354	1001	287	1031	27	1058
233	900	45	924	391	951	377	972	422	1001	371	1031	439	1060
273	900	173	924	168	953	405	972	75	1007	108	1033	525	1060
275	900	203	924	224	953	19	975	96	1007	330	1033	49	1062
333	900	215	924	435	953	121	975	351	1007	340	1033	297	1062
441	900	365	926	131	954	133	975	386	1007	498	1033	405	1062
21	902	403	927	135	954	15	977	405	1007	75	1034	168	1063
35	903	433	927	305	956	63	977	55	1009	411	1036	208	1063
160	903	455	927	347	956	207	977	148	1009	21	1039	285	1063
217	903	31	930	143	959	374	977	99	1010	88	1039	370	1063
220	903	279	930	164	959	480	977	115	1012	279	1039	463	1065
221	903	177	932	312	959	178	979	301	1012	364	1039	476	1065
263	903	231	932	395 ,	959	177	982	385	1014	418	1039	7	1071
278	903	275	932	422	959	277	982	186	1015	412	1041	50	1071
322	903	387	932	18	961	481	982	258	1015	439	1042	56	1071
117	905	447	932	130	961	230	983	447	1015	41	1044	281	1071
341	905	455	932	393	961	342	983	466	1015	71	1044	436	1071
123	906	417	935	103	964	222	985	484	1015	361	1044	361	1078
187	906	217	937	231	964	3	986	135	1020	10	1047	445	1078
143	908	316	937	313	964	121	988	461	1020	430	1047	230	1079
204	911	207	938	433	964	161	990	495	1020	470	1047	282	1079
260	911	45	942	441	964	297	990	317	1022	141	1049	342	1079
378	911	24	943	201	966	39	991	7	1023	227	1049	24	1081
91	913	334	943	36	967	171	991	43	1023	290	1049	235	1081
129	913	450	943	130	967	193	991	127	1023	293	1049	318	1081
439	913	77	945	210	967	466	991	294	1025	327	1049	348	1081
183	916	79	945	400	967	472	991	306	1025	357	1049	423	1081
243	916	94	945	31	969	62	993	383	1025	390	1049	525	1081
77	918	112	945	74	969	367	993	35	1026	159	1050	407	1082
36	919	154	945	308	969	223	994	375	1026	371	1050	189	1084
В.1. Неприводимые многочлены над полем GF(2)
215
Таблица В.7
Неприводимые трехчлены над полем GF(2) вида 1 + X1 + Хт, 1085 т 1219
t	т	t	т	t	т	t	т	t	т	t	т
62	1085	503	1098	333	1116	189	1140	173	1169	196	1191
189	1086	35	1100	405	1116	413	1140	207	1169	212	1191
217	1086	93	1100	479	1116	419	1140	27	1170	173	1193
321	1086	165	1100	495	1116	539	1140	267	1170	281	1196
112	1087	209	1100	283	1119	357	1142	133	1174	519	1196
240	1087	245	1100	329	1119	461	1142	476	1175	405	1198
445	1087	407	1100	62	1121	227	1145	16	1177	114	1199
457	1087	497	1100	107	1121	506	1145	64	1177	171	1201
481	1087	519	1100	113	1121	131	1146	70	1177	360	1201
91	1089	117	1102	176	1121	243	1146	126	1177	388	1201
148	1089	65	1103	203	1121	23	1148	186	1177	287	1202
206	1089	71	1103	427	1122	221	1148	288	1177	43	1204
283	1089	164	1103	105	1126	90	1151	412	1177	129	1204
400	1089	189	1103	309	1126	125	1151	375	1178	387	1204
466	1089	434	1103	561	1126	241	1153	491	1178	459	1204
79	1090	465	1103	27	1127	268	1153	25	1180	559	1204
243	1090	21	1105	171	1127	415	1153	99	1180	513	1206
23	1092	57	1105	317	1127	499	1153	77	1182	273	1207
65	1092	96	1105	465	1127	541	1153	405	1182	423	1207
77	1092	321	1105	512	1127	75	1154	425	1182	511	1207
ИЗ	1092	363	1105	103	1129	307	1156	87	1183	118	1209
143	1092	439	1105	135	1129	513	1156	108	1183	145	1209
169	1092	195	1106	208	1129	245	1158	136	1183	290	1209
201	1092	327	1108	551	ИЗО	249	1158	134	1185	356	1209
353	1092	417	1110	129	1134	66	1159	317	1185	243	1210
455	1092	549	1110	189	1134	129	1159	386	1185	363	1210
479	1092	13	1111	321	1134	424	1159	171	1186	463	1210
57	1094	40	1111	441	1134	365	1161	75	1188	203	1212
261	1094	238	1111	9	1135	409	1161	153	1188	567	1212
139	1095	321	1111	36	1135	551	1161	251	1188	257	1214
383	1095	531	1111	106	1135	19	1164	261	1188	605	1214
476	1095	107	1113	298	1135	85	1164	287	1188	302	1215
538	1095	217	1113	277	1137	161	1164	327	1188	322	1215
14	1097	238	1113	313	1137	189	1166	395	1188	393	1217
86	1097	280	1113	458	1137	513	1166	413	1188	91	1218
303	1097	310	1113	31	1138	133	1167	507	1188	215	1218
83	1098	59	1116	183	1138	265	1167	525	1188	471	1218
87	1098	227	1116	141	1140	114	1169	233	1190		
216
Приложение В. Таблицы неприводимых многочленов
Таблица В.8
Неприводимые трехчлены над полем GF(T) вида 1 + X1 4- Хт, Y11& С т < 1374
t	т	t	т	t	т	t	т	t	т	t	т
413	1220	193	1239	421	1260	315	1284	129	1319	629	1350
555	1220	466	1239	483	1260	153	1286	52	1321	39	1351
255	1223	610	1239	545	1260	441	1286	490	1321	150	1351
549	1223	616	1239	585	1260	470	1287	337	1324	201	1351
588	1223	54	1241	589	1260	622	1287	555	1324	241	1351
234	1225	165	1241	77	1263	99	1289	397	1326	382	1351
547	1225	501	1241	346	1263	204	1289	277	1327	508	1351
167	1226	203	1242	119	1265	212	1289	372	1327	565	1351
27	1228	395	1242	338	1265	242	1289	379	1327	371	1353
193	1228	403	1242	371	1265	609	1289	466	1327	607	1353
433	1230	479	1242	467	1265	201	1294	640	1327	255	1354
105	1231	25	1246	552	1265	38	1295	73	1329	131	1356
265	1231	69	1246	576	1265	198	1297	364	1329	275	1356
355	1231	421	1246	7	1266	337	1297	95	1332	117	1358
390	1231	14	1247	447	1266	565	1297	193	1332	98	1359
453	1231	27	1247	345	1268	399	1298	243	1332	140	1359
496	1231	90	1247	333	1270	75	1300	407	1332	455	1359
517	1231	585	1247	17	1271	175	1300	617	1334	533	1359
151	1233	187	1249	53	1271	217	1300	392	1335	595	1359
172	1233	237	1249	380	1271	475	1300	647	1335	56	1361
247	1233	97	1252	450	1271	525	1300	75	1337	75	1361
256	1233	265	1252	168	1273	607	1300	102	1337	195	1361
368	1233	409	1252	357	1273	77	1302	344	1337	378	1361
520	1233	577	1252	495	1273	325	1302	408	1337	655	1362
427	1234	589	1255	217	1276	326	1305	315	1338	239	1364
49	1236	289	1257	427	1276	418	1305	459	1338	285	1364
119	1236	347	1257	541	1276	39	1306	511	1338	497	1364
151	1236	595	1257	189	1278	495	1308	125	1340	1	1366
301	1236	21	1260	385	1278	631	1308	189	1340	134	1367
317	1236	135	1260	637	1278	333	1310	305	1340	567	1367
441	1236	195	1260	216	1279	476	1311	507	1340	88	1369
153	1238	231	1260	418	1279	569	1311	539	1340	360	1369
4	1239	261	1260	229	1281	164	1313	348	1343	427	1369
10	1239	295	1260	392	1281	354	1313	360	1343	181	1372
56	1239	335	1260	547	1281	389	1313	553	1345	609	1374
58	1239	381	1260	596	1281	19	1314	553	1348		
146	1239	385	1260	231	1282	195	1314	237	1350		
154	1239	405	1260	223	1284	511	1314	477	1350		
В.1. Неприводимые многочлены над полем GF(2)
217
Таблица В.9
Неприводимые трехчлены над полем GF(2) вида 1 + X* 4- Хт, 1375 < т 1510
t	т	t	т	t	т	t	т	t	т	t	т
52	1375	259	1399	649	1414	655	1431	575	1463	140	1487
126	1375	264	1399	282	1415	387	1433	645	1463	237	1487
321	1375	540	1399	377	1415	363	1434	39	1465	276	1487
397	1375	589	1399	392	1415	503	1434	522	1465	717	1487
586	1375	92	1401	342	1417	83	1436	311	1466	252	1489
637	1375	364	1401	466	1417	357	1438	181	1468	279	1490
684	1375	550	1401	682	1417	322	1441	439	1468	307	1492
100	1377	679	1401	33	1420	442	1441	709	1468	94	1495
248	1377	127	1402	273	1420	465	1441	49	1470	241	1495
183	1380	355	1402	595	1420	395	1442	101	1470	561	1495
455	1380	81	1404	705	1420	595	1444	569	1470	679	1495
130	1383	99	1404	49	1422	421	1446	649	1470	49	1497
12	1385	221	1404	497	1422	195	1447	657	1470	332	1497
171	1385	403	1404	573	1422	301	1447	733	1470	448	1497
237	1385	429	1404	645	1422	342	1447	25	1471	563	1497
608	1385	513	1404	15	1423	663	1447	393	1471	608	1497
617	1385	549	1404	228	1423	721	1447	622	1471	685	1497
659	1385	567	1404	289	1423	13	1449	77	1473	25	1500
219	1386	569	1404	310	1423	83	1449	143	1473	35	1500
455	1386	585	1404	334	1423	176	1449	271	1473	225	1500
599	1386	661	1404	631	1423	301	1449	311	1473	275	1500
11	1388	47	1407	28	1425	515	1449	488	1473	285	1500
417	1388	98	1407	88	1425	521	1449	21	1476	365	1500
129	1390	119	1407	343	1425	706	1449	265	1476	375	1500
577	1390	260	1407	611	1425	315	1452	467	1476	455	1500
3	1391	272	1407	616	1425	297	1454	665	1476	555	1500
84	1391	413	1407	103	1426	52	1455	69	1478	735	1500
236	1391	553	1407	27	1428	182	1455	49	1479	749	1500
363	1391	620	1407	45	1428	307	1455	50	1479	80	1503
525	1391	194	1409	423	1428	314	1457	280	1479	178	1503
300	1393	464	1409	557	1428	422	1457	368	1479	565	1503
342	1393	383	1410	631	1428	567	1457	434	1479	246	1505
663	1393	447	1410	33	1430	243	1458	32	1481	311	1505
97	1396	531	1410	621	1430	567	1458	183	1481	366	1505
339	1396	125	1412	17	1431	729	1458	311	1481	599	1508
601	1398	153	1412	332	1431	185	1460	716	1481	623	1508
55	1399	429	1414	445	1431	485	1460	411	1482	189	1510
220	1399	589	1414	514	1431	627	1460	85	1486		
218
Приложение В. Таблицы неприводимых многочленов
Таблица В. 10
Неприводимые трехчлены над полем GF(2) вида 1 + X* + Хт, 1511 т 1641
t	т	t	т	t	т	t	т	t	т	t	т
278	1511	225	1534	723	1561	767	1577	765	1601	537	1620
288	1511	404	1535	95	1562	782	1577	783	1602	573	1620
500	1511	46	1537	167	1562	731	1578	317	1604	621	1620
692	1511	157	1537	567	1562	755	1578	153	1606	633	1620
399	1513	445	1537	7	1564	647	1580	577	1606	745	1620
690	1513	75	1540	405	1564	675	1580	87	1607	17	1623
702	1513	319	1540	77	1566	677	1580	291	1607	152	1623
299	1514	365	1542	117	1566	121	1582	350	1607	272	1623
277	1516	445	1543	497	1566	381	1582	438	1607	472	1623
69	1518	496	1543	509	1566	20	1583	528	1607	69	1625
285	1518	678	1543	513	1566	128	1583	231	1609	146	1625
405	1518	44	1545	569	1566	356	1583	309	1609	401	1625
220	1519	119	1545	127	1567	414	1583	771	1612	476	1625
492	1519	229	1545	225	1567	417	1583	103	1615	561	1625
549	1519	262	1545	319	1569	683	1583	268	1615	648	1625
705	1519	63	1548	386	1569	743	1583	279	1615	603	1628
733	1519	221	1548	679	1569	574	1585	182	1617	741	1630
229	1521	273	1548	706	1569	399	1586	235	1617	668	1631
464	1521	505	1548	736	1569	519	1586	238	1617	147	1633
467	1521	189	1550	667	1570	85	1588	488	1617	163	1633
544	1521	353	1550	501	1572	159	1588	500	1617	208	1633
27	1524	557	1551	585	1572	229	1588	538	1617	406	1633
293	1524	667	1551	17	1575	169	1590	545	1617	796	1633
327	1524	252	1553	38	1575	301	1590	637	1617	227	1634
473	1526	393	1553	68	1575	337	1590	655	1617	683	1634
373	1527	477	1553	127	1575	15	1591	754	1617	37	1636
415	1527	479	1553	181	1575	456	1591	800	1617	493	1636
487	1527	500	1553	224	1575	681	1591	802	1617	663	1636
520	1527	635	1553	518	1575	568	1593	211	1618	173	1638
610	1527	99	1554	616	1575	3	1596	27	1620	217	1638
60	1529	135	1554	679	1575	111	1596	33	1620	397	1638
186	1529	65	1556	709	1575	243	1596	227	1620	721	1638
207	1529	9	1558	763	1575	697	1596	243	1620	427	1639
563	1529	119	1559	341	1577	791	1596	297	1620	709	1639
642	1529	587	1559	350	1577	643	1599	339	1620	287	1641
207	1530	339	1561	701	1577	749	1599	405	1620	319	1641
359	1530	493	1561	716	1577	548	1601	465	1620	382	1641
591	1530	558	1561	735	1577	651	1601	495	1620	637	1641
В.1. Неприводимые многочлены над полем GF(2)	219
Таблица В.11
Неприводимые трехчлены над полем GF(2) вида 1 4- X1 + Хт, 1642 т 1822
t	т	t	т	t	т	t	т	t	т	t	т
231	1642	129	1678	285	1703	727	1735	759	1764	349	1791
310	1647	709	1678	590	1703	853	1735	250	1767	512	1791
469	1647	20	1679	52	1705	861	1735	623	1767	682	1791
494	1647	42	1679	162	1705	403	1737	327	1769	114	1793
757	1647	204	1679	217	1705	267	1738	560	1769	254	1793
434	1649	279	1679	633	1705	259	1740	882	1769	69	1798
660	1649	479	1679	744	1705	515	1740	279	1770	685	1798
579	1650	537	1679	93	1708	711	1740	607	1770	312	1799
583	1650	668	1679	211	1708	869	1742	371	1772	321	1799
727	1650	135	1681	303	1708	173	1743	117	1774	374	1799
803	1650	373	1681	201	1710	302	1743	829	1774	502	1801
45	1652	610	1681	178	1711	506	1743	486	1775	843	1802
53	1655	802	1681	465	1711	602	1743	771	1775	747	1804
16	1657	31	1687	250	1713	369	1745	217	1777	101	1806
105	1657	139	1687	332	1713	702	1745	544	1777	497	1806
520	1657	391	1687	425	1713	764	1745	801	1777	581	1806
37	1660	648	1687	626	1713	255	1746	859	1777	123	1807
445	1660	758	1689	221	1716	783	1746	635	1778	438	1807
615	1660	805	1689	377	1716	567	1748	815	1778	525	1807
763	1660	826	1689	113	1719	457	1750	457	1780	700	1807
99	1663	359	1692	268	1719	481	1750	57	1782	521	1809
319	1663	489	1692	611	1719	482	1751	81	1782	734	1809
808	1663	625	1692	300	1721	775	1753	105	1782	171	1810
176	1665	835	1692	531	1721	99	1756	245	1782	283	1810
349	1665	501	1694	684	1721	165	1759	585	1782	427	1810
376	1665	29	1695	39	1722	105	1764	439	1783	545	1814
488	1665	201	1697	839	1722	199	1764	520	1783	163	1815
271	1666	420	1697	261	1724	231	1764	559	1783	698	1815
459	1668	768	1697	749	1724	273	1764	214	1785	736	1815
202	1671	822	1697	753	1726	297	1764	364	1785	856	1815
292	1671	459	1698	94	1729	371	1764	392	1785	479	1817
406	1671	767	1698	118	1729	413	1764	452	1785	495	1818
90	1673	225	1700	216	1729	453	1764	574	1785	871	181.8
134	1673	311	1700	820	1729	469	1764	676	1785	11	1820
605	1673	441	1700	862	1729	539	1764	724	1785	45	1820
755	1674	567	1700	461	1734	603	1764	819	1788	335	1820
363	1676	825	1700	418	1735	611	1764	593	1790	359	1820
413	1676	161	1703	651	1735	735	1764	190	1791	779	1820
220
Приложение В. Таблицы неприводимых многочленов
Таблица В. 12
Неприводимые трехчлены над полем GF(2) вида 1 4-Х* + Хт, 1823 т 1979
t	т	t	т	t	т	t	т	t	т	t	т
684	1823	885	1854	261	1871	67	1911	811	1935	746	1953
735	1823	39	1855	345	1871	161	1911	231	1937	842	1953
893	1823	136	1855	806	1871	172	1911	297	1937	875	1953
9	1825	607	1855	199	1873	196	1911	930	1937	925	1953
759	1825	633	1855	763	1873	304	1911	747	1938	279	1956
273	1828	807	1855	253	1878	371	1911	113	1940	291	1956
343	1828	837	1855	341	1878	392	1911	177	1940	89	1958
381	1830	688	1857	174	1879	469	1911	11	1943	371	1959
51	1831	709	1857	613	1879	616	1911	60	1943	409	1959
99	1831	785	1857	852	1879	644	1911	158	1943	771	1961
511	1831	788	1857	370	1881	686	1911	519	1943	783	1961
771	1831	809	1857	892	1881	770	1911	528	1943	965	1961
518	1833	13	1860	669	1884	791	1911	960	1943	99	1962
670	1833	27	1860	867	1884	462	1913	91	1945	135	1962
881	1833	31	1860	833	1886	530	1913	288	1945	639	1962
243	1836	279	1860	353	1887	639	1913	294	1945	747	1962
891	1836	341	1860	392	1887	477	1918	328	1945	21	1964
53	1838	527	1860	652	1887	705	1918	358	1945	113	1964
465	1838	555	1860	800	1887	793	1918	652	1945	735	1964
836	1839	713	1860	29	1889	105	1919	51	1946	801	1966
66	1841	761	1860	497	1889	344	1919	603	1948	26	1967
710	1841	871	1860	371	1890	680	1919	709	1948	197	1967
873	1841	149	1862	667	1890	720	1919	919	1948	236	1967
339	1844	797	1862	931	1890	848	1919	9	1950	449	1967
375	1844	260	1863	873	1895	468	1921	121	1951	596	1967
447	1844	293	1863	235	1900	327	1924	759	1951	809	1967
557	1844	527	1863	297	1900	357	1926	17	1953	866	1967
623	1844	592	1863	525	1900	25	1927	35	1953	175	1969
705	1844	685	1863	733	1902	151	1927	70	1953	546	1969
901	1846	53	1865	945	1902	168	1927	178	1953	585	1969
180	1847	521	1865	778	1903	31	1929	266	1953	165	1974
257	1847	738	1865	930	1903	553	1929	280	1953	245	1974
596	1847	762	1865	344	1905	277	1932	287	1953	301	1974
614	1847	11	1866	358	1905	637	1932	413	1953	365	1974
768	1847	367	1866	424	1905	413	1934	532	1953	745	1974
920	1847	891	1866	946	1905	103	1935	560	1953	841	1975
49	1849	121	1870	931	1906	236	1935	605	1953	238	1977
412	1849	253	1870	945	1908	382	1935	650	1953	748	1977
В.1. Неприводимые многочлены над полем GF(2)
221
Таблица В. 13
Неприводимые трехчлены над полем GF(2) вида 1 4- X1 4- Хт, 1980 т 2000
t	т	t	т	t	т	t	т	t	т	t	т
33	1980	435	1980	161	1983	672	1985	546	1991	15	1994
63	1980	545	1980	967	1983	774	1985	896	1991	307	1996
125	1980	759	1980	311	1985	891	1986	103	1993	367	1999
297	1980	845	1980	584	1985	555	1988	124	1993	585	1999
307	1980	875	1980	597	1985	133	1990	717	1993	732	1999
363	1980	113	1983	668	1985	217	1990	762	1993		
В. 1.2. Неприводимые трехчлены вида 1 4- Хп 1 4- Хп
степени п, 2 < п 34 353
Таблица В. 14 сгенерирована программой из дипломной работы
Р. А. Хохлова (МГУ). Она содержит все неприводимые трехчлены вида
1+Xn-1 +ХП степени n,2 п 34353. В таблице «—» означает, что много-
член не порождает нормальный базис или, что многочлен не примитивен.
Знаком «4-» отмечены примитивные многочлены, знак «?» указывает, что
значение параметра не вычислялось; С — сложность нормального базиса.
Таблица В. 14
Неприводимые трехчлены над GF(2) вида 1 4- Хп~[ 4- Хп степени п, 2 п 471
п	Сложность С	Примитивность	п	Сложность С	Примитивность
2	3	4-	532	140621	4-
3	5	+	865	373 677	4-
4	9	-4	900	404029	4-
6	17	4-	1366	931 525	9
7	21	4-	2380	2 830981	9
9	41	—	3310	5 475 793	9
15	105	4-	4495	—	9
22	225	4-	6321	19 973 077	9
28	405	—	7447	27 728493	9
30	449	—	10198	51 991 681	9
46	1009	—	11425	65 261489	9
60	1789	4-	21846	238611 729	9
63	1913	4-	24 369	296 889089	9
127	—	4-	27 286	9	9
153	—	4-	28 713	9	9
172	14 729	—	32 767	9	9
303	45 893	—	34 353	9	9
471	110 201	4-			
222
Приложение В. Таблицы неприводимых многочленов
В.1.3. Неприводимые пятичлены степени п, 8 С п 290
В таблице В. 15, сгенерированной программой Р. А. Хохлова (МГУ),
представлено по одному неприводимому пятичлену тех степеней в диапа-
зоне от 8 до 290, для которых не существует неприводимых трехчленов.
Таблица В. 15
Некоторые неприводимые пятичлены 1 + Хк -h X1 4- Хт 4 Хп
над полем GF(2) степени п, 8 п 290
к	1	т	п	к	1	т	п	к	1	т	п	к	1	т	п
1	3	4	8	2	4	7	83	5	6	8	158	2	4	5	222
1	3	4	13	1	2	8	85	2	3	5	160	3	8	9	224
1	3	5	16	2	6	7	88	3	6	7	163	3	7	10	226
1	2	5	19	1	5	8	91	7	8	10	164	4	9	10	227
1	3	4	24	6	9	10	96	3	8	9	165	1	4	10	229
1	3	4	26	1	3	6	99	2	3	15	168	2	4	9	232
1	2	5	27	1	6	7	101	2	5	6	171	1	6	9	235
2	3	7	32	1	3	4	104	2	5	8	173	1	4	7	237
1	4	6	37	4	7	9	107	2	3	11	176	3	5	8	240
1	5	6	38	2	4	5	109	1	2	4	179	1	5	8	243
3	4	5	40	3	4	5	112	1	6	7	181	1	4	6	245
3	4	6	43	2	3	5	114	7	8	9	184	1	2	11	246
1	3	4	45	5	7	8	115	5	6	7	187	10	14	15	248
2	3	5	48	1	2	4	116	2	5	6	188	2	4	7	251
2	3	4	50	1	2	5	117	2	5	6	189	1	2	7	254
1	3	6	51	1	3	4	120	6	7	8	190	2	5	10	256
1	2	6	53	1	2	6	122	1	2	7	192	2	6	10	259
2	4	7	56	5	6	7	125	2	3	8	195	4	6	7	261
2	4	7	59	1	2	7	128	2	4	9	197	4	8	9	262
1	2	5	61	2	3	8	131	2	3	5	200	2	6	9	264
1	3	4	64	2	8	9	133	2	3	6	201	3	6	8	267
1	2	5	67	2	3	5	136	1	7	8	203	1	6	7	269
2	5	6	69	1	7	8	138	2	5	9	205	2	3	9	272
1	3	5	70	3	5	8	139	5	9	10	206	9	10	11	275
3	9	10	72	1	4	10	141	1	3	9	208	3	6	12	277
1	3	6	75	2	3	5	143	8	10	11	211	2	5	9	280
2	5	6	77	2	4	7	144	2	5	6	213	5	7	12	283
3	5	6	78	7	9	10	149	1	3	7	216	5	7	10	285
2	4	9	80	2	3	6	152	1	4	8	219	1	10	11	288
1	3	8	82	2	5	6	157	2	6	8	221	2	3	5	290
В.2. Неприводимые трехчлены над полем GF(3)
223
В.2.	Неприводимые трехчлены над полем GjF(3)
В таблицах В.16, В.17, В.18 даны неприводимые трехчлены над полем
GF(3) степени не выше 255. Данные этих таблиц заимствованы из рабо-
ты [27].
Таблица В. 16
Неприводимые трехчлены над полем GF(3) вида 2 4- X1 + Хт, 2 т 255
t	т	t	т	t	т	t	т	t	т	t	т
1	2	26	43	70	93	108	143	8	187	5	238
2	3	3	44	48	95	56	144	11	188	24	239
1	4	28	45	16	96	24	145	116	191	8	240
4	5	5	46	12	97	8	147	32	192	88	241
1	6	32	47	4	99	3	148	12	193	115	242
2	7	8	48	25	100	73	150	55	194	122	243
2	8	50	51	70	101	2	151	26	195	31	244
4	9	7	52	25	102	18	152	79	196	148	245
2	11	22	53	50	103	94	153	29	198	13	246
2	12	1	54	5	104	12	155	164	199	122	247
4	13	26	55	32	107	26	156	3	200	50	248
1	14	3	56	2	108	22	157	88	201	76	249
2	15	20	59	88	109	61	158	8	203	26	251
4	16	2	60	2	111	32	159	50	204	98	252
16	17	30	61	6	112	4	160	78	205	12	253
7	18	26	63	70	113	19	162	61	206	73	254
2	19	3	64	7	114	80	163	10	208	26	255
5	20	2	67	32	115	15	164	40	209		
16	21	52	69	15	116	22	165	7	210		
5	22	20	71	52	117	92	167	122	211		
8	23	28	72	2	119	28	168	65	214		
4	24	30	73	4	120	24	169	36	215		
6	25	9	76	40	121	43	170	4	216		
4	26	16	77	25	124	20	171	132	217		
20	27	13	78	52	125	19	172	26	219		
2	28	26	79	49	126	166	173	15	220		
4	29	2	80	8	127	73	174	89	222		
1	30	40	81	6	128	12	176	12	224		
20	31	32	83	48	131	52	177	16	225		
5	32	14	84	88	133	11	178	68	227		
28	33	16	85	44	135	38	180	72	229		
14	36	26	87	57	136	40	181	73	230		
6	37	6	88	136	137	25	182	30	232		
26	39	64	89	80	139	2	183	91	234		
1	40	19	90	59	140	20	184	26	235		
40	41	74	91	64	141	64	185	9	236		
7	42	10	92	65	142	47	186	70	237		
224
Приложение В. Таблицы неприводимых многочленов
Таблица В. 17
Неприводимые трехчлены над полем GF(3) вида 1 4- 2Х1 4- Хт, 3 < т < 255
t	т	t	т	t	т	t	т	t	тп	t	т
1	3	6	46	30	94	24	145	24	194	59	249
1	5	15	47	47	95	2	146	26	195	104	250
2	6	6	50	12	97	8	147	38	198	9	251
2	7	1	51	19	99	2	151	35	199	7	253
4	9	13	53	31	101	59	153	88	201	16	254
2	10	14	54	2	102	32	154	62	202	26	255
2	11	11	55	47	103	12	155	3	203		
1	13	8	58	26	106	22	157	9	205		
4	14	17	59	3	107	52	158	94	206		
2	15	7	61	9	109	32	159	40	209		
1	17	10	62	22	ПО	80	162	89	211		
8	18	26	63	2	111	59	163	6	214		
2	19	10	66	19	113	22	165	36	215		
5	21	2	67	32	115	54	166	85	217		
4	22	1	69	52	117	71	167	18	218		
3	23	4	70	34	118	24	169	25	219		
3	25	20	71	2	119	32	170	4	222		
2	26	1	73	1	121	20	171	16	225		
7	27	12	74	14	122	7	173	38	226		
4	29	16	77	52	125	52	174	11	227		
4	30	14	78	52	126	52	177	72	229		
5	31	26	79	8'	127	26	178	64	230		
5	33	40	81	27	131	59	179	104	234		
2	34	2	82	15	133	37	181	26	235		
2	35	27	83	4	134	34	182	70	237		
6	37	16	85	44	135	2	183	4	238		
4	38	34	86	1	137	64	185	5	239		
7	39	26	87	34	138	46	186	88	241		
1	41	13	89	59	139	8	187	2	242		
10	42	34	90	5	141	94	190	121	243		
1	43	1	91	40	142	71	191	97	245		
17	45	23	93	35	143	12	193	122	247		
В.2. Неприводимые трехчлены над полем GF(3)
225
Таблица В. 18
Неприводимые трехчлены над полем GF(3) вида 1 4- 2Xl + Хт, 3 < т 255
t	т	t	т	t	т	t	т	t	т	t	т
1	2	1	43	23	93	35	143	65	187	5	238
1	3	3	44	47	95	56	144	11	188	5	239
1	4	1	45	16	96	73	145	71	191	8	240
1	5	5	46	81	97	43	147	32	192	117	241
1	6	15	47	19	99	3	148	81	193	115	242
1	5	8	48	25	100	73	150	55	194	121	243
2	8	1	51	31	101	125	151	49	195	31	244
5	9	7	52	25	102	18	152	79	196	97	245
3	11	13	53	47	103	59	153	29	198	13	246
2	12	1	54	5	104	129	155	35	199	125	247
1	13	11	55	3	107	26	156	3	200	50	248
1	14	3	56	2	108	69	157	113	201	59	249
7	15	1	59	9	109	61	158	3	203	9	251
4	16	2	60	13	111	127	159	50	204	98	252
1	17	7	61	6	112	4	160	9	205	7	253
7	18	37	63	19	113	19	162	61	206	73	254
11	19	3	64	7	114	59	163	10	208	229	255
5	20	11	67	83	115	15	164	49	209		
5	21	17	69	15	116	77	165	7	210		
5	22	51	71	65	117	71	167	89	211		
3	23	28	72	3	119	28	168	65	214		
4	24	1	73	4	120	37	169	59	215		
3	25	9	76	1	121	43	170	4	216		
7	26	25	77	25	124	151	171	85	217		
7	27	13	78	73	125	19	172	25	219		
2	28	53	79	49	126	7	173	15	220		
25	29	2	80	119	127	73	174	89	222		
1	30	41	81	6	128	12	176	12	224		
5	31	2	83	27	131	83	177	209	225		
5	32	14	84	15	133	11	178	11	227		
5	33	31	85	61	134	59	179	14	228		
1	35	13	86	91	135	38	180	79	229		
14	36	37	87	57	136	37	181	73	230		
13	37	6	88	1	137	25	182	30	232		
7	39	13	89	59	139	181	183	91	234		
1	40	19	90	59	140	20	184	83	235		
1	41	17	91	5	141	121	185	9	236		
7	42	10	92	65	142	47	186	167	237		
Приложение С
Таблицы ОНБ
С.1. ОНБ размерности п, 2 < п < 30
В таблице С. 1 указаны все оптимальные нормальные базисы для q = 2
и 1 п 30, приведены минимальные многочлены генераторов этих ба-
зисов и матрицы А умножения, заданные перечислением координат еди-
ничных элементов. Например, запись вида А : (i, j) = (4, 3)( 1,0) означает,
что элемент на пересечении строки 4 и столбца 3 единичный и элемент
на пересечении строки 1 и столбца 0 тоже единичный (нумерация строк
и столбцов начинается с нуля). При составлении таблицы использованы
данные, полученные посредством компьютерных программ, разработан-
ных студентами П. И. Артемьевой (МЭИ) и Р. А. Хохловым (МГУ).
Таблица С.1
Таблица оптимальных нормальных базисов размерности от 1 до 30
п = 1 — ОНБ 1 типа, минимальный многочлен веса 2.
Матрица умножения:
(0,0)
п = 2 — ОНБ 1 типа, минимальный многочлен веса 3.
Матрица умножения:
(0,1) (1,0) (1,1)
п — 3 — ОНБ 3 типа, минимальный многочлен: 1 4- X2 4- X3,
Матрица умножения:
(0,1) (1,0) (1,2) (2,1) (2,2)
п = 4 — ОНБ 1 типа, минимальный многочлен веса 5.
Матрица умножения:
(0,2) (1,2) (1,3) (2,0) (2,1) (3,1) (3,3)
п = 5 — ОНБ 2 типа, минимальный многочлен: 1 4- X1 4- X2 4- X4 4- X5.
Матрица умножения:
(0,1) (1,0) (1,3) (2,3) (2,4) (3,1) (3,2) (4,2) (4,4)
С.1. ОНБ размерности п, 2 п 30
227
Продолжение таблицы С. 1
п = 6 — ОНБ 2 типа, минимальный многочлен: 1 4- X* 1 4- X4 4- X5 4- X6.
Матрица умножения:
(5,3) (5,5)
п = 9 — ОНБ 2 типа, минимальный многочлен:
1 + X1 + X4 + X5 + X6 + X8 + X9.
Матрица умножения:
(0,1)	(1,0)	(1,4)	(2,4)	(2,7)	(3,6)	(3,8)	(4,1)	(4,2)
(5,6)	(5,7)	(6,3)	(6,5)	(7,2)	(7,5)	(8,3)	(8,8)
п = 10 — ОНБ 1 типа, минимальный многочлен: веса 11.
Матрица умножения:
(0,5)	(1,5)	(1,6)	(2,3)	(2,7)	(3,2)	(3,8)	(4,7)	(4,9)
(5,0)	(5,1)	(6,1)	(6,8)	(7,2)	(7,4)	(8,3)	(8,6)	(9,4)
(9, 9)
п = 11 — ОНБ 3 типа, минимальный многочлен:
1 + X2 + X3 + X4 + Xs + х'° + х".
Матрица умножения:
(0,1)	(1,0)	(1,8)	(2,6)	(2,8)	(3,4)	(3,5)	(4,3)	(4,9)
(5,3)	(5,7)	(6,2)	(6,9)	(7,5)	(7,10)	(8,1)	(8,2)	(9,4)
(9,6) (10,7) (10,10)
п = 12 — ОНБ 1 типа, минимальный многочлен: веса 13.
Матрица умножения:
(0,6)	(1,6)	(1,7)	(2,8)	(2,10)	(3,5)	(3,9)	(4,7)	(4,10)
(5,3)	(5,11)	(6,0)	(6,1)	(7,1)	(7,4)	(8,2)	(8,9)	(9,3)
(9,8)	(10,2)	(10,4)	(11,5)	(11,11)
п — 14 — ОНБ 2 типа, минимальный многочлен:
1 + X1 + Xs + X9 + х12 + х13 + X14.
Матрица умножения:
(0,1)	(1,0)	(1,5)	(2,5)	(2,8)	(3,10)	(3,12)	(4,7)	(4,13)
(5,1)	(5,2)	(6,8)	(6,12)	(7,4)	(7,11)	(8,2)	(8,6)	(9,10)
(9,11)	(10,3)	(10,9)	(11,7)	(11,9)	(12,3)	(12,6)	(13,4)	(13,13)
228
Приложение С. Таблицы ОНБ
Продолжение таблицы С. 1
п — 18 — ОНБ 1 типа, минимальный многочлен: веса 19.
Матрица умножения:
(0,9)	(1,9)	(1.Ю)	(2,4)	(2.Н)	(3,12)	(3, 15)	(4,2)	(4,13)
(5,6)	(5,14)	(6, 5)	(6,15)	(7,14)	(7, 16)	(8,12)	(8,17)	(9,0)
(9,1)	(Ю, О	(Ю, 13)	(И.2)	(11,16)	(12,3)	(12,8)	(13,4)	(13,10)
(14,5)	(14, 7)	(15,3)	(15,6)	(16, 7)	(16,11)	(17,8)	(17, 17)	
п = 18 — ОНБ 2 типа, минимальный многочлен:
1 + X + X2 + Xs + X9 + X10 + X12 + X13 + X16 + X17 + X18.
Матрица умножения:
(0,1)	(1,0)	(1,8)	(2,5)	(2,8)	(3,14)	(3,16)	(4,7)	(4,13)
(5,2)	(5,9)	(6, 12)	(6, 16)	(7,4)	(7,17)	(8,1)	(8,2)	(9,5)
(9,14)	(Ю, 11)	(Ю, 12)	(11,10)	(11,15)	(12,6)	(12,10)	(13,4)	(13,15)
(14,3)	(14,9)	(15,11)	(15,13)	(16,3)	(16,6)	(17,7)	(17,17)	
п = 23 — ОНБ 3 типа, минимальный многочлен:
1 + X4 + X6 + X7 + X8 + х16 + х20 + X22 + X23.
Матрица умножения:
(0,1)	(1,0)	(1,19)	(2,9)	(2,19)	(3,12)	(3,15)	(4,5)	(4,6)
(5,4)	(5,13)	(6,4)	(6,16)	(7,13)	(7,21)	(8,Н)	(8,Н)	(9,2)
(9,20)	(10,15)	(10,17)	(Н,8)	(11,14)	(12,3)	(12,20)	(13,5)	(13,7)
(14,И)	(14,16)	(15,3)	(15,10)	(16,6)	(16,14)	(17,10)	(17,21)	(18,8)
(18,22)	(19,1)	(19,2)	(20,9)	(20,12)	(21,7)	(21,17)	(22,18)	(22,22)
п = 26 — ОНБ 2 типа, минимальный многочлен:
1 + х1 + х2 + X4 + х5 + х16 + х'7 + X18 + X20 + X21 + X24 + X25 + X26.
Матрица умножения:
(0,1)	(1,0)	(1,17)	(2,17)	(2,21)	(3,8)	(3,14)	(4, Ю)	(4,12)
(5,7)	(5,23)	(6,19)	(6,22)	(7,5)	(7,13)	(8,3)	(8,22)	(9, Ю)
(9,П)	(Ю,4)	(Ю,9)	(Н,9)	(11,23)	(12,4)	(12,15)	(13,7)	(13,20)
(14,3)	(14,18)	(15,12)	(15,24)	(16,20)	(16,25)	(17,1)	(17,2)	(18,14)
(18,21)	(19,6)	(19,24)	(20,13)	(20,16)	(21,2)	(21,18)	(22,6)	(22,8)
(23,5)	(23,11)	(24,15)	(24,19)	(25,16)	(25,25)			
С.1. ОНБ размерности п, 2 п 30	229
Окончание таблицы С. 1
п = 28 — ОНБ 1 типа; минимальный многочлен: веса 29.
Матрица умножения:
(0,14)	(1. 14)	(1,15)	(2,16)	(2, 19)	(3, 17)	(3,26)	(4, 13)
(4,18)	(5, 15)	(5,19)	(6,8)	(6, 20)	(7,Н)	(7,21)	(8,6)
(8, 22)	(9, 23)	(9,25)	(Ю, 17)	(Ю, 24)	(И-7)	(11,25)	(12,20)
(12,26)	(13,4)	(13, 27)	(14,0)	(14, 1)	(15, 1)	(15,5)	(16, 2)
(16, 22)	(17,3)	(17, 10)	(18,4)	(18,21)	(19, 2)	(19, 5)	(20,6)
(20,12)	(21,7)	(21, 18)	(22, 8)	(22,16)	(23,9)	(23, 24)	(24,10)
(24, 23)	(25,9)	(25,11)	(26, 3)	(26,12)	(27,13)	(27, 27)	
п = 29 — ОНБ 2 типа, минимальный многочлен:
1 + х' + х2 + х16 + х17 + х18 + х24 + х25 + х26 + X28 + X29.
Матрица умножения:
(0,1)	(1,0)	(1,21)	(2,6)	(2,21)	(3, 13)	(3, 18)	(4,Н)
(4, 27)	(5, 17)	(5,20)	(6, 2)	(6, 22)	(7,13)	(7, 25)	(8,9)
(8,10)	(9,8)	(9,14)	(10,8)	(Ю, 26)	(П,4)	(4,14)	(12,17)
(12, 24)	(13,3)	(13, 7)	(14, 9)	(14,Н)	(15, 24)	(15,26)	(16, 19)
(16, 23)	(17,5)	(17,12)	(18,3)	(18,22)	(19, 16)	(19, 27)	(20, 5)
(20, 28)	(21,1)	(21,2)	(22, 6)	(22, 18)	(23, 16)	(23, 25)	(24, 12)
(24,15)	(25,7)	(25,23)	(26, 10)	(26, 15)	(27,4)	(27, 19)	(28, 20)
(28,28)
п — 30 — ОНБ 2 типа, минимальный многочлен:
	1 +Х1	+ X16 + X17 + X24 + X25 + X28 + X29 + X30.					
Матрица умножения:							
(0,1)	(1,0)	(1,6)	(2,6)	(2, 22)	(3,12)	(3, 19)	(4, 17)
(4,28)	(5,21)	(5,29)	(6,1)	(6, 2)	(7,19)	(7, 22)	(8, 10)
(8,15)	(9, 14)	(9, 27)	(10,8)	(Ю, 20)	(11,14)	(11,18)	(12,3)
(12, 23)	(13,17)	(13,26)	(14,9)	(14,11)	(15,8)	(15,23)	(18,11)
(16,25)	(16, 27)	(17,4)	(17,13)	(18,21)	(19, 3)	(19,7)	(22, 7)
(20,10)	(20, 28)	(21,5)	(21,18)	(22, 2)	(23, 12)	(23,15)	(24, 25)
(27,9)	(24, 26)	(25, 16)	(25, 24)	(26, 13)	(26, 24)	(27, 16)	(28,4)
(28,20)	(29, 5)	(29, 29)					
230
Приложение С. Таблицы ОНБ
С.2. ОНБ размерности п, 30 < п < 1013
Ниже помещена таблица, сгенерированная программой П. И. Арте-
мьевой (МЭИ), содержащая размерности полей GF(2n) при 30 < п < 1013,
в которых существуют оптимальные нормальные базисы определенного
типа и приведены (в виде списков степеней одночленов) минимальные
многочлены генераторов этих базисов. В этой таблице мы не приводим
вычисляемые программой матрицы А, Т ввиду их громоздкости.
Таблица С.2
Таблица размерностей полей GF(2n) при 30 < п < 1013, в которых существуют
оптимальные нормальные базисы определенного типа, и минимальных многочленов
генераторов этих базисов
п = 33 — ОНБ 2 типа, минимальный многочлен:
0 1 16 17 24 25 28 29 30 32 33
п = 35 — ОНБ 3 типа, минимальный многочлен:
0 2 3 16 18 19 24 26 27 28 32 34 35
п = 36 — ОНБ 1 типа, минимальный многочлен веса 37
п = 39 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 16 20 22 23 24 32 36 38 39
п — 41 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 32 33 36 37 38 40 41
п — 50 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 32 33 34 40 41 42 44 45 48 49 50
п = 51 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 32 34 35 40 42 43 44 48 50 51
п = 52 — ОНБ 1 типа, минимальный многочлен веса 53
п = 53 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 32 33 34 36 37 40 41 42 48 49 50 52 53
п = 58 — ОНБ 1 типа, минимальный многочлен веса 59
п = 60 — ОНБ 1 типа, минимальный многочлен веса 61
п = 65 — ОНБ 2 типа, минимальный многочлен:
0 1 32 33 48 49 56 57 60 61 62 64 65
п = 66 — ОНБ 1 типа, минимальный многочлен веса 67
С.2. ОНБ размерности п, 30 < п < 1013	231
Продолжение таблицы С. 2
п = 69 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 32 33 34 36 37 48 49 50 52 53 56 57 58 64 65 66 68 69
п — 74 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 32 33 34 36 37 40 41 42 48 49 50 52 53 64 65 66 68 69 72 73 74
п = 81 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 16 17 32 33 40 41 44 45 46 64 65 72 73 76 77 78 80 81
п = 82 — ОНБ 1 типа, минимальный многочлен веса 83
п = 83 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 16 18 19 32 34 35 40 42 43 44 64 66 67 72 74 75 76 80 82 83
п = 86 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 32 33 36 37 38 40 41 64 65 68 69 70 72 73 80 81 84 85 86
п = 89 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 16 17 20 21 22 24 25 32 33 36 37 38 64 65 68 69 70 80 81 84 85 86 88 89
п = 90 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 16 17 18 20 21 24 25 26 32 33 34 36 37 64 65 66 68 69 80 81 82 84 85 88 89 90
п = 95 — ОНБ 3 типа, минимальный многочлен:
0 16 24 28 30 31 32 64 80 88 92 94 95
п — 98 — ОНБ 2 типа, минимальный многочлен:
0 1 2 16 17 18 24 25 26 28 29 64 65 66 80 81 82 88 89 90 92 93 96 97 98
п = 99 — ОНБ 3 типа, минимальный многочлен:
0 2 3 16 18 19 24 26 27 28 64 66 67 80 82 83 88 90 91 92 96 98 99
п = 100 — ОНБ 1 типа, минимальный многочлен веса 101
п = 105 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 64 65 68 69 70 72 73 80 81 84 85 86 96 97 100 101 102 104
105
п = 106 — ОНБ 1 типа веса 107
п = 113 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 64 65 72 73 76 77 78 96 97 104 105 108 109 НО 112 113
тг = 119 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 8 64 68 70 71 72 96 100 102 103 104 112 116 118 119
232
Приложение С. Таблицы ОНБ
Продолжение таблицы С.2
п = 130 — ОНБ 1 типа, минимальный многочлен веса 131
п = 131 — ОНБ 3 типа, минимальный многочлен:
0 2 3 64 66 67 96 98 99 112 114 115 120 122 123 124 128 130 131
п = 134 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 64 65 68 69 70 96 97 100 101 102 112 113 116 117 118 120 121 128 129 132
133 134
п — 135 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 64 68 70 71 96 100 102 103 112 116 118 119 120 128 132 134 135
п = 138 — ОНБ 1 типа, минимальный многочлен веса 139
п = 146 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 16 17 18 64 65 66 72 73 74 76 77 80 81 82 96 97 98 104 105 106 108
109 128 129 130 136 137 138 140 141 144 145 146
п = 148 — ОНБ 1 типа, минимальный многочлен веса 149
п = 155 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 16 18 19 20 24 26 27 64 66 67 68 80 82 83 84 88 90 91 96 98 99 100 128 130 131
132 144 146 147 148 152 154 155
п = 158 — ОНБ 2 типа, минимальный многочлен:
0 1 16 17 24 25 28 29 30 64 65 80 81 88 89 92 93 94 96 97 128 129 144 145 152 153 156
157 158
п = 162 — ОНБ 1 типа, минимальный многочлен веса 163
п — 172 — ОНБ 1 типа, минимальный многочлен веса 173
п = 173 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 16 17 18 32 33 34 40 41 42 44 45 64 65 66 72 73 74 76 77 80 81 82
128 129 130 136 137 138 140 141 144 145 146 160 161 162 168 169 170 172 173
п = 174 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 16 17 32 33 40 41 44 45 46 64 65 72 73 76 77 78 80 81 128 129 136 137
140 141 142 144 145 160 161 168 169 172 173 174
п — 178 — ОНБ 1 типа, минимальный многочлен веса 179
п = 179 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 32 34 35 40 42 43 44 48 50 51 64 66 67 72 74 75 76 128 130 131 136
138 139 140 160 162 163 168 170 171 172 176 178 179
С.2. ОНБ размерности п, 30 <п < 1013
233
Продолжение таблицы С. 2
п= 180 — ОНБ 1 типа, минимальный многочлен веса 181
п — 183 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 8 32 36 38 39 40 48 52 54 55 64 68 70 71 72 128 132 134 135 136 160 164 166
167 168 176 180 182 183
п = 186 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 32 33 34 36 37 48 49 50 52 53 56 57 58 64 65 66 68 69 128 129 130 132 133
160 161 162 164 165 176 177 178 180 181 184 185 186
п = 189 — ОНБ 2 типа, минимальный многочлен:
0 1 2 32 33 34 48 49 50 56 57 58 60 61 64 65 66 128 129 130 160 161 162 176 177 178
184 185 186 188 189
п = 191 — ОНБ 3 типа, минимальный многочлен:
0 32 48 56 60 62 63 64 128 160 176 184 188 190 191
п — 194 — ОНБ 2 типа, минимальный многочлен:
0 1 2 32 33 34 48 49 50 56 57 58 60 61 128 129 130 160 161 162 176 177 178 184 185
186 188 189 192 193 194
п = 196 — ОНБ 1 типа, минимальный многочлен веса 197
п = 209 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 16 17 32 33 40 41 44 45 46 128 129 136 137 140 141 142 144 145 160
161 168 169 172 173 174 192 193 200 201 204 205 206 208 209
п = 210 — ОНБ 1 типа, минимальный многочлен веса 211
п — 210 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 16 17 18 32 33 34 40 41 42 44 45 128 129 130 136 137 138 140 141 144
145 146 160 161 162 168 169 170 172 173 192 193 194 200 201 202 204 205 208 209 210
п = 221 — ОНБ 2 типа, минимальный многочлен:
0 1 2 16 17 18 24 25 26 28 29 32 33 34 128 129 130 144 145 146 152 153 154 156 157
160 161 162 192 193 194 208 209 210 216 217 218 220 221
п = 226 — ОНБ 1 типа, минимальный многочлен веса 227
п = 230 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 16 17 20 21 22 24 25 128 129 132 133 134 144 145 148 149 150 152 153 192
193 196 197 198 208 209 212 213 214 216 217 224 225 228 229 230
п = 231 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 16 20 22 23 24 128 132 134 135 144 148 150 151 152 192 196 198 199 208 212
214 215 216 224 228 230 231
234
Приложение С. Таблицы ОНБ
Продолжение таблицы С. 2
п — 233 — ОНБ 2 типа, минимальный многочлен:
О 1 4 5 6 8 9 16 17 20 21 22 128 129 132 133 134 136 137 144 145 148 149 150 192 193
196 197 198 200 201 208 209 212 213 214 224 225 228 229 230 232 233
п = 239 — ОНБ 3 типа, минимальный многочлен:
0 8 12 14 15 16 128 136 140 142 143 144 192 200 204 206 207 208 224 232 236 238 239
п — 243 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 И 12 128 130 131 136 138 139 140 192 194 195 200 202 203 204 224 226 227
232 234 235 236 240 242 243
п = 245 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 128 129 130 132 133 136 137 138 192 193 194 196 197 200 201 202 224
225 226 228 229 232 233 234 240 241 242 244 245
п = 251 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 128 130 131 132 192 194 195 196 224 226 227 228 240 242 243 244 248 250 251
п = 254 — ОНБ 2 типа, минимальный многочлен:
0 1 128 129 192 193 224 225 240 241 248 249 252 253 254
п = 261 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 128 129 130 132 133 192 193 194 196 197 224 225 226 228 229 240 241 242
244 245 248 249 250 256 257 258 260 261
п = 268 — ОНБ 1 типа, минимальный многочлен веса 269
п = 270 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 128 129 136 137 140 141 142 192 193 200 201 204 205 206 224 225 232
233 236 237 238 240 241 256 257 264 265 268 269 270
п = 273 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 16 17 128 129 136 137 140 141 142 144 145 192 193 200 201 204 205
206 208 209 224 225 232 233 236 237 238 256 257 264 265 268 269 270 272 273
п = 278 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 128 129 132 133 134 136 137 144 145 148 149 150 192 193
196 197 198 200 201 208 209 212 213 214 224 225 228 229 230 232 233 256 257 260
261 262 264 265 272 273 276 277 278
п — 281 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 16 17 20 21 22 24 25 128 129 132 133 134 144 145 148 149 150 152 153 192
193 196 197 198 208 209 212 213 214 216 217 224 225 228 229 230 256 257 260 261
262 272 273 276 277 278 280 281
п = 292 — ОНБ 1 типа, минимальный многочлен веса 293
С.2. ОНБ размерности п, 30 < п < 1013	235
Продолжение таблицы С. 2
п = 293 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 16 17 18 20 21 24 25 26 32 33 34 36 37 128 129 130 132 133 144 145 146 148
149 152 153 154 160 161 162 164 165 192 193 194 196 197 208 209 210 212 213 216 217
218 256 257 258 260 261 272 273 274 276 277 280 281 282 288 289 290 292 293
п = 299 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 8 10 11 16 18 19 20 32 34 35 36 40 42 43 128 130 131 132 136 138 139 144 146
147 148 160 162 163 164 168 170 171 192 194 195 196 200 202 203 208 210 211 212 256
258 259 260 264 266 267 272 274 275 276 288 290 291 292 296 298 299
п = 303 — ОНБ 3 типа, минимальный многочлен:
0 8 12 14 15 16 32 40 44 46 47 128 136 140 142 143 144 160 168 172 174 175 192 200
204 206 207 208 256 264 268 270 271 272 288 296 300 302 303
п = 306 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 32 33 34 40 41 42 44 45 48 49 50 128 129 130 136 137 138 140 141
160 161 162 168 169 170 172 173 176 177 178 192 193 194 200 201 202 204 205 256 257
258 264 265 266 268 269 288 289 290 296 297 298 300 301 304 305 306
п — 309 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 32 33 34 36 37 40 41 42 48 49 50 52 53 128 129 130 132 133 136 137 138
160 161 162 164 165 168 169 170 176 177 178 180 181 192 193 194 196 197 200 201 202
256 257 258 260 261 264 265 266 288 289 290 292 293 296 297 298 304 305 306 308 309
п = 316 — ОНБ 1 типа, минимальный многочлен веса 317
п = 323 — ОНБ 3 типа, минимальный многочлен:
0 2 3 32 34 35 48 50 51 56 58 59 60 64 66 67 128 130 131 160 162 163 176 178 179 184
186 187 188 256 258 259 288 290 291 304 306 307 312 314 315 316 320 322 323
п = 326 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 32 33 36 37 38 48 49 52 53 54 56 57 64 65 68 69 70 128 129 132 133 134 160
161 164 165 166 176 177 180 181 182 184 185 256 257 260 261 262 288 289 292 293 294
304 305 308 309 310 312 313 320 321 324 325 326
п = 329 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 32 33 36 37 38 40 41 48 49 52 53 54 64 65 68 69 70 72 73 128 129 132 133
134 136 137 160 161 164 165 166 168 169 176 177 180 181 182 256 257 260 261 262 264
265 288 289 292 293 294 296 297 304 305 308 309 310 320 321 324 325 326 328 329
п = 330 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 32 33 34 36 37 40 41 42 48 49 50 52 53 64 65 66 68 69 72 73 74 128
129 130 132 133 136 137 138 160 161 162 164 165 168 169 170 176 177 178 180 181 256
257 258 260 261 264 265 266 288 289 290 292 293 296 297 298 304 305 306 308 309
320 321 322 324 325 328 329 330
236
Приложение С. Таблицы ОНБ
Продолжение таблицы С. 2
п = 338 — ОНБ 2 типа, минимальный многочлен:
О 1 2 8 9 10 12 13 16 17 18 32 33 34 40 41 42 44 45 64 65 66 72 73 74 76 77 80 81 82
128 129 130 136 137 138 140 141 144 145 146 160 161 162 168 169 170 172 173 256 257
258 264 265 266 268 269 272 273 274 288 289 290 296 297 298 300 301 320 321 322
328 329 330 332 333 336 337 338
п — 346 — ОНБ 1 типа, минимальный многочлен веса 347
п = 348 — ОНБ 1 типа, минимальный многочлен веса 349
п = 350 — ОНБ 2 типа, минимальный многочлен:
0 1 16 17 24 25 28 29 30 32 33 64 65 80 81 88 89 92 93 94 128 129 144 145 152 153 156
157 158 160 161 256 257 272 273 280 281 284 285 286 288 289 320 321 336 337 344
345 348 349 350
п — 354 — ОНБ 2 типа, минимальный многочлен:
0 1 2 16 17 18 24 25 26 28 29 64 65 66 80 81 82 88 89 90 92 93 96 97 98 128 129 130
144 145 146 152 153 154 156 157 256 257 258 272 273 274 280 281 282 284 285 320
321 322 336 337 338 344 345 346 348 349 352 353 354
п = 359 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 16 20 22 23 24 64 68 70 71 80 84 86 87 88 96 100 102 103 128 132 134 135 144
148 150 151 152 256 260 262 263 272 276 278 279 280 320 324 326 327 336 340 342
343 344 352 356 358 359
п = 371 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 64 66 67 72 74 75 76 96 98 99 104 106 107 108 112 114 115 128 130
131 136 138 139 140 256 258 259 264 266 267 268 320 322 323 328 330 331 332 352
354 355 360 362 363 364 368 370 371
п = 372 — ОНБ 1 типа, минимальный многочлен веса 373
п = 375 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 8 64 68 70 71 72 96 100 102 103 104 112 116 118 119 128 132 134 135 136 256
260 262 263 264 320 324 326 327 328 352 356 358 359 360 368 372 374 375
п = 378 — ОНБ 1 типа, минимальный многочлен веса 379
п — 378 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 64 65 66 68 69 96 97 98 100 101 112 113 114 116 117 120 121 122 128 129 130
132 133 256 257 258 260 261 320 321 322 324 325 352 353 354 356 357 368 369 370
372 373 376 377 378
п = 386 — ОНБ 2 типа, минимальный многочлен:
0 1 2 64 65 66 96 97 98 112 113 114 120 121 122 124 125 256 257 258 320 321 322 352
353 354 368 369 370 376 377 378 380 381 384 385 386
С.2. ОНБ размерности п, 30 <п < 1013
237
Продолжение таблицы С. 2
п = 388 — ОНБ 1 типа, минимальный многочлен веса 389
п = 393 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 64 65 68 69 70 72 73 96 97 100 101 102 104 105 112 113 116 117 118 256
257 260 261 262 264 265 320 321 324 325 326 328 329 352 353 356 357 358 360 361
368 369 372 373 374 384 385 388 389 390 392 393
п = 398 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 64 65 72 73 76 77 78 96 97 104 105 108 109 НО 112 113 256 257 264
265 268 269 270 320 321 328 329 332 333 334 352 353 360 361 364 365 366 368 369
384 385 392 393 396 397 398
п = 410 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 16 17 18 20 21 24 25 26	64 65 66 68 69 80	81 82 84 85	88 89 90	96 97 98 100
101 256 257 258 260 261 272 273	274 276 277	280	281 282	320	321	322	324	325	336
337 338 340 341 344 345 346 352	353 354 356	357	384 385	386	388	389	400	401	402
404 405 408 409 410
п = 411 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 16 18 19 20 24 26 27 64 66 67 68 80 82 83 84 88 90 91 96 98 99 100 256 258 259
260 272 274 275 276 280 282 283 320 322 323 324 336 338 339 340 344 346 347 352
354 355 356 384 386 387 388 400 402 403 404 408 410 411
п = 413 — ОНБ 2 типа, минимальный многочлен:
0 1 2 16 17 18 24 25 26 28 29 64 65 66 80 81 82 88 89 90 92 93 96 97 98 256 257 258
272 273 274 280 281 282 284 285 320 321 322 336 337 338 344 345 346 348 349 352
353 354 384 385 386 400 401 402 408 409 410 412 413
п — 414 — ОНБ 2 типа, минимальный многочлен:
0 1 16 17 24 25 28 29 30 64 65 80 81 88 89 92 93 94 96 97 256 257 272 273 280 281 284
285 286 320 321 336 337 344 345 348 349 350 352 353 384 385 400 401 408 409 412
413 414
п — 418 — ОНБ 1 типа, минимальный многочлен веса 419
п = 419 — ОНБ 3 типа, минимальный многочлен:
0 2 3 16 18 19 24 26 27 28 32 34 35 64 66 67 80 82 83 88 90 91 92 256 258 259 272 274
275 280 282 283 284 288 290 291 320 322 323 336 338 339 344 346 347 348 384 386
387 400 402 403 408 410 411 412 416 418 419
п = 420 — ОНБ 1 типа, минимальный многочлен веса 421
п = 426 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 16 17 18 20 21 32 33 34 36 37 40 41 42 64 65 66 68 69 72 73 74 80 81
82 84 85 256 257 258 260 261 264 265 266 272 273 274 276 277 288 289 290 292 293
296 297 298 320 321 322 324 325 328 329 330 336 337 338 340 341 384 385 386 388
389 392 393 394 400 401 402 404 405 416 417 418 420 421 424 425 426
к
238
Приложение С. Таблицы ОНБ
Продолжение таблицы С.2
п = 429 — ОНБ 2 типа, минимальный многочлен:
О 1 2 8 9 10 12 13 16 17 18 32 33	34 40 41	42 44 45 64	65 66 72	73 74 76 77	80 81 82
256 257 258 264 265 266 268 269	272 273	274	288	289	290	296	297 298	300	301 320
321 322 328 329 330 332 333 336	337 338	384	385	386	392	393	394 396	397	400 401
402 416 417 418 424 425 426 428 429
п = 431 — ОНБ 3 типа, минимальный многочлен:
0 8 12 14 15 16 32 40 44 46 47 64 72 76 78 79 80 256 264 268 270 271 272 288 296 300
302 303 320 328 332 334 335 336 384 392 396 398 399 400 416 424 428 430 431
п = 438 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 32 33 36 37 38 40 41 48 49 52 53 54 64 65 68 69 70 72 73 256 257 260 261
262 264 265 288 289 292 293 294 296 297 304 305 308 309 310 320 321 324 325 326 328
329 384 385 388 389 390 392 393 416 417 420 421 422 424 425 432 433 436 437 438
п = 441 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 32 33 36 37 38 48 49 52 53 54 56 57 64 65 68 69 70 256 257 260 261 262 288
289 292 293 294 304 305 308 309 310 312 313 320 321 324 325 326 384 385 388 389
390 416 417 420 421 422 432 433 436 437 438 440 441
п = 442 — ОНБ 1 типа, минимальный многочлен веса 443
п = 443 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 32 34 35 36 48 50 51 52 56 58 59 64 66 67 68 256 258 259 260 288 290 291 292
304 306 307 308 312 314 315 320 322 323 324 384 386 387 388 416 418 419 420 432
434 435 436 440 442 443
п = 453 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 32 33 34 36 37 48 49 50 52 53 56 57 58 256 257 258 260 261 288 289 290 292
293 304 305 306 308 309 312 313 314 384 385 386 388 389 416 417 418 420 421 432
433 434 436 437 440 441 442 448 449 450 452 453
п = 460 — ОНБ 1 типа, минимальный многочлен веса 461
п = 466 — ОНБ 1 типа, минимальный многочлен веса 467
п = 470 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 32 33 36 37 38 40 41 256 257 260 261 262 264 265 272 273
276 277 278 288 289 292 293 294 296 297 384 385 388 389 390 392 393 400 401 404 405
406 416 417 420 421 422 424 425 448 449 452 453 454 456 457 464 465 468 469 470
п = 473 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 16 17 20 21 22 24 25 32 33 36 37 38 256 257 260 261 262 272 273 276 277 278
280 281 288 289 292 293 294 384 385 388 389 390 400 401 404 405 406 408 409 416
417 420 421 422 448 449 452 453 454 464 465 468 469 470 472 473
С.2. ОНБ размерности п, 30 < п < 1013
239
Продолжение таблицы С. 2
п = 483 — ОНБ 3 типа, минимальный многочлен:
0 2 3 16 18 19 24 26 27 28 256 258 259 272 274 275 280 282 283 284 384 386 387 400
402 403 408 410 411 412 448 450 451 464 466 467 472 474 475 476 480 482 483
п = 490 — ОНБ 1 типа, минимальный многочлен веса 491
п = 491 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 8 10 11 16 18 19 20 256 258 259 260 264 266 267 272 274 275 276 384 386 387
388 392 394 395 400 402 403 404 448 450 451 452 456 458 459 464 466 467 468 480
482 483 484 488 490 491
п = 495 — ОНБ 3 типа, минимальный многочлен:
0 8 12 14 15 16 256 264 268 270 271 272 384 392 396 398 399 400 448 456 460 462 463
464 480 488 492 494 495
п = 508 — ОНБ 1 типа, минимальный многочлен веса 509
п = 509 — ОНБ 2 типа, минимальный многочлен:
0 1 2 256 257 258 384 385 386 448 449 450 480 481 482 496 497 498 504 505 506 508
509
п = 515 — ОНБ 3 типа, минимальный многочлен:
0 2 3 256 258 259 384 386 387 448 450 451 480 482 483 496 498 499 504 506 507 508
512 514 515
п — 519 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 256 260 262 263 384 388 390 391 448 452 454 455 480 484 486 487 496 500 502
503 504 512 516 518 519
п = 522 — ОНБ 1 типа, минимальный многочлен веса 523
п = 530 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 16 17 18 256 257 258 264 265 266 268 269 272 273 274 384 385 386
392 393 394 396 397 400 401 402 448 449 450 456 457 458 460 461 464 465 466 480
481 482 488 489 490 492 493 512 513 514 520 521 522 524 525 528 529 530
п — 531 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 16 18 19 256 258 259 264 266 267 268 272 274 275 384 386 387 392
394 395 396 400 402 403 448 450 451 456 458 459 460 464 466 467 480 482 483 488
490 491 492 512 514 515 520 522 523 524 528 530 531
п = 540 — ОНБ 1 типа, минимальный многочлен веса 541
п = 543 — ОНБ 3 типа, минимальный многочлен:
0 16 24 28 30 31 256 272 280 284 286 287 384 400 408 412 414 415 448 464 472 476
478 479 480 512 528 536 540 542 543
240
Приложение С. Таблицы ОНБ
Продолжение таблицы С. 2
п = 545 — ОНБ 2 типа, минимальный многочлен:
0 1 16 17 24 25 28 29 30 32 33 256 257 272 273 280 281 284 285 286 288 289 384 385
400 401 408 409 412 413 414 416 417 448 449 464 465 472 473 476 477 478 512 513
528 529 536 537 540 541 542 544 545
п = 546 — ОНБ 1 типа, минимальный многочлен веса 647
п = 554 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10	16 17 18 20 21 32 33 34 36 37	40 41 42 256 257 258	260	261 264 265
266 272 273 274	276	277 288	289	290 292	293	296 297	298	384 385	386	388 389 392
393 394 400 401	402	404 405	416	417 418	420	421 424	425	426 448	449	450 452 453
456 457 458 464	465	466 468	469	512 513	514	516 517	520	521 522	528	529 530 532
533 544 545 546 548 549 552 553 554
п = 556 — ОНБ 1 типа, минимальный многочлен веса 557
п = 558 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 16 17 32 33 40 41 44 45 46 256 257 264 265 268 269 270 272 273 288
289 296 297 300 301 302 384 385 392 393 396 397 398 400 401 416 417 424 425 428
429 430 448 449 456 457 460 461 462 464 465 512 513 520 521 524 525 526 528 529
544 545 552 553 556 557 558
и = 561 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 32 33 40 41 44 45 46 48 49 256 257 264 265 268 269 270 288 289 296
297 300 301 302 304 305 384 385 392 393 396 397 398 416 417 424 425 428 429 430
432 433 448 449 456 457 460 461 462 512 513 520 521 524 525 526 544 545 552 553
556 557 558 560 561
п — 562 — ОНБ 1 типа, минимальный многочлен веса 563
п = 575 — ОНБ 3 типа, минимальный многочлен:
0 32 48 56 60 62 63 256 288 304 312 316 318 319 384 416 432 440 444 446 447 448 512
544 560 568 572 574 575
п — 585 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 32 33 36	37 38 40 41	48 49 52	53 54 64 65 68 69 70	72 73 256 257 260 261
262 264	265 288	289	292 293	294	296 297	304	305 308 309	310	320 321	324	325	326
328 329	384 385	388	389 390	392	393 416	417	420 421 422	424	425 432	433	436	437
438 512	513 516	517	518 520	521	544 545	548	549 550 552	553	560 561	564	565	566
576 577 580 581 582 584 585
п = 586 — ОНБ 1 типа, минимальный многочлен веса 587
п = 593 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 16 17 32 33 40 41 44 45 46 64 65 72 73 76 77 78 80 81 256 257 264 265
С.2. ОНБ размерности п, 30 < п < 1013
241
Продолжение таблицы С. 2
268 269 270 272 273 288 289 296 297 300 301 302 320 321 328 329 332 333 334 336 337
384 385 392 393 396 397 398 400 401 416 417 424 425 428 429 430 512 513 520 521 524
525 526 528 529 544 545 552 553 556 557 558 576 577 584 585 588 589 590 592 593
п = 606 — ОНБ 2 типа, минимальный многочлен:
0 1 16 17 24 25 28 29 30 32 33 64 65 80 81 88 89 92 93 94 256 257 272 273 280 281 284
285 286 288 289 320 321 336 337 344 345 348 349 350 384 385 400 401 408 409 412
413 414 416 417 512 513 528 529 536 537 540 541 542 544 545 576 577 592 593 600
601 604 605 606
п = 611 — ОНБ 3 типа, минимальный многочлен:
0 2 3 16 18 19 24 26 27 28 64 66 67 80 82 83 88 90 91 92 96 98 99 256 258 259 272 274
275 280 282 283 284 320 322 323 336 338 339 344 346	347	348 352	354	355 384	386
387 400 402 403 408 410 411 412 512 514 515 528 530	531	536 538	539	540 576	578
579 592 594 595 600 602 603 604 608 610 611
п = 612 — ОНБ 1 типа, минимальный многочлен веса 613
п = 614 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 16	17 20 21	22 24 25 64 65 68 69	70 80 81	84	85 86 88	89 96 97 100	101	102
256 257 260	261	262	272	273	276 277	278	280 281	320	321 324	325	326 336	337	340
341 342 344	345	352	353	356	357 358	384	385 388	389	390 400	401	404 405	406	408
409 512 513	516	517	518	528	529 532	533	534 536	537	576 577	580	581 582	592	593
596 597 598 600 601 608 609 612 613 614
п = 615 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 16 20 22 23 24 64 68 70 71 80 84 86 87 88 96 100 102 103 256 260 262 263 272
276 278 279 280 320 324 326 327 336 340 342 343 344 352 356 358 359 384 388 390
391 400 404 406 407 408 512 516 518 519 528 532 534 535 536 576 580 582 583 592
596 598 599 600 608 612 614 615
п = 618 — ОНБ 1 типа, минимальный многочлен веса 619
п = 618 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 16 17 18 20 21 64 65 66 68 69 72 73 74 80 81 82 84 85 96 97 98 100
101 104 105	106 256	257	258 260	261	264 265	266	272 273	274	276	277	320 321	322
324 325 328	329 330	336	337 338	340	341 352	353	354 356	357	360	361	362 384	385
386 388 389	392 393	394	400 401	402	404 405	512	513 514	516	517	520	521 522	528
529 530 532	533 576	577	578 580	581	584 585	586	592 593	594	596	597	608 609	610
612 613 616	617 618
п = 629 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 64 65 66 68 69 72 73 74 96 97 98	100	101	104	105	106	112	113	114	116
117 256 257 258 260 261 264 265 266 320 321 322	324	325	328	329	330	352	353	354	356
357 360 361 362 368 369 370 372 373 384 385 386	388	389	392	393	394	512	513	514	516
242
Приложение С. Таблицы ОНБ
Продолжение таблицы С. 2
517 520 521 522 576 577 578 580 581 584 585 586 608 609 610 612 613 616 617 618
624 625 626 628 629
п = 638 — ОНБ 2 типа, минимальный многочлен:
0 1 64 65 96 97 112 ИЗ 120 121 124 125 126 256 257 320 321 352 353 368 369 376 377
380 381 382 384 385 512 513 576 577 608 609 624 625 632 633 636 637 638
п = 639 — ОНБ 3 типа, минимальный многочлен:
0 64 96 112 120 124 126 127 256 320 352 368 376 380 382 383 384 512 576 608 624 632
636 638 639
п = 641 — ОНБ 2 типа, минимальный многочлен:
0 1 64 65 96 97 112 113 120 121 124 125 126 128 129 256 257 320 321 352 353 368 369
376 377 380 381 382 512 513 576 577 608 609 624 625 632 633 636 637 638 640 641
п — 645 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 64 65 66 68 69 96 97 98 100 101 112 113 114 116 117 120 121 122 128 129 130
132 133 256 257 258 260 261 320 321 322 324 325 352 353 354 356 357 368 369 370
372 373 376 377 378 512 513 514 516 517 576 577 578 580 581 608 609 610 612 613
624 625 626 628 629 632 633 634 640 641 642 644 645
п = 650 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9	10 64 65 66	68 69 72	73 74 96 97 98 100 101 104 105 106 112 113 114 116
117 128	129	130	132 133	136	137	138	256 257	258	260 261	264	265 266	320	321 322
324 325	328	329	330 352	353	354	356	357 360	361	362 368	369	370 372	373	512 513
514 516	517	520	521 522	576	577	578	580 581	584	585 586	608	609 610	612	613 616
617 618 624 625 626 628 629 640 641 642 644 645 648 649 650
п = 651 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 8 10 11 64 66 67 68 72 74 75 96 98 99 100 104 106 107 112 114 115 116 128 130
131 132 136 138 139 256 258 259 260 264 266 267 320 322 323 324 328 330 331 352 354
355 356 360 362 363 368 370 371 372 512 514 515 516 520 522 523 576 578 579 580 584
586 587 608 610 611 612 616 618 619 624 626 627 628 640 642 643 644 648 650 651
п = 652 — ОНБ 1 типа, минимальный многочлен веса 653
п = 653 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10	12 13 64	65 66 72 73	74 76 77	96	97 98 104 105 106 108 109	112	ИЗ 114
128 129	130	136	137	138 140	141	256 257	258	264 265	266	268 269 320	321	322 328
329 330	332	333	352	353 354	360	361 362	364	365 368	369	370 512 513	514	520 521
522 524	525	576	577	578 584	585	586 588	589	608 609	610	616 617 618	620	621 624
625 626 640 641 642 648 649 650 652 653
п = 658 — ОНБ 1 типа, минимальный многочлен веса 659
С.2. ОНБ размерности п, 30 <п < 1013
243
Продолжение таблицы С. 2
п — 659 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 16 18 19	64 66 67	72	74 75 76	80 82 83 96 98 99 104 106 107 108	128
130 131 136	138 139	140	144 146	147	256 258	259	264 266	267 268	272	274 275	320
322 323 328	330 331	332	336 338	339	352 354	355	360 362	363 364	512	514 515	520
522 523 524	528 530	531	576 578	579	584 586	587	588 592	594 595	608	610 611	616
618 619 620 640 642 643 648 650 651 652 656 658 659
п — 660 — ОНБ 1 типа, минимальный многочлен веса 661
п = 676 — ОНБ 1 типа, минимальный многочлен веса 677
п = 683 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 8 10 11 16 18 19 20 32 34 35 36 40 42 43 64 66 67 68 72 74 75 80 82 83 84 128
130 131 132 136 138 139 144 146 147 148 160 162 163 164 168 170 171 256 258 259 260
264 266 267	272 274	275	276 288	290 291	292	296	298	299	320	322	323 324	328	330
331 336 338	339 340	512	514 515	516 520	522	523	528	530	531	532	544 546	547	548
552 554 555	576 578	579	580 584	586 587	592	594	595	596	640	642	643 644	648	650
651 656 658	659 660 672	674 675 676 680 682 683
п — 686 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 16 17 32 33 40 41 44 45 46 64 65 72 73 76 77 78 80 81 128 129 136 137
140 141 142 144 145 160 161 168 169 172 173 174 256 257 264 265 268 269 270 272 273
288 289 296 297 300 301 302 320 321 328 329 332 333 334 336 337 512 513 520 521
524 525 526 528 529 544 545 552 553 556 557 558 576 577 584 585 588 589 590 592
593 640 641 648 649 652 653 654 656 657 672 673 680 681 684 685 686
п = 690 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 32 33 34 40 41 42 44 45 48 49 50 64 65 66 72 73 74 76 77 128 129
130 136 137 138 140 141 160 161 162 168 169 170 172 173 176 177 178 256 257 258 264
265 266 268	269 288	289	290	296	297	298	300	301	304	305	306	320	321 322	328	329
330 332 333	512 513	514	520	521	522	524	525	544	545	546	552	553	554 556	557	560
561 562 576	577 578	584	585	586	588	589	640	641	642	648	649	650	652 653	672	673
674 680 681	682 684 685	688 689 690
п = 700 — ОНБ 1 типа, минимальный многочлен веса 701
п = 708 — ОНБ 1 типа, минимальный многочлен веса 709
п = 713 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 32 33 36 37 38 40 41 48 49 52 53 54 128 129 132 133 134 136 137 160 161
164 165 166 168 169 176 177 180 181 182 192 193 196 197 198 200 201 256 257 260 261
262 264 265 288 289 292 293 294 296 297 304 305 308 309 310 512 513 516 517 518
520 521 544 545 548 549 550 552 553 560 561 564 565 566 640 641 644 645 646 648
649 672 673 676 677 678 680 681 688 689 692 693 694 704 705 708 709 710 712 713
244
Приложение С. Таблицы ОНБ
Продолжение таблицы С.2
п = 719 — ОНБ 3 типа, минимальный многочлен:
О 8 12 14 15 32 40 44 46 47 48 128 136 140 142 143 160 168 172 174 175 176 192 200
204 206 207 256 264 268 270 271 288 296 300 302 303 304 512 520 524 526 527 544 552
556 558 559 560 640 648 652 654 655 672 680 684 686 687 688 704 712 716 718 719
п = 723 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 16 18 19 32 34 35 40 42 43 44 128 130 131 136 138 139 140 144 146
147 160 162 163 168 170 171 172 192 194 195 200 202 203 204 208 210 211 256 258 259
264 266 267 268 272 274 275 288 290 291 296 298 299 300 512 514 515 520 522 523
524 528 530 531 544 546 547 552 554 555 556 640 642 643 648 650 651 652 656 658
659 672 674 675 680 682 683 684 704 706 707 712 714 715 716 720 722 723
п = 725 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 16 17 18 20	21 32 33 34	36 37 40 41 42 128 129	130	132	133	136	137
138 144 145 146 148 149 160	161	162	164	165	168 169 170 192 193	194	196	197	200	201
202 208 209 210 212 213 256	257	258	260	261	264 265 266 272 273	274	276	277	288	289
290 292 293 296 297 298 512	513	514	516	517	520 521 522 528 529	530	532	533	544	545
546 548 549 552 553 554 640 641 642 644 645 648 649 650 656 657 658 660 661 672
673 674 676 677 680 681 682 704 705 706 708 709 712 713 714 720 721 722 724 725
п = 726 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 32 33 36 37 38 40 41 128 129 132 133 134 136 137 144 145
148 149 150 160 161 164 165 166 168 169 192 193 196 197 198 200 201 208 209 212 213
214 256	257	260	261	262	264	265	272 273	276	277	278	288 289	292	293	294	296	297
512 513	516	517	518	520	521	528	529 532	533	534	544	545 548	549	550	552	553	640
641 644	645	646	648	649	656	657	660 661	662	672	673	676 677	678	680	681	704	705
708 709	710	712	713 720	721 724 725 726
п = 741 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4	5 16 17 18 20 21	24 25 26 128	129	130	132	133	144	145	146	148	149	152 153
154 192	193 194	196	197	208	209 210	212	213	216	217	218	224	225	226	228	229 256
257 258	260 261	272	273	274	276 277	280	281	282	512	513	514	516	517	528	529 530
532 533	536 537	538	640	641	642 644	645	656	657	658	660	661	664	665	666	704 705
706 708 709 720 721 722 724 725 728 729 730 736 737 738 740 741
п = 743 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 16 20 22 23 24 128 132 134 135 144 148 150 151 152 192 196 198 199 208 212
214 215 216 224 228 230 231 256 260 262 263 272 276 278 279 280 512 516 518 519
528 532 534 535 536 640 644 646 647 656 660 662 663 664 704 708 710 711 720 724
726 727 728 736 740 742 743
п = 746 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 16 17 18 20 21 128 129 130 132 133 136 137 138 144 145 146 148 149
192 193 194 196 197 200 201 202 208 209 210 212 213 224 225 226 228 229 232 233 234
256 257 258 260 261 264 265 266 272 273 274 276 277 512 513 514 516 517 520 521 522
С.2. ОНБ размерности п, 30 < п < 1013
245
Продолжение таблицы С. 2
528 529 530 532 533 640 641 642 644 645 648 649 650 656 657 658 660 661 704 705
706 708 709 712 713 714 720 721 722 724 725 736 737 738 740 741 744 745 746
п = 749 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 16 17 18 128 129 130 136 137 138 140 141 144 145 146 192 193 194
200 201 202	204 205	208	209 210	224	225 226	232	233 234	236	237	256	257 258	264
265 266 268	269 272	273	274 512	513	514 520	521	522 524	525	528	529	530 640	641
642 648 649	650 652	653	656 657	658	704 705	706	712 713	714	716	717	720 721	722
736 737 738	744 745	746	748 749
п = 755 — ОНБ 3 типа, минимальный многочлен:
0 2 3 8 10 11 12 128 130 131 136 138 139 140 192 194 195 200 202 203 204 224 226 227
232 234 235 236 240 242 243 256 258 259 264 266 267 268 512 514 515 520 522 523
524 640 642 643 648 650 651 652 704 706 707 712 714 715 716 736 738 739 744 746
747 748 752 754 755
п — 756 — ОНБ 1 типа, минимальный многочлен веса 757
п = 761 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 128 129 132 133 134 192 193 196 197 198 224 225 228 229 230 240 241 244
245 246 248 249 256 257 260 261 262 512 513 516 517 518 640 641 644 645 646 704
705 708 709 710 736 737 740 741 742 752 753 756 757 758 760 761
п = 765 — ОНБ 2 типа, минимальный многочлен:
0 1 2 128 129 130 192 193 194 224 225 226 240 241 242 248 249 250 252 253 256
257 258 512 513 514 640 641 642 704 705 706 736 737 738 752 753 754 760 761 762
764 765
п = 771 — ОНБ 3 типа, минимальный многочлен:
0 2 3 128 130 131 192 194 195 224 226 227 240 242 243 248 250 251 252 512 514 515
640 642 643 704 706 707 736 738 739 752 754 755 760 762 763 764 768 770 771
п = 772 — ОНБ 1 типа, минимальный многочлен веса 773
п = 774 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 128 129 132 133 134 192 193 196 197 198 224 225 228 229 230 240 241 244
245 246 248 249 512 513 516 517 518 640 641 644 645 646 704 705 708 709 710 736
737 740 741 742 752 753 756 757 758 760 761 768 769 772 773 774
п = 779 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 8 10 11 128 130 131 132 136 138 139 192 194 195 196 200 202 203 224 226 227
228 232 234 235 240 242 243 244 512 514 515 516 520 522 523 640 642 643 644 648
650 651 704 706 707 708 712 714 715 736 738 739 740 744 746 747 752 754 755 756
768 770 771 772 776 778 779
246
Приложение С. Таблицы ОНБ
Продолжение таблицы С.2
п = 783 — ОНБ 3 типа, минимальный многочлен:
О 8 12 14 15 128 136 140 142 143 192 200 204 206 207 224 232 236 238 239 240 512
520 524 526 527 640 648 652 654 655 704 712 716 718 719 736 744 748 750 751 752
768 776 780 782 783
п — 785 — ОНБ 2 типа, минимальный многочлей:
0 1 8 9 12 13 14 16 17 128 129 136 137 140 141 142 144 145 192 193 200 201 204 205
206 208 209 224 225 232 233 236 237 238 512 513 520 521 524 525 526 528 529 640
641 648 649 652 653 654 656 657 704 705 712 713 716 717 718 720 721 736 737 744
745 748 749 750 768 769 776 777 780 781 782 784 785
п = 786 — ОНБ 1 типа, минимальный многочлен веса 787
п = 791 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 8 16 20 22 23 128 132 134 135	136 144	148	150	151 192	196	198	199 200	208
212 214 215 224 228 230 231 232 512	516 518	519	520	528 532	534	535	640 644	646
647 648 656 660 662 663 704 708 710	711 712	720	724	726 727	736	740	742 743	744
768 772 774 775 776 784 788 790 791
п = 796 — ОНБ 1 типа, минимальный многочлен веса 797
п = 803 — ОНБ 3 типа, минимальный многочлен:
0 2 3 16 18 19 24 26 27 28 32 34 35 128 130 131 144 146 147 152 154 155 156 160 162
163 192 194 195 208 210 211 216 218 219 220 512 514 515 528 530 531 536 538 539
540 544 546 547 640 642 643 656 658 659 664 666 667 668 672 674 675 704 706 707
720 722 723 728 730 731 732 768 770 771 784 786 787 792 794 795 796 800 802 803
п = 809 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 32 33 36 37 38 40 41 128 129 132 133 134 136 137 144 145
148 149 150 160 161 164 165 166 168 169 192 193 196 197 198 200 201 208 209 212 213
214 512	513 516	517	518	520	521 528	529	532	533	534 544	545	548	549	550	552 553
640 641	644 645	646	648	649	656 657	660	661	662	672 673	676	677	678	680	681 704
705 708	709 710	712	713	720	721 724	725	726	768	769 772	773	774	776	777	784 785
788 789	790 800 801	804 805	806 808 809
п = 810 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10	16 17 18 20 21 32 33 34	36 37 40 41	42 128 129 130 132	133	136	137
138 144 145 146	148 149 160 161 162	164	165	168 169	170 192 193 194 196	197	200	201
202 208 209 210	212 213 512' 513 514	516	517	520 521	522 528 529 530 532	533	544	545
546 548 549 552	553 554 640 641 642	644	645	648 649	650 656 657 658 660	661	672	673
674 676 677 680 681 682 704 705 706 708 709 712 713 714 720 721 722 724 725 768
769 770 772 773 776 777 778 784 785 786 788 789 800 801 802 804 805 808 809 810
п = 818 — ОНБ 2 типа, минимальный многочлен:
0 1 2 8 9 10 12 13 32 33 34 40 41 42 44 45 48 49 50 128 129 130 136 137 138 140 141
160 161 162 168 169 170 172 173 176 177 178 192 193 194 200 201 202 204 205 512 513
С.2. ОНБ размерности п, 30 < п < 1013
247
Продолжение таблицы С.2
514 520 521 522 524 525 544	545	546 552 553 554 556	557	560 561 562 640 641	642	648
649 650 652 653 672 673 674	680	681 682 684 685 688	689	690 704 705 706 712	713	714
716 717 768 769 770 776 777	778	780 781 800 801 802	808	809 810 812 813 816	817	818
п = 820 — ОНБ 1 типа, минимальный многочлен веса 821
п = 826 — ОНБ 1 типа, минимальный многочлен веса 827
п = 828 — ОНБ 1 типа, минимальный многочлен веса 829
п = 831 — ОНБ 3 типа, минимальный многочлен:
0 32 48 56 60 62 63 128 160 176 184 188 190 191 192 512 544 560 568 572 574 575 640
672 688 696 700 702 703 704 768 800 816 824 828 830 831
п = 833 — ОНБ 2 типа, минимальный многочлен:
0 1 32 33 48 49 56 57 60 61 62 64 65 128 129 160 161 176 177 184 185 188 189 190 512
513 544 545 560 561 568 569 572 573 574 576 577 640 641 672 673 688 689 696 697
700 701 702 768 769 800 801 816 817 824 825 828 829 830 832 833
п = 834 — ОНБ 2 типа, минимальный многочлен:
0 1 2 32 33 34 48 49 50 56 57 58 60 61 64 65 66 128 129 130 160 161 162 176 177 178
184 185 186 188 189 512 513 514 544 545 546 560 561 562 568 569 570 572 573 576
577 578 640 641 642 672 673 674 688 689 690 696 697 698 700 701 768 769 770 800
801 802 816 817 818 824 825 826 828 829 832 833 834
п = 846 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 32 33 40 41 44 45 46 48 49 64 65 72 73 76 77 78 128 129 136 137 140
141 142 160 161 168 169 172 173 174 176 177 512 513 520 521 524 525 526 544 545 552
553 556 557 558 560 561 576 577 584 585 588 589 590 640 641 648 649 652 653 654
672 673 680 681 684 685 686 688 689 768 769 776 777 780 781 782 800 801 808 809
812 813 814 816 817 832 833 840 841 844 845 846
п = 852 — ОНБ 1 типа, минимальный многочлен веса 853
п = 858 — ОНБ 1 типа, минимальный многочлен веса 859
п — 866 — ОНБ 2 типа, минимальный многочлен:
0 1 2 16 17	18 24 25 26 28 29 64 65 66 80 81 82 88 89 90 92 93	96 97 98 128	129	130
144 145 146	152 153	154	156 157	512	513 514	528	529	530	536	537	538	540	541	576
577 578 592	593 594	600	601 602	604	605 608	609	610	640	641	642	656	657	658	664
665 666 668	669 768	769	770 784	785	786 792	793	794	796	797	832	833	834	848	849
850 856 857 858 860 861 864 865 866
п — 870 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 16 17 20 21 22 24 25 64 65 68 69 70 80 81 84 85 86 88 89 96 97 100 101 102
248
Приложение С. Таблицы ОНБ
Продолжение таблицы С.2
128 129 132 133 134 144 145 148 149 150 152 153 512 513 516 517 518 528 529 532 533
534 536 537 576 577 580 581 582 592 593 596 597 598 600 601 608 609 612 613 614 640
641 644 645 646 656 657 660 661 662 664 665 768 769 772 773 774 784 785 788 789
790 792 793 832 833 836 837 838 848 849 852 853 854 856 857 864 865 868 869 870
п = 873 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9 16 17 20 21 22 64 65 68 69 70 72 73 80 81 84 85 86 96 97 100 101 102 104
105 128 129 132 133 134 136 137 144 145 148 149 150 512 513 516 517 518 520 521 528
529 532 533 534	576	577	580	581	582	584 585	592	593 596	597 598	608	609 612	613
614 616 617 640	641	644	645	646	648	649 656	657	660 661	662 768	769	772 773	774
776 777 784 785	788	789	790	832	833	836 837	838	840 841	848 849	852	853 854	864
865 868 869 870	872	873
п = 876 — ОНБ 1 типа, минимальный многочлен веса 877
п = 879 — ОНБ 3 типа, минимальный многочлен:
0 8 12 14 15 16 64 72 76 78 79 80 96 104 108 НО 111 128 136 140 142 143 144 512 520
524 526 527 528 576 584 588 590 591 592 608 616 620 622 623 640 648 652 654 655
656 768 776 780 782 783 784 832 840 844 846 847 848 864 872 876 878 879
п = 882 — ОНБ 1 типа, минимальный многочлен веса 883
п = 891 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 64 66 67 68 96 98 99 100 112 114 115 116 120 122 123 128 130 131 132 512 514
515 516 576 578 579 580 608 610 611 612 624 626 627 628 632 634 635 640 642 643
644 768 770 771 772 832 834 835.836 864 866 867 868 880 882 883 884 888 890 891
п = 893 — ОНБ 2 типа, минимальный многочлен:
0 1 2 64 65 66 96 97 98 112 ИЗ 114 120 121 122 124 125 128 129 130 512 513 514 576
577 578 608 609 610 624 625 626 632 633 634 636 637 640 641 642 768 769 770 832
833 834 864 865 866 880 881 882 888 889 890 892 893
п = 906 — ОНБ 1 типа, минимальный многочлен веса 907
п = 911 — ОНБ 3 типа, минимальный многочлен:
0 8 12 14 15 64 72 76 78 79 96 104 108 ПО 111 112 512 520 524 526 527 576 584 588
590 591 608 616 620 622 623 624 768 776 780 782 783 832 840 844 846 847 864 872
876 878 879 880 896 904 908 910 911
п = 923 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 16 18 19 20 24 26 27 64 66 67 68 80 82 83 84 88 90 91 96 98 99 100 512 514 515
516 528 530 531 532 536 538 539 576 578 579 580 592 594 595 596 600 602 603 608
610 611 612 768 770 771 772 784 786 787 788 792 794 795 832 834 835 836 848 850
851 852 856 858 859 864 866 867 868 896 898 899 900 912 914 915 916 920 922 923
С.2. ОНБ размерности п, 30 < п < 1013
249
Продолжение таблицы С. 2
п = 930 — ОНБ 2 типа, минимальный многочлен:
0 1 2 16 17 18 24 25 26 28 29 32 33 34 64 65 66 80 81 82 88 89 90 92 93 512 513 514
528 529 530 536 537 538 540 541 544 545 546 576 577 578 592 593 594 600 601 602 604
605 768 769 770 784 785 786 792 793 794 796 797 800 801 802 832 833 834 848 849
850 856 857 858 860 861 896 897 .898 912 913 914 920 921 922 924 925 928 929 930
п = 933 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 16 17 18 20 21 24 25 26 32 33 34 36 37 64 65 66 68 69 80 81 82 84 85 88
89 90 512 513 514 516 517 528 529 530 532 533 536 537 538 544 545 54,6 548 549
576 577 578 580 581 592 593 594 596 597 600 601 602 768 769 770 772 773 784 785
786 788 789 792 793 794 800 801 802 804 805 832 833 834 836 837 848 849 850 852
853 856 857 858 896 897 898 900 901 912 913 914 916 917 920 921 922 928 929 930
932 933
п — 935 — ОНБ 3 типа, минимальный многочлен:
0 4 6 7 16 20 22 23 24 32 36 38 39 64 68 70 71 80 84 86 87 88 512 516 518 519 528 532
534 535 536 544 548 550 551 576 580 582 583 592 596 598 599 600 768 772 774 775
784 788 790 791 792 800 804 806 807 832 836 838 839 848 852 854 855 856 896 900
902 903 912 916 918 919 920 928 932 934 935
п = 938 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 8 9 10 16 17 18 20 21 32 33 34 36 37 40 41 42 64 65 66 68 69 72 73 74 80 81
82 84 85 512 513 514	516	517 520	521 522	528	529 530	532	533	544	545 546	548 549
552 553 554	576 577	578	580 581	584 585	586	592 593	594	596	597	768 769	770 772
773 776 777	778 784	785	786 788	789 800	801	802 804	805	808	809	810 832	833 834
836 837 840	841 842	848	849 850	852 853	896	897 898	900	901	904	905 906	912 913
914 916 917 928 929 930 932 933 936 937 938
п = 939 — ОНБ 3 типа, минимальный многочлен:
0 2 3 4 8 10	11 16 18	19 20 32 34 35 36 40	42 43 64	66	67 68 72	74 75 80	82 83 84	512
514 515 516	520 522	523	528	530	531	532	544	546	547	548	552	554	555	576	578	579
580 584 586	587 592	594	595	596	768	770	771	772	776	778	779	784	786	787	788	800
802 803 804	808 810	811	832	834	835	836	840	842	843	848	850	851	852	896	898	899
900 904 906 907 912 914 915 916 928 930 931 932 936 938 939
п = 940 — ОНБ 1 типа, минимальный многочлен веса 941
п = 946 — ОНБ 1 типа, минимальный многочлен веса 947
п = 950 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 8 9	32 33 36	37 38 40 41	48 49 52	53 54 64	65	68 69 70	72 73 512 513 516 517
518 520 521	544 545	548	549 550	552	553	560 561	564	565 566	576 577	580	581 582
584 585 768	769 772	773	774 776	777	800	801 804	805	806 808	809 816	817	820 821
822 832 833	836 837	838	840 841	896	897	900 901	902	904 905	928 929	932	933 934
936 937 944 945 948 949 950
250
Приложение С. Таблицы ОНБ
Окончание таблицы С. 2
п = 953 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5	6 32	33	36 37 38	48	49 52 53	54
518 544	545	548	549	550	560	561	564	565
769 772	773	774	800	801	804	805	806	816
837 838	896	897	900	901	902	928	929	932
56 57 64	65	68 69 70	512	513	516	517
566 568	569	576	577	580	581	582	768
817 820	821	822	824	825	832	833	836
933 934	944	945	948	949	950	952	953
п — 965 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 32 33 34 36 37 48 49 50 52 53 56 57 58 512 513 514 516 517 544 545 546 548
549 560 561 562 564 565 568 569 570 768 769 770 772 773 800 801 802 804 805 816
817 818 820 821 824 825 826 896 897 898 900 901 928 929 930 932 933 944 945 946
948 949 952 953 954 960 961 962 964 965
п = 974 — ОНБ 2 типа, минимальный многочлен:
0 1 8 9 12 13 14 32 33 40 41 44 45 46 48 49 512 513 520 521 524 525 526 544 545 552
553 556 557 558 560 561 768 769 776 777 780 781 782 800 801 808 809 812 813 814
816 817 896 897 904 905 908 909 910 928 929 936 937 940 941 942 944 945 960 961
968 969 972 973 974
п — 975 — ОНБ 3 типа, минимальный многочлен:
0 8 12 14 15 32 40 44 46 47 48 512 520 524 526 527 544 552 556 558 559 560 768 776
780 782 783 800 808 812 814 815 816 896 904 908 910 911 928 936 940 942 943 944
960 968 972 974 975
п — 986 — ОНБ 2 типа, минимальный многочлен:
0 1 2 4 5 16 17 18 20 21 24 25 26 32 33 34 36 37 512 513 514 516 517 528 529 530 532
533 536 537 538 544 545 546 548 549 768 769 770 772 773 784 785 786 788 789 792
793 794 800 801 802 804 805 896 897 898 900 901 912 913 914 916 917 920 921 922
928 929 930 932 933 960 961 962 964 965 976 977 978 980 981 984 985 986
п = 989 — ОНБ 2 типа, минимальный многочлен:
0 1 2 16 17 18 24 25 26 28 29 32 33 34 512 513 514 528 529 530 536	537	538	540	541
544 545 546 768 769 770 784 785 786 792 793 794 796 797	800 801	802	896	897	898	912
913 914 920 921 922 924 925 928 929 930 960 961 962 976	977 978	984	985	986	988	989
п = 993 — ОНБ 2 типа, минимальный многочлен:
0 1 16 17 24 25 28 29 30 512 513 528 529 536 537 540 541 542 768 769 784 785 792 793
796 797 798 896 897 912 913 920 921 924 925 926 960 961 976 977 984 985 988 989
990 992 993
п = 998 — ОНБ 2 типа, минимальный многочлен:
0 1 4 5 6 16 17 20 21 22 24 25 512 513 516 517 518 528 529 532 533 534 536 537 768
769 772 773 774 784 785 788 789 790 792 793 896 897 900 901 902 912 913 916 917
918 920 921 960 961 964 965 966 976 977 980 981 982 984 985 992 993 996 997 998
С.З. Возможные размерности ОНБ п, 998 < п < 10 000
251
С.З. Возможные размерности ОНБ п,
998 < п < 10 000
Приведенная ниже таблица С.З — таблица размерностей полей GF(2n)
при 998 < п < 10 000, для которых существуют оптимальные нормаль-
ные базисы (ОНБ) составлена на основе компьютерных вычислений
по программе, разработанной в дипломной работе Р. А. Хохловым (МГУ).
В скобках после размерности указан тип базиса (если для рассматрива-
емого поля одновременно существуют базисы типа 1 и 2, то в скобках
стоит 1,2; другие варианты не встречаются). Таблица для п 1000 име-
ется, например, в [53, 72] (см. также таблицу С.2). В этой таблице мы
не приводим вычисляемые программой матрицы А, Т и минимальные
многочлены ввиду их громоздкости.
Таблица С.З
Таблица размерностей ОНБ. В скобках после размерности указан тип базиса (если
для рассматриваемого поля одновременно существуют базисы типа 1 и 2, то в скобках
стоит 1, 2; другие варианты не встречаются)
1013(2)	1014(2)	1018(1)	1019(3)	1026(2)	1031(3)	1034(2)	1041(2)
1043(3)	1049(2)	1055(3)	1060(1)	1065(2)	1070(2)	1090(1)	1103(3)
1106(2)	1108(1)	1110(2)	1116(1)	1118(2)	1119(3)	1121(2)	1122(1)
1133(2)	1134(2)	1146(2)	1154(2)	1155(3)	1166(2)	1169(2)	1170(1)
1178(2)	1185(2)	1186(1)	1194(2)	1199(3)	1211(3)	1212(1)	1218(2)
1223(3)	1228(1)	1229(2)	1233(2)	1236(1)	1238(2)	1251(3)	1258(1)
1265(2)	1269(2)	1271(3)	1274(2)	1275(3)	1276(1)	1278(2)	1282(1)
1289(2)	1290(1)	1295(3)	1300(1)	1306(1)	1310(2)	1323(3)	1329(2)
1331(3)	1338(2)	1341(2)	1346(2)	1349(2)	1353(2)	1355(3)	1359(3)
1370(2)	1372(1)	1380(1)	1394(2)	1398(2)	1401(2)	1409(2)	1418(2)
1421(2)	1425(2)	1426(1)	1430(2)	1439(3)	1443(3)	1450(1)	1451(3)
1452(1)	1454(2)	1463(3)	1469(2)	1478(2)	1481(2)	1482(1)	1492(1)
1498(1)	1499(3)	1505(2)	1509(2)	1511(3)	1518(2)	1522(1)	1530(1)
1533(2)	1539(3)	1541(2)	1548(1)	1559(3)	1570(1)	1583(3)	1593(2)
1601(2)	1618(1)	1620(1)	1626(2)	1636(1)	1649(2)	1653(2)	1659(3)
252
Приложение С. Таблицы ОНБ
Продолжение таблицы С.З
1661(2)	1666(1)	1668(1)	1673(2)	1679(3)	1685(2)	1692(1)	1703(3)
1706(2)	1730(2)	1732(1)	1733(2)	1734(2)	1740(1)	1745(2)	1746(1)
1749(2)	1755(3)	1758(2)	1763(3)	1766(2)	1769(2)	1773(2)	1778(2)
1779(3)	1785(2)	1786(1)	1790(2)	1791(3)	1806(2)	1811(3)	1818(2)
1821(2)	1829(2)	1835(3)	1838(2)	1845(2)	1850(2)	1854(2)	1859(3)
1860(1)	1863(3)	1866(1,2)	1876(1)	1883(3)	1889(2)	1898(2)	1900(1)
1901(2)	1906(1)	1923(3)	1925(2)	1926(2)	1930(1)	1931(3)	1938(2)
1948(1)	1953(2)	1955(3)	1958(2)	1959(3)	1961(2)	1965(2)	1972(1)
1973(2)	1978(1)	1983(3)	1986(1)	1994(2)	1996(1)	2001(2)	2003(3)
2006(2)	2009(2)	2010(2)	2026(1)	2028(1)	2039(3)	2045(2)	2046(2)
2049(2)	2052(1)	2055(3)	2063(3)	2066(2)	2068(1)	2069(2)	2078(2)
2079(3)	2082(1)	2098(1)	2109(2)	2114(2)	2115(3)	2121(2)	2126(2)
2129(2)	2130(1,2)	2140(1)	2141(2)	2163(3)	2174(2)	2178(2)	2181(2)
2186(2)	2195(3)	2198(2)	2212(1)	2220(1)	2223(3)	2225(2)	2231(3)
2236(1)	2241(2)	2242(1)-	2246(2)	2253(2)	2258(2)	2266(1)	2268(1)
2273(2)	2291(3)	2292(1)	2295(3)	2301(2)	2308(1)	2310(2)	2318(2)
2319(3)	2332(1)	2338(1)	2339(3)	2345(2)	2351(3)	2356(1)	2361(2)
2370(1)	2388(1)	2391(3)	2393(2)	2394(2)	2399(3)	2406(2)	2415(3)
2436(1)	2438(2)	2451(3)	2458(1)	2459(3)	2466(1,2)	2471(3)	2475(3)
2476(1)	2478(2)	2483(3)	2486(2)	2493(2)	2501(2)	2505(2)	2511(3)
2519(3)	2525(2)	2529(2)	2530(1)	2538(1,2)	2543(3)	2548(1)	2549(2)
2553(2)	2556(1)	2559(3)	2573(2)	2578(1)	2585(2)	2589(2)	2594(2)
2613(2)	2615(3)	2620(1)	2630(2)	2651(3)	2654(2)	2658(1)	2666(2)
2675(3)	2676(1)	2682(1)	2692(1)	2693(2)	2698(1)	2699(3)	2703(3)
2706(1)	2715(3)	2721(2)	2738(2)	2739(3)	2740(1)	2741(2)	2750(2)
С.З. Возможные размерности ОНБ п, 998 < п < 10 000
253
Продолжение таблицы С.З
2753(2)	2759(3)	2763(3)	2778(2)	2781(2)	2786(2)	2788(1)	2795(3)
2796(1)	2802(1)	2811(3)	2818(1)	2819(3)	2823(3)	2825(2)	2829(2)
2836(1)	2841(2)	2842(1)	2846(2)	2850(1,2)	2858(2)	2860(1)	2870(2)
2871(3)	2874(2)	2889(2)	2891(3)	2895(3)	2903(3)	2906(2)	2908(1)
2913(2)	2919(3)	2921(2)	2925(2)	2934(2)	2938(1)	2939(3)	2951(3)
2956(1)	2961(2)	2962(1)	2963(3)	2969(2)	2993(2)	3005(2)	3010(1)
3014(2)	3018(1)	3023(3)	3026(2)	3033(2)	3036(1)	3050(2)	3065(2)
3066(1)	3071(3)	3082(1)	3086(2)	3098(2)	3099(3)	3101(2)	3105(2)
3114(2)	3123(3)	3131(3)	3134(2)	3138(2)	3143(3)	3149(2)	3155(3)
3158(2)	3161(2)	3171(3)	3179(3)	3183(3)	3186(1)	3189(2)	3194(2)
3198(2)	3202(1)	3234(2)	3245(2)	3252(1)	3273(2)	3275(3)	3298(1)
3299(3)	3303(3)	3306(1)	3309(2)	3318(2)	3322(1)	3326(2)	3329(2)
3345(2)	3346(1)	3350(2)	3351(3)	3354(2)	3359(3)	3366(2)	3370(1)
3381(2)	3389(2)	3390(2)	3401(2)	3411(3)	3412(1)	3413(2)	3414(2)
3431(3)	3434(2)	3441(2)	3449(2)	3453(2)	3455(3)	3458(2)	3460(1)
3466(1)	3468(1)	3473(2)	3474(2)	3485(2)	3490(1)	3491(3)	3495(3)
3498(1)	3506(2)	3509(2)	3513(2)	3516(1)	3519(3)	3521(2)	3532(1)
3534(2)	3538(1)	3539(3)	3546(1)	3551(3)	3554(2)	3556(1)	3563(3)
3570(1)	3579(3)	3580(1)	3593(2)	3603(3)	3605(2)	3609(2)	3612(1)
3614(2)	3618(2)	3621(2)	3623(3)	3626(2)	3636(1)	3641(2)	3642(1)
3653(2)	3658(1)	3665(2)	3674(2)	3676(1)	3690(1)	3700(1)	3705(2)
3708(1)	3725(2)	3729(2)	3732(1)	3738(2)	3749(2)	3753(2)	3758(2)
3761(2)	3770(2)	3773(2)	3774(2)	3778(1)	3779(3)	3786(2)	3791(3)
3794(2)	3795(3)	3796(1)	3801(2)	3802(1)	3803(3)	3810(2)	3821(2)
3834(2)	3843(3)	3845(2)	3850(1)	3851(3)	3852(1)	3858(2)	3863(3)
254
Приложение С. Таблицы ОНБ
Продолжение таблицы С.З
3876(1)	3878(2)	3879(3)	3894(2)	3906(1)	3911(3)	3914(2)	3916(1)
3922(1)	3926(2)	3930(1)	3938(2)	3939(3)	3941(2)	3946(1)	3950(2)
3953(2)	3959(3)	3966(2)	3974(2)	3975(3)	3988(1)	4002(1)	4012(1)
4018(1)	4019(3)	4020(1)	4026(2)	4034(2)	4043(3)	4046(2)	4055(3)
4058(2)	4061(2)	4073(2)	4085(2)	4089(2)	4090(1)	4092(1)	4098(1)
4109(2)	4110(2)	4115(3)	4118(2)	4121(2)	4131(3)	4132(1)	4134(2)
4138(1)	4145(2)	4146(2)	4155(2)	4156(1)	4181(2)	4193(2)	4211(2)
4214(2)	4215(3)	4218(1)	4221(2)	4223(2)	4228(1)	4233(2)	4242(1)
4252(1)	4256(2)	4258(1)	4260(1)	4263(3)	4269(2)	4271(3)	4281(2)
4282(1)	4286(2)	4298(2)	4299(2)	4304(2)	4311(3)	4313(2)	4323(3)
4331(3)	4334(2)	4338(2)	4346(2)	4348(1)	4349(2)	4356(1)	4362(1)
4365(2)	4370(2)	4372(1)	4373(2)	4391(3)	4396(1)	4401(2)	4403(2)
4409(2)	4410(2)	4418(2)	4419(3)	4430(2)	4433(2)	4443(2)	4450(1)
4461(2)	4466(2)	4475(3)	4481(2)	4482(1)	4484(2)	4485(2)	4492(1)
4499(2)	4503(3)	4505(2)'	4506(1)	4514(2)	4516(1)	4524(2)	4529(2)
4546(1)	4551(3)	4563(3)	4575(2)	4580(2)	4586(2)	4590(2)	4599(3)
4601(2)	4602(1)	4610(2)	4613(2)	4619(3)	4620(1)	4628(2)	4636(1)
4641(2)	4646(2)	4655(3)	4659(3)	4661(2)	4668(2)	4670(2)	4671(2)
4674(2)	4685(2)	4690(1)	4695(3)	4698(2)	4709(2)	4710(2)	4716(2)
4718(2)	4722(1)	4733(2)	4739(2)	4745(2)	4766(2)	4769(2)	4773(2)
4775(3)	4786(1)	4788(1)	4793(2)	4800(2)	4806(2)	4809(2)	4812(1)
4814(2)	4821(2)	4830(2)	4838(2)	4839(3)	4848(2)	4866(2)	4871(3)
4874(2)	4876(1)	4883(2)	4895(3)	4901(2)	4916(2)	4925(2)	4929(2)
4932(1)	4935(3)	4941(2)	4943(3)	4950(2)	4953(2)	4956(1)	4961(2)
4970(2)	4972(1)	4974(2)	4983(3)	4986(1)	5002(1)	5010(1)	5018(2)
С.З. Возможные размерности ОНБ п, 998 < п < 10 000
255
Продолжение таблицы С.З
5033(2)	5034(2)	5039(3)	5045(2)	5046(2)	5049(2)	5050(1)	5051(3)
5055(2)	5058(1)	5066(2)	5069(2)	5070(2)	5075(2)	5076(1)	5081(2)
5088(2)	5090(2)	5098(1)	5106(1)	5111(2)	5123(2)	5126(2)	5129(2)
5133(2)	5135(3)	5136(2)	5144(2)	5146(1)	5150(2)	5156(2)	5165(2)
5170(1)	5171(2)	5178(1)	5184(2)	5188(1)	5195(3)	5199(2)	5213(2)
5226(1)	5229(2)	5231(3)	5238(2)	5243(3)	5249(2)	5250(2)	5260(1)
5279(3)	5283(2)	5294(2)	5300(2)	5303(2)	5306(2)	5308(1)	5315(2)
5319(3)	5328(2)	5332(1)	5333(2)	5343(2)	5345(2)	5354(2)	5361(2)
5366(2)	5386(1)	5394(2)	5399(2)	5415(3)	5418(2)	5423(3)	5426(2)
5429(2)	5430(2)	5433(2)	5441(2)	5442(1)	5444(2)	5445(2)	5454(2)
5474(2)	5476(1)	5482(1)	5486(2)	5489(2)	5493(2)	5500(1)	5501(2)
5506(1)	5513(2)	5523(2)	5528(2)	5534(2)	5535(2)	5541(2)	5543(2)
5546(2)	5556(1)	5562(1)	5565(2)	5572(1)	5579(3)	5585(2)	5588(2)
5598(2)	5606(2)	5619(2)	5630(2)	5636(2)	5639(2)	5650(1)	5655(3)
5658(1,2)	5675(3)	5682(1)	5684(2)	5691(3)	5692(1)	5699(3)	5700(1)
5711(3)	5716(1)	5718(2)	5721(2)	5740(1)	5741(2)	5748(1,2)	5751(3)
5759(3)	5763(2)	5774(2)	5778(1)	5789(2)	5793(2)	5796(2)	5808(2)
5810(2)	5812(1)	5816(2)	5826(1)	5838(2)	5842(1)	5844(2)	5849(2)
5850(1)	5858(2)	5859(2)	5868(1)	5871(3)	5889(2)	5891(3)	5894(2)
5900(2)	5903(3)	5906(2)	5910(2)	5913(2)	5915(3)	5919(3)	5922(1)
5933(2)	5938(1)	5943(2)	5948(2)	5951(3)	5954(2)	5963(2)	5966(2)
5969(2)	5984(2)	5986(1)	5990(2)	5993(2)	6005(2)	6010(1)	6020(2)
6021(2)	6024(2)	6028(1)	6035(2)	6048(2)	6052(1)	6053(2)	6059(2)
6066(1)	6071(3)	6074(2)	6078(2)	6080(2)	6098(2)	6100(1)	6101(2)
6105(2)	6113(2)	6119(2)	6125(2)	6126(2)	6130(1)	6131(2)	6134(2)
256
Приложение С. Таблицы ОНБ
Продолжение таблицы С.З
6138(2)	6140(2)	6150(2)	6161(2)	6172(1)	6173(2)	6186(2)	6189(2)
6195(2)	6196(1)	6200(2)	6202(1)	6206(2)	6210(1,2)	6216(2)	6218(2)
6225(2)	6228(1)	6236(2)	6243(3)	6245(2)	6255(3)	6268(1)	6269(2)
6273(2)	6276(1,2)	6288(2)	6294(2)	6298(1)	6305(2)	6306(2)	6309(2)
6316(1)	6318(2)	6322(1)	6323(2)	6326(2)	6329(2)	6348(2)	6369(2)
6371(3)	6372(1)	6378(1)	6381(2)	6388(1)	6390(2)	6395(3)	6396(1)
6399(2)	6404(2)	6410(2)	6414(2)	6426(2)	6444(2)	6449(2)	6453(2)
6455(3)	6458(2)	6459(2)	6461(2)	6468(1)	6470(2)	6479(2)	6483(2)
6489(2)	6490(1)	6491(3)	6500(2)	6518(2)	6521(2)	6524(2)	6546(1)
6551(2)	6554(2)	6573(2)	6575(2)	6579(2)	6581(2)	6591(2)	6593(2)
6614(2)	6618(1)	6620(2)	6636(1)	6645(2)	6652(1)	6654(2)	6656(2)
6658(1)	6663(3)	6665(2)	6669(2)	6690(1)	6698(2)	6700(1)	6705(2)
6708(1)	6725(2)	6728(2)	6731(2)	6732(1)	6734(2)	6738(2)	6743(2)
6756(2)	6761(2)	6762(1)	6768(2)	6778(1)	6780(1)	6783(2)	6788(2)
6798(2)	6802(1)	6806(2)	6809(2)	6813(2)	6824(2)	6826(1)	6828(1)
6839(2)	6843(2)	6845(2)	6848(2)	6854(2)	6855(3)	6861(2)	6864(2)
6868(1)	6878(2)	6879(2)	6881(2)	6882(1)	6898(1)	6899(2)	6903(2)
6906(1)	6914(2)	6915(2)	6916(1)	6920(2)	6929(2)	6938(2)	6939(2)
6941(2)	6946(1)	6948(1)	6950(2)	6953(2)	6960(2)	6965(2)	6966(2)
6970(1)	6983(3)	6998(2)	6999(2)	7004(2)	7005(2)	7012(1)	7014(2)
7016(2)	7018(1)	7025(2)	7026(1)	7040(2)	7042(1)	7043(3)	7053(2)
7068(1)	7071(2)	7074(2)	7076(2)	7079(3)	7086(2)	7103(3)	7108(1)
7110(2)	7121(2)	7146(2)	7151(2)	7170(2)	7173(2)	7186(1)	7193(2)
7194(2)	7203(2)	7205(2)	7209(2)	7210(1)	7211(2)	7218(1)	7223(2)
7228(1)	7230(2)	7236(1)	7242(1)	7252(1)	7259(2)	7266(2)	7268(2)
С.З. Возможные размерности ОНБ п, 998 < п < 10 000	257
Продолжение таблицы С.З
7271(3)	7274(2)	7275(3)	7278(2)	7282(1)	7306(1)	7310(2)	7313(2)
7314(2)	7319(2)	7326(2)	7328(2)	7330(1)	7334(2)	7348(1)	7349(2)
7358(2)	7361(2)	7368(2)	7370(2)	7373(2)	7379(2)	7385(2)	7389(2)
7398(2)	7406(2)	7410(1)	7413(2)	7415(2)	7421(2)	7425(2)	7433(2)
7434(2)	7439(2)	7443(3)	7445(2)	7450(1)	7458(1)	7461(2)	7464(2)
7469(2)	7473(2)	7476(1)	7478(2)	7484(2)	7491(2)	7498(1)	7506(1)
7515(2)	7516(1)	7522(1)	7526(2)	7530(2)	7538(2)	7540(1)	7541(2)
7545(2)	7546(1)	7548(1)	7550(2)	7553(2)	7565(2)	7569(2)	7572(1)
7574(2)	7580(2)	7586(2)	7588(1)	7593(2)	7602(1)	7613(2)	7620(1)
7629(2)	7631(2)	7634(2)	7642(1)	7643(2)	7649(2)	7656(2)	7659(3)
7665(2)	7668(1)	7674(2)	7686(2)	7688(2)	7690(1)	7691(2)	7695(3)
7706(2)	7713(2)	7716(1)	7719(2)	7721(2)	7730(2)	7746(2)	7748(2)
7755(3)	7756(1)	7763(2)	7784(2)	7788(1)	7790(2)	7803(2)	7814(2)
7820(2)	7821(2)	7823(2)	7824(2)	7828(1)	7830(2)	7833(2)	7835(2)
7841(2)	7852(1)	7863(2)	7865(2)	7868(2)	7869(2)	7874(2)	7876(1)
7880(2)	7882(1)	7883(3)	7886(2)	7893(2)	7895(2)	7898(2)	7900(1)
7901(2)	7904(2)	7906(1)	7911(2)	7929(2)	7932(1)	7940(2)	7943(3)
7948(1)	7950(2)	7953(2)	7959(2)	7961(2)	7979(3)	7985(2)	7995(2)
8000(2)	8003(3)	8016(2)	8031(2)	8033(2)	8034(2)	8043(3)	8051(2)
8052(1)	8063(2)	8068(1)	8069(2)	8092(1)	8093(2)	8094(2)	8096(2)
8108(2)	8111(2)	8114(2)	8115(3)	8116(1)	8122(1)	8126(2)	8133(2)
8136(2)	8146(1)	8150(2)	8159(2)	8166(2)	8169(2)	8170(1)	8174(2)
8178(1)	8181(2)	8190(2)	8205(2)	8210(2)	8213(2)	8218(1)	8220(1)
8223(3)	8226(2)	8236(1)	8238(2)	8240(2)	8242(1)	8243(3)	8246(2)
8259(2)	8264(2)	8268(1)	8273(2)	8280(2)	8283(3)	8286(2)	8290(1)
258
Приложение С. Таблицы ОНБ
Продолжение таблицы С.З
8292(1)	8301(2)	8303(3)	8309(2)	8310(1)	8325(2)	8336(2)	8346(2)
8349(2)	8351(2)	8362(1)	8373(2)	8381(2)	8386(1)	8393(2)	8411(2)
8414(2)	8421(2)	8422(1)	8428(1)	8441(2)	8442(1)	8446(1)	8450(2)
8451(3)	8465(2)	8466(1)	8471(3)	8481(2)	8489(2)	8490(2)	8493(2)
8505(2)	8510(2)	8512(1)	8513(2)	8523(2)	8526(2)	8538(1)	8546(2)
8549(2)	8553(2)	8561(2)	8562(1)	8568(2)	8572(1)	8579(3)	8583(2)
8591(3)	8594(2)	8596(1)	8598(1)	8601(2)	8603(2)	8604(2)	8608(1)
8619(2)	8626(1)	8628(2)	8649(2)	8658(2)	8663(3)	8666(2)	8668(1)
8675(3)	8676(1)	8679(2)	8692(1)	8693(2)	8694(2)	8698(1)	8709(2)
8715(2)	8721(2)	8730(1)	8735(2)	8738(2)	8740(1)	8741(2)	8746(1)
8754(2)	8759(3)	8786(2)	8789(2)	8798(2)	8799(3)	8802(1)	8806(1)
8811(2)	8813(2)	8818(1)	8820(1)	8834(2)	8836(1)	8841(2)	8853(2)
8856(2)	8866(1)	8873(2)	8874(2)	8886(1)	8891(2)	8894(2)	8903(3)
8913(2)	8918(2)	8919(3)	8922(1)	8925(2)	8931(3)	8932(1)	8945(2)
8951(3)	8954(2)	8955(3).	8961(2)	8962(1)	8968(1)	8969(2)	8970(1)
8978(2)	8979(3)	8988(2)	8990(2)	8994(2)	8998(1)	9006(2)	9010(1)
9021(2)	9023(2)	9028(1)	9029(2)	9038(2)	9044(2)	9048(1)	9058(1)
9059(2)	9066(2)	9071(3)	9074(2)	9084(2)	9090(2)	9095(3)	9105(2)
9114(2)	9125(2)	9126(2)	9134(2)	9144(2)	9150(1)	9155(2)	9160(1)
9164(2)	9172(1)	9180(1)	9183(3)	9189(2)	9202(1)	9206(2)	9213(2)
9216(2)	9220(1)	9221(2)	9226(1)	9230(2)	9240(1)	9246(2)	9256(1)
9260(2)	9270(2)	9276(2)	9282(1)	9292(1)	9293(2)	9296(2)	9318(2)
9322(1)	9330(2)	9335(3)	9336(1)	9340(1)	9342(1)	9348(1)	9350(2)
9356(2)	9359(3)	9365(2)	9370(1)	9371(3)	9374(2)	9378(2)	9386(2)
9393(2)	9396(1)	9418(1)	9419(3)	9420(1)	9429(2)	9432(1)	9434(2)
С.З. Возможные размерности ОНБ п, 998 < п < 10 000
259
Окончание таблицы С.З
9436(1)	9449(2)	9455(3)	9458(2)	9459(3)	9466(1)	9473(2)	9478(1)
9479(3)	9486(2)	9489(2)	9490(1)	9504(2)	9506(2)	9518(2)	9525(2)
9532(1)	9534(2)	9538(1)	9539(2)	9543(2)	9546(1)	9569(2)	9570(2)
9578(2)	9581(2)	9586(1)	9590(2)	9600(1)	9603(3)	9606(2)	9609(2)
9612(1)	9615(2)	9618(1)	9624(2)	9628(1)	9629(2)	9642(1)	9650(2)
9659(3)	9660(1)	9666(2)	9676(1)	9686(2)	9689(2)	9693(2)	9695(2)
9696(1)	9701(2)	9711(2)	9713(2)	9716(2)	9720(2)	9731(2)	9732(1)
9734(2)	9741(2)	9748(1)	9750(2)	9753(2)	9765(2)	9766(1)	9770(2)
9771(2)	9776(2)	9785(2)	9791(2)	9798(2)	9801(2)	9802(1)	9830(2)
9832(1)	9848(2)	9849(2)	9850(1)	9854(2)	9858(1)	9863(2)	9869(2)
9875(3)	9881(2)	9882(1)	9900(1)	9906(1)	9909(2)	9922(1)	9926(2)
9930(2)	9933(2)	9940(1)	9944(2)	9945(2)	9948(1)	9959(2)	9963(2)
9968(2)	9974(2)	9981(2)	9986(2)	9989(2)	9995(3)	9998(2)	
Приложение D
Примеры исполнения MQV-протокола
В таблицах D.1 и D.2 даны примеры исполнения MQV-протокола рас-
пределения ключей при исходных данных из примера 2.2.3 на с. 92.
В примерах применяется так называемый полиномиальный шестнадца-
теричный код, цифры которого соответствуют следующим элементарным
многочленам
0о0,	1й1,	2н1,	ЗШ+Х,
4нГ,	5О1+Х2,	6<->Z+X2,	7^i+X+X2,
8н13,	9-Н1+Т3,	av-X+X3,	bv-1+Х+Х3,
мХ2+Х3,	<1Ш+Х2+Х3,	е^Х+Х2+Х3,	f^l+X+X2+X3
Полиномиальный бинарный код, содержащий коэффициенты мно-
гочлена в порядке возрастания степеней переменной слева направо, по-
лучается из полиномиального шестнадцатеричного кода заменой цифр
следующими четверками двоичных символов
О о 0000,	1 о 1000,
4 о 0010,	5^1010,
8 о 0001,	9 <->1001,
с <-> ООП,	do 1011,
2 о 0100,	3<->1100:
6 <->0110,	7 <->1110,
а о 0101,	6 о 1101
енОШ,	/нПП.
Вычисления осуществлены с использованием программного алгебра-
ического процессора ECMPEIGF2n разработанного под руководством
авторов студентами МЭИ А. Б. Дроздовым и Ал. И. Мамонтовым с исполь-
зованием библиотеки программных функций, созданной с участием сту-
дентов МЭИ П. И. Артемьевой, В. С. Гамова, Я. Ю. Грачева, и Е. В. Шеста-
кова.
Таблица D.1
Пример исполнения MQV-протокола распределения ключей
E(F) Y2 + XY = X3 + X1 + 1,
р(Х) = 1 + х + х1 + т8 + х163,
Р = (d42149e09429d/4563ecl816488c92de89/93a9&2,
ccd 18d6cc3042c4c 17а213506345с80965ас 1 d476),
Примеры исполнения MQV-протокола
Продолжение таблицы D 1
кА = 12,
кв = 123,
dA = 345,
dB = 4567,
Qa = (aA,bA) = dAP = (474/a2c826al319456366c990e98a/2dbl42397e2,
4469са11/046е1е334992е684490462577/392803),
Qb = (aB, bB) = dBP = (83del 16505042/669/0/2 Ic9e97a5/e6a828210/7,
03c c7e4821382660537946c8/de/4231 /4eec669e77),
Ra = (xA,yA) = kAP = (64977666e87e8610246e2e415952/527eee928643,
c67e28ed76137е756с37654/186e716/64e5ac546),
Rb = (xB,yB) = kBP = (a5684e246044/cl26e9832417513387e474290547,
56864137/09/5/79а8а660/е44с4/4148е68ае2с6),
(oaQa) = (а78е5060619409а/914/2345се54646а4с2312/04,
63/05e8521083a4884361 a 18c93174391 c9661542),
Xa(o,aQa) = (738984e3ada682466c8de2d486/db3e/3d843/021,
5е8481ее2/48079аеа248с913a02/019938647аа5),
(aBQB) = (е54/4327610/е67а1а6ае6460е464//06448640еЗ,
4е284942396а60940506636са6/6774с6628е6407),
xB(aBQB) = (2с50566108а146а15сЗЗ/4536/994865а/а648975,
3129а/769а653/968с066е729210/154dc2469 la7),
UA = RB + xB(aBQB) = (de462338/d9629325e26908/a7876c8a66c757l51,
a62c82815c3/839/9Oc312687ea69522c898O6O/1),
UB = RA + xA(aAQA) = (806/9cc508453439962672c5/8619/448l5cee/e,
eOaeal2b/e88261d8cc2O/a7cl/791c723c3/5O77),
dAUA = (c/6987ce3d9/224904c36e734e65/20246671b5d2,
3694d862abd3c57c7181 c00c6/6/03a8c 14468044),
kAUA = (679939&e030ec98ab965465b30054ee74a9281841,
ba 17e4c //75е4152a7bbb52a2bc8a7136a6630e65),
xAdAUA = (a&/3e/685c538e6195384/64/4al48ac6a423e573,
46536285463165c67al238851201c8cbc45239e53),
aAxAdAUA = (/12aa9686/45551a9&4l492bell/92835436a73e5,
bdd 13c 13c71 a536555/0e94/04eec930367/81/5),
dBUB = (92764e4485e8140ebe77/5/8cee//408a/305762,
55067с/14466865428546847e/2a6016405882877),
262
Приложение D. Примеры исполнения MQV-протокола
Окончание таблицы D. 1
kBUB = (/8ee4d95672247/c499626el433939988018e6803,
6d4101c25272932645164ed2c756566d8d365ce97),
xBdBUB = (cd93e/7d6498566d2d4689c()//a8/668664ea5aa,
d05e972c3207/2162a218c60/5/cd0c971300d2a3),
aBxBdBUB = (60201643e7661/6e84325633100a6469588el57e5,
86dd4cc39377/9cea3055//c390/dl340d4992377),
WA = kAUA+xAaAdAUA = (2dd76c369d46815926673509597595cc43c/addd,
62799368d6d62dc6664777ee3342218526ad6/876),
WB = kBUB + xBaBdBUB = (2dd76c369d46815926673509597595cc43c/addd,
62799368d6d62dc6664777ee3342218526ad6/876).
Таблица D.2
Пример исполнения MQV-протокола в поле малого порядка
E(F) y2 + XY = Х3 + Х2+ 1,
р(Х) = 1 + X + X15,
Р = (0d7,7591),
kA = 12,
fcB=123,
d^ =345,
- dB =4567,
Qa = (aA, bA) = dAP = (25d5, /642),
Qb = («в, bB) = dBP = (ac82,2781),
Ra = (xA,yA) = kAP =(dle7, 7984),
Rb = (xB, yB) = kBP = (48d5, d986),
aAQA =(a607,9424),
Xa^aQa) =(ee41,9&d),
QbQb =(4&a6, 506),
Xb(<1bQb) =(a6cl, lc57),
UA = RB + xB(aBQB) = (4eb/, 75cl),
UB = Ra + хаМа) = (4677, 595),
UA =(/6e4,/0el),
dAUA =(5591,3922),
kAUA =(Hd6,c536),
Qa = (aA, bA) = dAP = (25d5, /642),
QB = (aB, bB) = dBP = (ac82, 2781),
Примеры исполнения MQV-протокола	263
Окончание таблицы D.2
xAdAUA=(Jdei,7fa4),
aAxAdAUA = (3d95,81/4),
UB =(4677,595),
dBUB = (8eO6,ce63),
=(c8/7,dd>2),
xBdBUB = (c/05,4d/2),
aBxBdBUB = (0613,6e95),
WA = kAUA + xAaAdAUA =(d936, 32a3),
В = kBUB + xBaBdBUB = (d936, 32e3).
Литература
1.	Айерленд К., Роузен М. Классическое введение в современную теорию чисел.
М.: Мир, 1987.
2.	Алферов А. П., Зубов А. Ю., Кузьмин А. С., Черемушкин А. В. Основы криптогра-
фии. М.: Гелиос АРВ, 2001.
3.	Болотов А. А., Гашков С. Б., Фролов А. Б., Часовских А. А. О методах имплемен-
тации арифметических операций в криптографических системах // Известия
РАН. Теория и системы управления. 2002. № 1. С. 86-96.
4.	Болотов А. А., Гашков С. Б., Фролов А. Б., Часовских А. А. Элементарное введение
в эллиптическую криптографию: Алгебраические и алгоритмические основы.
М.: КомКнига/URSS, 2006.
5.	Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО,
2003.
6.	Введение в криптографию / Под ред. В. В. Ященко. М.: МЦНМО-ЧеРо, 1998.
7.	Гашков С. Б. Кочергин В. В. Об аддитивных цепочках векторов, вентильных
схемах и сложности вычисления степеней // Дискретный анализ. 1992. № 52.
С. 22-40.
8.	Гашков С. Б., Чубариков В. Н. Арифметика. Алгоритмы. Сложность вычисле-
ний. М.: Изд-во МГУ; Дрофа, 2005.
9.	Глухов М.М., Елизаров В. ГГ, Нечаев А. А. Алгебра. Т. 1, 2. М.: Гелиос АРВ,
2003.
10.	Кнут Д, Искусство программирования на ЭВМ. Т. 2. Киев: Вильямс, 2000.
11.	Коблиц Н. Курс теории чисел'и криптографии. М.: ТВП, 2001.
12.	Лидл Р., Нидеррейтер X. Конечные поля. М.: Мир, 1988.
13.	Нечаев В. И. Элементы криптографии. М.: Высшая школа, 1999.
14.	Саломаа А. Криптография с открытым ключом. М.: Мир, 1996.
15.	Соловьев Ю. П., Садовничий В. А., Шавгулидзе Е. Г, Белокуров В. В. Эллиптиче-
ские кривые и современные алгоритмы теории чисел. Ижевск: ИКИ, 2003.
16.	Шнейер Б. Прикладная криптография. М.: Триумф, 2002.
17.	Bach Е. A note to square roots in finite fields. IEEE Trans // Inform. Theory. 1990.
36. P. 1494-1498.
18.	Bach E., Shallit J. Algorithmic number theory. Cambridge, Massachusetts; L.: MIT
Press, 1996.
19.	Bailey D. И, Paar C. Optimal extension fields for fast arithmetic in public-key
algorithms. CRYPTO 98 // Lecture Notes in Computer Science. 1998. № 1462.
P. 472-485.
20.	Bailey D. И, Paar C. Efficient arithmetic in finite field extensions with application
in elliptic curve cryptography // J. of Cryptology. 2001. Vol. 14. № 3. P. 156-173.
21.	Balasubramanian R., Koblitz N. The importability that an elliptic curve has subex-
ponential discrete log problem under Menezes—Okamoto—Vanstone algorithm //
J. of Cryptology. 1998. 11. P. 141-145.
Литература
265
22.	Barreto P.S.L.M., Kim H. Y., Lynn В., Scott M. Efficient algorithms for pairing-
based cryptosystems Crypto 2002 // LNCS. 2002. 2442. P. 354-368.
23.	Barreto P. S. M. L., Galbraith S., О h’Eigeartaigh C. and Scott M. Efficient pairing
computation on supersingular abelian varieties // Cryptology ePrint Archive, Report
2004/375. 2004.
24.	Scott M. and Barreto P. S. M. L. Compressed pairing CRYPTO 2004, LNCS 3152.
2004. P. 140-156 (update version: Cryptology ePrint Archive, Report 2004/303.
2004).
25.	Bellare M., Micali S. Non-interactive oblivious tranasfer and applicatioms // Advances
in Cryptology: Crypto-89. Heidelberg ate.: Springer-Verlag. P. 547-557.
26.	Bellare M., Rivest R. Translucent Cryptography — An Alternative to Key Escrow, end
its Implementation via Fractional Oblivious Transfer. MIT/LCS Technical Report
683. 1990.
27.	Bertoni G., Guajardo J., KumarS., Orlando G., PaarC., Wolinger T. Efficient GF(pm)
Arithmetic Architectutes for Cryptographic Applications, LNCS 2612. 2003. P. 158-
175.
28.	Blake I., Murhty K. and Xu G. Refinements of Miller’s Algorithm for Computing
Weil/Tate Pairing // Cryptology ePrint Archive. Report 2004/065.
29.	Blake I., Seroussi G., Smart N. Elliptic curves in cryptography. Cambridge University
Press, 1999.
30.	Blake I., Seroussi G., Smart N. Advances in elliptic curve cryptograhy. Cambridge
University Press, 2005.
31.	Boheh D. and Franklin M., Identity-based encryption from the Weil pairing // SIAM
J. on Computing. 2003. 32. P. 586-615.
32.	Boneh D., Lynn B. and Shacham H. Short signatures from Weil pairing // J. of Cryp-
tology. 2004. 7. P. 297-319.
33.	Brickell E., Gordon D., McCurley K, Wilson D. Fast exponentiation with precompu-
tation // Proc. Eurocript’1992, Balatonfured, Hungary.
34.	Ciet M., Joye M., Lauter K., Montgomery P. L. Trading inversions for multiplications
in elliptic curve cryptography // Cryptology ePrint Archive, Report 2003/257, 2003.
35.	Ciet M. Lange T., Sica F. and Quisquater J-J. Improved algorithms for efficient
arithmetic on elliptic curve using fast endomorphisms, Proceedings of Eurocrypt.
2003. Warsaw, Poland, LNCS 2656, 388-400.
36.	Cohen H., Myaji A. and Ono T. Efficient elliptic curve exponentiation using mixed
coordinates. Asiacrypt’98, LNCS 1514. P. 51-65.
37.	Coppersmith D. Fast evaluation of logarithms in fields of characteristic two, IEEE
Trans // Inform. Theory 1984. 30. P. 587-594.
38.	Dimitrov V. S., Imbert L., Mishra P. K. Fast elliptic curve point multiplication using
double-base chains. Preprint. 2004.
39.	Duursma I. and Lee H.-S. Tate pairing implementation for hyperelliptic curves
У2 = Xp - X 4- d. Asiacrypt-2003, LNCS 2894. 2003. P. 111-123.
40.	Duursma I. and Lee H.-S. Tate pairing implementation for tripartite key agreement //
Cryptology ePrint Archive, Report 2003/053. 2003.
41.	Eisentrager K., Lauter K., Montgomery P. L. Fast elliptic curve arithmetic and
improved Weil pairing evaluation. CT-RSA 2003, LNCS 2612. 2003. P. 343-354.
266
Литература
42.	Frey G., Muller M., Ruck H. The Tate pairing and the discrete logarithm applied to
elliptic curve cryptosistems, IEEE Trans // Inform. Th. 1999. 45. 5. P. 1717-1719.
43.	Fong K, Hankerson D., Lopez J- H., Menezes A. Field inversion and point halving
revisited // IEEE Tracs. on Comp. 2004. Vol. 53. №8. P. 1047-1059.
44.	Galbraith S. Supersingular curves in cryptography, Asiacrypt-2001, LNCS 2248. 2001.
P. 495-513.
45.	Galbraith S. D., Harrison S. D. and Soldera D. Implementing the Tate pairing,
ANTS V, LNCS 2369. 2002. P. 324-337.
46.	Galbraith S., Menezes A. Algebraic curves and cryptography. Preprint. 2005.
47.	Galbraith S., Rotger V. Easy decision Diffie—Hellman groups // LMS Journal of
computation and mathematics. 2004. 7. P. 201-218.
48.	Granger R., Page D. and Stam M. On small characteristic algebraic tori in pairing
based cryptography // Cryptology ePrint Archive, Report 2004/132. 2004.
49.	Exponent group signature schemes and efficient identity based signature schemes
based on pairings // Cryptology ePrint Archive, Report 2002/012.
50.	The Oakley key determination protocol // IETF RFC. 1998. 2412. Nov.
51.	Itoh K, Takenaka M., Torii N., Temma S., Kurihara Y. Fast implementation of public-
key cryptography on DSP TMS320C6201, CHES’99, LNCS 1717. 1999. P. 61-72.
52.	Joux A. One round protocol for tripartite Diffie—Hellman // Lecture Notes in
Computer Science. 2000. 1838. P. 385-393.
53.	Jungnickel D. Finite fields: Structure and arifmetics. Wissenschaftsverlag, 1995.
54.	IEEE 1363, Standard specification for public-key cryptography, 2000.
http://grouper.ieee.org/groups/1363/index.html.
55.	ISO/IEC 14888-3 Information technology — Security techniques — Digital signa-
tures with appendix. 1998.
56.	ISO/IEC 15946 Information technology — Security techniques — Cryptograhic
techniques, based on elliptic curves. 1999.
57.	Izu T., Takagi T. Efficient computation of the Tate Pairing for the large MOV
degrees. ICISC 2002, LNCS 2587. 2003. P. 283-297.
58.	Kerins T., Marname ИК P., Popovici E. M., and Barreto P. S. L. M. Efficient hardware
for Tate pairing calculation in characteristic three. Preprint. 2004.
59.	Knudsen E. Elliptic scalar multiplication using point having. ASIACRYPT’99 Lecture
Notes in Computer Science 1716. P. 135-149.
60.	Koblitz N. Hyperelliptic cryptosystems. J. of Cryptology, 1. 1989. P. 139-150.
61.	Koblitz N. Algebraic aspects of Cryptography. Springer-Verlag. 1998.
62.	Koblitz N. Constructing elliptic curves cryptosystems in characteristic 2. Crypto’90 //
Lecture Notes in Computer Science 537. P. 156-167.
63.	Koblitz N. An elliptic curve implementation of the finite field digital signature algo-
rithm, LNCS 1462. 1998. P. 327-33.
64.	Koblitz N., Menezes A. Pairing-based cryptography at high security levels. Preprint.
2005.
65.	Kwon S. Efficient Tate pairing computation for supersingular elliptic curves over
binary fields // Cryptology ePrint Archive, Report 2004/303, 2004.
66.	Lay G., Zimmer H. Constructing elliptic curves with given group order over large
finite fields. Algorithmic number theory // Lecture Notes in Computer Science.
1994. 877. P. 250-263.
Литература
267
67.	Lercier R. Finding good random ellilptic curves for cryptosystems defined GF(2n}
Eurocript-97 // Lecture Notes in Computer Science. 1997. 1233. P. 379-392.
68.	Lopez. J., Dahab R. Improved algorith for elliptic curve over GF(2n) SAC’98 //
Lecture Notes in Computer Science. 1999. № 1556. P. 201-212.
69.	Lopez L, Dahab R. Fast multiplication on elliptic curve over GF(2n) without pre-
computation. CHES 2000 // Lecture Notes in Computer Science. 2000. № 1965
P. 317-327.
70.	Menezes A. J., Vanstone $. Elliptic Curve Cryptosystems and their implementation //
Journal of Cryptology. 1993. №6. P. 209-224.
71.	Menezes A. J., Vanstone S, Okamoto T. Reducing elliptic curve logarithms to loga-
rithms in a finite field. IEEE Trans // Inform. Th. 1993. Vol. 39. № 5. P. 1639-1647.
72.	Menezes A. J., Oorschot P. van, Vanstone S;A. Handbook of Applied Cryptography.
New York; London; Tokio; Boca Raton: CRC Press, 1997.
73.	Miller V The Weil pairing, and its efficient calculation //J. of Cryptology. 2004. 17.
P. 235-261.
74.	Miyaji A., Nakabayashi M., Takano S. New explicit conditions of elliptic curve traces
for FR-reduction // IEICE, E84-A. 2001. P. 1234-1243.
75.	Montgomery P. Speeding the Pollard and elliptic curve methods of factorization //
Mathematics of computation. 1987. Vol. 48. P. 243-264.
76.	Morain F. Building cyclic elliptic curves modulo large prime. Eurocript-91 // Lecture
Notes in Computer Science. 1991. 547. P. 328-336.
77.	Okamoto T., Pointsheval P. The Gap Problems: a new class of problems for for the
security of cryptographic primitives, PKC 2001, LNCS 1992. 2001. P. 104-118.
78.	Page D., Smart N. and Vercauteren F. A comparison of MNT curves and supersingular
curves. Preprint. 2002.
79.	Page D., Smart N. P. Hardware implementation of finite fields of characteristic
three Ц CHES 2002. LNCS, 2002.
80.	Paterson K. G. ID-based signatures from pairings on elliptic curves // Cryptology
ePrint Archive, Report 2002/004.
81.	Rabin M. How to exchange secrets by oblivious transfer // Ntcn. Report TR-81.
Aiken Computational laboratory, Hardvard University, 1981.
82.	Robertson J. Solving the generalized Pell equation //
http://hometown .aol.com/jpr2718.
83.	Rosing M. Implementing Elliptic Curve Cryptography. 32 Lafayette Pace. Grinvich:
Manning Publicatiobs Co., 1998.
84.	Santis A. de, Persiano G. Public-randomness in public key cryptography // Proceen-
ings EUROCRYPT 90. 1991. Vol. 473. P. 46-62.
85.	Santis A. de, Di Crescenzo, Persiano G. Zero-Knowledge arguments and pablic key
cryptography // Information and Communication. 1995. 121. 1. P. 23-40.
86.	Schoof R. Nonsingular plane cubic curves over finite feilds // J. Combinat. Theory.
1987. Vol.A46. P. 183-211.
87.	Schroeppel R., Orman FL, Malley S’O., Spatschek O. Fast key exchange with elliptic
curve systems. CRYPTO 95 // Lecture Notes in Computer Science. №963. 43-56.
88.	Schroeppel R. Elliptic curve point having wins big // 2nd Midwest Arithmetical
Geometry in Cryptograhy Workshop, Urbana, Illinois, November 2000.
268
Литература
89.	Scott М. Complex Multiplication programm //
ftp .compapp. dcu. ie/pub/crypto/cm .exe.
90.	Standards for efficient cryptography group SEC-1: Elliptic curve cryptography //
http://www.secg.org.
91.	Standards for efficient cryptography group SEC-2: Recommended elliptic curve
domain parameters // http://www.secg.org.
92.	Silverman J. The Arithmetic of Elliptic Curves. Springer, 1986.
93.	Smart N. P. An identity based authenticated key agreement protocol based on Weil
pairing // Electronic Letters. 2002. Vol. 38. P. 630-632.
94.	Smart N. P. How secure are elliptic curves over composite extension fields. Preprint.
2000.
95.	Solinas J. Efficient arithmetic on Koblitz curves // Designs, Codes and Cryptography.
2000. 19. 195-249.
96.	Tijdeman R. On the maximal distance between integers composed of small primes //
Composito Mathematica. 1974. 28. P. 159-162.
97.	Verheul E. Evidence that XTR is more secure than supersingular elliptic curve cryp-
tosystems // J. Cryptology. 2004. 17. P. 277-296.
Предметный указатель"
Алгебраическая кривая 83, I
Алгебраическое замыкание 73, I
Алгоритм Берлекемпа 112, I
— возведения в степень в конечном
поле малой характеристики
185, I
-------в мультипликативной группе
21, I
-------с фиксированной базой 209,
I
—	вычисления аддитивного кратного
элемента 22, I
—	Гаусса 199
—	деления многочленов
классический 168, I
—	Дуурсма—Ли 169
----без извлечения корней 173
----в характеристике два 175
----без извлечения
квадратных корней 175
----ускоренный 173
—	Евклида 26, 1
----бинарный расширенный 35, I
----для вычисления обратного
элемента по модулю 34, I, 35, I
----расширенный 30, I, 31, I
— инвертирования
в полиномиальном или
нормальном базисах 182, I
— Кронекера 80, I
— Коновальцева 69, I
— Миллера 138
----бинарный	156
* В указатель	также	включены	тер-
мины из книги	«Элементарное	введе-
ние в эллиптическую криптографию: Ал-
гебраические и алгоритмические основы»
(М.: URSS, 2006) [4], которая публикуется
параллельно с настоящим изданием. Эти
термины помечены знаком I.
---, вариант 160
---тернарный 142, 156
---ускоренный 141
—	модулярной композиции 123, I
—	обращения матрицы 204
—	определения порядка точки
эллиптической кривой 83
-------элемента группы 22, I
— поиска образующего элемента
группы вероятностный 23, I
-----------точек эллиптической
кривой, вероятностный 84
---элемента максимального
порядка группы 24, I
—	почти инверсный 190, I
— приведения матрицы
к диагональному виду 202
---матрицы к треугольному виду
199
---по модулю «малочлена»
базовый 170, I
---«малочлена» обобщенный
175, I
—	проверки невырожденности
матрицы 201
-	Р. Шуфа 108, I
—	сложения и удвоения точек
эллиптической кривой 9
— тестирования на неприводимость
114, I
— умножения вектор-строки
на матрицу 206
---матрицы на вектор 197
---многочленов гибридный 154, I
------- классический 150, I
-------представленных
элементарными многочленами
153, I
— «четырех русских» 66, I, 122, I
270
Предметный указатель
— Штрассена умножения матриц
125, I
Алгоритмы с матрицами 196
Аномальные несуперсингулярные
кривые 54
-------, их эндоморфизмы 57
-------, кольцо эндоморфизмов 57
-------, норма эндоморфизма 59
Базис векторного пространства 44, I,
58, I
— поля полиномиальный 59, I
----нормальный 59, I
------гауссов 73, I
----оптимальный 72, I
----стандартный 59, I
Базисы Гауссовы нормальные 274, I
-------, алгоритм возведения
в степень 293, I
-------, генераторы ГН Б 292, I
-------, сложность умножения 278, I
-------, таблица умножения 283, I
-------, умножение в ГНБ 276, I
— редундантные 297, I
Быстрая линейная алгебра 65, I
Быстрое инвертирование
в стандартном базисе
с помощью модулярной '
композиции многочленов 222, I
— возведение в степень с помощью
модулярной композиции
многочленов 219, I
Вес полинома 25, I
Выбор точки эллиптической кривой,
суперсингулярный случай 81
---------, несуперсингулярный
случай 82
Вычет 32, I
Вычисление следа в полях
характеристики два 49
Гауссовы периоды 226, I
Гипотеза Артина 227, I
— Шольца об аддитивных цепочках
200,1
Глубина схемы 66, I
Группа 15, I
—	абелева 16, I
—	аддитивная 16, I
—	коммутативная 16, I
—	конечная 17, I
—	конечно-порожденная 101, I
—	мультипликативная 16, I
—	тривиальная 17, I
—	циклическая 17, I
—	Div (Е) дивизоров кривой 125
Две модификации алгоритма
умножения 156, I
Двоичная запись Бута 208, I
---минимальная
с отрицательными цифрами
207, I
— система уравновешенная 207, I
Двоичной записи длина А(п) 197, I
---сумма цифр i/(n) 197, I
Делимое 18, I
Делитель 18, I
Дерево степеней для аддитивных
цепочек 200, I
Дивизор 125
— главный 126
Дискриминант 86, I
Евклидовы кольца 60
---, деление с остатком 60
---, наибольший общий делитель
60
---, обратимые элементы 60
---, простые элементы 60
Извлечение квадратных корней
в конечном поле 75, I
Изоморфизм 25, I
Инвариант (;-инвариант) 86, I
Инволютивный закон 89, I
Индекс подгруппы в группе 19, I
Искажающее отображение 148
Касательная 84, I
Предметный указатель
Квадратичный вычет по модулю р
74, I
— невычет по модулю р 74, I
Квадратичная сумма Гаусса 76, I
Квадратные корни в полях
характеристики два 53
— уравнения в полях характеристики
два 48
Классы вычетов по модулю тп 18, I
—	конгруэнтности 32, I
---по модулю тп 18, I
—	эквивалентности 17, I
Кольцо 23, I
—	многочленов 25, I
---по модулю многочлена 33, I
—	с единицей 24, I
Конечного расширения поля степень
44, I
Корень многочлена 40, I
Кортеж 69, I
Кривая гиперэллиптическая рода g
130
—	гладкая 84, I
—	неособая 84, I
—	несуперсингулярная 88, I, 109, I
—	суперсингулярная 88, I, 109, I
—	Ферма 84, I
—	эллиптическая 84, 1
Кривые изоморфные 86, I
—	Коблица 54
—	над полем характеристики два
суперсингулярные 20
		несуперсингулярные 25
Криптосистема Эль-Гамаля,
эллиптический вариант 93
Критерий подгруппы 19, I
Левые смежные классы 19, I
Лемма Оливоса 202, I
—	Пиппенджера о графах
аддитивных цепочек 201, I
Линейная комбинацией векторов
58, I
Линейно зависимые векторы 58, I
— независимые векторы 58, I
Линейное представление 29, I
271
Метод аддитивных цепочек 32
—	бинарный построения аддитивных
цепочек 197, I
—	использования операции
ополовинивания 45
—	Карацубы 162, I
—	Лопеса—Дахаба использования
проективных координат 43, I
—	множителей построения
аддитивных цепочек 198, I
—	Монтгомери 37, 40
---быстрого возведения в степень
214, 1
---в проективных координатах 42
Минимальные многочлены
оптимальных нормальных
базисов 261, I
Минимальный многочлен элемента
48, I
Многочлен круговой 50, I
—	малого веса 171, I
—	над полем 25, I
—	нормированный 25, I
—	примитивный 49, I
—	характеристический элемента 56, I
—	элементарный 147
Многочлены Диксона 262, I
—	Чебышева 262, I
Множество DivQ(E) дивизоров
нулевой степени 126
Множитель секретности (или
безопасности) 129
Модификация классического
алгоритма умножения 154, I
Модулярная композиция 122, I
Наибольший общий делитель целых
чисел 18, I
------элементов кольца 28, I
Несуперсингулярные кривые над
полем GF(2n) 25
Норма элемента 56, I
Нормальное множество 59, I
Нормирующий множитель 27, I
Носитель дивизора 125
Область целостности 24, I
272
Предметный указатель
Односторонняя функция 97
Операция вычитания 17, I
— деления 17, I
---на ненулевой элемент в поле
39, I
— инверсии 16, I
Операция ополовинивания 45
— сложения многочленов 26, I
— умножения многочленов 26, I
Оптимальные нормальные базисы
70, I
-------второго типа 227, I
-------, алгоритм построения
235, I
------перВ0Г0 типа 226, I
-----------, алгоритм построения
230, I
-------третьего типа 227, I
-------, алгоритм построения
239, I
Ориентированный граф 196, I
Остаток от деления 18, I, 28, I
Отношение конгруэнтности
по модулю m 18, I, 32, I
— эквивалентности 17, I
Периоды типа (п, к) 280, I
Подгруппа 19, I
—	главная 55
—	кручения 99, I
Подполе 24, I
Поле 24, I
—	Галуа 25, I
—	конечное 25, I
—	простое 25, I
—	разложения многочлена 46, I
Полуслед 50
Полюс функции 133
Поля циклотомические 296, I
Порядок группы 17, I
—	кривой 104, I
—	мультипликативной группы поля
40, I
—	ненулевого элемента поля 40, I
— неприводимого над GF(p)
многочлена 55, 1
—	полиномиальной функции 133
—	поля 25, I
—	рациональной функции в точке
126
—	точки кривой 99, I
—	элемента 17, I
—	эллиптической кривой 104, I
Последовательности Люка 55
Представитель класса
нормированный 27, I
Примитивный корень fc-й степени
из 1 42,I
—	элемент по модулю р 42, I
---поля 42, I
Проективная замена координат 84, I
Проективное пространство 36
Проективные координаты 36
Проблема дискретного логарифма 84
— Диффи—Хеллмана 84
--- билинейная 121
---для эллиптических кривых 86
---, распознающий вариант 121
Простые числа Мерсенна 185
---Солинаса 143
---Ферма 185
Протокол Диффи—Хеллмана
распределения ключей,
классическая версия 85
— Менезеса—Кью—Венстоуна
распределения ключей
(MQV-протокол) 90
— Месси—Омуры распределения
ключей для классической
криптосистемы 86
---------, аддитивный вариант 85,
88
—	передачи с забыванием 106
—	электронной жеребьевки 115
Прямая сумма групп 101, I
Разложение на неприводимые
множители над полем 46, I
Размещение данных
на эллиптической кривой 82
Ранг кривой 101, I
Расширение поля алгебраически
замкнутое 85, I
Предметный указатель
273
----конечное 44, I, 42, I
----простое 42, I
------алгебраическое 43, I
---------степени п 43, I
Расширенная гипотеза Римана ERH
227, I
Расширенный алгоритм Евклида
30, I, 31, I
Рациональная функция на кривой
133
Редуцирование Монтгомери 215, I
Решение квадратных уравнений 76
------, несуперсингулярный случай
80
Свойство нулевого разглашения 116
Символ Кронекера—Якоби 79, I
— Лежандра 76, I
Скалярное умножение
на несуперсингулярных кривых
39
----на суперсингулярных кривых 31
Скручивание кривой 107, I
— несуперсингулярных кривых над
полем GF(2n) 27
След точки 151
— элемента 55, I
----абсолютный 55, I
Сложение и удвоение точек кривой
над полем характеристики три
13
-----------большой
характеристики 11
------несуперсингулярной кривой
над полем характеристики два
14
------суперсингулярной кривой
над полем характеристики два
16
Сложность нормального базиса 70, I
— схемы 66, I
Спаривание 120
— Вейля 125
— Тейта 143
Степень вложения 145
— дивизора 126
-	MOV
(Menezes—Okamoto—Vanstone)
129
Степень многочлена 25, I, 83, I
— полиномиальной функции 132
— элемента 16, I
Схема из функциональных элементов
66, I
—	логическая 66, I
—	умножения многочленов
декомпозиционная 163, I
Таблица неприводимых трехчленов
208, 221
--пятичленов 222
—	оптимальных нормальных базисов
226
—	размерностей ОНБ 251
Теорема А. Брауэра 198, I
—	двойственности Оливоса 202, I
—	Куммера 265, I
—	Лагранжа 19, I
—	Люка 265, I
—	о группе главных дивизоров 127
—	о порядке степени элемента 20, I
—	Ферма малая 20, I
—	Хассе 105, 1
—	Хассе—Вейля 105, I
—	Чебышева 228, I
—	Э. Страуса о векторных
аддитивных цепочках 201, I
-	Э. Яо 202, I
—	Эйлера 20, 1
Тип группы 109, I
Точка бесконечно удаленная 84, I
—	инфлекции 90, I
—	кратности А: 96, I
—	кривой 83, I
—	кручения 99, I
--порядка г 124
—	неособая 83, I
Трюк Шамира 213, I
Удвоение итерированное 163
274	Предметный указатель
Умножение многочленов
с использованием таблицы
152, I
— Монтгомери 215, I
Уравновешенный т-адический код 61
------минимальный 61
Утроение точки 154
Факториальные кольца 61
Фактор-множество 17, I
Форма Вейерштрасса 84, I
Характеристика поля 39, I
Хэш-функция 96
Цепочка двойственная 201, I
—	линейная 199, I
Цепочки аддитивные 196, I
—	векторные аддитивные 201, I
—	, двойственный граф 201, I
—	кратчайшей векторной аддитивной
длина Z([n15..., nm]) 201, I
---длина Z(n) 196, I
---линейной длина Г(п) 200, I
—	с нулевым весом удвоений 204, I
—	с операцией вычитания 4.6.26, I
Циркулянтная матрица 60, I
Частное 18, I
Числа взаимно простые 18, I
— циклотомические 283, I
Число примитивных многочленов
50, I
Электронная подпись 96
--Эль-Гамаля с возвратом
сообщения, эллиптический
вариант — схема
Nyberg-Rueppel 102
—	цифровая BLS-подпись 122
Элемент нейтральный 16, I
—	образующий 17, I
—	обратный 16, I
—	противоположный 16, I
—	симметричный 16, I
—	, сопряженный с элементом поля
54, I
—	функциональный 66, I
Элементы сопряженные 51, I
Эллиптический интеграл 85, I
Эндоморфизм Фробениуса 57
Якобиевые координаты 161