В.Б. Полонский, Е.М. Рабинович, М.С. Якир
УЧИМСЯ
РЕШАТЬ ЗАДАЧИ
ПО ГЕОМЕТРИИ
А

Творческий союз учителей Украины
Ассоциация учителей математики
В.Б. Полонский
Е.М. Рабинович
М.С. Якир
УЧИМСЯ РЕШАТЬ
ЗАДАЧИ
ПО ГЕОМЕТРИИ
Учебно-методическое пособие
Рекомендовано Министерством
образования Украины
Киев
«MaricTD-S»
1996

ББК 22.151.Оя721
П52
Полонский В.Б., Рабинович Е.М., Якир М.С.
Учимся решать задачи по геометрии. Учеб.-метод.
пособие. — К.: «Магистр-S», 1996. — 256 с.
ISBN 966-557-011-0
Рекомендовано Министерством
образования Украины
Пособие, написанное в форме конспекта
опытного учителя, содержит более 1000 задач с большим
числом примеров, их решениями и разбором. На
большом и разнообразном материале авторам
удалось систематизировать по методам решений
основные типы задач школьной планиметрии. В
основе систематизации также лежит принцип от
простого к сложному.
Для учащихся 7-11 классов, абитуриентов,
преподавателей математики.
_ 1602050000-025 - -
П <jg без объявл. ББК 22.151.Оя721
ISBN 966-557-011-0 © Полонский В.Б.,
Рабинович Е.М.,
ЯкиР м-с> 1996
© «Maricrp-S», 1996

От авторов
Это не сборник задач, хотя в книге их
более 1000. Несмотря на большое число
разобранных примеров, это и не решебник,
наличие которого у ученика так раздражает
учителя. Скорее всего, это добротный
конспект, написанный учителем не только для
«служебного пользования», но и дидактический
материал, который удобно положить на парту
каждому ученику.
Кратко остановимся на содержании
каждой главы. Материал главы I уместно
использовать на начальном этапе изучения основных
тем планиметрии. Как нам кажется, форма
условия задач (готовые чертежи) позволяет
более наглядно и динамично «войти» в тему.
Известно, что задача может служить не
только целью, но и средством обучения.
Учиться решать задачи с помощью ключевых
(опорных, базисных) — идея древняя. Особенность
главы II состоит в том, что читатель получает
возможность окунуться сразу во всю
планиметрию, увидев ее, как единое целое.
Глава III посвящена как традиционным
методам, так и оригинальным приемам
решения задач.

Как научиться видеть, что решение
данной задачи требует рассмотрения нескольких
случаев, а не «хвататься» за разбор того,
который лежит на поверхности? Глава IV
помогает ответить на этот вопрос.
Работа над книгой распределилась
следующим образом. Глава I написана Е.М.
Рабиновичем, главы II и III написаны совместно
всеми авторами, глава IV написана В.Б.
Полонским и М.С. Якиром.
Авторы выражают искреннюю
благодарность П.И. Горнштейну, предоставившему
обширнейший архив геометрических задач,
А.Г. Мерзляку и М.Е. Рабиновичу, чьи ценные
советы способствовали улучшению рукописи.

Глава I
Геометрия на готовых чертежах
7 КЛАСС
7.1. Смежные и вертикальные углы.
7.2. Признаки равенства треугольников.
7.3. Равнобедренный треугольник.
7.4. Признаки параллельности прямых.
7.5. Признаки параллельности прямых.
7.6. Сумма углов треугольника.
7.7. Сумма углов треугольника.
7.8. Прямоугольный треугольник.
7.9. Окружность.

Геометрия на готовых чертежах
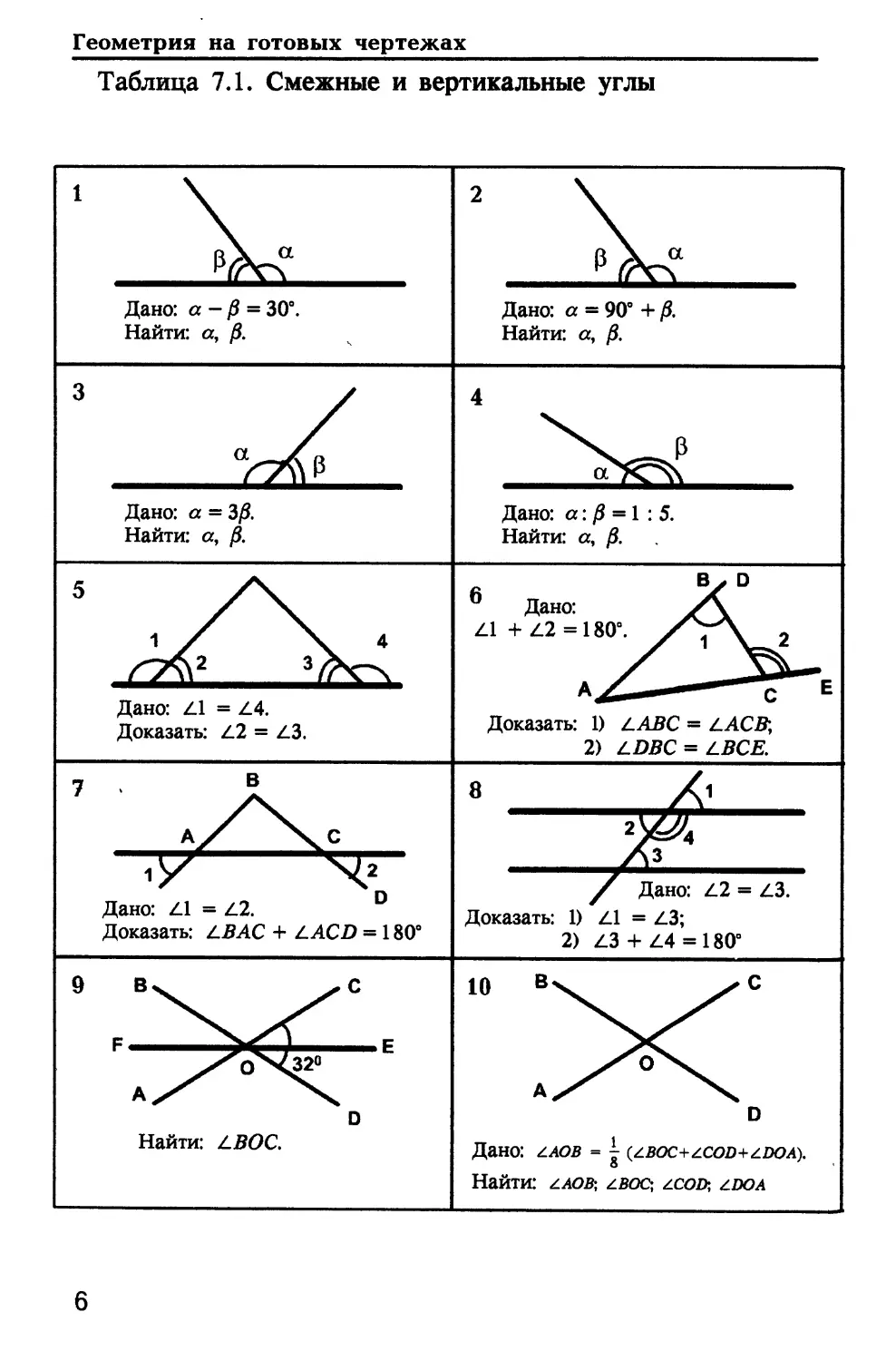
Таблица 7.1. Смежные и вертикальные углы
Дано: a-fi = 30°.
Найти: а, р.
/
Дано: а = 3/3.
Найти: а, р.
Дано: Z.1 = Z4.
Доказать: Z.2 = Z.3.
.А.
Дано: П = Z.2. D
Доказать: ABAC + LACD = 180°
9 В^ ^С
D
Найти: Z50C.
2 \
Дано: а = 90° + Д
Найти: а, /?.
4
Дано: а: /9 = 1 : 5.
Найти: а, р.
0 Дано: У\
П + Z.2 = 180°. /7\_ 2
Доказать: 1) LABC = LACR,
2) LDBC = LBCE.
8 /i
/ Дано: L2 = Z.3.
Доказать: 1) Z.1 = Z.3;
2) Z.3 + Z4 = 180°
10 ВЧ. ^Хс
D
Дано: z^os = ^ (zsoc+zcod+zdo^).
О '
НаЙТИ: гИАОВ] ЛВОС; Z.CO&, £DOA

Геометрия на готовых чертежах
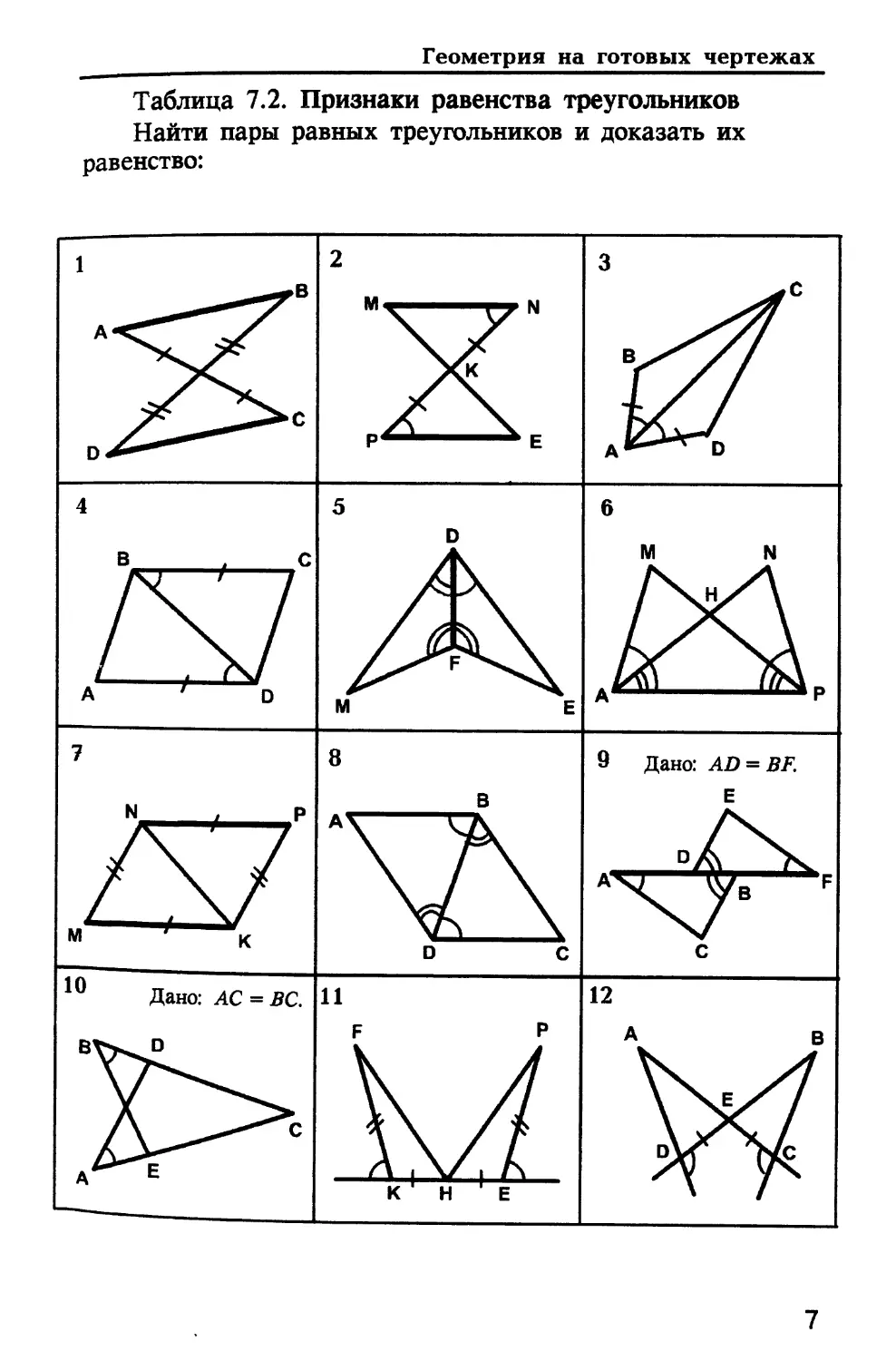
Таблица 7.2. Признаки равенства треугольников
Найти пары равных треугольников и доказать их
равенство:
М
9 Дано: AD = BF.
"Ч ув F
11
12
j |
К ■ Н ' Е

Геометрия на готовых чертежах
Таблица 7.3. Равнобедренный треугольник
Доказать: АЛВС — равнобедренный.
D Е
Дано: BD = BE.

Геометрия на готовых чертежах
Таблица 7.4. Признаки параллельности прямых
Параллельны ли прямые а и Ы
1
3
5
7
а
b
а
ь у
а
b
а р
b
7
Мл»
/too
с/
400Х
(до0
7
/
Д180°-а
Е
\/
М
2
4
6
8
a
b
a
b
a
b
a
b
\e
1
D
4
i
A
K/
/
^65°
V50
\
7
С
В
дв
А Дано: АВ-ВС.
f A

Геометрия на готовых чертежах
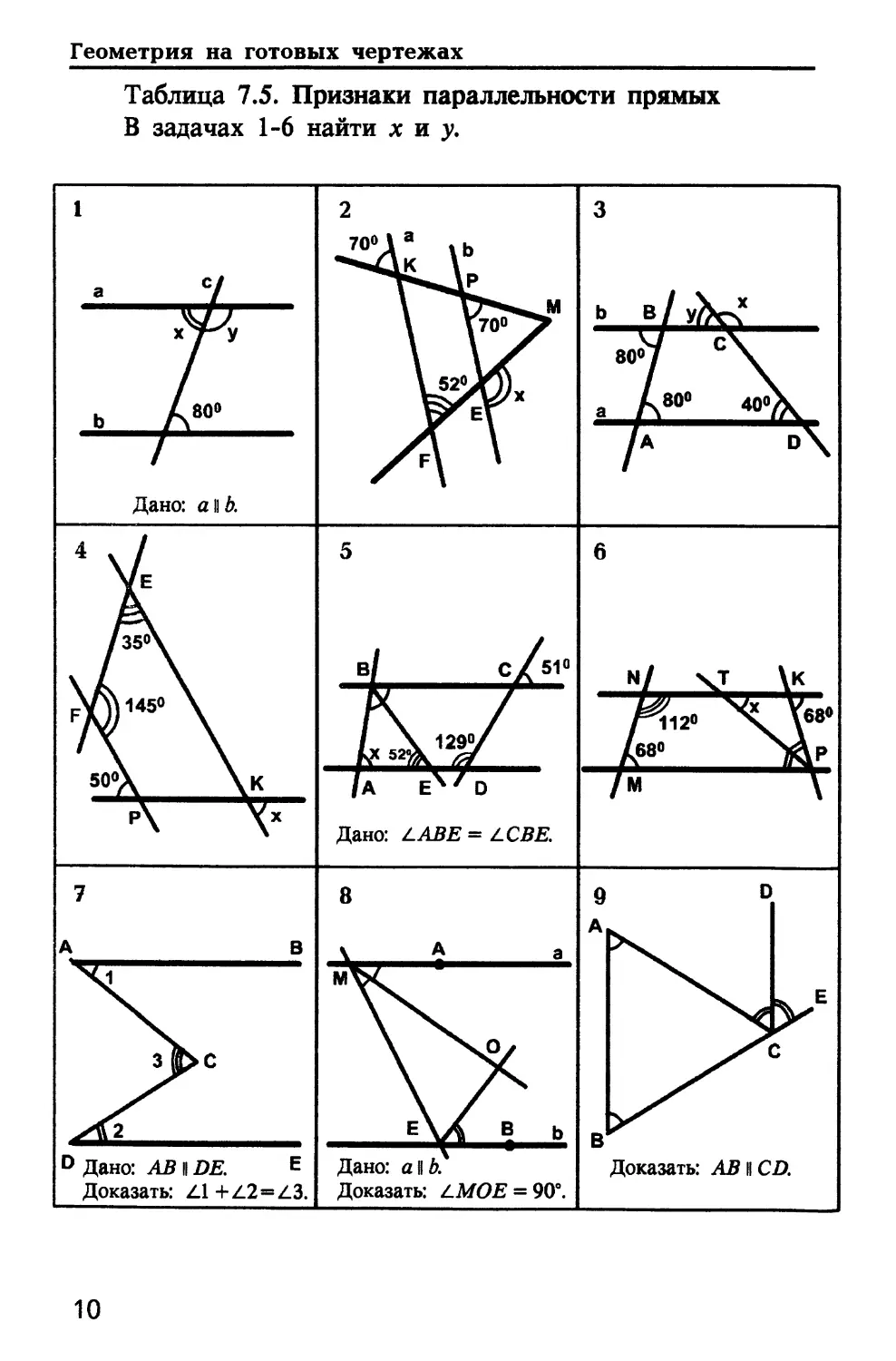
Таблица 7.5. Признаки параллельности прямых
В задачах 1-6 найти х и у.
Дано: а\\Ь.
70°
50°
Ч '
Дано: LABE= LCBE.
D Дано:
Доказать:
Дано: all/?.
Доказать: LMOE- 90°.
Доказать:
10

Геометрия на готовых чертежах
Таблица 7.6. Сумма углов треугольника
Найти неизвестные углы ЬАВС.
1
А
4
7
10
/
А
V
1
С1
/
/
А
/
/
в
45tSw
с
\
\
»в
дВ
\
70°Д
dc
\
\
\130°
С
2
110е
5
С
8
11
/
А
i
\
N
1
ч
1
/
к
/
f
ВА
\
дВ
А
■■■■■
дВ
\
\
С
X 1зо°
V\
в
\
с
Дано:
ABHCD.
\ D
С
3
А
6
40°^
9
/
А
12
А
j
/
/
4.
в
/
\
1
\i100
у\
С
В
А
105еJ
(1
С
\125°
С
В
\
л
с
11

Геометрия на готовых чертежах
Таблица 7.7. Сумма углов треугольника
Найти: LABC.
Найти: LABC.
Доказать:
LABC < LADC.
А С
Доказать: L\ > Z.2.
Дано: а\\Ь.
Доказать:
Zl +Z.2+Z.3=360e.
7 Найти ошибку:
В
Найти: LEKC.
12

Геометрия на готовых чертежах
Таблица 7.8. Прямоугольный треугольник
Найти равные треугольники (задачи 1-3).
5 А
300
А С
Найти: АВ.
Найти: ВС.
И0
60°
Найти: ВС.
Е 7 С
Найти: АВ.
Найти: АЕ.
Дано: АВ - ВС.
Доказать: AD - СЕ.
13

Геометрия на готовых чертежах
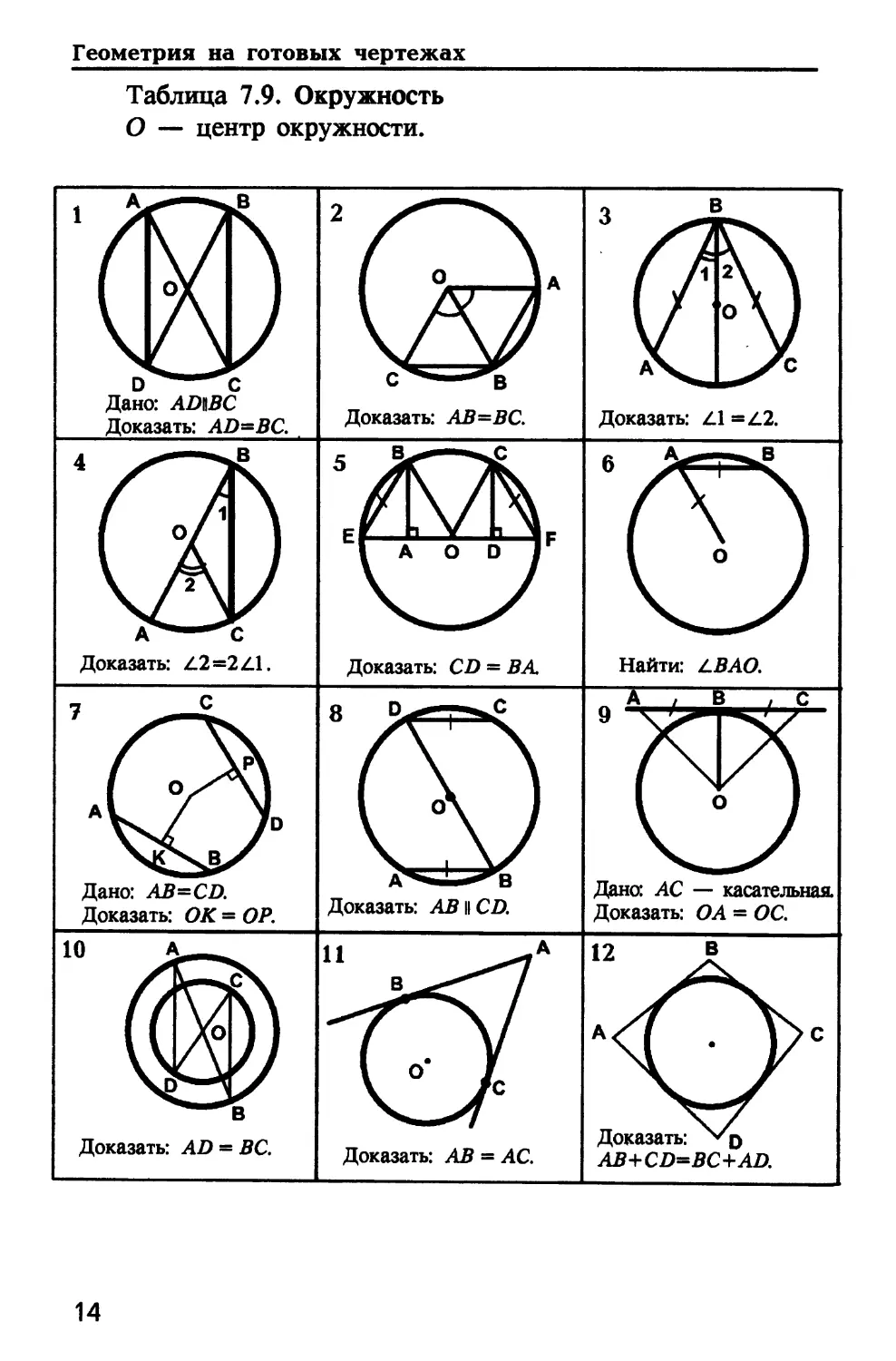
Таблица 7.9. Окружность
О — центр окружности.
D С
Дано: ADWC
Доказать: АР-ВС.
Доказать: АВ=ВС.
Доказать: Z2=2Z.l.
Доказать:
Найти: LBAO.
Дано: AB-CD.
Доказать: ОК = ОР.
Доказать: АВ и CD.
Дано: АС — касательная
Доказать: О А = ОС.
10
Доказать: AD = BC.
Доказать: АВ = АС.
Доказать: о
AB+CD=BC+AD.
14

Геометрия на готовых чертежах
8 КЛАСС
8.1. Определение и признаки параллелограмма.
8.2. Определение и признаки параллелограмма.
8.3. Свойства параллелограмма.
8.4. Свойства параллелограмма.
8.5. Свойства параллелограмма.
8.6. Трапеция.
8.7. Теорема Фалеса.
8.8. Средняя линия треугольника и трапеции.
8.9. Неравенство треугольника.
8.10. Решение прямоугольных треугольников.
8.11. Теорема Пифагора.
8.12. Декартовы координаты на плоскости.
8.13. Декартовы координаты на плоскости.
8.14. Векторы на плоскости.
8.15. Векторы на плоскости.
15

Геометрия на готовых чертежах
Таблица 8.1. Определение и признаки параллелограмма
Доказать, что ABCD — параллелограмм.
1
в с
A D
4
В С
v\
A D
7
В С
A D
Дано: АЛОВ = ACOD.
2
В М с
л/
А К D
5
в с
А ' D
8
В С
A D
Дано: ААВС = ACDA
3
В С
A D
6
В С
IXJ
A D
9
С Е
К А
Дано: АКСЕ —
параллелограмм.
16

Геометрия на готовых чертежах
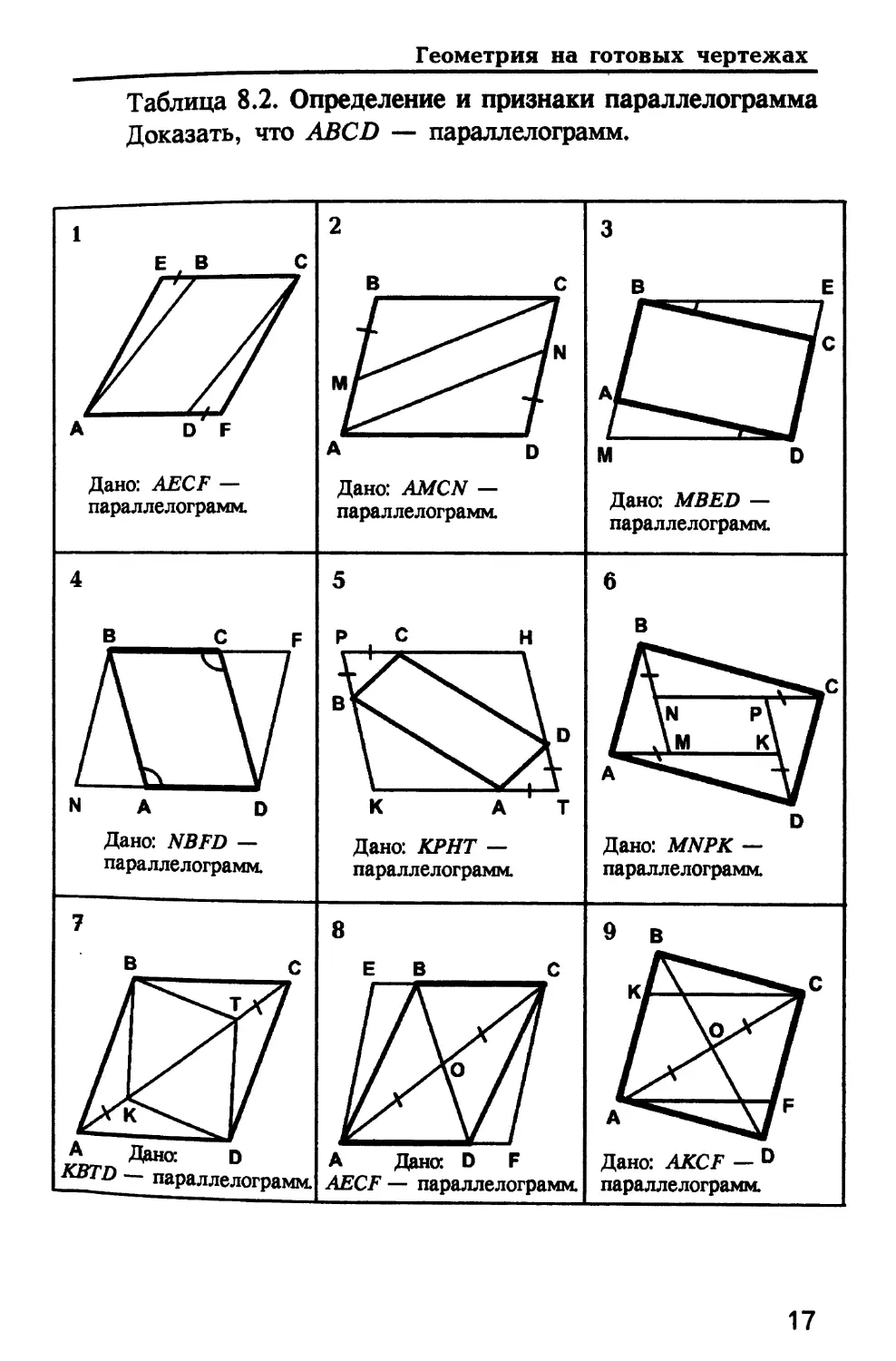
Таблица 8.2. Определение и признаки параллелограмма
Доказать, что ABCD — параллелограмм.
е в
D F
Дано: AECF —
параллелограмм.
Дано: AMCN —
параллелограмм.
Дано: MBED —
параллелограмм.
N A D
Дано: NBFD —
параллелограмм.
Дано: КРИТ —
параллелограмм.
Дано: MNPK —
параллелограмм.
— параллелограмм.
А Ддна D F
AECF — параллелограмм.
Дано: AKCF — D
параллелограмм.
17

Геометрия на готовых чертежах
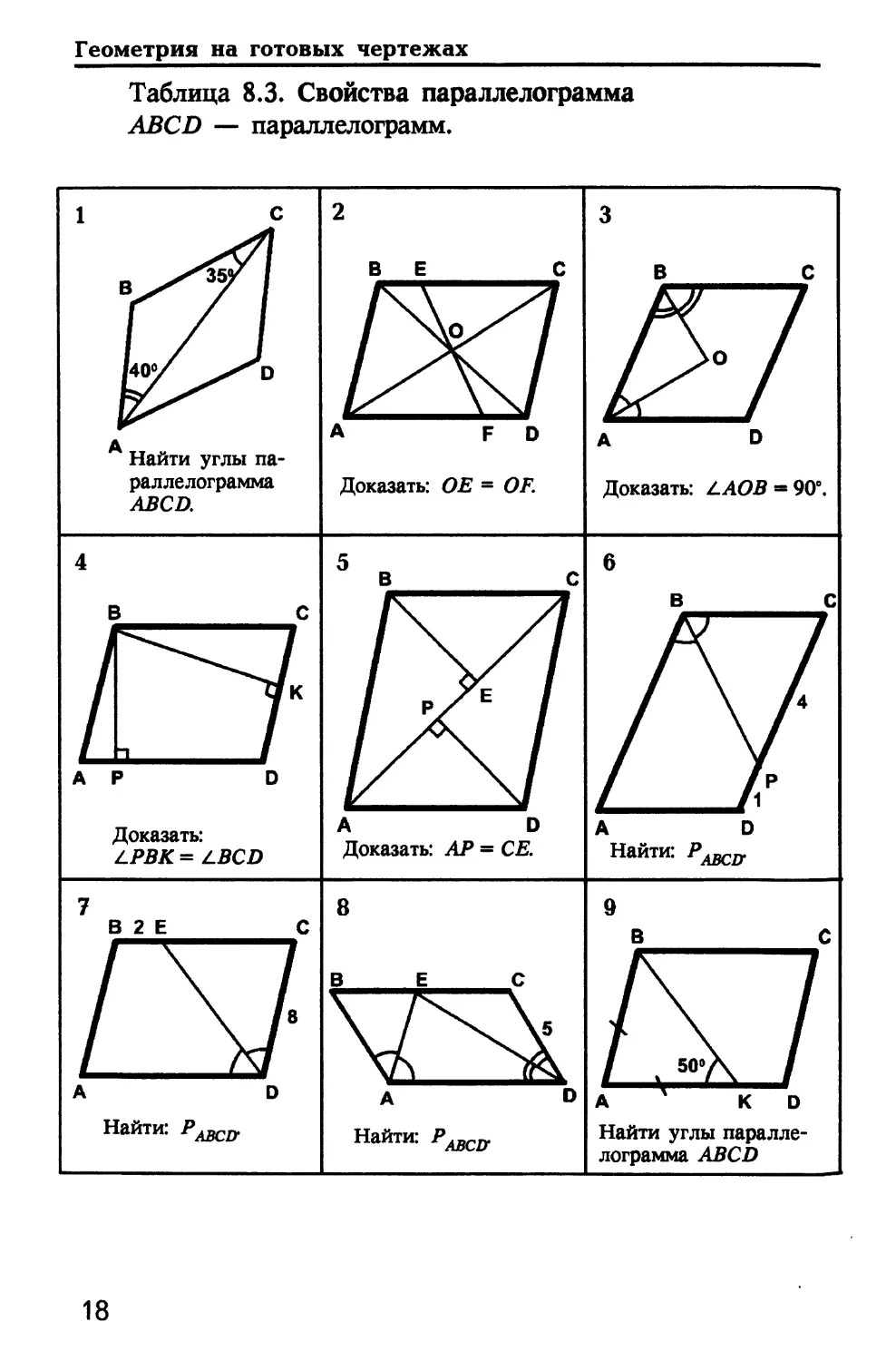
Таблица 8.3. Свойства параллелограмма
ABCD — параллелограмм.
Найти углы
параллелограмма
ABCD.
В Е
A f D
Доказать: ОЕ = OF.
7
Доказать: LAOB = 90°.
о-
А Р
Доказать:
LPBK= LBCD
A D
Доказать: АР = СЕ.
Найти: Р
АВСГГ
В 2 Е
Найти:
Найти: Р
АВС1Г
А К D
Найти углы
параллелограмма ABCD
18

Геометрия на готовых чертежах
Таблица 8.4. Свойства параллелограмма
ABCD — прямоугольник
ABCD — ромб
в _с
£7
А М N D
Доказать: BN = СМ.
Найти: LBDC.
9
AM D
Доказать: ВМ = BN.
A D
Найти: АСОЦ LACB.
10 в
A D
Найти: LABC.
А Е D
Доказать: BE = DF.
A D
Дано: ОЕ = 4.
Найти: АС.
zv
A D
Найти: LBAD.
Доказать: ОК = ОР.
8
20^
В \
А
A D
Доказать:
ромб.
А7
A D
Найти: /.BAD.
к Доказать: KB = KD.
19

Геометрия на готовых чертежах
Таблица 8.5. Свойства параллелограмма
Дано: ABCD — ромб.
Доказать:
LABF= LCBE.
М
Дано: ABCD — ромб.
Доказать:
LMBD=LDBP.
Дано: ABCD — ромб.
Найти углы ABCD.
В
Дано: ABCD —
параллелограмм.
Доказать: ABCD — ромб.
A D
Дано: ABCD —
параллелограмм.
Доказать: MNPK —
прямоугольник.
Дано: ABCD — ромб.
Найти: LBAD.
A D
Дано: ABCD — квадрат.
Доказать: BFDE — ромб.
Дано: ABCD — квадрат.
Доказать: A.B.C.D. —
квадрат.
A D, ' D
Дано: ABCD — квадрат.
Доказать: AfixC{Dx —
прямоугольник.
20

Геометрия на готовых чертежах
Таблица 8.6. Трапеция
ABCD — трапеция.
A D
Доказать: LAOB = 90°.
A D F
Доказать: ВС = DF.
A D
Доказать: АВ = CD.
6
В С
ВаС
А Е D
Дано: BE i CD.
Найти углы трапеции.
Найти углы трапеции.
А Е b D
Найти АЕ и ED.
7 В 5 С
i E D
Дано: AD = 15.
Найти: СЕ.
9 В 5 С
А 30
Найти: ВС.
Е А
Дано: AD = 15.
Найти: периметр
трапеции.
21

Геометрия на готовых чертежах
Таблица 8.7. Теорема Фалеса
Теорема о пропорциональных отрезках.
Дано: / II т II п.
Найти: AK:KF:FE.
Дано:
Найти: х.
В Дано: KPHDE.
Найти: х.
Дано: /Ш = 30
Найти: х и у.
Дано: АС I ГО IPK.
Найти: х и у.
А 4 М 6 С
Найти: KN: NC.
А 6 Е 2,5 С
Найти: АК: KF.
A D
Дано: ABCD —
параллелограмм.
Доказать: BM=MN=ND.
АР С
Найти: АР: PC.
22

Геометрия на готовых чертежах
Таблица 8.8. Средняя линия треугольника и трапеции
А 10 С
Дано: EFlAC.
Найти: PBEF
А
Ух5
А С
Дано: MNWAC.
Найти: Р
ABC
Найти: РАПГ.
А\в\с\
5 В_аС
A D
Дано: ABCD —
трапеция. Доказать:
АО = ОС.
А D
Дано: ABCD —
трапеция.
Найти: EF, ME, FN.
Доказать: MNPK
параллелограмм.
Дано: ABCD — ромб.
Доказать: MNPK —
прямоугольник.
Дано: AF= FC, BP = PD.
Доказать: EFKP —
параллелограмм.
А Е D
Дано: ABCD —
трапеция; ME IIС Д
Доказать: ME = CD/2.
10 в
11 В
м
А К ' D
Дано: ABCD —
трапеция.
Доказать: АВ = CD.
12 В 2 С
А 8 D
Дано: ABCD —
трапеция.
Найти: х, yt z.
A D
Дано: ABCD —
трапеция.
Найти: х, у.
23

Геометрия на готовых чертежах
Таблица 8.9. Неравенство треугольника
Существует ли треугольник ABC?
1
В
А 6 С
2
В
А 10 С
3
А 7 С
Дано: АВ = ВС = 10
В каких пределах меняется х?
4 в
А х с
7 В
А
Аас
5 в 8
А С
8
В
А 6 С
6 в
А
А х С
9
в
А х С
Дано: xSN
Дано: ААВС — равнобедренный. Найти АВ.
10
В
А
А 8 С
И
С
А х В
12
Л
А 8 С
24

Геометрия на готовых чертежах
Таблица 8.10. Решение прямоугольных треугольников
Найти х и у.
А у D
Дано: ABCD —
прямоугольник.
М
х
Р
A D У
А У D В
Дано: АВ = т
8 С
9 в б
120»
2V3
Дано: ABCD —
трапеция.
10
В5С

11
12
A ED
Дано: ABCD —
трапеция. AD = х
,120°
i Т. i
А Е В
Дано: BD = у.
25

Геометрия на готовых чертежах
Таблица 8.11. Теорема Пифагора. Пропорциональные
отрезки в прямоугольном треугольнике
Найти х и у.
Дано: АВ = 13.
Найти ошибку.
Дано:
АС = 8, BD = 6.
А 5 Е D
Дано: ABCD —
параллелограмм.
20
A D
Дано: ABCD —
квадрат.
Дано: АК = 8.
10 А
12
В 5 С
А Е С
Дано: ABCD —
трапеция; AD = 9.
26

Геометрия на готовых чертежах
Таблица 8Л 2. Декартовы координаты на плоскости
Определить координаты вершин прямоугольника ABCD.
С (6; 4)
D х
Е
А
\
-5;1)
0
У
С(5;3)
D
X
3 ,
0
У
В
А(2;-2)
С(10;6)
х
D
Найти координаты точки С:
В(3;0)
Дано^
Записать уравнение окружности:
11
12
А(0;-6)
27

Геометрия на готовых чертежах
Таблица 8.13. Декартовы координаты на плоскости
4У
О х
Сравнить АВ и АС
М(5;12)
Найти: sin a, cos а, tga
Составить уравнение прямой:
4
0
У
1;4)
X
1У
Р(-3;2)
А(2;ЗЬ
30
10
У
(4;1Ь
Найти противоречие:
13
х=-3
28

Геометрия на готовых чертежах
Таблица 8.14. Векторы на плоскости
a d
Дано: ABCD — квадрат.
Указать равные векторы.
Дано: ABCD — ромб.
Указать равные векторы.
В(2;7)
Найти:
(6;3)
(3:2) S
у/ (4;2)
Равны ли векторы
а и Ь1
Найти координаты
вектора AM.
Дано: ABCD — ромб, АС-16;
BD - 10. Найти
координаты векторов АВ и AD.
С(5;2)
9
А(-4;3) D(-1;4)
Доказать: ABCD —
параллелограмм.
Дано: ABCD —
параллелограмм. Доказать:
Ш5Ш
A D
Дано: ABCD —
параллелограмм. Доказать:
ВЕ+ЁР+РС=СР+АС.
10
в
в
Выразить DE через С А
Выразить РК через
О А и ОА
29

Геометрия на готовых чертежах
Таблица 8.15. Векторы на плоскости
Выразить вектор х через векторы а и b (ABCD — параллелограмм)
€3
Доказать: а + Ъ + с = 0.
120°
120°
С В
Дано: |5| -| 5| =| с\
5 Дано: ABCD —
прямоугольник.
в с
Найти;
| AB+AD-DC-OLli .
А(4;4)
В(3;7) С(-4;8)
Найти: cos LB.
А
4
0
Найти:
У
6
ОА
•ОР.
в
ж
г
(
Р
X
Найти
ошибку.
С(4;3)
10
11
Ч6О° 6
О ^В
I5I-2J5I-3.
Найти: | 5+5|, | 5-5|.
12
В(3;4)
Записать уравнение
прямой МР,
касательной к окружности.
А(-2;3)
С(4;2)
Записать уравнение
высоты BD.
30

Геометрия на готовых чертежах
9 КЛАСС
9Л. Подобные треугольники.
9.2. Первый признак подобия треугольников.
9.3. Второй и третий признаки подобия треугольников.
9.4. Вписанные углы.
9.5. Вписанные углы. Угол между касательной и хордой.
9.6. Решение треугольников.
9.7. Решение треугольников.
9.8. Правильные многоугольники.
9.9. Площадь треугольника.
9.10. Площадь четырехугольника.
9.11. Площадь четырехугольника.
9.12. Площади фигур.
9.13. Площади фигур.
9.14. Площадь круга и его частей.
31

Геометрия на готовых чертежах
Таблица 9Л. Подобные треугольники
Дано: ААВС ~ bAfifiv Найти х, у, z:
z С А, 6 С,
Дано: -££- = 3.
А 8 С А, 4 С,
А у С Л 5 С,
z С,
с С А, 20 С,
Дано: а: Ь: с = 4: 3:5.
A z С А, с С,
Дано: a:b:c = 5:6:l. PABCssl0%.
32

Геометрия на готовых чертежах
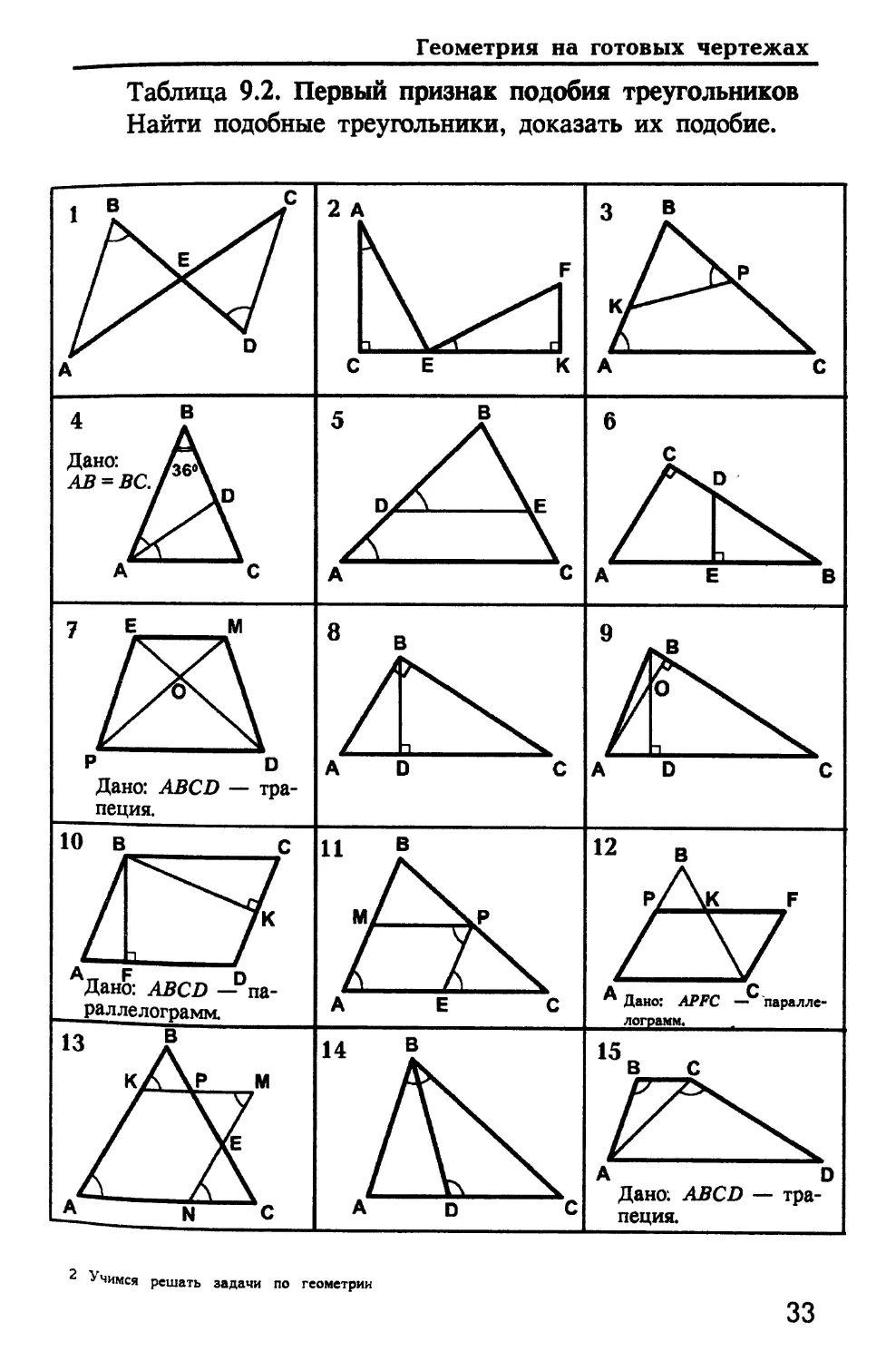
Таблица 9.2. Первый признак подобия треугольников
Найти подобные треугольники, доказать их подобие.
2 а
С Е
Дано:
АВ = ВС.
/ \
7 Е М
Р D
Дано: ABCD —
трапеция.
A D
10 в
11 ?
Дано: ABCD —°па-
раллелограмм
12 в
рАк
/V
Дано: APFC — пара л ле-
13
с/\р м
14
15
В С
N С
A D
Дано: ABCD —
трапеция.
Учимся решать задачи по геометрии
33

Геометрия на готовых чертежах
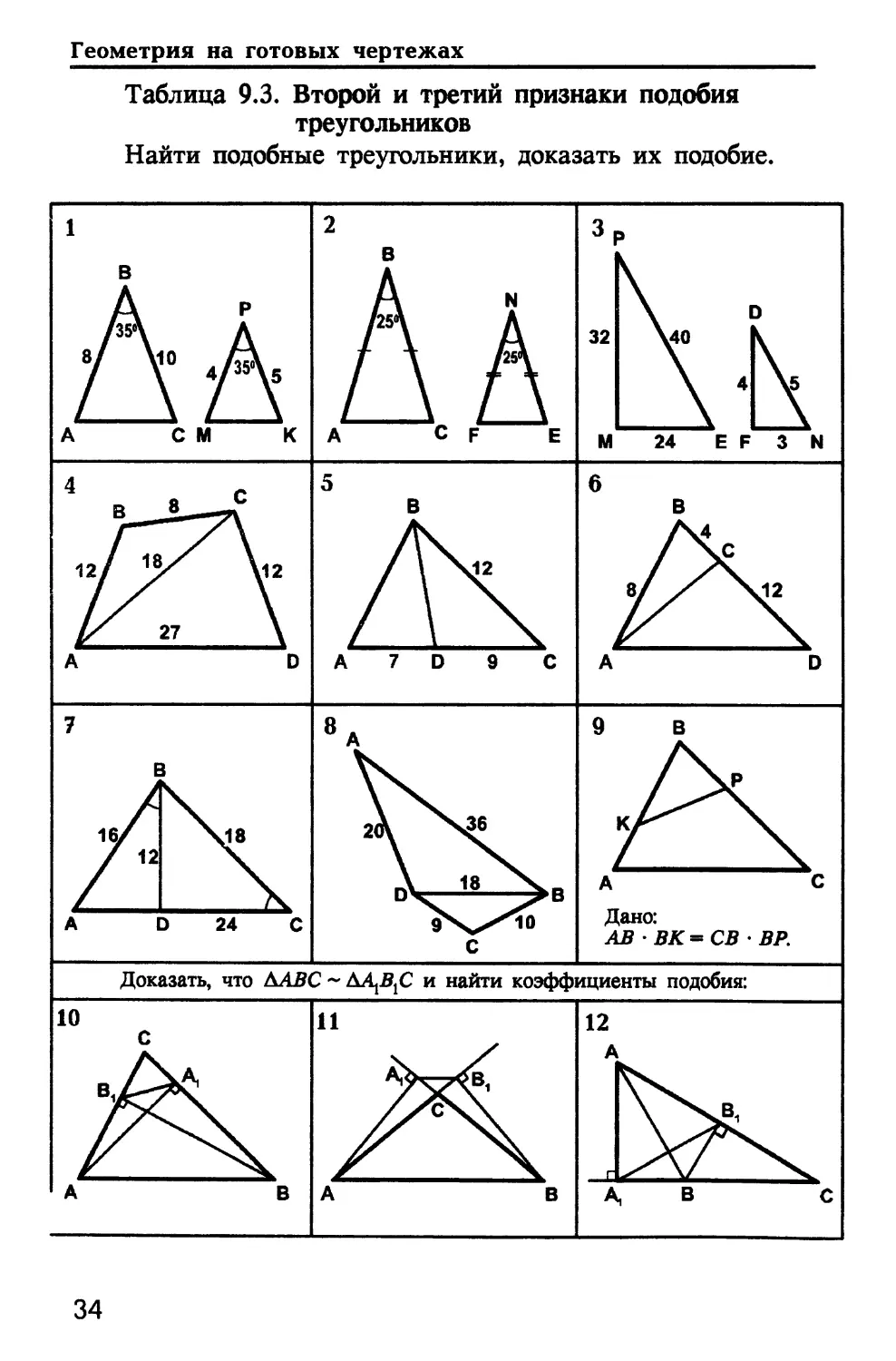
Таблица 9.3. Второй и третий признаки подобия
треугольников
Найти подобные треугольники, доказать их подобие.
32
М 24 Е F 3 N
А 7 D 9 С
D 24 С
Дано:
АВ ВК=СВ ВР.
Доказать, что ААВС ~ AA^Bfi и найти коэффициенты подобия:
10
12
А в
34

Геометрия на готовых чертежах
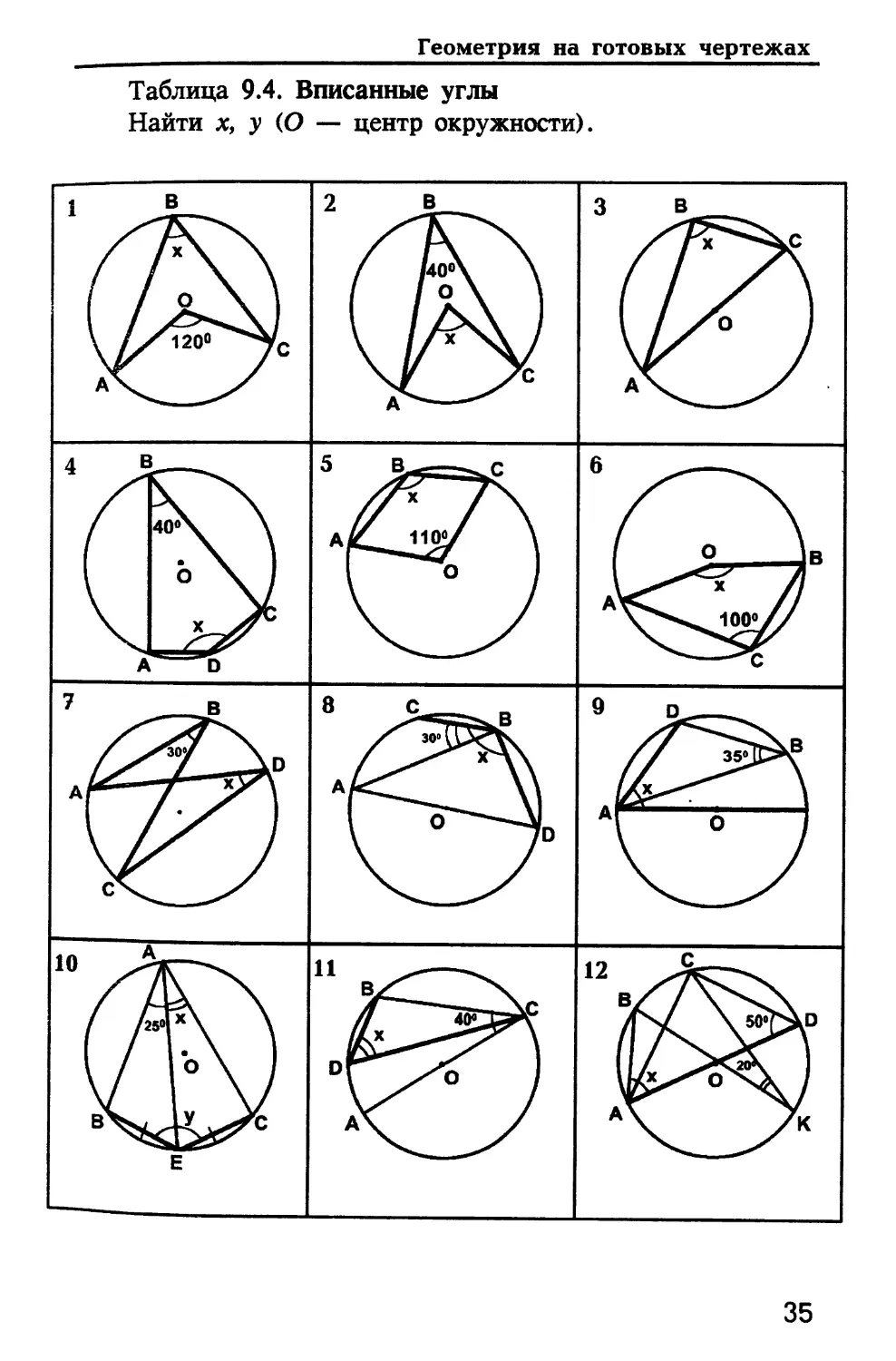
Таблица 9.4. Вписанные углы
Найти х, у (О — центр окружности).
3 В
9 D
35

Геометрия на готовых чертежах
Таблица 9.5. Вписанные углы. Угол между касательной
и хордой
О — центр окружности, В — точка касания
Найти: LCBE
Найти: LABC
Найти: LADB
Найти: LABE
Найти: LAMK
Найти:
9 N
Найти: LKFP
Доказать: tsADK~ AFEK,
Найти: ME
Доказать:
AABD-ABCD
■а
Доказать: ЛЯ2= AD • АС
Доказать:
36

Геометрия на готовых чертежах
Таблица 9.6. Решение треугольников
Найти х:
АдС
7 в
A D С
Дано: АС-Ь
A D С
Найти: АС
37

Геометрия на готовых чертежах
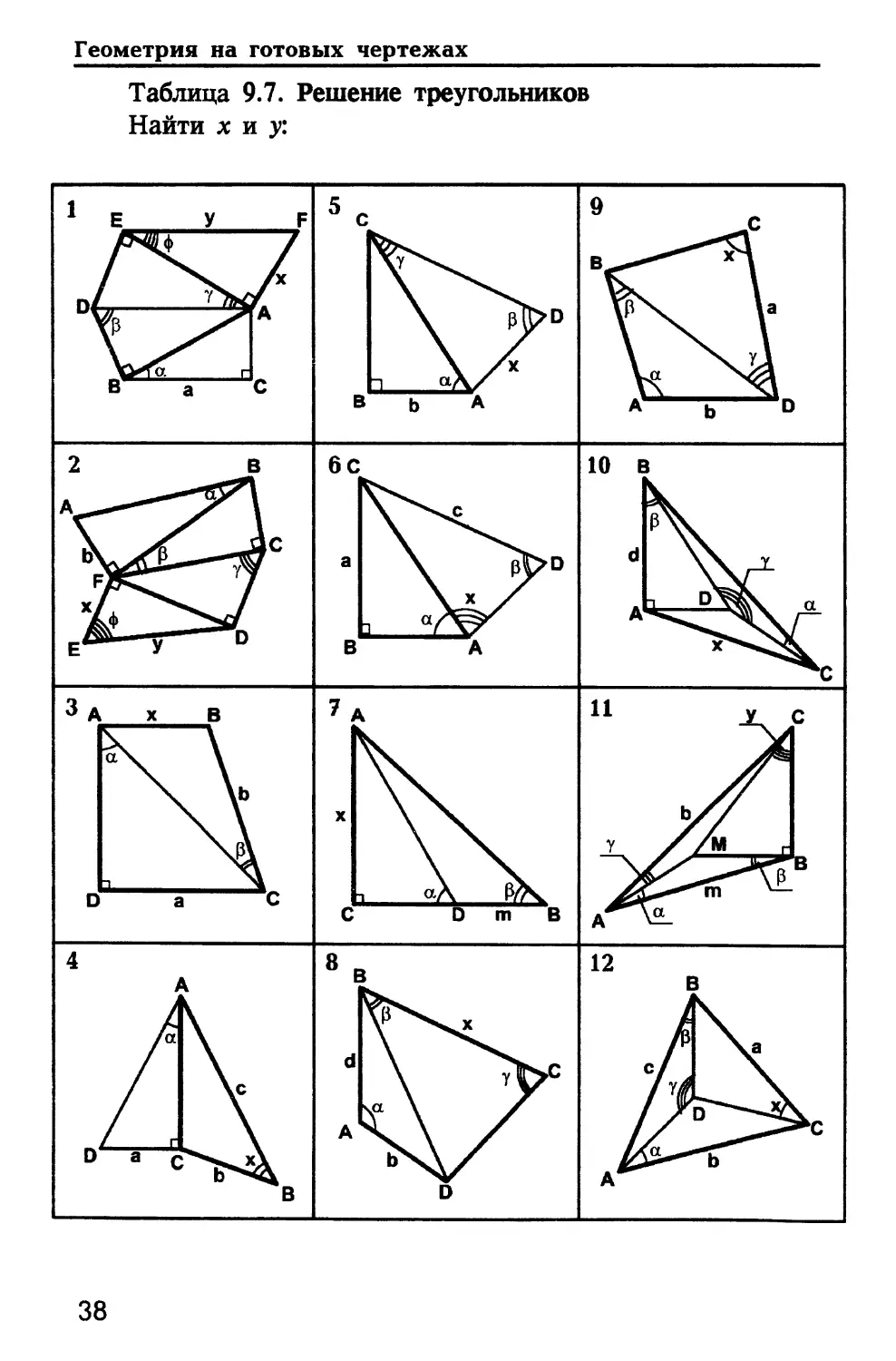
Таблица 9.7. Решение треугольников
Найти х и у:
В b
10 в
38

Геометрия на готовых чертежах
Таблица 9.8. Правильные многоугольники
а — сторона многоугольника, R (г) — радиус описанной
(вписанной) окружности, О — центр многоугольника
Найти количество сторон
многоугольника
Зная один из элементов
(a, R или г), найти два других
150°
А Р
А К F
39

Геометрия на готовых чертежах
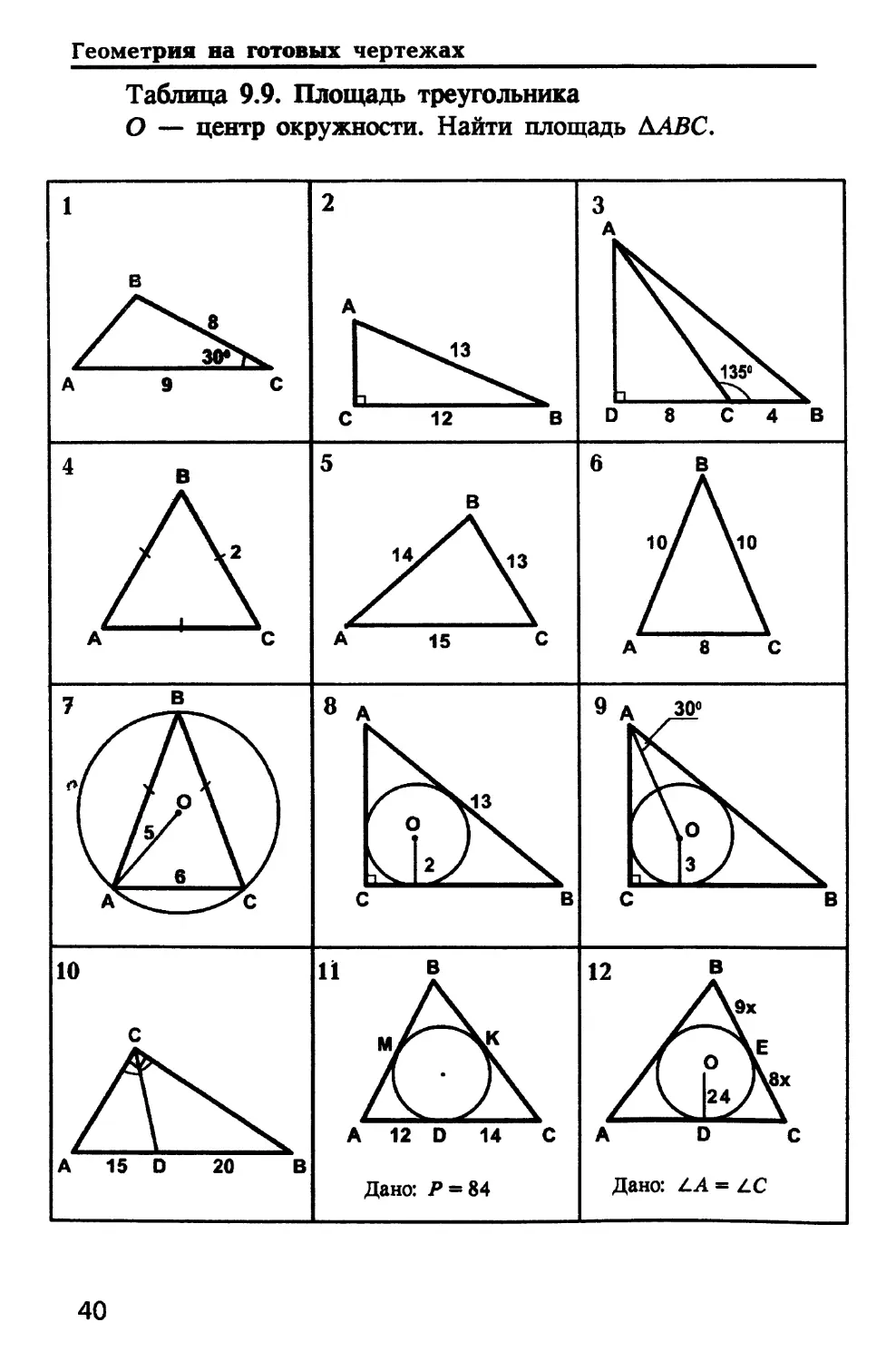
Таблица 9.9. Площадь треугольника
О — центр окружности. Найти площадь ААВС.
АЭС
13
С 12 В
D 8 С 4 В
В
6 В
А 15 С
А 8 С
9 а 30°
10
12
9х
А 15 D 20 В
А 12 D 14 С
Дано: Р = 84
A D С
Дано: LA- LC
40

Геометрия на готовых чертежах
Таблица 9.10. Площадь четырехугольника
Найти площадь ABCD:
Прямоугольник
Параллелограмм
Ромб
А
А
6
В
/
В
/
50°
15
8
/
D
С
/
С
/
Дано: АС = 8,
10
и
АЗЕ
А 4 Е » D
11
А Е D
A F D
12
A D
Дано: АС = 8, BD-b
41

Геометрия на готовых чертежах
Таблица 9.11. Площадь четырехугольника
Найти площадь трапеции ABCD:
1
I
A
4
В
/
/
4
-\
E
названа
Дано: AD
В
I
A
7
13
/
A
10
В
A
!
B
/
7
о
7
17
С
\
= 7
С
5M
b
с
\
к
!\
\
D
\
D
D
D
2
7
/
A
5
/
A
8
A
11
25
i
/
A
В
/
/
п
E
Дано:
в
в
/-
в
г
■■■■
6
13
г У
37
11
28
С
\
л
= 5
С
л
с
л
\
D
\
D
С
У
12
D
\
D
3
В
/
3
5
А
С
>
/
F 2
Дано: ABH.FE
6
В 7
/ у
А 25
9
В ^
А
12
В 2 С
V
А 18
Дано: АС = 7,
С
!5
\
BD
\
D
\
D
D
s
D
= 15
42

Геометрия на готовых чертежах
Таблица 9Л 2. Площади фигур
с
Найти отношение площадей -=Д:
5 в
A D
Дано: ABCD —
трапеция
A D
Дано: ABCD —
Дано: ABCD —
трапеция
43

Геометрия на готовых чертежах
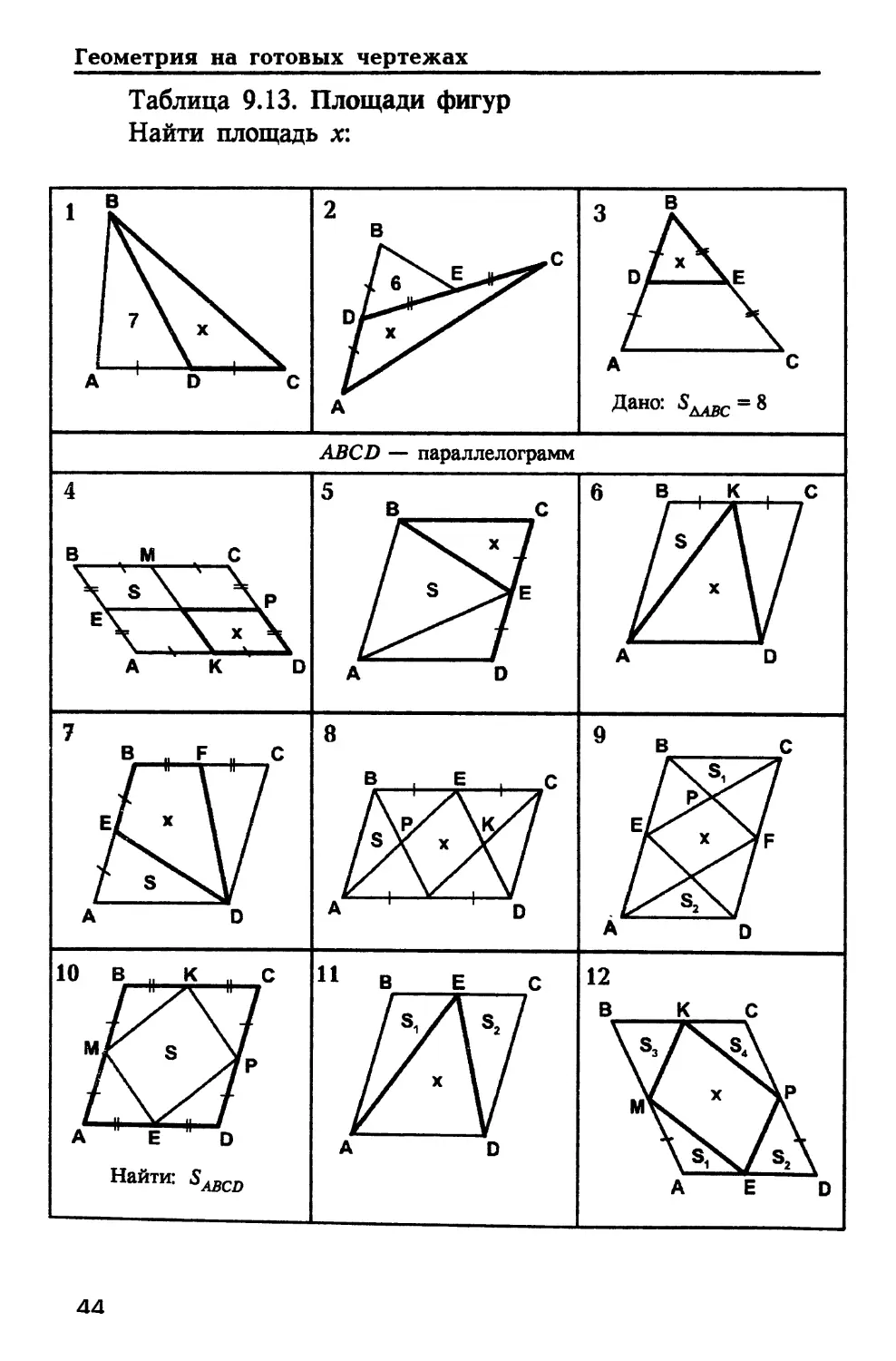
Таблица 9.13. Площади фигур
Найти площадь х:
А
Дано:
ABCD — параллелограмм
ВМС
у. у ч.
*\ \Л
А К D
В „ F
11
ВЕС
Найти: S
ABCD
А Е D

Геометрия на готовых чертежах
Таблица 9.14. Площадь круга и его частей
R — радиус круга, О — центр.
Найти площадь заштрихованной фигуры.
Дако: Rl=5\
Дано:
0; Д2=6;
I
Дано: R = 6
г
Дано: ASC-D —
прямоугольник; R^ = Ц2 = 1
О, 20
Дано: /^ = ^2 =
= R4 = 2. Я5 = 3
9 О
15
О4
of
Дано:
10
/I
Г1
А Ю
Дано: Л =
Дано:
Дано: Ry = R2
45

Глава II
Метод ключевых задач
§1. Параллельные прямые,
пересекающие стороны угла
Ключевая задача.
Если Afix || А2В2 (рис. 1), то
О А, _ ОВ1
~ОА2 " ~ОВ2
О А, _ ОВ,
АЛ "ЧЧ
Решение. О
Поскольку
ДОЛД ^
Рис. 1
по первому признаку, то
соответственные стороны этих треугольников пропорциональ-
ОА. OB. AA
вы. Отсюда _ = _ = -р-. Имеем:
ОА1 _ ОВ1 ОА2 _ ОВ2
ОА,-
ОД O5j
ОД OJ5/ ДА2 ВХВ2
Примеры.
Задача 1.
Даны три отрезка a, b и с. Построить такой отрезок
46

Метод ключевых задач
В, х
Рис 2
Решение.
На сторонах произвольного угла отложим отрезки
ОА1 = а, А1А2 = й, ОВХ = с (рис. 2). Соединим точки Д и В{.
Проведем А2В2 \\ А1В1. Теперь
а с
можно записать -г- = „ „ .
Ь ВХВ2
Следовательно, отрезок
ВХВ2 является искомым.
Задача 2.
В равнобедренном
треугольнике ABC
{АС = СВ) проведена
медиана СС{ и
биссектриса ЛД.
Найти LACB,
если АА1 = 2ССГ
Решение.
Проведем ClD\\AAl (рис. 3). Поскольку АСХ = СХВ, то
— средняя линия треугольника АА^В, значит,
т.е. треугольник CCXD — равнобедренный.
Пусть LACCX = LCfB = Z-C^q = а. Тогда
LCAC, = ZC^q = 90° - a, Z^q = LDCiB = 45° - f •
По свойству внешнего угла треугольника запишем
LCDC, = LDC.B + LDBCV
т.е. а = 45° - ^ + 90° - а. Отсюда 2а = 108°, LACB = 108°.
Задача 3.
Высота ВК ромба ABCD, опущенная на сторону AD9
пересекает диагональ АС в точке М. Найти MD, если известно,
что Я* = 4, AK: ATZ) = 1: 2.
47

Метод ключевых задач
Решение.
Проведем OL±AD
(рис. 4). Имеем
ВО = О£>, ВК II ОЦ
тогда
PL DO
LK OB =
т.е. DL = LK.
Учитывая, что AK:KD- 1:2,
получаем АК = XL.
Поскольку КМ || OL, то
КМ — средняя линия
треугольника AOL.
Имеем:
следовательно,
4
М
1.
Отсюда
MD = BM = BK-MK= 3.
Задача 4.
В равнобедренном треу- С
гольнике ABC (АС = АВ)
отношение высоты AD к основанию ВС равно
взята на стороне АВ так, что АМ-^АВ. Найти величину
угла МСВ.
Решение.
Проведем DF \\ СМ (рис. 5). Так как CD = DB, то
MF = /В, а с учетом АЛ/ = ~г^^ получаем AM = Mf. Отсюда
. Имеем:
Следовательно, LECD = 30°.
48

Метод ключевых задач
Упражнения
1.1. Построить отрезок -т-, где а и Ъ — длины данных
отрезков.
1.2. Высота CD треугольника ABC делит медиану ВМ в
соотношении 3:1, считая от вершины В. В каком отношении
CD делит сторону АВ, считая от вершины А1
1.3. В треугольник вписан прямоугольник так, что две
его вершины лежат на боковых сторонах, а две — на
основании. Диагонали треугольника параллельны боковым
сторонам. В каком отношении вершины прямоугольника делят
боковые стороны?
1.4. Высота треугольника делит основание в отношении
3:7. В каком отношении серединный перпендикуляр к
основанию делит боковую сторону?
1.5. В треугольнике ABC проведены медианы AM и ВК.
Через середину ВК проведена прямая, параллельная AM. В
каком отношении эта прямая и точка М делят сторону ВС,
считая от вершины В!
1.6. М и Р — середины смежных сторон AD и DC
параллелограмма ABCD. МС и РВ пересекаются в точке К.
Найти ВК:КР.
1.7. В треугольнике ABC А^ лежит на ВС и ВА1: Afi =
= 1:3, Сх — середина АВ. Найти АК: К^, где К т- точка
пересечения АА^ и ССГ
1.8. D — середина стороны АС треугольника ABC. Q —
точка пересечения медиан треугольника DBC. Прямая AQ
пересекает сторону ВС в точке М. Найти ВМ: МС.
1.9. В остроугольном треугольнике ABC длины медиан
ВМ, CN и высоты АН равны соответственно 4, 5 и 6. Найти
площадь треугольника ABC.
1.10. В равнобедренном треугольнике ABC (АВ = ВС)
ортоцентр делит пополам расстояние между центром
описанной окружности и основанием. Определить cos LABC.
1.11. В треугольнике ABC АВ = АС = 75. ВС = 90.
Вершины В и С соединены с серединой О высоты, проведенной
из вершины А. ВО и СО пересекают стороны АС и АВ
соответственно в точках Вх и С,. Найти площадь
четырехугольника ОС \ВХ.
49

Метод ключевых задач
1.12. Длина основания АС треугольника ABC равна 3, а
медианы AD — 4. Высота BE делит медиану AD пополам.
Найти площадь треугольника ABC.
1.13. В остроугольном треугольнике ABC через вершину
В и середину стороны CD проведена прямая. В каком
соотношении эта прямая делит сторону АС, считая от вершины
А, если LBAC = a, LCBA=fl.
1.14. В треугольнике ABC АС>АВ, а угол при вершине
А равен а. На стороне АС взята точка М так, что
АВ = МС. Пусть Е — середина отрезка AM, D — середина
отрезка ВС. Найти LCED.
1.15. На сторону ВС ромба ABCD опущена высота DE.
Диагональ АС пересекает высоту DE в точке F так, что
DF :FE = 5:1. Найти сторону ромба, если АЕ = 5.
1.16. Медиана BD и биссектриса АЕ треугольника ABC
пересекаются в точке М, причем AM:ME- 3:1, АЕ = й,
AD = а. Найти площадь треугольника ABD.
1.17. В треугольнике ABC на основании АС взяты точки
Р и Q так, что AP<^Q. Прямые ЯР и BQ делят медиану
ЛМ на три равные части. Известно, что PQ = 3. Найти ЛС.
1.18. В треугольнике ABC точки Р и Q лежат на стороне
АС, а прямые ВР и BQ делят медиану М на три равные
части. Известно, что ВР = BQ, АВ = 9, ДС =11. Найти ЛС.
1.19. Через вершину В треугольника ABC проведена
прямая, параллельная биссектрисе угла С и пересекающая
продолжение стороны АС в точке D. Определить, в каком
отношении прямая АЕ делит сторону ВС, если Е — середина
BD и АС:СВ = Ь:а.
1.20. В прямоугольном ААВС (Z.C = 90°) через вершину
Л и середину высоты CD проведена прямая, пересекающая
катет ВС в точке М. Доказать, что СМ: MB = cos2 A.
50

Метод ключевых задач
§2. Середины сторон четырехугольника
Ключевая задача.
Середины сторон выпуклого четырехугольника являются
вершинами параллелограмма, площадь которого равна
половине площади
данного
четырехугольника.
Решение. А -
Отрезки FM и
KN (рис. 6)
являются средними
линиями треугольников
ABC и ADC
соответственно. Тогда
м
FM || AC, FM = ^ АС и KN \\ AC, KN = ^АС.
Отсюда FM = KN, FM || KN и, следовательно,
четырехугольник FMNK — параллелограмм.
Пусть площадь четырехугольника ABCD равна S.
Отсюда SFBM + SKDN
4 s- Аналогично SFAK + SMCN = ^ S.
Получаем S
FhfNK = 5 - (S^M + SKDN
7%" S*
Примеры.
Задача 1.
Доказать, что в выпуклом четырехугольнике сумма
квадратов диагоналей в два раза больше суммы квадратов отрезков,
соединяющих середины противоположных сторон.
Решение.
Воспользовавшись теоремой о сторонах и диагоналях
параллелограмма, имеем FN2 + МК2 = 2 (FM2 + MN2) (рис. 7).
51

Метод ключевых задач
Учитывая, что FM = ^ АС и MN = ^ AD, получаем
FN2
Задача 2.
Диагонали
трапеции взаимно
перпендикулярны,
длина одной из них рав-А
на 6 см. Длина
отрезка,
соединяющего середины
оснований, равна 4,5 см.
Найти площадь
трапеции.
Решение.
Пусть К и М
(рис. 8) — середины
боковых сторон трапеции.
FN = 4,5, АС = 6 и
LBOA = 90°.
Так как KF || АС и
KN || BD, то LNKF = 90° и
KFMN — прямоугольник.
Тогда из прямоугольного
треугольника FKN получа-
N
Рис. 8
ем: KN=^FN2 - KF2 = V4,52 - З2 =
JKFMN
KFKN
2 #
9VT
а так как S
ABCD
2SKFMN> T0
Ответ: 9V5".
Упражнения
2.1. Доказать, что середины сторон прямоугольника
являются вершинами ромба.
52

Метод ключевых задач
2.2. Доказать, что середины сторон ромба являются
вершинами прямоугольника.
2.3. Доказать, что середины сторон равнобедренной
трапеции являются вершинами ромба.
2.4. Доказать, что если отрезки, соединяющие середины
противоположных сторон выпуклого четырехугольника,
равны, то диагонали четырехугольника перпендикулярны.
2.5. Доказать, что если отрезки, соединяющие середины
противоположных сторон выпуклого четырехугольника,
перпендикулярны, то диагонали четырехугольника равны.
2.6. Середины сторон трапеции являются вершинами
ромба. Определить вид трапеции.
2.7. Доказать, что отрезки, соединяющие середины
противоположных сторон выпуклого четырехугольника, и
отрезки, соединяющие середины диагоналей, пересекаются в одной
точке.
2.8. Доказать, что если отрезки, соединяющие середины
противоположных сторон выпуклого четырехугольника, делят
его на четыре равновеликие части, то такой
четырехугольник — параллелограмм.
2.9. В трапеции ABCD сумма внутренних углов,
прилежащих к основанию AD> равна 90°. К и L — середины
оснований трапеции, М и N — середины диагоналей.
Докажите, что MN = АХ.
2.10. В выпуклом четырехугольнике ABCD АВ = CD.
Через середины диагоналей АС и BD проведена прямая,
пересекающая АВ и CD в точках MnNсоответственно. Докажите,
что LBMN= LCNM.
2.11. Доказать, что площади выпуклых
четырехугольников, у которых середины сторон совпадают, равны.
2.12. Середины сторон двух шестиугольников совпадают.
Доказать, что площади шестиугольников равны.
2.13. Дан равносторонний треугольник ABC. С центром
в точке А радиусом АВ описана дуга ВС. М — произвольная
точка дуги ВС, отличная от В и С. Середины хорд МС и
MB соединены отрезками с серединами сторон АВ и АС
соответственно. Доказать, что полученные отрезки взаимно
перпендикулярны.
53

Метод ключевых задач
§3. Медиана, проведенная к гипотенузе
Ключевая задача 1.
В прямоугольном треугольнике длина медианы,
выходящей из вершины прямого угла, равна половине длины
гипотенузы.
Решение.
На луче СМ
отложим отрезок
MD, равный от- ^
резку СМ (рис. 9). А ^\^ SF
В
четырехугольнике ACBD
диагонали точкой
пересечения делятся
пополам, значит, Рис 9
ACBD —
параллелограмм. Однако LACB = 90°, значит, ACBD —
прямоугольник. Отсюда СМ= 2CD~ 2^'
Следствие. Центр описанной окружности прямоугольного
треугольника лежит на середине гипотенузы.
Ключевая задача 2.
Если в треугольнике длина медианы равна половине
длины основания, к которому она проведена, то этот треугольник
прямоугольный.
Решение.
Проведя вышеописанное дополнительное построение,
приходим к выводу, что ABCD — это параллелограмм с равными
диагоналями, т.е. прямоугольник. Отсюда LACB = 90°.
Примеры
Задача \.
BD — медиана прямоугольного треугольника ABC
(LB = 90°). Пусть К — точка касания стороны AD
треугольника ABC с окружностью, вписанной в этот треугольник.
Найти углы треугольника ABC, если К делит AD пополам.
54

Метод ключевых задач
Решение.
Пусть N — точка касания
окружности со стороной BD
треугольника BDA (рис. 10). Имеем
DK = DN = х. Поскольку К —
середина AD, то АР = АК = х. По
свойству медианы, проведенной
к гипотенузе, BD = AD = 2х.
Отсюда BN = ВР = х. Значит,
треугольник ABD —
равносторонний. Имеем LA = 60°, Z.C = 30°.
В
Р
Рис. 10
Задача 2.
Найти основания АВ и
CD трапеции ABCD, у которой АВ = 2С£> = 2AD, ЛС = а,
Решение.
Проведем СЕ \\ AD
(рис. 11). Пусть AD = х.
Тогда
АВ = 2DC = 2х.
Но АЕ = DC = х. Отсюда
СЕ= ^АВ. Значит, Z..4GB = 90°. Имеем
Е В
Рис. 11
— медиана треугольника АСВ.
+ СЯ2 = Vo2 + й2.
Упражнения
3.1. Доказать, что сумма расстояний от оснований двух
высот треугольника до середины его третьей стороны равна
третьей стороне.
3.2. Медиана, проведенная к гипотенузе прямоугольного
треугольника, равна т и делит прямой угол в отношении
1:2. Найти стороны треугольника.
3.3. В треугольнике ABC медианы, выходящие из вершин
А и С, взаимно перпендикулярны. Найти отношение
медианы, проведенной к стороне АС, к стороне АС.
55

Метод ключевых задач
3.4. В треугольнике ABC медианы ВВХ и ССХ пересекаются
в точке М и взаимно перпендикулярны. Найти МЛ, если
ВВ{ = 36, ССХ = 15.
3.5. Доказать, что высота и медиана прямоугольного
треугольника, проведенные к гипотенузе, образуют угол, равный
разности острых углов треугольника.
3.6. Гипотенуза прямоугольного треугольника в 4 раза
больше проведенной к ней высоты. Найти острый угол
треугольника.
3.7. В треугольнике ABC стороны АВ и АС равны
соответственно 8 и 7, ABAC = 120°. Найти расстояние от
основания высоты, опущенной на АС, до середины ВС.
3.8. В треугольнике ABC медианы BD и AF пересекаются
под прямым углом в точке О, причем ВО = AD. Найти
отношение радиусов окружностей, описанных около
треугольников BOF и АОВ.
3.9. Длина средней линии трапеции равна 5, а длина
отрезка, соединяющего середины оснований, — 3. Углы при
большем основании равны 30° и 60°. Найти основания
трапеции и ее площадь.
3.10. Периметр параллелограмма ABCD 80 см.
Биссектрисы углов А и D пересекаются в точке М такой, что ВС
делит AM пополам. Найти стороны параллелограмма.
3.11. На продолжении наибольшей стороны АС
треугольника ABC отложен отрезок СМ = ВС. Доказать, что LABM —
тупой.
3.12. В трапеции ABCD (AD \\ ВС) MN — средняя линия.
Биссектриса угла ABC пересекает ее в точке Р. Доказать,
что LAPB = 90°.
3.13. В прямоугольном треугольнике ABC LA = a,
LC = 90°. Через точки А и С и середину гипотенузы проведена
окружность радиуса R. Найти радиус окружности, вписанной
в треугольник ABC.
3.14* М и N — середины сторон ВС и CD параллелограмма
ABCD. Докажите, что если DMJ.АС, то BN:CD = 3:2.
56

Метод ключевых задач
§4. Соотношения в прямоугольном
треугольнике
Ключевая задача.
В прямоугольном треугольнике ABC, в котором
Л С = 90°, CD — высота (рис. 12), имеют место следующие
соотношения:
1) AC2 =AD • АВ;
2) ВС2 = BD-AB;
3) CD2 = AD • DB;
AC2 AD^
} ВС2 BD'
Решение. Рис ц
-AC -AZ)
ДАС2) со ДАВС по первому признаку. Отсюда -т= = "т^»
'). Из подобия треугольников BCD и АЕС
аналогично получаем второе соотношение.
Поскольку LACD= LCBD, то /SACD со ABCD. Тогда
DB ~~CD'Ciy- BD AD*
Четвертое соотношение непосредственно следует из
первых двух.
Примеры
Задача 1.
Построить квадрат, равновеликий данному
прямоугольнику.
Решение.
Пусть длины соседних
сторон прямоугольника а и Ь. Бели
х — длина стороны искомого
квадрата, то х2 = ab.
Следовательно, надо по двум заданным^
отрезкам а и Ъ построить такой Рис* 13
отрезок дс, чтобы х = >ldb. На одной прямой отложим два
отрезка AD = an DB = b (рис. 13).
57

Метод ключевых задач
На отрезке АВ как на диаметре построим полуокружность.
В точке D восстановим перпендикуляр к АВ. Этот
перпендикуляр пересечет полуокружность в точке С. Отрезок CD —
сторона искомого квадрата. Действительно, LACD = 90°
(вписанный угол, опирающийся на диаметр). Тогда имеет место
третье соотношение, т.е. CD = VAD • BD - yfaF.
Задача 2.
Диаметр АВ окружности
равен 1. На нем отложен
отрезок АС длиной а.
Проведена также хорда AD длиной
Ъ (рис. 14). Из точки С
восстановлен перпендикуляр к д
АБ, пересекающий хорду
AD в точке .Е, а из точки
D опущен перпендикуляр
DF на АВ. Оказалось, что
AE-AF. Докажите, что Ри 4
Решение.
AF
LADB = 90°, DF±AB, тогда AD = у/АВ • AF. Отсюда
AI? AC AW
- ALr ? = AE. AAEC со /SADF. Запишем ^ = ^
AB
Й2
AD
Упражнения
4.1. Диаметр АВ разделен на отрезки АС = 8 и ВС = 5.
Из точки С проведен к нему перпендикуляр CD длиной 6.
Определите положение точки D относительно окружности.
4.2. Высота, опущенная на гипотенузу прямоугольного
треугольника, делит ее на отрезки 24 и 54. Найдите катеты.
4.3. Катет прямоугольного треугольника равен 6,
проекция его на гипотенузу — 2. Найти гипотенузу и второй катет.
4.4. Один катет прямоугольного треугольника равен 6, а
проекция другого катета на гипотенузу — 5. Найдите
гипотенузу.
58

Метод ключевых задач
4.5. Определите катеты прямоугольного треугольника, у
которого перпендикуляр, опущенный из вершины прямого
угла на гипотенузу, больше одного из отрезков гипотенузы
на 3 и меньше другого на 4.
4.6. Определите меньший катет прямоугольного
треугольника и длину перпендикуляра, опущенного из вершины
прямого угла на гипотенузу, если больший катет треугольника
меньше гипотенузы на 2 и больше прилегающего к нему
отрезка гипотенузы на 1,6.
4.7. Один из катетов прямоугольного треугольника равен
15, а проекция другого катета на гипотенузу равна 16. Найти
радиус окружности, вписанной в треугольник.
4.8. Найти площадь круга, вписанного в прямоугольный
треугольник, если проекции катетов на гипотенузу равны 9
и 16.
4.9. Через вершину прямого угла прямоугольного
треугольника с катетами 6 и 8 проведен перпендикуляр к
гипотенузе. Вычислите площади образовавшихся треугольников.
4.10. Определите площадь равнобедренной трапеции, у
которой основания 10 и 26, а диагонали перпендикулярны
боковым сторонам.
4.11. Диагональ равнобедренной трапеции равна 3V13 и
перпендикулярна боковой стороне. Разность оснований равна
8. Определите площадь трапеции.
4.12. Определите высоту равнобедренной трапеции, если
ее диагональ перпендикулярна боковой стороне, а разность
квадратов оснований равна 25.
4.13. Дана равнобедренная трапеция, средняя линия
которой 9, площадь равна 54 и диагональ перпендикулярна
боковой стороне. Определите основание трапеции.
4.14. В окружность вписана трапеция, боковая сторона
которой равна 15, средняя линия 16 и большее основание
является диаметром окружности. Определите площадь
трапеции.
4.15. В окружность вписана трапеция, средняя линия
которой равна 16, боковая сторона больше меньшего основания
на 8 и большее основание является диаметром окружности.
Определить высоту трапеции.
4.16. В полукруг единичного радиуса вписана трапеция
так, что ее основание лежит на диаметре. Найти площадь
трапеции, если ее периметр равен 5.
59

Метод ключевых задач
4.17. Диагонали прямоугольной трапеции взаимно
перпендикулярны, и большая из них точкой пересечения делится
на отрезки, равные 36 и 34. Определите основание трапеции.
4.18. Перпендикуляр, опущенный из вершины тупого угла
ромба на его сторону, делит большую диагональ на отрезки,
равные 3,5 и 12,5. Определить сторону и меньшую диагональ
ромба.
4.19. Площадь прямоугольного треугольника равна 2V3".
Определите его высоту, проведенную к гипотенузе, если она
делит прямой угол в отношении 1:2.
4.20. Окружность, построенная на катете прямоугольного
треугольника как на диаметре, делит гипотенузу в отношении
1:3. Найдите углы треугольника.
4.21. На катете АС прямоугольного треугольника ABC
как на диаметре построена окружность. Она пересекает
гипотенузу АВ в точке D, АС = b, AD: DC = 4:3. Найти
расстояние от точки В до центра окружности.
4.22. Дан ромб ABCD {LA — острый). На прямой АВ
выбрана точка F так, что LCFA = 90°. Отрезки DF и ВС
взаимно перпендикулярны. Определить cos Л.
4.23. В остроугольном треугольнике ABC проведены
высоты AD и ВР. На высоте AD взята точка М, а на ВР —
точка N так, что LBMC = LANC = 90°, MN = 4 + 2 VT,
LMCN = 30°. Найти биссектрису угла С треугольника
MCN.
60

Метод ключевых задач
§5. Вписанный угол
Ключевая задача.
Вписанные углы, опирающиеся на одну дугу, равны.
Решение.
Вписанный угол равен половине градусной меры дуги,
на которую он опирается. Отсюда следует справедливость
доказываемого утверждения.
Следствие. Вписанный угол, опирающийся на диаметр,
прямой.
Примеры
Задача 1.
Четырехугольник ABCD
вписан в окружность. Его диагонали
пересекаются в точке К.
Окружность, проходящая через А, В
и К, пересекает ВС и AD в
точках М и N. Доказать, что
КМ = KN.
Решение.
LDAC = LDBC (рис. 15) как
вписанные, опирающиеся на одну
дугу. Тогда градусные меры дуг
NK и КМ равны. Но равные дуги
стягивают равные хорды, значит,
NK = KM.
Задача 2.
Доказать, что у всех
трапеций, вписанных в данную
окружность, с общей боковой сто- В
роной АВ отношение высоты и
средней линии постоянно.
Решение.
Для всех трапеций
градусная мера дуги АВ (рис. 16)
постоянная. Следовательно, вели-
РИС. 16
61

Метод ключевых задач
чина угла BDA не изменяется, т.е. tg LBDA — величина
J3\jf
постоянная. Имеем tg LBDA = -rj=r. Осталось лишь заметить,
Ми
что длина отрезка MD равна средней линии трапеции.
Задача 3.
В окружности радиуса R
проведены две пересекающиеся
перпендикулярные хорды АВ и CD.
Докажите, что АС2 + BD2 = 4R2.
Решение.
LABC + LDCB = 90° (рис. 17).
Следовательно, сумма
градусных мер дуг АС и DB равна
180°. Значит, если отложить
хорду АК = DB, то градусная мера Рис. 17
дуги САК станет равной 180°.
Отсюда LCAK- 90° и СК — диаметр. Имеем
AC2
= АС2 + АК2 = СК2 = 4Д2.
Упражнения
5.1. Один из углов прямоугольного треугольника равен
35°. Под каким углом виден каждый его катет из центра
описанной окружности?
5.2. Высота, опущенная из вершины С вписанного в
окружность треугольника ABC, продолжена до пересечения
с окружностью в точке Е. Эта точка соединена с точкой D,
диаметрально противоположной вершине С. Доказать, что
DE || АВ.
5.3. Биссектриса угла В треугольника ABC пересекает
описанную окружность в точке D. Доказать, что AADC —
равнобедренный.
5.4. Доказать, что сторона треугольника, лежащая против
угла ъ 30°, равна радиусу окружности, описанной около
треугольника.
5.5. Доказать, что для любой точки X окружности,
описанной около прямоугольника ABCD, сумма ХА2 + ХВ2 +
+ ХС2 + XD2 — величина постоянная.
62

Метод ключевых задач
5.6. Хорда АВ перпендикулярна радиусу ОМ и делит его
пополам. Найти величину углов АОВ и ВАМ.
5.7. Вне окружности с центром О взята точка М.
Окружность, диаметром которой является ОМ, пересекает
данную окружность в точках А и В. Доказать, что МА и MB —
касательные к окружности с центром в точке О.
5.8. Построить прямоугольный треугольник по гипотенузе
и проекции одного из катетов на гипотенузу.
5.9. Угол при вершине равнобедренного треугольника
равен 40°. Одна из боковых сторон служит диаметром
полуокружности, которая делится другими сторонами на три дуги.
Найти градусные меры этих дуг.
5.10. Через вершины В и С треугольника ABC проходит
окружность, пересекающая стороны АВ и АС в точках К и
М соответственно. Доказать, что ААВС ю ААМК. Найти
МК и AM, если АВ = 2, ВС = 4, АС = 5, АК = 1.
5.11. Две окружности пересекаются в точках А и В.
Через точку А проведены диаметры AD и АС. Доказать, что
точки В, С и D лежат на одной прямой.
5.12. Две окружности пересекаются в точках А и В. Через
В проведена секущая, пересекающая окружности в точках
С и D. Доказать, что величина угла CAD постоянная для
всякой секущей, проходящей через точку В.
5.13. Окружность, построенная на стороне
параллелограмма как на диаметре, проходит через середину соседней
стороны и точку пересечения диагоналей. Найти углы
параллелограмма.
5.14. Две окружности пересекаются в точках М и К.
Через М и К проведены прямые АВ и CD соответственно,
пересекающие первую окружность в точках А и С, а вторую —
в точках В и D. Доказать, что AC \\ BD.
5.15. В окружности проведены диаметр АВ и хорда BD.
На диаметре выбрана точка О и проведена окружность с
центром О, касающаяся хорды в точке К и исходной
окружности в точке А. Докажите, что АК — биссектриса угла
DAB.
5.16. Окружность, построенная на большем основании
трапеции как на диаметре, касается меньшего основания и
пересекает боковые стороны, деля их пополам. Найти меньшее
основание трапеции, если радиус окружности равен R.
63

Метод ключевых задач
5.1 7. Центры вписанной и описанной окружностей
треугольника ABC лежат по разные стороны от прямой АВ.
Длина стороны АВ равна радиусу описанной окружности.
Чему равен угол АОВ, где О — центр вписанной окружности?
5.18. В треугольник ABC вписана окружность, касающаяся
его сторон в точках L, М, N. Докажите, что треугольник
LMN — всегда остроугольный.
5.19. На стороне CD квадрата ABCD выбрана точка N
CN 1
так, что -™ = лг-_ i« Через точки В nN проведена прямая,
пересекающая окружность, описанную около квадрата, в
точке К. Найти величину угла KCD.
5.20. Продолжение медианы треугольника ABC,
проведенный из вершины А, пересекают описанную около
треугольник окружности в точке D. Найти длину отрезка ВС,
если длина каждой из хорд АС и DC равна 1.
5.21. В остроугольном треугольнике высоты, проведенные
через вершины В и С треугольника ABC, пересекают
описанную окружность в точках Вх и Сх. Определить угол А
треугольника ABC, если прямая ВХСХ проходит через центр
описанной окружности.
5.22. В круг вписан равнобедренный треугольник ABC,
АВ = ВС = с. Через точку А проведена хорда АК = т,
пересекающая ВС в точке М. Найти длину отрезка AM.
5.23. Высоты треугольника продлены до пересечения с
описанной окружностью. Доказать, что отрезки этих линий
от ортоцентра до окружности делятся соответственными
сторонами пополам.
5.24. Пользуясь одной линейкой, проведите
перпендикуляр к заданному диаметру из заданной точки, лежащей вне
окружности.
5.25. Вершина А остроугольного треугольника ABC
соединена отрезком с центром О описанной окружности. Также
проведена высота АН. Докажите, что LBAH = LOAC.
5.26. Треугольник ABC — равнобедренный (АВ = ВС).
BD — медиана. Вокруг треугольника ABD описана окружность
радиуса 4. Эта окружность пересекает сторону ВС в точке
Е. BE: ЕС = 7:8. Найдите периметр треугольника ABC.
5.27. В четырехугольнике ABCD, вписанном в
окружность, через вершины А и В и точку Р пересечения диагоналей
64

Метод ключевых задач
проведена окружность, пересекающая сторону ВС в точке
Е. Докажите, что если АВ = AD, то CD = СЕ.
5.28. Окружности Sx и S2 пересекаются в точках А и В.
Центр окружности Sx лежит на S2. Хорда АС окружности
Sj пересекает S2 в точке D. В и О лежат по разные стороны
от АС. Докажите, что OD ± ВС.
5.29. Продолжения высот остроугольного треугольника
ABC пересекают описанную окружность в точках Mv M2,
Мг Докажите, что в треугольнике М]М2Мг высоты
треугольника ABC являются биссектрисами.
5.30. Биссектриса внешнего угла при вершине С
треугольника ABC пересекает описанную окружность в точке D*
Докажите, что AD = BD.
5.31. На хорде АВ окружности S с центром О взята точка
С. Описанная окружность треугольника АОС пересекает
окружность S в точке D. Докажите, что ВС = CD.
5.32. Из вершины тупого угла А треугольника ABC
опущена высота AD. Из точки D радиусом AD описана
окружность, пересекающая стороны треугольника АВ и АС в точках
М и N соответственно. АВ = с, AM = m, AN = п.
Найдите АС.
5.33. Две окружности пересекаются в точках Аи В. Через
точку К первой окружности проводятся прямые КА и KB,
пересекающие вторую окружность в точках Р и Q
соответственно. Докажите, что хорда PQ второй окружности
перпендикулярна диаметру КМ первой окружности.
5.34. В остроугольном треугольнике ABC сумма величин
углов А и В в полтора раза больше величины угла С. Длина
меньшей стороны АС равна 3. Найти длину высоты BD, если
известно, что отрезок, соединяющий точку D с центром
описанной окружности, виден из вершины В под углом 6е.
3 Учимся решать задачи по геометрии
65

Метод ключевых задач
§6. Угол между касательной и хордой
Ключевая задача. D
Угол TAB между
касательной AT и хордой АВ (рис.
18) измеряется половиной
градусной меры дуги АтВ.
Решение.
Проведем диаметр AD.
LABD = 90° как вписанный,
опирающийся на диаметр.
Понятно, что LDAT = 90°.
Следовательно,
LBAT = LADB =
Примеры
Задача 1.
Две окружности
пересекаются в точках А и В. Через
точку В проводится прямая,
пересекающая окружности в
точках С и А а затем через
точки С и D проводятся
касательные к этим
окружностям (рис. 19). Докажите,
точки A, D, С и Р — точка
пересечения касательных —
лежат на одной окружности.
Доказательство.
Рис. 19
L\ = L2, A3 = Z4, L\ + LA = 180° - ADPC.
Отсюда L2 + Z.3 = 180° - LDPC, т.е.
LDAC + LDPC = 180°.
Значит, вокруг четырехугольника DACP можно описать
окружность.
66

Метод ключевых задач
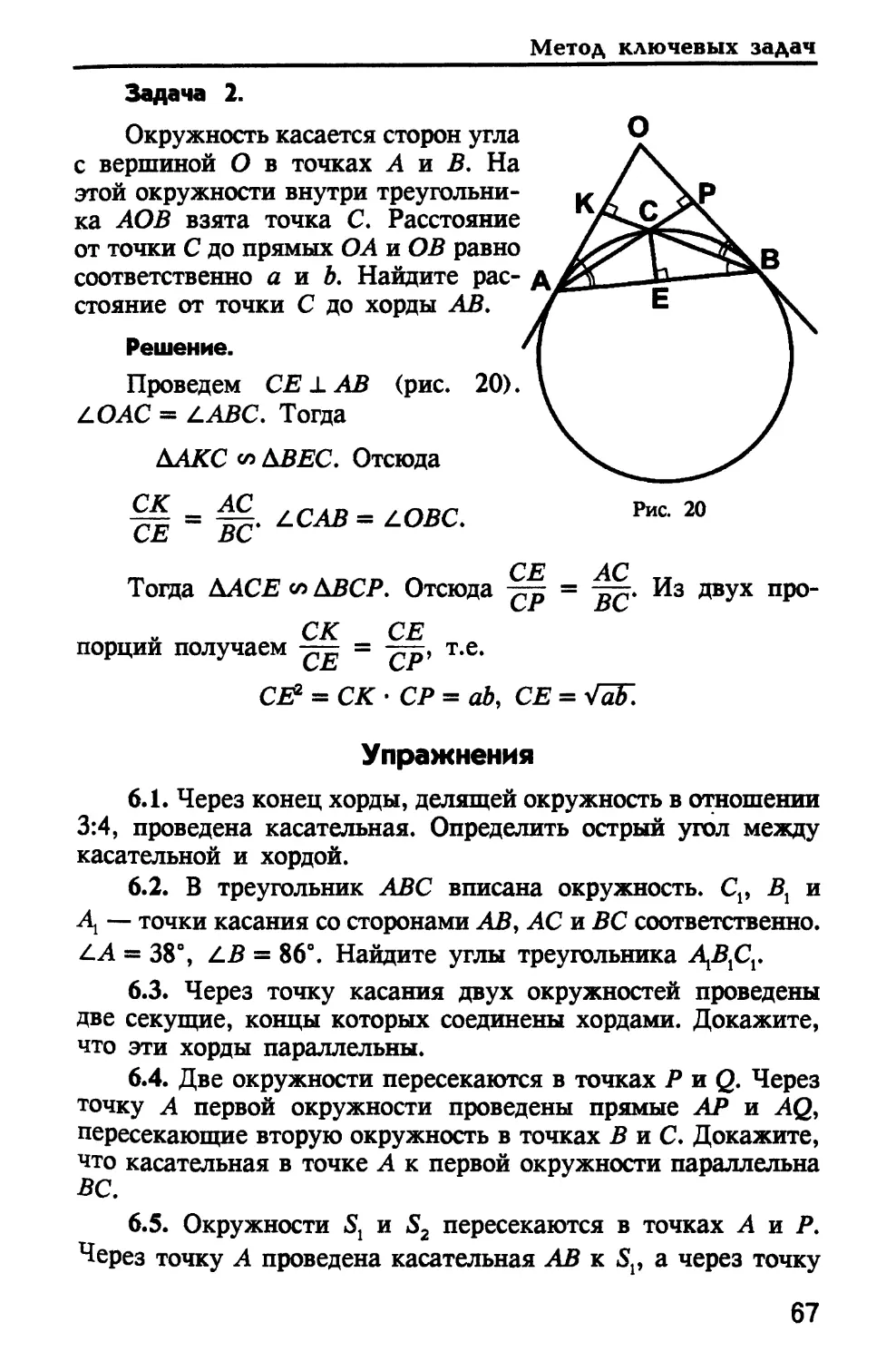
Задача 2.
Окружность касается сторон угла
с вершиной О в точках А и В. На
этой окружности внутри
треугольника АОВ взята точка С. Расстояние
от точки С до прямых О А и ОВ равно
соответственно а и Ь. Найдите
расстояние от точки С до хорды АВ.
Решение.
Проведем СЕ ± АВ
LOAC = ААВС. Тогда
В
(рис. 20).
ААКС со АВЕС. Отсюда
Рис. 20
СЕ АС
Тоща ЬЛСЕ со АВСР. Отсюда -^р = -дТу Из двух про-
СК СЕ
порции получаем -^ = -^, т.е.
С& = СКСР = aby СЕ = VaF.
Упражнения
6.1. Через конец хорды, делящей окружность в отношении
3:4, проведена касательная. Определить острый угол между
касательной и хордой.
6.2. В треугольник ABC вписана окружность. Cv Bx и
А1 — точки касания со сторонами АВ, АС и ВС соответственно.
LA = 38°, LB = 86°. Найдите углы треугольника AfixCv
6.3. Через точку касания двух окружностей проведены
две секущие, концы которых соединены хордами. Докажите,
что эти хорды параллельны.
6.4. Две окружности пересекаются в точках Р и Q. Через
точку А первой окружности проведены прямые АР и AQ,
пересекающие вторую окружность в точках В и С. Докажите,
что касательная в точке А к первой окружности параллельна
ВС.
6.5. Окружности St и S2 пересекаются в точках А и Р.
Через точку А проведена касательная АВ к Sp а через точку
67

Метод ключевых задач
Р — прямая CD \\AB (BE S2, С G S2, D G Sx). Доказать, что
ABCD — параллелограмм.
6.6. ЛВ — основание равнобедренного треугольника
ABC, Доказать, что окружность, касающаяся сторон угла
АСВ в точках А и В, проходит через точку О — центр
вписанной окружности треугольника ABC.
6.7. Две окружности разных радиусов с центрами О{ и
О2 пересекаются в точках А и В. К эти окружностям проведена
общая касательная. Точки касания С и D лежат по ту же
сторону от линии центров, что и точка В. Найдите LOXAO2,
если LCAD = а.
6.8. К двум окружностям, пересекающимся в точках М
и К, проведена общая касательная. Докажите, что если А и
В — точки касания, то LAMB + LAKB = 180°.
6.9. В треугольнике ABC (LC = 90°) на катете АС
построена окружность, пересекающая АВ в точке Е. Через тцчку
£ проведена касательная, пересекающая катет ВС в точке
D. Докажите, что треугольник BDE — равнобедренный.
6.10. Касательная в точке А к окружности, описанной
около треугольника ABC, пересекает ВС в точке Z>, AE —
биссектриса треугольника ABC. Докажите, что AD = АЕ.
6.11. Через центр окружности со{ проведена окружность
со2. А и В — точки пересечения окружностей. Касательная
к окружности со2 в точке В пересекает со{ в точке С. Докажите,
что АВ = ВС.
6.12. Окружности Sx и S2 пересекаются в точке А. Через
нее проведена прямая, пересекающая S{ в точке В, a S2 в точке
С. Через точки С и Б проведены касательные, пересекающиеся
в точке D. Докажите, что величина угла ВВС постоянна.
6.13. Две окружности касаются друг друга внешним
образом в точке D. Прямая касается одной из них в точке А,
а другую пересекает в точках В и С. Докажите, что точка
А равноудалена от прямых DB и CD.
6.14. Из точки С окружности на хорду АВ опущен
перпендикуляр CD. Из концов хорды опущены перпендикуляры
АЕ и BF на касательную к окружности в точке С. Докажите,
что С&=АЕ- BF.
68

Метод ключевых задач
6.15. Две окружности пересекаются в точках А и D.
АВ и АС — хорды, которые касаются каждой их окружностей.
АИ2 BD
Докажите, что
6.16. Окружность проходит через вершины В, С и D
трапеции ABCD и касается боковой стороны АВ в точке В.
Основания трапеции а и Ь. Найдите диагональ BD.
6.17. Около треугольника ABC описана окружность.
Прямая / касается окружности в точке А. Через точку D стороны
АВ проведена прямая DE \\ I, EG AC. АЕ = 5, AD = 6,
ЕС = 7. Найти BD.
6.18. Через центр О окружности, описанной около
остроугольного треугольника ABC, проведена прямая,
перпендикулярная СО и пересекающая отрезки АС и ВС в точках
Е и F соответственно. Вычислите длину отрезка CF, если
известны длины сторон АС = Ь, ВС = а и длина отрезка ЕС
равна d.
6.19. Из точки А проведены секущая и касательная к
окружности радиуса R. Пусть В — точка касания, a D и
С — точки пересечения секущей с окружностью, причем
точка D лежит между Л и С. Известно, что BD — биссектриса
ААВС, ее длина равна R. Найдите расстояние от точки А до
центра окружности.
6.20. Из точки вне окружности проведены касательная
и секущая, причем точки касания и точки пересечения
секущей с окружностью являются вершинами некоторой
трапеции. Найдите отношение оснований трапеции, если
известно, что угол между касательными равен 60°.
6.21. Через точку А окружности проведена хорда АВ,
затем касательная в точке В. Диаметр, перпендикулярный
радиусу ОА, пересекает касательную в точке С, а хорду (или
ее продолжение) — в точке D. Докажите, что ВС = CD.
6.22. В угол с вершиной S вписана окружность,
касающаяся сторон в точках А и В. М — точка на окружности.
MKjlAB, MP±AS, ME±BS. Докажите, что MA? = MP • ME.
6.23. В треугольнике ABC биссектриса угла А пересекает
сторону ВС в точке D. Перпендикуляр к этой биссектрисе,
проведенный через середину М отрезка AD, пересекает
прямую ВС в точке N. Докажите, что прямая NA — касательная
к окружности, описанной около треугольника ABC.
69

Метод ключевых задач
§7. Величина угла, вершина которого лежит
внутри [вне! окружности
F
внутри
Ключевая задача 1.
Величина угла ABC (рис. 21)
равна полусумме градусных мер
дуг АтС и EnF.
Решение.
Проведем хорду FC.
LABC = LAFC + LECF =
АтС +
Ключевая задача 2.
Величина угла ЛВС (рис. 22)
равна полуразности градусных
мер дуг АтС и EnF.
Решение.
Проведем хорду AF.
LABC = LAFC - LEAF =
Примеры
Задача 1.
Через середину С дуги АВ проведены
две прямые CD и СЕ, пересекающие
хорду AS в точках Н и F. Доказать, что
около четырехугольника DHFE можно описать окружность
(рис. 23).
Рис. 22
Доказательство.
LDHF= ^(
LDEF= ^
70

Метод ключевых задач
Отсюда LDHF + LDEF ••
"2
180е.
m
+ kjACB)
Задача 2.
В окружность вписан четы
рехугольник ABCD. Его
противоположные стороны CD и АВ,
ВС и AD продолжены до
взаимного пересечения в точках
N и F (рис. 24). Докажите, что
биссектрисы углов BFA и AND
перпендикулярны.
Доказательство.
S — точка пересечения биссектрис.
LKND = \
Рис. 23
Отсюда
Аналогично дока
зывается, что
= ^ (kjMC +
+ kjAE + \.
LESM
Рис. 24
2 (wJ5M +
+ kjKD)
71

Метод ключевых задач
Получаем: LMSP = LESM. Значит,
LMSP = LESM = 90°.
Упражнения
7.1. Из точки А вне окружности проведена секущая,
пересекающая окружность в точках В is. С. Дуга ВС содержит
112°. Касательная AD делит эту дугу в отношении 7:9.
Найдите LBAD.
7.2. Хорды АВ и CD пересекаются в точке М.
LAMC = 40°. Дуга AD больше дуги ВС на 20°.
Найдите wAD.
7.3. Окружность разделена точками А, В, С и D так, что
kjAB : \^ВС : ^jCD : <jDA = 3:2:13:7. Хорды AD и БС
продолжены до пересечения в точке М. Найдите LAMB.
7.4. Диаметр АВ и хорда CJ9 пересекаются в точке М.
LCMB = 73°, дуга ЯС содержит 110°. Найдите градусную
меру дуги AD.
7.5. Окружность разделена точками А, В, С и D так, что
suAB: w£C: \^CD: \^DA = 2:4:5:7. Проведем хорды АС и
AD, они пересекаются в точке М. Найдите LAMB.
7.6. Из концов дуги АВ, содержащей 48°, проведены
хорды АС и BD так, что LDMC, образованный пересечением
хорд, равен LDNC, где N принадлежит дуге CD. Найдите
градусную меру дуги CD.
7.7. Диагонали четырехугольника ABCD пересекаются в
точке М, а прямые АВ и CD — в точке ЛГ. LAMD = 108°,
LAND = 24°. Найдите Z.ARD и Z.5DC, если около ABOD
можно описать окружность.
7.8. В круге с центром О и радиусом R проведена хорда
АВ и продолжена на расстояние ВС = R. Через точки С и
О проведена секущая CD. Точка С лежит дальше от D, чем
от О. Докажите, что LAOD = 3LACD.
1.9. На окружности взяты четыре точки. Середины
образованных дуг попарно соединены отрезками. Доказать, что
среди этих отрезков есть по крайней мере два
перпендикулярных.
7.10. Около треугольника ABC описана окружность.
AAl, BBV ССХ — биссектрисы углов треугольника, причем
72

Метод ключевых задач
точки Д, Вх и С{ лежат на окружности. Докажите, что
BBV CC{ перпендикулярны сторонам треугольника AfixCv
7.11. Точка М лежит на диаметре АВ окружности с
центром О. С и D — точки окружности по одну сторону от
АВ, причем LCMA = LDMB. LCMD = а. Найдите LCOD.
7.12. Доказать, что биссектриса внешнего угла А
треугольника ABC, вписанного в окружность, параллельна хорде,
соединяющей середины дуг АВ и АС.
7.13. В окружности проведена хорда. На меньшей из
образовавшихся дуг взята точка и через нее проведена
касательная. Найдите на касательной точку, из которой хорда
видна под наибольшим углом.
7.14. На сторонах выпуклого четырехугольника как на
диаметрах построены четыре круга. Докажите, что они
полностью покрывают четырехугольник.
7.15. По стороне правильного треугольника катится
окружность радиуса, равного его высоте. Докажите, что угловая
величина дуги, высекаемой на окружности сторонами
треугольника, всегда равна 60°.
7.16. Диагонали равнобедренной трапеции ABCD
пересекаются в точке Р. Докажите, что центр О ее описанной
окружности лежит на описанной окружности треугольника
АРВ.
7.17. Из точки М, взятой вне круга, проведены к нему
касательные МА и MB. Прямая AD перпендикулярна
диаметру BD. Докажите, что DE = ЕА, где Е — точка
пересечения МС и AD.
73

Метод ключевых задач
§8. Формула а = 2R sin a
Ключевая задача.
Хорда окружности равна
произведению диаметра на синус
вписанного угла, опирающегося на эту хор-
Решение.
Проведем диаметр AD (рис. 25)
LADB = a, LABD = 90° как
вписанный, опирающийся на диаметр.
Отсюда АВ = AD sin а.
Примеры
Задача 1.
В четырехугольник ABCD вписана окружность. Диагонали
его пересекаются в точке О. Пусть Rv R2, Rv R4 — радиусы
окружностей, описанных около треугольников ABO, ВОС,
COD и AOD. Докажите, что R{ + R3 = R2 + R4.
В
Решение.
Заметим, что синусы всех
углов при вершине О (рис. 26)
равны. Тогда
я - ^ - ВС
1 "" 2 sin a' 2 "" 2 sin а'
CD = AD
3 2 sin а' 4 2 sin а' Рис# 26
Поскольку в четырехугольник ABCD можно вписать
окружность, то АВ + CD = ВС + AD. Отсюда следует
справедливость доказываемого равенства.
Задача 2.
В треугольнике ABC точка М лежит на стороне АВ, точка
N — на стороне АС. Через точки М, ЛГ, Б, С проходит
окружность радиуса V3" (рис. 27). Найдите длину отрезка
AM, если ВС = 3, AM: М# = 2:1, Z.A4C = 30°.
74

Метод ключевых задач
Решение.
ВС = 2R sin LBNC,
где R — радиус
окружности, R = VT. Отсюда
sin LBNC =
Значит, LBNC = 120° или _ _
LBNC = 60°. РиС* 27
Если LBNC = 120°, то ZA/V5 = 60°. Следовательно,
LABN = 90° и МЛГ — диаметр, что противоречит условию.
Остается LBNC = 60°. Имеем LCMB = 60°, LAMC = 120е,
2LMCM = 30°, AM = МС.
Пусть MB = х, тогда МС = 2х. К треугольнику МВС
применим теорему косинусов. 9 = х2 + 4.x2 - 2х • 2х • у.
Отсюда х = VT, A/V/ = МС = 2 V31
Упражнения
8.1. В треугольнике ABC точка Л/ принадлежит отрезку
ВС. Докажите, что отношение радиусов описанных
окружностей вокруг треугольников АМВ и MAC не зависит от
выбора точки М на стороне ВС.
8.2. Основания равнобедренной трапеции равны 36 и 12.
Определить радиус окружности, описанной около трапеции,
если ее боковая сторона равна 16.
8.3. Радиус окружности, описанной около треугольника,
равен Л, его углы — а, /?, у. Найдите площадь треугольника.
8.4. Углы треугольника а и /J. Найдите отношение его
площади к площади описанного круга.
8.5. В окружность радиуса R вписан треугольник с углами
15° и 60°. Найдите его площадь.
8.6. В равнобедренной трапеции основания равны 21 и
9, высота — 8. Найдите радиус описанного круга.
8.7. Из точки М на окружности проведены три хорды:
MN =1, МР = 6, MQ = 2. При этом LNMP = LPMQ.
Найдите радиус окружности.
75

Метод ключевых задач
8.8. В треугольнике ABC £A = 5T, LC = 63°, радиус
описанной окружности R. А\ и ССХ — высоты. Найдите
радиусы окружностей, описанных около треугольников
АССХ и АСАХ.
8.9. Докажите, что окружность, проходящая через
ортоцентр треугольника и две его вершины, равна окружности,
описанной около треугольника.
8.10. В треугольнике ABC LA = 37°, F — точка
пересечения биссектрис АД и ССХ. Радиусы окружностей, описанных
около треугольников BAfi{ и FC^ равны. Найдите угол С.
8.11. Угол В треугольника ABC равен 60°. Радиус
описанной окружности равен 2. Найдите радиус окружности,
проходящей через А и С и центр окружности, вписанной в
треугольник ABC.
8.12. Дан квадрат ABCD. О — центр окружности,
вписанной в треугольник ABC. Луч АО пересекает окружность,
описанную около квадрата, в точке Т. Найдите отношение
ВС: ВТ.
8.13. В равнобедренном треугольнике центр вписанной
окружности делит высоту, проведенную к основанию, на
отрезки 5 и 3, считая от вершины. Найти радиус описанной
окружности.
8.14. Из точки М, двигающейся по окружности,
опускаются перпендикуляры на фиксированные диаметры АВ и
DC. Докажите, что длина отрезка, соединяющего основания
перпендикуляров, не зависит от выбора точки М.
8.15. Перпендикуляр, восстановленный к стороне АВ
треугольника ABC в ее середине, пересекает высоту, проведенную
из вершины В, в точке К, а серединный перпендикуляр к
стороне ВС пересекает эту же высоту в точке М. Радиус
окружности, описанной около треугольника ABC, равен R.
ВК = а. Найдите ВЫ.
8.16. Четырехугольник ABCD, диагонали которого
взаимно перпендикулярны, вписан в окружность. N — точка
пересечения диагоналей четырехугольника, AD: ВС = 1:2, R —
радиус описанной окружности. Найдите отношение ВС : R.
8.17. В окружность радиуса R вписана трапеция ABCD
с острым углом при основании AD, равным а. Известно, что
биссектриса угла С проходит через центр описанной
окружности. Найдите площадь трапеции.
76

Метод ключевых задач
8.18. В треугольнике ABC угол В равен 120е. На стороне
АВ взята точка М, на стороне ВС — точка N так, что
AM = 2МБ, CN = 2BN. Около четырехугольника AMNC
описана окружность радиуса 1. Найдите площадь
треугольника ABC.
8.19. Дан треугольник со сторонами АВ = 4, ВС = 3 и
7
АС = 5. На стороне АВ взята точка Z> так, что DB = ^. Через
точки С, D и В проведена окружность, пересекающая АС в
точке Е. Найдите длину отрезка BE.
8.20. На стороне АС остроугольного треугольника ABC
найдите такую точку, чтобы расстояние между ее проекциями
на две другие стороны было наименьшим.
8.21. Прямоугольник ABCD вписан в окружность.
Биссектриса угла А пересекает эту окружность в точке К, а
сторону ВС в точке Р. Известно, что ВК = 2ВР. Найдите
отношение ВР: ВС.
8.22. Противоположные стороны вписанного
четырехугольника равны аиЬ. Угол между диагоналями, обращенный
к заданным сторонам, равен а. Найдите радиус описанной
окружности.
8.23. Две окружности радиусов R и г пересекаются в
точках А и В и касаются прямой в точках С и D. Найдите
радиус окружности, описанной около треугольника ACD.
8.24. Около треугольника ABC описана окружность. Из
произвольной точки М окружности проведены
перпендикуляры MN и МК на прямые АВ и АС соответственно. Для
какой точки М длина отрезка NK максимальна?
77

Метод ключевых задач
§9. Свойства пересекающихся хорд
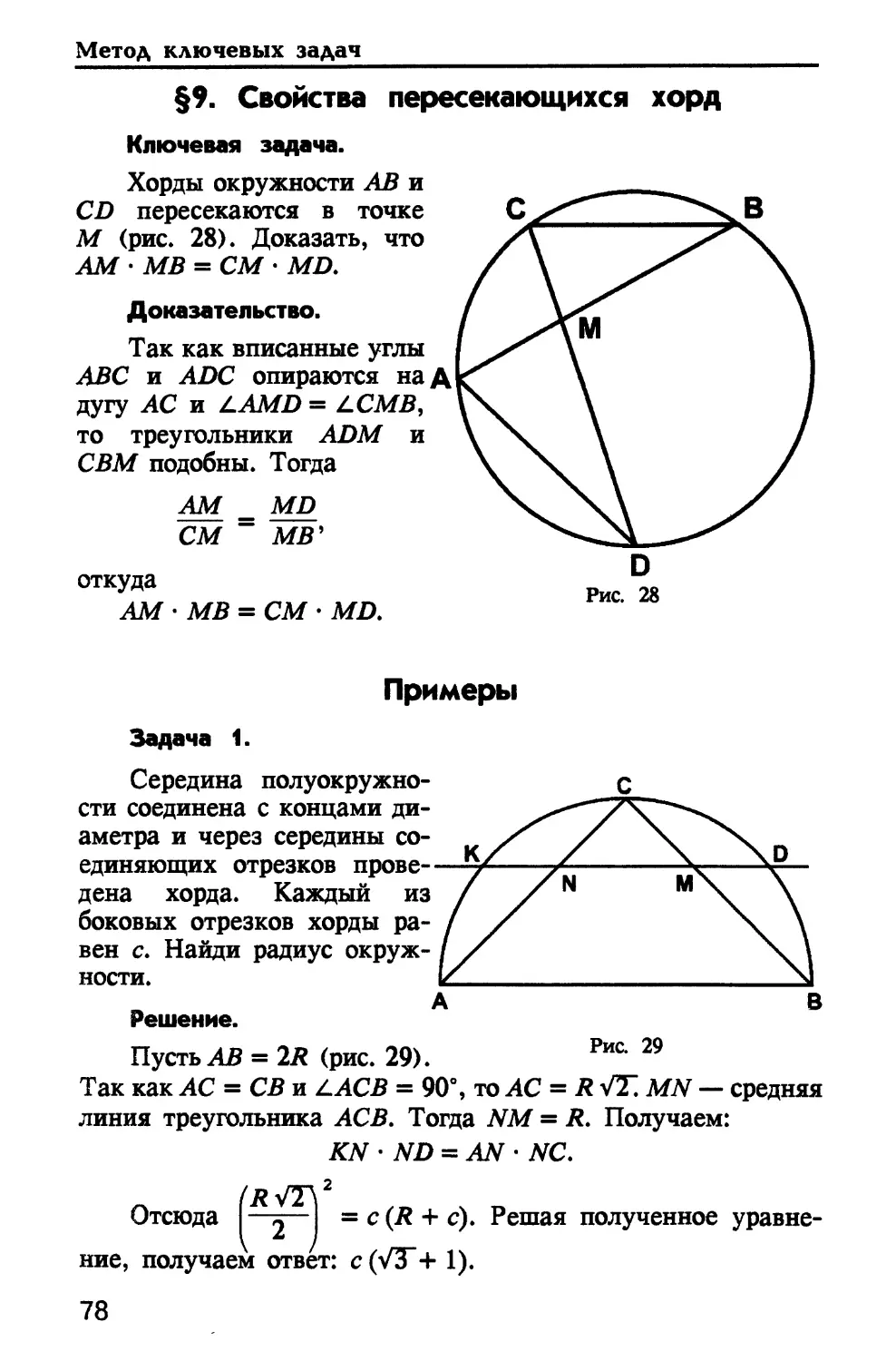
Ключевая задача.
Хорды окружности АВ и
CD пересекаются в точке
М (рис. 28). Доказать, что
AM MB = CM- MD.
Доказательство.
Так как вписанные углы
ABC и ADC опираются над
дугу АС и A AMD = LCMB,
то треугольники ADM и
СВМ подобны. Тогда
AM MJD
_
СМ " MB'
откуда
AM
MD.
Примеры
Задача 1.
Середина
полуокружности соединена с концами
диаметра и через середины
соединяющих отрезков
проведена хорда. Каждый из
боковых отрезков хорды
равен с. Найди радиус
окружности.
N
В
Рис. 29
Решение.
Пусть АВ = 2R (рис. 29).
Так как АС = СВ и LACB = 90°, то АС = Л vT МЛГ — средняя
линия треугольника ЛСВ. Тоща JVM = R. Получаем:
NC.
Отсюда —2— =c(R + c). Решая полученное
уравнение, получаем ответ: с (VT+ 1).
78

Метод ключевых задач
Задача 2.
В круге с центром О
радиуса R проведен диаметр
АВ и через середину радиуса
АО — хорда CD, которая
видна из середины радиуса
ОБ под прямым углом. Най--
ти расстояние от центра
окружности до хорды CD.
Решение.
Опустим
перпендикуляры из точек МиОк хорде
CD (рис. 30). ОР — средняя
линия треугольника MNL, a
значит, OP = w
Рис. 30
Кроме того, СР = PD и
CL = ND, LD = CN.
Из прямоугольного треугольника CMD
ML2 = CL- LD = NDCN = BN • NA.
3R
Учитывая, что BN = у
R
= -у, получаем:
ML
и ОР =
RVT
у/Т
Ответ: R^f.
4
Упражнения
9.1. Перпендикуляр из точки окружности на радиус,
равный 34 см, делит его в отношении 8:9, считая от центра.
Определить длину перпендикуляра.
9.2. Медиана, выходящая из вершины А треугольника
ABC, продлена до пересечения в точке А с описанной
окружностью. Найти длину АА\ если медиана равна m, a
сторона ВС = а.
9.3. Середина D полуокружности соединена с концами
диаметра АС. Хорда BE параллельна АС и делится хордами
AD и DC на три равные части. М — точка пересечения хорд
AD и BE. Найти длину отрезка DM, если AD = а.
79

Метод ключевых задач
9.4, Дана точка Р, удаленная на 7 см от центра
окружности радиуса 11 см. Через эту точку проведена хорда длиной
18 см. Каковы длины отрезков, на которые делится хорда
точкой Р?
9.5* В окружность вписан равнобедренный треугольник,
основание которого равно 10 см, а боковая сторона — 12 см.
Через середину высоты треугольника проведена хорда,
параллельная его основанию. Найти длину хорды.
9.6. В окружность вписан треугольник, одна из сторон
которого равна 21 см. Параллельно той стороне, через точку
пересечения медиан, проведена хорда. Отрезки хорды,
расположенные вне треугольника, равны 8 и 11 см. Определить
неизвестные стороны треугольника.
9Л. В окружность вписан треугольник ABC и в нем
проведены медианы AF и ВК. Медиана AF продолжена до
пересечения с окружностью в точке D. Определить стороны
АС и ВС, если ВК = 63 см, AF = 45 см и FD = 24,2 см.
9.8. Два отрезка АВ и CD пересекаются в точке М так,
что МА = 7 см, MB = 21 см, МС = 3 см, MD = 16 см. Лежат
ли точки А, 2?, С, D на одной окружности?
9.9. Через точку Р, лежащую на общей хорде АВ двух
пересекающихся окружностей, проведена хорда КМ первой
окружности и хорда LN второй окружности. Докажите, что
четырехугольник KLMN вписанный.
9.10. Доказать, что из всех хорд, проходящих через
заданную точку, расположенную внутри окружности, но не
являющуюся ее центром, наименьшая та, которая этой точкой
делится пополам.
9.11. Высоты AD и BE остроугольного треугольника
ABC с ортоцентром Н продлены до пересечения с описанной
окружностью в точках Dx и Ех. АН = HDV ВН = EEV Найти
углы треугольника ABC.
9.12. Сторона АВ треугольника ABC является хордой
некоторой окружности. Стороны АС и ВС лежат внутри
окружности, продолжение АС пересекает окружность в точке
Д а продолжение ВС — в точке Е. Найти радиус окружности,
если АВ = АС = CD = 2 и СЕ = VT.
9.13. Медиану AD треугольника ABC продлили до
пересечения с описанной окружностью в точке Е. Найти углы
треугольника ABC, если известно, что 4AD = 2АВ = АЕ.
80

Метод ключевых задач
9.14. АС и BD — диагонали ромба ABCD. Окружность,
описанная около треугольника ABD, пересекает большую
диагональ АС в точке Е. Определить диагонали ромба, если
АВ = 20 см, а СЕ = 7 см.
9.15. Равнобедренный треугольник ABC (АВ = ВС) вписан
в окружность, и его медиана AD продлена до пересечения с
окружностью в точке Е. AD = 27 см, DE = 16 -~ см. Определить
стороны треугольника.
9.16. Вокруг треугольника ABC описана окружность.
Медиана AD продлена до пересечения с этой окружностью в
точке Е. Известно, что АВ + AD = DE, LBAD = 60°, АЕ = 6.
Найти площадь треугольника ABC.
9.17. Около треугольника ABC описана окружность, в
которой через точку пересечения биссектрис треугольника
проведена хорда, параллельная стороне АС. Сторона АВ равна
30 см и делит хорду на отрезки, равные 8 см и 25 см.
Определить неизвестные стороны треугольника.
9.18. Внутри окружности проведены две пересекающиеся
хорды так, что точки их пересечения удалены от центра
3
окружности на -= ее радиуса и делят хорды в отношениях
1:1 и 4:9. Найти угол между хордами.
9.19. На окружности взята точка ^ис центром в точке
К проведена окружность, касающаяся диаметра первой
окружности в точке Е и пересекающая ее в точках Р и М.
Доказать, что РМ делит КЕ пополам.
81

Метод ключевых задач
§10. Касательная и секущая, проведенные
к окружности из одной точки
Ключевая задача.
AT —
касательная к окружности
(рис. 31). Тогда
А7* = АС • АВ.
Решение.
LATB = ^
Значит,
LATB = LTCB.
Следовательно,
ААТВ со ААТС.
AT АВ
Отсюда -77Г = ~т^9
т.е. AT2 = АС • ЛЯ.
Следствие.
АВ • ЛС = 4М • АЛГ
(рис. 32).
Примеры
Задача 1.
В угол вписаны
две окружности. А и
5 — точки касания
первой окружности
со сторонами угла, м М1
Al и В{ — второй. От- Рис- 33
резок ABt пресекает эти окружности в точках С и Сг
Докажите, что АС = ЯД (рис. 33).
82

Метод ключевых задач
Решение.
Понятно, что ААХ = ВВХ. Имеем:
AAf = ABx- АСХ = (АС + ССХ + СХВХ)(АС + ССХ),
вв% = вха • вхс = (од + схс + сахвд +
Отсюда АС + CCj = 2?^ + CCV т.е.
Задача 2.
На боковой стороне
АВ равнобедренного
треугольника как на диаметре
построена окружность.
Окружность пересекает
основание АС в точке М
и боковую сторону ВС в
точке N. Найдите длины
отрезков MN и NC, если
АС = а и АВ = *.
Решение.
Так как АВ — диа-С
метр окружности, то Рис*
LAMB = 90° (рис. 34). Тогда ВМ — высота равнобедренного
треугольника. Отсюда AM = ~, LNBM = LMBA.
Следовательно, Wj
о2
= wMA и MN = МЛ = |. Имеем: CN CB =
= СМ • СМ. Отсюда G/V =
Упражнения
10.1. Из внешней точки к окружности проведена секущая,
проходящая через ее центр, и касательная, равная половине
секущей. Доказать, что отрезок касательной относится к
радиусу, как 4:3.
10.2. Из точки Л, взятой вне круга, проведены две
секущие ABC и ADE (АВ и AD — внешние отрезки секущих)
и хорды BD и ЕС. Докажите, что AABD со ААСЕ.
83

Метод ключевых задач
10.3. Из точки А, не лежащей на окружности, проведены
к ней касательная и секущая. Расстояние от точки А до точки
касания равно 16 см, а до одной из точек пересечения секущей
с окружностью равно 32 см. Найдите радиус окружности,
если секущая удалена от ее центра на 5 см.
10.4. Из внешней точки проведена к окружности секущая
2
длиной 12 см и касательная, длина которой составляет -^
внутреннего отрезка секущей. Определите длину касательной.
10.5. На одной из сторон прямого угла выбрали две точки:
одну на расстоянии 6, а другую — 24 от вершины. Проведена
окружность, проходящая через выбранные точки и
касающаяся другой стороны угла. Найдите расстояние от вершины
угла до точек касания.
10.6. Через вершину острого угла равнобедренного
прямоугольного треугольника проведена окружность, которая
проходит через середину гипотенузы и касается продолжения
противолежащего катета. Найдите радиус этой окружности,
если длина катета равна а.
10.7. Из точки А, расположенной вне круга с центром в
точке О радиуса R, проведена секущая АСВ (С лежит между
А и В). Окружность, построенная на отрезке ВС как на
диаметре, касается отрезка АО в точке D. Найдите длину
отрезка AD, если АО = а.
10.8. Катеты прямоугольного треугольника равны а и Ь.
На отрезках гипотенузы, определенных основанием
перпендикуляра, опущенного на гипотенузу, описаны
полуокружности. Найдите длины отрезков катетов, находящихся внутри
этих полуокружностей.
10.9. Окружность касается стороны ВС треугольника
ABC в ее середине, проходит через А, а отрезки АВ и АС
пересекает в точках D и Е соответственно. Найти угол
о
ВАС, если ВС = 12, AD = 3,5, ЕС
10.10. Боковая сторона равнобедренного треугольника
является диаметром окружности, которая отсекает от второй
боковой стороны отрезок, равный -=-, а от основания отрезок,
равный 6 (отрезки расположены вне окружности). Определите
медиану, проведенную к боковой стороне треугольника.
84

Метод ключевых задач
10.11. На одной из сторон треугольника, равной 12, как
на диаметре построена окружность, которая отсекает от двух
других сторон отрезки, равные 1 и 1,25 (отрезки расположены
вне окружности). Определите неизвестные стороны
треугольника.
10.12. Две окружности радиусов R и г (R>r) касаются
внешним образом в точке А. Через точку В, взятую на
большей окружности, проведена касательная ВС к меньшей
окружности. Найдите длину отрезка ВС, если хорда АВ = а.
10.13. Две окружности радиусов R и г (R > г) касаются
внешним образом в точке А, Через точку В, взятую на
большей окружности, проведена касательная ВС к меньшей
окружности. Определите длину отрезка АВ, если ВС = а.
10.14. Окружность радиуса R с центром О проходит через
вершины А и В треугольника ABC, пересекает отрезок ВС
в точке М и касается АС в точке А. Найдите СМ, если
10.15. Точка В лежит между точками А и С. На АВ и
АС как на диаметрах построены окружности. К отрезку АС
в точке В проведен перпендикуляр до пересечения с большей
окружностью в точке D. Из точки С проведена касательная
СК к меньшей окружности. Докажите, что CD = СК.
85

Метод ключевых задач
§11. Отношение площадей треугольников,
имеющих общую высоту (основание)
Ключевая задача 1.
Пусть М — произвольная точка стороны АС треугольника
ABC. Тогда
Решение.
Проведем высоту
BD треугольника ABC
(рис. 35). Отрезок BD
будет также высотой
треугольников МВС и
АВМ. Имеем: S^M = ^BD • AM, SMBC = -^
MC. Отсюда
Ключевая задача 2
Площади
треугольников ABC и
ADC (рис. 36)
относятся как высоты,
проведенные к
основанию АС.
Решение.
Проведем высоты
ВЫ и DN
треугольников ABC и ADC. Тогда
Отсюда
: DN.
Примеры
Задача 1.
Данный параллелограмм разделите на три равновеликие
части прямыми, выходящими из одной вершины.
86

Метод ключевых задач
Решение.
Пусть ВВХ и ВВ2 — искомые прямые (рис. 37). Если
площадь параллелограмма S, то S^» = ^ S, S^^ = т* S. По-
В С
скольку треугольники
АВВ1 и ARD имеют
общую высоту, то их
площади относятся
как основания, т.е.
Рис. 37
-3°*2 *
Аналогично
доказывается, что д
СЯ2: CD = 2:3.
Отсюда следует
алгоритм построения:
разделить каждую из
сторон AD и DC
параллелограмма в
отношении 2:1, считая
от вершин А и С.
Задача 2.
В окружность
вписан
четырехугольник ABCD,
причем AS является
диаметром окружности.
Диагонали АС и BD
пересекаются в точке
М (рис. 38).
Известно, что ВС = 3,
3
СМ = -т9 а площадь треугольника А#С втрое больше площади
треугольника ACD. Найдите длину отрезка AM.
Решение.
Понятно, что LACB = 90°, а значит, J?C — высота
треугольника АСВ. Проведем DK ± АС. Поскольку треугольники
87
Рис

Метод ключевых задач
ADC и ABC имеют общее основание, то их площади
относятся как высоты. Отсюда S^c: SACD = ВС: DK.
Следовательно, ВС :DK= 3:1, т.е. DK = ^BC = l. Пусть LMBC = a.
Тогда из треугольника МСВ tga = j. LDAC = LDBC = a.
Поскольку LADB = 90° и DK ± AM, то LKDM = а. Имеем
АМ = АК + КМ \ ^
Упражнения
11.1. Докажите, что медиана треугольника делит его на
две равновеликие части.
11.2. В трапеции ABCD (ВС \\ AD) M — точка
пересечения диагоналей. Докажите, что SABM = SMCD.
11.3. Середина одной из диагоналей выпуклого
четырехугольника соединена с концами другой. Докажите, что
полученная ломаная делит четырехугольник на две
равновеликие части.
11.4. Если диагональ выпуклого четырехугольника делит
другую диагональ пополам, то она делит пополам и площадь
четырехугольника. Доказать.
11.5. Разделите данный треугольник на три равновеликие
треугольника прямыми, выходящими из одной вершины.
11.6. В треугольнике ABC на медиане ВЫ взята точка
К так, что ВК: КМ =1:2. Найдите отношение площадей
треугольников АВК и ABC*
11.7. Площадь трапеции делится диагональю в отношении
3:7. В каком отношении она делится средней линией, считая
от меньшего основания?
11.8. В прямоугольнике ABCD точка К делит сторону
АВ в отношении АК: KB = 3:4, а точка М делит сторону
CD в отношении DM: МС = 5:3. В каком отношении КМ
делит площадь прямоугольника?
11.9. В треугольнике ABC точка М делит сторону АС в
отношении AM: МС = m : л. К — произвольная точка отрезка
ВМ. Докажите, что площади треугольников АВК и ВКС
относятся, как т : п.
88

Метод ключевых задач
11.10. Внутри треугольника ABC выбрана точка М так,
что площади треугольников АМВ, ВМС, АМС равны.
Докажите, что М — точка пересечения медиан,
11.11. На прямой, соединяющей середины оснований
трапеции, взята точка и соединена со всеми вершинами трапеции.
Доказать, что треугольники, прилегающие к боковым
сторонам трапеции, равновелики.
11.12. В трапеции ABCD на боковой стороне АВ взята
точка М так, что MB: AM = m. Найдите отношение площади
треугольника BCD к площади треугольника MBD, если
отношение длин оснований ВС и AD равно к.
11.13. Через середину высоты равнобедренного
треугольника проведены две прямые, соединяющие ее с вершинами
основания. Какую часть площади треугольника составляют
каждая из 6 частей, на которые эти две прямые разрезают
треугольники?
11.14. В равностороннем треугольнике ABC, площадь
которого равна 5, отложены от вершины В на сторонах ВА и
ВС отрезки ВМ = BN = ^ АВ. Точки М и N соединены с
точками А и С. Отрезки AN и СМ пересекаются в точке D.
Найдите площадь четырехугольника MBND.
11.15. Длина боковой стороны трапеции равна а, а
расстояние от нее до середины противоположной стороны равно
Ь. Найдите площадь трапеции.
11.16. В треугольнике ABC из точки Е стороны ВС
проведена прямая, параллельная высоте BD, которая пересекает
сторону АС в точке F. Отрезок EF делит треугольник ABC
на две равновеликие части. Найдите длину отрезка EF, если
BD = 6, AD: DC = 2 : 7.
11.17. Через вершину В треугольника ABC проведена
прямая, параллельная биссектрисе угла С и пересекающая
продолжение стороны АС в точке D. Пусть Е •— середина
отрезка BD. Определите, в каком отношении прямая АЕ делит
площадь треугольника ABC, если известно, что длина стороны
АС равна Ъ, а длина стороны ВС равна а.
11.18. Дан треугольник ABC. Продолжим его сторону
АВ за вершину В отрезком ВР таким, что ВР = АВ; сторону
АС — за вершину А отрезком AM таким, что AM = СА;
сторону ВС — за вершину С отрезком КС таким, что
89

Метод ключевых задач
КС = ВС. Во сколько раз площадь треугольника РКМ больше
площади треугольника ABC?
11.19. На продолжении сторон АВ, ВС, CD и DA
четырехугольника ABCD соответственно за точки В, С, D и
А откладываются отрезки ВВХ = АВ, CCj = ЯС, ЯД = CD,
AAl = DA Найдите площадь четырехугольника AlBlC1Dl, если
площадь четырехугольника ABCD
равна 5. в
11.20. Е, F, К, L — середины
сторон четырехугольника ABCD
(рис. 39). Докажите, что сумма
площадей треугольников ALM,
BNE, CPF, KQD равна площади,
четырехугольника MNPQ. А
11.21. В треугольнике ABC
проведена медиана BD, а через Рис
ее середину и вершину А —
прямая /. В результате такого построения треугольник разбит на
три треугольника и один четырехугольник. Найдите площади
этих фигур, если площадь треугольника ABC равна S.
11.22. На стороне АВ треугольника ABC взята точка D,
делящая ее в отношении т: п, считая от вершины А, а на
стороне ВС точки Е и F, делящие ее в отношении p:q:r,
считая от вершины В. Найдите отношения площадей
треугольников DEF и ABC.
11.23. В треугольнике ABC точки К и N — середины
сторон АВ и АС соответственно. Через точку В проведена
прямая, которая пересекает АС в точке F, a KN — в точке
L так, что KL: LN =3:2. Определите площадь
четырехугольника AKLF, если площадь треугольника ABC равна 40.
11.24. Диагональ выпуклого четырехугольника делит
пополам отрезок, соединяющий середины двух
противоположных сторон этого четырехугольника. Докажите, что эта
диагональ делит пополам и площадь четырехугольника.
11.25. Дан выпуклый я-угольник. Построить
равновеликий ему выпуклый (п - 1)-угольник.
11.26. В треугольник ABC вписана окружность с центром
О. Прямая ВО пересекает эту окружность в точках М и N,
а отрезки АО и СО пересекают эту окружность соответственно
в точках Р и Q. Найдите отношение площадей треугольников
MPN и MQN, если LA = a, LC = у.
90

Метод ключевых задач
§12. Отношение площадей подобных
треугольников
Ключевая задача.
Отношение площадей подобных треугольников равно
квадрату коэффициента подобия.
Решение.
Пусть ААВС со AAlBlCl и коэффициент подобия равен к.
Проведем высоты BD и B{D{ (рис. 40). Имеем:
AlCi.
Рис. 34
Тогда
jBDAC k-Bfi.kAfi,
Примеры
Задача 1.
В четырехугольнике ABCD сторона АВ равна стороне
ВС, диагональ АС равна стороне CD, а угол ABC равен углу
A CD. Радиусы окружностей, вписанных в треугольники
ABC и ACD, относятся, как 3:4. Найдите отношение площадей
этих треугольников.
Решение.
Поскольку треугольники ABC и ACD равнобедренные и
их углы при вершинах равны, то они подобны. Радиусы их
вписанных окружностей относятся, как 3:4, значит,
коэффициент подобия равен к = -т. Тогда площади этих треуголь-
д
ников относятся, как Л2 = -т-£*
91

Метод ключевых задач
Задача 2.
Внутри
треугольника ABC выбрана
точка М. Через эту точку
проведены прямые,
параллельные сторонам
треугольника (рис. 41).
Площади трех образо-д
вавшихся треугольни- та АЛ
— — — гИС. 41
ков равны Sv S2, S3.
Найдите площадь треугольника ABC.
Решение.
Понятно, что указанные в условии треугольники подобны
треугольнику ABC. Пусть SENM = Sv SMQF = S2, SPMK = S3,
с 1Ж }/K ЕМ ^5Г РК т/К MF ^
S. Имеем: -^ = ^с' 7# = ЛС'7# = ЛС• Отсюда
VS7+VS7 ЕМ + Р/С + М/1 _ АР + РК + КС _
т.е. S = (^ ^
Упражнения
12Л. В прямоугольном треугольнике катеты относятся,
как 3:4, а высота, проведенная к гипотенузе, делит площадь
треугольника на части, разность которых равна 84 см2.
Найдите площадь всего треугольника.
12.2. Площадь прямоугольного треугольника разделена
пополам прямой, перпендикулярной гипотенузе. Найдите
расстояние между этой прямой и вершиной меньшего из острых
углов, если больший катет равен 20 см.
12.3. Через середину Е высоты BD равнобедренного
треугольника ABC (АВ = ВС) проведена прямая MN \\ АВ, М
принадлежит АС, N принадлежит ВС. Найдите площадь
треугольника CMN, если площадь треугольника ABC равна 32.
12.4. Провести прямую, параллельную основанию данного
треугольника и такую, которая делит его на две равновеликие
части.
12.5. Высота остроугольного треугольника равна 4. Она
делит основание на две части, относящиеся как 1:8. Найти
92

Метод ключевых задач
длину отрезка, параллельного высоте и делящего треугольник
на две равновеликие части.
12.6. Высота, опущенная на гипотенузу прямоугольного
треугольника, делит его на два треугольника, площади
которых 6 и 54. Найдите гипотенузу.
12.7. Основание треугольника делится высотой на отрезки,
длины которых 14 и 36. Перпендикулярно к основанию
проведена прямая, делящая площадь данного треугольника
пополам. На какие части эта прямая разделила основание
треугольника?
12.8. В каком отношении, считая от вершины, нужно
разделить боковую сторону треугольника двумя прямыми,
параллельными основанию, чтобы площадь треугольника была
разделена на три равновеликие части?
12.9. чИз середины основания треугольника проведены
прямые, параллельные сторонам. Докажите, что площадь
получившегося параллелограмма в 2 раза меньше площади
треугольника.
12.10. На стороне АС треугольника ABC взята точка Е,
через которую проведены прямые EF \\ АВ и ED || ВС.
Докажите, что SBDEF = 2 у/S^e ' SEFC.
12.11. Точки D и Е, К и L, М и N делят соответственно
стороны АС, СВ и ВА треугольника ABC на три равные части.
Докажите, что площадь четырехугольника, образованного
пересечением прямых BD, BE, KN и LM равна <* площади
треугольника ABC.
12.12. Основания трапеции относятся, как т: п. Найти,
в каком отношении делится площадь трапеции ее
диагоналями.
12.13. Площадь треугольника равна а. Каждая сторона
треугольника разделена в отношении т:п:т. Определить
площадь шестиугольника, вершинами которого служат точки
деления.
12.14. Из внешней точки А к окружности проведены
касательная АВ и секущая ACD. АС : АВ = 2: 3. Площадь
треугольника ABC равна 20. Найдите площадь треугольника ABD.
12.15. В треугольнике ABC MN \\ AC, KN \\ АВ. Площади
треугольников BMN и NKC равны соответственно S{ и S2.
Найдите площадь треугольника ABC.
93

Метод ключевых задач
12.16. В треугольнике ABC из вершины А проведена
прямая, пересекающая сторону ВС в точке D, находящейся
между точками В и С, причем CD :ВС = а [а < -~1. На
стороне ВС между точками В и D взята точка £ так, что
CD = /ХЕ, и через нее проведена прямая, параллельная АС
и пересекающая АЕ в точке F. Найдите отношение площадей
трапеции ACEF и треугольника ADC.
12.17. В квадрате каждая вершина соединена с серединой
стороны, лежащей между двумя следующими вершинами
(считая вершины в одинаковом порядке). Соединительные
прямые образуют своим пересечением квадрат. Докажите,
что его площадь составляет -^ площади данного квадрата.
12.18. Внутри выпуклого четырехугольника ABCD
выбрана точка М. Она симметрично отображена относительно середин
Tv Т2, Т3, Т4 его сторон. Полученные точки Мр М2, М3, М4
соединены так, что получился выпуклый четырехугольник.
Докажите, что его площадь не зависит от выбора точки М.
12.19. Дан параллелограмм ABCD. Прямая, проходящая
через вершину С, пересекает прямые АВ и AD в точках К
и L. Площади треугольников КВС и CDL равны Р и Q.
Найдите площадь параллелограмма ABCD.
12.20. В треугольнике ABC через основание D высоты
BD проведена прямая, параллельная стороне АВ, пересека-
BJC
ющая сторону ВС в точке К. Найдите отношение -^, если
площадь треугольника BDK составляет у^ площади
треугольника ABC.
12.21. Отрезок АВ есть диаметр круга, а точка С лежит
вне этого круга. Отрезки АС и БС пересекаются с окружностью
в точках D и М соответственно. Найдите угол CBD, если
площади треугольников DCM и АСВ относятся как 1:4.
12.22. В треугольнике ABC угол С равен 30°, а угол А —
острый. Перпендикулярно стороне ВС проведена прямая,
отсекающая от треугольника ABC треугольник CNM (точка
N лежит между В и С). Площади треугольников CNM и
ABC относятся, как 3:16, NM:BH= 1:2, ще ## — высота
треугольника. Найдите отношение АН: НС.
94

Метод ключевых задач
12.23. В треугольнике ABC ME \\ AC, MF \\ АВ (точки
Е, М, F лежат соответственно на сторонах АВ, ВС, СА).
Площадь параллелограмма AEMF равна -rg площади
треугольника ABC. Найдите отношение ВЫ: МС.
12.24. Площадь ромба ABCD равна 2. В треугольник
ABD (BD — диагональ ромба) вписана окружность, которая
касается стороны АВ в точке К. Через точку К проведена
прямая KL, параллельная диагонали AC (L лежит на стороне
ВС). Найти величину угла BAD, если известно, что площадь
треугольника KBL равна а.
12.25. Дана равнобедренная трапеция, у которой длина
верхнего основания вдвое меньше длины нижнего.
Определить, в каком отношении делит нижнее основание прямая,
которая параллельна диагонали, проходит ниже нее и отсекает
треугольник площадью в 4 раза меньше площади трапеции.
12.26. Из точки Р, лежащей на гипотенузе АС
прямоугольного треугольника ABC, проведен перпендикуляр РМ к
АС, который делит треугольник на две равновеликие фигуры.
Найдите площадь треугольника ABC, если АР= а, СР = 6.
95

Метод ключевых задач
§13. Площади треугольников, на которые
четырехугольник разделен диагоналями
Ключевая задача.
Доказать, что если
выпуклый четырехугольник
ABCD (рис. 42) разделен
своими диагоналями на
треугольники с площадями Sv
S2, S3 и S4, то
Sx • S3 = S2 • S4.
Решение.
Треугольники ABO и
Рис. 42
СВО имеют общую высоту ВК, а значит, -—■ = -рг=. Анало-
-ф = -zr= (DF — общая высота треугольников ADO и
CDO). Приравнивая левые части полученных равенств, по-
лучаем
S4
у откуда S{- S3 = S2- S4.
Примеры
Задача 1.
В трапеции ABCD (AB \\ CD) АВ = 1, DC = 2. Обозначим
точку пересечения диагоналей этой трапеции через F. Найти
отношение суммы площа- А В
дей треугольников ABF is.
CDF к сумме площадей
треугольников
BFC.
AFD
Решение.
Покажем, что
площади треугольников AFD и
BFC (рис. 69) равны.
Действительно,
SAFD
- SDAC "" SD
BFC
'' SCBD " SDFC*
96

Метод ключевых задач
Но SDAC = SCBD (высоты АК и ВМ этих треугольников
равны и DC — общее основание).
Пусть S^p = Sv a Sapd = SBFC = S2. Так как треугольники
АВ 1
ABF и CDF подобны, причем -уг-= = ^, то SCI)F = 4SV
Используя ключевую задачу, имеем S{ • 4S{ = S2, или S2 = 2Sr Тогда
Sabf*
SAFDA
h &CDF
1- SBFC
S, + 4S,
2S2 "
5Sl
- 2S2
5S,
= 4S,S
5
' 4'
Ответ:
5
4'
Упражнения
13.1. В трапеции ABCD (АВ \\ CD) О — точка пересечения
диагоналей АС и BD. Площади треугольников АВО и CDO
равны соответственно 10 и 40. Найти площадь трапеции.
13.2. Четырехугольник разделен диагоналями на четыре
треугольника. Наименьшие площади трех из них равны 10,
20 и 30. Найти площадь данного четырехугольника.
13.3. Площадь трапеции равна 3, основания относятся
как 1:2. Найти площади треугольников, на которые трапеция
разделена диагоналями.
13.4. В треугольнике ABC на стороне АС взята точка
М, а на стороне ВС — точка N. Отрезки AN и ВМ
пересекаются в точке О. Найти площадь треугольника CMN, если
площади треугольников ОМА, ОАВ и OBN соответственно
равны Sv S2, Sr
13.5. О — точка пересечения диагоналей выпуклого
четырехугольника ABCD. Известно, что SAOB, SBOC, SCOD, S^^ —
натуральные числа. Доказать, что произведение этих
площадей является точным квадратом.
13.6. Диагонали выпуклого четырехугольника ABCD
пересекаются в точке О. Какую наименьшую площадь может
иметь этот четырехугольник, если
Saob = 4 см2, SCOD = 9 см2?
13.7. Равнобедренная трапеция ABCD (AD \\ ВС, AD > ВС)
описана около окружности с центром О. О{ — точка пересе-
4 Учимся решать задачи по геометрии

Метод ключевых задач
чения диагоналей трапеции. Площади треугольников АО{В и
АОВ равны 3 и 4. Найти углы трапеции.
13.8. Через точку Л, лежащую вне окружности, проведены
две прямые. Первая прямая пересекает окружность в точках
В и Е, вторая — в точках Си/). Прямые ВС и DE
пересекаются в точке К, лежащей вне окружности. Известно, что
SKBE = 7 SBCDE И SKBE = 4SABC НаЙТИ "О^'
98

Метод ключевых задач
§14. Признак параллельности сторон
четырехугольника
Ключевая задача.
Если в выпуклом четырехугольнике ABCD площади
треугольников ABD и ACD равны, то ВС параллельно AD.
Доказать.
В
Решение.
Так как AD — общая
сторона треугольников
ABD и ACD (рис. 44), то
их высоты ВК и СМ равны,
а следовательно, ВСМК —
прямоугольник и ВС || AD.
Примеры
Рис. 44
Задача 1.
В равнобедренном прямоугольнике ABC AB=1,
LABC = 120°. Через середину D стороны АС проходит прямая,
которая пересекает ВС в
точке Е и продолжение
АВ в точке F. Площади
треугольников BEF и DEC
равны. Найти длину отрезка
EF.
Решение.
Покажем, что FC \\ BD
(рис. 45). Действительно,
В
SDEC
SFEC И
SPEC>
SFBC
а значит, 5
BD — средняя линия в треугольнике AFC и, следова-
тельно, FC = 2BD=l. DC = -=-. Из прямоугольного треу-
FDC
гольника FCD FD = у/FC2 + С& = ^р.
99

Метод ключевых задач
Так как Е —• точка пересечения медиан треугольника
AFC, то EF= \f£>= -у.
Ответ: -=-.
Упражнения
14.1. В выпуклом четырехугольнике ABCD Е — точка
пересечения диагоналей. Доказать, что AD параллельна ВС
тогда и только тогда, когда SABE = SCED.
14.2. Отрезок, соединяющий середины двух
противоположных сторон выпуклого четырехугольника, разделил его
на два равновеликих четырехугольника. Доказать, что эти
стороны параллельны.
14.3. Каждая диагональ четырехугольника делит его на
треугольники одинаковой площади. Доказать, что этот
четырехугольник — параллелограмм.
14.4. В равностороннем треугольнике ABC со стороной
а проведена прямая, пересекающая АВ и ВС в точках М и
Р, а продолжение АС — в точке N так, что SMBP = SCNP =
= 8ШРС. Найти ВЫ и ВР.
14.5. В выпуклом четырехугольнике ABCD E —
точка пересечения диагоналей. Известно, что S^£ = SDCE = 1,
sabcd * 4> AD = 3- Найти ВС.
14.6. В выпуклом четырехугольнике ABCD О — точка
пересечения диагоналей. Доказать, что если 5^С1)= (^SAOD +
+ VSCOB )2, то Л^ параллельно ^С.
14.7. В выпуклом четырехугольнике ABCD E — точка
пересечения диагоналей. SABE = SCED. Площадь ABCD больше
площади треугольника ABE не более, чем в четыре раза.
Найти CD, если АВ = VT
14.8. Докажите, что если два треугольника,
получающиеся при продолжении сторон выпуклого четырехугольника до
их пересечения, равновелики, то одна из диагоналей
четырехугольника делит другую пополам.
14.9. Дан выпуклый пятиугольник ABCDE. SABC= «5^=
= Scde = sdea = seab = S- Найти площадь ABCDE.
100

Метод ключевых задач
§15. Угол между биссектрисами внутренних
односторонних и смежных углов.
Ключевая задача.
Доказать, что угол между биссектрисами внутренних
односторонних углов при параллельных прямых (смежных
углов) равен 90°.
Рис. 46 Рис. 47
Решение.
Очевидно, что угол между биссектрисами равен
^ в случае внутренних односторонних углов
180° -
(рис. 46) и —=^- Для случая смежных углов (рис. 47). Так
как а+/?= 180°, то как в одном, так и в другом случае
биссектрисы перпендикулярны.
Примеры.
Задача 1.
Окружность, вписанная в
трапецию. ABCD (AD || ВС), касается
сторон АВ и CD в точках К и М
соответственно. Доказать, что
М
АК- КВ =
Решение.
MD (рис. 48).
Рис 48
Так как СВА и DAB —
внутренние односторонние углы при параллельных ВС и AD, a
ВО и АО — их биссектрисы, то LAOB = 90°. Аналогично
LCOD = 90°. В прямоугольных треугольниках АОВ и DOC
ОК2 = АККВ, ОМ2 = СМ • MD.
101

Метод ключевых задач
Кроме того, OK = ОМ как радиусы одной окружности.
Тогда, приравняв правые части полученных равенств, получаем
доказываемое свойство.
Задача 2.
В прямоугольном треугольнике ABC с катетами 3 и 4
вершина С прямого угла соединена с серединой D гипотенузы
АВ. Найти
расстояние между центрами
окружностей,
вписанных в
треугольники ACD и BCD.
Решение.
Так как DO{ и
DO2 (рис. 49) — бис-^
сектрисы смежных
углов, то
треугольник OXDO2 — прямоугольный и Ofi*2 = DOf + DO?.
Рис* 49
DOX = DN- O{N, DO2 = DF- O2F.
Так как CD- AD- DB, то DN и DF — высоты, OXN и
O2F — радиусы вписанных окружностей в равнобедренные
треугольники CD А и CDB соответственно. DN = 2, DF = ^,
3 2
OXN'= 2> O2F= -5- (проверьте самостоятельно). Тогда
4'
^ а ПО
6' а Ol°2
V25
25
36
Ответ:
5VT3"
—ту-.
Упражнения.
15.1. В параллелограмме ABCD проведены биссектрисы
внутренних углов, пересекающиеся в точках Р, Е, М, К
соответственно. Доказать, что РЕМК —- прямоугольник.
15.2. В трапецию вписана окружность радиуса 6. Точка
касания делит одно из оснований на отрезки 9 и 12. Найти
стороны и площадь трапеции.
102

Метод ключевых задач
15.3. AM и AN — биссектрисы внешнего и внутреннего
углов (соответственно) треугольника ABC. LABC — LBCA =
= 90°. Доказать, что AM = AN.
15.4. Из основания высоты СН прямоугольного
треугольника ABC (AC = 90°) проведены биссектрисы: НЕ
треугольника СНА и HF треугольника СНВ. Доказать, что точки С,
Е, F и Я лежат на одной окружности, причем вторая —
точка К — пересечения этой окружности с гипотенузой АВ —
основание биссектрисы СК треугольника ABC.
15.5. Биссектриса внешнего угла при вершине А
треугольника ABC пересекает продолжение стороны ВС в точке
Е. Доказать, что если АЕ в два раза больше высоты
треугольника, опущенной из вершины Л, то один из углов В и
С треугольника на 60° больше другого.
15.6. Дан параллелограмм ABCD с острым углом А. На
стороне AD взята точка К так, что ВК — биссектриса угла
ABC. СК — биссектриса угла BCD. Найти отношение
периметра параллелограмма к радиусу окружности, описанной
около треугольника ВКС.
15.7. Около окружности описана трапеция ABCD
(AD || ВС). Расстояния от центра О окружности до вершин
А и В равны соответственно а та. Ь. Определить sin LBAD и
высоту трапеции.
15.8. В прямоугольной трапеции, высота которой 2й, на
стороне, перпендикулярной основанию, как на диаметре
описана окружность, которая касается противоположной стороны
трапеции. Найти произведение длин оснований трапеции.
15.9. К окружности проведены касательные, касающиеся
ее в концах диаметра АВ. Произвольные касательные к
окружности пересекают эти касательные в точках К и М
соответственно. Доказать, что АК • ВМ — константа.
15.10. Доказать, что отрезок, соединяющий центры
вписанной и вневписанной окружностей, делится описанной
окружностью пополам.
15.11. В треугольнике ABC 2LC = 90°, CD — высота.
AC = 3, СВ = 4. Найти расстояние между центрами
окружностей, вписанных в треугольники ACD и DCB.
15.12. В трапецию ABCD (ВС || AD) вписана окружность
с центром в точке О. Доказать, что
1 . 1 = 1 . 1
OJ? ОС1 СМ?'
103

Метод ключевых задач
15.13. В трапеции ABCD {ВС \\ AD) биссектрисы
внутренних углов А я В пересекаются в точке М, а биссектрисы
углов С и D — в точке N. Доказать, что длина отрезка
MN равна полуразности суммы оснований и суммы боковых
сторон.
15.14. В ровсб вдисана окружность. Прямая, касающаяся
этой окружности в точке Р, пересекает стороны АВ, ВС и
продолжение стороны AD соответственно в точках JV, Q и
М так, что MNiNP: PQ = 7 :1: 2. Определить tg LBAO.
104

Метод ключевых задач
§16. Расстояние от вершины треугольника до
точки касания вписанной окружности
со стороной.
Ключевая задача 1.
Пусть М, N, Р — точки касания вписанной окружности
со сторонами АВ, ВС, АС соответственно (рис. 50). Тогда
AM = р - a, BN = р-Ъ,
СР = р - с, где р —
полупериметр треугольника
ABC, a — длина стороны
ВС, Ъ — длина АС, а с
длина АВ.
Решение.
По свойству
касательных, проведенных из одной
точки, имеем
AM = АР = х,
= BN = у, CN=CP = z.
Тогда 2х + 2у + 2z = 2р,
х + у + z = р,
Аналогично
= p- с.
Ключевая задача 2.
Пусть М и N — точки
касания вписанной окружно- А
сти со сторонами АВ и ВС Рис' 51
треугольника ABC. X — произвольная точка дуги MN
(рис. 51). EF — отрезок касательной, проведенной к
окружности в точке X. Тоща периметр треугольника EBF не зависит
от выбора точки X и равен 2 (р - Ь), вде р — полупериметр
треугольника ABC, A — длина стороны АС.
Решение.
Периметр треугольника EBF равен ЕВ + BF + FE =
105

Метод ключевых задач
= ЕВ + BF + ЕХ + XF = BE + ЕМ + BF + FN =
= MB + BN= IBM = 2 (р - 6).
Примеры.
Задача 1.
Две вершины треугольника закреплены в точках А и В,
а третья вершина переме-
щается в плоскости так,
что разность расстояний
от нее до точек В и А —
величина постоянная.
Доказать, что центры
окружностей, вписанных в
треугольники ABC, лежат
на одной прямой.
Решение.
__ Рис. 52
Пусть К — точка
касания вписанной окружности со стороной АВ (рис. 52). Если
р — полупериметр треугольника ABC, то
АВ - {ВС
2
АС)
— величина постоянная. Следовательно,
все окружности, вписанные в треугольники ABC, касаются
стороны АВ в одной и
той же точке. Поэтому
их центры лежат на
прямой, проходящей через
точку К
перпендикулярно АВ.
Задача 2.
В треугольнике
проведены три прямые,
параллельные его сторонам
и касающиеся вписанной
окружности. Они
отсекают от данного треуголь-
ника три треугольника
106
К
N Q
Рис. 53

Метод ключевых задач
(рис. 53). Радиусы окружностей, описанных около них, равны
Rv R2, Rv Найти радиус окружности, описанной около данного
треугольника.
Решение.
Периметры треугольников ASK, EBF, TCQ соответственно
равны 2 (р — а), 2 (р — ft), 2 (р — с). Каждый из этих
треугольников подобен треугольнику ABC. Периметры подобных
треугольников относятся как их соответственные линейные
элементы. Имеем:
R± _ 2 (р - а) ^2 _ 2 (р - ft) ^з _ 2 (р- с)
R 2р ' R 2р ' R 2р '
где R — радиус описанной окружности треугольника ABC.
Отсюда д = = = 1.
Тогда R = Rx + R2 + Rr
Упражнения.
16.1. Доказать, что для треугольника ABC (AB = с,
ВС = а, АС = ft) имеет место равенство г = (р — a) tg у.
16.2. В треугольнике ABC с периметром 2р длина стороны
АС равна a, Z.AJ9C = а. Вписанная в треугольник окружность
с центром О касается ВС в точке К. Найдите площадь
треугольника ВОК.
16.3. Доказать, что в прямоугольном треугольнике радиус
а + ft - с
вписанной окружности равен ^ » где а и ft — длины
катетов, с — длина гипотенузы.
16.4. Катеты прямоугольного треугольника равны 8 и 15.
Чему равно расстояние от вершины прямого угла до центра
вписанной окружности?
16.5. Радиус окружности, вписанной в прямоугольный
треугольник, равен полуразности катетов. Найдите углы
треугольника.
16.6. В треугольник ABC со сторонами ВС = а, АС = 2а
и углом С = 120° вписана окружность. Через точки касания
этой окружности со сторонами АС и ВС и через вершину
В проведена вторая окружность. Найдите ее радиус.
107

Метод ключевых задач
16.7. Доказать, что площадь прямоугольного треугольника
равна произведению отрезков, на которые точка касания
вписанной окружности делит гипотенузу.
16.8. Доказать, что если площадь треугольника равна
произведению отрезков, на которые разбивается его сторона
точкой касания вписанной окружности, то треугольник —
прямоугольный.
16.9. Дан параллелограмм ABCD. В треугольники ABC,
ACD, ABD и BCD вписаны окружности. Докажите, что точки
касания окружностей и диагоналей параллелограмма —
вершины прямоугольника.
16.10. Доказать, что если в выпуклый четырехугольник
ABCD можно вписать окружность, то окружности, вписанные
в два треугольника ABC и ADC, касаются друг друга.
16.11. В треугольнике ABC со сторонами АВ = V3~,
ВС = 4, АС = VT" проведена медиана BD. Окружности,
вписанные в треугольники ABD и BDC, касаются BD в точках
М и N соответственно. Найдите MN.
16.12. На основании АС равнобедренного треугольника
ABC расположена точка £>, при этом AD = a, DC = й.
Окружности, вписанные в треугольники ABD и DBC, касаются
BD в точках М и N соответственно. Найдите MN.
16.13. В прямоугольный треугольник вписана окружность.
Точка касания делит гипотенузу в отношении 2:3. Найти
стороны треугольника, если центр вписанной окружности
удален от вершины прямого угла на расстояние V3T
16.14. В треугольник со сторонами 6, 10 и 12 вписана
окружность. К окружности проведена касательная так, что
она пересекает две большие стороны. Найдите периметр
отсеченного треугольника.
16.15. В треугольник с периметром, равным 20, вписана
окружность. Отрезок касательной, проведенной к окружности
параллельно основанию, заключенный между сторонами
треугольника, равен 2,4. Найдите основание треугольника.
16.16. В равнобедренный треугольник с основанием 12
вписана окружность, а к ней проведены три касательные так,
что они отсекают от данного треугольника три малых
треугольника. Сумма периметров малых треугольников равна 48.
Найдите боковую сторону данного треугольника.
16.17. В равнобедренный треугольник вписана
окружность. Точки касания делят каждую боковую сторону на
108

Метод ключевых задач
отрезки длиной тип, считая от вершины. К окружности
проведены три касательные, параллельные каждой из сторон
треугольника. Найдите длину отрезков касательных,
заключенных между сторонами треугольника.
16.18. В треугольнике ABC К и L — точки касания
стороны АВ с вписанной и вневписанной окружностями
соответственно. Докажите, что AL = ВК.
16.19. В треугольник постоянного периметра 2р вписана
окружность. К этой окружности проведена касательна,
параллельная стороне треугольника. Найдите наибольшую
возможную длину отрезка касательной, концы которой
принадлежат сторонам треугольника.
16.20. Окружность радиуса 1 вписана в треугольник
ABC, в котором cos LABC = 0,8. Эта окружность касается
средней линии треугольника ABC, параллельной стороне
АС. Найдите длину стороны АС.
109

Метод ключевых задач
§17. Свойства биссектрисы угла треугольника.
Ключевая задача.
Если BD — биссектриса угла В треугольника ABC
с,ч AD AB
(рис. 54), то -^ = -££. М
Решение.
Проведем CM \\ BD (рис. 54).
Тогда LABD = LBMC и
LBCM = LDBC.
Поскольку LABD = LDBC,
LBMC = LMCB. Отсюда ВМ ••
АВ АВ
ВМ ВС
Имеем: -=гр;
Примеры.
Задача. А
Расстояние от вершины прямого
угла до гипотенузы равно а, а до точки
пересечения биссектрисы меньшего
угла с меньшим катетом равно ft. Найдите
длину меньшего катета.
Решение.
МР ± NK (рис. 55), МР = a.NE —
биссектриса угла N, ME = ft. Пусть
LMNK = а, тоща LPMK = а. Имеем:
ME MN п А
= cos а. С другой стороны,
cos a
МК.
МР
MX*
аЪ
Отсюда
a-V
МК-Ъ
Ответ:
МК'
аЪ
а-Ъ
D
Рис. 54
Е
Рис. 55
К
AD = m,
110
Упражнения.
17.1. В треугольнике ABC LC = 90°, CD — биссектриса,
' п. Найдите катеты треугольника.

Метод ключевых задач
17.2. В прямоугольный треугольник вписана
полуокружность так, что диаметр лежит на гипотенузе, а центр делит
гипотенузу на отрезки длиной 15 и 20. Найдите радиус
полуокружности.
17.3. Точка на гипотенузе, равноудаленная от обоих
катетов, делит гипотенузу на отрезки длиной 30 и 40. Найдите
катеты треугольника.
17.4. В прямоугольный треугольник с углом 60° вписан
ромб со стороной, равной 6, так, что угол в 60° у них общий
и все вершины ромба лежат на сторонах треугольника.
Найдите стороны треугольника.
17.5. В равнобедренном треугольнике основание и боковая
сторона равны соответственно 5 и 20. Найдите биссектрису
угла при основании треугольника.
17.6. Найдите биссектрисы острых углов прямоугольного
треугольника с катетами 24 и 18.
17.7. В треугольнике ABC биссектрисы BD и АЕ углов
В и А пересекаются в точке О. Определите АС, если АВ =
= 12, АО:ОЕ = 3:2 и AD:DC = 6:7.
17.8. В треугольнике ABC AD — биссектриса угла А.
АВ + BD = DC + А С. Докажите, что данный треугольник
равнобедренный.
17.9. Окружность радиуса R касается сторон АВ и ВС
треугольника ABC в точках К и М соответственно. Известно,
что центр окружности лежит на стороне АС> М — середина
стороны ВС, длина отрезка ВК в два раза больше длины
отрезка АК. Найдите площадь треугольника.
17.10. Равнобедренный треугольник ABC {АВ = ВС)
вписан в окружность. Диаметр AD пересекает сторону ВС в точке
Е, при этом DE: АЕ = к. Найдите отношение СЕ: ВС.
17.11. Углы А и В треугольника ABC соответственно
равны 30° и 50°. Докажите, что стороны треугольника связаны
соотношением а = —т—, где ВС = а, АС = Ь, АВ = с.
17.12. Отрезок AD является биссектрисой прямоугольного
треугольника ABC (AC = 90°). Окружность радиуса
VHTпроходит через точки А, С и D и пересекает гипотенузу АВ в
точке Е так, что АЕ: АВ = 3 :5. Найдите площадь
треугольника ABC.
17.13. Сторона АС треугольника ABC делится основанием
D биссектрисы угла В на отрезки 12 и 3. Найдите радиус
111

Метод ключевых задач
окружности с центром на прямой АС, проходящей через точки
В и D.
17.14. В треугольнике ABC биссектриса угла ВАС равна
а. Окружность, построенная на этой биссектрисе как на
диаметре, делит соответственно стороны АВ и АС в отношении
2:1 и 1:1, считая от вершины А. Найдите площадь
треугольника ABC*
17.15. В окружность вписан квадрат ABCD. Хорда АЕ
проходит через середину М его стороны CD. В каком
соотношении хорда BE делит сторону CD1
17.16. В круге проведены две хорды АВ и CD,
пересекающиеся в точке М. К — точка пересечения биссектрисы угла
BMD с хордой BD. Найдите отрезки ВК и KD, если
BD = 3 и площади треугольников СМВ и AMD относятся,
как 1:4.
17.17. В треугольнике ABC проведены биссектрисы AD и
CF (точка D лежит на стороне ВС> а точка F — на стороне
АВ). Найдите отношение площадей треугольников ABC и
AFD, если известно, что АВ = 21, АС = 28, СВ = 20.
17.18. В треугольнике ABC биссектриса BE и медиана
AD перпендикулярны и имеют одинаковую длину, равную 4.
Найдите стороны треугольника ABC.
17.19. Дана равнобедренная трапеция ABCD (AD || ВС,
AD>BC). Точки К и F — середины сторон ВС и AD
соответственно. На стороне АВ как на диаметре построена
окружность, касающаяся прямой KF в точке Р и пересекающая
сторону AD в точке N. Е — точка пересечения прямых АР
и BN. Докажите, что BE:EN = DN: NA.
17.20. В равнобедренном треугольнике ABC (АВ = ВС)
биссектрисы BD и AF пересекаются в точке О. SDOA: SB0F =
= 3:8. Найдите АС: АВ.
17.21. N — середина стороны АС равностороннего
треугольника ABC, Z — точка на высоте BN. Прямая AZ
пересекает окружность, описанную около треугольника ABC в
точке Р. Найдите отношение ВР: PC, если BN = 1BZ.
17.22. В равнобедренном треугольнике ABC (АВ = ВС)
проведена биссектриса AD. Площади треугольников ABD и
ADC равны соответственно Sx и S2. Найдите АС.
112

Метод ключевых задач
§18. Второй признак подобия треугольников.
Ключевая задача.
Доказать, что если в треугольниках ABC и A^Bfa
выполняется соотношение -т-^- = -г-^ и ABAC = LBXAJCV то такие
треугольники подобны.
Доказательство сформулированного утверждения можно
найти в любом школьном учебнике.
Примеры.
Задача 1.
В треугольнике ABC на
медиане ВМ выбрана точка
К так, что
LMKC = LBCM.
Доказать, что
LAKM = LBAM*
А М С
Решение. Рис. 56
Так как треугольники ВМС и СМК (рис. 56) подобны
. ВМ МС „
по первому признаку подобия, то -г—^ = -==-. Учитывая,
ПАП ЛИЛ ВМ AM
что МС = AM, получаем -ттт = -jrrz и, следовательно,
треугольники АВМ и КАМ подобны (LKMA = LAMB). Отсюда
LBAM = LAKM.
Задача 2.
В
остроугольном треугольнике
ABC АА1 и ВВХ —
высоты. Доказать,
что треугольник
\ВХС подобен
треугольнику ABC.
Рис. 57
113

Метод ключевых задач
Решение.
В прямоугольном треугольнике AAfi (рис. 57) -~-т =
СВ.
^ cos LACB, а следовательно,
= cos LACB. Аналогично
Со
СА СВ.
-^гт = т^тэ = cos ^-АСВ, и треугольники Afifi и ABC подобны
с коэффициентом подобия к = cos LACB.
Упражнения.
18.1. В треугольнике ABC LBAC = 45°, LABC = 75°.
Радиус окружности, описанной около ААВС, равен R. А\ и
BBt — высоты, Н — точка их пересечения. Найти
радиусы окружностей, описанных около треугольников А1В1С и
аан.
18.2. В треугольнике ABC АВ = 8, ВС = 12, АС = 16.
Точка D делит АС на отрезки AD = 7 и DC = 9. Найти BD.
18.3. Из точки А проведены два луча AM и AN. На луче
AM взяты точки Я и В, а на луче A/V — точки С и D так,
что АН • Ав = АС • AD. Доказать, что точки Н, В, С и D
лежат на одной
окружности.
18.4. Из точки, „
М, лежащей вне ок-/ " "--—""
ружности, проведев
два луча, пересекаю-^
щие окружность в
точках А, В, С и D
(рис. 58). Доказать,
что треугольники
АМС и £>М£
подобны.
18.5. Отрезок АВ есть диаметр круга, а точка С лежит
вне этого круга. Отрезки АС и 5С пересекаются с окружностью
в точках D и М соответственно. Найти угол CBD, если
площади треугольников DCM и АСВ относятся как 1:4.
18.6. Окружность, построенная на стороне АС
треугольника ABC как на диаметре, проходит через середину стороны
Рис. 58
114

Метод ключевых задач
ВС и пересекает сторону АВ в точке D так, что AD = ^ АВ.
Найти площадь треугольника ABC, если АС = 1.
18.7. Равнобедренный треугольник ABC с основанием
АВ = 12 имеет длину боковой стороны 10* Окружность,
построенная на боковой стороне как на диаметре, пересекает
остальные стороны в точках Я и Р. Найти площадь
четырехугольника АНРС.
18.8. В треугольнике ABC на средней линии DE,
параллельной АВ, как на диаметре построена окружность,
пересекающая стороны АС и ВС в точках М и N. Найти MN, если
ВС = а, АС = Ъ, АВ = с.
18.9. На стороне АВ треугольника ABC взята точка М
такая, что -г^= = -у. Известно, что LBAC - 45° и LABC =
= 75°. Найти LACM.
18.10. На общей
хорде двух пересекающихся
окружностей взята точка
М и через нее проведены
хорды ABnCD (рис. 59).
Доказать, что
LMDB = LMAC.
18.11. Через
середину Е отрезка AM (M при-
надлежит стороне СВ)
треугольника ABC и его вершину С проведена прямая,
пересекающая АВ в точке D, причем АЕ2 = ЕС • ED. Доказать,
что точки A, D, М и С лежат на одной окружности.
18.12. В остроугольном треугольнике ABC проведены
высоты BD и СЕ. Из вершин 5 и С к прямой ££> проведены
перпендикуляры BF и (Ж. Доказать, что EF = 1Ж.
18.13. В треугольнике ABC проведены высоты АН, ВК
и CL. Доказать равенство АК BL • СИ = AL ВН СК =
= НК- KLLH.
18.14. Точка М, лежащая вне круга с диаметром АВ,
соединена с точками А и Б. Отрезки МА и MB пересекают
окружность в точках С и D соответственно. Площадь круга,
вписанного в треугольник АМВ, в 4 раза больше площади
круга, вписанного в треугольник CMD. Найти LAMB.
115

Метод ключевых задач
18.15, В треугольнике ЛВС ЛИ — высота (Я
принадлежит отрезку ВС). Выполняется соотношение: АН2 = ВН • СН.
Доказать, что ABAC = 90°.
18.16. Доказать, что если между сторонами а, Ъ и с
треугольника существует зависимость о2 = й2 + be, то углы
А и В, противолежащие сторонам а и Ь, удовлетворяют
равенству LA = 2 LB.
116

Глава III.
Избранные методы и приемы
§1. «Удлинение» медианы
Дополнительней построение — один из наиболее
эффективных приемов решения геометрических задач. Однако
такие построения чаще всего связаны с серьезными
трудностями. Хорошо, если условие задачи подсказывает, как
дополнить чертеж.
В
Во многих
задачах, связанных
с медианой, ее
«удвоение» или
«удлинение» на
треть приносит
результат.
Приведем ха-А
рактерный
пример.
М
Рис. 60
Задача 1.
В трапеции ABCD (ВС \\ AD) M и N — середины
оснований ВС и AD. AC = VW, BD = 1, MN = 2. Найти площадь
трапеции.
Решение.
На прямой AD (рис.
60) отложим отрезок
DK = ВС. Так как
DBCK —
параллелограмм, то BD = СК = 1.А
Проведем CF || MM
Несложно показать, что
F — середина АК.
Кроме того, SBAC = 5^
(равные основания и
высоты). Тогда очевидно,
что StBrn = S.™
к
abcd

Избранные методы и приемы
Таким образом, задача свелась к поиску площади
треугольника АСК по двум сторонам АС = VT3", СК = 1 и медиане
к третьей стороне CF=2. «Удвоим» медиану CF (рис. 61).
Так как AF = FK и CF = FT, то АСКТ — параллелограмм.
По теореме о сторонах и диагоналях параллелограмма
АК2 + СТ2 = 2 (АС2 + СК2). Отсюда АК = 4. Остальное просто
Ответ:
Упражнения.
1.1. Построить треугольник по двум сторонам и медиане
к третьей стороне.
1.2. В равнобедренном треугольнике с боковой стороной,
равной 4, проведена медиана боковой стороны, равная 3.
Найти основание треугольника.
1.3. Основание равнобедренного треугольника равно
4vT~, а медиана боковой стороны 5. Найти длины боковых
сторон.
1.4. Стороны АВ и АС треугольника ABC равны 8 и 6.
В каких пределах изменяется медиана AMI
1.5. Доказать, что если две стороны и медиана,
проведенная к третьей стороне, одного треугольника соответственно
равны двум сторонам и медиане к третьей стороне другого
треугольника, то такие треугольники равны.
1.6. В треугольнике ABC АВ = с, ВС = а, АС = Ъ. Найти
длину медианы AM.
1.7. Найти отношение суммы квадратов всех медиан
треугольника к сумме квадратов всех его сторон.
1.8. Найти углы, образованные медианой ВВХ со сторонами
ААВС АВ и ВС, если АВ = 6, ВС = 8, ВВ{ = 5.
1.9. Доказать, что медиана треугольника меньше
полусуммы заключащих ее сторон.
1.10. Докажите неравенство: -~р < тх + т2 + тг < 2р, где
mv m2, m3 — медианы, ар — полупериметр треугольника.
1.11. Внутри угла взята точка М. Провести через М
прямую так, чтобы отрезок, заключенный между сторонами
угла, делился точкой М пополам.
118

Избранные методы и приемы
1.12. В треугольнике ABC LBAC-a, £ABC=P>
LACB = <р. Медиана AM = т. Найти площадь треугольника.
1.13. В треугольнике ABC медиана ВМ перпендикулярна
стороне ВС. АВ: ВС = 2:1. Найти LABC.
1.14. Даны две концентрические окружности. Доказать,
что сумма квадратов расстояний от точки одной окружности
до концов диаметра другой окружности не зависит ни от
выбранной точки, ни от выбранного диаметра.
1.15. Найти отношение площади треугольника к площади
треугольника, стороны которого равны медианам данного.
1.16. Построить треугольник по трем медианам.
1.17. Дан прямоугольник ABCD. Доказать, что для любой
точки М плоскости МА2 + МС2 = MB2 + MD2.
119

Избранные методы и приемы
§2. Метод вспомогательной площади
Ключом к решению многих задач становится работа с
понятием, на которое в условии не дано намека. Нередко
такой вспомогательной величиной служит площадь.
Примеры.
Задача 1.
В прямоугольном треугольнике ABC (Z.C = 90°) CD —
высота (рис. 62). Радиусы
окружностей, вписанных в
треугольники ACD и DCB,
соответственно равны гх и
г2. Найдите рад; ус
вписанной окружности в
треугольник ABC.
Решение. д
Пусть площади
треугольников ACD, DCB,
ABC соответственно равны
Sv S2, S. Очевидно, что
AACD c/> AABC и
ACBD с/> ААВС.
Площади подобных
треугольников относятся, как
квадраты соответственных
линейных элементов.
Имеем:
Л = ^ _£ =- !l A D2D1 В
S **' S **' Рис. 63
где г — радиус окружности, вписанной в треугольник ABC.
Отсюда
Задача 2.
В треугольник ABC вписаны две касающиеся друг друга
окружности так, что одна касается сторон АВ и АС, а другая —
120

Избранные методы и приемы
ЛВ и ВС. Доказать, что сумма радиусов этих окружностей
больше радиуса окружности, вписанной в данный треугольник.
Решение.
Проведем касательные CD: и CD2 к данным окружностям
(рис. 63) ♦ Понятно, что SABC < SACD + SBCD.
Тогда pr ^ p{r{ + р2г2, где p, pv p2, r, rp r2 — полупериметры
и радиусы вписанных окружностей соответственно
треугольников ABC, ACDV D2CB. Имеем
Поскольку р,<р и р2<р, то — < 1 и — < 1. Отсюда
Упражнения.
2.1. По данным катетам а и Ъ определите высоту,
проведенную к гипотенузе.
2.2. Стороны треугольника равны 13, 14 и 15. Найдите
наименьшую высоту.
2.3. Стороны треугольника равны 5 и 8, угол между ними
60°. Найдите высоту, опущенную на третью сторону.
2.4. Доказать, что сумма расстояний от любой точки,
лежащей внутри равностороннего треугольника, до его сторон
не зависит от выбора этой точки.
2.5. Доказать, что сумма расстояний от любой точки,
взятой внутри правильного многоугольника, до всех прямых,
содержащих его стороны, есть величина постоянная.
2.6. Доказать, что сумма расстояний от любой точки
основания равнобедренного треугольника до боковых сторон
не зависит от положения точки на основании.
2Л. Решите ключевую задачу §17 главы II методом
площадей.
2.8. В треугольнике длины двух сторон равны 6 и 3.
Найдите длину третьей стороны, если полусумма высот,
проведенных к данным сторонам, равна третьей высоте.
2.9. Построить треугольник по двум сторонам, если сумма
соответствующих им высот равна третьей стороне.
121

Избранные методы и приемы
2.10. Докажите, что для всякого треугольника имеет место
равенство т~ + тг + т- = —, где г — радиус вписанной ок-
К пь пс г
ружности.
2.11. В треугольник со сторонами а, Ъ, с вписан полукруг
с диаметром, лежащем на стороне с. Найдите радиус этого
полукруга.
2.12. Радиусы двух пересекающихся окружностей равны
17 и 39, а расстояние между центрами 44. Определите длину
общей хорды.
2.13. Высоты параллелограмма 1\ и h^, а периметр 2р.
Найдите стороны,
2.14. Определить острый угол ромба, в котором сторона
есть среднее пропорциональное между диагоналями.
2.15. В треугольнике ABC AC = a, BD ± AC, BD = А,
г — радиус вписанной окружности. Найдите расстояние от
центра вписанной окружности до вершины В.
2.16. Прямая проходит через вершину В равнобедренного
треугольника ABC (AB = ВС), пересекая его основание АС в
точке D. Известно, что LABD = ^ LABC и AD: DC = 3 : 4.
Острый или тупой угол АВС1
2.17. Доказать, что биссектриса AL треугольника ABC
равна . с • cos -у, где а = ABAC, Ъ = АС, с = AS.
2.18. В треугольнике АЯС проведены медианы АК и
СМ. Оказалось, что LBAK = LBCM = 30°. Доказать, что
треугольник ABC равносторонний.
2.19. Внутри треугольника ABC взята точка О. Прямые
АО, ВО, СО пересекают стороны треугольника в точках \,
Bv Cx соответственно. Доказать, что
АС В\ СВ.
с^Ас'М= <теорема Чевы)*
2.20. Доказать, что диагонали вписанного
четырехугольника относятся, как суммы произведений его сторон,
сходящихся к концам этих диагоналей:
АС: BD = (АВ • AD + ВС • CD) : (АВ ВС + CD AD).
122

Избранные методы и приемы
2.2L Стороны треугольника образуют арифметическую
прогрессию. Доказать, что биссектриса среднего по величине
угла есть геометрическое место точек, сумма расстояний от
которых до сторон треугольника есть величина постоянная.
2.22. Внутри треугольника ABC взята точка О. Прямые
АО, ВО и СО пересекают стороны треугольника ABC в точках
Д, В1 и С{ соответственно. Доказать, что
ОА ОВ. ОС
_i I L j_ L 1
Ad, И\ СС, ~
123

Избранные методы и приемы
§3. Метод вспомогательной окружности
По-видимому, вспомогательная окружность — одно из
наиболее эстетичных дополнительных построений. Скорее
всего, это связано с тем, что «увидеть» окружность там, где ее
нет, уже само по себе нетривиально. Однако мы надеемся,
что после изучения настоящего параграфа у читателя будут
чаще возникать «круги перед глазами».
Ключевая задача 1.
Если в четырехугольнике сумма противоположных углов
равна 180°, то вокруг него можно описать окружность.
Решение.
Пусть в четырехугольнике ABCD LABC + LADC = 180°.
Построим окружность, проходящую через точки А, В и С
(это всегда
возможно). Допустим, что
эта окружность не
проходит через
точку D, a nepece-Bi
кает сторону AD в
точке Д — рис. 64
(случай, когда
окружность
пересекает продолжение \^ \ ^^7ъл
стороны AD,
рассматривается
аналогично). Посколь- Рис. 64
ку
четырехугольник ABCDX вписан
в окружность, то LABC + LADf, = 180°. Отсюда LDX = LD,
чего быть не может, так как LADfi — внешний для
треугольника CDDV Следовательно, построенная окружность
проходит через точку D.
Примеры
Задача 1.
Доказать, что высоты AHV BH2, СНг остроугольного
треугольника ABC делят пополам углы треугольника HXH2HV
124

Избранные методы и приемы
Решение.
Поскольку LAHbH + LHH^ = 180°, то вокруг
четырехугольника АНЪНН2 можно описать окружность (рис. 65). Тоща
LHbAH = LHZH2H как
вписанные, опирающиеся на
одну дугу. Аналогично
доказывается, что
Но LBAH = LBCH, так как/
они дополняют угол ABC дс
90°. Отсюда
LHZH2H = LHXH2H.
Таким же способом
доказывается, что
Задача 2.
В треугольнике ABC LB = 60°,
и ССХ — биссектрисы,
пересекающиеся в точке О (рис. 66).
Докажите, что СЦ = OCV
Решение.
ACiOA{ = LAOC
Рис. 66
180° - (LOAC + LOCA) =
180° - ~ (LBAC + LBCA) = 180° - ~ (180° - LABC)
Следовательно, LCXB\ + АС1ОА1 = 180°, т.е. вокруг
четырехугольника ОС{ВА^ можно описать окружность. Поскольку
О — точка пересечения биссектрис треугольника, то
АС{ВО = LOBAl. Значит, w СХО = w O^, а равные дуги
стягивают равные хорды, т.е. ОСХ = ОА1.
125

Избранные методы и приемы
Упражнения.
3.1. Из точки Р, расположенной внутри острого угла
ВАС, опущены перпендикуляры РСХ и РВХ на прямые АС и
АВ соответственно. Докажите, что LCXAP = LCXBXP.
3.2. Дан прямоугольный треугольник ABC (ZC = 90°).
На катете ВС выбрана произвольная точка М. Из точки М
проведен перпендикуляр MN на гипотенузу АВ. Докажите,
что LANC = LAMC.
3.3. Внутри треугольника ABC взята произвольная точка
О. Из нее опущены перпендикуляры ОМ, OF и ОР на стороны
АВ, ВС и АС соответственно. Докажите, что
LAOC = LAMP + LPFC.
3.4. В прямоугольник ABCD вписан равносторонний
треугольник АР К так, что вершина К лежит на стороне ВС, а
Р — на CD. KH — высота этого треугольника. Докажите,
что треугольник ВНС — равносторонний.
3.5. Вершины А и В треугольника ABC с прямым углом
С скользят по сторонам прямого угла с вершиной Р. Докажите,
что точка С при этом перемещается по отрезку.
3.6. Дан угол а с вершиной в точке А и точка М внутри
угла. В и С — основания перпендикуляров, опущенных из
точки М на стороны угла. MB = а, МС = й. Найдите AM.
3.7. Из произвольной точки М внутри данного угла с
вершиной А опущены перпендикуляры МР и MQ на стороны
угла. Из точки А опущен перпендикуляр АК на отрезок
PQ. Докажите, что АРАК = LMAQ.
3.8. Расстояние между основаниями двух высот ВМ и
BN ромба ABCD вдвое меньше диагонали BD. Найдите углы
ромба.
3.9. Дан прямоугольный треугольник ABC (ZC = 90°).
На его гипотенузе построен квадрат ABFD, М — его центр.
Докажите, что LACM = LMCB.
3.10. В выпуклом четырехугольнике ABCD
противоположные углы А и С — прямые. На диагональ АС опущены
перпендикуляры BE и DF. Докажите, что СЕ = FA.
3.11. Внутри угла АОВ взята точка М, проекциями
которой на стороны угла являются точки Мх и М2. Докажите,
чт0 Somxm2m к 2 OM2 Sin
126

Избранные методы и приемы
3.12. Дан квадрат ABCD, О — его центр, К — середина
ВС, М — середина OD. Найдите LAMK.
3.13. Дан треугольник ABC. BH — его высота. В
треугольник вписан полукруг с центром О на АС. М и N — точки
касания со сторонами АВ и ВС. Докажите, что LMHB =
= LBHN.
3.14. К окружности проведены две касательные. Доказать,
что длина перпендикуляра, опущенного из произвольной
точки окружности на хорду, соединяющую точки касания, есть
среднее пропорциональное между длинами перпендикуляров,
опущенных из этих точек на касательные.
3.15. Внутри прямоугольника ABCD выбрана точка
М так, что LBMC + LAMD = 180°. Найдите сумму углов
ВСМ и MAD.
3.16. В треугольнике ABC LACB = 120°. Я — точка
пересечения высот, О — центр описанной окружности, М —
середина дуги АСВ. Доказать, что НМ = МО.
3.17. Дан квадрат ABCD. Точки Р и Q лежат
соответственно на сторонах АВ и ВС, причем ВР = BQ. Пусть Н —
основание перпендикуляра, опущенного из точки В на отрезок
PC. Найдите угол DHQ.
3.18. На сторонах АВ и CD прямоугольника ABCD взяты
точки К и Е так, что ВК = СЕ. Из точки К опущен
перпендикуляр КО на диагональ АС. Найдите угол ВОЕ.
3.19. На сторонах АВ, ВС и АС треугольника ABC взяты
соответственно точки D, E, F, для которых DE = BE и
FE = СЕ. Доказать, что центр описанной около треугольника
ADF окружности лежит на биссектрисе угла DEF.
Ключевая задача 2.
Если точки В и С лежат в одной полуплоскости
относительно прямой AD, причем LABD = LACD, то точки А, В,
С и D принадлежат одной окружности. Доказать.
Решение.
Предположим, что точка С не лежит на окружности,
описанной около треугольника ABD. Тогда возможны два
случая:
а) С лежит вне данной окружности (рис. 67). Тогда
LACD = LAKD - LCDK.
127

Избранные методы и приемы
В
Рис. 67 Рис- 68
Но по теореме о вписанном угле LABD = LAKD и,
следовательно, LACD < LABD.
6) С лежит внутри окружности (рис. 68). Здесь
LACD = LAKD + LCDK и LACD > LABD.
Полученные противоречия и доказывают нужное
утверждение.
Примеры
Задача 1.
На медиане AM
треугольника ABC взята точка К так,
что LBKM=LABC (рис. 69).
Доказать, что LCKM = LACB.
Решение.
«Удвоим» медиану AM (уже
знакомый читателю прием).
LBCD = LABC = LBKD.
Таким образом, точки С, К, В,
D принадлежат одной
окружности. Тогда LCKD = LCBD (как Рис 69
опирающиеся на общую дугу
CD), но LCBD = LACB. Откуда LCKD = ААСВ.
128

Избранные методы и приемы
Упражнения
3.20. Определить площадь трапеции, у которой длины
оснований равны 10 и 26, а диагонали перпендикулярны
боковым сторонам.
3.21. Найти геометрическое место оснований
перпендикуляров, опущенных из данной точки А на прямые,
проходящие через данную точку В.
3.22. В выпуклом четырехугольнике ABCD проведены
диагонали АС и BD. Известно, что AD = 2, LABD = LACD =
= 90°, и расстояние между точками пересечения биссектрис
треугольников ABD ъ ACD равно у/Т. Найти длину
стороны ВС.
3.23. В остроугольном треугольнике ABC CCX и АА1
высоты. Доказать, что серединный перпендикуляр к СД
проходит через середину АС.
3.24. В остроугольном треугольнике ABC CCX и АА1
высоты. Из точек А и С на прямую Afit проведены
перпендикуляры AF и СК. Доказать, что FCX = К\.
3.25. Из вершины А квадрата ABCD проведены два луча,
образующие угол 45°. Один пересекает сторону ВС в точке
E, диагональ BD — в точке Р, другой — сторону CD в точке
F, а диагональ BD — в точке Q. Доказать, что SilffF = 2SAPQ.
3.26. В треугольнике ABC проведены биссектриса BE и
высота АН. LBEA = 45°. Доказать, что LEHC = 45е.
3.27. Окружность, вписанная в дельтоид ABCD (АВ = ВС,
CD = AD), касается его сторон АВ, ВС и AD в точках К,
М и N соответственно. Диагональ АС пересекает отрезок
MN в точке Р. Доказать, что точки А, К, Р, N лежат на
одной окружности.
3.28. На сторонах АВ, ВС и СА треугольника ABC
отмечены точки Ct, <Лр jBj соответственно. Оказалось, что
АС, ВА СВ.
Доказать, что треугольники ABC и AlBlCl подобны.
3.29. На стороне АВ треугольника ABC вне треугольника
построен квадрат с центром в точке О. На стороне АС построен
квадрат вовнутрь треугольника с центром в точке М. Дока-
5 Учимся решать задачи по геометрии

Избранные методы и приемы
зать, что точки О, М и D (D — основание высоты к стороне
ВС) лежат на одной прямой.
Ключевая задача 3.
Доказать, что если точки
О и С находятся в одной (в
разных) полуплоскостях
относительной прямой AS, причем
ОА = ОВ и LAOB = 2LACB
UAOB = 2 (180° - LACB)), то
точки А, В и С лежат на
окружности с центром в точке О.
Доказательство.
Рассмотрим случай, когда
точки О и С лежат в одной
полуплоскости. Предположим, что
точка С лежит вне окружности
с центром с точке О и радиусом Рис 70
О А = ОВ (рис. 70). Тоща
LAOB = lLACfi = 2 (Z.4CJ5 + LCAC{).
Если же точка С лежит внутри
окружности (рис. 71), то
LAOB
В
Случай, когда точки О и С
лежат в разных полуплоскостях,
рассмотрите самостоятельно.
Примеры
Задача 1.
В выпуклом
четырехугольнике ABCD АВ = AD = 10, LBAD = 100°, LBCD
длину диагонали АС.
Решение.
Заметим, что 2 (180° - LBCD) = 100° = LBAD (рис. 72).
Тогда точки В, D и С лежат на окружности с центром в
точке А.
Ответ: ЛС = 10.
В
РисГ 71
130е. Найти
130

Избранные методы и приемы
Упражнения.
3.30. В трапеции ABCD
(AD || ВС) угол ADB в два раза
меньше угла АСВ. ВС = АС = 5,
AD = 6. Найти площадь
трапеции.
3.31. В треугольнике ABC
ABAC ш 30°, LABC = 80°.
Внутри треугольника выбрана точка
К такая, что треугольник ВСК —
равносторонний. Найти АКАВ.
3.32. Вне равностороннего
треугольника ABC (но внутри угла АСВ) выбрана точка М
так, что LAMC = 20е и LBMC = 30°. Найти LACM.
3.33. Вне равнобедренного треугольника ABC (AB = АС),
но внутри угла ABC, выбрана точка М так, что LBMC =
= 40е, а 21БМЛ = 10°. Найти LBAM, если LABC = 50е.
3.34. Внутри квадрата ABCD взята точка М такая, что
LMAC = Z.MOD = а. Найти ZABM.
3.35. В выпуклом четырехугольнике ABCD ABAC = 25°,
£ВСА = 20°, £BDC = 50\ LBDA = 40°. Доказать, что
Л4 = DB = £>С.
Удобно, когда некоторый класс задач объединяет
одна ключевая идея. К сожалению, такая четкая
классификация возможна не всегда. Часто
выручает опыт, интуиция и сообразительность.
Думаем, что приобрести подобный опыт
читателю помогут следующие примеры и упражнения.
Примеры.
Задача 1.
В четырехугольнике три тупых угла. Доказать, что из
двух его диагоналей больше та, которая проведена из вершины
острого угла.
Решение.
Построим на отмеченной диагонали как на диаметре
окружность. Тогда две другие будут лежать внутри
окружности, и отрезок, из соединяющий, меньше диаметра.
131

Избранные методы и приемы
Задача 2. В
В квадрате ABCD со
стороной 1 на сторонах АВ к ВС
выбраны соответственно точки
Р и Q так, что периметр
треугольника PBQ равен 2.
Найдите величину угла PDQ.
Решение.
Проведем окружность с
центром в точке D радиуса 1.
Очевидно, что она касается
сторон квадрата в точках А и С Рис- 73
(рис. 73). Любая касательная к дуге АС отсекает от квадрата
треугольник, периметр которого равен 2 (ключевая задача 2,
§ 16, глава II). Пусть PQ не касается проведенной окружности.
Если PQ не имеет общих точек с окружностью, то проведем
касательную PXQX || PQ. Периметр треугольника PXBQ{ больше
периметра треугольника PBQ — очевидно. С другой стороны,
их периметры равны по 2. Аналогично можно получить
противоречие, если отрезок PQ пересекает окружность. Итак,
точка D является центром вневписанной окружности
треугольника PBQ. Имеем LPDQ = 180° - ^ (LAPQ + LPQC) =
= 180° - ^ ■ 270° = 45°.
Упражнения.
3.36. Можно ли разместить равносторонний треугольник
со стороной 3 внутри круга радиусом V10?
3.37. Через точку Р, лежащую на общей хорде АВ двух
пересекающихся окружностей, проведена хорда КМ первой
окружности и хорда LN второй окружности. Доказать, что
LNKM = LNIM.
3.38. На одной стороне угла с вершиной в точке О
выбраны точки А и В, на. другой — D и С так, что
ОВ • ОА = ОС • OD. Докажите, что ABAC = LBDC.
3.39. В остроугольном треугольнике ABC AHV BHV
СНЪ — высоты, Н — точка их пересечения. Докажите, что
АН НН^ВН • НН2 = СН • ННУ
132

Избранные методы и приемы
3.40. Восстановите квадрат по четырем точкам, каждая
из которых лежит соответственно на каждой из сторон
квадрата.
3.41. На одной стороне угла с вершиной О даны точки
А и В. Найдите на второй стороне такую точку X, чтобы
угол АХВ был наибольшим.
3.42. Определите углы треугольника, в котором медиана,
биссектриса и высота, выходящие из одной вершины
треугольника, делят соответствующий угол на четыре равные
части.
3.43* Высота и медиана, выходящие из одной вершины
треугольника и расположенные внутри него, образуют со
сторонами треугольника, выходящими из той же вершины,
равные углы. Доказать, что данный треугольник
прямоугольный или равнобедренный.
3.44. Докажите, что квадрат биссектрисы угла
треугольника равен разности между произведением боковых сторон
и произведением отрезков основания.
3.45. Четырехугольник ABCD вписан в окружность.
Биссектрисы углов В и С пересекаются на стороне AD. Докажите,
что AB + CD- AD.
3.46. Длины основания CD, диагонали BD и боковой
стороны AD трапеции ABCD равны между собой и равны р.
Длина боковой стороны ВС равна q. Найдите длину
диагонали АС.
3.47. Постройте треугольник ABC по точке А> центру
описанной окружности и точке пересечения биссектрисы угла
А со стороной ВС.
3.48. Постройте прямоугольный треугольник ABC
(Z.C = 90е) по точкам А и В и точке М, лежащей на
биссектрисе угла С.
3.49. В треугольнике ABC AA>90°. На стороне ВС
найдите такую точку X, что АХ = VAX • ХС.
3.50. Внутри угла с вершиной О взята точка. Провести
через нее прямую так, чтобы треугольник, отсекаемый от
угла этой прямой, имел заданный периметр.
3.51. В треугольнике ABC с углом при вершине 2*, равном
120°, проведена биссектриса BD. Найдите отношение сторон
треугольника АВ и АС, если известно, что BD: DC - к.
133

Избранные методы и приемы
3.52. В треугольнике ABC проведены биссектрисы АА1,
ВВХ и CCV Найдите сумму углов ВС{В{ и BAlBv если известно,
что угол ABC равен 120°.
3.53. В треугольнике ABC LB = 100% СЕ — биссектриса.
На стороне АС выбрана точка D так, что LDBC = 20°. Найдите
величину угла CED.
134

Избранные методы и приемы
§4. Применение центральной симметрии
Напомним некоторые определения и свойства.
1. Точки Л и А называются симметричными
относительно точки О, если О — середина отрезка АА*.
2. Преобразование фигуры, при котором каждой точке
этой фигуры сопоставляется точка, симметричная ей
относительно заданной точки О, называется центральной
симметрией с центром О.
3. Центральная симметрия является движением.
Следовательно, симметричные фигуры равны.
4. Ограниченная фигура не может иметь более одного
центра симметрии.
5. Если прямые ^ и /2 симметричны относительно точки
О, то I, || lr
6. Если четырехугольник имеет центр симметрии, то он
является параллелограммом.
Примеры.
Задача 1.
Две окружности пересекаются в точке М. Провести через
М прямую, пересекающую окружности в точках А и В так,
что
Заметим, что при симметрии окружности Sx (рис. 74)
относительно точки М точка В переходит в точку А. Таким
образом, точку А можно получить как пересечение
окружностей S2 и S/. В — точка
пересечения S{ и прямой AM.
Задача 2.
Окружность пересекает
стороны ВС, СА, АВ треугольника
ABC в точках Ах и Л2, Bv и Bv
Cj и С2 соответственно. Докажите,
что если перпендикуляры к
сторонам треугольника, проведенные
через точки А1, Вх и Cv пересе-
Рис. 74
135

Избранные методы и приемы
каются в одной точке, то и перпендикуляры, проведенные к
сторонам через А>, В2 и С2, тоже пересекаются в одной точке.
Решение.
Перпендикуляры, проведенные в точках Д, Bv Cv
симметричны перпендикулярам в точках А2> В2> С2 соответственно
относительно центра окружности О (докажите).
Следовательно, фигуры, образованные этими тройками перпендикуляров,
симметричны относительно точки О. То есть перпендикуляры
в точках А2у В2, С2 пересекаются в точке, симметричной М
Ш — пересечение перпендикуляров в точках Д, Bv С)
относительно О.
Упражнения
4.1. Провести через данную точку прямую так, чтобы
она разделила площадь данного параллелограмма пополам.
4.2. Вершины одного параллелограмма лежат на сторонах
другого — по одной вершине на каждой стороне. Доказать,
что диагонали обоих параллелограммов пересекаются в одной
точке.
4.3. Две прямые, проходящие через центр
параллелограмма ABCD, пересекают сторону ВС в точках М и N, а
сторону AD — в точках К и F. Доказать, что MN = KF.
4.4. М — середина отрезка, соединяющего центры двух
равных окружностей* Прямые, проходящие через точку М,
пересекают одну из окружностей в точках Л и В, а другую —
в К и F. Доказать, что АВ = KF.
4.5. Параллелограмм ABCD разбит своими диагоналями
на треугольники АОВ, ВОС, COD и DOA. К, L, М, N —
точки пересечения медиан этих треугольников. Доказать, что
KLMN — параллелограмм.
4.6. Внутри окружности дана точка М. Через эту точку
проведите хорду АВ так, что AM = MB.
АЛ. Постройте отрезок с серединой в данной точке и
концами на двух данных прямых.
4.8. Постройте отрезок с серединой в данной точке и
концами на данной окружности и данной прямой.
4.9. Внутри острого угла заданы точки А и С. Постройте
параллелограмм ABCD так, чтобы точки В и D лежали на
сторонах угла.
136

Избранные методы и приемы
4.10. Постройте квадрат с центром в данной точке О и
точками MhjV, принадлежащими двум соседним сторонам
квадрата.
4.11. Постройте квадрат с центром в данной точке О и
точками М и N, принадлежащими двум противоположным
сторонам или их продолжениям.
4.12. Постройте ромб с центром в данной точке и тремя
вершинами на трех данных прямых.
4.13. Постройте ромб с центром в данной точке и тремя
вершинами на трех данных окружностях.
4.14. Построить параллелограмм ABCD, вершины
которого А и С лежат на прямой а, а вершины В и D — на
прямых Ъ и с соответственно.
4.15. Дана прямая а и две окружности по разные стороны
от нее. На прямой взят отрезок CD. Постройте треугольник
ABC так, чтобы точки А и В лежали на окружностях, а
отрезок CD являлся медианой.
4.16. Даны две концентрические окружности S{ и 52.
Проведите прямую, на которой эти окружности высекают три
равных отрезка.
4.17. Построить ромб, центр которого лежит в данной
точке, а три стороны или их продолжения касаются трех
заданных окружностей.
4.18. Докажите, что прямые, проведенные через середины
сторон вписанного четырехугольника перпендикулярно
противоположным сторонам, пересекаются в одной точке.
4.19. Пусть Р — середина стороны АВ выпуклого
четырехугольника ABCD. Докажите, что если площадь
треугольника PCD равна половине площади четырехугольника
ABCD, то ВС || AD.
137

Избранные методы и приемы
§5. Применение осевой симметрии
L Точки Л и Л' называются симметричными
относительно прямой /, если прямая / перпендикулярна отрезку
АА и проходит через его середину,
2. Преобразование фигуры, при котором каждой точке
этой фигуры сопоставляется точка, симметричная ей
относительно заданной прямой /, называется осевой симметрией с
осью /.
3. Осевая симметрия является движением, а
следовательно, симметричные фигуры равны.
Примеры.
Задача 1.
В прямоугольном треугольнике ABC (Z.C = 90°) медиана
AM = m проведена к меньшему катету и образует с большим
угол 15е. Найти площадь
треугольника.
Решение.
Построим точку К,
симметричную точке М относительно прямой
АС (рис. 75). Тоща
АКАС = АМАС и S
Имеем S
ЛВС
2S
КАС '
JKAM
\т2 sin 30е = ^г.
2 4
Задача 2.
Даны прямая АВ и
точки С и D по одну сторону
от нее. На прямой АВ
построить такую точку X,
чтобы I LAXC - LBXD\ = 90°.
Решение. А
Отобразим точку С
симметрично относительно
прямой АВ, получим точку Сг
138
В
Рис. 76

Избранные методы и приемы
На отрезке DC{ как на диаметре строим окружность. Она
пересекает прямую АВ в точках Х1 и X (рис. 76). Они и есть
искомые. Покажем это.
90° - LCXXD = LCXXA + LAXD =
= LAXC + 180е - LDXB, т.е.
90° = 180е + LAXC - LDXB, LDXB - LAXC = 90е.
Для точки Хх рассуждения аналогичны.
Упражнения
5.1. Даны прямая MN и точки А и В в разных
полуплоскостях относительно MN. Через А и В проведите лучи так,
чтобы угол между ними делился MN пополам.
5.2* Точки А и В лежат по одну сторону от прямой /.
Найдите на прямой / такую точку X, чтобы лучи ХА и ХВ
образовывали с прямой / равные углы.
5.3. Построить треугольник ABC, если заданы точки А
и В и прямая /, на которой лежит биссектриса угла С.
5.4. На каждой стороне угла M0N взяты по две точки
А, В и А1, В1 так, что О А = ОА1 и ОВ = ОВХ. Доказать, что
прямые Afi и АВХ пересекаются на биссектрисе угла MON.
5.5. В окружности проведены две неравные параллельные
хорды. С помощью одной линейки найдите середины этих
хорд.
5.6. Через вершину А треугольника ABC и точку D,
лежащую на стороне ВС, проведена прямая. Найдите на этой
прямой такую точку X, из которой отрезки BD и DC были
бы видны под равными углами.
5.7. Построить треугольник ABC, если даны прямая АВ
и серединные перпендикуляры к сторонам ВС и СА.
5.8. Построить треугольник ABC, если даны вершина А
и прямые, на которых лежат биссектрисы углов В и С
5.9. Построить параллелограмм ABCD по вершине D и
серединным перпендикулярам к сторонам АВ и ВС
5.10. Построить ромб ABCD по серединам М и N сторон
АВ и ВС и точке Е, лежащей на прямой АС.
5.11. Построить треугольник ABC по двум сторонам АВ
и АС и разности углов В и С
139

Избранные методы и приемы
5.12. Построить трапецию по боковым сторонам,
основанию и разности углов при этом основании.
5.13. Дан угол ABC, равный 45е, и точки М и N внутри
угла. Построить равнобедренный треугольник, вершина
которого лежит на одной стороне, основание — на другой, а
боковые стороны проходят через точки М и N.
5.14. Дана прямая I til точки А и В по одну сторону от
нее. Найдите на прямой / такую точку X, чтобы сумма
АХ + ХВ была минимальна.
5.15. Точки А и В расположены по разные стороны
относительно прямой /. Найдите на прямой I такую точку Ху
чтобы величина \АХ-ХВ\ была наибольшей.
5.16. Доказать, что из всех треугольников с постоянными
основанием и высотой, проведенной к этому основанию,
равнобедренный имеет наименьший периметр.
5.17. На стороне АС остроугольного треугольника ABC
дана точка М. На сторонах АВ и ВС найдите такие точки
N is. P, чтобы периметр треугольника MNP был наименьшим.
5.18. Дан острый угол ABC и точка Р внутри него.
Найдите на сторонах В А и ВС точки М и N, чтобы периметр
треугольника MPN был наименьшим.
5.19. Дан острый угол ABC и точки М и N внутри него.
Найдите на сторонах угла такие точки Р и Q, чтобы периметр
многоугольника PMNQ был наименьшим.
5.20. Докажите, что площадь четырехугольника ABCD
не превосходит АВ • CD + ВС • AD.
5.21. Точка М лежит на диаметре АВ окружности радиуса
R. Хорда CD проходит через М и пересекает АВ под углом
45е. Докажите, что СМ2 + DM2 = 2Д2.
5.22. Построить ромб так, чтобы одна его диагональ имела
заданную длину d и принадлежала данной прямой /, концы
другой диагонали принадлежали соответственно прямой и
данной окружности.
5.23. Построить квадрат, у которого одна диагональ лежит
на данной прямой, а концы другой диагонали принадлежат
соответственно данным прямой и окружности.
5.24. Построить четырехугольник ABCD, у которого
диагональ АС является биссектрисой угла А, зная длины его
сторон.
5.25. Даны прямая АВ и точки С и D по одну сторону
от нее. На прямой АВ постройте такую точку Ху чтобы
LAXC ш 2LBXD.
140

Избранные методы и приемы
5.26. Окружности с центрами О и О{ расположены по
одну сторону от прямой АВ. На прямой АВ найдите такую
точку X, чтобы касательные, проведенные из нее к двум
данным окружностям, составляли с прямой АВ равные углы.
5.27, Через точку М основания АС равнобедренного
треугольника ABC проведена прямая, пересекающая прямые
ВА и ВС в точках N и Р. Докажите, что
NA PC
NM РМ*
5.28. На биссектрисе внешнего угла С треугольника
ABC взята точка М, отличная от С. Докажите, что
МА + МВ > СА + СВ.
141

Избранные методы и приемы
§6. Применение преобразования поворота.
1. Преобразование фигуры F в фигуру /", при котором
каждая точка X фигуры F переходит в такую точку X*
фигуры F\ что ХО = ХО и LXOX = а, где О — заданная
точка и а — данный угол, 0<а<я, называется
преобразованием поворота фигуры F около точки О на угол а.
2. Если точка X — образ точки X при повороте вокруг
точки О на угол а, то этот факт будем записывать так:
3. Преобразование поворота есть движение.
Примеры.
Задача 1.
На стороне ВС равностороннего треугольника ABC
отмечена точка D и на отрезке CD как на стороне построен
равносторонний треугольник
CDE вне треугольника ABC.
Точки К yl M — середины
отрезков AD и BE соответственно.
Докажите, что треугольник
СКМ — равносторонний.
Решение.
Рассмотрим
преобразование поворота с центром в точке
С на угол 60е (рис. 77). Тощад*
. Отсю- рис. 77
да образом отрезка BE при
данном преобразовании будет
отрезок AD. Поскольку М и К — середины этих отрезков, то'
1ф (М) = К. Следовательно, СК = CM, LKCM = 60е, т.е.
треугольник СКМ — равносторонний.
Задача 2.
На стороне CD квадрата ABCD отмечена точка Е.
Биссектриса угла ВАЕ пересекает сторону ВС в точке F. Доказать,
что АЕ = ED + BF.
142

Избранные методы и приемы
Решение.
Рассмотрим поворот с цен- 1
тром А на угол 90% Тоща
*7(Д) = Я, *Г (Я) = Яр
причем 2?! лежит на ВС (рис, 78).
Тогда DE = BE[ (напомним,
что поворот есть движение, а
значит, переводит фигуру в
равную). Имеем:
BF=DE + BF.
Рис. 78
Поскольку LEXAB = LEAD, то
LFAD.
Ho LFAD = LBFA, следовательно, LEXAF = LEXFA.
Отсюда AEX = EyF = DE + JW.
Упражнения.
6.1. Дан угол ABC и внутри него точка М. Построить
равнобедренный прямоугольный треугольник с вершиной в
точке М так, чтобы две другие его вершины лежали на
сторонах угла.
6.2. Дан угол ABC и внутри него точка М. Построить
равносторонний треугольник с вершиной в точке М так, чтобы
две другие его вершины лежали на сторонах угла.
6.3. В данный квадрат впишите равносторонний
треугольник так, чтобы одна из его вершин совпала с вершиной
квадрата, а две другие принадлежали сторонам квадрата.
6.4. Даны две окружности и точка М вне этих
окружностей, Постройте прямоугольный равнобедренный
треугольник с вершиной в точке М так, чтобы две другие вершины
лежали на данных окружностях.
6.5. Внутри треугольника ABC отмечена точка Р. Найдите
на сторонах ВС и АС точки К и М такие, что РК = РМ и
LKPM =45°.
6.6. Даны окружность, квадрат и точка Р. Постройте
равнобедренный треугольник РАВ (РА = РВ)> вершины А и
В которого принадлежат окружности и стороне квадрата, а
LAPB = 45е.
143

Избранные методы и приемы
6.7. Через центр квадрата проведены две взаимно
перпендикулярные прямые. Докажите, что отрезки этих прямых,
заключенные внутри квадрата, равны.
6.8. Через центр равностороннего треугольника проведены
две прямые, угол между которыми равен 60°. Докажите, что
отрезки этих прямых, заключенные внутри треугольника,
равны.
6.9. Постройте равносторонний треугольник так, чтобы
вершины принадлежали трем данным параллельным
прямым.
6.10. Постройте квадрат так, чтобы три его вершины
принадлежали трем данным параллельным прямым.
6.11. На сторонах АВ и АС треугольника ABC построены
квадраты ABMN и ACQP во внешнюю сторону. Докажите,
что МС = ВР, МС ± ВР.
6.12. На сторонах АВ и AD квадрата ABCD отмечены
точки КиМсоответственно так, что АК + AM = АВ. Найдите
угол КОМ, те О — центр квадрата.
6.13. На сторонах АВ и АС равностороннего
треугольника ABC отмечены точки КиМ соответственно так, что
АК + АМ = АВ. Найдите угол КОМ, где О — центр
треугольника.
6.14. В равнобедренной трапеции ABCD на боковых
сторонах АВ и CD отмечены точки КиМ соответственно так,
что АК = СМ. Меньшее основание ВС трапеции равно боковой
стороне, а острый угол трапеции равен 60°. Найдите угол
КОМ, ще О — середина AD.
6.15. В ромбе ABCD с тупым углом А, равным 120°, на
сторонах АВ и AD отмечены точки КиМ соответственно
так, что ВК « AM. НАйдите угол КСМ.
6.16. Впишите в окружность два равных треугольника с
соответственно перпендикулярными сторонами.
6.17. Внутри квадрата ABCD взята точка К и на отрезке
АК как на стороне построен квадрат АКЕМ, сторона КЕ
которого пересекает сторону AD квадрата ABCD. Докажите,
что В К = DM.
6.18. На прямой / взяты последовательно точки А, В и
С, а на отрезках АВ и АС по разные стороны от прямой
/ построены равносторонние треугольники ABD и ACN.
Докажите, что середины К и L соответственно отрезков DC и
144

Избранные методы и приемы
DN и точка А служат вершинами равностороннего
треугольника.
6.19. На прямой / взяты последовательно точки А, С,
Е. На сторонах АС и СЕ по одну сторону от прямой /
построены равносторонние треугольники ABC и CDE. Точки
К и М — середины отрезков AD и BE соответственно.
Докажите, что треугольник СКМ — равносторонний.
6.20. Угол С треугольника ABC равен 120°. Доказать,
что 1С = а ,, где 1С — длина биссектрисы, выходящей из
вершины С, АС = й, БС = а.
6.21. Из точки Р, расположенной внутри равностороннего
треугольника ABC, сторона АВ видна под углом 150°.
Доказать, что отрезки АР, ЯР, СР могут служить сторонами
прямоугольного треугольника.
6.22. Внутри равностороннего треугольника ABC выбрана
точка Р так, что АР2 + ВР2 = СР*. Доказать, что
LAPB = 150е.
145

Избранные методы и приемы
§7. Применение гомотетии.
1. Гомотетия с центром О и коэффициентом к
(отличным от нуля) — это преобразование, при котором каж-
ддй точк^ X ставится в соответствие такая точка Х\ что
ОХ-кОХ.
2. Гомотетия отрезок переводит в отрезок.
3. Гомотетия сохраняет величину угла.
4. При гомотетии прямая переходит в параллельную
прямую или сама в себя.
Примеры.
Задача 1.
На продолжениях медиан АК, BL и СМ треугольника
ABC взяты точки Р, Q, R так, что ^ ^
MR = j СМ. Найти
Решение.
Заметим, что
OP = OQ OR
АО ОВ " ОС
(рис. 79).
Это означает, что
треугольник PQR
гомотетичен треугольнику ABC с
коэффициентом
гомотетии k = - -г. Тогда
если
= 1.
Рис. 79
с _25е _25
w " 16 ^ " 16
25
16*
Задача 2.
Ответ: -£.
10
BJBj, CCj — высоты остроугольного треугольника
ABC. Доказать, что радиус окружности, описанной около
146

Избранные методы и приемы
треугольника Afifc в
два раза меньше
радиуса окружности,
описанной около
треугольника ABC.
Решение.
Пусть М, N и Р —
точки пересечения
высот с окружностью,
описанной около
треугольника ABC (рис. 80).
Докажем, что
НА1
Действительно,
Рис. 80
= 90е - LABAl.
Но углы ВААХ и МСВ равны как вписанные,
опирающиеся на общую дугу MB. Тоща LMCAl = LHCA, и так как
САХ ± ИМ, то треугольник НСМ равнобедренный и НА1 =
= ДМ. Аналогично НВХ = B{N и HCl = CtP. Теперь ясно, что
треугольник Afifi^ гомотетичен треугольнику MNP с
коэффициентом гомотетии к = 2 и R
HNP
ABC
~" "**
Упражнения.
7.1. Через точку касания двух окружностей проведены
две секущие и их вторые точки пересечения с каждой
окружностью соединены хордами. Доказать, что эти хорды
параллельны.
7.2. Две окружности касаются в точке К. Прямая,
проходящая через точку К, пересекает эти окружности в точках
А и В. Доказать, что касательные к окружностям, проведенные
через точки А и В, параллельны.
7.3. Две окружности касаются внутренним образом,
причем меньшая проходит через центр большей. Доказать, что
всякая хорда большей окружности, проходящая через точку
касания, делится меньшей окружностью пополам.
147

Избранные методы и приемы
7.4. Найти геометрическое место точек — середин хорд
данной окружности, выходящих из одной точки этой
окружности.
7.5. Две окружности касаются внутренним образом в
точке О. В произвольной точке М внутренней окружности
проведена к ней касательная, пересекающая вторую
окружность в точках А и В. Доказать, что LAOM = LMOB.
7.6. Дан угол ABC и точка Р внутри него. Провести через
точку Р прямую так, чтобы ее отрезок внутри угла делился
в отношении 1:2.
7.7. Дан угол ABC и точка М внутри него. Постройте
окружность, касающуюся сторон угла и проходящую через
точку М.
7.8. Внутри угла АОВ дана точка М. Найти на луче
О А точку, одинаково удаленную от М и луча ОВ.
7.9. Внутри угла АОВ дана точка М. Найти на луче
ОА точку, расстояние от которой до точки М вдвое больше,
чем до луча ОВ.
7.10. На плоскости даны точки А и В и прямая /. По
какой траектории движется точка пересечения медиан
треугольников ABC, если точка С движется по прямой Z?
7.11. Радиус окружности, описанной около треугольника
ABC, равен R. Вычислить радиус окружности, описанной
около треугольника, вершины которого являются серединами
медиан данного.
7.12. Дан треугольник ABC и произвольная точка Р.
Доказать, что точки, симметричные точке Р относительно
середин сторон ABC, являются вершинами треугольника,
равного данному.
7.13. Доказать, что прямая, проходящая через точки
пересечения диагоналей и боковых сторон трапеции, делит
ее основание пополам.
7.14. Докажите, что точки, симметричные произвольной
точке относительно середин сторон квадрата, являются
вершинами некоторого квадрата.
7.15. Построить треугольник по периметру и двум углам.
7.16. Построить треугольник по двум углам и радиусу
описанной окружности.
7.17. Построить треугольник по отношению двух сторон,
величине угла между ними и радиусу вписанной окружности.
148

Избранные методы и приемы
7.18. Впишите в данный треугольник другой треугольник,
стороны которого были бы параллельны трем данным прямым.
7.19. Впишите в данный треугольник квадрат, две
вершины которого лежат на основании треугольника, а две
другие — на боковых сторонах.
7.20. Вписать в данный треугольник ABC прямоугольник
с отношением сторон 2:5 так, чтобы большая сторона
прямоугольника принадлежала бы основанию АС, а две вершины
лежали бы на сторонах ВА и ВС.
7.21. Докажите, что точка пересечения медиан М, точка
пересечения высот Н и центр описанной окружности О
треугольника ABC принадлежат одной прямой, причем
ИМ-ЮН (прямая Эйлера).
149

Избранные методы и приемы
§8. Метод координат.
1. Бели точка А имеет координаты х{ и yv В — х2 и у2>
2. Если точка М — середина отрезка АВ, то ее координаты
*2 д У! + У2
И
2 И 2 •
3. Уравнение окружности с центром в точке К (а; Ь) и
радиусом R имеет вид (х - а)2 + (у - А)2 = Л2.
4. Общее уравнение прямой ах + by + с = 0, где
а2 + Й2 # 0.
5. Уравнение невертикальной прямой у = кх + 1.
Примеры.
Задача 1.
Найдите геометрическое место точек, сумма квадратов
расстояний от которых до верпган А и В треугольника ABC
равна квадрату расстояния до
третьей его вершины —
точки С.
Решение.
В задачах на метод
координат важно удачно, а
точнее, выгодно выбрать систему
координат. В нашей задаче
удобно принять середину
отрезка АВ — точку О — за
начало отсчета и «положить»
отрезок АВ на ось абсцисс
Рис. 81
(рис. 81). Выберем единичный отрезок так, чтобы А (-1; 0)
и В (1; 0). Пусть координаты точки С (a; ft), а точка
М (х; у) принадлежит искомому ГМТ. Тогда МЛ2 + М52 =
= МС?. Причем последнее можно считать необходимым и
достаточным условием принадлежности точки М
искомому ГМТ. Имеем:
(х + I)2 + f + (х - I)2 + f = (jc - а)2 + (у - Ъ)2.
После надлежащих преобразований получим:
150

Избранные методы и приемы
(х + а)2 + (у + й)2
2 (о2 + й2 - 1).
А2<1, то искомое ГМТ —
Теперь ясно, что если
пустое множество.
Если о2 + й2 = 1, то (х + а)2 + (у + й)2 = 0, и ГМТ состоит
из одной точки D (— а; - й), симметричной точке С
относительно начала координат.
Если а2 + й2 > 1, то имеем окружность с центром в точке
D(- а; - й) и радиусом У ^
Задача 2.
В треугольнике ЛВС
LACB = 60% а радиус
окружности, описанной около этого
треугольника, равен R = 2 VT.
На стороне АВ взята точка D
так, что AD = 2D2? и при этом
CD = V2T Найдите площадь
треугольника ABC.
Решение.
Имеем
Рис. 82
АВ = 2R sin 60° = б.
Тогда AD - 4, DB = 2. Выберем систему координат как в
предыдущей задаче (рис. 82). Тоща координаты точки
D (1; 0). Поскольку LAOB = 120°, то ОЕ = VT, а координаты
точки О(0; VT). Пусть координаты точки С(х; у). Она
лежит на двух окружностях: одна с центром в точке О и
радиусом 2VT, другая — с центром в точке D радиусом
V2". Имеем систему
Решив систему, получим у = VI", у= -VT. Заметим, что
\у\ — это длина высоты, выходящей из точки С треугольника
ABC. Тоща S = ^АВ • \у\ = 3 VT.
Ответ: 3VT.
151

Избранные методы и приемы
Упражнения.
8.1. Найдите множество точек плоскости, разность
квадратов расстояний от которых до двух данных точек постоянна.
8.2. На плоскости даны точки Аи В. Найдите множество
точек плоскости, удаленных от А на расстояние вдвое большее,
чем от В.
8.3. На плоскости даны точки Л и В. Найдите
геометрическое место точек М таких, что AM2 + 2ВМ2 = 6АВ2.
8.4. На плоскости даны две точки А и В. Точка С
перемещается в плоскости так, что длина медианы AD
треугольника ABC остается неизменной. Найдите множество
точек С.
8.5. На плоскости даны точки А и В. Найдите множество
С точек плоскости таких, чтобы в треугольнике ABC медиана
AD была равна стороне ВС.
8.6. Найдите ГМТ плоскости, сумма квадратов расстояний
от которых до вершин данного треугольника — величина
постоянная.
8.7. Найдите множество точек плоскости, сумма квадратов
расстояний от которых до двух противоположных вершин
данного прямоугольника равна сумме квадратов расстояний
до двух других его вершин.
8.8. На данном отрезке АВ берется произвольная точка
C. По одну сторону от АВ на отрезках АС и СВ строятся
квадраты. Найдите множество середин отрезков, соединяющих
центры этих квадратов.
8.9. Окружность вписана в ромб ABCD с углом 45е.
Доказать, что для любой точки М окружности имеет место
равенство МА2 + MB2 + МС2 + М& = | АВ2.
8.10. Окружность вписана в ромб с углом 60°. Расстояние
от центра окружности до ближайшей вершины равно 1.
Докажите, что для любой точки Р окружности имеет место
равенство РА2 + РВ2 + PC2 + PD* = 11.
8.11. В треугольнике ABC на стороне ВС выбрана точка
D. Докажите, что имеет место равенство
АВ2 • DC + АС2 • BD - А& • ВС =
= BCDCBD.
152

Избранные методы и приемы
8.12. Дан треугольник ЛВС, М — его центроид. Докажите,
что для любой точки X плоскости имеет место равенство
ХА2 + ХВ2 + ХС2 = AM2 + ВЫ2 + СМ2 + ЪХМ2.
8.13. В правильном шестиугольнике ABCDEF стороны
АВ и CD продолжены до их пересечения в точке К. Докажите,
что МК2 = МЯ2 + Л/С2, ще М — произвольная точка
окружности, описанной вокруг шестиугольника.
8.14. В квадрат ABCD вписана окружность единичного
радиуса. Доказать, что для любой точки М этой окружности
имеет место равенство МА2 • МС? + MB2 • MD2 =10.
8.15. В круг вписана трапеция MNPQ (MQ \\ NP). А —
произвольная точка прямой, содержащей диаметр,
параллельный основаниям трапеции. Доказать, что
AM2 + А<£ = AN2 + AI*.
8.16. Докажите теорему о свойстве сторон и диагоналей
параллелограмма: сумма квадратов диагоналей
параллелограмма равна сумме квадратов его сторон.
8.17. На прямой / даны три точки А, В и С так, что
точка В лежит между А и С. По одну сторону от прямой /
построены равносторонние треугольники АМВ и BNC.
Докажите, что середина отрезка МС, середина отрезка NA и точка
В являются вершинами равностороннего треугольника.
8.18. Хорда АВ стягивает дугу окружности, равную 120°.
Точка С лежит на этой дуге, а точка D лежит на хорде
АВ. При этом AD = 2, BD = 1, CD = VT. Найдите площадь
треугольника ABC.
8.19. В параллелограмме ABCD на диагоналях АС и
BD взяты соответственно точки Р т Q так, что АР*.PC =
= 2:3, BQ: QD = 1: 4. Найдите PQ, если АВ = 5, AD = 3,
LADB = 90°.
153

Избранные методы и приемы
§9. Применение векторов
1. Если М — середина отрезка АВ, то
OM = ^(OA + ОВ).
2. Для того, чтобы точки Л, В и С принадлежали одной
-# -* -*
прямой, необходимо и достаточно ХВ « а ХА + р ХС, где
X — произвольная точка, aa+jS=l
3. Если М — точка пересечения медиан треугольника
ABC, a X — произвольная точка, то
ХМ = | (ХА + ХВ + iC).
4. Чтобы из попарно неколлинеарных векторов а, ^и
смможно было составить треугольник, необходимо и достаточно
5. Для того, чтобы векторы <Ги ^были перпендикулярны,
необходимо и достаточно <?- 2Г= 0.
Примеры
Задача 1.
Докажите, что из медиан
треугольника можно составить
треугольник.
Решение.
Пусть А4р BBV ССХ — меди- в.
аны треугольника ABC (рис. 83).
Тогда
АА, = ^ (АВ - СМ),
В
Рис. 83
Отсюда
+ Щ + СС, = 5!
154

Избранные методы и приемы
Задача 2.
На плоскости даны точки
А и В. Найти множество точек
С этой плоскости таких, что
медианы треугольника ЛВС,
проведенные из вершин А и
перпендикулярны.
Решение.
Введем систему координат
так, что А(0; 0), В(1; 0)
(рис. 84). Пусть С(х; у).
Тоща Л,
шВ\%
И
Рис.
Имеем
2 ' гу
Из условия перпендикулярности медиан получаем
^ = 0.
Отсюда I х - ij
Таким образом, точка С принадлежит окружности с
центром в середине отрезка АВ и радиусом w АВ. Доказательство
того, что каждая точка (за исключением М и N) окружности
удовлетворяет условию, мы оставляем читателю.
Упражнения
9.1. Точка пересечения средних линий четырехугольника
совпадает с точкой пересечения его диагоналей. Доказать,
что четырехугольник — параллелограмм.
9.2. Доказать, что в четырехугольнике отрезок,
соединяющий середины диагоналей, проходит через точку
пересечения средних линий и делится в этой точке пополам.
9.3. Точка М — середина отрезка АВ, точка М —
середина отрезка АВ'. Доказать, что середины отрезков
АА, ВВ' и ММ лежат на одной прямой.
155

Избранные методы и приемы
9.4. Докажите, что медианы треугольника пересекаются
в одной точке и делятся ею в отношении 2:1, считая от
вершины*
9.5. Докажите, что точка пересечения диагоналей
трапеции, точка пересечения ее боковых сторон и середины
оснований принадлежат одной прямой.
9.6. Дан четырехугольник ABCD, середины сторон АВ и
CD и точка пересечения диагоналей которого принадлежат
одной прямой. Докажите, что АВ || CD,
9.7. Середины сторон АВ и CD, ВС и DE пятиугольника
ABCDE соединены отрезками. Середины Н и К
полученных отрезков снова соединены. Докажите, что НК || АЕ и
9.8. В четырехугольнике ABCD точки MhJV- середины
диагоналей АС и BD. На прямых AD и ВС взяты точки Р и
Q так, что РМ || BD и QN \\ АС. Доказать, что PQ || АВ.
9.9. На стороне AD и на диагонали АС
параллелограмма ABCD выбраны соответственно точки М и N так, что
^AD и ^
Доказать, что точки М, N и В принадлежат одной прямой.
9.10. В треугольнике ABC биссектриса AD делит сторону
BD 1
ВС в отношении -~f\ = -v ^ каком отношении медиана СЕ
делит эту биссектрису?
9.11. Точки D, Е и F лежат на сторонах треугольника
BD СЕ 2 AJF 1
ABC так, что ^ = 3, -^ = ^ и — = ^. Доказать, что
прямые AD, БЕ и С/1 проходят через одну точку.
9.12. На сторонах АВ, ВС и СА треугольника ABC выбраны
точки /", М, # соответственно так, что -== = ттт? — ттт»
Доказать, что точки пересечения медиан треугольников
ABC и FMN совпадают.
9.13. Дан четырехугольник и точка М. Доказать, что
точки, симметричные точке М относительно середин сторон
данного четырехугольника, являются вершинами
параллелограмма.
156

Избранные методы и приемы
9.14. Точки L и М — середины противоположных сторон
АВ и CD четырехугольника ABCD. Доказать, что для того,
чтобы четырехугольник был трапецией, необходимо и
достаточно ил = ^ (AD + вс).
9.15. В правильном треугольнике ABC на стороне ВС
выбрана точка Ми из нее опущены перпендикуляры MN и
МК на стороны АВ и АС. Кроме того, проведены отрезки
KN и ОМ (О — центр треугольника), пересекающиеся в
точке Р. Доказать, что NP = КР.
9Л6. В треугольнике ABC АВ = 4, АС = 10,
д
= 60°. Точка N принадлежит стороне ВС и -т= = 3.
Найти AN.
9.П. BD — медиана треугольника ABC. LDBC = 90е,
^^AB. Найти LABD.
4
9.18. В треугольнике ABC на сторонах £С и АС
соответственно выбраны точки D и Е так, что 2Ф = CD,
АЕ = 2СЕ. Найти jg, если ii)l5£n LABC = 60°.
9.19. В параллелограмме ABCD точка К — середина
стороны ВС, а точка М — середина стороны CD. Найти
AD, если АК= 6, ЛМ= 3, Z£AM= 60°.
9.20. В треугольнике ЛЯС Z£ = 90\ Медианы AD и
#Е взаимно перпендикулярны. Найти LACB.
9.21. В треугольнике ABC LBAC = 60°, А0 = 6, АС = 4.
Найти угол между медианами 2Ш и CF.
9.22. В прямоугольном треугольнике ABC (LC = 90е)
АС = а, ВС = a VT. Доказать, что медианы АМХ и СМ2
перпендикулярны.
9.23. Дан выпуклый четырехугольник ABCD. LA - 65°,
LD = 85°, АВ = V3", CD = 3. Найти длину отрезка,
соединяющего середины сторон AD и ВС.
9.24. В четырехугольнике ABCD диагонали АС и ЯО
взаимно перпендикулярны и пересекаются в точке О.
ОВ = ОС= 1, ОА ж 8, О£> = 7.
Найти угол между прямыми АВ и DC.
157

Избранные методы и приемы
9.25. В трапеции ABCD боковая сторона АВ
перпендикулярна основаниям AD и ВС. Точка Е — середина стороны
CD. Найти отношение -^, если АЕ = 2АВ и АЕ ± CD.
9.26. Доказать, что в произвольном треугольнике ABC
АВ* + ВС2 + СА2
ctg LA + ctg LB + ctg LC = j^ .
9.27. Пусть М и N — середины сторон CD и Di?
правильного шестиугольника ABCDEF, a P — точка пересечения
отрезков AM и БАГ. Найти угол между прямыми AM и BN.
158

Глава IV
Многовариантные геометрические задачи
Как правило, первый этап решения геометрической
задачи — это выполнение чертежа, соответствующего условию.
В подавляющем большинстве задачи школьного учебника
предполагают однозначную геометрическую трактовку: задача
построения чертежа по исходным данным имеет одно решение.
Естественно, такая практика формирует определенный
стереотип, результатом которого являются неполные решения
определенного класса геометрических задач, а именно таких,
где заданные параметры не позволяют выполнить чертеж
одновариантно. Подобные задачи нередко встречаются на
вступительных экзаменах и, естественно, являются
традиционно сложными для абитуриентов.
Настоящий пункт ставит перед собой цель не только
познакомить учащихся с задачами указанного типа, но и
попытаться раскрыть некоторые причины, ведущие к
неоднозначной трактовке условия.
Понятно, что предлагаемый материал принесет
максимальную пользу, если читатель попытается решить задачи
самостоятельно и сравнить свои решения с авторскими.
§1. Условие задачи не определяет взаимное
расположение точек и фигуры
Примеры
1) Точка или принадлежит отрезку АВ> или ему не
принадлежит, но лежит на прямой АВ.
2) Точки лежат или в одной полуплоскости относительно
заданной прямой, или в разных. То же и с полупространством.
3) Различные положения центра описанной окружности
или ортоцентра треугольника в зависимости от вида
треугольника (остроугольный, прямоугольный, тупоугольный).
Задача 1.
Длина окружности, описанной около равнобедренного
треугольника, равна 20л;. Найдите площадь этого
треугольника, если его основание равно 12.
159

Многовариантные геометрические задачи
Решение.
Очевидно радиус окружности
равен 10. Нетрудно догадаться, что в
данную окружность можно вписать
два равнобедренных треугольника с
заданным основанием (рис. 85). В
первом треугольнике LCX — острый, V
во втором LC2 — тупой (случай,
когда L Сх = L С2 = 90° числовые
данные задачи исключают).
I случай. Рис 35
Имеем АВ = 2R sin LC^ где Л —
радиус окружности. Отсюда sin LCX = ^. Поскольку LCX —
4
острый, то cos LCX = ^. По теореме косинусов
А& ж 1АС\ - 1АС\ • cos LCV
Далее, получаем АС* = 360. Площадь ААСХВ равна
5 = 2АС* sin LC\ = 1^#
II случай.
3 4
Здесь также sin LC2 - -=, но cos LC2 = - tf, так как
LC2 — тупой. Теперь, придерживаясь вышеизложенной схемы
решения, легко установить, что площадь ААС2В равна 12.
Ответ: 108 или 12.
Задача 2.
ABCDE —правильный пятиугольник. Точка М обладает
таким свойством, что ADEM — равносторонний. Найти
величину угла АМС.
Решение.
Так как внутренний угол правильного пятиугольника
равен 108°, то
LMDC = LEDC - LEDM ж 108е- 60° = 48° (рис. 86).
160

Многовариантные геометрические задачи
В силу того, что AMDC —
равнобедренный (MD = DC), то
LDMC = \ (180° - 48е) = 66е.
Аналогично устанавливаем, что
£ЕМА = 66°. Отсюда LAMC =
= 360е - (60е + 66° + 66е) - 168°.
Однако приведенное решение
не является полным.
Действительно, в условии задачи не сказано,
что точка М лежит внутри
пятиугольника. Поэтому возможен
второй случай (рис. 87):
LMDC = LMDE +LEDC = 60°+
+ 108° = 168е.
Так как AMDC —
равнобедренный (MD = DC), то Z.CMD = 6\
Аналогично получаем LAME = 6°.
Следовательно,
LAMC =LEMD - 2 LCMD =
= 60е- 12е = 48е.
Ответ: 168е или 48е.
Задача 3.
Найти длины сторон АВ и АС
треугольника ABC, если ВС = 8, а
длины высот, проведенных к АС и ВС, равны соответственно
6,4 и 4.
Решение.
Обозначим основание высоты, проведенной к стороне АС,
через Bv а к стороне ВС — Д. Выразив площадь ААВС двумя
способами, получим А\ - ВС = ВВХ • АС. Отсюда 4 • 8 =
= 6,4ЛС, ЛС = 5.
Обратим внимание читателя, что на данном этапе
решения задачи мы преднамеренно не делали никаких ссылок на
рисунок. И это можно понять. Ведь любая ссылка на готовый
6 Учимся решать задачи по геометрии
161

Многовариантные геометрические задачи
чертеж зафиксировала бы
положение точек ДиБ, относительно
отрезков ВС и АС соответственно. Но
это положение зависит от вида
треугольника ABC. Однако условие
задачи умалчивает, остроугольный он
или тупоугольный. (Случай
прямоугольного треугольника очевидно
не реализуется.)
Таким образом, для полного
решения задачи надо разобрать
четыре случая: ДАЯС — остроугольный,
LA — тупой, LB — тупой, LC —
тупой. Вместе с тем более
внимательный анализ показывает, что
этот перебор можно сократить.
Действительно, так как
Рис. 88
то угол В тупым быть не может.
I случай.
Треугольник остроугольный
(рис. 88). Из ААА^С
А1С ш V AC* -AAf m 3.
Тоща Ар = ВС - Af = 5.
Bi A
Рис. 89
Из
II случай.
LA — тупой (рис. 89). Из
Рис 90
ABBfi ВХС = V5C2- ВВ% = 4,8,
т.е. В1С<АС, что не
соответствует рисунку. Значит, этот случай не реализуется.
Читатель может задать вопрос: зачем же рассматривать
ту ситуацию, которая не существует? Но, как говорят в
народе, легко быть крепким задним умом.
Ill случай.
LC — тупой (рис. 90). Заметим, что отрезок СВХ по-
прежнему равен 4,8. Но в разбираемой ситуации это не
приводит к противоречию. Из ААВ.В
162

Многовариантные геометрические задачи
АВ:
Задача 4.
В круг радиуса R
вписана трапеция так, что
расстояние от центра круга до
одного из ее оснований вдвое
меньше соответствующего
расстояния до другого
основания. Найти периметр
трапеции, если известно, что
один из ее углов равен 60°.
Решение.
[ = УТЗТ
Ответ: У?Ги 5 или V137 и 5.
6
Рис. 91
Так как в условии задачи не сказано, вде лежит центр
круга (внутри или вне трапеции), то необходимо рассмотреть
два случая. (Случай, когда центр круга принадлежит одному
из оснований трапеции, условие задачи исключает.)
На рис. 91 О — центр круга, MN X AD, ON = 2OM, О
принадлежит отрезку MN. Проведем ВР ± AD. Учитывая
условие, LABP = 30°. Пусть ОМ = х, тогда NO = 2х, ВР = 3*.
Из AOBN BN = УЛ2-
ААВР АР = у^р = хуГ5~. Имеем:
из ААОМЛМ=УЛ2-х2, из
-х? -ху/Т.
Тогда
- 4х> = УД2 - х2 - xVT.
Отсюда после несложных пре-
п
образований получаем х = у.
Следовательно, ON = 2х =
— R — противоречие.
Аналогично можно
показать, что случай, когда
ОМ = 2ON, не реализуется.
Рассмотрим второй случай
(рис. 92).
Рис. 92
163

Многовариантные геометрические задачи
Рассуждая, как и в первом случае, для х получаем урав-
х Л RVT ^
нение
Отсюда х
Т7Г
Тоща ис-
« ПЛУТ
комый периметр равен —=—. (Предлагаем читателю в этом
убедиться самостоятельно.)
Ответ:
URy/T
Задача 5.
Угол ABC равен 60°, причем АВ = ВС = а. Окружность
Ох касается АВ в точке А, а окружность О2 касается ВС в
точке С, кроме того, эти окружности касаются друг друга
внешним образом. Найти радиусы окружностей, если
известно, что их отношение равно двум.
Решение.
Если известно, что
окружность касается прямой
в данной точке, то отсюда
еще не следует
однозначность положения ее центра
в одной из полуплоскостей,
определяемых прямой.
Этот факт нередко служит
источником
неопределенности геометрической
задачи. Как раз здесь мы
столкнулись с подобной
ситуацией. Действительно,
каждый из центров Ох или Рис. 93
О2 может находиться как внутри угла, так и вне его.
I случай.
Ясно, что ОХА ± АВ и О2С ± ВС. К — точка пересечения
прямых ОХА и О2С (рис. 93). Легко установить, что LAKC =
= 120е. Поскольку АВ = ВС, то ААВК = АСВК по гипотенузе
и катету. Отсюда LABK = АСВК = 30е. Тогда АК = СК =
з •
164

Многовариантные геометрические задачи
Пусть О2С = г. По условию ОХА = 2г. Далее
Отсюда после
необходимых преобразований
получаем
V3T-3VT
г = ^ а.
II случай.
Понятно, что
LOfiC - 30°.
Тоща О,С = ~-t a
(рис. 94).
Ill случай.
Имеем
3 '
:. 95).
Применим к АОгКО2 теорему косинусов. Имеем
*•
- 2
Рис. 94
IV случай.
Как и в первом случае, определяем, что LOXKO2 - 120°,
LABK= LCBK= 30е (рис. 96). Далее
165

Многовариантные геометрические задачи
Рис. 95
Рис. 96
Опять-таки применяем теорему косинусов к АО{КО2
166

Многовариантные геометрические задачи
V3T+3VT
Отсюда г = -А а.
Ответ:
V3T-3V3" V35"-3V3"
а и
а, или
, или
-, или
а и
6 н 3
V3T+3VT
Задача 6.
Два ромба ABCD и АМНК>
имеющие общую вершину А,
расположены так, что стороны
АВ и AM образуют угол в 30е.
Известно, что углы при
вершине А обоих ромбов равны 60°,
площадь пересечения ромбов
равна 5VT, а площадь их
объединения равна 23VT. Найти
площадь каждого из ромбов.
Решение.
Наверное, прочитав условие этой задачи, сразу сложно
представить соответствующую «картинку». Однако этот
«недостаток» в качестве приложения имеет и свои преимущества.
Возможно, попытки выполнить чертеж подскажут читателю,
что одновариантно это сделать нельзя.
Нарисуем ромб ABCD с углом А, равным 60е (рис. 97).
Поскольку по условию стороны AM и АВ образуют угол в
30°, то сторона AM может лежать или на луче AMV или на
луче АМ2. Однако, нарисовав ромб АМНК в каждом из двух
случаев, мы увидим, что фигуры (пересечение ромбов) будут
симметричны относительно АС, а значит, равны. Поэтому
принадлежность точки М лучу АМ{ или лучу АМ2 не будет
источником многовариантности в данной задаче.
Но более внимательный подход покажет, что форма
пересечения ромбов зависит от положения вершины Н на
луче АВ.

Многовариантные геометрические задачи
I случай.
АН < АВ (рис. 98). Пусть стороны
ромбов ABCD и АМН К соответственно
равны а и Ь. Поскольку острые углы
этих ромбов содержат по 60°, то
2 ' а ^амик ~ 2 *
Рис. 98
В рассматриваемом случае
пересечение ромбов — это треугольник АН К, а объединение
состоит из ромба ABCD и треугольника АМН. Учитывая
условие, составляем следующую систему:
23VT,
5VT.
Отсюда получаем а = 6, Ъ = 2VT Однако теперь не надо
спешить с какими-либо выводами, а проверить, удовлетворяет
ли найденный результат
рассматриваемой геометрической
конфигурации. Из ААКН с помощью
теоремы косинусов
устанавливаем, что АН = 2VT3^ Таким
образом, АН>АВ, что противоречит
рассматриваемому случаю.
II случай.
АВ<АН<ЗАВ (рис. 99).
Здесь пересечение ромбов —
это четырехугольник АВЕК,
объединение состоит из ромба ABCD
и двух треугольников АМН и
ВНЕ. Из ААМН по теореме косинусов устанавливаем, что
АН = bVT. Тогда ВН = ЫТ- а. Легко показать, что
АВЕН ш 90е, LEBH ш 60е.
Рис. 99
Отсюда SBHE = ■* g-^ . Осталось
отметить, что
, a S
168

Многовариантные геометрические задачи
Теперь можно составить систему
, cNT (VJb-afVT _ „-
4 2 8 ~ '
(VJb-afVT _ .„г
4 " 8 " 5V3'
После надлежащих преобразований легко получить
\а = 4VT,
Если Ъ = 2V5"", то АН = 6VT> a = 4VT", что соответствует
рассматриваемому случаю. Если Ь = 4VT, то
АН = 4VF> a = 2VF.
И этот результат подходит. Таким
образом, площади ромбов
принимают одно из двух значений
16УТили 12VT.
Ill случай.
АН > ЗАВ (рис. 100). Теперь
пересечение ромбов — это
треугольник ABC, а объединение
состоит из ромба АМН К v треугольника
ACD. Имеем
23VT,
4
5V3:
4
Отсюда _
Однако АН = bVT= 6VT< За = 6V5", что не удовлетворяет
рассматриваемому случаю.
= 12УТили
Ответ: SABCD = 16\Ти
16V3:
169

Многовариантные геометрические задачи
Задача 7.
Основанием пирамиды SABCD служит прямоугольник
ABCD, диагональ BD которого составляет со стороной ВС
угол а. Все боковые ребра пирамиды имеют длину /, а
величина угла ASC равна 2/}. Пирамида пересечена плоскостью,
равноудаленной от всех ее вершин. Определить площадь
сечения пирамиды этой плоскостью.
Решение.
Заметим, что если плоскость пересекает отрезок в его
середине, то концы отрезка равноудалены от этой плоскости
(докажите
самостоятельно). Следовательно,
секущая плоскость, о которой
говорится в условии,
должна пересекать ребра
пирамиды в их серединах.
Возможны три
принципиально различных
положения секущей плоскости.
I случай.
М, N, Р, Q —
середины соответственно ребер
AS, BS, CS, DS (рис. 101). рис Ю1
Так как боковые ребра
пирамиды равны, то ее вершина проектируется в центр
описанной окружности основания, в данном случае в точку
пересечения диагоналей прямоугольника.
Из AOSC ОС = /sin/З. АС = ЮС = 2/sin/3.
Sabcd
sin (180° - 2а) = 2Z2 sin2£ sin 2а.
Четырехугольник MNPQ гомотетичен прямоугольнику
ABCD с коэффициентом гомотетии -= и центром S.
Следовательно, SMNPQ- -rSASCD = iyl2s\n2fism2a.
II случай.
М, N, P, Q — середины соответственно ребер АВ, SB,
SC, DC (рис. 102). Очевидно MNPQ — трапеция, причем О
170

Многовариантные геометрические задачи
принадлежит MQ, MQ = ВС,
NP = -у MQ. Несложно
показать, что
MQ = 21 sin /3 cos а.
Проведем ОТ ± ВС. L —
точка пересечения прямых ST
и NP. Так как
MQ ± пл. SOT,
то OL ± MQ.
Очевидно SL = LT, тоща Рис 102
III случай.
А#, N, P, Q —
середины соответственно
ребер ЛД i45, 5S, ЯС
(рис. 103).
По аналогии со
вторым случаем можно
показать, что
-т12 sin/3 sin a x
х Vl-sin2/3sin2a.
Предлагаем читателям в этом убедиться самостоятельно.
171

Многовариантные геометрические задачи
§2. В условии задачи фигурируют две
касающиеся окружности, но не указан
способ касания: внешний или внутренний. В
задаче даны две точки, делящие
окружность на две дуги, кроме того
известно, что некоторая прямая касается
окружности, но не указано, на какой
из двух дуг лежит точка касания
Задача 8.
Дан отрезок длины 20. Три окружности радиуса 4 имеют
центры в концах отрезка или в его середине. Найдите радиус
четвертой окружности, касающейся трех данных.
Решение.
°р °2> °з — центры окружностей радиуса 4 (рис. 104).
Причем оръ = 20, О2 — середина отрезка Ору О4 — центр
окружности, касающейся трех данных. Пусть искомый
радиус равен х. Тоща Ор4 = х + 4, О4О2 = х - 4. Для
прямоугольного треугольника Ор4О2 (докажите самостоятельно,
что О4О2 ± Орг) (х + 4)2 = (х - 4)2^+ 102.
Отсюда х = 6,25.
Рис. 104
Опять-таки может создаться впечатление, что получен
окончательный ответ. Но на самом деле это не так, потому
что существует еще одно совершенно иное положение
четвертой окружности — рис. 105. Имеем:
172

Многовариантные геометрические задачи
Рис. 105
ОАОХ- О4О2= *-4, О4Ог = х + 4.
Проведем О4К ± ОХО2. Очевидно О{К = = КО2 = 5. Из
АО4КО2 О4К2 = (х - 4)2 - 52. Из ДО4*О3
О4К2 = (*+4)2- 152.
Получаем (х - 4)2 - 52 = (х + 4)2 - 152. Отсюда х = 12,5.
Заметим, что существуют еще четыре случая положения
центра четвертой окружности (центрами могут быть точки,
симметричные точке О4 относительно прямой ОХОЪ или
относительно точки О2). Очевидно, что эти случаи будут давать
уже ранее полученные результаты.
Ответ: 6,25 или 12,5.
Задача 9.
Две окружности радиусов R и г (R > г) касаются в точке
Л. Определить сторону равностороннего треугольника, одна
из вершин которого в точке А, а две другие лежат на разных
окружностях.
Решение.
Нетрудно догадаться, что полное решение требует
рассмотрения двух случаев: данные окружности касаются
внешним образом (рис. 106) и внутренним (рис. 107).
173

Многовариантные геометрические задачи
Пусть искомая
сторона правильного
треугольника равна а.
Рассмотрим первый
случай (рис. 106).
Пусть
LOXAB = а,
0°<а<90в.
Рис. 106
Тогда
- 120° - а.
Из
равнобедренного треугольника ОХАВ по теореме синусов находим, что
а = 2R cos а, аналогично из АО^С а = 2r cos (120е - а). Имеем
а = 2r cos (120е - а) = - г cos а + rVTsin а = - г cos a +
+ VTrVl-cos2a = -^
Отсюда a (2R + г) =
+ 4Rr + 4r>) =
Во втором случае (рис. 107)
легко показать (предлагаем
читателям это сделать
самостоятельно), что если ААВС
равносторонний и точка Oj лежит
внутри круга с центром О2, то
точки С и В лежат в разных
полуплоскостях относительно
прямой ЛОГ
Пусть LBAO{ = а. Тогда
/П АС - 60° - « Рис' 107
Аналогично из равнобедренных треугольников OjAE и
получаем соответственно
a = 2R cos a, a = 2R cos (60° - a).
174

Многовариантные геометрические задачи
Отсюда нетрудно установить, что а = *ы ' -.
V RT ~ RT т г
Заметим, что если О1 лежит вне круга (или на
окружности) с центром О2, то точки В и С лежат в одной
полуплоскости относительно АО{ (или точка С лежит на АО{), и
ответ в этом случае не изменится.
Л RrVT RrVT
Ответ: * ., -или
Задача 10.
Расстояние между центрами двух окружностей равно Юг.
Одна из окружностей имеет радиус 5г, вторая 6г. Некоторая
прямая пересекает меньшую окружность в точках Л и В и
касается большей в точке С. Найти длину хорды АВ> если
АВ = 2ЯС.
Рис. 108
Решение.
Учитывая величины радиусов окружностей и расстояние
между их центрами, устанавливаем, что данные
окружности имеют две общие точки (рис. 108). О2С ± АВ. Проведем
°ici II О2С, ОД || Cfi. Очевидно OlClCAl — прямоугольник и
175

Многовариантные геометрические задачи
АСХ = Cfi. Пусть АСХ = С{В = х. Тоща, учитывая условие,
ВС = х.
Отсюда ОД = 2*. Пусть ОХСХ = у. Имеем
ОД - О2С - А1С - Ьг - у
Из ДОда 25^ = х2 + >^.
Из АОДО2 100л2 = 4ДС2 + (6г - у)2. После несложных
преобразований устанавливаем, что 2x=2rV2T~, т.е. АБ= 2л/2П
Рис. 109
Было бы хорошо, если читатель заметит, что
приведенное решение не является полным. В самом деле,
проведем касательную к большей окружности перпендикулярно
Орг (рис. 109). Здесь точка С принадлежит прямой ОгО2, и
условие АВ = 2ВС очевидно выполняется. Из АО{АС А(?=
= ОХА2 - Of? = 25г* - 16/* = 9/*. Итак, АВ = 2БС = 6г.
Ответ: 2п^П~или 6г.
Задача 11.
Дан равнобедренный треугольник ABC (АВ - ЯС). В
точке М к окружности, вписанной в треугольник, проведена
касательная, перпендикулярная к стороне ВС. D — точка
пересечения касательной со стороной ВС. Определить площадь
176

Многовариантные геометрические задачи
треугольника ABC, если радиус вписанной окружности равен
г, а площадь треугольника MBD равна S.
Рис. Ш
Рис. ПО
Решение.
Известно, что
работать с крупным
чертежом удобней,
чем с маленьким.
Как нам кажется,
этот тривиальный
факт в данной задаче
играет решающую роль.
На рис. ПО построены равнобедренный треугольник ABC
и вписанная в него окружность. MD — касательная, о которой
говорится в условии.
А если чертеж увеличить? — рис. 111. Теперь несравнимо
легче заметить, что можно провести еще одну касательную
M{DV удовлетворяющую условию. (Ведь на рис. ПО вписанная
окружность почти «не оставила места» для касательной
I случай.
К — точка касания вписанной окружности со стороной
ВС. Очевидно OMDK — квадрат. Тоща MD = r. Так как
2S
JMBD
то BD
25
—. Далее, ВК •
DK= = —
Из
&ОВК:
яо= V —
177

Многовариантные геометрические задачи
Отсюда Ц
(iV4S2 + 4&
25
г
II случай.
АОВК-ЛСВЕ.
- ЕС ЕС ГВЕ
А \2 /1 # о i
г2 + 2/ + г г ~V4S2 + 4Sr* + 2/^*4
•
Покажем схематичное решение.
MiOKDl — квадрат, ВDx = у-, ВК = *f-r, BO
S
-45/*+ 2/,
_ (во + oEfr _ (Jv*1 - «* + а* + И ,»
^ 5ЛГ 25 -г2
Ответ:
§3. В задаче фигурируют объекты,
которым приписываются определенные
свойства, но не указан порядок
соответствия между множеством
объектов и множеством их свойств
Примеры.
1) В условии сказано, что треугольник ЛВС
равнобедренный, но не сказано, какие пары сторон равны.
178

Многовариантные геометрические задачи
2) Точка М делит
отрезок АВ на отрезки
длиной а и Ь. При этом не
уточнено, какой из них
равен а, а какой — Ь.
3) Известно, что угол
между пересекающимися
прямыми АВ и CD равен
а. Однако не указано, какой из углов —
AMD или АМС (М — точка пересечения
прямых) — острый.
Задача 12.
Дан ромб со стороной, равной 1, и
л
острым углом при вершине, равным -jr.
Точка К лежит на стороне ВС, причем
ВК = КС. Найти расстояние от вершины
В до прямой АК.
Решение.
Условие задачи нас «привязывает» к
вершине В. Но при этом мы не знаем,
является ли угол В острым или тупым.
I случай.
Рис. 113
5л
-g- (рис. 112). Проведем ВЕ±АК. Отрезок BE —
= ^ABBKsin LB = \sin$ = \.
2 4 6 8
Из ААВК по теореме косинусов
искомый. Имеем: 5
АК
V
АВ2 + ВК2 - 2АВ
АК
II случай.
ж
-£ (рис. 113). Имеем:
179

Многовариантные геометрические задачи
1
1
BE-
2S
ABK
1
AK
Ответ:
Задача 13.
Длины соседних сторон
вписанного в окружность
четырехугольника отличаются на 1.
Длина наименьшей из них
также равна 1. Найти радиус
окружности.
Решение.
Пусть ABCD —
четырехугольник, о котором говорится
в условии. Например, ВС — его
наименьшая сторона, ВС = 1.
АВ и CD соседние с ВС стороны.
Поэтому АВ
или
2V5-2V3"
1
2V5-2V3"'
Рис. 114
CD = 2. Сторона AD должна отличаться от
соседней стороны, равной 2, на единицу. Поэтому для AD
возможны два значения: AD =3 или AD = 1.
I случай.
AD = 3 (рис. 114). Так как хорды АВ и CD равны, то
ВС || AD и ABCD — равнобедренная трапеция. Проведем
BE X AD. Легко показать, что АЕ= = =1, DE- 2. Из
Из ABED BD=VT. Ясно, что
равен R. Тоща
ААВЕ
LBAD = 60°.
Пусть радиус окружности
= 2R sin 60е. Отсюда R
II случай.
AD=1 (рис. 115). Очевидно ABCD —прямоугольник.
Зная стороны прямоугольника, легко показать, что его радиус
V5~
V5
описанной окружности равен -у-
Ответ:
V2T vT
или
180

Рис. 115
Многовариантные геометрические задачи
Задача 14.
Периметр трапеции равен
112. Точка касания вписанной
в трапецию окружности делит
одну из боковых сторон на
отрезки, равные 8 и 18. Вычислить
основания этой трапеции.
Решение.
Пусть ABCD —трапеция, о
которой говорится в условии.
М — точка касания вписанной
окружности с боковой стороной
AS. По условию точка М делит
АВ на отрезки, равные 8 и 18.
Налицо неопределенность:
неизвестно, какой из отрезков —
AM или MB — равен 8, а
какой 18.
Сделаем чертеж — рис. 116.
Имеем ОМ LAB, LBAO -
= LOAD, LABO ш LOBC. Угол
BAD — острый, угол ABC —
тупой. Отсюда LMAO < LMBO,
следовательно, АМ>МВ, а значит, AM = 18, MB « 8. И,
казалось бы, неопределенность условия задачи исчезает. Однако
здесь сработал глубоко укоренившийся стереотип: изображать
трапецию с двумя острыми углами при большем основании.
Таким образом, нельзя утверждать, что LBAD — острый.
Он может быть и тупым — рис. 117 (случай, когда LBAD
585 90°, условие задачи исключает, так как AM*MB).
I случай.
LBAD — острый (рис. 116). LBAD +LABC = 180°. Сле-
довательно, LAOB = 90°. Из ААОВ ОМ = = ЧАММВ = 12.
Так как в данную трапецию можно вписать окружность,
112
то АВ + CD = ВС + AD - ^ = 56. Отсюда CD = 30.
Пусть СТ = х, тоща DT = 30 - х. Из ACOD
ОТ2 = СТ- TD, 144 = х (30 - х).
Рис. 116
181

Многовариантные геометрические задачи
Отсюда х = б или х = 24. Поскольку угол ADC — острый,
то СТ < TD. Значит, СТ = 6, Г£> = 24. CW=CT = 6, 2МС-
= £>Г = 24 (N я К — точки касания окружности с
основаниями трапеции). BN=BM = 8, ЛК = ЛМ= 18. Отсюда
ВС = 14, AD = 42.
II случай.
LBAD — тупой (рис. 117).
Поскольку в предыдущем
случае для нахождения длин от- М\
резков СТ и TD мы не
использовали порядок соответствия
чисел 8 и 18 длинам отрезков
AM и MB, то сразу можем ут-
верждать, что СТ - 6, TD - 24.
Отсюда легко получить ЯС = 24, AD = 32.
Однако и сейчас решение задачи нельзя считать полным.
В самом деле, углы при большем основании трапеции не
обязательно острые, но (!) один из них непременно острый.
А если отрезки с длинами 8 и 18 лежат именно на боковой
стороне, которая в двух рассмотренных случаях образовала
острый угол с основанием? (На наших рисунках это сторона
CD.) Придется рассмотреть и этот случай.
Будем пользоваться теми же рисунками. Итак, СТ - 8,
TD - 18, MB = х. Имеем знакомое уравнение 144 = х (30 -
- *). Его корни х = 6 или х = 18. Для рис. 116 MB = 6, а
для ри$. 117 MB = 18. Дальше — понятно.
Ответ: 14 и 42 или 24 и 32.
Сделаем одно замечание. Порой «алгебра» геометрической
задачи может навести на мысль о многовариантности. Так,
в только что разобранной задаче наличие двух корней
х = 6 и х = 18, наверное, могло бы стать своего рода
подсказкой. Ведь даже если учащийся «зевнул» второй случай,
то необходимость проверки реализации полученного
промежуточного результата, возможно, сыграла бы свою роль.
Задача 15.
В треугольнике ABC LA = 75е, LB = 45°. На стороне
СК
СА берется точка К так, что -^- = 3. На стороне СВ берется
182

Многовариантные геометрические задачи
точка М так, что прямая
КМ отсекает от
треугольника ABC треугольник, ему по-
V"hM
добный. Определить -j=r.
Решение.
С большой степенью
вероятности первая идея,
которая может возникнуть, —
это выбрать точку М так, А
чтобы КМ || АВ. В этом
случае LCKM = 75е. Однако ес-
*"*■ 118
45е, то мы также получим
ли провести КМ так, что LCKM
треугольник, подобный данному.
На рис. 118 этим двум случаям соответствуют точки
Мх и М2.
Для подобных треугольников ABC и КСМХ запишем
КМ, СКЪ
АВ " АС " 4'
Для подобных треугольников А В С и
KM.
C1C
~СВ' ПуСТЬ
П° теореме
М2 С К имеем
С* А
=
sin 75
т. Отсюда СВ =
= 2х (1 + V3). Таким
образОМ ^M2_CiC_
ооразом, ^ -C5~
3 3 (V3"- 1)
Ответ: -г или ч . s
4 4
Задача 16.
В правильной треугольной призме две вершины верхнего
основания соединены с серединами противоположных сторон
нижнего основания. Угол между полученными прямыми
равен ~э. Найти объем призмы, если длина стороны основания
равна а.

Многовариантные геометрические задачи
Решение.
На рис. 119 изображена
правильная треугольная
призма. D — середина ребра АВ,
Е — середина ребра ВС. По
условию угол между прямыми
А1Е и C{D равен ^.
Следовательно, возможны два случая:
1) jLAflC^LDOE**^;
2) LApD = LCpE = \.
J Рис. 119
Рассмотрим первый случай. Очевидно, что
равнобедренная трапеция, тогда DO = ОЕ = DE = ^
средняя линия ААВС) и Ар = О CJ = ^Cj = а. Отсюда
За
-~. Высота призмы
Я
•АЕ*= V Иг -
2 '
Объем призмы V = S
авс н - 4
8
л
Для второго случая имеем L Е А1 С{ = -г. Проведем
ЕТ ± A1CV Тогда
Из
А1Е = —— = —2~-. Следовательно,
что невозможно, так как А^Е — наклонная, а АЕ — ее
проекция на плоскость АВС.
Ъагу/Т
Ответ:
8 Ф
184

Рис. 120
Многовариантные геометрические задачи
Задача 17.
В основании пирамиды —
правильный треугольник со
стороной V5". Боковые грани
пирамиды равновелики. Одно из
боковых ребер равно 3VT. Найти
объем пирамиды.
Решение.
Так как ребра основания
данной пирамиды равны, а
боковые грани равновелики, то
равны и высоты боковых
граней, проведенные из вершины
пирамиды. А отсюда следует,
что равны прямоугольные
треугольники, образованные
высотой пирамиды и высотами
боковых граней. Следовательно,
боковые грани данной
пирамиды образуют равные углы с
плоскостью основания. Значит
(докажите самостоятельно!), точка
О — проекция вершины
пирамиды на плоскость ABC —
равноудалена от прямых,
содержащих стороны основания.
Тогда возможны два
случая: О — центр вписанной
окружности ААВС и О — центр вневписанной окружности.
Рассмотрим первый случай (рис. 120).
Очевидно в этом случае пирамида является правильной,
и DA = DB = DC ж 3vT, АО
Высота пирамиды Н = DO
Объем пирамиды V = ^ S^
Рис. 121
У/А& - ОА2
„ 1 3V3"
Если О — центр вневписанной окружности (рис. 121),
то легко показать, что АО = 2АК = 3VT (К — середина ВС).
Следовательно, AD*3VT. Отсюда
Имеем
185

Многовариантные геометрические задачи
Н =OD =
- ОС?
1
3
3V3"
2V3~=3.
Ответ: 2\/Тили 3.
Задача 18.
Через вершину Вх куба ABCDA^Bfi^ проведена
плоскость, пересекающая ребра ВС и АВ и образующая с гранью
ABCD угол а, причем в
сечении получен равнобедренный
треугольник. Найти площадь
сечения, если ребро куба
равно а.
Решение.
Пусть секущая плоскость
пересекает ребра ВС и АВ
соответственно в точках N
и М.
Возможны три случая:
основанием равнобедренного
треугольника может служить
MN, или ВХМ, или BXN
(очевидно достаточно из двух
последних случаев рассмотреть
один).
I случай.
Здесь М Вх = NBV Тогда
MB = BN и BD± MN
(рис. 122).
По теореме о трех
перпендикулярах ВХЕ ± MN и,
следовательно, LBXEB = a.
Shmv ЕВ • ME
cos а ""
Рис. 122
Рис. 123
cos а
BE?
cos а
cos а
sin2 а
II случай.
Имеем МВ{ = MN. AMBXB = AMBN по гипотенузе и
катету, тогда В Вх = BN. Следовательно, N=C (рис. 123).
Проведем BE ± МС. LBXEB = а. Пусть СМ = х. Отсюда
1,86

Многовариантные геометрические задачи
Имеем MB *
a sin a
"~V-cos2a#
С — НАГ41 J
^мвхс 2
СВ ш
мс-
1
a2. 5J5 = actga.
J5£. Тоща V^-a2
a sin a
f- cos 2a
a
sina "
• a = xactga,
a2
2 V-cos 2a'
_ a2 cos a
Ответ: =— ила
sin a
Задача 19.
S — вершина треугольной пирамиды SABC. Боковые
ребра пирамиды равны, а боковые грани равновелики. Найти
объем пирамиды, если известно, что боковые ребра равны по
U а LASB ш 2а.
Поскольку боковые грани равновеликие равнобедренные
треугольники с равными боковыми сторонами, то синусы
плоских углов при вершине S равны, т.е.
sin LASB = sin LBSC = sin LASC.
Отсюда возникает необходимость в рассмотрении трех
случаев.
I случай.
LASB ш LASC = LBSC «
2а.
Воспользуемся хорошо
известным фактом, что проекция
прямой SC на плоскость ASB
содержит биссектрису угла ASB.
Наверное, для нас более
привычно (удобно)
рассматривать проекцию бокового ребра
на основание пирамиды, чем на
боковую грань. Поэтому
«положим» данную пирамиду на
боковую грань AS В (рис. 124).
Рис. 124
187

Многовариантные геометрические задачи
СК ± ил. ASB, LASK = LKSB ж а. По теореме о трех
косинусах (подробно об этой теореме можно прочитать в [1 ])
cosZ.CSB = cosLCSKcosLBSK, т.е. cos 2a = cosLCSKcosa.
Отсюда cos LCSK = -zzTZ"* Объем пирамиды
cos a
Я SASB ' СЛГ- qT"
sin LCSK-.
1
cos22a Z3sin2a
5— =—5—
cos2 a 3
rz—A . 2
V3 -4 sin2a.
Обратим внимание читателей, что при нахождении объема
пирамиды нам было безразлично, принадлежит ли точка К
грани ASB или нет.
Рис. 125
II случай.
Z.CSA = LBSA = a,
Рис. 126
= n-2a (рис. 125).
AQ ± ил. CSB, LCSQ = LQSB = ^ - а. Имеем cos
cos LASQ • cos Z.ASQ, cos 2a = cos Z.4SQ-cos [ -^ - a j,
cos 2a
cos Z.A5Q
1
sin a
1 I2
^ • у sin (jt - 2a) • Z • sin LASQ =
188

Многовариантные геометрические задачи
- X sin 2a V1 -
0
III случай.
LBSC =£ASC
cos2 2a
sin2 a
= зг-2а,
I
LAi
3cos2a
3
JB = 2a
V4sin:
(рис.
1 a —
126).
1.
Предлагаем читателю самостоятельно установить, что
здесь мы получим результат, совпадающий с ответом в I
случае.
/3sin2a /т—Т-Г1— /3cos2a
V3 4
Л /sina /т—Т-Г1— /cosa jA . 2 Г
Ответ: —~— V3 - 4sin а или —^— ^4 sm a " * •
Упражнения
1.1. Две боковые стороны треугольника 26 и 30, а высота,
опущенная на третью сторону, — 24. Вычислить медиану
треугольника, проведенную к третьей стороне.
1.2. Точка М удалена от сторон угла в 60° на расстояния
уТи 3 VT (основания перпендикуляров, опущенных из М на
стороны угла, лежат на сторонах, а не на их продолжениях).
Прямая, проходящая через М, пересекает стороны угла и
отсекает треугольник периметра 12. Найти площадь этого
треугольника.
1.3. Около равнобедренного треугольника ABC
(АС = ВС) описана окружность радиуса R. Угол С
треугольника имеет величину a ia< -^l. Точка Е — середина дуги
ВС описанной окружности. Найти радиус окружности,
касающейся внешним образом описанной окружности в точке Е
и прямой АВ.
1.4. Две прямые, перпендикулярные стороне АС
треугольника ЛВС, делят этот треугольник на три равновеликие
части. Известно, что отрезки этих прямых, заключенные
внутри треугольника, равны между собой и равны стороне
АС. Найти углы треугольника ABC.
1.5. Каждый плоский угол трехгранного угла с
вершиной 5 имеет величину 60°. На ребрах трехгранного угла
взяты соответственно точки А, В и С так, что SA - 2а,
SB = SC = а. Найти радиус сферы, касающейся ребер угла и
плоскости ABC.
189

Многовариантные геометрические задачи
1.6. В основании пирамиды SABCD с вершиной S лежит
равнобокая трапеция ABCD с меньшим основанием АВ - а
и острым углом а. Высота SO пирамиды равна А. Прямая
АО пересекает сторону CD в точке К, являющейся ее
серединой. Найдите угол, образованный боковой гранью SBC
с плоскостью основания, если АО : ОК = 8 : 1 и
LAOB = 90°.
1.7. Основанием призмы АВСАВХСХ служит правильный
треугольник ABC, длина стороны которого равна 2а.
Ортогональной проекцией призмы на плоскость ABC является
трапеция с боковой стороной АВ и площадью в два раза больше
площади основания. Найти высоту призмы, если АВХ = Ь.
1.8. В основании правильной четырехугольной пирамиды
SABCD лежит квадрат ABCD с длиной стороны, равной а.
Плоскости боковых граней образуют с плоскостью основания
пирамиды углы, равные а. На сторонах AD и ВС основания
взяты точки Е и F так,что АЕ = ^ а и CF = w. Через эти
точки проведена плоскость, составляющая с плоскостью
основания пирамиды угол /3. Найти площадь получившегося
сечения.
1.9. Длина апофемы боковой грани правильной
треугольной пирамиды равна к. Пирамида пересечена плоскостью,
равноудаленной от всех ее вершин. Найдите площадь
получившегося сечения, если боковое ребро пирамиды составляет
с плоскостью ее основания угол величиной /3.
1.10. Дан отрезок длины 2. Три окружности радиуса 2
имеют центры в концах отрезка и в его середине. Найдите
радиус четвертой окружности, касающейся трех данных.
1.11. В треугольнике ABC АВ - с, ВС - а, АС т А,
sin ABAC = |, sin LABC = -^, Sa + 13* + 65с = 320. Найти
а, Ь и с.
1.12. Основанием пирамиды SABCD служит
прямоугольник ABCD, длина диагонали которого равна </, a LCAD-
= <р. Плоскости противоположных боковых граней ASB и CSD
составляют с плоскостью основания пирамиды углы,
величиной а и 2а соответственно. Определите объем пирамиды, если
известно, что AS - BS.
190

Многовариантные геометрические задачи
1.13. В прямоугольном параллелепипеде
АВ = а, ВС = a VT. Угол между прямыми СВХ и BDX равен
45°. Найти АА1.
1.14. Дан куб с основаниями ABCD и АДС^Д, где
АД || ЭД || CCj || DDV В угол Л куба вписан шар радиуса
R = 0,5. Найти радиус шара, касающегося граней
трехгранного угла куба с вершиной С и данного шара, при условии,
что ребро куба а - 1,5.
1.15. В основании четырехугольной пирамиды лежит
выпуклый четырехугольник, две стороны которого равны б, а
две другие равны 10. Высота пирамиды равна 7. Все боковые
грани пирамиды наклонены к плоскости основания под углом
60°. Найти объем пирамиды.
191

Ответы. Указания. Решения.
Глава I.
7 класс.
Таблица 7.1. 10. 40°; 140°; 40°; 140°. Указание: Пусть
LAOB = х, тоща LCOD = х, LBOC = LAOD = 180° - х.
Получаем уравнение х = ^г (360° *- х).
Таблица 7*2. 6. AAMH = APNH (по II признаку), т.к.
LMAP = Z.ATA4, ZMA4 = LNAP, АР — общая сторона.
AAMH = APNH (по II признаку), т.к. AM = PN, LAMH =
= Z./W# (из равенства ААМР и АРМА), LMAH
180е - LAHM -
LNPH = 180е - Z.AWP - LPNH).
Таблица 7.3. 6. Указание: LAEB = LCEB. 9. Указание:
воспользоваться равенством AADF и ACDE, откуда
Z.JDAF = Z£>C£ и ZAEC = ^Л/С.
Таблица 7.4. 8. Да. Решение. LBAC = Z.5CA = 80°, тогда
АВАР = 80° - 40° = 40°, LKPA = Z.PAK: = 40°,
откуда LPAC = LAPK и а\\Ь.
Таблица 7.5. 6. 34°. Решение. LNMP + LMNK = 180е,
откуда МС || МР, LMPK = 68°, Z.J^P7 = 34е. Отсюда
LPTK-LTPM^ 34°. 7. Указание: через точку С провести
прямую, параллельную АВ. 8. Доказательство. LAME Л-
+ LBEM- 180°, тоща
Z.OME + Z.CXEM = 0,5 {LAME + Z££M) = 90е,
тоща из ДМЕО: ZMOJS = 90°.
Таблица 7.6. 12. 30е, 60е, 90е.
Таблица 7.7. 1. 90е Решение. LABD+LBAD+ LCBD +
+ LDCB = 180е; 2 (LABD + Z.CAD) = 180е, LABC = 90е. 2.
80е. Решение. LABC = 180° - 2 (ZCMC + Z.OCM) =
- 180° - 2 (180° - LAOC) = 180° - 2 • 50° - 80°.
5. 360°. 8. 20е. Решение. LDFB = 110°, LADC = 140°, откуда
LA = 20е. 9. 180е - (а + 0 + у). Указание: LBEC = а + /3.
192

Ответы. Указания. Решения.
Таблица 7-8. 3- AABD = ADCA; AABE = ADCE. 4. 8.
Указание: отложить на луче ВС отрезок CD = ВС. Рассмотреть
AABD. 8. 14. Указание: показать, что ААВЕ —
равнобедренный.
Таблица 7.9. 3. Указание: рассмотреть АЛОВ и АВОС.
5. Доказательство. АВОЕ = ACOF (по III признаку), откуда
ВА = CD как соответствующие высоты. 8. Доказательство.
ACOD = AAOB (по III признаку), откуда LD-LB и
DC || ВА. 12. Доказательство. Пусть точки М, N, Р, К —
точки касания сторон АВ, ВС, CD и DA с окружностью
соответственно. Тогда AM = АК, ВЫ = ВЛГ, СЛГ = СР,
DP = DK (задача 11), АВ + CD = ЛМ + MB + СР
+ BN + NC + KD = AD + ВС.
8 класс.
Таблица 8.1. 9. Доказательство. Проведем АС. АС
пересекает ЕК в точке О. СО = ОА, ВО = ОК-КВ,
OD = OE- DE. Так как ОК = ОЕ, то ОВ = = OD. Значит,
ABCD — параллелограмм.
Таблица 8.2. 3. Доказательство. Так как £М || DE, то
LABC = LADC. LBAD = LBCD (как соответствующие
внешние углы AAMD и АСЕВ). Отсюда ABCD — параллелограмм.
6. Доказательство. ABNC = ADKA (по первому признаку),
откуда ВС = AZ). Из равенства ААВМ = ACDP: АВ. = CD.
Значит, ABCD — параллелограмм. 8. Указание: доказать
равенство треугольников АВОС и AiXM. 9. Указание: доказать,
что ААОВ « ACOD.
Таблица 8.3. 4. Доказательство. LPBK + Z.4DC =
= 180°, Zi4Z>C + LBCD ш 180°, откуда Z.PB* = LBCD. 5.
Доказательство. Из равенства ААВС и АСДЛ (по III признаку):
LPAD = LBCE. AADP = ДСЕВ (по гипотенузе и острому
углу). Отсюда АР = СЕ.
Таблица 8.4. 3. Решение. Из АВОЕ (LE = 90°, LB =
= 30°) OB = 2ОЕ = 8, В£> = 2ОВ = 16. ЛС = BD = 16.
Таблица 8.5. 3. Решение. Пусть LDBE = х, тоща
2х. Из Д£££>: д; + 2х + 120е - 180°. х = 20°.
40е. Тогда LADC = ZABC ■ 80°, LBAD = Z.BCD =
= 100°. 5. Доказательство. LBAN + LABN = ^ (LBAD +
7 Учимся решать задачи по геометрии --

Ответы. Указания. Решения.
+ LABC) = 90°, откуда из AABN LN = 90е. Тогда LMNP =
= 90°. Аналогично для других углов MNPK. 6. 60°. Указание:
показать, что ABCD — равносторонний. 8. Доказательство.
А1В1 = ВХСХ = Cfix = £>Д (из равенства: АА1ВВ1 = ЩССХ =
= AC1DD1 = ADlAAl). Пусть LBBXA^ = а, тогда
LBAlB{ = ZC^q = 90° - а.
LA,B£X = 180° - (а + 90° - а) = 90°.
Значит, Afifi^ — квадрат.
Таблица 8.6. 5. 60°, 60°, 120°, 120°. Решение. LBCA =
= LCAD (как внутренние накрест лежащие), LCAD =
= ABAC = ^ Z.jB^£> = | Z.ADC. Пусть /.СЛ£) = х. Из AACjD:
х + 2х = 90°; х = 30°; LCDA = Z^^D = 60°, LABC =
= LBCD = 120°. 6. ^-^; ^у^. 7. 10. Указание: ААСЕ —
равнобедренный. 8. 15. Указание: треугольники ABD и
БСР — прямоугольные равнобедренные. Провести BE ± AD.
9. 40. Решение. LBCE = LCED = 30°, ZO^D = LOEA +
+ Z^OJE1, откуда LAOE = Z5OC = 30°. АВОС и ДОЛЕ —
равнобедренные. ВО = ОА = АЕ = 5. Из AECD (Z.C = 90°,
LE = 30°): CJ5 = ^ED = 10. PiWCD = 5 + 15 + 10 + 10 = 40.
8 7
Таблица 8.7. 3. 6. 4. я; = 16, у = 14. Решение. - = ^~—•
X о\)~-Х
х = 16, у = 14. 5. х = 2,5; у = 4,375. 6. 1:3. Решение. Проведем
КЕ \\ВМ. АЕ:ЕМ = АК:КВ, откуда АЕ = ЕМ=2.
KN:NC = EM:MC = 2:6= 1:3.
7. 4:1. 9. 1:2.
Таблица 8.8. 1. 14. 3. 20. Решение. РАВС =AlBl + BlC1+
+ AlCl = ^(АВ + ВС + АС) = 20°. 5. ^-^; |; |. Решение.
MJ51 — средняя линия ДАВС, ME = |> Аналогично, FN = f.
^^ = MN - 2МЕ = —2 а = —9—ф ^# Указание: провести
диагонали BD и ЛС. 8. Указание: EF и РК — средние линии
194

Ответы. Указания. Решения.
ДАВС и ADBC соответственно. 9. Указание: провести
BF || CD. 11. 5; 6; 7. 12, 4 и 6. Решение. Для трапеции
РВСК: ^у^ = х. Для трапеции AMND: ~^ = у. Решая
систему, получаем: х = 4, у = 6.
Таблица 8.9. 3. Нет. ЛС + ВС = 7 + ЯС, ЛВ = 10 + ЯС,
т.е. А£>ЛС + 2?С, что невозможно. 4. xG(l;9). Указание:
ВС -АВ<х<АВ + ВС. 8. х е (2; 10). Указание: продлить
медиану CD на ее длину (точка Д). Рассмотреть ACBD{. 9. 2.
10. 7 или 8. 11. 7.
Таблица 8.10. 3. Z(cosatg2a - sin a); ^ Решение.
Из ДЛЯС: AC = Zcosa, £>С = /sina. Из ААВС: У = ^^;
БС = /cos a tg 2a. x = ВС - DC = /cos a tg 2a - / sin a.
4. m (sin ft - cosjS tg 08 - a)). 6. m cos a; m cos2 a. 7. ctg a x
x sin/?; ctgacos/S. 9. 8. Решение. Проведем BE±AD.
£ABE = 30°. Из AAB£: AE = BEtg30° = 2. AD = AE + ED=
= 8. 10. 7. Решение. Из ДС£Х>: ED = СЕ ctg ACDE = 1.
= ВС + 2ED = 5 + 2 = 7. И. -у-. Решение. Из АЛ£>С:
£С = 4. Из ДАВ£: 5JE: = AE tg 30° =
. 12.
Таблица 8.11. 1. Решение. AD = 13 - 3 = 10. Из ДАОС:
АС = У100- 16 = V&T. Из Д1)БС: БС = 5. Из ДАВС: АС =
= Vl32-52 = 12. 12 *>/М~. BD*3 2. 4V3"h Ьу/Т. 6. 12;
16. Решение. Из ДАВС: tg ZABC = ^| = |. Из ACDB:
tg ZC5Z) = -. - = |. Пусть х = 3*, )> = 4k. (3*)2+ (4*)2= 202,
Л = 4, х = 12, >> = 16. 7. 3VT7! Пусть Ai) = у, тогда
= 8 - у. Из ДЛМ£>: MZ)2 = б2 - f. Из ДМ/Ж: MJ92 =
= 42 - (8 - у)2 = 36 - f = 16 - (8 - у)2, у = Ц-. Из AAMD:
х = V б2 - ЙЛ 2 = 3 VTT: 8. 12 VTT и 18 VTT. Указание:
CD = VAD^DW- 36. 9. 2 vT3^ 10. 3 VX Решение.
AB- AD. ЪЬ = АВ(АВ- 5). AB = 9.
195

Ответы. Указания. Решения.
Из ААВС: х = VАВ2 - АС2 = 3 V5~. 11. 12vTh 16. Решение.
Из ДАОС: CD = V3T. Из ДАВС: 32 = 2 - ДР. BD =16. у =
18. Из &CDB: х = ЯС = V162 + 32 = 12Vi: 12.
4V2:
Таблица 8.12. 7. (х - 2)2 + (>> - 2)2 = 4. 8. (х + З)2 +
+ (у - 4)2 = 25. 12. (х - 2)2 + у2 = 1.
4
Таблица 8.13. 3. 0,8; -0,6; - ^. 5. х= - 3 6. у= 195х.
8. у = - vTjc + 4 VT. Решение. у = кх + Ъ — общее уравнение
прямой, к = tg 120°= - V3~. у = - у/Тх + й. Так как у (4) = 0,
то -4vT+ft = 0, £ = 4VT. y=-VTx + 4V3". 10. 5у-3х +
+ 7 = 0. Указание: к и х находятся из системы
4* + *=1,
- к + й = - 2.
11. Решение. Прямая у = — 3 не пересекает окружность.
Таблица 8.14. 4. Да. Решение, а = (2; 1), Ъ = (2; 1). 5.
(- 3; 6). 6. АВ (8; 5), AD (8; - 5). 7. Доказательство.
АВ (6; -2), Ъд (6; - 2). faK как АВ = DC, то АВ = DC и
АВ || DC и ABCD — параллелограмм. 8. Доказательство.
Ш ББ " ' ю. e
2 Ш. 11. ~РК = ~2 (QA " ^)- 12- Указание: продлить
медиану J5M на ее длину.
— —/1*~ — 1 — —
Таблица 8.15. 1. х = а - ^ А. 2. х = ^ (а - *). 3. х = Ь -
— ^ 5. 4. Доказательство. Сложив по правилу
параллелограмма векторы "а иЪ, получим вектор d такой, что \d\ =
= 161 = ial, так как параллелограмм, построенный на
векторах Ъ и 5 будет ромбом с тупым углом 120°, а меньшая
диагональ такого ромба равна его стороне, d и с равны по
модулю и противоположно направлены, поэтому d + с = 0,
т.е. а + 6 + с = 0. 5. Указание: сложить векторы а и с. 6. 6,5.
Решение. AB + AD = AC, AC-~DC = AD, AD -7)3 = !
196

Ответы. Указания. Решения.
_ 1 ЙЛ • ВС
\А0\ = 6,5. 7. - -тг* Указание: cos Z.5 = -= =-. 8. 8.
v:) \ВА\ • \ВС\
9. АВ АС # 0. 10. VET, VT Решение.
13
V4 + 9 + 2 • 2 • 3 • 0,5
11. y = 9-x. Решение. ОМ (2; 2). Пусть точка Е(х;у)
лежит на прямой МР. Тоща ME (х - 4; у - 5). ME • ОМ = 0.
2х - 8 + 2у - 10 = 0, у = 9 - х. 12. у = 6* - 14.
9 класс.
Таблица 9.1. 3. 10,5; 7,5. 4. 20; 18; 16. Указание: к =
= -^ =2. 5. 16; 12. Решение. а:Ь:с = х:у:20 = 4:3:5.
х = 4*, у = ЗА, 20 = 5*, Л - 4. х = 16, у = 12. 6. 30; 36; 42.
Таблица 9.2. 4. AABC^ACAD (по двум углам). 8.
ААВС со ДАОЯ со Д#£>С. 9. AMP* со ANEK со ДЛГРО соДМЕО.
12. ААВС со АРВК со Л/С*. 13. ДАБС со ДЯЯР со ДМЕР со
Таблица 9.3. 5. ААВС со ABDC Доказательство. LC —
общий, ^ = ^ = ^. 9. ААВС со APJ3J:. Доказательство.
АВ ВС
LB — обпщй, -^ = -д£. 10. ДАС5 со АА1СВ1. Доказатель-
АС
cmeo. LC — обпщй. Из AACAl: cos LC = -^-, из АВСВХ:
BJC AC BJC
cos Z.C = -^г, -^ = ~^ = cos LC. k = cos Z.C. 11. ДАВС со
со ДЛДС, Л = cos ZC. 12. ААВС со ДЛДС, ik = cos LC.
Таблица 9.4. 1. 60е. 3. 90е. 4. 140е. 6. 160е. 9. 55°.
Решение. Проведем DC. LDCA = LDBA = 35е, LADC = 90е.
Из AADC: LDAC = 55°. 10. 25е; 130°. Решение. Проведем
ВС. LBCE ж LBAE = 25е, LBCE = LCBE = LCAE = 25°,
50е, LBEC= 130°. И. 50е. 12. 60е. Решение.
LBAD = ZA4C + Z.CAD. LBAC ■ 20°,
ZCAD = 40е, Z5AD = 60е.
197

Ответы. Указания. Решения.
Таблица 9.5. 1. 50е. 3. 70°. Решение. LAEB = 100%
LDBE=LEAB = 30°, LEDB = LAEB - LDBE = 70е'. 4. 30°
6. 50°. 7. а + /3. 8. Доказательство. LDAE = LDFE,
DK
LDKA = LEKF, ADAK со AEFK (I признак), откуда -™ =
АК
KF = AK • KE. 9. 2. Указание: воспользоваться
результатом задачи 8. 11. Доказательство. Проведем ВС и
BD. AABD со ААСВ (см. задачу 10). -т^ = -т^, АВ2 = ЛС X
х AD. 12. Указание: провести из точки Р касательную к
окружности и воспользоваться результатом задачи 11.
Таблица 9.6. 1. 3VT. 2. V3T. 3. 1. в
_ a sin (а + р) т sin у
5' sin а • 7' Sin(a+fl- Р*шен"&
тт а ^or. *и ^В ,D msiny
Из AABD: —.—ъ = ~~:—\ АВ = —:—я^-.
smp sin у sinp
Из ААВС: -Л **
sin
_ msin^Ssiny __
sin(a+/3)'
Л й sin a sin (а + /?) ui
8' sin /3 sin у • у«**ш«* найти Рис- 127
AS из ААВС, затем рассмотреть
ДАб/>. 9. 12. Решение. Из ДАВС:
у А 132+ 142- 152 5
cos LA = —^—г^—т-j— = т^ • s
2-13-14 13 io
Из AABD: BD = АВ sin LA = 12. 10. 1 и З. Решение.
£ + 16 - 2 • 4 • x • ^ = 13. x2 - Ax + 3 = 0, x = 1, x = 3. Для
обоих случаев неравенство треугольника выполняется.
11 2 VI 2 sin2 a _ 4 sin a cos /?
' Y 8т2(а+£) sin(a+£) •
Решение. Продлим медиану BD на ее длину (рис. 127).
198

Ответы. Указания. Решения.
Рассмотрим ABCD.. Из ABCD.: ВС = ?"S1°1. Из ADBC:
' ' sin (а + р)
_ \J 2 2w2sin2a 4m2 sin «cos ft
**" Y m i2(+ft) 8ш(«+)8) *
2 sin2 a 4 sina cos (i
+ sin2(a+/8) " sir' ' m *
12, 15° или 105°. Решение. Из ДЛЯС:
sin 30° si
12 ?; sinZC=^s 1) Z.C = 45° 2) ZC=135°;
2
1) х = 105°, 2) х = 15°.
АА5С: АВ = ——; из ДАВ£): AD = ^-^; из AADE:
cos a' cosasin/3'
ш а ату
cos a sin p
- У Ц У y
"" cosasin^' y~ cos a sin/S cos ^>#
ftcos^si
- 2ЛС • * • cos^, ще
а . й2 + с2 - a2 ctg2a _ isiny
5"' 4' cosx We ' 5* cos a sin/3-
, . с sin 5 sin a y
о. sinx= (возможны два значения угла).
m sin a sin/3
sin(a-/3) ф
8. x= -^^sinOS + y), 5D
sin у ^ y
9. sin x = -jojpr • 5D, ще
b sin a „^
BD =
sinp
10. V^D2 + DC2 + L4Z> • £>Csin(y -£), щ
199

Ответы. Указания. Решения.
MR
т.
BD sin (a
msina
sin(« + £
+ y)
+ O2
ВС-
V A5
2 1
C£>
' ('
is i
x-y/Mt
'tf + m2
csin^2
siny 1
'Jhm сехъ. (rt 4- л^^
с sin 03 + y)
siny '
26c sin/3 sin a
siny
. 360° ie , ,0 n.
шение. 180° (л - 2) = 150° n, n = 12. 3. 9. Решение. Первый
способ: LABC = 140е, далее как в задаче 2. Второй способ:
так как сумма внешних углов выпуклого многоугольника
360е, то п ш 360е: 40е = 9. 4. 10. 5. г = | ctg ^, Л =
Таблица 9.9. 3. 16. Указание: AC = DCVT= 8 у/Т. 7. 27.
Решение. Проведем АО±ЛС. Из ДАОХ>: OD = 4, Bi> =
= ВО + OD « 9. Si4ec = ^ • 6 • 9 = 27. 8. 30. Решение. Для
ЬАВС
= с + г. р = 13 + 2 = 15. S - р • г ш 15 • 2 = 30. 9. 27 +
+ 18 VT. Решение. Проведем ОЕ ± АС. Из ААОЕ: АЕ = 3V31
АС ш 3 VT+ 3. Из ААВС: АВ = 2 (3 V3~+ 3).
S = ^ • 2 (3 + 3 V3") • (3 + 3 V3~) ~ =
. + VTf.
10. 294. Решение. AC.CB~AD.DB = 3:4. Пусть ЛС ■ Зх,
ВС « 4х (3*)*+ (4л)2= 352, 5ж = 35, х = 7. ЛС = 21, ВС - 28.
5 ■ | • 21 • 28 = 294. 11. -336. Решение. AM = AD = 12,
С* =С£> = 14, ВК = ВМ= (84 - (2 • 12 + 2 • 14)) : 2 = 16.
АВ = 28, ВС = 30, АС = 26, 5= у/р(р - а)(р - Ь)(р - с) - 336.
200

Ответы. Указания. Решения.
12. 3000. Решение. Из ABCD (DC = Sx, LD = 90°)
BD = \5х. Рдцс = 25*. S^. = 25* • 24 = ^ • 16л • 15л, * = 5,
S = 600 • 5 = 3000.
Таблица 9.10. 3. 78. Решение. Из ДАВС: В£ = V4 • 9 =
= 6- 5авс = ^ • 6 • 13 = 39, Яддсд = 25^, = 78. 4. 60. Решение.
Пусть АЕ = /С = ж. Из ДАВС: х (16 + х) = 36, * = 2. АС
=20, 5^^=30, 5^^=60. 7. 20VT Решение. Из ДАВЯ: АБ
4 \/3~ '
^4. Из
= 20 VT 8. 12 VT Решение. S^ = ^ • 4 • 3 • sin 45" =
sabcx»= 4scob:= 12 ^ n- 1404- Решение. AB:AF = BE:EF =
= 13:5. AB = 13x, AF » 5x. Из ДА5/1: 5f = 12x = 36, л - 3.
AD = AB = 39, S = 39 • 36 = 1404. 12. 320. Решение. Из
АВОС: 4л2 - 64, х - 4, ВС = 20, S = 2 • 8 • 20 = 320.
Таблица 9.11. 3. 25. Решение. Проведем СК \\ АВ.
DF = FK= 2. DK=4, AD = 7. S = ^y^ • 5 = 25. 4. 25 VT.
Указание: АЕ- ^(AD + BQ- 5. 625. Указание: h = -yX
x (AD + ВС). 6. 192. Решение. Проведем СЕ ± AD.
АЕ = ^ • (25 + 7) - 16.
Из ДАСЕ: СЕ = V202 - 162 = 12. S = 12 • 16 = 192. 7. 144. 8.
120 у/Т. Решение. Из ДАСХ>: AZ> = 12 VT, АС = 24. Проведем
BE ±АС. АЕ = ЕС= 12. Из АВЕС: ВС = Ц^ = 8 VT.
sabcd= 8V3^12V3. 12=120V3~: 9. 3630. Решение. Из
ACOZ) (Z.CO£> = 90°): О£ = г = V25 • 36 = 30, АВ - 2г = 60.
s^d = ^ (АВ + CD) • АВ = ^ (60 + 61) • 60 = 3630. 10. 49 |.
11. 468. Решение. Проведем СЕ\\АВ. СЕ = 25, ££>=17.
S -204 Л 25сдо 2'204 24 ? 11 + 28
х 24 = 468. 12. 42. Указание: провести СЕ || BD. Найти
201

Ответы. Указания. Решения.
Таблица 9.12. 2. 6:5. 5. 37:12. Решение.
9 . 5 — 4 • 3 37
SX:S2 = (S{ + S2 - S2):S2 = -^—^ = y^*
8. 5:4. Решение. Sx: S2 = BK.KD = S3: S4 = 5:4. 9. 2:7.
10. 1:3. 12. 1. Решение.
С
Таблица 9.13. 5. у. Решение.
= SAED = ^ S
7. 2S. 8. 2S. 9. Sx + S2. Решение. Проведем EF. SPEF= SPBC=
= sv sfke = sakd = S2 <см- заДачУ 12 таблица 9.12).
= Sx + S2. 10. 2S. Решение. Проведем МР. МВСР и
параллелограммы. SMBCP = 2SMKp9 SMADP = 2SM£/,,
S— 9 /'с -i-C \-ie
AD\*U \ yiEir РЛЛ.МГ/
11. Sj + S^ 12. SJ + 52 + S3 + S4 Указание: провести МР,
рассмотреть параллелограммы МВСР и MADP.
Таблица 9.14. 2. 60тг. 4. 24л. 5. Гу - ^ч Л2. Решение.
R V ** „ Я/С < /> *-e rt ni I *^" T ** 1 ^
~о т • о.
4 ' ^х "" 360°
-4jr-9jr = 300-13тг. 10. 12,5 я. 11. 16-
Т" (Iп + "2") * 8* 30° ~ 13л:* Решение. SOOJDO = 15 • 20 =
- An. Решение.
*охо2оъол = 42 = 16. SMNPK = 16 - Ал.
12. 16 VT- 8л:. Решение. йорл = ^-^- = 16 VT.
smnk = 16 VT- 0,5 • л: • 42 = 16 vT- 8л:.
202

Ответы. Указания. Решения.
Глава II.
§1. 1.2. 2:3. Указание: проведите MN \\ CD. 1.3. 1 : 2.
Указание: воспользуйтесь тем, что диагонали прямоугольника
точкой пересечения делятся пополам. 1.4, 2:5. 1.5. 3:1:4.
Указание: воспользуйтесь тем, что медианы треугольника
точкой пересечения делятся в отношении 2:1, считая от
вершины. 1.6. 4 : 1. Указание: провести PL || AD, где L
принадлежит отрезку МС. 1.7. 4:3. Указание: провести AJ) || ССГ
1.8. 3:2. Указание: BE — медиана треугольника DBC.
Провести DP || ЕТ || AM (точки
Р и Т лежат на стороне ВС).
1.9. 2 VT+ 8. Указание: пусть
£ — точка пересечения
медиан треугольника ABC.
Провести
EF1.BC.
N
Применить теорему Пифагора
к треугольникам EBF и EFC.
2
1.10. j. Указание: проведем
высоты BE и СМ (рис. 128).
Через центр О описанной
окружности проведем KN || AM.
Проведем EF \\ AM. cos LABC = j£. 1.11. 450. Указание:
провести DK \\ CCX. Показать, что АС{: AB = 1: 3. Провести
М
AD, N принадлежит AD. 1.12. 6 VT. Указание: проведем
DF JL АС. Пусть О — точка пересечения высоты BE и медианы
AD. Показать, что ВЕ = 4ОЕ и AE = EF = FC. 1.13.
sin (a + /?)
Указание: О
sin a cos/Г
кает АС в точке К. Провести
КР AD t tA a
"" = tJd» 1*14. ■=-. Указание: провести DK
середина высоты CD. ВО пересе-
КА РА + КР
СК
АВ. По-
~КР
203

Ответы. Указания. Решения.
М
N Q
Рис. 129
1.15. Ц-.
казать, что ЕК = KD. 1.15. -у\ Указание: провести
ОК±ВС. Пусть EC = z. Показать, что BK = KE = 2z. Из
ADEC найти cos LDCE. Применить теорему косинусов к
треугольнику ABE. 1.16. Указание: провести DF || АЕ. Доказать,
что ВМ = MD. Отсюда AM — высота AABD. 1.17. 10,
Указание: провести ML \\ DT \\ BQ (рис. 129). Показать, что Q —
середина АС. Тогда Е — точка пересечения медиан ДАВС.
2 20
Провести EN \\ ВР. АР = PN = |PQ и т.д. 1.18. ^ Указание:
как в предыдущей задаче, показать, что 5Q — медиана.
Провести ВК±АС. Установить, в каком отношении точка
К делит основание АС. К треугольникам АВК и СВК при-
а + Ъ
менить теорему Пифагора. 1.19. —т—. Указание: доказать,
что ВС яв CD. Провести СР || АБ. 1.20. Решение. Через
вершину С провести прямую, параллельную прямой AM и
пересекающую продолжение стороны ВА в точке & Имеем:
СМ _ КА AD ADAB АС2
АВ
MB
АВ
АВ
АВ2
= cos2 LA.
§2. 2.6. Указание: данная трапеция является равнобокой.
2.7. Указание: докажите, что четырехугольник EKFM —
параллелограмм (рис. 130). 2.8. Указание: докажите, что высоты
треугольников AML и LKD, проведенные из вершин М и
К соответственно, равны. Отсюда следует, что AD || MK.
Аналогично ВС || МК (рис. 131). 2.10. Докажите, что треугольник
РЕК (Р, Е, К — середины отрезков АС, ВС и #D
соответственно) равнобедренный. 2.12. Указание: рассмотрим один
204

Ответы. Указания. Решения.
из данных
шестиугольников (рис. 132).
Пусть О — середина
диагонали CF. Тоща
ABCDEF
В
2.13. Указание:
докажите, что середины
сторон
четырехугольника АВМС являются
вершинами ромба. А
§3. 3.2. 2/W, /н,
mVT. 3.3. 3:2. Указа-ъ
ние: если ВВХ —
медиана, аМ- точка
пересечения медиан, то
1
3.4. 26. 3.6. 15е, 75°.
Указание: проведите
медиану к гипотенузе.
А
L
Рис. 131
3.7. 6,5. 3.8. vT9~: 2 VT. Указание: искомое отношение равно
АВ: BF. Показать, что LOAD = 30е. 3.9. 2; 8; 2 .
Указание: М и N — середины оснований (рис. 133). Проведем
МР || ЛЯ и МК || CLD. Отсюда LPMK= 90°. ЗЛО. 8 см,
С Т D
205

Ответы. Указания. Решения.
32 см. Указание: доказать, что LAMD- 90° (рис. 134).
Провести медиану ME. Доказать, что ЕК || АВ. 3.11.
Указание: отложить на стороне АС отрезок DC = СМ. Имеем:
DC = СМ = ВС. 3.12* Указание: показать,что MB = МР.
3.13.
2i*sin2a
.
Указание: если
— середина АВ, то
1+ctg^
LFCA = /.Л4С = а. Применить теорему синусов к
треугольнику CFA. 3.14. Указание: см. задачу 3.3.
§4. 4.1. Точка D лежит внутри окружности. 4.2. 18 V3",
12 VT. 4.3. 16; 12 vT. 4.4. 9. 4.5. 15; 20. 4.6. 6; 4,8. 4.7. 5.
Указание: воспользоваться формулой г = х , где а и
й — катеты, с — гипотенуза. 4.8. 25 я. 4.9. 8,64; 15,36. 4.10.
216. Указание: воспользуйтесь тем, что высота
равнобедренной трапеции, опущенная из вершины тупого угла, делит
большее основание на отрезки, один из которых равен средней
линии трапеции, а другой — полуразности оснований. 4.11.
54. 4.12. 2,5. 4.13. 5 и 13. 4.14. 192. Указание: докажите,
что данная трапеция равнобедренная и ее диагонали перпен-
3 V3"
дикулярны боковым сторонам. 4.15. 12. 4.16. —т—. 4.17. 45
Рис. 135
206

Ответы. Указания. Решения.
и 80. 4.18. 10 и 12. 4.19.
VT. 4,20. 30°, 60°, 90°.
Указание: точка
пересечения окружности с
гипотенузой является
основанием высоты,
выходящей из прямого угла
данного прямоугольного
треугольника. 4.21. Ъ.
4.22. cos LA =
Указание: провести
FE || ВС (рис. 135). А
Пусть сторона ромба 1. Рис* 136
Тогда BF = cos LA, FC = sin LA. 4.23. 7 + 4 V3~. Указание:
MC2 = ДС • DC, ЛГС2 = AC • PC. cos LBCA = ~ = ^. От-
ЛС ВС
сюда MC-NC (рис. 136).
§5. 5.1. 110° и 70°. 5.5. Указание: треугольники АХС и
BXD — прямоугольные. 5.6. 120° и 30°. 5.9. 100°, 40°, 40°
5.10.
4
2
-=. Указание: докажите, что LAKM
Рис. 137
F D
= LMCB. 5.13. 60°, 120°.
Указание: доказать, что
данный параллелограмм —
ромб. 5.14. Указание:
воспользуйтесь тем, что сумма
противоположных углов
вписанного
четырехугольника равна 180°. 5.15. Указа- д
ние: докажите, что
ОК || AD. 5.16. 2R (vT- 1).
Указание: LAED = 90°, DE = ЕС. Отсюда AACD —
равнобедренный (рис. 137). АС = 2R. Аналогично доказывается,
что BD = 2R, т.е. трапеция равнобедренная. 5.17. 165°.
Указание: докажите, что LAOB = 90° + ^ LACB. 5.18. Указание:
пусть О — центр вписанной окружности. Докажите, что точка
О лежит внутри треугольника NLM. 5.19. 15°. Указание:
докажите, что tg LNBC = -т^-. 5.20. у/Т. Указание: пусть Е —
207

Ответы. Указания. Решения.
середина ВС. Докажите, что
ААЕС^ААВС. 5.21. 45°.
5.22. —. Указание: докажи-
т
те, что ААВМ со ААКВ. 5.23.
Указание: докажите, что
LMAH=LKAH (рис. 138).
5.24. Указание: если в
треугольнике проведены две
высоты, то третью можно
построить с помощью одной
линейки. 5.25. Указание:
проведите диаметр через
точку А. 5.26. 20. Указание:
LAEB = 90°. 5.28. Указа-
что
ние: докажите,
LBOD = LDOC. 5.30.
LACB = 180е - 2а. 5.31.
п • с
У проведем
Рис. 138
Указание: если LACD = а, то
Указание: LAOD= 2LABD. 5.32.
m
Указание:
= 90°. LMEA
LABD ■
диаметр АЕ (рис. 139).
ДМАЛГ со ААВС.
E
Рис. 139
5.33. Указание: докажите, что если LBAK = а, то LPQK = а.
Легко показать, что ZM£# = 90°-a (рис. 140). 5.34.
6 cos 12е cos 18°. Указание: LC = 72е. Проведем диаметр BE
(рис. 141). LBEA = LBCA = 72е. LOBC = 12е.
§6. 6.1. 45°. 6.2. 71е, 62°, 47°. 6.3. Указание: проведите
общую касательную к данным окружностям через точку ка-
208

Ответы. Указания. Решения.
В
Рис. 140 Рис.
сания. 6.4. Указание:
докажите, что LPBC = LPQA.
6.6. Указание: докажите,
что середина дуги АВ есть
центр вписанной
окружности в треугольник АСВ. 6.7.
2а. 6.11. Указание:
докажите, что LABO = LOBC, где/
О — центр окружности с
6.13. Указание: через точку)
D проведите общую
касательную. Пусть CD
пересекает окружность в точке F
(рис. 142). Докажите, что
DA — биссектриса угла
FDB. 6.14. Указание:
докажите, что ДАЕС со ACDB, AACD^ACFB. 6.16. Указание:
докажите, что AABD со ADCB. 6.17. 4. Указание: докажите,
что AADE со ДЛСВ. 6.18. —. Указание: проведите касательную
к окружности в точке С. Докажите, что AEFC со ААВС. 6.19.
- 2 . 6.20. —^—• 6«22. Указание: докажите, что АМАК со
со АВМЕ, АМВК со АМАР. 6.23. Указание: докажите, что
= ZABC.
Рис.
209

Ответы. Указания. Решения.
М
N
Рис. 143
§7. 7.1. 7°. 7.2. 150°. 7.3. 72°. 7.4. 144°. 7.5. 70°. 7.6. 156°.
7.7. 66° и 24°. 7.10. Указание: продлите DM до пересечения
с окружностью в точке Dx. \~*AC = kjADv 7.13. Указание:
искомой точкой является точка касания. 7.17. Указание:
АС пересекает ВМ в точке N (рис. 143). LN= -~
Отсюда AM = M/V = БМ. Л£> || ЯЛГ и т.д.
§8. 8.2. —g—• Указание: радиус окружности, описанной
около трапеции ABCD (ВС || AD) равен радиусу окружности,
описанной около треугольника ACD. Найдите диагональ АС
2
и sin AD. 8.3. 2R2 sin a sin/S sin у. 8.4. — sin a sin/? sin (a
8.5. —-т—. 8.6. 10,625. 8.7. 2 V fi • Указание: NP = PQ.
Примените теорему косинусов к треугольникам MNP и
MPQ и найдите cos LPMQ. 8.8. R -у-. 8.9. Указание: если
Я — ортоцентр, то ZAtfC = 180° - LB. 8.10. 83°. Указание:
докажите, что svn LB = sin LA^FCV 8.11. 2. 8.12. V2 + VT.
25
8.13. -j-. Указание: пусть О — центр окружности, 2? — точка
касания со стороной АВ. Покажите, что BE = 4. Найдите
sin LA. 8.15. —. 8.16. —^-. Указание: AAND^ABNC. 8.17.
а 5
2R2 sin3 а. Указание: докажите, что LCAD -all.
210

Ответы. Указания. Решения.
9VT
8.18. ~52~- Указа"
ние: Докажите,
что треугольник
ABC —
равнобедренный. 8.19. -у.
Указание:
докажите, что DC —
диаметр окружности.
8.20. Искомая
точка — это
основание высоты
треугольника,
провеРис. 144
денной из вершины 2?. Указание: через вершину В и
основания перпендикуляров проведите окружность. 8.21. -гт,
8.22.
Указание: сумма градусных мер
2 sin a
дуг, которые стягивают хорды аи i, равна 2а. Тогда если
хорды отложить от одной точки окружности, то угол между
ними будет 180° - а. 8.23. y/W. Указание: LCO^A = 2LACD
и LAO2D = 2 A ADC (рис. 144). 8.24. AM — это диаметр.
Указание: точки A, N, М, К лежат на одной окружности.
§9. 9.1. 8 у/ТТсм. 9.2. ^ * 4т\ |
нт
\ 9.3- |. 9.4. 6 см и 12 см.
9.5. 13 см. 9.6. 30 см и 33 см.
9.7. 42 см и 66 см. 9.8. Нет.
Указание: воспользуйтесь
методом от противного. 9.9.
Указание: воспользуйтесь
следующим утверждением: концы
отрезков АВ и CD,
пересекающихся в точке М, при-д
надлежат одной окружности,
если AM- MB = CM • MD.
Сформулированный факт
легче всего доказать,
используя метод от противного. 9.10.
Указание: пусть AM = х,
MB = уи V3qT= а (рис. 145).
рис# 145
211

Ответы. Указания. Решения.
Воспользовавшись
неравенством между средним
арифметическим и
средним геометрическим, полу-
чим а
X + V
—s-S
или
х + у > 2а. Очевидно, что
равенство возможно лишь
при условии х = у. 9.11. -т,
arctg 3, -j- - arctg 3.
Указание: докажите, что
Рис. 147 Рис. 148
9.12, Vy. Указание: несложно получить ВС = 2 V2" (рис. 146).
Но тоща i4^ + ^C2 = 5C2, откуда Z.5i4C = 90°. 9.13. 30е,
30°, 120е. 9.14. 32 см и 24 см. 9.15. 42 см, 42 см, 24 см.
9 V3"
9.16. . . Указание: обозначим CD = DB = х> AD = у. Тоща
DE = 6 - уу АВ as 6 - 2у. Получаем jc2 = у (6 - у). Второе
уравнение можно получить, применив теорему косинусов в
треугольнике DAB. 9.17. 27 см и 28,5 см. Указание:
докажите, что треугольники OLC и ONA — равнобедренные
(рис. 147). 9.18. arcsinjr. Указание: докажите, что
LAMD= LMON (рис. 148), ще ON ± DC. 9.19. Указание:
212

Ответы. Указания. Решения.
KF- FT = PFFM и
DFFE = PF- FM
(рис. 149).
Получим KF FT = DF- FE.
Тогда
(КЕ - FE)(KE + FE) =
= DF • /Е, или
КЕ? = FE? + DFFE =
= /Я (FE + DF) = FE
Отсюда /Я= ^
10.2. Указание:
воспользуйтесь вторым признаком
подобия треугольников. 10.3.
13 см. 10.4. 6 см. 10.5. 12. 10.6.
™. 10.7. Vo2-*2. Указание:
из точки А проведите
касательную АК (рис. 150). Докажите,
что AD = АК. 10.8. , . „ ,
. 10.9. 90°. Указание:
найдите стороны А£ и АС. 10.10.
11. 10.11. 8 и 10. 10.12.
а V 1 + -^ . Указание: пусть
А8 пересекает меньшую ок- Рис 150
ружность в точке К. АОВА со ДАЩ, где О и Ot — центры
соответственно большей и меньшей окружностей. 10.13.
Указание: AADO{ соДАВО (рис. 151). 10.14.
R (Vsin^ + ctg2** - sin/3).
Указание: выразите длины отрезков АС и
заданные углы.
через Л и
213

Ответы. Указания. Решения.
11.6. 1:6.
11.7. 2:3. Указание:
основания трапеции
относятся как 3:7.
11.8. 59:53.
Указание: у трапеций
КВСМ и KMDA
общая высота,
следовательно, их
площади относятся как
полусуммы (суммы)
оснований. 11.9.
Указание:
воспользуйтесь тем, что ес-
В
ЛИ -г-
О
а- с
b-d
k (ml
и -§ ;
а
то
= k. 11.11.
т
11.13.
Указание: SBCD: S
™ ^DMC "" 4'
е — с — _
(рис. 152).
Указание: проведите DN || AF. Докажи-
1
те, что BF: FC
ab. Указание: проведите PQ || АВ
(рис. 153). Площадь
трапеции ABCD равна площади
параллелограмма ABQP.
9VW а + Ъ
11.10. —«—• 11.1/. —т—.
7 Ъ
Указание: докажите, что
треугольник BCD —
равнобедренный. Проведите
СР || АЕ. 11.18. 7.
Указание: проведите отрезкид
MB, PC, KA.
214
1 : 2. 11.14. -5. 11.15.
Рис. 153

Ответы. Указания. Решения.
11.19. 5S. Указание: проведите отрезки AlB, BXC, CXD, DXA.
11.20. Указание: проведите диагонали четырехугольника
ABCD. 11.21. ^, |, ||.
Указание: проведите от- АпИ
резок DK, ще К — точка
пересечения прямой / со
стороной ВС. 11.22.
Atg 11 24
(т + п)(р + q + г)'
9. 11.25. Указание:
проведем / || АЛ (рис. 154). .
. Ап_{ — искомый
(п - 1)-угольник. 11.26.
cos (у/2)
^Й2) до"
кажите следующую
лемAi
Рис. 154
му: если в треугольнике ABC О — точка пересечения
биссектрис, то LAOC = 90° + ^ LABC. Имеем:
LMOP = 90° + Ц и LMNP = 45° + J (рис. 155).
Аналогично LMOQ = 45° + т-
MQQN
и т.д.
В А
Рис. 155
§12. 12.1. 300 см2. 12.2. IOVTcm. 12.3. 32. 12.5. 3. 12.6.
20. 12.7. 20 и 30. 12.8. 1: (VT- 1): (V3~- VT). 12.10.
Указание: докажите, что
= ^7. 12.12. тп:т2: тп: п2. Ука-
215

Ответы. Указания. Решения.
зание: пусть О — точка пересечения диагоналей трапеции
ABCD (ВС || AD). Выразите площади треугольников АВО,
OCD, ВОС через площадь треугольника AOD. 12.13.
(т + п)(3т + п)
-— N—-z—^ • а. Указание: покажите, что треугольники,
(2/w + ft)
образованные в результате деления, подобны исходному
треугольнику. 12.14. 25. Указание: AABCu>AABD. 12.15.
12.16.
4 (1 - а). Указание: В С
_ ВС-BE
а " 2ВС '
А Е D
— = 1 - 2а Рис. 156
12.18. Указание: докажите, что площадь четырехугольника
MlM2MiMA в четыре раза больше площади четырехугольника
Г,Г2Г3Г4. 12.19. 2V^J. 12.20. 3:1 или 1:3. Указание: пусть
= х, КС = у. Тогда SMC: S^ - у*: (* + у)2, SBKD: SDKC -
1
х: у. 12.21. 30°. Указание: \ = ± 12.22.
^ С5 • АС • sin С
1:3. Указание: SBHC:SMNC=
12.23. 5:1 или 1:5. Указание: S^ •
/МЛЛ2_ 1
\ВН) "4-
S
^, 12.24. 2arcsinVa". Указание: S^iS^^
рмс ML,
= KB2 :AB* = BE*: AB2 = sin2 LBAE. 12.25.
3
(рис. 156). Указание: SACD: Si4BC = AjD : £C = 2, 5i4BCI) = ^ x
3 "",. 12.26.
AfC: i4C =
216

Ответы. Указания. Решения.
§13. 13.1. 90. 13.2. 120.
13.3. 1/3, 2/3, 4/3, 2/3.
Указание: докажите, что
JANM
JMBC
(рис. 157).
Тогда
AM
МС
s4
SA + S3 + x x '
где S4 и х — площади
треугольников NOM и
CMN соответственно.
13.5. Указание: ум-
ножте почленно равен-д
ства
S2S4
и
Указание: решение задачи сводится к исследованию функции
;ите,
VT
S (х) = 13 + х + ™. 13.7. 60е и 120°. Указание: докажите,
что АВ •
AD + BC
и 5
Указание: докажите, что
ABCD
SKCE
Sdce
4S
АОВ
ALE
ED'
§14. 14.3. Указание: рассмотрев равенства
Sl + S2
и Sx
докажите, что Sx = S3 и S2 = S4. 14.4. -5-, -j-. Указание:
докажите, что МС \\ BN (рис. 159) и воспользуйтесь
подобием треугольников МРС и NPB. 14.5. 3. Указание: если
ТО S
4ДО
^. Тоща 2 + S + •£ < 4, откуда S = 1.
Теперь несложно показать, что ABCD — параллелограмм.
14.6. Указание: SAarn = SAnn + S,
а»
2^^500,, но
217

Ответы. Указания. Решения.
^ABCD "~ ^AOD
^СОВ "*" ^АОВ """
Теперь, воспользовавшись
С С — С С ТТП1Г21
^AOD *COB "" *АОВ °COD> ПОКа'
жите, что SAOB = Scoz>. 14.7.
V7~. 14.8. Указание:
воспользуйтесь следующим
свойством: точки
пересечения боковых сторон, точки
пересечения диагоналей, а
также середины
оснований трапеции
принадлежат одной прямой. 14.9.
S. Указание: пусть
. Так как
трапеция, то
Тогда (S - Sj)2 = SSV
§15. 15.1. Указание: все четыре^
биссектрисы попарно
перпендикулярны. 15.2. 21, 15, 7, 13, 168. Указание:
АР = AM =12 (рис. 161). Кроме того, OK2 = CK KD и
ОР2 = АРРВ. 15.3. Указание: покажите, что LBNA = 45°.
15.4. Указание: покажите, что LECK = LEHK = 45е (здесь
АС>ВС). 15.5. Указание: докажите, что LAFE= 60° WjF —
биссектриса внутреннего угла при вершине А). 15.6. 6.
Указание: докажите, что АК = АВ и DK = DC. Кроме того,
LBKC = 90°, а следовательно, БС — диаметр окружности,
218

Ответы. Указания. Решения.
описанной около треугольника
Х)/СС/. JLD. /. ~j> rj, / у "TsT* *Э*о.
ctr "^ о^ у аг *t* о'
А2. Указание:
ВС = СЕ, ^i) = Z)£ (рис. 162).
OE = ^AB = h. LCOD = 90°.
Тогда СХЁ2 = СЕ • Ш). 15.9. Указание:
AKBM = KD- DM = OD2 = R2
(рис. 163).
15.10. Указание: докажите, что в
прямоугольном треугольнике ОВО{ NB =
= ЛГО (рис. 164). 15.11. VT. 15.12.
Указание:
В
A D
Рис. 162
О К
2S
АОВ
ОАОВ
АВ
OCOD
О&
ОМ- CD
(рис. 165).
15.13. Указание: докажите, что точки
М и N принадлежат средней линии
трапеции. 15.14. у. Указание: пусть
АДГ = а, ЛГР = х, PQ = 2х, MW = 7х
(рис. 166). МО и OQ — биссектрисы
углов QMD и MQC. Отсюда
LMOQ = 90° и
OP = VMP • PQ = 4х.
Из подобия треугольников NBQ и
получаем:
Рис. 165
219

Ответы. Указания. Решения.
mm*tANmll&+A,
Кроме того,
КВ.
Получаем
а[х + ^
Отсюда а =
16*2.
Рис. 166
§16. 16.2. |(p-a)2tg~ 16.4. Зу/Т. 16.5. 30% 60е, 90е.
16.6. а V у ♦ Указание: найдите АВ по теореме
косинусов. Пусть М и N — точки касания вписанной окружности
соответственно со сторонами ВС и AC. CN = р - АВ. Найдите
iW по теореме косинусов. LBMN = 150°. 16.7. Указание: если
JT — точка касания с гипотенузой АЯ, то АК = i - г,
ВС = а-г. АК - КВ = (а- r)(b- г) и т.д. 16.8. Указание:
имеем S = V/> (р - а)(р - *)(р - с) = (р - *)(р - а). 16.9. Ука-
зание: К, М> L, N — точки касания (рис. 167). Имеем:
ОК-АО-АК- f -
Аналогично вычисляется длина каждого из отрезков ОМ,
OL, ON. 16.10. Указание: пусть Кх и К2 — точки касания
В С
Рис. 167
220

Ответы. Указания. Решения.
вписанных окружностей с диагональю АС. К{К2^ \АС-
СК2)\. Осталось показать, что К{К2= 0. 16.11.
. 16.12. lg2 *'• 16ЛЗ- 6> 8> 10- 1бЛ4- 16- 16Л5- 4
6. Указание: воспользуйтесь тем, что периметры подобных
треугольников относятся как соответственные стороны. 16.16.
18. 16.17. —т-т>~ и , о * 16.19. -тр. Указание: пусть
/Я + Lfl YYI -т Lit 4
длина стороны, параллельной касательной, равна а.
Покажите, что длина отрезка касательной равна — (р - а). Функцию
X
f(x) = — (p — x) исследуйте на наибольшее значение. 16.20.
Р
3. Указание: пусть D — точка касания вписанной окружно-
« л п пп \/1 + cos В
сти со стороной АВ. BD = V уз
«17. 17.1. ; , / , I о ,
e Vm2 + л2 Vm2 + л2
17.4. 9, 9VT, 18. 17.5. 6. Указание: найдите отрезки, на
которые биссектриса делит
боковую сторону треугольника.
Определите косинус угла при
основании треугольника. 17.6. 9V5",
COS IS
П). 17.2. 7. 17.3. 42 и 56.
8 y/W. 17.7. 9. 17.9.
зание: АВ:ВС
20
3:4. 17.10.
. Ука-
2k
Указание: проведем высоту ВК
(рис. 168). ВО — биссектриса
треугольника ABE. Имеем:
СЕ _ ВС-BE _
ВС" ВС
Рис. 168
BE
ОЕ
17.11. Указание: проведите биссектрису CD. AABC v>AADC.
Воспользуйтесь также теоремой о биссектрисе. 17.12. 32.
Указание: АС = АЕ> АС:АВ = Ъ:5. 17.13. 4. Указание:
проведите биссектрису внешнего угла при вершине В. Она
221

Ответы. Указания. Решения.
пересекает прямую АС в
точке К. DK — диаметр
искомой окружности.
Покажите, что АК:КС = АВ:ВС.
В,
17.14.
7о2У55Г
Указание:
ЛВ: АС = 3:4.
17.15. 1:2. Указание:
LCEL= LLEM=45%
tg LMCE = tg LMAD = 2
(рис. 169).
17.16. 1 и 2. Указание:
AAMD со АСМВ с
коэффициентом подобия 2, т.е.
MB:MD = 1:2. 17.17. 1:4.
Указание: SAFD: SABD =
Рис. 169
В
AF
АВ
AF
AF + BF
1
" 1 + BFIAF
Аналогично найдите отно-
шение
SABD:
_. 17.18.
Г, 2VTT, 3VX Указание:
AABD — равнобедренный. Проведите DK || BE. 17.19.
Указание: проведем BN (рис. 170), BN±AD, LEAN = LEAB.
17.20. 1:2. Указание: пусть SA
JBOF
1
8*,
JAOB
AB
AD
- 2 ЛС " ГС
2~ 5x
1
BO
OD
JABO
AB
AC
AB
^ - Зх
17.21.
2AD " 6х
1:12. Указание: РА — биссектриса угла 5РС. Проведите
222

Ответы. Указания. Решения.
2 Vs (S + S )
NM || АР. 17.22* —1, * —- Указание: проведем высоту
MSf S2
Sf - S2
ВК. Пусть LEAD = LDAC = a. cos la =
АС =
§18. 18.1. *.
Указание: докажите, что
точки С, Bv Я, А ле-А D
жат на одной окруж- ис* д
ности. 18.2. 6. Указание: нужно за- -
ВС 12 3
метить, что -г^ = тт = т <РИС- 171),
9 3
~д7^ = То = 7> а следовательно,
ВС DC * Hi
~In == ~пп> откуда следует подобие "/
треугольников ВСА и DCB. 18.3.
Указание: из условия следует, что д~""^~~~~""""^-
А 12 А Гу ^
^77 = -717' а значит, треугольники Рис- 172
ABD и ЛСЯ подобны (рис. 172).
Тогда LACH = LABD, откуда ^АВЯ + LHCD = 180°. 18.4.
Указание: воспользуйтесь ключевой задачей параграфа. 18.5.
30°. 18.6. -=-. 18.7. -т^г. Указание: 5„ов = 5^В4 cos2
18.8. —-—д~т -. 18.9. 15°. Указание: докажите, что
~ВС = ^' откуда Z^CM = ABAC = 45°. 18.10. Указание:
AM CM
так как AM - MB = РМ • МК = СМ • МД то
М£>
18.11. Указание: из условия следует, что ^^ = -г= и так
как АЕ = ЕМ, то
223

Ответы. Указания, Решения.
АЕ
ЕС
ЕР
ЕМ*
18Л 2. Указание: из
прямоугольного треугольника BDC
(рис. 173)
DC = ВС cos LACB, а
Я* = DC cos LCDK =
= ВС cos
но так как
В
Рис. 173
LCDK = LADE = Z.ABC, то
DK = ВС cos LACB cos Z. ABC.
Аналогично JSf = ВС cos ZACS cos LABC. 18.14. 60°. 18.16.
Указание: из условия
следует, что
__а Ъ
b + c ~ а'
а значит, треугольники
DBC и ВАС (рис. 174)
подобны.
Глава III.
§1. 1.1. Указание: «удвоив»
данную медиану ВМ (рис. 175),
постройте треугольник ВСК. 1.2. VW.
Указание: «удвоив» медиану боковой
стороны (рис. 176), воспользуйтесь а
теоремой о сторонах и диагоналях
параллелограмма. 1.3. 6. 1.4.
Указание: AD = 2AM (рис. 177). Из
неравенства треугольника следует, что
DC - AC<AD<AC + CD. Отсюда
DC-AC ^ АХЛ ^ АС Л-CD
224

Ответы. Указания. Решения.
Рис. 176
\<АМ<1.
1.5. Указание: ABDC
(рис. 178), откуда CM=CXMV
1.6.
V2A2 + 2с2 - а2
arccos -с,
arccos -=.
1.7. y- 1.8.
4
Указание:
«удвоив» медиану
ЭД (рис. 179),
рассмотрите
треугольники ABD и
1.9. Указание:
< ВС + CD
1.10. Указание:
правое неравенство
легко следует из
предыдущей
задачи. Для
доказательства левого
неравенства используется неравенство треугольника для
треугольников АОВ, АОС, ВОС (рис. 180), где О — точка
пересечения медиан. 1.11. Указание: алгоритм построения
2m2 sin a sin fi sin <p
Рис. 178
ясен из рис. 181. 1.12.
1.13. 120 .
2 sin2 a + 2 sin2 <p - sin2 a
Указание: в треугольнике BDC (рис. 182) Z.5iX: = 30°. 1.14.
Указание: если М — выбранная точка (рис. 183),
8 Учимся решать задачи по геометрии
225

Ответы. Указания. Решения.
Рис. 181
А С
Рис. 180
выбранный диаметр, а О —
общий центр окружностей,
то 2 (MA2
= MM2
1Л5. д.
4R2.
Указание: рас-
смотрите треугольник OCD
(рис. 184), где О — точ-
D ка пересечения медиан,
a ED = OE. 1.16.
Указание: «удлинив» медиану
ВВ{ (рис. 185) на треть,
постройте треугольник
ОСМ. В полученном
треугольнике медиана
2СА- Стороны
Рис. 182
ВА и ВС находятся
аналогично. 1.17. Указание:
в треугольнике MBD,
«удвоив» медиану МО,
рассмотрите
параллелограмм BMDM{:
MB2 + М& =
_ В& + MM2
- 2
(рис. 186).
226

Ответы. Указания. Решения.
В
„ А лг
. 2.4. Указание: со-
Рис. 186
едините выбранную точку с вершинами треугольника.
Площадь равностороннего треугольника равна сумме площадей
трех образовавшихся треугольников. 2.7. Указание:
1
s лп jAB BD- sin a
ABD *\aJ a*
Ш = 1
JDBC
BD • ВС • sin a
227

Ответы. Указания. Решения.
2.8. 4. 2.9. Указание: покажите, что третья сторона равна
——-г, где а и Ъ — данные стороны. 2.11.
n/L ph
р — полупериметр. 2Л2. 30. 2ЛЗ. т-А-, , +, . 2Л4. 30°.
2.15. 2^V4r4 + o2(A-2or)2. 2.16. Угол тупой. Указание:
пусть LABD = а, тогда LDBC = 2а. S^ : SDBC = 3:4, т.е.
*" "~ sin а 3
= -т. 2.17. Указание: SBAr + .
1
2Л8. Указание: 8ШО = Scox (О — точка пересечения
медиан), ААМО&АСОК, значит, МО = ОК и т.д. 2Л9. Указа-
ние: ^1 = §^£( *£ = ^, ^ = fe 2.20.
DC - AC
"ABD
ABADBD ВС CD- BD
2.22. Указание: проведите BHX X AC, OH2 ± AC. Покажите,
OBl SAOC
что -^ = -^ и т.д.
§3. 3.4. Указание: вокруг четырехугольников АВКН
и НКСР можно описать окружности. 3.5. Указание: до-
кажите, что величина угла СРВ постоянна. 3.6.
Va2* & + 2abcosa тг ^ ^D лъж
-г- . Указание: найдите СЯ. AAf — диаметр
sin ее
окружности, описанной около четырехугольника АСМВ. 3.7.
Указание: LAPQ = LAMQ. 3.8. 30е и 150е. Указание: опишите
окружность вокруг четырехугольника MBND. 3.9. Указание:
вокруг четырехугольника АСВМ можно описать окружность.
ЗЛО. Указание: пусть LBDC = a, LBDA = £. Выразите длины
228

Ответы. Указания. Решения.
отрезков СЕ и AF через радиус В
круга, описанного около четырех- ""
угольника ABCD, и углы а и /3.
3.11. Указание:
МХМ2 = ОМ • sin LAOB.
3.12. 45е. Указание: пусть КО
пересечет сторону AD в точке Z1
(рис. 187). Очевидно, что ABKF —
прямоугольник. FM — средняя
линия треугольника AOD, значит, А
LFMO = 90°. Тогда точки А> В,
К, М и F лежат на одной
окружности. 3.13. Указание:
вокруг четырехугольника OMBN
можно описать окружность.
3.14. Указание: вокруг
четырехугольников МАХС и CXBN
(рис. 188) можно описать
окружность. Докажите, что
ААХС со АСХВ
Рис. 188
по первому признаку. 3.15. 90°.
Указание: постройте треугольник AMXD, равный
треугольнику ВМС, так, чтобы точка Мх лежала вне прямоугольника.
3.16. Указание: LAOB =120°, LAHB = 60°. Вокруг
четырехугольника АОВН можно описать окружность. Найдите ее
центр. 3.17. 90°. Указание: пусть ВН пересекает сторону
квадрата в точке F. Докажите, что AF = BQ. Точки F, Я,
Q, С, D лежат на одной окружности. Найдите ее диаметр.
3.18. 90е. 3.19. Указание: пусть О — центр описанной
окружности треугольника ADF. LDOF = 2LA. Докажите,
что LFED= 180° - 2ZA 3.20. 216..3.21. Окружность с
диаметром АВ, исключая точку А. 3.22. VT. Указание:
докажите, что LAED = LAFD =135° (Е и F — точки пересечения
биссектрис треугольников ABD и ACD), откуда точки А, £,
F и D лежат на одной окружности. 3.23. Указание: точки
А, С, Ср Ац принадлежат окружности с диаметром АС* 3.24.
Указание: отрезок MN делят хорду СХА^ пополам. Кроме
229

Ответы. Указания. Решения.
того, MN — средняя линия
трапеции AFKC. 3.25.
Указание: LEAQ = LQBE = 45°
(рис. 189), следовательно,
около BAQE можно описать
окружность и LAQE = 90°.
Тоща из прямоугольного
треугольника AQE
АЕ = VTAQ.
Аналогично
AF=VTAP.
3.26. Указание:
проведите биссектрису НМ
треугольника АН В (рис. 190).
Тогда LAEQ = LAHQ =
= 45е и, следовательно,
вокруг четырехугольника
HEAQ можно описать
окружность. Далее исполь-_
зуйте, что С
LHEQ = AHAQ.
И
В
Рис. 190
Bi С
в
Рис. 191 Рис* 192
3.27. Указание: заметьте, что LAKN = LKMN = LNPA
(рис. 191). 3.28. Указание: проведите СХА2 \\АС (рис. 192).
АС, СА2
—L и В{А2 || АВ. Отсюда
СВ.
Тогда jj-д
230

Ответы. Указания. Решения.
LCXABX =
и точки Сх$ Ах> А2У Вх
принадлежат одной
окружности. Не забудьте рассмот- g
реть случай, когда А1
принадлежит отрезку СА2. 3.29.
Указание: описав
окружности около
четырехугольников OADB и ADMC,
покажите, что
3.30. 22. Указание: проведите
окружность с центром в точке
С и радиусом СВ (рис. 193).
Поскольку LACB = 2LADB, то
точка D лежит на этой
окружности. Из прямоугольного
треугольника CHD найдите высоту
С#. 3.31. 20°. Указание: точки
А, В, С лежат на окружности с
центром в точке К. 3.32. 20°.
Указание: точки С, В, М лежат
на окружности с центром в
точке А. 3.33. 160°. 3.34. 90° - 2а. Указание: покажите, что
Z.A/V/C=135° (рис. 194). Тогда точки А, М, С лежат на
окружности с центром в точке В. 3.35. Указание: опишите
окружность около треугольника ABC (рис. 195) и докажите,
что D — ее центр. 3.36. Можно. 3.37. Указание: докажите
методом от противного, что g
если отрезки КМ и NL
пересекаются в точке Р, причем
KPPM = NP- PL, то точки
Рис. 194
Ку N, М и L лежат на одной А
окружности. 3*38. Указание:
проведя окружность через
точки А, В и С, докажите
методом от противного, что
точка D лежит на этой
окружности. 3.39. Указание:
опишите окружность вокруг
231

Ответы. Указания. Решения.
треугольника ABC. Пусть АН{ пересекает окружность в точке
i4j, ВН2 — в точке Bv СНг — в точке Сх. Докажите, что
ННХ = ЯД, НН2 ш ВД, ННЪ = НЪСХ. 3.40. Указание: пусть
Мр М2, М3, М4 — заданные точки. На отрезках М{М2 и
М3М4 как на диаметрах постройте окружности. Этим
окружностям принадлежат две противоположные вершины
квадрата. Диагональ квадрата делит дуги этих окружностей
пополам. 3.41. Искомая точка X такая, что ОХ2 = ОБ • ОА. 3.42.
90е, 67,5% 22,5е. Указание: опишите окружность вокруг
данного треугольника. Продлите медиану до пересечения с
окружностью. 3.43. Указание: опишите окружность вокруг
данного треугольника. Продлите медиану до пересечения с
данной окружностью. 3.44. Указание: опишите окружность
вокруг данного треугольника. Продлите биссектрису до
пересечения с окружностью. Воспользуйтесь теоремой о хордах.
3.45. Указание: обозначим точку пересечения биссектрис
через М. Опишите окружность вокруг треугольника ВМС.
Пусть она пересекает AD в точке К. Докажите, что треу-
гольники KDC и АМВ — равнобедренные. 3.46. V4/*2 - я2.
Указание: постройте окружности с центром в точке D и
радиусом р. 3.49. Указание: опишите вокруг треугольника
ABC окружность. Постройте ГМТ середин хорд, проходящих
через А. 3.50. Указание: постройте окружность, касающуюся
сторон угла в точках Рх и Р2 так, что ОРХ = ОР2 = р, вде
р г- заданный полупериметр. 3.51. к. Указание: проведите
биссектрису AF. Продлите сторону АВ за точку В. Теперь
становится очевидным, что F — центр вневписанной
окружности треугольника ABD. Отсюда DF — биссектриса угла
BDC. 3.52. 150°. Указание: докажите, что А1 и Сх — центры
вневписанных окружностей соответственно треугольников
ЛВВ{ и СВВг. 3.53. 10°. Указание: продлите сторону СВ за
точку В. Докажите, что Е — центр вневписанной
окружности треугольника BDC. N В Р
§4. 4.1. Нужная пря- / '^РТ^Г 7
мая проходит через центр /^
параллелограмма. 4.2. Ука- AZ^^ О/
зание: пусть О — точка пе- /^ 7
ресечения диагоналей
ABCD (рис. 196). При сим-
метрии относительно ОМ D К
Рис 196
232

Ответы. Указания. Решения.
точка А переходит в точку
С и отрезок MN — в отрезок
РК. Аналогично NP
переходит в КМ. То есть при
симметрии относительно точки
О KMNP переходит в себя.
4.4. Указание: при
симметрии окружности
относительно М отрезок АВ переходит
в KF. 4.5. Указание: точки
К и М, L и N симметричны
относительно центра
параллелограмма. 4.6. Указание:
А и В — точки пересечения
1
Рис. 197
данной окружности и окружности, симметричной ей
относительно точки М. 4.8. Указание: рассмотрите симметрию
данной прямой относительно данной точки. 4.9. Указание:
найдите середину отрезка АС, а далее воспользуйтесь решением
задачи 4.7. 4.10. Указание: найдите образы точек М и N при
симметрии относительно О. Теперь воспользуйтесь решением
задачи 3.40. 4.12. Указание: точку С (рис. 197) можно найти
как точку пересечения прямых /2 и ^', где Z/ — образ прямой
^ относительно точки О. 4.14. Указание: вершины В и D —
точки пересечения прямых Ъ и с\ с и <f соответственно, где
dud' — образы прямых с и d относительно середины отрезка
АС. 4.15. Указание: отобразите одну из окружностей
симметрично относительно точки D. Точка пересечения второй
окружности с полученной — вершина треугольника. 4.16.
Указание: отобразите меньшую
окружность S{ симметрично
относительно любой
принадлежащей ей точки А. Пусть
В — точка пересечения
полученной окружности с
окружностью S2. Тоща АВ —
искомая прямая. 4.18.
Указание: докажите, что данные
прямые являются образами
серединных
перпендикуляров к сторонам
четырехугольника ABCD (рис. 198)
Рис.
233

Ответы. Указания. Решения.
при симметрии относительно точки пересечения отрезков
КМ и NL. 4.19. Указание: пусть точка £? симметрична D
относительно точки Р. Площадь треугольника PCD равна
сумме площадей треугольников РВС и РВ1У. Заметьте, что
точка В лежит на отрезке DC.
§5. 5.1. Указание: постройте точки А1и Bv симметричные
соответственно точкам А и В относительно прямой MN. 5.6.
Указание: отобразите симметрично одну из вершин В или
С относительно прямой AD. 5.7. Указание: отобразите прямую
АВ относительно каждого из данных серединных
перпендикуляров. 5.10. Указание: через точку Е проведите прямую,
параллельную прямой MN. 5.11. Указание: если треугольник
ABC отобразить симметрично относительно серединного
перпендикуляра к стороне ВС, то можно увидеть треугольник,
в котором известны две стороны и угол между ними. 5.12.
Указание: через одну из вершин проведите прямую,
параллельную боковой стороне. Задача сводится к предыдущей.
5.13. Указание: пусть точка Мх симметрична точке М
относительно стороны АВ. На отрезке MXN как на диаметре
постройте окружность. Точка ее пересечения со стороной АВ
есть вершина искомого треугольника. 5.15. Указание:
отобразите точку А симметрично относительно прямой /. 5.16.
Указание: вершина треугольника лежит на прямой, параллельной
основанию. Расстояние между этими прямыми равно высоте
треугольника. Задача сводится к задаче 5.14. 5.17. Указание:
отобразите точку М симметрично относительно сторон ВА и
ВС. Полученные точки соедините. 5.20. Указание: проведите
серединный перпендикуляр к диагонали АС. Пусть точка В{
симметрична В относительно проведенной прямой. SABCD =
= S^cd* 5.21. Указание: пусть Сх и Dl — точки, симметричные
точкам С и D относительно АВ. Хорда CXD имеет постоянную
длину, так как стягивает дугу постоянной градусной меры.
5.22. Указание: отобразите данную окружность симметрично
относительно прямой /. Полученная окружность пересекает
дачную прямую в одной из вершин ромба. 5.24. Указание:
пусть точка Вх симметрична точке В относительно АС. Вх
лежит на AD. В треугольнике BfiD известны все три стороны.
5.25. Указание: пусть точка Dx симметрична точке D
относительно прямой АВ. Постройте окружность с центром в точке
234

Ответы. Указания. Решения.
D{ и радиусом -jDDv
Проведите из точки С касательную
к построенной окружности.
5.27. Указание: постройте
прямую NXPV симметричную
прямой NP относительно
прямой АС (рис. 199). Nt
принадлежит ВА, Рх —■ ВС*
ANAM со
5.28. Указание: пусть
точка Вх симметрична точке В
относительно биссектрисы.
Вх лежит на прямой АС. Рис. 199
Пусть точка А1 симметрична точке А относительно той же
биссектрисы. AM + MB = \М + MB > \В.
§6. 6.1. Указание: рассмотрите поворот с центром М на
угол 90°. Пусть образ прямой ВС пересекает прямую В А в
точке N, т.е. R™ (ВС) = В1С1 и ВХСХ C\BA = N. Тогда
R-^XB^) = ВС, R-J°\N) = K,
причем К принадлежит ВС. Итак, MN = МК, LNMK = 90е.
6.7. Указание: рассмотрите поворот с центром в центре
квадрата на угол 90°. 6.9. Указание: пусть даны прямые а1,
о,, аъ, причем а^ лежит в полосе прямых ai и аъ. Выберем
на Og произвольную точку О и рассмотрим поворот R%\
Пусть R%' (а^ = а\. Точка пересечения прямых а\ и а^ —
одна из вершин искомого треугольника. 6.11. Указание:
рассмотрите поворот с центром в точке А на угол 90°. 6.12.
90°. Указание: рассмотрите поворот с центром в точке О на
угол 120°. 6.13. 120°. Указание: рассмотрите поворот с
центром в точке О на угол 120°. 6.14. 120°. Указание: докажите,
что AD = 2BC. Рассмотрите поворот с центром в точке О на
угол 120°. 6.15. 60°. 6.17. Указание: рассмотрите поворот с
центром в точке А на угол 90°. 6.20. Указание: пусть
R-6°t(A)=Al,AAl
где CD — биссектриса угла С.
CD,
235

Ответы. Указания. Решения.
ААА^В со ACBD.
6.21. Указание: &* (Р) = Рх.
РХВ = PC, AP = PJP,
LPXPA = 60е.
§7. 7.1. Указание:
рассмотрите гомотетию с центром в точке
касания, при которой центр одной
окружности переходит в центр
второй. 7.3. Указание:
окружности гомотетичны с
коэффициентом к = 2 и центром гомотетии
в точке А (рис. 200). 7.4. Если
М — данная точка, а О —
центр окружности, то искомое
ГМТ — окружность с
диаметром ОМ у исключая точку М.
Указание: рассмотрите гомоте-
тию с центром в точке М и
Рис. 201
коэффициентом k = -у. 7.5.
Указание: пусть А1 и В{ —
точки пересечения ОА и ОВ с
меньшей окружностью (рис. 201). Так как окружности
гомотетичны с центром О, то АХВ1 \\ АВ и отрезки ОХМХ и ОХМ —
серединные перпендикуляры к А1ВХ и АВ соответственно.
Остается заметить равенство дуг А1М и MBV 7.6. Указание:
рассмотрите гомотетию с центром в точке Р у. коэффициентом
к = - 2. 7.7. Указание: постройте произвольную окружность,
касающуюся сторон угла А.
(рис. 202) и примените
гомотетию с центром В и
коэффициентом k =
7.8. Указание: на луче
ОА выберем
произвольную точку А'. Проводим»
А'В'±ОВ и А'М=АВ'
Ш' лежит на луче ОМ)
Рис. 202
236

Ответы. Указания. Решения.
(рис. 203). Примените
гомотетию с центром в точке
ОМ
О и коэффициентом дмгтг.
7.10. По прямой, парал-
дельной прямой /. 7.11. -т.
7.12. Указание:
треугольник с вершинами в
полученных точках гомотети-0
чен треугольнику с
вершинами в серединах сторон с
коэффициентом k = 2. 7.15.
Указание: постройте
треугольник АДСР подобный
данному, а затем
примените гомотетию с центром в
любой из вершин и ко-
р
эффициентом -j^-. 7.18.
В
Рис. 203
Указание: постройте
треугольник так, чтобы его сто- А
роны были параллельны
данным прямым, а две вер- \
шины принадлежали
сторонам данного треугольника.
Затем примените
гомотетию с центром в вершине
данного треугольника. 7.19.
Указание: постройте
квадрат К*LIMN*, а затем
примените гомотетию с
центром в точке А (рис. 204).
7.21. Указание:
докажите, что треугольник Aflfa
(рис. 205) гомотетичен треугольнику ABC (В{С{ || ВС,
А{С1 || AC, AlBi || АВ) с коэффициентом к = - 2 и центром в
точке М.
§8. 8.1. Прямая, перпендикулярная отрезку,
соединяющему данные точки. Указание: выберите начало координат
Рис. 205
237

Ответы. Указания. Решения.
в середине данного отрезка. Ось абсцисс содержит этот
отрезок. 8.2. Окружность. Указание: пусть начало координат в
точке А. Положительная полуось совпадает с лучом [АВ).
Уравнение окружности будет \х - ^ + / - ?>• 8.3. Окруж-
ность, центр которой делит отрезок АВ в отношении 2:1,
считая от вершины А, радиусом -~АВ. 8.4. Окружность без
точек пересечения с прямой АВ, Указание: выберем систему
координат, как в предыдущей задаче. Бели координаты точки
С (х; у), то D Iх 2 ; оП • 8.5. Окружность с центром на прямой
АВ без точек пересечения с прямой АВ. 8.6. окружность с
центром в центроиде данного треугольника или сам центроид.
8.7. Вся плоскость. Указание: введите систему координат с
центром в точке пересечения диагоналей прямоугольника и
осями, параллельными его сторонам. 8.8. Отрезок, длина
которого равна -уАВ. 8.9. Указание: выберите систему
координат так, чтобы начало совпало с точкой пересечения
диагоналей ромба, а оси содержали диагонали. Если М(х;у)> то
х2 + / = -д-. 8.11. Указание: выберите систему координат с
центром в точке В> ось абсцисс совпадает с лучом ВС. 8.12.
Указание: выберите систему координат, как в предыдущей
задаче. 8.13. Указание: выберите начало координат в центре
окружности и осями, совпадающими с осями симметрии
шестиугольника. 8.15» Указание: пусть начало координат
совпадает с центром окружности. Ось ординат содержит диаметр,
о котором говорится в условии. 8.17. Указание: выберем
начало координат в точке .А, ось абсцисс совпадает с лучом
АС. Приняв стороны равносторонних треугольников за а и Ь,
найдите длины отрезков BQ, BP, QP. 8.18. Указание: см.
задачу 2. 8.19. —^—. Указание: выберите начало координат в
точке D, ось абсцисс — [DA), ось ординат — [DB).
§9. 9.1. Указание: пусть О — точка пересечения
диагоналей четырехугольника ABCD (рис. 206). Точки М и N —
середины сторон ВС и AD соответственно. Обозначим
OB = ZT, OC-t. Тоща
238

Ответы. Указания. Решения.
М
, а
Так как ОМ и ON — колли-
неарны, то
дк = к дм или
Отсюда (к-^а)а^ф-к)£
но так как аи*- некол-
линеарны, то & = а = /J.
Имеем:
- з;
а
- о),
а следовательно, ВС
Аналогично можно показать,
что А5 || CD. 9.3. Указание:
если точки К, L и Р —
середины отрезков А4', ММ
и АВ' соответственно, то
), a
= ^ (АВ
9.5. Указание:
Рис. 208
^ + (X!) (рис. 207).
Из подобия треугольников AOD и СОВ:
ОМ = ^
Для доказательства принадлежности точек К, F и М одной
прямой используйте подобие треугольников ВКС и AKD.
239

Ответы. Указания. Решения.
9.7. Указание: докажите, что
вектор НК коллинеарен
вектору MF (рис. 208). 9.9.
Указание: пжт l ™
В
N
(рис. 209).
2
9.10. -~. Указание:
|ся (рис. 210).
Рис. 210
Приравняйте
коэффициенты в полученных
равенствах и учтите, что а + /3
= 1. 9.11. Указание: най-
дите отношение
Рис. 211
(рис. 211) и докажите, что
векторы АО и CXD коллинеарны (О — точка пересечения
BE и CF). 9.12. Указание: если Mt и М2 — точки
пересечения медиан треугольников ABC и DEF, то
Cf).
240

Ответы. Указания. Решения.
9.15. Указание: введите
систему координат (рис.
212): С(1;0), К(х;0),
М(х; (l-x)V3Qi
Если
n \-%ят~
Pj — середина JVx, то
' 2 4
Докажите, что
С х
Рис. 212
9.16. —2—• Указание: AN = -тАВ + -г АС. Далее полученное
равенство возведите в скалярный квадрат. 9.17. 30°. 9.18.
> Указание:
\вА. С
3
учетом AD • BE = 0 и LABC = 60° получите уравнение
9.19. 4. 9.20. arctg-y% 9.21.
11\^Г
arccos-
182 '
9.22. Указа-
ние:
CM2 ш i
+ СВ), С
l (рис.213).
Рис. 213
-* -> V2T~ 3V130
Проверьте, что СМ2 • АМХ = 0. 9.23. -у. 9.24. arccos j
Указание: введите систему координат с центром в точке
о
пересечения диагоналей. 9.25. ^. Указание: введите систему
координат так, что Л(0;0), B(0;p), C(l;p), D(k;0). Тогда
241

Ответы. Указания. Решения.
, Р
, АЕ
±±.Е\
2 ' гу
-1; -р).
Теперь из условий АЕ • CD = 0 и IАЕ\2 = 4 IABI2 получите
систему для к и р. 9.26. Указание:
АВ ic i% JC
м-BCsinB
ВССА
2S
Далее воспользуйтесь тем, что
2(АВ • АС + Л5 • ВС +
9.27. 60°. Указание: введите систему координат в центре
шестиугольника.
Глава IV.
1.1. 4V3T или 2 V193. Решение. I случай. Основание
высоты BD принадлежит стороне АС (рис. 214). Пусть
АВ = 26, ЯС = 30, BD = 24. Тогда находим
AD
- BE? = V262 - 242 = 10,
DC = V5C2 - Б!)2 = V302 - 242 = 18.
Отсюда ЛС = AD + DC = 28.
Для того, чтобы вычислить длину
медианы ВЫ, достроим треугольник
А8С до параллелограмма А8СК.
Теперь, применяя теорему о сторонах
и диагоналях параллелограмма,
имеем ВК2 + АС? = 2 (АВ2 + ВС2).
Подставляя числовые данные,
находим
J5/C = 8 V3T, ВМ = ^ВК=4ЛТ.
II случай. Основание высоты
лежит на продолжении стороны
242
Рис. 214

Ответы. Указания. Решения.
(рис. 215). В этом случае
AC =DC - AD = 8.
Теперь, воспользовавшись
тем же приемом, что и в первом
случае, несложно получить
ВЫ = \77Г= 2VTW.
1.2. 4VT. Решение.
Любопытно, что в этой задаче не
реализуется именно тот случай,
который первым приходит в
голову.
I случай. Пусть точка М
расположена внутри данного угла
(рис. 216). MjF= VT, M£>= 3VT,
Рис. 215
ABC
12, ABAC = 60°.
Обозначим АС = х, АВ = у.
По теореме косинусов с учетом
введенных обозначений
ВС = Vx2 + у2 - лу.
Отсюда получаем уравнение
х + у + Vx2 + у2 - ху = 12.
Для того, чтобы получить еще одно уравнение, выразим
площадь треугольника ВАС двумя способами. С одной стороны
а С
+ 3VJx. Теперь можно записать систему уравнений
• у2 - ху = 12,
ху = 2у + 6х,
которая, как несложно убедиться, решений не имеет.
II случай. Рассмотрим ситуацию, когда точка М
расположена так, как показано на рис. 217.
Сохраним соответствующие обозначения.
Очевидно в этом случае система уравнений выглядит так:
-xy = 12,
ху = 6х - 2у.
243

Ответы. Указания. Решения.
Полученная система имеет единственное решение х = 4,
уш4.
1.3. Если
/ ос\
R cos a + sin ~-
<^, то —* ^
I - sin ^
или
R [cosa - suitt
если ^ < а < w» то
_ / .а
Л cos а + sin w
ж
; если а-^у то
(cos a + sin ?• J
или
1 - sin ^
R (sin ^- - cos a)
Рис. 217
1 - sin w
Решение. Здесь
источником второго
решения является
неоднозначное положение
точки Е на описанной
окружности.
Действительно, ведь выбор дуги
ВС может быть сделан
двумя способами.
I случай (рис. 218).
Обозначим радиус ок- А
ружности с центром в
точке Ох OtN = х. Тоща
ОО^ОЕ + ЕО^ R + x.
Кроме того, LO£>M = LBCD = ^ как углы со взаимно
перпендикулярными сторонами, a LBOD = а как угол, равный
половине центрального угла, опирающегося на дугу АВ.
N
Рис. 218
244

Ответы. Указания. Решения.
Из треугольника Орм
ОХМ = ООХ sin LOXOM =
= (R + х) sin ^.
С другой стороны
ОХМ = Oj ЛГ - МЛГ =O{N-
-OD = x- Rcosa.
Получаем уравнение
х - R cos a = (R + х) sin ^.
_ / . а\
R cos а + sin ^
ч/ТСЮДа X — .
1 - sin -у
^7
м
с
/
Рис. 219
С
0 \1
II случай (рис. 219). Здесь,
сохраняя прежние обозначения,
ее
имеем: ОХМ = (R + х) sin ^,
Решая уравнение (R + х) sin ^ = R cos a + х, получаем
С
= —^
sin у- cos а]
1 - sin -^г
Теперь важно не
сделать преждевременный
вывод, что решение
задачи завершено.
Действительно, нетрудно
ж
понять, что при а<-~
точки О и Ох находятся
в одной полуплоскости
относительно прямой
АВ, а при a = -у
(точки Е и А совпадают), задача вообще не имеет решения.
Л/
Рис. 220
245

Ответы. Указания. Решения.
Итак, рассмотрим случай а<-~ (рис. 220).
OXN — радиус окружности с центром в точке Ог Пусть
O{N = ОХЕ = jc, тогда Op = R + х. Несложно установить, что
LOQK = ^, £BOD = a, OD = Rcosa и OK=OD-KD =
= OD - OXN = R cos a - jc. С другой стороны, из треугольника
ООХК О К = = (Л + х) sin тт. Получаем уравнение
а
(R + x) sin w = R cos a - x.
/
cos а
Отсюда х =
L
- sinT
1.4. arctg V5", arctg V5~,
л: - 2 arctg V5~ или arctg -^
б
A
"*Т-«—«^ Д' Mi) к 'С
Решение. I случай. Углы
и ЯСМ — острые (рис. 221).
Рис. 221
ATM J. ЛС, £tf J. i4C и NM = EK = AC.
Кроме того, S^f/f = SCEK = 7 S,,™.
Покажем, что треугольник ABC равнобедренный.
Действительно, треугольники AjVM и C£J^ равновеликие
прямоугольные и имеют пару равных катетов NM = ЕК.
Отсюда следует, что AANM = АСЕК и Z.ААС = LBCA.
Поскольку SCBD= ту S.^, SCEK = т5,™ и ACBD со
со АСЕК, то несложно получить
BD _уЗ
0,5 £/Г
246

Ответы. Указания. Решения.
Отсюда LBCD =LBAC = arctg V(T, a LCBA = л - 2 arctgVTT
II случай. Рассмотрим
ситуацию, когда один из углов,
прилежащих к стороне АС, тупой (рис.
222). Здесь
NM
и
= "ВКЕ =
Проведем отрезки QC и BD
параллельно NM и EF, а также
отрезок DQ (F и Т — точки
пересечения прямой ЕК с отрезками
AD и DQ соответственно). Понят-
но
Рис. 222
DF а значит, |^ = ^> откуда EK = FT = NM.
BE
BQ DC'
Теперь заметим, что SKBE = SFTD (каждый из этих
треугольников имеет высоту, равную DF), а следовательно,
SFTD = SMNA, откуда с учетом равенства FT = NM сразу
вытекает, что треугольник AQD равнобедренный.
Покажем, что отрезки NM и TF делят треугольник
AQD на три равновеликие части. Для этого достаточно
доказать, что S
AQD
JABC*
Действительно,
SAQLC + SQBL,
AQD -
+ SCLZ), но SQBL = SCL£) (здесь мы использовали известное
свойство трапеции, в данном случае трапеции DCQB).
Остальное несложно, и мы предлагаем читателю
завершить решение самостоятельно.
1.5. - + /ц > Решение. Здесь существование второго
решения обусловлено тем, что центр сферы может лежать как
в одном, так и в другом полупространстве относительно
плоскости ABC (на рис. 223 это точки Ох и О2).
I случай. Центр сферы расположен в одном
полупространстве с точкой S. Удобно рассматривать правильный
тетраэдр с боковыми ребрами SA = SBX = SCX = 2а, а треугольник
247

Ответы. Указания. Решения.
Рис. 223 Рис. 224
ABC как сечение этого тетраэдра. Ясно, что центр сферы
расположен на высоте SQ тетраэдра АвДя.
Рассмотрим треугольник ASD (рис. 224). SD = AD =
= crfT, AS = 2а. Г и F — точки касания сферы с прямыми
AS и АР соответственно. AQ = 2 QD.
Легко получить SQ = 2а У ^. Проведем QL || АР.
DL _ QQ _ 1 QM _ LP _ LP^ _ \
U" QA~V MS " PS " JD " 3*
V 3
Отсюда Ц = § и MS
-
Пусть Щ = -FOi = x. Из треугольников JSOj и FO{M
« H0 sin
tg
sin
tg
»/ж-, откуда x s - + JH * Второй
татель может рассмотреть самостоятельно.
248
и
LFOXM
MQ = 2УГ
-4Q 5 Ф
Имеем cos Z. /ЦМ = -тя»-. Теперь получаем уравнение

Ответы. Указания. Решения.
1.6. arctg
ЗА
V3~a sin (a + arcsin -
arctg ■
или
sin f <
VTa arcsin (a + arcsin
2V7V
7 j
Рис. 225 Рис. 226
Решение. I случай. Точка О расположена внутри трапеции
ABCD (рис. 225).
Пусть ОК = х, ЛО = 8*, АК = ВК=9х. Треугольники
АОВ и ВОК прямоугольные (LAOB = £В(Ж = 90е).
Имеем ВО
^(9х)2-хг =4xVT.
= 12x.
V(8x)
Отсюда 12x = а и *=т^« Введем обозначения ZABO =/3,
= 180° - a - arcsin |.
Проведем O£ -L БС. Из треугольника ОБЕ
^§ = f • Тогда
—s—
in f
/ 2
sin fa + arcsin-j
Угол SEO — искомый.
50
V5a sin (a + arcsin ^
249

Ответы. Указания. Решения.
II случай. Точка О расположена вне трапеции (рис* 226).
Сохраним прежние обозначения. Теперь АК = KB = 1х.
ВО = У(7х)2 -
2VT
y Дальнейшее
решение аналогично
приведенному в первом
случае.
1.7. Уй2 - 7а2 или
4xVT, AB = V(8*)2 + (4W3)2 = AxJT,
Решение. I случай.
Грань AAjCjC
перпендикулярна плоскости осно- Рис 227
вания (рис. 227).
Так как площадь трапеции АВВ2С2 в два раза больше
площади треугольника ABC, то площади параллелограмма
ВСС2В2 и треугольника ABC равны. Отсюда можно заключить,
что СС2 = FCX --у АС = а. Но тогда A1F = А2С = а, а значит,
точка А2 — середина отрезка АС. А2С2 = Л2С + СС2 = 2а.
Кроме того, А2В2 = АВ = 2аиВ2С2 = ВС = 2а, т.е. треугольник
А2В2С2 равносторонний. Имеем:
СВ2= ovT, AB2- у/АС2+ С&2=^(2а)2+ (аУЗ)2= aVT
Отсюда 5^2 = у1Щ-Щ = У*2-7а2.
II случай. Грань BBfifi перпендикулярна плоскости
основания (рис. 228).
Аналогично первому случаю можно показать, что точка
В2 — середина стороны 5С треугольника ABC. Тогда
^J52 = а УЗ"! Из треугольника АВ2В1
вхв2 =
= = У*2-За2.
1.8* Бели ортогональная проекция сечения принадлежит
большей части основания пирамиды, то
_ 2a2 sin а / 2 sin a cos/8
~9sin(a+)S) 11+ sinCa+^
250

Ответы. Указания. Решения.
при ^€[0;arctg(3tga)],
sin а
2 sin a cos
при /?Е rarctg(3tga);^"|; если ортогональная проекция
сечения принадлежит меньшей части основания пирамиды, то
_ a2 sin a /_ sin а cos/8 \
9 sin (а + /8) [ sin (а + /3) J'
Решение. Пусть ABCDS — данная пирамида (рис. 229).
М и ЛГ — точки
пересечения ребер S-A и SJ9 с
секущей плоскостью. AT, AfJ^ ; ^С/
Q и Р — середины
отрезков АВ, MN и .Е/7
соответственно,
Ясно, что
четырехугольник ENMF —
равнобедренная трапеция с
основаниями EF и MN.
В треугольнике KQP
КР
_ QP = K
i i
Отсюда
=
sin (л: - (а + /3)) sin a sin ^3*
2а sin а г,_ 2а sin В
*g3sin(
Из подобия треугольников ABS и NMS
>л ал ""
а
MN _ SQ
Sic sk'
и, так как SK = •=—^—, получаем
ММ = АВ(1-Щ=а(1-
Тогда
_ EF+NM _ 2а2 sin a / 2 sin а cos/8\
5^mf - 2 ' У 9 sin (а+^3) ^ sin (а+£) J *
in^cosa\
in(a+/S)J
251

Ответы. Указания. Решения.
Рис. 229 Рис. 230
Ясно, что приведенное решение соответствует той
геометрической конфигурации, когда точка Q принадлежит
отрезку KS (в том числе и вырожденные случаи Q = К и
Q = S). В этом случае /? изменяется от 0 (Q = X) до
arctg(3tga) (Q = S).
Рассмотрим случай^ G Farctg (3 tga); -у! (рис. 230). Здесь
=P> LQTO = а, РТ = |. Тогда из треугольника PTQ
asina апп/З
8-a) и iy~ 3sinOS-ay
Из подобия треугольников DCS и NMS
MN _SQ_ST-TQ TQ
CD~ ST~ ST Sr
и
JEFMN
EF + MN a2 sin a
2 FQ " 9 sin ф - a)
_
2 sina cos /?
sin (p - -
Осталось рассмотреть тот случай, когда ортогональная
проекция сечения принадлежит меньшей из двух частей
основания пирамиды, т.е. прямоугольнику EFCD (рис. 231).
В этом случае LQPT = )3, /3 €
Дальнейшее решение аналогично приведенному в первом
случае.
252

Литература
1. Габович MS. Алгоритмический подход к решению
геометрических задач. — К.: Рад. школа, 1989. — 160 с.
2. Галицкий М.Л., Гольдман AM., Звавич Л.И. Курс
геометрии 8-го класса в задачах. — Львов, 1991. — 96 с —
(Квантор; N7).
3. Горнштейн П.И., Мерзляк AJH., Полонский В.Б.,
Якир М.С. Подводные рифы конкурсного экзамена по
математике. К.: Евроиндекс Лтд, 1994. — 240 с.
4. Готман Э.Г., Скопец З.А. Решение геометрических
задач аналитическим методом. М.: Просвещение, 1979. —
128 с.
5. Крайзман М.Л. Розв'язування геометричних задач
методом координат. — К.: Рад. школа, 1983. — 127 с.
6. Кушнир И.А. Построение треугольника (Энциклопедия
решения задач). — К., 1993. — 71 с.
7. Лоповок Л.М. Сборник задач по геометрии 6-8
классов. — К.: Рад. школа, 1985. — 104 с.
8. Парахневич В.А., Парахневич Е.В. Сборник задач по
геометрии. — Мн.: Нар. асвета, 1972. — 176 с.
9. Прасолов В.В. Задачи по планиметрии. 4.2. — 2-е
изд., перераб. и доп. — М.: Наука, 1991. — 240 с.
10. Рабинович ЕМ. Равновеликие треугольники в
задачах // Математика в школе. — 1993. — N3. — с. 63-65.
11. Рабинович ЕМ. Сборник задач по планиметрии на
готовых чертежах. — К., 1996.
12. Рыбкин Н.А. Сборник задач по геометрии. Часть I.
Планиметрия. — Изд. 18-е. — Учпедгиз, 1952. — 120 с.
13. Саранцев Г.И. Сборник задач на геометрические
преобразования. — М.: Просвещение, 1975. — 112 с.
14. Сборник задач по математике для поступающих во
втузы. Под ред. М.И.Сканави. — М.: Высшая школа, 1988. —
431 с.
15. Цыпкин А.Г., Пинский А.И. Справочник по методам
решения задач по математике для средней школы. — 2-е
изд., перераб. и доп. — М.: Наука, 1989. — 576 с.
16. Шарыгин И.О. Учимся решать задачи по геометрии //
Математика в школе. — 1989. — № 2-4.
253

ОГЛАВЛЕНИЕ
Глава I. Геометрия на готовых чертежах 5
Глава П. Метод ключевых задач 46
§1. Параллельные прямые, пересекающие стороны
угла 46
§2. Середины сторон четырехугольника 51
§3. Медиана, проведенная к гипотенузе 54
§4. Соотношения в прямоугольном треугольнике . 57
§5. Вписанный угол 61
§6. Угол между касательной и хордой 66
§7. Величина угла, вершина которого лежит
внутри (вне) окружности 70
§8. Формула а = 2R sin a 74
§9. Свойства пересекающихся хорд 78
§10. Касательная и секущая, проведенные к
окружности из одной точки 82
§11. Отношение площадей треугольников,
имеющих общую высоту (основание) 86
§12. Отношение площадей подобных треугольников 91
§13. Площади треугольников, на которые
четырехугольник разделен диагоналями 96
§14. Признак параллельности сторон
четырехугольника 99
§15* Угол между биссектрисами внутренних
односторонних и смежных углов 101
§16. Расстояние от вершины треугольника до
точки касания вписанной окружности со стороной 105
§17. Свойства биссектрисы угла треугольника ... ПО
§18. Второй признак подобия треугольников .... 113
Глава III. Избранные методы и приемы 117
§1. «Удлинение» медианы 117
§2. Метод вспомогательной площади , 120

§3. Метод вспомогательной окружности 124
§4. Применение центральной симметрии 135
§5. Применение осевой симметрии 138
§6. Применение преобразования поворота 142
§7. Применение гомотетии 146
§8. Метод координат 150
§9. Применение векторов 154
Глава IV. Многовариантные геометрические задачи . . 159
§1. Условие задачи не определяет взаимное
расположение точек и фигуры 159
§2. В условии задачи фигурируют две касающиеся
окружности, но не указан способ касания:
внешний или внутренний. В задаче даны две
точки, делящие окружность на две дуги, кроме
того известно, что некоторая прямая касается
окружности, но не указано, на какой из двух дуг
лежит точка касания 172
§3. В задаче фигурируют объекты, которым
приписываются определенные свойства, но не
указан порядок соответствия между множеством
объектов и множеством их свойств 178
Ответы* Указания. Решения 192
Литература 253

Учебно-методическое пособие
ПОЛОНСКИЙ Виталий Борисович,
РАБИНОВИЧ Ефим Михайлович,
ЯКИР Михаил Семенович
УЧИМСЯ РЕШАТЬ ЗАДАЧИ
ПО ГЕОМЕТРИИ
Под редакцией авторов
Художник Жураковская ОН.
Технический редактор Вербовиков A.M.
Корректор Рабинович М.Е.
Сдано в набор 15.07.96 г. Подписано в печать 16.09.96 г.
Формат 84*1081/^2. Бумага офсетная № 1.
Печать офсетная. Гарнитура Тайме. Усл.-печ.л. 13,44.
Уч.-изд.л. 22,7. Тираж 10 000 экз. Заказ № 0216239
МСП Научно-практический, учебно-методический центр
«Магистр-S» Творческого союза учителей Украины
252030, Киев-30, ул. Б. Хмельницкого, 16/18.
Тел. 229-89-29.
Отпечатано с готовых фотоформ на комбинате печати
издательства «Пресса Украины»
252047, г. Киев-47, пр-т Победы, 50.