i алкин В.Я., > ячугов Д.Ю. ' ш
КОНКУРСНЫЕ ЗАДАЧИ
ОСНОВАННЫЕ НА ТЕОРИ
ЧИСЕЛ
учебное посоС тя абитуриентов и пп . ников
Москва, 2002
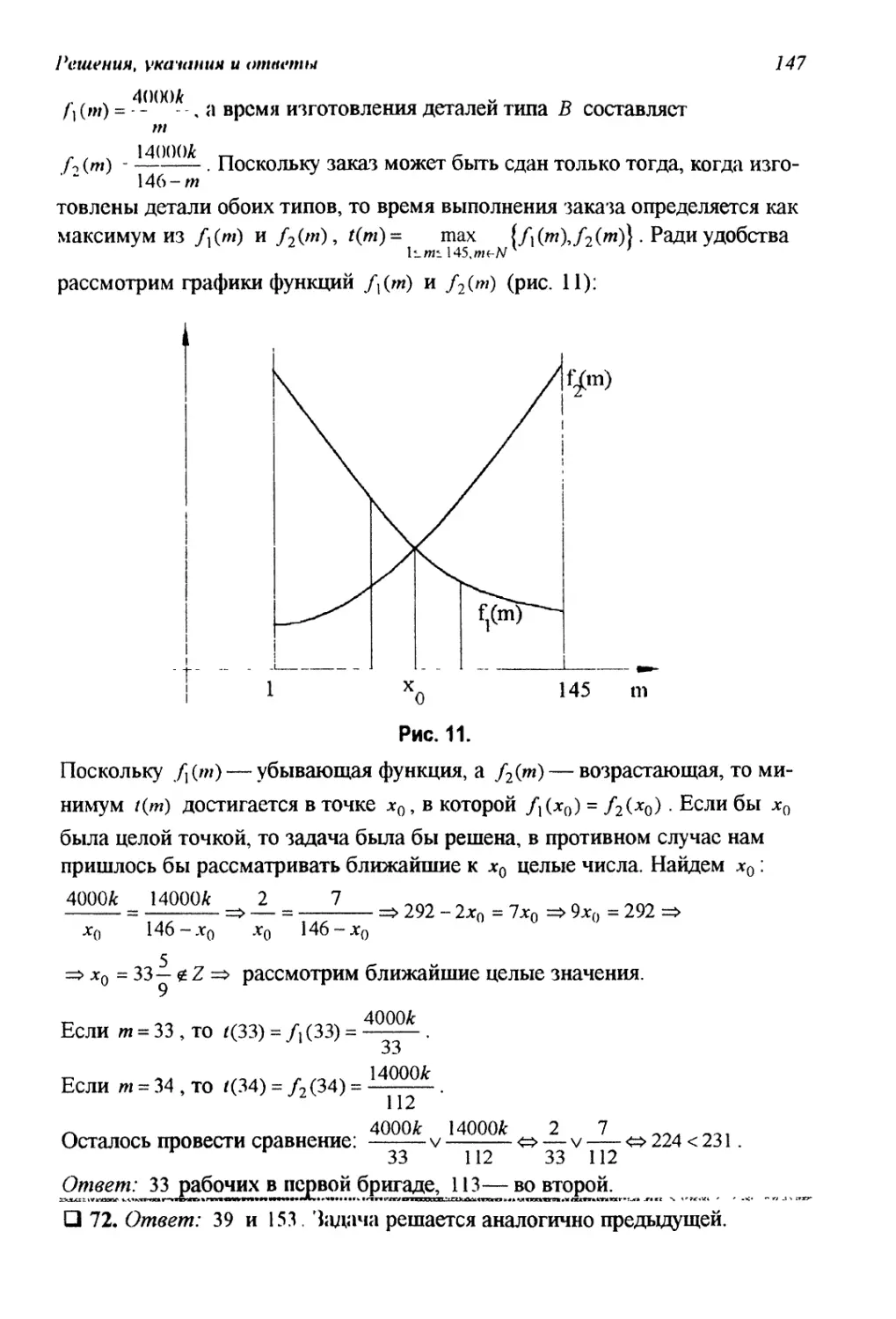
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. М. В. ЛОМОНОСОВА
ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И
КИБЕРНЕТИКИ
Галкин В.Я., Сычугов Д.Ю., Хорошилова Е.В.
КОНКУРСНЫЕ ЗАДАЧИ,
ОСНОВАННЫЕ НА ТЕОРИИ
ЧИСЕЛ
учебное пособие для абитуриентов и школьников
Москва, 2002
УДК 373:512
ББК 22. 1Я 729
К645
Галкин В.Я., Сычугов Д.Ю., Хорошилова Е.В.
Конкурсные задачи, основанные на теории чисел.
— М., факультет ВМиК МГУ 2002 — 180 стр.
Рецензенты: академик Ильин В. А., доцент Леонтьева Т. А.
В данном пособии в пределах школьного курса математики и
программы вступительных экзаменов рассматриваются элементы теории
чисел. Излагается необходимый теоретический материал. Особое внимание
уделено задачам. Проводится разбор основных типов задач, в том числе
конкурсных задач практически всех факультетов МГУ за последние 37 лет
и других вузов. В конце каждого раздела приводится большое число задач
для самостоятельной работы. В конце книги даны решения задач или
указания к решению и ответы.
ISBN 5-89407-125-9
© Галкин В.Я., Сычугов Д.Ю., Хорошилова Е.В., 2002
3
Рецензия
на книгу Галкина В.Я., Сычугова Д.Ю., Хорошиловой Е В
"Конкурсные задачи, основанные на теории чисел”
Задачи и вопросы, связанные с элементами теории чисел, нередко
вс1рсчаются на вступительных экзаменах. Прежде всего, это задачи с нату-
ральной и целочисленной арифметикой. На устном экзамене встречаются
задачи, связанные с делимостью, сократимостью дробей, а также с доказа-
юльством рациональности либо иррациональности какого-либо числа. На-
конец, нельзя не упомянуть задачи по тригонометрии, в которых при отборе
корней возникают диофантовы уравнения.
Между тем в школе натуральная и целочисленная арифметика изуча-
с1ся в младших классах, и к моменту вступительных экзаменов многие ус-
певают ее основательно забыть. Учебных пособий для абитуриентов, в ко-
юрых изучение теории чисел органично сочеталось бы с разбором конкурс-
ных задач, практически нет. (И это несмотря на огромное количество посо-
бий для поступающих в ВУЗы!)
Данная книга, на мой взгляд, удалась. Авторы, опытные преподавате-
ли факультета ВМиК МГУ, практически не выходят за рамки школьной
программы и в то же время дают теоретический материал, достаточный для
подготовки в любой ВУЗ. Особое внимание уделяется разбору конкурсных
задач и методам их решений.
Книга написана понятным и простым языком, и в то же время с долж-
ной степенью математической строгости. Это обстоятельство делает ее при-
(одной как для проведения классных и групповых занятий, так и для само-
сюятельного изучения.
Книга, несомненно, окажется полезной школьникам старших классов,
абитуриентам, школьным учителям для проведения факультативных заня-
1ий, а также преподавателям подготовительных курсов и репетиторам.
В.А. Ильин, академик
Российской Академии Наук
4
Оглавление
ВВЕДЕНИЕ...................................................5
ГЛАВА 1. НАТУРАЛЬНЫЕ ЧИСЛА.................................8
§1	. Введение в натуральные числа.......................8
§2	. Делимость, простые и составные числа............ .10
§3	. Делимость с остатком..............................19
§4	. Наибольший общий делитель и наименьшее общее кратное. 21
Задачи для самостоятельной работы......................24
ГЛАВА 2. ЦЕЛЫЕ ЧИСЛА..................................... 32
§	1. Задачи на делимость...............................32
§2	. Диофантовы уравнения первого порядка с двумя неизвестными...37
§3	. Диофантовы уравнения второго и высших порядков... 43
§4	. Неравенства в целых числах........................63
§5	. Системы уравнений и неравенств в целых числах.... 68
§6.	Задачи с параметрами и целые числа................ 74
§7	Экстремальные задачи с целыми числами.............. 83
Зад	ачи для самостоятельной работы........................96
ГЛАВА 3. РАЦИОНАЛЬНЫЕ ЧИСЛА..................................103
§1	. Свойства числовых дробей. Сократимые и несократимые дроби 103
§2	. Представление рациональных чисел десятичными дробями. 109
§3	. Разные задачи с рациональными числами............111
Задачи для самостоятельной работы.....................116
ГЛАВА 4. ИРРАЦИОНАЛЬНЫЕ ЧИСЛА .........................  120
§1	. Некоторые теоретические положения..............  120
§2	. Доказательство иррациональности некоторых чисел..123
§3	. Разные задачи с иррациональностью................126
Задачи для самостоятельной работы.....................129
РЕШЕНИЯ, УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ.....................132
Глава 1...............................................132
Глава 2.............................................. 152
Глава 3...............................................166
Глава 4.............................................. 174
ЛИТЕРАТУРА.............................................. 179
5
Введение
Задачи и теоретические вопросы, содержащие элементы теории чисел,
весьма часто встречаются на вступительных экзаменах по математике в
МГУ и других ВУЗах. На письменных экзаменах к таковым прежде всего
относятся задачи с натуральной и целочисленной арифметикой. В качестве
примера можно привести те текстовые задачи, в которых неизвестные ве-
личины по своей природе могут принимать только натуральные значения
(вспомним задачу о землекопах из стихотворения С. Маршака!). Встреча-
ются также абстрактные формулировки задач типа "‘Решить в целых числах
уравнение f (л, у) = 0 ”, либо ‘"Решить в натуральных числах неравенство
fix) > о ", либо "‘Решить в натуральных числах систему неравенств...” и т.д
Нельзя нс упомянуть и о примерах из области тригонометрии, когда при
решении и (или) отборе корней приходится решать диофантовы уравнения
На устном экзамене, помимо упомянутых типов, встречаются еще за-
дачи на доказательство рациональности либо иррациональности какого-
либо числа, а также задачи, связанные с сократимостью дробей, делимо-
стью или не делимостью и др. В программе по математике к устным экза-
менам в МГУ имеются вопросы ‘"Признаки делимости на 2,3,5,9,10".
"Свойства степеней с натуральными и целыми показателями”, "’Свойства
корней /2-й степени”, “Свойства степеней с рациональными показателями”,
а также вопрос ""Свойства показательной функции и ее график”, для пра-
вильного ответа на которые необходимо понимание, что такое веществен-
ное число, если не на строгом математическом, то хотя бы на интуитивном
уровне.
Между тем учебные пособия для абитуриентов, в которых изложение
)лсментов теории чисел сопровождалось бы разбором конкурсных задач,
практически отсутствуют. В школе натуральная и целочисленная арифме-
1ика изучаются в младших классах, и к моменту вступительных экзаменов
многие успевают ее весьма сильно забыть. Имеющиеся действительно хо-
рошие книжки по целочисленной арифметике (например, [1,2]) выходят
довольно далеко за пределы программы для поступающих, что затрудняет
их использование при подготовке к вступительным экзаменам. Необходи-
мый для подготовки к ответам на билеты материал можно найти в
11.4,23,24], однако в силу специфики данйых книг их авторы нс имели воз-
можности рассмотреть много задач и тем более провести хоть какую-либо
классификацию типов задач и методов решений Аналогичное замечание
можно сделать и по поводу статей в журнале ""Квант” [8-10]. Наилучшее, на
наш взгляд, изложение материала имеется в [5], однако к настоящему вре-
мени придумано множество новых конкурсных задач, да и данная книга
6
уже стала библиографической редкостью.1 В вышедшей недавно в целом
весьма удачной книге [25] теории, а также разбору новых конкурсных задач
с целыми числами посвящена небольшая по объему глава. Поэтому боль-
шое количество трудных и оригинальных задач остались за ее пределами.
Все это определило стиль нашей книги. Мы сознательно не включали
в нее ничего, что выходило бы за рамки школьной программы. Мы ориен-
тировались на школьника, готовящегося к вступительным экзаменам Точ-
но также и задачи рассматривались в подавляющем большинстве конкурс-
ные и решались они чисто “школьными” методами.
Книга написана на основе лекций, читаемых авторами в лектории
МГУ, на подготовительных курсах факультета ВМиК МГУ, а также в Шко-
ле Молодого Предпринимателя экономического факультета МГУ. Матери-
ал подается следующим образом. Последовательно изучаются натуральные,
целые, затем рациональные, и, наконец, вещественные числа. Особое вни-
мание уделено задачам.
Многие задачи авторские. К конкурсным и олимпиадным задачам на-
ми всегда указан источник заимствования (для МГУ дан только факультет в
сокращенном написании и иногда отделение и год, для большинства других
ВУЗов дается их старое или новое название и год). Мы хорошо понимаем,
что придумать новую задачу гораздо сложнее, чем ее решить. Сами были в
шкуре составителей. В последние годы в большинстве самых разных пуб-
ликаций, в том числе и солидных, у конкурсных задач стыдливо опускается
источник их появления, а это самый настоящий плагиат. Не зная авторов
задач, но указывая ВУЗ, факультет и год, мы отдаем хоть и косвенное
должное составителям. Для остальных задач мы указываем источник, если
нам удалось найти какую-либо ссылку.
Всякое теоретическое положение иллюстрируется примерами и кон-
курсными задачами. Проводится разбор основных типов задач, начиная от
самых простых и заканчивая достаточно сложными. В конце каждого раз-
дела даны задачи для самостоятельной работы, а в конце книги — их реше-
ния или указания с ответами.
Мы в основном рассматривали конкурсные задачи МГУ за последние
37 лет. однако книга содержит еще небольшое количество олимпиадных
1 В 1996 году книга [5] была переиздана. Имеющийся в ней теоретический
материал был приведен в соответствие с современной программой для по-
ступающих в МГУ, однако новые конкурсные задачи в ней, к сожалению,
не появились. Ввиду того, что название книги изменено, в нашем списке
литературы она упоминается как [6].
7
задач [11-16], а также задач других ВУЗов. Последнее обстоятельство по-
зволяет использовать книгу как пособие для подготовки в любой ВУЗ.
Мы надеемся, что эта книга окажется полезной школьникам старших
классов, абитуриентам, школьным учителям, ведущим основные и факуль-
тативные занятия по математике, а также репетиторам.
Мы приносим глубокую благодарность академику В. А. Ильину, взяв-
шему на себя труд написать рецензию на наше пособие. Особенно приятно
услышать в свой адрес похвалу от автора большой серии популярнейших
учебников по высшей математике Выражаем также благодарность доцен-
там факультета ВМиК МГУ Иновенкову И.Н., Панферову В.С., Леонтьевой
Т.А , а также Голубеву В.И., которые прочитали рукопись и сделали ряд
ценных замечаний.
ГЛАВА 1
Натуральные числа
.t> 1 *.• Г, ,'И/Л	А . • . iti - » 'А ->• г-
§1. Введение в натуральные числа
1.	Натуральные числа и системы счисления
В школьном курсе математики изучаются натуральные, целые, рациональ-
ные и вещественные числа (в математических школах и классах затраги-
ваются и комплексные числа). Последние числа в программу по математи-
ке для поступающих в вузы не входят, и поэтому мы их не рассматриваем.
Числа 1,2,3,...,2002,... являются натуральными. Натуральное число —
одно из основных понятий математики. Крылатая фраза, принадлежащая
Кронекеру: ^Натуральные числа создал Бог, остальное — творение рук
человеческих.”1 Множество всех натуральных чисел принято обозначать
заглавной латинской буквой N.
Множество натуральных чисел замкнуто (не выводит за пределы) относи-
тельно арифметических операций сложения и умножения. Это означает,
что если сложить два любых натуральных числа, то результатом будет на-
туральное число. То же самое относится к операции умножения Операции
вычитания и деления могут вывести за пределы множества N.
В десятичной позиционной системе счисления (арабской) натуральное чис-
ло п представляется в виде
п = акак_\ ...а2а} а() = ак 10* +ак_} • 10*-1 + ... + Л] • 101 +а0 • 10°,
где , (i = 0,... Д) цифры от 0 до 9, причем ак * 0
Помимо десятичной системы счисления существуют другие, например,
двоичная, которая применяется при записи чисел в памяти компьютеров.
В ней всякое натуральное число раскладывается по степеням двойки, при-
чем цифры а{ могут принимать только значения 0 или 1.
1 Леопольд Кронекер (1823 - 1891) — известный немецкий мтемишк ' ha фраза
была сказана им на Берлинском собрании ес1ссг1и)испыгн1слсй и 188<> i
Глава 1. Натуральные числа	9
2.	Задачи с десятичной системой счисления
С использованием десятичной системы счисления решается немало кон-
курсных задач арифметики натуральных чисел.
-< - Г1ГС»** » • а	«Vf Ч-Ч О'ГГЦЧТ» СГТМУЯ СЖГГХТгг 4r*WV*1-T	*г*» <т- 1	i	If
□ Пример 1. (Физфак, 1965)1 Доказать, что число Л/ = 11L .1-222...2 при
2и	п
любом натуральном п является полным квадратом
Решение. М = (999^- 2-999^91/9 = (102"-1-2(10”-1))/9 =
2п	п
= (102и - 2 • 10” +1)/9 = ((10й -1)/З)2 = (ЗЗЗддЗ)2
п
• , • - ’.У • Т-1»' ШТ^Г.ЧГПТМИМ'Л.Г >-.l.'.ir4K.1>AI».v<	'.'Т J. .•’(•XHWV/.TV Ч.	IV. <
□	Пример 2. Найти последнюю цифру числа З1999
Решение. З1999 = 34‘499 П = 81499 • 27. Первый множитель оканчивается на I,
следовательно, исходное число должно оканчиваться на 7.
□	Пример 3. Расшифровать равенство MM + NKN = PQQl\ где буквами
Л/, У, Р, Q обозначены неизвестные цифры в десятичной записи чисел.
Решение. Поскольку двузначное число ММ <100, трехзначное число
\JKN < 1000, a PQQP > 1000, то равенство может достигаться лишь в случае
/^1^/4-:= 9 и (9 = 0. Перепишем частично расшифрованное равенство
Л/Л/ +ЭМ) = 1001. Отсюда следует М = 2 (так как только цифра 2 при сло-
жении с цифрой 9 дает в младшем разряде единицу). Остается лишь вос-
становить значение цифры К : 9 АГ 9 = 1001 -22 = 979 или К = 7
Ответ: 22 + 979 = 1001.
__ » к. м» * 4 AIM	Л4Л« "ЛГа.	'V* <•	•<	< *• '	««
□	Пример 4. Показать, что число, имеющее в десятичной записи вид
abcabc, где а, Ь , с — цифры, а * 0 , делится на 7 , 11, 13.
Решение. abcabc = a 105 +Ь • 104 + с-103 +а • К)2 + 6 • 101 + с-10° =
= 100100а + 100106 + 1001с = 1001(102а + 106 +с) = 7-11-13 abc,
что и требовалось показать.	I
1 Далее факультеты МГУ будут указываться без ссылки на МГУ
10
Конкурсные задачи
§2. Делимость, простые и составные числа
1.	Простые и составные натуральные числа
Пусть п и т — натуральные числа, п делится нацело (без остатка) на
т , если существует натуральное число к такое, что п = тк . Числа п , т
и к при этом называют соответственно делимым, делителем и частным.
Обозначение делимости нацело натурального числа п на натуральное чис-
ло т символически таково: п : т (п кратно т).
Натуральное число называется четным, если оно делится нацело на 2,
и нечетным в противном случае.
Определение делимости без остатка позволяет разделить все натуральные
числа на простые и составные.
Натуральное число, большее единицы, называется простым, если оно де-
лится без остатка лишь на единицу и на само себя. Примерами простых чи-
сел могут служить 2,3,5,7,11,13,17,..., 1999. Натуральные числа, большие
1 и не являющиеся простыми, называются составными. Например, числа
4,30,33,1991,2001 —составные. Сама единица по определению не явля-
ется ни простым, ни составным числом.
Если натуральные числа п и т делятся нацело на натуральное число к ,
то число к называется общим делителем чисел п и т. Числа, не имею-
щие никаких других общих делителей, кроме 1, называются взаимно про-
стыми Например, 4 и 25 — взаимно простые числа.
Приведем без доказательства следующие теоремы (доказательства можно
найти в книге [1]).
Теорема 1. Простых чисел бесконечно много.
Замечание. Данную теорему впервые доказал Евклид методом “от против-
ного”. Попробуйте сделать это самостоятельно.
Теорема 2. (основная теорема арифметики).
Всякое натуральное число п > 1 представимо в виде произведения степе-
ней простых чисел р}, р2,..., рк‘
" = Р}' Р22 -'Pic *
причем числа т}, т2,..., тк являются натуральными и для каждого п
определены однозначно. Это представление единственно с точностью до
перестановки сомножителей.
Например, 63 = З2 • 71, и иным способом разложить это число в произведе-
ние простых сомножителей нельзя.
Глава I. Натуральные числа	Л
2.	Задачи на свойства простых чисел
Рассмотрим несколько задач, связанных со свойствами простых чисел.
t T.-’i	л*	«гь»	-jriA.r^ vsjttvzv. —	t kun с.	t • н*
□	Пример 1.11усть р — простое число и р > 3. Доказать, что р2 -1
делится нацело на 24.
Решение. Применим формулу разности квадратов р2-1=(р-1)0 + 1). По-
скольку р — простое число, большее 3, то р — нечетное число. Поэтому
числа р -1 и р +1 являются четными. Данные числа представляют собой
два последовательных четных числа, поэтому одно из них делится на 2,
а другое — на 4. Значит, (р - 1)(р +1) делится на 8.
Докажем теперь, что упомянутое произведение делится также и на 3.
Числа р ~ 1, р , р +1 являются последовательными. Это значит, что одно
из них обязательно делится на 3 . Но число р не может делиться на 3, так
как р — простое и большее 3. Значит, на 3 делится либо р -1, либо р +1,
и поэтому р2 -1 делится на 24 .
Для решения следующей задачи нам понадобится
Утверждение. Если a,beN и если а\к,Ь\к, то (докажите сами!)
Y) (а+Ьу.к ,	2) если я-6 > 0 => (а-/>):£ .
□	Пример 2. Пусть р , q — простые, р > q > 3. Доказать, что (р2 - q2): 24.
Решение, р2 -q2 = (р2 - 1) - (q2 -1), и задача сводится к предыдущей
Замечание. Попробуйте решить эту задачу вторым способом, разложив
р2 - q2 на множители и проведя рассуждения, аналогичные изложенным
в примере 1.
3.	Составные числа и формулы сокращенного
умножения
Для доказательства факта, что то или иное число является составным,
в ряде случаев можно использовать формулы сокращенного умножения.
Рассмотрим два примера.
□ Пример 3. Доказать, что число 210 + 512 является составным.
Решение. 210+512 = (25 )2 + (56 )2 =(25 +56)2 -2-25-5б =
= (25 + 56)2 -(23 • 53)2 = (25 +56 +23-53)-(25 +56 -23-53)
I)	Конкурсные нн)ачи
Далее (2s И6 |2* 53)>1, (25 +56 -2’-5*) .• I (докажите последнее неравен-
ство самостоятельно). Итак, исходное число представлено в виде произве-
дения двух натуральных чисел, каждое из которых больше I Следова-
тельно, оно составное.
- 7 г >» г •чгТ'ЧГ'Г| vt»i	j ”• -j	r - < * • tst
'□ Пример 4. Доказать, что число 222333 + 333222 не является простым.
Решение. 222333 + 333222 = (2221И)3 +(33374)3 Далее это выражение раскла-
дывается на произведение целочисленных сомножителей как сумма кубов,
что и доказывает утверждение.
Замечание. Формулы сокращенного умножения применяются при реше-
нии задач натуральной и целочисленной арифметики весьма часто, поэто-
му мы еще не раз вернемся к ним.
4. Применение основной теоремы арифметики
Разберем несколько конкурсных задач, идея решения которых основана на
применении основной теоремы арифметики.
Ф Пример 5. (ВМК, 1986) В академическом собрании сочинений, включаю-
щем менее 20 томов, число томов с художественными произведениями
кратно числу томов с письмами, которых, в свою очередь, в 3 раза меньше,
чем томов с публицистикой. Если число томов с художественными произ-
ведениями увеличить в 2 раза, то их станет на 14 больше, чем томов с пись-
мами. Сколько томов с публицистикой в собрании сочинений?
Решение. Пусть X, L, Р — количество томов, содержащих соответственно
художественную литературу, письма и публицистику. Имеем систему
X = kL,
. Р = 3/
y . р? 7	™ (Подставим X = kL.P = 3L)
2Х=Л + 14
Разложим 14 в произведение простых сомножителей 14 = 2-7, кроме того,
14 = 1-14 Так как 2k -1 — число нечетное, то может быть лишь
2£ -1 = 1, 2k -1 = 7 Проанализируем эти два случая.
1) 2k - 1 = 1 => k = 1, тогда L = 14 и (к +4)Л = 70 > 20 не годится.
2) 2к -1 = 7 => к = 4 , тогда L = 2 и (к + 4)Л = 16 < 20 годится. При этом
Р = 3L = 6
L„k е N,
(к + 4)Р< 20,
(2k-V)L = 14.
()твет • 6 томов
Рассмотрим более сложную задачу.
/ 'natta I Натураньны? чигча	13
• '	Uv ,»*	9«« w < • . 14 V4 •/ ' i	s* > . Lu*. V—л«Л
Hi Пример 6. (BMK, 1982) Ila заводе было несколько одинаковых прессов,
ппампующих детали, и завод выпускал 6480 деталей в день. После рекон-
струкции вес прессы заменили на более производительные, но тоже одина-
ковые, а их число увеличилось на 3. Завод стал выпускать в день 11200
деталей. Сколько прессов было первоначально?
Решение. Пусть Р — количество прессов до реконструкции, А — произ-
водительность прессов старого типа, т — производительность прессов
нового типа (деталей в день). Из условия задачи следует
Р < к „т е N ,
к < т, Р > 1,
' У’А = 6480 = 24-34-5,
(1> + 3)m = 11200 = 2б •5" •7
Второе условие дает
24-З4-5	26•52-7 j	?	s
А =---=---<--------— ш, 34-(Р + 3)<22-5-7Л 81F + 3 < 140Л
Р Р + 3
Р> — = 4—
59	59
Итак, Ре N . Р > 5 .
Из разложения числа (Р + зр т следует, что Р + 3 нс делится на 3 Значит,
не делится на 3 и число Р. Следовательно, в разложении числа Р на про-
стые сомножители присутствует только 2 (степень не выше четырех) и 5
(степень не выше 1).
Если Л = 24, то Р + 3 содержит множитель 19, что невозможно из послед-
него равенства.
Если Р = 23, то Р + 3 содержит множитель 11, что невозможно
Если Р - 2 4 • 5 , то Р 4- 3 = 83 , что невозможно.
Если Р = 23 • 5, то Р + 3 = 43 , что невозможно
Если Р ~ 22 • 5 = 20 , то Р + 3 = 23 , что невозможно
Наконец, если ^ = 2- 5 = 10, то Р + 3 = 13, что невозможно
Остается только Р = 5 .
Ответ: первоначально было 5 прессов
Наконец, рассмотрим еще одну достаточно сложну^ задачу; также решае-
мую при помощи основной теоремы арифметики
□ Пример 7. (Эконом., 1993) За время хранения вклада в банке проценты
по нему начислялись ежемесячно сначала в размере 5 % в месяц, затем
12%, потом 11—% и, наконец, 12 5 % в месяц. Известно, что под действи-
9
ем каждой новой процентной ставки вклад находился целое число месяцев.
14	Конкурсные задачи
а по истечении срока хранения первоначальная сумма вклада увеличилась
на 104- %. Определить срок хранения вклада.
6
Решение. Пусть по 1-ой процентной ставке вклад в банке пролежал т}
месяцев, по 2-ой процентной ставке — т2 месяцев, по 3-ей и 4-ой — т3
и т4 месяцев. Заметим, что 5 % соответствуют . Это означает, что ко-
гда вклад находился под действием 1-ой процентной ставки, он каждый
21	3
месяц увеличивался в — раза. Далее, 12% соответствуют — и за время
„ „	.	28
действия 2 -ои процентной ставки вклад каждый месяц увеличивался в —
раза. Аналогично получим, что за время действия 3 -ей процентной ставки
10	.
каждый месяц вклад увеличивался в — раза, а за время действия 4 -ои
9 о
ставки — в - раза. За все время сумма согласно условию задачи увеличи-
8
1	49
лась на 104- %, т.е. в — раза. Обозначим за $ первоначальную сумму де-
нег и составим уравнение
Г 2£yV28pfloppy'4 _ $,49
К <2oJ 1,25) I, 9 ) 1,8;	24
После преобразований получим
2 Г'1 -28W2 10^ -9"м -24 = 20w* -25W2 -9^ -8™4 -49
Разложим числа, стоящие в левой и правой частях последнего равенства,
на простые множители:
22m2 + m3+3	f2m4 + l $т5 ^тх+т2 _	З2™3	7 2
и воспользуемся тем фактом, что всякое натуральное число разлагается на
произведение простых сомножителей единственным образом (по основной
теореме арифметики). Это означает, что степени при 2, 3, 5 и 7 в левой и
правой частях равенства совпадают:
2т2 + т3+3 = 2гщ + 3w4,
W] + 2ш4 4-1 = 2m3,
т3 = W] + 2ni2,
+rn2 = 2.
Решая эту систему уравнений, получим
Wj = 1, ni2 = 1, т3 =3, rn4 = 2,	+т2 ♦ пц I т4 - 7
Ответ: вклад хранился 7 месяцев.
Замечание. Из уравнения пц + т2 = 2 и условии Ш), ш >W мгновенно сле-
дус! Ж| т: 1 . Это обстоятельство сильно упрощаем решение системы.
Глава 1. Натуральные числа	15
5. Признаки делимости и связанные с ними задачи
В программу по математике для поступающих в МГУ включено доказа-
тельство признаков делимости на 2, 3, 5, 9, 10. Рассмотрим эти и некоторые
другие признаки. Поскольку все эти признаки являются и необходимыми,
сформулируем их в терминах достаточности и необходимости (<=>).
Пусть п акак_}...а2а}а^ - ak\tf + ак _j 1 О*-1 + ... + а1101 + а()10°. Тогда
1.	Число п делится нацело на 2 <^> а0:2.
2.	Число п делится нацело на 4 <=>	:4.
3.	Число п делится нацело на 8 <=>
5.	Число п делится нацело на 9 <=>	:9.
1=0
6	Число п делится нацело на 5 <=> я0:5.
7.	Число п делится нацело на 25 <=> Л|П() :25.
8	Число п делится нацело на 10 <=>	-Л)
9.	Число п делится нацело на 11 <=> сумма цифр. занимающих нечетные
места, отличается от суммы цифр, занимающих четные места, на число,
делящееся на 11.
Например, 103785 делится на 11, так как 1-04-3-7 + 8-5 = 0.
Рассмотрим в качестве примера доказательство делимости на 3.
Доказательство достаточности. Воспользуемся десятичной системой
счисления и представим п в виде
п = акак_\ ...а2а\а§ — ак • 10^ +ак _]  10^ ^ + .. + • 10^ + а® • 10 —
= ^(999...9 + 1) + а^_|(999...9 + 1) + ... + ^(9 + 1) + а0 =
к	к-\
— (ак • 999...9 + ак-\ * 999 ...9 +... + • 9) + (ак + ак_] +... + #□).
к	к-}
Числа вида 999...9 делятся без остатка на 3. Поэтому сумма чисел внутри
первых скобок делится без остатка на 3, и делимость числа п на 3 опреде-
ляется вторыми скобками. Остается заметить, что в последних — сумма
цифр числа п.
Необходимость доказывается из этого же представления.
16	Конкурсе ые зада чи
Признак делимости на 9 доказывается аналогично. Прочие признаки дели-
мости докажите самостоятельно в качестве упражнения, либо обратитесь к
[1,3,4].
Разницу между необходимостью и достаточностью продемонстрируем на
следующем замечательном примере.
9 Пример 8. Доказать следующий признак делимости если сумма цифр
числа т равна сумме цифр числа 2т , то т: 9
Доказательство. Если т -а() +10^ +102а2 +. ,а 2т =Ь() 4-106] +102Ь2 +.. —
конечные числа в десятичной записи, то
т = 2т — т = 4- 4- Ь2 4-... 4-4- 99/>2 4-... — (<7g 4- 4- а2 4-... 4- 9(7] 4-99(72 4-...) =
= [0 4-9(Z>] - (7|) 4-99(/>2 - а2) 4-... ]: 9.
Ответ на вопрос "является ли этот признак и необходимым9” (т.с верно ли
обратное утверждение?) — отрицательный. Например, число 333 делится
на 9, но суммы цифр у чисел 333 и 666 очевидно не равны.
Проверьте, что наименьшее из чисел, делящихся на 9, у которых сумма
цифр не равна сумме цифр удвоенного числа, есть 144
I СЬ. ЛПМЬМ	т	Gd'KXXXJOXr J.T.AtlkaJj'-	kw. -.XU. ~ u л
□ Пример 9. Найти цифру Л\ при которой число 5А'793Л'4 делится наце-
ло на 3.
Решение. Воспользуемся признаком делимости на 3:
5 4- X 4- 7 4- 9 4- 3 4- X 4- 4 = 2X 4- 2 8 = 2 (X 4-14): 3 .
Непосредственной подстановкой вместо Лг цифр 0, 1, ,9 получаем, что
при А = 1,4,7 указанное число делится нацело на 3.
Ответ: {1,4,7}
Пользуясь признаками делимости на 2, 3, 5, 9, 10, можно строить признаки
делимости на произведения этих чисел, скажем, на 6, 18, 22, 55 и т.п.
__________ к
Например, п-акак_}. z7jO0 :18 <=> л0:2 и :9
(=0
'Кс	I ' ‘Т^ <ГГ-О>к> ХД131. ’	. С	.4	X 'Х.1»	‘	S. > ж.
Й Пример 10. (Физфак, 1964) Найти все числа вида « = 34А57 такие, что
п делится без остатка на 36.
Решение. Разложим 36 на произведение взаимно простых сомножителей:
36 = 9 4. Очевидно, что должны выполняться оба признака делимости —
на 4 и на 9. Поскольку' признак делимости на 4 использует только две по-
следние цифры в числе, то удобнее начинать с него. Итак, 5F = 5O 4- Y
должно делится на 4 Отсюда следует, что 7 = 2 или 7 = 6
Глава 1. Натуральные числа
17
Пусть У = 2. Тогда 34%52 должно делиться на 9, т.е. сумма цифр числа
5 = з + 4 + X +5 + 2 = 14 + X должна делиться на 9. Отсюда: Az=4 и
пх = 34452.
Пусть У = 6 . Тогда 5 - 3 + 4 + Л' + 5 + 6 = 18 + X должно делиться на 9. Отсю-
да X - 0 либо X = 9 и н2 - 34056 и = 34956 .
Ответ: таких числа три пх = 34452, п2 = 34056,	- 34956
6. Задачи на доказательство делимости
Обсудим задачи, связанные с доказательством самого факта делимости.
Иногда при доказательстве делимости оказывается полезной формула сум-
мы членов геометрической прогрессии.
ф Пример 11. Доказать, что 36 9 73697 -1 делится без остатка на 3696
Решение. Рассмотрим сумму членов геометрической прогрессии
S = l + 36971 + 36972 + З6973 + +36973096 =	-—
3697-1
Поскольку в левой части равенства стоит целое число, то и в правой части
равенства стоит целое число, что и доказывает утверждение.
Замечание. Эту же задачу можно решить при помощи одной из формул
сокращенного умножения.
При доказательстве делимости натуральных чисел порой является эффек-
тивным метод математической индукции. Подробное изложение метода
имеется в [5,6]. Начнем с простой задачи.
ф Пример 12. Доказать, что при любом натуральном п число (и3 +2н) • 3.
Решение. Воспользуемся методом математической индукции.
1) При п = 1 w3 + 2н = 3:3 => утверждение при п = 1 верно.
2) Пусть утверждение верно при п = к , то есть (к3 + 2к): 3
Докажем, что из этого следует справедливость утверждения при п = к +1,
то есть что (к +1)3 + 2(к +1): 3 .
В самом деле,
(А+1)3 + 2(А + 1) = А3 + 3р + ЗА + 1 +2А' + 2 = (А3 + 2А) + 3(А2 + А +1).
Первое слагаемое делится на 3 по индуктивному предположению, второе
слагаемое также делится на 3 Следовательно, и вся сумма делится на 3.
Утверждение доказано.
18	Конкурсные задачи
Замечание. Эту задачу можно легко решить и без индукции, рассматривая
остатки от деления числа п на 3.
Теперь рассмотрим более сложную задачу.
 — --тп- -1—»»ППМ'И«ЛТ-Г‘|Г|П-Г.^~ГГ-ГТ.ТГГ'1Т-|ГТ*1 —*^-*~* —**	—	<<»»»,  /л
□ Пример 13. Доказать, что при любом целом неотрицательном п число
11”+2 4-122л+1 делится на 133.
Решение. Воспользуемся методом математической индукции.
1) При п = 0 . 11”ь2 +122”+1 = 112 4-121 = 133 ==> утверждение верно.
2) Пусть утверждение верно при п = к > 0, то есть (11^+2 + 122Zr+1): 133.
Докажем, что из этого вытекает справедливость утверждения при п = к +1.
] j(/c+i)+2	- i i*’3 +122*+3 = 1М1^+2 +122 -122Ь1 =
= 1111*’2 4-(133 4-11)-122Л+1 = 1 Н11*+2 4-122/ж) 4-133-122*11
Первое слагаемое делится на 133 по индуктивному предположению, второе
также делится на 133. Следовательно, и вся сумма делится на 133. Утверж-
дение доказано.
Наконец рассмотрим задачу, предлагавшуюся на Пятой Соросовской
Олимпиаде 1999 года для школьников 11 класса (16].
Пример 14. Найдите все натуральные числа, меньшие чем 10s, которые
делятся на 1999 и у которых сумма цифр в десятичной записи равна 25
Решение. Очевидно, что данную задачу при наличии достаточного време-
ни можно решить «тупым перебором». Мы же приведем рассуждения, по-
зволяющие этот перебор существенно упростить.
Будем для удобства записей обозначать сумму цифр натурального числа т
символом 5(»/). Пусть п — одно из чисел, удовлетворяющих условию
задачи. Тогда
п е ТУ,
=, A<_L2L = 5O-^_ => Д-<5()
« = 19994, ке N.	1999	1999
5 («) = 25
Представим число п в виде произведения п = (2000 -1)4 = 24 • 1000 - 4 =
= (24 - !)• 1000 4-999 - (4 - 1). Из последнего равенства следует, что сумма
цифр у числа п равна 5(«) = 5(24 -1) 4- 27 - 5(4 - 1), поэтому
5(24 - 1) - 5(4 - 1) 4-27 = 25 или 5(24 - 1)-5(4 - 1) =-2 . Обозначим 4-1=»/
и получим уравнение 5(2»/ 4-1) - 5(»/) = -2, где 0 < »/ < 49.
Обозначим через а и Ь число десятков и единиц числа »/, тогда
»/ = 10а 4- Ь, где 0 < а < 4,0 < Ь < 9, и рассмотрим два случая
Глава I. Натуральные числа	19
1)	Если 0 < b < 4 , ТО 5(2w + l) = 2а +2fc + l,S(m) = а +Ь , поэтому
S(2m ч-1) — S(m) = а+ 6 + 1^-2=> в этом случае решений нет.
2)	Если 5<6<9, TO S(2m + 1) = (2а +1) 4-(2Л 4 1 - 10) - 2а +2Ь- 8 , поэтому
S(2m 4-1)- S(m) = а + b-% = -2 или а 4-b = 6 .
О < а < 4,
5 < h < 9,
а 4- b = 6,
a,b е Z
к
Л] =0,
6| = 6
Д2 ~
Ь2 =5
=> т} = 6 => к} = 7 => щ 1999 • 7 = 13993,
=>т2 = 15=>*2 = 16=>м2 = 1999-16 = 31924. "
Ответ • 1 1993 и 31924.
§3	. Делимость с остатком
Понятие делимости с остатком основано на следующем утверждении,
доказательство которого можно найти в 11 ].
Теорема. Для любого натурального числа п и натурального к,п>к суще-
ствует и притом единственная пара целых неотрицательных чисел р и
q таких, что n-k-pig, где целое число р называется неполным част-
ным от деления п на к , а число q называется остатком, причем
()<</<«-!. В частном случае при q = 0 число п делится на к нацело.
□ Пример 1. а) 14 = 2-7 4-0 (м = 14, к = 7, р = 2, <? = 0);
Ь) 25 = 7-34-4 (п = 25, к = 7, р = 3, q = 4)
1. Задачи, основанные на рассмотрении остатков
Решение многих задач целочисленной арифметики основано на рассмот-
рении возможных остатков от деления, и это будет демонстрироваться
на протяжении всей книги.
□ Пример 2. (Филфак, 1969) Остаток от деления некоторого натурального
числа п на 6 равен 4, остаток от деления на 15 равен 7. Чему равен оста-
ток от деления числа на 30 ?
Решение. По условию
п = 6к 4- 4,
п = 15т 4- 7
5п =30*4-20, _
4п = 60т 4-28
= Ч)(к - 2т) -8 = 30(* - 2w -1) 4-22 = 30/ 4- 22.
Ответ: 22.
20	Конкурсные задачи
□ Пример 3. Доказать, что при любом целом т число т(т2 +5) делится
без остатка на 6.
Решение. Представим т в виде т-бр + q , где р — целое число, а оста-
ток q принимает одно из значений 0, 1, 2, 3, 4, 5
Если <7 = 0, то m = 6/j =>t?2(w2+5) кратно 6,
если <7 = 1, то т = 6р +1
=>т(т2 +5) = (6р + 1)(36/Г +12р + 6) = 6(6р + 1)(6р2 +2р + 1) кратно 6 .
если q = 2 . ТО т = 6р +2
=>т(т2 4-5) = (6/?4-2)(36/?2 4-24р4-9) = 6(Зр4-1)(12р2 4-8/7 4-3) кратно 6.
если <у = 3, то т = 6 р а 3
=>т(т2 +5) = (6/7 ч- 3)(36/Г I 36/; 4-14)--6(2/> 4-1)(18/;2 4-18/7 4-7) кратно 6 ’,
ССЛИ <7 = 4 , ТО т = 6р +4
т(т2 4-5) = (6р 4-4)(36р2 4-48р 4-21) = 6(3/7 4-2)(12/Г 4-16/; 4-7) кратно 6 ;
если q = 5 , ТО т = 6р 4- 5 =>
т(т2 4-5) = (6р 4-5)(36р2 4-60/7 4-30) = 6(6р 4- 5)(6р2 4- Юр 4- 5) кратно 6 .
Замечание. Эту задачу можно было бы решить и вторым способом, коро-
че. т (т2 4- 5) = т3 4- 5т = т3 -т + 6т - т(т2 -1) + 6м = (т -\)т(т 4-1)4-6>и
Число 6т делится на 6, число (т -\)т(т 4-1) также делится на 6, как про-
изведение трех последовательных натуральных чисел.
□	Пример 4. Доказать, что сумма квадратов двух последовательных целых
чисел при делении на 4 дает в остатке 1 .
Решение. Пусть т — произвольное целое число. Тогда
т2 + (m + l)2 = 2(т2 + т) +1 = 2w(w4-l)4-l.
Первое слагаемое содержит произведение двух последовательных целых
чисел т(т + \\ которое, как известно, всегда делится на 2 Следовательно,
первое слагаемое делится нацело на 4 и при этом остаток равен 1.
□	Пример 5. (Стэндфордский университет, США) Доказать, что нет такого
числа в последовательности 11,111.111 1,1 1111.. ., которое является квадра-
том целого числа.
Решение. Каждый член п указанной последовательности, начиная с треть-
его, представим в виде п ЮОш i 11 I(25т » 2) з 1. где т — неотрицатель-
Глава 1. Натуральные числа	21
ное целое число. Поэтому п нечетно и при делении на 4 дает остаток 3.
С другой стороны, числа вида (2А +1)2 при делении на 4 имеют остаток 1.
2.	Пример сочетания нескольких методов
Наконец, существуют задачи, при решении которых приходится комбини-
ровать рассмотрение остатков с каким-либо иным приемом (например,
с использованием формул сокращенного умножения или с анализом цифр)
□ Пример 6. Доказать, что при всех целых п число п5 - п делится на 30.
Решение, п5 - п -п(пА	-V)(n2 +1) = (п - 1)н(л + 1)(л/2 4 1)
Числа п -1, н, п +1 — последовательные, поэтому одно из них делится на 3
и по крайней мере одно — на 2. Итак, делимость на 6 мы уже доказали.
Чтобы доказать делимость произведения на 5, достаточно рассмотреть все
остатки от деления числа п на 5. Сделайте это самостоятельно
§4. Наибольший общий делитель и
наименьшее общее кратное
1.	НОД и связанные с ним задачи
Если натуральные числа И| и //? делятся нацело на одно и то же натураль-
ное число т , то т называется их общим делителем Наибольший из об-
щих делителей двух (или нескольких) чисел называется их наибольшим
общим делителем и обозначается НОД{п} ль)
Первый способ нахождения НОД основан на разложении чисел hj и п2
на простые множители и поиске наименьшей степени вхождения того
или иного простого множителя в каждое из чисел »] ль О втором способе
(алгоритме Евклида) будет рассказано ниже
□	Пример 1. (Мое. гос. акад, тонкой хим. технологии, 1997) Найти НОД(54С12)
Решение. 54 = 21 • З2, 72 = 22 • З2 => 7Л9Д(54,72) = 21 • З2 = 18.
Если НОД(п^п2) = I, то, как указывалось выше, числа »| и п2 являются
взаимно простыми
□	Пример 2. Решить систему
22
Конкурсные задачи
т+п- 20,
НОД(т,п) = 5,
т,п е W
Решение. НОД (т.п) = 5=>т = 5k, п = 51, где k, I е /V ==> 5к + 51 = 20 => к +1 = 4.
Так как М — взаимно простые числа, то для к,/ получим решения
(3,1); (1,3). Далее находим т.п .
Ответ: (5, 15), (15, 5).
□ Пример 3. Доказать, что при всех натуральных значениях п наиболь-
ший общий делитель чисел н2 4-10/2 + 21 и w2+9/1 + 18 равен и+3.
Доказательство, п2 + Юп + 21 = (п + 3)(п +7), п2 + 9п +18 = (п + 3)(н + 6)
число и+3 является делителем обоих рассматриваемых чисел. Далее, по-
скольку числа п + 6 и п + 7 — последовательные и поэтому взаимно про-
стые, то число п + 3 — наибольший общий делитель.
□	Пример 4. (г. Уфа, блиц-олимпиада 1998, 11 класс) Доказать, что при всех
целых к выполняется НОД(2к + 1, 9 к +4) - 1.
Решение. Пусть х е N и пусть
f(2A'+l):x,	((8/с + 4):х,	[к':х,	.
\(9к + 4):х	|(9Л +4)^ ^ \(2к + 1)!х =>1 :-v	~ 1
□	Пример 5. Найти наибольший общий делитель чисел 11111111 и
111... 111 (сто раз повторяется единица).
Решение. При делении большего из чисел а = Щ_3 на меньшее число
100 раз
h = 11111111 получим неполное частное q = 10000000... 10000000 10000
I I раз
и остаток г = 11И, т.е.
а =	+ 1111, a-bq= 1111.
Отсюда видно, что всякий общий делитель а и Ь (в том числе и наиболь-
ший) является также и делителем числа 1111. Но число 1111 само делит
числа а и Ь (легко проверить), а, значит, оно и есть их НОД.
/ 'пава 1. Натуральные чисна	23
2.	НОК и связанные с ним задачи
Наименьшее натуральное число, которое делится нацело на данные нату-
ральные числа И] и п2, называется их наименьшим общим кратным и
обозначается НОК(w1 ,«2).
Правило нахождения НОК также основано на разложении чисел п},п2 на
простые множители и поиске наибольшей степени вхождения всех про-
стых множителей в числа И] и п2. О втором способе будет сказано ниже.
I	/’.I'f-rv .ТГ*2ТГГ-?Л"1г	»• Т**ГГГГ^Г*Т1»	<-• l- f Г —I	t
□ Пример 6. Найти ЯСЖ(42Д8).
Решение. 42-21 з'-7‘, 18 - 21 - З2 => Я67К(42,18) = 21 -32-7’ -126
□ Пример 7. Доказать, что при всех натуральных значениях п наимень-
шее общее кратное чисел п2 + 6н + 9 и п + 4 равно п3 + 10п? + ЗЗп + 36.
Доказательство, п2 + 6п + 9 = (и + З)2. Поскольку числа п + 3 и п +4 взаим-
но простые, то их наименьшее общее кратное равно их произведению. Сле-
довательно, НОК(п2 + 6и + 9,?;+4) = (гГ +6и + 9)(л+4) = л3 +10н2 + 33н + 36 .
□ Пример 8. (ВМК, 1978) Совокупность А состоит из различных натураль-
ных чисел. Количество чисел в А больше семи. Наименьшее общее кратное
всех чисел из А равно 210. Для любых двух чисел из А их наибольший об-
щий делитель больше единицы. Произведение всех чисел из А делится на
1920 и не является квадратом никакого целого числа Найти числа, из ко-
торых состоит А.
Решение. Каждое число из А должно делить число 210- 2 3 5 7. Значит,
все числа из Л раскладываются только на простые множители 2. 3, 5, 7 в
степенях не выше первой. По условию произведение всех чисел делится на
1920 = 27•3•5 . Поэтому среди искомых чисел должно быть не менее семи
четных. Но только восемь четных чисел являются делителями числа 210
2, 2-3 = 6, 2-5 = 10, 2-7 = 14, 2-3-5 = 30,
2-3-7 = 42, 2-5-7 = 70. 2-3-5-7 = 210.
Если число 2 е А , то любое другое число из А делится на 2, ведь любой
общий делитель больше 1. Поэтому А = {2. 6, 10, 14, 30, 42, 70, 210}, но
произведение есть полный квадрат, что не разрешается. Итак. 2 g А , зато
оставшиеся семь четных чисел принадлежат А . Пусть к — одно из нечет-
ных чисел из А . Так как НОД чисел 6 и А больше или уавен 3 .то А: 3 .
Аналогично к\5 и к: 7 . Значит, к : (3-5 7) и А = 3-5-7 = 105. Осталось убе-
диться, что все условия задачи соблюдаются.
Ответ: А = {6,10.14,30,42.70,105,210}.
24
Конкурсные задачи
3.	Теорема о свойствах НОД и НОК
Следующая теорема отражает свойства НОК и НОД ( здесь к.т.п —
натуральные числа)
Теорема. 1) НОД(т.п} НОК(т.н} = тп.
2)	ИОД(кт.кн} - к • НОД(т.п).
3)	НОК(кт.кп) = к • ИОК(т.п}.
4)	НОД(шп + \) = \.
5)	Если п >т , то НОД (шт) = НОД(н -т,т).
6)	НОД (шт) = ИОД(т.г), где г — остаток от деления п на т.
Утверждения 1 — 6 докажите самостоятельно, для чего воспользуйтесь
основной теоремой арифметики и соображениями делимости.
На свойствах 5, 6 основан алгоритм Евклида нахождения НОД(т.п). Так,
НОД(\ 125,725) = 7/(9Д(400,725) = НОД (400,325) = /7ОД(75,325) =
= НОД(75,25) = 25 .
Пользуясь свойством 1 и алгоритмом Евклида, находят НОК(т,п).
□ Пример 9. Найти /ЯЛК*(63,28)
Решение. Задача решается в два действия
1) Воспользуемся свойством 6:
НОД (63,28) = ИОД (7,28) = 7 .
2) НОК(632Я>) = 63 • 28 /7ОД(63,28) - 63 • 28 7 = 252.
Задачи для самостоятельной работы
MAWtW.ll.te1 ‘И- *	4|> t -44 Mte «bteA. »*. .w wZ4ol«A>MUi.	Ate-Ь V UU . '	4	i :	- -	j
□	1. Расшифровать равенство PPQ - Р = MRMM .
□	2. Найти все пары натуральных чисел т ин, удовлетворяющих равен-
ству 2т -2п = 1984
□	3. Доказать, что ни при каком натуральном п число п4 + 2п3 + 2п2 +2п +1
не может быть полным квадратом.
□	4. Доказать, что натуральное число, сумма цифр которого равна 24, не
может быть полным квадратом.
□	5. Доказать, что число, оканчивающееся на 17, ни можш быть полным
квадратом.
Глава 1. Натуральные числа	25
□ 6. Сумма цифр некоторого числа п равна 366. Может ли это число быть
полным квадратом?
□ 7. Найти предпоследнюю цифру числа, которое является полным квад-
ратом и оканчивается на 5 .
□ 8. Доказать, что числа 16, 1156, 111556, 11115556,.., являются полными
квадратами.
□ 9. Найти последнюю цифру числа 19971"7.
□ 10. Доказать, что разность между трехзначным числом и числом, запи-
санным теми же цифрами, но в обратном порядке, либо равна нулю, либо
нс может быть квадратом целого числа.
□ 11. Найти цифру X , при которой число 12^ 347Л’ делится на 8
□ 12. Доказать, что 7191 -1 делится на 6.
□ 13. Доказать, что любое число, десятичная запись которого состоит из
Зп единиц, делится на 37 .
□	14. Доказать, что при всех натуральных п число •|(24m+2 + 1) — целое,
и при п > 1 — составное.
□	15. Доказать, что при любом натуральном п числа вида 23л-7и-1 де-
лятся на 49
□	16. Пусть т , п у к — натуральные числа и m + н + & делится без остатка
на 6. Доказать, что в этом случае делятся без остатка на 6 числа
т3+п3+к3 пт5+п3+к.
□	17. Про натуральные числа т и п известно, что т2+п2 делится без
остатка на 3. Доказать, что в этом случае числа т и п по отдельности
также делятся на 3 .
□	18. Доказать, что утверждение, сформулированное в предыдущей зада-
че, останется справедливым, если 3 заменить на 7.
□	19. Пусть р>5 — простое число. Доказать, что /?4-1 делится без ос-
татка на 48.
□	20. Доказать, что для всех натуральных чисел т , п таких, что т > п,
число тп(т2 -п2) делится без остатка на 6.
□	21. Доказать, что при натуральных п число d-п делится на 6.
□	22. Доказать, что произведение любых четырех последовательных нату-
ральных чисел делится нацело на 24 .
26	Конкурсные шдачи
□ 23. Доказать, что при любом натуральном п число ns -5п3 + 4w делится
без остатка на 120.
□ 24. Делится ли на 81 число, запись которого состоит из 81 единицы ?
□ 25. Доказать, что из любых 52 целых чисел можно выбрать два числа
так, чтобы либо их сумма, либо их разность делилась на 100.
□ 26. Известно, что длины сторон прямоугольного треугольника являются
целыми числами. Доказать, что в этом случае верны утверждения:
1) хотя бы одна из длин сторон треугольника делится на 3 ;
2) хотя бы одна из длин сторон треугольника делится на 5 .
□ 27. Доказать, что число abed делится нацело на 101 тогда и только то-
гда, когда ab - cd = 0 .
□ 28. Доказать, что из 18 последовательных трехзначных чисел хотя бы
одно делится без остатка на сумму своих цифр.
□ 29. Найти максимальное п , при котором число 500’ делится на 7"
□ 30 Известно, что п-1 делится нацело на 2, п-2 делится нацело на 5.
Доказать, что н+3 делится нацело на 10 .
□	31. Может ли натуральное число делиться нацело на 8 , а при делении на
12 давать в остатке ю ?
□	32, Число т при делении на 4 дает в остатке 1, а при делении на 5
даст в остатке 2. Чему равен остаток от деления числа т на 20 ?
□	33. Доказать, что любая натуральная степень числа 15 при делении на 7
даст остаток 1.
□	34. Доказать, что число пА +64 составное при всех натуральных п .
□	35. Доказать, что если одно из чисел 2п -1, 2п + 1 является простым, то
второе цз них является составным, где п — натуральное число, п > 2 .
□	36. Найти все целые п . при которых модуль трехчлена п~ -7н + 10 явля-
ется простым числом.
□	37. Найти все простые числа р такие, что р1 +13 — тоже простое
□	38. Числа Р и 2/> + 1 являются простыми и р > 3 . Доказать, что число
4р + 1 составное
□	39. Доказать, что следующие числа:
о 1990
1)	т = 23	-1.
S
2)	п = 2s -1 (пятерка выписана сто раз).
3)	k = 22 2381 +55 5177
Глава 1. Натуральные числа
27
являются составными.
□ 40. Найдется ли такое натуральное п , при котором число 2п +п2 окан-
чивается на 5 ?
□ 41. Найти последнюю цифру числа 9999"
□ 42. Какой цифрой оканчивается число 9906 - I ?
□ 43. Коля и Витя живут в одном доме. На каждом из пажей во всех подъ-
ездах дома расположено по 4 квартиры. Коля живот на s паже в квартире
№ 8V а Витя — на 3 этаже в квартире № 169. Сколько пажей в их доме?
□ 44. В 13-томном справочнике сплошная нумерация страниц Сколько
страниц в одном томе, если в каждом из томов их поровну, а сумма номе-
ров первых и последних страниц равна 39390.
□ 45 Расставить между цифрами 1,2,3,4 и 5 знаки матема гичсских дей-
ствий так, чтобы результатом этих действий было число 2()
□ 46. Найти трехзначное число, равное кубу суммы его цифр
□ 47. Шестая степень натурального числа п записывае!ся в десятичной
системе семью цифрами 2, 4, 5, 8, 8, 9, 9, расположенными в некотором
порядке. Найти п .
□ 48 Известно, что а + а 1 — натуральное число. Доказать, что а4 in 4 —
также натуральное число.
□ 49. Если все цифры некоторого натурального числа п переписать в об-
ратном порядке, то новое число будет в четыре раза больше первоначаль-
ного. Найти хотя бы одно такое число п .
□ 50. Некоторое натуральное число п оканчивается на 2. Если двойку
перенести с последнего места на первое, то число удвоится. Найти п .
□ 51. Найти хотя бы одно натуральное п , которое делится на 11 без ос гаг-
ка, а при делении на 2,3..10 дает в остатке 1.
□ 52. Найти наименьшее натуральное число, в записи которого задейство-
ваны все цифры от () до 9, и такого, что оно делится без остатка на 36 .
□ 53. Найти минимальное натуральное число, которое при делении на 2,
3, ..., 10 дает в остатке соответственно 1,2, ..., 9.
□ 54. Известно, что «-1 делится без остатка на 15, а 1001 делится без
остатка на п +1. Найти п .
□ 55. (ВМК, 1971) В киоске были проданы одинаковые комплекты, состоя-
щие только из синих и красных карандашей, причем в каждом комплекте
число синих карандашей более чем на 3 превосходило число красных. Ес-
ли бы в каждом комплекте число синих карандашей увеличили в 3 раза, а
число красных — в 2 раза, то число синих карандашей в одном комплекте
28	Конкурсные задачи
превосходило бы число красных не более чем на 16, а общее число всех
проданных карандашей равнялось бы 81. Определить, сколько продано
комплектов и сколько в каждом комплекте синих и красных карандашей.
□ 56. (Психфак, 1975) Найти все целые положительные решения уравнения
Зх2 + Зху + 2х - у = 56.
□ 57. (Психфак, 1975) Найти все целые положительные решения уравнения
2х2 - 2ху 4 х + Зу = 36.
□ 58. (Физфак, 1983) После деления некоторого двузначного числа на сумму
его цифр в частном получается 7, а в остатке 6. После деления этого же
двузначного числа на произведение его цифр в частном получается 3 и в
остатке 11. Найдите это двузначное число
□ 59. (Эконом., 1983) На факультет подано от школьников на 600 заявлений
больше, чем от производственников. Девушек среди школьников в 5 раз
больше, чем девушек среди производственников, а юношей среди школь-
ников больше, чем юношей среди производственников, в п раз, причем
6 < п < 12 (и— целое число). Определить общее количество заявлений,
если юношей среди производственников на 20 больше, чем девушек среди
производственников.
□ 60. (Эконом., 1983) В магазине продаются красные и синие карандаши.
Красный карандаш стоит 17 копеек, синий карандаш — 13 копеек. На по-
купку карандашей можно затратить не более 4 рублей 95 копеек. При за-
купке число синих карандашей нс должно отличаться от числа красных
карандашей более, чем на пять. Необходимо закупить максимально воз-
можное суммарное количество красных и синих карандашей, при этом
красных карандашей нужно закупить как можно меньше. Сколько красных
и сколько синих карандашей можно закупить при указанных условиях?
□ 61. (Психфак, 1984) Найдите все натуральные трехзначные числа, каждое
из которых обладает следующими двумя свойствами:
1) вторая цифра числа в 2 раза меньше последней его цифры;
2) сумма самого числа с числом, получающимся из него перестановкой
первой и третьей его цифр, делится на К) без остатка.
□	62. (ВМК, 1986) Число двухкомнатных квартир в доме в 4 раза больше
числа однокомнатных, а число трехкомнатных квартир кратно числу одно-
комнатных. Если число трехкомнатных квартир увеличить в 5 раз, то их
станет на 22 больше, чем двухкомнатных. Сколько всего квартир в доме,
если известно, что их не меньше 100?
□	63 (Эконом., 1986) Линию, связывающую города А и В, обслуживают са-
молеты трех типов. Каждый самолет первого, второго и третьего типа мо-
жет принять на борт соответственно 230, ПО и 40 пассажиров, а также 27,
12 и 5 контейнеров. Все самолеты линии могут приняв на борт одновре-
Глава 1. Натуральные числа	29
менно 760 пассажиров и 88 контейнеров. Найдите число действующих на
линии самолетов каждого типа, зная, что их общее число не превосходит 8.
□ 64. (Эконом., 1986) В течение нескольких дней двое рабочих изготовляли
специальные детали, причем ежедневная выработка деталей у каждого ра-
бочего была постоянной. В итоге за все эти дни второй рабочий сделал на
к деталей больше, чем первый, где’число к удовлетворяет неравенству
127 < к < 132. Если бы первый рабочий увеличил ежедневную выработку в
два раза, то за то же количество дней он изготовил бы на 77 деталей боль-
ше, чем второй. Сколько дней рабочие изготовляли детали? Какова была
ежедневная выработка у каждого из рабочих?
□ 65. (ВМК, 1987) С завода на стройку нужно перевезти 24 больших и 510
маленьких бетонных блоков. Доставка блоков осуществляется автомаши-
нами, каждая из которых вмещает 44 маленьких блока и имеет грузоподъ-
емность 10 тонн Масса маленького блока 0.2 тонны, большого — 3.6 тон-
ны, большой блок занимает место 14 маленьких. Найдите минимальное
число рейсов, достаточное для перевозки всех блоков.
□ 66. (Эконом., 1990) Натуральные числа а, 6,с, взятые в указанном по-
рядке, образуют возрастающую геометрическую прогрессию, знаменатель
которой является целым числом. Числа 2240 и 4312 делятся без остатка на
Ь и с соответственно. Найдите числа а , Ь, с, если известно, что при ука-
занных условиях сумма а + Ь + с максимальна.
□ 67. (ИСАА, 1991) При перемножении двух натуральных чисел, разность
которых равна 10, была допущена ошибка: цифра сотен в произведении
увеличена на 2 . При делении полученного (неверного) произведения на
меньший множитель получены частное 50 и остаток 25. Найти множил ели.
□ 68. (Филфак, 1991) Представить 1991 как произведение простых чисел
□ 69. (Мех.-мат., 1992) Мастер делает за 1 час целое число деталей, большее
5, а ученик — на 2 детали меньше. Один мастер выполняет заказ за целое
число часов, а два ученика вместе — на 1 час быстрее. Из какого количест-
ва деталей состоит заказ?
□ 70. (Мех.-мат., 1992) Один рабочий на новом станке производи! за 1 час
целое число деталей, большее 8, а на старом станке — на 3 делали меньше
На новом станке один рабочий выполняет дневную норму за целое число
часов, а два рабочих вместе выполняют норму на старых станках на 1 час
быстрее. Из какого числа деталей состоит дневная норма, если производи-
тельность рабочих одинакова?
□ 71. (Эконом., 1992) Цех получил заказ на изготовление 2000 деталей
типа А и 14000 деталей типа Б. Каждый из 146 рабочих цеха затрачивает на
изготовление одной детали типа А время, за которое он мог бы изготовить
2 детали типа Б. Каким образом следует разделить рабочих цеха на две
бригады, чтобы выполнить заказ за наименьшее время, при условии, что
30	Конкурсные HiOtviH
обе бригады приступят к работе одновременно и каждая из бригад будет
занята изготовлением деталей только одного типа?
□ 72. (Эконом., 1992) Фабрика получила заказ на изготовпе-ние 1005 деталей
первого типа и 2010 деталей второго типа. Каждый из 192 раОочих фабри-
ки затрачивает на изготовление 2 деталей первого типа время, за которое
он может изготовить 1 деталь второго типа. Каким образом сисдусг разде-
лить рабочих на две бригады, чтобы выполнить заказ за наименьшее время,
при условии, что обе бригады приступят к работе одновременно, и каждая
из бригад бу дез занята изготовлением деталей только одного типа?
□ 73. (Эконом., 1993) Техническая реконструкция предприятия была прове-
дена в четыре этапа Каждый из этапов продолжался целое число месяцев и
сопровождался падением производства. Ежемесячное падение производст-
ва составило на первом этапе 9-^%, на втором — на треть6*4 — 4%
Д	ГТ
и на четвертом — 6-" о в месяц. По окончании реконструкции перво-
4
начальный объем производства на предприятии сократился на 46%. Опре-
делить продолжительность периода реконструкции
□ 74. (Психфак, 1994) Абитуриенты сдавали экзамены в течение 3-х дней в
одних и тех же аудиториях Число экзаменовавшихся в каждый день аби-.
туриентов в каждой аудитории было равным числу аудиторий. Если бы
экзамены проводились в другом корпусе, то их можно было бы провести за
два дня, используя каждый день одни и тс же аудитории, причем каждый
день в каждой аудитории абитуриентов удалось бы рассадить по рядам так,
что число рядов, а также число людей в ряду было бы равным числу ис-
пользуемых аудиторий. Найти минимальное возможное число абитуриен-
тов, которое могло бы быть проэкзаменовано при этих условиях.
□ 75. (Психфак, 1994) Собранные на бахче арбузы уложили в одинаковые
контейнеры, положив в каждый контейнер одинаковое число арбузов. Ко-
гда третью часть всех контейнеров погрузили в автомобили, то число по-
груженных контейнеров оказалось равно числу арбузов в одном контейне-
ре. Пятая часть всех собранных арбузов была продана магазином в течение
нескольких дней, причем каждый день продавалось одно и то же число
арбузов, равное квадрату числа дней продажи Какое минимальное число
арбузов может быть собрано?
□ 76. (ИСАА, 1998) При перемножении двух натуральных чисел произведе-
ние было ошибочно увеличено на 372. При делении полученного (невер-
ного) произведения на меньший сомножитель получилось в частном 90
и в остатке 29. Найти эти числа
□ 77. (ВМК, 1982) На фабрике несколько одинаковых по i очных линий вмес-
те выпускали в день 15000 банок консервов После реконструкции все по-
точные линии заменили на более производительные, но 1акжс одинаковые.
Глава 1. Натуральные числа	31
а их количество увеличилось на 5. Фабрика стала выпускать 33792 банки
в день. Сколько поточных линии было первоначально?
□ 78. (ВМК, 1978) Совокупность А состоит из различных натуральных чи-
сел. Количество чисел в Л не меньше восьми. Наименьшее общее кратное
всех чисел из А равно 462 Для любых двух чисел из А их наименьшее об-
щее кратное меньше 250. Произведение всех чисел из Д умноженное на 9,
является кубом целого числа. Найти числа, из которых состоит А.
□ 79 (ВМК, 1986, устный экзамен) Сколько раз двойка входит в разложение
на простые сомножители произведения (и +!)(// + 2)(л + 3) (2н -1)2«. п е N ?
Конкурсные задачи других ВУЗов
□ 80. (МИФИ, 1976) Произведение двузначного числа и числа, записанного
теми же цифрами в обратном порядке, равно 2450. Найдите это число
□ 81. (МИФИ, 1976) Найдите пары натуральных чисел, разность квадратов
которых равна 45.
□ 82 (МАДИ, 1997) Сколько существует четырехзначных чисел, которые в
600 раз больше суммы своих цифр?
□ 83. (МГТА, 1997) Какое трехзначное число равно кубу цифр его единиц,
а также квадрату числа, составленного из его второй и третьей цифр?
□ 84. (Воронежский гос. ун-т,1997) Найти все натуральные числа п , для кото-
рых число w2 +1 делится без остатка на п +1
□ 85. (Мос. гос. академия прикладной биотехнологии, 1995) Найти двузначное
число, если известно, что при делении этого числа на сумму его цифр
в частном получается 4 и в остатке 3; если же из искомого числа вычесть
удвоенную сумму его цифр, то получится 25.
□ 86. (Мос. автомобилестроительный институт, 1993) Если двузначное число
разделить на сумму его цифр, то в частном получится 3 и в ослике 7
Если же взять сумму квадратов цифр этого числа и вычесть из нес произве-
дение тех же цифр, то получится первоначальное число. Найти это число
□ 87. (МГИМО, 1995) Партию деталей решили поровну разложить по ящи-
кам. Сначала в каждый ящик положили по 12 деталей, но при эюм оста-
лась одна деталь. Тогда из одного ящика вынули все детали, и в оставшие-
ся ящики удалось разложить детали поровну. Сколько деталей было в пар-
тии, если в каждый ящик помещается не более 20 деталей?
□ 88. (МИФИ) Разность цифр двузначного натурального числа А равна 4,
а сумма квадратов цифр/1 больше произведения\его цифр на 37. Найти А
ГЛАВА 2.
Целые числа
Числа О, 1, - к 2, -2, 3, -3, ... являются целыми. Множество целых чисел
обозначается Z. Множество Z замкнуто относительно операций сложения,
вычитания и умножения. Это означает, что сумма двух целых чисел всегда
является целым числом. То же самое относится к операциям вычитания и
умножения Операция деления может вынести за пределы множества це-
лых чисел. Например, 5 +3 = 8 е Z, 5-3 - 2г Z, 5 • 3 = 15 е Z, £ Z.
В данной главе мы будем рассматривать основные типы и методы решения
уравнений и неравенств в целых числах, системы уравнений и неравенств,
целочисленные задачи с параметрами, экстремальные задачи с целыми
числами. При этом мы нс будем касаться целых чисел в тригонометрии.
Прежде всего мы рассмотрим задачи, связанные с делимостью.
§1. Задачи на делимость
1. Делимость нацело
Условимся в этой главе под “числом” всегда понимать целое число (если
не оговорено противное).
Число а делится на число 6*0 нацело (а\Ь), если существует число с
такое, что а = b-с. При этом а называется делимым, Ь — делителем,
ас — частным.
Например, а = 212, 6 = -53, а:Ь , поскольку выполнено равенство
212 = -53-(-4), с=-4 —частное.
Отметим, что частное определено однозначно. Достаточно предположить
противное: существует q такое, что а = Ь-с}. Из равенства Ьс = Ьсх следует
6 (с - q) = 0 , а из последнего равенства, поскольку 6*0, получаем с = q ,
т. е. частное единственно.
2. Делимость с остатком
Деление чисел нацело выполнимо не всегда (4 на 3 нацело не делится), т. е.
множество Z не замкнуто относительно операции деления. Поэтому целе-
Глава 2. Целые числа	33
сообразно наряду с делением нацело рассмотреть и другую, более общую
операцию, которая всегда выполнима, а в случае выполнимости деления
нацело совпадает с ним. Такой операцией будет деление с остатком.
Разделить число а на число 6 + 0 с остатком — значит представить
число а в виде
a-qb+r,	(1)
где q и г  целые и 0 < г < j 6 | При этом а и b по-прежнему называют
де чимым и делителем, q - неполным частным, а г остатком.
Отметим, что указанные числа q и г определены однозначно (докажите это
самостоятельно!). Если остаток г равен нулю, то а делится нацело на Ь На-
пример.
1)	при а = 106, 6 = 13 будет 106 = 8-13 + 2;
2)	при а = 106, 6 = -13 будет 106 = (-8)-(-13)+ 2 ;
3)	при а = -106, Ь = 13 будет -106 = (-9)-13 + 11;
4)	при « = -106, 6 = -13 будет-106 = 9(-13) + 11;
5)	при	<7	=	13, 6 = 106 будет 13 = 0-106 + 13 ;
6)	при	</=	13, 6 = — 106 будет 13 = 0-(-106)+ 13;
7)	при	«	=	-13, 6 = 106 будет-13 = (-!)• 106 + 93;
8)	при	«	=	-13 , 6 = -106 будет -13 = 1-(-106) + 93 .
□ Пример 1. Какие числа нужно поставить в равенстве (1), определяющем
делимость целого числа а с остатком г,
1) <7 = 40-49+г,
2) а =40-(-49) + г ,
если известно, что остаток г наибольший из возможных?
Решение.
1) а) если делителем 6 является число 40, то по условию г = 39 и
39+40-49 = 39+ 1960 = 1999 = а .
б) если делителем является число 49, то г = 48 и имеем равенство
48+ 40-49 = 48 +1960 = 2008 = « .
2) в) если делитель 6 = 40, то из условия следует г = 39 и
39 + 40 - (-49) = 39 -1960 = -1921 = « .
г) если делитель 6 =-49, то г =48 и 48- 1960 = -1912 = а .
34
Конкурсные задачи
Ответ:
1) 1999 = 40-49 + 39 ИЛИ 2008 = 40-49 + 48 .
2) -1921 = 40-(-49) + 39 или -1912=40-49 + 48.
Следующие задачи на делимость с остатком — достаточно простые, хотя и
параметрические.
Tmrt«n arrrrar	^тг»ю иишижл «ut»’» " шиьепачоггтче * ‘C'r'~-vxv,rr'-*rr-.rrrar	"• -г -уг 9 > -*
□ Пример 2. Разделить целое число:
а) п на п -2;	б) п2 + и+1 на и+ 2 с остатком.
Решение и ответ записываются одновременно.
0-(-2)+0 при // = 0,
(-1).(-1) + 0 при и = 1,
деление невозможно при п = 2,
3-1+0 при п-3,
2-2 + 0 при w = 4,
1-(и-2)+2 при п = -1,-2,-3,-4, ±5, ±6, ..;
б)
п2 +и + 1
0-2 + 1 при и = 0;
1-1+0 при и = -1;
1-3+0 при и = 1;
деление невозможно при п = - 2;
2-2 + 0 при л = -3;
(н-1)-(п +2) + 3 при п = 2,3,±4,±5,...
3.	Несколько задач на делимость
Сознаемся, что в главе I при постановке задач на делимость натуральных
чисел мы иногда лукавили: в некоторых задачах делимость имеет место
для всех целых чисел (а не только для натуральных), скажем, в примере 13.
С другой стороны, мы пользовались делимостью и отрицательных чисел,
как в примере 2. Надеемся, что после прочтения настоящей главы все недо-
разумения читателей будут сняты.
-	4 Ылй	W I	от «♦*)*<»*<**» •*.»« <*•	*• * • it ’Ж *•**>* *•*>•* 1 V '
□	Пример 3. Доказать, что разность любого двузначного числа и числа,
записанного теми же цифрами, но в обратном порядке, делится на 9.
Решение. ah-ba = 10а + b -(10Z? + а) = 9а - 9Ь = 9 • (а -Ь).
Заметим, что разность ab-ba может быть положительной, отрицательной
или нулем, так же как и а - Ь .
-ПК Г	«п-ч *стжг*”- «w-жг	***Г IV V ЛЯГ». 7*-»' F -ъ. S \	ч ЛГЧМ ’.У1СЯГ»— ».* ГГГТ • V .« -	- <
□	Пример 4. Неполное частное от деления трехзначного числа на сумму
его цифр равно 13, а остаток равен 23. Найти все целые числа, обладающие
ЭI им свойством.
Глава 2. Целые числа
35
Решение. Обозначим трехзначное число xyz. Тогда по условию
100х + 10у + z = (х+у + z)-13 + 23 Значит, 87х-\v-12z = 23 Такое равенство
в целых числах невозможно: левая часть делится на 3, а правая — нет.
Ответ: таких чисел не существует
НД1 ЛГТ**ГЛЛГ»	р. ftUTtra >4>rv**	„ , Л i	f
□	Пример 5. Доказать, что если abc делится на 37, то и Ьса, и cab тоже
делятся на 37.
Решение. Заметим, что число ааа : 37, так как ааа = а • 10? ♦ а 10 + а = а  111,
а 111:37. Тогда abc-aaa-b-a с-а\У1 (двузначное число, делящееся на
37, как разность чисел, делящихся на 37, может быть и отрицательным чис-
лом). Умножим последнее число на 10, получим b-а с-а 0:37 Сложим
это число с ааа:37, тогда Ьса: 37. Действуя аналогично: вычитая из Ьса
число ЬЬЬ потом умножая на 10 и складывая с ЬЬЬ, получим, что и
cab: 37.
4.	Обобщенные формулы сокращенного
умножения
Их две. Одна обобщает формулы а2 -Ь2 и а3 -Ь3 для любого натурально-
го показателя степени п > 2
an-bn^(a~b\an-} -van 2b + ... + abn~2 + ЬпХ).	(2)
Вторая обобщает формулу а3 + Ь3 для положительного нечетного показа-
теля степени я = 2А+1, А: = 1,2,...
a2k^b2k^(a + b\a2k	(3)
Для доказательства достаточно в обеих правых частях раскрыть скобки и
привести подобные члены, при этом сокращаются все слагаемые, кроме
первого и последнего. Проведите выкладки и убедитесь, что правые части
формул (2) и (3) равны левым частям.
5.	Применение обобщенных формул сокращенного
умножения в задачах на делимость
Формулы (2) и (3) при целых а и Ь с успехом^ используются при решении
задач на делимость разностей или сумм степеней целых чисел.
□ Пример 6. Доказать, что числа вида 132” — 1 делятся нацело на 168
36	Конкурсные задачи
Решение. 132"-1 = (132)" -1 = 169" -1" = (169-1)-(169"“' + 169"'2+ .. +
+169 + 1) = 168/, где / = 169" 1 -+169” 2 +... +169 + 1 — целое число.
□ Пример 7. Доказать, что числа вида 134"+2 +1, где п = 0, 1, 2, . ,
делятся на 170.
Решение. 1 з4”*2 +1 = (132 )2”+| +1 = 1692"*1 +12"+1 = (169 +1) • (1692” -1692” 1 +
+ ... -169+ 1) = по-/, где / = 1692” -1692"'1 + ... -169 + 1 — целое число.
е,	«». »-e-* Mi	« и >> . w. X'Wi . w.h:.'. «г -v + -
□	Пример 8. Доказать, что при всяком натуральном п числа Звп - 26п
делятся нацело на 35.
Решение. Прежде чем использовать формулу (2) преобразуем заданную
разность 36м-26м =(36)м-(26)м = 729м-64м =(729-64)-(729м ’4-729м’2 64* +
+ ... +64"-1) = б65 /, где / — целое число, написанное во вторых скобках
Поскольку 665 5 • 7 • 19, то имеет место делимость нс только на 35, но и на
19, и на 665.
.1111 Мк И41М>	lx*..	/*. .	.и < <AW-r	ж.	А-.
□	Пример 9. Доказать, что при всех натуральных нечетных п числа
3<>м -ь26м делятся нацело на 793.
Решение. Воспользуемся формулой (3) при нечетном п
З6п + 2Ьп = (З6)п 4- (26)м = 729м + 64м = (729 4- 64)• (729м"1 -729м 2 641 + ... -
-7291-64м 2 + 64м 1) = 793/, где / — число, написанное во вторых скобках
Убедитесь, что 793 — не простое число, а составное.
Формулы (2) и (3) позволяют утверждать, что для целых а и b 1) разность
одинаковых натуральных степеней делится на разность оснований, и 2)
сумма одинаковых натуральных нечетных степеней делится на сумму ос-
нований. Это мы видели в разобранных примерах и будем неоднократно
использовать в дальнейшем
6.	Комбинированные методы решения задач
на делимость
□	Пример 10. Доказать, что 1110 -1 делится на 100.
Решение. По формуле сокращенного умножения (2) получаем
II10 -1 = 1110 -I10 =(11-1). (Н9 4-1 I8 4-... 4-1 14-1) = 10/.
Глава 2. Целые числа	37
Второй сомножитель / представляет из себя сумму десяти слагаемых, каж-
дое из которых, очевидно, оканчивается на единицу. Значит, / оканчивается
нулем и поэтому делится на 10. Делимость на 100 доказана.
□	Пример 11. (Устный экзамен ВМК, 1986). Доказать, что число 29 + 299
делится на 100.
Решение. Идея решения видна из преобразований.
29+ 299= 29-(1 + 290) = 29 (1+(210)9) = 29 (19+1()249 ) 2"-1025-/
В последнем равенстве использована формула (3) при 2А ♦ I - 9, где / —
целое число: I - 1-210 +220 - ...-271) +28<)
Поскольку 1025 = 25 41, а 29=4-27, то последнее произведение заведомо
делится на 100.
□	Пример 12. (Геолог. 1999, устный экзамен) Доказать, что число
Ю1999 -1999 делится нацело на 9.
Решение. Запишем заданное число следующим образом
101999 -1999 = (101999 -1,9")-1998.
Слагаемое в скобках делится на разность оснований, т с на 10-1 = 9. Вто-
рое слагаемое делится на 9 по признаку' делимости (сумма цифр равна 27).
Болес сложные задачи приведены в конце главы II.
§2. Диофантовы уравнения первого порядка
с двумя неизвестными
1. Основные определения и теоремы
Неоднородным диофантовым уравнением первого порядка с двумя неиз-
вестными х, у (названо по имени александрийского математика Диофанта,
жившего в 3 в н.э.) называется уравнение вида
тх + ну = k	(1)
где т, н, к, х, у е Z, к: * 0 .
Однородным диофантовым уравнением первого порядка с двумя неиз-
вестными х,у называется уравнение вида <
тх 4- ну = 0 ,	(2)
где т, н, х, yeZ.
38	Конкурсные задачи
Сформулируем несколько теорем относительно свойств решений уравне-
нии (1) и (2). Часть из этих теорем очевидна, а доказательство других мож-
но найти в [2] либо [8).‘
Т1ЮРЕМА 1 Если свободный член к в уравнении (1) не делится на наи-
больший общий делитель (НОД) чисел т и т то уравнение (1) не имеет
целых решений.
Например, уравнение 34х- VIу = 3 в целых числах неразрешимо, поскольку'
3 не делится нацело на 17.
Пусть теперь к делится на НОД (пц п). Проведя такое деление, мы добьемся
того, что коэффициенты т и п в уравнении (1) станут взаимно простыми
числами.
ТЕОРЕМА 2. Если коэффициенты тип уравнения (1) взаимно простые
числа, то это уравнение имеет по крайней мере одно решение.
Пусть мы нашли какое-либо решение уравнения (1) (как это сде-
лать мы обсудим чуть позже). Оказывается, что и все остальные решения
этого уравнения могут быть выражены через (xj, у}).
ТЕОРЕМА 3. Если коэффициенты тип уравнения (1) являются взаимно
простыми числами, то это уравнение имеет бесконечно много решений.
Все эти решения описываются формулами
Г X = X] + nt,
[ у - V] - ml,
где (xj, у|) - какое-либо решение уравнения (1), reZ.
Далее сформулируем утверждение, устанавливающее связь между реше-
ниями уравнения (1) и уравнения (2).
'ТЕОРЕМА 4. Если пары чисел (хиу|) и (х2,у2) — решения уравнения (1),
то пара чисел = xj -х2 и у^~ у}- у2 — решения уравнения (2).
Из данной теоремы следует, что всякое решение уравнения (1) является
суммой какого-либо частного решения (1) и решения уравнения (2).
И, наконец, совсем просто решается уравнение (2)
ТЕОРЕМА 5. Если т и п взаимно простые числа, то всякое решение
уравнения (2) имеет вид
( х = пк,
[ у = -тк, к eZ.
1 Мы сознательно не приводим доказательств этих гсорсм, поскольку в программу
для посгунающих в ВУЗы их доказательство не входш
Глава 2. Целые числа	39
,	ч -мье,, xa*^wb<«.v*^	>	*	• aJ^»j	„. -г .. *;*	-	”	~и/
Обсудим теперь, как искать решения уравнения (1). В силу теоремы 1 и
сформулированного сразу за ним замечания мы будем рассматривать слу-
чай, когда числа т и п — взаимно простые.
2. Метод рассмотрения остатков от деления
Этот способ удобно применять, если хотя бы один из коэффициентов т, п
невелик по модулю. Пусть это будет, например, т.
Перепишем уравнение (1) в виде
тх = к-пу	(3)
Левая часть уравнения (3) делится нацело на т. Значит, должна делиться
нацело на т и правая часть данного уравнения
Рассматривая всевозможные остатки / отделения у на т, / = (), 1,т~\,
мы получим, что при одном значении / из указанного промежутка будет
делиться на т и правая часть (доказательство этого утверждения имеется
в [8] ). Поскольку число т невелико по модулю, то перебор вариантов бу-
дет тоже невелик.
□ Пример 1. Решить уравнение Зх-4у = 1 в целых числах
Решение. Перепишем уравнение в виде Зх = 4у +1. Поскольку левая часть
уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмот-
рим три случая
1.	Если у = Зт, где те /, то 4 у 4-1 = 12м +1 не делится на 3
2.	Если у = Зм 4-1, то 4у +1 = 4 (3/н + 1) + 1 = 12м + 5 не делится на 3.
3.	Если у = Зм + 2, то Ду +1 = 4 (Зт + 2) + 1 = 12/?? + () делится на 3, поэтому
Зл = 12т+9 => х-Дт 4-3, откуда следует
хч	[ .г = 4m 4-3,
Ответ: 4	где произвольное те/ .
[ у = Зт 4-2,
Описанный только что способ удобно применять и в том случае, если чис-
ла т и н не малы, но зато разлагаются на простые сомножители
□ Пример 2. (Филфак, 1969) Указать хотя бы одну пару целых положитель-
ных чисел т, п таких, что 36m - 25н = 1.
Решение. Перепишем уравнение в виде 25?? - 3(\п -1
I. Число слева делится на 5, следовательно, должно делиться на 5 и число
справа. Рассмотрим всевозможные остатки от деления т на 5
1. Если т = 5т} , то 36м-1 = 180м| -1 не делится на 5.
40	Конкурсные задачи
2, Если т = 5пц +1, то 36/л -1 = 36(5mj +1) -1 = 180,^ + 35 делится на 5.
В рассмотрении других остатков нет необходимости, так как при других
остатках правая часть делиться на 5 не будет (докажите это сами).
Итак, 25н = 180???] -35 или 5п = 36??/] - 7 .
Далее будем рассуждать аналогично
II. Число слева делится на 5. следовательно, делится на 5 и число справа
1.	Если	= 5т2. то 36//J) - 7 = 180ш2 -7 не делится на 5
2.	Если	= 5т2 +1 , то 36ш, - 7 = 36(5?н2 +1) - 7 = 180»ь +29 не делится на 5.
3.	Если = 5т2 + 2 , то 36/Hj -7 = 36(5ш2 +2)-7 = 18()/и2 +65 делится на 5.
В рассмотрении других остатков нет необходимости.
III. Итак, 5п = 180???2 +65. н = 36т2 + 13 Осталось выразить m через т2.
( п - 36т2 + 13,
[ т =	+1 = 5(5т2 +2) + 1 - 15т2 + 11
Оказалось, что исходное уравнение имеет бесконечно много решений. По-
скольку по условию задачи нам достаточно указать одну пару, то выберем,
например, т2 = 0 . Тогда т = 11, п = 13.
Отвепг т = 11, и = 13
3. Метод последовательного уменьшения по
модулю коэффициентов
Метод рассмотрения остатков становится неэффективным, если числа \т'
и |w| являются большими простыми числами. Чтобы убедиться в этом,
достаточно рассмотреть уравнение 79 v - 23* = 1
В книге [2] изложен алгоритм решения уравнения (1) (алгоритм Евклида),
основанный на применении цепных дробей. Однако цепные дроби с сере-
дины 50-х годов в школьную программу не входят. Поэтому мы изложим
алгоритм, основанный на последовательном уменьшении по модулю
коэффициентов при неизвестных.
Начнем с примера.
□ Пример 4. Решить в целых числах уравнение 79у - 23х = 1.
Решение. 1. Сравним коэффициенты при неизвестных по модулю. В на-
шем случае |23|<|79| Проведем деление с остатком: 79-23 -3 + 10 и пере-
пишем исходное уравнение в виде 23* = 79у -1 - (23 • I з 10)у -1 =
= 69у +1 ду-1 => 23х-б9р = 10^-1. Левая часть последнего уравнения де-
лится нацело на 23, поэтому должна делиться на 23 и правая часть:
Юр -1 = 23/ => 10у = 23/ +1, где / < 7. / новое неизвестное.
Глава 2. Целые числа
41
2.	Полученное новое уравнение по inny точно такое же, как исходное.
Однако коэффициенты при ней шестых в нем уменьшились по модулю.
Повторим процедуру уменьшения коэффициентов еще раз:
Юу = 23/ 4-1 = (2• 10 F 3)/ ♦ I > IOv -20/ = 3/ + 1 =>3t +1 = 10м , где и — новое
неизвестное, и t Z .
3.	Проведем процедуру уменьшения коэффициентов в последний раз:
3/ +1 = Юм = (3- 1м t 1)м	3/ -9м +1 = и => и - 3(/ -Зм) +1 = Зп + 1, где п е Z .
4.	Нам осталось выразить х и у через п. Поскольку и = Зп +1, то
а) 3/ = Юм -1 = Ю(3н +1) - 1 = 30»+9 =>/ = Юн+ 3 ;
в) Юу = 23/ +1 = 23 (Юн + 3) +1 = 230и + 70	у = 23и + 7 ;
С) 23х = 79у-1 = 79(23н + 7)-1=79-23и + 552=>х = 79и + 24.
„	[х = 23и + 7,
Ответ: <	где ne'Z .
[у = 79и + 24,
Из рассмотренного примера становится очевидно, что в общем виде урав-
нение тх + пу = к решается при помощи следующих действий:
1.	Выбор наименьшего по модулю коэффициента (пусть \т\ < |н|).
2.	Проведение процедуры уменьшения коэффициентов. Это делается
при помощи деления с остатком.
Пусть п = /|m| + q , где 0 < q < |w| - 1, тогда тх + пу
тх 4- (/\т | + q )у = к => тх + 1\т\у = к - qy .
Левая часть последнего уравнения делится на т. Значит, должна делиться
на т и правая часть: к - qy = mt, где / е Z, / — новое неизвестное.
3.	Повторение процедуры уменьшения коэффициентов. Новое уравнение
отличается от старого только тем, что его коэффициенты по модулю
меньше коэффициентов старого. Так как |и| конечно, то мы за конечное
число раз повторения процедуры добьемся того, что коэффициент при од-
ном из новых неизвестных будет по модулю равен 1. Значит, относительно
этого неизвестного задача решена.
4.	Возврат от новых уравнений к исходному.
Рассмотрим последний пример решения диофантова уравнения.
□ Пример 5. 11х-12у = 1, x,yeZ.
1.	11х - 11у = у + 1
2.	у +1 = 11/ =5> у = 11/-1
3.	11х = 12у+ 1 = 12-(11/-1)+ 1 = 12-11/-11, => х = 12/-1.
[х = 12/-1.
Ответ: <	/ е Z.
г	|у=11/-1,
42	Конкурсные кОачи
4.	Задачи с диофантовыми уравнениями первого
порядка
Рассмотрим, во-первых, задачи, связанные с нахождением общего члена
нескольких арифметических прогрессий.
□ Пример 6. (Психфак, 1967) Найти сумму чисел, одновременно являющих-
ся членами арифметических прогрессий: 2,5,8..и 2 и 7,12,17,.. ,157.
Решение. Члены первой прогрессии описываются формулой
ап = 2 + 3(и -1), где п = 1, 2,..., 111 Члены второй прогрессии — формулой
Ьк - 7 + 5(k -1), где k = 1, 2,..., 31 Для того чтобы найти общий член про-
грессии, надо решить уравнение в натуральных числах ап - Ьк , т.е.
2 + 3(п -1) = 7 + 5(к -1) ИЛИ 3(и-1) = 5£.
Число слева делится на 3, а значит, должно делиться на 3 и число 5к . Но
это может быть только, если к = Зт . Поэтому формула общего члена двух
прогрессий имеет вид см =7+5(Зш-1) = 15ш+2, где 15т + 2 <, 157, откуда,
следует, что т = 1,2,..., К). Поэтому сумма общих членов равна
17 + 152
Яобщ =-------10 = 169-5 = 845.
Ответ: 845.
Рассмотрим более сложную задачу
□ Пример 7. Известно, что последние члены двух арифметических про-
грессий ах = 5, а2 = 8, ..., ам и А, =9,	= 14, ...,/^ совпадают, а сумма
всех общих членов равна 815. Найти М и К .
Решение. Очевидно, что ат = 5 + 3 • (т -1), где 1 ш < Л/ , Ьк = о + 5 {к -1),
где 1 < к < К. Для нахождения общего члена составим и решим диофантово
уравнение 5 + 3-(т-1) = 9 + 5-(£-1) <=> Зт = 5к 4 2 .
Левая часть полученного уравнения делится на 3, значит, должна делиться
на 3 и правая часть. Рассматривая всевозможные остатки от деления к на 3,
(сделайте это самостоятельно!) получим, что
к = Зп - 1 , 3ш = 5(3п 1)42- 15n -1 , где 1 < н < У .
Определим М Нетрудно видеть, что общие члены обоих арифметических
прогрессий сами составляют арифметическую прогрессию, поэтому
SN = —+ 15jV~1 • JV = 815 <=> 15,V2 + 13W-1630 = 0 <=> N = 10
fX'=3A/-l = 29,
\M = 5jV-1=49.
Ответ: К = 29 , M = 49 .
Глава 2. Целые числа
43
§3. Диофантовы уравнения второго и
высших порядков
1.	Типы уравнений второго порядка
Диофантовым уравнением второго порядка с двумя неизвестными называ-
ется уравнение вида
Ях2 +Вы + (У +Dx+Ey + F=O,	(1)
где х, yeZ — неизвестные, Л, В, С, L), Е, F &Z — коэффициенты, при-
чем хотя бы одно из трех чисел Л, В, С не равно нулю.
Составим дискриминант уравнения
d = I32-4AC.	(2)
Несмотря на кажущуюся сложность уравнения (1), мы скоро убедимся, что
при помощи замены переменных оно сводится к одному (и только к одно-
му) из трех простейших уравнений типа:
х2 + Е}у + Ь\ =0 (соответствует d = 0),	(3)
х2 +Q у2 + 1<\ =0 , где С\ > 0 (соответствует d < 0 ),	(4)
х2 ~С}у2 +F] = 0, где б", > 0 (соответствуй d '• о).	(5)
Здесь х, у — новые целые неизвестные, Q, Ех„ Ц е Z — новые целые ко-
эффициенты. Тип уравнения при преобразованиях не меняется.
Уравнения (3), (4), (5), в зависимости от типа, а также от дополнительных
свойств коэффициентов могут:
а)	вообще не иметь целых решений;
б)	иметь конечное число целых решений;
в)	иметь бесконечное число целых решений.
Мы сначала изучим свойства простейших уравнений, а затем покажем, как
уравнение (1) свести к одному (и только одному!) из трех типов (3), (4), (5).
2.	Уравнение типа +
Перепишем уравнение (3) в виде
E1y = -(x2+F1).	(6)
44
Конкурсные задачи
2а. Случай, когда Ех = ±1
Если Е} = 1 то уравнение (6) уже решено. В этом случае получается беско-
нечно много решений:
Г х - произвольное целое,
[y = -x2-F}.
Аналогичные формулы и результат получаются, если Е} = -1
2Ь. Случай, когда Е{ * ±1
Если Е} * ±1, то правая часть уравнения (6) делится на Ех Будем искать х
В виде х = тЕ} + q , где т € Z, q & Z, 0 < q < \Е} | -1 . Тогда
Е} у = ~(т2Е2 + 2тЕх q + q2 +1<\ ) = -Е} (т2Е} + 2mq) -(q2 + F}), откуда следует,
что q2 +F} должно делиться нацело на Е}. Итак, уравнение (6) можно ре-
шать перебором остатков.
□ Пример 1. Решить уравнение х2 +1 = 5у в целых числах.
Решение.
1.	Если х - 5т , то 25т 2 +1 нс делится на 5.
2.	Если х = 5т + 1,то (5m+l)2 +l=25m2+10m+2 тоже не делится на 5.
3.	Если х = 5т + 2, то (5т + 2)2 +1 = 25m2 + 20m + 5 делится на 5 В этом
случае имеем решения
Г х = 5т + 2, т - произвольное целое,
[у = 5т2 +4т + 1.
4.	Если х = 5т+3, то (5т + 3)2 +1 = 25т2 + 30ш + 10 делится на 5. В этом
случае решения
{х = 5т + 3, т - произвольное целое,
у = 5т2 +6т + 2.
5.	Если х = 5т + 4 , то (5т + 4)2 +1 = 25т2 + 40m + 17 не делится на 5.
Г х = 5т + 2 ,	f х = 5т + 3 ,
Ответ: <	0 или <	9	где т е /
[у = 5пГ +4т +1 [у = 5пГ + 6т + 2,
Замечание 1 Как мы убедились, в отличие от уравнений первого порядка,
разрешимость может быть при нескольких значениях остатка q.
Замечание 2. У нас получились две бесконечные серии решений, которые
не пересекаются, так как 5m+2 * 5т +3 .
Замечание 3. Эти серии можно объединить в одну, переписав ответ в виде
Глава 2. Целые числа	45
(х = 5т ± 2,
<!	где т — произвольное целое,
[у = 5т ±4т + 1.
Может оказаться так, что ни при каких 0 < q s |Л’] | -1 q2 +Fj нацело на
не делится, и тогда уравнение (3) не имеет целочисленных решений.
□ Пример 2. (ВМК, 1997, устный экзамен) Доказать, что уравнение х2 +1 = Зу
не разрешимо в целых числах.
Решение. Правая часть уравнения при всех у е Z делится на 3. значит,
должна делиться и левая часть. Рассмотрим всевозможные остатки от деле-
ния числа х на 3. Если х = Зт, то 9w2 +1 = Зу и левая часть уравнения не
делится на 3. Следовательно, в этом случае равенство невозможно.
Случаи х = Зтн + 1 и х = Зт + 2 рассматриваются аналогично.
Итак, мы убедились, что уравнение типа (3) либо имеет бесконечно много
целых решении, либо не имеет их вообще.
3. Уравнение типа x^Cjj^+Fj =0, где с\>0
Этот случаи самый простой. Перепишем уравнение в виде
х2+С} у2 =,	(1)
откуда следует
1.	Если F, > 0, то решений нет, так как х2 +(^ у2 > О, -Г} < о .
2.	Если Ej = О. то единственным решением (4) является х = о, у = 0.
3.	’Если Fx < 0 , то из (7) вытекают неравенства
Неравенства (8) задают на плоскости (х, у) прямоугольник с центром
в начале координат и со сторонами 2^-/3 , 2^-Г}/С} . Поскольку внутри
такого прямоугольника существует только конечное число точек с цело-
численными координатами, то становится ясно, что:
1. Число решений уравнения (4) может быть чс более, чем конечным
(а может и вообще нс быть). Например, уравнение х2 + 2у2 = 5 решений
в целых числах не имеет, а уравнение х2 + 2у2 = 9 имеет шесть решений
(х = ±3, у = 0), (х = 1, у = ±2), (х = -1, у = ±2). Заметим, однако, что число
решений всегда является четным Докажите это утверждение сами.
46	Конкурсные задачи
2. Уравнение (4) допускает решение перебором. Действительно, чтобы
решить данное уравнение, достаточно проверить все точки с целочислен-
ными координатами, удовлетворяющие условиям (8).
Таких точек, однако, может оказаться много, и тогда возникает чисто тех-
ническая проблема: как отбросить заведомо неприемлемые варианты
(иными словами, как организовать перебор.) В этом случае очень полез-
ными оказываются соображения симметрии, делимости, а иногда — при-
менение формул сокращенного умножения.
□ Пример 3. Решить в целых числах уравнение Зх2 + 8у2 = 515 .
Решение. Прежде всего выпишем оценки:
И< 13
Из этих оценок следует, что простым перебором решать это уравнение
крайне нерационально, так как прямоугольнику {	‘ ’ принадлежат
[|у|< 8
27-17 = 459 точек с целочисленными координатами. Надо привлекать до-
полнительные соображения.
1. Прежде всего ясно, что если (х0, у0) — решение нашего уравнения, то
и (х0, — у0), (-х0, у0), (-х0, -у()) —также решения. Поэтому достаточно
рассмотреть случаи х 2 о , у > о. Изображением множества таких точек
являются узлы решетки на рис. 1.
Итак, 0 < х < 13, 0 < х < 8 . Однако число вариантов перебора все еще оста-
ется слишком большим (14-9 = 126). Привлечем соображения делимости.
2. Перепишем исходное уравнение в виде Зх2 + 8у2 = 512 + 3 или
3-(х2 -1) = 8-(64-у2).
Из последнего уравнения следует, что х2 -1 делится на 8, а 64 -у2 должно
делиться на 3. Это выполнено (убедитесь сами), если х = 2т +1, у = 3k ± 1.
При условиях 0 < х < 13, 0 < х < 8 получим, что х может принимать значе-
ния 1, 3, 5, 7, 9, 11, 13, ау— 1, 2, 4, 5, 7, 8. Оставшиеся "подозрительные”
точки отмечены на рис. I символом "жирная точка".
Глава 2. Целые числа
47
Рис. 1. Иллюстрация к анализу «подозрительных» точек:
1. «решетка» — после этапа 1;
2. «жирные точки» — после этапа 2;
3. «квадратики» —после этапа 3;
4. кольцевая часть — после этапа 4.
Нетрудно подсчитать, что осталось 42 ’'подозрительных” точки, что все
еще слишком много. Однако соображения делимости далеко не исчерпаны.
3. Перепишем уравнение в виде 8 • (х2 +у2) = 515 + 5у2, откуда следует, что
х2 + у2 делится на 5. Проведем анализ остатков от деления х и у на 5:
. ( х = 5/,
a)	i где /, peZ .
[ У = 5/7,
В этом случае решений нет, так как тогда х2:25, у2:25 , а 515 нацело на 25
не делится.
(х = 5/±1,
б)	с .о	Гре Z.
[у = 5/7 ± 2,
С учетом предыдущего получим, что если х = 1, 9, 11, то у = 2, 7, 8.
fx = 5Z±2,
в)	i с , где /, peZ .
[ у = 5р ± 1,
С учетом предыдущего получим, ггго если х = 3, 7, 13, то у = 1, 4.
Оставшиеся "подозрительные” точки на рис. i помечены символом "квад-
ратик”. Нетрудно посчитать, что число "подозрительных” точек сократи-
лось до 16. Это все еще много.
4. Для уменьшения числа "подозрительных" точек используем неравен-
ства (мы уже учитываем, что х*0, ^*0):
Конкурсные задачи
а)	8х2 +8у2 > Зх2 +8/ = 515 > 512, или х2 I Г > 64 .
б)	515 = Зх2+8у2 > Зх2+3v2 или 3-(х2 + у’)- 515.
Два последних неравенства позволяют утверждай, что "подозрительные”
точки Moiyr лежать только внутри кольца 64 • х » у
обстоятельство позволяет уменьшить число “подозрительных” точек до 8:
Осталось проверить найденные ’’подозрительные” точки, удовлетворяют
ли они уравнению (сделайте сами). Получается, что < и < явля-
ются решением. С учетом симметрии получим 8 решений.
( х = ± 1	( х = ± 13
Ответ: <! и <
[ у = ± 8	[ у = ± 1
Итак, все закончено и с уравнением типа (4). Видно, что, несмотря на его
простоту, при ’’нехороших” коэффициентах организация перебора может
быть весьма трудоемкой.
В заключение данного пункта заметим, что уравнение вида
+ Еу + Е = 0 ,
(9)
где С>0, легко приводится к виду (4). Для этого умножим (9)
на 4С2 и выделим полный квадрат
4С 2х2 + С [(2Су + Е )2 - Е~ ] + 4С 2F = 0, или
4( ’ 2х2 + С (2Су + Е)2 + 4С 2F - СЕ2 = 0.
Далее остается только ввести новые целые переменные:
f z = 2Сх,
\t = 2Cy + E
и переобозначить коэффициенты.
4.	Уравнение типа х2 -Qy2 + Ft =0, где о
Уравнение (5) из всех трех типов является наиболее сложным. Чтобы упро-
стить изложение, разделим тип (5) на три подтипа:
х2 - т2у2 4-/*[ * 0 , где w,/*j < Z,
х2-С| у2 - ], где <’| -О, Г’, « Z, С, /ш2,
х2 (’| г2 I /'i 0 . где (‘| « 0, (’| < Z, (’t / т\ Е} -1 .
(Ю)
(П)
(12)
Глава 2. Целые числа
4.1	Уравнение подтипа х2 -т2у2 +fx =о
Применим формулу разности квадратов
(x-my)(x + my) = ~F1 .
Поскольку х, у, теZ , то и х-ту, х + ту — тоже целые. Разложим число
на произведение всевозможных целых сомножителей:
(х~ту)(х + ту) =-Fx = p^qx = p2q2 = • • = Pnqn •
Далее осталось решить в целых числах системы уравнений:
х- ту = рх I х-ту = р2
х + ту = qx ’ [х + ту = q2
х~ту = рп
x + my = qn
□	Пример 4. Решить уравнение х2 -4у2 = 13 в целых числах.
Решение. Применим в левой части формулу разности квадратов:
(х-2у)(х + 2у) = 13, причем числа х-2у и х + 2у в силу замкнутости мно-
жества целых чисел относительно операций сложения, вычитания и умно-
жения являются целыми. Поскольку 13 — простое число, то оно может
быть разложено на произведение двух целых чисел лишь четырьмя спосо-
бами: 13 = 13 1 = 1-13 = (-13)(-1) = (-1)-(-13). Рассмотрим эти случаи.
Jx-2y = 13,	*i=7, Jx-2y = l’,	*2 =7,
[х + 2у = 1	у,=-3;	?1х + 2у = 13^ у2=3;
(х-2у = -13, хз ~ “7,	(х-2у = -\,	х4=-7,
в}\х + 2у = -1	Уз=3; гф + 2у = -13 у4 = -3.
Так как всякое целое число -F} может быть разложено в произведение це-
лых сомножителей лишь конечным числом способов (докажите это утвер-
ждение сами при помощи основной теоремы арифметики), то и число ре-
шении уравнения (10) — не более, чем конечное. Может оказаться так, что
уравнение (10) вообще не имеет целых решений.
□	Пример 5. Решить уравнение х2 - 9у2 =22 в целых числах.
Решение. Применим формулу разности квадратов, (х - Зу)(х +3у) = 22.
Можно разлагать 22 во всевозможные произведения целых сомножителей,
но можно поступить и проще. Заметим, что х-Зу и х + Зу различаются на
бу , то есть на четное число. Это означает, что сомножители х - Зу и
хч-Зу либо оба четные, либо оба нечетные. Значит, их произведение либо
нечетное, либо делится на 4. Но число 22 четное и на 4 не делится.
Ответ: нет решений.
50	Конкурсные задачи
4.2	Уравнение подтипа х2-С1у2=1,
Это уравнение является вспомогательным при построении решения более
сложного уравнения (12). Две пары целых решений (х = ± 1, у = 0) очевид-
ны. Далее ясно, что если пара натуральных чисел (х, у} является решени-
ем, то и пары (± х, ± у) также являются решениями. Поэтому множество
всех решении уравнения (11) строится через положительные решения. На
вопрос, сколько таких решении может быть, отвечает следующая лемма.
Лемма. Если уравнение (11) имеет хотя бы одно решение (х0,у0), где
х0, д е Л' , то тогда таких решений бесконечно много.
Доказательстпо. Пусть пара натуральных чисел (х0,у0) — решение урав-
нения (11). Тогда
(хо -	+ V^-Уо) = 1	(13)
возведем равенство (13) в квадрат
(х0 - ^С\Уо)2 (*о + V^-Уо)2 =
= 1(*0 +?1У<Ь-^(.2хоУо)][(х2 +С1У2) + у[с^(2х0у0)] = \ .	(14)
Обозначим
(15)
У\=2*оУо-	(16)
Нетрудно заметить, что xb yj е N, что Х| > х0, у( >у0 и, как следует из
(14), пара (х|, ух) является решением уравнения (9), то есть
^i-VQJi)(^+Vc3'i) = i-	(17)
Перемножим соотношения (13) и (15) и получим
[(х0 - т[С\Уо)(х} -JC\y\)] • [ (х0 + у]~С\ Уо)(х] +у[С}У\)] =
[Сад	+*1№)М(*о*1 +QУоУ])+Е\(ЛУ1 +х1>'о)]- (18)
Обозначим
х2 =ад + С]УоУ} ,
У2 = хоУ\+х\Уо-
Аналогично, числа (х2,_у2) являются натуральными, удовлетворяют урав-
нению (11) и неравенствам: х2 > х,, у2 > v,.
Далее по индукции ясно, что (k +1) -с решение уравнения (11) имеет вид *
Мы '<>** •	,	П9)
И*,| хп vk 4 vt}xk ,	v >
Глава 2. Целые числа	51
где к = 0,1, 2,.... Лемма доказана.
ui nt^.urmaniii.ihiiwtww*	l»гтг>
□	Пример 6. Найти три различных решения уравнения х2-2у2 = 1, х, у е N.
Решение. Первая пара легко подбирается х0 = 3, у0 = 2. Далее воспользу-
емся формулами (17)
jq =32 + 2 - 22 =17 , ух = 2-(3-2) = 12 ;
х2 =3-17+ 2 2-12 = 99 , уг = ЗЛ2 + 2-17 - 70 .
[3	(17	(99
Ответ:	< ,	<	;	{
[2	[12	[70
Нам теперь остается выяснить, существует ли хотя бы одно решение урав-
нения (11) в натуральных числах. Соответствующая теорема приведена в
[2]. Метод ее доказательства основан на применении цепных дробей, и мы
вынуждены ограничиться только формулировкой.
ТЕОРЕМА 1. Существует по крайней мере одно решение уравнения (11)
в натуральных числах.
Согласно сформулированной выше лемме, это означает, что уравнение (11)
имеет бесконечное множество решений в натуральных числах. Среди всех
решений выберем (ль,у0) такое, что точка (х0,у0) оказалась наименее уда-
ленной от начала координат, и назовем его нормальным решением. Оказы-
вается, что все решения уравнения (11) можно выразить через нормальное.
ТЕОРЕМА 2. [ 2 ] Все решения в натуральных числах уравнения (11) могут
быть выражены через нормальное решение из формул (19).
«WWV'MWW'WfWWVVWMmMNBWVVWnWVWWmWVWVVWVWmWPfWmmWNmWVVWWWmWmWVV'NmVVWtVmVl <	w
□	Пример 7. Найти все натуральные решения уравнения х2 - Пу2 = 1.
Решение. Нормальное решение ищется подбором: л0 = 8, у0 = 3. Далее
пользуемся формулами (19)
f = $хк + ^Ук >
[УАг+1 =*Ук + Зхк , где к = 0, 1, 2, ...
4.3	Уравнение подтипа x2-Clty2 = -F15 т2 eN , Ft
Для уравнения типа (12) справедлива
Лемма. Если уравнение (12) имеет хотя бы одно решение в натуральных
числах, то тогда таких решений бесконечно много.
Доказательство. Пусть пара натуральных чисел (^, jpo) является решени-
ем уравнения (12), а натуральные числа (xk,yk) являются решениями
уравнения (11). Применим формулу разности квадратов
52
Конкурсные задачи
(х0 +ТОРо)(*о - fe) = " >
(•*£ +т[С\Ук')(* хк ~ ^С\Ук} — 1 •
Перемножим два последних соотношения и получим
[ (х0^ + С} Уо У к)	(-*0 У к + Уохк) И (хохк + с\ У о Ук) +	(io У к + Уохк) ] =	,
откуда следует, что натуральные числа (хк+}, ук+])
хк+\ = хохк+С\УоУк>
Ук+\ ~хоУк +Уохк> где к = 0,1,2,...,
являются решениями уравнения (12).
(20)
Замечание. Формулы (20), вообще говоря, не описывают все решения
уравнения (12). Более подробно см. [2].
□ Пример 8. Найти три различных натуральных решения уравнения
х2-2у2=5.
Решение. Первую пару £0 = 5, у0 = 3, нетрудно найти. Далее воспользуемся
результатами примера 6 и вспомним, что числа xQ = 3, у0 = 2, и х, = 17,
У! =12 являются решениями уравнения х2 -2у2 =1. И, наконец, применим
формулы (18)
jq =5-3 + 2-3-2 = 27, ух = 5-2+3-3 = 19 ;
х2 =5-17 + 2-3-12 = 157, у2 =5-12+3-17 = 111.
Гх0 = 5, р!=27,	Jx2=157,
Ответ: < Л < ;	< /
[уо=3; 1у1=19'
Коренное отличие уравнения (11) от уравнения (12) состоит в том, что это
последнее может вообще не иметь решений.
□ Пример 9. (ВМК, 1997, устный экзамен) Решить в целых числах уравнение
х2-7у2 = 5.
Решение. Перепишем уравнение в виде х2 - 5 = 7у2, откуда следует, что
левая часть уравнения должна делиться на 7. Рассмотрим всевозможные
остатки от деления х на 7:
если х = 7к, то х2-5 = 49&2-5 не делится на 7;
если х = 7&±1, то х2-5 = 49Л2±14Л-4 не делится на 7;
если х = 7£±2, то х2-5 = 49£2 ±28£-1 не делится на 7;
если х = 7к±з, то х2 -5 = 49£2 ±42^+4 не делится на 7;
()твет: нет решений.
Глава 2. Целые числа	53
Замечание. Разумеется, можно было бы рааллотретъ случаи х=7к ,
x = 7Jt + l, x=7fc+2, ... , х = 7£+6, во это менее экономично.
Итак, уравнение вида (12) либо вообще не имеет решений, либо имеет их
бесконечно много.
В заключение пункта заметим, что уравнение
х2-Су2+Dx+Ey+F = O, где DхО ,	(21)
переводится в уравнение (5) так же, как уравнение (9) переводится в урав-
нение (4). Проделайте выкладки самостоятельно.
5.	Приведение уравнения Ахг +Вху+Суг +Dx+Ey + F = $
к каноническому виду
Опишем процедуру замены переменных в уравнении (1). Основная осо-
бенность всех преобразований состоит в том, что новые неизвестные и но-
вые коэффициенты уравнений должны оставаться целыми числами. Это
обстоятельство и определяет некоторую громоздкость вычислений.
5.1 Случай, когда л = с=о
В этом случае дискриминант d = В2 > 0. Уравнение (1) принимает вид
Вху + Dx+Еу+F = О.	(20)
Умножим уравнение (20) на 4/1
4В2лу + 4BDx+4BEy+4BF = 0.
Далее введем вспомогательные (нс окончательные) целые переменные
Z« х, I-х—у.
Тогда
4ду = (х+у)2-(х-у)2 = z2-Z2t
2х - (х + у) + (х-у) = z + t,
2y = (x + y)-(x-y) = z~/.
Подставив последние соотношения в (20), получим
S2(?-/2)+2BD(z + r)+2BE(z-O+4M'=0.
B2z2 -B2t2 + IB(D + E)z + 2B(D-E)t + ABF~0.
Выделим полные квадраты.
{[Bz+(D+E)]2-(D+E)2} - {[Bl-(D-E)\2 -(l)-Ef}+4BF = 0.
Введем окончательные целые переменные
Bz
54	Конкурсные задачи
и приведем уравнение к виду
w2 -v2 + 4BF-4DE = 0 .
Обозначив 4BF - 4DE = Fx, получим уравнение типа (10)
и1 - v2 = -Fx .
Казалось бы, последнее уравнение можно решать, применяя формулу раз-
ности квадратов и разлагая -Fx на целые сомножители. Но сейчас удобнее
сразу вернуться к старым переменным.
и2 - V2 — {и +v)(u - v) =
= {[Bz^(D + E)]+[Bt-(D-E)]}{[Bz + (D+E')]-[Bt-(D~E)]} =
= [B(z+ t) + 2E][B(z-t) + 21)] = [2Bx + 2E]-[2By + 2D] =
= 4(Bx + E)(By + D) = -F].	(21)
□ Пример 10. Решить уравнение в целых числах ху + х - у = 2.
Решение. Минуя промежуточные переменные, сразу приведем уравнение
к виду (21), для чего проведем последовательно преобразования
4ху + 4 (х - у) = 8 ;
(х+у)2 - [(х-у)2-4(х-у)]=8;
(х + у)2-[(х-у-2)2-4| =8;
(х + у)2-(х-у-2)2 =4;
(х+у + х-у-2)(х+у-х + >> + 2) = 4;
4(х - 1)(у +1) = 4 ;
(х-1)(_у + 1)=1 = 11 = (-1)(-1).
al = =>/х = 2’	51 P~l = -1’ => Jx = 0’
' |у+1 = 1	{^ = 0;	(^ + 1 = -1	[>> = -2.
г>	[2,	(0.
Ответ: < ’	< \
Иногда для решения (20) бывает удобнее не приводить его к каноничес-
кому виду (10), а сразу воспользоваться стандартными "школьными” сооб-
ражениями делимости нацело.
Для этого перепишем уравнение (20) в виде
y(Bx + £)=-(ZXr + F)	(22)
Если Е делится нацело на В, то тогда имеет место решение
Е
х —--,
В
у - любое целое.
Если Вх+Е = к (1)х >/• ’), где к t /, то тогда получим решение
55
Глава 2. Целые числа
I х - любое целое,
Если же эти условия не выполняются, то тогда выражение (22) можно раз-
делить на Вх + Е
Dx+F
у =--------,
Вх+Е
и искать, при каких целых х число у является также целым.
□ Пример 11. (ИСАА, 1997) Найти все пары целых х и у, удовлетворяющих
уравнению Злу+ 16х + 13у+ 61 = 0 .
Решение. Перепишем уравнение в виде
у (3х + 13) =-(16х + 61) .
Выражение Зх +13 не обращается в нуль ни при каких целых х, поэтом)' мы
можем все поделить на 3х + 13
16х + 61	15х + 65 + х-4	_ 4-х
у =-------=---------------= —5 +----.
3х + 13	3х + 13	3х + 13
Поскольку у — целое, то дробь также должна быть целым числом,
4-х	,	,
------= к , где к е Z .
Но тогда Зк — тоже целое число
_	12-Зх 25-Зх-13	25
Зх --------=------------------1.
3х + 13 3х + 13 3х + 13
~	25
Отсюда следует, что------ — целое число, поэтому
3х + 13
(3х + 13 = ±1, ±5, ±25,
[xgZ.
Далее после несложных вычислений получается
_ (х = -4, [х = -6, (х = 4,
Ответ:	<
(у = 3; у = -7; у = -5.
5. 2 Случай, когда Л*0, В = С = 0
Уравнение (1) принимает вид
Ах2 +Dx + Ey + F = O.	(23)
Дискриминант (23) равен нулю. Этот случаи выделен нами как отдельный
только потому, чтобы на простом примере пояснить, какие выкладки сле-
дует проводить в общем случае.
Умножим уравнение (23) на 4А и выделим полный квадрат
4Л2х2 + 4ADx + 4AEy+ 4AF = 0 ,
56
Конкурсные задачи
(2Ax+D?+4AEy+4AF-D2 =0.
Обозначим
lAD+x-u:' 4AF-D2 =Fl ; 4АЕ = Е},
и получим окончательный вад уравнения
и2 +Ду+/^ = 0.
Нетрудно видеть, что это уравнение типа (3).
ГИЯМПТГ IИОПЖИИ JWIЧЧИИОТМ ——Ч—Г~ ~ ~П'ТТ—ИМШГИШШГТП  Г-"Г ЛИ"--—ЮТГТГ  "Г
□ Пример 12. Решить в целых числах уравнение Эх2 +2х+Зу-2 = 0.
Решение. На практике нет необходимости приводить уравнение к виду (3),
а достаточно воспользоваться соображениями делимости. Перепишем ис-
ходное уравнение в виде
3у = 2-2х-3х2,
откуда следует, что 2-2х должно делиться на 3.
а)	Если х = 31,то 2х-2 = 6к-2 не делится наЗ;
6)	Если х = ЗА+1,то 2х—2 = 61 делится на 3;
в)	Если х = 31+2,то 2х-2 = 6А+2 не делится на 3.
Итак, х = 31+1. Остается найти
у _ 2-2,-Ь* _ 2-2(М + 1>-3)»^ , и +, )2
{х = 31*1,
у —2А-(ЗА + 1) . где к - произвольное целое.
5. 3 Случаи, когда в, с — любые числа
Итак, сейчас перед нами наиболее общий тип уравнения (1). Так же как и в
предыдущем пункте, умножим уравнение на 4 А и получим
4А2х2+4АВху+4АСу2 +4ADx+4AEy+4AF = 0.
Нашей первой целью является избавление от произведения ху. Для этого
выделим полный квадрат
(2Ах+Ву)2—В2у2 +4АСУ2 +4ADx+4AEy+4AF = 0.
Введем новую целую переменную z - 24х+Бу, тогда 4Ах = 2z - 2Ву,
Z2-{В2-4AC)y2+D(2z-2By)+4AEy+4Ar>’-0. или
(z+D)2-(B2-4AC)y2+(4AE-2BD)y + 4A/> I)2 О.
Осталось ввести новую целую переменную
и - t 1 />,
переобозначить коэффициенты
Глава 2. Целые числа
57
4AE-2BD = EX, 4AF-D2=FX,
и вспомнить, что В2-4 АС = d . Тогда уравнение (1) примет вид
и2 -dy2 + Exy + Fx - 0 .
Возможны 3 случая:
если d = 0 , то мы сразу получаем тип (3);
если d <0, то при Ех получаем уравнение типа (9), которое перево-
дится в тип (4); если же Ех = 0, то уравнение типа (4) получается сразу;
если d > 0 , то при Ех * о получаем тип (21) (переводится в тип (5)), либо
мы сразу получаем уравнение типа (5).
Соответствующие типам (3), (4), (5) примеры рассмотрены выше
6. Почему диофантово уравнение второго
порядка приводится только к одному
из трех типов (3), (4), (5)? 1
Нам осталось выяснить, почему уравнение (1) можно привести только к
одному из типов (3), (4), (5). Идея доказательства состоит в следующем.
Напомним, что типу (3) соответствует дискриминант d = 0 , типу (4) соот-
ветствует d < 0 , а типу (5) — d > 0.
Если мы покажем, что при замене переменных знак дискриминанта не ме-
няется, то это и будет означать, что тип уравнения изменить нельзя.
Доказательство. Прежде всего отметим, что коэффициенты D, Е, F на дис-
криминант никак не влияют, и их можно не учитывать.
Рассмотрим выражение вида
Ах2 +Вху + Су2.
Выражению (24) соответствует дискриминант
d=B2-4AC .
Заменим переменные в (24):
gu +hv = х,
ри +qv-y.
Здесь w, v — новые целые переменные, g, h,p, q — коэффициенты перехода.
Прежде всего отметим, что переход от переменных (л, у) к переменным
(м, v) должен быть взаимно однозначным. Это означает, что система урав-
нений (26) с неизвестными w, v при любой правой части (ж, у) должна
иметь единственное решение. Из теории систем линейных уравнении
(24)
(25)
(26)
1 Приводимое здесь доказательство хотя и является простым, но в школьную прог-
рамму не входит Поэтому при желании данный пункт можно пропустить
58	Конкурсные задачи
с двумя неизвестными 1 следует, что это возможно тогда и только тогда,
когда главный определитель системы (26) А = gq - ph # 0.
Перепишем выражение (24) через новые переменные
A(gu + hv)2 + B(gu+hv)(pu + qv) + C (pu + qv)2 =
= (Ag2 + Bgp + Cp2)u2 + (2Agh + Bgq + Bhp + 2C pq) uv + (Ah2 +Bhq + Cq2)v2 =
= A} u2 4- B\ uv + Cjv2 .	(27)
Подсчитаем дискриминант d} в выражении (27)
di = B2-4A}C} =
= (2Agh + Bgq + Bhp+2Cpq)2 -4(Ag2 + Bgp + Cp2)(Ah2 + Bhq + Cq2) =
= 4A2g2h2 + B2g2q2 + B2h2p2 +4C2p2q2 + 4ABg2hq+4ABgh2 p+KACghpq +
+ 2B2ghpq + 4BCgpq2 4- 4BChp2q - 4A2g2h2 - 4ABg2hq - 4A( g2q2 -
- 4ABgh2p - 4B2ghpq - 4BCgpq2 -4ACh2p2 - 4BC hp2 q - 4C2 p2 q2 -
= ^(g V + h2p2 4- 2ghpq-4ghpq ) - 4AC (g2q2 +h2p2 - 2ghpq) =
= (B2 - 4 AC )(g2q2 - 2ghpq + h2p2) = (B2 - 4 AC )(gq - hp)2 = d  Л2 .
Итак, мы вывели формулу
d} =
откуда следует, что дискриминанты выражений (24) и (27) либо одновре-
менно положительны, либо одновременно отрицательны, либо одновре-
менно равны нулю. Еще раз напомним, что в уравнении типа (3) дискри-
минант равен нулю, в уравнении типа (4) — меньше нуля, и в уравнении
типа (5) — больше нуля. Отсюда вытекает, что
1) уравнения типа (3), (4), (5) не переводятся друг в друга;
2) всякое уравнение типа (1) может быть приведено только к одной из
канонических форм (3), (4), (5).
Утверждение доказано.
7,	Приемы решений уравнений в целых числах
второго и высших порядков
Мы только что изложили теорию уравнений второго порядка в целых чис-
лах. Ясно, что приведение к одной из канонических форм (3), (4) или (5)
является одновременно и универсальным методом решения. Однако, как
это бывает и в жизни, универсальный метод часто не является самым эко-
1 ' ha теория опять-таки исключена из школьной программы. Однако конкурсные
UUUI4H па системы уравнений встречаются, потгому теорию лучше знать. Рекомен-
дуем киши 15. б|
Глава 2. Целые числа	59
комичным и эффективным. Полезно знать еще и "школьные’' приемы ре-
шения. Такие приемы порой работают и для уравнений высших порядков.
7.1 Соображения делимости, основная теорема
арифметики, НОД и НОК двух чисел
г.а*жжнллялм»»1ггв«хкгла^и?«л1п\х>.м»1 vixjuu глж»	д
□ Пример 13. (Психфак, 1975) Найти целые положительные решения урав-
нения 2х2 + 2ху-х+у = 112 .
Решение. Заметим, что данное уравнение является линейным относитель-
но у, и перепишем его в виде
у (2х +1) = 112+ х-2х2 .
Поскольку х, у е N, то 2х + 1*0 и поэтому
112 + Х-2Х2 112 + 2х-(2х2 +х)	2х + 112	2х + 1 + 111
У  ------------------------------L - -х 4-------= -X +----------=
2х + 1	2х + 1	2х + 1	2х + 1
1 Н1
= -х +1 +------ е N ,
2х + 1
откуда следует, что 111: (2х + 1). Так как натуральными делителями числа
111 являются лишь 1,3,37 и 111, то возможны 4 случая:
а)	2х +1 = 1, тогда х = 0, у = 112 , x*N\
б)	2х +1 = 3, тогда х = 1, у - 37 , х, у е N ;
в)	2х + 1 = 37, тогда х = 18, у = -14, y*N ;
г)	2х + 1 = 111, тогда х - 55 , у = -53 , y*N,
Ответ: х - 1, у = 37 .
Замечание. Решение уравнения путем приведения к каноническому виду
оказывается значительно более трудоемким.
Рассмотрим задачу, ключом к решению которой является основная теорема
арифметики.
□ Пример 14. (Эконом., 1994) Найти все целочисленные решения системы
(7889? =2875/,
Решение. Разложим числа 7889 и 2875 на простые множители:
7889 = 23 • 73, 2875 - 23 • 53. После сокращения на 23 и извлечения кубиче-
ского корня первое уравнение системы примет вид 7х = 5у . Так как 5 и 7 —
взаимно простые числа, то из последнего равенства вытекает, что число у
RGJVKHQ делиться на 7. Из условия |у| < 8,1 следует, что yj = -7, у2 = 0 и
Уз = 7. Остается найти значения х1, х2 и х3.
Ответ: (-5; -7), (0; 0), (5; 7).
60	Конкурсные задачи
Покажем теперь, как работает идея выделения НОД (х, у) и перехода
к взаимно простым числам
• -> v. г.-rrriicr»» nuuM'utu'pnrintrr»^	TJv>rT»nmttJM5m» п_'-<.г1«г»жгл.т.>1.татгг	i	... п 4	t < к т
□ Пример 15. (Химфак, 1995) Найти все пары целых чисел т и п, удовлетво-
ряющих уравнению т2 + атп-Ьп2 = 0 , где а = 1953100 , b = 1995100 .
Решение. Нетрудно заметить, что пара чисел (0; 0) является решением.
Пусть (wo^'2o) — ненулевое решение уравнения, и пусть d = НОД^т^пД.
Тогда пара взаимно простых чисел т ~ тД d, п = пД d также является ре-
шением нашего уравнения (докажите это). Далее ясно, что
1) т и п нс могут быть одновременно четными (они взаимно простые),
2) по соображениям делимости не может также быть, что одно из чисел
четное, а другое — нечетное (так как числа а нЬ — нечетные),
3) также по соображениям делимости невозможен случай, когда т и п - -
нечетные.
Следовательно, ненулевых решений нет.
Ответ: (0,0)
7.2 Метод разложения на множители
Иногда при решении уравнений в целых числах полезно применять метод
разложения на сомножители.
□	Пример 16. Решить в целых числах уравнение х2 - ху - 2у2 = -5.
Решение. Разложим выражение в левой части на сомножители.
X2-лу-2/ = (х+у)(х-2у) = -5 = (-5)-( J) = (5)-(-l) •
Поскольку х и у — целые, то выражения в круглых скобках слева также
являются целыми, и нам надо рассмотреть два случая:
Jx + y = -5	(х = -3	fx+v = 5	(х = 3
[ х - 2 у = 1	[ у = -2	[ х - 2у = 1	[ у = 2
(-3	[3
Ответ: < и <
1-2	12
Замечание. Данный метод сработал потому, что уравнение z2-z-2 = 0
имеет целые корни.
Метод разложения на множители применим и при решении уравнений
высших порядков.
□	Пример 17. (Мех.-мат., 1966) Найти все целые решения уравнения
2л2_у2+,у2 - 6л2 -12 = 0 .
Глава 2. Целые числа
б]
Решение. Представим выражение в левой части уравнения в виде
у2(2х2 +1) - 3(2х2 +1) - 9 = О или (2х2+1)(у2 - 3) = 9 .
Поскольку х и у целые, то 2х2 +1 и у2 - 3 также являются целыми числами.
Болес того, 2х2 +1 — натуральное число. Число 9 может быть разложено
в произведение натуральных чисел одним из следующих способов.
9 = 1 9 = 3-3 = 91. Поэтому надо рассмотреть три случая
. f 2х2 +1 = 1,	_ (2х2 +1 =3, ч [2л2+1 = 9.
3) 1 ?	бМ .	в) 1 о
(У -3 = 9;	[^-3 = 3;	[у“-3 = 1;
В случаях а) и б) целых решений нет, а система в) имеет решения
z ч	[ Xi = 2 ,	( as = 2 , f х? = -2 ,
Ответ: < 1 -	< “ n s
Vj = 2 ;	( у-> = -2;	= 2;
-2,
-2.
7.3 Метод решения уравнения относительно
одного из неизвестных
При решении алгебраических уравнений с несколькими неизвестными
в целых числах порой бывает эффективен метод разрешения уравнении
относительно одного из неизвестных.
’ «. " *	1 .-.«St. . • ' >»х	>NUB»4*
□ Пример 18 (Мех.-мат., 1966) Найти все целочисленные решения уравне-
ния 2х2 - Злу - 2 у2 = 7 .
Решение. Рассмотрим уравнение как квадратное относительно х. Нетрудно
видеть, что его дискриминант равен 25у2 +56. Поскольку нас интересуют
лишь целочисленные решения, то дискриминант должен быть квадратом
целого числа, то есть 25у2 +56 = К2, откуда следует (К -5у)(К + 5у)« 56
Рассмотрев все варианты разложения числа 56 на целые множители, в ито-
ге получим
( X, = 3 ,	| Хэ = -3 ,
Ответ. 1 .	< ~	.
(У1 ~ Р- [У2 =“1 
Замечание. Задача также решается с помощью разложения на множители.
□ Пример 19 (ВМК, 1996) Найти все целочисленные решения уравнения
10V*-2/ +х2у2 +29/ -113х2 +171 = О
Решение. Представим уравнение в виде
10х4 - (113-у2)х2 - (2у4-29у2 - 171) = О
и рассмотрим его как квадратное относительно х2 (биквадратное). Заме-
тим, что его дискриминант D равен
D = (y2-ИЗ)2 + 40(2у4-29у2-171) = 81у4 -1386у2 +5929 = (9v2-77 )2
62
Следовательно,
Конкурсные задачи
2 _(113-/)±(9/-77)
Л1 Э — ----------------------
1	ОЛ
и исходное уравнение можно представить в виде
5
.2 19-у2>
2
= 0,
откуда немедленно получаем совокупность двух уравнений
5.V2 =2у2 + 9
2х2 +у2 =19.
Первое уравнение не имеет целочисленных решений, так как его левая
часть кратна 5, а остаток от деления на 5 правой части, как легко показать,
может принимать лишь значения 1, 2, 4. Решения второго уравнения нахо-
дятся подбором: 19-2х2>0, |х| < ^19/4 <4 ;
х = 0, ±1, ±2 нс годятся, а х = ±3 дают решения.
Ответ: (3; 1), (3; -1), (-3,1), (-3,-1).
7*4 Пример нестандартного решения
В заключение данного параграфа рассмотрим уравнение, имеющее "стан-
дартный” вид, но решаемое нестандартным способом.
□ Пример 20 (Химфак, 1997) Найти все пары целых чисел (х, у), удовле-
творяющие уравнению (х2 + у2) (х + у - 3) = 2ху.
Решение. В силу неравенства о среднем арифметическом и среднем гео-
метрическом х2 +у2 >2|ху|, причем знак равенства достигается тогда и
только тогда, когда | х | = | у |.		
Так как x+y-3eZ,л	го равенство	возможно, только если:
1)	=> X 4 |х+у-3=1	= у = 2; f х = 3,	2)\х1~у\ 1 => 0; [х+у-3=1
fх+у-3=0, J = 0	Ь=о р = 0. Ду = з;	4)р!+/-0.	„р.о;
5)Р = ^ 7 (х + у-3 = -1	0;	6)р=--\ , => 0. [ х + у - 3 = -1 /1	[0, Ответ: 1	<	<	< [2; [0; 13; 10.
Глава 2. Целые числа	63
§4. Неравенства в целых числах
В данном параграфе мы коснемся специфики задач на доказательство и ре-
шение неравенств в целых числах. Эта специфика, порожденная дискрет-
ностью неизвестного, может, как мы сейчас убедимся, проявляться весьма
интересно и разнообразно.
1.	Пример неравенства, справедливого только на
множестве Z
Прежде всего отметим, что условие принадлежности аргумента множеству
Z может само по себе играть определяющую роль Одно и то же неравен-
ство может оказаться справедливым, если рассмотреть его на Z, и неспра-
ведливым, если рассмотреть его же на множестве вещественных чисел.
□ Пример 1. (Филфак, 1970) Доказать, что 11и2 - 14л + 3 > о при всех п е Z
( 7V 16
Решение. Поскольку 11и2 -14 п+3 = 111 и - — 1 - —. то достаточно прове-
рить неравенство лишь при « = 0 (3>0) и п-\ (0£0).
2.	Математическая индукция как метод решения
неравенств
В следующем примере для решения используется метод математической
индукции.
□	Пример 2. (Психфак, 1972) Найти все целые решения неравенства
л - 1 < log6(x+ 3).
Решение. Допустимые х определяются из условия х + 3 > о, х е Z , т. е.
х = -2, -1, 0, 1, ... Начнем последовательно проверять:
1)	х = -2 — очевидно решение: -3 < log61 = 0;
2)	л = -1 —решение: -2<log62 —отрицательное число меньше положи-
тельного;
3)	х = 0 — решение: -1 < 0 < log6 3 следует из транзитивности неравенств;
4)	л = 1 — решение: 0<log64 — вытекает из свойств логарифмической
функции. Для остальных целых х неравенство не выполняется. Докажем
это по индукции:
х	п -1 > log6(n +3), и>2, neN.
База индукции: п = 2 и 1 > log6 5 очевидно ^ерно
Индуктивный переход: для любого целого п = к > 2 , если выполнено
64
Конкурсные задачи
Zr - 1 > log6 (А*+3),
то и выполнено для п = k +1
(А+1) - 1 = А > log6 (А'+4) = log6 [(Zr+3) +1 ].
Прибавим к неравенству (*) по 1 и проверим, что справедливо неравенство
log6(A+3) + l >log6(A+4).
В самом деле. logf)(A +3) + 1 = log6 (6к +18) > logG (к +4). поскольку
6А + 18 > А + 4, 5к +14 > о , что верно для любого к > 2 . Индуктивный пере-
ход обоснован
Ответ: х = {-2, -1, 0, 1}.
3.	Метод перебора и проблема его организации
При решении неравенств в целых числах часто применяется очень эффек-
тивный метод — перебор. Причем метод перебора часто работает и в том
случае, когда традиционные "школьные” методы решения неравенств ока-
зываются неэффективны.
log3(8x-7)
□ Пример 3. (Психфак, 1973) Найти все целые числа х, удовлетворяющие
3 log о (21-5х)
неравенству 22
Решение. Допустимые х определяются системой неравенств
21 - 5л > О,
8х-7>0,
х eZ
х<21 '5.
х>7/8.
х eZ
Г 7/8 < лг < 21/5
| xeZ
<=> х= 1,2; 3; 4.
Подставляем последовательно найденные х в неравенство, предварительно
его упростив.
3
32 + 21оез(8х-7) > (21-5х)2 .
3
1) х = 1. Тогда 32 + 21оез‘=33> 162 <=> 33>43 4 о 33>64,
и неравенство нс выполнено.
2) X - 2 . Тогда U I 21"*	- 16 • 11 •’ о Кг .> 11’ <=> 1296 >1331,
и неравенство нс выполнено.
3) х = 3. Тогда 32 + 21<>в ,17 > 32 t-2? Зб>62 <» 362 > 63 <=> 6>1,
и неравенство выполнено.
з
4) х = 4. Тогда 32 + 2loe ,2S > 32 -I 22 = 36 > I2 =1,
и неравенство выполнено.
Глава 2. Целые числа	65
Ответ: х - 3, х = 4.
В только что рассмотренном примере число вариантов (четыре) было отно-
сительно невелико. Многие конкурсные задачи, однако, составлены так,
что простым перебором обойтись либо просто нельзя, либо это будет неоп-
равданно трудоемко. В этом случае необходимо организовать перебор,
привлечь дополнительные соображения и отбросить заведомо неприемле-
мые варианты.
□ Пример 4. (Филфак, 1976) Найти все целые z, удовлетворяющие неравен-
ству z + \ < ^6-z.
Решение. Допустимые z определяются из системы
[ Z 4- 1 > О,
=> -l<z<6 => z = -1, 0,1, 2, 3,4, 5, 6.
16 - z > О
Заметим, что левая часть неравенства увеличивается с ростом z, а правая —
уменьшается. Это обстоятельство позволяет упростить перебор.
1.	При z = -1 неравенство очевидно выполнено.
2.	При z = 0 имеем < ^6 — верно.
3.	При z = 1 ^2<^5 <=> (^2)24 < (^5)24 •» 24 = 16 < 53 = 125 — верно.
4.	При z = 2	> ^4 , так как З4 = 81 > 43 = 64.
В силу Сделанного выше замечания, необходимости в проверке значений
z = 3,4, 5,6 нет. Эти числа решениями не являются.
Ответ: z = -1,0,1.
Замечание. Эту идею можно применить при решении предыдущей задачи.
' 1°8 о (21 —5х)	।
В самом деле, 22	— функция убывающая, а 32 + 2 3	—
функция возрастающая. Организуйте перебор самостоятельно (при этом
число вариантов сокращается с четырех до трех).
Отметим, что для применимости метода перебора условие х е Z вовсе не
обязательно. Достаточно чтобы область определения неравенства была
дискретным множеством.
□ Пример 5. (Филфак, 1982) Найти все числа х, удовлетворяющие одновре-
менно следующим условиям:
^-log1/5 (х + 8) > log1/5 (х-4) и 11.2-х —целое положительное число.
Решение. Перепишем неравенство в виде log !/s ^х +8 > log 1/s (х-4)
и замени^ его равносильной системой неравенств
66
Конкурсные задачи
Гх-4 > 0,	[х>4,
<! .-- <=>	<=> х > 8 .
|^х + 8<х-4	[я-9х + 8>0
Второе условие задачи (11 2 - х) е N дает
1)	11.2-х = 1, х = 10.2;
2)	11.2-х = 2, х = 9.2*;
3)	11.2-х = 3, х = 8 2.
Для остальных натуральных п - 4, 5, 6, ... неравенство х>8 не выполнено.
Ответ: х1 = 8 2 ; х2 = 9.2 ; х3 = 10 2 .
Следующая задача также решается перебором. Она интересна тем, что в
ней неизвестное начинает играть как бы роль параметра (в данном случае
основание логарифма).
□ Пример 6. (Биофак, 1975) Найти все целые п, удовлетворяющие неравен-
ству
2п
2 cos —
7
у{п+5 - 1
^10-/1
Решение.
1)
0 < 2cos - п + 8 < 1
7
у[п + 5 -1
^Ю-л
Так как 2cos—>2cos—=1, то 2cos—+ 7</i<2cos —+ 8 и, следова-
7	6	7	7
тсльно, п = 9 . Однако при п = 9 имеем /14 -1 > 1, т. е. второе неравенство
нс выполнено.
2)
2тг
2cos---и + 8 > 1,
7
V«-5 -1 >710-н
п < 2cos — + 7
7
yjn + 5 > yj 10-п +1
-3<н<8,
п + 4 > 10 - п + 2д/10- /1
-3 < п < 8,
п -3 > /10 - я
4 <и < 8,
и2 - Sn - 1 > 0
<=> п - 6, 7; 8 .
Ответ: 6, 7, 8.
67
Глава 2. Целые числа
4.	Метод интервалов
При решении неравенств в целых числах часто применим и “старый доб-
рый” метод интервалов.
□ Пример 7. (Филфак, 1972) Определить, сколько целочисленных решений
имеет неравенство (и2 - 2) (7/2 -22)(и2 - 52)(п2 - 152) <0 .
Решение. Методом интервалов по л2 определяем решения (см рис. 2)
2 < и2 < 22 ; 52 < п2 < 152 . Дальше подбором находим
77 = ±2, ±3; ±4; л = ±8; ±9; ±10; ±11; ±12.
Ответ: 16 решений.
В следующей задаче комбинируется метод интервалов (для нахождения
ОДЗ) и метод перебора (для отыскания решения).
□ Пример 8. (Мех.-мат., 1996) Найти все целочисленные решения неравен-
ства д/х3- 5х-3 < 6 - х .
Решение неравенства ищем среди целых решений системы (неравносиль-
ной)
|х3-5х-3>0,	|х(х2-5)>3,
16 - х £ 0	| х 6.
Во-первых, первое из неравенств системы очевидно выполнено при
х = 3, 4, 5, 6. Подстановкой проверим, что х~3 — решение исходного
неравенства, а остальные значения х — нет.
Во-вторых, при х = 0, 1,2 первое неравенство системы не выполнено, в
чем нетрудно убедиться при помощи проверки.
В-третьих, при х = -1 выполнено как первое неравенство системы, так и
исходное неравенство: ^-1 + 5-3 = 1 < 7 .
В-четвертых, при х = -2,-3, ... очевидно не выполнено условие разреши-
мости (первое неравенство системы).
Ответ: х = -1; х = 3.
- 5х 4- 2у 4- 4z = -1,
2х 4- Зу - 6z = -2 ,
3x-5y4-2z=3
-5x4- 2у 4- 4z = -1,
1 lx-12 v -= 7.
68	Конкурсные задачи
5.	Неравенства с несколькими неизвестными
В заключение данного параграфа рассмотрим пример неравенства в целых
числах с несколькими неизвестными.
□ Пример 9. (Мех.-мат., 1990) Найти все тройки целых чисел (х, у, z), удо-
влетворяющих неравенству
log2(2x4-3y-6z4-3)4-log2(3x-5y 4-2z-2) + log2(2y4-4z-5x4-2) > z“ -9z4-17.
Решение. Так как логарифмы определены для положительных чисел, т. е.
2x+3y-6z 4-3 е ТУ , Зх-5у 4-2z-2 е ТУ , 2у 4-4z - 5х + 2 е ТУ ,
и, кроме того, выполняется равенство
(2х4-3у - 6z 4-3) 4- (Зх - 5у +2z - 2) 4- (2у + 4z - 5х 4-2) = 3 ,
то отсюда следует система
2у 4-4z-5x4-2 = 1,
« 2х 4-Зу -6z 4-3 = 1,	<=>
Зх - 5у 4-2z - 2 - 1
Итак, каждый логарифм равен нулю, и поэтому из исходного неравенства
следует
z2-9z + 17<0	<=> |(9-УТз)<г<|(9+УТЗ)
Атак как ^(9-У13)> ^(9-3) = | > 2 и ^-(9 + ^13) <|(9ч 4)--у,то
z = 3, 4, 5, 6
Проверьте, что при z = 3 , 5, 6 последняя система не имссг целых решений
относительно х и у. А при z = 4 получаем х = 5 , у = 4 .
Ответ: v 5 , у = 4, z = 4
§5. Системы уравнений и неравенств
в целых числах
При решении систем уравнений и неравенств в целых числах соображения
делимости, методы разложения на множители и перебора используются
в полном объеме. Разумеется, что для систем организация разумного пере-
бора будет еще более существенной. Новым моментом становится то, что
для систем с двумя неизвестными (неважно, уравнений или неравенств)
весьма полезной оказывается графическая интерпретация.
69
Глава 2. Целые числа
1.	Разложение на множители
Рассмотрим несколько примеров применения этого метода. Первый при-
мер интересен тем, что система из двух уравнений и трех неизвестных
имеет конечное число решений (за счет целочисленности неизвестных).
□	Пример 1. Решить в целых числах систему уравнений
f ху 4- z - 94 ,
| x + yz - 95 .
Решение. Вычитая из первого уравнения второе, получаем
^(y-l)+z(l-y) = -l,	- >	( V-1)(X~Z) = -1 .
Отсюда либо
=> у = 2 , z 32 , х = 31 ’,
либо
x-z = 1
=> у = 0 , г - 95 , z - 94 .
Ответ: (31, 2, 32), (95; 0; 94).
Метод разложения на множители работает и в том случае, если мы имеем
смешанную систему уравнений и неравенств.
□	Пример 2. (ВМК, 1995) Найти все целые числа п и т такие, что
2пт 4-Зю = 10 И п + т £ 5 .
Решение. Из первого условия следует, что т (2п + 3) = 10
Заметим, что число т — целое, а число 2л+ 3 — целое и нечетное.
Так как их произведение равно 10, то возможны лишь варианты:
-	[ т = 2,	.	о _
!• S о г => л = 1	"> т+п = 3<5 не годится;
[ 2п + 3 - 5
-	f т = - 2,	.	лп
2.	’	=> и = -4 т + п = -6 < 0 не годится:
2и + 3 = - 5
2п +3 = -1
=> п = -2 => ю4-п = -12<5 не годится.
[ю = 10
Ответ: <	.
[ п = -1.
70
Конкурсные задачи
2. Организация перебора
Как уже не раз говорилось, разумная организация перебора позволяет рез-
ко сократить число вариантов. Рассмотрим задачу, в которой перебор ор-
ганизуется исходя из условий положительности дискриминанта.
• .д,» О	3»	<rrrr^-> \-CUf-> ч~ tz»*k .«I ЛГГ41 I и -Л zWfz » u
□ ПримерЗ. (Эконом., 1973) Найти все пары чисел (х, у), для которых
выполняются одновременно следующие условия:
а)	2х2-ху+9 = 0,
б)	2х2+у2<81,
в) х — целое.
Решение.
2х2-ху + 9 = 0 => D = y~ -72 > 0 => у2 >72, х*0,
2х2+у2<81 => 2х2 < 81 -у2 < 81 -72 = 9 => х = ±1,±2,
X G Z .
1.	При х = 1, у = 11, 2х2+у2>81 не годится;
2.	при х = -1, у = -11, 2х2 +у2 > 81 не годится;
3.	при х = 2, у = — * = 8.5, 2х2 + у2 = 8+	= 80.25 <81 годится:
х	4
4.	при х = -2, у = -8.5, 2х2 + у2 < 81 годится.
f X] = 2,	[ х2 = - 2 ,
Ответ: <	4
[у1 = 8.5;	[у2 = - 8.5.
В следующей задаче для сокращения числа вариантов применяется опера-
ция пересечения множеств.
□ Пример 4. (Биофак, 1992) Найти все пары целых чисел (р, q), удовле-
творяющие одновременно двум неравенствам:
p2 + q2 < 18/7-20^-166,
32p-q~ > р" 4- 12(/ +271.
Решение. Выделяя полные квадраты, перепишем неравенства в виде
(р - 9)2 + (</+ 10)2 < 15,	(1)
 (/>-16)2+(<?+6)2 <21,	(2)
р, <7 е Z .
Из неравенства ( 1 ) с учетом р, q е Z следует
1. (р-9)2<15 => |р-9|<3 => -3</>-9<3 => 6<р<12;
(3)
71
(4)
с учетом p, q g Z следует
|p-16|^4 => -4:S/>-16<4 => 12<p<20;
(5)
(6)
( 1 ), ( 2 ) и получим
Глава 2. Целые числа
2. (д +10)* 2 <15 =>
Из неравенства ( 2 )
1. (р-16)2<21 =>
2. (д + 6)2<21 => |д + 6|<;4 =>
Из неравенств ( 3 ), ( 5 ) следует, что единственное целое число р , которое
может удовлетворять одновременно неравенствам ( 1 ) и ( 2 ), это р = 12.
Подставим р = 12 в
(д + 10)2 <6,
 (д + 6)2 <5,	=>
д eZ
q G Z
qeZ
-%<>q<, -4,
q e Z
=> q ~ - 8 .
п ]Р = 12’
Ответ: <
[д = -8.
Рассмотрим задачу, для решения которой уже вполне допустимым являет-
ся применение графических методов. (Мы пока этого не делаем.)
□ Пример 5. (Отд. прикл. социологии филос. ф-та, 1986) Найти все пары це-
лых чисел (х, у), удовлетворяющих системе
2х2 + 2у2+24х- 28^+167 < 0 .
'5
х + 2у < — .
'	2
Решение. Перепишем условие задачи в виде
X2 + 12х + 36 +у2 - 14у- + 49+ ’у -36-49 <0,
„	15
х 4- 2 у < — ,	<=>
2
x, у g Z;
(x + 6)2 + (y-7)2<|
и 15
X 4- 2 у < --- ,
2
X , у G Z .
Первое неравенство в системе имеет пять пар целочисленных решений:
72	Конкурсные задачи
|jq=-6, Jx2=-5, jx3=-6. |х4 = -7, fvs=-6,
[У1=7,	[У2	[Уз = 8,	[>>4=7;	(У5=6
Условию х + 2у<~ удовлетворяют две пары: (х4,у4) и (.rs,y5).
П	1	= " 7 > /	=• " <
Ответ:	s
[у4~7;	[у5=6.
Замечание. Решите эту же задачу с применением графических методов.
3.	Пр именение графики
При решении систем с двумя неизвестными важную роль приобретает гра-
фическая интерпретация уравнений и неравенств. Хотя чисто графическое
решение строгим не является (и соответственно, задача, решенная чисто
графически, как правило, полностью не засчитывается!), графики играют
вспомогательную роль и служат источником идей. Рассмотрим примеры.
□ Пример 6. (Эконом., 1983) Сколько точек с целочисленными координата-
ми находится внутри криволинейной трапеции, образованной осью абс-
цисс, прямыми х = 3/2 , х = 129 и графиком функции у = log2x? Точки, ле-
жащие на границе указанной криволинейной трапеции, не учитывать
Решение. Построим график функции у = log2 х (по оси х для удобства
изображения масштаб задан неравномерно)
▲
У
Рис. 3.
Заметим, что (рис. 3):
1.	для каждого целого х, 3 < х < 4, число точек с целочисленными коор-
динатами внутри фигуры равно 1;
2.	для каждого целого х, 5 < х < 8, число таких точек 2;
3.	для каждого целого х, 9 < х < 16, число таких ючек 1.
4.	для каждого целого х, 17 х 32 , число таких ючек 4,
Глава 2. Целые числа	73
5.	для каждого целого х, 33 < х <, 64, число таких точек 5;
6.	для каждого целого х> 65 < х < 128 , число таких точек 6.
Следовательно, общее число точек с целочисленными координатами равно
п = (4-3 + !)• 1 + (8-54-1)2 + (16 - 9 + 1) 3 + (32-17 + 1) 4 +
4 (64-3341). 5 4 (128-6541).6 - 2-144-248-3 416-4 432-5 464-6 =
= 2 + 8 + 24 + 64 + 160 + 384 = 642 .
Ответ: 642 точки.
□ Пример 7. (Биофак, 1997 и фунд. мед., 1997) Найти все пары натуральных
чисел (г; и), удовлетворяющие одновременно двум неравенствам
ht+AI <22и-2и\
(4w>7z + 14.
Решение. Во-первых, разрешим оба неравенства относительно t
2 ,,	47
/ < -и +1 lw-,
2
4
t < — и -2.
7
Для решения задачи необходимо найти все точки плоскости Out, обе коор-
динаты которых натуральные числа, расположенные под прямой (и воз-
4	_	~	2	47
можно на ней) t = — и - 2 и под параболой / = -ir +11« - —.
Если и < 5 , то t < — и-2<—-2 = у < 1, т. е. нужных нам точек (м, /), при
и < 5 нет. Если и = 8, то из первого неравенства системы получаем, что
47 1
/<-64 + 11-8- — = у . Если же и > 9 , то первое неравенство дает / < 0, по-
этому точек (w, /) при н £ 8 тоже нет
74	Конкурсные задачи
Если и = 6, то система принимает вид
47 r 1
t < -36 + 66-= 6—;
2	2
-6-2 = 1—.
7	7
Значит, t = 1.
Если и = 7, то система принимает вид
47	1
Г <-494-77- —= 4—,
2	2
4
£<-•7-2 = 2,
7
т. е. t = 1 или t = 2.
Ответ: щ = 6 ,	= Г, и2 = 7 , t2 = 1; и3 = 7 ,	= 2 .
§6. Задачи с параметрами и целые числа
В данном параграфе мы будем рассматривать задачи, в которых либо неиз-
вестные, либо параметры (либо и то, и другое) принимают целочисленные
значения. Как правило, такие задачи являются весьма сложными, хотя есть
и исключения.
1.	Задачи с натуральными и целочисленными
параметрами. Отбор параметров
Условия принадлежности параметров множествам натуральных либо це-
лых чисел порождают и методы решения таких задач. Мы сейчас покажем
на двух примерах, как можно организовать процедуру “перебора парамет-
ра". Как всегда, мы начнем с относительно простой задачи.
□ Пример 1. (Геолог., 1974) Определить, при каких целых значениях к сис-
тема уравнений
(aretgx)2 4- (arccosy)2 = л 2 к ,
arctg х 4- arccosy = —
имеет решения, и найти все эти решения.
Решение. Обозначим и = aretgx , v = arccosy и запишем исходную систему
в виде
Глава 2, Целые числа
75
u* 1 2 3 4 + v2 -п2ку
и 4-v = —, keZ.
2
|й|<у, 0<V<7T.
(*)
5д-2	с 2
Так как 0<w2 +v2 < — +тг2 =------, то 0<л2к <-— , т. е. к = 0 или к = 1.
\2)	4	4
При £ = 0 система (*) очевидно не имеет решений.
При к = 1 ее решения суть = /|, v1 = z2; н2 = h., v2 = , гДе zi и h. корни
квадратного уравнения
2 7Г	ЗТГ 2 Л	7Z ГТ
Г----1----= 0, Zi 2=-Т-</7 .
2	8	1,2 4	4 У
Второе решение не подходит (v2 > 0, 4 < 0). А первое решение дает нам
arctg х = — (1 - JV),
4
arccos у = — (1 + ^~7);
у = cos [-(14-/7) I
(4	)
Ответ: к = 1
Для организации "перебора" вовсе не обязательно, чтобы множество зна-
чений параметра было конечным. Рассмотрим следующий пример.
□ Пример 2. (Географ., 1987) Найти все натуральные значения параметра Ь,
1
при каждом из которых выражение -------- имеет смысл для каждой пары
Х4-у’4-3
чисел (х,у), где х<0 и у<0, для которой выражение 1g(ху-Ь) также
имеет смысл.
Решение. Рассмотрим отдельно значения Ь = 1; Ъ = 2 и 6 = 3,4, •
3	3
1. Если Ь <2, то пара чисел х0 = --, у0 = - — такова, что
9
хоуо-6 = — -Ь > 0, и lg(x0y0-6) определен. В то же время х0 4-у0 4-3 = 0,
4
так что дробь не определена.
2. Если Ь > 3 , 6 е , то требуются условия ху >Ь , х<0, ^<0, х4-^4-3^0
одновременно.
Пользуясь неравенством о среднем арифметическом и среднем геометри-
ческом двух положительных чисел, находим
-х-у > 2^(-х)(-у) = 2<fxy > 2y[b £ 2-^3 .
Конкурсные задачи
Отсюда х+у+3 = 3 - (-х - у) < 3 - 2^3 < О и, следовательно, не обращается в
нулытривсех Ь"г.З.
Ответ: /> = 3,4,5, ...
Итак, как мы только что убедились, при решении задач с натуральными и
целочисленными параметрами необходима организация процедуры ’'пере-
бора”. Ясно, что чем точнее мы будем учитывать специфику входящих в
условия задач функции, тем эффективней будет данная процедура.
2.	Различные задачи с целыми числами
на квадратный трехчлен
Казалось бы, нет ничего более традиционного для "школьной” математики,
чем задачи с квадратным трехчленом. Однако введение параметра плюс
требование целочисленности решения позволяют создавать оригинальные
и трудные задачи даже на таком материале.
□ Пример 3. (Геолог., 1995) Найти все значения параметра а, при которых
неравенство 9* х <20- 3х + а не имеет ни одного целочисленного решения.
Решение. Обозначим 3х = у > 0 и тогда неравенство принимает вид
/(>') = /-20y-a<0.
Вершина параболы — в точке у0 = 10.	a \ / ( J )	/
Чтобы не было целых корней, надо, чтобы	Y	/
у = 9 не входил в решение неравенства	\	/
(рис. 5), т. е. /(9)> 0 <=>
9\ 10
81-20-9-л > 0 , а <-99.
Рис. 5.
Ответ: а <-99.

□ Пример 4. (Четвертая Соросовская олимпиада школьников 1997 — 1998,
II очный тур, 11 класс.) Найдите все значения параметра а, при которых суще-
ствует ровно 1998 целых х, удовлетворяющих неравенству
2
х - лх + а < 0 .
Решение. Обозначим заданный квадратный трехчлен через
/	\	2
г / \	2	I 7Г । ТЕ
J(x) = x -лх + а = |х-+ а------.
Гпава 2. Целые числа	77
Так как вершина х0 - * удовлетворяет неравенствам ~ < х0 < 2, то мно-
жество решений перавснсгна содержит ровно 1998 целых чисел в том
и только в том случае, koi да парабола у = f(x) расположена так, как
показано на рис. 6, т. е. ровно 999 целочисленных точек справа от —:
2,3,..., 1000 , и ровно столько же целых чисел слева от —:
Значит, корни трехчлена должны удовлетворять системе неравенств
-998 <"(«•-V*2-4«) -997,
1000<-1(л+^л2-4а) < 1001,
решив которую относительно ау получим ответ. Проделайте это сами.
Можно рассуждать и по-другому: в множество решений попадают числа
л- = -997 и х = 1000, не попадает х = 1001. Значит, искомые значения а яв-
ляются решениями системы неравенств
[/(-997) < 0,
|/(1001) > 0
Ответ: 1001 (я -1001) < а < -997 (тг +997).
□ Пример 5. (Эконом., 1992) Найти все значения параметра q, при каждом
из которых число целочисленных решений неравенства
х2 -5(х-1) + 3|х~7|-7 < 0 максимально.
Решение. Перепишем исходное неравенство в виде
3 [х - q | < q - х2 + 5 (х - 1) ,
раскроем модуль:
9972+ 997л+а<0,	100,^ _ 100(2 < а < _9972 _99Ъг
10012 - 1001л- + а > 0
78
Конкурсные задачи
-q + x2 -5х + 5 <3(x-q)<q-x2 +5х-5
и, упростив, перейдем к системе неравенств
4q > х2 - 2х 4- 5,
2q < —х2 4- 8х - 5.
Заметим, что, казалось бы, совершенно необходимое неравенство
q -х2 +5(х-1) > 0 для корректного раскрытия модуля учитывать в задаче
вовсе не нужно: оно следует из системы, достаточно вычесть второе нера-
венство из первого.
Запишем систему неравенств в виде двойного неравенства относительно q
1	2	1	5	1	2 л 5	/ч
—х2 х 4- — < q < х + 4х .	(*)
4	2	4	2	2
Из транзитивности неравенств получаем неравенство на х
—х2 х + — < х2 +4х~— , х2 -6x4-5 О, 1 < х < 5 .
4	2	4	2	2
Учитывая, что х е Z, имеем следствие из неравенства (♦):
5	7
х = 1 О 1 <> q <> I ;	х-2 <=> — < q < — ;	х-3 <=> 2 < q < 5;
4	2
х = 4 <=> —	; х - 5 <=> 5 <> q <.5 .
4 4	2
Ключом к задаче является следующая таблица-рисунок:
5	13 7
1 4	2	3 Т 2 4
Рис. 7.
Просматривая таблицу-рисунок сверху вниз, замечаем, что, во-первых,
максимальное число целых решений будет три (2, 3, 4 или 3, 4, 5), а, во-
13	7	1
вторых, это будет при — < q < — или в изолированной точке q = 5
13	7
Ответ: — <q<—\ q = 5 .
4	2
Глава 2. Целые числа	79
Замечания: 1. Авторское решение [22] содержит красивую идею — пере-
ход в плоскость (л, q) (неизвестного и параметра) и явный изъян — чисто
графическое решение в этой плоскости.
2. Идею этого решения (таблица-рисунок) сообщил нам В. И. Голубев.
3. Системы уравнений и неравенств с целыми
параметрами или целыми решениями
В системах с целочисленными параметрами проблема отбора значений па-
раметра (по сравнению со случаем одного уравнения) значительно услож-
няется. По существу, организация отбора значений параметров начинает
играть ключевую роль.
□ Пример 6. (Химфак, 1983) Найти все целые значения т, при которых
система уравнений
| х2 -4(2х-2-2т-ш2) = у(8 - 2л -
[х2 - 12х + 40 + у(у-2х + 12) = 4m(zw + l)
имеет решения. При найденных значениях т решить эту систему.
Решение. Перепишем систему в виде
(х2 + у2 + 2ху-8х-8у + 16-8 + 8m + 4m2 = 0,	f (х + у-4)2 = 8-8т -4m2,
|х2 +у2 -2ху -12х + 12у +36 + 4 = 4т2 + 4т	|(-х + у+6)2 = 4m2 I 4т - 4
Условия разрешимости системы записываются как
/8-8п?-4/и2 > О, (т2 +2т-2 < 0,	< т < л/З-1,
l')	<=> 1 ?	<==> 1 о
[4т~ +4т -4 > 0 (т +ш-1 > 0	[ яг +ги -1 > 0
[ т = -2; -1, 0,
<=> s 2	1	<=> т- -2 .
[т +т -1 > 0
При этом система принимает вид
f (х+у-4)2 = 8,
| (-*+>> + 6)2 =4
и распадается на совокупность четырех линейных систем.
| х+у = 4 ± 2-^2,
[ - х + у = ± 2 - 6.
80	Конкурсные задачи
Рассмотрим теперь обратную ситуацию, когда параметр не является це-
лым, но требуется найти целочисленное решение смешанной системы ура-
внений и неравенств
□ Пример 7. (Психфак, 1985) Найти все значения параметра а, при каждом
из которых существует единственная пара целых чисел х и у, удовлетво-
ряющая условиям
-15л2 + 11ху-2у2 = 2,
*<У,
2а2 х + Зау < 0.
Решение. Сперва найдем решение задачи без третьего неравенства. Пере-
пишем уравнение в виде
-15х2 + 1 Ьу-2у2 = (Зх-у)(2у -5х) = 7 .
Отсюда имеем совокупность из четырех систем:
Зх-у = 7, (3x-y = l, f3x-y = -7, |Зх-у = -1,
2у-5х = 1, |2у-5х = 7, ( 2у - 5х = - I, (2у-5х = -7
Решениями этих систем являются соответственно
(15; 38), (9, 26), (- 15, - 18), (-9: -26) .
Из них только пары (15, 38) и (9; 26) удовлетворяют неравенству х < у .
Таким образом, требуется найти все а, при каждом из которых выполня-
ется только одно из неравенств
2а2 • 15 + 3а • 38 < О
или
2а2-9 + За-26 < 0.
После упрощения неравенства примут вид
За1 +19а < 0 ; За2 +13я < 0 . Решая их, получим
<а<0; -“«,<().
5	3
Условию задачи удовлетворяют все числа из промежутка
13	19
	< а <	,
3---------5
который и составляет
Ответ: при - — < а < - —.
Завершим данный пункт рассмотрением особо трудных задач.
□ Пример 8. (ВМК, 1989) Найти все значения параметра а, при каждом из
которых уравнение
Глава 2. Целые числа	81
.	а2 + 4тг2 I 4	г------------------------------
log j ---------------------------J (х - 5 + 1Олг— 34)(|яг - х| — а + тс + 2) =0
~4х-х“~2(л - 2тг)|бг -2лг| + 4тга
имеет по крайней мере одно целочисленное решение.
Решение. Сначала преобразуем знаменатель дроби Л(х, а)
Ь(х„ а) = ~х2 + 4х-4 -2 |х-21 (а-2тг)+ 4тга+ 4 =
= -|х-2|2 -2\х-2\(а-2л)~(а-2я)2 + (а-2л)2 + 4ла + 4 =
= а2 + 4тг2 +4 -(|х -2| + а ~2л)2 <а2 +4лг2 +4 .
Написанное неравенство выполняется при всех х. Значит, дробь, являю-
щаяся аргументом у логарифма, при любом х нс меньше единицы, а сам
1 Г1
логарифм — < 1 неположителен.
V л J
Затем, второе слагаемое в уравнении, очевидно, тоже неположительно.
Сумма двух неположительных слагаемых равна нулю, только когда оба
слагаемых равны нулю одновременно. Следовательно, исходное уравнение
равносильно системе (параметрической) двух уравнений с одним неиз-
вестным
| |х-2| + я-2лг = 0,
}(х-5 + 1()7г-34)(|7г-х|-а + лг + 2) = О,
относительно которой спрашивается: при каких а она имеет хотя бы одно
целочисленное решение?
Подставляя а из первого уравнения
а = 2л - |х - 2|
во второе, получим следующее уравнение
(х - 34 + 5 |х - 2|) (|х-тг | - тг+2 + |х - 2|) = 0 ,
равносильное совокупности пары уравнений.
х-34 + 5 |х-2 | = 0
|х-лг| + |х-2|-лг + 2 = 0
х - -6 е Z, х - — £ Z,
3
|х-7г| + |х-2|-лг+2 = 0
х - -6
|x-zr| + |x-2| = (7r-x) + (x-2)
х - -6,
х = 2, х = 3.
Итак, найдено три целых корня: xj = -6, х2 = 2 , х3 = 3 . Соответствующие
им значения а из (1) составляют
ответ:	-2л - 8 , а2 = 2л , а3 - 2л -1.
Следующая задача при стандартном начале интересна и необычна своим
концом — логической работой с совокупностью трех линейных уравнений
82	Конкурсные задачи
относительно одного натурального неизвестного и одного искомого пара-
метра.
□ Пример 9. (Психфак, 1999) Найти все значения параметра а, при каждом
из которых ровно пять различных наборов (x,y,z) натуральных чисел
удовлетворяют системе
112х2 -4х-2ху + 3у-у = 0,
[ ayz+axz + аху > xyz.
Решение. Решим сначала первое уравнение смешанной системы в нату-
ральных числах, переписав его в виде
^(2л-3) = 12х2-4х-9
Так как при натуральном х будет 2х - 3 * 0, то
12х2-4х-9	12
у =----------= бх + 7 +----.
2х-3	2х-3
Значит, 2лг-3 —делитель 12, т.е. 2х-3 =-1,1,2,3,4,6,12 и х равно 1,2
или 3, а соответствующие у = 1, 31 и 29. Подставив найденные пары (хуу)
в неравенство исходной системы, получим совокупность
2az + а> z \
33az + 62л > 62z;
32az Ч-87« > 87z
Нам нужно выяснить, при каких а эта совокупность имеет ровно 5 нату-
ральных решений Z.
Если а < 0, то таких решений нет, если а > i , то первому неравенству
удовлетворяют все натуральные z. Значит, 0 < а < i, но при таких а послед-
ние два неравенства вообще не имеют решений в натуральных числах.
Итак, нужно найти те а (0 < а < ~), при которых неравенство
а
2az + a > z <=> z < ---
1-2а
имеет ровно 5 натуральных решений z, т.е.
Г	1	0<а<-,	1
а 1 V V	2 5-10а<а, <=> -	0 < а	< —,	г	, 9 ’	5	6 _	z	—	< а	—
5<———26		5 а 2 6	11	13
1 - 2а	сч 1 VI о	J1 1-2а 13
(>тнст: — <а< — .
11	13
Глава 2. Целые числа
83
§7. Экстремальные задачи с целыми
числами
1.	Вводные замечания и вводная задача
Экстремум — это обобщающее понятие, означающее либо максимум, либо
минимум. При этом минимум — наименьшее значение функции или наи-
меньший член последовательности, а максимум — наибольшее значение
функции или наибольший член последовательности. В нашей книге рас-
сматриваются задачи трех типов:
найти экстремум фунции целочисленного аргумента (последовательности);
найти целочисленный экстремум функции вещественного аргумента;
найти целочисленный экстремум последовательности.
Ввиду дискретности аргумента (либо функции) при решении таких задач
применяются специальные методы.
□ Пример 1. Журнал состоит из п вложенных друг в друга двойных лис-
тов. На каком двойном листе сумма чисел, обозначающих номера страниц,
будет 1) наибольшей, 2) наименьшей ?
Решение. На левой части двойного листа с номером т страницы пронуме-
рованы с начала, а на правой — с конца. Нетрудно подсчитать, что на ш-ом
двойном листе будут номера страниц 2>л-1 и 2т с начала, а также
4и - 2т + 2 И 4п - 2т +1 С конца.
Сумма страниц на m-ом листе равна
2т - 1 + 2т + 4п- 2т +1 + 4п - 2т + 2 = 8и + 2
и не зависит от номера т.
Ответ: сумма страниц будет наибольшей и одновременно наименьшей
8и+2 на любом из п двойных листов.
Замечание. Одна из немногих задач, где исследуемая функция оказывается
постоянной величиной (константой).
2.	Экстремум квадратного трехчлена
с целочисленным аргументом
При поиске максимального (минимального) значения квадратного трех-
члена может оказаться так, что абсцисса х0 вершины параболы не является
целым числом. В этом случае экстремум достигается на целом числе, бли-
жайшем к лг0.
84	Конкурсные задачи
□ Пример 2. Найти наибольший член числовой последовательности
ап = -2п2 +27-45, и = 1,2,...
Решение Введем функцию у(х) = -2х2 + 27^-45 . Ес максимум достигает-
27
ся в точке х = — , но это число не целое.
4
Чтобы понять, как найти максимальное у(х) при хе 2 , обратимся к гра-
фику функции (рис. 8).
27	27
Заметим, что функция возрастает при х < — и убывает при х > -- Так как
27	27
7----<------б, а график квадратичной функции симметричен относи-
4	4
тельно прямой х = х0, то максимальный член ап — седьмой.
Ответ: ат^ = а7 = 46
□ ПримерЗ. (Геолог., 1999) Дана арифметическая прогрессия с третьим
членом, равным -13, и с седьмым членом, равным 3 Найти наименьшее
возможное значение суммы первых п членов такой прогрессии.
Решение. Условия задачи приводят к системе уравнений относительно а,
и d (первого члена и разности прогрессии)
аз ~ а\ + 2^7 = -13,
а~!=	+ 6d = 3.
Ее решение нетрудно найти: а} = -21, d = 4 .
Сумма первых п членов (как квадратичная функция п )
2a\+d(n-Y)	-42 + 4(и-1) о2 z 23 ч
\	?------“w =------у-----п = 2пл-23и = 2(н~- — п) =
Глава 2. Целые числа
85
J 2 э 23 232 232
= 2 п -2п-----+---------
4	16	16
529
8
достигает минимального значения при натуральном щ ближайшем к
23	3
— = 5 —, т. е. п - 6
4	4
Итак, minS„ = S6 = 2 • 62 - 23• 6 = 6(12 - 2.3) = -6  11 = -66
Ответ: -66
Замечание. Способ решения двух последних задач основан на том. что
график параболы симметричен относительно прямой, проходящей через ее
вершину и параллельной оси ординат. Для не квадратичной функции этот
способ может оказаться неверным.
3. Как искать экстремум, если /(и) не является
квадратным трехчленом ?
Иногда работает такая схема рассуждений. Введем функцию f(x) такую,
что f(n) = ап. Для определенности рассмотрим поиск максимума.
Пусть f (х) возрастает при х < и убывает — при л .• л() Если л() < / , то
задача решена. Если же нет, то надо сравнивать значения / при двух бли-
жайших к х0 целочисленных значениях аргумента.
□ Пример 4. Найти наибольший член последовательности
		п -	27 4	+ 46—, 8		27 если п< —; 4
fn ~ '	46- 8		-5		27 п	 4	27 если п> — 4
Решение. Будем рассуждать аналогично решению примера 2 Введем
функцию f(x) вида
27
если х< —,
4
27
если х > —
4
Рассмотрим график функции f(x). (рис. 9)
86
Конкурсные задачи
27	27
Как нетрудно видеть, /(л) возрастает при *<— и убывает при х^~
27
Вот только график ее несимметричен относительно прямой х = — ,
и повторение рассуждений предыдущей задачи оборачивается ошибкой.
27	27
Решение первое (ошибочное). Так как 7— <------6, то аП1ах = а7 .
4	4
27
Решение второе (правильное). Так как /(л) возрастает при х^ — -> то
97
/(!) = «! </(2) = и2 <...</(б) = а6. Далее, /(х) убывает при х-~^, п0~
этому имеем /(7) = а7 > /(8) = д8 > /(9) = и9 >... Значит, максимальный
член последовательности — либо ав , либо а7 . Сравним их.
г 27	i	13
а б = 6----+ 46— = 46----= 45—,
4	8	8 4	8
лЛ 27^1	1 5	7
а7 = 46—5 7-----= 46--------- 44—.
8	V 4 )	8 4	8
Итак, а6 > а7 !
7
Ответ: атлк = а< =44 — .
ШаЛ	О	g
Метод “поиска ближайших целых чисел” может работать и для функций
более сложного вида.
□ Пример 5. (Эконом., 1971) Найти максимальный член последователь-
ности
о	25
ап = -2лГ + 20и -48 +-----------, где п = 1,2,...
(5и-31)2 +10
Решение. Обозначим ап = Ьп + с„ , где
87
Глава 2. Целые числа
Ь„=-2п2 +20и-48 = 2-2(п-5)2, с„ =-----.
'	7	" (5и-31)2+10
Рассуждая аналогично решению предыдущей задачи, мы приходим к вы-
воду, что max bn = Ь5 и что max сп = с6 . Поэтому либо max ап = а5, либо
max ап = а6 . Проведем сравнение а5 и а6. Поскольку
о 25	25	п 25 117
46 И 6	п 5	46	46
117
Ответ: max а„ = as =--.
п 3 лг
□ Пример 6. (Геолог., 1997) Стоимость изготовления т коробок пропор-
циональна 17 + 5m+m2. Определить количество коробок, при котором
стоимость изготовления одной коробки минимальна.
Решение. Пусть /(х) = х+ —, а>0 и х > 0. Если > х2 > 0 , то
х
f(x})-f(x2) = x}-x2 4- — -—= (Х! -х2)(1-— ).
*1 Х2	XjX2
Если xj >х2 >4а , то /(х0 >/(х2). Значит, /(х) возрастает на множестве
'/а<х<сю . Если 0<xj<x2<V^, то /(^])</(х2). Следовательно, /(х)
убывает на множестве 0 < х £ 4а .
Стоимость одной коробки по условию
С/ 17 + 5m+m2	17	17	1 с 17	2
S(m) =----------= т +— + 5; 5(4) = 4 + — + 5 = 13—; 5(5) = 5 + — + 5 = 13—.
т	т	4	4	5	5
Ответ: т-4.
4.	Задачи, в которых экстремум — целое число
Рассмотрим несколько задач, в которых, в отличие от предыдущего случая
(аргумент дискретен), требуется найти целочисленный экстремум функции.
□ Пример 7. (Химфак, 1997) Из сосуда, содержащего чистый спирт, отлили
| часть и добавили такое же количество воды. Потом отлили | часть сме-
си и добавили такое же количество воды. Так проделали к раз (включая
первое переливание). Каково наименьшее значение к, при котором про-
центное содержание спирта в сосуде станет меньше 10%?
Решение. После /-го ( / = 1,2,... Д) переливания в сосуде останется чистого
2
спирта - от его количества до этого переливания.
88
Конкурсные задачи
Без особого труда проверяется, что при / = к - 6 имеем
(2У-64 _L 32 -f2f
La J ~ 729 < 10 < 243 "4-V
Ответ: к = 6.
□ Пример 8. (Химфак, 1997) н насосов различной мощности наполняют
бассейн водой. Первый насос, работая автономно, может наполнить весь
бассейн за 2 часа, второй — за 4 часа, ..., н-й — за 2п часов. Каким должно
быть наименьшее число насосов л, чтобы все п насосов, работая одновре-
менно, наполнили бассейн быстрее, чем за I час и I минуту? Можно ли
наполнить бассейн водой быстрее, чем за 1 час?
Решение. За 1 час работы первый насос наполняет ~ часть бассейна, вто-
рой ----— часть....п-й-----— бассейна. Значит, работая одновременно,
22	2п
п насосов за 1 час наполняют часть бассейна, равную
Поэтому:
за 1 час наполнить полностью бассейн нс смогут никакое число насосов;
п насосов, работая одновременно, наполняют бассейн за -!--- часов
--PT
I 2 )
Нам нужно найти наименьшее натуральное решение неравенства
Легко проверить, что
1 <j_ _i_ nV
64 < 61 < 32 “Ы
Ответ: н = 6, нет.
Пример 9. (Мех.-мат., 1995) Найти наибольшее целое число и, удовлетво-
ряющее неравенству
3-22л+1 +2” <1.
Решение. Пусть 2Л = / > 0 . Неравенство переписывается в виде
6t2 +t-l <0 .
Глава 2. Целые числа	89
хг	1	1 гл Л 1 I	1
Корни трехчлена h =	= “ • Из / > О и ~2<1<~з полУчасм 1 у т.с.
2” < з ’ П < log2 J = “1о^23< “1 Значит, наибольшее целое п = -2 .
Ответ: п = -2.
ттххи•жгпрц>ж«ж»>»4&ахп««1джяии1хтх«*»11»»гоижи>«»ж*хж1лиичж|»*1«п1»г«атд»х1дсгтжжж11пгпггтит<гашддуяп1тг.«я»пмгошагтз>и« ^---'"тх.гчжеилххсзгv
□ Пример 10. На какую наибольшую степень числа 2 делится выражение
п2 + 4т? 4-33 при целых значениях «?
Решение. Перепишем данное выражение в виде п2 +4п 4- 33 = п(п +4) 4- 33.
Так как числа п и п + 4 имеют одинаковую четность, то делимость на 2 есть
тогда и только тогда, когда п нечетно. Подставив п = 2к -1, получим
п(п + 4) + 33 = 4к2 +4к + 30 = 2(2к2 4-26 + 15).
Выражение делится на 2, но не делится на 4.
Ответ: на первую.
5.	Неравенства, делимость и перебор
Нс следует забывать, что мы имеем дело с дискретным (целочисленным)
аргументом, и все приемы, использующие перебор (ограниченный), а так-
же соображения делимости, остаются в силе.
□ Пример 11. (Географ., 1979) В школьной газете сообщается, что процент
учеников некоторого класса, повысивших во втором полугодии успевае-
мость, заключен в пределах от 2,9% до 3,1%. Определить минимально воз-
можное число учеников в таком классе
Решение. Пусть п — число учеников в классе, из них т учеников повысили
успеваемость, так что процент учеников, повысивших успеваемость
— • 100% . По условию имеем оценки
п
2,9%<г —-100% <3,1% .	(1)
п
Тт	1000	1000
Из последнего неравенства следует п г	> 32 > т с « 33.
Легко заметить, что если « = 33 и т = 1, то неравенства (1) выполнены.
Значит, минимально возможное число учеников равно 33.
Ответ: 33.
Следующая пара задач весьма поучительна. Разобрав их, нетрудно понять,
насколько усложняется задача по мере роста ее размерности (изделия двух
типов и трех типов). Начнем с простой.
90	Конкурсные чадачи
□	Пример 12. (Эконом, веч. отд. и отд. менеджмента, 1996) В контейнер упа-
кованы изделия двух типов. Стоимость и вес одного изделия составляют
400 тыс. руб. и 12 кг для первого типа и 600 тыс. руб. и IS кг для второго.
Общий вес изделий 321 кг. Определить минимальную и максимальную
возможную суммарную стоимость находящихся в контейнере изделий.
Решение. Обозначим через тип количество изделий первого и второго
типов соответственно. Необходимо найти минимальное и максимальное
значение (в тыс. руб.) величины суммы S - 400/// + 600« . где
12/л + 15л = 321, т.п = 0,1,2,3,...
Выразив т через п из второго равенства и подставив его в первое, получим
5 = 100(107+//) .
Учитывая ограничение
4/л+5л = 107, /л, л = 0,1,2,3,...,
находим наименьшее возможное значение п = 3 и наибольшее возможное
значение л = 19. При л = 3 5 = 11000 тыс. руб., при л = 19 5 =12600 тыс
руб.
Ответ: 11000 тыс. руб. и 12600 тыс руб.
Увеличим размерность задачи до трех. Теперь нам придется решать дио-
фантово уравнение с тремя неизвестными.
□	Пример 13. (Эконом, 1996) В контейнер упакованы комплектующие
изделия трех типов. Стоимость и вес одного изделия составляют 400 тыс.
руб. и 12 кг для первого типа, 500 тыс. руб. и 16 кг — для второго типа, 600
тыс. руб. и 15 кг — для третьего типа. Общий вес изделий равен 326 кг.
Определить минимальную и максимальную возможную суммарную стои-
мость находящихся в контейнере комплектующих изделий.
Решение. Обозначим через л/, л и к количество изделий первого, второго
и третьего типов соответственно. Необходимо найти минимальное и мак-
симальное значение величины (в тыс. руб.)
5 = 400л/+ 500л+ 600& , где 12л/ + 16л + 15£ = 326, т.п, к = 0,1,2,...
Из последнего равенства следует, что к — четное, т е. к = 21, / = 0,1,2,..,
значит, 6/// + 6л + 157 = 163 .
Из этого равенства следует, что число I нечетное, т. е. / = 2р +1,
// = 0,1,2,..., значит, Зл/+4л + 15р = 74 .
Отсюда следует, что 74-4л делится нацело на 3, т. с. л при делении на 3
дает остаток 2, т. е. л=3</ + 2, ^ = 0,1,2,..., значит,
/л f Лд + 5р = 22, т.д.р = 0,1,2,...
Глава 2. Целые числа	91
Из этого равенства с учсюм к -2(2р +1), >? = З7 + 2 , выражая т через р и q,
получаем окончательно
5 = 100(110-,/ ♦ ЛрГ 7 = 0,1, 2,...
Простым перебором находим наименьшее значение 5 = 10500 при р = 0,
7 = 5, т - 2 и наибольшее значение 5 = 12600 при р = 4 , 7 = 0, т = 2 .
Ответ: 10500 тыс. руб., 12600 тыс. руб.
Вообще, размерность три и выше, как правило, порождает сложности при
решении как в рассуждениях, так и при вычислениях. Еще один пример.
□ Пример 14. (Эконом., 1997) Имеются три пакета акций. Общее суммарное
количество акций первых двух пакетов совпадает с общим количеством
акций в третьем пакете. Первый пакет в 4 раза дешевле второго, а суммар-
ная стоимость первого и второго пакетов совпадает со стоимостью третье-
го пакета. Одна акция из второго пакета дороже одной акции из первого
пакета на величину, заключенную в пределах от 16 тыс. руб. до 20 тыс.
руб., а цена одной акции из третьего пакета не меньше 42 тыс. руб. и не
больше 60 тыс. руб. Определить, какой наименьший и наибольший процент
от общего количества акций может содержаться в первом пакете.
Решение. Пусть к, т и п — количество акций в первом, втором и третьем
пакетах соответственно; х, у и z — цены (в тыс. руб.) одной акции в этих
пакетах соответственно. Необходимо найти пределы изменения величины
р^—--------100(%),
к + т 4- п
причем из условий задачи следует смешанная система
[к+т=п, kx + my = nz, Акх = ту,
|16<у-х<20, 42<z<60.
Положив 7 =	, получаем
7+ 5qy	50
х = —, z = —— и р =  -----.
4	4(1 + 7)	1 + <7
Неравенства исходной системы перепишем в виде
[ 64	80
---- < у < ----,
4-7	4-7
168-1^- < у < 240--^
5?	5q
Эта система имеет решения тогда и только тогда, когда
92
Конкурсные задачи
Л-< 240-1^
4-9 5q
1AR 1 + ’ < 80
loo----S ---
5q 4-q
7
3
Так как p - --, то из последнего неравенства следует 12,5 < р < 15.
1+9
Ответ: 12,5 % и 15%,

При поиске экстремума перебором по-прежнему важной остается задача
отбрасывания заведомо неприемлемых вариантов (организация перебора).
□ Пример 15. (Эконом., 1990) Натуральные числа а,Ь,с, взятые в указан-
ном порядке, образуют возрастающую геометрическую прогрессию, зна-
менатель которой является целым числом. Числа 2240 и 4314 делятся без
остатка на Ь и с соответственно. Найти числа а,Ь,с. если известно, что
при указанных условиях сумма а + Ь + с максимальна.
Решение. Пусть q — знаменатель прогрессии, тогда b = aq, с = aq2.
2240 = 2б5-7 '.(aq)
4314 = 23 • 72 11 :(а92)
(1)
(2)
Из условий (1) — (2) следует, что ни число а, ни число q нс могут содер-
жать множителей 5 и 11. Воспользуемся основной теоремой арифметики
и выпишем систему условий:
a = 2ni7r\ rn,n^Z,
q = 2p7r, p,reZ, p,r>0,
n + r<\	(следует из условия (1)),
m+2p<3	(следует из условия (2)),
Р + г > 0	( прогрессия возрастающая),
5 = « + 6 + c = (2w7n(l+2p7r+22/772г)) -> max.
Далее заметим, что 5 возрастает по каждому из аргументов т, п, р, г Зна-
чит, максимум может достигаться, только если (и = 1, г = ()), либо
(п = \., г = 1) и (т = 1, р = 1), либо (т = 3, р о). Вариант
(и = г - 0, т = 3, р = 0) невозможен, так как р + г = 0 Значит, осталось
3 случая*
( п = 1, г = 0, т = 1,	р = 1)	=>	а	- 21 71 14	,	q	=	21	7° - 2
а = 14, 6 = 28, с = 56	>	5 98;
( w = 0, г = 1, m = 1,	/; = I )	'>	а	21 7° - 2	,	q	= 21	71	= 14	=>
=> л = 2, 6 = 28,	с V)2	>	5-422;
Глава 2. Целые числа	93
( и = 0, г = 1, m = 3, р = 0 ) => а = 237° = 8 , q = 2°7'= 7 =>
=> л = 8, /> = 56, с =392 => .S'= 456.
Ответ: а = 8, b = 56, с = 392 .
Замечание. Если не заметить возрастание 5, то число вариантов резко уве-
личивается (до 18).
Рассмотрим оригинальную задачу на нахождение максимума с использо-
ванием нюансов делимости нацело.
□ Пример 16. (Мех.-мат., тестирование, 1997) Группа солдат может быть пе-
редислоцирована на новое место двумя способами: либо на двух автобусах
за несколько рейсов, либо тремя автомобилями, причем в этом случае чис-
ло рейсов каждого будет на один меньше. Транспорт во всех случаях пол-
ностью загружен. Какое максимально возможное количество солдат можно
перевезти, если в автомобиль входит на 7 человек меньше, чем в автобус?
Решение. Пусть г — число рейсов автобусов, каждый из которых вмещает
ровно п солдат (меЛ(, г £2, и >8) Тогда для группы из Л/ солдат по
условию имеем систему двух уравнений в целых числах
J 2т = М,
[3(г-1)(л-7) = М,
и требуется найти максимальное М е N .
Идея решения задачи основана на том, что НОД (п,п~7) = 7 • В самом де-
ле, пусть п = dl\ и п-7 = dl2, где d — общий делитель и lxJ2e N. Тогда
7 = d (/j - /2), и, значит, d -1 или d = 7 .
Следовательно, н = 7/ (/еЛ ), и приравнивая в системе правые части, по-
лучим уравнение в целых числах 2г/ = 3(г -1) ( / -1).
Заметим, что г > 2 , / > 3 (при / = 2 г = -3, что невозможно). Упростим по-
следнее уравнение: г/-3г-3/ + 3 =0. Заметим также, что значения / = 3
или г = 3, очевидно, не являются решениями уравнения. Далее,
3/-3	3/-9+6	о 6
г = ---- = -------- = 3 +-----.
1-3	1-3	1-3
Отсюда следует, что 1-3 = Г, 2; 3; 6 и / = 4; 5; 6. 9
Составим таблицу.
/	г	п = 71	N = 2т
4	')	28	504
5	6	И	420
6	5	42	420
9	4	6 1	S04
94	Конкурсные задачи
Из таблицы видно, что у командиров есть 2 автобуса по 28 человек и нуж-
но сделать 9 рейсов, или 3 автомобиля по 21 человеку и нужно сделать
8 рейсов. Второй вариант: командиры располагают парой автобусов вмес-
тимостью 63 человек и проделывают 4 рейса, или имеют три автомобиля
по 56 человек и назначают 3 рейса. Во всех случаях
Ответ: максимальное число перевезенных солдат 504.
В заключение рассмотрим несколько задач математических олимпиад.
□ Пример 17. (Третья Соросовская олимпиада школьников 1996 — 1997, III (фи-
нальный) тур, 10 класс.) Найти наименьшее натуральное п, при котором вы-
полняется равенство sin п° - sin (1997//)° .
Решение. Исходное равенство равносильно совокупности двух следующих
(вытекают из условия равенства синусов):
1997л-и = 36ОЛ , k,meNy	499и = 90&;
1997» = 180 « t 360m	|_ 111» = 10(2лм +1).
Первое равенство выполняется при « = 90/, к =499р , и наименьшим п бу-
дет натура. >ное число 90
Второе равенство выполняется при наименьшем п = 10 (т = 55).
Ответ: наименьшее п = 10
□ Пример 18. (V Соросовская олимпиада школьников 1998 — 1999, III (финаль-
ный) тур, 11 класс.) Известно, что числа а, Ь и с являются различными после-
довательными членами арифметической прогрессии, все они больше 1000,
и все — квадраты натуральных чисел. Найдите наименьшее возможное
значение Ь.
Решение. Обозначим а = а2 Ь = Ь2 и c = q2. Можно считать ах <Ь} <с}
(если прогрессия убывающая, то переименуем числа). Кроме того, по усло-
вию су! >32. Пусть Ъх ~а} + t, где t — натуральное. Имеем
2а2 +4tax + 2t2 -а2 +с2 , q2 + 4Zq + 2t2 = С|2 ,
(а} + 2t)2 -с2 = 2t2 , (q + 2t + c} )(а{ + 2t-c} ) = 2t2 .
Обозначим теперь р = ах + 2/ + q , q = q + 2/ - q . Из равенства p - q = 2q =>
=> p, q — одной четности, а из основного уравнения pq-2t2 =>
( р ~2п,
\	=> t = 2v
[ q = 2т
Далее, имеем систему уравнений
Глава 2. Целые числа
95
p + q
ay+2t = ---- = n + rn
1	2
p-q
Cl = ---- = n-m .
1	2
2v2 = nm ,
t = 2v
a} = n + m - 4v > 32 ,
c} = n - m > 34,
2v2 = nm ,
by = n + m - 2v -> min.
Заметим, что by = (n + m -4v) + 2v > 32+2v и m > 1 => n > 35
2v2 = nm > 35 v > 5 . Рассмотрим случаи:
1. v = 5 , тогда	2. v = 6, тогда
nm = 50,	nm - 72,
n + m > 52,	n + m > 56 ,
' n-m > 34,	0 ;	’«-«/> 34,	« = 72, m = 1 => by - 71 12 = 61
n > 35,	n > 35,
m > 1,	m > 1,
3. v = 7, тогда
nm = 98,
n + m > 60,
n-m >34, => « = 98, «/= 1 => b} = 99-14 = 85;
n > 35,
m > 1,
4. v = 8 , тогда
nm = 128,
n + m > 64,
* n - m > 34,
n > 35,
m > 1,
« = 128, «/ = 1 ==> by = 129-16 = 113;
«=64, «/ = 2 by = 66-16 = 50;
5. v > 9 , тогда by > 32 + 2v > 32 + 18 = 50
Итак, minfy = 50, при этом a = 342, b = 502, c = 622.
Ответ: min b = 2500 .
Задачи д ля самостоятельной работы
•	лл*деыии14<1Лг«1 > 1 Лк '	'X1XJC*4«W»XMF г-”л*гтл- '** чад-у/мджо ' * ' •	л-^мл< г ’ г.л'4 j 4Л»а *•
□ 1. Разделить целое число:
а) п на п-1; б) п2 + н + 1 на и + 1 с остатком.
□	2. Доказать, что если (mn + pq) делится на т-р, то и (mq+np) тоже
делится на т-р , где т, п, р, q е Z . т* р.
□	3. Доказать, что числа вида к54 -к22 делятся на 10 при любом целом к.
□	4. Доказать, что при делении двух целых чисел на их разность получа-
ются равные остатки, а (неполные) частные отличаются на единицу'.
□	5. Доказать, что число 25S +1 делится на 11.
□	6. Доказать, что если а -1 делится на к™ , то ak -1 делится на Л",+1
(к, тиа — натуральные числа, к * 1)
□	7. Доказать, что число N = 3105 +4l()S одновременно делится на
7;13 ; 49,181, 379
□	8. Доказать, что число 721 -487 делится на 288.
□	9. Доказать, что число 22 22555S + 55552222 делится на 7.
□	10* Решить уравнение в целых числах 19х - 21 р = 2 .
□	11. Найти все целые неотрицательные т и //, удовлетворяющие уравне-
нию 19ш+84« = 1984
□	12. Решить уравнение в целых числах 20л-9^ = з и найти сумму трех
наименьших положительных х, являющихся корнями данного уравнения.
□	13. Найти сумму первых ста общих членов двух арифметических
прогрессий 0, 7, 14, ... и 3, 7, 11, ..
□	14. Известно, что последние члены двух арифметических прогрессий
= 3, а2 = 9..aL и = 4, Ь2 = 14, . ., Ьм совпадают и что сумма всех
общих членов прогрессии равна 1140. Найти L и А/
□	15. (Мех.-мат., 1993, устный экзамен) Решить в целых числах уравнение
х2 = 9у2+7.
□	16. Решить в целых числах уравнение р2 - 2pq - 3q2 = -3 .
□	17. Решить в целых числах уравнение ху = х+у.
□	18. Решить в целых числах уравнение ^m+Jn = п .
□	19. Доказать, что уравнение х2 + 2 = 5у не разрешимо в целых числах.
□	20. (ВМиК, 1998, устный экзамен) Доказать, что уравнение х2-5у2=3
нс имеет решений в целых числах.
□	21. Найти все целые и, удовлетворяющие уравнению
Глава 2. Целые числа
97
3	3	3	3	4
м(м+3) (w 4-3)(w-F6) (н + 6)(м + 9) (и+ 9)(и + 12) ~ 15
□	22. (ИСАА, 1998) Найти все пары целых чисел х и у„ удовлетворяющих
уравнению Злу + 14х + 17у + 71 = 0 .
□	23. (Химфак, 1997, май) Найти все пары целых чисел, удовлетворяющих
уравнению (гм2 + m2)(mi + m-5) = 2tmm .
□	24. (Химфак, 1995) Найти все пары целых чисел п и т, удовлетворяющих
уравнению м? + апт-Ьп2 = 0, где а ~ 174350, b = 1995100 .
□ 25. (Эконом., 1989) Решить уравнение в целых числах
9х2у2 + 9лу2 + 6х2у + х2 + 2у2 +18лу 4- 5х 4- 7 у 4- 6 = 0 .
□	26. (ВМиК, 1996, апрель) Найти все целочисленные решения уравнения
14х4 -5у4 -Зх2у2 + 82у2 -125х2 +51=0.
□	27. (Филфак, 1970) Доказать, что 5м2 -бм + 1>0 при всех целых п.
□	28. (Психфак, 1972) Найти все целые решения неравенства
2х +1 < 2 log2(x +3).
□	29. (Психфак, 1973) Найти все целые х, удовлетворяющие неравенству
22'о824х>40+21"в 1(4 2х)
□	30. (ВМиК, 1996, устный экзамен)1 Решить неравенство в целых числах
п/^2<]6^.
□	31. (Мех.-мат., 1995) Найти наибольшее целое число м, удовлетворяющее
неравенству 4-32/r+l + Зк < I.
□	32. (Филфак, 1982) Найти все числа х, удовлетворяющие одновременно
следующим условиям:
logl/2^<log1/2(3-x) и х +—целое число.
□	33. (Филфак., 1971) Сколько целочисленных решений имеет неравенство
(м2 -3)(м2 -33)(м2 -103)(м2 -203) <0?
□	34. (Мех.-мат., 1996) Найти все целочисленные решения неравенства
7х - х3 - 5 < х + 4 .
□	35. (Мех.-мат., 1990) Найти все тройки чисел х,у, z, для которых спра-
ведливо неравенство
1	3	2	2 п .1
у/7 + 2x-4y+3z y2y + 3z-5x	^3x + 2y-5z-4
□ 36. (Мех.-мат., 1971) Решить в целых числах систему неравенств
1 Обратите внимание на ссылку на аналогичную задачу в основном тексте
98
Конкурсные пк)ачи
х + у>25,
< у <2х + 18,
у > х2 + 4х.
□ 37. (Эконом., 1973) Найти все целые числа А, Л/, N, удовлетворяющие
одновременно следующим условиям:
«) ЗА" + 5AY = 207V - 69,
б)	2АГ + ЗЛ/= 137V - 50,
в)	К+М +N <60,
г)	Л'>12.
□ 38. (Эконом., 1973) Найти все пары чисел (х,у). для которых выполня-
ются одновременно следующие условия:
а)	х2 - 2л^+12= 0,
б)	х2 + 4/<60,
в) х - целое.
□ 39. (Эконом., 1983) Сколько точек с целочисленными координатами на-
ходится внутри криволинейной трапеции, образованной осью абсцисс, пря-
мыми х = 50, х = 244 и графиком функции у = log3 (х +1) ? Точки, лежащие
на границе указанной криволинейной трапеции, не учитывать.
□	40. (Отд. прикл. социологии филос. ф-та, 1986) Найдите все пары целых
чисел (х, у), удовлетворяющих системе
\2х2 +2у2 - 12х+ 20у+65 < 0,
14х + 2у > 3.
□	41. (Биофак, 1992) Найти все пары целых чисел {т.п). удовлетворяю-
щих одновременно двум неравенствам:
т2 + п2 < 16т-22и-171,
ЗОлг - п2 > 252 + 14л + т2.
□	42. (Эконом., 1994) Найти все целочисленные решения системы
|7875х3 = 1701/,
[|х|^5
□	43. (Биофак, и фунд. мед., 1997) Найти все пары натуральных чисел (/, и),
удовлетворяющие одновременно двум неравенствам:
12/+ 2м2 < 24м-63,
[5и > 12/ + 11.
□	44. (ВМиК, 1995) Найти все целые числа п и т такие, что
4ш2+Зл?п = 13 и п-т>%.
/ 'natui 2, Цыы* числи	99
□	45. (Психфак, 1985) Найди те вес значения а, при каждом из которых су-
ществую единственная пара целых чисел (х, у), удовлетворяющая уравне-
нию Ъ' ♦ 11гр ♦ Юр*’ 7 и двум неравенствам: х + у> 0, 4а2х-3оу< о
□ 46. (Геолог., 1974) Определить, при каких целых значениях к система
arccosx ♦ (aicsmy)2 = 7г/с2/4,
(aicsin р)2 arccosx = я2 / 16
имеет решения, и найти вес эти решения.
□	47. (Геолог, 1995) Найти все значения параметра а, при которых нера-
венство 16х < 30 -4х - а нс имеет ни одного целочисленного решения.
□	48. (Географ., 1987) Найти все отрицательные целые значения параметра
1
а, при каждом из которых выражение------ имеет смысл для каждой
у-х-3
пары чисел (х, у), где х < 0 и у > 0, для которой выражение 1g (а - ху)
также имеет смысл.
□	49. (Эконом., 1992) Найти все значения параметрад, при которых число
целочисленных решений неравенства х2 4- 5 (х +1) + 3 |х - р| + р < 0 макси-
мально.
□	50. (ВМиК, 1998, устный экзамен) Найти вес целые значения а, при которых
х2 +(а + 5)х + 5а + 1 можно разложить в произведение (х + />)(х ♦ г) двух
сомножителей с целыми Ь и с.
□	51. (Химфак, 1983) Найти все целые значения л, при которых система
уравнений
4х(х-у - п - 1) + у(у + 2л 4-х) + 2п2 = 0,
у(2х -у -4) + 12л2 = х2 -4х + 12л + 8
имеет решения. При найденных значениях л решить эту систему.
□	52. (Психфак, 1985) Найти все значения параметра а, при каждом из ко-
торых существует единственная пара целых чисел хну, удовлетворяющих
условиям
Зх2 + 11ху + 10/ = 7,
’ х + у > 0,
4а2х-3ау < 0.
□	53. (ВМиК, 1989) Найти все значения параметрад, при каждом из которых
уравнение
J (х + Зр - Зя - 4) (\х + я | 4- р - 2;г + 2) + log я+	------= о
2(р-я)1х + 2)-х-4х + 2ря
имеет по крайней мере одно целочисленное решение.
100
Конкурсные taOa'iti
□ 54. Найти наименьший член послсдова1слыюсги ап =п~ -9п + 5.
и = 1,2, ... .
□ 55. (Эконом., 1971) Найти минимальный член последовательности
ап = п2 - 8м 4-15--------, п = 1, 2, . . .
(Зп-16)2+6
□ 56. На какую наибольшую степень числа 2 может делиться выражение
а2 +4п - 33 при целых значениях а?
□ 57. (Геолог., 1997) Стоимость изготовления п банок пропорциональна
24 4// +-//“. Определить количество банок, при котором стоимость изго-
товления одной банки минимальна.
□ 58. (Геолог., 1999) Дана арифметическая прогрессия с третьим членом,
равным 15, ис восьмым членом, равным -5. Найти наибольшее возмож-
ное значение суммы первых п членов такой прогрессии
□ 59. (Географ., 1979) При подведении итогов соревнования вычислено, что
процент числа членов бригады, перевыполнившей план, заключен в преде-
лах от 92,5% до 93,5%.Определить минимально возможное число членов
такой бригады.
□ 60. (Мех.-мат., тестирование, 1997) Группа солдат может быть передисло-
цирована на новое место двумя способами, либо на двух автобусах за не-
сколько рейсов, либо пятью автомобилями, причем в этом случае число
рейсов каждого будет на два меньше. Транспорт во всех случаях полно-
стью загружен. Какое максимально возможное количество солдат можно
перевезти, если в автомобиль входит на 15 человек меньше, чем в автобус9
□ 61. (Эконом., 1990) Натуральные числа А, / и т, взятые в указанном по-
рядке, образуют возрастающую геометрическую прогрессию, знаменатель
которой является целым числом. Числа 2835 и 2646 делятся без остатка на /
и т соответственно. Найти числа А, I и т, если известно, что при указанных
условиях сумма к 4-/ + т максимальна.
□ 62. (Химфак, 1997) Из сосуда, содержащего чистый спирт, отлили |
часть и добавили такое же количество воды Потом отлили ~ часть смеси
и добавили такое же количество воды. Гак проделали п раз (включая пер-
вое переливание). Каково наименьшее значение л, при котором процентное
содержание спирта в сосуде станет меньше 30% 9
□ 63. (Химфак, 1997) т насосов различной мощности наполняют бассейн
водой Первый насос, работая автономно, может наполнить весь бассейн за
3 часа, второй — за 9 часов...т-й — за 3™ часов Каким должно быть
наименьшее число насосов ш, чюбы все т насосов, работая одновременно,
наполнили бассейн быстрее, чем за 2 часа и 1 минуту? Можно ли напол-
нить бассейн водой быстрее, чем за 2 часа?
Гнана 2. Цецыс lin(‘liu
101
□	64. (Эконом., веч отд. и отд. менеджмента, 1996) В контейнер упакованы
изделия двух типов. (стоимость и вес одного изделия составляют 300 тыс.
руб и 15 кг для первого типа и 400 тыс. руб. и 18 кг для второго типа Об-
щий вес изделий равен 279 кг. Определить минимальную и максимальную
возможную суммарную стоимость находящихся в контейнере изделии
□	65. (Эконом., 1996) Партия товара упакована в коробки трех типов. Вес и
стоимость содержимого одной коробки составляет 9 кг и 320 тыс. руб. для
первого типа, 6 кг и 150 тыс. руб. для второго типа, 4 кг и 120 тыс. руб. для
ipeibcro типа. Суммарная стоимость товара равна 4180 тыс. руб. Опреде-
лить наибольший и наименьший общий вес партии товара
□	66. (Филфак, 1986) В ящике находится 13 красных шаров и 17 белых ша-
ров. Разрешается проводить в любом порядке и в любом количестве сле-
дующие операции:
а)	увеличить на 2 число красных шаров и одновременно уменьшить на I
число белых шаров;
б)	увеличить на 1 число красных шаров и одновременно увеличить на 2
число белых шаров;
в)	уменьшить на 2 число красных шаров и одновременно увеличить на 1
число белых шаров;
г)	уменьшить на 1 число красных шаров и одновременно уменьшить на 2
число белых шаров.
Можно ли, совершая такие действия, добиться того, чтобы в ящике оказа-
лось 37 красных и 43 белых шаров ? Ответ обоснуйте.
□	67. (ВМиК, 1998, устный экзамен) Доказать, что ч-Зич-5 нс делится на
121 ни при каком целом п.
□	68. (Геолог., 1999, май) Найти такое двузначное число, что сумма квадра-
та числа его единиц и удвоенного квадрата числа его десятков в три раза
больше разности числа 14 и произведения цифр этого числа.
□	69. (МАДИ, 1996) Попарные суммы пяти целых чисел Xj, х2, х3, х4, х5
равны 0,2,4,4,6,8,9,11,13,15 Найти наименьшее и наибольшее из
этих пяти чисел
□	70. (Четвертая Соросовская олимпиада школьников 1997 — 1998, II очный тур,
9 класс.) Найдите все значения параметра а. при которых существует ровно
2 целых значения х, удовлетворяющих неравенству х2 + 5 л/2 х + а < 0
102	Конкурсные задачи
Конкурсные задачи последних лет
г>- ^нгг;(.г лгги-<г-.	-г.
□ 71. (Ф-т наук о материалах, 2000) Сколькими нулями оканчивается число
2000’
□ 72. (ИСАА, 2000) Определить сумм} всех таких натуральных чисел п , для
которых числа 5600 и 3024 делятся без остатка на л и п + 5 соответственно.
□ 73. (Соцфак. 2000) Найти все значения параметра а , при каждом из ко-
торых отношение решений квадратно! о уравнения
? > 1
(<724-|)r* I 4л +--= О
а 4-1
является целым числом. Кратные корни учитываются дважды.
□ 74. (Мех.-мат., 2001) Найти псе нары (т, п) натуральных чисел, меньших
1000, для которых сумма т1 tmn ♦ ')п? делится на 352.
□ 75. (Мех.-мат., 2001) Найти псе числа, кратные числу 72 и имеющие деся-
тичную запись вила 74Л'23У , где .V. } — цифры.
ГЛАВА 3
Рациональные числа
ЖЙМ»МГ>«*К*Н1№К-ГЛ JWyC-
§1. Свойства числовых дробей. Сократимые
и несократимые дроби
1. Определения. Основное свойство дроби.
Замкнутость множества Q
Рациональным числом называется дробь вида — , где т е Z, п е N Число
п
т называется числителем дроби, а число п сс знаменателем.
Замечание. Иногда встречается другое определение: рациональным чис-
лом называется дробь вида —, где meZ, не/, п*0 Равносильность
п
двух определении докажите самостоятельно.
Обозначение множества всех рациональных чисел — Q. Это множество
включает в себя множества натуральных и целых чисел: N cz Z с (2 по’
скольку любое целое число т можно записывается дробью
т
т- —.
1
Для рациональных чисел qx и q2 аксиоматически вводятся правила сложе-
ния 91+^2 и умножения qx q2. Операции вычитания q} - q2 и деления —
(для q2 * 0) определяются как обратные к сложению и умножению. В ре-
зультате получаются следующие правила действии с дробями:
_ т} т2 _ +(т2пх
Ч\ +Я1~ — + — ----------г~^— >
п\	п2	WP’2
Ж]	т2 пгхп2 - т2п}
Я] ~ <12 =-------=------------->
w]	w2	Л1П2
Шу nij	ПЪПЬ
Я\’Я2=~' — =
Л] n 2	пхп2
qx пи nt2	nixn2	,	~
— = —L ’ —— -...... -.	( q^	0,	то есть пъ * 0 ).
q2 n} n2	nxm2
104	Конкурсные задачи
Замечание. Правила арифметических операций устроены именно так, что
для целых q} и q2 они автоматически переходят в операции над целыми
числами.
Из сформулированных правил следует замкнутость множества рациональ-
ных чисел относительно четырех арифметических операций. Это означает,
что если к рациональным числам q} и q2 применить арифметическую опе-
рацию (в случае деления <?2 * °), то результат будет рациональное число
Из последней формулы следует основное свойство дроби: для любого це-
лого числа п * 0 справедливо равенст во
Рп
q qn
„	3	6	12	68	4	14
Например, - = — ,3 = —.	= —, —
5 10	4	221 13 -4
-7 _ 7
Т"^2
7
2
Продемонстрируем, как работает замкнутость множества Q относительно
арифметических операций.
□	Пример 1, (ВМК, 1995, устный экзамен) Доказать, что если числа а + b и
ah рациональны, то число a'+b' также рационально.
Решение. Воспользуемся формулой суммы кубов двух чисел
a3 + b3 = (а+6)(а2 -ab + b2) = (а + b)[(a + b)2 -3ab].
Поскольку’ числа а 4- Ь , ab и 3 рациональны, а множество Q замкнуто
относительно четырех арифметических операций, то и а3 + b3 е Q .
Множество Q не замкнуто относительно операции извлечения корня лю-
бой степени. Это означает, что если k е Q, р е Q, то число tfp вовсе нс
обязательно является рациональным (даже если р неотрицательно). На-
пример, у[2 &Q (см. следующую главу). В этой связи возникают задачи:
при определенных дополнительных условиях доказать, что tfp является
рациональным числом. Рассмотрим пример.
□	Пример 2. (ВМК, 1996, устн. экзамен) Известно, что числа а , Ь и Та - 4b
рациональны (а > 0, 6 > 0, а *Ь). Доказать, что в этом случае рациональны
также числа -Ja и y[b .
Решение. Из условий задачи и замкнутости () относительно четырех
арифметических операций следует рациональность числа у/a +y[b
Глава 3: Рациональные числа
105
г~ ГГ а-Ъ
\а +у/Ь - —т=-=•.
4а - Jb
Значит, рациональными оказываются 4а и 4b :
4а - ~^4а +4ь)+(4а -4ь)]. 4ь = -i\(4а + 4ь)-(4а - 4ь)].
2. Правильные, неправильные и смешанные дроби
Положительная дробь — (/? е ?/, <? е У) называется правильной, если
Я
р <q .и неправильной, если p>q.
Числитель неправильной дроби можно единственным образом переписать
в виде р - И' q + г , где п — натуральное число, аг — целое число, удов-
летворяющее условию 0 < г < q При г ф 0 неправильную дробь можно за-
р	г	г тт г
писать в виде — = и + — -п— Число п— при этом называется смешанной
Я	Я	Я	я
дробью, где п — целая часть, а — — дробная часть.
Я
8	31
Например, — — правильная дробь, —----неправильная дробь. Последнее
31	1
число можно переписать в виде смешанной дроби = ю-
I
3. Сократимость и несократимость дробей. Задачи
Если числа р и q не имеют общих простых делителей, то дробь — назы-
я
вается несократимой. Так, дробь — несократима, а — сократима.
□ Пример 3. Сократить дроби:
, 3325	4199	ч 18087	, 19110055
a)----; б)----; в)-----? г)------.
3350	1292	11377	11466033
Решение сводится к нахождению НОД числителя и знаменателя.
133
а)	дробь сокращается на 25, получили ;
106
Конкурсные задачи
б)	дробь сокращается на 17 19 = 323, получили —;
в)	дробь несократима;
г)	дробь равна (не находя НОД, заметим, что числитель делится на 5,
знаменатель — на 3).
Рассмотрим несколько задач на исследование сократимости дробей.
□ Пример 4. Сократима ли при каких-нибудь натуральных п дробь
? Ответ обосновать.
5»+ 8
Решение. Будем искать общие множители для числителя и знаменателя.
Пусть 3n4-5 = pm, 5и + 8 = р<7, где р,т nq — натуральные числа, а /?>о
— общий множитель. Умножим первое из соотношений на 5, второе — на
3 и вычтем одно из другого. В результате получим
1 = 5рт - 3pq = р (5т - 3<?).
Итак, мы разложили единицу на произведение двух натуральных чисел,
что возможно в единственном случае р = 1, 5т - 3q = 1. Следовательно,
дробь несократима ни при каких п .
2и^ — 1
□ Пример 5. Доказать, что дробь------- несократима при целых п .
п 4-1
Решение. Пусть п +1 = kl, где к * 1 Докажем, что тогда 2и2 -1 не делится
на к . Для этого преобразуем число 2п2 -1
2п2-1 = 2и2-2 + 1 = 2(и-!)(«+1) + 1 = 2(п-1)А/ + 1 =/с [2(й-1)/| + 1
— не делится на к . Утверждение доказано.
□ Пример 6. При каких натуральных значениях н дробь -———• явля-
7и + 3
стся правильной и несократимой? Укажите все такие дроби.
Решение. Дробь является правильной, если ~~ п*— < 1,
7н + 3
1)
2)
п2-8и+12<0 => (и-6)(л-2)<0 > 2<»<6 => 3<«<5.
При п = 3 дробь сокращается на 3.
77
При п = 4 дробь несократима и равна —.
Гпава 3: Рациональные числа	107
35
3)	При п = 5 дробь также несократима и равна —.
( Т7\	( 3SA
Ответ: п - 4 — , п = 5 — .
>	<•	'V»tSruyratXrt».eeei5BXOl.LA X.'
л3 —8
□	Пример 7. Найти все целые п, когда дробь-------------целое число.
«4-2
Решение. Преобразуем дробь к виду -—- = п2 - 2п 4- 4 - ——. Дтя того
«4-2	«4-2
чтобы дробь была целым числом, необходимо и достаточно, чтобы «4-2
являлось делителем 16, то есть «4-2 = ±1, ±2, ±4, ±8, ±16.
Ответ: {-18,-10,-6,-4,-3,-1,0,2,6,14}
а2 4- 3
□	Пример 8. Доказать, что дробь —-------- несократима при а е Z .
а4 4- 7а2 4-11
Решение. Перепишем данную дробь в виде —------------а—-t.2----- Пусть
(а2 4-3)2 4-(а2 4-3) - 1
числитель данной дроби делится на целое число к * 0, ± 1. Но знаменатель
дроби на к делиться не может, так как два слагаемых делятся на к, а
третье — нет. Следовательно, дробь несократима.
□	Пример 9. (ВМК, 1972, устный экзамен). Найти все целые I , при которых
дробь ——- сократима. При этом сокргпима на какое число?
Решение. Пусть к * ±1 — общий делитель числителя и знаменателя. Тогда
(5/ 4-6 = кт, (40/4-48 = 8/™,
[8/4-7 = Аи [40/4-35 = 5/™
Вычтем из первого равенства второе и получим 13 = £(8m-5«)	13-Аг =>
дробь может быть сократима только на ±13. Чтобы выяснить, при каких /
это возможно, решим уравнение в целых числах:
5/4-6 = 13m, l,m е Z
Напоминаем, что это уравнение можно решить двумя способами:
1) рассмотреть всевозможные остатки от деления на 13;
2) воспользоваться процедурой уменьшения коэффициентов (см. главу 2).
Решив уравнение (сделайте это самостоятельно), получим I = 13s4-4, s&Z
Ответ: при / = 13s+ 4, где s eZ , дробь сократима на ±13 .
J08	Конкурсные задачи
И, наконец, рассмотрим задачу "олимпиадного” типа.
□ Пример 10. (Пятая Соросовская олимпиада школьников 1998-1999, II (очный)
тур, 10 класс.) Сократите дробь
123456788...87654321
1234567899...987654321 ’
если цифра 8 в числителе встречается 2000 раз, а цифра 9 в знаменателе - -
1999 раз. (В результате надо получить несократимую дробь.)
Решение 1. Пусть N = 11...1, п = 1234567 . Тогда числитель (zl) дроби равен
2007
.4 =п- 102()()7 +8W -п = и(1О2007 - 1)ч-8Л' /\'(9« + 8). Заметим, что
9/2 4- 8 = (10 - 1)« 4- 8 = (12345670 - 1234 S67) t 8 - 11111111. Обозначим послед-
нее число через к Знаменатель дроби (В) равен
В = (107/4-8)102007 И)Л/ (10/2 I 8) (10// I 8)(1О2007 - 1)4-9W = Л'(90//-81) =
А А
= iV(10A 4-1). Значит, дробь можно сократить на N и — =	— • Пусть d
— общий делитель к и 10А 4-1, тогда d — делитель 1, поэтому последняя
дробь несократима.
Ответ, дробь можно сократить на Д' =	,
"2067"
в результате получим несократимую дробь	•
Решение 2. Рассмотрим число а = 11...1, где количество единиц равно
2007. Сложим в столбик 8 чисел: а , а • 10, а • 100,..., а - Ю7. Гак как каждое
из этих чисел получается из предыдущего сдвигом влево на 1 разряд и до-
писыванием в конце нуля, то при суммировании в каждом столбце, кроме
семи крайних слева и семи крайних справа, получим 8 и в целом — числи-
тель т данной в задаче дроби. Если же сложить в столбик 9 чисел а .
а -10 , а -100,..., п- Ю8, то получим знаменатель п данной в задаче дроби
Таким образом имеем т = ар, n = aq , где р = 1JLJ, q =	. Отсюда
Н	9
т р
— = — , причем р и q — взаимно просты, так как q - К)// ь 1 и, следова-
ть Я
тсльно, если бы р и q имели общий делитель /• > 1, то 1 = q - 10/> делилось
бы на г.
()твет: —, где р = 11...1, q ~ 11...1.
8	9
Глава 3: Рациональные числа
109
§2. Представление рациональных чисел
десятичными дробями
1. Определения различных десятичных дробей
Если знаменатель q обыкновенной дроби -- равен ненулевой степени
7
числа 10, то — можно записать в виде конечной десятичной дроби
Я
и	^4	2714	6
Например, обыкновенные дроби —, -------,------можно записать в виде
10	100	100
конечных десятичных дробей: 0.4, 27.14, -0.06 Такие дроби называют
конечными потому, что у них после запятой конечное число цифр.
Бесконечной периодической десятичной дробью называется десятичная
дробь, у которой после запятой стоит бесконечно много цифр, причем одна
цифра или упорядоченная группа цифр, начиная с некоторого разряда по-
сле запятой, повторяется. Эта повторяющаяся цифра или группа цифр на-
зывается периодом. Например,
1)	17,145454545 = 17,1(45), период равен 45 .
2)	1,343343343...=1,(343), период равен 343.
Справедлива следующая теорема, которую приведем без доказательства.
Теорема. Всякое рациональное число представимо в виде либо конечной,
либо бесконечной десятичной периодической дроби, и, наоборот, всякая
конечная или бесконечная десятичная периодическая дробь может быть
представлена в виде рационального числа.
Например,
7	354
1)	_ = 0.777... - 0.(7),	2) ------= 0.354000... = 0.354 (0) = 0.354 .
9	1000
3)	— = 0.11222... = 0 11(2),	4) — = 1.455. .. = 1.4(5).
900	90
по
Конкурсные задачи
2. Перевод обыкновенных дробей в десятичные
и наоборот
Обыкновенную дробь можно перевести в десятичную периодическую при
помощи обычного деления “столбиком”, например,
1)	1 = 0.(3), так как при делении 1 на 3 “в столбик” получим
0.333 . = 0 (3);
2)	1 = 0,(142857);
47
3)	— = 1,5(6).
30
Первый способ перевода бесконечной периодической десятичной дроби в
обыкновенную основан на вычислении суммы бесконечно убывающей
геометрической прогрессии:
✓	.	ар+\ар 1	ар >гк
"ар^ар+\ар+2 -“р+к) = а^а]а2 ар +....~^Тк---------
, ар + 1ар + 2 ар+к	, арл\ар+2”‘ар\к
+ _1L. = а(ъа}а?. .ап +	f—
ю'”гк	' lo^ci-io’*)

□ Пример 1. Перевести 0.11(7) в обыкновенную дробь.
Решение. Воспользуемся формулой суммы членов бесконечно убывающей
геометрической прогрессии
011(7) = 011 + —1—+ —1—+ —-—+...-
1000 10000 100000
= 0.11+1^1^1 = 0.1]+— = 11+^- = ^12 !1 = 21.
1-1/10	900	100 900	900	900 450
Второй способ (без использования формулы суммы прогрессии).
Обратимся к предыдущему примеру.
Обозначим х - 0,11(7) = 0,11777 ... Тогда ЮОл = 11,(7) = 11,777 . . Вычтем из
100л: число х. ЮОх -х = 99х = 11,777...-0,11777. = 11,66000.. = 11,66 , поэтому
_ 11.66 _ 1.06 _ 106 _ 53
99 “ 9 ” 900 " 450 *
Глава 3: Рациональные числа	111
4н*/«НмЛ'4»* .ММ»ШР.Ч<»+^ ^aA.'VA. X/* WL X.**	f —4-x
□	Пример 2. Представить x - 2,2(75) в виде обыкновенной дроби.
Решение. Воспользуемся вторым способом. 1 000* = 2275,(75). Вычтем
2253	273
Юл = 22,(75) и получим 990х = 2253, откуда следует х -	= 2-^ •
Ответ: 2—
990
v	« м* WJWWV.I' >»»»ИНММР' ЛЛфуММл WfpwiWWj*	< Г|<» » »<	>»*» 1 -- .Г«*т*гг^ « •*г—'•< Э*гж вЭ**»г» »'»'• V f****»^ • 4>м><
□	Пример 3. (Геолог. 1994) Какое из чисел больше: 2ТГ7 или 8,(24) ?
Решение. 1) Представим 8,(24) в виде обыкновенной дроби, для чего обо-
значим 8,(24) = х . Тогда ЮОх - х = 99х = 824,(24) - 8,(24) = 816 , откуда сле-
816 272
дует х =--=-----.
99	33
2	) Итак, надо сравнить числа 'ijrj и , или, в удобной для задач на
сравнение чисел форме записи, 2V17v-^-. Далее для краткости будем
использовать обозначения avboc vd. Это означает, что числа а и Ь
связывает один и тот же знак отношения (меньше, равно или больше), что
и числа с и d. Проведем цепочку сравнений:
2Vn V—« V17 V—= i^<=>17vl71^i<;;.332 =1089 >1088=17-64 .
33	33	33	ЗЗ2
Значит, и во всей цепочке сравнений число слева больше
Ответ: 2^17 >8,(24).
§	3. Разные задачи с рациональными
числами
В этом параграфе мы рассмотрим несколько задач, связанных со свойства-
ми рациональных чисел. В наибольшей степени эти задачи характерны для
устного экзамена, хотя есть и исключения.
112
Конкурсные задачи
1.	Пример с дробями
□ Пример 1. Определить наибольшее отношение трехзначного числа к
сумме его цифр.
Решение. I lyc i ь т, п и к — соответственно число сотен, десятков и еди-
ниц, тлцк с {0.L2. О} он + о Рассмотрим отношение
100m + Юн ч к _ !()()(/// г п т£) -90л-99£ _ Ю() _ 90н+99£ < 1()()
т + п + к	т + н \ к	tn + п+к
Нетрудно видеть, что оценка достигается (неравенство обращается в ра-
венство), если п = к = 0 .
Ответ: максимальное отношение равно 100 .
2.	Преобразование произведений и сумм
Идея решения следующей задачи основана на весьма часто используемом в
математике приеме, когда сомножители в произведении преобразуются
так, что почти все из них сокращаются (аналогично поступают и с сумма-
ми большого числа слагаемых: их стараются преобразовать таким же обра-
зом, чтобы почти все слагаемые взаимно уничтожились).
□ Пример 2. (Эконом., 1965) Найти произведение
Решение. Обозначим произведение через П.
п _ 22 - I З2 -1 42 -1	992 - I I (Ю? -1 _
22 З2 42	992	I002
1-3 2-4 3-5 4-6	97-99 98 100 99-101 _ 101	101
22 З2 42 52	982	992	I002	2-100 200
/->	101
Ответ: -----.
200
Итак, если мы имеем дело с большим числом сомножителей (слагаемых),
то всегда ли надо попытаться «свернуть» произведение (сумм})? Не всегда.
В следующем примере попытка «сворачивания» уводит от решения.
Глава 3: Рациональные числа	113
>.!>	KvWlta	J .-t. '»>*'	5 1 ...... Ч'	IT . .г г	, V.J< . ..
□ Пример 3. Может ли сумма
111	1
- + - + — + ...+ —
2 3 4	п
при каком-то п оказаться равной целому числу7
Решение. Возьмем слагаемое с наибольшей степенью двойки, входящую в
знаменатель. Эта наибольшая степень будет только в одной дроби
2к
При приведении этих дробей к общему знаменателю числители всех дро-
бей будут четными, кроме числителя, где знаменателем является 2к. Зна-
чит, числитель суммы нечетен, тогда как знаменатель четен.
Ответ: не может.
э , 1 1 1 1 „
Замечание. Подумайте, почему выражение ^i=l+~ + - + —+ +~ свер-
о 1	I 1	1
нуть не удается, а выражение 5, = —+— +-------+ ...+------- прекрасно
1-2 2-3 3-4	«•(« + !)
сворачивается? Вычисли re 52 самостоятельно
3.	Примеры уравнений в рациональных числах
При решении уравнений в рациональных числах очень часто бывает
плодотворной идея подстановки рациональной зависимости между не-
известными. Разумеется, зависимость следует подбирать так, чтобы она
упрощала исходное уравнение
□ Пример 4. Найти все рациональные числа х,у, удовлетворяющие урав-
нению х2 + у2 = 1 .
Решение. Пара чисел является решением нашего уравнения. Заме-
тим (см. рис. 10), что у любой прямой, проходящей через точку (0;1) и точ-
ку (л.у) с рациональными координатами такими, что х2 + у2 = 1, угловой
коэффициент наклона будет рациональным числом. Поэтому всякое реше-
ние исходного уравнения представим в виде у = Лг +1, где Л
114
Конкурсные задачи
Дальнейшие вычисления несложны
(Лх+1)2+?=1 => (Я2 + 1 )*2 + 2Лх = 0,
(решение х = 0, у = 1 нами уже учтено)
(Л2 4- 1)х 4- 2Л = 0 => х = —, _у=14-Ях = --— , где Я .
Л2 4-1	14-Я2
Чтобы получить окончательный ответ, представим Я в виде несократимой
дроби Я = — :
п
2тп
т2 4- Г
Ответ:
2тп
тп +п
где т„п eZ, т2 + п2 * 0 .
1лл 7£iz«xttwutr««-rcai3<srrjs3z3sxDXBax№Kxrxr/mrmJKKnra^aTxrvKBuсг»1асти>впви»*хвЯ1ХИ1»*’С«*Л1тии«ии,»’лт'7<’:>43-'..ггд»-к»хгг	.'i
□ Пример 5. (Психфак, 1976) Решить уравнение xlog,oX = з^10810*2-1. Дока-
зать, что все его корни являются рациональными числами.
Решение. Сведем уравнение к квадратному, для чего прологарифмируем
его по основанию 10.
(1g*)2 =lg5 + (21g^-l)lg2, (Igjr)2 -2lg2• Igj + Igy = 0,
115
Глава 3: Рациональные числа
Igx = lg2±^(lg2)2 -lg| = Ig2 + V(lg2)2-21g2 + lg2+lg5 =
= lg2 ±V(lg2)2 -21g2 + l = Ig2 ± (Ig2 - 1).
Откуда следует
1) (lg х)] = 1 ИЛИ Xj = 10 ,
2) (lgx)2 =2lg2-l = lg^ = lg| или Х2 = |.
2
Но числа 10 и — —рациональные.
2
Ответ: jq = 10; х2 = —• Эти числа рациональные.
4.	Приближения рациональными числами
В заключение главы приведем два непростых примера, предлагавшихся на
устных экзаменах факультета ВМК в 1992 году.
□ Пример 6. Указать какое-нибудь рациональное число а такое, что
I sin 81° - а |< 0,01.
Решение. Имеем цепочку равенств и неравенств
sin8 Г = cos9° = 71-sin2 9° = J1 - sin2 — >
V 20
>> Vl-(0,16)2 = Vo,9744 >0,98,
так как sin — < — < 0,16 (использовано известное неравенство sinx < х при
20 20	r	г
о < х < -к» и неравенство — я < 3.2).
Итак, 0.98<sin81°< 1, и, следовательно, годится « = 099, потому что из
последних неравенств вытекает
0,98 - 0,99 = -0,01< sin 81°-0,99 <0,01= 1-0,99, | sin 81°-а| < 0,01.
Ответ: например, а = 0,99.
Замечание. Если вычислить sin 8 Г с четырьмя значащими цифрами, то
будем иметь sin 81° = 0,9877....
116	Конкурсные задачи
□ Пример 7. Указать какое-нибудь рациональное число а такое, что
<о,1
Решение. Заметим, что
т = .. 12	= 10(718 + 717); 4,24 < 718 < 4,25, 4,12 <717 <4,13
Tii-Tn
Значит,
83,6 = 10(4,24 + 4,12) < ш • 10(4,25 + 4,13) = 83,8
и, следовательно, годится а = 83.7, поскольку из последних неравенств
-0,1 < т - 83,7 < 0,1, \т - 83,7|< 0,1
Ответ: например, и - 83 7
Замечание, т = 83,657... с тремя значащими цифрами после запятой.
Задачи для самостоятельной работы
□	1. Представьте число — в виде десятичной периодической дроби.
□	2. Представьте число 0 87(15) в виде правильной дроби.
□	3. Докажите, что сумма двух периодических десятичных дробей суть
конечная десятичная либо бесконечная периодическая дробь.
□	4. Известно, что числа а,Ь и 4а + 4ь являются рациональными. Дока-
зать, что в этом случае являются рациональными числа 4а и 4b .
□	5. Сократима ли при каких-нибудь натуральных п дробь +-- ? Ответ
4п +3
обосновать.
□	6. Доказать, что дробь вида х = может быть сократима только на
4п + 2
2	(здесь п — натуральное число).
□	7. Доказать, что дробь п * несократима при натуральных п
п“ +1
Глава 3: Рациональные числа
117
□	8. При каких целых п сократима дробь х =	*1 ?
и2 4-л 4-3
□	9. При каких натуральных п дробь 1 несократима?
п2 -1
□	10. При каких п е Z дробь " будет целым числом?
п - 1
□	И. Доказать, что если две положительные несократимые дроби в сумме
равны 1 , то их знаменатели равны.
<хУ°е,зХ 13
□	12. (Психфак, 1976) Доказать, что корни уравнения	= у- явля-
ются рациональными.
□	13. При каких целочисленных значениях параметра т корни уравнения
х2 ч- тх ч-1 = 0 являются рациональными числами?
□	14. При каких целочисленных значениях параметра т корни уравнения
х2 4-л 4-ш = 0 являются рациональными числами?
□	15. (Геолог., 1994) Какое из чисел больше: 2^14 или 7,(48) ?
□	16. При каких цифрах A/./V значение дроби Лг =	наибольшее?
□	17. Докажите, что между любыми двумя рациональными числами rj <г2
существует бесконечно много рациональных чисел.
□	18. Пусть числа а и Ь, представленные десятичными дробями
а = а^,а}а2а3 .. и Ь = Ь^ЬХЬ2ЬУ. ' являются рациональными. Докажите, что
число х, десятичная дробь которого построена по правилу
хп = max{art,6n} = если hfl' будет также рациональным,
если л
И Л 5	*"
□	19. Доказать, что если tga, tg/? — рациональные числа, т.п — нату-
ральные числа и tg(wa), tg(пр), ty(ma+np) существуют, то tg(wa4-/?/?)
рациональное число.
□	20. При каких целых а корни уравнения ах2 4- (2а - 1)х 4- (а - 2) = О ра-
циональны?
118	Конкурсные задачи
□	21. Решить уравнение х2 + 2у2 - 1 в рациональных числах.
□	22. Решить уравнение х2 + 3 = 2х+у2 в рациональных числах.
□	23. Уравнения х2 +рх + q = 0 и х2 + тх +п = 0 с целыми коэффициента-
ми p,q,m,n имеют общий нецелый корень. Доказать, что р-п, q-m .
□	24. Указать такое рациональное число а , что |cos9°-a|< 0,01.
□	25. Указать такое рациональное число а , что
<0,1 .
Конкурсные задачи других ВУЗов
□	26. (МИФИ, 1976) Рассматривается дробь, знаменатель которой меньше
квадрата числителя на единицу. Если к числителю и знаменателю приба-
вить по 2 , то значение дроби будет больше, чем j, если же из числителя и
знаменателя вычесть по 3, то дробь останется положительной, но будет
меньше . Найдите дробь.
□	27. (МАИ, 1977) Знаменатель несократимой дроби на 2 больше числителя.
Если у дроби, обратной к данной, уменьшить числитель на 3 и вычесть из
полученной дроби данную дробь, то получится ~. Найдите дробь.
□	28. (МАДИ) В дроби 0,(25) вычеркнули первую справа от нуля цифру.
Найти отношение вновь полученного числа к исходному.
/8-1-3 F1 ч- / 8 — 3 /У
□	29. (МИСИС) Выяснить, является число х=' ->™ *—.......v рацио-
^3+^5-V3-V5
нальным или нет.
Задачи математических олимпиад
- ~	- у-1_Г‘	..‘-Г Tr.--L-rJlinnrrJ-* “	• “ V • - ‘Г-ТТ <М	I Л X «?>•’-* f
□	30. (Четвертая Соросовская олимпиада школьников 1997-1998, II (очный) тур, 11
класс) Найдите все целые п , для которых log2^i(«2 +2) является рацио-
нальным числом.
Глава 3: Рациональные числа	119
□ 31. (Пятая Соросовская олимпиада школьников 1998-1999, I (заочный) тур, 8
класс) Даны две правильные обыкновенные дроби. У первой — числитель
на 5 меньше знаменателя, у второй — числитель на 1998 меньше знамена-
теля. Может ли у их суммы числитель быть больше знаменателя?
□ 32. (Пятая Соросовская олимпиада школьников 1998-1999, III (финальный) тур,
9 класс) В качестве доказательства того, что правильный ответ еще не озна-
чает правильность решения, учитель привел следующий пример. Возьмем
19
дробь —. После зачеркивания 9 в числителе и знаменателе (“сокращения”
1	1999
на 9) получаем верный ответ — дробь - ! Точно так же дробь можно
“сократить” на три девятки. (Зачеркнуть в числителе и знаменателе 999.) А
возможно ли, чтобы в результате подобного “сокращения” также получил-
ся бы правильный ответ, равный - ? (Рассматриваются дроби вида —.
3	аЗ
Здесь буквой а мы обозначили несколько цифр, следующих в одинаковом
порядке в числителе после 1, а в знаменателе перед 3. “Сокращаем” на а )
ГЛАВА 4
Иррациональные числа
•>» ' *♦	^«и^гмъ«^г'Г1Л>пст*л»»'Мт	< Hw.-vtttMa .-»?►. г» »•.'ti:^'*jw •
§1. Некоторые теоретические положения
1. Определения и основные утверждения
Иррациональным числом называется число, представимое в виде беско-
нечной непериодической десятичной дроби. Из сформулированной в пре-
дыдущей главе теоремы следует, что такое число не может быть представ-
ши
лево в виде — , где тип — целые, и * 0.
п
Множество рациональных и иррациональных чисел образуют множество
действительных (вещественных) чисел, которое принято обозначать
буквой R . Как следует из вышесказанного, множество вещественных чи-
сел состоит из всевозможных десятичных дробей, как конечных, так и бес-
конечных, периодических и непериодических. Множества натуральных,
целых, рациональных и действительных чисел связаны между собой сле-
дующими включениями: N с Z с Q с R
2. Арифметические операции и операции
извлечения корня. Результаты операций
Множество R замкнуто по отношению ко всем чшырсм арифметическим
действиям, а также по отношению к операции извлечения корней нечетной
степени. Операция извлечения корней четной счспсни определена только
для неотрицательных вещественных чисел. Доказательство этих фактов
выходит за рамки школьной программы.
Замечание. В программу устного экзамена по математике для поступаю-
щих в МГУ включен вопрос «Свойства степеней с натуральными и целыми
показателями. Свойства арифметических корней п-и степени. Свойства
степеней с рациональными показателями» Отмстим, что на устных экза-
менах не требуют строгого доказательства факта существования корней.
Обсудим теперь результаты операций. Начнем с примера, впервые рас-
смотренного Пифагором в 4 веке до н э.
Глава 4: Иррациональные числа	121
ЯЫ^ДМЛЛ1|Ьй*1Т»»«.»»пм»*ЬИ11ИИИ|1ашММ4М»»—ч.чйЬдчмйПП»»» 1ЧЖТИГЖ1МГ »|АЫ^Ьмм^дстл»»м»»1«»л1»1«л«»ж»»ххг»лж.ж«ст.х^.апгтт-хюигхх»гстгч^,»л«цЬ»<»«иг.ж1
□ Пример 1. Доказать, что V2 — число иррациональное.
Доказательство проведем от противного. Предположим, что ^2 — pa-
ционально. Тогда V2 = —•, где — — несократимая дробь (любую дробь
п	п
можно привести к несократимому виду, поэтому такое предположение до-
пустимо). Тогда т2 = 2п2. Поскольку правая часть делится на 2, то и левая
часть должна делиться на 2, т.е. т2 д&а&тся на 2. Но тогда и т делится на 2
(в самом деле, если т нечетно, то и т2 также нечетно). Следовательно,
существует некоторое к eZ : т = 2к . Подставим это значение в равенство
т2 = 2п2 => 4к2 = 2п2. Из последнего равенства вытекает, что п2 делится на
2, и, в свою очередь, п также делится на 2. Получили, что дробь — сокра-
п
тимая. Противоречие доказывает утверждение об иррациональности V2 .
Замечание 1, Подробнее о методах доказательства иррациональности тех
или иных чисел будет рассказано в §2.
Замечание 2. Аналогично можно доказать иррациональность чисел
V5, V2, у/з и т.д.. Однако проще и удобнее воспользоваться более об-
щей теоремой, которую мы сейчас сформулируем и докажем.
Теорема 1. Пусть т е N , 2 £ £ е W . Тогда число является либо нату-
ральным, либо иррациональным.
Доказательство. Пусть Цт не является ни натуральным, ни иррациональ-
ным. Но тогда это число — дробное и ^m=plq. Отсюда следует
m=(plq)k . Но последнее равенство невозможно, так как слева — целое
число, а справа — дробное.
□	Пример 2. Доказать, что числа V21, V2, V? иррациональны.
Указание. Для доказательства этих фактов либо воспользуйтесь теоремой
1, либо повторите метод Пифагора “от противного”.
Обсудим теперь результаты арифметических операций с иррациональ-
ными числами. .
Теорема 2. Если произвести любую из четырех арифметических операций
над иррациональным и рациональным числами (для случая операций умно-
122	Конкурсные задачи
жения и деления необходимо потребовать, чтобы рациональное число не
было равным нулю), то в результате получится иррациональное число.
Доказательство. Рассмотрим случай операции сложения. Пусть z — ир-
рациональное число, ц — рациональное число и х = z+q . Если предполо-
жить, что х — рациональное число, то это противоречит равенству
z = х - q, поскольку множество рациональных чисел замкнуто относитель-
но операции вычитания. Остальные случаи рассматриваются аналогично.
Результатом арифметической операции над двумя иррациональными чис-
лами может быть как рациональное, так и иррациональное число. Рассмот-
рим несколько примеров.
□	Пример 3. Указать пару иррациональных чисел таких, что
а)	их сумма — иррациональна (Ответ: например, у/з и V$ );
б)	их сумма — рациональна (Ответ: например, 1 - VI и 4^ У
в)	их произведение — иррационально (Ответ: например, 4з и у[5 У,
г)	их произведение — рационально (Ответ: например, \-4з и \+4зу,
д) их разность — иррациональна (Ответ: например, у/5 и 4з );
е)	их разность — рациональна (Ответ: например, VI+ 1 и у/1 у
ж)	их отношение — иррационально (Ответ: например, 4з и VI );
з)	их отношение — рационально (Ответ: например, - sVI и 4з).
у/3
Заметим, что корень любой степени из иррационального числа а есть все-
гда число иррациональное.
В самом деле, достаточно предположить, что tfa - —	, как мы тут же
Я
( \п	( \п
получим противоречие: — eQ,a*Q, но — =а .
уя)	\я)
Более интересен вопрос: может ли быть рациональным числом , где а и
Р — иррациональны? Ответ положительный. Приведем два примера
1. а/у =(VI)log236 =6 (иррациональность VI уже доказана, а иррацио-
нальность числа log2 36 будет доказана ниже, в §2).
Глава 4: Иррациональные числа	123
(	^2
2. а? = 72 Доказательство забавно. Мы не можем доказать при
/-V2	.
помощи “школьных методов”, рационально число 72 или нет. Но, если
V2 рационально, то пример уже построен. Если же нет (иррационально),
то, поскольку 72 — иррационально, то = (72	= 721 2 = 2.
§2. Доказательство иррациональности
некоторых чисел
В данном параграфе мы рассмотрим исключительно конкурсные задачи
“школьного типа”. В таких задачах доказательство иррациональности ка-
кого-либо числа может быть проведено двумя методами:
1) показать, что данное число представимо в виде бесконечной десятич-
ной непериодической дроби;
2) от противного.
В качестве иллюстрации первого способа рассмотрим число
х - 0.1 ()() 1000100001..., в десятичной дроби которого группа нулей каждый
раз увеличивается на единичку. Очевидно, что такая десятичная дробь яв-
ляется непериодической, и, следовательно, число х — иррациональное.
Что же касается метода ”от противного”, то им решается основная масса
конкурсных задач.
Замечание. Об иных, нс входящих в школьную программу, методах дока-
зательства иррациональности чисел можно прочитать в [21].
1.	Примеры из радикалов
Рассмотрим несколько задач на доказательство иррациональности выраже-
ний с радикалами.
□	Пример 1. Доказать иррациональность числа 7з +77 .
1 Данное число является иррациональным Эта задача была решена А. О. Гельфон-
дом в начале 50-х годов.
124
Конкурсные задачи
„	т-г	Д Д т
Доказательство. Предположим противное, то есть что уЗ + v7 = — е Q .
/ \Х	_ I Z X Z.
Тогда (л/з +V7)* 2 = IO + 2V2T = I — I и поэтому Jli = — — -10
\nJ	2 \пJ
Но число V21 — иррациональное. Противоречие.
□	Пример 2. Доказать иррациональность числа V2 + Vz .
Доказательство. Предположим противное, т.е.
2.	Задачи, решаемые при помощи соображений
делимости. Пр имер из логарифмов
Порой, пользуясь доказательством иррациональности “от противного”,
привлекают соображения делимости (нацело либо с остатком).
□ Пример 3. Доказать, что log23 —иррациональное число.
Решение. Предположим противное, т.е. log23 = т/п . Поскольку log23 > 0,
то т и п — натуральные числа. Тогда по определению логарифма
2т1п =3 или 2W = 3”. Последнее равенство невозможно, так как в его ле-
вой части стоит четное число, а в правой части — нечетное.
□ Пример 4. Доказать, что log2 36 —число иррациональное.
Доказательство. log2 36 = log2 (22 • З2) = 2 + 2log2 3 — и задача свелась к пре-
дыдущей.
Глава 4: Иррациональные числа	125
я*'.илм>£'лъ.и7*(-. vs.
□ Пример 5. Доказать, что число 73и+2 при любом натуральном п есть
число иррациональное.
Доказательство. Обозначим 73и4-2 = р .
1)	Пусть р eN . Проведем анализ остатков от деления р на 3 :
а)	р = 3к =>р2 =9к2 *Зп + 2=> этот случай невозможен;
б)	р = Зк + 1 р2 = 9 к2 + 6к + 1 Зп + 2 => этот случай невозможен;
в)	р = Зк + 2^>р2 = 9к2 4- Ш +4 = 9к2 4- Ш 4-4-34- 1 * Зп +2 => и этот
случай невозможен;
2)	Пусть р - — е Q и число — — несократимая дробь. Тогда
п	п
Л
р1 =3/24-2 = —- .
п2
Но это равенство невозможно: слева — целое число, а справа — не целое.
3.	Доказательство иррациональности значений
тригонометрических функций
Доказательство иррациональности некоторых значений тригонометриче-
ских функций происходит методом “от противного’9 при помощи формул
тригонометрии.
Пример использования формулы тангенса суммы двух аргументов.
□ Пример 5. Доказать, что tg5° является иррациональным числом.
Доказательство. Воспользуемся тем фактом, что если tg а е £ , tg р e Q
tga 4- teB
и tg(a 4- р) существует, то тогда tg(a 4- Р) = —--также рационально.
1 - tga • tg/3
Предположим противное. Тогда tglO°=——— также является рацио-
l-(tg5°)2
нальным числом, поскольку арифметические операции с рациональными
числами не выводят за пределы множества Q. Рассуждая аналогично, при-
дем к выводу, что tgl5°= tg(10°+5°) = tg(Q]'()o^5o — рациональное число.
Повторяя операцию прибавления 5° несколько раз ( и не выходя при этом
/з
за пределы множества рациональных чисел), получим, что tg3O°=-~ так-
126	Конкурсные задачи
же является рациональным числом, то есть число — рационально. По-
лученное противоречие завершает доказательство.
Рассмотрим более сложную задачу, в которой используются формулы ко-
синуса двойного и тройного угла.
□ Пример 7. Доказать, что cos2° — иррациональное число.
Доказательство. Заметим, что если cos.y е О, то тогда
cos2x = 2cos2 х- 1 € Q, cos3x = 4 cos3 x - 3cosx g Q,.
Пусть cos 2° c Q => cos 6° g Q => cos 18° e Q => cos 36° e Q cos 72° e Q .
Ho cos 72° = sin 18° = —1 g Q. Противоречие.
Замечание 1. Напомним, как вычисляется sin 18°, например,
cos54°= sin36°=>
=> 4 cos318°-3 cos 18° = 2 sin 18° cos 18° => 4 cos218°-3 - 2 sin 18° =>
=>4(1 - sin2 18°) -3 = 2sinl8°=> 4sin2 18°+2sin 18°-1 = 0, но sinl8°> 0, поэтому,
решая квадратное уравнение относительно sin 18°, мы должны выбрать
75-1
положительный корень => sin 18° =	.
Замечание 2. Из иррациональности cos2° следует иррациональность чисел
sin Г, cos 1° Докажите это самостоятельно.
§3. Разные задачи с иррациональностью
Встречаются задачи, где не сразу видно, что для их решения требуется
привлекать соображения об иррациональности какого-либо числа.
1. Доказательство непериодичности функций
Прежде всего, дадим определение периодической функции.
Функция /(х) называется периодической, если существует число Т > 0
такое, что:
1) для любого х из области определения функции D(f) числа х + Т,
х-Т также принадлежат D(f);
/ 'пава 4: Иррациональные числа	127
2) для любого .г из /)(/) верно равенство /(*) = f(x + T) = f(x-T).
Всякое число 7’ * о, удовлетворяющее данным условиям, называется пери-
одом функции / (л) Наименьшее из этих чисел называется главным пери-
одом. Из школьного курса математики известно, что функции y = sinx,
v = cosx — периодические, и что их главный период равен 2 я.
□ Пример 1. Доказать, что функция f(x) = cosx • cos^/Lc непериодическая.
Решение. Предположим, что это не так и что существует число Т > о, для
которого для всех леГ(/) выполнено равенство/(х) = /(х + Г). Возьмем
х = 0 и получим, что /(0) = /('/’) = 1. Поскольку 1 cos z | не превосходит 1,
то отсюда следует, что cosТ = cosV27 = ±1 или Т = кт, ^2Т = пн. где ан, п
— либо одновременно четные, либо одновременно нечетные целые числа
А раз так, то отношение ш/и = Т2 является рациональным числом, что
неверно. Полученное противоречие завершает доказательство.
2. Нестандартное тригонометрическое уравнение
Всем известно, что число п — иррациональное (доказательство эго го фак-
та от абитуриентов и школьников не требуется). Рассмотрим задачу, идея
решения которой основана на иррациональности числа л .
□ Пример 2. (Геогр. ф-т, 1996, предварит, экз.) Решить уравнение
| + 1 | । - 1 |
cos -------х • cos -------х I = 1 .
V 6	)	6	)
Решение. Поскольку |cos а|< 1, то возможны лишь случаи, когда либо оба
сомножителя равны 1, либо -1.
1) Пусть
12 лай _
—— ,m e Z,
Зу/тт 4-1	12яш _ 12ЯП
‘З?1- .»eZ W7 + 1 ъ[я-\
3V л - 1
Если m = п = 0 , то х = 0.
Пусть х * 0, тогда m * 0, п о и
128
Конкурсные задачи
т 3>/л +1 г~ т + п
— = —=-------
п зА-1 3(т-п)
2
т + п
3(т-п)
но последнее равенство невозможно, так как л — иррациональное число,
а число справа — рациональное.
2) Случай, когда оба сомножителя равны -1 рассматривается аналогич-
но.
Ответ: х = 0.
3. Нестандартные задачи с квадратным
уравнением
□ Пример 3.(Фил. фак., 1971) Докажите, что если р и q — целые числа,
причем р2-4q2 = 4pq, ТО р = q = 0 .
Решение. Если q = 0 , то р = 0 .
Пусть 7^0. Поделим уравнение на q2 и, обозначив x = p/q, получим
х2 - 4х - 4 = 0 Корни полученного квадратного уравнения х}2 = 2 ± 2^2 —
иррациональные числа (докажите самостоятельно), и, следовательно, ра-
венство Х| 2 = р! q невозможно. Доказательство завершено.
* 'V*fW¥	«OW/HWWlrr	**»• re*»/ »W* r^r1	*Trt / -< Л
□ Пример 4. Один из корней уравнения х2 + рх + q = 0 равен 1 + 4з .Найти
р и q , если известно, что они рациональные.
Решение. Подставим число 1 + 4з в уравнение:
(1 + Л)2+(|+Л)р + q = 0 , то есть (2 + р)л/з = -(4 + р 4- <?) .
В последнем равенстве справа стоит рациональное число. Следовательно,
число слева тоже должно быть рациональным. Это возможно только в од-
ном случае, когда множитель р 4- 2 равен нулю. Но тогда должно равнять-
f р 4- 2 = 0,
ся нулю и р 4- q 4-4 . Решая систему j	получим
Ответ: p-q = -2.
Глава 4: Иррациональные числа	129
Задачи для самостоятельной работы
101ИВУМШ1П1ТДЖГВ01ГЖ«Т»Т*ГЖДЛ «<ЛЛГ»ЖМ*Я<ДВВ>»»ВМ4И» МЯЖВВВЖДДЯВКВСЫЖЛИВДИД <Л.МГАЖА*".«ЖЖА.г 'Ж ‘ vm. J’X4fcK*l£ZCDt>	t МЛГ/ г Ъ*^Л1	».
□ 1. Доказать, что для любых двух рациональных чисел а < Ь найдется
иррациональное число х такое, что а < х < Ь .
□ 2. Доказать, что для любых двух иррациональных чисел а<р найдется
рациональное число а такое, что а <а<р.
□ 3. Доказать, что число х = 012345678910111213... (после запятой выписа-
ны подряд все натуральные числа) является иррациональным.
□ 4. Пусть числа а = «0>а1а2 -ак- и b = bQyb}b2 . Ьк .. ( ак и Ьк — цифры в
десятичной записи) являются иррациональными. Будет ли иррациональ-
ным число с = c0,cjc2 ..ск , где цифра ск определяется по следующему
\ак, если ак>Ьк, _
правилу: ск = тах(а4Л)=М еаш ак<Ьк? Ответ обосновать.
□ 5. Пусть цифры числа 0,11235. определяются по следующему правилу:
ак + ак , J, если ак +ак+} < К),
ак +ак и - 10, если ак +ак±} >10
Какое это число: рациональное или нет? Ответ обосновать.
□ 6. Доказать, что число ^0.3 является иррациональным.
□ 7. Доказать, что a) V5 — иррациональное число; б) Jp .... иррацио-
нальное число, где р простое.
□ 8. Является ли log2 7 числом рациональным или нет? Ответ обосновать.
□ 9. Доказать, что log1636 — иррациональное число.
□ 10. Доказать, что если т и п — взаимно простые числа, то iogw п —
иррациональное число.
□ И. Доказать, что cos5° —иррациональное число.
□ 12. Доказать, что cos6° — иррациональное число.
□ 13. Доказать, что sin 5° —иррациональное число.
□ 14. Доказать, что sin20° — иррациональное число.
□ 15. Доказать, что cos20° — иррациональное число.
□ 16. Доказать, что sin 10° —иррациональное число.
□ 17. Доказать, что cos!0° —иррациональное число.
□ 18. Доказать, что sm25° —иррациональное число.
ак + 2 =
130	Конкурсные задачи
□ 19. Доказать, что квадратный корень из любого натурального числа,
оканчивающегося на 2, является иррациональным числом.
□ 20. Доказать, что квадратный корень из любого натурального числа,
оканчивающегося на 15, является иррациональным числом.
□ 21. Доказать, что функция у = cosx+cosV3x является непериодической.
□ 22. (Филфак., 1971) Доказать, что если р и q — целые числа, причем
р2 - 9<у2 - Gpq, ТО р - q = 0 .
□ 23. Пусть р — рациональное число, q — произвольное вещественное
число, и уравнение х2 + рх + q = 0 имеет два различных вещественных кор-
ня и х2 . Доказать, что числа и х2 либо являются одновременно ра-
циональными, либо одновременно иррациональными.
□ 24. (Мехмат, устн. экз.) Существуют ли иррациональные числа а и р та-
кие, что уравнение х2 + ах + p-Q имеет рациональный корень?
□ 25. Написать уравнение с целыми коэффициентами, одним из корней
которого является xj = ^5 + 7з .
□ 26. Доказать, что корни уравнения х2 + рх + <7 = 0, где p.q —нечетные
числа, иррациональны.
□ 27. Могут ли числа 2,	, 9/2 быть членами (не обязательно последо-
вательными):
а)	одной и той же арифметической прогрессии?
б)	одной и той же геометрической прогрессии?
□ 28. Может ли уравнение х2 + px + q = 0 с рациональными коэффициен-
тами р и q иметь иррациональные корни:
а)	л, х2=^?
б)	х, =-Л, х2 = —?
в)	X] = 1-V7, х2 = 1 + V7 ?
□ 29. Доказать, что если хотя бы один из корней уравнения х2 + рх + q = 0
с целыми коэффициентами р и q рационален,, то оба корня этого уравне-
ния — целые (предполагается, что уравнение имеет два корня).
□ 30. Найти рациональные корни уравнения 2 х = Зу.
131
Глава 4: Иррациональные числа
□	31. (Геогр. ф-т, 1996, предварит, экз.) Решить уравнение
л/5 + l . (45-1	я-1 , п
2 I 2	2)
□	32. (ВМК, 1986, устный экзамен) Рационально или иррационально число
Уз )/>2-б7з)о
ч/гТз+д 2>/з-4
□	33. (Третья Соросовская олимпиада школьников 1996-1997, 9 класс,
III финальный тур) Каким, рациональным или иррациональным, является
число
|^-2=—» + -	'	+<Ло + Й) ?
□ 34. Дана треугольная пирамида, у которой три плоских угла при одной
вершине прямые. Произведение площадей трех треугольников, примы-
кающих к этой вершине, равно 9. Проверьте, что объем такой пирамиды —
иррациональное число.
Решения, указания и ответы к задачам
Глава 1
□ 1. Решение. Так как PPQ — трехзначное число, Р — однозначное, а
MRMM —четырехзначное, то Р не меньше 3.
1)	Если Р = 3, то 990 = 330 • 3 < 33Q • 3 339 • 3 = 1017 => единственное число
вида MRMM , попадающее в указанный промежуток, есть число
Ю11=>2 = 7=> 337-3=1011.
2)	Если Р = 4 , то 1760 £ 442 • 4 < 1796 => ни одно число вида MRMM в этот
промежуток не попадает => нет решений.
3)	При Р = 5, 6, 7 рассуадения аналогичны, при этом решений нет.
4)	Если Р = 8,то 7040 ^882-8^7112 => единственное число вида MRMM из
этого промежутка, есть 7077, это число нечетное => нет решений.
5)	Если Р = 9 , то 8910 < 992 ’9 8991 => возможно только MRMM = 8988 , но
это число не делится на 9 => нет решений.
Ответ: 337-3 = 1011.
□	2. Указание. Представить 1984 в виде 1984 = 64 -31 = 2б(25-1) и
воспользоваться основной теоремой арифметики.
Ответ: (7И=Р’
= 6
□	3. Доказательство следует из неравенств
(и2 +и)2 <и4 +2и3 +2и2 +2и + 1 < (н2 +п + 1)2 , так как п2 + и и п2 + м + 1 —
два подряд идущих натуральных числа.
У».	JB4f« w ww wwwmhhwmw —wy	f-rm'Tvr-''' » - •* “
□ 4. Доказательство от противного. Пусть п = к2, тогда и:3, так как сум-
ма цифр 5 = 24:3. Следовательно, к: 3. Значит, п = к2:9, но 24 не делится
нацело на 9. Получили противоречие.
^тгд»»»те^1мти1ттгг<№«1япппги>^.Гт«.1..»......Диг.....М||».Ж.«тити». tf.» xewajujouU! .*<-> > «•> и
□ 5. Указание. Рассмотреть всевозможные числа вида п -10£	, где
о < т < 9 , и показать, что при возведении в квадрат п нс может
оканчиваться на 7.
□	6. Указание. Доказательство аналогично задаче 4.
Ответ: не может.
□	7. Решение, п = ЮЛ +5 =>и2 -- I (М)Лт’ 1(Ш +25. Следовательно, предпо-
следняя цифра числа п2 есть 2
Решения, указания и ответы	133
□	8. Указание. С помощью умножения в столбик показать, что справед-
п л-1	( л-1 V
ливоравенство: 111...1555...56 = 333...34
□	9. Решение. Число, оканчивающееся на семерку, при возведении в сте-
пень 1,2,3,4,5,6,... оканчивается на 7,9,3,1,7,9,3,1,.. , то есть последняя цифра
меняется периодически с периодом 4. Так как 1997 = 1996 +1 = 4 • 499 +1, то
последняя цифра числа 19971997 есть 7.
ТЧ/МГУЛНМД1ЯИШ«|глiiHLiinmiMwrHBjrwtwnu	I.П«'ТЖ..»»1ГЛ»И>1ЯГТГ<Л1МТ1П»»ИИП«TTtЮЛ -•* ' *	-
□ 10, Решение, mnk-knm = 100m + 1 On + £ -100& - 10и - m = 99(m-&). Число
99(m - k) • 11, но не делится нацело на 112, поэтому не может быть пол-
ным квадратом.
 »«»«<»wrjrrK»w«x»»Ar»»x»«wwv»WMWJW)n,»»»•>я	^гтг»»кгт-'тл, ~»>-w«xxx«rv.> - ,<• «»»> <«- » > тп
□ 11. Указание. Воспользоваться признаком делимости на 8 .
Ответ: X = 2 .
ХЛМА* «ЖКЖ4>в»ХЧ«АМММХМПМ.«ММг ЖД4АММ«»ГЖ.'1>4ЛМи1<»1ШЖЖК0аВИгга*аВХЕЕЖПХККМ>ЛКЖЖШиг<*ЛЛ«МД«М 4Ч)^*1^ЙИ*Д«А*»*1В*«-КЮММ^Ыич*Лв*ЛЛ4а*иИИ1аиЖв(»Ж*4 v к. MJ.tr JO. / >
□ 12. Решение. Воспользуемся формулой суммы геометрической прогрес-
7191 -1 7^’ ~ 1
сии 1 + 7 + 72 +.. ,+7190 = ——— = —-—. Так как в левой части равенства
стоит натуральное число, то это и доказывает, что (7191 -1): 6.
м t 1»л	Ь-Здлааимлъ	X-4S,» *XXMWJU»X>^a£niXXaA*i24«4JbUUUM14HL< vr	ЛА a »IUKVIML.> •	i
□	13. Указание. Для доказательства достаточно применить деление в
столбик, поскольку 111:37.
□	14. Указание.
1) 24л+2 оканчивается на 4 — доказывается с помощью индукции по п.
2) 24w+2 +1 = (22л+1 +1)2 - 2 • 22л+1 = (22л+1 - 2Л+1 + 1)(22л+1 4-2"+1 +1).
1*«W ’ »ЛТ,ч W!«yi-l^Vr2Vri<VlTrVinnSW*MH49B4tnr,>r7rtt»iz.<»<'y s вде«НГ«ЯЛНи1.“Я№»^<Г ГЛ»4ЖТ»-*гтЯИ»«*эт&»‘»«в«ЧЧИ>>^-‘1 ГсЛ»*» ч». 'ккпвапя .  * I Ч
□	15. Указание. Воспользоваться методом математической индукции.
гл > Ашжшамвшшмыиижматымлм.'жи- u'AwntUHU»iiiHHW<irMniH> т,»и>ммгтьшюлт>г.с^иу.4ым^лкмыь,и.~п ииг.»>»«11чгаииям.^.л »* .
□	16. Указание. Рассмотреть всевозможные остатки от деления чисел
т , п , к на 3, с учетом условия задачи.
1Г ц-п Г-r.Bintm----------------------- --1ГИГПГ"- 1-----•  -------—  ‘
□	17. Метод аналогичен предыдущей задаче.
rr»*wv< IX»иг»,-л г»<.c«Mrtnnw»«.иI«.1Д»»>«>л>»ТУ <гггг/г»гчем«Д|ччи»ц'МИМ«Г1*х<...«»г«».о»	, •- —,r\.мт»-.,. . >v ’ »« »%»•>' г»гк-г- -
□	18. Метод аналогичен предыдущей задаче.
г.—ги» «пах, <»,.<«.»»*.и> **'* < »>	.. < >	»ч
□	19. Указание. Утверждение (р4 -1):48, где р —простое число,
доказывается аналогично утверждению (р2 -1): 24 (см. пример в тексте),
кр 'МАМ1«едзпЕвдоп';тайпжя1?шжтат<1Жг<ЧУМ«№ЯЕШямв№*ы1эадозд«ят	л--*». .
□	20. Указание, к = тп(т - п\т+п). Докажите сначала, что к:2 . Для это-
го рассмотрите всевозможные остатки от деления т и п на 2.
Для доказательства к\3 также рассматриваются всевозможные остатки от
деления т и п на 3.
*тм1км*'4Л'-«««•	лиг*_*»,'ил»и*лч« - »• ч ft.TR.iM>> .lh>	> ~~ и '	<
□ 21. Задача решается на выбор одним из двух способов:
разложением на множители; методом математической индукции.
134	Конкурсные задачи
г	’UA.4LAW^UX^*>'*<4.SiV ~«и * Л*	нк’.« ?t '	•' i ) jrfJ
□ 22. Решение. Среди четырех последовательных чисел найдется по край-
ней мере одно, которое делится на 3 => п(п » 1Хн + 2Х« + 3) : 3 . Также среди
четырех последовательных чисел найдется два подряд идущих четных чис-
ла, поэтому одно из них должно делиться на 4 п(п + 1Х« + 2Х« + 3) • 8 .
JT ^•fYTFFrWlinFflirFUr^	”*Г« ?’)Л	•. ** * »TT£>3vA	'* *1 1 '’*>*. V__
□ 23. Решение. Заметим, что п5 -5п3 4-4w = (w-2X«-lX« + lXw + 2). Сре-
ди пяти последовательных чисел по крайней мере два последовательных
четных — делится на 8; по крайней мере одно число, делящееся на 3 и одно
число, делящееся на 5.
j 7'.гчаа<пкГ. чтти?^дхл’^.к;дла1.'?,ъ акл 4..1и	х	—•* jxsx-л г »	it
□ 24. Решение. Представим число п в следующем виде
9 групп
81	9	9	9
п = 111...1 = 111...1 111...1... 111...1 и заметим, что при делении п на 9 обра-
зуется число, состоящее из 9 одинаковых групп цифр. Следовательно, сум-
ма цифр числа ~ делится на 9 => п:81.
Ч И*	V* *4"	*> » Z--4.. : • ’ . • г V -V - /ч . »’ ' < < 1 .S "С *
□ 25. Указание. Взять возможные остатки от деления данных 52 чисел на
100 и заметить, что либо сумма, либо разность остатков будет кратна 100
□ 26. Решение. Докажем сначала вспомогательное утверждение: для того
чтобы натуральное число было полным квадратом, необходимо, чтобы оно
заканчивалось на одну из следующих цифр' 0, 1, 4, 5, 6 или 9. (Вспомога-
тельное утверждение доказывается при помощи рассмотрения всевозмож-
ных остатков п2 =(10р + д)2).
Докажем теперь утверждение задачи. Для выполнения условия
м2 = „2 +к2, где т,п,к — натуральные числа, необходимо, чтобы хотя бы
один остаток от деления т.п или к на 10 был бы равен 0 или 5 (докажи-
те при помощи рассмотрения всех допустимых остатков 0.1,4,5,6,9 ).
Представив п2 = (т + к\т - к), рассмотрите все остатки от деления т и к
на 3 . Во всех случаях получите н2:3, а значит, и п-З.
□ 27. Решение. Представим число в виде
ri^d = 1000а + 100fe + 10с + d = (1010 - 10> +(101 -_Tg> +_10с + d =
= 101(10а + b) + [ 10с + d - (10а + 6)j = 101(10а + b) + cd - ab,
откуда и следует утверждение задачи.
□ 28. Доказательство. Среди 18 подряд идущих чисел одно обязательно
делится на 18. Обозначим это число N и докажем, что N делится на сум-
му своих цифр S . Так как М : 18, то N • 9, а значит, и сумма цифр 5
числа N делится на 9 . Но, так как W — число трехзначное, то 5 может
Решения, указания и ответы
135
быть равно только 9, 18 или 27 .Трехзначное число с суммой цифр 27 есть
999, и оно на 18 не делится. Значит, случай S = 27 исключен и может быть
только 5=9 или 18 => N : 5 .
-»г	• ><» г-н uir:	л*гяул ,	.> л	г — _
□	29. Решение. 500’ = 1-2• 3-. .-500. Среди чисел 1,2, .,500 имеется
= 71 число, делящееся на 7 . Среди них имеется — = 10 чисел, де-
лящихся на 72. и есть еще
1 и	7
— = ] —одно число, делящееся на 7 . Сле-
довательно, п = 71 +10 +1 = 82 .
п*ххл лдмьм	jttUM'Avtxan	-✓ и,* «д 1 кГЧСЖМММЛ*	, -ь. » л.»-	J	-*• ’
□	30. Указание. Рассмотреть всевозможные остатки отделения п на К).
'ттжтмппдза.шзл	к нхипгшшруи-тх	Aj-rvncr и*	• <
□	31. Ответ, нс может.
Доказательство. Пусть и = 12m +10. Если т — четное число, то
п = 12(2А:) +10 = 24k +10 — не делится нацело на 8 Если т — нечетное
число, то п = 12(2 А: + 1) +10 = 24k +22 — не делится нацело на 8 .
•	» тиг	'•чм’члммлтгн »- «WT4 w'r^rwrwTB	ъ • *аг	> ♦-ли • •	4 --
□	32. Решение. По условию задачи
т = 4k + 1 => 5m = 20^+5, т = 5п + 2 4т = 20и + 8 Вычтем два полученных
равенства. Получим т = 20(£ - п) - 3 = 20(Аг - п - 1) + 17
Ответ: 17
‘	• к \ »	а.” 4» «- . Г	A V44M	t>r -	♦- «. V г « ч	. Ьч V ч **•<' *	• f	' »ч *'* *
□	33. Указание. Представить 15 в виде 15 = 72 + 1 и доказать по индук-
ции, что число 7 2 +1 в любой натуральной степени оканчивается на 1.
□ 34. Решение, п4 +64 = и4 + 16н2 +64 -16w2 = (п2 + 8)2 -(4w)2 =
= (н2-4н+8)(к2+4и + 8).
- *" w ‘ -ы. 4 ’-Г'ллзгтгггл-г^г-яг i лггалпогах^ тга гл ихх-г* - г	•.	• •	хт: j »<„	- .*•> > "> v -.»»•*•	•	•
□ 35. Решение. Числа 2" -1, 2”, 2" +1 представляют собой три подряд
идущих натуральных числа. Следовательно, одно из них делится нацело
на 3. Но число 2” не делится нацело на 3 . Значит, одно из чисел 2п -1,
2п +1 кратно 3. В то же время 2п - 1 > 22 -1 = 3, так как по условию задачи
п > 2. Значит, одно из чисел 2" - 1, 2п +1 является составным.
□ 36. Решение. Поскольку |п2 - 7н +101 = \п - 211п - 51, то число
р2 - 7п +1 о| может быть простым только тогда, когда либо |л - 2| = 1, либо
|и - 5| = 1. Рассмотрим случаи.
1)	н = 1, |л2 -7?/ + К) р I 7 ♦ 10 = 4 — составное число:
2)	?г = з, |и2-7п +101 .л 9 21 ♦ 10-9 —составное число;
3)	и = 4 , |и2-7п +10| |1б 28 । 1о| 2 —простое число;
136
Конкурсные задачи
4)	и = 6, |и2-7и + 10|= |36-42+10| = 4 —составное число.
Ответ: при п = 4 .
□ 37. Решение. 1) если р — нечетное число, то р2 +13 — четное и
/Г +13 > 2 — составное;
2)	если р = 2 (единственное простое четное число), ю р2 + 13 = 17.
Ответ: р -2 .
'» *	•» ’♦-KZ-T V ’ »»	-	I ’ л- • • -»	к	» »•	:*
□ 38. Решение. Покажем, что из условия задачи следует, что р = 3k + 2 .
В самом деле, если р = Зк и р > 3, то р не является простым. Если
Р = Зк: + 1, то 2р +1 = 2(3к +1) +1 = 6к + 3 — это число не является простым.
Итак, р = Зк + 2 . Тогда Ар +1 = 4(3£ + 2) +1 = 12Лг + 9 — составное число.
/TTTU »	>^t***4 t	•» /? Г •'Ч.Г'ТтМПг •»! t *>	* • г»-ягт/*г» rF*vrrwr О’Т • f * < -** |Г •. Г' ГЧ'Т’ГК r\V» t
□ 39. Указание. Воспользоваться формулами сокращенного умножения.
1) т =	-1 = (р-1Хр2 + р + 1);
5
2)	п =	- I = (r/-l)(f/4 + q3 +q2 + <? + !), где q = 2s (пятерка выписана 99
раз);
3)	к = г3 + s3 = (г + s)(r2 -rs + s2), где p,q,i\seN .
‘«ИГ V ’mill fh , ITY *• /Ш‘ ’• »• ’ •	- •» * >r« t»v« ’ 1 I*’ '• 1 -» * - »••»»•» - м % » •
□ 40. Ответ: такого натурального n не существует.
Указание. Показать, что последняя цифра числа 2п + п2 представляет со-
бой периодическую последовательность, не содержащую 5.
♦ 4 44АЛ ‘	•* ‘Г" • '	HfW4G*Jb> Л*	и‘4Л*» < •* •MH'.V '-VW » •> >> <•’».	• 4
□ 41. Решение. Заметим, что число, оканчивающееся девяткой, при возве-
дении в нечетную степень оканчивается на 9, а при возведении в четную
степень оканчивается на 1 . Число 9999" — нечетное, следовательно, чис-
ло 9999""9 оканчивается на 9.
□ 42. Указание. 9906 -1 оканчивается нулем. См. предыдущую задачу.
□ 43. Решение. Пусть К — номер подъезда Коли, V — номер подъезда
Вити, М — число этажей. Номер квартиры Коли заведомо больше номера
любой квартиры, расположенной в том же подъезде этажом ниже, и не
превосходит максимального номера квартиры, расположенной на той же
лестничной площадке. Аналогичные условия на номер квартиры Вити:
Л/ е 7V,
А(К - 1)Л/ + 4(5 - 1) < 83 < А(К - 1)М + 4- 5,
‘ 4(Г - \)М +4(3 - 1) < 169 < 4(И - 1)Л/ + 4 • 3,
М > 5 (wo крайней мере 5 этажей в доме есть)
V
Решения, указания и ответы
137
K,V,M eN,
63 < 4(Л - 1)Л/ < 67 => 4(Л - 1)М = 64,
4	157 < 4(Г - 1)М < 161 => 4(Г - 1)AY = 160,
Л/>5
U
ку.м e.V,
(К - \)М = 16 => 16: М => М = 1,2,4,8,16,	л / _ «
< (Г - 1)Л/ = 40 => 40: М => М = 1,2,4,5,8,10,20,40,	М ~ 8
М > 5
Ответ. 8 этажей
•	ь ъ» • » «1 »v гчл»л* -<	-«с	ЛАЛЛАН -JU4 . х. лл». <- *	*_д С + * J AUJUUTЛ^. . А» т *. »«i~ I \
□	44. Решение. Пусть в каждом томе k eN страниц. Тогда 1-й том начи-
нается со страницы номер 1 , заканчивается страницей с номером к Вто-
рой том начинается со страницы к +1, а заканчивается (2к +1) -й страни-
цей. Рассуждая по индукции получим, что том номер М начинается со
страницы номер к(М -1)4-1, а заканчивается страницей с номером Ш ,
где 1 < М <13. Поэтому сумма первых и последних номеров равна
5 = Л| +62 = [14-(Zr4-l)4- (2к 4-1) 4- 4- (12к 4-1)] 4-[к + 2к 4-... 4- 13/с | =
= 1 + 12Л + * 13+—-13 = 13(6fc + l) + 13-7A = 13(13A + l) = 39390 => fc = 233
2	2
Ответ: 233 страницы.
- V м* /VI	ч 1 UU/i Л	**. «.-V/-».' ►WJM’JU'IK'’ *-•	'ы«> Д п kUUv4kU4 iWJU,	,	« nil	» j «Г	.Л.	.
□ 45. Ответ: (1+2-3 + 4)-5 = 20 ,
□	46. Решение. Пусть 5 — сумма цифр трехзначного числа, тогда
100 <S3 < 1000 . Из неравенства следует, что 5 может принимать только
значения 5,6,7,8,9 . Среди указанных чисел условию задачи удовлетворяет
лишь 8 , так как 8я = 512, 54-14-2=8 (докажите перебором).
Ответ: 512.
• • «мт и «/	» *j гл \ "/	А*-< 3 ♦ U V' •« ИР ХЧЯГВ Uk WA1UCVQ»! Л >. -л* < < * ’ •*	’ ’*’»! VACUUM
□	47. Решение. 106 < 2458899 = Nmm < п6 < Мт.л. = 9988542 < 15б =>
=>10<//<15. Далее, поскольку’ 9 4-9 4-84-84-54-44-2 = 45 , то и:3. Следова-
тельно, п —только 12 . Однако необходимо проверить, действительно ли
126 записывается указанными цифрами: 126 = 46 • З6 = 212 • З6 = 4096 • 729 =
= 2985984. Иначе задача не имела бы решения.
Ответ' и = 12.
Ч < «	г-J • V.iJXk г. 4, и.	JtJtO	Г/	А Г Л-.* <	' Ц ч < 1.ХОГ
□	48. Решение. Обозначим т = а* 4-а“4 . Заведомо т > 0 . Далее
т = а4 +а~4 =(а2 +а 2 )2 - 2 = | (а 4- а~] )2 - 2 ]2 - 2 е Z . Отсюда meN .
।	* пя»л-х г» зггзтзггхгл:• •»**»*•'лг»-। ««	»uwtirnno»*ir»	ттг » х»тхт.тГАт^1 ч	f .	»
□	49. Решение. Обозначим т =а}а2.. ак_}ак, I =4т = акак_]...а2а] .Прове-
дем ряд рассуждений.
138	Конкурсные задачи
1)	Так как разрядность чисел т и / совпадают, то может быть только
ах = 1, либо а} = 2. Но ах = 1 не годится, так как в этом случае число / бы-
ло бы нечетным. Итак, т = 2д2••	1 = 4m = akak-v--a2~ •
2)	Ввиду того, что разрядности чисел т и I совпадают, 0 < а2 < 4 По при-
знаку делимости на 4 число л22:4 =>а2 - 1,33,7,9 . Получается, что а2 = 3
либо 1 . Но значение а2 = 3 не годится, потому что 23 - 4 > 90, и тогда число
/ имело бы вид / = 9^-j ...32, а число т имело бы вид 23 . ak j 9 , и равен-
ство / = 4m было бы невозможным а2 = 1 , I = акак _ j. .12 ,
т - 21 ..ак_хак,^=> из равенства / = 4 m сразу следует, что
ак - 8 => т = 21...аА:_18 , I = 4m - Ъак j 12.
3)	Из последнего равенства видно, что ак_} > 4 . В то же время путем под-
бора можно убедиться, что для того, чтобы число / оканчивалось на 12,
необходимо, чтобы акч было равно 7 или 2 => ак_х=7 => т = 21...78,
/ = 87... 12. Нетрудно видеть, что 2178-4 = 8712 , и что одну такую пару чи-
сел мы нашли (больше по условию и не требуется).
Ответ: и = 2178 .
□ 50. Решение. Пусть п = х2 = 10х+2, т = 2х = 2-10* +х, где к — число
десятичных цифр в записи числа п . Из условия In = m получаем уравнение
2(10x4-2) = 2-10*+х , или 19х = 210*-4 = 2(10* -2) =>(10*-2):19 Число
10* — 2 состоит из цифр 10* -2 = 99^98 . Для нахождения числа к будем
к цифр
делить 999...98 в столбик на 19 . Поскольку 38:19 , нам следует ожидать
появления остатка 3 .
139
Решения, указания и ответы
999... 98119_____________
95	5263157894736842
49
119
114
59
57
29
12
109
95
149
133
169
152
179
171
89
76
139
133
69
И
129
114
159
152
79
76
38
38
О
15 девяток
Итак, I()* — 2 = 999.. 9 8, или к = 16. Откуда
х = 2( 10к - 2) /19 = 2  5263157894736842 = 10526315789473684 .
Ответ: п = 105263157894736842 .
□ 51. Решение. 1) Напишем сначала общую формулу числа т , которое
делится на 2Д4Д ,10 . Поскольку
2 = 21,3 = З1,4 = 22,5 = 51,6 = 21 • З1,7 = 71,8 = 23,9 = З2,10 = 21 -51, то
т = к-23 -З2 -51 -71 = 2520* , где * е W .
2) Всякое число вида п = т +1 = 2520Л + 1 при делении на 2,3,4,...,9,10 будет
давать в остатке 1 . Нам осталось подобрать число к так, чтобы «:11. Для
этого заметим, что 2520 =229 114-1 и поэтому получаем
п = 2520k ч-1 = (229 • 11 +1)£ +1 = 229 • 11 ♦ к + к +1, откуда следует, что мини-
мальное значение к = 10 и wmm = 25201.
Ответ: 25201.
140	Конкурсные задачи
•>й^ы«анил?*^*м*м4*ы<1жив»1ммиииш».м«л«»м*<4^м««в^*ныь4,ле‘'1*’-’►ъеа*.»'..-* v?<	. .
□ 52. Решение. Так как 36 = 9 • 4, то число п должно делиться без остатка
на 9 и на 4.
1)	Выясним сначала, будет ли число, в записи которого цифры 0,1,2, 9
появляются только по одному разу, делиться на 9 . Сумма цифр
5 = 0 +1 + 2+ +9 = 45 достаточно, чтобы каждая цифра появлялась только
один раз.
2)	Далее воспользуемся признаком делимости на 4 . Двузначное число,
составленное из двух последних цифр, должно делиться на 4 .
3)	Первая цифра должна быть значащей. Так как нам нужно минимальное
число п, то это 1 => w = 1....
4)	Вторая цифра может быть нулем . Из оставшихся цифр 2,3, ,9 можно
выбрать двузначное число, делящееся на 4 (например, 96).
5)	Третья цифра может быть 2 -> из оставшихся цифр можно выбрать дву-
значное число (например, 96), делящееся на 4,=>м = 102....
6)	Рассуждая аналогично, приходим к выводу, что п = 102345 ... Из остав-
шихся цифр 6,7,8,9 можно выбрать двузначные числа, делящиеся на 4 , а
именно 68,96,76 . Следовательно, п} = 1023457968,п2 = 1023457896,
п3 = 1023458976 => «min = п2 .
Ответ: « = 1023457896.
□	53. Решение. Формула числа т , делящегося на 2,3,4,. ,9,10 (см. задачу
51), имеет вид т - 2520/с, где k eN . Если рассмотреть число вида
т = 2520k -1, то при делении на 23,4, .. ,10 будет получаться остаток
133, ,9 . Поскольку нам нужно «min , то к = 1 и п = 2519
Ответ: « = 2519.
□	54. Решение.
f(^-l):15,
1001:(« +1),
И Е N
Поскольку 1001 = 91 • 11 = 7 • 11 • 13, то возможны случаи:
1)	п +1 = 7 => « -1 = 5 — не делится нацело на 15;
2)	« +1 = 11 п -1 = 9 — не делится нацело на 15;
3)	и +1 = 13 =>« -1 = 11 — не делится нацело на 15 ;
4)	« +1 = 11 «7 = 77 =>«- 1 = 75:15 =>« = 76 ;
5)	« + 1 = 13-7 = 91 =>«-1 =89 —не делится нацело на 15 ;
6)	«+ 1 = 13-11 = 143 =>«-1 = 141 —не делится нацело на 15;
7)	« +1 = 7 • 11 • 13 = 1001 => « -1 = 999 — нс делится нацело на 15 .
Ответ: « = 76 .
Решения, указания и ответы	141
>’ <• •	►’(*«/.. VI У'кЖ’.а.	V 'Л~ 1 «	4.Л л. ‘ г.'МЛ-'--, г,Л» ‘
□	55. Решение. Пусть г и Ь — число красных и синих карандашей в од-
ном комплекте, к — число комплектов. Из условия задачи следует
^We^ (1),
6 - г > 3 (2),
k > 1 (3),
0<36-2г < 16 (4),
(36+2г)£ = 81 (5)
Из условия (2) следует: b > 3,
поэтому 36 4-2г > 9.
Так как к > 1, то из условия (5)
и соображений делимости вытекает
= 3, Зг+26 = 27
г, b g N,
b - г > 3,
О <36-2г <16,
36+2г = 27 (6)
^Из (6) следует' делимость г на 3,
поэтому следует проверить
г = 3,6,9,12. Из них неравенствам
<(2) и (4) удовлетворяет только г = 3 J
= 3,
[к = 3.
Ответ: 3 комплекта, по 7 синих и по 3 красных карандашей в каждом.
□	56. Решение. Зх2 +3лу + 2х-у = 56,x,y &N или y(3x- 1)= 56-2x-3x2,
_ 56 - 2x ~ 3x2 _ 3x2 + 2x - 56 _ 3x2 - x + 3x - 56
или У ~	~	~	;
3x -1	3x -1	3x -1
3x - 56
"зГ-Г
Зх -1 - 55
Зх -1
x +1 —= ——— x -1 Так как x, у g /V , to
3x - 1 3x - 1
-----g jV (3x - 1 g jV) . Отсюда возможны случаи:
Зх - 1
э
1)	Зх -1 = 1 х = j не годится;
2)	Зх - 1 = 5	Зх = 6,х = 2.у = у - 2 - 1 = 11 -3 = 8 =>	— решение,
3)	Зх - 1 = 11	Зх = 12,х = 4, v = — - 4 - 1 = 0 нс годится,
11
4)	Зх - 1 = 55,х = — & N .
3
(у - э
Ответ. X’
(у ~ 8-
w	| > . м*	*♦ -» ’УХЖ < Л’ ♦< •/	*• ** *Г» *- «•<-<» •'AXTirr^ ' • -	- v	Ч	» V V. .
□	57. Задача решается аналогично предыдущей.
Ответ: х, = 9.= 9,х2 = 1,у2 - 33 .
□	58. Решение, х = тп = 10w + н . Получим систему
142
Конкурсные задачи
Зт -6п = 6=>т = 2п 4- 2,
10™ + л = Зтп + 1 1.
10™ + п = 7(™ + п) + 6,
10™ + п = Зтп + 11,
™ g Z, 1 < ™ 9,
п g Z, 0 < п < 9
10(2л +2) + п - Зл(2л + 2) + 11 = б//2 +6// + 11 => 6л2 -15н - 9 = 0 . т. е.
, 2 .	, п	5±V25 + 24	5±7 5 + 7 .	,	. Q
2п - 5// - 3 = 0 => л, о =-------=-----=------= 3, т = 2п + 2 = 8 .
4	4	4
Ответ: х = 83.
□ 59. Решение. Обозначим к — число юношей-школьников, / — число
девушек-школьниц, ™ —число юношей-производственников, р — число
девушек-производственниц. Получим систему уравнений
k,l,m,p,n g
к + / = ™ + р + 600,
/ = 5р,
< к - пт,
к,р,п е W,
к + 5 р- р + 20 + р + 600,
к - п(р + 20),
k,p,n G W,
к + Зр = 620,
к - п(р + 20),
т = р + 20,
(Так как пр + 20л + Зр = 620.
р(п + 3) = 620 - 20 л,	то
р, л g N,
20(31 -п)
Р =--------—
_ 20(31 -л/) _
? п + 3
20(-3 - л + 34)
= -20 +	= -20 +	.
н+ 3	п + 3
п = 6 не годится, так как 680 не делится нацело на 9 ;
л = 7,р = 68-20 = 48 (!);
п = 8 г=> 680 не делится нацело на 11 ;
п = 9 => 680 не делится нацело на 12 ,
п = 10 => 680	не делится	нацело	на	13 ;
п = 11	680	не	делится	нацело	на	14;
п = 12	680	не	делится	нацело	на	15 .
Итак, п =	7,р =	48, Л = п(р +	20) = 7(48 + 20) = 68• 7 = 476,
/ = 5р = 5-48 = 240,™ = р+ 20 = 68,4: + /+ ™ + р = 476+ 240+ 68 +
+ 48 = 832.
1)
2)
3)
4)
5)
6)
7)
Ответ: всего было подано 832 заявления.
Л‘> «	4	-	-г-	•	-	iWWHTWlV'-'TW.' I '• >	. J. 4 - С	.	>
□ 60» Решение. Пусть к — число красных карандашей, с — синих. Тогда
к gZ,к >0,
с eN9
17Л + 13с<495,
Решения, указания и ответы	143
Заметим, что при замене одного красного карандаша на синий происходит
экономия 4 коп., а сумма к +с не меняется. Поэтом}7 минимально возмож-
ное число красных карандашей определяется соотношением с ~к s.
с е TV,	(с g JV, < 17(с - 5) + 13с < 495,	ЗОс < 495 - 85 = 410, = с + с- 5 = 2с-5-> max,	12с - 5 —> max. к = с - 5	к - с - 3	с е N. => J 41	2 |с< — =13-. 3	3
Ответ: 13 синих и 8 красных.
□ 61. Решение.
X = тпк = 100>н 4- Юн + к,
т,п,к g Z.
1 < т < 9, 0 < п < 9, 1 < к < 9,
2п = к
Шт + 1 Он + к + 1 00А + 1 Он + т = [ 101(ш + к} + 20н{10 => (т + к)АО
=> т + к = 10
X = 100w + Юн + А,
т.п,к gZ,
И < т < 9, 0 < н < 9, I < к < 9,
т + к = 10,
2н = к
а)	к = 2,п = 1,т = Ъ=>х} =812 ,
б)	к = 4,н = 2, т = 6 => х2 = 624 ;
в)	к = 6, п = 3, т = 4 =>	= 436 ;
г) к = 8, п = 4, т = 2 х4 = 248 .
>	~ >*	Л- < .	•»	*4	л * -•«	. М»,	- 1	4»	Ответ: 248, 436, 624, 812.
□ 62. Решение. Пусть Е — число однокомнатных квартир в доме, D —
число двухкомнатных, Т — трехкомнатных.
E,D,T eN'	(г? 'г D = 4E, ^ТЕ- п Л.'У'У	=> Р = 4Я=>]5Г=4£ + 22.	=>  IXrJioo,	iVrV-100’ E + D + T--)	[5Д+/-?	Е.Т Г-Е' 5Т -4Е = 22. 5Е + Т > 100
[Е,к eN, ^Т = кЕ,к eN =>Я(^ + 5)-?=> \5кЕ-4Е = 22,=> [кЕ +5Е>100	(ЕЛ G^ ^Е(5А-4)=22, Е(А + 5)>100
Из второго уравнения следует, что возможны четыре случая:
1)	Е = 1, тогда 5к -4 = 22, Зк = 26 к £ X ;
2)	Е = 2, тогда 5А - 4 = 11.А = 3,Е(А+ 5) = 2(3 + 5) = 16 < 100 — не годится;
3)	Е = 11, тогда 5А-4 = 2, 5А = 6 => А £ ТУ ;
144
Конкурсные задачи
4)	Е = 22,5k - 4 = 1Д = \JE(k 4-5) = 22-6 = 132 > 100 — годится.
Ответ: 132 квартиры.
□ 63. Решение. Пусть т — число самолетов 1 -го типа, п — число само-
летов 2-го типа, к — число самолетов 3-го типа.
т,п,к &N,
230m 4-110» 4-40^ = 760,
27m 4-12»-г 5£ = 88,
m 4- n 4- к < 8
пцп,к g /V,
23m 4-1 In 4- 4k - 76, 4m 4- n 4- к = 12
27m 4-12» 4- 5k = 88, к = 12 - 4nt - n
nt + n + k <%
nt,n g JV,
23m 4-11» 4-4(12 - 4m -») - Int + ln 4-48 = 76,
in 4-» 4- (12 - 4m - ») < 8,
4m + n < 12
nt,11 g TV,
m 4-n - 4.
nt
- лт -ч =5* jm	z,	IZ— Д
4m 4- 4 - nt - 3nt 4- 4 < 12 => 3nt <8	I
nt,n,k,d еК,
127 < к < 132,б7 > 1,
J](n -nt)d = к,
(2nt-n)d=77
Ответ: 2 — первого типа, 2 — второго, 4 —третьего.
□ 64. Решение. Пусть первый рабочий изготавливал m деталей в день,
второй — п , а работали они d дней, причем по условию d > 1.
ni,n,k,d g /V,
127 <к ^132,d >1,
/с .
n-nt = — е N,
d
77
2nt - ii = — g /V
d
Поскольку TT:d, d > 1, to d может принимать только 3 значения:
1)	d =! . Этот вариант невозможен, так как ни одно число к, 126 < к < 132
не делится на 7 .
2)	d-11. Этот вариант невозможен по аналогичной причине.
3)	d = 11. Тогда к = 132, так как 132:11 и других значений к таких, что
126 < к < 132,/Н1, нет.
Подставим найденные значения и в систему (2):
[» -nt - 12, Jm = 19,
|2т-п = 7 [n = 3l
Ответ: первый рабочий изготавливал в день 19 деталей, второй — 31.
Всего работали 11 дней.
A’-VJK.LMAA-'J «.	v	ЛЖ ЖКАЛГХ	V Г» •'UlMV	«• ««ЛАА «Я»-* •* lWt.ul.uL .1 О.	ОА. »» f	Ч 4» < J
□ 65. Решение. Пусть п — минимальное число рейсов, за которое можно
перевезти груз. Определим п при помощи следующих рассуждений.
1)	Общий вес блоков составляет 24  1.6 + 51 о• 0,2 = 188,4 т. Так как макси-
мальная грузоподъемность машины Ю тонн, то для перевозки груза требу-
ется не менее 19 рейсов, » ’19 (шраничсние по грузоподъемности).
Решения, указания и ответы	145
2)	Обозначим как "место” объем маленького блока, тогда объем большого
блока составляет 14 "мест”. Всего объем перевозимого груза равен
24 • 14 + 510 • 1 = 846 “мест”. Так как 44 • 19 < 846 < 44 • 20 , то отсюда следует,
что п > 20 (ограничение по объему).
3)	Итак, меньше чем за 20 рейсов обойтись нельзя. Если мы укажем спо-
соб, как обойтись за 20 рейсов, то задача будет решена.
Один грузовик можно загрузить по максимуму одним из трех способов:
а)	2 блока больших и 14 маленьких (10 тонн, 42 "места”);
б)	1 блок большой и 30 маленьких (9,6 тонн, 44 "места”);
в)	44 маленьких блока (8,8 тонн, 44 "места”).
Весь груз можно перевезти за 20 рейсов: сделать 12 рейсов типа "а” (24
больших и 168 малых блоков), а оставшиеся 510-168 = 342 малых блока
можно перевезти за 8 рейсов, так как 8- 44 = 352 > 342
Ответ- за 20 рейсов
□ 66. Решение. Обозначим b = ak,c = ak2.
а М е .V,
224() = 2°-5’7:‘(dl),
4312--23 5° 72 11:(аА2),
<з(1 +А + А'~ ) —> max.
Далее, числа а.к также разложим на простые множители
d=2W25w$7W7llw” , fc = 2',25',57'bll"1’ , где m^nt eZ.m,^ £0. Из условий
делимости следуют неравенства.
« = 2"'27п,\
к = 2п*1п\
т2уП2,т7уп7 е/'
ПИ , «2' т7 > п7 -
т7 + н7 < l,m2 + 2w2 - 3,
л(1 + А + Р) -> max
Заметим, что при одновременном увеличении т.н величина а(\+к+к2)
растет. Поскольку нам нужен максимум этой величины, то достаточно рас-
смотреть условия т7 +п7 = 1,т2 + 2н2 = 3 . Возможны 4 случая:
1)	т2 = 3,н2 = 0,ш7 = 1,н7 = 0 . Тогда а = 237* = 54,А* = 2°7° = I . Этот случай не
годится, так как прогрессия не является возрастающей.
2)	т2 = 3,п2 = 0,ш7 = О.„7 = 1 Тогда а = 237" = 8,А = 2°?’ = 7,
h = ак = 56,с = 392,a +- /> + с -- а(к2 + А + I) = 456 .
3)	т2 = 1.и2 = 1.ш7 = 1.н, - 0 . Тогда а = 2’7' = 14,А = 2’7° = 2,
b - ак = 28,с = ак2 = 56,а -♦ /м г 14 ♦ 28 + 56 = 98 .
146	Конкурсные задачи
4)	m2 = 1,и2 = l,m7 = 0,и7 = 1 Тогда а =2*7° =2,А =2’7'= 14,
b = ак = 28,с = ак2 - 392,а +Ь + с = 434 .
Ответ: а = &,Ь = 56, с = 392 .
Ч* *.	' v >•*, vrr»*Fef t*V»t 9 •* » ГЧП •**'<.rt > tro” » *»	‘	>
□ 67. Решение. Обозначим сомножители т и n.
т.п € ТУ,
m - n - 10 => m - n 4-10,
mn 4- 200 = 50/2 4- 25,
цифра сот си в nm может быть увеличена на 2
(й + 10)и4'200 = 50/2 4-25 =>//2 -40и4-175 = 0
1) пх =-- 5,wj = 15 => тхщ = 75 => цифра сотен отсутствует.
2) п2 = 35,т2 = 45 т2н2 = 1575 => цифра сотен может быть увеличена на 2
Ответ. 45 и 35.
□ 68. 1991=11 181. Указание. Воспользоваться признаком делимости на
11 и затем доказать, что 181 — простое число.
Оэтст1ждята;цхка1х>1ажм1дцкци«жмх«»жж1мдж1п>1жи1«1111»>»имм11д>ыл1^1л>сдаяхспссгтгэтгжтгг1поо1х*ж»>»оасооашиажкстг4х1хкгг^с’'^_тх«^. t <
□ 69. Решение. Пусть мастер делает п деталей в час и выполняет заказ из
Л/ деталей за к часов. Имеем систему уравнений и неравенств
пк = Л7,
‘ ‘nXM^N," М' пк = 2(-" ”	- пк = 2п +4£ - 4 =>
п > 5
п(к - 2) = 4к - 4 . Видно, что к = 2 не является решением =>
4Аг-4 44:-8-ь4 А 4	A./t
-------------------- 4 -}.- откуда следует, что 4: (к - 2)
к ~ 2 к 2 к ~ 2
1)Если £ - 2 = 1,4; = 3, то w = 4+—= 8,Л/ = *н = 24 .
к-2
2) Если к - 2 = 2,4: = 4 , то п = 4 + ~ — = 6,Л/ = кп = 24 .
к -2
4
3) Если к - 2 = 4,4: = 6 , то п = 4 4-----= 5, не годится, так как п > 5
к - 2
Ответ: заказ из 24 деталей.
□	70. Указание. Задача решается аналогично предыдущей
Ответ: 36 деталей.
• /м	Г / /К I, S* 1 5 ч. ч(	. Г«.^.<Ж4.4^.%АЛЛПДАА«А*1а1 «»пАЧ«»-<4 t •••»•. Г«* Г
□	71. Решение. Обозначим трудоемкост ь детали типа В через к челове-
ко-часов, тогда трудоемкость детали типа Л составляет по условию 2к
человеко-часов. Тогда трудоемкость изготовления деталей типа А состав-
ляет 40004: человеко-часов, дст алей гипа В — 140004: человеко-часов
Пусть в первую бригаду выделено 1 - т < 145 человек, тогда во вторую —
146-W человек. При лом время изготовления деталей типа А составляет
Решения, указания и отпеты
147
f} (щ) = -	, а время изготовления деталей типа В составляет
т
(т) - 14()()(-- . Поскольку заказ может быть сдан только тогда, когда изго-
146- т
товлены детали обоих типов, то время выполнения заказа определяется как
максимум из Д(ш) и f2(m), t(m)~ max	{Д (/и),/2 (m)|. Ради удобства
wi 145,m< W v	;
рассмотрим графики функций J\(m) и f2(m) (рис. 11):
Рис. 11.
Поскольку /}(т) — убывающая функция, а f2(m) — возрастающая, то ми-
нимум t(m) достигается в точке xQ, в которой /i(x0) = /2(хо) Если бы х0
была целой точкой, то задача была бы решена, в противном случае нам
пришлось бы рассматривать ближайшие к х0 целые числа. Найдем х0:
40004:	14000/с	2
------ = ------- —S  
х0	146-х0	х0
7
-------=> 292 - 2х0 = 7х0	9х0 = 292
146-х0
=> х0 = 33— g Z рассмотрим ближайшие целые значения.
Если т = 33 , то /(33) = /j (33) =	•
Если т = 34 , то /(34) = f2(34) = ~~~~~ •
~	40004: 140004:	2	7
Осталось провести сравнение: --------v--------<=> — v — <=> 224 < 231.
33	112	33 112
Ответ: 33 рабочих в первой бригаде, 113— во второй.
□ 72. Ответ: 39 и 153. Задача решается аналогично предыдущей.
148	Конкурсные задачи
□ 73. Решение. Пусть К — объем производства предприятия до реконст-
рукции По условию задачи сначала в течение щ месяцев падение произ-
водства составляло 9—%
(что соответствует умножению на —), далее —
в течение месяцев — на 8-% (умножение на —). далее — в течение
°4
т3 месяцев — на 4% (умножение на —), и, наконец, в течение т4 меся-
цев — на 6 —% (умножение на —). В результате сохранилось 54%
4	16
первоначального уровня.
1 J/H2 24m3 l5m4 50 = J 12m2 25m3 lfm4 2? раздагая обС части ра_
венства на простые множители и пользуясь основной теоремой арифмети-
ки, получим систему уравнений:
>И| 4- Зт3 4-1 = 2т2 4- 4т4
т3 4- т4 = т2 4- 3,
4-т4 4-2 = 2т3,
= т2
1т2 ~ 3^3 + 4ти4 = 1,
- т2 4- т3 4- т4 = 3,
т2 - 2т3 4- т4 = --2
- 2т3 4- 5ш4 = 4,
- т3 4- 2т4 = 1
т4 = 2
тщ ~ 3

- т2 -2 =>т} 4- т2 4- т3 4- т4 - 9
Ответ. 9 месяцев
□ 74. Решение. Обозначим число абитуриентов через п . Пусть к — чис-
ло аудиторий в 1-м корпусе, т — число аудиторий во 2-м корпусе. Тогда,
согласно условию задачи, число абитуриентов п равно Зк2, а, с другой
стороны, — 2т3. Поэтому п = 3к2 = 2т3, где njc,m е N . Воспользуемся
основной теоремой арифметики: к = 2РгЗр' , т = 24234' и подставим пред-
ставления к , т в уравнение
3-22р232^ =2.23<?2 3^з или
2р2 - 3q2 4-1,
2/>3 +1 = 3?3,
Р2-> Рз>Я2’Яз
Р2>РЗ>Я2^ЯЗ ^°-
Минимально возможные значения	» ПРИ которых возможно
равенство, это q2 = 1,р2 = 2,^3 = 1,р3 = 1 =>н = 3-22 232 =2433 = 4 32 .
Ответ: 432 .
□ 75. Ответ: 16875. Задача решается аналогично предыдущей.
Решения, указания и ответы
149
□ 76. Решение. Пусть т и п — сомножители, причем т > п . Из условия
т.п е У,
т > п > 29 {так как ПРИ делении 1
7 ^на п остаток равен 29J ’
тп + 372 = 90л + 29
т.п е У,
т > п > 29,
и(90-от)=343=73.
поэтому' возможен
лишь один случай п = 49	90 - т = 7 ==> т - 83 все условия выполнены.
Ответ: {"'=49'
.	-X т - '•	t
□ 77. Аналогичная задача решается в §2.
Ответ ‘ 6
□ 78. Аналогичная задача решается в §2.
Ответ: J - {123,7,11,14,22,77}
□ 79. Решение. Умножим и разделим данное произведение на 1 2 ... п.
1-2- ...(2л - 1)2//	2-4 ..-(2л -2)2л
(л + 1)(л + 2)...(2л-1)2л =--------—=1-3-5• .. (2л-I)---------------— ~
1 • 2 • • п	1 • 2 •. . • л
= 1 3 • 5 •• (2л - 1) 2".
Впереди 2п стоит произведение нечетных чисел.
□ 80. Решение. Пусть X — неизвестное число, т
п — число единиц. Из условия задачи следует
Ответ: п
число его десятков.
Д' = 10/?/ + п.
т.п е N.
• 1<т<9,
I < п < 9,
(1 От + л/Юл + т) = 2450
X = 10m + п.
т.п g X.
1<т<9,
1 < п < 9,
101тл + 10(т2 + //2 ) = 2450
Из последнего уравнения по соображениям делимости следует, что тп
должно делиться на 10 . Но тогда возможны варианты.
1)	т - 5,п = 2	(либо	п = 2.т = 5).	при этом	52 • 25 = 1300, нс годится;
2)	т = 5,л = 4	(либо	т - 4. л = 5),	при этом	54 • 45 = 2450 .
3)	т = 5.п = 6	(либо	т = 6, л = 5),	при этом	56•65 = 3980. не годится;
4)	т = 5,// = 8	(либо т = 8,// = 5).	при этом	58 • 85 = 4930 . не годится.
Ответ: 54 и 45.
□ 81. Решение. э •> . w ч лс . лс < п
\пг - гГ = (т - п\т + п) = 45 = 1 45=3 15 = 5 9
(Других вариантов быть не может, так как т -п <т + п .)
1) ( ?=lk=>lw’ %2?'
7 \т + /? = 45	(?7| = 22.
150
Конкурсные задачи
ЛИ] = 23, \т2 = 9, jm3 = 7,
«I =22, рь [пз
ри - п = 3	\т2 = 9,
' \т 4- п - 15 pt2 = 6;
о ч рл - п = 5, рн3 = 7,
' ' рн 4- п = 9	= 2,
Ответ.
I J.	МХуЩ	. - 1 — >#>.	».'< - Д.— * * > -Um -Л JKi^Vv.
□ 82. Решение. Пусть п — искомое число, a.b.c.d — его цифры в поряд-
ке старшинства (а — старшая). Тогда
L,Z? с\с7 е< 9 0<b,c d9,	Из последнего равенства сле-
р/ = 1000а+ 1006 + 10с + </ = 600(а + b + c + d)	г
дует, что п делится на 100 , поэтом}' с = d = 0, откуда следует
а-Ь е Z,	а [у е /
< 1 < а < 9, 0 < b < 9,	< 1 < а < 9,0 < b < 9 => а = 5.6 = 4,// = 5400
10н+6 = 6(а+6) 4а = 5Ь
Ответ, такое число одно (н = 5400).
□ 83. Решение. Пусть т = 100а + 106 + с, тогда
а.Ь.с eZ.ni е К.
100 < т < 1000,
« 1 < а.Ъ < 9. 0 < с < 9,
100а 4-106 + с = с3 - т^>	>100.
100<з 4- 106 + с = (106 4- с)2	100(а - 62 ) + 106(1 - 2с) = с2 - с
Из последнего равенства следует, что с2 - с делится на К) и с3 > 100 . По-
этому могут годиться только с = 5,с = 6, с = 9 Проверим их.
1)	Если с = 5 , то т = 53 = 125 =>а = 1,6 = 2 , но 125 *212.
2)	Если с = 6, то т = 63 =216=>а = 2,6 = 1, но 216* 122.
3)	Если с = 9 , то т = 73 = 729 =>а = 7,6 = 2, 729 = 272 .
Ответ, т = 729 .
• ’*> Ди*» V-V*	*•'«* V ,	к тг , <* .««*<'• < ч	*»	—и ** - >»* -А t ч « • -	<• —
г-1 л j wj	и24-1	(н^—1)4-2	2
□ 84. Решение. ------= 2------<---= п - 14----, откуда следует, что
п + 1	7/4-1	п 4- 1
2:(л? 4-1). С учетом neN получаем ответ.
Ответ: п = 1.
□ 85. Решение. X = Юн/ -ьн , тогда
и/,п е Z,	т.п eZ,	т.п е Z,	
Г VI VI о VI S VI	1 ти £ 9, 0 п s 9,	<	1 СЛ VI VI О VI 5 VI	\т - 4.
10/н + и = 4(н/4-н)+3, 1 От 4- п - 2(т + п) = 25	6т - Зп = 3, 8m - п - 25	2т -п = 1, 8m - п = 25	" |и = 7
Ответ: 47.
151
Решения, указания и ответы
•*» » . - B4Az4,**..b.-,1S<44	-Л .4 ЛММ. » И	. г - < -SS,4< Л.,«
□ 86. Решение. X = \От + п . тогда
т.п е Z,
т.н е Z.
1 < т < 9, 0 < п < 9,
Юли 4- п = 3(т + л?) 4- 7,
т2 + п2 - mn = 1 Оли 4- п
1 < ли < 9, 0 < и < 9,
7т - 2и = 7,
т~ 4-и2 -тп= \()т + п
В принципе, из первого уравнения можно выразить ли через п и подста-
вить во второе, но лучше поступить проще. Заметим, что из первого урав-
нения следует, что н должно делиться на 7. Поскольку п — десятичная
цифра, то возможны два случая:
1) л/ = 0 => w = 1, но тогда т~ +722 -mn = I * Юти +Л7 = !()=> этот случай нс
подходит;
2) п = 7 т = 3 , тогда ли2 + п2 -тп = 9 + 49 - 21 = 37 —1 Оллл + н
Ответ 37.
□ 87. Решение. Пусть всего было Л/ деталей и Ь ящиков Тогда
M.b е N, М = 126 + 1,	6 еЛ\6> 1,	beN,b>\,	6 (Ч N,6 > 1,
М 	е N 6-1 — <20, |{’;1	126 + 1 	е /V. 6-1 >^.20, 6-1	Л 1 ]2(/>-1)+1\ 6-1	"	’	>2. 13 (-V, Ь 1 12 '„"г21’
Из второго условия следует, что 13 делится нацело на b - 1. Если 6 - 1 = 1,
то не выполняется третье условие. Следовательно,
6 -1 = 13 ь = 14 => М = 12-14 + 1 = 169 .
()твет 169 деталей.
□ 88. Решение. Числа а+ 4 на (и>0) удовлетворяют уравнению
а2 + (а + 4)2 = а (а + 4)+ 37 , или а2 + 4а - 21 = 0 .
Ответ: 37 или 73.
Глава 2
п =
а)
б)
□ 1. Решение и ответ записываются одновременно:
О - ( -1) 4- 0 при п = О
деление невозможно при п - 1
2-14-0 при п = 2
1 (п - 1) + 1 при п = - 1 , - 2 , ± 3 , ± 4 ,
1-1 + 0 при п = О
деление невозможно при п = - 1
' +1 =
3-1 + 0 при п = - 2
п • (п + 1) + 1 при п = 1 . 2 , ± 3 ,
□ 2. Решение. Имеем тп + pq = к(т- р), к е Z
этого равенства mq + np Тогда после переноса
Прибавим к обеим частям
пт + pq получим
mq + пр = к (ш - р) + mq 4- пр - тп - pq - к (т - р) + q(m - р) + п(т - р) -
= (т- р)(к + q - т) ,
т. с. (mq 4- пр\. (т - р), что требовалось доказать.
□ 3. Решение. А54 -к~ = А22(АЛ2 -1)-А22(А16 +1)(А16
= А-22(А-16 + 1)(А8 + 1)(А4 + 1)(А2 + 1)(А + 1)(А -1).
1)	Это произведение очевидно делится на 2, так как произведение
(A--l)A' (или £(£ + !)) четно.
2)	Если к = 5/, то утверждение очевидно.
3)	Если к = 5/ + 1, то один из двух последних сомножителей делится на 5 ;
если к - 51 ± 2 , то к2 +1 делится на 5 . Проверьте это самостоятельно.
Замечание: мы доказали делимость указанного числа даже на 30.
□	4. Решение. Пусть т. п e Z и т-п = а . Тогда если т = qa + г (0 < г < а),
то п = т - а - qa + г - а = a(q -1) + г , что и требовалось доказать.
□	5. Указание. 255 + 1 =(2s)ll+l -32й +1п =(32 + !)•/-33/ = 11-3/, /eZ.
□	6. Решение. ак -1 = (д-1)(дАг"1 + ак~2 +...+Я1 +<z(,) =
= (а-\)\(ак~}-\) + (ак~2-1) + ... + (а]-\) + к].
По условию а -1 делится на кт , следовательно, а - 1 делится и на к . Зна-
чит, каждое слагаемое в квадратных скобках делится на разность основа-
ний а -1, а оно делится на к (последнее слагаемое равно к ). Отсюда и из
делимости д-1 на кт следует делимость ак -I на к”' - к = кт"'}.
Решения, указания и ответы	153
4'.г\иаыт »ni »и«ттип.ы1и<»м»и<>«»я»рдиаг*..»мм1/^м.-мги1ым<^>плм«^нд>ц|«*м1жсгм*?ц<мд»тд5«сг»*й>^«х.у^«,ч.пд.>7	'.,
□ 7. Решение. Делимость на 7 очевидна: сумма оснований равна 7 при
нечетном показателе в формуле (3), глава 2, §1.
Далее заметим, что 105 = 3-5-7 и, значит.
1)	З105 + 4105 = З3'35+43 3s=2735+ 6435 = (27 + 64) = 7-13;
2)	3105 + 4105 = (35)21 +(45)21 :(35 +45) = 7 181;
3)	3'05 + 4105 = (З7)'5 + (47)'5 : (З7 + 47 ) = 49 • 379 .
7	d лод,	ота wixu..ancrjty дз	.lj а^1ГАлижхизаа».гг.1г«*ггг^. .лхэх *	- х Л
□ 8. Решение. 721 - 487 = 7 • 720 - 7 - 480 = 7(4910 -1) - 480 =
= 7(49-1)(499 +498 + ... + 1)-48-10 = 48[7(499 + 498 +... + 49+ 1) -10].
Так как 49 = 8-6 + 1, то 49* = 6т +1, где meN . Достаточно воспользо-
ваться формулой бинома (кто знает) или доказать индукцией по к . Теперь
выражение в квадратных скобках принимает вид (и е М)
7(би +10) - 10 = 7- би +60 = 6(7и +10).
Итак, все исходное выражение записывается как
721 -487 = 48 • 6(7и +10) = 288(7и +10),
т. е делится нацего m J288.
□	9. Решение. Имеем, сначала добавляя и вычитая 45555, а потом вычитая
и добавляя 42222 , с помощью формул (2) и (3), глава 2, § 1, получим
22225SSS +5 5 5 52222 = (2222ssss +45555)+ (55552222 -42222) + 42222 -45555 =
= 2226 q} + 5551-g2 -42222 (4П33 -1) = 7-318-q} + 7-793-g2 - 42222 (641111 -1) =
= 7• Р} + 7 р2 - 42222(64 -1)-9, = 7(р, + р2) -7 • 9</3  42222 =
= 7(Р| +р2 + Рз) = 7р ,
где q,, р,, р е Z , / = 1,2.3.
□	10. Решение. 1) Перепишем уравнение в виде 19л = 21у + 2 =
= 19 у + 2 у + 2 2у + 2 = 19х - 19 у
2)	Первый шаг процедуры уменьшения коэффициентов. Правая часть
полученного уравнения делится нацело на 19, следовательно, должна
делиться на 19 и левая часть, 2y + 2 = \9t => 2у + 2-18/ = /
3) Второй и последний шаг процедуры уменьшения коэффициентов.
Левая часть :2 => Р2 => t = 2n.
4)	Получение зависимости х иу через и: 2у + 2 = 19/ =38н => у = 19н-1
19х = 21у+ 2 = 21(19и-1)+ 2 = 21 -19//-19 х = 21п-\.
(х = 21п-1,
Ответ:	где п е Z .
[у = 19и -1,
□ 11. Указание. Решить диофантово уравнение в целых числах и учесть,
что т > 0 , п > 0
154
Конкурсные задачи
[wi = 100, f/мо =16,
Ответ. <	<
[??! =1,	[и2 - 20
□ 12. Решение. 1) Перепишем уравнение в виде
19х -19 у = 3 - х ,
откуда следует, что 3-х делится на 19, поэтому
2) х-3 = 19л, ИЛИх = 19и + 3, где neZ.
3) По условию задачи требуется решить уравнение, то есть вьфазить у
через л : 19у = 20х-3 = 20(19и + 3)-3 = 20-19и+ 57 , илиу = 20«+3.
4) Осталось найти сумму трех наименьших положительных х :
при п = 0 х{} = 3 ; при п = 1 х, = 22 ; при п = 2 х2 = 41 .
(х = 19н+3,
Ответ: <	сумма равна 66
[у = 20л + 3,
□ 13. Решение. Имеем ат = 1т , bk = 3 + 4(к -1) = 4к -1. Найдем формулу
общего члена двух прогрессий; для чего решим диофантово уравнение
1т = 4к -1, т, к е Z . (Решите уравнение самостоятельно!)
Получим к = 1п + 2 , откуда следует формула общего члена
Сп = 7 + 28(н-1), 1 < л < 100
Осталось найти сумму первых ста общих членов:
S|„.ze>.„WJ„.
Ответ: 138950
□ 14. Ответ: L = 47 , М = 56 . Аналогичная задача решается в тексте.
□ 15. Решение.
fx2=9v2 + 7,	| (х-3у)(х + 3у) = 1 • 7 = 7-1 = (-1)(-7) = (-7)(-1),
|x,yeZ	[x^yeZ.
Поэтому надо рассмотреть 4 случая:
1) JX"3'V = L	f*l=4’	2) Р"3^ = "1’	Рг2=-4’
[х + Зу = 7	[ V] = 1,	[х + 3 у = -7	(уз = -1,
[х-3у = 7,	Гх3=4,	[х-Зу = -7,	[х4 = -4,
3) л	=> s	4)1	=> *(
|х + 3у = 1	|j>3 = -1,	[r + 3y = -l	|у4 = 1.
[л, = 4, |хп = -4, f х3 = 4,	[,v4 = -4,
Ответ: <	< “	<	<
bi = l-	Ьз = -1. 1у4 =1
- Т	r?ir" <-1 ч-г, > л м Г75» ТГ .-.ТЛТ  r<wr>ri4r. .1-	• Tr'Tnf I’UH'HVrrn'™	< •. S	I,’
□ 16. Решение.
[p2-2pq-3q2=~3. f(p + 7)(/; Зе/) =-3 = 1(-3) = (-1)3 = 3(-1) = (-3)1 ,
I p,qfEZ\	\ p.q^Z
Далее решается аналогично предыдущей задаче.
Решения, указания и ответы
155
|Р1 =0, IP? = °’
Ответ: <Г < 2
171=1;	[72=“1;
Рз =2.
,73 = 1.
Р4 = -2,
74 = “I-
□ 17. Решение. <	’ => у(х-!) = х. Поскольку х = 1 не является
[х,у е Z,
решением, то у -
= 1 +----. Откуда следует, что 1: (х -1) =>
□ 18. Решение.
*1=2.
71 =2
2)
х2 = 0.
У2 =°
Ответ:
х2 = О
т[т +
m,neZ:
т, п е Z,
=> у/п=п2-т => 4n=k,keZ,k>().
Откуда следует
Ответ'
п = к\
т=к4 -к,
где к е Z, к > 0 .
□ 19. Решение. <
|х,у е Z.
Поскольку 5у:5 , то (х2 + 2): 5 .
Рассмотрим все возможные остатки отделения х на 5.
1)	Если	х = 5т , то х2 + 2 = 25m2 +2 — не делится нацело на 5.
2)	Если	х = 5т + 1.то х2 + 2 = 25m2 + 10т + 3 — не делится нацело на	5.
3)	Если х = 5т + 2 . то х2 + 2 = 25т2 + 20т + 6 — не делится нацело на 5.
4)	Если	х = 5т + 3 , то х2 + 2 = 25т2 + 30m + 11 — не делится нацело	на	5.
5)	Если	х - 5т + 4 , то х2 + 2 = 25m2 + 40m + 18 — не делится нацело	на	5.
Откуда следует неразрешимость уравнения в целых числах.
□	20. Задача решается аналогично предыдущей.
□	21. Решение. Заметим, что п ф 0, п ф -3, п -6, п - 9, п ф -12 и преоб-
разуем левую часть уравнения:
3	3	3	3
и(и + 3) (и + 3)(л + 6) (7?+6)(п+9) (и + 9)(и+12)
1 W 1	1 И 1 I
---+-------------+-------------
n+6j ^и+6 n + 9y + 9 и + 12
156
Конкурсные задачи
_£__J_______4_
п п +12 15
откуда следует п(п +12) = 45 или и2 4-12и-45 = 0, И|=-15, л2=3
Ответ: щ =-15, п2 =3
**>	1 6». :а4»ыь»Н4*М'»м**г‘нч**Ы'* ►rtttWJH/wniNW'fru;'*'	-ч '
□ 22. Решение. Перепишем уравнение в виде у(3х +17) = -(14x4-71) По-
скольку xeZ , то Зх +17 * 0 , и можно разрешить уравнение относительно у
14x4-71 о 42x4-213	42x4-238-25 э 1л 25
у =---------=z> Зу =-------------=----------------=> 3v=-144--------------.
3x4-17	3x4-17	3x4-17	'	3x4-17
25
Поскольку Зу и 14 — целые, то-----------------тоже целое => 25 : (Зх 4-17),
3x4-17
[3x4-17 = ±1, ±5, ±25,
откуда следует	=> ^ =-4, х2 =-6, х^ =-14
fxj=-4,	(х2=-6,	1х3=-14.
Ответ: <	5	4
[у=-3,	[у2 = -13, [уз = -5
*•» <•	т*гь 4 > г’.лп-ч Iтгсяггвр-.^лгяи-’ *	г; r;rt,r»,> czzct ivm kirrn-’tw/ у »w*r , * - «
□	23. Аналогичная задача решается в тексте.
Ответ: (3,3). (5.0). (0:5).
-	<tt. 1»д«гл > иич<к,ч< -«лял* к-л.икм.хаи/г? ,»>w.	.чл-тхл» Tuasxijcorn ir . v - mei n	> c
□	24. Аналогичная задача решается в тексте.
Ответ- ш = (), п = ().
< 4 U tU J Л'/Ч< »м V '<7*Ч<ХГГ/ М-1ГХХХЖЛ I • 1“1 ЯХЯХ кг « Р-.-'ЯЛ». дха«	Г Л ДЖл/ i 4 Г f *	1 - •* У	•
□ 25. Решение. Перепишем уравнение в виде
(9у2 4- бу 4-1 )х2 4-(9у24-18у + 5)х + (2у2 4-7у4-6) = 0
V 4-2
и решим его как квадратное относительно х , откуда получим Х| = -----------,
3 V 4- 1
2р + 3 D
х2 = —:-- Решая два последних уравнения в целых числах, получим
2
Ответ: <{	<
1°;
< /V .с *ЧГ »Т » J ч I	»»	<•<	*’».*••	'• V» >	'f*	» -	•» »	«t с*^ t - \ -г 4 t onwtlbr* • t
□	26. Аналогичная задача рассматривается в тексте.
[х = 2, [х = -2.
Ответ- <	<
7	(	3 V 4
□	27. Решение. 5п -6//4-1 = 5|н-~I -у. Проверяем ближайшие к вер-
<3	4^
шине параболы I у, - — I целые значения п = о и 1. Имеем 1 > 0 и 0 > о.
□	28. Указание. После подстановки х = -2, -1,0 J неравенство
2/14-1 >2log2(«4-2) доказать методом математической индукции.
Решения, указания и ответы	157
' Ь- ♦	АХЧГ.<О Л’» -	?	/.«<'	---	i
□	29. См. решение аналогичной задачи в основном тексте.
Ответ' л- = 4 .
□	30. Решение. Допустимые* ^5^>q*	-2<х<5. xeZ.
Затем упростим исходное неравенство (возведем в четвертую степень):
VT+2 <
Теперь последовательно подставляем
1)	х = -2 , неравенство очевидно выполнено.
2)	х = -1. неравенство очевидно выполнено;
3)	л* = 0 , V2<^5?	<=>	24 = 16 < 53 = 125 , выполнено;
4)	х = 1, ^3<^4 ?	<=>	34=81 > 43 =64, нет.
Дальше проверять не надо из-за монотонности.
Ответ, х - -2 , л = -1. х = 0
□	31. Аналогичная задача решается в тексте.
Ответ, к =-2.
ч « v< и t. V». ••J I v| Jf '4	Ш i ip*-*.-'*" % Ч-Т <4 -	* •*	*
□	32. Аналогичная задача решается в тексте.
..	5	8
Ответ'	*.	= -,	*2	= ~•
1	3	3
□ 33. Решение, (п2-3)(л/2-33)(>г-103)(?г-2ОЗ)< 0, neZ.
Введем переменную х = н2 и пользуемся методом интервалов (см рис. 12).
Рис. 12
Отсюда следует, что неравенство имеет решения при
3 < п~ < 33 п = ±2, ±3, ±4, ±5,
103<н2<203 => // = ±11.±12,±13,±14
Всего 16 решений.
Ответ 16 решений.
□ 34. Указание. Условия разрешимости
позволяют рассмотреть 5 случаев
1)	х = -4 не подходит;
2)	* = -3;
7х-х3-5>0.	(*(*“- 7) <-5,
х + 4>0	1л‘>-4
158	Конкурсные задачи
3)	х = -2,-1,0 нет решений;
4)	х = 1.2;
5)	х = 3,4,5.... нет решений.
Ответ • х - -3. х = 1. х = 2
□	35. Аналогичная задача решается в тексте.
Ответ: х = -3. у = -3, z = ~ 4
□	36. Решение.
X + V > 25.
2х 418 > v > 25 - х Зх > 7.
у <2x418.
Л	2x418 > у > х~44х => х“+2х-18<0
X, у € Z
-1	< г < -1 + ^19 . а так как (-1 - V?9) е (-6. -5).
(-1 + д/Й)) е (3.4). — е (2.3), то единственное х е Z . которое может быть
решением системы, это х = 3 Подставим в исходную систему и получим
у >22.
< v < 24, v - 22,23, 24
у >21
ответ: Х|=3- ^ = 3- Г = 3-
[У] = 22.	[ у 2 = 23. |уз = 24
□ 37. Решение. Выразим М и У через К . Из первых двух уравнений
следует, что 5N = К 4 43. 5Л / = К 4103 . Отсюда из соображений делимости
получим К = 5L 42 . где LeZ .
[5Л’= 5Л 42 443 = 5Л 445 У -Л4 9,
|5Л/=5Л424103 = 5Л4105 => Л/= />421.
Х' = 5Л42>12.
К 4 ЛУ 4 .V = 51 j 424/>494/>421 = 7/>4 32 < 60
Решения, указания и ответы
159
K = 5L + 2y
M=L+2\,
N = L + 9
Ответ:
□ 38. Решение.
х2 - 2ху 4-12 = О,
х2 4-4у“ < 60,	=>
х е Z
4у“ < 60 - х~ => 4у“ < 60,
л2 =60-4/ <60-48 = 12.
X € Z
х ф О,
х2 4-12 х 6
У~-------= —4-— ,
2х 2 х
12<>-2<15,
х2<12.
хе Z
Решив эту систему, получим
/=3.	1х; =-3,
Ответ' <	<
|У1 = 3 5,	[у2 -•-3 5
* .1 tr ***-<**т1 *•	varr-»». «zz'tok * *гву**-/»»	. », л-v >	* • - -» - i.
□	39. Ответ: 743 Аналогичная задача решается в тексте.
□	40. Ответ: (3,-4), (4,-5) Аналогичная задача решается в тексте.
□	41. Ответ: (11,-9) Аналогичная задача решается в тексте.
Ч <r»v r7.-rrrr*^IT!?«WWr:crWA^K«-*	HW*-r ,	•J-’.'V * »
□	42. Ответ: (-3.-5), (0,0), (3,5) См. решение в тексте.
□	43. Аналогичная задача решается в тексте.
(w = 5,	[ и = 6,	I и - 6,	[м = 7.
Ответ: \	\	\	\
[/ = 1.	р=1;	р = 1,	|/ = 1,
□	44. Аналогичная задача решается в тексте.
1т = -13,
Ответ' <
1/7=17
160
Конкурсные задачи
□ 45, Решение.
Зл2 + 1 \ху + Юу" -1.
л' + у О,
Да ~х - Зау < О
I.	Прежде всего решим в целых числах квадратное уравнение Зх2 + 1 lxv+10y2 = (x + 2v)(3x + 5v) = 7 = 7 1 = 1 -7 = (-7)-(-1) = (-!)• (-7)
	[х + 2у = 7,	[х = -33,	(х + 2у = 1.	(х = 9. [З.г + 5у = 1	|у = 20,	[Зх + 5у = 7	[у = -4, jx + 2y = -7,	fx = 33,	f.r + 2y = -l,	J.v = -9, |3x + 5y = -l	|y = -20;	(Зх + 5у = -7	|.v = 4
и	Из четырех пар чисел неравенству v + у > о удовлетворяют пары
	(х = 9,	(х = 33. |у = -4	[у = -20
III	Подставим найденные значения л.у в неравенство Да2х-3ау<{) :
36а2+12а = 12(3а2 +«)<(),	(1)
132а2+60а = 12(11а2+5а) <0 .	(2)
Из условия задачи следует, что нам надо найти значения а . при которых
выполняется только одно из неравенств (1), (2)
Так как неравенство (1) имеет решение < а < (), а неравенство (2) —
решение - ~ < а < о, то лишь одно из неравенств выполняется при
5	1	5	1
---< а < —. так как----< —
11	3	11	3
п ( 5 И
Ill 3 J
□	46. Аналогичная задача решается в тексте.
Ответ: к = 2. t) 2=cos—, у12=±1.
□	47. Аналогичная задача решается в тексте.
Ответ• а > 224 .
□	48. Указание. Начнем проверять условия задачи последовательно при
а = -1. -2. -3;.... Убедимся, построив конкретный пример, что <7 = -1 и
а = -2 не годятся. Далее как в аналогичной задаче из текста.
Ответ: а = -3. -4, -5,...
Решения, указания и ответы	161
17	7
□	49. Ответ: при р = -5,-----< р < -- . Аналогичная задача решается
в тексте.
□	50. Решение. Пусть при всех х е R выполнено равенство
х2 - (а + 5)х + 5а + 1 = (х4-6)(х4-с) = х2 +(b +с)х + Ьс . Тогда получим систем}7
а, Ь, с е Z,
Ь 4- с = - (а + 5),
Ьс = 5а 4-1
а, Ь, с е Z,
с = -(а + b 4-5),
Ьс = 5а 4-1
a.b е Z,
- b(a + b 4- 5) = 5а 4-1
a, b е Z,
э	—
-а(Ь 4-5) = -(b“ + 5Ь 4-1)
а. h е Z,
Л2+5/> + 1	,	1
а =----------= -Ь-------
Ь+5	Ь + 5
Отсюда следует, что Ь + 5 = ± 1, поэтому Ь} = - 6, 62 = ~4
Ответ:	=7, а2 = 3 .
• * ik » » ПОТА* V-' лл - \	- »*• +* ****	t	» ' - »	- *	-
□ 51. Указание. Переписать систему в виде
(у -2x4-й 4-1)2 -(н 4-1)2 4-2м2 = 0,
(У-Х4-2)2 = 12и2-12и-4
Написать условия разрешимости
I + 2п -п2 >0,
4(3>Г -Зи-1) >0
-2н -1 <0,
Зн2-Зн-]>0
1-72 <п< \+Ц.
Зп2 - Зп -1 > 0
« = 0.1,2,
Зм2 - 3« -1 > 0
п - 2 .
Решить совокупность из четырех линейных систем.
Ответ: п = 2. (2-275,-475), (2+275,475), (-275,-2-475),
(275,475-2).
з-	—о--	.г * г -u »iv (^*'нш;£глтх;.	l * ' л .1. »•	мхзгочч.
□	52. Аналогичная задача решается в тексте.
z.	5	1
Ответ:-------< а < —.
11	3
I	f .	Г-ГГЧ* S*	Л ч*	*№>!'•,> СЧ i *,V “•/ИГ*. 'Л * «* I	TJ5, < ' /	<«/	« -
□	53. Указание. Выделяя полный квадрат у знаменателя дроби
Я2 4- р2 4- 4 - (| X 4- 2 | 4- 71 - р)2 < ЯГ2 4- /?2 4- 4
и учитывая выписанную оценку сверху, переходим от уравнения к равно-
сильной системе
1*4-2 | -р 4-7Г = 0,
(х 4- Зр - Зтт - 4 )( |х 4- 71 I 4-р - 2тг 4- 2) = 0,
которая распадается на совокупность двух систем:
162
Конкурсные задачи
Далее задача решается аналогично рассмотренной в тексте.
Ответ: р}= я , р2 = я + \, р3 = я+3 .
-**ЖК»ГЕП1 rywrVV*3TSS5P*V*»*<<* *»	ГТТК-ЧГ -МГ»’»»*ПТ»'Г,^ЗГ	’WHO <Г »	’VrFWV X “ П1ми»д» А • '<*» *
□ 54. Решается так же, как и задача в тексте, но минимум по п достигает-
ся в двух точках: п = 4 и п = 5.
Ответ: а4 = а5 - -15 .
‘гаг гглтжжс»»»*г*« -* <ч wti4 l tri п-ъул. »«<ч t *!•*• .v w	/%**»**•<.«*•»» '**’*▼» ‘«r»- »-*•*» mn* .**•*»». «-* * -i * 7 ‘ •’*
□ 55. Решение. Обозначим an=bn-cn, где bn = и2 - 8н +15 = (и - 4)2 -1,
9	9
сп = —----~ • Далее, min bn = b4 = -1. max сп =	= — , так как
16	16	99
---5<6-------. Но поскольку а4=-1-----------------------------<0--=а5, то минимальный
3	3	22	7
член четвертый.
Z.	31
Ответ: а4 =----
22
Г -к	• эг'*\г>илгг;лгпосеж>^гж« »T««*trr. тп»-г»1лсстотпаяпЕиагая ХЯПО«Ж-. ” KT'XIXXX’V % т» *.*х > • - .. 1 - о
□	56. Решение. Перепишем данное выражение
п2 +4н -33 = п(п + 4)-33 .
Так как числа п и п + 4 имеют одинаковую четность, то данное выражение
делится на 2 тогда и только тогда, когда п — нечетно. Подставив
п = 2k 4-1, ПОЛуЧИМ, ЧТО
и(и+4)-33 = 4£2 + 12^-28 = 4(/с2 + Зк-7).
Заметим, что выражение в скобках не делится на 2 ни при четных к . ни
при нечетных к .
Ответ: вторую
»•<	...	Л, Л ММСММЖ.ЪМСМтеСМ''”**'». ’Z.M* ’* 45. X	•
□	57. См. решение аналогичной задачи в основном тексте.
Ответ: п-5.
□	58. См. решение аналогичной задачи в основном тексте.
Ответ: maxSn = S6 = 78 .
□	59. Ответ: 14 .
-	чи. здх1Жлхгм,«’де *'>•>»« л *эттаг»- г'нп«лг?~ххпклг*7'иэ»ыиа>1хуп1лм	»	• •
□ 60. Решение. Обозначения см. в основном тексте.
pV = 2ra,
[?/= 5(г-2)(п -15).
Докажем, что НОД (п, п -15) = 15 аналогично разобранному примеру. Под-
ставим п = 15/ и придем к уравнениям
fW = 215r/,
[N = 5 • 15 (r-2)(Z-l).
Решения, указания и ответы
163
По аналогии НОД (г,г-2) = 2. Подставим г = 2q и, исключив N, перей-
дем к уравнению второго порядка
2/</= 5(/-1)(<? - 1) , 3lq-5q = 5l-5.
51 - 5 ,	2/	1	,	1
q —-------— 1 Ч------— 1 Ч------------= 1 Ч---:——
31-5	31-5	(3/-5)/2/	\ +
2/
Для того чтобы q было целым, необходимо (и достаточно), чтобы
/-5 = 0. Итак, имеем / = 5, q = 2 и г = 4, w = 75. Значит, 2т = 600.
Ответ: 600.
□ 61. Аналогичная задача решается в тексте.
Ответ: А = 27, / = 189, т = 1323 .
-	<vl<r «X/	.<#«• hWVM •‘/MUK'dMtf''«t*	*• j rOAttiUAMtCltM «<Л. Г~Г ’» S * ’	”»» V .«X -<«
□	62. Аналогичная задача решается в тексте.
Ответ: л = 6 .
□	63. См аналогичную задачу в тексте.
Ответ: т-5 \ нет.
□	64. Аналогичная задача решается в тексте.
Ответ: 5700 тыс. руб. и 6100 тыс. руб.
П г t, tMJ J -W	b*.it*4A'.VV'VAM.'U‘J v 1*- 1 r«U«AKM	Л<е>.>Л*%иЧМ’Л«Л1Г» М4ЛГ 4J04AW	‘	’	«- * '
□	65. Аналогичная задача решается в тексте.
Ответ: 123 кг, 158 кг.
►	- *»'/-’TVTomr im"iTminTmtr ^TErurj—va» * mn»rr чг <-iTT#k*n—т^ч<х^1г*»»жк»^»хтг»сж?Л?г«»ж»*«м’г1 г .	- i t rutitycrj-rrt st?
□ 66. Решение. Пусть сделано а операций первого типа, Ь операций вто-
рого типа, с —третьего и d —четвертого. Тогда
\3 + 2a+b-2c-d = 37.
17 - а+ 2Ь + с - 2d = 43, =>
a,b,c,d е Z, а,6,с,^>0
2а Ч- b - 2с - d - 24,
- а+2Ь +с - 2d = 26,
abb,c,d е Z, a,6,c,d>0.
Умножим второе уравнение на 2 и сложим с первым. В результате полу-
чим 5(6 - d) = 76, что невозможно, так как 76 не делится на 5 .
Ответ: нельзя.
□ 67. Для того чтобы трехчлен «2+3« + 5 делился на 121, необходимо,
чтобы он же делился на 11. Представим п в виде п = 1 \к + q и рассмотрим
всевозможные остатки ^ = 0,1,2,...,10. При подстановке выясняется, что
единственным значением q , когда п2 ч- Зл ч- 5 делится на 11, является q = 4 .
Но при 9 = 4: и2 +3п+ 5 = (11Л+4)2 +3(11/с+4) + 5 = 121Р +121^ + 33 — не де-
лится на 121.
□ 68. Решение. л = 10шч-« , Тогда w,«gZ, 0 <| т|, |п | < 9, |т | ф0, т.п —
одного знака.
164
Конкурсные задачи
п2 + 2т2 = 3(14-/пл) => п2 + 3тп + 2т2 =42 => (п + т)(п + 2т) =
= 42 = 1-42 = (-1)-("42) = 2 21 = (-2)-(-21) = 3-14 = (-3)• (-14) = 6• 7 = (-6)-(-7) =
= 7-6 = (-7)4-6) = 14-3 = (-14)4-3) = 21-2 = (-21)-(-2) = 42-1 = (-42) (-1)
Заметим, что \(п + 2т)-(п+т)\ = \т\<9 у поэтому первые шесть и послед-
ние шесть вариантов не годятся. Остается рассмотреть случаи
. ч f«4-w = 6,
1) <	=> т = 1, п - 5, х = 15,
л 4- 2т = 7
{п + т = -6,
=> т - -1, п = - 5, х = -15,
п + 2т = -7
3) <	’ => nt = -1, п = 8 — не годится, так как т, п — разных знаков.
п 4- 2т = 6
4)	’ r=> m = 1, w = - 8 — не годится, так как т .п - - разных знаков;
+ 2т = -6
Ответ: х = ± 15
□ 69. Решение. Занумеруем числа в порядке возрастания, так что
Л| < х2 <	< х4 < xs. Отсюда следует
[х] 4- А'2 -	+ х3 - Л*1 + х4 - *1 + ЛЧ - х2 +XS - *3 + XS - Л4 + *5 '
[Л*] 4- Х3 < Х2 + Х$ < Х2 + Х4 < Х3 + Х4 S Л’з 4 Х5 .
Заметим, что в выписанных неравенствах встречаются все десять возмож-
ных попарных сумм. Наименьшими среди них, как видно, являются х, 4-х2
и Л] 4-х3, а наибольшими — х3 + х5 и х4 4-xs. Таким образом получаем сис-
тему четырех уравнений с пятью неизвестными
х, 4- х2 = 0 ,	( 1 )
л*1 4- х3 = 2,	(2 )
\34-Л5=13,	(3)
х44-х5=15	(4)
Чтобы получить пятое уравнение заметим, что каждое из чисел
Л], л-3, л3, л4, х5 встречается во всех попарных суммах 4 раза, поэтому
4 (л‘| 4- х2 4*х3 4-Jt4 4-Х<5) = 0 4-24-44-44-64-84-94-114-134-15 = 72
~Aq 4- Х2 4- Х3 4- Х4 4-	— 18	( 5 )
Сложим теперь первое, второе и четвертое уравнения системы и получим
X! 4- (xj +х2 4-х3 4-х4 4-х5) = 17. откуда следует Х| = -1 . Далее нетрудно полу-
чить х5 = 10 .
Ответ: наименьшее число равно -1, наибольшее число равно 10
Решения, указания и ответы
165
□	70. Решение. Рассмотрим функцию /(х) = х2 +5^х + а. Ее графиком
с	„	5-72
является парабола с вершиной в точке	, и прямая х = х0 — ось
симметрии этой параболы. Рассмотрим целочисленные точки оси х и рас-
положим их в порядке возрастания расстояния относительно оси симмет-
рии. Поскольку -4<—-<-3.5 (проверьте!), получим последовательно
-4,-3,-5,-2,.... Полезно сделать рисунок, как в примере основного тек-
ста. Условие задачи будет выполнено, если меньший корень jq будет
- 5 < xj < -4, а больший х2---3 < х2 < -2 . Подставляя сюда корни и ре-
шая систему неравенств относительно а , получите ответ.
Но можно рассуждать иначе. Приходим к простой системе неравенств
f/(-3)<(),
1/(-5)>0
-25 + 25-72 <а<-9 + 15ч/2 .
25-25-72 +а>0
Ответ: 25(-Т2-1)<а<;3(5-72-3).
□	71. Указание. Представить число 2000! = 1 • 2 • 3-• 2000 по основной тео-
реме арифметики в виде 2^2 • З^3 • 5^5 • 7^7 •...• pkkp и подсчитать число к5.
Среди чисел 1-2-3-...-2000 имеется 2000:5 = 400 делящихся на 5,
2000.25 = 80 делящихся на 25 = 52 , 2000.125 = 16 делящихся на 125 = 53, и,
наконец, 2000 = 3-625 + 125 , т.е. 3 делящихся на 625 = 54 . Итак,
к5 =400 + 80 + 16 + 3 = 499 .
Легко сообразить, что нулей у 2000! будет ровно ks = 499 .
UtHlKKOW»»» Ч1«М1ММЫ«	ИМ**» l.hA»	. м. > »<
□ 72. Решение. 1. Ищем п е N , чтобы два числа
„	5600 25-52-7 х, х, 3024 24-33-7
Nj =----=---------е N и М2 ~~--------------G ™ •
п п	п + 5	п + 5
Если п делится на 5, то п + 5 тоже делится на 5 . Но этого быть не может
из-за второго условия — 3024 не делится на 5 . Значит, п = 2к - 7т, где
Аг = 0; 1; 2, 3; 4; 5, а т = 0, 1
2. Перебор, начиная с 1) т = 0 , при этом п = 2к = _1, 2, 4; 8; 16,32 , а
п + 5 = 6; 7; 9,13; 21;37 должно делить 3024 . Подходящие п подчеркнуты.
2) т = 1, при этом п = 2к • 7 = 7,14; 28, 56,112, 224, а
п + 5 = 12; 15; 33; 61; 117; 229 — только 12 делит 3024.
Вывод: искомые числа п . 1,2,4,7,16, а их сумма 1+2 + 4 + 7 + 16 = 30.
166	Конкурсные задачи
... ---—---...  ..штрихи	ibnKf.-л. •лЛ.*? .>4.	—-
□ 73. Ответ: а = ! (/ ±J/2 + 4Z -4) , где /-—, п - - 5,-4,-3; - 2
2	(л + 1)2
или п - 1,2,..., 17
, , I,	. .inm. iw.ww«Hi-~n i   г-1 < w.'»WT>r «ГК-ИГГМ*ИЛ|Г|w in> i. i« "*««	' - - r»i:.->r'v4 - -
□ 74. Указание. 4 (m2 + mn + 9n2):352 ,(2m + n)2 4-35«2 =352k =>(2m +n)2 : 35 ,
2m 4-« = 35/ }52/4-35«2 = 352&=>«2:35 и « = 35/, а, следовательно, m = 35p.
Ответ: 282 пары (35/;35/;), где p, / = 1,2,..., 28.
□ 75. Аналогичная задача решается в главе 1, §2, пример 10.
Ответ: 740232 : 749232
Глава 3.
I **.	'>1	X 11%	UAbXX'iAbU--	»> -аАЛ/ т	*»
□ 1. Решение. 23:17 = 1,3529411764705823529... = 1,(352941176470582).
'' s -’«rx.oaxtwjxxri г’1с^’хж1»л»»1гаа^«дагйж^«г»опжпотх1ссаогстапи«жлчяо£х.^«>х<>4«>т»ггпахп>ч«лгглу.<с’п.> ’	' •	•’
□ 2. Решение. 0,87(15) = 0,87+ -Ц- + Д- + -Ц-+... = 0.87 + Д--------------------------------------------—
104	106 К)8	104 1-10
= 0,87 + 15-------= 0,87 +-----------= 0,87 +--------=---------------------------=-=-.
0,99	99	3300	3300	3300 1650
□	3. Решение. Поскольку две периодические десятичные дроби представ-
ляют собой рациональные числа, то и их сумма — рациональное число, а,
следовательно, конечная десятичная либо бесконечная десятичная перио-
дическая дробь.
I t-. • « -Trr>ni<\r-rw.-u - .гг.1г..Г1<~“чт^гпл.>ттгг”И« я- -	.... a.i.- i	».»	w ”
□	4. Решение. По условию числа а.Ь и Ja + 4b — рациональны. Отсюда
следует рациональность числа 4b -4а =	• Значит, рациональны
2
2
»»к	»« '	- мммм«»»м «•„	ч+мле*
□	5. Ответ: дробь несократима.
Указание. Аналогичная задача решается в тексте.
.vi.auс»> .-' а. --jxextrист,.-улэппог, ха rucawaauctttf^wnaxaansaxxuJ^x-xxMxxi’tnxxsuxccrp ':аааиг. Сх , ,	. .	•.
□	6. Задача решается аналогично предыдущей.
□	7. Решение. Пусть k > 1 — общий делитель чисел п2 +1 и п2 - п +1, то-
гда выполнены равенства п2 +1 ~ kl и п2 - п +1 = кт . Поскольку
п = (п2 +1)- (н2 -« + !) = к(1-т), то тогда и число л делится на к . Но если
число п делится на к , то и п2 делится на к , а число п2 4-1 на к не делит-
ся Противоречие.
Решения, указания и ответы
167

□ 8. Решение. Пусть k — общий делитель чисел и1 2 3+2и+4 и и2 +п + 3.
Тогда выполнены равенства
п2 + 2п+4 = кт,
=> п +1 = к(т - /) — делится на
п2 + п 4- 3 = к1
к . Из последнего условия следует, что
\п2 4-2и 4-4 = (и 4-1)2 4-3 - делится на к,
|и2 4-п4-3 = (п4-1)2 -(«4-1)4-3 - делится на к.
Поэтому числа п2 4-2/? 4-4 и п2 4-и 4-3 могут иметь только общий делитель,
равный 3 . Выясним, при каких п это возможно.
1)	Если п = Зр , то п2 4-2/7 4-4 нс делится на 3 .
2)	Если /7 = 3/74-1, ТО п2 4-2/7 4-4 = (Зр4-1)2 4- 2(3/74-1)4-4 = 9/?2 4- 12/74-7 НС
делится на 3.
3)	Если п = Зр 4-2 , то
п2 4-2н 4-4 = (3/7 4- 2)2 4-2(3/7 4-2)4-4 =9/?2 4-18/7 4-12 делится на 3.
п2 + п + 3 = (Зр + 2)2 4-(3/?4-2) 4-3 = 9/72 4-15/74-9 делится на 3.
Ответ: при п = 3р 4-2, р е Z .
□ 9. Указание. Способом, аналогичным рассмотренному в предыдущей
задаче, выясним сначала, при каких п дробь сократима? Оказыва-
/72 -1
ется, что это так
□ 10. Решение.
п-} = ±1, ±5.
□ 11. Решение.
при п = Зк 4-1. Дал
3n+2 _ 3(n-l) + 5
n - 1	n -1
олли*/	>м.
m к
— 4-—= 1,
/7 I
« т,п, к, I &N,
m к
— y— - несокрап
зйшее очевидно.
Ответ: при /? = Зк, // = Зк 4- 2, к е Z .
5 ~
4----, Откуда следует
п -1
Ответ: {-4, 0, 2,6}.
т к	. .	,
=>---F — = 1 => ml +кп = nl .
п I
1) Перепишем последнее равенство в виде: nl - ml = кп => кп-.l. но А’ и /
общих множителей не имеют =>/?:/.
2) Перепишем равенство в виде nl - кн = ml => тГ.п , но т и п общих
множителей не имеют =>/•//.
3) Так как P.nm'.l .то н = /
□ 12. Решение. Решим уравнение
168	Конкурсные задачи
-л .	'	lively.,	«И.<мЛЛ
10gBx 13
= —, для чего прологарифми-
руем его по основанию 13. Получим квадратное уравнение
(logl3x)2-(log13 X)-(10gl37) = 1 -log)37,	откуда	следует
logi37±(log,3 7-2) Отсюда не-
2	2
трудно найти Xj 2.
Ответ: х1 = 13, х2 = —,Х) ,х2 е <2 •
□ 13. Решение. Если D = т2 - 4 > 0 (то есть	|т| > 2,т е Z ), то
-т±ут2-4	„
xj 2 =---------. По условию X) 2 eQ . Так как т — число целое, то
т2 -4 — целое. Это означает, что Jm2 -4 либо число целое, либо ирра-
циональное.
Пусть 4т2 -4 =ke'Z,k>0. Тогда, с учетом т - к < т + к получим
т2 -4 = к2 =>(w-^Xm + Ar) = 4 = (-4)(-l) = l-4 = 2-2 = (-2X-2). 4 случая:
|м + А: = 4,
2)	<	=> т <£ Z,
\т-к =1
т - k = -1
\т + к=2, т = 2.
3) <!	=><
]т -к = 2	1^ = 0;
т + к = -2,	(т = -2,
т-к~-2 [к = 0.
Ответ: при т = ± 2 .
□ 14. Решение, х2 + х+т = 0, х е £>, т g Z . Сначала выясним условие раз-
[meZ,
решимости квадратного уравнения: D = 1 - 4т > 0 => < Тогда
(т < 0.
-1 ± Vl -4/w А
*1,2 =----;----- Аналогично предыдущей задаче получим
2
^\-4т =keN!=> -4m = Z:2-l = (A-l)(/c + l)=>/c = 2/ + l=> -4w = 2/(2/+2) =>
т =-1(1 + 1), 0 < I е Z .
Ответ: при т = -/(/ +1), где / е Z,/ > 0 .
••	-ЛНГ**ЧТГ^	*• У-^ntt *♦ **»	> w Г» - * *** Н »v	»TK f I* ’•- *	>. » +. t.	e	V к'ОЧл. •!
□	15. Ответ: 2-Jl4 < 7.(48).
Указание. Аналогичная задача решается в тексте.
-р'1'э;'жх1«ампхшшхшгиаоишхадешзиг>.'.1МС1Я 4.'Гл*>Ас4>.<1	> « г	i г r.i’ ’,’wix > i	_s
□	16. Ответ: при М = 9,N - 0 .
Решения, указания и ответы	169
Указание. Докажите, что при увеличении Л/ значение дроби увеличивает-
ся при любом У. И, наоборот, при уменьшении N значение дроби увели-
чивается при любом М.
□	17. Указание. Все числа вида =r,+(r2-r1)/2w, где ле.¥. удовлетво-
ряют неравенству г} <гп <г2 и являются рациональными.
□	18. Решение. Так как а и Ь — рациональные числа, то представляю-
щие их десятичные дроби будут либо конечными, либо бесконечными пе-
риодическими. Докажем, что и число х будет представлено либо конечной,
либо бесконечной периодической дробью.
а)	Если обе дроби	и	конечны, то и число х будет
представлено конечной дробью, следовательно, в этом случае г — рацио-
нальное.
б)	Если одна из дробей, например	— конечная, а другая.
— бесконечная периодическая, то, начиная с некоторой позиции,
цифры дроби *0Л|*2-*з будут совпадать с цифрами дроби <^оЛЛ2^з ’ а’
следовательно, число х будет представлено периодической дробью, следо-
вательно, и в этом случае число х будет рациональным.
в)	Наконец, пусть обе дроби а^аха2а3 и Ь^.Ь}Ъ2ЬУ. являются бесконеч-
ными периодическими. Пусть периодичность первой дроби начинает про-
являться с /-й цифры и период состоит из к цифр, а у второй дроби перио-
дичность начинает проявляться с т-й цифры и ее период состоит из п
цифр. Тогда цифры дроби х^х}х2х3 будут начинать повторяться с цифры
номер Az = max(/,m), и цифры дроби х будут повторяться через Л/ кп
позиций. Следовательно, дробь х0.Х|Х2х3 будет периодической, следова-
тельно. и в этом случае х будет рациональным числом
□ 19. Решение. Если tga — рациональное число, то tg2a = -^~- также
1 -
является рациональным числом (результат арифметических действий с ра-
ч гт	. tg2a + tga
циональными числами есть рациональное число). Далее tg За =---------
1 - tg2a • tga
также рациональное число. Рассуждая по индукции, приходим к выводу,
что tgwa —рациональное число. Аналогично tgw/? —также рациональ-
ное число. И, наконец, tg (та + пр) =	----рациональное число.
1 - tgwa* tgH/7
□ 20. Решение. Заметим, что уравнение ах2 + (2а-\)х + а-2 = 0 является
линейным, если а = о, и квадратным, если а * о . Рассмотрим эти случаи.
1) Если а = 0 , -х — 2 = 0 => г - - 2 (рациональное)
170
Конкурсные задачи
2) Если а * 0, то условием разрешимости квадратного уравнения является
неравенство 4а +1 > 0 Поскольку а е Z , 0 # 0, то это означает а е N .
г-г	ът	-(2a-l)±V4a +1 z.
Пусть а е N , тогда 9 = —-------------е Q . Это может быть только если
а,
74л 4-1 = k е N или 4а = к2 -1 - (к -1) (к i I) Но, поскольку а е N , то равен-
ство может быть выполнено только если А -1 и А + 1 — два последователь-
ных четных числа. Итак, к -1 = 2п, к Н = 2п + 2 и поэтому 4а = 2п(2п 4-2)
или « = «(« + !) (*). Осталось заметить, что случай « = () соответствует
п = 0 и тоже описывается формулой (*).
Ответ' при а = и(и + 1), где п е Z , п > 0 .
□ 21. Решение. Заметим, что х = 1,у - о — решение нашего уравнения.
Если О,у) — какое-либо иное его решение, то в силу того, что х,у е О ,
х — 1
верно ---е Q и поэтому = Ху 4-1, где X е Q. Подставим рациональную
у
зависимость х от у в исходное уравнение.
(Ху 4-1)2 4- 2у2 = 1 ==> (Л2 4- 2)у2 4-2Ау = 0 (решение х - 1,у = 0 уже учтено)
=> (Л2 4-2)у 4-2Х = 0 => у = —,х - --	. Осталось представить X несо-
X2+2	2U2
кратимой дробью X = — , и тогда получим
п
Ответ:
2н~ - т2
x = ~2--Г'
<	+ ш	где т„п е Z .
_ 2пт
2п2 + т2
□	22. Решение. Пусть у - х = а е Q . Подставляя у = х 4- а в уравнение, име-
ем х1 4-3 = 2х4-(л4-л)2, 2(а 4- !)л* = 3-л2, х = ——-— (а #-1). и, следователь-
2(0 4-1)
но,
у=х+а=
а2 4- 2а 4-3
2(0 4-1)
3-0“	0“ 4-20 4-3	,
Ответ: х =--------, у =---------, где -1 а е О.
2(0 4-1)	2(0 4-1)
□	23. Решение. Если . х() — общий корень уравнений, то, подставляя его в
оба уравнения и вычитая их, получим х0(р - т) = п - q .
Если р - т, то все доказано (х0 0), и, следовательно, п - q = 0.
нений, получим, приводя
(и-^)2 +(р-тХрп-дт) = 0 .
противоречивому равенству
целое число. Остается р = т
Решения, указания и ответы	171
Если р * т, то добьемся, чтобы п - q и р-т были бы взаимно простыми.
сокращением. Теперь, подставляя	~—— в любое из двух данных урав-
р-т
к общему знаменателю и упрощая,
Поделив почленно на р - т * 0, приходим к
(" - я)2	*
-—^- = mq-np — слева дробь, справа —
р-т
И q = п.
□	24. Заметим, что cos9° = sin 81°, и задача свелась к уже рассмотренной.
□	25. Решение аналогично примеру, рассмотренному в тексте.
т= '° ^ = 10(712+-ЛТ). 3,31<7п <3,32; 3,46 < 712 < 3,47
712-711
67,7 = 10 • (3,31 + 3,46) < т < 10  (3,32 + 3,47) = 67,9.
Ответ: а = 67,8 .
□ 26. Решение. Пусть х = —, но п - т2 - I, поэтому
п
те/,
т
Л=^7’
т + 2	2
т2 + 1
„?-4 Ю
Нетрудно видеть, что т*±\.т*±2.т*() (при т = 0 не выполняется по-
следнее неравенство). Следовательно, поскольку т — целое, то т2 - 4>0
и мы получаем из последнего неравенства т > 3. Отсюда вытекает
т 6	> 3,
* Зт + 6>т2 +1,
10m-30<w2 -4
'j	4
т -Зм + 5<0, =>и/ = 4,и = 15,х =—
w2-IOm+26>0	15
Ответ: —
15
т 6 Z,
т _ 1 пГ - 1 Зт + 30 = 0 .
т т + 2	15
□ 27. Решение
т
х = —,
п
т.п е Z,
• т.п - взаимно простые, т- 1 _
п = т + 2,
п-3 т_ 1
, т п 15
1) т} = 10, но тогда п} = 12 и дробь сократима.
2) т2 = 3, тогда п2 = 5, дробь несократима.
172
Конкурсные задачи
з
Ответ: —.
5
□ 28. Решение. Пусть х = 0.(25) = 0.252525. и у = 0,5252525... Рассмотрим
25
100х = 25,2525. и вычтем х . Тогда 99х = 25 и х = — .
99
С другой стороны, имеем 1 000 у = 525,2525... и вычтем из него К) у = 5.2525 ..
Тогда 990у = 520 и у -	.
у 52 25 52	2
Искомое соотношение — = — — = — = 2— = 2.08 .
х 99 99 25	25
Ответ: 2,08.
□ 29. Решение. Упростим данное число х >() следующим образом
16 4-2^64-63
6 -2л/9^5
Ответ: рациональное (даже целое).
□ 30. Решение. Пусть заданное число рационально, т.е.
log2n_|(?r+2) = -, 0^, dtZ.
Я
Так как п2 + 2 > 2п -1 при любом целом н , то log2п i (и2 + 2) > 1 при лю-
бом натуральном п > 2 Значит, d и q — натуральные числа и
(н2 2 У7 = (2/1 - 1)с/, т.е. у чисел п2 + 2 и 2// - 1 одни простые делители.
Если р — общий простой делитель п2 + 2 и 2// -1. то
п2 + 2 = pN,
2п - 1 = рЛ/,
где N и К! — натуральные. Исключим в левой части п . Для этого первое
равенство домножим на 4. а второе — на (2н +1) и вычтем почленно одно
из другого. Получим 9 = 4 (л2 +2)-(2н - 1)(2и +1) = (4N ~(2п + ЦМ )p=kp .
k — целое. Значит, р — делитель 9, т.е. р = 3 . Следовательно, числа
п2 + 2 и 2н -1 являются степенями тройки:
н 4-2 = 3 ,
2л - 1 = з'.
причем т > /. Поскольку 9 = 4(и2 + 2)-(2л-1)(2л+ 1) = 4-3"' - (З1 + 2)-31 -
= 3' (4-3™ '-3'-2).то / = 2. ш = 3 Тогда» = 5
Ответ. п = 5 .
Замечание 1. Решение написал В С. Панферов.
Решения, указания и ответы	173
Замечание 2. Ответ п = 5 был у многих учеников, но они его получили
"тупым” подбором, не зная, при каком п остановиться.
Li j-aa'i .ч.-^ .   ..
□	31. Решение. Идея: если знаменатели дробей достаточно велики и каж-
дая из дробей больше ~, то сумма больше 1.
D	3995	2002
Возьмем, например, ------ и------.
4000	4000
Ответ, может.
Iga^.a
□	32. Решение. Пусть дробь формально сократима, т.е. =4= = — . Про-
аа ...ад д
п
ведем последовательность эквивалентных преобразований:
д-10" + д-а-10"“1 + д-а-10"~2 + ...+ да-10 + да =
= 10-а-10"“1 + 10-а-10"~2+... + 10а + д,
аСО-дНЮ”'1 + 10"’2 + .. + 101 +10°) = д(10"-1),
a(10-g)HLJ = g99979
п	п
Так как 999.. 9 = 9-111...!, то получаем уравнение а(10-д) = 9д При нали-
п	п
чии ограничений на а и д система
1<а<9,
* 1 < д 9,
а (10 - д) = 9д
имеет только два решения: а = 6, д = 4 и а = 9, д = 5 . Таким образом суще-
ствуют только два класса формально сократимых дробей, а именно
п _ 166...6 п _ 199...9
'<б)4 = 66^ И Г(9)5 = ^5 ' 
Как следствие мы имеем, что дробь вида а формально не сократима
аа...аЗ
ни при каком 1 < а < 9 .
Глава 4.
□	1. Решение. Рассмотрим линейную функцию вида y(t} = a + t(b - а), где
t € [0; 1]. Нетрудно видеть, что у(/) строго возрастает на [0; 1] и что мно-
жеством се значений является отрезок [ а\ Ь ]. Тогда число
(ЛД Лч	1Ч fVsT , (vr
у — = а + -(Ь-а) удовлетворяет условиям: 1) а<у — <6; 2) у —
2
7
7
2
2
2
V2 /L ч
— иррациональным, так как а —рациональное, а — (Ь-а) —иррацио-
нальное.
□	2. Решение. Пусть для определенности а > О и р > 0 . Представим числа
а и р в виде десятичных дробей: а = а^аха2аъ , Р-Ь^,ЪхЬгЪъ где л()
и Ло — целые части чисел а и р .
Поскольку а и р — иррациональные числа, то десятичные дроби будут
бесконечными и непериодическими. Поскольку а < р , то найдется номер
к такой, что а0 =	’•••»%-] -Ьк-\'ак <^>к • Возьмем конечную деся-
тичную дробь а = Ьо,Ь}Ь2...Ьк . Тогда а — рациональное, и а <а<р
□	3. Решение. Пусть это не так, тогда х — периодическая дробь. Предпо-
ложим, что период х = 0,1234567891011121314 .. начинается с и-й позиции
после запятой и состоит из к цифр. Так как в ряде натуральных чисел при-
сутствует число 10"+* = 1 000_0 , и это число заведомо находится после
к нулей
п -й позиции после запятой, то получается, что в области периодичности
дроби имеются подряд п + к нулей. Но поскольку период состоит из к
цифр, то отсюда следует, что все цифры периода — нули. Это противоре-
чит алгоритму построения числа х .
.................................... ........................ XX-UBCJ .
□	4. Решение. He обязательно. Приведем пример.
1) Построим число а по следующему правилу: а = 0,8а28а48«б8. , где по-
следовательность десятичных цифр с четными номерами [а2к] — непе-
риодическая и а2к <8. Тогда а —иррациональное число.
2) Построим число Ь по следующему правилу: Ь = 0,^8/>38/>58 ., где по-
следовательность десятичных цифр с нечетными номерами (Z>2*+i} — не“
периодическая и 62*+i 8 •
Решения, указания и ответы	175
&
Тогда число с, где ck = тах{а^ ,Ьк}, имеет вид с = 0,888...= — — рациональ-
ное число.
л*	'г* -тчм*п«♦*	*.• м.г	» t. и л "г«
□	5. Решение. Поскольку каждая цифра данной дроби, начиная с третьей,
определяется двумя предыдущими, то признаком периодичности дроби
является повторение двух цифр ата„п} =ат+кат^.кп . Выпишем дробь
а = 0,П2358314594370774156178538190998752796516730336954932572910П.. =>
число а — рациональное.
□	6. Решение. Пусть = J— =~ — несократимая дробь. Тогда
V10 п
3	* 2
— =	3/22 = Юли2	число л2:Ю => л:Ю,и = ЮЛ => 300Л2 =
10 п2
Юли2 => ЗОЛ2 = т2 => лн2:10 => пгЛО => т = 10/ => п = 10Л,т -10/ ==> противоре-
чие с предположением несократимости.
□ 7. Доказательство можно провести двумя способами:
1) аналогично предыдущей задаче;
2) сослаться на теорему 1.
□ 8. Решение. Пусть 0 < log2 7 = —, где т,п е Л' => 2” =7 => 2т = 7” , но
п
2т не делится нацело на 7, а 7”:7=> противоречие =>log27 — иррацио-
нальное число.
□ 9. Доказательство аналогичное предыдущей задаче.
□ 10. Предположим противное. Пусть logmw = —, где p,q<EN . Тогда
Я
mp/q = п или тр = nq . Но последнее равенство невозможно, так как т и
п — взаимно простые числа, и поэтому тр и nq — также взаимно про-
стые числа.
г*ж«ч,гл*ь-»<»сг\*^ «глл чгк (имн*.- urv* • л уj<r>. v-r.rtv	st*»	у	x yr.»w\ лгз »-•- *	.	s t . i
□ 11. Пусть cos5° eQ => cos 10° = 2cos2 5° -1 eQ => cos30° =	=
4cos310°- 3cos 10° g()=>V3 eg —противоречие.
В»»»».»»	».»И^Ла.Г.а»МДДЫЛИЛД»>Г|>1« ММ1КЫ«и»М»Л. «11»	. ...	>«ЗДК<г. /
□ 12-17. Доказательство аналогичное.
176	Конкурсные задачи
г	j^rs3SS4KjasM№»amKnуапыгияямллям»»шпипгумьт«Ю№«>т^итгп«гтарь.^*йД»А.-1и»/л*~-\к.«ам »».*м kv««h< мл . w - >'. -
□ 18. Пусть sm25°6 2=>sm75o=3sm25o^sm325°eP- Но sin75°= cos 15° =
= cos(45°-30°) = g Q . Противоречие.
4
□ 19. Указание. Достаточно показать, что V10Z/+2 g N .
, »^ххгг^ХА4А1оаакжмиг/м ж^м.ждмхжп)Х2*жа«ж»4пж0оошдехшодо<*дж)ииысмшшжж&«*вммии1хА>*вк)скхжикммдхдодлхъх.ж * и> axcaaja*^ • * s < *
□ 20. Задача решается аналогично предыдущей.
□ 21. Решение. у(х) = cosx+ со$4зх,у((У) = 2 . Пусть у(х) —периодическая
и пусть Т>0 — период. Тогда у(х + Т) = у(х) для любого xeR , в частно-
[ cosT = 1, (Т = 2nk, г- п
сти, у(Г) = у(0) = 2=>^ г-	г- =>уЗ=----------противоречие.
[cosV37, = l |у37’ = 27гн к
□ 22. Решение. Решим уравнение р2 -6pq-9q2 = 0 в целых числах. Если
q = 0, то /? = (). Пусть q*0. Обозначим х = — еQ и поделим уравнение на
q2. Тогда х2-6х-9 =0,х = 3±2«/з е£?=> уравнение х2-6х-9 = 0 рацио-
нальных корней не имеет ==> уравнение р2 -6pq-9q2 =0 нс имеет иных
целых решений, кроме р = q = 0.
' *•'•”*«	ггт->’-г*«г\жгт-ч w «virrvT•’•гч> .iivii пт.	। % * i п «» • »- > * г» »
□ 23. Предположим противное. Пусть х1 е Q, х2 . Но тогда согласно
теореме Виета ~(х| + х2) = р * Q , что противоречит условию задачи.
-- •. чи» ^члтл»ч*. л,али-1« ъд.лсж<х»4г * »улл.	* *л-«> «ьдегл*».* д^мг^гкгжяажжмжхх» *	глалжжйл^-» • * *г . >*•	•
□ 24. Существует. Например, построим приведенное квадратное уравне-
ние, имеющее корни у/2 и i. Согласно обратной теореме Виета это урав-
? f I— 1	л/2*
ненис имеет вид х - V2+-х + —= 0. Поэтому в нашем примере
( г- 1А	72
а = -\у2 + —) — иррациональное и р = 2L--------------------------------также иррациональное.
r«rv»> TV ГО ^tASnU'*r*nMMr<tn*t»T'*9Tr>*rrvvrrr<nv«	iTaTzr mrYW Y>XYW«r«rV«> > . •'Гжаеж%АХГ»АК>ЗГ’1Г* ft	.!*(#<	- Ц”'*’
□ 25. Например, уравнение х4-16х2+4 = 0.
Замечание: уравнение второй степени написать нельзя.
..КЧ-7 лмт , -Г -ч kV, rrvJ(<vZ^T ЖМГЛ	»-r*t Ъ*-Г -	-	*
+ / 2 _ д
□	26. Решение. х} 2 = —~ ~	, поэтому достаточно показать, что
р2 -4q не может быть квадратом целого числа. Пусть это не так и
^р2 ~	> где m g Z . Но тогда m — число нечетное, так как р и q —
Решения, указания и ответы	177
нечетные, поэтому т = 2k + 1 и мы получаем ^р2 -4q = 2k +1 =>
4q = (2k + I)2 - p1 = (2k + I)2 - (21 + l)2 (число p — нечетное). Из послед-
него равенства следует 4q = (2k + I)2 - (21 +1)2 =
= (2k - 2l)(2k + 21 + 2) = 4(k - l)(k + I + 1) => q = (k - l)(k + I + 1) =
= (k - l)(k - I +1 + 21) = (k - l)(k - I +1) + 2l(k - /). Но последнее равенство
невозможно, так как q — число нечетное, а число (к -l)(k - I + 1) + 2l(k -1)
четное.
□	27. Ответ: а) не могут, б) могут.
г~	9
а)	Пусть 2 = Я| + (т - l)d - ат, у]6 = а} +(п - \)d = ап, — = Я| +(к - 1)е/ = ак
_ ак -а к-н 2	9-2V6 тт к - п
Тогда —-----~ =-----= ~-----=-----— . Но ------ — рациональное чис-
ак-ап1 к-т 9_^	5	к-т
2
9-2-Тб
л о, а---------иррациональное — противоречие.
б) Пусть 2 = b}qm 1
l п 1 L 9 q2
= Ь\Я =^П' - = 3
= ь]Як-' =ьк.
Тогда
2(к п)
^к _ ак-т _
Ьт~Ч
ь„ U
откуда
следует
(к-т)(к- п) _ Г 3
"<2.
4(к - н) = 3(к - т) или к ч- Зт = 4п .Последнее возможно, например, если
Г- 9
к = \т = 1,и = 2 . Поэтому числа 2,<6,— могут, например, являться первым,
вторым и пятым членами геометрической прогрессии
или
или

□ 28. а) Не может, так как по теореме Виета
5
6-У5
-у- = -р Q , а по условию задачи р е Q.
б)	Не может, так как xj • х2 = q = - О .
V5
в)	Может. Например, уравнение г2 - 2х - 6 = 0 .
178	Конкурсные задачи
I 2
□ 29. xj 2 =	—— e Q. Согласно теореме 1 число <jp2 -4q либо
иррациональное, либо целое. Иррациональность невозможна, иначе бы
•vi,2 & Q • Следовательно, ^р2 -4q — целое. Тогда есть две возможности.
1)	р —нечетное, тогда ^р2-4q —нечетное, и числа -р±^р2 -4q —
четные => х},х2 eZ .
2)	р — четное, тогда ^р2 ~4q — четное, и числа - р ± ^р2 ~4q — чет-
ные => хьх2 е Z .
* v-tv* - *» ’^чг*нч»1м<‘1м<у*л«л	и *^vr*>»wrt4tT«vi»n¥rwww*ww<'WWJnt£’HAt'-'<»r,*r',.m ч*-«. t •/$>»»>*	» t i)v<<	* » т -г
□ 30. Решение. 1) При х = у ~ 0 2х - Зу = 1.
2) Пусть х * 0, тогда и у * 0. Прологарифмируем уравнение по основанию
2 и получим — = logo 3 . Но последнее равенство невозможно, так как — —
У ~	У
рациональное число, a log23 —иррациональное.
□	31. Аналогичная задача решается в тексте.
Ответ: х = 0 .
А> ft/	ГИТО»ТО*Г»Т»ГЯ*1ГГл«ТО™»*Г*ГГГЛ>ГМ*гтТЛ<те»«^	’tnwi	“<Т»<Т-Н < 9 MWHWW» fct t
□	32. Решение. Преобразуем заданное число следующим образом
Уз _ 7б(2-Уз) = Уз + Уз = Л 1 +	1
^3 + 2-Уз + 1 2(Уз-2) ^/(Уз +1)2 У25/2-УЗ ^Уз + 1 74-2-Уз,
Ответ: не только рациональное, но и целое.
□	33. Решение. Домножим числитель и знаменатель первой дроби на
Vs - V3 , а второй дроби — на Ш - у/2 и воспользуемся формулой разло-
жения разности кубов на множители. Получим ^5-^3+^3-^2=^5-^2,
что дает с последней скобкой 5-2=3.
Ответ: рациональное.
k AW*»W tf-tt ’•	€.	»«*ОНЫ* А**»ТС Г tr	* м 1	е- 9 «,
□	34. Решение. Обозначим длины ребер, выходящих из данной вершины
через а.Ь и с. Имеем
у =zL.2L.c=Lyl(abc)2 = ^.1^..^..— =	,
32 б’	6 V 2 2 2	3 N 1 2 3
где 5и52 и 53 —площади примыкающих треугольников.
По условию получаем V = ^2 .
179
ЛИТЕРАТУРА
1.	Воробьев Н.Н. Признаки делимости. — М., Наука, 1988.
2.	Гельфонд А.О. Решение уравнения в целых числах. —М., Наука, 1983.
3.	Будак А.Б., Щедрин Б.М. Элементарная математика. Руководство для
поступающих в МГУ. — М., Издат. отдел УНЦ ДО МГУ, 2002.
4.	Якушева Е.В., Попов А.В., Якушев А.Г. Математика. Ответы на воп-
росы. Теория и примеры решения задач. — М., Федеративная Торговая
Компания, 1997.
5.	Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для
поступающих в ВУЗы. —М., 1976.
6.	Дорофеев Г.В., Потапов М.К., Розов Н.Х. Математик;! для поступающих
в ВУЗы. —М., изд. «Дрофа», 1996.
7.	Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.Н. Алгебра.
Задачник 10-11 кл.. Учебное пособие для общеобразовательных заведений
— М., изд. «Дрофа», 1996.
8.	Соловьев Ю. Неопределенные уравнения первой степени. Приложение к
журналу «Квант»., 1994, №2, стр. 32-40.
9.	Гальперин Г. Просто о простых числах. Там же, стр. 4-13.
10.	Егоров А.А. Деление с остатком и сравнение по модулю. Там же, стр.
14-22.
11.	Шустер Ф.М., Фельдман А.М., Гуревич В.Ю. Сборник олимпиадных
задач по математике. — Минск, 1962.			
12. Первая Соросовская олимпиада	школьников	1994-1995.	— м.
МЦИМО, 1995. 13. Вторая Соросовская олимпиада	школьников	1995-1996.	— м.
МЦИМО, 1996. 14. Третья Соросовская олимпиада	школьников	1996-1997.	— м.
МЦИМО, 1997. 15. Четвертая Соросовская олимпиада	1 школьников	1997-1998.	— м
МЦИМО, 1998.
16.	Пятая Соросовская олимпиада школьников 1998-1999	— М.:
МЦИМО, 1999.
17.	Рождественский В.В., Панкратов Е.В , Мельников И.И , Вавилов В.В.
Математический тренинг. — М., 1997.
18.	Мельников И.И., Олехник С.Н., Сергеев И.Н. Математика. Задачи
вступительных экзаменов с ответами и решениями (1993-1997 гг.) МГУ.
Учебно-научный центр довузовского образования. М.,1998.
19.	Задачи вступительных экзаменов по математике (1998 г.) Под общ.
ред. Григорьева Е.А. — М., Изд-во МГУ, 1998.
20.	Федотов М.В., Хайлов Е II Алгебра Устный экзамен по математике.
— М., Изд-во МГУ, 1999.
180	Конкурсные задачи
21.	Нивен А. Числа рациональные и иррациональные. — М., «Мир», 1966.
22.	Справочник для поступающих в Московский университет. — М., Изд-
во МГУ, 1993.
23.	Будак А.Б., Щедрин Б.М. Элементарная математика. Методические
указания к ответам на теоретические вопросы билетов устного экзамена по
математике. — М., факультет ВМиК МГУ, 2000.
24.	Кравцев С.В., Макаров Ю.Н., Лукашенко Т.П., Нараленков М.И., Чир-
скии В.Г., Шавгулидзе Е.Т. Математика. Ответы на вопросы, теория и
примеры решения задач — М., изд-во "Экзамен”, 2001.
25.	Кравцев С.В., Макаров Ю.Н., Максимов М. И., Нараленков М.И., Чир-
скии В.Г. Методы решения задач по алгебре: от простых до самых
сложных. —М., изд-во "Экзамен", 2001.
В. Я. Галкин, Д, Ю. Сычугов, Е. В. Хорошилова
Конкурсные задачи, основанные
на теории чисел
Издательский отдел факультета ВМиК МГУ
(Лицензия ИД № 05899 от 24.09.01.)
Изд. лиц. ИД № 00510 от 01.12.99.
Подписано в печать 01.03.2002. Формат бОхОО1/^.
Печать офсетная. Бумага газетная.
Печ. л. 11,25. Тираж 1000 экз. Заказ 619.
ООО “МАКС Пресс”, 107066, г. Москва, Елоховский пр., д. 3, стр. 2.
Тел. 939-38-90, 939-38-91, 928-10-42.
Тел./факс 939-38-91.
Отпечатано в Производственно-издательском комбинате ВИНИТИ,
140010, г. Люберцы Московской обл., Октябрьский пр-т, 403.
Тел. 554-21-86.