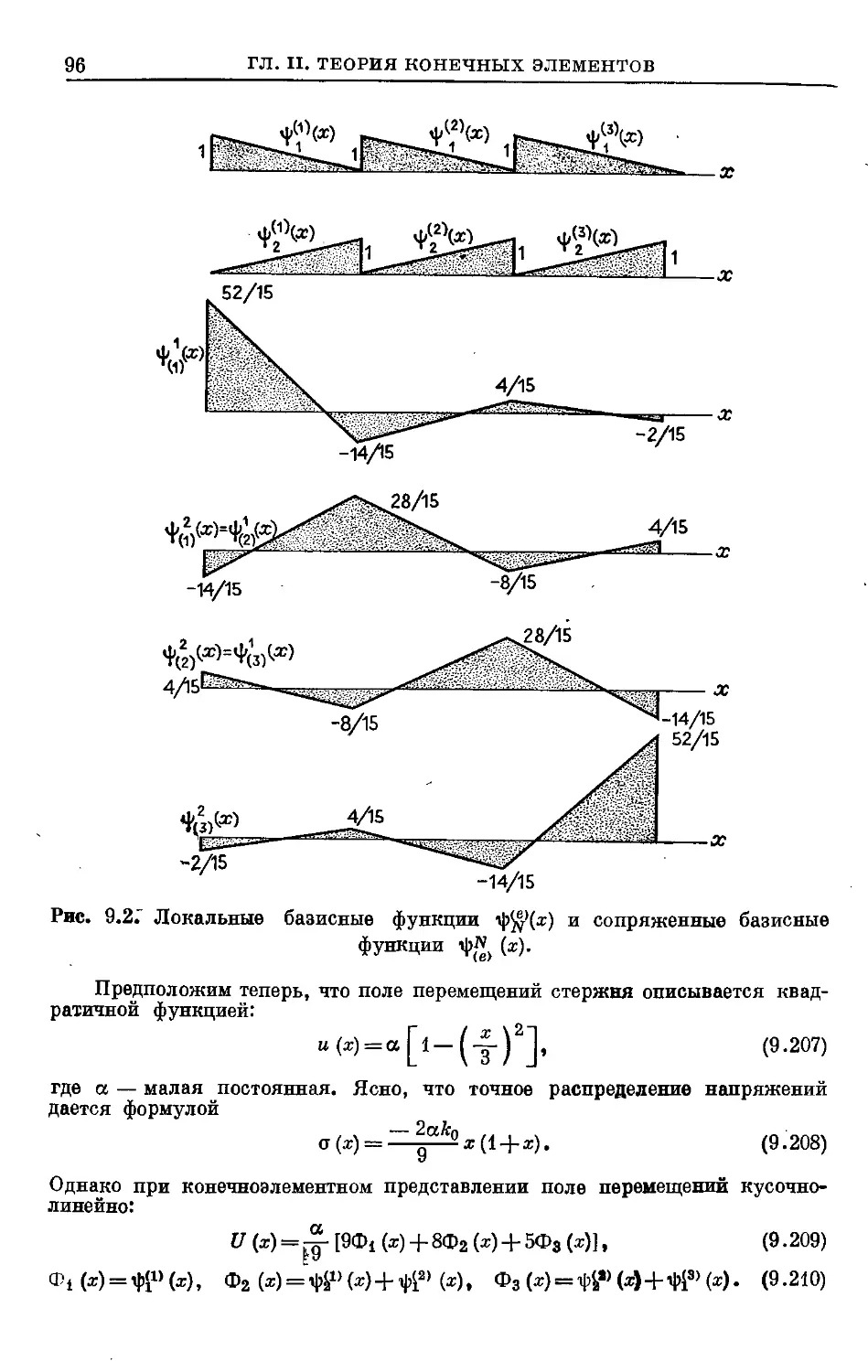
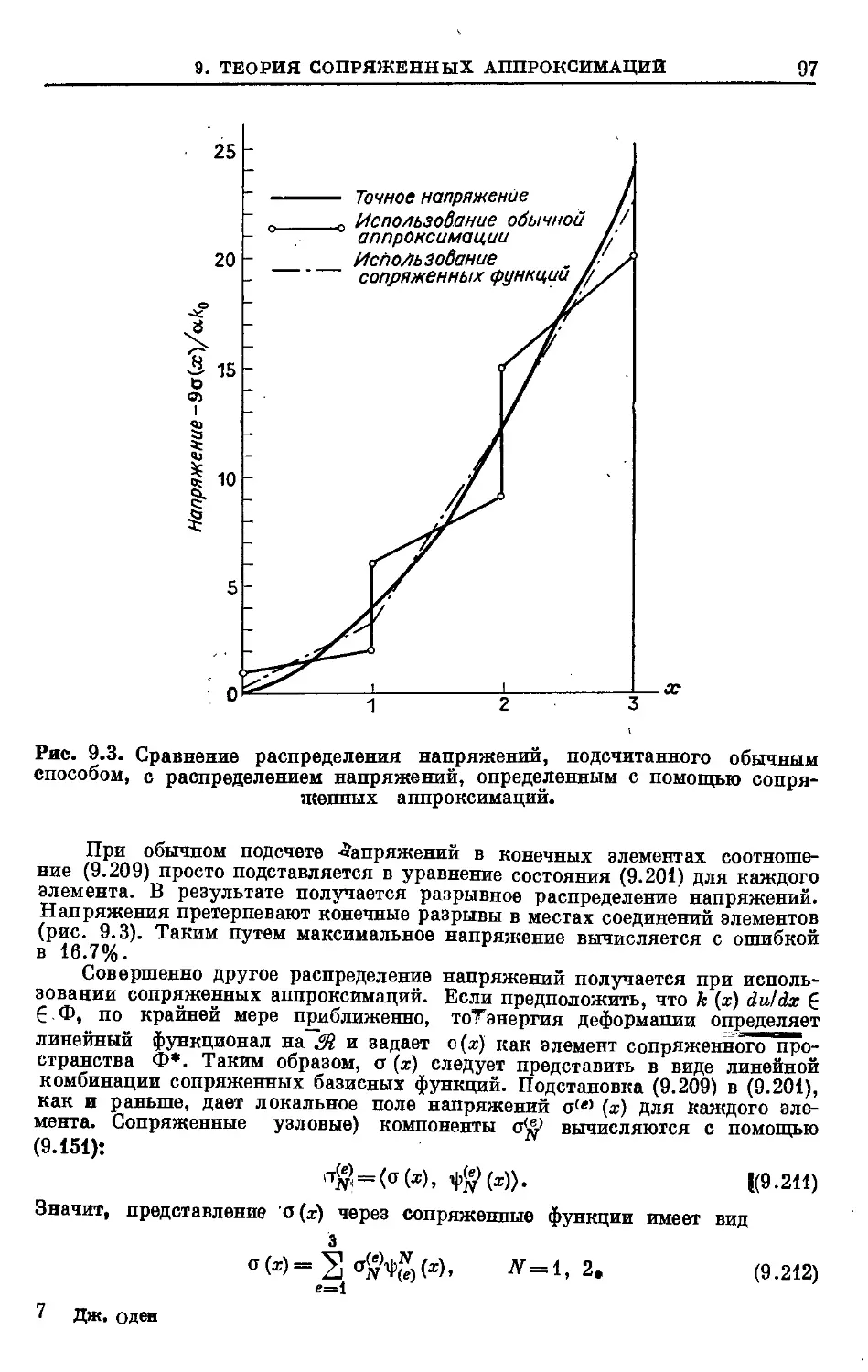
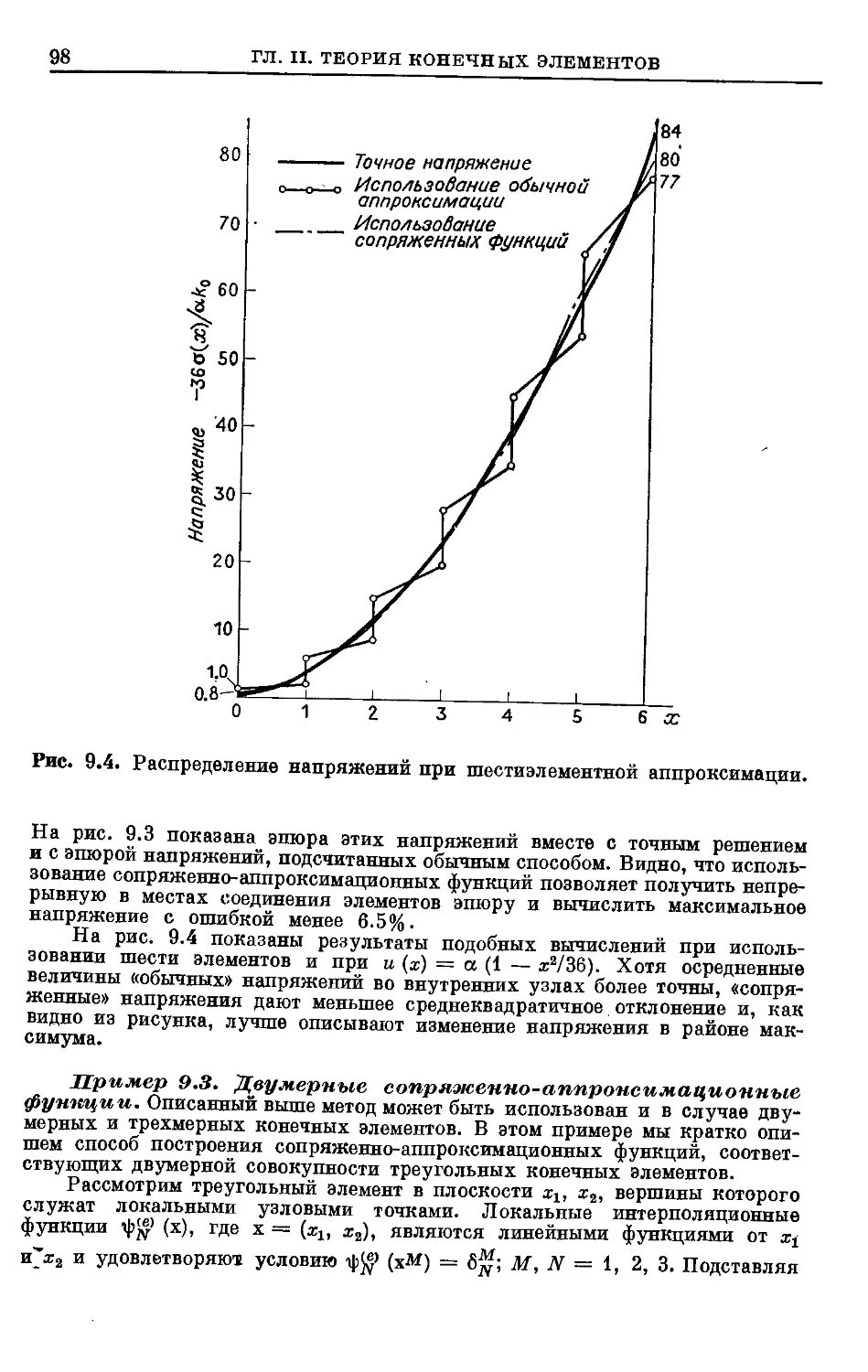
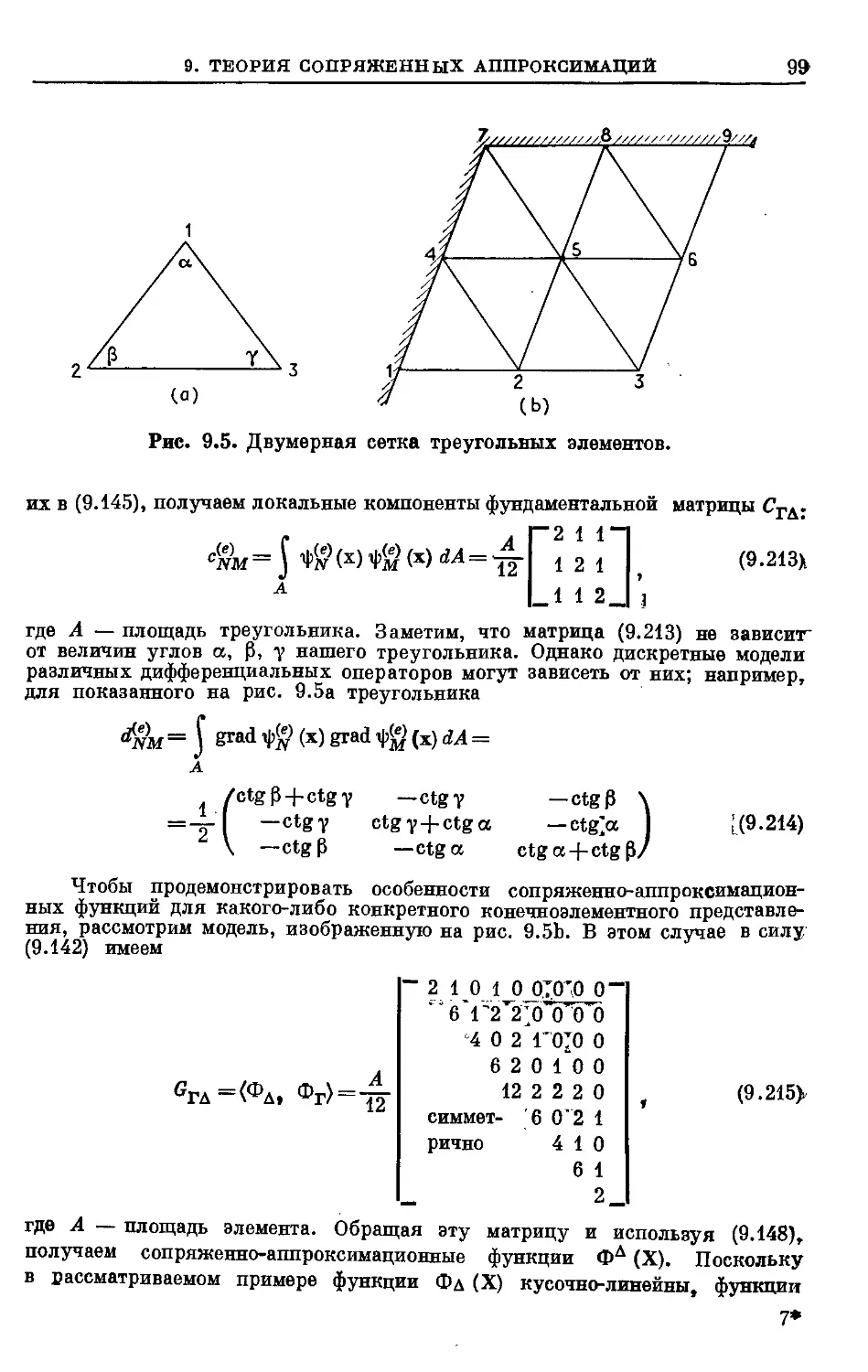
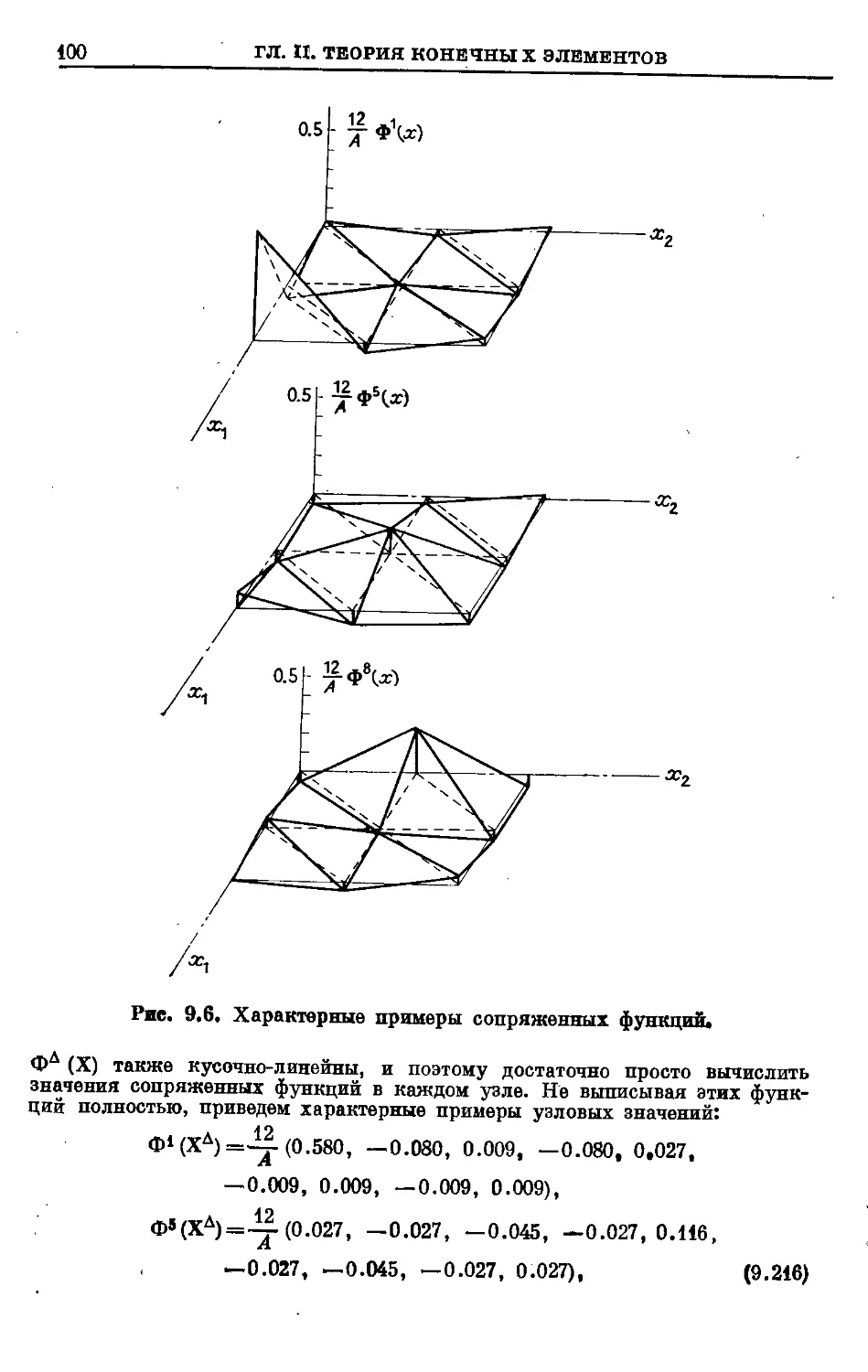
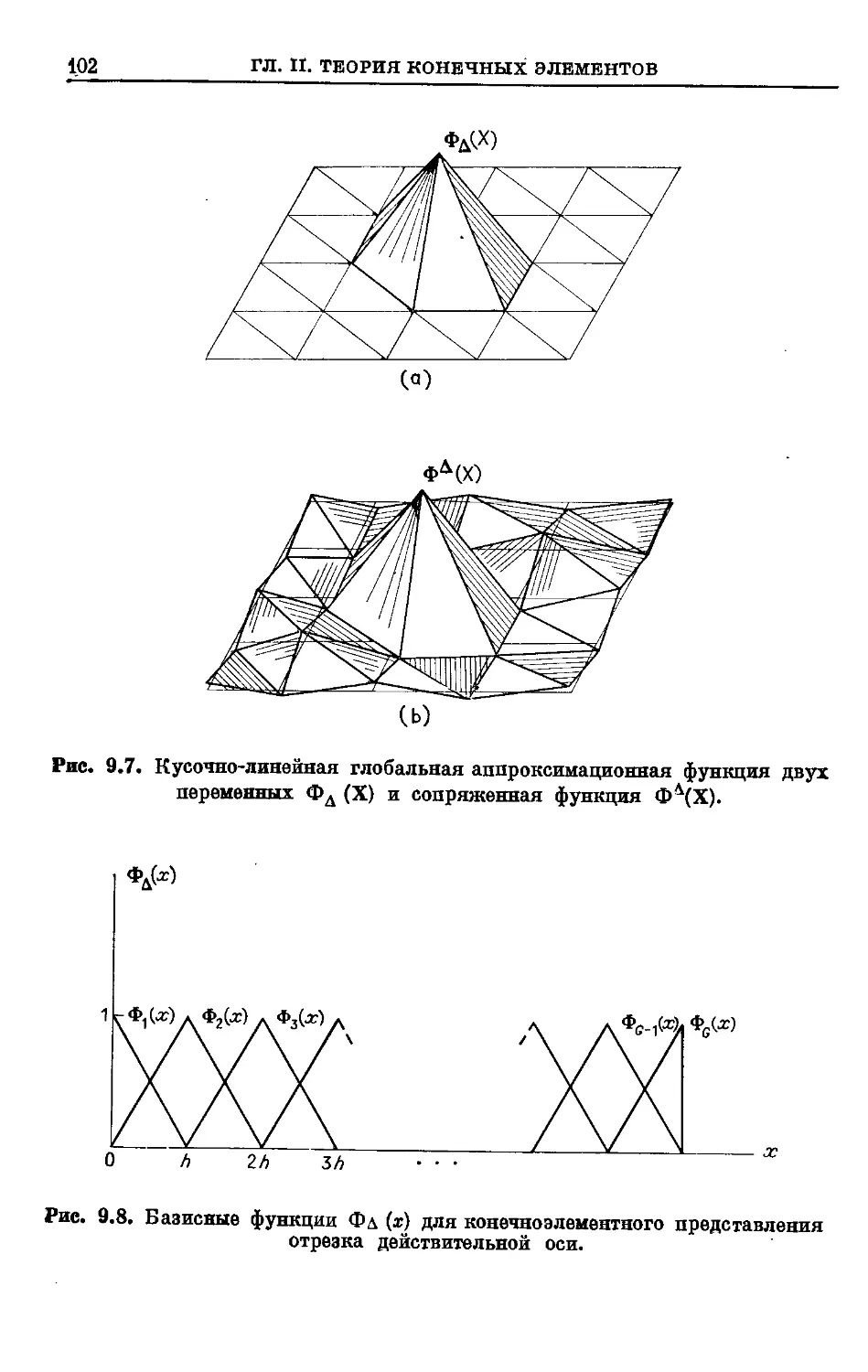
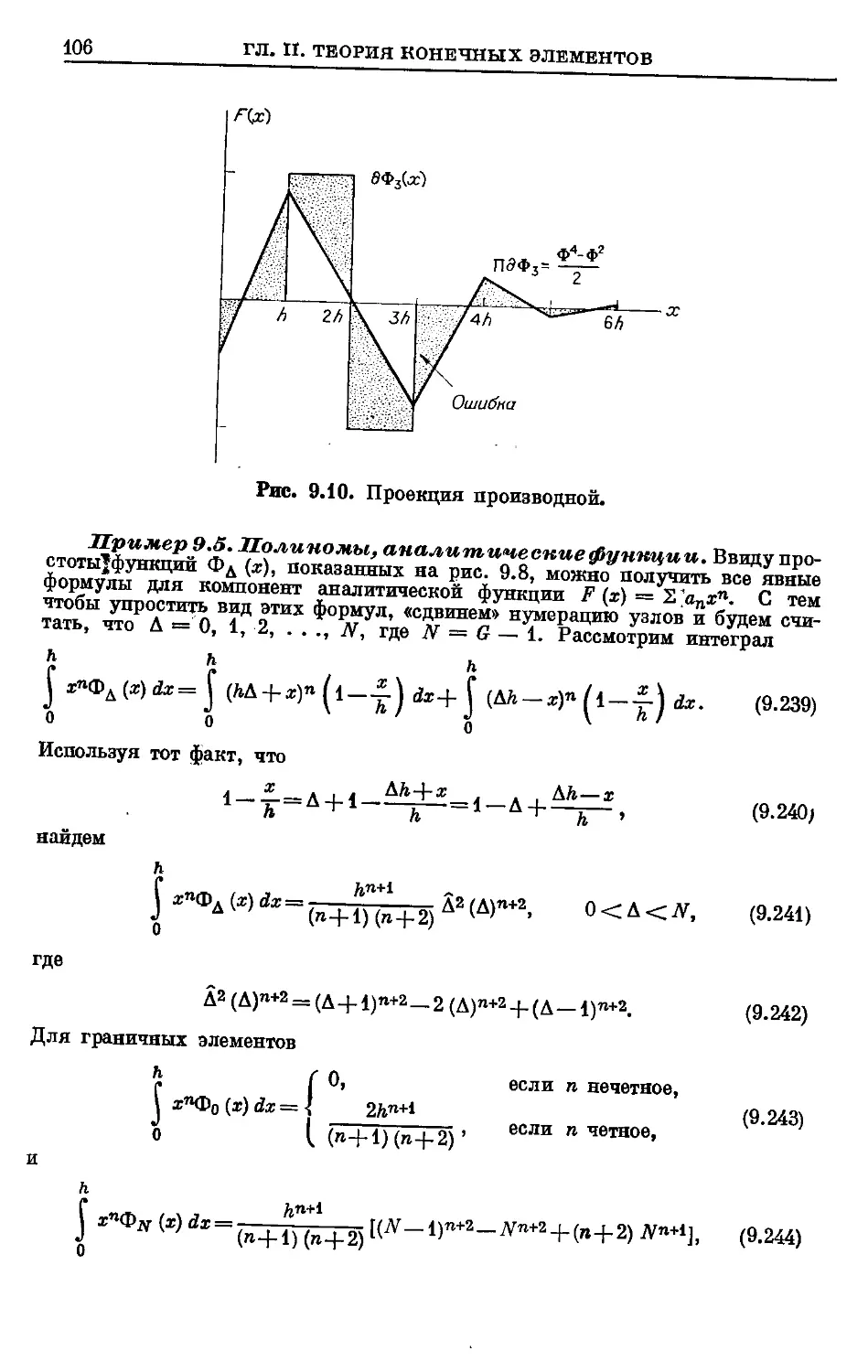
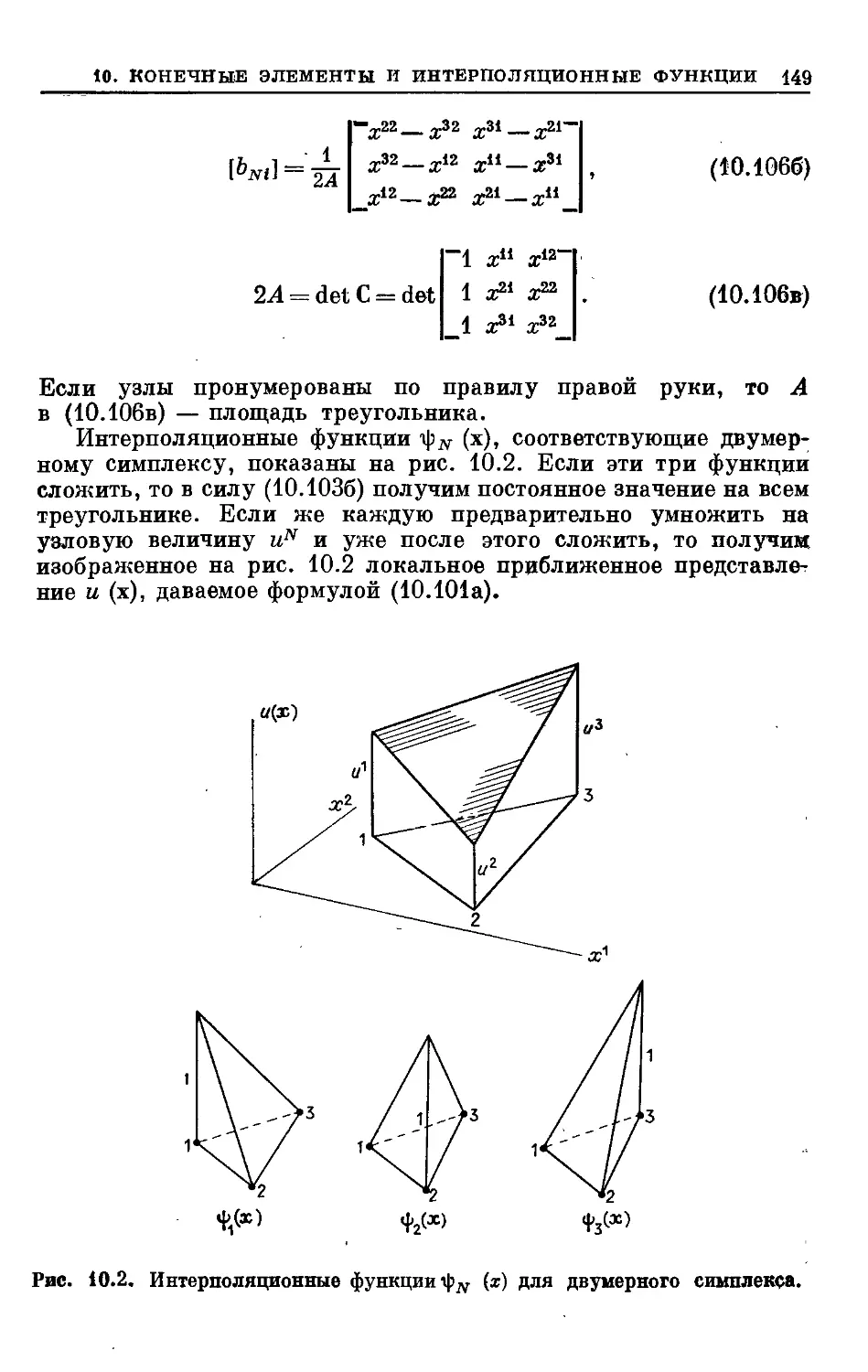
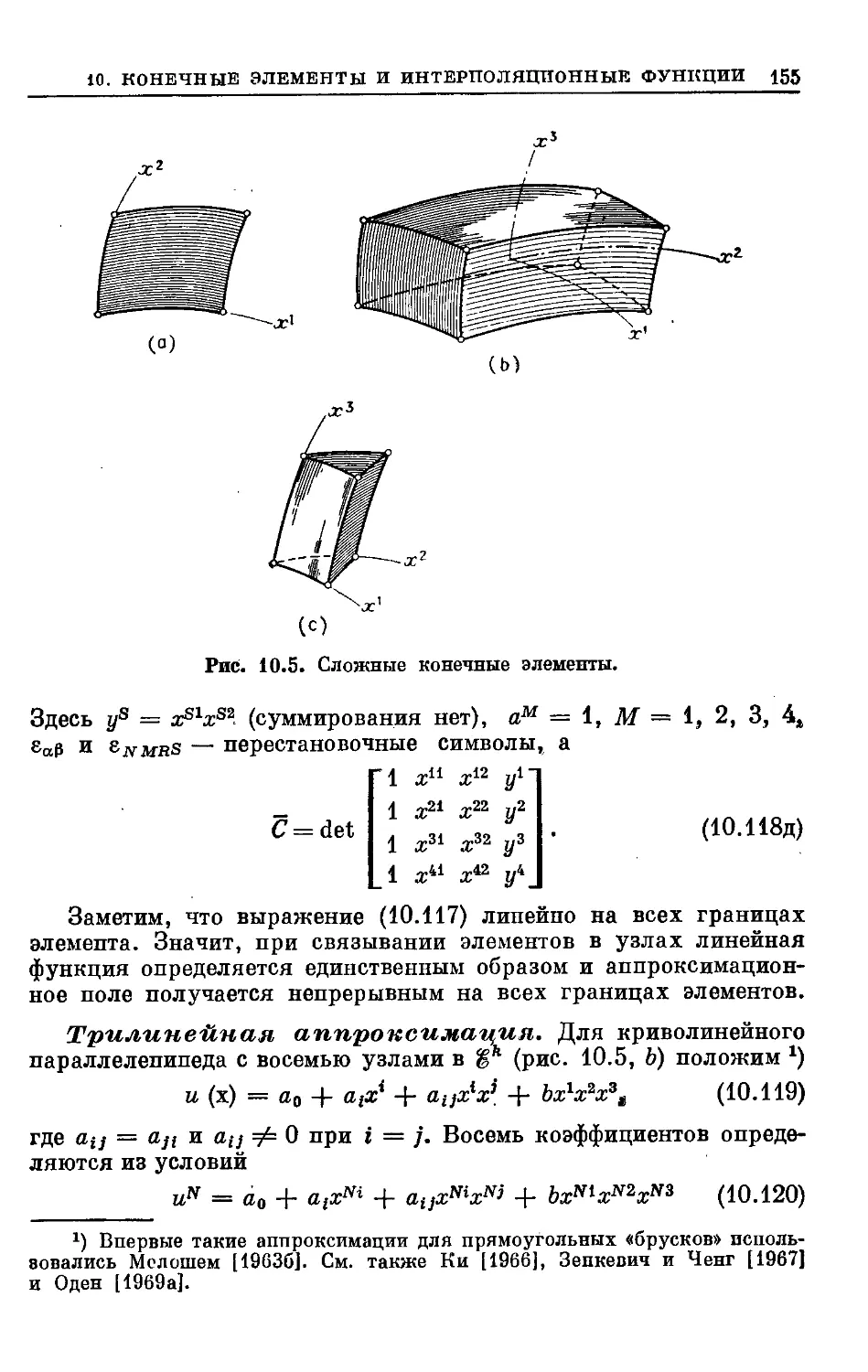
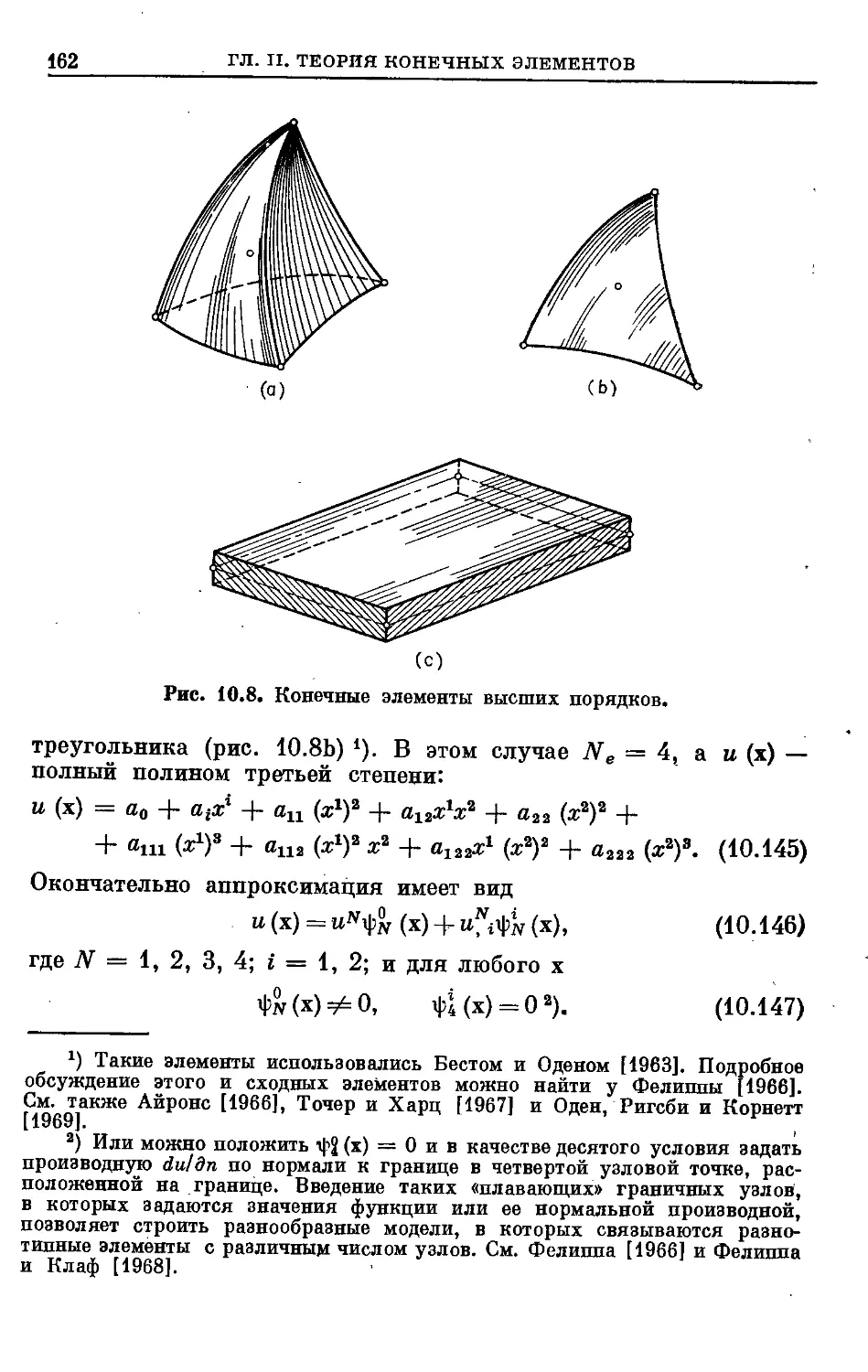
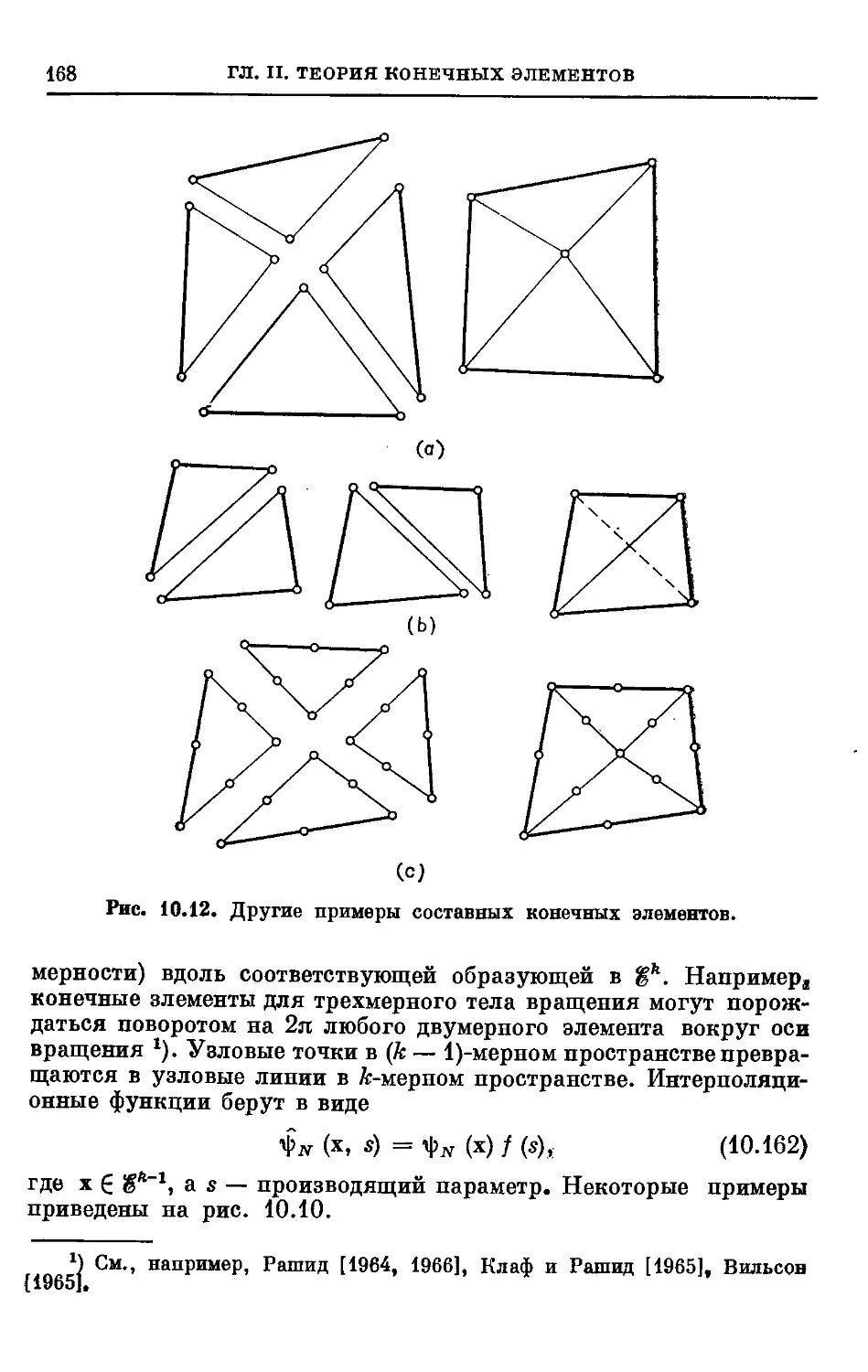
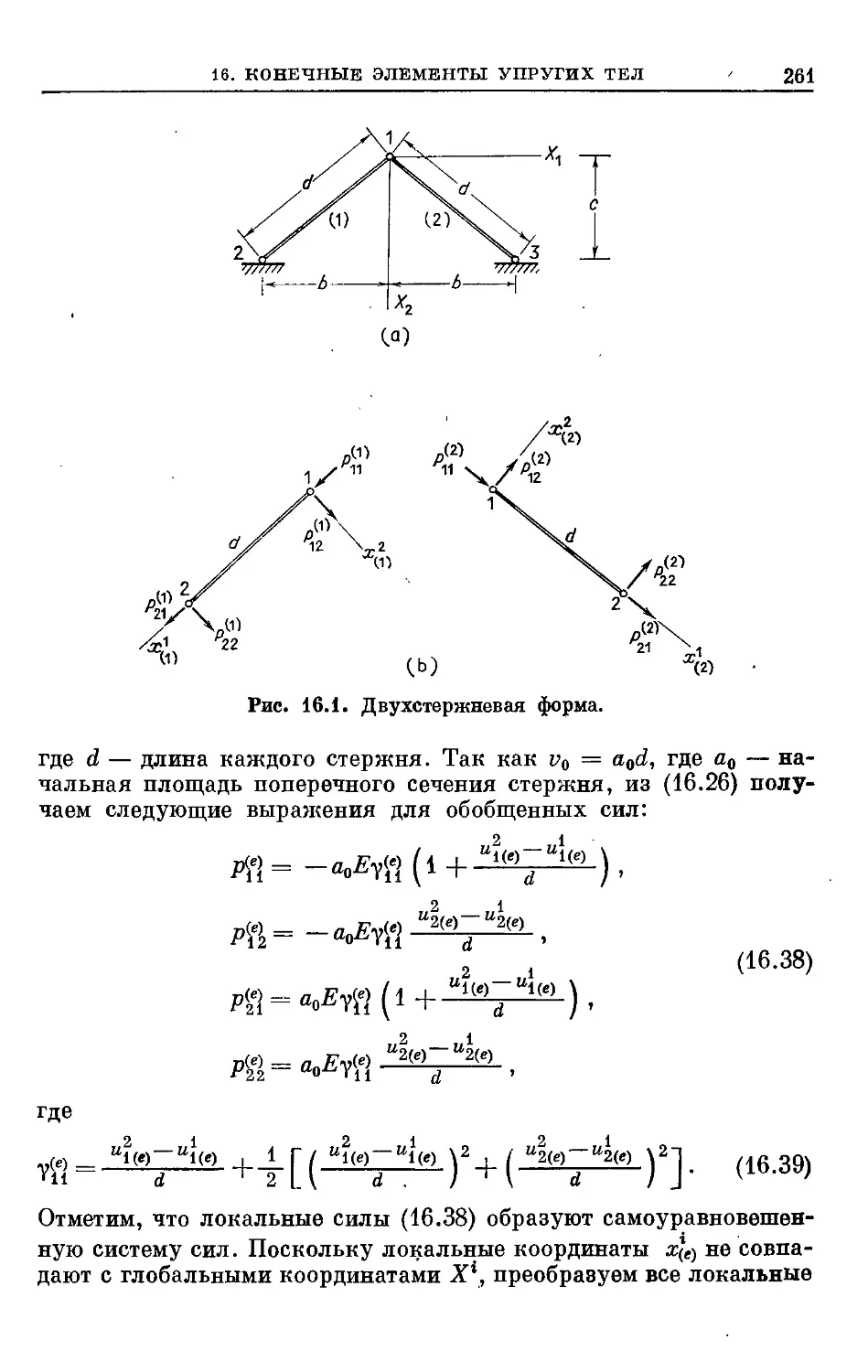
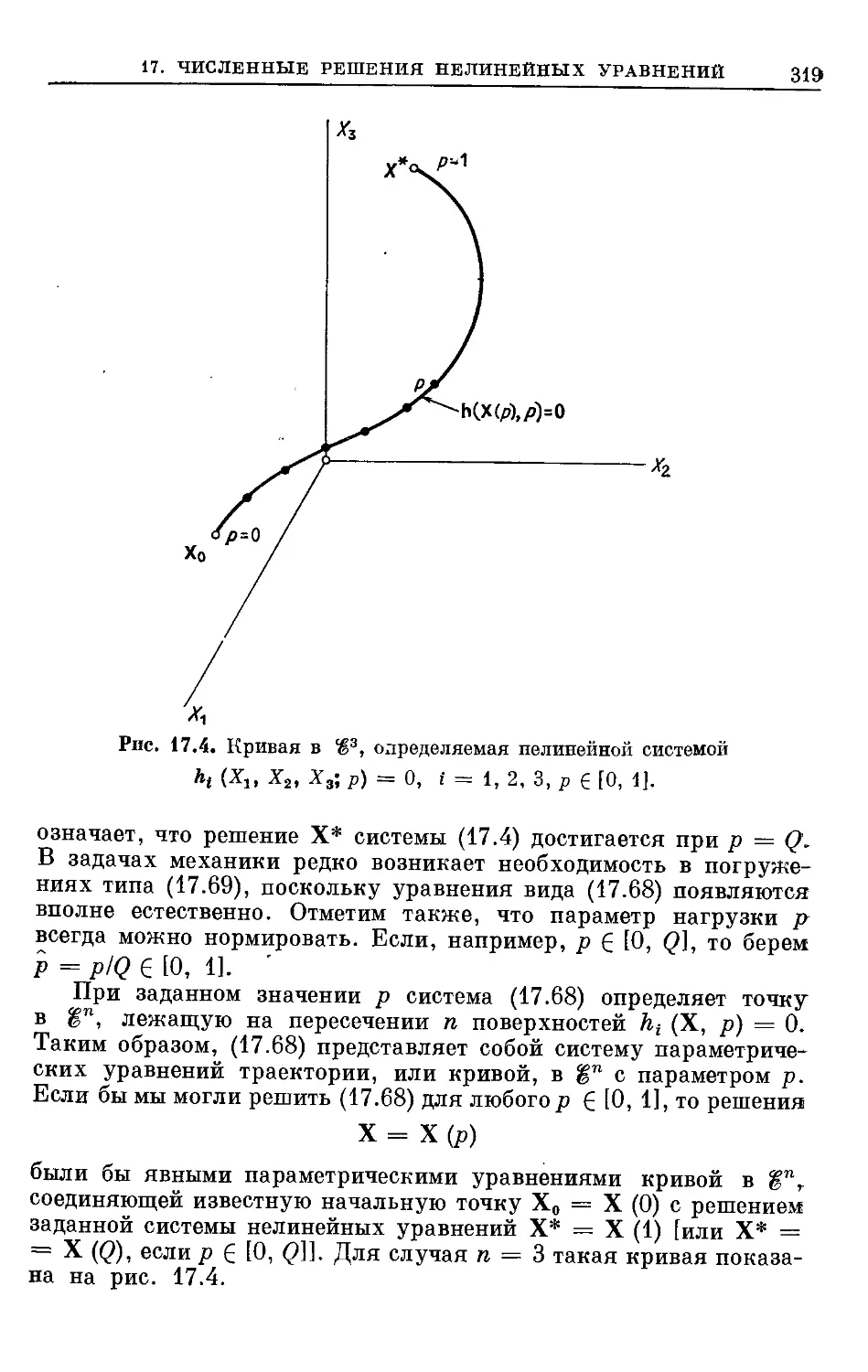
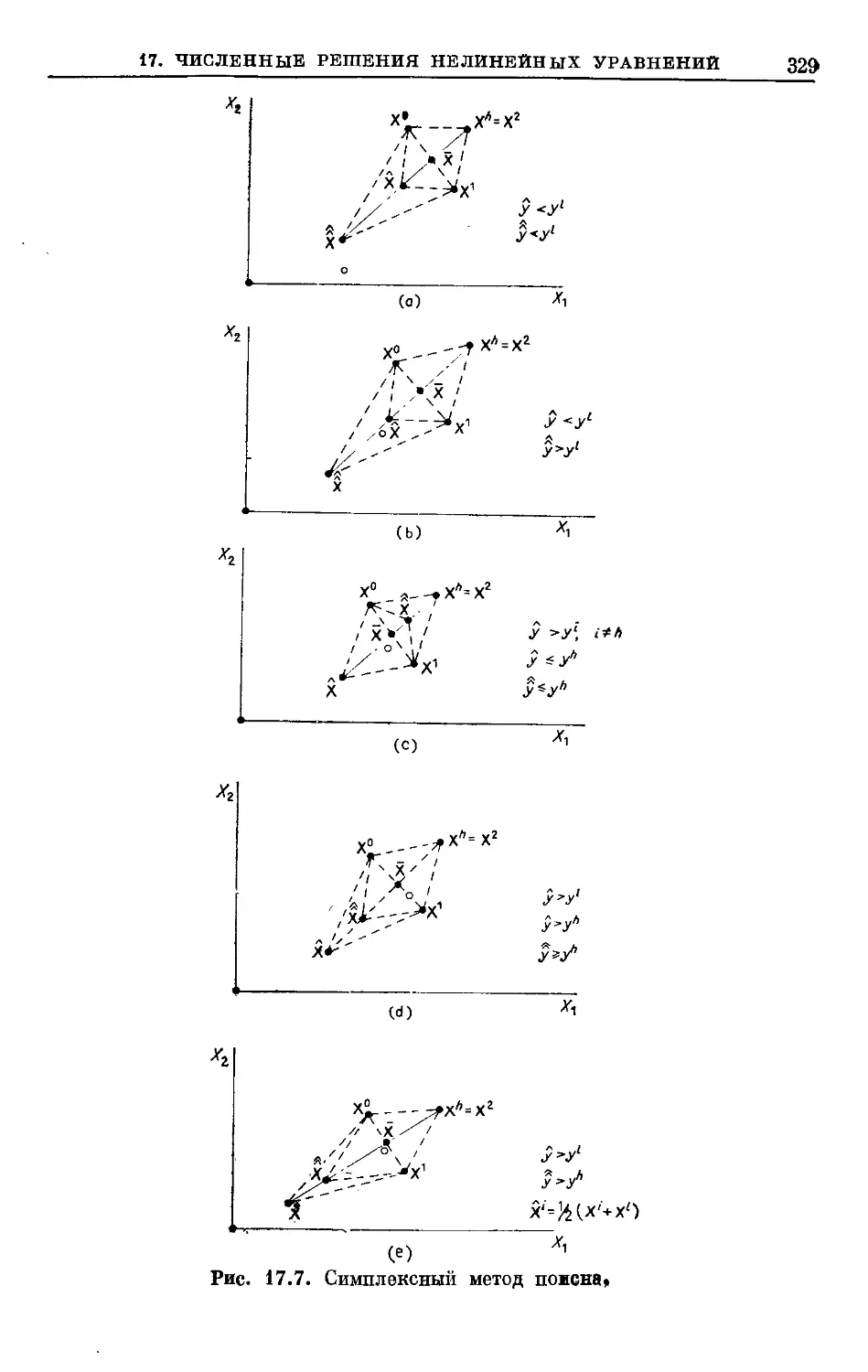
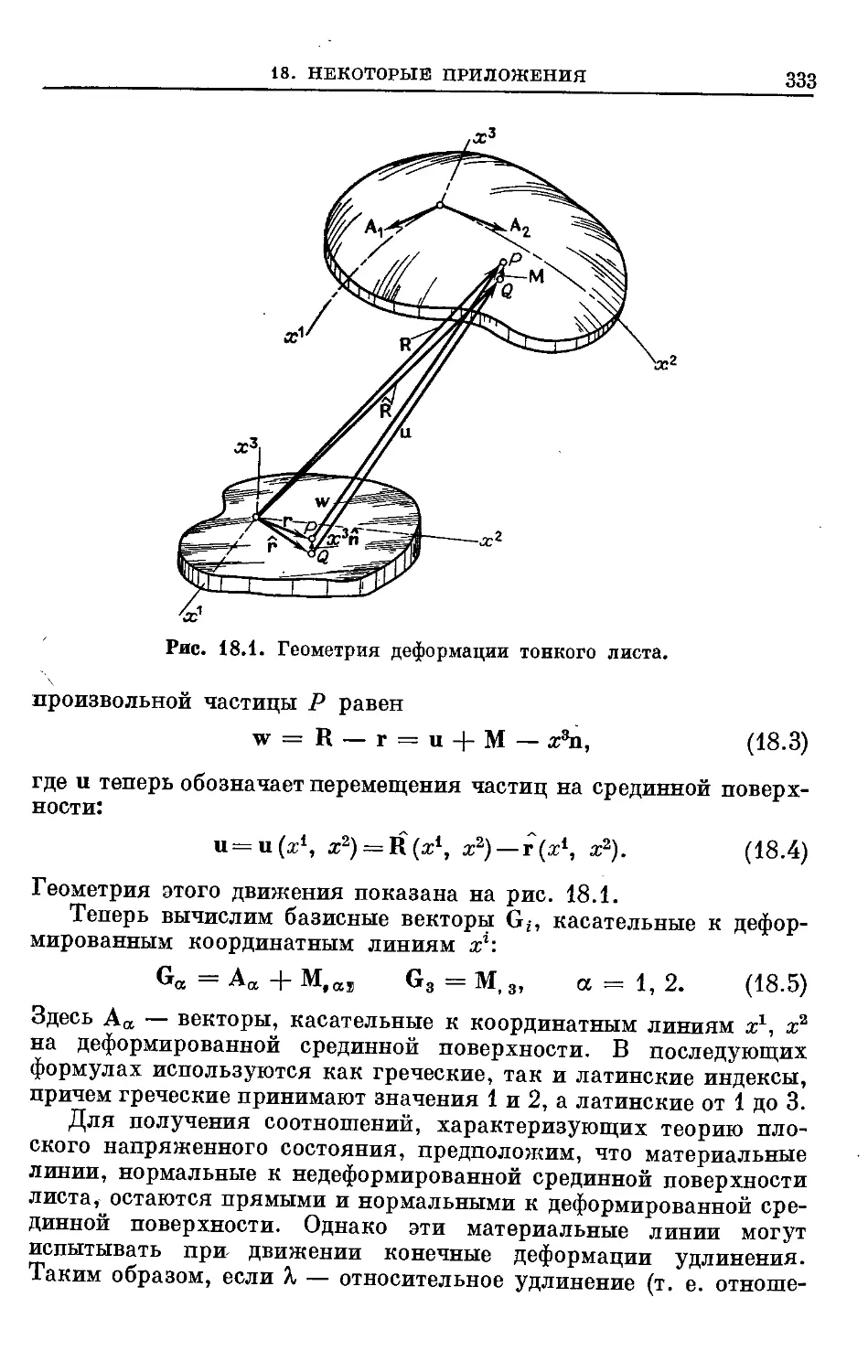
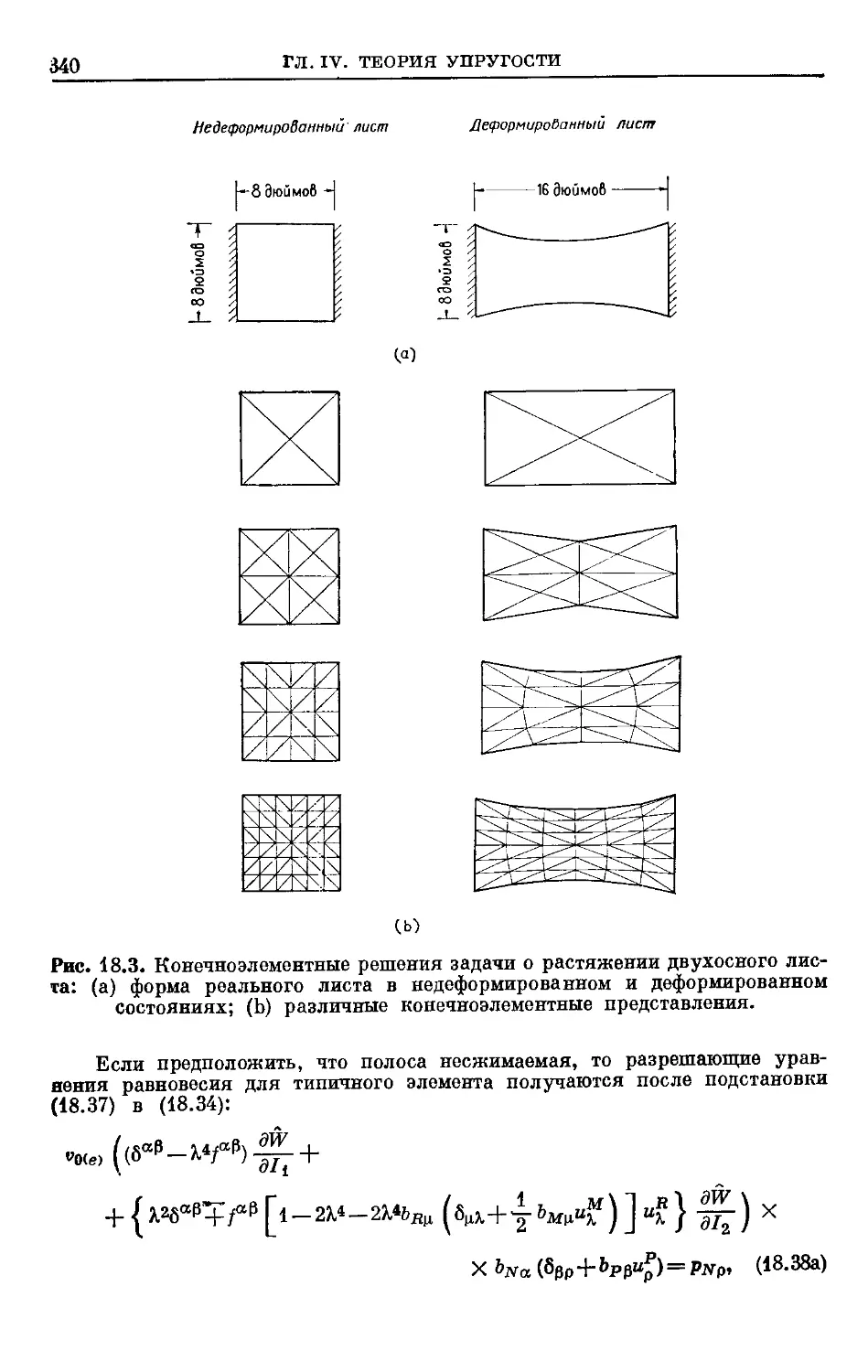
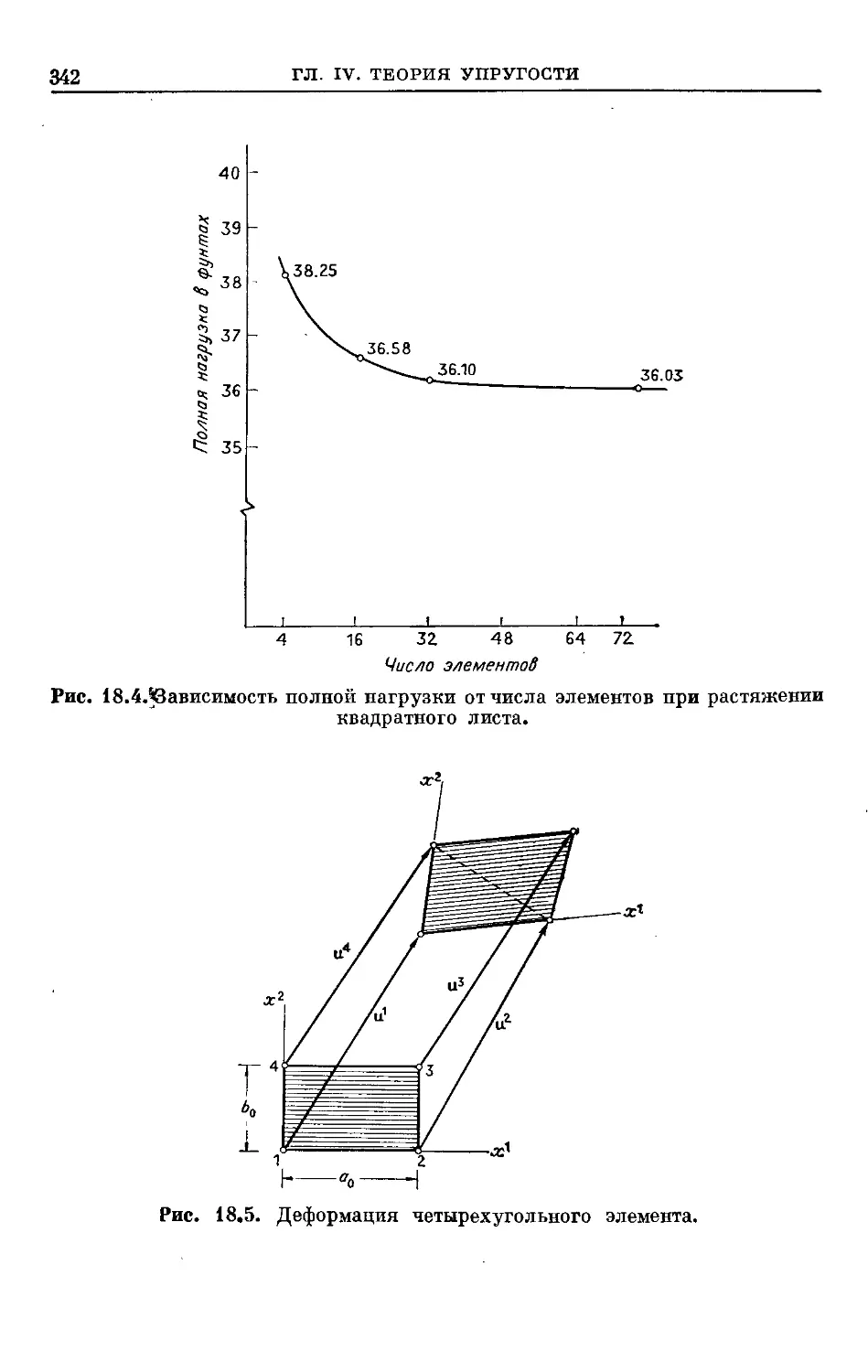
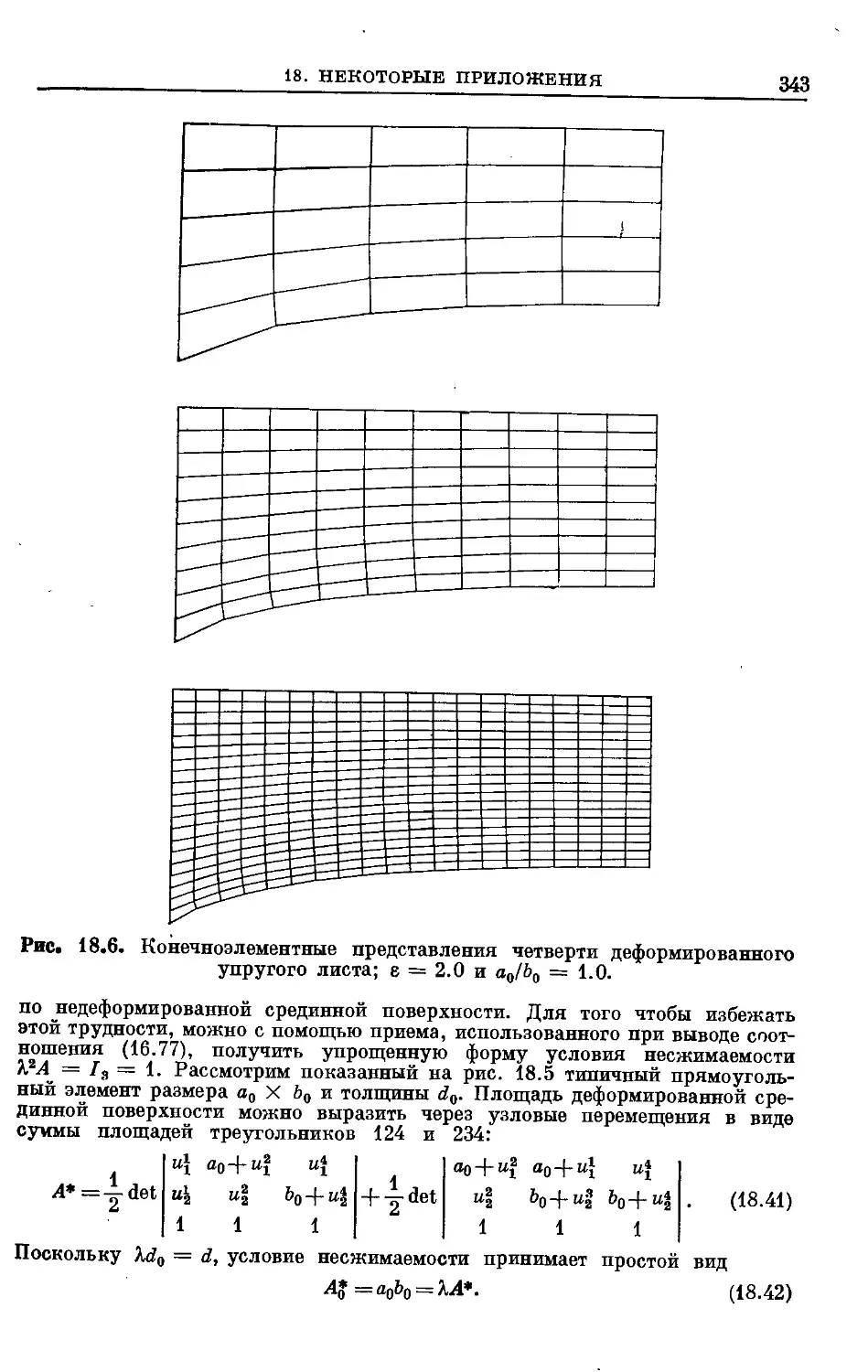
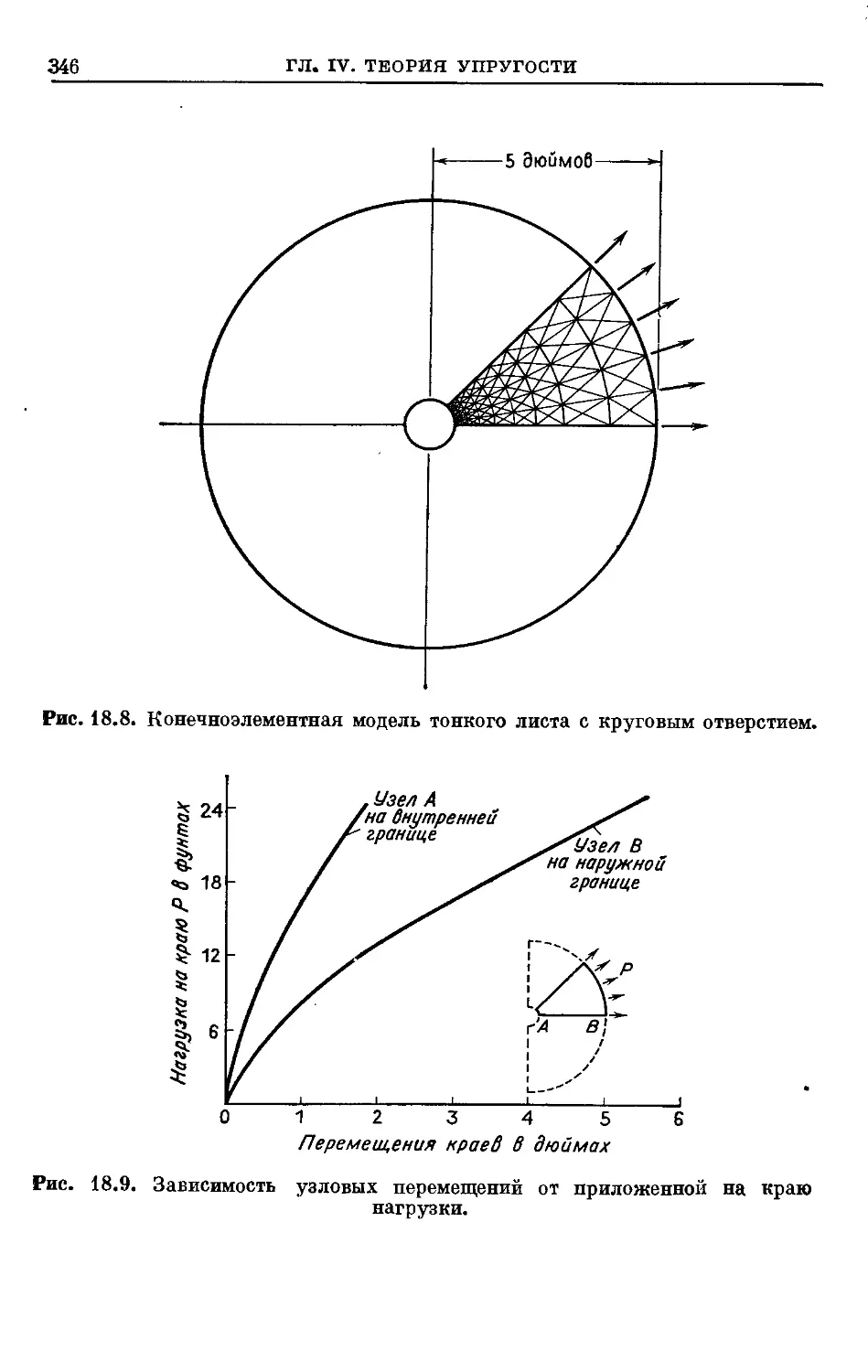
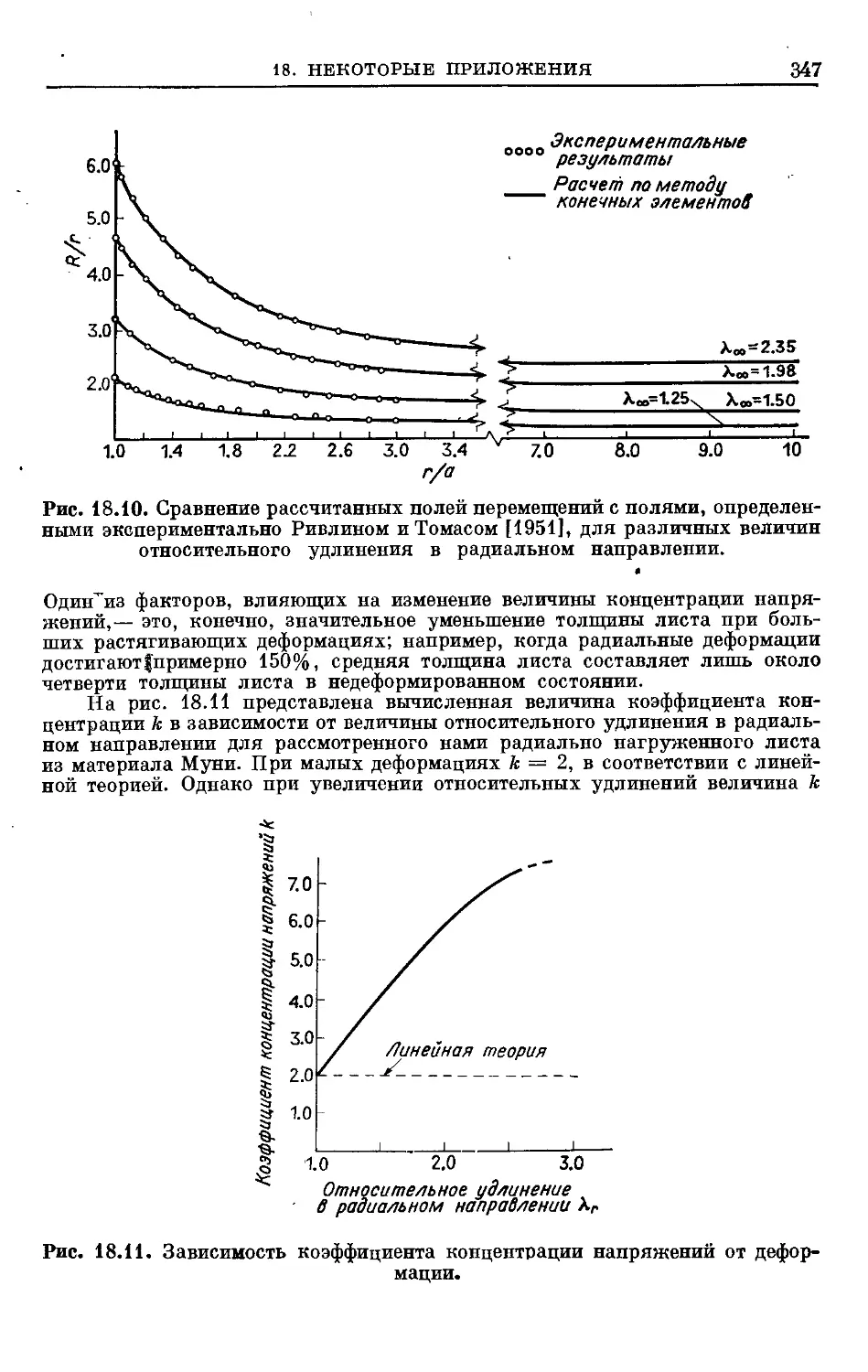
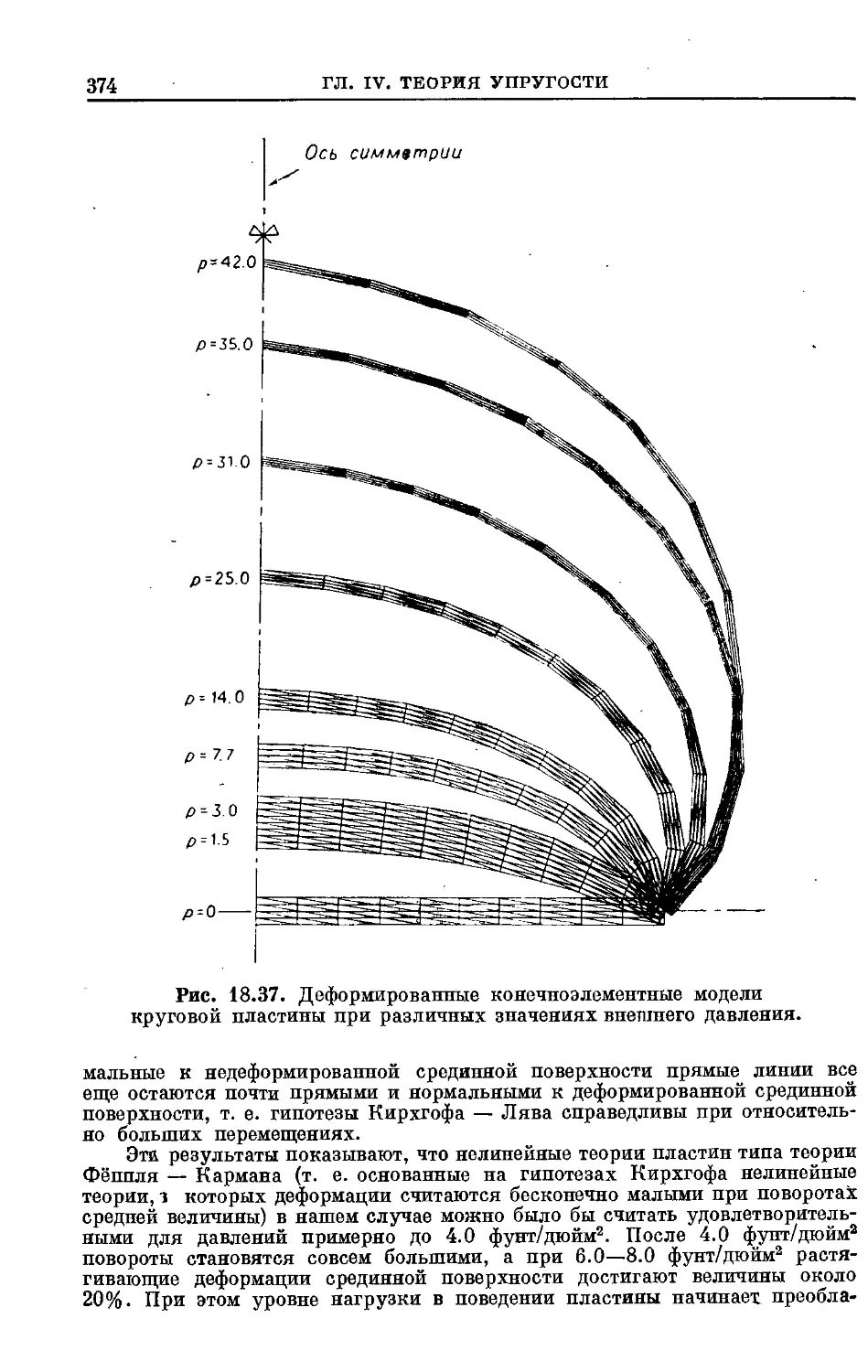
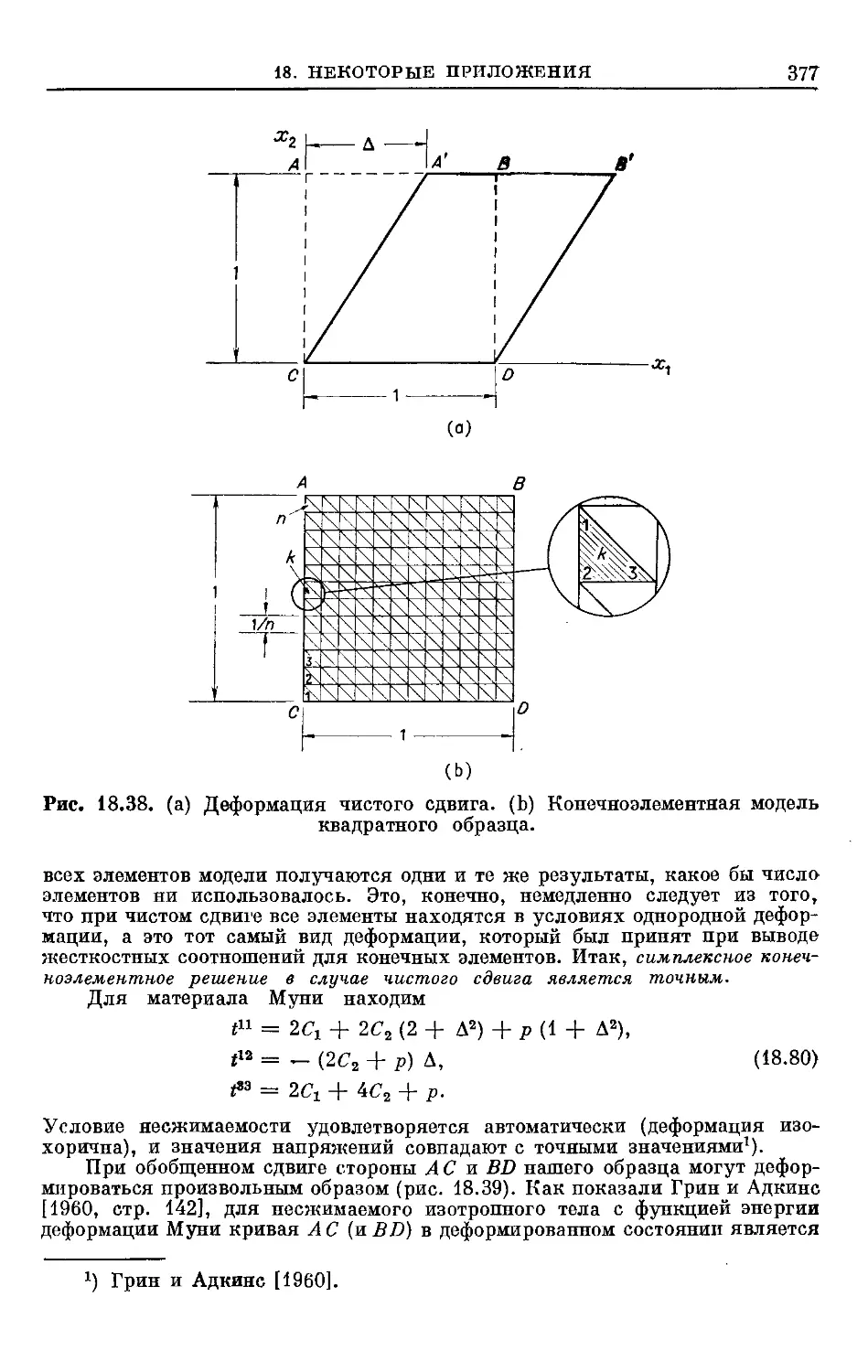
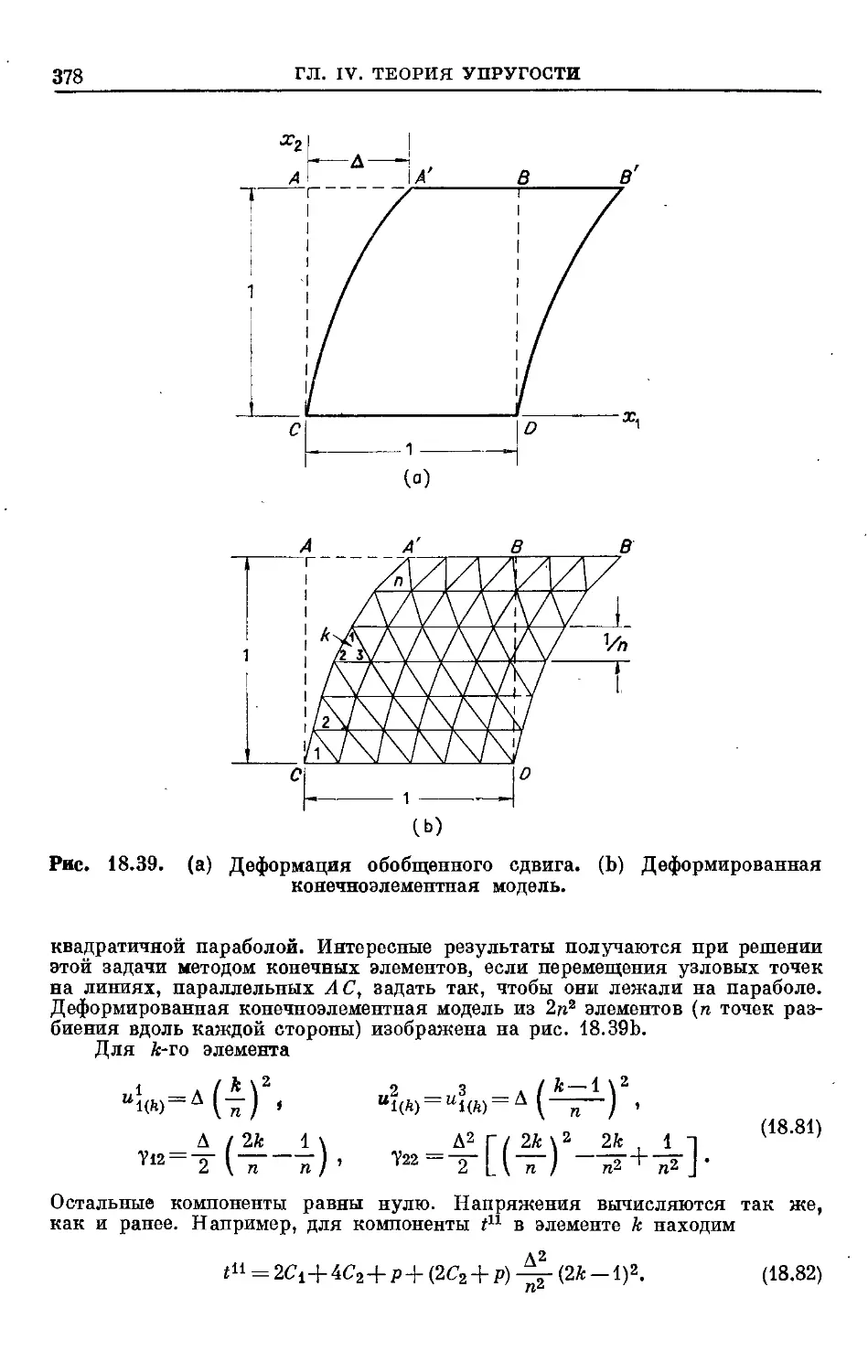
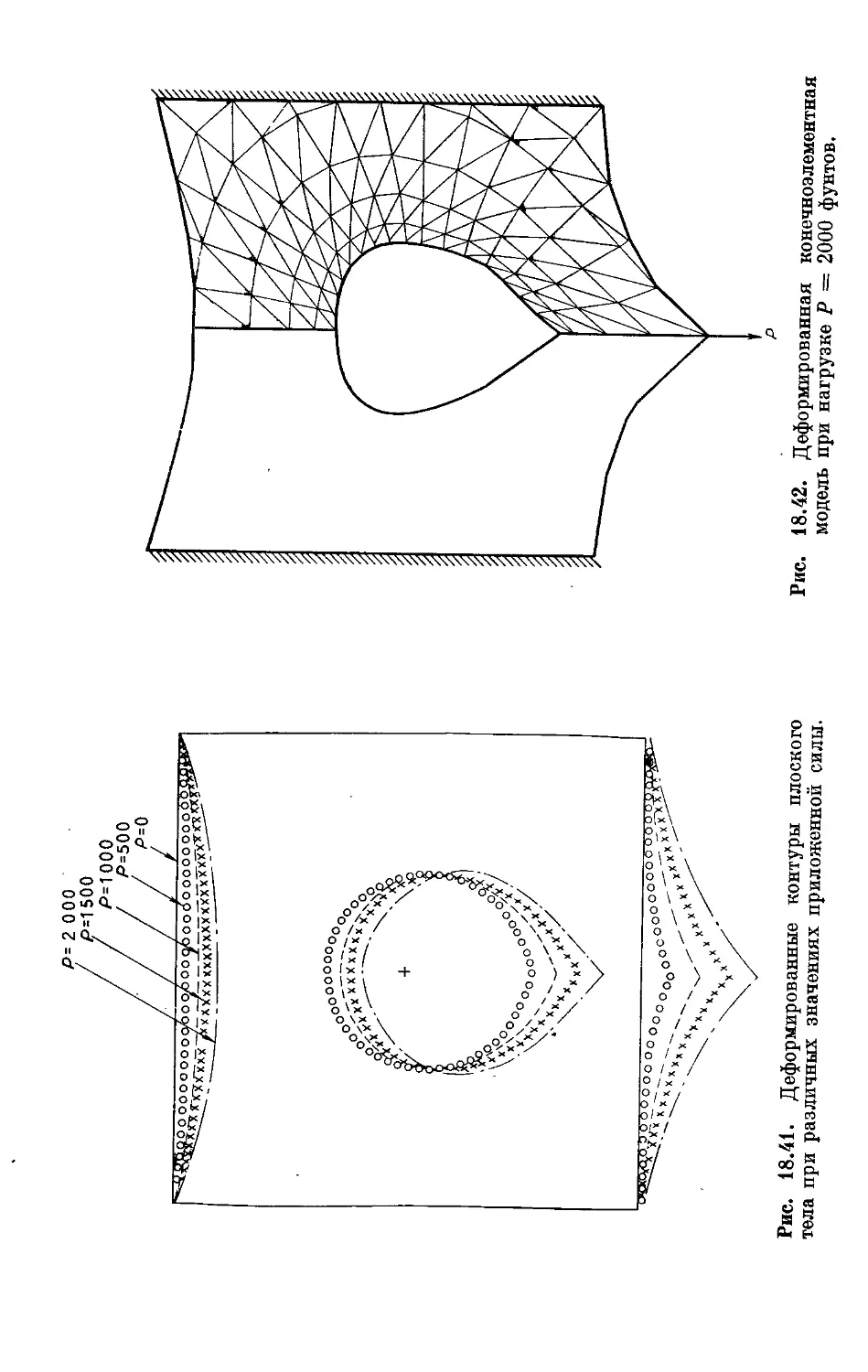
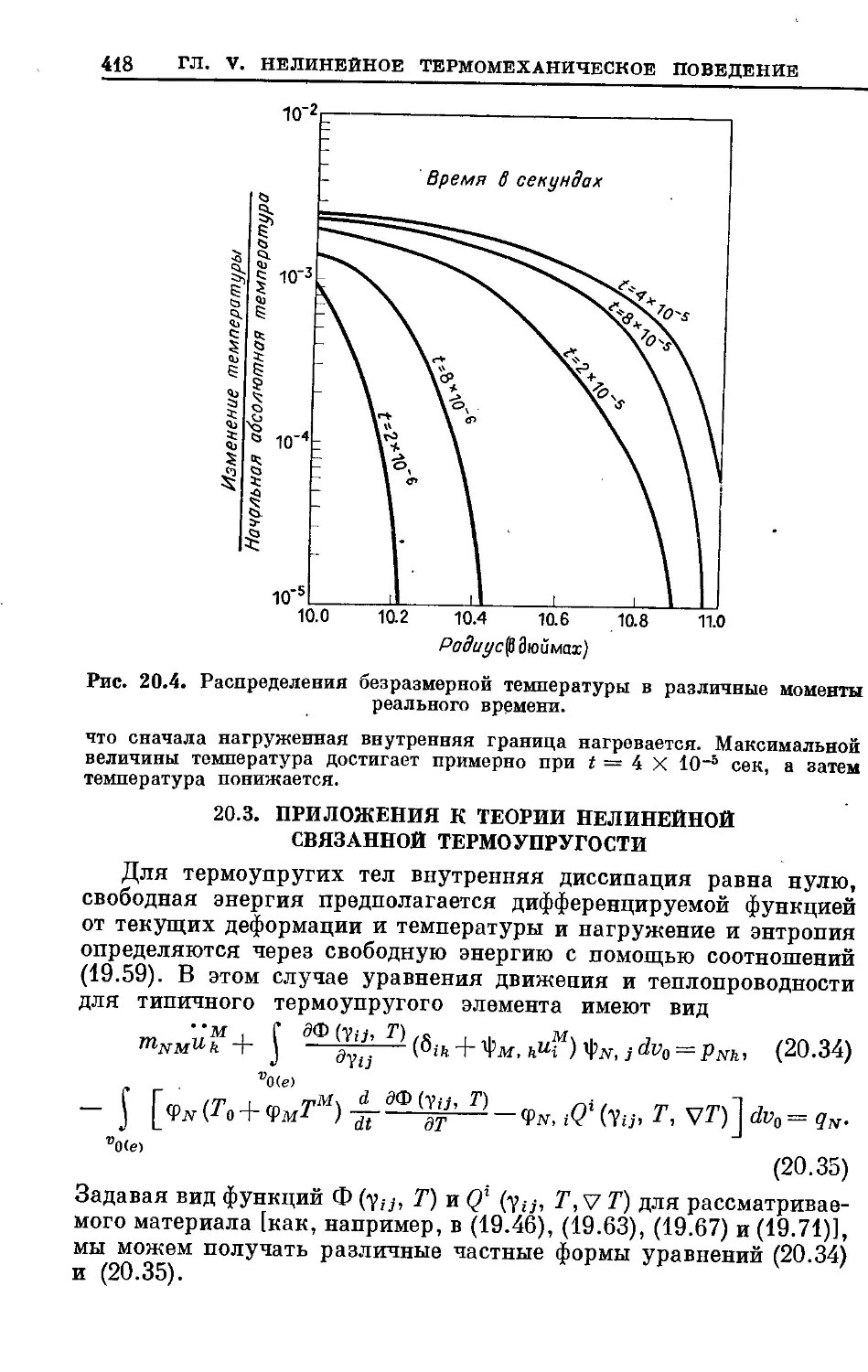
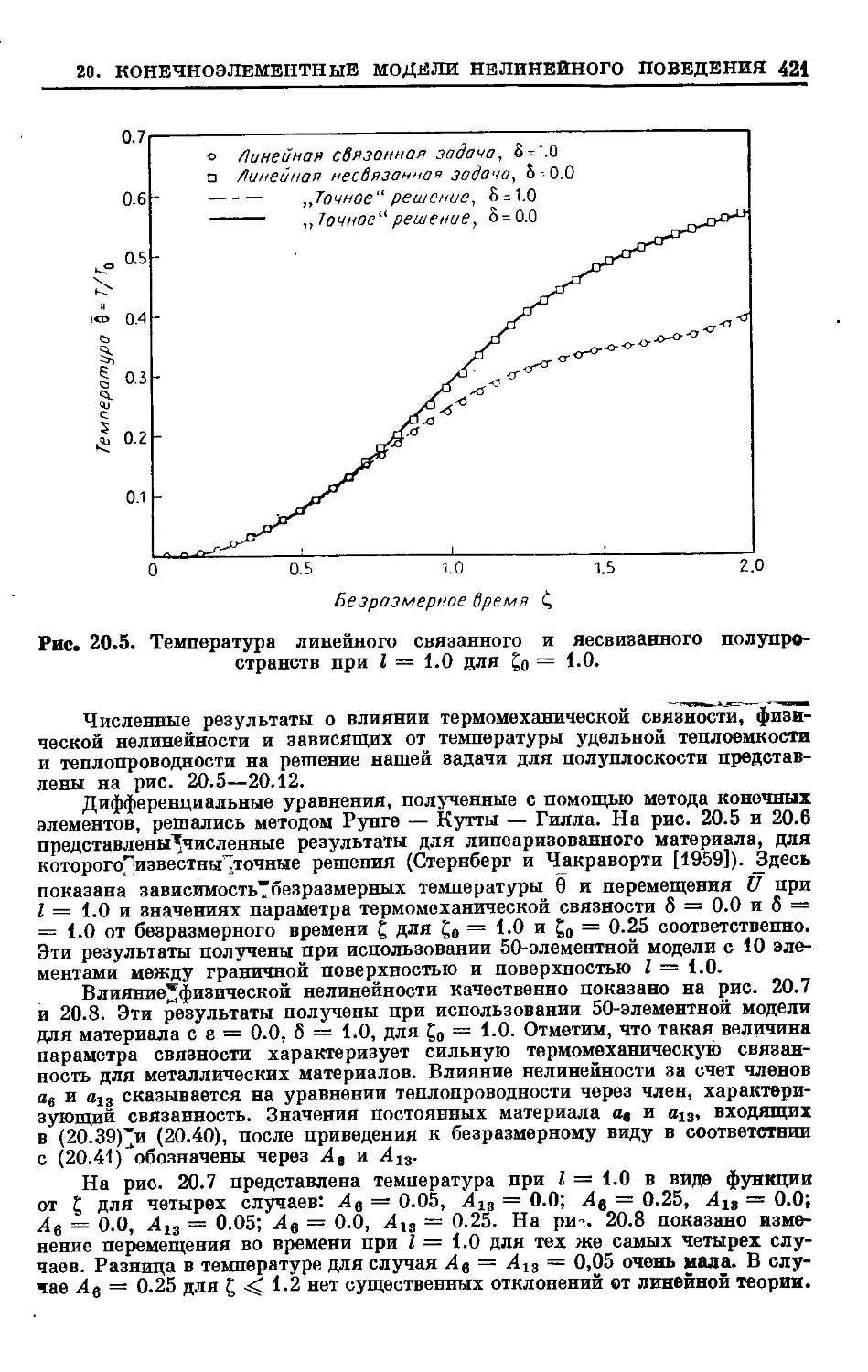
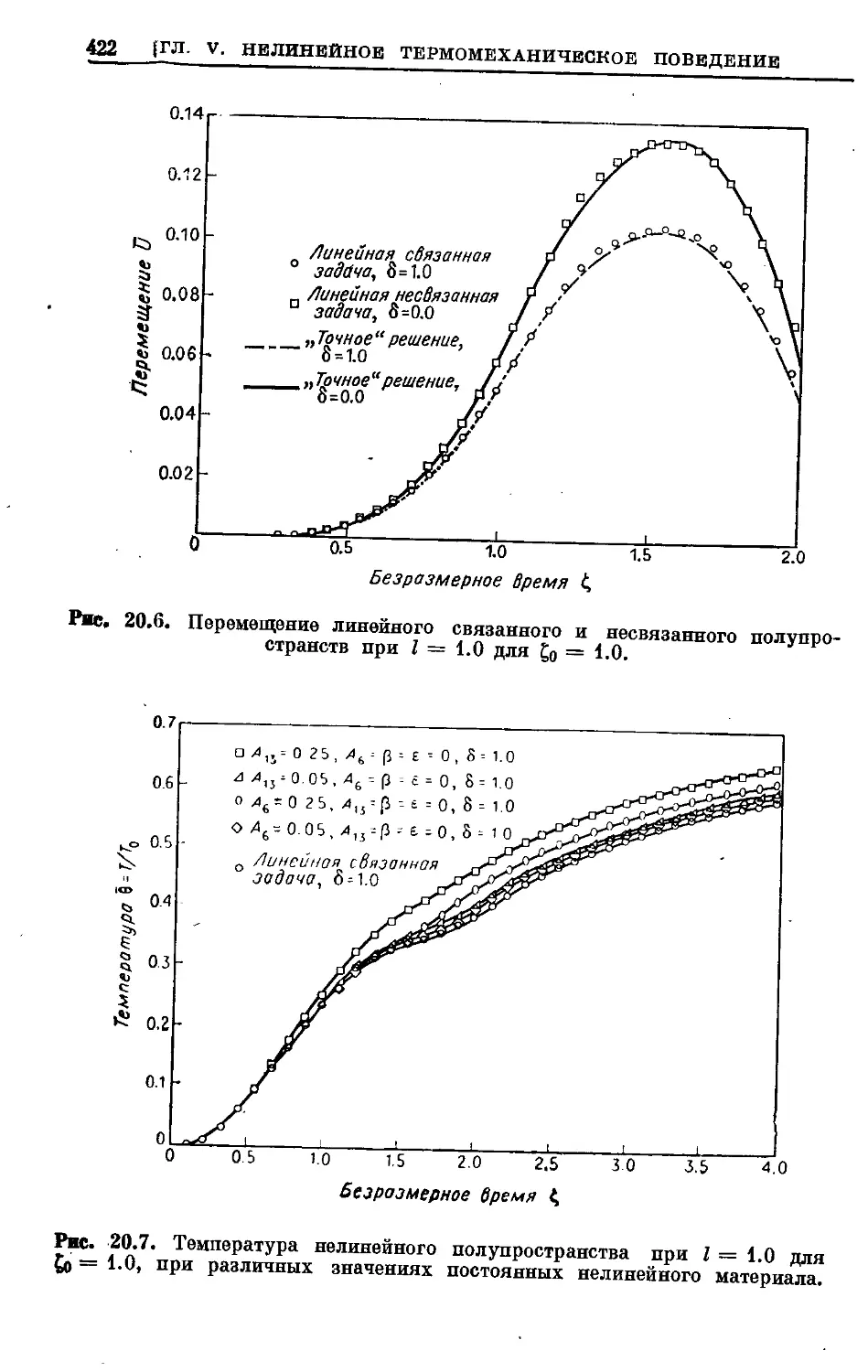
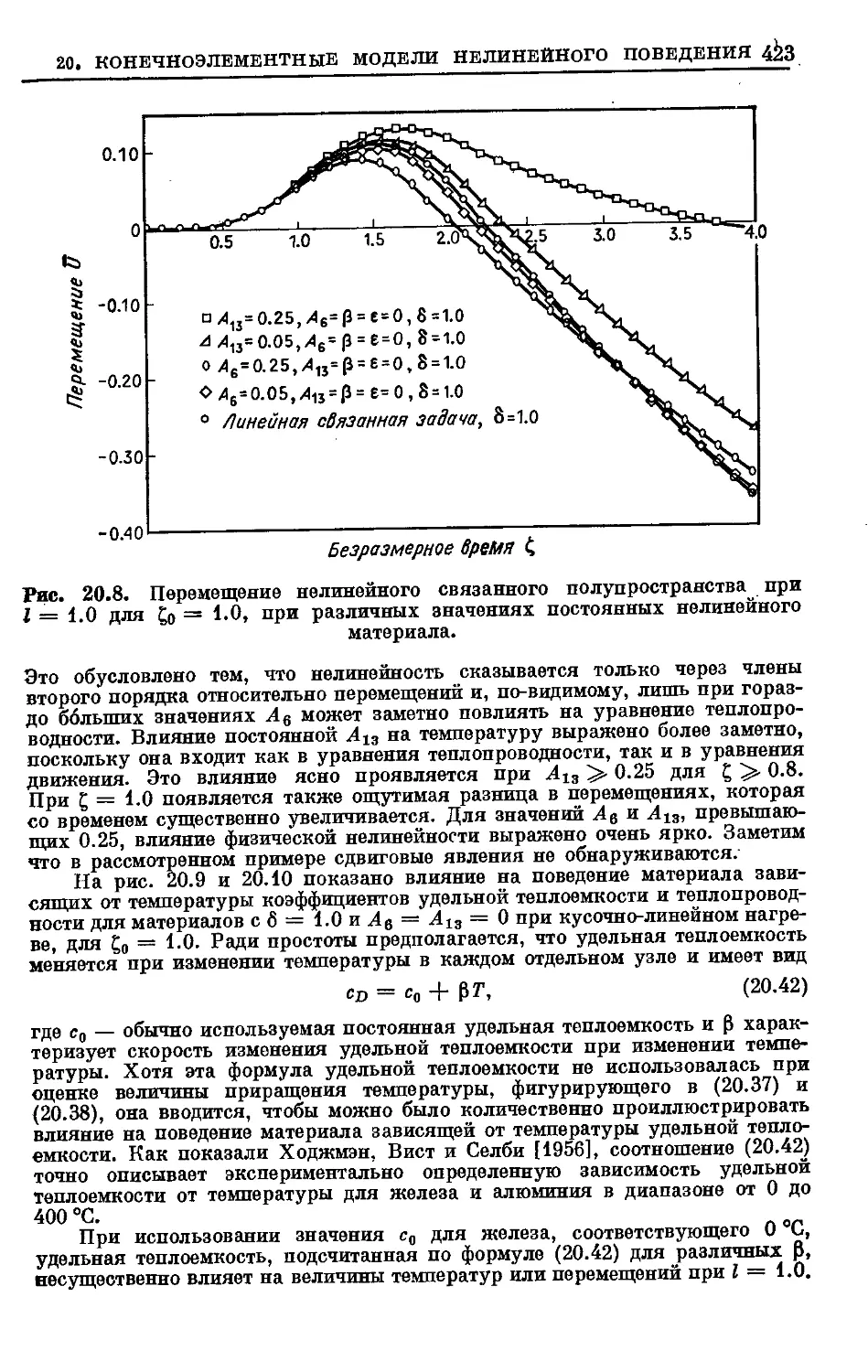
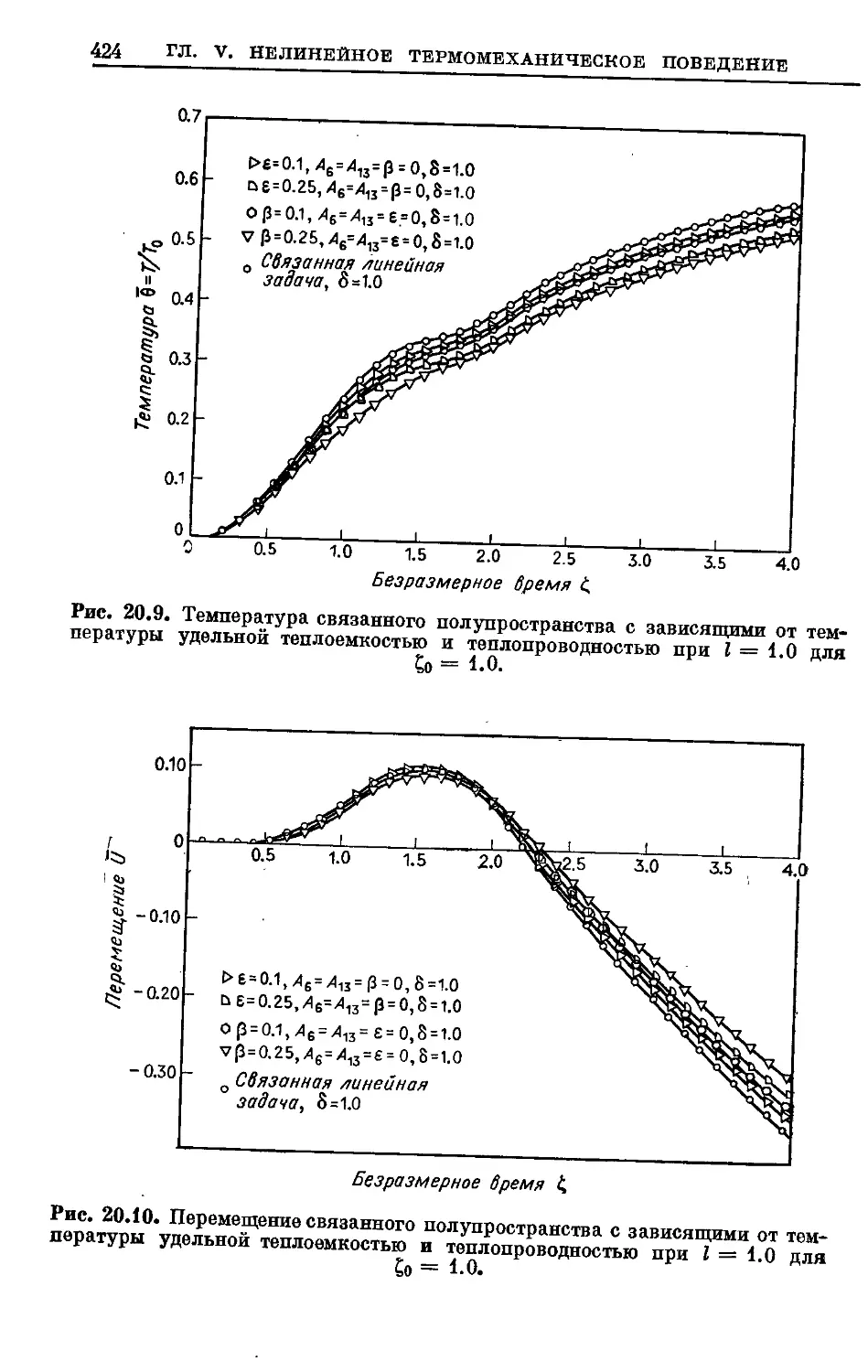
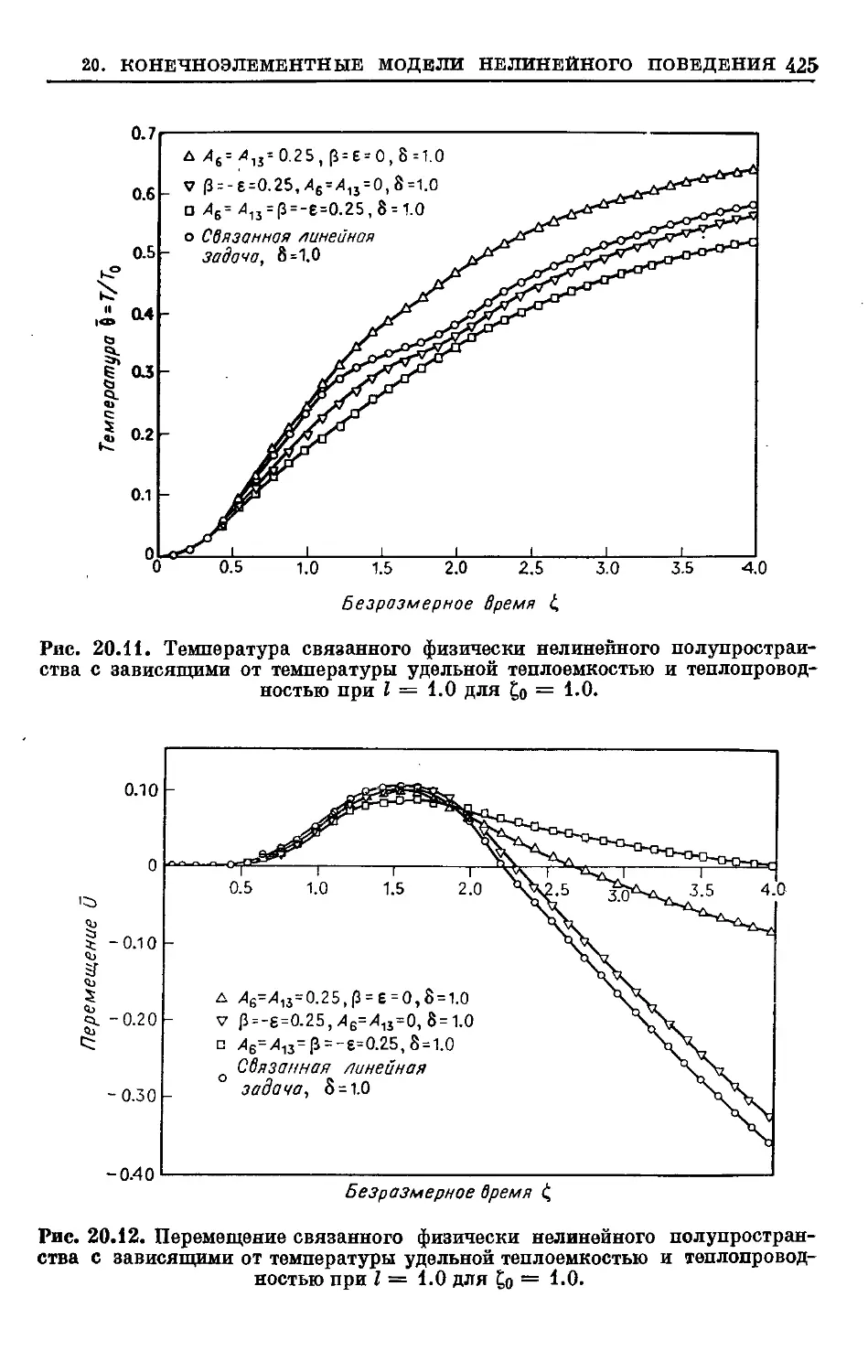
Text
с-4/ _ _
Дж.Оден
элементы
вйёлинейной
механике
сплошных
Издательство
Мир
Advanced Engineering Series
Irving H. Shames, Consulting editor
Finite elements
of nonlinear continua
J. T. Oden
Professor of Engineering Mechanics
The University of Alabama in Huntsville
MCGRAW-HILL BOOK COMPANY
New York • St. Louis • San Francisco • Dflsseldorf • Johannesburg
Kuala Lumpur • London • Mexico • Montreal • New Delhi • Panama
Rio de Janeiro • Singapore • Sydney • Toronto
1972
Дж. ОДЕН
Конечные элементы
в нелинейной механике
сплопшых сред
Перевод с английского
А. М. ВАСИЛЬЕВА
Под редакцией
Э. И. ГРИГОЛЮКА
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1976
УДК 51&.5+531 + 532+536
0-4/
Книга посвящена систематическому изложению одного
изТновейших методов численного анализа — метода конечных
элементов — и его приложений к широкому классу нелиней-
нелинейных задач механики сплошных сред и строительной механики.
Понятие конечного элемента служит тем звеном, которое
объединяет основы механики сплошных сред и современные
методы численного анализа и дает инструмент для получения
количественной информации о нелинейных процессах. Хотя
основное внимание уделено решению задач механики твердо-
твердого тела, материал излагается таким образом, что результаты мо-
могут быть применены и в ряде других областей математической
физики, таких, как динамика разреженных газов или теория
электромагнетизма.
Книга представляет значительный интерес для инженеров-
исследователей и научных работников, занимающихся вопро-
вопросами нелинейной механики и ее практическими приложениями.
Она полезна преподавателям, аспирантам и студентам старших
курсов.
Редакция литература по математическим наукам
Дж. Оден
Конечные элементы в нелинейной механике сплошных сред
Редактор В. Авербух. Художник Н. Дронова
Художественный редактор В. Шаповалов. Технический редактор Н. Иовлева
Сдано в набор 26/Ш 1976 г. Подписано к печати 28/IX 1976 г.
Бумага тип. JSI4 2 60x901/16 14,50 бум. л. 29 усл. печ. я., Уч.-изд. л. 28.02
Изд. № 1/8004 Цена 2 р. 13 к. Зак. 01310
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени Московская типография № 7 «Искра революции»
Союзполиграфпрома при Государственном комитете Совета Министров СССР по делам
издательств, полиграфии и книжной торговли.
Москва, К-1, Трехпрудный пер., 9
20305-043
О . 43-76 © Перевод на русский язык, «Мир», 1976
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Развитие вычислительных машин и численных методов открыло
большие перспективы использования конечноэлементного анализа
при исследовании проблем механики и проектировании современ-
современных конструкций и аппаратов.
Предлагаемая вниманию читателя монография представляет
собой систематизированное изложение метода конечных элементов,
охватывающее многочисленные частные публикации, главным
образом на протяжении последнего десятилетия. В ней рассматри-
рассматриваются линейные и нелинейные проблемы механики сплошных
сред. И хотя главное внимание сосредоточено на вопросах механи-
механики твердого тела, общность изложения и наличие большого числа
примеров, иллюстрирующих приложения теории, позволяют рас-
распространить описанные в книге методы на случай нелинейной
механики жидкости, а также электромагнитных процессов в непре-
непрерывных телах.
В книге сначала дана общая теория конечных элементов для
сплошных нелинейно деформируемых сред, когда нелинейность
обусловлена и внутренним сопротивлением материала внешним
воздействиям, и конечными перемещениями узлов элемента.
Затем строятся элементы, пригодные для решения термомеханиче-
термомеханических задач, и конечноэлементные модели материалов с памятью.
При исследовании конечно-деформируемых сред установлены
матрицы жесткости для большого класса изопараметрических
элементов упругих тел. Подробно описаны и проанализированы
методы численного решения нелинейных уравнений. Приведены
конкретные результаты численных расчётов для ряда типичных
задач.
Завершает монографию обширный список литературы, вклю-
включающий в себя около 400 наименований. При переводе в него добав-
добавлено несколько работ. Они помечены звездочкой.
Эту книгу можно рекомендовать всем, интересующимся пробле-
проблемами приближенного решения задач механики сплошных сред.
Э. И. Григолюк
Посвящается
Барбаре
ПРЕДИСЛОВИЕ
Книга посвящена описанию метода конечных элементов и его
приложений к широкому классу нелинейных задач механики сплош-
сплошных сред и строительной механики. Особое внимание уделено
решению задач механики твердого тела, однако основы мето-
метода изложены с достаточной степенью общности, допускающей
применение, например, к нелинейным задачам гидродинамики,
электродинамики, теории дифференциальных уравнений в част-
частных производных. Рассмотрены также различные численные мето-
методы решения больших систем нелинейных уравнений.
Интерес к численным исследованиям в области механики сплош-
сплошных сред возник у меня в результате продолжительных занятий
нелинейной механикой, когда я уяснил громадные возможности,
предоставляемые современными ЭВМ для решения нелинейных за-
задач, и осознал, что практическая ценность современных нелиней-
нелинейных теорий поведения конструкций и материалов определяется
в первую очередь их применимостью к конкретным задачам.
Несколько лет назад1 я занялся анализом возможности приме-
применения метода конечных элементов к изучению больших деформа-
деформаций упругих тел. Неожиданный успех уже первых исследований
(некоторые из результатов этих исследований вошли в настоящую
книгу) вдохновил меня, и я решил заняться нелинейными сплош-
сплошными средами общего вида. В последующие годы я подготовил
и прочел в Алабамском университете в Хантсвилле курс лекций
по применениям метода конечных элементов в нелинейной механи-
механике, в котором я попытался объединить основы механики сплошных
сред и современные методы численного анализа. При таком объеди-
объединении каждый из этих предметов приобретает новое содержание
и значение. Нелинейные теории поля в механике ценны уже не
только тем, что они представляют собой элегантное обобщение
классических теорий, но и тем, что с помощью электронных машин
они становятся источником получения количественной информации
о действительных происходящих в природе нелинейных явлениях.
Понятие конечного элемента с его простотой и общностью служит
тем самым звеном, которое соединяет вместе эти различные предме-
предметы, причем соединяет их способом, который в ретроспективе выгля-
ПРЕДИСЛОВИЕ
дит гораздо естественнее многих классических приемов приклад-
прикладной механики.
При отборе материала для книги я не стремился к тому, чтобы
дать исчерпывающий набор решений для всех типов нелинейных
задач. Моей целью было описать общий и физически наглядный
метод получения дискретных моделей сплошной среды и предста-
представить образцы применения этого метода к исследованию характер-
характерных нелинейных задач механики твердого тела. После усвоения
основных принципов читатель сможет сам приложить метод
к целому ряду не рассмотренных в книге задач.
Для того чтобы книгу можно было читать независимо от других
источников, в гл. I приведены вводные сведения о методе конечных
элементов и некоторые сведения по кинематике сплошной среды,
а также напоминаются характеристики напряженного состояния
и фундаментальные законы сохранения массы и количества дви-
движения. ¦ ' ¦
В гл. II излагается общая теория конечных элементов. При
этом свойства конечноэлементных моделей полей общего вида
представлены в форме, пригодной для пространств любой конечной
размерности. Рассматриваются различные типы конечноэлемент-
конечноэлементных моделей, а также критерии сходимости метода и некоторые
приложения к линейным и нелинейным дифференциальным урав-
уравнениям, волновым явлениям и динамике разреженных газов.
Кроме того, в зтой главе подробно обсуждаются понятия сопря-
сопряженных подпространств и сопряженных аппроксимаций.
Гл. III посвящена механике типичного конечного элемента
сплошной среды. Она начинается с изложения соответствующих
термодинамических понятий и принципов, за которым следует
вывод локальной и глобальной форм закона сохранения энергии
для сплошных сред. Используя теорию, развитую в гл. II, мы
далее выводим из закона сохранения энергии общие кинематиче-
кинематические соотношения и уравнения движения и теплопроводности для
конечного элемента сплошной среды. В главу включен также крат-
краткий обзор теории определяющих уравнений и указан вид опреде-
определяющих уравнений для дискретных моделей полей перемещений
и полей температур.
В гл. IV рассматриваются приложения метода конечных эле-
элементов к нелинейным задачам теории упругости. Глава начинается
с обзорного изложения теории конечных упругих деформаций.
Затем выводятся нелинейные жесткостные соотношения для упру-
упругих тел и приводятся решения ряда задач, в том числе задач
о конечных деформациях несжимаемых тел вращения, растяжении
и раздувании упругих мембран, конечной плоской деформации
несжимаемых упругих тел. В эту главу включен также обзор
различных методов решения больших систем нелинейных урав-
уравнений.
ПРЕДИСЛОВИЕ
Глава V посвящена изучению неупругого поведения, причем
особое внимание уделяется термомеханически простым материалам
и материалам с памятью. Выводятся общие уравнения движения
и теплопроводности для конечных элементов таких материалов
и описывается ряд применений этих уравнений к некоторым
избранным задачам, в частности к задачам линейной и нелиней-
нелинейной связанной термоупругости и нелинейной связанной термо-
вязкоупругости.
Я обнаружил, что написание книги является нелинейной зада-
задачей, решение которой требует многих итераций. Поскольку в на-
настоящем своем виде этот текст очень мало отличается от нескольких
предыдущих итераций, я публикую его с надеждой, что он может
служить приближенным решением стоявшей передо мной задачи.
Однако нелинейная прикладная механика — еще очень юная об-
область исследований, растущая все быстрее с каждым днем. Так что
последовательность еще далеко не сошлась. Если эта книга послу-
послужит начальным приближением для последующих итераций, она
сыграет предназначенную ей роль.
Я признателен за поддержку, полученную при подготовке
книги от ряда коллег и учеников. Особенно полезными были
замечания и предложения профессоров X. Браули и Г. Агирре-Ра-
миреса. Весьма плодотворным было для меня обсуждение ряда
вопросов с профессорами Т. Дж. Чангом и Дж. Вемпнером. Пер-
Первые варианты некоторых глав этой книги распространялись среди
студентов, и я искренне благодарен им за их отзывы. Особенно
я признателен Дж. Ки, Д. Бхандари, У. Армстронгу, Т. Сато,
Дж. Поу и Д. Кроссу. Мой долг выразить благодарность НАСА
и Научно-исследовательскому отделу воздушных сил США, при
поддержке которых были осуществлены исследования, способ-
способствовавшие возникновению ряда изложенных в книге идей.
Моя большая благодарность сотрудникам издательства Мак-
Гроу-Хилл, особенно Джеку Мейзелу, за терпеливость и старатель-
старательность, с которой они выверили огромное количество математиче-
математических символов и верхних и нижних индексов в моей рукописи.
Мне доставляет удовольствие поблагодарить также миссис
Д. Уиджент, которая с энтузиазмом взялась за перепечатку всей
рукописи и с большим подъемом проделала эту огромную работу.
В заключение, но далеко не в последнюю очередь, я хочу
выразить признательность той, которой посвящена эта книга.
Ее ободряющие слова, помощь в чтении корректур и многие
личные жертвы, принесенные ради того, чтобы я мог завершить
работу, я всегда буду помнить с благодарностью.
Дж. Т. Оден
Глава I
Предварительные сведения
1. ВВЕДЕНИЕ
В первой половине двадцатого века основная часть литературы
по механике твердого тела и строительной механике касалась
приложений к различным краевым задачам давно сформулирован-
сформулированных линейных теорий. Конечно, были отдельные замечательные
исключения: работы, приведшие к возрождению и усовершенство-
усовершенствованию классических теорий пластичности и вязкоупругости; раз-
разрозненные, хотя частично и успешные попытки создания единой тео-
теории поведения материалов; и большое число исследований геомет-
геометрических нелинейностей, связанных с «сохранением нелинейных
членов». Однако для большинства инженеров и научных работни-
работников практические приложения механики твердого тела сводились
к решению линейных задач.
Причина этого вполне понятна, поскольку до недавнего прош-
прошлого поведение реальных конструкций можно было адекватно
описывать линейными теориями. Например, деформации большин-
большинства конструкций при рабочих нагрузках обычно были едва раз-
различимы невооруженным глазом, а известно, что при малых дефор-
деформациях и установившихся однородных температурах уравнения
состояния для таких распространенных материалов, как сталь
и алюминий, можно без особых погрешностей считать линейными.
В последнее время ситуация резко изменилась. Начиная
с 1950 г. широкое применение нашли многие новые материалы,
поведение которых уже нельзя описать классическими линейными
теориями. Термовязкоупругость зарядов твердотопливных двига-
двигателей, закритическое поведение гибких конструкций, использова-
использование сильно деформируемых надувных конструкций, нелинейное
поведение полимеров и синтетических материалов — вот лишь
несколько новых областей исследования, стимулировавших инте-
интерес к нелинейной механике твердого тела. Сейчас уже сформули-
сформулирована теория упругости в общем виде, предложены новые нели-
нелинейные теории вязкоупругости и термовязкоупругости и вырабо-
выработаны основные, ставшие уже общепризнанными, принципы получе-
получения уравнений состояния нелинейных материалов. Девизом совре-
современных изысканий в области нелинейного поведения материалов
10 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ^
стала максимальная общность, и к* настоящему времени уже пред-
предложено несколько теорий, описывающих диапазон сред от упругих
твердых тел до термовязких жидкостей.
Несмотря на успехи в создании нелинейных теорий поведения ма-
материалов и конструкций, те, кто сталкивается с феноменом нелиней-
нелинейности в практической деятельности, располагают очень малой коли-
количественной информацией. Нелинейные теории приводят к нелиней-
нелинейным уравнениям, а это означает, что классические методы анализа
сразу становятся неприменимыми. Число точных решений нели-
нелинейных задач, имеющихся во всех опубликованных работах
по нелинейному поведению материалов и конструкций, можно
пересчитать по пальцам, но и они, все без исключения, относятся
лишь к телам простейших геометрических форм при простейших
граничных условиях. Часто применяется «полуобратный метод»,
когда вид деформированного тела предполагается известным зара-
заранее (©итуация, которую редко встретишь на практике), но даже
ж в этом случае для получения количественных результатов
на заключительном этапе обычно используются численные методы.
Этот дефицит количественной информации — в некотором смы-
смысле ирония судьбы, поскольку одновременно с последними дости-
достижениями в нелинейной механике твердого тела появилось наиболее
мощное из когда-либо существовавших средств получения количе-
количественной информации — ЭВМ. Но, с одной стороны, специалисты
в области вычислительной математики все свое внимание уделяли
таким новым областям, как кибернетика и нелинейное програм-
программирование, с другой стороны, механики были увлечены чисто тео-
теоретическими аспектами механики сплошных сред. А на стыке
лежит плодороднейшая земля, настоящая благодатная нива —
численный анализ нелинейных сплошных сред. Это сплав совре-
современных теорий сплошной среды и современных методов численно-
численного анализа, на основе которого с помощью ЭВМ можно получать
количественную информацию о нелинейном поведении материалов
и конструкций. Систематическое исследование части этой проме-
промежуточной территории и составляет содержание книги.
2. КОНЦЕПЦИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Для получения количественных решений в нелинейной меха-
механике сплошных сред часто приходится прибегать к численным
методам. Однако независимо от того, какие первоначальные пред-
предположения и методы использовались, чтобы сформулировать зада-
задачу, если для получения результатов привлекаются численные
методы, сплошная среда фактически аппроксимируется в процессе
решения некоторой дискретной моделью. Этим подсказывается
логическая альтернатива классического подхода — с самого начала
представлять сплошную среду при помощи дискретной модели.
2. КОНЦЕПЦИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ Ц
В этом случае дальнейшая идеализация при составлении уравне-
уравнений иди при их решении может и не понадобиться. Один из таких
подходов, основанный на идее кусочной аппроксимации непрерыв-
непрерывных полей, получил название метода конечных элементов. Просто-
Простота и общность этого метода делают его удобным средством решения
широкого класса нелинейных задач.
При классическом подходе исследование сплошных сред начи-
начинают обычно с изучения свойств бесконечно малых элементов рас-
рассматриваемого континуума. Устанавливают соотношения между
средними значениями различных величин, связанных с рассма-
рассматриваемыми бесконечно малыми элементами, а затем, устремляя
размеры элементов к нулю при неограниченном возрастании их
числа, получают дифференциальные уравнения в частных произ-
производных или интегральные уравнения, описывающие поведение
тела.
В противоположность этому классическому подходу при ис-
использовании метода конечных элементов начинают с изучения
свойств элементов конечных размеров. При установлении этих
свойств могут использоваться уравнения, описывающие поведение
континуума, но размеры элементов остаются все время конечными,
интегрирование заменяется конечным суммированием, а диффе-
дифференциальные уравнения в частных производных заменяются,
скажем, системами алгебраических или обыкновенных дифферен-
дифференциальных уравнений. Сплошная среда с бесконечным числом
степеней свободы представляется, таким образом, дискретной
моделью, имеющей конечное число степеней свободы. При этом
если удовлетворяются некоторые условия полноты, то с увеличе-
увеличением числа конечных элементов и уменьшением их размеров пове-
поведение дискретной системы приближается к поведению «непрерыв-
«непрерывной системы»— сплошной среды. Существенной особенностью
такого подхода является то, что он в принципе применим к досле-
доследованию конечных деформаций физически нелинейных анизотроп-
анизотропных неоднородных тел любой геометрической формы при произ-
произвольных краевых условиях.
2.1. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Идея представления непрерывных функций с помощью кусоч-
кусочной аппроксимации отнюдь не нова. В зачаточном виде идеи интер-
интерполяции использовались по всей видимости уже в древней Вави-
Вавилонии и Египте и, следовательно, опередили математический анализ
больше, чем на две тысячи лет. Много позже восточные математики
пытались оценить магическое число я, приближенно определяя
площадь единичного круга. Представляя круг в виде совокупно-
совокупности большого, но конечного числа прямоугольников или много-
многоугольников и принимая за площадь круга сумму их площадей,
12 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
они достигли точности почти в сорок значащих цифр. Наконец,
Ньютоном и Лейбницем был создан математический анализ, кото-
который позволил сформулировать большинство задач математической
физики с помощью дифференциальных уравнений в частных про-
производных и интегральных уравнений. Впрочем, частые неудачи
попыток использования классических аналитических методов при
решении этих уравнений, с одной стороны, и пришествие ЭВМ —
с другой, привели к тому, что все большее число современных
исследователей применяют приближенные методы численного
анализа. Интересно, однако, отметить, что при этом они во многих
случаях подсознательно прибегают к более примитивным концеп-
концепциям, чем использованные при получении решаемых урав-
уравнений.
Идея представления конструкций в виде набора дискретных
элементов восходит к раннему периоду исследования конструкций
летательных аппаратов, когда, например, крылья и фюзеляжи
рассматривались как совокупности стрингеров, обшивки и рабо-
работающих на сдвиг панелей. Хренников [1941] ввел «метод карка-
каркасов»— предшественник общих дискретных методов строительной
механики — и применил его, представляя плоское упругое тело
в виде набора брусьев и балок. Топологические свойства некото-
некоторых типов дискретных систем изучались Кроном [1939] *), который
разработал универсальные методы анализа сложных электрических
цепей и строительных конструкций. Курант [1943] 2) дал прибли-
приближенное решение задачи кручения Сен-Венана, используя кусочно-
линейное представление функции искажения в каждом из тре-
треугольных элементов, совокупностью которых заменялось попереч-
поперечное сечение тела, и формулируя задачу с помощью принципа
минимума потенциальной энергии. Пример применения Курантом
метода Ритца содержит в себе все основные моменты процедуры,
известной теперь как метод конечных элементов. Аналогичные идеи
использовал позже Пойа [1952]. «Метод гиперокружностей», пред-
предложенный в 1947 г. Прагером и Сингом [1947] и подробно исследо-
исследованный Сингом [1957] 3), легко может быть приспособлен для
«конечноэлементных» применений; он проливает новый свет на
приближенные методы решения некоторых краевых задач мате-
математической физики. В 1954 г. Аргирис и его сотрудники 4) начали
публикацию серии работ, в которых они далеко развили некоторые
обобщения линейной теории конструкций и представили методы
х) См. также, например, Крон [1944а, 19446, 1953, 1954, 1955].
2) См. также Курант, Фридрихе и Леви [1928].
3) Синг [1957] говорит о линейной интерполяции на треугольных обла-
областях; очевидно, что применение им «полиэдральных графов» и «пирамидаль-
«пирамидальных функций» — как раз в духе метода конечных элементов.
4) Аргирис [1954, 1955, 1956, 1957], Аргирис и Келси [1956, 1959, 1960
1961, 1963], Аргирис, Келси и Кэмел [1964].
3. МЕХАНИКА СПЛОШНЫХ СРЕД 13
исследования дискретных конструкций сложных конфигураций
в форме, удобной для использования ЭВМ.
Первое формальное изложение метода конечных элементов,
вместе с методом жесткостей для совокупности элементов принад-
принадлежит Тэрнеру, Клафу, Мартину и Топпу [1956], которые при
исследовании задач о плоском напряженном состоянии использо-
использовали для описания свойств треугольного элемента уравнения
классической теории упругости. Именно Клаф [1960] первым ввел
термин «конечные элементы» в своей более поздней работе, посвя-
посвященной плоским задачам теории упругости. В последующие годы
о методе конечных элементов было написано несколько сотен
статей. Обширные списки литературы можно найти в ряде книг
я обзорных статей об этом методе 1).
3. МЕХАНИКА СПЛОШНЫХ СРЕД
В последующих параграфах нашей главной целью будет разра-
разработка общих методов построения конечноэлементных моделей
непрерывных полей и использование этих моделей при исследова-
исследовании нелинейных задач строительной механики и механики сплош-
сплошных сред. Уравнения, описывающие поведение сплошной среды,
можно разделить на четыре группы: 1) кинематические; 2) динами-
динамические, например законы сохранения; 3) термодинамические
и 4) определяющие уравнения (уравнения состояния). Термодина-
Термодинамические принципы, излагаемые в гл. III, являются удобным
средством получения общих уравнений движения и теплопровод-
теплопроводности для конечных элементов сплошных сред. Определяющие
уравнения устанавливают соотношения между кинематическими,
динамическими и термодинамическими переменными и, таким
образом, характеризуют материал, из которого состоит сплошная
среда. Общие положения теории определяющих уравнений обсуж-
обсуждаются в гл. III, а в гл. IV и V рассматриваются определяющие
х) См., например, труды конференций и сборники статей под редакцией
Вёбеке [1964а, 1971], Зенкевича и Холистера [1965], Рыдзевского [1965],
Пшеменецкого, Бейдера, Бозича, Джонсона и Микитова [1966], Холанда
и Белла [1969], Рована и Хэккетта [1969], Бёрки, Бейдера, Микитова, Пше-
Пшеменецкого и Ширка [1969] и Галлагера, Ямады и Одена [1970]; книги Пестела
и Лекки [1968], Галлагера [1964], Мартина [1966а] и Зенкевича и Ченга
[1967]. В книге Пшеменецкого [1968] приводится свыше 400 работ о методе
конечных элементов. Имеется ряд обзорных статей и докладов, например
Аргирис [1958, 1966а, 19666], Уоррен, Кастл и Глория [1962], Парр [1964,
1967], Фелиппа и Клаф [1968]. См. также диссертацию Фелиппы [1966].
Сингхал [1969] составил перечень 775 работ, относящихся к методу конечных
элементов и матричным методам расчета конструкций. Более поздние обзоры:
Зуданс [1969], Зенкевич [1970]. Обзорные статьи, посвященные исключи-
исключительно приложениям к нелинейным задачам: Маркл [1970], Мартин [1970],
Оден [1969а, 19706].
14 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
уравнения для ряда материалов. Остальная часть этой вводной
главы посвящена краткому описанию кинематических и динами-
динамических соотношений для сплошных сред.
4. КИНЕМАТИКА
Кинематика, в ее традиционном понимании, изучает движение
тел без рассмотрения причин, вызывающих его. Она описывает
геометрические, характеристики движения, и ее основные понятия
образуют важную часть основ механики сплошных сред. Здесь
мы дадим обзор некоторых наиболее важных кинематических соот-
соотношений, которые используются в дальнейшем 1). Остальные кине-
кинематические соотношения вводятся в последующих разделах по
мере надобности.
4.1. ГЕОМЕТРИЯ И ДВИЖЕНИЕ
Тело — это бесконечное множество частиц, которым можно
поставить во взаимнооднозначное соответствие упорядоченные
тройки вещественных чисел, называемых координатами частиц.
Каждой частице можно приписать некую меру, называемую массой;
мы будем предполагать, что масса абсолютно непрерывна в том
смысле, что при стремлении к нулю произвольного объема тела
то же самое происходит и с его массой. Расположение множества
частиц, образующих тело, в какой-либо момент времени называется
конфигурацией тела. Более строго, конфигурация — зто гладкое
отображение тела на некоторую" область трехмерного эвклидова
пространства. Последовательность отображений, определяющих
конфигурации тела в различные моменты времени t (т. е. однопара-
метрическое семейство конфигураций), называется движением тела.
Разумеется, понятия тела и движения очень близко знакомы
нам по нашему повседневному опыту, и взятый нами при их
определении несколько формальный тон для большинства пресле-
преследуемых в книге целей не является необходимым. Формальные
определения помещены здесь лишь для того, чтобы указать на до-
дополнительный смысл некоторых аппроксимаций, которыми мы
будем заниматься в следующих главах.
х) За небольшими исключениями используются обозначения, введенные
в книге Грина и Зерны [1968, стр. 53—61]. Подробное изложение кинематики
сплошных сред с историческим обзором содержится в работе Трусделла
и Тулина [1960, стр. 241—463]. Формальное аксиоматическое изложение
кинематики приведено у Трусделла и Нолла [1965, стр. 48—56], а также
у Трусделла [1966а, стр. 17—25] [см. также книгу Трусделла *[1972]. —
РедЛ
4. КИНЕМАТИКА 15
Рассмотрим непрерывное трехмерное тело в некоторой началь-
начальной (отсчетной) конфигурации Со. Для идентификации частиц
поставим в соответствие каждой частице х упорядоченную тройку
вещественных чисел xt = {хи х2, х3), называемых материальными
координатами частицы х. Чтобы придать числам xt геометрический
смысл и описать движение тела относительно конфигурации Со,
введем в трехмерном пространстве фиксированную прямоуголь-
прямоугольную систему декартовых координат zh называемых пространствен-
пространственными координатами 1). В качестве материальных координат х(
возьмем числа, равные соответствующим декартовым координатам
z{ точки пространства, занимаемой частицей х, когда тело находит-
находится в конфигурации Со. Таким образом, величины xt с геометриче-
геометрической точки зрения являются декартовыми координатами части-
частицы х относительно системы координат zt в момент^ когда тело
находится в начальной конфигурации. Начало х% = @, 0, 0)
материальной системы координат обозначается через о, а про-
пространственной — через 0. К моменту х = t @ ^ т ^ t) движение
тела переводит его из начальной конфигурации в некоторую новую
конфигурацию С, и частица х перемещается в новое положение Р,
пространственные координаты которого обозначаются через z^ (т).
Таким образом, декартовы координаты частицы в любой момент
времени т суть zt (т), а при т = 0 координаты zt (т) и xt совпадают
[*, @) = xt] 2).
Мы можем описать движение тела относительно конфигурации
Со, установив функциональную зависимость zt от Х( и времени.
Таким образом, мы предполагаем, что zt — однозначные функции
от xt и т, которые непрерывно дифференцируемы нужное число
раз всюду, за исключением, возможно, некоторых особых точек,
кривых или поверхностей. Итак,
zt = zt (xx, x2, xs, т). D.1)
Далее, будем считать, что существует единственное обращение
функций D.1) и что
j (x, т)
Говорят, что функции D.1) определяют движение тела.
Подчеркнем, что тройки вещественных чисел х{ используются
только как метки, приписываемые материальным частицам тела.
Числовые значения хи определяющие некоторую частицу в Со,
г) Материальные координаты часто называют лагранжевыми, а простран-
пространственные — эйлеровыми. — Прим. ред.
2) Заметим, что поскольку xt и zt — прямоугольные декартовы коорди-
координаты в Со, место индекса (вверху или внизу) не имеет значения. Мы будем
использовать для обозначения координат частицы в Со какяг, так и аг«,
а в С — как zt, так и z{. Однако в конфигурации С имеет смысл писать х1
вместо xt.
16
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
определяют ту же самую частицу во всех конфигурациях тела.
Мы можем считать эти метки-числа координатами, написанными
прямо на теле, так что они непрерывно движутся вместе с телом,
когда то переходит из Со в некоторое другое положение. Отсюда
следует, что координаты xt, прямоугольные в Со, в С уже, вообще
Рис. 4.1. Геометрия движения из конфигурации Со в конфигурацию С.
говоря, криволинейные: прямые линии, параллельные осям xt
в Со, становятся в С кривыми, а координатные плоскости в Со
превращаются в С в криволинейные поверхности. Такие координа-
координаты называют еще конвективными или вмороженными. Поскольку
использование этих координат приводит к весьма простым кине-
кинематическим соотношениям, именно они чаще всего применяются
в механике твердого тела.
Радиус-вектор произвольной частицы х, занимающей в кон-
конфигурации Со положение Ро, обозначается через г, а радиус-вектор
той же самой частицы, занимающей в конфигурации С положе-
положение Р, обозначается через R. Если ij обозначают ортонормирован-
ные базисные векторы, касательные к осям z$, то
г = ед D-3)
D.4)
4. КИНЕМАТИКА 17
Вектор
u = R — r = Mjij D.5)
называется вектором перемещения, а функции иг = мг (хи
х2, хг, т) — компонентами перемещения. Геометрия движения
из Со в С показана на рис. 4.1.
4.2. ПЕРЕМЕЩЕНИЕ И ДЕФОРМАЦИЯ
Пусть ds0 — линейный элемент в Со, a ds — тот же самый
элемент в С; тогда
dsl — dr-drssdxidxi, D.6)
ds* = dR.dR**dzidzi. D.7)
Инвариант
ds2 — ds20 D.8)
является мерой деформации тела. Если всюду в теле ds* — dsl = 0,
то движение тела называется абсолютно жестким движением.
Если в точке х инвариант ds2 — dsl Ф 0, то говорят, что в этой
точке тело находится в деформированном состоянии.
В соответствии с D.4) и D.5)
dR = R,mdxm = zUmiidxm^Gmdxm, D.9)
где
Gms=sZi,mii = im+U m = Fim + Wi,m)ij- D.Ю)
Здесь запятая означает частную производную по Xi (например^
zUm == dzildx™; uUm == диг1дхт), a 8im — символ Кронекера. Век-
Векторы Gm касательны к деформированным (конвективным) коорди-
координатным линиям хт. Заметим, что функция (8jm + иг т) переводит
начальные касательные базисные векторы i^ в касательные векторы
Gm в С. Функции
Zi.m = бг-т + UUm D.11)
называются градиентами деформации.
Подставляя D.9) в D.7), получим
ds2 == Gtj dx4x\ D.12)
где
Gi)^GrGj = GJi. D.13)
Функции Gij являются ковариантными компонентами метрического
тензора для конфигурации С в конвективной системе координат хг.
Их иногда называют компонентами тензора меры деформации
Грина. Ввиду D.10) и D.13)
Gi} f^wffiblX'^fyJJtlJjFfM + um,ium,j. D.14)
2 Дж, Оден
•18 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Возвращаясь к D.8), можно выразить инвариантную меру де-
деформации в виде
ds2 — ds20 = 2y¦„ dxl dx\ D.15)
где
Уи =-Три - &ti). D.16)
Поскольку выполнение условия ds2 — ds^ =^=0 указывает, что части-
частица х тела находится в деформированном состоянии, функции ytj
служат мерами деформации. Они представляют собой компоненты
симметричного тензора второго порядка, называемого тензором
деформации Грина — Сен-Венана. Так как ds = ds0 при уц = 0
(и наоборот), необходимым и достаточным условием того, чтобы
движение тела было абсолютно жестким, является обращение
в нуль компонент деформации повсюду в теле. Заметим также,
что поскольку Ytj = Yji, всегда можно найти для данной точки Р
в С ортогональную систему координат, такую, что ytj = пц — 0
при i =^ )'. Направления осей этой системы координат называются
главными направлениями деформации, а компоненты деформации
по главным направлениям — главными деформациями.
Подставляя D.14) в D.16), получаем соотношения, связывающие
перемещения с деформациями:
4ii = \{Ui,i + Ui,i + um,iUm,j). D.17)
Хотя градиенты перемещений utj в общем случае не симметрич-
симметричны (т. е. Ujj Ф Ujj), их можно выразить в виде суммы компонент
симметричного тензора е^ и антисимметричного тензора и>ц, где
- в«ВЕ4(»1.у + »Л|) = вд, D.18а)
«°Ms4-(»i.y — »/.i)=— ан- D.186)
Величины etj и и>ц соответственно называются компонентами
тензора бесконечно малой деформации и тензора поворота. Ясно,
что
utj = еа + со/;- D.19)
и
dut — uitj dxj = (еи + аи) dxK D.20)
Компоненты деформации можно выразить через etj и со^-.
Подставляя D.19) в D.17), получаем
У И = eii + -2 (emi + «mi) (emj + d>mj). D.21)
При деформации очень гибких тел, таких, как пластины и оболоч-
оболочки, часто можно считать, что величины etj — бесконечно малые
4. КИНЕМАТИКА 19
первого порядка, а компоненты o>j7- велики по сравнению с ними 1).
Тогда приближенно
Если же и etj и o»j7- (а значит и utj) — бесконечно малые первого
порядка, то можно пренебречь их произведениями и квадратами
по сравнению с первыми степенями, и соотношение D.22) сводится
просто к
уи = еи. D.23)
Заметим, что при этом в случае ец = 0 (жесткое движение) форму-
формула D.20) принимает вид
йщ = atj dx}. D.24)
Это — бесконечно малое перемещение без деформации, представ-
представляющее собой жесткий поворот линейных элементов йхг.
4.3. ИНВАРИАНТЫ ДЕФОРМАЦИИ
Для каждого тензора второго порядка можно построить три
функции его компонент, постоянные во всех системах координат.
Эти функции называются инвариантами тензора. Главные инва-
инварианты тензора Gtj, обозначаемые через 1и 12, /3, называются
главными инвариантами деформации. Они определяются форму-
формулами:
Ii = 8irGTi, D.25а)
/2 = у Fir8hGriGsj- W'GijGrs), D.256)
/3= det GU~G, ¦ D.25в)
или, с учетом D.16):
/, = 3 + 2Ti;, D.26а)
/2 = 3 + 4?п + 2 {УпУи -уиуп), D.266)
/3 = 1 + 1уа + 2 (УпУл-уиУп) + y ^ШеыУггУпУы, D.26в)
гДе Ун = ЬггУп, а перестановочные символы е^к и е™' обозначают
знаки соответствующих перестановок.
В дальнейшем понадобятся выражения для частных производ-
производных инвариантов по деформациям. Замечая, что
См. Новожилов [1948, стр. 172].
2*
20 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
находим:
°Г =2бтп, D.28а)
= 4 [бтп A + Vii) -6nr6msYrS], D.286)
= 2бтп A4- 2ун) — 46nr6msvs + 4еЫйеп'*7^Тй1 . D.28в)
4.4. ИЗМЕНЕНИЯ ОБЪЕМА И ПЛОЩАДИ
Формула для элементарного объема в Со имеет простой вид:
dv0 = dxx dxt dx3. D.29)
После деформации векторы it dxt (суммирования нет), образующие
ребра прямоугольного объема dv0, становятся векторами Gt dxt.
Значит, в деформированном теле этот объемный элемент имеет
новый объем:
do = | Gi • (G2 x G8) | dx1 dx% dx\ D.30)
.Нетрудно установить, что
\Gi-(G^G3)\ = \zu}\ = V\G^\=Vh = VG. D.31)
Таким образом,
do = VG dxi dx2 dxs = ]/"G dv0 = V~T3 dva. D.32)
Деформации^ при которых объем не изменяется, называются
изохорическими. Ясно, что в случае изохорических деформаций
/, = 1 D.33)
Для того чтобы описать изменение элементов площади, удобно
ввести новое множество векторов G1, нормальных к координатным
доверхностям хг в деформированном теле х):
*0* <4-34>
Здесь eiik = Etjh — уже упоминавшиеся перестановочные симво-
символы, a G = | Gt) | = /s. Векторы G1 взаимны с векторами Gt,
т. е.
0{.С^ = б}. D.35)
Далее, функции
C^G'.G* D.36)
1) Термины «недоформированное тело», «деформированное тело» и т. д.
яе надо, конечно, понимать буквально. Под деформацией понимается дефор-
деформация относительно некоторой начальной конфигурации, причем не всегда
возможно или удобно выбирать начальную конфигурацию, соответствующую
естественному, свободному состоянию тела.
4. КИНЕМАТИКА 21
являются контравариантными компонентами метрического тензора
для С в конвективной системе координат х1, и тензор G11 обратен.
к тензору Gtj. В начальной конфигурации Со векторы, скажем
f, dx2 и is dx3, служат сторонами элементарной прямоугольной
даощадки dA10 координатной плоскости хх. Вектор it = i2 X is
нормален к dA10, и
dA10 = | i2 X i3 | dx2 dxa = dx2 dx3. D.37)
После деформации первоначально плоская площадка dAl0 стано-
становится криволинейной поверхностью dAy со сторонами, образуемы-
образуемыми векторами G2 dx2 и Gs dx3. Вектор Y^GG1 — G2 X G3 нормален
it dAt. Таким образом,
dAt = | G2 x Gs | dx2 dx3 = /GG11 dx2 dx3, D.38a)
G11 = G1^1 — квадрат длины вектора G1. Аналогично, эле-
элементарные площадки dAi0 и dA30 координатных плоскостей хг
и х3 в С0 переходят в деформированном теле в dA2 и dA3, где
^ D.386)
D.38в)
4.5. СКОРОСТЬ, УСКОРЕНИЕ И СКОРОСТЬ ДЕФОРМАЦИИ
Скорость v частицы определяется как скорость изменения ее
положения во времени. Если измерять зто изменение относительно
начальной конфигурации Со, то
v = R = yji", D.39)
где точка сверху означает частную производную по времени (т. е.
R = dR/df). Поскольку по определению конвективные координаты
частицы х1 не изменяются во времени (т. е. xi = 0), из D.4) и D.5'
следует, что
vt = ii=Ui. (АЛО)
Аналогично ускорение а частицы — это скорость изменения
во времени ее скорости. Относительно конфигурации Со
D.41)
ai = Vi = Zi=ut. D.42)
При исследовании деформаций сплошных тел полезно знать
скорость, с которой происходит деформирование. Естественной
Мерой скорости деформации является скорость изменения во вре-
22 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
мени инварианта ds2 —
ds2 — dsl = ds2. D.43)
Вследствие D.15) имеем
dx{ dx\ D.44)
гДе Ун = dytj/dt — скорости изменения компонент тензора дефор-
деформации. Подставляя сюда D.17), находим
ds* = 2 (8mi + um, t) um, j dxi dxi = 2zm, tum, j dxl dx>, D.45)
и в силу D.19)
d? = 2zm, t (em] + am}) dxl dx*. D.46)
• •
Функции в]т и (ujm называют соответственно компонентами
тензора скоростей бесконечно малых деформаций и тензора скоро-
скоростей поворота *). Повторным дифференцированием D.46) по време-
времени можно найти деформации и скорости перемещений высших
порядков.
4.6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
Кинематические соотношения, выведенные выше, нетрудно
записать в форме, справедливой для произвольной криволинейной
системы координат. Например, пусть ?г — криволинейные коорди-
координаты в начальной конфигурации Со, задаваемые преобразованиями
gf = g* (xu x2, х3),: D.47)
xt = хг A\ Ъ\ Is).
Координаты ?1 также следует рассматривать как конвективные,
и их точно так же, как хif можно использовать для описания
начальной конфигурации тела Со.
Базисные векторы gt, касательные к координатным линиям ?г,
и векторы g\ нормальные к координатным поверхностям ?г при
т = 0, определяются выражениями
8« = -&»»» e'—gt-im, D.48а,б)
а ковариантные и контравариантные компоненты соответствующе-
соответствующего метрического тензора имеют вид
gu = grgit ё" = ё-ё- D.49а,б)
1) В оригинале spin tensor. — Прим. ред.
5. ДИНАМИКА 23
Вектор перемещения и в этой криволинейной системе координат
записывается в виде
п = ш&* = и?%, D.50)
где Wt и wl — ковариантные и контравариантные компоненты
вектора и в системе координат ?г. Аналогичные формулы справед-
справедливы, конечно, в этой системе координат и для других векторов.
Компоненты тензора деформации определяются теперь выра-
выражениями
и видно, что ytj = 7o> определяемым формулами D.17), только
в том случае, когда gtj = btj. Соотношения между деформациями
и перемещениями принимают вид
Чи = у (Щ ¦¦ i + Щ: i + wTiwm..j), D.52)
где двоеточие означает ковариантное дифференцирование по
координатам |г, т. е.
"*:i = -Sr- r>m- D.53a)
^• = ^-+Г)ти;т, D.536)
где Г]^ — символы Кристоффеля второго рода для начальной
конфигурации Со:
rift = _^»_ilL. D.54)
Главные инварианты деформации представляются в виде
Л = Л-т_= 3 + 2gimymJ, _ D.55а)
/2 = 3 + igimymi 4- 2 (gimg"ftymiVnft -gimgnhymkym), D.556)
где g = | g f/ |.
С помощью преобразований, подобных использованным при
получении формул D.48) — D.55), можно записать в криволиней-
криволинейных координатах ?г и другие формулы, которые были ранее выве-
выведены в декартовых координатах.
5. ДИНАМИКА
Наряду с кинематическими можно сформулировать и некоторые
динамические соотношения, которые справедливы для всех сплош-
сплошных сред. Они следуют из основных законов механики, а не из
24 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
чисто геометрических рассуждений. Это — локальные уравнения
движения, получаемые из уравнений количества движения и мо-
момента количества движения, и динамические краевые условия,
формулируемые на основе понятия напряжения *). В последую-
последующих главах при рассмотрении конечноэлементных моделей будет
требоваться, чтобы эти уравнения движения и динамические
краевые условия удовлетворялись только в некотором осреднен-
ном смысле для некоторого конечного объема среды. Таким обра-
образом, речь будет идти об удовлетворении глобальных уравнений
движения для конечных объемов материала и о выполнении дина-
динамических краевых условий только в отдельных точках. В связи
с этим динамические соотношения не играют столь важной роли
в построении дискретных моделей сплошных сред, как изложен-
изложенные в предыдущем параграфе кинематические соотношения. Тем
не менее они являются фундаментальными не только для механики
вообще, но и для нашего приближенного анализа, поскольку при
построении любой аппроксимационной теории необходимо ясное
понимание явления, описываемого приближенно.
5.1. ЗАКОН СОХРАНЕНИЯ МАССЫ И УРАВНЕНИЯ
КОЛИЧЕСТВА ДВИЖЕНИЯ И МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
Приведем некоторые определения и законы, на которых осно-
основывается механика сплошных сред.
Закон сохранения массы. Каждое тело обладает неко-
некоторой неотрицательной аддитивной инвариантной характерис-
характеристикой, называемой массой. Масса тела сохраняется (не изменяется)
при любом его движении.
Предположим, что масса тела абсолютно непрерывна, т. е.
что существует функция р называемая массовой плотностью,
представляющая массу единичного объема тела. Если р0 и р —
массовые плотности данного тела в конфигурациях Со и С, то
в соответствии с вышеприведенным законом
pQdv0= ^ pdv. E.1)
С учетом D.32) можно также записать
^(9o-YGP)dvo = O. E.2)
"о
х) Для более подробного изучения этих законов см., например, Трусделл
и Тупин [1960, стр. 465—491] или Эринген [1962, стр. 82—111], [1967, стр. 93—
113]. „.
5. ДИНАМИКА 25
Поскольку это должно выполняться для любого объема, получаем
0=v^p0' E*3)
Уравнение E.3) называется уравнением неразрывности.
Определение 1. Количество движения J тела о/К опреде-
определяется формулой
J= j у dm, E.4)
где v — поле скоростей, а т — масса.
Определение 2. Момент количества движения S4'0 тела ой
относительно точки 0 определяется формулой
,= \ Rxvdm, E.5)
где R — радиус-вектор относительно точки 0, v — поло скоростей,
a m — масса.
Если масса абсолютно непрерывна, то dm в E.4) и E.5) можно
заменить на p[dv.
Уравнение количества движения. Производная по
времени количества движения равняется результирующей F(H)
всех сил, действующих на тело:
4r = F(B, E.6)
Уравнение момента количества движения.
Производная по времени момента количества движения отно-
относительно точки О равняется результирующему моменту М(Н)
относительно точки 0:
^ М(Л). E.7)
dt
5.2. ВНЕШНИЕ СИЛЫ И НАПРЯЖЕНИЯ
Внешние силы, действующие на сплошное тело4 можно разде-
разделить на две категории: A) массовые (или объемные) силы и B) по-
поверхностные силы. Массовые силы обусловлены внешними причи-
причинами и характеризуются плотностью — силой, приходящейся
на единицу массы (или объема) тела. Предполагается, что эти
плотности представляют собой непрерывные функции, определен-
определенные во всем объеме тела. Поверхностные силы (или поверхностные
усилия) действуют на граничных поверхностях тела. Они обуслов-
26 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
лены воздействием различных тел друг на друга через граничные
поверхности и характеризуются величиной поверхностной силы,
приходящейся на единицу площади граничной поверхности.
Предполагается, что плотности поверхностных сил представляют
собой кусочно-непрерывные функции.
В результате взаимодействия между собой частиц тела в нем
возникают также внутренние силы. Поскольку сила, с которой
какая-либо частица действует на соседние, равна и противополож-
противоположна по направлению силе, с которой эти соседние действуют на нее,
равнодействующая всех внутренних сил равна нулю. Чтобы оха-
охарактеризовать количественно внутренние силы, рассмотрим произ-
произвольную частицу х в деформированном теле и проведем через нее
некоторую поверхность А. Пусть N обозначает результирующую
внутреннюю силу, действующая на часть тела, расположенную
с одной стороны А, а —N — силу (реакцию), действующую на часть
тела, расположенную с другой стороны А. Рассмотрим малый
элемент АА поверхности А вблизи х. Пусть AN — результирую-
результирующая внутренняя сила на АА; тогда'вектп.о/> напряжения а в точке х
определяется следующим образом:
о= lim -7-T, E.8)
Вектор напряжения а представляет собой силу на единицу площа-
площади в деформированном теле. Ясно, что а зависит не только от N,
но и от ориентации площадки АА.
Если вектор напряжений в точке х отнести к базисным векто-
векторам Gj в деформированном теле, то его можно представить в форме
a = cijw;Gj, E.9)
где аг} — контравариантные компоненты тензора напряжений 1),
измеряемых на единицу площади в деформированном теле в кон-
конвективных координатах х\ а nt — ковариантные компоненты
единичного вектора в точке х, нормального к проходящей через
нее поверхности, на которой действует о. Говорят, что функции ог\
определяют напряженное состояние в точке х. Индексы у о13
имеют следующий смысл. Первый индекс указывает на направление
нормали к поверхности, на которой действует ог}, а второйиндекс—
на направление компоненты напряжения.
Смешанные и ковариантные компоненты напряжений можно
вычислить с помощью метрического тензора Gtj, определенного
формулой D.13):
oii = Gimom\ ва = С)тоГ. E.1Оа,б)
х) Величины а" иногда называют компонентами второго тензора напря-
напряжений Пиолы — Кирхгофа; см. Трусделл и Нолл [1965, стр. 124, 125].
Компоненты л3т = гт,го^ первого тензора напряжений Пиолы — Кирх-
Кирхгофа в общем случав не симметричны.-
5. ДИНАМИКА 27
Впоследствии мы покажем, что для монополярных сред тензор вг'
симметричен и поэтому о[3 = о^., = oi. Заметим, что физические
компоненты напряжений «гу, отнесенные к единичным векторам
вычисляются по формуле1)
Si, = o~u _L ; здесь по г и j суммирования нет. E.11)
Величины stj не являются компонентами тензора.
В соответствии с определениями напряжений и поверхностных
сил, в точках граничных поверхностей деформированного тела
вектор напряжения должен равняться плотности поверхностной
силы. Это условие
o = S E.12)
в граничных точках называется динамическим краевым условием
или краевым условием в напряжениях 2). Если поверхностную силу
отнести к базису Gj, то
сг{4 = ^, E.13)
где nt — ковариантные компоненты единичного вектора, нор-
нормального к граничной поверхности деформированного тела, a S3 —
контравариантные компоненты вектора S.
Поскольку в механике твердого тела обычно предполагается,
что априори известна форма тела в некоторой начальной конфи-
конфигурации, то часто бывает удобно определять напряженное состоя-
состояние в точке с помощью тензора напряжений t11 в конвективных
координатах хг, но измеренных на единицу площади в недеформи-
рованном теле 3). Компоненты tx} и о11 в одной и той же системе
координат связаны между собой соотношением
E.14)
Если t — вектор напряжений, измеряемых на единицу площади
недеформированного тела, то вместо E.9) имеем
j E.15)
где «, — компоненты единичной нормали п к недеформированной
поверхности, отнесенной к базису i; в начальной конфигурации:
П = И;1;. E.16)
') В предположении, что криволинейные координаты Xi ортогональны.—
Прим. перев.
2) При постановке нелинейных краевых задач возможны и другие фор-
формулировки краевых условий в напряжениях; см., например, Савин [1968,
стр. 637, 638].— Прим. перев.
3) См. Грин и Адкинс [I960, стр. 12—14].
28 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
5.3. ЗАКОНЫ ДВИЖЕНИЯ КОШИ
Используем теперь уравнения количества и момента количества
движения для получения локальных уравнений движения, приме-
применимых к любой частице х в конфигурации С. Пусть F обозначает
плотность массовых сил, a S — плотность поверхностных сил.
Тогда в соответствии с E.4) и E.6)
•^-Jvprfy = F№)= J Fpdv+ Js<M. E.17)
v v А
Учитывая E.12) и E.13) и с помощью формулы Грина — Гаусса ')
преобразуя интеграл по замкнутой поверхности в интеграл по огра-
ограниченному этой поверхностью объему, получаем
[ S dA та \ oi5ntGs dA = ( -4=- -A- (VG oijGj) dv. E.18)
J •! J 1/ G дхг
A A v '
Предположим теперь, что v, v и р непрерывны в v. Вследствие
закона сохранения массы d (p dv)ldt = 0. Поэтому E.17) можно
переписать в форме
]; = 0, E.19)
где а = v — ускорение. Так как E.19) справедливо для любого
объема, подынтегральное выражение должно обращаться в нуль.
Следовательно,
7J=-(/ea^)il+pF = pa. " E.20)
С другой стороны, E.20) можно записать в форме
с$ + р** = ря', E.21)
где точка с запятой означает ковариантнов дифференцирование
по конвективным координатам хг, т. е.
o$ = ff?«+f?malm + rS,a« . E.22)
где Т\т — символы Кристоффеля второго рода для деформирован
ного тела:
TLJ^gL, т>о. E.23)
dzr '
Уравнение E.21) называется первым законом движения Коши.
х) У нас ее обычно называют формулой Гаусса — Остроградского, —
Прим. ред.
5. ДИНАМИКА 29
Часто бывает удобно записывать уравнение движения в величи-
величинах, отнесенных к начальной конфигурации Со. Учитывая E.3)
и E.14) и замечая, что
Y = FiGj = F)ih E.24)
а = ajGj ='ujiit E.25)
Fj^Zm.jF7", u} = zm,jam, E.26а,б)
видим, что E.21) можно преобразовать к виду
(<V Л i + PoFm = Po'um. E.27)
Возвращаясь к уравнению момента количества движения,
получаем 1)
-|- j R х vpdv = М{Н) = j R x Fp dv + j R x SdA. E.28)
v v A
Проводя аналогичные рассуждения и используя E.20), получим
локальное уравнение момента количества движения
GixVGa^Gj^O, E.29)
или, в другой форме,
гто» = 0. E.30)
Отсюда следует, что
crij = ан E.31)
или4 с учетом E.14),
tij = tH. E.32)
Уравнение E.30) называется вторым законом движения Коши.
Уравнения E.31) и E.32) показывают, что вследствие этого закона
тензоры напряжений а11 и tt3 симметричны. Таким образом, из девя-
девяти компонент напряжения независимы только шесть.
х) Мы ограничиваемся здесь изучением монополярных сред, так что
возможность существования моментных напряжений, объемных или массо-
массовых моментов и т. д. не рассматривается.
Глава II
Теория конечных элементов
6. ВВОДНОЕ ИЗЛОЖЕНИЕ ОСНОВНЫХ ИДЕИ
МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Метод конечных элементов можно трактовать как систематиче-
систематический способ аппроксимации непрерывной функции дискретной
моделью, представляющей собой множество значений заданной
функции в некотором конечном числе точек области ее определе-
определения в совокупности с кусочными аппроксимациями этой функции
на некотором конечном числе подобластей. Эти подобласти назы-
называются конечными элементами, и локальная аппроксимация
функции на каждом конечном элементе единственным образом
определяется значениями этой функции в конечном числе предва-
предварительно выбранных точек области ее определения. Таким обра-
образом, при построении конечноэлементной модели заданной функции
поступают следующим образом:
1. В области определения функции фиксируют конечное число
точек и определяют значения функции в этих точках. Выб-
Выбранные точки называют узловыми точками или просто
узлами.
2. Область определения функции приближенно представляют
в виде совокупности конечного числа непересекающихся
подобластей, называемых конечными элементами. Таким
образом, моделью области определения функции является
совокупность конечных элементов, связанных между собой
надлежащим образом в узлах на их границах.
3. Заданную функцию локально аппроксимируют на каждом
конечном элементе непрерывными функциями, однозначно
определяемыми значениями функции (а возможно, и значе-
значениями ее производных вплоть до некоторого порядка)
в узловых точках, принадлежащих зтим элементам.
Важной особенностью метода конечных элементов является то,
что первоначально при локальной аппроксимации функции на ко-
конечных элементах их можно рассматривать независимо друг от
друга. Это значит, что каждый элемент можно считать совершенно
изолированным от всей совокупности и аппроксимировать функ-
функцию на этом элементе с помощью ее значений в узлах независимо
6. ВВОДНОЕ ИЗЛОЖЕНИЕ ОСНОВНЫХ ИДЕЙ
31
от того, какое место займет рассматриваемый элемент в связанной
модели, и от поведения функции на других конечных элементах.
Таким образом, имеется возможность создания каталога разно-
разнообразных конечных элементов с произвольными узловыми значе-
значениями локальной аппроксимирующей функции. Мы можем затем
выбирать из этого каталога те конечные элементы, которые нужны
для аппроксимации области определения заданной функции и ее
значений.
6.1. ОДНОМЕРНАЯ ЗАДАЧА
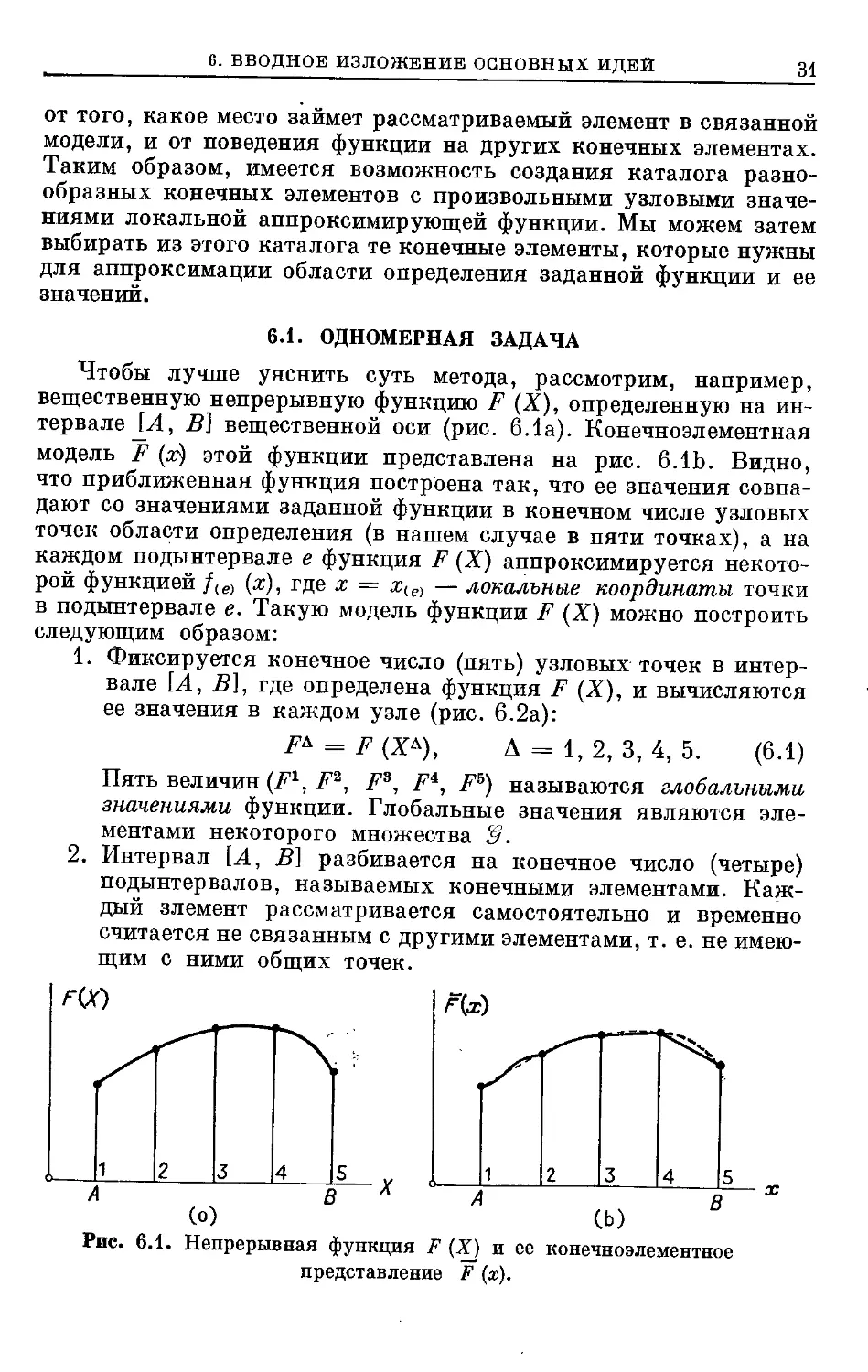
Чтобы лучше уяснить суть метода, рассмотрим, например,
вещественную непрерывную функцию F (X), определенную на ин-
интервале [А, В] вещественной оси (рис. 6.1а). Конечноэлементная
модель F (х) этой функции представлена на рис. 6.1Ь. Видно,
что приближенная функция построена так, что ее значения совпа-
совпадают со значениями заданной функции в конечном числе узловых
точек области определения (в нашем случае в пяти точках), а на
каждом подынтервале е функция F (X) аппроксимируется некото-
некоторой функцией /(е) (х), где х = xie) — локальные координаты точки
в подынтервале е. Такую модель функции F (X) можно построить
следующим образом:
1. Фиксируется конечное число (пять) узловых точек в интер-
интервале [А, В], где определена функция F (X), и вычисляются
ее значения в каждом узле (рис. 6.2а):
F* = F (Хд), А = 1, 2, 3, 4, 5. F.1)
Пять величин (F1, F2, Fs, F*, F5) называются глобальными
значениями функции. Глобальные значения являются эле-
элементами некоторого множества &.
2. Интервал [А, В] разбивается на конечное число (четыре)
подынтервалов, называемых конечными элементами. Каж-
Каждый элемент рассматривается самостоятельно и временно
считается не связанным с другими элементами, т. е. не имею-
имеющим с ними общих точек.
А В Л
(о) (Ь)
Рис. 6.1. Непрерывная функция F (X) и ее конечноэлементное
представление F (х).
32
ГЛ. И. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
3. Для каждого элемента е устанавливается система локальных
координат х(е). Заданная функция локально аппроксими-
аппроксимируется на е функцией /(й (х) == /(е) (xie)), которая в узлах 1
и 2 на концах подынтервала принимает значения $е) и ffe)
(рис. 6.2Ь). Восемь значений (/Jd, /fi), /<2), . . ., /Д)) можно
рассматривать как элемент некоторого множества X. Вели-
Величины /(I) (N = 1, 2) называются локальными значениями
функции, соответствующими элементу е.
4. Интервал [А, В] отображается на подынтервалы [а(е), bie)]
(е = 1, 2, 3, 4) с помощью простых отношений инцидент-
инцидентности, связывающих глобальные координаты Хл различных
узлов с локальными координатами х{е):
r2 _ ri уз
Г2 Г1 — у2
^C) — x\k)= х4»
F.2)
Эти отношения допускают две различные интерпретации.
Если временно рассматривается один отдельный элемент,
D)
Рис. 6.2. Глобальные значения и локальные аппроксимации функции F (X)
6. ВВОДНОЕ ИЗЛОЖЕНИЕ ОСНОВНЫХ ИДЕЙ 33
то отношения типа xfa = X2 и х\%) = Ха описывают вло-
вложение элемента в связанную модель интервала [А, В].
Таким образом, они описывают связывание конечноэлемент-
ной модели. С другой стороны, отношения типа X* = х*з) =
= ЖD) описывают разбиение отрезка на конечные элементы.
Как будет показано позже, эти интерпретации по математи-
математической природе совершенно различны.
5. Между глобальными значениями функции F^ (А = 1, 2, 3, 4,
5) и локальными значениями /^ (е = 1, 2, 3, 4; N = 1, 2)
устанавливается связь с помощью простых отношений
инцидентности вида:
/1 — pi f2 — /1 — рг
hi) > Ju)~42)~I '
УB) УC) ^ ' 'C) /D) Г ' *> -0'
которые непосредственно следуют из F.2) в силу того, что
значения функций F (X) и /(е) (х) находятся во взаимно
однозначном соответствии с точками X и xie) их областей
определения.
6. Ввиду того, что теперь локальные аппроксимирующие
функции однозначно определяются через глобальные зна-
значения F^ посредством формул F.3), их рассматривают сов-
совместно; окончательная модель функции F (X) имеет простой
вид
_ 4 _
F(x)=%fw(x,Fl,F*, ...,^5), • F.4)
гДе fie> (xi F1, F2, . . ., F5) — локальные функции, выражен-
выраженные через соответствующие глобальные значения.
При построении конечноэлементных моделей других функций,
скажем G (X), Н (X) и т. д., определенных на других интервалах
вещественной оси, не слишком много выигрывается, если строить
локальные аппроксимации для каждого подынтервала, выбираемо-
выбираемого в области определения функции, совершенно независимо. Как
указывалось ранее, мы можем локально определить функцию
на произвольном отрезке с помощью произвольных узловых зна-
значений, и эта одна и та же локальная аппроксимация может исполь-
использоваться многократно для построения дискретных моделей целого
множества различных функций путем придания нужных значений
произвольной длине отрезка и задания нужного положения узлов
в модели области определения рассматриваемой функции. Мате-
Математически зто достигается введением отношений инцидентности
типа F.2), которые устанавливают связь между глобальными коор-
координатами ХА и локальными координатами х^е). Подобным же
8 Дж. оден
34 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
образом произвольность локальных узловых значений /(е) устра-
устраняется отношениями типа F.3), которые позволяют выразить /(е)
через соответствующие глобальные значения F^.
Описанные выше зависимости, существующие между связан-
связанной моделью и отдельными конечными элементами, а также между
глобальными и локальными узлами, математически могут быть
описаны двумя довольно простыми отображениями. Рассмотрим
сначала любой элемент некоторой совокупности fl* непересекаю-
непересекающихся интервалов: %* = {[яц), xfi)], [х}2), жB2)], . . ., [жD), хЩ.
Пусть Л — отображение, которое вкладывает некоторый фикси-
фиксированный интервал е в соответствующее место в интервале [А, В].
Это отображение Л: [х\е), ж(|)] -*¦ [А, В] осуществляется так *):
X = 2 A~Nx(e)i e фиксированно, F-5)
N=1
где Д = 1, 2, ..., 5 и
,е) ¦ х, если узел Д связанной модели
соответствует узлу N элемента е F.6)
противном случае.
D)
Например, в равенствах F.2) для четвертого элемента Л^ = 0s
если Д ф 4, 5, и в соответствии с F.2)
4 DL 1 DL 2 1
{1, ее
со
О в
D), D) D) D)
так как Л* =Л| = 1 и Л* =Л? = 0.
(е)
Отображение Л описывает вложение интервала [а(е), ble)]
в интервал [А, В] и называется привязыванием элемента е к модели
области определения функции. С другой стороны, совокупность
таких отображений
A) B) C) D) E)
Л = {Л, Л, Л, Л, Л}
х) Отношения инцидентности, подобные этому, были введены Кроном
[1939] и рядом других авторов. Аргирис [1954] использовал аналогичные
преобразования в своем методе перемещений. Форма, использованная в F.5),
подобна предложенной Висманном [1962, 1963, 1966] для конечноэлемент-
ного расчета больших деформаций упругих тел. Эти преобразования исполь-
использовались при исследовании нелинейных задач Оденом [напр., 1967а, 19676,
1969а, 19696]. Равенство F.5) является просто формальной математической
формулировкой связывания модели. Практически оно записывается с помо-
помощью соответствующей нумерации узловых точек. Необходимость полностью
(Ю.
определять массив Л^ возникает редко.
6. ВВОДНОЕ ИЗЛОЖЕНИЕ ОСНОВНЫХ ИДЕЙ 35
можно рассматривать как отображение нашей совокупности 91*
непересекающихся интервалов на «связанный» интервал [А, В].
Говорят, что отображения Л осуществляют связывание конечно-
элементной модели.
(е) (е)„
Транспозиция отображения AN обозначается через ?2Д; она
интерпретируется как отображение множества ?/ глобальных
точек Xs в множество X локальных точек х$у
т№ _ У OWYA Cfi 8^
х..— zj «дЛ . \v-°;
() д=1
Элементы массива ?2Д определяются по существу так же, как
и элементы массива Л^:
A, если узел N элемента е соответствует узлу А
QN = \ связанной модели, /g g\
i 0 в противном случае.
Например, если рассмотреть узел х\з) (рис. 6.2), то
, C), C) C) C), C)
х?3) = QJX1 + QfZ2 + Q3X3 + Q4Z4 + Q|X6. F.10)
C) C)
Но по определению йд = 0, если А Ф 4, a Q4 = 1. Таким образом,
Отображение QA означает просто перенумерацию целочислен-
целочисленных меток, приписанных различным узловым точкам модели.
(е)
В некотором смысле Q можно рассматривать как отображение
конечного подмножества интервала [А, В] в подмножество конеч-
конечных подынтервалов. По зтой причине совокупность Q таких
отображений будет называться разбиением [А, В] на конечные
элементы. • * ¦
(О. (е)
Ясно, что массивы AN и ?2Д можно использовать для того,
(е) (е)
чтобы образовать композицию Л Q = /е, где Ie — тождественное
отображение совокупности локальных узлов элемента е на себя:
2
Д=1
N, М=1, 2. F.12)
Здесь fijtf — символ Кронекера. Можно также образовать ком-
композицию Q Л = Iq, где fff — отображение совокупности гло-
3*
36 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
бальных узлов, соответствующих элементу е, на себя:
{бг, если узлы Хл, Хг принадлежат эле-
элементу е,
л г IP. \ ч\
О, если узлы X , X не принадлежат (оло)
элементу е,
А, Г=1, 2, 3, 4, 5.
Возвращаясь теперь к F (X), напомним, что заданная функция
F (X) осуществляет взаимно однозначное соответствие между ее
значениями F = F (X) и точками X области ее определения.
Таким образом, любой локальной или глобальной точке, фигури-
фигурирующей в равенствах F.7) или F.8), соответствует локальное
или глобальное значение функции. На это соответствие ясно ука-
указывает то, что отношения F.3) по форме идентичны отношениям
F.2). Отсюда следует, что для фиксированного е можно записать
jb F.14)
/й= 2 (&>Л. F.15)
Д1
6.2. ДВУМЕРНАЯ ЗАДАЧА
Прием, использованный в одномерном случае, можно исполь-
использовать и при построении конечноэлементных моделей функций,
определенных на двумерных областях. Рассмотрим, например,
скалярную функцию Ф = Ф (X, Y), определенную в некоторой
замкнутой области % плоскости X, Y (рис. 6.3). Зафиксируем
некоторое конечное число G точек и пометим их последовательно
числами 1, 2, . . .f G. Значения Фл в этих точках задаются форму-
формулой
фл = ф(Хл), F.16)
где Хл — точка под номером А с координатами (Хл, Ул).
Аппроксимируем область Щ некоторой совокупностью Е под-
подобластей ге, точки которых задаются локальными координатами
х(е) = (xie), y(e)). Локальные аппроксимации заданной функции
на каждом элементе обозначим через q\e) (x), а их значения
в узлах х?) — через ф^, где N = 1, 2, . . ., Ne, Ne — общее
число узлов элемента е. Связывание и разбиение модели осуще-
6. ВВОДНОЕ ИЗЛОЖЕНИЕ ОСНОВНЫХ ИДЕЙ
37
ствляются с помощью отношении инцидентности
Ne (e) G (е)
N=i в Д=1
F.17а, б)
а локальные значения связаны с глобальными посредством отобра-
отображений
Ne (<0 G (e)
Ф = 2 Л^ф(е) и Ф(е)= 2 йдФЛ- F.18а,б)
N=1 Д=1
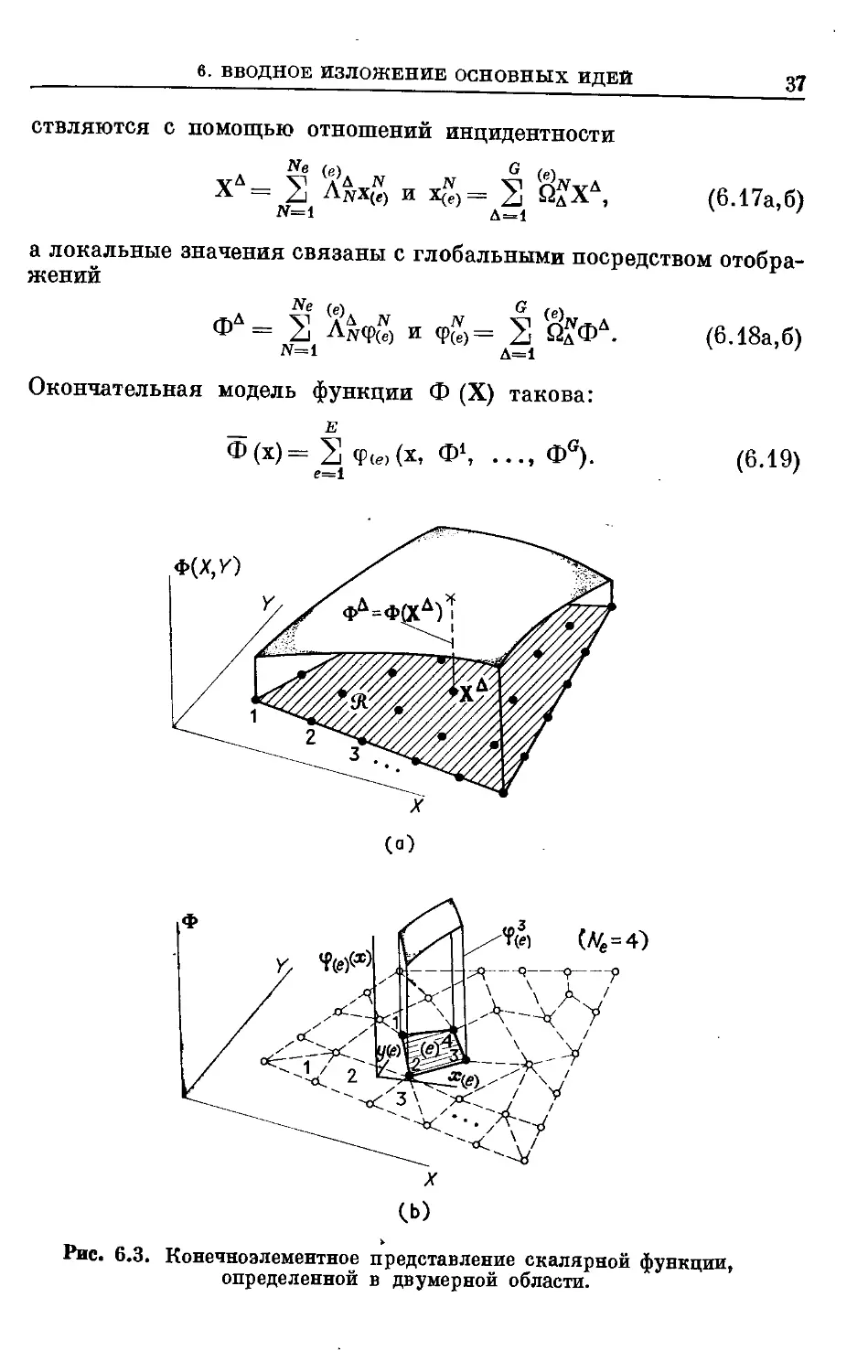
Окончательная модель функции Ф (X) такова:
Ф(х)= 2 Ф(.)(х,
е=1
F.19)
(ЛЬ = 4)
¦<3 wfS<L /
Рис. 6.3. Конечноэлементное представление скалярной функции,
определенной в двумерной области.
38 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ
ФУНКЦИИ ОБЩЕГО ВИДА г)
Мы изложили в предыдущем параграфе основные идеи метода
конечных элементов. Займемся теперь их обобщением, с тем чтобы
построить конечнозлементные представления произвольных функ-
функций, определенных на пространствах любой конечной размерно-
размерности к.
7.1. НЕКОТОРЫЕ ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ МАТЕМАТИКИ
Изложим кратко ряд понятий и фактов 2), полезных при исследовании
свойств общих конечноэлементных моделей непрерывных полей.
Мы используем обычные теоретико-множественные обозначения3).
Например, о ? «*? означает «о принадлежит множеству ^?»; о (f ^ означает,
что о не принадлежит ^f; js J — что Л является подмножеством ?8,
а^с J — что ^f является собственным подмножеством &. Запись вида
^t = {о | о обладает свойством Р} используется для указания множеств,
все элементы которых обладают определенным свойством Р. Равенство двух
множеств, записываемое в виде ^f = ,38, означает, что ^ s«58 и «58 S «^?.
Объединение, пересечение и разность двух множеств ^и J обозначаются
соответственно через ^ \\ ,53, <? [~| М и ^?\«53. Прямое (декартово) произ-
произведение двух множеств <? и «38 — это множество ^f X «58 упорядоченных
пар (а, Ъ), т.е. ^ X М = {(а, Ь) | а 6 af, Ь € .38}.
Пусть ^f — подмножество «58. Элемент 6 ? «58 называется точкой накоп-
накопления или предельной точкой множества «^?, если в любой окрестности Ъ
(т. е. в любом открытом множестве, содержащем Ъ) имеется точка множе-
множества Л, отличная от Ь. Иначе говоря, если Ь — точка накопления для ^f,
то любая окрестность Ъ содержит бесконечное число точек множества jt.
Множество, состоящее из ^ и всех его точек накопления, называется замы-
замыканием Л;. Если Ж и «58 — два таких множества, что замыкание ^f содержит
в себе «58, то говорят, что J% плотно в «58. Если же замыкание ^f равно «38,
то говорят, что J% всюду плотно в «58.
Термины «функция», «отображение» и «преобразование» используются
как синонимы и имеют следующий смысл: если даны два множества ^f и «58,
то отображение F множества ^ в множество «58, обозначаемое символом
F: ^ ->¦ «58,— это правило, которое каждому элементу в?^ ставит в соот-
соответствие один и только один элемент F (а) ? «58- формально F — это такое
подмножество произведения ^ X «58, что (а, Ъ) 6 F и (а, с) ? F =Ф Ь = с,
где символ =Ф читается «влечет за собой». Множество Л называется обла-
областью определения функции F, а элемент F (о) 6 М — образом элемента а
при отображении F или значением функции в точке а. Вся совокупность
образов F (j?) = {/ (а) | а 6 ^f} называется образом отображения F. Ото-
х) Материал этого параграфа в основном соответствует статьям Одена
|1969а, 19696]. См. также Оден [19676], Оден и Агирре-Рамирес [1969].
2) Некоторые из этих понятий рассматриваются подробнее в § 9 и 10.
3) См., например, Биркгоф и Маклейн [1941], Мур [1962] или Мак-Кой
[I960]. Доступно и полно линейная и абстрактная алгебра изложены в книге
Мостова, Сэмпсона и Мейера A963), а также у Финкбейнера [1966] и Гройба
[1963]. С основами функционального анализа можно ознакомиться по кни-
книгам Колмогорова и Фомина [1972] Люстерника и Соболева [1965] или Тэй-
лора [1958].
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 39
бражение F называется отображением ^f на «38, если F (<?) = «38, и назы-
называется взаимно однозначным, если / (о) = / (Ъ) =Ф а = Ъ. Если Е: «^? -*¦ «38
взаимно однозначное отображение на, то для каждого Ь g «38 существует
единственный элемент а 6 Jf, такой, что Ь — f (а), т. е. существует обратная
функция F-h M -»- Л-
Группой "§ называется алгебраическая система, состоящая из множе-
множества J# и операции „ * " (отображения из jt X jt в jb), ставящей в соответ-
соответствие каждой упорядоченной паре (а, ft) элементов а, Ь ? jl- третий эле-
элемент с ?^, обозначаемый через с — а * Ъ, такая, что
1° (а * ft) * с = а*(Ъ * с);
2° существует элемент е ? ^f, удовлетворяющий условию е * а =
= о * е = о для любого о ? ^f;
3° для любого а^ существует элемент а ? ^, такой, что о*а =
= а * а = е.
Если а * b = b * а, то группа "§ называется абелевой (или коммутативной).
Пусть R означает поле действительных (или комплексных) чисел, т. е.
множество частично упорядоченных действительных (комплексных) чисел
с обычными операциями сложения и умножения. Линейным (или векторным)
пространством V называется абелева группа, образуемая множеством эле-
элементов а, Ь, . . ., иногда называемых векторами, и операцией +', назы-
называемой векторным сложением, в совокупности с отображением RX f3^- СУ°,
называемым скалярным умножением, которое удовлетворяет следующему ус-
условию: для каждой пары чисел а, р" ? R и каждой пары векторов а, Ь ? "У0
1° (ар) a = а (pa);
2° (а + Р) a = аа + Pa;
а (а + Ь) = аа + оЖ;
3° 1а = а.
В дальнейшем, если только не будет сделано специальной оговорки, под
R понимается поле действительных чисел.
Максимальное число к линейно независимых элементов векторного про-
пространства V называется его размерностью. Для обозначения пространства
размерности к используется символ <?oh. Базисом пространства "У0 размер-
размерности к называется всякое множество к линейно независимых элементов
этого пространства. Любой вектор а ? "У0 является линейной комбинацией
элементов базиса.
Подмножество S линейного пространства "У0 с операциями векторного
сложения и скалярного умножения называется подпространством "У0 в том
и только в том случае, когда оно само является линейным пространством.
Если % и dT —¦ подпространства линейного пространства "У0, то суммой
$ и 3~, обозначаемой через $ + ЗГ, называется множество элементов вида
в + t, где s ? %, t ? 3~. Пересечение "§ П &~ подпространств % и 3" —
это в соответствии с общим определением множество элементов, принадле-
принадлежащих одновременно обоим подпространствам. Как % + 3~, так и Ъ П &
являются подпространствами V1. Если % -{- 9~ = f3 и? f\ ?Г == 0, где
0 — пустое множество, то 'У0 называется прямой суммой "§ и 3~; это.
записывается так: V = "§ ф 3~.
Часто в линейном пространстве "У0 можно каждому элементу а поста-
поставить в соответствие неотрицательное действительное число, обозначаемое
через |[ а || и называемое нормой а, такое, что выполнены условия:
1° II а II ^ 0, причем равенство выполняется в том и только в том слу-
случае, если а = 0;
2° !| Яа || = | X | || а || для любого скаляра X;
3° | а + Ы| < || а || + || Ь ||.
40 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Линейное пространство, в котором определена норма, называется нормиро-
нормированным линейным пространством. Понятие нормы является обобщением
обычного понятия длины вектора.
Последовательность ах, а2, . ¦ ., ап, . . ., элементов нормированного
линейного пространства (записывается коротко {ап}), обладающая свойством
lim у ат — ап || = 0, называется последовательностью Коши. Если суще-
7П,П-*-оо
ствует а0, такое, что lim || ап — а0 || = 0, то говорят, что последователь-
П-*ос
ность {ап} сходится (или сходится по норме || -||) к а0. Ясно, что если после-
последовательность {ап} сходится, то она является последовательностью Коши.
Иногда последовательность элементов линейного пространства может схо-
сходиться к элементу, не принадлежащему этому пространству. Если в норми-
нормированном линейном пространстве каждая последовательность Коши схо-
сходится к элементу этого же пространства, то оно называется полным. К каж-
каждому неполному нормированному линейному пространству всегда можно
добавить дополнительные элементы, так, что получающееся в результате
пространство, называемое пополнением исходного пространства, будет пол-
полным нормированным линейным пространством. Полное нормированное линей-
линейное пространство называется банаховым пространством. Если каждая после-
последовательность элементов пространства обладает сходящейся подпоследова-
подпоследовательностью, то пространство называется компактным.
Пусть J^i и Мч. — банаховы пространства, 2 — произвольное под-
подпространство Зх и А — отображение (функция) 2 в &2. В этом случае А
обычно называют оператором. Говорят, что множество 2 есть область опре-
определения оператора А, а множество всех элементов из Мг вида Л а, где а ?
6 2,— образ оператора А.
Оператор А называется аддитивным, если
А (а + Ь) = А& + АЪ,
и однородным, если
А (Ха) = X (Аа),
где X — произвольное действительное число и а, Ь ? 2. Если оператор А
аддитивен и однороден, то он называется линейным; в противном случае —
нелинейным. Оператор А ограничен, если существует положительное действи-
действительное число М, такое, что
Ма|| <М || а ||,
где символы || || означают нормы в пространствах J8i или 3&v
Сумма двух операторов Ах и Л2 определяется формулой
(Ах + А2) а = Аг& + Л2а,
а умножение оператора А на скаляр X — формулой
(ХА) а = Х(А&).
Можно показать, что совокупность всех линейных ограниченных операторов
в банаховом пространстве & сама образует банахово пространство, если
некоторым естественным образом ввести норму оператора.
Среди операторов особый интерес представляют функционалы. Опера-
Оператор Ф называется функционалом, если пространство его значений является
множеством действительных чисел. Таким образом, линейный функционал —
это оператор Ф (а) = X, где а ? 2> и Я, — действительное (или комплексное)
число, такой, что Ф (ka.) = ХФ (а) и Ф (а + Ь) = Ф (а) + Ф (Ь). Совокуп-
Совокупность всех ограниченных линейных функционалов на банаховом простран-
пространстве сама является банаховым пространством при соответствующем опреде-
определении нормы функционала, которое обозначается через ,38* и называется
сопряженным к пространству J8.
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 41
Пространством со скалярным произведением называется линейное про-
пространство, в котором определено скалярное произведение. Под скалярным
произведением понимается отображение 'У0 X 'У0 в R, ставящее в соответ-
соответствие каждой паре элементов (а, Ь) ? 'У3 X 'У0 неотрицательное действитель-
действительное число, обозначаемое через (а, Ь), которое, удовлетворяет следующим
аксиомам:
1° (а, а) >• 0, причем равенство выполняется тогда и только тогда,
когда а = 0;
2° (а, Ь) = (Ь, а);
3° <А,а + цЬ, с) = X (а, с) + ц (Ь, с).
Понятие скалярного произведения позволяет ввести понятия ортогональ-
ортогональности (элемент а ортогонален элементу Ь, если (а, Ь) = 0) и длины (|| а || =
= 1Л(а, а)). Отсюда следует, что каждое пространство со скалярным произ-
произведением является нормированным линейным пространством. Бесконечно-
Бесконечномерное банахово пространство со скалярным произведением, полное по нор-
норме || а || = у (а, а), называется гильбертовым пространством.
Часто оказывается возможным определить скалярное произведение эле-
элементов двух различных векторных пространств 'У0 и 'У0 над одним и тем же
полем скаляров как отображение пар (а, а), где а ? 'У3 и "а ? 'У3, во множе-
множество действительных чисел. При этом требуется, чтобы для любых а и а
1° (Яа+цЬ, а"> = Я,<а, а>+ц <Ь, а);
, Ь);
3° (а, а) = 0 при фиксированном аЕ5^=фа=О и (а, а) = О
при фиксированном а ? V =Ф а = 0.
В этом случае "У0 и Ч/3 называются дуальными пространствамих). Если
gj — базис "У0 и g* — базис V и (gt, gi) = б|, то говорят, что эти базисы
образуют биортогональный базис для "У0 и ?/э. С алгебраической точки зрени я
нет существенной разницы между пространством 'У0, дуальным к простран-
пространству 'У0 со скалярным произведением, и сопряженным к "У0 пространством
'У3*; фактически "У0 изоморфно сУа*. Вследствие этого термины «дуальное про-
пространство» и «сопряженное пространство» часто используются как синонимы.
Всякое пространство со скалярным произведением является метриче-
метрическим пространством; обратное утверждение, несправедливо. Метрическое
пространство ¦— это совокупность элементов X, Y, Z, . . ., называемых точ-
точками, вместе с функцией d (X, Y) (метрикой), ставящей в соответствие каж-
каждой паре точек X и Y некоторое неотрицательное действительное число. Это
число называется «расстоянием между» точками X и Y. Должны выполняться
следующие три аксиомы метрики:
1) d (X, X) = 0;
2) d (X, Y) = d (Y, X);
3) d (X, Y) < d (X, Z) + d (Z,l Y).
Пол агая d (X, Y) = || X — Y || или d (X, Y) = У {X — Y, X — Y), не-
нетрудно видеть, что каждое нормированное линейное пространство, а сле-
следовательно, и каждое пространство со скалярным произведением является
метрическим пространством. Метрическое пространство <М называется
сепарабелъным, если в нем существует счетное всюду плотное множество.
х) В этом случае говорят также, что пространства СУ° и У® находятся
в двойственности.— Прим. ред.
42 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
В последующих параграфах будет удобно говорить о точках Амперного
пространства, не вводя каких-либо систем координат. Это достигается с по-
помощью понятия точечного пространства %h. Говорят, что непустое мно-
множество Mh образует точечное пространство %h, ассоциированное с про-
пространством ^« со скалярным произведением, если существует функция
g: ?kh X Лк -*¦ <^°h со следующими свойствами:
1° для каждого X ? ?%h и каждого а 6 lJ/Dh существует единственный
элемент Y 6 Мк, такой, что g (X, Y) = а;
2° если g (X, Y) = a, g (X, Z) = Ь и g (Y, Z) = с, где X, Y, Z ?
б ?Яи и а, Ь, с ? уъъ, то а + Ь = с.
Элементы X, Y, . . . ? ?ffi называются точками. Далее, говорят, что век-
вектор g (X, Y) = а есть разность между точками X и Y, и удобно писать
g (X, Y) = X - Y = а.
Размерностью точечного пространства %h называется размерность простран-
пространства fz'h.
Таким образом, разность между двумя точками Y, X является вектором
XY = Y — X. Однако в дальнейшем, когда это не будет вызывать недоразу-
недоразумений, мы будем предполагать, что фиксирована некоторая точка 0^ 6
€ %h, называемая началом, так что под X можно понимать просто вектор
X — О,* = 0i»X — радиус-вектор точки X относительно точки 0<g. Каж-
дому X (или X — О») можно поставить в соответствие набор к действитель-
ных чисел X = (X1, X2, . . ., Xh), называемых координатами точки X.
Эти координаты определяются выбором базиса cV3h. Например, если в каче-
качестве базиса ^k взято ортонормированное множество векторов {ilt i2, ...
. . . ifc} (т. е. <!., ip = Ьи, i, / = 1, 2, . . ., к), то X - 0% = X4t, где
по повторяющемуся индексу производится суммирование от 1 до к, при
этом X* называются декартовыми координатами, а пространство %h назы-
называется эвклидовым точечным пространством. Отметим, что в общем случае
координаты X1, X2, . . ., Xh не обязательно декартовы и пространство %h
не обязательно эвклидово.
Под г-окрестностью JT (Хо) точки Хо ? %h понимается открытый шар,
определяемый как множество всех X ? %h, для которых d (Хо, X) < г,
где г — действительйое число, называемое радиусом этого шара. Пусть
S1 — некоторое подмножество %h, т. е. <fjP a %h. Точка X ? %h назы-
называется внешней точкой для <ЦР, если существует окрестность X, не содержащая
точек множества <ЦР. Если в каждой окрестности X имеются хотя бы одна
точка, принадлежащая <ЦР, и хотя бы одна, не принадлежащая $, то X назы-
называется граничной точкой для JP. Множество всех граничных точек множества
^Р называется его границей и обозначается через д^Р.
Пусть ^! и dii — непустые подмножества %h. Если ^ и ^fa не имеют
общих элементов, т. е. пересечение ^ П *&г пусто, то ^г и ^#» называются
непересекающимися (или дизъюнктными). Множество tf cz %"¦ называется
несвязным, если <ЦР = ^ [} <?г, где jtr и ^2 — непустые непересекающиеся
множества. В противном случае оно называется связным.
Некоторые связные подмножества ,5# с %h принято называть областями
А-мерного пространства %h. А именно областью называется открытое связ-
связное подмножество %h вместе со всеми своими граничными точками, с частью
их или вообще без них. Если область ?Я не содержит своих граничных точек,
то она называется открытой областью; если же М содержит все свои гра-
граничные точки — то замкнутой областью. Ясно, что область не обязательно
должна быть открытой или замкнутой. Если для всех X 6 31 норма || X || =
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 43
= || X ¦— Осе II < М, гДе М — некоторая положительная константа, то
область & ограничена, а если область 31 одновременно замкнута и ограни-
ограничена, то она компактна 4).
Мы будем в основном рассматривать аппроксимации различных непре-
непрерывных функций, определенных на компактных подмножествах А-мерного
точечного пространства %h. Более точно, пусть 2Г — некоторое множество
элементов Т, U, V, . . ., в значительной мере произвольных. Почти во всех
ваших приложениях величины Т будут действительными или комплексны-
комплексными числами, векторами или тензорами^ заданного порядка. Нами будут рас-
рассматриваться отображения: F: М -*¦ У , которые ставят в соответствие каж-
каждой точке X некоторого компактного подмножества М пространства %k
элемент Т ? 3~. Для обозначения таких функций мы будем использовать
запись Т = F (X), где Т — значение функции в точке X. Область М есть
область определения функции F (X). Предполагается, что F непрерывна
на М, т. е. для каждой точки Хо принадлежащей Л, F (X) ->¦ F (Хо) при
d (X, Хо) -»¦ 0. Отсюда следует, что образ F (М) тоже компактен. Если при
этом F — взаимно однозначная функция, то существует F и F называют
тогда топологическим отображением или гомеоморфизмом.
7.2. ЗАМЕЧАНИЯ ОБ ОБОЗНАЧЕНИЯХ
В последующем изложении постоянно используются индексные
обозначения и хорошо известное соглашение о суммировании.
Индексированная величина есть общий элемент некоторого упоря-
упорядоченного массива. Для получения всех элементов этого массива
надо придать каждому индексу все значения от 1 до верхнего
допустимого для этого индекса предела. По всем повторяющимся
индексам, если только они не заключены в скобки, производится
суммирование по всем допустимым значениям этих индексов.
Например, равенства F.5) и F.14) можно записать в виде
Л =ANX(e) И /< =ANf(e),
где суммирование производится по повторяющемуся индексу от 1
до Ne, где Ne — общее число узлов элемента е. Равенства F.8)
и F.15) можно записать в форме
а:(е)="ДАа И /(е) = "д/' ;
суммирование производится по повторяющемуся индексу А от 1
до G, где G — общее число глобальных узлов связанной модели.
Для обозначения того факта, что символ относится к типичному
(общему) конечному элементу, он наделяется идентификационной
меткой, в качестве которой обычно используется буква е. Эта
буква является пометой, а не индексом, и во избежание путаницы
она обычно заключается в скобки.
Часто будет необходимо различать глобальные величины (т. е.
величины, относящиеся к совокупности конечных элементов)
и локальные (т. е. относящиеся к отдельному конечному элементу).
Напомним, что речь идет о конечномерном пространстве.— Прим. ред.
44 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
За небольшими исключениями, для обозначения глобальных
величин используются прописные буквы. Строчные латинские
индексы используются для обозначения элементов массива или
компонент векторов и тензоров. Прописные греческие и латинские
индексы используются для обозначения величин, определенных
в узловых точках дискретной модели, причем греческие индексы
относятся к глобальным узлам связанной модели, а латинские —
к локальным узлам отдельных непересекающихся конечных эле-
элементов.
7.3. ДИСКРЕТНАЯ МОДЕЛЬ ОБЛАСТИ ?Я
Ясно, что построение конечноэлементной модели области А
пространства Щк не зависит от полей F (X), для которых 'Я может
быть областью определения. Дискретная модель <Я- строится
следующим образом.
1. В % фиксируется конечное число G точек, которые обозна-
обозначаются через X1, X2, . . ., Xе или, в сокращенной записи,
Хл (А = 1, 2, . . ., G). Эти точки называются глобальными
узловыми точками или глобальными узлами. Конечное мно-
множество {X1, X2, . . ., Xе} этих точек обозначается через аЯ-%.-
2. Область °Л приближенно представляется другой областью А,
которая содержит все узловые точки М- Разность °Л\°А
будем обозначать через ??е и называть областью отклонения.
Если множество 'Яг пусто, то f и f равны. Очевидно,
что fix <= Ш.
3. Теперь рассмотрим конечное число Е не связанных между
собой подмножеств ге пространства Шк, называемых конеч-
конечными элементами. Хотя в конечном счете мы хотим «связать»
зти элементы вместе, чтобы получить всю область М, мы
пока считаем все конечные элементы замкнутыми и непере-
непересекающимися, не допуская даже частичного совпадения
их границ. Границу любого элемента будем считать отлич-
отличной от границ всех других элементов, хотя в связанной
модели граничные точки двух конечных элементов могут
совпадать. Эта дизъюнктность составляет фундаментальное
свойство конечных элементов. Математически оно выражает-
выражается следующим образом:
Ti Л rj =0, i Ф /; i, / = 1,2,.. ., Е, G.1)
где, напомним, 0 — пустое множество. Объединение
будем называть несвязанной или несобранной областью.
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 45
4. Рассмотрим типичный конечный элемент ге, который пока
считается полностью изолированным от совокупности дру-
других элементов. В тех случаях, когда это удобно, для локаль-
локальной идентификации точек в ге будет использоваться символ
х(й) х). Иногда под этим символом удобно понимать локаль-
локальный радиус-вектор точки в ге относительно некоторой
фиксированной начальной точки оее. Можно также под-
подразумевать под х(в) упорядоченный набор к действительных
чисел х<е) = (х1(в), ?2<е), • • ., xft(e)), называемых локальными
координатами точки элемента е. Однако на данном этапе
удобно говорить о локальных точках, не прибегая к нача-
началам или системам координат.
В ге фиксируем конечное число Nе точек; обозначим их соот-
соответственно через х?ф xfe), . . ., х^е, или, более кратко,
Х(«) (N = 1,2,...-, Nе). Эти точки называются локальными
узловыми точками или просто локальными узлами. Конечное
множество {xfc), xfe), • • ., xfef} локальных узлов элемента
ге обозначается через ^?*(е>-
5. До сих пор подобласти ге никак не были связаны с °А. Свя-
Связанность дискретной модели для 3? достигается с помощью
отображения аЛ* на ft или каждого элемента Я^е) на 3?х-
По очевидным соображениям это отображение называется
связыванием элементов (оно преобразует несвязанную область
Ш* в связанную область ГЯ). Если предположить на время,
что существует надлежащее соответствие между узлами
подобласти ге и узлами в ??, то связанность модели дости-
(е) _
гается с помощью отображения Л: "S*fe) —>¦ 3?х (е фикси-
фиксировано) следующим образом:
A = ANX(e), G.3)
где A = 1,2,. . ., G, no N производится суммирование от 1 до
(е)д
Ne, a An определяются выражениями, аналогичными F.6),
а именно,
(р1 ( 1, если для связанной модели узел А в М
А% — < совпадает с узлом N в ге, G.4)
^ 0 в противном случае.
В G.3) под ХЛ и х$) понимаются точки пространства %и,
а не радиус-векторы (иначе вместо Хл надо было бы просто
г) Буква е является идентификационной меткой элемента, и не имеет
никакого значения, где она расположена. Наряду с символом х<е> для локаль-
локального обозначения точек в ге мы будем использовать и символ х<е).
46 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
подставить вектор ХА — В<е>, где В(в) — радиус-вектор
начала щ^ относительно начала ХА). Вопрос «переноса»
начальных точек оге в 0е и т. д., таким образом, несуществен,
поскольку отображение просто указывает, какие точки
в ffi*(e) инцидентны заданной точке в 9гх. Вследствие этого-
говорят, что функция Ajv определяет отношение инцидент-
инцидентности между 9г'х и ^х(е) (Ш1Ж & и ^?*)- Поскольку задание
узловых точек в М и 3?*(е) произвольно, требуется, чтобы
соответствие, обеспечивающее связанность, существовало-
для всех точек в % и %*, так что G.3) дает также отображе-
отображение 91 в Ш*. Таким образом, совокупность
A) B) (Е)
Л= {Л, Л, ..., Л}
отображений элементов отображает всю совокупность 9i
в М*.
6. Процедура, обратная связыванию элементов в модель,
называется разбиением. Процесс разбиения 92 на конечные
элементы предполагает просто перенумерацию глобальных
узловых точек, связанных с элементом, таким образом,
чтобы новая нумерация соответствовала схеме, принятой
для локальных узлов. Это достигается с помощью отобра-
отображения Q множества J?x в %*(е), задаваемого формулой
Х(е) = "дЛ , У' •3/
где по повторяющемуся индексу А производится суммирова-
ние от 1 до G, а ?2Д определяются формулами
{1, если узел N элемента ге совпадает
с узлом А связанной модели М, G.6)
О в противном случае.
Массив Q\ — это просто результат транспозиции массива
Лдг, определенного формулами G.4).
Очевидно, что для фиксированного элемента ге композиция
(е) («)
Л Q есть тождественное отображение 1е множества локаль-
локальных узлов "Л* в себя:
" = 8n- G.7)
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИИ ОБЩЕГО ВИДА 47
(е) (е)
Аналогично композиция ь2 Л есть отображение Iq сово-
совокупности глобальных узлов, соответствующих элементу е
в себя:
(e)N(e) f бд, еСЛИ Х*", X* 6 Ге,
QaAjv = ^ г д ('-о)
I, 0, если X , X $ ге.
Совместимость. Ясно, что границы элементов и располо-
расположение узлов в них должны быть такими, чтобы, будучи объединен-
объединенными вместе, наши непересекающиеся элементы могли образовать
дискретную модель области %. Существование функции Аи, кото-
которая связывает элементы в единое целое, зависит от расположения
узлов в конечных элементах и на их границах и от соответствия
между этими узлами и глобальными узлами ХЛ в области М-
Рассмотрим два конечных элемента ге и г/ с границами дге
и drj. Пусть эти конечные элементы примыкают друг к другу
в связанной модели 91. Тогда части дг'е и дг) этих границ должны
отображаться в некоторую общую границу в 2?, которую будем
называть межэлементной границей элементов те и г/. Должны
выполняться следующие условия:
1. Каждой точке х(в) ? дг'е соответствует точка x(fy 6 дг).
2. Если связывание элементов переводит х(в) ? дг'е в точку
Хб Ш, то оно переводит точку х(^> ? дг), которая по усло-
условию 1 отвечает х(в), в ту же самую точку X.
3. Каждой локальной узловой точке х$) 6 дг'е соответствует
некоторая локальная узловая точка х^ 6 дг).
4. Каждому локальному узлу х^) ? ге соответствует один-един-
один-единственный узел ХЛ ? М, и связывание элементов переводит
Хф в соответствующий ему узел ХЛ.
Перечисленные выше требования будем называть условиями
совместимости для дискретной модели. Они являются необходи-
(«>д
мыми и достаточными условиями существования функции An,
и ими обеспечивается возможность подогнать элементы друг к дру-
другу так, чтобы они образовали дискретную модель области М.
Очевидно, множества точек, составляющих дг'е ж дг) в ffl*, в соот-
соответствии с условием 2 отображаются на межзлементную границу
в №. Условия 1—3 обеспечивают связывание элементов в их
узлах при отображении и отсутствие разрывов и пересечений гра-
границ конечных элементов в связанной модели. Условие 4 учитывает
возможность введения внутренних узлов (локальных узлов ге,
которые не попадают на границу элемента) и гарантирует сущест-
48 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
вование соответствующих узлов в М. Из условий 1—3 немедленно
вытекает следующее интересное следствие:
5. Если отображение G.3) переводит локальный узел х??) ?дг"е
в узловую точку Хл 6 М, то оно переводит локальный узел
*(/) 6 dr'f, соответствующий х(е), в ту же самую узловую
точку ХЛ.
Отметим, что узловая точка ХЛ, о которой говорится в усло-
условии 5, находится на межэлементной границе в М-
Кратность граничные точек. Пусть X — точка,
лежащая на межэлементной границе. Говорят, что эта точка имеет
кратность т, если в ней встречаются т конечных] элементов.
Если же точка X не лежит на межэлементной границе, то ее
кратность т = 0.
7.4. ДИСКРЕТНАЯ МОДЕЛЬ ФУНКЦИИ F
Описав способ построения конечноэлементной модели подмно-
подмножества М пространства Шк, вернемся к задаче построения дискрет-
дискретной модели непрерывной функции F: М -*¦ ?Г. Мы начинаем
с построения изложенным выше методом конечноэлементной
модели М области М определения функции F. Эта модель М будет
служить областью определения другой функции F, которая долж-
должна аппроксимировать F. Далее поступаем так.
1. Значение F (X) нашей функции в глобальном узле Хл ? М
обозначаем через FA:
F* = F (Хл). G.9)
Величины FA называются глобальными значениями функции
F (X); множество глобальных значений {F1, F2, . . ., FG}
обозначается через и называется глобальным множеством,
соответствующим функции F (X).
2. Теперь рассмотрим совокупность °Л* несвязанных конеч-
конечных элементов ге. Каждый конечный элемент ге считается
областью определения некоторой локальной функции, обо-
обозначаемой через Ье), того же типа, что и F. Локальная
функция f(e> и значения функции f<e' (x) определены только
для х ? ге- Хотя в конечном счете после связывания между
собой конечных элементов, дающего М, эти локализованные
функции будут соединены для получения аппроксимации
заданной функции F, пока они рассматриваются порознь,
совершенно независимо от F (X) и друг от друга. Функция
1<е>. (х) называется ограничением F (X) на ге.
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЯ ОБЩЕГО ВИДА 49
3. Значение f(e> (x) локальной функции f(e> в локальном узле
х^, элемента е обозначается через ife):
f(?, = f(e>(x(%). G.10)
Величины f^( называются локальными значениями функций,
соответствующих элементу ге. Упорядоченные множества
локальных значений {ffX), . . ., Щ\},
обозначаются через Хе и называются локальными множе-
множествами. Их объединение обозначается через X:
Х= U Хе.
4. Локальные функции аппроксимируются на соответствующих
им конечных элементах непрерывными функциями вида
, ГЙ), G.11)
где функции i]5(e) (x, f^() определены так, чтобы они облада-
обладали следующим свойством:
ifo, (х$, f?>) = С) в узле хм 6 г.. G.12)
Поэтому в узловых точках элемента значения функций i]5(e)()
совпадают со значениями локальных функций х).
Как правило, удобно выбирать аппроксимирующие'функции
i]5(e)(x, f^), линейно зависящие от узловых значений f(^,:
Ъл(*, f(iI)) = fW(x), G.13)
где по повторяющемуся индексу N производится суммирова-
суммирование от 1 до Nе, a t^f (х) обозначает Nе скалярнозначных
функций, соответствующих конечному элементу е. Вслед-
Вследствие G.12)
) = 6#, хм^х(^ге, G.14)
где бм (М, N = 1, 2, . . ., Ne) — символ Кронекера 2).
Функции oj)j?' ( ) сходны с интерполяционными полиномами
х) Отметим, что если локализованные функции f(e' дифференцируемы
класса С (г >• 1), то возможно построить функцию if(e), у которой не только
Значения в узлах совпадают со значениями f^, но и величины первых г част-
частных производных совпадают с величинами соответствующих производных
функции f<e> (x). Такие аппроксимации высшего порядка будут рассмот-
рассмотрены в § 8.
2) ДрУгие свойства локальных интерполяционных функций рассмат-
рассматриваются в § 9 и 10.
4 Дш. Одев
50 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Лагранжа. Однако в рассматриваемом случае они не обяза-
обязательно являются полиномами.
С учетом G.13) равенство G.11) записывается в виде
fw(x) = f(Vw)W. G.15)
5. Конечноэлементная модель F (X) получается в результате
связывания всех наших непересекающихся элементов с по-
помощью преобразования G.3) и последовательных отображе-
(е)
ний Л: Xg-^-'S локальных множеств Хе в глобальное
множество &, определяемых (для фиксированного е) фор-
формулой
F4=&w, G.16)
(е)
где An задается формулой G.4). Иначе говоря, совокуп-
совокупб
ность отображений
М
В
М, ()
Л = 2 Л отображает X = \j Xe в У.
е=1 е=1
о. L другой стороны, массив li\, определяемый формулой
G.6), может использоваться для разбиения § на Xе:
ff = $?F\ G.17)
7. Окончательная дискретная модель функции такова:
w G.18)
2
или, с учетом G.16) и G.17) *),
Q
F (х) = 2 ipj?(x) Q%FA = Фд (х) F\ G.19)
х) Строго говоря, последующее соотношение справедливо в М всюду,
за исключением множества меры нуль. Если, например, X — точка межэле-
межэлементной границы в ?Н кратности т и Т — нужное значение дискретной модели
функции F (X) в X, то G.19) дает тоТ вместо Т. Для того чтобы избежать этого
осложнения, можно просто переопределить Фд (х) с помощью функции г (х),
которая равна единице, когда кратность точки X есть нуль, и равна крат-
кратности т этой точки, когда т^=0 [например, вместо Фд (х) использовать
Фд (х)/г (х)]. Впредь соотношения G.18) — G.20) будут применяться с согла-
соглашением, что на межэлементных границах вводится множитель 1/г(х). В про-
пространствах с мерой это замечание несущественно, поскольку любые две
функции, равные всюду, за исключением множества меры нуль, считаются
равными, ибо интегралы Лебега от двух функций, равных всюду, за ис-
исключением множества меры нуль, равны между собой. См., например, Кол-
Колмогоров и Фомин [1972].
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 51
Здесь Фд (х) — глобальные аппроксимационные функции,
определяемые равенством
2(&«(х). G.20)
е=1
Очевидно, что для х ? ге
Для узловой точки х^( ? ге, совпадающей с Хл в связанной
модели,
F
7.5. ПРИМЕРЫ
Широкие возможности использования метода конечных эле-
элементов обусловлены тем, что можно подробно исследовать аппро-
аппроксимацию заданной функции F (X) в пределах некоторой малой
подобласти области ее определения независимо от поведения
функции в других подобластях. Это, например, означает, что при
использовании концепции конечного элемента для исследования
поведения твердого тела можно выделить типичный конечный
элемент тела, аппроксимировать различные поля локально на
элементе и полностью описать поведение элемента с помощью этих
аппроксимаций независимо от его положения в модели, характера
связей с примыкающими к нему элементами и поведения других
элементов модели. После получения локальных аппроксимацион-
ных полей на типичных конечных элементах полная модель поля
получается с помощью отображений G.17) и G.19).
Для уяснения основных положений метода рассмотрим несколь-
несколько простых примеров.
Пример 7.1. Спалярная функция па двумерной области.
Рассмотрим сначала область Si двумерного пространства ^2 (рис. 7.1, а),
являющуюся областью определения скалярной функции Ф (X) рассмот-
рассмотренного в п. 6.2 типа. Точка X ? 31 задается координатами X1 и Ха, так
что можно записать
Ф = Ф (X1, X2).
Для простоты рассмотрим довольно грубую модель 31 области 31, состоя-
состоящую только из семи узлов и двух конечных элементов (рис. 7.1, Ъ). Так что
С=7и? = 2. Заметим также, что границы области 31 выбраны так, чтобы
она достаточно хорошо аппроксимировала 3i\ область отклонения Me на
рисунке заштрихована. Хотя всегда желательно, чтобы <Я возможно лучше
аппроксимировала область 31 или даже совпадала с ней, часто оказывается
невозможным или нецелесообразным выбирать в качестве границ 31 гра-
границы М. Это частично обусловлено тем, что предпочтительнее использовать
конечные элементы простейших форм, для того чтобы легко можно было
4*
62
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
1
f
2/
С
o5
-'
v4
r6
)
(а)
(Ь)
со Чо (d) ^
Рис. 7.1. Модель области в %2, состоящая из двух конечных элементов.
строить интерполяционные функции i|w (x). Кроме того, в последующем
от функций ij)^' (x) придется потребовать удовлетворения некоторым условиям
непрерывности в связанной модели, которые в свою очередь могут наложить
жесткие ограничения на форму границ конечных элементов. Таким образом,
в общем случае гладкая граница М аппроксимируется кусочно гладкой
границей ~?Я.
Возвращаясь к глобальному описанию дискретной модели для Ф (X),
пометим узлы в ~Ш цифрами от 1 до 7. Тогда если Фд (Д = 1, 2, . . ., 7) —
вначения нашей функции в узлах, то глобальное множество "§ будет таково:
{Фд}=
Ф2, Ф8, Ф«, Ф5, фб, Ф'}.
G.21)
Пометим два конечных элемента, показанных на рис. 7.1, с и d, симво-
вами A) и B) и введем в них системы локальных координат X(d = (x}v, х?ъ)
и хB)= (ж}2), ж?2))- На этом этапе элементы считаются никак не связанными
друг с другом; системы локальных координат ж^,, х?1} или xfa, xf2) могут
не совпадать с системой глобальных координат X1, X2. Отметим, однако,
что при исследовании задач, подобных рассматриваемой, удобно выбирать
все локальные системы совпадающими с глобальной. При этом связывание
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 53
элементов сводится просто к установлению соответствия между глобальными
и локальными узлами, пронумерованными различными способами.
Обозначим узлы элемента A) цифрами 1, 2, 3 и 4 (Ne=1 = JVX = 4),
а узлы элемента B) цифрами от 1 до 5 (Ne=i = Nt — 5). Части функции
Ф (X), определенные на элементах A) и B), обозначим через q>(D (х^) и
ФB) (хB>) соответственно (не путать с функциями, введенными формулами
G.19) и G.20)). Для простоты будем считать, что системы локальных коорди-
координат X(d и ХB) совпадают с системой глобальных координат X, т. е. локаль-
локальные функции можно обозначать просто через фA} (х) и фB) (х), а глобальную
функцию — через Ф (X) или Ф (х).
Значения локальной функции ф^ (x) в четырех узлах элемента A)
суть cpji), cpfu, ер,3!, и ф^,, а значения ф<2) (х) в пяти узлах элемента B) —
Ф^г,, ф<2н • • ., ф?2)- Таким образом, локал-ные множества ?х и 55г для
элементов записываются в виде
r = i, 2, 3, 4, 1
Г-1,2,3,4.5, К ™
/ *y\1 fil" fTl3 rf~4 I TJ //n]V I fml /T^2 fY^U fY^4 fY^5 \ /7 OO\
— ITAH т<1)» tA)' T(D/ iy'1 J—ItB)' TB)i тB)* tB)j tBj/" ^'•fcifc'/
В каждом конечном элементе строим аппроксимации локальных полей
Ф1 (х) » ФA> (х) = fJut']1' (x) -f фц^г1' (х) + фцМ1' (х) + Фа)^1' (х), - G.23а)
Ф2 (х) » фB> (х) = фB>"Ф1а) (х) + ФB2)'ф2г) (х) + 4>h№2> (х) + ф^гЖ2' (х) + фргЖ2' (х),
G.236)
или, более кратко,
фB) (X) » Ф^,'Ф^) (Х),
где функции ifjj' (x) обладают свойством G.14).
Предположим, что точки границ 23 и 15 элементов A) и B) находятся
во взаимно однозначном] соответствии с точками отрезка 26 в связанной
модели Hi (показанного на рис. 7.1, b пунктиром) и что соответствие между
всеми узловыми точками в М* и М отвечает условиям совместимости. Ясно,
что, если, исходя из области ?k, осуществлять ее разбиение на конечные эле-
элементы, всегда можно выбрать элементы и узловые точки таким образом, чтобы
«0.
условия совместимости удовлетворялись. Введем массив Л^ по формуле
(е)
G.4) и свяжем наши элементы в единую модель Ф (X) отображениями Л: %е-*-
ФЛ = Л^ф^, G.25)
где е = 1, 2; N = 1, 2, 3, 4 при е = 1 и JV = 1, 2, 3, 4, 5 при е = 2|
А = 1, 2, 3, 4, 5, 6, 7. Имеем:
е=1: Ф1 =
Ф2 Л?
Л}1+ + Л1ф?1) =
G'26а)
B) B)
Л|фЬ,+ ... + Л
B) B
л!1++л
54 . ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
B) B)
ф4 = л?ф?2) 4- ... 4- Л|ф?2) = фC2), G.266)
B) B)
Точно так же
фй = $лфА' G-27)
или 58
<i)
G.28)
B)_ B)_ B)
Таким образом,
Ф4 = ф?2„ Ф5 = ф?2„ Ф6 = Ф?1,=Ф?2), G.29)
Окончательно, дискретная модель функции Ф (X) такова:
_ 2 _ _ _
Ф (х) = /1 ф(е) (х) = фи) (хL" фB) (х), G.30)
или в силу G.23)
Ф (х) =-- iftM1' (х) + трКЖ (х) 4- Ф&,^»(х) 4- ФцЖ1' (хL- фЬЖ2) W 4-
4- «pfi^i1» (x) 4- ф?2Ж2) (х) 4- Ф?2Ж2) (х) 4- чЬМп (х)- G.31)
Используя G.29), получаем
Ф (х) = Ф1^1» (х) 4- Ф2 № (х) 4- ^i2) (х)] 4- Ф^г2' (х) 4- Ф4^2) (х) 4-
4- ФЩ2) (х) 4- Ф6 №и (х) 4- ti2) (x)] 4- Ф7г|>D1);(х), G.32)
чем и заканчивается построение конечноэлементной модели для Ф (X).
Нетрудно убедиться, что Ф (х) совпадает с Ф (X) в семи узловых точ-
точках ?Ц и что в остальных точках Ф (X) достаточно хорошо аппроксимируется
функцией Ф (х). По определению функции г|)^> (х) тождественно равны нулю
в элементе B), a ifj^' (х) — в элементе A). Например, если точка х элемен-
элемента A) находится вблизи узла Xе области М, то можно положить ijw (x) = 0
и заметить, что ipi1' (x), i|4lJ (х) и г^1' (х) -*¦ 0, а г|)а) (х) -*¦ 1 при х -+¦ Xе.
Если же точка х принадлежит элементу B), то ф^> (х) = 0 и тр[2) (х), г|J2) (х),
*?2> (х) и г|)<,2> (х) ->¦ 0, а г|I2> (х) -* 1 при х -* X6.
Узловая точка X6 имеет кратность 2, так как она лежит на границе двух
лементов. Следовательно '), ввиду G.32)
Ф (Хб) =
Подобные же соотношения справедливы и для других граничных точек.
*) См. примечание на стр. 50
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 55
Отсюда следует, что наша аппроксимация Ф (х) непрерывна в узловых
точках 2 и 6 межэлементной границы 26. В дальнейшем мы будем требовать,
чтобы форма элементов и свойства функций г|)$' (х) обеспечивали непрерыв-
непрерывность Ф (х) во всех точках межэлементных границ.
Пример 7.2. Преобразования локальных координат. Как
видно из предыдущего примера, введение системы локальных координат
часто является лишь формальностью, призванной подчеркнуть тот факт,
что при построении локальных аппроксимаций /(е) (х) отдельные конечные
элементы рассматриваются независимо от других. Часто модели можно
строить, используя одни и те же координаты и в глобальных и во всех локаль-
локальных системах, и вся разница между ними — формальная разница в обозна-
обозначении локальных и глобальных узловых точек. Однако в некоторых случаях
использование систем локальных координат, отличных от глобальных, имеет
существенное значение. Как правило, эти случаи характеризуются тем, что
окончательная конечноэлементная модель представляет собой ансамбль
конечных элементов некоторой размерности, вложенных в пространство
более высокой размерности, скажем локальные поля/(е) (х) определены в про-
пространстве размерности п, а окончательная модель — в пространстве размер-
размерности к > п. Одним из примеров такого типа является трехмерная ферма,
состоящая из брусьев, локальное поведение которых может быть описано
одномерными функциями. Локальные системы используются также в тех
случаях, когда ориентация или расположение элемента в связанной модели
либо его форма таковы, что введение локальных систем облегчает построение
функций tyffl (х).
Рассмотрим простой пример области М, состоящей из нескольких пло-
плоских фигур, которые, будучи связанными вместе, образуют кусочно-глад-
кусочно-гладкую поверхность в трехмерном пространстве. Предполагается, что каждая
плоская фигура имеет относительно простую форму многоугольника (напри-
(например, треугольника, прямоугольника, шестиугольника). Удобно каждую
такую плоскую фигуру считать конечным элементом, принять М = ?Я
и выбрать в качестве узловых точек элементов вершины многоугольников.
Во многих приложениях с помощью подходящего набора таких плоских
конечных элементов может представляться какая-либо гладкая поверхность,
но сейчас это для нас несущественно.
Для описания геометрии модели введем систему глобальных координат
Хг (i = 1, 2, 3), для простоты прямоугольных декартовых. Кроме того,
в каждом конечном элементе введем свою систему локальных координат
x\o (i = 1. 2, 3), тоже 'прямоугольную декартову, у которой оси х\е) и xfe)
лежат в плоскости элемента е, а ось xfe) перпендикулярна этой плоскости.
Эта конечноэлементная модель изображена на рис. 7.2.
Мы решаем задачу аппроксимации кусочно-непрерывного поля Ф (х),
которое локально для каждого конечного элемента является двумерным.
Другими словами, если ф(е) (х) — локальное поле, соответствующее эле-
элементу ге, то ф(е) (х) — функция только локальных координат х}е), х?е>
в плоскости элемента е:
Ф(в)=Ф(е) D)- 4))> е=1'2- • • •-Е- <7-33)
Поступая обычным образом, обозначим через ф^> значения локальных
полей в локальных узлах каждого элемента и аппроксимируем локальные
поля функциями вида
Ф(« = *Й> D)' ХЬ) Ч#)- ^ = 1. 2, ..., Ne. G.34)
56
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рис. 7.2. Совокупность плоских двумерных элементов,
вложенных в трехмерное пространство.
Тогда окончательная модель запишется так:
ф (х)=
G.35)
В соответствии с G.35) для вычисления приближенного значения поля
в какой-либо точке, не являющейся узлом; необходимо указать элемент, кото-
которому принадлежит эта точка и ее локальные координаты в системе х\еу Гло-
Глобальные координаты X1 служат для идентификации положения элементов
и узлов в модели и используются для ее связывания, а в описании аппрокси-
аппроксимирующего поля Ф (х) (формула G.35)) не участвуют. Однако в некоторых
случаях удобно рассматривать все в одной общей системе координат, за кото-
которую естественнее всего выбрать систему глобальных координат X1.
Для того чтобы осуществить связывание модели и дать описание аппрок-
аппроксимирующего поля в системе глобальных координат, введем другие системы
локальных координат хг(е) (i = 1, 2, 3), совпадающие с X1. Это означает,
что в каждом элементе оси ж?е) параллельны осям X*, а начала всех систем
х\е) совпадают с началом системы Xi. Локальные координаты х\е) и х\е) свя-
связаны между собой преобразованиями
¦(*)'
,=V*i,-'
G.36)
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 57
где aj — направляющие косинусы осей X1 (или х\е)) относительно осей х%е),
а В\еу — глобальные координаты начала системы х\е) относительно начала О
системы X1. Величины aj обладают обычными свойствами:
(e)i
(е).
det a]=l.
Связывание и разбиение модели осуществляются отображениями
где
V)
G.37>
G.38>
G.39)
Здесь xfj — локальные координаты узла ./V элемента е (x^Jc = 0).
Локальные интерполяционные функции ipjy* (x) выражаются через вспо-
вспомогательные координаты zje) с помощью формул G.36), а соотношение G.35>
принимает вид
W
G.40)
где
j
ff \ а-(х! Д' )]. G.41)
В G.41) вместо ж?е)|можно написать Хг, если известно, что функции tyffi (x>
отличны от нуля лишь в соответствующем конечном элементе.
Пример 7.3. Векторные поля. Предыдущий пример относился
к скалярному полю, заданному на эвклидовом пространстве в прямоуголь-
Рис. 7.3. Область опреде-
определения векторного поля
V(X), заданного в двумер-
двумерном неэвклидовом про-
пространстве.
58 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ных декартовых координатах. Однако метод конечных элементов применим
практически к любым векторным или тензорным полям, определенным как
на эвклидовых, так и на неэвклидовых пространствах в произвольных криво-
криволинейных координатах.
Для подтверждения этого рассмотрим векторное поле V (X), заданное
на некоторой области М произвольного (неэвклидова) пространства %к,
точки которого определяются криволинейными координатами X1 (i =
= 1, 2, . . ., к). Одна такая область в двумерном пространстве изображена
на рис. 7.3 в виде ансамбля криволинейных конечных элементов. Пусть
v(e) (х) — локальное векторное поле, соответствующее элементу е. a gt(e)
и gje) — естественные ковариантные и контравариантные базисные векторы,
«вязанные с системой координат at . Тогда
v<e> = vle)8i<e) = vUe)g\ey G-42)
где v\e) и vi(e) — соответственно контравариантные и ковариантные компо-
компоненты локального векторного поля.
Предполагается, что векторные функции gi(c) и gje, заданы заранее
и каждую компоненту v}e, или vj(e) можно рассматривать как скалярное поле
на гр. Таким образом, можно воспользоваться аппроксимациями4)
?Р = 4>1#М' G-436)
где vfe] и v^ey — контравариантные и ковариантные компоненты локального
поля в узловой точке N элемента е. На основании G.42) имеем
^Д, G.44)
где v,e, — значение локального векторного поля в узловой точке N эле-
элемента ге:
G.46)
Окончательно конечноэлементная модель векторного поля описывается фор-
формулой
v(x) = 2Q*vM>$(*)- G-47)
е
*) Ортогональные криволинейные координаты для построения конечных
элементов цилиндрических оболочек использовались Богнером, Фоксом
и Шмитом [1966, 1967] и другими авторами. Общие конечноэлементные
представления ковариантных и контравариантных компонент векторов
в неэвклидовых пространствах типа G.35) применялись Оденом [1968а]
при исследовании тонких оболочек. См. также Вемпнер, Оден и Кросс [1968],
Вемпнер [1969] и Оден и Вемпнер [1967]. Эргатудис, Айронс и Зенкевич
{1968а, 19686] и Ахмад, Айронс и Зенкевич [1969] рассмотрели семейства
«изопараметрических» конечных элементов с криволинейными границами.
Подбирая полиномы с помощью заданных граничных точек, эти авторы сумели
построить конечные элементы, аппроксимирующие достаточно общие гра-
границы. Более подробно такие элементы будут рассмотрены в п. 10.4.
7. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ФУНКЦИЙ ОБЩЕГО ВИДА 59
Интересно отметить, что в рамках изложенной ранее теории можно построить
ДРУГУЮ аппроксимацию V (X). Вместо G.43) положим
v(e) = v,e)(xJV)^(x) G.48)
и запишем
V(« = t&|>#(x). G.49)
Аппроксимации G.44) и G.49) совпадают в узлах, но различаются в дру-
других точках элемента. В самом деле,
v<,, (х) = 1|#> (х) (*$%$)*) = Ч# « (»
в то время как
у(е) (х) = tf$ (х) vfj%f (х) = ф$ (х) 4)g(C) (*), G.51)
где
«$I = 8е«> (*W), в|«)М = вмЛ G.52а, б)
В аппроксимации G.50) V(e) (х) определяется через постоянные базисные
векторы g[5J)i> g(V)(e) B узловых точках. В аппроксимации же G.51) v(e) (x)
определяется через базис в точке х, и такая аппроксимация, вообще говоря,
лучше. Общая форма записи G.47) для глобальной аппроксимации в обоих
случаях одинакова.
Пример 7.4. Тензорные поля. Точно тот же метод может быть
применен и к тензорным полям. Пусть, например, Т (X) — поле тензоров
второго ранга на некоторой области М, a t(e) (x) — локальное поле, соот-
соответствующее элементу е. Тогда 4)
t(e, (х) = ^Не) 0 gJ(e) = t\^gHe) 0 giw = tf{e)gie) 0 gJ(e) =
= *»(«)«(«) ®gfe). G-53)
где t\3e) и tlj{e) — контравариантные и ковариантные компоненты, a i1^
и t^ — смешанные компоненты тензора t(e) (x). Они аппроксимируются так:
где г(%!;, . . ., г^у — значения соответствующих компонент в узловой
точке N элемента е. Это означает, что
t(e)(x) = t(^«(x), G.55)
где
i.2V _ fNij,f(e) ^ Je) __ fNi „(e) ,-j. „i _
Если T — глобальные значения тензорного поля Т (X), то
t^ = Q^TA. G.57)
') Символы gi 0 gj, gt 0 gi, . . ., gi 0 gi используются для обозна-
обозначения тензорных произведений базисных векторов gi и gi (i, / = 1, 2, . . •
. . ., Л). Каждое из множеств диад gt 0 g^, gt 0 g?, g4 0 gh gl 0 g' слу-
служит базисом соответствующего А2-мерного векторного пространства тензоров
второго ранга.
60 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Окончательно конечноэлементное представление тензорного поля имеет вид
2 ?
Отметим, что опять, используя вместо текущих значений g(e)J (x), g<e) (x)
их значения в узлах gBV)i и giN^ey даваемые формулами G.52), можно постро-
построить другую аппроксимацию типа G.50).
Пример 7.5. Линейная интерполяция. Для полноты изложе-
изложения и удобства дальнейших ссылок вернемся к рассмотренной в п. 6.1 одно-
одномерной задаче и приведем один из простейших примеров конечноэлементной
модели непрерывной функции. Рассмотрим снова действительную функцию
F (X), заданную на замкнутом интервале А ¦< X < В действительной оси
(рис. 6.1). Начнем, как всегда, с фиксации некоторого числа узловых точек
в области [А, В], причем возьмем А = 1, В = G. На рис. 6.1, а показан
случай, когда G = 5. Вычисляем в этих точках значения функции F1 =
= F (X1)," . . ., F° = F (XG). На рис. 6.2, & показаны отдельные конечные
элементы, которые, будучи связанными друг с другом, представляют собой
подынтервалы интервала [А, В]. Для выполнения условий совместимости
модели мы в каждом конечном элементе задаем два локальных узла в конце-
концевых точках подынтервалов. Локальная функция, соответствующая элемен-
элементу е, обозначается через /(е) (х), а локальные значения функций в локальных
узлах 1 и 2 элемента обозначаются через Це) и ffe) (рис. 6.2, Ь).
Пока все сказанное является просто повторением изложенного ранее.
Теперь же рассмотрим локальные функции додробнее. Каждое локальное
поле аппроксимируется функцией вида
^ |) f)*B)(*)- G-59>
В качестве иллюстрации возьмем линейные интерполяционные функции
,1,(е)(„\ w _' lh(e)/_\___Z___ifL п йПя Й\
где L(e) =xfe) — x\e) представляет собой длину элемента. Подчеркнем»
однако, что на функции г|>^> (х) пока не было наложено никаких ограничений,
кроме условия непрерывности внутри элемента и условий G.14). Хотя в рас-
рассматриваемом примере эти функции взяты линейными, в общем случае они
могут быть и нелинейными. В самом деле, добавляя к функциям G.60) любое
произведение любых непрерывных функций, обращающихся в нуль в узлах
x\ei и xfe), мы получим другие функции г|)^> (х), которые тоже удовлетворяют
условиям G.14) *).
Замечая, как обычно, что
где N = i, 2 и Д = 1, 2, ..., G, окончательно получаем такое выражение
для конечноэлементной модели F (X) при кусочно-линейной аппроксимации:
') Например, добавляя в правые части равенств G.60а) и G.606) сла-
слагаемые С (x(ei — х[е>)т(х{е> — xf>)n, где т, п > 0, замечаем, что по-преж-
по-прежнему if)Je) fo) = l,x|)Je) (х2) = 0 и г]5Bе) (Xl) = 0, i|;fe) (х2) = 1. Дополнительные
требования к функциям г|5(^, (х) рассматриваются в § 10.
8. ПРЕДСТАВЛЕНИЯ ВЫСШЕГО ПОРЯДКА 61
8. ПРЕДСТАВЛЕНИЯ ВЫСШЕГО ПОРЯДКА
Изучив основные свойства конечноэлементных моделей непре-
непрерывных функций, перейдем к вопросу построения конечноэле-
конечноэлементных представлений высшего порядка.
8.1. ОБЩИЕ СВОЙСТВА МОДЕЛЕЙ ВЫСШЕГО ПОРЯДКА
Рассмотрим опять непрерывную функцию F (X) = F (X1, X2, ...
. . ., Хк), определенную на некоторой области С'Л пространства Щк.
Если у F (X) существуют и непрерывны в J? частные производные
до порядка р включительно, то можно построить представления
высшего порядка, которые не только совпадают с локальными
значениями функций f(e) (x) в каждом узле конечного элемента,
но еще и обладают частными производными порядка г^р, сов-
совпадающими с частными производными заданной функции в узлах
конечного элемента.
Удобно считать, что точки в gft — это наборы из к глобальных
координат Хг (i = 1, 2, . . ., к), которые связаны с локальными
координатами х\е, (i — 1, 2, . . ., к; е = 1, 2, . . ., Е) посредством
преобразования
у» yi/,.' «2 ft > .q ..
Л. —Л. (J-(e)i x(e)i •••) x(e))i \Р-Ч
причем предполагается, что для каждого е существуют единствен-
единственные обратные преобразования
•^(е) — (?) \ 1 "^- ) • • • > -^*- / • (о. /.)
Для локальных представлений высшего порядка вместо G.11)
используется более общая формула:
f(«) /х\ _ JJ (х. fN . tN . fN . \ /Q Оч
в которой применено обозначение
ife) hi,., ir = : : ~ > (8.4)
где iu н, . . ., ir = 1, 2, . . ., к. Функции Н(е) () в (8.3) определяют-
определяются таким образом, чтобы они обладали следующими свойствами:
1. сама Н(е) (х; . . .) и все ее частные производные по хг обра-
обращаются в нуль при х $ ге;
2. Н(е)(хм; ...) = $, хмеге;
(8.5)
4. — - = I(e).iiio...,-M XMI
62 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Свойства функций Н(е) ( ) внутри элемента сходны со свой-
свойствами интерполяционных полиномов Эрмита (хотя они и не обя-
обязательно являются полиномами) *). В связи с этим функции Н(е) ()
называются обобщенными интерполяционными функциями Эрми-
Эрмита. Как правило, их удобно выбирать такими, чтобы их частные
производные были линейными относительно узловых значений
соответствующих частных производных локального поля f(e) (x):
где ц, i2, . . ., ir = 1, 2, . . ., k, а N = 1, 2, . . ., Ne. Тогда (8.3)
принимает вид
F(c> (х) = «° (х) + S !*, tfj?1 (x) + S (I f*. «^ (x)) + . . .
¦••+SIS (••• S f(?),^...^fN)ili2-'-!>W)], (8.7)
?i=i 12=11 ir=ii--i
где А; — размерность нашего пространства, и по повторяющемуся
индексу N — производится суммирование от 1 до Nе. Скалярные
функции г|)$ (х), г|5^)г (х), . . ., г|з^)г112-г(х) обладают следую-
следующими свойствами:
1. Функции ^°(х), #(i), . . ., ip%)iii2-ir (x) и все их
частные производные обращаются в нуль при х (J ге;
2. Среди множества функций г|э$г112""гг (х), х 6 ге, только
те отличны от нуля, для которых г2 ^ г2 ^ г3 ^ . . .
3. Во всяком узле хм 6 ге
° если s^=r,
];б^ ... 6&, если s = г.
f
= I
Здесь бм, 6}\ , . . ., 8fs — символы Кронекера, s = 0,1, 2, ...
. . ., т; ij< г2 < . . . < ir; jt < /2 < . . . < /r; ij, г2, . . .
. . ., ir, /l5 /2, . . ., /r = 1, 2, . . ., &; k — размерность про-
пространства; r ^ m; M, N = 1, 2, . . ., JVe.
x) Интерполяционные формулы Эрмита и конечноэлементные представле-
представления высшего порядка при построении дискретных моделей одномерных и дву-
двумерных скалярных полей использовались многими авторами, среди прочих
Богнером, Фоксом и Шмитом [1966], Пестелом [1966], Фелиппой [1966],
Диком и Пайэном [1967], а также Точером и Харцом [1967]. Начальные све-
сведения об интерполяционных полиномах Эрмита можно найти во многих
книгах по численному анализу (например, у Гильдебранда [1956]). Родствен-
Родственные вопросы кусочной интерполяции и представлений высшего порядка рас-
рассматривались Курантом [1943], Фортом [1948], Биркгофом и Буром [1965],
Ланхаром и Чу [1968] и другими авторами.
8. ПРЕДСТАВЛЕНИЯ ВЫСШЕГО ПОРЯДКА 63
Указанные свойства обеспечивают совпадение значений функ-
функции f(C) (x) и ее частных производных по хг до порядка т включи-
включительно со значениями f(C) (x) и ее соответствующих производных
во всех узловых точках элемента е.
Если представление высшего порядка f(C) (x) и его частные
производные до порядка т включительно содержат по крайней
мере один элемент множества ty($44'" гт (х) и ни одного элемен-
элемента порядка выше, чем т, то f<e) (x) называется представлением
(т + 1)-го порядка функции f(e> (x). Так, G.15) есть представле-
представление первого порядка. Отметим, что в представлении (т + 1)-го
порядка нормированные функции Эрмита i$v'° (x) не являются
функциями Лагранжа i|)$' (x), входящими в G.15). Это объясняется
тем, что в G.15) не накладывалось никаких ограничений на произ-
производные функции ty'jy (x), в то время как производные порядка
г ^ т функций ipjv>0 (x) должны обращаться в нуль во всех узло-
узловых точках конечного элемента. Действительно, от функции
fF) (x) в представлении первого порядка G.15) требовалось лишь,,
чтобы она совпадала с f(C) (x) в локальных узлах. Таким образом,
только для представления первого порядка ty'ff (х) и г|$>0 (х)
обязаны совпадать.
При осуществлении связывания конечноэлементных моделей,
основанных на представлениях высшего порядка, необходимо вве-
ввести дополнительные глобальные и локальные множества узловых
значений функций F (X) и f<e) (x) и их частных производных.
Например, можно положить
ihi %...ir} (8.9)
и
%Ъ) = {^(«)}; •?(«) = {he), г}' • ¦ • '> %(еJ' ' ' *' = ike), ЧН ¦ ¦ ¦ »г}» (
где Ffb . . ., Ffj ,- ,- —значения различных частных производ-
производных от F (X) в узловой точке А области ffl. Отметим, что по опре-
определению
*?« = -^. 1Й.«=^--*.". (8.11)
Итак, для осуществления связывания и разбиения системы вместо
G.16) и G.17) надо использовать
(8-12)
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
tN ЙлГрД *N OX) рА&У
1(е) = УдГ , I(e), i= { Г.^д,
,, U (8.13)
N вхг эх» pA gw v '
w'ii = "a?—'дТ >r5 л' '¦¦'
или, в общем виде,
h...hiiA. (8.14)
N дХ" дХ}* дХ»
f
() () (
Часто локальные координаты х\е, можно выбирать совпадаю-
совпадающими с глобальными координатами X*. Тогда дХ11дх\е) — Ь)
и (8.14) сводится к
i(e), Щ2. .Лг~ ^дР,Йг2. • -Ь- (8.15)
Ясно, что построение и использование представлений высшего
порядка, вообще говоря, гораздо сложнее, чем использование
представлений первого порядка. Вопрос о том, окупаются ли
повышением точности те трудности, которые связаны с построени-
построением представлений высшего порядка, еще не выяснен. Отметим,
что, поскольку производные F t t ,л часто сами являются непре-
• 12'" г
рывными функциями, можно использовать представления первого
порядка не только для F (X), но и для ее производных.
8.2. ПРИМЕРЫ
Рассмотрим кратко некоторые примеры конечноэлементных ¦
представлений высшего порядка.
Пример 8.1. Представление второго порядка. Представление
второго порядка локального поля, определенного на каком-либо элементе
двумерного пространства, имеет вид
f<«> (х) = f^#° (x) + $}i rfp (x) + f&, 2г|#2 (х), (8.16)
где N = 1, 2, . . ., Ne. Первые частные производные от f(e» (x) таковы:
(8-17)
5x2 =i(e)^N, 2 + f(e), ltjv, 2 + f(e), 2^N, 2'
где для большей ясности в некоторых местах опущена идентификационная
метка элемента (е) и не указана явно зависимость tyNli и т. д. от х (т. е. if>lv,l =
8. ПРЕДСТАВЛЕНИЯ ВЫСШЕГО ПОРЯДКА 65
Требуется, чтобы в узловых точках хм? ге выполнялись] равенства
f<«> (хм) = fM ?el (xM) = fM l, Щ (xM) = fM 2. (8.18a, б, в)
Значит, для всех узлов хм ? re
Ч&( l (xM) = y°Nt 2 (xM) = t]v, 2 (xM) = ^ t (xM) = ^ (xM) = ^ (хм} = 0
(8.19)
и, кроме того,
^(xM) = ^ (хм) = г|>2 (хм) = бм={ *' если xN = xM> (820)
I 0, если x Ф x .
Как отмечалось ранее, локальные узловые значения производных t,e* t
и f^2 и глобальные значения F\ и Fa2 перед связыванием элементов должны
быть отнесены к общей системе координат. В рассматриваемом случае
f?)=(^FA, F&=(A%i^y (8.21а, б)
f&^-^-bV.. fAi=w°
(8.21b, г)
'(е), 2= 9х2 "д^.а- F,2 = 3X2 AJVf(e), а' (8-zlS. e)
где а=1, 2. Окончательно наша модель имеет вид
Е
F (х) = 2 $д [^° (х) FA + -tjj- ^ (х) F*. ] , (8.22)
e=i Ж(«)
где JV = 1, 2, . . ., Ne; A = f, 2, . . ., G; a, P = 1, 2.
Пример 8.2. Эрмитова интерполяция. Здесь мы коротко рас-
рассмотрим представление высшего порядка действительной функции F (X),
определенной на интервале А < X < В (см. рис. 6.1). После выбора гло-
глобальных узлов и конечных элементов построим локальную аппроксимацию
/<е) (х) на типичном конечном элементе. На этот раз функции /<е) (х) выберем
такими, чтобы в узловых точках, являющихся концами конечного элемента,
значения /<е> (х) и dfie) (x)ldx совпадали со значениями /<е) (х) и df(e) (x)ldx.
Локальные и глобальные координаты можно взять совпадающими.
Одной из аппроксимаций, удовлетворяющих этому требованию, является
кубичный полином
где
г(,о(х) = 1—3|2 + 2|3, (8.24а)
\|)§ (х) = 3|2 — 2g3, (8.246)
г|)^ (х) = L(e) (| — 2|2-J-E3)i (8.24в)
i|>i(z) = — Z,(e)(i2-i3), (8.24г)
5 Дж. Одея
66 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
) — х(е)
Легко проверить, что
7(е)(^1)=/(е), 7(е)И = /Bе),
(8.26)
He), 1' cte ~ *(
dx '(e), 1' dx ~'(«), I*
Функции (8.24) являются хорошо известными интерполяционными поли-
полиномами Эрмита, а полином (8.23) — единственным полиномом третьей сте-
степени, удовлетворяющим условиям (8.26). Используя полином пятой сте-
степени, можно дополнительно к (8.26) добиться, чтобы значения второй произ-
производной полинома в каждой узловой точке совпадали со значениями
<Р/(е) (x)/dx2. Вообще если в узловых точках задавать dnf(e) (x)/dxn, то можно
обойтись полиномом степени 2ге + 1. Подчеркнем, что полином (8.23) —
всего лишь одна из бесчисленного множества функций, удовлетворяющих
условию (8.26).
Окончательно конечноэлементная модель F (X) описывается формулой
F (х) = ^| /^е, (х) = 2j Яд [wn (x) F "b^jv (x) F i]> (8.27)
е е
где N=1, 2 и Д = 1, 2, ..., G.
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИИ х)
Одним из самых фундаментальных свойств конечноэлементных
аппроксимаций является то, что рассмотренные ранее интерполя-
интерполяционные функции ч|)$' (х) образуют базис некоторого конечномер-
конечномерного подпространства пространства SB, которому принадлежит
аппроксимируемая функция F (X). В случае когда на Ш задано
скалярное произведение, функции г])др (х), как правило, не орто-
ортогональны, и это наводит на мысль о построении другой системы
функций, которые называются сопряженно-аппроксимационными,
функциями. В этом параграфе подробно рассматривается понятие
сопряженно-аппроксимационной функции и показывается, что
эти функции обладают некоторыми определенными свойствами,
основополагающими для методов аппроксимации вообще и метода
конечных элементов в частности.
9.1. СОПРЯЖЕННЫЕ ПРОСТРАНСТВА И БИОРТОГОНАЛЬНЫЕ БАЗИСЫ
В п. 7.1 уже говорилось, что совокупность всех линейных
функционалов на линейном пространстве V сама является линей-
линейным пространством V*, называемым сопряженным к V. Можно
*) Этот параграф основан на работе Браули и Одена [1971]. См. также
Оден и Браули [1971а].
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 67
показатьг- что для некоторых пространств со скалярным произве-
произведением сопряженное пространство изоморфно дуальному простран-
пространству У (надо использовать скалярное произведение для построе-
построения линейных функционалов на У).
Пусть 98 — банахово пространство (полное нормированное
линейное пространство) и 38* — его сопряженное. Пусть 38 ж 38*
оба сепарабельны, т. е. в !% и в 38* существуют счетные всюду
плотные множества элементов. Тогда говорят, что последователь-
последовательности {хп} ? 98 и {уп} ?38* образуют счетный биортогоналъный
базис для 98 и 98*, если выполняется условие
У* (х,) = 6} (9.1)
и если для любых if Ж и yf J1* справедливы разложения
*=3 а**|, 2/=2 ая*. (9.2)
г=1 1=1
Здесь уг (х) — линейные функционалы, определенные на 38, а схо-
сходимость рядов (9.2) — это сходимость по норме в 98 и 38* соот-
соответственно:
IU- S. а**1 \\ -*¦ 0, \\ у- S ajy11| -* 0. (9.3)
1= 1 i= 1
Из (9.1) и (9.2) следует, что коэффициенты а1 и at задаются выра-
выражениями
а1 = f (х), а( = у (xt). (9.4)
Важным свойством сепарабельных пространств является то,
что при заданном счетном биортогональном базисе возможно пред-
представить 98 я. 98* ъ виде прямой суммы конечномерного и бесконеч-
бесконечномерного пространств:
п оо
х =2 alxt+ 2 а*хи (9.5а)
i=l i=n+l
71 со
»=Se«»'+ S «гУ{- (9-56)
i=l i=n+l
Разложения (9.5) определяют операторы проектирования П:
& -+&' жП.*: 98* -+98*' пространств 38 и 38* на конечномер-
конечномерные подпространства 98' и ig>*' соответственно, т. е.
Ш=2аЪ;г, n*y=Se,y*. (9.6)
i=i i=i '
5*
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Это означает, что каждый элемент х 6 98 единственным обра-
образом представим в виде суммы элемента Их ? 98' и элемента вида
i=n+l
принадлежащего некоторому подпространству 98" пространства 98
(т. е. 98 = 98' ф 38"). То же самое можно сказать и об элементах
у 6 Я*, т. е. J>* = #•' ф 98*", ж у = П*у + у", где П*г/ 6
€#•', а
г=п+1
Подпространства $?*" и 98*' являются ортогональными дополне-
дополнениями к 98' и 98" соответственно, и 98', 38*' и 4?", 98*" образуют
дуальные пары.
9.2. СОПРЯЖЕННЫЕ ПОДПРОСТРАНСТВА
Для простоты мы ограничимся рассмотрением гильбертовых
пространств, т. е. полных бесконечномерных пространств со ска-
скалярным произведением. Гильбертовы пространства обладают весь-
весьма удобным свойством: они самосопряжены в том смысле, что топо-
топологическое сопряженное к гильбертову пространству изоморфно
ему. Напомним, что гильбертово пространство SB является также
банаховым пространством, так как S3 полно по норме || х \\ =
= У (х, х), где (ж, х)—определенное на SB скалярное произведение.
Таким образом, рассматривается гильбертово пространство SB,
элементами которого будут функции, определенные на некоторой
ограниченной области Ш эвклидова и-мерного пространства.
Элементы пространства SB обозначаются через F (X), G (X), . . .,
где X— точка области Ш. Скалярное произведение на SB X SB
обозначается через (F, G), и используется обычная норма || /*" II =
VW
Для многих приложений важен частный случай, когда SB —
пространство квадратично интегрируемых функций на "Л. При
этом скалярное произведение двух элементов F (X) и G (ХL при-
принадлежащих SB, определяется формулой
(9.7)
где под интегралом понимается интеграл Лебега. Функции F (X)
и G (X) ортогональны, если (F, G) = 0. Для любой функции
F (X) 6 SB
(F, FX+oo. (9.8)
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 69
Представим &8 в виде суммы двух подпространств Фи d',
где Ф — подпространство конечной размерности G. Для осуще-
осуществления этого разложения выберем в качестве базиса подпростран-
подпространства Ф какое-нибудь множество G линейно независимых функций
{Фд (X)} х) пространства Зв, где А = 1, 2, . . ., G. Тогда каждый
элемент F (X) ? SB можно представить в виде суммы некоторого
элемента подпространства Ф и некоторого элемента подпростран-
подпространства Ж:
F(X) = F(X) + F(XJ), (9.9)
где F (X) 6 Ф и F (X) ?$в'. Поскольку множество {Фд (X)} обра-
образует базис для Ф, каждый элемент F (X) 6 Ф можно единственным
образом представить в виде линейной комбинации функций
Фд (X):
F (X) = /™ФД (X), (9.10)
где по повторяющемуся индексу А производится суммирование
от 1 до G. Коэффициенты F& называются компонентами F (X)
относительно базиса {Фд (X)}.
Заданием множества функций Фд (X) определяется оператор
проектирования П: Ш -> Ф, который отображает Ш на конечно-
конечномерное подпространство. Таким образом, мы можем записать
F(X) = UF (X). (9.11)
Необходимо иметь в виду, что функции Фд (X) не обязательно
ортогональны. Введем симметричную G X G-матрицу
СДГ^(ФД, Фг>, А, Г = 1,2, . . .,<?, (9.12)
которая называется фундаментальной матрицей 3) подпростран-
подпространства Ф. Функции Фд (X) ортогональны в том и только в том случае,
х) Использование в качестве индекса символа Д, который ранее приме-
применялся для идентификации глобальных узлов, не случайно. Далее в п. 9.6
будет показано, что_функции Фд (X) образуют базис для конечноэлементных
аппроксимаций на 31.
2) Излагаемый здесь подход не использует сепарабельности &6 и при-
пригоден для пространств более общего вида. Если &€ сепарабельно, то часто
ищут бесконечное множество базисных функций Фд (X) и тогда
оо
F (X) = 2 рА ФД (Х)'
Здесь же мы просто определяем подпространство Ф, строя некоторое мно-
множество линейно независимых функций. Способ построения такого множества
базисных функций рассматривался в п. 7.4 и изучается более подробно
в п. 9.6.
3) Матрица Сдг иногда называется матрицей Грама базисных функций
{Фд}. Если пространство Ш комплексное, то для Сдг транспонированная
матрица совпадает с комплексно сопряженной.
70 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
когда
Сдг = с(Д)бдг, (9.13)
где бдг — символ Кронекера, т. е. Фд (X) ортогональны, если
матрица Сдг диагональна.
Поскольку {Фд (X)} — множество линейно независимых функ-
функций, матрица Сдг регулярна и элементы ее непосредственно вычи-
вычисляются по формулам (9.12). Матрицу, обратную к Сдг4 обозна-
обозначим через Сдг4 т. е.
(СдГ)-1^Сдг, (9.14)
или
СдЛСлг=б?, (9.15)
где А, Л, Г = 1, 2, . . ., G. Матрицы Сдг и Сдг играют важную
роль в теории сопряженных аппроксимаций.
Опишем теперь Сопряженное пространство Ф*,; введя конеч-
конечный набор {Ф4} линейных функционалов на Ф. Пусть {ФЛ (X)} —
множество G линейно независимых функций на %% удовлетворяю-
удовлетворяющих условию
(фд, Фг) = бг. (9.16)
Напомним, что сопряженное пространство Si* для пространства
&8 — это совокупность всех линейных функционалов, определен-
определенных на Щ. Поскольку (9.16) определяет множество G линейных
функционалов на $6 и функции Фд (X) линейно независимы, мно-
множество {ФЛ (X)} определяет проекцию П* пространства &6* на не-
некоторое конечномерное подпространство Ф*, которое является
сопряженным к Ф. Согласно (9.16), два множества {Фд (X)}
и {Ф4 (X)} образуют счетный биортогональный базис для Ф.
Множество {Ф4 (X)} будем называть сопряженным базисом для Ф.
Соотношение (9.16) выражает свойство, которым должны обла-
обладать функции Ф4 (X), чтобы их можно было считать сопряженны-
сопряженными базисными функциями. Однако этого свойства недостаточно для
однозначного определения совокупности независимых функций
Ф4 (X). Для устранения этой неопределенности построим функ-
функции Фл (X) по формулам
Ф4 (X) = Сдг Фг (X), (9.17)
где Сдг — матрица, обратная к фундаментальной матрице (см.
(9.14)). Тогда имеем также
Фд (X) = СдГФг (X). (9.18)
Легко показать, что функции Фд (X), определяемые формулами
(9.17), линейно независимы. В самом деле^
(X) = 0 =>- К* = 0х А = 1, 2, . . ., G.
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 71
Отсюда яснОд что если
КАФ* (X) = ЯдСдгФг (X) = 0х
то КАСАТ = /Р1 == 0. Но это означает, что КА = 0, ибо Сдг —
положительно определенная матрица. Таким образом,
КАФ* (X) = 0 =* Яд = 0 (А = 1, 2, . . ., G),,
и, значит, функции ФА (X) линейно независимы. Кроме того, умно-
умножая (9.17) скалярно на Фг (X), находим
<Ф\ Фг> = <СДЛФЛ, Фг> = Сдл <ФЛ, Фг> = С^Сап (9-19)
или в силу (9.15)
<фд, фг> = 8Л, (9.20)
что в точности совпадает с условием (9.16). Это означает, что (9.17)
единственным образом определяет биортогональный базис под-
подпространств Ф и Ф*.
Из (9.17) непосредственно получаются два важных свойства
пространства Ф*. Во-первых, заметим, что вследствие (9.17)
каждый элемент множества {ФА (X)} является линейной комби-
комбинацией первоначальных базисных функций Фд (X). Поэтому
функции ФА (X) из Ф* принадлежат и Ф, значит, Ф и его сопряжен-
сопряженное Ф* совпадают, т. е. подпространство Ф самосопряженное.
Следовательно, каждый элемент F (X) 6 Ф можно представить
в виде линейных комбинаций либо функций Фд (X), либо функций
Фл (X). Вместо (9.10) можно записать
F(X) = FAOA(X) = FA$)A(X), (9.21)
где коэффициенты FA можно рассматривать как компоненты F (X)
относительно базиса Фх (X). Запись (9.21) позволяет считать FA
и F& ковариантными и контравариантными компонентами F (X).
Во-вторых1 мы видим, что
<фд, фг) = САЛ {Фл, Фг> = Сдлб1, (9.22)
или
фГ) = сдг. (9.23)
Поэтому обратной к фундаментальной матрице САт подпростран-
подпространства Ф является фундаментальная матрица сопряженного под-
подпространства Ф*.
Возвращаясь к (9.21), отметим, что
(F, Фд> = (/^ГФГ, Фд) = FT {Фг, Фд) = ^А, (9.24)
(F, Фд) = {/?ГФГ, Фд> = /"г {Фг, Фд) = FA4). (9.25)
*) С_нругой стороны, если функция F (X) известна, то в качестве ком-
компонент F (X) лучше брать FA = (F, ФА) вместо (9.24) в FA = {F, Фд)
вместо (9.25); см. п. 9.3.
72 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Кроме того, в силу (9.17) и (9.18) компоненты FA и FA связаны
между собой соотношениями
/•а = C^FC, (9.26)
^д = Сдг^, (9-27)
так что с помощью фундаментальных матриц можно «поднимать»
и «опускать» индексы компонент функций из Ф.
Скалярные произведения и нормы. Пусть F (X) и
G (X) — две функции, принадлежащие подпространству Ф:
F (X) = ^лФд (X) = ^ДФА (X),
(9.28)
G (X) = ?ЛФД (X) = СДФА (X).
Тогда скалярное произведение F и G определяется формулами
(F, G) = <^лФд, СгФг> = (^Фд, СГФГ) ==
= (^дФл, СгФг) = (/'дФА, СГФГ), (9.29)
или
(F, G) = CATFAGT = FhGh = FAGA = CATFAGT. (9.30)
В частности,
||Ff = (F, F) = CATFAFT = ^FA = CAVFAFT^0, (9.31)
чем доказана отмечавшаяся ранее положительная определенность
матрицы Сдг.
Аффинные преобразования. Пусть {Гд (X)} — еще
одно множество G линейно независимых функций. Если это
множество является подмножеством Ф, то всегда можно найти
матрицу А\, описывающую аффинное преобразование множества
{Гд} в {Фд}. При этом если матрица АА невырождена, то ее
обратная АТА преобразует {Фд} в {Гд}:
Фд(Х)=ЛдГг(Х), ГД(Х) = ЦФГ(Х): (9.32)
Аналогично можно показать, что
ФЛ(Х) = 2АГГ(Х), ГА(Х) = ^ФГ(Х). (9.33)
Пусть Fh и F% — компоненты некоторого элемента F (X) ? Ф
относительно нового биортогонального базиса {Т*д}, {ГА}. Легко
показать, что если функция F (X) инвариантна относительно пре-
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 7$
образований типа (9.32) и (9.33), то
F$ = A$Fr, F*A = AVAFV, (9.34>
). (9.35)
Отметим также, что
$$ i^ (9.36>
(9.37>
где
(Гд, Гг)=Сдг, <ГЛ, ГГ> = СДГ, (Гд, ГГ) = бг. (9.38)
Формулы (9.32) и (9.33) описывают довольно частные случаи
изменения базиса, поскольку предполагалось, что функции Гд (X}
принадлежат подпространству Ф. Нетрудно ввести множество»
базисных функций, не принадлежащих Ф. В этом случае преоб-
преобразований типа (9.32) и (9.33) не существует.
Резюме. В виде краткого резюме повторим изложенные ранее
основные положения и результаты. Для аппроксимации функции
F (X) прежде всего определяется конечномерное подпространство
Ф заданного гильбертова пространства SB, которому принадлежит
F (X). С этой целью фиксируется какая-либо совокупность G
линейно независимых элементов Фд (X) пространства SB. Проек-
Проекция элемента F (X) 6 SB на подпространство Ф обозначается через;
F (X); она может быть выражена в виде линейной комбинации,
базисных функций Фд (X) (т. е. F(X) = ^АФД (X); Д = 1, 2, ...
. . ., G). Затем строится еще одно множество сопряженных базис-
базисных функций ФА (X) по формулам
Фд (X) = СдгФг (X). (9.39).
Здесь САГ — матрица, обратная к невырожденной положитель-
положительно определенной матрице Сдг, определяемой соотношением
Сдг = (Фд, Фг>, (9-40)
где ( , ) — скалярное произведение в SB. Ясно, что
Фд(Х) = СДГФГ (X). (9.41)
Так как формулы (9.39) единственным образом определяют множе-
множество сопряженных базисных функций, удовлетворяющих условию^
(фЛ, ФГ) = 6Г, (9.42)
два множества функций {Фд (X)} и {ФА (X)} образуют счетный
биортогональный базис для Ф. Кроме того, поскольку (9.42)»
74 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
явно задает множество из G линейных функционалов на Ф, то
¦функции {Фл (X)} образуют базис G-мерного пространства Ф*,
сопряженного с Ф. Таким образом, элементы Ф* представляются
в виде линейных комбинаций функций Фл (X) (т. е. F* (X) =
= /"ДФЛ (X); Д = 1, 2, . . ., G). Однако (9.17) показывает, что
каждая функция Фл (X) является линейной комбинацией перво-
первоначальных базисных функций. Это означает, что ФЛ (X) ? Ф
ш, следовательно, пространства Ф и Ф* совпадают. Отсюда следу-
следует, что каждый элемент F (X) ? Ф можно единственным образом
представить в виде линейной комбинации как функций Фд (X),
так и функций ФЛ (X). Действительно,
F (X) = FДФД (X) = ^ДФЛ (X), (9.43)
где
F* = {F, ФЛ>, /1д = (ЛФд>, (9.44)
«ли
FA = CATFr, FA = CATFr. (9.45)
Скалярное произведение двух функций и норма функции в Ф
определяются формулами (9.30) и (9.31). Наконец, аффинные пре-
преобразования биортогонального базиса в пространстве Ф описывают-
описываются формулами (9.32) и (9.33).
9.3. НАИЛУЧШАЯ АППРОКСИМАЦИЯ
Рассмотрим теперь задачу определения наилучшей аппрокси-
аппроксимации заданной функции F (X) ? SB в пространстве Ф, базисом
которого является заданное множество функций Фд (X). Под
-«наилучшей аппроксимацией» мы понимаем элемент из Ф, бли-
ближайший к F (X) относительно естественной метрики
d [F (X), G (X)] = \\F(X)-G (X) || в SB.
Пусть Лл — произвольные G чисел, так что ЛЛФД (X) ? Ф.
Нам надо определить ЛЛ, минимизирующие функционал
/ (ЛА) = (F — ЛАФД, F — ЛДФД>, (9.46)
который ввиду равенства / (Лл)- = d2 [F (X), ЛАФД (X)] является
мерой расстояния между F (X) и ЛДФД (X). Возвращаясь к (9.9)
и (9.25), мы видим, что
(F, Фд) = (F + F, Фд) = FA + FA, (9.47)
где использовано обозначение (F, Фд) = FA. Используя этот
«факт и (9.30), убеждаемся, что (9.46) можно переписать в виде
/ (Лд) = CArF*FT +1| F ||2 + 2F*FA - 2ЛЛ (F^ + /д) + СДГЛЛЛГ.
(9.48)
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 75
Для того чтобы найти ЛЛ, которые минимизируют / (Лл), положим
Л1ф- = 0 (9.49)
и решим эту систему линейных уравнений. Мы получим
. (9.50)
Смысл этого результата станет понятен, если заметит^ что,
подобно (9.47),
(F, ФЛ> = {F + F, ФЛ> = FA + C^Fr = Л*,а. (9.51)
Таким образом, наилучшей аппроксимацией заданной функции
F (X) в подпространстве Ф является функция F (X) ? Ф> компо-
компоненты которой относительно базиса {Фд} равны, скалярным про-
произведениям F (X) с сопряженными базисными функциями Фл (X).
Отметим, что в приложениях, как правило, F (X) — неизве-
неизвестная функция, и лучшее, что можно сделать,— это использовать
компоненты FA и РА, определенные формулами (9.24) и (9.25).
Однако если функция F (X) задана, то коэффициенты, определяю-
определяющие ее наилучшую аппроксимацию в Ф, находятся с помощью
(9.51). Если через Ffb) и F&1 обозначить коэффициенты наилуч-
наилучшей аппроксимации, то
, ФЛ>, Ff = F& + {P,<I>b). (9.52)
В случае когда можно получать коэффициенты F^ и /дЬ) в фор-
форме (9.52), нетрудно установить еще одно интересное свойство под-,
пространств Ф и Ф*. В этом случае вместо (9.43) используется
соотношение
F (X) = *$,ФД (X) = ^Ь)ФЛ (X). (9.53)
Тогда1)
= (F-F, Фд> = 0,
а - л (9.54)
(F, ФЛ> = {F-F, Фл} = 0,
т. е. пространство Ф (или Ф*) является ортогональным дополне-
дополнением к М' (или Si*')- Далее предположим, что (9.53) и (9.54)
выполняются; тогда мерой Е ошибки представления функции
F (X) ее проекцией F (X) = U.F (X) будет
(9.55)
J) Определяемый последующими формулами выбор F, при котором функ-
функция F — F ортогональна к Ф, мотивируется классической теоремой о проек-
проекциях в гильбертовых пространствах. См. теорему 10.8.
76 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
поскольку F и F ортогональны. Так как в общем случае норма
|| F || может быть неограниченной, ошибка Е мала только в том
случае, если функция F (X) близка к подпространству Ф.
Обобщение. Нетрудно обобщить приведенные выше резуль-
результаты на случай дуальных несамосопряженных пространств. Корот-
Коротко остановимся на этом. Пусть JF и "§ — дуальные пространства,,
элементами которых являются функции, обозначаемые через / и g,;
и пусть (/, g) — скалярное произведение «между» JF и §. Далее,
пусть Ф — некоторое конечномерное подпространство Bf, af—
дуальное ему подпространство в &'. Пространства Ф и W поро-
порождаются биортогональным базисом Фд ? Ф, WA 6 ^. где
(ФД) ?г) = ё1\ Д,Г=1, 2, ...,G. (9.56)
Если F и G1) — проекции / и g на Ф и W, то
F = Р*ФА, G = <?Д?А, (9.57)
где по повторяющимся индексам производится суммирование
от 1 до G, а
/¦д = (д чгД), Gh = (g, Фд). (9.58)
Пусть ЛАФД и Мд^д — произвольные элементы из Ф и f.
Рассмотрим билинейный функционал
/ (Л*, Мт) = (/ - ЛдФд, g - МГЧТ), (9.59)
который после некоторых выкладок можно записать в виде
/ (Л*, Мт) = (f-F,g-G)+ {F* - Л* > (Gt - Mr >• (9.60)
Ясно, что при подстановке любой из определяемых формулами
(9.57) проекций второй член в (9.60) обращается в нуль. Если
мы введем линейное положительно определенное регулярное
отображение к пространства JF в !§, такое, что х (Ф) cz W, то
х определяет матрицу хгд == (Фд, х (Фг)), такую, что
хгдЛд = Мт. (9.61)
Поэтому функционал / (ЛА, Мт) = / (ЛА, xrQAQ) является поло-
положительно определенной квадратичной формой
/ (Л*) = <f — F,x(f — F)) + хдг (Ла - F&) (Лг - FT). (9.62)
Следовательно, если Лд выбраны в соответствии с (9.58), то функ-
функционал (9.62) принимает минимальное значение.
х) Не нужно путать это G с размерностью подпространства Ф. — Прим*
перев.
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 77
9.4. НЕКОТОРЫЕ СВОЙСТВА СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
Предположим, что мы расширили пространство &8 таким обра-
образом, что оно включает в себя функции типа дельта-функции
Дирака х) б (X — А), А 6 'Я, определяемой условиями
f О, Х=^А, с
6(Х-А) = { v . \(X-A)d« = l. (9.63)
I oo, A = A, J
М
Здесь А — фиксированная точка области 9.
Пусть Д (X — А) — проекция функции Дирака б (X — А)
на подпространство Ф:
Д (X — А) = Пб (X - А) = ДДФД (X) = ДДФД (ХJ (9.64)
где в соответствии с (9.24) и (9.25) [или (9.44)]
ДД = <б (X -А), Фд (Х)> = Фд (А), (9.65)
Дд = (б (X - А), Фд (X) > = Фд (А). (9.66)
Следовательно,
Д (X — А) = Фд (А) Фд (X) = Фд (А) ФД (X). (9.67)
Таким образом, значения функций ФЛ (X) (или Фд (X)) в произволь-
произвольной точке А 6 А равны компонентам ДЛ (или Дд) проекции дельта-
функции б (X — А) на Ф.
Отметим, что в то время как функция б (X — А) отлична от
нуля только в точке А, проекция Д (X — А) может быть отличной
от нуля почти всюду в области определения функций из Ф. Однако
основные свойства функции б (X — А) сохраняются при проек-
проектировании П: Ш -»- Ф. Например, видно, что
(Д(Х-А), ^(Х)> = (ФД(А)ФА(Х), ^ГФГ(Х)) =
= ФД(А)^Г(ФЛ, Фг> =
= /'ЛФд(А) = /?(А). (9.68)
В частности^ если F (X) = 1 является элементом пространства Ф,
то
(Д (Х-А), 1) = 1. (9.69)
Чтобы установить еще одно свойство функций Фд (X), пред-
предположим, что в % фиксировано конечное число G узловых точек
х) Напомним, что б (X — А) не является квадратично интегрируемой
функцией. Поэтому наши результаты, касающиеся наилучшей аппроксима-
аппроксимации элементов из &6, к ней неприменимы. Однако проекция Пб (X — А)
корректно определена.
78 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Хл (А = 1, 2, . . ., G). Предположим, далее, что функция Фд (X)
в узле Хг равна единице, а в других узлах обращается в нуль, т. е.
ФД.(ХГ) = 81. (9.70>
Тогда проекция дельта-функции (9.64) принимает вид
А (X - XT) = Фд (Хг) Ф* (X) = фг (X). (9.71)
Базисные функции Фд (X), обладающие свойством (9.70), будем
называть нормализованными относительно G узлов Хд. В п. 9.&
рассматривается способ построения таких нормализованных базис-
базисных функций для конечноэлементных аппроксимаций. Равенство-
(9.71) показывает, что сопряженные функции ФА (X) представляют
ёобой проекции дельта-функций б (X — Хд) узлов ХА.
Моменты и объемы. В некоторых приложениях, в случае
когда Ш — гильбертово пространство со скалярным произведе-
произведением, задаваемым формулой (9.7), удобно ввести в рассмотрение?
моменты М& и МА, определяемые формулами
Ш, (9.72>
к
j ChTMT. (9.73>
Тогда
j F(X) dft = F*M& = FbM*. (9.74>
Если предположить, что F (X) = 1 g Ф и функции Фд (Х>
нормализованы относительно G узловых точек (условие (9.70))f
то эти функции будут удовлетворять еще и условию
S 1. (9.75)
S
Д=1
Тогда моменты (9.73) можно представить в форме
G
Мл = СЛГЖг = Слг j Фг(Х) 2 Фл (X) d%, (9.76)
М А=1
ИЛИ
Л/л = САГ2 <Фг, Фл). (9.77)
А=1
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
Но <ФГг Фд> = Ста% так что
G G
МА = 2 САТСГА = 2 6д = 1 • (9-78)
Л=1 Л=1
Аналогично
С С
МА= 2 (Фд, ФЛ>= 2 СдЛ. (9.79>
Л=1 Л=1
Заметим, что
G G
2 МА = j 2 Фд(Х)йй= jd^ = r, (9.80>
д=1 ,% д=1 ^?
где 5^' — объем области Ш. Отметим также, что
в в
r = \m= 2 2 сдг- (9.81>
^? д=1 r=i
Таким образом, если выполнено условие (9.75), то сумма всех эле-
элементов фундаментальной матрицы Сдг равна объему области 9?
определения функций из Ф. Кроме того, в силу (9.74) и (9.78)
с
j F{X)dn= 2 *д- (9-82)
Заметим еще, что если базисные функции Фд (X) удовлетворя-
удовлетворяют условиям (9.70) и (9.75), то
F(X*) = F* = CArFr. (9.83>
Значит, среднее значение F (X) в области °1г, определяемое интегра-
интегралом (9.82), неравно сумме значений F (X) в узлах ХЛ, а равно сумме
сопряженных значений FA = Сдг/t. Мы видим, что FA есть значе-
значение F (X) в узловой точке ХА, в то же время как F^ — среднее
значение F (X) в окрестности Хд.
9.5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
В этом пункте мы кратко рассмотрим некоторые свойства
аппроксимаций линейного оператора Х- Как правилоа приходится
иметь дело с уравнениями типа
XF (X) = G (X), (9.84)
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где X — линейный оператор, отображающий элемент F (X) гиль-
гильбертова пространства &8 в элемент G (X) другого гильбертова
пространства Ш функций, определенных на той же самой области
Ш, что и функции из &8. Для простоты будем пока считать, что
¦Ш = Ш, т. е. что Х\$в -+&&. Тогда XF (X) €<$?, и можно гово-
говорить о проекции UXF (X) на подпространство Ф:
UXF (X) = ?Дфд (X) = ?ДФ* (X). (9.85)
Здесь
?А = <ФД, nXF)t ?д = (Фд, USSF). (9.86)
'Очевидно, что
nXF(X) = UXF(X) + nXF(X). (9.87)
Для упрощения дальнейших рассуждений предположим, что
«операторы П и X коммутируют, т. е.
UX = XU. (9.88)
Хорошо известно, что (9.88) в большинстве случаев выполняется
лишь приближенно. Разность XII — ИХ является мерой того,
насколько хорошо подпространство Ф соответствует рассматривае-
рассматриваемой задаче. Очевидно, равенство (9.88) предполагает, что <55ФД а
cz Ф. При выполнении условия коммутирования (9.88) можно
¦считать, что
nXF(X) = XTIF(X) = O (9.89)
и
YIXF (X) = XUF (X) = XF (X) = F*XOA (X). (9.90)
Тогда в силу (9.86)
LA = LwFT = L-AvFv и LA = L*rFr = L*TFr, (9.91)
где
Ьдг= (Фд, #Фг>, Ьдг = (Фд,, ХФГ), (9.92а, б)
LAT = (ФА, ХФТ), ЬАТ = <ФА, ?Фг>. (9.92в, г)
Ясно, что действие оператора X на Ф описывается матрицами
LAV, . . ., L.p. Отсюда следует, что
UXF (X) = LArFTQ)* (X) = LATF^ (X) =
= ?л1>гФд(Х) = ?Аг/?'ГФд(Х). (9.93)
Аппроксимация уравнения (9.84) в Ф принимает вид
e4(X). (9.94)
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 81
Приравнивая соответствующие компоненты, получаем
LVr = GA. (9.95)
Если матрица LAr невырождена1 то
F* = N*TGr, (9.96)
где N^r — матрица, обратная к LAr, и приближенное решение
уравнения (9.84) имеет вид
(9.97)
енный
(9.98)
В гильбертовом пространстве $В оператор Хх сопряженный
к X, определяется соотношением
Для выбранных нами аппроксимаций имеем
или
LrAGrGA = LrbFTG\ (9.99)
где
?дг = (фг, ?фд>. (9.100)
Это означает, что
?гд = Ьдг. (9.101)
Как и следовало ожидать, матрицей сопряженного оператора X
служит матрица, транспонированная к матрице оператора X.
Аппроксимации некоторых линейных операторов будут рас-
рассмотрены в качестве примеров в § И.
Задачи о собственных значениях. Рассмотрим две
эадачи о собственных значениях
%iG. (9.102)
Используя наши аппроксимации^ эти уравнения можно предста-
представить в виде
(L*r — №6x')Fr = 0 (9.103)
и
(LAr-;\,CAr)Gr = 0. (9.104)
Известно, что множества собственных значений матрицы и транс-
транспонированной к ней совпадают. Далее, всегда можно выбрать
биортогональные множества собственных функций, причем если
6 Дж. Оден
82 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
все собственные значения различны,, то единственным образом.
Пусть Ft® и Сд — собственные векторы, соответствующие соб-
собственным значениям Ха и Яр матриц ZAr и LAr. Тогда
(9.106)
= бар. (9.107)
В частности, если функции Фд (X) являются собственными функ-
функциями линейного оператора X в SB, то сопряженные функции
Фд (X) будут собственными функциями сопряженного оператора X.
Другими словами,
ХФА(Х) = Л(Д)ФД(Х). (9.108)
Если оператор X самосопряжен, то собственные функции Фд (X)
и ФЛ (X) совпадают: Фд (X) = Фд (X) (с точностью до констант).
Лроизводные сопряженных аппроксимаций. Один
из наиболее распространенных линейных операторов — оператор
частного дифференцирования. Рассмотрим некоторые свойства
производных аппроксимационных функций. Пусть d^F (X) обозна-
обозначают частную производную функции F (X) ?&8- Будем предпола-
предполагать, что dy,F (X) существует и что производные базисных функций
Фд (X) тоже принадлежат подпространству Ф, т. е. <ЗцФд ? Ф
(это последнее предположение, конечно, не всегда справедливо).
Введем в рассмотрение массив
^Г = (^ФЛ, Фг). (9.109)
В соответствии с (9.11)
Д ^ГФГ(Х). (9.110)
Возникает важный вопрос: при каких условиях проекцию
(9.110) можно использовать для аппроксимации производных
от сопряженных функций Фд (X)? Другими словами, когда мы
имеем право считать, что
^ФЛ(Х) = ^ГФГ(Х). (9.111)
Ответ на этот вопрос дает следующая теорема.
Теорема 9.1. Равенству (9.111) эквивалентны следующие
условия:
а. д^П = Шц на Ф.
б. д»Ф с= Ф.
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 83
в. Ф есть пространство решений некоторой системы линей-'
них дифференциальных уравнений с постоянными коэффициентами.
Доказательство. Схема доказательства такова. Мы покажем^
что из (9.111) следуют условия а и в, из а следует б, а из &
следует (9.111).
(9.111) =4* а. Действительно,
ГО„ФЛ (X) = Df Фг (X) = <урд (X) = д» [ПФЛ (X)]
для каждой функции ФЛ (X) ? Ф.
а =^ б. В самом деле, д№ (Ф) = дцПФ = П (д^Ф), з
П (д^Ф) с Ф по определению.
б => (9.111). Поскольку дц (Ф) сг Ф, то д^Фд (X) является
линейной комбинацией функций Фд (X), что и утверждается
равенством (9.111).
(9.111) =з- в. Это немедленно следует из того, что множество
{Фд} представляет собой полное решение уравнения
дрХд = СдГ1)ц ГЛ.
в =ф- (9.111). Систему линейных дифференциальных уравне-
уравнений порядка п всегда можно свести к системе уравнений перво-
первого порядка. Следовательно, <9иФд (X) содержатся в Ф. Дока-
Доказательство завершено.
Предполагая, что условия теоремы выполнены, можно с помо-
помощью (9.111) получить производную любого элемента F (X) =
= ГАфд (X) ? Ф:
d^FW^D^F^riX). (9.112)
Однако соотношение
Ш^(Х) = 1>^дФг(Х) (9.113)
может не выполняться, если только на Ф не наложить дополни-
дополнительные условия
а'. д^П = Шц в SB.
б'. д„ (Ф) с Ф.
Можно показать, что условия (9.113), а' и б' эквивалентны.
Если предположить, что эти дополнительные условия тоже
выполнены, то операция дифференцирования д^в $ё приближенно
описывается с помощью массива Z^, определяемого формулой
(9.109), а производные высших порядков представляются с помо-
помощью степеней D^r. Действительно, вводя дискретные операторы
Dtx = DtACAQI%T (9.114)
и
^ ?Л[Й (9.115)
6*
84 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
легко показать, что, например,
^ (9.116)
(9.117)
J div а d% = D*rA%MT, (9.118)
(F, d^^D^FbGr, (9.119)
$ (9.120)
T (9.121)
и т. д. Отметим также, что можно использовать дискретные опера-
операторы и других типов, такие, как
^V дг = {дрФ&
_д.
U]i,t Г == ('ТА.'-'
Ви1,ьт = {дъ.Фь
и т. д. Тогда
„ Фг)=Сд
ЛД _ sjAAq
. ЗцФГ)
Фд(Х) = Г
ФЛ(Х) = Г
/-I Г) МЛ
П-Д /1
|i, ЛГ, LI», Г = ^ГЛ
»и,дгФГ(Х) = ?)^
>^ГФГ(Х) = ^Г(
Л?>и,дгФГ(Х) = 1
(9.122)
тлДЛ /-тгДЛ тл
L»n =6 />ц, гл,
(9.123а, б)
(9.124)
'дФг(Х), (9.125)
Dr(X), (9.126)
^дФг(Х). (9.127)
Ясно, что с помощью операторов (9.122) — (9.124) можно получить
другие формулы, соответствующие формулам (9.116) —(9.121).
Производные порядка выше двух подсчитываются по общей
формуле
(9.128)
Следует сказать, что дополнительные условия а' и б' (и даже
более слабые условия а, б, в) редко выполняются в приложениях.
Однако мы будем предполагать, что размерность G может быть
взята достаточно большой, с тем чтобы эти условия выполнялись
хотя бы в некотором приближенном смысле. Интересно отметить,
что если эти условия не выполняются, то производная проекции
постоянной величины не обязательно равна нулю! Некоторые
другие факты будут отмечены ниже при описании конкретных
примеров.
. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 85
9.6. ПРИЛОЖЕНИЯ К КОНЕЧНОЭЛЕМЕНТНЫМ АППРОКСИМАЦИЯМ
Для того чтобы применить изложенную теорию сопряженных
аппроксимаций к конечноэлементным аппроксимациям, необходи-
необходимо выяснить природу базисных функций Фд (X), используемых
для конечноэлементных представлений функций F (X). С этой
целью, следуя описанной в § 6 и 7 процедуре, представим область
^? областью Ш, состоящей из совокупности Е конечных элементов
ге, которые связаны между собой в G глобальных узловых точках
Хд (А = 1, 2, . . ., G). Как обычно, внутри каждого элемента
(е)
выбираем Ne локальных узловых точек х^O так что х^, = &2^ХЛ,
а для фиксированного е имеет место равенство Хд = А%х^е), где
(е) (е)
An и ?2д — массивы, определяемые формулами G.4) и G.6).
Для упрощения обозначений будем пока предполагать, что систе-
системы локальных и глобальных координат хе и X совпадают, так что
для записи точки в 9? можно использовать символы х и X. В случае
необходимости подчеркнуть, что точка принадлежит определенно-
определенному элементу, мы, как и прежде, будем использовать идентифика-
идентификационную метку (е).
Рассмотрим гильбертово пространство &8, элементы которого
являются функциями, определенными в области 'Я, и напомним,;
что проекция П: $8 -*¦ Ф определяет G-мерное подпространство
в S8, порождаемое функциями Фд (X). В случае конечноэлемент-
конечноэлементных аппроксимаций областью определения функций в подпро-
подпространстве Ф является совокупность конечных элементов ffl. Таким
образом, в "Л
F(X)ttF(X) = FA<Z>A(X), (9.129)
где, если функции Фд (X) нормализованы в узлах ХЛ в соответ-
соответствии с (9.70),
= FA. (9.130)
Метод конечных элементов предполагает использование спосо-
способа получения (9.129) и при локальных рассмотрениях. Пусть Р'*'
обозначает проекцию Ж на iV„-мерное подпространство W(C) функ-
функций, определенных в ге, т. е. Р(С}: SB -*• ^(е). Опишем эту проек-
проекцию, введя систему Nе линейно независимых локальных базисных
функций i^jv' (x), нормализованных в локальных узловых точках:
^(x*) = 6?, ' (9.131)
где М, N = 1, 2, . . ., Nе. Локальная проекция функции F (X)
определяется формулой
F (9.132)
86 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где локальная аппроксимация /(?) (х) единственным образом
выражается в виде линейной комбинации локальных базисных
функций (см. G.15)):
7 &#. (9.133)
Вследствие (9.131) компоненты ffey представляют собой значения
локальных аппроксимаций в локальных узлах:
/<" (г") = /(^(хМ) = /(W = /й, (9.134)
и, как обычно,
/й 8>д F* A
(9.135)
Для установления связи локальных функций i^jv' (x) с глобаль-
глобальными функциями Фд (X) потребуем, чтобы функция г^ (x) было,
ограничением Фд (X) на элементе ге, что записывается так:
\|>$(х) = Л&Фд(х); (9.136)
здесь под Фд (х) понимается Фд (X) только для X 6 ге- Это соот-
соотношение определяет вложение Л: Ф -*• W и следует из того
факта, что значения г^' (х) и Фд (X) находятся во взаимно одно-
однозначном соответствии с точками их областей определения ге
и М. Для х ? ге справедливо также соотношение
фд (X) = S^Spiv (x) при фиксированном е, (9.137)
и почти всюду4) в аА
JL (е)
(9.138)
Из определений Pie> и П ясно, что
Л
(9.139)
Мы видим, что при тех же оговорках, которые были сделаны отно-
относительно (9.138), равенство (9.130) можно переписать в виде
/(X) = ^дФд (X) = | Н&|$ (х) = S /<Ж (*). (9.140)
или, в силу (9.133),
*) См. подстрочное примечание на стр. 50. Отметим, что (9.138) опре-
определяет базисные функции Фд (X) именно так, как они были введены ранее
формулами G.20).
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 87
Фундаментальные свойства конечноэлементных
аппроксимаций. Описав базисные функции Фд (X) для
конечноэлементных аппроксимаций, мы можем применить к ним
изложенную ранее общую теорию сопряженных аппроксимаций.
Подставляя (9.138) в (9.12), получаем фундаментальную матрицу
подпространства Ф для конечноэлементных моделей
Е Е (е) (/)
Сдг = (Фд, Фг> = 2 2 0№<ф8\ФЙ>. (9-142)
Однако локальные аппроксимирующие функции г^* (х) определе-
определены так, что их носители почти не пересекаются, так что
0, еф1. (9.143)
Значит, (9.142) можно переписать в виде
СДГ= S &Й^м, (9.144)
где c(nm — локальная фундаментальная матрица подпростран-
подпространства ?(<?>:
<#м = <4#, V&- - (9-145)
На первый взгляд кажется -естественным использовать матрицу
с'хм и ее обратную для построения множества локальных сопря-
сопряженных базисных функций, как это делалось раньше при опреде-
определении ФЛ (X). Однако мы тогда ограничились рассмотрением
пространств Ф и Ф*, содержащих только непрерывные функции.
А так как от функций г|)$' (х) требуется только лишь, чтобы они
образовывали непрерывные базисные функции Фд (X) по форму-
формулам (9.138), нет никаких оснований ожидать, что в достаточной
степени произвольная линейная комбинация 2 (c'nm) -1 '
_
будет тоже непрерывной в М. Поэтому необходим другой подход.
Определим локальные сопряженные аппроксимации для конеч-
конечноэлементных представлений с учетом этого замечания. Для нача-
начала рассмотрим линейный функционал, соответствующий взятию
скалярного произведения функции
F(X) = /?ЛФД (X) = 2 $д^Ч$ (х) = ^ДФЛ(X) (9.146)
е
с произвольной функцией G (X) ? Ф*, которая также является
суммой Е локальных аппроксимаций:
88 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где
ФА(Х) = САГФГ(Х) = СЛГ 2 QtVn(x)- (9.148)
е
Имеем
(F, G) = F^Gt, = FbGA = F* <2 Йд4$ (х), G), (9.149)
е
где
Сд = (G, Фд) = 2 few (9.150).
е
и использовано обозначение
g(N = {G, 0$). (9.151)
Видно, что в противоположность (9.135) глобальные значения 6гд
в глобальной узловой точке А получаются в результате суммирова-
суммирования всех локальных значений gffi в локальных узлах, инцидентных А.
Позднее мы остановимся на этом подробнее.
Возвращаясь к (9.147), мы можем теперь определить системы
локальных сопряженных базисных функций, поскольку
G (X) = 2 8д ?#ФЛ (X) = 2 1{в) (х), (9.152)
е е
что наводит на мысль положить
?е) (х) = ^Чй (х), N = l,2,...,Ne, (9.153)
где в силу (9.152)
frt..
(9.154)
Это равенство определяет локальные сопряженные базисные
функции для элемента е конечноэлементной аппроксимации. Вслед-
Вследствие (9.138) имеем
«Й(*)=82Г^|1ЙГ*2«- (9.155)
Соотношение (9.155) весьма важно: оно показывает, что «ло-
«локальные» сопряженные базисные функции для элемента е являются
линейными комбинациями базисных функций всех Е конечных
элементов. Таким образом, функции т$*а (х) не обязаны иметь
локальные носители; фактически для каждой локальной функции
г|з^ (х) носителем служит вся связанная область "А. Это означает,
что обычный прием вычисления локальных значений сопряженных
аппроксимаций с помощью локальных узловых значений gffi (напри-
(например, вычисление напряжений элемента по аппроксимации пере-
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 89
мещений) не вполне точен. Для того чтобы локальная сопряженная
аппроксимация была согласована с определенным на Ф линейным
функционалом (например, энергией), необходимо рассматривать
всё в базисе, имеющем своей областью определения всю совокупность
конечных элементов. Эти свойства локальных сопряженных аппро-
аппроксимаций будут продемонстрированы на примерах в п. 9.8.
Заметим, что
{йЛ il/e)) = йNCAr У йг^ (Фм *|)д') (9.156)
поэтому, ввиду (9.145),
(9.157)
где M, N, R = 1, 2, . . ., Ne и Д, Г = 1, 2, . . ., G. Ясно, что мно-
множества функций ¦ty'ff (x) и г|)^, (х) не образуют локального биорто-
гонального базиса для функций из Ч*4*'.
После того как базисные функции Фд (X) и Фд (X) для конеч-
ноэлементных представлений определены формулами (9.138) и
(9.148), просто получить и другие величины, нужные при конечно-
элементных аппроксимациях. Например, из (9.72) и (9.73) полу-
получаем
Е м G
Мь = j Фд (X) dm = 2 W = S <?дг, (9-158)
где
J (9.159)
| 1. (9.160)
Далее, если мы введем локальный дискретный оператор
^%m=(<VI$,A (9.161)
то в соответствии с (9.109) и (9.122)
D», дг = 2 $?$r4e! wm, (9.162)
< = СДЛСГЙ I ЙлЧ%м. (9.163)
Например,
dyf (X) = S &&(^ NMF*<Z>T (X). (9.164)
90 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Дискретные операторы Z)?? и В fix, задаваемые формулами (9.114)
и (9.115), для конечноэлементных моделей имеют вид
B №<*» NM)(^ №#W, (9.165)
Й&«?1»). о. 166)
Нетрудно получить соотношения, подобные (9.116) — (9.121) или
(9.122) — (9.128), в форме, соответствующей конечноэлементным
аппроксимациям. Для этого надо подставить в них (9.162), (9.163),
(9.164) или (9.165). Поскольку это делается очень просто, подробнее
останавливаться на этом не будем.
В случае линейного операторного уравнения типа (9.84) рас-
рассмотрим его локальную форму
P^XF (X) = P^G (X), (9.167)
которую^ мы аппроксимируем с помощью соотношений
Pie)XF (X) ^ ?P(e)F (X) = Xf{e) (x) = /Й?Ч$ (х) (9.168)
(9.169)
Таким образом, в пределах конечного элемента
fyXytf (x) = ggflW (x). (9.170)
Вводя обозначение
1<$N = (i|)($, X^n), (9.171)
имеем
hjNj(e) = С.ГШё(е). (УЛ/ А)
Локальные матрицы типа Imn часто вырождены, поскольку локаль-
локальным функциям /<е) (х) пока позволяется принимать произвольные
значения на локальных границах дге элементов. Поскольку
(«) («)
f?e) = Q%Fv и g(e) = arGT, (9.173)
(е)
умножая (9.172) на Од и суммируя по е, получаем
F 2j Од tjfjvOr == G 2j Од CjifjyOr. (9.174)
е е
Полагая
(9.175)
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ 91
и замечая, что
приходим к равенству
LbTFT = GA, (9.177)
которое эквивалентно (9.95). Отметим, что приведенные рассужде-
рассуждения основывались на предположении о перестановочности X
и Р(С). Другие подходы, применимые как к линейным, так и к
нелинейным операторам, будут рассмотрены в § 10 и в примерах
§ 11 (а также в п. 9.8).
9.7. ОБОБЩЕННЫЕ СОПРЯЖЕННЫЕ ПЕРЕМЕННЫЕ1)
В качестве некоторого обобщения изложенной теории сопря-
сопряженных аппроксимаций рассмотрим способ построения обобщен-
обобщенных сопряженных переменных для других линейных функцио-
функционалов.
Пусть E° и &~ — два пространства, элементами которых являют-
являются функции S (X) и Т (X), определенные в одной и той же области
fi cr Щк. В рассматриваемом случае значения функций S (X)
и Т (X) могут быть векторами, тензорами и т. д. Пусть имеется
некоторое отображение, ставящее в соответствие каждой паре
функций [Т (X), S (X)] 6 3~ X of вещественную функцию G (X),
Хб й. Бинарную операцию, которая для заданного X отобра-
отображает пару [Т (X), S (X)] в G (X), будем обозначать символом *, т. е.
G (X) = Т (X) * S (X). (9.178)
Пусть, далее Q — функционал на &~ X <5°, определяемый равен-
равенством
Q [Т (X), S (X)] = j T (X) * S (X) AM, (9.179)
м
где интеграл в правой части — интеграл Лебега. Потребуем, чтобы
функционал Q [Т (X), S (X)] = Q [T, S] был билинейным, т. е.
чтобы выполнялись равенства
Q [оТх + РТ2, S] = а<? [Tlt S] + р<? [Т„ S],
(9.180)
Q [Т, oSx + PS2] = aQ [Т, SJ + р<? [Т, S2],
х) См. Оден [1969а, 1971а]; дальнейшие обобщения см. у Одена и Редди
[1973].
92 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где аир — скаляры. Значит, при фиксированном S (X) формула
(9.179) определяет линейный функционал на $~. Совокупность
всех таких линейных функционалов образует сопряженное про-
пространство к 3'. Будем называть S (X) и Т (X) сопряженными отно-
относительно Q.
Нас будет интересовать следующая задача: при заданной
конечноэлементной аппроксимации Т (X) функции Т (X) найти
соответствующую модель S (X), согласующуюся с (9.179). Значение
термина «согласующаяся» станет ясным позднее.
Для решения этой задачи рассмотрим типичный конечный
элемент ге аппроксимации °А области ??, ограничениями полей
Т (X) и S (X) на которой являются соответственно t(e) (x) и s(e) (x).
Локально, положим
gM [t, s] = J t(e) (x) * s(e) (x) dre. (9.181)
re
В конечноэлементной модели локальные аппроксимации поля
Т (X) имеют вид
t(e> (х) » Р> (х) = %$% (х), х 6 ге, (9.182)
так что вместо (9.181) имеем
дм «?« = $•*#, N = 1, 2, ..., Ne, (9.183)
где
$ j$s(e)(x)dre. (9.184)
Величины Sjy' (е = 1, 2, . . ., Е; N = 1, 2, . . ., Ne) назовем
локальными обобщенными значениями функции S (X) в узле N
элемента е, согласующимися г) с аппроксимацией t(e) (x) и функ-
функционалом Q.
Глобально положим
Е
2<7(e). (9-185)
где
Q
T (X) = ТДФД (X) = Тд 2 Q?i|$ W• (9-186)
x) Термин «согласующийся» применительно к конечноэлементным
аппроксимациям был введен Арчером [1963, 1965] в связи с аппроксимациями
распределений сил и масс по методу конечных элементов.
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
93
©
Рис. 9.1. Совокупность конечных элементов.
Далее, можно написать
# = TA*SA, Д = 1, 2, ...,G, (9.187)
где SA — глобальное обобщенное значение S (X) в узле Хд:
бд = j Фд (X) S (X) dМ = 2 ^д j 4n (x) s(e) (x) dre (9.188)
М
Из (9.184) и (9.188) видно, что
е=1
(9.189)
Таким образом, в противоположность простому отношению инци-
инциQ
дентности tjj, = Q^TA между локальными и глобальными значе-
значениями Т (х), глобальное значение вд сопряженного поля в узловой
точке А связанной модели равно сумме локальных значений Sjy'
во всех элементах, связанных в А, причем узлы N этих элементов,
значения в которых являются слагаемыми суммы, инцидентны
узлу А.
Например, в глобальной узловой точке 1 двумерной связки
конечных элементов (рис. 9.1)
Т1 = tfx> = tf2) = tf3> = tf4>. (9.190)
94 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Однако для сопряженного поля
Si = s'1) + sf4-s<3' + s^. (9.191)
Отметим, что
?=TA*SA=2$)*s#. (9.192)
е
Важно иметь в виду, что
ТЛ = Т(ХЛ), но SA=^S(XA). (9.193)
Сопряженная аппроксимация в % описывается более сложными
формулами:
Е
S (X) » SAOA (X) = 2 в« (х), (9.194)
SM(x) = e#i|$(x), <,(х) = &АГ3(Йг*й(х). (9.195)
9.8. ПРИМЕРЫ
Для лучшего уяснения изложенных идей приведем несколько
примеров, в которых используются сопряженные аппроксимации.
Пример 9.1. Механическая работа. Начнем с простого примера,
в котором используется элементарное понятие работы. Рассмотрим два век-
векторных поля U (X) и F (X), определенных в области ?R пространства %ъ.
Если U (X) — то поле, которое аппроксимируется, то
~П (х) = 2 и(е) (х) =2 Q^$ (х) ид. (9.196)
е е
Пусть векторная функция U (X) описывает поле перемещений некоторого
непрерывного тела, a F (X) — поле действующих на тело сил. Тогда ?<е> —
работа локального поля сил f<e>(x) на перемещениях U(e) (x), a * означает обыч-
обычное скалярное произведение векторов (* = -):
>= J
J ()y% (9.197)
Те
Здесь f^y' — согласующаяся обобщенная сила в узловой точке N:
fW(i)^(i)ire. (9.198)
Наконец, глобальные значения узловых сил получаются в результате век-
векторного сложения всех локальных узловых сил в узлах связанной модели:
Функционал Q в этом случае представляет собой полную работу узловых
сил Рд на соответствующих перемещениях узлов иЛ:
^=UA-FA = 2u^-f^. (9.200)
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
95
Пример 9.2. Вычисление напряжений. Чтобы продемонстриро-
продемонстрировать значение сопряженных функций т!$е) (х), приведем простой пример 1),
относящийся к расчету напряжений в модели, основанной на аппроксимации
поля перемещений.
Рассмотрим неоднородный стержень, напряжения а (х) в котором опре-
определяются формулой
du(x)
их
(9.201)
Здесь и (х) — поле перемещений, а модуль к (х) считается линейной функ-
функцией:
, (9.202)
где к0 — константа, характеризующая материал стержня.
Для простоты воспользуемся довольно грубым конечноэлементным пред-
представлением, в котором фигурируют лишь три одномерных элемента единич-
единичной длины. Локальные базисные функции tyffi (х), соответствующие типич-
типичному элементу е, возьмем линейными относительно локальной координаты |:
,1,(е) ii\ л Е ,i,(e) (%\ Е /а 9ПЧ\
Локальные фундаментальные матрицы таковы:
'й>м = <*й> -*^~
2 1
Определяя путем сопоставления узлов операторы инцидентности
ставляя (9.204) в (9.142), получаем
г — L
°дг—g"
1
0
0
1
4
1
0
0
1
4
1
0'
0
1
2
26—7 2—1
— 7 14 -4 2
2 —4 14 —7
— 1 2—7 26
(9.204)
и под-
(9.205)
С помощью (9.155) теперь можно определить сопряженные базисные функции:
Ч>Ь> (*) =-& Wi1' (x)-7 [1|)^> (x) + ^i*> (*)] + 2 M>i« (*) + Ф1ю (*)] - ^3) И},
]- 4
Я|)B2) И = 1|>C) (ж) =
] - 7*i»> (x)},
Функции я|)]|' (ж) и i|>(Jf, (ж) изображены на рис. 9.2.
См. Оден и Браули [1971а].
(9.206)
96
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
-X
-X
52/15
-а?
-2/15
-14/15
Рис. 9.2." Локальные базисные функции tyfflx) и сопряженные базисные
функции чЫ* (х).
Предположим теперь, что поле перемещений стержня описывается квад-
квадратичной функцией:
(9.207)
где а — малая постоянная. Ясно, что точное распределение напряжений
дается формулой
(9.208)
Однако при конечноэлементном представлении поле перемещений кусочно-
линейно:
U (х) = rj- [9Ф4 (*) + 8Ф2 (*) + 5Ф3 (*)],
(9 • 209)
(х)- (9-210)
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
97
25 h
20 Ь
СП
I
15
10
Точное напряжение
Использование обычной
аппроксимации
Исполь зование
сопряженных функций
Ряс. 9.3. Сравнение распределения напряжений, подсчитанного обычным
способом, с распределением напряжений, определенным с помощью сопря-
сопряженных аппроксимаций.
При обычном подсчете -Запряжений в конечных элементах соотноше-
соотношение (9.209) просто подставляется в уравнение состояния (9.201) для каждого
элемента. В результате получается разрывное распределение напряжений.
Напряжения претерпевают конечные разрывы в местах соединений элементов
(рис. 9.3). Таким путем максимальное напряжение вычисляется с ошибкой
в 16.7%.
Совершенно другое распределение напряжений получается при исполь-
использовании сопряженных аппроксимаций. Если предположить, что к (х) duldx ?
? Ф, по крайней мере приближенно, тоТэнергия деформации определяет
линейный функционал на Sft и задает о (х) как элемент сопряженного про-
пространства Ф*. Таким образом, а (х) следует представить в виде линейной
комбинации сопряженных базисных функций. Подстановка (9.209) в (9.201),
как в раньше, дает локальное поле напряжений а(е> (х) для каждого эле-
элемента. Сопряженные узловые) компоненты а^-' вычисляются с помощью
(9.151):
Значит, представление о (х) через сопряженные функции имеет вид
3
2#' ЛГ=1> 2» <9-212)
з
е=1
7 Дж. оден
98
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
80
70
50
Точное напряжение
Использование обычной
аппроксимации
Использование
сопряженных функции
84
80
77
§.30
I
20 -
10
1 2
Рис. 9.4. Распределение напряжений при шестиэлементной аппроксимации.
На рис. 9.3 показана эпюра этих напряжений вместе с точным решением
и с эпюрой напряжений, подсчитанных обычным способом. Видно, что исполь-
использование сопряженно-аппроксимационных функций позволяет получить непре-
непрерывную в местах соединения элементов эпюру и вычислить максимальное
напряжение с ошибкой менее 6.5%.
На рис. 9.4 показаны результаты подобных вычислений при исполь-
использовании шести элементов и при и (х) = а A — я2/36). Хотя осредненные
величины «обычных» напряжений во внутренних узлах более точны, «сопря-
«сопряженные» напряжения дают меньшее среднеквадратичное отклонение и, как
видно из рисунка, лучше описывают изменение напряжения в районе мак-
максимума.
Пример 9.3. Двумерные сопряженпо-аппронсимациопные
функции. Описанный выше метод может быть использован и в случае дву-
двумерных и трехмерных конечных элементов. В этом примере мы кратко опи-
опишем способ построения сопряженно-аппроксимационных функций, соответ-
соответствующих двумерной совокупности треугольных конечных элементов.
Рассмотрим треугольный элемент в плоскости хх, х2, вершины которого
служат локальными узловыми точками. Локальные интерполяционные
функции г|)$> (х), где х = {хи х2), являются линейными функциями от хх
¦а~х% и удовлетворяют условию i|)jy' (хМ) = б^; м, N = 1, 2, 3. Подставляя
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
(а)
Рис. 9.5. Двумерная сетка треугольных элементов.
их в (9.145), получаем локальные компоненты фундаментальной матрицы Сгд:
(9.213А
J
где А — площадь треугольника. Заметим, что матрица (9.213) не зависит"
от величин углов а, Р, у нашего треугольника. Однако дискретные модели
различных дифференциальных операторов могут зависеть от них; например,
для показанного на рис. 9.5а треугольника
= J
А
/ctgP
= -5-1 —
\ —
ctgP+ctgv —ctgv
ctgv ctgv+ctga
ctgP —ctga ctga + ctgB/
—ctgP \
—ctg> 1
ga + ctgB/
1.(9.214)
Чтобы продемонстрировать особенности сопряженно-аппроксимацион-
ных функций для какого-либо конкретного конечноэлементного представле-
представления, рассмотрим модель, изображенную на рис. 9.5Ь. В этом случае в силу
(9.142) имеем
2 10 1 0 ОЖр 0-
симмет-
рично
4 0 2 ГОТО 0
6 2 0 1~0 0
12 2 2 2 0
6 0 1
4 1 0
6 1
2_
(9.215>
где А — площадь элемента. Обращая эту матрицу и используя (9.148),
получаем сопряженно-аппроксимационные функции Фд (X). Поскольку
в рассматриваемом примере функции Фд (X) кусочно-линейны, функции
7*
100
ГЛ. И. ТЕОРИЯ КОНЕЧНЫ X ЭЛЕМЕНТОВ
Рис. 9.6. Характерные примеры сопряженных функций.
Фл (X) также кусочно-линейны, и поэтому достаточно просто вычислить
значения сопряженных функций в каждом узле. Не выписывая этих функ-
функций полностью, приведем характерные примеры узловых значений:
)=ii @.580, —0.080, 0.009, —0.080, 0,027,
—0.009, 0.009, —0.009, 0.009),
ф«(Хд)=-Я@.027, -0.027, -0.045, -0.027,0.116,
—0.027, —0.045, —0.027, 0.027),
(9.216)
9. ТЕОРИЯ СОПРЯЖЕННЫЙ АППРОКСИМАЦИЙ
101
=-^.(— 0.009, 0.000, 0.027, 0.018,
—0.027, —0.054, —0.045, 0.214, —0.080).
Эти функции показаны на рис. 9.6.
Заметим, что в общем случае двумерной кусочно-линейной аппроксима-
аппроксимации глобальная аппроксимациониая функция Фд (X) является «пирамидаль-
«пирамидальной», как показано на рис. 9.7,а. Она достигает максимального значения
в узловой точке Л и обращается в нуль в элементах, не содержащих узла Л.
Сопряженно-аппроксимационная функция ФА (X) также имеет максимальное
вначение в узловой точке Л, но она принимает ненулевые значения во всех
элементах рассматриваемой области (рис. 9.7,6).
Пример 9.4. Кусочно-линейные аппронсимационны* функ-
функции одной переменной. В качестве доведенного до конца со всеми под-
подробностями и в то же время простого примера проиллюстрируем предыдущие
рассуждения, подробно рассмотрев кусочно-линейные аппроксимационные
функции, возникающие при делении интервала / на G — 1 равных подынтер-
подынтервалов длины h при условии, что Фд (ж) обращается в нуль во всех*у8лах,
кроме узла хА = АЛ (рис. 9.8). В этом случае
где Л = 2, .,., G — 1;
dx, а фундаментальная матрица имеет вид
2 1 0
1 4 1
0 1 4
0
0
0
О ..
О ..
О ..
Пусть Ап обозначает определитель n-го порядка
4 1 0 ... О О О
1 4 1 ... О О О
О 1 4 ... О О О
4.1 0
14 1
0 1 2
(9.217)
0 0 0
0 0 0
0 0 0
4 10
1 4 1
0 1 4
(9.218)
Эти определители удовлетворяют рекуррентному соотношению
Поскольку
4n+i —
определители
2 1 О ... О О
1 4 1 ... О О
О 1 4 ... О О
n.i = 0.
0 0 0
0 0 0
4 1
1 4
2 1 О
14 1
О 1 4
0 0
0 0
0 0
0 0 0
0 0 0
4 1
1 2
(9.219)
(9.220)
102
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ФдУО
ФЛ(Х)
Рис. 9.7. Кусочно-линейная глобальвая аппроксимационная функция двух
переменных Фд (X) и сопряженная функция Ф4(Х).
ФД*)
0
2/> ЪЬ
Рис. 9.8. Базисные функции Фа (х) для ковечвоэлемевтвого представлевия
отрезка действительной оси.
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
103
являются линейными комбинациями А^, а именно
Bn = 2An-i-An-2 = An-2An-i, (9.221)
С„ = Л„-25„_1 = ЗЛ„.2, (9.222)
то они тоже удовлетворяют соотношению (9.219). Рекуррентное соотноше-
соотношение (9.219) допускает два независимых решения в виде членов геометрической
прогрессии_ ah = a", bh = а"", где а = 2 + У3~= 3.732050808 и а =
= 2 — "j/^3 = 0.267949191 удовлетворяют квадратному уравнению
аа — 4а + 1 = 0. (9.223)
Определители А^ и В^ представляются в виде линейных комбинаций а*
и а.-*:
Ah=y(ah—а-ь-2), #ft = 1/2 (а"+«-"), (9.224)
где у = а/(а — а-1) = 1.077350269. Начальные члены последовательностей
Ah, Bh приведены в табл. 9.1, при составлении которой использовано соот-
соотношение
AMfc = Ak+1-2Ak + Ah-i = 2Ah. (9.225)
Теперь ожно найти матрицу, обратную к фундаментальной матрице:
в.
G-T
*-» в.
G-2
Д<Г;
(9.226)
при А > Г элементы матрицы находятся из условия симметрии СЛГ = СГЛ<
Для примера выпишем матрицу при G = 7:
390Л
1,351
-362
97
— 26
7
— 2
1
— 362
724
— 194
52
— 14
4
— 2
— 7
— 194
679
— 182
49
— 14
7
-26
52
— 182
676
— 182
52
— 26
7
— 14
49
— 182
679
— 194
97
— 2
4
— 14
52
— 194
724
— 362
1
— 2
7
— 26
97
—362
1.351
(9.227)
Соответствующие сопряженные функции показаны на рис. 9.9.
Таблица 9.1
к
—2
—1
0
1
2
3
4
—1
0
1
4
15
56
209
AAh
1
1
3
11
41
153
0
2
8
30
112
Bh
7
2
1
2
7
26
97
ABh
0
—5
—1
1
5
19
71
А»*
4
2
4
14
52
104
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рис. 9.9. Сопряженные функции, соответствующие базисным функциям,
изображеннымХна рис. 9.8.
В качестве проверки можно вычислить, насколько точно выполняется
равенство
лгд=
= \ OA(x)dx.
С учетом (9.224) формула (9.226) принимает вид
сдг_, цм-г Уз («A+a-A-|-2)(«G-r+g-G+r)
° ~1~а) ~Т aG_a-G+Z
В пределе при G —»¦ оо для Д яэ Г « G/2 имеем
для любых Д, Г,
яли
•?
1 —а-1 а-2 —а-3 ...
— а-1 1 —а а-2 —а
... -а-* 1 -а-1 а-2
—а-1 1 —а-1
(9.228)
(9.229)
1(9.230)
Рассмотрим приближенные выражения для производных от функций,
соответствующих изображенным на рис. 9.8 кусочно-линейным базисным
функциям. Поскольку производные ЗФД (х) разрывны, очевидно, что условие
перестановочности дП = Пд (см. теорему 9.1) не выполняется. Все же имеет
9. ТЕОРИЯ СОПРЯЖЕННЫХ АППРОКСИМАЦИЙ
105
смысл ввести матрицы DAr и ВАГ в соответствии с формулами (9.122) и (9.124):
2?дг == f фд дФт dx, ВАГ = f афд аФг dx. (9.231)
31 31
Матрица ВАГ симметрична, a DAT почти антисимметрична, так как
f Фд дФт dx= — С Фг аФд dx при 1< Д, Г < G. (9.232)
Эти матрицы в явной виде таковы:
¦—1 10 0 ...
0 О"
— 1
0
0
0
1
—1
0
0
0
0
—1
0
0
-1
2
— 1
0
0
1
0
0
0
0
1
0
0
0
—1
2
0
0
...
...
0
0
-1
0
0
0
0
-1
0
¦ . •
• . .
...
• • •
0
0
0
—1
0
0
0
—1
0
0
0
1
0_
0
0
0
2
—1
о-
0
0
—1
1
(9.233)
(9.234)
Ж
является достаточно хорошей аппроксимацией, в то время как
дР « 2?ДГ^АФГ (х) (9.235)
— довольно грубой, что показано на рис. 9.10, где оператор DAT применен
к базисной функции Ф3 (х). Это объясняет, почему вычисление ВАГ через
DAF по формулам (9.116) дает плохую аппроксимацию. С другой стороны,
(9.231) свидетельствует о том, что —Лдг можно использовать лля вычисле-
вычисления вторых производных:
(х) ж—BLTF^T (z), (9.236)
у б (х — Д/»I =
вместо (9.115), (9.117). Действительно,
ГО2фд= п Г-^- S (х — Ah-2h) — у S (х—
(9.237)
г*
а это не что иное как взятый с множителем ilh центральный разностный'опе-
ратор второго порядка в точке х = (Д — I) h с шагом h; отсюда следует, что
= -Ядг. (9.238)
106
ГЛ. И. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
FW)
Рис. 9.10. Проекция производной.
Пример 9.5. Полиномы, аналитические фунпции. Ввиду про-
стоты|функций Фд (х), показанных на рис. 9.8, можно получить все явные
формулы для компонент аналитической функции F (х) = 2'anin. С тем
чтобы упростить вид этих формул, «сдвинем» нумерацию узлов и будем счи-
считать, что Д = 0, 1, 2, ...,7V, где N = G — 1. Рассмотрим интеграл
ft ft h
J *«ФД (x) dx= j (hA + *)" (l—I") &+ j (M —ж)» (l—f") *».
0 0
Используя тот факт, что
{x) dx =
найдем
где
Для граничных элементов
) dx=
ьп+1
Д2 (Д)
п+2>
о < Д < ЛГ,
О,
если п нечетное,
»+2)' если га четное'
(9-239)
(9.240;
(9.241)
(9.242)
(9.243)
(х) Д« =
(9.244)
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ Ю7
откуда для больших N
j,^(,)d^(ra+1^+2)("+2)iVn. (9.245)
о
Возвращаясь теперь к F (х) = 2 апхП< нетрудно видеть, что для конеч-
ноэлементных аппроксимаций
2 апх* « FA<DA (ж) = FA<DA (ж), (9.246)
п
где для наилучшего приближения
д, 2 «**")=2 ап <фА. *»>=Sа» Jфд (ж) жП dx>
п п п J?
(9.247)
или
= S S [ «й J
1 0
е=1 О
Таким образом, получаем
(9.249)
где
2
о
— вторая первообразная для F (х), а оператор Д2 определяется формулой
(9.242).^Для граничных элементов
± AF-*(Nh) (9.250)
где F-1 — первообразная, а Д — разностный оператор первого порядка.
Ясно, что для очень больших N
FA = hP
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ
И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
При изложении теории конечных элементов до сих пор в основ-
основном рассматривались элементы произвольной формы с произволь-
произвольным числом узловых точек. Локальные аппроксимации /<е)(х)
на каждом элементе описывались с помощью интерполяционных
функций ^n (х)> точная форма которых за редкими исключениями
не указывалась. Однако в практических приложениях теории
надо отказываться от этой общности и рассматривать конкретные
типы элементов и соответствующих им интерполяционных функ-
функций. При построении различных конечноэлементных моделей,
как правилог требуют, чтобы отдельные элементы имели достаточно
108 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
простую геометрическую форму и чтобы интерполяционные функ-
функции тоже были простыми, обычно полиномами. Если к этому доба-
добавить, что выбор функций tJjjv' (x) должен обеспечивать непрерыв-
непрерывность F (х) на межэлементных границах и сходимость F (х) к F (х)
при уменьшении размеров элементов *), то станет ясно, что и на
форму допустимых конечных элементов, и на вид интерполяцион-
интерполяционных функций накладываются довольно серьезные ограничения.
В этом параграфе рассматриваются конечноэлементные модели
операторных уравнений и вопросы сходимости для широкого клас-
класса элементов. Кроме того, приводятся примеры некоторых допусти-
допустимых конечных элементов и соответствующих им интерполяцион-
интерполяционных функций.
10.1. ОПЕРАТОРЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Как правило, нам приходится иметь дело с решением задач^
сводящихся к уравнениям вида
® (и) = h (ЮЛ)
где и = и (х) — элемент некоторого нормированного линейного
пространства Т', в общем случае состоящего из функций, задан-
х) Синг [1957, стр. 207—213] исследовал сходимость полиэдральных
функций, возникающих в результате линейной интерполяции на треуголь-
треугольных областях. Его исследования непосредственно применимы к соответствую-
соответствующим конечноэлементным моделям, но относятся, как и более ранняя работа
Куранта [1943], лишь к представлениям первого порядка. Исследования
по сплайн-функциям и бикубичной интерполяции Биркгофа и Гарабедяна
[1960] и Биркгофа и де Бура [1965] применимы к конечноэлементным аппрок-
аппроксимациям гладких поверхностей; в связи с этим см. также Алберг, Нильсон
и Уолш [1967]. Мелош [1963а] получил достаточное условие монотонной
сходимости конечноэлементного расчета задач о малых прогибах пластин
на основе энергетического подхода, а Вёбеке [19646, 1965, 1966] исследовал
границы применимости различных коиечноэлементных решений задач линей-
линейной теории упругости. Вопросы сходимости метода конечных элементов для
некоторых краевых задач рассматривались Фридрихсом и Келлером [1967],
Варгой [1967] и Сиарле, Шульцем и Варгой [1967]. Подробное исследование
сходимости конечноэлементных представлений для одного класса линейных
операторных уравнений проведено Ки [1966] и Арантесом э Оливейрой
[1968, 1969, 1971]. Гибридные модели рассматривались Тонгом и Пайэном
[1967], а свойства полноты и сходимости некоторых типов конечноэлемент-
конечноэлементных аппроксимаций изучались Маклеем [1963, 1967], Джонсоном и Маклеем
[1968], Дании [1968], Зламалом [1968], Гелем [1968], Валцем, Фултоном
и Сайрусом [1969], Табанде [1970], Брэмблом и Зламалом [1970]. Исполь-
Использование «холмистых функций» для конечноэлементных представлений обсуж-
обсуждается в работе Бабушки [1970], а вопросы устойчивости, погрешности
и сходимости некоторых конечноэлементных аппроксимаций исследованы
Фиксом и Стрэнгом [1969], Стрэнгом [1970] и Фридом [1971]. Некоторые
подробности, относящиеся к критериям сходимости и полноты, изложены
в работе Фелиппы п Клафа [1968]. См. также Клаф и Точер [1966], Грин,
Джонс, Маклей и Строум [1969], Оден и Браули [19716], а также Оден [1970в,
1У / J.OJ*
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ Ю9
ных в некоторой открытой области % Л-мерного эвклидова про-
пространства и на ее границе дШ, а / = / (х) — элемент другого нор-
нормированного пространства 41 (часто 41 = V) и &". V ->¦ 41 —
оператор из У* в 41; более точно, & отображает некоторое под-
подмножество 35 пространства V, называемое областью определения
оператора еТ5, в 41. Кроме уравнения A0.1), решение должно удов-
удовлетворять некоторым краевым условиям на д91.
Большинство методов аппроксимации состоит в построении
последовательностей (пп) аппроксимаций для и в линейных под-
подпространствах пространства Т, сходящихся в некотором смысле
к и, так чтобы имела смысл символическая запись:
jlim ^ (пп) = & (и).
Однако может случиться, что область 35 определения оператора &
не содержит елементов ип, тогда необходимо расширить область
определения оператора ЗР таким образом, чтобы она принадлежала
некоторому полному нормированному пространству (была плотна
в нем). Прежде чем развивать эти идеи в связи с конечноэлемент-
ными аппроксимациями^ напомним ряд основных понятий.
Последовательности Коши и полнота. Рассмотрим
вещественное нормированное линейное пространство!^, т. е. норми-
нормированное линейное пространство, элементы которого можно умно-
умножать на вещественные числа. Пусть и обозначает элемент про-
пространства Т, а || и || — его норму. Если каждому положительному
целому числу п поставить в соответствие некоторый элемент
ип 6 У% то совокупность и1, и2, . . ., ип, . . ., записываемая {ип},
образует последовательность в Т. Говорят, что последователь-
последовательность {ип} в Т имеет предел B*^f, если для любого г >¦ 0 суще-
существует целое число т, такое, что || ип — и* || < е при всех п > т.
Если это имеет место, то говорят, что последовательность {ип}
сходится к пределу и* по норме || и || и пишут lim un = и*
п -* °о
или, более обстоятельно, lim \\ ип — и* || = 0.
П -*¦ оо
Последовательность {ип} называется последовательностью Ко-
Коши, если lim || ит — ип || = 0, т. е. если для любого е > 0
т, п -» оо
существует целое число N, такое, что || ит — ип \\ << г при всех
т, п > N. Ясно, что каждая сходящаяся последовательность
является последовательностью Коши, поскольку если и* — пре-
предел {ип}, то || ит - ип || = || (ит - и*) - (ип — и*) || <
< || т * || + || ип - и* || < е, где e=gl + ea, a
|| || 82 при m > N и || ип — и* ||< е2 при п > N.
Таким образом, || ит — ип \\<С г при т, п > N. Однако обрат-
обратное утверждение неверно, поскольку может случиться, что после-
НО ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
довательность {ип} ? У «сходится» к пределу и* $ У. Широко
известным примером неполного метрического пространства являет-
является пространство рациональных чисел; например, последователь-
последовательность {1, 3/4, 13/15, . . .} сходится к иррациональному числу я/4
и, следовательно, не сходится в пространстве рациональных
чисел.
Если каждая последовательность Кощи элементов нормирован-
нормированного линейного пространства У сходится к элементу этого про-
пространства, то говорят, что пространство У полно. Полное норми-
нормированное пространство называется банаховым пространством. Если
У неполно, его всегда можно вложить в некоторое полное про-
пространство Т', называемое пополнением У. Пространство f назы-
называется пополнением пространства У, если У является подпро-
подпространством в Т и всюду плотно в нем. Термин «всюду плотно»
означает, что У является замыканием У$т. е. что каждый элемент
и ? V как угодно близок к некоторому элементу и пространства У
в том смысле, что для любого s > 0 существует элемент и ? У t
такой, что || и — м || <; е. Для нормированных пространств
свойство полноты, конечно, зависит от используемой нормы.
Практически процесс пополнения неполного пространства сво-
сводится к добавлению к пространству предельных точек последова-
последовательностей Коши этого пространства (конкретнее, можно попол-
пополнить пространство, построив классы эквивалентности последова-
последовательностей Коши, так что если и — класс эквивалентности, то
и = lim и™, где {и71} ? У). В качестве важного примера рас-
га ->• со
смотрим У = SS — пространство со скалярным произведением,
определяемым формулой
{и, v)= ^uvdjg, A0.2)
М
где интеграл принимается в смысле Лебега. Здесь и и v — функ-
функции, заданные на М и || и \\ = (и, иI/2 < оо. Предположим, что Ш
состоит из функций и ? С0 (М), т. е. непрерывных на 91 функций.
В этом случае SS неполно: можно построить последовательность
непрерывных функций, сходящуюся к разрывной функции. Изве-
Известным примером служит последовательность
ип(х) =
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ Щ
Каждый член этой последовательности непрерывен при х ? [0, 1],
но она сходится по норме || и \\ = (и, и >*/2 к разрывной функции
скачка и* (x)=h(x — 72). Более того, невозможно сделать и* (х)
непрерывной, изменяя ее значения на множестве меры нуль. Чтобы
пополнить $в, поставим в соответствие последовательностям
{ип}, {у™} ? SB предельные точки и*, v*, причем под и* = v*
будем понимать lim || ип — vn || = 0. Тогда {и*, v*) =
т, п -* оо
= lim {ип, vn) и || и* || = lim || ип ||. То что такой процесс
П -V ОО П -»¦ ОО
пополнения приводит к цели, гарантируется знаменитой теоремой
Хана — Банаха 1): Всякий непрерывный линейный функционал
(в нашем случае g (и) = (и, у>), определенный на линейном под-
подпространстве У нормированного линейного пространства У,
можно продолжить на все пространство с сохранением нормы.
Следовательно, в качестве \\ и* || можно взять ту же самую норму,
первоначально определенную лишь на неполном пространстве SB.
В нашем примере пополнением SB является L2 {ffi) — простран-
пространство квадратично суммируемых функций на %. Пространство
С° {%) плотно в L, (Й), т. е. для любой функции и* 6 L2 {%)
можно построить такую последовательность непрерывных функ-
функций ип ? С0 (%), что для любого е > 0 существует N, удовлетво-
удовлетворяющее условию: || и* — ип \\ <С г при п > N. Другими слова-
словами, любая квадратично интегрируемая функция в 91 может быть
аппроксимирована непрерывной функцией. Так как по теореме
Вейерштрасса о равномерной аппроксимации любая непрерывная
функция и ? С0 (J2) может быть равномерно аппроксимирована
некоторым полиномом р 2), то для каждого п существует полином
рп, такой, что | ип (х) — рп (х) | ^ е (е > 0) для всех х ^ 92.
Отсюда следует, что для ограниченной области ^? выполняется
неравенство \\ ип—рп || << г', где г' зависит от 91, так что
II и* — рп ||< || и* - ип || + II ип — рп' ||< е + е' при п > N.
Таким образом, любую квадратично суммируемую функцию тоже
можно аппроксимировать в среднем полиномом.
Более общим образом, пространство SB можно считать про-
пространством функций и ? (У (^?); т. е. функций, непрерывных в fi
(или в Ш + д9?) вместе со своими частными производными до
порядка г включительно. Тогда если вместо A0.2) положить
/ . ди, dv , дги дЧ ,
•••+-я—я з——з з—\dM, A0.3)
^ e*lt ^i2 ... dxir dxh dxi2... dxir ) v
x) См. Колмогоров и Фомин [1972], стр. 169—170.
2) Если область ?Я ограничена. — Прим. ред.
Ц2 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где (%, хг, . . ., xk) = х — точка области 91, ix + i» + . . .
. . . + ir = r, i < /. h < fa < • • • < ir и i, /, ilt i8, . . ., ir =
= 1, 2, . . ., к, то, как легко увидеть, J# неполно в норме || и || =
= (и, иI/2. Пополняя Ш подобным описанному выше способом^
получим пространство,; обозначаемое через 2/ (ffl) v).
Счетная система элементов <plt ф2, . . ., ф„, . . . нормированного
пространства "Г называется полной, если множество линейных
комбинаций элементов этой системы всюду плотно в f, т. е. если,;
каков бы ни был элемент и ? У, для каждого е > 0 найдутся такие
числа alt . . ., a,N (где N зависит от « и от е), что
l|2ll (Ю.4)
Ясно, что если в пространстве имеется счетн я полная система^
то оно сепарабельно.
Линейные операторы2). Рассмотрим комплексное гиль-
гильбертово пространство $$, элементы которого и, v, w,...—функции,
определенные в некоторой области 3? пространства Mh- Скалярное
произведение в SS опять обозначается через {u,v) ж опять || и\\ —
= (и, иI/*, но теперь (и, v)= (v, и), где (v, и) обозначает число,
комплексно сопряженное числу (v, и). В большинстве приложе-
приложений элементами и, v, . . . 6 Si являются квадратично суммируемые
функции (т. в. и 6 Ь^ ($?)), так что скалярное произведение
{и, v) определяется формулой A0.2) с v, замененным на v.
Рассмотрим оператор & = X, определенный на некотором
плотном (линейном) подпространстве 3) пространства St. Будем
J) Пространство L\ C1) состоит из функций, которые не только квадра-
квадратично суммируемы в М, но и обладают обобщенными производными в смысле
?2 всех порядков до г включительно. Под обобщенной производной порядка
г в смысле Ь% от функции и понимается интегрируемая функция w, такая, что
где ф — любая г раз дифференцируемая функция, которая вместе со всеми
своими производными обращается в нуль в некотором пограничном слое
области 3?; таким образом", и может не быть г раз непрерывно дифферен-
дифференцируема в М, но она должна быть квадратично интегрируема. [Пространство,
которое состоит из определенных в 31 функций с интегрируемой р-й степенью,
имеющих обобщенные производные до порядка г включительно, называется
пространством Соболева W? {3t).\ Более подробные сведения можно найти
у Михлина [1952] или Михлина и Смолицкого [1965].
2) Материал этого раздела заимствован в основном из Книг Михлина
[1952, 1970].
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ ЦЗ
использовать следующие определения г), касающиеся операто-
оператора X.
Оператор X называется линейным, если он аддитивен и одно-
однороден, т. е. если для любых двух элементов и, v 6 3D и скаляров
«!, - оса справедливо равенство X (а^и + atv) — агХ (и) +
+ а»Х (v). Отсюда следует, что X @) = 0.
Оператор X называется симметричным, если для любых двух
элементов и, v 6 35 имеет место тождество {Хи, v) == (и, Xv).
В нашем случае, когда пространство S3 комплексное, для того
чтобы оператор S3 был симметричным, необходимо и достаточно,
чтобы (Хи, и) было всегда вещественным. В случае когда S3 —
вещественное пространство, для того чтобы оператор X был сим-
симметричным, необходимо, чтобы он удовлетворял некоторым допол-
дополнительным условиям.
Оператор X называется положительно определенным, если для
любой функции и ? 35 справедливо неравенство (и, Хи) ^ 0,
причем (и, Хи) = 0 тогда и только тогда, когда и = 0; всякий
положительно определенный оператор X симметричен.
Оператор X называется ограниченным с нижней и верхней гра-
границами сх и са, если для любой функции и ? 35 выполнены нера-
неравенства сг || й || ^ || Хи || ^ с2 || и ||.
Пусть оператор X ограничен, тогда наименьшая верхняя гра-
граница называется нормой оператора X и обозначается через || X ||.
Таким образом, || Хи ||< || X || || и ||.
Оператор X называется положительно ограниченным снизу,
если существует такая постоянная у Ф 0, что (и, Хи ) ^ у2 || и ||*
для любой функции и ^ 35.
Если для каждой последовательности {и71} элементов обла-
области 3), для которой lim || ип — и* \\ = 0, справедливо соотноше-
п -*- оо
ние lim || Хип — Хи* \\ = 0, то оператор X непрерывен в и*.
п -*¦ оо
Оператор °М с областью определения 3)т называется расшире-
расширением (или продолжением) оператора X с областью определения 351,
если 3i cz 3)т и оЛи = Хи для каждого и ? 35i.
Линейный оператор X на $8, значениями которого являются
вещественные или комплексные числа, называется линейным функ-
функционалом. Каждый ограниченный линейный функционал I на S3
имеет вид 1и = (и, v), где v — некоторый единственным образом
определяемый элемент S3 (строго говоря, v принадлежит сопряжен-
сопряженному пространству S3*, т. е. пространству всех линейных непре-
непрерывных функционалов на &8\ но в рассматриваемом случае
S3 = S3*).
Рассмотрим задачу решения уравнения
Хи = /, A0.5)
J) Некоторые из них уже приводились выше, — Прим, ред.
8 Дж, оден
114 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где X — линейный оператор, определенный на плотном в $8 мно-
множестве 35, а / — заданный элемент SB. Помимо уравнения A0.5)
имеется еще некоторое краевое условие
= g (Ю.6)
на dffi, где 38 — тоже линейный оператор. Сначала рассмотрим
случай однородных краевых условий, т. е. случай, когда g = 0;
тем самым мы пока ограничимся множеством 35, элементы ко-
которого удовлетворяют условию 38 и = 0 на dj?.
Сформулируем три важные теоремы *), касающиеся решения
уравнения A0.5).
Теорема 10.1 (единственность). Если оператор X
в уравнении A0.5) положительно определен, то это уравнение
имеет не более одного решения.
Доказательство. Доказательство довольно просто. Предполо-
Предположим, что Хиг = Хи2 = /• Тогда и = их — и2 удовлетворяет
условию Хи = 0. Поскольку X положительно1 определен,
{и, Хи) = 0 =^ и = 0. Следовательно, иг = и2.
Теорема 10.2. Пусть X — положительно определенный
линейный оператор, и пусть уравнение A0.5) имеет решение и*.
Тогда функционал
J (и) = (Хи, и) — (и, /> — </,'«> (Ю.7)
принимает минимальное значение при и = и*. Обратно, если
в области определения 3) функционала X существует функция
и*, реализующая минимум функционала J (и), то и* является
решением уравнения A0.5). (Здесь пространство $8 комплексно.)
Доказательство. Пусть и* удовлетворяет условию Хи* = /,
и пусть т] — произвольный элемент 35. Тогда вследствие сим-
симметричности X
Поскольку оператор X положительно определен, {Хг\, г\) ~^-
;> 0. Следовательно, если v — произвольный элемент из 35
вида v = и* + Л с т] Ф 0, то
J (v) = J (и*) + {Хг\, т] > > / (и*).
Поэтому функционал / (v) принимает минимальное значение
при v = и*. Это доказывает первую часть теоремы.
См. Михлие [1970, стр. 86].
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ Ц5
Доказательство второй части основывается на том факте,
что всякий элемент и ?$в, ортогональный ко всем элементам г\
плотного в $? множества 35, равен нулю. Пусть т] ? 35. Тогда
/ (и* + вт|) — / (и*) > 0,
если и* реализует минимум функционала / (и). Используя
A0.7), можно получить
е2 {Хг\, л > + 2е Re [ {Хи* - /, т) >] > 0,
что возможно только тогда, когда Re [ {Хи* — /, т]> ] = 0,
ибо е может быть здесь любым вещественным числом. Заменив
Л на щ, получим Im [{Хи* — /, т]>] = 0. Следовательно,
{Хи* —/, т]> = 0.
Это означает, что элемент Хи* — / ортогонален ко всем эле-
элементам т] множества 3), плотного в $8. Так может быть только
в том случае, если Хи* = /, что и доказывает теорему.
К сожалению, эта теорема основывается на некоторых важных
предположениях, которые во многих случаях могут быть неспра-
несправедливыми. Во-первых, мы предполагали, что в 35 существует
элемент и*, который удовлетворяет уравнению A0.5) и минимизи-
минимизирует функционал A0.7). На вопрос о существовании элементов,
реализующих минимум функционала / (и), ответ частично дается
приводимой ниже теоремой, в которой используются понятия
энергетической нормы и сходимости по энергии. Кратко поясним
их. Новое определение скалярного произведения [и, v] = {Хи, v)
приводит к новому определению нормы в 35, а именно || и \\% =
= [и, и]1/2. Эта норма называется энергетической нормой или
энергией элемента и. Если последовательность {ип} 6 35 такова,
что для любого е > 0 мы имеем \\ ип — и \\% < е при п > N *),
то говорят, что {ип} сходится к и по энергии. Аналогично счетная
система элементов ф1? <р2, . . . называется полной по энергии, если
эта система полна относительно энергетической нормы.
Легко показать, что если оператор X положительно ограничен
снизу, то сходимость по энергии последовательности {ип} к и*
влечет за собой сходимость в среднем {и71} к и*. При отыскании
элементов и*, минимизирующих функционал / (и), мы будем
требовать, чтобы решение уравнения A0.5) обладало конечной
энергией, т. е. чтобы \\ и* \\% < оо. Условие на оператор X, необ-
необходимое для существования элемента и*, минимизирующего функ-
функционал / (и), дается следующей теоремой 2).
х) То есть если эта последовательность сходится к и в энергетической
норме. — Прим. ред.
2) Доказательство ее имеется у Михлина [1970, стр. 89—90]. См. также
статью Фридрихса [1934], где впервые рассмотрена эта задача и доказа-
доказана теорема.
8*
¦116 ГЛ. П. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Теорема 10.3 (существование). Пусть J (и) —функци-
—функционал вида A0.7). Элемент и* с ограниченной энергией, минимизиру-
минимизирующий J (и), существует только в том случае, если оператор X
положительно ограничен снизу.
Однако даже в том случае, когда оператор X положительно
ограничен снизу, может случиться, что 35 не содержит элемента,
минимизирующего / (и). В этом случае 3) не является полным
по норме || и \\cg, и необходимо расширить X (и 3)), чтобы получить
полное пространство. Процесс расширения осуществляется сле-
следующим образом.
1. Пусть 38 — полное нормированное линейное пространство
и X — линейный положительно ограниченный снизу опера-
оператор, определенный на 35 а 38. Построим новое простран-
пространство 38% функций с конечной энергией, в котором скалярное
произведение [и, v] задается формулой
[u,v] = {Хи, v)t
а норма — формулой
|| и \\х = [и, u]V\
2. Если 3S% неполно, пополним его, как описывалось ранее г).
Тогда каждый элемент и ? 38% либо принадлежит 351 либо
является пределом некоторой последовательности {и71} 6 35 %
т. е. Km || и — ип \\% -> 0 (по определению пополнения,
П-VOO
35 плотно в 38% по энергетической норме ||-||^).. Можно
показать (см. Михлин [1970]), что каждый элемент и 6 38SS
принадлежит также и 38; кроме того, если простран-
пространство 38 сепарабельно, то и 38% сепарабельно.
3. Расширим область определения функционала / (и) до всего
пространства 38%. Это можно сделать, если в определении
функционала / (и) положить {Хи, и) = || и \\]g и заметить,
что
Следовательно, линейный функционал 1и = (и, f) огра-
ограничен в 38%, и существует единственный элемент и* про-
пространства 38% (а значит, и 38), такой, что {и, /> = [и, и*].
г) И результат дополнения обозначим тем же символом &Ва,. — Прим.
ред.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ Ц7
Таким образом, для и 6 <&В%
/(И) = ||«-И*|Й;-||И*|&
и min / (и) = / (и*) = —1| м* ||jg. Продолженный функ-
функционал записывается в виде
/ (и) = [и, и] — [и, и*] — [и, и*],
или
/ (и) = [и, и] — 2 Re [и, и*]. A0.8)
4. Поскольку {и, /> = [и, и*], существует оператор elmd^,
такой, что и* — e?f, и можно показать, что он ограничен
и положительно определен. Если e?f = 0, то (и, f) = 0
и элемент / ортогонален ко всем элементам множества 3)\
плотного в &8<g. Следовательно, аЛЦ = 0 =ф / = 0, а это
означает существование ©f. Если и* ?3), %и* =/ и
и* — <Mf, то оМ~ги* = Хи*. Значит, для каждого элемента
м65 справедливо равенство оМ~хи = Хи и 3)^-1 Э 3)%.
Отсюда следует, что оператор еМ'1 является расширением
оператора X на ffl%.
В случае неоднородных краевых условий функционал / (и)
следует видоизменить. Предположим, например, что SB = L2 (ffi) —
вещественное пространство, оператор X в уравнении A0.5) поло-
положительно определен и существует решение уравнения A0.5).
Рассмотрим случай, когда решение должно удовлетворять неод-
неоднородному краевому условию A0.6) на д<Я, где функция g диффе-
дифференцируема нужное число раз, а граница д'Я по крайней мере
кусочно-гладка. Представим и в виде суммы двух частей v и w,
где v удовлетворяет однородному краевому условию 3§v = 0.
Ясно, что v минимизирует функционал
/ (v) => (Xv, v) -2 <v,J), A0.9a)
где
/ = / -Xw. A0.96)
Поскольку v = и — w, имеем;
J(v) = J (и) + Q1 (щ w)-J (w), A0.10)
где
& (и, w) = (и, Xw) — {Хи, w). A0.11)
Во многих случаях Q1 (и, w) = 0. Если же нет, то будем пред-
предполагать, что Q1 (и, w) представимо в виде
Q1 (и, w) = Q(u) + P (w). A0.12)
118 ГЛ. П. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Таким образом, полагая R (w) = P (w) — / (w), мы можем при-
привести A0.10) к виду
/ (v) = / (и) + Q (и) + R (w). A0.13)
Здесь R (w) есть скаляр, зависящий только от w и не дающий
вклада в градиент функционала J (v), в то время как Q (и) пред-
представляет краевые условия и выражается в форме поверхностных
интегралов по гиперповерхности d%. Таким образом, решение
уравнения A0.5), удовлетворяющее краевому условию A0.6),
получается в результате минимизации нового функционала
/ (и) = (Хи, и) —2 (u,fY+Q (и), A0.14)
где, очевидно, I (и) = J (и) — R (w).
Для иллюстрации другого подхода к этой проблеме предполо-
предположим, что оператор X* является формально сопряженным к операто-
оператору X, т. е.
uXv — vX*u = b (и, v), A0.15)
где b (и, v) — так называемый билинейный конкомитант опера-
оператора X. Интегрируя A0.15), получаем
(и, Xv) — {v, Х*и) = В (и, v), A0.16)
где В (и, v) определено на д%. Если краевые условия таковы, что
В {и, v) = 0, то оператор X* называется сопряженным оператору
X. Тогда вместо A0.7) используем
/ (и) = (и, Х*и) + В(и,и)-2 </, и). A0.17)
Ясно, что в случае однородных краевых условий В (и, и) = 0,
{и, X* (и)) = {и, X (и)) ж A0.17) сводится к A0.7) (в предполо-
предположении, что пространство 36 вещественно).
Нелинейные операторы. Многие из положений, выска-
высказанных относительно линейных положительно определенных опе-
операторов, могут быть обобщены и распространены на случай нели-
нелинейных операторов и неположительных линейных операторов.
Кратко рассмотрим этот вопрос. Пусть V — банахово простран-
пространство, элементы которого обозначаются через и, и 3* — нелинейный
оператор, определенный на Т. Нам понадобится ряд определений.
Определение 1. Пусть Р — оператор, определенный на V.
Если для некоторого и ? V при любом h ?У
limll — (^(u + ah)— &>(u)) — G$> (и, К) 11 = 0, A0.18)
а-,-0 II а П Л '
где а — вещественное число, то G35 (и, h) называется дифферен-
дифференциалом Гатпо оператора S5 в точке и при приращении h.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ Ц9
Из определения следует, что дифференциал Гато однороден,
но не обязательно линеен. Можно показать *), что если оператор а?5
имеет дифференциал Гато в каждой точке некоторого выпуклого
множества Q с У, то для любых и, и -\- h ? Q выполняется
условие Липшица
|| & (и + К) - & (и) || < || GP (и + ah, h) ||
при а 6 @, 1).
Более сильным определением дифференциала для нелинейных
операторов служит
Определение 2. Если для некоторого и ? f
& (и + К) —® (и) = б#> (и, h) + а> (и, h), A0.19)
где бгТ5 (и, h) есть линейный оператор относительно h g f и
lim -JL-1| со (и, h) ||-> 0, A0.20)
||h||->-0 II "II
то бгР (и, К) называется дифференциалом Фреше оператора $*
в точке и (при приращении К), а со (и, h) — остаточным членом
(или просто остатком).
Ясно, что если существует бе?5 (и, h), то существует и G& (и, h).
Однако обратное неверно. Если дифференциал Гато линеен отно-
относительно h, то можно записать
G® (и, h) = DG® (и) (Л);
DgSP (и) называют производной Гато в 'точке и. Аналогично
можно записать
6<fP (и, h) = Ф' (и) (Л);
?Р' (и) называют производной Фреше оператора $* в точке и.
Если производная DquP1 (и) существует в некоторой окрестности
JT (и0, г) = {и | || и — и0 || ^ г} точки и0 и непрерывна в и0
(т. е. lim || GGaft (u0) — DG^ (un) || -»- 0 для любой последова-
П-*-оо
тельности {un}, сходящейся к и0), то существует также 69* (и0, h)
и 8& (и0, h) = G® (щ, К).
Дифференциал Фреше называется локально равномерным на мно-
множестве fief, если для любого е > 0 существуют такие т] (е, и0),
б (е, и0) > 0, что для всех и ? JT (и0, у\) выполняется неравенство
|| со (u, h) || < е || h || при || h \\ < б. Если производная &' огра-
ограничена и локально равномерна в jfT (u0, г), то она непрерывна
в Ж (щ, г) [Вайнберг, 1956].
х) Вайнберг [1956]; там же приводятся достаточные условия линейности
дифференциала Гато по приращению.
120 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Определение 3. Пусть К (и) — дифференцируемый по Фреше
функционал, определенный на множестве Q с: У, и пусть {и, v) —
скалярное произведение «между» У и сопряженным ему простран-
пространством у*. Оператор &, определяемый формулой
, h) = lim—
«->о а
называется градиентом г) функционала К (и). При этом пишут
еР (и) = grad К (и). [Если К (и) дифференцируем по Гато, то
grad К (и) называется слабым градиентом, если же К (и) диффе-
дифференцируем по Фреше, то сильным градиентом.]
Определение 4. Оператор $чУ-*-У* называется потен-
потенциальным оператором на некотором множестве Qcf, если суще-
существует такой функционал К (и), что grad К (и) = $Р (и) для
любого и ? Q.
Можно показать, что необходимым и достаточным условием
потенциальности оператора $". f* -*¦ У* в JT (щ, г) является
симметричность (8оР (и, кг), ht) в следующем смысле:
<б<^ (и, h^, ht) = <б# (u,hz), кг) для всех Ник2^У и и 6
6 JP (и0, г), причем {8оР (и, hj, h2) предполагается непрерывным
в JT (и0, г).
Определение 5. Точка щ ? У, такая, что К (и) ^ К (и0)
или К (и) ^ К (и0) для всех и 6 Ж (щ, г), называется экстремаль-
экстремальной точкой функционала К (и). Если grad К (и0) = 9, где 0 —
нулевой элемент пространства У*, то и0 называется критической
точкой функционала К (и).
Сформулируем важную теорему, доказанную Вайнбергом
[1956].
Теорема 10.4. Пусть & — потенциальный на JT (и0, г) опе-
оператор. Тогда существует функционал К, единственный с точно-
точностью до константы, градиентом которого является $*. Этот
функционал определяется формулой
?(«)=] {&(uo + s(u-uo)), u-uo}ds + Ko, A0.21)
о
где Ко — К (и0) — произвольная константа.
Ясно, что теорема 10.4 представляет собой существенное обоб-
обобщение теоремы 10.2. В самом деле, если потенциальный оператор &
линеен, но не положительно определен или если оператор.^5 нели-
*) Таким образом, градиент — это частный случай производной. —
Прим. ред.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 121
неен и существуют решения уравнения A0.1), то можно с помощью
формулы A0.21) построить соответствующий функционал К (и),
градиентом которого является оР, и рассматривать задачу нахож-
нахождения решений уравнения A0.1) как задачу нахождения критиче-
критических точек функционала К (и). Принцип поиска таких решений^
для которых grad К (и*) = 0, будем называть экстремальным
принципом для оператора $".
Чтобы наглядно продемонстрировать, что A0.21) действительно-
является обобщением A0.7), положим и0 = 0, Ко = 0, Т = Шг
где SB — вещественное гильбертово пространство, и
® (и) = Xu-f,
где X — симметричный положительно определенный оператор и»
уравнения A0.5). По теореме 10.4 оператор $f> (и) является гра-
градиентом функционала
1 1 1
К(и)= [ {X (su) — /, и) ds = \ s (Хи, и) ds— f (/, и) ds.
0 0 0
Интегрируя, получаем4
где / (и) — квадратичный функционал A0.7).
Хотя мы не будем подробно останавливаться на вопросе суще-
существования и единственности решений нелинейных операторных
уравнений г) или существования относительного минимума соот-
соответствующих функционалов, интересно тем не менее отметить,
что для большого класса нелинейных операторов можно сформули-
сформулировать условия, аналогичные наложенным на линейный опера-
оператор X. Например, нетрудно доказать, что для нелинейного потен-
потенциального операторного уравнения оРи = / существует хотя бы
одно решение, если дифференциал Фреше положительно ограничен
снизу, т. е. если существует такая постоянная у, что
<60» (и,Л),Л>>т1 \\h\\2 (Ю.22>
и, следовательно, функционал К (и) ограничен снизу. Далее,
в случае когда К (и) — функционал на компактном подмножестве
пространства У, точка и*, в которой К (и) имеет относительный
минимум, существует, если
Ь*К («, h, h) > || h || Я. (|| h II), A0.23)
1) Для ознакомления с такого рода вопросами см. Саати [1967] или
Вайнберг [1956].
122 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где 0 < к (s), lim к (s) = оо и 82К (и, h, h) — второй дифферен-
S->oo
циал Фреше функционала К (и). Любая минимизирующая после-
последовательность для К (и) [т. е. любая последовательность {ип},
такая, что lim К (ип) = min К (и)] сходится по норме S8 к неко-
п->оо
торому пределу, называемому обобщенным решением задачи мини-
минимизации функционала A0.21). Ясно, что A0.23) представляет
собой обобщение на случай банаховых пространств обычного усло-
условия относительного минимума функции в критической точке.
В самом деле, мы можем написать
K(u + h) = K(u) + 8K(u,h) + ~82K(u,hah)+... . A0.24)
Поэтому, если grad К (и) = 9, т. е. если и — критическая точка
для К (и), положительность К (и) в JP (и, г) следует из того, что
квадратичная форма 82К (и, h, h) удовлетворяет неравенству
<10.23).
В заключение укажем одно имеющее фундаментальное значе-
значение свойство потенциальных операторов. Рассмотрим нелиней-
нелинейное операторное уравнение!
®и = /, A0.25)
и пусть $Ри = ffiu — / — потенциальный оператор из V в W*,
являющийся градиентом функционала К (и). Предположим, что
решение и* уравнения A0.25) существует и является критической
точкой для К (и). Тогда]
grad К (и*)^7#и*Д)=:0;
или
<!Ри* —/, А) = 0. A0.26)
Поскольку h — произвольный элемент пространства Т% это озна-
означает, что образ & (и*) решения уравнения A0.25) ортогонален
к Т. Это наблюдение лежит в основе общего метода построения
конечноэлементных аппроксимаций решений нелинейных опера-
операторных уравнений J).
10.2. КОНЕЧНОЭЛЕМЕНТНЫЕ АППРОКСИМАЦИИ
При конечноэлементных аппроксимациях mhJb общем случае
имеем дело со следующей задачей. Пусть Ш — пространство со
скалярным произведением; обычно это гильбертово пространство
L\ C1), элементами которого являются функции F (х), определен-
определенные в некоторой области *Ш пространства %h. [Как правило, нас
См. изложение метода Галеркина в п. 10.3,
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 123
будут интересовать случаи, когда сама функция F (х) и ее произ-
производные вплоть до порядка г + 1 кусочно-непрерывны и квадратич-
квадратично интегрируемы в %.] Далее, пусть &8 — другое пространство,
элементами которого являются функции F (х), х?%, класса
С (9Z), г <с р. Требуется построить такую последовательность
линейных подпространств Ф1, Ф2, . . . пространства $ё конечных
размерностей щ, п2, . . ., не обязательно вложенных друг в друга,
что для каждой функции F (х) ? 38 существует последовательность
функций F1 (х) ? Ф1, F2 (х) 6 Ф2, . . ., удовлетворяющая условиям
lim [| F(x)-Fn(x) || = lim || F, t (x)-^(x) || = ...
n->oo n->oo
... = lim || F, ili2... im (x) - F, ilh ... im (x) || = 0. A0.27)
П->оо
Здесь ||• || обозначает нормы в $8 ти$В\ ilt i2, . ¦ ., im = I, 2, . . ., к;
P', im.. .im = dmF/dxu dxH . . . dxim, где it < i2 <_. . . <_im.
Функции Fn (x) образуют последовательность {Fn} в SS- Члены
этой последовательности получаются в результате построения
измельчения модели 5?. При измельчении области % число
элементов ге и глобальных узлов G бесконечно увеличивается,
причем каждая точка х 6 °А содержится в сколь угодно
малом элементе, а класс каждого элемента и соответствующих
ему интерполяционных функций не изменяется. Например, если
"Я a g2 состоит из треугольных элементов, на которых исполь-
используются линейные интерполяционные функции ор$' (х1, х%), то
и каждое измельчение J? должно состоять из треугольных эле-
элементов и линейных интерполяционных функций. Если каждый
узел и каждая межэлементная граница в модели 3? являются
узлом и межэлементной границей и в ее измельчении, то измель-
измельчение называется регулярным, в противном случае — нерегу-
нерегулярным.
Чтобы придать понятию измельчения количественное выраже-
выражение, введем понятие диаметра конечного элемента ге. Пусть х?
и х) — произвольные точки элемента ге. Диаметр бе элемента
ге — это максимальное расстояние между точками ге, т. е. бе =
= max || xf — х§ ||; х|, х^ 6 ге. Мерой мелкости б конечноэлемент-
ной модели служит максимальный диаметр ее элементов: б =
= max {81, б2, . . ., бя}. Пусть 91 — некоторая конечноэлемент-
ная модель, а °Л' — ее измельчение; °Л' равномерно, если б' < б,
где б' — мера мелкости 3?'. Пусть б и б' — наименьшие диаметры
элементов моделей % и Щ'. Если б' < б, то измельчение 91' назы-
называется равномерно утончающимся. Впредь мы будем предполагать,
что все измельчения регулярны и равномерны, а меры мелкости
124 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
б (Г) последовательности измельчений З?1, %2, . . ., ffiT, . . .,
удовлетворяют естественному требованию lim б (Г) = 0. Кроме
Г-^оо
того, мы будем считать, что в последовательности измельчений
для всех элементов используются локальные аппроксимационные
функции одного и того же вида.
Ясно, что наша первая задача — разработать метод построения
последовательности {F"}. Для этого мы, как обычно, представляем
область Я моделью Я, состоящей из конечного числа связанных
в общих узловых точках и непрерывно соединенных на меж-
межэлементных границах подобластей ге. Опять ограничение функции
F (х) на ге будем обозначать через /(е> (х), где для простоты не
делается различия между локальными и глобальными координата-
координатами (х<е) = X). Предполагается, что локальное конечноэлементное
представление имеет вид
A0.28)
Здесь N_== 1, 2, . . ., Ne\ f*e), /?)>ь . . ., $уи...ь — значения
функции /<е> (х) и ее частных производных вплоть до r-го порядка
в узловой точке N, а локальные интерполяционные функции
ор$° (х), . . ., ap$tlt2-" 'гг (х) или* тождественно равны нулю для
какого-либо узла N, или являются обобщенными эрмитовыми
интерполяционными функциями (см. п. 8.1). Общее число незави-
независимых членов в выражении A0.28) называется степенью свободы
элемента. Далее будут также использоваться следующие пред-
предположения и допущения: A) локальные представления /(в) (х)
и глобальные представления F (х) единственным образом опреде-
определяются главными узловыми значениями /^, /й, *, . . .,/(I), и.. .гг»
входящими в A0.28), и соответствующими глобальными значения-
значениями F&, F&i, . . ., F&it . для всех моделей области аА; B) идентифи-
идентификационная метка элемента (е) для простоты не пишется, и зависи-
зависимость функций ap^r, apjv, . . ., ор1^' ¦ 'гг от х явно не указывается.
Удобно ввести следующие определения.
Определение 1. Конечноэлементные аппроксимации / (х)
образуют семейство (или класс) JFr, если в каждой из них хотя
бы в одной узловой точке используются значения частных произ-
производных порядка г.
Например, / (х) = fNty% -f /Sjftipp определяет некоторое се-
семейство 3FZ конечноэлементных аппроксимаций. Придавая все-
всевозможные вещественные (или комплексные) значения параметрам-
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 125
коэффициентам fN, f, уь> получаем все функции этого семейства JFa*
Представление / (х) = fNty% + f,iih^ih определяет некоторое дру-
другое семейство &z.
Определение 2. Пусть / (хе) и g (хе) задают два семейства
конечноэлементных аппроксимаций. Функции / (хе)_и g (xe) назы-
называются г-эквивалентными на элементе ге области Й, если
\\1(xu)-g(xe)\\^Kbre, ХеЧГе, A0.29)
где бе — диаметр элемента ге, а К — положительная постоянная,
не зависящая от бе.
Если соотношение A0.29) справедливо для всех элементов
области Шх то оно определяет отношение эквивалентности для
семейств определенных на ?? функций. Диаметр бе рассматривает-
рассматривается как параметр. Для семейства {ЙТ} измельчений, мерой мелко-
мелкости которых служат б (Г), выполнены неравенства бе ^ б (Г),
и поэтому бе -»¦ 0 при б (Г) -»¦ 0. Понятие г:эквивалентности имеет
смысл только по отношению к заданной норме. Если не будет
делаться специальных оговорок, мы будем иметь дело с равномер-
равномерной эквивалентностью функций, определяемой неравенством
II/ — ? II = I/ — ? I ^ КЬге. Например, при достаточно малых
бе функция / (хе) = 1 + хе + #е + 36 sin xe 2-эквивалентна функ-
функции 1 + хе + ^е> а функция / (хе) = sin xe 3-эквивалентна функ-
функции хе. Две функции / (хе) и g (xe), 1-эквивалентные между собой,
в пределе при б -»¦ 0 равны почти всюду. Таким же образом если
значения / и g в точках хе отличаются только членами порядка б?,
т. е. если
= *(*.) +0F;), (Ю.зо)
то / и g являются r-эквивалентными на г е. Под О (б?) понимается
функция от б? (и, возможно, от хе), обладающая свойством
JL 10F.0 | = 0.
Определение 3. Пусть f€) (x) определяет некоторое семей-
семейство jFr конечноэлементных аппроксимаций на ге. Положим
G(x)=J(e)(x)~F(x). A0.31)
Семейство ,^гг называется r-допустимым для аппроксимации F (х)
по отношению к норме ||-||, если
|()I,|| ||().,fJl...ir|| = 0. A0.32)
6->-0 6-^0
126 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Ясно, что если JFT является r-допустимым, то /, й..лг и Р,ч..лт
по меньшей мере 1-эквивалентны на ге.
Если конечный элемент семейства JFr имеет d степеней свободы,
то значение / (х) в точке х представляет собой наложение значений
d линейно независимых функций, принадлежащих <рт. Говорят,
что эти линейно независимые функции характеризуют «единичные
моды» элемента. Хотя обычно принимается, что значение / (х)
в точке х можно сделать любым при помощи соответствующего под-
подбора амплитуд единичных мод, для нас важна возможность при-
придать функции / (х) нужное значение в нормированном пространстве
лишь с точностью до членов порядка бе. Это приводит нас к сле-
следующей теореме.
Теорема 10.5. Пусть f принадлежит некоторому классу
г-допустимых конечноэлементных аппроксимаций и {-эквивалентна
некоторому полному полиному х), содержащему т членов. Тогда
степень свободы d элемента ге не больше т.
Доказательство. Ясно, что коэффициенты полного полинома,
содержащего т независимых членов, могут быть найдены путем
приравнивания его т значений значениям функции / и некото-
некоторых ее производных в узлах элемента ге. Тогда по определению
d = т. Однако если два или более членов имеют общий коэф-
коэффициент, то d <lm. Значит, в общем случае d ^.т. Если же
функция / лишь 1-эквивалентна полному полиному, содержа-
содержащему т членов, то все сказанное остается справедливым, с той
разницей, что значения / и некоторых ее частных производных
в узлах могут принимать заданные значения только с точностью
до членов порядка бе.
Предыдущие определения и теорема 10.5 характеризуют неко-
некоторые общие свойства конечноэлементных аппроксимаций, удоб-
удобные для равномерного приближения заданной функции F (х).
Однако, как указывалось ранее, при получении конечноэлемент-
конечноэлементных решений краевых задач требуется полнота базисных функций
по энергии. Для решения вопроса полноты по энергии необходимо,
конечно, уточнить тип оператора X, входящего в определение
энергетического скалярного произведения. Мы ограничимся рас-
рассмотрением вопроса полноты для довольно широкого класса
линейных положительно ограниченных снизу дифференциальных
х) Под полным полиномом степени п от к переменных понимается поли-
полином, содержащий (п + к)\ In \к\ независимых членов; коэффициенты его,
однако, не обязательно независимы.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 127
операторов порядка 2р вида *)
s=0 i^ i2 »ft=0 г1
2
V 1 J2 •'ft
где jj4- i2+ • • • +ift = 7i + /2+ • • • + 7ь = Р и ^14'•••¦4—набор
ограниченных непрерывно дифференцируемых функций в %, сим-
симметричных по индексам iu i2, . . ., ih, jt, . . ., jh и положительных
в том смысле, что для любого х ? йД справедливо HepaBeHCTBo>
а;*1^'2 . . . хгьА}1г ] []^ xji . . . х h >- у2 || х ||2, у > 0. Предположим
также, что и 6 3t<g удовлетворяет однородным краевым условиям
на д^, вследствие чего после интегрирования по частям скалярное
произведение {и, Xv) можно представить в виде]
(и, Xv) = [и, v] = j dpuAdvvd№, A0.34)
Ж
где для простоты записи введено обозначение
n ¦ • ¦ n toi • • • dx\ h h dx\ ... dx)
8=0 ij, г2, ..., tft=0 H »ft ^l Jft
^•¦'г jft=0
A0.35)
Тогда энергетическая норма записывается так:
|| и ||jg = [и, и] = j дриАдри йМ, A0.36)
и можно показать, что если у! — верхняя граница для А (например,
max | А (х) | s?C А), то
\\u-v\\2?<^MA max \9p(u-v)\z. A0.37)
Расстоянием по энергии будет d% (и, v) = || и — v |[jp. '
Понятно, что от A0.36) можно перейти прямо к A0.7) или A0.8)
и получить вариационную формулировку дифференциального
уравнения в частных производных Хи = /, в которой фигурирует
х) Это — незначительное обобщение примера, рассмотренного Фелиппой
и Клафом [1968].
428 гл. п. теория конечных элементов
функционал
J(u)=\ (ЬриАдри —2м/) dM. A0.38)
Я
Квадратичные функционалы вида A0.38) (т. е. функционалы,
включающие производные порядка р) называются функционалами
класса Ср~1. В вариационной задаче для функционала класса С
краевые условия для и, содержащие производные до порядка
р — 1 включительно, называются главными (или геометрическими)
краевыми условиями, а условия, содержащие производные порядка
р, р + 1, •••> 2/? — 1,— естественными краевыми условиями.
Производные и до порядка р — 1 включительно называются глав-
главными производными. При построении аппроксимаций для A0.36)
и A0.38), как правило, мы будем требовать, чтобы и имело непре-
непрерывные главные производные в % + дШ (т. е. и 6 Cv~x (92 + дЩ)
л чтобы производные и порядка р были квадратично интегрируемы
(т. е. дри 6 L2 СЩ)- Если оператор X положительно определен,
этот класс функций плотен в SSjg.
После этих замечаний докажем следующую важную теорему *).
Теорема 10.6. Пусть d — степень свободы конечного элемен-
элемента ге, локальное конечноэлементное представление f (х) на котором
принадлежит семейству Jzrr. Тогда с помощью локальных базисных
функций г|$ (х), арг# (х), . . ., т|$ ¦¦1г (х) можно получить после-
последовательности аппроксимаций, полные по энергетической норме
A0.36), если выполнены следующие условия:
а. функция f (x) по крайней мере ^-эквивалентна полиному,
содержащему d членов;
б. семейство в?г содержит подсемейство <?Р функций, которые
вместе со своими производными до порядка s являются т-эквивалент-
ными соответствующим производным полных полиномов степени
г + 1, где s^r+1, т^ р -\- 1 — s;
в. г + 1 = р-
Доказательство. Заметим, что если теорема справедлива, в слу-
случае когда / (х) полином из d членов, включающий в себя полный
полином степени г + 1 = Р, то в пределе при стремлении меры
х) Эта теорема является обобщением доказанной Арантесом э Оливей-
рой [1968] теоремы, в которой рассматривались только полиномиальные
приближения. Важно четко представлять, что в этой теореме речь идет
о локальных условиях полноты конечноэлементных аппроксимационных
функций; т. е. функции, удовлетворяющие условиям этой теоремы, обеспе-
обеспечивают только локальное выполнение неравенства A0.51), а фундаменталь-
фундаментальное глобальное условие конечности энергетической нормы может при этом
не выполняться. Во избежание этого впоследствии на элементы семейства 2Fr
будет наложено дополнительное условие /--соответственности (см. определе-
определение 4 на стр. 135).
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 129
мелкости б к нулю она справедлива и для всех / (х), которые
1-эквивалентны таким полиномам. Поэтому предположим, что
7 (х) — полином из d членов с d независимыми коэффициентами
и что мы можем выделить в нем полный полином р (х) степени
р = г + 1, коэффициенты которого могут принимать произ-
произвольные постоянные значения. Значит, / (х) можно использо-
использовать для описания элементов с d степенями свободы (см. теоре-
теорему 10.5).
Пусть F (х) — элемент из ЗВ%, где оператор X имеет вид
A0.33). Поскольку X имеет порядок 2р, можно на ге предста-
представить F (х) в виде
F <х*>'«, ¦ • • vi К -<> • • • 4+1 - *w>. <10-39>
где FN, F F, . . . — значения функции F (х) и ее производных
в узловой точке xN, а точка х* расположена «между» xN и х.
Пусть g5" cr З'т содержит полином степени р, коэффициенты ко-
которого можно приравнять первым р членам разложения A0.39).
Тогда если К — верхняя граница для | F (х), ^...ij+i |, то
\F(x)-p (х) \<^щ !(бе)р+1, A0.40)
где b = (p + k)l/[(p 4-1)! (к—'1)\] — число членов степенир + 1
по к переменным хи а бе — диаметр элемента. Аналогично
с помощью последовательного дифференцирования получаем
^IFer1-5, A0.41)
где К — положительная постоянная.
По предположению р (х) ? Jzrr. Значит, р (х) можно записать
в виде
i...ir^--V(x), A0.42)
где г = р — 1. Пусть g (х) — элемент из jFr, который может
совпадать с главными производными F (х) в каждой узловой
точке xN элемента гв. Тогда
р (х) - g (х) = (р" - g») г|^ (х) + (Р% - gNJ % (х) + ...
••• + (Р..Л-^1...1Г)Ф^"'Г(х). (Ю.43)
Для того чтобы выражение A0.28) (или A0.42)) было безраз-
безразмерно однородным, необходимо, чтобы локальные интерполя-
9 Дж. Оден
130 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ционные функции г|^, ty%N, • ¦ •, были представимы следующим
образом: •
A0.44)
Здесь I — характерный размер элемента, % — безразмерные
локальные координаты (например, ?г = xjl), а фдг, <Pn, ¦ • ¦
. . ., q>N"'tr — безразмерные базисные функции, не зависящие
от абсолютных размеров элемента. Предполагается, что эти
функции ограничены на ге, т. е. для всех xjl ? re существуют
положительные постоянные К0, К1, . . ., 1С, такие, что
|q&(g)| -К0, \^A)\^К\ ..., | <$'¦¦* (S) \^КГ.
Отсюда следует, что если бе—диаметр элемента, то
:^. (ю.45)
Отметим также, что
\^А;\;г*Лт(х)\<каы~т- (Ю.46)
Следовательно, возвращаясь к A0.43), имеем
A0-47)
при любых значениях индексов iu i2, . . ., ir.
В силу A0.41)
где s = 0, 1, 2, . . ., г. Подставляя это в A0.43) и принимая
во внимание A0.46), получаем
IP(x), v..ip-g(x),it.. лр\<Ше, A0.49а)
где г
И =
а г = р — 1. Заметим, что при получении A0.49а) мы пред-
предполагали] существование а|$; \иТ. Лт-и (х) в г«> хотя порядок
представления g (х) только г.
Ю. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 131
Из A0.49а) и A0.41) видно, что х)
l1l1i A0.50)
при любом / = 0, 1, 2, . . ., р, где С; = М + ЬК/(р + 1 — у)!.
Таким образом, в обозначениях A0.35) имеем
|dp(F(x)-g(x))|<C8e, A0.51)
где С — не зависящая от бе постоянная. Подставляя A0.51)
в A0.37), получаем
\\F--g\\2x^reCZA(8e)Z, A0.52)
где подразумевается, что F и g зависят от х. Если б — мера
мелкости связанной конечноэлементной модели (т. е. б =
= max {бь б2,..., бЕ}) и если глобально нормы A0.52) приводят
к конечной энергии, то \\ F — g \\х ^ %С2Лб2, где С -^ макси-
максимальная из постоянных С для всех элементов. Ясно, что для
последовательности глобальных аппроксимаций, порождае-
порождаемых представлениями в классе ЛРГ и соответствующих регуляр-
регулярным равномерным измельчениям, б -*¦ 0, Hm \\ F — g \\v — 0.
6-.-0
Поэтому построенные таким образом глобальные базисные
функции полны по энергии. Для того чтобы показать теперь,
что достаточно, чтобы р (х),^...^, где р (х) ? IS, были лишь
тп-эквивалентны р (х)_ 4|.. _is, где/? (х) полный полином степени р,
заметим, что в соответствии с A0.41) и A0.48)
Значит, A0.50) справедливо при 8е-*-0, поскольку т ^>
^ р + 1 — s. Этим заканчивается доказательство теоремы.
Для лучшего понимания теоремы полезно разобрать простой
иример. Положим 'Й. = Щ} и рассмотрим линейный оператор
dx2
х) Если / (х) — полином степени q и р -\- 1 — j! ^ 2 (q + 1 — р), то при-
приводимая ниже оценка A0.50) согласуется с оценкой погрешности Фикса
и Стрэнга [1969]. Подробно такие оценки погрешности рассмотрены Фридом
[1971]; в работе Фикса и Нассифа [1972] можно найти оценки погрешностей
для параболических уравнений. См. также Корнеев [1967], Бабушка [1971],
Маклей [1971] и Оден [19716].
9*
132 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Пусть область 3)х состоит из функций и (х) ? С2 [а, Ь], которые
удовлетворяют условиям и (а) = и (Ь) = 0. Заметим, что в силу
этого условия
Значит^ оператор X симметричен, положительно определен и
ь
и п2 f /d(u — у)\2 , ., \d(u — v) 2 .
II» —1|у= J (-W"^) <k<(b-g)max| Kdx . A0.53)
В этом случае р = 1 и г = 0.
Предположим теперь, что отрезок [а, Ь] разбит на Е конечных
элементов, длины которых суть б1; б2, . . ., бя, и рассмотрим класс
конечноэлементных представлений первого порядка вида
(Ю.54)
где с целью удобства опять используется символ х для обозначе-
обозначения локальных координат (х\е) = 0, х\е) = бе). Предполагается,
что функция he (x) обладает свойствами
he @) = 0, he Fв) = бе A0.55)
и вид функции he (x) один и тот же для всех элементов. Ясно, что
если h (x) задана, то функция /(е) единственным образом опреде-
определяется на элементе ге своими значениями /^, в узлах элемента.
Пусть U (х) — произвольный элемент области 35g (или ее рас-
расширения), и пусть U1, С/2, . . ., UG — значения U (х) в глобаль-
глобальных узлах. Без ущерба для общности мы можем рассмотреть
подынтервал, соединяющий узлы 1 и 2. С помощью теоремы Тэйло-
Тэйлора легко показать, что
^ (Е/2_ С/*) = V (х) + ± [U" (х) (б.- х?- U"'(*•) х*],
где U" (х) = dU/dx, U" (х) = cPUldx*, х 6 1х\ х2},
< х* < х.
Возвращаясь к A0.54) и временно опуская метку е, имеем
Таким образом, если / совпадает с U (х) в узлах, то
]' (х)- V (х) - (h' (x)-l) U' (х) +
+ ±h' (х) [U" Aс) (б - xf - U" (х*) х*\
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 133
для х?ге. Пусть | h' (x) К А, | U' (х) |< В и | U" (х) |< С
для всех х ? [a, ft]. Тогда
где D^.AC. Следовательно, если б — мера мелкости связанной
модели и F (х) — глобальная аппроксимация, соответствующая
То (Х), ТО
IIF-U ]\%<(Ь-а) [В | h'-l \ + D8]\ A0.56)
Значит, lim \\ F — U \\% ф 0, если h' (x) не является по меньшей
б-* о
мере {-эквивалентной единице, т. е. \ h' — 1 | =?^ К8.
В рассматриваемом примере р = 1, так что в соответствии
с теоремой 10.6 достаточно использовать класс #"° конечноэлемент-
ных представлений (т. е. класс представлений, в которых задаются
только значения самой функции в узловых точках и которые
содержат функции, по крайней мере 1-эквивалентные полным
полиномам степени р = г+1 = 1,т. е. в нашем случае полиному
первой степени а + Ъх). Действительно, если ifo (х) = 1 — х/8,}
то h (х) = х и \ h' — 1 | = 0. Однако функция h (x) должна быть
лишь {-эквивалентна х.
Чтобы подчеркнуть это, заметим, что можно выбрать целое
множество функций, удовлетворяющих условиюA0.55). Например:
2° h (x) = Ье 4
3° h(x) = x + x(x — 6e)m, A0.57)
и т. д. В примере 1 производная h' (x) не является 1-эквивалентной
единице, так как \ h' (х) — 1 | = | 1 — я/2 cos (nx/28e) |. Поэтому
конечноэлементные модели, построенные с помощью функций
такого типа, не будут полными по энергии. С другой стороны,
в примерах 2° и 3° соответственно имеем \ h' — 1 | ^ 26^/3 +
+ 1364е/90 + . . . и | h' — 1 К (т - 1) 8?. Значит, при доста-
достаточно малом 8е во втором примере Ы будет 2-эквивалентной едини-
единице, а в третьем пг-эквивалентной. Функция примера 4 тоже допу-
допустима, поскольку можно показать, что Ь! (х) — 1 -f О (8).
Примеры A0.57) и теорема 10.6 позволяют сделать интересные
наблюдения:
134 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
1. Локальные интерполяционные функции не обязательно дол-
должны быть полиномами.
2. В тех случаях, когда локальные интерполяционные функ-
функции — полиномы, они не обязательно должны быть полными
полиномами. Действительно, для функционалов класса Ср~1
(или энергетических норм, содержащих производные порядка р)
они должны лишь включать в себя полные полиномы степени ^р.
Из теоремы 10.6 вытекает такой общий критерий выбора пол-
полных по энергии локальных интерполяционных функций х).
Теорема 10.7. Пусть выполнены условия а — в теоремы 10.6.
Тогда функции /(е) (х) и всем ее частным производным до порядка
р = г -\- 1 могут быть приданы в те значения, отличающиеся от
произвольных постоянных не более чем членами порядка 8е.
Доказательство. Это утверждение непосредственно следует
из теоремы 10.6, поскольку ЛРТ содержит функции р (х), кото-
которые по крайней мере 1-зквивалентны полным полиномам степе-
степени р с произвольными коэффициентами. Например, что-
чтобы придать постоянное значение К частной производной
dm+nf/(dx1)m (дх2)п порядка m -\- п, где m + n =?^ р, можно
просто приравнять коэффициент одночлена (xl)m (я2)™ полного
полинома степени р величине Klm\ п\, а все остальные коэф-
коэффициенты полинома приравнять нулю-
х) При конечноэлементном исследовании изгиба пластин Бейзли, Ченг,
Айронс и Зенкевич [1966] предложили в качестве критерия полноты («схо-
дпмости») условия, что функции перемещений не должны допускать «дефор-
мации^элемента в результате его жесткого движения» и что функции пере-
перемещений должны допускать постоянные «деформации» и кривизны в эле-
элементе. Аналогичные требования выдвигались ранее Айронсом и Дрейпером
[1965]. Поскольку рассматриваемый ими функционал принадлежит классу
С1, их критерий означает требование допустимости постоянных значений
функции перемещений и ее первых и вторых частных производных на каж-
каждом элементе. Доказательство для полиномиальных аппроксимаций позже
было дано Арантесом э Оливейрой [1968]. Теорема 10.7 показывает, что эти
постоянные значения должны допускаться только при б -*¦ 0. К сожалению,
многие авторы в последующем трактовали критерий, предложенный Бейзли
и др., слишком буквально и использовали требования «жесткого движения»
и «постоянства деформации» как фундаментальные условия полноты для
всех конечноэлементных аппроксимаций полей перемещений. Однако нетруд-
нетрудно проверить, что можно построить удовлетворяющую требованиям полноты
теоремы 10.7 конечноэлементную аппроксимацию поля перемещений упру-
упругого тела, которая не приводит к жесткому движению или постоянной дефор-
деформации при конечном бе. В этом можно убедиться, беря в теореме 10.6 в каче-
качестве xi криволинейные координаты (например цилиндрические, тогда иг =
= const не приводит ни к жесткому движению, ни к постоянной деформа-
деформации, в то время как иг = а + Ъг допустимо для задач класса С0). Жесткие
движения и постоянные деформации должны получаться только в пределе
при б -> 0. С другой стороны, Мюррей [1970] показал на численных приме-
примерах, что включение жестких движений в элементы конечных размеров может
существенно ускорить сходимость.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 135
Условия теорем 10.6 и 10.7 представляют собой основу для
построения конечноэлементных аппроксимаций. Важно, однако,
добавить к ним требование соответственности х).
Определение 4. Семейство lfT конечноэлементных аппро-
аппроксимаций называется г-соответственным (или просто соответствен-
соответственным), если на совокупности элементов, образующих связанную
модель, глобальные аппроксимации F (х) и все их частные произ-
производные до порядка г включительно непрерывны на межэлементных
границах.
Таким образом, соответственные конечноэлементные аппрокси-
аппроксимации F (х) ? С2 {%). Требование соответственности обусловлено
упоминавшимся ранее обстоятельством, что в вариационной задаче
класса Cp-1 область определения функционала состоит из функций
и 6 Ср~1 (9г), частные производные которых порядка р принадле-
принадлежат L2 ($)', в случае нарушения этого требования могут появлять-
появляться неограниченные энергетические нормы (см. примечание
на стр. 128). С одной стороны, использование соответственных
конечноэлементных аппроксимаций обеспечивает необходимую для
решаемой задачи степень гладкости функций, но, с другой сторо-
стороны, оно накладывает дополнительные ограничения на форму эле-
элементов. В п. 10.4 будут приведены примеры допустимых конечно-
-элементных аппроксимаций.
10.3§ КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ ОПЕРАТОРНЫХ УРАВНЕНИЙ
В этом пункте кратко рассмотрены некоторые методы построе-
построения конечноэлементных моделей для уравнений вида A0.1) и A0.5)
с линейными и нелинейными операторами. Методы, которые успеш-
успешно могут использоваться для построения моделей, никоим образом
не ограничиваются разобранными ниже примерами.
х) Термины «соответственность» (conforming) и «несоответственность»
(nonconforming) в связи с непрерывностью конечноэлементных аппроксима-
аппроксимаций введены в статье Бейзли, Ченга, Айронса и Зенкевича [1966]. Требование
непрерывности было выдвинуто Мелошем [1963а], см. также Ки [1966].
Бейзли и др. показали, что в некоторых случаях требование непрерыв-
непрерывности может быть чрезмерно сильным, однако их результаты указывают,
что для несоответственных элементов сходимость может зависеть от их ориен-
ориентации в конечноэлементной модели. Арантес э Оливейра [1968] отметил, что
в некоторых случаях может допускаться разрывность производных порядка
г — р — 1; например, в задачах с заданными условиями скачка на поверх-
поверхностях, которые во всех измельчениях конечноэлементной модели являются
межэлементными границами. Разрывность производных порядка г может
допускаться на некоторых поверхностях внутри элемента для равномерных
регулярных измельчений моделей из составных элементов (см. п. 10.4.6).
См. также Айронс и Дрейпер [1965] и Клаф и Точер [1966].
136 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Метод Ритца *). Наиболее часто для получения конечно-
элементных аппроксимаций различных краевых задач используется
метод Ритца. Существенные черты метода уже в значительной мере
ясны из нашего обсуждения вопроса полноты в предыдущем пунк-
пункте. Остановимся на них более подробно. Пусть X — симметричный
линейный положительно ограниченный снизу оператор.Рассмотрим
уравнение
Хи = /, A0.58)
где / — элемент из L2 (??), а область определения оператора X
обозначается через 35 {35 =s=3)g). Предположим, что решение и
должно удовлетворять однородным краевым условиям на д%.
Как указывалось ранее, задача решения уравнения A0.58) может
рассматриваться как задача минимизации функционала
/ (и) = (Хи, и)-2 if, и) A0.59)
при условии, что решение и* принадлежит 35 или сколь угодно
близко к элементам множества 35 по норме ||-1|. Здесь / — элемент
пространства $8, причем &в вещественно. Область 35 плотна
в полном пространстве Ш%, получаемом пополнением пространст-
пространства со скалярным' произведением [и, v] = (Хи, v) для элементов
из 35. Пусть к = min / (и). Последовательность {ип} ? ffl% назы-
называется минимизирующей последовательностью, если lim / (ип) =
= / (и*) = к. Метод Ритца состоит из следующих этапов:
1. Определение полной по энергии системы элементов (фа, ф2, ...)
в Ш%- Элементы <рг- могут быть взяты из 35, поскольку SS
плотно в $в%. Пусть Ф— конечномерное подпространство,
порожденное первыми п элементами системы.
п
2. Построение аппроксимации ип = 2 а;Фг Для функции
г=1
и'вФс помощью выбора at, минимизирующего / (и) в Ф.
Можно показать 2), что полученная таким образом после-
последовательность аппроксимаций {ип} является минимизирую-
минимизирующей последовательностью для / (и). Кроме того, если опера-
оператор X положительно ограничен снизу, то lim || u* — un\\g=
П-*оо
= 0.
х) Этот хорошо известный метод был предложен Ритцем [1908, 1909]
как обобщение метода, использовавшегося Рэлеем [1877].
2) См. Михлин [1952]. Если fn == Хип и оператор X неограничен, то
может случиться, что lim || fn — / || =? 0. Однако fn сходится слабо к /
П-^оо
в том смысле, что lim (/„—/, g) — 0 для всех g 6 36% или даже для всех
П-+оо
g 6 $6, если нормы || /п || ограничены в совокупности.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 137
Предположим, что нам требуется построить конечноэлементное
решение линейного уравнения A0.58). Начинаем с построения
конечноэлементной модели 'Я для области 91 + &% и модели для и:
Е/(х) = 2 ^)(х) = С7дФд(х),
е=1
Фд(х) = Цй^>(хI A0.60)
,.N &W/A.
Ще) = "Д U ,
здесь предполагается, что функции Фд (х) полны по энергии.
Локальной аппроксимацией для и на элементе ге в соответствии
с A0.60) будет
п(е)(х) = <г|$(х). A0.61)
Пусть теперь 1т — ограничение оператора X на функции, опре-
определенные на ге. Тогда, если решение уравнения A0.58) минимизи-
минимизирует функционал A0.59), ограничение / (и) на ге можно записать
в виде
/(f)(«) = A и)-2 (и, /> A0.62)
и
Е
J(u)=% /W(u), - A0.63)
е=1
где под ми/ понимаются их ограничения на ге. Подставляя A0.61)
в A0.62), получаем
/е) (и») = 1%и&& -2/#4, (Ю.64)
где М, N = 1, 2, ...,Ne, a
№n = И(Ж Ш f# = (/, г|$>. A0.65)
Аналогично, подставляя A0.60) в A0.59), получаем для глобаль-
глобальной аппроксимации
/ (С7А) = LATUAUr — 2FbUA,: A0.66)
где А, Г = 1, 2, . . ., G и
?дг = (#ФД, Фг>, ^д = </, Фд>. A0.67)
В силу A0.63)
LATUAUT-2FAUA = 2
e=l
= S A^КУ?/г-2/ЙУ). A0.68)
e=l
138 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Локально ре) (uN) принимает минимальное значение, если
^Ф- = 0 = 2Z« - 2/&>, A0.69)
или
#>*«<" = /#. A0.70)
С учетом A0.60) и A0.63) из A0.70) получаем глобальное требова-
требование
L^IF = Ft, A0.71)
откуда в соответствии с A0.66) следует, что dJ (С/А)/д?/д = 0.
Решив A0.71) относительно UT, получаем функцию Е/гфр (х),
являющуюся аппроксимацией Ритца для решения и* уравнения
A0.58) в подпространстве Ф.
Кратко рассмотрим вопрос сходимости последовательности
аппроксимаций Ритца. Как и в предыдущем пункте, рассмотрим
последовательность подпространств Ф1, Ф2, . . . пространства SS,
порождаемых функциями Фд (х), Ф| (х), . . ., которые строятся
из локальных конечноэлементных аппроксимаций обычным обра-
образом. Эта последовательность получается в результате использо-
использования регулярных равномерных измельчений модели "А, мера
мелкости которых б -> 0; предполагается, что базисные функции
каждого подпространства r-соответственны и полны по энергии
в смысле теоремы 10.6.
Пусть и* = и* (х) — функция в Ш, которая действительно
минимизирует функционал / (и); пусть U = U (х) — глобальная
конечноэлементная аппроксимация и*, которая минимизирует
J (и) в n-мерном подпространстве Фп, определяемом допустимой
конечноэлементной моделью; и пусть G = G (х) — элемент из Ф™,
совпадающий с функцией и* и ее главными производными в узло-
узловых точках. Ограничением ge (x) функции G (х) на ге является
функция, определяемая соотношением A0.43). Поскольку по пред-
предположению множества базисных функций Фд (х), Фд (х), . . .,
порождаемых равномерными регулярными измельчениями, полны
по энергии (относительно некоторого содержащего и* класса
функций), можно ввиду A0.52) для любого е > 0 найти такое
целое N, что расстояние по энергии от и* до G будет меньше е1^2
при и > N, где п — размерность подпространства Ф™, т. е.
при n>N. A0.72)
Тогда поскольку / (G) = djy (и*, G) —1| и* \\% = d2?(u*, G)-\-J(u*)
(см. A0.8)), то
J(G) — J(u*)<e при n>N, A0.73)
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 139
или lim / (G(n)) = J(u*). [Напомним, что d%(u*, G)l>0.] Ясно, что
П-»оо
J (и*)</ (?/)</ (G);_значит,
J(U) — J(u*)<^J(G) — J(u*). (ЮЛА)
Таким образом, при п > N выполняется неравенство J (U) —
— / (и*) < е. Следовательно, lim / (Un) = / (и*) = min / (и),
П-+.ОО
т. е. последовательность конечноэлементных аппроксимаций функ-
функционала / (и) сходится к минимуму / (и*), если базисные функции
Фд (х) полны по энергии. Заметим также, что если Ш вещественно,
а оператор X самосопряжен, то
a%(U, u*) = [U — u*, U — u*] = [U,U]—2[U,u*] + [u*,u*] =
= J(U)-J(u*). A0.75)
Поэтому dx A1(Щ, и*) < е при п > N, и расстояние по энергии
между Um и и* стремится к нулю при неограниченном возраста-
возрастании п. Конечно, может случиться, что XU^ = рП) не сходится
к / = Хи* (см. Михлин [1952]). _
Отметим, что если измельчения %г построены так, что Ф1 cz
с= Ф2 ci . . . Ф™ с . . ., то соответствующие аппроксимации Рит-
ца обладают свойством
/(f/1)>/(t72)>... J(Un)>...>/(и*). A0.76)
Сходимость в этом случае монотонна *). Однако монотонная сходи-
сходимость не означает сходимости к / (и*). Тем не менее можно утвер-
утверждать, что если Фг+1 гэ Фг, i = 1,2,. . ., и если базисные функции
аппроксимаций полны по энергии относительно некоторого содер-
содержащего и* класса функций, то / (Un) монотонно сходится к / (и*).
Метод взвешенных невязок 2). Общий метод построения
конечноэлементных моделей нелинейных уравнений содержит
в себе идею взвешенных невязок. Рассмотрим, например, уравнение
& (и) = U (Ю.77)
где З5 — нелинейный оператор, определенный на некотором мно-
множестве 3). Пусть
¦ Ще)(х) = и^%)(х) A0.78)
1) Условие ф*+1 zd Ф1 в качестве достаточного условия монотонной схо-
сходимости соответственных конечноэлементных аппроксимаций предложил
Мелош [1963а]. Это условие исследовал также Ки [1966].
2) Подробный обзор применений метода взвешенных невязок дан Фин-
лейсоном и Скривеном [1966]. Изложение метода можно найти у Эймса [1965]
или Крэндалла [1956]. Приложения этого метода к конечноэлементным аппро-
аппроксимациям линейных дифференциальных уравнений рассматривались Лео-
Леонардом и Брэмлеттом [1970].
140 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
— конечноэлементная аппроксимация для и на типичном конечном
элементе ге\ для удобства изложения предположим, что м(е) (х) ?
6 ZB&u), где 1Р(е) — ограничение оператора ^ на функции, опре-
определенные в ге. Функция
г1а (х) = 0»<« (пш) - Г (Ю.79)
называется невязкой, соответствующей элементу ге. Ясно, что
если г(е) (х) = 0, то м(е) является решением уравнения A0.77)
в ге. Метод взвешенных невязок состоит в выборе множества
весовых функций w'ff (х), N = 1, 2, . . ., Nе, таких, что г(е) (х)
обращается в нуль в смысле некоторого взвешенного среднего в ге.
Как правило, требуют, чтобы
$ = 0, A0.80)
е
или, с учетом A0.79),
*$("?))-/$(«» = 0, A0.81)
где
J 'М W *Ъ. A0-82а>
А») = j fe) (x) и;й (х) dre A0.826)
и ^м(^й) в обшем случае нелинейно относительно щеу Глобально
имеем
(е) (в)
И^д (х) = S Йд ^ (х), ы« = Qf^A, (Ю.83а, б)
1
5Рд (С/Г) = S йМ (ЙГ/С7Г), J^= 2 QT/^U, A0.83b, г)
е=1 е=1
или
$a(Ut)-FT = 0. A0.84)
Решения нелинейных уравнений A0.84) обеспечивают глобальное
обращение в нуль взвешенной средней невязки, т. е. выполнение
равенства
j [ffl (UfOT (x)) -/ (х)] WA (x) dM= 0. A0.85)
Ж
Различные типы методов осреднения различаются выбором весовых
функций We (х).
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 141
Заметим, что A0.80) и A0.85) являются условиями ортогональ-
ортогональности: невязка делается ортогональной некоторому подпростран-
подпространству, порождаемому весовыми функциями WA. Природа подпро-
подпространства опять-таки зависит от выбора этих весовых функций.
Идея поиска таких элементов п в линейном подпространстве Ф,
что и — п ортогонально Ф, основывается на классической теореме
^ проекциях, фундаментальной для большинства методов осред-
осреднения .
Теорема 10.8. Пусть 36 — гильбертово пространство
иФ — замкнутое подпространство в 36¦ Для каждого и ? 36 суще-
существует единственный элемент п* ? Ф, такой, что \\ и — п* || <С
<С || и — п || при всех других п ? Ф- Кроме того, необходимым
и достаточным условием минимальности расстояния \\ и — п* \\
является ортогональность и — п* подпространству Ф.
Доказательство. Вариант этой теоремы был доказан в п. 9.3.
Сейчас приведем более подробное доказательство. Сначала
предположим, что элемент п* ? Ф минимизирует d2 (и, п) =
= || и — м ||, но и — п* не ортогонально Ф. Тогда
{и — п*, и) = X Ф 0. Пусть пх = п* + Хп. В этом случае
\\и — щ\\2 = \\и—п*\\2—(и—п*, Ы)~{Ы, и—п*) + \Х\2 =
здесь мы предположили, что || п || = 1, что не уменьшает
общности. Это соотношение показывает, что если и — п*
не ортогонально Ф, то п* не минимизирует сР (и, п), вопреки
первоначальному предположению. Таким образом, если п*
минимизирует <Р (и, п), то и — м* ортогонально Ф. Для того
чтобы доказать, что если и — м* ортогонально Ф, то п* —
единственный вектор в Ф, минимизирующий сР1 (и, п), заметим,
что для любого п ? Ф
Следовательно, \\ и — п || > || и — п* \\ при и Ф п*.
Отметим, что единственность и ортогональность не зависят
от полноты пространства 36.- В случае когда 36 полно (т. е.
когда 36 — гильбертово пространство), можно доказать и суще-
существование п*. Пусть X = inl || и — п ||, п ? Ф, и пусть {м™} —
последовательность в 36\ такая, что lim \\ и — пп \\ -> X.
П->оо
Тогда
142 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ИЛИ
Поскольку Ф — линейное подпространство, пт + йп 6 Ф- От-
Отсюда следует, что
\\пт— мп||2<2||йт— u\\2 + 2\\lin — uf — 4Я2,
и так как || пт — и || ->- X при та-voo, это означает, что
|| пт — пп || -*¦ 0 при т, п ->- с». Поэтому {мт} является после-
последовательностью Коши в замкнутом подпространстве Ф. Сле-
Следовательно, она имеет предельную точку п* ? Ф- Поскольку
|| и — пп || непрерывна, \\ и — п* || = X, чем и заканчивается
доказательство.
Метод Галёркина. Пожалуй, наиболее мощным средством
получения приемлемых конечноэлементных моделей нелинейных
уравнений является метод осреднения Галёркина *). Являясь по
существу частным случаем метода взвешенных невязок (и обобще-
обобщением метода Ритца), он основан на рациональном выборе весовых
функций wN (x) в' соответствии с видом используемой конечно-
элементной аппроксимации.
Основы метода удобно показать на примере, в котором & (и) =
= ?Р (и) — / — потенциальный оператор, а аР (и) — нелинейный
оператор из уравнения A0.77). Как отмечалось в п. 10.1, оператор
(Э5 (и) можно считать градиентом функционала К (и), критически-
критическими точками которого являются решения уравнения Ф (и) = 0.
Поэтому на основании A0.26)
(S5 (и*) — /, h) = 0, A0.86)
где h — произвольный элемент пространства, которому принадле-
принадлежат м, аи* — критическая точка функционала К (и). Если конеч-
ноэлементная аппроксимация м(е> (х), определяемая формулой
A0.78), только приближенно удовлетворяет соотношению A0.77),
то определяемая формулой A0.79) невязка г(е) (х) не обязательно
будет ортогональна всем h. Однако коэффициенты аппроксимации
х) Метод был описан в статье Галёркина [1915] [а еще раньше — в рабо-
работах Бубнова *[1913 1914], почему его правильнее было бы называть методом
Бубнова. — Ред.] и использовался в применении к конечным элементам
Оденом [1967а, в, 19696], Сабо [1969], Сабо и Ли [1969а, б] и другими. В ста-
статьях Сабо этот метод применяется к построению конечноэлементных моделей
задач плоской статической упругости и изгиба упругих плит, когда он по
существу совпадает с методом Ритца. Однако метод Галёркина естественно
приводит к более явным формулировкам условий на границах конечных
элементов. Большинство из конечноэлементных формулировок глав III
и V этой книги могут рассматриваться как приложения метода Галёркина.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 143
и^е) можно выбрать так, чтобы невязка г(е) (х) была ортогональна
конечномерному подпространству, порождаемому интерполяцион-
интерполяционными функциями i|$p (х) [или, что то же самое, Фд (х)]. Локально
это равносильно соотношению
(®V{u{e))-f\ h) = 0. A0.87)
Но поскольку теперь h = h (x) — произвольный элемент из Ф,
его можно представить в виде h = h^tyff (x). Поэтому
{^{u(e))-f\ ,|#>йй = О. A0.88)
Равенство A0.88) должно выполняться при любых коэффициентах
hfe). Это означает, что
0. (Ю.89)
Таким образом, мы получили систему нелинейных уравнений для
коэффициентов и^у Ясно, что в случае, когда (и, v) — \ uvdre,
A0.89) принимает вид
A0.90)
Сравнивая это уравнение с A0.80), видим, что метод Галёркина
по существу является методом взвешенных невязок с весовыми
функциями и$, (х) = tyffl (x). Отметим также, что в этом случае
формулы A0.82) для р$ (u?e)) и Щю) принимают вид
е>) = \ ^е) (ФМ) № (х) dr., /g(w) = j fe) (x) 4$ (x) dre.
A0.91)
Наконец, заметим, что если if* содержит производные по пара-
параметру t (времени) и м(в) = ufe) (t) tyff (x), то метод Галёркина
приводит к системам дифференциальных уравнений A0.81) [где
PW (u?e) (t)) и /$(«,) (t) определяются формулами A0.91)] относитель-
относительно и^е) (t) для каждого конечного элемента.
Метод наименьших квадратов. В качестве послед-
последнего примера метода для построения конечноэлементных моделей
кратко рассмотрим метод наименьших квадратов. В этом методе
мерой ошибки е аппроксимации п<е) является квадрат нормы
невязки:
е= ||rte) ||2 = <r(e), r(e)>._ A0.92)
Метод наименьших квадратов заключается в том, что коэффициен-
коэффициенты uft) выбирают таким образом, чтобы мера ошибки е была мини-
144 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
мальной. Используя A0.79), получаем
e = {^(^4))-f\ &{е)(фи%)-?% A0.93)
Условие
|<^> (i0'94)
приводит к системе уравнений
$?(*$)-Л? = 0, A0.95)
где
A0.96а, б)
Соответствующая A0.95) глобальная форма уравнений получается
обычным способом. Сравнивая A0.94) с A0.80), видим, что метод
наименьших квадратов по существу есть частный случай метода
взвешенных невязок, соответствующий выбору весовых функций
wf (х) = drw 1ди% = д&м (п^Iди%у
10.4. ПРИМЕРЫ КОНЕЧНЫХ ЭЛЕМЕНТОВ
В п. 10.2 было установлено, что соответственные конечноэле-
ментные аппроксимации, которые удовлетворяют условиям полно-
полноты, даваемым теоремами 10.6 и 10.7, можно использовать для
построения приемлемых приближенных решений большого класса
физических задач. В этом пункте мы дадим несколько примеров
локальных интерполяционных функций ¦$% (х), г|з]у (х), ...
. . ., i|)lV*r (x)i которые приводят к глобальным базисным функ-
функциям, удовлетворяющим этим условиям [т. е. F (х) 6 С4" (й) и функ-
функции F (х) с ее производными до порядка г -\- 1 можно на каждом
элементе ге придавать значения, по крайней мере 1-эквивалент-
ные произвольным постоянным] х). Для удобства мы будем рас-
рассматривать приближения скалярной функции U (х) локальными
аппроксимациями п(е) (х), имея в виду, что такие же локальные
интерполяционные функции \р% (х), г|э]у (х) ... можно использо-
использовать и для представления векторных и тензорных функций (см.
примеры 7.4 и 7.5). Кроме того, поскольку мы будем рассматривать
х) Каталоги различных приемлемых конечных элементов составлены
целым рядом авторов. См., например, Аргирис [1966а], Аргирис, Фрид
и Шарпф [1968а, 19686, 1968в], Аргирис и Шарпф [1968], Аргирис и Фрид
11968], Аргирис, Бак, Шарпф, Хилбер и Маречек [1969], Зенкевич и Ченг
{1967], Фелиппа [1966], Фелиппа и Клаф [1968].
0. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 145
типичный конечный элемент, идентификационную метку элемента
временно писать не будем. Отметим, что наиболее часто используе-
используемой функциональной формой интерполяционных функций являют-
являются полиномы *). Это объясняется их простотой, удобствами их
использования при вычислениях (например, при численном инте-
интегрировании) и тем, что при полиномиальных представлениях, как
правило, проще проверять выполнение условий полноты и соот-
соответственности.
10.4.1. Симплексные модели 2). Простейшими среди всех конеч-
конечных элементов являются так называемые симплексные модели 3),
образующие топологические симплексы в том пространстве, в кото-
которое вложен конечный элемент. При симплексных представлениях
локальные поля и (х) аппроксимируются линейными относительно
координат хх функциями:
и (х) = а0 + atx\ i = 1, 2, . . ., к. A0.97)
Здесь а0, а1л а2, . . ., ak суть к -f- 1 постоянных, которые надо
определить. В fc-мерном пространстве фиксируем к -\- 1 узловых
точек (Nе = к + 1) и вычисляем значения A0.97) в каждом узле х^:
и (xN) == uN = а0 + atxNi,
i = 1, 2, . . ., к, N = 1, 2, . . ., к + 1. A0.98а)
Соотношения A0.98а) представляют собой систему к -f- 1 уравне-
уравнений относительно к + 1 величин а0, вх, . . ., ak. Удобно переписать
х) Подчеркнем, что в общем случае интерполяционные функции не обя-
обязательно должны быть полиномами. Действительно, на это ясно указывают
примеры A0.57). Крахула и Полемус [1968], например, использовали функ-
функции получающиеся добавлением к основным полиномам подходящих рядов
Фурье. Общие вопросы применения полиномиальных аппроксимаций в ме-
методе конечных элементов рассмотрены Фелиппой [19С6], Дании [1908] и Сил-,
вестером [1969].
2) Симплексом в ft-мерном пространстве называется выпуклое множе-
множество S, определяемое совокупностью к + 1 вершин (узлов) Nt, N2, . . .
. . ., Л^ь+ц не лежащих в одной (к — 1)-мерной гиперплоскости. Это ыно-
ft+l ft+l
жество S состоит из всех точек у вида у = ^] ci^t< гДе °i ^-® и ^] ct = i:
i=l i=l
См., например, Грейвс [1956, стр. 146—150] или Гройб [1963, стр. 253, 254].
В эвклидовых пространствах %h симплексами являются, например, тетраэдр
D узла) в трехмерном пространстве %3, треугольник (три узла) в двумерном
пространстве %2 и отрезок прямой B узла) в одномерном пространстве %1.
3) Симплексные модели связаны с использованием линейных интерполя-
интерполяционных функций в элементе, и они одними из нерпых применялись в методе
конечных элементов. См., например, Тэрнер, Клаф, Мартин и Топп [1956],
Синг A957], Галлагер, Пэдлог и Бсйлард [1962]. Свойства симплексных аппро-
аппроксимаций исследовались Висманном [19,63], Оденом [1967а, 19676, 1969а],
Фелиппой [1966], Оденом и Агирре-Рамиресом [1969] и другими. Симплекс-
Симплексные модели для пространств более высокой размерности обсуждались Одв-
нбм [1969а] и Фридом [1969а].
10 Дж. Оден
146
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
A0.98а) в матричной форме
-1
1
1
_1
xn
xu
x3i
rft+l, 1
X2Z
X3Z
-pft+l, 2
xlh -,
... X2h
... X3h
xh+l,k_
' do '
-ah-
=
¦ vl -
u3
.uk+\ .
ИЛИ
Са = и,
, A0.986)
A0.98в)
где С — матрица коэффициентов уравнений A0.486) размера
(к + 1) X (к -f- 1). Уравнение A0.98в) будет иметь единственное
решение при условии, что матрица С невырождена. Таким обра-
образом, для единственности требуется, чтобы
det С Ф 0. A0.99)
Условие A0.99) можно трактовать как условие того, что к -f- 1
узловых точек х^ не лежат в одной (к — 1)-мерной гиперплоскости.
Предполагая, что A0.99) выполнено, решаем уравнение A0.98в)
и получаем
а = С-% A0.100)
Соотношение A0.100) позволяет линейно выразить коэффициенты
а0, аг, . . ., ah через узловые значения uN локальной функции
и координаты узловых точек хт. Подставляя A0.100) в A0.97),
после упрощений получаем искомую локальную аппроксимацию х):
и (х) = uNtyN (х), N = 1, 2, . . ., к + 1, (Ю.101а)
где в рассматриваемом случае интерполяционные функции линей-
линейны относительно локальных координат хг:
yN (х) = aN + bmxl. A0.1016)
Величины aN и bNi с помощью A0.100) выражаются через коорди-
координаты узлов хт. В частности, если Сц (г, / = 1, 2, . . ., к + 1) —
элемент г-й строки и /-го столбца матрицы С, то 2)
aN = -^-cofactor (Cm),
A0.102а)
A0.1026)
х) Такие линейные интерполяционные функции иногда называются
барицентрическими координатами симплекса. См. Гройб [1963, стр. 253].
2) Ниже cofactor означает «алгебраическое дополнение». — Прим. ред.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 147
где
С = det С. A0.102в)
Функции tyN (x), х ? ге, обладают следующими свойствами:
ft+i
^(х)>0, S *wW = l- A0.103a, б)
ЛГ=1
Кроме того, для любой узловой точки хм ? гв
i|>w(x«O = e?f. A0.103b)
Кратко суммируем важные свойства симплексной модели.
1. Число Ne узловых точек симплексного элемента на единицу
больше размерности пространства, в котором располагается
элемент (Ne = к -\- 1).
2. Локальные аппроксимации и (х) [и интерполяционные функ-
функции гр№ (х)] являются линейными функциями локальных
координат хх.
3. Выполняются требования полноты и непрерывности. Линей-
Линейная функция в %h единственным образом определяется
заданием ее значений в к -f- 1 точках, находящихся в общем
положении. Поскольку локальные функции и (х) линейны
на границах элемента, соединение двух симплексных эле-
элементов вместе сводится к заданию одинаковых узловых
значений соседних локальных аппроксимаций в двух точках
на их межэлементной границе. Значит, локальные поля
совпадают во всех точках межэлементных границ, а гло-
глобальные базисные функции Фд (х) всюду непрерывны. Чтобы
проверить, что A0.101) может представлять постоянные
значения м(е> (х) на элементе, достаточно положить каждое
узловое значение uN = X, где к — произвольная постоянная.
Тогда в силу A0.1036) и (х) = X для всех х 6 ге.
4. Требование непрерывности, упомянутое в C), выполняется
при произвольной ориентации элемента, т. е. для выполне-
выполнения требований непрерывности не обязательно, чтобы грани-
границы элемента были координатными линиями. (Как будет видно
впоследствии, этим свойством обладают не все соответствен-
соответственные конечные элементы.)
5. Интерполяционные функции гр№ (х) удовлетворяют соот-
соотношениям A0.103) (это свойство, конечно, присуще не только
симплексным моделям).
Рассмотрим некоторые частные виды интерполяционных функ-
функций A0.1016) для пространств размерности к ^ 3.
10*
148
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рис. 10.1. Симплексные конечные элементы, Ne = к + 1.
Симплекс в трехмерном пространстве. В трех-
трехмерном эвклидовом пространстве симплексная модель представляет
собой тетраэдр с четырьмя узлами (см. рис. 10.1, а). Имеем
С =
X
i2
1 а* Ж22 Я23
1 я31 я32 я33
1 я41 я42 ж43
A0.104)
aJV="
6C
— 1
Rm
A0.105a)
A0.1056)
где Ej/fc и bnrst соответственно трех- и четырехмерные перестано-
перестановочные символы, N, R, S, Т — 1, 2, 3, 4; i, j, k, m = 1, 2, 3;
P(^m = iH», если i = m, и p"™ = 1, если i Ф m. Далее,
| С | = | det С | = 6v, A0.105b)
где v — объем тетраэдра.
Симплекс в двумерном пространстве. В двумерном
эвклидовом пространстве симплекс — это треугольник с тремя
узлами (см. рис. 10.1, Ь). Имеем
A0.106a)
—x2ixi2
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 149
[bNt] = -тт
-32 -12 ~11 ,.31
а;12—Ж22 ж21 —а;11
A0.1066)
= det С = det
х22
х32
A0.106»)
Если узлы пронумерованы по правилу правой руки, то А
в (Ю.Юбв) — площадь треугольника.
Интерполяционные функции tyN (x), соответствующие двумер-
двумерному симплексу, показаны на рис. 10.2. Если эти три функции
сложить, то в силу A0.1036) получим постоянное значение на всем
треугольнике. Если же каждую предварительно умножить на
узловую величину uN и уже после этого сложить, то получим
изображенное на рис. 10.2 локальное приближенное представле-
представление и (х), даваемое формулой A0.101а).
Рис. 10.2. Интерполяционные функции i!pN (x) для двумерного симплекса.
150 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Что касается погрешности симплексных аппроксимаций в %г,
то Синг 1) доказал, что если конечноэлементная аппроксимация
к<|!) совпадает в узлах с заданной функцией и, то
A0Л07>
где К — граница | и,и |, бв — диаметр элемента, а 0 — наиболь-
наибольший из углов треугольника. Этот результат можно рассматривать
как предостережение при построении равномерных измельчений
симплексных моделей: избегать длинных, заостренных треугольни-
треугольников с малыми внутренними углами. Очевидно, что равносторонние
треугольники дадут по оценке A0.107) наименьшую погреш-
погрешность.
Симплекс в одномерном пространстве. В одномер-
одномерном эвклидовом пространстве симплексная модель состоит из
двух узлов, соединенных отрезком прямой линии (рис. 10.1, с).
Если положить х1 = х, то
_i ! A0.108)
где L = xz—я1. Значит,
!>,(*) = ?!=?¦, ,|,8 (*) = ?=?!. (Ю.109)
Это — знакомые нам линейные интерполяционные функцци Лаг-
ранжа G.60).
Криволинейные симплексные модели. Во всех при-
приведенных соотношениях, относящихся к симплексным моделям^
характер локальных координат хг совершенно произволен, и поэто-
поэтому нет никаких оснований требовать, чтобы они были прямоуголь-
прямоугольными декартовыми. Действительно, х1 может быть произвольной
криволинейной системой «вмороженпых» координат, а простран-
пространство, в котором расположен конечный элемент, может быть неэв-
неэвклидовым. В общем случае можно использовать криволинейные
х) Синг [1957, стр. 211]. Подобные результаты были получены Ки [1966].
Ему удалось показать, что для трехмерного симплекса
где 9 — наибольший из углов, образованных ребрами любой треугольной
грани, а ф — наибольший из углов, образованных содержащей угол 9 гранью
с остальными гранями тетраэдра.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 151
/С=3
к=г
(с)
Рис. 10.3. Криволинейные симплексные модели.
симплексные модели типа показанных на рис. 10.3. Функции и (х)
в этом случае линейны относительно криволинейных координат х\
и непрерывность на межэлементных границах сохраняется.
Естественные координаты. При построении локаль-
локальных интерполяционных функций часто бывает удобно использовать
специальные координаты t,t, называемые естественными или, в слу-
случае двумерных симплексов, координатами площади *). В fc-мерном
пространстве координатами t,t служит набор к -\- 1 чисел, опре-
определенных так, чтобы они обладали свойствами
^(xw) = 6f, Ci + C»+... + bm=l. A0.110)
Таким образом, ?,¦ = const является параметрическим уравнением
гиперплоскости, параллельной г-й грани элемента, а ?; = 0 есть
уравнение самой грани. Естественными координатами узлов
1, 2, . . ., Ne = к + 1 являются A, 0, 0, . . ., 0), @, 1,0,.. ., 0),
. . ., @, 0, 0, . . ., 1). Для треугольного элемента естественными
координатами центра тяжести 0 являются ?х = AJA, '?2 = AJA
и ?3 = А3/А, где Аг, А2, Ая — площади частей треугольника,
образованных сходящимися к точке 0 от узлов 1, 2, 3 линиями
[т. е. Аг — площадь треугольника B, 0, 3), А^ — треугольника
C, 0, 1), А3 — треугольника A, 0, 2)], а А = Аг + А2 + А3 —
общая площадь треугольника. Это объясняет использование тер-
термина «координаты площади». Ясно, что эти координаты являются
х) См., например, Тэйг и Керр [1964], Аргирис [1966а], Зенкевич и Ченг
[1967], Стриклин [1968] и Фрид [1969а]. В общей постановке этот вопрос
рассмотрен Фридом [1969а], а вопросы использования таких коордппат для
различных типоа конечных элементов исследованы Фелиппой [1966].
152 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
безразмерными и «вмороженными», т. е. не зависящими от выбора
внешних систем отсчета и формы элемента.
Как указано Фридом [1969а], полезно ввести линейное аффин-
аффинное преобразование координат ?* в х1 посредством соотношений
*' = У%, * * 1, 2, .... ft, / = 1, 2, .... ft, ft +1 A0.111а)
и
*"+i = Ci 4- С* + • • • 4- Cft+i. A0.1116)
Тогда можно определить матрицу Ctj (i, j = 1, 2, . . ., к -\- 1)
со свойствами
С„ = -^1 = 1, Ci+itiJ'^- = yi}, A0.112а, б)
det Са = С, A0.112в)
где С — определитель A0.102в). Далее, можно показать [Фрид,
1969а], что если
4^ = -?-cofactor (CMt]), A0.112г)
то
я я
i Л О Ь 7 Л О 1г I ^ МП А АЧ\
I = J.,Z, ...,/?, / ^ 1, ^, . . ., К -j- 1. ^ 1U. х LO)
±г = Аи±, i = l,2,...,A,
При к ^ 3 имеем Ац = ЛЦ)а^, где Аф—площадь (длина)
/-грани элемента, а ац — направляющий косинус угла между xtl
и нормалью к А]. Можно показать, что отсюда следует такое
выражение для производной по направлению единичного векто-
вектора п:
± = ±А}щаФ A0.114)
Кроме того, как было отмечено тем же Фридом, полное множество
полиномов степени М может быть получено перебором всевозмож-
всевозможных комбинаций iu i2, . . ., ip в членах вида Ц1Ц2 ¦ ¦ ¦ ?№+1 с
h ~Ь 'г + • • • + ip = М. Это обстоятельство можно использо-
использовать при интегрировании полиномов относительно естественных
координат по конечным элементам х).
10.4.2. Комплексные модели. Комплексными моделями мы будем
называть конечные элементы с Nе > * + 1, с помощью которых
можно добиться межэлементной непрерывности, не требуя, чтобы
границы элемента были координатными линиями 2).
1) См. Стриклин [1968].
8) Такие элементы использовали Вёбеке [1965], Аргирис [1965а, 19656,
1965в], Фелиппа [1966], Зенкевич и Ченг [1967] и другие.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 153
(с)
Рис. 10.4. Комплексные конечные элементы.
=1, Ne-Z
Например, можно использовать квадратичную аппроксимацию
и (х) = а0 4- а&* + а,%ркз?, A0.115а)
где а{] = а л и ?, / = 1, 2, . . ., к. Соответствующие интерполя-
интерполяционные функции имеют вид
Мрп (х) = aN + бм*1 4- с^яУ, A0.1156)
где cNtj = с^,-. Коэффициенты aN, bNt, cNij, как и ранее, опре-
определяются в результате решения Ne уравнений, соответствующих
вычислению значений A0.115 а) в каждой узловой точке.
При квадратичной аппроксимации можно использовать эле-
элементы такой же формы, как и в симплексной модели, но с дополни-
дополнительными узлами. Например, в качестве трехмерного комплекс-
комплексного элемента можно использовать криволинейный тетраэдр типа,
показанного на рис. 10.4, а. В этом случае Ne = 10, к = 3. Верши-
Вершины тетраэдра являются узловыми точками, а расположение
остальных шести узлов достаточно произвольно (оно должно лишь
быть таким, чтобы определитель из элементов матрицы С не обра-
обращался в нуль). Удобно расположить эти узлы симметрично в сере-
серединах ребер тетраэдра.
Для двумерной модели Ne = 6 и можно использовать тре-
треугольный элемент с шестью узлами, показанный на рис. 10.4, Ъ.
Отметим, что вдоль каждой стороны функция и (х) квадратична.
Поскольку квадратичная функция единственным образом опре-
определяется тремя независимыми величинами, при соединении сосед-
соседних элементов непрерывность сохраняется. Зламал [1968] пока-
вал, что для такого элемента
154 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где м,{ и uf] совпадают в узлах, К — верхняя граница для | ы, ijh \%
Зе — диаметр элемента, а 9 — наибольший угол в треугольнике.
В одномерном случае Ne = 3 и можно использовать элемент,
показанный на рис. 10.4, с. Отметим, что связывания таких одно-
одномерных элементов в концевых точках недостаточно для определения
квадратичной функции в элементе. В этом случае необходимо
задать значение локальной аппроксимации во внутренней узловой
точке. То обстоятельство, что один из узлов обязательно является
внутренним, существенно отличает одномерную комплексную
модель от подобных моделей в пространствах более высокой раз-
размерности.
10.4.3. Сложные1) модели. В сложных моделях для достиже-
достижения межэлементной непрерывности нужно, чтобы границами
элемента были координатные линии. Приведем несколько при-
примеров.
Билинейная аппроксимация 2). Для криволинейного
злемента в|2с четырьмя узлами {рис. 10.5а)
и (х) = а0 + аах°- + ЪхЧг. A0.116)
Четыре коэффициента а0, аи а2, Ъ определяются из условий
lxNZ, A0.117)
где а = 1, 2; N = 1, 2, 3, 4 и по N суммирования нет. Решая
A0.117) и подставляя результат в A0.116), как обычно, получаем
соотношение вида и (х) = uNtyN (x). В рассматриваемом случае
^ (х) = aN + bNax« +7Nxlx2, A0.118a)
где
^x^ys, A0.1186)
bNa = 4- zNMRsZataMxRPys, A0.118в)
х) В оригинале multiplex. — Прим. ред.
2) Билинейные аппроксимации в прямоугольных координатах исполь-
использовали Галлагер, Раттингер и Арчер [1964], Аргирис [1965в], Зенкевич и Ченг
11967] и др. Криволинейные элементы были описаиы Эргатудисом, Айронсом
и Зенкевичем [1908а] и Оденом [1969а]. Криволинейные неэвклидовы били-
билинейные аппроксимации использовались Вемппером, Оденом и Кроссом
11968].
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 155
(Ь)
Рис. 10.5. Сложные конечные элементы.
Здесь ys = ж81^82. (суммирования нет), ам — 1, М = 1, 2, 3, 4»
еар и SjvjfHS — перестановочные символы, а
'1 хи xi2 ц
= det
1 x2i
1 x3i
у2
x®-
Заметим, что выражение A0.117) липейпо на всех границах
элемента. Значит, при связывании элементов в узлах линейная
функция определяется единственным образом и аппроксимацион-
ное поле получается непрерывным на всех границах элементов.
Трилинейная аппроксимация. Для криволинейного
параллелепипеда с восемью узлами в Шн (рис. 10.5, Ъ) положим х)
и (х) — а0 -\- atx + aijXixJ + Ьхххгхгш A0.119)
где ai] = а^г и а,-; ^= 0 при i = /. Восемь коэффициентов опреде-
определяются из условий
„N = а0 + агхт + ai}xNixNJ + bxmxN2xN3 A0.120)
х) Впервые такие аппроксимации для прямоугольных «брусков» псполь-
вовались Молошем [19636]. См. также Ки [1966], Зепкевич и Ченг [1967]
и Оден [1969а].
156 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ
(суммирование по N не производится), так что и (х) можно записать
в виде
и (х) = uN$N (х), N = 1, 2, . . ., 8. A0.121)
Если начало системы координат расположено в центре элемента, то
A0.122а)
-f(l +?)(!- Л) A-0.
|~ С),
где
?= —, Л = 4г, Z = — ; A0.1226)
я о с
предполагается, что границами элемента являются плоскости
х1 = ±а, я2 = ±Ъ ш х3 = ±с Отметим, что функция и (х) линей-
линейна на всех границах элемента, так что непрерывность на меж-
межэлементных границах при связывании элементов обеспечена.
Призматические элементы. Локальные аппроксима-
аппроксимации вида г)
и (х) = а0 + atx% + х3 (сх1 + dx2), A0.123а)
\pN (x) = aN + ^jvi-z1 + cNxlx3 + d^-A:3 A0.1236)
соответствуют призматическим элементам типа, показанного на
рис. 10.5, с.
Лараллелепипеидалъные элементы. Для криволи-
криволинейных параллелепипеидальных элементов с двадцатью узлами
(см. рис. 10.6, а) применяются локальные аппроксимации вида 2)
и (х) = по + агх1 + аг,хУ + (z1J (b2x* + Ь3х3) + (л;2J (с^1 + с3х3) +
4- (х3J (d^ + d2x2) + xWx3 (e0 + е(хг), A0.124)
J) См. Ки [1966].
2) См. Эргатудис, Айронс и Зенкевич [1968а, 19686].
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 157
(«О ~ W
Рис. 10.6. Криволинейные параллелепипеидальные конечные элементы.
где аг] — пц. Для элемента с тридцатью двумя узлами1) (рис. 10.6,6)
используются аппроксимации, содержащие наряду со всеми чле-
членами A0.124) дополнительно члены
П
+ h
A0.125)
где git = 0 при i Ф j.
10.4.4. Изопараметрические элементы. Построение криволи-
криволинейных конечных элементов, описанное в предыдущем пункте,
основано на предположении, что система локальных внутренних
криволипейных координат известна заранее и что локальные поля
могут быть аппроксимированы соответствующими полиномами
относительно этих координат. Однако во многих задачах границы
столь сложны, что практически невозможно подобрать систему
координат, в которой они были бы координатными линиями.
Границы элементов в лучшем случае могут служить только аппро-
аппроксимацией действительных криволинейных границ. Наилучшая
аппроксимация криволинейных границ достигается с помощью
криволинейных изопараметрических конечных элементов 2). Пост-
Построение таких элементов основано на идее подбора полиномиальных
кривых, проходящих через заданные точки на границе. Подбор
осуществляется практически так же, как и аппроксимация локаль-
локальной функции и (х) на каждом элементе.
Предположим, например, что х1, хг, х3 — система прямоуголь-
прямоугольных декартовых координат в %3. Преобразование х1 в произволь-
х) См. работы, указанные в предыдущем подстрочном примечании.
2) Одпп тип сдвиговых изопараметрических элементов был использован
Тэпгом [1961]. Эту идею обобщили и подробно разработали Эргатудис [1966],
Эргатудис, Айронс и Зенкевич [19С8а, 19686]. См. также Ахмад, Айронс
и Зенкевич [1969] и Фелиппа и Клаф [1968].
158 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ную систему криволинейных координат осуществляется соотно-
соотношениями
Б* = ? (х\ х\ х2), A0.126)
причем предполагается, что существует обратное преобразование
х* = х1 &\ %\ Г). A0.127)
В практических приложениях координаты хг могут быть локаль-
локальными координатами типичного конечного элемента, однако форма
соотношений A0.127), требуемых для описания заданной границы,
может быть очень сложной и к тому же меняться от элемента
к элементу. Подберем аппроксимацию преобразования A0.127),
которую можно было бы использовать для границ различной
формы. Естественно обратиться к полиномиальным аппроксима-
аппроксимациям вида
хг = а* + 4l} + ajhl%h +.... A0.128)
Поступая таким же образом, как и при построении локальных
аппроксимаций и (х), вычисляем A0.128) в конечном числе Ne
узловых точек, расположенных, как правило, на границе элемен-
элемента, и приходим к системе уравнений
хт = ai + a%m + a)hlNilim +..., A0.129)
где хт и ?w* — соответственно декартовы и криволинейные
координаты узла N. Решая систему A0.129) и подставляя резуль-
результат в A0.128), получаем такую аппроксимацию нашего преобра-
преобразования координат:
** = $n A) *т- A0.130)
Интерполяционные функции г|з^ (?) являются полиномами по ?*
и удовлетворяют обычным условиям:
Ne
2гЫЮ = 1, ^A)>0. A0.131а, б)
Эти же самые интерполяционные функции г|з^ (|) можно
использовать и для аппроксимации локального поля и (|) на
элементе: и (|) = uNtyN (|).
Легко проверить, что функции tyN (|) автоматически обеспе-
обеспечивают возможность представления линейных вариаций (и посто-
постоянных первых производных) функции и (%) на элементе *). Возьмем,
например,
и = а0 + а,х1 = и1* г|5„ (|). A0.132)
См. Эргатудис, Айронс и Зенкевич [1968а].
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
Рис. 10.7. Примеры изопараметрических конечных элементов
(по Эргатудису, Айронсу и ЗенкевичуЦ1968а]).
Поскольку uN = а0 + а{хтх имеем
3
W-1
A0.133)
Первый член в силу A0.131а) равен а0, а второй в соответствии
с A0.130) равен aix%, т. е. A0.132) представляет собой тож-
тождество.
Эргатудис, Айронс и Зенкевич [1968а] использовали различные
полиномиальные аппроксимации для получения криволинейных
элементов типа показанных на рис. 10.7. Можно использовать
и изопараметрические элементы типа показанных на рис. 10.6.
Доказано, что функции, соответствующие элементам, изображен-
изображенным на рис. 10.7, в общем случае удовлетворяют требованиям
полноты, обеспечивают получение постоянных производных и удо-
удовлетворяют условиям непрерывности на межэлементных грани-
границах. Для представленного на рис. 10.7, а элемента соотношение
A0.128) принимает вид
xh = ah0 +
(PJ, A0.134>
где i, j, к = 1, 2, a^ = а& и предполагается, что уравнения
|l = ±1 определяют границы элемента. Тогда
1* (I) = т A4- l^Ni) A + ?f2)-4 [1 -(S1J! [
? *1] [1-(?)*], (Ю.135)
N = 1, 2, .. .x 8. В случае элемента (Изображенного на рис. 10.7, Ъг
¦wA) = ж A + П*1) A + Е^2) {9 [(I1J + (I2J] -10} A0.136а)
160
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
для N = 1, 2, 3, 4 (только для узлов в углах). Для узлов, распо-
расположенных в точках ?1 = ±1, |2 = ±-а", имеем
О
), A0.1366)
а в точках |2=±1, ^ = ±-5-
yN (|) = *- [1 _ (|iJ] (i + |i^i) A4. ^2) A0.136b)
Таким образом, A0.128) в этом случае принимает вид
\A1)Ч2 +
K?2, A0.137)
и выражения для т|з^ (^) аналогичны. Если элемент имеет форму,
показанную на рис. 10.7, с, то, в матричной записи,
A0.138а)
где в случае расположения узлов в точках ?г = 0, ±1
A0.1386)
10.4.5. Примеры элементов высших порядков. В большинстве
приложений, рассматриваемых в последующих параграфах, мы
ограничиваемся копечноэлементными представлениями первого
порядка. Однако для полноты картины приведем ряд примеров
конечноэлементных представлений высших порядков1).
Представления высших порядков в Щ1. В случае одномерного
пространства мы используем, конечно, обычные интерполяцион-
интерполяционные функции Эрмита, рассмотренные в § 8 (см. формулы (8.23) —
х) Ряд примеров элементов высших порядков был рассмотрен Фелиппой
[1966], который классифицировал их по признаку «С-д-совместимости».
По этой классификации элемент относится к С-О-совместному типу, если на
межэлементных границах непрерывны только сами локальные функции.
Если же непрерывны и первые q частных производных, то элемент считается
C-q-совместимым. В соответствии с определением 10.2 элемёпт С-д-совмести-
мого типа является q-соответственным. Кроме того, Фелиппа классифициро-
классифицировал элементы по признаку существования внутренних узловых точек, числу
степеней свободы и т. д. См. также Фелиппа и Клаф [1968J.
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 161
(8.26))г например для представления второго порядка
и (х) = а0 + агх 4- а2х2 + dgX3, A0.139)
или
и(х) = и"Ъ%(х) + иЦу%(х), tf=l,2, A0.140)
где
A0.141)
Ь = хг—х1. A0.142а, б)
Представление третьего порядка на одномерном элементе с дву--
мя узлами получается при использовании полинома пятой сте-
степени х):
и (х) = а0 + ахх + а2х2 + пдх3 -J- а4ж* + а5л;5. A0.143)
В каждой узловой точке задаются и (х), du (x)/dx и d2u (x)/dxz.
В общем случае для одномерных элементов с двумя узлами
представление га-го порядка получится, если взять в качестве и (х)
полный полином степени га -f- 2 и задать в обеих узловых точках
и (х), du (x)/dx, . . ., dnu {x)ldxn.
Представление второго порядка в Щ3. Функция и(х)
и ее первые частные производные задаются в каждой из четырех
вершин тетраэдра, и и (х) берется в виде полного полинома третьей
степени (рис. 10.8аJ):
и (х) = а0 + сцхг + al}Xlxi + ai/j^Vx*, A0.144)
где i, j, k = 1, 2, 3; a^ = aji, aijk = atkj = ajik- Независимых
параметров а0, . . ., а,цк двадцать, а узлов пока 4. Пятый узел
можно расположить произвольно, но обычно удобно помещать
в его центре тяжести.
Представление второго порядка в %а. Аппроксимацию
второго порядка функции и (х1, х2) на треугольной области можно
построить, задавая и (х1, х2) в четырех узловых точках и первые
частные производные и (х),а в трех узловых точках — вершинах
х) См. Ланхар и Чу [1968].
2) См., например, Аргирис [1965а].
11 Дж. оден
162
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рис. 10.8. Конечные элементы высших порядков.
треугольника (рис. 10.8Ь) '). В этом случае Ne = 4, а и (х) —
полный полином третьей степени:
и (х) = а0 + atxl + аХ1 (ж1J + а12х1х2 + а22 (х2J +
+ «in (х1K + «ii2 {х1У х2 + а122^ (X2)* + а222 (я2)». A0.145)
Окончательно аппроксимация имеет вид
и (х) = uNty% (x) + u^ityx (x), A0.146)
где N = 1, 2, 3, 4; i = 1, 2; и для любого х
ф!(х) = 02). A0.147)
х) Такие элементы использовались Вестом и Оденом [1963]. Подробное
обсуждение этого и сходных элементов можно найти у Фелиппы [1966].
См. также Айронс [1966], Точер и Харц [1967] и Оден, Ригсби и Корнетт
[1969].
2) Или можно положить г|?2 (х) = 0 и в качестве десятого условия задать
производную duldn по нормали к границе в четвертой узловой точке, рас-
расположенной на границе. Введение таких «плавающих» граничных узлов,
в которых задаются значения функции или ее нормальной производной,
позволяет строить разнообразные модели, в которых связываются разно-
разнотипные элементы с различным числом узлов. См. Фелиппа [1966] и Фелиппа
и Клаф [1968].
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 163
Размещение четвертого узла произвольно, но логично поме-
поместить его в центре тяжести.
Зламал [1968] доказал, что если конечно элементная аппрокси-
аппроксимация и(е) совпадает с непрерывно дифференцируемой функцией,
у которой существуют четвертые производные во всех узловых
точках (три вершины и центр тяжести), и если производные функ-
функций Ф~> и и совпадают, то
*6' и l"-"(e)l<-drF*6«. <10-148a>
где 8 — наибольший из углов треугольника, К — верхняя грани-
граница для | uti]hi |, а бе — диаметр элемента.
Представление третьего порядка в %г.~ Представ-
Представление третьего порядка на треугольном элементе в двумерном про-
пространстве получается при использовании полного полинома пятой
степени х) относительно х1 и х2:
и (х) = а0 + а%хг + аихгх' + ai]kxlx'xh +
+ атпх^хнхт + S|ito»jVAV. A0.1486)
Учитывая зависимости между выписанными членами, устанавли-
устанавливаем, что в таком полиноме пятой степени 21 независимый пара-
параметр. Двадцать одно условие получается в результате задания и,
u,i, и,2, и,и, и,12 и и,,22 в трех вершинах треугольника и нормаль-
нормальных производных ди/дп в средней точке каждой иэ сторон. В этом
случае и имеет вид
и (х) = и»$% (х) + uN^ (x) + uNirt% (x) + uNn<pN, (x), A0.149)
где N = 1,2, 3, N' = 4, 5, 6, (pN' (xN) = 0, dyN, (хм')/дп = 6Jv'-
Вершины пронумерованы цифрами 1, 2, 3, а середины сторон —
цифрами 4, 5, 6.
Зламал [1968] показал, что
где | i | ^^ 4, а ЛГ — верхняя граница для шести производных от ц-
х) Такой элемент впервые был предложен, по-видимому, Витхумом
[1966]; для исследования упругих пластин его использовали Босхард [1968],
Белл [1969], Аргирис, Фрид и Шарпф [1968в], Аргирис и Бак [1968]. Свой-
Свойства сходимости для этого элемента исследовал Зламал [1968]. Возможны,
конечно, представления более высоких порядков. Брэмбл и Зламал [1970],
например, предложили общий метод полиномиальных аппроксимаций
на треугольниках, в которых полином относительно х1 и х2 степени Am + 1
определяется заданием всех его производных до порядка 2т в вершинах,
производных порядка 2го — 1 в центре тяжести и производных по нормали
в г -\- 1 равностоящих узловых точках на каждой стороне треугольника
(г = 1, 2 т).
И*'
{64 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Замечания о других элементах высших поряд-
порядков. Наиболее широко конечноэлементные модели высших поряд-
порядков использовались в связи с приложениями к задачам изгиба тон-
тонких пластин и оболочек. При использовании теорий, основанных на
гипотезах Кирхгофа — Лява, деформации элемента пластины или
оболочки описываются полем перемещений точек срединной поверх-
поверхности и первыми производными этого поля. Вследствие этого для
непрерывности всего поля перемещений требуется не только непре-
непрерывность перемещений срединной поверхности, но и непрерывность
первых частных производных г). Это в совокупности с требовани-
требованием, что модель должна обеспечивать возможность описания случая
постоянных кривизн 2), приводит к значительным трудностям
построения соответственных конечных элементов 3). Эти трудно-
трудности — один из многочисленных примеров того, как упрощающие
предположения (например, гипотезы Кирхгофа — Лява, предпо-
предположение о несжимаемости и т. д.), предназначавшиеся первона-
первоначально для того, чтобы облегчить применения теории, существенно
усложняют построение удобных конечноэлементных моделей.
Практически очень часто при использовании более фундаменталь-
фундаментальной (неупрощенной) теории проще строить приемлемые конечно-
элементные модели.
В качестве примера полностью совместимой двумерной конечно-
элементной модели третьего порядка, соответствующей прямо-
прямоугольному элементу пластины (см. рис. 10.8, с) или криволинейно-
криволинейному четырехугольному элементу оболочки (Богнер, Фокс и Шмит
[1967]), приведем функцию
3 3
A0.151)
*) Проблему непрерывности можно обойти, отказавшись от гипотез
Кирхгофа — Лява и используя аппроксимации первого порядка перемеще-
перемещений и углов поворота. См., например, Мелош [1966], Утку [1966], Утку
а Мелош [1967], Вемпнер, Оден и Кросс [1968] и Оден и Вемпнер [1967].
2) Это требование, по-видимому, впервые было выдвинуто Айронсом
и Дрейпером [1965] и подробно рассмотрено в статье Бейзли и др. [1966].
См. примечание на стр. 134.
3) В первых работах по методу конечных элементов для тонких пла-
пластин требованиями непрерывности и полноты, включая требования возмож-
возможности описания (в пределе) постоянных деформаций (кривизн и кручений),
как правило, пренебрегали, и было предложено много недопустимых эле-
элементов. Интересный обзор ранних работ сделан Фелиппой [1966, стр. 215—
219]. Сравнение некоторых прямоугольных и треугольных элементов, при-
применявшихся до 1965 г., проведено Клафом и Точером [1966]. Бейзли, Ченг,
Айронс и Зенкевич [1966] использовали несоответственные треугольные эле-
элементы, а Клаф и Точер [1966] получили полностью совместимый треуголь-
треугольный пластинчатый элемент, применив композицию трех кубичных полиномов.
Полностью совместимый прямоугольный пластинчатый элемент был построен
Богнером, Фоксом и Шмитом [1966]. Ряд элементов для пластин и оболочек
был предложен при аппроксимации напряжений или напряжений и переме-
перемещений вместе; см., например, Бест [1963], Пайэн [19646], Вёбеке [1966], Герр-
ианн [1966] и Пайэн и Тонг [1969а, 19696].
10. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ 165
Шестнадцать коэффициентов Crs определяются таким образом,
чтобы и (х), ди (х)/дхг и д2и (х)/дх1 дх2 принимали заданные значе-
значения в четырех узлах, размещенных в углах. Интерполяционными
функциями в этом случае являются двумерные интерполяционные
функции Эрмита, и и (х) можно записать в виде
и (х) = un$n (х) + «>n (x) + uN12^2 (х), A0.152)
где N = 1, 2, 3, 4. Выражения для функций ¦$%, tyh, г]$ в орто-
ортогональных координатах можно найти в статье Вогнера, Фокса
и Шмита [1967].
10.4.6. Дополнительные замечания о конечноэлементных моде-
моделях. В заключение этого параграфа сделаем ряд замечаний общего
характера относительно свойств конечноэлементных моделей.
Замечание 1. Дополнительные параметры. На-
Напомним, что в соответствии с G.7) локальная аппроксимация
в общем случае имеет вид
u(x) = Y(x, it"), A0.153)
где функция ? ( ) должна удовлетворять условию
? (хм, uN) = uM. A0.154)
Мы использовали специальную линейную форму
u(x) = u^N(x), A0.155)
требуя, чтобы
4>w(x*) = 6#. A0.156)
Однако условия A0.154) будут выполнены и в том случав!
если положить г)
и (х) = u^N (x) + х (х), A0.157)
где % (х) — любая функция, обращающаяся в нуль в узлах:
X (х") = 0. A0.158)
Пайэн [1964а] показал, что можно получить уточненные конечно-
элементные модели, задав функцию % (х) в виде полинома
X (х) = Ъ0+ Ъгх' + bijx'x3 + .... A0.159)
Например, при билинейной аппроксимации A0.116) можно взять
и (х) = иРЦргт (х) + я*з* (а - х1) (Ъ - *2) (Ьо "+ ^х1 +
+ Ь3 (х1J +...), A0.160)
х) Пример аппроксимации, обладающей таким свойством, приведен
в подстрочном примечании на стр. 60.
166
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рис. 10.9. Неэвклидовы симплексные,
комплексные и сложные конечные элементы.
где а и Ь — длины сторон элемента, а начало системы координат х1
помещено в точке @,0). Дополнительные параметры Ъо, Ъх, Ь2, . . ¦
должны быть определены из вспомогательных условий, связанных
с рассматриваемой задачей (например, условия минимума потен-
потенциальной энергии).
Крахула и Полемус [1968] использовали вместо A0.159) ряды
Фурье, т. е. вместо A0.160) —
+ х*х*(а-х*)(Ь-х*) 2
sin
sin-
A0.161)
m=ln=l
Замечание 2. Неэвклидовы элементы. Еще раз отме-
отметим, что описанные ранее элементы могут рассматриваться не только
в эвклидовых пространствах. Элементы в римановом простран-
пространстве строятся так же легко, если надлежащим образом определено
само пространство. Например, двумерные симплексные, комплекс-
комплексные и сложные элементы на римановой поверхности получаются
с помощью формул A0.106), A0.115) и A0.118), если рассматри-
рассматривать хх как внутренние поверхностные координаты. Эти модели
показаны на рис. 10.9.
Замечание 3. Производные элементы. Часто бывает
удобно строить модели в fc-мерном пространстве, порождаемые дви-
движением (к — 1)-мерной области (или области еще более низкой раз-
Образующая
Рис. 10.10. Примеры производных элементов.
Рис 10.11. Составные призматические конечные элементы)
168
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рис. 10.12. Другие примеры составных конечных элементов.
мерности) вдоль соответствующей образующей в Щк. Например^
конечные элементы для трехмерного тела вращения могут порож-
порождаться поворотом на 2я любого двумерного элемента вокруг оси
вращения х). Узловые точки в (к — 1)-мерном пространстве превра-
превращаются в узловые линии в й-мерном пространстве. Интерполяци-
Интерполяционные функции берут в виде
$N (x, s) = qN (x) / (s), A0.162)
где х ? %к~х, as — производящий параметр. Некоторые примеры
приведены на рис.
10.10.
М См., например, Рашид [1964, 1966], Клаф и Рашид [1965], Вильсон
A965].
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 169
Замечание 4. Составные элементы 1). Отметим, на-
наконец, что путем объединения двух или более базисных элементов
описанных выше типов можно построить множество так называемых
составных элементов. Некоторые примеры представлены на рис.
10.11 и 10.12: призматический элемент, полученный в результате
объединения пяти симплексных тетраэдров (рис. 10.11); четырехсто-
четырехсторонний элемент, полученный соединением четырех треугольных сим-
симплексов (рис. 10.12а); плоский четырехсторонний элемент, образо-
образованный наложением четырех треугольников (рис. 10.12Ь); и четы-
четырехсторонний элемент, полученный в результате соединения четы-
четырех комплексных треугольных элементов (рис. 10.12, с).
И. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
Для того чтобы применять изложенные выше понятия к линей-
линейным или нелинейным задачам, нужно еще располагать средствами
перехода от соотношений, выполняющихся в точке, к соотноше-
соотношениям, выполняющимся в некоторой конечной области. При реше-
решении дифференциальных уравнений в частных производных такой
переход от соотношений в точке к соотношениям в области может
осуществляться с помощью вариационной постановки задачи или
с помощью других методов, таких, как метод взвешенных невязок,
метод Галёркина и т. д. В ряде физических задач он может осу-
осуществляться с помощью локальных и глобальных форм законов
сохранения термодинамики и электродинамики. В этом параграфе
мы рассмотрим несколько примеров.
11.1. КОНЕЧНЫЕ ЭЛЕМЕНТЫ
В ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ ОБЛАСТИ2)
Поскольку описанные ранее конечноэлементные модели в прин-
принципе могут использоваться для аппроксимации функций в про-
пространствах любой размерности, вполне естественно рассмотреть
их применение для представления функций в четырехмерной
пространственно-временной области.
Рассмотрим, например, скалярную функцию Ф (X1, X2, Xs, t).
Ясно, что можно положить X* = t и считать функцию Ф ( ) опре-
1) Составные элементы использовались целым рядом исследователей.
Вот некоторые из них: Висманн [1962], Беккер и Брисбейн [1965], Аргирис
[1966а], Клаф и Точер [1966], Фелшша [1966], Перси [1967], Зенкевич и Ченг
[1967], Хьюджес и Эллик [1969].
а) Использовать конечные элементы в пространственно-временной обла-
области предложили независимо Никелл и Сэкмэн [1968], Оден [19696] и Фрид
[19696]; данное здесь изложение основано на работе Одена. См. также Арги-
Аргирис и Шарпф [1969].
170 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
деленной на четырехмерном пространстве, точки которого задают-
задаются координатами Xх (i = 1, 2, 3, 4). Если область определения
представлена в виде набора из Е четырехмерных подобла-
подобластей, то можно рассмотреть локальную аппроксимацию поля
Ф(е) (х1, х2, Xs, х*) на типичном конечном элементе е:
Ф« = ф^(х), A1.1)
где интерполяционные функции 1р$ (х) являются функциями от
х1, х2, Xs, х*. Вообще говоря, процесс связывания элементов состо-
состоит в простом применении методов, изложенных в § 7. Однако под-
подробности использования моделей при решении задач распростра-
распространения волн, дифференциальных уравнений гиперболического
и параболического типов и т. д. можно разобрать только на кон-
конкретных примерах.
Щвумериые задачи. Для того чтобы проиллюстрировать
использование конечных элементов в пространственно-временной
области, рассмотрим простой пример одномерного упругого стержня
длины L с поперечным сечением А под действием заданной силы Р (t)
на свободном конце или при заданном начальном перемещении
и (х, 0) = / (х). В обычных конечноэлементных моделях продоль-
продольное перемещение и = и (х, t) аппроксимируется одномерными
интерполяционными функциями tyN (x) (N — 1, 2, . . ., Ne),
помноженными на являющиеся функциями времени узловые пере-
перемещения. Мы же сейчас будем считать перемещения и^ значения-
значениями локального поля uW (x, t), определенного в некоторой области
двумерного пространства (х, t). Интерполяционные функции
являются функциями как продольной координаты х, так и време-
времени t, т. е. tyN = ipjv (x, t). Для типичного конечного элемента
uV(x,t) = u?e)qN(x, t). A1.2)
Лагранжев потенциал S для линейно упругого стержня с моду-
модулем упругости Е и массовой плотностью р равен
t V
I I ^1 С /л\ j. /~, /\ Jf /A A O\
« a
где v — объем стержня и —^ Sa (t) и (xa, t) = — Sx (t) и (хг, t) —
a
— ?2 (t) и (x2,t) — потенциал сил S1 (t) и St (t) на концах рас-
рассматриваемого участка стержня. Таким образом, для типичного
конечного элемента е
г\ 1 (е) М N | N (с) /Л 4 /\
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 171
где
dvdt
• \ at 01 ox ox i
t v
%= J J
Р#= j 2 5« (*)!*(*«.*)*• A1.6)
t a
В этих выражениях интегрирование производится по отрезку
времени, «захватываемому» элементом.
Из A1.4) видно, что лагранжиан ? обладает интересным свой-
свойством: в отличие от обычного случая он не является функциона-
функционалом от скорости. Действительно, ? является обычной, функцией
узловых значений перемещений, которые в принятой нами поста-
постановке не зависят от времени. Однако принцип Гамильтона х)
использовать все равно, конечно, можно, так что
б^е) = -Йг «4 = 0, A1.7)
а мы получаем
aSfVw + P# = 0. A1.8)
Связывание элементов в общую модель осуществляется обычным
для двумерных конечноэлементных моделей способом.
Одномерные волны. Важно отметить, что техника решения
записанных выше конечноэлементных уравнений совершенно
не такова, как в задачах эллиптического типа. Уравнение A1.8)
есть конечнозлементный аналог гиперболического волнового урав-
уравнения
где а —
Для иллюстрации этой техники рассмотрим простой пример,
в котором локальное поле задано в виде линейной симплексной
аппроксимацииз
A1.10)
где а, Ъ% с — постоянные и N = 1, 2, 3. В этом случае конечный
элемент представляет собой треугольник в двумерном простран-
х) Который правильнее было бы называть принципом Гамильтона —
Остроградского.— Прим. ред.
172
ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
u(r,t)
Рис. 11.1. Конечные элементы в пространственно-временной области,
стве, показанный на рис. 11.1. Видно, что
^1 (*> t) = -??¦ [(Xzt3—X3t2) + (h— t3) X + (X3—Xz) t],
^ -t2)x+ (xz -Xi) t],
где A — площадь элемента в плоскости х, t. Например, для заштри-
заштрихованного элемента на рис. 11.1 мы с помощью A1.11) и A1.8)
устанавливаем, что при такой довольно грубой аппроксимации
локальные уравнения принимают вид
=4) - 4>- ^ D) - 4))>
A1.12)
где Pn — —k2pN/ApA и К2 = k2a2/h2.
Предположим, что и @, t) = и (L, t) = 0, и (х, 0) = / (х)
и ди (х, O)fdt = 0 — заданные краевые и начальные условия и что
используется система конечных элементов, изображенная на
рис. 11.2. Решение осуществляется следующим образом:
1. Принципиальным моментом является то, что каждый раз
следует рассматривать только один ряд элементов (первый
ряд соответствует промежутку 0 ^ t <J к, второй — проме-
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
173
u{x,t)
.**A^i<'~*
/
Рис. 11.2. Пример распространения решения во времени.
зкутку к <! t <J 2/с и т. д.). Глобальные значения С/л пере-
перемещений граничных узлов в соответствии с краевыми усло-
условиями приравниваются нулю: U1 — U6 (=Un = Ule =
= ...) = 0, U5 = U10 (=U15 = U20 = ...) = 0. Перемеще-
Перемещения внутренних узлов, соответствующих t = 0, принимают
заданные значения, т. е. U2 = f (h), Us = / Bfe), C/4 =s
= / (ЗА) и т. д.
2. Поскольку перемещения С/4, 77s, ?7* принимают заданный
значения, соответствующие глобальные обобщенные
«силы» (сопряженные переменные) Р2, Р3, Pi обращают-
обращаются в нуль. Неизвестными в получающихся уравнениях
P2{U\ IP) = P,(IP, U*) = Pk(U*, C/8) = 0 A1.13)
являются узловые значения W, Ua, U9, характеризующие
эпюру перемещений через к секунд. Поскольку каждое из
уравнений A1.13) содержит только одну неизвестную,
величины U7, U8 и U9 сразу выражаются через заданные
узловые значения перемещений при t — 0.
3. Далее рассматривается следующий ряд элементов (к ^ t ^
^ 2к). Перемещения U12, U13 и Uu находятся из условий
pi __ ре _ р» — о Затем рассматривается третий ряд эле-
элементов и т. д.
Таким образом, конечнозлементное решение распространяется
во времени точно так же, как и при обычных явных конечноразно-
стных схемах.
Отметим, что в случае, когда на конце бруса приложена изме-
изменяющаяся во времени нагрузка, а начальные перемещения не зада-
174 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ны, способ решения таков же, с той лишь разницей, что U5, U10,. . .
. . . ф 0 и вместо A1.13) величины Р2, Р3> Р* (и Рц Ре» • • •)
принимают заданные ненулевые значения.
Устойчивость. Довольно грубая симплексная модель,
использованная в приведенном выше примере, является простейшей
конечнозлементной моделью для задач рассматриваемого типа.
В более сложных волновых задачах можно ожидать повышения
точности при использовании аппроксимаций высших порядков
или при увеличении числа степеней свободы элементов. Тем не
менее интересно отметить, что для внутреннего узла показанной
на рис. 11.12 системы (например, узла 8)
-2P8 = 0 = (-U3-2U» + Ui3)+Xz(lP-2U8 + U»), (ИЛА)
что в точности совпадает с центрально-разностной аппроксимацией
первого порядка для уравнения A1.9). Значит, можно восполь-
воспользоваться критерием Куранта, Фридрихса и Леви [1928] для того,
чтобы сделать вывод об устойчивости описанной схемы решения.
В соответствии с этим критерием решение неустойчиво при к > 1
и с увеличением' К неустойчивость становится сильнее; при К < 1
решение устойчиво, но с уменьшением К точность уменьшается;
при К = 1 решение устойчиво и может быть сделано сколь угодно
близким к точному решению уравнения A1.9).
Динамические системы. Нетрудно применить изложен-
изложенные ранее идеи к случаю динамических систем более общего вида.
Пусть, например, u (x, t) обозначает поле перемещений. Рас-
Рассмотрим локальную конечноэлементную аппроксимацию
ие = MpN (x) u" (t). A1.15)
Узловые величины nN являются функциями времени, так что
можно построить конечноэлементную аппроксимацию uN на «зле-
менте времени» [tt, tt]. Например, при использовании эрмитовой
интерполяции по времени получаем х)
ue(x, *) = *M
где а = 1,2, u% = uN(ta), u% = du"(ta)/dt и ввиду (8.24)
где | = t/h, h = At — длина элемента времени и для простоты
используется локальный отсчет ^ = 0, t2 = h.
См. Фрид [19696].
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 175
Рассмотрим динамическую систему, для которой
t, A1.18)
и
где х — кинетическая энергия, U — V — потенциальная энер-
энергия, & D — работа сил вязкости. Поскольку подынтегральное
выражение содержит интегралы от перемещения и и его градиентов
по объему среды, подстановка A1.16) в A1.18) приводит к соот-
соотношению
1 Г2 • •
So = 4" ) (mNM"N • uM - kNMи" ¦ им + 2р„ • u* + 2cNMи". u«) dt,
A1.19)
где mNM, kNM и cNM — соответственно матрицы масс, жесткостей
и демпфирования для нашего элемента, а рдг = р^ (t) — вектор
обобщенной силы в узле N х). Здесь
и" @ = Ф? (*) и^ + Ф? (*) и?. (И .20)
Если мы возьмем для р^ (t) такую аппроксимацию по времени:
Pw@ = *a(*)Pw. (И-21)
о = 1, 2, то, подставляя A1.20) и A1.21) в A1.19), получаем
«(в)= J^lVMUa-Up +^iVMUa-Up +CWMUa-Up +
+ ^Ркиа-и^ + 4оР^-«р+41Р^-ир), (И.22)
где
8 PJf ^ A1.23a)
A1.236)
A1.23b)
A1.23r)
A1.24а)
A1.246)
x) Более подробно матрицы масс и жесткостей и обобщенные силы для
конечных элементов рассматриваются в § 13 и 16.
176 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
q>7q>sdt, A1.24в)
t\
h
dao = j 2г|заф^ dt, A1.24r)
к
dai = \ 2*|заф? dt A1.24д)
(i
при r, s = О, 1.
Из принципа Гамильтона следует, что
Значит,
A (Д§?№ + С%%) iif + 4oPn = 0,
A1.25)
После связывания конечных элементов (в пространстве и времени)
я использования краевых и начальных условий из A1.25) получаем
систему линейных уравнений относительно и^ и и„ • Таким обра-
образом, в противоположность рассмотренной ранее схеме для примера
распространения волны эта конечноэлементная модель приводит
к неявной (и, следовательно, часто безусловно устойчивой) схеме
интегрирования.
11.2. КОНЕЧНЫЕ ЭЛЕМЕНТЫ В КОМПЛЕКСНОЙ ПЛОСКОСТИ.
УРАВНЕНИЕ ШРЁДИНГЕРА
Волновое уравнение Шрёдингера из квантовой механики запи-
записывается в терминах комплексной волновой функции %. Посмотрим,
как строятся конечноэлементные аналоги уравнений Шрёдингера
для х и для комплексно-сопряженной функции % в случае, когда
частица массы т находится под воздействием потенциального поля
V(x) = V (x, у, z).
Волновая функция % (х, t) может быть записана в виде
X (х, t) = u (х, t) + iv (x, t), A1.26)
где i = Y—1- Комплексно-сопряженная функция % (х, t) =
= и (х, t) — iv (x, t), и произведение % (х, t) % (x, t) с физической
точки зрения характеризует плотность вероятности в момент
времени t нахождения частицы в положении, определяемом коор-
координатами х. Ограничиваясь рассмотрением типичного конечного
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 177
элемента е, локально аппроксимируем действительную и мнимую
части функции % (х, t) следующим образом:
и<е> (х, t) = HpN (x) 4), у<е> (х, t) = ypN (x) 1$, (Н.27а, б)
где Ще), v^e) — зависящие от времени узловые значения функций
и (х, t) и v (x, t). Тогда
W. (И-28а)
. A1.286)
где
ХЙ = 4, + ww. XW = "W - fyW- (H.29a, 6)
Лагранжева плотность L(e) для нашего элемента равна х)
-^(xl-fx)-xFx, A1.30)
где h — постоянная Планка; варьируя функции % и х. мы должны
минимизировать ? = \ \ ] \ ?(е) ^^? ^*-
Подставляя A1.28) в A1.30) и требуя, чтобы
dLW d
получаем пару уравнений:
— « + ^^^-7^ = 0, A1.31a)
^Г^Г = О, (Н.316)
где
2 j iv, i (x) dre, A1.32a)
(x) dre A1.326)
T2w = j Ум (x) F (x) $N (x) dre. A1 .32b)
Уравнения A1.31) представляют собой дискретную интерпре-
интерпретацию волновых уравнений Шрёдингера для конечного элемента.
х) См. Морс и Фешбах [1958],
12 Дж. оден
178 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Величины &Pmn%^/2ju и h^MNY^J^ni являются обобщенными
каноническими моментами в узловой точке N элемента, а
(h%a^N/8nbn) — Ymjv — дискретным эквивалентом оператора Га-
Гамильтона для частицы, находящейся в конечном элементе е.
11.3. ОДНО НЕЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
Кратко рассмотрим конечноэлементную формулировку одной
нелинейной краевой задачи, состоящей в нахождении функции
и (х, у), определенной в некоторой замкнутой области 31 эвклидо-
эвклидовой плоскости и удовлетворяющей там нелинейному дифференци-
дифференциальному уравнению
= f(z, у) A1.33)
при однородном условии
и (*) = 0 A1.34)
на граничной кривой Г. Здесь V2 = дЧдх* -\- д2/ду2, их = ди/дх
и % = ди/ду.
Поступая, как указано в п. 10.1, вводим нелинейный оператор
®(u) = f — 2uv4—ul — ul, A1.35)
так что A1.33) можно записать в виде
® (и) = 0. A1.36)
Нетрудно показать, что ffi — потенциальный оператор; действи-
действительно, в соответствии с A0.19)
= — 2(V2uh—uxhx— Uyhy), A1.37)
где h — произвольная функция, удовлетворяющая условию
A1.34). Если g — еще одна такая функция, то
{65s (и, Л), g)-(№(u, g), fe> =
= — 2 \ [gV2uh — hV2ug— g (uxhx + Uyhy) + h (uxgx + uvgy)] d<% =
k
= — 2 j \gvSp-h — huVzg + g (uxhx + uyhy)— h (uxgx + uygy)\ &"Л.
A1.38)
Поскольку
j guvzh&П = - j [hx ± (gu) + hy± (g«)] йП + j gu? ds
Я~ г
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 179
и т. д., а интеграл по контуру обращается в нуль, ибо g и h удов-
удовлетворяют условию A1.34), последний интеграл в A1.38) равен
нулю и
(б^ (и, h), g) = (8& (и, g), h). A1.39)
Эта симметричность и показывает, что оператор аР потенциален.
Следовательно, по теореме 10.4 существует функционал К (и),
определяемый формулой A0.21), градиентом которого является
(Э5 (и). Замечая, что
— (Я5 (то), ")=
где т — параметр, интегрируя последовательно по частям и ис-
иольэуя A1.34), находим, что
то), и) = С [Зх2и(и2х + ul) + uf] йП. A1.40)
к
Подставляя A1.40) в A0.21) (с s, замененным на т, и м'о = Ко — 0)
и выполняя интегрирование, получаем функционал
К(и)= J [u(ui + ul) + uf]dfi:_' A1.41)
' Легко проверить, что оР (и) действительно является градиентом
для К (и):
= a^[h (ы* + «у) + 2и (uxhx + uuhv) + hf) dft +
m
a? j [u (fc« + Ц) + 2h (ujix + uyhv)
yi. A1.42)
j
m.
Поскольку h = 0 на Г, первый интеграл в правой части A1.42)
после интегрирования по частям можно записать в виде
—a J hBuv2u + ul + ul — f)d%,
так что
lim — [К (и + ah) — К (и)] = f & (и) KdM = <<3V(u), h),
Л
Следовательно,
grad К (и) = &> (и), A1.43)
12*
180 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
и в точке и*, удовлетворяющей уравнению A1.36)s
grad К (и*) = 0t A1.44)
т. е. и* является критической точкой функционала К (и).
Возвращаясь теперь к построению конечнозлементной модели
Уравнения A1.33), представим 31 в виде совокупности Е конечных
элементов М и обозначим через &(е) (и) ограничение К (и) на эле-
элемент е. Тогда приближенно
.Е
где
j %J (J re. A1.46)
Локально на типичном элементе ге имеем u(e> (xt у) = и$-$рг (хг у) и
A1.47)
где
, A1.486)
М, N, R = 1,; 2, . . ., Л^е. Локально и(е> реализует экстремум &(е)
в подпространстве, порождаемом функциями г|5$ (a;s y)s если коэф-
коэффициенты ще) выбраны так, чтобы
=0. A1.49)
Используя A1.47), приходим к системе квадратных уравнений
2(е) ,,*f,,^ I Ле) п /л л сЛ\
где
^IMN == &IMN ~T~ "®NMI* (ll.Ol)
Поскольку
uN — ONn& (\ \ C19^
H,(p\ Z^Z bi A L/ • I J. л. ¦ «J^r I
tJV[t) --Zi J \ /
из A1.47) и A1.45) вытекает, что
К (и) = АЛГАиА17ти* + FiU\ A1.53)
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 181
где
Е /с\ /с\ re\ Е /е\ l-
Ллгд = 2 ЙлЛЧ'мн, ^л= S Йл/^- A1.54а, б)
е=1 е=1
Окончательно конечноэлементный аналог уравнения A1.33) полу-
получается из условий dK(u)ldU^ = 0 [или непосредственно под-
подстановкой A1.52) в A1.50) и результата этой подстановки в A1.546)];
/лгдС/ГСЛ + *л = 0, A1.55)
где
Ллгд = ЛЛГл4-2Лгл. A1-56)
Используя теперь краевые условия (т. е. полагая С/д = 0 в узлах
Д на границе М), мы видим, что A1.55) дает нам систему квадрат-
квадратных уравнений относительно неизвестных узловых значений С/Л,
Методы решения таких систем нелинейных алгебраических урав-
уравнений рассматриваются в § 17.
11.4. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ. УРАВНЕНИЕ БОЛЬЦМАНД
В статистической механике разреженных газов (свободное
молекулярное течение без столкновений) встречаются задачи,
в которых успешно можно использовать конечноэлементные модели
в шестимерном [г-пространстве. Молекулярная плотность предпо-
предполагается достаточно низкой, а температура достаточно высокой,
так что каждая молекула газа может рассматриваться как клас-
классическая частица с определенным положением и импульсом. Пове-
Поведение содержащегося в некотором объеме газа в классической
кинетической теориих) описывается функцией распределения
/ (х, v, t), определенной таким образом, что она характеризует
число молекул, находящихся в момент времени t в элементарном
«объеме» dQ шестимерного фазового пространства (хг, х2 и жа
задают положение молекулы, а ж4 = vt, хь = v2, хв = v3 суть
компоненты ее скорости). В отличие от классической механики,
в которой имеют дело только со средними скоростями, величины
i?i, v2 и v3 считаются независимыми от хг, х2 и х3. Укажем в общих
чертах, как строятся конечноэлементные аппроксимации таких
функций распределения 2).
Рассмотрим уравнение Больцмана для функции распределения
/ (х, v, t) при неустановившемся состоянии для модели столкно-
столкновения Батангера — Гросса — Крука (БГК) в условиях отсут-
) См., например, Хуанг [1963].
2) Такие конечноэлементные аппроксимации рассматривались в статьям
Одеиа [19696], Брэмлетта и Мэллета[1970] и Агирре-Рамиреса, Одена и By
[1970]. Наше изложение основано на последней статье.
182 гл. ii. теория конечных элементов
ствия внешних сил:
| -^-. A1.57)
Здесь v — (микро)скорость, х — радиус-вектор, F — максвеллов-
ское распределение и т — время столкновения.
В принципе можно было бы непосредственно построить конечно-
элементную модель A1.57) с помощью шестимерных конечных
элементов в (^-пространстве, поскольку все необходимое для такого
построения было подготовлено в § 7. Например, можно было бы
представить область дискретной моделью М, являющейся сово-
совокупностью шестимерных элементов (скажем, симплексов), и запи-
записать для ограничения функции / (х, v, t) на типичный элемент:
[Г> (х, v, t) « /^ (t) г|$ (*„ х2, ..., х6), A1.58)
N = 1, 2, . . ., Ne (Ne > 7). Используя метод взвешенных невя-
невязок, мы получили бы аналог A1.57) для типичного элемента в виде
= У(я), (Н-59)
где /(^ = с?/(^/сЙ (для сокращения письма введем х* — (хи х2,..., хв))
A1.60a)
Q l
<e) m=l
A1.606)
1^ = {4 F}$ (x*)dQ- A0.60b)
Все дальнейшие рассуждения по существу те же.
К сожалению, записанные выше уравнения чрезвычайно трудно
использовать в практических расчетах, и поэтому целесообразно
поискать другую конечноэлементную модель. Для иллюстрации
одной из таких возможностей скомбинируем основные идеи метода
конечных элементов и метода Канторовича *) [1933]. Предполо-
Предположим, что в области Q функция / (х, v, t) приближенно представи-
ма в виде
/(X, V, t)= 2 Са(х, t)Qa(v), A1-61)
а=1
1) Точнее, метода Бубнова — Власова.— Прим. ред.
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 183
где са и Qa — некоторые функции указанных аргументов, аи —
некоторое целое число. Поскольку равенство A1.61) является
лишь приближенным, можно с помощью A1.57) определить невязку
п
а=1
Тогда при соответствующем выборе весовых функций W$ (v)
из условий
ОО
ШЖр (v) R dv = 0 A1.63)
— ОО
получим систему дифференциальных уравнений
дса . , А I * V* П Ш (К/\
где по повторяющемуся индексу а производится суммирование
от 1 до и и
а = И1wp (v) Qa (v) dv' bpa=Ш*
— oo —oo
A1.65)
Теперь можно приступить к построению конечноэлементной
модели для A1.64). Представляя М (пространственную область
определения функций са (х, t)) в виде некоторой совокупности
элементов, запишем для типичного элемента е
A1.66)
Локальная невязка ге для каждого элемента равна
Ге = apal|5jv (х) Са(е) + [Ьра • grad Tjjjy- (х) -f- u^a^N (х)] са(е) — -^pt
A1.67)
гДе С<х,(е) = dca(e)/dt. Из уСЛОВИЯ
J^(x)r.dre = O A1.68)
получаем конечнозлементное уравнение
'JV i/i. та , -* л \Н И,» — П Н1 6Q\
184 гл. п. теория конечных элементов
где
г(е)
*MN
= J Ум (x) grad xjjjv (x) dre, A1.70)
идентификационная метка элемента е для простоты опущена.
Используя соотношения
(е) ^ (е)
е?(е) = Ж, *&.= 2 й^|м, A1.71)
придем к системе дискретных уравнений для связанной системы:
OfiaAuCi + (Ь„а • В?д + аЬАть) Ci-F$T = 0, A1.72)
где
АТА = ААТ= 2 ОгГ^»Ра,
Е е (И-73)
вгд= 2 ^ваА
Уравнения A1.72) представляют собой систему дифференциальных
уравнений относительно узловых величин Ct- Отметим, что после
нахождения Са (t) можно с помощью A1.61) построить дискретную
модель функции распределения:
/ (х, v, t) = 2 Ci (*) Фа (х) Qa (v), A1.74)
a=l
где
Неустановившееся куэттовское течение. В ка-
качестве примера рассмотрим течение между двумя параллельными
пластинами, расположенными на расстоянии d друг от друга
и ускоряющимися в противоположных направлениях от состояния
покоя до некоторой постоянной скорости U12 (рис. 11.3). Удобно
ввести постоянную р = (m/2kT)i/2, где т — молекулярная масса,
к — постоянная Больцмана, а Т — температура. Направив ось х
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
185
1 2
1 п-Ъ
d n
X
-/////////////////////л
-CZz
— 6/2
и/г~- 7777O777-л
/////////////////////////у,
Рис. 11.3. Модель куэттовского течения между параллельными пластинами.
перпендикулярно течению, введем безразмерную координату %
и безразмерную скорость с соотношениями
? = -J, c = pv. A1.75)
Предположим, что функция распределения / имеет вид
/ (I, с, t) = п0р3я-з/2 ехр (-с2) [1 + ф* (?, с, t)\, A1.76)
где п0 — число, характеризующее плотность, а ф* — функция
возмущения. Для линеаризированной задачи течения без изме-
изменения плотности и температуры можно принять, что функция;
возмущения ф* имеет вид
Ф* (|, с, t) = С/сгф (|, сх, t), A1.77)
и линеаризированное одномерное уравнение Больцмана для модели
столкновения БГК принимает вид
A1.78)
где а — число, обратное числу Кнудсена. Интересующие нас
величины макроскопической скорости течения qz (|, t) и вязкого-
сдвигового напряжения xXz (|, t) определяются формулами
оо
^- = 4" J ехр(-^)Ф(|, С, t)dl,
A1.79)
где xxz = —U12 У л — свободная молекулярная1) величина
сдвигового напряжения.
1) В оригинале free molecular; отсюда индекс fm.— Прим. ред.
186 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Для получения приближенного решения уравнения A1.78)
по методу конечных элементов рассмотрим полиномы Эрмита,
определяемые формулой
^-^), ь = 0, 1, .... (Ц.80)
-Множество функций ?\ в A1.61) введем следующим образом:
¦Функции Н% (?) ортогональны на (—оо, оо) относительно веса
«хр ( —j ?2 J. Кроме того,
XC, = ? Л1 у Jt. \L L.OciJ
Предположим, что аппроксимация функции ф имеет вид
п
фA, сх, 0=2 сх{1, t)ux{cx), A1.83)
тде Qx определяется формулой A1.81), и найдем невязку:
п
-"= Zj 1Р ~aj~ (s» t) + сх -g|- (ё, 04-ася,(ё, 0)^мс*) —
g, 0, A1-84)
где
оо
A1.85)
Уравнение A1.64) теперь принимает вид
4^ ^ 0, A1.86)
где
Wt(g)Qfc(OdC, A1.87)
• оо
11. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
187
0.1 0 2 0.3 0.4 0.S
Относительное расстояние от пластины ?,- x/d
Рис. 11.4. Профили скоростей для различных моментов времени.
Неустановившееся куэттовское течение.
0.1 0.2 • 0.3 0.4 0.5
Относительное расстояние от пластины i^-x/d
Рис. 11.5. Распределение сдвиговых напряжений для различных моментов
времени. Неустановившееся куэттовское течение.
188 ГЛ. II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Ввиду ортогональности функций Qx удобно выбрать \?$ (?) =
= Qp (?) (т.е. использовать метод Галёркина). Взяв для примера
в A1.83)п = 2, найдем, что
дсх дс*
-^- + ?¦^-^+©^^ = 0, A1.88)
где
[ад=¦§[; 5
а 6 = 4 + 1^8/27. Формулы A1.79) принимают вид
Яг (Е. <) 2
Окончательное уравнение для типичного конечного элемента
таково:
ЛмА + {E^BMN + D^AMN) 4.) = 0. A1.91)
Численные результаты, полученные при использовании формул
A1.90) и A1.91) для п = 2, показаны на рис. 11.4 и 11.5. Они очень
хорошо согласуются с решениями, найденными другими методамих)
х) См., например, Хуанг и Гидденс [1967].
Глава III
Термомеханическое поведение
конечных элементов сплошной среды
12. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕРМОДИНАМИКИ
Хотя рассмотренные общие приемы построения дискретных
моделей в принципе применимы к любым непрерывным полям, мы
«будем заниматься главным образом термомеханическими явления-
явлениями, поскольку именно с ними связаны наиболее важные проблемы
нелинейной механики твердых тел. Термодинамические законы
естественным образом устанавливают связь кинематических и ди-
динамических переменных с другими величинами, характеризующи-
характеризующими термодинамическое состояние тел. Глобальные энергетические
законы сохранения дополняют локальные уравнения сохранения
количества движения и момента количества движения. Их можно
использовать для получения конечнозлементных уравнений, удов-
удовлетворяющих, по крайней мере в некотором осредненном смысле,
основным физическим законам (например, законам движения
Коши) для конечных объемов тела.
Кратко изложим некоторые термодинамические понятия и зако-
законы *), являющиеся исходными при выводе общих уравнений сохра-
сохранения энергии и уравнений движения для конечных элементов
нелинейных сплошных сред.
12.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
В термодинамике отдельную часть физической вселенной или
отдельное количество материи, идентифицированное для иссле-
исследования, называют системой. Если между системой и ее окруже-
окружением не происходит обмена материей, то говорят, что система
1) Обсуждение основ термодинамики применительно к теории сплош-
сплошных сред имеется у Колемана [1964], Трусделла [19?6а, 19666] и Эрингена
11967]. См. также монографию Трусделла [1969] [и *[1972].— Ред.]. Обзор
приложений к изучению деформируемых тел можно найти в ряде книг и ста-
статей. Вот некоторые из них: Био [1955, 1956], Боли и Уэйнер [1960], Фын
11965]. Изложение классической термодинамики имеется у Хатсопуласа
и Кянэна [1965]. Вопросы прикладной термодинамики необратимых про-
процессов освещены Майкснером [1943], Эккартом [1948], Пригожиным [1947,
1961], Де Гроотом и Мазуром [1962].
190 ГЛ. 111. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
замкнута; если система не взаимодействует с окружающей средой г
то говорят, что она изолирована. Таким образом, некоторое коли-
количество материи, выделенное для изучения его поведения, незави-
независимое от других количеств материи, не взаимодействующее и не-
обменивающееся материей с окружающей средой, является -замк-
-замкнутой изолированной системой.
Совокупность информации, которая полностью характеризует
систему во всех отношениях, описывает состояние системы. В общем
случае информация, характеризующая состояние системы в задан-
заданный момент времени, представляет собой значения некоторых
функций, называемых параметрами состояния или переменными
состояния и описывающих различные свойства системы.
Естественной и фундаментальной характеристикой состояния:
каждой термомеханической системы является то, насколько она
горяча или холодна в данный момент времени. Описывается сте-
степень нагрева или охлаждения с помощью обычного понятия темпе-
температуры. Температура 8 — зто вещественное число, показываемое-
термометром *). Если тело нагревается, то его температура повы-
повышается, если охлаждается, то понижается; во всем остальном»
шкала, в которой мы измеряем температуру, совершенно произ-
произвольна.
Экспериментальные исследования показывают, что безотноси-
безотносительно к масштабу используемого термометра существует темпера-
температура, ниже которой никакая система не может быть охлаждена-
Другими словами, температура ограничена снизу. Если точная-
нижняя грань принята за нуль, то температура называется абсо-
абсолютной и при любом масштабе|
9>0. A2.1}
Работа определяется обычным путем; например, работа силы F
при перемещении dn равна F-du. Конечно, для систем общего вида
работу можно выразить многими разными способами.
При исследовании механического поведения сплошных тел мы.
имеем дело с механической мощностью Q, развиваемой действующи-
действующими на тело внешними силами. Мощность является мерой скорости,.
х) В некоторых работах по классической термостатике понятие темпе-
температуры вводится в связи с определением равновесного состояния системы-
Если переменные состояния системы не зависят явно от времени и система
сама по себе не стремится изменить свое состояние (т. е. изменения могут
происходить только вследствие внешних причин), то говорят, что система
находится в равновесии. Постулат, гласящий, что две системы, каждая из ко-
которых пребывает в равновесии с третьей системой, пребывают в равновесии
и между собой, обычно называют нулевым законом термодинамики. Можно
показать, что равновесие трех систем означает существование у них общей
переменной состояния, называемой температурой. Любая из этих трех (или
большего количества) систем может играть роль термометра, который пока-
показывает температуру на некоторой удобной, но произвольной шкале. См.
Уэплз [1952].
12. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕРМОДИНАМИКИ I9f
с которой зти силы совершают работу (Q = F-dn/dt). Если F и S —
плотности объемных сил и поверхностных усилий, действующих.
на тело объема v с площадью поверхности А и массовой плотно-
плотностью р, то механическая мощность тела Q задается формулой
= j pF-vdv+ Js.vcL4,
где v = v (x, t) — поле скоростей.
С понятием работы тесно связано понятие энергии. Энергия —
это, попросту говоря, способность совершать работу. Это аддитив-
аддитивная скалярная мера, приписываемая количествам материи и харак-
характеризующая способность всех сил, которые могут быть связаны
с данным количеством материи (или с любой его частью), совер-
совершать работу. Работа всегда совершается благодаря изменению»
энергии, и различные классификации энергии отражают природу
сил, совершающих работу при изменении энергии.
Энергия, которой обладает механическая система в силу ее дви-
движения, называется кинетической энергией (энергией движения).
В механике сплошных сред кинетическая энергия к тела с массо-
массовой плотностью р, занимающего объем v, определяется так:
х = -± j pvvdv. A2.3>
v
Кроме кинетической энергии тело может обладать внутренней
энергией U, обусловленной способностью сил, действующих внут-
внутри тела, совершать работу. При рассмотрении сплошных тел мы
будем предполагать, что существует плотность внутренней энер-
энергии е, представляющая собой внутреннюю энергию единицы массы
тела. Тогда
U=^pedv. A2.4)
В элементарных курсах механики часто рассматривается
лишь чисто механическое поведение твердых тел, характеризуемое-
изменениями кинетической и внутренней энергий и механической
мощностью, развиваемой внешними силами. Однако в природе
поведение твердых тел редко ограничивается только механически-
механическими эффектами. Когда над телом совершается работа, оно, как
правило, нагревается. С другой стороны, когда два тела, находя-
находящихся при различных температурах, приводятся в контакт друг
с другом, то, как показывает опыт, от одного тела к другому пере-
передается энергия и зтот процесс может сопровождаться совершением
работы. Эта передаваемая *) вследствие разности температур
В единицу времени. — Прим, ред.
192 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
энергия называется скоростью нагрева или скоростью тепловой
работы и обозначается через Q.
Полный приток теплоты к телу складывается из теплоты, воз-
викающей в результате действия источников внутри тела и прито-
притока теплоты в тело из окружающей среды. Для измерения первой
части теплоты введем тепловую плотность г, характеризующую
поступление тепла на единицу массы х), обусловленное источника-
источниками внутри тела. Для измерения второй части рассмотрим произ-
произвольный элемент поверхности тела с площадью dA и внешней еди-
единичной нормалью п. Теплота, проходящая через dA, равняется
•q-ndA, где q — вектор теплового потока, или просто тепловой
поток. Полная скорость нагрева задается формулой
<?= J prdv+ J q-ndA. A2.5)
12.2. СОХРАНЕНИЕ ЭНЕРГИИ. ПЕРВЫЙ ЗАКОН
Опыт показал, что все различные энергии системы аддитивны
и что, какие бы изменения энергии ни имели места и каковы бы
ъи были при этом скорости работы и нагрева, внутренняя энергия
системы всегда такова, что в сумме никаких утечек энергии не про-
происходит. Этот закон сохранения энергии вводится как фундамен-
фундаментальная аксиома механики 2):
Закон сохранения энергии. Сумма скоростей изменения
¦во времени кинетической и внутренней энергий равна сумме скорости
работы, совершаемой над системой, и изменений всех других энер-
энергий системы в единицу времени:
x+*7 = Q + S?a, A2.6)
a
где, как и ранее, точка означает взятие производной по времени,
а Еа (а = 1, 2, . . .) — механический эквивалент поступления
анергии a-го рода (например, тепловой энергии, электрической
энергии, химической энергии) в единицу времени3).
При исследовании термомеханических явлений мы в основном
имеем дело с механическими энергиями и их взаимным превраще-
превращением в теплоту, т. е. из всех «энергий на единицу времени» Еа мы
рассматриваем только скорость нагрева Q, так что A2.6) принимает
вид
# , A2.7)
х) В единицу времени.— Прим. ред.
2) Три другие фундаментальные аксиомы механики приведены в п. 5.1.
3) См. Эринген [1962],
12. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕРМОДИНАМИКИ 193
Этот результат известен как первый закон термодинамики; он
является фундаментальным при исследовании термодинамического
поведения сплошных тел.
Равенство A2.7) иногда называют глобальной формой первого
закона, поскольку оно относится к конечному объему материала.
В случае достаточной гладкости рассматриваемых величин с помо-
помощью теоремы Грина — Гаусса можно получить локальную форму
первого закона, служащую выражением энергетического баланса
в точке сплошной среды. Чтобы получить эту локальную форму,
рассмотрим текущую конфигурацию твердого тела С (мы поль-
пользуемся обозначениями, введенными в гл. I). Фиксируем систему
внутренних координат хг, первоначально прямоугольных декарто-
декартовых в конфигурации Со, естественными базисными векторами
которой являются введенные в гл. I взаимные векторы Gt и G*.
В начальной конфигурации базис образован ортонормальными
векторами it, и прямоугольные (пространственные) координаты
точки в С, представляющие собой «бывшие» координаты хг в Со,
обозначаются, как и раньше, через zt. Поле скоростей v, поле
ускорений а и поле теплового потока q задаются соотношениями
u A2.8а)
A2.86)
A2.8b)
где ummqm — прямоугольные декартовы компоненты перемещений
и теплового потока относительно координат хг в начальной конфи-
конфигурации С„.
Вспоминая (см. E.12) и E.13)), что
S = SjGJ = a = aiiniGj, A2.9)
мы видим, что
Q = J pF'vs dv + j а%
A
= j
A2.10)
где точка с запятой означает ковариантное дифференцирование
по конвективным координатным линиям хг. Аналогично
Q= j prdv+ j QjnjdA= \ (pr+V-q)dv, A2.11)
v A v
13 Дж. Оден
194 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где V-q = (?tft. и
и=т чг
что в силу закона сохранения масс дает
A2.12)
Подставляя A2.4), A2.10), A2.11) и A2.12) в A2.7), упрощая
и группируя члены, получаем
J [(of. + pF - pa') Vj - (ре - a%:, -Q\j- pr)] dy = 0. A2.13)
В первой скобке мы узнаем члены, входящие в первый закон
движения Коши E.21). Значит, если удовлетворяется уравнение
Количества движения, то первая скобка обращается в нуль. Остаю-
Остающийся интеграл должен обращаться в нуль для любого объема.
В предположении непрерывности подынтегрального выражения
вторая скобка тоже должна обращаться в нуль, и мы приходим
к следующей локальной форме первого закона термодинамики:
pe = a%;i + Q\j + pr. A2.14)
Компоненты векторов и тензоров в A2.14) отнесены к коорди-
координатам хх в деформированном теле. Соотношение A2.14) можно
записать и в других видах. Например, компоненты иг, vi поля
A2.8а) связаны с компонентами скорости в прямоугольных декар-
декартовых координатах начального состояния соотношениями
vt = zmtium, vl=—um, A2.15а, б)
где запятая обозначает обычное дифференцирование по xt. Далее,
Vj;-i= (Zm,iUm);i = ZmjUmii, A2.16)
и в силу D.44), D.45) и симметричности тензора аг}
ouvj ¦ {= aiJzm< }ит< i = ai; Fm; + um_,) um, i = oi3yih A2.17)
где уц — тензор деформаций (см. D.16) и D.17)). Величина
oxlvjti = ог1уи иногда называется мощностью напряжений. Если
q — вектор теплового потока на единицу площади в недеформи-
рованном теле, то
V A2.18)
12. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕРМОДИНАМИКИ 195
Подставляя A2.17) и A2.18) в A2.14), получаем
? i^iti + pr. A2.19)
С учетом A2.4) и A2.5) соотношение A2.19) дает
U= ^a%jdv + Q. A2.20)
Таким образом, A2.7) можно также записать в виде
Q. . A2.21)
Представляет интерес еще одна локальная форма записи зако-
закона сохранения энергии. Пусть е и h обозначают соответственно
внутреннюю энергию и скорость притока теплоты на единицу
недеформированного объема. Тогда
е = рое и h = рог. A2.22а,б)
Вспоминая, что, согласно E.14), напряжение на единицу
поверхности недеформированного тела, отнесенное к координатам
х1 в деформированном теле, равно ?} = У&у*', и подставляя
A2.22) в A2.19), получаем другую форму записи соотношения
A2.14):
e = Pyu + qt.t+h. A2.23)
12.3. ЭНТРОПИЯ. НЕРАВЕНСТВО КЛАУЗИУСА - ДЮГЕМА
Наряду с абсолютной температурой 0 мы будем считать фунда-
фундаментальным свойством всех термодинамических систем энтро-
энтропию Н х). Также как и энергия, энтропия важна для нас только
в связи со своими изменениями, которые накладывают ограниче-
ограничения на Q/в. Мы предполагаем, что энтропия — аддитивная функ-
функция, присущая любому количеству материи. Таким образом, общая
энтропия тела равна сумме энтропии его частей. В случае сплош-
сплошных тел мы предполагаем, что Н абсолютно непрерывна относи-
*) В классической термостатике понятие энтропии обычно Ъводят, пытаясь
представить вариацию Q dt тепловой энергии в виде точного дифференциала.
При этом Q dt делят на абсолютную температуру, результат Q dt/Q обозна-
обозначают через dH и Н называют энтропией. К сожалению, такое определение
применимо только к очень ограниченному классу термодинамических явле-
явлений и теряет смысл для необратимых процессов. Мы предпочитаем ввести
энтропию как самостоятельное фундаментальное свойство материи и опре-
определить его роль в термодинамике деформаций с помощью неравенства Клау-
зиуса — Дюгема и его следствий. Этот подход был развит Колеманом и Нол-
лом [1963], Колеманом и Мизелом [1964], Трусделлом [1966а, 1969] и Эрин-
геном [1967]. [См. также Трусделл *[1972].— Ред.]
13*
196 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
тельно массы, так что существует функция г\, называемая удельной
энтропией или энтропией на единицу массы, такая, что
H=^pr\dv. A2.24)
V
Далее, мы предполагаем, что общее изменение энтропии сплош-
сплошного тела в единицу времени может происходить не только в резуль-
результате изменения Я, но и в результате притока энтропии через гра-
граничные поверхности тела и, возможно, поступления энтропии
от источников внутри тела. Полное производство энтропии в теле
определяется формулой
Г = /}— Г e-ndA — \ psdv, A2.25)
A v
где е — вектор потока энтропии, as — поступление энтропии
за единицу времени на единицу массы от внутренних источников.
Фундаментальной аксиомой термодинамики является постулат
неотрицательности Г:
Неравенство Клаузиу са—Дюгема. Общее производство
энтропии всегда неотрицательно:
Г > 0. A2.26)
В принятом нами способе изложения неравенство A2.26) пред-
представляет собой формулировку второго закона термодинамики.
Согласно A2.25) неравенство Клазуиуса — Дюгема означает, что
#> \ e-ndA+ \ psdv, A2.27)
A v
т. е. скорость изменения общей энтропии Н никогда не меньше
суммы притока энтропии через поверхность тела и производства
энтропии внутренними источниками. При соответствующих пред-
предположениях гладкости соотношения A2.24) и A2.27) дают
s. A2.28)
Величины ens всегда можно представить в виде х)
е=Ч- + ё,- s = _L + 7, A2.29а, б)
*) Во многих работах величины е и s полагаются равными q/9 и г/9
ab initio. См., например, Колеман и Нолл [1963], Колеман и Мизел [1964]
или Трусделл [1966а]. Величины~ё и s (см. A2.29а б)) ввел Эринген [1967,
стр. 128—129]. Он называет «простым термомеханическим процессом» про-
процесс, в котором 1Г = 0 и = 0. Мюллер [1967] довольно подробно исследовал
случай, когда е, вф- 0; величина е рассматривается им как фундаменталь-
фундаментальная зависимая переменная наряду с тепловым потоком q.
12. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕРМОДИНАМИКИ 197
где q/9 — приток энтропии, обусловленный притоком теплоты,
г/0 — производство энтропии внутренними источниками, обуслов-
обусловленное притоком тепла от них, а е и s — соответственно приток
и производство энтропии, обусловленные всеми прочими эффек-
эффектами. Поскольку нас интересует главным образом термомеханиче-
термомеханическое поведение, целесообразно принять е = 0 и s = 0, так что
e = -i, s = -J-. A2.30а, б)
Подставляя A2.30) в A2.28), получаем неравенство
qV9 + pr A2.31)
которое можно трактовать как локальную форму неравенства
Клаузиуса — Дюгема для случая, когда справедливы соотноше-
соотношения A2.30).
12.4. СВОБОДНАЯ ЭНЕРГИЯ И ВНУТРЕННЯЯ ДИССИПАЦИЯ
В теории теплопроводящих материалов удобно ввести удельную
свободную энергию ар, определяемую формулой
ар = е - т)9, A2.32)
и внутреннюю диссипацию б, определяемую формулой
A2.33)
Из определений A2.32) и A2.33) следуют соотношения
ре = о1}уи + рвг\-8 A2.34)
и
9у = ои'уи — рт]0 — б. A2.35)
Подставляя A2.34) в A2.14), получаем важный результат:
^ A1.36)
который представляет собой локальную форму закона сохранения
энергии в терминах удельной энтропии т), внутренней диссипа-
диссипации б и тепловых переменных q и г. Подставляя A2.36) в A2.31),
приходим к общему диссипационному неравенству х):
4 . A2.37)
См. Колеман [1964].
198 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Обычно принято также вводить неравенство Клаузиуса — Планкаг)
8 = p9Ti-V-q-pr>0. A2.38)
Заметим, что можно получить и другие формы записанных выше
соотношений, относя величины к недеформированной (начальной)
конфигурации. В частности, пусть |, ф и с обозначают соответ-
соответственно энтропию, свободную энергию и диссипацию на единицу
объема в начальной конфигурации:
t = Рол, A2.39)
Ф = Р«Ж A2.40)
о = YG8. A2.41)
Тогда
Ф = е —10,. A2.42)
° = ***Уи- (Ф + ЭД, A2.43)
и вместо A2.34) —A2.36) мы получаем
е=Г% + д%-о, A2.44)
4> = ?>уи-ф-в, A2.45)
i . A2.46)
12.5. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
Под термодинамическим процессом мы понимаем всякое множе-
множество функций, включающее в себя движение zt (x, t) и поля 0 (х, t),
о%0 (х, t), q (x, t)t и r\ (x, t), определенные в точках х в моменты
времени t, при условии, что эти функции удовлетворяют уравне-
уравнениям количества и момента количества движения и закону сохра-
сохранения энергии для любой части тела. В каждый заданный момент
времени эти функции определяют термодинамическое состояние
тела. Для классификации термодинамических процессов будем
использовать обычную терминологию: процесс называется изотер-
изотермическим, адиабатическим, изэнтропическим или изоэнергетиче-
') Эта терминология предложена Трусделлом [1966а, стр. 245]. [См.
также Трусделл, *[1972].— Ред.] Соотношение A2.38), вообще говоря, не
следует из A2.37), за исключением некоторых случаев, например случая
квазиупругого поведения. В классической термостатике б в A2.37) не фигу-
фигурирует, и это неравенство означает, что тепло никогда не течет против гра-
градиента температуры. Трусделл [1966а] истолковывает присутствие б в A2.37)
как указание на возможность потока тепла против градиента температуры
при подводе достаточного количества локальной энергии. Мы будем исполь-
использовать в качестве фундаментального диссипационного неравенства неравен-
неравенство A2.37).
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 199
ским, если соответственно 0, Q, Н или U равняется нулю. Если
функции состояния, включая градиенты деформации, не зависят
от х, то процесс называется однородным.
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА
Располагая основными механическими и термодинамическими
законами и общим понятием конечноэлементной модели непрерыв-
непрерывного поля, объединим их теперь вместе и получим общие конечно-
элементные формулировки поведения конечноэлементных моделей
сплошных сред.
13.1. КИНЕМАТИКА КОНЕЧНОГО ЭЛЕМЕНТА
Рассмотрим сплошное тело, которое в начальной конфигурации
Со занимает некоторую область М трехмерного эвклидова про-
пространства. Геометрия тела и внешние ограничения (связи) произ-
произвольны, и на тело может воздействовать любая система внешних
сил и тепловых потоков. Для описания движения тела введем,
как и ранее, систему внутренних глобальных координат, обозначае-
обозначаемых через Хг, которые временно для простоты будем считать пря-
прямоугольными декартовыми в начальной конфигурации Со. Прямо-
Прямоугольные декартовы координаты в произвольной конфигурации С
в некоторый момент времени t ^> 0 частицы х, которая первона-
первоначально занимала положение X = X (Хг) в Со, будем обозначать
через Zt и будем говорить, что функции
Zt = Zt (X, t) A3.1)
описывают движение тела.
В 'соответствии с изложенным в гл. II построим дискретную
модель тела, состоящую из конечного числа Е связанных соот-
соответствующим образом в узловых точках конечных элементов.
Внутри каждого конечного элемента ге тела введем систему вну-
внутренних локальных координат х\е), которую для простоты времен-
временно будем считать прямоугольной декартовой в начальной конфи-
конфигурации С0(е) элемента е. Прямоугольные декартовы координаты
частицы х в произвольной конфигурации С<е) элемента ге в неко-
некоторый момент времени t ^> 0, которая первоначально находилась
в точке х = х (хг) в С0(е), будем обозначать через zi(e) и будем
говорить, что функции
Не) = Че) Ы, t) ¦ A3.2)
описывают движение элемента е.
200 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Пока точная форма каждого элемента, число узлов и характер
связей не имеют особого значения, но мы будем считать, что основ-
основные требования совместимости удовлетворены и"что поэтому сово-
совокупность элементов, соединенных друг с другом, образует связан-
связанное целое. Если это так и если Xдг обозначают глобальные коор-
координаты какого-либо узла в глобальной системе, а х™ — локальные
координаты этого же узла в элементе ге, то связанность модели
достигается с помощью отображения
?$ = foAi, A3.3)
где
^=«К^ A3-4)
(e)N
QA — обычный массив инцидентности, определяемый формулами
G.6); 1 = 1, 2, 3; N = 1, 2, . . ., Ne; А = 1, 2, . . ., G; е =
= 1, 2, . . ., Е. В A3.4) величины ал суть направляющие косинусы
(е) (в). .. (е)
углов между X1 и #L и а^а^ = 8 , det oj = 1. Аналогично если
требования совместимости выполнены в процессе всего движе-
движения, то
^ = ^«, A3.6)
где ZAt = Zf — прямоугольные координаты в С узла, который
определялся координатами ХЛг в Со, а г^ — соответствующие
локальные координаты узла в С(е), который в С0(«) имел коорди-
координаты ж?\
Поле глобальных перемещений Ut = С/г- (X, f) определяется
формулой
?/,- = гг - Х„ A3.7)
где Xt = X1, а поле локальных перемещений, соответствующее
элементу ге,— формулой
Щ(е) = Z{(e) — Ще) ¦ A3.8)
в гло-
глоA3.9)
Таким образом, компоненты перемещения узловой точки А в гло-
глобальной системе суть
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 201
а компоненты перемещения узловой точки N элемента ге —
(с)
Из A3.4), A3.6) и A3.10) следует, что если uf{e) = ajuP(e), то
и*е) = Щ^. A3.11)
Для завершения построения конечной модели поля перемеще-
перемещений U нужно построить соответствующие аппроксимационные-
функции для каждого конечного элемента. Ради простоты рассмо-
рассмотрим лишь представления первого порядка. Построение представ-
представлений высших порядков хотя и более громоздко, но осуществляет-
осуществляется непосредственным применением метода, описанного в § 8.
Итак, для элемента ге имеем
, A3-12)
где a|)te> (x) — локальные интерполяционные функции для этого
элемента. Соответственно
jjy$ (х), A3.13)
или, с учетом A3.11),
Ui = 2 SIЩ (X) Uf = Фд (X) Ut. A3.14)
е
Соотношения A3.12) и A3.14) дают дискретную модель поля
перемещений U. Теперь нетрудно определить поле скоростей V
и поле ускорений А:
г й 2#П# 1315>
At = V, = U, = 2 ^ (х) ^д *^о A3-16)
• . * " А
где Ui и Ui — компоненты скорости и ускорения в узловой точке
А связанной глобальной системы, т. е.
Vt = Uf, At = Ut- A3.17а, б)
Отметим также, что
»«•> = «&,!#(*). «i(e) = <e)^(x), A3.18а, б)
где
"й, = 8д !? = »&. A3.19а)
"QUt A3.196)
202 ГЛ. Ш. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Соотношения A3.15) и A3.16) показывают, что наше конечно-
элементное представление представляет поля перемещений, скоро-
скоростей и ускорений в виде произведений функций одних простран-
пространственных переменных на узловые значения, являющиеся функция-
функциями одного времени. Ясно, что производные по времени высших
порядков от U получаются последовательным дифференцировани-
дифференцированием соотношения A3.14):
bi*t%V$(x)(Q%Ut. A3.20)
е
Имея конечноэлементную модель поля перемещений, нетрудно
вычислить все другие величины, характеризующие деформацию
конечноэлементной модели тела. Например, для типичного конеч-
конечного элемента ге градиенты деформации суть
Компоненты тензора деформации в соответствии с D.17) имеют вид
»!i2.j). A3-22)
—
. №., К А+«чМмМ • <13-23>
а компоненты тензора скоростей деформации —
Значит,
Тензор меры деформации Gtj для нашего элемента задается, конеч-
конечно, формулой
$ A3.25)
так что главные инварианты D.25) можно получить просто под-
подстановкой A3.22) в D.26).
Интересно отметить, что для симплексных моделей
е), A3.26)
где адг и Ъ%\ определены формулами A0.102) [а также A0.105),
A0.106) и A0.108)]. Значит,
^Nj = bN1, A3.27)
где для простоты идентификационная метка элемента (е) опущена.
Таким образом, для симплексных моделей
A3.28)
g> = \ {ufbNl + ufbNj + bytbUJu»u«), A3.29)
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 203
g> = -I [ufbm + ufbN] + bNibM] (lj[u« + и«й«)], A3.30)
х1, A3.31)
J? = Ьа + bNiuf + 6^Mf + bNibuiu»u«. A3.32)
Мы видим, что для симплексных моделей при использовании
прямоугольных декартовых координат относительно начальной
конфигурации каждый конечный элемент находится в состоянии
однородной деформации1). Градиенты деформации и компоненты
тензора деформации постоянны в каждом элементе.
13.2. ЭНЕРГИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Воспользуемся теперь фундаментальным свойством конечно-
элементных моделей: для описания локальных аппроксимаций
на каждом элементе различные элементы ге можно считать никак
не связанными между собой. Таким образом, мы можем временно
сосредоточить внимание на одном типичном элементе ге из ансамб-
ансамбля, представляющего сплошную среду, и мыслить этот элемент
как изолированный от всей остальной системы. Опять для удоб-
удобства и простоты не будем писать идентификационную метку эле-
элемента (е), за исключением тех случаев, когда это может привести
к недоразумению.
Итак, рассмотрим типичный конечный элемент ге с массовой
плотностью р,е) = р(е) (х) и объемом vie) в произвольной конфигу-
конфигурации С(е). В начальной конфигурации Со (в) эти величины обозна-
обозначаются через р0(е) = р0(е) (х) и v0 (fi) . В соответствии с A3.12)
и A3.18) поля перемещений, скоростей и ускорений для нашего
элемента имеют вид
«! = и?1Ых), A3.33а)
ut = i?\pN(x), A3.336)
ut = u?yN(x), A3.33в)
х) Деформация называется однородной в случае, когда каждая прямая
линия деформируется снова в прямую; см. Трусделл и Тупин [1960, стр. 285].
Градиенты деформации A3.28) постоянны в элементе; плоскости деформи-
деформируются в плоскости, прямые — в прямые. Однако симплексные модели поля
перемещений не всегда приводят к состояниям однородной деформации. Если,
например, начальные координаты не прямоугольные декартовы, то дефор-
деформация, соответствующая симплексной модели поля перемещений, в общем
случае не будет однородной. В цилиндрической системе координат (г, z, 6),
например, перемещение ит = к приведет к окружной деформации, зависящей
от г. Имеется ряд случаев однородной деформации, представляющих особый
интерес (например простой сдвиг, однородное растяжение). В этих случаях
конечноэлементная модель дает точное описание кинематики деформации.
См. Оден [19686, 1970а] и Оден и Агирре-Рамирес [1969].
204 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
причем подразумевается, что uf зависят от времени. Поэтому все
кинематические соотношения для этого элемента могут быть
с помощью формул A3.22) — A3.25) записаны через компоненты
узловых перемещений щ и их производные по времени щ и uf.
Кинетическая энергия. Теперь возможно вычислить
энергии, связанные с термомеханическим поведением элемента.
Обращаясь сначала к A2.3), для кинетической энергии и(е) элемента
получаем
1 (* 1С**
и(е) = -2~ ) pv-vdi; = -2- \ pou-udi;o. A3.34)
"(в) "ОМ
В настоящем контексте мы предпочитаем относить движение к на-
начальной конфигурации элемента Сош. Подставляя A3.336)
в A3.34), находим
^ A3.35)
(е)
ИЛИ
к A3-36)
где mNM — симметричная матрица размера iVe X Nе, называемая
согласованной матрицей масс г) для элемента и определяемая
формулой
™nm = \ '¦Ро (х) i|3jv (х) \EМ (х) di;0. A3.37)
(е)
Ясно, что матрица mNM распределяет общую массу по узлам в виде
дискретных узловых масс таким образом, что кинетическая энергия
движения Nе дискретных узловых точек равна кинетической энер-
энергии, обусловленной непрерывными полями р0 (х) и и (х) в элементе.
Скорость изменения кинетической энергии элемента равна
4e) = mNMuMu»; A3.38)
здесь мы воспользовались свойством mNM = mMN. Отметим, что
хе можно интерпретировать как мощность, развиваемую «инер-
х) Этот термин был введен Арчером [1963], который использовал эпитет
«согласованная», чтобы подчеркнуть, что масса элемента распределена по
узлам некоторым специальным образом, согласованным с предполагаемым
полем скоростей ipN (x) iiN, а не просто без разбора разбросана по узловым
точкам, как это часто делается. Позже Арчер [1965] распространил эту идею
дальше и ввел согласованные силы. Обобщение этих идей, которым занимались
Оден [1969а], Оден и Агирре-Рамирес [1969], а также Браули и Оден [1971],
лежит в основе теории сопряженных аппроксимаций, изложенной в § 9.
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 205
ционными» силами тнмщ в узле N. При такой интерпретации
mNMui видно, что если ускорения всех узлов равны нулю, за
исключением, скажем, узла К, то инерционная сила в узле ./V равна
mNKUi . Если кроме того ui = 1, то сила в узле N просто равна
mNK. Таким образом, элемент mNK согласованной матрицы масс
можно интерпретировать как инерционную силу в узле N, обуслов-
обусловленную единичным ускорением узла К. А свойство симметрии mMN =
— mNM можно интерпретировать как динамическую форму закона
взаимности Максвелла: сила в узле N, обусловленная единичным
ускорением в М, равна силе в узле М, обусловленной единичным
ускорением в N.
Интересно посмотреть, какой вид принимает A3.36) при исполь-
использовании симплексных моделей. В этом случае^ (х) = aN + bNixl и
mNM = moaNaM + (aNbMl -f bNiaM) 5г + ЬтЪм1Г\ A3.39)
где т0 — полная масса элемента, sl — первые моменты массы,
а Г° — тензор моментов инерции относительно начала системы
локальных координат х1:
то= \ Ро(х)^у0, sl= \ р0(х)хгAи0, A3.40а, б)
с0(е) »0(е)
f>= f po(x)xixidvo. A3.40b)
Массив aNaM распределяет массу по узлам, а массив bNibMj
распределяет по узлам инерцию вращения элемента, приводя
к дискретным узловым эквивалентам.
•
Отметим еще, что величину и(е) можно представить в виде ска-
скалярного произведения
*<«= J poa-u^v^o- A3.41)
е0(е)
Значит, в соответствии с (9.181) поле инерционных сил роа сопря-
жено полю скоростей и относительно скорости изменения кинети-
кинетической энергии.
Внутренняя энергия. Полная внутренняя энергия
элемента записывается в виде
U(e)= j edvQ= j pedv, A3.42)
206 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
где е и е — введенные ранее удельные внутренние энергии. Ско-
Скорость изменения внутренней энергии равна
Um= j edv0. A3.43)
v0(e)
Напомним (см. A2.23)), что е можно выразить через мощность
напряжений №уц, тепловой поток и поступление тепла от вну-
внутренних источников. Значит, Е/(е) тоже можно представить в виде
tlly ijdvo-\-Qle), A3.44)
<е>
или
С7(й)= f ai}yijdv + Q{e), A3.45)
где Q{e) — общая скорость нагрева элемента е.
С учетом A3.23) получаем
tuyu = tli^Nt t (8}k + и^Ум, j) Uk, A3.46)
где подразумевается, что tytfj зависят от х. Поэтому
A3.47)
= j
(е>
¦
Мало что еще можно сказать о виде С/(е), не зная характеристиче-
характеристических свойств материала, из которого состоит элемент.
Механическая мощность. Возвращаясь к A2.2), ука-
укажем, что внешние силы F и S сопряжены полю скоростей и элемента
относительно механической мощности Q. Пусть F (х) — действую-
действующая на элемент объемная сила на единицу недеформированного
объема, a S — поверхностная сила, отнесенная к конвективным
координатам хг, но измеренная на единицуплощадиЛ0в начальной
конфигурации [S = t = Р'п^у, см. E.15)]. Тогда механическая
мощность, развиваемая действующими на элемент внешними
силами, равняется
fi(r)= ( F(x)-$N(x)uNdv0+ j S-\pN(x)uNdA0, A3.48)
(e>
где A0 = Ao(e) — площадь поверхности элемента в начальной
конфигурации. Поступая так же, как и при рассмотрении кине=
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 207
тической энергии, запишем
Це) = 1>-^ + 1>-8„, A3.49)
где
fw= j F(x)ypN(x)dv0 A3.50)
= J
A3-51)
A0<e>
Величина f jv является обобщенной силой в узле N элемента, обусло-
обусловленной объемными силами F (x), a aN — обобщенной силой в узле N,
обусловленной поверхностными силами S (х). Силы sN служат
дискретными аналогами напряжений для конечноэлементной моде-
модели. В них выражается влияние контакта элемента с окружающей
средой (например, с соседним конечным элементом). Обобщенные
силы iN и sN иногда называют согласованными обобщенными сила-
силами, поскольку они вычисляются способом, согласованным с при-
принятым полем скоростей, а именно обобщенные силы fN + sK
определяются так, чтобы механическая мощность, развиваемая
сосредоточенными узловыми силами при движении с узловыми
скоростями и^, равнялась мощности, развиваемой непрерывными
полями F (x), S (х) и и (х).
Важно отметить, что действительные поверхностные силы S (х)
наблюдаются наЛи только в деформированном элементе, т. е. эти
силы в общем случае зависят от деформации и, следовательно,
являются функциями узловых перемещений и^. Точная форма
этой зависимости определяется характером приложенных нагру-
нагрузок, начальной формой элемента и видом интерполяционных
функций ijjjy (x) *). Пока нам достаточно будет писать просто
S = S (х), а впоследствии мы будем определять поверхностные
усилия через градиенты перемещений для каждого случая нагру-
жения и каждого рассматриваемого типа конечного элемента.
х) В гл. IV, например, показывается, что в случае равномерного давле-
давления р мы имеем
V
что для конечного элемента дает
St = -P V&-, п, (вт + *„, ти?) G$.
Здесь G<e) и 6^?™ — тоже функции от щ ,j. К счастью, для конкретных форм
¦флг (х) возможны существенные упрощения. См. § 16—20.
208 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Пусть \>N обозначает полную обобщенную силу в узловой
точке N:
Pn = *n + в*. A3.52)
Ее компоненты равны
Pni = frtt + sNt, A3.53)
или
j St(x)MpN(x)dA0. A3.54)
A0(e
Теперь A3.49) принимает вид
r0<e> A0(e)
0{e) = uff-pw = iI?W,, A3-55)
где N = 1, 2, . . ., Ne и i = 1, 2, 3.
Скорость нагрева. Полную скорость нагрева конечного
элемента обозначим через Q{e) и этим ограничимся. На данном этапе
конкретные формы представления Q{e) приближенными полями
не имеют значения, поскольку они не влияют на вид уравнений
движения элемента. Производство энтропии и теплопередача
в конечном элементе будут рассмотрены позднее *).
13.3. СОХРАНЕНИЕ ЭНЕРГИИ В КОНЕЧНОМ ЭЛЕМЕНТЕ
Если ограничиться рассмотрением термомеханического пове-
поведения, то закон сохранения энергии в конечном элементе в соот-
соответствии с A2.7) имеет вид
(«. A3-56)
где, согласно A3.38), A3.47) и A3.55),;
' A3.57а)
(• .. •
t7(g) = V t Vfljy, j (Од -f- V|JM, jWtr) UVqU^ -f- V<e;, A3.576)
J . ft ft '
"(He)
Q(e) = -pNi -)- ц^, A3.57в)
<?(e) = <?(«• A3.57r)
Подставляя A3.57) в A3.56), получаем уравнение энергетического
баланса для случая термомеханического поведения конечного
См. п. 13.8.
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 209
элемента:
u?u»+ J t™qN,mFn + $M, jU?) dvou? = pNiu?. A3.58)
Заметим, что поскольку мы заменили скорость изменения внутрен-
ней энергии е в выражении для Е/(е) правой частью соотношения
A2.23), скорость нагрева Q{e) не входит в A3.58). Еще раз отме-
отметим, что A3.58) справедливо для любых материалов без каких-
либо ограничений на порядок и величину градиентов деформации.
Для получения конкретных форм уравнения A3.58) для различных
материалов нужно исключить t1' с помощью уравнений состояния.
13.4. ОБЩИЕ УРАВНЕНИЯ ДВИЖЕНИЯ КОНЕЧНОГО ЭЛЕМЕНТА
Теперь нетрудно написать общие уравнения движения для
типичного конечного элемента сплошной среды. Обращаясь
к A3.58), мы видим, что каждый член содержит компоненты узло-
узловой скорости и?, являющиеся функциями одного времени. Поэто-
Поэтому уравнение энергетического баланса можно переписать следую-
следующим образом:
[mNMuf + j ^Wim(e;i+i|)M,yuM)di;e-pwl]uW = 0. A3.59)
Как обычно, по повторяющимся индексам производится суммиро-
суммирование по всем допустимым для них значениям: N, М = 1, 2, . . .
. . ., iVe; i, /, m = 1, 2, 3. Соотношение A3.59) представляет собой
закон сохранения энергии для конечного элемента. Поскольку этот
закон справедлив при произвольных движениях элемента, он дол-
должен быть справедлив и при любых значениях узловых скоростей
щ . «Разворачивая» в A3.59) суммирование по повторяющимся
индексам N ш i ш рассматривая каждый член, мы убеждаемся, что
если A3.59) выполняется при произвольных щ , то член, стоящий
в скобках, должен обращаться в нуль при всех значениях N ж i.
Таким образом,
f A3.60)
<е>
Уравнение A3.60) представляет собой общее уравнение движения
конечного элемента сплошной среды 1). Это система 3./Ve уравнений
1) Это уравнение и некоторые другие его формы были выведены Оденом
|1967в, 19696, 1970а]. См. также Оден и Кубица [1967], Оден и Агирре-Рами-
рес [1969] и Оден [19706]. Отметим, что этот же результат можно получить
14 дж. оден
210 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
относительно узловых перемещений и их производных по времени.
Снова конкретные формы уравнения A3.60) могут быть получены
после того, как специализирован материал. Тогда tl} можно выра-
выразить через узловые температуры, величины и?, щ , . . ., предысто-
предыстории изменения этих величин и т. д. и таким образом исключить
из уравнений движения. В представленном выше виде уравне-
уравнение A3.60) является дискретным эквивалентом первого закона
движения Коши E.27) и выражает баланс количества движения
в некотором осредненном смысле для элемента ге.
13.5. ГЛОБАЛЬНЫЕ ФОРМЫ УРАВНЕНИЯ ДВИЖЕНИЯ
Уравнение A3.60) описывает движение типичного конечного
элемента. Для получения уравнений движения всего ансамбля
А * А *' * А
элементов используем обозначения С/4, Е/{ и С/{ для глобальных
значений компонент перемещения, скорости и ускорения узла А
связанной модели. Тогда в соответствии с A3.11) — A3.20) имеем
N (e)N A
МЦе) — Ъ&\и i I (Lo.Vldf
u$e) = Q%U?, A3.616)
j.N О 77. l\°sMn\
где для простоты временно принято, что локальные координатные
(«)¦
линии x%iei параллельны глобальным X1 (т. е. а} = б}).
Пусть Рд — глобальное значение обобщенной силы в узле А
связанной модели. Тогда полная механическая мощность, разви-
развиваемая в модели, равна
A3.62)
с помощью понятия «виртуальной работы». А именно, рассматривая энергию,
обусловленную произвольной вариацией 8uf узловых скоростей, получаем
уравнение, идентичное A3.59), с той лишь разницей, что и f за скобкой за-
заменяется на бuj. Далее используется то соображение, что баланс энергии
должен сохраняться при произвольных вариациях узловых скоростей (см.
Оден и Агирре-Рамирес [1969]). С другой стороны, можно рассматривать
вывод уравнения A3.60) как приложение метода Галёркина, в соответствии
с которым уравнения движения Коши E.27) умножаются на «произвольную»
функцию u^tyff (x) и интегрируются по объему элемента. Однако произве-
произведенный здесь вывод физически более нагляден и естественнее связан с основ-
основными физическими законами.
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 211
где А = I, 2? . . .^ G. Однако Q можно также представить в виде
суммы
Е
Q= 2 Q(e), A3.63)
е=1
где Qle) определяется формулой A3.55). Тогда
Pa-U^Jp^-u^. A3.64)
Подставляя сюда A3.616), находим
(Рд-2&#)-йЛ = 0, A3.65)
е
что дает
Рд=2!ОдРЙ\ A3-66)
е=1
или, в покомпонентной записи,
Рм=3$кр(&- A3-67)
Этот результат,; конечно, сразу следует также из определения
сопряженных полей (см. (9.189)). Однако данный здесь вывод
приводит к разумной физической интерпретации обобщенных
сил Рд. Снова мы видим, что обобщенные силы Рд и р^ сопряжены
скоростям UA и nN относительно механической мощности Q.
Силы Рд вычисляются таким образом, что механическая мощ-
мощность, развиваемая в результате «дискретных» движений UA,
такова же, как и механическая мощность, развиваемая во всех
элементах модели; таким образом, равенство A3.64) можно интер-
интерпретировать как утверждение об инвариантности механической
мощности для модели. Равенства A3.66) и A3.67) показывают,
что глобальная обобщенная сила в узле Д связанной модели
является векторной суммой локальных обобщенных сил в узлах
р$} всех элементов, соединяющихся в узловой точке А связанной
модели (см. (9.191)).
Прежде чем двигаться дальше, стоит отметить еще одно свойство
обобщенных сил Рд. Подставляя A3.52) в A3.66), получаем
Рд = FA + SA, A3.68)
где
FA = | <Ъ&\ A3-G9)
¦ A3.70)
e=l
14*
212 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Ясно, что величина FA является глобальной обобщенной силой
в узле А, обусловленной распределенными в нашей сплошной среде
объемными силами F (х). Если предположить, что поле F (х)
задано, то локальные обобщенные силы i(ff для каждого элемента
можно вычислить, используя A3.50). Тогда FA в каждой узловой
точке связанной модели находится по формуле A3.69).
Величина Эд представляет собой глобальную обобщенную
силу в узле А, обусловленную поверхностными силами S (х).
Однако локальные значения s$> являются дискретными аналогами
напряжений в конечноэлементной модели. Таким образом, для
любого внутреннего узла величина sffl характеризует действие
¦одного элемента на другой (т. е. это дискретный эквивалент кон-
контактных сил). Значит, для внутренних узлов имеет место равен-
равенство г)
Эд = 0 A3.71)
"и A3.68) сводится к
Рд = FA. A3.72)
Однако для узлов, расположенных на границе, в общем случае
Эд Ф 0 и справедливо A3.68).
Возвращаясь к построению глобальных уравнений, преобра-
преобразуем узловые перемещения, скорости и ускорения в A3.60)
с помощью A3.61):
J .&#)**,. A3.73)
в0(е>
Наконец, подставляя A3.73) в A3.67) и производя упрощения,
получаем глобальные уравнения движения для всего ансамбля
конечных элементов:
Рп (t) = MTJJf + GVi (t) + Ягд (t) Ut, A3.74)
где
аМО A3-75)
J) Может случиться, что поле напряжений претерпевает конечные раз-
разрывы на некоторых поверхностях в теле. Тогда SA можно использовать
в качестве дискретного эквивалента скачка в узлах на таких поверхностях.
В этом случае вместо A3.71) имеем SA = [SA], где
fed = 2 ЯЭД?
е
— скачок силы S в узле Л связанной модели.
Е
(t)=y,Qrbji J i$№.mdv0, ' A3.76)
e=1 в0(е>
¦pi
=2^г(^ j tftyftntifl.idvo. A3.77)
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 213
Е
Q
Обозначения Gn (t) и т. д. указывают на зависимость от тензора
напряжений t. Массив Жгд является глобальной согласованной
матрицей масс всего ансамбля конечных элементов. Величины
Gn (t) и Нть (t) должны быть представлены в виде функций или
А "Л
функционалов от Ui , Ui , . . . и/или их предыстории после вве-
введения уравнений состояния, характеризующих материалы элемен-
элементов. Локальные значения узловых перемещений, скоростей и уско-
ускорений для каждого элемента определяются по формулам A3.61)
после решения уравнений A3.74). Значения этих полей в произ-
произвольных внутренних точках находятся из A3.12) и A3.18), а ком-
компоненты тензоров деформаций и скоростей деформаций в случае
надобности определяются по формулам A3.22) и A3.23). Узловые
силы р$\ для каждого элемента можно вычислить, используя
A3.60). В последующих разделах будут рассмотрены различные
частные формы уравнений A3.60) и A3.74).
Если оси систем локальных прямоугольных координат x\ei
не параллельны осям глобальных координат Xх, то надо незначи-
незначительно видоизменить приведенные выше соотношения. А именно,:
вместо A3.61) и A3.67) в этом случае надо ввиду A3.4) и A3.6)
использовать соотношения
?) ^ A3.78а,б)
(«)(е)„..А Д
iQgut Р
$) ЯЦр%у A3.78в,г)
Далее поступают точно так же, как* описано выше.
13.6. УРАВНЕНИЯ ДВИЖЕНИЯ В КООРДИНАТАХ ОБЩЕГО ВИДА
Все уравнения, полученные в этом параграфе до сих пор, осно-
основывались на предположении,; что локальные координаты х1.
в начальной конфигурации элемента прямоугольные декарто-
декартовы. Общий вид предыдущих уравнений, справедливый при любом
выборе внутренних криволинейных координат в начальной конфи-
конфигурации, более громоздок, но получить его нетрудно 1).
См, Оден и Агирре-Рамирес [1969] и Оден [1970а],
214 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Пусть Ще) — произвольная система криволинейных координат
в элементе ге в конфигурации С0(е) с ковариантными и контра-
вариантными базисными векторами gj(e) и g,*, (см. D.48)). Для
удобства мы опять опускаем идентификационную метку элемента
и пишем просто ?\ gt и g\ Поле перемещений типичного элемента
записывается так:
u(e, = Щ A, t) gl = wl A, t) gl; A3.79)
здесь wt и wl — ковариантные и контравариантные компоненты
перемещения. Отметим, что векторы gt и g* тоже являются функ-
функциями от ?1.
Для конечного элемента используем представления
wt = w* $N A) или wl = v?in^N(Q. A3.80а,б)
Компоненты тензора деформаций в этом случае суть
; vs*=4-(««-«.j+er ».»+».*•«. у). A3.81)
где и; = дп1д%3. Другие кинематические величины подсчитывают-
ся аналогичным образом.
Замечая, что
^(^ )>» A3.82)
и
^ (^) , A3.83)
где r?jj — символы Кристоффеля второго рода для §* в С0(е)
(см. D.54)), поступаем точно так же, как и ранее, и получаем
вместо A,3.60) следующее уравнение движения для типичного
конечного элемента:
°0(e)
-^м^Г^Г^)йг;07уМ« = р1?, A3.84)
где tyN,q = dtyN (|)/5|9, a tqi — тензор напряжений на единицу
площади в С0(е), отнесенный к конвективным координатам ?*
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 215
в С(е). Вместо этого можно использовать уравнение
v0(e)
v0(e)
% = pm, A3.85)
? N A3.86a,6)
Если координатные линии \\е) параллельны глобальным коор-
координатным линиям S' в С, то
u$=Q?PFA\ *4e) = {kwt A3.87а,б)
П = 2йЖ), Рд, = ЕЙ4. A3.88а,б)
е е
Если %\е) и Зг не параллельны, то для того, чтобы отнести компо-
компоненты к общему базису, надо в A3.87) и A3.88) включить дЪ>\еIдЕ>
и дЕЧдЩп.
Глобальные уравнения движения имеют вид
4 A3.89)
или
MrJvf + Gri (t) + Н^г (t) Wi = Pri, A3.90)
где ЛГгд определяется по формуле A3.75), за тем исключением, что
вместо tyN (x) используется tyN (?), и
Q? j V8^T}d A3.91)
йУо, A3.92)
е v0(e)
(t) = 2 Or Sf J *'j №м, An, A + ^M^iv, 9Г^ -
A3.93)
Заметим, что в случае, когда Ще) — прямоугольные декартовы
координаты (Ще) = х\е)), мы имеем Т)к = 0, gu = giJ = 6),
wf = wNi = uf, a A3.84) и A3.85) сводятся к A3.60). Точно так
же Gr = ^ = Gri,. а ЯГДтРГАт и S?MWt сводятся к
216 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Отметим, что менее точная, но значительно более простая фор-
форма уравнений движения в произвольных координатах получается,
если вместо аппроксимации компонент и>, и и>* использовать
векторное представление и(е) = г(з^и^,, где u^( = u(e) (х^). Как
отмечалось в п. 7.5 (см. G.48) — G.52)), это эквивалентно отнесе-
отнесению и(е) к постоянным базисным векторам g5v', и g^ce), являющим-
являющимся средними значениями базисных векторов g; и g1 в узлах. Тогда
вместо A3.82) и A3.83) мы имеем
~Щ1~~~ЩГ W gBV "'
и уравнения A3.84) и A3.85) сводятся к уравнениям
, q (б* + 1>M. jU>m) dv0 = p^f A3.95)
A3-96)
vQ(e)
Здесь опять \|)jv, g = d$N (Q/dlq.
13.7. ПРЕДСТАВЛЕНИЯ ВЫСШИХ ПОРЯДКОВ
Конечноэлементные представления высших порядков строятся
по существу тем же способом, с помощью которого была получена
формула A3.60). Для полноты изложения посмотрим, как пишут-
пишутся локальные уравнения движения для представления третьего
порядка.
Рассмотрим такую локальную аппроксимацию для поля пере-
перемещений:
«1 = ФДО + ^И& +*?"!%. A3"97>
где ¦флг, г|;]у и if* — локальные интерполяционные функции, опи-
описанные в § 8, а и?, uij и i4jfe — значения компонент перемещений.
и их первых и вторых производных в узловой точке N элемента.
Здесь i, j, к = 1, 2, 3, причем для функций xf^ предполагается,
что j ^ к, так что всего этих функций 6Ne. Напомним (см. (8.8)),
что функции if?^, oEjv и ifjv обладают свойствами
из.»)
"' -о, "*""
дхг дх1 дхг
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА 217
Отметим, что иногда при построении представлений третьего поряд-
порядка для ut удобно исключать некоторые функции г|здг, г|з^, ^w-
Замечая, что
подставляем A3.99) в A2.7) и, используя A2.2), A2.3), A3.45)
и D.17), после некоторых алгебраических преобразований получа-
получаем следующую запись закона сохранения энергии для элементам
Рт"? + Рм»?,3 + Рггтк,}* = °- A3.100)
Здесь PNl, PNij и PNijh — функции от uf, u^j, ufjh и их произ-
производных по времени (см. A3.102)). Поскольку A3.100) должно.
' N ' N 'N
выполняться при произвольных значениях щ , щ^ и щ^и, мы
заключаем, что
Pni = Pnu = Pmih = 0. A3.101)
Это приводит к трем системам уравнений движения для конечног»
элемента:
?0(e>
^w.^i.fc dvo = dTNh, A3.102)
0(e)
°0(e)
Здесь
^Ч ^ лмг + г|,«лмг8) A3.103)
°0(e) 0(e)
0(e) B0(e)
да<грО1 A3.104)
°0(e)
218 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
j Sh\p°NdA0,
) A0(e)
m= J PoPhVNd
vO(e) Л0(е>
°0(e)
Массивы /rajvM, Ijvm, ¦ • •, #3vm" представляют собой матрицы рас-
распределенных по узлам массы, инерции вращения и «инерции
высшего порядка», a pNk, cHnu и №rNk — обобщенные узловые силы,
моменты и моменты высших порядков, соответствующие обобщен-
обобщенным узловым перемещениям uf и их первым и вторым производ-
производным.
Глобальные уравнения движения получаются с помощью пре-
преобразований вида
OV/7 ,,N nTT
= «At/ft, U ^у = Уд(УЙ1у,
(lo.lOo)
Подобным же образом можно получить представления любого
порядка. Поскольку метод их построения ясен, больше на этом
-останавливаться не будем.
13.8. ЭНТРОПИЯ И ТЕПЛОПЕРЕДАЧА В КОНЕЧНЫХ ЭЛЕМЕНТАХ
Для построения конечноэлементных моделей тепловых явлений
вам надо вернуться к понятиям энтропии, скорости нагрева и тем-
температуры, рассмотренным в § 12. Естественно возникает вопрос
о том, какую из имеющихся в нашем распоряжении термодинами-
термодинамических переменных (абсолютная температура, тепловой поток,
градиент температуры, поток энтропии и т. д.) избрать в' качестве
первичной, независимой переменной. Всюду в дальнейшем этот
вопрос решается исходя из следующего соглашения. При построе-
построении конечноэлементных моделей физического явления в качестве
первичных независимых переменных мы выбираем те, которые в этом
явлении наиболее естественным образом наблюдаются или изме-
измеряются. Например, в таком чисто механическом явлении, как
деформация твердого тела, очевидной и простейшей характеристи-
характеристикой является перемещение частиц относительно друг друга. Если
известны поле перемещений и законы поведения материала, то
можно вычислить все остальные механические величины, например
тензор деформаций, скорость, градиенты деформации. Для тепло-
13. ТЕРМОМЕХАНИКА КОНЕЧНОГО ЭЛЕМЕНТА ' 219
вых явлений очевидной характеристикой является изменение тем-
температуры. Температура — наиболее естественная доступная для
измерений величина, описывающая тепловое поведение системы,
и поэтому она принимается за первичную независимую перемен-
переменную *).
При построении конечноэлементных представлений температу-
температуры в типичном конечном элементе мы можем локально абсолютную
температуру аппроксимировать так:
е(„ (х, t) = e* (t) <pN (x)% A3.106)
где (Pjv (х) — локальные интерполяционные функции [обозначение
cpjv (x) = ф$' (х) используется вместо обычного tyN (x) для того,
чтобы подчеркнуть, что тип локальной аппроксимации температу-
температуры не обязательно должен совпадать с типом локальных аппрокси-
аппроксимаций полей перемещений tyN (x) uN]. В большинстве случаев
удобно представлять абсолютную температуру в виде суммы
известной начальной температуры То (х) и изменения температу-
температуры Т (х, t):
6 (х, t) = Го (х) + Т (х, t). A3.107)
В классической термостатике То (х) обычно принимается постоян-
постоянной и предполагается, что | Т (х, t) | <^ То. При использовании
соотношения A3.107) для типичного элемента принимается
Г(е) (х, t) = Т» ФЯ (х)> A3.108)
так что абсолютная температура в элементе задается формулой
6 (х, t) = То (х) + T»yN (x)% A3.109)
где подразумевается, что TN зависят от t. Напомним, что N =
= 1, 2, . . ., Ne и что идентификационная метка элемента для
простоты опущена.
В соответствии с A2.46)
6 I = Qi.t + h + ax A3.110)
где ? — энтропия на единицу объема в Со, h — поступление тепла
от внутренних источников на единицу объема в Со и а — удельная
внутренняя диссипация. Для построения конечноэлементной моде-
х) Выбирая u (x, t) и 9 (х, t) в качестве первичных переменных, мы по
существу используем так называемую «аксиому причинности». По Эрингену
11967, стр. 145], «движение материальных точек тела и их температуру сле-
следует рассматривать как самоочевидные наблюдаемые характеристики термо-
термомеханического поведения тела. Остальные величины, входящие в уравнения
баланса масс, моментов, производства энергии и сохранения энергии (напри-
(например напряжения, энтропия, тепловой поток и т. д.), являются «причинами» ...»
Предполагается, конечно, что внешние воздействия, такие, как объемные
силы, источники тепла и некоторые поверхностные усилия или перемещения,
заданы заранее; см. § 14.
220 ГЛ. Ш. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ли процессов производства энтропии и теплопередачи в типичном
конечном элементе умножим A3.110) на Т (х, t):
Т%1 = Tqlti + Th + Та. A3.111)
Замечая, что
Tqu = {Tqt),i - T.tqt, A3.112)
перепишем A3.111) в виде
Тк - T.tqt = (Tqii.t + Th+ Та. A3.113)
Подставляя A3.108) и A3.109) в A3.113), интегрируя по эле-
элементу и с помощью теоремы Грина — Гаусса преобразуя интеграл
от первого слагаемого в правой части A3.113) в поверхностный
интеграл, получаем
J
х) [То (х) + Фм (х) Тм] |(
°0<e>
где
qN(x)hdv0 + J qint(pN(x)dA0, A3.115)
»0(<0 A0(e)
aN= f or(x, i) yN(x)dy0. A3.116)
Здесь qN — обобщенная нормальная компонента теплового потока
в узле N элемента е, a aN — обобщенная диссипация в узле N.
Поскольку A3.114) должно выполняться при произвольных
TN то
.A3.117)
Это — общее уравнение теплопередачи для конечного элемента х).
Глобальная форма уравнения теплопередачи для всего ансамбля
4) Такого типа конечноэлементные формулировки впервые были даны
Оденом и Агирре-Рамиресом [1969]; см. также Оден и Кросс [1969], Одеа
[19б9г, 19706] и Оден и Поу [1970]. Конечноэлементные постановки класси-
классической задачи теплопередачи впервые были представлены Вильсоном и Никел-
лом [1966] и Беккером и Парром [1967], использовавшими вариационный
принцип. Исследование нелинейных задач теплопередачи методом конечных
элементов было произведено Агирре-Рамиресом и Оденом [1969]. В гл. V
мы подробно рассмотрим такие задачи.
14. УРАВНЕНИЯ СОСТОЯНИЯ 221
элементов такова:
j
»0(е)
i;o) = ^A + 2A, A3.118)
где 3~v —глобальное значение изменения температуры в узле Г
связанной системы, a Qд и 2 д — глобальные значения qN и aN
в узле А:
<?л= S &$> A3.119)
е=1
¦Д (e)w ел
^д = ^/j ййД Ojy . ^1O. l^AJJ
е=1
Отметим, что нормальные компоненты теплового потока q(iii
в A3.115), подобно контактным силам S (х), определены для нас
только на материальных поверхностях в деформированном теле.
Следовательно, qN в общем случае зависят от деформации элемен-
элемента. Для различных граничных условий можно ввести ряд частных
форм qN l). Отметим также, что тепловой поток qt в интеграле
по объему в формуле A3.117) является в общем случае функцией
или функционалом температуры и возможно градиентов перемеще-
перемещений и/или их предыстории и что конкретный вид таких функциона-
функционалов зависит от материала, из которого состоит элемент. Точно
также вид функции производства энтропии ?(е) зависит от свойств
материала.
Представленный выше вывод соотношений, описывающих теп-
теплопередачу в конечных элементах, носит вводный характер. Более
подробно эти соотношения исследуются в гл. V. Там же дается
интерпретация различных входящих в соотношения величин.
Мало что еще можно сказать о форме уравнений, описывающих
теплопередачу в конечноэлементных моделях, пока нет сведений
о материале элемента и пока не установлены уравнения состояния
для ?(е) и qHe) (или ф(е), Щ} и qHe)).
14. УРАВНЕНИЯ СОСТОЯНИЯ
Уже несколько раз отмечалось, что для того, чтобы общие
Уравнения движения и теплопередачи конечного элемента (напри-
(например, A3.60) и A3.117)) можно было приложить к конкретным зада-
задачам, необходимо ввести соответствующие уравнения состояния
(или определяющие соотношения) для напряжений, теплового
г) См. Оден и Кросс [1969].
222 ГЛ. Ш. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
потока, энтропии и, возможно, внутренней энергии или свободной
энергии. В этом параграфе кратко излагаются некоторые аксиомы
теории определяющих соотношений, образующие основу для
построения уравнений состояния идеальных материалов х).
14.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Напомним, что в предыдущем параграфе мы установили, что>
в качестве независимых переменных в уравнениях состояния
используются движение z = z (x, t) [или, что то же самое, поле
перемещений и = и (х, t) = z (x, t) — х] и температура 0 =
= 0 (х, t) [или, что то же самое, изменение температуры Т =
= Т (х, t) = 0 (х, t) — То (х). В качестве зависимых переменных
состояния используются тензор напряжений аг', вектор теплового
потока q, плотность энтропии т| и плотность свободной энергии ijr
(плотность внутренней энергии е при этом можно определить как
)
Мы знаем, что два количества материала одного размера, веса,
цвета и формы могут вести себя совершенно различно при одина-
одинаковых воздействиях внешних сил и потоков тепла. Следовательно,,
поведение данного образца зависит от физических свойств мате-
материала. При этом обычно считается, что приближенное представле-
представление об этих свойствах дают лабораторные испытания. Однако
вопрос об экспериментальном определении свойств материалов
сам по себе чрезвычайно сложен. Даже если бы мы могли уста-
установить совокупность экспериментов, которые показывали быг
как некоторые компоненты напряжения меняются при изменениях
температуры и некоторых компонент деформации и скоростей
деформации, трудно ожидать, что на основе ограниченного числа
эмпирических соотношений мы получим описание свойств мате-
материала для достаточно широкого диапазона деформаций и темпе-
температур. Другими словами, эмпирическая формула может описывать
поведение материала для довольно специальных процессов дефор-
деформирования, воспроизводимых в лаборатории, но та же самая
формула может давать совершенно неудовлетворительные резуль-
результаты при других деформациях. Для того чтобы избежать таких
трудностей, надо установить некоторые правила, которым должны
удовлетворять уравнения состояния материала, чтобы они давали
удовлетворительные результаты для всех классов деформаций
и температур, которые предполагается исследовать. Во-вторых,
х) Подробное изложение теории определяющих соотношений см. у Трус-
делла и Нолла [1965] и Эрингена [1962, 1967] [а также у Трусделла *[1972].—
Ред.]. Хорошими вводными руководствами могут служить книги Трусделла
[1966а] и Эрингена [1967]. Краткое изложение имеется во многих учебниках
по механике сплошных сред, например у Джаунземиса [1967], Лея [1968],
Мэлверна [1970].
14. УРАВНЕНИЯ СОСТОЯНИЯ 223.
нужно иметь точный вид уравнений состояния, согласующийся
с этими правилами, для того чтобы знать, что измерять в лаборато-
лаборатории при исследовании имеющихся в нашем распоряжении образцов
материала. Следует, конечно, иметь в виду, что уравнения состоя-
состояния характеризуют идеальные материалы, действительные матери-
материалы лишь приближенно отвечают различным классификациям
по форме уравнений состояния. Кроме того, надо иметь в виду,-
что можно построить уравнения состояния, описывающие задан-
заданный материал лишь приближенно — только в определенном диапа-
диапазоне температур и деформаций.
14.2. ФИЗИЧЕСКАЯ ДОПУСТИМОСТЬ,
ДЕТЕРМИНИЗМ, РАВНОПРИСУТСТВИЕ
При выборе правил, которыми надо руководствоваться при
построении уравнений состояния, достаточно очевидными пред-
представляется следующие три. Во-первых, мы уже уделили много
внимания локальным формам пяти основных физических законов
сохранения: закона сохранения массы, уравнений баланса коли-
количества движения и момента количества движения, закона сохра-
сохранения энергии и неравенства Клаузиуса — Дюгема г):
A4.1)
Было бы довольно неразумно требовать выполнения законов A4.1)
и при этом выбирать уравнения состояния, которые по каким-либо
причинам приводят к их нарушению. Таким образом, в качеств©
общего правила мы устанавливаем необходимость согласованно-
согласованности уравнений состояния с законами A4.1). Это правило иногда
называют принципом физической допустимости.
Правило 1 (физическая допустимость). Все уравне-
уравнения состояния должны согласовываться с основными физическими
законами сохранения: законом сохранения массы, уравнениями
баланса количества движения и момента количества движения,
законом сохранения энергии и неравенством Клаузиуса — Дюгема.
Второе самоочевидное правило называется принципом детерми
низма. Опыт показывает, что из всего диапазона значений пара
х) См. соотношения E.3), E.21), E.31), A2.14) и A2.31),
224 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
метра времени т от —оо до настоящего момента t и далее до -)-00
заведомо можно исключить значения, большие, чем t; если бы это
было не так, это означало бы, что поведение тела каким-либо
образом зависит от движения и температуры в будущем. Таким
образом, мы"исключаем какую бы то ни было зависимость поведе-
поведения материала от будущих событий. Однако поведение в прошлом
может влиять на поведение материала в настоящий момент; други-
другими словами, переменные состояния (a", q, tj, -ф) определяются
движением и температурой вплоть до настоящего времени вклю-
включительно.
Правило 2 (детерминизм). Значения переменных состоя-
состояния (аг}, q, т|, 1|з) в материальной точке х тела в момент времени t
определяются предысторией движения и температуры всех точек
тела.
Пусть Т (х, t) — al'Gi <S> Gj — тензор напряжений в частице х
в момент времени t. Предположим на минуту, что уравнения состоя-
состояния имеют вид
Т(х, *) = $[*(х', *), 9(х\ *), х, *],
q (x, t) = Q [z (x\ s), 9 (x', s), x, *],
t|(x, t) = jT[z(x\ *)9(x\ s), x, t), ( -)
я|>(х\ t) = W[z(x', s), 9(x\ *), x', *],
где ? и Q — соответственно тензорный и векторный, a jjT иТ —
скалярные функционалы г) от предыстории z (x', s), 9 (х', s),
х' G M, s ^ t, и обычные функции от х и t. В A4.2) в каждом из
четырех уравнений состояния используется одна и та же совокуп-
совокупность независимых переменных [z (x', s), 9 (х\ s), x, t], для того
чтобы избежать всяких предубеждений, которые мы могли при-
приобрести, имея дело с классическими теориями. Например, закон
теплопередачи Фурье утверждает, что 2) q = i?V9, а закон Гука
устанавливает, что компоненты напряжения являются линейными
комбинациями компонент деформации. В более общих теориях,
включающих явления диссипации, возможны случаи, когда
и напряжения и тепловой поток зависят от деформации, от 9, V9
л т. д. В принципе, с помощью правила 1 о физической допустимо-
допустимости можно исключить зависимость Т, q, т| или i|) от некоторых
J) Автор понимает здесь под функционалом всякую (не обязательно ве-
тцественнозначную) функцию, областью определения которой служит мно-
множество функций. — Прим. ред.
%) Градиенты движения и температуры допускаются в качестве аргу-
аргументов функционалов состояния в силу принципа локального действия, рас-
рассматриваемого в следующем пункте.
14. УРАВНЕНИЯ СОСТОЯНИЯ 225
из переменных, но в качестве меры предосторожности мы всегда
начинаем с предположения, что все функционалы состояния (или
определяющие функционалы) зависят от одной и той же совокуп-
совокупности независимых переменных. Этот принцип называется прави-
правилом равноприсутствия.
Правило 3 (равнопрису тствие). Любая величина,
фигурирующая в качестве независимой переменной в каком-нибудь
одном уравнении состояния, должна присутствовать во всех
уравнениях состояния.
14.3. ЛОКАЛЬНОЕ ДЕЙСТВИЕ
Четвертое правило, иногда называемое принципом локального
действия или принципом окрестности, накладывает некоторые
ограничения на гладкость определяющих функционалов в окрест-
окрестности материальной точки х.
Правило 4 (локальное действие). На зависимые пере-
переменные состояния в точке х несущественно влияют значения неза-
независимых переменных в материальных точках, удаленных от х.
Это правило имеет важное значение для конечноэлементных
приложений. Предположим, что функции u (x, t) = z (x, t) — х
и Т (х, t) = 0 (х, t) — То (х) аналитичны в окрестности JT (х„, г)
частицы х0 ? №. Тогда и (х, ()иГ (х, t) можно разложить вблизи
х0 в ряды Тэйлора вида
U (X, t) = U (Хо, t) + U, i (Хо, t) {Хг - Х\) +
+ ~и и (хо, t) {х1-х\) {J-x{) +..., A4.3)
Т (х, t) = Т (хо, t) + T, t (xo, t) {xl - х\) +
±ij.., A4.4)
где х 6 Ж (х0, г). Предположим, что мы фиксировали конечное
число К точек в jjT (х0, г) и обозначили их через х1, х2, . . ., хк,
причем К ^- 4. Множество {xw} этих точек определяет множество
радиус-векторов dN = xN — х0, исходящих из х0- Вводя обозна-
обозначения
uN(t) = u(xN, t), A4.5)
TN(t) = T(xN,t), A4.6)
видим, что можно вычислить A4.3) и A4.4) в каждой точке хм ?
€ Ж (х0, т) и получить 2К соотношений:
u*(O = u(xo, t) + u,i(x0,t)dm + ±u „(so, t)dmdmj+..., A4.7)
TN (t) = T (xo, t) + T,t (xo, t) dm +jT,u (xo, t) dNidmJ +.... A4.8)
15 дж. Оден
226 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
В свете конечноэлементных аппроксимаций ясно, что значения
uN (t) eP (t) — это просто узловые перемещения и температуры
в узловой точке xN конечного элемента Ж (х0, г). Аксиома локаль-
локального действия позволяет утверждать, что если г достаточно мало,
то поля u (x, t) vl T (x, t) в/1 (х0, г) с достаточной степенью точно-
точности могут представляться лишь конечным числом членов рядов
A4.3) и A4.4). Это означает, что для х ? JP (х0, г) поля u (x, t)
и Т (х, t) единственным образом могут быть определены по их
значениям в конечном числе точек окрестности jfP (x0, г), и именно
это и является основой использования конечноэлементных аппро-
аппроксимаций в механике сплошных сред. Действительно, заметим,
что A4.3) можно переписать в виде
и (х, t) = а @ + Ь, (*) х* + с„ (*) х*х* + . . ., A4.9)
где
a (t) = и (хо, t) — u i (хо, t) х\ + -j u tJ (xo, t) х\х>0 +..'.,
¦ bt (t) = и,, (х0, *) - ц „ (х0, t) 4 + ~ и m (хо, *) х{х\ + ..., A4.10)
Cij (*) = у», И (Х0. t) —-И, lih (Хо. 0 х\ +4 U- Шт (ХО, t)x*X™+....
Аналогичное соотношение можно записать для Т (х, t) исходя из
A4.4). Если в A4.9) используются, например, только два члена,
то а и Ьг можно определить из четырех условий
uN (t) = u (xN, t) = a (t) + bt (t) xN\ N = 1, 2, 3, 4,
A4.11)
в чем мы узнаем обычную симплексную аппроксимацию для тетра.
эдральной окрестности (конечного элемента).
Возвращаясь к A4.3) и A4.4), мы видим, что вследствие пра-
правила локального действия определяющие функционалы могут
содержать не только предыстории движения z (x, t) и температуры
0 (х, t), но и различные градиенты (производные) этих функций.
Таким образом, если определяющие функционалы достаточно
гладки, то их аргументами кроме движения z (x, s) и температуры
0 (х, s) могут быть их градиенты
zu (x, s), z,t) (x, s), . . ., z,ili2..ti (х, s), . . . ,
A4.12)
0,г (х, s), Q,tj (x, s), . . ., O.ijij...^ (x, s), ....
Материалы, которые характеризуются функционалами от преды-
предыстории различных градиентов высших порядков, иногда называют
непростыми материалами градиентного типа х).
*) Трусделл и Ноля [1965, стр., 111] называют материалы свойства кото-
которых зависят от градиентов до порядка Л^, материалами дифференциального
типа порядка N.
14. УРАВНЕНИЯ СОСТОЯНИЯ 227
Особый интерес представляет подкласс материалов, для кото-
которых важны лишь градиенты первого порядка. Напомним, что
однородное движение относительно начальной койфигурации Со —
это движение вида
z(x, 0 = «.i W(^-a:J) + «e(*). A4.13а)
где хв — фиксированная частица в Со, a ze (t) — произвольное,
не зависящее от х жесткое движение. Аналогично однородная
температура — это температура вида
е (х, t) = е„ (*) («* - 4) + в» (*)• A4.136)
В этих выражениях г,г и 0,* не зависят от х (т. е. z,t и 0,* зависят
только от х0 и t). Пусть (х, t) и 0 (х, t) — движение и температу-
температура в х, и пусть z (x, f) и 0 (х, t) — однородные движения и темпера-
температура. Для каждого е >. О существует б > 0, такое, что || z — z || <
< е (и | 0 — 0 | < е) при || х — х0 || < б, за исключением, воз-
возможно, некоторых сингулярных точек, линий или поверхностей,
т. е. всегда можно выбрать окрестность х0, достаточно малую для
того, чтобы движение и температура точек этой окрестности были
как угодно близки к однородным движению и температуре. В дей-
действительности это представляет собой обоснование большинства
симплексных конечноэлементных аппроксимаций, которые физиче-
физически означают, что движение и температура однородны в конечной
окрестности материальной точки. Далее, если функционалы состоя-
состояния, например ? [ ], достаточно гладки, так что || ?[z (x', s),
0 (х\ s), х, t] — ? [z (x\ s), (х\ s), x, t] || < e? для всех
|| z — z || < e, где || || — надлежащим образом определенная
норма, а х', х ? JP (х0, б) и т. д., то в соответствии с A4.13) каж-
каждый функционал состояния можно записать как функционал от
предыстории х) z (x, t), zt (x, t), 0 (х, t) и 0<г (х, t) и функцию
от х и t. Материалы такого типа называются простыми материала-
материалами. Используя стандартные обозначения для предыстории 2) дви-
движения и температуры:
z* (х,; s) = z (х, t — s)t
t > 0, A4.14)
0* (х, s) = 0 (х, t - s)t
г) В следующем пункте мы исключим зависимость функционалов состоя-
состояния от некоторых из этих переменных; см. A4.21).
2) См., например, Колеман [1964], Трусделл и Нол* [1965] или Трусделл
[1966а] [а также Трусделл *[1972].— Ред.].
15*
228 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
видим^ что для простых материалов A4.2) принимает вид
Т(х, *) = ?[z'(s), zU(s), e'(s), Qli(s), x, t],
q;(x, t) = Q [z* (s), «I г (*), 0f (*), 9| i (*), x, t], ,, . , _
. , . , A4.15)
j| (x, *) = JT [z* (*), zU (*), 9* («), 0|i (*), x, *],
¦ (x, t) = w [zf (s), *;,(«), ef («), e!j (*), x, ty,
здесь подразумевается, что zf (s), z'i (s) зависят от х; таким обра-
образом, наши предыстории в силу гипотезы локального действия
зависят от х, а не от х'. Дальнейшие упрощения форм функциона-
функционалов состояния для простых материалов рассматриваются ниже.
14.4. НЕЗАВИСИМОСТЬ ОТ СИСТЕМЫ ОТСЧЕТА И СИММЕТРИЯ
Очевидно, что поведение материала не зависит от выбора систе-
системы пространственных координат. Например, если удлинение
образца материала пропорционально величине «растягивающей
силы», то этот же закон пропорциональности должен быть засви-
засвидетельствован различными наблюдателями при различных движе-
движениях, использующими для исследования поведения образца раз-
различные системы отсчета.
Для того чтобы перевести это на язык математики, обозначим
через z |(x, t) и z (x, t) две пространственные системы координат,
различающиеся между собой на ортогональное преобразование
a (t)t сдвиг времени i = t — аи перенос с (t):
zi(x,?) = aw(*)*j(*. t) + ct(t). A4.16)
Здесь ct-ij = a), cttftmj « 8tm и det (аи) = ±1- Ортогональные
преобразования типа A4.16) называются преобразованиями наблю-
наблюдателя, поскольку они устанавливают связь между движениями
одной и той же материальной точки, наблюдаемыми двумя различ-
различными наблюдателями. То обстоятельство, что определяющие
функционалы должны быть инвариантны относительно таких пре-
преобразований, известно как аксиома независимости материала
от системы отсчета или аксиома материальной объективности;
эта аксиома представляет собой важное средство, позволяющее
устанавливать дополнительные ограничения на форму функцио-
функционалов состояния.
Правило 5 (материальная независимость от
системы отсчета). Уравнения состояния инвариантны
относительно преобразований наблюдателя.
14. УРАВНЕНИЯ СОСТОЯНИЯ 229
В соответствии с этим правилом определяющий функционал,
скажем ? [ ] [см. A4.2)], должен быть таким, что
? [z (х\ в), 9 (х', *), х, *] =$ [«V. 4 е (х'- *). х> 4 A4-17)
где z (x', s) определяется формулой A4.16) с t, замененным на
«прошлое время» s.
Рассмотрев два частных случая преобразования наблюдателя
A4.16), мы получим сейчас два важных следствия из принципа
независимости материала от системы отсчета. Рассмотрим, во-пер-
во-первых, случай временного сдвига, когда а = t, ац = 8tj, ct (s) = 0.
Тогда z (x', s) = z (x\ s + t), t = t — a = 0 и, для примера,
T = S[*(x\.* + *). 9(x',s + f), x, 0]. A4.18)
Однако можно ввести новый параметр времени s = t — s, 0 ^
^ s ^ оо, так что s + t = t — s. Тогда . ;
T = ?[z(x', t—1), 9(x', t — s), x, 0]. A4.19)
Отсюда следует, что определяющие функционалы не зависят от
времени и являются функционалами от предыстории z (x', t — s) =
= zf (х', s) и 0 (х', t — s) = 0f (x', s). Второе следствие получается
в результате рассмотрения того частного случая, когда A4.16)
является жестким переносом системы координат: atj = 6tj, a = 0,
с (s) =. — z(x, s). Тогда z (x', s) = z (x', s) — z (x, s), и, учитывая,
что определяющие функционалы явно не зависят от времени,
а также принимая s = s, получаем
'{Г = Z [z (x\ t — s) — z(x, t — s), G (x', t — s), x]. A4.20)
Однако, согласно принципу локального действия (правило 4),
z(x', t — s) — z(x, t — s) = z, t (x, i —s) (ж'4—xl) +
+ jz,tJ(x, г-з)(х'1-хг)(хГз-х>)+..., A4.20а)
9(x', t—*) = 9(x, ^ — *) + 9,j(x, *—*)(«'* —a;f)+ A4.206)
Таким образом, определяющие функционалы зависят от\предысто-
рий градиентов движения, а не от предыстории самого движения.
Обращаясь к A4.15), мы видим, что вследствие принципа неза-
независимости материала от системы отсчета уравнения состояния
для простых материалов имеют вид:
т(х, «) = ?[*!«(*), ef(S), е;«(*), х],
q(x, t)=Q[*!i(*). 9*(*), e|i(*), x],
* . , A4.21)
T)(x, t) = jr[zU(s), в'(*), е|,(*), x],
Ц»(х, t) = 1Ift*!i(*), e'(*), e|i(*), x],
где опять подразумевается, что предыстории зависят от х.
230 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Еще одно приложение правила 5 связано с рассмотрением част-
частного случая преобразования A4.16), когда с (s) = 0, а — 0,
a a1 (s) = [atj (t — s)] произвольно (т. е. случая произвольной
непрерывной предыстории жестких вращений пространственной
системы координат); оно часто приводит к значнтельному упроще-
упрощению вида определяющжх функционалов. В этом случае для прос-
простых материалов
%Ца* (*) L|4 (*), 0f («), а* (в) 9|,(в), х] =
= e(*)S[i|i(e), ef(s), efi(s), x]«T(t). A4.22)
Любой определяющий функционал должен иметь форму, инвари-
инвариантную относительно преобразований вида A4.22).
Преобразования пространственной системы координат типа
A4.16) наводят на мысль о возможности инвариантности относи-
относительно преобразований материальных систем отсчета. Такие
преобразования имеют смысл, если мы рассматриваем материалы,
обладающие некоторыми свойствами симметрии в начальной кон-
конфигурации Со- Пусть Со и С* — две начальные конфигурации
тела, описываемые материальными координатами х и х* соответ-
соответственно. Движением тела будет тогда z (х, t) илж z (x*, t) в зависи-
зависимости от того, какая конфигурация используется в качестве
отсчетной. Если зафиксировать текущую конфигурацию, то,
очевидно^
^ ^ A4.23)
Далее, можно найти невырожденное линейное унимодулярное пре-
преобразование St которое переводит Со в С* в том смысле, что dx*i =
= S\j dx' (или dx* =!. S dx). Соотношение A4.23) показывает, что
градиенты деформации относительно Со а С* связаны между
собой так:
gx*i
A4.24)
Если, например, Т = ?[z'j (x, s), x] (предыстория температуры
временно для простоты опущена), то такжеТ = ?* [z'i* (x*, s), x*],
а это означает, что функционалы ? [ ] и ?* [ ] должны удовлет-
удовлетворить соотношению
Z[zti(x, s), х] = ?•[*.'«(*, s)S~\ Sx + b], A4.25)
где Ь указывает на возможный перенос системы х относительно х*.
Теперь предположим, что свойства материала в двух различных
конфигурациях Са и С* одинаковы (плотности р0 и р* предпола-
14. УРАВНЕНИЯ СОСТОЯНИЯ 231
гаются равными). Тогда, опуская перенос Ь, имеем
%[**,i(x, s), x] = S[*|i(x, *) S-1, Sx], A4.26)
где det S = ±1 (поскольку р*, == | det S | p0).
Совокупность унимодулярных отображений S, которые сохра-
сохраняют форму функционала инвариантной, образуют группу изотро-
изотропии определяющего функционала. Групповое свойство х) следует
из того, что совокупность невырожденных унимодулярных преоб-
преобразований S образует мультипликативную группу & относитель-
относительно операции взятия композиции линейных преобразований (т. е.
матричного умножения), а именно если Slt S2, S3 ? &, то S^ ? &
(ибо det SiSs = det Si det S2 = ±1), S;1S1 = I, S~\ l?$ и
Si (S2S3) = (S^) S3. Предположим, что две произвольные началь-
начальные конфигурации Со и С* связаны между собой отображением
8: Со -*¦ С* и функционалы реакции материала ? в Со и С* суть
соответственно ? [ ] и ?* [ ]. Предположим также, что эти функ-
функционалы имеют группы изотропии Z/ и §*¦ Тогда если Hf§,
то ? [z|i (x, s) = ?* [ z|{ (x, s) SHS], и это означает, что SHS 6
? §*. Две группы^ и Ь*, связанные между собой соотношениями
типа SHS = Н*, гдеН* ? &* и S ?§, называются сопряженны-
сопряженными группами. Поскольку наши отображения взаимно однозначны
и групповые свойства при таких отображениях сохраняются,
группы "§ и S* изоморфны. Значит, группы изотропии функцио-
функционала, соответствующего любым двум связанным между собой
унимодулярным преобразованием начальным конфигурациям, изо-
изоморфны. Это свойство иногда называют материальным изоморфиз-
изоморфизмом.
Группа "§ для данного материала является подгруппой полной
группы 11 всех унимодулярных преобразований и может содер-
содержать (а может и не содержать) группу О ортогональных преобра-
преобразований. Поведение материала можно охарактеризовать в соот-
соответствии со свойствами группы изотропии для функционалов
состояния этого материала. Например, если для отсчетной конфи-
конфигурации Со группа изотропии "§ совпадает с ортогональной груп-
группой 0 или содержит ее, то материал называется изотропным,
а конфигурация Со называется естественным или недеформирован-
ным состоянием. Для изотропных материалов мы принимаем S = а
и устанавливаем, что а? [z'i (x, s), х] аг = ? [az'{ (x, s) аг,ах].
С другой стороны, если & с О, то материал называется ани-
аотропным в Со. Далее, если 0 э &, материал называется про-
простым твердым телом, а если "§ — полная унимодулярная груп-
группа, то — простой жидкостью. Наконец, если мы к локальным
«тестам» типа dx* = S dx присовокупим, как в A4.25), и перенос
г) См. п. 7.1.
232 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
х* = Sx + d, то в случае изменения ? [ ] вследствие наличия
переноса b материал называется неоднородным. Если же % [ ]
не зависит от Ь, то материал называется однородным.
Определяющие функционалы для всех идеальных материалов
обладают группой изотропии некоторого определенного типа,
и мы можем в качестве руководящего принципа для упрощения
формы функционалов сформулировать шестое правило, называемое
принципом материальной симметрии:
Правило 6 (материальная симметрия). Форма урав-
уравнений состояния должна быть инвариантна относительно группы &
унимодулярных преобразований материальной системы отсчета.
Отметим, что если для однородных материалов мы возьмем
S = I, то для любого b справедливо равенство ? [ъ\г (х, s), x] =
= ? [z*,- (x, s), х + b], что возможно, только когда Z [ ] не зави-
зависит явно от х. Значит, для однородных материалов можно не
включать х в число аргументов определяющих функционалов.
Другие правила. Кроме сформулированных шести аксиом
возможно установить ряд других правил, которым надлежит
следовать при построении уравнений состояния. Поскольку основ-
основными являются правила 1—6, мы лишь упомянем здесь еще два
других правила. Во-первых, ясно, что определяющие функциона-
функционалы должны согласовываться с размерностью величин: все члены,
входящие в уравнения состояния, должны иметь одинаковую
размерность. Во-вторых, часто вводится «аксиома памяти» *),
в соответствии с которой предполагается, что текущие значения
переменных состояния несущественно зависят от их значений
в отдаленном прошлом. Это предположение является аналогом
принципа локального действия в области времени и по существу
накладывает на z (x, t) требования гладкости по переменной t.
Если, например, функция z (x, t) достаточно гладка и допускает
разложение вида
z (х, 9) = z (x, t) + z (x, t) (t-1) + ... + -I z (x, t) (i- t)n +...,
A4.27)
где tQ ^ t ^ t, если t0 достаточно «далеко», так что поведение
при t <C t0 не влияет существенно на поведение в момент t, то
определяющие функционалы можно свести к функциям от текущих
скоростей z (x, t), z (x, t), . . ., z"(x, t) [и, конечно, 6 (х, t), 6 (х, t), ...
х) Современная формулировка дана Колеманом и Ноллом [1961]. См.
также Трусделл и Нолл [1965] и Колеман [1964] [и Трусделл *[1972].— Ред.].
Как указывает Эринген [1967, стр. 153], формально понятие затухающей
наследственности было введено Странео [1925]. Мы рассмотрим это понятие
позднее в п. 19.1.
14. УРАВНЕНИЯ СОСТОЯНИЯ 233
п
. . ., 6 (х, t)]. Такие материалы называются материалами скорост-
скоростного типа. Для материалов скоростного типа может, однако,
потребоваться необычно высокая дифференцируемость z (х, t)
и 6 (х, t), так что для достижения большей общности аксиому
памяти лучше записывать, используя функциональную форму
уравнений состояния, которая требует лишь интегрируемости
функций z'j (х, s), 6* (х, s) и т. д.
Мы не придаем такого же значения аксиоме памяти, как сфор-
сформулированным ранее шести правилам, потому что во многих
случаях она очевидным образом неприменима (например, для
упруго-пластических материалов). Однако это правило может
быть полезным при исследовании некоторых задач термовязко-
упругости; мы рассмотрим его подробнее в гл. V.
14.5. ОПРЕДЕЛЯЮЩИЕ ФУНКЦИОНАЛЫ ДЛЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Располагая некоторым набором определяющих функционалов,
которые удовлетворяют всем основным принципам теории опреде-
определяющих соотношений, можно получить представления этих функ-
функционалов, пригодные для конечноэлементных исследований. Рас-
Рассмотрим, например, случай однородного простого термомехани-
термомеханического материала, характеризуемого уравнениями состояния
вида
Т(х, t) = %[*', i(*, *), в*(*. *), 0*i(x, *)],
q(X, o = Q[«!i(*. *), e*(x, *), e?i(x, *)], 0Q4
. . t A4. lo)
T)(x, t) = jT[zU(x, s), 6'(x, *), e*t(x,s)],
i|>(x, t) = W[zU(x, s), 6'(х, *), 91,A, *)].
Для типичного конечного элемента е имеем:
zt (x, t) = xt + Ui (t) гр^ (х),
Zt, j (X, t) = бу + U? (t) ^N, j (X), 2g
9(х, t) = T0 + TN(t)yN(x),
Э,г(х, t) = TIt(t)iflftt(x)t
где опять для простоты идентификационная метка элемента опуще-
опущена и То (х) = То — постоянная начальная температура. Обозна-
Обозначая предыстории узловых перемещений и температур через
T"(t) A4-30)
234 ГЛ. III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
видим, что A4.28) можно переписать в виде
Т(х, t) = %[u^(s), Tm)(s)],
q(x, *) =
],
w/« A4.31)
, Tm(s)],
), Tm(s)],
где
, (x) u?(t)(s), T0 + <pN (x) Гад («), f Wf, (x)
A4.32).
Таким образом, для конечных элементов зависимые переменные
Т, q, ц и г|з в точке х внутри элемента являются функционалами
от полных предыстории узловых перемещений и изменений тем-
температуры. Аналогичные заключения получаются и для более
общих материалов градиентного типа. Отдельные примеры будут
рассмотрены в гл. IV и V.
Глава IV
Теория упругости
при конечных деформациях
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ
В этой главе исследуется приложение метода конечных элемен-
элементов к задачам теории упругости при конечных деформациях х),
т. е. к задачам об очень больших деформациях упругих тел, когда
не накладывается никаких ограничений на порядок величин
перемещений, градиентов перемещений и компонент тензора дефор-
деформаций. При этом в качестве частных случаев получаются различ-
различные дискретные модели задач классической теории упругости при
бесконечно малых деформациях. Однако прежде чем рассматривать
свойства дискретной модели, надо охарактеризовать механические
свойства материалов, которые считаются упругими.
15.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Теории, относящиеся к упругим материалам, являются старей-
старейшими теориями о поведении деформируемых тел. В 1678 г., напри-
например, Гук [1678] 2) дал следующее описание одного класса упругих
тел: «Совершенно очевидно, что Правило, или Закон, Природы
для каждого упругого тела состоит в том, что возникающая в нем
сила, или напряжение, стремящаяся возвратить тело в его есте-
естественное состояние, всегда пропорциональна расстоянию, или
смещению, от этого естественного состояния...» Хотя мы теперь
знаем, что закон пропорциональности Гука не обязателен для
упругих тел (и фактически редко выполняется при конечных
упругих деформациях), такие материалы тем не менее действитель-
действительно обладают «естественными состояниями»; в эти состояния тела
х) С изложением теории упругости при конечных деформациях и реше-
решениями некоторых задач можно ознакомиться по книгам Грина и Зерны
[1968] и Грина и Адкинса [1960].
2) Гук пришел к своему закону пропорциональности в 1660 г. и опуб-
опубликовал его в виде анаграммы в 1676 г. Исторический обзор развития тео-
теории упругости можно найти в статье Трусделла [1952]. Эта статья была пере-
переиздана в 1966 г. (см. список литературы). Отметим также старую книгу Тод-
хантера и Пирсона [1893].
236 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
возвращаются после снятия внешних нагрузок по произвольной
программе.
Таким образом, если мы намереваемся дать более точное описа-
описание упругих тел, то у нас имеются два напрашивающихся отличи-
отличительных их признака. Во-первых, термодинамические процессы
в упругих телах должны быть обратимы в том смысле, что ни
в одной точке тела нет диссипации. Во-вторых, поведение упругого
тела не должно зависеть от предыстории деформирования; напри-
например, напряжение в любой частице упругого тела определяется
только текущей деформацией — в противном случае возвращение
тела в начальное состояние различными процессами деформиро-
деформирования могло бы привести к различным напряжениям. В дальней-
дальнейшем мы увидим, что второй отличительный признак приводит
к более слабым ограничениям на определение упругих тел, чем
первый.
15.2. УПРУГИЕ МАТЕРИАЛЫ
Определение упругих материалов основывается непосредствен-
непосредственно на наблюдении, что напряжения в таких материалах зависят
только от величин деформаций в текущий момент времени. Мате-
Материал называется упругим, если напряжения в нем в произволь-
произвольный момент времени t зависят только от локальной деформации
в этот момент времени и не зависят от предыстории деформиро-
деформирования. Это означает, что уравнения состояния для упругих мате-
материалов имеют вид
a« = S«(Gr.), A5.1)
где 2*J (Grs) — функция текущей деформации, характеризуемой
текущим значением тензора деформации относительно некоторой
фиксированной конфигурации (G^- = б^- + %Уи)- Ясно, что вместо
Grs в A5.1) можно использовать любую другую эквивалентную
меру деформации, например уц или ъЛ. Кроме того, понятно, что
среди аргументов функции поведения (реакции) материала 2 " ( )
должно присутствовать х, чтобы можно было описывать поведение
неоднородных тел. Однако для удобства мы не будем указывать
явно зту зависимость.
Поскольку в определении упругих материалов термические
переменные (например, 6, r\, q1) не фигурируют, теория упругости
описывает только механическое поведение материалов. Следова-
Следовательно, A5.1) можно назвать уравнением механического состояния.
Сравнивая A5.1) с A4.21), мы замечаем, что упругие материалы
образуют специальный подкласс простых материалов: A) свойства
этих материалов не зависят от температуры и ее предыстории,
и B) напряжения в них зависят лишь от «постоянных» предыстории
деформирования, т. е. предыстории, при которых деформация
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 237
во все моменты в прошлом равна текущей деформации *). Таким
образом, можно сказать, что упругие материалы образуют простой
подкласс простых материалов..
Если рассмотреть A5.1) с точки зрения изложенных в § 14
аксиом состояния, то очевидно, что принципы детерминизма
и локального действия соблюдены и что в данном случае принцип
равноприсутствия несуществен, поскольку имеется только одно
уравнение состояния. Физически допустимые процессы для неко-
некоторых упругих тел будут указаны в следующем параграфе. Имея
в виду требования независимости от выбора системы координат и
материальной симметрии, можно сказать, что функция реакции
S1^ должна быть инвариантной относительтГвсех преобразований
наблюдателя вида A4.16) и относительно * преобразований ма-
материальной системы отсчета, принадлежащих группе изотропии
материала. В частности, если все ортогональные преобразования
« = [a?j (t)]принадлежат группе изотропии упругого материала
и если
K, A5.2)
то материал изотропен. С другой стороны, при преобразовании
материальных координат х = Sx должно выполняться равенство
а1' = 2ij (G), где G = SGS и 21* (G) = SSij (G).S-1. Отметим
также, что, поскольку Gt] безразмерно, функция Ег' (Grs) должна
иметь размерность напряжений.
Особый интерес представляют изотропные материалы A5.2).
В этом случае ог3 является изотропной функцией симметричного
тензора Gtj и 2 (G) можно записать в относительно простом виде.
Предполагая, что функция 2 (G) аналитична относительно G,
мы можем представить ее в виде ряда по степеням G:
2(G)=a0I + a1G + a2G2+... + anG"+.... [A5.3)
Здесь ао,,ах, . . ., ап —скалярные функции компонент Gu тензо-
тензора G. По теореме Кэли — Гамильтона, примененной к квадрат-
квадратным матрицам третьего порядка, матрица G удовлетворяет своему
характеристическому уравнению:
, A5.4)
где /х, /2, /3 — главные инварианты 2) тензора G. Значит, G3 и все
более высокие степени G можно выразить через G2, G, 1 и главные
инварианты G. Таким образом, 2 (G) является аналитической
х) Трусделл и Нолл [1965, стр. 123] показали, что теория упругости
применима ко всем простым материалам в статике, т. е. к простым материалам
в состоянии равновесия, находившимся в состоянии равновесия во все вре-
времена в прошлом.
2) См. D.25).
238 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
изотропной функцией от G в том и только в том случае, когда ее
можно представить в виде
A5.5)
где х0, хг и х2 — скалярнозначные полиномы от инвариантов Ilt
/2, /3. Поскольку единичный тензор 1 в конвективных координа-
координатах х1 имеет компоненты G%i, Gtj или 8}, из A5.5) следует, что урав-
уравнение состояния для изотропного упругого тела может быть запи-
записано в виде
t i • A5.6)
о] = хоб) 4- x16im6"GJ-rGms + x28lrGT}
и т. д. С другой стороны, если в качестве материальных координат
выбрать криволинейные координаты |г в начальной конфигура-
конфигурации С о, то
0" = XoG" + XigirghGrs + Krf",
а\ = щЬ) + xlgimgrsGjTG + x^G
где g%} — контравариантный метрический тензор в Св.
15.3. ГИПЕРУПРУГОСТЬ, ТЕРМОДИНАМИЧЕСКИЕ ОСНОВЫ
Другое определение упругих материалов можно получить исхо-
исходя из понятия обратимости. Рассмотрим классический пример
силы F (х), действующей на частицу при движении ее из одной
точки в другую. Напомним, что независимость работы W от пути,
пройденного частицей, означает существование некоторой диффе-
дифференцируемой- функции текущего положения W (х), называемой
потенциалом-, градиент которой равен силе F (х) = VW (х). Рабо-
Работа, совершаемая такими консервативными силами на замкнутом
пути, равна нулю. При этом говорят, что F «порождается» потен-
потенциальной функцией W. В том же духе мы можем считать, что про-
процесс деформации, описываемый, например, тензором меры дефор-
деформации Gtj или тензором деформации yi}, представляет собой «путь»,
пройденный сплошным телом.. При этом «силой», совершающей
работу, будет, конечно, тензор напряжений ali. Обратимость
упругих деформаций и независимость от пути (от предыстории
деформации) для упругих тел приводят нас к предположению
о существовании некоторой дифференцируемой функции деформа-
деформаций, скажем Е {уц), которая порождает напряжения. Таким обра-
образом, мы предполагаем, что существует потенциальная функция
Е (ум), называемая плотностью энергии деформации, такая, что
рЕ = о*}уи. A5.8)
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 239
Тогда
pE(yij) — p——yij = o™yi] A5.9)
и.1'2)
Чтобы отличать упругие материалы, как они были определены
в предыдущем пункте, от материалов, удовлетворяющих соотно-
соотношению A5.10), последние будем называть гиперупругими. Таким
образом, материал называется гиперупругим, если напря-
напряжения в теле выводятся из функции энергии деформации с помощью
соотношения A5.10).
Чтобы обосновать существование потенциальной функции Е(уг^
исходя из изложенных в § 12 термодинамических законов, напом-
напомним, что, согласно A2.14), A2.35) и A2.36), локальный закон сохра-
сохранения энергии можно записать в одном из следующих видов:
A5.11)
A5.12)
A5.13)
Законы сохранения массы и баланса количества движения при
этом локально удовлетворяются. Поскольку обратимость дефор-
деформаций упругих тел предполагает равенство нулю внутренней
диссипации б, A5.11) и A5.12) можно переписать в виде
A5-14)
A5.15)
Из предыдущих рассуждений ясно, что в определяющие законы
упругих тел должны входить только текущие значения независи-
независимых переменных состояния, а не их предыстории. В соответствии
с этим рассмотрим класс материалов, удовлетворяющих A5.14)
х) Ясно, что, взяв плотность энергии деформации в виде функции от ytjr
а не Gtj, мы не нарушили общности, поскольку ytj = (Gtj — 6fj)/2. Пусть,
например, Е (уи) = A/2) Ё (Gi}); тогда pi = A/2) рЁ = A/2) р (dE/dGrs)X
X (dGrJdyl}) ytj, и вместо A5.10) мы будем иметь oli = p (дЁ/dGjj).
2) Во избежание недоразумений необходимо иметь в виду, что при диф-
дифференцировании Е по уц все остальные компоненты, включая yjt, считаются
постоянными A9^ /)• Следовательно, соотношение A5.10) в действительности
надо было бы записать в виде а'з = A/2) р [(дЕ/ду^) + (dE/dyjt)]. Чтобы
избежать этой громоздкой записи, условимся, что во всех последующих фор-
формулах для любого тензора Atj под д/дАц понимается A/2) [(dldAi}) +
4- (д1дАн)].
240 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
и A5.15), для которых свободная энергия является дифференцируе-
дифференцируемой функцией текущих значений деформации (характеризуемой
тензором деформации), температуры и градиентов температуры *),
т. е.
г|> = V (yti, 6, 9,0. A5.16а)
Согласно принципу равноприсутствия 2), все другие определяющие
функции (а", т], Q1) должны быть функциями тех же самых пере-
переменных:
, 9,8.0, A5.166)
Ч^Л*(Чц, 9, Э, 0, A5.16в)
Qi = &i(yii, в, 0,0- A5.1бг)
Поскольку ф = е — т]6, вместо A5.16а) можно использовать вну-
внутреннюю энергию
е = S (уи, л, е.0; A5.17а)
тогда
а" = 2"G„, л. е.0, A5-176)
8 = в(т„, т|, 8,0, - A5.17в)
С1 = §*(?», Л, 9,0- A5.17г)
Ясно, что
f ^e+^7e-fe A5Л8)
A5.19)
Подставляя A5.18) и A5.19) в неравенство Клаузиуса — Дюгема
A2.31), применяя A2.33) и A2.36) и производя перегруппировку
членов, получаем
( )^4I A5.20а)
. A5.206)
х) Для неоднородных и анизотропных материалов опять следует в число
аргументов функции V ввести х и, возможно, некоторые преимущественные
направления dfe. Однако для простоты записи из всех аргументов указы-
указываются лишь ytj, 9 и 9ift, а зависимость от х и d^ подразумевается.
а) См. правило 3,' п. 14.2.
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 241
Так как эти соотношения должны выполняться для любых угя Л>.
8 и 8,ft, мы заключаем, что
ЯЧГ ЯР
о ' = р—— = р-т—, A5.21а)
oyij "Ун
Т1=—Ж' 0 = 4f' A5.216, в)
^- = #Г = 0. A5.21г)
Равенства A5.21г) показывают, что если 6 = 0, то свободная
энергия материалов типа A5.16) и внутренняя энергия материалов
типа A5.17) не зависят от градиентов температуры 0^. Ввиду
A5.21а) и A5.216) это означает, что ам, Н и т| тоже не зависят от
0,^. Значит, вместо A5.16) можно написать
., Э),
'9)'
, 9,0,,),
где
а вместо A5.17)
. Л),
0G,7, Л).
A5-24)
где
2ij(YM- Л) = Р-^г и в(То, Л) = ||- A5.25)
Сравнивая A5.22) с A4.15), видим,что уравнения A5.22) описывают
частный класс простых материалов, поведение которых зависит
только от текущих значений ytj и 0, а не от их предыстории х).
Материалы, описываемые уравнениями A5.24), называются совер-
совершенными 2) материалами.
Попытаемся определить термодинамические процессы и урав-
уравнения состояния, допускающие существование потенциальной
х) С другой стороны, A5.22) можно считать уравнениями состояния
любого простого материала в состоянии «теплового равновесия» (Трусделл
и Нолл [1965, стр. 300]). См. подстрочное примечание на стр. 189.
2) Эта терминология используется Трусделлом и Ноллом [1965, стр. 296].
16 дж. Оден
242 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
функции типа использованной в A5.10). С этой целью рассмотрим
сначала изотермические процессы в материалах, описываемых
уравнениями A5.22). Для таких процессов температура 0 постоян-
постоянна, так что 6 = 0 и можно написать i|) = W (уи). Тогда A5.15)
и A5.21) дают
P4>ayv °и Р A56>
Далее, рассмотрим иззнтропические процессы в материалах,
описываемых уравнениями A5.24). Для таких процессов г| = О
и можно записать е = S (уц)- Тогда A5.14) и A5.21) дают
% Ц^ A5.27)
Сравнивая A5.26) и A5.27) с A5.8) и A5.10), видим, что теория
гиперупругости применима к изотермическим процессам в классе
простых материалов, характеризуемом соотношением A5.22), и к
изэнтропическим процессам в совершенных материалах. В первом
случае энергия деформации ассоциируется со свободной энергией,
а в последнем — с внутренней. Более общим образом предположим,
что второе из уравнений A5.24) разрешимо, так что г| представимо
в виде функции от у ц и 6. Тогда можно исключить г\ из остальных
уравнений состояния A5.24), так что в них будут фигурировать
лишь функции от ун и 0. Отсюда можно сделать вывод, что теория
гиперупругости применима и к изотермическим, и к изэнтропиче-
изэнтропическим процессам х) в совершенных материалах и в простых мате-
материалах класса A5.22) (или, что то же самое, к изотермическим
и изэнтропическим процессам во всех простых материалах в состо-
состоянии теплового равновесия).
С точки зрения A5.21а) ничто, конечно, не мешало нам полу-
получить ог' из потенциала W (уц, 0) для любых термодинамических
процессов в материалах, характеризуемых уравнениями A5.22).
Однако в этом случае мы получили бы теорию термоуптругости,
поскольку напряжения зависели бы и от ytj, и от 0. Термоупру-
Термоупругостью мы займемся в следующей главе, а здесь ограничимся рас-
рассмотрением чисто механического поведения материалов. Таким
образом, в остальной части этой главы мы всеми тепловыми эффек-
эффектами пренебрегаем и сосредоточиваем свое внимание на материа-
материалах, характеризуемых только одной определяющей функцией —
энергией деформации Е (уц) или функцией 2*' (Grs) из A5.1).
*) Рассматривая члены, входящие в уравнение энергии, можно было бы
также исследовать изоэнергетические процессы (е = 0) в материалах, опи-
описываемых соотношением A5.14), для которых г\ = ЛГ (у^, е). В этом случав
энергия деформации ассоциируется с удельной энтропией,
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 24Я
15.4. ПОЛНЫЕ ПОТЕНЦИАЛЫ
Заметим, что если внешние силы F и S тоже порождаются
потенциальной фунцией V, например
V=— \ pF-udv- \ S-udA, A5.28)
v ' А
то можно определить полную потенциальную энергию П тела
как сумму
П = U + V, A5.2»)
где U — полная энергия деформации
A5.30|
Используя обычный прием вычисления вариаций П, соответ-
соответствующих допустимым вариациям би$ поля перемещений (т. е. ва-
вариациям, удовлетворяющим всем наложенным на деформацию
кинематическим ограничениям), интегрируя по частям и учитывая
A5.10), получаем следующее выражение для первой вариации
полной потенциальной энергии:
6П
= j (a«. + P^j) Swj dv. A5.31)
V
Мы знаем, что если тело находится в равновесии, то выражение,
стоящее в скобках в соотношении A5.31), равно нулю. Таким обра-
образом, приходим к известному принципу стационарности потенци-
потенциальной энергии: из всех допустимых полей перемещений упругого
тела поля, отвечающие состояниям статического равновесия, выде-
выделяются тем, что им соответствуют стационарные значения пол-
ной потенциальной энергии FП = 0). Более того, можно пока»
зать, что если мы имеем состояние устойчивого равновесия, то Ц
при этом принимает минимальное значение.
В более общем случае динамики консервативных систем можно
расширить понятие полной энергии, включив в нее кинетическую
энергию. Лагранжев потенциал L определяется формулой
L = к — U, A5.32)
где к — кинетическая энергия, выражение которой дается форму-
формулой A2.3). Принцип Лагранжа (или принцип Гамильтона для
консервативных систем) гласит, что из всех движений, переводящих
16*
244 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
консервативную систему из одной конфигурации в другую за интер-
интервал времени (t0, t±), происходящие в действительности выделяются
тем, что они придают стационарное значение FА = 0) интегралу
действия А, где
=\bdt.
t
A5.33)
15.5. ФУНКЦИЯ ЭНЕРГИИ ДЕФОРМАЦИИ
Обычно предполагается, что размеры и форма упругого тела
известны нам в начальной конфигурации Со, в идеальном случае
отвечающей недеформированному состоянию материала. По этой
причине удобнее использовать вместо Е (уц) упругий потенциал
W (Уи), отнесенный к единице объема v0 недеформированного тела.
В силу закона сохранения массы
W = р0Е, A5.34)
где р0 — массовая плотность в Со (р0 = V^Gp). Следовательно,
вместо A5.10) мы имеем
у 1 т A535)
1 YG dytJ V ;
С другой стороны, тензор напряжений f13, определяемый форму-
формулой E.14), можно вычислить так:
t^^-^L. A5.36)
дуй
Ниже приводятся некоторые свойства и различные формы
функции энергии деформации W.
Анизотропные мате риалы. Группы изотропии анизот-
анизотропных материалов обычно подразделяются на 12 различных типов,
каждый из которых определяет особый класс анизотропии. Первые
11 соответствуют 32 кристаллическим классам в соответствии
с классификацией кристаллов в минералогии *) и принадлежат
шести основным типам кристаллических систем: триклинной,
моноклинной, ромбической, тетрагональной, кубической и гекса-
гексагональной. Опишем вкратце эти 11 кристаллических типов 2).
Чтобы сделать это, надо перечислить правосторонние вращения S,
порождающие группы изотропии & для каждого типа материала,
1\ е. те вращения, которые, вместе с обратными к ним, дают после
х) См. Дана и Хёрлбат [1969].
2) Подробности можно найти у Смита и Ривлина [1958], Грина и Адкин-
са [1960], Трусделла и Нолла [1965] [см. также Трусделл *[1972, стр. 194].—
Ред.].
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 245
взятия всевозможных конечных произведений все элементы груп-
группы. Пусть Sn'P обозначает правостороннее вращение на угол |5
(О < р < 2я) относительно оси, направленной вдоль единичного
вектора п. Тогда наши 11 кристаллических типов инвариантны
относительно следующих преобразований '):
триклинная система: кубическая система:
1) I, -I, 6) SibIt, S'2'*, Sn'2n/3,
моноклинная система: 7) Sll'It/2, Si2'"/2, Si3'"/2,
2) S 3> , гексагональная система:
ромбическая система: 8) S'3' 2я/3,
3) SilJ\ Si2'", 9) S11"*, Si3'2lt/3,
тетрагональная система: Ю) S'3' п/3,
4)Si3-"/2, И) S11"", 81я'я/3.
5) Si3'"/2, Sib",
Здесь i, — ортонормалыше базисные векторы, а п = (ix + i2 + i3]
К этим одиннадцати можно добавить двенадцатый тип анизо-
анизотропии, называемый трансверсальной изотропией, группа изотро-
изотропии которого порождается тождественным преобразованием I
и преобразованием S's- 0, где Р — произвольный угол, заключенный
между 0 и 2я. Так называемые ортотропные материалы относятся
к типам 3, 5, 6 и 7; их группы содержат отражения относительно
трех взаимно перпендикулярных плоскостей.
Чтобы продемонстрировать, как можно использовать группы
изотропии для упрощения вида W, рассмотрим один пример анизо-
анизотропного материала с моноклинной симметрией, для которого
функция энергии деформации является полиномом относительно
компонент деформации уи, уг2, ?зз! Vi2> V13 и Таз- Поскольку
W(у) = W (SyS) для всех S, принадлежащих группе изотро-
изотропии материала, для группы, порождаемой S'3' я, имеем
w (Vii. V22, 7зз, V12, Y13. V23) = W (yllx Y22, ?зз, V12, — Vis. —V23)
A5.37)
Воспользуемся известной теоремой теории групп 2) о том, что
величины (at + bt)/2 и (atbj + п]Ьг)/2 (i, j = 1, 2, . . ., п) образу-
образуют полиномиальный базис для полипомов, симметричных относи-
относительно переменных (аг, а2, . . ., ап) и (Ьь 62, • • •> Ьп). Положим
(alt а2) = —фг, Ъ2) = (у13, у23) и по указанной теореме получим,
что в рассматриваемом примере функция W может быть пред-
J) См. Трусделл и Ноля [1965, стр. 83]
2) См. Г. Вейль [1946].
246 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
ставлена в виде полинома относительно семи величин уп, у22, 7зз»,
Yi2i V?3' V23 и Vi3?23- Аналогичные приемы можно использовать
в для других классов анизотропных материалов х).
Полиномиальное представление. Если предположить,
что функция W(ytj) аналитична относительно своих аргументов у и,
то функцию энергии деформации можно представить в виде ряда
W(ytj)=^Wt(yu), A5.38)
где Wi (уц) — однородный полином степени i относительно у^.
Соотношение A5.38) можно переписать в виде
W = Wo + E%j + ±Eijmnyijymn + 4Eijmn"yijymnyrs +..., A5.39)
где Wo — произвольная постоянная, a Ei}, Eijmn, Ei}mnrs, . . .
называются коэффициентами упругости порядка 0, 1, 2, ...
соответственно. Для однородных тел коэффициенты упругости
представляют собой характеризующие материал постоянные.
Поскольку оба тензора alj (или ?3) и уц симметричны, коэффици-
¦ енты упругости всех порядков тоже симметричны по индексам
из каждой последовательной пары индексов:
Eij = EH,
?ijmn _ jj-jimn __ jja'mm. __ jj-mnij /| rj ^Q\
cnjmnrt pjimnrs pijnmrs _ pijmnsr pijsrmn pmnrsij prsijmn
Из A5.36) следует, что для этого класса гиперупругих материалов
tU = е« + Ei3mnymn + Eijmnrsymnyrs +.... A5.41)
Ясно, что при утп = 0 будет f' = Е1'1. Следовательно, Е1* суть
«начальные напряжения» в начальной конфигурации Со. Если
конфигурация Со выбрана так, что она соответствует естественно-
естественному ненапряженному состоянию, то можно положить Е11 = 0.
Тогд^а, опуская несущественную постоянную Wo, A5.39) можно
записать в виде
W = ± Eijmnytjymn +1 Е»™"Ъ1УтпуГ1 +.... A5.42)
Сохраняя только конечное число членов в представлении A5.42).,
можно получить различные приближенные теории гиперупругости.
Например, кладя в основу предположение, что деформации ytj
«малы», можно получить функцию энергии деформации для клас-
классической теории упругости при малых деформациях, если сохранить
*) Полный перечень инвариантов полиномиальных разложений W для
различных групп изотропии приведен Смитом и Ривлином [1958].
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 247
в A5.42) оТдещ первый член х):
W = ±-Ei}mnyi}ymn. A5.43а)
В зтом случае
tij'' = Е1}тпутп. A5.436)
Хотя компоненты деформации у и в A5.43) и предполагаются беско-
бесконечно малыми, эти соотношения могут и не привести к линейной
теории, поскольку ytj могут нелинейно зависеть от градиентов
перемещений ut, j. Функция энергии деформации для классической
линейной теории упругости получается из A5.43) при предполо-
предположении, что, кроме yij, и вращения со^ (а значит, и ut,j) бесконечно
малы. При этом уг] = etj, где ец — тензор бесконечно малых
деформаций, определенный формулой D.18а), и
mn. A5.44а,б)
Материалы, подчиняющиеся закону A5.436) или A5.446),
называются гукоеыми.
Теория гиперупругости второго порядка получается из A5.42)
при сохранении членов, содержащих коэффициенты упругости
до второго порядка включительно:
1 Eyuymnyrs% A5.45а)
tH = Eiimnynn + Eijmn"ymnyTs. A5.456)
Аналогичным образом, .сохраняя дополнительные члены в выра-
выражении A5.42), можно получить различные теории более высоких
порядков.
Из рассмотрения A5.41), A5.436) и A5.456) видно, что прибли-
приближенные теории упругости можно получать, просто разлагая функ-
функцию реакции материала 2г' (Grs) = 213' Frs + 2yrs) по степеням
Grs или yrs. Такие разложения по форме совпадают с приведенны-
приведенными выше выражениями для f'. Однако соответствующие коэффи-
коэффициенты упругости иногда могут и не совпадать. Более подробно
^обстоятельство будет рассмотрено в конце параграфа.
Изотропные материалы. Поскольку группой изотропии
для изотропных гиперупругих материалов является полная ортого-
ортогональная группа, имеем W {угу) = W (ocfvmna"). Можно показать,
что W в этом случае является функцией главных инвариантов
yij, или, что более удобно, главных инвариантов Gtj'.
_____ W=W (Ilt I2, /,), A5.46)
J) Понятно, что функция, определяемая формулой A5.43а), отличается
от функции A5.42). Однако в обоих случаях удобно обозначать ее одинаково.
Обозначение W используется для различных форм энергии деформации и в по-
последующем, если это не может вызвать недоразумений.
248 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
где 1Х, /2 и /3 определены соотношениями D.25). Для материалов
с функцией энергии деформации такого типа
~ ah дУи + ai2 dytj + д13
или, с учетом D.28),
tij = 2 ™- 8ij + 4 -|? [6W A + угг) - б*VI +
+ 2 -^-[буA + 2?Гг)-2б{)-бЧг + 28™я8^Тт,.?„8]. A5.48)
Для получения приближенных форм W опять естественно рас-
рассмотреть разложение по степеням инвариантов
^=2 S SCrrt(/i-3)'(/a-3)'(/s-l)*, ^„00 = 0. A5.49)
r=0 s=0 (=0
Оставляя, например, только линейные относительно инвариантов
члены, получим аппроксимацию
W = С100 (I, - 3) + С010 (Л - 3) + С001 (/„ - 1). A5.50)
Другая полиномиальная аппроксимация была предложена Кава-
ной [1969] х), предположившим, что
W = А,К\ + А2К2 + АЯК\ + А,К,К2 + АЪК2 +
+ AeKil + A7K2lK2 + A8KiK3 + A9Kl, A5.51)
где А1, . . ., Л9 — постоянные материала, а Кг, К2 и К3 — инва-
инварианты тензора деформации:
Кг = угг, К2 = 4ts4ts, K3 = Vj/V<rV/r- A5.52)
Таким образом, A5.51) содержит члены до четвертого порядка
включительно относительно компонент деформации. С другой
стороны, /ь /2 и /3 с помощью D.26) можно выразить через компо-
компоненты деформации и найти выражения коэффициентов Crst через
коэффициенты упругости, входящие в A5.42). Для изотропных
материалов число независимых коэффициентов упругости Е1'тп,
E^mnrs, . . . минимально. Например, коэффициенты упругости
первого порядка выражаются только через два коэффициента Ла-
Ламе % и ц по формуле
Eiimn = J^llgmn + ц F™6in + gingim^ A5.53)
а коэффициенты упругости второго порядка изотропных упругих
материалов определяются формулой
Eiimnrs = ^giigmngre + ^ ^giigmngrs_ gijgmsgnr^ +
+ E38im8jn8rs + ?6im6sn6rj. A5.54)
г) В этой работе приводятся значения постоянных Ах, , . ,, Ад, полу-
полученные из экспериментов на пористом полиуретане.
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 24!>
Здесь Ег, Е2, Е3 и Ек — модули упругости второго порядка г)
изотропных упругих материалов. Можно показать, что для изо-
изотропных гиперупругих тел Е2 -f- Е3 = 2 (X — fi), т. е. существует
только три независимых модуля упругости второго порядка.
Несжимаемые тела. Известно, что многие упругие при
конечных деформациях материалы деформируются без заметного-
изменения объема. Такие материалы относятся к несжимаемым упру-
упругим материалам. Практически все решения задач теории упругости
при конечных деформациях получены именно для таких материа-
материалов. Кроме того что все движения несжимаемых материалов про-
происходят без изменения объема, их характерной особенностью-
является то, что тензор напряжений не полностью определяется
деформацией. Действительно, ясно, что к напряжениям в дефор-
деформированном несжимаемом материале можно добавить с любым
множителем напряжения, которые обычно связаны с изменением
объема, т. е. произвольное гидростатическое давление. При этом
деформация тела не изменяется. Другими словами, дополнитель-
дополнительное приложение гидростатического давления к несжимаемому
упругому телу изменяет напряжения в нем, но не влияет на дефор-
деформации или, для гиперупругих материалов, энергию деформации.
Поскольку изохорическим движениям соответствует равенство-
единице третьего главного инварианта /3, уравнение состояния
для несжимаемых материалов имеет вид
A5.55)
где h — гидростатическое давление, a GTS должны быть такими^
чтобы удовлетворялось условие несжимаемости
/3 = 1. A5.56)
Для гипер упругих материалов A5.56) можно считать ограничи-
ограничительным условием. Вводя в этом случае
-l), A5.57)
где К — множитель Лагранжа, имеем вместо A5.36)
tU=W+X*?2-=W+hGti. A5.58>
Здесь 2Х приравнено гидростатическому давлению h, а уц удовлет-
удовлетворяет условию A5.56).
х) Для таких материалов, как железо и медь, коэффициенты второго
порядка экспериментально определены Сигером и Баком [I960]. См. также
Сигер [1964]. Теории третьего порядка исследовались Джоном [1958] и дру-
другими. Краткий обзор вопроса дан Трусделлом и Ноллом [1965, стр. 230].
См. также Сакади [1949] и Шенг [1955].
250 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Вследствие A5.56) функция энергии деформации для изотроп-
изотропных несжимаемых гиперупругих тел является функцией только
первых двух главных инвариантов:
W = W (Ilt /2). A5.59)
Поэтому соотношения A5.47) — A5.48) принимают виц
tH ow aii ¦ ew ai2 h ai3 =
h
dl2 dyu ' dyt]
^- [8ij A + yrr) -
+ 2h [6i} A + 2Vrr) -28ir8hyST + 2eimnehsymryns]. A5.60)
Для различных материалов предложен ряд аппроксимаций
функции W Aг, /2). Полиномиальные аппроксимации в общем
•случае можно записать в виде
W= 2 § Crs(/i-3)r(/2-3)«, CM = 0. A5.61)
г=0 s=0
Известный и наиболее часто используемый случай полиномиаль-
полиномиальной аппроксимации A5.61), характеризующий материал Муни *)
(Муни [1940]), получается при сохранении лишь линейных отно-
относительно 11 и /2 членов:
W = С1 {1Х - 3) + С2 (/, - 3). A5.62)
Здесь С1 = С10, С2 = С01. Обнаружено, что этот закон Муни
позволяет удовлетворительно описывать деформации некоторых
натуральных и вулканизированных резин в довольно широком
диапазоне. Однако эксперименты на натуральных резинах при
деформациях, превышающих 450 -г- 500 процентов, указывают
на отклонения от закона Муни.
Используя гауссовскую кинетическую теорию для резинопо-
добных материалов, Трилор [1958] пришел к так называемой
неогуковой форме
W = С {1г — 3). A5.63)
Однако, за исключением некоторых вулканизированных резин
<, органическими наполнителями, A5.63) приводит к результатам,
лишь весьма грубо согласующимся с экспериментальными.
Основываясь на результатах многочисленных экспериментов
на резинах, Ривлин и Саундерс [1951] предложили в качестве более
общей формы функции энергии деформации
W = C1(I1-3) + F (/, - 3), A5.64)
*) Используя закон Муни, Ривлин [1949а, 19496] решил целый ряд задач.
По этой причине функцию A5.62) иногда называют функцией энергии дефор-
деформации .материала Муни — Ривлина. См. также Ривлин [1948а, 19486].
15. ОСНОВЫ ТЕОРИИ УПРУГОСТИ 251
где вид функции F A2 — 3) может быть различным для разных
типов материалов. Для F (/2 — 3) подыскивались различные поли-
полиномиальные аппроксимации. Клоснер и Сегал [1969], например,
предположили, что F (/2 — 3) есть кубический полином относи-
относительно (/2 — 3) 1):
W=CX (/х - 3) + С2 G2 - 3) + С3 A2 - 3)а + С4 (/а - ЗK.
A5.65)
Однако не все предлагавшиеся полиномиальные аппроксимации
для W имеют вид A5.64). Можно, например, рассмотреть квадра-
квадратичную относительно A1 — 3) функцию 2):
W = С, (I, -3) + В1 (I, - ЗJ + С2 (/, - 3). A5.66)
А вот форма функции энергии деформации для резин, наполнен-
наполненных серой, предложенная Бидерманом [1958] 3):
W = CX (Ъ -3) + В1 (I, - ЗJ + В, (I, - ЗK + С, (/, - 3).
A5.67)
Не во всех предлагавшихся для W формах функция F (/2 — 3)
в A5.64) берется в виде полинома по /2 — 3. Используя негаус-
совскую молекулярную теорию 4), Джент и Томас [1958] пришли
к предположению, что 8F (/2 — 3)/д12 = С/12, где С — постоян-
постоянная материала. Харт-Смит [1966] Б) подробно рассмотрел эту
теорию и предложил экспоненциально-гиперболический закон:
A5.68)
Александером [1968] предложены такие формы:
W = С,G, -3) + С2G2-3) + С3In h~l+k A5.69)
и
W = с, ( еВД-зя d/t + С2 G2-3) + С3 In /2~3+fel , A5.70)
J) Такая аппроксимация хорошо согласуется с результатами экспери-
экспериментов для натуральных резин при'/j, /2 < 8.
2) Такая форма для W была предложена Исихарой, Хасицумэ и Тати-
баной [1951], которые получили ее, используя негауссовскую молекулярную
теорию для резин. Александер [1968] показал, что она дает не очень хорошие
результаты при некоторых испытаниях на одноосное растяжение. Другая
«трехконстантная» теория была предложена Синьорини [1955].
3) Хотя по некоторым сообщениям форма A5.67) прекрасно согласуется
с одноосными экспериментами, она, как заметил Александер [1968], плохо
согласуется с двухосными экспериментами Трилора [1944].
4) Томас [1955].
5) См. также Харт-Смит и Крисп [1967]
252 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
где С1; С2, С3, кякг — постоянные материала. Соотношение A5.69)
соответствует форме Ривлина — Саундерса A5.64), а A5.70) объе-
объединяет в себе характерные черты форм A5.64) и A5.68) и хорошо
согласуется с экспериментами на хлоропреновом каучуке.
В качестве последнего примера упомянем функцию энергии
деформации для силиконового каучука, предложенную Хатчин-
Хатчинсоном, Беккером и Лэнделом [1965] *):
W = Сх (/j - 3) + Bi (/j — ЗJ + В2 A -е№-3)) + В3 A - е^-з)).
A5.71)
Эта форма W приводит к результатам, хорошо согласующимся
с данными как одноосных, так и двухосных испытаний.
Условия интегриру емости. Не каждый упругий мате-
материал является гиперупругим. Действительно, всечто нужно для того,
чтобы материал можно было назвать упругим,— это чтобы его
определяющее уравнение согласовывалось с изложенными в § 14
принципами и определяло тензор напряжения в виде функции
текущих значений Gti (или уц). Для того же, чтобы упругий мате-
материал был гиперупругим, необходимо выполнение равенства
|^ A5.72)
где 21' (Grs) — функция реакции, определенная формулой A5.1)
Таким образом, A5.72) можно рассматривать как систему диффе-
дифференциальных уравнений в частных производных для функции
энергии деформации W. Если эти уравнения интегрируемы, то
упругий материал, характеризуемый функцией 2" (Grs), будет
и гиперупругим.
Рассмотрим, например, изотропный упругий материал, опре-
определяющее уравнение которого имеет вид A5.6). В этом случае
мы требуем, чтобы
dW dh , dW dl2 dW dl3
dl\ dyj j dlo dyj j dlo dy; j '
где %a = I^GXa, a = 0, 1, 2, так что ха — функции главных
инвариантов /15 /2, /3. С учетом D.16) и D.28)
Эти равенства можно рассматривать как систему дифференциаль-
дифференциальных уравнений в частных производных для функции энергии
См. также Сан Мигель [1965].
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 253
деформации W. Условия ее интегрируемости таковы:
дК2 , dtti ,
Соотношения A5.75) являются необходимыми и достаточными
условиями того, чтобы изотропный упругий материал был и гипер-
гиперупругим. Аналогично, хотя и несколько сложнее, можно получить
условия интегрируемости для анизотропных упругих материалов х).
Поскольку невыполнение их означает возможность диссипации
энергии^ упругих телах, в большинстве последующих рассмотрений
будет предполагаться, что условия интегрируемости удовлетворены.
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ^ЕЛ
Вследствие существенно нелинейного характера уравнений
теории упругости при конечных деформациях количественные
решения почти всех задач, имеющих практическое значение, полу-
получаются лишь численно. Метод конечных элементов благодаря его
простоте и общности является наиболее удобным способом форму-
формулировки нелинейных задач теории упругости для их численного
решения 2). В этом параграфе будут получены общие уравнения
движения и равновесия для типичных конечных элементов упру-
упругих тел.
16.1. НЕЛИНЕЙНЫЕ ЖЕСТКОСТНЫЕ СООТНОШЕНИЯ
Напомним (см. A3.60)), что общее уравнение движения типич-
типичного конечного элемента сплошной среды имеет вид
tk^N,j(8ki + yM,kuM)dv0 = pm A6.1)
Ve)
х) См. Трусделл и Нолл [1965, стр. 302].
2) Конечноэлементные постановки задач нелинейной теории упругости
при конечных деформациях были даны Оденом [19676]. Приложения к задачам
о плоском напряженном состоянии рассматривали Оден [1966а], Беккер
[1966], Питерсон, Кэмпбелл и Геррманн [1966], Оден и Сато [1967а, 19676],
а также Оден и Кубица [1967]. Задачи о конечной плоской деформации решал
методом конечных элементов Оден [19686], а приложениями к случаю трех-
трехмерных тел и в частности тел вращения занимались Оден и Ки [1970, 1971а].
См. также Немат-Нассер и Шатов [1970] и Хофмайстер, Гринбаум и Ивенсен
[1970]. Кавана [1969] использовал этот метод в связи с экспериментальными
работами по теории упругости при конечных деформациях. Имеется обзор
Одена [1969в], содержащий ссылки на работы по родственным вопросам.
Хотя часть представленного далее материала основана на упомянутых рабо-
работах, этот материал излагается здесь в несколько большей общности.
254 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
(идентификационная метка элемента е для удобства опущена).
Здесь mNM — согласованная матрица масс, определяемая форму-
формулой A3.37), pNi — обобщенные узловые силы, задаваемые форму-
формулой A3.54), a ipjv, j = &tyN (xj/dx1 — градиенты локальных интер-
интерполяционных функций \pN (x). Поскольку для упругих материалов
thi определяется соотношением A5.1) (напомним, что thi =
= y^Go*'), уравнения движения упругого конечного элемента
таковы:
j lj A6.2)
где в соответствии с A5.1) 1h} [G%n (u*)] = 2fti (и?). Для гипер-
гиперупругих конечных элементов, используя A5.36), можно записать
mNMu^ -f- I -г-—ipW] у Fft^-(-ipjvf. ku^) dv0 — Put. A6.3)
*0(e)
В этих уравнениях N, M, R = 1, 2, . . ., Ne, где Л^е — общее-
число узловых точек элемента е, a i, j, к, т, п, s = 1, 2, 3.
При статическом (или квазистатическом) поведении упругих
• • т, *
тел можно опустить инерционные члены mNMui в A6.2) и A6.3)т
что дает нам уравнения равновесия типичного конечного элемента
в виде
Коэффициенты при узловых перемещениях в A6.4) называются
жесткостями, а соотношение A6.4) — нелинейным жесткостным
соотношением. Если элемент упругий, но не гиперупругий, то
в A6.4) просто следует заменить dWldytj на ]/G 2ft^ (uf). Подстав-
Подставляя в соотношение A6.4) соответствующие выражения для W,
например рассмотренные в п. 15.5, можно найти специальный
вид, который принимает это соотношение для различных типов
гиперупругих конечных элементов.
Приведем несколько примеров.
1. Аналитическая функция W {уц). Аналитическая функция
энергии деформации задается формулой A5.38). Уравнение A6.4)
принимает вид
00
2 J
A6.5)
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 255
2. Сжимаемые анизотропные тела. Функция W имеет вид
A5.42). В этом случае
(Eh}mnymn + Ehimn"ymnyTS + • • •) Ч>*. i X
"(Не)
Х(вы + Ч>*.*0&>о = Д«. A6.6)
Здесь Ehimn, Ehimms, . . . обладают свойствами симметрии A5.40),
и в соответствии с A3.22) для конечного элемента
Ум, »«• A6-7).
3. Теория упругости второго порядка. Функция PF (уц) опре-
определяется формулой A5.45а). В уравнении A6.6) сохраняются
только коэффициенты упругости второго порядка.
4. Большие повороты, бесконечно малые деформации. В этом
случае W (угу) задается формулой A5.43а), a ytj — формулой
A6.7), причем считается, что величины у^ «малы». В результате
мы приходим к таким нелинейным жесткостным соотношениям
для гуковых материалов:
rO(e>
A6.8)
где M, N, R, S = 1, 2, . . n Ne, a i, j, k, m, n, s — 1» 2, 3. Есла
ввести обозначения
то соотношение A6.8) можно записать более компактно:
j Ek}mnyR,myNijasnbkidvouf = pNi. A6.10)
5. Классическая теория упругости при малых деформациях.
В этом случае W определяется выражением A5.44а), и для конеч-
конечного элемента имеем
? iU?. A6.11).
Градиенты перемещений tyNt гщ f<;4HTaroTCH бесконечно малыми.
Тогда аи = btj = 8{j, и A6.10) сводится к линейному жесткостно-
му соотношению:
A6.12)
0(e)
256 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Вводя обозначение
*1ш = j Ei3mn^M<m^Ntjdv0, A6.13)
(е)
соотношение A6.12) можно записать в виде
Ьнм1% = Рт, A6.14)
где компоненты pNi векторов р$ теперь не зависят от uf- Массив
кг$м представляет собой хорошо известную матрицу жесткости
для линейно-упругих материалов. Сравнивая A6.13) с A6.8),
получаем интересную интерпретацию введенных выше функций
asn и bki (см. A6.9)). На основании A6.12) член Ек1тп можно рас-
рассматривать как «матрицу жесткости» единичного куба упругого
материала. Остальные члены осуществляют линейное преобразо-
преобразование этой матрицы в матрицу, связанную со всем конечным эле-
элементом. В линейной теории эти преобразования осуществляются
членами tyMt m и tyNl] из A6.12), а в случае больших вращений
дополнительно появляются функции аш и bki. В соответствии
с A6.8) локальные жесткости преобразуются не конгруэнтно,
как это имеет место в линейном случае, и члены, осуществляющие
это преобразование, являются функциями от градиентов переме-
перемещений. Этот момент особенно ярко проявляется при использова-
использовании различных специальных форм i!pN (x).
i ¦ »
6. Изотропные упругие тела. Функция энергии деформации
определяется формулой A5.46), так что A6.4) принимает вид
SW dh i 9W д!2 | dW dlj
v0(e>
+ ^M,kuf)dv0 = pNi, A6.15)
или, ввиду A5.48),
б" + 4 ™
- б + 4
+ 2 -§- [8hj A + 2yrr) - 26hr8hysr + 2skmVrsymryns] } X
X i|3jv, j Fftг + \|зм, huf) dv0 = pm. A6.16)
Здесь yrs задаются формулой (fl6.7), a
)%- A6.17)
Из приведенных примеров ясно виден общий способ получения
уравнений равновесия для любого типа сжимаемого упругого
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 257
элемента: чтобы получить соответствующие уравнения движения,
надо просто добавить член mNMu^n считать щ , pNi и т. д. функ-
функциями времени. Уравнения, описывающие поведение несжимаемых
упругих элементов, требуют особого внимания. Они будут рас-
рассмотрены в следующем пункте.
Симплексные модели1). Жесткостные соотношения прини-
принимают особенно простую форму, если используются линейные интер-
интерполяционные функции в симплексной аппроксимации:
yN(x) = aN + bNix\ A6.18)
где aN и bNi определены выражениями A0.105), A0.106) и A0.108).
Здесь Nе = к + 1, где к — размерность пространства, a i =
= 1,2, . . ., к. Функции A6.18) являются локальными базисными
функциями для линейного элемента с двумя узлами в одномерных
задачах, треугольного элемента с тремя узлами в двумерных зада-
задачах и тетраэдрального элемента с четырьмя узлами в трехмерных
задачах. Рассмотрим трехмерный случай (Ne = 4; к = 3).
Замечая, что
yNli = bNi, A6.19)
мы видим, что в нашем случае в соответствии с A3.29) и A3.39)
(aNbM] + aMbN]) sj + bNibM]l", A6.20)
M, A6.21)
A6.22)
где ро и v0 — массовая плотность и объем элемента в начальной
конфигурации, s? — моменты массы относительно системы локаль-
локальных координат х\е), а Г3 — тензор массовых моментов инерции
в системе х\е).
В соотношении A6.20) предполагается, что элемент однороден,
т. е. что р0 (х) = Ро = const. Хотя это, вообще говоря, не имеет
места, тем не менее это хорошее и удобное приближение, если раз-
размеры элемента взяты достаточно малыми. При использовании сим-
симплексных моделей неоднородных тел каждый конечный элемент
обычно (и мы будем следовать этому обычаю) считается однород-
однородным, а неоднородность материала учитывается приписыванием
различных свойств различным конечным элементам. Таким обра-
образом, для симплексных элементов функцию энергии деформации
и ее производные по ytj можно считать не зависящими от х1, так
что их можно вынести за знак интеграла по объему в A6.3). Отсюда
1) См. Оден [19676].
17 Дж. Одея
258 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
следует, что нелинейные жесткостные соотношения для симплекс-
симплексных элементов имеют вид
^llf A6.23)
В рассмотренных выше частных случаях уравнение A6.23)
принимает следующие формы:
1. В случае когда W — аналитическая функция от ytj,
оо
^ A6.24)
2. Для сжимаемых анизотропных тел
n + 4-bsnuss) (8hi + bMhuf)uf
X (8ki + bMkuf) u*u*+ ... = pNi, A6.25)
где M, N, K, R,S, T = 1, 2, 3, 4 и i, j, к, m, n, p, q,r,s = 1, 29 3.
3. Уравнения для теории упругости второго порядка полу-
получаются, если в A6.25) отбросить все коэффициенты упругости
выше второго порядка.
4. Симплексные жесткостные соотношения при бесконечно
малых деформациях, но больших поворотах получаются из A6.25),
если сохранить один первый член в левой части этого соотно-
соотношения J):
Fsn + ^~bSnul) EkjmnbRm(8hi+bMhuf) uf = pNi. A6.26)
5. Симплексные представления для классической теории упру-
упругости при малых деформациях получаются в результате подстанов-
подстановки A6.19) в A6.12) 2):
A6.27)
В этом случае матрица жесткости A6.13) принимает вид
A6.28)
х) Приводимое ниже соотношение впервые получено Висманном [1963].
См. также Висманн [1966].
2) Различные формы приводимого ниже соотношения найдены Галлаге-
ром, Пэдлогом и Бейлардом [1962]. Оно является одним из первых линейных
жесткостных соотношений, полученных для трехмерных конечных элементов
упругих тел.
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 259
Сделанное ранее замечание относительно преобразований Е1'тп
теперь легче понять: в линейной теории Elimn преобразуется
в жесткостное соотношение элемента с помощью матриц YvifiMm
и YvobNj, в то время как для кинематически нелинейного случая
A6.26) преобразования осуществляются различными матрицами:
VU~obNj (8m + l/2fcsnu?) и VvobBm (8ki + bMhuf), элементы кото-
которых зависят от узловых перемещений.
6. Наконец,, для симплексных моделей изотропных упругих
тел вследствие A6.15) имеем
A6.29)
или, ввиду A6.16),
vobNj
RT
- 6ftr6'5 {bRsuf + bRruf
u)
- 8kr8h (bRsuf + bRTuf + bRsbSTu$usp)
S) x
X (bKnuf + bKsu% + bKnbTsuful)} ) (8H + bMhuf) = pNi, A6.30)
где, как обычно, M, N, К, R, S, T = 1, 2, 3, 4 и i, /, к, m, n,p, r, s=
= 1, 2, 3.
Отметим, что соотношения A6.23) — A6.30) могут быть приме-
применены и к одномерным и двумерным элементам, если просто изме-
изменить область допустимых значений индексов: для одномерных
элементов М, N, . . ., S, Т — 1, 2 и i, j, . . ., г, s = 1; для двумер-
двумерных элементов М, iV, . . ., S, Т = 1, 2, 3 и i, j, . . ., г, s = 1, 2.
Кроме того, эти соотношения можно использовать для описания
движения одномерных и двумерных элементов в пространстве
более высокой размерности. Например, ,для трехмерного набора
одномерных элементов (ферма или рама) М, N, . . ., S, Т = 1, 2
и i, ]', . . ., г, s = 1, 2, 3. Для плоских конструкций из одномерных
элементов М, N, . . ., S, Т == 1, 2 и i, j, . . ., г, s = 1, 2. Для
трехмерного набора двумерных элементов (например, мембраны)
М, N, . . ., S, Т = 1, 2, 3 и i, j, . . ., г, * = 1, 2, 3.
Глобальные формы. Возвращаясь к общей форме жестко-
стных соотношений A6.4), напомним, что для применения их к ти-
типичному конечному элементу е достаточно все величины енабдить
17*
260 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
идентификационной меткой элемента:
"o(e>
В соответствии с A3.11) и A3.67) имеем
^*Ai = S ®ЬР$1 И и«е) = ^Д^' A6.32)
где йд — булево преобразование, характеризуемое, например,
формулой F.9), Е — общее число конечных элементов, a PAt
и Ui — компоненты обобщенной силы и перемещения в узле А
связанной модели. Отсюда следует, что глобальная форма нели-
нелинейных жесткостных соотношений для совокупности упругих
конечных элементов имеет вид
1
Aб.зз)
где А, Г = 1, 2, . . ., G; М, N = 1, 2, . . ., Ne; i, j, к = 1, 2, 3.
Динамические уравнения, описывающие поведение совокупности
упругих элементов, получаются просто добавлением в A6.33)
слагаемого M^rUi, где Л/дг — глобальная матрица массы A3.75).
Сравнивая A6.33) с A3.76) и A3.77), видим, что в нашем случае
V$jHtdv0, A6.34)
Ядг = 2 № j ^ ^) ^ . dVo. A6.35)
В качестве простого примера глобальной формы жесткостных
соотношений для конкретного типа материала рассмотрим пока-
показанную на рис. 16.1 двухстержневую форму, изготовленную
из изотропного гукова материала. В этом случае при использова-
использовании указанных в части (Ь) рисунка локальных координат можно
положить
?1Ш = Е, Eiimn = 0, i, /, т, п ф 1, A6.36)
где Е — модуль Юнга. Используя симплексное представление
A6.18), находим, что
$N,l=bNi, 6ц=— &21= J". A6.37)
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ
261
rzz
11 ч/А
/f-
(.ь)
Рис. 16.1. Двухстержневая форма.
где d — длина каждого стержня. Так как v0 = aod, где aQ — на-
начальная площадь поперечного сечения стержня, из A6.26) полу-
получаем следующие выражения для обобщенных сил:
e)—u2(e)
d
A6.38)
где
Отметим, что локальные силы A6.38) образуют самоуравновешен-
самоуравновешенную систему сил. Поскольку локальные координаты х\е) не совпа-
совпадают с глобальными координатами X1, преобразуем все локальные
262 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
величины к общей системе отсчета в соответствии с A3.11):
A6.40а)
A6.406)
где
' —b с
Замечая, что QJ = QJ = п\ = Ь| = 1, а все другие йд = 0 и
что в силу концевых условий U\ = U\ = 0, локальные обоб-
обобщенные силы можно выразить через глобальные узловые переме-
перемещения U\ следующим образом:
р«}'= -а0ЕУ™ [l +'JL(bU-cV)] ,
^^ao^YiV-^^ + bF),
р«» = - a0Ey[? [1 - ±- (bU + cV)] , A6.42)
и т. д., где U\ = U, U\ = V и
I A6.43)
Преобразуя A6.42) в соответствии с A6.406)f получаем
U—b)t
A6.44)
Ввиду A3.67) глобальные силы в узле 1 связанной модели оконча-
окончательно записываются в виде
Рн = -т-. [2 (Ь2 - cV) + IP + У2],
" A6.45)
Эти уравнения 1) представляют собой уравнения равновесия в
уэле 1. '
Некоторые их решения см. у Одена [1971в].
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 263
В частном случае, когда деформации симметричны относитель-
относительно оси хй, имеем U = 0, Р1г = р[\> -(- р[? = 0 и остается только
одно уравнение:
^2с). A6.46)
Из уравнений A6.45) и A6.46) видно, что в рассматриваемой сим-
симплексной модели получается кубичная зависимость обобщенных
сил от узловых перемещений. Согласно A6.46) Р12 является кубич-
кубичным полиномом третьей степени относительно V с тремя корнями
V = 0, с, 2с. Значит, при заданной нагрузке Р12 могут существо-
существовать три равновесные конфигурации, т. е. теперь уже нельзя
ожидать единственности поля перемещений при заданной нагруз-
нагрузке, как это было в линейной теории.
Если V очень мало, то уравнение 16.46 можно линеаризовать:
A6.47)
Выражение в правой части зависит от высоты конструкции с.
В принципе ничто не мешает нам рассматривать случай с = О,
когда оба стержня расположены на одной прямой. В этом случае
линеаризованное решение не существует и поведение конструкции
можно предсказать только на основе нелинейной теории.
При неконсервативном нагружении узловые силы Ри и Р12
в уравнениях A6.45) должны, вообще говоря, представляться в виде
функций от узловых перемещений. Рассмотрим, например, ситуа-
ситуацию, когда в узле 1 приложена сила Q, которая всегда нормальна
к элементу 1. Тогда
Рц = -§г(с — У), .'A6.48a)
pa = JL(b + U), A6.486)
где
d*2 = d2 + 2 (bU — cV) + U2 + V2. A6.49)
16.2. НЕСЖИМАЕМЫЕ МАТЕРИАЛЫ *¦)]
Хотя в некоторых точных решениях задач теории упругости
при конечных деформациях предположение о несжимаемости
приводит к ряду упрощений, при использовании метода конечных
элементов этого не происходит. Напомним, что напряжения,
') Линейные задачи для несжимаемых тел рассматривались многими
авторами. Бесконечно малые осесимметричные деформации несжимаемых
упругих тел вращения были изучены Беккером и Брисбейном [1965]. Их
исследования основаны на одной вариационной теореме Геррманна [1965],
которую можно получить исходя из более общей теории, развитой Трусделлом
264 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
возникающие в несжимаемом материале, не полностью опреде-
определяются деформацией или энергией деформации. Действительно,
W определяет напряжения в несжимаемых гиперупругих телах
лишь с точностью до аддитивной скалярнозначной функции h,
называемой гидростатическим давлением, которое не совершает
работы в процессе деформирования тела. В конечноэлементных
приложениях гидростатическое давление является дополнитель-
дополнительной неизвестной величиной в жесткостных соотношениях. Условие
несжимаемости A5.56) должно выполняться, по крайней мере
приближенно, во всей дискретной модели. Поскольку практически
во всех известных уравнениях состояния сильно деформируемых
упругих материалов (например, натуральных и синтетических
резин, полимеров, твердых топлив) зти материалы предполагаются
несжимаемыми, исследование конечных деформаций несжимаемых
тел — важная часть теории упругости при конечных деформациях.
С учетом A5.55), A5.58) и A6.1) жесткостные соотношения для
несжимаемых конечных элементов можно записать в виде
p1{i A6.50)
или, для гиперупругих элементов,
V)
(^ ) A6.51)
»0(е)
где h = hle> (x, t) — локальное гидростатическое давление, соот-
соответствующее элементу е. Узловые перемещения и% должны быть
такими, чтобы удовлетворялось условие несжимаемости. Для
конечных элементов его простейшей очевидной аппроксимацией
является осредненное условие несжимаемости:
A6.52)
°0(е)
При выборе декартовых материальных координат в начальной
конфигурации С0(е) возможны некоторые упрощения в записи
и Тупином [1960]. Другие приложения, относящиеся к линейным несжимае-
несжимаемым материалам, даны Тэилором, Пистером и Геррманном [1968], Тонгом
[1969], Ки [1969], Хьюджесом и Элликом [1969]. Приложениями к случаю
конечных деформаций несжимаемых упругих тел занимались Оден [19676,
19686] и Оден и Ки [1970, 1971а]. Решения ряда задач о плоском напряжен-
напряженном состоянии, включая задачи о конечных деформациях, получены, напри-
например, у Одена и Сато [1967а] и Беккера [1966]; в этих задачах часто удается
избежать обычных трудностей, связанных с соблюдением условия несжимае-
несжимаемости и расчетом гидростатического давления.
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ . 26!>
A6.52). Вспоминая, что
/3 = (let Gij = det zm, iZmJ = (det zm, t) (det zm, }) = ,
= (det zu jJ,\ A6.53)
где zm< t = 8mi -f- i!pNi tUm — градиенты деформации, условие A6.52)
можно записать в таком более удобном виде: ;
[det(8mi + TpN<iu%Wdv0-v0 = 0. A6.54)
»0(е)
Другие формулировки условия несжимаемости будут рассмотре-
рассмотрены ниже.
Ни в A6.50), ни в A6.51) ничего не предполагалось относитель-
относительно характера изменений h (x) в конечном элементе. Возможна
сделать несколько предположений. Простейшей локальной аппро-
аппроксимацией для h (x, t), и зачастую приводящей к наименьшему
числу дополнительных неизвестных, является аппроксимация
нулевого порядка, т. е. предположение, что h постоянно в эле-
элементе:
hie)(x) = h%\ A6.55)
где hft — постоянная. В динамических задачах/ конечно, tf
считается функцией времени. Для трехмерного конечного элемен-
элемента A6.51) совместно с A6.54) представляет собой систему 3Ne
уравнений относительно SNe + 1 неизвестных и™ (М = 1,2,...
. . ., Ne; i = 1, 2, 3) и Щ). Еще одно уравнение, необходимое для
получения полной системы, следует из локального условия несжи-
несжимаемости A6.52) или из других его формулировок, например
A6.54). Таким образом, для состоящей из Е элементов дискрет-
дискретной модели, у которой не заданы компоненты перемещений в G
глобальных узлах, аппроксимация A6.55) приводит к системе
3G + Е уравнений (уравнения равновесия и условия несжимае-
несжимаемости) относительно 3G компонент перемещений и Е гидростатиче-
гидростатических давлений в элементах. Отметим, что для сжимаемых материа-
материалов такая модель приводит к системе только 3G уравнений.
Вместо A6.55) можно использовать какую-нибудь более общую
аппроксимацию гидростатического давления, как, например,
h(e)(x) = hNyN(x), A6.56)
где tyN (x) — та же самая совокупность локальных интерполяци-
интерполяционных функций, что использовалась для аппроксимации полей
перемещений. Тогда A6.51) принимает вид
,ku?I)dv0 = pm. A6.57)
266 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Однако в этом случае A6.57) является системой 3We уравнений
относительно Ше неизвестных (hR и uf; M, R = 1, 2, . . ., Ne;
i = 1, 2, 3), в то время как при аппроксимации A6.56) мы имеем
систему 37Уе + 1 уравнений. Поскольку локальное условие несжи-
несжимаемости в форме A6.52) дает только одно дополнительное уравне-
уравнение для каждого элемента, очевидно, что если мы будем поступать
так же, как и в случае постоянного гидростатического давления,
то не получим достаточного для решения задачи числа уравнений.
С этой трудностью мы справимся следующим образом. Пусть
Н^ (А = 1, 2, ..., G) — значение гидростатического давления
в узле А связанной модели. Тогда
A6.58)
и глобальная форма соотношения A6.57) принимает вид
0(е)
A6.59)
где А, Г, Ф = 1, 2, . . ., G; M, N, R = 1, 2, . . ., Ne; i, j, к =
= 1, 2, 3. Если в связанной модели заданы т компонент п узловых
перемещений, то A6.59) представляет собой систему 36? — т
уравнений относительно 46? — т неизвестных. Это означает, что
в рассматриваемом случае следует потребовать выполнения усло-
условия несжимаемости в каждой узловой точке, а не в каждом элемен-
элементе. Для получения нужных условий преобразуем «непрерывное»
условие несжимаемости /8 = 1 в эквивалентное локальное условие
для узловой точки, введя величину г)
i)<fo0. A6.60)
Ще)
Если Шд — глобальное] значение величины (ш)м в узле А свя-
связанной модели, то, как следует из G.16) и (9.189),
(iii)S = лЪИд и Шд = 2 $д (Ш)#. A6.61а, б)
е=1
Тот факт, что в этих равенствах фигурирует Шд, а не ША, гово-
говорит о том, что величины Шд являются компонентами некоторой
функции на конечномерном подпространстве Ф*, сопряженном с
пространством Ф, порождаемым глобальными базисными функциями
2) Интерпретацию величины (iii)$ в свете вариационных принципов
мы дадим в п. 16.4,
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 267
Равенство A6.616) показывает, что П1Д является суммой локаль-
локальных вкладов (ш)!^ от всех элементов, соединяющихся в узле А
связанной модели. Вспоминая (см. (9.82) и т. д.), что зти ковариант-
ные величины являются средними значениями III (X) в окрестно-
окрестности узла ХА, можно убедиться, что обращение Шд в нуль в каж-
каждой из G глобальных узловых точек означает выполнение условия
несжимаемости в среднем во всей связанной конечноэлементной
модели. Таким образом, мы полагаем
в
Шд=2 Од J №(W-l)dvo = 0, A6.62)
e=1 B0(e)
Д = 1, 2, . . ., G. Условия A6.62) вместе с 3G — т жесткостными
соотношениями A6.59) образуют полную систему AG — т неза-
независимых уравнений относительно 46? — т неизвестных Ut9 ffA.
Отметим, что использование постоянного в элементах гидро-
гидростатического давления A6.55) не обязательно приводит к меньше-
меньшему числу неизвестных, чем более сложная аппроксимация A6.56).
Действительно, A6.55) приводит к 3G — т -\- Е уравнениям, в то
время как A6.56) — к 4G — т; нетрудно привести примеры, когда
Е > G. С другой стороны, часто при использовании A6.55) и A6.54)
условие несжимаемости в связанной модели выполняется точнее.
В некоторых случаях оказывается даже возможным удовлетво-
удовлетворить условиям несжимаемости в каждом конечном элементе точно.
При вычислениях применение осредненных условий несжимае-
несжимаемости A6.62) удобнее, чем A6.54), поскольку связывание дискрет-
дискретной модели для h (x) осуществляется с помощью A6.58) точно так
же, как и связывание модели поля перемещений. К тому же A6.56)
позволяет, как правило, точнее определить гидростатическую
часть тензора напряжений, а использование рассмотренных в § 9
сопряженных аппроксимационных функций позволяет преодолеть
многие трудности, связанные с расчетом напряжений в конечных
элементах.
Следует отметить, что использование для гидростатического
давления аппроксимаций более высокого порядка, чем для поля
перемещений, может привести к увеличению числа неизвестных
без заметного повышения точности 1). На самом деле, если напря-
напряжения в элементе определяются обычным образом (т. е. из локаль-
локальных уравнений состояния после определения перемещений и гид-
гидростатического давления), то порядок лекальных аппроксимаций
гидростатического давления должен быть меньше порядка аппро-
аппроксимации перемещения. Возьмем, например, однородную сим-
симплексную модель в декартовых координатах. В этом случае гради-
х) См. Хьюджес и Эллик [1969].
268 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
енты перемещений и часть тензора напряжений, определяемая
энергией деформации, постоянны в каждом конечном элементе.
Поэтому вполне естественно предположить, что и гидростатическое
давление в каждом конечном элементе постоянно. Тем не менее
локальные напряжения, вычисленные при аппроксимациях дав-
давления и перемещения одинакового порядка, можно использовать
для определения распределения напряжений с помощью рассмот-
рассмотренных в § 9 сопряженных аппроксимаций. Мы обсудим этот вопрос
в следующем параграфе. Отметим также, что возможно построить
не постоянную в элементе аппроксимацию h (x), порядок которой
ниже порядка аппроксимации перемещений. Можно,, например,
для перемещения использовать билинейную аппроксимацию в пло-
плоском четырехугольном элементе, а аппроксимацию для гидроста-
гидростатического давления получить, разбивая элемент на два (или более)
треугрльника, внутри которых h предполагается постоянным.
Основываясь на приведенных рассуждениях, примем в качестве
общего правила в наших последующих рассмотрениях несжимае-
несжимаемых элементов, что порядок аппроксимации гидростатического
давления меньше или равен порядку аппроксимации поля пере-
перемещений.
Возвращаясь теперь к общим нелинейным жесткостным соот-
соотношениям для несжимаемых элементов A6.51), мы можем выписать
их для различных типов несжимаемых гиперупругих материалов.
Для изотропных материалов W является функцией первых двух
главных инвариантов 1г и/2. Соотношение A6.15) принимает вид
°0(e)
A6.63)
или, в соответствии с A6.16),
°0(е)
- 28kr8hyST + 2ehmne?rsymryns]} $N<, (8ki + rpM, huf) dv0 = pNi, A6.64)
где h = tyNhN или h = h0.
Если W выражается в виде полинома относительно инвариан-
инвариантов, как, скажем, в A5.61), то в A6.64) надо подставить
r=0 s=0
оо оо
2 ^
Г=0 8=0
A6.65)
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 269
Важный частный случай материала Муни получается, когда
СЛХ7 ЯТЛ7
~ = Ci и ^к = Сг, A6.66)
где С\ и С% — постоянные; если С2 = 0, то получаются уравне-
уравнения для неогуковых элементов. Различные другие формы урав-
уравнения можно получить, подставляя выражения для W, опреде-
определенные формулами A5.65) — A5.71).
Симплексные модели. Для симплексных моделей можно
записать уравнения в более явном виде. Поскольку
Щ _ dig d?ftj _ dla n — \ 9 Hfi fi7\
)--^-^—^, а-1,2, (lb.b/)
dyh] rN"
то при Yif, задаваемом формулой A6.21),
j% = 2bNh {bhi + bMhuf), A6.68a)
^ = 2bNm (8tk + bMhuf) { 26mft [l + bPs( 8rs +4 bRsuf ) uf] -
A6.686)
bImbJku]uj)
A6.68b)
где /, /, К, M, TV, P, R = 1, 2, 3, 4 и i, /, &, m, re, p, g, r, s, t =
= 1, 2, 3. Поэтому жесткостные соотношения для однородных
несжимаемых изотропных конечных элементов принимают вид
Nm
28mh [l + bPj ( 6r; +1
+ bImbJkUjuj)} -щ
+ 2bP}
Mi + bImbJhu]u]) +
) (в 4Ь^) Х
=рм; A6.69)
270 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Здесь предполагается, что гидростатическое давление постоянно,
т. е. hm (х) = /г(ое). Если же лучше считать, что h (x) меняется
по линейному закону внутри элемента [т. е. h (x) =
= (aN + bNixl) hN], то h0 в A6.69) следует заменить на mQhQ,
где Ttiq — локальные моменты, определяемые формулой (9.159).
Для симплексных представлений
mQ= \ \\>Qdv0— \ (aQ + bQiXl)dvo = voaQ + bQislv), A6.70)
°0(е) ю0(е)
где S(B) = \ хг dv0 — первые моменты объема относительно мате-
«0
риальных координат a;^.
При й(в> (х) = h$ A6.69) представляет собой систему 12
уравнений относительно 13 неизвестных и?, h0. К этим уравнениям
надо добавить условие несжимаемости A6.52) или A6.54). Заме-
Заметив, что для симплексных моделей
A6-71)
условие несжимаемости получим в виде
det(emf + bMa?) = l. A6.72)
К этому же результату можно прийти другим путем. Три ребра
конечного тетраэдрального элемента в недеформированном теле
образует тройка векторов
л = (х\-х\)ц, Ъ = {х1-х\)ц, с = (х*-х\)ц, A6.73)
где i, — ортонормальные базисные векторы в С0<е>- Начальный
объем элемента равен одной шестой смешанного произведения
зтих векторов:
v0 = 1а-(Ь X с) = 1 sijk (хЬ-х\) (х?-х)) D-4). A6.74)
Векторы, образующие ребра тетраэдра после деформации, таковы:
а = (ж? + и?— х\ — u\)iu
, A6.75)
— х\— и\)\и
и объем деформированного элемента равен
v = -i а • (Ь X с) = 1 sijk(z!-z\) (zf-z)) (zi-z\), A6.76)
где Zi = Xi + щ — пространственные координаты смещенных
узлов. Поскольку мы требуем, чтобы v — v0, то после некоторых
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 271
выкладок получаем
±(xf + uf-х\-и\
A6.77)
Раскрыв скобки в левой части и сравнивая результат с A0.96)»
можно найти коэффициенты bNi и убедиться, что A6.77) и A6.72)
совпадают между собой. Таким образом, для симплексных аппро-
аппроксимаций условие несжимаемости для дискретной модели выпол-
выполняется точно.
Если предположить, что гидростатическое давление в элементе
изменяется по линейному закону, то надо записать условия несжи-
несжимаемости в каждой узловой точке в соответствии с A6.60) и A6.62).
Для симплексных моделей локальное условие имеет вид
(iii)® = mM{[det(8im + bNiu%)]*-l}, A6.78)
где тм определено формулой A6.70), а глобальное —
S Qfrng {[det Ftm + Ь&ОК)]»- 1} = .0. A6.79)
e=l
16.3. ОБОБЩЕННЫЕ СИЛЫ И НАПРЯЖЕНИЯ
Мы уже несколько раз отмечали, что обобщенные силы в уздах
p$i представляют собой результирующие напряжений на поверх-
поверхностях в деформированном теле, отнесенных к конвективным
материальным координатам х\е) и, конечно, объемных сил. Таким
образом, узловые силы могут меняться и по величине и по направ-
направлению в процессе деформирования тела и в общем случае должны
выражаться через перемещения и их градиенты. В этом пункте
мы етавим себе цель найти выражения для обобщенных сил, учи-
учитывающие их зависимость от деформации.
Напомним (см. § 13), что выражения для обобщенных сил
получаются из условия сохранения локальной механической
мощности в следующем смысле:
j pri", A6.80)
A(e)
где F — объемная сила на единицу массы в С(е), S — поверхност-
поверхностное усилие на единицу деформированной площади, и — вектор
скорости, pN — обобщенная сила в угле N и uN — скорость узла
N. Поскольку u (x, t) = uN (t) г|з№ (х) и u = uN (t) tyN (x), векторы
р№ обобщенных узловых сил представляются в виде 1)
Pn = lN + ew, A6.81)
1) См. A3.52) и A3.54).
272 гл. iv. теория упругости
где fjv и Sjv — обобщенные силы, обусловленные соответственно
объемными и поверхностными силами:
tjt= J р (х) т|>к (х) F (x, t)dv и sN= j ^(x)S(x, t)dA.
Че) Л(е)
A6.82)
Векторы pN можно выразить в виде линейных комбинаций
ортонормальных базисных векторов i^ в начальной конфигурации
или ковариантных базисных векторов Gif касательных к конвек-
конвективным координатным линиям х\е) в деформированном элементе,
т. е.
A6.83)
где N=1, 2, ..., Ne и i — l, 2, 3. Поскольку
Gj = zm, jim = (8mi + um, t) im = FroJ + $M, {u%) im, A6.84)
то
PNi = tN Fml + ipMJmWf )• A6.85)
Аналогично можно записать
i A6.86)
. A6.87)
так что
*w= j P(/il>wdi;oif= j pF^G^dy, A6.88)
где подразумевается, что функции ро» р,; ^i, ^, ifjv и Gy зависят
от х.
Обращаясь к вкладу в рк' поверхностных сил, заметим, что
последние могут измеряться на единицу площади недеформирован-
ной поверхности dA0 или на единицу площади деформированной
поверхности dA, так что поверхностная сила, действующая на
элемент, равна
J Sd40= j SdA. A6.89)
Здесь
Л0(е)
S^t^niG, и S^a^ntG/, A6.90)
где txi и a*' — тензоры напряжений в конвективных координатах,
измеренных на единицу недеформированной и деформированной
площадей соответственно (t11 = ^Gol}), П( — компоненты единич-
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 273
ной нормали к dA0 и ni — ковариантные компоненты единичной
нормали к dA. Таким образом,
j dA, A6.91)
л0(е) A(e)
или, с учетом A6.84),
Sjv= J ti3nt (бм + \рм, )Um ) \|V dA0\m =
Л°(е) A6.92)
Важной особенностью теории деформирования твердых тел
является то, что обычно предполагается известной форма тела
в некоторой начальной конфигурации. Поэтому и естественно
и удобно, как мы это уже и делали раньше, рассматривать движение
тела и изучать его поведение относительно начальной отсчетной
конфигурации. При этом декартовы компоненты обобщенной силы
в узле N имеют вид
= J
A6.93)
где St = ti3'ni.
Определение вклада объемных сил в pNi [см. A6.93)] не вызы-
вызывает особых затруднений, поскольку компоненты Ft (x, t) пред-
предполагаются заданными для всех значений х и t. Однако вычисление
поверхностного интеграла в A6.93) требует некоторого внимания.
Рассмотрим, например, случай, когда на поверхность конечного
элемента действует нормальное усилие q = q (x, t), т. е. когда
q — переменное давление. Результирующая сила на элементарной
площадке dA деформированного элемента выражается так:
A6.94)
где n = «jG1 — единичный вектор нормали к dA.
Напомним, что
^ d4o,, A6.95а, б)
A6.95b)
где dAt и dAoi — проекции dA и dA0 на координатные поверхности
в деформированном и недеформированном теле соответственно.
Подставляя A6.95) в A6.94), после некоторых выкладок находим,
18 дж. оден
274 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
что
§'=^Уё(Ркпк, A6.96)
где для данного конечного элемента
. ku?) (в„ + грм, ,11?),
Таким образом, если не учитывать объемных сил, мы получаем
в этом случае из A6.93)
,,"Г)^Л0. A6.98)
Л0(е>
Для симплексных моделей удобно предположить, что р0Рг
и §' постоянны в каждом элементе. Тогда A6.93) сводится к
Pni = PoFimN + & (8п + bMjv?) mtf°\ A6.99)
где mN — момент первого порядка, задаваемый формулой A6.70), и
qNdA0. A6.100)
Л0(е)
Если величина q в A6.98) тоже постоянна, то для такого типа
нагружения
pNi = qVGG3knk (8n + MpM,}uf) m&>. A6.101)
Аппроксимации1). Выражения A6.93) и A6.99) показывают,
что даже в случае относительно простых нагружения и геометрии
конечного элемента обобщенные узловые силы являются достаточ-
достаточно сложными функциями узловых перемещений. Поэтому есте-
естественно попытаться найти упрощенные приближенные выражения
для этих сил. Опишем один довольно общий метод аппроксимации,
заключающийся в представлении деформированной поверхности
произвольного элемента в виде совокупности плоских треуголь-
треугольных или четырехугольных элементов, нагрузка на которые пред-
предполагается равномерно распределенной.
Рассмотрим поверхность конечного элемента произвольного
вида (типа показанной на рис. 16.2), испытывающую большие пере-
перемещения и искажения формы, вызванные произвольной системой
поверхностных усилий.
Объемные силы мы не рассматриваем, поскольку они легко
учитываются с помощью A6.88). Безотносительно к действительно-
действительному виду локального поля перемещений иг = ij3jvuf деформирован-
Мы следуем здесь работе Одена [1970г].
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ
275
Рис. 16.2. Аппроксимация деформированной поверхности^элемента.
ную поверхность представим совокупностью плоских элементов,
как правило треугольной формы, узловые точки которых совпа-
совпадают с узловыми точками недеформированной поверхности элемен-
элемента. Приложенные поверхностные усилия будем предполагать
равномерно распределенными на каждом плоском элементе. Если
элемент достаточно мал, то, используя множество его подэлемен-
тов, можно обеспечить хорошую аппроксимацию для достаточно
произвольных нагрузок. Сосредоточим наше внимание на типичном
плоском треугольном подэлементе площади а. Пусть п, ег и е2 —
ортонормальная тройка векторов, причем п есть нормаль к а
в деформированном элементе. Результирующую силу, действую-
действующую на а, можно записать в виде
S = a (qon + S& + S2e2), A6.102)
где q0, 51! и S2 — заданные постоянные нормальные и касательные
компоненты поверхностной силы на единицу деформированной
площади а. Предположим, что треугольная поверхность, на кото-
которой действует сила S, проходит через узлы 1, 2 и 3 деформирован-
деформированной поверхности элемента. С помощью приема, аналогичного
18*
276 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
использованному при выводе различных форм условия несжимае-
несжимаемости в предыдущем пункте, найдем, что радиус-векторы смещен-
смещенных положений узлов 1, 2 и 3 относительно начальной конфигура-
конфигурации равны суть
Rw = r» + n* = ?p{5+i*f)i!. i,N=l,2,[3. A6.103)
Две стороны нашего треугольника образованы векторами
А = R2 — R1 и В = R3 — R1, A6.104)
так что площадь его поверхности задается формулой
а = -¦ [А х В | = -i VAiAtBjBj - Afi^Bj, A6.105)
-¦ [А х В | = -i
а единичная нормаль п — формулой
n = -^AxB = -^BmAiBjik. A6.106)
Еслив например, взять
e' = W=^' |A6Л07)
то
y — | A | В] A6.108)
и A6.102) сведется к
[ 1A6.109)
Соответствующие обобщенные силы pN можно теперь полу-
получить, просто равномерно распределив S по всем узлам, так что
Pjv = -g- S (N = 1, 2, 3). Можно поступить по-другому и положить
где
Поскольку первый способ проще, воспользуемся им и запишем
{ qZ (ж? + и? — х\ — и\) (x3j-\-u] — x) — и})
j + Щ — х\ — и\) (xj + Щ ~ х\ — щ)
¦+¦ l{4+ur-xl-ul)(xr+ur-xl-ul)]V2
{xl + u%-xi-u\)-S2[{x2r + ul-xl-u\)x
i/2 } A6.110)
для всех N (N = 1, 2, 3).
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 277
Подчеркнем, что силы pN не следует путать с обобщенными
силами рдг, фигурирующими в жесткостных соотношениях для
элемента. Если на внешней нагруженной поверхности находятся R
узлов элемента, то результирующая локальная обобщенная сила
в узле N элемента определяется формулой
Б' (е)
PiV = S Qj? PNm A6.111)
e=i
где Е' — число плоских подобластей, использованных в представ-
представлении поверхности элемента, N = 1, 2, . . ., R и iV' = 1, 2, 3.
Отметим также, что не всегда возможно или удобно определять ег
соотношением A6.107). В зависимости от характера приложенной
нагрузки для ех можно использовать и другие определения. Факти-
Фактически базисные векторы е1 и е2 в плоскости а не обязательно долж-
должны быть ортогональны и можно просто принять ех = А/| А |
и е2 = В/| В |. В этом случае A6.110) сводится к
4 [?в (*? + uf - х\ - и}) (xl + и) — х$— и}) +
4"
. aS? (ж1 + и1 — х\ — и\) aSf(xh-\-uu — x\ — uk)
+ qXj + Г
н
qJ' A
где Sf и S* — компоненты вектора S/a по направлениям е, и е:, а
i/z A6.1126)
A6.112b)
В важном частном случае, когда S = доап — равномерно рас-
распределенная нормальная сила, получаются особенно простые
выражения для обобщенных сил р„:
4 * + и* — х\ — и\) (х$ + и$—х}~и)). A6.113)
Описанный выше способ можно использовать и в двумерных
задачах. При этом криволинейная граница деформированного тела
заменяется совокупностью прямолинейных отрезков, как показано
на рис. 16.3. Если S — приложенное к поверхности равномерно
распределенное усилие на единицу длины, а п и е — единичные
векторы, нормальный и касательный к деформированной поверх-
поверхности , то
S = L* (?on + Se). A6.114)
Здесь q0 n S — нормальное и касательное усилия на единицу
длины^ а
^-^)]1/2, A6.115).
278
|ГЛ. IV ТЕОРИЯ УПРУГОСТИ
X,
Рис. 16.3. Аппроксимация деформированной границы двумерного тела.
где а=1, 2. Нетрудно убедиться, что
п^±(Ь*2ц + ЬП2), A6.116a)
e = ^;(Lfl1-L!ia), A6.1166)
где
Lf = L1 + uJ-»l, L*2 = L2 + ul-ul. A6.116b)
Здесь Lx = x\ — x\, L2 = x\ — x\ — проекции линии, соединяю-
соединяющей узлы 1 и 2, на оси хх и ж2 недеформированного элемента. Соот-
Соответствующие обобщенные силы равны
= -j [ft
= 4 to
\- u\) + 5 (La + «2 - u*)
A6.117)
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 279
Для каждого N (N = 1, 2). В частном случае одной нормальной
нагрузки (S = 0) эти формулы сводятся к
^а = ^-(-1)Са>ера?1, A6.118)
где а, р = 1, 2 и еар — двумерный перестановочный символ.
Напряжения 1). После определения узловых перемещений
Ui и Ще) локальные выражения для деформаций и энергии дефор-
деформации можно получить, подставляя локальные поля перемещений
в соотношения, связывающие между собой деформации и переме-
перемещения, и затем подставляя результат в соответствующие локаль-
локальные выражения для функции энергии деформации элемента. Напря-
Напряжения элемента могут быть вычислены с помощью уравнений
состояния A5.1) и A5.36). Однако вычисленные таким образом
напряжения в общем случае будут иметь конечные разрывы
на межэлементных границах и в лучшем случае будут лишь грубыми
средними значениями действительных напряжений элемента.
Непрерывное распределение напряжений можно легко получить,
используя введенное в § 9 понятие сопряженно-аппроксимацион-
ных функций.
Пусть til) — локальный тензор напряжений элемента е, опре-
определяемый локальными уравнениями состояния для элемента (нап-
(например, для гиперупругих элементов tfe) = dWie)/dylij). Разрывное
Распределение напряжений в связанной модели, порождаемое
этими локальными напряжениями, описывается всюду, за исклю-
исключением множества меры нуль, формулой
TU= 2 #)(*, *)• A6.119)
Здесь предполагается, что преобразования от локальных коорди-
координат к глобальным уже осуществлены. Будучи разрывными, гло-
глобальные напряжения ~Ti3 = Т" (X, t) не принадлежат конечно-
конечномерному подпространству Ф или его сопряженному Ф*, порождае-
порождаемым глобальными базисными функциями Фд (X) или ФА (X) соот-
соответственно. Однако легко можно вычислить проекцию Ti} = ПГг;
напряжения Т13 на сопряженное пространство Ф*:
Г3 = Т%ФА (X), A6.120)
где
1 = (Тг\ Фд>= j Г3'ФкйМ, A6.121)
х) Сг.. Оден и Браули [1971а], а также Оден и Ки [1971а].
280 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
причем интегрирование производится по всей связанной области.
Величины Т%1 (А = 1, 2, . . ., (?) называются согласующимися
компонентами напряжения в узле А связанной конечнозлементной
модели.
Локальные формы соотношения A6.120) можно получить,
вспомнив, что х)
фд (X) = 2 Q2Y# (х) и Фа (X) = СЛГФГ (Х),,A6.122а, б)
е
где Слг — матрица, обращенная к Сдг, а
САТ = (Фд, Фг>- A6.122b)
Для типичного конечного элемента полагаем
#(« = <$), *w>= J $)Ч%^„ A6.123)
»0(е)
и получаем 2) локальную аппроксимацию
$> = #«!&(*). A6-124>
где в соответствии с (9.154) и (9.155)
^ (х) = Q>A (X) =(&АГ Д Qr^cg (х). A6.125)
В приложениях локальные поля A6.124) играют второстепен-
второстепенную роль, поскольку согласующиеся напряжения в каждом узле
можно получить непосредственно из A6.121).
16.4. ФОРМУЛИРОВКИ С ИСПОЛЬЗОВАНИЕМ
ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
Во многих случаях удобно переформулировать конечноэлемент-
ные постановки задач теории упругости в терминах полной потен-
потенциальной энергии каждого конечного элемента. Возвращаясь
к нелинейному жесткостному соотношению A6.4) для гиперупру-
гиперупругих элементов, заметим, что если обе его стороны умножить
на произвольную вариацию Ьи? узловых перемещений, то получим
0 = Plffiu?. A6.126)
J) См. (9.138), (9.144) и (9.148).
2) См. (9.153).
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 281
А так как
8U(e)=
»0(е) »0(е)
8U(e)= J
°0(е)
^f *w.i(eki + i|>M.k»f N<di;o, A6.127)
•0(О "J
мы видим, что входящий в A6.126) интеграл можно рассматривать
как вариацию полной энергии деформации элемента, обусловлен-
обусловленную вариацией обобщенных перемещений uf. Таким же образом,
если записать
8F(e)=-p№6uf, A6.128)
то выражение в правой части A6.126) оказывается вариацией
локальной потенциальной энергии внешних сил F(e) = —JPjv;"^-
Ясно, конечно, что в действительности потенциал F(e, может
не существовать, тем не менее Vie) в A6.128) можно искусственно
трактовать как потенциал, если использовать надлежащие обоб-
обобщенные силы, обсуждением которых мы занимались в предыдущем
пункте, и если считать эти силы не зависящими от вариаций и1?.
При этих условиях соотношение A6.126) можно переписать так:
J , A6.129)
_eB
dui
где я(е) — полная потенциальная энергия элемента е:
(е) = J WwdD0-pmu». A6.130)
*0(е)
Жесткостное соотношение для типичного элемента принимает вид
—- = 0-— \ —?-dvo — pNi, A6.131)
duV J ди-
1 "ОМ
а полная потенциальная энергия всей совокупности элементов
равняется
Е
П= 2 n(e> = ^7 + V, A6.132)
е=1
где
[7=2 ^7», V= S Vw A6.133)
e=l e=l
282 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Поскольку
i(e)
ЯСНО, ЧТО
Следовательно,
Е
U=y. \ W,e)dv0-
Vi (вЧ (в)
¦>.ut=-pAiy
PmV?.
A6.134)
f. A6.135)
A6.136)
Глобальные жесткостные соотношения получаются из условий
равновесия
i|Etf = 0, A6.137)
из которых вытекает, что
Е аи/ с .N
Так как
Q" ^л Hfi -1 чал
видно, что A6.138) можно переписать в виде
Рм= S ^Д J -^r^.i («Af+ *м, /&Cf) ^o, A6.140)
1 ki
что согласуется с A6.33).
Для несжимаемых материалов надо использовать вместо
видоизмененную функцию энергии деформации W = W
+ h (I3 — 1). При этом
A6.141)
е=1 в0(е)
и условие 6П = 0 приводит к уравнениям равновесия и к услови-
условиям несжимаемости. Действительно, если Л = hNtyN, то
A6.142)
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 283
откуда следует, что и дП/ди?, и dWdhN равны нулю. Условие
га
от
dU/duf = О дает A6.57), а в соотношении
r = J $n (h-l)dv0 = (iii)N = 0 A6.143)
мы узнаем условие несжимаемости A6.60).
При рассмотрении динамических явлений строится локальный
потенциал Лагранжа Z(e) для каждого элемента путем вычитания
я<е) из кинетической энергии:
1(е) = ще)-лЮ = ^-тым^и?-лЮ. A6.144)
Глобально
Е
L=2/w = x-n = i-Mir^[-n. A6.145)
е=1
Минимизация интеграла действия А [см. A5.33)] приводит к урав-
уравнениям движения Лагранжа:
d _JL ??_ = o, A6.146)
* got 9uf '
которые для совокупности конечных элементов имеют вид
jJl JjL-O. A6.147)
Здесь дП/dUf равно правой части соотношения A6.138). В A6.147),
конечно, дП/ди? ф 0 и U? = U? (t).
16.5. УРАВНЕНИЯ В ПРИРАЩЕНИЯХ1)
В этом пункте мы займемся важной задачей вывода уравнений
движения конечного элемента в приращениях. Временно снимем
ограничение упругости и вернемся к общему случаю движения
элемента произвольной сплошной среды. Затем мы посмотрим,
какой специальный вид примут наши уравнения в случае упругого
поведения элемента при приращении воздействий.
х) Основные идеи, используемые при выводе линейных форм уравнений
в приращениях, описывающих поведение деформируемых тел, принадлежат
Коши [1829] и Сен-Венану [1868]; в последующем их неоднократно выдвигали
заново. Современное полное изложение теории деформаций при приращениях
дано Био [1965]. Техника приращений широко применяется в приложениях
метода конечных элементов. Впервые она была использована Тэрнером [1959]
и Аргирисом [1959] при исследованиях с помощью метода конечных элементов
геометрически нелинейных задач теории упругости и упругой устойчивости.
Обзор относящихся сюда работ вплоть до 1965 г. сделан Мартином [19666].
Многие из конечноэлементных формулировок в приращениях, полученные
до 1968 г., неполны, поскольку они не учитывают надлежащим образом изме-
284 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Общие уравнения. Уравнения движения конечного элемен-
элемента для случая больших деформаций и произвольных свойств материа-
материала в существенной степени нелинейны. Однако во многих прило-
приложениях удобно рассматривать линеаризованные формы этих урав-
уравнений относительно малых возмущений движения, наложенных
на произвольное движение элемента. Такие формы уравнений
в приращениях оказываются особенно полезными в задачах стати-
статической и динамической устойчивости, пластичности и задачах
о статическом и квазистатическом поведении упругих тел.
Рассмотрим движение типичного конечного элемента, перево-
переводящее его к моменту времени t из начальной конфигурации С0(е)
в конфигурацию C(t\ В более поздний момент времени t -\- At
элемент будет занимать конфигурацию C^t+м, близкую к С[е) ¦
Пусть щ , ttf, Si, F° и uf, t%\ St, Ft — узловые перемещения,
напряжения, поверхностные усилия и объемные силы в конфигу-
конфигурациях С(е) и Ct+bt соответственно. Тогда
A6.148)
где ?f, s'3, R( и Вг — приращения величин uf, $', ?? и Р\ при
движении из Cf} в Cf+м-
Под 5 г здесь понимаются декартовы компоненты поверхностно-
поверхностного усилия на единицу начальной (недеформированной) площади,
отнесенные к начальной конфигурации С0{е), т. е. в соответствии
с A6.92) и A6.93):
Si = tmjnm (8}i + грм, juf) = S} (8n + грМ; juf). A6.149)
Таким образом, если
о
оО сЗ /r i i т\/Т\ /л а л с/~\\
с^г =оо (Oji -f- vpM, jU. ), (lb.loU)
TO
")], A6.151)
нений нагружения и поворотов элемента. Относительно общие формы урав-
уравнений в приращениях для конечных элементов были получены Ягмаи [1968],
Хиббитом, Марклом и Райсом [1970], Оденом [1969в, 19706] и Мартином
[1970]. Обзор результатов можно найти у Одена [1969в], Мартина [1970]
и Каваи [1970]. В настоящем пункте материал излагается по работе Одена
и Ки [19716].
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 285
где приращения 8S3 величин S1 в общем случае также являются
0 м м
функциями от щ , t% и изменяются в процессе нагружения.
Например, в случае равномерного давления q0 из A6.96) вытекает,
что
8S3 = 8q0VG0Ghjnh + qo[(8/В)Ghjnk + }ГЩFGW) nk) + О (e2),
A6.152)
где Go и G*> — детерминант и контравариантные компоненты тен-
тензора деформации в С\е); 8q0, 8 YG и &Gk' — приращения величин
q0, YG и Gki, причем q0 считается заданным, а б ]Лб? и 8Gk' обусло-
обусловлены приращениями деформации. Слагаемое О (е2) обозначает
члены высшего порядка относительно приращений 8q0, 8G и 8Gh3.
Поскольку в общем случае можно положить
N kj dG>{xu?) „
8GJ б?
8GJ = у, б?{ , A6.153)
члены в квадратных скобках в A6.152) являются линейными функ-
функциями от tf. Поэтому с точностью до членов первого порядка отно-
относительно приращений узловых перемещений и приложенных
нагрузок мы можем представить 8S3 следующим образом:
6# = $(!м Г0)8Г + Р&(и?, !%)&. A6.154)
Здесь Т\ — действительные заданные усилия в конфигурации Cf\
не зависящие от деформации, 8Тг — заданное приращение величи-
величины Т\, a Ql и Рм — функции, определяемые только состоянием
тела в Cte) (до приложения приращений 8Тг). Из A6.150) и A6.151)
вытекает, что
Rt = Si — Si =
= 57о*м. it? + (bji + ^M.juf1) (Ql8Tr + P^). A6.155)
Значит, обобщенные узловые силы в С\%м можно представить
в виде
A6.156)
где
P°Ni= J Pou°1>w<&>o+ J Si(8n + ^M,juf)^NdA A6.157)
A
(e) A0(e)
286 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
j
А0(е)
j ^^ A6.158)
Возвращаясь к общим уравнениям движения A3.60), подставим
туда A6.148) и A6.156). Получим уравнение
°0(е)
+ 1рм,Д^ + 1рм,^)^0 = Р^ + ^г, A6.159)
которое можно переписать так:
NJif + j C'ipiv, m (Ьп + Ум, juf) dv0-p%.] + mNM'(M +
v0(e)
@ (e)
+ j Sm}\bN,m$M,)dvolT = rm. A6.160)
Поскольку величины им, fj' и р??г должны удовлетворять уравне-
уравнениям движения элемента, когда он находится в конфигурации Cf\
выражение в квадратных скобках в A6.160) должно обращаться
в нуль. Кроме того, последний интеграл в левой части A6.160)
содержит произведение тензора приращений напряжений, линей-
линейных относительно ?f и их предыстории, на приращения узловых
перемещений %%. Следовательно, это слагаемое имеет порядок
выше первого относительно приращений ^ и может быть опущено.
Таким образом, мы приходим к системе линейных уравнений
mNMli + ] t^o'^N,m^M.jdvoli1 +
\ ^N,m(8ji + ^M,juf)dv0 = rNi. A6.161)
Это и есть общие уравнения движения конечного элемента в при-
приращениях.
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 28?
В общем случае тензор напряжений в любой частице является
функционалом от градиентов деформации, их предыстории, тем-
температуры, ее предыстории и, возможно, градиентов температуры
и т. д. В конечноэлементных моделях функционал реакции для
напряжений может быть выражен в терминах узловых значений
перемещений, температур и их предыстории и представляет собой
функцию от х и, возможно, некоторых преимущественных направ-
направлений dfe в начальной конфигурации. Следовательно, тензор при-
приращений напряжений sm3 можно определить как линейный функ-
функционал от значений и предыстории узловых перемещений, тем-
температур и т. д. Рассмотрим, например, специальный класс простых
материалов, для которых
tv= ?tf(uw«(*)) A6.162)
s=0
(зависимость от х явно не указана). Если предысториям uN&> (s)
и текущим значениям узловых перемещений uN сообщить малые
вариации t,N^' (s) и t,N, то напряжение Р1 получит соответствую-
соответствующую вариацию s13, где
**»= |0(и»(*)(*) + Е№(|)(*)) —*и. A6.163)
«=о
Если функционал %г} ( ) удовлетворяет надлежащим услови-
s=0
ям гладкости, то можно записать
si} = ?*» (о»<« (*)) + б ?'j (uw<»> (*)) | t,Nm (*)) + ... -1\ A6.164)
s=0 s=0
где б S° ( | ) — первая производная Фреше функционала Чг3 ( ),
s=0 s=0
а вертикальная черта в аргументе функционала указывает, что
производная линейна относительно следующей за чертой величи-
величины, в нашем случае — относительно предыстории t,Nm (s). Под-
Подставляя A6.162) в A6.163) и сохраняя лишь члены первого поряд-
порядка по t,N и gW(t) (s), убеждаемся, что s11 является линейным функ-
функционалом от предыстории приращений узловых перемещений:
где
-- &гз u"O (s) ? u (s)), A6.165)
s=0
<5i} (uW) (s) | EW@ (*)) = б Zi3' (uwW (s) 1 gN(t) (в)). A6.166)
s=0 s=0
288 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Уравнения движения в приращениях A6.161) для конечных эле-
элементов материала рассматриваемого типа принимают вид
s=0
(()|())^(J ^,^f)^o = rive. A6.167)
B0(e)
Упругие элементы. В частном случае упругих конечных
элементов тензор напряжений является функцией от текущих значе-
значений Gtj или уц, и тензор приращений напряжений может быть пред-
представлен в виде линейной функции от приращений t,f. Рассмотрим,
например, гиперупругий элемент, для которого функция энергии
деформации W (ytj) аналогична относительно компонент деформа-
деформации. Если W (уц) — энергия деформации на единицу объема
элемента в конфигурации С*е), то энергия деформации в произ-
произвольной близкой конфигурации С1+д* равна
j
A6.168)
где byij — вариация тензора деформации, обусловленная прира-
приращением величины и^:
A6.169)
Таким образом, тензор напряжений в возмущенной конфигурации
имеет вид
*Vb+*LM /У 8утп+..., A6.170)
или, с точностью до членов первого порядка относительно прира-
приращений деформации,
^ = i»+W^ <16Л71>
где tli = dW/dyi}. Значит,
sii = ti}-t$ = Ciimn&Vmn, A6.172)
где
ij зт т A6.173)
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 289
Замечая, что Сгзтп обладают следующими симметриями:
rAjmn __ y-ijimn гЛтгп _ gtnnij /aq /rj/л
и подставляя A6.169) в A6.172), получаем
Итак, тензор приращений напряжений для упругого элемента
является линейной функцией от приращений узловых перемеще-
перемещений, а также линеен относительно приращений деформаций 8ytj.
Однако поведение при приращениях не является упругим в смысле
классической (линейной) теории упругости, поскольку дополнитель-
дополнительные напряжения зависят не только от дополнительной бесконечно
малой деформации ец, но также от перемещений uf *). Действи-
тельноа если Cijmn = Ei}mn, то предположение, что si} = Eijmnemn,
привело бы к выражению для напряжений E%imntyNt mt^. Это
отличается от правильного выражения на довольно значительную
величину Eiimn\pNt тг|зм, „u^f, которая учитывает, в частности,
влияние поворота элемента.
Приращение жестиостей. Часто оказывается удобным
ввести матрицы (массивы) приращений жесткости, которые линейно
действуют на приращения перемещений ?f. Обращаясь к A6.158),
A6.161) и A6.175), введем следующие сокращенные обозначения:
A6.176)
с0(е)
j t^Nm^M$ihdv A6.177)
A6.178)
T A6.179)
A0(e)
j ? o. A6.180)
A0(e)
*) См. Трусделл и Ноля [1965, стр. 250]. К сожалению, во многих конеч-
ноэлементных исследованиях ошибочно утверждается^обратное.
19 Дж. оден
290 гл. IV. теория упругости
Здесь к$м — матрица приращений жесткости, Gnm — матрица
начальных напряжений х), D$m — матрица начального поворота 2),
R%nm — матрица начального нагружения 3) и 8р Nt — прираще-
приращения обобщенных узловых сил, обусловленные заданными прира-
приращениями внешних нагрузок. В этих обозначениях уравнения
движения элемента в приращениях принимают вид
mNM'i? + (к$м + G%M + D%M + R%M) If = 8pNi. A6.181)
Следует отметить, что вопреки тому, что утверждается во мно-
многих работах, матрица приращений жесткости к$м не совпадает
с обычной матрицей жесткости к%^м классической линейной теории
упругости, определяемой формулой A6.13). Действительно, к^м
сводится к к$м только в том частном случае, когда Ciimn = Eiimn.
Беря различные частные случаи A6.181), можно получить
постановки ряда специальных задач. Например, если к$м = кг^м
и элемент не испытывает значительных поворотов в невозмущенной
конфигурации, то из условия
dot (А#„+ <#„) = 0 A6.182)
можно найти классическую критическую нагрузку (соответствую-
(соответствующую статической потере устойчивости). Однако случаи довольно
значительных поворотов элемента до потери устойчивости не так
уж редки, и поэтому в общей ситуации необходимо к матрицам
в A6.182) добавить D1?m и Rnm- Если 8pNi приравнять нулю,
3)Эта матрица называется также матрицей «геометрической» жесткости
или «касательной» жесткости; см., например, Тэрнер, Дилл, Мартин и Мелош
[1960], Тэрнер, Мартин и Вейкл [1964] или Аргирис, Келси и Кэмел [1964],
Аргирис [1965а]. Мартин [19666] подробно исследовал эту матрицу для
частных видов элементов, а общую формулу получил Оден [19666] способом,
несколько отличающимся от излагаемого здесь. Ранее в литературе, посвя-
посвященной приложениям метода конечных элементов к геометрически нелиней-
нелинейным задача матрица Gl^M использовалась для того, чтобы «подправлять»
линейную матрицу жесткости в конце каждого этапа приращения нагрузки.
К сожалению, если не вводить новые материальные координаты в деформи-
деформированном элементе после каждого приращения — как это делали, например,
Мюррей и Вильсон [1969а, 19696],— то ясно, что этот метод неверен.
г) Важность использования матрицы Dlj$M в некоторых нелинейных
задачах показана Марклом [1968], который называл ее «матрицей начальных
перемещений». Используемый здесь термин введен Оденом и Кубицей [1967].
См. также Оден [1969в, 19706] и Хиббит, Маркл и Райе [1970].
8) Значение введения поправочных членов на нагрузку в уравнения
в приращениях было отмечено Оденом [1969д] и Оденом и Ки [1970]. Различ-
Различные формы' матрицы i?jyM были впервые гпредложены Хиббитом, Марклом
и Райсом [1970]. Однако их формы не совпадают с A6.179).
16. КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПРУГИХ ТЕЛ 294
a mNMt,i оставить в уравнениях, то их можно использовать для
исследования задач динамической устойчивости *).
Несжимаемые элементы. Для несжимаемых материалов
необходимо ввести в рассмотрение приращения гидростатических
давлений элемента. Поступая точно так же, как и при выводе уравне-
уравнений A6.161), но используя в качестве отправной точки уравнения
движения несжимаемых элементов A6.57), мы вместо A6.181)
получим
где Н1^м — матрица начальных давлений
г . о„
ik Г ~ dG } (и ) р
•" NM = \ "'О Т~м ^N] ("im "Ь ^рР, mui )
J I дК
h
A6.183)
dv0
A6.184)
JNi(8h)= j 8hGh0}\pNtJ(8ih + ^Mthuf)dv0. A6.185)
Щ(е)
Здесь h0 — гидростатическое давление в невозмущенном элементе
(например, h0 = tyRhf) и 8h — приращение гидростатического дав-
давления (например, 6Л = tyR8hR). Напряжения Ц' и Gl^M не являют-
являются теперь полными напряжениями, они представляют собой части
тензора начальных напряжений, обусловленные деформацией-
в момент времени t.
К уравнениям A6.183) надо, конечно, добавить условия несжи-
несжимаемости в приращениях
detZ«iJ8«Vsi20sZ0j<ipM,r^()]tf = O, A6.186a)
"о «о
где
°Г- A6.1866)
х) Некоторые частные случаи, относящиеся к динамической устойчивости
элементов при периодических начальных напряжениях, рассматривались
Хаттом [1968] и Брауном, Хаттом и Саламой [1968]. Много работ посвящен»
использованию дискретных моделей при расчете скоростей флаттера само-
самолетных конструкций; см., например, Бисплингхофф, Эшли и Халфмэн [1955J
или более позднюю работу Карьяппы, Сомашекара и Шаха [1970]. Барсоум
[1970] исследовал некоторые вопросы динамической устойчивости в связи
с конечноэлементными аппроксимациями тонкостенных балок.
19*
292 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
В случае если используются условия несжимаемости в узлах, мы
применяем условие A6.62) «в приращениях»:
3&дв(ш)# = 0, A6.187)
где
б(ш)#= J ^J^p-dvtf. A6.188)
v0(e) *
16.6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
Все приведенные до сих пор в этом параграфе уравнения были
получены в предположении, что материальные координаты х\е)
являются прямоугольными декартовыми в начальных конфигу-
конфигурациях С0(в) конечных элементов. Нетрудно, однако, записать
зкесткостные соотношения в форме, справедливой в любой системе
материальных координат. Вспоминая (см. A3.79) и A3.80)),
что в общем случае
»» = »igi = «'ig1, A6.189)
ш{ = ш™гЫ1). wi = w^N(l), A6.190)
где gj и gl — ковариантные и контравариантные базисные векторы
системы локальных криволинейных материальных координат |\
и что
dW
ij где
из A3.84) и A3.85) получаем нелинейные жесткостные соотно-
соотношения для гиперупругого элемента
IdW г i i i
~лГ. [Р/Фл?, о— гР^Г,-G+ ('Фм, j^pN, qOm + ФАгФN, q^mj —
«0(е)
— Фм, rtN^mq — ^M^N^mj^lq) WMm\ d,V0 = p*N A6.192)
И
lSiq^N,p+gqrtN^ip + (^M, q^N, pSf — \|?M\pN, рТ% +
d»o = Pwi- A6.193)
Здесь
a^MS) j^|Li^. A6.194)
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 293
В динамических задачах необходимо, конечно, в формулы
A6.192) и A6.193) добавить инерционные члены тями>ш и пг^мЩ-
Поскольку получение различных видов этих уравнений для раз-
разных систем криволинейных координат осуществляется стандарт-
стандартным образом, мы на этом останавливаться не будем.
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕ ЛИНЕЙНЫХ [УРАВНЕНИИ
Из теории, изложенной в предыдущих параграфах, ясно, что
статическое поведение конечных элементов при конечных упругих
деформациях описывается большими системами нелинейных алге-
алгебраических и трансцендентных уравнений. Хотя системы нелиней-
нелинейных уравнений встречаются в прикладных задачах механики уже
в течение нескольких веков, общих методов получения их точных
решений не существует. Таким образом, неизбежно приходится
использовать численные методы, и в общем случае решение можно
получить лишь с некоторой заданной степенью точности. В этом
параграфе мы обсудим основные идеи, на которых основываются
некоторые схемы численных решений больших систем нелинейных
уравнений х).
17.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Задача состоит в следующем. Рассматривается система п
нелинейных уравнений:
h (Xu Xt, . . .,: Хп) = 0,;
П (Хи Х„ . . ., Хп) = 0, A7.1)
fn (Xi, X2f . . ,j Xn) — 0,
и требуется найти удовлетворяющие этой системе значения X, где
X представляет собой га-мерный вектор независимых неизвестных»
A7.2)
х) Мы даем лишь относительно краткий обзор. Более подробно с этими
вопросами можно ознакомиться по книге Ортеги и Рейнболдта [1970]. Общие
свойства и методы решений нелинейных уравнений описаны в книгах Саати
и Брэма [1964] и Саати [1967] и в ряде обзорных статей; см., например, Брукс
[1958, 1959], Спэнг [1962], Флетчер [1965], Бокс [1966], Зойтендейк [19661,
Айзаксон и Келлер [1966], Ковалик и Осборн [1968], Пауэлл [1969].
294 гл- iv. теория упругости
В конечноэлементных приложениях, как правило, компонентами
вектора X являются компоненты узловых перемещений и, возмож-
возможно, гидростатические давления в элементах или в узлах, а уравне-
уравнения A7.1) суть глобальные жесткостные соотношения и условия
несжимаемости.
Часто мы будем использовать обозначение
f(X) = {/l(X)}, A7.3)
так что A7.1) можно записать в виде га-мерного векторного урав-
уравнения
f(X) = O. A7.4)
Другую постановку задачи можно получить, рассматривая
норму
F (X) = || f (X) ||2 = fт (X) ? (X) = /^ (X) + ... + /Д (X), A7.5а)
ЕЛИ
J A7.56)
Если X и ft (X) вещественны, то для любого X
F (X) > 0. A7.6)
Ясно, что равенство в A7.6) имеет место только в том случае, если
все /г (X) = 0, а это возможно лишь когда X удовлетворяет A7.4).
Поэтому задача решения системы нелинейных уравнений A7.4)
эквивалентна задаче нахождения значений X, при которых функ-
функция F (X), определенная формулой A7.5), достигает минимума.
В приложениях к задачам нелинейной теории упругости нет,
конечно, надобности искусственно строить вспомогательную функ-
функцию F (X), которую надо минимизировать для получения решений
жесткостных уравнений (уравнений равновесия), поскольку мы
уже имеем такую функцию в лице полной потенциальной энер-
энергии П, задаваемой формулой A6.136). Таким образом, задачу
нахождения решений системы нелинейных уравнений равновесия
типа A7.4) всегда можно свести к задаче нахождения таких X,
которые минимизируют П (X) (или, в обтием случае, F (X)) *).
^Геометрические понятия. Удобно считать X точкой
или вектором га-мерного пространства %п. Для каждой пары элемен-
элементов X, Y 6 Г имеем X + Y - Z => (Хг + Yu . . ., Хп + Yn) 6 Шп
х) Такой подход к решению задач нелинейной теории упругости для
конечноэлементных моделей использовался Богнером, Мэллетом, Миничем
и Шмитом [1965], которые называли его «энергетическим» подходом. См.
также Мэллет и Шмит [1967], Шмит, Богнер и Фокс [1968], Богнер [1968],
Фокс и Стэнтон [1968], Шмит и Монфортон [1969]. Аналогичный подход,
во в сочетании с другим методом минимизации, применял Беккер [1966].
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 295
и аХ = (аХх, . . ., аХ ) ? Шп, где а — вещественное число. Мож-
Можно ввести скалярное произведение Х-Х = ХТХ = XtXt, i =
= 1, 2, . . ., га; эвклидову норму [| X || = j/"X-X; понятие орто-
ортогональности (X-Y = 0 <?=> X _L Y) и углы в %п (cos 6 =
= Х- Y/1| X || || Y ||, где 6 —«угол между» X и Y). Отметим, что
в некоторых случаях удобнее использовать вместо эвклидовой
нормы yxtXt максимум-норму
l|X||max = max|Xj|, ? = 1,2, ...,га.
Некоторые результаты, излагаемые ниже, справедливы для случая
банаховых пространств общего вида (или легко обобщаются на этот
случай).
Вектор X называется единичным вектором, если || X || = 1;
система п взаимно ортогональных единичных векторов ег образует
ортонормированный базис пространства %п; каждый вектор
X ? %п можно единственным образом представить в виде линей-
линейной комбинации векторов е;, а именно X = Х^г. Большинство
геометрических понятий трехмерного пространства можно сформу-
сформулировать^ так, чтобы они имели смысл и для %п. Например, если
Хо — заданная точка, а "к — произвольное вещественное число,
то множество всех векторов X, удовлетворяющих условию
X = Хо + XN, A7.7)
определяет прямую линию, проходящую через Хо в направлении N.
Аналогично множество точек, удовлетворяющих условию
(X - Xo)-N = 0J A7.8)
образует (га — 1)-мерную гиперплоскость с нормалью N.
Пространство %п или некоторое его подпространство служит
областью определения 3) функций /г (X) из A7.1). Если для любых
двух точек Хъ Х2 ? 3) прямолинейный отрезок X = аХг +
+ A — а) Х2 @ ^ а ^ 1), соединяющий их, сам принадлежит 3),
то область называется выпуклой. Как правило, мы будем предпола-
предполагать, что наши выпуклые области открыты, т. е. что для каждого
Хо 6 SB существует шар || X — Хо || <С г, все элементы которого
тоже принадлежат SS. Множество JT (Хо, г) = {X | || X — Хо || <С г}
называется открытым шаром радиуса г с центром Хо, а множество
Jit* (Хо, г) — {X | || X — Хо || ^ г} — замкнутым шаром. Множе-
Множество аР (Хо, г) = {X | || X — Хо || = г} есть сфера радиуса г
с центром Хо. Функция вида / (X) = С, где С — постоянная,
описывает поверхность в %п. Таким образом, система A7.1)
описывает совокупность га поверхностей в %п; точка их пересече-
пересечения X и служит искомым решением системы.
При другом подходе мы рассматриваем функцию F (X) [или
П (X)] из A7.5) как скалярнозначную функцию с областью опре-
296 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
деления SS. Полагая F (X) = С, где С — постоянная, мы опре-
определяем (п — 1)-мерную поверхность уровня функции F (X). Реше-
Решения системы A7.1) — это те точки области определения функции
F (X), в которых она достигает относительного минимума. Скорость
изменения функции F (X) в точке X при движении из нее в направ-
направлении единичного вектора N задается, как обычно, производной
по направлению N, т. е. равна g-N, где g — градиент функции
F(X):
Кривая в %п описывается параметрическим уравнением вида
X = X (к) и векторы dX (k)/d% касательны к кривой. На всякой
поверхности уровня F (X) = С скорость изменения функции
F (X) вдоль любой кривой на этой поверхности dF/dk = 0 =
= g-dX/dX; это значит, что g направлено по нормали к поверхно-
поверхности уровня. Далее, если dX произвольно и образуете градиентом g
угол 0, то dF = || g || || dX || cos 0. Следовательно, в направлении
градиента @ = 0) скорость изменения функции F (X) максимальна.
Методы решения. В большинстве численных схем, приме-
применяемых для решения нелинейных уравнений, начинают с некото-
некоторого пробного приближенного решения Хо, которое называется
нулевым приближением. Далее тем или иным способом строится
последовательность приближений, которая должна сходиться
к решению нашей системы.
Численные методы, которые мы будем рассматривать, можно
разбить на две группы: итерационные методы и неитерационные
методы. В итерационных методах последовательность прибли-
приближенных решений строится с помощью фиксированного набора
операций. В неитерационных методах точки подбираются слу-
случайно. Как правило, в итерационных методах нулевое прибли-
приближение выбирается произвольно, а последующие получаются
с помощью рекуррентных формул вида
ХГ+1 = ХГ + ГБГ. A7.10)
Здесь Хг — приближенное решение на r-и шаге процесса, назы-
называемое r-й итерацией, a XrDr — поправка; Dr есть n-мерный век-
вектор, определяющий направление поправки, а 1Г — скаляр, опре-
определяющий ее величину. Из сопоставления A7.10) с A7.7) ясно,
что, используя рекуррентные формулы такого типа, мы продви-
продвигаемся к решению вдоль отрезков прямых, соединяющих последо-
последовательные приближения. Добавляя в A7.10) члены, содержащие
приближения Xr~*, Xr~2, . . ., можно, конечно, получить рекур-
рекуррентные формулы более высокого порядка, основанные на квадра-
квадратичной, кубичной и т. д. интерполяции.
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 297
Некоторые,, специальные итерационные схемы определения
минимума функций F (X) = fT (X) f (X) вида A7.5) относят к мето-
методам спуска; если F (Xr+1) ^ F (Хг), то мы как бы «спускаемся»
от значения функции в нулевом приближении Хо к значению
в минимизирующей точке X*, где F (Х*) = 0. К наиболее важным
методам спуска относятся так называемые градиентные методы,
в которых при выборе направления движения к минимуму ис-
используется градиент функции F (X). Итерационные методы
поиска, напротив, не связаны с вычислением градиентов. Эти
методы построены по такому принципу: среди ряда приближений
ищутся минимизирующие F (X), затем вместо этих приближений
образуются новые, так что на каждом этапе поиска используются
только те приближения, которые в совокупности дают более близ-
близкое к минимуму значение.
К указанным методам примыкают некоторые общие итерацион-
итерационные методы, основанные на непосредственном рассмотрении нели-
нелинейной системы A7.1) или на ее последовательных линеаризациях.
К ним относятся мощный метод Ньютона — Рафсона и методы
продолжений типа метода последовательных нагружений. Заме-
Заметим, наконец, что большинство итерационных схем можно считать
видоизменениями давно известного метода последовательных при-
приближений, который органически связан с фундаментальным поня-
понятием неподвижной точки оператора и принципом сжимающих ото-
отображений.
В следующем пункте мы кратко остановимся на этом принципе
ввиду его общематематического значения и ретроспективной связи
с другими итерационными методами. В остальном параграф посвя-
посвящен описанию наиболее важных итерационных и неитерацион-
неитерационных методов решения нелинейных уравнений.
17.2. НЕПОДВИЖНЫЕ ТОЧКИ И СЖИМАЮЩИЕ ОТОБРАЖЕНИЯ
Рассмотрим нелинейный оператор ЗР, который отображает про-
пространство %п (или в более общем случае банахово пространство Т)
в себя. Всякая точка X ? %п (или Т), удовлетворяющая условию
® (X) = X, A7.11)
называется неподвижной точкой оператора еР. Задача отыскания
решений уравнения A7.11) называется задачей о неподвижных
точках оператора еР.
Любое уравнение можно переформулировать как задачу о не-
неподвижной точке. Если, например, задано уравнение
Q (X) = Y, A7.12)
то можно положить
& (X) = X + Q (X) - Y. A7.13)
298 гл. IV. теория упругости
Тогда решение уравнения A7.12) будет неподвижной точкой опера-
оператора & (X), введенного формулой A7.13). Точно так же задачу
отыскания решения уравнения A7.4) можно свести к задаче
о неподвижной точке, если взять ИР (X) = X — f (X).
Неподвижные точки оператора $> (X) можно искать методом по-
последовательных приближений. Пусть Хо — нулевое приближение,
т. е. какое-то пробное решение уравнения A7.11). Если & (Хо)
несущественно отличается от Хо, то естественно считать X1 =
= & (Хо) уточнением Хо. Далее, точно так же X2 = # (X1) слу-
служит возможным уточнением X1. Продолжая этот процесс, мы стро-
строим последовательность {Хг} последовательных приближений
к неподвижной точке X оператора & (X) с помощью формулы
Хг'х = 0» (ХО, г = 0, 1, 2, .... A7.14)
Если ввести степени оператора
0*0 = 7, 0*'** = 0*@*г), r = 0, 1, 2, ....
то
X1 = 0» (Хо) = 0* @* (Хо)) = S51 (Хо),
X2 = ® (X1) = № @" (Хо)) = &2 (Хо), ....
Таким образом, A7.14) можно записать в виде
Xr+i ^ ^r+i (Хо^ A7.15)
Определение *). Оператор $>, отображающий банахово про-
пространство У в себя, называется сжимающим отображением (или
отображением сжатия) в замкнутом шаре
JT(X0, r) =
если существует такое вещественное число X @ ^ X <С l)j что для
любых X, Y 6 Ж (Хо, г) выполняется условие Липшица
II 0*(Х) - 0* (Y) || .< А, ||-X - Y ||. A7-16)
Постоянная Липшица X называется коэффициентом сжатия.
х) Хотя нас в основном интересуют нелинейные операторы в %п, это
определение и все теоремы этого пункта справедливы для произвольных
банаховых пространств. Отметим также, что понятие сжимающего отображе-
отображения легко распространить на случай общих метрических пространств. Пусть
X и f — метрические пространства с метриками d (Хх, Х2) и р (Ylt Y2)
соответственно. Отображение 3й из X в f называется сжимающим в шаре
JT (Хо, г)= {X \ d (Хо, X) < г}, если существует такой коэффициент сжа-
тш_0 < Я< 1, что р (# (Xj), 3° (Х2)) < Ы (Xlt X2) для любых ХЪ Х2 6
е лг (х0. г).
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 29Й
Теорема 17.1 (принцип сжимающиж отображе-
отображении). Пусть аР (X) — отображение сжатия в JT (Хо, г) с коэффи-
коэффициентом сжатия X, и пусть Хо удовлетворяет условию
L A7.17)
||
Тогда:
а. Последовательность {Хг}, построенная с помощью формулы
Xr+1 = SP> (Хг), сходится к некоторой точке X* ? JT (Хо, г0).
б. X* есть неподвижная точка оператора а/15.
в. X* — единственная неподвижная точка оператора & в шаре
Jf (XO1 г).
Доказательство. Чтобы доказать а, покажем сначала, что если
выполнено условие A7.17), то все итерации Xr+1 = ^ (Хг)
будут находиться в шаре JT (Хо, г0). Применим метод матема-
математической индукции (т. е. проверим, что наше утверждение
верно для г = 1, и покажем, что из его справедливости для
п = г следует справедливость для п = г -f 1). Поскольку
X1 = &> (Хо), имеем в силу A7.17)
|| X1 - Хо || = A - %) г0 < г0.
Значит, X1 6 Ж (Хо, г0). Предположим, что || Хо— Хг || ^ г0
для итераций X1, X2, . . ., Хг. Тогда
|| Хг+1 — Хг || = || &> (Хг) — fl5 (X1") || <
<X || Хг-Хг-* || = % || № (X1"-1)-® (Хг-2) ||< -
Отсюда следует, что
|| Хг+1-Х0|| = || (Хг+1-Хг)
<ЦХг+1-Хг
1 -V) го+ Г A -Я,) г„+ ... + A-Х) г0
или
Следовательно, Xr+1 6 Ж (Хо, г0). Таким образом, мы доказа-
доказали, что все итерации принадлежат шару jjT (Хо, г0).
Покажем теперь, что итерации {Хг} образуют последова-
последовательность Коши. Действительно, для любого т
|| Хт—Хтп|| = || (Хю-ХП1в1) + (Хт#1-Хт*2)-1- ...
300 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
| Хт - Xm+i || +1| Xm+i -
A-Г)г0. A7.18)
Так как X фиксированно и 0 ^ X <С 1, то для любого е > 0
можно найти такое целое N (е), что || Хт — Xm+n || < е при
B>0nm>JV (например, при заданном е можно взять такое
N, что lN< е/г0; тогда || Хт - Xm+n ||< е A — Хп)< е
при т "> N). Поэтому последовательность {Хт} является
последовательностью Коши.
Если X* — предел этой последовательности, то X* 6
?jjP (Хо, г0). Этим завершается доказательство утверждения а.
Поскольку
|| <^ (Хг) — X* /| = || Xr+1 — X* ||
и, как было показано, lim || Xr+1 — X* || = 0, ясно, что
lim ||> (Хг) — &> (X*) || =Го. Далее, || № (Хг) — S5 (X*) ||<
<1 Хг — X* ||; следовательно, lim @> (Хг) = ^ (X*) = Х*,;
Г->оо
т. е. X* — неподвижная точка оператора а?5. Этим доказано б.
Заметим, что б следует также из а ввиду непрерывности ffis
вытекающей из условия A7.16). Действительно, если lim Xr =
Г->со
= X*, то
lim ® (Хг) = <^ (X*) = X*.
г-
Остается показать, что точка X* — единственная неподвиж-
неподвижная точка в JT (Хо, г0). Предположим, что X — другая непод-
неподвижная точка в JT (Хо, г0). Тогда
у х*-х ц = || ^(х*)—
что, конечно, невозможно. Тем самым теорема полностью
доказана.
Отметим, что первое утверждение теоремы 17.1 можно записать
так (см. A7.15)):
X0). A7.19)
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 301
Если справедливо соотношение A7.19), то будем говорить, что
точка X* достижима из Хо, а множество всех точек, из которых
X* достижима, назовем областью достижимости. Нетрудно
показать, что в случае, когда выполнены условия теоремы 17.1Ж
X* достижима из любой точки шара jfT (Хо, г0). Действительно,
поскольку
видно, что || аР (X) — X1 || ^ кг0, т. е. $> отображает jfT (Хо, г0)
в меньший шар JP (X1, %,r0) с J/' (Хо, г0). Вообще, устремляя
в A7.18) п к бесконечности, получаем
|| Хг - X* ||< Я.рг0. A7-2°)
т. е. ®г отображает ~JT (Хо, г0) в ~JT (Xr, Vr0).
Отметим, что любая последовательность {Хг} с Xr ?
? JP (Xr, %rr0) также будет сходиться к X*. Это дает возможность
использовать при построении последовательных приближений
к X* аппроксимации оператора а?5.
Схематически решение задачи о неподвижной точке методом
последовательных приближений для одномерного случая показано
на рис. 17.1. В случаях (а) и (Ь) мы имеем сходящиеся схемы, при-
причем в случае (а) итерации образуют монотонно возрастающую
последовательность, а в случае (Ь) — осциллирующую. В случае
(с) оператор е?5 имеет две неподвижные точки, X* и X*. Однако
точка X* недостижима методом последовательных приближений,
потому что не существует содержащего ее шара, в котором аР (X)
является отображением сжатия: если е — малое положительное
число, то нулевое приближение Хо = X* + е приводит к расхо-
расходящейся последовательности, а Хо = X* — е. порождает после-
последовательность, сходящуюся к X*, а не к X*.
Рассмотрение одномерных задач о неподвижной точке, пред-.
ставленных на рис. 17.1, наводит на мысль, что сходимость метода
последовательных приближений (и все остальные утверждения
теоремы 17.1) гарантирована, когда тангенс угла наклона кривой
z = if* (X) по модулю меньше единицы (т. е. | аР' (X) \ ^ % < 1).
Это действительно так, и доказывается это без особого труда.
Возникает вопрос, имеет ли место аналогичное утверждение для
n-мерного случая. Ответ на этот вопрос также утвердителен.
В самом деле, если еТ5 = Р — оператор, отображающий %п в себя
302
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Рис. 17.1. Метод последовательных приближений для некоторых
одномерных задач о неподвижных точках.
и имеющий непрерывную производную в JT (Хо, г), то, как следует
из теоремы Тэйлора х),
l (V)
\Xj-Yj\
для любых двух точек X и Y 6 Ж (Хо, г), где \г некоторая точка
шара Л'(Хо, г), лежащая на отрезке, соединяющем X и Y. Если
х) См. Айзаксон и Келлер [1966]. Дополнительные сведения об отобра-
отображениях сжатия можно найти у Ролла [1969] или Ортеги и Рейнболдта [1970].
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 303
мы воспользуемся максимум-нормой || X || = max | Xt |, то
li
Следовательно, при | dPt (\l)/dXj | ^ Х/п, 0 ^ X <С 1, имеем
|| Р (X) - Р (Y) ||< X || X - Y ||,.
т. е. Р является отображением сжатия в JT (Хо, г) и, значит,
справедливы все заключения теоремы 17.1.
Возвращаясь к A7.4), заметим, что можно построить много
таких операторов Р (или аР)^ неподвижными точками которых
будут решения уравнения A7.4). Пусть, например, А (X) —
любая невырожденная матрица размера п X п. Тогда если поло-
положить
Р (X) = X - А (X) f (X),
то ясно, что Р (X) = X ==> А (X) f (X) = 0. Но А (X) f (X) = 0 =ф
=^> f (X) = 0, поскольку по предположению матрица А (X) невы-
невырождена при любом X. Рекуррентная формула в этом случае имеет
вид
Xr+1 = Р (Хг) = Xr —A (Xr) f (Xr). A7.21)
Выбирая различным образом А (X), можно по формуле A7.21)
построить множество итерационных схем. Если, например,
А (X) = А есть постоянная матрица, то A7.21) определяет так
называемый метод хорд. Если в качестве А (X) взять матрицу,
обратную к матрице Якоби:
а (X) = J-1 (X) = [dft (X)/dXj]-\
то получится метсд Ньютона — Рафсона (см. п. 17.4). Если же
положить А = J (Хо), то получится модифицированный метод
Ньютона — Рафсона. Перечень этих примеров можно было бы
продолжить и далее.
17.3. МЕТОДЫ СПУСКА И ГРАДИЕНТНОЙ МИНИМИЗАЦИИ
Используя в качестве отправной точки A7.10), рассмотрим
некоторые итерационные методы минимизации функции F (X) =
= fT (X) i (X). Эти методы отличаются выбором V и Г г, часть из
них относится к методам спуска IF (Xr+1) ^ F (Хг)], а в других
используются градиенты (или «сопряженные» градиенты) функции
F (X). Поскольку в большинстве этих методов фигурируют неко-
некоторые аппроксимации градиента g, их обычно называют градиент-
градиентными методами.
304 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Покоординатные методы. Один иэ простейших спосо-
способов выбора вектора направления Dr в A7.10) — задать его в виде
Dp = eJ, A7.22)
где е; есть n-мерный единичный вектор:
с5=@, 0 0, 1, 0 ...0} A7.23)
(единица на ;-м месте).
Таким образом, каждый раз изменяется лишь одна компонента
вектора Хг. Выбор этой компоненты может осуществляться произ-
произвольно, или же могут вводиться дополнительные условия, опре-
определяющие номер компоненты jf, изменяющейся на данном шаге
итерации. Методы такого типа называются покоординатными
методами (или, подробнее,методами покоординатной релаксации).
В покоординатных методах Хг обычно определяется следующим
образом. Предположим, что F (X) аналитична в окрестности
точки Хг. Тогда справедливо разложение
i, j=l
Величины d2F (X)/dXi dXj являются компонентами симметрич-
симметричной матрицы Н размера п X п, называемой матрицей Гессе функ-
функции F (X):
TdF (X) М7,„
и
S dx ^ = ег-РГ' A7-26)
г=1
где gr = 'VF (Хг) — градиент функции F (X) в точке Хг. Таким
образом, если ограничиться квадратичными членами, то
F (Хг + ЬЧУ) = F (Xr) + %Y ¦ Dr + у (^rJ DrTHDr. A7.27)
Предположим, далее, что поверхность уровня в окрестности точ-
точки Хг выпукла, т. е. для любых X и Y иэ этой окрестности
F [аХ + A — a) Y]< aF (X) + A - a) F (Y) при 0 < а < 1.
Тогда условие того, что величина Хг при заданном Dr определяет
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 305
Рис. 17.2. Последовательные движения в методе покоординатной релаксации,
максимальный шаг в направлении минимума, имеет вид
dF(Xr+XrDr)
откуда
s
г=1
dXt
DrTHDr
n n r
у у d*F(Xr)
A7.28)
Поскольку в покоординатных методах Dr задается формулой
A7.22), то
ir.D' = rf.. ^UW = Hlm^^^r) , A7.29)
20 дж. оден
306 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
где gTj есть /-я компонента градиента g в точке Xr, a Hq)Q) — эле-
элемент матрицы Гессе Н в точке Хг, стоящий на пересечении /-й
строки и;-го столбца. Таким образом, в покоординатных методах
Г=—-?-. A7.30)
Направление /-го шага в A7.22) и A7.30) в принципе произволь-
произвольно. Образчик последовательных движений в покоординатном
методе представлен на рис. 17.2.
Примером одновариантного метода, в котором ej выбираются
не произвольно, может служить известный релаксационный метод
Саутвелла *). В этом методе номер / того места в A7.23), на котором
стоит единица, соответствует той координате, которая обеспечивает
максимальное локальное уменьшение F (X), т. е. / выбирается
из условия
|| OF {ХгIдХ3 || = max | dF (Xr)/dXt \.
l
Ясно,,; что возможны многочисленные модификации я улучшения
этого метода.
Метод наискорейшего спуска. Напомним, что направ-
направлением максимальной скорости возрастания функции F (X) является
направление ее градиента g (X). Следовательно, —g (X) пред-
представляет собой направление максимального спуска в X. Полагая
Dr=-g(X''), A7.31)
мы получаем метод наискорейшего спуска Коши [1847].
Величину шага Я,г, соответствующую направлению A7.31).
можно вычислить по формуле A7.28). Таким образом, для каждого
г направление вектора Xr+1 — Хг является направлением наиско-
наискорейшего убывания F (X).
Нетрудно доказать существование решений и сходимость итера-
итерационного процесса в том случае, когда F (X) является квадратич-
квадратичной дважды непрерывно дифференцируемой функцией в области SD
и ее матрица Гессе положительно определена.
Теорема 17.2. Пусть F (X) — квадратичная функция вида
Т Т A7.32)
где матрица! Н положительно определена. Пусть, далее, {Хг} —
такая последовательность точек, что
х) См., например, Саусвелл [1940, 1946] и Аллен [1954].
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 307
где %т определяется формулой A7.28), a gr — градиент:
g
Тогда
а. Существует единственная точка X*, в которой функция
F (X) достигает минимума.
б. Последовательность {Хг} сходится к X*.
Доказательство *). Поскольку Н — положительно определен-
определенная матрица, существует такая невырожденная матрица К,
что КТК = Н. Поэтому A7.32) можно переписать в виде
2F (X) = (YT + bTK) (Y + K~lTb) + (А — Ь^'Ч)),
где Y = КХ. Таким образом, 2F (X) > А — ЬТН-Ч) для всех
X, и равенство достигается в том и только в том случае, если
Y = —К~1тЬ, т. е. если X + Н~Ч> = 0. Поэтому минимум
F (—Н~Ч)) существует и единствен. Этим доказано утвержде-
утверждение а теоремы.
Чтобы доказать утверждение б, обозначим через X* =
= —Н-1Ь точку, в которой F (X) достигает минимума. Условие
lim || X* — Xs" |[ = 0 равносильно в рассматриваемой ситуа-
Г-*-оо
ции условию
\im[F(Xr) — F(X*)] = 0,
которое мы сейчас и докажем.
Пусть Ег = Хг — X*'— ошибка на r-м шаге. Тогда
F (Хг) — F (X*) = F (X* + К) — F (X*) = -i ErTHEr.
Если со — собственное значение матрицы Н, то НХ = иХ
и й = ХТНХ/ХТХ.
Обозначим через со отношение наименьшего собственного зна-
значения матрицы Н к наибольшему. Тогда соХтХ ^ ХТНХ ^
^ ХТХ для любого X. Следовательно,
F(Xr)-F(Xr+i) (grVJ
F(Xr)-F(X*) (g^HgrHg'Vigr)
где 0 < со ^ 1, ибо матрица Н положительно определена. При
выводе этого неравенства используется то обстоятельство, что
НЕГ = Н (Хг - X*) = НХГ + Ь = gT. Вычитая обе части
неравенства из единицы и производя упрощения, получаем
F (Xr+1) - F (X*) < A - со) [F (Хг) - F (X*)].
В изложении этого доказательства мы следуем Саати и Брэму [1964].
20*
308 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Поэтому, если Хо — нулевое приближение, то
F(Xp)-JP(X*)<(l~(o)r[ii'(Xo)-F(X*)]. A7.33)
Поскольку 0 < и <; 1, правая часть этого неравенства стре-
стремится к нулю при неограниченном возрастании г; значит,
F(Xr) — F (X*) -> 0, чем и завершается доказательство.
Если F (X) не является квадратичной функцией, то итерацион-
итерационный процесс все же может сходиться в смысле A7.33) при условии,
что Хо достаточно близко к X* — настолько, чтобы квадратичные
члены в разложении F (X) преобладали над членами высших поряд-
порядков. Доказательства сходимости, основанные на этом соображе-
соображении, называются доказательствами, основанными на квадратичной
сходимости. Теорему 17.2 можно обобщить на случай произ-
произвольной дважды непрерывно дифференцируемой функции F (X),
матрица Гессе которой в точке минимума X* положительно
определена.
Теорема 17.31). Пусть F (X) — вещественнозначная дважды
непрерывно дифференцируемая функция, определенная на выпуклой
области пространства %п. Пусть Хо — произвольная точка,
такая, что замкнутое множество 'ё = {X: F (X) ^ F (Хо)}
ограничено и для любого вектора X 6 У выполняется неравенство
| ХТНХ | ^ аХтХ, где Н — матрица Гессе функции F (X), а а —
положительное число. Пусть, далее, Xr+1 = Xr -\~ %rgr, где gr —
градиент функции F (X) в точке Хг ? § и %г удовлетворяет условию
F (Хг+ Я,у) < F (Хг + *¦?) при любом X > 0. Тогда: а) некото-
некоторая подпоследовательность {Хг>т} последовательности {Хг} схо-
сходится к точке X* 6 S, в которой g (X*) = 0; б) F (Хг'т) моно-
монотонно убывает и стремится к F (X*) — локально минимальному
значению функции F (X); в) если X* — единственная точка локаль-
локального минимумаТв S* то сама последовательность {Хг\ сходится
к X*.
Выбор ХТ в соответствии с A7.28) обеспечивает оптимальный
размер шага для квадратичной функции F (X). При этом F (X)
убывает за один шаг на максимально возможную величину. Если
F (X) не является квадратичной функцией или если требуется
оптимальность Хг для заданного числа п шагов, а не для одного
шага, то к более быстрой сходимости может привести и другой
выбор %'.
Методы сопряженных градиентов2). Так называемый
метод сопряженных градиентов минимизирует квадратичные функ-
х) Доказательство этой теоремы можно найти у Гольдстейна [1962].
См. также Саати и Брэм [1964].
2) См. Хестинзи Штифель [1952], а также Флетчер и Ривс [1964]. Более
общее изложение имеется у Дэниэла [1967].
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 309
ции и переменных зар итераций, гдер^га. Чтобы продемонстриро-
продемонстрировать идею метода, перепишем квадратичную функцию A7.32) в виде
F(X) = F0 + ^(X-X*)JH(X-X*), A7.34)
где X* — точка, в которой F (X) принимает минимальное значе-
значение. Тогда
g (X) = VF = Н (X - X*). A7.35)
Как обычно, положим Xr+1 = Хг -f- VDr. Предположим, что
векторы D°, D1, . . ., D", указывающие направления последова-
последовательных движений, линейно независимы, и введем обозначение
or = KW. Имеем
= xr~q + aT-q + a1"**1 + ... + o7",
или, для п-ш итерации,
X" = Xr+1+ "S a*. A7.36)
5=r+l
Поэтому
n-1
Поскольку НХ* = 0 и HXr+1 = gr+1, то
Отсюда следует, что
gnTDr = g^+i)TDr+ S ^D9THDr. A7.37)
g=r+i
Предположим теперь, что векторы D°, D1, . . ., D" являются
Н-сопряженными в том смысле, что
D9THDr = 0, q^=r. A7.38)
Тогда в силу A7.37) для всех г имеем
gnTDr = 0. A7.39)
Поскольку D°, D1, . . ., D™ линейно независимы, они образуют
базис нашего «-мерного пространства. Поэтому A7.39) означает, что
gn = 0. A7.40)
310 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Значит,
H(X"-X*) = gn = 0,
и вследствие положительной определенности Н,
X" = X*. A7.41)
Таким образом, минимум достигается после п итераций или
раньше, если на каком-либо шаге Хп окажется равным нулю.
Основное требование A7.38) метода сопряженных градиентов
может быть удовлетворено различными способами. В общем случае
полагаем, как обычно,
D°=-go=-V/'(Xo) A7.42а)
и
Dr+1 = - gr+1 + prDr, A7.426)
где рг выбирается так, чтобы удовлетворялось условие A7.38),
т. е. чтобы
Dr+lTHDr= -
Отсюда
„г+1ТТ
A743)
Определенные таким образом векторы направлений Dr являются
линейно независимыми и Н-сопряженными.
Если F (X) — не квадратичная функция A7.34), а функция
общего вида, то матрицу Гессе Н надо определять для каждого
цикла. В этом случае вывод о сходимости за п итераций становится,
строго говоря, неверным, но и для неквадратичных функций
часто наблюдается относительно быстрая сходимость за п циклов.
Кроме того, в случае неквадратичной функции F (X) иногда более
удобно размеры шагов Хг подбирать способом, отличным от A7.28).
Метод переменных матриц. Метод переменных
матриц, предложенный Давидоном [1959] и обобщенный Флетчером
и Пауэллом [1963], является мощным итерационным методом
спуска, позволяющим находить локальные минимумы нелинейных
функций нескольких переменных. Метод основан на обычном
предположении, что члены второго и более низких порядков в раз-
разложении Тэйлора преобладают над всеми другими членами в окрест-
окрестности локального минимума. Напомним, что для квадратичной
функции п переменных вида A7.32) точкой минимума является
X* = —Н-1Ь. В методе переменных матриц, однако, обратная
матрица Н не вычисляется непосредственно. Вместо этого вво-
вводится аппроксимирующая ее матрица G, в качестве которой перво-
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 311
начально можно взять любую положительно определенную сим-
симметричную матрицу. Матрица G видоизменяется при r-й итерации
с использованием информации, полученной при движении в напра-
направлении
D' = -Gy. A7.44)
Видоизменение осуществляется таким образом, чтобы вектор пере-
перемещения а1 к минимуму вдоль прямой X = Xr -f- KDr был соб-
собственным вектором матрицы Gr+1H. Это гарантирует, что G
приближается к матрице Н, определенной в точке минимума.
Обычно Go принимают равной единичной матрице, при этом началь-
начальный шаг совершается в направлении наискорейшего спуска.
После определения Dr из соотношения A7.44) величина V
подбирается таким образом, чтобы значение F (Xr -f- XrSr) было
минимальным по сравнению со всеми другими значениями на пря-
прямой Xr -f- XSr. Процесс осуществляется следующим образом.
Полагаем
Xr+1 = Xr + or, A7.45)
где аг = А/ТУ. Вычисляем F (Хг+1), учитывая, что arTgr+1 = О,
и определяем
Yr = gr+1-gr. A7.46)
Тогда
A7.47)
где
• Ar = -^V, A7.48а)
ar Y
Далее весь процесс повторяется исходя из точки X741 с исполь-
использованием градиента gr+1 и матрицы Gr+1. Величина расстояния
от минимума при r-й итерации задается формулой
d-f^H-'VyI^ A7.49)
которую можно приближенно записать так:
cf »(DrVI/2 A7.50)
(ибо Gr приближается к Н при r-> cxd). Итерационный процесс
заканчивают, когда d? станет меньше некоторой заданной величи-
величины или когда каждая] компонента Dr станет меньше заданной
постоянной.
312 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Можно показать, что если F (X) — квадратичный функционал,
то описанный метод сходится за то ^ п итераций. Действительно,
из A7.46) следует, что
Yr = HXr+1-HXr = Hor.
Таким образом,
Gr+1Hor = Grrr + ar
ar Ha?
= or. A7.51)
Мы можем считать, что Н и G' суть вполне определенные сим-
симметричные положительно определенные матрицы. Тогда для каж-
каждого г = 0, 1, . . ., п — 1 определена итерация Хг Ф Н~Ч) = X*.
В противном случае Хг = X* и процесс сходится для г < п.
Из предыдущего обсуждения сопряженных градиентов мы знаем,
что X" = Н~Ч), если D0, . . ., W являются /Г-сопряженными.
Рассмотрим следующие два соотношения:
A7.52а)
A7.526)
Из A7.51) видно, что они справедливы при к = 1. Покажем, что
если они выполняются для к, то они верны и для к -+- 1. Из перво-
первоначального выражения для градиента gft = a -f HXft следует, что
g" = а + Н (Xi+1 + ai+i + oi+2 + . .. + о"),
откуда
gh = g;« + Н (oi+1 + oi+2 + . . . + о*).
Значит, для всех i ^.k, i ф к,
так что A7.52) верно для к ^.п. Отсюда следует, что Хп = Н~1Ь.
Соотношение A7.52а) показывает, что GnH имеет п линейно неза-
независимых собственных векторов с единичными собственными зна-
значениями. Поэтому GnH = I, что и требовалось доказать.
17.4. МЕТОД НЬЮТОНА — РАФСОНА
Теперь рассмотрим мощный и хорошо известный метод Ньюто-
Ньютона — Рафсона и его модификацию. Этот метод широко применяется
в нелинейных задачах механики твердых тел и, в частности, строи-
строительной механики.
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 313
Вернемся опять к системе нелинейных уравнений A7.4) и пред-
предположим, что разность между начальной точкой Хо и решением
является малым вектором АХ. Если функция f (X) достаточное
число раз дифференцируема в Хо, то можно воспользоваться раз-
разложением Тэйлора:
f (X) = f (Хо + АХ) = f (Хо) + Jo (X - Хо) + . . . = 0, A7.53)
где Jo — матрица Якоби в точке Хо:
]- A7-54>
Если в A7.53) ограничиться только линейными членами, то полу-
получим
(О « f (Хо) + Jo (X - Хо),
откуда
X = Хо - J-Ч (Хо). A7.55)
Это значение X, конечно, лишь приближенное, но его можно
использовать в качестве начального на следующем шаге итераци-
итерационного процесса. В общем случае получаем рекуррентную формулу
Xr+1 = Xr-Jrf(Xr). A7.56)
Процесс повторяется до тех пор, пока не получим | AXj | < 8
для некоторого заранее заданного 8.
Проиллюстрируем метод Ньютона — Рафсона на классическом
примере функций одной переменной. Начиная с пробной точки XOt
вычисляем / (Хо) и /' (Хо) и подсчитываем новое значение X1 =
= Хо — / (X0)/f (Хо). Как показано на рис. 17.3а, это означает
спуск по касательной к функции / (X) в точке Хо. Если /' (X)
в какой-либо точке обращается в нуль, итерации Ньютона —
Рафсона, как видно из рис. 17.ЗЬ, могут расходиться.
Отметим, что в соответствии с A7.56) на каждом шаге итера-
итерационного процесса нужно обращать матрицу Якоби Jr размера
п X п. Этого можно избежать, применяя модифицированный ме-
метод Ньютона — Рафсона, в котором используется лишь матрица
Якоби из первого шага. В этом методе вместо A7.56) применяется
рекуррентная формула:
Xr« = Xr_j-lf (Хг}_ A7.57)
Ясно, что модифицированный метод Ньютона — Рафсона является
частным случаем упомянутого в п. 17.2 метода хорд, соответствую-
соответствующим выбору J в качестве матрицы А из A7.21). Хотя необходи-
необходимое для достижения требуемой точности число итераций при
использовании модифицированного метода, как правило, гораздо
больше, общий объем вычислений и затраты времени могут быть
314
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
I
Сходимость
метода
Ньютона-Рафсона
Сходимость
модифицированного
метода
х°
(с)
Рис. 17.3. Стандартный и модифицированный методы Ньютона — Рафсона.
значительно меньше, чем при использовании обычного метода
Ньютона — Рафсона. Схематично сопоставление модифицирован-
модифицированного и немодифицированного методов представлено на рис. 17.3а
и с; в последнем случае видно, что во всех итерациях исполь-
используется начальный наклон /' (Хо).
Метод Ньютона — Рафсона и его модифицированный вариант
успешно применялись на практике для решения больших систем
нелинейных уравнений. Важная роль этих итерационных методов
связана и с их теоретической ценностью, поскольку для них суще-
существует ряд теорем, позволяющих ответить на вопросы о суще-
существовании и единственности решения, сходимости и скорости
сходимости итерационного процесса на основе сведений о началь-
начальной точке Хо и о значениях | dfJdXj | и | d^fJdX] дХк |. Кроме
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИИ 315
того, результаты о существовании и единственности решений
и о сходимости метода Ньютона — Рафсона решения нелинейных
алгебраических и трансцендентных уравнений можно обобщить
на случай нелинейных операторов в банаховых пространствах.
Приведем без доказательства некоторые теоремы о нелиней-
нелинейных уравнениях 1).
Теорема 17.4. Система нелинейных уравнений:
U (X) = 0, i = 1, 2, . . ., п,
XT = {Xl, . . ., Хп},
имеет решение, которое можно получить методом Ньютона —
Рафсона, если выполнены следующие условия:
а. Матрица Якоби Jo невырождена и
HJ-4K5, A7.58)
где В — некоторое положительное число.
б. ||Х1-Х0|[<Л, A7.59)
где А — некоторое положительное число.
в. a^ixi <С для *. /. *=1. 2, .... п. 1A7.60)
При этом решение X* удовлетворяет оценке
||X*-XO||<A-/T=2^)^, A7.61)
где
A7.62)
Теорема 17.5. Если выполнены все условия теоремы 17.4 и
дХ^дХ ^А i, j, k = l, 2, ..., п A7.63)
в области
#-, A7-64)
то решение X* единственно.
На r-м шаге итерационного процесса
а нам нужно, чтобы
lim||X*-Xr|| = 0,
J) См., например, Ролл [1969].
316 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
т. е. чтобы для любого заданного положительного е существовало
такое целое т, что
|| X* — Хг||<е при г>т.
Поэтому мы должны постоянно, начиная с нулевого приближения,
следить за величиной || Jrlf (Xr) ||, которая позволяет удержи-
удерживать в нужных границах последовательные итерации. Если суще-
существование J^1 уже установлено, оценка нормы матрицы, обратной
к матрице Якоби, на следующем шаге зависит от оценки модуля
вторых производных \fi,jk I и получается с помощью теоремы
о среднем значении. Отсюда условие A7.60).
Метод Ньютона — Рафсона можно рассматривать как еще один
метод минимизации, во многом похожий на методы наискорейшего
спуска. Предположим, что
и с точностью до квадратичных членов
Выберем ог так, чтобы
Но
„л dF(К )
ёг qxJ- ~
ттТ дгР (X )
Таким образом, метод Ньютона — Рафсона характеризуется век-
вектором поправки
ог = ХТу= _Er-1gr=[-4J'i]1ri] A7.65)
и
Xr+1 = Xr-H'"V = Xr-JrF. A7.66)
Следует отметить, что в методе Ньютона — Рафсона (как, впро-
впрочем, и в большинстве градиентных методов) на каждом шаге ите-
итерационного процесса требуется знание величины dftldXj. Однако,
за исключением отдельных случаев, вычисление большого массива
производных либо вообще невозможно, либо требует чересчур
много времени. Поэтому удобно использовать конечно-разностные
аппроксимации для J. Используя, например, для dfJdXj разно-
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 317
стную аппроксимацию вперед, зададимся малым АХ,- = h и запи-
запишем
,,
1
Тогда производные dfJdXj не надо вычислять аналитически и при
составлении вычислительных программ в памяти машины требует-
требуется хранить только п функций /г (X), а градиенты их уже не тре-
требуются.
17.5. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ НАГРУЖЕНИИ *)
По-видимому, наиболее часто используемым методом решения
систем нелинейных уравнений, встречающихся в задачах нелиней-
нелинейной теории упругости, является метод последовательных нагру-
жений. Будучи в некоторых чертах сходным с методом Ньютона —
Рафсона, этот метод обладает рядом особенностей, делающих его
особенно полезным в приложениях к физическим задачам. Во-пер-
Во-первых, каждый шаг итерационного процесса допускает ясную физи-
физическую интерпретацию. А именно рассматривается нагружение
деформируемого тела приращением нагрузки бр, которое считается
достаточно малым, так что реакция тела на это приращение линей-
линейна. После приложения каждого приращения нагрузки выписывает-
выписывается новое жесткостное соотношение и осуществляется следующее
приращение нагрузки. Продолжая этот процесс, мы получаем
полную картину нелинейного поведения тела в виде последова-
последовательности кусочно-линейных шагов. Поскольку до приложения
нагрузок тело, как правило, находится в естественном ненапря-
ненапряженном состоянии, вопрос о выборе начального приближения
отпадает. Действительно, если X обозначает вектор неизвестных
узловых перемещений, то мы просто полагаем Хо = 0, что дает
начальную точку, соответствующую недеформированному состоя-
состоянию тела. В случае же, когда тело несжимаемо, мы приравниваем
нулю узловые перемещения и вычисляем гидростатические давле-
давления в недеформированном состоянии. Они и служат компонента-
компонентами начальной точки Хо.
Поскольку каждый его шаг имеет вполне определенный физи-
физический смысл, метод последовательных нагружений позволяет
*) В литературе методы последовательных нагружений фигурируют под
самыми разнообразными названиями: например, описываемые здесь расчет-
расчетные схемы часто называют методами погружения, методами продолжения
или методами переменных параметров. Методы погружения использовались
при исследовании вопросов существования решений нелинейных операторных
уравнений и для решения нелинейных функциональных уравнений. См.,
скажем, работы Гавурина [1958], Давиденко [1965] и Мейера [1968]. Имеется
исторический обзор Фиккена [1951]. Сводное изложение методов продолже-
продолжения и дополнительные ссылки на литературу читатель найдет в книге Ортеги
и Рейнболдта [1970].
318 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
получить гораздо больше сведений о поведении тела, чем просто
величины перемещений при заданной системе нагрузок. Действи-
Действительно, естественным образом получается полный набор решений,
соответствующих различным частям нагрузки. Это позволяет
исследовать промежуточные состояния на устойчивость и при
необходимости производить соответствующие видоизменения про-
процедуры для определения точек бифуркации и нахождения много-
многозначных решений.
Приступим к описанию метода. Опять начнем, с рассмотрения
системы п нелинейных уравнений вида A7.4), но теперь будем
предполагать, что каждое уравнение помимо неизвестного векто-
вектора X содержит еще некоторый вещественный параметр р, т. е.
будем рассматривать систему вида
h (X, р) = 0. A7.68)
Здесь h есть n-мерный «вектор нелинейных уравнений» относитель-
относительно компонент n-мерного вектора X, а параметр р, вообще говоря,
связан с заданной нагрузкой. Если на тело действуют п независи-
независимых нагрузок, то все равно можно получить систему типа A7.68),
представляя полный вектор нагрузок Р в виде рА, где Л — посто-
постоянный вектор. Если в задаче параметр р не присутствует сам
естественным образом (как в задачах строительной механики),
то систему уравнений вида A7.68) можно получить, осуществляя
погружение нашей нелинейной системы A7.4) в некоторое одно-
параметрическое семейство с помощью оператора, обычно называе-
называемого оператором гомотопии, например, такого *):
h (X, р) = а (р) g (X) + р (р) i (X), G7.69а)
где а (р) и Р (р) — вещественнозначные функции, a g (X) —
векторнозначная функция, подобранная таким образом, что если
Р 6 [0, Q] (Q — вещественное число), то
h (Хо, 0) = 0
и
h (X*, Q) = 0,
где X* — решение системы A7.4). Можно, например^ положить
h (X, P) = (Q- p) (X - Хо) + pi (X). A7.696)
Тогда
h (Xo, 0) = 0
и
h (X*, Q) = Qi (X*) = 0
См. Мейер [1968].
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
319
Рис. 17.4. Кривая в %3, определяемая нелинейной системой
ht (Xu Хг, Х3; р) = О, i = 1, 2,3, Ре [0, 1].
означает, что решение X* системы A7.4) достигается при р — Q.
В задачах механики редко возникает необходимость в погруже-
погружениях типа A7.69), поскольку уравнения вида A7.68) появляются
вполне естественно. Отметим также, что параметр нагрузки р
всегда можно нормировать. Если, например, р ? [0, Q], то берем
P=P/Qe to, 1]. '
При заданном значении р система A7.68) определяет точку
в %п, лежащую на пересечении п поверхностей ht (X, р) = 0.
Таким образом, A7.68) представляет собой систему параметриче-
параметрических уравнений траектории, или кривой, в Г с параметром р.
Если бы мы могли решить A7.68) для любого р 6 [0, 1], то решения
X = X (р)
были бы явными параметрическими уравнениями кривой в %пг
соединяющей известную начальную точку Хо = X @) с решением
заданной системы нелинейных уравнений X* = X A) [или X* =
= X @, если р ? [0, Q]). Для случая п = 3 такая кривая показа-
показана на рис. 17.4.
320 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Итак, X = X (р) есть отображение отрезка [0, 1] в некоторое
множество 3 а §п. Будем предполагать, что это отображение
удовлетворяет соотношению A7.68) для всех р 6 Ю, 1], что оно
непрерывно дифференцируемо по р на отрезке [0, 1] и что функция
h: %n X [0, 1]-»-Г в A7.68) имеет непрерывные частные произ-
производные по X и р. Таким образом, A7.68) удовлетворяется для всех
значений р из отрезка [0, 1]. Следовательно, если X — решение,
соответствующее некоторому значению р, а X + 6Х — другое
решение, соответствующее р + fy>, где 8р — приращение р, то
h (X, р) = h (X + 8Х, р + 8р) = 0. A7.70)
В силу предположенной дифференцируемое™ h (X, р) имеем
h (X + 6Х, р + 8р) = Ь <Х, р) + Ях (X, р) 6Х +
+ hp (X, р) Ьр + <о (X, р, 6Х, 8р), A7.71)
где Нж — матрица размера п X п, a hp и <о — и-мерные векторы^
определяемые соотношениями
A7-72a)
hp(X, р) = [М-Й] A7.726)
и
<о(Х, р, 6Х, Ьр) =
Здесь
Итерационная схема приближенного решения уравнения A7.68)
немедленно получается из A7.70) и A7.71), если предположить,
что 8р и | 8Xi | достаточно малы, чтобы в A7.71) можно было сохра-
сохранить только линейные члены. При этом
Нх (X, р) 6Х + hp (X, р) 8р « 0.
Следовательно, если Щ1 (X, р) существует в точке (X, р), то
6Х=-Щ1(Х, p)hp(X, р)Ьр. A7.73)
Это непосредственно приводит к методу последовательных нагру-
жений. А именно, пусть р ? [0, Q], X @) = Х° и матрица Нх (X, р)
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
321
Рис. 17.5. Процесс последовательных нагружений.
невырождена для всех рассматриваемых значений р. Разделим
отрезок [О, Q] на М частей:
О = Ро < Pi < Рг < • • • < Рм = Q,
так что
м
Ьрг = Рг—Рт-1 и <?=2брг. A7.74а, б)
Тогда кривая X = X (р) получается с помощью формул
Х'+* = X' - Н? (Хг, рг) Ър (Хг, рг
i, A7-75)
где г = О, 1, . . ., М — 1.
Этот процесс для одномерного случая [h (X, р) = 0] изображен
на рис. 17.5. Если только h (X, р) не является идеально линейной
функцией, после конечного числа М приращений нагрузки всегда
возникает в результате некоторая ошибка 8. Если в какой-нибудь
точке (Хг, рт) матрица Н (Хг, рт) вырождена, процесс, конечно,
не проходит. В этом случае необходимо модифицировать уравне-
уравнения, изменяя, например, масштаб параметра или определяя новую
начальную точку вслед за точкой (Хг, рг) с помощью, скажем,
метода Ньютона — Рафсона. Если в самом начале det Нж (Хо, 0) =
= 0, надо выбирать новое нулевое приближение \'о. Значение Х^
может соответствовать нулевому значению некоторого нового
параметра р' — р (X, р).
Интересно отметить, что все рассмотренные в п. 16.5 соотноше-
соотношения в приращениях содержатся в A7.72). Мгновенные жесткости
21 Дж. Оден
322 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
&1ш A6.176), матрица начальных напряжений Gnm A6.177)
и матрица начальных поворотов D1nm A6.178) могут быть отожде-
отождествлены с матрицей Нж A7.72а). Матрица начальных нагрузок
R%nm A6.179) соответствует определяемой формулой A7.726)
матрице hp, а при помощи A6.180) можно получить приращение
нагрузки Ър.
Модификации. Возможны некоторые модификации и усо-
усовершенствования процедуры, описываемой соотношением A7.75).
Если приращение Ьрт достаточно мало, есть основания полагать, что
векторы Хг, г — 0, 1, . . ., определенные соотношением A7.75),
дадут неплохую аппроксимацию решения A7.68). Однако для
нелинейных систем на каждом шаге процесса неизбежно появляют-
появляются погрешности (см. рис. 17.5), которые будут накапливаться при
движении вдоль кривой X = X (р). Один из путей повышения
точности метода последовательных нагружений — использование
каждой точки Хг, определяемой соотношением A7.75), в качестве
начальной точки для метода Ньютона — Рафсона. Поскольку Х,г
вообще говоря, близко к X (рг), для уменьшения погрешности sr
до желательных пределов обычно требуется лишь небольшое число
итераций. Таким образом, для каждого г осуществляется процесс
где X1-0 = Хо, Хг+1- ° = Xr'mr, т = 0, 1, 2, . . ., тг - 1, при
г <; М; при г = М берутся т = 0, 1, 2, .... Таким образом,
после каждого приращения нагрузки 8рг выполняется тг итера-
итераций Ньютона — Рафсона, а после последнего приращения нагруз-
нагрузки (г = М) осуществляется такое число итераций, какое нужно
для получения сколь угодно близкого к X* = X (Q) значения X.
Действительно, можно показать 1), что если матрица Нж (X, р)
существует, невырождена и непрерывна по р и если существует
непрерывный при всех р вектор X (р), то существуют такое раз-
разбиение отрезка [0, Q] и такие целые числа тпх, т2, . . ., тм_х, что
lim {Xм-m} = X(Q) = X*.
7П->-оо
С некоторыми видоизменениями по существу такой же процесс
может использоваться для получения многозначных решений
уравнения A7.68). А именно если матрица Н* (Хг, рг) почти выро-
вырождена [т. е. если det Нж (Хг, рг) « 0] при некотором рг, то, сохра-
сохраняя рТ постоянным, введем новую точку Хо = Хг + А, где А —
*) Доказательство можно найти в книге Ортеги и Рейнболдта [1970].
Для случая равномерных приращений 8рг = QIM Мейер [1968] получил
оценки размера шага, требуемого для того, чтобы решение X* было дос-
достижимо методом Ньютона — Рафсона из последней итерации Xм.
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
323
о Метод последовательных нагрутснии
х Тот же петод б сочетании с методом
Ньютона —Рафсона
I
9х
/
\
V
Рис. 17.6. Нахождение многозначных решений с помощью комбинирования
метода последовательных нагружений и метода Ньютона — Рафсона.
некоторый постоянный вектор. Точка Хо служит начальной точ-
точкой для итераций Ньютона — Рафсона. В случае сходимости про-
процесса он определяет новую начальную точку (X*, рг), из которой
можно возобновить процесс последовательных нагружений с мень-
меньшими, чем прежде, приращениями нагрузки или даже с ёрг+1 <; 0.
Ясно, что можно установить ряд признаков для определения знака
и величины приращения брГК1 и вектора А. На рис. 17.6 представ-
представлен пример применения описываемого метода к нахождению много-
многозначных решений в одномерной задаче.
Отметим, что каждая точка Хг, определяемая по формуле
A7.75), может быть подправлена на каждом шаге с помощью
любого другого метода, а не только метода Ньютона — Рафсона.
Если, например, мы можем построить такую функцию Р (X, р),
что
h (X, р) = X - Р (X, р) = 0, A7.77)
то каждую точку Хг в A7.75) можно подправить с помощью мето-
метода последовательных приближений: при любом р точка X (р)
является неподвижной точкой оператора Р (X, р) и
¦vTt m+I __ p /vri '
Р),
A7.78)
где X1'0 = Хо, Xr+1'° = Xr'mr, т = 0, 1, 2, . . ., т - 1 при
г < М ит = 0, 1,2, ... при г = М- Возможны и другие выборы
подправляющего итерационного процесса.
Численное интегрирование. Предположим, что пара-
параметр нагрузки р сам является известной непрерывной функцией
21*
324 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
вещественной переменной s ? [0, оо). Тогда, если, вернувшись
к соотношению A7.73), разделить обе его части на беи совершить
предельный переход при 6s ->¦ 0, мы получим систему нелинейных
дифференциальных уравнений первого порядка:
Х = К(Х, s)p, A7.79)
где
К (X, s) = -т (X, р (*)) Ър (X, р (*)). A7.80b)
Поэтому можно считать, что процесс последовательных нагруже-
ний соответствует численному интегрированию системы уравнений
A7.79).
U*' Действительно, одним из простейших методов численного инте-
интегрирования является метод Эйлера, в соответствии с которым
интервал [0, S] разбивается на подынтервалы точками 0 = s0 <
<•'«! < s2 < . . . < sM = S и Х аппроксимируется разностным
отношением
Это приводит к формуле интегрирования
Ясно, что если p==shj> = 1,to A7.81) совпадает с A7.75), т. е.
метод последовательных нагружений A7.75) является просто
результатом применения метода Эйлера к дифференциальному
уравнению A7.79).
Это замечание наводит на мысль, что использование вместо
A7.75) и A7.81) более сложных методов численного интегрирова-
интегрирования может обеспечить большую точность решения нелинейной
системы A7.68). Это, вообще говоря, верно, поскольку погреш-
погрешность метода Эйлера имеет порядок h = 6s, в то время как можно
указать много других методов интегрирования, имеющих погреш-
погрешность порядка hm, т > 1. Для примера укажем на методы Рунге —
Кутты х) четвертого порядка, в которых К (Хг, sr) h в формуле
г) Подробное изложение различных методов Рунге — Кутты, включая
исторический обзор, содержится в книге Коллатца [1966]. Вопросы исполь-
использования метода Рунге — Кутты в методах последовательных нагружений
(методах продолжения) обсуждаются в работах Киснера [1964] и Давиденко
[1965]. См. также Хайслер, Стриклин и Стеббинз [1971] и Оден [1971в].
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 325
A7.81) (при р = 1, 8sr+1 = h) заменяется на
AXr= S [*,Z,, A7.82а)
i0
i=0
где
i-i
Z0 = K(Xr, *г) и Z; = K(Xr+ S PijZj", sr + a;/i). A7.826)
Метод Рунге — Кутты с коэффициентами Рунге получается,
если взять ц0 = fig = цх/2 = ц2/2 = 1/6, ах — а2 = «3/2 = 1/2
и Рю = Р21 = Рзг/2 = 1/2, р20 = Рзо = 0; коэффициенты Кутты
имеют вид ц0 — цх/3 = ц2/3 = ц3 = 1/8, ах = а2/2 = а3/3 = 1/3
и Рю = — Рго = 1/3, Рзо = Psi = —Р31 = Рзг = 1, а коэффициен-
коэффициенты Гилла таковы: \к0 = ц3 = 1/6, fij = A — 1/]/л2)/3, ji2 =
= A + 1/К2)/3, а3 = 2а2 = 2ох = 2р10 = 1, р81 = -1//2,
Рго = —Рю — Psi» P«i = 1 + Рз1> §32 = 1 — Рз1 и Рзо = 0.
С другой стороны, методы Эйлера или Рунге — Кутты можно
использовать для определения начальных точек Хо, X1, . . ., Хт
так называемого метода поправок и предсказаний. Воспользуемся
тем, что на A7.79), а следовательно и на метод последовательных
нагружений, можно смотреть как на задачу решения системы
нелинейных интегральных уравнений
s
J K(X@, C)dC A7.83а)
о
Здесь мы для простоты приняли р = 1. Если Хг = X (sr), то
можно записать
K(X@, C)dC; A7.836)
j
тем самым предполагается, что известен процесс изменения X
от Хо до Xr"m (т. е. значения Хо, X1, . ... Xr~m). Интеграл в A7.836)
можно приближенно представить квадратурной формулой типа *)
j r-j+a
j К (X (С), С) dt,» h 2 Р,К (Xr-j+a, sr-j+a). A7.84)
Sr-m )=0
Здесь используется q -f- 1 промежуточных точек между sr_m
и sr+1; р7- суть весовые коэффициенты, а а = 1 или 0. Если а = 0,
J) Квадратурные формулы такого типа используются в § 20 для решения
систем нелинейных интегро-дифференциальных уравнений.
326 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
то говорят, что формула A7.84) открыта справа, если же а = 1,
то говорят, что она закрыта справа. Пусть г ^ max {/re, n, q, t},
тогда метод поправок и предсказаний для численного интегрирова-
интегрирования задается правилами
Xr+1 = Xr-m + ^|№(Xr-,-+i) Sr_/+l) + /lp0K(Xri, sT+l), A7.85a)
Xr+i = Хг_„ + ft 2 Mt (Xr~ , *г_,). A7.856)
Таким образом, (t -f- 1)-точечная открытая справа квадратурная
формула используется для определения предсказания A7.856),
а (Я + 1)-точечная закрытая справа квадратурная формула —
для определения поправленного значения A7.85а). Если, например,
t = га = 3, q = /re = 0, 24ц = E5, —59, 37, —9) и 240 =
= (9, 19, —5, 1), то формулы A7.85) дают метод Адамса — Моул-
тона х).
Использование приемов численного интегрирования в методе
последовательных нагружений совместно с корректировкой резуль-
результатов после каждого этапа с помощью метода Ньютона — Рафсо-
на, по-видимому, представляет собой один из наиболее эффектив-
эффективных способов решения больших систем нелинейных уравнений.
17.6. МЕТОДЫ ПОИСКА
Вернемся к вопросу о решении нелинейных уравнений путем
минимизации функционала F (X) типа A7.5). Рассмотрим ряд
примеров методов итерационного и неитерационного поисков,
которые могут успешно применяться, когда неудобно (или невоз-
невозможно) вычислять градиенты функционала F (X).
Симплексный метод поиска. В симплексном методе
поиска, как показывает само название, используются симплексы 2).
Симплекс в ^-мерном пространстве образуется множеством к + 1 то-
точек (называемых его вершинами) р0, ри ..., ри, не лежащих в од-
одной (к — 1)-мерной гиперплоскости. Симплекс of состоит из всех
точек у, удовлетворяющих условию
y=%ctPt, A7.86а)
i=0
!) См. Айзаксон и Келлер [1966, стр. 388].
2) Напомним, что в одномерном пространстве симплекс — это отрезок,
соединяющий две точки [ра, рх]. В случае к — 2 симплекс состоит нз точек,
расположенных внутри и на границе треугольника. Для к = 3 симплекс
состоит из точек, расположенных внутри и на границе тетраэдра, и т. д.
См. Нелдер и Мид [1964].
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 327
где
ft
e«>0, S «1 = 1- A7.866, в)
i=0
Когда рассматривается задача нахождения тг-мерного векто-
вектора X*, минимизирующего функцию F (X), вектор X можно счи-
считать точкой в тг-мерном пространстве. В симплексном методе п + 1
пробных точек Х°, X1, . . ., X" берутся в качестве вершин симплек-
симплекса в тг-мерном пространстве. Затем подсчитываются величины
г/° = F (Х°), у1 = F (X1), . . ., уп = F (Хп). A7.87)
Пусть yh = F (Хл) и у1 = F (Х() являются соответственно
максимальной и минимальной из этих величин. После исключения
точки ХЛ, соответствующей наибольшему значению у (т. е. yh)
мы находим «центр тяжести» X оставшихся точек по формуле
п
Х = —У.Х*. A7.88)
г=0
Затем строится прямая в тг-мерном пространстве, соединяющая
точки ХЛ и X. Произвольная точка X на этой прямой может быть
задана формулой
Х = A+а)Х-аХЛ; A7.89)
число а называется коэффициентом отражения. Обычно а задает-
задается заранее и положительно, так что точки X и X находятся по раз-
разные стороны от ХЛ (т. е. X ближе к минимуму). Далее вычисляется
величина
y = F(X). A7.90)
Здесь возможны различные случаи. Например:
!• У < У1 — это значит, что мы нашли новый минимум и мож-
можно двигаться дальше в том же направлении, в котором мы
пришли к точке X. Находим новую точку
-yX,. [A7.91)
где у >- а > 0. Если у = F (X) •< у1, то можно построить
новый (улучшенный) симплекс, положив у = у1', т. е.
вводя новую «вершину минимума», а все остальные верши-
вершины оставив неизменными, и продолжить процесс.
2» У > У1 (или у > у1) — процесс идет неправильно. В этом
случае надо заменить точку максимума точкой X (или X)
и повторить процесс.
328 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
3. у > уг, i Ф k — в этом случае A7.91) дает не лучшее напра-
направление и ХЛ надо переопределить, взяв в качестве точки
максимума ту из точек ХЛ или X, которая соответствует
меньшей величине у. Затем находим новую точку
Х=рХЛ + A —Р)Х, A7.92)
где 0 <; Р < 1 — коэффициент сжатия. Если у = F (X) ^
^ yh, то yh заменяется на у и процесс повторяется. Если
у > yh, сжатие ничего не дает; в этом случае все надо начать
сначала с новыми начальными значениями Хг, в качестве
которых можно взять, например,
Х1 = -^-(Хг + Х1), A7.93)
Итерации продолжаются, пока не будет достигнут ми-
минимум.
Хотя симплексный метод предполагает осуществление множе-
множества проб и итераций, доказано, что он достаточно эффективен при
решении некоторых нелинейных систем в тех случаях, когда
не проходят другие методы. Особенно эффективен этот метод при
решении больших систем линейных неравенств. Поэтому он гораз-
гораздо чаще применяется в нелинейном программировании, чем при
решении систем нелинейных уравнений.
Возможны многие модификации и улучшения симплексного
метода поиска. Скажем, можно предпринять меры для того, чтобы
симплексный метод не приводил к не представляющей интереса
точке минимума, если известен единичный куб тг-мерного про-
пространства, в котором находится нужный минимум. Функция пере-
переопределяется таким образом, чтобы ее значения вне куба были
сколь угодно большими, тогда любая попытка выйти за пределы
куба завершится возвращением внутрь куба и процесс сойдется
к искомому минимуму.
На рис. 17.7 показаны возможные пути симплексного поиска
в двумерном пространстве. Поиск начинается (см. (а)) с выбора
трех начальных точек Х°, X1, X2, определяющих симплекс. Пред-
Предположим, что X2 = ХЛ соответствует наибольшему значению у
1уг = / (X2) > у0, у2 > у1]. Вычисляем по Х° и X1 их среднее зна-
значение X и проводим прямую A7.89) до новой точки X. На рис. (а)
представлен случай, когда у < у1, так что вычисляется новое
значение X. Поиск в этом случае успешен. На рис. (Ь) тоже у <; у1,
но дальнейшее продвижение в X не дает желаемого результата,
поскольку у > у1. Следовательно, в этом случае X берется в каче-
качестве новой точки, соответствующей минимальному значению.
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 329
к~
1 \ .•
/ - ^
X*
о
/Г
X /
х
х*=х
2
У
У
<У'
<У1
(а)
°=х'
(Ь)
(с)
у >у{
X,
У'У"
" vX.
>/
Рис. 17.7. Симплексный метод поисна»
330 • ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
На рис. (с) показан случай, когда возникает необходимость в сжа-
сжатии, поскольку у > у1. Новое значение ХЛ принимается равным X,
так как у < уь, далее ХЛ опять заменяется на X, поскольку ока-
оказывается, что у ^ yh. Случай, изображенный на рис. (d), сходен
с показанным на рис. (с), за исключением того, что ХЛ сохраняет
свою первоначальную роль, ибо у > yh. Наконец, на рис. (е)
сжатие не дает нужного результата, и необходимо брать новые
начальные точки. Начальные значения Х°, X1, X2 = Хг заменяют-
заменяются на Хг = -q-(Xl -f Хг), где Х( — точка, соответствующая наи-
меньшему начальному значению у1 = F (Х().
Методы случайного поиска. В методах случайного
поиска начальные пробные, тючки не определяются точно. Они
выбираются случайно в соответствии с некоторой тг-мерной функ-
функцией плотности вероятности. Функция плотности обычно берется
«плоской», что означает равную вероятность выбора в качестве
начальных любых точек заданной области.
В методе чисто случайного поиска просто в области, где мини-
минимум заведомо существует, случайно выбирают пробные точки
в соответствии с некоторым фиксированным распределением веро-
вероятностей. После проверки определенного числа точек считается,
что минимум достигается в точке, соответствующей наименьшему
из полученных значений функции. Требуемое число пробных
точек можно определить, исходя из распределения вероятности.
Если предположить, что минимум равновероятно может нахо-
находиться в любой точке тг-мерного (гипер)куба со стороной d и что
изменения независимых переменных ограничены величиной 6^,
то отношение объема соответствующего кубика к объему всего
куба равно
(^Г- .A7.94)
Вероятность того, что пробная точка не лежит в кубике, равна
1 — а. Из элементарных вероятностных соображений следует,
что вероятность неуспеха р проб составляет A — а)р. Вероятность
же того, что по крайней мере одна точка попадет в кубик, рав-
равняется
Swmi — (l — a)v. A7.95)
Отсюда
р=
— a)
Здесь S — доверительный уровень, ар — требуемое число точек.
В таблице 17.1 приведены некоторые типичные числовые значения.
17. ЧИСЛЕННЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
331
Таблица 17.1
0.1
0.05
0.025
0.01
0.005
Зависимость
0.8
16
32
64
161
322
числа проб
0.9
22
45
91
230
460
р от а и S !>
0.05
29
59
119
299
598
0.99
44
90
182
459
919
Видно, что требуемое число точек быстро возрастает при умень-
уменьшении а.
Ставится условие *), чтобы число пробных точек не зависело
от числа независимых переменных. Это означает, что величина
а должна быть постоянной. Следовательно, с увеличением п вели-
величина 8N!d также увеличивается. Таким образом, точность «на одну
переменную» уменьшается, так как размеры кубика растут.
Подставляя A7.94) в A7.96), получаем
п
Р- In [1-(
Если предположить, что величина (8N/d)n мала, то знаменатель
можно приближенно заменить первым членом разложения
A7.98)
При этом получим
Число требуемых точек растет почти экспоненциально с увеличе-
увеличением размерности. Для доверительного уровня S, равного 0.9,
имеем
. р*2,3 (-?¦)". A7.99)
Спэнг [1962] сравнил это число с числом точек, требуемым при
поиске с помощью простой кубической решетки с шагом б^, когда
за минимум принимается наименьшее из значений в узлах решетки.
Это последнее число равно
Ш- <17100)
Брукс [1958].
332 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
т. е. приблизительно в два раза меньше, чем при чисто случайном
поиске. Все равно такой поиск практически редко применяется
при больших п, поскольку р по-прежнему возрастает по экспонен-
экспоненциальному закону x)i
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
В этом параграфе представлены приложения описанной теории
к некоторым задачам теории упругости при конечных деформаци-
деформациях. Все приводимые ниже примеры относятся к изотропным телам.
18.1. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
В теории плоского напряженного состояния рассматриваются
тонкие тела, у которых компоненты напряжений в одном из напра-
направлений заданы и напряженное состояние в произвольной частице
является по существу двумерным.
Упругие мембраны. Рассмотрим тонкий лист из однород-
однородного упругого материала, ограниченного поверхностямиxs=±d0/2,
начальная толщина d0 которого в общем случае является функцией
от хг и х2. В первоначально плоском недеформированном листе
положение произвольной частицы Р определяется радиус-вектором
г = г(ж1, х2) + х3п, A8.1)
где г (х1, х2) — радиус-вектор частицы Q в плоскости х1, х2 и п —
единичный вектор нормали к недеформированной срединной
поверхности.
Предположим, что лист совершает движение, переводящее его
из начальной конфигурации Со в другую конфигурацию С. Поло-
Положение частицы Р относительно фиксированной системы отсчета
в Со определяется радиус-вектором
R = R(a;1, х2) + М(х\ х2, х3), A8.2)
где R (х1, х2) — радиус-вектор частицы Q на деформированной
срединной поверхности и М (х1, х2, х3) — вектор, соединяющий
частицы Р и Q в деформированном теле. Вектор перемещения w
*) Для уменьшения необходимого числа точек Спэнг [1962] разработал
квазиитерационный метод поиска. В этом методе предполагается, что
минимум находится в окрестности группы точек, соответствующих наимень-
наименьшим значениям. После проведения некоторого количества проб вокруг этой
группы строится меньший гиперкуб. Далее процесс повторяется. Хотя число
пробных точек, случайно выбираемых на каждом шагу, здесь не так велико,
как при чисто случайном поиске, доверительный уровень при этом уже не
удается оценить, так как вероятности зависят от исследуемой функции.
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 333
Ряс. 18.1. Геометрия деформации тонкого листа.
произвольной частицы Р равен
w = R — r = u + M — ahx, A8.3)
где и теперь обозначает перемещения частиц на срединной поверх-
поверхности:
х1, х2) = К.(х1, хг) — г (ж1, хг). A8.4)
Геометрия этого движения показана на рис. 18.1.
Теперь вычислим базисные векторы G;-, касательные к дефор-
деформированным координатным линиям хг:
G* = Аа + М,а% G3 = М, з, а = 1, 2. A8.5)
Здесь Аа — векторы, касательные к координатным линиям х1, х2
на деформированной срединной поверхности. В последующих
формулах используются как греческие, так и латинские индексы,
причем греческие принимают значения 1 и 2, а латинские от 1 до 3.
Для получения соотношений, характеризующих теорию пло-
плоского напряженного состояния, предположим, что материальные
линии, нормальные к недеформированной срединной поверхности
листа, остаются прямыми и нормальными к деформированной сре-
срединной поверхности. Однако эти материальные линии могут
испытывать при движении конечные деформации удлинения.
Таким образом, если Я, — относительное удлинение (т. е. отноше-
334 • гл- IV- теория упругости
ние деформированной длины к недеформированной) в направлении
х3 при х3 = 0, то вектор М в формуле A8.2) записывается в виде
М (х1, х2, х3) = Ка*п, A8.6)
где п — единичный вектор нормали к деформированной срединной
поверхности. И X и п являются функциями от х1 и х2. При таком
определении М соотношения A8.5) принимают вид
Ga = Аа + х3 (Xn),a, G3 = Ял. A8.7)
Замечая, что п-Аа = 0, получаем для компонент тензора меры
деформации Gtj такие выражения:
G« • Gp = Aafi - 2Xa*Baf> + № (*3J B^Bfr + (x3J X, „*,, p,
Ga3 = Ga-G3=-Xx3X,a, A8.8)
GM = G,-G, = a,8, a, p, Я,= 1, 2.
Здесь 4ap и Бар — ковариантные компоненты соответственно
первого и второго фундаментальных тензоров деформированной
срединной поверхности, а Ва — смешанные компоненты второго
фундаментального тензора:
ЛхЭ = Аа-АЭ) 5аЭ=—Аа-П3, Ba = A^Bfia. A8.9)
В последнем из этих соотношений AW — контравариантные ком-
компоненты первого фундаментального тензора деформированной
срединной поверхности (так что Аа>"А^ = бр или Аа& = А™-Ар»
где А"-Ар = Sjj).
В принципе, подстановка соотношений A8.8) в D.16) приводит
к выражениям для компонент тензора деформации, соответствую-
соответствующим теории Кирхгофа конечных деформаций пластин. Сейчас,
однако, нас интересует упрощенный вариант соотношений A8.8),
который отвечает теории очень тонких мембран. Поэтому ограни-
ограничимся рассмотрением деформаций симметричных относительно
срединной поверхности достаточно тонких тел, так что Gtj по суще-
существу постоянны по всей толщине. В этом случае X = d/d0 и вместо
A8.8) имеем
Gae = Aafi, Ga3 = 0, С33 = Я2. A8.10)
Компоненты деформации в этом случае равны
4 = -1(Я,а-1). A8.11)
Главные инварианты тензора деформации принимают вид
A8.12)
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 335
где 6°^, еР** — двумерные перестановочные символы (е12 = —е21 =
= 1, е11 = е22 = 0) и
А = det (Aafi) = ±-г«№»АаХА^. A8.13)
Отметим также,: что, поскольку
Аа = Й,а(а:1, *2) = ia + o,ei A8.14)
где и — вектор перемещения частиц срединной поверхности, ком-
компоненты деформации равны
YaS = ~2 ("a, S + "Э. а + "ft, <x"fc, p),
733 = 4 (А2-1), A8.15)
Таз = 0,
где а, р = 1, 2 и А; = 1, 2, 3.
Предположим, что лист изготовлен из однородного изотропного
гиперупругого материала с энергией деформации на единицу неде-
формированного объема W. Тогда локально
W A1г /2, h) = ti}yu = *aP7a(> + t33y3S, A8-16)
A8Л7)
где тензор напряжений ?' определяется соотношениями
С учетом A8.11) и A8.12) имеем
A8.186)
^ ^^ A8.18в)
где
ep A8.19)
Нормальную компоненту напряжений t33 можно определить
из краевых условий на деформированной срединной поверхности.
Пусть, например, ql и q2 обозначают давления, приходящиеся
на единицу площади деформированной срединной поверхности
и приложенные соответственно к поверхностям х3 = —d/2 и х3 =
= -\-dl2. Тогда приближенно "ht33 = —qt VА н^ поверхности
—d/2 и %t33 = —q2 У А на поверхности -\-dl2. Для тонких мембран
можно также использовать аппроксимацию Я233 = —q У А, где
336 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Ч — (<7i + <7г)/2 — среднее давление. Однако поскольку в очень
тонких мембранах величины мембранных напряжений ?, как
правило, во много раз превышают t33, обычно просто полагают
t33 = 0 и сводят таким образом задачу к задаче об определении
двумерного напряженного состояния. В последующих рассужде-
рассуждениях мы будем считать, что i33 « 0.
Для несжимаемых материалов 13 = 1 и W является функцией
лишь от /х и /2. В этом случае вместо (8.12) можно записать
12 = ± + Х2Ьаее«ЧЫА^, [A8.20)
Х*=(±.г<#вР»Аа9А)#)''1-
Определяющие уравнения для несжимаемых мембран имеют вид
A8-21б>
где W = W (Jlt I2) ah — гидростатическое давление. Величину
гидростатического давления h можно определить из условия
t33 « 0:
h=-X2~ ^баР4ар. A8.22)
Поэтому A8.21а) можно переписать так:
[ ^)]^, A8.23)
а ^3 = t33 = 0.
Мембранные элементы. Располагая кинематическими
соотношениями, записанными в терминах перемещения срединной
поверхности, мы можем теперь вывести уравнения равновесия для
конечных элементов упругих мембран. Рассматривая типичный
элемент е с Nе узлами, мы, как обычно, представляем локальное
поле перемещений в виде
ы{ = 1ЫЛ*2)<, A8.24)
где ui — компоненты перемещений частицы х1, я2 на срединной
поверхности и N = 1, 2, . . ., Ne;i = 1, 2, 3. Тогда в соответствии
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 337
с A8.15) имеем
Для сжимаемых материалов Я,2 можно аппроксимировать на
элементе следующим образом:
Я2 = qN (хх, *,) ц*, A8.26)
где \iN == (А,2)^ — значение К2 в узле iV. Для несжимаемых мате-
материалов можно получить выражение Я-2 через мембранные деформа-
деформации уа$, если подставить A8.11) в A8.20):
I2 = A + 2у« + 2гаЧ^уаРу^Г1. A8.27)
Поскольку t33 fa 0, уравнения равновесия конечного элемента
мембраны имеют вид
ftvi =
ди1?
'o(e) "o(e>
Если предположить, что начальная толщина недеформированного
элемента d0 постоянна, и обозначить площадь недеформированной
срединной поверхности через А*, то уравнение A8.28) примет вид
A8.29)
Обобщенные узловые силы pNi определяются соотношениями
A6.93), которые в нашем случае действия поперечных нагрузок
более удобно записать так:
+ J ^(б^ + ^.ви^)^^', ^)Л18, A8.30a)
= J FtyNdA*0+ J 5«^d48, , A8.306)
где F* (ж1, x2) — компоненты объемных сил на единицу площади
недеформированной срединной поверхности и S*} — поверхност-
поверхностные усилия на единицу площади недеформированной срединной
поверхности в конвективных координатах хг [см. A6.96)]. Для
приложенных касательных сил на кривой Г, являющейся границей
срединной поверхности элемента, можно использовать двумерный
вариант формулы A6.98). Однако в последующем мы предпочитаем
применять аппроксимации обобщенных сил типа A6.113), A6.117)
и A6.118).
22 дж. Оден
338 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
В случае сжимаемых материалов жесткостные соотношения для
элементов изотропных мембран получаются подстановкой A8.18а)
и A8.26) в A8.29). Произведя эту подстановку, найдем
X ipw, « (брг + tpM, fuf) dA% = Рт, A8.31)
где
iVe величин цй = (Х2)й определяются из условия, что Z33 должно
в среднем на элементе обращаться в нуль. С учетом A8.18в) полу-
получаем в каждой узловой точке
H- <)8-33>
3iVe уравнений A8.31) вместе с Nе уравнениями A8.33) образуют
систему ANe уравнений относительно ANe неизвестных и** и \iN.
Если предполагается, что величина Я,2 постоянна в каждом элемен-
элементе, скажем Я,2 = [i0, то в A8.31) надо просто заменить ч(зн(хв на \i^
и к SNe уравнениям равновесия добавить одно условие:
которое получается из A8.33) заменой я|з^ на единицу.
Для изотропных несжимаемых материалов вместо A8.31)
имеем
2do { {F«р_я,*/-|1)-^+[л.аввЧ/в|1A-2я,*-2я,*т;)]-^.} х
? рт, A8.34)
где /*Р определяется по формуле A8.32) и, согласно A8.27),
ы
»
X
X (фя, ли? + 1>Я. nuJ + ipH. я*р. ^K)]'1 • A8'35>
Здесь i, y, fc = 1, 2, 3; a, p, Л, ц = 1, 2; TV, Л/, P, R = 1, 2, . . ., ЛГ..
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
339
Рассмотрим теперь ряд частных случаев уравнений A8.34)
и обсудим численные результаты, получающиеся при их примене-
применении к конкретным задачам.
Растяжение упругого листа. Для начала рассмотрим относитель-
относительно простую задачу о растяжении на заданную величину тонкого упругого
листа. Тонкое прямоугольное тело защемлено по противоположным краям
и растягивается в своей плоскости, как показано на рис. 18.2. Узловые
силы|на сторонах х2 = +6/2 равны нулю, а компоненты uj* узловых пере-
перемещений на границе х1 = +а/2 заданы равными +а (е — 1)/2, где е —
относительное удлинение в направлении координатной линии х1. Эта задача
соответствует испытаниям так называемых двухосных полос, широко исполь-
используемым для описания предельных свойств таких материалов, как резины,
полимеры, твердые топлива и клеи. Несмотря на простоту формулировки,
точного решения задачи о поведении двухосных полос при конечных упру-
упругих деформациях, по-видимому, не существует. Что же касается получения
численных решений, то использование метода конечных элементов в случае
этой задачи особенно удобно, поскольку на границах заданы (отличные от
нуля) перемещения, а не усилия, так что не приходится исследовать изме-
изменения формы нагруженных поверхностей.
Сначала рассмотрим симплексную аппроксимацию локальных полей
перемещений, соответствующую набору треугольных элементов. В этом
случае
$N (x\ х2) = aN + bNa xa A8.36)
A8.37)
Здесь N = 1, 2, 3; а,
лами A0.106).
= 1, 2; а массивы aN и bNa определяются форму-
формуЬ
т
Рис. 18.2. Растяжение упругого двухосного листа.
22*
340
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
ИедеформироВанный лист Деформированный лист
|~8Эюймов -1
-16 Зюймоб -
2 ,
\
\
\
/
/
7
\
ы
\
/^
/
7
N
\
\
/
/
7
/
/
/
>
/
Л/\/\
/
/
/
ъ,
u^~-—
W
Рис. 18.3. Конечноэлементные решения задачи о растяжении двухосного лис-
листа: (а) форма реального листа в недеформированном и деформированном
состояниях; (Ь) различные конечноэлементные представления.
Если предположить, что полоса несжимаемая, то разрешающие урав-
уравнения равновесия для типичного элемента получаются после подстановки
A8.37) в A8.34):
X bNa
) = Pnp, A8.38a)
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 341
X
X (bBVi%+bBiiUb+bRi.bpViu*u*)']~i , A8.386)
где yo<e> = ^о^4*(е) — начальный объем элемента и а, Р, %, ц, р = 1, 2)
М, N, P, R = 1, 2, 3. Эти уравнения применимы к симплексным элемен-
элементам любого несжимаемого изотропного гиперупругого материала. Для
материала Муни W (/i, /2) имеет вид A5.62), и потому
Ж и Ж * ( }
Заметим, что случай С2 = 0 соответствует так называемым неогуковым
материалам. Большинство из приводимых здесь численных результатов
относится к материалам Муни.
На рис. 18.3 представлены численные результаты, полученные Оденом
и Сато [1967а] х) при применении уравнений A8.38) к конкретной задаче
о растяжении двухосной полосы. В этом примере рассматривалось растяже-
растяжение квадратного резинового листа толщиной 0,05 дюйма со стороной 8,0 дюй-
дюйма, при котором первоначальная длина листа увеличивается в два раза
(е = 2). Предполагалось, что материал листа является материалом Муни
с постоянными С1 = 24.0 фунт/дюйм2 и С2 = 1.5 фунт/дюйм2. На рисунке
показана форма деформированного листа, получающаяся при различных
разбиениях на конечные элементы. Возникавшие в процессе вычисления
системы нелинейных уравнений решались методом Ньютона — Рафсона.
Начальные точки определялись с помощью малого числа итераций Нью-
Ньютона — Рафсона для довольно грубой конечноэлементной модели листа.
Эти результаты затем использовались в качестве начальных значений для
более мелкой сетки, причем начальные значения перемещений в дополни-
дополнительных узлах определялись линейной интерполяцией.
Для сравнения с экспериментальными данными представляет интерео
определение результирующей силы F, которую требуется приложить к гра-
границе в горизонтальном направлении для получения величины относитель-
относительного удлинения 8 = 2. Величина F для каждой сетки конечных элементов
получается простым суммированием компонент в направлении оси х1 обоб-
обобщенных сил на границе. В рассматриваемом примере значения для резуль-
результирующей силы монотонно сходятся при измельчении сетки к «36.0 фунта
(см. рис. 18.4).
Другой подход к решению задачи о двухосной полосе методом конеч-
конечных элементов применил Беккер [1966], который пользовался билинейной
аппроксимацией локального поля перемещений:
) =ajf + bNaxa + м,
Здесь N = 1, 2, 3, 4, а массивы aN, Ъ^а и cjv определяются формулами
A0.118). Однако прямая подстановка A8.40) в A8.35) приводит к очень слож-
сложному выражению для №, которое в соответствии с A8.34) надо интегрировать
х) Ранее конечноэлементное исследование конечных деформаций тонких
упругих мембран было проведено Оденом [1966а], а конечные плоские дефор-
деформации упругих листов с помощью конечноэлементных моделей изучал Бек-
Беккер [1966]. См. рис. 18.6 и 18.7.
342
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
40
Iм
* 36
38.2S
36.03
4 16 32 48 64 72
Число элементов
Рис. 18.4.48ависимость полной нагрузки от числа элементов при растяжении
квадратного листа.
Рис. 18.5. Деформация четырехугольного элемента.
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
343
-
_
-—
-—¦—
— ¦ '
_ ¦—
1 ¦
i
Рис. 18.6. Конечноэлементные представления четверти деформированного
упругого листа; е = 2.0 и ао/Ьо = 1.0.
по недеформированной срединной поверхности. Для того чтобы избежать
этой трудности, можно с помощью приема, использованного при выводе соот-
соотношения A6.77), получить упрощенную форму условия несжимаемости
i?A = 1Я = 1. Рассмотрим показанный на рис. 18.5 типичный прямоуголь-
прямоугольный элемент размера а0 X Ьо и толщины d0. Площадь деформированной сре-
срединной поверхности можно выразить через узловые перемещения в виде
суммы площадей треугольников 124 и 234:
«1 «0 + «1
4*=4det
tit
u\ ao-\-u\
1
-idet
1
0 + 1 К
Ъ0+и$ Ъ0+и\
1 1
A8.41)
Поскольку kd0 = d, условие несжимаемости принимает простой вид
A8.42)
344
Гл. IV. ТЕОРИЯ УПРУГОСТИ
1.10
1.05
(Ь)
Рис. 18.7. Линии равных напряжений в деформированном упругом листе:
(а) осевые нормальные напряжения; (Ь) поперечные нормальные напряжения;
8 = 1.5 и а0/Ьо = 1.0.
Следовательно, вместо A8.35) можно взять
k=aobo/A*. A8.43)
Остальные члены в A8.34) при локальном определении иа по формуле A8.40)
представляют собой полиномы относительно хх и хг.
Вместо того чтобы получать в явном виде жесткостные соотношения для
таких четырехугольных элементов, Беккер предпочел свести задачу к задаче
нахождения значений узловых перемещений, минимизирующих полную
потенциальную энергию П (UA), которая вычислялась с использованием
аппроксимации A8.40). Этот подход, описанный в п. 17.1, можно исполь-
использовать в сочетании с любым из рассмотренных в § 17 методов минимизации
функционала. Приводимые здесь решения получены с помощью модифициро-
модифицированного метода покоординатной релаксации (см. п. 17.3). Численные резуль-
результаты Беккера представлены на рис. 18.6 и 18.7.
На рис. 18.6 показана четверть первоначально квадратного листа из мате-
материала Муни, растянутого в е = 2,0 раза при различных конечноэлементных
представлениях. Безразмерные постоянные Муни Сх и С2 были приняты рав-
равными соответственно 8 и 1, что позволило получить результаты, хорошо
согласующиеся с экспериментами на резиновых листах.
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 345
На рис. 18.7 показаны линии уровня осевых и поперечных нормальных
напряжений при растяжении квадратного листа в случае увеличения его
первоначальной длины в 1,5 раза (е = 1,5). Эти линии уровня значительна
отличаются от определенных с помощью теории бесконечно малых деформа-
деформаций несжимаемых тел *), по которой, в отличие от теории конечных деформа-
деформаций материалов Муни, отношение поперечного напряжения к осевому не зави-
зависит от относительного удлинения е и постоянных материала.
Лист с круговым отверстием. Ривлин и Томас [1951] экспери-
экспериментально изучили поведение тонкого кругового резинового листа с неболь-
небольшим центрально расположенным круговым отверстием при осесимметричном
растяжении в плоскости листа. Как показывают эксперименты Ривлина
и Саундерса [1951] на этом же материале, его свойства можно удовлетвори-
удовлетворительно охарактеризовать с помощью функции энергии деформации в форме
Муни при значениях постоянных Сх = С2/0.08 = 18.35 фунт/дюйм2. Экспе-
Эксперименты Ривлина и Томаса проводились на образце, который в недеформи-
недеформированном состоянии имел диаметр 5.0 дюйма, толщину 0.0625 дюйма и отвер-
отверстие диаметром 1.0 дюйма. По наружному краю листа прикладывались
радиальные нагрузки и замерялись перемещения при различных величинах
относительного удлинения в радиальном направлении.
Опишем результаты исследования этой же задачи методом конечных эле-
элементов 2) с использованием симплексной модели A8.38). Полная конечно-
элементная модель, применявшаяся при исследовании, изображена на
рис. 18.8. В силу симметрии фактически рассматривался только один октант.
После построения связанной модели обобщенные силы в узлах на внутренней
окружности приравнивались нулю, а обобщенные силы, действующие в узло-
узловых точках на наружной окружности, задавались таким образом, чтобы
они представляли равномерно распределенную радиальную нагрузку. Полу-
Полученные нелинейные уравнения равновесия решались методом последова-
последовательных нагружений, что позволило получить полные сведения о поведении
листа в процессе деформирования.
На рис. 18.9 показано вычисленное изменение ^перемещений узловых
точек на внутренней и наружных границах в зависимости от величины сили
Р, действующей на одной восьмой части наружной границы. Видно, что
с увеличением нагрузки материал размягчается: при малых нагрузках
он довольно жесток и наклон S кривой, соответствующей внутренней границе,
составляет 77 фунт/дюйм, в то время как при больших деформациях поведе-
поведение почти линейно и S « 22 фунт/дюйм. Заметим, что по линейной теории
получаются перемещения наружной границы, составляющие лишь 28%
от даваемых нелинейной теорией.
На рис. 18.10 представлено сравнение рассчитанных перемещений с пере-
перемещениями, определенными экспериментально Ривлином и Томасом для
различных величин относительного удлинения Я в радиальном направлении
при г = оо. В качестве безразмерной ординаты взято отношение радиуса
в деформированном состоянии к его величине в недеформированном состоя-
состоянии, а в качестве абсциссы — безразмерное расстояние г/а от центра отвер-
отверстия, где г — радиальная координата точки в недеформированном теле
и. а — недеформированный радиус центрального отверстия. Результаты рас-
расчета с использованием конечноэлементной модели очень хорошо согласуются
с экспериментом.
Для рассмотренных в этом примере формы листа и условий нагружения
линейная теория упругости дает коэффициент концентрации напряжений,
равный 2 (т. е. а22 (а)/а11 (оо) = 2). Однако на самом деле коэффициент кон-
концентрации напряжений зависит от величины деформации и свойств материала.
х) Уильяме и Шейпери [1962].
2) Эти результаты получены Оденом и Ки [1971а].
346
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Рис. 18.8. Конечноэлементная модель тонкого листа с круговым отверстием.
на наружной
границе
0 1 2 3 4 5 G
Перемещения краев В дюймах
Рис. 18.9. Зависимость узловых перемещений от приложенной на краю
нагрузки.
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
347
Экспериментальные
результаты
Расчет по методу
конечных элементов
J
г"
-,
Хоо
Х,»=1.25Ч \о
\
=2.35
,= 1.98
.=1.50
1.0 1.4 1.8 12. 2.G
3.0 3.4
г/а
V=-
7.0
8.0
9.0
10
Рис. 18.10. Сравнение рассчитанных попей перемещений с полями, определен-
определенными экспериментально Ривлином и Томасом [1951], для различных величин
относительного удлинения в радиальном направлении.
Один^из факторов, влияющих на изменение величины концентрации напря-
напряжений,— это, конечно, значительное уменьшение толщины листа при боль-
больших растягивающих деформациях; например, когда радиальные деформации
достигают|'примерно 150%, средняя толщина листа составляет лишь около
четверти толщины листа в недеформированном состоянии.
На рис. 18.11 представлена вычисленная величина коэффициента кон-
концентрации к в зависимости от величины относительного удлинения в радиаль-
радиальном направлении для рассмотренного нами радиально нагруженного листа
из материала Муни. При малых деформациях к = 2, в соответствии с линей-
линейной теорией. Однако при увеличении относительных удлинений величина к
3.0
Относительное удлинение
в радиальном направлении аг
Рис. 18.11. Зависимость коэффициента концентрации напряшений от дефор-
деформации.
348
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
также увеличивается и достигает примерно 6 при Я,ю=^2.0. Этот результат
согласуется с выводами Янга [1967] о концентрации напряжений в матери-
материалах My ни.
Одноосное растяжение листа с круговым отверстием.
Рассмотрим задачу об однородном растяжении тонкого первоначального квад-
квадратного однородного листа с центрально расположенным круговым отвер-
¦^—Недеформированная
граница
(Ь)
Рис. 18.12. Недеформированная и деформированная конечноэлементная
модель одноосно растягиваемого квадратного листа с круговым отверстием.
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
349
1.6-
Расчет по методу
конечных элементов
Результаты
эксперимента
2.4
Рис. 18.13. Сравнение результатов расчета с экспериментальными результа-
результатами Сегала и Клоснера [1970] по определению формы деформированного
отверстия.
стием. Начало материальной системы координат х1, х2 расположим в центре
отверстия, а оси х1 и х2 направим параллельно сторонам листа. Лист растя-
растягивается в направлении х1, а его ширина в направлении х2 поддерживается
постоянной.
Эта задача возникла в связи с экспериментами Сегала и Клоснера [1970]
на листах из эластичной резины, функция энергии деформации для которой
имеет вид, существенно отличный от формы Муни. После ряда испытаний
на образцах из некоторых несжимаемых эластичных резин х) они предло-
предложили кубичную по /2 функцию энергии деформации, определяемую выра-
выражением A5.65). Таким образом, функция энергии деформации содержит
четыре постоянные материала. Из опытов на образцах из натурального
каучука были определены приближенные значения этих постоянных: Сг =
= 20.28 фунт/дюйм2, С2 = 5.808 фунт/дюйм2, С3 = —0.7200 фунт/дюйм2
и С4 = 0.04596 фунт/дюйм2. Затем на квадратном образце из того же мате-
материала со стороной 6.5 дюйма толщины 0,079 дюйма и с круговым отверстием
диаметра 0.5 дюйма были проведены опыты, в которых определялись пере-
перемещения и форма листа после деформирования. Образец испытывался по опи-
описанной выше программе при одноосном растяжении.
Кратко рассмотрим результаты конечноэлементного исследования этой
задачи2). На рис. 18.12а показана конечноэлементная модель четверти
листа, состоящая из 192 симплексных элементов. Уравнения A8.38) с уче-
учетом соответствующих краевых условий приводят к системе 198 уравнений
относительно компонент перемещений узловых точек. Присутствие члена
(/2 — ЗK в выражении для функции энергии деформации обусловливает
появление в уравнениях равновесия каждого элемента членов, содержащих
двенадцатую степень перемещений узловых точек. Коэффициент поперечной
1) Клоснер и Сегал [1969].
2) Оден и Ки [1971а].
350
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
.=1.365
Расчет по методу
конечных элементов
Результаты
эксперимента
12
1.56 рассчитанное
,f ^"\1.54 замеренное
0.04
0
-0.04
1.21 рассчитанное
замеренное
Рис. 18.14. Сравнение рассчитанных перемещений с экспериментально опре-
определенными Сегалом и Клоснером.
деформации Я, входящий в уравнения равновесия в четвертой степени, дает
перемещения в степени —4. Перемещения узловых точек в направлении оси
х1 при х1 = +3.25 полагались равными друг другу и растяжение листа осу-
осуществлялось за счет задания приращений равномерной нагрузки в узловых
точках на границе в направлении оси х1. Таким образом, система нелинейных
уравнений равновесия решалась методом последовательных нагружений,
описанным в п. 17.5.
На рис. 18.12Ь показана деформированная система конечных элементов
при Xi = 2. Мы видим, что круговое отверстие вытягивается и становится
эллиптическим, а радиальные лучи приобретают заметную кривизну.
На рис. 18.13 показана в большем масштабе четверть отверстия после дефор-
деформации. Для сравнения приводятся два профиля отверстия: полученный
в результате расчета и определенный экспериментально Сегалом и Клосне-
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ' 351
?ом — при значениях относительного удлинения Xxi = Х%, равных 1.0,
.36 и 1.46. Соответствие между рассчитанными и замеренными в опытах
перемещениями очень хорошее.
На рис. 18.14 произведено сравнение перемещений вдоль осей х1 и я2,
определенных расчетным путем и полученных в опытах Сегала и Клоснера,
при различных величинах относительного удлинения Ях. Опять соответствие
очень хорошее. Лишь при малых значениях ^ наблюдается различие в рас-
рассчитанных и замеренных вертикальных перемещениях узловых точек, рас-
расположенных на оси х2. Это в основном обусловлено тем, что использованные
в расчетах приращения нагрузки приводили не в точности к тем же самым
относительным удлинениям, которые замерялись в опыте. Кроме того, можно
думать, что при малых относительных удлинениях точность эксперименталь-
экспериментального определения перемещений снижается.
Влияние вида функции энергии деформации. Интересно срав-
сравнить численные решения одной и той же задачи, полученные при использо-
использовании различных видов функции энергии деформации W. Для примера рас-
рассмотрим задачу об одноосном растяжении квадратного листа с круговым
отверстием (рис. 18.12) для следующих семи различных видов функции энер-
энергии деформации: 1) неогукова форма A5.63), 2) форма Муни A5.62), 3) форма
Клоснера — Сегала A5.65) (использованная в предыдущем примере), 4) фор-
форма Исихары — Хасицумэ — Татибаны A5.66), 5) форма Бидермана A5.67),
6) экспоненциальная форма Харт-Смита A5.68) и 7) экспоненциальная форма
Александера A5.70).
При проведении сравнения постоянные материала определялись по
экспериментальным данным Трилора х), полученным для восьмипроцентной
сернистой резины. Они дают такие значения постоянных для материалов
первых пяти типов: С = Сг = 27.02 фунт/дюйм2, С2 = 1.42 фунт/дюйм2,
С3 = —0.959 фунт/дюйм2, С4 = 0.0612 фунт/дюйм2, В1 = —0.27 фунт/дюйм2,
В2 = 0.00654 фунт/дюйм2. Таким образом, коэффициенты при одинаковых
членах во всех полиномиальных формах функции энергии деформации совпа-
совпадают между собой. Для харт-смитовой формы A5.68) данные Трилора при-
приводят к следующим значениям коэффициентов: G = 22.75 фунт/дюйм2,
кг = 0.00028, к2 = 1.20. Наконец, если потребовать совпадения одинаковых
членов в A5.68) и A5.70) и воспользоваться, после соответствующего пере-
пересчета, экспериментальными результатами Александера 2), то можно полу-
получить значения постоянных, входящих в A5.70): С2 = 1.34 фунт/дюйм2,
С3 = 26.55 фунт/дюйм2.
Результаты расчета величины силы, приложенной в направлении оси
Xi к границам хг = +а/2, в зависимости от относительного!удлинения Я при
?i = ±оо (см. рис. 18.12) для различных видов функции энергии деформации
представлены на рис. 18.15 3). Недостаточность экспериментальных данных
не позволила точно определить постоянные, входящие в форму Александера,
для резины, на которой проводил эксперименты Трилор. Этим, по-видимому,
объясняется разница в начальном наклоне кривых для материала Алексан-
Александера и других материалов. Для относительных удлинений Я от 1.0 до 2.0 пове-
поведение материала Александера заметно отличается от поведения других рас-
рассматриваемых материалов. Однако для больших значений относительного
удлинения, как видно из рис. 18.16, это отличие|не так заметно. При 2.0 <sj
<Sj Я < 5.5 одноосное поведение неогукова материала и материала Муни
практически линейно, в то время как экспоненциальные формы Харт-Смита
и Александера и квадратичная форма Исихары — Хасицумэ — Татибаны
*) Трилор [1944, 1958].
2) Александер [1968].
3) Численные результаты, представленные на рис. 18.15—18.18, и их
анализ принадлежат Одену и Ки [1972].
352
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
S4 -
56 -
e 40 -
I 32
¦a 24
5:
16 -
8 -
1.0
;
-
/'
/ &
- /w
w
y'
/
r
n
ддлл Исихары-Хасицумз-Татибаны
+++++ Бидермано
ooooo Клоснеро—Сегола
п п d d Хорт - Смита
—•— Александера
i i i i i
1.2 1.4 1.6 1.8 2.0
Относительное удлинение к
2.2
2.4
Рис. 18.15. Зависимость силы в направлении оси х г на границах xx = + а
от относительного удлинения X при л^ = + оо для различных видов функции
энергии деформации.
описывают ужесточение материала. Поведение материалов Клоснера —¦
Сегала и Исихары — Хасицумэ — Татибаны при % > 2.0 не исследовалось.
Существенно, что одноосное поведение, характеризуемое рис. 18.15
и 18.16, почти нечувствительно к виду функции энергии деформации. Следо-
Следовательно, экспериментов при одноосном нагружении описанного типа недо-
недостаточно для точного описания свойств материала. Подобные же выводы были
сделаны Александером [1968] в связи с одноосными испытаниями тонких
полос.
Однако деформированная форма центрального отверстия более чувстви-
чувствительна к виду функции энергии деформации. На рис. 18.17 и 18.18 показаны
160
н
°120
80
^ 40
НеогукоВа.
'•' Муни
д д дд Исихары-Хасицумэ —Татибаны
+++++ Бидермана
о о о о Клоснера—Сегала
а а а а Харт - Смита
—.— Александера
1.0
1.5
2.0
5.0
5.5
2.5 3.0 3.5 4.0 4.5
Относительное удлинение X
Рис. 18.16. Зависимость силы на краю от относительного удлинения X.
6.0
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
353
Неогуково
o.S
Муни
дддд Исихары-Хасиц-умэ-Татиданы
+ + + + Бидермано
о о о о Клоснеро-Сега/ia
? ??п Хорт - Смита
—-— Александеро
Не деформированное
'отверстие
э о о о о т
oooooooeoo
0.5
1.0
Ж, (вюймы)
Рис. 18.47. Деформированная форма четверти центрального отверстия при
одноосном растяжений силой 64.0 фунта.
рассчитанные профили четверти деформированного отверстия для сил Р
величиной 64 и 160 фунтов соответственно. Понятно, что при этом величина
относительного удлинения X при хх = +оо для разных материалов различна.
При Р = 64 ф. центральное отверстие для материала Клоснёра — Сегала
имеет гораздо более уплощенную форму, чем для других материалов. При
меньших нагрузках (соответствующих величинам относительно удлинения X
от 1 примерно до 2) профили, определенные расчетным путем, прекрасно
Неогуково
Муни
++ + *+ Бидермано
апааа Хорт-Смита
—— Александеро
^•1.0
'г
jfo.5
Не деформированное
'отверстие
хЛ (Эюймы)
Рис. 18.18. Деформированная форма четверти центрального отверстия при
одноосном растяжении силой 160.0 фунта.
23 дж. Оден
354 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
согласуются с результатами измерений Клоснера и Сегала [1969]; однако
в этой работе нет экспериментальных данных для больших значений X.
При Р = 64 ф. (рис. 18.17) формы отверстий для неогукова материала
и материала Муни очень близки, но при больших нагрузках (рис. 18.18)
наблюдается значительное отличие поперечных перемещений при х2 = d/2.
Напротив, для материалов Харт-Смита и Бидермана различие профилей при
Р = 160 ф. менее выражено, чем при Р = 64 ф. Хотя материал Александера
несколько жестче, чем материал Харт-Смита, профили отверстия для них
близки по форме в довольно широком диапазоне изменения относительного
удлинения. Профиль отверстия для материала Бидермана близок к профилю
для материала Исихары — Хасицумэ — Татибаны при Р = 64 ф. и мате-
материала Харт-Смита при Р = 160 ф.
Раздувание упругих мембран1). Применим теперь уравненияA8.34)
к более общей задаче о раздувании мембран под действием нормального
к срединной поверхности давления. Используя опять симплексное]^пред-
симплексное]^представление, приходим к локальным соотношениям
B, = «wBf + bwpA.f, A8.44)
где aN и bNft — те же самые массивы, что и в A8.37) [и A0.106)]. Теперь,
однако, цг и иУ отличны от нуля, и вместо A8.38а) имеем локально
f)=pNv A8.45)
где а, Р, ц = 1, 2; N, M, R, P, i, к = 1, 2, 3. Рассмотрим случай, когда
каждый элемент нагружен равномерным давлением д„, так что, согласно
A6.113),
PNk = -g" Я&Ш (*? +•»? -4 ~ иЬ («J
-g
где, по крайней мере локально, х^ = 0.
Харт-Смитом и Криспом [1967] приведены экспериментальные и теоре-
теоретические данные о поведении первоначально плоской круглой резиновой
мембраны диаметром 50.8 мм и толщиной 0.2 мм под действием равномер-
равномерного давления 0.097 кг/мм2. Исходя из этих экспериментальных данных и мо-
молекулярной теории Джента и Томаса [1958] 2), Харт-Смит и Крисп предло-
предложили для функции свободной энергии формулу A5.68), в соответствии с кото-
которой
|? 4?? A8-47>
Здесь С, кх и к% — постоянные материала. Поскольку для резиноподобных
материалов &х лежит в диапазоне от 0 до 0.0004, a fc2 — в диапазоне от 0
до 1.5, функции в A8.47) приближенно равны постоянным Муни Сх и С2,
в предположении, что 1г и /2 постоянны в каждом элементе, так что постоян-
постоянные Муни для элементов могут быть вычисл'ены с помощью A8.47) и экспе-
г) Конечноэлементные решения ряда задач о раздувании и конечных
деформациях тонких упругих мембран получены Оденом [1966а], Оденом
и Сато [1967а, 19676], Оденом и Кубицей [1967]. См. также Оден [1971в]..
2) См. также Харт-Смит [1966].
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
355
Рже. 18.19. (а) Конечноэлементная модель круговой мембраны. (Ь) Типичный
сектор с углом 30°.
риментальных данных Харт-Смита и Криспа. На рис. 18.19 показана исполь-
использованная конечноэлементная модель, а на рис. 18.20 приведен профиль разду-
раздутой мембраны, отвечающий численным результатам, полученным при реше-
/нии соответствующей системы нелинейных уравнений методом Ньютона —
Рафсона *). Для сравнения на том же рисунке приведены профили по Харт-
Смиту и Криспу. Заметим, что довольно грубая сетка элементов приводит
к результатам, хорошо согласующимся с экспериментальными данными:
максимальная разница между вычисленными и замеренными перемещениями
составляет около 6%. За исключением незначительного изменения верти-
вертикального перемещения центрального узла, по существу такие же результаты
получаются при использовании средних значений постоянных Муни Сг =
= 9.5 Ct = 1.75 кг/см2 во всей модели.
Следует указать на сильную нелинейность задач этого типа. На рис. '18.21
показана зависимость величины относительного удлинения Хр в вершине
раздутого листа от внутреннего давления. Эти результаты были получены
Оденом и Кубицей [1967] в испытаниях круговых дисков из чистого натураль-
Эти результаты принадлежат Одену и Кубице [1967].
23*
356
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
—°— Метод конечных элементов
Результаты 1 „ _
эксперименте/К ларт-Шит
Теория J " Крисп
(см)
Рис. 18.20. Сравнение профиля раздутой мембраны, рассчитанного методом
конечных элементов, с профилями, определенными экспериментально и тео-
теоретически.
1 2 3 4 5 6
Относительное удлинение
В вершине Кр
Рис. 18.21. Зависимость величины относительного удлинения от внутреннего
давления.
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 357
ного каучука толщиной 0.0173 см и 38.1 см в диаметре. Диски нагружались
последовательно в несколько этапов внутренним давлением приблизительно
до 100 мм водяного столба. Исследование поведения диска методом конечных
элементов при предположении, что материал диска является материалом
Муни с постоянными Сг = 1.14 кг/см2 и С2 = 0,14 кг/см2, позволило полу-
получить профили, хорошо согласующиеся с результатами эксперимента. Из ри-'
сунка видно, что при давлении приблизительно 90 мм водяного столба отно-
относительное удлинение в центре неоднозначно. Это указывает на неустойчи-
неустойчивость (при растяжении). Такая особенность поведения обычно вызывает зна-
значительные затруднения при проведении расчетов. Однако, используя метод
Ньютона — Рафсона и разумно выбирая пробные значения (начальные точ-
точки), удалось успешно решить эту задачу при заданной величине внутреннего
давления х).
18.2. НЕСЖИМАЕМЫЕ УПРУГИЕ ТЕЛА ВРАЩЕНИЯ 2)
Рассмотрим упругое тело вращения с поперечным сечением
произвольной формы. Будем предполагать, что положения мате-
материальных частиц в начальной конфигурации тела характеризуют-
характеризуются конвективными (внутренними) цилиндрическими координатами
I1 = г, |2 = z и |3 = 6. Деформация тела определяется полем
перемещений и = и (г, г, 6) и его градиентом и,г = ди1д\1. Ниже
мы ограничиваемся рассмотрением лишь осесимметричных дефор-
деформаций, для которых u = u (r, z) и поле перемещений определяется
радиальной и осевой компонентами % и м2- В этом случае соотно-
соотношения между деформациями и перемещениями сводятся к следую-
следующим:
+ Uu, aU% > A8.48a)
A8.486)
где Yag(a, (}, ц — 1, 2) — ковариантные компоненты тензора
деформаций, мй = и1* и
Я = 1 + -^-. A8.49)
Функция X = X (г, z) представляет собой относительное удлинение
в окружном направлении, т. е. % — отношение длины окружного
1) Оден [1971в].
2) Применениям метода конечных элементов к линейным задачам о сим-
симметричных бесконечно малых деформациях гуковых тел вращения посвящены
работы Рашида [1964, 1966] и Клафа и Рашида [1965]. Вильсон [1965] рас-
рассмотрел линейную задачу о произвольных бесконечно малых деформациях
осесимметричных упругих тел, а Беккер и Брисбейн [1965] построили конеч-
ноэлементные модели для исследования бесконечно малых деформаций"несжи-
маемых тел вращения. Приложения к общей-задаче о конечных освсиммет-»
ричных деформациях несжимаемых тел вращения даны в статье Одена и Ки
[1970], на основе которой и написан этот пункт.
358 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ¦:'
волокна в деформированном теле к его первоначальной длине
в начальной конфигурации.
Если, как и раньше, мы предположим, что тело изотропно
и гиперупруго, то функцию энергии деформации W можно пред-
"ставить как функцию от главных инвариантов тензора меры
деформации. Для рассматриваемого типа деформаций
A8.50)
где
q> = l+2-y2 + 2e«Pe**y«x'Yfti ' A8.51)
и, как обычно, 8аР — двумерный перестановочный символ. Следо-
Следовательно,
» = 2 W- бар + 2
- б + 2 -
^Э ), A8.52а)
A8.526)
= 2 -§*. + 4 A + Tg) Ц- + 2 -I* Ф. A8.52в)
Для несжимаемых материалов W = W (Ii, /2), /3 = 1 и
3 = 2 -gt баэ + 2 -|Г [баЭ A + Я2) + 2ё«*вЭ*Ы +
(баЭ + 28^8Р^Й), A8.53а)
A8.536)
A8.53в)
где h — гидростатическое давление.
Коиечпоэлемеитиые аппроксимации. Построим ди-
дискретную модель нашего тела вращения, представив его в виде сово-
совокупности Е конечных элементов вращения (см. рис. 18.22). Следуя
обычной процедуре, выделяем типичный конечный элемент е и ап-
аппроксимируем локальное поле перемещений иа (I1, |2) на этом эле-
элементе следующим образом: иа = tyN (?\ ?2) и?, где ?*= г и |2 = z.
Ковариантные компоненты метрического тензора в недеформиро-
ванном теле имеют простой вид: gu = g22 = 1, ?3з = г2 и gij = О
(i Ф у); символы Римана — Кристоффеля таковы: Г,33 = Г^ =
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
359
Рис. 18.22. Конечноэлементная модель тела вращения.
= 1/г, Г*3 = —г, а все остальные T)h = 0. Поскольку и3 =
= dujd^3 = 0, имеем и ™р = ufр = иа, р. Подставляя все это
вместе с A8.53) в A6.192) и производя упрощения, получаем сле-
следующие уравнения равновесия для изотропного несжимаемого
конечного элемента вращения:
SW
dW
"
v0(e)
+ 2
ди
SW
dui
di2
dl.
du
N
ди.
ди"
A8.54)
где h = ijj^fe^ — гидростатическое давление в конечном элементе
и dv0 = 2nr dr dz. Сюда надо еще добавить условия несжимаемо-
несжимаемости типа A6.54) или A6.62).
У прощенные формы. В различных рассматриваемых далее
приложениях будет использоваться упрощенная форма уравнений
A8.54), получаемая при использовании симплексных элементов
и соответствующей аппроксимации для У?. В случае симплексных
элементов Nе — 3; гидростатическое давление считается постоян-
постоянным в каждом элементе, и, как обычно, иа = aNUa -f- bN1ru,a +
360 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
-f- bNiziia, где aN и bNa определяются соотношениями A0.106).
Тогда
cM^wf, A8.55а)
A8.556)
i A8.55b)
и
N ^ivp V"<* I "MP^a/i (lb.Oba)
<X
—лГ = 2—81а(а^ -\-bN$x$), A8.566)
-^V = 2bNX F? + bmu%) [8? + yptl (ePPe^t* + e&ef*)]. A8.56b)
К сожалению, интегрирование тех членов в A8.54), которые
содержат определяемое формулой A8.55в) относительное окруж-
окружное удлинение X, приводит к очень сложным логарифмическим
выражениям. Для того чтобы избежать этих сложностей, будем
использовать вместо A8.55в) аппроксимацию X, вычисленную
исходя из среднего радиального перемещения по элементу и стре-
стремящуюся с уменьшением размеров элемента к точному значению X:
Х = 1+^-. A8.57)
г
Здесь ^иг — среднее радиальное перемещение узлов и средняя
радиальная координата узлов:
«1 = 4-К+ "' + "?), 7 = i-(r1 + r2-j-r3). A8.58)
Относительное удлинение X считается при этом постоянным в эле-
элементе, и вместо A8.56в) мы используем соотношение
СЛ о Л /ciVl I cJV2 i ciV3\ slot /iQ '-iQV
a r
После этих упрощений A8.54) принимает вид
-f (-Щ- + Ш) bNX (б? + Ъм#?) [Ь{ + 7рц (еРРеМ + е*е*»)]} = pNa,
A8.60)
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 36f
где v0 = 2пгА0, а Ао — площадь недеформированного поперечного
сечения элемента. Узловые силы вычисляются с помощью спосо-
способов, описанных в п. 16.3. Например, при действии на границу
элемента равномерных нормальных усилий интенсивности q мы
в соответствии с A6.118) используем
Р1а = Р2а = (-1)(а)8Эа4?Л(^ + Й+^ + и12)8аЭ^, A8.61)
где L\ = Lp — проекции линии, соединяющей узлы 1 и 2 на оси
|р после деформации (|х = г, |2 = г).
Поскольку A8.60) представляет собой систему шести уравнений
относительно семи неизвестных hie) и Ua, надо еще записать усло-
условие несжимаемости для элемента. Оно получается простым при-
приравниванием друг другу объемов деформированного и недеформи-
недеформированного элементов:
v (uN) — vo = O. A8.62)
Здесь
и v = 2n(r + ui) A; A8.63)
«[Иг определяются по формулам A8.58), а А и Ао суть площади
деформированного и недеформированного поперечных сечений
кольцевых элементов:
A8.64а>
p=i
з
А = | Т 2 &mnp^3 (х? + и«) (х»> + и») . A8.64б>
p=i
Задача о бесконечном цилиндре. Сначала рассмотрим конечные-
осесимметричные деформации бесконечно длинного толстостенного цилиндра,
нагруженного внутренним давлением. Эта задача представляет особый инте-
интерес, поскольку здесь мы имеем один из немногих случаев, когда результаты
можно сравнить с известными точными решениямиг), и, кроме того, эта
задача одномерна, что позволяет записать нелинейные жесткостные соот-
соотношения в особенно простой форме.
Для описания осесимметричных (радиальных) деформаций можно постро-
построить конечноэлементную модель тонкого диска, используя рассмотренные-
ранее треугольные конечные элементы вращения, как показано на рис. 18.23а.
Хотя задачу можно существенно упростить, если приравнять радиальные-
перемещения расположенных на одной вертикали друг против друга узло&
/ и /', метод конечных элементов подвергнется гораздо более суровому
испытанию, если допустить независимые перемещения всех узлов в радиаль-
радиальных направлениях. При этом модель из Е конечных элементов приводит
к2?+2 нелинейным уравнениям относительно Е -\- 2 неизвестных узловых
перемещений и Е гидростатических давлений в элементах.
Грин и Зерна [1968].
362
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Рис. 18.23. Конечноэлементные представления бесконечного цилиндра.
В качестве первого примера рассмотрим полый цилиндр из материала
Муни с С-1 = 80 фунт/дюйм2, С2 = 20 фунт/дюйм2, внутренний радиус кото-
которого 7.00 дюйма, а наружный — 18.625 дюйма. Цилиндр нагружен внутрен-
внутренним давлением р = 128.2 фунт/дюйм2 4). Эпюры перемещений и гидростати-
гидростатического давления для случая Е = 10 B2 неизвестных) представлены на
рис. 18.24. Видно, что при таком довольно грубом представлении есть невна-
чительная разница в величине узловых радиальных перемещений вертикаль-
вертикально противолежащих узлов. А именно, в случае 10 элементов эта разница
г) Точное решение для такого цилиндра получено Балтруконисом
и Вайшнавом [1965].
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
363
5.0
>1 4-°
«I
* 3.0
1
3 2.0
I
,t 1.0
-120
l<t
ПО
-100
-90
-80
— Точное решение A28.2 фунт/Эюпм2)
- -а Верхний ряд узлов
—о Нижний ряд узлов
—— Точное решение A28.2 фунт/Вюйм2)
о Средние значения для
конечных элементов
7.0 10.0 15.0 18.625
Недеформированное расстояние по радиусу в дюймах
Рис. 18.24. Эпюры перемещения и гидростатического давления.
достигает 5%, но средние значения перемещений верхних и нижних узлов
Отличаются от точных лишь на 1%. При такой крупной конечноэлементной
сетке гидростатические давления в элементах являются лишь весьма грубыми
средними значениями. Значения, отмеченные на рисунке, получены осред-
осреднением гидростатических давлений в соседних (верхних и нижних) элементах,
причем предполагается, что эти значения гидростатическое давление прини-
принимает в средних по радиусу точках между узлами. Для решения системы нели-
нелинейных уравнений, полученных в этом примере, использовался метод после-
последовательных нагружений, описанный в п. 17.5. На рис. 18.25 представлены
напряжения в элементах, полученные осреднением главных напряжений
в соседних по вертикали элементах, для модели, состоящей из 20 элементов.
Видно, что результаты очень хорошо согласуются с точным решением.
Другая конечноэлементная модель задачи о бесконечном цилиндре полу-
получается при использовании тонких цилиндрических конечных элементов,
показанных на рис. 18.23,Ь. Хотя численные результаты для этой новой моде-
модели практически совпадают с результатами для моделей типа показанной
иа рис. 18.23, а, жесткостные соотношения, выведенные из одномерных кине-
364
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
2
*2 400
1
Точное решение
Решение по методу
конечных элементов
s
го
§
50
^-100
Лг
7.0 18.625
Рис. 18.25. Напряжения в цилиндре.
матических соотношений, гораздо проще соотношений, соответствующих
двумерным элементам.
Для одномерного элемента единичной высоты из материала Муни нели-
нелинейные жесткостные соотношения таковы:
где
=у (ri+r2),
2r
A8.65)
A8.66)
A8.67)
Условие несжимаемости для этого случая записывается так:
1 = Я2Д2, A8.68)
а обобщенная сила в узле на внутренней или внешней границе, обуслов-
обусловленная соответственно внутренним или внешним давлением р, равна
i 1*)p, A8.69)
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
365
150г
12S
I!
100
I
75
50
2S
0.
— Точное решение
о 40 приращений нагрузки
Д 20 приращений нагрузки
п 10 приращений нагрузки
0 1.0 2.0 3.0 4.0 5.0
Перемещение внутреннего узла 8 дюймах
Рис. 18.26. Кривые зависимости между давлением и перемещением,
полученные методом последовательных нагружений.
где положительный знак отвечает случаю, когда р — внутреннее давление
(N — узел на внутренней границе), а отрицательный знак отвечает внешнему
давлению (N — узел на наружной границе).
На рис. 18.26—18.30 представлены численные результаты, полученные
при решении приведенной выше задачи для толстостенного цилиндра
¦(гвнутр = 7.00 дюйма, гнар = 18.625 дюйма, Сх = 80 фунт/дюйм2, С2 =
= 20 фунт/дюйм2) с помощью уравнений A8.65) — A8.69). Решения полу-
получены для различных значений внутреннего давления в диапазоне от 0 до
150 фунт/дюйм2. Для этого материала при внутреннем давлении
150 фунт/дюйм2 возникают деформации порядка 150%, так что поведение
цилиндра не может быть описано в рамках классической теории малых
деформаций.
Система нелинейных уравнений решалась описанным в п. 17.5 методом
последовательных нагружений. На рис. 18.26 изображена зависимость
внутреннего давления от радиального перемещения внутреннего узла, полу-
полученная при нагружений соответственно в 10, 20 и 40 этапов для девяти конеч-
конечных элементов. Для давлений менее 100 фунт/дюйм2 при 40 этапах нагруже-
ния ошибка накапливается сравнительно малая.
Чтобы читатель мог составить представление о скорости сходимости
конечноэлементных решений, на рис. 18.27 показаны отношение перемещения
внутренней поверхности цилиндра к его точному значению и отношение
гидростатического давления в примыкающем к внутренней границе элементе
к среднему на элементе точному значению гидростатического давления в зави-
зависимости от числа элементов. Как и следовало ожидать, конечноэлементная
Перемещение
Гидростатическое давление
I I I 1 I I L
2
3 4 5 6
Число элементов
8
Рис. 18.27. Сходимость ковечноэлементных решений.
1.4 г-
Число элементов
Рис. 18.28. Сходимость напряжений в элементе, примыкающем к внутренней:
границе.
130
110
J 90
E
I 70
0)
!
I
50
30
10 -
-а™ (точное значение)
-а11 (девять элементов)
Средние значия^
узловых напряжений
7.0 10.0 15.0 18.GZS
Расстояние по радиусу{Ь Эюймаж)
Рис. 18.29. Эпюры напряжений а11 и а22.
400
R о33(девять элементов)
300
н
о
200
I
100
R2a3Z(точное значение)
•—V
Средние значения
узловых напряжений
7.0 10.0 15.0 18.625
Расстояние по радиусу^ Эюпмах)
Рис. 18.30. Эпюры величины, пропорциональной напряжению о33-
368
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
модель цилиндра жестче самого цилиндра. Перемещение внутреннего узла
быстро и монотонно сходится снизу к точному значению. Гидростатические
давления сходятся, конечно, медленнее, но уже для пяти элементов они
отличаются от точных значений всего на 1.5%.
Довольно быстрая монотонная сходимость гидростатического давления
на рис. 18.27 не может, однако, служить указанием на сходимость напряже-
напряжений в элементах, даже несмотря на то что доля гидростатического давления
в окончательных значениях напряжений может быть весьма значительной.
Максимальная разница между точными значениями напряжений и вычис-
вычисленными по методу конечных элементов имеет место в первом (ближайшем
к внутренней границе) элементе. На рис. 18.28 представлено отношение
напряжений в этом элементе к точным средним по элементу значениям в зави-
зависимости от числа элементов. Мы видим, что сходимость не для всех компо-
компонент является монотонной снизу, и не для всех компонент она такая же
быстрая, как для гидростатического давления. Тем не менее для девятиэле-
ментного приближения, как видно из рис. 18.29 и 18.30, эпюры напряжений,
подсчитанные методом конечных элементов, хорошо согласуются с точными
эпюрами.
Толстостенный сосуд. Рассмотрим осесимметричные деформации
толстостенного несжимаемого упругого сосуда, изображенного на рис. 18.31.
Материал впять считаем материалом типа Муни с постоянными Cj =
= 80 фунт/дюйм2 и С2 = 20 фунт/дюйм2. Сосуд нагружен внутренним давле-
давлением 190 фунт/дюйм2 по границе ВС. Часть границы АВ свободна от нагру-
нагрузок. Размеры недеформированного тела указаны на рисунке.
Рис. 18.31. Толстостенный высокоэластичный сосуд, нагружаемый
внутренним давлением.
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
369
Рис. 18.32. Недеформированное и деформированное сечения сосуда
(в масштабе).
Вследствие симметрии достаточно рассмотреть только один квадрант.
Конечноэлементная модель состоит из 48 элементов, соединенных друг с дру-
другом в 35 узловых точках. При заданных краевых условиях имеем 113 неиз-
неизвестных: 48 гидростатических давлений в элементах и 65 компонент узловых
перемещений. При использовании этой конечноэлементной модели для каж-
каждого элемента получаем нелинейные жесткостные соотношения полиномиаль-
полиномиального вида, содержащие шестые степени неизвестных узловых перемещений
и гидростатических давлений.
Для решения системы нелинейных уравнений использовался метод
последовательных нагружений, причем нагрузка задавалась в девятнадцать
этапов приращениями по 10 фунтов. В рекуррентных формулах использо-
использовались приближенные значения градиентов, вычисленные по конечноразно-
стным формулам с шагом AXi = 0.0001.
Деформированная и недеформированная совокупности конечных эле-
элементов показаны в масштабе на рис. 18.32. Поскольку объемы конечных
элементов не изменяются, большое увеличение радиуса приводит к значи-
значительному уменьшению площади поперечного сечения. Видн(?, что прямые
24 дш. оден
370
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
700
700
-50 0
1500 1000
Рис. 18.33. Линии уровня радиальных напряжений tn и окружных «напря-
«напряжений» R2tss (в фунт/дюйм2 и фунтах соответственно).
радиальные линии в недеформированном теле существенно искривляются
в процессе деформации. Как и следовало ожидать, максимальные деформа-
деформации и напряжения возникают в прилежащих к внутренней границе элементах
вблизи соединения цилиндрической и тороидальной частей сосуда. Макси-
Максимальные окружные деформации имеют порядок 400%. Величины напряже-
напряжений в элементах получены способом, описанным в п. 16.3. Линии уровня для
компонент напряжений i11 и Л2*83 представлены на рис. 18.33.
На рис. 18.34 показано деформированное тело после 14, 17 и 19 этапов
нагружения (соответствующие величины внутренних давлений: 140, 170
140 170
190
Рис. 18.34. Деформированные сечения сосуда для величин внутреннего дав-
? ления 0, 140, 170 и 190 фунт/дюйм2. <
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
371
10 20
30 40 50
Время t
(о)
80
в
у
у
уУ
<У_
D
У
у
у
у
у
У
у
у
^У
у
у
у
у
у
у
у
у*
у
у
у
у
У
у
у
У
у
у
у
/У
у
у
у
у
у
У
у
X С
\
^^
\
\
\
\,
\
\
\
^4^
N
\
ч
ч
"\
N
\^
\,
\
I
Рис. 18.35. (а) Процесс нагружения первоначально плоской круговой пласти-
пластины. (Ь) Конечноэлементная модель пластины.
и 190 фунт/дюйм2). Для исследования поведения при более высоких давле-
давлениях было осуществлено 11 дополнительных нагружений по 10 фунт/дюйма
с доведением давления до 300 фунт/дюйм2. Наблюдалось радикальное изме-
изменение формы на каждом таком этапе после 190 фунт/дюйм2, что указывает
на ярко выраженное уменьшение жесткости при увеличении нагрузки. При
давлении 300 фунт/дюйм2 деформации получились совершенно нереально
большими, а площади поперечного сечения некоторых элементов почти
обратились в нуль. Это означает, что для получения правдоподобных дефор-
деформаций при давлениях выше 190 фунт/дюйм2 надо давать меньшие приращения
нагрузки.
Изгиб и раздувание круговой пластины1). Одно из интересных
приложений метода конечных элементов к исследованию осесимметричных
тел связано с изучением квазистатического поведения свободно опертой
круговой пластины под действием меняющегося по кусочно-линейному зако-
закону внешнего давления (см. рис. 18.35а). Недеформированная пластина диа-
диаметром 15 дюймов и толщиной 0.5 дюйма изготовлена из изотропного несжи-
Здесь воспроизводятся результаты, полученные Оденом и Ки [1971а].
24*
372
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Расходимость, обусловленная
размером приращения
Линейная
теория
i
5 10 15 20
Перемещение центра^ Зюимах)
25
Рис. 18.36. Зависимость поперечного перемещения центра пластины
от величины приложенного давления.
маемого материала типа Муни с постоянными Сх = 80 фунт/дюйм2 и С2 =
= 20 фунт/дюйм2. Конечноэлементная модель пластины изображена на
рис. 18.35, 6; отметим, что для наглядности на этом рисунке толщина пре-
преувеличена. Исследование проводилось описанным ранее методом последова-
последовательных нагружений. Внешнее давление прилагалось в виде отдельных прира-
приращений (один этап нагружения соответствует единице времени на рис. 18.35,а)
от 0 фунт/дюйм2 до максимального значения 43.7 фунт/дюйм2. Разгрузка
пластины осуществлялась по тому же закону в обратном порядке. Заметим,
что внешние нагрузки в этой задаче неконсервативны; поверхность нагружае-
нагружаемых элементов при увеличении давления существенно меняется и по пло-
площади, и по ориентации.
Предварительные исследования задачи вскрыли чрезвычайную зависи-
зависимость предсказываемого поведения от выбора размеров приращения нагрузки.
Это иллюстрируется рис. 18.36, где показана зависимость поперечного пере-
перемещения центра пластины от величины давления. Видно, что поведение
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 373
быстро отклоняется от пресказываемого линейной теорией после достижения
давления всего лишь 1 фунт/дюйм2. Далее кривая идет вверх почти линейно
при изменении давления от 3 до 28 фунт/дюйм2, а при дальнейшем повышении
давления наклон постепенно снижается. Поскольку трудно, если вообще
возможно, предвидеть такое поведение до выбора размера приращения,
вначале было получено несколько пробных решений с помощью грубых
конечноэлементных моделей для различных постоянных приращений. Эти
решения изображены на рисунке пунктирными линиями. Характерным для
слишком большой величины приращения является большое перемещение
на начальном этапе без последующего увеличения перемещений некоторых
узлов при неограниченном возрастании давления. Кроме того, нарушается
локальное равновесие сил в элементах и конечноэлементная модель претер-
претерпевает нереалистичные искажения. В рассматриваемой задаче для описания
поведения пластины при давлении всего лишь 3 фунт/дюйм2 пришлось исполь-
использовать 30 приращений нагрузки; дальнейшее же повышение давления до
40 фунт/дюйм2 было осуществлено за 25 этапов.
Рассчитать поведение пластины при давлении, превышающем
42 фунт/дюйм2, оказалось невозможным без модификации конечноэлемент-
ной модели. Это связано с численной неустойчивостью процесса последова-
последовательных нагружений и с несжимаемостью элементов; при деформациях поряд-
порядка 500% площади поперечных сечений некоторых конечных элементов почти
обращаются в нуль, поскольку объем кольцевых элементов не меняется,
и это приводит к плохой обусловленности матриц Якоби. Для того чтобы
преодолеть это затруднение, необходимо до наступления неустойчивости
приостановить процесс последовательных нагружений и построить новую,
улучшенную конечноэлементную модель деформированного тела. Началь-
Начальные значения узловых перемещений для новой модели можно получить линей-
линейной или квадратичной интерполяцией результатов, вычисленных по перво-
первоначальной модели. При этом целесообразно перед возобновлением процесса
последовательных нагружений осуществить несколько итерационных циклов
Ньютона — Рафсона для дальнейшего уточнения узловых перемещений
и гидростатических давлений.
Предположение о несжимаемости материала в задачах такого типа
может приводить и к другим трудностям при проведении расчетов. Предпо-
Предположим, например, что край АВ (см. рис. 18.35Ь) защемлен, а не свободно
оперт и что пластина нагружается внешним давлением по изображенной
на рис. 18.35а программе. При малом увеличении давления узловые точки,
расположенные, скажем, на CD, будут перемещаться приблизительно верти-
вертикально, так что все элементы в прямоугольнике А В CD будут приближенно,
в состоянии однородного чистого сдвига. Поэтому любые величины верти-
вертикальных перемещений лежащих на CD узлов приведут к изохорическим
(сохраняющим объем) деформациям. Следовательно система нелинейных
уравнений (уравнения равновесия и условия несжимаемости) не будет иметь
единственного решения. Если возможно в таких случаях переписать исход-
исходные уравнения так, чтобы получить «детерминированную» систему, то ука-
указанных неприятностей можно избежать, используя другие конечноэлемент-
ные модели, как правило с элементами неправильной формы на границах.
Результаты расчета деформированной конечноэлементной модели пла-
пластины для различных значений действующего давления представлены на
рис. 18.37. Видно, что в рассмотренном примере линейная теория дает удо-
удовлетворительные результаты только примерно до восьми приращений нагруз-
нагрузки по 0.1 фунт/дюйм2. При давлениях приблизительно от 0.8 до 1.0 фунт/дюйм2
растягивающие деформации все еще малы, но повороты уже становятся
ощутимыми. Деформации остаются малыми (менее 5%) вплоть до того, как
давление достигает величины примерно 4.0 фунт/дюйм2. При этом уровне
давления повороты некоторых элементов достигают 50°. Сдвиговые и попе-
поперечные деформации при нагрузке такого уровня малы; первоначально нор-
374
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Ось симметрии
Р--0
Рис. 18.37. Деформированные конечноэлементные модели
круговой пластины при различных значениях внешнего давления.
малыше к недеформированной срединной поверхности прямые линии все
еще остаются почти прямыми и нормальными к деформированной срединной
поверхности, т. е. гипотезы Кирхгофа — Лява справедливы при относитель-
относительно больших перемещениях.
Эти результаты показывают, что нелинейные теории пластин типа теории
Фёппля — Кармана (т. е. основанные на гипотезах Кирхгофа нелинейные
теории, з которых деформации считаются бесконечно малыми при поворотах
средней величины) в нашем случае можно было бы считать удовлетворитель-
удовлетворительными для давлений примерно до 4.0 фунт/дюйм2. После 4.0 фунт/дюйм2
повороты становятся совсем большими, а при 6.0—8.0 фунт/дюйм2 растя-
растягивающие деформации срединной поверхности достигают величины около
20%. При этом уровне нагрузки в поведении пластины начинает, преобла-
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ " 375
дать мембранный характер, т. е. она больше раздувается, чем изгибается.
При 25 фунт/дюйм2 поперечные деформации достигают 20%, а повороты
некоторых элементов превышают 90°. При максимальном давлении
в 43.7 фунт/дюйм2 возникают деформации порядка 500%, элементы вблизи
опоры поворачиваются на 128°, толщина пластины уменьшается с 0.5 дюйма
до примерно 0.15 дюйма и пластина принимает сильно искаженную форму,
показанную на рисунке.
18.3. КОНЕЧНАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
Теорию конечной плоской деформации изотропных гиперупру-
гиперупругих тел можно трактовать как частный случай обсуждавшейся
в предыдущем пункте теории для осесимметричных тел. Рассмотрим
однородное твердое тело в условиях плоской деформации, парал-
параллельной плоскости х1, х2. Кроме того, тело может быть подвергнуто
равномерному растяжению в направлении оси Xs, характеризуемо-
характеризуемому относительным удлинением %. Тогда 7аР определяются форму-
формулами A8.48а), уаа = 0 и yi3 = -^ (Я,2 — 1), где теперь к — изве-
известная постоянная. Главные инварианты тензора меры деформации
имеют вид
Где Y? = Vaa =
T = 4GiiV22-Yi2Y2i) = 2e<^eP^apY^- A8.71)
При изохорических деформациях /3 = 1 и A8.70) можно пере-
переписать так:
1± = с— ш,
A8.72)
/2 = с — АЛр,
где
c = l-t-Jl2-|--p- = const. A8.73)
Следовательно, для изотропных несжимаемых тел при конечной
плоской деформации
A8.74а)
A8.746)
A8.74b)
376 ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
Конечноэлементные приближения 1). Следуя обыч-
обычной процедуре, получаем уравнения равновесия изотропного не-
несжимаемого конечного элемента при плоской деформации в виде
v0<e)
+ 2 (¦^ + k2hy»e^N,»yllX}dv0 = pNa. A8.75)
Для симплексных аппроксимаций A8.75) сводится к
A + X2) Ц-
+ 2 (|? + Х%) г-нтту^} =pNa. A8.76)
Условие несжимаемости имеет простой вид
Ао = А, A8.77)
где v4o и А определяются по формулам A8.64). Предполагается,
что величина X задана заранее. Обобщенные силы определяются
с помощью методики, описанной в п. 16.3. Для равномерно рас-
распределенных нормальных усилий pNa задается формулой A8.61).
Чистый и обобщенный сдвиг. Сначала рассмотрим примеры при-
применения уравнений A8.76) к ряду довольно простых задач о конечной пло-
плоской деформации, для которых известны точные решения.
Для удобства будем считать, что функция энергии деформации материала
имеет вид Муни. Классическая задача о чистом сдвиге представляет собой
задачу о конечных плоских деформациях прямоугольного блока, в котором
прямые линии, параллельные, скажем, оси хи перемещаются относительно
друг друга в направлении оси уи оставаясь при этом прямыми и параллель-
параллельными в деформированном теле. Образец в форме куба, претерпевающий чистый
сдвиг, показан на рис. 18.38.
Пусть А, В, С и D — угловые точки образца, и пусть Д — полное
горизонтальное перемещение точек А я В относительно точек С и D. Пред-
Предполагая, что Я = 1, и используя конечноэлементную модель, изображенную
на рис. 18.38Ь, найдем, что для k-то элемента на прямой АС (заштрихованного
на вынесенной увеличенной части модели)
Г ° 4
L 1 o
[bNa] = n\ -1 -i\ A8.78)
l -kA
!(*)- —
„1 „2
Нетрудно подсчитать, что Vn = V23 = V33 = 0. V12 = V21 = A/2 и V22 =
= Д2/2. Таким образом, компоненты деформации не зависят от п (и к) и для
См. Оден [19686].
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
377
Рис. 18.38. (а) Деформация чистого сдвига. (Ь) Конечноэлементная модель
квадратного образца.
всех элементов модели получаются одни и те же результаты, какое бы число
элементов ни использовалось. Это, конечно, немедленно следует из того,
что при чистом сдвиге все элементы находятся в условиях однородной дефор-
деформации, а это тот самый вид деформации, который был принят при выводе
жесткостных соотношений для конечных элементов. Итак, симплексное конеч-
ноэлементное решение в случае чистого сдвига является точным.
Для материала Муни находим
iii = 2d + 2С2 B + Д2) + р A + Д2),
*12 = - BС2 + р) Д, A8.80)
«83 = 2Сг + 4С2 + р.
Условие несжимаемости удовлетворяется автоматически (деформация изо-
хорична), и значения напряжений совпадают с точными значениями1).
При обобщенном сдвиге стороны АС ш BD нашего образца могут дефор-
деформироваться произвольным образом (рис. 18.39). Как показали Грин и Адкинс
[1960, стр. 142], для несжимаемого изотропного тела с функцией энергии
деформации Муни кривая А С (и BD) в деформированном состоянии является
Грин и Адкинс [1960].
378
ГЛ. IV. ТЕОРИЯ УПРУГОСТИ
la)
X,
Рис. 18.39. (а) Деформация обобщенного сдвига. (Ь) Деформированная
конечноэлементная модель.
квадратичной параболой. Интересные результаты получаются при решении
этой задачи методом конечных элементов, если перемещения узловых точек
на линиях, параллельных АС, задать так, чтобы они лежали на параболе.
Деформированная конечноэлементная модель из 2д2 элементов (п точек раз-
разбиения вдоль каждой стороны) изображена на рис. 18.39Ь.
Для к-то элемента
)=ul(ft)=A
/ 2к
V12=t\—~
Д2
2к \2 2fe , 1
) +
A8.81)
Остальные компоненты равны нулю. Напряжения вычисляются так же,
как и ранее. Например, для компоненты tn в элементе к находим
-р- Bft —1
A8.82)
18. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
379
Рис. 18.40. Несжимаемое плоское тело с центральным отверстием под дей-
действием приложенной на границе сосредоточенной силы Р и конечноэлемент-
ная модель этого тела.
Плоское тело с круговым отверстием. В качестве последнего
примера кратко опишем численные результаты конечноэлементного решения
задачи о конечной плоской деформации несжимаемого квадратного образца
из резины типа Муни с центрально расположенным круговым отверстием х).
Образец защемлен по двум противоположным сторонам (другие стороны
свободны), и на него действует сосредоточенная сила, приложенная в сере-
середине стороны под отверстием, как показано на рис. 18.40. Размеры недефор-
мированного тела в плане 10 X 10 дюймов, первоначальный диаметр цен-
центрального отверстия 4.0 дюйма, а постоянные Муни приняты равными Сх =
= 80 фунт/дюйм2, С2 = 26 фунт/дюйм2. Использованная при решении конеч-
ноэлементная модель показана на рис. 18.42. Внешняя нагрузка Р вели-
величиной в 2000 фунтов прикладывалась в 20 этапов, по 100 фунтов на
каждом.
Рассчитанный деформированный контур тела при различных уровнях
внешней нагрузки показан на рис. 18.41, а на рис. 18.42 представлена дефор-
деформированная конечноэлементная модель при Р = 2000 фунтов. Как и следо-
следовало ожидать, в точке приложения нагрузки деформация сингулярна. Дефор-
Деформации достигают порядка 50%, и главный «диаметр» искаженного сердце-
сердцевидного отверстия увеличивается до 5 дюймов. .
См. Оден и Ки [1971а].
P=2 000
Рис. 18.41. Деформированные контуры плоского
тела при различных значениях приложенной силы.
Рис. 18.42. Деформированная конечноэлементная
модель при нагрузке Р = 2000 фунтов.
Глава V
Нелинейное термомеханическое
поведение сплошных сред
В этой главе мы применим общие уравнения движения и тепло-
теплопроводности, выведенные в гл. III для конечных элементов сплош-
сплошной среды, к нелинейным задачам о термомеханическом поведении
твердых тел. Хотя в принципе все дело сводится к простой под-
подстановке в эти общие уравнения определяющих уравнений рассма-
рассматриваемого материала, характер и сложность получаемых систем
уравнений, а также методы их численного решения могут быть
должным образом оценены лишь при изучении конкретных приме-
примеров. На последующих страницах сначала излагается теория про-
простых материалов с памятью, а затем рассматриваются частные
виды определяющих функционалов, согласующиеся с этой теорией.
В заключение строятся конечноэлементные модели таких материа-
материалов и описывается их применение к ряду характерных нелинейных
задач.
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ
Общеизвестно, что механическая работа сопровождается выде-
выделением тепла, и обратно, нагревая тело, можно производить меха-
механическую работу. Известно, далее, что свойства многих материалов
могут меняться со временем и могут зависеть от температуры
и скорости деформирования. Например, пластмассы, полимеры,
биологические ткани и многие металлы могут продолжать дефор-
деформироваться при неизменных приложенных нагрузках, и скорость
этого деформирования может быть очень чувствительной к изме-
изменениям температуры. Поведение материалов такого типа может
зависеть не только от текущих значений деформации и температу-
температуры, но и от их предыстории. В общем случае поведение таких
материалов характеризуется также диссипацией энергии, что
отличает их от рассмотренных ранее гиперупругих материалов.
Термомеханическое поведение большого класса диссипативных
материалов описывается термодинамической теорией простых
материалов; основные положения этой теории и будут изложены
в последующих пунктах.
382 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
19.1. ТЕРМОДИНАМИКА ПРОСТЫХ МАТЕРИАЛОВ *)
.Напомним [см. § 14, в частности A4.27)], что термомеханически
простые материалы характеризуются четырьмя определяющими
уравнениями, представляющими напряжение, тепловой поток,
плотность энтропии и свободную энергию в виде функционалов
от предыстории деформации, температуры и, возможно, градиентов
температуры. Для удобства мы предполагаем, что материал одно-
однороден, т. е. что за начальную конфигурацию принята некоторая
однородная конфигурация Со. В этом случае определяющие функ-
функционалы и плотность р = р0 не зависят от частицы материала х.
Используя тот факт, что уц = у (zm_ izm% j—8tj), и принцип
локального действия, в качестве независимых переменных состоя
ния выбираем предысторию деформации \г (х, s) = \ (х, t — s),
где \ (х, t) — тензор деформации в х в момент t, предысторию тем-
температуры 8' (х, s) = 8 (х, t — s) и текущий градиент температуры
g (x, t) = V8 (х, t). Таким образом, мы рассматриваем класс про-
простых материалов, описываемых определяющими уравнениями вида
1 V() () g()]
Т= $ [у* (s), в* (s); g(t)),
1° A9-1)
r\ = jr[y*(8), e'(*); g(*)],
q= 5 [V'(*). e'(«); g(«)l,
где гр и т] — плотности свободной энергии и энтропии, Т =
= al'Gf ® Gj — тензор напряжения, q — тепловой поток,
ОО OQ
а 4f, . . ., О, — соответствующие определяющие функционалы
Пределы у функционалов в A9.1) указаны для того, чтобы под-
подчеркнуть, что параметр, характеризующий прошлое время, изме-
изменяется от 0, что отвечает текущему моменту, до оо. Зависимость
ip, Т, т] и q от х и t, равно как зависимость \г (s), в' (s), g (t) от х,
явно'не указывается.
4) Механическая теория простых материалов создана Ноллом [1958];
она была распространена на случай термомеханических явлений Колеманом
[1964] и получила дальнейшее развитие в совместных работах Колемана и его
сотрудников. См., в частности, статьи Колемана, Гуртина и Херреры [1965],
Колемана и Гуртина [1965а, 19656] и Колемана и Мизела [1967], на которых
основано наше изложение.
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 383
Заметим, что вид функционалов Ч', . . ., Q может отличаться
от вида функционалов, скажем, в A4.28) вследствие другого выбора
меры деформации. Отметим также, что в соответствии с приведен-
приведенным в п. 14.2 правилом равноприсутствия аргументами всех
определяющих функционалов служит одна и та же совокупность
переменных.
Для облегчения последующих рассмотрений удобно ввести
понятие прошлой предыстории. Суть дела сводится просто к обо-
обособлению текущего значения функции от всех ее значений в прош-
прошлом. Пусть, например, и (s) — вещественнозначная функция
на интервале s ? [0, оо), и пусть фиксировано некоторое значение t;
тогда функция и* (s) = и (t — s), как и ранее, называется (полной)
предысторией и в момент t. Ограничение полной предыетории
и*(з) на открытый интервал @, оо) называется прошлой предысто-
предысторией для uf(s) и обозначается через и\ (s), т. е.
u?(s) = u(* —s), 0<s<oo. A9.2)
Таким образом, полную предысторию и* (s) можно представить
в виде пары [и\ (s), и* @)].
Возвращаясь к A9.1), выразим определяющие функционалы
через прошлые предыстории yl (s), 0' (s), а не'через полные пред-
оо оо
ыстории y'(s)> б' (s)- Вводя новые функционалы Ч', . . ., Q
s=0 s=0
формулами
i [?«r(e), #(*); y- 6, g]= i [?*(*), 6*(*); g] A9.3)
«=0 s=0
и т. д., где ?(Г 9 и g— функции от х и t, вместо A9.1) получаем:
со
т|)= Ф 1у'г(8), 0'(s); y, 6, g].
s=0
T= S [\i(s), 6*(e); Y, 0, g],
A9-4)
л —^" Ev* (*). eJ(*); v, e, g].
0
q a [\l(), j(); Y, , g]
s=0
Для того чтобы быть физически допустимыми, функционалы
A9.4) должны быть такими, чтобы не нарушались основные физи-
физические законы, описывающие термомеханическое поведение (пра-
(правило 1 п. 14.2). В частности, требуется, чтобы удовлетворялись
384 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
локальные формы закона сохранения энергии и неравенства Кла-
зиуса — Дюгема 1):
р\|> = o%iytj — ртH — б,
I A9.5)
p0T)_V.q+-g-q.g —рг>0,
где б — плотность внутренней диссипации.
Для проверки допустимости определяющих соотношений A9.4)
путем их подстановки в A9.5) требуется вычислять производные
по времени от определяющих функционалов. Это приводит к необ-
необходимости использовать дифференцирование по Фреше, описанное
в п. 10.1 [см. A0.19)]. В набранном петитом тексте мы воспроизведем
в новой форме и разовьем далее нужный математический аппарат.
Свойства гладкости функционалов^ Пусть 86 — вещественное
нормированное линейное пространство, элементами которого являются
определенные на @, оо) вещественнозначные функции и, с нормой || и \\.
Пусть, далее, 86 — пространство вещественнозначных функций и на [0, оо),
таких, что ограничение иг функции и на @, оо) принадлежит 86. Простран-
Пространство 86* также можно наделить структурой нормированного линейного
пространства, введя норму
|| и |[+ = || ur(s) || +1 и @)|. A9.6)
оо
Пусть К — дифференцируемый по Фреше [см. A0.19)] функционал,
8=0
определенный для всех и ? 86*. Тогда для произвольной функции h ? 86*
(+) = К (и) + б+ К (u\h) + a(u,h), A9.7)
s=0 s=0 s=0
оо оо
где 6 К (и | К) — первый дифференциал Фреше функционала К 2), а оста-
s=o s=0
ток со (и, К) удовлетворяет условию
lira —Цг ||ш(м, й)||+=0. A9.8)
U II h 1Г
, оо
Мы предполагаем, что дифференциал 6Tif (и | h) непрерывен по совокуп-
s=0
,оо
ности и и h; вертикальная черта в 6TZ (и \ К) указывает на то, что диффе-
s=o
ренциал линеен по h.
В случае iV-кратной дифференцируемости нашего функционала выпол-
выполняется соотношение
JV
К (u+h)= К (и)+ У. -i-8+n К (u\h,h, ..., h) + aN(u, h), A9.9)
s=0 s=0 *-* nl s=0
n=l
') Cm. A2.31), A2.33) и A2.35).
2) В точке и при приращении h.~ Прим. ред.
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 385
, оо
где 6 К~ (и | hu h2, . . ., hn) (при фиксированном и) есть симметричная
8=0
n-линейная форма на <SS?+ (т. е. отображение произведения <55?+ X ЯК?* X ...
... X 8& в поле вещественных чисел) и
lhn ¦ bl.tw 1|и№(Ц.*)Н*-»-0- A9.10)
оо
Число 6tTl ЛГ (м | hu h3, . . ., hn) называется Я-дифференциалом Фреше
«=о
оо
функционала Я в точке и *).
«=о
, оо
Удобно переписать б К (и \ h) в форме, в которой подчеркивается раз-
»=о
личие между функцией и и ее ограничением ит на @, оо). Это достигается
введением вместо К (и) другого функционала К, определяемого соотно-
8=0 8=0
шением
К Ив); и>]= К (и), A9.11)
8=0 8=0
где v (s) = щ (s) — ограничение функции и на @, оо) ж w = и @). Тогда
оо
наш «полный» дифференциал Фреше функционала К (и) примет вид
8=0
где
б+ К (и|А) = 6 К [v(s);w\hr(s)] + D К [v (e); w] h @), A9.12)
8=0 8=0 8=0
б К [v(s);w\hr(s)]= К [v+hr;w]— К (v; w) — ш(у, hr), A9.13a)
8=0 «=0 8=0
D К [v(s);w]=-?- К [v(s);w]. A9.136)
8=0 ""> 8=0
CO ОО
Ясно, что DK [ ; ] h @) — линейная функция от /г @), а 8К [ ; \ hr] — линей-
8=0 8=0
ный функционал от hr (s).
Нетрудно распространить изложенное на пространства более общего
вида. Опишем один важный для нас частный случай. Пусть Г обозна-
обозначает упорядоченную пару (Т, Р), где Т — произвольный тензор второго
ранга на %s и р — скаляр. Множество таких пар обозначим через ^ и вве-
введем на этом множестве бинарные операции сложения и умножения на скаляр,
положив по определению
а-Г = («Т, сф), A9.14)
х) При приращениях йь . . ., hn.— Прим. ред.
25 дж. Оден
386 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
где Ti = (Tf, Рх), Г2 = (Та, Pj) 6 ^ и а - скаляр. Алгебраическая система
(dt> +i •) представляет собой 10-мерное линейное пространство f*10 с нуле-
нулевым элементом О = @, 0). Далее, в f010 можно ввести скалярное произве-
произведение, например по формуле
IVr2 s (ft, Га> = triyrj + р,р2, A9.15)
Где tr — след, а символ Т, как обычно, обозначает транспонирование. Тогда
появляется естественная норма:
цг|.1о=1Л(Т7Т>. A9.16)
Множество С10, состоящее из таких элементов Г = (Т, Р), для которых
det Т ф 0 и р > 0, образует конус в 9°10.
Рассмотрим теперь банахово пространство Ш прошлых предыстории,
образованное измеримыми по Лебегу отображениями из @, оо) в f°la, с нор-
нормой || Г ||, называемой нормой на прошлых предысториях, которое обладает
следующими свойствами *):
1. Если Гх е 36, Г: @, оо) -»- ^10 и || Г ||0 < II Гх Но почти всюду
в @, оо), то || Г || < ]| Ti |. Кроме того, если {Г„} 6 36, || Гп || <
| Л (s) 1|0, причем функция Л измерима,
Л || < К.
К < оо и || Гп («'
то Л 6 36 и lim || Г„ || =
П-
2. Каков бы ни был элемент Q ? ^10, в &6 существует такая функция
ю, что «> (s) = Q для всех s ? @, оо).
3. Пусть С10 С 9^10 — упомянутый выше конус: С10 = {Г = (Т, Р) | Г €
? ^Ю; detT^O, р > 0}. Конус С10 является образом некоторого
конуса % а &€, обладающего тем свойством, что принадлежащие
ему абсолютно непрерывные функции, чьи производные принадле-
принадлежат &в, плотны в нем.
4. Если Г ? ffi, то 5ert(s)J и ?еГ (s) g <§? для каждого е > 0 , где
5ЕГ (s) = Г (s — е) при s 6 (е, оо) и 0 при s 6 @, е], a SeT (s) =
= Г (s + е) при всех s ^ @, оо).
Помимо &6, можно определить банахово пространство Sf6 полных
предыстории, образуемое множеством измеримых по Лебегу функций Г4,
отображающих [0, оо) в СУТЛЯ и имеющих конечную норму: || Г* II < оо.
Здесь Гг — класс эквивалентности в 36 , отвечающий ограничению функ-
функции Г' на @, оо). Норма в &6 , называемая нормой на полных предысториях,
определяется формулой
1|Г<||+ = ЦГ?|| + ||Г<(О)||о- A9.17)
Элементы в ffif*', соответствующие функциям Г', отображающим [0, оо)
в конус С10, образуют конус ^ в &&*.
Пусть теперь К — непрерывный функционал, определенный на ^Т(Х)^ЭЗ>
8=0
где ^3 — трехмерное векторное пространство. Тогда
К [Г<; v]= К [Г'Г;Т, Ў], A9.18)
8=0 8=0
См. Колеман и Мизел [1967].
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 387
оо
где v ? У®3- В предположении, что функционал К непрерывно дифференци-
дифференцируем по Фреше, можно записать
оо оо оо
К [Г1+Ф; Г + О, v+w]= К [Г1;Г, v] + 6 К [Г*;Г, у|Ф] +
8=0 8=0 8=0
оо оо
+DT К [Ti; Г, v]-fi+9v К [Г|.;Г , vj-w+co^; Г, v, Ф, Q, w), A9.19)
8=0 8=0
где Ф 6 &6, w 6 ^°3, каждый «частный» дифференциал Фреше непрерывен
оо
по совокупности своих аргументов, ЬК [ ; , | ] обозначает дифференциал
8=0
Фреше по &6, ду — обыкновенное частное дифференцирование по V,
оо оо оо
DT К [Г*; Г, v]-fi= К [Г1; Г + fi, v]- 1 [Г1; Г, v] —
.8=0 Т 8=0 Г 8=0
-а(Т*т;Т, v, О), A9.20)
где ш = о (|| О Цо), и
г || со (Г^.; Г, v, Ф, Q,w)||
— а> M4-II о и 4-1—Г
IIФ11+11 O|lo+lw|-0 L I' <pll + ll"llo+J w|
оо
т. е. о» = о (|| Ф || + || О ||0 + | w |). Если К [ ; , ] рассматривать как функ-
8=0
СО
цию параметра г, то скорость изменения К [ ; , ] по t можно вычислить,
используя A9.19) и свойство 4 пространства^?. Обозначая dKldt через К (Z),
получаем г)
а СО СО
6=0 8=0
со
+ av Д [Г*Г; Г, v] .;(*), A9.22)
где
гг — Т~г(т) =~rf~r'-W A9.23)
для почти всех s 6 @, °о).
Затухающая память. Хотя в большей части последую-
последующих рассмотрений нам не потребуется конкретизировать вид нормы
||-||, входящей в соотношение A9.6) и последующие соотношения,
Колеман и Мизел [1967, стр. 262].
25*
388 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
для многих важных приложений целесообразно ввести норму в Щ,
характеризующую затухание памяти. В физическом понимании
материал имеет затухающую память, если на его текущее поведе-
поведение не оказывает существенного влияния его поведение в отдален-
отдаленном прошлом. Математически это свойство можно описать, рас-
рассматривая описанное ранее нормированное линейное простран-
пространство 38 как гильбертово пространство &8ц), для чего вводится
некоторая фиксированная монотонно убывающая квадратично
интегрируемая функция влияния i (s) x), которая непрерывна
на [0, со) и удовлетворяет условию lim i (s) = 0. Скалярное
s->0
произведение двух элементов и, v 6 SS^y определяется при этом
формулой
оо
(и, v) = j и (s) v (s) i2 (s) ds, A9.24)
и нормой, входящей в A9.6), будет
оо
|| и || = [ j и2 (s) i2 (s) ds]1/2 . A9.25)
о
В случае пространства Ш более общего вида, состоящего из эле-
элементов Г = (Т, Р), можно использовать в качестве нормы, харак-
характеризующей затухание памяти, например, такую норму:
о о
+ [tr Т @) Тт @)]1/2 +1P @) |. A9.26)
Некоторые основные свойства термомехани-
чески простых материалов. Для того чтобы применить
изложенную выше теорию дифференцирования в нормированных
пространствах к определяющим функционалам A9.4), необходимо
выяснить структуру соответствующих нормированных про-
пространств. С этой целью временно будем использовать другие обо-
обозначения. Пусть Л (t) — упорядоченная пара [\ (t), 0 (t)], т. е.
первый член А — это деформация, тензор второго ранга, а вто-
второй — абсолютная температура 0, скаляр. Таким образом, Л
является элементом рассмотренного ранее пространства 5^0. Тогда
Л' (s) обозначает пару предыстории l\* (s), 0* (s)] и Х\ (s) — огра-
ограничение Л* (s) на @, оо). Уравнения A9.4) в этих обозначениях
') < — от английского influence (влияние).— Прим. ред,
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 389
можно переписать так:
со со
i|>= f [Л?(*); Л, g], T= S [Aj(*); A, g],
S= 0 S= О
- - A9-27)
r\=jr[AU*)\ л- g]. ч= о [A'(s); л- gi-
s=0 s=0
oo oo
Из A9.18) ясно, что Ч' , . . ., Q являются функционалами,
s=0 s=0
определенными на прямой сумме пространства полных предысто-
предыстории Ш^ и пространства f3, которому принадлежит g (t). Таким
образом, по формуле A9.22) можно определить скорость изменения,
со
скажем, функционала W:
8=0
^=6? [Al; Л, g|A^] + Z?Af [Л,; Л, g]-A(t) +
s=0 s=0
СО
W[Al; A, g].g(t). A9.28)
CO
Здесь б W [ ; ,] — дифференциал Фреше, Z?a — оператор, опре-
s=0
деленный соотношением A9.20), и ds — обычный оператор частно-
частного дифференцирования. Расписывая А через компоненты у в 6,
A9.28) можно представить в виде
s=0 s=0 *=0
CO CO
+ A)? [ — ]9 + dg? [ — ]-g, A9.29)
где для простоты записи введено обозначение [ — ] = lyl, 0';
Y, Э, g]. Операции б7, бе, Dv и Z?e определяются очевидным обра-
образом, аналогично операциям б и DA, введенным в A9.28). При вычи-
вычислениях бывает удобно использовать эти определения в следующей
форме:
оо оо
6V? [-|hr] = lim-^{? [Y'+ahr, 0j; y, 6, g]}, A9.30a)
69 ^ [-|pr] = lim^r{Y [Y*. 6^+apr; Y, в, g]}, A9.306)
s=0 a-»0 oa s=0
DVV [~]-b=\im^-{W [?;, QU Y+«h, 9, g]}, A9.30b)
s=0 a->0 ('a s=0
r{^ [Yr. 6'; Y. e + aP, g]}- A9.30r)
390 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
Таким образом, частное дифференцирование по уг] и 0 обычно
осуществляется по формулам A9.30в) и A9.30г).
Возвращаясь к первому соотношению A9.5) и вспоминая A2.35),
переписываем неравенство Клаузиуса — Дюгема в виде
<тУ7«-Р(* + Лв)+-д-*'в>°- A9.31)
Определяющие функционалы A9.27) должны быть такими, чтобы
ни при каких термодинамических процессах, происходящих
в материалах, неравенство A9.31) не нарушалось.
Обращаясь к индексным обозначениям и подставляя A9.27)
и A9.29) в A9.31), приходим к условию
(!«[_]_ро f [_])уц_Р(лв| [_]+.!• [_j)e-
8=0 8=0 8=0 8=0
- P6V I [ -1 и*,] - рве i [ -1 #] -
¦'«=0 8=0
-pdg.$ l-]gt + j О{[-]^>0. A9.32)
*s=0 ° 8=0
При фиксированных прошлых предысториях уЬ(Г), 0* и фиксиро-
фиксированных значениях уц, 0 и gt величины ytj, 0 и gt могут меняться
произвольно. Для того чтобы A9.32) выполнялось при любых
• ¦ *
значениях ytj, 8 и gt, необходимо, чтобы коэффициенты при них
обращались в нуль, а остальные члены были положительными
при всех значениях t:
со
dg.W [ — ] = 0, A9.33а)
«=о
Iw[-] = p0v f [-], A9.336)
«=о у«=о
J*[_] = _0ef [_], A9.33b)
S—0 8=0
-P{6V f [-iY«r)]+eef [—;e*]>+-l qj[-]^>o. A9.ззг)
lJs=0 »=0 ° 8=0
С учетом этих результатов и соотношения A2.33) внутренняя дис-
диссипация задается формулой
б = - р {б7 I [ -1 y\j(r)] + бе Т [ -1 #]}. A9.34)
^8=0 8=0
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 391
На основании A9.33) и A9.34) можно установить следующие
фундаментальные свойства термомеханически простых матери-
материалов *):
оо
1. Функционал свободной энергии W [ — ] не зависит от гра-
8=0
диента температуры g [это следует из A9.33а)].
оо оо
2. Определяющие функционалы Z1' [ — ] и JT [ — ] для
8=0 8=0
напряжений и энтропии определяются по функционалу сво-
свободной энергии; следовательно, они тоже не зависят от g
[это следует из A9.336) и A9.33в)].
3. Внутренняя диссипация определяется по функционалу сво-
свободной энергии соотношением A9.34); она удовлетворяет
общему диссипационному неравенству A9.33г).
Из свойств 1 и 2 следует, что простой материал характеризует-
характеризуется только двумя определяющими функционалами, один из которых
описывает свободную энергию, а другой — тепловой поток; напри-
например:
S;°Vr4' Г4'Т' ' A9.35)
8=0
Напряжение, энтропия, внутренняя диссипация и внутренняя
энергия определяются функционалами
aij= %{}[угг, 0'; Y> 6]==рД„..? [\l, &1; \, 0], A9.36а)
8=0 US=0
оо оо
ц = ЛГ[у1, 0'; ?, 0]= — DeY [yl, 0*; у, 0], A9.366)
8=0 8=0
оо оо
6=iJ [y', 0'; Y' 0]=—р{6V.Ф [Yr, 0*; y. 0IyW)] +
8=0 У8=0
s=0
[Yr, Bj; Y, в |6t]}, A3.36b)
= e[?i, 6^; Y. в] s= A -6De) * [Y*. в'; Y, в]. A9.36г)
8=0 S=0
Кроме A9.36), определяющие функционалы должны удовлетво-
удовлетворять принципу материальной независимости от системы координат,
*) Колеман [1964].
392 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
рассмотренному в п. 14.4, и должны иметь форму, инвариантную
относительно принадлежащих группе изотропии материала уни-
модулярных преобразований. Отметим, что в большинстве прило-
приложений этой теории к однородным телам вместо г|з, аг\ r\, Q1 и б
мы_предпочитаем использовать величины <р = рогр, t1' = |^Сстгз,
I = РоЛ» 4t — &im YGQm и о = б YG. Конечно, все основные
выводы и, за исключением незначительных видоизменений, форма
уравнений при этом сохраняются. В следующем пункте мы кратко
рассмотрим формы определяющих функционалов для некоторых
материалов. %
19.2. ЧАСТНЫЕ ФОРМЫ УРАВНЕНИИ СОСТОЯНИЯ
ДЛЯ ПРОСТЫХ МАТЕРИАЛОВ
При получении частных форм определяющих функционалов
для различных материалов естественно прежде всего попытаться
использовать разложения функционала свободной энергии х),
подобно тому как в § 15 использовались разложения функции
энергии деформации. Хотя экспериментальных данных, подтвер-
подтверждающих возможность использования таких разложений для
конкретных нелинейных материалов, недостаточно, линеаризации
определяющих функционалов, полученные таким образом, согла-
согласуются с классическими теориями линейной термо-вязко-упругости
и термоупругости. Для наших настоящих целей достаточно рас-
рассмотреть один типичный пример возможной формы этих функцио-
функционалов.
Тензорнозначную и скалярнозначную функции 0* (s) и 0* (s),
определенные формулами
О' (в) = 0, 0' (в) = 0, 0 < s < оо, A9.37)
оо
будем называть нулевыми предысториями. Если 3F [\г, 0'] —
8=0
функционал от полных предыстории \ (s)» " (s) T0> используя
A9.9) и накладывая соответствующие условия гладкости на
*) Идея представления различных определяющих функционалов в виде
разложений типа разложения Тэйлора (с производными Фреше), члены кото-
которых, вообще говоря, представляют собой многократные интегралы от преды-
предыстории деформации и/или температуры, использовалась целым рядом авто-
авторов. Например, различные изотермические случаи рассматривались Грином
и Ривлином [1957, 1960], Грином, Ривлином и Спенсером [1959], Колеманом
и Ноллом [1960], Чэконом и Ривлином [1964], Пипкином [1964, 1966] и дру-
другими. Некоторые авторы (в их числе У орд и Онат [1963]) пытались исполь-
использовать усеченные разложения при экспериментальном исследовании некото-
некоторых вязко-упругих и термо-вязко-упругих материалов, хотя в этом направ-
направлении сделано еще очень мало. Иной подход к определению свободной энергии
предложил Шейпери [1968]. См. также Лианис [1965] и Мак-Гуирт и Лиа-
нис [1969].
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 393
SF [ — ], можно построить обобщенное разложение Тэйлора для
s=0
оо
функционала 3F [ — ] в окрестности нулевых предыстории A9.37):
s=0
JF [0' (*) + у' (*), 0' (*) + 6' («)] = #¦ [0*] +
S=0 8=0
+ бт If [0* | у' (*)] + 8eJF [0* | в' (в)] +
s=0 s=0
s—0
-i- бе ^[0*| 6' (в), в( («)]+..., A9.38)
s=0
ОО
где 0* = [0' (s), 0' (s)]. С другой стороны, JF [ — ] можно выра-
8=0
зить через прошлые предыстории yr (s), Qr (s) с помощью нового-
функционала
&[yl 6'; Y, 6] = #[y', 6'] A9.39)
s=0 s=0
и вместо A9.38) записать
v . + Y + ][]
s=0 s=0
+ 6V I" [0* | v«] +6e# [0* | e*r] +D,^ \0*].y + DeF [0*]
s=0 s=0 s=0 s=0
+ 4-6? I" [0*| v', v'l + «vSe I" [0* | yl, Ql) +¦
/! s=0 s=0
+ 6V?)T # [0* | Y* ] • Y + 6TA> & I5* IV*] 9 +
e=0 s=0
21 s=0 2! s=0 2! s=0
A9.40)
где 0* = @', 0'; 0, 0).
oo oo oo
Если положить вр [ — ] = W [ — ], где W [ — ] — функцио-
s=0 s=0 s=0
нал свободной энергии, то, обрывая разложение A9.40) на том
394 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
или ином члене, можно получить определяющие функционалы для
различных материалов. Ахенбах, Фогель и Геррманн [1968,
•стр. 13] х) предложили следующую форму функционала свободной
энергии, получаемую из A8.40) при сохранении только членов
не выше третьей степени по у, 6 и их предысториям:
Ф = Л + Abu + АЬиТ + А1уцТ* + А{1тпуцутп + АТпуцутпТ +
*=0
-\-BiT-\-BzT2'-\-B3T:i. A9.41)
оо
Здесь Ф — функционал свободной энергии на единицу недефор-
8=0
мированного объема, Т = 6 — То — отклонение от некоторой
постоянной отсчетной температуры То и 2)
°° л оо j со
= Ф [ — ] + ¦<>-of-Ф [— |?г> * г] ~Г ~7Т Оу Ф 1 — lYr» YrJ +
s=0 ^ «=0 ^ «=0
|Y и+
8=0 ° S=0
8=0 ^ s=0
A9.42а)
<х> оо оо ,
'•' 8=0 8=0 S=0
f 1 б^Ф [ — |Г*, Г^ + бубуФ [ —|y'. ^г]}, [A9.426)
^ 8=0 8=0
^••¦°г{Ф [ —]+бгФ [-^'Ц-б^Ф [-|y']}. A9.42b)
J; 8=0 8=0 S=0
{rDy..D*T<h [ —], A9.42r)
?Л i?0 f -1 + 4?01 -1T']>• («.42д)
?т..?)т ?>ГФ[-], A9.42е)
d) В этой работе рассматривается лишь одномерный случай.
2) Заметим, что члены 6ТФ [— | у[] и беФ [— I 6^] не входят в A9.42),
поскольку эти функционалы обращаются в нуль при постоянных предысто-
риях деформации и температуры.
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 395
s=0 s=0 «=0
2 s=0 Г> 2 Ts=0 Г' Г
A9.42ё)
Ф [ —| Y(]}. A9.42ж)
"s=0 " ~s=0 " ' ' "s=0 r
1Ф [ — ], A9.42s)
s=0
где ф[_|..] = ф
s=0 s=0
= De. Более конкретно, можно ввести такие зависящие от дефор-
деформации и температуры интегральные коэффициенты1):
»Y*7"*7". A9.43a)
А? = Е* + G[iimn * ymn + M[li •T + M? . Т *Г +G'2i}mn » упп » Г,
A9.436)
« ? У <" A9.43в)
A9.43г)
4jmn = v G\}mn @) + N'iimn * т> A9.43д)
% A9.43e)
»Vu*?". A9-43ё)
^ A9.43ж)
В, = {Л@). A9.43з)
Здесь Ru, R12, . . ., GCmn, M», . . ., Ln, D™, . . ., Fx - ядра,
характеризующие материал, a ¦ означает оператор свертки, дей-
действующий (при соответствующей замене переменных) следующим
Ахенбах, Фогель и Геррманн [1968, стр. 5].
396 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
образом:
t t
Ки » Y * Y' = \ \ днтП V — Su t—s2) ft; (Si) Лу"? (S2) dsi dsz, A9.44a)
0 0
t t t
R112* Y * Y' *T' = j j J /?iT2" (t — sut-s2,t — s3) уtj (*j) X
0 0 0
x _Ym^_f2 ^з_ ^Sl ds2 ds3, A9.446)
A9.44b)
Предполагается, что нижний предел интегрирования — это тот
момент времени, когда начинается деформирование тела. Под-
Подставляя A9.41) в A9.36а) и A9.366) и вспоминая, что t1'=
i [-\=DyO [-] и %=Роц =
s=0 s=0
^ [ — ] = — DTO [ — ], приходим к следующим опре-
s=0 s=0
деляющим уравнениям для напряжений и энтропии:
tij = Avl + ДТ + ЩТ* + 2А{ГпуПп + 2А1ГпЧшпТ, A9.45а)
-l = Bt + 2B2T + ЗВ3Т* + А%1 + 2А%,Т + А^тпуиупп. A9.456)
Функционал внутренней диссипации получается точно таким
же образом с использованием A9.36в).
Ясно, что, сохраняя большее число членов в разложении A9.40),
можно аналогичным образом получить теории высших порядков.
Интересно отметить, что приравнивание нулю 6' (s) и 6 (t)
в A9.45а) дает классические определяющие уравнения линейной
изотермической вязкоупругости. С другой стороны, если наши
интегральные коэффициенты заменить константами, то A9.45а)
сводится к уравнению состояния для класса термоупругих мате-
материалов с зависящими от температуры свойствами. Ниже мы рас-
рассмотрим этот класс материалов подробнее.
Чтобы завершить описание материала, необходимо к A9.45)
добавить определяющее уравнение для теплового потока q. Среди
множества форм, которые могут быть использованы для функцио-
оо
нала Q [ — ], упомянем предложенный Кристенсеном и Нахди
s=0
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 397
[1967] линейный закон:
оо
Q*= J K»(t-s)^^-ds, A9.46)
о
где хгз (t — s) — ядро теплопроводности. Вместо этого закона
можно использовать обобщенный закон Фурье:
Qi=Zii[\tr,TU\,T}T.}, A9.47)
s=0
ОО .
где х" [ — ] — функционал от указанных аргументов. Если
s=0
оо. .
и'3 [ — ] заменить постоянной кг}, то A9.47) сводится к клас-
s=0
сическому закону теплопроводности Фурье.
Термореологически простые материалы. Резуль-
Результаты экспериментов на разнообразных вязкоупругих материалах
позволяют выделить важный подкласс материалов с памятью, обыч-
обычно называемых термореологически простыми материалами *). А
именно среди аморфных высокополимеров, которые при заданной
постоянной (во времени и в пространстве) температуре приближен-
приближенно подчиняются законам линейной и нелинейной вязкоупругости,
есть группа материалов, свойства которых меняются особенно
просто при изменении температуры: кривые, характеризующие
зависимость свойств материала от времени при разных постоян-
постоянных температурах, построенные в логарифмической шкале времени
(по оси абсцисс откладывается In t), получаются друг из дру-
друга сдвигом. Это явление представляет собой основную харак-
характеристику термореологически простых материалов; она позволяет
установить отношение эквивалентности между температурой и In t.
Чтобы лучше уяснить суть дела, рассмотрим определяющий
закон A9.45а). Для случая изотермических деформаций изотроп-
изотропных линейных вязкоупругих тел он сводится к такому закону:
{t-s)^ds, A9.48)
где у'ц и у — девиаторные и дилатационная компоненты yi},
а / (t — s) и К (t — s) — модули релаксации. Для термореологи-
термореологически простых материалов модули релаксации при постоянной
температуре Т будем записывать в виде функций от In t; напри-
х) См. Шварцл и Стэйвермэн [1952] или Уильяме, Лэндел и Ферри [1955].
Сводное обсуждение вопроса можно найти у Коста [1969], см. также Лианис
1968].
398
ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
а-
о.
¦о
¦5:
I
Логарифм t
Рис. 19.1. Явление смещения для термореологически простых материалов.
мер, / (t — s) запишем в виде Ет (In t). Тогда свойство смещения
выражается равенством
Ет (In t) = ET(j [In t + f (Г)], A9.49)
где / (Т) — функция смещения относительно То, такая, что
dfldT > 0 и / (То) = 0. Оно означает, что кривая модуля релакса-
релаксации при увеличении Т сдвигается к меньшим временам, как пока-
показано на рис. 19.1. Если ввести коэффициент смещения Ъ (Т) фор-
формулой
Ь (Т) = ехр / (Л, A9-50)
то модуль релаксации /г (t) при постоянной температуре Т будет
удовлетворять условию
JT(t) = Ет (In t) = ЕТо [In t + lnb(T)] =
= ETo{ln[ib(T)]} = JTo(t,). A9.51)
Величина
? = № (Л A9.52)
называется приведенным временем. Если удается обратить A9.52)
и получить t = g (?), то A9.48) можно переписать в виде
ds " J os
0
A9.53)
где ^(х, S) = ^[x, g(Q], ih(x, ?) = Vy[x, g(S)], Y>, D=Y[x, g(C)] и
s — f (s). Таким образом, будучи преобразованы к приведенно-
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 399"
му времени, определяющие уравнения для термореологически
простого материала принимают такой же вид, как в изотермическом
случае.
Хотя приведенные выше рассуждения относятся лишь к частно-
частному случаю линейного поведения тела при различных постоянных
температурах, основные идеи можно обобщить на случай конечных
деформаций тел при неустановившихся и непостоянных в про-
пространстве температурах х). Если, например, предположить, что-
свойства релаксации в частице х зависят лишь от текущей темпера-
температуры Т (х, t) в этой частице, то можно постулировать, что прира-
приращение приведенного времени А? связано с приращением реального
времени At соотношением At, = Ъ [Т (х, t)] At. Тогда вместо
A9.52) получаем
t
?J(x, *) = j Ъ [Т (х, *)] ds. A9.54>
о
Ясно, что при постоянной (во времени и в пространстве) темпера-
температуре A9.54) сводится к A9.52). Тэйлор, Пистер и Гудро [1970]
предложили другой вариант, согласно которому приведенное
время ? зависит от предыстории как температуры, так и скорости
ее изменения:
I (х, t) 1 \ Ъ [Т (х, >)?$&±] Л. 1A9.55)
о
Возможны и другие обобщения.
В качестве характерного примера определяющего функциона-
функционала для свободной энергии термореологически простого материала
приведем функционал, рассмотренный Костом [1969, стр. 55] 2):
Ф[-]=Фо+ I Л" (?-?А&- V f(t-s)^
5 ds о ds
-Si) b— S2)—26r(L, — Si, Q — S2)] X
о о
x) Обобщение теории термореологически простых материалов на случай
нелинейных сред было осуществлено Лианисом [1968], и эта обобщенная тео-
теория была успешно применена при описании конечных деформаций стирол-
бутадиенового каучука в экспериментах Мак-Гуирта и Лианиса [1969].
2) Этот вид функционала является обобщением предложенного Кристен-
сеном и Нахди [1967].
400 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
jn) \
J
^п dsl(ls2-
J J dSi ds2
J J
J
-~\ \°*&-~'i,Z-k)%-§-dkds2, A9.56)
где для компактности записи все величины преобразованы к при-
приведенному времени, т. е. уи (х, ?) = угу Iх. S (S)l> ^ (х. ^) =
= 71 [х, g (?)], ф (х, S) = Ф [х, g (S)]L г = g (Q, S = / @ опреде-
определяется соотношением A9.54), sx = f (sx), s2 = / (s2). В A9.56)
функции?>^ (),?¦(,), G ( , ) ni ( , ) — это ядра, характеризую-
характеризующие материал, а а — постоянная материала. Приводя A9.56)
к реальному времени и пренебрегая членами, обусловленными
дТ (х, t)ldxt, после подстановки A9.56) в A9.36) и выполнения
дифференцирования получаем такие выражения для t1'', | и а:
ti} = Dij @) + 8im8jn \ 2G [f (t) — g] fe ds +
t t
3 J ds J d"s
J ds J
о о
= / @) + 3aK @) v,, + <M @) 71 (t) -
t t
"- f-f [3aiTE)]vJJ(/(*)-*)tfi-[4-[^(e)]71(/(O-e)tfa, A9.576)
CT= —F И "I"
-i- (( «{[/()slf /@^}^^
z j Jo "' 3sj ds2
t t
+ \ \A.
J J ol
0 О
t t
"о \ \ 'я7{о^[/@ — si> /(^) — S2l}~^—^--dsids2. A9.57b)
0 0
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 401
В этих соотношениях К (s) = К @, s), G (s) = G @, s), M (s) =
= м @, s) = ЪК @, s) — 2G @, s) и Jl (s) = Л @, s). Ясно, что
дг' @) — начальные напряжения в материале. Ядра К (s)uG (s) —
это объемный и сдвиговый модули релаксации, а — коэффициент
линейного температурного расширения, а оМ @) Т связано с удель-
удельной теплоемкостью материала. Заметим, что хотя сами соот-
соотношения A9.57) применимы лишь к случаю бесконечно малых
деформаций твердых тел при малых градиентах температуры, вводя
функцию ?, = } (t), можно получить определяющие уравнения^
существенно нелинейные относительно Т (х, t).
Термоу пру гость. Важный класс простых материалов ха-
характеризуется свободной энергией, зависящей лишь от текущих
значений ytj и Т, а не от их предыстории. Такие материалы назы-
называют термоупругими х). Рассмотрим, например, случай, когда сво-
свободная энергия на единицу недеформированного объема изотроп-
изотропного термоупругого твердого тела является дифференцируемой
функцией от текущих деформации ytj (t) и температуры Т (х, t) =
= e(x,*)-7V
q>(x,t) = O(yij,T). A9.58)
Тогда в соответствии с A9.36а) и A9.366) 2)
а из A9.36в) следует, что для термоупругих тел
о = 0. A9.59в)
Поступая так же, как при получении соотношений A9.42),
рассмотрим однородное изотропное твердое тело, для которого
Ф ( ) есть аналитическая функция от Г я некоторых инвариантов
тензора ytj, например
ф = Ф (/„ /„ /8, Л, A9-60)
где
J\ = Чш
J, = 1/2 (v,,v« - Yi/Yu). A9-61)
/3 = det yu.
x) Cm. A5 22) и A5.23). Теория термоупругости возникла более века
назад в работе Дюамеля [1837]. Линейная теория подробно изложена в раз-
различных книгах и обзорных статьях, например у Боли и Уэйнера [1960],
Чэдвика [1960], Новацкого [1962], Паркуса [1964, 1968] и Джонса [1965].
2) Поскольку предполагается существование дифференцируемой потен-
потенциальной функции Ф (у, Т), было бы более точно называть материал, описы-
описываемый соотношениями A9.59), «гипертермоупругим».
26 д«, Одеи
402 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
Разлагая A9.60) в степенной ряд по Г и инвариантам деформа-
деформаций х), получаем
Ф = й0 + aj/j + a2/2 + a3J3
aiZJ\T + auJ* + ai5J22 + а16^3 +..., A9.62)
где a0, au ... — постоянные материала. Для простоты ограничим-
ограничимся рассмотрением свободных от напряжений в недеформированном
состоянии материалов, свободная энергия которых является
функцией, не содержащей членов выше четвертого порядка отно-
относительно деформаций и третьего относительно приращений тем-
температуры. В этом случае а0 и а17, а18, а19, . . . равны нулю. Отме-
Отметим, что при определении класса таких материалов не делается
никаких предположений относительно величин деформаций и тем-
температуры, просто выделяется класс термоупругих материалов,
функции свободной энергии которых имеют указанный вид.
В случае термоупругости при конечных деформациях приемле-
приемлемые теории могут быть построены при использовании относительно
простых форм функции свободной энергии. Например, один из
несжимаемых термоупругих материалов типа Муни характери-
характеризуется функцией свободной энергии вида
ф = a1J1 + aji + anT2 + aJxT, A9.63)
где
«i = 2 (С1! + 2С2), а2 = 4С2 A9.64)
и Сг, Сг — обычные постоянные Муни для изотермического случая.
Кроме этого, должно удовлетворяться следующее условие несжи-
несжимаемости:
J* + {Ji + р* = 0. A9.65)
В соответствии с A9.59а, б) и A5.58) напряжения и энтропия
задаются соотношениями
*1> = а^ + а2 (/,6" - &imVnymn) + bija8T+
+ h[26ij A+4/2) + 4/, F1j- 28imVnymn) + 45imVnymk Bynh-bnk)],
A9.66a)
l=-2aiT-abyH, A9.666)
где h — произвольное гидростатическое давление.
Если градиевты перемещений удовлетворяют неравенству
I ui,j I <С 1> то справедливы классические соотношения 2ytj =
х) Подобные разложения использовались Диллоном [1962] при формули-
формулировании нелинейной теории термоупругости. Другие законы связи напряже-
напряжений с деформациями для термоупругих тел предложены Рейнером [1958]
и Йиндрой [1959]. Данное здесь изложение основано на работе Одена [1969г],
см. также Оден и Поу [1970].
19. ТЕРМОМЕХАНИКА МАТЕРИАЛОВ С ПАМЯТЬЮ 403
= ии + Ujit между деформациями и перемещениями и в качестве
характеристики физически нелинейного термоупругого твердого
тела можно использовать
ф = а2/2 + а8/8
+ ак/i?72 + anJaT + а13Т3 + alsJ\T + auJ\
A9.67)
Здесь предположено, что члены выше четвертого порядка не дают
существенного вклада в свободную энергию. В зтом случае
ti} = б" [a2/i + a3J2 + 2abJi + 3a6/* + a8T + ae/2
— У и («а + яз/i + at/i + anT + 2a15/2 + a16/^) + ytkyjk (a3 + al6Jt),
A9.68a)
— I = 2aiT + a8Jt + la^Jj: + anJ2 + За^Т2 + alvT\. A9.686)
Отмечая, что определяющие уравнения A9.68) слишком сложны
для практических применений в задачах исследования напряже-
напряжений, Диллон [1962] х) предложил упрощенный вариант пред-
представления A9.67), основанный на следующих предположениях
и опытных фактах:
1. Предполагается, что линеаризованный вариант соотношений
A9.68) совпадает с классическими соотношениями, описы-
описывающими линейное изотропное термоупругое твердое тело.
Тогда
аг = -2|i, а5 = V, (Я, + 2|i), а8 = -а (ЗЯ, + 2|i),
—2Тач = с, A9.69)
где Я, и (г — постоянные Ламе, а — коэффициент линейного
температурного расширения и с — удельная теплоемкость
при постоянной деформации. [Заметим, что соотношение
а7 = —с/2Т несовместимо с соотношением A9.686), которое
было выведено в предположении независимости а7 от Т,
однако это противоречие существует и в линейной теории,
где с вводится как постоянная, удовлетворяющая условию
V-q=cT при постоянной деформации.]
2. Удельная теплоемкость дается формулой
cd = с - 2 (Т + То) (За18Г + alo/i). A9.70)
Предполагается, что cd = с = const, так что а]0 = а12 = 0.
3. Если нагрев материала при сжатии равен по величине охла-
охлаждению при растяжении, то требуется, чтобы а1Я = 0.
х) Приводимые результаты, а именно A9.71) и A9.72), представляют
собой незначительное обобщение результатов Диллона.
26*
404 ГЛ. V. НЕЛИНЕЙНОЕ |ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
4. Эксперименты на многих материалах типа металлов пока-
показывают, что соотношение между дилатационными компо-
компонентами напряжения и деформации линейно в большей
области, чем соотношение между девиаторными компонента-
компонентами. На основании этого члены четвертого и более высоких
порядков относительно деформации опускаются (а14 = а15 =
= а1в = 0), но член anJ2T сохраняется, так как он пред-
представляет собой нелинейную составляющую девиатора дефор-
деформации.
При этих упрощающих предположениях выражение для функ-
функции Ф ( ) сводится к
Ф = -2(г/2 + a3J3 + -|- (К + 2(г) /* + ae/J + a,7* -
—а (ЗА, + 2ц) JXT + ae/i/i + alxJ2T. A9.71)
Таким образом^
j * 3a,/; - a (ЗЯ, + 2|i) T + ae (/2 + J\) + аи/,Л +
B\1 — a3Jt — fltg/i—aHT)+a3yihy]kt A9.72a)
?= — 2а777 + а(ЗЯ, + 21г)/1—аи/2. A9.726)
Соотношения A9.71) и A9.72) выписаны только как пример
одной из возможных упрощенных форм определяющих уравнений
для нелинейных термоупругих тел. Отбрасывая или сохраняя те
или иные члены в степенном разложении A9.62), можно получить
ряд других форм функции свободной энергии, приводящих к нели-
нелинейным определяющим уравнениям для напряжений и энтропии.
Вопрос о том, какая из форм больше подходит для заданного мате-
материала, может быть решен лишь на основе экспериментов. При
отбрасывании нелинейных членов уравнения A9.71) и A9.72)
сводятся к классическим уравнениям линейной изотропной термо-
термоупругости. Полагая а3 = а6 = а9 = 0, получаем уравнения для
нелинейного относительно девиаторных деформаций материала,
описанного Диллоном [1962]. Случай, когда либо а3, либо ав, либо
а9 ф 0, соответствует материалу с умеренно нелинейными дилата-
дилатационными свойствами. При чисто дилатационных деформациях
выражение для \ совпадает с выражением, используемым в клас-
классической теории.
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО
ТЕРМОМЕХАНИЧЕСКОГО ПОВЕДЕНИЯ СПЛОШНЫХ СРЕД
В этом параграфе строятся конечноэлементные модели термо-
термомеханического поведения твердых тел и рассматриваются их при-
приложения к характерным задачам нелинейной термо-вязко-упруго-
сти и термоупругости.
20. КОНЕЧНОЭЛТСМЕНТНЬТЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 405
20.1. КОНЕЧНЫЕ ЭЛЕМЕНТЫ МАТЕРИАЛОВ С ПАМЯТЬЮ1)
Пусть и? (х, t) = i$> (х) «&, @ и Т<е) (х, 0 = <р# (х) Т%> @ -
локальные аппроксимации полей перемещений и приращений тем-
температуры на типичном элементе е конечноэлементной модели тер-
оо
момеханически простого тела, и пусть для зтого элемента <р<е) [ —],
«=о
ОО ОО 00
?,е>[ — 1, Jf(t)\ — ] и (?je) [—] —определяющие функционалы для
*=0 »=0 «=0
соответственно свободной энергии на единицу начального
объема, тензора напряжений, энтропии на единицу начального
объема и теплового потока. В силу соображений, высказанных
в предыдущем параграфе, мы предпочитаем выражать ф(в) [ — ]
?=0
через прошлые предыстории Yr<e>i 6?(е> деформации и температуры
и их текущие значения yL> @)» ®*<е> @)« Заметим, что полные
предыстории деформации и температуры для нашего конечного
элемента можно записать в таком виде (мы временно для простоты
опускаем идентификационную метку элемента е):
B0.1)
, B0.2)
х) Задачи ьязкоупругости, ползучести, термоупругости и термо-вязко"
упругости в конечноэлементной подстановке исследовались целым рядом
авторов. Среди первых работ по ползучести и термоупругости укажем работы
Пэдлога, Хаффа и Холловея [1960], Тэрнера, Дилла, Мартина и Мелоша
[1960], Галлагера [1061], Галлагера, Куинна и Пэдлога [1961], Галлагера,
Пэдлога и Бейларда [1962], Уоррена [1962]. См. также обзор Уоррена, Кастла
и Глории [1962].
Исследованием задач линейной вязкоупругости с помощью метода конеч-
конечных элементов занимались Кинг [1965], Чанг [1966], Уайт [1969] и другие
авторы, а конечноэлементные модели изотермических задач для нелинейных
вязкоупругих тел рассматривали Оден [1967а, 1970а] и Донг, Пистер и Дан-
хэм [1968]. Линейную задачу теплопроводности изучали с использованием
конечных элементов Вильсон и Никелл [1966] и Беккер и Парр [1967];.одна
нелинейная задача теплопроводности была решена Агирре-Рамиресом и Оде-
ном [1969].
Неустановившееся линейное термоупругое поведение твердых тел при
заданных температурных полях изучал Виссер [1966], а Фудзино и Осака
[1969] исследовали методом конечных элементов теплопроводность и распрвг
деление температур в твердых телах; см. также Бесселинг [1966]. Задачи
неустановившейся связанной линейной термоупругости рассматривались
Никеллом и Сэкмэном [1968] и Оденом и Кроссом [1969], а решения ряда
нелинейных задач динамической связанной термоупругости были получены
Оденом [1969] и Одевом и Поу [1970]. Построением общих конечноэлементных
моделей термомеханического поведения простых материалов занимались
Оден и Агирре-Рамирес [1969] и Оден [19706]. Конечноэлементный анализ
вопросов, связанных с теплопроводностью и движением термовязкоупругих
материалов, был дан Тэйлором и Чангом [1966], Тэйлором, Пистером и Гудро
[1970], Костом [1969], Оденом и Армстронгом [1971], Оденом [1971г].
406 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
где подразумевается, что y\j (s),tyNi, 0* (s) и q>N являются функция-
функциями от х. В формулах B0.1) и B0.2) uf{i) (s) и Тт) (s) — предысто-
предыстории узловых значений компонент перемещений и изменения тем-
температуры (отклонений от некоторой постоянной во времени и в
пространстве отсчетной температуры То) в узле N элемента. Следо-
Следовательно, в соответствии с A9.36) определяющие уравнения для
элемента можно записать с помощью функционалов от предыстории
и? и Т":
Ф<«> = Г(е> [u?w, If»; nN, T\ B0.3а)
«=0
u",r"], B0.36)
«=о
S(e)= !Q(e) lUr , 1T , U , 1 J, (ZU.OB)
»=0
д1=1\е){и^\Т^\^,Т\ B0.3г)
v' »=o
Здесь ufw, T?®—ограничения uN(t — s), TN(t — s) на @, oo),
«=0 №=0
Y [x, um @)], 0 [x, TNit> @)]}, B0.4a)
д t?{Y(X) uf}) 0(X
Y [x, uW) @)], 0 [x, T™ @)]}, B0.46)
|() [ = - Д, Ф» {^ (x, u^>), tf (x, Tf\
Y [x, um) @)], 0 [x, Tm @)]}, B0.4b)
*=0 »=0
Y [x, u"» @)], 0 [x, rW(t) @)], Tm)V<pN (x)} B0.4r)
и для простоты введено обозначение [u^<*>, T*?V); uN (t), TN (t)] =
= [u^'), TN№]. Аналогично внутренняя диссипация для элемента
задается соотношением
()()uN,^], B0.5)
8=0
где
- ®(е) [ - ] = 6V Ф(е) [ +1 u?(t>] + б9 Ф(е) [ +1 ff»]. B0.6)
0 0 0
V [ 1
»=0 «=0
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 407
Здесь использовано обозначение
[ +1 i?»l - {V; (ж, nf»), в* («,!*»);
у [х, иГ} @)], 0 [х, Т™ @)] | Щ (х, s) и$?}, B0.7а)
где «6@, оо),
f%l(x,s) = ±1pN,mzin(s)(8jn6mi + 6in&jm) B0.76)
и zlk,n(s)—предыстории градиентов перемещений:
4.«(s) = Snft + г|>м, „uf(t) (s). B0.7b)
Массив B0.76) дает возможность рассмотреть преобразование
й»= -?тЬ»М = -?j^ = -У»5« W- B0-8)
Подставляя B0.3) и B0.5) в A3.60) и A3.117), получаем общие
уравнения движения и теплопроводности для конечных элементов
термомеханически простых сред:
#[ ]^<т(и + рм,^H рт, B0.9)
»=0
rO(e>
" dvo = gN + aN, B0.10)
где pNi nqN — компоненты обобщенных сил и нормальные компо-
компоненты теплового потока в узле N, задаваемые формулами A3.54)
и A3.115), а обобщенная диссипация aN в узле A3.116) определяет-
определяется по формуле
N= \ S(el[uw» ^«Цр^. B0.11)
%
'О(е)
Поскольку глобальные формы зтих уравнений получаются
непосредственно применением соотношений A3.74) — A3.77) и
A3.118) — A3.120), мы не будем их здесь приводить.
Интересно отметить, что B0.9) можно по аналогии с A6.131)
переписать в виде
Pm = mNrfl"+ [ V^'tv'.e'l^o, - B0.12)
408 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
где
оо оо
' \ е'; y» 0
оо..
&[ ]
0 ди
B0.13)
А
Точно так же в B0.10) вместо d §ш [uW>, Т*ЩШ можно
»=о
использовать
-i- Z)TJV Ф(е> [Y(, 0'] = Z)9 Ф(е) [Y,«, 6<; у, 0] -JL f ". B0.14)
Понятно, что в соотношениях B0.11) — B0.13) y' и 0* должны
быть выражены (или определены) через предыстории узловых
величин u N<-t'> и TNW. Таким образом, конкретные формы уравне-
уравнений движения и теплопроводности для элементов можно получать,;
непосредственно используя функционал свободной энергии и функ-
функционал теплового потока данного материала. В следующих пунктах
рассматриваются приложения этих уравнений к некоторым задачам
термо-вязко-упругости и неустановившейся термоупругости.
20.2. ПРИМЕНЕНИЕ К СЛУЧАЮ ТЕРМОРЕОЛОГИЧЕСКИ
ПРОСТЫХ МАТЕРИАЛОВ
В случае термореологически простого материала, определяемо-
определяемого соотношениями A9.56), A9.57) и, скажем, A9.46), удобно пре-
преобразовать входящие в них величины к приведенному времени ?,.
Если действительное (неприведенное) время можно выразить через
приведенное, т. е. существует g (?) = t, и b W (x, ?,)] == b [6 (х, t)]—
коэффициент смещения A9.50) (здесь 0 = То + Т), то для любой
функции действительного времени t (и х)
/(х, *) = />, ?N[§(х, ?)], B0.15)
где f = df/d?. Отсюда следует, что
uf = S@)uf,
uf = S2 @) uf + b @) 5 @) uf, B0.16)
и т. д. (подразумевается, что величины щ1, 0 и др. зависят от ?).
Подобные же соотношения имеют место для ^, ^' и а.
20. КОНЕЧНОЭЛЕМВНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 409
В качестве конкретного примера рассмотрим материал, опре-
определяемый соотношениями A9.46), A9.56) и A9.57). Предположим,
что р0? « р^о? и 2уи = utj + Ujt. Тогда, преобразуя получаю-
получающиеся уравнения к приведенному времени с помощью B0.15)
и B0.16), мы приходим к следующим уравнениям движения и теп-
теплопроводности термореологически простого элемента в^приведен-
ном времени:
диУ
м • -* \ 2G(? —s)—i-ds +
bl \
ds
3K(^ — s)^K-ds = pNh(t,), B0.17)
0
о 6
J J
J J
EC
J
B0.18)
410 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
Здесь s = f(s), /—функция, определяемая соотношением B0.15), и
J
"(Не)
(е>
=Y J
"o<
WMA = " J
= a J
o<e>
(e)
B0.19)
^Miv= J Фм. iVn, t dv0,
v0(e)
««, =-g- J фм^лг, i'l'L, / dv0,
= J
г0<е)
=-2- J
°0<e)
*0(e>
Чтобы получить численные решения уравнений B0.17) и B0.18)»
мы предположим, что ядра в интегралах, входящих в этп уравне-
уравнения, относятся к ядрам материалов с затухающей памятью, т. е.
материалов, на поведение которых в текущий момент времени
несущественно влияют значения деформаций и температур в отда-
отдаленном прошлом. Выполнения этого свойства обычно достигают.
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 411
принимая, что ядро представимо в виде «распадного» ряда Прони;
типичное ядро К (?) представляется в виде ряда
B0.20)
1=1
где Ki и v,- — экспериментально определяемые постоянные
(vj >• 0) и С >• 0. Что касается ядер вида G (?, 5')» то часто пред-
предполагают, что они удовлетворяют условию
С (Б - Б', Б - Г) = G B5 - Б' - Г), B0.21)
так что в соответствии с B0.20) можно записать
<?(Б-Б\ Б-Б')= 2 (|)
i=; B0.22)
и т. д., где Я,г — положительные постоянные.
Рассмотрим теперь типичный интеграл, входящий в записанные
ранее определяющие уравнения; например,
5')-^MC- B0.23)
Удобное для численных аппроксимаций представление интеграла
B0.23) можно получить, разбивая интервал приведенного времени
[0, 51 на г подынтервалов [?m, tm^h те = 1,2, ...,г+1. Исполь-
Используя для ядра, входящего в B0.23), представление B0.20), имеем
ign}=s G*~yh S J •+t'/X| чг к- B0-24>
i=l m=l Em
Если hm = 5ти — ?m — шаг по времени, то интегралы в B0.24)
можно приближенно вычислить с помощью правила Симпсона:
а
ехр
412 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
Далее производные duf/dt, надо заменить разностными аппрокси-
аппроксимациями. Будем предполагать, что uf между узлами т — 1, т,
т + 1 меняется по квадратичному закону; тогда производные
аппроксимируются с погрешностью О (h2). Подставляя разностные
аппроксимации производных в B0.25), после перегруппировки
членов получаем следующее выражение для интеграла* B0.23):
н («. V' B0-26)
»
где
/jl (u, Я) = Я («f, к,) ехр [~УМ] + С (wf, Я,), B0.27а)
г-1
Я (щ , Xt) — 2
m—i
, 2
B0.276)
С (uf, %t) = i $?+«- «&-«) ехр ( ^) +
j;^ J +
^±^]. B0.27в)
В B0.27а) предыстории Н (uf, А.г) отделены от текущих значений
С (uf, А.,), т. е. величина интеграла в текущий момент ?г + К
получается добавлением к сумме, накопленной к моменту времени
?r, члена, соответствующего интервалу времени между 1Г и ?r + hr.
Под uf(m), м,чт-1) и т. д. понимаются uf (t,m), uf(lm — hm) и т. д.
При использовании обозначений B0.27) уравнения движения
и теплопроводности термореологически простого конечного элемен-
элемента принимают вид
_ т и-Л-т' и-Л-(п h Л V Г Т-(
k
+ Ъ{мю 2 K%J" («, v)- c*w 2 ^/" (Л v), B0.28a)
—-/и (Г, v) —
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 413
2 ^
h
, v) + ftWJlf 2 ^/f (Л е). B0.286)
После связывания элементов получается система существенно
нелинейных ди^реренциальных уравнений относительно узловых
вначений и?, TN и их предыстории.
Пример. Неустановившееся поведение термовязпоупругого
толстостенного цилиндра1). В качестве иллюстрации применим
B0.28) к задаче о бесконечно длинной толстостенной круговой цилиндрической
трубе при заданных механических и температурных воздействиях на ее внут-
внутренней и наружной границах. Для конечноэлементной аппроксимации компо-
компонент перемещений и температуры воспользуемся симплексными аппроксимаци-
аппроксимациями урк (г) = dpj + bNr, n=l, 2, где av и6№— постоянные, зависящие только
От протяженности конечного элемента в радиальном направлении [для эле-
элемента, заключенного «между радиусами» гх и г2, ах = —а2 = —1/(га — rt),
6j = г2/(г2 — rt), 62 = rll(r2 — rt)]. Подставляя эти интерполяционные функ-
функции в массивы B0.19), получаем все коэффициенты уравнений дискретной
модели, не зависящие от свойств материала.
Далее надо определить вид функции смещения 6 (9). Уильямсом, Лэнде-
ром и Ферри [19551 для широкого класса полимеров, жидких полимеров,
органических и неорганических стекол была предложена следующая эмпи-
эмпирическая формула для Ь (9):
lg о @) = —^.
р + 0 —10
Здесь а и 3 — постоянные. Согласно экспериментальным данным (Эринген
[1967]), при [ 0 — То /< 50 °С мы имеем a « 9 и р я* 100, так что если
Го = 0 "С, то
B0.29)
где для нашего конечного элемента Т = <pN (г) Тк = (aN + Ь^г) TN. Пере-
Переходя к приведеняому времени, получаем
Ъ @") = 10*, [6 = (Ъ In 10) х, B0.30а,б)
где
?*>»(**" Bо.зов)
и f * представляется, как и выше, с помощью разностей второго порядка.
1) Этот пример был рассмотрен Оденом и Армстронгом [1971]; ем. также
Оден, Чанг и Ки [1971].
414 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
При численном интегрировании текущее значение Ъ (9) считается посто-
постоянным на каждом шаге, так что бит отстают от текущих значений на вели-
величину, соответствующую размеру текущего шага hr. В конце каждого шага
по времени значения бит пересчитываются, и эти пересчитанные значения
используются на следующем отрезке времени для определения узловых пере-
перемещений и температур. При этом матрицы массы mj^ и m']^'N удается пред-
представить в особенно простом виде:
т% = 2я 1п A0) хМNM, B0.31а,б)
(aNbM-\-aMbN)(rl-r\) bNbM (r§ — r\)
+
+
bNbM (r§ — r\)
+ 2 J"
B0.31b)
Здесь принято yN (r) « aN + bN (rx -j- r2)/2. Аналогичным образом вычис-
вычисляются и другие интегралы в уравнениях движения и теплопроводности.
Если пренебречь объемными силами и внутренними тепловыми источ-
источниками, то выражения для обобщенных сил и тепловых потоков принимают
вид
PN = rN(aN + bNrN)SN(Z), qN=rN(aN + bNrN)QN(Q B0.32a, б)
(по N суммирования нет), где SN (?) и Qy (?) — заданные функции приве-
приведенного времени. Можно также взять в качестве заданных произвольно
зависящие от времени узловые перемещения и температуры. В задачах с кон-
конвективной теплопередачей полагаем
QN = fN<X-T%), B0.33)
где fN — коэффициент теплопроводности в узле N и Т% — температура
окружающей среды вблизи границы цилиндра х).
Завершим постановку задачи. Мы рассматриваем гипотетический матери-
материал, для которого р0 = 10~3 фунт сек^дюпм4, а = 10~5 дюйм/дюйм °С, ядро
дилатационной релаксации К (?) = 10 X 105 ехр ( — ?/10~5 ) + 5 X
X Ю5 ехр (—t/oo) фунт/дюйм2, ядро сдвиговой релаксации G (g) = 1 X
X 105 ехр (—J/IO) + 0.1 X 105 ехр (—tj°°) фунт/дюйм2 и ядро теплопро-
теплопроводности в законе наследственного типа A9.46) х (?) = 0.10 ехр (—J/10-5) +
4- 0.01 ехр (—?/оо) фунт/дюйм °С сек.
Теперь применим записанные выше соотношения для изучения поведе-
поведения цилиндра с внутренним радиусом 10.0 дюйма и наружным радиусом
11.0 дюйма, стенка которого, имеющая толщину 1.0 дюйма, разбита на двад-
двадцать 0.05-дюймовых элементов. Систему нелинейных дифференциальных
уравнений, описывающую поведение этой модели, интегрируем, используя
упомянутую ранее явную квадратичную схему; однако вследствие наличия
нелинейных членов наследственного типа на каждом шаге по времени полу-
получается система нелинейных алгебраических уравнений относительно текущих
значений узловых перемещений и температур. В приводимых ниже примерах
эти уравнения решались методом Ньютона — Рафсона.
Начальные значения для метода Ньютона — Рафсона определяются
из начальных условий [если, например, иN (?„) = иN (?o) = TN(?o)=
= * (So) = 0, то^центрально-разностные аппроксимации производных и
• ••••••
и fN непосредственно позволяют выразить uN, 7iN, fN и t nb момент вре-
времени ?0 + h через значения uN и fN при ?0 + h]. Подсчитанные таким обра-
J) Более подробное обсуждение вопросов моделирования различных
краевых условий можно найти у Одена и Кросса [1969].
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 415
8ом начальные значения подставляются в B0.28), и в результате опреде-
определяются перемещения и температуры при ?0 + h и величина т (см. BО.ЗОв)),
которые используются на втором шаге по времени. На этом втором шаге для
различных производных опять используется квадратичная аппроксимация
Umi-i «C Um+i — 4мт + um_i)/2fe. Таким образом находятся начальные
данные для итерационного процесса Ньютона — Рафсона. После того как
процесс сойдется с заданной степенью точности, добавляется новое прираще-
приращение приведенного времени и процесс продолжается.
Напряжения в элементах подсчитываются в конце каждого шага по вре-
времени путем подстановки узловых перемещений и температур в определяю-
определяющие уравнения для напряжений A9.57а). Все величины (узловые перемеще-
перемещения, температуры и напряжения в элементе) подсчитываются в виде функций
приведенного времени, а затем преобразуются к реальному времени с помо-
помощью соотношения Д* = Д?/6[9(?)], где Д? =h — приращение приведен-
приведенного времени и 6 (9) определяется формулой B0.30а). Реальное время на
(г + 1)-м шаге равно, следовательно, tT + Mb [9 (?)].
Отметим, однако, что м и t определяются для приведенного вре-
времени, отличного от приведенного времени, при котором определяются напря-
напряжения; а именно, коэффициент смещения для узловых значений м и f
определяется изменением температуры одного-единственного узла, тогда
как тензору напряжений отвечает коэффициент смещения, определяемый
температурным полем всего элемента и потому зависящий от изменений тем-
температуры в каждой точке элемента. В первом случае мы просто полагаем
приращение реального времени Д*г, относящееся к узловым значениям
цг, Тт, равным h/br, где Ъг — (глобальное) значение 6 (9) в узле Г. Во вто-
втором случае (для напряжений) приращение реального времени Д?(е) для эле-
элемента е принимается равным Л/Ь(е>, где 6(е) — среднее значение коэффициента
смещения для элемента е.
В качестве примера рассмотрим динамическое поведение цилиндра при
мгновенном нагружении давлением р = iOh (t) фунт/дюйм2 \h (t) — единич-
единичная ступенчатая функция] по внутренней границе и краевых условиях кон-
конвективного теплообмена. Коэффициенты теплопроводности на внутренней
и наружной границах равны соответственно 0.1 и 1.0 дюйм фунт/дюйм2 °С сек.
Предполагается, что внутренние источники тепла отсутствуют; начальная
температура цилиндра и окружающей среды принята равной 300 °К. Изме-
Изменение температуры, таким образом, происходит вследствие термомеханиче-
термомеханических эффектов. Для рассматриваемых параметров материала и условий
нагружения установившееся состояние достигается примерно через 10~* сек.
Для сравнения можно также получить решение в изотермическом случае
при пренебрежении тепловыми эффектами, если положить 6 = 1, 6 = 0
и принять за переменную интегрирования реальное время.
Результаты расчета волн окружных и радиальных напряжений в раз-
различные моменты реального времени для изотермического и неизотермиче-
неизотермического процессов приведены в виде безразмерных графиков на рис. 20.1
и 20.2; эпюры перемещений показаны на рис. 20.3. Хотя эпюры напряжений
и перемещений для изотермического и неизотермического процессов соответ-
соответствуют различным моментам времени (так как для неизотермичзского про-
процесса все величины надо преобразовывать к реальному времени), результаты
указывают на запаздывание неизотермических волн напряжений и заметное
уменьшение амплитуды.
Окружные напряжения вначале сжимающие, но затем при t = 10~3 сек
они почти всюду в цилиндре становятся растягивающими. Для прохождения
1.0-дюймовой толщины цилиндра изотермической волне окружных напряже-
416
ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
Изотермический
процесс
Неизот ернический
процесс
Время в секундах
Рис. 20.1. Распространение напряжений в термореологически простом
цилиндре. Зависимость безразмерного окружного напряжения от расстояния
по радиусу для различных моментов реального времени.
-1.0
-0.8-
.§ -0.6 -
I
«3
-0.4-
-0.2-
10.0
10.2
10.4 10.6
Родиуф Зюймаос]
11.0
Рис. 20.2. Распространение напряжений в термореологически простом
цилиндре. Зависимость безразмерного радиального напряжения от расстоя-
расстояния по радиусу для различных моментов реального времени.
20. КОНЕЧНОЭЛЕМЕНТН ЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 417
КГ3
ю
-4
10"9
-f=5*1Cf
Изотермический
процесс
Неизотермическии
процесс
Время в секундах
10.0
10.2
11.0
10.4 10.6 10.8
Радиус^) дюймах)
Рис. 20.3. Эпюры радиальных напряжений для различных моментов реаль-
реального времени.
ний^требуется примерно 2.5-Ю сек, а неизотермической волне — примерно
4.0 -10 сек. Эпюры перемещений при изотермическом и неизотермическом
процессах качественно подобны. На наружной границе неизотермические
перемещения больше изотермических, а на внутренней границе меньше. Это
в основном обусловлено величинами коэффициентов теплопроводности на
границах. Отметим, что приведенные численные результаты получены при
использовании приращений приведенного времени величины 10~в сек; на
каждом шаге по времени наблюдалась довольно быстрая сходимость итераций
Ньютона — Рафсона.
На рис. 20.4 представлены результаты расчета изменения температуры
по толщине цилиндра для различных моментов реального времени. Видно,
27 Дж. Оден
418 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
§;
to
J4.
*i
С:
<ь
i
10-2
о
2>
e
<э
p.
| 10-3
s
1
I
О 10-4
I
a-
10"s
i
Время в секундах
: \ \ \A\
- v1 V \ \ \
- v * \ \ \
I \ \ \
Г \ \
II 11 1 II
10.0 10.2 10.4 10.6 10.8
РодиуфЬюймах)
11.0
Рис. 20.4. Распределения безразмерной температуры в различные моменты
реального времени.
что сначала нагруженная внутренняя граница нагревается. Максимальной
величины температура достигает примерно при t = 4 X 10 сек, а затем
температура понижается.
20.3. ПРИЛОЖЕНИЯ К ТЕОРИИ НЕЛИНЕЙНОЙ
СВЯЗАННОЙ ТЕРМОУПРУГОСТИ
Для термоупругих тел внутренняя диссипация равна нулю,
свободная энергия предполагается дифференцируемой функцией
от текущих деформации и температуры и нагружение и энтропия
определяются через свободную энергию с помощью соотношений
A9.59). В этом случае уравнения движения и теплопроводности
для типичного термоупругого элемента имеют вид
::м . г дФ (Уи, т) ,л
, dv0 = pNh, B0.34)
ЧКе)
d дф\
~di
Г)
dT
v0(e)
B0.35)
Задавая вид функций Ф (у1}, Т) и Ql (ytj, T, V Т) для рассматривае-
рассматриваемого материала [как, например, в A9.46), A9.63), A9.67) и A9.71)],
мы можем получать различные частные формы уравнений B0.34)
и B0.35).
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 419
Пример. Нелинейное термоупругое полупространство.
В качестве характерного примера приложения уравнений B0.34) и B0.35) к за-
задаче о неустановившемся поведении нелинейной термоупругости рассмотрим
нелинейный вариант задачи Даниловской *), т. е. задачи о неустановившемся
поведении термоупругого полупространства при переменном во времени
нагреве его границы. Предполагается, что при бесконечно малых деформа-
деформациях поведение материала описывается нелинейным определяющим законом
типа A9.71), A9.72а) и A9.726) [мы также удерживаем член а^з в A9.67)]
а тепловой поток описывается нелинейным законом Фурье:
4i = *о A + в Г) Тл,
где. х0 — теплопроводность при Т = 0 и е — параметр материала. Тогда
B0.34) и B0.35) принимают вид
°0(е)
-j (а3+ад) (yrryss-yrsyrs)-a $Х+2ц) Т
То ]
+ Bц—агутт—а9у;т — аиТ) yij+a3yiryir | 6ifti|)w,) dvo = pNht B0.37)
fN (*) [2а7Г — а (ЗЯ+ 2ц) угг+ аи (ТГгТ«—ТгЛм) +
°0(е)
+ 6a12rr+2e1S7rrY«<i]d»o- j Xo{l + eT)&iMN,iTt}dDo = gN*, BOJ38)
°0(е)
здесь X и [х — постоянные Ламе; ^а — коэффициент линейного температур-
температурного расширения; а3, ае, ат, ад, an, a12 и ai3 — постоянные материала; уц =
tf f/ n
Рассмотрим изотропное физически нелинейное термоупругое полупро-
полупространство х :> 0 из материала, которому отвечают уравнения B0.37) и B0.38),
при одноосных движениях, описываемых формулами
щ = и (ж, *), и2 = и3 = 0.
Граничная поверхность а^ = 0 считается свободной от напряжений, и пред-
предполагается, что она1 равномерно нагревается по кусочно-линейному закону
вида
Т1 = 0 при — oo<t<0,
при
при t0<t<oo,
J) Впервые несвязанная линейная задача была рассмотрена В. И. Да-
Даниловской [1952], чье имя и получила эта задача. Решения связанной линей-
линейной задачи в явном виде были даны Стернбергом и Чакравортл J1959J,
а конечноэлементные решения — Никеллом и Сэкмэном [1968] и Оденом
и Кроссом [1969]. Излагаемое, здесь обобщение на нелинейный случай при»
надлежит Одену и Поу [1970]. . . :.,.„;;
27*
420 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
где Тг — вачальвая температура поверхности, Tf — конечная температура
поверхности и t0 — время нагрева границы. Поскольку предполагается,
что первоначально тело находится в покое, перемещения и напряжения при
температуре Tj удовлетворяют начальным условиям
Л*. 0) = 0, дЛ< '*• 0)t= 0, 0 < х < oo.g
at
Для простоты мы используем симплексные \аппроксимации (полей [пере-
[перемещений |и температуры в элементе, так что?_
где
"¦w (*) = aN + bmx, N = 1, 2.'t
При этом уравнения движения и теплопроводности для^твпичного конечного*
элемента принимают вид:
B0.39а)
¦ fWD(T)T0 ,j L0^
92 e
Ч—р-«в ("i-^^-^-^ + TzJt"?^^), B0.396)
!^^), B0.40а)
-12)-^.Чз (щ-иг) (и^ъ), B0.406)
где L—длина элемента. Введем безразмервые перемеввые:
B0.41a)
Д20.416)
В выписанных выше соотношениях I — характерная длина, t — реальное
время, «о — начальный коэффициент теплопроводности, сд (Т) — завися-
зависящая от температуры удельная теплоемкость при постоянной деформации,
Яиц — постоянные Ламе, а — коэффициент линейного температурного
расширения, S — параметр термомеханической связности.
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 421
0.7
0.6
к? °'5
ю> 0.4
0.2
0.1
о Линейная связанная задача, S = 1-0
d Линейная несвязанная задача, 5--0.0
„Точное" решение, 8 = 1.0
„Точное11 решение, 5 = 0.0
0.Б 1.0
Безразмерное время
1.5
2.0
Рис. 20.5. Температура линейного связанного и яеевизанного полупро-
полупространств при I = 1.0 для ?0 = 1-0.
Численные результаты о влиянии термомеханической связности, физи-
физической нелинейности и зависящих от температуры удельной теплоемкости
и теплопроводности на решение нашей задачи для полуплоскости представ-
представлены на рис. 20.5—20.12.
Дифференциальные уравнения, полученные с помощью метода конечных
элементов, решались методом Рунге — Кутты — Гилла. На рис. 20.5 и 20.6
представлены^численные результаты для линеаризованного материала, для
которогоПизвестны^точные решения (Стернберг и Чакраворти [1959]). Здесь
показана зависимостьТбезразмерных температуры 9 и перемещения U при
I = 1.0 и значениях параметра термомеханической связности S = 0.0 и S =
= 1.0 от безразмерного времени ? для ?0 = 1.0 и ?0 = 0.25 соответственно.
Эти результаты получены при использовании 50-элементной модели с 10 эле-
элементами между граничной поверхностью и поверхностью I = 1.0.
Влияние^физической нелинейности качественно показано на рис. 20.7
и 20.8. Эти результаты получены при использовании 50-элементной модели
для материала с 8 = 0.0, S = 1.0, для ?0 = 1.0. Отметим, что такая величина
параметра связности характеризует сильную термомеханическую связан-
связанность для металлических материалов. Влияние нелинейности за счет членов
ав и а13 сказывается на уравнении теплопроводности через член, характери-
характеризующий связанность. Значения постоянных материала ав и ai3, входящих
в B0.39)~и B0.40), после приведения к безразмерному виду в соответствии
с B0.41) обозначены через At и А13.
На рис. 20.7 представлена температура при I = 1.0 в виде функции
от ? для четырех случаев: Ав = 0.05, А13 = 0.0; А6 = 0.25, А13 = 0.0;
Ае = 0.0, А13 — 0.05; Ае = 0.0, Axs — 0.25. На ри-. 20.8 показано изме-
изменение перемещения во времени при I = 1.0 для тех же самых четырех слу-
случаев. Разница в температуре для случая Ае = А13 = 0,05 очень мала. В слу-
случае Ag = 0.25 для ? ^ 1.2 нет существенных отклонений от линейной теории.
422 (ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
0.14
0.12
S 0.08
В 0.06
0.04
0.02
Линейная связанная
0 задача, 8=1.0
Линейная несвязанная
а задача, 8=0.0
„ Точное " решение,
8=1.0
„ Точное" решение,
8=0.0
V
0.5 1.0 1.5
Безразмерное время 4
2.0
Рие. 20.6. Перемещение линейного связанного и несвязанного полупро-
полупространств при I = 1.0 для ?о = 1.0.
с*.
0.7
0.6
0.5
0 3
0,2
0.1
OLa
a >«,j= 0 25, Аь -- C = Е = 0, 8-- 1.0
A xt13 - 0. 05 , Ak = р = с = 0, 8= 1.0
о Аь- 0 25, Ап-р = е = 0, 8 = 1.0
ОИ6=0. 05,-413-P = ?i0,S =
Линейная связанная
задача, 6 = 1.о
о
1.0 1.5 2.0 2.5
Безразмерное время <
3.0
i.b
4.0
Рве. 20.7. Температура нелинейного полупространства при I — 1.0 для
{о = 1.0, при различных значениях постоянных нелинейного материала.
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 423
0.10
$ -сю
|
? -0.20
-0.30
-0.40
5 3.0 3.5 4.0
л /A3=o.O5,-vp = e=o, 8=1-
о A6= 0.25, /413= p = 6 = 0,8 = 1.0
0 Линейная связанная задача, 8=1.0
Безразмерное время t,
Рис. 20.8. Перемещение нелинейного связанного полупространства при
I = 1.0 для ?о = 1-0, при различных значениях постоянных нелинейного
материала.
Это обусловлено тем, что нелинейность сказывается только через члены
второго порядка относительно перемещений и, по-видимому, лишь при гораз-
гораздо больших значениях Ав может заметно повлиять на уравнение теплопро-
теплопроводности. Влияние постоянной А13 на температуру выражено более заметно,
поскольку она входит как в уравнения теплопроводности, так и в уравнения
движения. Это влияние ясно проявляется при А1з !> 0.25 для Z, !> 0.8.
При ? = 1.0 появляется также ощутимая разница в перемещениях, которая
со временем существенно увеличивается. Для значений А@ и А13, превышаю-
превышающих 0.25, влияние физической нелинейности выражено очень ярко. Заметим
что в рассмотренном примере сдвиговые явления не обнаруживаются.
На рис. 20.9 и 20.10 показано влияние на поведение материала зави-
зависящих от температуры коэффициентов удельной теплоемкости и теплопровод-
теплопроводности для материалов с б = 1.0 и Ag = Ai3 = 0 при кусочно-линейном нагре-
нагреве, для ?0 = 1.0. Ради простоты предполагается, что удельная теплоемкость
меняется при изменении температуры в каждом отдельном узле и имеет вид
cD = «о + РГ, B0.42)
где с0 — обычно используемая постоянная удельная теплоемкость и Р харак-
характеризует скорость изменения удельной теплоемкости при изменении темпе-
температуры. Хотя эта формула удельной теплоемкости не использовалась при
оценке величины приращения температуры, фигурирующего в B0.37) и
B0.38), она вводится, чтобы можно было количественно проиллюстрировать
влияние на поведение материала зависящей от температуры удельной тепло-
теплоемкости. Как показали Ходжмэн, Вист и Селби [1956], соотношение B0.42)
точно описывает экспериментально определенную зависимость удельной
теплоемкости от температуры для железа и алюминия в диапазоне от 0 до
400 СС.
При использовании значения с0 для железа, соответствующего 0 СС,
удельная теплоемкость, подсчитанная по формуле B0.42) для различных Р,
несущественно влияет на величины температур или перемещений при I = 1.0.
424 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
0.5 1.0 1.5 2.0 2.5 3.0
Безразмерное время <
3.5
4.0
Рис. 20.9. Температура связанного полупространства с зависящими от тем-
температуры удельной теплоемкостью и теплопроводностью при I = 1.0 для
?о = 1.0.
0.10
0
-0.10
-0.20
-0.30
„ Ir^^' I
0.5 1.0
-
t>? = 0.1 Ae~ /4-17= |3 =
Ь ?=0.25,/1g=/413= |3
О |3 = 0.1 >>4g=/4i3:=?
1.5
0,8=1.0
о Связанная линейная
задача, 8=1.0
V
2.0 ^
!7 I
|&(?5
I
3.0
I
3.5 4.0
Безразмерное время 4
Рис. 20.10. Перемещение связанного полупространства с зависящими от тем-
температуры удельной теплоемкостью и теплопроводностью при I = 1.0 для
Со = 1.0.
20. КОНЕЧНОЭЛЕМЕНТНЫЕ МОДЕЛИ НЕЛИНЕЙНОГО ПОВЕДЕНИЯ 425
II
r
Темт
V.I
0.6
0.5
0.4
O5
0.2
0.1
0
д А6=Ап--о.гъ, р=е = о
о ^e^is^P^630-25-8
о Связанная линейная
задача, 8=1.0
8=1.0 ^r**J*"~^*^
= 1.0 л*****^ s*&?%%*
I I I I
0.5 1.0 1.5 2.0 2.5 3.0
Безразмерное Время i,
3.5
4.0
Рис. 20.11. Температура связанного физически нелинейного полупростран-
полупространства с зависящими от температуры удельной теплоемкостью и теплопровод-
теплопроводностью при I = 1.0 для ?о = 1.0.
V |3 = -6=0.25,/46=/413=0, 8=1.0
? /46=/413=|J = -e=0.25, 8 = 1.0
Обязанная линейная
задача.
-0.40
Безразмерное время
Рис. 20.12. Перемещение связанного физически нелинейного полупростран-
полупространства с зависящими от температуры удельной теплоемкостью и теплопровод-
теплопроводностью при I = 1.0 для ?о = 1-0.
426 ГЛ. V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ
Представленные на рис. 20.9 и 20.10 результаты, характеризующие влияние
величины Р на поведение материала, получены при использовании удельной
теплоемкости железа при 0 °С и значениях Р = 0.25 и 0.1 и 8 = 0.0. При
Р = 0.1 величина со примерно удваивается, а при р = 0.25 удельная тепло-
теплоемкость увеличивается примерно на 250% с изменением температуры до
Т = 1.0. Аналогично значение 8, вычисленное на основании эксперименталь-
экспериментальных данных (Якоб, [1962]) для железа, по существу не влияет на значения
температур и перемещений для проявляющего линейные свойства материала
с р = 0.
Другие случаи, представленные на рис. 20.9 и 20.10, отвечают значе-
значениям 8 = —0.1 и —0,25, которые характеризуют соответственно 10- и 25-про-
25-процентное уменьшение теплопроводности для Т = 1. Такое уменьшение тепло-
теплопроводности с увеличением температуры согласуется с экспериментальными
данными для ряда металлов, например железа (Якоб [1962]).
Эти результаты показывают, что соответствующие действительности
значения ей р вызывают понижение температуры в материале со временем.
Температурные эффекты сказываются на уравнениях движения через пара-
параметр термомеханической связности. Они вызывают уменьшение перемещений
при I = 1.0.
На рис. 20.11 и 20.12 показано совместное влияние нелинейных членов
Ag и А1з и зависящих от температуры теплопроводности и удельной тепло-
теплоемкости на поведение материала при кусочно-линейном нагреве для ?0 =
= 1.0. Приведенные кривые отвечают значениям постоянных материала
Ав = А13 = 0.25, Р = 8 = 0; А6 = А1з = 0, Р = 0.25, 8 = —0.25; Ав =
= А13 = р = 0.25, е = —0.25.
СПИСОК ЛИТЕРАТУРЫ
В этот список включены лишь работы, использованные при написании
книги. Курсивные числа в скобках в конце каждого описания указывают
параграф и/или пункт, где имеется ссылка на работу.
Авила (J. Avila)
[1970] Continuation methods for nonlinear equations, doct. diss., Univ.
of Maryland, College Park A7.5)
Агирре-Рамирес, Оден (G. Aguirre-Ramirez, J. T. Oden)
[1969] The finite element technique applied to heat conduction with tem-
temperature dependent thermal conductivity, Heat Transfer Division,
ASME Winter Meeting, Nov. 16—20, ASME Paper 69-WA/HT-34
A3.8, 20.1)
Агирре-Рамирес, Оден, By (G. Aguirre-Ramirez, J. T. Oden, S. T. jWu)
[1970] A numerical solution of the Boltzmann equation by the finite ele-
element technique, Proc. 7th Inter. Symp. Rarefied Gas Dyn., Univ.
degli Studi di Pisa, Pisa, June 29 — July 3, Academic Press,
Inc., N.Y. A1.4)
Айзаксон, Келлер (Б. Isaacson, H. В. Keller)
[1966] Analysis of numerical methods, John Wiley & Sons, Inc., N.Y.
A7, 17.2, 17.5)
Айронс (В. Irons)
[1966] Engineering application of numerical integration in stiffness method,
AIAA /., 4, 2035—2037. [Русский перевод: Ракетная техника
и космонавтика, 4 A966), № 11, 213—216.] A0.4)
Айронс, Дрейпер (В. Irons, К. J. Draper)
[1965] Inadequacy of nodal connections in a stiffness solution for plate ben-
bending, AIAA J., 3, № 5, 961. [Русский перевод: Ракетная техника
и космонавтика-, 3 A965), № 5, 206—207.] A0.2, 10.4)
Алберг, Нильсон, Уолш (J. H. Ahlberg, E. N. Nilson, J. L. Walsh)
[1967] Теория сплайнов и ее приложения, «Мир», М., 1972. A0)
Александер (Н. Alexander)
[1968] A constitutive relation for rubber-like materials, Inter. J. Eng. Sci.,
6, № 9, 549-563. A5.5, 18.1)
Аллен (D. N. de G. Allen)
[1954] Relaxation methods, McGraw-Hill Book Company, N.Y. A7.3)
Арантес э Оливейра (E. R. de Arantes e Oliveira)
[1968] Theoretical foundations of the finite element method, Inter. J.
Solids Struct., 4, 929—952. A0, 10.2)
[1969] Completeness and convergence in the finite element method, Proc.
2d Conf. Matrix Methods Struct. Mech., AFFDL-TR-68-150 (Oct.
15—17, 1968), Wright-Patterson AFB, Ohio, 1061—1090. A0)
l) Звездочкой помечены работы, добавленные при переводе. Для пере-
переводных книг год в квадратных скобках — это, как у автора, год выхода
оригинального издания; год выхода перевода приводится на обычном месте
в самом описании. Если он предшествует году в квадратных скобках, то это
означает, что перевод был выполнен с более раннего издания.— Прим. ред.
428
СПИСОК ЛИТЕРАТУРЫ
/1971]
Лргирис
[1954]
[1955]
[1956]
[1957]
[1958]
[1959]
[1965а]
[19656]
[1965в]
[1966а]
[19666]
Аргирис,
[1968]
Аргирис,
[1969]
[1956]
[1959]
[1960]
[1961]
[1963]
Аргирис,
[1964]
The Convergence theorems and their role in the theory of structures,
IUTAM Colloq. High Speed Computing Elastic Struct., Liege. A0)
(J. H. Argyris)
Energy theorems and structural analysis, Aircraft Eng., 26, 347—
356, 383—387, 394. B.1, 6.1)
Energy theorems and structural analysis, Aircraft Eng., 27, 42 —
58, 80—94, 125-134, 145-158. B.1)
The matrix analysis of structures with cut-outs and modifications,
Proc. 9th Inter. Congr. Appl. Mech., sec. II, Mechanics of Solids,
September. B.1)
The matrix theory of statics, Ingr. Arch., 25, 174—192. B.1)
On the analysis of complex structures, Appl. Mech. Rev., 11, 331 —
338. B.1)
Recent developments of matrix theory of structures, Tenth Meeting
of the AGARD Structures and Materials Panel, Aachen, Germany.
A6.5)
Matrix analysis of three-dimensional elastic media, small and large
deflections, AIAA J., 3, 45—51. [Имеется русский перевод в книге:
Дж. Аргирис, Современные достижения в методах расчета кон-
конструкций с применением матриц, Стройиздат, М., 1968, 215—239.]
A0.4, 16.5)
Tetrahedron elements with linearly varying strain for the matrix
displacement method, /. Roy. Aeron. Soc, 69, 877—880. A0.4)
Triangular elements with linearly varying strain for the matrix
displacement method, /. Roy. Aeron. Soc, 69, 711—713. A0.4)
Continua and discontinue, Proc. Conf. Matrix Methods Struct.
Mech., AFFDL-TR-66-80 (Oct. 26—28, 1965), Wright-Patterson
AFB, Ohio. B.1, 10.4)
Matrix displacement analysis of plates and shells, Ingr. Arch., 35,
102—142. B.1)
Бак (J. H. Argyris, К. Е. Buck)
A sequel to Technical Note 14 on the TUBA family of plate elements,
/. Roy. Aeron. Soc, 72, № 675, 977—983. A0.4)
Бак, Шарпф, Хилбер, Маречек (J. H. Argyris, К. Е. Buck,
D. W. Scharpf, H. M. Hilber, G. Mareczek)
Some new elements for the matrix displacement method, Proc. 2d
Conf. Matrix Methods Struct. Mech., AFFDL-TR-68-150 (Oct. 15—
17, 1968), Wright-Patterson AFB, Ohio, 333—366. A0.4)
Келси (J. H. Argyris, S. Kelsey)
Structural analysis by the matrix force method with applications to
aircraft wings, Wiss. Ges. Luftfahrt Jahrb., 78—98. B.1)
The analysis of fuselages of arbitrary cross-section and taper, Air-
Aircraft Eng., 31, 62—74, 101-112, 133-143, 169-180, 192—203,
224-256, 272-283. B.1)
Energy theorems and structural analysis, Butterworth, London. B.1)
The analysis of fuselages of arbitrary cross-section and taper, Air-
Aircraft Eng., 33, 34, 71-83, 103-113, 164-174, 193-200, 227—238.
B.1)
Modern fuselage analysis and the elastic aircraft, Butterworth,
London. B.1)
Келси, Кэмел (J. H. Argyris, S. Kelsey, H. Kamel)
Matrix methods of structural analysis: A precis of recent develop-
developments, в сб.: В. Fraeijs de Veubeke (ed.), «Matrix Methods of Struc-
Structural Analysis», AGARDograph 72, Pergamon Press, Ltd., Oxford,
1—164. Кроме того, эта работа опубликована под названием «Recent
advances in matrix methods of structural analysis» в «Progress in the
Aeronautical Sciences», vol. 4, Pergamon Press, Oxford. B.1, 16.5)
СПИСОК ЛИТЕРАТУРЫ 429
Аргирис, Фрид (J. H. Argyris, I. Fried)
[1968] The LUMINA element for the matrix displacement method, J. Roy,
Aeron. Soc, 72, 514—517. B, 10.4)
Аргирис, Фрид, Шарпф (J. H. Argyris, I. Fried, D. W. Scharpf)
[1968a] The HERMES 8 element for the matrix displacement method, /.
Roy. Aeron. Soc, 72, 613—617. A0.4)
[19686] The TET 20 and TEA 8 elements for the matrix displacement me-
method, /. Roy. Aeron. Soc, 72, 618—623. A0.4)
[1968b] The TUBA family of plate elements for the matrix displacement
method, /. Roy. Aeron. Soc, 72, 702—709. A0.4)
Аргирис, Шарпф (J. H. Argyris, D. W. Scharpf)
[1968] The SHEBA family of shell elements for the displacement method,
/. Roy. Aeron. Soc, 72, № 694, 873—883. A0.4)
[1969] Finite elements in space and time, /. Roy. Aeron. Soc, 73, № 708,
1041—1044. Кроме того, опубликовано в Nucl. Eng. Design., 10,
№ 4, 456-464. A1.1)
Арчер (J. S. Archer)
[1963] Consistent mass matrix for distributed mass system, /. Struct.
Div. ASCE, 89, 161—178. (9.7, 13.2)
[1965] Consistent matrix formulation for structural analysis using finite
element techniques, AIAA /., 3, 1910—1918. [Русский перевод:
Ракетная техника и космонавтика, 3 A965), № 10, 155—166.]
(9.7, 13.2)
Ахенбах, Фогель, Геррманн (J. D. Achenbacb, S. M. Vogel, G. Herrmann)
[1968] On stress waves in viscoelastic media conducting heat, в сб.: Н. Раг-
kus, L. I. Sedov (eds.), «Irreversible Aspects of Continuum Mecha-
Mechanics and Transfer of Physical Characteristics in Moving Fluids»,
Springer-Verlag N.Y. Inc., N.Y., 1—15. A9.2)
Ахмад, Айронс, Зенкевич (S. Ahmad, В. M. Irons, О. С. Zienkiewicz)
[1969] Curved thick shell and membrane elements with particular reference
to axisymmetric problems, Proc. 2d Conf. Matrix Methods Struct.
Mech., AFFDL-TR-68-150 (Oct. 15—17, 1968), Wright-Patterson
AFB, Ohio, 539—572. G.5, 10.4)
Бабушка (I. Babuska)
[1970] Approximation by hill functions. Tech. Note BN-648, Univ. of
Maryland, College Park. A0)
[1971] The rate of convergence for the finite element method, SI AM J.
Nwner. Anal., 8, № 2, 304—315. A0.2)
Балтруконис, Ваишнав (J. H. Baltrukonis, R. N. Vaishnav)
[1965] Finite deformations under pressurization in an infinitely long, thick-
walled elastic container ideally bonded to a thin elastic case, Trans.
Soc. Rheol., 9, 273—291. A8.2)
Барсоум (R. Barsoum)
[1970] A finite element formulation for the general stability analysis of
thin-walled members, doct. diss., G rnell Univ.. Ithaca. N.Y. A6.5)
Бейзли, Чент, Айронс, Зенкевич (G. P. Bazeley, Y. K. Cheung, В. М. Irons,
О. С. Zienkiewicz)
[1966] Triangular elements in plate bending — Conforming and non-confor-
non-conforming solutions, Proc. Conf. Matrix Methods Struct. Mech., AFFDL-
TR-66-80 (Oct. 26—28, 1965), Wright — Patterson AFB, Ohio,
547—576. A0.2, 10.4)
Беккер (Е. B. Becker)
[1966] A numerical solution of a class of problems of finite elastic defor-
deformation, dpct. diss., Univ. of California, Berkeley. A6, 16.2, 17.1,
18.1)
430 список литературы
Беккер, Брисбейн (Е. В. Becker, J. J. Brisbane)
[1965] Application of the finite element method to the stress analysis of
solid propellent rocket grains, Spec. Rep. S-67, vol. 1, Rohm and
Haas Co., Huntsville, Ala. A0.4, 16.2, 18.2)
Беккер, Парр (E. В. Becker, С. Н. Parr)
[1967] Application of the finite element method to heat conduction iu
solids, Tech. Rep. S-117, Rohm and Haas Redstone Research Labo-
Laboratories, Huntsville, Ala. A3.8, 20.1)
Белл (К. Bell)
[1969] A refined triangular plate bending finite element, Int. J. Numer.
Methods Eng., 1, № 1, 101—122. A0.4)
Бёркв, Бейдер, Микитов, Пшеменецкий, Шерк (L. Berke,9 R. M. Bader,
W. J. Mykytow, J. S. Pr?emieniecki, M. H. Shirk)
[1969] (ред.) Proc. 2d Conf. Matrix Methods Struct. Mech., AFFDL-TR-
68-150 (Oct. 15—17, 1968), Wright-Patterson AFB, Ohio. B.1)
Бесселинг (J. R. Besseling)
[1966] Matrix analysis of creep and plasticity problems, Proc. Conf. Matrix
Methods Struct. Mech., AFFDL-TR-66-80 (Oct. 26—28, 1965),
Wright-Patterson AFB, Ohio, 665—678. B0.1)
Бест (G. C. Best)
[1963] A formula for certain types of stiffness matrices of structural ele-
elements, AIAA /., 1, 478—479. [Русский перевод: Ракетная техника
и космонавтика, 1 A963), № 1, 242.] A0.4)
Бест, Оден (G. С. Best, J. T. Oden)
[1963] Analysis of shell-type structures, Eng. Res. Rep. 157, General Dyna-
Dynamics, Fort Worth, Texas, December. A0.4)
Бидерман В. Л.
[1958] Вопросы расчета резиновых деталей, в сб. «Расчеты на проч-
прочность», вып. 3, Машгиз, М., 40—87. A5.5, 18.1)
Био (М. A. Biot)
[1955] Variational principles in irreversible thermodynamics with application
to viscoelasticity, Phys. Rev., 97, № 6, 1463—1469. A2)
[1956] Thermoelasticity and irreversible thermodynamics, /. Appl. Phys.,
27, № 3, 240—257. A2)
[1965] Mechanics of incremental deformation, John Wiley & Sons, Inc.,
N.Y. A6.5)
Биркгоф, де Бур (G. Birkhoff, С. de Boor)
[1965] Piecewise polynomial interpolation and approximation, в сб.:
H. L. Garabedian (ed.), «Approximation of Functions», Elsevier
Publ. Co., Amsterdam, 164—190. (8.1, 10)
Биркгоф, Гарабедян (G. Birkhoff, H. L. Garabedian)
[I960] Smooth surface interpolation, /. Math. Phys., 39, 258—268. A0)
Биркгоф, Маклейн (G. Birkhoff, S. MacLane)
[1941] A survey of modern algebra, The Macmillan Co., N.Y. G.1) v
Бисплинтхофф, Эшли, Халфмен (R. L. Bisplinghoff, H. Ashley, R. L. Halfman)
[1955] Аэроупругость, ИЛ, М., 1958. A6.5)
Богнер (F. К. Bogner)
[1968] Finite deflection, Discrete element analysis of shells, doct. diss.,
Case Western Reserve Univ., Cleveland, Ohio, также Tech. Rep.
AFFDL-TR-67-185, Wright-Patterson AFB, Ohio, December. A7.1)
Богнер, Мэллет, Минич, Шмит (F. К. Bogner, R. H. Mallett, M. D. Minich,
L. A. Schmit, Jr.)
[1965] Development and evaluation of energy search methods of nonlinear
structural analysis, Tech. Rep. AFFDL-TR-113, Wright-Patterson
AFB, Ohio. A7.1)
СПИСОК ЛИТЕРАТУРЫ 431
Богнер, Фокс, Шмит (F. К. Bogner, R. L. Fox, L. A. Schmit, Jr.)
[1966] The generalization of interelement, compatible stiffness and mass
matrices by the use of interpolation formulas, Proc. Conf. Matrix
Methods Struct. Mech., AFFDL-TR-66-80 (Oct. 26—28, 1965),
Wright-Patterson AFB, Ohio, 397—443. G.5, 8.1, 10.4)
[1967] A cylindrical shell discrete element, AIAA /., 5, № 4, 745—750.
[Русский перевод: Ракетная техника и космонавтика, 5 A967),
№ 4, 170—175.] G.5, 10.4)
Бокс (М. J. Box)
[1966] A comparison of several current optimization methods, and the us&
of transformations in constrained problems, Computer J., 9, 67—
77. A7)
Боли, Уэйнер (В. A. Boley, J. H. Weiner)
[1960] Теория температурных напряжений, «Мир», М., 1964. A2, 19.2}
Босхард (W. Bosshard)
[1968] Ein neues vollvertragliches endliches element fur Plattenbiegung,.
Abhandlungen IVBH, Zurich, 1—14. A0.4)
Браули, Оден (H. J. Brauchli, J. T. Oden)
[1971] Conjugate approximation functions in finite element analysis, Quart.
Appl. Math., 29, № 3, 65-90. (9, 13.2)
Браун, Xarr, Салама (J. Б. Brown, J. M. Hutt, A. E. Salama)
[1968] Finite element solution to dynamic stability of bars, AIAA J.,
6, № 7, 1423—1425. [Русский перевод: Ракетная техника и кос-
космонавтика, 6 A968), № 7, 251—253.] A6.5)
Брукс (S. H. Brooks)
[1958] A discussion of random methods for seeking maxima, /. Operations
Res., 6, 244—251. A7, 17.6)
[1959] A comparison of maximum seeking methods, /. Operations Res., 7,
430-457. A7, 17.6)
Брэмбл, Зламал (J. Bramble, M. Zlamal)
[1970] Triangular elements in the finite element method, Math. Computersr
24, № 112, 809—820. A0, 10.4)
Брэмлетт, Мэллет (Т. Т. Bramlette, R. H. Mallett)
[1970] A finite element solution technique for the Boltzman equation, /.
Fluid Mech., 42, I, 177—191. A1.4)
Бубнов И. Г.
*[1913] Отзыв о работе проф. С. П. Тимошенко «Об устойчивости упругих
систем», Сборник С.-Петербургского института инженеров путей
сообщения, вып. 81, 33—36; также: Избранные труды, Судпром-
гиз, Л., 1956, 136—139. A0)
*[1914] Строительная механика корабля, ч. 2, Типография Морского
мин-ва, СПБ, 515—541. A0)
Вайнберг М. М.
[1956] Вариационные методы исследования нелинейных операторов, Гос-
техиздат, М. A0.1)
Валц, Фултон, Сайрус (J. E. Walz, R. E. Fulton, N. J. Cyrus)
[1969] Accuracy and convergence of finite element approximations, Proc.
2d Conf. Matrix Methods Struct. Mech., AFFDL-TR-68-150 (Oct.
15—17, 1968), Wright-Patterson AFB, Ohio, 995—1027. A0)
Варга (R. S. Varga)
[1967] Hermite interpolation-type Ritz methods for two^point boundary
value problems, в сб.: J. H. Bramble (ed.), «Numerical Solutions of
Partial Differential Equations», Academic Press, Inc., N.Y., 365—
373. A0)
432 СПИСОК ЛИТЕРАТУРЫ
Вейль (Н. Weyl)
[1946] Классические группы, их инварианты и представления, ИЛ, М.,
1947. A5.5)
Вемпнер (G. A. Wempner)
[1969] Finite elements, finite rotations, and small strains of flexible shells,
Int. J. Solids Struct., 5, 117—153. G.5)
Вемпнер, Оден, Кросс (G. A. Wempner, J. T. Oden, D. A. Kross)
[1968] Finite element analysis of thin shells, /. Eng. Mech. Div. ASCE,
J94, № EM6, 1273—1294. G.5, 10.4)
Вёбеке (В. М. Fraeijs de Veubeke)
[1964a] (ред.) «Matrix methods of structural analysis», Pergamon Press,
Ltd., Oxford. B.1)
[19646] Upper and lower bounds in matrix structural analysis, в только чт*
указанном сборнике [1964а]. A0)
[1965] Displacements and equilibrium models in the finite element method,
в сб.: О. С. Zienkiewicz, G. S. Holister (eds.), «Stress Analysis»,
John Wiley & Sons, Inc., N.Y., 145—197. A0, 10.4)
[1966] Bending and stretching of plates — Special models for upper and
lower bounds, Proc. Conf. Matrix Methods Struct. Mech., AFFDL-
TR-66-80 (Oct. 26—28, 1965), Wright-Patterson AFB, Ohio,
863—886. A0, 10.4)
[1971] (ред.) «High-speed Computing of Elastic Structures», Proc. IUTAM
Sym. High-speed Computing Elastic Struct., August, 1970, Liege.
B.1)
Вильсон (Б. L. Wilson)
[1965] Structural analysis of axisymmetric solids, AIAA J., 3, 2269—2274.
[Русский перевод: Ракетная техника и космонавтика, 3, A965),
№ 12, 124—131.] A0.4, 18.2)
Вильсон, Никелл (Б. L. Wilson, R. Б. Nickell)
[1966] Application of the finite element method to heat conduction analy-
analysis, Nucl. Eng. Design, 4, № 3, 276—286. A3.8, 20.1)
Висманн (J. W. Wissmann)
[1962] Numerical analysis of nonlinear elastic bodies, Eng. Res. Rep.
ERR-AN-157, General Dynamics/Astronautics, September. F.1,10.4)
[1963] Numerische Berechnung nichtlinearer elasticher Koerper, Diss.,
Hannover. F.1, 10.4, 16.1)
[1966] Nonlinear structural analysis; tensor formulation, Proc. Conf. Matrix
Methods Struct. Mech., AFFDL-TR-66-80 (Oct. 26—28,1965), Wright-
Patterson AFB, Ohio, 679—696. F.1, 16.1)
Виссер (W. Visser)
[1966] A finite-element method for the determination ol Non-stationary tem-
temperature distributions and thermal deformations, Proc. Conf. Matrix
Methods Struct. Mech., AFFDL-TR-66-80 (Oct. 26—28, 1965),
Wright-Patterson AFB, Ohio, 925—943. B0.1)
Витхум ф. Withum)
[1966] Berechnung von Platten nach dim Ritzschen Verfahren Mithilfe
Dreieckformiger Maschennetze, Mitt. Inst. Statik Tech. Hochschule
Hannover, vol. 9. A0.4)
Гавурин М. К.
[1958] Нелинейные функциональные уравнения и непрерывные аналоги
итеративных методов, Известия Вузов, Математика, № 5 F),
18-31. A7.5)
Галёркин Б. Г.
[1915] Стержни и пластинки. Ряды в некоторых вопросах упругого равно-
равновесия стержней и пластинок, Вестник инженеров, 1, JSIs 19, 897—
908. A0.1, 10.3)
СПИСОК ЛИТЕРАТУРЫ 433
Галлагер (R. H. Gallagher)
[1961] Matrix structural analysis of heated airframes, Proc. ASD Symp.
Aerothermoelasticity, ASD-TR-61-645, November. B0.1)
[1964] A correlation study of methods of matrix structural analysis, Per-
gamon Press, Ltd., Oxford. B.1)
Галлагер, Куинн, Пэдлог (R. H. Gallagher, J. F. Quinn, J. Padlog)
[1961] Deformational response determinations for practical heated wing
structures, Proc. AIR-ONR Symp. Struct. Dyn. High Speed Flight,
Los Angeles. B0.1)
Галлагер, Пэдлог, Бейлард (R. H. Gallagher, J. Padlog, P. O. Bijlaard)
[1962] Stress analysis of heated complex shapes, /. Amer. Rocket Soc, 32,
700—707. [Русский перевод: Ракетная техника, 32 A962), № 5,
52-61.] A0.4, 16.1, 20.1)
Галлагер, Раттингер, Арчер (R. H. Gallagher, I. Rattinger, J. S. Archer)
[1964] A correlation study of methods of matrix structural analysis,
AGARDograph 69, Pergamon Press, Ltd., Oxford. A0.4)
Галлагер, Яма да, Оден (R. H. Gallagher, Y. Yamada, J. T. Oden)
[1970] (ред.) «Recent Advances in Matrix Methods in Structural Analysis
and Design», Proceedings of the U.S.— Japan Seminar on Matrix
Methods in Structural Analysis and Design, Tokyo, 1969, Univ.
of Alabama Press, Univ. B.1)
Геррманн (L. R. Herrmann)
[1965] Elasticity equations for incompressible and nearly incompressible
materials by a variational theorem, AIAA J., 3, № 10, 1896—1900.
[Русский перевод: Ракетная техника и космонавтика, 3 A965),
№ 10, 139—144.] A6.2)
[1966] A bending analysis for plates, Proc. Conf. Matrix Methods Struct.
Mech., AFFDL-TR-66-80 (Oct. 26—28, 1965), Wright-Patterson
AFB, Ohio, 577—602. A0.4)
Гель (J. J. Goel)
[1968] Construction of basic functions for numerical utilization of Ritz'a
method, Numerische Math., 12, 435—447. A0)
Гильдебранд (F. B. Hildebrand)
[1956] Introduction to numerical analysis, McGraw-Hill Book Co., N.Y. (8.1)
Гольдстейн (A. A. Goldstein)
[1956] Cauchy's method ot minimization, Numerishe Math., 4, 146—150.
A7.3)
Грейвс (L. M. Graves)
[1956] The theory of functions of real variables, 2d ed., McGraw-Hill Book
Co., N.Y. A0.4)
Грин, Адкинс (A. E. Green, J. E. Adkins)
[1960] Большие упругие деформации и нелинейная механика сплошной
среды, «Мир», М., 1965. E.2, 15, 15.5, 18.3)
Грин, Джонс, Маклей, Строум (В. Е. Greene, R. E. Jones, R. W. McLay,
D. R. Strome)
[1969] On the application of generalized variational principles in the fi-
finite element method, AIAA J., 7, № 7, 1254—1260. [Русский пе-
перевод: Ракетная техника и космонавтика, 7 A969), № 7, 47—
55.] A0)
Грин, Зерна (А. Е. Green, W. Zerna)
[1968] Theoretical elasticity, 2d ed., Oxford Univ. Press, London. D, 15,
18.2)
Грин, Ривлин (A. E. Green, R. S. Rivlin)
[1957] The mechanics of nonlinear materials with memory. I, Arch. Rat.
Mech. Anal., 1, 1—21 A9.2)
[1960] The mechanics of nonlinear materials with memory. Ill, Arch. Rat.
Mech. Anal., 4, 387—404. A9.2)
28 Дж. Оден
434 СПИСОК ЛИТЕРАТУРЫ
Грин, Ривлин, Спенсер (А. Е. Green, R. S. Rivlin, A. J. M. Spenser)
[1959] The mechanics of nonlinear materials with memory. II, Arch. Rat.
Mech. Anal., 3, 82—90. A9.2)
Гройб (W. H. Greub)
[1963] Linear Algebra, 2d ed., Academic Press, Inc., N.Y. G.1, 10.4)
Гук (R. Hooke)
[1678] Lectures de potentia restitutiva, or of spring, Explaining the power
of springing bodies, брошюра, воспроизведенная в книге:
R. Т.г Gunther, «Early Science in Oxford», vol. 8, 1931, 119—152.
A5.1) -
Давиденко Д. Ф.
[1965] О применении метода вариации параметра к построению итера-
итерационных формул повышенной точности для определения численных
решений нелинейных интегральных уравнений, ДАН, 162, № 3,
499-502. A7.5)
Давидон (W. С. Davidon)
[1959] Variable metric method for minimization, AEC Res. Develop. Rep.
ANL-5990 (rev.). A7.3)
Дана, Хёрлбат (J. D. Dana, C. S. Hurlbut)
[1959] Dana's manual of mineralogy, 17th ed., John Wiley & Sons., Inc.,
N.Y. A5.5)
Даниловская В. И.
[1952] Об одной динамической задаче термоупругостя, ПММ, 16, № 3,
341—344. B0.3)
Дании (Р. С. Dunne)
[1968] Complete polynomial displacement fields for finite element method,
/. Roy. Aeron. Soc, 72, 245—246. A0, 10.4)
Де Гроот, Мазур (S. R. DeGroot, P. Mazur)
[1962] Non-equilibrium thermodynamics, North-Holland Publ. Co., Am-
Amsterdam. A2)
Джаунземис (W. Jaunzemis)
[1967] Continuum mechanics, The Macmillan Co., N.Y. A4)
Джент, Томас (А. N. Gent, A. G. Thomas)
[1958] Forms of the stored (strain) energy function for vulcanized rubber,
/. Polymer Sci., 28, 625—628. A5.5, 18.1)
Джон (F. John)
[1958] On finite deformations of elastic isotropic material, Inst. Math.
Sci. Rep. IMM-NYU 250, N.Y. Univ. A5.5)
Джонс (D. J. Johns)
[1965] Thermal stress analysis, Pergamon Press, Ltd., Oxford. A9.2)
Джонсон, Маклей (M. W. Johnson, Jr., R. W. McLay)
[1968] Convergence of the finite element method in the theory of elasticity,
/. Appl. Mech., ser. E, 35, № 2, 274—278. [Русский перевод: Труды
Американского общества инженеров-механиков, Прикладная меха-
механика, 35 A968), сер. Е, № 2, 68—72.] A0)
Дик, Пайэн (A. L. Deak, Т. Н. Н. Pian)
[1967] Application of the smooth-surface interpolation to the finite element
analysis, AIAA J., 5, N° 1, 187—189. [Русский перевод: Ракетная
техника и космонавтика, 5 A967), № 1, 235—237.] (8.1)
Диллон (О. W. Dillon, Jr.)
[1962] A nonlinear thermoelasticity theory, /. Mech. Phys. Solids, 10,
123—131. A9.2)
Донг, Пистер, Данхэм (R. G. Dong, K. S. Pister, R. S. Dunham)
[1968] Mechanical characterization of nonlinear viscoelastic solids for itera-
iterative solution of|boundary-value problems, Struct. Mater. Res. Rep.
68—11 Structural Engineering Laboratory, Univ. of California,
Berkeley. B0.1)
СПИСОК ЛИТЕРАТУРЫ 435
Дэниэл (J. W. Daniel)
[1967] The conjugate gradient method for linear and nonlinear operator
equations, SI AM J. Numer. Anal., 4, 10—25. A7.3)
Дюамель (J. M. C. Duhamel)
[1837] Second memoire sur les phenomenes thermomechaniques, /. Ecole.
Polytech., 15, № 25. A9.2)
Зенкевич (О. С. Zienkiewicz)
[1970] The finite element method: from intuition to generality, Appl.
Mech. Rev., 23, № 3, 249—256. [Русский перевод: Механика, № %
A974), 90-103.] B.1)
Зенкевич, Холистер (О. С. Zienkiewicz, G. S. Holister)
[1965] (ред.) «Stress Analysis», John Wiley & Sons, Inc., N.Y. B.1)
Зенкевич, Ченг (О. С. Zienkiewicz, Y. К. Cheung)
[1967] The finite element method in structural and continuum mechanics,
McGraw-Hill Book Co., N.Y. [Русский перевод 2-го изд.: О. Зенке-
Зенкевич, Метод конечных элементов в технике, «Мир», 1975.] B.1, 10.4)
Зламал (М. Zlamal)
[1968] FOn the finite element method, Numerische Math., 12, 394—409. A0,10.4)
Зойтендейк (G. Zoutendijk)
[1966] Nonlinear programming: A numerical survey, SI AM J. Control,
4, 194—210. (/7)
Зуданс (Z. Zudans)
[1969] Survey of advanced structural design analysis techniques, Nuet.
Eng. Design, 10, № 4, 400—440. B.1)
Исихара, Хасицумэ, Татибана (A. Isihara, N. Hashitsume, M. Tatibana)
[1951] Statistical theory of rubber-like elasticity. IV (Two-dimensional
stretching), /. Chem. Phys., 19, 1508—1512. A5.5)
Йиндра (F. Jindra)
[1959] Warmespannungen, hei einem nichtlinearen Elastizatatsgeset, Ing,
Arch., 38, 109—116. A9.2)
Каван (Т. Kawai)
[1970] Finite element analysis of the geometrically nonlinear problems,
в сб.: R. H. Gallagher, Y. Yamuda, Oden (eds.), «Recent Advances
in Matrix Methods in Structural Analysis and Design», Proceedings of
the U.S.— Japan Seminar on Matrix Methods in Structural Analysis
and Design, Tokyo, 1969, Univ. of Alabama Press, Univ. A6.5)
Кавана (К. Т. Kavanagh)
[1969] The finite element analysis of physically and kinematically non-linear
elastic solids, doct. diss., Univ. of California, Berkeley; также опуб-
опубликовано как Struct. Mater. Res. Rep. 69-4, Structural Engineering
Laboratory, Univ. of California, Berkeley, April. A5.5, 16)
Канторович Л. В.
[1933] Один прямой метод приближенного решения задачи о минимуме
двойного интеграла, ИАН СССР, VII сер., Отделение матема-
математических и естественных наук, № 5, 647—652. A1.4)
Карьяппа, Сомашекар, Шах (В. Kariappa, R. Somashekar, С. G. Shah)
[1970] Discrete element approach to flutter of skew panels with in-plane
forces under yawed supersonic flow, AIAA J., 8, № 11, 2017—2030.
[Русский перевод: Ракетная техника и космонавтика, 8 A970),
№ И, 120—126.] A6.5)
Ки (S. W. Key)
[1966] A convergence investigation of the direct stiffness method, doct.
diss., Univ. of Washington, Seattle. A0, 10.2, 10.3, 10.4)
[1969] A variational principle for incompressible and nearly incompressible
anisotropic elasticity, Int. J. Solids Struct., 5, № 9, 951—964. A6.2)
28*
436 список литературы
Кинг (I. P. King)
[1965] On the finite element analysis of two-dimensional stress problems
with time dependent properties, doct. diss., Univ. of California,
Berkeley. B0.1)
Киснер (W. Kisner)
[1964] A numerical method for finding solutions to nonlinear problems,
SJAM J. Appl. Math., 12, № 2, 424—428. A7.5)
Клаф (R. W. Clough)
[1960] The finite element method in plane stress analysis, /. Struct. Div.,
ASCE, Proc. 2d Conf. Electronic Computation, 345—378. B.1)
Клаф, Рашид (R. W. Clough, Y. R. Rashid)
[1965] Finite element analysis of axisymmetric solids, /. Eng. Mech. Div.,
ASCE, 91, № EMI, 71-85. A0.4, 18.2)
Клаф, Точер (R. W. Clough, J. L. Tocher)
[1966] Finite element stiffness matrices for analysis of plate bending, Proc.
Conf. Matrix Methods in Struct. Mech., AFFDL-TR-66-80 (Oct.
26—28,1965), Wright-Patterson AFB, Ohio, 515—546. A0,10.2,10.4)
Клоснер, Сегал (J. M. Klosner, A. Segal)
[1969] Mechanical characterization of a natural rubber, PIBAL Rep. 69-42,
Polytechnic Inst. of Brooklyn, N.Y. A5.5, 18.1)
Ковалик, Осборн (J. Kowalik, M. R. Osborne)
[1968] Methods for unconstrained optimization problems, American Elsevier
Publishing Co., Inc., N.Y. A7)
Колеман (В. D. Coleman)
[1964] Thermodynamics of materials with memory, Arch. Rat. Mech. Anal.,
17, 1—46. A2, 12.4, 14.3, 14.4, 19.1)
Колеман, Гуртин (В. D. Coleman, M. Б. Gurtin)
[1965a] Waves in materials with memory. III. Thermodynamic influences
on the growth and decay of one-dimensional acceleration waves,
Arch. Rat. Mech. Anal., 19, 266—298. [Воспроизведено в сб.:
С. Truesdell (ed.), «Wave Propagation in Dissipative Materials»,
Springer-Verlag, Berlin, 1965.] A9.1)
[19656] Waves in materials with memory. IV. Thermodynamics and the
velocity of general acceleration waves, Arch. Rational Mech. Anal.,
19, 317—338. [Воспроизведено в том же сборнике.] A9.1)
~ tin, R. I. ~~
Колеман, Гуртин, Херрера (В. D. Coleman, M. E. Gurtin, R. I. Herrera)
[1965] Waves in materials with memory. I. The velocity of one-dimensional
shock and acceleration waves, Arch. Rat. Mech. Anal., 19, 1—19.
[Воспроизведено в том же сборнике.] A9.1)
Колеман, Мизел (В. D. Coleman, V. J. Mizel)
[1964] Existence of caloric equations of state in thermodynamics, /. Chem.
Phys., 40, 1116—1125. A2.3)
[1967] A general theory of dissipation in materials with memory, Arch.
Rat. Mech. Anal., 27, 255—274. A9.1)
Колеман, Ноля (В. D. Coleman, W. Noll)
[1960] An approximation theorem for functionals with applications in con-
continuum mechanics, Arch. Rat. Mech. Anal., 6, 355—370. A9.2)
[1961] Foundations of linear viscoelasticity, Rev. Mod. Phys., 33, 239—249.
A4.4)
[1963] The thermodynamics of elastic materials with heat conduction, and
viscosity, Arch. Rat. Mech. Anal., 13, 167—178. A2.3)
Коллатц (L. CoIIatz)
[19661 Численные методы решения дифференциальных уравнений, ИЛ,
М., 1953. A7.5)
Колмогоров А. Н-, Фомин С. В.
[1972] Элементы теории функций и функционального анализа, 3-е изд.,
«Наука», М. G.1, 7.4, 10.1)
СПИСОК ЛИТЕРАТУРЫ 437
Корнеев В. Г.
[1967] Сопоставление метода конечных элементов с вариационно-разно-
вариационно-разностным методом решения задач теории упругости, Изв. ВНИИР
им. Веденеева, 83, 286—307. A0.2)
Кост (Т. L. Cost)
[1969] Thermomechanical coupling phenomena in non-isothermal viscoelaa-
tic solids, doct. diss., Univ. of Alabama, University. A9.2, 20.1)
Коти (A. L. Cauchy)
[1829] Sur l'equilibre et le mouvement interieur des corps consideres comma
des masses continues, Ex. Math., 4, 293—319; Oeuvres, vol. 9, 342—
369. A6.5)
[1847] Methods general e pour la resolution des systemes d'equations simul-
tanees, C.R., 25, 536—538. A7.3)
Крахула, Полемус (J. L. Krahula, J. F. Polhemus)
[1968] Use of Fourier series in the finite element method, AIAA J., 6, № 4,
726—728. [Русский перевод: Ракетная техника и космонавтика,
6 A968), № 4, 210—211.] A0.4)
Кристенсен, Нахди (R. М. Christensen, P. M. Naghdi)
[1967] Linear non-isothermal viscoelastic solids, Acta Mech., HI/1, 1—12.
A9.2)
Крон (G. Kron)
[1939] Tensor analysis of networks, John Wiley & Sons, Inc., N.Y. B.1, 6.1\
[1944a] Tensorial analysis and equivalent circuits of elastic structures, J.
Franklin Inst., 238, 399—442. B.1)
[19446] Equivalent circuits of the elastic field, /. Appl. Mech., 66, 149—
167. B.1)
[1953] A set of principles to interconnect the solutions of physical systems,
/. Appl. Phys., 24, 965—980. B.1)
[1954] A method to solve very large physical systems in easy stages, Proe.
IRE, 42, 680—686. B.1)
[1955] Solving highly complex structures in easy stages, /. Appl. Mech.,
22,!" 235—244. B.1)
Крэндалл (S. H. Crandall)
[1956] Engineering analysis: a survey of numerical procedures, McGraw-
Hill Book Co., N.Y. A0.3)
Курант (R. Courant)
[1943] Variational methods for the solution of problems of equilibrium and
vibrations, Bull. Amer. Math. Soc, 49, 1—23. B.1, 8.1, 10)
Курант, Фридрихе, Леви (R. Courant, К. О. Friedrichs, H. Lewy)
11928] Uber die partiellen Differenzengleichungen der mathematischen
Physik, Math. Ann., 100, 32—74. [Русский перевод: УМЕ, 8
A941), 125—160.] B.1, 11.1)
Ланхар, Чу (Н. L. Langhaar, S. С. Chu)
[1968JP Piecewise polynomials and the partition method for ordinary diffe-
differential equations, в сб.: «Developments in Theoretical and Applied
Mechanics», vol. 4, Proceedings, Southeastern Conference on Theore-
Theoretical and Applied Mechanics, Pergamon Press, Ltd., Oxford, 553—
564. (8.1, 10.4)
Лей (D. C. Leigh)
[1968] Nonlinear continuum mechanics, McGraw-Hill Book Co., N.Y. A4)
Леонард, Брэмлетт (J. W. Leonard, Т. Т. Bramlette)
[1970] Finite-element solution of differential equations, /. Struct. Div.,
ASCE, 96, № EM6, 1277—1284. A0.3)
Лианис (G. Lianis)
[1965] Integral constitutive equations of nonlinear thermo-viscoelasticity,
School Aeron. Astronautics Eng. Sci. Rep. AA & ES 65-1, Purdue
Univ., Lafayette, Ind. A9.2)
438 список литературы
[1968] Nonlinear thermorheologically simple materials, 5th Int. Congr.
Rheol., Kyoto, Japan. A9.2)
Лурье А. И.
¦[1970] Теория упругости. «Наука», М. D)
Люстерник Л. А., В. II. Соболев
[1965] Элементы функционального анализа, 2-е изд., «Наука», М. G./)
Майкенер (J. Meixner)
[1943] Zur Thermodynamik der irreversiblen Prozesse, Z. Angew. Phys.
Chem., B, 53, 235—263. A2)
Мак-Гуирт, Лианис (С. W. McGuirt, G. Lianis)
[1969] Experimental investigation of non-linear non-isothermal viscoelasti-
city, Int. J. Eng. Sic, 7, 579—599. A9.2)
Маклей (R. W. McLay)
[1963] An investigation into the theory of the displacement method of
analysis for linear elasticity, doct. diss., Univ. of Wisconsin, Madi-
Madison. A0)
[1967] Completeness and convergence properties of finite element displace-
displacement functions — A general treatment, AIAA 5th Aerospace Sci.
Meeting, AIAA Paper 67-143, N.Y. A0)
[1971] On certain approximations in the finite element method, /. Appl.
Mech., 38, № 1, 58—61. [Русский перевод: Труды Американского
общества инженеров-механиков, Прикладная механика, сер. Е,
38 A971), № 1, 58—61.] A0.2)
Мак-Кой (N. McCoy)
[1960] Introduction to modern algebra, Allyn and Bacon, Inc., Boston. G.1)
Маркл (p. V. Marcal)
[1968] Effect of initial displacements on problems of large deflection and
stability, Proc. ASCE Joint Specially Conf. Optimization Nonlinear
Probl., Chicago, April. A6.5)
[1970] Finite element analysis with material nonlinearities — Theory and
practice, в сб.: R. H. Gallagher, Y. Yamada, J. T. Oden (eds.),
«Recent Advances in Matrix Methods in Structural Analysis and
Design», Proc. of the U.S.— Japan Seminar on Matrix Methods in
Structural Analysis and Design, Tokyo, 1969, Univ. of Alabama
Press, Universitjs. B.1)
Мартин (Н. С Martin)
[1966a] Introduction to matrix methods of structural analysis, McGraw-
Hill Book Co., N.Y. B.1)
[19666] On the derivation of stiffness matrices for the analysis of large deflec-
deflection and stability problems, Proc. Conf. Matrix Methods Struct.
Mech., AFFDL-TR-66-80 (Oct. 26—28, 1965), Wright-Patterson
AFB, Ohio, 697—716. A6.5)
[1970] Finite element formulations of geometrically nonlinear problems,
в сб. «Recent Advances in Matrix Methods in Structural Analysis
and Design» (см. Маркл [1970]). B.1, 16.5)
Мейер (G. Meyer)
[1968] On solving nonlinear equations with a one-parameter operator im-
imbedding, SIAM J. Numer. Anal, 5, 739—752. A7.5)
Мелош (R. J. Melosh)
[1963a] Basis of derivation of matrices for the direct stiffness method, AIAA
J., 1, 1631—1637. [Русский перевод: Ракетная техника и космо-
космонавтика, 1 A963), № 7, 169—176).] A0, 10.2, 10.3)
[19636] Structural analysis of solids, /. Struct. Div. ASCE, 89, 205—223.
A0.4)
[1966] A flat triangular shell element stiffness matrix, Proc. Conf. Matrix
Methods Struct. Mech., AFFDL-TR-66-80 (Oct. 26—28, 1965),
Wright-Patterson AFB, Ohio, 503—514. A0.4)
СПИСОК ЛИТЕРАТУРЫ 439
Михлин С. Г.
[1952] Проблема минимума квадратичного функционала, ГИТТЛ, М.— Л.
A0.1, 10.3)
[1970] Вариационные методы в математической физике, 2-е изд., «Наука»,
М. A0.1)
Михлин С. Г., Смолицкий X. Л.
[1965] Приближенные методы решения дифференциальных и интеграль-
интегральных уравнений, «Наука», М. A0.1)
Морс, Фешбах (P. M. Morse, H. Feshbach)
[1953] Методы теоретической физики, т. 1, ИЛ, М., 1958. A1.2)
Мостов, Сэмпсон, Мейер (G. D. Mostow, J. H. Sampson, J. P. Meyer)
[1963] Fundamental structures of algebra, McGraw-Hill Book Co., N.Y.
G.1)
Муни (М. Mooney)
[1940] A theory of large elastic deformation, /. Appl. Phys., 11, 582—592.
A5.5)
Myp (J. T. Moore)
[1962] Elements of abstract algebra, The Macmillan Co., N.Y. G.1)
Мэлверн (L. E. Malvern)
[1970] An introduction to the mechanics of a continuous media, Prentice-
Hall, Inc., Englewood Cliffs., N.J. A4)
Мэллетт, Шиит (R. H. Mallett, L. A. Schmit, Jr.)
[1967] Nonlinear structural analysis by energy search, /. Struct. Div.
ASCE, 93, № ST3, 221—234. A7.1)
Мюллер (I. Miiller)
[1967] On the entropy inequality, Arch. Rat. Mech. Anal., 26, 118—141.
A2.3)
Мюррей Д., Вильсон (D. W. Murray, E. L. Wilson)
[1969a] Finite element large deflection analysis of plates, /. Eng. Mech.
Div. ASCE, 95, № EMI, 143—165. A6.5)
[19696] Finite-element postbuckling analysis of thin elastic plates, AIAA J.,
7, № 10, 1915—1920. [Русский перевод: Ракетная техника и кос-
космонавтика, 7 A969), № 10, 115—121.] A6.5)
Мюррей К. (К. Н. Murray)
[1970] Comments on the convergence of finite-element solutions, AIAA
J., 8, 815—816. [Русский перевод: Ракетная техника и космонав-
космонавтика, 8 A970), № 4, 277—279.] A0.2)
Нелдер, Мид (J. A. Nelder, R. Mead)
[1964] A simplex method for function minimization, Computer J., 7, 308
A7.6)
Немат-Нассер, Шатов (S. Nemat-Nasser, H. D. Shatoff)
[1970] A consistent numerical method for the solution of nonlinear elasticity
problems at finite strains, Dep. Aerospace Mech. Eng. Sci. Tech.
Rep. 2, January. A6, 16.1)
Никелл, Сэкмэн (R. E. Nickell, J. J. Sackman)
[1968] Approximate solutions in linear coupled thermoelasticity, /. Appl.
Mech., ser. E, 35, № 2, 255—266. [Русский перевод: Труды Аме-
Американского общества инженеров-механиков, Прикладная механика,
35 A968), сер. Е, № 2, 51—60.] A1.1, 20.1, 20.2)
Новацкий (W. Nowacki)
[1962] Thermoelasticity, Pergamon Press, Ltd., Oxford. A9.2)
Новожилов В. В.
[1948] Основы нелинейной теории упругости, ГИТТЛ, М.— Л. D.2)
Нолл (W. Noll)
[1958] A mathematical theory of the mechanical behavior of continuous
media, Arch. Rat. Mech. Anal., 2, 197—226. A9.1)
440 СПИСОК ЛИТЕРАТУРЫ
Оден (J. Т. Oden)
[1966а] Analysis of large deformations of elastic membranes by the finite
element method, Proc. IASS Int. Congr. Large-span Shells, Lenin-
Leningrad. A6, 18.1)
[19666] Calculation of geometric stiffness matrices for complex structures,
AIAA J., 4, № 8, 1480—1482. [Русский перевод: Ракетная техника
и космонавтика, 4 A966), № 8, 21 —217.] A6.5)
[1967а] Numerical formulation of a class of problems in nonlinear viscoelas-
ticity, Advan. Astronautical Sci., 24, June. F.1, 10.3, 10.4, 16.1,
20.1)
[19676] Numerical formulation of nonlinear elasticity problems, /. Struct.
Div. ASCE, 93, № ST3, 235—255. F.1, 7, 10.4, 16, 16.1, 16.2)
[1967b] Finite element applications in linear and nonlinear thermoelasticity,
в сб. «The Discrete and Continuum Concepts in Micro and Macro
Mechanics», EDM Specialty Conf., ASCE, Nov. 8—10, 1967, Raleigh,
N.C., 32—35. A0.3, 13.4)
[1968a] Calculation of stiffness matrices for thin shells of arbitary shape,
AIAA J., 6, № 5, 969—972. [Русский перевод: Ракетная техника
и космонавтика, 6 A968), № 5, 256—258).] G.5)
[19686] Finite plane strain of incompressible elastic solids by the finite
element method, Aeron. Quart., 19, 254—264. A3.1, 16, 16.2, 18.3)
[1969a] A general theory of finite elements. I. Topological considerations, Int.
J. Numer. Methods Eng., 1, № 2, 205—221. F.1, 7, 9.7, 10.4, 13.2)
[19696] A general theory of finite elements. II. Applications, Int. J. Numer.
Methods Eng., 1, № 3, 247—259. {6.1, 7, 10.3, 11.1, 11.4, 13.4)
[1969b] Finite element applications in nonlinear structural analysis, Proc.
Symp. Appl. Finite Element Methods Civil Eng., Vanderbilt Univ.,
Nashville, Тешь, 419—456. B.1, 16, 16.5)
[1969r] Finite element analysis of nonlinear problems in the dynamical
theory of coupled thermoelasticity, Nucl. Eng. Design, 10, № 4,
465—475. A3.8, 19.2, 20.1)
[1969д] Discussion of finite element analysis of nonlinear structures, /.
Struct. Div. ASCE, 95, № ST6, 1379—1381. A6.5)
[1970a] A generalization of the finite element concept and its application to
a class of problems in nonlinear viscoelasticity, Developments in
Theoretical and Applied Mechanics, IV, ed. by D. Friederick (Pro-
(Proceedings, 4th SECTAM, March 1968), Pergamon Press, Oxford,
581—592. A3.1, 13.4, 13.6, 20.1)
[19706] Finite element formulation of problems of finite deformation and
irreversible thermodynamics of nonlinear continua, в сб.: R. H. Gal-
Gallagher, Y. Yamada, J. T. Oden (eds.), «Recent Advances ingMatrix
Methods in Structural Analysis and Design», Proceedings of the
U.S.— Japan Seminar on Matrix Methods in Structural Analysis and
Design, Tokyo, 1969, Univ. of Alabama Press, University. B.1, 13.4,
13.8, 16.5, 20.1)
[1970b] Finite-element approximation of a class of nonlinear operators, SI AM
Soc. Indus. Appl. Math., Fall Meeting, Boston, Mass. A0)
[1970r] Note on an approximate method for computing nonconservative
generalized forces on finitely deformed finite elements, AIAA J.,
8, № 11, 2088—2090. [Русский перевод: Ракетная техника и кос-
космонавтика, 8 A970), № 11, 215—217.] A6.3)
[197la] The theory of conjugate projections in finite element analysis, NATO
Advanced Study Institute on Finite Element Methods in Continuum
Mechanics, Lisbon. (9.7)
[19716] Finite Element Formulation of Nonlinear Boundary-value Problems,
NATO Advanced Study Institute on Finite Element Methods in
Continuum Mechanics, Lisbon. A0, 10.2)
СПИСОК ЛИТЕРАТУРЫ 44t
[1971в] Finite element approximations in nonlinear elasticity, NATO Ad-
Advanced Study Institute on Finite Element Methods in Continuum
Mechanics, Lisbon. A6.1, 17, 18.1)
[1971r] Finite element approximations in nonlinear thermoviscoelasticity,
NATO Advanced Study Institute on Finite Element Methods in-
Continuum Mechanics, Lisbon. B0.1)
Оден, Агирре-Рамирес (J. Т. Oden, G. Aguirre-Ramirez)
[1969] Formulation of general discrete models of thermomechanical behavior
of materials with memory, Int. J. Solids Struct., 5, № 10, 1077—
1093. G, 10.4, 13.1, 13.2, 13.4, 13.6, 13.8, 20.1)
Оден, Армстронг (J. Т. Oden, W. H. Armstrong)
[1971] Analysis of nonlinear, dynamic coupled thermoviscoelasticity prob-
problems by the finite element method, Computers and Structures, 1,
603-621. B0.1, 20.2)
Одев, Браулв (J. Т. Oden, H. J. Brauchli)
[1971a] On the calculation of consistent stress distributions in finite element
applications, Int. J. Numer. Methods Eng., 3, № 3, 317—325. (9,
9.8, 16.3)
[19716] A note on accuracy and convergence of finite element approximations.
Int. J. Numer. Methods Eng., 3, 291—294. A0)
Оден, Вемпвер (J. Т. Oden, G. A. Wempner)
[1967] Numerical analysis of arbitrary snell structures under arbitrary static
loadings, Univ. Alabama Res. Inst. Rep. 47, November. G.5, 10.4)
Оден, Ки (J. Т. Oden, J. E. Key)
[1970] Numerical analysis of finite axisymmetric deformation of incompres-
incompressible elastic solids of revolution, Int. J. Solids Struct., 6, 497—518.
A6, 16.2, 16.5, 18.2)
[1971a] Analysis of finite deformations of elastic solids by the finite element
method, Proc. IUTAM Colloq. High Speed Computing Elastic
Struct., Liege. A6, 16.2, 16.3, 18.1, 18.2, 18.3)
[19716] On some generalizations of the incremental stiffness relations for
finite deformations of compressible and incompressible finite ele-
elements, Nuc. Eng. Design, 15, 121—134. A6.5)
[1972] On the effect of the form of the strain energy function on the solution-
of a boundary-value problem in finite elasticity, Computers and
Structures, 2, 585-592. A8.1)
Оден, Кросс (J. Т. Oden, D. A. Kross)
[1969] Analysis of general coupled tnermoelasticity problems by the finite-
element method, Proc. 2d Conf. Matrix Methods Struct. Mech.,
AFFDL-TR-68-150 (Oct. 15—17, 1968), Wright-Patterson AFB,
Ohio, 1091—1120. A3.8, 20.1, 20.2, 20.3)
Оден, Кубица (J. Т. Oden, W. K. Kubitza)
[1967] Numerical analysis of nonlinear pneumatic structures, Proc. Int.
Colloq. Pneum. Struct., Stuttgart, May, 82—iO7.[A3.4,16,16.5,[18.1}
Оден, Поу (J. Т. Oden, J. Рое)
[1970] On the numerical solution of a class of problems in dynamics coupled
thermoelasticity, Developments in Theoretical and Applied Mecha-
Mechanics, V (Proceedings, 5th SECTAM, April 1970), ed. by D. Frederik,
Pergamon Press, Oxford. A3.8, 19.2, 20.1, 20.3)
Оден, Реддв (J. Т. Oden, J. N. Reddy)
[1973] Note on an approximate method for computing consistent conjugate
stresses in elastic finite elements, Int. J. Numer. Methods Eng., 6,
№ 1, 55—61. (9.7)
Оден, Ригсби, Корнетт (J. Т. Oden, D. M. Rigsby, D. Coraett)
[1969] On the numerical solution of a class of problems'in a linear first strain»
gradient theory of elasticity, Int. J. Numer. Methods Eng., 1, № 2,
159—174. A0.4)
442 СПИСОК ЛИТЕРАТУРЫ
Оден, Сато (J. Т. Oden, T. Sato)
[1967а] Finite strains and displacements of elastic membranes by the finite
element method, Int. J. Solids Struct., 1, 471—488. A6, 16.2, 18.1)
[19676] Structural analysis of aerodynamic deceleration systems, Advan.
Astronautical Sci., 24. A6, 18.1)
Оден, Чанг, Ки (J. Т. Oden, Т. J. Chung, J. E. Key)
[1971] Analysis of nonlinear thermoelastic and thermoplastic behavior of
solids of revolution by the finite element method, Proc. 1st Intern.
Conf. Struct. Mech. Reactor Tech., Berlin. B0.2)
Ортега, Рейнболдт (J. M. Ortega, W. C. Rheinboldt)
[1970] Итерационные методы решения нелинейных систем уравнений
со многими неизвестными, «Мир», М., 1975. A7, 17.2, 17.5)
Пайэн (Т. Н. Н. Pian)
[1964а] Derivation of element stiffness matrices, AIAA J., 2, № 3, 576—
577. [Русский перевод: Ракетная техника и космонавтика, 2
A964), № 3, 210.] A0.4)
[1Э646] Derivation of element stiffness matrices by assumed stress distri-
distributions, AIAA J., 2, 1333—1336. [Русский перевод: Ракетная
техника и космонавтика, 2 A964), № 7, 219—222.] A0.4)
Пайэн, Тонг (Т. Н. Н. Pian, P. Tong)
[1969а] Basis of finite element method for solid continua, Int. J. Numer.
Methods Eng., 1, 3—28. A0.4)
[19696] Rationalization in deriving element stiffness matrix by assumed
stress approach, Proc. 2d Conf. Matrix Methods Struct. Mech., AFFDL-
TR-68-150 (Oct. 15—17, 1968), Wright-Patterson AFB, Ohio, 441 —
470. A0.4)
Яаркус (H. Parkus)
[1964] Methods of solution of thermoelastic boundary value problems,
в сб.: A. M. Freudenthal, B. A. Boley, H. Liebowitz (eds.), «High
Temperature Structures and Materials», Proceedings of the Third
Simposium on Naval Structural Mechanics, Pergamon Press, Ltd.,
Oxford. A9.2)
[1968] Thermoelasticity, Blaisdell Publishing Co., Waltham, Mass. A9.2)
Парр (С. Н. Parr)
[1964] The application of numerical methods to the solution of structural
integrity problems of solid propellent rockets. I, Solid Rocket
Struct. Integrity Abstr., Solid Rocket Structural Integrity Infor-
Information Center, Univ. of Utah, Salt Lake City. B.1) .
[1967] The application of numerical methods to the solution of structural
integrity problems of solid propellent rockets. II, там же. B.1)
Пауэлл (М. J. D. Powell)
[1969] A survey of numerical methods for unconstrained optimization,
SI AM Rev., 12, № i, 79—97. A7)
Перси (J.^H. Percy)
[1967] Quadrilateral finite element analysis in elastic-plastic plane-stress
analysis, AIAA J., 5, № 2, 367. [Русский перевод: Ракетная
техника и космонавтика, 5 A967), № 2, 229—230.] A0.4)
Пестел (Е. С. Pestel)
[1966] Dynamic stiffness matrix formulation by means of Hermitian polyno-
polynomials, Proc. Conf. Matrix Methods Struct. Mech., AFFDL-TR-66-80
(Oct. 26—28, 1965), Wright-Patterson AFB, Ohio, 479 — 502. J (8.1)
Пестел, Лекки (Е. С. Pestel, F. A. Leckie)
[1968] Matrix methods in elasomechanics, McGraw-Hill Book Co., N.Y. B.1)
Питерсон, Кэмпбелл, Геррманн (F. E. Peterson, D. M. Campbell, L. R. Herr-
Herrmann)
[1966] Nonlinear plane stress analysis applicable to solid propellent rocket
grains, Bull. 5th Meeting Interagency Chem. Rocket Propellent
СПИСОК ЛИТЕРАТУРЫ
443
phenomenes irreversibles, Desoor,
Group — Working Group on Mech. Behavior, GPIA Pub]. 119,
vol. 1, 421—455. A6)
Пипкин (А. С Pipkin)
[1964] Small finite deformations of viscoelastic solids, Rev. Mod. Phys.,
36, 1034-1041. A9.2)
[1966] Approximate constitutive equations, в сб.: S. Eskinazi (ed.), «Modern
Developments in the Mechanics of Continue», Academic Press,
Inc., N.Y., 89—108. A9.2)
Пойа (G. Polya)
[1952] Sur une interpretation de la methode des differences finies qui peut
fournir des bornes superieures ou inferieures, C.R., 235, 995. B.1)
Прагер, Синг (W. Prager, J. L. Synge)
[1947] Approximations in elasticity based on the concept of function spaces,
Quart. Appl. Math., 5, 241—269. B.1)
Пригожий (I. Prigogine)
[1947] Etude thermodynamique des
Liege. A2)
[1961] Введение в термодинамику необратимых процессов, ИЛ, Mt,
1960. A2)
Пшеменецкий (J. S. Przemieniecki)
[1968] Theory of matrix structural analysis, McGraw-Hill Book Co., N.Y,
B.1)
Пшеменецкий, Б ей дер, Бозич, Джонсон, Микитов (J. S. Przemieniecki,
R. M. Bader, W. F. Bozich, J. R. Johnson, W. J. Mykytow)
[1966] (ред.) Proc. Gonf. Matrix Methods Struct. Mech., AFFDL-TR-66-80
(Oct. 26—28, 1965), Wright-Patterson AFB, Ohio. B.1)
Пэдлог, Хафф, Холловей (J. Padlog, R. D. Huff, G. F. Holloway)
[1960] Unelastic behavior of structures subjected to cyclic, thermal, and
mechanical stressing conditions, WADD-TR-60-271, Wright-Patter-
Wright-Patterson AFB, Ohio. B0.1)
Рашид (Y. R. Rashid)
[1964] Solution of elasto-static boundary value problems by the finite ele-
element method, doct. diss. Univ. of California, Berkeley. A0.4, 18.2)
11966] Analysis of axisymmetric composite structures by the finite element
method, Nucl. Ejig. Design, 3, 163—182. A0.4, 18.2)
Рейнер (М. Reiner)
[1958] Реология, «Наука», М., 1965. A9.2)
Ривлин (R. S. Rivlin)
[1948a] Large elastic deformations of isotropic materials. I. Fundamental
concepts, Phil. Trans. Roy. Soc, A 240, 459—490. A5.5)
[19486] Large elastic deformations of isotropic Materials. IV. Further deve-
developments of the general theory, Phil. Trans. Roy. Soc. A 241, 379—
397. [Воспроизведено в сб.: «Problems of Non-linear Elasticity»,
International Science Series, Gordon and Breach, Science Publishers,
Inc., N.Y., 1965.] A5.5)
[1949a] Large elastic deformations of isotropic materials. V. The Problem of
flexure, Proc. Roy. Soc, A 195, 463—473. [Воспроизведено в том
же сборнике.] A5.5)
[19496] Large elastic deformations of isotropic materials. VI. Further results
in the theory of torsion, shear, and flexure, Phil. Trans. Roy. Soc,
A 242, 173—195. [Воспроизведено в том же сборнике.] A5.5)
Ривлин, Саундерс (R. S. Rivlin, D. W. Saunders)
[1951] Large elastic deformations of isotropic materials. VII. Experiments
on the deformation of rubber, Phil. Trans. Roy. Soc, A 243, 251 —
288. A5.5, 18.1)
444 СПИСОК ЛИТЕРАТУРЫ
Ривлин, Томас (R. S. Rivlin, A. G. Thomas)
[1951] Large elastic deformations of isotropic materials. VIII. Strain distri-
distribution around a hole in a sheet, Phil. Trans. Roy. Soc, A 243, 289—
298. A8.1)
Ритц (W. Ritz)
[1908] Uber eine neue Methode zur Losung gewisser Randwertaufgaben,
Gottingener Nachrichten, Mathematik und Physik, Klasse, 236—
248. A0.3)
[1909] Uber eine neue Methode zur Losung gewisser Variationsprobleme der
mathematischen Physik, /. Reine Angew. Math., 135, № 1, 1. A0.3)
Рован, Хэккетт (W. H. Rowan, Jr., R. M. Hackett)
[1969] (ред.) Proc. Symp. Appl. Finite Element Methods Civil Eng., School
of Engineering, Vanderbilt Univ., Nashville, Tenn. B.1)
Ролл (L. B. Rail)
[1969] Computational solution of nonlinear operator equations, John Wiley
& Sons, Inc., N.Y. A7.2, 17.4)
Рыдзевский (J. R. Rydzewski)
[1965] (ред.) Theory of arch dams, Pergamon Press, Ltd., Oxford. B.1)
Рэлей (Sir John William Strutt, Lord Rayleigh)
[1877] Теория звука, Гостехиздат, М., 1955. A0.3)
Саати (Т. L. Saaty)
[1967] Modern nonlinear equations, McGraw-Hill Book Co., N.Y. A0.1, 17)
Саати, Брэм (Т. L. Saaty, J. В ram)
[1964] Nonlinear mathematics, McGraw-Hill Book Co., N.Y. A7, 17.3)
Сабо (В. A. Szabo)
[1969] Principles of discretization of continuous structures, doct. diss.,
State Univ. of N.Y., Buffalo. A0.3)
Сабо, Ли (В. A. Szabo, G. С Lee)
[1969a] Derivation of stiffness matrices for problems in plane elasticity by
Galerkin's methods, Int. J. Numer. Methods Eng., 1, No. 3, 301—
310. A0.3)
[19696] Stiffness matrix for plates by Galerkin's method, /. Eng. Mech.
Div. ASCE, 95, No. EM3, 571—585. A0.3)
Савин Г. Н.
*[1968] Распределение напряжений около отверстий, «Наукова думка»,
Киев. E.1)
Сакади (Z. Sakadi)
[1949] On elasticity problems when the second order terms of the strain are
taken into account. II, Mem. Fac. Eng. Nagoya Univ., 1, 95—107.
A5.5)
Can Мигель (A. San Miguel)
[1965] On the characterization of multiaxial data in terms of the strain
energy concept, Bull. 4th Meeting Interagency Chem. Rocket Pro-
pellant Group — Working Group Mech. Behavior, CPIA Publ.
94U, vol. 1, 169—178. A5.5)
Саусвелл (R. V. Southwell)
[1940] Relaxation methods in engineering science: A Treatise on approxi-
approximate computation, Oxford University Press, London. A7.3)
[1946] Relaxation methods in theoretical physics: A continuation of the
treatise, vol. 1 (vol. 2, 1956), Oxford University Press, London. A7.3)
Сегал, Клосиер (A. Segal, J. M. Klosner)
[1970] Stress concentration in an elastomeric sheet subject to large deforma-
deformations, PIBAL Rep. 70-ll,fPolytechnic Inst. of Brooklyn, March. A8.1)
Сен-Венаи (A. J. С. В. de Saint Venant)
[1868] Formules de 1'elasticite des corps amorphes que des compressions per-
manentes et inegales ont rendus heterotropes, /. Math. Pures Appl.,
13, 242—254. A6.5)
СПИСОК ЛИТЕРАТУРЫ 445
Сиарле, Шульц, Варга (P. G. Ciarlet, M. H. Schultz, R. S. Varga)
[1967] Numerical methods of high-order accuracy for nonlinear boundary
value problems, Numerische Math., 9, 394—430. A0)
Сигер (A. Seeger)
[1964] Discussion to paper by Foux, в сб.: М. Reiner, D. Abir (eds.), «Second-
order Effects in Elasticity, Plasticity, and Fluid Dynamics», Procee-
Proceedings of the International Symposium, Haifa, April 23—27, 1962,
Pergamon Press, Ltd., Oxford (distributed by the Macmillan Co.,
N.Y.). A5.5)
Сигер, Бак (A. Seeger, 0. Buck)
[1960] Die experimentalle Ermittlung der elasctischen Konstanten hoherer
Ordung, Z. Naturforsch., 15a, 1056—1067. A5.5)
Силвестер (R. Silvester)
[1969] Higher-order polynomial triaugular finite elements for potential
problems, Int. J. Eng. Sci., 7, No. 8, 849—861. A0.4)
Синг (J. L. Synge)
[1957] The hypercircle method in mathematical physics, Cambridge Univ.
Press, Cambridge. B.1, 10, 10.4)
Сингхал (А. С Singhal)
[1969] 775 selected references on the finite element method and matrix
methods of structural analysis, Civil Eng. Dept., Rep. S-12, Laval
Univ., Quebec, January. B.1)
Синьорини (A. Signorini)
[1955] Solidi incomprimibili, Ann. Mat. Рига Appl., 147—201. A5.5)
Смит, Ривлип (G. F. Smith, R. S. Rivlin)
[1958] The strain energy function for anisotropic elastic materials, Trans.
A MS, 88, 175—193. A5.5)
Спэнг (H. A. Spang III)
[1962] A review of minimization techniques for nonlinear functions, SIA~M
Rev., 4, № 4, 343-364. A7, 17.6)
Стернберг, Чакраворти (E. Sternberg, J. G. Chakravorty)
[1959] On inertia effects in a transient thermoelastic problem, /. Appl.
Mech., 26, № 4; Trans. AS ME, ser. E, 81, 503—509. B0.3)
Странео (Р. Straneo)
[1925] Sull'expressione dei fenomeni ereditari, Atti Accad. Naz. Lincei
Rend., ser. 6, 1, 29—33. A4.4)
Стриклин (J. A. Stricklin)
[1968] Integration of area coordinates in matrix structural analysis, AIAA
J., 6, № 10, 2023. [Русский перевод: Ракетная техника и космонав-
космонавтика, 6 A968), № 10, 252.] A0.4)
Стрэнг (G. Strang)
[1970] The finite element method andjapproximation^theory, Sym. Numerical
Sol. Partial Differential Equations, Univ. of Maryland, College
Park. A0)
Табанде (N. Tabandeh)
[1970] Convergence of the finite element method, doct. diss., Lousiana State
Univ., Baton Rouge. A0)
Тодхантер, Пирсон (I. Todhunter, K. Pearson)
[1893] A history of the theory of elasticity and of the strength of materials
from Galilei to Lord Kelvin, Cambridge Univ. Press, Cambridge.
A5.1)
Томас (A. G. Thomas)
[1955] The departures from the statistical theory of rubber elasticity, Trans.
Faraday Soc, 51, 569—582. (^5.5)
Тонг (Р. Tong)
[1969] An assumed stress hybrid model for an incompressible and near-in-
near-incompressible material, Int. J. Solids Struct., 5, 455—461. A6.2)
446 список литературы
Тонг, Пайэн (P. Tong, Т. Н. Н. Pian)
[1967] The convergence of finite element method in solving linear elastic
problems, Int. J. Solids Struct., 3, 865—879. A0)
Точер, Харц (J. L. Tocher, B. J. Hartz)
[1967] Higher-order finite elements for plane stress, /. Eng. Mech. Dit.
ASCE, 93, № БМ4, 149-172. (8.1, 10.4)
Трилор (L. R. G. Treloar)
[1944] Stress-strain data for vulcanized rubber under various types of defor-
deformation, Trans. Faraday Soc, 40, 59. A5.5, 18.1)
[1958] Физика упругости каучука, ИЛ, М., 1953. A5.5, 18.1)
Трусдепл (С. Truesdell)
[1952] The mechanical foundations of elasticity and fluid dynamics, /.
Rat. Mech. Anal., 1, 125—300 (исправления: там же, 2 A953),
595—616, 3A954), 801). [Воспроизведено в сб. «Continuum Mecha-
Mechanics I: The Mechanical Foundations of Elasticity and Fluid Dyna-
Dynamics», Gordon and Breach, Science Publishers, Inc., N.Y., 1966.}
A5.1)
[1966a] The elements of continuum mechanics, Springer-Verlag N.Y. Inc.,
N.Y. D, 12, 12.3, 12.4, 14, 14.3)
[19666] Thermodynamics of deformation, в сб.: R. J. Donnelly, R'. Herman,
I. Prigogine (eds.), «Non-equilibrium Thermodynamics Variatio-
nal Techniques and Stability», Univ. Chicago Press, Chicago.
A2)
[1969] Rational thermodynamics, McGraw-Hill Book Co., N.Y. A2, 12.3}
*[1972] Первоначальный курс рациональной механики сплошных сред,
«Мир», М., 1975. A2)
Трусделл, Нолл (С. Truesdell, W. Noll)
[1965] The nonlinear field theories of mechanics, в «Encyclopedia of Phy-
Physics», vol. HI/3, Springer-Verlag, N.Y. Inc., N.Y. D, 5.2, 14, 14.3,
14.4, 15.2, 15.3, 15.5, 16.5)
Трусделл, Тупин (С. Truesdell, R. Tcupin)
[1960] The classical Field theories, в «Encyclopedia of Physics», vol. HI/1
(Principles of Classical Mechanics and Field Theory), Springer-
Verlag N.Y. Inc., N.Y. D.5, 13.1, 16.2)
Тэйг (I. C. Taig)
[1961] Structural analysis by the matrix displacement method, English
Elec. Aviation Ltd. Rep. S-O-17. A0.4)
Тэйг, Kepp (I. C. Taig, R. I. Kerr)
[1964] Some problems in the discrete element representation of aircraft
structures, в сб.: В. Fraeijs de Veubeke (ed.), «Matrix Methods of
Structural Analysis», AGARDograph 72, Pergamon Press, Ltd.,
Oxford, 267—315. A0.4)
Тэйлор Р., Пистер, Геррманн (R. L. Taylor, K. S. Pister, L. R. HerrmaimV
[1968] On a variational theorem for incompressible and nearly incompres-
incompressible orthotropic elasticity, Int. J. Solids Struct., 4, 875—883.
A6.2)
Тэйлор Р., Пистер, Гудро (R. L. Taylor, K. S. Pister, G. L. Goudreau)
[1970] Thermomechanical analysis of viscoelastic solids, lit. J. Numer.
Methods Eng., 2, 45—59. A9.2, 20.1)
Тэйлор Р., Чанг (R. L. Taylor, T. Y. Cbang)
[1966] An approximate method for thermoviscoelastic stress analysis,
Nucl. Eng. Design, 4, 21—28. B0.1)
Тэйлор Э. (A. E. Taylor)
[1958] Introduction to Functional Analysis, John Wiley & Sons, Inc.,
N.Y. G.1)
СПИСОК ЛИТЕРАТУРЫ 447
Тэрнер (М. J. Turner)
[1959] The direct stiffness method of structural analysis, 10th Meeting
AGARD Struct. Mater. Panel, Aachen. A6.5)
Тэрнер, Дидл, Мартин, Мелош (М. J. Turner, E. H. Dill, H. С. Martin,
R. J. Melosh)
[1960] Large deflections of structures subjected to heating and external
loads, /. Aerospace Set, 27, 97—102, 127. A6.5, 20.1)
Тэрнер, Клаф, Мартин, Топп (М. J. Turner, R. W. Clough, H. С Martinr
L. P. Topp)
[1956] Stiffness and deflection analysis of complex structures, /. Aeron.
Sci., 23, № 9, 805—823, 854. B.1, 10.4)
Тэрнер, Мартин, Вейкл (M. J. Turner, H. С. Martin, В. С. Weikel)
[1964] Further developments and applications of the stiffness method,
в сб.: В. М. Fraeijs de Veubeke (ed.), «Matrix Methods in Structural
Analysis», AGARDograph 72, Pergamon Press, Ltd., Oxford, 203—
206. A6.5)
Уайт (J. L. White)
[1969] Finite elements in linear viscoelasticity, Proc. 2d Gonf. Matrix
Methods Struct. Mech., AFFDL-TR-68-150 (Oct. 15—17, 1968),.
Wright — Patterson AFB, Ohio, 489—516. B0.1)
Уильяме, Лэндел, Ферри (M. L. Williams, F. R. Landel, J. D. Ferry)
[1955] The temperature dependence of relaxation mechanisms in amorphous-
polymers and other glass forming liquids, /. ACS, 77, 3701—3707.
A9.2, 20.2)
Уильяме, Шейпери (M. L. Williams, R. A. Schapery)
[1962] Studies of viscoelastic media, Calif. Inst. Tech. Rep. ARL 62-366.
A8.1)
Уорд, Онат (I. M. Ward, E. T. Onat)
[1963] Nonlinear mechanical behavior of oriented polypropylene, /. Meek*.
Phys. Solids, 11, 217—229. A9.2)
Уоррен (D. S. Warren)
[1962] A matrix method for the analysis of buckling of structural panel*
subjected to creep environments, AF Flight Dyn. Lab. Rep. ASD-
TR-62-740. B0.1)
Уоррен, Кастл, Глория (D. S. Warren, R. A. Castle, R. C. Gloria)
[1962] An evaluation of the state-of-the-art of thermomechanical analysis of
structures, AF Flight Dyn. La':- Лев. WADD-TR-61-152. B.1, 20.1)
Утку (S. Utku)
[1966] Stiffness matrices for thin triangular elements of nonzero gaussian
curvature, AIAA 4th Aerospace Sci. Meeting Paper 66-530, Los
Angeles, June 27—29. A0.4)
Утку, Мелош (S. Utku, R. J. Melosh)
[1967] Behavior of triangular shell element stiffness matrices associated
with polyhedral deflection distributions, AIAA 5th Aerospace Sci.
Meeting Paper 67-114, N.Y., January 23—27. A0.4)
Уэплз (G. Whaples)
[1952] Caratheordory's temperature equations, /. Rat. Meek. Anal., 1,
301—307. A2.1)
Фелиппа (С. A. Felippa)
[1966] Refined finite element analysis of linear and non-linear two-dimen-
two-dimensional structures, doct. diss., Univ. of California, Berkeley. B.1,
8.1, 10.4)
Фелиппа, Клаф (С. A. Felippa, R. W. Clough)
[1968] The finite element method in solid mechanics, Symp. Numerical
Soln. Field Probl. Continuum Mech., Durham, North Carolina, April
5—6. B.1, 10, 10.2, 10.4)
448 список литературы
Фиккен (F. Ficken)
[1951] The continuation method for nonlinear functional equations, Comm.
Pure Appl. Math., 4, 435—456. A7.5)
Фикс, Нассиф (G. Fix, N. Nassif)
[1972] On finite element approximations to time-dependent problems, Nume-
rische Math., 19, № 2, 127—135. A0.2)
Фикс, Стрэиг (G. Fix, G. Strang)
[1969] Fourier analysis of the finite-element method in Ritz-Galerkin theory,
Studies Appl. Math., 48, 265—273. A0)
Финкбейнер (D. T. Finkbeiner II)
[1966] Introduction to matrices and linear transformations, 2d ed., W. H.[Fre-
H.[Freeman and Co., San Francisko. G.1)
Финлейсон, Скривен (В. A. Finlayson, L. E. Scriven)
[1966J The method of weighted residuals — A review, Appl. Math. Rev.,
19, № 9, 735—748. A0.3)
Флетчер (R. Fletcher)
[1965] Function minimization without evaluating derivatives, Computer J.,
8, 33-51. A7)
Флетчер, Пауэлл (R. Fletcher, M. J. D. Powell)
[1963] A rapidly convergent descent method for minimization, Computer J.,
6, № 2, 163—188. A7.3)
Флетчер, Ривс (R. Fletcher, С. М. Reeves)
[1964] Function minimization by conjugate gradients, Computer J., 7,
149—154. A7.3)
Фокс, Стэнтон (R. L. Fox, E. L. Stanton)
[1968] Developments in structural analysis by direct energy minimization,
AIAA J., 6, № 6, 1036—1042. [Русский перевод: Ракетная техника
и космонавтика, 6 A968), № 6, 55—63.] A7.1)
Форт (Т. Fort)
[1948] Finite differences, Clarendon Press, Oxford. (8.1)
Фрид (I. Fried)
[1969a] Some aspects of the natural coordinate system in the finite element
method, AIAA J., 7, № 7, 1366—1368.[|Русский перевод: Ракетная
техника и космонавтика, 7 A969), № 7, 187—188.] A0.4)
[19696] Finite-element analysis of time-dependent phenomena, AIAA J.,
7, № 6, 1170—1172. [Русский перевод: Ракетная техника и космо-
космонавтика, 7 A969), №|6, 210-212.] A1.1)
[1971] Discretization'and round-off error in the finite element analysis of
elliptic boundary value problems and eigenvalue problems, doct. diss.,
Massachusetts Inst. of Technology, Cambridge. A0.2)
Фридрихе (К. О. riedrichs)
[1934] Spektraltheorie halbbeschrankter Operatoren und Anwendung auf
die Spektralzerlegung von Differentialoperatoren, Math. Ann., 109,
456-487. A0.1)
Фридрихе, Келлер (К. О. Friedrichs, H. В. Keller)
[1967] A finite difference scheme for generalized Neumann problems, в сб.:
J. H. Bramble (ed.), «Numerical Solution of Partial Differential
Equations», Academic Press, Inc., N.Y. A0)
Фудзино, Осака (Т. Fujino, К. Ohsaka)
[1969] The heat conduction and thermal stress analysis by the finite element
method, Proc. 2d Conf. Matrix Methods Struct. Mech., AFFDL-TR-
68-150 (Oct. 15—17, 1968), Wright-Patterson AFB, Ohio, 1121 —
1164. B0.1)
Фын (Y. С Fung)
[1965] Foundations of solid mechanics, Prentice-Hall, Inc., Englewood
Cliffs, N.J. A2)
СПИСОК ЛИТЕРАТУРЫ 449
Хайслер, Стриклин, Стеббинз (W. E. Haisler, J. A. Stricklin, F. J. Stebbins)
[1971] Development and evaluation of solution procedures for geometrically
nonlinear structural analysis by the direct stiffness method, Proc.
AIAA/ASME 12th Struct., Struct. Dyn., Mater. Conf., Anaheim,
Calif. A7.5)
Харт-Смит (L. J. Hart-Smith)
[1966] Elasticity parameters for finite deformations of rubber-like materials,
Z. Angew. Math. Phys., 17, 608—625. A5.5, 18.1)
Харт-Смнт, Крисп (L. J. Hart-Smith, J. D. C. Crisp)
[1967] Large elastic deformations of thin rubber membranes, Int. J. Eng.
Sci., 5, № 1, 1—24. A5.5, 18.1)
Хатсопулас, Кинэн (G. N. Hatsopoulas, J. H. Keenan)
[1965] Principles of general thermodynamics, John Wiley & Sons, Inc.,
N.Y. A2)
Хатт (J. M. Hutt)
[1968] Dynamic stability of plates by finite elements, doct. diss., Oklahoma
State Univ., Stillwater. A6.5)
Хатчинсон, Беккер, Лэндел (W. D. Hutchinson, G. W. Becker, R. F. Landel)
[1965] Determination of the stored energy function of rubber-like materials,
Bull. 4thTMeeting Interagency Chem. Rocket Propulsion Group —
Working Group Mech. Behavior, CPIA Publ. 94U, vol. 1, 141—152.
A5.5)
Хестинз, Штифель (M. R. Hestens, E. Stiefel)
[1952] Method of conjugate gradients for solving linear problems, /. Res.
Nat. Bur. Std., В 49, 409—436. A7.3)
Хнббит, Маркл, Райе (Н. D. Hibbit, P. V. Marcal, J. R. Rice)
[1970] A finite element formulation for problems of large strain and large
displacement, Int. J.\ Solids) Struct., 6, № 8, 1069—1086.
A6.5)
Ходжмэн, Вист, Селби (С. D. Hodgman, R. С. Weast, S. M. Selby)
[1956] Handbook of chemistry and physics, Chemical Rubber Publishing
Co., Cleveland. B0.3)
Холанд, Белл (I. Holand, K. Bell)
[1969] (ред.) «Finite Element Methods in Stress Analysis», Tapir Press,
Trondheim, Norway. B.1)
Хофмайстер, Гринбаум, Ивенсен (L. D. Hofmeister, G. Greenbaum, D. A. Even-
sen)
[1970] Large strain, elasto-plastic finite element analysis, Proc. Uth
AIAA/ASME Struct. Structural Dyn. Mater. Conf., Fort Collins,
Colo., April. A6)
Хренников (A. Hrennikoff)
[1941] Solution of problems in elasticity by the framework method, /.
Appl. Mech., 8, A169—175. B.1)
Хуанг, Гидденс (А. В. Huang, D. P. Giddens)
[1967] The discrete ordinate method for the linearized boundary value
problems in the kinetic theory of gases, в сб. «Rarified Gas Dynamics,
5th Symposium», vol. 1, Academic Press, Inc. N. Y., 481—504.
Ш.4)
Хуанг К. (К. Huang)
[1963] Statistical mechanics, John Wiley & Sons, Inc., N.Y. A1.4)
Хьюджес, Эллик (Т. J. R. Hughes, H. Allik)
[1969] Finite elements for compressible and incompressible continua, Proc.
Symp. Civil. Eng., Vanderbilt Univ., Nashville, Tenn., 27—62.
A0.4, 16.2)
Чант (Т. Y. Chang)
[1966] Approximate solutions in linear viscoelasticity, doct. diss., Univ.
of California, Berkeley. B0.1)
29 Дж. Оден
450 СПИСОК ЛИТЕРАТУРЫ
Чэдвик (P. Chadwick)
[1960] Thermoelasticity. The dynamical theory, в сб.: I. N. Sneddon and
R. Hill (eds.), «Progress in Solid Mechanics», vol. 1, North-Holland
Publishing Co., Amsterdam. A9.2)
Чэкон, Ривлин (R. V. S.Chacon, R. S. Rivlin)
[1964] Representation theorems in the mechanics of materials with memory,
Angew. Math. Phys., 15, 444—447. A9.2)
Шварцл, Стэйвермэн (F. Schwarzl, A. J. Stayerman)
[1952] Time-temperature dependence of linear viscoelastic behavior, /.
Appl. Phys., 23, 838—843. A9.2)
Шейпери (R. A. Schapery)
[1968] On the application of a thermodynamic constitutive equation to
various nonlinear materials, School Aeron. Astronautics Eng. Sci.
Rep. AA & ES 68-4, Purdue Univ., Lafayette, Ind. A9.2)
Шенг (Р. L. Sheng)
[1955] Secondary elasticity, Chinese Assoc. Advan. Sci. Monograph, ser. 1,
vol. 1, № 1. A5.5)
Шиит, Богнер, Фокс (L. A. Schmit, Jr., F. K. Bogner, R. L. Fox)
[1968] Finite deflection structural analysis using plate and shell discrete
elements, AIAA J., 6, № 5, 781—791. [Русский перевод: Ракетная
техника и космонавтика, 6 A968), № 5, 17—29.] A7.1)
Шмит, Монфортон (L. A. Schmit, Jr., G. R. Monforton)
[1969] Finite deflection analysis of sandwich plates and cylindrical shells
with laminated facings, Proc. 10th AIAA/ASME Struct. Structural
Dyn. Mater. Gonf., New Orleans, April. A7.1)
Эймс (W. F. Ames)
[1965] Nonlinear partial differential equations in engineering, Academic
Press, Inc., N.Y. A0.3)
Эккарт (С. Eckart)
[1948] The thermodynamics of irreversible processes. IV. The theory of
elasticity and anelasticity, Phys. Rev., 72, № 2, 373—382. A2)
Эргатудис (I. Ergatoudis)
[1966] Quadrilateral elements in plane analysis, M.S. thesis, Univ. of
Wales, Swansea. A0.4)
Эргатудис, Айронс, Зенкевич (I. Ergatoudis, В. M. Irons, О. С. Zienkiewicz)
[1968а] Curved isoparametric, «quadrilateral» elements for finite element
analysis, Int. J. Solids Struct., 4, 31—42. G.5, 10.4)
[19686] Three dimensional analysis of arch dams and their foundations, Proc.
Symp. Arch. Dams., 21—34. G.5, 10.4)
Эринген (А. С Eringen)
[1962] Nonlinear theory of continuons media, McGraw-Hill Book Co.,
N.Y. E, 12.2, 14)
[1967] Mechanics of continue, John Wiley & Sons, Inc., N.Y. E, 12, 12.3,
13.8, 14, 14.4, 20.2)
Ягмаи (S. Yaghmai)
[1968] Incremental analysis of large deformations in mechanics of solids
with applications to axisymmetric shells of revolution, doct. diss.,
Univ. of California, Berkeley; также Struct. Eng. Lab. Rep. SESM
68-17, Univ. of California, Berkeley. A6.5)
Якоб (М. Jakob)
[1962] Heat transfer, vol. 1, John Wiley & Sons, Inc., N.Y. B0.3)
Янг (W. H. Yang)
[1967] Stress concentration in a rubber sheet under axially symmetric
stretching, /. Appl. Mech., 34, 942—946. [Русский перевод: Труды
Американского общества инженеров-механиков, Прикладная меха-
механика, 34 A967), сер. Е, № 4, 220-224.] A8.1)
ИМЕННОЙ УКАЗАТЕЛЬ
Авила (J. Avila) 427
Агирре-Рамирес (G. Agirre-Ramirez)
8, 38, 145, 181, 203, 204, 209, 210,
213, 220, 405, 427, 441
Адкинс (J. E. Adkins) 27, 235, 244,
377, 433
Айзаксон (Е. Isaacson) 293, 302, 326,
427
Айронс (В. Irons) 58, 134, 154, 156—
159, 162, 164, 427, 429, 540
Алберг (J. H. Ahlberg) 108, 427
Александер (Н. Alexander) 251, 351 —
354, 427
Аллен (D. N. de G. Allen) 306, 427
Арантес э Оливеира (Е. R. de Arantes
е Oliveira) 108, 128, 134, 135, 427
Аргирис (J. H. Argyris) 12, 13, 27,
144, 151, 152, 154, 161, 163, 169,
283, 290, 428, 429
Армстронг (W. H. Armstrong) 8, 405,
413, 441
Арчер (J. S. Archer) 92, 154, 204,
429, 433
Ахенбах (J. D. Achenbach) 394, 395,
429
Ахмад (S. Ahmad) 58, 157, 429
Бёрки (L. Вегке) 13, 430
Бидерман В. Л. 251, 351—354, 430
Био (М. A. Biot) 189, 283, 430
Биркгоф (G. Birkhoff) 38, 62, 108,
430
Бисплингхофф (R. L. Bisplinghoff)
291, 430
Богнер (F. К. Bogner) 58, 62, 164,
165, 294, 430, 431, 450
Бозич (W. F. Bozich) 13, 443
Бокс (М. J. Box) 293, 431
Боли (В. A. Boley) 189, 401, 431
Босхард (W. Bosshard) 163, 431
Браули (Н. J. Brauchli) 8, 66, 95,
108, 204, 279, 431, 441
Браун (J. E. Brown) 291, 431
Брисбейн (J. J. Brisbane) 169, 263,
357, 430
Брукс (S. H. Brooks) 293, 331, 431
Брэм (J. Bram) 293, 307, 308, 444
Брэмбл (J. Bramble) 108, 163, 431
Брэмлетт (Т. Т. Bramlette) 139, 181,
431, 437
Бубнов И. Г. 142, 182, 431
Бур, де (G. de Boor) 62, 108, 430
Бхандари (D. R. Bhandari) 8
Бабушка (I. Babuska) 108, 131, 429
Бак (К. Е. Buck) 144, 163, 249, 428,
445
Балтруконис (J. H. Baltrukonis) 362,
429
Барсоум (R. Barsoum) 291, 429
Бейдер (R. M. Bader) 13, 430, 443
Бейзли (G. P. Bazeley) 134, 135,
164, 429
Бейлард (Р. О. Bijlaard) 145, 258,
405, 433
Беккер (Е. В. Becker) 169, 220, 252,
253, 263, 264, 294, 341, 344, 357,
405, 429, 430, 449
Белл (К. Bell) 163, 430, 449
Бесселинг (J. R. Besseling) 405, 430
Бест (G. С. Best) 162, 164, 430
Вайнберг М. М. 119—121, 431
Вайшнав (R. N. Vaishnav) 362, 429
Вальц (J. E. Walz) 108, 431
Варга (R. S. Varga) 108, 431, 444
Вейкл (В. С. Weikel) 290, 447
Вейль Г. (Н. Weyl) 245, 432
Вемпнер (G. A. Wempner) 8, 58,
154, 164, 432, 441
Вёбеке (В. М. Fraeijs de Veubeke) 13,
108, 152, 164, 432
Вильсон (Е. L. Wilson) 168, 220, 290,
357, 405, 432, 439
Висманн (J. W. Wissmann) 34, 145,
169, 258, 432
Виссер (W. Visser) 405, 432
Вист (R. G. Weast) 423, 449
Витхум (D. Withum) 163, 432
29*
452
ИМЕННОЙ УКАЗАТЕЛЬ
Власов В. 3. 182
By (S. Т. Wu) 181, 427
Гавурин М. К. 317, 432
Галёркин Б. Г. 142, 432
Галлагер (R. H. Gallagher) 13, 145,
154, 258, 405, 433
Гарабедян (Н. L. Garabedian) 108,
430
Геррманн Дж. (G. Herrmann) 394,
395, 429
Геррманн Л. (L. R. Herrmann) 164,
253, 263, 264, 433, 442, 446
Гель (J. J. Goel) 108, 433
Гидденс (D. P. Giddens) 188, 449
Гильдебранд (F. В. Hildebrand) 62,
433
Глория (R. С. Gloria) 13, 405, 447
Гольдстейн (A. A. Goldstein) 308, 433
Грейвс (L. M. Graves) 145, 433
Грин Б. (В. Е. Greene) 108, 235, 244,
377, 392, 433
Грин Э. (А. Е. Green) 14, 27, 361,
433, 434
Гринбаум (G. Greenbaum) 253, 449
Гройб (W. H. Greub) 38, 145, 146, 434
Гудро (G. L. Goudreau) 405, 446
Гук (R. Hooke) 235, 434
Гуртин (М. Е. Gurtin) 382, 436
Давиденко Д. Ф. 317, 324, 434
Давидон (W. С. Davidon) 3iO, 434
Дана (J. D. Dana) 244, 434
Даниловская В. И. 419, 434
Дании (Р. С. Dunne) 108, 145, 434
Данхэм (R. S. Dunham) 405, 434
Де Гроот (S. R. DeGroot) 189, 434
Джаунземис (W. Jaunzemis) 222, 434
Джент (А. N. Gent) 251, 354, 434
Джон (F. John) 249, 434
Джонс (D. J. Johns) 108, 401, 433,
434
Джонсон (М. W. Johnson, Jr.) 13,108,
434, 443
Дик (A. L. Deak) 62, 434
Дилл (Е. Н. Dill) 290, 405, 447
Диллон (О. W. Dillon, Jr.) 402—404,
434
Донг (R. G. Dong) 405, 434
Дрейпер (К. J. Draper) 134, 135, 164,
427
Дэниэл (J. W. Daniel) 308, 435
ДюамельA. М. С. Duhamel) 401, 435
Зенкевич (О. С. Zienkiewicz) 13, 58,
134, 144, 151, 152, 154-159, 164,
169, 429, 435, 450
Зерна (W. Zerna) 14, 235, 361, 433
Зламал (М. Zlamal) 108, 153, 163,
431, 435
Зойтендейк (G. Zoutendijk) 293, 435
Зуданс (Z. Zudans) 13, 435
Ивенсен (D. A. Evensen) 253, 449
Исихара (A. Isihara) 251, 351—354,
435
Йиндра (F. Jindra) 402, 435
Каваи (Т. Kawai) 284, 435
Кавана (К. Т. Kavanagh) 253, 435
Канторович Л. В. 182, 435
Карьяппа (В. Kariappa) 291, 435
Кастл (R. A. Castle) 13, 405, 447
Келлер (Н. В. Keller) 108, 293, 302,
326, 427, 448
Келси (S. Kelsey) 12, 290, 428
Керр (R. I. Кегг) 151, 446
Ки (S. W. Key) 108, 135, 139, 150,
155, 156, 253, 264, 279, 284, 290,
345, 349, 351, 357, 371, 379, 413,
435, 441, 442
Кинг (I. P. King) 405, 436
Кинэн (J. H. Кеепап) 189, 449
Киснер (W. Kisner) 324, 436
Клаф (R. W. Clough) 13, 108, 127,
135, 144, 145, 157, 160, 162, 164,
168, 169, 357, 436, 447
Клоснер (J. M. Klosner) 251, 349,
350-354, 436, 444
Ковалик (J. Kowalik) 293, 436
Колеман (В. D. Coleman) 189, 195—
197, 227, 232, 382, 386, 387, 391,
392, 436
Коллатц (L. Gollatz) 324, 436
Колмогоров А. Н. 38, 50, 111, 436
Корнеев В. Г. 131, 437
Корнетт (D. Cornett) 162, 441
Кост (Т. L. Cost) 397, 399, 405, 437
Коши (A. L. Cauchy) 283, 306, 437
Крахула (J. L. Krahula) 145, 166, 437
Крисп (J. D. С. Crisp) 251, 354—356,
449
Кристенсен (R. M. Christensen) 396,
399, 437
Крон (G. Кгоп) 12, 34, 437
Кросс (D. A. Kross) 8, 58, 154, 164,
220, 221, 405, 414, 419, 432, 441
ИМЕННОЙ УКАЗАТЕЛЬ
453
Крэндалл (S. H. Crandall) 139, 437
Кубица (W. К. Kubitza) 209, 253,
290, 354, 355, 441
Куинн (J. F. Quinn) 405, 433
Курант (R. Gourant) 12, 62, 108,
174, 437
Кэмел (Н. Kamel) 12, 290, 428
Кэмпбелл (D. M. Campbell) 253, 442
Ланхар (Н. L. Langhaar) 62, 161, 437
Леви (Н. Lewy) 12, 174, 437
Лей (D. С. Leigh) 222, 437
Лейбниц (G. W. Leibniz) 12
Лекки (F. A. Leckie) 13, 442
Леонард (J. W. Leonard) 139, 437
Ли (G. С. Lee) 142, 444
Лианис (G. Lianis) 392, 397, 399,
437, 438
Лурье А. И. 438
Лэндел (F. R. Landel) 252, 397, 413,
447, 449
Люстерник Л. А. 38, 438
Мазур (P. Mazur) 189, 434
Майкснер (J. Meixner) 189, 438
Мак-Гуирт (С. W. McGuirt) 392, 399,
438
Мак-Кой (N. McCoy) 38, 438
Маклей (R. W. McLay) 108, 131,
433, 434, 438
Маклейн (S. MacLane) 38, 430
Маречек (G. Mareczek) 144, 428
Маркл (Р. V. Marcal) 13, 284, 290,
438, 449
Мартин (Н. С. Martin) 13, 145, 283,
290, 405, 438, 447
Мейер (G. Meyer) 38, 317, 318, 322,
438, 439
Мейзел (J. Maisel) 8
Мелош (R. J. Melosh) 108, 135, 139,
155, 164, 290, 405, 438, 447
Мид (R. Mead) 326, 439
Мизел (V. J. Mizel) 195, 196, 382,
386, 387, 436
Микитов (W. J. Mykytow) 13, 430, 443
Минич (М. D. Minich) 294, 430
Михлин С. Г. 112, 114—116, 136,
139, 439
Монфортон (G. R. Monforton) 294, 450
Морс (P. M. Morse) 177, 439
Мостов (G. D. Mostow) 38, 439
Муни (М. Моопеу) 250, 351—353,
439
Мур (J. Т. Мооге) 38, 439
Мэлверн (L. E. Malvern) 222, 439
Мэллетт (R. H. Mallett) 181, 294, 430у
431, 439
Мюллер (I. Muller) 196, 439
Мюррей Д. (D. W. Murray) 290, 439
Мюррей К. (К. Н. Murray) 134, 439
Нассиф (N. Nassif) 131, 448
Нахди (P. M. Naghdi) 396, 399, 437
Нелдер (J. A. Nelder) 326, 439
Немат-Нассер (S. Nemat-Nasser) 253,
439
Никелл (R. E. Nickell) 169, 220, 405,
419, 432, 439
Нильсон (Е. N. Nilson) 108, 427
Новацкий (W. Nowacki) 401, 439
Новожилов В. В. 19, 439
Ноля (W. Noll) 14, 26, 195, 196, 222,
226, 227, 232, 237, 241, 244, 245,
249, 253, 289, 382, 392, 436, 439, 446
Ньютон (I. Newton) 12
Оден (J. Т. Oden) 13, 34, 38, 58, 66,
91, 95, 108, 131, 142, 145, 154, 155,
162, 164, 169, 181, 203, 204, 209,
210, 213, 220, 221, 253, 257, 262,
264, 274, 279, 284, 290, 324, 341,
345, 349, 351, 354, 355, 357, 371,
376, 379, 402, 405, 413, 414, 419,
427, 430—433, 440, 441
Онат (Е. Т. Onat) 392, 447
Осака (К. Ohsaka) 405, 448
Осборн (М. R. Osborne) 293, 436
Ортега (J. M. Ortega) 293, 302, 317,
322, 442
Пайэн (Т. Н. Н. Pian) 62, 108, 164,
165, 434, 442, 446
Паркус (Н. Parkus) 401, 442
Парр (С. Н. Parr) 13, 220, 405, 430,
Пауэлл (М. J. D. Powell) >293, 310,
442, 448
Перси (J. H. Percy) 169, 442
Пестел (Е. С. Pestel) 13, 62, 442 -
Пипкин (А. С. Pipkin) 392, 443
Пирсон (К. Pearson) 235, 445
Пистер (К. S. Pister) 264, 405, 434,
446
Питерсон (F. E. Peterson) 253, 442
Пойа (G. Polya) 12, 443
Полемус (J. F. Polhemus) 145, 166,
437
Поу (J. Рое) 8, 220, 402, 405, 419, 441
Прагер (W. Prager) 12, 443
454
ИМЕННОЙ УКАЗАТЕЛЬ
Пригожий (I. Prigogine) 189, 443
Пшеменецкий (J. S. Przemieniecki)
13, 430, 443
Пэдлог (J. Padlog) 189, 443
Райе (J. R. Rice) 284, 290, 449
Раттиягер (I. Rattinger) 154, 433
Рашид (Y. R. Rashid) 168, 357, 436,
443
Редди (J. N. Reddy) 91, 441
Рейнболдт (W. С. Rheinboldt) 293,
302, 317, 322, 442
Рейнер (М. Reiner) 402, 443
Ривлин (R. S. Rivlin) 244, 246, 250,
345, 247, 392, 433, 434, 443-445,
450
Ривс (С. М. Reeves) 308, 448
Ригсби (D. M. Rigsby) 172, 441
Рита. (W. Ritz) 136, 444
Рован (W. H. Rowan, Jr.) 13, 444
Ролл (L. В. Rail) 302, 315, 444
Рыдзевский (J. R. Rydzewski) 13, 444
Рэлей (Sir John William Strutt,
Lord Rayleigh) 136, 444
Саати (Т. L. Saaty) 121, 293, 307, 308,
444
Сабо (В. A. Szabo) 142, 444
Савин Г. Н. 27, 444
Сайрус (N. J. Cyrus) 108, 431
Сакади (Z. Sakadi) 249, 444
Салама (А. Е. Salama) 291, 431
Сан Мигель (A. San Miguel) 252, 444
Сато (Т. Sato) 8, 253, 264, 341, 354,
442
Саундерс (D. W. Saunders) 250, 345,
443
Саусвелл (R. V. Southwell) 306, 444
Сегал (A. Segal) 251, 349—354, 436,
444
Селби (S. M. Selby) 423, 449
Сен-Венан (A. J.C1B. de Saint Venant)
283, 444
Сиарле (Р. G. Ciarlet) 108, 445
Сигер (A. Seeger) 249, 445
Силвестер (R. Silvester) 145, 445
Синг (J. L. Synge) 12, 108, 145, 150,
443, 445
Сингхал (А. С Singhal) 13, 445
Синьорини (A. Signorini) 251, 445
Скривен (L. E. Scriven) 139, 448
Смит (G. F. Smith) 244, 246, 445
Смолицкий X. Л. 112, 439
Соболев В. И. 38, 438
Сомашекар (R. Somashekar) 291, 435
Спенсер (A. J. M. Spenser) 392, 434
Спэнг (Н. A. Spang III) 293, 331,
332, 445
Стеббинз (F. J. Stebbins) 324, 449
Стернберг (Е. Sternberg) 419, 421, 445
Странео (P. Straneo) 232, 445
Стриклин (J. A. Stricklin) 151, 152,
324, 445, 449
Строум (D. R. Strome) 108, 433
Стрэнг (G. Strang) 108, 131, 445, 448
Стэйвермэн (A. J. Staverman) 397, 450
Стэнтон (Е. L. Stanton) 294, 448
Сэкмэн (J. J. Sackman) 169, 405,
419, 439
Сэмпсон (J. H. Sampson) 38, 439
Табанде (N. Tabaiideh) 108, 445
Татибана (М. Tatibana) 251, 351 —
354, 435 ;
Тодхантер (I. Todhunter) 235, 445
Томас (A. G. Thomas) 251, 345, 347,
354, 434, 444, 445
Тонг (P. Tong) 108, 164, 264, 442, 446
Топп (L. Р. Торр) 13, 145, 447
Точер (J. L. Tocher) 62, 108, 135, 162,
164, 169, 436, 446
Трилор (L. R. G. Treloar) 250, 251,
351, 446
Трусделл (С. Truesdell) 14, 24, 26,
189, 195, 196, 198, 203, 222, 226,
227, 232, 235, 237, 241, 244, 245,
249, 253, 263, 289, 446
Тупин (R. Toupin) 14, 24, 203, 264,
446
Тэйг (I. С. Taig) 151, 157, 446
Тэйлор P. (R. L. Taylor) 264, 405, 446
Тэйлор Э. (А. Е. Taylor) 38, 446
Тэрнер (М. J. Turner) 13, 145, 283,
290, 405, 447
Уайт (J. L. White) 405, 447
Уиджент (D. Wigent, Mrs.) 8
Уильяме (М. L. Williams) 345, 397,
413, 447
Уолш (J. L. Walsh) 108, 427
Уорд (I. M. Ward) 392, 447
Уоррен (D. S. Warren) 13, 405, 447
Утку (S. Utku) 164, 447
Уэйнер (J. H. Weiner) 189, 401, 431
Уэплз (G. Whaples) 190, 447
Фелиппа (С. A. Felippa) 13, 62, 108,
127, 144, 145, 151, 152, 157, 160,
162, 164, 169, 447
ИМЕННОЙ УКАЗАТЕЛЬ
455
Ферри (J. D. Ferri) 397, 413, 447
Фешбах (Н. Feshbach) 177, 439
Фиккен (F. Ficken) 317, 448
Фикс (G. Fix) 108, 131, 448
Финкбейнер (D. Т. Finkbeiner II)
38, 448
Финлейсон (В. A. Finlayson) 139,
448
Флетчер (R. Fletcher) 293, 308, 310,
448
Фогель (S. M. Vogel) 394, 395, 429
Фокс (R. L. Fox) 58, 62, 164, 165,
294, 431, 448, 450
Фомин С. В. 38, 50, 111, 436
Форт (Т. Fort) 62, 448
Фрид (I. Fried) 108, 131, 144, 145,
151, 152, 163, 169, 174, 429, 448
Фридрихе (К. О. Friedrichs) 12, 108,
115, 174, 437, 448
Фудзино (Т. Fujino) 405, 448
Фултон (R. E. Fulton) 108, 431
Фын (Y. С. Fung) 189, 448
Хайслер (W. E. Haisler) 324, 449
Халфмен (R. L. Halfman) 291, 430
Харт-Смит (L. J. Hart-Smith) 251,
351—356, 449
Харц (В. J. Hartz) 62, 162в 446
Хасицумэ (N. Hashitsume) 251, 351—
354, 435
Хатсопулас (G. N. Hatsopoulas) 189,
449
Хатт (J. M. Hutt) 291, 431, 449
Хатчинсон (W. D. Hutchinson) 252,
449
Хафф (R. D. Huff) 405, 443
Херрера (R. I. Неггега) 382, 436
Хестинз (М. R. Hestens) 308, 449
Хёрлбат (С. S. Hurlbut) 244, 434
Хиббит (Н. D. Hibbit) 284, 290,
449
Хилбер (Н. М. Hilber) 144, 428
Ходжмэн (С. D. Hodgman) 423, 449
Холанд (I. Holand) 13, 449
Холистер (G. S. Holister) 13, 435
Холловей (G. F. Holloway) 405, 443
Хофмайстер (L. D. Hofmeister) 253,
449
Хренников (A. Hrennikoff) 12, 449
Хуанг А. (А. В. Huang) 188, 449
Хуанг К. (К. Huang) 181, 449
Хьюджес (Т. J. Hughes) 169, 264,
267, 449
Хэкетт (R. M. Hackett) 13, 444
Чакраворти (J. G. Chakravorty) 419,
421, 445
Чанг (Т. Y. Chang) 405, 413, 442,
446, 449
Ченг (Y. К. Cheung) 13, 134, 135,
144, 151, 152, 154, 155, 164, 169,
429, 435
Чу (S. С. Chu) 62, 161, 437
Чэдвик (P. Chadwick) 401, 449
Чэкон (R. V. S. Chacon) 392, 450
Шарпф (D. W. Scharpf) 144, 163, 169,
428, 429
Шатов (Н. D. Shatoff) 253, 439
Шах (С. G. Shah) 291, 435
Шварцл (F. Schwarzl) 397, 450
Шейпери (R. A. Schapery) 345, 392,
447, 450
Шенг (P. L. Sheng) 249, 450
Шерк (М. Н. Shirk) 13, 430
Шмит (L. A. Schmit, Jr.) 58, 62, 164,
165, 294, 430, 431, 439, 450
Штифель (Е. Stiefel) 308, 449
Шульц (М. Н. Schultz) 108, 445
Эймс (W. F. Ames) 139, 450
Эккарт (С. Eckart) 189, 450
Эллик (Н. Allik) 169, 264, 267, 449
Эргатудис (I. Ergatoudis) 58, 154,
156-159, 450
Эринген (А. С. Eringen) 24, 189, 192,
195, 196, 219, 222, 232, 450
Эшли (Н. Ashley) 291, 430
Ягмаи (S. Yaghmai) 284, 450
Якоб (М. Yakob) 426, 450
Ямада (Y. Yamada) 13, 433
Янг (W. H. Yang) 348, 450
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
абелева группа 39
абсолютная температура 190
абсолютно жесткое движение 17
аддитивный оператор 40
адиабатический процесс 198
аксиома материальной объектив-
объективности 228
— независимости материала от систе-
системы отсчета 228
анизотропный материал 231
базис 39
банахово пространство 40
барицентрические координаты 146
билинейный конкомитант 118
биортогональный базис счетный 67
вектор 39
— напряжения 26
— перемещения 17
вершина 326
взаимная однозначность 39
вмороженные координаты 16
внешняя точка 42
внутренняя диссипация 197
— энергия 190
всюду плотно 38
выпуклая область 295
геометрические краевые условия 128
гильбертово пространство 41
гиперупругий материал 239
главная деформация 18
главное направление деформации 18
главные краевые условия 128
— производные 128
главный инвариант деформации 19
глобальное значение 31
— — обобщенное 93
— множество 48
— перемещение 200
глобальный узел 44
гомеоморфизм 43
градиент деформации 17
градиентный метод 297
граница 42
границы оператора 113
граничная точка 42
группа 39
— изотропии 231
гуков материал 247
движение 14
двойственность 41
декартовы координаты 42
деформация 20
диаметр элемента 123
дизъюнктность 42
динамическое краевое условие 27
дифференциал Гато 118
— Фреше 119
— — локально равномерный 119
достижимая точка 301
дуальные пространства 41
единичная мода 126
единичный вектор 295
естественное состояние 231
естественные координаты 151
— краевые условия 128
задача Даниловской 419
закон взаимности Максвелла 205
— сохранения массы 24
— — энергии 192
— термодинамики второй 196
— — нулевой 190
— — первый 193
законы движения Коши 28—29
закрытая справа квадратурная фор-
формула 326
замкнутая система 190
измельчение 123
— нерегулярное 123
— регулярное 123
изолированная система 190
изопараметрический элемент 157
иеотермический процесс 198
изотропный материал 231
изохорическая деформация 20
изоэнергетический процесс 198—199
изэятропический процесс 198
инвариант тензора 19
интерполяционные функции Эрмита
обобщенные 62
инцидентность 32
итерационный метод 296
итерация 296
кинетическая энергия 190
класс СР 128
— &г 124
количество движения 25
коммутативная группа 39
компактность 40
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
457
комплексная модель 152
компоненты перемещения 17
конвективные координаты 16
конечный элемент 30
консервативная сила 238
конфигурация 14
координаты 14
коэффициент отражения 327
— сжатия 298, 328
— смещения 398
коэффициенты упругости 246
краевое условие в напряжениях 27
кратность граничной точки 48
кривая 296
кристаллические типы 245
критическая точка 120
лагранжевы координаты 15
линейное пространство 39
линейный оператор 40
— функционал 113
локальное значение 33, 49
— — обобщенное 92
— множество 49
— перемещение 200
локальные координаты 31, 45
локальный узел 45
масса 14
массовая плотность 24
— сила 25
материал Александера 251, 351—353
— анизотропный 231
— Бидермана 251, 351—353
— гиперупругий 239
— градиентного типа 226
— гуков 247
— дифференциального типа 226
— изотропный 231
— Исихары — Хасицумэ — Татиба-
ны 251, 351-353
— Клоснера — Сегала 251, 351—353
— Муни 250, 351—357
— Муни — Ривлина 250
— неогуков 250, 341, 351—353
— неоднородный 232
— однородный 232
— ортотропный 243
— скоростного типа 233
— совершенный 241
— термореологически простой 397
— термоупругий 401
— упругий 236
— Харт-Смита 251, 351—353
материальная независимость от
системы отсчета 228
материальные координаты 15
материальный изоморфизм 231
матрица Гессе 304
— Грама 69
— начального нагружения 290
— — поворота 290
— начальных давлений 291
— — напряжений 290
— приращений жесткости 290
— Якоби 313
межэлементная граница 47
мера деформации 18
— мелкости 123
метод Адамса — Моултона 326
— Бубнова 142
— Бубнова — Власова 182
— взвешенных невязок 139
— Галёркина 142
— гиперокружностей 12
— градиентный 297
— Канторовича 182
— каркасов 12
— наименьших квадратов 143
— наискорейшего спуска 306
— Ньютона — Рафсона 303, 312
— •— ¦— модифицированный 303, 313-
— переменных матриц 310
— поиска 297
— покоординатной релаксации 304
— поправок и предсказаний 326
— последовательных нагружений 317"
метод последовательных приближе-
приближений 298
— Ритца 136
— Рунге — Кутты 324
с коэффициентами Гилла 325-
Кутты 325
Рунге 325
— Саусвелла 306
— случайного поиска 330
— сопряженных градиентов 308
— спуска 297
— хорд 303
метрика 41
метрическое пространство 41
механическая мощность 190
минимизирующая последователь-
последовательность 136
модель БГК 181
модули упругости второго порядка
249
момент количества движения 25
мощность напряжений 194
напряженное состояние 26
начало 42
невязка 140
458
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
недеформированное состояние 231
неитерационный метод 296
нелинейный оператор 40
неогуков материал 341, 351—353
неоднородный материал 232
непересекающиеся множества 42
неподвижная точка 297
непрерывный оператор 113
неравенство Клаузиуса — Дюгема 196
— Клаузиуса — Планка 198
несвязанная область 44
несобранная область 44
неэвклидов элемент 166
норма 39
— на полных предысториях 386
— — прошлых предысториях 386
— оператора 113
нормализованные базисные функции
78
нормированное пространство 40
нулевое приближение 296
нулевой закон термодинамики 190
область 42
— достижимости 301
— замкнутая 42
— определения 38, 40
область отклонения 44
— открытая 42
обобщенная диссипация 220
— производная в смысле L2 112
— сила 207
обобщенное решение задачи миними-
минимизации 122
обобщенный тепловой поток 220
образ 38, 40
обратная функция 39
общее диссипационное неравенство
197
ограниченность 43
ограниченный оператор 40, 113
однородная деформация 203
— температура 227
однородный материал 232
— оператор 40
— процесс 199
оператор 40
— гомотопии 318
определяющие уравнения 13
определяющий функционал 228
ортогональность 68
ортонормированный базис 295
ортотропный материал 243
остаточный член 119
открытая справа квадратурная фор-
формула 326
— область 295
отношение инцидентности 46
отображение 38
— на 39
параллелепипеидальный элемент 156
параметр состояния 190
переменная состояния 190
перестановочные символы 19
плотность 38 ,
— энергии деформации
поверхностная сила 25
поверхность 295
— уровня 296
покоординатные методы 304
полная по энергии система 115
— система 112
полное производство энтропии 196
полнота 110
положительно ограниченный снизу
оператор 113
— определенный оператор 113
пополнение 40, 110
последовательность Коши 40, 109
поступление энтропии от внутренних
источников 196
потенциальный оператор 120
поток энтропии 196
правило равноприсутствия 225
предельная точка 38
предыстория 383
— полная 383
— прошлая 386
преобразование 38
— наблюдателя 228
приведенное время 398
привязывание 34
призматический элемент 156
принцип Гамильтона 243
— детерминизма 224
— Лагранжа 243
— локального действия 225
— материальной симметрии 232
— окрестности 225
— сжимающих отображений 299
— стационарности потенциальной
энергии 243
— физической допустимости 223
продолжение оператора 113
производная Гато 119
— Фреше 119
производный элемент 166
простая жидкость 231
простое твердое тело 231
простой материал 227
пространственные координаты 15
пространство Соболева 112
прямая сумма 39
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
459
равновесие 190
равномерная эквивалентность 125
равномерно утончающееся измель-
измельчение 123
равномерное измельчение 123
радиус-вектор 42
разбиение 33, 35, 46
размерность 39
расстояние 41
расширение оператора 113
самосопряженность 71
свободная энергия 197
связность 42
связывание 33, 35, 45
семейство 2Fr 124
сепарабельность 41
сжатие 298
сжимающее отображение 298
сильный градиент 120
симметричный оператор 113
симплекс 143, 326
симплексная модель 145
симплексный метод поиска 326
система 189
скалярное произведение 41
— умножение 39
скорость деформации 21
— нагрева 192
— тепловой работы 192
слабый градиент 120
сложная модель 154
совершенный материал 241
согласованная матрица масс 204
согласованные силы 207
соответственность 135
сопряженное пространство 40
сопряженные группы 231
сопряженный базис 70
— оператор 81, 118
составной элемент 169
состояние системы 190
степень свободы элемента 124
сумма 39
сфера 295
сходимость по энергии 115
тело 14
температура 190
тензор бесконечно малой деформации
18
— деформации Грина — Сен-Вана-
на 18
— меры деформации Грина 17
— напряжений 26
— — Пиолы — Кирхгоффа второй
26
— — — — первый 26
— поворота 18
— скоростей бесконечно малых де-
деформаций 22
— — поворота 22
теорема Хана — Банаха 111
теория гиперупругости второго по-
порядка 247
— Фёппля — Кармана 374
тепловая плотность 192
тепловой поток 192
термодинамический процесс 198
термореологически простой мате-
материал 397
термоупругий материал 401
точечное пространство 42
точка накопления 38
трансверсальная изотропия 245
трилинейная аппроксимация 155
удельная теплоемкость 401, 403, 420,
425
— энтропия 196
узел 30
узловая точка 30
упругий материал 236
уравнение неразрывности 25
— количества движения 25
— момента количества движения 25
— состояния 13
условие несжимаемости 249
условия совместимости 47
физические компоненты напряжений
27
формально сопряженный оператор
118
фундаментальная матрица 69
функционал 40
— состояния 228
функция 38
— влияния 388
шар 42
эвклидово точечное пространство 42
эйлеровы координаты 15
экстремальная точка 120
экстремальный принцип 121
энергетическая норма 115
энергия 115
энтропия 195
С-д-совместимость 160
г-допустимость 125
г-эквивалентность 125
Оглавление
Предисловие редактора перевода 5
Предисловие 6
Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ 9
1. Введение . . . . 9
2. Концепция конечных элементов 10
2.1. Исторические замечания И
3# Механика сплошных сред . . , 13
4. Кинематика 14
4.1. Геометрия и движение 14
4.2. Перемещение и деформация 17
4.3. Инварианты деформации 10
4.4. Изменения объема и площади 20
4.5. Скорость, ускорение и скорость деформации 21
4.6. Криволинейные координаты 22
5. Динамика 23
5.1. Закон сохранения массы и уравнения коли-
количества движения и момента количества дви-
движения . : 24
5.2. Внешние силы и напряжения 25
5.3. Законы движения Коши 28
Глава II. ТЕОРИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ 30
6. Вводное изложение основных идей метода ко-
конечных элементов 30
6.1. Одномерная задача 31
6.2. Двумерная задача 36
7. Конечноэлементные модели функций общего вида 38
7.1. Некоторые предварительные сведения из ма-
математики 38
7.2. Замечания об обозначениях 43
7.3. Дискретная модель области М 44
Совместимость . 47
Кратность граничных точек 48
7.4. Дискретная модель функции F 48
7.5. Примеры 51
Пример 7.1. Скалярная функция на
двумерной области 51
ОГЛАВЛЕНИЕ 461
Пример 7.2. Преобразования локальных
координат 55
Пример 7.3. Векторные поля .... 57
Пример 7.4. Тензорные поля .... 59
Пример 7.5. Линейная интерполяция . 60
8. Представления высшего порядка 61
8.1. Общие свойства моделей высшего порядка 61
8.2. Примеры 64
Пример 8.1. Представление второго
порядка 64
Пример 8.2. Эрмитова интерполяция . 65
9. Теория сопряженных аппроксимаций .... 66
9.1. Сопряженные пространства и биортогональ-
ные базисы 66
9.2. Сопряженные подпространства 68
Скалярные произведения и нормы . . 72
Аффинные преобразования 72
Резюме 73
9.3. Наилучшая аппроксимация 74
Обобщение 76
9.4. Некоторые свойства сопряженных аппрокси-
аппроксимаций 77
Моменты и объемы 78
9.5. Линейные операторы 79
Задачи о собственных значениях ... 81
Производные сопряженных аппроксима-
аппроксимаций 82
9.6. Приложения к конечноэлементным аппро-
аппроксимациям 85
Фундаментальные свойства конечноэле-
ментных аппроксимаций 87
9.7. Обобщенные сопряженные переменные . . 91
9.8. Примеры 94
Пример 9.1. Механическая работа . . 94
Пример 9.2. Вычисление напряжений . . 95
Пример 9.3. Двумерные сопряженно-ап-
проксимационные функции .... 98
Пример 9.4. Кусочно-линейные аппрок-
симационные функции одной пере-
переменной 101
Пример 9.5. Полиномы, аналитические
функции 106
10. Конечные элементы и интерполяционные функ-
функции 107
10.1. Операторы в нормированных простран-
пространствах 108
Последовательности Коши и полнота 109
Линейные операторы 112
Нелинейные операторы . 118
10.2. Конечноэлементные аппроксимации . . 122
10.3. Конечноэлементные модели операторных
уравнений 135
Метод Ритца 136
Метод взвешенных невязок 139
Метод Галёркина 142
462 ОГЛАВЛЕНИЕ
Метод наименьших квадратов 143
10.4. Примеры конечных элементов .... 144
10.4.1. Симплексные модели 145
10.4.2. Комплексные модели 152
10.4.3. Сложные модели 154
10.4.4. Изопараметрические элементы . . 157
10.4.5. Примеры элементов высших поряд-
порядков 160
10.4.6. Дополнительные замечания о ко-
нечноэлементных моделях 165
11. Некоторые приложения 169
11.1. Конечные элементы в пространственно-
временной области 169
Двумерные задачи 170
Одномерные волны 171
Устойчивость 174
Динамические системы 174
11.2. Конечные элементы в комплексной плоско-
плоскости. Уравнение Шрёдингера 176
11.3. Одно нелинейное дифференциальное урав-
уравнение в частных производных 178
11.4. Кинетическая теория газов. Уравнение
Больцмана 181
Неустановившееся куэттовское течение . 184
Глава III. ТЕРМОМЕХАНИЧЕСКОЕ ПОВЕДЕНИЕ КОНЕЧНЫХ
ЭЛЕМЕНТОВ СПЛОШНОЙ СРЕДЫ 189
12. Предварительные сведения из термодинамики . 189
12.1. Основные определения и понятия . . 189
12.2. Сохранение энергии. Первый закон . . 192
12.3. Энтропия. Неравенство Клаузиуса — Дю-
гема 195
12.4. Свободная энергия и внутренняя дисси-
диссипация 197
12.5. Термодинамические процессы 198
13. Термомеханика конечного элемента 199
13.1. Кинематика конечного элемента . . . 19&
13.2. Энергия конечных элементов 203
Кинетическая энергия 204
Внутренняя энергия ' 205
Механическая мощность 206
Скорость нагрева 208
13.3. Сохранение энергии в конечном элементе 208
13.4. Общие уравнения движения конечного эле-
элемента 209
13.5. Глобальные формы уравнения движения. 210
13.6. Уравнения движения в координатах обще-
общего вида 213
13.7. Представления высших порядков .... 216
13.8. Энтропия и теплопередача в конечных эле-
элементах 218
14. Уравнения состояния 221
14.1. Вводные замечания 222
ОГЛАВЛЕНИЕ 465
14.2. Физическая допустимость, детерминизм,
равноприсутствие 223
14.3. Локальное действие 225
14.4. Независимость от системы отсчета и сим-
симметрия 228
Другие правила 232
14.5. Определяющие функционалы для конеч-
конечных элементов 233
Глава IV. ТЕОРИЯ УПРУГОСТИ ПРИ КОНЕЧНЫХ ДЕФОР-
ДЕФОРМАЦИЯХ 235
15. Основы теории упругости 235
15.1. Вводные замечания 235
15.2. Упругие материалы 236
15.3. Гиперупругость, термодинамические ос-
основы 238
15.4. Полные потенциалы . . . 243
15.5. Функция энергии деформации .... 244
Анизотропные материалы 244
Полиноминальное представление . . . 246
Изотропные материалы 247
Несжимаемые тела 249
Условия интегрируемости 252
16. Конечные элементы упругих тел 253
16.1. Нелинейные жесткостные соотношения . . 253
Симплексные модели 257
Глобальные формы 259
16.2. Несжимаемые материалы 263
Симплексные модели 269
16.3. Обобщенные силы и напряжения .... 271
Аппроксимации 274
Напряжения 279
16.4. Формулировки с использованием потен-
потенциальной энергии 280
16.5. Уравнения в приращениях 283
Общие уравнения 284
Упругие элементы 288
Приращение жесткостей 289
Несжимаемые элементы 291
16.6. Криволинейные координаты 292
17. Численные решения нелинейных уравнений . 293
17.1. Вводные замечания 293
Геометрические понятия 294
Методы решения 296
17.2. Неподвижные точки и сжимающие ото-
отображения 297
17.3. Методы спуска и градиентной миними-
минимизации 303
Покоординатные методы 304
Метод наискорейшего спуска .... 306
Методы сопряженных градиентов . . 308
Метод переменных матриц 310
17.4. Метод Ньютона—Рафсона 312
17.5. Метод последовательных нагружений . . 317
Модификации 322
464 ОГЛАВЛЕНИЕ
Численное интегрирование 323
17.6. Методы поиска 326
Симплексный метод поиска 326
Методы случайного поиска 330
18. Некоторые приложения 332
18.1. Плоское напряженное состояние . . . 332
Упругие мембраны 332
Мембранные элементы 336
Растяжение упругого листа 339
Лист с круговым отверстием .... 345
Одноосное р'астяжение листа с круговым
отверстием 348
Влияние вида функции энергии дефор-
деформации 351
Раздувание упругих мембран .... 354
18.2. Несжимаемые упругие тела вращения . . 357
Конечноэлементные аппроксимации . . 358
Упрощенные формы 359
Задача о бесконечном цилиндре ... 364
Толстостенный сосуд 368
Изгиб и раздувание круговой пластины . 371
18.3. Конечная плоская деформация .... 375
Конечноэлементные приближения . . 376
Чистый и обобщенный сдвиг .... 376
Плоское тело с круговым отверстием . 379
Глава V. НЕЛИНЕЙНОЕ ТЕРМОМЕХАНИЧЕСКОЕ
ПОВЕДЕНИЕ СПЛОШНЫХ СРЕД 381
19. Термомеханика материалов с памятью . . . 381
19.1. Термодинамика простых материалов . . 382
Свойства гладкости функционалов . . 384
Затухающая память 387
Некоторые основные свойства термоме-
ханически простых материалов . . . 388
19.2. Частные формы уравнений состояния для
простых материалов 392
Термореологически простые материалы . 397
Термоупругость 401
20. Конечноэлементные модели нелинейного термо-
термомеханического поведения сплошных сред ... 404
20.1. Конечные элементы материалов с памятью 405
20.2. Применение к случаю термореологически
простых материалов 408
Пример. Неустановившееся поведение
термовязкоупругого толстостенного ци-
цилиндра 413
20.3. Приложения к теории нелинейной связан-
связанной термоупругости 418
Пример. Нелинейное термоупругое полу-
полупространство 419
Список литературы 427
Именной указатель 451
Предметный указатель 456
ПОПРАВКА
Стр. 5, строка 8 снизу: вместо 13 к. следует читать 14 к.