Text
,,'i',
.
j' rЕО
Т
ИЯ
\ j, ;<,.':";/> : 6 " '.... 8 .
" " l' ,
, 1 '.;:: r
"
l'
, I
t
Н. Н. НИКИТИН
rЕОМЕТРИЯ
у Ч Е Б Н И К Д Л Я 6 8 К Л А С С О В
и 3 Д А Н И Е 16 e
Уmверждё/1, Министерством nросвещенuя РСФСР
ИЗДАТЕЛЬСТВО «ПРОСВЕЩЕНИЕ» МОСКВА 1971
513 (075)
Н-62
ОТ ИЗДАТЕЛЬСТВА
По решению Министерства просвещения СССР
в 15-е издание учебника
внесены дополнения и уточнени ,
предложенные академиком А. Н. KOA},f,OZUP06blAi
НиКОАйи Никифорович Никитин
rЕОМЕТРИЯ
Учебник для 6 классов
Редактор И. с. Комиссарова. Переплёт художника Б. л. Николаева.
Технический редактор Е. В. Б даН08а. Корректор Р. Б. ШтутAUJН.
СдаНо в набор 24/11 1970 f. Подписано К печати 24/XII 1970 r f)OX90t . Бумаrа типоrраф.
екая НII З. Печ. л. 13. Уq.-иэд. л. 12,18. Тираж 1500 Tы.. (1 ОOl з (00000) экэ.
Издательство «ПРОС8ещение Комитета по печати при Совете Министров РСФСР.
Москва, З-А проезд Марьиной рощи. 41.
Саратовский пo.nиrрафический (омбинат Росrnавполиrpафпрома Комитета ПО печати
IlpB Совете Министров РСФСР. Саратов, уn. Черяышевскоro, 59. Заказ 562.
иева без переплёта 16 коп., переплёт бум. 7 коп., коленкор 15 коп.
6-8
rЛАВА I
ОСНОВНЫЕ понятия.
1. ЧТО' ТАКОЕ rЕО.'WЕТРИЯ.
Мы приступаем к изучению HOBoro учебноro предмета. Называ-
ется этот учебный предмет r е о м е т р и Я. Слово это rреческое.
В переводе на русский язык оно означает з е м л е м е р и е.
rеометрия возникла ещё в rлубокой древности, Коrда людям
пришлось заниматься измерение'М" расстояний, вычислять площади
земельных .участков разнообразной формы и различных размеров,
составлять планы земельных участков, определять по плану их
настоящие раЗl\1еры, вычислять вместимость различных сооруже.
ний, сосудов.
Несколь о тысяч лет назад в древнем Еrипте были выработаны
правила, которыми пользовались люди при вычислении различных
расстояний, площадей и объёмов.
Е)кеrодные разливы реки Нил надолrо затопляли плодородную
долину реки и смывали следы rраниц между земельными участка-
ми. После разлива еrиптяне должны были находить свои земельные
участки и снова восстанавливать их rраницы. Всё это было связано
со СЛОЖНЫl\fИ измерительными, чертёжными и вычислителЬНЫ\IИ
работами.
Еrиптяне вели оживлённую торrовлю с rреками. rреки позаим-
ствовали знания у еrиптян, дополнили, уточнили их, постепенно
развили и привели в систему. Особенно MHoro в деле развития reo.
метрии сделал rреческий учёный-математик Евклид, живший две
тысячи двести лет назад. Разработанную им науку он изложил в
тринадцати книrах, которые назвал «Начала».
«Начала» Евклида содержали сведения не только по rеометрии,
но и по арифметике. По образцу евклидовых «Начал» составляются
школьные учебники и по настоящее время. В некоторых странах
долrое время школьники изучали rеометрию по переводу «Начал»
ЕВI<,пида.
В настоящее время содер>кание rеометрии значительно разно-
образнее и сложнее. На уроках rеометрии мы более подробно озна-
к.?мимся с тем, какими вопросами она занимается и что составляет
ее содержание.
3
2. rЕОМЕТРИЧЕСКОЕ ТЕЛО. ПОВЕРХНОСТЬ. ЛИНИЯ. ТОЧКА.
Окружающие нас предметы мы можем изучать по-разному.
Например, о школьном здании можно сказать, что оно кирпичное
(или деревянное), тёмно-красное (или друrоrо цвета); ствол берёзы
белый; листья на деревьях зелёные (или жёлтые). О чернильнице
може 1 сказать, что она сделана из пластмассы, что она чёрная.
Классная комната светлая, тёплая. Яблоко румяное, сочное, вкус-
ное.
Однако на занятиях по rеометрии в окружающих предметах
нас не интересуют ни материал, из KOToporo они сделаны, ни цвет,
ни то состояние, в каком они находятся (твёрдое, жидкое); всем
этим занимаются на уроках естествознания, фи ики, химии.
При изучении rеометрии нас будут интересовать фор м а и
раз м е р.ы преД 1етов. Например, и деревянный, и картонный,
и проволочный куб НО ИТ одно и то же название куб (черт. 1).
Эти предметы сделаны из различноrо материала, но имеют одну
и ту же форму, отличаются только своими размераl\1И.
Точно так же футбольный мяч, деревянный шар, резиновый
мяч, мыльный пузырь имеют одну и ту же форму форму шара
(черт. 2).
Если не обращать внимания на физические свойства предмета
(материал, из KOToporo он сделан, цвет и т. д.), а рассматривать
только форму предмета и ero размеры, то этому преДl\1ету можно
дать название r е о м е т р и ч е с к о r о т е л а.
На чертеже 3 дано изображение здания MOCKoBcKoro rосудар-
CTBeHHoro университета имени М. В. Ломоносова.
Рассматрив я ero с rеОl\1етрической точки зрения, мы обращаем
ВНИl\lание на ero размеры, взаимное расположение отдельных час-
тей, их форму. I
Если пройти по комнате в каКО 1-нибудь направлении, то можно
в конце концов дойти до
стены. Дальше идти нельзя..
Комната с этой стороны or-
раничена, имеет rраниuу.
То же самое получится,
U ..
если мы поидем по комна-
те в друrом направлении.
Если в комнате под-
бросить вверх мяч или ка-
кой-нибудь друrой лёrкий
предмет, то он долетиТ до
потолка и ударится о Hero.
ВЫХОДИТ, что комната or-
раничена не только с бо..
ков, но также сверху и
снизу. rраница тела есть
поверхность.
ЧЕРТ. )
\' ',",\ \ \ Q
\: , . '} I I I . : ' .' . .
I .
":' ':1' . ..
........... .. .\............
. .
-
ЧЕРТ. 2
4
ЧЕРТ. 3
За поверхность можно условно принять,
например, лист бумаrи, если пренебречь ero
толщиной; таким образом, поверхность мож-
но представить себе отдельно от reoMeT-
рическоrо тела.
Если часть поверхности белоrо листа
бумаrи закрасить какой нибудь краской.
(черт. 4), то закрашенная часть будет от- ЧЕРТ. 4
деляться от белой части листа линией.
- Линия оrраничивает закрашенную часть поверхности листа бу.
маrи. rраница поверхности есть линия.
За линию МdЖНО условно принять, например, натянутую или
ненатянутую нить.
Линию условно можно изобразить мелом на доске или каран-
дашом на листе бумаrи. --------
Таким образом, ЛИНИIО lvtожно представить себе отдельно от
поверхности, если пренебречь толщиной получающихся изобра-
жений.
Если взять часть какой нибудь линии, то концаl\IИ её будут
точки.
в
8
д.
р
8
С
8 Е
Ч1:: РТ & 5
ЧЕРТ. 6
8
За точку ,{ожно условно принять то изображение, OTopoe по-
лучится на листе бумаrи, если на этот лист надавить концом остро
отточенноrо карандаша. Таким образом, точку MOiKHO представить
себе отдельно от линии, если пренебречь размерами получающихся
изобра)l{ений.
Отметим мелом на доске несколько точек, чтобы различать эти
точки, можно их пронумеровать или обозначить каждую точку
буквой.
В reометрии принято обозначать точки заrлзвными буквами
латинскоrо алфавита. На чертеже 5 изображены: точка А, точка В,
('
точка С, точка D, точка Е.
Таким же образом мы можем отметить точки на листе бумаrн.
На поверхности земли точки отмечаются колышками, иноr да
ставится столбик (черт. 6).
3. ПРЯМАЯ. ЛУЧ. ОТРЕЗОК.
Первое представление о прямой линии можно получить, натянув
между двумя точками А и В шнур (черт. 7). Так получится, однако,
не вся прямая, а только её отрезок, заключённый между точкаl\.tи
А и В. На чертеже 8 отрезок АВ продолжен до краёв классной
доски. Но прямая, часть которой видна на чертеже, продолжается
и дальше неоrраниченно в обе стороны.
BOKpyr себя вы найдёте MHoro отрезков прямой: край стола,
край листа БУI\1аrи. Если аккуратно сложить лист бумаrи, то
линия сrиба будет прямолинейным отрезком (черт. 9). Постарайтесь
во всех этих случаях представить себе всю прямую, на которой
лежит какой либо отрезок. Укажите, например, точки, в которых
прямая, проходящая по краю стола, пересекает стены класса.
В rеометрии отвлекаются от практических трудностей, возни-
кающих при желании продолжить отрезок очень далеко, и считают,
что каждая прямая линия уже продолжается в обе стороны Heorpa
ниченно, что у неё совсем нет «концов». Только такую бесконечно
ЧЕРТ, 1
6
ЧЕРТ. 8
продолжающуюся в обе стороны линию называют в rеометрии пря-
мой линией или просто п р я м о й. Сформулируем пер в о е
с в о й с т в о прямой.
1. Прямая бес"он,еч,н,а.
Сформулируем в т о р о е важное с в о й с т"в о прямой.
2. Через любь/,е две точи" про-
ходит пря..мая, и при",о.м толь"о
одна.
На этом свойстве прямой основана
проверка линейки. Если мы на бумаrе
обозначим две точки и ч рез них каран-
дашом аккуратно проведем по краю ли-
нейки линию, а затем повернём линейку
v u ..
друrои сторонои и снова проведем по
краю линейки через те же точки друrую
-;
линию и если при ,:этом линии сольют-
СЯ, то линейка правильная (черт. 11).
Если же линии не сольются, то это по-
u
кажет, что линеика сделана неправиль-
но (черт. 12). r """. ..""""'.. .."""""''''''' !
Прямая линия на доске или на бума- J
re обозначается или одной малой буквой
латинскоrо алфавита, или двумя больши-
ми буквами, поставленными в двух раз- r : M....... ......... ....... . ..... o ..
личных точках этой прямой (черт. 13).
Если на прямой линии отметим ка- F . ' "
кую-нибудь точку, то получим два луча
(черт. 14).
ЧЕ РТ 9
.... ...
ЧЕРТ. 10
ЧЕРТ. 11
ЧЕРТ. 12
1
д
.
8
.
л у ч о м называют часть
u
..'IИ8ИИ, оrраниченную с ОДНОИ стороны
(черт. 15). Луч также обозначается или
одной fалой буквой латинскоrо алфа-
вита, или двумя большими буквами, из
которых одна ставится в начале луча.
Часть прямой, оrраниченная с обеих
СТОРОН, называется о т рез к о м n р я.
м о й (черт. 16).
Отрезок, как и прямая линия, обоз-
начается.или одной буквой, или двумя.
В последнем случае эти буквы обозна-
чают концы отрезка (черт. 16).
Линия, состоящая из нескольких
отрезков, не лежащих на одной пря-
мой, называется л о м а н о й
u
прямои
---- 8
а
. .....
ЧЕРТ. 18
Луч
д
.
/7уч
ЧЕРТ. 14
"
"
О,. "
/
r
.
д в
ЧЕРТ. 15
а
д
8 ....
о)
б)
ЧЕРТ. 16
ЧЕРТ. 17
(черт. 17, а). Если КОljЦЫ ломаной сов-
падают, то такая ломаная называется
3 а l\{ к н У т о й (черт. 17, б).
/
.......
; ...............
4. ПЛОСКОСТЬ.
IJ
Познакомимся ещё с одним осно-
вным понятием rеометрии по-
нятием п л о с к о с т и. Первое пред-
ставление о плоскости можно получить,
рассматривая поверхность стола, или поверхность спокойноЙ
БОДЫ в сосуде, или в пруде в тихую прrоду. Однако во всех этих
случаях мы имеем дело не со всей плоскостью, а только с её частью.
Чтобы получить правильное представление о плоскости в TO 1
смысле, как это слово понимают в rеометрии, надо представить
себе поверхность стола или озера продолженной неоrраниченно.
Мысленно можно представить себе, например, как плоскость по-
верхности стола при её продолжении разрезает стены комнаты и
проходит в соседней комнате по поверхности друrоrо стола (если
он 'имеет ту же вь}соту, как и стол в нашей комнате, черт. 18).
ЧЕРТ. Н)
8
ОБJ
ЧЕРТ t 19
Стараясь представить себе наrлядно плоскость, надо опираться
u
на следующее о с н о в н о е с в о и с т в о n л о с к о с т и:
Если через две точ"и nлос"ости nроведена прямая,
,пО все точии этои nрямои лежат на тои же плос-
"ос тц.
Так как отрезок и луч являются част ми прямой, то из основ-
u u
Horo своиства плоскости вытекает, что отрезок, или .,Т}уч, имеющии
с плоскостью две общие точки, целиком лежит на этой плоскости.
Точки, линии и поверхности, взятые отдельно или в комбина-
циях друr с друrО1\1, образуют r е о м е т р и ч е с к и е Ф и r у -
р ы (черт. 19).
Часть rеометрии, которая занимается изучением фиrур, все
u
части которых расположены на однои плоскости, называется п л а-
н и м е т р и е й.
Часть rеометрии, занимающаяся изучением фиrур, которые не
1orYT быть помещены в одной плоскости, называется с т е р е о-
м е т р и е й.
5. СРАВНЕНИЕ ОТРЕЗКОВ. ДЕЙСТВИЯ НАД ОТРЕЗКАМИ.
1. Равные и неравные отрезки.
Отрезки называются. равными, если они MorYT быть наложены
u
один на друrои так, что концы их совпадут.
Пусть HaI\1 даны два отрезка АВ и CD (черт. 20, а). Наложим от-
резок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и
отрезок АВ направим по отрезку CD. Если точка В совпадает с
точкой D, то отрезки АВ и CD равны; АВ == CD.
Сравним два отрезка КО и ЕМ (черт. 20, 6). Наложим отрезок
КО на отрезок' ЕМ так, чтобы точки К и Е совпали. Отрезок КО на-
правим по отрезку ЕМ. Если точка О окаж тся rде-нибудь между
точками Е и М, то rоворят-..t. что отрезок ЕМ больше отрезка ко;
отрезок КО меньше отрезка ЕМ.
Записывается это так: ЕМ > ко, КО < ЕМ..
д 8
. . Е М
. . .
с D К О
. . . .
а) б)
ЧЕРТ. 20
9
2. Построение отрезка, paBHoro данному, с помощью циркуля.
Построение отрезка, paBHoro данному отрезку АВ (черт. 21),
выполняется с помощью циркуля таким образом: одну ножку цир-
куля устанавливают на один конец отрезка АВ", а друrую на
друrой ero I{OHeu И, не меняя раствора циркуля, переносят ero на
д
I
в N
I .... --- .... I
р
I ---
ЧЕРТ. 21
некоторую прямую так, чтобы конец одной ножки отметил какую-
нибудь точку N, тоrда конец друrой ножки циркуля отметит неко-
торую точку Р на этой ж прямой. Отрезок NP будет равен отрез..
ку АВ.
3. Сложение и вычитание отрезков.
Чтобы найти сумму двух отрезков, например АВ и CD
(черт. 22, а), надо взять прямую линию и на ней некоторую точку,
наПрИl\1ер точку N(черт. 22,6), затем с помощью циркуля отложить
д
.
в
,1 .
N
р
I
м
1 ------
с
I
D
I
---- 1
й}
5)
ЧЕРТ. 22
На этой прямой от точки N сначала отрезок NP, равный отрезку
АВ, а потом от ero конца в том же направлении отложить отрезок
р М, равный отрезку CD. Отрезок N М будет называться суммой
отрезков А В и CD. Это записывают так:
N М == А В + CD.
Таким же образом находится ..сумма нескольких отрезков
(черт. 23):
MN == АВ + CD + ЕР.
При епожении отрезков, как и в арифметике при сложении чи-
сел, выполняются законы пере мести тельный и сочетательн..ый:
д
I
С
I
Е
I
8
I
D
I
АВ + CD == CD + АВ;
(А В +CD)+ ЕР ==А В +( CD + ЕР).
С D
I I
F
I
м
I
N
I ....
д
I
к
I
8
I
ЧЕ 1->1 t 2;j
ЧЕРТ. 24
10
Чтобы найти разность двух отрезков АВ и CD (черт. 24), надо
на большем отрезке (АВ) от конца ero, например точки А, отложить
меньший отрезок (CD). Оставшаяся часть (КВ) большеrо отрезка
и будет разностью этих отрезков: АВ CD == КВ.
4. Умножение и деление отрезка на целое число.
а) Умножить отрезок АВ на целое число, например на 5,
это значит, что отрезок АВ надо взять слаrаемым 5 раз (черт. 25):
БАВ == MN.
Отрезок MN есть произведение отрезка АВ на число 5.
6) На чертеже 25 отрезок MN составлен из пяти равных отрез-
ков, т. е. отрезок MN разделён на пять равных частей. Каждый
1
из них составляет часть отрезка MN.
5
в) Чтобы разделить отрезок на равные части с помощью цир-
куля, поступают таким образом. НаПРИl\1ер, если нужно разделить
отрезок на две равные части, то циркуль раздвиrают на rлаз так,
чтобы раствор циркуля составлял примерно половину отрезка.
Затем на данном отрезке от ero конца последовательно один за дру-
rим откладывают этим раствором циркуля два отрезка. Если полу-
ченная сумма отрезков будет 1\1еньше данноrо отрезка, то раствор
циркуля увеличивают; если сумма окажется больше данноrо отрез-
ка, то раствор циркуля уменьшают. Так, постепенно исправляя
ошибку, MO)I{HO отыскать довольно точно половину отрезка (черт. 26).
Таким же образом, выполняется приближённое деление отрез-
ка на 3, 4, 5 и Т. д. равных частей. Только в этом случае надо брать
111 u 345
на rлаз 3; 4; 5; ... отрезка и откладывать взятыи отрезок , , ...
раз, смотря по тому, на сколько равных частей надо разделить дан-
ный отрезок.
9 6. ИЗМЕРЕНИЕ ОТРЕЗКА. СВОЙСТВО ОТРЕЗКА.
1. Измерение отрезков.
Измерение отрезка производится с помощью масштабной линей-
ки (или сантиметровой ленты). Выполняется измерение отрезка
следующим образом. Если ну}кно ИЗ1\1ерить длину отрезка АВ
'-.....
I I
Д 8
t t
I I
М N
I ,
. I
ЧЕРТ. 25 ЧЕРТ 26
11
(черт. 27), то надо совместить точку А с тем делением линейки,
против KOTOpOrO стоит цифра О. Затем надо направить масштабную
u u
линеику по отрезку и посмотреть, против KaKoro деления линеики
будет точка В. -..
Число, соответствующее этому делению, и покажет длину изме-
ряемоrо отрезка. Длина.отрезка АВ равна 32 мм.
При измерении отрезка используется также и циркуль. Сначала
одну ножку циркуля устанавливают на один конец ИЗ fеряемоrо
отрезка, а друrую на друrой ero конец (черт. 28). aTeM, не ме..
няя раствора циркуля, переносят ero на масштабную линейку
так, чтобы конец первой ножки совпал с начальной (нулевой) чер..
той линейки, тоrда конец второй ножки циркуля покажет длину
измеряемоrо отрезка (черт. 29). Длина этоrо отрезка равна 53 мм.
Сложение и вычитание отрезков, а также умножение и деление
их на целое число можно ВЫПОЛнять так: измерить данные отрезки
с помощью масштабной линейки или сантиметровой ленты и затем
выполнить указанные действия над полученными числами. Так,
чтобы сложить или вычесть, например, отрезки АВ и CD, сначала
измерим их. Пусть оказалось АВ == 27,4' см, CD == 19,8 см.
Тоrда сумма этих отрезков АВ + CD == 27,4 + 19,8 ==
== 47,2 (см), а, разность А В .........
....... CD == 27,4 19,8 == 7,6 (см).
Чтобы умножить, например,
отрезок АВ на 3, нужно измерить
длину ero и полученное число' yrvt-
ножить на 3.,
Если АВ равно 27,4 СМ, то
АВ · 3 == 27,4 · 3 == 82,3 (см).
Чтобы разделить отрезок на рав-
ные части с помощью масштабной
u u
ли неи к и , надо измерить данныи от.
резок и полученное число разделить
на данное число частей. Например,
если длина отрезка равна 48 ММ, а
нужно ero разделить на шесть рав-
ных частей, то на каждую часть
придётся по 8 .мМ.'
д в
. .
rb' ' III IIIIIIII IIIIIIIII IIIIIII}
ЧЕРТ. 28
12
ЧЕРТ I 27
ЧЕРТ. 29
2. Длина ломаной, свойство от-
резка.
Длиной ломаной называется СУМ-
ма длин составляющих ее отрез-
ков.
Например, длина. ломаной на
черте}l{е 30, а равна
2 + з + 2 +/4 == 11 (см).
Отметим важные свойства отрезка прямой линии: отреЗО1е пря.
.мой "ороче любой ло.маноii l соединяющей ezo "онцы.
Так, на обоих чертежах 30, б и 30, в длина ломаной ABCDF боль-
ше длины отрезка АР.
3 а м е ч а н и е. Можно высказать и более общее утверждение:
отрезок прямой короче, чем любая друrая линия, соединяющая
ero концы (черт. 30, 2). Но точный смысл этоrо утверждения будет
вам понятен только тоrда, коrда вы познакомитесь с точным опре-
u
делением длины произвольнои линии.
7. ПРОВЕШИВАНИЕ ПРЯМОЙ ЛИНИИ НА ПОВЕРХНОСТИ ЗЕМЛИ.
Для провеш'ивания, т. е.
u
проведения прямых линии на
зе!\fле, пользуются вехами.
Вехи это колья, заострён-
ные с QДНОЙ стороны. Обыкно"
венно вехи бывают длиной в
1 .! 2 м. Для лучшей види..
2
мости вехи закрашивают в два
цвета (чаще Bcero в красный и
белый).
Слово «провешивание» и об..
разовалось от слова «веха».
Если нужно провешить пря..
мую линию между двумя точками
А и В, положение которых дано,
то сначала в этих точках ставят-
ся вехи; затем между ними
устанавливается промежуточ-
ная веха С так, чтобы вехи
А и С закрывали веху В
(черт. 31).
Если расстояние от ТQ И А
до точки В большое, то прихо-
дится ставить ещё вехи между
точками А и С и между С и В.
Вообще при провешивании пря-
мой линии на ровной поверхно"
сти земли необходимо, чтобы рас..
стояние между вехами было от
50 до 100 м, а на холмистой
от ........ 10 до 50 м.
а)
д
F
о)
в
д
F
с
2)
ЧЕРТ. 30
18
Иноrда ПРИХОДИТСЯ провешить прямую линию, направление ко..
торой задано двумя вехами, поставленными в точках А и В. В ЭТОl'v1
случае прямая линия продолжается в нужном направлении за веху
В так, чтобы следующую веху С закрывали вехи А и В (черт. 32).
. ,О
.-. . ...
.-
.--.-,.,.
.. .....-.:
.
""
...,
. ....-
ЧЕРТ, 31
"
. "
O " ..
;'
..". . #}, ......... ........III!I' .
41" . .. -
-" ...... ..,..
" ..-
"", _., " ..... ..", ....,.",.. ,.._tI
11"' : .. '" ... ....... ?.....,...
"ои'.!" ': ,......
. I ..",.. ""'. .......... "
* ,.A...... , ::
Затем ставятся следующие вехи так, чтобы их закрывали две
ранее поставленные вехи.
Необходимо, чтобы все вехи стояли вертикально. Правильность
вертикальноrо направления проверяется с помощью отвеса. OTBec
это шнур, на конце KQТOpOrO имеется небольшой rруз (черт. 33).
J---"""
.... -' .,.,
. .,., . . '"',..--4
. -. т., .... ..
..., .... ".. .. -со.. .
..... .......... . . ....--.
,. ,. .
пr ........... :...----- .
................,.... .. . ;.
;о . ------- . - _ I
......... .. ..
- . -=:_
-->--
....,.-
;.
.......
.....
..../')""1'1' "
,'(;)
.,.,.
."
"""""""::-
,...
ЧЕ РТ. 32
", ", --.J ....... ....
", - >
" . ........., ..,...--,....,.,..."...
....... ?./. .'1 ,. """....., ..: ,.., . I (, .......
,..."".. , , . ... ........ --
.......... ./ -: :;;..o.-.-. "",,-:: - -
...,.- /:/ ;", .
,."U" ./'" ............,.....:. ............ '"('&Iod' 'LP: ,,'
.2V "./ /. .... " ,"';
, " ( .., - ... ..........." ( ... .. ,"""%, l' о'/. .
""'I ',.' " ",'."' ,...,...-; J ........
r- , ., .,
. Jv ,'.{ __ r-;",'
.. 0.0
14
Упражнения.
1. Начертить отрезок и разделить ero с помощью
масштабной линейки на 2 равные части (на
з,' 4, 5, 8, 1 О равных частей).
д
I
с
,1
А
,
8'
I
D
I
с
I
в
I
ЧЕРТ. 34
ЧЕРТ. 35
2. Начертить отрезок и приближёНIIО разделить
ero с помощью циркуля на 2 равные части
(на 3, 5, 8 равных частей).
3. Сколько Bcero отрезков на чертеже 34? на чер-
теже 35? -
. '"
t ....... "v.'
.. . ......,.... ".
-.::::::::. ;: \' \ " I
"411"1'.'" ,.':..1' , ...\. . "'",
. '''''''r,;:, ... \ \1\' ,
' ,У,...:... ::::-,. ,,
ЧЕРТ. 33
8. ИЗМЕРЕНИЕ РАССТОЯНИЙ В КОМНАТЕ И НА МЕСТНОСТИ.
Измерение расстояний в комнате, например: длины, ширины,
высоты её, высоты и ширины окон и т. д. .....-.... про изводится С помо"
щью метра или рулетки.
Рулетка представляет собой неширокую ленту, металлическую
u u
или из плотнои ткани, на которои нанесены деления на метры и
сантиметры. Длина рулетки обыкновенно бывает 10 м и 20 М.
ДЛЯ сохранности и удобства пользования рулетка заключается
в кожаный или картонный футляр (черт. 36).
Расстояние па поверхности земли измеряется с помощью рулет..
ки или металлической мерной ленты длиной 20 м (черт. 37).
Иноrда расстояния измеряются с помощью полевоrо циркуля
(черт. 38). Расстояние 1\1ежду ножками полеВОI'О циркуля берётся
или 1 м, или 2 м.
ЧЕРТ. 36
ЧЕРТ t 37
15
Можно расстояние измерить
шаrами, но для этоrо нужно
предварительно уз ать длину
cBoero шаrа и уметь переводить
полученное число шаrов в
метры.
Чтобы узнать длину cBoero
шаrа, нужно отмерить расстоя..
ние длиной в 10 или 20 м и про..
шаrать ero несколько раз, за-
писывая каждый раз полученное
число шаroв. Затем найти сред"
нее число шаrов. Например,
1
получилось 30 шаrа, затем 32 ша..
2
2м
ЧЕРТ. 38
пусть первый раз на 20 м
1
ra,. 31 шаrа, 30 шаrов 1 .
2
(30 + 32 + 31 + 30 ): 4 == 31.
Разделиu 20 ом на среднее число шаrов (31), найдём среднюю
длину шаrа: 0,65 ом (с точностью до 0,01).
После этоrо полезно составить ДЛ!, себя такую таблицу:
Число Метры Число Метры Число Метры
шаrов шаrов шаrОВ
1 0,6 10 6,5 100 65,0
2 1,3 20 13,0 200 135,0
3 1,9 30 20,0 300 195,0
4 2,6 40 26,0 400 260,0
Б 3,2 50 32,5 500 325,0
. 6 3,9 60 39,0 600 390,0
7 4,5 70 45,5 700 455,0
8 5,2 80 52,0 800 520,0
9 5,8 90 58,5 900 585, О
По этой таблице леrко переводить полученное число шаrов в
метры. Например, если при измерении какоrо-либо расстояния
получилось 724 шаrа, перевод их в метры может быть выполнен
так:
700 шаrов == 455 .м
20 шаrов == 13 м
4 шаrа == 2,6.м
724 шаrа 470 м
1
K.м
2
1 За полшаrа принимается неПОJJНЫЙ шаr.
16
УпраJJCн,еIZUЯ.
1. Измерить длину, ширину и высоту cBoero класса, своей комнаты.
2. Провешить прямую линию на школьном дворе или на каком нибудь зе-
мель ном участке.
3. Измерить расстояние между двумя какими нибудь пунктами с помощью
мерной цепи или рулетки или с помощью полевоrо циркуля.
4. Составить таблицу для перевода своих шаrов в метры.
5. Измерить шаrами расстояние от своей квартиры до школы и перевести' в
метры.
6. Определить на rлаз расстояние между какими-нибудь пунктами, затем из-
мерить то же расстояние шаrами и перевести в .метры. Вычислить, какой
процент составляет ошибка, полученная при определении расстояния на
rлаз.
9. уrол. ДЕЙСТВИЯ НАД УrЛАМИ.
1. Определение уrла.
У2ЛО.JJl называется часть плос1tостu, 02ранuченная
дву.м.я лучаJfШ с общuм. начало.м.
Примеры уrлов изображены на чертеже 39. Рассматривая этот
чертёж, надо понимать, что весь уrол изобразить на чертеже нельзя,
как нельзя на чертеже изобразить и весь луч. Каждый уrол в дей..
ствительности продолжается неоrраниченно. На нашем чертеже
заштрихованы только части изображённых там уrлов.
Точка, из которой выходят оrраничивающие уroл лучи, назы-
вается в ерш и 11 О Й уrла, а сами эти лучи с т о р о н а м и
у r л а (черт. 40).
Если начертить на плоскости два луча ОА и ОС, то они разделя..
ют плоскость на две части. Мы получим не один уrол, адва (черт. 41).
Часто при изображении уrла чертят только выходящие из
вершины начаЛЬН Iе участки ero сторон, а ту часть плоскости, ко..
торую хотят указать, обозначают дужкой, как это сделано на чер"
теже 42.
Уrол обозначается или одной большой буквой, поставленной
у вершины уrла, например А или В (черт. 42, а), или тремя буква..
.;
" /
..... ........-:
/
"""--
ЧЕ РТ. 39
11
Вершина
/
/
/
O
O
I
I
1,
\
,
/
ЧЕРТ. 40
ЧЕРТ. 41
ми, ИЗ которых одна ставится при вершине уrла, а две друrие
у каких-нибудь точек сторон, например L Аве или L ACD
(черт. 42, б). Буква, стоящая при вершине уrла, всеrда записыва-
ется между двумя друrими буквами. Иноrда уrол обозначают циф-
рой, поставленной внутри уrла (черт. 42, в).
в д Д8C
Д
Д с
"
"
LIiCD
I О)
О) I D 6)
I
ЧЕРТ. 42
Укажем ещё один способ получения уrлов. Если возьмём луч АС
(черт. 43) и будеl\1 поворачивать ero BOKpyr точки А против часовой
стрелки вплоть до положения АВ, то ero последовательные поло-
жения «заметут» уrол со сторонами АС и АВ.
Продолжая вращать луч в том же направлении, мы будем по-
лучать всё новые уrлы. Может наступить такой момент, коrда оба
луча будут составлять прямую линию (черт. 44). Такой уrол назы-
вается раз в ё р н у т ы м уrлом. Леrко понять, что развёрну-
' /
/
/
В /
./
о P 0t'\a
/'" C{f\o
O p o a
C{fI
Вершина
-'
д
(If\
с
--- ---
в
с
ЧЕРТ, -t3
ЧЕРТ. 44
18
()
с
в
с
а)
б)
ЧЕРТ. 45
ТЫЙ yroJi есть часть плоскости, оrраниченная прямой, т. е. п о л у-
п л о с к о с т ь (черт. 44).
Если продолжать вращение луча ещё дальше, чем на чертеже 44,
будем получать новые уrлы (черт. 45, а), пока луч не вернётся
в своё начальное положение (черт. 45, б). Будем считать, что луч
в ходе CBoero вращения «замёл» самый большой воз ложный уrол,
называемый п о л н ы f'1 уrЛО 1.
3 а м е ч а н и е. Заметьте, что, введя понятие о «полном yr..
ле», мы отступили от первоначальноrо определения уrла. Полный
уrол в сущности есть вся плоскость (черт. 45, в), а не её часть, or.
раниченная двумя лучами.
2. Сравнение уrлов по величине.
Уrлы азываются р а в н ы м и, если их можно совместить на..
ложением. Равенство уrлов обозначается так:
L АВС === L D рр (черт. 46).
В(Е)
D
F
ЧЕРТ. 46
ЧЕРТ. 47
Развёрнутые уrлы при наложении MorYT быть совмещены.
Отсюда все развёрнутые УZЛbl равны между собой.
Полные уrлы при наложении также MorYT быть совмещены.
Следовательно, все полные УZЛbl равны .между собой.
Если уrол 1 можно наложить на уrол 2 так, что одна из сторон
уrла 1 совместится со стороной уrла 2, но при этом у,rол 1. составит
только часть уrла 2 (черт. 47), то rоворят) что уrол 1 fеньше yr-
ла 2, а уrол 2 больше уrла 1.
19
8
с
ЧЕРТ t 48
fI
с
ЧЕРТ 49
д
м
ЧЕРТ. 50
,"
.,,"
ЧЕРТ. 51
....
о
ЧЕРТ. 52
20
3. Действия над yr Jlами. Биссек-
Триса yr ла.
Если один уrол приложить к дру-
rOfvlY так, что они будут иметь общую
вершину и сторону, а внутренние
области уrлов не будут налеrать друr
на друrа, то полученный таким обра-
зом уrол будет называться суммой
этих уrлов (черт. 48).
L АВ С . Ll + L2, или LABC==
== L КВС + L АВК.
L КВС является раз н о с т ь ю
уrлов АВ С и А В К: .
L КВС == L АВС L А.ВК.
Точно так же L АВК == L ABC
L КВС.
Можно получить сумму не толь'ко
двух, но И нескольких уrлов (черт. 49):
LABC== LDBC +LKBD+LABK.
При сложении уrлов выполняют-
u о
ся переместительныи и сочетательныи
законы, как и при сложении отрез-
ков.
Если взять сумму нескольких рав-
ных уrлов, т. е. один и тот же уrол
по торить слаrаемым несколько раз
(черт. 50), то полученный уrол будет
результатом Уf\.Iножения уrла на це-
лое число:
L АОМ == 5 L С. С4Ледовательно, L с
1
будет равен L АОМ; L БОМ ==
5
== LAOM. LFOM == LAOM.
5 ' 5'
4
L КОМ == L АОЛ1.
5
Луч, делящий yroJl пополам, на-
зывается б и с с е к т р и с о й yr ла
(черт. 51).
Полный уrол равен сумме двух
pa BёpHYTЫX уrлов (чер-r. 52), а раз-
.. U
вернутыи уrол равен половине пол-
Horo уrла.
4. Прямой уrол.
80зьмём лист бумаrи и на одной стороне ero, как показано на
чертеже 53, обозначим точку В, которую примем за -вершину раз..
вёрнутоro уrла; стороны этоrо уrла обозначим через BD и вс.
Если лист бумаrи соrнём так, чтобы сrиб прошёл через точку В,
а лучи BD и ВС совпали, то развёрнутый уrол разделится H два
равнЫХ уrла. Каждый из них. будет составлять половину разверну..
Toro уrла. Уzол, равный половине развёрнуmоzо уzла, на-
зывается nРЯАtЫ.м. У2ЛО.Аt. LABC == LABD (черт. 53).
Д
д
D С
D С I
в
ЧЕРТ. 53 ЧЕРТе 5-'
Так как все развёрнутые уrлы равны между собой, то и все
прямые уrлы, как половины равных уrлов, также равны между
собой. Величина прямоrо уrла обозначается буквой d: L АВС ==
== d; L ABD == d. Развёрнутый уrол равен 2d. Полный уrол равен
4d (черт. 54).
10. ПЕРПЕНДИКУЛЯР 1( ПРЯМОЙ.
ПОСТРОЕНИЕ ПЕРПЕНДИI(УЛЯРА 1( ПРЯМОЙ.
1. Перпендикуляр к прямой. Основные свойства перпеНДИI<уляра.
Прямые линии, образующие между собой пря иые yr ЛЫ, на-
зываются взаимно перпендикулярными. .
Прямые АВ и CD (черт. 54) взаимно
перпендикулярны.
Перпендикулярность прямых обозна..
"-
чается знаКО 1 . На чертежах 53 и 54
АВ DC и DC ..L АВ.
Каждая из этих прямых называется пер
пеНДИКУЛЯрО 1 к друrой. АВ перпенди- D
куляр к DC, и CD перпендикуляр к АВ.
К данной прямой через данную на
.,
неи точ"у АtОЖНО провести тOiJb"O
один nерпеltdu«уляр (черт. 55).
д
'К
,
I
I
I
I
,О
I
I
I
,
L/ 8
с
ЧЕ1>Т. 55
21
'"
I
д
0/
/
/
I
/
I
I
/
в
с
ЧЕРТ. 56
ЧЕРТ. 57
ЧЕРТ. 58
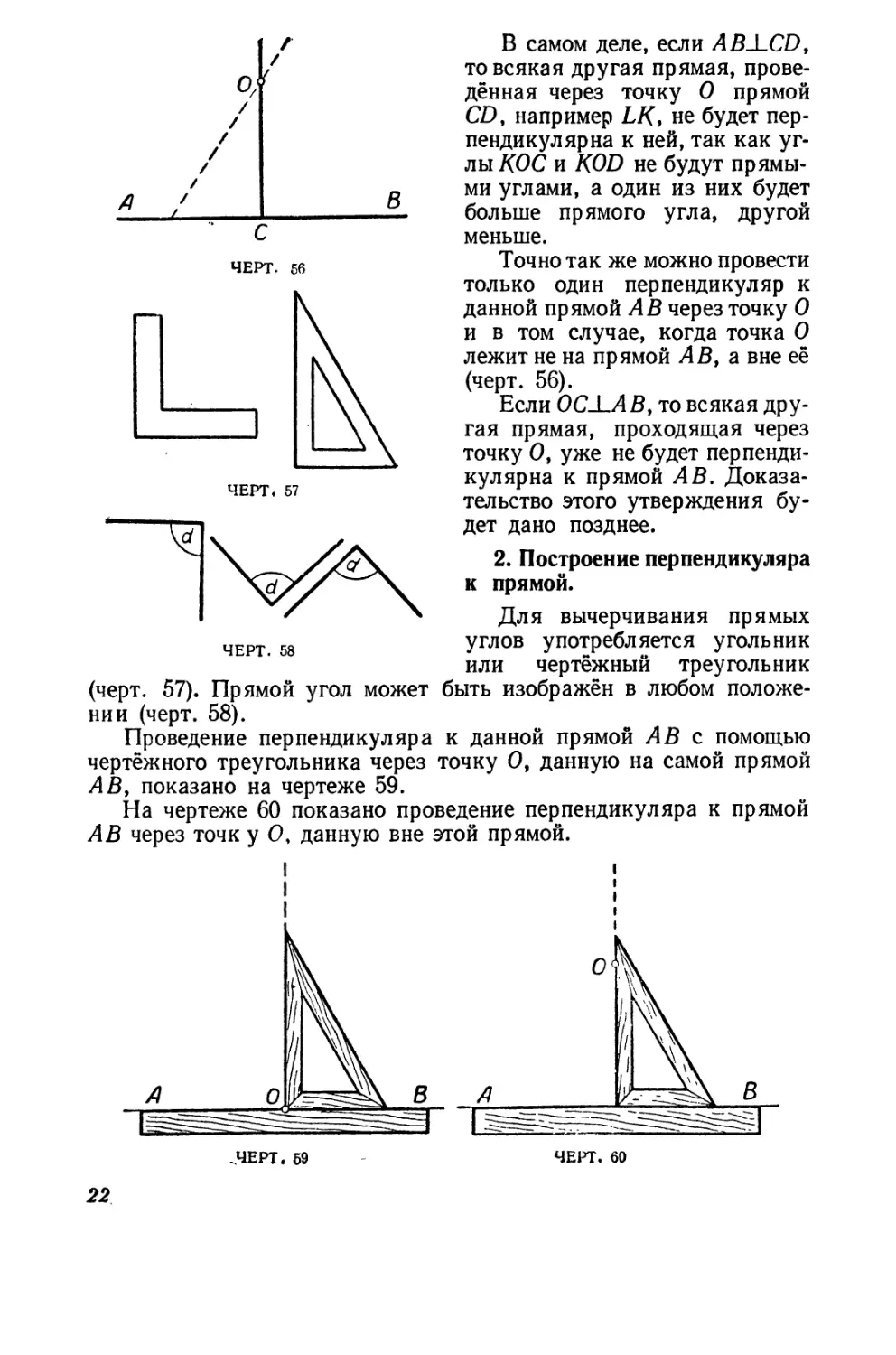
в самом деле, если А B.l...CD,
то всякая друrая прямая, прове-
дённая через точку О прямой
CD, например LK, не будет пер-
о
пендикулярна к неи, так как yr-
лы КОС и KOD не будут прямы-
ми уrлами, а один из них будет
больше прямоrо уrла, друrой
меньше.
Точно так же можно провести
только один перпендикуляр к
данной прямой АВ через точку О
и в том случае, коrда точка О
лежит не на прямой АВ, а вне её
(черт. 56).
Если OC AB, то всякая дру-
rая прямая, проходящая через
точку О, уже не будет перпенди-
кулярна к прямой АВ. Доказа-
тельство этоrо утвер ения бу-
дет дано позднее.
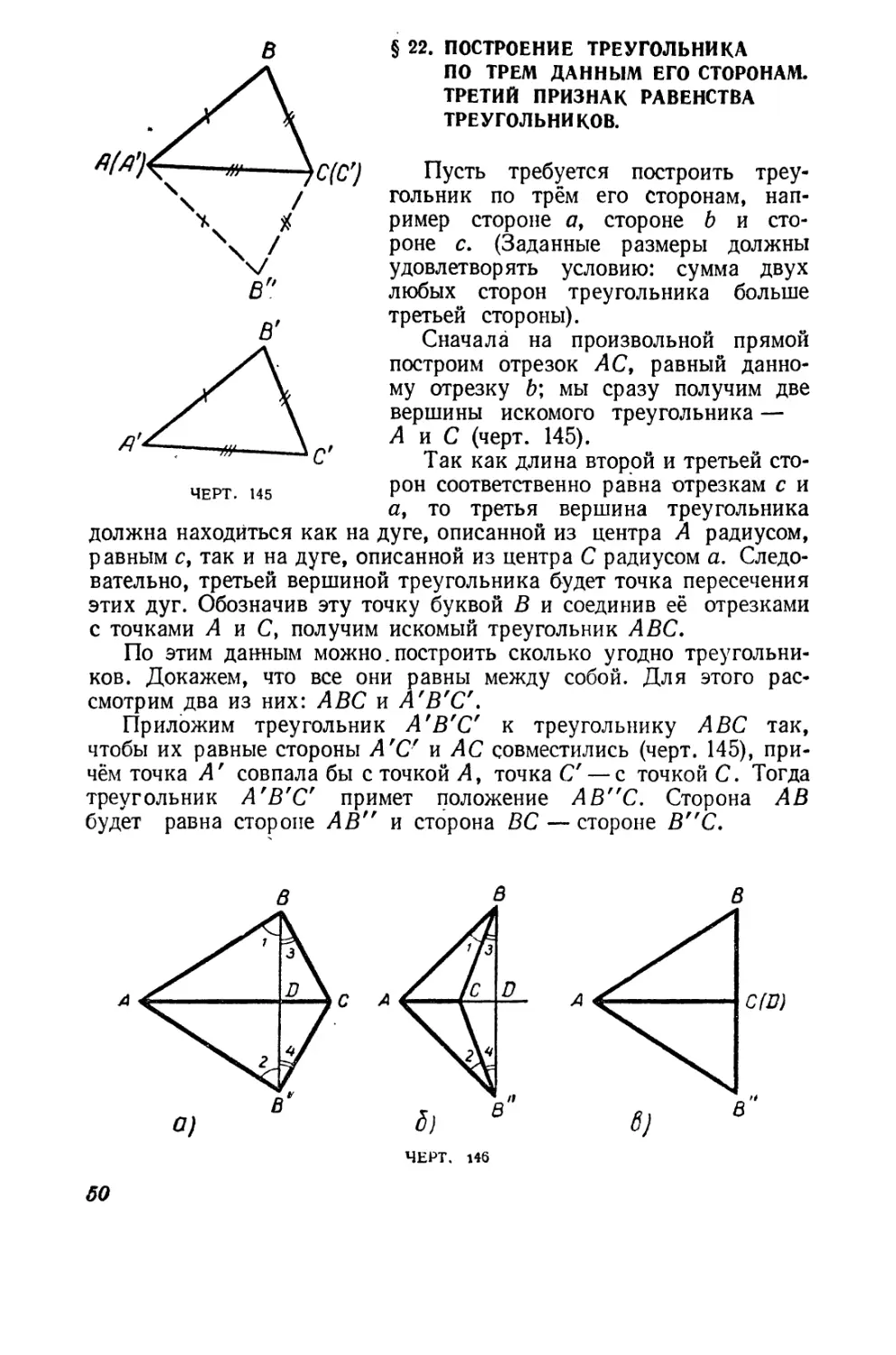
2. Построение перпендикуляра
u
К прямои.
Для вычерчивания прямых
уrлов употребляется уrольник
.. о
или чертежныи треуroльник
быть изображён в любом положе-
(черт. 57). Прямой уrол может
нии (черт. 58).
Проведение перпендикуляра к данной прямой АВ с помощью
чертёжноrо треуrольника через точку О, данную на самой прямой
АВ, показано на чертеже 59.
На чертеже 60 показано проведение перпендикуляра к прямой
АВ через точк у о. данную вне этой прямой.
I
I
I
А О
ЧЕРТ. 59
22.
д
.........
ЧЕРТ, 60
3. Проверка чертёжноrо треуrОJlьника.
Чтобы проверить чертёжный треуrольник, надо начертить пря-
мую линию, взять на ней какую-нибудь точку И, приняв ,луч за СТО-
u
РОНУ уrла, построить при помощи треуrольника прямои уrол с
вершиной в данной точке. Затем чертёжный треуroльник надо пе-
ревернуть, приложить той же стороной прямоrо уrла к этой пря-
МОЙ в противоположном направлении от вершины и построить
второй прямой уrол с вершиной в той же точке. Если начерченные
прямые совпадут (черт. 61), то чертёжный треуrольник верен, если
же не совпадут, то треуrольник не верен (черт. 62).
"
.
\
t. ·
'\ ' \
I "
: 8,. ",
I ""
I '. \
L.......... ".
f\\
:,
I -.
: I \
, ,\\
. \. \
I \,.
I \ \
L.. ....... ..
ЧЕРТ!\ 61
4. Уrлы острый и тупой.
Уrлы, большие развёрнутоrо.
Так как все прямые уrлы равны меж-
ду собой, то прямой уrол может быть
принят за меру уrлов.
Уrол, меньший прямоrо, называется
острым уrлом (черт. 63).
Уrол, больший прямоrо, но меньший
развёрнутоrо, называется тупым
(черт. 64).
MorYT быть уrлы и б6льшие раэвёр-
HYToro (черт. 65). Однако мы оrраничим-
ся рассмотрением ТОЛЬКО тех уrлов,
которые меньше развёрнутоrо; уrлы же,
большие развёрнутоrо, мы рассматри-
вать не будем, кроме Тех случаев, коrда
это будет особо oroBopeHo.
5. Эккер.
Для построения прямых уrлов на
земной поверхности применяется осо-
бый прибор, который называется ЭК-
Керам.
ЧЕРТ. 62
ЧЕРТ. б5
ЧЕРТ. 63
ЧЕРТ. 64
23
ЧЕРТ. 66
Эккер представляет собой два бруска, укреп-
лённых под прямым уrлом. На концах брусков
ставятся булавки или тонкие rвозди так, чтобы
прямые, соединяющие их (черт. 66), QЫЛИ вз -
имно перпендикулярны. Эккер укрепляется на
треножнике или на палке.
Чтобы построить на зеf\1ле прямой уrол, надо
наметить вершину уrла, а эккер поместить так,
чтобы тdчка пересечения взаимно перпендику"
лярных прямых (на чертеже они изображены
пунктиром) оказалась на одной отвесной линии
с намеченной вершиной уrла на местности. За-
тем по направлению булавок одноrо бруска
провешить одну ПрЯl\1УЮ линию, а по направле-
нию булавок BToporo бруска вторую ПрЯМУIО
(черт. 67).
I .
.
ЧЕРТ. 67
Если надо провести прямую, перпендикул ярную к данной пря-
мой в данной точке, то эккер ставится над этой точкой так, чтобы
направление булавок одноrо бруска совпадало с направлением
данной прямой. Затем по направлению друrоrо бруска провешива-
ется вторая прямая, которая с данной прямой образует прямой
уrол, т. е. перпендикулярна к ней.
Упражнения.
1. Начертить ПРЯМУIО, взять на ней точку и провести с J10МОЩЬЮ чертёж-
Horo треуrольника перпендикуляр к данной прямой через данную. точку.
24
2. Начертить прямую, взять точку вне утой прямой и С помощью ертёж-
Horo треуrольника провести прямои перпендикуляр, проходящии через
данную точку.
3. Назвать все уrлы, которые имеются на чертежах 68 и 69 (не считая yr-
лов, которые бо.пьше развёрнутоrо).
о
ЧЕРТ. 68
д
"
,
,
,
,
"
с
о
с
'-.ЕРТ. 69
ЧЕРТ. 70
4. Вырезать из плотной бумзrи квадрат. Разрезать ero на две paB: ыe час-
ТИ, как покаэзно на чертеже 70, и из полученных двух фиrур составить
фиrуры, изображённые на черте)I{е 71, а. б, в, 2, д, е, ж, З. . .
8)
2)
/
/
е)
Ж)
ЧЕРТ. 71
11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ уrлы.
1. Смежные yr..YJbI.
Если МЫ ПРОДОЛЖИМ сторону какоrо нибудь уrла за ero верши-
ну, то ПОЛ УЧИМ два уrла (черт. 72): L АВС и L CBD, у которых
одна сторона ве общая, а две друrи.е АВ и BD составляют прямую
Линию. \
Два yr па, у которых одна сторона общая, а две друrие соста-
вляют прямую линию, н зываются с м е ж н ы м и уrпами.
Смежные уrлы можно получить и таКИ 1 образом: если из какой-
нибудь точки ПРЯМОЙ проведём луч (не лежащий на данной ПРЯМОЙ),
То ПОЛУЧИМ смежные уrлы. Например, L ADF и L FDB ....... уrлы
смежные (черт. 73).
25
д"-- ....
D
ЧЕРТ tJ 72
F
"
/
"
/
"
/
fFY\
D В
ЧЕРТ. 73 ЧЕРТ. 74
д
Смежные уrлы MorYT иметь самые разнообразные положения
(черт. 74).
Смежные уrлы в сумме составляют развёрнутый уroл, поэтому
су-м.ма двух сJи,ежных У2лов равна 2d.
Отсюда прямой уroл можно определить как уrол, равный сво-
ему смежному уrлу.
Зная величину одноro из смежных уrлов, мы можем найти ве.
личину друrоrо смежноrо с ним уrла.
Например, если один из смежных уrлов равен : d, ТО второй
д
"
"-
"
"-
"
,,/0
"
",
,,/
''''с
'Е
ЧЕРТ. 75
ЧЕРТ 16
26
уrол будет равен:
3 2
2d d == 1 d.
5 5
2. Вертикальные yr лы.
Если мы продолжим стороны уrла
за ero вершину, то получим вертикаль-
ные уrлы. На чертеже 75 уrлы БОР и
АОС ....... вертикальные; уrлы АОВ и
СОР также вертикальные.
Два уrла называются в е р т и к а л Ь-
Н Ы м и, если стороны OAHoro yr ла явля-
ются продолжениями сторон друrоrо
yr ла.
Пусть L 1 == ! d (черт. 76). Смежный
8
7 1
с ним L 2 будет равен 2d....... d, т. е. 1 d.
8 8
Таким же образом можно вычислить, чему
1 7
равны L 3 и L 4 : L 3 == 2d 18 d == g d ;
L 4 == 2d d == 1 d (черт. 77).
МЫ видим, что L 1 == L 3 и L 2 == L4.
Можно решить ещё несколько таких же
задач, и каждЫЙ раз будет получаться один
и тот же результат: верти"альные уz.лы
равны tежду собой.
Однако, чтобы убедиться в том, что вер-
тикальные уrлы всеrда равны между собой,
недостаточно рассмотреть отдельные числовые
примеры, так как выводы, деланные на ос-
нове частных примеров, иноrда MorYT быть и
ошибочными.
Убедиться в справедливости свойства вертикальных 'уrлов необ-
ходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
L а + L с == 2d;
L Ь + L с == 2d
(так как сумма Сl\1ежных уrлов равна 2d).
Отсюда L а + L с == L Ь + L с
(так как и левая часть этоrо равенства равна 2d, и правая еro часть
тоже равна 2d).
В это равенство входит один и тот же уrол с.
Если мы от равных величин отнимем поровну, то И останется
поровну. В результате получится: L а == L Ь, т. е. вертикальные
уrлы равны между собой.
При рассмотрении вопроса о вертикальных уrлах мы сначала
объяснили, какие уrлы называются вертикальными, т. е. дали
о п р е Д е л е н и е вертикальных уrлов.
Затем мы высказали суждение (утвержде-
ние) о равенстве вертикальных уrлов и в спра..
ведливости этоrо суждения убедились путём
доказательства. Такие суждения, справедли-
вость которых надо доказывать, называются
теоремами!. Таким образом, в данном
параrрафе мы дали определение вертикаль-
ных уrлов, а также высказали и доказали
теорему об их свойстве.
В даль ейшем при изучении rеометрии нам
постоянно придётся встречаться с определе-
Ниями и доказательствами теорем.
1 В дальнейшем в тексте теоремы будем выде-
ЛЯТЬ кружочками.
ЧЕРТ. 77
с
ЧЕРТ. 78
ЧЕРТ. 79
ЧЕРТ.. 80
21
ЧЕРТ. 81
Упражнения.
3. Сумма уrлов, имеющих общую вершину.
На чертеже 79 Ll, L2, L 3 и L4 рас-
"
положены по одну сторону прямои И имеют
общую вершину на этой прямой. В сумме
.. U
эти уrлы составляют развернутыи уrол, т. е.
L 1 + L 2 + L 3 + L 4 == 2d.
На черте}ке 80 Ll, L2, L 3, L4 и L 5
иrvrеют общую вершину. В сумме эти уrлы сос..
тавляют полный уrол, т. е. L 1 + L 2+
+ L 3 + L 4 + L 5 == 4d.
1. Один из смежных уrлов равен 0,72 d. Вычислить уrол, составленный
биссектрисами этих смежных уrлов.
2. Доказать, что биссектрисы двух смежных уrлов образуют прямой уrол.
3. Доказать, что если два уrла равны, то равны и их сме}кные уrлы.
4. Сколько пар смежных уrлов на чертеже 81?
5. Может ли пара смежных уrлов состоять из двух острых уrлов? из двух ту..
пых уrлов? из ПрЯ lоrо и тупоrо уrлов? из прямоrо и oCTporo уrлов?
6. Если один из смежных уrлов пр'ямой, то что можно сказать о величине
смежноrо с ним уrла?
7. Если при пересечении двух прямых линий один уrол прямой, то ЧТО можно
сказать о величине остальных трёх уrлов? j
12. ОКРУЖНОСТЬ. KPyr.
1. Радиус. Хорда. Диаметр.
Если 1\.fbI paCKpOel\f циркуль и укрепим конец одной ножки в ка-
кой нибудь точке плоскости, а друrую ножку будем вращать, не
меняя раствора циркуля, так, чтобы её конец двиrался по плоскос"
ти (черт. 82), то этот конец опишет кривую линию, все точки ко..
торой находятся на равном расстоянии от одной и той же точки.
Если вращение продолжать до тех пор, пока кривая окажется
замкнутоЙ, то получим о к р у ж н о с т ь.
28
ЧЕРТ 82
о к р у ж н о с т ь ю называется кривая
замкнутая линия на плоскости, все точки
которой находятся на одинаковом рас-
.,
стоянии от однои точки; эта точка назы-
вается Ц е н т р о м о к р у ж н о с т и.
Часть плоскости, оrраниченная окруж-
ностью, называется к р у r о м (черт. 83).
Отрезок прямой, соедиНЯЮЩИЙ точку
окружности с её центром, называется р а-
диусом (черт. 84).
Так как все точки окружности находят-
ся от центра на одном и том же расстоя-
u u
нии, то все радиусы однои и тои же ок"
ружности равны между собой. Радиус
обыкновенно обозначается буквой R или ,.
Точка,взятая внутри окружности, на-
ходится от её центра на расстоянии, мень-
шем радиуса. В этом леrко убедиться, если
через данную точку провести радиус
(черт. 85). Точка, взятая вне окружности,
находится от её центра на расстоянии,
большем радиуса. В этом леrко убедиться,
если соединить данную точку с центром ок-
ружности (черт. 85).
Отрезок прямой, соединяющий две
u
точки окружности, называется хор Д о и.
Хорда, проходящая через центр, назы-
вается Д и а м е т р о м (черт. 84). Диаметр
обыкновенно обозначается буквой D. Диа-
метр равен двум радиусам:
D == 2,.
Так как все радиусы одноrо и тоrо'же
Kpyra равны между собой, то и все диа-
метры данноrо Kpyra равны между собой.
· Т е о р е м а. Хорда, не про ходящая че-
рез центр "pyz.a, .м.еньше диаметра,
проведённоz.о в тоя же иpyz.e.
в caMOl'f деле, если проведём какую ни-
будь xopд , например АВ, и соединим её
концы с центром О (черт. 86),то УВИДИl\f,
что хорда А В меньше ЛОl\fаной линии
АО + 08, т. е. АВ < 2" а так как 2, ==
== D, то А В < D .
0"'r r'f'o
,оj;жнОС
ЧЕРТ. 83
ЧЕРТ. 84
Д'
ЧЕРТ. 85
ЧЕРТ. 8 r
ЧЕРТ. 87
29
Если Kpyr переrнуть по диаметру (черт. 87), то обе части Kpyra
и окружности СОВl\1естятся. Д и а м е т р Д е л и т к р у r и о К-
р У ж н О с т ь н а Д в е р а в н ы е ч а с т и.
Два Kpyra (две окружности) называются р а в н ы м и, если их
можно наложить друr на друrа так, чтобы они сопместились.
Поэтому два Kpyra (две окружности) с раВНЫI\'lИ радиусами равны.
2. Дуrа кружности.
Часть окружности называется д у r о й.
Слово «дуrа» иноrда заменяется знаком v. Дуrа обозначается
двумя или тремя буквами,. из которых две ставятся на концах дуrи,
а третья у какой-нибудь точки дуrи. На чертеже 88 обозначены
две дуrи: v АСВ и v ADB. .
В том случае, коrда дуrа меньше полуокружности, она обычно
обозначается двумя буквами. Так, дуrу ADB можно обозначить
v АВ (черт. 88). О хорде, которая соединяет концы дуrи, rоворят,
что она стяrивает дуrу.
Если передвинуть дуrу АС (черт. 89, а) так, чтобы она скользила
ПО,данной окружности, и если при 3ТОМ она совпал'ает с дуrой NM,
то vAC== )NM.
ЧЕРТ. 88
й)
б)
ЧЕРТ. 89
На чертеже 89, б дуrи АС и АВ не равны ме}кду собой.
rlачинаются обе дуrи в точке А, но одна дуrа (v А В) составл я-
ет только часть друroй дуrи (v АС). Поэтому v АС > v АВ;
v АВ < v АС.
Упражнения..
1. Сформулируйте определения, которые приведены в данном ПСф(\rраq:е.
2. Сформулируйте теоремы, которые доказаны в данном параrра е.
13: ЦЕНТРАЛЬНЫЙ уrол. ИЗМЕРЕНИЕ Уrлов.
1. Центральный уrол.
Ц е н т р а л ь н ы м у r л о м называется уrол, образованный дву-
мя радиусами одноrо и Toro же Kpyra.
ВО
L АОВ ........ центральный (черт. 90). Дуrа
А В называется соответствующей централь-
ному уrлу АйВ.
Полному уrлу соответствует ося окруж-
ность.
Развёрнутому уrлу соответствует дуrа, paB
иая половине окружности.
llрямому уrлу соответствует дуrа, равная
части окружности.
4
Ф Теорема. Если в одно.м. и то.м. же "pyze два централь..
IlblX уzла равны, "lO равны и СОО"lвеmствующие ия дуzи.
Докажем это. Возьмём окружность, JI0СТРОИМ В ней два равных
центральных уrла (черт. 91). Пусть L АОВ == L COD. Вращая
L АОВ BOKpyr ,центра О, можно совместить ero с уrлом COD,
так как эти уrлы равны между собой (такое условие принято на-
ми). Если же уrлы АОВ и COD совместятся, то в силу равенства
радиусов совместятся и концы дуr АВ и CD. (Точка А совместится
с точкой D, и точка В совместится с точкой С.) Следовательно,
СОВ 1естятся и сами дуrи А В и CD, так как все точки этих дуr на-
ходятся на одинаКОВОf\1 расстоянии от центра, т. е. v АВ == v CD.
Докажем обраТНУIО теорему.
ЧЕРТ. O
е т е о р е м а. Если в одно.м. и тоя же 1(, pyze две дуzи равны,
пlO равны " соответствующие и.м. центральные УZЛbl.
в самом деле, так как дуrа АВ равна дуrе CD (черт. 91), то
дуrа АВ, скользя по окружности, f\10жет совместиться с дуrой CD,
при этом точки А и В совместятся соответственно с точками D и с.
Но в этом случае радиус ОА совместится с радиусом OD, а радиус
ОВ совместится с радиусом ОС, т. е. уrол АОВ равен уrлу COD.
Эти две теоремы справедливы и для равных KpyroB.
Вторая теорема называется о б р а т н о й по отношению к
первой потому, чт В первой теореме доказь вается равенство дуr,
если равны центральные уrлы, во второи В
же теореме, наоборот, доказывается равен-
ство центральных уrлов, если равны дуrи.
2. Измерение уrлов. rрадус дуrи и уrла.
Сравнивая уrлы по величине, мы отмеча
ли, что уrлы MorYT быть равными или нерав-
ными. Уrол может быть равен прямому, боль-
ше прямоrо, меньше прямоrо. Однако это
даёт H I лишь приблизительное представ..
ЧЕРТ. 91
31
пение о величине TOro или иноrо
уrла. Острые уrлы, как и тупые,
IorYT значите.ПЬНО отличаться один
от ДРуrоrо.
Чтобы более точно определять
величину уrлов, применяются осо-
бые меры дуr и уrлов.
Для измерения дуr служат ду..
rOBbIe rpaдycbI, а для измерения
уrлов ....... уrловые.
Д у r о в ы м r р а Д у с о М, или
1
rрадусом дyrи, называется 360 часть
ЧЕРТ. 92 окружности (черт. 92).
rpaдyc дуrи в свою очередь делится на 60 равных частей, назы-
ваемых дуrовыми минутами, а минута делится на 60 равных час-
теЙ, называемых дуrовыми секундами.
Если Д у rа составляет , нап р име р, 25 о У сти ТО ro-
360 кр жно ,
варят: дуrа содержит 25 rpa-
дусов. Обозначается это так:
250. Если дуrа содержит 25 rpa-
дусов 40 минут и 15 секунд, то
это записывается так: 25°40'15".
Всякому rpaдycy дуrи соот-
ветствует центральный уrол
(черт. 92), который называется
у r л о в ы м r. р а Д у с о м. По-
этому между числом уrловых
rрадусов центральноrо уrла и
числом дуrовых rрадусов соот-
ветствующей ему дуrи сущест-
вует такое соответствие: сколь-
ко дуrовых rрадусов содержит
дуrа какоrо-нибудь центрально..
ro уrла, столько же уrловых
rpaдYCOB содержит и соответст-
u u u
вующии этои дуrе центральныи
уrол, и, наоборот, сколько уrло-
вык rрадусов содержит цент-
ральный уrол, столько же ду-
rOBbIX rрадусов содержит дуrа
этоrо центральноrо уrла. При..
нято rоворить, что центральный
уrол измер яется дуrой, на кото-
рую он опирается.
32
ЧЕРТ. 93
ЧЕРТ. 94
На чертеже 93 изображены два центральных уrла. Дуrа пер во-
ro содержит 30, столько же уrловых rрадусов содержит и центраЛЬ 4
нЫЙ уroл. ВТОрОЙ центральный уrол содержит ВО, столько же дуrо.
вык rpaдYCOB содержит и соответствующая ему дуrа.
Такое соответствие между числом уrловых' rрадусов централь-
Horo уrла и числом дуrовых rрадусов соответствующ й ему дуrи
даёт возможность измерять уrлы и строить их.
Уrловой rрадус составляет часть полноrо уrла. Так как
360
полные уrлы равны между собой, то и уrловые rрадусы равны меж.
ду собой.
Развёрнутый уrол равен 180 уrловым rрадусам, прямой уrол
. И u 1
равен 90 уrловым rpaдycaM. наче, уrловои rрадус составляет
180
м 1
часть развернутоrо уrла, или часть прямоrо уrла.
90
Уrловой rрадус, как и дуrовой, делится a 60 равных частей,
называемых м и н у т а м и, которые в свою очередь тоже деЛЯТСЯ4
на 60 равных частей, называемых с е к у н Д а м и.
Диаметр Луны виден наl\1И приблизительно под уrлом в 30'.
Человеческий rлаз может видеть только те предметы, которые на-
ходятся под уrлом зрения больше 1'. Поэтому rорошина с расстоя.
ния в 1 КМ не видна человеческим rлазом, так как уrол зрения в
1 , ,
этом случае составляет меньше .
Все уrловые rрадусы равны между собой, но этоrо нельзя ска-
зать о дуrовых rрадусах (черт. 94). Длина дуrовоrо rрадуса из.
меряется в зависимости ---от длины радиуса.
Че f больше радиус окружности, тем больше длина дуrовоrо rpa..
дуса. Так, например, длина дуrовоrо rрадуса земноrо меридиана
(или экватора) приблизительно равна 110 КМ.
Ду rOBbIe rpaдycbI равны только в одной окружности и в равных
окружностях.
3. Транспортир.
Для измерения уrлов, а
также для построения уrлов
существует прибор, называе-
мый транспортиром (черт. 95).
Он состоит из линейки, к ко.
u
торои присоединена ПОЛУОК"
ружность. Центр полуокруж--
ности отмечен небольшим вы-
резом или штрихом на. диа-
метре полуокружности.
.Дуrа полуокружности раз..
делена на rрадусы оТ О до 1800.
2 н. Н. НИКИТИН
в
s
It
2
о
з
2
4
ЧЕРТ. 95
33
ЧЕРТ. 96
ЧЕРТ. 97
с
4. Измерение yrJloB с по-
мощью транспортира.
Измерение уrлов с по-
мощью транспортира про-
изводится следующим об-
разом.
Пусть нам нужно из-
мерить L АВС (черт. 96).
Сделаем этот уrол цент-
ральным. Для этоrо сов-
местим центр транспорти-
ра с вершиной L А ВС (с
точкой В). Направим диа..
метр транспортира по од..
ной стороне LABC (по ВС),
тоrда друrая сторона уrла
покажет, сколько rрадусов
содержит дуrа измеряемо-
ro уrла. В данном случае
она содержит 520, следо-
вательно, L АВС будет
равен 52 уrловым rраду.
сам. На чертеже 97 показа..
но измерение тупоrо уrла
ВОС. Уrол вое равен 120°.
Записывается это так:
L Аве == 520. L ВОС ==
== 1200.
5. Построение yr лов с
помощью транспортира.
Пусть требуется пост-
роить уrол в 500 по данноЙ
8 ero вершине О и по данной
стороне ОВ. Совместим
центр траспортира с точ-
кой О. Таким обраЗО f,
уrол, который мы строим,
делаем центральным.
НапраВИ 1 диаметр транспортира по пряrvl0Й ОВ (черт. 98) и отсчи-
таем по дуrе транспортира справа от нуля 500. Поставим против
500 точку С и соединим её с точкой О (вершиной уrла). Мы полу-
чим искомый LCOB, равный 500.
Если Hal\1 прямая не дана и не указана точка, которая должна
быть вершиной yr ла, а просто сказано: построить уrол в 1250,
то мы сначала проведё 1 nроизвольную прямую и rде нибудь на
ЧЕРТ. 98
34
ней возьмём точку О, которую примеNI за вершину уrла, и таким iKe
образом построим требуемый уrол.
6. Приближённое деление уrла на равные части.
Можно разделить уrол на несколько равных час ей помощью
транспортира. Для этоrо надо измерить уrол, число rpaдYCOB
уrла разделить на данное число частей и построить требуемые уrлы.
Упражнения
1. Какой уrол составляют минутная и часовая стрелки в 1 час ПОПОЛУДНII
(в 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 часов)?
2. Начертить прямой уrол с помощью транспортира. Провести в нём из ero
вершины луч. Измерить отдельно 1 и L2, наЙтИ их сумму. Вычислит
процент поrрешности по отношению к прямому yr лу (900).
3. Измерить уrлы фиrуры, помещённой на чертеже 99, и найти их сумму.
4. Измерить уrлы фиrуры, помещённой на чертеже 100, и найти их сумму.
5. Построить несколько уrлов и разделить их на
2, 3, 4, 5 равных частей с помощью тран.
спортира,
ЧЕРТ. 99
ЧЕРТ. 100
"Астролябия.
Для измерения и построения уrлов на местности служат спе..
циальные приборы, называемые уrломерами.. Простейшим из этих
приборов является а с т р о л я б и я, её упрощённая схема дана
на чертеже 1 О 1.
. °fl . 0;1 .
ЧЕРТ. 101
35
Основной частью астролябии служит Kpyr (лимб) с делениями
от О до 3600. На ось, проходящую через центр Kpyra, 'насажена ме-
. u
таллическая или деревянная линеика так, что она может вращать-
ся около этой оси. На концах линейки находятся два диоптра, ко..
торые используются для установки линейки в определённом поло-
жении. Один из диоптров, называемый rлазным диоптром, имеет
узкую вертикальную щель. В друrом диоптре щель более широ-
кая, в ней установлен вертикально волосок или тонкая проволока.
Этот диоптр называется предметным. Линейка вместе с диоптрами
называется а л и Д а Д о й. Наружные края алидады скошены,
и на них имеются указатели (штрихи или выступы) для отсчёта
делений на Kpyre.
Весь прибор устанавливается на треножнике.
8. Уровень. Для Toro чтобы Kpyr
астролябии (лимб) при-
нял rоризонтальное по-
ложение, что очень важ-
но для точности при
измерении уrлов, упот-
ребляется особый При-
ЧЕРТ. 102 бор, называеrvIЫЙ у р о в-
н е м (черт. 102).
-Основной частью уровня является стеклянная трубка, запаян-
ная с обоих концов. Трубка эта заполняется спиртом или эфиром,
причём в трубке оставляется небольшой пузырёк воздуха. Если
положить уровень на rоризонтальную плоскость, то пузырёк воз-
духа будет находиться в середине трубки; если же плоскость
не будет rоризонтальной, то пузырёк воздуха переместится к одному
из концов трубки. Уровень устанавливается на лимбе по край-
ней мере в двух различных направлениях. Таким образом, наблюдая
за положение { пузырька воздуха, можно установить, будет ли дан-
ная плоскость rоризонтальной или она будет иметь уклон в ту или
друrую сторону.
В целях большей прочности и удобства пользования прибором
трубка уровня заключается в металлическую оправу, в которой
оставляется небольшое оконце для наблюдения за поло)кением пу-
зырька воздуха. Уровень укрепляется на металлической пластин-
ке. Иноrда на поверхности Kpyra астролябии закрепляются не.
подвижно два уровня в .различных направлениях. .
Применяется ур'овень и как саl\fостоятельный при бор, с помощыо
KOToporo можно проверить rоризонтальность любой плоскости или
u
прямои линии.
При выполнении строительных работ вместо уровня нередко
лрименяется более упрощённый прибор, называемый в а т е р"
36
n а с о м (черт. 103). Он состоит из двух
деревянных планок, соединённых под
ПРЯМЫ I уrлом. На одной из планок под-
вешен шнур с rрузиком (отвес).
В случае rоризонтальноrо поло)ке-
ния проверяемой плоскости отвес сов-
падает с направлением планки; если
проверяемая плоскость не rоризонталь-
на, отвес уклоняется от этоrо направ-
ления (черт. 104).
9. Измерение уrлов
при помощи астролябии.
ЧЕРТ. 103
Предположим, нужно измерить на
1\1естности уrол АСВ (черт. 105).
Вершину уrла (точку С) отмечают ко-
лышком длиной в 25 30 см, треножник
с астролябией устанавливают над точкой С так, чтобы отвес, под..
вешенный к центру Kpyra, находился как раз над выступающим из
земли кол ЫШКОl\11 , а плоскость Kpyra астролябии была rоризон
тальной.
После ЭТоrо алидаду устанавливают так, чтобы её положение
совпало с ОДНИ1\1 из направлений СА или СВ, например с направле-
нием СА. Вначале алидаду устанавливают на rлаз, а затем, смот-
ря в узкуLO щель rлазноrо диоптра, перемещают алидаду до тех
ЧЕРТ. 104
. :'''' :
-"".>. "
."":;--.
ЧЕРТ. 105
37
ЧЕРТ, 106
ЧЕРТ. 107
пор, ПОI<а волосок преДf\.fетноrо диоптра не закроет предмет А.
После этоrо отмечают деление Kpyra, против KOToporo находится
указатель одноrо из двух диоптров.
Затем алидаду устанавливают по направлению СВ и отмечаlоr
деление Kpyra, против KOToporo находится указатель Toro же диоп-
тра.
Разность отсчёто& и даст уrол между направлениями СВ и СА,
т. е. уrол АСВ (черт. 106).
Если отсчёты на А и В окажутся по разные стороны нуля, то
величину уrла можно определить по противоположным MeTKa 1
алидады.
Описанный выше прибор даёт небольшую точность.
С целью повышения точности измерений используются более
совершенные приборы. На чертеже 107 показан один из таких
приборов (теодолит).
Упра3lснения
1. При измерении уrла с помощью астролябии получили отсчёты 250 и 750.
Чему равен измеряеl\IЫЙ уrол?
2. При измерении уrла с помощью астролябии получили отсчёты 350 И 340 Q .
Чему равен измеряемый уrол?
у к а э а н и е. Для' решения задачи реКО:Vlендуем сделать чертё ж.
r /1 А В А 11
E!!r"
ТРЕуrопьниии.
14. ПОНЯТИЕ О мноrоуrОЛЬНИКЕ.
Часть плоскости, оrраниченная замкнутой ломаной линией,
называется м н о r о у r о л ь Н И К О м.
Отрезки этой ЛО1\1аной линии называются с т о р о н а м и
l'vlноrоуrольника; АВ, ВС, CD, DE, БА (черт. 108) CTOpOHЫ мно"
rоуrольника ABCDE.
Длина замкнутой ломаной, оrраничивающей мноrоуrольник,
называется ero пер и м е т ром.
Мноrоуrольник называется в ы п у к л ы м, если он располо-
жен по одну сторону от любой своей стороны, неоrраниченно про-
долженной за обе вершины.
l\\ноrоуrольник MN Р КО (черт. 109) не будет выпуклым, так
как он расположен не по одну сторону прямой КР.
Мы будем рассматривать только выпуклые мноrоуrольники.
Уrлы, составленные двумя соседними сторонами мноrоуrоль-
ника, называются ero в н у т р е н н и м и у r л а м и, а вершины их ........
в ерш и н а м и мноrоуrольника.
Отрезок прямой, соединяющий две несосеДНtlе вершины l\'IHOro-
уrольника, называется Д и а r о н а лью мноrоуrольника.
АС, AD диаrонали lноrоуrольника (черт. 108).
Уrлы, смежные с внутренними уrлами мноrоуrольника, на-
зываются внешними уrлами мноrоуrольника (черт. 110).
В зависимости от числа уrлов (сторон) мноrоуrольник называ.
ется треуrольником, четырёхуrольником, пятиуrольником и т. д.
Два мноrоуrольника называются равными, если их l\fОЖНО со-
вместить наложением. '-...
с м
р,
,
"
,
,
,
д
,/
/"
N
о
ЧЕРТ, 108
ЧЕРТ. 109
ЧЕРТ 110
39
15. ТРЕуrольник и ErO ЭЛЕМЕНТЫ.
1. Треуrольник обозначается треl'vIЯ заrлавными буква:\1И, сто-
ящими при ero вершинах: Для сокращения записи слово «треуrоль-
ник» заменяют знаком . Треуrольник, изображённый на черте-
же 111, можно записать так: АВС.
Сторону треуrольника принято обозначать той же буквой, что
и вершину уrла, противолежащеrо этой стороне, но малой буквой.
Так, например, на чертеже 112 сторона ве обозначена буквой а,
так как она лежит п.ротив уrла А; сторона СА обозначена буквой Ь,
так как она лежит против уrла В; сторона АВ обозначена буквой с,
так как она лежит против уrла С.
Если продолжим какую нибудь сторону треуrольника, то полу"
чим уrол, СlVlе)кный с ОДНИ 1 из внут-
ренних уrлов треуrольника. Такой
уrол называется в н е ш н и м уrЛО 1
треуrольника.
При каждой вершине треуrольни-
ка может быть построено по два
внешних уrла (черт. 113).
2. Если из какой-либо вершины
треуrольника опустим перпендикуляр
на противоположную сторону, то
получим отрезок, который назы-
вается в ы с о т о й треуrольника
(черт. 114).
Сторону треуrольника, к которой
проведена высота, принимаIОТ за о с..
н о в а н и е треуrольника.
Высота может быть проведена к
любой стороне треуrольника. Иноrда
высота треуrольника пересекает не
само основание треуrольника, а ero
продолжение. Так, на чертежах 115 и
116 высоты AD и ЕМ пересекают
продолжения оснований 8е и FK.
в каждом треуrольнике можно
провести три высоты. Если аккурат-
но провести все высоты треуrольника,
'fO можно заl\.lетить, что все высоты
треуrольника или их ПрОДОЛ)I{е-
ния пересекаlОТСЯ в одной точке
(черт. 117, 118). Если же высоты или
их продолжения пересекутся не в
одной точке, то можно с уверен-
ностью СI<азать, что черте/I{ сделан
веточно.
д
Вершина
ЧЕРТ. 111
д
ЧЕРТ. 112
ЧЕРТ, 113
40
Высота треуrольника обозначается
буквой h, к кgторой присоединяется
u u
обозначение тои стороны, к которои
она проведена: h a , h b , hc (черт. 117).
3. Если соединить какую-нибудь
вершину треуrольника с серединой
u u
противолежащеи еи стороны, то полу-
ЧИl\1 отрезок, который называется м е-
Д и а н о й треуrольника (черт. 119).
Медиана обозначается буквой т, к
которой присоединяется обозначение
той стороны, к середине которой
она проведена: та' т ь , те (черт. 120).
В каждом треуrольнике можно
провести три медианы. Если прово-
дить их аккуратно, то в любом тре-
уrольнике медианы пересекутся в од-
ной точке (черт. 120).
4. Отрезок биссектрисы уrла тре-
уrольника от ero вершины до противо-
дежащей стороны называется б и с-
с е к т р и с о й треуrольника. Биссек-
триса обозначается буквой l, к которой
д
F
Е
"
ЧЕР r. 116
ЧЕРr 117
д
в
ЧЕРТ. 119
в
д
F
к
ЧЕРТе J 14
...........
д
....
8
ЧЕРТ! 115
о
Е К
, .//FI ........""
J( I I ......
"./ \ I I
\ I 1
\ I I
, 11
'
ЧЕРТ. 118
в
д
ЧЕРТ. 120
41
в
д
ЧЕРТ! 121
присоединяется обозначение уrла,
из вершины Koтoporo она проведе-
на: lA , lB, lc (черт. 121). Биссектри-
сы треуrольника (так же как, высо-
ты и медианы) пересекаются в одной
точке (черт. 121).
Стороны и уrлы треуrольника,
а также ero высоты, l\lедианЫ,
биссектрисы называ ся элемен-
тами треуrольника. Слово «эле.
мент» значит «составная часть».
Упражнения
1. Начертить несколько треуrольников и провести в каждом из них с по.
МОЩЬЮ чертёжноrо треуrольника по три высоты.
2. Начертить несколько треуrольников и провести в каждом из них по три
медианы. .
3. Начертить неСI{ОЛЬКО треуrольников и провести в кажДОМ из них по три
биссектрисы.
16. виды ТРЕуrольников в ЗАВИСИМОСТИ
ОТ СРАВНИТЕЛЬНОЙ ДЛИНЫ ИХ СТОРОН И ВЕЛИЧИНЫ Уrлов.
"
1. ВИДЫ треуrольников в зависимости от сравнительной ДЛИНЫ
их сторон.
Треуrольник, у KOToporo все три стороны имеют различные
ДЛИНЫ (черт. 122), называется раз н о с т о р о н н и lVI.
ЧЕРТ. 122
ЧЕРТ. 123
Треуrольник, у KOToporo две стороны равны (черт. 123), назы-
вается р а в н о б е д р е н н ы rvl.
Сторона равнобедренноrо треуrольника, не равная двум друrим
сторонам, обыкновенно принимается за ero основание (если не сде-
лано особой оrоворки).
Треуrольник, у KOToporo равны все три стороны, называется
р а в н о с т о р о'н Н И М (черт. 124).
42
2. Зависимость между сторонами
треуrОJJьника.
В треуrольнике каждая TopOHa
отрезок, а две друrие ero стороны
составляют ломаную линию t соединя-
ющую концы этоrо отрезка. Поэтому
8 "аждая сторона треУ20ЛЬНU1lа.
.меньше CYM.JJlbl двух друz.их ezo
сторон (9 6).
В АВС (черт. 125) АС +ВС >
?АВ.
Если от обеих частей этоrо нера-
венства отнимем по ве, то получим
АС > АВ........ ве, Т. е.
8 сторона треуz.ольнияа больше
разности двух друz.их ez.o сторон.
3. Виды треуrОJJЬНИКОВ в зависи-
мости от величины их yr лов.
Треуrольник, у KOToporo все три
уrла острые, называется о с т р о..
у r о л ь н ы м.
Треуrольник, в котором есть пря-
мой уrол, называется п р я м о..
у r о л ь н ы м.
Стороны треуrольника, заключаю-
u
Iцие прямо уrол, называются к а т е-
т а 1\1 И, а сторона, лежащая против
прямоrо уrла, называется r и п о т е-
н у зой (черт. 126).
Треуrольник, в КОТОрО1\1 есть ту-
пой уrол, называется т у п о у r о л ь..
н ы I\1 (черт. 127).
17. СИММЕТРИЯ ОТНОСИТЕЛЬНО
ПРЯМОЙ.
ЧЕРТ. 124
с
д
ЧЕРТ. 125
Е
Q)
Е
...-'\
е;:,.,
":)0
?
\i)
,.,.
1. Фиrуры, симметричные друr' дрyrу.
Начертим на листе бумаrи чернилаI\1И какую-нибудь фиrуру, а
карандашом вне её произвольную ПрЯI\lУЮ. Затем, не давая чер-
нилам высохнуть, переrнёI\1 лист бумаrи по этой прямой так, чтобы
одна часть листа налеrла на друrую. На этой друrо части листа
получится, таким образом, отпечаток данной фиrуры. Если затем
лист бума rи. опять распрямить, то на Hё 1 окажутся две фиrуры,
d
Катет
ЧЕРТ I 126
ЧЕРТ 127
43
которые называются с и м l'vI е т р II Ч..
Н Ы м и относительно данной пря..
l'vl0Й (черт. 128).
Две фиrуры называются СИМ-
метричными относительно некоторой
прямой, если при переrибании плос"
кости чертежа по этой прямой они
совмещаются.
Прямая, относительно которой
данные фиrуры симметричны, назы
вается их о сью с и 1\1 М е т р и и.
Из определения СИl\Iметрпчных
фиrур следует, что ВСЯI{ие СИl\llметрич
ные фиrуры равны.
Получить си лметричные фиrуры
можно и не пользуясь переrибанием
ПЛОСКОСТИ, а с помощью I"еометричес-
Koro построения. Пусть требуется
построить точку С', симмеТРИЧНУIО
данной точке С относительно прямой
АВ. Опустим ИЗ точки С перпенди"
куляр CD на прямую АВ и на про-
должении ero отложим отрезок DC' ==
== DC. Если переrнём плоскость черте-
жа по АВ, то точка С СОВl'vlестится
с точкой С': точки С и С' симметрич-
ны (черт. 129).
Пусть требуется теперь пос-
троить отрезок C'D', симметричный
ЧЕРТ. 130 данному отрезку CD относительно
прямой АВ. Построим точки С' и D', симметричные точкам С
и D. Если переrнём плоскость черте)ка по АВ, то ТОЧКИ С и D
совместятся соответственно с точками С' и D' (черт. 130). Поэто-
му отрезки CD и С 'D' совместятся, они будут СJIl\Iыетричны.
д' М 'о А
T
E .e Е
1 в
, D' 1t D
.с
C' N r с
ЧЕРТ. 128
д
с'
с
8
ЧЕРТ. 129
Д
с'
с
D
в
в'
44
ЧЕРТ. 131
Построим теперь фиrуру, симметричную данному мноrоуrольни-
}(У ABCDE относительно данной оси сймметрии MN {черт. 131).
Для решения этой задачи опустим перепендикуляры Аа, ВЬ, Се, Dd
и Ее на ось симметрии MN. Затем на продолжениях этих перпен-
дикуляров отложим отрезки аА' == Аа, ЬВ' == ВЬ, еС' == Се; dD' ==
=== Dd и еЕ' == Ее.
Мноrоуrольник А' B'C'D'E' будет СИl'лметричным мноrоуrоль-
нику ABCDE. Действительно, если переrнуть чертёж по прямой
MN, то соответствующие вершины обоих мноrоуrольников совмес-
тятся, а значит, совместятся и сами мноrоуrольники; это и доказы-
вает, что мноrоуrольники ABCDE и А 'B'C'D'E' симrvlетричны от..
носительно прямой MN.
2. Фиrуры, состоящие из симметричных частей.
Часто встречаются rеометрические фиrуры, которые какой ни-
будь прямой разделяются на две симметричные части. Такие фиrу-
ры называются с и rvl 1\1 е т р и ч н ы м и.
ЧЕРТ t 132
а)
о)
ЧЕРТ. 133
ЧЕРТ. 131
Так, например, уrол':"'" фиrура симrvlетричная, и биссектриса
уrла является ero осью симметрии, так как при переrибании по
ней ,одна часть уrла совмещается' с друrой (черт. 132).
В Kpyre осью симметрии является ero диаметр, так как при пере-
rибании по нему один полукруr совмещается с друrи:м (черт. 133).
Точно так же симметричны фиrуры на чертежах 134, а, Ь. .
Симметричные. фиrуры часто встречаются в природе, строитель-
стве, в украшениях. Изображения, помещённые на чертежах 135
и 136, симметричны.
45
/............"""'
.;.. ----
, z
':;. ;", . -....... "
. r''1''....-
. /;;, / '.
. ,......".... -;;.../. ,-.
ЧЕРТ. 135
Следует заметить, что симметричные фиrуры совместить прос-
тым передвижением по плоскости можно лишь в некоторых случаях.
Чтобы совместить симмет-
ричные фиrуры, как прави-
ло, необходимо одну из них
повернуть обратной стороной.
18. СВОЙСТВА РАВНОБЕДРЕН..
HOrO ТРЕуrОЛЬНИI(А.
Построим равнобедренныIй
треуrольник А ВС и проведё f
в нём биссектрису уrла, зак"
Лlочённоrо между равными
сторонами АВ и СВ. Равно..
бедренный треуrольник раз..
бился на два треуrольника
ЧЕРТ. 136 ABD и CBD (черт. 137).
Переrнёl\1 l\lысленно плос..
I{ОСТЬ чертеiка по биссектрисе BD, так, чтобы правая часть её сов-
пала с левой. Тоrда сторона Ве пойдёт по стороне ВА, так как
L 1 == L2, и точка е совпадёт с точкой А, так как 8е == ВА.
Следовательно, при переrибании чертежа по BD треуrольник
BDC совместился с треуrольником BDA, Т. е. биссектриса BD яв-
ляется осью симметрии треуrольника АВС.
Отрезки CD и DA совместились, т. е. сторона АС в точке D
разделилась пополам.
Следовательно, BD будет не только биссектрисой треуrольиика
А ВС, но и ero медиаНОI\.
46
JТrлы BDC и BDA совместились, следова..
'I'еЛЬНО, они равны. Но в то же время ОНИ
смежные, поэтому каждыи из них равен пря-
МОМУ уrлу. Значит, BD является вь!сотой
треуrольника.
Уrлы С А совместились, следовательно,
ОНИ равны. Отсюда:
е 1. Биссеипlриса У2ла при вершине рав-
нобедренноzо треуzольни«а является
ezo осью симмет..йии.
8
ЧЕРТ. 137
. 2. Биссе«mриса уzла n1)и вершине равнобедренноzо тре-
УZОЛЬНU1(,а в то же вреJНЯ является ezo JНeдиaпoй и выео-
.,
тои.
Так как из вершины треуrольника можно провести только одну
биссектрису, одну медиану и одну высоту, то медиана, проведён-
ная к основанию равнобедренноrо треуrольника, яВляется и бис-
сектрисой, и высотой, точно так же и высота является и биссектри-
сой, и медианой.
. 3. Уzлы при основании равнобедренноzо т 1Jеуzольн""а
равны .между собой.
о 4. В равносторонне.м ntJJеУZОЛЬНU1(,е все внутренние yz.. .
Лbl равны .между собой. '
19. ПОСТРОЕНИЕ ТРЕУrольников по ОДНОМУ
ИЛИ ДВУМ ЭЛЕМЕНТАМ.
Пусть требуется построить треуrольник по данной стороне й.
Так как об уrлах треуrольника и о друrих ero сторонах ничеrо не
сказано, то можем построить сколько уrодно различных треуrоль-
ников, у которых одна сторона будет равна отрезку а (черт. 138).
Пусть требуется построить треуrольник по данному уrлу а.
В этом случае также можно построить СI{ОЛЬКО уrодно различных
треуrольников, имеющих данный уrол (черт. 139).
Q
1\ / 1'\
l' / /)( /\1/1
""- .j'Л>(>,)../ \ I I
I /1/ //У-х-" \ \ I I
. jjf '/ ' \\'
wi: .,
а
ЧЕРl. 138
ЧЕРТ & 139
Q
t
Ь
'"
,
....... '
" ,
....... "
...... ...... ........"
...... ....... ........ .......'
"-000. .......
ь
ЧЕРТ "140
41
..
/',
/ '
/ \
/ / \
/ / \ \
/ / \ \
/ // \ \
/ / \ \
/ / \ \
/ / \
_ .Li,.... rt tl. ___
L
ЧЕРТ f 141
,
t
Q
л
," \
А \\
I , \ \
, \\
, '\\
" , \\
,' \
'
а
ЧЕРТ. 142
Точно так же можно построить сколько уrодно различных тре-
уrольников по двум сторонам, или по двум уrлам, или по уrлу
и стороне (черт. 140, 141, 142).
Таким образом, если будут заданы только один или два элемен-
та треуrольника, то по этим элеl\Iентам можно построить сколько
уroдно различных треуrольников.
Перейдём теперь к построению треуrольников не по одному и
не по двум, а по трём ero элементам.
20. ПОСТРОЕНИЕ ТРЕУrОЛЬНИКА
ПО ДВУМ ДАННЫМ Ero СТОРОНАМ и уrлу МЕЖДУ НИМИ.
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУrОЛЬНИК08.
8
А
,
8
ЧtРТ. 143
48
с
Пусть требуется построить треуrоль-
ник, одна сторона KOToporo равна, нап-
ример, 35 .м.м, друrая сторона равна
32 .м.м и уrол, эаключённый fvlежду эти-
ми сторонами, равен 460.
Построим с помощью транспрртира
L А, равный 460, и на ero сторонах
отложим отрезки АВ и АС, соответст-
венно равные 35.мм и 32 .м.м (черт. 143).
Соединив точки В и С, получим иска..
мый треуrольник АВС. По Tel\1 же дан..
ным ПОСТрОИ1\1 друrой треуrольник
ЬА'В'С'.
По этим данным мы можеl\1 построить
сколько уrодно треуrольников. )loKa.
жем, что все они равны между собой.
Для этоrо рассмотрим любые два из
них: АВ С и А'В'С'.
НаложимдА'В'С' Ha АВС так,
чтобы вершины А' и А совrvlестились.
Сторону А'С' направим по стороне АС'.
Тоrда точка С' совместится с точкой С, потому что А 'С' АС.
Сторона А' В' пойдёт по стороне АВ, так как LA' == L А.
Точка В' СОВl\lестится с точкой В, так как А'В' === АВ. Если точки
С и С', В и В' совместились, то совместятся и стороны В'С' иве.
Треуrольники АВС и А' В'С' совпали, значит, они равны.
. Таким образом, еслu две стороны, и уzол между ними одно-
zo т.оеУZОЛЬНU1(,а соответственно равны, дву.м сторона.м
и уzлу .Idежду ни,М,ц друzоzо треУZОЛЬНURа, то та1(,ие
"lJJеуzольнu1(,U равны .между собой.
Назовём это пер в ы м признаком равенства треуrольников.
21. ПОСТРОЕНИЕ ТРЕУrОЛЬНИКА ПО СТОРОНЕ И ДВУМ
ПРИЛЕЖАЩИМ К НЕЙ УrЛАМ. ВТОРОЙ ПРИЗНАК РАВЕНСТВА
ТРЕУrОjlhНИКОВ.
Пусть требуется построить тре..
уrольник, одна сторона KOToporo
равна, например, 40 мм, а уrлы,
прилежащие к ней, равны 500 и 480.
На произвольной прямой постро-
им отрезок АС, равный 40 мм. Затем
на этом отрезке при точке А постро-
им уrол, равный 500, а при точке c
уrол, равный 480 (черт. 144).
Если мы достаточно продолжим
стороны этих уrлов, то они пересе-
кутся в некоторой точке В. Полу-
чим треуrольник АВС.
По этим данным можно построить
сколько уrодно треуrольников. До-
. кажем, что все они равны между
собой. Для этоrо рассмотрим два из
них: АВС и А'В'С'.
Наложим 6. А' В'С' на 6. АВС
так, чтобы совместились равные
стороны АС и А'С'. Тоrда сторона А'В' пойдёт по стороне АВ,
так как LA' == L А, и сторона С' В' пойдёт по стороне СВ, так
как L С' == L С. Точка В' одновременно должна быть и на сто-
роне АВ, и на стороне СВ, следовательно, она совместится с точ-
кой В, так как дне прямые l\fOryT пересечься только в одной точке.
Треуroльники АВС и А' В'С' совпали, значит, они равны.
. Таким образом, если сторона и два nрилежащuх " ней У2ла
одноzо треУZОЛЬНURа соответственно равны стороне и
дву.м п-рилежащи.м " ней У2лам друzоzо треУZОЛЬНU1(,а, тО
та1(,ие треуzольни"u равны между собой.
Назовём это в т о р ы м признаком равенства треуrольников.
в
д
.,
в
д
ЧЕРТ. 144
с
с"
49
8
22. ПОСТРОЕНИЕ ТРЕуrОЛЬНИI(А
по ТРЕМ ДАННЫМ Ero СТОРОНАМ.
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА
ТРЕуrольни КОВ.
..
л/д')
С(С} Пусть требуется построить треу..
rольник по трём ero сторонам, нап-
ример стороне а, стороне Ь и сто..
роне с. (Заданные размеры должны
удовлетворять условию: сумма двух
любых сторон треуrольника больше
третьей стороны).
Сначала на произвольной прямой
ПОСТРОИ l отрезок АС, равный данно-
му отрезку Ь; мы сразу получим две
вершины искомоrо треуrольника
А и С (черт. 145).
Так как длина втор.ой и третьей сто-
рон соответственно равна отрезкам с и
а, то третья вершина треуrольника
должна находиться как на дуrе, описанной из центра А радиусом,
равным с, так и на дуrе, описанной из центра С радиусом а. Следо..
вательно, третьей вершиной треуrольника будет точка пересечения
этих дуr. Обозначив эту точку буквой В и соединив её отрезкаl\1И
с точками А и С, получим искомый треуrольник АВС.
По этим даННЫl\1 можно _ построить сколько уrодно треуrольни-
ков. Докажеl\f, что все они равны между собой. Для этоrо рас..
смотрим два из них: АВС и А'В'С'.
Приложим треуrольник А' В'С' к треуrольнику Аве так,
чтобы их равные стороны А 'С/ И АС СОВl\1естились (черт. 145), при-
чём точка А' совпала бы с точкой А, точка С' с точкой С. Тоrда
треуrольник А' В'С' примет у!оложение А В"С. Сторона АВ
будет равна стороне АВ" и сторона 8С стороне В"С.
" /
'1..
, /
'у
B '
8'
д'
с'
ЧЕРТ. 145
8
8
в
А
с
А
А
С{[))
B
О)
8)
,
8
О)
ЧЕРТ. 146
60
Соединим отрезком прямой точки В и В" и найдём точку D
пересечения этоrо отрезка с прямой АС. Приходится различать
три случая: 1) точка D лежит между точками А и С (черт. 146, а);
2) точка D лежит вне отрезка АС (черт. 146, 6); 3) точка D совпада..
ет с одним из концов отрезка А С (черт. 146, в).
Проведём доказательство в первом случае. В ЭТОl\I случае име..
ем два равнобедренных треуrольника
..BAB" и
BCB", у которых
Ll == L2, а L 3 == L 4, откуда
LB == Ll + L 3 == L 2 + L 4 == L В".
Следовательно, по первому признаку равенства треуrольников
ABC == 6.АВ"С, но тоrда 6 АВС == 6 А 'В'С'.
Аналоrично проводится и доказательство в двух друrих слу-
чаях. Мы доказали, что
. Если три стороны одНО20 треУ20льник.а соответственно
равны тре.м. сторонам- дРУ2020 треУ20Аьна"а, то та1(,ие
mреУ20ЛЫlиии равны .между собой. .
Назовём это т р е т ь и м признаком равенства треуr_ольников.
3 а м е ч а н и я. 1. Во всех трёх признаках равенства тре..
уrольников в число трёх данных элементов входит хотя бы одна
сторона треуrольника.
2. В равных треуrольниках против равных сторон лежат рав-
ные уrлы и, обратно, против равных уrлов лежат равные стороны.
23. жt:сткость ТРЕуrОЛЬНИI(А.
Если возьмём три металлические или
деревянные планки, закрепим их концы
(булавка
IИ или rвоздиками) так, чтобы
получить треуrольник, то увидим, что нам
не удастся изменить форму полученноrо
треуrольника (черт. 147).
Треуrольник
фиrура ж ё с т к а я.
Если заданы три ero стороны, то форма
треуrольника уже не может измениться.
Это вытекает из только что доказанноrо ЧЕРТ. 147
признака равенства треуrольников.
Стропила зданий имеют вид треуrольников. Это придаёт им
крепость и устойчивость (черт. 148, а).
При устройстве садовой калитки обязательно прибиваIОТ план-
ку (доску), иноrда две планки, чтобы получились треуrольники.
Это придаёт крепость калитке; иначе её скоро перекосит (черт. 148, б)
На чертеже 149 также показано, как пользуются на практике
жёсткостью треуrольника.
51
24. ПОСТРОЕНИЕ yr ЛЛ,
PABHOrO ДАННОМУ.
Дан уrол ВАС (черт. 150),
требуется с помощью циркуля и
линейки построить уrол, рав-
ный уrлу ВАС.
Реш е н и е. Проведем пря-
мую линию и обозначим на ней
произвольную точку о. Из Bep
шины А данноrо уrла ВАС как
из центра произвольным радиу-
сом опише 1 дуrу так, чтобы она
пересекла обе стороны данноrо
уrла. Обозначим точки пересе-
чения буквами К и М. Потом тем
ж е ра диусом из точки О как из
центра проведем дуrу так, чтобы
она пересекла взятую наt1И пря-
мую. Обозначим' точку пересече
ния буквой N. После этоrо
возьмем циркулем расстояние
КМ и из точки N как из центра
опишем дуrу радиусом, равным
расстоянию КМ, так, чтобы она
пересекла дуrу, описанную из
точки О, в какой нибудь точ
ке Р.
Проведя прямую ОР, полу
чим уrол PON, равный уrлу
ВАС. Чтобы убедиться в paBeH
стве этих уrлов проведем отрез-
ки МК и N Р, получим два треуrолника К АМ и Р О N, которые
равны по 3-МУ признак у равенства треуrольников.
Следовательно, L. РО N == L В АС, так как эти yr лы лежат в
равных треуrольниках против равных сторон.
с
А
м
ЧЕР1. 150
52
а
/
С .-
...... .d.
-==...
..............................
I 1, :
I j 't..
.... ... И:-
1 "", ....;.. "::'" "' .
./' ...........tI'
..;
.
. .\ '."
r
б
ЧЕРТ. 148
о
}N
9 25. ПОСТРОЕНИЕ ТРЕУrОЛЬНИI(А по ТРЕМ ЭЛЕМЕНТАМ.
ЧЕТВЁРТЫЙ СЛУЧАЙ ПОСТРОЕНИЯ ТРЕуrольников.
Треуrольник имеет три стороны и три уrла. В 20, 21 и 22
ыы разобрали три случая построения треуrольников по трёl\1 из
ЭТИХ шести «элем:ентов треуrольника). Рассмотрим теперь все раз-
личные способы выбора трёх элементов треуrольника из шести
указанных. Таких способов шесть:
1) две стороны и уrол l\1ежду ними;
1)
I
2)
"1
2) сторона и два прилежащих к ней уrла;
3) три стороны;
З)
4}
5)
6)
4) две стороны и уrол, противолежащий одной
из них;
5) сторона, один уrол, прилежащий к ней,
и друrой противолежащий;
6) три уrла.
Пятым и шестым случаЯl\1И l\IbI займёмся позднее, а сейчас рас-
Сl\IОТРИМ четвёртый случай.
Пусть даны две стороны а и Ь и уrол а, противолежащий сто-
роне а. На произвольной прямой построим отрезок АС, равный
отрезку Ь, и на ЭТОl\1 отрезке, с вершиной в точке А, строим уrол,
равный а. С центром в точке С проведём окружность радиуса а.
Эта окружность либо вовсе не пересечётся со второй стороной уrла
(черт. 151, а), либо будет Иl\1еть со второй стороной уrла одну общую
точку (черт. 151, 6), либо, наконец, пересечётся со второй стороной
I /
/
В i
д ь С Д Ь
Б) б)
ЧЕРТ. 151
53
уrла в двух точках (черт. 151, в). Таким образом, задача построе-
ния треуroльника по двум сторонам а и Ь и уrлу а, противолежа
щему стороне а, может иметь два решения, одно решение или
Вовсе не Иl\1еть решений.
На черте}l{е 151, в треуrольники АВС и АВ'С не равны. По--
этому нельзя сказать, что из равенства двух сторон и уrла, про..
4<тиволежащеro одной из сторон, одноrо треуrольника cooTBeTCTBYIO
щим сторонам и уrлу друrоrо треуrольника вытекает равенстпо
треуrольников.
26. свойство ВНЕШНЕrо уrЛА ТРЕуr..оЛЬНИКА.
. т е о р е м а. Внешний уzол 8СЯк.оzо lпреуzольнuк.а больше
"аждоzо 8HympeHHezo уzла треуzольнu""а, не сяежноzо
с ",ия.
Дано: L BCD
Е внешний уrол треу-
rольника АВС.
Надо доказать, что
LBCD>LB и LB,CD>
> L А (черт. 152).
Д о к а з а т е л ь С т-
в о. Для доказатель-
ства выполним в пер-
вую очередь построе-
ние, в результате KOTO
poro внешний уrол BCD
разобьётся на две чаСТlI.
1. Проведём медиану АО треуrольника А ВС.
2. ПРОДОЛЖИl\'1 её на отрезок ОЕ, равный АО.
з. Проведёы отрезок ЕС.
После этоrо раССl\10ТРИМ треуrольники АОВ и СОЕ. В этих тре-
уrо.пьниках
в
д
с
ЧЕРТ 152
D
АО == ОЕ }
ВО == ОС
Уrлы АОВ и СОЕ равны, как вертикальные ( 11).
Следовательно, треуrольник АОВ равен треуrольнику СОЕ
(по двум сторонам и уrлу, заI{лючённому между ними, т. е. по
1-l\1У п,ризнаку равенства треуrольников, 20).
Из равенства треуrольников следует, что L В == L ВСЕ, TaI{
как они ле}l{ат в равных треуrольниках против равных сторон АО
и ОБ. rlo уrол ВСЕ только часть внешнеrо уrла BCD, поэтому весь
внешний уrол BCD БОЛЫllе BHYTpeHHero уrла В. Таким же спосо
бом доказывается, что внешний уrол BCD больше BHYTpeHHero yr-
ла А (в этом случае построение надо начать с проведеllИЯ i\'iедианыI
треуrОЛЬf:Iика АВС к стороне АС).
по построеНИIО.
54
Из этой теоремы вытекают следствия, важные для доказатель-
ства некоторых теорем. .
С л е Д с т в и е 1. В тупоуzольноя lпреуzольни"е" IltОЛЬ1(,О
один YZOA тупой, остальные ocтJJble, так как внеIП"
и и и
нии уrол, смежныи с тупым внутренним уrлом, острыи, ПОЭТО..
и и
му каждыи из остальных внутренних уrлов тоже острыи.
С л е Д с т в и е 2. В пря.моуzольноAf, т t)еУZОЛЬНU1(,е толь-
1(,0 один уzол пfJЯ,М,Ой, остальные острые,' так как внеш.
u u и
нии уrол, смежныи с ПрЯМЫlVI внутренним уrлом, тоже пр ямои, по..
и и
этому каждыи из остальных внутренних уrлов острыи.
С Л е Д с т в и е 3. Из точ1(,U, вЗЯ:tlОЙ вне прямой, мож-
но провесп-еи " этой прямой толь"о один перпендu1(,УЛЯР,
и
так как, предположив, что из взятои точки проходит и
второй перпендикуляр к данной прямой, мы получили бы тре..
уrольник, внешний уrол KOToporo равняется внутреннему уrлу,
и .
не смежному с ним, что противоречит доказаннои теореме.
э 27. РАВЕНСТВО прямоуrольных ТРЕуrОЛЬНИI(ОВ.
1. Первые два признака равенства
прямоуrольных треуrольников.
Мы установили, что для равенства двух треуrольников доста..
точно, чтобы три элемента одноrо треуrольника были равны соот.
ветствующим элементам друrоrо треуrольника, при этом непремен"
но в число этих элементов дол)кна входить хотя бы одна сторона.
Так как все прямые уrлы равны lVIежду собой, то прямоуrольные
треуrо.пьники уже имеют по одному равному элементу, именно по
равному прямому уrлу.
. Отсюда следует, что п.rJЯм'оуzольные mреуzольнu1(,U равны:
1) если к,аmеты одноzо т.rJеуzольнu"а соответственно
равны катета.:n друzоzо треуzольни1(,а (черт. 153);
2) если катет и прилежащий острый уzол одноzо
треуzольни"а соответственно равны "а тет у u пfJuлежа-,
ще,М,у ос.тро,М,у уzлу.друzоzо пt1Jеуzольнuк,а (черт. 154).
ЧЕРТ. 153
ч рr. 154
55
Упра3lснения
1. Можно ЛИ построить треуrольник по стороне и двум уrлам, если оба за-
данных уrла будут прямые? оба тупые? один прямой, друrой тупой?
2. Построить треуrольник по трём ero сторонам, если ero стороны соответст-
венно равны:
а) 6 с'м, 5 с'м, 7 с'м;
б) 5 с'м, 7 с'м, 8 с'м.
з. Можно ли построить треуrольник, если стороны ero будут соответст-
венно равны:
а) 1 О с'м, 6 с'м, 4 с'м;
б) 48 мм, 32 мм, 8 ,м,м?
Если нельзя построить эти треуrольники, то почему?
4. Построить прямоуrольный треуrольник с помощью циркуля и чертёж-
Horo треуrольника по двум ero катетам.
2. Две задачи на построеl:'ие прямоуrольных треуrольников.
А
с==5,4см
ЧЕРТ. 155
в
3 а Д а ч а 1 . П 0-
строить пРЯМОУ20ЛЬНЫЙ
mреУ20ЛЬНИ1\, по следую-
щим данным: 2ипотену-
за с == 5,4 СМ, L А ===
== 380.
Реш е н и е (черт.
155) .
1. На прямой MN
откладывае 1 отрезок
АВ == 5,4 СМ.
2. Строим уrол КА В,
равный 380.
3. Из точки В опус-
каем с помощью чертёж-
Horo треуrольника
перпендикуляр ве на
прямую АК.
Треуrольник АВС
отвечает условию зада-
чи.
с:5,4см
А
м
I
с==З8мм
J K
,l/
N
3 а Д а ч а 2. По-
строить пРЯМОУ20ЛЬНЫU
треУ20ЛЬНИ1\, по следую-
щим данным: 2ипотенуза
с == 38 .мм, катет Ь ==
== 26 мм.
I
Ь==26нм
Ь==26нм
м
с
в
ЧЕРТ. 156
56
Реш е н и е (черт. 156).
1. На произвольной прямой MN берём точку С и проводим
СК ..L MN.
2. На прямой СК откладываем отрезок СА === 26 ММ.
3. Из точки А как из центра раДИУСО f, равным отрезку с ==
== 38 .мМ, описываем дуrу так, чтобы она пересекла прямую MN,
например, в точке В.
4. Точки А и В соединяем отреЗКОl\f.
Треуrольник АВС отвечает условию задачи.
Докажем теперь две теоремы, устанавливающие ещё два при-
знака равенства прямоуrольных треуrольников.
3. Теорема о признаках равенства прямоуrольных треуrольников.
Теорема 1. Если zuпome-
"уза и острый уzол од"оzо
треуzольнu«а соответственно
равны zuпотенузе и острому
уzлу друzоzо треуzольнu«а,
то та«ие пря.моуzольные тре-
уzольни«и равны.
Чтобы доказать эту теорему,
построим два прямоуrольных
треуrольника АВС и А' В'С', У
которых уrлы А и А' равны, rи..
потенузы АВ и А' В' также равны,
а уrлы С и C' прямые (черт. 157).
l-Iаложим треуrольник А' В' С' на
треуrольник АВС так, чтобы вер-
шина А' совпала с вершиной А, rи-
потенуза А ' В' с равной rипоте..
нузой АВ. Тоrда вследствие ра-
венства уrлов А и А' катет А 'С'
пойдёт по катету АС; катет В'С'
совместится с катетом ВС: оба они
перпендикуляры, проведённые к
одной прямой АС из одной точки
В ( 26, следствие 3). Значит, вер"
шины С и С' совместятся.
Треуrольник АВС совместится
с треуrольником А ' В' С'. Следо..
вательно, ABC == A'B'C'.
Эта теорема даёт 3 й признак
равенства прямоуrольных тре-
уrольников. (по rипотенузе и ОСТ-
рому уrлу).
в
В'
d d
Д С с'
ЧЕРТА 15Z
Д Д'
с
в С'
в'
м N
С(С') в'
ЧЕРТ. 158
51
. Теорема 2. Если 2ипоmенуза и 1lатет одНО20 тР,е...
yzoAbItU1(,a соответственно равны zипотенузе и 1lате-
ту дJУ2020 треуzольни"а, то тa иe nря.м.оуzольные
треуzольнu1(,U равны.
Чтобы доказать это построим два прямоуrольных треуrольника
АВС и А' В'С', у которых уrлы С и С' ПРЯl\1ые, катеты АС и
А 'С' равны, rипотенузы АВ и А' В' также равны (черт. 158).
Проведём прямую MN и отметим на ней точку С, из этой точки
проведём перпендикуляр СК к прямой MN. Затеl\1 ПрЯl\10Й уrол
треуrольника АВС наложим на прямой уrол КСМ так, чтобы вер-
шины их совместились и катет АС пошёл по лучу СК, тоrда ка-
тет ВС пойдёт по лучу СМ. ПРЯl\10Й уrол треуrольника А'В'С'
наложим на ПРЯlVI0Й уrол KCN так, чтобы вершины их совмести-
лись и катет А 'С' пошёл по лучу СК, тоrда катет С' В' пойдёт
по лучу CN. Вершины А и А' совпадут вследствие равенства ка-
тетов АС и А'С'.
Треуrольники АВС и А' В'С' составят вместе равнобедреННLIЙ
треуrольник ВАВ', в котором АС оках{ется высотой и биссектрисой
а значит, и осью симметрии треуrольника ВАВ' ( 18). Из этоrо сле.
дует, что АВС == A'B'C'.
Эта теорема даёт 4..й признак равенства прямоуrольных тре..
уrольников (по rипотенузе и. катету).
4. Перпендикуляр к отрезку,
.. u
проведенныи через ero середину.
. 'Т е о р е м а. Всякая точ,к.а, лежащая на nерпенда/(,УЛЯ,fJе,
nJJоведенном. II оmрезк.у ч,еlJез ezo середину, одина"ово
удалена от 1l0ltцов этоzо о трезк. а , (черт. 159).
Пусть прямая БО перпендикулярна к отрезку АВ и АО == ОВ.
Возьмём на ЕО произвольную точку К и докажем, что А/( == ВК.
Прямоуrольные треуrо.пьники АОК и ВОК равны по ДВУ I кате-
там: АО == ОВ по УС.ПОВИI<?, КО общая сторона. Следовательно,
\ АК == КВ. Так !{ак точ-
[ ка К взята ПРОИЗ80ЛЬНО,
то и всякая друrая точка
.перпендикуляра ЕО оди..
наково удалена от кон..
цЬв отрезка АВ.
Если же мы возьмём
какую"нибудь точку Р на
плоскости, не находящу-
юся на перпендикуляре
/
/
/
/
I
I
Е
к
,
,
,
,
,
,
р
К ,/""\
,/ \
/ " \
/ "' \
/ " \
// "
д
о
в
д
о
8
ЧЕРТ! 159
ЧЕРТ. 160
58
До сих пор при решении задач на
построение l\lbI пользовались цирку-
7IeM, линейкой, чертёжным треуrоль-
ником и транспортиром. Решим теперь
р ЯД задач на построение с помощыо
только двух инструментов циркуля
и линейки.
3 а д а ч а 1. Разделить данный
оmрезок пополам.
Дан отрезок АВ, требуется разде-
лить ero пополам.
Реш е н и е. РаДИУСОl\I, БОЛЬШИl\f
половины отрезка АВ, опишем из
точек А и В как из центров пересекаю-
UJ,иеся дуrи (черт. 161). Через точки
'пересечения этих дуr проведём прямую CD, которая пересечёт
отрезок АВ в некоторой точке К и разделит ero этой точкой по-
полам: АК == КВ.
ЕО, то отрезки РА и РВ не будут рап-
ны (черт. 160). СоеДИНИ1v1 точку К
(ТОЧI{У пересечения ЕО и АР) с точ-
}{ой В. ВК + кр > РВ, но но ДOKa
занному ранее АК == ВК, ПОЭТО fУ
АК + КР > РВ, или АР>РВ, Т. е.
вся«ая t/zоч«.а, не паходящаяся
на перпенди"уляре ЕО, неоди--
наиО80 удалена' от "онцов ont,--
резuа АВ. .
Упражнения..
1. Построить равносторонний треуrоль-
ник по да нной ero стороне.
2. В следующих задачах дополнить усло-
вие неДостающими данными, чтобы
реше ние каждой задачи было единст
венным:
а) Построить равнобедренный Tpe
уrольник по данному ero основанию.
б) Построить прямоуrольный треуrоль-
ник по данному ero катету.
В) Построить прямоуrольный тре-
уrольник по данной ero rипотенузе.
28. ПОСТРОЕНИЯ ЦИРКУЛЕМ
И ЛИНЕЙКОЙ.
д
в
ЧЕРf. iol
к
J ,
I \
I \
/ \
I -\
/ ,
1 \
I \
I \
, \
I ,
11
о
N
в
м
ЧЕРТ. 162
11 М\
\ .
\
\
\
\
\
\
в
Е
ЧЕРТ. 163
69
Докал{ем это. Соединим точки А и В с точками С и D. CAD ==
== CBD, так как по построению АС == СВ, AD == BD, CD .........
общая сторона.
Из равенства этих треуrольников следует, что L АСК ==
== L ВСК, т. е. СК является биссектрисой уrла при вершине
равнобедренноrо треуrольника АСВ. А биссектриса уrла при вер"
JIIине равнобедренноrо треуrольника является и ero медианой, т. е.
прямая CD разделила отрезок АВ пополам.
3 а д а ч а 2. Провести перпендикуляр к данной прямой АВ
через точку О, находящуюся на этой прямой.
Дана 'прямая АВ и точка о, лежащая на этой прямой. Требу-
ется провести перпендикуляр к прямой АВ, проходящий через
точку О.
Реш е н и е. Отложим на прямой АВ ОТ точки О два равных
отрезка ОМ и ON (черт. 162). Из точек М и N как из центров одним
и Tel\,f же радиусом, БОЛЬШИl\f ом, опишем две дуrи. Точку их пере-
сечения К соеДИНИ f с точкой о. ко медиана в равнобедренном
треуrольнике MKN, следовательно, КО АВ (э 18).
3 а д а ч а 3. Провести перпендuкуляр к данной пря.мой АВ
через точку С, находящуюся вне этой прямой.
Даны прямая АВ и точка С вне этой прямой, требуется про-
вести перпендикуляр к прямой АВ, проходящий через точку С.
Реш е н и е. Из точки С как из центра опишем дуrу таким
радиусом, чтобы она пересекла прямую АВ, например, в точках
М и N (черт. 163). Из точек М и N как из центров одним и тем
же радиусом, большим половины MN, опишем дуrи. Точку их пе..
ресечения Е соединим с точкой С и с точками М и N. Треуrольники
СМЕ и CNE равны по трём сторонам. Значит, Ll == L2 и СЕ
является биссектрисой уrла С в равнобедренном треуrольнике MCN,
а следовательно, и перпендикуляром к прямой АВ (э 18).
29. ПОНЯТИЕ О ТЕОРЕМЕ И АКСИОМЕ.
1. Понятие о теореме.
в предыдущих параrрафах путём рассуждений мы установили, или,
l{aK rоворят, доказали, ряд свойств различных rеометрических фиrур.
Например:
Сумма двух смежных уrлов равна 2d ( 11).
Вертикальные уrлы равны между собой ( 11).
Если в одном и том же Kpyre центральные уrлы равны, то равны и со-
ответствующие им дуrи ( 13).
Такие математические предложения, в правильности которых мы убеж-
даемся путём рассуждения (доказательств), мы называли т е о р е м а м и.
Каждая теорема состоит из двух частей: из условия и заключения.
Условие обыкновенно начинаеТСR со слова «если», а заключение со сло-
ва «то». Условие ТО, что дано; заключение то, что надо доКазать.
60
Например:
..
Условие Заключение
.
1 Если два уrла смежные, то сумма их равна 2d.
2 Если два уrла вертикальные, то они равны между собой:.
3 Если в одном и том же Kpyre то равны и соответствующие
центральные уrлы равны, им дуrи.
4 Если каждое слаrаемое делит- то и сумма этих слаrаемых
ся на какое.нибудь число, разделится на это число.
5 Если сумма цифр какоrо-ни- то и само это число разде-
будь числа делится на 9, лится на 9.
Последние дв е теоремы (4.я и 5-я) известны нам из рифметики. Зна-
ЧИТ, и там мы уже встречались с теоремами.
2. tTeOpeMbl прямая и обратная.
Если в теореме условие сделать заключением, а заключение....... услови-
ем, то первая теорема будет называться п р я м о Й, а вторая о б-
р а т н о Й, а обе теоремы вместе в 3 а и м н о о б р а т н ы м И.
Прямая теорема
1
Если в одном и том же Kpyre
центральные уrлы равны, то рав-
ны и соответствующие им дуrи,
Если сумма цифр какоrо-ни-
бу дь числа делится на 9, то 11
само это число разделится на 9.
Если два yr ла смежные, то
сумма их равна 2d.
Если два уrла вертикальные,
то они равны между собой.
Если ка ждое ела raeMoe делит-
ся на какое нибудь число, то и
сумма этих слаrdемых делится
на это число.
Обратная теорема
Если в одном и том же Kpyre
дуrи равны, то равны и соответ-
ствующие им центральные уrлы.
Если число делится на 9, то и
сумма цифр этоrо числа делится
на 9.
Если сумма двух уrлов равна
2d, то они см жные (?).
Если два уrла равны между со-
бой, то/ они вертикальные (?).
Если сумма нескольких слаrае-
мых делится на какое.нибудь чис-
ло, то и каждое слаrаемое де-
лится на это число (?).
Если верна прямая теорема, то это ещё не значит, что верна и обратная
ей теорема.
В приведённых примерах для 1.й и 2 й теорем обратные теоремы верны.
Что )ке касается теорем 3.й, 4-й и 5.й, то здесь обратные тееоремы не верны.
В самом де.nе, можно иметь два уrла, сумма которых равна 2d, но они
MorYT быть не смежными.
Если есть два равных уrла, то это не значит ещё, что они обязательно
вертикаль ные.
2
3
4
5
61
Сумма двух или нескольких слаrаемых может делиться, например, на
10, но это не значит, что каждое из этих cпaraeMbIx делится на 10.
Например, сумма 71 и 19 делится на 10 (90 : 10 == 9), но ни 71; ни 19
на 10 не делятся.
Отсюда следует сделать такой вывод: если доказана справедливость
какой нибудь теоремы, то это ещё не значит, что справедлива и обратная Teo
рема. Она так же нуждается в доказательстве, как и прямая теорема.
3. Понятие об аксиоме.
Некоторые свойства rеометрических фиrур принимают без доказательств.
Например:
Через всякие две точки можно .провести прямую линию, и притом толь.
ко одну ( 3).
Отрезок прямой линии короче соединяющей еrq,концы ломаной (9 6, п. 2).
Такие математические предложения, которые принимаются без до.
каззтельств, называются а к с и о м а м и.
В каждом доказательстве теоремы приходится ссылаться на ранее
установленные предложения. Поэтому ясно, что изложение rеометрии дол
ЖНО начинаться с аксиом. Из аксиом можно выводить теоремы, из этих тео.
рем новые теоремы и т. д. Но не приняв сначала ни одной аксиомы, нель.
зя сдвинуться с места. В 9 37 мы познакомимся ещё с одной аксиомой
(аксиомой параллельности), обсуждение которой сыrрало особую роль вис.
тории rеометрии.
Вы видит.е, что наш учебник оrраничивается указанием некоторых п р"'и.
м е р о в аксиом. Кроме этих аксиом, мы опирались и на некоторые друrие
допущения, принятые без доказательств, Т. е. по существу на не сформулиро-
ванные явно аксиомы.
Совершенно cTporoe изложение rеометрии без скрытых, невысказанных
допущений, только на основе явно высказанных аксиом дело трудное.
Число аксиом, необходимых для TaKoro изложения rеометрии, оказывается
довольно большим. 1( вопросу о построении rеометрии на основе аксиом вы
ещё вернётесь в IX Классе.
Упражнение.
"
Сформулировать две теоремы, обратные теоремам: \1) ,«Если треуrольник
р,\внобедренный, то биссектриса уrла при вершине совПадает с ero высотой»;
2)'«Если треуrольник равнобедренный, то медиана, проведённая к основанию,
совпадает с ero высотой», и доказать их справедливость.
9 30. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И уrЛАМИ
ТРЕуrОЛЬНИКА.
. т е о р е м а 1. П роти8 большей стороны 8 mреУZОЛЬНU1(,е
лежит и БО.4ьший уz.ол.
Пусть в д АВС сторона АВ больше стороны вс. Докажем,
что уrол С, лежащий против большей стороны АВ, больше уrла А,
лежащеrо против меньшей стороны ве (черт. 164).
Отложим на стороне АВ от точки В отрезок BD J равный стороне
ве, и соеДИНИ1\1 отрезком точки D и с.
Треуrольник D ве равнобедренный.
62
Уrол BDC равен уr.лу BCD, так как
они лежат против равных сторон в тре-
уroльнике.
Уrол BDC внешний уrол треуrоль-
ника ADC, поэтому он больше уrла А.
Так как L BCD == L BDC, то и уrол
BCD больше уrла А: L BCD>L А. Но
уrол BCD составляет только часть Bcero
уrла С, поэтому уroл С будет и подавно
больше уrла А.
Доказать самостоятельно ту же Teope 1Y
по чертежу 165, коrда BD == АВ.
В 18 мы доказали, что в равнобедрен-
ном треуrольнике уrлы при основании
равны, т. е. в треуrольнике против равных
сторон лежат равные уrлы. Докажем те-
перь обратные теоремы.
. т е о р е м а 2. Против равных yz...
лов в треуzольни1(,е лежат ирав..
нрю CтOJJOHbl.
Пусть в L АВС L А ==L С (черт. 166).
Докажем, что АВ==ВС, т. е. треуrоль-
НИI{ Аве равнобедренный.
Между сторонаl\1И АВ и ВСмо)кет быть
только одно из трёх соотношений:
1) АВ > ВС;
2) А В < ВС;
3) АВ == ВС.
Если бы сторона АВ была больше ВС, то
уrол С был бы больше уrла А, но это про-
тиворечит условию теоремы, следовательно,
АВ не может быть больше ВС.
Точно так же АВ не может быть мень-
ше ВС, так как в этом случае уrол е был
бы меньше уrла А. ЧЕРТ. lбб
Следовательно, возможен только третий случай, т. е.
АВ == ВС.
Итак, мы доказали: против равных уrлов в треуrольнике- ле-
жат и равные стороны. )
· т е о р е м а 3. Против большеzо уzла в mреуzольни"е
лежит БОЛЬUlая сторона.
Пусть в треуrольнике АВС (черт. 167) L С > L В.
Докажем, что АВ > АС. Здесь также может быть одно из трёх
следующих соотношений:
в
с
д
ЧЕРТ. 164
в
с
\
\
\
\
А ..... .... ........... ..... ..... .... D
ЧЕРТ. 165
в
д
63
1) АВ == АС;
2) АВ < АС;
3) АВ > АС.
8
Если бы сторона АВ была равна
стороне АС, то L С был бы равен L В.
Но это противоречит условию теоремы.
Значит, АВ не может равняться АС.
Точно так же АВ не может быть
f\fеньше АС, так как в ?том случае уrол ЧЕРТ. 161
С был бы меньше уrла В, что также противоречит данному
ловию.
Следовательно, возможен только один случай, а именно:
д
ус.
АВ > АС.
Мы доказали: против большеrо уrла в треуrольнике лежит и
большая сторона.
С л е Д с т в и е. В пряМ,оуzолы-l,О-М тJJеУZОЛЬНU1(,е 2U II
потенуза больше л..юбоzо из ezo 1(,атетО8.
31. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ К ПРЯМОЙ.
1. Проекция отрезка на прямую.
Если через какую-нибудь точку, взятую вне ПрЯl\fОЙ, про..
U u
вести прямую, перпендикулярную к неи, то отрезок от данном
u
точки до прямои для краткости называют одним словом пер п е и-
Д и к у л я р.
Отрезок СО перпендикуляр к прямой АВ. Точка О назы..
вается о с н о в а н и е м перпендикуляра СО (черт. 168).
Если прямая, проведённая через данную точку, пересекает
u "
друrую прямую, но не перпендикулярна к неи, то отрезок ее от
u U u
даннои точки до точк пересечения с друrои прямои называют
н а к л о н н о й к этой прямой.
Отрезок Ве наклонная к прямой Ай. Точка С называется
о с н о в а н и е 1\1 наклонной (черт. 169).
Если из концов какоrо-нибудь отрезка опустим перпендикуляры
u u
на произвольну прямую, то отрезок прямои, заключенныа t\.fеж..
С
д
о
8
в
/
д с о
ЧЕРТ! f69
ЧЕРТ f 168
64
8 М IK
д
I I , Р
, I I
Е д' В' О К (Р') С
ЧЕРТ. 170
tt
ду основаниями перпендикуляров, называется про е к Ц и е и
о т рез к а на эту прямую.
Отрезок А' В' проекция отрезка АВ на ЕС. Отрезок ОМ'
также называется проекцией отрезка ОМ на ЕС.
Проекцией отрезка КР, перпендикулярноrо к ЕС, будет точка
К' (черт. 170).
2. Свойства перпендикуляра и наклонных.
. Теорема 1. Перпенди«уляр, проведённый из 1lа"ой.
нибудь точки 1(, прямой, .меньше вся«ой на1(,лонноii,
nроведённой из тои же точки « этой прямой.
Orрезок АС (черт. 171) является перпе дикуляром к прямой
ОВ, а АМ одна из наклонных, проведённых из точки А к пря"
мой ОВ.
Требуется доказать, что АМ > АС.
В t6. МАС отрезок АМ является rипотенузой, а rипотенуза
больше каждоrо из катетов этоrо треуrольника (9 30). Следова-
тельно, АМ > АС. Так как наклонная АМ взята нами произ-
u
вольно, то можно утверждать, что всякая наклонная к прямои
больше перпендикуляра к этой прямой (а перпендикуляр короче
всякой наклонной), если они проведены к ней из одной и той же
точки.
Верно и обратное утверждение, а именно: если отрезок АС
(черт. 171) меньше вся'коrо друrоrо отрезка, соединяющеrо точку А
с любой точкой прямой ОВ, то он является перпендику.ляром к
ОВ. В самом деле, отрезок АС не может
быть наклонной к ОВ, так как тоrда он не Д
был бы самым коротким из отрезков, соеди-
няющих точку А с точками прямой ОВ.
Значит, он может быть только перпенди-
куляром кОВ.
Длина перпендикуляра, опущенноrо из
u
даннои точки на прямую, принимается за
р а с с т о я н и е от данной точки до О М С В
u u
ЭТОН прямои. ЧЕРТ. 171
3 н. Н. НИКИТИН
65
. Теорема 2. Если две на"лонные,
nроведённые " nря.мой из одной
.,
и тои же пtОЧIlU, равны, ,по рав--
ны и их nрое"ции.
Пусть ВА и ВС наклонные, ПрОБе-
дённые из точки В к прямой АС (черт.
172), причём АВ == вс. Нуя{но дока-
зать, что равны и их проекции.
Для доказательства опустим из точ-
ки В перпендикуляр ВО на АС. Тоrда
АО и ОС будут проекции наклонных АВ
и Ве на прямую АС. Треуrольник АВС
равнобедренный по условию теоремы.
ВО высота этоrо треуrольника. Но
высота в равнобедренном треуrольни-
ке, проведённая к основанию, является
в то же время и медианой этоrо тре-
уrольника ( 18).
Поэтому АО == ос.
.
. т е о р е I а 3 (обратная). Если две
на"ЛОllные, nроведённые 1(, nрямоii
из одной и 1пой же тОЧl(,ll, име--
ют равные nрое"ции, то они рав..
ны .между собой.
Пусть АС и СВ наклонные к пря-
мой АВ (черт. 173). CO...LAB и АО==ОВ.
Требуется доказать, что АС == ВС.
В прямоуrольных треуrольниках
АОС и ВОС катеты АО и ОВ равны.
СО общий катет этих треуrольни-
ков. Следовательно, AQC == ВаС.
Из равенства треуrольников вытека-
ет, что АС == ВС.
. Т е о р е м а 4. Если из одной и той
же точ"и проведены " пряJНОЙ
две наилонные, то та иЗ них боль--
ше, 1l0торая имеет большую про--
е"цuю на ату пряJНУЮ.
Пусть АВ и ВС наклонные к пря-
мой АО; BO...L АО и АО>СО. Требует-
ся доказать, что АВ . ВС.
1) Наклонные расположены по одну
сторону перпендикуляра.
Уrол АСВ внешний по отношению
к прямоуrолъному трsуrольнику СОВ
66
8
ЧЕРТ. 172
с
ЧЕРТ 173
8
д
ЧЕРТ. 174
в
ЧЕРТ. 115
(черт. 174), а поэтому LAC8>L СОВ, С
Т. е. он тупой. ОтСlода следует, что
АВ > СВ.
2) Наклонные расположены по обе
стороны перпендикуляра.
Для доказательства отложим на АО
от точки О отрезок ОК == ОС и соединим
точку К с точкой В (черт. 175). Тоrда по К О
TeOpel'vIe 3 имеем: ВК === ве, но АВ>ВК,
следовательно, АВ > ве, т. е. теорема ЧЕРТ. 176
справедлива и в этом случае.
8 т е"'о р е м а 5 (обратная ). Если из одной и той же точи"
проведены" прямой две на«лонные, то большая на..
«донная иMeetп и большую прое«цuю на эту пря.м,ую.
Пусть КС и Ве наклонные к прямой КВ (черт. 176), СО ...L КВ
и КС > Ве. Требуется доказать, что КО > ОВ.
Между отрезками КО и 08 может быть, только одно из трёх
соотношений: 1) КО < ОВ; 2) КО == ОВ, 3) КО > ОВ.
КО не может быть меньше 08, так как тоrда по теореме 4 нак-
лонная КС была бы меньше наклонной ВС, а это противоречит ус-
ловию теоремы.
Точно так же КО не может равняться ОВ, так как в этом слу-
чае по теореме 3 ке == 8С, что тоже противоречит условию теоремы.
Следовательно, остаётся верным только последнее соотношение,
а именно, что КО > ОВ.
32. НЕКОТОРЫЕ СВОЙСТВА ОКРУЖНОСТИ,
ПЕРПЕНДИКУЛЯРА К ОТРЕЗКУ,
ПРОВЕДJ::нному ЧЕРЕЗ ErO СЕРЕДИНУ,"
и БИССЕКТРИСЫ УrЛА.
1. О к Р у ж н о с т ь. Все точки окружности обладают одним и
тем же свойство , а именно: все они находятся на одном и том же
В расстоянии от центра, равном радиусу дан-
,/" ной окружности.
Д ,/ Любая точка плоскости, не лежащая на
/)1' данной окружности, этим свойством уже не
Oct'/ обладает. Расстояние от центра до всякой
точки, лежащей внутри данной окруж-
ности, меньше радиуса этой окружности
(черт. 177):
ЧЕРТ!. 177
ОА < R.
З*
67.
Расстояние от центра до всякой точки, лежащей вне этой
окружности, больше радиуса:
ОВ > R.
Фиrура (например, линия), все точки которой обладают одним и
v v
тем же своиством, а ни одна из друrих точек плоскости этим свои-
ством не обладает, называется
rеометрическим местом
т о ч е к, обладающих данным свой-
ством.
Окружность можно опреде-
лить так: r е о м е т р и ч е с к о е
м е с т о т о ч е к плоскости, одина-
.. v
ково удаленных от однои точки
v
этои плоскости, называется окруж-
ностью.
2. Пер п е н Д и к у л я р к
о т рез к у, про в е Д ё н н ы й
ч е рез е r о с е р е Д и н у. в 27 было доказано, что всякая
точка, лежащая на перпендикуляре, проведённом к отрезку через
ero середину, одинаково удалена от концов этоrо отрезка (см. черт.
159); всякая же точка плоскости, не находящаяся на этом пер-
пеНf{икуляре, этим свойством не обладает (см. черт. 160). По-
этому можно сказать, что перпендикуляр, проведённый к отрез-
ку через ero середину, есть r е о м е т р и ч е с к о е м е с т о т 0-
ч е К, каждая из которых одинаково удалена от концов этоrо от-
резка.
3. Б и с с е к т р и с а у r л а. Все точки биссектрисы уrла
обладают одним общим СВОЙСТВО!\1: каждая из них находится на
одинаковом расстоянии от сторон этоrо уrла.
Пусть луч Ай является биссектрисой уrла ВАС (черт. 178).
Возьмём какую-нибудь произвольную точку Е на биссектрисе
АО и опустим из неё на стороны уrла перпендикуляры:
о
д
с
N
ЧВРТ. 178
68
в
д
Е
с
ЧЕРТ I 119
8
с
ЧЕРТ. 180
EN ...L АС и БЛ1 АВ. Мы П)cJ1УЧИМ два треуrольника АЕМ
и AEN.
Треуrольники эти прямоуrольные по построению, сторона
АЕ является общей, а L 1 == L 2 по условию. Отсюда следует,
что 6 АМЕ === L ANE ( 27, п. 3) и ЕМ == EN, т. е. точка Е
ОJ.инаково удалена от сторон уrла ВАС. Так как точка Е была
взята на биссектрисе произвольно, то можно утверждать, что
II всякая точка биссектрисы АО одинаково удалена от сторон
L ВАС.
Всякая же точка О, находящаяся не на биссектрисе АР (черт. 179),
неодинаково удалена от сторон этоrо уrла.
ОПУСТИfi1 из точки О перпендикуляры ON и ОЕ на АВ и АС и
докаже l, что ON не равняется ОБ.
Из точки К пересечения биссектрисы АР и перпендикуляра
ОБ ОПУСТИl\1 перпендикуляр КМ на АВ. По доказанноrvlу.ранее
КМ == КБ, кроме Toro, МК + КО > МО, тоrда и ЕК .+ КО >
> МО, т. е. ОЕ > ОМ. Но МО > NO, так как MO rипотену-
за, а NO катет в треуrольнике MON. Поэтому ОБ и подавно
больше ON.
Следовательно, всякая точка, не лежащая на биссектрисе уrла,
неодинаково удалена от сторон этоrо уrла.
Биссектриса yr ла есть r е о м е т р и ч е с к о е м е с т о т о-
ч е к, каждая из которых одинаково удалена от сторон этоrо yr ла.
Она я-вляется осью симметрии уrла.
4. 3 а д а ч а. Поспzроить биссектрису У2ла, т. е. разделить
У20Л пополаht.
Дан уrол АВС, требуется разделить ero пополам:
На сторонах данноrо уrла АВС (черт. 180) от ero верши-
ныI В ОТЛОЖИl\1 равные отрезки ВМ и BN. Из точек М и N од-
ним и тем же раДИУСОl\i описываем дуrи. Точку К пересечения
этих дуr соеДИНИl\1 с точкой В. Луч ВК будет биссектрисой данноrо
уrла АВС.
Чтобы доказать это, соединим точку К с точкаl\1И М и N и срав-
ним треуrольники ВМ К и BN К:
ВМ == BN }
МК == NK
по построению.
ВI<.. общая сторона.
Следовательно, ВМК == BNK.
Отсюда L МВК == L NBK, так как они лея{ат против равных
сторон в двух равных треуrольниках, Т. е. ВК служит биссектрисой
уrла АВС.
69
o
CJ
й)
д)
и)
/
/
О)
8)
2)
е)
Ж)
'> (
З)
К)
/1)
М)
ЧЕРТ. 181
Упражнения.
1. Вырезать из плотной бумаrи квадрат. Разрезать ero на три треуrо.7JЬНИ-
ка, как покаЗ2НО на чертеже 181, и из полученных треуrольников соста-
вить фиrуры, изображённые на чертежах а, б, 8, z., д, е, ж, Э, и, К, л, М.
2. Доказать, ЧТ9 высоты, проведённые из вершин уrлов при основании рап-
нобедренноrо треуrольника на ero боковые стороны, равны.
3. Доказать, что медианы, проведёНIIые к рапным сторонам равнобедрен-
Horo треуrольника, равны.
rЛАВА ///.
ПАРАлпЕIlЬНЫЕ ПРЯМЫЕ.
33. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯАiЫХ ЛИНИЙ.
1. Определение параллеJIЬНЫХ прямых.
с
а
F
/
",
"
"
о ti!. ... .......... м N
ЧЕРТ 182
ЧЕРТ, 183
Прямые линии называются пер е с е к а ю Щ и м и с я, если
они имеют только одну общую точку.
Так, наПрИ 1ер, прямые АВ. и CD имеют только одну общую
точку О, эти пряrvtые пересекающиеся. Прямые ЕР и MN также
пересекаЮlциеся (черт. 182, 183).
Две прямые, лежащие в одной плоскости и не имеющие ни
одной общей точки, называются параллельными (черт. 184).
Параллельность прямых обозначается знаком II.. Если пря-
мые АВ и CD параллельны, то пишут: АВ 11 CD.
Представление о параллельных прямых дают нам линии вразли..
нованных ученических тетрадях (в линейку и в клетку), противопо"
ЛО}l{ные края листа' бумаrи, тетради, стола, переплёты оконных рам.
2. Параллельные отрезки.
Если два отрезка расположены на параллел ных прямых лини..
ях, то эти отрезки также называются пар а л л е л ь н ы м и. На
чертеже 185 АВ 11 CD, отрезки MN и
ЕР, расположенные на них, будут
параллельными.
Точно так же называются парал-
лельныrvlИ два отрезка, если при не-
оrраниченном продолжении их обра-
зуются параллельные прямые
(черт. 186).
д
--
8
с
...
D
ЧЕРТ. 184
'11
34. уrлы МЕЖДУ ДВУМЯ
ПРЯМЫМИ И СЕКУЩЕЙ.
Если две прямые АВ и CD
пересечёl\l третьей прямой ЕР
(черт. 188), то ПОЛУЧИl\1 восемь
уrлов (не считая развёрнутых),
из них четыре уrла располо-
жены BOKpyr одной точки пе-
ресечения этих прямых и четы-
ре уrла BOKpyr друrой точки
пересечения.
Прямая ЕР, пересекающая
обе прямые АВ и CD, называется
их секущей.
Четыре уrла, располо)кенные
?vlежду прямыми АВ и CD, Т. е.
уrлы 3, 4, 5, 6, называются
внутренними уrлами, а уrлы 1,
2, 7, 8 внешними.
Эти восемь уrлов 1Y10ЖНО раз-
личны!\! обраЗОl\1 объединить па-
рами.
В заВИСИl\10СТИ от их положения относительно ПРЯl\lЫХ и секу-
u
щеи этим парам уrлов дают различные названия.
Уrлы 1 и 5, 2 и 6, 3 и 7, 4 и 8 называются с о о т в е т с т-
в е н н ы м и.
Уrлы 3 и 6, 4 и 5 называются в н у т р е н н и м и н а к р е с т
л е ж а Щ и м и.
3. Свойство двух fJ
перпендикуляров к
u u u
ОДНОИ И тои же прямои.
8 Теорема. Если две nря С
.lНыe АВ и CD nерnенди1(,У"
лярны 1(, одll0Й и тOli же
nРЯ.lНОЙ MN (черт. 187), то
они параллельны.
В самом деле, если бы АВ
и CD были не паралле.пьны,
т. е. имели бы общую точку,
например точку О, то тоrда из
одной и той же точки О на пря-
мую MN было бы опущено два
перпендикуляра, а этоrо быть
не MO)l{eT (Э 26).
12
м N
, I
в
Е F
I I
D
ЧЕРТ. 18"}
в /'-
/D /
/c/
/
/
LIEPT. 186
А
с
м
N
в
D
ЧЕРТ. 187
ё
с
5 6
7 8
F
D
ЧЕРТ. 188
r Уrлы 1 и 8, 2 и 7 называются в н е ш н и м и н а к р е с т л е-
ж а Щ и м и.
Уrлы 3 и 5, 4 и 6 называются в н у т р е н н и м и о Д н о с т о;.
р О Н Н И М и.
Уrлы 1 и 7, 2 и 8 называются в н е ш н и м и о Д н о с т о р о н-
н и м и.
35. ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ прямых.
Теорема о том, что два перпендикуляра к одной прямой парал-
лельны (9 33), даёт признак параллельности двух прямых. Можно
вывести более общие признаки параллельности двух прямых.
1. Первый признак параллельности.
. Если при nересе",ении двух nря-мых третьей внутрен-
ние на"рест лежащие уzлы равны, то эти прямые
nараллеЛЬНbl.
Пусть прямые АВ и CD пересечены прямой ЕР и L 1 == L 2.
Возъмём точку О середину отрезка KL секущей ЕР (черт. 189).
ОIjусТИм из точки О перпендикуляр ОМ на прямую АВ и пер-
пендикуляр ON на прямую CD. Докажем, что точки М, О, N ле-
жат на одной прямой MN. Рассмотрим два треуrольника OLM и
OKN.
Эти треуrольники прямоуrольные, так как OM...L АВ, а
OiV CD. L 1 == L 2 по условию, ОК == OL по построе-
нию, следовательно, эти треуrольники равны (э 27).
Из равенства этих треуrольников следует, что LMOL== LKON.
Чтобы доказать, что точки М, О и N лежат на одной прямой, рас-
Сl\10ТРИМ L MON.
L МОК + L MOL == 180°, но L MOL == L KON,
следовательно, L МОК + L KON == 180°, Т. е. L' MON развёрну-
u
тыи, а это значит, что точки
М, О и N лежат на одной пря-
Д М В мой. ОМ ...L АВ, ON ...L CD,
а значит, MN перпендикулярна
А В и CD.
Таким образом, прямые АВ
и CD перпендикулярны к од-
D ной и TO же прямой MN, сле-
довательно, они параллельны
(э 33), что и требовалось ДOKa
заТЬ.
с
N
ЧЕРТа 189
'/3
с
8
2. Второй признак паралJlеJlЬНОСТИ.
Посмотрим, будут ли параллель-
ны прямые АВ и CD, если при пе-
ресечении их третьей прямой ЕР рав-
ны соответственные yr лы.
Пусть какие-нибудь соответствен-
ные уrлы равны, например L 3==
==L2 (черт. 190). L3==L 1, как yr-
лы вертикальные; значит, L 2 будет
равен L 1. Но уrлы 2 и 1 внут-
ренние накрест лежащие уrлы, а мы
уже знаем, что если при пересече-
u
нии двух прямых третьеи внутрен-
ние накрест лежащие уrлы равны,
то эти прямые параллельны. Следо-
вательно, АВ 11 CD.
. Если при пересечении двух nря
81
.мых Illpembeu соответственные
уzлы равны, то эти две nРЯ"
.мые параллельны.
,Д
D
'Н;РТ. 190
ЧЕРТ. 191
На этом-свойстве основано построение параллельных прямых
U ..
при помощи линеики и чертежноrо треуrольника.
Выполняется это следующим образом.
Приложим треуrольник к линейке Ta , как это показано на
чертеже 191. Будем передвиrать треуrольник так, чтобы одна
ero сторона скользила по линейке, а по какоfi-либо друrой сто-
роне треуrольника проведём несколько прямых. Эти прямые бу-
дут параллельны.
3. Третий признак параллеJlЬНОСТИ.
с
Пусть нам известно, что при пересечении двух прямых АВ и
CD третьей пр мой сумма каких-нибудь внутренних односторонних
уrлов равна 2d (и и 180°). Будут ли в этом случае ПРЯl\1ые АВ и CD
Е пар аллельны (черт. 192)?
Пусть L 1 и L 2 внутренние од'"
В носторонние уrлы и в сумме составляют
2d. Но L 3 + L 2 == 2d, как уrлы
смежные. Следовательно, L l_ + L 2==
== L 3 + L 2. Отсюда L 1 == L 3,
D а эти уrлы внутренние накрест лежа-
щие. Следовательно, АВ 11 CD.
ЧЕРТ "192
д
14
д
D
8
с
ЧЕРТ. 1 9 3
д
D
8
с
ЧЕРТ. 194
. Если nplt пересечении двух прямых третьей сумма
внутпенних односпzоронних уzлов равна 2d то эти две
прямые па.rJаллельны.
У1lражнение.
Доказать, что прямые параллельны: а) если внешние накрест .лежащие
уrлы равны (черт. 193); б) если сумма внешних односторонних уrлов
равняется 2d (черт. 194).
э 36. РЕЙСМАС. МАЛКА.
в столярной мастерской приrvlеняется прибор, называе-
мый рей с м а с о м. Он употребляется для Toro, чтобы края
изrотовляемоrо бруска были параллельны. Устройство рейсма-
са и работа с ним показаны на чертежах 195 и 196.
Один край дерев нноrо брус-
ка Быструrивают точно по пря-
10Й, а затем к нему приклады-
вают реЙСl\1ас и ведут ero по
бруску. Металлический шпенёк
вычертит прямую, параллель-
ную краю бруска.
При столярных и плотнич- ЧЕРТ. 195
ных работах употребляется ещё
прибор, называемый м а л к о й
(черт. 197). Он ПРИl'vlеняется в тех
случаях, коrда нужно провести
несколько параллельных пря-
f'лыIx линий, идущих под опреде..
лённым уrлом к какой-нибудь
прямой, например при разметке
rнёзд для ступеней лестницы
(черт. 198) .
Малка....... это две пластинки,
соединённые винтом. ОНИ МО-
ryт быть поставлены ПОД любым ЧЕРТ. 196
15
ЧЕРТ. 197
ЧЕРТ. 198
уrЛОl\1 друr J{ друrу и удерживаться в это { положении ВИНТОl\11.
Одна .пластинка скользит вдоль КрОl\fКИ доски, а по краю друrой
пластинки чертятся параллельные линии.
37. АКСИОМА ПАРАЛЛЕЛЬНОСТИ ЕВКЛИДА.
3 а Д а ч а. Через точку М, взятую вне прямой А В, провести
прямую, nараллельную прямой АВ.
Пользуясь доказанными теоремами опризнаках параллельно-
сти прямых, 1\10ЖНО эту задачу решить различными способами.
Решение. l й способ
(черт. 199) .
Проводим MN АВ и через
точку М проводим CD MN; по..
лучаеl\I CD MN и АВ MN.
На основании теоремы 33 заКЛIО..
чаеl\l, что CD 11 А В.
2 й с п о с о б (черт. 200).
Проводим МК, пересекающую АВ
ПОД любым уrлом а, и через точку М
проводим ПрЯf\ЛУЮ ЕР, образующую
с прямой МК уrол ЕМК, равный yr
лу а. На основании TeOpel\'lbI Э 35
заключае1\1 , что ЕР 11 АВ.
Решив данную задачу, можем
считать доказаННЫIvI, что через лю
бую точку М, взятую вне прямой
АВ, можно провести прямую, ей па-
раллельную. Возникает ЕОПрОС:
сколько же прямых, параллельных
данной ПрЯl\fОЙ и проходящих через
с
м
D
11
N
8
ЧЕРТ j 111
Е
.8
F
д
к
ЧЕРТ. 200
16
даннуЮ точку, мо}кет существовать?
u
Практика построении п?зволяет
предполаrать, что существует только
одна такая прямая, так как при тща-
тельНО выполненном чертеже прямые,
проведённыIe различными способами
через одну и ту же точку параллель-
но одной и той же прямой, слива.
ются.
В теории ответ на поставленный вопрос даёт так называемая
а]{сиома параллельности Евклида; она формулируется так:
....."
с.............. --.. --.. о __.... --- .... .,. к
.... " ......
--- --- ......
....--- ...................
д
8
ЧЕРТ. 201
ч ереэ точ,IlУ, взятую вне данной пря.моii, .можно про..
вести тОЛЬ1l0 одну пря.мую параллельную этой
прямоii.
На чертеже 201 через точку О проведена прямая СК, параллель-
ная прямой АВ.
Всякая друrая прямая, проходящая через точку О, уже не бу-
дет параллельна прямой АВ, а будет её пересекать.
В начале настоящеrо курса было сказано о том, что rеометрия
возникла в rлубокой древности и что особенно 1Horo для её разви-
тия сделал rреческий математик Евклид.
Евклид сформулировал аксиому параллельных в таком виде:
«Если --при пересечении двух прямых третьей cYMI\1a внутренних
односторонних уrлов меньше двух прямых, то эти две прямые пере-
секаются с той стороны от секущей, с которой сумма внутренних
уrлов меньше двух прямых».
Можно ДОI<азать, что аксиома параллельных в формулировке
Евклида равносильна принятой нами.
Более двух тысячелетий после Евклида мноrие математики пы-
таЛI1СЬ доказать математичеекое предложение, выраженное аксио-
мой параллельных, опираясь на друrие принятые ЕВКЛИДОl\f аксио-
мы, но всеrда их попытки оказывались безуспеШНЫ IИ.
Только в начале XIX века великий русский учёный, профессор
Казанскоrо университета Николай Иванович Лобачевский показал,
что, используя все друrие аксиомы Евклида, это математическое
предложение доказать нельзя. ПРИНИl\1а вместо аксиомы парал-
лельных, что через точку вне прямой можно провести не одну, а
u u
несколько прямых, параллельных даннои прямои, можно построить
новую rеометрию, ЛQrически столь же стройную, как и обычная
евклидова rеометрия. В этой новой rеомеТRИИ Лобачевскоrо ниrде
u ·
не встречается противоречии.
Аксиомы обычной евклидовоЙ rеометрии выражают свойства
окружающеrо нас реальноrо пространства, проверенные на прак-
ТИКе. Но проверка эта имеет всеrда лишь приближённый характер.
77
Можно считать установленным, что в знакомой нам на практике
части пространства с очень большой точностыо оправдываются
все теоремы rеометрии Евклида.
Мы не f\10жем здесь останавливаться на взrлядах современной
физики по вопросу о rеометрии реальноrо пространства в косми-
ческих масштабах. Мноrие учёные считают, что в масштабах, да..
леко превышающих размеры солнечной системы и rалактики,
rеО lетрия реальноrо пространства может и отличаться от евкли"
u
довои.
38. ЗАВИСИМОСТЬ МЕЖДУ УrЛАМИ, ОБРАЗОВАННЫМИ
ДВУМЯ ПАРАЛЛЕЛЬНЫ1\1И ПРЯМЫМИ И СЕКУЩЕЙ.
Мы знаем, что две прямые параллельны, если при пересечении
их третьей прямой равны COOTB TCTBeHHыe уrлы, или внутренние
или внешние накрест лежащие уrлы, или сумма внутренних или
сумма внешних односторонних уrлов' равна 2d. .
Докажем, что верны и обратные теоремы, а именно:
· Если две параллельные пря.мые
.,
пересеч,ень, третьеи, то:
1) соответственные уzлы
равны,.
2) внутренние на1'рест ле..
жащие уzлы равны,.
3) Вl;tешние на1(,рест лежа..
щие уzлы равны,.
4) су.мМ,а внутренних одно...
сторонних уzлов равна 2d;
5) суМ,М,а внешних односто-
-ронних уzлов равна 2d.
/l
с
ЧЕРТ. 202
с
Д....................
D
.....................К
ЧЕРТ. 203
д
м
D
с D
N
ЧЕРТ. 204
78
в
в
8
Докажем, например, что если две
параллельные прямые пересечены
u u
третьеи прямоя, то соответственные
уrлы равны.
Пусть прямые АВ и CD параллель..
ны, а MN их секущая (черт. 202).
Докажем, что OOTBeTCTBeHHыe уrлы
1 и 2 равны между собой.
ДОПУСТИl\1, что L 1 и L 2 не рав"
ны. Тоrда при точке О можно пост..
роить L МОК, соответственный и
равный L 2 (черт. 203).
Но если L МОК == L 2, то цря..
мая ОК будет параллельна CD (9 3&).
Получили, что через точку О про-
ведены две ПРЯ iые АВ и ОК , парал-
лельные прямой CD. Но этоrо быть не
может (Э 37).
Мы пришли к противоречию, по-
TO 'IY что допустили, что- L 1 и L 2 М
не равны. Следовательно, наше до-
пущение является непраВИЛЬНbIМ и:
L 1 должен быть равен L 2, т. е.
соответственные уrлы равны.
Установим соотношения между ос..
та.пьными уrлами. Пусть прямые АВ
и CD параллельны, а MN их секу-
щая (черт. 204).
Мы только что доказали, что в
ЭТОl\i случае соответственные уrлы
равны. Положим, что какие-нибудь
два из них Иf\iеют по 1190. Вычислим М
величину каждоrо из остальных шес-
ти уrлов. На основании свойств смеж-
ных и вертикальных уrлов мь! по-
лучим, что четыре уrла из восьми
будут И1vlеть по 1190, а остальные
по 610.
Оказалось, что как внутренние,
T8I{ и внешние накрест лежащие yr-
лы попарно равны, а сумма внутрен-
них или внешних односторонних yr-
лов равна 1800 (или 2d).
То же самое будет иметь место и
при люБОf\1 друrом значении равных
соответственных уrлов.
/i
в
с
D
N
ЧЕРТ I 205
/l
N
8
с
D
ЧЕРТ. 206
д
в
с
D
F
ЧЕРТ. 207
с л е Д с т в и е 1. Если каждая из двух пря.мых АВ 11,
CD параллельна одной и той же третьей прямоii ММ,
то пe08bJ,e две прямые паралле/l,ьныl между c060lt
(черт. 205).
В самом деле, проведя секущую ЕР (черт. 206), получим: а) Ll ===
== L 3, так как АВ 11 MN; б) L 2 == L 3, так как CD 11 MN.
Значит, L 1 == L2, а это уrлы COOТBeTC BeHHыe при прямых
АВ и CD и секущей ЕР, следовательно, прямые АВ и CD парал-
nелЬНЫ.
С JI е Д с т в и е 2. Еедll, прямая перпендzжулярна " одной
",з двух парадледьных пРЯ.AlbIХ, то она пepneHдu1(,Y
дярна и " дpy oa (черт. 207).
19
В самом деле, если ЕР L АВ, то L 1 ==d; если АВ
L 1 == L 2.
Следовательно, L2 == d, т. е. EP...L CD.
39. СУММА ВНУТРЕННИХ уrлов ТРЕуrОЛЬНИКА.
8
fI CD, то
т е о р е м а. CY.A-Iма внутренних уzлов mреуzольниuа
равна дву.А! прямым уzла-м.
Возьмём какой"нибудь треуrольник АВС (черт. 208). Обозна-
чим ero внутренние уrлы цифрами 1, 2 и 3. Докажем, что
L 1 + L 2 + L 3 == 2d.
Проведём через какую"нибудь вер-
шину треуrольника, например В,
прямую М/Х параллельно АС.
При вершине В мы получили три
уrла: L 4, L 2 и L 5. Их сумма
'составляет рззвёрнутый уrол, следо..
вательно, она равна 2d.
L 4 + L 2 + L 5 == 2d.
м
д
ЧЕРТ. 208. .
Но L 4 == L 1 это внутренние накрест лежащие уrлы при
параллельных прямых MN и АС и секущей АВ.
L5 == L 3 это внутренние накрест лежащие yr ль! при па-
раллельных прямых MN и АС и сеI{ущей ВС.
Значит, L 4 и L 5 можно заменить равными им L 1 и L 3.
Следовательно, L 1 + L 2 + L.3 == 2d, или 1800. Теорема до-
казана.
2. Свойство внешнеrо yr ла треуrольника.
8 r е о р е rvl а. Вllешнии уzол т{Jеуzольни-ка. равен су.мяе
двух В1l.утренних уzлов, не с-межных с ним.
Б самом деле, в треуrольнике АВС (черт. 209) L 1 + L 2 ==
2d L 3, но и L.BCD, внешний уrол этоrо треуrольника, не
С lежнЫЙ с L 1 и L 2, также равен 2d L 3.
Таким образом,
L 1 + L"2 == 2d L 3; 8
L BCD == 2d L з.
Следовательно, сl + L 2 == L ВС D.
Выведенное \ свойство вIkшнеrо yr-
па треуrольника уточняет содержание
ранее доказанп6й теоремы о внешнеl\1
уrле треуrольника (9 26), в которой
утверждалось только, . что внешний D
уrол треуrО.;'1ьника больше аждоrо ЧЕРТ. 209
80
BHYTpeHHero уrла '1реуrольника, не смежноrо с пим; теперь >Jl;e"yc-
танавливается, что внешний уrол равен сумме обоих вцу ренних
уrлов, не смежныIx с ним.
3. Свойство прямоуrольноrо треуrольника с yr oM в ЗО
са Т ео р е м а. Катет nря.м.ОУZОЛЬНОZО треуzольни"а
лежащий против уzла в 30°, равен половине 2ипо..
теНУЗbl.
Пусть в прямоуrольном треуrольни"
ке АСВ уrол В равен 300 (черт. 210).
Тоrда друrой ero острый уrол будет
равен 600.
Дока)l{ем, что катет АС равен поло-
пине rипотенузы АВ.
Продолжим катет АС за вершину
ПрЯl\10rо уrла С и отложим Ьтрезок СМ,
равный отрезку АС. Точку М соединим
с точкой В. Полученный треуrольник
ВСМ равен треуrольнику АСВ (э 27).
МЫ видим, что каждый уrол треуrоль-
ника АВМ равен 600, следовательно, этот треуrольник равно-
сторонний. .
Катет АС равен половине АМ, а так как АМ равняется АВ,
то катет АС будет равен ПОЛQвине rипотенузы АВ.
в
\
\
300 \
\
\
,
\
,
,
,
... ...__.l
С М
ЧЕРТ. 210
Упражнения.
1. Чему равна сумма двух острых уrлов прямоуrольноrо треуrольника?
2. Начертить треуrольник. С помощью транспортира измерить ero уrлы и
найти их сумму. .
Вычислить, какой процент по отношению к 180 q составляет допущенная
поrрешность при измерении уrлов треуrольника. .
3. Доказать, что биссектрисы двух внутренних односторонних уrлов, обра-
зованных двумя параллельными и секущей, составляют прямой уrол.
4. Доказать, что прямоуrольные треуrольники равны, если катет и проти-
волежащий ему уrол одноrо прямоуrольноrо треуrольника равны катету и
противолежащему уrлу друrоrо IJрямоуrольноrо треуrольника.
5. Построить прямоуrольный треуrольник:
а) по катету и прилежащему острому ) rлу;
б) по катету и противолежащему острому уrлу..
6. Доказзт,ь, что если в прямоуrольном треуrольнике катет равен поло-
вине rипотенузы, то уrол, лежащий про ив этоrо катета, равен зо q .
.3.9a. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ О ПОСТРОЕНИИ
. ТРЕуrольников И ПРИ3НАКАХ РАВЕНСТВА ТРЕУrольнико
Вернемся. теперь J{ шести задачам о построении треуrольника по трём
элементам из 25. Теперь нам ясно, что, зная два уrла треуrольника, можно
81
IlаЙ'j. ,. третиЙ. Если известны уrлы а иР, то третий уrол l' равен
l' == 2d a p.
Леrко произвести и соответствующее rеометрическое построение: по-
строив уrлы а и с общей веРUIИНОЙ О по разные стороны от прямой ОМ
(черт. 211, a)t найдём уrол
Это замечание позволяет свести пятый случай построения треуrольника КО
второму. Второй признак равенства треуrольников теперь можно высказать в
такой форме: если сторона и два уrла одноro треуrольника равны соответствую.
ШJI:\I стороне и уrлам BTOpOro треуrольника, то треуrольники равны. Приме-
няя сформулированный таким образом второй признак ра-
венства треуrольников, надо только следить за тем, что-
бы считать соответствующими уrлы, противолежащие со-
отвеТСТВУI0ЩИМ сторонам. НесоблюдеIiие этоrо правила
моrло бы привести к ошибочным выводам: на чертеже
211, б треуrольники АВС и А' В' С' имеIОТ равные сторо-
ны АС == А 'С' и уrлы А == А', В == В', но треуrоль-
ники не равны.
Что касается шестоrо способа выбора трёх элементов
треуrольника, то мы видим теперь, что задание трёх
уrлов треуrольника не даёт ничеrо HOBoro по сравнению
с заданием двух уrлов. Если заданные три уrла в сумме
равны двум прямым, то можно построить сколько уroд-
но неравных треуrольников с этими уrлами (черт. 211, в).
Если же сумма заданных уrЛОБ не равна двум прямым,
то построить треуrольник нельзя.
м
о
N
р
а)
L. N О Р == 2 d ...... а ...... == "у .
BVC
Д
в'
6)
д'
82
oj
ЧЕРТ_ 211
40. уrлы С СООТВЕТСТВЕННО ПАРАЛЛЕЛЬНЫМИ
И ПЕРПЕНДИКУЛЯРНЫМИ СТОРОНАМИ.
1. Уrлы с соответственно параЛЛeJIЬНЫМИ сторонами.
Возьмём на плоскости две точ-
ки С и О и из этих точек прове-
дёrvl две пары лучей СА 11 ОМ и
св 11 ON так, чтобы уrлы А СВ
и MON были или оба острые С
(черт. 212, а) или оба тупые (черт.
212, б) .
Уrлы АСВ и MON ........ уrлы с
соответственно параллельными
сторонами. Докажем, что эти уrлы
равны между собой. Д
Пусть СВ пересекает ОМ в
точке D. L АСВ == LMDB, как
соответственные уrлы при парал-
лельных АС и МО и секущей СВ.
L MDB == L MON, как соответ-
ственные уrлы при параллельных
СВ и ON и секущей МО, но тоrда
L АСВ ==L MON. Следовательно,
. Уz,Лbl С соответСlпвенно па..
раллеЛЬНblми сторона.ми рав-
НЫ, если они оба ост.рые или
оба тупые.
cv
8
N
8
о N
Ь)
ЧЕРТ. 212
Построим два острых уrла АСВ
и MON с соответственно парал-
лельными сторонами (черт. 213):
СА 11 МО и СВ "ON....... и про-
должим за вершину О стороны
уrла MON.
При вершине О образовались
два тупых уrла ЕОМ и FON (так
как смежный с ними уrол MON
по построению острый). .
Каждый из них в сумме с уrлом MON составляет 2d, а так как
L MON == L АСВ, то L АСВ + L МОЕ == 2d и L АСВ +
+ L FON == 2d. Следовательно,
с
I
1=-
ЧЕРТ. 213
в
N
е Уzлы, с соответственно параллельными сторонами 8
су.,п.ме СОСflzавЛЯЮtп 2а, если один из них острый, а
друzоit т,пой.
83
Построим произвольный острый
уrол АВС. Проведёl\1 через вер-
шину уrла лучи, перпендикуляр-
.
ные к ero сторонам, так, чтобы
они образовали острый уrол.
ВО J.... Ве и ВК АВ (черт.
214). Мы получим новый уrол
ОВК. Стороны уrлов Аве и ОВК
взаимно перпендикулярны.
L АВС == d ....... L СВК;
L ОВК == d L СВК.
Отсюда следует, что LA ВС==
=== L ОВК.
Постр им произвольный тупой
уrол АОВ и через ero вершину
проведём лучи, перпендикулярные
к ero сторонам, так, чтобы они
образовали тупой yrofl'. ОК J....OA
и ое J.... О В (черт.' 215), уrо.п
КОС тупой. Стороны уrлов
АОВ и КОС взаимно перпенди-
кулярны, поэтому
L АОВ == d + L КОВ;
L КОС == d + L КОВ.
Отсюда следует, что
L АОВ == L кос.
. у ZЛbl С соответствеН1l0 пе 0--
nендU1lУЛЯРНЫ/ttи сторонами
равны /ttежду собой, если
они оба OCnlpble или оба
тупые.
ПОСТрОИl\1 произвольный острый уrол АОВ и проведём через
ero вершину перпендикуляры к ero сторонам так, чтобы они об-
разовали острый уrол (черт. 216). Получим: L КОМ == L АОВ.
Продолжим сторону ОК за вершину о. Стороны уrла ЕОМ перпен-
дикулярны сторонам уrла АОВ. При этом L ЕОМ тупой, так
как смежный с ним L МОК....... острый. L КОМ + L БОМ == 2d
(как уrлы смежные). Но L КОМ по ранее доказаННОlVlУ равен
L АйВ. Следовательно, и L АОВ + L ЕОМ == 2d.
. У2ЛЫ С соответственно перпендU1lулярными cmopOHa}"tu
8 сум..ме составляют 2а, если один из них острый, а
и. &1
дру 20и тупои.
2. Уrлы с соответственно
перпендикулярными сторонами.
84
д
в /
l' С
r\
I \
I \
I \
I \
о,. 'к
ЧЕ1>Т. 214
к
.."
.."
,,"
.."
"
в
I
I
I
. ,t
C 1
ЧЕРТ. 215
Е\ Д
\\
О), в
I \
I \
I \
I ,
м: ',к
ЧЕРТ. 216
Мы раСС!\'lатривали уrлы, состав..
ленные взаимно перпеНДИКУЛярНЫ tИ
сторонами, коrда они имели оБЩУ10
вершину. Выведенные нами свойства
будут справедливы и в том случае,
коrда уrлы не будут иметь общей О
вершины. 1\
Построим: произвольный острый \
уrол АОВ и через какую нибудь точку , \'
С (черт. 217) проведём лучи СБ ОА к', ,Е'
и СК ОВ так, чтобы уrол КСЕ был
u
тоже острыи.
Yr"ТIbI АОВ и КСЕ составлены взаиrvIНО перпендикулярными
сторона!\IИ. Докажем, что они равны ме}кду собой. Для этоrо через
точку О (вершину L АОВ) проведём ОК' 11 СК и ОБ' 11 СЕ.
L КСБ == L К'ОБ', так как они составлены взаимно параллель-
ными сторон ми и оба острые. Но L К'ОБ' == L АОВ по дока..
за нному. Следовательно, L АОВ == L КСЕ.
Если продолжим сторону СЕ за вершину уrла, мы получим
L МСК, смежный с L КСЕ. L МСК + L KCE==2d, но LKCE==
L АОВ. Поэтому L АОВ + L МСК == 2d.
.
,М
\
\
8
[
.
к
ЧЕРТ. 217
,
41. ПРАКТИЧЕСКИЕ РАБОТЫ НА МЕСТНОСТИ.
1. Проведение параллельных прямых на местности.
Пусть на!\1 нужно провести прямую, параллельную имеющейся
изrороди АВ (черт. 218), на данном от неё расстоянии, например на
расстоянии 20
Для решения этой практической задачи провешим с ПО!\/IОЩЬЮ
9ккера из точки С прямую, перпендикулярную к ПрЯ!\10Й АВ, и на
ЧЕРТ. 218
85
ней отложим отрезок CD длиной 20 М. В точке D установим эккер
так, чтобы направление одноrо бруска эккера совпало с направле-
нием CD. .
По направлению BToporo бруска эккера провешим прямую MN.
Она будет параллельна прямой АВ.
Докажите это с помощью какоrо"нибудь признака параллель..
ности двух прямых линий, приняв CD за секущую прямых АВ
и MN.
2. Съёмка плана земельноrо участка,
имеющеrо форму мноrоуrольника.
а) С ъ ё .f К а п л а н а з е м е л ь н о r о у ч а с т к а, и м е-
ю Щ е r о фор м у т р е у r о л ь н и к а.
Пусть нам нужно начертить план земельноrо учаСТI<а, имеюще-
ro фОр1\1У треуrольника, стороны KOToporo равны, например, 120 м,
95 м и 70 м (черт. 219).
Приняв 1\1асштаб l\lиллиметр за один метр, ПОСТрОИ1\1 треуrоль-
НИК, стороны KOToporo соответственно равны 120 мм, 95 мJи и 70.мм.
Получим план данноrо нам земельноrо участка, построенный в
Jvl асшт абе, р ав HOI\1 0,001.
При вычерчивании плана масштаб должен выбираться в за..
висимости от размеров участка и от размеров листа бумаrи,
на KOTOpO 1 будет изобра)кён
план.
б) С ъ ё м к а п л а н а з е-
м е л ь н о r о у ч а с т к а,
и 1\1 е ю Щ е r о фор м у ч е..
. T ы р ё х У r о л ь н и к а.
Пусть требуется начертить
план четырёхуrольноrо участка,
стороны KOToporo равны, напри..
'мер, 200 м, 180 At, 160 М и 195 м
(черт. 220). Провешим диаrональ
9Toro четырёхуrольника, на-
пример АС, и ИЗ1\1ерим её
длину. Пусть она будет рап..
н а 21 О '.м.
Выбрав подходящий fасштаБJ
построим сначала один треуrоль-
ник, треуrольник АВС, а зате 1
к стороне АС пристроим второЙ
треуrольник ADC. В результате
получим план данноrо нам уча-
стка, построенный в выбранном
масштабе.
86
120 м
ЧЕРТ. 219
160М
D
/ С
/
,
,
/
/
,
/
/
/
,
/
/'
/
/
/
/
,
/
,
,
,
/
с)
'f.I()
А
200м
\!ЕРТ, 220
в
Если надо начертить план земельноrо участка, имеющеrо форму
пятиуrольника или шестиуrольника, то поступаем так же: разби-
ваем этот мноrоуrольник на треуrольники, измеряем длины их
сторон, выбираем подходящий масштаб и последовательно строим
треуrольники, располаrая их на чертеже в том же порядке, как
они расположены на самом зеrvtельном участке.
3. Определение расстояния между двумя точками,
одна из которых недоступна.
Чтобы определить расстояние между точками А и В, разделён"
НЫМИ рекой (черт. 221), строим при точке В с помощью эккера пря..
мой уrол ABN. На прямой BN откладываем последовательно два
равных отрезка ве и CD. Точки С и D отмечаем вехами. При точке
D строим прямой уrол BDK. Продолжение отрез а АС пересечёт
прямую DK в некоторой точке Е. DE == АВ. Доказать самостоя-
тельно правильность решения.
ЧЕРТ. 221
4. Определение расстояния между двумя доступными
точками, разделёнными препятствием (черт. 222).
Пусть требуется определить расстояние между точка и А и В.
Провешим произвольную прямую, примем её за ось симметрии
и построим с помощью эккера ТОЧКИ А' и В', СИМ .fетричные задан..
'НЫМ. Отрезок, соеДИНЯЮIЦИЙ построенные точки, имеет иско.МУЮ
длину, Т. е. А' В' == АВ. .
87
., .., ::::::=--:::::=J )
s )--::; ..J
. -==-
:?! 1 . . '
........................... :=- ............. c......;;; ,.....
1 7:::::: ... . -. . _ l .7 ,.'- """""'..
p r:- v - ", .. _--..
A. ...,....""'. н,. ,.....
, ... "",.....,"".. .....
в
\
.\
\ ,
", :: \.-
.,;..,..",... \
\ '-...
,.....
..... .. \ ..
..............' """........................ \
"""'-"""" . 1. ............ "................ J
.... ,../. ' \ ",-<. """". , " .............., " ,I \ ......
"","' .rr '\ "'" ...." ....;.-- -: """,. f\oW "
/: ... А i"'" ....... ........ ---= - ---- ,.,/'- '"'
, . ' 'К П '\ ...... ...... ........ ........... ....... ...... ....... ....... ........ \
,. 7" /"7 .; (, .,. "'" ........ 8 '
'у. \м · с..... ' ..
......
......
...... ......
- .. ....
....................
ЧЕРТ. 222
Упражнения
1. На школьном дворе провести прямую, параллельную какой нибудь дан-
ной прямой (изrороди, забору, стене школьноrо здания).
2. Отметить вехами rде нибудь вблизи школы земельный участок треуrоль-
ной формы и начертить ero план.
з. Начертить план какоrо нибудь земельноrо участка четырёхуrольной фор-
мы (например, школьноrо участка или участка, занимаемоrо оrородом,
садом; или предварительно на открытой ровной площадке обозначить
вехами вершины какоrо-нибудь четырёхуrольника и нанести ero на план).
[ЛАВА /V
.
ЧЕТЫРЁхуrОПЬНИНII.
42. СУММА ВНУТРЕННИХ уrлов ЧЕТЫРЁхУrОЛЬНИКА.
. т е о р е м а. Сумма внутренних уzлов чеmь/,рёхуzоль"шеll
равна 4d.
В четырёхуrо..Т!ьнике ABCD (черт. 223) проведём диаrональ АС.
Тоrда четырёхуrольник разобьётся на два треуrольника АВС и
ACD. L 1 + L в + L 2=== 2d, L 3+
+ L D + L 4 === 2d. Отсюда полу
чим: L 1 + L в + L 2 + L 3 +
+ L D + L 4 === 4d.
Но L 1 + L 3 === L А, а L 2 +
+ L 4 == L С.
Следовательно,
L А + L в + L с + L D === 4d.
8
д
с
ЧЕРТ. 223 D
Упражнения.
1. Начертить четырёхуrольник и построить отрезок, равный ero периметру.
2. MorYT ли все 4 внутренних уrла четырёхуrольника быть тупыми?
3. MorYT ли все 4 BHYTpeHH,!ix уrла четырёхуrольника быть острыми?
4. Начертить четырёхуrольник. С помощью транспортира, измерить ero yr-
лы и найти их сумму. Вычислить, какой процент по отношеНИIО к истин-
ной сумме внутренних уrлов четырёхуrольника составляет допущенная
поrреш ность.
5. Построить четырёхуrольник по четырём ero сторонам и одной из диаrо-
налей. '
6. Построить четырёхуrольник по четырём ero сторонам и одному из уrлоI3.
э 43. ПАРАulЛЕлоrРАММ.
1. Определение параллелоrрамма
Если пару параллельных прямых пересечём друrой парой парал--
лельных прямых, то ПОЛУЧИl\'l четырёхуrольник, у KOToporo проти--
воположные стороны попарно параллельны.
В четырёхуrоль.никах ABCD и EFNM (черт. 224) BD 11 АС и
АВ 11 CD; ЕР 11 MN и ЕМ 11 FN.
Четырёхуrольник, у KOToporo противоположные стороны попар-
но параллельны, называется параллелоrраммом.
89
2. Свойства параллелоrрамма.
8 Т е о р е м а 1. Диаzональ nа]Jал-
ледоzражжа делит ezo на два
равных треуzольника.
Пусть имеется параллелоrрамм
ABCD (черт. 225), в котором ЧЕРТ. 224
АВ 11 CD и АС 11 BD.
Требуется доказать, что диаrональ делит eI'o на два равных
треуrольника.
Проведёrvl в параллелоrраМf'ле ABDC диаrональ СВ. ДокаlI(ем,
что Ь СА В == CDB.
Сторона СВ общая для этих треуrольников; L АВС == L BCD,
как внутренние накрест лежащие уrлы при параллельных АВ и
CD и секущей СВ; L АСВ == L CBD, тоже как внутренние накрест
лежащие уrлы при параллельных АС и BD и секущей СВ ( 38).
д
в
,,'"
,,"
",.",rd
"
D
ЧЕРТ, 225
ЧЕРТ. 226
Отсюда Ь САВ == Ь CDB.
Таким же путём можно доказать, что диаrональ AD разделит
параллелоrрамм на два равных треуrольцика ACD и ABD.
С л е Д с т в и я. 1. П роmuвоположные УZЛbl параллело-
zpaAtMa равны жежду собой.
L А == L D, это следует из равенства треуrольников САВ
и CDB. Аналоrично и L С === L В.
2. Противоположные сторонь' параллелоzра lм'а рав-
ны между собой.
АВ == CD и АС == BD, так как это стороны равных треуrоль..
ников и лежат против равных уrлов
. т е о р е м а 2. Диаzонали nараллелоzра.м.ма в точке их neloe-
сечения делятся nоnола.м.
Пусть ВС и AD диаrонали параллелоrрамма ABCD
(черт. 226).
Докажем, что АО == OD и СО == ОВ.
90
Для этоrо сравним какую нибудь пару противоположно рас-
положенных треуrольников, например i:l АОВ и 6. COD.
В этих треуrольниках АВ == CD, как противоположные сторо-
вЫ параллелоrрамма;
L 1 == L 2, как уrлы внутренние накрест лежащие при параЛ 40
l17JельНЫХ АВ и CD и секущей AD;
L 3 == L по той же причине, так как АВ 11 CD и СВ их
ССI<ущая (9 38).
Отсюда следует, что Д АОВ == Ь COD. А в равных треуrоль",
никаХ против равных уrлов лежат равные стороны. Следовательно,
АО == OD и СО == ОВ.
. Т е о р е м а 3. Cy.м.JНa уzлов, прилежащи,х " одной стОрОllе
параллелоzра.м.ма, равна 2d.
Доказать самостоятельно.
3. Признаки параллелоrрамма.
. т е о р е м а 1. Если противоположные стороны "eтblpl.. -
уzольнииа попарно paBHbl, то этот чеmырёхуzолЬНuк,......
параллело zppMAt.
Пусть в четырёхуrольнике ABDC (черт. 227) АВ == CD и
АС == BD. Дока)кем, что при этом условии АВ 11 CD и АС " BD, Т. е.
четырёхуrольник ABDC параллелоrрамм. Соединим отрезком
какие нибудь две противоположные вершины этоrо четырёхуrо.пьни",
ка, например С и В. Четырёхуrольник ABDC разбился на два
равных треуrОJ!ьника: САВ и i:l CDB. В самом деле, сторона СВ
у них общая, АВ == 9D и АС == BD по условию. Таким образом,
три стороны одноrо треуrольника соответственно равны трём сторо-
Haf\1 друrоrо, поэтому 6. САВ == Ь CDB.
В равных треуrольниках против равных сторон лежат равные
уrлы, поэтому L 1 == L 2 и L 3 == L 4.
Уrлы 1 и 2 являются внутренними накрест лежащими уrлами
при пересечении прямых АВ и CD
прямой СВ. Следовательно, АВ 11 CD.
Точно так же уrлы 3 и 4 являют-
ся внутренними накрест лежащими yr-
лами при пересечении прямых СА и
BD прямой СВ, следовательно,
СА "BD (9 35).
Таким образом, противоположные С
стороны четырёхуrольника ABDC по-
парно параллельны, следовательно, он
параллелоrра JМ, что И требовалось до.
казать.
8
"
"
"
"
"
,
"
"
ЧЕРТ. 221
91
Пусть в четырёхуrольнике
ABDC АВ == CD и АВ 11 CD. До-
}{а)кем, что при этих условиях че
тырёхуrольник ABDC пар алле-
лоrраМ 1 (черт. 228).
Соединим отрезком СВ вершины С и В. Вследствие параЛЛeJlЬ-
ности прямых АВ и CD уrлы 1 и 2, как 'уr.пы внутренние накрест
лежащие, равны ( 38). Тоrда треуrольник САВ равен треуrоль-
нику CDB, так как сторона СВ у них общая, АВ == CD по условию
теоремы и L 1 == L 2 по доказанному. Из равенства этих Tpe
уrольников BЫTeKa T равенство уrлов 3 и 4, так как они лежат
против равных сторон в равных треуrольниках.
Но уrлы 3 и 4 это внутренние накрест лежащие уrлы, обра
З0ванные при пересечении прямых АС и BD прямой СВ, следова..
тельно, АС 11 BD ( 35), т. е. четырёхуrо ьник ABDC парал...
лелоrрамм.
"'8 Т ео рема 2. Если две проти-
вополОжные сторонь!, четы-
рёхуzольнu"а равны и парад-
дельны, то этот четырех-
уzольнuи параллелоzраМ.Аt.
Упражнения.
с
в
ЧЕРТ. 228
1. Доказать, что если диаrонали четырёхуrольника в точке их взаимноrо
пересечения делятся пополам, то этот четырёхуrольник паралле-
лоrрзмм.
2. Доказать, что четырёхуrольник, у KOToporo сумма внутренних уrлов,
, прилежащих к и:аждой из двух соседних сторон, равна 2d, есть парал-
лелоrрамм.
3. Построить параллелоrрамм по двум сторонам и уrлу между ними:
а) используя параллельность противоположных сторон параллело-
rpaMMa;
б) используя равенство противоположных сторон параллелоrрамма.
4. Построить параллелоrрамм по двум смежным сторонам и диаrонали.
5. Построить параллелоrрамм по двум ero диаrоналям и уrлу между ними.
6. Построить параллелоrрамм по ero стороне и двум диаrоналям.
44. ПОДВИЖНОСТЬ ПАРАЛЛЕлоrРАММА (ШАРниРноrо).
Параллелоrрамм в отличие оТ треуrольника не является жёст"
кой фиrурой. Если построить модель параллелоrрамма так, чтобы
стороны ero соединялись друr с друrом с помощью шарниров, то
u
такои параллелоrрамм окажется подвижным: стороны ero можно
вращать, изменяя уrлы между ними. Это свойство параллелоrрамма
вытекает.из 10ro, что по данным сторонам можно строить паралпе-
лоrраммы с различными внутренними Уfлами (черт. 229).
92
- - - - I
\
ЧЕРТ, 229
о такой фиrуре rоворят, что
она не жёсткая. На чертеже 230
показано использование свой..
ства нежёсткости фиrуры.
ЧЕРТ 230
45. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ.
в 9 17 были рассмотрены фиrуры, симметричные относительно
прямой, которая называлась осью симметрии.
В rеометрии рассматривается и друrой вид симметрии, которая
называется Ц е н т р а л ь н о й с и м м е т р и е й или симметри
u U
еи относительно точки, называемом it е н т р о м с и м м е т р и и.
93
1. Центрально симметричные точки.
"! ..."
'Если возьмём какую нибудь точку О, проведём через He riря
мую и отложим на этой прямой по разные стороны от точки О рав-
ные отрезки ОВ и ОС (черт. 231), то получим две точки В и С,
ц е н т р а л ь н о с и м м е т р и ч н ы е относительно точки О.
Точка О называется u е н т р о м симметрии
этих точек.
_ Центрально симметричными относительно
центра О называются две точки, которые
u u u
лежат на однои прямом, Проходящеи Через
центр о, на равных расстояниях от цент-
ра о.
Если повер нуть отрезок ОС во..
Kpyr точки О на 180$, то точки С и В совпадут.
с
",/,/'
О /
Р
/
/
В //
,
ЧЕРТ. 231
Две фиrуры называются центрально симметричными относи..
тельно центра о, если при повороте одной из них BOKpyr этоrо
центра на 1800 они'. совместятся всеми своими точками.
2. Центрально симметричные отрезки.
Возьмём две пары центрально симметричных точек относительно
точки О (черт. 232): ОВ == ОВ' и ос == ОС'. Соединиl' f1трезками
точки В и С, В' и С'. Получим отрезки ве
и В' С', концы которых центрально сим-
метричны относительно точки о.
Если повернём чертёж BOKpyr точки О
на 180 G , то точки в' и С' займут COOTBeTCT
венно положение точек В и С. Отрезки
В'С' и 8е совместятся, они центрально
симметричны. Ценmрально СU.Al.меmрич- В
ные ОtnIJезl(,U равны.
8'
с
",
",
",
..... О ",
...... ./
* ........ м'
;"'... ..... ......
", ......
"
",
",
ЧЕР-Т, 232
3. Центрально симметричные треуrольники.
в
с'
Возьмём три пары централь-
но симметричных точек относи...
тельно какой",нибудь точки О
(черт. 233):
ОА == ОА', ОВ == ОВ'
и ОС == ОС'.
Соединив точку А с точками
В и С, а точку А' с точками
......
...... /
...... '"
...... /
..... /
........
//0 "
/ ,
/ "
"
/1'
с
ЧЕРТ. 233
94
8'
в' И С', получим два треуroльника. Эти треуrольники центрально
симметричНЫ относительно точки О, являющейся центром сим-
метрИИ.
При повороте чертежа BOKpyr ТОЧКИ О на 180 Э точки А', С' и В'
займуТ соответствен но положение точек А, С и В, т. е. 6. А' С' В' и
6 АСБ совместятся.
Центрально симметричные тpeyzO/l,bHU1(,U равны.
Точно так же равны и любые симметричные фиrуры.
4. Симметрия параллелоrрамма.
Большое число фиrур обладает тем СВОЙСТВОМ, что при повороте
плоскости чертежа на 1800 BOKpyr некоторой точки новое положе..
вие фиrуры совпадает с пер оначальным. Такие фиrуры называются
центрально симмеТРИЧНЫlvl-И. Пар ал..
Д В лелоrрамм принадлежит к числу та..
" ".-,,/ ких фиrур, он центрально симметри..
',о"."''" чен относительно точки пересечения
",,><, ero диаrоналей (черт. 234).
".,- "
".,,"', В самом деле, так как ОС == ОБ
С D и ОА == OD, то точки С и В, а
также А и D симметричны относи..
ЧЕРТ. 2ЗI тельно центра о. Если паралле..
лоrрамм повернуть на 1800 BOKpyr точки пересечения ero диаrо..
налей, то новое положение параллелоrрамма СОБпадёт спервона..
чальным.
46. ЧАСТНЫЕ виды ПАРАЛЛЕлоrРАММОВ.
1. Прямоуrольник.
Построим прямой уrол А. Обозначим на ero сторонах две произ..
вольные точки В и С (черт. 235). Через точку В проведём прямую,
параллельную АС, а через точку С
проведём прямую, параллеТIЬНУЮ АВ.
Точку пе р есечения этих П р ямых обо.. B 'D
значим буквой D (черт. 236). Мы .........................ч
получили параллелоrрамм ABDC, I
в котором L А == d. Нет руд но дока..
8
,С
D
d
Д
с
д
с
ЧЕРТ. 235
ЧЕРТ, 236
98
зать, что в этом параллелоrрамме все внутренние уrлы бу..
дут прямые.
В самом деле, LB + L А ==2d, как уrлы внутренние односто...
ронние при параллельных прямых АС и BD и секущей АВ. Но
L А == d, следовательно, и L В == d. Кроме Toro, L А == L D и
L В == L С, ка к противоположные уrлы параллелоrрамма. Та..
ким образом, все уrлы этоrо параллелоrрамма прямые.
Параллелоrрамм, у KOToporo все уrлы прямые, называется
п р я м о у r о л ьн И К О 1\'1.
2. Свойства прямоуrольника.
Так как п рямоуrольник есть параллелоrрамм, То он обладает
всеми ero св ойствами (9 43).
1. Диаrональ прямоуrольника делит ero на два. равных тре...
уrольника. .
2. Диаrонали прямоуrольника в точке их пересечения делятся
пополам.
3. Противоположные стороны прямоуrольника равны между
собой, равны также и противоположные уrлы ero.
Кроме этих свойств, прямоуrольник обладает ещё следующим
свойством: диаzоналu nря.моуzольнuиа равны.
Докажем это свойство. Возьмём прямо...
С уrольник ABCD, проведём в нём две диа..
rонали (черт. 237) АС и BD и докажем,
что они равны между собой. .
Сравним два треуrольника ABD и
ACD. Сторона AD у них общая и АВ ==
== DC. Кроме Toro, они прямоуrольные.
D Следовательно, они равны между собой,
ЧЕРТ. 237 поэтому А С == BD.
У п р а ж н е н и е. Докажите, что если диасонали параллело..
2раМм'а равны, то этот nараллеЛО2рам'м' nРЯМОУ20ЛЬНUК.
Этим свойством прямоуrольника пользуются в столярных и сле-
сарных мастерских для проверки, насколько точно сделаны те или
иные детали или предметы, которые должны иметь прямоуrольную
форму, например: крышка стола, дно или боковая стенка ящика,
рамка для картины и т. д.
Если противоположные стороны четырёхуrольника попарно рав"
ны и равны ero диаrонали, то он должен быть прямоуrольником.
В противном же случае он Не будет иметь форму прямоуrольника
и потребует соответствующеrо исправления.
в
" ,,'"
, /
'" /
" /
,.."< '"
,," "
/" ",
.
д
3. Построение прямой, все точки которой находятся на данном
расстоянии 1 от данной прямой.
Если через точку А, находящуюся на расстоянии 1 от данной
прямой МС, провести прямую, параллельную MC, то любая точ"
96
1< ка этой прямой будет находиться
на расстоянии 1 от прямой МС,
(черт. 238).
Если АВ == 1 и ОР ...L МС, то
С ОР === АВ === 1 (как противополощ"
ные стороны прямоуrольника).
Кроме прямой АК, по друrую
сторону М С l\-IОЖНО построить ещё
прямую EN, обладаIОЩУЮ тем же
свойством: ВА' == РО' == 1. Точ
ки плоскости, не лежащие на пря
МЫХ АК и EN, этим свойством не обладаIОТ. -
Прямые АК и EN ЯВЛЯIОТСЯ rеометрическим местом точек, от.
стоящих от данной прямой .МС на расстоянии 1.
Эти две прямые симметричны относительно данной прямой. '
д о
м : J ! р
I I
/ I I
I I
--- -.& ..... .... ....................":"
[д' о' N
ЧЕРТ. 238
4. Ромб.
Построим уrол и на ero сторонах отложим от вершины А равные
отрезки АВ === АС (черт. 239). Через точку В проведём прямую, па
раллельную АС; через точку С прове
дём прямую, П,араллельную АВ . Точку
пересечения этих прямых обозначим че
рез D. Мы получили параллелоrрамм
ABDC, причём BD === АС, CD == АВ,
как ПРОТИВОПОЛО}l{ные стороны парал
лелоrрамма. Отсюда BD == АС === АВ ::.:=
=== DC. Д
Параллелоrрамм, ,у KOToporo все сто.
роны равны, называется ромбом.
в /D
.. .... ...... r
/
/
'f
/
/
/С
ч Е Р Т. 2 J9
5. Свойства ромба.
Так как ромб есть параллелоrрамм, то он обладает - все tИ ero
свойствами.
1. Диаrональ ромба делит ero на два равных треуrольника.
2. Диаrонали ромба в точке их пересечения делятся пополам.
3. Противоположные стороны ромба равны между собой, равны
и противоположные уrлы ero.
Кроме TOI'O, ромб обладает ещё следующими свойствами:
а) диаzонали ро.мба 8заu,AfНО n,!рnендU"УЛЯРНbl,.
б) диаzональ РО.Аtба делит уzол. ezo nопола.м.
4 11. Н. Никитин
97
в ромбе ABCD проведём две диаrона..
ли АС и BD (черт. 240), пересекающие..
ся в точке о, и докажем, что АС ...L BD,
а диаrональ АС делит уrол/ С по-
полам. В равнобедренном треуrольнике
BCD отрезок СО является медианой, а
следовательно, и высотой, и биссектри-
сой уrла с. Отсюда AC.L BD и L 1 ===
== L 2. .
Так же до к ззывается, что диаrональ АС делит попал ам уrол А,
а диаrОНaJIЬ BD делит пополам уrлы В и D.
6. Квадрат.
Построим прямой уrол. и на ero сторонах отложим равные отрез..
ки АВ и АС (черт. 241).
Через точки В и С проведём прямые, параллельные сторонам АС
и АВ. Точку пересечения их обозначим
через D. Мы получили четырёхуrольник, в
котором:
а) противоположные стороны попарно
параллельны, следовательно, это пара ле...
лоrрамм;
б) все уrлы прямые, следовательно, это
прямоуrольник;
в) все стороны равны, следовательно,
это ромб.
Прямоуrольник, в котором все сторо"
роны равны, называется квадратом
(черт. 242) .
Может быть дано и такое определение
квадрата: ромб, у KOToporo все yr JlЫ пря..
мые, называется квадратом.
8 'D
__ '--:-' _ _ _ _ __ .....с
J
I
I
I
I
I
I C
д
ЧЕРТ,241
D
ЧЕРТ. 240
7. Свойства квадрата.
Так как квадрат является и параллело..
rpaMMOM, и прямоуrольником, и ромбом, то
он обладает всеми их свойствами.
квадрата делит ero на два равных треуrоль..
ЧЕРТi 242
1. а) Диаrональ
ник а.
б) Диаrонали квадрата в точке их пересечения делятся пополам.
в) Противоположные стороны квадрата равны между собой,
равны и противоположные уrлы ero. (Свойства параллелоrрамма.)
2. Диаrонали квадрата равны. (Свойство прямоуrольника.)
3. а) Диаrонали квадрата взаимно перпендикулярны.
б) Диаrональ квадрата делит ero уrол пополам. (Свойства ромба.)
98
8. Симметрия прямоуrольника, ромба и квадрата.
Так как прямоуrольник, ромб и квадрат являются паралле--
ЛОI'раммами, то точка пересечения диаrоналей этих фиrур являет
ся также их центром симметрии.
Прямоуrольник, ромб и квадрат, кроме Toro, и'меют ещё оси
симrvlетрии. В прямоуrольнике осями симметрии являются прямые,
проходящие через середины противоположных сторон (черт. 243).
"
/
,
I
I
I
.... ......---..... + ---
I
I
I
I
ЧЕРТ, 243
/
/
" , /
,1/
*
/1'
/ 1 '\.
/ I '
/ '\.
I
ЧЕРТ. 244
/
"
ЧЕРТ. 245
в ромбе осями симметрии являются две еро диаrонали (черт. 244).
Квадрат имеет четыре оси симметрии (черт. 245), которые ука...
эаны для пря-моуrольника и ромба.
Упражнения.
1. Перечислите изученные свойства параллелоrрамма.
2. Перечислите изученные свойства прямоуrольника.
з. Перечислите изученные свойства ромба.
4. Диаrонали четырёхуrольника взаимно перпендикулярны. Значит ли, что
этот четырёхуrольник ромб? При каком до.
полнительном условии он будет ромбом?
5. Построить ромб по данной стороне и прилежа-
щему уrлу.
6. Построить ромб по двум ero диаrоналям.
7. Построить квадрат по данной ero стороне.
8. Построить квадрат по ero диаrонали.
9. Приложить двустороннюю линейку сначала к
одной стороне произвольноrо уrла А, а затем
к друrой стороне и провести две прямые, парал.
лельные сторонам этоrо уrла (черт. 246). Точку
С пересечения этих двух прямых соединить с вершиной уrла и дока-
зать, что прямая АС разделит L::A пополам. -
10. В следующих задачах дополнить условие недостающими данными, что.
бы решение было единственным:
а) построить ромб по данной ero стороне;
б) построить прямоуrольник по данной ero стороне;
В) построить ромб по данному уrлу;
r) построить паралле лоrрамм по данной ero стороне.
I '"
с/",'"
.
///
// /
", /
/",'" /
д
/
/
ЧI:РТ. 216
4*
99
11 Вырезать квадрат, разрезать ero на части, как
показано на черте)ке 247, и составить нз них
фиrуры, приведённые на этом чертеже.
а)
u
/'
[]2]
д)
О)
z) д) е) ж)
О/ /
З) и) 1<) 17)
lJ
М) Н) О) n) Р}
:::) [)
с) т) у)
ЧЕРТ. 247
47. СВОЙСТВО ОТРЕЗКОВ, ОТСЕКАЕМЫХ ПАРАЛЛЕЛЬНЫМИ
ПРЯМЫМ И НА СТОРОНАХ УrЛА.
. Теорема. Если на одной стороне уzла отложить рав-
ные отрез"и и через их "онцы провести nараллельные
пря-мые, nересе"ающие друzую сторону уzла, то и на
этой стороне уzла отложатся равные .между собой
отрез"и.
Пусть на стороне АВ уrла ABN отложены рав ные отрезки
ВМ == МК == КС (черт. 248) и через точки деления М, К и С про
ведевы параллельные прямые, пер ее екающие сторону BN Toro же
yrJla.
100
На этой стороне образовались три отрез..
ка: ВМ', М'К' и К'С'.Требуется доказать,
что ВМ' == м' к' == К'С'.
Для доказательства через точки М' и
К' проведём прямые, параллельные АВ.
1\\ы получим треуrольники ВММ', М' ЕК'
и К' РС'. Сравним эти треуrольники.
Сначала срааним треуrольники МВМ' и
М'ЕК'. В этих треуrольниках имеем: L-l ==
== L 2, как соответственные уrлы при па...
раллельных ВА и М' Е и секущей BN;
L 3 == L 4, как острые уrлы 1 с соответст...
венно парал лельными сторонами (АВ 11 М' Е
и ММ' 11 КК'). ВМ == МК по построению,
МК == М'Е, как противоположные стороны
параллелоrрамма. Следовательно, ВМ==М'Е.
Таким образом,
ВММ' ===
М' ЕК' (по стороне и двум приле..
)Е(ащим к ней уrлам). Отсюда следует, что ВМ' == М'К'. Так же
l\fОЖНО доказать, что ВМ' == К'С', т. е. ВМ' == М'К' == К'С'.
При доказательстве Teope
lbI мы откладывание отрезков начали от
вершины уrла, но теорема справедлива и для Toro случая, коrда
откладывание отрезков будет начато не от вершин уrла, а
от любой точки eI'o стороны. (Докажите это самостоятельно.)
В этом случае вершину уrла на чертеже можно не отмечать
(черт. 249).
Теорема справедлива и для случая, коrда прямые КО и МР
параллельны.
3 а д а ч а. Разделить данный оmрезок на n равных частей.
Пусть отрезок АВ (черт. 250) НУ}l{НО разделить на 5 равных
частей. Для этоrо из точки А ПОД каким
нибудь уrлом к отрезку
r1B проnедём луч и от вершины
4
отло}ким на нём последовательно 5
равных отрезков. Конец, последнеrо
к
м
I
I
I
I
N
L
д
I
I
I
О
.l
ЧЕРТ. 249
в
с'
N
ЧЕРТ. 248
ЧЕРТ. 250
1 У r лы З
й и 4
Й MorYT Оl<аза7ЬСЯ оба тупыми, но и в этом случае они
останутся равными, а потому доказательство теоремы не изменится.
101
отрезка, точку С 5 ' соеДИН!I\f отрезком ПрЯ\fОЙ с ТОЧКОЙ В и через
точки деления С 1, С 2 , С З' C проведём прямые, параллельные ВС 5 .
Эти прямые разделят данный отрезо на 5 равных частей.
Подобным образом всякий отрезок можно разделить на любое
число равных частей.
48. СРЕДНЯЯ ЛИНИЯ ТРЕуrОЛЬНИI(А.
8 т е о р е м а. Отрезо", соединяющий середины двух сторон
и
треуZОЛЬНU1(,а, параллелен третье" стороне тре УZОЛЬНU..
"а и равен ее половине.
Д а н о: В треуrо,пьнике АВС АМ == ВМ и СК == ВК.
Н а Д о д о к а з а т ь: 1) МК 11 АС;
2) МК == АС .
2
Доказательство. Продолжим МК на отрезок КЕ==МК
н точку С соединим с точкой Е (черт. 251).
Рассмотрим треуrольники МВК и КЕС.
еК == КВ по условию, }
КБ == МК по построению, следовательно,
L 1 == L 2, как вертикальные; МВК === КЕС.
Из равенства этих треуrольников следует: 1) ЕС == МВ И t
значит, ЕС == АМ; 2) L4 === L3,
но это уrлы внутренние накрест
лежащие при прямых ЕС и
МВ и секущей ВС, следователь
но, ЕС lf МВ, и, значит, ЕС 11
rJ АМ .
Рассмотрим теперь четырёх-
уrольник АМЕС. В нём. ЕС ==
== АМ и ЕС 11 АМ, поэтому
АМЕС параллел{)rрамм (9 43,
n. 3). .
Из этоrо следует:
1) МЕ 11 АС,
МК 11 АС;
. 2) ME AC, и, значит, МК A .
Отрезок, соединяющий середины двух сторон треуrольника,
называется с р е Д н е й л и н и е й треуrольника.
и,
значит,
в
А
Е
с
ЧЕРТ. 25]
Упражнения.
1. Доказать, что прямая, проходящая через середину какой либо стороны
треуrольника параллельно друrой ero стороне, делит третью сторону
треуrольника пополам.
2. Доказать, что отреЗI{И, соединяющие последовательно середины сторон
любоrо четырёхуrольника, образуют параллелоrрамм.
у к а з а н и е. Провести в четырёхуrольнике диаrонали.
102
З. Диаrонали четырёхуrольника равны 38 ММ и 36 ММ. Вычислить периметр
параллелоrрамма, образованноrо отрезками, соеДИНЯIОЩИМИ середины
сторон этоrо четырёхуrольника.
49. ТРАПЕЦИЯ.
Четырёхуrольник, у KOToporo две противоположные стороны
параллельны, а друrие две не параллельны, называется трапе-
цией.
На чертеже 252 у четырёхуrольника ABDC АВ 11 CD, АС =F BD.
ABDC трапеция. Параллельные етороны трапе'ции назы..
ваются её о е н о в а н и я м и; АВ и CD основания трапе..
ции. Оетальные две етороны называютея б о к о в ы м и с т о р О..
Н а м и трапеции; А С и BD боковые с тароны трапеции.
в
д
в
d
о
ЧЕРТ 252
ЧЕРТ. 253
ЧЕРТ. 25!
Если боковые стороны равны, то трапеция называетея р а в н о..
бедре.нной.
Трапеция АВаМ равнобедренная, так как АМ == ВО (черт. 253).
Трапеция, у которой одна из боковых сторон перпендикулярна
к основанию, называетея п р я м о у r о л ь н о й (черт. 254).
С р е Д н е й л и н и е й трапеции называется отрезок, еоеди
няющий середины боковых сторон трапеции.
· Т е о р е м а. Средняя линия трапеции параллельна 1(,аждо-
./НУ из ее оснований и равна их полусу.мAtе.
Д а н о: ОС средняя
линия трапеции ABDK,
T. e. ОК == ОА и ВС == CD Д
(черт. 255). _
Н а Д о Д о к а 3 а т ь:
1) ОС 11 KD и ОС 11 АВ
2) ОС == KD + АВ .
2
Д о к а з а т е л ь е т в о. К Е
Через точки А и С проведём ЧЕРТ. 255
ПРямую, пересекающую
продолжение оенования KD в некоторой точке Е.
В треуrольниках АВС и DCE: ВС =СD по условию; Ll == L2,
как вертикальные, L 4 == L 3, как внутренние накреет
103
JIежащие при параллельных АВ и КБ и еекущей BD. Следователь...
но, АВС == д DCE.
Отсюда АС == СЕ, Т. е. ОС является ередней линией треуrоль
ника КАЕ.
Следовательно (9 48)
1) ОС 11 КБ, И, значит, ОС 11 KD и ОС 11 АВ;
2) ОС == КЕ == KD + ED , но DE==AB (из равенства треуrольни
2 . 2
ков АВС и DCE), поэтому отрезок DE можно заменить равным ему
отреЗКО1v1 АВ. Тоrда получим:
ОС == KD + АВ .
2
Теорема доказана.
Упражнения.
1. Доказать, что сумма внутренних уrлов трапеции, прилежащих к каж
дай боковой стороне, равна 2d. .
2. ДОJ<азать, что уrлы при основании равнобедренной трапеции равны.
3. Доказать, что если уrлы при основании трапеции равны, то эта трапеция
равнобедренная.
4. Доказать, что диаrонали равнобедренной трапеции равны ме}l(ДУ собой.
5. Доказать, что если диаrонали трапеции равны, то эта трапеция paBHO
бедренная.
б. Доказать, что периметр фиrуры, образованной отрезками, соединяю
щими середины сторон четырёхуrо,льника, равен сумме диаrоналей это.
ro четырёхуrольника.
7. Доказать, что прямая, проходящая через середину од ной из боКОВЫХ
сторон трапеции параллельно её основаниям, делит друrую боКОВУIО
сторону трапеции пополам.
50. СВОЙСТВА МЕДИАН ТРЕуrОЛЬНИКА.
;8 т е о р е м а. Все три .медианы, треуzольника пересекают..
ся 8 одной точ"е..
Пусть в треуrольнике АВС (черт. 256) AD и ВЕ........ медианы,
nересекающиеся в точке о. Дока}l{ем, что и отрезок NC, nроходя--
щий через третью вершину
этоrо треуrольника и точку
О, будет также медианоЙ,
Т. е. AN == NB.
J1ля доказательства через
точку Е nроведём EF 11 AD,
тоrда СР == FD. Разделим
отрезок BD I!ополам; пусть
DK == КВ. Получим п! ==
== n2 == п 3 == пl" как поло
С вины равных отрезков CD
и BD.
в
104
Через точку К проведём KS 11 AD; тоrда т! == т2 === rп з , Т8I{
как KS 11 OD 11 ЕР и n" == nз == п2.
Через точки S и Е проведём SP 11 ON и EQ 11 ON, тоrда 14 ==
== 1 з == 12' так как SP 11 ON 11 Е Q и mз == m2 == mt. KpQMe TOI'O,
12 == l f , так как АЕ == ЕС и EQ 11 CN. Отсюда l == I з == 12 == 1.,
НО '4 + lэ == NB, а 12 + 11 == NA.
Следовательно, AN == NB, Т. е. NC является также медианой
треуrольника АВС.
Таким образом, все три медианы треуrольника пересекаются в
одной точке.
l(po fe Toro, мы видим (черт. 256), что отрезок. ОБ составляет
1 ·
ВЕ. Аналоrично мож но доказать, чтр отрезок ON составляет
3
1 1
CN и отрезок OD составляет AD. ТЭJ<ИМ образом, то""а
3 3
lzересе'l,ения .медиан в mреуzольни"е отделяет от каж-
дой медианы mретью часть, считая от COOnZ8emcmBY-
.,
ющеи стороны.
rЛАВА v
ИЗМЕРЕНИЕ ПJlОЩАДЕI
rЕОМЕТРИЧЕСКИХ Фиr Р.
51. ПОНЯТИЕ ОБ И3МЕРЕНИИ ПЛОЩАДЕЙ. ПАЛЕТКА.
В жизни часто приходится вычи лять площади rеоl\lетрических
фиrур.
НаПРИl\Iер, приходится определять площадь поля, оrорода,
спортивной площадки или определять площадь пола в здании, пло..
щадь стен или окон в комнате.
При всяком измерении необходимо заранее иметь меру, с ко..
торой сравнивается измеряеl\fая величина. При взвешивании упот
ребляются меры веса: килоrрамм, rpaMM, тонна, центнер. Время
измеряется часами, минутами, секунда fИ.
При измерении длины отрезка мы сравниваем ero с метром, caH
тиметром или с какой нибудь друrой мерой длины. При измерении
уrлов пользуемся уrловыми rрадуса!\П'I, минутами.
Точно TaKiKe при измерении площадей rеометрических фиrур
пользуются особыми мерами, с которыми сравниваются эти
фиrуры.
Такими мерами являются квадраты, стороны которых равны
какой нибудь ,Т}инейной мере: leTpy, дециметру, сантиметру, мил...
пиметру. При измерении площадей, имеющих большие размеры,
за меру l\10жет быть принят квадрат, сторона KOToporo равна кило...
метр у .
I<вадрат, сторона KOToporo равна какой нибудь линейной еди
нпце, называется l{вадратной едини цей: к в а Д р а т н ы м м е т..
р о м, к в а Д р а т н ы м с а н т и м е т р о М, к в а Д р а т н ы м
к и л о м е т р о м и Т. Д., В зависимости от ТОl'О, какой линейной
мере равняется сторона квадрата, принятоrо' за еди ницу измерения.
Измерить площадь какой-нибудь, rеометрической фиrуры
значит узнать, сколько тех или иных квадратных единиц содер-
жится в фиrуре, площадь которой измеряется.
П а л е т к а. В тех случаях, коrда измерение площади какой
нибудь фиrуры не требует большой точности, а также коrда фиrу
ра, площадь которой требуется измерить, оrраничена криволинеЙ..
ным контуром (черт. 257), для измерения площади употребляется
особый прибор, называемый п а л е т к о Й.
Палетка представляет собой прозрачную плаСТII пку, на которую
наносится масштабная квадратная сетка, например, со стороной
квадрата, равной 1 СМ.
106
Эта пластинка накладываетея на фиrуру, площадь которой тре-
буется измерить (черт. 258).
Сначала подечитывается чиело квадратов, полностью' уклады-
вающихея в данной фиrуре; на чертеже 258 их 26. Затем подсчиты-
вается чиело квадратов, пересекаемых контуром фиrуры; на черте-
же их 21.
Каждый из неполных квадратов принимаетея за половину квад-
рата, таким образом, их общая площадь приближённо составит
21 : 2 == 10,5 квадрата.
ЧЕРТ. 257
ЧЕРТ. 258
Общее число квадратов, заключающихся в измеряемой фиrуре,
таким образом, составит 26 + 10,5 36,5 квадрата. Если, на-
ПрИ fер, каждый квадрат в действительности еоответствует 1 кв. м,
то измеряемая площадь еоставит 36,5 кв. М.
Однако измерение площадей с помощью палетки не отличается
точностью, утомительно, поэтому на практике чаще Beero пользу..
ются более еовершенными и точными епоеобами измерения площа-
дей, которые по существу еводятея к измерению длин отрезков и
использованию особых формул.
В последующих параrрафах мы расемотрим некоторые формулы,
е которыми наиболее часто приходитея иметь дело на практике.
52. ПЛОЩАДЬ прямоуrОЛЬНИI(А.
Пусть нужно определить площадь прямоуrольника, одна сто-
рона KOToporo равна, например, 5 СМ, а сторона, смежная с ней,
равна 3 с.м, или, как принято rоворить, оенование данноrо прямо-
уrольника равно 5 СМ, высота 3 с.м (черт. 259, а).
Если отложим на основании и высоте прямоуrольника от верши-
ны А отрезки, равные 1 с.м, и через полученные точки деления про-
ведём прямые, параллельные сторонам прямоуrольника (черт. 259,6),
то прямоуrольник окажетея покрытым сеткой квадратов (как палет-
кой). Вдоль основания AD уложится 5 квадратов, т. е. етолько,
сколько сантиметров составляет длина оенования прямоуrольника.
Таких полос получится 3, т. е. етолько, сколько сантиметров со-
101
ставляет высота прямоуrольника. Поэтому вся площадь прямо..
уrольника составит
5 кв. см · 3 === 15 К8. СА!.
Рассмотрим теперь случай, коrда ДЛИНЫ сторон прямоуrольника
выражены дробными числами. Например, пусть основание пря-
моуrольника а == 5,4 см, а высота h == 1,6 СМ.
Чтобы определить площадь прямоуrольника, выразим длины ero
сторон в l\fиллиметрах:
а == 54 МА!, 11 == 16 Af.M.
в
ЗСN
с
в
с
2см
lс""
11
: : : : D
ICN 2 сн Зен 4сн SCM
11
D
а)
6)
ЧЕРТ. 259
Тоrда площадь прямоуrольника, выраженная в квадратных мил-
лиметрах, будет равна произведению чисел 54 и 16, т. е.
S == (54 . 16) КВ. ММ.
Чтобы получить ответ в квадратных сантиметрах, надо число, вы..
ражающее площадь прямоуrольника в квадратных миллиметрах,
разделить на число, показывающее, сколько квадратных миллимет"
ров составляют один квадратный сантиметр, т. е. на (10 .10) кв. .мм,
так как квадратный сантиме'тр это прямоуrольник, длина и
ширина KOToporo содержат по 10 мм.
Получим:
S == ( 54. 16 ) ' КВ. см == ( 54 . 16 ' ) КВ. СМ == (5,4 . 1,6) кв. СМ.
10. 10 10 10
Таким образом, чтобы вычислить площадь прямоуrОЛЬНИl<а, надо
число, выражающее длину основания прямоуrольника, умножить
на число, выражающее длqну ero высоты в fepax Toro же наимено-
вания. Произведение этих чисел и выразит площадь прямоуrоль-
ника в квадратных l\lCpaX Toro же наименования.
· Для l<раТI\ОСТИ rоворят: пЛОlцадь пря.моуzольнu"а равна
nро"зведению ezo основания на высоту. .
Записывается это так: S === а · h, rде S площадь прямоуrоль..
Ника, а ero основание, h высота, выраженные в мерах одноrо
наименования.
1(j8
В тех случаях, коrда основа-
ние и высота прямоуrольника
выражены в мерах различноrо
наименования, необходимо пред-
варительно выразить их в мерах
одноrо наИl\fенования.' Напри-
мер, если основание прямо-
уrольннкаравноl,15м, а высо-
та равна 24 СМ,то нужно или
1,15 м выразить в сантиметрах,
или 24 см выразить в долях мет-
p a. Получим: или 115 см х
х 24 см == 2760 КВ. см, или
],15 А! х 0,24 м == 0,276 КВ. М.
2760 кв. см записывается ещё и
TaK: 2760 см 2 , а 0,276 КВ. м мож-
но за писать Tal<: 0,276 м 2 .
Л'\ О)l{ИО и друrим способом
проверить справедливость фор-
мулы площади прямоуrольни-
иа, т. е. формулы S == ah, для
случаев, коrда одно или оба
измерения прямоуrольника вы-
ражаются дробными числами. На
чертежах 260, а, б, В изображены
таиие прямоуrольники.
Чтобы определить площадь
J110боrо прямоуrольника, напри-
мер, в квадратных сантимет-
рах, достаточно подсчитать, ЧЕРТ. 260
'"'
ск лько ивадратных сантиметров полностью окрывают данныи
прямоуrольник.
Такой подсчёт покажет, что:
на чертеже 260, а площадь прямоуrольника равна 9 КJJ. см;
на чертеже 260, б площадь прямоуrольника paBtla 15 КВ. см;
на чертеже 260, В площадь прямоуrольника равна 3,6 кв. см.'
Если вычислим площадь каждоrо из данных прямоуrольников
по формуле S == ah, то получим точно такие же ответы. Значит,
формула S == ah для данных прямоуrольников еправедлива.
Подобны м обраЗО1.f можно убедиться в еправедливости формулы
S == ah для любоrо прямоуrольника.
Доказать справедливость формулы S == ah ДЛЯ прямоуrольника,
1
у Koтoporo а == 3 з см и h == 2,5 см.
Упражнения.
1. Вычислить площадь прямоуrольнина, длину ИЛИ высоту по следую-
щим Данным:
4,5.2= 9(хб.сн)
('\1
4,5 см
.
а)
6'2,5= 15 (lffJ.CN)
(...)
\r)
б с 1'1
Б)
2, .1,5 = 1,6 (lf8. СМ)
I О, 5 кд. см 0,5 хд см Ц2
. 1 кб,сн 1 хб.СМ OJ
2,4 см
t
д)
109
а h S а h S
1 30 см 6 см 9 48 см ..... 240 CAt 2
2 1 м 20 см 8 см 10 56 САС 1120 c.м
3 14 f,И 6 Аf М 11 30 см 1 ,2м2
4 1 ,8 см 5 мм 12 ...... 250 с м 1 м 2
5 12 км 8 км 13 0,7 м 0,56 м 2
6 125 км 140 ! 14 0,9 м О, 72 м 2
7 1,? м 65 СМ 15 0,06 к м ..... 0,3 км 2
8 1 км 125 М 760 м 16 ..... 0,33 км 0,56 км'2
2. Вычислить площадь стен вашеrо класса
(вашей комнаты) и составить формулу,
обозначив длину класса через а, шири-
ну ..... через Ь и высоту..... через с.
3. Вычислить площадь фиrуры, изображённоir
на чертеже 261, разбив её на прямо-
уrольники и принимая 1 .мм за 1 м.
4. Вычислить площадь школьноrо двора
(школьноrо оrорода).
53. ПЛОЩАДЬ КВАДРАТА.
ЧЕРТ. 261
Так как квадрат есть прямоуrольник,
у KOToporo основание и высота равны, то
для вычисления площади квадрата доста-
точно измерить одну ero еторону и полу-
ченное число возвести в квадрат, т. е. по-
множить само на себя. Полученное число и
выражает площадь данноrо квадрата.
Если сторону квадрата обозначить че-
рез а, то площадь ero будет равна а 2 .
S квадрата === а · а === а 2 (черт. 262).
о
а
ЧЕРТ, 262
УпражнеНttR.
1. Вычислить. площ.здь квадрата, если ero сторона равна 4 см (8 САС, 12 ММ,
1 ,2м, 4,5 КМ, 4 м 50 см, 0,4 м, О, 15 .м).
2. Сколько квадратных метров содержит участок в одии rektap-, если он имеет
форму квадрата со стороной, равной 100 м?
з. Сколы{о квадратных метров содержит ар, если он имеет форму квадрата
со стороноК., равной 10 м?
4. Сколько аров содержит reKTap?
110
54. ТАБЛИЦА КВАДРАТОВ ЧИСЕЛ.
При вычислении площадей различных квадратов приходится
возводить число в квадрат. Чтобы ускорить и облеrчить выполнение
этой операции, обыкновенно пользуются таблицами квадратов
чисел.
В школе пользуются четырёхзначными математическими табли
цами В. М. Брадиса, в которых дано подробное описание их устрой-
ства и объяснено, как ими пользоватьея.
55. ИЗВЛЕЧЕНИЕ I(ВАДРАтноrо I(ОРНЯ.
ТАБЛИЦА КВАДРАТНЫХ I(ОРНЕА ИЗ ЧИСЕЛ.
Возведение числа в квадрат является несложной операцией,
в особенности если пользоваться таблице квадратов чисел. He
сколько сложнее обратная операция извлечение из числа KBaд
paTHoro корня.
Пусть, например, перед нами поставлена задача: «Н айти CTO
рону квадрата, площадь KOToporo равна ;'00 кв. см.).
Если обозначить CTO QHY квадрата через х, тоrда х 2 == 100.
Значит, х это число, квадрат KOrOporo равен 100. Такое число
называется квадратным корнем из 100 и записывается так: V 100 .
Знак V называется р а Д и к а л о м.
В данной задаче можно леrко подобрать ответ к ней: V 100 ==
10. Точно так же леrко устно решаются такие задачи: JI 121 ==
11; V I44 == 12; V 400 == 20; V 900 == 30 и т. д.
Труднее решить задачу, коrда приходится извлекать квадрат-
ный корень из мноrозначноrо числа, например из 1296, 47 841 и
т. д. В этом случае дело значительно облеrчается, если восполь-
зоваться таблицами В. М. Брадиса, в которых указаны приёмы из-
влечения точных и приБЛИ}J{ённых KBa paTHЫX корней из чисел.
56. ПРАI(ТИЧЕСI(ИЕ РАБОТЫ.
1. Вычислить площадь пола вашеrо класеа, коридора.
2. Вычислить площадь пола вашей комнаты (квартиры).
3. Вычислить площадь окна вашеrо класса (без переплётов)\.
П p м е ч а н и е. Площадь окна без переплётов называется
u
световои площадью.
4. Вычислить световую площадь всех окон вашеrо класса и
найти её отношение к площади пола. Вычислить то же для вашей
комнаты.
5. Измерить площадь какоrо нибудь земельноrо учаетка, имею-
(цеrо форму прямоуrОJIьника, и выразить её в reKTapax и арах.
6. Вычислить площадь земельноrо участка прямоуrОJIЬНОЙ фор-
МЫ по следующим данным (результат выразить в apax) :
111
Длина Ширина Пло щадь
(в арах)
30 АС 2::> М
48 м 32 А'
12 АС 7,5 .м
9,4 м 6,8 А'
7. Вычислить площадь зе lельноrо участка прямоуrольной фор-
мы по следующим данным:
57. РАВНОВЕЛИКИЕ фиrуры.
Вычислить площади прямоуrольников, изображённых на черте-
жах 263, 264, 265,
20м
1'\,)
Q
l
tr
ч:>
t
........
I
25м
32м
ЧЕРТ. 263
ЧЕРТ. 264
ЧЕРТ. 265
Измерения этих прямоуrольников (длина и ширина) различны,
однако площади их оказались равными. rеометрические фиrуры,
площади которых равны, называются р а в н о в е л и к и м и.
УпражнеНUfl.
1. Для "ришкольноrо оrорода решили отвести земельный участок площадью
в адин reKTap. Какую длину и ширину мо}кет иметь пришкольный оrород
прямоуrольной формы?
2. Для опытной делянки решили отвести участок в один ар. Какую длину и
ширину может иметь этот учаСТQК, если он будет иметь форму прямоуrоль-
ника?
з. Сделать необходимые измерения и вычислить площадь прямоуrольника
АВСО (черт. 266), а затем построить несколько равновеликих ему пря-
МОУ rоль ни ков.
4. Какая разница между равными фиrурами и равновеликими?
58. ТЕОРЕМА ПИФАrОРАl.
Пусть дан прямоуrольный треуrольник, етороны KOToporo
l!, Ь и с (черт. 267).
Построим на ero сторонах I{вадраты. Площади этих К8адратов
соответетв енно раЕНЫ а 2 , Ь 2 и с 2 . Докаже f, что с 2 == а 2 + Ь 2 .
1 П И Ф а r о р rреческий учёныЙ, живший около 2500 лет назад (564
473 rr. ДО нашей эры).
112
Построим два квадрата мкор и
М' K'O P' (черт. 268, 269), приняв за
сторону каждоrо из них отрезок, рав-
НЫЙ сумме катетов прямоуrольноrо тре..
уrольника АВС. Выполнив в этих квад-
ратах пос роения, показанные на чер-
тежах 268 и 269, мы увидим, что квадрат
мкор разбился на два квадрата е пло..
Ul.адями а 2 и Ь 2 и четыре равных прямо-
уrольных треуrольника, каждый из ко-
торых равен прямоуrольному треуrоль-
нику АВС. Квадрат М' К'О' р' раз"
бился на четырёхуrольник (он на чер-
теже 269 заштрихован) и четыре прямо
уrольных треуrольника, каждый из KO
торых также равен треуrольнику АВС.
Заштрихованный четырёхуrольник
Евздрат, так как стороны ero равнЫ
(!(аждая равна rипотенузе треуrольника
АВС, т. е. С), а уrлы прямые (L 1 +
4 L 2 == 900, откуда L 3 == 900).
Таким образом, еумма площадей
квадратов, построенных на катетах (на
чертеже 268 эти квадраты заштрихова-
НЫ), .равна площади квадрата мкор
без суммы площадей четырёх равных
треуrольников, а площадь квадрата,
nOCTpoeHHoro на rипотенузе (на черте-
же 269 этот квадрат тоже заштрихо-
ван), равна площади I{вадрата М' К'О' Р',
paBHoro квадрату МКОР, без суммы
площадей четырёх таких же треуrоль-
ников. Следовательно, площадь квад-
рата, nOCTpoeHlIoro на rипотенузе пря-
моуrольноrо треуrольника, равна еум-
ме площадей квадратов, построенных
на катетах.
Получаем формулу с 2 == а 2 + Ь 2 , rде
с rИl10тенуза, а и Ь катеты прямо-
уrольноrо треУI'ольника.
Теорем,У Пифаrора кратко принято
формулировать так:
8 Квадрат zипОntен.узы "п fNJ -
уюА IJОIO fW ", _a. ра-
вен сумме "вадраmов "ате-
тО8.
8
с
д
D
ЧЕРТ. 266
02 а
с ь
Ь 2
ЧЕРТ. 267
р
о
ь
о
,
аЗJ "
"
"
. ,
'"
\
\
, '"
\ b
\
\ /
\ / <//// :i
\. '///.
ь
а
ь
м а
,
к
ь
ь О'
а
ь
о
м'
а к'
ЧЕРТ. 269
11З
1--1з формулы с 2 а 2 + Ь 2 можно получить такие формулы:
а 2 == с 2 Ь 2 ; Ь 2 == с 2 а 2 .
Этими формулами можно пользоваться для наХ9ждения неиз-
вестной стороны прямоуrольноrо треуrольника по двум данным ero
СТОРЕ>нам. Например: а) если даны катеты а == 4 см, Ь == 3 см, то
можно найти rипотенузу (с): с 2 == а 2 + Ь 2 , т. е. с 2 == 4'2 + 32;
с 2 === 25, откуда с == V 25 == 5 (см);
б) если даны rипотенуза с == 17 см и. катет а == 8 см, то 'можно
найти друrой катет (Ь):
Ь 2 == с 2 а 2 , т. е. Ь 2 == 172 82; Ь 2 == 225,
откуда Ь == V 225 == 15 (см).
Сл е Д с т в и е. Если в двух пря.JНОУZОЛЬНЫХ треуzоль-
никах АВС и A 1 B t C 1 2ипотенузы с и С . равны, а "атет
Ь треуzольНtt"а АВС больше катета Ь 1 треуzольнu"а
A 1 B 1 C i , то "атет а треуzольнu"а АВС .меньше "aпle..
",а аl треуzольнu"а А 1 В 1 С 1 . (Сделать чертёж, ИЛЛIОСТРИРУ-
ющий это следствие.)
В самом деле, на основании теоремы Пифаrор,а получим:
а 2 == с 2 Ь 2 ;
а1 2 == С1 2 b .
В записанных формулах уменьшаемые равные, а вычитаемое
в перЕОЙ q:ормуле больше Еычитаемоrо во второй формуле, сле-
довательно, первая разность меньше второй, т. е. a 2 <ai. Orкуда
а < af.
Упражнения.
1. Пользуясь чертежом 270, доказать теорему Пифаrора nля рвянобедренно-
ro прямоуrольноrо треуrольника.
2 Один катет прямоуrольноrо треуrОJlьника равен 12 см, друrой 5 см. Вы-
числить длину rИП01енуэы 910ro треуrольника.
3. rИП01енуэа прямоуrольноrо треуrольника равна 10 с,м, один из катетов ра-
вен В СМ. Вычислить ДЛИI:lУ друrоrо катета 910ro треуrольника.
-1 rипотенуза прямоуrольноrо треуrольника равна 37 СМ, один из ero катетов
равен 35 С,м. Вычислить ДЛИНУ ДРуrоrо катета 910ro треуrольника.
5. Построить квадрат, по площади вдвое больший данноrо.
6 Построить квадрат, по площади вдвое меньший данноrо.
у к а э а н и е. Провести в д-анном квадрате диаrонали. Квадраты, по
строенные на половинах этих диаrоналей, будут искомыми.
7. Катеты прямоуrольноrо треуrОJ1ьника соответственно равны 12 см и 15 см.
Вычислить ДЛИНУ rипотенузы 9Toro треуrольника с точностью до
О, 1 СМ .
8. rип<>тенуэа пря'моуrольноrо треуrОJlьника равна 20 СМ, один из ero ка-
тетов равен 15 СМ. Вычислить длину друrоrо катета с точностью
до 0,1 см.
114
/
/
/
/ Q
/
/
с
ЧЕРТ. 270
jffi
ЧЕРТ. 271
9. Какой ДЛИНЫ должна быть лестница, чтобы её можно было приставить к
окну, находящемуся на высоте 6 м, если нижний конец лестницы должеli
отс оять от здания на 2,5 .м? (Черт. 271.)
Пусть требуется найти площадь параллелоrра lма АВСО
(черт. 272, а). Примем сторону АВ за основание' параллелоrрамма
и из вершин D и С проведём высоты DM и СК. Площадь получен-
Horo прямоуrольника MKCD равна произведению' МК на DM.
Треуrольники ADM и ВСК рав-
ны, так как они имеют по равной rи-
потенузе и по равному катету:
AD == ВС и DM == СК.
Параллелоrрамм ADCB состоит
из трапеuии MDCB и треуrольника
ADM, прямоуrольник MDCK состо-
ит ИЗ той }I{e трапеции MDCB и тре-
уrольннкэ ВСК, который равен
треуrольнику ADM. Следовательно,
площадь параллелоrраМr\tа равна
площади прямоуrольника. Orсюда
площадь параллелоrрамма равна
также произведению МК на DM.
Но МК == АВ (М К == DC == АВ),
поэтому площадь параллелоrрамыа
. будет равна произведению АВ на DM,
т. е. площадь nараллелоzра.м.ма
!JавняеmСR "произведеНllЮ ezo ос-
нования на высоту.
59. ПЛОЩАДЬ ПАРАЛЛЕлоrРАММА.
а)
р
м
в
с
I
Ih
I
..........L
К
а
6)
D
с
д
I
I
Ih
I
I I
...L ...... ......
в Е F
ЧЕРТ. 272
115
Sп ра.'Jле.Тfоrрамма== й. h, rде а основание параллмоrрамма и h ...... ero
высота.
Несколько иное рассуждение придётся применитъ для вывода
формулы площади параллелоrрамма, изображённоrо на чертеже
272, б, rде ABCD данный параллмоrрамм, а EFCD ......... вспомоrа-
u
'Iмьныи прямоуrольник.
1. Доказать, что если на отрезке АВ как на основании построить несколько
парзллелоrраммов, второе основание которых будет лежать на прямой
МК, параллельной АВ, то все ЭТ параллелоrраммы будут равновелики
(черт. 273).
2. Вычислить площадь параллело-
rрзмма по следующим данным:
3. Площадь параллелоrрамма рав-
на 128 кв. м; основание ero равно
16 м. Вычислить длину высоты
параллелоrрамма.
4. Площадь параллелоrрамма рав-
на 720 кв. см; высота ero равна
12,5 С.". Вычислить длину OCH<r
вания параллелоrрамма.
60. ПЛОЩАДЬ ТРЕуrольни КА.
Пусть требуется определить площадь треуrОЛЬНIII<а АВС. Про-
ведём через вершины ero 'с и В (черт. 274) прямые, параллельные
сторонам АВ и АС. Мы получим параллелоrра ABCD. Площадь
ero равна произведению основания АВ на высоту СО. Параллело-
rpaMM ABDC состоит из двух равных треуrольников АВС BCD.,
следовательно, площадь тре-
у.rольника АВС равна половине
площади параллелоrрамма, т. е.
J
S ABC == АВ · СО. Orсюда,
. 2
8 площадь треУ20льн""а рав-
на половине про"эведе--
н"я е20 основания на 86/--
соту.
м
к
д в
ЧЕРТ. 273
Упражнения.
с D
"""""'--- """7
I
I
/
I
I
\
11,
ЧЕРI. 274
116
SABCD == SAFCD SBCF,
SEFCD == SAFCD SADE, но
f::::a ВСР == д ADE, следовательно,
SAВCD == SEFCD == CD · CI"', т. е.
SABCD == а · h.
.й
h
s
25 .мм
48м
]6,2 с'м
1,4.м
З, 2 с,м
] 4 мм
30 м
]2,5 СМ
25 СМ
14 .м,М
S h
=:::i.. .
.
Эту формулу можно представить в таком виде:
а h
S л == · h или S л == а · .
I 2
Выразить эти формулы словами.
Упражнения.
1. Доказать, что площадь прямоуrольноrо треуrольника pa Ha половине
произведения ero катетов.
2. ВЫ ЧИСJIIIТЬ П.псщадь треуrольника по следующим данным: t
3. Площадь треуrольника равна
360 КВ. см (288 КВ. с,м). Основа-
ние ero равно 72 С,М. Вычислить
высоту треуrольника.
4. Ilлощадь треуrольника равна
240 К8. .м'м, высота ero равна
200 ,мм (30 М,М, 8 c t). Вычислить
основание треуrольника.
5. Через вершину С треуrольника
АВС проведена прямая СК, I!a-
раллельная стороне треуrольника
АВ (черт. 275). Доказать, что все
треуrольники, построенные на стороне АВ как на основании с вершиной
на прямоЙ СК, равновелики.
r
......
,
l,
с"
Основание
Высота
Площадь
32 см
1 ,м 15 см
1,2 м
42,5 ,мм
18 сМ
64 см
1,4 м
18 .мм
С"' К
о
6. Сделать необходимые построения
и измерения и вычислить:
а) площадь треуrольника АОВ
(черт. 276);
б) площадь треуrольника СВК
(черт. 277).
61. ПЛОЩАДЬ ТРАПЕЦИИ. В
Пусть нам нужно узнать, К
чему равняется площадь трапе- ЧЕРТ. 277
ЦИИ ABCD (черт. 278). ПрОБе-
дём в ней диаrональ DB. Трапеция разобьётся на два треуrоль-
ника ADB и DCB. Обозначим высоту трапеции и треуrольников
через 11, а площади треуrольников AD В и D ве через S 1 и S 2"
Тоrда ·
ЧЕРТ. 273
S АВ. h .
1 ,
2
А
ЧЕРТ. 216
с
Масштаб 0;001
S DS . h
2 ·
, 2
117
D С
, I
,
, I h
,
, I
,
, I
, I
,
А В
ЧЕРТ. 278
Следовательно, площадь всей тра-
пеции выразится так:
S АВ · h DC · h
ABCD == + ==
2 2
== ( АВ +- DC) h == АВ + DC . h.
2 2
8 Площадь трапеции равна про"эведеНItЮ пОЛУС,AlAl6l е8
..
основаНlt1t на высоту.
а+Ь -
Sтрапеции == . h, rде а и Ь основания трапеции, а /1 ее
2
высота.
Упражнения.
1. Най!и ПЛОlцадь трапеции по следующим данным:
а Ь h S
38 см 25 с"и 12 см
45 , 5 с.м 16 , 8 с.м 75 см
425 .мм 328 .м"И 12 СА!
2. Площадь трапеции равна 480 КВ. см; высота её равна 12 с"и; одно из
оснований на 6 с.м больше друrоrо. Вычислить основания этой трапеции.
3. Площадь трапеции равна 960 КВ. м; одно основание её равно 60 м, дру-
roe 36 .м. Чему равна высота этоЙ трапеции?
4. Площадь трапеции равна 1200 КВ. см, высота её равна 24 см. Одно оснdйа-
ние больше друrоrо в 3 раза. Вычислить основания этой трапеции.
5. Сечение канавы имеет форму трапеции (черт. 279), Одно основание её
равно 90 с'м, друrое 56 см; высота трапеции 65 с.м. Вычислить площадь
сечения этой канавы.
6. Сделать необходимые построения и измерения и вычислить площадь тра-
пеции АВСК (черт. 280).
1/
в
ЧЕРТ. 279
ЧЕРТ. 280
118
По данному плану и масштабу (черт. 281) вычислить площадь пруда.
у к а з а н и е. Сделать необходимые измерения и сначала вычислить
площадь большоrо прямоуrольника, а затем из ero площади вычесть
сумму площадей фиrур 1 11, принимая их З3 треуrольники и трапеuии.
7.
ЧЕРТ. 281
62. ПЛОЩАДЬ произвольноrо
мноrоvrольни КА.
Пусть требуется вычислить пло-
щадь произвольноrо четырёхуrольни-
ка ACDB (черт. 282). Проведём в нём
диаrональ, например AD. Получим
два треуrольника ABD и ACD, пло-
щади которых вычислять умеем. За..
тем находим сумму площадей этих
треуrольников. Полученная сумма и
будет выражать площадь данноrо
четы рё х у rол ь н И 1( а.
Если нужно вычислить площадь
пятиуrОЛЬНИI<а, то поступаем таким
же образом (черт. 283) Из одной ка..
кой нибудь вершины проводим диа-
rова-пи. Получим три треуrольника,
площади которых можем вычислить.
Значит, можем найти и площадь дан-
Horo пятиуrольника. Так же поступа..
ем при вычислении площади любоrо
м ноrоуrольника.
Упражнения.
1. Сделать необходимые построения и
измерения и вычислить площадь
четырёхуrольника, изображённоro на
чертеже 284.
2. По данному плану земельноrо участ-
ка вычислить ero площадь (черт. 285).
,4
8
ЧЕРТ. 282
ЧЕРТ. 283
масштаб 0,01
ЧЕРТ. 284
Нпr.штаб 0,001
ЧЕРТ. 285
ТЛАВА VI
r
ПРЯМАЯ ПРИЭМА.
ПОВЕРХНОСТЬ И О&lIЁМ прямоl ПРИЭМЫ.
63. КУБ.
1. Построtиие модели куба.
На чертеже 286 изображена выкройка, или, как её принято на-
зывать, раз в ё р т к а, поверхноети куба. Она еостоит из шести
равных квадратов. Если эту развёртку eorHYTb по указанным на
чертеже пунктирным линия f и еклеить отмеченные одинаковыми
пометками стороны квадратов, то ПО.ПУЧИ 1 поверхность rеометри-
чеекоrо тела, называемоrо к y
б о М. К
Под номером 287 дан чертёж
куба, а п()д HO iepoM 288 рису-
с
д
в
I
. I
I
I
ЧЕРТ. 2 7
ЧЕРТ. 286
ЧЕ РТ. 288
HOI{ куба. Куб оrраничен шеетью равными квадратами, которые
называютея ero r р а н я м и. На риеунке видны только три ero
rрани, а на чертеже можно видеть все шесть rраней. Любые две
противоположные rрани куба называются ero о е н о в а н и я м И,
тоrда остальные четыре ero rрани нззываютея б о к о в ы м и
r р а н я м и; отрезки, которые получаются пр" пересечевии rpa-
ней куба, называются ero р ё б Р а м и. У куба 12 рёбер. Все ОIlИ
равны между еобой.
120
При пересечении трёх rрзней куба образуются точки, I{OTOpbIe
называются ero в ерш и НЗ1\-1 и. У куба 8 вершин.
2. Взаимное положение рёбер и rраней куба.
Противоположные rрани куба параллельны. Плоскости, в ко-
торых лежат эти rрани, не пересекаются, Т. е. не имеют общих то-
чек. Параллельные плоскости мы наблюдаем на мноrих окружаю-
щих нас предметах; наПРИ1\1ер, плоскости пола и потолка в комнате
параллельны.
Две полуплоскости с общим краем делят пространство на две
части. Каждая из этих частей называется Д в у r р а н н ы f У r-
ЧЕРТ. 289
ЧЕРТ. 290
ЧЕРТ. 291
л о М. МЫ буде!tf рассматривать только меньшую из этих частей.
Двуrранный уrол оrраничен двумя полуплоскостями, которые
nрилеrают к общей прямой, называемой p e б р о м Д в у r р а Н-
н о r о у r л а. Оrраничиваю:цие двуrранный уrол ПQЛУПЛОСКОСТИ
называются ero rранями.
Двуrранные уrлы бывают острые (черт. 289), прямые (черт. 290)
и тупые (черт. 291). Под прямым уrлом пересекаются TaK)I{e етены
в комнате, стены и потолок, стены и пол. Плоскости, пересекаю-
щиеся под ПРЯМЫ f уrлом, называются перпендикулярными.
Рёбра куба, находящиеся на одной rрани (черт. 287), или пере-
секаются под прямым уrлом (ЕА АВ, KC' БG и т. д.), или
параллельны (ЕР 11 АВ, 8е 11 кр и т. д.).
3. Скрещивающиеся прямые.
Рёбра куба, например ке и АВ (черт. 287), не параллельны,
но и не пересекутся, сколько бы их ни продолжать. Прямые, кото-
рые не параллельны и не пересекаются, называются с к р е Щ и-
в а 10 Щ И М И е я. Леrко получить модели скрещивающихся пря-
мых. Например, две иrлы, из которых одна положена на стол, а
друrая воткнута в стол так, что не пересекает первую, представляют
собой модель двух екрещивающихся прямых (черт. 292). Эrи две
прямые не пересекзются и не параллельны; леrко убедиться, что
через них нельзя провести ПЛОСКОСТ .
121
Точно так же, если взять две дощечки, поместить их параллель-
на друr друrу и затем на одну из них положить палочку в на..
правлении, например, с юrа на еевер, а на друrую в направле..
нии с запада на восток, то эти две палочки образуют модель скре..
щивающихся прямых (черт. 293).
Эти две ПРЯIvIые тоже не пересекаются, не параллельны, и через
них также нельзя провести плоскость.
W O
ЧЕРТ. 292
ЧЕРТ. 293
Найдите модели скрещивающихся прямых на окружающих
предметах, например, в классной комнате.
4. Прямая, перпендикулярная к плоскости.
Рассматривая куб (черт. 287), заметим, что ребро FB образует
прямые уrлы с рёбрами ВС и АВ, лежащими на нижнем основаltии
куба. Эrо же ребро РВ образует прямые уrлы с любой прямой, про..
ведённой в плоскости основания куба через точку В. Ребро FB
является перпендикуляром к плоскости основания куба.
Пер п е н Д и к у л я р о м к п л о е к о с т и называется
пр ямая, которая пересекает плоскость в какой"нибудь точке н
перпендикулярна к любой пряrvlОЙ, проведённой в этой плоскости
через ту же точку.
Чтобы провести перпендикуляр
к плоскости, берут два чертёжных
треуrольника и ставят их так,
чтобы два катета лежали на плос..
кости, как показано на чертеже
294, а друrую пару катетов сов..
1ещают. Эrи два катета и образуют
перпендикуляр к данной плоско..
. сти. На чертеже 294 прямая А В
перпендикулярна к плоскости Р.
Перпендикулярность прямой
АВ к плоскости Р леrко прове..
р
ЧЕРТ. 294
122
рить: для эrоrо надо nзять ещё один чертёжный треуrольни : 11 не..
сколько раз в различных положениях приложить ero к двум пер"
вым треуrольникам так, чтобы ero катет всякий раз совмещался с
катетом АВ. Тоrда друrой катет TpeTbero треуrольника всё время
будет находиться в плоскости Р. Значит, можно считать прове..
ренным, что прямая АВ образует прямые уrлы с любой прямой,
- u -
проведеннои на плоскости через ее основание, т. е. является пер-
пендикуляром к плоскости.
Описанный опыт с двумя треуrольниками делает правдоподоб.
u
нои такую rипотезу.
8 Если прямая, nересекающая плоскость в ка"ОЙ НU"
будь то""е О, перпендикулярна " двум, nрямы.м, прове..
денны,М, на плоскости через точ"у О, то эта прямая
nерпендикулярна 1(, пЛОС1(,осmи.
Сформулированное предложение даёт нам признак перпенди-
кулярности прямой И плоскости. В курсе IX класса оно доказы-
вается.
Orметим ещё два предложения, которые тоже примем без до..
казательства:
1) через любую точку можно провести перпендикуляр к дан-
ной плоскости, и притом только один;
2) через любую точку 1vIОЖНО провести плоскость, перпенди-
u u ,
кулярную К даннои прямои, и притом только одну.
Возьмём на ребре двуrранноrо уrла точку и проведём через эту
точку плоскость, перпендикулярную ребру (черт. 295). В сечении
получим плоский уrол. rрадусная
мера этоrо плоскоtо уrла и счи..
тается мерой Двуrранноrо уrла 1 .
Если этот плоский уrол острый,
прямой или тупой, то и дву"
rранный уrол считается соответ"
ственно острым, прямым или
тупым.
Леrко проверить, что в силу
этоrо определения двуrранные yr..
ЛЫ, образуемые rранями куба,
действительно прямые, как и бы-
ло сказано в п. 2.
5. Измерение дауrранных yr ЛОВ.
, I
ЧЕРr, 295
1 fрадусная мера не зависит от выбора точки на ребре.
123
6. Площаяь поверхности куба.
Чтобы вычислить площадь поверхности куба, достаточно вы-
u
числить площадь однои ero rрани и полученное число помножить
на 6. Если ребро куба обозначить через а, то площадь поверхности
одной ero rрани будет равна а 2 , а площадь всей поверхности куба
(полная поверхность) составит 6а 2 .
S == 6а 2 , rде S площадь полной поверхности куба.
Площадь поверхности ero оснований составит 2а 2 . Площадь
поверхности боковых ero rранеЙ составит 4lt .
Упра:JlснеНtlЯ.
1. Ребро куба раВIIО 8 СА! (10 см, 12 CAt, 20 C..4t). Вычислить площадь всей
ero поперхности; площадь оснований; площадь ero боковой поверхности.
2. Площад() полной поверхности куба равна 150 К8. СМ (600 К8. С-М,
216 кв. СМ, 864 К8. CAt). ВЫЧИСЛИТЬ
длину ero ребра.
3. Площадь боковой поверхности куба
равна 100 К8. см (64 ко. СМ,
324 КВ. см, 576 К8. СМ). Вычислить
.... площадь ero полноii поверхностн.
4. Сделать из плотной бумаrи модель
куба, ребро Koтoporo ра оно 8 CAI.
У К а з а н и е. Для Toro чтобы
полученное rео lеТJ1нческое тело со.
храняло CBOIO q:OPMY, У развёртки
куба необходимо сделать неболь.
шие закраины (черт. 296). Если их
подклеить, они составят каркас, ко.
LIEPT.. 296 торый придаст неоБХОДИ fУЮ жёст.
кость модел и.
5. Сколько потребуется белил дЛЯ ОК.
раски с обеих сторон бака (б з
КРЫШКИ); IIмеющеrо форму куба с ребром в 80 см, если на окраску 1 кв. /;t тре..
буется белил 0,25 ке?
64. ПРЯМАЯ ПРИ3МА.
1. На чертеже 297 изображена разверт-
ка поверхности rеометрическоrо тела.
Она состоит из двух квадратов и четы-
p x равных прямоуrольников.
Если ЭТУ развёртку corHYTb ,!Iадле)l{а..
щим образом по пунктирным линиям, то
получим поверхность rеометрическоrо тела,
называемоrо п р я м о й ч е т ы р ё х у r о л ь-
н о й при з м о й. у этой призмы все боко-
вые рёбра перпендикулярны к плоскости
основания.
124
I
I I I
I I I
I I I
I I I
I I I
I I I ,
.
4[Pf а 297
Под HOMepo ' 298, а дан чер-
тё}к такой призмы, а на чер-
теже 298, б её рисунок.
Развёртка поверхности пря-
мой четыр хуrольной призмы
может состоять и из шести пря-
моуrольников (черт. 299). Под
номером 300 дан чертёж такой
приз:мы, а на чертеже 301 дан
её рисунок.
Прямая четырёхуrольная
призма имеет, как и куб, 6
rраней, 12 ребёр и 8 вершин.
Призма, все rрани которой
прямоуrольники, называется
п р я м о у r о л ь н ы м п а-
р а л л е л е п и п е Д о М.
Длина и ширина основания
прямоуrольноrо параллелепипе-
u
да считаются длинои и шири-
ной с а м о r о пар а л л е л е-
п и п е д а, а любое из ero бо-
ковых рёбер принимается за
в ы с о т у п р я м о у r о л ь-
Horo параллелепипеда.
Длина, ширина и высота пря-
моуrольноrо цараллелепипеда
называlОТСЯ ero и з м е р е н и-
я м и.
Прямоуroльный параллеле-
пипед является весьма распро-
странённой фиrурой в ОКРУ- ЧЕРТ. 300
жающей действительности. Фор- ,
му прямоуrольноrо параллелепипеда име дома, комнаты,
шкафы, кузов rрузовоЙ машины, железобетонные плиты ДЛЯ по-
u
сrроики домов, кирпич и т. д.
а)
I
I
I
I
I
....
б)
'.'0 , .
............ ; : ....
'. : ,,
.....:. '1:
": ::' .: :,
6: .;:
:"..,; .
{....:::,.::. .
'" ..
.1,'
<: ,
.. ""....,""".
'( . ....' .'
. .., 1
';J!' , ..
ЧЕРТ. 298
---- I
I I
I I I
1 I 1
I I I
. 1 1 1
I I I
-- I
.
ЧЕРТ. 299
I
I
I
I
I
I
I
'
. \..
;.\\ ;.. , ::::. '. ' .
..., I " Ь
1-& :{:..' :o\= ,:
..1;>..':....'...... 'Ol\.
't{, lI; :,
ЧЕРТ. 301
Упражненuя.
1. Начертить прямоуrольный паралле.лепипед. Указать:
а) параллельные, пересекающиеся, скрещивающиеся прямые;
б) параллельные плоскости, перепендикулярные плоскости;
В) прямые, перпендикулярные к плоскости.
2. Сформулировать определение:
а) параЛЛeJJЬНЫХ прямых;
б) скрещивающихся прямых;
В) прямых, перпенднкупярны.х к плоскости.
3. Построить модели:
а) снрещиваlОЩИХСЯ ПРЯМЫХ;
125
б) Двуrранных уrлов.
4. Сформулировать признак перпендикулярности прямой к плоскости.
5. Объяснить, как построить плоскость, перпендикулярную к данной прямой.
2. Прямая призма может иметь в основании не только квадрат
или прямоуrольник, но и любую друrую прямолинейную фиrуру:
параллелоrраМ 1, трапецию (черт. 302), треуrОJIЬНИК (черт. 303)
I
.1
I
I
I
; , .
... :":." .... \
ЧЕРТ. 302
и вообще мноrоуrольник. В прямой ПРИЗ fе за высоту принимает-
ся любое из её боковых рёбер.
В прямой призме, у которой основаниями с.пужат траf1еции,
параллеЛЬНЫf\'IИ rранями являются только основания и одна пара бо-
I
I
I
I
I
I
...... --- ,
ЧЕРТ. 303
коВЫХ rраней (черт. 302). В прямой призме, у которой основаниями
служат трапеции, параллелоrраммы или треуrольники, MorYT быть
как прямые, так острые и тупые двуrранные уrлы.
3. Вычисление площади поверхности прямой призмы.
Площадь боковой поверхности или, короче, боковой поверх-
ностью прямой призмы называется сумма площадей её боковых
rраней. ПЛощадью полной поверхности или, короче, полной поверх-
126
ностыо прямой ПРИЗ 1Ы называется сумма площадей обоих основа-
ний и площади БОI{ОВОЙ поверхности.
Площади боковых rраней и оснований вычисляются по соответ-
ствующим формулам. .
Упражнения.
1. Длина, ширина и высота прямоуrольноrо параллелепипедз равны соот-
ветственно 12 см, 8 см и 20 см. Вычислить площадь ero полной повеРХНОСТJI,
сумму площадей оснований и площадь боковой поверхности.
2. Обозначив длину, ШИРJIНУ И высоту прямоуrольноrо параллелепипеда
через а, Ь и с, выразить в ВИде формулы: 1) сумму площадей оснований,
2) площадь боковой поверхности, 3) площадь полной поверхности.
3. Вычислить площадь полной поверхности прямой призмы, имеющей в ос-
новании параллелоrрамм, по следующим данным:
Основание Высота Вторая СТО- Высота
парал- па рап- . рона парал- S
лелоrрамма лелоrрамма лелоrрамма п ризмы
а) 1 О см 6 с-м I 8 с-м 25 см I
I
б) 8, 5 с-м 7 ,2 см 7 , 8 с-м 1 ,2 см
в) 12 см 0,5 м 0,7 м 35 см
4. Чисто обрезанная доска имеет в длину 6,5 11, ширина её 32 см, толщина
4 см. Вычислить площадь её полной поверхности.
5. Вычислить площадь полной поверхности вашей классной комнаты и её
боковую поверхность.
6. Вычислить площадь полной поверхности прямой призмы, основание ко-
торой имеет форму paBHocTopoHHero треуrольника со стороной в 8 см, а
высота призмы равна 20 см.
7. Вычислить площадь полной поверхности прямой призмы, основание ко-
торой имеет форму равнобедренной трапеции с параллельными сторонами
в 12 см и 9 см, высота трапеции равна 6 см, а высота самой призмы
р а R н а 1 А! 15 см.
8. Вычислить площадь полной поверхности прямой призмы, основание ко-
торой имеет <t;OPMY прямоуrольноrо треуrольника с катетами в 25 см и
18,1 см, а высота призмы равна 38 см.
9. Вычислить площадь полной поверхности моделей призм, имеющихся в ма-
тематическом кабинете школы, сделав преДfJарительно необходимые из-ме-
рения.
10. На плотной бумаrе начертить развёртку поверхности ,двух прямоуrоль-
ных параллелепипедов: с квадратным основани м и с основанием, име-
ющим форму прямоуrольника, и сделать из этих развёрток два пря..
моуrольных параллелепипеда.
11 На плотной бумаrе начертить развёртки поверхности призм с основа-
ниями в виде параллелоrрамма, трапеции, paBHocтopoHHero треуrоль
ника, прямоуrольноrо треуrольника, разностороннеrо треуrольника и
сделать из этих развёрток модели прямых призм.
121
65. ПОНЯТИЕ ОБ ИЗМЕРЕНИИ ОБЪ МQ8.
ДЛЯ изrvlерения объёмов тел ПОЛЬЗ.уются особыми мерами.
Такими мерами являются кубы, рёбра которых равны какой-
нибудь линейной мере: метру, дециметру, сантиметру, миллимет-
ру. Куб, ребро KOToporo равно какой-нибудь линейной единице,
называется кубической единицей: кубическим feTpoM, кубическим
u u u
дециметром и т. Д., В зависимости от Toro, какои линеинои мере
равняется ребро куба, принятоrо за единицу измерения.
Мы можем представить себе куб, ребро KOToporo равно кило-
l\feTpy, тоrда получается кубический километр.
Чтобы измерить объём какоrо-нибудь тела, надо узнать, сколь-
ко тех или иных кубических единиц содержится в этом теле.
В некоторых случаях объём можно определить непосредственно
опытным путём. Например, если нужно узнать, сколько кубических
дециметров воды или какой-нибудь друrой жидкости помещается в
некотором сосуде, достаточно взять полый кубический дециметр
и путём переливания узнать, скольким кубическим дециметрам рав-
няется объём (или, иначе, вместимость) измеряемоrо сосуда.
Однако измерить объём путём непосредственноrо опыта далеко
не всеrда возможно. Чаще Bcero объём rеометрическоrо тела при-
.. u
ходится устанавливать лишь путем вычислении на основании осо-
бых правил, выведенных для различных rеометричесн:их тел, имею-
щих ту или иную форму.
66. КУБИЧЕСКИЕ МЕРЫ.
1. Зависимость между метрическими мерами объёма.
Посмотрим, какая зависимость существует между кубическим
метром и кубическим дециметром. Если на основании кубическоrо
метра мы будем устанавливать кубические дециметры, то их в один
u
СЛОИ уложится столько, сколько
квадратных дециметров содержится в
основании куба, т. е. 10. 10 == 100
I<убических дециметров (черт. 304).
ВЬ1сота этоrо слоя будет равна одному
дециметру; чтобы заполнить кубиче-
скими дециметраl\fИ весь куб, нуж-
но будет заполнить 10 таких слоёв
по 100 кубических дециметров в
каждом, т. е. Bcero в кубическом мет-
ре уложится 10. 10 · 10 == 1000 ку-
бических дециметров. Таким обра-
зом, 1 'куб. метр== 1000 куб. деци-
метров. ЧЕРТ. 304
128
Так же мы можем вычислить, сколько содержится в кубическом
метре кубических еантиметров.
1 куб. метр == 100 · 100. 100 == 1 000 000 куб. сантиметров.
Рассуждая таким же образом, мы найдём, что:
1 куб. метр == 1000 · 1000 · 1000 == 1 000 000 000 куб. миллимет-
ров.
1 куб. дециметр == 10 · 10 · 10 == 1000 куб. сантиметров.
1 куб. дециметр == 100 · 100 · 100 == 1 000 000 куб. миллиметров.
1 куб. еантиметр == 10 · 10 · 10 == 1000 куб. миллиметров.
2. Объём куба.
Вообu е, если длину ребра куба мы обозначим через а, то, для
Toro чтобы вычислить ero объём, нужно длину ребра возвести
в куб, т. е. а · а · а. Получаем формулу:
l V == аЗ, rде v........ объём куба, а ........ ero ребро.
67. ОБЪ М прямоуrольноrо ПАРАЛЛЕЛЕПИПЕД1\.
1. ВЫВОД ФОРМУЛЫ объёма прямоуrольноrо пар8JIJIмепипеда,
измерения KOToporo выражены целыми числами.
Пусть оам нужно вычислить объём прямоуrольноrо паралле-
пепипеда, длина оенования KOToporo равна 20 см, ширина........ 12 см
и высота 5 см (черт. 305).
Площадь основания этоrо параллелепипеда будет равна 20 · 12 =:1
::::: 240 (кв. см). Значит, на ero основании в один слой можно уло.
жить 240 кубических сантиметров. Bcero таких слоёв будет пять.
Объём данноrо параллелепипеда будет равен 240 : 5 == 1200 (куб. см).
Если длину основания прямоуroльноrо параллелепипеда обоз-
начим через а, ширину ero........ через Ь и высоту параллелепипе-
да ........ через с, то получим формулу:
V==abc, rде V объём прямоуrоль-
Horo параллелепипеда
Произведение аЬ выражает площадь
основания прямоуrольноrо параллелепи-
педа, а с........ ero высоту. Следовательно,
в этом случае объём прямоуrольноrо
параллелепипеда равен произведению
площади ero основания на высоту.
При м е ч а н и е. Длина, ширина и вы.
сота параллелепипеда должны быть измерены
ОДНОЙ и той же мерой. ЧЕРТ. 305
t 5 н. Н. НИКИТИН
129
2. ВЫВОД формулы объёМ8 прямоуrольноrо, пар аJJJlмеп и педа,
измерения KOToporo выражены дробными числами.
Пусть нужно вычислить объём прямоуrольноrо параллелепипе.
да, у KOToporo все или некоторые измерения выражены дробными
числами. Например, длина равна 18,5 М, ширина 12,4 м, высо-
та 10,4 М. Выразим эти измерения прямоуrольноrо параллеле-
пипеда в дециметрах; тоrда длина данноrо параллелепипеда будет
равна 185 дм, ширина 124 дм, высота 104 дм, т. е. измерения
ero выразятся целыми числами. В таком случае объём V прямо-
уrольноrо параллелепипеда, как доказано, вычисляется по формуле
V == (185 · 124 '. 104) -куб. дм.
Чтобы объём выразить в кубических метрах, надо число, выра-
жающее объём в кубических дециметрах, разделить на число, по-
казывающее, сколько кубических дециметров составляют 1 куби-
ческий метр, т. е. на 103.
Получим:
V == ( 185. 124. 104 ) К б. м == ( 185 . 124 . ] 04 ) К у б. Af
1 У 10 lО 10 ......
== (18,5 · 12,4. 10,4) куб. М.
Таким образом, объём прямоуrольноrо параллелепипеда выра-
жается формулой V == аЬс и в том случае, коrда длина й, ширина Ь
и высота с выражаются дробными числами в единицах одноrо и
Toro же наименования.
Полученную формулу можно также записать в виде V == (аЬ) с;
аЬ выражает площадь основания параллелепипеда, поэтому полу-
ченная формула показывает, что
. Об'lJёж nРЯAlОУ20ЛЬН020 параллелеnипеда равен произве..
дению площади е20 основания на BblCOтy.
68. оБы!M ПРЯМОЙ ПРИЗМЫ.
1. Объём прямой треуrольной npизм,,
Пусть требуется найти объём прямой треуrольной призмы,
площадь основания которой равна S, а высота равна h == АА' ==
ВВ' == СС' (черт. 306).
Начертим отдельно основание призмы, т. е. треуroльник АВС
(черт. 307, а), и достроим ero до прямоуroльника, для чеrо через
вершину В проведём прямую КМ 11 АС и из точек А и С опустим на
ЕЛу прямую перпендикупяры AF и СЕ. Получим прямоуrольник
АСЕР. Проведя высоту BD треуrольника АВС, увидим, что пря-
моуrопьник АСЕР разбился на 4 прямоуroльных треуroльника.
Причём Ll ВСЕ == д BCD и д ВАР == д BAD. Значит, liпo-
180
щадь I1рямоуrольника ACEF вдвое
больше. площади треуrольника
АВС, Т. е. равна 28.
К данной rfризме с основанием
АВС пристроим призмы с основа-
ниями ВСЕ и ВАР и высотой h
(черт. 307, 6). Получим прямо-
уrольный параллелепипед с основа-
нием АСЕР.
Если этот параллелепипед рас-
сечём плоскостью, проходящей че-
рез прямые BD и ВВ', то увидим,
что прямоуrольный параллелепи-
пед состоит из 4 призм С основания-
ми BCD, ВСЕ, BAD и ВАР.
Призмы с основаниями BCD и
ВСЕ MorYT быть совмещены, так как
основания их равны ( BCD ==
== ВСЕ) и также равны их боко-
вые рёбра, являющиеся перпенди-
кулярами к одной плоскости. Зна-
чит, объёмы этих призм равны.
Также равны объёмы призм с ос-
нованиями BAD и ВАР.
Таким образом, оказывается,
что объём данной треуrольной
призмы с основанием АВС вдвое
меньше объёма прямоуrольноrо
параллелепипедз с основанием
ACEF.
Нам известно, что объём пря-
моуrольноrо параллелепипеда ра-
вен произведению площаДА ero ос-
нования на высоту, Т. е. в данном
случае равен 2Sh. Orсюда объём
данной прямой треуrольной приз-
мы равен 8h.
· ОбfJё.м. прямой mреуzо.льной
nрuзJныl равен произведению
площади e основания на вы..
соту.
2. Объём прямой мноrоуrольной
прнзмы.
Чтобы найти объём прямой
мноrоуrольной призмы, например
6*
д'
с'
в
Ч.1:.!JТ, З06
с
к F
д'
F'
в Е
м
(1)
D'
I
I
В' I
I
I
I
I
I
D 1
F
ЧЕ 1. 301
в Е
6)
131
ЧЕРТ. 308
Упражнения.
пятиуroльной, с площадью основания 3 и высотой h,
рззобьём её на треуrольные призмы (черт. 308).
Обозначив площади основания треуrольных лризм
через S f, 32 И S з, а объём данной мноrоуrольной
призмы через У, получим:
V == 8th + S2h + 8 з h,
или
V == (8. + 82 + 8 з )h.
И окончательно: V == Sh.
ТаКИl\1 же путём выводится формула объёма
прямой призмы, имеющей в основании любой мно.
rоуrольник. Значит,
. Объём любой пnя.мой nрUЗ./f/bl равен nроиз-
ведению площади её основания на высоту.
1. Вычислить объём прямой призмы, имеющей в основании параллелоrрамм, ПО
следующим данным:
Основание Высота Высота Объём
па ра-л- па рап- ПрИ3МЫ п риэм Ы
ле.лоrраммз лелоrрамма
а) зо с.м 8 САС 45 c.w
б) 17 ,5 см 6, 4 см 35 с.м
в) 6,5 .м 4,8 .м 10 АС
r) 4 ,8 дАС 35 САС 0,4 М
2. ВЫЧИCJ1ить объём прямой ПрIlЗМЫ, имеюа еЙ в основан ии треуrоЛЬНИК, по сле-
дующим данным:
Основание Высота Высота Объём
треуrольника .
треуrольника nризмы призмы
а) 1"8 с.м 9 см 20 c .
б) 0,7 АС О , 65 .м 1,2 АС
в) 0,65 АС 48 см 1,5' АС
З. Вычислить объём прямой призмы, имеющей в основании равносторон-
ний треуrольник со стороной в 12 САС (32 СМ, 40 см). Высота призмы 60 САС.
4. Вычислить объём прямой призмы, имеющей в основании прямоуrольный
треуroльник с катетами в 12 см и 8 см (16 САС и 7 см; 9 м и б АС). Высота
призмы 0,3 .м.
б. Вычислить объём прямой приэмы, имеющей в основании трапецию с па-
ралле.льными сторонами в 18 см и 14 (JI н высотой В 7,5 C4t. Высота приэ-
мы 40 см.
6. Вычислить объём вашей классной комнаты (4ИЗJ<ультурноrо зала, своей
комнаты) .
132
7. Полная поверхность куба paB
на 150 см 2 (294 см', 864 с.м 2 ).
ВЫЧИСJlИТЬ объём этоrо куба.
8. Длина строительноro кирпи
ча 25,0 СМ, ширина ero
12,0 СМ, толщина 6,5 см.
а) Вычислить ero объём.
6) Определить ero вес, если
1 кубический сантиметр кир-
пича весит 1,6 е.
9. Сколько штук строительноrо
кирпича потребуется для по-
стройки сплошной кирпичной
стены, имеющей форму пря
моуrольноrо параллелепипе-
да, длиной 12 АС, шириной
0,6 АС и высотой 1 О.м? (Разме-
ры кирпича взять из упраж
нения 8).
10. Длина чисто обрезанной ДОС-
ки равна 4,5 АС, ширина
35 см и толщина 6 см.
а) Вычислить её объём. б) Оп-
ределить её вес, если 1 ку-
бический дециметр ДОСКИ ве-
сит 0,6 ке.
11. Сколько тонн сена можно
уложить в сеновал, покры-
тый двускатной крышей (черт.
3(9), если длина сеновала
равна 12 АС, ширина 8 АС, высота..... 3,5 .м и высота конька крыши равна
1,5 АС? (Удельный вес сена принять за 0,2).
12. Требуется выкопать канаву длиноЙ 0,8 км; в разрезе канава должна иметь
форму трапеции с основаниями в 0,9 АС и 0,4 .м, и rлубина канавы ДОJlжна
равняться 0,5 ! (черт. 310). Сколько кубометров земли придётся при ЭТОМ
вынуть?
ЧЕРТ I 309
......
ЧЕРТ. 3]0
rпABA VII
ОИI8УНlНОСТЬ 11 ир r. ЦИJlИНДР.
f 69. ПОСТРОЕНИЕ ОКРУЖНОСТИ ПО TP M ДАННЫМ ТОЧ КАМ.
З а Д а ч а. Через три точки, не лежащие на одной прямой, про.
вecпlU окружность.
Пусть нам даны три точки А, В и С, не лежащие на одной пря.
мой (черт. 311). Соединим эти точки отрезками АВ и ВС. Чтобы най.
ти точки, равноудалённые от точек А и В, разделим отрезок АВ
пополам и через ero середину (точку М) проведём прямую, пер-
пендикулярную к АВ. Каждая точка этоrо перпендикуля'ра оди-
наково удалена от точек А и В ( 27, п. 4).
Чтобы найти точки, равноудалённые от точек В и с, разделим
отрезок БС пополам и через ero середину (точку N) проведё 1 пря.
мую, перпендикулярную к ВС. Каждая точка этоrо перпендику.
ляра оди аково удалена от точек В и С.
Точка О пересечения этих перпендикуляров будет находиться
на одинаКОВО 1 расстоянии от данных точек А, В и С (А О == ВО ==
== СО). Если мы, приняв точку О за центр Kpyra, радиусом, рав-
ным АО, проведём окружность, то она пройдёт через все данные
точки А, В и С.
Точка О является единственной точкой, которая может служить
центром окружности, проходящей через три точки А, В и С, не
лежащие на одной прямой, так как два пер-
пендикуляра к отрезкам АВ и ВС MorYT пе-
ресечься только в одной точке. Значит, зада
ча имеет единственное решение.
При м е ч а н и е. Если три точки А.
В и С будут лежать на одной прямой, то за-
дача не будет имеТI? решения, так как пер-
пендикуляры к отрезкам АВ и ВС будут
параллельны и не будет существовать точ-
ки, одинаково удалённой от точек А, В,
С, т. е. точки, которая моrла бы служить
центром искомой окружности.
Если соединить отрезком ТОЧI{И А и С и середину этоrо отрезка
(точку К) соединить с центром окружности О, то ОК будет перпен-
дикулярна к АС (черт. 311), так как в равнобедренном треуrоль.
нике АОС ОК является медианой, поэтому ОК АС.
, I
.-- *..
..... ..... ....L ...... -:.... С
, I К', /
'')IM N>/
" /
,
ЧЕРТ. 311
134
С л е д с т в и е. Три nерnендшеуД,яра 1(, cтOPOHQ,.Af, тре-
уzольнuяа, nроведенные через их серединь" nересе"а-
ются в одной точ"е.
70. ДИАМЕТР, ПЕРПЕНДИКУЛЯРНЫЙ К ХОРДЕ.
. Т е о р е м а 1. Диаметр, nерпендияулярныii " .хорде, де..
лит эту хорду и стяzиваемые ею дуzи пополам.
Пуеть диаметр АВ перпендикулярен к хорде CD (черт. 312).
Требуется доказать, что СЕ == ED,
vCB == vBD, vCA == vDA.
Соединим точки С и D с центром ок-
ружности о. В равнобедренном треуrоль-
нике COD отрезок ЕО является высотой,
проведённой из вершины О на основание
CD; следователЬНО,ОЕ является и медиа-
но й и биссектрисой, т. е. СЕ == ED и,
L 1 == L 2. .
Но L 1 и L 2 суть централnные
уrлы.
Отсюда равны и соответствующие им
дуrи, а именно vCB == v BD. Дуrи СА
и DA также равны между собой, как
дополняющие равные дуrи по полуокружности.
. т е о р е м а 2 (обратная). Диаметр, nроведённыii через се..
редину хорды, не nроходяu еii через цеНlпр, перnендlШУ--
лярен, " ней и делит дУZll, Сlпяzива!!мые хордой, пополам.
Пусть диаметр АВ делит хорду CD пополам. Требуется дока-
зать, что АВ J.... CD, vCB == vBD и v СА' == v AD (черт. 313).
Соединим точки С и D с центром кру-
ra. Получим равнобедренный треуrОЛЫ-IИI{
COD, в котором ОК является медианой,
а значит, и высотой. Следовательно,
А BJ....CD, а отсюда (по теореые 1) следует,
что vCA == vAD; vCB == \ /BD.
. Т е о р е м а 3 (обратная). ДиаАlепtр, 11pO-
ведённый через сеuедину д)'zu, делит
пополам хорду, стяzuваЮЩУ10 эту
дуzу, и nерпендllJ(,улярен " Эlпой
хорде.
Пусть диаметр АВ делит дуrу CBD
пополам (черт. 313). Требуется доказать,
что СК == KD и АВ J.... CD.
Соединим центр Kpyra О с точкаТ\1И С и D. В равнобе)I.ренном
треуrольнике COD отрезок ОК является биссектрисой уrла COD,
так KaJ{ по условию TeOpel\'lbI vCB==vBD, поэтому ОК будет и ме..
дианой и высотой Э"тоrо треуrолъника. Следовательно, диаметр
АВ проходит через середину хорды и 'перпендикулярен к ней.
д
ЧЕРТ. 312
д
в
ЧЕРТ. 313
135
f 71. ЗАВИСИМОСТЬ МЕЖДУ ХОРДАМИ И дУrАМИ.
Докажем ряд теорем, устанавливающих зависимость между
u u
хордами и их дуrами в ОДНОIl и тои же окружности или в равных
окр ужностях.
При этом будем иметь в виду дуrи, меньшие полуокружности.
. Теорема 1. Равнь/,е дуzu стяzu-
ваюmся равными ХО,йда.ми.
Пусть дуrа АВ равна дуrе СК. Тре-
буется доказать, что и хорда АВ равна
хорде СК (черт. 314).
Д о к а з а т е л ь с т в о. Соединим
концы хорд с центром окружности
точкой о. Полученные треуrольники
АОВ и КОС равны, так как имеют по
две соответственно равные стороны (ра-
диусы одной окружности) и по ,равно-
му уrлу, заключённому между этими сто-
рона1\1И (эти уrлы равны как централь-
ные, соответствующие равным дуrам). Следовательно, АВ == СК.
. т е о р е м а 2 (обратная). Равные хорды сmяzuвают рав-
нью дуzu.
Пусть хорда АВ равна хорде СК.
Требуется доказать, что дуrа АВ равна дуrе СК (черт. 314).
Д о к а з а т е л ь с т в о. Соединим концЬ! хорд с центром ОК-
ружности точкой о. Полученные треуroльники АОВ и. КОС
равны по трём соответственно равным сторонам. Следовательно, рав-
ны уrлы АОВ и СОК; но уrлы эти центральные, соответствующие
дуrам АВ и СК; из равенства этих уrлов следует равенство дуr:
v АВ == v СК.
. т е о р е м а 3. Большая д,zа Сnl,яzивается и большей
хордой.
Пусть дуrа АВ больше дуrи СК (черт. 315).
Требуется доказать, что хорда АВ
больше хорды СК.
Д о к а 3 а т е л ь с т в о. Пере-
двинем по окружности дуrу СК так,
чтобы точка К совместил ась с точкой
А, тоrда точка С займёт положение
С' на дуrе А В между точками А и В,
дуrа СК примет положениедуrи АС',
а хорда СК примет положение хорды
АС'. Проведём радиусы в точки А,
В и С'. Опустим из центра О перпен-
Дикуляры ОЕ и OD на хорды АВ и
АС'. В треуroльнике аРЕ от-
резок ОЕ катет, а отрезок
к
-8
ЧЕРТ. 315
136
8
ЧЕРТ. 311
ОР rипотенуза, поэтому OF > ОБ, а значит, и OD > ОЕ.
Рассмотрим теперь треуrольники ОАDи ОАЕ. В этих треуrоль..
никах rипотенуза ОА общая, а катет ОЕ меньше катета OD, тоrда
по следствию из теоремы Пифаrора ( 58) катет АЕ больше катета
AD. Но эти катеты составляют ПОЛОВИНbI хорд АВ и АС', значит,
и хорда АВ больше хорды АС'. Вследствие равенства хорд АС'
и СК получаем АВ > СК. ,
. Теорема. 4 (обратная). Большая хорда сmяzuваеm и
большую дуzу.
Пусть хорда АВ больше хорды СК.
Требуется доказать, что дуrа АВ больше дуrи СК (черт. 315).
Между дуrами АВ и СК может существоват? только одно из
трёх следующих соотношений:
v АВ < v СК;
v АВ == v СК;
vAB> v СК.
Но дуrа АВ не может быть меньше дуrи СК, так как тоrда по
прямой теореме хорда АВ была бы меньше хорды СК, а это проти-
.Боречит условию теоремы.
Дуrа АВ не может быть равна дуrе СК, так как тоrда хорда
А8 равнялась бы хорде СК, а это тоже противоречит условию.
Следовательно, v АВ > v СК.
72. СВОЙСТВО дУr,
3АКЛЮЧ ННЫХ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ХОРДАМИ.
.
. т е о р е м а. Дуzи, за"люч,ённые JНежд, параллельны.ми
xopдa.мu, равны.
Пусть хорда АВ параллельна хорде CD (черт. 316). Требуется
доказать, что v АС == v BD. Проведём М
диаметр MN АВ. Так как CD 11 АВ,
то MN CD. Переrнём чертёж по диа-
метру MN так, чтобы правая часть совпа-
ла с левой.
Тоrда точка В совпадёт с точ кой А, так
как они симметричны относительно оси
NM (АВ MN по построению и АК ==
== КВ).
Аналоrично точка D совпадёт с точкой N
С. Orсюда vAC == v BD. ЧЕРТ. 316
9 73. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ.
1. Возможны следующие три случая взаимноrо положения
прямой и окружности:
131
в
' d J
'у
,..
к
ЧЕРТ. 3 I 7
ЧЕРТ. 318
ЧЕРТ. ЗJ9
1) Прямая не имеет е окружностью ни одной общей точки
(черт. 317).
2) Прямая е окружностью имеет только одну общую tочку
(черт. 318).
..Прямая, имеющая е окружностью только одну общую точку,
называется к а е а т е л ь н о й к окружности.
3) Прямая имееr е окружпоетью две общие точки (черт. 319).
Такая прямая называется е е к у щей.
2. Теоремы о касателыIйй к окружности.
. Теорема 1. ПРЯм'ая, nеrJпен/Jи. УЛJ:,DнаJl, " радиусу 8
"Оllечн,ой ezo' точ"е, лежащей на о"ружн,ости, Яд-
.,
ляется "асательнои " о"ружн,ости.
Пусть ОМ радиус окружности, CD ОМ (черт. 318).
Требуется доказать, что CD каеательная к окружности.
Д о к а з а т е л ь е т в о. Если ОМ CD, то расстояние от
центра О до любой друrой точки прямой CD больше радиуеа ОМ,
следовательно, всякая точка прямой CD, кроме точки М, лежит
вне Kpyra. Поэтому точка М единетвенная общая точка прямой
CD и окружности, а это означает, что CD касательная к окруж-
ноети.
· т е о р е м а 2 (обратная). Касаlllельная " о"ружности
перnенди"улярн,а " радиусу этой о"ружн,осmu, nрове-
денн,о.му в mочяу "асан,ия.
Пусть прямая CD ......... касательная к окружности и М точка
касания.
Требуетея доказать, что CD ОМ (черт. 318).
Д о к а 3 а т е л ь с т в о. Еели прямая CD каеаетея окружности
в точке М, то веякая друrая точка прямой CD будет находиться
u
вне Kpyra, оrраниченноrо это и окружностью, следовательно, рас-
стояние от каждой точки прямой CD дО центра, кроме ТОЧI{I1 М,
будет больше расетояния ОМ радиуса окружности. Значит,
этот радиуе есть наименьший из отрезков, еоединяющих точку О
с точками прямой CD, поэтому ОМ CD.
138
3. Свойство дуr,
заключённых .между касатеJlЬНОЙ и параллельной ей хордой.
. т е о р е м а. Дуzu, за"люч, нные .между касательно;;' и
параллельн,ой ей хордой, равны.
Пусть касательная А В и хорда СО параллельны. Точка Е
точка касания прямой АВ с окружностью О (черт. 320). Требуется
доказать, что vCE == vED. Для доказательства соединим точку
касания Е с центром Kpyra.
ОЕ АВ, а так как CD 11 АВ, то ОЕ CD, а перпендику.
.. U U
ляр к хорде, проведенныи из центра тои же окружности, делит
стяrиваемую ею дуrу пополам. Следовательно, v СЕ == v ED.
4. Построение касательной Д 8
к окружности.
З а Д а ч а. Построить прямую, ка-
сапzельную к окружности в данной её
точке .
Дана окружность О, требуется про- О
вести прямую, касательную к этой ок-
ружности в точке М (черт. 321).
Проведём радиус ОМ и через конеч-
ную ero точку М проведём прямую
КМ, перпендикулярную к радиусу. ПО ЧЕРТ.. 320
доказанному paH прямая КМ будет
касательной к окр'ужности.
t 74. ВЗАИМНОЕ ПОЛОЖЕНИЕ
ДВУХ ОКРУЖНОСТЕА.
Прямая, проходящая через центры
u u
двух окружностеи, называется л и н и е и
Ц е н т ров.
Рассмотрим взаимное расположение
u
двух окружностеи.
1.0кружности не имеют
о б щей т о ч к и.
а) Окружности лежат одна вне друrой.
В ЭТО f случае расстояние между
центрами больше суммы радиусов:
00' > R + , (черт. 322).
б) Одна окружность лежит внутри
u
друrои.
В этом Случае расстояние между
центрами меньше разности радиусов:
00' <R , (черт. 323), так как R '==
00' + м N.
ЧЕРТ. З2[
ЧЕРТ. J22
139
2. О к Р у ж н о е т и и м е ю т т о л ь к о о Д н у о б щ У ю
точку. .
Такие окружности называются касающимися. В этом случае
точка касания лежит на линии центров и расстояние между цент-
рами равно:
а) cYM?vle их радиусов: 00' == R + r (внешнее касание, черт.
324) ;
б) разности их радиусов: 00' == R r (внутреннее касание,
черт. 325).
3. О к р у )к Н О е т и пер е с е к а ю т с я (черт. 326).
В этом случае расстояние между центрами меньше суммы ради-
усов и больше их разности:
00' < R + " 00' > R , (Э 16).
Справедливы и обратные предло-
жения:
1) если 00' > R + r или
00' < R " то окружности не име-
ют общей точки;
2) если 00' == R + r или 00' ==
=== R " то окружности касаются;
З) если 00' < R + , и
00' > R ', то окру}кности пере-
секаются.
Все предложения, изложенные
в 74, даны без доказательства. Они
MorYT быть cTporo доказаны, как и
друrие предложения.
ОКРУ)I{НОСТИ, имеющие общий
центр, называются к о н ц е н т р и-
ч е е к и м и. При равных радиуеах
они СОВ 1ещаются, при различных ра-
диусах не имеют ни одной общей
точки (черт. 327).
ЧЕРТ. 323
ЧЕРТ. 324
140
ЧЕРТ. 325
ЧёРТ, 326
Ч1:Рl. 321
75. свойство КАСАТЕЛЬНЫХ, ПРОВЕДЕННЫХ К ОКРУЖНОСТИ
из ОДНОЙ ТОЧ КИ.
. т е о р е м а. Если из "a"Oli-нибудь то",,," провести две
касательные 1(, окружности, то их отрезки О"' дан-
ной то",ки до точе1(, касания равны .между собой "
центр окружности находится на биссе1(,.""рисе уzла,
образованноzо этU.Аlи "асаlnельны,.ми.
Пусть АВ и АС касательные к окружности О (черт. 328).
Требуется доказать, что АВ == АС и
ОА является биссеI{ТРИСОЙ уrла А
Т. е. L 1 == L 2.
Треуrольники аВА и ОСА прямо-
уrольные, так как касательные АВ и
АС перпендикулярны к радиусам 08 и
ОС в точках В и С. Сторона ОА общая.
Катеты ОВ и ОС равны, как радиусы
одноrо и Toro же Kpyra. Прямоуrоль-
ные треуrольники аВА и ОСА равны
по rипотенузе и катету. Orсюда АВ ==
== АС и L 1 == L 2, т. е. ОА есть биссек-
триса уrла'. А.
На этом свойстве касательных основа..
но устройство прибора, называемоrо ц е н..
v
т р о и е к а т е л е м, которыи нередко
прим няется в столярных и слесарных мас-
терских для отыскания центра Kpyra на
различных деталях. Центроискатель
(черт. 329) представляет собой уrол, со-
ставленный из двух деревянных или ме-
таллических пластинок, в котором приде-
лана биссектриса этоrо уrлз.
Центроискатель прикладывают к КРУ-
ry так, чтобы пластинки стали касательными, и проводят пря-
мую по биссектрисе уrла. Затем центроискатель поворачивают И
снова проводят прямую по биссектрисе уrла. Точка пересечения
этих двух прямых и определит центр Kpyra.
д
ЧЕРТ. 328
1/
1,
r'
,
1\ I
l' I ./
I '" .t-. .... ...... .......
ЧЕРТ. 329
76. ВПИСАННЫЕ И НЕКОТОРЫЕ друrИЕ уrлы.
1. Вписанный уrол.
Уrол. вершина KOToporo. находится на окружности, а сторон..
являются хордами, называется вписанным.
Уroл АВС вписанный уroл. Он опирается на дуrу АС, за-
КJIючённую между ero сторонами (черт. 330).
141
. т е о р е м а. Вписанный уzол UЗJНеряется половиной д,-
ZU, на "оторую он опирается.
Это надо понимать так: вписанный уrол содержит столько уrло..
вых rрадусов, минут и секунд, сколько дуrовых rрадусов, минут
и секунд содержится в половине дуrи, на которую он опирается.
При доказательстве этой теоремы надо рассмотреть три случая.
Пер вый с л у чай. Центр Kpyra лежит на стороне вписан..
Horo yr ла (черт. 331).
Пусть L АВС вписанный уrол и центр Kpyra О лежит на
стороне ВС. Требуется доказать, что он измеряется половиной ду.
rи А С. .
Соединим точку А с центром Kpyra. Получим равнобедренный
Ь АОВ, в котором АО == ОВ, как радиусы одноrо и Toro же Kpyra.
Следовательно, L А == L В. L АОС является внешним по отно-
шению к треуrольнику АОВ, \ поэтому L АОС == L А + L в
1
( 39, п. 2), а так как уrлы А и В равны, то L В составляет
2
L АОС.
Но L АОС ИЗ Iеряется дуrой АС, следовательно, L В измеря-
ется половиной дуrи АС.
Например, если v АС содержит 60018', то L В содержит 3009'.
В т о рой с л у чай. Центр Kpyra лежит между сторонами
вписанноrо уrла (черт. 332).
Пусть L ABD вписанный уrол. Центр Kpyra О лежит между
ero сторонами. Требуется доказать, что L ABD измеряется поло-
виной дуrи AD.
ДЛЯ доказательства проведём диаметр ВС. Уr.ол ABD разбился
на два уrла: L 1 и L 2.
L 1 измеряется половиной дуrи АС. а L 2 измеряется полови-
ной дуrи CD, следовательно, весь L А BD измер яется v А С +
2
+ v CD, т. е. половиной дуrи AD. Например, если v AD со-
2
держит 1240, то L В содержит 620.
8
д
ЧI:::.Pi. ЗJO
14
в
с
ЧЕРТ. ЗJl
ЧЕРТ. 332
д
м
8
ЧЕРТ. 333
в
а)
с
о)
ЧЕРТ. з:н
т р е т и й с л у чай. Центр Kpyra лежит вне ВПkсанноro
уrла (черт. 333). Пусть L MAD вписанный уrол. Центр Kpyra
О находится вне уrла. Требуется доказать, что L MAD измеряет-
ся половиной дуrи MD.
Для доказательства проведём диаметр АВ. L MAD==LMAB......
1
L DAB. Но L МАВ измеряется v МВ, а L DAB измеря-
2
1 1
ется v DB. Следовательно, L MAD измеряется...... (v мв
2 2
1
...... v DB), т. е...... v MD. Например, если v MD содержит
2
48°38'16", 1'0 L MAD содержит 24°19'8".
С л е Д с т в и я. 1" Все вписанные УZЛЫ, оnu.рающu.еся на
одну и ту же дуzу, равны .между собой, так как они изме-
ряются половиной одной и той же дуrи (черт. 334, а).
2. Вписанный УlОЛ, опирающu.йся на диаметр, --- пря-
мой, так как он опирается на половину окружности. Половина
окружности содержит 180 дуrовых rpaдYCOB, значит, yrOJI, опи-
рающийся на диаметр, содержит 90 уrловых [радусов (черт. 334, 6).
2. Уrол, образованный касательной и хордой.
е Т е о р е м а. У zол, образованный
касательной и хордой, из.меряет-
ся половиной дуzи, за"лючённой
.Аtежду ezo сторона.ми.
Пусть L САВ составлен хордой СА и
касательной АВ (черт. 335). Требуется
доказать, что он измеряется полови-
ной vCA. Проведём через точку С пря-
мую CD U АВ. Вписанный LACD измеря-
8
с
ЧЕРТ. ззь
148
!J
ЧЕРТ. 336
fVI
б)
ЧЕРТ. 337
ется ПОЛОВИНОЙ дуrи AD, но v AD ::=: vCA, так как они заКЛЮJtены
между касательной и параллельной ей хордой. Следовательно,
L DCA измеряется половиной дуrи СА. Так как данный L СА В :==
== L DCA, то и он измеряется половиной дуrи СА.
Упражнения.
1. На чертеже 336 найти касательные к окружностям блоков.
2. По чертежу 337,а доказать, что уroл АВС измеряется полусуммой дуr
АС и DK.
3. По чертежу 337,6 доказать, что уrол АМ В измеряется полуразностью
дуr АВ и СЕ.
4. Через точку А, лежащую внутри Kpyra, с помощью чертёжноro треуrоль-
ника провести хорду так, чтобы она в точке А раздепилась пополам.
5. С помощью чертёжноro треуrольника разделить дyry на 2, 4, 8, .. равныХ!
частей.
6. Описать данным радиусом окружность, проходящую через две данные точки.
Сколько решений имеет задача?
7. Сколько окружностей можно провести через данную точку?
77. ДЛИНА ОКРУЖНОСТИ.
В ряде случаев длину окруж-
ности можно определить непос-
редственно измерением. Напри-
мер, чтобы узнать, чему равна
длина окружности ведра, стака-
на (черт. 338, rде окружности
обозначены пунктиром), нужно
окружность обвести шнуром,
затем выпрямить ero и измерить
полученный отрезок. Но таким
образом измерить длину окруж-
144
ЧЕРТ. зза
ности не 8сеrда возможно. Обыкнозенно длину окружности
определяют по длине диаметра (или радиуса).
Проделайте такой опыт. Измерьте длину какой-нибудь окру>к"
ности и её диаметр. Затем узнайте, во сколько раз длина окружности
больше длины cBoero диаметра, т. е. найдите отношение окружности
к своему диаметру. Проделайте это несколько раз, беря различные
ОI(РУЖНОСТИ. У вас всеrда отношение окружности к своему диаметру
бvдет больше 3 и меньше 4. Точные вычисления показали, что это
о;'ношение выражается беско»ечной непериодической десятичной
дробью 3,141592... .
Число, показывающее отношение окружности к своему диаметру,
соrласились обозначать rреческой буквой 1[ (пи).
Обыкновенно при вычислениях длины окружности оrраничива..
ются сотыми долями И принимают 1[ 3,14.
Если длину ОКРУЖНОСТИ обозначить БУI{ВОЙ С, диаметр бук..
вой D, радиус буквой " то получим для вычисления длины ок-
ружности такую формулу: С == D1[, или С == 2r1[. Обыкновенно при-
нято писать: С == 1f.D, или С == 21[r.
Упражнения.
1. Вычислить длину окружности, если D == 10 си (20 см, 4 м, 0,5 м).
2. Вычислить длину окружности, если, == 15 СА! (75 м,и, 3 м, 0,2 A-t).
З. Длина окружности равна 628 .мм (9,42 ..4t). ВЫЧIIСЛИТЬ её диаметр и радиус.
4. Диаметр колеса автомобиля равен 0,75 м. Какое расстояние прошё.,'1 аnтомо-
биль, если ero колесо сделало 2000 оборотов?
5. Деталь, имевшая в поперечнике 160 мм, при обработке на токарном стаJl"
ке делала 300 оборотов в минуту. Вычислить первоначальную скорость ре-
зания этой детали в секунду.
6. Сосна на высоте 0,5 м от повеРХIiОСТИ земли имела в ОКРУЖ:1I0СТИ 280 СМ.
Вычислить её толщину (диаметр) на этой высоте.
78. ДЛИНА дуrи в пО.
Чтобы найти длину дуrи в пО, надо сначала определить длину
дуrи в 10, для чеrо длину окружности разделить на 360, а затем по
лученный результат У IНОЖИТЬ на n.
2лrп Л,rп
Получаем формулу: 1 == == , rде 1 ----- длина дуrи.
360 180
79. ПЛОЩАДЬ KPyrA.
Разделим окружность на возможно большее число равных час..
теЙ'I,все."полученные точки деления еоединим с центром окружно-
сти, а соседние друr с друrом хордами.
Таким образом ПОЛУЧИ f ряд равных равнобедренных треуrоль..
ников (черт. 339).
ah
Площадь каждоrо треуrольника равна , rде а....... основа-
, 2
ние ero, h высота. Сумма площадей всех треуrольников составит
6 н. Н. НИКИТИН
146
ЧЕРТ. 339
ah ап/l
.n == . При большом числе делений
2 2
сумма площадей треуrольников становится
весьма близкой к площади Kpyra, сумма сс-
нований aп K длине окружности С, а высо-
та h I{ радиусу Kpyra '.
Поэтому
аn/l С, 2лr · r 2
== == nr .
2 2 2
С увеличением числа делений (n) точность этоrо равенства
можно сделать еколь .уroдно высокой. На еамом деле, можно
считать, ЧТО
s == 1tr 2 ,
rде S --....а площадь Kpyra.
CTporoe обоснование подобных рассуждений, содержащих «пере-
ход К пределу» при неоrраниченном возрастании числ.а п, даётся
в етарших классах.
УпражнениR.
1. Вычислить площадь Kpyra, если ето радиус равен 5 см (35 см, 3 м, 0,5 м,
150 ММ).
2. Вычислить площадь Kpyra, если диаметр ero равен 20 см (15 см, 200 ММ,
2 М, 0,4 М).
з. Длнна окружности крута 94,2 СМ. Вычислить площадь этоro Kpyra.
4. Длина окружности цилиндра в машине равна 628 .мМ. Вычислить площадь
поршня для этоrо цилиндра.
Сектором называется часть Kpyra, or-
раниченная двумя радиусами и дуrой. На
чертеже 340 сектор АОВ заштрихован.
Чтобы найти площадь сектора, дуrа
KOТOporo содержит пО, надо площадь кру-
ra разделить на 3600 и полученный ре-
зультат умножить на n.
П Ф S Пf"2п S
олучаем ормулу:, 360 ' rде ....... площадь
Обозначив
I 80. ПЛОЩАДЬ С.ЕКТОРА.
Н6
".
в
ЧЕРТ. 340
сектора.
т==
180
длину дуrи, стяrивающей сектор, можно формулу для площади
сектора записать в виде
I
S == mr.
2
81. ЦИЛИНДР.
1. Образование ци.rJ.I:ндра.
в окружающей нас действительности встречается MHoro пред-
метов, имеющих форму цилиндра, например ведро (черт. 341), кон-
сервная банка (черт. 342), пенал (черт. 343), кусок проволоки Kpyr..
лоrо сечения и т. д. .
Цилиндр может быть образован вращением прямоуrольника
BOKpyr одной из ero сторон (черт. 344, 345).
--- --- ....
'" "
" ,/
I ...... ......
I
I
I
I .....
t"
'...... ......-#fI#
ЧЕРТ. 341
ЧЕРТ _ 342
ЧЕРТ 343
ЧЕРТ 344
Цилиндр- имеет два. основания, которые являются круrами, и бо-
ковую поверхность, которая называется Ц и л и н Д р и ч е с к о й
поверхностью (черт. 346).
.-.- ..........................
,..- .........
./ "
,
"-.. ./
I " --.... .-.-. ",
I ....... .... .....
.......- ---. ......
.-.-. ,
v/ ,
\ /
" .",-"
...... ...... .... ."..
.
Оснобанuе
ЦUlIuндричеСКЙR
поберхнос то
.....- --- ...... ......
,,'" '"
I '\
Оснобоние
ЧЕРТ 345
ЧЕРТ". 346
6*
141
2пr.h
h
ЧЕРТ. 347
ЧЕРТ. 348
2. Развёртка поверхности цилиндр
Если боковую поверхность цилиндра развернуть и положить
11а плоскость, то получим прямоуrольник (черт. 347). .
Развёртка полной поверхности цилиндра состоит из прямоуrоль-
ника, длина KOToporo равна длине окружности основания цилинд-
ра, а высота высоте цилиндра, и двух KpyroB (черт. 348).
3. Площадь поверхности цилиндра.
Площадь каждоrо основания цилиндра paBHa1tr 2 , площадь обоих
оснований составит 2пr 2 (9ерт. 348).
Площадь боковой поверхности цилиндра равна площади прямо-
уrольника, основание Koтoporo равно 2лr, а высота равна высоте
цилиндра h, т. е. 21trh.
Полная поверхност ь цилиндра составит: 2пr + 21trh ==
== 23tr (, + h).
Упражнения.
). Радиус основания цилиндра равен 8 с..и, высота ero 20 CJI. Вычислить:
а) сумму площадей ero оснований,
б) площадь ero ооковой поверхности,
в) полную поверхность цилиндра.
2. Водосточная труба имеет в поперечнике 20 CJI, её длина 12 AI. Сколько
пистов оцинкованноrо же.пеза нужно заroтoвить для такой трубы, ec
.ли площадь каждоrо листа равна 2 кв. AI, а отходы при работе составля-
ют 10% заroтoвленноro железа?
з. Сколько пистов белой жести потребуется на устройство цилиндрическоro
бака с крышкой, есЛИ радиус основания бака должен быть 0,40 АС, 3 вы-
сота бака 0,75..и? На отходы при работе требуercя добавить к площа-
ди поверхности бака 5%.
Площадь одноrо писта белой жести равна 1,8 ка. АС.
... Выполнив необходимые измерения, вычилить боКОВУЮ н ПОЛНУЮ поверх-
ности модели 11.ИJJИ н.цра , ИNеющеrосв в математическом кабинете ш.копы.
148
4. Объём цилиндра.
Объём цилиндра ВЫЧИСЛЯIОТ по той же фор..
муле, что и объём прямой призмы, Т. е. для вы..
числения объёма цилиндра площадь ero основа..
ния (11:,2) умножают на высоту h.
V ци.'1индра' == 11:,2. Il.
Получение формулы объё fа цилиндра мо}кно
пояснить таким рассуждением. Пусть дан ци-
линдр, впишем в Hero ПРЯl\.IУЮ призму,
Т. е. построим внутри цилиндра такую ПРЯl\lУЮ
лризму, основаниями котороЙ служат 1\1 Horo-
уrольники, вписанные в основание цилиндра
(черт. 349). Вершины таких мноrоуrольников
л жат на окружностях оснований цилиндра. Объём (V') этой приз--
мы выразится формулой: V' == 8'h, rде 8' площадь основан я
призмы, h высота призмы. Если при ЭТО!\1 за основание призмы
взять мноrоуrольник с очень большим ЧИСЛО f очень малых сто..
рон, то площадь основания призмы будет весьма мало отличаться
от площади Kpyra, служащеrо основанием цилиндра, а объём
призмы будет весьма мало отличаться от объёма цилиндра. Если
пренебречь этими различиями в размерах, то объём цилиндра (V)
выразится следующей формулой: V == Sh, rде 8 площадь осно"
вания цилиндра, 11 ero высота.
Заменив 8 через л,2, rде r радиус основания цилиндра, по-
лучим формулу объёма цилиндра:
. V == '1tr 2 h.
При м е ч а н и е. В формуле V == Sh поставлен знак точноrо, а не
приближённоrо равенства, хотя на основании проведённоrо рассуждения мы
моrли бы ero ечитать приближённым, но в старших классах средней школы
доказывается, что р апеНСТ80 V == Sh точное, а не приближённое.
Упражнения.
1. Вычислить объём цилиндра, если диаметр ero основания равен 16 см,
а высота цилиндра равна 25 см.
2. колько кубических дециметров (литров) воды помещается в баке, имею-
щем форму цилиндра, если радиус основания ero равен 30 см, высота
равна 0,6 м?
3. Бревно имеет цилиндрическую форму. Диаметр ero основания равен
ЗА см. Длина бревна 7,2 М. Сколько кубометров древесины содержи'I'
это бревно? .
4. Цистерна для молока имеет цилиндрическую форму. Диаметр основания
её равен 1,2 м. Длина цистерны 2 м. Сколько литров молока может
вместить эта цистерна?
5. Сколько весит стальной вал цилиндрической формы, если радиус ero ос-
ования равен 75 мм, а длина 1,6 АС и если кубический дециметр ero
весит 7,8 KZ?
6. Вычислить объём модели цилиндра, имеющеrося в ШI{ОЛЬНОМ математи-
ческом кабинете.
7. Вычислить объём ведра, употребляемоrо в домашнем хозяйстве и иыеlО-
щеrо форму цилиндра.
\
,
l'
I
I
I
1
I
I
ЧЕРТ. 349
rЛАВА VIII
ПРОПОРЦИОНАПЬНОСТЬ ОТРЕЗКОВ.
ПОДО&ИЕ Фиrур.
82. ОТНОШЕНИЕ ОТРЕЗКОВ.
1. Определение.
Отношением двух отреЗКОII называется отношение тех чисел,
которые выражают ДJlИНЫ этих отрезков, при условии, что отрезки
измерены единицами одноrо наименования.
В арифметике отношением одноrо числа к друrому называетея
чаетное от деления первоrо числа на второе, поэтому можно ека-
зать, что отношением одноrо отрезка к друrому является частное от
деления длины первоrо отрезка на длину BToporo, еели длины от-
резков выражены в единицах одноrо наименования.
Отношение одноrо отрезка к друrому обычно изображаетея
АВ
в виде чаетноrо (дроби): .
CD
Еели даны два отрезка А В == 6 см и CD == 4 см, то отношение
6
отрезка АВ к отрезку CD равно , т. е.
4
АВ 6 АВ
CD == 4' или CD == 1,5.
в этом случае делимое (А В) называетея предыдущим членом ОТ-
ношения, делитель (CD)........ ПОCJlедующим членом отношения, а
частное (1 ,5) отнощением.
4
Orношение отрезка CD к отрезку АВ равно 6' Т. е.
CD 4 CD 2
............... == и л и == .
АВ 6 ' АВ 3
Это отношение в десятичных дробях придётея выражать при-
ближённо: CD 0,67 (с точностью до 0,01 с избытком), так как
АВ
CD
== 0,6666... .
АВ
Если длины отрезков выражены приближённо, то отношение
тоже получится приближённым.
160
D АВ
6,5
Пусть АВ
6.5 см, С
2,7 СМ, тоrда
СО 2,7'
AB '
2 4
СО '
(с точностью до 0,1 с HeДOCTaTKO
I).
2. Независимость отношения от принятой единицы измерения.
Пусть мы имеем два отрезка, ДЛИНЫ которых выражены в мет-
рах. Например: АВ == 6..41, ОС == 2..41. Найдём их отношение:
АВ
6
3 ос
2
1
ОС
2"
' АВ
6
3.
Измен.ится ли величина отношения, если мы длины этих отрез-
ков выразим в друrих мерах, например в сантиметрах?
Тоrда АВ == 600 с.м, ОС == 200 СМ. Найдёl\{ их отношение:
АВ
600
3 ос
200
1
ОС
200
, АВ
600
3.
Orношение отрезков в TO
1 И друrом случае не изменилось, так
как для выражения длин отрезков в сантиметрах 1\1bI оба члена. от..
ношения АВ и ос. умножили на одно и то же число (на 100). Зна-
чит, отношение отрезков не зависит от выбора единиц измерения.
Необходимо лишь, чтобы длины обоих отрезков были выражены
мерами одноrо и Toro же наименования.
Упражнения.
1. Найти отношение отрезков АВ и CD при условии, если: а) АВ == 12 см,
СО == 3 см; б) АВ == 2 .м, CD == 80 см.
2. Найти отношение отрезков АВ и CD с точностью до 0,1 и 0,01 при усло
вии, если: а) АВ == 7 см; CD == 3 см; б) АВ == 13 см, CD == 7 см.
3. Измерить отрезки т и n (черт. 350) и Jfайти отношения:
m
1 . т
п
n
n
и
т
ЧЕРТ. 350
83. ПРОПОРЦИОНАЛЬ.НЫЕ ОТРЕЗI(И.
ИЗ арифметики известно, что равенство двух отношений пазы-
16 20 2 4
ваетен пропорцией. Например:
==
.
==
. То же самое
4 5' 3 6
имеем и в rеометрии: если даны две пары отрезков, ar.ношения ко-
а 4
торых равны, то можно составить пропорцию. Если
==
и
Ь 3
Ml
==! (черт. 351), то получим пропорцию а == ; отрезки й, Ь, с
d 3 Ь d
и d называются про пор Ц и о н а л ь н ы м и.
а
Отношение Ь называется, как и в арифметике, п рвым отношением,
с вторым отношением; а и d называются крайними членами
d
пропорции, Ь и с средними членами.
о
с
ЧЕРТ. 351
ь
d
в пропорции можно ПО v1енять местами отношения; можно
переставить крайние члены, средние члены; можно переставить
те и друrие одновременно.
а с
ПОСI{ОЛЬКУ В пропорции == под буквами подразумеваlОТ чис-
Ь d
ла, выражающие длины отрезков,' то произведение крайних чле-
нов её равно произведению средних членов. Отсюда, зная три чле-
на пропорции, f\10ЖНО найти неизвестный четвёртый её член. Так,
а с a.d
в пропорции == х == ..
х d с
Отметим ещё некоторые свойства пропорций, КОТОРЫ.!\.IИ придёт-
ся в дальнейшем пользоваться при доказательстве некоторых теорем
и при решении задач.
а) Если три члена одной пропорции соответственно равны трём
членам друrой пропорции, то равны и четвёртые члены этих про-
порций.
Если == и == , то х == у. в самом деле, х == ь.с
ь х Ь У а
Ь.с Ь.с
У == , т. е. и х и у равны одному и тому же числу .
а а
б) Если в пропорции равны предыдущие члены, то равны и по-
а а
CJIедующие, т. е. если == , то х == у.
х у
Чтобы убедиться в ЭТО f, перестаВИ I средние члены в этой про-
nорции. Получим: == . Но == 1. Следовательно, и х == 1. А
а у а у
это возможно лишь в том случае, коrда числитель и знаменатель
дроби равны, т. е. Х == у.
в) Если в пропорции равны последующие члены, то равны и пре-
дыдущие, т. е. если х == У , то х == у.
а а
. В сnр-аведливости этоrо свойства предлаrается вам убедиться
самостоятельно. Для этоrо проведите рассуждение, аналоrичное
ПJ?едыдущему.
162
,4 1 12 см r B
а
С l 5см I D х
,
[ , 18см ( р Ь
M tr-- х I N У
ЧЕРТ. 352 ЧЕРТ. 353
УnражнеllllЯ.
1. На чертеже 352 изображены четыре пропорциональных отрезка, причём
АВ EF
== . Определить длину отрезка MN.
CD MN
2) На чертеже 353 изображены четыре nропорциональных отрезка, причём
а Ь
== и а == Ь. Чему равен у, если х == 28 Mht?
х У
84. ПОСТРОЕНИЕ ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКОВ.
(!t Т е о р е м а. Если две прямые пересечь неСКОЛЬ1lими парал-
лельными пРЯМ-Ьtми, то отношение двух отрезков,
8/ 8/
110лучивши.хся на первои nрямои, равно опtношению соот-
ветств,ющих оmреЗ1l0В на второй прямой. (Черт. 354.)
Докажем теорему для случая, коrда ОТ80шения отрезков BЫ
ражаются рациональными числами, т. е. дробями вида , rде р
q
и q натуральные числа.
Ее 5
На чертеже 355 ........ == , т. е. четверть отрезка АВ уклады-
АВ 4
вается ровно пять раз в отрезке ВС. Надо доказать, что отношение
5
отрезков В'С' и А' В' тоже равно .
4
в' с' D'
д'
д де D
.
а)
д
6)
}
ЧЕРТ. 3М
153
с
с'
/1'
в'
ЧЕРТ. 355
Разделив отрезок АВ на четыре
части, а отрезок ВС на пять равных
частей, получим девять равных отрез-
ков. Через точки деления проведём
прямые, параллельные прямым АА',
ВВ', СС'. На прямой т' получим то..
же девять равных отрезков (СМ. 947),
причём в отрезке А' В'уложится четы-
ре этих отрезка, а в отрезке В'С'
пять (черт. 355).
ПОЭТО IУ
В'С' 5 8С
............... .........
А' В' 4 АВ ·
То же рассуждение 10ЖНО провести и в случае любоrо отноше-
ния.!!..., rде р и q натуральные числа.
q
Ничеrо не ИЗ tенится в ходе доказательства и в случае друrих
указанных на чертеже 354 случаев взаимноrо расположения отрез-
ков.
А'В' C'D'
Так, в случае а) == ,
АВ CD
АВ' В' С'
в сл у ча е б) == ...............,
АВ ве
АВ А' В'
в сл у чае B ) == .
АС А'С'
f 85. ЗАДАЧИ НА ПОСТРОЕНИЕ.
3 а д а ч а 1.. Построить отрезки, nрОnOрЦllОflаЛЬflЬte двум
дaHHbl.М оmрезкам АВ II CD (черт. 356).
Реш е н и е. 1. Проводим две произвольные прямые LM' и NK.
2. На одной из них, например на LM, откладываем отрезки
А'В' и C'D', соответственно равные отрезкам АВ и СО.
3. Через точки А', В', С' и D' проводим ряд параллель..
ных прямых в любом направлении, но так, чтобы эти прямые
пересекли вторую прямую N К.
А
С
N
L
ЧЕРТ. 356
164
Отрезки ЕР и PQ, получив
шиеся на второй прямой, про
порциональны данным отреЗ 4
АВ ЕР
кам АВ иСD"т. е. == .
CD PQ
Задача имеет сколько уrод..
НО решений, так как парал
лельные секущие можно про
водить в друrих направлени...
ях и отрезки EF и Р Q бу...
дут иметь друrую длину, оставаясь пропорциональными отрезка 1
АВ и CD.
3 а д а ч а 2. Разделить отрезок в данном отношении.
Пусть требуется разделить отрезок АВ (черт. 357) на две части
так, чтобы они относились, как 4 и 5. Для этоrо нужно данный от..
с
11
ЧЕРТ. 357
резок разделить на 4 + 5 9 равных частей. Подобные задачи
решались ранее (947). На данном отрезке АВ выделим отрезок АС,
равный 4 частям, тоrда СВ будет равен 5 таким частям:
АС 4
СВ == 5'
Упражнения.
1. Три отрез]{а имеют длину 1 о- см, 8 см и 5 см.
Какую длину должен иметь четвёртый отрезок, чтобы эти четыре от-
резка были пропорциональны?
2. Начертить отрезок и разделить ero в отношении 2 к З.
86. ПОНЯТИЕ О ПОДОБИИ фиrур.
На чертежах 358 361 изображены попарно фиrуры, которые
отличаются своими размерами, но имеют одинаковую форму: на
чертеже 358 равносторонние треуrольники, на чертеже 359.......
квадраты, на чертеже 360....... два Kpyra, на чертеже 361 ....... пдна
и та )I{e д аль, но изображённая в разных масштабах.
6
D
о
6
ЧЕРТ. 358
ЧЕРТ. 359
ЧЕРТ. ЗБО
ЧЕРТ. Збl
166
46
45
зз
зз
34
35
З6
46
о
Джанкой
о
Симферополь
СеВастополь
З
35
Jб
.1
З5
Jб
48
46
о
ДЖQНКОЙ
'5
rе8астополь
зз
З5
З6
]'1
ЧЕРТ, 362
В окружающей нас деЙСТВИТeJlЬНОС
ти часто встречаются такие предметы
или их изображения, кохорые бывают
сходны по своей форме, но отличаются
своими размерами, например отличающи
еся размерами фотоrрафии одноrо и тo
u
ro же лица, карты земнои поверхности
(черт. 362), планы зданий (черт. 363) JI
т. д. Такие фиrуры называют подобны
ми. Для обозначения подобия фиrур
употребляется знак ").
l
ЧЕРТ. 363
87. ПОДОБНЫЕ ТРЕуrольники.
1. Определение подобных треуrольников.
Рассмотрим два чертёжных прямоуrольных треуrольника с ост-
рыми уrлами в 600 и 300 (черт. 364).
Стороны BTOpOro треyrольника по сравнению с первым умень-
шены в два раза.
АВ 2' АС 2' ВС == 2.
А' В' , А'С' , В'С'
У этих треуrОJIЬНИКОВ уrлы попарно равны. Стороны, лежащие про-
тив равных уrлов, пропорциональны:
АВ == АС == ВС == 2.
А'В' А'С' В'С'
Такие треуrОJiЬНИКИ называют л о Д о б н ы м и. Стороны,
лежащие против равных уrлов, называются с х о Д с т в е н н ы м и.
Таким образом, подобными называются пtреУ20дьн,1Жи, у "О..
торых У2ЛЫ попарно равны, а сходсmвен.ные сmороныпро..
по.рцuoнальны. Подобие тре-
уrольников записывается так:
f:J. АВС N f:J. А' В'С'.
Отношение сходственных
сторон подобных фиrур назы-
вается к о э Ф Ф и ц и е н т о м
п о Д о б и я. В данном слу-
чае коэффициентом подобия
треуrольников АВС и А 'В'С'
будет число 2.
Если же взять отношения
А' В' В'С' А'С'
АВ == ВС == АС ' то коэф
фицие т подобия БУДf!f ра- А
2
вен
в
в'
д'
с'
с
ЧЕРТ. 364
181
в
А
ЧЕРТ. 365
в
А
к
ЧЕРТ. 366
ПОЛУЧИ I :
2. Свойство прямой, параллепьноА
какой-либо стороне треуrОJlьиика.
Проведём в треуrольнике АВС пря..
мую DE параллельно стороне АС
(черт. 365).
Получим треуrольник DBE. Дока..
}I{eM, что 6 АВС с\) 6 DBE. Вследствие
параллельности сторон DE и АС L 1 ==
== L 2 и L 3 == L 4. Уrол В является
общим для этих треуrольников. С лед о..
вательно, уrлы этих треуrольников по..
парно равны.
Так как DE 11 АС, то АВ == ве .
DB ВЕ
Проведём через точку Е прямую,
параллельную стороне АВ (черт. 366).
Получим: ВС == АС , но АК == DE.
_ ВЕ АК
Поэтому
с
8С АС
ВЕ DE .
Сопоставляя полученную пропорцию
с пропорцией
АВ ВС
DB ВЕ '
АВ ВС АС
== == т. е.
DB ВЕ DE'
сходственные CTOPOfIbI треуrольников Аве, и DBE нропорiiцонаJlЬ
ны. Раньше БЫ,[{9 Аоказано, что. уrлы этих тре.уrольников попарно
равны. Значит, . . Авс с\) Д DBE. СлеДQвательно,
. Прямая, провед нная паралле.льно ka".r.Jii-л.р,бl) стороне
mреУZОЛЬНUf;'а, O!1'ce"aeт'- от Hezo.. тjJp,z,О-д'ЬН.If, подо б..
Hblii даflНОМУ.
88. ТРИ ПРИ3НАКА ПОДОБИЯ ТР.ЕvrОJlЬНИКО8.
. т е о р е м а 1. Два 'l"ре.уz,ОЛЬНU1€.а подабitы, есди, два уzла
одноzо mpe,ZOAb'H1/,'ka соощветственно р(jвнЬ4 дву,М yz.-
лая друzоzо. .. .
Пусть в треуrольниках Аве- и А'В'С' L А == L. A ,;
LB:::=L 8'1. Доказать, что ABeC'\."' А'В'С' (черт. 367). Прежде
1 В подобных тр У ольника,, вершины COOTBefci eHHO равных yrJlOB ' часто
обоЗI ачают одинаJ{ОВЫМИ буквами.
,.168
Ecero отметим, что из равенства двух уrлов данных треуrольников
следует, что и третьи уrлы их равны, т. е. L С == _ С'.
Отло}ким от верши;ны В, например, на стороне АВ треуrольни-
ка А ЕС отрезок ВМ, равный отрезку А 'В'. Из точки М проведём
прямую MN 11 АС. Мы получили L MBN, который подобен L АВС
( 87). Но L MBN== L А' В'С', так как L B==L В' по условию
'Теоремы; сторона МВ == А' В' по построению; L BMN == L А'
(L BMN и L А' порознь равны одному и тому же L А).
Если A1BN "'L АВС, ToL А'В'С' N 6. АВС. Эта теорема
выражает l й признак подобия треуrольников.
С л е Д с т в и я. 1. Равносторонние
треуzольнuкu подобны.
2. Равнобедренные nlреуzольни-
«и подобны, если они и-м.еют по
равно-м.у уzлу IlfJU вершине или
nJJll основании.
3. Два пря-м.оуzольных тре-
УZОЛЫ-lиl(а подобны, если они и.ме-
юm по равному OC11lpOMY УZЛУ.
4. Равнобедренные nрЯ.АfО-
уzольные треуzольнuки подобны.
. т е о р с м а 2. Два rtlреуzольни«а по-
добны, если две стороны одноzо
пlреуzольника nРОnQрциональны
дву.м сторона-м. друzоzо треуzоль-
ника u, УZЛbl, лежащие .между ни..
.ми, равны.
Пусть в треуrольниках АВС и А'В'С'
АВ == ВС и L В == L В'.
А' В' В'С'
Требуется доказать, что Д АВС
., L А' В'С' . (черт. 368).
Для доказательства отложим, на-
пример, на стороне АВ треуrольника
АВС от верщины В отрезок ВМ, равный
отрезку А' В:. Через точку М проведём
прямую MN '! АС. Полученный тре-
уrольник М BN подобен треуrольнику
АВС (9 87). Докажем, что L MBN == А
== 8 А' В'С'. В этих треуrольниках
L B==L В' по условию теоремы, МВ ==
== А 'В' по построению. Чтобы убедиться
в равенстве сторон BN и В'С', составим
АВ ве .
nропорцию == (она вытекает И3
МВ BN
nараллельности АС и MN) и сравним
.. u
ее с пропорциеи, которая дана
в
д
с
В'
,
д
с'
ЧЕРТ. 361
в
с
в'
A' C'
ЧЕРТ. 368
169
АВ 8С
в УСЛОВIIИ TeopervlbI: == . в этих
А' В' В'С'
двух пропорциях имеется по три оди-
наково расположенных равных члена,
следовательно, равны и четвёртые их
члены, т. е. В'С'== BN. Отсюда следует
равенство треуrольников М BN и А 'В' С'.
Так как 6 MBN N 6АВС, то, следо- Д
вательно., и 6 А' В'С' С"\.) L АВС.
Эта теорема выражает 2..й признак
подобия треуrольников.
С л е Д с т в и е. Прямоуzольные
пlреуzольнuки подобны, если ка-
тeпlbl одноzо из них пропорцио..
нальны катетам друzоzо.
Q Т е о р е м а 3. Два rпреуzольни"а по-
()обны, если т..ои стороны одноzо
111реуzольника пропорциональны
п"рё"к сmороная друzоzо треуzоль-
ника. .
П у сть в Т р е у rольниках АВС и А'В'С' АВ === ВС == АС ( че р т. 369 ) .
А' В' В'С' А'С'
Требуется доказать, что 6 ABCC"\.'\L А'В'С'.
ДЛЯ доказательства отложим на стороне АВ треуrольника АВС
от вершины В отрезок ВМ == А' В'. Из точки М проведём прямую
MN fI АС. ПолученныЙ треуrольник MBN подобен треуrольнику
АВС. Следовательно, АВ == ВС == АС . Докажем, что 6 MBN ==
МВ BN MN
== А'В'С'. Для доказательства сравним две пропорuии:
АВ ВС АВ ВС
== и == . в этих П ро по р циях имеется по три одина-
МВ NB А'В' В'С'
ков о раСПОЛО)J{енных равных члена, следовательно, равны и четБёр..
тые члены их, т. е. BN == В'С'. Сравним ещё две пропорuии:
АВ АС АВ АС
== и == . в этих П р опо р циях также имеется по три
МВ MN А' В' А:С'
одинаково располо)кенных равных члена, следовательно, равны и
четвёртые члены их, т. е. MN == А 'С'. Оказалось, что три сторо-
ны дВМN равны трём сторонам L А' В'С', а именно: МВ == А 'В';
BN == В'С' и MN == А 'С'. Следовательно, дМВN == А 'В' С',
а д АВС С"\.)Д А'В'С'.
Эта теорема выражает 3-й признак подобия треуrОЛЬНИКОБ.
в
с
в'
д'
с'
ЧЕРТ. 369
Упражнения.
\. В двух подобных треуrольвиках АВС и А' В'С' стороны АВ, ВС и АС
соответственно раяны 20 СА[, 18 СМ и 15 С,Л,t. Сторона А'С' треуrольника
А'В'С' равна 10 СА!. Чему равны стороны А'В' и В'С'?
160
2. Треуrольники АВС и А' В'С' подобны. Стороны АВ, 8е и АС треуrоль..
ника АВС соответственно равны 20 см, 15 с'м и 12 см. I(о ициент подо"
бия треуrольников равен 2,5. Вычислить периметр треуrольника А' В'С'.
(Два решения.)
89. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ СВОЙСТВ
ПОДОБНЫХ ТРЕуrольников.
Свойства подобных треуrольников очень широко применяются
на практике. Они находят своё применение при изrотовлении раз..
личных приборов, механизмов, при проведении измерительных ра..
(от, при решении различных задач на вычисление и построение.
Ниже приводится описание некоторых таких работ.
1. Деление отрезка на равные части
с помощью пропорциональноrо цир-
куля.
Пропорциональный циркуль приме-
lIяется в тех случаях, коrда нужно не-
большой отрезок разделить на несколь-
ко равных частей (черт. 370). Состоит
пропорциональный циркуль из двух HO
жек одинаковой длины, скреплённых
таким образом, что они MorYT вращать-
ся BOKpyr винта О. Кроме Toro, блаrо..
даря прорезям этот винт может переме-
щаться, вследствие чеrо размеры плеч
ножек MorYT изменяться по нашему же..
АО
ланию; таким образом, отношения
СО 08
и MorYT быть выбраны произвольно.
ОО
Предположим, нам нужно разделить
отрезок на пять равных частей (черт.
371). Для этоrо винт О должен быть
укреплён таким образом, чтобы отноше-
АО СО
ние плеч и равнялось 5.
ОВ OD
ЭТО леrко сделать по тем делениям и
цифрам, которые проставляются по кра-
ям прорезей. Затем ножки циркуля
раздвиrаются и устана ливаlOТСЯ так,
чтобы концы ножек А и С совпадали с
концами данноrо отрезка т. Тоrда рас-
стояние между ножками D и В будет
1
составлять отрезка т. Это следует из
5
подобия треуrольников АОС и DOB.
D В
>
д
t
ЧI:РТ. 370
д
т
.С
ЧЕРТ. 371
161
Затем циркуль поворачивается и на отрезке т ОТКЛ3J1,ывается
отрезок DB; он отложится ровне 5 р2З.
2. Построение и измерение отрезков с помощью
поперечноrо масштаба.
Для построения и измерения отрезков с возможно большей сте-
пенью точности применяется прибор, называемый поп е р е ц..
н ы м м а с ш т а б о м. Устройство ero видно из чертежа 372.
На произвольной прямой ОК от точки О откладываются вправо
отрезки, принятые за единицу. Влево от точки О откладывается
такой же единичный отрезок ОВ. В точке В к прямой ВК восставля..
ется перпендикуляр, на котором от точки В откладываются 10 рав-
НЫХ ПРОИЗВОЛЬНЫХ отрезков, и через полученные точки деления
1, 2, 3, ..., 1 О проводятся прямые, параллельные прямой ВК. Из то-
чек О, 1, 2, 3 прямой ОК проводятся к ней перпендикуляры, пере-
секающие проведённые параллельные прямые. Отрезок ОВ делится
на 10 равных частей, как и отрезок AD. Затем точки деления ниж-
Hero отрезка ОБ соединяютс с точками деления BepXHero отрезка
AD, но так, чтобы нулевое деление нижнеrо отрезка было соединено
с первым делением BepXHero отрезка, а деление 1 нижнеrо отрез-
ка с делением 2 BepxHero отрезка и т. д.
«Цена>, (значение) делений на поперечном масштабе такова:
каждое деление между наклонными параллелями равно О) 1; деле-
ния внутри треуrольника с вершиной О соответственно равны 0,01;
0,02 и т. д.
Используют поперечный масштаб следующим образом: если нуж-
HO на данной прямой построить отрезок, равный, например, 1,4
единицы, то помещают одну ножку циркуля в точку с цифрой 1 на
луче ОК, а друrую ножку циркуля........ в точку, помеченную на ОТ-
резке ВО цифрой 4. Получается отрезок, равный],4 единицы, ко-
u
торыи И переносится на указанную прямую.
Если нужно построить отрезок, равный 2,35 единицы, то поме-
щают одну ножку циркуля в точку пересечения перпендикуляра,
помеченноrо цифрой 2 (на луче ОК), и rоризонтальной параллели,
помеченной цифрой 5. Зате1v! вторую ножку циркуля устанавливают
на пересечении параллели 5 с прямой, идущей от деления 3 ниж-
А987б5 4 321D
10
э
8
7
6
5
4
3
2
1
В 98765 4 З 21 О
I \ , I I
N м
1
2
J
к
ЧЕРТ. 372
16
Hero отрезка ВО (черт. 372). Получаем отрезок MN, равный 2,35
единИЦЫ, который переносится на указанную прямую.
Если требуется измерить какой-нибудь отрезок СР, данный вне
поперечноrо масштаба, то поступае.\f так:
1. Ставим ножки циркуля в точки С и Р, затем переносим цир-
куль на поперечный масштаб, помещая одну ножку на такую отмет-
ку луча ОК, чтобы друrая ножка оказалась внутри отрезка ВО.
2. Передвиrаем циркуль параллельно ВК дО Toro момента, Kor-
u "
да вторая ножка окажется на однои из наклонных параллелеи.
3. По местоположению ножек циркуля определяем длину от-
резка СР.
3. Определение высоты предмета.
Пусть нужно определить высоту какоrо-нибудь предмета, на-
пример высоту дерева (черт. 373). Поставим по отвесу на rОРИ30Н-
тальной площадке на некото-
ром расстоянии от основания
дерева шест с вращающейся
планкой (изображённый на чер-
теже отдельно), планку устано-
вим по направлению на вер-
шину дерева, как это показано
на чертеже 373. Отметим на по-
верхности земли точку В, яв-
u
ляющуюся точкои пересечения
прямой А' А с rоризонталъной
площадкой.
Прямоуrолъные треуrольни-
ки А 'С' В и АСВ подобны, так
как они имеют по равному ост-
рому уrлу В. Измерив расстоя-
ния С' В и СВ и найдя отноше-
ние их, мы найдём коэффициент
подобия этих треуrольников.
Например, если расстояние С' В == 18 м, а СВ == 1,5 м, то
18
коэффициент подобия будет равен == 12. Если длина ка-
1,5
тета АС составит, например, 1,8 М. то высота дерева составит
1,8. 12 21,6 (м).
в
ЧЕРТ. 313
4. Определение расстояния до недоступной точки.
Пусть надо определить расстояние от пункта А дО В, находяще-
rося rде-нибудь в недоступном месте, например на островке, ОКРУ-
жённом водой (черт. 374). Примем пункты А и В за rеометричес-
кие точки. Провешим по возможности на ровном месте отрезок АС
и измерим ero. Пусть длина отрезка составит, например, 120 .11.
163
Измерим с помощью астролябии уrлы
А и С. Пусть они составят 620, 540.
На листе бумаrи в масштабе 0,001 по..
строим треуrольник А' В'С' с уrлами
n 620 и 540 (черт. 375). Этот треуrоль..
ник будет подобен треуrольнику АВС.
Коэ<1x}Jициент подобия их будет равен
1000. На чертеже измерим отре-
зок А' В'. Пусть длина ero будет равна
142 мм. Помножим длину А' В' на
коэффициент подобия этих треуrольни"
ХОВ, получим: 142. 1000== 142 000 (м.«),
что составит 142 м. ЭТО и будtт ис-
KO 10e расстояние 'от пункта А до
пункта В. В целях достижения наи-
большей точности необходимо осо..
бенно тщательно ИЗ fерить уrлы тре..
уrольника АВС и, кроме Toro, отре..
зок АС взять таким образом, чтобы
L В не был слишком мал, так как Tor..
да значительно уменьшится точность
результата.
П р а к т и ч е с к и е р а б о т bJ.
u
мастерскои металлическии пропорциональныи
120м
ЧЕРТ. 374
в'
А'
с'
ЧЕРТ & 375
1. Сделать в
циркуль.
2. Начертить поперечный масштаб, приняв за единицу 1 дм.
3. Определить расстояние до какоrо"нибудь недоступноrо
пункта.
4. Определить высоту какоrо"нибудь предмета: здания, мачты,
дерева.
90. ПОДОБИЕ мноrоуrольников.
Два одноимённых мноrоуrОJlьника называются подобными, еCJIИ
yrJlbl одноrо из них соответственно равны yrJlaм дрyrоrо, а сход-
ственные стороны мноrоyrольников ПрОПОрЦИОНaJlЬНЫ.
О Д н о и м е н н ы м и называlОТСЯ мноrоуroльники, имеющие
о Д н н а к о в о е число сторон (уrлов).
D
Е
164
D'
с
с'
ЧЕРТ. 376
с х о Д с т в е н н ы м и называются стороны подобных мно-
rоуrольников, соединяющие вершины соответственно равных yr..
лов (черт. 376). Так, например, чтобы мноrоуrольник ABCDE был
подобен мноrоуrольнику А' B'C'D' Е', необходимо, чтобы L А ==
== L А'; L В == L В'; L С == L С'; L D == L D'; L Е ==
== / Е' и, К р оме Toro , ,АВ == 8е == CD == DE == ЕА
А' В' В'С' С' D' D' Е' Е' А'
. т е о р е м а. Два подобны.: Аfноzоуzольнuиа диаzонаЛЯМtt,
llровед нными из вepUlUH любой пары соответственно
равных уzлов, разбuваJотся на одинаковое число подоб-
ных lпреуzольников.
Пусть мноrоуrольники ABCDE и A'B'C'D'E' подобны
( ч р т. 377 ) т. е. АВ == 8е == CD == DE == ЕА и L А == L А'
, А' В' В' С' С' D' D' Е' Е' А' ,
L.. В == L В', LC == L С', L D == L D', L Е == L Е'.
В обоих l\IноrоуrолыIкахx из вершин каких"нибудь соответ-
ственно равных уrлов, например из вершин А и А', проведём
диаrонали. Мы видим, что мноrоуrольники разБИЛIIСЬ на оди-
наковое число треуrольников. L{oKa-
жем, что эти треуrольники подобны,
а именно: Д АВС N 6. А'В'С';
6. ACD ) 6. А 'C'D' и ADE N
('\." 6. А' D' Е'.
Подобие треуrольников АВС и
А ' В'С' вытекает из равенства уrлов
В и В' и пропорциональности сторон
АВ 8е
А'В' В'С"
Рассмотрим треуrольники ACD и
А 'C'D'. Из подобия треуrольников
АВС и А' В'С' следует, что L 1 == LЗ.
В данных, м ноrоуrольниках L С ==
== L С', поэтому и L C L 1 ==
== L С' L 3, т. е. L 2 == L 4;
из п,одобия тех же треуrольников еле-
дvет, что ВС == АС . В то же В р емя
J В'С' А'С'
ВС DC
ИЗ У словия теоремы имеем: == ;
В'С' D'C'
так как первые отношения этих про-
Упражнения.
1. Будут ЛИ подобны два любых квадрата?
2. Будут ЛИ подобны два любых прямоуrольника?
3. Будут ли подобны два любых ромба?
Е
D
I
/
I
I
I
I ;1'
I /
I "
-"
с
,4 в
о'
с'
11' 8'
ЧЕРТ. 377
165
порций равны, то должны быть равны и вторые отношения их, т. f .
АС DC
-==
А'С' D'C"
В треуrольниках ACD и А 'C'D' имеем по равному уrлу, эаКЛIО-
чённому между пропорционалыIмии сторона?\IИ, следовательно,
Д ACD N д А 'C'D'.
Подобие треуrольников AD Е и A'D' Е' следует из Toro, чтс,
L Е == L Е' ( по У словию ) и АЕ == ED ( по оп р еделению по-
А'Е' E'D'
добных мноrоуrольников). Таким образом, эти треуrольники имеюr
по равному уrлу, заключённому между пропорциональными сторо-
нами. Следовательно, Д AED N д А' E'D'. Теорема доказана.
3 а м е ч а н и е. Подобные треуrольники расположены в по-
добных мноrоуrольниках в одном и том же порядке. .
Мы рассмотрели два подобны.х пятиуrольника. Таким же путём
может быть построено доказательство для любых подобных мно-
rоуrольников.
Упражнение.
Дано (черт. 377): 6. АВС с';) А'В'С'; ACD с';) A'C'D' и дАЕD с';)
NA A'E'D'.
Доказать, что мноrоуrольники ABCDE и А' B'C'D' Е' подобны.
91. ОТНОШЕНИЕ ПЕРИМЕТРОВ ПОДОБНЫХ мноrоуrольников.
Сначала рассмотрим свойство ряда равных отношений. Пусть
2 4 6 8 2 H U..
имеем, например, отношения: 1 == 2 == "3 == 4 ==. аидем СУМ-
u
МУ предыдущих членов этих отношении, эатем сумму их последую-
u м 2+4+6+8
щих членов и наидем отношение этих сумм, получим: ==
1+2+3+4
20 .
== == 2. То же самое мы получим, если возьмём ряд каких-ни-
10
б u 2 4 6 8 10 2 Н u
удь друrих отношении, например: == == == == == . аи-
3 6 9 12 15 3
дём сумму предыдущих членов этих отношений и сумму после-
ДУЮЩИХ, а затем найдём отношение этих сумм, ПОЛУЧИ f:
2+4+6+8+10 30 2
3 + 6 + 9 + 12 + 15 == 45 == 3 ·
В том и друrом случае сумма предыдущих членов ряда равных
.
отношении относится к сумме последующих членов этоrо )ке ряда,
как предыдущий член любоrо из этих отношений относится к свое-
му последующему.
166
Мы вывели это свойство, рас-
смотрев ряд числовых примеров. Оно
может быть выведено cTporo и в об-
щем виде.
Теперь рассмотрим отношение пе- Е
риметров подобных мноrоуrольников.
Пусть мноrоуrольник ABCDE по-
добен м ноrоуroльнику А ' В/ C'D' Е'
(черт. 378). Из подобия этих M-Horo-
АВ ве
У rольников след у ет, что == ==
- А' 8' В'С'
== CD == DE == ЕА . На основании
С' D' D' Е' Е' А'
выведенноrо нами свойства ряда рав-
ных отношений можем написать:
D
а
D'
С'
АВ + 8е + CD + DE + БА АВ
А'В' + В'С' + С'о' + D'E' + Е'А' A'B"
Сумма предыдущих членов взятых
нами отношений представляет собой периметр первоrо IHO-
rоуrольника (Р), а сумма последующих членов этих отношений
представляет собой периметр BToporo мноrоуrольника (Р'), значит,
р АВ
ЧЕРТ. 378
р' А' В'
Следовательно, neplUlempbl подо6н,6и .Afн,ОZО,ZО/l,ЬНIШО8
относятся "а" UJ& сходственные стороны.
92. ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ фиrур.
Рассмотрим отношение площадей двух квадратов. Если сторону
одноrо квадрата обозначим через т, а сторону друroro через п,
то площади будут соответственно равны т" и п 2 (черт. 379). Обо-
значив площадь первоrо квадрата
через S, а площадь BToporo........ че..
рез-S', получим:
S т 2
==: , т. е.
S' п'
1. Отношение площадей квадратов.
. площади "вадратов отно-
сятся uate "вадрап,ы ltX сто-
ро Н.
Полученную формулу можно пре
образовать так: == ( ) I.
S' n
I
I I
.... .... r ..... ..,.... .....
I I
........j.....---.J .....
I I
I I
D
п
т
ЧЕРТ. 379
161
в
/1
с
в'
д' о'
ЧЕРТ. 380
Значит, можно сказать, что отно-
шение площадей двух квадратов рав-
но квадрату отношения их сторон.
На чертеже 379 отношение сторон
квадратов равно 3, отношение их пло-
щадей равно 32 == 9.
2. Отношение площадей двух
подобных треуrольников.
Пусть АВС С\) А' В'С' (черт.
3ВО). Из подобия треуrольников сле-
дует, что L А == L А'; L В == L В'
и L С == L С'.
АВ. 8С АС
К ро ме тoro, в
А' В' В'С' А'С' .
этих треуrольниках из вершин В и
В' проведём высоты и обозначим их
через h и h'. Площадь первоrо тре-
AC.h
уrольника будет равна ,a пло-
2
А'С' .h'
щадь Bтoporo треуrОJ1ьника
2
Обозначив площадь первоrо треуrольника через S, а площадь
, S АС. h S АС h
BТO p oro че р ез S пм у чим: == или == · .
, S' А'С' . h' , S' А'С' h'
Из подобия треуrольников АВО и А' В'О' (они подобны, потому
что прямоуroльные И, кроме Toro, имеют по равному острому уrлу,
h АЯ АВ АС
а именно LА==LА' ) след у ет: == . Но == . Следовател ь-
h' А' В' А' В' А'С'
h АС S АС h h
но, == . Заменив в фор м у ле == ................ отношение P aBHbJM
h' А'С' S' А'С' . h' h'
АС S АС АС S (АСУ'
ем у отношением , по лучим : == ............... · , или == . Итак,
А'С' S' А'С' А'С' S' (А'С')3
площади подобных треУ20ЛЬН""'О8 относятся "а" квад-
раты ехооственньи сторо".
S ( АС ) 2
Полученную формулу можно преобра30ВЗТЬ так: s' ;:: А/С' ·
Значит, можно сказать, что отношение площадей двух подобных
треуroJJЬНИКОВ равно квадрату отношения их сходственных сторон.
3. Отношение площадей подобных мноrоуrОJlЬНИКОВ.
Пусть ABCDE и A'B'C'D'E' подобные мноrоуrольники
(черт. 381). ИэвеС1НО, что ABCN А'В'С',дАСD N A'C'D',
168
l::l ADE "'., 6. А' D' Е' ( 90). Кроме Toro,
ПЛ. ABC (АВ)2 ПЛ. лАСD
.
пл. A'B'C' (А'В')2' пл. .6.A'C'D'
(CD)2. ПЛ. БАDЕ (DE)2 Т
==, ==. ак как
(С' D' )2 пл. , А' D' Е' (D' Е' )2
вторые отношения этих пролорций раБ"
ны, что вытекает из подобия м Horo..
пл. Ь.АВС пл. БАСD
УI'ОЛЬНИКОВ то ==
, пл. БА' В'С' пл. б А'С' D'
== пл. 6 ADE == (АВ y . Использ у я СБОЙ"
пл. 6A'D'E' (А'В')2
СТЕО ряда равных отношений, получим:
ПЛ. 6АВС + пл. 6ACD + ПЛ. 6ADE
пл. ь. А' В'С' + пл. А' С' D' + ПЛ. f:::, А' D' Е'
( АВ ) 2 S ( АВ ) 2
== или == rде S и s'........
(A'B') ' S' (А'8')2'
площади данных подобных мноrоуrоль-
ников. Следовательно,
д
с
в'
ЧЕРТ. 381
. Площади подобных .мНО20У20льни"ов относятся 1ta1t
"вадрап-,ы, сходственных сторон. Полученную ФОР 1УЛУ мож"
НО привести к ТЗ K01\t У вид у : === ( АВ ) 2.
S' А'В'
Упражнения.
1. Сторона первото квадрата больше стороны второто квадрата в 2 раза (в 5 раз).
Во сколько раз площадь nepBoro квадрата больше площади BТOporo
квадрата?
I
2. Сторона nepBoro квадрата составляет "3 (0,1) стороны Bтoporo квадрата.
Какую часть площаДЬ nepвoro квадрата составляет от пnощади BТOpOro
квадрата?
з. Коэффициент подобия в подобных мноrоуrOJlьниках равен 4 ( ; 0,4; 2,5).
Чему равно отношение их площадей?
4. Отношение площадей подобных мноroуrольников равно 36 (100; 0,09).
Чему равно отношение сходственных сторон этих MHoroy ronb н иков?
t 93. . ПОСТРОЕНИЕ ПОДОБНЫХ ФИf)'Р.
1. Построение подобных треуrольников.
Мы уже знаем, что для построения треуroльника, подобноrо
данному, достаточно из какой-нибудь точки, взятой на стороне
треуrOJJьника, провести прямую, параллельную cropoHe Tpeyroпb-
169
в
д
41
ЧЕРТ. 332
Е
с
д
в.,
ЧЕРТ. 383
ника. Получим треуrольник, по...
добный данному (черт. 382):
L:l АСВ С\) д А 'СВ'.
с
3. Съёмка. плана земельноrо участка.
а) Съёмка плана производится с
помощью особоrо прибора, называе-
MOro l\{ е н 3 у Л О Й (черт. 384).
Мензула представляет собой квад-
ратную доску, помещённую на "ре-
НО!КНlIке. При вычерчивании плана
доска приводится в rоризонтальное
поло,кение, что проверяется с помо-
щью уровня. Для проведения прямых
линий по нужному направлению
употребляется алидада, снабжённая
диоптрами. В каждом диоптре имеется
110
2. Построение подобных
мноrоуrольников.
Дпя построения мноrоуrольни-
ка, подобноrо данному, l\{bI l\.fo>l<eM
поступить таким образом: разобь-
.. U
ем данныи мноrоуrольник диаrона-
лями, проведёННЫfvlИ. из какой-
либо ero вершины, на треуrольни-
ки (черт. 383). На какой-нибудь
стороне данноrо мноrоуrольни-
ка ABCD Е, например на стороне
АЕ, возьмём какую-нибудь точку
Е' и проведём прямую, параллель..
ную стороне ED, дО пересечения
её с диаroналью AD, например, в
точке D'. Из точки D / проведём
прямую, параллельную стороне
DC, дО пересечения её с диаrональю
АС в точке С/. Из точки С'прове-
дём ПрЯ .Iую, параллельную стороне
СВ, дО пересечения со стороной АВ в точке В'. Полученный fvlHoro..
у.rольник А В' С' D 'Е' подобен данному мноrоуrольнику A,BCD Е.
Справедливость этоrо утверждения доказать самостоятельно.
Если требуется построить м ноrоуrольник, подобный данному,
с указанным коэффициентом подобия, то исходная точка Е/ берётся
на стороне АЕ или её продолжении соответственно данному коэф"
фициенту подобия.
черт t J84
прорезь, в которой
натянут волосок, что
позволяет достаточно
точно наводить алидаду
в нужном направлении.
На мензулу кнопками
укрепляют лист белой
бумаrи, на котором и
вычерчивается план.
Для Toro чтобы снять
план с земельноrо уча-
стка ABCDE, выби-
рают внутри участка
какую нибудь точку О
так, чтобы из неё были
видны все вершины зе-
мельноrо участка (черт.
385). С помощью вил-
ки с отвесом (черт. 386) устанавливают мензулу так, чтобы точка
О, отмеченная на листе бумаrи, приходилась против избранной на
участке точки О. Затем из точки О на листе бумаrи, прикреплёННQМ
к м:ензуле, прочерчивают при помощи алидады лучи в Ii8праВJIеЩlЯХ
точек А, В, С, D и Е; измеряют расстояния ОА, ОБ, ОС, ОП JI
ОЕ и откладывают на этих лучах в принятом м асштабе отрезКII
ОА', ОВ', ОС', OD', и ОЕ'.
Точки А', В', С', D' и Е' соединяют. Получается'мноroуroль-
ник А' B'C'D' Е', представляющий собой п.пан данноro земельноro
участка в принятом масштабе.
Описанный нами способ мензульной съёмки называется п 0-
лярным.
Существуют и друrие способы съёмки плана с помощью мен-
зулы, о которых можно прочитать в специальных руководствах по
U ..
мензульнои съемке.
На каждом плане обыкновенно даётся
масштаб, по которому можно установить ис-
тинные размеры снятоrо участка, а также
и ero площадь.
На плане также указывается направле-
ние стран света.
П р а к т и ч е с к а я р а б о т а. Сде-
е .. е
лать в школьнои мастерскои простеишую мо-
дель мензулы и снять с её помощью план
какоrо нибудь небольшоro эемельноrо участка.
б) Съёмку плана эемельноrо участка мо-
жно произвести с помощью астролябии.
Пусть надо снять план земельноrо уча-
(1
r
I
ЧЕРТ. 388
B
____ ---- l'
", ---- ---- l'
,
Д "' I , ...
\ " r .
"" , 8' , ·
\ "А I '
\ ,-Q/ ,
\ " , с' ..... ...............
\ ,," Е , / С
l---"" \ //
E " \ /
'" \ /
" \ /
........ /
.:
ЧЕРТ. 385
171
стка АВСОЕ. Возьме f одну из
вершин участка, например А, за
исходную и с помощью астролябии
измерим уrлы при вершине А,
т. е. L 1, L 2, L 3 (черт. 387).
Потом с помощью мерной цепи
измерим расстояния АЕ, AD, АС
и АВ. В зависимости от размеров
участка и размеров листа бумаrи,
на который наносится план, выби
рается масштаб для вычерчивания
плана.
При точке А, которую прини
маем за вершину мноrоуrольника,
строим три уrла, соответственно
равные L 1, L2 и L3; затем в
избраННОl\f l\lасштабе на сторонах
этих уrлов от точки А' отклады
Баем отрезки А'Е', A'D', А'С' и
А' В', соединив отрезками точки
А' и Е', Е' и D', D' и С', С' и В',
в' и А', получим мноrоуroльник 'B C'D'E', подобный MHoro
уrОЛЬНИI<У ABCDE. Это будет план данноrо земельноrо участка,
начерченный в избранном масштабе.
д
в
Е
д'
в'
Е'
о'
ЧЕРТ. 387
rЛАВА /Х
триrОНОМЕТРIIЧЕСКИЕ ФУНКЦИИ
OCTPOrO yr IIА.
На основании равенства и подобия треуrольников мы имели
ВОЗМОЖНОСТЬ решить ряд задач, связанных с определением рас..
стояний, измерить которые непосредственно не представлялось
БОЗl\iОЖНЫМ. Например, МЫ находили расстояние до недоступной
точки, высоту предметов, расстояние между пунктами, разделён-
ными каким-нибудь препятствием, и Т. д.
Такие работы име большое практическое значение, однако
при их выполнении мы получали недостаточно точные результаты.
Если результаты, полученные нами, моrли удовлетворять нас,
коrда мы имели дело с фиrурами небольших размеров, то они со-
вершенно не iоrли бы удовлетворить нас в силу своей неточности,
если бы мы имели дело с фиrурами, имеющими большие размеры.
Кроме Toro, без уrломерноrо инструмента мы не в состоянии были
находить размеры уrлов, имея в своём распоряжении только лишь
длину ,-ех или иных отрезков; например, по длине сторон произ-
вольноrо треуro.льника мы не моrли определять величину ero уrлов.
Однако в математической науке существуют такие приёмы, ко-
торые обеспечивают необходимую точность измерений, несмотря
на значительные размеры избранных для измерения расстояний, а
кроме тоro, дают возможность по длине тех или иных отрезков опре-
делять размеры нужных нам уrлов и длины неизвестных отрезков.
Овладение такими приёмами связано с изучеНИеАf TaI{ назы-
ваемых триrонометрических функций. К ознакомлению с некото-
рыми из них мы и переходим .
94. ОПРЕДЕЛЕНИЕ триrОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
1. Соответствие между отношением сторон и ВeJlИЧИНОЙ
острых yrJlOB В прямоyrольном треyrОJlьнике.
Пусть имеется какой-нибудь произвольный острый уroл, на-
пример L ВАС == а (черт. 388). На стороне АВ Б03ЬМём произволь-
ную точку М и опустим из неё перпендикуляр MN на сторону АС.
Получим прямоуrольный треуrольник MAN.
Возьмём отношения ero сторон попарно:
173
A1N
(отношение катета, ПРОТИ80-
АМ
лежащеrо уrлу а, к rипотенузе);
AN
(отношение катета, при-
АМ
лежащеrо к уrлу а, к rипотенузе);
MN
(отношение катета, ПРОТИБО-
AN
лея{ащеrо yr лу а, к катету при-
л е)l{ащем У) ;
АМ
(отношение rипотенузы к ка-
MN
тету, противолежащему уrлу а);
АМ
(отношение rипоrенузы к
AN
катету, прилежащему к уrлу а);
AN
(отношение катета, приле-
MN
жащеrо к уrлу а, к катету про-
тиволежащему).
Мы получили 6 отношений.
Величина этих отношений не за..
висит от Toro, rде на стороне АВ
мы возьмём точку М. Так, если
вместо точки М мы возьмём на
стороне АВ какую--нибудь точку
l\1'(черт. 388), то новый треуrольник AM'N' будет подобен
треуrольнику MAN и потому ни одно из отношений не изменится.
Значит, взятому уrлу а соответствуют одни и те же опреде...
лённые значения каждоrо из отношений. Возьмём теперь дру"
rой острый уrол, L В' АС === Р (например, больший уrла а), и
на стороне АВ' отметим точку Р так, чтобы АР == АМ (чер1'.
389). Как увидим ниже, подобный выбор точки Р Не повлия
ет на общность рассуждений. Опустив из' точки Р перпендику'"
ляр PD на сторону АС, получим прямоуrольный треуrольник
APD. Составим отношения сторон этоrо треуrольника в том же
порядке, как и для треуrольника MAN:
11
в
N
N'
ЧЕРТ. 38
д
п'
с
ЧЕРТ. 389
с
PD
.
АР '
AD: РО . АР.
АР . AD' ' PD '
АР . AD
AD ' PD'
Эти отношения не изменятся, если точку Р переместим в люБУIО
точку Р' луча АВ'. Значит, взятому значению уrла р соответствует
определённое значение каждоrо из отношений.
174
Однако есл!! мы сравним значения соответствующих отношений
для уrла а и для уrла , то увидим, что они различны:
PD =1= MN , так как АР == АМ, а PD> MN;
АР АМ
AD AN АР == АМ, а AD < AN;
АР =1= АМ ' так как
PD MN PD > MN, AD < AN
AD =1= AN ' так как а и, следовательно,
первое отношение больше BToporo и т. Д.
Таким образом, выходит, что каждому размеру oCTporo yr
ла соответствует определённое значение каждоrо отношения
сторон. Справедливо и обратное утверждение: каждому зна..
чению отношения сторон соответствует определённый размер
уrла.
На этом основании можно считать, что отношения сторон прямо...
уrольноrо треуrольника являются Ф у н к Ц и я м и е r о о с т р о...
r о у r л а. Эти функции называются т р и r о н о м е т р и ч е.-
с к и м и Ф у н к Ц и я м и у r л а.
Перейдём к более подробному их рассмотрению.
Возьмём прямоуrольный треуrольник АВС и обозначим ero
стороны буквами й, Ь и с (черт. 390). Рассмотрим сначала .функ
ции уrла А.
а
Отношение называется синусом уrла А, т. е. синусом
с
.уrла А называется отношение катета, про-
тиволежащеrо этому yrJlY, к rипотенузе.
Ь
Отношение называется к о с и н у с о м
с
уrла А, Т. е. косинусом yrJla А называется
отношение ка тета, прилежащеrо к этому
уrлу, к rипотенуэе.
а
Отношение называется т а н r е н с о м
Ь
уrла А, т. е. TaHreHCOM yr,'1a А называется
отношение катета, npотнволежащеrо атому
yrJlY, к катету npнлежащему.
2. Определение триrонометрических функций.
в
А
о
ь
с
ЧЕРТ 1 890
118
ь
Отношение называется к о т а н r е н с о м уrла А, т. е.
а
KOTaHreHCOM yr па А называется отношение катета, прилежащеrо
к этому yrny, к катету противолежащему.
Отношение !.. называется с е к а н с о м уrла, А.
ь
с
Отношение...... называется к о с е к а н с о 1\1 уrла А.
а
Наиболее употребительными являются первые четыре функuии:
синус, косинус, TaHreHC и I<OTaHreHC.
Эти .функции уrла А обозначаются так: sin L А, cos L А,
tg L А и с tg L А;
а ь а Ь А
== sin L А; == СО$ L А; b == tg L А; a == ctg L ·
с с '
Установим теперь функuии для L В.
синус уrла В, == sin L В;
с с
а
косинус уrла В,
с
== COS L В;
с
ь
.... ......... TaHreHC yr па В,
а
ь
== tg L. В;
а
....... KoтaHreHC уrла В, а == ctg L В.
ь ь
Упражнения.
1. (Устно.) Начертить прямоуrОJlЬНЫЙ треуrольник С катетами 3 с.м и 4 СА!.
Вычислить С ПОМОЩЬЮ теоремы Пифаrора длину rипотенузы, а затем
синус, КОСИНУС, TaHreHC и KOT8HreHC острых уrлов треуrолыIка..
2. Начертить прямоуrольный треуrольник АВС С катетами: АС == 18 .м.м,
8е == 24 .мм, вычислить с помощью теоремы Пифаrорз ДЛИНУ rипотену-
зы АВ и найти СИНУС, косинус, TaHreHC и KOTaHrellC уrла А, а затем синус,
КОСИНУС, танrеис и котзнrенс уrла В.
з. Начертить произвольный прямоуrольный треуrольник, измерить ero стороны
в миллиметрах и найти СИНУС, КОСИНУС, TaHreHC и KOTaHreHC острых yr ЛОВ
треуrольника с точностью до 0,01.
95. ПОСТРОЕНИЕ уrЛА ПО ЗАДАННОМУ ЗНАЧЕНИЮ
ОДНОЙ из ErO триrОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
4
1. Построить уzол, тaHzeHC кoтopozo равен .
5
Ilостроим С помощью чертёжноrо треуrольника прямой уrол
и на ОДНОЙ ero стороне отложим от вершины 5 произвольных мае..
176
штабных единиц, а на друrой 4
(черт. 391). Соединив точки А и В,
получим прямоуrольный треуrоль..
ник АВС.
L А будет искомым, так как
tg L А == : .
2. Построить уаол, синус которо-
3
ао равен 5'
Построим прямой уrол и на одной
ero стороне отложим от вершины от-
резок СВ, равный трём произвольны {
масштабным единицам (черт. 392).
Из точки В как из центра ра-
диусом, равным 5 тем же масшта
ным единицам, опишем дуrу, пересе--
кающую друrую сторону прямоrо yr-
ла. Точку пересечения обозначим
буквой А. Соединив точки А и В,
ПОЛУЧИ I прямоуrольный треуrольник
АВС. .Р L А ...... искомый, так как
sin L:A ==!.
5
3. Построить уаол, косинус коmo...
5
роао равен 6".
Построим прямой уrол и на од-
u
нои ero стороне отложим от вершины
уrла отрезок АС, равный 5 произ
вольным масштабным единицам
(черт. 393). Из точки А как из центра
радиусом, равным 6 тем }I{e масштаб
ным единицам, опишем дуrу, пересекающую друrую сторону при..
Moro уrла. Точку пересечения обозначим буквой В. Соединив точ.
ки А и В, получим прямоуrольный треуroльник АВС.
L А ....... искомый, так как cos L А ==!.
6
Так как каждый из катетов прямоуrольноrо треуrоль ника
всеrда Iеньше rипотенузы, то синус и косинус любоrо oCTporo
уrла всеrда меньше 1.
Что касается сравнительной величины катетов, то каждый из
них может быть и больше и меньше друrоro. Поэтому tg L А 1-1
ctg L А MoryT быть выражены любым положительным числом.
Каждый из них может быть ме ньше единицы, больше единицы и
равен единице.
7 н. Н, ННК IТИII
А
с
ЧЕРТ. 391
в
д
с
ЧЕРТ. 392
g
д
с
ЧЕРТ. 393
l1Т
t 96. ЗНАЧЕНИЯ триrОНОМЕТРИЧЕСКИХ функций
НЕКОТОРЫХ yr ЛОВ.
Найдём значения триrонометрических функций для уrлов в 300,
450 и 600.
1) Для уrла в 300.
Возьмём прямоуroльный треуrОJlЬНИК с острым yrJIOM в 300
(черт. 394). Обозначим длину rипотенузы АВ через с и выра-
зим длины катетов.
с
ве == , как катет, лежащий против уrла в ЗО 8 .
2
Катет АС найдём по теореме Пифаrора.
АС == .У AВ2 8(;2 == V c' ==' У" З: == с 3 ·
с о
аВС 2 1 ВС 2
Тоrда sin 30 == == == ..... == 0,5; tg 300 == ==
АВ о 2 АС с ./3
2
1
==- ..........
vз
113
==............ 0,5774;
3
сУЗ
cos 300 == АС == ....!.... == уз 0,8660.
АВ о 2
2) Для yrJIa в 450.
Возьмём прямоуrольный тре-
уrольник с острыми уrJIами по 450
(черт. 395). Обозначим длину rипот
вузы АВ через с и выразим длины
катетов. АС == ве, следовательно, по
теореме Пифаrора АВ2==2ВС2, откуда
АВ2 2AВ 2с 2
В (;2 ....... ............... ...... ..........
...... 2 ...... 4 ..... 4'
Значит 8е == 1 [ 2с2 ...... с JI2
, r 4 ...... 2 ' ОДНО-
временно и АС == с JI2 .
2
сУ2
Т . 45 0 ве 2
оrда Sln == АВ == с
== У2 0,7071;
2
tg 450== 8С == 1;
АС
в
А
ЧЕРТ 394
в
д
ЧЕPr а 395
118
cos 45:> == !3 С === v2 0,7071.
АВ 2
3) Д л я У r л а в 600.
Значения триrонометрических функций для уrла в 6O можно
найти из Toro же треуrольника, из Koтoporo нашли значения триrо-
нометрических функций для уrла в З0са (черт. 394), так как если
L А == 300. то L В == 60(;).
Тоrда
sin 600 == АС == уз O,8660; tg60° == АС == VЗ- 1,7321;
АВ 2 ВС
cos 600 == вс == == 0,5.
АВ 2
Составим теперь таблицу значений триrонометрических ФУНК-
ций для уrлов в 30са, 450 и 600.
Уrол I Синус I Косинус , TaHreHC
1 . VЗ уз
30 Q ..... == 0,5 ........... 0,8660 ........... 0,577 4
2 2 3
450 1/2 0,7071 У2 1
0,7071
2 2
I уз 1
600 0,8660 ....... == 0,5 уз 1,7321
2 2
Рассматривая эту таблицу, можно заметить, что СИНУС и тан"
reHC oCTporo уrла в о з р а с т а ю Т при увеличении уrла, а ко..
синус при увеличении уrла У б ы в а е Т.
При уменьшении уrла синус и таиrенс убывают, а косинус воз-
растает.
Упражнения.
1. Пользуясь чертежом, рассмотреть изме-
нение триrонометри еских функций в
связи с изменением уrла (черт. 396).
2. Значения триrонометрических функций
острых уrлов помещены в математиче-
ских таблицах В. М. Брадиса. Под-
робное описание таблиц и указания
к их использованию даны 8 самих
таблицах.
Пользуясь таблицами Брадиса, рассмот-
реть изменение триroнометрически
ФУНКЦИЙ в связи с изменением yrna.
r-
д
с'" С"
ЧЕРf. 396
с'
119
I 97. триrОНО \1ЕТРИЧЕСКИЕ функции ДОПОЛНИТЕЛЬНЫХ
Уrлов.
Дополнительными уriIа 1И называются два уrла, которые в
сумме составляют 900-. Такими уrлами, в частности, являются
острые уrлы прямоуrольноrо треуrольника.
. Уrлы А и В в прямоуrольном треуrольнике АСВ (черт. 397)
являются дополнительными уrлами, так как L А + L В == 900;
L А == 900 L В; L В == 900 L А.
Рассмотрим соотношения между триrонометрическими функ-
пиями дополнительных уrлов.
а а .
1) sin L:A == ; cos LB == , Т. е. синус данноz,о уzла ра-
с с
вен "осин усу дополнительноzо уzла.
2) cos LA == ; sin L:B == , т. е. "осинус данноzо уzла
с с
равен синусу дополниlпельноzо уzла.
а а
3) tg LA == ; ctg L:B == , т. е. тан"
ь b
z,eHC данноzо уzла равен "oтaHzeHCY
дополниtпельноzо уzла.
4) ctg L:A == ; tg L:B == , т. е. "отан,..
а а
z.eHC данноzо уzла равен тaпzeucy
допОЛllиl1lельноzо уzла.
Знание соотношений между триrономет"
рическими функциями дополнительных yr.. Д
u
лов важно для понимания устроиства три..
roнометрических таблиц.
t 98. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ
И уrлАМИ в прямоУrольном
ТРЕУrОЛЬНИКЕ.
Пусть дан прямоуrольный треуrольник
АВС (черт. 398). Обозначим ero стороны через
й, Ь и с. По определению триrонометрических
функций: == sin L А; == cos L В; .!!... :=J
С С С
.== sin L В; ! == cos L А. Отсюда а ==
с
==с sinLA == с cos LB; Ь ==с sin LB ==с cos LA,.
Т. е. "атеm nРЯА,оуzолыtоzо тpeYZOAb-
ни"а равен zunоmенуэе, у.мн,оженноit На
синус уzла, nроmUSОАежащеzо этожу А.
катету, или на "осин,с ,zAa, пpll.4e-
.жащеzо " не..".
180
в
а
с
ь
ЧЕРТ. 397
в
а
ь
с
ЧЕРТ. 398
Из TOrO }ке прямоуrольноrо треуrЬльника имеем, что
== tg L А, отсюда а == Ь tg L. А; == ctg LA, откуда Ь ==
ь а
=== а ctg LA, т. е. катет пря;моуzольноzо треуzолыш"а
равен дрУZОAlУ катету, умноженному на maHzeHC уzла,
противолежащеzо первому катету, или на "oтaHzeHC
уzла, прилежащеzо " nepBoAlY Kaпlemy.
99. РЕШЕНИЕ ПРЯI'\10уrольных ТРЕуrОЛЬНИКО8.
Выведенные нами соотношения дают возможность решать пря
моуrольные треуrольники, т. е. по некоторым данным элементам
треуrольника находить все остальные.
Рассмотрим несколько примеров.
1. Даны zunотенуза nРЯМ,ОУ20ЛЬНО20 треуzольника u один из
есо острых уzлов. Найти катеты этО20 треУ20льника и второа
острый усол.
Пусть rипотенуза с == 82,0 см; L А == 420 (черт. 399). Вычие.
лить длину катетов а и Ь и величину уrла В. Прежде Bcero оп-
ределим величину L В. L В == 900 ...... L А == 90<J ...... 42<J == 48().
Чтобы вычислить длину катета а, найдём по таблицам значе-
ние синуса уrла в 420, sin 42 G == 0,6691. Так как а == csin LA,
получим: а == 82,0. 0,6691 54,9 (см).
Второй катет треуrольника мож-
но вычислить различными способа-
ми. Используя значение уrла А, на...
ходим: Ь == с cos 420, или Ь == 82,0 х
Х 0,7431 60,9 (см).
Все неизвестные элементы Tp
уrольника АВС вычислены.
Длину катета Ь можно найти из
равенства Ь == с sin L В, т. е. Ь==
== с sin 48 Э .
Пользуясь таблицами квадратов
чисел, можно также вычислить катет
Ь и на основании теоремы Пифаrора
Ь V822 552.
2. Даны ка/пет nРЯМОУ20ЛЬНОZО тре..
У20льника u один из е20 острых У2лов:
Н айти ёиnoтенузу, вmoрой катет
эmo20 mреуеольнuка и второй острый
УZОЛ.
в
Q
IJ
ь
а
ЧЕРТ. 399
д
в
а
ь
с
ЧЕРТ. 400
181
Пусть катет а равен 25 сом, уrол А равен 32 G (черт. 400). Бычие..
пить длину rипотенузы С, длину катета Ь и величину уrла В.
L В == 900 ...... L А == 900 ....... 320 == 580;
а == с sin L'A' откуда с == а ; С == 25 ; с == 25 47 (см);
, sin LA sin 3Z> 0,5299
а 25
а == Ь tg / А; Ь == tg LA ; Ь == 0,6249 40 (см).
Все неизвестные элементы треуrольника АВС вычислены.
Можно было и в данно й зад аче приме нить иные способы решения.
Например: Ь == V с 2 ....... а 2 1/ 472 252 40 (см). .
З. Даны два катета nРЯМОУZОЛЬНОZО треуzольни1(,Q" найти ezo
2иnoтенузу и величину острых УZЛ08.
Пусть катет а равен 21 см, а катет Ь равен 18 соМ (черт. 401).
Вычислить длину rипотенузы с и величину уrлов А и В.
Найдём сначала (пользуясь теоремой Пи..
фаroра и таблицами квадратов чисел) длину
rипоте нузы с:
с == 1/ а 2 +Ь 2 ; с == 1/212+ 182 28 (см).
Найдём величину одноrо из острых yr..
JlОВ, используя равенство ==tg LA; tg LA==
ь
== 21 1,1667. Откуда L А 49 Э (с точ"
18 А
ностью до l О ), тоrда L В 41°.
4. ' Даны катет u 2иnoтенуза nрямоуzоль
НО20 треуzольнuка. Катет а == 52 см, 2И"
noтенуза с == 67 см. Решить треуzольник (самостоятельно).
3 а м е ч а н и е. Для решения прямоуroльных треуrольников
рекомендуется широко пользоваться Jlоrарифмической линейкой и
различными таблицами.
в
а
ь
с
ЧЕРТ. 401
100. уrол ПРЯМОЙ с плоскостью.
При выполнении различных практических измерительных работ
на местности часто приходится использовать уrлы, образуемые
прямой с плоскостью.
Уrол прямой с плоскостью оп..
ределяется следующим образом.
Пусть имеется плоскость и какая..
нибудь прямая, пересекающая эту
плоскость (черт. 402), например
прямая АВ пересекает плоскость
р в точке А. Чтобы опред
v u о
лить уrол этон прямои сданнои
плоскостью, из какой нибудь точ"
I
I
I
___L .....
с'
ЧЕРТ. 402
182
ки С прямой АВ опустим перпендикуляр СС' на данную плос..
кость Р.
Через точки А и С' проведём на плоскости Р прямую АС'.
L БА С' и будет уrлом, образованным прямой АВ с данной плос..
костью Р.
101. ПРАКТИЧЕСКИЕ ЗАДАЧИ С ПРИМЕНЕНИЕМ тРиrОНОМЕТРИИ.
Мы уже имели дело с различными практическими задачами,
которые решали или на основании равенства треуrольников, или
на осно вании их подобия. .
Знание триrонометрических функций позволяет нам решать т.а..
кие задачи более совершенными методами и с боЛЬ--
шей точностью.
Рассмотрим несколько таких задач.
1. Определить высоту предмета, 1(, основанию ко..
тОрО20 noдойти нельзя.
Например, нужно определить высоту те--
левизион ой антенны, которая отделена от
нас рекой (черт. 403).
Рассмотрим прямоуrольный тре--
уrольник ACD. В этом треуrольнике
мы можем с помощью астролябии
измерить уrол А. По..
ложим, он равен 420.
В треуrольнике BCD
измеряем LDBC, пусть
он равен 47<а.
Решение.
о
CD
............. ==
АС
== tg 420; CD == tg 470;
8С
АС== CD .
tg 4 '
CD
ве tg 470 (точки А, В, е находятся на одной прямой).
АС....... ВС == CD CD ; AC BC == CD ( 1
tg 420 tg 470 tg 420
АС Бе == CD ( t I )
0,9004 1,0724.
Расстояние АС ВС, т. е. АВ, может быть непосредственно
измерено, пусть оно равно 12,0 м, тоrда
12,0 == CD (1,1106 0,9325) == CD · 0,1781.
Откуда CD == 12 67,4 (м).
0,1781
I
/f
//
//
//
//
//
//
//
, /
, /
/ /
/ /
/ /
/ /
/ /
/ / '-"-
...::t2°A47 8
Д C
I В I
ЧЕРТ. 403
I ) ;
tg 470
.188
Для окончательноrо определения высоты антенны к 67,4 м еле..
дует прибавить высоту прибора, с помощью KOToporo определяли
уrлы А и В. Если высота прибора, например, составляла 1,40 м, то
окончательно высота антенны будет равна 67,4 + 1,40 == 68,8 (м).
2. Определить расстояние между nунктамu А и В, разделен--
Hbl.Ми npenf:lmcmвueM.
а) Пусть требуется найти расстояние от пункта А до пункта
В, находящеrося за рекой (черт. 404).
Строим при помощи астролябии или эккера при точке А прямой
уrол ВАС. Взяв на прямой АС произвольную точку D, с помощыо
астролябии измеряем уrол ADB;
пусть он равен 440. Измеряем рас--
стояние AD; пусть оно составит
120 At.
Torlla АВ == tg 440, или АВ ==
120
== 120.tg 44° 120.0,9657 116 (м).
б) Пусть нужно определить рас--
стояние от пункта А до пункта
В, между которыми находится вод--
ное пространство (черт. 405).
Принимая точку А за вершину
уrла, строим прямо й уrол ВАМ.
На прямой АМ фикс ируем какую--
нибудь точку С, находящуюся от
точки А на расстоянии, например,
200 A-t. С помощью астролябии
определяем уrол АСВ. Пусть он
будет равен 480. Тоrда АВ == tg 480,
АС
или АВ == 1,1106.
200
Откуда АВ == 1,1106 · 200
222 (м).
Практические раба..
ты:
1. Определить в окружающей обстановке высоту какоrо"нибудь
предмета, к основанию KOToporo подойти нельзя.
2. Определить расстояние до какой"нибудь недоступной точки.
в
,
/" /' , .... ......,
1" ""'.....
I .... .....
..",.... ,..
t , ......
А ь-- ... ..... ... ..... ..... .... ....
D
ЧЕРТ. 404
Д?"
I ', .
I ................
I v .......,.,....... ...
/r. 1
1, .о В 1\
I · \ ",
'. ,,
I '" >-: .::
'>'" .....
, ",,
Cf'-'
I
/М
ЧЕРТ. 405
102. СУММА ВНУТРЕННИХ И ВНЕШНИХ Уrлов
выпуклоrо мноrоУrОЛЬНИКА.
При съёмке плана земельноro участка, имеющеro форму MHoro-
уroЛЬНИК8, необходимо производить проверку правильнасти изме-
рения ero yrпoB.
184
I
/
/
".
"'"
;'
;'
;'
;'
/"
.......
/
-,-'
I
I
I
" /
'* .. ...
/ ,
/ ,
/ ,
// ,
.............
ЧЕРТ. 406
ЧЕРТ. 407
ЧЕРТ. 408
Для этоrо HY}I{HO знать, как находить сумму внуТренних и внеш-
них уrлов любоrо мноrоуrольника. К рассмотрению этоrо вопроса
мы и перейдём.
Возьмё f мноrоуrольник, имеющий n сторон (черт. 406).
Диаrонали, выходящие из одной какой"либо вершины mhoro--
уrольникз, разделяют ero на (n 2) треуrольника, так как каж-
дый из этих треуrольников содержит по одной стороне мноrоуrоль...
НИI{а, за исключением двух крайних треуrольников, содержащих
по две стороны МНОl"оуrольника. Следовательно,
8 Сумма внешних уzлов .мНОZОУZОЛЬНIЖа равна 2d. (п 2).
Возьмём мноrоуrольник, имеющий n сторон, и построим при
каждой ero вершине по одному внешнему уrлу (черт. 407).
1\\ы получим n пар смежных уrлов. Сумма их равна 2d · п.
Сюда входят все внутренние и внешние уrлы мноrоуrольника. Но
так как сумма внутренних уrлов мноrоуrольника равна 2d (n ...... 2),
то сумма внешних уrлов, взятых по одному при каждой вершине
равна 2dп...... 2d (n 2) 2dn...... (2dn ...... 4d) 2dn...... 2dn +
+ 4d == 4d. Следовательно,
8 Сумма внешних уzлов любоzо вЬ/,nУIlЛОZО .мноzоуzольни..
"а, вэяmь,х по одному при "аждоit e o вершине, рав-
на 4d.
Упражнения.
1. Пользуясь чертежом 408, вывести друrим способом формулу для выч --
пения суммы внутренних yrпoB JIюбоrо выпуклоrо мноrоуrольника.
2. Вычиcnить сумму внутренних уrлов пятиуrольника, шестиуrольника,
восьмиуrопьника, двенадцатиуrопьника.
3. Применить выведенную формупу для вычиcnения суммы внутренних yrпoB
выпуклоro мноrоуrопьника ДJlЯ четырёхуroпьника и треуrопьника.
4. Сколько сторон (уrлов) имеет мноrоуroпьник, еспи сумма Qнутренних
yrnoB ero равна 12 d?
5. Может nи сумма внутренни yrnoB мноroУroJlьника быть выражен а не-
чётным числом d?
188
f 103. съЕМКА ПЛАНА ЗЕМЕльноrо УЧАСТКА
с ПОМОЩЬЮ АСТРОЛЯБИИ путЕм ОБХОДА ПО КОНТУРУ.
Съёмка плана в этом случае производится так: измеряются по
следовательно все уrлы мноrоуrольника и все ero стороны. Затем
в принятом масштабе (в зависимости от размеров участка и лис
та бумаrи, на который наносится план) строится мноrоуrольник
с сохранением величины уrлов. Стороны мноroуrольника YMeHЬ
шаются соответственно принятому масштабу.
Полученный мноrоуrольник на плане будет подобен мноrоуrоль..
иику в натуре, так как уrлы этих мноrоуroльников будут COOTBeT
ственно равны, а .сходственные СТО}IOны пропорциональны.
Умение точно вычислять сумму внутренних уrлов любоrо вы..
пуклоrо мноrоуrольника даёт нам возможность делать проверку
правильности измерения уrлов при съёмке. плана.
Пусть мы имеем план земельноrо участка, имеющеrо форму
выпуклоrо мноrоуrольника, например шестиуroльника.
По выведенной нами формуле сумма внутренних уrлов шести
уrольника равна 2d (6 ....... 2), Т. е. 8d, или 720(3. У нас же в резуль..
тате измерений получилось не 720'J, а, например, 718 . Таким об
разом, мы допустили ошибку в 2(1. Такая ошибка вполне допусти
ма. Она может быть объяснена недостаточным совершенством из..
мерительных приборов, неточной их установкой, нашей неопыт..
"остью, неточностью измерений и т. д. .
Если эту ошибку разложить поровну на все 6 уrлов, то она со-
ставит менее 0,50 на каждый уrол. В таких случаях так и посту..
пают: допущенную ошибку распределяют поровну между всеми
уrлами мноrоуrольника.
Если же расхождение будет более значительным, например в
10......20<3' то необходимо вторично и возможно тщательнее выпол"
нить необходимые измерения. .
Ошибки при съёмке плана MorYT быть и при измерении и на..
несении на план длин отрезков, поэтому они также ДОЛЖНЫ под..
u
верrаться тщательноя проверке.
rЛАВА х
-.,.
ВПИСАННЫЕ
И описАнныE мноrо rОIlЬНИИИ.
104. ОПРЕДЕЛЕНИЯ.
Если все вершины мноrоуrольника лежат на окружности, 1'0
мноroуrольник называется в п и с а н н ы м в окружность, а OK
ружность ....... О П и с а н н о й около мноrоуrольника (черт. 409).
ЧЕРТ. 409
ЧЕРТ.. 410
Если все стороны мноrоуrольника являются касательными
окружности, то мноrоуrольник называется о п и с а н н ы м около
окружности, а окружность называется в п и с а н н о й в MHOro-
уroльник (черт. 410).
9 105. ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕуrольники.
8 т е о р е м а 1. 0"0/1.0 всяsоzо mреУZОАьнияа .мОЖНО Oпlt--
сать О"ружность.
Описать окружность около треуrольника ....... это значит постро-
ить такую окружность,_ которая проходила бы через ero вершины,
" u
т. е. через три точки, не лежащие на однои прямои.
В 69 была решена задача: «Через три точки, не лежащие на
одной прямой, провести окружность». При этом было установлено,
что задача всеrда имеет решение, и только одно.
На этом основании можем утверждать, что около любоrо тре-
уrольника можно описать окружность, и притом только QДНУ.'
187
Как видно из решения той же задачи,
центром окружности, описанной около тре-
уrольника, является точка пересечения пер..
пендикуляров, восставленных к сторонам
треуrольника из их середин.
е т е о р е м а 2. Во вся"ий "lреУZОЛЬНtt"
..,ОЖНО вписать 01(,РУЖlI0сmь.
Пусть дан АВС (черт. 411). Проведём
биссектрисы двух уrлов треуrольника, на..
пример уrла А и уrла В. Опустим из точ..
ки их пересечения О перпендикуляры на
стороны треуrольника АВС: OM...L АС,
ОК ...L АВ и OP...L ВС.
Все эти перпендикуляры равны между со..
бой: ОР == ОК == ОМ (так как ОР == ОК и
ОМ == ОК, то и ОР == ОМ, 9 32).
Следовательно, если из точки О как из центра радиусом, рав-
ным ОК, описать ОI<РУЖНОСТЬ, то прямые АВ, ВС и АС будут ка-
сательными к окружности О, так как они перпендикулярны к ра-
диусам в конечной их точке на окружности. ..
Таким образом, окружность О будет вписанной в треуrольник
АВС.
С л е Д с т в и е. Все три биссе1(,mрисы mреуzольни1(,а nе-
ресе"аются в одной тОЧ:llе.
В д АВС (черт. 411) соединим центр окружности О с вершиной
С треуrольника и докажем, что ОС является биссектрисой L С.
Для этоrо сравним два прямоуrольных треуrольника: мое
и РОС. Они равны по rипотенузе (ОС) и катету (01\1 == ОР).
Следовательно, L 1 === L 2, т. е. ОС является биссектрисой
уrла С.
Таким образом, все три биссектрисы треуrольника пересекаются
u
В однои точке.
. При м е ч а н и е. Пересечение биссектрис треуrольника в од-
нои точке отмечалось еще в начале настоящеro курса, но Tal\1 это
свойство было дано без доказательства.
t 106. СВОЙСТВА ВПИСАННЫХ
И ОПИСАННЫХ ЧЕтыр хУrольников.
8 Теорема 1. Сумма противоположных УZЛО8 вписаН-
HOZO четырехуzольни"а ра8на 180°.
Пусть в окружность с центром О вписан четырёхуrольник
ABCD (черт. 412). Требуется доказать, что L А + L с == 1800 и
L В + L D == 1800.
L. А, как вписанный в окружность О, измеряется v BCD.
2
L С, как вписанный в ту же окружность, измеряется.!... u BAD.
2
в
J<
.А
ЧЕ РТ. 411
188
с
Следовательно, сумма уrлов А и
С измеряется ПОЛУСУМJ\10Й дуr BCD
и BAD, в сумме же эти дуrи состав-
ляют окружность, т. е. имеют 3600.
Отсюда L А + L С == 3600 : 2== 1800.
Аналоrично ДОI<азывается, что и
L В + L D == 1800. Однако это мож-
но вывести и и HbIJ\I путём. Мы зна-
ем, что сумма внутренних уrлов вы-
пуклоrо четырёхуrольника равна 3600.
Сумма уrлов А и С равна 1800, зна-
чит, на сумму друrих двух уrлов че-
тырёхуrольника остаётся тоже 1800.
I Т е о р е м а 2 (обратная). Если в
четырех,zольнияе cYMAfa двух
п,rJотивоположных уzлов рав-
на 1800 t то о"оло ma"ozo ч,е-
тыlёхуzольнuяаa можно опи-
сать о"ружность.
Пусть сумма противоположных
уrлов четырёхуrольника ABCD рав-
на 1800, а именно L А + L С ==
== 1800 и L В + L D == 1800
(черт. 412).
Док а жеJ\1, что около TaKoro четы-
рёхуrольника можно описать окруж-
ность.
Д о к а 3 а т е л ь с т в о. Через
любые 3 вершины этоrо четырёх-
уrольника можно провести окруж-
ность, например через точки А, В и
с. rде будет находиться точка D?
Точка D может занять только од-
- v
но из следующих трех положении:
оказаться внутри Kpyra, оказаться
вне Kpyra, оказаться на окружности
Kpyra.
Допустим, что вершина окажется
внутри Kpyra и займёт положение D'
(черт. 413). Тоrда в четырёхуrоль..
нике ABCD' будем иметь:
L В + LD' ==2d.
Продолжив сторону AD' ДО пересечения с окружностью в ТОЧ"
ке Е и соединив точки Е и С, получим вписанный четырёхуrОЛЬНИ$
АВСЕ, в котором по пр мой теореме
L В + L Е == 2d.
в
А
о
ЧЕРТ. 412
ЧЕРТ. 413
ЧЕРТ. 414
1.,
Из ЭТИХ двух равенств следует:
L D' == 2d L В; L Е == 2d ...... L В;
откуда
L D' == L Е,
но этоrо быть не может, так как L D', как внешний относительно
треуrольника CD'E, должен быть больше уrла Е. Поэтому точка D
не может оказаться внутри Kpyra.
Так же доказывается, что ,вершина D не может занять положе..
ние D" вне Kpyra (черт. 414). .
Остаётся признать, что вершина D должна лежать на окруж-
ности Kpyra, т. е. совпасть с точкой Е, значит, около четырёхуroль..
ника ABCD можно описать окружность.
С л е Д с т в и я. 1. Вон.р,z, BCRSOZ,O nРЯAf,оуz,ОАьнива Af,ОЖ..
НО описать он.р,жность.
2. Bo"pyz, равнобедренной трапецtШ .можно описать
о"ружность.
В обоих случаях сумма противоположных уrЛО8 равна 1800.
8 Т е о р е м а З. В oпиCaHHOAf, ч,еп"ЫР JCуz,ОАьни"е C,MAfbl
противоположных сторон равны.
Пусть четырёхуrольник ABCD опи..
сан около окружности (черт. 415), т. е.
стороны ero АВ, ВС, CD и DA каса-
тельные к этой окружности. Требуется
доказать, что АВ + CD == AD + ВС.
Обозначим точки касания буквами
М, N, К, Р. На основании свойств ка-
сательных, проведённых к окружности
из одной точки (9 75), имеем:
АР == АК;
ВР == ВМ;
DN == DK:
CN == СМ.
ЧЕРТ. 4)5
Сложим почленно эти равенства. Получим: АР + ВР + DN"+
+ CN == АК + вм + DK + СМ, т. е. АВ + CD == AD + ве,
что и требовалось доказать.
у пражне","я.
1. В описанном четырёхуrольнике два противоположных yrпa относятся
как 3 : 5, а друrне ДВа относятся как 4 : 5. ОпреДeJIИТЬ величину этих
уrлов.
2. В описанном четырёхуrольнике сумма двух противоположных сторон равна
45 см. Остальные две стороны ОТНОСЯТСЯ как 0,2 : 0,3. Найти длину 9ТИ
сторон.
110
rЛАВА Х/
ПРАВИIlЬНЫЕ мноrоуrОIlЬНИКИ.
107. ОПРЕДЕЛЕНИЕ.
МноrоуrОJlЬНИК называется n р а в и JI Ь -
н Ы м, если равны все ero стороны и равны все
уrлы (черт. 416).
Из правильных мноrоуrольников мы пока
U ..
изучали только правильныи четырехуrольник
(квадрат) и правильный треуroльник (рав"
носторонний треуrольник).
Упражнения.
1. Можно ли назвать правильным четырёхуrольни-
ком любой прямоуrопьник? Ромб?
2. Будет ли правильным треуrольник, имеющий равные уrлы?
ЧЕРТ. 416
108. ПОСТРОЕНИЕ ПРАВИЛЬНЫХ мноrоуrольников.
. т е о р е м а 1. Если о"ружность разделить на равные части и
то.,,,и деле'ния последовательно соединить хорда.ми, то полу-
чu.м nравuльны.й .мН020уzольни" (вписанный).
Пусть окружность О разделена, например, на 5 равных частей (это можно
сделать с помощью транспортира) и точки деления последовательно соеди-
lieHbI хордами (черт. 417). Полученный мноrоуrольник правильный, так как:
во первых, все стороны ero равны, как хорды, стяrивающие равные дуrи;
BO BTOpЫX, все уrлы ero равны, как вписанные, опирающиеся на равные
дуrи.
Будем иметь то же самое, если разделим окружность на любое ЧИС.l0
равных частей.
. т е о р е м а 2. Есди о"ружность разделить на равные .,асти и
через то.,,,и деления провести касательные" ней, то получит-
ся правильны,й .IIно оуzольни" (описанный), вершина.ми "оторо-
20 б,дут служить то.,,,и пересе.,ения "асательных, nровед'н,-
ных 'tереэ соседние то.,,,и "асания (черт. 418).
А
Е
ЧЕРТ. 417
ЧЕРТ. 418
191
в справедливости этоrо можем убедиться следующим образом. Соеди-
ним хордами точки касания; получим ряд треуrольников, каждый из кото-
рых составлен двумя касательными и хордой. Эти треуrольники равнобедренные
(на основании свойств касательных, проведённых к окружности из какой-
нибудь точки вне её). Кроме тoro, все они равны между собой, так как имеIОТ
по "равной стороне (хорды, стяrивающие в Kpyre равные дуrи) и по два равных
у rла (все они составлены касательной и хордой и измеряются половинами равных
дуr) .
Отсюда следует, что построенный мноrоуrолыlкK правильный, так как
имеет равные стороны и равные уrлы.
109. СВОЙСТВА ПРАВИЛЬНЫХ мноrоуrольников.
. Т е о р е м а 1. О"оло любоzо правильноzо .AlHOZ о УZОЛЬНIt"а МОЗ1СНО
описать о"ружность.
Пусть ABCDEF (черт. 419)...... правильный мноrоуrольник; надо доказать,
что около Hero можно описать оКружность.
Мы знаем, что всеrда можно провести окружность через три точки, не
nежащие на одной прямой; значит, всеrда можно провести окружность, КО-
'[орая пройдёт через три любые вершины правильноrо мноrоуrольника, на-
пример через вершины Е, D и С. Пусть ТОЧI<а О центр этой окружности.
Докажем, что эта окружность пройдёт и через четвёртую вершину мноrоуrоль-
ника, например через вершину В.
Отрезки ОЕ, OD и ОС равны между собой, и каждый равен радиусу окруж-
IiОСТИ. Проведём ещё отрезок ОВ; про этот отрезок сразу нельзя сказать, что
он также равен радиусу окружности, это
надо доказать.
Рассмотрим треуrольник-и OED и ODC,
они равнобедренные и равные, следователь-
но, L. 1 == L 2 == L 3 == L 4.
Если внутренний yroп данноrо MHoro..
уrопьника равен а, то L 1 == L 2 ::::а
а а
==L.3==L4== ; но если L4== ,ТОИ
2 2
а
L 5 == , т. е. L. 4 == L. 5.
2
Orcюда заключаем, что А О CD
== А ОСВ и, значит, ОВ == ОС, т. е. отрезок 08
равен радиусу проведённой окружности. Из
этоrо следует, что окружность пройдёт и че-
рез вершину В правильноrо мноrоуrольника.
Таким же приёмом докажем, что по-
строенная окружность пройдёт и через все
остальные вершины мноrоуrольника. Зна
чит, эта окру>кность будет описанной около
данноrо правильноrо мноrоуrолыIка.. Тео-
рема доказана.
. Т е о р е м а 2. В любой правильны/i, МНО-
zоуzольни" МОЖНО вписать о"руж-
ность.
Пусть ABCD EF ...... правильный MHoro-
уrопьник (черт. 420), надо доказать, что в
Hero можно вписать окружность.
Из предыдущей теоремы известно, что
окопо правильноrо мноrоуrольника можно
описать окружность. Пусть точка О...... центр
этой окружности. Соединим точку О с верши..
Е
ЧЕРТ. 419
F
с
ЧЕРТ. 420
192
в
нами мноrоуrольника. Полученные треуrОЛЫ-IИКИ OED, ODC и т. д. равны
между собой, значит, равны и их высоты, проведённые из точки О, т. е.
ОК == OL === ОМ == ON == ОР == OQ.
Поэтому окру>кность, описанная из точки О как из центра радиусом, рав-
ным отрезку ОК, пройдёт через точки К, L, М , N, Р и Q, и высоты треуrоль-
ников будут радиусами окружности. Стороны мноrоуrольника перпендику-
JIЯРНЫ к радиусам в этих точках, поэтому они являются касательными к этой
окружности (9 73). А это значит, что построенная окружность вписана в данный
правильный мноrоуrольник.
Такое же построение можно выполнить для любоrо правильноrо MHoro"
уrольника, следовательно, вписать окружность можно в любой правильный
,
мноrоуrольник.
С л е Д с т в и е. О"ружnостu, описанная ОI'ОЛО правильноzо
.Аfноzоуzольни"а и Вnt"санная в Hezo, имею", общий центр.
а п р е Д е ,,1 е н и я. 1. Центром правильноrо мноrоуrольника называется общий
центр окружностей, описанной около 9Toro мноrоyrольиика и вписанной в Hero.
2. Перпендикуляр, опущенный из центра правильноrо мноrоуrольника на
ero сторону, называется апофемой правильноrо мноrоуrольника.
110. ВЫРАЖЕНИЕ СТОРОН ПРАВИЛЬНЫХ мноrоУrольников
ЧЕРЕЗ РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ.
С помощью триrонометрических функций можно выразить сто-
рону любоrо правильноrо мноrоуrольника через радиус описанной
около Hero окружности.
Пусть АВ сторона правильноrо п-уrольника, вписанноrо в
Kpyr радиуса ОА == R (черт. 421). Проведём апофему OD правиль-
Horo мноrоуrольника и рассмотрим прямоуrольный треуrольник
AOD. В ЭТОlvl треуroльнике
L. AOD == L. АйВ == . 3600 == 1800 ;
2 2 n n
AD == А40 · sin L AOD == R sin 180" ,
n
НО АВ == 2AD и потому АВ ==2R sin 1800 .
n
Длина стороны правильноrо n-уrольника,
вписанноrо в Kpyr, обозначается обычно
а п , ПОЭТОl\IУ полученную формулу можно
записать так: 6
. 1800
а п == 2R sln . ЧЕРТ. 421
n
Следствия. 1. Длина стороны правильн,оzо шести-
уzольн,и"а l BпиcaHHOZO в "pyz радиуса RI выражаетс
форм.УЛОЙ а в == RI так как
а в == 2R sin 1800 == 2R sin 300 == 2R == R.
6 2
2. Длина стороны правильн,оzо ч,еmь/'р хуzольниltа
(ltвадраmа), BпиcaHHOZO 8 "pyz радиуса R, выражается
фор.мулоii а, == R у"2, так как
193
й" == 2R sin 1800 == 2R sin 450 == 2R -v 2 == R V"2:
4 2
3. Длина сто por,bl nравuльноzо треуzольниl(,а, впи-
€tlHHOZO в "pyz радиуса R, вь'ражаеmся фор.мулой
аз == R V3, так как
1800 1/3.......
а з === 2R sin == 2R sin 600 == 2R == R V 3.
з 2
t 111. ПОСТРОЕНИЕ ПРАВИЛЬНЫХ ШЕстиуrОЛЬНИКА,
ТРЕуrОЛЬНИКА И ЧЕтЫРЕхуrОЛЬНИКА с ПОМОЩЬЮ
ЦИРКУЛЯ И ЛИНЕЙКИ.
1. Чтобы построить правильный шестиуrольник, достаточно
u
провести окружность и последовательно, одну за друrои построить
хорды, равные радиусу. По доказанному эти хорды равны сто-
ронам правильноrо шестиуrольника, вписанноro в Kpyr. Полу-
"
чим правильныи шестиуrольник. ,
2. Чтобы построить правильный треуrольник, построим сперва
правильный шестиуrольник, как указано в пункте 1, а затем соеди-
ним отрезками вершины этоrо шестиуrольника через одну. Полу-
"
чим правильныи треуrольник.
3. Чтобы построить правильный четырёхуrольник (квадрат),
достаточно провести в Kpyre два взаимно перпендикулярных диа-
метра и концы их соединить отрезками. Получим правильный че-
тыёхуrольник..
f 112. ПЛОЩАДЬ ПРАвильноrо мноrоуrОЛЬНИКА.
Пусть дан. правильный п-уrольник (черт. 422). Требуется опре-
ДeJIЦТЪ ero площадь. Обозначим сторону l\fноrоуrольника через а
и центр через О. Соединим отрезками центр с конца1\fИ какой-либо
стороны мноrоуrольника, получим треуrольник, в котором прове-
дём апофему мноrоуrольника.
ah
Площадь этоrо треуrольника равна . Чтобы определить
2
площадь Bcero мноrоуrольника, нужно площадь одноrо треуroльника
умножить на число треуrольников, т. е. на
ah aпh
n. Получим: S == · n == ............., но аn рав-
2 2
няется пери метру мноroуrольника. Обозначим
ero через Р. Окончательно получаем:
S == Ph , rде S площадь правильноrо мно-
2
rоуrольника, Р .......ero периметр, h апофема.
. Площадь правUЛЬНО20 .мНОZОУ20ЛЬНlЖа
о равна половине nроuзведения ezo nери-
ЧЕРТ. 422 .метра на апофе.му.
rЛАВА Х/I
ПJlОЩАДИ ПОВЕРХНОСТЕ.
Н о&ъЁМЫ rЕОМЕТРНЧЕСКНХ ТЕJI.
113. ПРАВИЛЬНАЯ ПРИ3МА.
1. Определения.
Призма называется n р а в и л ь н о Й, если основаниями её служат
правильные мноrоуrольники и боковые ребра перпендикулярны к
основаниям.
В зависимости от числа уrлов в основании призма называется
треуrольной, четырёхуrольной, пятиуrольной и т. Д.
На чертежах 423, 424, 425 даны изображения и развёртки по-
v . .. u
верхностеи правильных призм: треуrольнои, четырехуrольнои и
u
шестиуrольнои.
Боковыми rраня!\{и любой правильной призмы служат прямо-
уrольники.
ЧЕРТ. 423
-- I
I I I
I I I
I I I
I I I
! I I
I I I
--
ЧЕРТ. 424
.: .
:
llJB
ЧЕРТ. 425
I
I
. I
I
I
2. 8ычис.л-ение площади поверхности правильной призмы.
Основаниями правильной призмы являются правильные l\IHOrO-
уrольники, поэтому для вычисления площади основания такой
приэмы применяем 'формулу:
S ==.!..!!:. ( 112).
2
Боковые rрани представляют собой равные прямоуrольники,
поэтому для вычисления площади боковой поверхности данной
приэмы достаточно вычислить площадь одной боковой rрани и
умножить на их число.
Для вычисления полной поверхности данной призмы надо найти
сумму площадей двух оснований и боковой поверхности.
Упражнения.
1. Вычислить площади поверхностей указанных в таблице правильных приэм,
имеющих высоту, равную 25 см.
Название ПрН3М
Радиус ОК-
ружности,
описанной
около осно-
вания
ПЛощадь
боковой по-
вер Хиости
Площадь
полной по
вер ХноСти
ПЛощадь
основания
а) ПраВИJlЪная треуroль-
на я приэма . . . .. 6 с'м
б) ПраВИJJЬная четырёх-
уroльная призма 8 сАС
В) П раВИJJЬная шести-
уroльная n ризма " 5 сАС
196
При вычислениях рекомендуется пользоваться таблицами и поrарифмичес-
кой ,,'Iинейкоii.
2. Сделать необходимые измерения и вычислить площади поверхностей правиль-
ных призм, имеющихся в математическом кабинете школы.
3. Вычисление объёма правильной призмы.
Объём правильной призмы вычисляется так же, как и объём
всякой прямой призмы ( 68), по формуле: V == QH, rде V выра..
жает объём призмы; Q площадь основания; Н высоту приз..
мы (Т. е. длину боковоrо ребра).
Упражнения.
1. По данным в предыдущей таблице вычислить объёмы указанных в ней
правильных призм.
2. Вычислить объёмы правильных призм, имеющихся в математическом кабине-
те школы.
При вычислениях рекомендуется пользоваться таблицами и лоrарифмиче-
ской линейкой.
1 14. ПИРА 'ИДА.
1. Определения.
Пир а r.l и Д о й называется rеометрическое тело, оrраниченное
мноrоуrолы-lком,' называемым основанием пирамиды, и треуrоль-
никами с общей вершиной, которые называются боковыми rpa-
НЯМИ.
Общая вершина всех боковых rраней называется в ерш и-
11 О Й пирамиды.
В ы с о т о й пирамиды называется перпен,цикуляр, опущенный
из вершины пирамиды на её основание (черт. 426).
Пирамида, у которой основанием служит правильный м но..
rоуrольник, а высота проходит через центр основания, называется
п р а в и л ь н о й. Боковые rрани правильноiI пирам иды
равные между собой равнобедрен..
ные треуrольники.
Высота боковой rрани правиль...
u
нон пирамиды, опущенная из вер..
шины на сторону основания, на..
зывается а п о Ф е м о й- пирами..
ды.
На чертежах 427, 428, 429 даны
изображения и развёртки поверхно..
u
стен правильных пирамид: треуrоль..
u " u
нои, четырехуrольнои и шестиуrоль..
ной. На чертеже 430 изображены еrи..
петские пирамиды.
ЧЕРТ, 426
191
ЧЕРТ, 427
ЧЕРТ. 428
ЧЕРТ. 429
Упражнения.
СделатЬ развёртки правильных пирамид, изображённых на чертежах 427,
428, 429 и изrотовить из них модели пирамид.
2. Площадь поверхности пирамиды.
Чтобы определить площадь боковой поверхности пир амиды,
вздо найти сумму площадей всех её боковых rpаней.
Если к площади боковой поверхности пирамиды прибавить
площадь. её основания, пonучи я ПJlQЩадь полной поверхности
пирамиды.
198
ЧЕРТ. 430
Для краткости rоворят: БQковая поверхность пирамиды и пол...
иая поверхность пирамиды, опуская слово «площадь».
Упражнения.
в основании праВИJlЬНОЙ пирамиды тре-
уroJlЬНИК со стороной в 12 см. Апофема
пнрамиды ---- 20 СМ:
ВЫЧИСJlИТЬ: а) ПJlощадь основания,
б) боковую поверхность,
в) ПОJlНУЮ поверхность этой пирамиды.
Боковые rрани правипьной треуroJlЬНОЙ
пирамиды ---- равносторонние Tpeyroпь.
ники. Сторона основания равна а САС.
Вычислить боковую и ПОJlНУЮ поверх-
ность этой пирамиды (черт. 431).
Решить вторично эту задачу, раСПОJlОЖИВ
rрани пирамиды в виде параJlJlелоrрамма
(черт. 432). .
3. Объём пирамиды.
В старших классах средней школы
доказывается, что объём пирамиды со-
. 1
ставляет объёма призмы, имеющей
3
1.
2.
3.
ЧЕРТ. 431.
NV
а а
ЧЕРТ. 432
199
/1
/ L
....
//,
....r
.... ....
/
/
ЧЕРТ. 433
ЧЕРТ. 434
."
одинаковое основание с пирамидои и одну и ту же высоту
(черт. 433).
Следовательно, объём пирамиды вычисляется по формуле:
1
V== S.H
з J
rде V объём пирамиды, S площадь основания, Н........ высота
пирамиды.
Для иллюстрации этой формулы рекомендуется сделать из кар..
roна прямую четырёхуrольную призму и четырёхуrольную пира..
миду, имеющие равные основания и равные высоты. Если эту
пирамиду заполнить, например, песком и затем пересыпать ЭТОТ
1
песок в сделанную призму, то песок заполнит только 3" вмести..
мости призмы. Чтобы заполнить призму песком, необходимо триж..
ДЫ пересыпать в неё песок из заполненной пирамиды (черт. 434).
Упражнения.
По указанной выше формуле решить ряд задач по данным, помещённым в ниже-
следующей таблице:
Сторона Высота Длина
,N Название пврамиды основания пира- боковоro Об'Ь м
"ИДЫ ребра
1. Правильная четы рёх а) 25 см 40 см . . . .
уrольная пирамида б) 14 см . . . . 20 с'м . . . .
2. Правильная шести -
уrольная пирамида 9 САС 24 см . . .
З. Правильная треуrоль-
ная пирамида 14 САС 3D САС . .
200
115. конус.
1. ПОJlучение конуса.
Если вращать прямоуrольный треуrольник около одноrо из ero
катетов, то получится rеометрическое тело, называемое п р я м ы м
к р у r о в ы l\'1 К О Н У с о м 1 (черт. 435, 436, 437).
S Вершина
понуса
Основанием конуса является Kpyr.
rипотенуза прямоуrольноrо треуrольника, движение которой
образует боковую поверхность конуса, называется о б раз у ю-
щей конуса. Боковая поверхность конуса называется к о н и..
u
Ч е с к о и п о в е р х н о с т ь ю.
Высота прямоrо KpyroBoro конуса, опущенная из ero вершины
на основание, проходит через центр основания.
2. Раэвёртка поверхности конуса.
На чертеже 438 дано изображение развёртки конуса. Сектор
SAB развёртка боковой поверхности конуса, а Kpyr с центром
О основание конуса. Длина дуrи АВ, очевидно, равняется дли..
не окружности основания конуса
(2nR) , а радиус AS этой дуrи........ o
u
разующеи конуса.
Упражнение.
Начертить раэвёртку K0J:lYca в произвольном
масштабе и сделать модель прямоrо Kpyro-
Boro конуса.
З. ПJlощадь поверхности конуса.
ПЛощадь поверхности конуса (или А
просто поверхность конуса) равна
сумме площадей основания и боко-
u
вои поверхности.
I
/
Высота /
конуса
I
I
I: : ,
)<, .,./
OCHo{jaHue
Образующая S
:: b -- ;:о...
У.......
.... ....
, о
....--...... ..-,'
- -. -- .-
ЧЕРТ. 435
ЧЕРТ. 436
1 мы будем рассматривать только пря-
мой круrовой конус и бу».ем называть ero
просто к о н у с.
ЧЕРТ. 437
s
8
ЧЕРТ. 431
201
В предыдущем пункте мы рассмотрели понятие раэвёртки по..
верхности конуса. Будем обозначать через R радиус основания
конуса, а через l ...... длину образующей. Развёртка боковой поверх..
ности конуса есть сектор Kpyra радиуса 1, оrраниченный дуrой,
длина которой равна 2лR. По формуле площади KpyroBoro сектора
( 80) эта площадь равна
2nRl == nRl.
2
Площадь основания конуса paBHanR2. Поэтому площадь полной
поверхности конуса равна
пR2+ nRl == л',R (R + 1).
4. Объём конуса.
Объём конуса выражается такой же формулой, что и объём пн"
рамиды: V == Sh, rде v...... объём конуса, S....... площадь основа..
3
1
пия конуса, h....... ero высота. Окончательно V == ....... л'R1h, rде R ......
. з
радиус основания конуса.
Получение формулы объёма конуса можно пояснить таким рас..
суждением.
Пусть дан конус (черт. 439). Впишем в Hero правильную 'пи..
рамиду, т. е. построим внутри конуса такую пирамиду, вершина
которой совпадает с вершиной конуса, а основанием служит пра
вильный мноrоуrольник, вписанный в основание конуса. Объём
этой пирамиды выразится формулой: У' == ..!. 8'h, rде v'....... объём
3
пирамиды, S' ....... площадь её основания, h ....... высота пирамиды.
Если при этом за основание пирамиды взять мноrоуrольник
с очень большим числом сторон, то площадь основания пирамиды
будет весьма мало отличаться от площади Kpyra, а объём пирами..
ды ....... весьма мало отличаться от объёма кону..
са. Если пренебречь этими различиями в раз..
мерах, то объём конуса выразится следующей
формулой:
V == ..!.. Sh, rде У...... объём конуса, S.......
3
площадь основания конуса, h ...... высота кону-
са. Заменив S через пR 1 , rДе R ....... радиус кру"
1
ra, получим формулу: V == ....... nR1h, Bыpa
3
жающую объём конуса.
ЧЕРТ. 439
30:1
1
При м е q а н и е. В формуле V ...... Sh по.
3
ставлен знак точноro, а не приближённоro равенства,
хотя на основании проведёиноro рассуждеНИR мы
моrли бы ero считать примижённым, но' в старших классах.среднеА школы до-
t .
казывается, что равенство V == Sh точное, а не ПРJJближённое.
'" 3
у пр аж ",ения.
1. Вычислить полную поверхность конуса н ero объём по Данным, поме-
щённым в нижеследующей таблице:
Радиус ДЛRНа Полна. Объём
основ ани в образующей поверхнОсть
а) 3 САе 10 СМ . . . . . .
б) 5 СМ 13 СМ . . . . . .
в) 10 СМ 20 см . . . . . .
r) 11 СМ 35 см . . . . . .
2. Определить вес кучи песка, имеющей форму конуса с окружностью осно-
вания 15,7 м и с образующей в 6,8 м. (Удельный вес песка принять равным
1 ,5.)
З. Вычислить поверхность и объём конусов, имеющихся среди моделей reoMeT-
рических тел в математическом кабинете школы.
При всех вычислениях рекомендуется пользоваться таблицами и JIоrариф-
мической линейкоА.
116. ШАР.
Если вращать половину Kpyra BOKpyr ero диаметра, то получим
rеометрическое тело, называемое шар о м (черт. 440).
Центр Kpyra будет служить и центром шара, а диаметр Kpyra.......
диаметром шара. -
Поверхность шара называется шар о в о й п о в е р х н <r
с т ь Ю. Все точки шаровой повер..хности одинаково удалены от
центра шара.
--- - ...
'" "'-,
" ,
" ,
. I ,
, \
, \
ЧЕРТ. 440.
.
ЧЕРТ. 441
ЧЕРТ. 442'
203
Сечение шара' плоскостью всеrда имеет фОрl\fУ !<pyra (черт. 441).
Сечение, проходящее через центр Шара, называется большим кру"
rOM. Большой Kpyr делит шар на две равные части (черт. 442).
. Площадь поверхности шара (или просто поверхность шара)
равна учетверённой площади большоzо "pyza, т. е. 4nR2;
S==4пR2, или S == лD2. Эти формулы будут выведены в старших
классах школы.
Объём lпара равняется i пRЗ, V == nR3.
3 3
Получение формулы объёма шара можно пояснить таким рас-
суждением. В шар можно поместить весьма большое число пира-
мид с весьма малыми площадями оснований, расположив пирамиды
так, чтобы вершины их находились в центре шара, вершины ОСНО'"
ваний лежали на поверхности шара и своими боковыми rранями
пирамиды непосредственно примыкали одна к ДРУI"ОЙ (черт. 443).
ЧЕРТ. 443
ВЫСОТа каждой из построенных пирамид очень близка по длине
к радиусу (R) шара. Если пренебречь различием их длин, ТО объём
(v) каждой пирамиды можно выразить так:
1
v == ....... S R,
3
rде S площадь основания пирамиды.
Сумма объёмов (V') этих пирамид тоrда выразится формулой:
У' == 1. s' R, rде S' сумма площадей оснований пираl\.IИД. Сумма
3
эта (8') весьма близка к площади поверхности шара (8).
204
Сумма объёмов всех пирамид (V') весьма близка к объёму (у)
шара. Если пренебречь незначительными раЗЛИЧИЯl\!И в размерах
1
этих величин, то получим формулу: V == SR, по казывающую,
3
б " 1
что о ъем шара равен произведения площади поверхности шара
3
на длину радиуса. Обычно rоворят короче:
. Об'Оё шара равен.! произведения поверхности шара на
3
ezo радиус.
Подставив значение S == 41tR2, по,пучим формулу: V -= л'R3,
8
п[)3
или V == , rде D...... диаметр шара.
6
1
При м е ч а н и е. В формуле V == 3 SR поставлен знак точноro, а не
приближённоro равенства, хотя на основании проведённоrо рассуждения МЫ
моrли бы ero считать приб.пижённым, но в старших классах средней школы
. 1
доказывается, что равенство V == SR точное, а не приближенное.
3
Упражнения.
1. Вычислить объём шара, если ero радиус равен 5 СМ (8 см; 1 О см; 12 см).
2. Сколько весит чуrунный шар, если радиус ero равен 50 см? (Удельный
вес чуrуна принять равным 7.)
3. Определить объём футбольноrо мяча (предварительно сантиметровой лен-
той измерить окружность большоrо Kpyra и вычислить R).
4. Медный шар весит 1 О 1\2. Определить ero диаметр (удельный вес Me
равен 7,9).
5. Вычислить объём земноrо шара, приняв ero диаметр за 13000 км.
ЧЕРТ. 444
6. На чертеже 444 изображены три rеометрических тела: цилиндр, конус
и шар. Радиусы оснований цилиндра If конуса Р ВJ-Ibl радиусу шара.
Высоты цилиндра и конуса равны диаметру ЦJ!lP ,
Доказат8, что при этих условиях объём цилиндра равен сумме объёМО8 ко-
нуса и шара.
оrЛАВЛЕНИЕ
r л А В А 1. ОСНОВНЫЕ ПОНЯТИЯ.
i 1. Ч то такое rеометрия. . . . . . . . . . . . . . . . . . . 3
2. rеометрическое тело. Поверхность. ЛИНИЯ. Точка 4
3. Прямая. Луч. Отрезок .......... 6
4. Плоскость . . . . . . . . . . . . . . . . . . . 8
t 5. Сравнение отрезков. Действия над отрезками . . . . . 9
t 6. Измерение отрезка. Свойство отрезка . . . . . . . . . . 11
7. Провешивание прямой линии на поверхности земли . . . . 13
t 8. Измерение расстояний в комнате и на местности . . . . . . . . . 15
9. Уrол. Действия над уrлами .................. 17
10. Перпендикуляр к прямой. Построение перпендикуляра к пря-
мой . . . . . . . . . . . . . . . . . . ... . .
11. Смежные и вертикальные yr лы
12. Окружность. Kpyr .....
t 13. Центральныи уrол. Измерение yr лов
. . .
. .
21
25
28
. . . . 30
. . .
. . .
r л А В А 11. ТРЕvrольНИКИ.
14. Понятие о мноrоуrольнике . . . . . . . . . . . . .
f J5. Треуrольник и ero элементы . . . . . . . . . . . . . .
f 16. Виды треуrольников в зависимости от сравнительной длины
их сторон и величины уrлов . . . . . . . . . . 42
f 17. Симметрия относительно прямой . . . . . . . . 43
f 18. Свойства равнобедренноrо треуrольника ...... 46
f 19. Построение треуrольников по одному или двум элементам . . . . . 47
20. Построение треуrольника по двум дaHHblМ ero сторонам и yr лу
между ними. Первый признак равенства треуrольников . . . . . . 48
f 21. Построение треуroльника по стороне и двум прилежащим к ней
уrлам. Второй признак равенства треуrольников . . . . . . .
f 22. Построение тр уrольника по трём данным ero сторонам. Третий
признак равенства треуrольников . . . . . . . . . . . . . . . . . 50
f 23. ёCТKOCTЬ треуrольника .................. 51
24. Построение уrла, paBHoro данному ................ 52
f 25. Построение треуrольника по трём элементам. Четвёртый случай по
строения треуrольников ....... ...
f 26. Свойство внешнеrо уrла треуrольника ...
t 27. Равенство прямоуrольных треуrольников
28. Построения циркулем и линейкой
29. Понятие о теореме и аксиоме ...........
30. Соотношения между сторонами и уrлами треуrольника ...
31. Перпендикуляр и наклонная к прямой . . . . . . . .
f 32. Некоторые свойства окружности, перпендикуляра к отрезку, про-
ведённому через ero середину, и биссектрисы уrла . . . . . . . . . 67
39
40
49
. .
53
54
55
59
60
62
64.
. . . .
r л А В А 111. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
f 33. Взаимное положение прямых линий
34. Уrлы между двумя прямыми и секущей
f 35. Признаки параллельности двух прямых
f 36. Рейсмас. Малка ........
f 37. Аксиома параллельности Евклида ..
. . . .
. .
. .
. . .
71
. . . . 72
73
75
76
. . .
. . . .
. .
.
. . .
. . . . .
. . . .
206
38. Зависимость между yrnами, образованными двумя параллельяыми
прям и и сек ей ....................... 78
39. Сумма внутренних уrлов треуrольника .............. 80
39а. Заключительные замечання о построении треуrольников и признаках
равенства треуrольников . . . . . . . . . . . . . . . . . . 81
40. Уrлы с соответственно параллеЛЬНblМИ и перпендикулярными c:ropo.
нами . . . . . . . . . . . . 83
41. Практические работы на местности . . . . . . . . . . . . . . . 85
r л А В А VI. ЧЕтырЕх)'rольники.
42. Сумма внутренних уrлов четырёхуrольника . . . . . . . . 89
43. Параплелоrрамм . . . . . . . . . . . .
44. Подвижность параллелоrрамма (шарнирноrо) ... . . . . . . 92
45. Центральная симметрия ........ . . . . . . . . 93
9 46. Частные виды параллелоrраммов .... _ . . . 95
47. Свойство отрезков, отсекаемых параллельными прямыми на сторонах
48. С;:НЯЯ лин я. треу л н к · · : : : : : : : : : : .. : · · :gg
49. Трапеция . . . . . . . . . . . . . . . . . . . . . . ] 03
50. Свойства медиан треуrольника . . . . . . . . . . 104
r п А В А V. И3J'WЕРЕНИЕ ПЛОЩАДЕЙ rЕОМЕТРИЧЕСКИХ фиr}'р.
51. Понятие об измерении площадей. Палетка . . . . 106
52. Площадь прямоуroльника .............. . . . 107
53. Площадь квадрата . . . . . . . . . . . . . . . 11 О
9 54. Таблица квадратов чисел ................ . 111
55. Извnечение квадратноrо корня. Таблица квадратных корней из чи-
СМ ......... ....
56. Практические работы .....
57. Равновеликие фиrуры . . .
58. Теорема Пифаrора .
59. Площадь па раллелоrрамма .........
60. Площадь треуrолъника . .
9 61. Площадь трапеции . . . . . . . . . . .
62. Площадь произвольноrо мноrоуroлъника ....
r пА ВА VI. ПРЯМАЯ ПРИ3МА. ПОВЕРХНОСТЬ И ОБЪ2М ПРЯМОЯ ПРИ3М61.
63. Куб . . . . . . . . . . . . . . . . .
64. Прямая призма ..............
65. Понятие об измерении объёмов . .
66. Кубические меры . . . . . . . . .
9 67. Объём пр ямоуrольноrо параллелепипеда
68. Объём прямой призмы .......
rЛАВА VII. ОКР)'ЖНОСТЬ И KPvr. ЦИЛИНДР.
9 69. Построение окружности по трём данным точкам ... 134
70. Диаметр, перпендикулярный к хорде ..... . . . 135
71. Зависимость между хордами и дуrами . . . . . . . . . . . . . . 136
72. Свойство дуr, заключённых между параллельнblМИ хордами . . 137
9 73. Взанмное положение прямой и окружности ...........
74. Взаимное положение двух окружностей ... . . .. . . . . 139
Э 75. Свойство касательных, проведённых к окружности из одной
точки . . . . . . . . . . . . . . . .
76. Вписанные и некоторые друrие уrлы
77. Длина окружности ...................... 144
78. Дпина дуrи в пО .. . . . . 145
79. Площадь. Kpyra . . . . . . . . .
80. ПЛощадь сектора .. 146
81. Цили"iP . .. ...................... 147
. . .
. . 112
. . . .
115
116
117
119
120
124
128
. . .
129
130
. .
. . . .
. . .
141
.........
207
r л А В А VIII. ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ. ПОДОБИЕ Фиrvр.
t 82. Отношение отрезков . . . . .
f 83. Пропорциональные отрезки . . . . . . .
f 84. Построение пропорциональных отрезков
f 85. Задачи на построение . . . . .' . . .
f 86. Понятие о подобии фиrур .............
f 87. Подобные треуrольники ........
f 88. Три признака подобия треуrольников . . . . . . . . . .
f 89. Практическое применение свойств подобных треуrольников .
t 90. Подобие мноrоуrольников . . . . . . . . . . · ·
f 91. Отношение периметров подобных Мl:lоrоуrольников
f 92. Отношение площадей подобных фиrур .............
f 93. Построение подобных фиrур . . . . . . . . . . . .
r л А В А IX. тРиrОНОМЕТРИЧЕСКИЕ ФVНКЦИИ ос TPoro yr ЛА.
f 94. Определение триrонометрических функций ........... 173
f 95. Построение уrла по заданному значению одной из ero триrономет-
рических функций ............... . .. 176
f 96. Значения триrонометрических функций некоторых уrлов . . . . . 178
f rл. Триrонометрические функции дополнительных уrлов . . . . . . 180
S 98. Соотношения между сторонами и yr лами в прямоуrольном треуrоль
нике ..........................
t 99. Решение прямоуrольных треуrольников . . . . . . . . . . . .
t 100. Уrол прямой с плоскостью . . . . . . . . . . . . . . . . . . .
f 101. Практические задачи с применением триrонометрии ...,....
f 102. Сумма внутренних и внешних уrлов выпуклоrо мноrоуrольника ..
f 103. Съёмка плана земельноrо участка с помощью астролябии путём
обхода по контуру . . . . . . . . . . . . . . . . . . . . 185
r п А в А Х. ВПИСАННЫЕ И ОПИСАННЫЕ мноrоуrольники.
t 104. Определения . . . . . . . . . . . . . . . . . . . . . . . . 187
f 105. Вписанные и описанные треуrольники .............
f 106. Свойства вписанных и описанных четырёхуrольников ..... ,. 188
r п А в А XI. ПРАВИЛЬНЫЕ мноrоуrольники.
t 107. Определение . . · .:. · · · . . . . . . . 191
f 108. Построение правильных мноrоуrольников ... . . . .
f 109. Свойства правильных мноrоуrольников ............ 192
f 110. Выражение сторон правилыlхx мноrоуrОЛЬНИКО8 через радиус
описанной окружности .................... 193
f 111. Построение правильных шестиуrольника, треуrольника и четырёх-
уrольника с помощью циркуля и линейки ........... 194
t 112. Площадь правильноrо мноrоуrольника . . . . . . . . . . . .
r л А В А XII. ПЛОЩАДИ ПОВЕРХНОСТЕЙ И ОБЪ2МЫ rЕОМЕ.ТРИЧЕСКИХ ТЕЛ.
1 113. Правильная ПрИЗi\lа ..... .... . . . . . 195
114. Пирам ида. .... ............ . . . . 197
115. Конус. . . . . . . . . . . . . . 201
t 116. Шар ... . . . . . . . . . . . 203
. . .
150
151
153
154
155
157
158
161
164
166
167
169
. . .
. . . .
181
182
183
184