НОВОЕ В ЖИЗНИ, НАУКЕ, ТЕХНИКЕ
Серия «Математика, кибернетика», № 3, 1976 г.
Издается ежемесячно с 1967 г.
А. Н. Ефимов,
доктор технических наук
ПРЕДСКАЗАНИЕ
СЛУЧАЙНЫХ
ПРОЦЕССОВ
ИЗДАТЕЛЬСТВО «ЗНАНИЕ»
Москва 1976

Ефимов А. Н.
Предсказание случайных процессов. М.,
«Знание», 1976.
64 с. (Новое в жизни, науке, технике. Серия
«Математика, кибернетика», 3. Издается ежемесячно с 1967 г.)
В брошюре рассказывается об идеях и способах
предсказания значений случайных процессов. Рассматриваются
простейшие алгоритмы прогнозирования, демонстрируются свойства
прогнозирующих фильтров. Показаны основные свойства
алгоритмов прогноза в сочетании с алгоритмами суммирования и
циклического опроса. Рассматриваются технические устройства,
в которых используется операция прогнозирования. Брошюра
рассчитана на массового читателя.
СОДЕРЖАНИЕ
Предисловие 3
§ 1. Постановка задачи прогноза 6
§ 2. Исходные предпосылки 8
§ 3. Алгоритмы прогноза 14
§ 4. Прогнозирующий фильтр 20
§ 5. Прогноз и суммирование 31
§ 6. Прогноз в технике 40
§ 7. Особенности прогнозирования векторных
случайных процессов 47
§ 8. Экспертные оценки и прогноз 56
Алексей Николаевич Ефимов
ПРЕДСКАЗАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
Редактор В. И. Ковалев. Худож. редактор В. Н.
Конюхов. Техн. редактор Т. В. С а м с о н о в а. Корректор
Т. Ю. Дорогова
А 05851 Индекс заказа 64303
Сдано в набор 5/1 1976 г. Подписано к печати 18/11 1976 г
Формат бумаги 84Х1087з2 Бумага типографская № 3
Бум. л. 1,0 печ. л. 2,0 усл. печ. л. 3,36 уч.-изд. л. 3,29
Тираж 65520 экз. Заказ 2932 Цена 11 коп.
Издательство «Знание». 101835.
Москва, Центр, проезд Серова, д. 4.
Чеховский полиграфический комбинат Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли
г. Чехов Московской области
© Издательство «Знание», 1976 г,

ПРЕДИСЛОВИЕ
Способность предвидеть ход событий издревле
считалась у всех народов признаком ума и одаренности —
достаточно вникнуть в смысл слов «прозорливый» и
«недалекий», чтобы убедиться в этом.
Эта способность, присущая не только людям, но и
животным, была так основательно проверена многовековым
опытом, что сомневаться в ней не приходилось, но механизм
этого явления, источник этих способностей был настолько
загадочен, что без колебаний относился древними к разряду
сверхъестественного.
Информация о будущем добывалась по-разному.
Одиссей, например, должен был вызвать из недр Аида «Душу
пророка, слепца, обладавшего разумом зорким, душу Ти-
ресия фивского...» \ которая, напившись жертвенной
крови, обрела способность предсказать ему дальнейший путь
и препятствия на этом пути. За следующие десять веков
техника предсказаний существенно упростилась, но
научная база осталась той же: «Убийство (Калигулы) было пред-
вещено многими знаменьями. В Олимпии статуя Юпитера,
которую он приказал разобрать и перевезти в Рим,
разразилась вдруг таким раскатом хохота, что машины
затряслись, а работники разбежались...» 2.
Церковь за наукой права на прогноз не признавала из
принципиальных соображений: предсказывать будущее
можно лишь путем «откровения свыше», но никак не эмпирико-
дедуктивным путем.
Классическая наука в лице П. Лапласа провозгласила
полную предсказуемость мира. «Дайте нам мгновенные ко-
1 Гомер. Одиссея. М., «Художественная литература», 1967,
с. 539.
2 Г. Светоний. Жизнь двенадцати цезарей, М., «Наука»,
1966, с. 125.
1*
3

ординаты и скорости всех молекул Вселенной и мы
предскажем ее судьбу».
Классическая механика действительно могла бы
совершить и то и другое. Могла бы — если бы действовала в
классическом мире. Мир же оказался гораздо сложнее —
предсказывать его можно, это верно, но не безошибочно.
Закономерности прогноза выяснены лишь в последние
десятилетия. Предсказанные явления, значения и
ситуации входят в научный обиход и быт.
Сегодня авиапассажир, потерявший несколько часов
из-за неверного прогноза погоды, выражает недовольство
в адрес предсказателей теми же словами, что и в адрес,
например, лифтера, продержавшего его полчаса между
этажами. Мистический туман рассеялся, предсказания
случайных процессов ведутся сейчас на безупречной научной
основе и при помощи совершенной техники, но, к сожалению,
знания этих основ и методов распространены еще
совершенно недостаточно.
Теме «прогноз случайных процессов» не повезло — она
не попала ни в один из популярных учебников по теории
вероятностей и выпала, таким образом, из поля зрения
большинства инженеров и естественников.
Предполагая у читателя знания по теории вероятностей
в объеме книг Б. В. Гнеденко х и Е. С. Вентцель 2, автор
хочет продемонстрировать основные закономерности и
методы прогнозирования стационарных случайных
процессов. Автор рассчитывает также, что читатели легко
найдут в сфере своей практической деятельности проблемы,
к оценке и решениям которых смогут применить идеи и
методы прогнозирования.
Прогноз в технике чаще всего сводится к предсказанию
значений случайных процессов — режимов работы
технических устройств, либо воздействий на них со стороны среды.
Перечислить задачи прогноза, встречающиеся в технике,
в этой брошюре невозможно. Они имеют место почти во
всех областях — касается ли это чисто технологических
проблем или общих вопросов, связанных с развитием
техники. Мы приведем два примера, имеющих большую
общность и позволяющих проследить цели прогнозирования.
1 Б. В. Гнеденко. Курс теории вероятностей. М., Физмат-
гиз, 1961.
2 Е. С. Вентцель. Теория вероятностей. М., «Наука», 1964.
4

Первый пример, предлагаемый читателю, относится к
проблеме взаимоотношений человека и машины, или, говоря
более конкретно, поведения оператора за пультом ЭВМ.
Оператор в кресле перед пультом с умиротворяющими
зелеными огоньками, кажется, являет собой воплощение мечты
о легком и радостном труде. Внешнее впечатление,
разумеется, обманчиво. Раз оператор-наблюдатель вообще
посажен перед пультом, то неприятность должна наступить —
ее-то он и ждет, чтобы вмешаться. Состояние его, как
говорят, дискомфортно — он ждет выхода одного из
параметров за пределы нормы, но не знает, с какой стороны
надвигается опасность. Операторы, работающие за такими
пультами, быстро утомляются, увеличивается вероятность
ошибки.
Помогает им вычислительное устройство, следящее за
параметрами и прогнозирующее их ход. Если какая-либо
из наблюдаемых величин приближается к допустимой
границе и предсказывается ее выход из нормы, оператор
извещается об этом и может принять меры заранее либо
приготовиться к этому. В случае если прогноз не подтверждается
и параметр остается в норме, внимание оператора
переключается на другой объект с неблагоприятным прогнозом и т. д.
Петушок, подаренный царю Додону в сказке А. С. Пушкина,
представлял собой именно такое прогнозирующее
устройство. Второй пример — классический, относящийся к
истории развития кибернетики. Предоставим слово Н.
Винеру — «отцу кибернетики», создавшему теорию и методы
расчета прогнозирующих устройств.
«Задача управления огнем противовоздушной обороны
совсем не похожа на задачу артиллерийского обстрела
крепости, а скорее напоминает охоту на уток. Пока вы
стреляете, утка не остается на месте, и, если целиться в ту точку,
в которой утка находится в момент выстрела, то, когда
прилетит пуля, она окажется уже далеко. Поэтому нужно
стрелять с определенным упреждением и уметь оценивать
величину этого упреждения быстро и точно. Если такая
оценка окажется неверной, то вам, наверное, не удастся
выстрелить по этой же утке еще раз.
... В систему управления огнем ПВО приходится
вводить что-то эквивалентное таблице поправок, позволяющей
автоматически определять необходимое упреждение для
орудия с тем, чтобы самолет и снаряд оказывались в одной
и той же точке одновременно. Задача об этих поправках на
первый взгляд может казаться чисто геометрической, но
5

при более тщательном подходе к ее решению выясняется,
что оно сопряжено с необходимостью как можно более
точной оценки будущего положения самолета по данным
наблюдений его положения в прошлом»г. Добавим, что
координаты самолета изменяются случайно и что
источником этой случайности может служить сам пилот,
маневрирующий, чтобы обмануть артиллериста.
В качестве «пилота» и «артиллериста» здесь могут
выступать автоматические системы управления огнем ПВО и
противодействия на самолете.
В приведенной цитате сформулирована цель прогноза —
«возможно более точная оценка будущего положения» —
и основа предсказания — «... поданным наблюдений ...
положений в прошлом».
Итак, основой для суждения о будущем является
материал о поведении процесса в прошлом.
Здесь речь будет идти о предсказании значений
случайных процессов, относящихся к классу нормальных и эрго-
дических.
Методы статистического прогноза дают возможность
оценить будущие значения процесса по результатам
наблюдения прошлых и текущих значений, используя при этом
знание его вероятностных характеристик.
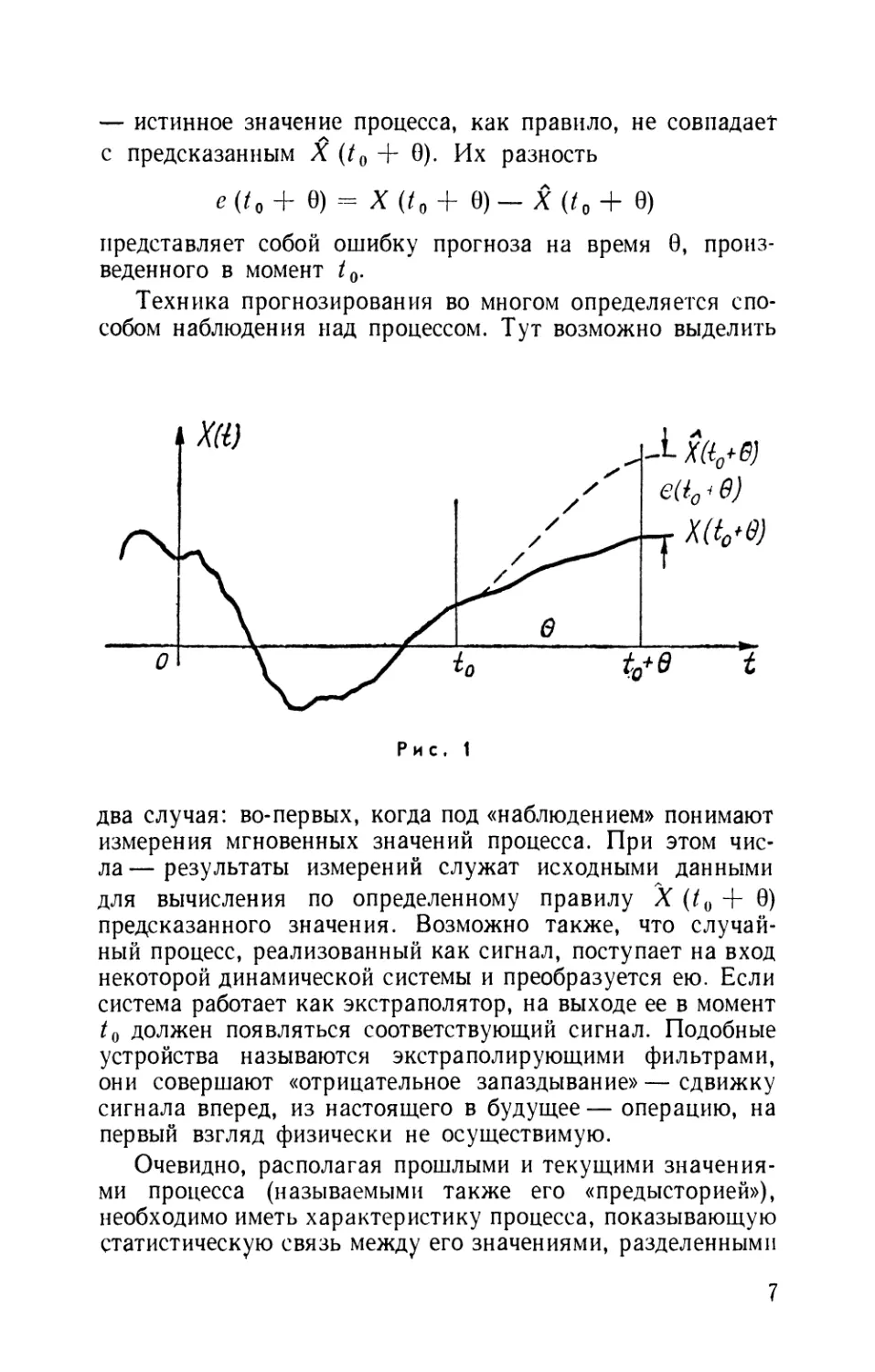
Пусть X (t) — стационарный гауссов случайный
процесс, наблюдавшийся некоторое время до момента /0 (рис. 1).
После t0 сведений о значениях процесса нет. Требуется
предсказать X (/0 + 6) — значение процесса в момент /0 + 6
через время 0, причем желательно сделать это «получше».
Если, предсказав значение X (t0 + 0), дождаться момента
/0+ 6 и произвести наблюдения, его результат X (t0 + 0)
1 Н. В и н е р. Я — математик. М., «Наука», 1964, с. 228.- • -
6
§ 1. ПОСТАНОВКА
ЗАДАЧИ ПРОГНОЗА

— истинное значение процесса, как правило, не совпадает
с предсказанным X (t0 + 0). Их разность
7
представляет собой ошибку прогноза на время G,
произведенного в момент /0.
Техника прогнозирования во многом определяется
способом наблюдения над процессом. Тут возможно выделить
Рис. 1
два случая: во-первых, когда под «наблюдением» понимают
измерения мгновенных значений процесса. При этом
числа — результаты измерений служат исходными данными
для вычисления по определенному правилу X (t0 + 0)
предсказанного значения. Возможно также, что
случайный процесс, реализованный как сигнал, поступает на вход
некоторой динамической системы и преобразуется ею. Если
система работает как экстраполятор, на выходе ее в момент
t0 должен появляться соответствующий сигнал. Подобные
устройства называются экстраполирующими фильтрами,
они совершают «отрицательное запаздывание» — сдвижку
сигнала вперед, из настоящего в будущее— операцию, на
первый взгляд физически не осуществимую.
Очевидно, располагая прошлыми и текущими
значениями процесса (называемыми также его «предысторией»),
необходимо иметь характеристику процесса, показывающую
статистическую связь между его значениями, разделенными

временным промежутком 9. Такой характеристикой
является корреляционная функция.
Чтобы вычислить предсказанное значение, нужно уметь
выбрать правило вычисления X (t{) + 0) — алгоритм
прогноза.
Для оценки качества прогнозирования нужно
условиться о каком-то критерии, так или иначе связанном с ошибкой
прогноза. Наиболее распространенным критерием является
средний квадрат ошибки:
Прогнозирование значений, которые случайный процесс
примет в будущем, возможно на основании анализа связи
между теми значениями, которые он принимал в прошлом
и принимает в настоящем. Для количественной
характеристики этой связи нам понадобится вспомнить о свойствах
системы случайных величин.
Регрессия
Пусть случайные величины X и Y объединены в
систему (ХК), подчиненную нормальному распределению с
плотностью:
§ 2. ИСХОДНЫЕ
ПРЕДПОСЫЛКИ
Мы будем пользоваться этим критерием, имея в виду,
что алгоритм прогноза должен выбираться так, чтобы ё1
был минимален.
Интуитивно ясно, что близкие значения можно
предсказать с большей точностью, чем удаленные, и что поэтому с
увеличением времени прогноза 0 средний квадрат ошибки
будет расти.
Для дальнейшего изложения нам необходимо вспомнить
о свойствах двумерного нормального распределения,
регрессии и корреляционной функции.

Здесь тх и ту — математические ожидания входящих
в систему компонент X и Y\ о2х и о* — их дисперсии,
есть коэффициент корреляции, а Кху — корреляционный
момент, характеризующий степень взаимозависимости
компонент.
Компоненты системы X и Y подчинены одномерным
нормальным законам N± (mx% ох) и N2 (my, ау), причем в силу
действующей между ними статистической связи изменение
одной из компонент влечет за собой изменение закона
распределения другой. Этот закон, вычисленный при условии,
что первая компонента X приняла определенное значение,
называется условным законом распределения и имеет вид:
есть плотность нормально распределенной условной
случайной величины Y/X.

Итак, при изменении одной из компонент (например, X)
вид закона распределения второй не изменяется, а меняется
лишь его параметр ту/х C) — условное математическое
ожидание. Условная же дисперсия D) от значения X не
зависит.
Зависимость ту/х от X линейна и называется
регрессией Y на X.
Аналогично прямая
есть линия регрессии X на Y.
Коэффициент корреляции /-определяет наклоны линий
регрессий: tg а = г ~—; tg (J = ——~— . Коэффициент
корреляции является мерой линейной связи между
компонентами системы. Он показывает, насколько хорошо в
среднем одна из величин может быть представлена в виде
линейной функции, от другой.
Пусть Y представима в виде суммы некоторой
линейной функции от X и остатка Z:
Y = I (X) + Z = (АХ + В) + Z. F)
Будем рассматривать Z = Y — / (X) как ошибку
приближения величины Y линейной функцией / (X) = АХ +
+В. Линейной функцией наилучшего среднеквадратическо-
го приближения называют такую функцию / (X), для ко-
торой средняя квадратическая ошибка приближения)Л\4[22]
принимает наименьшее значение. Можно доказать, что
такая функция существует и что для нее М [Z] = 0 г.
Будем искать нужную линейную функцию в виде:
1 См. Л. 3. Румшисский. Элементы теории вероятностей.
М., «Наука», 1970.

Очевидно, М [Z2] достигает наименьшего значения при
Аох — гоу = 0 и С = 0. Таким образом, линейная функция
наилучшего среднеквадратического приближения
Корреляционная функция
Стационарный случайный процесс X (t) обладает
вероятностными характеристиками, не зависящими от текущей
переменной (времени, например). Его математическое
ожидание тх (t) = тх = const и дисперсия Dx (t) = Dx =
const. Его корреляционная функция Кх (t, t')9 равная по
определению корреляционному моменту между сечениями
процесса X (t) и X (/'), не зависит от расположения
сечений / и /', а лишь от расстояния между ними т = V — /.
Корреляционная функция Rx (т) стационарного
процесса X (t) есть функция одного аргумента. Она четна:
Rx (т) = Rx (—т) и равна дисперсии в нуле: Rx @) = Dx.
На практике часто пользуются нормированной
корреляционной функцией
И
т. е. совпадает с уравнением регрессии C).
Линия регрессии, проведенная через совокупность
случайных точек, является наилучшим приближением и в более
сложных случаях — когда ее уравнение выражается,
например, полиномом.
Очень часто бывает, что вид зависимости между
компонентами системы (линейная, полиномиальная,
логарифмическая и т. д.) бывает известен из физических соображений,
а опыт устанавливает лишь параметры этой зависимости —
в нашем случае это тх\ m • ах\ or • г.
Функция Рд. (т), таким образом, равна коэффициенту
корреляции между сечениями процесса X (t) и X (t + т).
Очевидно, что р^ @) = 1.
Если стационарный процесс эргодичен, т. е. если
вероятностные характеристики его, вычисленные то ли путем
усреднения множества реализаций ансамбля, то ли путем
усреднения по времени одной достаточно длинной реали-

зации, оказываются одинаковыми, корреляционная
функция вычисляется весьма просто:
Рис. 2
в случайные моменты 0lt 02, Оу, ..., О,-, ..., образующие
простейший поток.
В силу свойств простейшего потока вероятность за
время т совершиться т переходам подчинена распределению
Пуассона и равна
Корреляционная функция
/?(т) == М [X (t) X (t + тI
вычисляется как математическое ожидание произведения
X (t) X (t -|- т), принимающего значения а2, если число
12
Здесь X (t) — центрированный процесс X (t)\ T— длина
реализации.
Для некоторых типов процессов корреляционная
функция может быть вычислена как, например, для процесса
типа «телеграфный сигнал».
«Телеграфный сигнал» X (t) (рис. 2) принимает значения
а и —а, причем переход от значения к значению совершается

переходов за время т четно, и —а2, если число переходов
нечетно:
R (т) - а- [Р @) + Р B) ... ] — а2 [Р A) + Р C) ... ].
Здесь в квадратных скобках — вероятности совершения
четного и нечетного числа переходов за время т.
Подставляя Р (т), получим:
13
Процесс, интервал корреляции которого был бы равен
нулю, являлся бы «абсолютно случайным» — связей между
его сечениями не было бы вовсе. Такой процесс, не
осуществимый физически, является, однако, очень удобной моделью
и носит название «белый шум».
В технических системах протекают случайные процессы,
имеющие весьма различные времена корреляции. Так,
например, для рабочих процессов мощного энергоблока
тепловой электростанции флюктуации яркости факела в
топке имеют интервал корреляции в доли секунды; в
минуты— температуры перегретого пара; десятки минут —
нагрузки генератора и расхода топлива и, наконец, до
десяти суток — теплотворной способности твердого топлива.
Ясно, что случайное изменение яркости пламени
(важная характеристика режима горения) по сравнению с
колебаниями теплотворной способности представляет собой
очень хорошее подобие «белого шума».
Методы корреляционного анализа случайных процессов
вошли в практику лишь с появлением средств вычисли-
Так как сумма в скобках равна ?-^\ то R (т) = aV-2^
и R @) = а2.
Одним из важных для практических расчетов параметров
случайных процессов является «интервал корреляции» —
время т0, в течение которого между сечениями процесса
сохраняется статистическая связь и корреляционный
момент между ними остается больше некоторого заданного
уровня, например \R (т) | > 0,05.
Иногда время корреляции т0 определяют, как половину
ширины основания прямоугольника единичной высоты,
площадь которого равна площади под кривой модуля
корреляционной функции:

тельной техники. Лет 15—20 назад некоторое
распространение получили специализированные вычислительные
устройства— коррелографы (корреляторы), предназначенные
для построения корреляционных функций.
Ранние коррелографы, построенные на
электромеханическом, механическом и даже гидравлическом принципе,
требовали ручной работы двух операторов, поздние
представляли собой автоматизированные цифровые устройства,
«поглощавшие» осциллограммы и выдававшие графики
корреляционных функций. Сейчас, однако, корреляторы почти
полностью вытеснены универсальными ЦВМ.
§ 3. АЛГОРИТМЫ
ПРОГНОЗА
Здесь мы познакомимся с несколькими
распространенными правилами вычисления предсказанных значений —с
алгоритмами прогноза.
Очевидно, алгоритм, указывая предсказанное значение,
должен связать с ним предысторию процесса и его
вероятностные характеристики. С другой стороны, качество
алгоритма определится дисперсией ошибки прогноза.
Мы будем рассматривать алгоритмы прогноза, линейные
относительно значений предыстории. Как будет показано,
для гауссовых процессов, оперировать которыми мы
условились выше, этот класс алгоритмов оказывается
наилучшим.
Рассмотрим несколько простейших линейных
алгоритмов.
Прогноз по последнему значению
Прогнозирование по последнему отсчету, называемое
также «ступенчатой экстраполяцией», или
«экстраполяцией нулевого порядка», заключается в том, что в качестве
предсказанного значения X (t0 + Э) принимается
значение X (t0):
X (t0 + 6) = X (t0). A0)
Предсказанное значение здесь не зависит от времени
прогноза 0, предыстория представлена лишь одной точ-
14

кой—последним значением X (t0)> вероятностные
характеристики не учитываются вовсе.
Алгоритм прогноза, как видно из A0), заключается в
умножении значения X (t0)—последнего отсчета на
единицу, т. е. не требует выполнения вообще никаких
вычислительных операций.
Прогноз, таким образом, можно выполнять, ничего не
зная о процессе, кроме последнего значения, и не
производя никаких вычислений. Очевидно, эти удобства, эта
экономичность должны чем-то оплачиваться. Они оплачиваются
низкой точностью.
Ошибка прогноза
e(t0 + 6) = X(t0 + 6)-X(/0+ 6)
здесь приобретает вид:
e(t0+ 9) = X(t0+ Q)—X(t0)9
а ее средний квадрат, если тх = 0,
?F) = M{[X(t + 6)-Х (ОН = o*-2Rx(B) +
+ о*х = 2 [ol—R(Q)l A1)
Средний квадрат ошибки прогноза растет от 0 при 9 = 0,
когда R @) = а*, до 2о2х при 0 = оо, когда R (об) = 0.
Хорош или плох этот способ прогноза, можно будет
сказать, лишь сравнив ошибку данного с ошибками других
алгоритмов. Простота же этого способа обеспечила ему пока
что наибольшее распространение как в технике
управления, где данные об управляемом процессе хранятся в ЗУ
и считываются в момент выработки управляющего
воздействия, так и в быту, когда, взглянув утром на термометр
за окном, мы и несколько часов спустя ориентируемся на
ту же температуру.
Прогноз по математическому ожиданию
Прогнозирование по математическому ожиданию
заключается в том, что в качестве предсказанного значения X (/0+
+ 6) принимается математическое ожидание процесса тх:
X (t0 + 9) = тх.
Как и в предыдущем случае, предсказанное значение
здесь не зависит от времени прогноза 9. Однако различие
заключается в том, что хотя информации о предыстории не
требуется никакой, нужны некоторые сведения о свойствах
процесса — о его математическом ожидании. Алгоритм
прогноза не требует выполнения никаких вычислительных
операций.
15

Рис. 3
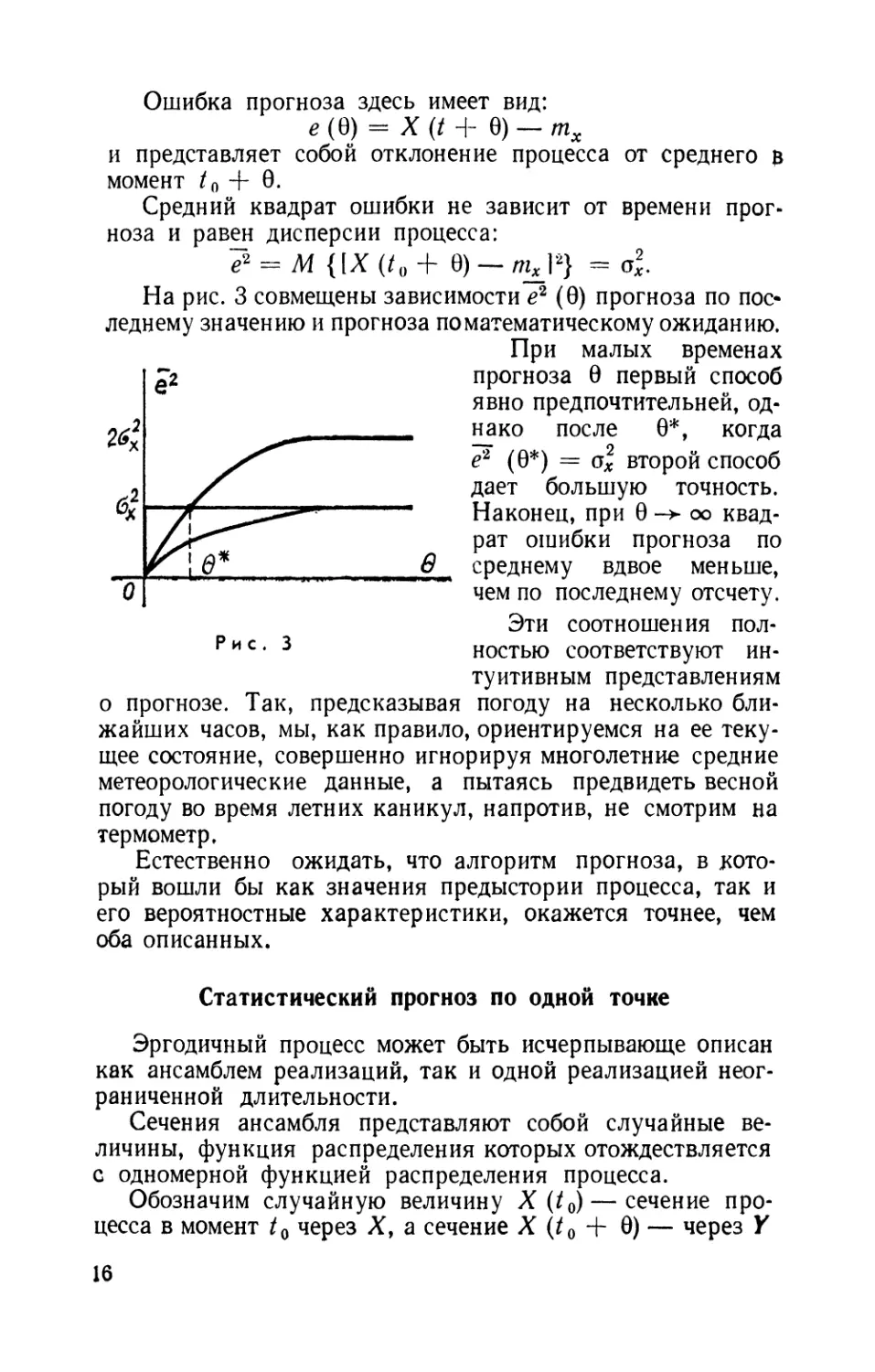
Ошибка прогноза здесь имеет вид:
е(В) = X(t + Q) — mx
и представляет собой отклонение процесса от среднего $
момент t0 + 0.
Средний квадрат ошибки не зависит от времени
прогноза и равен дисперсии процесса:
7* = М{1Х (/0 + 9) - /и*12} = oi
На рис. 3 совмещены зависимости е2 @) прогноза по
последнему значению и прогноза по математическому ожиданию.
При малых временах
прогноза Э первый способ
явно предпочтительней,
однако после 0*, когда
е1 @*) = ol второй способ
дает большую точность.
Наконец, при 0 ~> оо
квадрат ошибки прогноза по
среднему вдвое меньше,
чем по последнему отсчету.
Эти соотношения
полностью соответствуют
интуитивным представлениям
о прогнозе. Так, предсказывая погоду на несколько
ближайших часов, мы, как правило, ориентируемся на ее
текущее состояние, совершенно игнорируя многолетние средние
метеорологические данные, а пытаясь предвидеть весной
погоду во время летних каникул, напротив, не смотрим на
термометр.
Естественно ожидать, что алгоритм прогноза, в
который вошли бы как значения предыстории процесса, так и
его вероятностные характеристики, окажется точнее, чем
оба описанных.
Статистический прогноз по одной точке
Эргодичный процесс может быть исчерпывающе описан
как ансамблем реализаций, так и одной реализацией
неограниченной длительности.
Сечения ансамбля представляют собой случайные
величины, функция распределения которых отождествляется
с одномерной функцией распределения процесса.
Обозначим случайную величину X (t0) — сечение
процесса в момент t0 через X, а сечение X (t0 + 0) — через Y
16

и будем рассматривать систему (XY) двух случайных
величин — последнего значения предыстории и
предсказанного значения. Прогнозирующий алгоритм сформирован
так, что в качестве предсказанного значения X (t{) + 0)
назначает условное математическое ожидание величины Y
при условии, что X = X (t0):
X (t0 + 9) - ту/х.
Ошибка прогноза
е (t0 + 9) - X(t0 + 9) - X (t0 + Q) = Y- mylx
представляет собой отклонение случайной величины Y
от своего условного математического ожидания, а средний
квадрат ошибки ?2(9) = М [Y — ти/хJ] равен условной
дисперсии о*/х.
Вспоминая C), D), установим, что
X (/0 + 9) = тх/у = ту + гх1и -^— (Х — тх) A2)
и
?(8) - о~/х - ol A - г). A3)
Поскольку процесс X (/) стационарен, математические
ожидания и дисперсии сечений одинаковы:
°у ^ °х = а» ту = тх = т-
Коэффициент корреляции гху равен значению
нормированной корреляционной функции в 9;
rxy = p (9).
Теперь алгоритм прогноза принимает вид:
X (t0 + в) = m + р (9) [X (f 0)— /п], A4)
а средний квадрат ошибки оказывается зависящим от 9:
ет(9) - а2 [1 — р2 (9I. A5)
Алгоритм предполагает знание отклонения процесса от
среднего в момент t()y т. е. одной точки предыстории,
значения нормированной корреляционной функции р (9) и
математического ожидания.
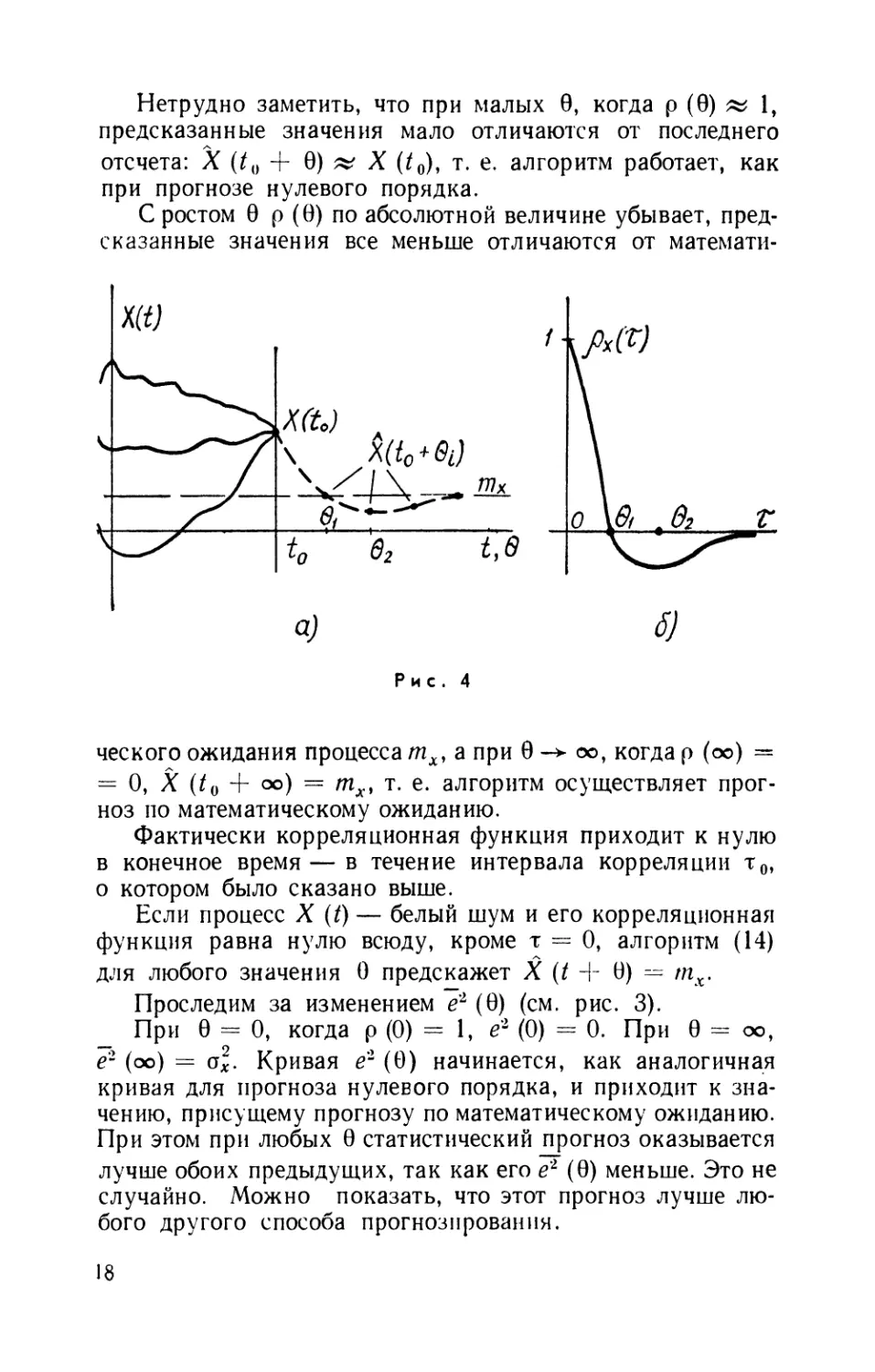
На рис. 4, а изображена предыстория процесса X (t),
а на рис. 4, б— его нормированная корреляционная
функция р (9). Прогноз производится на время 9Х, 92 ... 9/ ...
Точки, соединенные пунктиром на рис. 4, а, представляют
собой предсказанные значения X (t{) + 92), X (t0 + 92)...—
произведения отклонения X (t0) — тх на (> (9Х), р (9о)... .
2 Серия «Математика» № 3
м

Нетрудно заметить, что при малых 0, когда р @) « 1,
предсказанные значения мало отличаются от последнего
отсчета: X (t{) + 0) » X (t0)y т. е. алгоритм работает, как
при прогнозе нулевого порядка.
С ростом 0 р @) по абсолютной величине убывает,
предсказанные значения все меньше отличаются от математи-
Рис. 4
ческого ожидания процесса тх, а при 0 -*- оо, когда р (оо) =
= О, X (/0 + оо) = тх> т. е. алгоритм осуществляет
прогноз по математическому ожиданию.
Фактически корреляционная функция приходит к нулю
в конечное время — в течение интервала корреляции т0,
о котором было сказано выше.
Если процесс X (t) — белый шум и его корреляционная
функция равна нулю всюду, кроме т = 0, алгоритм A4)
для любого значения 0 предскажет X (t + 0) = тх.
Проследим за изменением е2 @) (см. рис. 3).
При 0-0, когда р@) = 1, е1 @) = 0. При 0 - оо,
е- (оо) = а*. Кривая е2 @) начинается, как аналогичная
кривая для прогноза нулевого порядка, и приходит к
значению, присущему прогнозу по математическому ожиданию.
При этом при любых 0 статистический прогноз оказывается
лучше обоих предыдущих, так как его е2 @) меньше. Это не
случайно. Можно показать, что этот прогноз лучше
любого другого способа прогнозирования.
18

Действительно, зависимость предсказанного значения
X (t0 + 0) как условного математического ожидания от
последнего отсчета X (/0) представляет собой уравнение
регрессии. Выше было показано, что уравнение регрессии
является функцией наилучшего среднеквадратичного
приближения. Следовательно, сечение пучка реализаций,
проходящих при /ft через точку X (t0) (см. рис. 4, а), будет
иметь средний квадрат отклонения относительно точки,
предсказанной по A4), меньший, чем относительно любой
другой, выбранной по иному, чем A4), правилу. Прогноз
A4) является для гауссовых процессов оптимальным.
Статистический прогноз по двум и более точкам
Итак, привлечение для прогнозирования все более
полной информации о процессе позволяет уменьшить ошибку
предсказания. По сравнению с простым переносом и
прогнозом по математическому ожиданию статистический
прогноз более эффективен именно потому, что использует
значения математического ожидания, корреляционной функции
и одной точки предыстории. Следует ожидать, что
использование двух или более точек предыстории позволит еще
больше повысить эффективность. Так и происходит.
Пусть теперь систему образуют три случайные
величины—сечения X (/2) = Z, X (/о) = Х\ X (/0 + 6) = Y.
Тогда предсказанное значение X (t0 + 6) = ти1х%г —
условное математическое ожидание сечения X (/0 f 6) при
условии, что предыдущие отсчеты приняли значения Z =-
- X (/2) и X = X (/„).
Выражение для предсказанного значения весьма
громоздко:
Средний квадрат ошибки растет медленнее, чем в
предыдущем случае, но в тех же пределах (см. рис. 3): е1 @) = 0,
е1 (оо) =-- а2.
Пример. Температура агрегата изменяется
случайно, корреляционная функция этого процесса приведена на
рис. 4. Измерения температуры производятся с частотой
2*
19

1 раз в минуту и используются для управления процессом.
Сравним ошибку экстраполяции на 0 ----- 1 мин при
различных алгоритмах:
а) дисперсия ошибки прогноза при ступенчатой
экстраполяции
? A) == 16 (°С)\
б) при статистической экстраполяции по одной точке
? A) = 14,0 (°СJ,
в) при статистической экстраполяции по двум точкам
? A) - 13,0 (°СJ.
Различие в эффективности алгоритмов невелико в силу
того, что время прогноза A мин) мало по сравнению с
временем корреляции G мин). Особенно незначителен выигрыш
при переходе к статистической экстраполяции по двум
точкам г.
Привлекая все новые точки предыстории, можно
улучшить прогноз, но не беспредельно. С одной стороны, ясно,
что предыстория, более удаленная чем на интервал
корреляции, не поможет делу: отсчет и прогноз окажутся
статистически не связанными и информации друг о друге не
дадут.
С другой стороны, слишком «частое» расположение
отсчетов внутри интервала корреляции также не имеет
смысла: отсчеты будут коррелированы очень сильно и будут
повторять друг друга*— то, что может быть сказано одним из
них, уже сказано соседом.
Существует предел уменьшения средней ошибки
прогноза, превзойти который принципиально невозможно.
Мы рассмотрели алгоритмы прогноза — правила
вычисления предсказанных значений в случае, когда процесс
представлен числовыми отсчетами.
1 См. Э. Л. И ц к о в и ч, Э. А. Т р а х т е н г с р ц.
Алгоритмы централизованного контроля и управления производством.
М., «Советское радио», 19G7.
20
§ 4. ПРОГНОЗИРУЮЩИЙ
ФИЛЬТР

Если процесс реализован как сигнал, прогнозирующее
устройство, на вход которого этот сигнал поступает,
должно выдавать на выходе его будущие значении.
Мы рассмотрим вначале физическую картину работы
такого устройства, не касаясь математической стороны дела.
Сейчас методы синтеза прогнозирующих фильтров
изучаются студентами ряда технических факультетов, но еще
недавно A0—20 лет назад) это входило лишь в аспирантские
курсы специалистов по связи и теории управления. Н.
Винер в книге воспоминаний «Я— математик» пишет, что в
1943—1944 гг., когда теория фильтрации и
прогнозирования была им разработана и изложена в секретном
отчете 1, переплетенном в желтый переплет, отчет этот получил
у инженеров прозвище «желтая опасность» из-за
содержащихся в нем «математических ужасов».
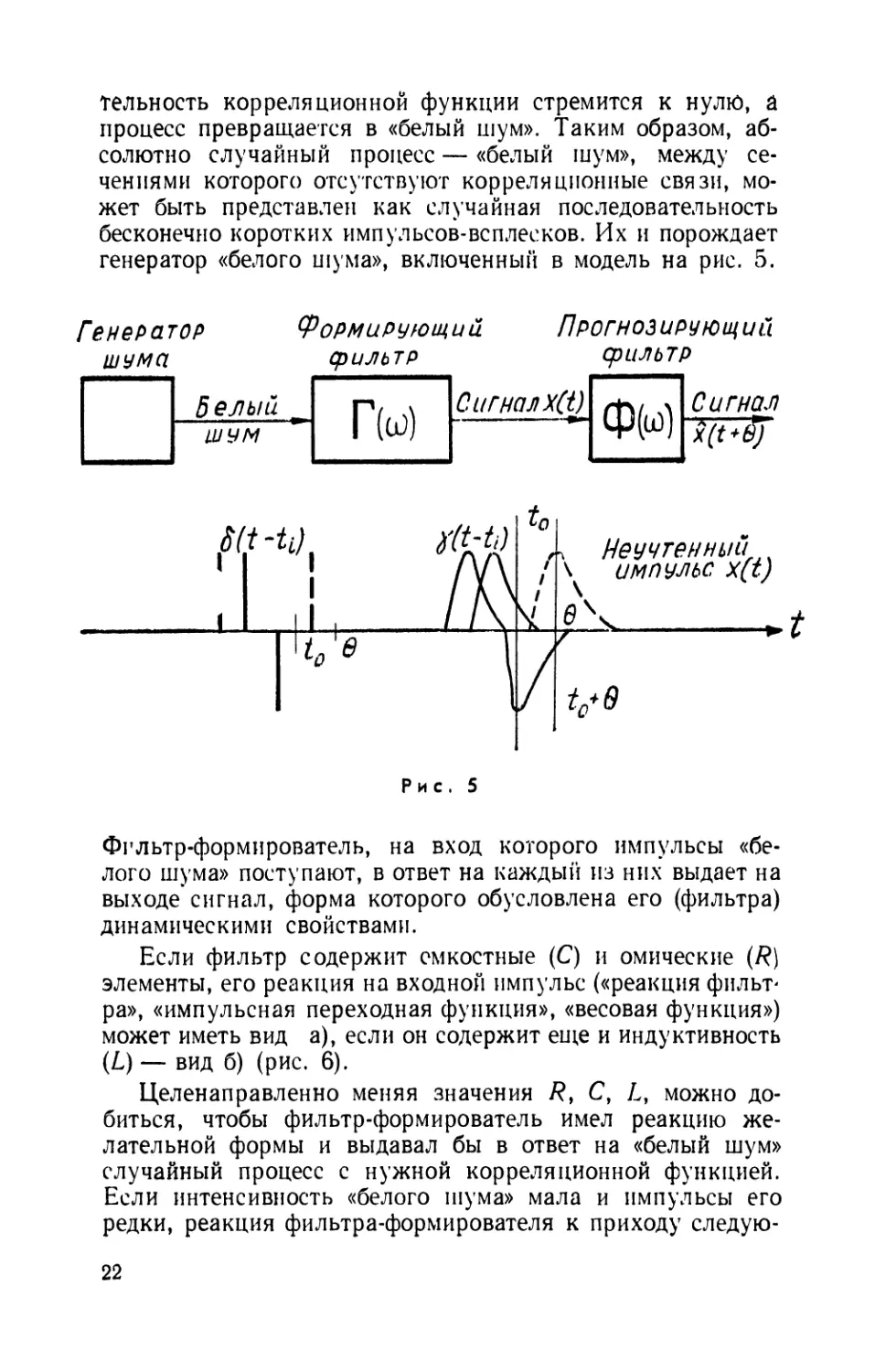
Модель случайного процесса
Записанная на осциллографе и магнитофоне реализация
случайного процесса при воспроизведении будет
воспринята, как шум. Другая реализация, другого рисунка, будет
воспринята и ухом, и специальными
приборами-анализаторами, как тот же шум. Реализации весьма различных
рисунков могут иметь одну и ту же корреляционную функцию.
Для удобства принято представлять случайные
процессы, как порождение некоторой модели-— системы,
состоящей из генератора «белого шума» и формирующего фильтра.
Простейшей моделью реализации случайного процесса
представляется наложение импульсов одной и той же
формы, возникающих в случайные моменты времени, как это
изображено на рис. 5. Некоторые случайные процессы
действительно имеют подобную микроструктуру, например
дробовый эффект, вызываемый эмиссией из катода
отдельных электронов, или радиоактивный распад, отдельные акты
которого наступают в случайные моменты.
Амплитуда и частота импульсов определяют дисперсию
процесса, а форма их — корреляционную функцию. Если
импульсы противоположных знаков возникают в среднем
одинаково часто, математическое ожидание процесса равно
нулю. Длительностью импульса определяется и интервал
корреляции. При неограниченном сужении импульсов дли-
1 Работа предназначалась для управления средствами
противовоздушной обороны.
21

тельность корреляционной функции стремится к нулю, а
процесс превращается в «белый шум». Таким образом,
абсолютно случайный процесс — «белый шум», между
сечениями которого отсутствуют корреляционные связи,
может быть представлен как случайная последовательность
бесконечно коротких импульсов-всплесков. Их и порождает
генератор «белого шума», включенный в модель на рис. 5.
Рис, 5
Фгльтр-формирователь, на вход которого импульсы
«белого шума» поступают, в ответ на каждый из них выдает на
выходе сигнал, форма которого обусловлена его (фильтра)
динамическими свойствами.
Если фильтр содержит емкостные (С) и омические (R)
элементы, его реакция на входной импульс («реакция
фильтра», «импульсная переходная функция», «весовая функция»)
может иметь вид а), если он содержит еще и индуктивность
(L) — вид б) (рис. 6).
Целенаправленно меняя значения R, С, L, можно
добиться, чтобы фильтр-формирователь имел реакцию
желательной формы и выдавал бы в ответ на «белый шум»
случайный процесс с нужной корреляционной функцией.
Если интенсивность «белого шума» мала и импульсы его
редки, реакция фильтра-формирователя к приходу следую-
22

щего импульса успевает затухнуть, если же импульсы
часты, сечение выходного сигнала представляет собой сумму
незатухших к этому моменту «хвостов» предыдущих
импульсов.
Физическая картина прогноза
В рамках избранной модели реализации «белого шума»
отличаются одна от другой расположением импульсов,
реализации процесса X (t) на выходе формирующего фильтра —
расположением его импульсов-реакций.
Реализации «белого шума» и X (t) изображены на рис. 5,
где момент t()— последняя точка предыстории, 9— время
прогноза. Для исчерпывающего задания реализаций
достаточно располагать набором точек О, 0lf ... 01 —
моментами появления импульсов и знать вид реакции фильтра-
формирователя — форму его выходного импульса. Так как
реакция фильтра известна, наблюдение за предысторией
сводится к фиксации моментов О, 0{, ... . Если бы в момент /0
поток импульсов из генератора «белого шума»
прекратился, на выходе формирователя еще некоторое время можно
было бы наблюдать сигнал— реакцию фильтра на
импульсы, пришедшие ранее.
Зная моменты их появления, можно было вы вычислить
с>мму этих «хвостов» в любой будущий момент t{) [ 6.
Это и было бы величиной X (t{) Н- 0) — предсказанным
значением процесса. Однако в момент t{) процесс не
прекращается — прекращается лишь наблюдение над ним,
состоящее в подсчете и фиксации пришедших на формирователь
импульсов «белого шума». Поэтому импульсы, поступившие
после момента t{)y не будут учтены наблюдателем, реакция
23
Рис. 6

на них фильтра-формирователя наложится на
предсказанное значение и составит е (t0 + 9), ошибку прогноза.
Истинное значение в момент t + В будет состоять из
предсказанной величины и ошибки:
X(t+Q) = Х(/„ + 0) + e(to+ 0). A6)
Очевидно, что при значениях 0, малых по сравнению со
временем корреляции, когда вероятность появления
неучтенного импульса мала, значение ошибки будет в среднем
мало. Однако с увеличением 0, когда «хвосты» учтенных
импульсов будут все более и более затухать, а неучтенных
появится все больше и больше, сигнал в момент t + Э станет
определяться в основном ошибкой. Когда 0 превысит
время корреляции, наблюдатель потеряет возможность
предсказать что-либо, кроме среднего значения.
Предсказывать «белый шум», естественно, нельзя — его
импульсы мгновенны и не имеют «хвостов». В связи с этим
стоит вернуться к примеру Н. Винера с упреждением при
стрельбе по самолету и обсудить следующий вопрос.
Предположим, что летчик, желая «переиграть»
зенитчиков, старается придать движению самолета случайный
характер. Самое большее, к чему он должен стремиться,
это придать движению штурвала характер «белого шума».
Предположим, штурвал достаточно легок и летчику это
удалось. Теперь, даже наблюдая движение штурвала,
предсказать его невозможно. Значит ли это, что и движение
самолета нельзя предсказать? Нет, не значит. Самолет играет
здесь роль формирующего фильтра, а движущийся
штурвал - роль генератора шума. Мы знаем, что процесс на
выходе формирователя предсказать возможно, причем чем
больше инерционность самолета по этому каналу
управления, тем более точным будет прогноз. Артиллеристу
поэтому полезнее наблюдать движение самолета, чем
следить за поведением летчика.
Свойства прогнозирующего фильтра
Предыдущие рассуждения показали, как должен был
бы действовать наблюдатель, желающий прогнозировать
импульсную модель случайного процесса, и даже
позволили оценить эффективность такого прогноза.
Теперь нужно выяснить, какими динамическими
свойствами должен обладать прогнозирующий фильтр, который,
будучи включенным после источника белого шума и фильт-
24

pa формирующего, выдавал бы на выходе X (t0+ б) —
предсказанное значение.
Обратимся к рис. 5.
Сумма ординат реакций фильтра-формирователя в
момент /0—последнее наблюдение предыстории процесса.
Сумма ординат в момент /0 + 0, если бы она стала
известной наблюдателю в момент /0, явилась бы предсказанным
значением Я (t0 -\- &). Следовательно, фильтр, который
сдвигал бы все импульсы-реакции формирователя на б
влево по временной оси, выполнял бы функции
прогнозирующего: в момент /о на его выходе наблюдалось бы
предсказанное значение!
Поскольку обе части выражения A6) описывают один
и тот же процесс, дисперсию (мощность) процесса можно
представить распределенной между точным значением и
ошибкой. При 0^0 мощность предсказанной
последовательности совпадает с мощностью точных значений, при
0 = оо мощность ошибки достигает дисперсии процесса.
Таким образом, дисперсия ошибки прогнозирующего
фильтра растет подобно ошибке оптимального прогноза
от 0 до а~\
Однако, можно ли вообще говорить о «сдвигании
сигнала вперед»? Осуществима ли физически такая операция?
Не противоречат ли такие попытки закону причинности?
На рис. 7 изображены импульсы «белого шума»,
вызванная им реакция фильтра-формирователя у (i) и резуль-
25
Рис. 7

тат сдвигания ее влево — реакция прогнозирующего
фильтра Р {t) = у (t+ 6). Существенно, что функция Р (/), как
реакция фильтра, существует лишь в области 6^0. При
в < 0 р (/) = 0 и закон причинности, таким образом, не
„нарушается.
Итак, реакция прогнозирующего фильтра р (/) — не
просто смещенная влево на Э по временной оси, но еще и
«отрезанная» слева фигура у (/).
Операция, которая сохранила бы часть фигуры у (t),
показанную пунктиром левее 9 = 0, конечно, физически
неосуществима.
Прогнозирующий фильтр «заглядывает в будущее» в
пределах физической законности: основываясь на прошлом
процесса и расплачиваясь за увеличение времени
предсказания возрастающей мощностью ошибки. Непонимание
этого лет 20—25 назад давало поводы объявлять
прогнозирование случайных процессов «идеализмом», а
кибернетику, широко использующую идеи прогноза, —
«лженаукой».
Элементы количественного описания прогнозирующего
фильтра
Этот раздел рассчитан на читателя, знакомого с
понятием «передаточная функция» и основными свойствами
преобразования Фурье.
Здесь будут получены выражения, описывающие
прогнозирующий фильтр и дисперсию ошибки прогноза.
Вернемся к рис. 5, на котором изображена модель,
содержащая источник «белсго шума», формирующий и
прогнозирующий фильтры. Источником шума и формирующим
фильтром моделируется случайный процесс X (/), значения
которого требуется прогнозировать.
Опишем эту часть модели. Импульсы у (t— /f),
появляющиеся в случайные моменты tt и образующие реализацию
процесса X (/), определяют своим видом корреляционную
функцию
26
Если стандартные импульсы затухают достаточно
быстро, к ним можно применить преобразование Фурье.

Пусть Г (со) — Фурье - изображение импульса у (t— tt):
27
Любопытно, что импульсы у (t) разлагаются в интеграл
Фурье, а сам процесс — нет.
Корреляционная функция оказывается связанной с
изображением Г ((о):
Но подобным образом — как взаимное преобразование
Фурье — связана с корреляционной функцией процесса
его спектральная плотность S (со). Следовательно,
S(a>)= |Г(со)|2.
Если у (t) сужаются, спектр процесса расширяется. При
импульсах бесконечно малой длительности процесс
превращается в «белый шум». Его корреляционная функция равна
нулю при всех т Ф О, а спектр неограниченно широк:
5шМ = I-
Пропуская «белый шум» через фильтр с частотной
характеристикой Г (со) и импульсной переходной функцией у (t),
получим процесс со спектральной плотностью
«(©)= Ь|Г(со)|*.
При этом импульсы белого шума превратятся в у (t).
Импульсная переходная функция (реакция)
последовательного соединения прогнозирующего и формирующего
фильтров, как было установлено, сдвинута влево по
сравнению с у (t):
Р@ = y(t+ В)
при условии Р (t) == 0, t<C 0.
Преобразование Фурье В (со) переходной функции Р {t):

равно произведению частотной характеристики
формирующего фильтра Г (со) и искомой частотной характеристики
прогнозирующего:
Для процесса с подобной корреляционной функцией
прогнозирующий фильтр оказался просто усилительным
звеном с коэффициентом передачи е~е. Значение
коэффициента передачи е~в совпадает со значением корреляционной
функции процесса при 0. Оказывается, прогнозирующий
28
Таким образом, синтез прогнозирующего фильтра
осуществляется в следующей последовательности:
а) находится Г (со) по спектральной плотности
прогнозируемого процесса;
б) вычисляется реакция у (t)\
в) вводится функция Р (t)\
г) определяется б (со) и Ф (со).
Пример. Пусть случайный процесс типа
«телеграфный сигнал» имеет параметры \i = l/2 иа= 1 и,
следовательно, корреляционную функцию
R (т) - е-М.
Подобной корреляционной функции соответствует
спектральная плотность
Искомая передаточная функция фильтра

фильтр выполняет ту же операцию, что и алгоритм
статистического прогноза по последнему значению: умножает
последнюю точку предыстории на значение нормированной
корреляционной функции при т — 0. Это может вызвать
недоумение—ведь фильтр должен учитывать всю
предысторию процесса, а учел опять лишь последнюю точку.
Дело в том, что «телеграфный сигнал» относится к
классу так называемых «марковских» процессов, на дальнейший
ход которых влияет лишь последняя точка предыстории.
Фильтр действительно учел всю предысторию, но
предыстория эта для выбранного процесса сосредоточена в
последней точке.
Выражение для ошибки
Ошибка как разность между точным и предсказанным
значениями процесса имеет вид:
2д
Ее спектральная плотность
S? (со) -5,(о))- 1 • |В(со)Г2,
где 1 — спектральная плотность «белого шума».
Интегрирование A7) дает:
Здесь следует вспомнить, что
персия процесса равна площади, ограниченной кривой
спектральной плотности, или, в физической
интерпретации, мощность процесса X (t) равна сумме мощностей,
приходящихся на элементарные частотные интервалы.
Равенство
называется равенством Парсеваля и имеет прозрачный
физический смысл: мощность процесса, подсчитанная по вре-

менной области, должна совпадать со значением,
полученным при суммировании мощностей, приходящихся на
элементарные частотные интервалы.
Вспоминая, что Р (/) = у (t + 6), ( ^? 0, получим:
1 А. С. Пушкин. Собр. соч., т. VII. М., «Наука», 1964, с. 144.
30
Но по равенству Парсеваля
Очевидно, как и для статистических алгоритмов, е2 @) =
-0 и ?(оо) = Dx.
Поскольку функция у2 (t) неотрицательна, зависимость
е2 @) неубывающая.
Значения A8) в рамках данной модели не могуг быть
уменьшены никаким другим способом прогнозирования.
Предсказывать процесс лучше, чем с ошибкой A8),
принципиально невозможно.
Естественно закончить этот параграф цитатой,
показывающей, что рассмотренная только что схема, отделяющая
закономерное развитие процесса от случайного источника
ошибок, интуитивно была понята достаточно давно:
«... Но провидение не алгебра. Ум человеческий, по
простонародному выражению, не пророк, а угадчик, он
видит общий ход вещей и может выводить из оного глубокие
предположения, часто оправданные временем, но невозможно
ему предвидеть случая — мощного мгновенного орудия
провидения ...»1.

§ 5. ПРОГНОЗ
И СУММИРОВАНИЕ
Предсказанные тем или иным способом значения
случайного процесса представляют собой, как правило,
исходный материал для выработки управляющего воздействия
либо принятия решения.
Процесс превращения исходных данных в управляющее
воздействие состоит из ряда математических и логических
операций над ними. Поскольку исходные
данные—значения случайных процессов либо последовательностей,
результаты их преобразований также случайны.
Пусть случайные процессы Х1 (/), Х2(/), ..., Хл (/),
образующие вектор X (/), измеряются одновременно, в
результате чего образуется совокупность чисел х19 л\2, ...,
хп. Предположим, далее, что некоторое вычислительное
устройство (ВУ) производит вычисления с использованием
совокупности {Хх, X 2, ..., Х„} и через время 6 выдает
наблюдателю результаты, образующие значение нового
случайного процесса
Ф(/+ в) = Ф(Х1, Х2, ..., Хп, 6),
Ф— закон (алгоритм) преобразования над числами {Xt}>
а в может быть временем, необходимым для вычислений по
алгоритму ф, или заданной задержкой, или временем
передачи данных по внутреннему каналу связи.
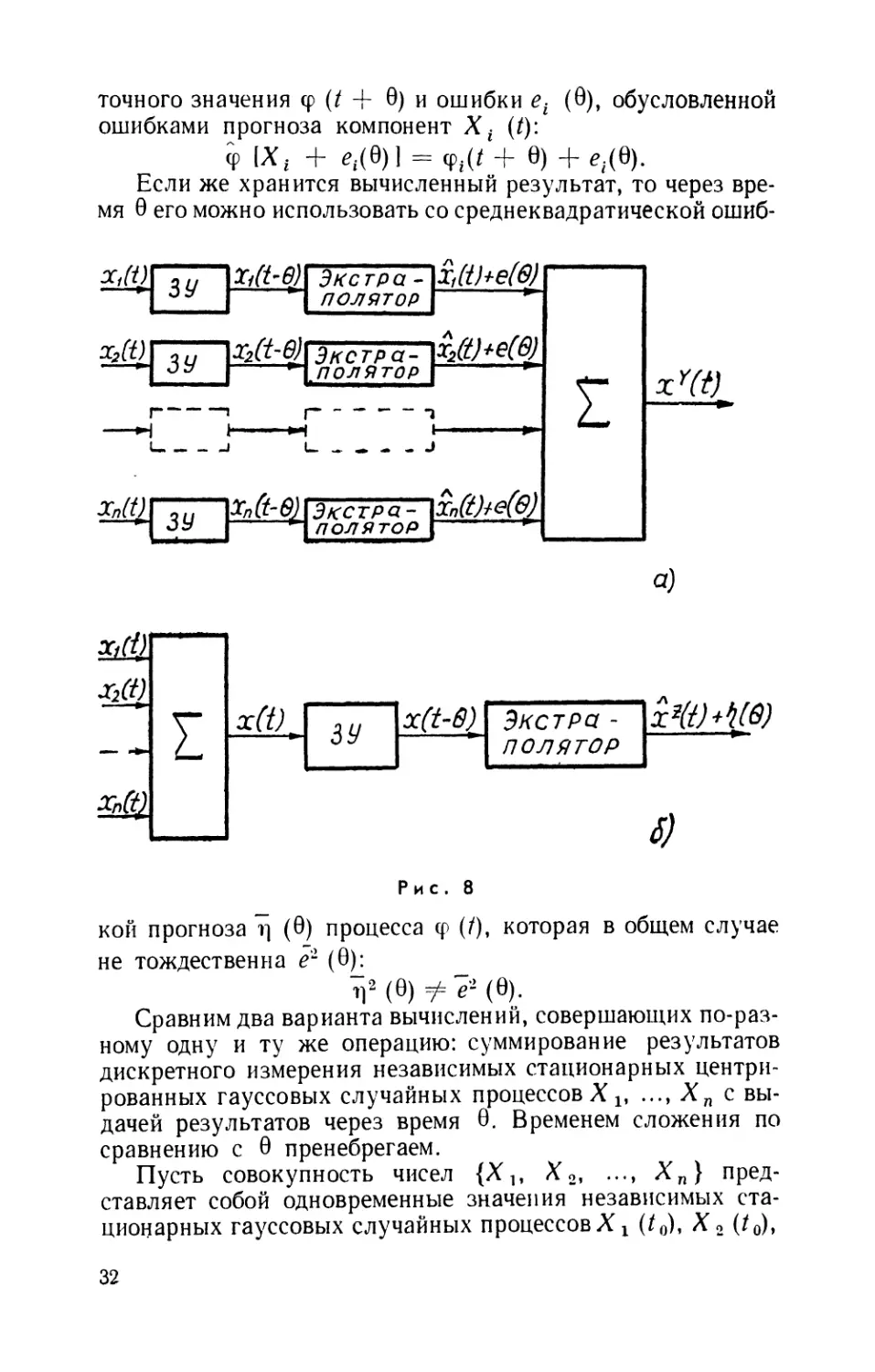
Очевидно, возможны два пути вычисления: хранить в
запоминающем устройстве (ЗУ) в течение времени В
исходные данные {Хг} и формировать результат перед
выдачей его наблюдателю или, напротив, сразу производить
вычисления и хранить в ЗУ их результат ф. Второй вариант
кажется более привлекательным в силу того, что система
получилась бы экономичнее: вместо запоминания п
исходных чисел нужна всего одна ячейка для хранения
результата. Однако оказывается, что эти вычислительные
процедуры дают разные значения ошибок прогноза на время 0.
Так, если хранятся результаты измерения процессов,
то вычисленный через время 6 результат будет состоять из
31

точного значения ср (/ + 0) и ошибки et (9), обусловленной
ошибками прогноза компонент Xt (t)\
Ф [X, + е.(9)] = ф.(/ + в) + *4(в).
Если же хранится вычисленный результат, то через
время в его можно использовать со среднеквадратической ошиб-
Рис. 8
кой прогноза г) F) процесса ф (/), которая в общем случае
не тождественна е1 F):
Сравним два варианта вычислений, совершающих
по-разному одну и ту же операцию: суммирование результатов
дискретного измерения независимых стационарных
центрированных гауссовых случайных процессов X v ..., Хп с
выдачей результатов через время 9. Временем сложения по
сравнению с 9 пренебрегаем.
Пусть совокупность чисел {X,, Х2, •. •, X п }
представляет собой одновременные значения независимых
стационарных гауссовых случайных процессовX х (/0), X2 (/0)»
32

..., Xn (t0) с корреляционными функциями #х (т), /?2 (т),
..., Rn (т), суммируемые с задержкой 6 по процедурам Y
или Z (рис. 8). Процедуры эти включают операцию
задержки (хранения в запоминающем устройстве), преобразующую
процесс X (t) в X (t— 9); восстановление после задержки
(прогнозирование), преобразующее процесс X (t — 0) в
X (/) = X (/) + е (/, 0)
и суммирование
ХУ(Ц=У(Х19 Х2, ..., Хп, в)= [Х1(/)+Х2 (/) +
+ ... + Хп (/I + 1ех (/, О) + е2 (/, 0)+ ... + <?„ (/, 0)];
X*(/) = Z(XlfA2f...,Xn, 0) = [Хх (/) + ... +ХП (/I +
+ ч (Л о).
Сумма Хк состоит из суммы точных значений
слагаемых и суммы ошибок прогноза слагаемых, a Xz —из
точного значения суммы слагаемых и ошибки прогноза суммы,
п
имеющей корреляционную функцию R (т) = 5^* ^' ^Р°~
1
цедуры Y и Z отличаются последовательностью операций
суммирования и задержки: если в первом случае в ЗУ
хранятся слагаемые, то во втором — сумма
X (/) = Х1(/)+Х2 (/) + ... +Xn(t).
Очевидно, процедуры суммирования равноценны в
смысле точности лишь в случае равенства входящих в эти вы-
п
ражения ошибок прогноза е2 @) = ^е? @) и тJ @). Одна-
ко возможен случай, когда
и, следовательно, операции прогноза и суммирования по
процедурам Y и Z приводят к различным ошибкам.
Для сравнения эффективности процедур Y и Z введем
критерий — разность дисперсий ошибок прогноза:
33
Знак критерия укажет более точную процедуру, а
значение— выигрыш, получаемый при ее применении.
Поскольку при малых временах 0 все е2 @) близки к
нулю, а при больших стремятся к установившимся значе-

при этих 0 процедуры Y и Z равноценны: Д@)^Д(оо) =0.
Если разность Д (В) при каких-либо в отличается от
нуля, она имеет по меньшей мере один экстремум. Это значит,
что существует время 0, при котором преимущество одного
из способов выражено наиболее ярко. Посмотрим, насколько
различается эффективность вычислительных процедур при
применении уже знакомых нам алгоритмов прогноза.
Прогноз по последнему значению
Среднеквадратичная ошибка прогноза в этом случае
определяется формулой A1):
?t(Q)~2 \Rt @)— /?t (вI.
При суммировании по процедуре У она примет вид:
34
ниям (к дисперсий для оптимальных статистических й к
двум дисперсиям при простом переносе):-
а по процедуре Z
Я5 (в) = 2 [/?2@)-/?2(9I.
Так как процессы не коррелированы, корреляционная
функция суммы процессов равна сумме корреляционных
функций слагаемых
Таким образом, оказывается
"?(в)Е=Н2(в),
Д @) = 0, следовательно, вычислительные процедуры Y
и Z равноценны по точности, но Z более экономична.
Прогноз по математическому ожиданию
Дисперсия ошибки прогноза здесь не зависит от
времени 6 и равна дисперсии процесса. Поскольку для
независимых процессов

процедуры Y и Z равноценны: Д (В) == 0.
а при алгоритме Z
B0)
B1)
где D^ и #2 (й) — дисперсия и корреляционная функция
с>ммы исходных процессов.
Поскольку исходные процессы независимы,
корреляционная функция их суммы равна сумме корреляционных
функций
Сравнение B0) и B2) покалывает, что дисперсии ошибок,
вообще говоря, различны. Их разность
всегда положительна. Это означает, чю всегда предиочти-
35
Статистический прогноз по одной точке
Перепишем выражение для дисперсии ошибки A5) в виде
Дисперсия ошибки при применении алгоритма Y будет
иметь вид:

тельней процедура К, в которой операция прогноза
предшествует суммированию.
При Э == 0 и 8 = оо Д @) = 0 и Д (оо) = 0. Процедуры
Y и Z равноценны.
В наиболее простом случае, когда дисперсии процессов-
слагаемых одинаковы и
Dt = D2-^ ... = Dn = D0f
разность дисперсий приобретает вид:
Это выражение позволяет увидеть любопытный факт.
Оказывается, что если все процессы-слагаемые имеют
одинаковые корреляционные функции
*i @) = Я, (9) - ... = R @),
Д @) == 0, т. е. обе вычислительные процедуры равноценны!
Действительно, при этом
Таким образом, более экономическую процедуру Z (при
этом занимается меньший объем памяти) можно
рекомендовать при прогнозировании процессов, имеющих одинаковые
корреляционные свойства.
Вспомним, что одинаковыми корреляционными
функциями обладают процессы с самыми различными «рисунками»
реализаций — «телеграфный сигнал» и синусоида со
случайной амплитудой и фазой.
Ниже на примере будут показаны наличие тахД(9)
и зависимость его величины от различия корреляционных
функций суммируемых процессов.
Прогнозирующий фильтр
До сих пор речь шла о мгновенных значениях, «отсчетах»
процессов-слагаемых и о результатах вычислений,
произведенных над ними.
Сейчас мы вновь будем говорить о случайных процессах
как о сигналах и о прогнозировании их значений как о
об

воздействии на эти сигналы специально подобранными
прогнозирующими фильтрами.
Естественно, что речь не может идти о выборе одной из
двух вычислительных процедур, отличающихся порядком
выполнения математических операций, — сейчас мы будем
сравнивать две структурные схемы: Y и Z.
Сигналы xt(t) поступают на элемент задержки,
осуществляющий «чистое запаздывание» сигнала на время в. В
технических системах запаздыванием обладают устройства,
передающие сигнал с конечной скоростью, — каналы
связи, трубопроводы, транспортеры либо специально
сконструированные «линии задержки», время запаздывания в
которых можно регулировать. Роль экстраполяторов
выполняют прогнозирующие фильтры, о которых речь шла
выше, а суммирование производится в звеньях, устройство
которых зависит от физической природы сигнала. Так,,
напряжения суммируются на усилителях с высоким входным
сопротивлением, токи — на потенциометрах, расходы
жидкостей — в коллекторах и т. д.
Структурные схемы Y и Z, отличаясь порядком
соединения этих звеньев, осуществляют над сигналами те же
операции, что и соответствующие вычислительные процедуры
над мгновенными значениями этих процессов.
В схеме Y сумматор выдает наблюдателю сумму
предсказанных значений, состоящую из суммы точных значений
и суммы ошибок. Сумма их дисперсий известна:
37
В схеме Z наблюдатель получает прогноз суммы про-
п
цессов — процесса X (t) = V Xt (t) с дисперсией ошибки
1
Здесь Yj@ — реакция фильтра, прогнозирующего
процесс-слагаемое Xt(t). Она (реакция) определяется
спектральной плотностью S.(co). Реакция фильтра y(t) в схеме Z
определяется спектральной плотностью суммарного
процесса 5 (со). Поскольку слагаемые независимы, спектраль-

Анализ его позволяет установить, что как при очень
малых, так и при очень больших 9 схемы У и Z равноценны:
Д @) = Д (оо) = 0. При одинаковых спектральных
плоскостях процессов X. (t) схемы также равноценны.
Если St (со) различны, то Д ((о)>0 и имеет хотя бы один
максимум. Схема Y дает лучшую точность, причем
существует задержка, при которой выигрыш наиболее ощутим.
Эффекты, таким образом, совпадают с наблюдавшимися
в предыдущем случае — при применении линейного
статистического прогноза по одной точке.
Физически преимущества схемы Y можно объяснить
таким образом.
Дисперсия ошибки прогноза растет с ростом 9 тем
быстрее, чем меньше время корреляции процесса, т. е. чем
шире его спектральная плотность.
При суммировании же некоррелированных процессов их
спектральные плотности складываются и суммарная плот-
38
ная плотность их суммы равна сумме спектральных
плотностей: '
Однако если |Г.(со)Г*(со) \=St((s) и |Г (со) Г*(со) |=
=5 (со), то выполнение условия
не влечет, вообще говоря, равенства
Это значит, что ц2(в)фе2(Щ и разность их
д (9)=^(9)—?(в)
отлична от нуля. Значение Д (9), выраженное через
спектральные свойства процессов, имеет вид:

ность оказывается по крайней мере не уже, чем самая
широкая из плотностей слагаемых.
Дисперсия ошибки суммы растет, таким образом,
быстрее дисперсии ошибок слагаемых.
Пример. Пусть спектральные плотности
суммируемых процессов ХхA) и X2(t) имеют вид:
где
Ранее было сказано, что А @)=Д (оо)=0.
Действительно, подстановка значений 9=0 и 8=оо обращает выражение
39
Корреляционные функции их соответственно
а спектральная плотность суммы
Ошибки прогноза для сигналов Хх(/), X2(t) и X (/) равны:

А @) в нуль. Это означает, что при достаточно малых и
достаточно больших 0 схемы Y и Z равноценны.
Пример подтверждает и вывод о равноценности
алгоритмов при сложении сигналов с одинаковыми
спектральными плотностями.
Так, при а!=а2 и равенстве функций S^co) и S2(co)
А F) обращется тождественно в нуль.
При 0<0<оо А (В) отлична от нуля, поскольку А @) =
= А (оо)- О, в этом диапазоне изменения 6 имеет экстремум.
Задержка, при которой наступает экстремум,
определяется параметрами спектральных плотностей слагаемых:
§ 6. ПРОГНОЗ
В ТЕХНИКЕ
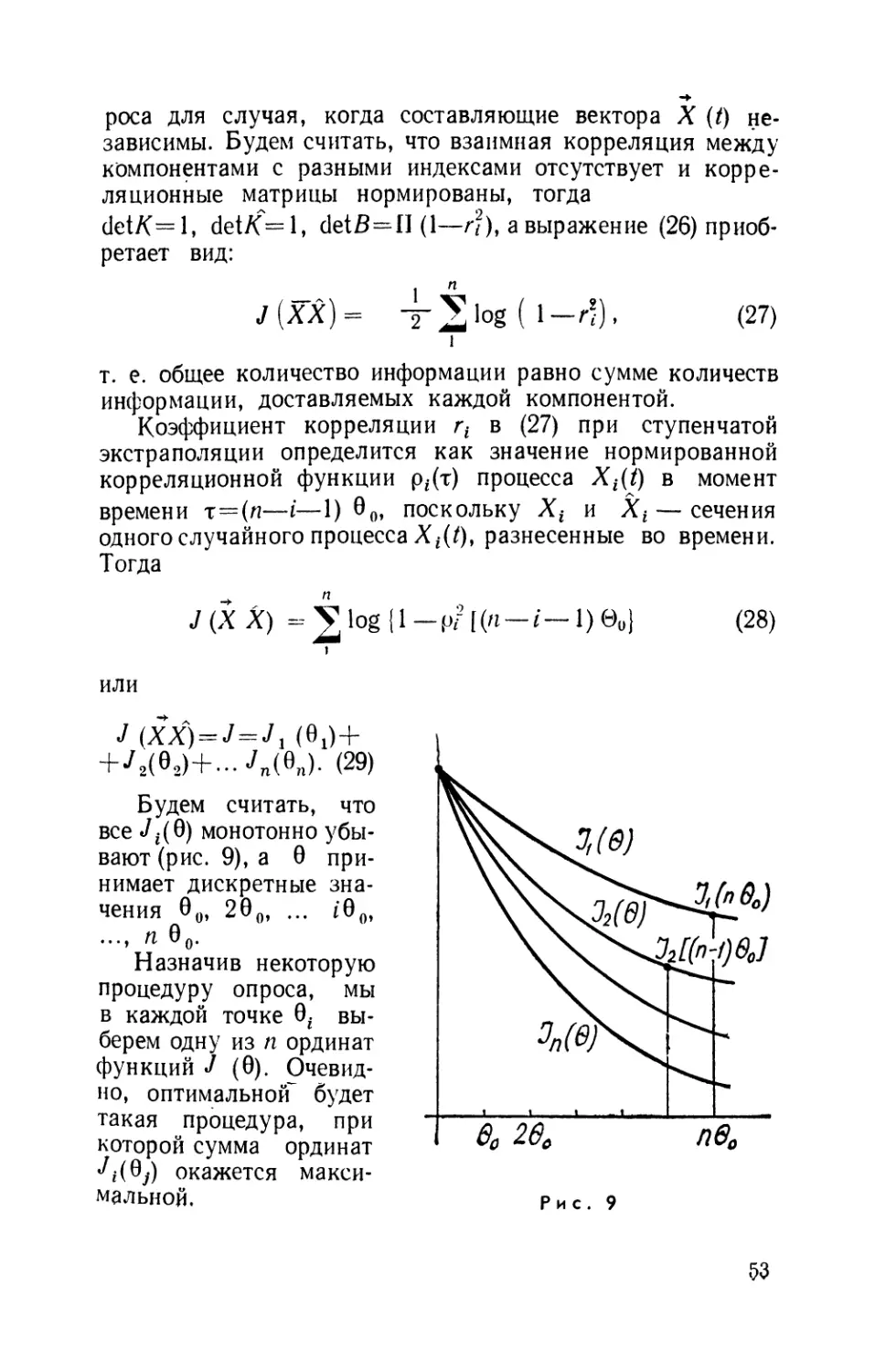
Итак, мы можем подвести некоторые итоги.
Предсказывать случайные процессы можно, не впадая в грех
нарушения закона причинности. При этом существует
принципиальный предел точности предсказания, наибольшего
приближения к которому можно добиться, вычисляя
предсказанное значение процесса по длительной предыстории и
привлекая все более полное вероятностное описание его.
Прогнозирование процесса не всегда производится
для использования будущих его значений. Применение
экстраполяции позволяет в настоящем получить больше
информации о прошлых значениях процесса, хранимых в
запоминающем устройстве. Мы увидим ниже, как
применение экстраполяторов в измерительных приборах и системах
связи позволяет более полно извлекать информацию из
измеряемых процессов и передавать ее более эффективным
образом.
Условием, необходимым для применения прогноза там,
где это может оказаться полезным, является возможность
достаточно быстро выполнить эффективный алгоритм
прогноза, обращаясь либо к вычислительной машине, либо к
устройству — экстраполятору. Последний может быть
дискретным — в этом случае это специализированное вычисли-
40

тельное устройство, либо непрерывным — тогда это
экстраполирующий фильтр.
Там, где прогноз является целью, как, например, в
метеорологии, либо важным условием достижения цели,
как, например, в зенитной стрельбе, прогнозирующие
программы для ЭВМ или прогнозирующие фильтры создаются
и используются давно и успешно.
Если же прогнозирование является вспомогательной
операцией при измерении, выработке управляющего
воздействия либо передаче информации, его применение в
настоящее время не всегда может быть обеспечено
необходимым машинным временем, либо подходящим арсеналом
вычислительных средств. Так, например, на современных
управляющих вычислительных машинах, как правило, нет
возможности при циклическом опросе организовать
восстановление хранимых результатов более эффективным
образом, чем при помощи прогноза нулевого порядка —
простого переноса. Следует ожидать, что с увеличением
арифметических и логических возможностей управляющей
вычислительной техники представится возможность
восстанавливать информацию из ЗУ более эффективно.
Обратимся к метеорологии. Именно эта область
деятельности наиболее тесно ассоциируется с понятием
«прогноз», поскольку именно прогноз погодных и других
геофизических факторов и является ее целью. Погоду
предсказывали задолго до появления статистических методов
прогнозирования, а, появившись, они не произвели переворота,
а лишь дополнили арсенал традиционных приемов. Вот как
пишет о соотношении случайного и детерминированного в
метеорологии Н. Винер.
«Недавно 1 по предложению Джона фон Неймана была
предпринята попытка решения задачи прогноза погоды,
при которой эта задача рассматривалась, как некоторая
очень сложная задача того же типа, что и астрономическая
задача об определении планетных орбит. Идея заключалась
в том, чтобы ввести все данные о начальном состоянии
атмосферы в сверхмощн>ю вычислительную машину, и
используя затем законы движения, выражаемые уравнениями
гидродинамики, рассчитать погоду на продолжительное
время вперед.
Однако основное препятствие на этом пути состоит в
том, что бюро прогнозов располагает лишь ограниченной
Книга И- Винера «Я — математик» вышла в 1956 г. (авт.)
41

информацией о состоянии атмосферы в отдельных точках,
разделенных колоссальными промежутками. Это
препятствие можно как-то преодолеть, лишь прибегнув к помощи
статистических методов. Поэтому наиболее
соответствующим природе задачи был бы метод, органически
объединяющий динамические и статистические соображения».
За время, прошедшее с момента, когда были написаны
эти строки, выработалась и методика такого объединения:
исходные данные прогнозируются на заданное время —
12, 24, 36 ч, а затем по ним методами динамической
метеорологии предсказывается погода.
Прогнозирующий алгоритм выбирается в зависимости от
времени прогноза. Предсказание погоды методом простого
переноса на сутки по принципу «завтра так же, как сейчас»
оправдывается в 70 % случаев. Для более точного прогноза
на сутки требуется учесть около 3000 различных
метеоизмерений, при прогнозе на трое суток их требуется уже 20 000.
Существует мнение, что процент оправдавшихся прогнозов
может быть в принципе повышен до 95—97%; это
указывает на сильную детерминированность метеорологических
процессов.
Отдельные геофизические процессы успешно
прогнозируются статистическими методами. Их вероятностные
характеристики определены на основании многолетних
наблюдений. Такие показатели, как уровень воды в реках,
количество выпавших осадков, сроки вскрытия и замерзания
рек, регистрируются в некоторых пунктах уже сотни лет
(сроки вскрытия Невы, например, с 1706 г.).
В системах управления управляющее воздействие
должно вырабатываться на основании измеренного отклонения
регулируемой величины от заданного значения. Это
отклонение экстраполируется, чтобы компенсировать
запаздывание или инерционность цепи обратной связи.
Существует значительный теоретический «задел» для
применения прогноза в целях повышения эффективности
автономных устройств, таких, например, как
телевизионные приемники и измерительные приборы.
В технике передачи сигналов существует несколько
способов повышения эффективности кодирования
сообщений при помощи операций, улучшающих согласование
статистических свойств кодируемых последовательностей и
канала.
Одним из наиболее известных способов согласования
является следующий: так называемое кодирование с пред-
42

сказанием—вычитанием или просто кодирование с
предсказанием. Источник сообщений соединен с запоминающим
устройством передатчика. Передатчик имеет экстраполятор,
прогнозирующий последующее значение входной
последовательности по предыдущим значениям, хранящимся в ЗУ.
Вычитающее устройство вычитает предсказанное
значение из действительной его величины и вырабатывает
сигнал ошибки
е(Ц=Х (tJ-X (/.),
который подается на вход кодирующего устройства. Кодер
кодирует сигнал ошибки и посылает его в канал. В
приемнике все происходит в обратном порядке. В нем также
имеются ЗУ и экстраполятор, который предсказывает то же
значение X (/;), что и экстраполятор передатчика.
Принимаемый сигнал путем декодирования вновь превращается
в сигнал ошибки e(tt). Далее он суммируется с
предсказанным значением X (/.) и, таким образом, восстанавливается
элемент сообщения X (tt). Теперь вместо значений
исходной последовательности X (tt) передается
последовательность ошибок предсказания е (tt). Если известно несколько
предыдущих значений -исходной последовательности, то
последнее значение может быть восстановлено по
известному значению е (/.). Таким образом, последовательность
е (tt) вместе с первыми значениями исходной
последовательности содержит всю информацию, заключенную в X (tt).
В чем же заключается преимущество такой системы и
какова тут роль эксграполятора? Ведь «заглядывайия в
будущее» тут не происходит. Действительно, на передающей
и на приемной стороне одновременно вычисляется
предсказанное значение X (/^), затем на передающей измеряют
X (/.) (дождавшись момента ^!), образуют и передают
разность е (ti) и прибавляют ее на приемной стороне к X (/,).
При этом преследуют две цели:
Во-первых, уменьшается мощность сигнала,
подлежащего передаче — e2<Dx;
во-вторых, кодирование с предсказанием преследует
цель превращения исходной последовательности X (tt) с
сильными статистическими связями в последовательность
е (tt) со слабыми статистическими связями между отсчетами.
Действительно, пусть последовательность отсчетов
нормированного сигнала X (/.) с нулевым математическим
ожиданием имеет корреляционную функцию (нормированную)
43

р (г,.). Каковы будут корреляционные связи между
соседними значениями ошибки оптимального статистического
прогноза по последнему значению?
Если отсчеты отделены промежутками времени А,
ошибка на Н-1-м шаге будет
ei+i=:Xi+—xn-i = P (д) ХГ~xni>
а ошибка на предыдущем шаге —
e^-Xr-X^.p (A) Xt_t-Xt.
Корреляционный момент между соседними значениями
ошибки
М и?Л+|] = Л« [(р (Д) X-Xi + i)(9 (A) *,_-*,)] =
= Р2(Д)Л1 IX^J-p^A* [Х^Х,-, 1-
-p(A)Af Щ]+М lXntXt].
Здесь М \XJ] — дисперсия последовательности,
равная единице, так как процесс X (t) нормирован;
М [Х,Х^] = М 1Х| + 1Х|] = Р(Д).
а М 1X^X^,1- рBА).
Теперь М UwJ = p(A) [р2 (A)—p BA)].
Для случая, когда корреляционная функция процесса
экспоненциальна р (т) — е , р2(Д)—е~2Л и р BА)-^е-'2Д и,
таким образом, М [eteni]- 0—последовательность
значений ошибок прогноза оказывается не коррелированной.
Вспомним, что для процесса с экспоненциальной
корреляционной функцией линейный прогноз по последнему
значению является одновременно и оптимальным.
Оптимальный прогноз дает тот же результат и в более общем случае.
Такая операция над сигналом называется декорреля-
цией, спектр сигнала е (/) после декорреляции расширяется
но сравнению с X (/), говорят, что сигнал приобретает шу-
моподобные свойства и появляется возможность кодировать
его более эффективно.
В периом случае, когда стремятся уменьшить мощность
ошибки прогноза, наилучшим оказывается, естественно,
оптимальное статистическое прогнозирование.
При декорреляции, когда стремятся минимизировать
энтропию последовательности значений ошибки прогноза
е (tt), может возникнуть ситуация, в которой наилучшим
окажется прогноз по последнему значению — простой
перенос!
Кодирование с предсказанием обещает быть особенно
эффективным в телевизионных системах будущего.
44

Действительно, телевизионный кадр («картинка»),
сменяемый 50 раз в секунду, почти ничем не отличается от
предыдущего (и от последующего). Изменения,
происходящие от кадра к кадру, составляют 2—5% информации, в
нем содержащейся. Применение в этой ситуации
кодирования с предсказанием означало бы, что ЗУ, содержащееся в
телевизоре, запоминает предыдущий кадр, экстраполятор
предсказывает следующий, а телецентр передает лишь
«поправку», составляющую незначительную долю той
информации, которая содержится в ЗУ.
Специалисты ожидают, что это позволило бы уменьшить
необходимую пропускную способность канала передачи
телеизображения в десятки раз.
Проблемой, не разрешенной и к настоящему времени,
является необходимость «упрятать» в обычные габариты
(и стоимость!) телевизора запоминающее устройство и
экстраполятор — по существу — специализированную
вычислительную машину.
Опыты над подобными системами уже проводились, но
запоминание и экстраполяция осуществлялись
универсальной ЭВМ, работавшей по специальной программе.
Большие выгоды сулит также применение экстраполя-
торов в измерительных приборах. При этом так же, как в
описанном выше примере, пользователь не подозревает,
что имеет дело с устройством, «прозревающим будущее».
Если измеряется гауссов случайный процесс с
дисперсией Dx = a* и нулевым средним, существует простое
правило выбора длины шкалы измерительного прибора. Шкала
с нулем посередине выбирается по «правилу 36»— по Збл.
в обе стороны от нуля. При этом прибор будет
«зашкаливать» в среднем не чаще чем 3 раза на 1000 измерений.
Приборы с «растянутой» шкалой позволяют измерять с
лучшей разрешающей способностью, но потери отсчетов
из-за зашкаливания при этом будут происходить чаще.
Применение экстраполятора в приборе позволяет
существенно «растянуть» шкалу.
Пусть, действуя по оптимальному статистическому
алгоритму, экстраполятор вычисляет на основании
нескольких предыдущих отсчетов предсказанное значение X (/+9),
равное условному среднему измеряемого процесса X (/).
Если теперь перенести середину шкалы в предсказанную
точку, прибор измерит отклонение истинного значения
X (/+6) от предсказанного X (/+9), т. е. ошибку прогно-
45

за е (/+6)! Но ошибка так же, как и измеряемый процесс,
подчинена нормальному закону с дисперсией е2(в). Поэтому
шкалу можно «растянуть», взявши ее величину равной
=h 3 ]/е2 (А) и получить, таким образом, более точное
измерение.
Обратим внимание на то, что экстраполятор здесь, как
и в системе передачи, осуществляет прогноз, если можно
так выразиться, скрытно от наблюдателя. Наблюдателю в
описанных системах предсказанные значения процессов не
предъявляются, они используются внутри системы. Цель,
с которой они используются, в обоих случаях одинакова —
улучшить технические характеристики систем, привлекая
информацию, извлеченную экстраполятором из
корреляционных связей между отсчетами.
Осуществление измерительных приборов с экстраполя-
торами технически более просто, чем телевизора с
предсказанием — вычитанием, однако поместить в цифровой
вольтметр, предназначенный для массового производства,
микропроцессор и „ЗУ сегодня еще экономически нецелесообразно.
Однако тенденция развития вычислительной техники
такова, что насыщение и источников
информации—измерительных приборов, и приемников ее элементами станет
возможным в ближайшем будущем.
По сведениям технической периодики так называемые
мини-ЭВМ, как показывает статистика, дешевеют в 10 раз
каждые 10 лет. Следующий этап миниатюризации и
специализации выводит на сцену микро-ЭВМ — вычислительные
машины, чьи процессор и запоминающее устройство,
выполненные на одном кристалле, будут стоить, по оценкам
экспертов, 1 доллар 1. Именно измерительные приборы и
явятся в первую очередь полем применения микро-ЭВМ.
Прогнозирование—не единственная операция по
первичной обработке данных, которую смогут выполнять
микро-ЭВМ непосредственно у источников информации.
Фильтрация, интерполирование, кодирование, выполненные «на
местах», позволят существенно уменьшить объем
информационного потока в системах управления, удешевить их
и повысить надежность. В сложных системах
телеуправления стоимость канала связи сравнима со стоимостью самой
системы управления.
1 Ф о с т е р. Направление развития архитектуры ЭВМ.—
«Зарубежная радиоэлектроника», 1973, № 8, с. 60,
46

§ 7. ОСОБЕННОСТИ
ПРОГНОЗИРОВАНИЯ ВЕКТОРНЫХ
СЛУЧАЙНЫХ ПРОЦЕССОВ
В системах управления и контроля приходится обычно
наблюдать не один процесс, а целую группу их, так или
иначе связанных друг с другом.
Так, при управлении движущимся в пространстве телом
наблюдаются его координаты, скорости и ускорения.
В системах сбора информации с временным разделением
каналов датчики опрашиваемой группы— источники
случайных процессов поочередно подключаются коммутатором
к измерительному прибору.
Опрос может производиться по программе, тогда
коммутатор подсоединяет в данный момент датчик, адрес которого
поступает из устройства управления, или по жесткой
схеме— циклически, в этом случае порядок подключения
датчиков сохраняется постоянным.
Результаты измерений направляются в запоминающее
устройство (ЗУ) — накопитель, где хранятся до завершения
цикла опроса, после чего совокупность измерений всех
процессов («ситуация») — «предъявляется» — поступает к
диспетчеру либо используется для выработки управляющего
воздействия на объект. После предъявления ситуация
стирается из памяти ЗУ — накопителя и цикл
повторяется.
Изучение закономерностей работы такой системы
приводит к необходимости решать весьма своеобразную задачу
прогнозирования, связанную с тем, что «диспетчер»
получает в конце цикла результаты измерений, произведенных
в разное время.
Пусть состояние объекта управления характеризуется
^-мерным стационарным гауссовым векторным случайным
->
процессом X (t) с компонентами Х1 (t), X., (<)» .., Хп (/),
вероятностные характеристики которого известны.
- >
Процесс X (t) задан своей- матрицей — строкой
математических ожиданий
| \mt | | = т;, mv ..., тх, ..., тп
47

и корреляционной матрицей
элементами которой являются взаимные корреляционные
функции между компонентами вектора, а элементами
главной диагонали — корреляционные функции компонент.
Предположим, что коммутатор подключает к
измерительному прибору компоненты Xt (t) в порядке
нумерации, причем время 6о, необходимое на подключение
источника, измерение и запись результата в ЗУ—накопитель,
одинаково для всех компонент.
Если результат измерения компоненты Хг (t) получен в
момент t{), то результат X2(t) — в момент ^0+90, X3(t) —
в момент времени /0+2бо. В общем случае для /-го
результата можно записать: XJrf0+(i—1) 001.
В силу конечности промежутка 90, определяемого
параметрами устройства сбора информации и ЗУ,
оказывается невозможным оценить ситуацию в моменты времени t0 ...
-> ->
tn, т. е. получить сечения вектора X (t0), X (tx) ... Вместо
мгновенного сечения вектора X (tt) в некоторый
определенный момент удается получить лишь «косое» его сечение,
занимающее время nQ0> определяемое быстродействием
системы и числом измеряемых компонент. Длительность
промежутка 00 и увеличение числа измеряемых параметров
приходится оплачивать потерей информации о состоянии
объекта управления.
Прежде всего следует выяснить вопрос о моменте, к
которому относится полученная в результате цикла опроса
ситуация. Это так называемая проблема датировки. Все
значения «косого» сечения вектора Xilt0+(i—1) 6J
следует отнести к какому-то из моментов t0, t0+Q0, ..., /0-Ив0,
называемому «датой» сечения.
Нетрудно показать, что выбор даты имеет значение для
точности оценки ситуации по результатам измерения
составляющих вектора. Сравним датировку tg--=t0—«начало
опроса» и tg~t0+(n—1) (п—1)90—«момент
предъявления ситуации».
4$

Отнесение всех отсчетов к начальному моменту означает,
что по результатам измерения, полученным через (/—I) 90
после даты, судят о том, какова была ситуация в момент t0.
Отнесение же всех п отсчетов к заключительному
моменту t0+(n—1) 90 означает, что по результатам измерения,
полученным за (п—i—1) 90 до даты, судят о том, какова
будет ситуация в момент t0+(n—1) 90.
Если в первом случае ни один отсчет из п не взят до
даты, то во втором ни один не взят после даты.
В случаях, когда информация о ситуации используется
диспетчером для принятия решения либо управляющим
устройством для выработки управляющего воздействия,
датировка производится именно моментом предъявления —
моментом, в который принимается решение, либо
формируется управление.
Датировка ситуации моментом ее предъявления всегда
требует для вычисления Xt(tg) операции
экстраполирования отсчетов на время (п—i—1) 60.
Итак, измеряя поочередно компоненты векторного
случайного процесса X (t), мы вместо сечения вектора в момент
t0 получаем его оценку X (t0)= Хх^0), Х2 (/0+^о) •••
--Xn[t0+(n—1) 90] — также случайный вектор,
компонентами которого являются предсказанные значения
компонент X (t).
—>
Значения компонент вектора X (/) в момент отсчета
отделены от даты различным промежутком времени. Так,
для компоненты X^t) он равен (п—1) 6 0, для Хь—(n—i) 90,
а для Хп (t) равен нулю, причем чем больше этот
промежуток, тем больше окажется и дисперсия ошибки прогноза.
Если процесс X (t) содержит независимые
составляющие, его корреляционная матрица диагональна и
дисперсия его ошибки экстраполяции представляет собой сумму
дисперсий ошибок компонент
49
Здесь е?[(п—i—1)90] — средний квадрат ошибки
экстраполяции i-u компоненты, есл,и порядок опроса
компонент совпадает с порядком их нумерации.
Выражение B4) показывает, что величина Е2 зависит от
порядка опроса компонент. Действительно, представим се-

Эти величины будут различны, если различаются
корреляционные функции переставленных компонент. Отсюда
можно сделать несколько существенных выводов.
Во-первых., ошибка прогнозирования векторного
случайного процесса зависит от последовательности прогноза
его компонент. Во-вторых, не задавшись этой
последовательностью, нельзя говорить об ошибке прогноза векторного
процесса. И наконец, естественно встает задача о выборе
такой последовательности измерения компонент, которая
обеспечила бы минимальное значение ошибки ?2, доставив
наблюдателю максимум информации о сечении процесса X (/0).
Информация о состоянии объекта управления,
получаемая в результате опроса, частично теряется к моменту
предъявления ситуации. Потери ее зависят от степени связи
предсказанного X (t0) и истинного X (?0), поэтому, назначая
различные процедуры опроса датчиков, получают
различные количества информации о состоянии объекта в момент
времени t0.
Оценим информационные потери при поочередном
прогнозе компонент и найдем процедуру, доставляющую
наблюдателю максимальное количество информации.
Рассмотрим n-мерные случайные векторные процессы
50
Если X—X^f), a Xi=Xt[t—(п—i) 0О1, значения Xt
и Xt представляют собой ординаты одного и того же
процесса, Xt(t), отделенные промежутком времени (*•—1) 90>
бе соотношение последовательностей нумерации и опроса
как л? = {1 х, 22, ...it .../;.../?„}, где числа в строке означают
порядок нумерации, а индексы — какой по счету была
измерена компонента. Внесем затем в процедуру опроса
инверсию: процесс Xt(t) будем измерять g-ым по счету, а
процесс Xg(t) — /-ым.
Значение Е% в первом случае будет:

и речь, очевидно, идет об алгоритме ступенчатой
экстраполяции.
Формула для вычисления количества информации в
векторе-оценке X (t) о векторе X (t) имеет вид:
Здесь /Х(Х) и f2{X) — плотности распределения
вероятностей случайных векторов X и X, a f {XX) — плотность
совместного распределения вероятностей компонент вектора
Так как вектор X имеет /г-мерное гауссово распределе-
ние, то оценка X будет иметь то же распределение.
Случайный 2/г-мерный вектор (X X) будет иметь также нормальное
распределение.
Для гауссовых процессов выражение B5) упрощается:
и определяет среднее количество информации, получаемое
наблюдателем за цикл. Выясним влияние
последовательности экстраполяции компонент на эту величину. В B6) входят
определители матриц /С, К и R. Рассмотрим их подробнее.
Матрица корреляционных моментов одномерного
распределения процесса X (/) К имеет вид:
/С= | \М (ВД) 11
и содержит в качестве элементов главной диагонали
дисперсии процессов Хъ Х2, ..., Х„, а в качестве элементов
строк и столбцов — начальные значения взаимных
корреляционных функций — элементов корреляционной
матрицы прогнозируемого процесса X (t).
Матрица корреляционных моментов одномерного
распределения процесса—оценки X (/) с компонентами Хх,
Х2, . 9Хп имеет вид:

и по-прежнему содержит в качестве элементов главной
диагонали дисперсии компонент прогнозируемого вектора X (t).
Как и у матрицы К, элементами строк и столбцов здесь
являются значения взаимных корреляционных функций Rfo)
из корреляционной матрицы B3). Различие между К и К
состоит втом, что здесь берутся значения Ru (т),
определяемые расстоянием между компонентами Xt и Xj в
процедуре опроса: элемент матрицы К имеет вид: /?^[(i—/) 90Ь
Поскольку взаимные корреляционные связи между
связанными процессами Xt(t) и Xj(t) с ростом времени затухают,
элементы матрицы К с увеличением абсолютной величины
разности i—/ уменьшаются. Наконец, подматрица Б,
входящая в матрицу /?, имеет вид:
в=\\м [х,х7.] ц= |/с,/[(п—/) е0]|.
Ее элементы характеризуют связь между процессами Хь
и Xjy принадлежащими различным векторам —
контролируемому X (t) и его оценке X (t). Элементы Kifl(n—j)Q0]
представляют собой значения взаимных корреляционных
функций Ru (т) с аргументами, равными интервалам,
отделяющим момент измерения /-ой компоненты от момента
предъявления ситуации.
Итак, зная корреляционную матрицу прогнозируемого
вектора и задав последовательность, можно определить
количество получаемой в результате опроса информации.
Считая, что процедура совпадает с порядком нумерации
компонент A, 2, ..., i, ..., /, ..., п), внесем в нее одну инвер.
сию, поменяв местами очередность компонент i и /.
Проследим, как изменяются при этом матрицы /С, К и В.
У матрицы К строки и столбцы с индексами i и / просто
меняются местами, причем значения переставленных
элементов не изменяются.
Матрица К в результате одной инверсии претерпит
более серьезные изменения. Аргументы строк останутся теми
же, 1-е и /-е строки и столбцы поменяются местами и, таким
образом, 4п—4 элемента приобретают новые аргументы.
Сходным образом изменится и матрица В.
Естественно, что значение детерминантов /С, К и В
после инверсии изменяется. Изменяется, естественно, и
величина J (X,X), определяемая величинами этих детерминантов.
Перейдем к планированию оптимальной процедуры оп~
52

роса для случая, когда составляющие вектора X (t)
независимы. Будем считать, что взаимная корреляция между
компонентами с разными индексами отсутствует и
корреляционные матрицы нормированы, тогда
det/C=l, det/(=l, detfl=II(l—r?)f а выражение B6)
приобретает вид:
B7)
т. е. общее количество информации равно сумме количеств
информации, доставляемых каждой компонентой.
Коэффициент корреляции rt в B7) при ступенчатой
экстраполяции определится как значение нормированной
корреляционной функции рДт) процесса X^f) в момент
времени т=(я—i—1) в0» поскольку Хг и Хь — сечения
одного случайного процесса Xt(t)9 разнесенные во времени.
Тогда
B8)
Рис. 9
53
или
J (XX) = J=Jl (Qx)+
+ ^(в2)+...^п(в„). B9)
Будем считать, что
все «/^(9) монотонно
убывают (рис. 9), а 0
принимает дискретные
значения 60, 20о, ... /0О,
..., п 60.
Назначив некоторую
процедуру опроса, мы
в каждой точке 0^
выберем одну из п ординат
функций J @).
Очевидно, оптимальной будет
такая процедура, при
которой сумма ординат
Л@/) окажется
максимальной,

Выбор оптимальной процедуры прогноза
Если число компонент вектора п невелико, можно
образовать все п! сумм ординат, выбрать наибольшую и
зафиксировать соответствующую ей процедуру, как
оптимальную. Однако уже при п=10 этот способ оптимизации,
называемый методом прямого перебора, становится слишком
трудоемким
Мы отыщем оптимальную процедуру, привлекая весьма
мощный метод динамического программирования, который
в нашем случае будет выглядеть очень просто и естественно1.
Представим, что все функции Jt(Q) убывают, но с
разной скоростью. Измерение первого процесса происходит
ft00 секунд тому назад, второго— (ft—1) 60 и т. д.
Назначим измерять первым тот из процессов, чьи
потери информации за время /г60 будут наименьшими. Для
этого среди ординат «^(ft^o) нужно выбрать наибольшую:
f1(Qi) = max Ji(nQ0) C0) есть количество информации,
оставшееся от первого измерения к моменту предъявления.
Функция, для которой выполняется это условие,
обозначена ^х(9). Действительно, при v=ft60 значение ^i(ft90)
больше, чем у остальных функций. Заметим, что
наибольшее значение среди этих п ординат при 0. = п90
отыскивается перебором их значений.
Второй номер следует присвоить процессу, функция
J2 F) которого удовлетворит соотношению:
/2(92) = max{/2[(ft-l) ej+^e,)}; C1)
/2(^2) — количество информации, оставшееся от первых
двух измерений к моменту предъявления при оптимальном
выборе первых двух шагов. Функция «^2(9) отыскивается
перебором п—1 значений функции /2(92).
Для отыскания процесса номер три берется соотношение
/з(ез) = тах{/з[(Аг-2) ео]+/2(Э2)} C2)
при переборе п—2 значений ординат при ®3=(п—2) 62.
Продолжая эту операцию, нумеруем последовательно
ft—1 процессов. Последний процесс Xn(t) определяется
однозначно -без перебора, удовлетворяя своей функцией
Jn(®) условию
fM = тах{/п(в0)+/п-1(в„_1)}. C3)
1 Е. С. Вснтцсл ь. Элементы динамического
программирования. М., «Наука>>, 1964»
54

Удовлетворяя подбором функций Л(б) ... ^п(б)
функциональные уравнения C0)—C3), мы совершим выбор
оптимальной процедуры изменения и экстраполяции
векторного процесса.
Каждое из уравнений C0)—C3) содержит в правой
части слагаемое, отысканное как максимальное на
предыдущем шаге, и слагаемое, максимизация которого должна
удовлетворить уравнение текущего шага.
Такой пошаговый выбор оптимальной процедуры, при
котором движение совершается в обратном порядке (у нас —
от момента, наиболее удаленного от точки предъявления
ситуации), характерен для метода динамического
программирования.
Все, что мы рассказали выше, относится к очень узкому
классу объектов—стационарным процессам, о которых
нам известны предыстория и вероятностные
характеристики. На самом деле процессы, которые необходимо
предвидеть, зачастую нестационарны. Нестационарность может
проявляться в изменении со временем их математических
ожиданий, дисперсий, корреляционных функций.
Очень часто предсказания требуют процессы, которые
не описываются количественными соотношениями,
измерить которые бывает затруднительно. Например, ответ на
вопрос, будет ли найден в заданный срок способ лечения
определенной болезни — тоже прогноз, но имеет ли это
отношение к рассмотренным задачам? А как отвечать на
вопросы о том, будет ли иметь спрос новый товар?
Существуют ли алгоритмы такого прогноза?
Что касается прогноза нестационарных процессов, то
с этой проблемой удается успешно справиться благодаря
применению адаптивных, или обучающихся
прогнозирующих фильтров (алгоритмов). Если прогнозируемый процесс
нестационарен, и это выражается в том, например, что его
корреляционная функция меняет вид с течением времени,
адаптивная система «изучает» процесс — периодически
определяет вид корреляционной функции и подставляет ее
значения в алгоритм прогноза, «улучшая» его.
Естественно, за свойство адаптивности, приобретаемое
системой, приходится платить усложнением алгоритмов, а
значит, и временем.
Прогнозирование качественных явлений зачастую не
может быть алгоритмизовано иногда по той причине, что
нам неизвестен сигнал, несущий информацию о будущем,
55

а иногда потому, что неизвестно, как по наблюдаемым
сигналам осуществлять прогноз.
Так, способность животных ощущать приближение
землетрясения, установленная достоверно, иллюстрирует
первый случай. Предполагают, что рыбы улавливают
изменения магнитного поля, предшествующего землетрясению.
Понятия «опыт», «интуиция» отражают ситуацию, когда
неясно, как вырабатывается прогноз. Существуют методы
учета интуитивных мнений опытных людей — их именуют
«экспертами» — для выработки прогноза событий.
Критерием при этом служит частота совпадений «произошло —
не произошло» предсказанное. Надежность подобных
прогнозов бывает весьма высокой — общеизвестно, например,
что подавляющее большинство научно-технических
предвидений Жюля Верна оправдалось
56
§ 8. ЭКСПЕРТНЫЕ
ОЦЕНКИ И ПРОГНОЗ
Итак, если предсказывать приходится явления, не
поддающиеся количественному описанию, или
алгоритмизировать не поддающийся прогнозу процесс, нужно «пойти и
спросить знающего человека». Сейчас Это называется
«получить экспертную оценку».
Прогнозирование такого рода получило существенное
распространение главным образом при планировании
научно-исследовательских работ и опытно-конструкторских
разработок. Ошибки при оценке затрат на создание новой
техники обычно бывают очень большими. Так, разработка
сверхзвукового пассажирского самолета «Конкорд» в 1962 г.
оценивалась в 170 млн. фунтов стерлингов, а в 1970 г.
возросла до 825 млн. Строительство нефтепровода через
Аляску, по подсчетам строителей, в 1969 г. требовало 900 млн.
долларов. Спустя несколько лет расходы оценивались
уже в 5,9 млрд., в марте 1975 г. называли сумму 7 млрд., а
чуть позже— уже в 10 млрд. — в И раз больше, чем было
предусмотрено первоначальной сметой.
Мы попытаемся проанализировать процедуру принятия
экспертных оценок в терминах рассмотренной выше общей

модели и выяснить существующее сходство и различие.
Экспертные оценки (в том числе будущих событий)
осуществляются в самом общем виде так.
Группе специалистов по определенной проблеме
предлагается система вопросов. Специалисты-эксперты,
определенным образом взаимодействуя, подготавливают ответы.
Ответы обрабатываются, на их основании вырабатываются
оценки или принимаются решения. Можно ли, наблюдая
такую группу в действии, отыскать аналогии с
прогнозирующим устройством, действующим по определенному
алгоритму, использующим сведения о предыстории и
закономерностях предсказываемого процесса?
Оказывается, в некоторой степени можно.
Будем рассматривать группу экспертов как
прогнозирующий механизм, состоящий из нескольких однотипных
блоков (экспертов), определенным образом соединенных
(взаимодействующих) друг с другом.
Каждый блок (эксперт), будучи специалистом,
располагает, во-первых, фундаментальными знаниями по
проблеме, во-вторых, текущей информацией — предысторией
развития процесса.
Каким именно образом каждый эксперт приходит к
ответу на тот или иной вопрос, неизвестно— в этом и
заключается основное отличие этого механизма от
прогнозирующего фильтра, однако процедура общения экспертов между
собой и правила согласования их мнений жестко
регламентированы. Эта процедура и система правил являются
алгоритмом функционирования всей системы в целом.
Получить оптимальный алгоритм формальным путем здесь,
разумеется, нельзя. Процедуры принятия групповых решений
были разными у разных народов и находились опытным или
интуитивным путем.
Древние германцы, согласно Тациту, проводили решения
в два приема, причем прибегали к недозволенным ныне
средствам:
«... На пиршествах они толкуют и о примирении
враждующих между собой, о заключении браков, о выдвижении
вождей, наконец, о мире и о войне, полагая, что ни в какое
другое время душа не бывает столь же расположена к
откровенности и никогда так не воспламеняется для
помыслов о великом... На следующий день возобновляется
обсуждение тех же вопросов, и то, что они в два приема
занимаются ими, покоится на разумном основании: они об-
с>ждают их, когда неспособны к притворству, и принима-
57

ют решения, когда ничто не препятствует их
здравомыслию» г.
Та же идея — сделать обсуждение как можно более
свободным и непринужденным — лежит в основе
современного метода «мозговой атаки». Здесь эксперты совместно
обсуждают проблему и свободно общаются друг с другом при
единственном ограничении — запрещается критика, что
способствует свободе высказывания. Все высказанные идеи
и мнения фиксируются и затем, на втором этапе,
происходит их анализ и отбор.
Все экспертные методы, предполагающие возможность
общения экспертов и унификации их мнений с целью
выработки единого решения, имеют тот общий недостаток, что
группа может скорее стремиться к компромиссу, чем к
истине. К тому же, став общим, мнение обезличивается, в
то время как анализ аргументов сторонников и в
особенности противников общего мнения может быть весьма
ценным.
Очень своеобразно выносились решения на выборах в
древней Спарте:
«Когда народ сходился, особые выборные закрывались в
доме по соседству, так, чтоб и их никто не видел, и сами они
не видели, что происходит снаружи, но только слышали бы
голоса собравшихся. Народ и в этом случае, как и во
всех прочих, решал дело криком. Соискателей вводили не
всех сразу, а по очереди, в соответствии со жребием, и
они молча проходили через Собрание. У сидевших взаперти
были таблички, на которых они отмечали силу крика, не
зная, кому это кричат, но только заключая, что вышел
первый, второй, третий, вообще очередной соискатель.
Избранным объявлялся тот, кому кричали больше и громче
других» 2.
Метод, при котором проводится индивидуальный опрос
экспертов, разработан в США в 60-х годах и получил
название «метод Делфи». Опрос экспертов производится в
форме анкет, предлагающих высказаться относительно
сроков, либо возможности произойти в будущем ряду
событий. Затем анкеты статистически обрабатываются,
анализируются аргументы относительно различных суждений
1 Т а ц и т. О происхождении германцев... Соч., т. 1. М.,
«Наука», 1969, с. 363.
2 Плутарх. Сравнительные жизнеописания. М., Изд. АН СССР,
1961, т. 1, с. 73.
58

и результаты обработки сообщаются экспертам. Затем опрос
повторяется, причем отмечается уменьшение разброса
оценок. Обычно приемлемое согласование мнений происходит
в результате трех-четырех циклов.
Анонимность экспертов в «методе Делфи» позволяет
избежать отрицательных влияний экспертов друг на друга,
однако результаты здесь оказываются очень
чувствительными к влиянию со стороны организаторов опроса,
составляющих анкеты.
Название «метод Делфи», попавшее в нашу литературу
из американских источников и кочующее теперь из работы
в работу, создает впечатление, что именно так
вырабатывались прогнозы — оракулы в храме Аполлона в Дель-
фах — прогностическом центре древнего мира. Мы
позволим себе привести длинную цитату из книги «Антенорово
путешествие в Грецию и Азию», чтобы рассеять это
впечатление:
«На рассвете, увенчавшись лаврами и держа в руках
ветвь, ... взошли мы в храм с бесчисленным множеством
народа... Каждый из вопрошавших вел за собою свою
жертву. Наша состояла в белом тельце ... Один из жрецов
ввел нас в святилище, или лучше сказать в вертеп, из
коего исходило испарение, вся окружность оного была
обвешана приношениями, свет помрачен курением фимиамов и
извержением паров, выходящих из пропасти, так что мы
не могли ничего различить. Самый треножник заслоняли
лавровые ветви и кожа змея Пифона...
Вошла Пифия в сопровождении двух жрецов и
святошей. Мы увидели шестидесятилетнюю старуху, тощую,
сухощавую, бледную, худо одетую, печальную, угрюмую;
чело ее увенчано было повязками, а голова лаврами, от коих
бросила она на священный огонь несколько листьев...
Испив воды, открывающей будущее, приблизилась она
потом к треножнику, но с упорностию противилась взойти
на него. Жрецы употребляли угрозы и насилие, дабы
заставить ее повиноваться. Она села на край жерла и,
напитавшись прорицательными испарениями, начала метаться,
краснеть и пенить; грудь ее поднялась, она испустила
жалобный вопль и ужасный стон; наконец, не в силах будучи
противостоять богу, одержавшему ее, хотела сойти с
треножника, но два жреца удержали ее силою. Тогда
разодрала она на себе покров, изорвала повязку и со страшным
в.оем произнесла грудью, ибо Пифии чревоволшебствуют,
несколько слов, которые жрецы старались заметить и за-
59

писать; после чего сошла, лишилась сил и самого почти
дыхания...
Мы бросились читать свои ответы. Я спрашивал в своей
записке, долго ли проживу, вот ответ: «Виноград
собирается прежде маслин». Фанор желал знать, счастлив ли
будет для него брак? Оракул ответствовал: «Сыне! Волы,
заложенные в плуг, рассекают землю, дабы поля произра-
щали плод». Долгое время искали мы смысл сих гаданий...»1.
Совершенно очевидно, что Пифия осуществить прогноз
не в состоянии. Она не обладает необходимой для этого
информацией — ни о предыстории процесса, ни о
закономерностях его развития. Пифия здесь — в лучшем случае
«генератор шума».
Роль «формирующего фильтра», роль экспертной
группы играют жрецы — образованные, искушенные в
политике, многоопытные люди. Критерий, который они
стремятся максимизировать, — доходы храма, поэтому когда
речь идет о пустячных вопросах массового посетителя, они
действуют по принципу «на любой вопрос — любой ответ»,
но, давая прогнозы и советы политического характера,
проявляют сугубую осторожность. Так, согласно
Геродоту, лидийский царь Крез, собираясь начать войну,
запросил Дельфийский храм и получил ответ, что, перейдя
границу, он разрушит большое царство. Крез после этого с
уверенностью начал поход и потерпел поражение. Однако
предсказание оказалось правильным — разрушенное
царство было его собственным.
Возвращаясь после довольно продолжительного
отступления к организации экспертных групп, отметим, что
«метод комиссий» и «метод Делфи» можно сопоставлять с
алгоритмами б) и а) соответственно рис. 8. Действительно,
при независимых экспертах их прогнозы фиксируются, а
лишь затем производится обобщение.
Каким требованиям должен отвечать эксперт —
основной элемент прогнозирующего механизма?
В книге С. Д. Бешелева и Ф. Г. Гурвича «Экспертные
оценки» приводится «портрет» идеального эксперта.
Основные его качества следующие:
— креативность — способность решать творческие
задачи, метод решения которых полностью или частично
неизвестен;
1 Антенорово путешествие в Грецию и Азию. Часть вторая, СПб.,
1803, с. 284—289.
60

— эвристичность — способность видеть или создавать
неочевидные проблемы;
— интуиция — способность делать заключения об ис-
иследуемом объекте без осознания пути движения мысли к
этому заключению;
— предикаторность — способность предсказывать или
предчувствовать будущие состояния исследуемого объекта;
— независимость — способность противопоставлять
предубеждениям и массовым мнениям свое собственное;
— всесторонность — способность видеть проблему с
различных точек зрения и т. д.1.
Вопрос о том, насколько специализированным должны
быть познания экспертов, остается предметом дискуссий.
Существует, например, мнение, что чрезмерная
профессиональная узость не позволяет преодолеть сложившиеся
представления и не даст такому эксперту возможности
предвидеть переломных моментов в развитии проблемы.
Во всяком случае очевидно, что запасом фундаментальных
знаний эксперт обладать обязан. Соотношения же между
глубиной и разнообразием определяются областью
прогнозирования, в которой работают эксперты.
«В промышленности большинство научных работников,
из числа которых формируются экспертные группы, можно
разделить на две категории: ученых-специалистов и ученых-
организаторов. Ученые-специалисты (специалисты узкого
профиля) обладают глубокими знаниями в узкой области
науки и техники и достаточно информированы о состоянии
дел в смежных областях, достижения в которых могут ими
использоваться в работе по специальности. Как правило,
эта группа научных работников имеет ученые степени,
большой стаж работы, печатные труды...
Ученые-организаторы (специалисты широкого профиля) — широко
эрудированные и информированные специалисты, обладающие
определенными знаниями по широкому кругу вопросов в
различных областях науки и техники...
При анализе комплексных проблем предпочтение должно
отдаваться ученым-организаторам и, наоборот, при
обсуждении специальных проблем — ученым-специалистам»2.
Таким образом, подбирая тех или иных экспертов,
«собирают» схему из адекватных задаче блоков.
1 С. Д. Б е ш е л е в, Ф. Г. Г у р в и ч. Экспертные оценки.
М., «Наука», 1973, с. 103.
2 Н. Н. К и т а е в. Групповые экспертные оценки. М.,
«Знание», 1973, с. 32—33.
61

Подобрать группу равноценных экспертов бывает
трудно, признание же их неравноценными заставляет так или
иначе вводить «вес» их мнений—количественную оценку
их значимости.
Оценка экспертов производится при помощи
специальных анкет, при ответе на которые кандидаты должны
продемонстрировать свои знания и способности. Анкета может
требовать от кандидата в эксперты самооценки — числовой
оценки своих знаний. Это позволяет делать заключения как
о степени подготовленности экспертов, так и о способности
критически ее оценить.
Другой критерий отбора экспертов—оценка
надежности их прошлых прогнозов. В качестве простейшей такой
оценки может использоваться частота подтвердившихся
прогнозов. Замечено, что эксперт чаще бывает прав, когда
утверждает возможность чего-либо, чем когда отрицает ее.
Широко известны ошибочные предсказания крупнейших
ученых о невозможности практического использования
фундаментальных открытий. Наиболее поразительным
представляется мнение Г. Герца о практической бесполезности
обнаруженных им электромагнитных волн.
Какова должна быть численность экспертов?
Очевидно, чтобы иметь право на коллективное суждение,
их не должно быть слишком мало, так как индивидуальное
суждение в этом случае могло бы иметь чрезмерно большое
влияние. С увеличением группы сильно усложняются
проблемы согласования мнений. Рекомендуют обычно группы из
10—20 экспертов.
Мы видели, что алгоритмы прогнозирования становились
более эффективными по мере привлечения все более длинной
предыстории. Как обстоит дело, если прогноз
осуществляется экспертами? Должны ли они помнить все этапы
предыдущего развития проблемы, допускаются ли «провалы» в
их памяти и, вообще, окажутся ли требования, которые
мы к ним предъявили, совместимыми со свойствами
человеческой памяти и психологией научно-технического
творчества?
В последнее десятилетие получены очень интересные
результаты, которые могут помочь ответить на подобные
вопросы, но, насколько нам известно, еще не
использовавшиеся при подборе экспертных групп.
Речь идет о том, что удается количественно оценить
справедливость выражения «новое—это хорошо забытое
старое».
62

При анализе отвергнутых заявок на изобретения было
замечено, что в них повторяются известные ранее, но
забытые и вновь найденные решения, чаще всего удаленные от
настоящего времени на определенный срок.
Повторные изобретения технических новинок
встречались редко, повторения музейных образцов также были
нечасты, повторялись обычно решения, найденные 10—15 лет
назад. Изучение этого факта позволило построить модель
рассеяния научно-технической информации во времени.
В потоке сведений, которым пользуются авторы заявок
(разработчики проблемы) в i'-й год, различаются две части:
Jtt — информация этого же года, известная разработчику,
и Ju—информация, ему неизвестная, а значит, и не
принимаемая им в расчет при выдвижении своих идей.
Общее количество информации J нормировано:
Jn (а)=0, так как только что возникшие идеи еще не стали
всеобщим достоянием и не достигли нашего разработчика
ни по одному из каналов обмена научно-технической
информацией (публикации, конференции и т. д.). Затем по мере
углубления в прошлое уровень информированности
возрастает, так как информация успевает попасть к
потребителю. Здесь, на глубине до 3 лет работают службы научно-
технической информации, стремящиеся сделать более
крутым передний фронт «информационной волны». Далее, на
глубине 10—15 лет начинается зона малой
информированности о технических идеях прошлого. Этот провал
информированности авторы модели объясняют разными причинами.
Например, тем, что то, что своевременно не стало известно
разработчику, так и остается неизвестным ему без
специальных историко-технических изысканий, или тем, что
человеческая память обладает способностью забывать то, что не
представляет непосредственного интереса в момент
ознакомления. Интересна и такая версия: число инженеров растет
очень быстро, удваиваясь каждые 5 лет . Так что лишь
четвертой части инженеров «есть что забыть» из сведений
десятилетней давности.
Еще шаг «в глубь времен» и Уи начинает расти —
начальный этап развития данного вида техники обычно хорошо
известен.
Таким образом, задавая группе экспертов вопросы о
будущем, следует иметь в виду, что они имеют весьма
специфические сведения о прошлом. Расчитывать на то, что их
63

прогноз будет базироваться на всей предыстории, нельзя.
Здесь уместно отметить, что от экспертов требуется нечто
большее, чем просто память о предыстории. Очевидно, они
должны знать или чувствовать закономерности,
управляющие предсказываемым процессом. Многочисленные
прогнозы явлений, развивающихся какое-то время
экспоненциально, основанные на наблюдаемом участке экспоненты,
являли собой явную нелепость. Жизнь очень быстро
опровергала их.
Так, на заре первой промышленной революции, когда в
Англии стремительно росла добыча угля и руды, количество
воды, которую приходилось откачивать из шахт, нарастало
еще быстрее. Откачка производилась вручную и было ясно,
что через несколько десятков лет все население страны
должно будет заниматься только ею. Этого не случилось, так как
была изобретена паровая машина.
В дальнейшем многие показатели промышленного
развития нарастали экспоненциально, давая поводы к
катастрофическим либо бессмысленным прогнозам. В настоящее
время быстрое нарастание количества управленческой и
научно-технической информации породило у некоторых
авторов рецидив подобных прогнозов. Так, в книге
И. С. Шкловского «Вселенная, жизнь, разум» («Наука», 1962)
«информационный взрыв» назывался в качестве возможной
причины гибели цивилизации. Очень характерно, что в
третьем, переработанном издании («Наука», 1973) эта
причина уже не фигурирует.
Напомним, что оптимальный статистический алгоритм
использует как информацию о закономерностях развития
предсказываемого процесса — корреляционную функцию,
так и отсчеты предыстории.
Как и для любых неформальных методов, эффективность
метода экспертных оценок будущего может быть
установлена только путем прямых сравнений предсказаний с
истинным ходом событий. Хотя успехи экспертных оценок
несомненны, сейчас еще нет готовых рецепторов проведения
прогнозов, гарантирующих нужную надежность. Однако
это, по-видимому, все же лучший из неформальных
способов предвидения.