Курс гравиразведки. - Миронов В.С.

Author: Миронов В.С.

Tags: прикладная геология и геофизика геологические методы поисков и разведки интерпретация результатов физика геология

Year: 1980

Similar

Теоретические основы обработки геофизической информации

Разведочная геофизика

Поиски и разведка месторождений полезных ископаемых

Инженерная геология для строителей

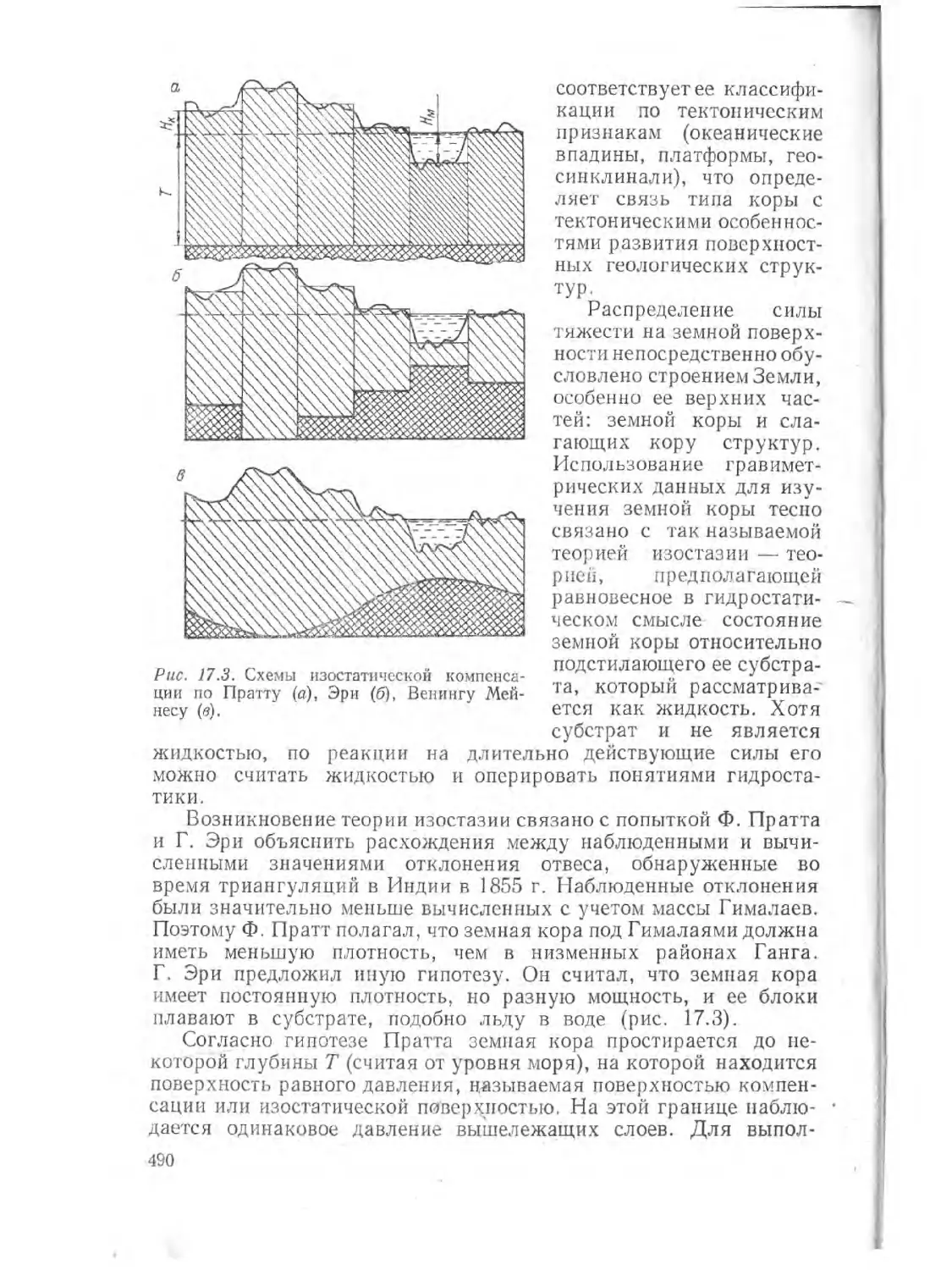
Text

В. С. Миронов
КУРС
ГРАВИРАЗВЕДКИ
Издание второе,
переработанное и дополненное
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебника для студентов вузов,
обучающихся по специальности
«Геофизические методы поисков и разведки
месторождений полезных ископаемых»
Ленинград „Недра"
Ленинградское отделение
1980
УДК 550.831 (075.8)
Миронов В. С. Курс граииря аведки. 2-е изд., перераб. и доп.—Л.:
Недра, 1980. — 543 с.
В книге рассмотрены теоретические основы гравитационной разведки, свой-
ства гравитационно! о потенциала и его производных, гравитационное поле
Земли; изложены принципы измерения элементов гравитационного поля; опи-
саны гравиметрические приборы, методика и техника гравиметрических изме-
рений; лапы принципы и методы геологической интерпретации гравитационных
аномалий, способы разделения гравитационного поля на составляющие; приве-
дены примеры применения гравиметрического метода при геологическом карти-
ровании, поисках и р.т всдке различных полезных ископаемых.
При подготовке второго издания книги были по возможности учтены дости-
жения в приборостроении, методике измерений и интерпретации гравитационных
аномалий.
Киша является учебником для студентов вузов, обучающихся по специаль-
ности «Геофизические методы поискан и разведки месторождений полезных иско-
паемых». Она может быть использована также инженерно-техническими работ-
никами геологе-геофизических организаций, занимающихся гравиметрическими
исследованиями.
Табл. 29, ил. 213, список лит. 22 назв.
Рецензент — кафедра геофизических методов исследования земной коры
Московского государственного университета им. М. В. Ломоносова.
20804—306
М 043(01)—80
104—80 19W05000U ©
Издательство «Недра», 1980
j Л*2ЮЫв» ода* f(
ПРЕДИСЛОВИЕ
КО ВТОРОМУ ИЗДАНИЮ
В годы, прошедшие со времени первого изда-
ния «Курса гравиразведки» (1972 г.), продолжалось развитие как
техники и методики измерений гравитационного поля, так и мето-
дов геологической интерпретации гравитационных аномалий. Это
потребовало существенного пересмотра отдельных глав книги.
В частности, более детально изложены вопросы абсолютных изме-
рений силы тяжести методом свободного падения, выбора плот-
ности промежуточного слоя при редуцировании, применения
вероятностно-статистического аппарата при интерпретации
гравитационных аномалий.
Некоторые разделы подверглись сокращению. Это касается,
например, способов измерения вторых производных гравитацион-
ного потенциала. Полностью исключить этот вопрос было бы не-
целесообразно, несмотря на тот факт, что производство варио-
метрической аппаратуры практически прекращено. При совре-
менном уровне техники вполне возможно создание портативных
высокопроизводительных гравитационных градиентометров,
потребность в которых давно назрела. В ряде стран уже ведутся
разработки такой аппаратуры.
В новом издании книги автор сохранил стиль и последователь-
ность изложения первого издания как наиболее методически
оправданные и проверенные на практике. Были исправлены опе-
чатки и неточности и учтены замечания и пожелания, высказанные
в отзывах на предыдущее издание.
г
ПРЕДИСЛОВИЕ
К ПЕРВОМУ ИЗДАНИЮ
Учебное пособие составлено на основе лек-
ций, читаемых автором на геологическом факультете Ленинград-
ского университета студентам-геофизикам в соответствии с про-
граммой курса «Гравиразведка», утвержденной для подготовки
геофизиков по специальности «Геофизические методы поисков
и разведки месторождений полезных ископаемых».
В книге автор стремился показать все стороны гравиразведки.
Книга состоит из четырех разделов, в которых изложены теория
гравитационного поля Земли, методы измерения силы тяжести
и вторых производных гравитационного потенциала, геологи-
ческое истолкование гравитационных аномалий и различные
аспекты применения гравиразведки в геологии.
Параллельно с лекциями проводятся лабораторные и практи-
ческие занятия, поэтому в книге дано довольно детальное описа-
ние гравнразведочной аппаратуры, настройки и наблюдений с ней,
практические приемы интерпретации гравитационных аномалий.
При составлении курса автор использовал существующие
учебники и учебные пособия по отдельным вопросам гравираз-
ведки, журнальные статьи и монографии.
Вполне естественно, что в книге, охватывающей все аспекты
гравиразведки, возможны отдельные упущения и ошибки. По-
этому автор заранее благодарен читателям за критические замеча-
ния, которые помогут улучшить содержание книги. Все замеча-
ния автор просит направлять по адресу: 199164, Ленинград,
В-164, Ленинградский государственный университет
им. А. А. Жданова, кафедра геофизических методов разведки
геологического факультета.
ВВЕДЕНИЕ
Гравиразведка — это сокращенное название
разведочной гравиметрии, или гравитационной (гравиметриче-
ской) разведки. Гравиразведка является одним из методов иссле-
дования геологического строения верхних частей Земли, поисков
и разведки полезных ископаемых. Она основана на изучении
свойств поля притяжения, источником которого являются массы
горных пород. На земной поверхности поле притяжения склады-
вается с полем центробежной силы, образуя поле силы тяжести,
или гравитационное поле. В разведочной гравиметрии приходится
использовать результаты измерений этого суммарного поля.
По объекту изучения гравиразведка является составной частью
более общей науки — разведочной геофизики, одной из приклад-
ных наук о Земле. По методу исследования (изучение физического
поля) гравиразведка является частью науки об измерении силы
тяжести — гравиметрии (от латинского gravitas — тяжесть и гре-
ческого ретресо — измеряю).
Следует отметить, что в настоящее время в понятие «грави-
метрия» вкладывают более широкий смысл: к гравиметрии относят
все вопросы научного и практического приложения результатов
измерения силы тяжести, используемых в различных отраслях
знания. В частности, оформилась как самостоятельная дисциплина
геодезическая гравиметрия, привлекающая результаты грави-
метрических измерений для исследования фигуры Земли.
Сила тяжести есть сила, с которой любое тело притягивается
к Земле. Начало экспериментальному изучению силы тяжести
было положено Г. Галилеем, проводившим опыты над падением
тел под действием силы тяжести. Он показал, что мерой силы
тяжести является ускорение, которое сила тяжести сообщает
свободно падающему телу. В 1590 г. Г. Галилей определил чис-
ленное значение ускорения свободного падения. В честь Г. Гали-
лея внесистемная единица ускорения (1 см в 1 с за 1 с) названа
гал.
В 1673 г. X. Гюйгенс установил, что сила тяжести может быть
определена из наблюдений за периодом качания маятника. Изме-
рени я силы тяжести того времени не отличались высокой точ-
ность ю и использовались в основном для оценки численного зна-
5
чоиия этой коштаи гы, поскольку прстполш алось, что сила тя-
жести па земной поверхности всюду нос гияпнл.
Первое свидетельство изменении i илы i и мч in с широтой было
получено в 1672 г. французским астрономом Ж. Рише, который
установил, что маятниковые часы отстают в низких широтах.
Правильное толкование этому факту дал II. Ньютон в 1687 г.
в третьем томе своего классического труда «Математические начала
натуральной философии». В этой работе И. Ньютон сформулиро-
вал закон всемирного тяготения и сделал попытку теоретически
определить фигуру Земли. Этим было положено начало грави-
метрии. Интерес к результатам измерения силы тяжести особенно
возрос со стороны астрономов и геодезистов после того, как
в 1743 г. А. Клеро показал возможность найти сжатие Земли по
гравиметрическим данным и вывел формулу изменения силы тя-
жести на земной поверхности.
Мысль о связи силы тяжести с внутренним строением Земли
впервые высказал М. В. Ломоносов. В 1753 г. он пытался постро-
ить прибор для регистрации вариаций силы тяжести во времени.
Развитию знаний о гравитационном поле способствовали ра-
боты К. Маклорена, П. Лапласа, А. Лежандра, С. Пуассона,
К- Гаусса, Д. Стокса, Д. Грина и других ученых, создавших
теорию потенциала физического поля, которая явилась теорети-
ческой основой не только гравиметрии, но и многих других отрас-
лей физики. Одновременно совершенствовались и методы измере-
ния силы тяжести. Усилиями Ф. Бесселя, X. Катера, Р. Штернека
маятники были превращены в приборы, позволяющие определять
силу тяжести с точностью до 10“8 ее значения.
В 1849 г. Д. Стокс доказал теорему, носящую теперь его имя,
которая позволяет находить фигуру Земли, используя только
гравиметрические наблюдения и не делая никаких предположений
относительно ее внутреннего строения. В 1887 г. па основе обобще-
ния гравиметрических измерений Ф. Гельмерт впервые вывел
формулу нормального распределения силы тяжести на земной
поверхности.
Создание в 1881 г. Р. Штернеком маятникового прибора для
относительных определений позволило перейти к массовым изме-
рениям силы тяжести, детальному изучению распределения ее
на земной поверхности. Накопленные сведения дали возможность
не только решать геодезические задачи, но и приступить к изуче-
нию внутреннего строения Земли. В 1872 г. И. И. Стебницкий
указал на связь уклонений отвеса в Восточном Закавказье с по-
гребенными массами, а в 1888 г. Ф. А. Слудский при изучении
гравитационной аномалии в районе Москвы определил глубину
залегания возмущающих масс, создающих эту аномалию.
Применению гравиметрии для решения геологических задач
способствовало изобретение венгерским физиком Р. Этвешем
в 1896 г. гравитационного вариометра, предназначенного для изме-
рения горизонтальных составляющих градиента силы тяжести
6
и кривизны уровенной поверхности. В 1902—1909 гг. Р. Этвеш
этим прибором выполнил первые измерения на Венгерской рав-
нине с геологической целью. Гравиметрические измерения для
геологии стали особенно широко применять после первой мировой
войны. В 1918 г. В. Швейдар использовал гравитационный варио-
метр для исследования солянокупольных структур в Германии,
с 1922 г. начинается применение вариометров в США.
В СССР внедрение гравиметрического метода разведки связано
с работами Особой комиссии по изучению Курской магнитной
аномалии, созданной в 1919 г. по инициативе В. И. Ленина.
Комиссия объединила ученых, которые стали основоположни-
ками разведочной геофизики в СССР: это — П. П. Лазарев,
П. М. Никифоров, А. А. Михайлов, Л. В. Сорокин, Г. А. Гамбур-
цев и др. С 1921 г. маятниковая и вариометрическая съемки про-
водились в районе КМА для поисков железистых кварцитов.
Положительные результаты работ способствовали широкому при-
менению гравиметрического метода и для решения других геоло-
гических задач.
В 1923 г. по инициативе геофизиков Горного института в Ле-
нинграде был организован первый в СССР научно-исследователь-
ский геофизический институт — Институт прикладной геофизики
(ИПГ), в котором работала группа гравиметристов под руковод-
ством Б. В. Нумерова: Н. Н. Михайлов, Н. Н. Самсонов, Н. Н. Че-
репанов, Э. Э. Фотиади и др. Научно-исследовательские работы
проводились как по конструированию гравиметрической аппара-
туры, так и по теории метода, истолкованию результатов наблюде-
ний, методике съемки.
Первые отечественные маятниковые приборы были созданы иод
руководством С. Е. Александрова в 1927 г. в Астрономическом
институте (Ленинград). В дальнейшем их разработкой занималась
группа Л. В. Сорокина в Государственном астрономическом ин-
ституте им. П. К- Штернберга (ГАИШ). Здесь же была разработана
маятниковая аппаратура для морских наблюдений, которые про-
водились на Черном, Каспийском, Охотском, Баренцевом и Япон-
ском морях.
Первые отечественные вариометры были созданы в ИПГ
в 1925 г. (П. Н. Никифоров). В дальнейшем они постоянно совер-
шенствовались. Начиная с 1935 г. был налажен серийный выпуск
гравитационных вариометров на заводе «Геологоразведка»
(М. Е. Абельский, С. А. Поддубный, С. К. Гирин). В 1955 г.
С. А. Поддубный разработал быстродействующий гравитационный
градиентометр, производительность которого была во много раз
выше, чем у вариометров.
Важное значение для упорядочения всех гравиметрических
исследований в СССР имело постановление Совета труда и обороны
от 20 сентября 1932 г. о проведении общегосударственной маятни-
ковой съемки. Этим постановлением определялась густота сети
(1 пункт на 1000 км2) и очередность районов съемки. К 1939 г.
7
г
была шкопчена маятниковая съемка европейской части СССР,
некоторых районов Западной Сибири и Средней Лани. Результаты
определений силы тяжести использовались для решения задач
региональной геологии, тектонического районирования геосинкли-
нальиых и платформенных областей (А. Д. Архангельский,
В. В. Федынский, Е. 11. Люстих и др.).
Первые работы по конструированию гравиметров были начаты
А. А. Михайловым в 1933 г. в ГАИШ. В Центральном научно-
исследовательском институте геодезии, аэросъемки и картогра-
фии (ЦНПИГАиК) М. С. Молоденский предложил конструкцию
металлического гравиметра, окончательная доводка которого была
завершена во Всесоюзном научно-исследовательском институте
геофизических методов разведки (ВНИИГеофизика) A. М. .Лозин-
ской, Л. В. Калишевой, П. И. Лукавченко, В. В. Федыиским и др.
В дальнейшем конструированием гравиметров занимались не-
сколько институтов: ВНИИГеофизика, Всесоюзный институт раз-
ведочной геофизики (ВИРГ). Институт физики Земли (ИФЗ АН
СССР).
В 1947 г. в ВИРГ был создан кварцевый гравиметр с жидко-
стной температурной компенсацией (С. А. Поддубный, Н. Н. Сам-
сонов), в 1950—1951 гг. во ВНИИГеофизике — кварцевый аста-
зированный гравиметр (К.. Е. Веселов, П. И. Лукавченко), на
основе которого завод «Геологоразведка» начал серийный выпуск
гравиметров ГАК.-ЗМ. Этот прибор послужил основой для раз-
работки целой серии более совершенных кварцевых гравиметров,
обладающих высокой точностью: ГАК-ПТ, ГАК-7Т и др.
К началу 50-х годов относятся работы по использованию
гравиметров для наблюдений на море. Создаются специальные
донные гравиметры (А. М. Лозинская, П. И. Лукавченко, В. В. Фе-
дынский, К- Е. Веселов), надводные приборы (К- Е. Веселов,
Е. И. Попов, Л. П. Смирнов и Др.), совершенствуется маятниковая
аппаратура для морских наблюдений (М. Е. Хейфец, С. Е. Алек-
сандров и др.). Проводятся также экспериментальные работы по
измерению силы тяжести с борта самолета (Ю. Д. Буланже,
Е. И. Попов, А. М. Лозинская и др.). Параллельно с совершен-
ствованием гравиметрической аппаратуры развивались методика
гравиметрических измерений с аппаратурой различных типов,
способы эталонирования, обработка результатов наблюдений.
Создание статических гравиметров позволило резко поднять
производительность и повысить точность измерений, что значи-
тельно расширило круг задач, решаемых гравиметрическим мето-
дом. Уже в 50-х годах стала возможной планомерная гравиметри-
ческая съемка масштаба 1 : 200 000. На отдельных площадях
проводится съемка масштаба 1 : 50 000 и крупнее. В перспективных
районах для поисков рудных тел выполняются гравиметрические
исследования в горных выработках (подземная гравиразведка).
Методы интерпретации гравитационных наблюдений и теорети-
ческие основы разведочной гравиметрии изложены в трудах
8
П. М. Никифорова, Б. В. Нумерова, Г. А. Гамбурцева, А. А. За-
морева, Н. Р. Малкина, Б. А. Андреева, А. К- Маловичко и дру-
гих ученых. На основе этих исследований решены задачи геологи-
ческого истолкования гравитационных аномалий. Назовем не-
которые из них.
Расчет гравитационного эффекта тел заданной формы, опре-
деление положения, формы и размеров тела по результатам грави-
метрических измерений рассматриваются в работах Г. А. Гамбур-
цева, Д. С. Микова, А. А. Непомнящих, О. Н. Шванка, А. А. Юнь-
кова, К- Ф. Тяпнина, А. К. Маловичко и др.
Разделение гравитационного эффекта нескольких тел, выра-
жение одних характеристик гравитационного поля через другие,
трансформации поля приводятся в трудах А. Н. Тихонова,
Ю. Д. Буланже, А. К- Маловичко, И. Г. Клушина, К. В. Гладкого,
Н. Р. Малкина, В. Н. Страхова, Б. А. Андреева и др.
Привлечению аппарата функций комплексного переменного
для интерпретации гравитационных аномалий посвящены ра-
боты С. В. Шалаева, В. Н. Страхова. Использование методов
интегральных преобразований, а также теории случайных функ-
ций рассматривается в работах К. В. Гладкого, И. Г. Клушина,
М. Г. Сербуленко, С. С. Серкерова, Л. А. Халфина и др.
В методику комплексной интерпретации результатов гравита-
ционных и других геофизических и геологических исследований
значительны?! вклад внесли А. Д. Архангельский, В. В. Федын-
ский, Ю. Н. Годин, Э. Э. Фотиади, Б. А. Андреев, С. И. Субботин
и др.
В настоящее время гравиразведка широко применяется при
решении самых разнообразных геологических задач, она является
одним из основных методов разведочной геофизики при реги-
ональных исследованиях, играет важную роль при поисках и
разведке различных полезных ископаемых. Особенно велико ее
значение при поисках месторождений нефти и газа, хромитов,
железных руд.
Дальнейшее развитие гравиразведки связано с совершенство-
ванием гравиметрической аппаратуры, повышением ее точности
и надежности, с автоматизацией процессов измерения и обработки
полученных материалов, созданием новых и улучшением уже
известных методов геологического истолкования гравитационных
аномалий, с рациональным комплексировапием разведочной грави-
метрии и других геофизических методов при решении конкретных
геологических задач.
f
Раздел I
ОСНОВЫ ТЕОРИИ
ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ
Глава 1
СИЛА ПРИТЯЖЕНИЯ И ЕЕ
ПОТЕНЦИАЛ
Сила притяжения
Сила тяжести g, распределение которой па
земной поверхности изучает гравиметрия, в каждой дайной точке
есть равнодействующая силы ньютонова притяжения F всей массы
Земли и центробежной силы С, вызванной вращением Земли
вокруг своей оси (рис. 1.1):
g = F + C. (1.1)
По сравнению с силон притяжения центробежная сила мала,
опа не связана с распределением масс в Земле и легко может быть
учтена. Основную компоненту силы тяжести составляет сила
притяжения, к рассмотрению которой мы и обратимся.
Согласно закону всемирного тяготения Ньютона две точечные
массы т и «Zj, расположенные на расстоянии г одна от другой,
взаимно притягиваются с силой
f = k (mm^r-), (1.2)
где k — гравитационная постоянная.
В системе СГС k = 6,673 10“8 см3/(г с2), в системе СИ k —
= 6,6720(41) 10 11 Н (м2/кг2) - - 6,6720(41) 10-11 м3/(кг с2), раз-
мерность dim k = LaM 1Т'2.
Сила притяжения, действующая на единичную массу, предста-
вляет собой напряженность поля притяжения и численно равна
ускорению, сообщаемому этой массе. Сила притяжения отличается
от ускорения только размерностью (размерность силы LMT~2,
размерность ускорения 7.Т'2). В точке с массой т, = 1 напряжен-
ность поля, обусловленного притяжением массы т, равна
F = k (т/г2).
(1-3)
10
Напряженность поля притяжения в
гравиметрии называют силой притяже-
ния или притяжением. Для краткости
термин «сила притяжения» сохраняется
и за ускорением, обусловленным силон
притяжения.
Сила притяжения представляет со-
бой вектор, направленный от притя-
гиваемой точки (с массой 1) к притя-
гивающей точке (массе).
Единица силы в системе СИ — нью-
тон [кг (м/с2)], в системе СГС—дина Р«с. 1.1. Силы тяжести g,
[г (см/с2) I; 1 дина = 10-Н. притяжения F и цептро-
п ' беж на я С.
В качестве единицы ускорения в
системе СИ принимается такое уско-
рение, которое получает масса 1 кг под действием силы 1 И, т. с.
[g] = 1 Н/1 кг — 1 м/с2.
Эту единицу на XV ассамблее Международного союза
геодезии и геофизики в 1971 г. было предложено называть
галилео (сокращенно G1 или Гл) в честь Г. Галилея, первым
измерившего ускорение свободного падения. Галилео—еди-
ница очень крупная: полное значение ускорения свободного па-
дения на Земле составляет 9,8 Гл. В гравиметрии более ши-
роко используется единица ускорения, называемая гал (также
в честь Г. Галилея). Гал—это ускорение, развиваемое массой
1 г под действием силы 1 дина: т. е. 1 гал 1 см/с2 10 2 Гл—
= 10 2 м/с2.
Для практических целей гал — единица также очень большая.
Поэтому обычно используют единицы более мелкие: миллигал
(мгал) и микрогал (мкгал); I мгал = 10-3 гал = 10® Гл =
= 10'® м/с2, 1 мкгал == 10’в гал = 10's мгал = 10“8 Гл =
= 10'8 м/с2.
Было предложено также применять единицу микрогалилео:
1 мкГл = Ю'в Гл = 10'* гал = 10'1 мгал = 1О'В м/с2.
В настоящее время наиболее широко распространенной еди-
ницей является миллигал. Но стандартом СЭВ 1052—78 его при-
менение допускается только до 1 января 1980 г. После этого срока
обязательной становится единица ускорения в системе СИ, т. е.
метр на секунду в квадрате. Чтобы облегчить сопоставление
материалов (карт, графиков), выраженных в разных единицах
(мгал, м/с2), примем за единицу измерения 10'® м/с2. Тогда
0,1 мгал = 0,1 • 10'® м/с2, 1 мгал = 110'® м/с2; 10 мгал = 10 X
X 10'® м/с2, т. е. первый сомножитель показывает значение уско-
рения в миллигалах.
Рассмотрим силу притяжения массы, распределенной в не-
котором объеме с плотностью а = о (|, ц, Q (рис. 1.2). Поместим
в точку В с координатами х, у, z массу, равную единице. В точке А
с координатами £, ц, £, находящейся в объеме v притягивающего
11
тела, выделим элементарную массу dm. Сила притяжения массы
dm в точке В
dF = k
dm
~r^~ ’
(1.4)
где
г- I х)'2 + (Г) - //) I ((, ?)-.
Проекции силы dF па оси ,v, у, г получим, умножив силу dF
на косинусы углов, которые образует вектор dF с осями координат:
dFx - dFcos(dF, x).-k j
dFtl = dF cos (dF, y) = k -%- ’ (1.5)
dF2 = dF cos (dF, z) = k !—. _L=_L. j
Сила притяжения F в точке В (х, у, z) всей массы, распределен-
ной в объеме v, может быть найдена интегрированием выражения
(1.4) по всему объему притягивающего тела. Аналогично получим
составляющие силы F по осям х, у, г:
F^k\^dm- F^k\^dnv, Fz^k\^-dni, (1.6)
ООО
где
dm — о di, dr\ di,.
Выражения (1.6) являются производными по х, у, z функции
U = k\(l/r)din, (1.7)
V
в чем легко убедиться непосредственным дифференцированием
функции U по координатам х, у, z:
= k $l=dLdm = Fx.
V
Рис. 1.2. Расположение притягива-
ющихся точек.
Аналогично могут быть полу-
чены две другие производные.
Таким образом,
Fx = dU/dx; Fy = dU/ду-
Fz = dU!dz. (1.8)
Функция U имеет то свойство,
что ее частные производные по
19
координатам притягиваемой точки рав-
ны составляющим силы притяжения
по ссответствующим осям координат.
Функции, обладающие таким свойством,
называются потенциальными. Функцию
U будем называть потенциалом при-
тяжения или гравитационным потен-
циалом. Выражение (1.7) определяет
потенциал притяжения масс, распре-
деленных внутри объема и, и является,
таким образом, объемным потенциа-
Рис. 1.3. Потенциал двой-
ного слоя.
лом.
Если допустить, что притягивающие массы расположены
только на поверхности 3 в виде слоя малой толщины h, то в этом
случае элементарная масса dm = о!г dS, где dS — элемент поверх-
ности 3. При этих условиях интеграл (1.7) примет вид
U = k [ о’(1/г) h dS.
s
Пусть при h -> 0 плотность о -> оо, но так, что
lim (о/г) = ц,
/1->0
где р есть конечная и непрерывная функция координат точки А
на поверхности 3. Тогда
U = k J р (l/г) dS.
s
Полученное выражение определяет потенциал простого слоя.
Функция [1 называется поверхностной плотностью простого слоя.
Пусть теперь на поверхности 3 распределен простой слой
с положительной поверхностной плотностью фр (рис. 1.3). На
расстоянии / по нормали от поверхности 5 расположена поверх-
ность 317 на которой распределен простой слой с поверхностной
плотностью —р так, что в точках этих слоев, находящихся на
одном отрезке нормали, плотности слоев равны по абсолютному
значению. Тогда сумма потенциалов двух простых слоев
U 4- = ( Р (1/г) dS - [ р (1/rJ dSr.
s s,
Имея в виду малость величины I по сравнению с расстояниями г
и можно считать dS dSt и
1 1 __ rt — г I cos <р _ / cos (п, г) _ д / 1 \ .
г гг ~ г Ci г2 — г2 ~ дп \ г ) '
Тогда
17 I и,.«J А 0.)^
13
Если теперь положить, что при I —> 0 произведение р/ стре-
мится к конечному, отличному от нуля пределу v, который назовем
плотностью двойного слоя, то получим потенциал двойного слоя:
S S
ПОТЕНЦИАЛ ПРИТЯЖЕНИЯ
И ЕГО ФИЗИЧЕСКИЙ СМЫСЛ
Для выяснения физического смысла потенциала притяжения
найдем его приращение dU при перемещении массы из точки В
с координатами х, у. z в точку В' с координатами х dx, у dy,
z + dz (рис. 1.4). Это приращение можно выразить через частные
производные от функции U:
dU = ^Ldx-\--^-dy-\-^-dz. (1.9)
дх 1 ду J 1 дг ' '
Обозначая косинусы углов, составленных направлением пере-
мещения s с координатными осями х, у, z, соответственно через
cos (s, х), cos (s, у), cos (s, z), а расстояние между точками В и В'
через ds, получаем
dx — ds cos (s, x);
dy = ds cos (.s, y);
dz ds COS (S, z).
(1.10)
Используя формулы (1.8) и (1.10), приводим выражение (1.9)
к виду
dU = ds [/•’, cos (s, x) Д Fy cos (s, y) -|- Fz cos (s, z)J.
Заменяя Fx, F,., Fz на F cos (F, x), F cos (F, y), F cos (F, z),
представляем
dU = F ds\cos(F, x)cos(s, x)-J-cos (F, //)cos(s, y) \
COS(/’, z)cos(s, z)|.
Рис. 1.4. Перемещение притягиваемой
точки в пространстве.
Так как выражение в квад-
ратных скобках равно cos (F, s),
получаем
dU — F cos (F, s) ds
или
dU = Fsds, (1.11)
где Fs — проекция силы притя-
жения на направление з.
14
Правая часть формулы (1.11) представляет собой произведение
силы Fs на путь ds, что равно работе. Таким образом, приращение
потенциала равно работе, которая производится действующей
силой для преодоления силы притяжения, создаваемой притяги-
вающей массой, при перемещении единичной массы из одной
точки в другую.
Отсюда следует, что
в
L/ = j F5 ds,
со
т. е. потенциал притяжения для некоторой точки В пространства
есть работа, которую совершают силы притяжения, обусловлен-
ные притягивающим телом, при перемещении под их действием
единичной массы из бесконечности в эту точку.
Уравнение (1.11) можно записать в виде
dU/ds = Fs. (1.12)
Таким образом, производная потенциальной функции по лю-
бому направлению равна составляющей силы по этому направле-
нию. Соотношения (1.8) являются частным случаем этого общего
свойства потенциальной функции.
Если направление s перпендикулярно к направлению силы F, то
cos(F, s) = 0; dU/ds = Fs = 0,
откуда
(У = с = const. (1-13)
Это выражение представляет собой уравнение эквипотенциаль-
ной (уровенной) поверхности, обладающей тем свойством, что
в любой ее точке сила притяжения направлена по нормали к этой
поверхности, а касательные составляющие силы равны нулю.
Значение силы на эквипотенциальной поверхности в общем случае
не является постоянным. Если направления s и F совпадают, то
cos (F, s) — 1 и
dUlds-=F. (1.14)
Величина ds в этом случае представляет собой расстояние
между двумя эквипотенциальными поверхностями U\ — с и U2 =
= с dU. Из формулы (1.14) следует, что расстояние между двумя
уровенными поверхностями обратно пропорционально действу-
ющей силе: если сила притяжения на участке уровенной поверх-
ности возрастает, то расстояние между поверхностями умень-
шается, и наоборот.
Поскольку приращение потенциала dU при переходе с одной
уровенной поверхности на другую постоянно и не зависит от
положения точки па этой поверхности, то приращение dU не
зависит от пути движения точки, а является функцией только
15
конечных точек перемещения. Отсюда следует, что приращение
потенциала dU по замкнутому контуру равно пулю.
Потенциал притяжения U является функцией, регулярной на
бесконечности, т. е.
liin (И/) -ЛМ, (1.15)
Z > Л»
где М — масса тела, создающего потенциал U.
При г -> с.о потенциал U обращается в нуль:
1- и f С dm J dm ,. М ...
Jim и ~ Iim — = lini ---------= um — — 0.
Г->ео Г>яо ** Г г Г Г >00 Г
Для доказательства равенства (1.15) запишем потенциал в точке
В, создаваемый по-разному распределенной массой М:
U k I (1/r) dm
V
— масса М распределена в объеме v;
L\ = k J (l/rj dm
V
— масса Л4 сосредоточена в точке объема v, ближайшей к точке В;
= k j" (1/га) dm
V
— масса M сосредоточена в точке объема V, наиболее удаленной
от точки В.
В этих формулах /у и га — соответственно расстояния от точки
В до ближайшей и самой удаленной от нее точек тела.
Тогда можно написать
V V V
или
k(M/r2)<U<k(M/ri).
Умножая это неравенство на г и переходя к пределу, получаем
lim (гД) Ш,
Г->оо
поскольку
lim (r/r2) lim (г/гх) ~ 1.
Г -> со Г~> сю
При рассмотрении основных свойств потенциальной функции
мы основывались только на общих выражениях (1.8) и (1.9),
справедливых для любых сил, имеющих потенциальную функцию,
16
Поэтому приведенные нами свойства справедливы не только для
сил притяжения, но и для всех других сил, для которых суще-
ствует потенциальная функция.
ВТОРЫЕ ПРОИЗВОДНЫЕ ПОТЕНЦИАЛА
ПРИТЯЖЕНИЯ И ИХ ФИЗИЧЕСКИЙ СМЫСЛ
Первые производные потенциала притяжения U по х, у и z
есть проекции силы притяжения на эти оси. Выясним физический
смысл вторых производных потенциала силы притяжения. По-
скольку потенциал U есть функция трех независимых переменных,
то он имеет шесть вторых производных:
94J дги дЧУ дгЦ д2Ц д-Ц
дх2 ’ ду* ’ дг* ’ дх ду ’ ду дг ’ дх дг
пли
и.ы, иуу, игг, и ху, иуг, ихг.
Производные U„, Uxy, UyS) определяют форму уровенной
поверхности в данной точке (рис. 1.5). Возьмем на этой поверх-
ности точку О и примем ее за начало координат, ось z направим по
нормали к уровенной поверхности. В этом случае координатная
плоскость хОу будет касательной плоскостью к уровенной поверх-
ности в точке б. Если через нормаль к уровенной поверхности
провести ряд плоскостей, то получим несколько так называемых
нормальных сечений уровенной поверхности, каждое из которых
будет плоской кривой. Угол, составленный какой-либо из секу-
щих плоскостей с координатной плоскостью хОг, обозначим через
ф. В дифференциальной геометрии известно выражение кривизны
1/р<Р нормального сечения в данной точке:
1/рф = г cos2 ср -ф- 2s sin ф cos ф ф- I sin2 ф,
где г, s, t — соответственно производные д2г!дхъ, (Fz/dx ду, d'z'dty,
если уравнение поверхности задано в виде
z = f(x, </) 0-16)
В нашем случае уравнение эквипотенциальной поверхности
имеет вид
U (х, у, z) = const, (117)
поэтому его надо преобразовать.
Дифференцируем это уравнение дважды по х, считая z функ-
цией X и у.
dU , dU дг „
дх ’’ дг ' дх ~ J’
d4J , дЧ/ дг дЧ/ f дг у <9аг л
дх3 ' дх дг дх ' дг3 \ дх ) дг дх3 ' ’ • ’
Поскольку координатная плоскость хОу является касательной
к уровенной поверхности, в начале координат имеем
дг/дх = 0; дг/ду ^0; dU/dz^U^.
Из равенства (1.18) получаем
Аналогичным образом, дифференцируя выражение (1.17) по х
и у, находим
s = (1.20)
дх ду иг - v
Дифференцируя выражение (1.17) дважды но у, имеем
z = .су- = ~ 77? UylJ' ^’21^
Получив выражения для г, s и Л определим кривизну нормаль-
ного сечения
1/Р.р = — (1Д4) (^ЛЛ- cos2 <р ф- Uiy sin 2ф + sin2 <р). (1.22)
Положив ф = 0 или л/2, получим нормальные сечения, совпа-
дающие с координатными плоскостями хОг и уОг:
l/Pxz = -(l/(/z)(/AA; 1/Рг,г = -(1/Пг)(/да. (1.23)
Среди бесчисленного множества нормальных сечений, определя-
емых уравнением (1.22), имеются два особых сечения: с мини-
мальной и максимальной кривизной. Эти сечения называются
главными нормальными. Чтобы найти их азимуты, надо решить
уравнение
18
(1.27)
Для этого Дифференцируем правую часть уравнения (1.22),
приравниваем ее нулю и решаем относительно <р. Обозначим иско-
мое значение ф через <р0. После дифференцирования получаем
—Uхх sin 2<р0 Д 2(7ед cos 2ф0 Д- ULIy sin 2<p0 = 0; (1.25)
tg2cpe = -2t/A.,/t/A, (1.26)
где
Из выражения (1.26) находим два значения угла <р0> различа-
ющиеся на л/2, это ф0 н ф0 Д л/2. Определим, какое из этих
решений дает нормальное сечение с максимальной кривизной
и какое — с минимальной. Пусть углом <р0 определяется сечение
с максимальной кривизной. Радиус максимальной кривизны
обозначим ртач, а минимальной рт1п. Вычислим значения кривизн
1/ртах и 1/pmin- Для этого в уравнение (1.22) подставим последова-
тельно фс и Фо I’ л/2. Тогда
1 /Ртах - — (1 /Уг) (Uxx COS3 ф0 -)- Uia sin 2ф0 Д- Um sin2 ф0); j
1/Ptntn == (l/C72-)(C/irsin3ip0 -t/VJ/sin2<r0 I //„,cos2(p(1). I
Найдем разность кривизн:
!----—— = -rj- (—UXIC cos 2фа - Чиху sin 2<p0 Д- Uuy cos 2<p0),
Ртах P min u г
ИЛИ
1/pmax— l/prala = (l/L/2)(t/Acos2<p0 — 2ВД, sin 2ф0). (1.28)
Из равенства (1.26) имеем
—2t/^ = t/Atg2<p0.
Подставляя значение —2Uxy в формулу (1.28), получаем
U г (1 Ртах 1/pinln) ~ Ь 8вс2ф0, (1.29)
Последнее равенство позволяет выбрать угол <р0 соответству-
ющим образом. Действительно, если 1/ршах есть максимальная
кривизна нормального сечения, то разность 1/ргаах — l/pmln поло-
жительна и произведение Иг (1/рт„ — 1/р[П,п) также положительно.
Отсюда следует, что и произведение (7дзес2фо тоже положитель-
но, т. е. для ф0 нужно взять квадрант, в котором cos 2ф0 имеет тот-
же знак, чго и Йд.
Величина
R(1/Pmax 1/Ртт)
19
называется вектором разности кривизн или вектором кривизны
и характеризует уклонение данной уровенной поверхности от
сферической; для сферы R 0. Соответственно величины
1/д =/?cos2(|>0 и 2UXU /?sln2<|ll
называются составляющими вектора кривизны. Очевидно, что
R = ^Ul+ (2l/w)2 •
Таким образом, производные Uxx, Um и Ux!/ определяют раз-
ность кривизн главных нормальных сечений уровенной поверх-
ности и их азимуты.
Рассмотрим физический смысл трех остальных вторых произ-
водных потенциала силы притяжения.
Производная U„ может быть представлена следующим
образом:
,, _ д_ ( дЦ_\ _ дЦ^
~~ дг \ дг / ~ дг ’
Так как ось г направлена по нормали к уровенной поверхности,
то U22 есть производная силы притяжения по вертикали, она
называется вертикальной составляющей градиента силы при-
тяжения.
Две другие производные UXz и UUl могут быть представлены
следующим образом:
.._____д / dU \ дЦг ' ,,____д f dU \ dU2
хг дх \ дг ) дх ’ иг ду \ дг ) ~ ду ’
т. е. эти производные являются составляющими градиента силы
притяжения в горизонтальной плоскости.
Геометрическая сумма этих двух векторов равна вектору
dUJds, характеризующему значение и направление наибольшего
изменения силы притяжения в горизонтальной плоскости. Длина
вектора dUJds вычисляется из равенства
диг1д.^уи2хг + и2уг,
его азимут относительно оси х определяется углом а:
tga =UyjUx..
По известным значениям UX2 и U,J2 или dUJds можно найти
составляющую градиента силы притяжения по любому направле-
нию в горизонтальной плоскости, проецируя вектор dUJds на это
20
направление. Например, если требуется определить проекцию
градиента силы притяжения на прямую р с азимутом р, то
dUJd? = (dUг!ds) cos (р — а) — (dU2/ds) cos a cos (i Д-
Д (dUz/ds) sin а sin р = Uxz cos Р -j- U нг sin p.
Остановимся на размерности и единицах рассмотренных нами
элементов гравитационного поля.
Поскольку первые производные потенциала притяжения
есть ускорения, имеющие размерность LT~\ то размерность вторых
производных Т~*. Единицы вторых производных [(см/с2)/см и
(м/с2)/м] во всех системах совпадают и могут быть представлены
как 1/с2. Единица, равная 1 • 10’0 1/с2, названа этвеш (Э) по имени
венгерского физика Р. Этвеша, впервые построившего прибор для
определения вторых производных. Если ускорение меняется
линейно, то его изменение в 0,1 мгал (0,1 10 5 м/с2) на расстоянии
1 км соответствует 1 Э (1 • 10"9 1/с2).
ОБЩИЕ ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ
ПРОИЗВОДНЫХ ПОТЕНЦИАЛА ПРИТЯЖЕНИЯ
Выражения производных гравитационного потенциала можно
получить из формулы (1.7), если задано расположение возмуща-
ющих масс относительно притягиваемой точки. В этом случае
потенциал притяжения в точке с прямоугольными координатами х,
у, z, лежащей вне тела V, определяется формулой
<т Д d n dt,
U(x, у, z)—k f-----------------------------775-.
J l(g-x)2 + (n-j/)24-U-2)2]1/2
(1.30)
В общем случае плотность тела о есть функция переменных
интегрирования rj, £. В гравиразведке обычно рассматривают
тела с постоянной плотностью. При этом условии сг выносят за
знак интеграла.
Для обозначения производных потенциала притяжения U
используют индексы, указывающие координаты, по которым ве-
дется дифференцирование. Дифференцируя равенство (1.30) по х,
у, z, получаем выражения для первых производных:
Ux (х, у, z) = ko j d£;
V
у, 2)=/га
V
U2(x, у, z)=ko
V
(1.31)
21
Повторное дифференцирование дает следующие выражения
для вторых производных:
., . , , г 2 (Е,— х)2 — (т) — у)2 — К — z)2 lt ,
Uxx (*. !/>?) = Ь J —---------------у,~-------------- dl dx\ <%,
V
,, , , , f 2(11—v)2 — (5 — x)2— (t—z)2 ,E ,
Ul/y (x, y, z) A<t j ——-U----lb_'------lb.—2_ rfg di] dZ, =
u
= feo-j[3(n-./)2 _^j^dT|dg.
V
u„ (x, у, z) = ka j *)a - (>1 -1/>2 _
V
Us(x, y, ?) = Uy!/(x, у, 2) — UXK(x, у, z) ==
= з/г(Т j di] t/?;
V
UX2 (.v, у, г) = d? dT]dS;
V
U,„ (x, у, г) = З/.’О j -(1".'^^-^ dg dn
V
Uxy (x, у, г) = 3/;a f dg di] dt,
(1.32)
где
r = У (I - x)2 + (Y| - уУ -НС - 2)2 .
22
Часто для вычислений бывает удобно начало координат по-
мещать в притягиваемую точку, т. е. полагать х — у = г = 0.
Тогда выражения (1.31) и (1.32) принимают вид
Uх (0, 0, 0) — ka j ~ d% dr) d£;
V
U„(0, 0, 0) = to j-^dgdr)dg;
V
Ux(0. 0, 0) = to [ -^-d^diidj;
(1.33)
Uxx(0, 0, 0)_^3to j’-^-dg dndS;
V
Uai(0, 0, 0) = 3toJ-^-dgdt]d£;
V
Uxy (0, 0, 0) = 3to j -|3- dg dr) dt;
V
c Ot2__712 _Y2
Uxx (0, 0, 0) = to J —L di- dn dS;
V
Um (0, 0, 0) = to J -n-—гУ~^2 d?= dn d^;
V
(0, o, 0) = ko [ dv, dg;
V
Us (0, 0, 0) = 3ko J dS dr) d?,
где
г = /^+ Ла + Г“-
23
Наряду с прямоугольной системой координат часто используют
вертикальную цилиндрическую систему г, а, связанную с прямо-
угольной соотношениями
5 — г cos а; 1] - г sin а; £ г;
d£r/i|d£- rdrdztla.
Взяв эти соотношения, получим следующие выражения для
первых и вторых производных потенциала:
t/, (0, 0, 0) Лю [ и r2 COS « II, — T^-r-dr az da; (г2+-г-)3'-
У Д0, 0, 0) = k0 i V r2 sill a * j j (л2 + г2)3/2 drdzda;
УДО, 0, 0) = H I’ (r2 Д. z2)3/2 d' dzda,
д,до, 0, 0) = H V r22cosa , , , (f2 । г2)5/2 W a?
(1.35)
t/,z(0, 0, 0) = 3toJ V r2z sin a , , , --в - dr dz da; (r + z*r2
У2г (0, 0, 0) = k<3 J V r(2z2-r2) . , , dr dz da;
гддо, 0, 0) = 3 A r r3 sin 2a , , , drdzda; J (r’ + г2)5у2 V
(7Л(0, 0, 0) = 3k<J Г r3 cos 2a , , , z, ox5/2 drdzda. J (г2 + г-)’/д
В горизонтальной цилиндрической системе координат, связан-
ной с прямоугольной соотношениями
g = р cos ф; п = у, £ = р Sin\p;
di, d i] dt, — p dp dy d<p,
24
выражения производных потенциала примут вид
(0, 0, 0) = ko | dP с1У с'<>
Uy (0, 0, 0) = ko ( dp dy dip;
иг (0, 0, 0) = ko J у-£—2 Ly dp dy dtp;
и.г (0, 0, 0) - J dpdr/dq;;
“ I (p +y)
Uyz(Q, 0, 0) = 3to f .dpdydy-,
J \P ~г У )
V
UZ2(Q, 0, Q) feg J pS t3 sin2a Ф -1Д- ^dpdydy-
J (p + у1)'»*
Uxy (0, 0, 0) = 3ko j ,P2^COS2^ dpdydv
~ (p +yj '
U* (0, 0/0) == 3ko J P^-^^-dpdydv.
(1.36)
При изучении гравитационного эффекта тел, размеры которых
по простиранию значительно больше их поперечных размеров,
можно считать, что гравитационное поле над серединой таких тел
почти равно полю тел, простирание которых бесконечно. Это пред-
положение существенно упрощает вычислительные операции,
незначительно снижая точность результата. Поэтому в грави-
разведке большое значение имеет понятие о двумерных телах,
т. е. отелах, простирающихся в одном измерении на бесконечность.
Форму двумерного тела целиком определяет его поперечное сече-
ние S. Двумерные тела можно рассматривать как цилиндрические,
полученные при движении образующей вдоль контура их попереч-
ного сечения.
Положим простирание двумерного тела параллельным оси у,
а плотность независимой от координаты ц. В этом случае основ-
ному свойству потенциала будет удовлетворять следующая функ-
ция, называемая логарифмическим потенциалом:
U(x, z)^ ko j J ln[(|-x)2 + (?^z)2]dg^. (1.37)
s
Чтобы показать, что эта функция является потенциалом при-
тяжения для двумерных тел, найдем значения составляющих Ux
и U2 силы притяжения по осям координат из формул (1.31). Для
25
этого необходимо проинтегрировать формулы (1.31) по г] в преде-
лах от —оо до Н-оо, что сведется к вычислению интеграла
/ = | (l/r3)dt]. (1.38)
-00
Взяв ряд простых интегралов, получим
у____________I________ ______________и —!/______________ | + “
’ (ё — лгГ2-F (С — г)г * [(5_х)2.|.(,|_!/)2 + (г_2П1/2 1.^'-
Учитывая это выражение, из формул (1.31) находим
Ux (х, z) = 2Z?cr J j
S
и ЛА 2) = 2*0 J j
3
(4 = 0.
(1.39)
Дифференцируя непосредственно выражение (1.37) по х и г,
можно убедиться в совпадении формул, полученных для Ux и 77.,
с уравнениями (1.39). Это доказывает, что выражение (1.37) яв-
ляется потенциалом притяжения в случае двумерных масс.
Дифференцируя повторно выражение (1.37) по координатам
притягиваемой точки, можно найти и вторые производные грави-
тационного потенциала двумерных тел:
Л,г (А г) = 4/го J j (£ х\& г) dl
S
Игг (х, z) = 7/л (а г) = 2/га [ j G ~ ~~ х)° dl d£;
s
(1-40)
где
-И?-2)*.
26
Помещая начало координат в притягиваемую точку, т. е. по-
лагая х = г = 0, и переходя к горизонтальной цилиндрической
системе координат, получаем
г r
I J I2 + i,2
s
£ dl dt
= 2А’о j" j cos ipclpdcp;
s
— 2ka | | sin <p dp dcp;
's
HMJ
s
£2-g2
<4(0, 0) =
ПД0, 0) = 2to [ f-sr™
s
ПЛ,(0, 0) = 4A’o J
*s
иг; (0, 0) = Уд (0, 0) = 2кв j j
s
= -2к а I [ -cos-~'-- dp d.ro.
J J P
s
sin 2<p . .
—dp dcp;
(141)
ПОТЕНЦИАЛ ПРИТЯЖЕНИЯ
СФЕРИЧЕСКОГО СЛЭЯ И ШАРА
Преимущество введения понятия «потенциал притяжения» как
функции, первые производные которой по координатам притяги-
ваемой точки являются составляющими силы притяжения по соот-
ветствующим осям координат, заключается в обобщении наиболее
фундаментальных свойств поля, таких как работа, сила, ускоре-
ние, и в возможности единообразного аналитического подхода
к их рассмотрению. Подобный подход к анализу потенциальных
полей возможен во всех точках поля, за исключением так называ-
емых сингулярных, или особых точек (полюсов). Отсюда очевидна
важность изучения особых точек поля, определения их положения
и отграничения таких точек «сферой безопасности» от остальной
части пространства при выводе аналитических выражений. Ука-
занное положение можно проиллюстрировать, рассмотрев потен-
циал притяжения простейших тел: сферического слоя и шара
(рис. Г. 6).
Введем сферические координаты р, ср, X с началом в центре О
сферического слоя радиусом R, толщину которого примем бес-
конечно малой. Полярную ось направим так, чтобы она проходила
через притягиваемую точку В, находящуюся вне шарового слоя.
Потенциал притяжения в точке В (р, 0, 0) от элементарного объема
dm, сосредоточенного в точке А с координатами ср, к, R, имеет вид
dU = k (I /г) dm, (142)
где г — расстояние между точками А и В,
2?
Ufft.U.O)
Рис. 1.6. Потенциал притяжения сферического слоя и шара.
Потенциал от всего сферического слоя получим интегрирова-
нием выражения (1.42) по всей поверхности слоя:
U-^k J(l/r)d/n. (j 43j
Элементарную массу dm можно выразить как произведение
поверхностной плотности р на элемент dS сферической поверх-
ности. Так как
dS = У?3 sin (f'dcpdX,
то
dm = p/?3sin (pdipdk. (1-44)
Из рассмотрения треугольника ОАВ следует, что
г® = R2 р= - 2Rp cos <р, (1.45)
где р — расстояние притягиваемой точки В от центра сферы 0.
28
Подставляя выражение (1.44) в формулу (1.43) и полагая
поверхностную плотность р. постоянной, получаем
U = /?р j j (Иг/г) sin гр dip dk. (1.46)
о о
Интегрирование по к в пределах от 0 до 2л дает
U = 2лЛр [ (R2/r) sin срг/(р. (1.47)
О
Для вычисления этого интеграла перейдем от переменной
интегрирования ср к переменной г.
Из уравнения (1.45) находим
г dr = Rp sin ср dtp,
откуда
R2 sin ср dip = (rR/p) dr. (1-48)
Подставим это выражение в формулу (1.47):
Р+Л
(7==2лАр j (R/pjctr. (1-49)
l>-R
Вынося R/p за знак интеграла как постоянную и выполняя
интегрирование по г, получаем
U = 4л#р (Ra/p) = k (М/р), (1.50)
где М — масса сферического слоя.
Отсюда следует, что потенциал притяжения однородного сфе-
рического слоя во внешней по отношению к нему области равен
потенциалу притяжения материальной точки с массой, равной
массе сферического слоя, и помещенной в его центре.
Сила притяжения сферического слоя в точке В ввиду сим-
метрии слоя направлена по прямой ОВ, совпадающей с осью р.
Используя основное свойство потенциальной функции, из фор-
мулы (1.50) находим силу притяжения сферического слоя во внеш-
ней точке В:
F = _ ди/др = k (М/р2). (1.51)
Такой же формулой выражается сила притяжения материаль-
ной точки с массой М на расстоянии р. Таким образом, поле одно-
родного сферического слоя во внешнем пространстве идентично
полю его массы, сосредоточенной в центре слоя.
Для потенциала точки В', расположенной во внутренней
области сферического слоя, аналогичные рассуждения приводят
к той же формуле (1.49). Нижний предел интегрирования в этом
29
случае будет другим, так как расстояние внутренней точки В'
от полюса N равно ON — OB' — R — р, поэтому
R+P
U = 2л/<р | (R/p)dr, (1.52)
Д-Р
откуда
U = 4л/гр/?. (1.53)
Вводя опять массу сферического слоя М, получаем
U=k(M/R). (1.54)
Для сферического слоя данной массы и радиуса это выражение
постоянно и не зависит от положения притягиваемой внутренней
точки, которое определяется расстоянием р. Поскольку значение
потенциала внутри сферического слоя постоянно, то все его произ-
водные равны нулю, в том числе и производная
— dU/dfy = F = O, (1.55)
т. е. во внутренней области однородного сферического слоя сила
притяжения равна нулю.
Однородный сферический слой конечной толщины можно рас-
сматривать как сумму бесконечного числа бесконечно тонких
слоев. Поверхностную плотность р бесконечно тонкого стоя мощ-
ностью dR можно выразить через объемную плотность ст:
р, = оДД (1.56)
Тогда интегрирование по R выражения (1.50) в пределах от
радиуса R внешней поверхности до радиуса Rx внутренней поверх-
ности даст формулу потенциала сферического слоя, имеющего
конечную мощность (R RJ, во внешней области:
j R\lR =±nk ~(R3 - R^ = k-^-, (1.57)
P R, * P
где M — масса сферического слоя, равная (4/3)ло(/?3 — У??).
-^Формула (1,57) при Rx = 0 выражает потенциал однородного
шара
U^~nko-~. (1.58)
Идентичность выражений потенциала во внешней области для
слоев бесконечно малой и конечной мощности и шара определяет
идентичность и производных потенциала. Дифференцируя по р
выражения (1.57) и (1.58), получаем силу притяжения сфери-
ческого слоя конечной мощности
„ dU 4 , R3 —R® , М .. -о,
—(1.59)
30
и силу притяжения шара
r ди 4 , R3 . М сп,
Р------г—= гглка-г-~ k-г-. (1.60)
dp 3 р2 р2 ' '
Для всех трех рассмотренных случаев выражения потенциала
и силы притяжения получились совершенно одинаковыми. Таким
образом, во внешней области поле однородных сферических слоев
бесконечно малой и конечной мощности, а также однородного шара
эквивалентно полю сосредоточенных в их центре масс, равных
массам оболочек или шара. Этот же вывод распространяется и на
неоднородный сферический слой и неоднородный шар, если не-
однородность зависит только от радиуса и не меняется по другим
координатам.
Для нахождения потенциала притяжения во внутренней точке
шара В' (см. рис. 1.6) проведем через эту точку вторую концен-
трическую сферу, которая разделит всю массу на две части: слой
So, по отношению к которому точка В' является внутренней,
и слой St, по отношению к которому точка В'может быть принята
внешней. Потенциал U в точке В' равен сумме потенциалов Uu
слоя So и слоя Si!
и = иа+ии
На основе равенств (1.53) и (1.57), учитывая пределы интегри-
рования, находим
к
(Д = 4."ito j= 2nto (Л2 — р2); (1-61)
р
U\ = ~ л/<!у (р3 — Д3). (1.62)
Суммируя Uo и i/j, получаем
О'=Р9-|-^=|г/еа('3/?г-р2ф2^). (1.63)
Для шара = 0, откуда
U = nko (3№ — р2). (1.64)
Дифференцируя это выражение по р, получаем силу притяже-
ния внутри однородного шара:
F =------- — 4- л top = k 41g-, (1.65)
0р 3 ‘ р2 v 7
где Мр = (4/3) лор3 — масса внутренней по отношению к точке В'
части шара; заметим, что Мр меняется с изменением р.
Внутри шара, как следует из формулы (1.64), потенциал дости-
гает максимума: t/raax = 2nto/?2 при р = 0 (рис. 1.7). С увеличе-
нием р до R потенциал уменьшается до 2/3 максимального: U —
31
= (4/3) гг/’о7?2. Сила притяжения F в центре шара равна нулю.
С возрастанием р ее значение увеличивается пропорционально
расстоянию от центра шара и на поверхности его достигает
(4/3) nkoR. Потенциал и сила притяжения, рассчитанные для
внутренней области шара, на его границе совпадают с их значе-
ниями, определенными по формулам (1.58) и (1.60) для внешней
области шара. С удалением от сферы потенциал и сила притяжения
уменьшаются обратно пропорционально соответственно первой
и второй степени расстояния от центра шара. При р-»• оо функ-
ции U —> 0 и F —> 0.
Из приведенного анализа следует, что потенциал притяжения
однородного шара и его первые производные являются конечными
и непрерывными функциями во всем пространстве. По-иному ведут
себя вторые производные гравитационного потенциала. Диффе-
ренцируя выражение (1.58) по р дважды, найдем, что в точках
пространства вне сферы
= (1.66)
Др- 3 ра ' '
на поверхности сферы, когда точка приближается к сфере извне,
d-U/dtf = (8/3) л/гсг. (1.67)
Для точек внутри сферы вторую производную получаем, диф-
ференцируя дважды выражение (1.64):
д2£7/(Эр2 = ~ (4/3) л/г<т.
(1.68)
32
Это значение производной сохраняется и на поверхности сферы,
когда точка приближается к ней изнутри:
d2U/dp2 = — (4/3) nko. (1.69)
Сопоставляя равенства (1.67) и (1.69), находим, что вторая
производная потенциала притяжения при переходе через поверх-
ность шара терпит разрыв и изменяется скачком на +4лА<т (см.
рис. 1.7). Знак скачка берется в зависимости от направления дви-
жения: «плюс» при переходе из внутренней области во внешнюю
и «минус» при движении в обратном направлении. Это свойство
вторых производных потенциала притяжения является весьма
важным, и к нему мы неоднократно будем возвращаться.
УРАВНЕНИЯ ЛАПЛАСА И ПУАССОНА
Обращаясь к общим интегральным выражениям (1.32), обра-
зуем сумму вторых производных потенциала притяжения:
4^ + + = зи f - z)2 _ ± j dm.
cbr2 1 ду2 1 дг1 j L г5 г8, J
(1-70)
Легко видеть, что для точек, не занятых притягивающими
массами,
\U = дЧЛдх2 ) дЧЛду2 ф dW/dz2 = 0. (1.71)
Полученное выражение называется уравнением Лапласа.
Функции, удовлетворяющие в некоторой области уравнению
Лапласа и являющиеся непрерывными в данной области вместе
со своими первыми и вторыми производными, называются гармо-
ническими. Таким образом, потенциал притяжения является
гармонической функцией во всем пространстве, не занятом при-
тягивающими массами. Гармоническими функциями являются
и все его производные вне притягивающих масс, в чем можно
легко убедиться двукратным дифференцированием по х, у и z
выражений (1.31), (1.32) и последующим сложением полученных
результатов.
Если же притягиваемая точка лежит внутри притягивающего
тела, то разности (£ — х), (ц — у) и (£ — z), а также величина г
могут стремиться к нулю. Поэтому подынтегральное выражение
в пределе примет вид 0/0. Для раскрытия неопределенности опи-
шем вокруг притягиваемой точки сферу конечного, но настолько
малого радиуса, чтобы плотность о сферы можно было считать
постоянной. Естественно, что сфера должна целиком находиться
внутри тела. Тогда потенциал U можно представить в виде суммы:
9
В. С. Миронов
33
где Ut — потенциал притяжения всего тела, за исключением
выделенной сферы, во внутренней точке (центре сферы); U.2 —
потенциал выделенной сферы.
Поскольку г для Ut нигде не обращается в нуль, U2 — функ-
ция гармоническая и Д^ = 0.
Для определения функции Дб/2 образуем из выражения (1.64)
частные производные по координатам х, у, г, неявно входящим
в нее через р:
44 = ~ 4 лЛор 17 = ~ 4 л/гп
Проделав аналогичное дифференцирование по у и г и сравнив
результаты, увидим, что
дгиъ/дуг — d-lJ2l'dz~дгиг/д.кг = — (4/3) л/го.
Суммируя вторые производные и учитывая, что ДОj = 0,
находим
ДО., = Д U = —4л/.ю. (1.72)
Полученное выражение, связывающее вторые производные
потенциала притяжения внутри области притягивающих масс,
называется уравнением Пуассона. Приведенное выше уравнение
Лапласа является частным случаем уравнения Пуассона, когда
поле рассматривается вне области притягивающих масс.
Таким образом, потенциал притяжения и все его производные,
если они заданы в некоторой области пространства вне притяги-
вающих масс, являются гармоническими функциями во всем про-
странстве, не занятом притягивающими массами. В области же
притягивающих масс в некоторых точках или сама потенциальная
функция или ее производные теряют свою непрерывность, т. е.
не являются гармоническими. Эти точки, в которых потенциал
теряет свои гармонические свойства, называются особыми. В ча-
стности, для шара вне притягивающих масс потенциал притяже-
ния (1.58) и все его производные всюду непрерывны и удовлетво-
ряют уравнению Лапласа во всех точках пространства. Точка
р = 0 (центр шара) является для потенциала и всех его производ-
ных особой точкой.
Особые точки потенциала притяжения и его производных
могут располагаться как внутри притягивающего тела, так и на
его поверхности. В последнем случае они совпадают с геометри-
ческими особенностями поверхности притягивающего тела: точ-
ками излома границы тела или угловыми точками. Зная положе-
ние особых точек, в некоторых случаях можно определить гео-
метрические параметры притягивающего тела.
34
ФОРМУЛЫ ГРИНА
Для выяснения других важных свойств потенциальных функ-
ций нам придется использовать математический аппарат, при-
меняемый при изучении пространственных функций. Основу уче-
ния о пространственных функциях составляют преобразования
Грина — Остроградского интегралов, взятых по объему, в интег-
ралы по поверхности.
Рассмотрим две функции Р (В, р, £.) и Q (J, т), £), непрерывные
вместе с их первыми производными в объеме v и на ограничива-
ющей его поверхности S.
Имея в виду тождество
о 1п ар_\ _ дР_ п д^Р_
01 к4 д$) - pg ' д1 * dtp '
можно написать
V dQ др lt „ дР V V п дгР ,е
J pg ' ag ‘ ag I J aga f='
Bl 51
Распространяя интегрирование на весь объем и, получаем
51 ’ll Ь -п2 Z, 1г
Ь 'Hl Л1 U
£2 Ла
-J j J Q~d$<h]dL. (173)
5i я» 5,
Элемент dr\dt является проекцией на плоскость yOz двух эле-
ментов поверхности S, а именно dSY и dS2, которые из этой поверх-
ности вырезаются бесконечно тонкой призмой с основанием dr)d£
(рис. 1.8). Угол наклона элемента поверхности S к координатной
плоскости yOz равен углу между внешней нормалью к S и положи-
тельным направлением оси х, т. е. для dSt этот угол тупой, для
dS2 острый. Поэтому
drfdfe = —dS^ cos (nlt x) = dS2 cos (n2, x)
г
Рис. 1.8. К преобразованию объемного интеграла в интеграл по
поверхности.
2*
35
7l2 £й wB Ля ^2
Hi tl «! 11! tl
- J J (c -f-) L£,(/i1 -J(Q -S-) U..cos x) ds^+
’ll Cl S
+ f (Q4r)L,cos(,;b x^-
Поскольку интегрирование ведется no i] и g в пределах значе-
ний этих переменных, соответствующих контуру проекции по-
верхности S на плоскость yOz, два последних интеграла можно
объединить в один, который распространяется на всю поверх-
ность S:
J Q cos (га, x) dS.
Введем в формулу (1.73) элемент объема dv = dgdi]dg, тогда
г дР dQ , f OP , v ,с f д^Р 1 Z1 ~л\
| dg * dg J J Q ^v. (1 *^4)
v S v
Аналогичные равенства могут быть написаны для производных
по т] и g. Суммируя все эти равенства и учитывая, что
Q cos (га, х) + cos (га, У) + cos (ге> г)] = <? 4тГ’
получаем
(1-75)
д2Р . д2Р , д2Р \ ,
pga Н 5ll2 । )av-
.40.=
J К dg 5g 1 Si] 5i] 1 5g 5g /
V
S v
Меняя в равенстве (1.75) P и Q местами, находим
Г / дР 5Q , дР dQ , дР 5Q \ ,
J < 5g ’ 5g + 5i] ’ 5r] + 5g ’ 5g )-
д’] <Эт]
d*Q d*Q dsQ \ ,
+ 5т]2 1 /
(1-76)
S v
Приравниваем правые части формул (1.75) и (1.76)
для сокращения записи обозначение
\Р = дЧ>)д1* ф- iPP/drf + д2Р/д^,
ВВОДИМ
и
36
отсюда
[ (Р &.Q — Q АР) dv = [ [P(dQ/dn] — Q (дР/дп)] dS. (1.77)
р s
Уравнение'(1.77) называется формулой Грина. Следует от-
метить, что в этой формуле производная берется по направлению
внешней нормали к поверхности S. Нормаль восстановлена на
элементе dS, и значение производной относится к точке на этом
элементе.
При Q const
| bPdv - [ (dP/dti)dS.
з S
(1-78)
Положим в этой формуле Р = 1/г, где г — расстояние точки А
(с текущими координатами р, ? внутри объема п) от некоторой
постоянной точки В (х, у, z),
ra = (g-x)4 (р-^ + ^-г)2.
Легко убедиться, что сумма производных
/ 1 \ аг / 1 \ -О
\ г / г г / at2 к Г / ~
следовательно, функция 1/г гармоническая во всей области, за
исключением точки В. Если точка В лежит вне объема и, то функ-
ция Р непрерывна во всех точках А внутри объема v и на поверх-
ности S, так как г =/= 0. Применяя формулу (1.78) и учитывая,
что А 4 (1/г) = 0, получаем
ЩФ>='М-1-)*=0- <179>
S о
Если точка В лежит внутри объема V, то применять формулу
(1.78) нельзя, так как функция 1/г терпит разрыв на элементе dv,
где точка А совпадает с В. Для того чтобы вычислить левую часть
выражения (1.79), примем во внимание, что в этом случае
AL(_L)dS = — = — dor, (1.80)
(‘.«к
s s
где <p — угол, составленный направлением г и нормалью к поверх-
ности S; ш — телесный угол, под которым из точки В виден эле-
мент поверхности dS.
37
Рис. 1.9. К определению значения
функции во внутренней точке.
Интеграл (1.81) равен взятой
с обратным знаком сумме углов
видимости замкнутой поверхнос-
ти S из точки В. Независимо
от формы поверхности эта сумма
равна 4л:
1 ж (Г?3 = --•" ILS2>
Пусть точка В лежит на по-
верхности S. В этом случае сумма
углов видимости соответствует по-
верхности полусферы с единич-
ным радиусом, лежащей по одну
сторону от касательной плоскости, проведенной к поверхности S
в точке В:
Ш4)
S
dS = — 2л
(1.83)
Сведя воедино результаты (1.79), (1.82) и (1.83), получим
S
— 4л (точка В внутри поверхности S);
— 2л (точка В на поверхности S); (1.84)
О (точка В вне поверхности S).
Обратимся теперь к формуле Грина (1.77); положим в ней
Q = 1/г, что даст
J(™7—-Г4',)* = ([рЖ-(-г)--7-Ж-]'<3- <185>
V S
Если точка В лежит вне поверхности 5, то во всех внутренних
точках объема у функция 1/г удовлетворяет уравнению Лапласа,
так что
- J ± bpdv + J-L. ljS _ J рф (ф) (IS _ 0. (1.86)
v S S
Если точка В лежит внутри поверхности S (рис. 1.9), формула
Грина может быть применена к той части области v, равной и',
которая получается, если из объема v выделить сферу безопас-
ности S', включающую в себя точку В. Тогда, применяя формулу
Грина (1.77), можно написать
- J ф ЛР* - J Р± (ф) dS - j ф-^-<« +
v' S S
+ <187)
S' S'
38
Пусть поверхность сферы безопасности S', окружающая точку
В, стремится к нулю. Рассматриваемая область v' при этом при-
ближается к объему v и интеграл в левой части выражения (1.87)
стремится к пределу ) (1/г) A Pdv. Интеграл [ Р (dr 1/дп) dS
v S'
имеет предел 4лР (В), поскольку при уменьшении размеров
поверхности S' все значения Р на ней отличаются сколь угодно
мало от значения Р в точке В, т. е. от Р (В), и поэтому
Р £ (4-)- р <й> J £ (-г) "s - ы т. (1.88)
S' S'
Смена знака в выражении (1.88) по сравнению с равенством
(1.82) произошла потому, что нормаль направлена внутрь поверх-
ности S'.
Предел интеграла | (1/г)(дР/дп) dS равен нулю: так как эле-
s'
мент dS поверхности S' пропорционален г2, следовательно, каж-
дый элемент интеграла пропорционален г, и поэтому весь интеграл
равен нулю.
Соединяя все эти результаты, из формулы (1.87) получаем
_ JJ-4P*+J-L (1.89)
V S S
Для случая, когда точка В находится на поверхности S, учи-
тывая выражение (1.84), в правой части формулы (1.89) вместо 4л
следует поставить 2л. Тогда, комбинируя последний результат
с формулами (1.86) и (1.89), имеем
v S S
4лР(В) (точка В внутри поверхности S);
2лР (В) (точка В на поверхности S); (1.90)
О (точка В вне поверхности S).
Полученное выражение называется фундаментальной формулой
Грина. Она позволяет вычислять значение любой функции Р,
непрерывной вместе с ее производными внутри поверхности S
и на ней, если известны сумма вторых производных АР во всех
внутренних точках и значения Р и дР!дп на поверхности S.
Из равенства (1.90) следует, что каждый из входящих в него
интегралов представляет собой потенциал. Действительно,
| r^APdv можно рассматривать как объемный потенциал масс,
V
плотность которых в каждой точке А равна АР. Интеграл
39
| г ' (дР/дп) dS представляет собой потенциал простого слой,
поверхностная плотность которого в каждой точке Л поверх-
ности 3 равна дР/дп. И, наконец, интеграл | Р(дг '/с)п) dS яв-
s
ляется потенциалом двойного слоя с плотностью Р.
Таким образом, всякая пространственная функция Р, удовлет-
воряющая поставленным выше условиям непрерывности, может
быть представлена как сумма потенциалов объемных масс, лежа-
щих внутри поверхности 3, и потенциалов простого и двойного
слоев, расположенных на этой поверхности.
ФОРМУЛЫ ГРИНА
ДЛЯ ГАРМОНИЧЕСКИХ ФУНКЦИЙ
Привлечение формулы Грина к изучению гармонических функ-
ций, к которым относится и потенциал притяжения, позволяет
выявить ряд важных свойств функций этого класса. Положим Р
в формулах (1.77), (1.78), (1.86) гармонической функцией (ДР =
= 0). Тогда непосредственно из условия (1.78) получим важную
формулу:
^(cW«)dS'=0, (1.91)
которая означает, что интеграл по замкнутой поверхности от
нормальной производной гармонической функции равен нулю,
т. е. значения нормальной производной функции Р, гармониче-
ской внутри поверхности 3, не могут быть заданы на ней произ-
вольно, а должны быть подчинены условию (1.91).
Из формулы (1.77) при условии, что обе функции Р и Q гармо-
нические внутри поверхности 3, получим
| [Р (dQ/dii) — Q (dP/dri)] dS = 0. (1-92)
Переходя к фундаментальной формуле Грина (1.90) и полагая
в ней ДР — 0, имеем
[ [pAZ-L^s =
Jr дп J on \ г /
S S’
4лР (В) (точка В внутри поверхности S);
—. 2лР(В) (точка В на поверхности 3); (1.93)
0 (точка В вне поверхности S).
Эта формула устанавливает, что значения функции Р, гармони-
ческой внутри поверхности 3, определяются в любой внутренней
40
точке В заданием значений самой функции и ее нормальной произ-
водной па поверхности 3.
Из формулы (1.93) легко получить известную теорему Гаусса
о среднем значении гармонической функции. Пусть 3 — поверх-
ность сферы радиусом R, тогда г = R и первый интеграл равен
нулю:
[ rl(dP/dn)dS R-1 [ (dP/dn)dS 0.
5 S
Для второго интеграла имеем
дг~1!дп = — cos ф/г = — R~\
так как направление нормали к поверхности сферы совпадает
с направлением R.
В результате из выражения (1.93) получаем
Р(В) ^[1/(4л/?2)] JPdS. (1.94)
s
Формула (1.94) выражает теорему Гаусса, согласно которой
значение гармонической функции во всякой внутренней точке В
равно интегральному среднему ее значений, взятых по поверх-
ности любой сферы, имеющей центр в точке В и лежащей целиком
внутри области и.
Положим в формуле Грина (1.90)
P = U,
где U — потенциал объемных масс, распределенных в объеме и.
Пусть о — объемная плотность; г — расстояние от точки В
до элемента поверхности S, ограничивающей объем и; тогда At/ =
= —4л/гст во всех точках объема и, и поскольку
— J г-1 At/ dv = 4nk j г-1о du — 4nU (В),
v °
то из формулы (1.90) следует
S S
0 (точка В внутри поверхности S);
— . —2лU (В) (точка В на поверхности 3); (1.95)
4nt/ (В) (точка В вне поверхности 3).
Для внешней точки В справедливо равенство
у(в> = -4гПФ-у-Г^(Ф)]‘в- 1'%)
§
4’
Это есть фундаментальная формула для потенциалов, показы-
вающая, что во всем пространстве, внешнем по отношению к по-
верхности' S, потенциал U определяется значениями самого по-
тенциала и его нормальной производной на поверхности S. По
своей структуре формула (1.96) аналогична формуле (1.93) для
гармонических функций во внутренней области. Для потенциаль-
ной функции важен один частный случай, не имеющий места для
гармонической функции, а именно, когда поверхность 5 есть по-
верхность уровня потенциала U. Пусть U — Uo на поверхности S.
В этом случае второй интеграл в формуле (1.96) приводится со-
гласно выражению (1.84) в зависимости от положения точки В
к следующему виду:
—4л(7а (точка В внутри поверхности S);
—2л7/() (точка В па поверхности S);
О (точка В вне поверхности S).
(1-97)
Подставляя этот результат в формулу (1.95), получаем
Uo (точка В внутри поверхности S);
Uu (точка В на поверхности S); .
U(В} (точка В вне поверхности 5).
(1.98)
Левая часть выражения представляет собой не что иное, как
потенциал простого слоя, если принять его поверхностную плот-
ность
р = — [ 1/(4л£)| (dU/dti).
(1-99)
Масса этого слоя равна всей массе М, заключенной внутри
уровенной поверхности 5, поскольку из формулы (1.78) следует:
| и dS = — [ 1/(4л£)| | (dU/дп)dS = j о dv = Л1. (1.100)
S Sv
Таким образом, мы получили следующий важный результат:
если распределить всю массу Л4, заключенную внутри уровенной
поверхности потенциала L/, на этой поверхности в виде простого
слоя так, чтобы плотность простого слоя была равна — [ 1/(4л/е) 1 X
X (dU/дп), то потенциал этого слоя во внешней точке будет иметь
то же значение, что и потенциал первоначального распределения
42
объемных масс внутри поверхности S. Такой слой называется
эквивалентным уровенным. Эквивалентное перераспределение масс
не изменяет внешнего поля. К этому надо добавить, что на внутрен-
ние точки эквивалентный слой не оказывает никакого действия,
поскольку при отсутствии масс внутри поверхности S функция U
будет гармонической внутри этой поверхности и постоянной.
Частный случай эквивалентного распределения мы уже рассма-
тривали: это эквивалентность сферического слоя и шара.
ЗАДАЧИ ДИРИХЛЕ И НЕЙМАНА
Формула (1.93) используется при решении задачи Дирихле:
определении гармонической функции Р вне поверхности 3 по ее
значениям, заданным на этой поверхности. Аналогичная задача
определения функции Р по ее нормальной производной дР/дп,
заданной на поверхности S, называется задачей Неймана.
Для решения задачи Дирихле необходимо в формуле (1.93)
исключить интеграл, содержащий дР!дп. Для этого выражение
(1.92) для двух гармонических функций Р и Q сложим с форму-
лой (1.93):
(1Л01)
S S
Полагая здесь
-г+«-® £(-М-в)-£. <|102>
получаем равенство
Р(В) = -J- (Q^-dS--Д- [P~dS. (1.103)
v ' 4л J дп 4л J дп ' '
S S
Для исключения дР/дп положим, что на поверхности S функ-
ция Q = — 1/г, тогда функция G на этой поверхности обращается
в нуль. Вводимая при этом условии функция G называется функ-
цией Грина. Имея в виду это условие, записываем
Р (В) = — 11 /(4 л) J j Р (dG/dn) dS. (1.104)
Полученное выражение является формальным решением за-
дачи Дирихле. Нахождение же функции Грина для конкретных
поверхностей представляет трудную задачу, которая решена
только для сравнительно небольшого числа случаев. Для поверх-
ности сферы радиусом R с центром О (рис. 1.10, а) функция Грина
имеет вид
G = l/r-(/?/p)(l//'), (1.105)
43
где г = ВА-, г' = В'А, при этом В есть точка, для которой ищем
значение функции Р; В' — сопряженная точка, лежащая на про-
должении прямой ОВ, условие сопряженности определяется ра-
венством 7?2 = рр'; р и р' — расстояния точек В и В' до центра
сферы; точка А — текущая точка внутри сферы.
Чтобы убедиться в правильности формулы (1.105), необходимо
доказать, что ее правая часть на поверхности сферы обращается
в нуль. Обозначив а — расстояние ОА и ср — угол АОВ, напишем
равенства
г3 = а2 ' р8 — 2ар cos ср;
г’2 — а2 р'2 — 2ар' cos ср.
(1.106)
После замены р' па R2/p получим
г'2 = а2 ]- R4/p2 — 2а (R2/p) cos ср. (1.107)
44
(1.108)
Если текущая точка А лежит на поверхности сферы (а = R),
то из равенств (1.106) и (1.107) следует
га =. R2 р2 — 2/?pcos <р;
г'2 = (№/р2) (R2 ф- р2 — 2/?р cos ср).
Подставляя полученный результат в формулу (1.105), находим
G = 1/г — (R/p) (p/R) (1/г) = 0.
Таким образом, убеждаемся, что выбранное для функции
Грина G выражение на поверхности сферы обращается в нуль,
что и необходимо было проверить для решения поставленной
задачи.
Найдем нормальную производную функции Грина на поверх-
ности сферы. Поскольку на сфере направление нормали совпадает
с направлением радиуса, то
дп 0R \ г / ' р dR \ г / ' '
имея в виду уравнения (1.108), получаем
dG д / I \ dr R д / 1 \ дг’
дп дг \ г / dR Г р dr1 \ г' ) dR ~
1 / R — р cos <р \ R 1 R (р — R cos qp) _
— уг ~ -
_ R —р cos <р R2 _ р — Л cos ср I [ j q,
г3 р2 г'3 ‘ \ ‘ /
Поскольку на поверхности сферы G = 0, из выражения (1.105)
находим
1/г = /?/(рг').
Использовав это соотношение, выразим в равенстве (1.110)
расстояние г' через г. Тогда
dG/dn = (₽а - pa)/(Rr8). (1 111)
Подставляя это выражение в формулу (1.104), получаем ра-
венство
Р(Я) = [(/?2-р2)/(4л/?)1 \(P/ra)dS. (1.112)
s
Формула (1.112) называется интегралом Пуассона, она опре-
деляет значение функции, гармонической внутри сферы ради-
усом R в любой внутренней точке В, через ее значение на сфере.
Таким образом, интеграл Пуассона решает внутреннюю задачу
45
Дирихле. Совершенно аналогично решается и внешняя задача
Дирихле — определение функции, гармонической вне сферы. Со-
ответствующая формула для этого случая отличается только зна-
ком, поскольку нормаль, внешняя по отношению к сфере, яв-
ляется внутренней относительно наружного пространства.
При неограниченном увеличении радиуса сферы в пределе
получаем плоскость (рис. 1.10, б), которая разделяет пространство
на две части: сопряженные точки В и В' лежат симметрично отно-
сительно этой плоскости. В этом случае R <х>, а р -> R и со-
гласно равенству (1.105).
G = l/r-I/r'. (1.113)
На плоскости вследствие того, что G = 0, а также из условия
симметрии имеем г — г’.
На основании равенства (1.113) записываем
dG/dn = — (1 /г2) cos (г, п) ф- (1 /г'2) cos (г', «).
Учитывая, что на плоскости г = г' и угол (г, п) — л — (г', п),
получаем
дО/дп = —(2/г2) cos (г, /1). (1-114)
Пусть ось г совпадает с направлением нормали к плоскости.
Тогда
z/r = cos (г, /г);
окончательно
Р(В) = [2/(2л)] J(P/r3)dS. (1.115)
s
Эта формула дает решение задачи Дирихле для плоскости.
Чтобы определить гармоническую функцию Р вне поверх-
ности S по значениям ее нормальной производной на этой поверх-
ности (задача Неймана), необходимо в фундаментальной формуле
Грина (1.93) исключить Р, тогда функция Р (В) будет выражена
только через дР1дп. Для этого применим формулу (1.92) к двум
гармоническим функциям Р и Q и сложим ее почленно с выраже-
нием (1.93), полагая при этом
Q+l/r = /7, (1.Ц6)
тогда
Р(В) =4- [н^-dS--^- \p-^-dS. (1.117)
' ’ 4л J дп 4л J дп ' 7
Остановимся подробнее на втором интеграле. Согласно усло-
вию (1.116)
f dS - f dS + dS,
J дп J дп 1 J дп \ г ) ’
s s s
46
но
[ (dQ/dn) dS — 0,
s
так как Q — гармоническая функция;
| (дг^/дп) dS = — 4л,
s
поскольку г — расстояние внутренней точки, для которой ищем
значение Р (5), от элемента поверхности dS.
Таким образом,
| (дН/дп) dS = — 4л, (1.118)
s
что дает право положить дН!дп = с, подчинив постоянную с усло-
вию
j (дН/дп) dS = с | dS = — 4л.
s s
Но j dS представляет собой площадь поверхности S, так что
s
с -- —4л/В; поэтому имеем
дН/дп = — 4л/5. (1.119)
Функция Н, выводимая под этим условием, называется харак-
теристической функцией Неймана. По форме уравнение (1.116)
напоминает функцию Грина, но отличается от нее тем, что на
поверхности 3 задается не условие 6 = 0, как в функции Грина,
а постоянство нормальной производной: дН/дп = с.
Подставляя значение (1.119) в формулу (1.117), имеем
(1.120)
Это выражение дает формальное решение проблемы Неймана,
так как, каковы бы ни были значения функции Р на поверхности 3,
второй интеграл есть некоторая постоянная, так что можно поло-
жить
Р (В) = [1/(4л)1 [ Н (дР/дп) dS + с.
S
(1-121)
Следует подчеркнуть, что в случае внутренней задачи Ней-
мана значения функции Р (В) определяются по нормальной произ-
водной дР!дп только с точностью до постоянной. Эту постоянную
47
легко найти для сферы. Действительно, для сферы S = 4лД2
и по теореме о среднем (1.94)
[1/(4лД2)] \PdS = P(O),
S
тогда
Д(В) = [1/(4л)1 \ H(dP/dn)dS + P(O). (1.122)
5
Интегрирование выполняется по поверхности сферы, а Р (О)
есть значение функции Р в центре этой сферы.
Для внешней задачи Неймана постоянная определяется из
условия, что на бесконечности Р = 0.
Построение характеристической функции Неймана даже для
сравнительно простых поверхностей довольно затруднительно.
Рассмотрим задачу Неймана применительно к бесконечной пло-
скости. В этом случае надо определить в одном из полупространств
гармоническую функцию Р, регулярную на бесконечности, по ее
нормальной производной, заданной на плоскости. Можно легко
убедиться, что характеристическая функция Неймана имеет вид
//= 1/г-Ь 1/Л (1.123)
где г — расстояние от точки В до текущей точки на плоскости,
принадлежащей тому же полупространству, что и точка В; г' —
расстояние от текущей точки на плоскости до сопряженной точки
В' (см. рис. 1.10, б).
Действительно, 1/г' — функция, гармоническая в полупро-
странстве, не включающем сопряженную точку. Нормальная
производная от Н
дН/дп = — cos (г, n)/r2 — cos (/-', ri)/r'2;
в точках самой плоскости, где г — г' и cos (г, п) = —cos (г', п),
эта производная обращается в нуль; на бесконечности функция
И = 0. Для точек самой плоскости имеем
Н = 2/г
и из формулы (1.122) получаем решение задачи Неймана для бес-
конечной плоскости:
Р(В) = [1/(2л)] \(l/r)(dP/dn)dS. (1.124)
48
Глава 2
ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ
СИЛЛ ТЯЖЕСТИ И ЕЕ ПОТЕНЦИАЛ
Материальная точка, расположенная
в Земле или на ее поверхности, испытывает воздействие силы
притяжения Земли и центробежной силы, вызванной вращением
Земли, а также силы притяжения других небесных тел. Совокуп-
ность этих сил представляет собой гравитационное поле Земли.
Мерой гравитационного поля является его напряженность (сила,
действующая на массу, равную единице), которая в гравиметрии
называется силой тяжести g.
Гравитационное поле Земли обычно рассматривают как поле
воздействия двух сил: силы притяжения и центробежной силы
Земли. Остальные силы (например, притяжение Луны и Солнца)
ввиду их малости не учитывают или изучают отдельно как времен-
ные изменения гравитационного поля Земли.
Общие свойства силы притяжения рассмотрены в главе 1.
Остановимся кратко на характеристике центробежной силы. Эта
сила возникает при вращательном движении массы вокруг не-
которой оси и направлена перпендикулярно к оси вращения.
Центробежная сила, действующая на единичную массу, численно
равна центробежному ускорению:
С — о2/р *= ®ар, (21)
где р — расстояние точки от оси вращения; v и со — линейная
и угловая скорости вращения точки.
Введем прямоугольную систему координат х, у, г с началом
в центре Земли, ось z направлена по оси вращения Земли. Центро-
бежная сила всегда параллельна плоскости хОу. Ее составляющие
по осям
Сх = С cos (р, х) = Л;
C„ = Ccos(p, у) = оА/; (2.2)
С.^0.
Центробежная сила (2.1) и ее составляющие (2.2) могут быть
представлены как частные производные функции
V = (со*/2) р2 = (соа/2) (.V2 Ь у2), (2.3)
которая называется потенциалом центробежной силы.
Продифференцировав дважды выражение (2.3), найдем
... dW . дгУ . д2У о 3 ..
АГ -х-й -1—5~-г 4- =* 2® , (2.4)
1 ')и ' dz* ' '
49
Сумма вторых производных потенциала центробежной силы не
равна нулю, следовательно, этот потенциал не является гармони-
ческой функцией. Потенциал центробежной силы и его производ-
ные непрерывны и конечны на конечном расстоянии от оси враще-
ния Земли.
Поскольку сила тяжести представляет собой геометрическую
сумму силы притяжения и центробежной силы, ее проекции на оси
координат могут быть выражены в виде
Wx = Ux-\-V/, Wy = Uy-\-Vy-, (2.5)
где
№ = £/-|-И (2.6)
— потенциал силы тяжести.
Сила тяжести может быть представлена как производная по
внешней нормали к уровенной поверхности
W = const, (2.7)
взятая с обратным знаком:
g = - dW/dn,
или
g = (2.8)
Меняя в формуле (2.7) значение постоянной, получаем различ-
ные уровенные поверхности. Одна из этих, поверхностей, а именно
та, которая совпадает с невозмущенной поверхностью воды
в океане, называется геоидом и принимается за фигуру Земли.
Понятие геоид (от греч. уц — Земля, 81600 — вид) было введено
в 1873 г. И. Листингом.
Геоид, совпадая на океанах со спокойной поверхностью воды,
продолжается под континентами так, что в любой его точке сила
тяжести направлена по нормали к геоиду. Положение геоида под
континентами можно наглядно представить, если мысленно про-
резать их сетью сообщающихся с океаном каналов, достаточно
узких, но без сил трения и капиллярности. Тогда вода океанов,
заполнив эти каналы, остановится на уровне, который и будет
соответствовать поверхности геоида.
Введение понятия геоид должно давать следующее после зем-
ного эллипсоида приближение к истинной фигуре Земли. Однако,
строго говоря, получается не совсем так. Первым приближением
фигуры Земли является сфера; вторым — эллипсоид вращения.
Переход от сферы к эллипсоиду (разница между полярной и эква-
ториальной полуосями около 20 км) значительно приблизил
аппроксимирующую поверхность к истинной поверхности Земли:
50
наибольшие отклонения в этом случае определяются рельефом
местности, т. е. они составляют обычно сотни метров и реже первые
километры. Поэтому следующее приближение должно было бы
учитывать именно эти отклонения истинной фигуры Земли от
идеальной. По современным данным геоид расходится с эллипсои-
дом на первые десятки метров (во всяком случае, не более чем на
100 м), т. е. уклонения геоида от истинной фигуры Земли являются
величинами того же порядка, что и у эллипсоида.
Таким образом, совпадая на океанах с физической поверхностью
Земли, геоид представляет собой следующее после эллипсоида
приближение к истинной фигуре Земли именно на океанах. Пере-
ход же от эллипсоида к геоиду на континентах не решает задачи
следующего приближения. К этому надо добавить, что геоид явля-
ется фигурой неправильной, т. е. в отличие от эллипсоида он не
может быть выражен аналитически, что исключает возможность
использования геоида при решении различных геодезических
задач. Но несмотря на все это, геоид имеет большое научное и
практическое значение. Относительно геоида определяют высоты
точек физической поверхности Земли. Поскольку геоид совпадает
с поверхностью невозмущенного океана, высоты над геоидом обычно
называют высотами над уровнем моря. Заметим, что измерить
высоты рельефа Земли над эллипсоидом непосредственно невоз-
можно. Можно только раздельно найти высоты геоида над эллип-
соидом и высоты физической поверхности Земли над геоидом.
Поэтому геоид как некоторое промежуточное звено позволяет
решать задачу определения истинной фигуры Земли.
Фигура Земли определяется силой тяжести, основной компонен-
той которой является сила притяжения, так как по сравнению
с ней влияние центробежной силы мало. Максимального значения
на поверхности Земли центробежная сила достигает па экваторе,
где она равна ®2а (а — радиус экватора), отношение этого значения
к силе тяжести gc на экваторе
q = M2a/gs. (2.9)
Подставляя сюда числовые значения ge, а и <о = 2л/86164
(в знаменателе число секунд в звездных сутках), получаем м‘“а =
= 3.4-10-2 м/с2; q = 1/288,4 = 0,00346883, т. е. q < 0,4%.
Центробежная сила, будучи перпендикулярной коси вращения
и направленной от центра Земли, уменьшает значение силы тяже-
сти на ы2а cos2 ср, где ср широта места. При движении от эква-
тора к полюсам центробежная сила уменьшается и на полюсах
становится равной нулю. Следовательно, сила тяжести на полюсе
на 1/288,4 больше силы тяжести на экваторе. Из-за формы Земли
сила тяжести на полюсе увеличивается еще на 1/549 своего значе-
ния (около 1,7-10 2 м/с2). Таким образом, суммарное изменение
силы тяжести на поверхности Земли составляет приблизительно
510’2 м/с2: от ge — 9,78 м/с2 на экваторе до gp = 9,83 м/с2 на
51
полюсе. Отношение разности силы тяжести на полюсе и экваторе
к силе тяжести на экваторе
h=fc-&)/£ = 1/189.
РАЗЛОЖЕНИЕ
ПОТЕНЦИАЛА СИЛЫ ТЯЖЕСТИ В РЯД
Точное значение потенциала силы тяжести
W = k j Г1 dm 4- (<о2/2) (х2 4 у2) (2.10)
определить невозможно, так как неизвестны расположение масс
в Земле и ее точная фигура. Поэтому ограничиваются приближен-
ным вычислением потенциала, которое выполняют при некоторых
допущениях.
Если предположить, что Земля представляет собой невращаю-
щийся шар с массой М и радиусом R, то выражение потенциала W
в точке на поверхности Земли принимает весьма простой вид:
W .. kM/R.
В целом форма Земли незначительно отклоняется от шара, и
поэтому можно для потенциала тяготения получить более конкрет-
ную, чем (2.10), формулу. Для этого подынтегральную функцию
1/г разложим в ряд и проинтегрируем его почленно, ограничивая
число членов сообразно с необходимой точностью. На основании
полученного в виде ряда уравнения для W найдем также в виде
ряда выражение для g. Сравнивая полученные таким образом ана-
литические значения g с наблюденными на земной поверхности,
можно найти коэффициенты этого ряда.
Расположим оси координат (рис. 2.1), как было указано выше
при выводе формулы (2.2). Обозначим расстояния от начала коор-
динат до точки А (£, т], £), где находится элемент массы dm, через
R и до точки В (х, у, г) через р, угол между радиусами-векторами р
и R — через у. Тогда можем написать
52
Разлагая это выражение в ряд по отношениям R/p, получаем
+ fC0SY I-4(7-)2(3cos2y-1) + '”ь(2-13)
Заметим, что коэффициенты при различных степенях R/p
в этом разложении есть так называемые сферические функции,
играющие важную роль во многих разделах математической фи-
зики, и в частности в теории потенциала. С использованием аппа-
рата сферических функций разложение (2.13) может быть записано
в виде
+ + + ••• I =
' Г' I- г Р J
= (2.14)
V Р +
где
Л(т)=1;
Pi (у) = cos у;
P,(y)-(l/2)(3cos2Y 1); (2J5)
Р3(у) = (1/2) (5 cos3 у — 3cosy)
— сферические функции первого рода с. одним аргументом у.
Все последующие члены разложения (2.14) могут быть найдены
по формуле
P«+i(Y) = ;7^^cosy/\(y)-^TP«-i(v). (2.16)
Теперь для потенциала силы тяжести W имеем следующее
выражение:
+-^c°sY + 4-(Ay‘!(3coS2v_i) + ...]f/m +
V
+ 4-“2(^ + '/‘л)- (2.17)
Можно показать, что полученный ряд абсолютно сходится, если
М/р < 1; при R/p > 1 ряд расходится. В случае R/p = 1 ряд
(2.17) сходится, за исключением точки, где cos у = 1 (если
cos2 у <7 1, ряд сходится везде!).
Интегрируем ряд (2.17) почленно:
= -у | dm + J R cos у dm +
~ | /?2 (3 cos2 у - 1) dm 4-----------Ь 4“ “2 ^2-18)
V
53
Интегрирование распространяется на весь объем Земли. Если
массу Земли обозначить /И, то первый член
(/л'р) | dm kM j>.
(219)
Для второго члена, имея в виду, что
cosy = (£х 4- Ez) (oR),
получаем
-4- f R cos у dm = -4- I '' dm
р2 J ' р“ J р
=р’ (х I =drn+у I iidm+2 Вdni)
k
р3
Интегралами типа Ed/гг определяются координаты центра
тяжести тела:
In — j Idm j | dm.
В нашем случае начало координат помещено в центре Земли,
следовательно, все три координаты центра тяжести должны быть
равны нулю, т. е. все три интеграла должны обращаться в нуль.
Поэтому
(/г/р2) | R cos у dm =0.
При интегрировании третьего члена уравнения (2.18) получим
J R'(3eos’v- l),to J [ +
При раскрытии скобки (£х (- г)у 4- |z) появятся интегралы
вида 2 | ±xv\y dm, 2 j Ex&dm, 2 | \\ijCzdm. Эти интегралы назы-
ваются в механике произведениями инерции. Они могут быть
превращены в нуль соответствующим выбором координатных
осей, которые должны совпадать с главными осями инерции.
В нашем случае ось z является одной из осей инерции, и поэтому
интегралы | ££dm и | rfcdm равны нулю. Чтобы выполнялось
условие | |i] dm = 0, надо оси х и у тоже совместить с главными
осями инерции. Так как при выборе системы координат направле-
ния осей Л' и у не были заданы, разместим их так, чтобы они совиа-
54
дали с главными осями инерции. В этом случае можно положить
| Ь] dm — 0. Теперь имеем
f г.2/о •’ / * f/о е2ха 4-T|V + t;2z3 02 \ j
2~г j R* (3 cos- v - 1) dm = — J (3-------p-----------R-) dm =
= ж [x21(3'2 ~ R1} dm+(3r|2 - R2) dm+z2f(,3?2 “ Ri} dm^ ’
(2.20)
Введем моменты инерции А, В и С относительно осей х, у, г.
Согласно изложенному выше это будут главные моменты инерции:
А = Jof-R2)^; B = J(|2 + ^)d/n; С = J (г + if)dm.
Подставляя эти обозначения в формулу (2.20), находим
(А/(2р3)] [ R2 (3 cos2 у - I) dm = [fe/(2p6) | |л-2 (С -ф В - 2Л) +
-Н/2(Л4 С-25) | г2(В + Л--2С)| =
— |&/(2р5)| |(3/2)(л2 —//2)(В — Л) (-
[(л-34 /г)/2 — z2] (2С — Л — В)}. (2.21)
Введем сферические координаты: геоцентрическую шпроту <р'
и долготу X, отсчитываемую от плоскости xOz, тогда
Л' = р cos <р' cos X; у = р cos q/ sin X; z = psintp'. (2.22)
Из равенства (2.21) имеем
[/г/(2р3)] | R3 (3 cos2 у — I) dm =
= [£/(2р8)| ((3/2) cos2 гр' cos 2Х (В - Л) +
+ (1-3sin2<p')[C-(Л-|-В)/21(. (2.23)
Теперь на основании формул (2.18), (2.19) и (2.23) можем напи-
сать выражение для потенциала силы тяжести
W = feM/p + [й/(2р3)| (1-3 sin2 ф') [С — (Л 4- В)/2] +
4 (3/4) (#/р3)(В — Л) cos2q/ cos 2X4- (1/2) cosp2cos2 q/. (2.24)
Эта формула является точной до малых второго порядка, если
за малую первого порядка считать сжатие Земли (~ 1/300). Ее
первый член представляет собой потенциал шара с массой, равной
массе Земли; второй, поскольку он зависит от широты, дает доба-
вочное действие экваториального вздутия Земли; третий, содержа-
щий долготу, учитывает неравномерное распределение масс по
долготе.
>D
Предположим, что Земля но внешней форме есть тело вращения,
близкое к шару. В этом случае оси х, у являются равноправными
и моменты инерции А и В равны между собой. Для сжатой у полю-
сов Земли С А и величина (С — А)/А мала (порядка сжатия
Земли). С учетом этого выражение потенциала W может быть
записано в более простом виде:
Г = kМ/р + (И2р3)] (С — Л) (1 — 3 sin3 Ф') ф-
-ф (1/2) со2р2 cos2 <р' (2.25)
или
(С —А) (I —3 sin2ср')
2р2тИ
। °>2P:1 1 .
+ >WC0S 'Р
(2.26)
ГЕОИД
Приравняв выражение (2.26) постоянной, получим уравнение
уровенных поверхностей, в число которых входит и геоид. Чтобы
получить уравнение геоида, необходимо соответствующим образом
выбрать постоянную. Для нахождения этой постоянной возьмем
какую-нибудь точку на геоиде и подставим координаты этой точки
в правую часть равенства (2.26). Пусть это будет точка пересечения
оси х с поверхностью геоида. Координаты этой точки ф' = О,
X = 0, р = а.
Подстановка всех величин в равенство (2.26) дает
const = (kM/a) 11 + (С - А)/(2а2М) + ю2а3/(2йЛ4)|. (2.27)
Таким образом, уравнение геоида имеет вид
kM_ Г, . (С —A) (1-3 sin2 ср') , coy 2 1 _
р [1 г 2р2Л1 2kM C0S J —
kM /. , С — А . ш2а2 \
— ~ V 1 + 2<AW + 2Ш /
или
с - — (1
2р2Л-1 И
3 sin2 ср')
। ь>У о ,1 /, С — А , со2а2 \ —1 ооч
+ 2Ш cos <₽ J (1 Ч- 2а*М + WW ) ‘ (2.28)
Введем для краткости следующие обозначения:
(С - Л)/(2п2Л4) = п; (o№/(kM) = q.
Равенство (2.28) представим в виде
1 I «(1- 3sinV) I -2y‘(/cos“'t'] х
X + « + (2.29)
56
Принимая во внимание, что все выводы мы делаем, сохраняя
лишь малые первого порядка, какими являются п и q, упростим
полученное выражение. В первом приближении р = а и вся правая
часть уравнения близка к единице. Так как отношения д2/ра и
р3/а8 умножаются на малые величины, то, заменяя эти отношения
единицей, делаем ошибку второго порядка. На этом же основании
во втором сомножителе сохраняем только главный член, перенося
остальные малые величины с обратным знаком в первый сомно-
житель. Тогда
р/а = 1 + п (1 — 3 sin2 ср') 4- (<//2) cos2 ср' — п — q/2.
Меняя cos3 q>' на 1 — sin2 ср', получаем уравнение геоида
р/д = 1 — (Зп + 9/2) sin2 ср'. (2.30)
Покажем теперь, что это есть выражение сфероида со сжатием
а = 3п+ q/2. (2.31)
Для этого напишем уравнение сфероида с полуосями а, а и Ь:
х2/аг -|- Уг/иг ф- z-/b2 ~= 1.
Сжатие этого сфероида а. — (а — Ь)/а. После замены координат
х, у, z координатами р, ср', К в соответствии с формулой (2.22)
уравнение сфероида примет вид
(р2 cos2 <р')/а2 4- (р2 sin2 <р')/й2 — 1. (2.32)
Подставив а (1 —а) вместо b в это уравнение, запишем отно-
шение
= (1 — а) (1 — 2а cos2 ср' 4~ cos2 ср') 1/2,
Разложив выражение во второй скобке в ряд и ограничившись
первой степенью а, вычислим
р/д = (1 — а) (1 ф- a cos2 ср') = 1 — а sin2 ср'. (2.33)
Сравнивая это равенство с уравнением (2.30), убеждаемся
в справедливости утверждения, что геоид очень близок (до малых
второго порядка) к сфероиду, сжатие которого определяется равен-
ством а — Зп 4- q!2. Этот вывод получен без каких-либо допуще-
ний относительно распределения плотности внутри Земли; пред-
полагается только, что Земля есть тело вращения, мало отличаю-
щееся от шара. Естественно, что вывод верен, если все массы
Земли находятся внутри геоида, так как только в этом случае
возможно разложение потенциала силы тяжести в ряд.
Более точное определение геоида представляет сложную проб-
лему, которая решается на основе геодезических и гравиметри-
ческих данных и по измерениям траекторий искусственных спут-
ников Земли.
57
СИЛА ТЯЖЕСТИ НА ПОВЕРХНОСТИ
УРОВЕННОГО СФЕРОИДА (ГЕОИДА)
Из определения силы тяжести следует, что на уровенной
поверхности она направлена по нормали к этой поверхности.
Поэтому чтобы получить силу тяжести g, необходимо найти произ-
водную потенциала W по направлению внешней нормали п, т. е.
g = —dW/dn. Однако направление нормали в уравнение (2.26)
явно не входит, но в нем есть направление радиуса р к центру
Земли. Для геоида направления п и р близки. Угол между нор-
малью п и плоскостью экватора равен географической широте ср,
а угол между направлением радиуса р и плоскостью экватора равен
геоцентрической широте ср'. Поэтому угол между нормалью п и
радиусом р равен ср ср'. Таким образом, дифференцирование
по р дает не полное значение силы тяжести g, а его проекцию на
направление р, равную g cos (ср — ср'). Так как угол ср — ср'
меняется от нуля на экваторе и полюсах до 11,6' на широте 45°,
то cos (ср — ср') принимает соответственно значения 1 и 0,999995.
Следовательно, величина g cos (ср — ср') может отличаться от g
максимально на 0,000005 своего значения. Можно пренебречь такой
малой величиной, если учесть, что и выражение (2.26) является
приближенным. Учитывая, что р и g противоположны по направ-
лению, можем написать
g ш - - dW'/dp.
Дифференцируя по р выражение (2.26) и заменяя ср' на ср
ввиду их близости, имеем
S - р2 [1 4“ 2рШ ( 3sin Ф) /гМ СОа Фj • (2 34)
Чтобы получить формулу для g на поверхности геоида, надо
в это выражение поставить вместо р его значение из уравнения
(2.30). Тогда
g = (kM/a2) [1 + (3cz2/p2) n (1 - 3 sin2 ср) -
— (p3/o3) q cos2 cp| [ 1 — (3n -f- <//2) sin2 cp]~2. (2.35)
Заменяя в первой квадратной скобке отношение а/p единицей,
разлагая выражение во второй квадратной скобке в ряд и ограни-
чиваясь только членами первого порядка малости, получаем
g = (kM/a1) [1 Зп (1 — 3 sin2 ср) —
— q cos2 ср] [ 1 + 2 (Зп + 7/2) sin2 ср] =
= (kM/a2) [ 1 -}- Зп -- q + (2<? — Зп) sin2 ср]. (2.36)
Подставляя в это выражение согласно формуле (2.31)
Зп = а — <?/2,
58
находим
g >== (kM/a2) {1 + « — (3/2) q ф- [(5/2) q — a] sin2 ф}. (2.37)
Выражение
(fe/W/a2)[l+«-(3/2)^]-^ (2.38)
представляет силу тяжести при ср — 0, т. е. на экваторе; отсюда
g = ge 1(5/2) q - a] [ 1 (3/2) q | apsirPrp}.
Введем еще обозначение
P == (5/2) q - a. (2.39)
Тогда, поскольку p малая первого порядка, во второй квад-
ратной скобке предыдущего выражения можно оставить только
первый член — единицу,
Таким образом, окончательно получим
g = £<(! — Р sin2 ср). (2.40)
Формулы (2.39) и (2.40) составляют так называемую теорему
Клеро. Первая из них, формула (2.39), определяет сжатие уровен-
ного земного сфероида через q и р. Вторая, формула (2.40), дает
закон нормального распределения силы тяжести на поверхности
уровенного сфероида (геоида).
Полагая в формуле (2.40) широту ср — ±90°, получаем силу
тяжести на полюсе
откуда следует
Р = (gp - geVge-
Таким образом, Р есть относительный избыток силы тяжести
на полюсе по сравнению с силой тяжести на экваторе.
Определив силу тяжести в двух точках на земной поверхности
с широтами и ф2, можно составить два уравнения с двумя
неизвестными ge и Р:
gi = &(l + Psin2Ti);
^2 = ^(1 +р£1П2фа).
Решив эти уравнения, можно найти ge и р. Для более уверен-
ного определения этих величин решают систему не для двух, а для
многих пунктов (методом наименьших квадратов).
НОРМАЛЬНОЕ
РАСПРЕДЕЛЕНИЕ СИЛЫ ТЯЖЕСТИ
Уравнение (2.40) справедливо только до малых второго порядка.
Если продолжить разложение ряда, то можно составить более
полную формулу — до малых третьего и более высоких порядков.
59
Уравнения (2.39) и (2.40) получены при допущениях, что форма
Земли есть эллипсоид вращения с малым сжатием и что вне этого
эллипсоида нет никаких масс. Возможно также найти уравнения,
подобные (2.40), в предположении, что Земля есть трехосный
эллипсоид с малым экваториальным сжатием. В этом случае общую
формулу можно представить в виде
£ = &[1 +₽sin2(p-p1sin22<p4-
+ cos2 q> cos 2 (X — %0) — • • •], (2.41)
т. е. в уравнении появляются члены, зависящие от долготы.
Если принять фигуру Земли за сфероид, то можно вывести
точную формулу распределения силы тяжести на нем. Этот вывод
сделан итальянским геодезистом К- Сомильяна, его формула
имеет вид
g = (age cos2 ср 4- bgpsin2 tp) (a2 cos2 <p -|- b~ sin2 <p)-1/2. (2.42)
Если в правой части этого равенства сделать подстановку
— ё^ёс = Р; (fl — b)la = а и разложить эту часть в ряд до
малых третьего порядка, то получим
£ = &(1 +Рз1п2ф — рхз1п22ф), (2.43)
где
Р = (5/2) 7 — а — (17/14)7»; (Зг = (5/8) aq — (1/8) a2, (2.44)
т. е. пришли к формуле Клеро с членами второго порядка.
Численные значения коэффициентов, входящих в правую часть
уравнений (2.41) или (2.43), т. е. значения ge, р, Pj (и т. д.), находят
сравнением формулы (2.43) с результатами гравиметрических
измерений. При этом каждое наблюдение силы тяжести дает одно
приближенное уравнение для определения этих коэффициентов.
Чтобы найти достаточно точные значения коэффициентов, необ-
ходимо иметь большое число наблюдений силы тяжести, равно-
мерно распределенных по поверхности Земли. В этом случае будем
иметь столько уравнений, сколько было наблюдений. Систему
этих уравнений решают способом наименьших квадратов. В на-
стоящее время пункты измерения силы тяжести на поверхности
Земли распределены очень неравномерно. По этой причине, а также
для сокращения вычислительной работы берут сравнительно не-
большое число уравнений. Поверхность Земли делят на площадки
со стороной в несколько градусов и все наблюдения на одной пло-
щадке осредняют для одного уравнения.
Коэффициенты р и рх связаны со сжатием Земли, и поэтому
их можно найти другим путем. Например, принять за уровенную
поверхность сфероид с определенным сжатием, по которому и
вычислить коэффициенты р и р:; наблюденные же значения силы
60
тяжести используются для нахождения ge. Решая систему уравне-
ний, получают числовые значения коэффициентов ge, 0, 0j и т. д.
Подставляя эти значения в формулу (2.41) или (2.43), находят
закон распределения силы тяжести на уровенной поверхности —
сфероиде, причем каждому уравнению соответствует вполне опре-
деленный сфероид со своим сжатием. Теоретическое значение силы
тяжести, вычисленное по уравнениям с числовыми коэффициен-
тами, называется нормальной силой тяжести и обозначается у;
само уравнение называется формулой нормального распределения
силы тяжести. Значение силы тяжести, вычисленное для принятого
сфероида, обозначается у0.
Формулы нормального распределения силы тяжести выводи-
лись многими авторами (И. Д. Жонголович, Н. П. Грушинский,
У. Хейсканен, У. Уотила), но в настоящее время только две из
них применяются па практике при обработке гравиметрических
измерений. Это формула Гельмерта 1901—1909 гг. и формула
Кассиниса 1930 г., принятая как международная. Приведем
некоторые из формул.
Формула Гельмерта выведена на основе около 1600 относитель-
ных измерений силы тяжести, распределенных по 9 широтным
зонам, каждая из которых была разделена на 10-градусные трапе-
ции. Формула имеет вид
= 978,030 (1 + 0,005302 sin2 ср - 0,000007 sin2 2<р). (2.45)
Этому уравнению соответствует эллипсоид со сжатием а =
= 1/298,2. Формула Гельмерта получила широкое распростране-
ние. В частности, до настоящего времени она применяется в СССР,
хотя при современной гравиметрической изученности Земли эту
формулу надо считать устаревшей. Использование именно этой
формулы связано с тем, что соответствующий ей эллипсоид имеет
сжатие, близкое к сжатию эллипсоида Красовского (а = 1/298,3),
который принят в качестве поверхности относимости при геодези-
ческих работах и, по-видимому, хорошо представляет всю Землю
(по современным данным ее сжатие 1/298,26). Переход на новую
формулу потребует большой вычислительной работы. В настоящее
время в формулу Гельмерта вносят поправку (—14-Ю'5 м/с2) для
привязки к новой потсдамской системе.
В 1930 г. на Международном геодезическом конгрессе в Сток-
гольме была принята в качестве международной формула Кас-
синиса
То = 978,049 (1 4- 0,0052884 sin2 ср - 0,0000059 sin2 2<р). (2.46)
Она получена на основе формулы Сомильяна по размерам между-
народного эллипсоида, т. е. коэффициенты 0 и 0Х вычислены по
формуле (2.43) для сфероида со сжатием а = 1/297, а из гравимет-
рических данных найдено только значение ge.
В 1971 г. на XV ассамблее Международного союза геофизики и
геодезии в Москве была рекомендована новая формула нормального
61
распределения силы тяжести, соответствующая так называемой
референц-систсмс 1967 г.:
уц = 978,0318 (1 |- 0,0053024 sin2 ф - 0,0000059 sin2 2ф). (2.47)
Для перехода от формулы Кассиниса к системе 1967 г. следует
вносить поправку, равную (—17,2 Д- 13,6 sin2 ср) 10"6 м/с2.
Формула Жонголовича 1952 г. выведена на основе 26 000 опре-
делений силы тяжести, из которых около двух третей приходится
на территорию СССР. Вся поверхность Земли была разделена на
площадки, равные по площади трапеции у экватора 10X10°.
Таких площадок получилось 410, в 229 из них имелись гравиметри-
ческие наблюдения. Для каждой из площадок было определено
среднее значение силы тяжести. Гравитационное поле, представлен-
ное таким образом, разлагалось в ряд по сферическим функциям.
Этим путем были получены следующие формулы нормального зна-
чения силы тяжести:
для сфероида
То = 978,0573 (1 + 0,0052837sin2ср -0,0000059sin22ср); (2.48)
а = 1/296,6;
для трехосного эллипсоида
Т„ - 978,0573 [ 1 | 0,005268 sin2 ф -
— 0,0000059 sin2 2ф Д- 0,0000155 cos2 ф cos 2 (X Д- 6°)]; (2.49)
«пип = 1/298,0.
У. Хейсканеном было предложено несколько формул: в 1924,
1928, 1938 и 1957 г. При выводе последней формулы поверхность
Земли была разбита на площадки 5x5°, для каждой из которых
определялось среднее значение силы тяжести. Эта формула имеет
вид:
для эллипсоида вращения (а — 1/297,2)
То = 978,0497 (1 Д- 0,0052902 sin2 ф - 0,0000059 sin3 2ф); (2.50)
для трехосного эллипсоида
То = 978,0516 [ 1 Д- 0,0052910 sin2 ф - 0,0000059 sin2 2ф Д-
+ 0,0000106 cos2 ф cos 2 (ХД-6°)].
Приведем уравнения нормального распределения силы тяжести,
полученные в последнее время.
Формулы Уотилы 1959 г.:
для двухосной Земли
То = 978,0496 (1 Д- 0,0052934 sin2 ф - 0,0000059 sin2 2ф); (2.51)
а= 1/297,4;
62
для трехосной Земли
Vo = 978,0516 [ 1 + 0,00529097 sin2 <р - 0,0000059 sin2 2<₽ +
+ 0,0000106 cos2 ф cos 2 (X + 6,5°)]; (2.52)
формула Грушинского
% = 978,0531(1 4- 0,0052883 sin2 <р - 0,0000059 sin2 2<р); (2.53)
а = 1/297,0.
У. Уотилой и Н. П. Грушинским выведены формулы нормаль-
ного распределения силы тяжести раздельно для Северного и
Южного полушарий. При этом получено значительное расхождение
между направлением большой экваториальной оси: по данным
У. Уотилы в Северном полушарии Хо == 3,5° 3, в южном 79,0° В;
по данным Н. П. Грушинского соответственно 15° 3 и 25° В.
Наличие асимметрии Северного и Южного полушарий Земли ставит
под сомнение возможность трактовать ее фигуру как трехосный
эллипсоид. К этому еще следует добавить, что направление боль-
шой экваториальной оси определяется с большим разбросом
(±30° в зависимости от используемых данных). Вероятно, измене-
ние экваториального радиуса Земли следует рассматривать как
крупную волну геоида, имеющую разный ход в Северном и Южном
полушариях.
При выводе формул нормального распределения силы тяжести
некоторые авторы (У. Хейсканен, И. Д. Жонголович, В. Каула)
одновременно вычислили и построили карты отклонений геоида
от сфероида (рис. 2.2).
Как уже отмечалось, из многочисленных нормальных формул
в настоящее время широко используются только две: формула
Гельмерта 1901 —1909 гг. и международная формула Кассиниса
1930 г. Причем гравиметрические наблюдения в СССР и странах
СЭВ обрабатываются по формуле Гельмерта, а в большинстве
стран Европы и Америки — по формуле Кассиниса.
В табл. 2.1 приведены нормальные значения силы тяжести,
вычисленные по формуле Гельмерта па каждый градус широты.
Переход от одной нормальной формулы к другой выполняется
очень просто — внесением небольших поправок. В табл. 2.2 даны
поправки уОм — уог, которые надо прибавить к нормальным
значениям силы тяжести, определенным по формуле Гельмерта,
чтобы перейти к международной формуле.
С запуском искусственных спутников открылась возможность
изучения гравитационного поля Земли по наблюдениям за их
орбитами. Движение спутника в поле силы тяжести Земли зависит
от этого поля. Если бы гравитационное поле соответствовало полю
сферы, то движение спутников происходило бы по эллиптическим
траекториям в соответствии с законами Кеплера. Но поскольку
внешнее гравитационное поле Земли отличается от поля сферы,
63
Таблица 2.1
Значения нормальной силы тяжести по формуле
Гельмерта 1901—1909 гг.
ф. гра- дус у0, 10"2 м/с2 Ф, гра- дус То, Ю'2 м/с2 ф. гра- дус То, 10~2 м/с2 ф. гра- дус То, 10'2 м/с2
0 978,0300 23 978,8182 46 980,7064 69 982,5464
1 ,0315 24 ,8841 47 ,7968 70 ,6061
2 ,0362 25 ,9521 48 ,8870 71 ,6633
3 ,0441 26 979,0222 49 ,9768 72 ,7180
4 ,0551 27 ,0942 50 981,0663 73 ,7701
5 ,0692 28 ,1682 51 ,1552 74 ,8196
6 ,0864 29 ,2439 52 ,2435 75 ,8665
7 ,1066 30 ,3213 53 ,3310 76 9105
8 ,1299 31 ,4002 54 ,4178 77 9518
9 ,1563 32 ,4806 55 ,5034 78 ,9902
10 ,1855 33 ,5625 56 ,5882 79 983,0257
11 ,2178 34 ,6456 57 ,6716 80 ,0583
12 ,2530 35 ,7299 58 ,7538 81 ,0880
13 ,2910 36 ,8154 59 ,8346 82 .1146
14 ,3319 37 ,9018 60 ,9141 83 ,1381
15 ,3756 38 9891 61 ,9918 84 ,1585
16 ,4221 39 980,0772 62 982,0679 85 ,1759
17 ,4711 40 ,1659 63 ,1423 86 ,1901
18 ,5226 41 ,2552 64 ,2148 87 ,2013
19 ,5771 42 ,3450 65 ,2853 88 ,2092
20 ,6337 43 ,4351 66 ,3539 89 ,2139
21 ,6929 44 ,5254 67 ,4203 90 983,2155
22 978,7543 45 980,6159 68 982,4842
то эти отклонения вносят возмущения в орбиты спутников, вызы-
вая их периодические изменения. Изучение вариаций элементов
орбит позволяет решить обратную задачу — найти параметры
гравитационного поля Земли. Особенно надежно определяется
Таблица 2.2
Поправки для перехода от формулы Гельмерта
к международной формуле
Ф> гра- дус Том — Тог* 10’2 м/с3 (р, градус Той— То г, 10'2 м/с2 Ф, градус Том Тог> 10“3 м/с3
0 4-0,0190t 30 Н-0,01658 65 -}-О,О0881о
5 ,018% 35 ,0157п 70 ,0078й
10 ,01873 40 ,0146и 75 ,0070(|
15 ,01844 45 ,0135ц 80 ,00644
20 ,0180, 50 ,012412 85 ,0060,
25 4-0,01738 55 60 ,011212 -1-0,0100ц 90 -1-0,0058“
3 В. С. Миронов
65
Рис. 2.2. Карта превышений геоида Кау.ча над сфероидом (а = 1/298,24).
Изолинии даны в метрах.
сжатие Земли, которое составляет по этим данным 1/(298,25±0,01).
Можно вычислить и коэффициенты разложения силы тяжести
в ряд, т. е. в конечном счете получить представление о распре-
делении силы тяжести на земной поверхности.
Расхождение значений g,. и р по различным формулам объясня-
ется недостаточной гравиметрической изученностью Земли. На-
копление данных позволит вывести новую, более точную, нормаль-
ную формулу, которая будет принята в качестве международной.
НОРМАЛЬНЫЕ ЗНАЧЕНИЯ
ВТОРЫХ ПРОИЗВОДНЫХ
ПОТЕНЦИАЛА СИЛЫ ТЯЖЕСТИ
Чтобы получить нормальные значения вторых производных
потенциала силы тяжести, достаточно принять за форму Земли
сфероид. Расположим начало координат на поверхности сфероида,
ось г — по нормали вниз, ось х —-по меридиану на север, ось у —
на восток в плоскости первого вертикала. Поскольку главные
сечения земного сфероида совпадают с меридианом и первым верти-
калом, то <р0 = 0; при этом из формулы (1.26) следует, что (U7(„)0 =
= 0. Примем RM — радиус кривизны меридиана, RN — радиус
кривизны первого вертикала. Известно, что
RM •= д(1 - е2) (1 - e2sin«<p)“3/2;
Rn = а(1 — e2sin2<p)~1/2;
е'1 = (а2 — Ь2)/а2,
(2.54)
где а и b — экваториальная и полярная полуоси земного сфероида;
е — его эксцентриситет.
Нормальное значение силы тяжести на сфероиде обозначим у0.
Тогда
(^хл)и = — У»/^м>
(rA)o = T„(l/Z?M- \/Rn).
Поскольку AIV' = 2(оа, нормальное значение
(11ZJ,, 2о? + То(1^м+ 1<0-
Найдем нормальные значения для Wxz и WK. Имеем
dx — Rm dy — Rn cos q> dX,
где фиХ — широта и долгота рассматриваемой точки.
Тогда
.IVZ ’I _ dg _ 1 , dg . , __ dg __ ___1____ ^g
' X2i> дх RM <?<р ’ ' г'г'° ду ~ cos ф дх
(16
(2.55)
(2.56)
. (2.57)
Пусть для силы тяжести g ее нор-
мальное значение у0 определяется одной
из нормальных формул, при этом огра-
ничимся только двумя членами:
Yo-=£e(i +₽sin2q?).
Тогда
dgldq = дуо/дф = sin 2<р;
dgidl. == ду0/дк = 0.
Подставляя эти значения в равенст-
ва (2.57), имеем
(^)0=(^M)sin2cp; (Гуг)о = 0. (2.58)
Рис. 2.3. Нормальные зна-
чения вторых производных
потенциала силы тяжести.
Формулы (2.55), (2.56), (2.58) позволяют найти нормальные
значения вторых производных потенциала силы тяжести (10““ 1/с2)
на поверхности земного сфероида (рис. 2.3), если известны м2,
0, а и е:
(1Г,г)0 = 8,11 sin 2<р;
= 0;
(№д)о = 5,12 (1 cos 2ф) = 10,25 cos2<p;
(^Л = °;
(№„)u = 3085,5 (1 -|- 0,000711 cos 2q).
(2.59)
ИЗМЕНЕНИЯ СИЛЫ ТЯЖЕСТИ ВО ВРЕМЕНИ
Гравитационное поле Земли рассматривалось в предположении,
что сила тяжести постоянна во времени. Однако вполне очевидно,
что сила тяжести не может оставаться всегда постоянной как
вследствие геологических и геофизических процессов, протекаю-
щих в Земле и приводящих к перераспределению масс внутри нее,
так и по причине разного положения Земли относительно Луны и
Солнца, а также других небесных тел. Поэтому необходимо оценить
порядок изменения силы тяжести.
Колебания силы тяжести можно подразделить на периодиче-
ские, связанные с вращением Земли вокруг своей оси, вследствие
чего меняется положение точки наблюдения на Земле относительно
Луны, Солнца и других небесных тел, и непериодические (вековые),
обусловленные внутриземными геологическими и геофизическими
процессами.
Проблема медленных (вековых) вариаций силы тяжести явля-
ется одной из важнейших в современной гравиметрии, поскольку
она затрагивает интересы физики, метрологии, геодезии, геофизики
и геологии. В частности, без точного знания силы тяжести в точке
3* 67
измерения невозможно установить эталонные значения силы тока
и давления; региональные и локальные изменения силы тяжести
могут приводить к уклонению отвеса, а следовательно, вносить
искажения в координаты пунктов, определяемые астрономическим
путем, и в высоты точек при нивелировании.
На протяжении последних 15—20 лет было сделано немало
попыток экспериментально обнаружить вековые вариации силы
тяжести как регионального, так и локального характера. В боль-
шинстве случаев выявленные изменения силы тяжести (порядка
0,001 -10~5 м/с2 в год) лежат в пределах погрешностей измерений.
При сравнении гравиметрических карт, составленных в разные
годы, были обнаружены изменения силы тяжести до 0,1 10~5 м/с2
в год. Однако эти результаты, вероятно, нельзя однозначно связы-
вать только с вариациями силы тяжести. Даже сопоставление
повторных наблюдений на специально оборудованных полигонах
в жестко закрепленных точках через длительные интервалы вре-
мени представляет большие трудности. Повторные же гравиметри-
ческие съемки проводились, как правило, по разной сети.
В самое последнее время появились некоторые фактические
данные, как будто бы подтверждающие существование вековых
вариаций силы тяжести. При повторных наблюдениях на специаль-
ных полигонах выявлены изменения силы тяжести, которые не
могут быть целиком объяснены погрешностью измерений. Инте-
ресно отметить, что существует корреляция изменений силы тяже-
сти с тектоническими особенностями региона, хотя и весьма слабая.
А. Сакума в Севре (Франция), проводя высокоточные абсолют-
ные определения силы тяжести, установил ее увеличение со ско-
ростью до 0,015 10'5 м/с2 в год. Вероятно, изменения силы тяжести
могут иметь периодический характер с амплитудой 0,06-1 (Г м/с3
и полупериодом 3 года. Пока же бесспорен факт повышения силы
тяжести в этом пункте за 4 года на 0,06 -10-5 м/с2.
О существовании вековых вариаций силы тяжести можно гово-
рить на основе теоретических предположений и некоторых косвен-
ных наблюдений. Прежде всего следует отметить, что неотектони-
ческие движения вызывают значительные изменения высоты от-
дельных точек земной поверхности. Материалы повторных нивели-
ровок убедительно показывают, что в некоторых районах верти-
кальные перемещения земной поверхности могут достигать не-
скольких сантиметров в год. Изменение высоты точки наблюдения
на 1 м приводит к изменению силы тяжести на 0,2-1Сй5 м/с2, что
вполне достаточно для измерения современными гравиметриче-
скими приборами. Внутри Земли могут происходить медленные
перемещения масс и колебания их плотности, что должно созда-
вать заметные вариации силы тяжести. Действительно, если
в слое мощностью 100 км плотность изменится на 0,001 г/см3, то это
приведет к изменению силы тяжести на 4- Ю-5 м/с2. В настоящее
время проводятся экспериментальные наблюдения по выявлению
вековых вариаций силы тяжести.
68
Периодические колебания
силы тяжести в основном вы-
зываются изменением поло-
жения Земли относительно
Луны и в меньшей степени
Солнца. Эти колебания силы
тяжести называются лунно-
солнечными вариациями или
возмущениями силы тяжести.
Возникают вариации следую-
щим образом (будем считать,
что Земля является абсолют-
но твердым телом). Сила
притяжения небесного све-
тила действует на каждый
Рис. 2.4. К изменению периодических
вариаций силы тяжести во времени.
элемент массы Земли. Для точек,
обращенных к светилу, притяжение больше, чем на противополож-
ной стороне Земли. Результирующая сила притяжения приложена
к центру тяжести Земли и направлена к светилу. Считая, что
центр тяжести испытывает все время одинаковое притяжение,
в двух точках земной поверхности, для которых светило нахо-
дится в зените и надире, будем иметь максимальное уменьшение
силы тяжести. При суточном вращении Земли каждая точка земной
поверхности будет дважды находиться в условиях, когда сила
тяжести минимальна. Кроме того, поскольку движение светил
происходит не по круговым, а по эллиптическим орбитам, на
вариациях силы тяжести сказывается также разная удаленность
светила от Земли.
• В действительности Земля не является абсолютно твердым
телом, поэтому вследствие своей упругости при изменении силы
притяжения она испытывает деформации: все точки перемещаются
в направлении светила, при этом точка, для которой светило нахо-
дится в зените, перемещается больше других. В зените и надире
па земной поверхности образуются выпуклости, возникает так
называемая приливная волна: Земля растягивается в направлении
к светилу и сжимается в направлении, перпендикулярном к нему.
Таким образом, по Земле все время пробегает волна приливного
вздутия, т. е. Земля непрерывно пульсирует. Особенно ярко эти
пульсации проявляются в океанических приливах, возникающих
под действием Луны и Солнца.
Лунно-солнечные вариации силы тяжести для абсолютно твер-
дой Земли можно оценить следующим образом. Пусть С — небесное
светило (Луна, Солнце); В — точка наблюдения на поверхности
Земли; О — центр тяжести Земли (рис. 2.4). Введем следую-
щие обозначения: т — масса небесного светила; rt и г — рас-
стояния от светила до пункта наблюдений В и до центра
Земли соответственно; углы гу и z — зенитные расстояния све-
тила для пункта наблюдений и для центра Земли; R — радиус
Земли.
69
Вариация силы тяжести в точке В равна разности проекций
векторов притяжения светила в точке В и в центре Земли на на-
правление ОВ:
fig = (km/rf) cos Zi 4- (km/r2) cos z. (2.60)
Исключаем из этой формулы zt и rtI имея в виду, что
cos zx — г cos z — R;
rl =. r3 4- R2 — 2rR cos z\
COS Zx = (r COS Z — R) (r2 4* C0S г)-1/2|
тогда
fig — km j — (r cos z — R) (r2 4- R2 — 2rR cos z)~3/21 =
= Ы|— [ 1 - (1-2 — cosz +72-) ] +
4-^(1-2-0052-1--^) }.
Разлагая выражение в степени (—3/2) по биномиальному ряду,
пол учаем
6g = km[1 -( 1 4- 3 -у- cosz • • ) j 4-
+ -^-(! 4З-7-cosz 1----)}^Am-J-(l - 3cos2z),
при этом пренебрегаем членами с сомножителем R2lr2 и выше.
Следовательно,
f>g = km (R/r3) (1—3 cos2 z). (2.61)
Введем принятое в астрономии обозначение sin Р = R/r —
горизонтальный параллакс, т. е. угол, под которым со светила
виден земной радиус. Тогда, принимая во внимание, что среднее
значение силы тяжести для шарообразной Земли
g == kM/R2,
где М — масса Земли, получаем
6g g sin3 Р (т/М) (1—3 cos2z) (2-62)
или
fig— (3,2) g sin3 P-Rn/М) (cos 2z 4- 1/3). (2.63)
Эта формула может быть использована для оценки лунно-сол-
нечных вариаций силы тяжести. Определим числовое значение
70
коэффициента —(3/2) g sin3 P (mlM) для Луны и Солнца. Изве-
стно, что отношение масс mlM для Луны равно 0,01227, для Солнца
332 000. Параллакс Солнца в течение года меняется в пределах
8,65—9,95", его среднее значение 8,80". Полагая g — 982-10’2 м/с2,
для Солнца получаем
Sgc == — 0,03788 (cos 2z ф- 1/3). (2.64)
Для Луны параллакс в течение месяца изменяется в пределах
53,5—61,6', его среднее значение 57'. Для Луны имеем
8§л = — 0,08226 (cos 2z + 1/3). (2.65)
Из формул (2.62) и (2.63) следует, что максимальное возмущение
силы тяжести небесным светилом происходит при его положении
в зените (z = 0) или в надире (г = 180°), минимальное при г — 90
и 270°; при z = 54° 44' и 125° 16' возмущение равно нулю. Соответ-
ственно поправки 8g принимают значения: для Солнца 8gCTmx =
= +0,06-10-®, SgCmln = — 0,03-10-Б м/с2; для Луны б£Лтах =
- +0,16-10-®, б£ЛпПп - -0,08-10-® м/с2.
Таким образом, максимальное изменение силы тяжести, обуслов-
ленное притяжением Луны, составляет приблизительно 0,25-10-®,
Солнца 0,1 -10~в м/с2, т. е. их суммарное влияние может достигать
0,3-10-® м/с2.
Значения 6g вычислены при условии, что Земля является абсо-
лютно твердым телом. На самом деле она обладает некоторой
пластичностью и под влиянием притяжения Луны и Солнца дефор-
мируется. В упругой твердой оболочке Земли возникает приливная
волна, которая смещает точку наблюдения В от центра Земли и тем
самым увеличивает амплитуду вариаций силы тяжести приблизи-
тельно в 1,2 раза. Высокоточные гравиметрические наблюдения
в стационарных условиях показывают, что лунные суточные
вариации на 15—20% больше, чем вычисленные по вышеприведен-
ным формулам.
В настоящее время точность относительных определений силы
тяжести настолько высока, что требуется вводить поправки и за
лунно-солнечные вариации. Для определения их числовых значе-
ний необходимо рассчитать для данного момента времени зенитные
расстояния z Луны и Солнца:
cos z = cos <р cos Д -j-sin <р cos A cos {Т — а),
где ф — географическая широта пункта наблюдения; а — прямое
восхождение; А — склонение Луны (Солнца); Т — время наблю-
дения.
Значения а и А следует брать из астрономического ежегодника.
На рис. 2.5 приведены графики суточного изменения силы тяжести
в разные фазы Луны на пунктах с разной широтой. Для учета
лунных суточных вариаций составлены специальные таблицы,
по которым можно получить поправки 8g по известному на данный
момент зенитному расстоянию г. Кроме того, ЦНИИГАиК каждый
71
Рис. 2.5. Лунно-солнечные вариации силы тяжести.
год публикует специальные графики, рассчитанные для всех суток
года; по этим графикам можно определять поправки за лунно-
солнечные вариации силы тяжести.
Глава 3
РЕДУКЦИИ СИЛЫ ТЯЖЕСТИ
ПОНЯТИЕ РЕДУКЦИЙ И ИХ ВИДЫ
Использование гравиметрических наблюде-
ний для геологических и геодезических целей предполагает сопо-
ставление и сравнение результатов этих наблюдений в границах
определенных территорий. Непосредственное сопоставление изме-
ренных значений силы тяжести оказывается невозможным, так
как наряду с неоднородным распределением масс в Земле, что и
является предметом исследований в гравиразведке, на силу тяже-
сти оказывают влияние географическое положение точек наблюде-
ний, их высота, окружающий рельеф.
Обычно представляют интерес не полные g, а только аномаль-
ные значения силы тяжести \g, которые получают, вычитая из
наблюденных g нормальные значения силы тяжести у в точках
измерения:
Ag ==£-?. (3.1)
Используя формулы (2.45)—(2.53), можно вычислить у0 — нор-
мальное значение силы тяжести некоторой идеальной Земли, пред-
72
ставляющей собой эллипсоид вращения с малым сжатием. По-
скольку в формулах для нормальных значений силы тяжести
учтено действие центробежной силы, которое не зависит от распре-
деления масс в Земле, а определяется лишь расстоянием до ее оси
вращения, то аномалии силы тяжести отражают только неоднород-
ное распределение масс и тождественно совпадают с аномалиями
притяжения.
Наблюденные значения силы тяжести g всегда относятся к фи-
зической поверхности Земли, на которой проведены измерения,
а нормальное значение у0 — к поверхности эллипсоида. Чтобы
получить аномалию силы тяжести, необходимо привести наблюден-
ное значение g к поверхности эллипсоида (обозначим приведенное
значение g,,) или же нормальное значение у0 — к физической
поверхности Земли. Эта операция осуществляется введением в зна-
чение силы тяжести некоторых поправок и называется редуциро-
ванием или приведением силы тяжести.
В принципе безразлично, редуцировать ли наблюденные значе-
ния силы тяжести па эллипсоид п определять аномалии на его
поверхности или же редуцировать нормальные значения на физи-
ческую поверхность Земли и вычислять аномалии на ней, т. е.
Ag = g-Y = £o-Yo- (3.2)
При геологических исследованиях редуцирование нормального
значения силы тяжести от поверхности эллипсоида к физической
поверхности Земли представляется более удобным, поскольку
аномальное гравитационное поле, отражающее распределение
масс внутри Земли, необходимо знать для реальной поверхности,
где проводились измерения, а не для поверхности эллипсоида.
При практическом осуществлении редуцирования используют
превышения земной поверхности относительно уровня моря (ге-
оида), а не относительно сфероида (нормального эллипсоида).
Поэтому величины g0 и у0 относятся к разным поверхностям, рас-
стояние между которыми равно превышению геоида над эллип-
соидом.
Аномалии силы тяжести, определенные таким образом, назы-
ваются смешанными в отличие от чистых аномалий, которые полу-
чают при сравнении наблюденных и нормальных значений, отне-
сенных к одной и той же поверхности. Амплитуда смешанных
аномалий зависит не только от плотностных неоднородностей
масс, ио и от превышений геоида над эллипсоидом. Выясним,
насколько отличаются смешанные аномалии от чистых, вычислен-
ных с учетом поправки за превышение геоида над эллипсоидом.
Пусть IF — нормальный потенциал силы тяжести, тогда уравне-
ние W = с дает уровенный сфероид, значение силы тяжести на
котором есть Yo- Если теперь действительный потенциал силы
тяжести приравнять постоянной с, то получим уравнение геоида,
сила тяжести на котором есть g0. Действительный потенциал силы
тяжести мало отличается от нормального, и его можно записать
73
в виде суммы W Т = с, где Т — аномальный (или возмущаю-
щий) потенциал, обусловленный плотностными неоднородностями
в Земле, Т величина малая по сравнению с W. Порядок малости Т
можно оценить исходя из следующих соображений. Пусть N —
расстояние между геоидом и сфероидом по нормали Тогда измене-
ние функции W при перемещении точки с поверхности эллипсоида
на поверхность геонда
(1W = Fs ds = с — (с -Т)=Т =
или
N - Т/у0.
(3.3)
Эта формула называется уравнением Брунса, она показывает,
что Т — величина одного порядка с N.
По современным данным (см. рис. 2.2) геоид отклоняется от
эллипсоида на несколько десятков метров, достигая максимального
расхождения в области Индийского океана. Поэтому, принимая,
как и раньше, за величину первого порядка малости отклонение
земного сфероида от шара (порядок сжатия сфероида), превышение
100 м можно отнести к малой второго порядка, т. е. потенциал Т
является величиной второго порядка малости по отношению к нор-
мальному потенциалу W.
Образуем аномалию силы тяжести
Г d(W + Т) I . Г (W •]
£° — L дп _|g+ L дп Js —
индексы g и s указывают на нормали к поверхности геоида и сфе-
роида.
Для приведения производных к одной поверхности (к сфероиду),
воспользовавшись разложением (dW/dri)s в ряд Тейлора, получим

(3.5)
формуле пренебрежем
силой и примем потен-
При вычислении производных в этой
сжатием сфероида, а также центробежной
циал W равным потенциалу притяжения шара с массой М и ра-
диусом Д. При этих условиях имеем
ап ар2 \ р / р3
Ц/=/г—;
Р
др2 \ р / р3
откуда
— 9/, — 9 Д»
дп2 /s ~ R ’
74
где
7fl = AOW).
Тогда
/ dW \ / d\V \ . о N ,
\ дп ) s \ дп / s “ R ”'’0’
„ N / дТ \
go То— 2 R То - ( дп )е-
(3.6)
Заменяя в уравнении (3.6) расстояние N его выражением (3.3)
и опуская индекс g у производной, поскольку из-за малости
потенциала Т безразлично, на какой поверхности брать его произ-
водную, получаем
£0_?0 = -277Я-д7Ж (3.7)
Это основное дифференциальное уравнение, связывающее ано-
малию силы тяжести с возмущающим потенциалом Т. Второй член
в правой части уравнения представляет силу, развиваемую воз-
мущающим потенциалом, и дает чистую аномалию. Первый же
член учитывает тот факт, что нормальные значения g9 и отно-
сятся к разных поверхностям, и показывает изменение силы тяже-
сти при переходе с поверхности сфероида на геоид. Это слагаемое
уравнения (3.7) называется членом Брунса. Из формулы (3.6)
видно, что косвенное влияние возмущающего потенциала, опре-
деляемого этим членом, пропорционально N — превышению геоида
над сфероидом.
Для геологических целей важны аномалии, причиной которых
являются плотностные неоднородности. Но эти аномалии искажа-
ются влиянием изменения превышений геоида над сфероидом.
Однако поскольку превышения меняются плавжгндлггнеббльших
территории искажения практически постоянны, то при геологи-
ческой интерпретации ими пренебрегают. Если же рассматри-
ваются территории порядка континентов, следует вводить поправку
за искажающее действие отклонения геоида от сфероида, макси-
мальное значение которой может достигать 40-ИГ5 м/с2.
Несмотря на кажущуюся простоту, вопрос о редукциях еще не
получил окончательного решения; до сих пор существует несколько
способов редуцирования, предложенных разными авторами. Мы
ограничимся рассмотрением только наиболее распространенных
при решении геологических задач редукций. Обычно используют
следующие поправки и соответствующие этим поправкам или их
комбинациям редукции силы тяжести.
Поправка за высоту — так называется поправка, которую
необходимо внести в нормальную силу тяжести, чтобы получить
ее значение в точке наблюдения при условии, что между этой точ-
кой и уровнем моря нет никаких притягивающих масс, поскольку
нормальное гравитационное поле рассчитано для сфероида, вне
75
которого ист никаких масс. Эту поправку часто называют редук-
цией и свободном воздухе или редукцией Фая.
Поправка за промежуточный слой —так называется поправка
за притяжение масс, расположенных между точкой наблюдения и
уровнем моря, которая как бы удаляет действие этих масс. Эту
поправку, сложенную с поправкой за высоту, называют редукцией
Буге.
Поправка за влияние рельефа окружающей местности (топогра-
фическая поправка) — эта поправка применяется при наличии
в районе крупных, резко выраженных неровностей рельефа. Она
приводит наблюденное значение силы тяжести к такому случаю,
как если бы точка измерений находилась на равнинной местности.
Поправка за рельеф—третья поправка, учитываемая редукцией
Буге. Она используется и другими редукциями.
I Оправка Прея — эта поправка вводится для получения наблю-
денных значений силы тяжести на поверхности геоида без удаления
или какого-либо перемещения масс, расположенных между точкой
наблюдения и геоидом. Такая поправка необходима при морских
подводных гравиметрических измерениях, когда требуется пере-
нести значение силы тяжести па уровень моря с учетом масс, под
которыми проводились наблюдения.
Кроме перечисленных редукций существует много других,
применение которых основано па различных предположениях
о распределении масс и соответствующем учете их влияния. Смысл
этих редукций состоит в том, чтобы уменьшить или исключить
гравитационный эффект, создаваемый предполагаемым или извест-
ным распределением масс в Земле. Примером может служить
изостатическая редукция. Согласно теории изостазии (см. главу 17)
всякому избытку масс над поверхностью геоида соответствует
такой же недостаток масс непосредственно под избыточными
массами. Тогда, принимая ту или иную гипотезу распределения
масс в верхней части литосферы, можно вычислить, как изменится
в данной точке сила тяжести, если внешние'' массы распределить
под поверхностью геоида.
Применяя различные редукции, получаем различные по ампли-
туде аномалии силы тяжести. В зависимости от использованной
редукции аномалия приобретает соответствующее название, на-
пример аномалия в свободном воздухе, аномалия Буге и т. д. При
геологических исследованиях необходимо привлекать такую редук-
цию, которая освобождала бы аномальное значение силы тяжести
от влияния всех факторов, не связанных с геологическим строением
изучаемого района, и подчеркивала бы гравитационный эффект,
обусловленный плотностной неоднородностью пород. Этому тре-
бованию достаточно хорошо удовлетворяет редукция Буге, кото-
рую обычно и применяют при составлении гравиметрических карт,
используемых для геологической интерпретации. При резком
рельефе дневной поверхности обязательно учитывают топографи-
ческую поправку.
76
Совершенно иным должен быть подход к выбору редукции, если
гравиметрические данные используются для изучения фигуры
Земли. В этом случае необходимо применять такие редукции,
которые не нарушают основных условий теории фигуры Земл i,
в частности не изменяют ее массы. Этим условиям удовлетворяют
редукции в свободном воздухе и изостатическая. Редукция Буге
здесь совершенно неприменима, поскольку не соблюдается требо-
вание сохранить полную массу Земли.
ПОПРАВКА
ЗА ВЫСОТУ ТОЧКИ НАБЛЮДЕНИЯ
И РЕДУКЦИЯ в СВОБОДНОМ ВОЗДУХЕ
Редукция в свободном воздухе заключается в приведении нор-
мального значения силы тяжести к точке наблюдения в предполо-
жении, что между этой точкой и уровнем моря нет притягивающих
масс.
Положим, что сила тяжести g определена в точке В (рис. 3.1)
на высоте h над уровнем моря (геоида). Нормальное значение силы
тяжести на уровне моря в точке В', являющейся проекцией точки
В на геоид, есть у0. Значение у0 должно быть редуцировано в точку
В на высоте/г. Так как разность g— ус мала, ограничимся в выра-
жении (2.36) силы тяжести на геоиде только первым членом,
заменив при этом а средним радиусом Земли R:
y0^kM/R2. (3.8)
Это ограничение равносильно предположению, что Земля пред-
ставляет собой шар. Поскольку высота h мала по сравнению с ра-
диусом Земли R, то поправку можно определить, дифференцируя
выражение (3.8) по R. Затем, переходя к конечным приращениям,
заменяем АТ? на h. Таким образом получаем
dy0/dh = dy0/dR = — 2/гЛ4/А*3 =
=-2y0/R.
Поправку за высоту вычис-
ляем по формуле
6g = -(2Vo/R)/i. (3.9)
Полагая для всей Земли
нормальное поле у0 равным сред-
нему значению (980-10"2 м/с2) и
расстояние R равным среднему
радиусу (6371 км), получаем
6g = — (2y0/R)h= 0,3086/г;
(3.10)
высота h выражается в метрах;
поправка 6g — в 10~5 м/с2.
Рис. 3.1. Редукция в свободном воз-
духе.
77
Коэффициент (—2у0/Д) в формуле (3.9) представляет нормаль-
ное значение вертикальной составляющей W„ градиента силы
тяжести, т. е. ее нормальное изменение с высотой. Таким образом,
уменьшение силы тяжести с высотой составляет приблизительно
0,3-Ю'5 м/с2 на каждый метр.
Корректируя редукцией в свободном воздухе поле у0, получаем
нормальное значение силы тяжести в точке наблюдения на высотеА:
у = у0 — 0,3086ft.
После введения поправки за высоту аномалия силы тяжести
ЛЯсв.и = ?-Т = £Г-То-Ь 0,3086ft. (3.11)
Полученная таким образом аномалия AgCB. п называется анома-
лией в свободном воздухе или аномалией Фая.
При выводе формул мы пренебрегли действием масс, располо-
женных между точкой наблюдения и уровнем моря. Эти массы
увеличивают наблюденное значение силы тяжести g, и, как след-
ствие этого, растет разность g — у, т. е. растет аномалия, причем
это увеличение тем больше, чем больше ft. Таким образом, анома-
лии силы тяжести с поправкой за высоту зависят от высоты пункта
наблюдений. Этот эффект становится особенно заметным в горных
районах, где аномалии в долинах всегда меньше аномалий на
вершинах.
Зависимость аномалий в свободном воздухе от высоты делает их
малопригодными для использования в геологических целях,
поскольку «эффект высоты» может значительно превосходить дей-
ствие плотностных неоднородностей и при резком изменении рель-
ефа полностью их маскировать. Иная ситуация в равнинных обла-
стях, где превышения точек наблюдений незначительны и влияние
слоя пород, заключенного между поверхностью наблюдений н
геоидом, остается постоянным.
Для исключения влияния промежуточного слоя пород и выделе-
ния эффекта аномальных масс приходится вводить дополнительные
поправки.
ПОПРАВКА
ЗА ПРОМЕЖУТОЧНЫЙ СЛОЙ
И РЕДУКЦИЯ БУГЕ
Влияние масс, расположенных между уровнем моря (геоида) и
точкой наблюдений, учитывается введением поправки за промежу-
точный слой. Предполагается, что действие масс между точкой
наблюдения и уровнем моря эквивалентно действию горизонталь-
ного бесконечно простирающегося во все стороны слоя, мощность
которого, равна высоте точки наблюдения над уровнем моря.
Притяжение этого слоя можно получить из общего выражени i
(1.31) для U г, если положить пределы интегрирования ±оо по
±оо по ц и 0, h по £.
78
Выполняя интегрирование в указанных пределах, находим
6g = 2nkah = 0,0419ст/г, (3.12)
где о — плотность пород промежуточного слоя.
Поскольку притяжение промежуточного слоя увеличивает
силу тяжести, наблюдаемую в точке В (см. рис. 3.1), то это притя-
жение вычитают. Сумму поправок за свободный воздух и проме-
жуточный слой учитывает редукция Буге. Аномалия силы тяжести
в редукции Буге
hg^g- уо -1-(0,3086 - 0,0419о)Л. (3.13)
По геологической эффективности аномалии в редукции Буге
имеют бесспорное преимущество перед аномалиями в свободном
воздухе. Поскольку в редукции Буге гравитационное действие
масс, расположенных между точкой наблюдений и уровнем моря,
устранено, то зависимость аномалий Буге от высоты пунктов изме-
рения значительно слабее, чем аномалий в свободном воздухе.
Обычно эта зависимость обратная, т. е. с увеличением высоты точки
наблюдения аномалия Буге уменьшается (в алгебраическом смы-
сле). Это связано с тем, что учитывая эффект промежуточных масс
как действие горизонтального слоя, мы вводим поправку несколько
большую, чем реальное влияние этих масс. Для более точного
учета промежуточных масс необходимо ввести еще поправку за
отклонение формы этих масс от плоского слоя (топографическую
поправку).
При вычислении аномалий в редукции Буге очень большое зна-
чение имеет плотность промежуточного слоя. Если эта плотность
сильно преуменьшена по сравнению со средней плотностью пород,
то аномалии Буге напоминают аномалии в свободном воздухе и
могут прямо коррелироваться с рельефом местности; при сильно
завышенной плотности наблюдается обратная корреляция.
При составлении сводных гравиметрических карт принята
единая плотность промежуточного слоя, равная 2,67 г/см3. Для
большей части земного шара это значение заведомо выше реаль-
ного, оно характеризует плотность верхней части кристаллической
земной коры, а также консолидированных палеозойских пород.
Для территории СССР с 1955 г. принята плотность промежуточного
слоя 2,3 г/сма. Для площадей, сложенных осадочными породами,
это значение ближе к реальному. Для отдельных районов необхо-
димо выбирать плотность промежуточного слоя, соответствующую
действительной.
РЕДУКЦИЯ ПРЕЯ
Цель этой редукции — привести на уровень геоида значения
силы тяжести, наблюденные па физической поверхности Земли, без
какого-либо перемещения масс. Такое редуцирование необходимо
79
осуществлять при измерениях силы тяжести под землей или под
водой.
Поправка Прея получается, если из поправки за свободный
воздух вычесть удвоенное действие промежуточного слоя, заклю-
ченного между точкой наблюдения и уровнем моря:
6^П = 0,3086/1-2-0,0419a/i. (3.14)
Эффект промежуточного слоя удваивают по следующим сообра-
жениям: находясь под точкой наблюдений, этот слои увеличивает
силу тяжести, а находясь сверху, когда точка перенесена на
уровень моря, уменьшает силу тяжести на ту же величину.
Следует отметить, что значение 2 0,0419пй совпадает с притяже-
нием однородным сферическим слоем точки, лежащей па его
поверхности. Поскольку действие такого слоя па внутреннюю
точку равно нулю, то редукция Прея, учитывая притяжение масс,
находящихся выше точки погружения, показывает изменение силы
тяжести при движении внутрь Земли.
Формула (3.14) может быть использована для определения сред-
ней плотности промежуточного слоя. Действительно, пусть извест-
ны значения силы тяжести на дневной поверхности и в шахте на
глубине Л. Тогда
о = (0,3086/1 - Ag)/(0,0838/0, (3.15)
где Ag — разность наблюденных значений силы тяжести на
поверхности и в шахте.
АНОМАЛИИ СИЛЫ ТЯЖЕСТИ НА МОРЕ
На морях и океанах геоид совпадает с физической поверхностью
Земли. Если гравиметрические измерения на этих акваториях осу-
ществляются на уровне геоида, то разность наблюденного и нор-
мального значения силы тяжести Ag = g — у, представляет ано-
малию, эквивалентную аномалии в свободном воздухе.
При измерении силы тяжести на надводном судне прибор может
располагаться несколько выше или ниже уровня моря; на подвод-
ной лодке прибор может находиться на несколько десятков метров
ниже уровня моря; при установке гравиметра на дне глубина
точек наблюдения совпадает с глубиной моря. Если прибор нахо-
дится несколько выше уровня моря, то для приведения наблюден-
ных значений к уровню моря вводится поправка за высоту (редук-
ция в свободном воздухе). При выполнении измерений ниже уровня
моря вводится поправка Прея, учитывающая притяжение слоя
воды между точкой наблюдений и поверхностью моря. Аномалия
силы тяжести в этом случае вычисляется по формуле
Agc„. „ - g - у, - 0,3086/г 4- 0,0838<т„/г, (3.16)
где Л — глубина погружения (принимается положительной); —
плотность морской воды (1,0.3 г/см”).
80
Тогда аномалия Прея
А.?п — g — То - 0,222/г.
При изучении акваторий часто используют аномалию Буге,
которую получают из аномалии в свободном воздухе, добавляя
поправку за промежуточный слой, мощность которого равна
глубине моря в точке наблюдения, а плотность равна разности
между плотностью земной коры и морской воды. Таким образом,
эта поправка «засыпает» океаны массами, доводя плотность воды
до плотности земной коры.
Строго говоря, такая аномалия не является аномалией Буге,
которая должна исключать действие расположенных выше геоида
масс, представленных в виде плоского слоя. На океанах массы за
поверхность геоида не выступают и, следовательно, поправка за
промежуточный слой равна нулю, т. е. аномалии Буге на океанах
совпадают с аномалиями в свободном воздухе. Поэтому аномалии
Буге на акваториях можно называть так только условно.
Формулы для вычисления условных аномалий Буге имеют сле-
дующий вид;
при наблюдениях на надводном судне (выше уровня моря)
AgB = g - Vo 4.0,3086/in 4 0,0419 (ст - 1,03) Н,
где/гп высота прибора над уровнем моря; Н - глубина моря, м;
при наблюдениях ниже уровня моря
^.g- Vo - 0,222/i 4- 0,0419 (о - 1,03) Я;
при измерениях па дне моря, когда h = Н,
AgB = g - Vo - (0,265 - 0,0419а) Я,
где о — плотность земной коры; глубины h и Н принимаются
положительными.
При необходимости следует вводить поправку за влияние
рельефа морского дна. Эта поправка учитывает эффект избытка
(недостатка) масс выше (ниже) уровня, проходящего через проек-
цию точки наблюдения на дно моря.
ПОПРАВКА
ЗА ВЛИЯНИЕ РЕЛЬЕФА МЕСТНОСТИ
Прежде всего необходимо заметить, что и понижения рельефа
(недостаток масс ниже точки наблюдения), и повышения релье ра
(избыток масс выше точки наблюдения) приводят к уменьшению
наблюденного значения силы тяжести. Действительно, массы,
расположенные выше точки наблюдения (рис. 3.2), создают верти-
кальную составляющую притяжения, направленную вверх, умень-
шая таким образом значение силы тяжести в этой точке. Недоста-
ток масс ниже горизонта также уменьшает силу тяжести. Таким
81
'-flTTl'1 образом, поправка за влияние релье-
лу фа дневной поверхности всегда по-
/i/'*' ложительна.
/'/' Чтобы рассчитать влияние релье-
--------------- фа, необходимо аппроксимировать
у/-------------его простыми геометрическими те-
х- лами, гравитационный эффект кото-
рых можно вычислить аналитически.
Обычно всю окружающую мест-
9 ность системой концентрических
Рис. 3.2. Влияние рельефа на окружностей с центром в точке на-
силу тяжести. 1 J
блюденпя и радиальных прямых де-
лят на ряд кольцевых секторов.
Действие реального рельефа в пределах каждого сектора заме-
няется действием криволинейной призмы с основанием, равным
кольцевому сектору, и высотой, равной средней высоте мест-
ности в пределах сектора. Влияние такой призмы можно опре-
делить аналитически. Просуммировав эффект всех секторов, по-
лучим поправку за влияние рельефа. Такую операцию осуществ-
ляют по всем секторам, исключая непосредственно прилегающие
к точке наблюдения, где для вычисления поправки используют
другие методы. Здесь прилегающий рельеф можно считать на-
клонной плоскостью, конической поверхностью и т. д.
Чтобы вывести уравнения для учета влияния рельефа, можно
использовать формулу для вертикальной составляющей притяже-
ния цилиндрического кольца в точке, расположенной на оси ци-
линдра (рис. 3.3). Взяв начало координат в этой точке, обратимся
к выражению (1.35) для функции U2 в вертикальных цилиндриче-
ских координатах. Вертикальную составляющую kg притяжения
цилиндрического кольца вычислим с помощью интеграла
2л га h
О Гг hl
(3.17)
где г, и г2 — радиусы внутренней и внешней цилиндри-
ческих поверхностей кольца; h и /гх — расстояния от точки
наблюдения до нижнего и верхнего оснований кольца.
Интегрирование удобнее выполнить сначала по а, затем
по г и г. После интегрирования по а и г получаем
h
Окончательно, после интегрирования по /1, находим
kg 2nku (j/*r'i ф- h2 — -1- hi j/"г; -ф /ij. (3.19)
82
При вычислении поправки
за влияние рельефа 1гх = О,
тогда
= 2пА’о r'i ф- li1 —
-И -]/Гг^+ /г2 + г2). (3.20)
Если цилиндрическое коль-
цо разделить вертикальными
плоскостями па п равных час-
тей, то притяжение каждого
кольцевого сектора, получен-
ного таким способом, будет в п
0
Рис. 3.3. К притяжению цилиндри-
ческого кольца.
раз меньше:
Again — (2зт/с<у/п) — Г т -j- /Г -ф- Гт — "j/"h -р rjn-j-ij, (3.21)
где гт и г,л+, — радиусы соседних окружностей.
Суммируя притяжение отдельных секторов, получаем поправку
за рельеф:
т Н
Xi Agnn.
Ill I
(3.22)
При малом значении отношения hl г можно упростить выражение
(3.21). Для этого его правую часть разложим по степеням отноше-
ний h/rm и h!rm+1 и ограничимся членами с (Л/r)2. При этих условиях
Л2
2г т 2r tn4j
И
Agnm^(nko/n)h*(llrm — l/rm+1).
(3.23)
В зоне, непосредственно прилегающей к точке наблюдения,
рельеф может быть представлен в виде наклонной плоскости.
В этом случае влияние кольцевых секторов можно выразить через
угол наклона плоскости 1 (рис. 3.4, а). Тогда исходное выражение
(3.17) следует интегрировать в пределах: по а от 0 до эх/2, по г
от 0 до R, по г от 0 до R tgi. После интегрирования по г и г полу-
чаем
П/2
Ag = 2hoR | (1 — cost) da. (3.24)
о
83
Рис. 3.4. К аппроксимации рельефа
ближней зоны наклонной плоскостью
(о), конусом (б), цилиндрическим
телом (в).
Для наклонной плоскости
tgi = tg /cos а.
После подстановки значения cost в формулу (3.24) получим
Л/2
Ag_2W j [1 — (1tg2/cos2a)—1/2] da (3,25)
о
или
Ag = 2/гсг/?
я/2
] (1 + tg27cos2a)~1/2 da
о
(3.26)
Интеграл, входящий в это выражение, можно представить
в следующем виде:
л/2 л/2
| (1 ф- tg2/cos2а)-1/2da = j (1 -ф tg2/ — tg2/sin2a)-1/2da =
о о
Л/2
= cas/ | (1 — sin2 /sin2a)~1/2 da. (3.27)
о
Это так называемый эллиптический интеграл первого рода,
неприводимый к элементарным функциям. Для его вычисления
подынтегральное выражение разлагают в ряд и затем почленно
84
интегрируют. Применяя этот способ к интегралу (3.27), получаем
ряд
Л/2
| (1 — sin21 sin2 а)-1/2 da =
о
= (л/2) 11 + (W sin2 / + |(1 -3)/(2 - 4)|2 sin41 Ц----------}. (3.28)
Значения этого интеграла табулированы по аргументу sin2 I.
Окончательно равенство (3.26) может быть записано в виде
Ag = nkoR ! 1 — cos [ 1 + (4") sin2 (o) sifl4 "b ’ ’ ’ ] j
(3.29)
или
Ag = л/?а/?(1 — cos/). (3.30)
При a = 2,0 г/см3 поправка
Ag = 0,0419/?(l - cos/). (3.31)
Когда рельеф центральной зоны аппроксимируют двумя полу-
плоскостями с углами наклона 7, и /2 вычислительная формула
(3.30) видоизменяется:
Ag = 0,0419/? (2-cos/t - cos/2). (3.32)
Если центральную зону рассматривают как конус, на вершине
которого располагается точка наблюдения (рис. 3.4, б), исходное
выражение (3.17) необходимо интегрировать в пределах: по г от 0
до /?, где 7? — радиус основания конуса; по z от г tg 1 до R tg 1,
где / — угол наклона образующей конуса. Тогда
2л R tg 1 к
Agf = AoJ J J
(I г tg 1 О
rz da dr dz
(г* -p z2)3/2
R R ig I
= 2rcfeo J— o- I dr = 2nJja/?tg I (1 — sin /). (3.33)
0 rig/
Если 1г — высота конуса, то формула примет вид
Ag = 2лАю/г (1 — sin 7). (3.34)
Когда центральную зону аппроксимируют цилиндром, из кото-
рого вынут конус (рис. 3.4, в), в выражении (3.33) пределы интегри-
рования no z будут 0 и 7? tg 7. В этом случае
Ag =^= 2лАю7? (1—cos/). (3.35)
85
МЕТОДЫ ВЫЧИСЛЕНИЯ
ПОПРАВКИ ЗА ВЛИЯНИЕ РЕЛЬЕФА
Чтобы практически применить выведенные выше формулы для
учета поправки за влияние рельефа местности, необходимо выбрать
соответствующие размеры радиусов г кольцевых зон и число секто-
ров на каждом кольце. На практике для ускорения вычисления
топопоправок применяют специальные таблицы и номограммы,
которые дают значение вертикальной составляющей притяжения
масс, заключенных в кольцах разных радиусов и разных высот.
Такого рода таблицы и номограммы составлены многими авторами
(Д. Ханфорд, 3. Хаммер, П. И. Лукавченко). Расчетные схемы
различаются только выбором радиусов г и числа секторов п, что
оказывает влияние на точность вычисления топопоправок.
В качестве примера рассмотрим таблицы и номограммы,
составленные П. И. Лукавченко. Таблицы и номограммы (рис. 3.5)
рассчитаны по формуле (3.21). По таблицам влияние рельефа можно
учитывать в радиусе до 30 км, а по номограммам — до 400 км.
150
5,м
1,0—
-7
7-
60-
.50
ЮЗ v22//l0:
too-
ls -
-15
90-
ijO- "S
0,8-'
07 -~3
6
6-.
0,6-
-4
0,5-.
35-t-6
30
28
26
-5 24--
7.2-
20-
18-
16-
-4
4-.
0.4--3
-3
40
L72 70
-fl
40
-4 30- _g
-7
14--3
-6
0,3-
-2
0,2
3-'
-2
12-'
-2
10-
20-.S
-4
V -
0,05-~
0-t-0
0-2
Зона 1
n 1
1-
04-0
2-10
2
6-~1
4-'
o^-o
10-20
3
6
2-
12
-1
8
s
20-50
4
8
r32
-3!
-30
-29
-28
-27
M 250- -
-15
3,0 Г2250lP[.22
-22"
'^450-
-20 .
-19
. ~'S400-
-17
-IB
-15.
'-13
T-z?
'-11300-
-10 -
.-9
-_8250-
--7
. 'b209
-5
~4
-3'S°-
-2
-.100-
l-o 0^4-0 o^-o
ЗОВ-
-21 i
20130-
-19
-13120-
-17
-46110-
-15 I
-14 100-
-a :
-12 go-
-25
--24
-23
-22
'-2!
-20
.-19
-18
-17
-'-16
'.-15
'.-14
'-13
-12
-11
-10
-9
'.'-8
'.'-7
:-6
--5
--3
+2
:'~1
. ^0
50-100 100-200
6
в
60
--И
~.-1O so-
50-
40
30
20
10-
-9
-8 70-
-7 :
-6 so-
-5
_-450
; -3 40
+ 2 30
I 20.
16
-14
-13™~1
-12
200-.
. -11
--_g2OO-
i50-. 8
. 7
-6.
150
-5
100-~4
-3
100
2
-21
.-20
'7/9450-7
.-10 -
'-17
'.-16 -
-'-!4 -
'-13 '
'_-l2350-
-11
-10 ' -
7_g300-_
8 --
7 --
250--
--5 •-
--5
-21
'-20
19
18
47
-16
45
44
43
42
41
10
9
8
7
6
5
4
3
2
1
4го°-.
з :
i’50-'
, tool
'лчг-:
50Д..1 .n
40- ' 50
20- o:
o^-o о
200-300 300-500 500-700 700-1000
7 8 9 10
is is ie 16
30
’ ' 80
a
о
-!
8
5
9
3
2
0
8
ю
Рис. 3.5. Фрагмент номограммы Лукавченко для вычисления поправок за влия-
ние рельефа на силу тяжести.
8G
Рис. 3.6. Палетки для вычисления влияния рельефа на силу тяжести.
В радиусе до 30 км вся местность представлена в виде 19 концентри-
ческих зон, каждая из которых разделена на несколько секторов.
В радиусе от 30 до 400 км содержится 8 кольцевых зон, также
состоящих из нескольких секторов. В радиусе больше 30 км вычис-
ление поправок проведено с учетом кривизны земной поверхности.
Номограммы представляют собой прямые вертикальные линии
с двумя шкалами: на левой нанесены высоты, на правой — топопоп-
равки. Каждая вертикальная линия соответствует одной зоне. Под
номограммами указаны внешний и внутренний радиусы зон, номера
зон и число отделений п в каждой из них. Поскольку' в зонах ради-
усом 30—400 км учтена кривизна земной поверхности, то поправки
здесь могут быть и положительными и отрицательными. Если пре-
вышения в зонах отрицательные, то поправки всегда положитель-
ные; если же превышения положительные, то поправки могут быть
и отрицательными и положительными. Поэтому для радиусов
30—400 км вычислены две номограммы: одна для отрицательных
превышений, другая для положительных.
Для определения средних превышений в секторах необходимо
иметь топографические карты различных масштабов. Для зон
в радиусе до 300 м нужны карты масштаба 1 : 1000—1 : 2000,
для зон до 30 км — 1 ; 10 000—1 : 50 000, а для зон больше
30 км — 1 : 100 000 и даже 1 : 500 000. Масштаб карты в общем
выбирают так, чтобы ширина узкой, внутренней, зоны в масштабе
была не менее 0,5 см. Для определения превышений на прозрачной
бумаге строят палетки в масштабе карты (на рис. 3.6 приведены
палетки для зон 4—6 и 15—18). Палетку накладывают центром на
точку, для которой надо вычислить топопоправку, и ориентируют
линией С—Ю по географическим координатным линиям карты. Для
каждого сектора палетки находят среднюю высоту сектора или'же
высоту в центральной точке сектора. По значению радиусов сек-
ира и его превышению относительно точки наблюдения определяют
87
поправку Ag для данного сектора. Сумма поправок по всем секто-
рам во всех зонах составляет топопоправку.
Определение топопоправки, как это можно видеть из описания
методики ее вычисления, является весьма трудоемким делом. Для
ускорения этой операции предложено несколько других способов,
отличающихся расположением зон и секторов и упрощением
исходной формулы, хотя существо всех способов одно и то же:
влияние действительного рельефа заменяется действием некоторых
правильных тел, которыми и аппроксимируется рельеф дневной
поверхности.
Так, в способе, предложенном Л. Д. Немцовым и А. И. При-
шивалко, рельеф представляется системой параллелепипедов
с квадратным основанием. Для этого поверхность разбивают на
квадраты различного размера. Точку наблюдений располагают
в центре начального квадрата. Этот квадрат окружен восьмью
квадратами такого же размера. Таким образом получается квадрат,
размер которого в 3 раза больше начального. К этому квадрату
в свою очередь примыкают восемь квадратов, размер каждого из
которых в 3 раза больше начального (и т. д.), т. е. в каждой после-
дующей зоне размер квадрата утраивается. Рельеф в пределах
начального квадрата аппроксимируют параболоидом четвертой
степени, действие остальных квадратов рассчитывают по формуле
вертикального параллелепипеда. Для определения топопоправки
составлены специальные таблицы и номограммы. Основным досто-
инством этого способа является возможность использовать однажды
снятые высоты для вычисления топопоправок в нескольких
пунктах.
Для уменьшения трудоемкости учета влияния рельефа без
снижения точности в ряде методов применяют разбивку местности
иа тела простой формы не «стандартную», а в зависимости от пове-
дения рельефа. Ограничимся здесь изложением метода, предло-
женного В. М. Березкиным и получившего довольно широкое
распространение. Чтобы ускорить определение поправки, В. М. Бе-
резкин рекомендует учитывать рельеф по его характерным точкам.
Этим уменьшается число необходимых превышений.
Сущность способа состоит в следующем. Если в исходной фор-
муле (3.17) выполнить интегрирование в пределах: по а от до
аи+1, по г от гт до rm+1, по г от 0 до h, то после интегрирования и
подстановки пределов по z получим
бп+1
= ЙО J J (1 - da dr. (3.36)
“n rm
Это выражение дает вертикальную составляющую притяжения
криволинейной призмы с основанием в виде криволинейной трапе-
ции. Полагая hlr малой величиной, упростим подынтегральное
88
Выражение, разложив его в ряд по степеням отношения h/r и огра-
ничившись только членами, содержащими ii-lr1. Тогда
&gam = (/гсг/2) j j (htyr2} dr da. (3,37)
При интегрировании по г положим, что с изменением радиуса
высота местности меняется по гиперболическому закону, т. е.
h = V (ZP/a2)/'2 — Ь2, (3.38)
где а и b — полуоси гиперболы.
Подставляя выражение (3.38) в равенство (3.37), получаем
&gnn ~ (ko/2) j I (b2/a2 — b2r2) dr da;
a,i 'rn
после интегрирования по г и а находим
Ag™ = Г(G1+i - rm) -I- b2 ( —’------Д) I (an+1 - a„). (3.39)
l и \ 'm+i rm / J
Для определения b2/a2 и b2 воспользуемся условиями, возни-
кающими на
границе участков интегрирования:
h\ = (b2l<r)rm - b1; )
й^+1-(г>'2/а2)г^+1_ b1. J
(3.40)
Решая эти уравнения относительно Ь2/а2 и Ь2, имеем
&_ = hn^—h2m .
а1 г- ____’
й‘2 r2 —h^r2
птг т-\~\
2 2
гт-\-1~гт
(3.41)
Подставив найденные значения b2/a2 и Ь2 в уравнение (3.39)
и положив одновременно, что ая+1 — ап = 2л/л, найдем
_ 2nko _ rm ,i — г,„ ( bm Am+1 \
Я 2 (rтц -|- rm) \ rm гm+1 J
Вводя обозначения
. 2
> = Гт+1 — Гт . р 2nkc _ пт
т 2 (Гщ-ц 4~ г,п) ’ т п гп1 ’
(3.42)
(3.43)
получаем
^gn,n = (Fm + Fm+1)Rm, (3.44)
что дает поправку за рельеф, представленный в виде одной криво-
линейной призмы.
89
При интегрировании вдо,'п. всего луча получим
rtl.
&g„= L Ag„,„ / а* ' . /Л) 1 '',('<> I -ь
-гЛЖ :- '<>) I ••• , Л.о. Н„ ,!>• (3.45)
Для определения функций Fm и А’,, составлена номограмма
(рис. 3.7), которая позволяет по h и г найти F,„ и В номо-
грамме приведены значения функций
74=Д„.4; 7т=Дл/4, (3.46)
что не изменяет общей поправки Ag;j, определяемой формулой
(3.45), которая в этом случае примет вид
&gn + Aj + F, (Д ' Д) Д • I Д1+1 U<„, I- Д,+1). (3.47)
Суммируя поправки по всем лучам, получаем поправку за
влияние рельефа
(3.48)
/1—0
Номограмма составлена для учета влияния рельефа в радиусе
30 км, число лучей 16, плотность о = 2 г/см3.
Практически топопоправку вычисляют следующим образом.
На прозрачной бумаге строят палетку, представляющую собой
16 лучей, проведенных из одной точки через равные углы. Центр
палетки накладывают на ту точку топографической карты, для
которой надо определить поправку. Вдоль каждого луча выбирают
характерные точки рельефа таким образом, чтобы они ограничи-
вали области, где изменение высот имеет более или менее одина-
ковый характер. Для этих точек устанавливают: гт — расстояние
до центра палетки, и h — превышение рельефа относительно цен-
тральной точки. По значениям гт и й с помощью номограммы на-
ходят функции Fm и Rm. Для определения Fm по горизонтальному
входу номограммы отмечают гт и по вертикальной шкале, направ-
ленной вверх, напротив h считывают значение функции Fm.
Для определения Rm по горизонтальному входу номограммы отме-
чают радиус г,п+1, а по вертикальной шкале, идущей вниз, на-
против гт считывают значение Rin. Определив все значения R,n
и F,lt, их подставляют в формулу (3.47). Следует отметить, что
для первых точек на радиусах всегда 7?0 = 2, поскольку г0 = 0.
Поэтому на номограмме нет значения Ro напротив rm+1 = 10.
Рассмотренный способ вычисления топопоправок дает некото-
рую экономию во времени, ио выбор характерных точек рельефа
субъективен и зависит от опыта вычислителя, что может ска-
заться на точности определения поправок.
90
/
FIO^m/c? h,M
8
0.6
0,5
0.4
14
-13
-12
-11
-10
1
- 16
-15
14
-13
т12
3
4
231
т126
10-
6
03 4-5
0,2- -4
в
-7
-6
-10
-в
-7
0,1-3 0,1-4 0,1-5 0.1-
-439
30- -422
-407
[394
г381
тЗВЗ--370
25-355^-358
-337 "
-323
-ЗЮ
-298
-348
-327
—317
л271
-253
-239
-226
20 26720-\-307
-276
-266
-255
-245
-237
-287
-277
267
!5- -20 >5- -215 >5- -235'5 257
-197
-165
-174
-163
204 )-226 \-247
-194
184
-174
-236
-7.16
-206 \226
-195 ,--215
r192
-169
-155
М3 Ю- -153 ю\/64 Ю-\-185 !5\-204
133 --143
56
45
35
1- 24
-22
-21
20
-18
т84
572
-61
-51
41
28
-27
-25
-23
-22
1.54
-144
-133
„„ „„ -122
92. 5 -102 5 -
-174
-163
-152
-140
- 727 5--141
113
97
79
56 1
-53
-50
-46
-43
-193
181
-168
- 155
-113 123 -133
--102 -113 -123
-92
5-62
-72
-61
-49
1-34
-32
-30
--26
-26
--103^-113
5 .
111 5-
98
-85
-69
48 I
46
-43
-40
-37
-126
-m
-88
-62
59
-55
52
-48
SO
- 78
-63
1-44 I
-42
-39
-37
-34
82
70
56
39
-37
42
31
-20
-19
-18
-17
-IS
--14 0,5- -16 R5- -20 «5- -24 05- -28 Off- -31
7/
-9
-6 0,1
Г
-18
-15
-12
-22
-19
- 75
-33
-30
-25
-21
18
—28
-24
20
-30
-26 -30
21
-35
-39
-34
28
-15
-13
-10 .... . _
7 0.1- ~9 0.1- -11 0.1- -12 0.1- -14 0,1- -15 0,1- -17 0,1- -20
25
10 20 30 50 70 100 150 200 250 300 400 500
10-

•50- -03370- 0,11 I- 0,4015- -029 2r -022 25- -Q)8 3- -0,29 4- -Ц22
U^JSO- -08050- -05770- -0,73 I--057'5- -Ц50 2- -Ц46 3- -0,50
104-134 28- -Ц1 за- -108 50- too 70-0961- -0.8615 -QS7 2- -0.67$ -Ц67
104-1,5020--133 20-133 50--1,20 70--1J2 ’--',0 $-0912--0,86
Ю 4/64 20- ->53 30- -148 SO- -[33 70- -Ц4 1-->2015--[08
Ю ^-(64 20- ->,53 30- -[48 SO- -1,33 70- -$4 1--,^.
Ю1-т 20- [6435 -1,57^- -143 70- -Ifl 1 - 133
10-48120- -ЦО S4- - >64 SO- -[56 70- -[51
i,7250-1,64
10 L12-5W--1.7580--!,^
10 4-1,8720-->8130--1,77
104->90^->85
104-1,92
Рис. 3.7. Номограмма Березкина для определения функций Fm и R,n.
91
Рис. 3.8. К определению превы-
шений рельефа по аэрофото-
снимкам.
написать
В настоящее время разработаны
и совершенствуются методы опреде-
ления поправки за влияние рельефа
на основе материалов аэрофотосъем-
ки. Это направление представляется
весьма перспективным, поскольку от-
крывается возможность автоматиза-
ции учета влияния рельефа местности,
кроме того, отпадает необходимость
в трудоемких и дорогостоящих гео-
дезических работах. Сущность мето-
да заключается в следующем.
Пусть фотосъемка местности вы-
полнена с двух точек О, и 0.2, разне-
сенных по горизонтали па некоторое
расстояние (рис. 3.8). Относительно
некоторой точки At на земной по-
верхности высота съемки равна Я;
угол видимости отрезка 0х02 из точ-
ки Аг равен Ф1. Если отрезок О±О2 рассматривать из точки А2,
близкой к Аг и имеющей относительно нее превышение ЛЯ, то
угол видимости этого отрезка будет гр2 = Ф1 Лер (прираще-
ние Дер имеет знак «плюс», когда точка А.г выше Л]). Можно
(Я ± ДЯ)/Я = (<рх ± Дер)/Ф1
или
ДЯ = Я (Дер/Ф1) = К Дер.
Таким образом, по аэрофотоснимкам местности с двух точек
при известной высоте съемки, определив коэффициент Я и угол Дер,
можно найти превышение ДЯ. Определение К и Дер проводится
на стереометре. Для автоматизации этого процесса и вычисления
поправок за влияние рельефа местности сконструированы спе-
циальные приставки к стереометру, позволяющие получать не-
посредственно значения топопоправок. Опыт использования аэро-
фотоснимков показывает, что для определения топопоправок с по-
грешностью (0,02.-4-0,05)-10-а м/с2 при превышениях до 500 м
нужны аэрофотоснимки масштаба 1 : 14 000—1 : 35 000. Преиму-
щества этого метода особенно очевидны в горных областях.
При вычислении топопоправки важно правильно определить
границы области, в пределах которой следует учитывать влияние
рельефа. В большинстве случаев предельный (максимальный)
радиус выбирают, оценивая гравитационное влияние рельефа за
пределами области, для которой рассчитывают топопоправку. Для
этого можно воспользоваться формулой (3.23). Положив г,„+1 = оо,
п = 4, получим гравитационное действие секториального ква-
дранта, высота которого 1г, а радиусы гт и оо;
Д^« = (л^/4)№(), (3.49)
S2
Задаваясь значением Agy, как погрешностью определения
топопоправки и находя по топокарте средние превышения рельефа
1г относительно точки наблюдения, вычисляют радиус учета влия-
ния рельефа гт. Обычно считают этот радиус достаточным, если
суммарное действие рельефа за пределами принятой во внимание
области не превосходит погрешности измерения силы тяжести или
же меняется линейно от точки к точке в пределах участка съемки.
При практическом вычислении поправок за влияние рельефа
вся область, в которой учитывается это влияние, делится, как
правило, на три зоны: центральную, среднюю и дальнюю. В цен-
тральной зоне поправку вычисляют или по данным непосредствен-
ных измерений превышений рельефа на местности, или аппрокси-
мацией рельефа правильной геометрической фигурой (наклонная
плоскость, конус и т. п.). В средней зоне поправку определяют
одним из методов, разобранных выше. В пределах дальней зоны
поправка чаще всего плавно меняется от пункта к пункту и яв-
ляется функцией только высоты точек наблюдений. В этом случае
для учета влияния дальних зон можно применять различные
интерполяционные способы, предварительно определив корре-
ляционную зависимость поправки от высоты пункта наблюдений.
Раздел IS
МЕТОДЫ
ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ
Глава 4
ЗАДАЧИ И СПОСОБЫ
ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ
ЗНАЧЕНИЕ ОПРЕДЕЛЕНИЙ СИЛЫ ТЯЖЕСТИ
ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ НАУКИ
Поведение силы тяжести па земной поверх-
ности начали изучать более двух веков назад. В настоящее время
на Земле ежегодно проводятся сотни тысяч новых определений
силы тяжести в различных условиях (на суше и море, в подземных
выработках и скважинах). Такое широкое распространение изме-
рений силы тяжести связано с использованием их для решения
ряда важнейших задач науки и практики, причем сфера прило-
жения определений силы тяжести все время расширяется вместе
с общим прогрессом науки и техники. Большинство определений
силы тяжести служит для изучения геологического строения иссле-
дуемых территорий, для поисков и разведки полезных ископаемых,
составляя основу разведочной гравиметрии — одного из методов
разведочной геофизики.
Знание распределения силы тяжести на земной поверхности
имеет огромное значение для геодезии, занимающейся изучением
фигуры Земли. Гравиметрические измерения являются неотъемле-
мой частью геодезических исследований. В частности, по грави-
метрическим данным найти сжатие Земли значительно проще,
чем по градусным измерениям.
Гравиметрические данные необходимо принимать во внимание
при запуске искусственных спутников Земли, поскольку для точ-
ного расчета орбит спутников надо знать распределение силы
тяжести на земной поверхности. С другой стороны, исследуя изме-
нения орбит спутников, получают богатый материал для изучения
гравитационного поля Земли.
Знание абсолютного значения силы тяжести играет важную
роль в метрологии, поскольку сила тяжести на экваторе g. яв-
94
ляется константой, необходимой при создании различных стан-
дартов и установлении единиц механических, магнитных и элек-
трических сил. Например, единица силы тока ампер определяется
как сила взаимодействия двух проводников определенной конфи-
гурации, возникающая при пропускании через них пеизменяю-
щегося тока. Сила взаимодействия проводников при этом уравно-
вешивается весом mg известной массы т.
Знание абсолютного значения силы тяжести хотя бы в одной
точке земной поверхности необходимо для приведения в единую
абсолютную систему всех гравиметрических измерений на земном
шаре, для изучения долгопериодических вариаций силы тяжести,
получения параметров формул ее нормального распределения.
Точное знание силы тяжести ge необходимо также для выражения
массы Земли в метрических единицах, что позволяет приводить
массы других небесных тел в таких же абсолютных единицах,
а не в относительных единицах массы Земли.
КЛАССИФИКАЦИЯ
МЕТОДОВ ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ
Для измерения силы тяжести принципиально могут быть ис-
пользованы разнообразные физические явления, которые зависят
от силы тяжести, например падение тела под действием силы
тяжести в пустоте, воздухе или жидкости, качание маятника,
поднятие жидкости в капиллярном сосуде, колебание струны,
растяжение пружины под действием груза. Однако, несмотря на
многообразие физических явлений, зависящих от силы тяжести,
только некоторые из них позволяют определить силу тяжести
с необходимой точностью.
Все существующие методы измерения силы тяжести могут быть
разделены на динамические и статические.
Динамическими называются такие методы, при которых на-
блюдается движение тела под действием силы тяжести, а непосред-
ственно измеряемой величиной является время, необходимое телу
для перехода из одного фиксированного положения в другое.
Статическими называются такие методы, при которых наблю-
дается изменение положения равновесия тела под действием силы
тяжести и некоторой силы, уравновешивающей ее, а непосред-
ственно измеряемой величиной является линейное или угловое
смещение тела с постоянной массой. Для уравновешивания силы
тяжести можно использовать силы различной природы. В настоя-
щее время в статических приборах уравновешивающей силой
служит упругое действие твердых тел (пружин, нитей, мембран
и т. д.).
При динамических методах измерения силы тяжести наиболее
часто используются следующие физические явления.
1. Колебания маятника, качающегося под действием силы
тяжести.
95
2. Колебания упругого маятника, качающегося под действием
силы тяжести и упругой силы, ей противодействующей.
3. Свободное падение тела.
4. Колебания струны, которая натянута подвешенной па ней
постоянной массой.
Измерения силы тяжести бывают абсолютными и относитель-
ными. При абсолютных измерениях определяют полное значение
силы тяжести в точке наблюдений. В этом случае кроме времени
измеряют линейные расстояния, например длину маятника или
путь, пройденный свободно падающим телом. При относительных
измерениях определяют не полное значение силы тяжести в точке
наблюдения, а приращение (разность) силы тяжести в данном
пункте относительно некоторого другого, исходного, значение
силы тяжести в котором обычно бывает известным.
Динамические методы определения силы тяжести могут быть
как абсолютными, так и относительными, статические — только
относительными.
Приборы, предназначенные для относительных определений
силы тяжести, называются гравиметрами. Гравиметры, в которых
использованы динамические принципы измерения силы тяжести,
называются динамическими; гравиметры, в которых использованы
статические принципы, — статическими.
Среди динамических методов получил широкое распростране-
ние на практике и господствовал в течение двух столетий маятни-
ковый метод, основанный на наблюдениях свободных колебаний
маятника. Другие динамические приборы (упругий маятник, струн-
ный гравиметр) появились в 30-х и 50-х годах нашего века.
Статические методы определения силы тяжести, хотя и были
предложены очень давно (первый гравиметр построил М. В. Ло-
моносов в 1753 г.), осуществились только в 30-х годах нашего сто-
летия. В настоящее время статические гравиметры являются
основными приборами для относительных определений силы
тяжести.
Глава 5
ДИНАМИЧЕСКИЕ МЕТОДЫ
ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ
ОСНОВЫ МАЯТНИКОВОГО
МЕТОДА ОПРЕДЕЛЕНИЯ СИЛЫ ТЯЖЕСТИ
Среди динамических методов измерения силы
тяжести главенствующее положение в течение длительного времени
занимал маятниковый метод, доведенный до высокой степени совер-
шенства. Маятником называется любое твердое тело, способное
96
совершать свободные колебательные
движения около горизонтальной оси.
Рассмотрим теорию колебаний мате-
матического маятника, представляюще-
го собой материальную точку М с
массой т, подвешенную на нерастяжи-
мой и невесовой нити ОМ длиной /
(рис. 5.1). Пусть маятник был откло-
нен от положения равновесия ОА на
угол а и начал совершать колебатель-
ное движение. В некоторый произволь-
ный момент времени t маятник зани-
мает положение ОМ, составляющее
угол <р с положением равновесия. Этот
угол называется углом элонгации. Си-
ла mg, действующая на точку М, мо-
жет быть разложена на две составляю-
щие: силу Р, действующую по направ-
лению ОМ, и перпендикулярную к ней
силу Q, направленную по касательной
к дуге AM.
ятник.
Первая составляющая уравновешивается сопротивлением точки
опоры О, вторая вызывает движение точки М в направлении
к точке А. Поскольку сила Q равна mg sin ф, то ускорение движе-
ния точки М есть g sin <р. С другой стороны, это ускорение равно
—l(d2q>/dt2), так как /<р есть путь, пройденный точкой М. Знак
минус указывает на уменьшение угла ф.
Дифференциальное уравнение движения маятника имеет вид
d2q!dt2 = — (§//) sin ф.
(5.1)
Умножив обе части уравнения на 2 (dq/dt) dt, после интегри-
рования по t получим
(d<p/di)2 == 2 (g/l) cos ф -ф с, (5.2)
где с — произвольная постоянная.
Чтобы найти с, обратимся к начальным условиям. В начале
движения при t = 0 маятник был отклонен на угол а и его скорость
была равна нулю, т. е.
Ф/=о =- (dcp/dt)^o — O. (5.3)
Подставив начальные условия (5.3) в уравнение (5.2), находим
с = — 2 (g//) cos а;
(dqldt)2 = 2 (g//) (COS q; — COS а). (5.4)
Уравнение (5.4) имеет физический смысл, если правая часть
положительна или равна нулю, т. е. когда cos <р > cos а. Это
возможно, если ф принимает значения в пределах от -фа до —а.
•I В. С- Миронов
97
Угол а соответствует максимальному отклонению маятника от
положения равновесия и называется амплитудой колебаний.
Время, необходимое маятнику для прохождения от одного край-
него положения -(-а до другого крайнего положения —а, назы-
вается периодом колебаний Т маятника.
Из уравнения (5.4) следует
dt — |/ l/(2g) (1/< cos<( — cosa)dcp. (5.5)
Интегрируя правую часть этого уравнения в пределах от —а
до -ра, имеем
Т Да
Т = j dt — f l/('2g) J ( 1/j cos cp — cos a) dip. (5.6)
о —a
Введя новую переменную sin (<p/2) - К sin ч|\ где A’ - sin (a/2),
после несложных преобразований получим
lt/2
Т = 2 |///g J (l/]/l — №sinsi|>)chp. (5.7)
о
Интеграл в выражении (5.7) нам уже встречался [см. формулу
(3.28)1, учитывая это, получаем
r=-nVTig{i -I- (4ysin2dr+(4^ysint-r+
I у 4 / & \ X» ' тг /
(2n — 1) 1
2n j
2 sin2"
a
~2
(5.8)
Если амплитуда колебаний маятника мала настолько, что ею
можно пренебречь, то равенство (5.8) при a = 0 примет вид
(5.9)
T = лУ l/g.
Это выражение можно получить также из дифференциального
уравнения движения маятника (5.J), положив в нем sin ср = ср.
Как следует из формулы (5.9), для малых амплитуд период
колебаний маятника не зависит от амплитуды. Это свойство маят-
ника называется изохронностью. При гравиметрических измере-
ниях амплитуда колебаний маятника не превышает 1°. Относи-
тельная погрешность измерений периода колебаний может быть
порядка 1-Ю-8. Тогда для второго и третьего членов формулы
(5.8) имеем соответственно 19-10"° и 8-10~10, т. е. второй член
формулы необходимо учитывать, а третьим и последующими
можно пренебречь, поскольку они малы. В этом случае период
колебаний маятника
Т = л I ///' 11 -т (1 /4) sin2 (a/2)]
(5.10)
98
или ввиду малости угла а
Т- л (1/16) сс2|. (5.11)
Практически осуществить математический маятник с необхо-
димой степенью точности невозможно. Поэтому при определениях
силы тяжести используют физический маятник.
ФИЗИЧЕСКИЙ МАЯТНИК
Под физическим маятником понимается любое твердое тело,
свободно вращающееся вокруг горизонтальной оси (рис. 5.2).
Пусть ось вращения проходит через точку О и направлена пер-
пендикулярно к плоскости чертежа, т. е. совпадает с координат-
ной осью х; ось z направлена вертикально вниз; оси х и у — гори-
зонтальные. Центр тяжести маятника находится в точке С на
расстоянии а от оси вращения. Положением прямой ОС вполне
характеризуется положение маятника в любой момент времени.
Пусть угол, составленный прямой ОС с осью z, равен <р. Тогда
уравнение движения твердого тела вокруг неподвижной оси
можно записать так:
/Л (d2<f/dt“) = S МЛ., (5.12)
где /л. и М, — момент инерции и момент сил относительно оси
вращения х.
Сумма моментов действующих сил
У, Мк = — Mga sin ip, (5.13)
где М — масса тела.
Уравнение движения принимает вид
/г (d2if/dt2) = —Mga sin ср (5.14)
или
d8<p/dZ2 — {gU) sin ф, (5.15)
где
/ = 4/(оЛ4). (5.16)
Выражение (5.15) совпадает с диф-
ференциальным уравнением движения
математического маятника (5.1). От-
сюда следует, что физический маятник
колеблется по тем же законам, что
и математический, только роль дли-
ны / в физическом маятнике играет
величина 1гх/(аМ). Эта величина на-
певается приведенной длиной физи-
ческого маятника.
4*
Отложив от оси вращения О через центр тяжести С отрезок,
равный приведенной длине физического маятника, найдем точку О',
которая называется центром качания. Сконцентрировав в центре
качания всю массу физического маятника, получим математиче-
ский маятник с тем же периодом колебаний, что и у физического
маятника.
Центр качания находится внутри тела. Его положение необ-
ходимо знать, чтобы определить приведенную длину физического
маятника при абсолютных измерениях силы тяжести. Отыскание
центра качания основывается на свойстве взаимных точек О и О'.
Момент инерции 1Х относительно оси вращения может быть выра-
жен через момент инерции 10 относительно оси, параллельной
оси подвеса маятника и проходящей через его центр тяжести:
4 = 4 + ^. (5.17)
Подставив это значение в формулу (5.16), найдем приведенную
длину маятника
I = 10/(аМ) + а. (5.18)
В правой части формулы (5.18) оба слагаемых всегда положи-
тельны, и поэтому I > а, т. е. приведенная длина физического
маятника всегда больше расстояния от центра тяжести маятника
до оси подвеса.
Пусть маятник качается вокруг оси, параллельной прежней,
ио проходящей через центр качания О'. Приведенная длина маят-
ника /' в этом случае может быть отличной от I, так как опа отве-
чает другой оси подвеса. Расстояние от оси вращения, проходящей
через точку О', до центра тяжести есть I—а, тогда
/' = /0/[(/ - а) /И] + (/ - а).
Заменяя длину I ее выражением (5.18), имеем
I' = а ф /0/(аМ) = I, (5.19)
т. е. приведенная длина маятника сохранилась прежней.
Точки 0 и О' являются взаимными: если через одну из них
проходит ось вращения, то другая является центром качания,
и наоборот. Поскольку в обоих случаях приведенные длины маят-
ника одинаковы, должен быть одинаков и период его колебаний.
Таким образом, если задана ось подвеса маятника, можно
отыскать центр качания. Этот принцип положен в основу оборот-
ного маятника, имеющего две параллельные оси качания, проходя-
щие через взаимные точки. Эти оси являются ребрами призм, на
которых поочередно качается маятник. Если периоды колебаний
совпадают, то приведенная длина оборотного маятника может быть
получена непосредственным измерением расстояния между приз-
мами.
Для твердого тела приведенная длина /' меняется в зависимости
от расстояния оси подвеса до центра тяжести. Из всех возможных
100
параллельных осей подвеса найдем такое ее положение (расстоя-
ние а), при котором приведенная длина / является минимальной.
Полагая / функцией а и дифференцируя уравнение (5.18), имеем
dl/da = ~/0/(о2Л!)+ 1 — О,
откуда
a (5.20)
Подставив это значение а в формулу (5.18), получим
/ = 2а. (5.21)
Уравнения (5.20) и (5.21) определяют такое положение оси
подвеса для данного твердого тела, при котором его приведенная
длина, а следовательно, и период колебаний будут минимальными.
Отвечающий этим условиям маятник называется минимальным.
Преимущество минимального маятника состоит в том, что неболь-
шие изменения в положении оси подвеса не сказываются суще-
ственно на приведенной длине, а следовательно, и на периоде
колебаний.
АБСОЛЮТНЫЕ
ОПРЕДЕЛЕНИЯ СИЛЫ ТЯЖЕСТИ
Абсолютное значение силы тяжести можно определить многими
методами. Наиболее часто применяют методы, основанные на
использовании оборотного маятника и свободного падения тела.
Первый оборотный маятник в виде металлического стержня
с укрепленными на его концах призматическими опорами скон-
струировал в 1818 г. X. Катер. Маятник мог качаться на каждой
из этих опор. Периоды качания на обеих опорах уравнивали, пе-
ремещая на стержне подвижный груз. По расстоянию между
призматическими опорами и периоду качания вычисляли значение
силы тяжести.
Более совершенную конструкцию оборотного маятника пред-
ложил Ф. Бессель, которая была осуществлена Репсолъдом
в 1864 г. В усовершенствованном виде такой маятник использо-
вался и в наше время для абсолютных определений силы тя-
жести. Ф. Бессель предложил и специальный метод наблюдений,
при котором можно не добиваться точного равенства периодов
качания маятника в двух положениях, а учитывать различие
в периодах введением соответствующих поправок. При этом сокра-
щается продолжительность наблюдений и отпадает необходимость
в регулировочных грузах.
Способ несовпадения периодов состоит в следующем. Пусть
выполнены наблюдения при двух положениях маятника с рас-
< гояпием I между осями и получены периоды 7\ и Т2, мало отли-
чающиеся от периода Т идеального маятника, для которого при-
веденная длина равна I. Тогда
7\ = л Vljg', Т2 = л,У12/§; T = n\'l/g. (5.22)
101
Из наблюдений известны 71( 7.., не известны /,, /2, /, Т. Состав-
ляя отношения из третьего и первого и третьего и второго выра-
жений (5.22) и возводя их в квадрат, имеем
r'/r'i ///,; T‘/t'; i/i,. (5.23)
Пусть расстояние от первой оси качания до центра тяжести
есть в,, а от второй осп а2, тогда
«1 + = I,
но
Zi = «j ф 1п/(вхМ)', 1г — а2 | /(|/(д2Л4).
Подставив эти выражения в формулу (5.23), исключив 10/М,
получим
Т2 (5.24)
Эта формула Бесселя решает поставленный вопрос. При Тг =
-= Т2 величина I = аг есть приведенная длина. Если же
Tj =4= Т2, то, чтобы определить 7, необходимо знать положение
центра тяжести маятника, т. е. и а2. Эти значения находят путем
специальных измерений.
При Oj = а2 знаменатель формулы (5.24) обращается в нуль.
Чтобы значение аг—а2 не было малой величиной, необходимо
сместить центр тяжести маятника к одному концу, при этом не
обязательно (и даже нежелательно) нарушать симметричную форму
маятника.
Точность определения абсолютного значения g зависит от точ-
ности найденных значений 7 и /. Логарифмируя и затем диффе-
ренцируя последнее из равенств (5.22), имеем
dglg = dlft-2dT/T
или, переходя к средним квадратическим погрешностям е, находим
(Ша ~ (2ег/7)2 + М)\ (5.25)
где 8Й, е7, с.-, — средние квадратические погрешности определе-
ния g, I и 7.
Современный уровень изготовления маятниковых приборов
позволяет рассчитывать на измерение g с погрешностью не больше
0,1-10~5 м/с2, т. е. относительная точность должна быть не ниже
11СГ7 (поскольку g 980-10~2 м/с2).
Приняв в выражении (5.25) принцип равных влияний, т. е.
эффект каждого слагаемого одинаковым, и относительную точ-
ность определения g равной 1• 10-7, найдем допустимую погреш-
ность периода 7 и приведенной длины /:
8Г = (1 /2 /2). 1(Н7 = 3,5-10-«7; е, = (1 /]/2) 1О’7/ =0,71 -10’7/.
Следовательно, если для определения силы тяжести исполь-
зуется секундный маятник (7 ^1 с, / «== 1 м), то погрешность
102
измерения периода 'Г не должна превышать 3,510-sc, а длины I
(1,071 мкм. Для более короткопериодного маятника, например
пол усеку иди ого (Т — 0,5 с, I = 0,25 м), допустимые погрешности
должны быть соответственно в 2 и в 4 раза меньше:
ег=1,8-10"8 с; щ =0,018 мкм.
Абсолютные определения силы тяжести проводились во многих
точках земного шара, но не все они обладают необходимой точ-
ностью.
Абсолютное значение силы тяжести необходимо знать хотя бы
в одной точке. В настоящее время таким пунктом является Потсдам-
ский геодезический институт. К этому пункту отнесены все гра-
виметрические съемки мира. Абсолютное значение силы тяжести
здесь было определено Ф. КюненомиФ. Фуртвенглером под руко-
водством Ф. Гельмерта в 1898—1904 гг. Наблюдения проводились
по пяти оборотным маятникам, изготовленным из тонкостенных
латунных трубок разных форм и массы. На основании 192 опре-
делений выведено абсолютное значение силы тяжести
g- — (981 274 ± 3).10“® м/с2.
Это значение силы тяжести было положено в основу мировой
гравиметрической системы, которая называется потсдамской.
В 1936 г. в Вашингтоне в Национальном бюро стандартов
США П. Хейлом и А. Куком, а в 1935—1938 гг. в Теддингтоне
(Англия) Д. Кларком проведены абсолютные определения силы
тяжести. Приведение их к Потсдаму показало, что они значи-
тельно расходятся и с ним и между собой: расхождение с Потсда-
мом составляет соответственно—17-КГ® и —13 10”5 м/с2.
Все рассмотренные определения силы тяжести сделаны одним
методом — методом оборотного маятника. При современном со-
стоянии техники точность этого метода не может быть повышена
из-за ряда трудно учитываемых факторов: удлинения маятника
под действием собственного веса, изгибов стержня и деформации
ножевых опор, стачивания ножей, сложности и неточности изме-
рения приведенной длины и др. Поэтому для определения абсо-
лютного значения силы тяжести желательно использовать прин-
ципиально другие методы, погрешности которых имеют иной, чем
для оборотного маятника, характер.
В настоящее время, когда измерение малых промежутков вре-
мени достигло точности 1 10"8—1-Ю-9, большое значение для
абсолютных определений силы тяжести приобретает метод свобод-
ного падения тела, или баллистический. Этот метод основан на
швисимости пути s, пройденного телом, от ускорения свободного
падения g и времени t:
s = g/2/2. (5.26)
103
Если бы удалое!, u iMepii и. расстояние s и время t от действи-
тельного начала движения, то силу тяжести можно было бы вы-
числить 110 формуле
g ---2s//2. (5.27)
Однако и начале движения при своем освобождении падающее
тело может получить небольшое дополнительное ускорение. По-
этому рас. niHiiiie s и время t нельзя отсчитывать от начального
момента; их значения следует измерять между точками, находя-
щимися на пути падения тела. Тогда
sz = -ф gi?/2, (5.28)
где ц, скорость тела в начале отсчета времени.
Отсюда следует, что при измерениях от произвольного начала
необходимо определить по крайней мере два значения пути 8г
и s2 и соответствующие им отрезки времени ф и /2. Тогда
2 (з2ф—ьт/2) 2 / s2 Sj X -j.
ё - ~ (5.29)
В СССР такие измерения были осуществлены в 1955—1966 гг.
в Ленинграде в Научно-исследовательском институте метрологии
И. Н. Агалецкнм, К. Н. Егоровым и А. И. Марциняком.
В 1958 г. работы по определению абсолютного значения силы
тяжести проводились в Париже Ш. Воле. Была применена кино-
съемка падающего жезла. Подобный метод использовал Г. Пре-
стон-Томас в Оттаве в Национальном исследовательском совете
Канады (1960 г.).
Основное влияние на точность силы тяжести, определенной
методом свободного падения тела, оказывает погрешность изме-
рения линейных расстояний. Вследствие структуры формулы
(5.29) относительная погрешность значения g в несколько раз
превышает относительную погрешность длины.
Влияние этого фактора можно исключить, если бросать тело
вертикально вверх и замечать время, за которое оно проходит
определенный участок пути при подъеме и при последующем
падении. Если s — длина этого участка; ф — интервал времени
между двумя пересечениями телом нижней границы участка;
/2 — то же для верхней границы участка, то сила тяжести
g -— 8s/(/j — /о). (5.30)
В этом случае относительная погрешность силы тяжести g
равна относительной погрешности длины Этот способ имеет и
другое преимущество: силы, действие которых на движение тела
пропорционально его скорости, не изменяют интервалов вре-
мени /j и /2. Именно к таким силам относится сопротивление воз-
духа, оставшегося в вакуумной камере.
Подобный метод определения силы тяжести был использован
А. Куком в Национальной физической лаборатории Теддингтона
104
Рис. 5.3. Схема установки для абсолютного определения силы тя-
жести (Национальная физическая лаборатория, Теддингтон).
и 1965 г. (рис. 5.3). Подброшенный катапультой 1 стеклянный шар 2
пролетает через два стеклянных блока 3, каждый из которых
имеет по две щели. Шар действует как линза, фокусируя свет
ламп 5, идущий от одной щели, на другую. Момент, когда шар
пролетает мимо щели, регистрируется светочувствительным ус-
тройством 4\ одновременно интерференционным способом изме-
ряется расстояние между блоками 3 путем сравнения с эталоном
длины 6.
Метод свободного падения усовершенствовал А. Сакума в Меж-
дународном бюро мер и весов в Париже. Он предложил вместо
105
Рис. 5.1. Принципиальная схема установки Сакумы.
шара подбрасывать рефлектор, имеющий форму прямого трех-
гранного угла, — уголковый отражатель (рис. 5.4). Расстояние
регистрируется с помощью лазерного интерферометра Майкель-
сона. Эталоном длины при измерениях пути служит расстояние
между парой фиксированных зеркал на концах кварцевой трубки,
которое контролируется интерференционным методом и выра-
жается через длину световой волны. Время регистрируется спе-
циальным электронным счетчиком.
Опорный луч, заданный импульсным источником белого 2
или монохроматического 1 света, падает на полупрозрачное
зеркало <?, которым делится на два пучка. Один из них, пройдя
через зеркало 3, отражается базисным фиксированным уголковым
отражателем 4 и падает на зеркало 5 или 6. Отразившись от них,
свет возвращается тем же путем на зеркало 3, откуда он направ-
ляется вверх на зеркало 7 и фотоумножитель 8, контролирующий
электронно-счетное устройство 9. Второй пучок света зеркалом 3
направляется вниз на движущийся уголковый отражатель 14,
от которого луч попадает па неподвижное зеркало 15 и затем возвра-
щается тем же путем на зеркало 7, фотоумножитель 8 и счет-
чик 9
106
Существует два положения движущегося уголкового отра-
жателя 14, при которых длина пути лучей, направленных зерка-
лом 3 вверх и вниз, одинакова. Это нижнее положение / (верхний
луч при этом должен отражаться от зеркала 6), и верхнее положе-
ние 11 (верхний луч отражается от зеркала 5). Расстояние между
этими положениями падающего отражателя равно точно половине
интервала I между зеркалами 5 и 6. Таким образом, интенсивные
вспышки белого света получаются при двух положениях подвиж-
ного уголкового отражателя.
Запуск импульсного источника 2 осуществляется монохрома-
тическим источником 1, свет которого распространяется тем же
путем, как и вспышки, с той лишь разницей, что он проходит через
зеркало 7, фильтр 10 и фотоумножитель 11. Когда уголковый отра-
жатель приближается к одному из двух положений, при котором
длины путей обоих лучей интерферометра равны, монохромати-
ческие интерференционные полосы создают на выходе фотоумно-
жителя 11 синусоидальный ток с частотой, зависящей от скорости
движущегося рефлектора. Этот сигнал принимается и усиливается
двумя контурами 12, настроенными на разные, по определенные
резонансные частоты. Когда рефлектор приближается к одному
из положений «равного расстояния», интенсивность монохромати-
ческого сигнала возрастает и он включает импульсный генера-
тор 13, который в свою очередь запускает импульсный источник
света как раз к моменту, когда вспышка вследствие интерферен-
ции белого света имеет максимальную интенсивность.
Следование луча к зеркалу или 5, или 6 обеспечивается отвер-
стием в зеркале 5 и двумя масками а и б. Отверстие в зеркале 5
может быть закрыто одной из этих масок. При наложении маски а
луч проходит через зеркало 5 и отражается от 6; при наложении
маски б луч отражается от кольца вокруг отверстия зеркала 5.
Механическая система с помощью мотора 16 меняет положение
масок, а также подключает электрические фильтры к соответ-
ственно настроенным контурам 12 для управления импульсным
генератором 13.
При работающей маске а вспышка происходит в тот момент,
когда уголковый отражатель проходит нижнее положение, а при
маске б — верхнее. Таким образом, получаются четыре последо-
вательные вспышки в моменты времени: Ту и 7'4 — в нижнем
положении при движении отражателя соответственно вверх и
вниз и работающей маске б; Т.2 и Т3 — в верхнем положении при
движении соответственно вверх и вниз и маске а. Время, необ-
ходимое для смены масок и включения электрических контуров,
составляет около 0,2 с. Интервал между зеркалами 5 и 6 (прибли-
зительно 1 м) измеряется с относительной точностью порядка
1 10-9 и контролируется перед и после каждого цикла. Счетное
устройство 9, запускаемое импульсами белого света через фото-
умножитель 8, определяет временные интервалы с погрешностью
0,5 10’а с.
107
Зная интервалы времени iL --- Ti — Т} и /а — Т3 — Т2 и
расстояние s = 1/2, значение силы тяжести вычисляем по фор-
муле (5.30). При точности определения расстояния и времени
порядка l-10"s погрешность абсолютного значения силы тяжести
составляет около 0,002- ИГ6 м/с2.
Небезынтересно отметить некоторые детали установки.
Подвижный уголковый отражатель состоит из трех взаимно
перпендикулярных зеркал, смонтированных на металлической
рамке. На этой же рамке укреплен идентичный второй комплект
зеркал так, что оптический центр отражателя располагается
в центре тяжести всего устройства. Этим исключается влияние
малых вращательных движений падающего отражателя. Чтобы
компенсировать действие микросейсм на результаты измерений,
всю установку монтируют на сейсмически стабилизированном
столе. В каждом из его углов находятся по два пьезоэлектрических
устройства, расположенных одно над другим; верхние вырабаты-
вают электрические сигналы при проявлении любых сил сейсми-
ческого происхождения; эти сигналы интегрируются и в противо-
фазе подаются на нижние пьезоустройства. В результате поверх-
ность стола перемещается так, что ликвидируются последствия
сейсмических движений основания.
Принцип свободного падения использован X. Фаллером и
Р. Хаммондом в Национальном бюро стандартов США для созда-
ния транспортабельной (масса около 1 т) установки для абсолют-
ных определений силы тяжести (рис. 5.5). В этой установке при-
менены свободно падающий уголковый отражатель и неон-гелие-
вый лазерный интерферометр.
Луч от лазера /, пройдя точечную диафрагму 2 и коллиматор 3,
падает на главное разделительное устройство 4, которое делит
его на две части: одна идет вверх на свободно падающий уголко-
вый отражатель 5, другая — на опорный уголковый отража-
тель 6. Интерференционная картина, образованная лучами, отра-
женными от падающего и опорного отражателей, представляет
Рис. 5.5. Схема установки
Фаллера—Хаммонда.
108
собой движущиеся полосы, которые регистрируются фотоумножи-
телем 7. Поскольку длина волны лазера хорошо известна, рас-
стояние, пройденное свободно падающим отражателем, опреде-
ляется числом интерференционных полос, зарегистрированных
в течение точно измеренного интервала времени. Электронный
счетчик определяет время между целым числом полос с точностью
до 1-10"9 с.
Первоначальная скорость падающего уголкового отражателя
неизвестна, поэтому измерения выполняются в течение двух вре-
менных интервалов tx и /2, а значение g определяется по формуле
(5.29), которая принимает вид
= Z [Л/а -ЛГХ _ к _________________Лй_\
й tl — \ ia tx ) ’
где A—длина волны лазерного луча; N± и Na — число полос,
сосчитанных за два временных интервала (интервалы имеют одно
и то же начало счета, причем обычно вдвое больше /2).
Измерения, выполненные на этой установке, показали, что
она обеспечивает определение силы тяжести с погрешностью
0,05 1(Г® м/с2. Для достижения такой точности требуется устра-
нить многие мешающие факторы. В частности, камера, где падает
уголковый отражатель, имеет высокий вакуум; приняты меры
для исключения электростатических и магнитных влияний.
Важно, чтобы луч, падающий на отражатель, был строго вертика-
лен. Это обеспечивается ртутным горизонтом 8: луч отражается
«сам на себя» и рассматривается в микроскоп 9. Для учета микро-
сейсм предусмотрен сейсмометр. Установка сконструирована таким
образом, что бросание уголкового отражателя выполняется авто-
матически; высота его падения 1 м. Выходные данные регистри-
руются цифропечатыо на ленте. Одно измерение состоит обычно
из серии в 50 падений и продолжается в течение 30 мин.
С этой установкой X. Фаллер и Р. Хаммонд провели определе-
ние абсолютного значения силы тяжести в целом ряда пунктов
Американского континента, в также в Севре и Теддингтоне. Их
результаты сходятся с данными А. Сакумы и А. Кука в пределах
0,1 - 1СГ5 м/с2.
В СССР работы по абсолютному определению силы тяжести
методом свободного падения с применением интерференционных
способов измерения расстояний были начаты в конце 60-х годов.
В Сибирском отделении АН СССР создан прибор со свободно
падающим уголковым отражателем, время падения около 0,5 .с,
высота 1,25 м. Одно измерение включает серию примерно из
200 циклов и длится около 40 мин. Погрешность определения
силы тяжести составляет 0,025- 10~s м/с2. Масса прибора около
600 кг, он может транспортироваться.
Разработка транспортабельных установок для абсолютных
определений силы тяжести методом свободного падения сделала
возможным создание сети абсолютных гравиметрических пунктов
109
Таблица 5.1
Абсолютные определении силы тяжести
Пункт .Автор Год Сила тяжести, 10'fi м/с2
наблюден- ная дн в потсдам- ской си- стеме g Rn—g
Потсдам Кюнен, Фурт- 1904 98 1 274,0 981 274,0 —
венглер Шуллер 1969 981 260,1 981 274,0 — 13,9
Вашингтон Кук, Хейли 1936 S80 088,6 980 105,0 — 16,4
Т ейт 1965 980 101,8 980 115,0 — 13,2
Тедди него н Кларк 1938 981 183,2 981 196,2 -13,0
Кук 1967 981 181,81 981 195,77 - 13,96
Фаллер 1969 981 181,86 981 195,76 -13,90
Ленинград Агалецкпй, Егоров, .Марциияк 1956 981 919,3 981 931,4 —12,1
Париж (Севр) Тулин 1958 980 927,7 980 940,5 — 12,8
Фаллер> 1969 980 925,96 980 939,86 — 13,90
Сакума 1970 980 925,93 980 939,87 — 13,94
Оттава Престон-Томас 1960 980 613,2 980 627,9 — 14,7
и введение поправки в потсдамскую систему (табл. 5.1). Совре-
менные измерения показали, что значение силы тяжести в мировом
исходном гравиметрическом пункте завышено на 14-10'6 м/с2; по
новейшим данным в Потсдаме g 981 260,1 • ИГ5 м/с5.
Результаты абсолютных измерений, выполненных X. Фалле-
ром, Р. Хаммондом, А. Сакумой, А. Куком, явились основой
для международной гравиметрической опорной сети 1GSN-71
(International gravity standartization net 1971). Эта сеть реко-
мендована к применению XV Генеральной ассамблеей Между-
народного союза геодезии и геофизики (Москва, 1971 г.).
Подавляющее большинство гравиметрических измерений, вы-
полненных во всем мире, являются относительными. Чтобы все
определения силы тяжести в различных частях земного шара
привести в единую, потсдамскую, систему, каждое государство
имеет один или несколько пунктов, которые служат исходными
для всех гравиметрических наблюдений в данной стране. Некото-
рые из этих исходных национальных пунктов непосредственно
связаны с Потсдамом.
Определение абсолютного значения силы тяжести с высокой
точностью имеет особо важное значение в метрологии при уста-
новлении разного рода эталонов. В геофизике, геодезии и гео-
логии обычно используются не абсолютные значения силы тя-
жести, а аномалии, получающиеся как разность наблюденного и
нормального значения. Важно следить, чтобы в формуле нор-
110
малыюго распределения значение ge было выражено в той же
исходной системе, что и наблюденное значение силы тяжести,
t В этом случае аномалии силы тяжести содержат постоянную
ошибку и не зависят от неточного значения силы тяжести в Пот-
сдаме. Однако это справедливо только в том случае, если постоян-
ная ошибка системы мала по сравнению с величинами, которые
в формуле нормального распределения принимаются за малые
первого порядка (в данном случае по сравнению с коэффициен-
том |3).
ОТНОСИТЕЛЬНЫЕ ОПРЕДЕЛЕНИЯ
СИЛЫ ТЯЖЕСТИ МАЯТНИКОМ
Определение абсолютного значения силы тяжести весьма
сложно, требует длительного времени и для детального изучения
распределения силы тяжести на земной поверхности малопри-
годно. Поэтому уже в начале прошлого века для этой цели стали
применять относительный метод определения силы тяжести маят-
ником. Идея этого метода состоит в том, что на ряде пунктов
проводят наблюдения с одним и тем же маятником неизменной
приведенной длины и из этих наблюдений находят или отношение,
или разность силы тяжести в пунктах наблюдения.
Действительно, пусть мы имеем маятник с приведенной дли-
ной /, которая в общем случае нам не известна. Определим период
колебаний 7\ этого маятника в пункте с известным значением
силы тяжести gx. После этого найдем период колебаний Т3 маят-
ника в пункте с неизвестным значением силы тяжести Д.;. Если
приведенная длина маятника в процессе наблюдений осталась
неизменной, то можно написать
TL = я У l/gj\ 7'., . л ( l/g2. (5.31)
Возведя эти равенства в квадрат и почленно поделив, получим
gz/gi = Т~х/Т^ или g-> — g\ (5.32)
В этих формулах приведенная длина 1, трудно поддающаяся
определению, исключена, поскольку ее значение принято постоян-
ным. В этом состоит преимущество относительного способа опреде-
ления силы тяжести маятником перед абсолютным.
Основная формула относительных определений силы тяжести
маятником может быть переписана в более удобном для вычисле-
ний виде. Положим
| АТ = 71(1 | АТ/Л).
Тогда
& = &(! i АТ/Т,)-3;
ш
разложив выражение в круглых скобках в ряд по степеням
малого отношения кТ/1\, получим
g2 -gi = Ag = - 2gt (ЬТ/Ti) 4- 3fft (A 7 "Г'О • (5.33)
В большинстве случаев в правой части разложения можно
ограничиться только одним первым членом,
МАЯТНИКОВЫЕ ПРИБОРЫ
ДЛЯ ОТНОСИТЕЛЬНЫХ ОПРЕДЕЛЕНИЙ
СИЛЫ ТЯЖЕСТИ
Первые маятниковые приборы для относительных измерений
силы тяжести были сконструированы и применены профессором
Дерптского университета Ф. Г. Парротом в 1829 г. Позднее (1881 г.)
они были усовершенствованы австрийским геодезистом Р. Штер-
неком. Вскоре после этого берлинский механик Штюкрат построил
четырехмаятниковый прибор, который в течение долгого времени
оставался основным инструментом для определения силы тяжести.
В дальнейшем были разработаны и созданы более совершенные
конструкции маятниковых приборов, улучшена методика наблю-
дений. К настоящему времени насчитывается более 30 конструк-
ций маятниковых приборов.
В 40-х—50-х годах, когда были созданы высокопроизводи-
тельные и точные гравиметры, являющиеся основными гравиме-
трическими приборами в настоящее время, использование маят-
ников в гравиметрической разведке полностью прекратилось.
Однако гравиметры еще не могут конкурировать с маятниками,
когда речь идет об измерении больших приращений силы тяжести
при создании сетей опорных пунктов пли об очень длительных
промежутках времени между повторными наблюдениями.
В эти же годы были разработаны маятниковые приборы вы-
сокой точности, что позволило применить их для создания эта-
лонных исходных пунктов при развитии опорных сетей. Совре-
менные методы регистрации периодов колебаний маятников,
использование кварцевых эталонов частоты для учета времени
дадут возможность в перспективе создать такие конструкции
маятниковых приборов, которые по производительности и точ-
ности не будут уступать гравиметрам. В то же время маятниковые
приборы не имеют недостатков, присущих всем гравиметрам,
а именно большого смещения нуль-пункта.
Маятники конструируют таким образом, чтобы выполнялось
основное требование—сохранение постоянства приведенной длины.
Каждый маятниковый прибор состоит из трех основных ча-
стей: маятников, штатива и счетчика (регистратора). В комплект
маятникового прибора входят также хронометр и радиоприемник.
Современный маятник (рис. 5.6) представляет собой стер-
жень 2, па верхнем конце которого укреплена головка (стремя) 3
И2
с ножом 4 из твердого материала (кварц или
агат) и зеркалом 5, на нижнем — чечевицеоб-
разный груз 1. По числу маятников приборы
делятся на двух-, четырех- и шестимаятни-
ковые.
Штатив прибора изготовлен в виде массив-
ной отливки и служит для подвески в нем
маятников. Штатив имеет площадки из твердого
материала (агат), на которые опираются ножи
маятников при качании; арретирующее устрой-
ство, поднимающее маятники с опорных пло-
щадок; пусковое устройство, обеспечивающее
запуск маятников с заданной амплитудой и
фазой; оптическое устройство(мостик), посред-
ством которого свет от регистратора попадает
на зеркала маятников и возвращается обратно
к регистратору. Штатив маятника сверху за-
крывается колпаком, предохраняющим маятник
от пыли, резких колебаний температуры и
давления.
Счетчик (регистратор) предназначен для
определения периода и амплитуды колебаний
маятников. Применяют три метода наблюдений
за периодом колебаний: визуальный, фотогра-
фический и фотоэлектронный с цифровой реги-
страцией. В соответствии с этим различается и
устройство счетчиков.
При визуальном наблюдении (метод сов-
падений) оператор в зрительную трубу следит
за положением световых бликов, посылаемых
хронометром к маятнику. Поскольку периоды
маятников несколько больше или меньше полусекунды, то поло-
жение блика все время меняется. Если блик в некоторый момент
времени находится на нити зрительной трубы, то он вновь вернет-
ся туда только по прошествии целого числа колебаний. Если это
заняло с секунд, то маятник совершил 2с — 1 колебаний в зави-
симости от того, больше или меньше полусекуиды его период.
Период колебаний маятника определяется формулой
Т = с/(2с + 1).
Рис. 5.6. Маятник.
(5.34)
Таким образом, метод совпадений является своеобразным но-
ниусом времени, повышающим точность определения периода коле-
баний. Естественно, что погрешность уменьшится в п раз, если
найти продолжительность не одного, а п интервалов.
Применение фоторегистрации повышает точность определения
периода колебаний маятника, но требует значительного времени
па обработку результатов наблюдений. В наиболее совершенных
Рис. 5.7. Комплект маятникового прибора ОВМ.
маятниковых приборах используются фотоэлектронные способы
определения периода и амплитуды колебания маятников.
В ЦНИИГАиК под руководством М. Е. Хейфеца сконструи-
рован высокоточный вакуумный двухмаятниковый прибор ОВМ
(рис. 5.7), специально предназначенный для создания сети опор-
ных гравиметрических пунктов.
В комплект прибора входят штатив 2 с подставкой 3 и двумя
маятниками, фотоэлектронный регистратор 4 колебаний маятника
и пульт управления 1.
В приборе использованы кварцево-металлические полусекунд-
пые маятники, стержень маятника изготовлен из плавленого
кварца, чечевица — из вольфрама, головка — из инвара. Преиму-
щество такого маятника перед цельнометаллическим заключается
в слабой зависимости периода колебаний от температуры. Чече-
вица прикреплена к кварцевому стержню в своем центре тяжести,
малое термическое расширение кварца не вызывает заметных
изменений приведенной длины маятника.
Маятниковый штатив герметизирован и имеет электрический
термостат. Арретирное устройство с корректором обеспечивает
одинаковую посадку маятниковых ножей на опорные площадки,
пусковое устройство — одновременный пуск маятников в противо-
фазе. При транспортировке маятники из штатива не вынимают,
в штативе имеется специальное зажимное устройство, исключа-
ющее перемещение маятников при перевозке. Управление всеми
операциями при наблюдениях с маятниковым прибором осуществ-
ляется с пульта управления через реверсивный двигатель.
Период колебания маятника определяют с помощью специаль-
ного фотоэлектронного регистратора (рис. 5.8). Луч света от
лампочки осветителя проходит через конденсор и собирается
в плоскости передающей диафрагмы, расположенной в фокусе
объектива 1. Из этого объектива выходит параллельный пучок
114
Пульт управления
Рис. 5.Я. Блок-схема маятникового прибора ОВМ.
света, который после нескольких отражений от зеркал маятников
п оптического мостика направляется в объектив 2. В фокальной
плоскости этого объектива расположена приемная диафрагма,
за которой находится фотоэлектронный умножитель ФЭУ. Прием-
ная диафрагма имеет три параллельные щели: центральную (для
измерения периода колебаний маятника) и две крайние (для опре-
деления амплитуды колебаний).
Многократное отражение луча света от зеркал маятников позво-
ляет уменьшить продолжительность светового импульса, пада-
ющего на ФЭУ, в п раз (п — число отражений луча от каждого
зеркала маятника). Световой импульс от маятника преобразуется
ФЭУ в электрический и поступает в формирующие каскады,
после которых импульс включает спусковое устройство, управ-
ляющее работой двух пересчетных схем. Одна из них служит для
измерения числа колебаний кварцевого генератора с частотой
100 кГц, а вторая фиксирует число колебаний маятника. После
некоторого наперед заданного четного числа колебаний маятника
счет прекращается. Период колебаний Т маятника получают деле-
нием числа колебаний Q кварцевого генератора, которое указы-
вается пересчетным устройством, на произведение известного
целого четного числа колебаний N и частоты со кварцевого гене-
ратора:
'Г — Q/(<o/V).
Амплитуду колебаний маятника определяют также фотоэлек-
। ровным способом, измеряя пересчетным устройством время пере-
мещения светового блика между двумя крайними щелями прием-
115
ной диафрагмы. Специальная шторка, которая срабатывает от
спускового устройства, перекрывает центральную щель, и им-
пульс от маятника проходит через крайние щели. Период колеба-
ний маятника определяют из наблюдений в течение 15 мин с по-
грешностью 2 1 ГГ8 с, что соответствует погрешности силы тя-
жести 0,1 10 5 м/с2.
В 1974 г. в ЦНИИГАиК создан новый маятниковый прибор для
высокоточных измерений, получивший название «Агат». При этом
были учтены недостатки маятникового комплекта ОВМ. Прибор
«Агат» сделан более компактным, в 3 раза снижена масса всего
комплекта, уменьшено потребление энергии питания, преду-
смотрена возможность работы на аккумуляторах, что позволяет
использовать прибор в полевых условиях. Погрешность опре-
деления периода маятников за 10 мин наблюдений составляет
1 10-8 с, что соответствует погрешности силы тяжести 0,06 X
X ИГ'1 м/с2.
ПОПРАВКИ
В НАБЛЮДЕННЫЙ ПЕРИОД КОЛЕБАНИЙ
МАЯТНИКА ДЛЯ УЧЕТА ВНЕШНИХ ВЛИЯНИЙ
Теория колебаний маятника разработана в предположении,
что маятник колеблется в пустоте, с постоянной амплитудой, на
твердом основании и т. д. В реальных же условиях наблюденный
период искажен действием различных внешних факторов: темпе-
ратурой, плотностью воздуха, неустойчивостью штатива. Чтобы
учесть искажающее действие внешних условий на период коле-
баний маятника, приходится вводить целый ряд поправок.
Для приведения полученного значения периода к бесконечно
малой амплитуде вводят поправку за амплитуду
Да = Т - —(T/4)sin2(a/2)^—(Т/16)а2. (5.35)
Изменения температуры сказываются на приведенной длине
маятника, а следовательно, и на периоде его колебаний. Поэтому
все наблюдения приводятся к одной температуре /0. Поправка
за температуру
А, /I (/- Q -АД/-/0)а + 4(4Ш), (5.36)
где А и Л, — статические, Л2 — динамический температурные
коэффициенты; dt/dh — часовой температурный градиент.
Температурные коэффициенты маятника определяют экспе-
риментально, наблюдая его колебания при постепенном умень-
шении или увеличении температуры. Чтобы ослабить влияние
температуры, маятники изготавливают из материалов с малым
коэффициентом линейного расширения (кварц, инвар) или при-
меняют термостатировапие.
Колебания маятника в воздухе осложняются потерей веса
в соответствии с законом Архимеда, изменением момента инерции,
116
вызванным прилипанием воздуха к маятнику, и Трением о воздух,
что увеличивает затухание маятника. Суммарное влияние этих
факторов учитывается эмпирической формулой
До =•- — BD - В' (5.37)
где В и В1 — барометрические коэффициенты, определяемые
экспериментально; D — плотность воздуха, определяемая но
показаниям барометра, психрометра и термометра.
Наблюденный период колебаний маятника измеряется в се-
кундах по хронометру или кварцевым часам. Поскольку любые
часы идут неточно, необходимо в наблюденный период ввести
поправку за суточный ход w хронометра:
Ч 115’77w-1C)'7’ <5’38)
Положив в этой формуле Т„ — 0,5 с, получим Дг -=w58wX
X ИГ7 с, т. е. для определения поправки с погрешностью до
1- 10 т с суточный ход хронометра надо знать до 0,02 с. Суточный
ход хронометра находят по радиосигналам точного времени, пере-
даваемым службой времени ведущих астрономических обсерва-
торий. При современных маятниковых наблюдениях вместо хроно-
метров используют термостатированные кварцевые часы. При
хорошем термостатировании (до 0,01° С) кварцевые часы в течение
длительного времени имеют ход менее 0,001 с в сутки, что прак-
тически исключает необходимость поправки за ход хронометра
и резко сокращает продолжительность наблюдений на пункте.
При колебаниях маятника верхняя часть штатива начинает
раскачиваться, что искажает наблюденный период колебаний.
Это явление называется сокачанием штатива. Для уменьшения
сокачания помещают в одной плоскости два одинаковых по длине
маятника и заставляют их раскачиваться с одинаковой амплитудой
в противофазе. Поскольку точно условие одинаковой длины не
выполняется, то оставшееся влияние сокачания штатива учиты-
вают введением поправки &та-
В современных маятниковых приборах для исключения по-
правки за сокачание штатива применяют особый метод наблюдении,
предложенный Ф. Венингом Мейнесом для маятников на неустой-
чивом основании (см. главу 8). Идея заключается в том, что на
одной подставке качаются в одной вертикальной плоскости два
практически изохронных маятника и фотопутем регистрируются
разности амплитуд и фаз этих маятников, свободные от возмуща-
ющих ускорений, действующих на штатив прибора. Этот метод
наилучшим образом исключает влияние сокачания штатива на
период колебаний маятника.
Все вычисленные поправки вносят в наблюденный период ко-
лебаний маятника и получают исправленный период
1 А/+ Ад А/д J (5.39)
117
Периоды определяют несколько раз и из исправленных пе-
риодов колебаний каждого маятника находят средний, который
используют для вычисления приращения силы тяжести по фор-
муле (5.33).
Маятниковые пункты, определенные в 1932—1945 гг., равно-
мерно размещены почти по всей территории СССР. В зависимости
от точности силы тяжести их относят к одному из трех классов:
с погрешностью (1 н-2)-10 5 м/с2 к первому классу, (2-~3)- 10“ м/с2
ко второму, (Зч-5)-10 8 м/с2 к третьему. Большинство маятнико-
вых пунктов, наблюденных до 1946 г., соответствует третьему
классу. В последующие годы по мере усовершенствования маят-
никовых приборов значительно повысилась точность определения
силы тяжести. В частности, кварцево-металлические маятниковые
приборы ЦНИИГАиК позволяют проводить измерения с погреш-
ностью, не превышающей 0,5 10 8 м/с2.
УПРУГИЙ МАЯТНИК
Кроме обычных маятников для определения силы тяжести при-
менялись упругие маятники, созданные в 30-х годах во Франции
Р. Леже и Ф. Хольвеком, а в СССР Г. И. Рудаковским и М. Е. Хей-
фецем.
Упругий маятник (рис. 5.9) представляет собой стержень,
обычно кварцевый, в нижний конец которого заделана плоская
пружина, изготовленная из элинвара. Если маятник под дей-
ствием силы тяжести и упругой силы пружины находится в равно-
весии, характеризуемом углом ср0, а затем, будучи отклоненным
от этого положения, начинает совершать колебательные движения,
то это движение можно описать уравнением
Рис. 5.9. Упругий
маятник.
/ (efep/d/2) — т (ср — ср0) + mgl sin ср, (5.40)
где 1 — момент инерции маятника; —т (ср —
— Фо) — момент упругой силы пружины; т —
постоянная упругости пружины; mgl sin ср —
момент силы тяжести.
Пренебрегая ср0 и принимая ввиду малости
угла sin ср яь ср, получаем
/ (d2cp/d(2) = —(т — mgl) ср. (5.41)
Уравнение (5.41) подобно уравнению движе-
ния обычного маятника. Поэтому период ко-
лебаний
7' = л У //(т — mgl); (5.42)
полагая H(jnl) = L, где L приведенная дли-
на упругого маятника, и т/(щ/) : с, получаем
Т — л ] Е/(с — g). (5.43)
118
Из этого уравнения следует, что период колебаний упругого
маятника определяется не полной величиной g, а разностью между
постоянной с и силой тяжести g. Значение с можно сделать весьма
близким к g, тем самым уменьшив требования к точности опреде-
ления периода. В сконструированных маятниках 1=6 см,
Т«3с, с — g^6,610-2 м/с2. Для измерения силы тяжести
с погрешностью 1 10~5 м/с2 период требуется найти с погреш-
ностью 2-10"4 с, что может быть обеспечено хорошим секундо-
мером в течение 10 мин.
По точности упругие маятники не уступали обычным маятни-
кам при значительно большей производительности, однако они
имели ряд существенных недостатков: сильную чувствительность
к наклону, очень быстрое затухание, изменение упругих свойств
пружины с течением времени. С появлением статических грави-
метров упругие маятники не применяются.
струнный гравиметры
К динамическим приборам для относительных определений
силы тяжести относятся струнные, или, как их иногда называют,
динамические, гравиметры. Идея струнного гравиметра была
впервые предложена в 30-х годах Л. И. Мандельштамом и
Г. П. Папалекси. Если подвесить массу на тонкой металлической
нити (струне), верхний конец которой закреплен неподвижно, то
натяжение струны, а следовательно, и период ее колебаний будут
зависеть от веса подвешенной массы, длины и веса струны. При
постоянных параметрах струны и груза изменения силы тяжести
проявляются в изменении частоты колебаний струны.
Первый макет действующего
струнного гравиметра был со-
здан в 1948 г, Р. Джильбертом
в Кембриджском институте гео-
дезии и геофизики. Испытания
проводились на подводной лод-
ке, при этом была получена
средняя квадратическая по-
грешность измерений2- 10-5м/с2.
В СССР несколько моделей
струнных гравиметров было
разработано во ВНИИГеофизи-
ке под руководством А. М. Ло-
зинской.
Рассмотрим схему струнного
гравиметра (рис. 5.10). Масса 1
подвешена на струне 2. Чтобы
можно было измерить частоту
колебаний струны, необходимо
сделать их незатухающими. Для
Рис. 5.10. Схема струнного гравиметра.
этого струна помещена между полюсами постоянного магнита 3 и
включена в колебательный контур с усилителем и положительной
обратной связью. Если на концы струны подать переменное напря-
жение, то струна начнет вибрировать. Изменение силы тяжести
регистрируется как изменение частоты генератора, что устанавли-
вается сравнением с частотой эталонного генератора. Чтобы обес-
печить необходимое демпфирование, массу делают из красной
меди в виде полого цилиндра и помещают ее между полюсами
магнита 4. От перемещения в горизонтальном направлении масса
удерживается тонкими горизонтальными нитями с малой упру-
гостью.
Частота колебаний идеально гибкой струны связана с силой
тяжести уравнением
! J_ 1 / HL = _L | ' (5 44)
1 ~ 21 V ?. 21 F п.$ ’ 1
где т — масса груза; I — длина, Z — линейная плотность, а —
объемная плотность, S — площадь поперечного сечения струны.
Логарифмируя и дифференцируя уравнение (5.44) по пере-
менным f и g, получаем связь изменения частоты с изменением
силы тяжести:
dg/g 2(d[/l). (5-45)
Отсюда следует, что для определения силы тяжести с погреш-
ностью 1-10”® м/с2 измерение частоты должно быть выполнено
с относительной точностью 0,5-10”6.
В струнном гравиметре ВНИИГеофизики в качестве струны
использована лента из бериллиевой бронзы сечением 0,25x0,05 мм
и длиной 50 мм; масса груза около 100 г, что дает частоту колеба-
ний струны около 1 кГц. Для определения силы тяжести с погреш-
ностью Г 10”® м/с2 частоту необходимо измерять до 5-10"4 Гц.
Приращение частоты !\f находят по счетчику фаз:
АМ{л^»1)/М. (5.46)
где п2 — zij — разность отсчетов; /2—4 — интервал времени счета.
Значение Af с допустимой погрешностью можно получить
за время менее 4 мин. При увеличении интервала времени счета
точность определения Д/ повышается.
Формула (5.44) справедлива только для идеально гибкой и ие-
растяжнмон струны. С учетом реальной жесткости струны в фор-
мулу вводится дополнительный множитель, при этом частота
колебаний струны повышается не более чем на 1—3%. Изменение
модуля упругости струны мало влияет на частоту ее колебаний,
поэтому действиетемпературы сказывается только на длине струны,
что является достоинством прибора. К достоинствам прибора надо
отнести также частотный выход результатов измерений, что
позволяет легко приспосабливать прибор для дистанционных
120
наблюдений, применять вычислительную технику. Некоторые
конструкции гравиметров разработаны для измерения силы тя-
жести па море и в буровых скважинах (см. главу 7).
Глава 6
СТАТИ Ч ЕС К И Е МЕТОДЫ
ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ
ОБЩИЕ СВЕДЕНИЯ
О СТАТИЧЕСКИХ ГРАВИМЕТРАХ
Статические методы измерения приращений
силы тяжести в настоящее время распространены наиболее ши-
роко. На статическом принципе создано несколько десятков раз-
личных конструкций гравиметров, и по объему наблюдений силы
тяжести статические гравиметры практически вытеснили маят-
никовые приборы.
Современные статические гравиметры — это легкие, портатив-
ные приборы, позволяющие измерять приращение силы тяжести
с высокой точностью при большой производительности, что и обес-
печило их широкое применение в гравиразведке. Большинство
современных гравиметров способны определять приращения силы
тяжести с погрешностью (0,14-0,02)-КГ5 м/с2, а специальные
гравиметры до 0,001 -КГ5 м/с2.
Продолжительность наблюдения с гравиметром на пункте
составляет 3—5 мин, т. е. производительность в основном зависит
от расстояния между пунктами и средств транспортировки прибо-
ров. Самый процесс наблюдений с гравиметрами значительно
проще, чем с маятниками.
Небольшая масса гравиметров позволяет использовать их
в различных полевых условиях, в малодоступных и труднопро-
ходимых районах. Специальные конструкции гравиметров можно
опускать на дно моря или устанавливать на корабле для морских
наблюдений.
Но наряду с такими важными преимуществами перед маятни-
ковыми приборами, как точность, высокая производительность
и транспортабельность, гравиметры имеют и ряд недостатков.
Наиболее существенным из них является смещение нуль-пункта,
происходящее вследствие необратимых изменений в материале,
из которого изготовлена упругая система гравиметра. Смещение
нуль-пункта, присущее в большей или меньшей степени всем гра-
виметрам, приводит к непрерывному изменению показаний. Для
контроля за нуль-нунктом приходится выполнять повторные на-
блюдения и вводить поправки.
Измеренные гравиметрами значения силы тяжести выражаются
в делениях шкалы прибора. Для вычисления приращения силы
121
тяжести в тех или иных конкретных единицах (миллигалах;
метрах на секунду в квадрате) необходимо установить переводной
коэффициент, называемый ценой деления гравиметра. Операция
определения цены деления называется эталонированием и является
одним из наиболее ответственных и сложных исследований грави-
метра (при маятниковых наблюдениях такой проблемы не суще-
ствует). Требуемая точность цепы деления гравиметра зависит
от максимального значения измеряемой разности силы тяжести,
а также от заданной погрешности наблюдений. Например, если
требуется измерить разность силы тяжести 1000-КГ6 м/с2 с по-
грешностью до 0,1-1СГ5 м/с2, то точность цены деления грави-
метра должна быть не ниже Г 10~4. Эталонирование гравиметра
с такой точностью является очень сложной задачей и требует
специальных исследований и приспособлений. Часто ограничи-
ваются точностью 1-10“8, в этом случае ошибка составляет 0,1 X
X Ю”6 м/с2 при измерении разности силы тяжести 100- 10~5 м/с3.
В отличие от маятниковых приборов, диапазон измерений
с которыми не ограничен, гравиметрами можно определять при-
ращения силы тяжести, амплитуда которых зависит от конструк-
ции гравиметров и их точности. Некоторые типы гравиметров
обладают большим, практически не ограниченным диапазоном
(3-:- 5)10 2 м/с2. Такие гравиметры получили название геодезиче-
ских, так как именно для геодезических целей приходится изме-
рять очень большие приращения силы тяжести. Большинство
гравиметров, используемых в гравиразведочной практике, обла-
дает диапазоном непрерывного измерения силы тяжести (100—j—
4-200) • 10”5 м/с2. Некоторые специальные типы гравиметров имеют
диапазон всего до 10- 10~ь м/с2.
Несмотря на ряд бесспорных преимуществ гравиметров перед
маятниковыми приборами, заменить их полностью гравиметры
пока не могут. Маятниковые приборы используют для создания
равномерной сети гравиметрических пунктов на всей поверхности
Земли, для привязки к этой сети наблюдений с гравиметрами и
приведения их в единую абсолютную систему.
Разнообразные конструкции статических гравиметров могут
быть объединены в группы по ряду общих признаков. По роду
упругой силы, которая уравновешивает силу тяжести, различают
три группы гравиметров: газовые, жидкостные и механические.
Газовые гравиметры — приборы, в которых сила тяжести
уравновешивается упругостью газа, заключенного в ограничен-
ном объеме, или давлением атмосферного воздуха. В настоящее
время эта группа гравиметров не имеет практического применения
из-за низкой точности, так как упругость газа очень сильно за-
висит от температуры.
Жидкостные гравиметры — приборы, в которых уравновеши-
вающей силой выступают капиллярные силы жидкости. Грави-
метры этого типа также не получили широкого распростра-
нения.
122
Механические гравиметры — приборы, в которых сила тяже-
сти уравновешивается упругостью твердых тел: металлов или
кварца. В настоящее время используются приборы только этой
группы. Механические гравиметры в зависимости от материала
упругой системы делятся на две подгруппы: металлические (упру-
гая система из металла или специальных сплавов) и кварцевые
(система из плавленого кварца).
Все статические гравиметры, по сути дела, являются высоко-
точными пружинными весами, на которых взвешивается один
и тот же груз постоянной массы. Мерой изменения силы тяжести
служит деформация упругого элемента. Регистрация деформации
осуществляется либо путем непосредственного отсчета положения
деформированной системы с помощью укрепленного на ней
индекса, либо, что наиболее распространено, компенсационным
способом. В этом случае с помощью вспомогательных устройств
создается дополнительное усилие, компенсирующее изменение
веса постоянной массы гравиметра, и упругая система приводится
в одно и то же — нулевое — положение. Усилие компенсацион-
ного устройства является мерой изменения силы тяжести.
В Советском Союзе основные требования к гравиметрической
аппаратуре для наземных и морских относительных измерений
силы тяжести устанавливаются государственными стандартами
(ГОСТ 14009—68. Приборы для гравиметрических исследований.
Типы. Основные параметры и нормы точности. ГОСТ 13017—73.
Гравиметры наземные. Основные параметры. Технические требо-
вания).
Согласно стандартам гравиметры в зависимости от их назначе-
ния подразделяются на следующие типы.
1. Наземные — для измерения приращений силы тяжести на
суше.
2. Донные — для измерений на дне водоемов.
3. Морские надводные — для измерений с надводных судов.
4. Морские подводные — для измерений с подводных судов.
5. Аэрогравиметры — для измерений с самолетов.
6. Скважинные — для измерений в скважинах.
7. Специальные — для измерений вариаций силы тяжести,
для съемки с космических аппаратов и т. п.
ФИЗИЧЕСКИЕ СВОЙСТВА
УПРУГИХ МАТЕРИАЛОВ,
ПРИМЕНЯЕМЫХ В ГРАВИМЕТРАХ
Главной частью любого гравиметра является его упругая, или
чувствительная, система, деформация которой под действием
веса груза служит мерой изменения силы тяжести. Упругая
система должна обладать высокой степенью постоянства упругих
свойств во времени, линейной зависимостью деформации от изме-
нения нагрузки и неизменностью упругих свойств при колебаниях
123
температуры. Для изготовления систем выбирают или специально
разрабатывают материалы, наилучшим образом удовлетворяющие
этим требованиям.
Применение упругих тел в механических гравиметрах основано
на законе Гука, согласно которому деформация упругого тела
пропорциональна напряжению. Однако закон Гука не полностью
описывает характер деформации тела под действием приложенного
к нему напряжения. Он является лишь первым приближением для
выражения действительной деформации тела, поскольку рассма-
тривает деформацию как чисто механическое движение, отвле-
каясь от физической природы упругих тел, их молекулярного
строения, влияния теплового движения и т. д.
По закону Гука деформация упругого тела (рис. 6.1) харак-
теризуется двумя коэффициентами пропорциональности: при рас-
тяжении и изгибе модулем Юнга Е
E(hL/L) -P^F/S,
а при кручении или сдвиге модулем сдвига G
GG = P = P/S,
где Р — нагрузка или напряжение, отнесенное к единице пло-
щади поперечного сечения; F — внешняя сила, приложенная
к телу; S — площадь поперечного сечения; L — первоначальная
длина; АЛ — удлинение при растяжении под действием напря-
жения, направленного по нормали к поперечному сечению; 0 —
угол сдвига, вызываемого касательным напряжением при кручении.
При определении механических характеристик материала со-
ставляют диаграмму деформации (рис. 6.2), на которой по оси
абсцисс откладывают относительное удлинение AL/L или угол
сдвига 0, а по оси ординат напряжение Р.
Рис. 6.1. Деформация упругого
тела.
Участок О А диаграммы со-
ответствует упругим обратимым
деформациям, удовлетворяющим
закону Гука. Напряжение,"при
котором прямая пропорциональ-
ность нарушается, называется
Рис. 6.2. Диаграмма дефор-
мации.
124
пределом пропорциональности (точка Р„).
На участке АВ деформация растет быст-
рее, чем на участке ОА, и носит частично
пластический характер. Наибольшее на-
пряжение, при котором с уменьшением
нагрузки еще не обнаруживается замет-
ной деформации, называется пределом
упругости (точка Ру). Практически пределы
упругости и пропорциональности не раз-
личаются между собой.
На участке ВС деформация растет поч-
Рис. 6.3. Упругое после-
действие.
ти без изменения нагрузки и носит целиком пластический харак-
тер. Материал начинает течь. На диаграмме образуется площадка,
почти параллельная оси абсцисс. Точка С характеризует поло-
жение, когда при постоянной нагрузке остаточная деформация
распространяется по всему объему тела, она называется пределом
текучести (точка Рт). Дальнейшее увеличение нагрузки вызывает
в материале способность вновь сопротивляться растяжению (или
сдвигу), но только до некоторого предела нагрузки. По достиже-
нии этого предела наступает разрыв (точка D). Нагрузка, дей-
ствующая в момент разрыва на единицу первоначальной площа-
ди поперечного сечения, называется пределом прочности или
временным сопротивлением R.
Экспериментальные исследования показывают, что закон Гука
справедлив только в некоторых пределах участка ОА, длина ко-
торого определяется точностью измерения. Упругие элементы
гравиметра могут работать удовлетворительно только в том слу-
чае, если они деформируются в пределах линейной зависимости
между деформацией и нагрузкой без следов остаточной деформации.
Остаточная деформация не должна превышать 1СГ8 от полной
деформации, что значительно меньше предела, который допускается
при проектировании многих других конструкций.
Каждый материал характеризуется своей диаграммой дефор-
мации. В частности, плавленый кварц имеет диаграмму, которая
обрывается, не дойдя до точки В, т. е. пределы прочности и упру-
гости практически совпадают. У металлов деформация суще-
ственно зависит от режима их термической и механической обра-
ботки. Применяя соответствующую технологию обработки метал-
лов, предел их упругости можно существенно повысить. Остаточ-
ная деформация снижается также с уменьшением нагрузки.
Полагают, что если напряжение не превосходит 20 % от предела
упругости, то остаточная деформация мала и на работу грави-
метра существенно не влияет.
Упругая деформация зависит от времени. Эта зависимость про-
является в упругом последействии, ползучести и упругом гисте-
резисе. Упругое последействие (рис. 6.3) состоит в том, что после
приложения внешней силы при постоянном напряжении Рг де-
формация принимает свое конечное значение не сразу, а прибли-
125
жается к нему асимптотически в течение некоторого времени.
При уменьшении напряжения от до Р2 новое значение деформа-
ции устанавливается также за некоторое время.
Для уменьшения упругого последействия пружины гравиме-
тров все время находятся в растянутом состоянии, близком к ра-
бочему. В металлических гравиметрах с арретирным устройством
пружина закрепляется в растянутом состоянии. В кварцевых
гравиметрах, где упругая система не арретируется, упругое после-
действие вызывает разную скорость смещения нуль-пункта в ста-
ционарных условиях и при транспортировке, когда упругий
элемент подвергается изменяющейся нагрузке. Как правило, при
транспортировке смещение нуль-пункта возрастает.
При измерении больших приращений силы тяжести, пере-
стройке диапазона измерений деформация пружины значительно
меняется. Упругое последействие проявляется в изменении пока-
заний гравиметра на одном и том же пункте в течение нескольких
минут. Поэтому при перестройке диапазона необходимо выждать
некоторое время, пока отсчет гравиметра не установится, т. е.
пока не будет достигнута окончательная деформация. Применяя
специальную термическую и механическую обработку металлов,
влияние упругого последействия можно уменьшить.
Ползучесть предсталяет собой процесс малой непрерывной
пластической деформации при длительно действующих постоян-
ных нагрузке и температуре. Ползучесть материала проявляется
начиная с некоторой температуры и увеличивается при повышении
температуры и нагрузки. Развитие ползучести в процессе работы
упругого элемента протекает в три этапа (рис. 6.4). Первый этап
(а) — скорость ползучести велика, но вследствие упрочения ма-
териала постепенно стабилизируется, принимая постоянное значе-
ние; второй этап (6) — скорость постоянна; третий этап (с) — из-за
разупрочения материала скорость возрастает и материал разру-
шается. Искусственным старением материала, подвергая его дей-
ствию повышенных температур и нагрузок, удается снизить пол-
зучесть до малых значений.
Упругий гистерезис состоит в том, что при повторяющихся
нагрузках и разгрузках деформаци
дый данный момент зависит не
только от действующей нагрузки,
но и от той, которая ей предшест-
вовала (рис. 6.5). При одной и
не строго одинакова и в каж-
Рис. 6.5. Упругий гистерезис.
126
той же нагрузке Р тело может иметь меньшую деформацию &LJL,
если до этого оно испытывало напряжение меньше Р, и большую
деформацию &.LJL, если предшествующее напряжение было
больше Р.
Все рассмотренные явления, выходящие за пределы действия
закона Гука, называются несовершенствами упругости. Источ-
ники их в настоящее время изучены еще недостаточно. Замечено,
что несовершенства упругости резко усиливаются при повышении
температуры. Именно температурные колебания являются тем
фактором, который оказывает на упругие системы гравиметров
наибольшее влияние. С изменением температуры изменяются раз-
меры и упругие свойства системы. Естественно, что влияние тем-
пературы надо уменьшить до значения, не превышающего чувстви-
тельности гравиметра. Решение этой задачи является одной из
сложнейших проблем как при изготовлении материала, так и при
конструировании самой системы гравиметра.
Изменение линейных размеров L тела при изменении темпе-
ратуры определяется коэффициентом линейного расширения мате-
риала а:
L = LO(1 Ч-а/),
где Lo — длина тела при I = 0° С.
Это равенство справедливо при малых изменениях темпера-
туры. При значительных перепадах температуры приходится
учитывать, что коэффициент а сам является функцией темпера-
туры: а а (0-
Модули упругости Е и G также зависят от температуры:
£ = £о(14-®0; G = G0(l-|-y/),
где е и у — температурные, или термоэластические, коэффициенты
модулей упругости первого и второго рода.
Коэффициенты 8 и у так же, как и а, являются функциями
температуры (табл. 6.1).
Таблица 6.1
Температурные коэффициенты материалов
Материал а, 10*в к, 10-« у, 10’“
Дюралюминий бронза фосфористая Сталь (разные марки) Киари плавленый Вольфрам "пшвар (разные сплавы) 1 luuopoKC 1 1 ч ичластик -(-23 + 17 + 10 : +12 +0,5 -1-4 -6 ч-+6 —583 —380 240+—280 + 120 —95 —40Ч-+20 —5++2 -5+0 —551 —411 —260-: -280 120 —06 —40 ч- -20 —Зч-+5 —4+0
127
Приведенные значения коэффициентов являются приближен-
ными, отражающими порядок указанных величин. Из таблицы
видно, что термоэластнческие коэффициенты значительно больше
коэффициента линейного расширения, они и определяют чувстви-
тельность гравиметра к температурным изменениям. Например,
если пружина изготовлена из материала с температурным коэф-
фициентом порядка 100-10"6, то при изменении температуры на
1° С показания гравиметра изменяются на 100- 10~6g, или на
100- 10 й м/с3. Чтобы избежать такого сильного влияния темпе-
ратуры, желательно иметь материалы с нулевыми или близкими
к пулю термоэластическимп коэффициентами.
Для изготовления упругих элементов металлических грави-
метров применяют специальные гравиметровые стали (элинвар,
изоэластик, ниворокс). Эти стали представляют собой железо-
никелевые сплавы, различающиеся между собой не столько со-
держанием железа и никеля, сколько малыми примесями других
элементов (например, бериллия), а также особенностями холодной
обработки и закалки. Эти сплавы менее подвержены упругому
последействию и ползучести. Но все железоникелевые сплавы
магнитны, поэтому изготовленные из них системы приходится
защищать от действия земного магнитного поля.
Кроме специальных гравиметровых сплавов упругие системы
изготавливают также из плавленого кварца. Плавленый кварц
имеет высокий предел упругости и прочности, обладает незначи-
тельным упругим последействием, немагнитен. Кварцевое стекло
сравнительно легко поддается обработке. Из него можно тянуть
тончайшие нити, навивать пружины и т. д. Однако плавленый
кварц обладает некоторыми существенными недостатками. У него
большой термоэластический коэффициент (-(-120- 10-е), который
к тому же сам является функцией температуры. Кроме того,
плавленый кварц с течением времени раскристаллизовывается,
что ухудшает его упругие свойства. Кварц отличается большей,
чем у сплавов, ползучестью, правда, достаточно постоянной
во времени.
Системы современных гравиметров изготавливают с пружинами
как из металла, так и из плавленого кварца. По точности измере-
ний нельзя определенно сказать, какой материал предпочтитель-
нее. В СССР наибольшее применение получили кварцевые грави-
метры.
ЭЛЕМЕНТЫ ТЕОРИИ
МЕХАНИЧЕСКИХ ГРАВИМЕТРОВ
Основной частью механического гравиметра является упругая
система. Деформация в упругой системе возникает под действием
веса груза или его момента, которые зависят от силы тяжести.
Приращение деформации упругого элемента и служит мерой изме-
нения силы тяжести.
128
Уравнение равновесия
При рассмотрении теории гравиметра будем полагать, что
система имеет только одну степень свободы и при изменении
силы тяжести масса может совершать или поступательное, или
вращательное перемещение.
Пусть х — деформация упругой системы, регистрируемая не-
которым индексом, связанным с перемещающейся массой. Тогда
момент массы упругой системы относительно оси вращения
М (х) = J г cos a dm,
V
где г — расстояние от оси вращения до элемента массы dm-,
а — угол, составленный направлением г с горизонтальной пло-
скостью.
Интегрирование распространяется на все массы системы.
Если значение g в объеме системы постоянно, момент силы тяже-
сти равен gM (х). Моменту силы тяжести противодействует мо-
мент W (х) внутренних упругих сил системы относительно оси вра-
щения. В общем случае упругая система может быть снабжена
дополнительными массами или пружинами для повышения чув-
ствительности к изменению силы тяжести, а также для настройки
гравиметра па рабочий диапазон измерений, приведения груза
в исходное (нулевое) положение и т. д. Поэтому момент W (х)
охватывает всю сумму моментов внутренних сил, возникающих
в результате деформации всех элементов упругой системы грави-
метра, т. е.
IF(x)^-S Wf(x).
i
Момент внешних сил, действующих на систему, в основном
определяется силой тяжести. Но кроме силы тяжести на упругую
систему могут оказывать действие магнитные и электрические поля
(если упругая система магнитна и способна электризоваться).
Поэтому в общем случае момент gM (х) определяется совокупным
действием всех внешних сил, действующих на систему:
ЯМ(х) = я£ М,.(х).
i
В момент измерения система гравиметра находится в состоянии
равновесия, т. е. сумма всех внешних и внутренних сил, действу-
ющих на систему, или сумма их моментов равна нулю. Тогда
уравнение равновесия системы с вращательным перемещением
массы можно записать в виде
gM(x) + F(x) = 0. (6.1)
В. С. Миронов
129
Для системы с поступательным перемещением массы вместо
моментов сил в уравнение равновесия войдут сами действующие
силы:
mg-\-fx—0, (6.2)
где т — перемещающаяся масса; х — полная деформация упру-
гой системы; / — жесткость упругой системы, зависящая от раз-
меров и упругости системы.
Упругая сила деформации и ее момент могут изменяться под
влиянием температуры i. Вес подвижного груза и его момент
зависят от температуры t, атмосферного давления р, угла наклона
системы |3. Поэтому в общем случае момент IF является функ-
цией аргументов х и I, а момент М — функцией аргументов х,
I, р и р. Тогда
gM (х, t, р, Р) + W (х, I) = 0. (6.3)
В дальнейшем изложении переменные, стоящие в скобках,
для краткости опускаются. Дифференцируя выражение (6.3) по
всем переменным, получаем основное уравнение упругой системы
гравиметра:
/ дМ J 0W \ dx . / о cW . ar \ dt . дМ dp
Ox r дх / dg b \Й dt а/ / dg ' g др ' dg
+ ё'4г'-4-~'1л',=о- (б-4)
1 s ар dg 1 ' '
Величина dx/dg характеризует изменение деформации упругой
системы в зависимости от приращения силы тяжести и называется
механической чувствительностью гравиметра; dgldt характеризует
влияние температуры на показания гравиметра и называется
температурным коэффициентом; dg/dp характеризует барометри-
ческий эффект гравиметра и называется барометрическим коэф-
фициентом; dg/dfi определяет зависимость показаний гравиметра
от угла наклона упругой системы.
Чувствительность гравиметра
Положив в основном уравнении t, р и |3 постоянными, получим
уравнение чувствительности гравиметра:
dg \& дх 1 дх / v '
Из этого уравнения следует, что чувствительность гравиметра
в общем случае зависит от х. Первым сомножителем является
масса или момент масс, а вторым — сумма производных по х
от силы тяжести и упругой силы или от моментов силы тяжести
п упругой силы, показывающих относительные скорости измене-
ния этих величин по сравнению с изменением х. Согласно урав-
130
нению равновесия моменты gM и W и их производные должны
иметь противоположные знаки. Очевидно, чем меньше второй
сомножитель (знаменатель) выражения (6.5) (сумма скоростей
изменения моментов силы тяжести и упругой силы), тем выше
чувствительность системы, т. е. чувствительность зависит от ха-
рактера изменения моментов М и W.
Рассмотрим гравиметр с поступательным перемещением массы.
Простейшей системой такого гравиметра является спиральная
пружина, работающая под действием груза на растяжение в пре-
делах пропорциональности. В этом случае, дифференцируя урав-
нение равновесия этой системы (6.2), имеем
dx/dg = — m/f = x/g, (6.6)
т. е. чувствительность гравиметра пропорциональна полной де-
формации х. Получить высокую чувствительность такой системы
можно либо увеличением массы, либо уменьшением жесткости
пружины, т. е. необходимы большие начальные деформации.
Однако такие деформации нежелательны, так как они ухудшают
работу упругого элемента. Поэтому в подобных системах достиг-
нуть высокой чувствительности нельзя. Такие системы называют
неастази рован иыми.
Положим теперь, что моменты W и М, а также их производные
по х меняются в зависимости от х. Как уже указывалось, dW/dx
и g (дМ/дх) определяют скорость изменения моментов упругой
силы и силы тяжести при вращательном перемещении масс или же
самих сил при поступательном перемещении масс. Когда сумма
производных, уменьшаясь с изменением х, стремится к нулю, то
чувствительность системы стремится к бесконечности. Построив
систему так, чтобы в некотором диапазоне изменения силы тя-
жести сумма g (дМ/дх) ф- dWIdx была близка к нулю, что озна-
чает почти одинаковую скорость изменения моментов силы тя-
жести и упругой силы при изменении деформации х, получим
систему с очень большой чувствительностью. Такую систему
называют астазированной.
Сущность операции астазирования состоит в уравнивании ско-
ростей изменения моментов силы тяжести и упругой силы на не-
котором участке изменения деформации х. Дегазирование поз-
воляет при небольших начальных деформациях упругого элемента
создать систему с высокой чувствительностью к приращению силы
тяжести. В узком диапазоне изменения силы тяжести астазиро-
ванная система становится эквивалентной неастазироваиной
с очень большой первоначальной деформацией.
Геометрически астазирование можно представить (рис. 6.6)
как уменьшение угла между касательными к кривым момента
силы тяжести уг = gM (х) и момента упругих сил уг = —W (х)
в точке их пересечения, соответствующей положению равновесия
системы. Сумма производных g (дМ/д.х) dW/dx представляет
собой сумму тангенсов углов наклона а касательных к оси х.
5* 131
Рис. 6.6. Изменение моментов чув-
ствительной системы гравиметра.
Чем меньше угол между касатель-
ными к кривым у, п тем боль-
ше чувствительность системы.
Если эти кривые только касаются
друг друга, то система находится
в положении неустойчивого рав-
новесия, Таким образом, астази-
рованная система должна харак-
теризоваться нелинейной зависи-
мостью хотя бы одной из сил
(или моментов сил) от изменения
деформации. Эти системы поэто-
му часто называют нелинейными.
Астазироваиие системы, т. е. достижение нелинейности функ-
ций gM (х) и IF (х), может быть выполнено различными способами:
особым расположением массы или пружины либо того и другого
вместе; введением дополнительных астазирующих масс, пружин;
созданием электрических или магнитных полей. В зависимости
от этого существуют многочисленные конструкции астазирован-
ных гравиметров.
Рассмотрим способы астазирования применительно к грави-
метрам вращательного типа, пользующимся наибольшим распро-
странением.
Астазироваиие массой
(гравитационное астазироваиие)
Рассмотрим систему в виде маятника, центр тяжести которого
находится выше оси вращения. Упругую силу, компенсирующую
момент силы тяжести, создает крутильная нить, являющаяся
осью вращения маятника (рис. 6.7, а).
В этом случае деформации х соответствует угол поворота а
и момент упругих сил пропорционален этому углу, т. е.
W = т (а -ф- а0),
где т — коэффициент пропорциональности; а0 — угол предвари-
тельного закручивания нити подвеса.
Момент силы тяжести
gM (а) = mgl,
где т — масса, I — плечо маятника.
132
Уравнение равновесия приобретает вид
mgl -ф т (а аи) = О,
а уравнение чувствительности
Д— — —ml (gm 4- 4 т') . (6.7)
dg \ - da. 1 / '
Очевидно, что большую чувствительность получим, когда
dllda < 0, а произведение gm (dl[da) близко к т. При этом условии
скорость изменения момента силы тяжести увеличивается, при-
ближаясь к скорости изменения момента упругих сил.
Было предложено несколько гравиметров, астазированных
массой. Однако на практике эти гравиметры широкого распростра-
нения не нашли из-за большой чувствительности системы к на-
клону. Заметим, что любая система гравиметра вращательного
типа при положении маятника выше оси вращения становится
системой, астазированной массой. Если центр тяжести маятника
расположен ниже осп вращения, то dt/da > 0 и приобрести высо-
кую чувствительность система не может.
Пусть dl/da 0, т. е. маятник находится в горизонтальном
положении. Для выполнения этого условия необходимо изменение
силы тяжести компенсировать какой-то дополнительной силой,
приводящей маятник в горизонтальное положение. Тогда момент
силы тяжести не зависит от а, в этом случае daldg = a0/g, т. е.
чувствительность системы пропорциональна полной деформации,
что соответствует неастазированной системе вращательного типа.
Такая система для получения высокой чувствительности требует
больших первоначальных деформаций.
Дегазирование пружиной
(упругое астазирование)
Рассмотрим систему, представляющую собой рычаг с массой,
удерживаемый в горизонтальном положении с помощью пружины
(рис. 6.7, б), т. е.
IE (a) = frbL,
где f — жесткость, ДТ — удлинение, г — плечо пружины.
Положим, что момент силы тяжести является постоянной вели-
чиной, т. е. при изменении силы тяжести изменение ее"момента
компенсируется некоторым дополнительным моментом. Тогда урав-
нение чувствительности имеет вид
\L (6.8)
dg \! da 1 * da / 7
Система будет астазированной, если f &.L (dr/da) > 0.
В этом случае
гд Г dr . г d М. п da
I -j------ fr —» 0 и -J---> оо.
' da 1 ' da dg
133
Лстазировапие массой достигалось введением отрицательной
величины dllda, что означало увеличение плеча силы тяжести
с увеличением g. При астазировании пружиной вводится положи-
тельная величина drlda, что означает уменьшение плеча упругой
силы с увеличением силы тяжести и, наоборот, увеличение плеча
упругой силы при уменьшении силы тяжести. Принцип астази-
рования пружиной используется во многих системах современных
гравиметров. При этом астазирующими элементами служат спе-
циальные дополнительные пружины или главная пружина, рас-
положенная определенным образом по отношению к рычагу маят-
ника.
Астазироваиие массой и пружиной
(гравитационно-упругое астазироваиие)
Рассмотрим систему, представляющую собой маятник с грузом,
удерживаемый пружиной так, что масса груза находится выше
оси вращения маятника (рис. 6.7, в). В этом случае уравнение
чувствительности
-^- = — + (6.9)
dg \5 da ' ' da ' 1 da / ' '
В этой формуле, третий член в скобках всегда отрицателен,
гак как отрицательна производная d MJda, (с уменьшением а
растет АЛ). Второй и первый члены могут быть и положительными
и отрицательными в зависимости от знака производной. Заметим,
что производная daJdg имеет смысл только тогда, когда она отри-
цательна. Если построить систему таким образом, чтобы сумма
первого и второго членов была положительной и по абсолютному
значению больше третьего члена на малую величину, то получим
систему с очень высокой чувствительностью. Для этого доста-
точно, чтобы производная dllda была отрицательна, a dr,'da. поло-
жительна. Эго означает, что с увеличением угла а плечо действия
пружины увеличивается, а плечо действия массы уменьшается.
Поэтому при увеличении а скорость изменения момента упругих
сил уменьшается, а скорость изменения момента силы тяжести
увеличивается, т. е. скорости сближаются.
Такой способ астазирования применен в гравиметрах, у кото-
рых центр тяжести масс расположен выше оси вращения и имеет
упругое астазирующее устройство.
Анализ чувствительности систем показывает, что для дости-
жения высокой механической чувствительности при небольших
размерах гравиметра астазированные системы имеют бесспорное
преимущество перед неастазированными. Это преимущество вы-
ражается в том, что высокая чувствительность в астазированных
системах обеспечивается при малой общей деформации упругого
элемента, что значительно улучшает его работу. Но в астазиро-
ванной системе смещение подвижного элемента зависит от изме-
нения силы тяжести нелинейно, что заставляет применять ком-
134
пенсационный метод измерения. В неастазированной системе эта
зависимость линейная в пределах всего диапазона измерений, но
для получения высокой чувствительности требуются большие де-
формации, что ухудшает механические свойства упругих элемен-
тов гравиметра.
Связь чувствительности системы
с периодом собственных колебаний
При сборке и регулировке гравиметра необходимо знать его
реальную чувствительность, так как при изготовлении отдельных
деталей гравиметра всегда существуют отклонения от заданных
расчетных параметров. О чувствительности гравиметра можно
судить по периоду собственных колебаний его упругой системы.
Найдем эту связь.
Для системы гравиметра с поступательным перемещением
массы собственные колебания системы вблизи положения равно-
весия описываются уравнением движения
+ = (6.10)
где т — масса подвешенного на пружине груза; х смещение
груза от положения равновесия; L — длина пружины; mg/L ~
— f — упругость пружины.
Решая это уравнение, находим период собственных колебаний
системы
Т = (6.11)
Чувствительность гравиметра
dx/dg = L/g;
подставляя это выражение в уравнение (6.11), имеем
Т — dx/dg или dx/dg"- Т2/п2. (6.12)
При вращательном перемещении массы уравнение собственных
колебаний системы около положения равновесия а = 0 имеет вид
= (“). ОМЗ)
где I — момент инерции системы относительно оси вращения;
а — угол отклонения системы от положения равновесия; УМ (а) —
сумма моментов внутренних и внешних сил, действующих на си-
стему и являющихся функцией угла а:
S М (а) = gM (а) + W (а). (6.14)
135
Поскольку упругая система гравиметра совершает малые ко-
лебания относительно положения равновесия, то £Л4 (а) можно
разложить в ряд по степеням малой величины а:
V1 V d У М («)
2,Л4 а = 2.Л4 («) -|-« +
terj а=0 ““ Ct - п
аг £ М (а)
Пренебрегая в разложении членами со степенью а выше первой
и имея в виду, что £/М (а)|а=о — 0> получаем уравнение движе-
ния в виде
, d3a ,
1 dt* ' “
(R.IG)
Решая это уравнение, находим период собственных колебаний
гравиметра вращательного типа
d^M(a) I
da rz=o
Имея в виду, что
‘‘ ЕМ = I dgM (а) , гЖ (а) \ _ dg I
da и_0 \, да ' da / ’ da |а=0 ’
получаем
-j /" / / rfa \ da Т3М ,
1 = п V лг(1г) ,,л" (bJ")
Если положить, что вся масса маятника гравиметра сосредо-
точена в центре тяжести, то
M = ml; I — nil2,
где I — расстояние от оси вращения до центра тяжести массы.
Тогда
if da . da 72 1 .п,
Т = л I/ —г~ I и -j— — -------г- (Ь. 19)
г dg dg л2 / v ’
Из формул (6.12) и (6.19) следует, что при увеличении периода
колебаний системы чувствительность растет пропорционально его
квадрату. Поскольку чувствительность у дегазированных систем
выше, то соответственно и период их колебаний значительно
больше, чем у пеастазированных.
Влияние температуры
При изменении температуры меняются упругие свойства,
длина плеч и рычагов системы. Все это приводит к нарушению
положения равновесия системы и, следовательно, к изменению
13G
показаний гравиметра. Изменение показаний при изменении
температуры на 1° С называется температурным коэффициентом
гравиметра.
Выражение температурного коэффициента получим из основ-
ного уравнения гравиметра (6.4), положив в нем производные
daddg, dp/dg, dfi/dg равными нулю, т. е. считая деформацию упру-
гой системы, давление воздуха и наклон прибора постоянными,
тогда
«ад
Зависимость моментов внешних и внутренних сил от темпера-
туры можно приближенно представить в следующем виде:
М = Л40(1 4-V+V); ^ = ^о(1(6.21)
где Л10 и Жо — моменты масс и упругих сил при некоторой исход-
ной температуре; t — изменение температуры от ее исходного
значения; и pj и р2 — соответственно линейные и квадра-
тичные эффективные температурные, коэффициенты упругой си-
стемы в целом, зависящие от коэффициентов линейного расшире-
и термоэластических коэффициентов материалов, из которых
изготовлены отдельные элементы упругой системы.
Дифференцируя уравнение (6.21) и подставляя результаты
в формулу (6.20), имеем
dg _ gM„ (А, + 2А2/) + Г0 (Pj + 2p.g/) /я оо>
dt м0(1 + Х^ + А3^)
Пренебрегая малыми величинами, содержащими произведения
вида и принимая во внимание, что IF0/Af0 — — g, получаем
выражение температурного коэффициента гравиметра
dg/dt = — g[(Хх — рх) 4- 2 (Х2 — р2) /]. (6.23)
Интегрируя это уравнение в интервале изменения темпера-
туры от до t2, определяем кажущееся приращение, силы тяжести,
регистрируемое гравиметром при изменении температуры на
Ы = 4 - tp.
bgii, = -g l(Xi - щ) Ai + (Xs - p2) Ai2|.
Температурное влияние на гравиметр зависит в основном от
линейного температурного члена — рх. Для большинства мате-
риалов, используемых в гравиметра?:, эффективный линейный
коэффициент определяется линейным термоэластическим коэф-
фициентом (см. табл. 6.1). Квадратичный температурный коэффи-
циент характеризует изменение температурного коэффициента
гравиметра с изменением температуры, т. е. нелинейность темпе-
ратурной характеристики. Его значение в основном зависит от
квадратичного термоэластического коэффициента упругого мате-
риала.
137
Из уравнения (6.23) следует, что для уменьшения температур-
ного коэффициента гравиметра необходимо подбирать материалы
с возможно малыми коэффициентами линейного расширения и
термоэластическими. Кроме того, можно найти такое сочетание
отдельных элементов упругой системы, чтобы сумма эффективных
коэффициентов л — р была близка к нулю; в этом случае темпе-
ратурный коэффициент гравиметра будет мал.
Чтобы ослабить температурное влияние, конструируют спе-
циальные термокомпенсационные устройства. При изменении тем-
пературы, нарушающем положение равновесия упругой системы,
эти устройства регулируют отдельные параметры системы таким
образом, что она возвращается в начальное положение равновесия.
Для этого необходимо, чтобы кажущееся изменение силы тяжести
А.щ, создаваемое температурным компенсатором при изменении
температуры, соответствовало уравнению
= bj 4- b2t2,
где Ьг и Ьг — некоторые эффективные коэффициенты температур-
ного компенсатора, зависящие от геометрических размеров ком-
пенсатора и температурных характеристик материала, из кото-
рого он изготовлен.
Для полной температурной компенсации необходимо, чтобы
— О,
т. е.
== —Ь^, Цз =: —
Конструкции термокомпенсационных устройств весьма разно-
образны. Во многих использован принцип биметаллических ком-
пенсаторов: два стержня из металлов с различными коэффициен-
тами линейного расширения, скрепленные с обоих концов, при
изменении температуры изгибаются. Помещая упругий элемент
гравиметра на одном из концов такой системы, можно создать
момент упругих сил, компенсирующий действие температуры.
В некоторых гравиметрах температурную компенсацию осуще-
ствляют, погружая упругую систему в жидкость, плотность кото-
рой изменяется с температурой. Тем самым создается выталкива-
ющая сила, действующая на массу системы. Можно использовать
в качестве упругих элементов несколько пружин с разными термо-
эластическими коэффициентами, подбирая их таким образом,
чтобы обеспечить нулевой температурный коэффициент системы
в целом.
Детальное устройство разных температурных компенсаторов
приведено при описании отдельных узлов гравиметров.
Теоретически с помощью термокомпенсационных устройств
температурный коэффициент гравиметров можно сделать равным
нулю. Однако добиться этого на практике весьма затруднительно
из-за ряда обстоятельств. Прежде всего, уравнять полностью
138
Рис. 6.8. Принципиальная схема элек-
трического термостата.
противодействующие влияния
при изменении температуры
удается только для ее некото-
рых определенных значений,
поскольку термомеханические
коэффициенты тел зависят от
температуры. Поэтому темпе-
ратурная компенсация осу-
ществляется только в пределах
некоторого интервала, внутри
которого находится температу-
ра полной компенсации. Кроме
того, при изменении температу-
ры разные части упругой си-
стемы в одно и то же время при-
нимают несколько разную тем-
пературу. Эта разница зависит
менения температуры, действия тепловых потоков внутри системы,
отношения коэффициентов теплоемкости и теплопередачи в отдель-
ных элементах и т. д. Для уменьшения разницы в температуре
от многих причин: скорости из-
отдельных частей чувствительная система гравиметра помещается
в специальные теплозащитные чехлы или устройства (например,
сосуд Дьюара), которые снижают скорость изменения темпера-
туры и обеспечивают более равномерное ее распределение по
всему объему системы гравиметра.
Наиболее полно влияние изменения температуры можно иск-
лючить, поместив упругую систему в термостат, внутри которого
поддерживается постоянная (до сотых и даже тысячных долей
градуса) температура. В настоящее время применяют только
электрические термостаты с одним или несколькими нагреватель-
ными слоями.
Электрический термостат (рис. 6.8) представляет собой тепло-
изолированный цилиндрический или прямоугольный сосуд, внутри
которого с помощью автоматического регулятора поддерживается
постоянная температура. Для этого применяют электромехани-
ческие регуляторы, состоящие из контактного термометра и элек-
тромагнитного реле.
Контактный термометр 1, включенный в цепь электромагнит-
ного реле 2, имеет два металлических контакта. Один постоянно
касается ртути в резервуаре термометра, другой впаян в капилляр
на такой высоте, что столбик ртути достигает его при определен-
ной температуре — температуре контактирования. Нагреватель-
ная обмотка 4 термостата соединена с аккумуляторной батареей 5
через контактный прерыватель 6. Пока столбик ртути не касается
контакта в капилляре, электрический ток течет только через
обмотку термостата и температура в термостате повышается. Как
только термометр нагреется до температуры контактирования,
цепь термометра замыкается и ток течет через обмотку реле.
139
Электромагнит размыкает цепь обмотки термостата, и термостат
начинает остывать. При остывании столбик ртути в термометре
опускается и размыкает цепь термометра, прерывая ток в обмотке
реле. Тогда якорь электромагнита опускается и замыкает цепь
обмотки термостата. Чтобы избежать образования нагара на кон-
тактах термометра и реле, через них пропускаются малые токи
и параллельно реле подключается искрогаситель 3. В некоторых
термостатах вместо электромеханических реле используют тран-
зисторы, а вместо термометров резисторы. Чтобы тепло не рас-
ходовалось очень быстро, сосуд с обогревательной обмоткой по-
мещен в теплозащитный кожух.
Наилучшим способом термостатирования является такой, когда
в термостате не одна, а несколько нагревательных обмоток,
обычно две-три, помещенных одна внутри другой. Каждая нагрева-
тельная обмотка имеет независимую терморегулировку; при этом
температура контактирования у каждого внутреннего термометра
должна быть на 2 -3‘ С выше, чем у внешнего термометра. Во
избежание тепловой инерции контактный термометр заделывают
в отверстие в нагревательном слое и обеспечивают хороший кон-
такт с этим слоем. Для нейтрализации действия магнитного поля,
вызванного током нагрева, обмотки термостатов наматываются
бифилярно.
Качество термостата характеризуется коэффициентом термоста-
тирования
Kt = А^н/А/В,
где — изменение наружной температуры; А/в — изменение
температуры внутри термостата.
Коэффициент термостатирования определяют эксперимен-
тально. Для этого гравиметру дают длительную отстойку при по-
стоянной внешней температуре. Измеряют температуру внутри
прибора и внешнюю. После этого внешнюю температуру изменяют
на 15—20° С ступенями по 3—5е С/ч. Отсчитывают температуру
внутри прибора и внешнюю. Строят график изменения темпера-
туры внутри прибора и внешней температуры во времени. По
отношению максимальных изменений температуры в приборе и
внешней температуры определяют коэффициент термостатирова-
ния. Из графика можно также определить сдвиг фаз — разницу
во времени между максимумами изменения внешней температуры
и температуры в приборе.
Как правило, двухступенчатые термостаты имеют коэффи-
циент термостатирования 150—-300, трехступенчатые 350—
500.
Для уменьшения температурных влияний даже термостатиро-
ванный гравиметр следует оберегать от резких колебаний тем-
пературы наружного воздуха. Для этого гравиметр помещают
в специальные теплоизоляционные контейнеры, в которых грави-
метры и транспортируют. Вынимают гравиметры только па корот-
ко
кое время для наблюдений. Измерения с термостатированным
гравиметром можно начинать только после того, как тепловой ре-
жим в нем установился. Для этого требуется не менее суток. Учи-
тывая это обстоятельство, нельзя отключать питание термостатов
при перерывах в наблюдениях даже в несколько дней, менять силу
тока и аккумуляторные батареи в процессе наблюдений. Для нор-
мальной работы термостатов необходимо, чтобы температура
внешнего термостата была на 5—6° С выше максимальной темпе-
ратуры окружающего воздуха.
Показателем установившегося температурного режима
является ритмичность работы внутреннего термостата, что отме-
чается по моментам включения и выключения контрольного ампер-
метра внутреннего термостата. При нормальной работе продол-
жительность нагрева и охлаждения внутреннего термостата
должна быть одинаковой. Это достигается настройкой термометров
внутреннего и внешнего термостатов на оптимальную разность
температур контактирования. Для экономичного расходования
энергии температуру термостатирования гравиметра устанавли-
вают применительно к температуре наружного воздуха в зависи-
мости от времени года и района работ.
Гравиметры без термостата имеют термометр для отсчета тем-
пературы системы. Вводятся соответствующие температурные
поправки, учитывающие влияние изменения температуры за время
наблюдений. Термометрами снабжаются и некоторые термостати-
рованные гравиметры. Однако исправить показания гравиметра
введением температурной поправки весьма затруднительно. Пре-
жде всего, показания термометра не отвечают действительной
температуре упругой системы, поскольку термометр и отдельные
части упругой системы имеют разную температуру. Эта разница
зависит от скорости изменения температуры и от ряда других
причин, не поддающихся учету. Практика наблюдений с грави-
метрами показала, что введение температурной поправки, как пра-
вило, ухудшает результаты наблюдений. Поэтому в настоящее
время температурные поправки не вводят, а изменения показаний
гравиметра учитывают общей поправкой за смещение нуль-
пункта прибора.
Температурный коэффициент нетермостатированных грави-
метров можно определить несколькими методами.
Метод петли является наиболее простым путем определения
температурного коэффициента и применяется, когда необходимо
найти приближенные значения коэффициента в некотором интер-
вале температур t2 — tr. Гравиметр нагревают до температуры t2
и затем начинают охлаждать до tt, с постоянной скоростью сни-
жения температуры. Затем снова нагревают прибор с тон же ско-
ростью, с которой он охлаждался. Как при нагревании, так и при
охлаждении прибора берут отсчеты температуры t и показаний
прибора s. На основе наблюдений строят кривую зависимости s
от I (рис. 6.9). Поскольку при одной и той же температуре имеется
141
Рис. 6.9. Определение температур-
ного коэффициента гравиметра
методом петли.
Рис. 6.10. Определение температур-
ного коэффициента гравиметра ме-
тодом двойной петли.
два наблюдения, то средняя кривая свободна от изменения нуль-
пункта. По ней и определяют температурный коэффициент.
Метод двойной петли позволяет установить температурный
коэффициент гравиметра более надежно, однако этот метод весьма
трудоемок и не. всегда может быть использован. Метод состоит
в следующем. Интервал температур t2 — tlt для которого надо
найти температурный коэффициент, разбивается на п более мел-
ких частей А/ так, что
Л
/а _ (1 = V
1=1
Гравиметр помещают в термокамеру, в которой поддержи-
вается температура /х и дают ему отстойку до тех пор, пока в пре-
делах чувствительности термометра температура внутри прибора
перестает изменяться. Снимают показание прибора sH
(рис. 6.10). Затем температуру в камере изменяют на А/х и вы-
держивают прибор при -у A tt, пока температура термометра
и упругой системы уравняется. Берут отсчет Затем по-
вторяют отсчет «А при температуре После этого снова изменяют
температуру на Д/х и после отстойки берут отсчет при
температуре /х -|- А/х. Таким образом получают двойную темпе-
ратурную петлю и на этом заканчивают определять изменения
Asj показаний гравиметра, соответствующие изменению темпера-
туры от /х до /j -|- Д/х. Отсчеты sn, s'llt s(1+M1, S/идп наносят
на график в функции времени Т. Разностями а — b и с — d опре-
деляются величины Asx, As[, т. е. изменение, показаний гравиметра
при изменении температуры от /х до -Г ^1- За окончательное
значение принимается величина
Ast = (Asi -|- As'i)/2.
После определения Asx по такой же программе находят As2,
As3 (и т. д.), соответствующие изменению температуры от /х -|- А/,
до 1г + \t1 -I- А/2 (и т. д.).
142
Определив все значения As,- последовательным суммированием
A/z и As,-, получают зависимость между показаниями гравиметрах
и его температурой t. Эту зависимость находят графически или
аналитически (способом наименьших квадратов).
Влияние атмосферного давления
Если упругая система гравиметра помещена не в герметичном
сосуде, то его показания изменяются с колебаниями атмосферного
давления. От атмосферного давления р зависит плотность воз-
духа р, а следовательно, и выталкивающая сила, действующая
по закону Архимеда на подвижные массы упругой системы грави-
метра. Изменение показаний гравиметра, связанное с ходом
атмосферного давления, называется барометрическим эффектом
и характеризуется барометрическим коэффициентом гравиметра.
Общее выражение для барометрического коэффициента можно
получить из формулы (6.4), положив неизменными деформацию х,
наклон р и температуру I:
/<р = М'1. (6.24)
с ар ь др
Барометрический эффект в гравиметре проявляется как кажу-
щееся изменение массы рабочего груза и, следовательно, момента
масс упругой системы. Каждая элементарная масса din упругой
системы при изменении плотности окружающей среды на вели-
чину dp испытывает по закону Архимеда кажущееся изменение
d (dm) — dp dv,
где dv — объем элементарной массы.
Кажущееся изменение момента масс всей системы
dM — dp р cos a dv — dpMa, (6.25)
V
где г — расстояние от оси вращения до объема dv; а — угол между
направлением г и горизонтальной плоскостью; Mv — | г cos adv —
V
объемный момент системы относительно оси вращения.
Поскольку система может быть изготовлена из материалов
с разной плотностью ст, введем эффективную плотность <Пф Упру-
гой системы, определяемую как отношение момента массы к мо-
менту объема:
ст5ф = М/М.с. (6.26)
Тогда из формул (6.25) и (6.26) имеем
dM/dp = Mv М/о?ф, (6.27)
143
Плотность воздуха определяется формулой
Р =
где р0 = 12,93- 1СГ4 г/см3 — плотность воздуха при температуре
0° С и нормальном давлении /?0 — Ю1 325 Па 1-105 Па; t — тем-
пература, °C.
Дифференцируя это выражение, находим
Др" = Ро [ Ро (1 -I- -273") ] ’ (6.28)
Подставив в формулу (6.24) величины (6.27) и (6.28), получим
барометрический коэффициент гравиметра
А.вз_^_^_,4.Л4-1=_(?_До_Гр/1 +
’’ dp ь др dp ь аэф L ' \ 273 / J
(6.29)
Барометрическую поправку найдем, взяв конечные значения
переменных,
Ag- -= Л'(, кр.
(6.30)
Из выражения (6.29) следует, что значение барометрического
коэффициента определяется плотностью материала массы упругой
системы, а именно: чем больше ее плотность, тем меньше баро-
метрический коэффициент, и наоборот. Например, для упругой
системы, изготовленной целиком из плавленого кварца (оэф —
= 2,2 г/см3), барометрический коэффициент в 10 раз больше (по
абсолютному значению), чем для системы из платины (<тЭф =
= 21,4 г/см3): соответственно —0,5-10"7 и — 0,05-10'7 м/с2 па
1 Па.
> Чтобы исключить влияние атмосферного давления, упругие
системы гравиметров помещают в герметически закрытые сосуды.
Есть гравиметры, у которых упругая система погружена в жид-
кость. Благодаря практической несжимаемости жидкости влияние
атмосферного давления на системы таких гравиметров ничтожно
мало. В гравиметрах вращательного типа барометрический эф-
фект можно свести практически к нулю барокомпенсатором
(рис. 6.11). Идея устройства и принцип действия барокомпенсатора
Рис. 6.11. Схема барометрической ком-
пенсации.
состоят в следующем. Полый
герметичный сосуд с малой
массой и большим объемом
располагают на конце рычага
упругой системы, противопо-
ложном грузу, на малом рас-
стоянии от оси вращения.
Очевидно, что объемный мо-
мент Л4-, всей системы будет
равен нулю при условии
144
равенства по абсолютному значению объемных моментов груза
и барокомпенсатора:
где гм и гк— плечи груза и барокомненсатора относительно осп
вращения.
В этом случае эффективная плотность oS(j, в выражении (6.26)
равна бесконечности и барометрический коэффициент Кр в фор-
муле (6.29) равен нулю.
Барокомпенсация осуществляется во многих гравиметрах
с вращательным перемещением массы, как астазированных, так
и неастазированных. Однако эта мера не может полностью за-
менить герметизацию системы, так как при быстром изменении
давления в негерметизированном корпусе возникает адиабати-
ческий температурный эффект, который вызывает изменение
показаний гравиметра. Адиабатический эффект становится за-
метным при транспортировке гравиметра на вертолете или само-
лете.
Наличие барометрического эффекта в гравиметрах послужило
предпосылкой для создания гравиметра-высотомера, позволя-
ющего одновременно измерять приращения силы тяжести и вы-
соты.
Влияние наклона гравиметра
При выводе основного уравнения гравиметра предполагалось,
что упругая система имеет одну степень свободы, т. е. может
вращаться только вокруг горизонтальной оси, а при малом на-
клоне оси упругой системы каждый ее элемент перемещается
в плоскости, перпендикулярной к оси вращения. При горизон-
тальной оси вращения перемещение элементов упругой системы
происходит в вертикальной плоскости.
Пусть р — угол наклона оси вращения упругой системы отно-
сительно горизонтальной плоскости. В наклонном положении
на систему действует не весь момент масс, а его проекция на пло-
скость, в которой происходит движение упругой системы, т. е.
МAI0cosp, (6.31)
где Мо — момент масс при горизонтальном положении оси вра-
щения.
Дифференцируя это выражение, находим
dM/dfi = —Л40 sin р. (6.32)
Зависимость показаний гравиметра от наклона получим из
уравнения гравиметра (6.4), положив деформацию х, темпера-
туру t и давление р неизменными:
dg/d^-g~M-\ (6.33)
146
Подставив сюда два предыдущих выражения, найдем
dg/Jp = gtg(3. (6.34)
Разлагая в ряд tg (3 и интегрируя выражение (6.34), получаем
о о
A£ = gj'tg[W = gj(p-r4F3+ =
—НгО +тг+ ) t6-3S>
Пренебрегая членами в четвертой степени и выше, имеем кажу-
щееся изменение (уменьшение) силы тяжести при наклоне оси
вращения системы от горизонта:
A^ = -^F/2). (6.36)
Аналогичную зависимость получим при наклоне гравиметра
в вертикальной плоскости, перпендикулярной к оси вращения
системы. В этом случае угол р будет означать отклонение исход-
ного положения рычага упругой системы от горизонтальной пло-
скости.
Формула (6.36) является уравнением параболы, вершина кото-
рой соответствует точке = 0. Из этой формулы следует, что
минимальная чувствительность гравиметра к наклону наступает
при [> = 0, т. е. когда центр тяжести масс лежит в одной гори-
зонтальной плоскости с осью вращения. Эта формула применима
ко всем гравиметрам с поступательным или вращательным пере-
мещением массы, как астазированным, так и иеастазированным.
Условию минимальной чувствительности к наклону удовлетворяют
все гравиметры, за исключением астази рован ных массой и массой
и пружиной, так как для астазироваиия этими способами необхо-
димо, чтобы центр тяжести системы находился выше оси вра-
щения. Системы таких гравиметров обладают очень большой чув-
ствительностью к наклону, из-за чего они и не получили широкого
распространения.
Если исходное положение упругой системы гравиметра гори-
зонтально с точностью до Г (0 = 1/3438), то ошибка в показаниях
гравиметра составит 0,04 10"5 м/с2. В таких гравиметрах для
установки системы в горизонтальное положение используются
уровни 1—0,5'. Чувствительность этих уровней позволяет при-
вести прибор в горизонтальное положение с точностью 0,5' и
выше, ошибка показаний гравиметра составит менее 0,01 ИГ “м/с2.
Следует иметь в виду, что погрешность Ag возрастает пропорци-
онально квадрату угла наклона. Необходимо следить за тщатель-
ностью крепления уровней и периодически проверять их юсти-
ровку.
Гравиметр имеет два уровня, жестко скрепленных с корпусом,
в котором находится упругая система. В гравиметрах вращатель-
146
а
Рис. 6.12. Зависи-
мость отсчета гра-
виметра от на-
клона.
ного типа один уровень (поперечный) располо-
жен вдоль оси вращения системы, вдоль этого
же направления находятся два нивелировочных
винта гравиметра. Другой уровень (продоль-
ный) перпендикулярен к первому и регули-
руется третьим нивелировочным винтом. Цель
регулировки уровней заключается в том, чтобы
при горизонтальном положении оси вращения
системы и рычага маятника вывести пузырьки
уровней на середину.
Гравиметр устанавливают на прочное осно-
вание и при помощи нивелировочных винтов
выводят пузырьки на середину уровней. Затем
для юстировки поперечного уровня каждый из
двух нивелировочных винтов, расположенных
вдоль этого уровня, поворачивают на 1—2
полных оборота (в противоположных направлениях), наклоняя
гравиметр в одну сторону, п берут отсчет. После этого гравиметр
теми же винтами постепенно возвращают в исходное положение,
беря отсчеты через четверть или половину оборота винтов. При
уменьшении наклона отсчет гравиметра увеличивается. Возвра-
тив гравиметр в исходное положение, наклоняют его, используя
те же винты, в противоположную сторону и также снимают отсчеты.
Убывание отсчетов показывает, что вершина параболы уже
пройдена. Затем снова приводят гравиметр в исходное положение.
Не трогая гравиметр с места, обрабатывают наблюдения.
Строят график зависимости отсчетов s гравиметра от наклона,
выраженного в оборотах п винтов (рис. 6.12). По оси абсцисс
наносят число оборотов винтов, по оси ординат — средние значе-
ния из двух отсчетов (при прямом и обратном ходе). В результате
получают параболу. Абсцисса оси симметрии параболы указы-
вает, при каком положении установочных винтов ось вращения
упругой системы горизонтальна. Установив нивелировочные винты
в это положение, регулировочными винтами уровня выводят его
пузырек на середину. После того как отрегулирован поперечный
уровень, аналогичным способом регулируют продольный. В этом
случае вращают только третий винт. Далее поступают так же,
как и при регулировке поперечного уровня.
При относительных определениях силы тяжести небольшая
погрешность в регулировке уровней практически не играет роли,
так как ошибка в показаниях гравиметра на исходном пункте
и на определяемом почти равны по значению и одинаковы по знаку.
При вычислении приращений силы тяжести ими можно пренеб-
речь.
Пусть ошибка в регулировке уровня равна |3. На исходном
пункте, где сила тяжести glt ошибка показаний гравиметра

147
а в определяемом пункте с силой тяжести g2 ошибка
^2-g2(P2/2).
В разности силы тяжести Ag = g2 — влияние неточности
установки уровня
Sg2-Sgi = Ag(fl2/2).
Вели Ag — 1000- 10 •г' м/с2, |> = 5', то
Ag-f- -- 1000- l()-s- 4-6 Лъ-У = = 0,001 • 10-й м/с2,
' ’ 2 2 \ 3438 / ’
что меньше погрешности измерений. Таким образом, регулировка
уровня с точностью 2—3 деления вполне достаточна, важно лишь
в течение рейса сохранять установку уровня постоянной. В про-
цессе полевых работ регулировку уровней необходимо периоди-
чески контролировать.
Влияние магнитного поля
Упругие системы гравиметров изготовляют из плавленого
кварца или на железоникелевых сплавах. Кварц —- немагнитный
материал, а железонпкелевые сплавы обладают некоторой магнит-
ностыо. Поэтому показания гравиметров с металлическими пру-
жинами зависят от влияния внешнего магнитного поля. Источ-
никами магнитного влияния являются магнитное поле Земли,
изменяющееся от пункта к пункту, а также местные магнитные
поля линий высоковольтных передач, электродвигателей и т. д.
Кроме того, пружины металлических гравиметров могут быть
случайно намагничены в процессе сборки и регулировки при
использовании намагниченного инструмента. При сборке таких
гравиметров металлические детали подвергают размагничиванию,
помещая их в сильное переменное постепенно убывающее магнит-
ное поле. От внешнего поля металлические упругие системы грави-
метров защищают специальными магнитными экранами из пер-
маллоя или армко-железа, что снижает его влияние в 5—10 раз.
Однако с течением времени упругая система все же намагничи-
вается. Поэтому металлические гравиметры необходимо пери-
одически проверять па магнитность и устранять ее.
Магнитное поле, действующее на систему, создает дополни-
тельный вращающий момент внешних сил, что искажает показа-
ния гравиметра. Эффект зависит от вертикальной Z и горизон-
тальной Н составляющих магнитного поля и азимута А, образу-
емого рычагом гравиметра с магнитным меридианом. Кажущееся
изменение силы тяжести SgM вследствие действия этих сил
A'/;//cos/l,
И8
где Kz и — вертикальный и горизонтальный магнитные коэф-
фициенты гравиметра.
Влияние горизонтальной составляющей Н обнаружить легко:
при наблюдении на одном и том же пункте отсчеты гравиметра
изменяются в зависимости от ориентировки прибора относительно
магнитного меридиана. Кривая зависимости отсчета от азимута А
представляет собой синусоиду, вершины которой соответствуют
положениям рычага, совпадающим с магнитным меридианом.
Амплитуда и знак синусоиды зависят от полярности и степени
намагниченности пружины.
Влияние внешнего магнитного поля и коэффициенты
и определяют, проводя наблюдения с гравиметром в кольцах
Гельмгольца. Установив кольца Гельмгольца горизонтально, на-
ходят влияние вертикальной составляющей Z. Расположив кольца
вертикально и меняя азимут колец, определяют влияние гори-
зонтальной составляющей Н. Напряженность h магнитного поля,
создаваемая кольцами Гельмгольца по линии, соединяющей
центры колец,
/I = 0,9/н//?,
где / — сила тока, проходящего через витки колец; и — число
витков; /? — радиус колец.
Сила тока должна быть такой, чтобы поле колец превышало
магнитное поле Земли в несколько раз. Постоянный ток пропу-
скают через кольца то в одном направлении, то в противополож-
ном. Берут два отсчета по гравиметру: s(+> — при положительном
направлении тока (условном), — при отрицательном. Магнит-
ные коэффициенты гравиметра

SZ — sz
2hz
S rj — s ,,
ПРИ Л = °-
Влияние горизонтальной составляющей магнитного поля Земли
может быть исключено достаточно полно в процессе полевых
наблюдений с гравиметром. Для этого прибор на всех пунктах
наблюдений с помощью буссоли устанавливают в одно и то же
положение относительно магнитного меридиана. Влияние гори-
зонтальной составляющей исключается также, если на каждом
пункте прибор ориентировать в двух противоположных ази-
мутах.
Совершенно иначе обстоит дело с влиянием вертикальной со-
ставляющей Z. Малое влияние горизонтальной составляющей Я
еще не гарантирует малого влияния вертикальной составля-
ющей Z. Как правило, поправки за влияние магнитного поля
Земли в отсчеты гравиметров не вводят, обычно стремятся раз-
магничиванием упругой системы и экранированием свести дей-
ствие магнитного поля к пренебрежимо малым значениям или
к нулю.
149
Регистрация малых перемещений
в гравиметрах
Измерение приращения силы тяжести гравиметром состоит
в измерении малых приращений деформации упругого элемента,
возникающих вследствие изменения веса постоянной массы, укре-
пленной на рычаге упругой системы. Процесс измерения малых
деформаций, как правило, складывается из двух основных действий.
1. Регистрация нулевого (исходного) положения подвижной
части упругой системы гравиметра.
2. Измерение приращения деформации упругого элемента при
возвращении упругой системы в исходное положение.
В процессе измерения эти два действия осуществляются одно-
временно с помощью специальных систем: регистрирующей и изме-
рительной. Необходимо заметить, что требования, предъявляемые
к указанным системам в отношении их точности и стабильности,
несравненно ниже требований к упругой системе гравиметра.
Действительно, при измерении силы тяжести с погрешностью
0,01 105 м/с2 относительная точность упругой системы достигает
порядка 1 10'8. ?1змеряемое приращение силы тяжести не может
быть больше чем 5- КГ2 м/с3 (разность силы тяжести между полю-
сом и экватором). Обычно же диапазон измерения силы тяжести
составляет (200 ч- 300)- 10”6 м/с2, в этом случае относительная
точность равна 1-1СГ4,
Характер регистрирующей системы гравиметра определяется
чувствительностью прибора и заданной точностью измерения силы
тяжести. В неастазированных гравиметрах с поступательным
перемещением массы деформация составляет приблизительно
0,1 мкм на 1-Ю"5 м/с2. Если требуется измерить силу тяжести
с погрешностью до 0,01- 10“° м/с2, то надо зарегистрировать поло-
жение подвижной части упругой системы до 0,001 мкм. В неаста-
зированных гравиметрах вращательного типа изменение угла
поворота при изменении силы тяжести на 110'5 м/с2 составляет
1—5", т. е. при той же погрешности 0,01- 10-6 м/с2 надо измерить
угол с точностью 0,01—0,05". Обеспечить такую точность весьма
трудно. В неастазированных гравиметрах регистрирующие си-
стемы отличаются высокой чувствительностью и сложностью.
В астазированных гравиметрах угловое перемещение массы во
много раз больше: на 1 10-Б м/с2 достигает 20—50". Поэтому реги-
стрировать положение равновесия в таких системах можно с мень-
шей точностью. Соответственно ослабляются требования и к реги-
стрирующей системе.
В зависимости от чувствительности упругой системы и заданной
точности измерений в гравиметрах используются и различные
регистрирующие системы: оптическая, электрическая, фотоэлек-
трическая.
Оптическая регистрация применяется во многих гравиметрах,
как астазированных, так и неастазированных. Система имеет или
150
Рис. 6.13. Оптические регистрирующие системы.
авто коллимационную зрительную трубу, или шкальный микро-
скоп с 200—600-кратным увеличением. При автоколлимационной
системе на подвижном рычаге упругой системы устанавливается
зеркало, по отклонению которого и судят о положении рычага
(рис. 6.13, а). Автоколлимационная зрительная труба имеет длин-
нофокусный объектив 3 и короткофокусный окуляр 1. В фокусе
объектива помещена пластинка 2 со шкалой, над которой рас-
положена осветительная призма 5. Шкала пластинки закрывается
призмой не полностью. Как правило, под призмой находится один
штриховой индекс. Свет лампочки 6, проходя через объектив,
проецирует этот индекс в виде параллельного пучка света. На его
пути расположено зеркало 4 рычага упругой системы, поэтому
изображение индекса попадает обратно на шкалу и в масштабе
1 : 1 изображается на самой шкале. Индекс и его изображение
совпадают. При отклонении рычага гравиметра изображение ин-
декса перемещается по шкале.
При регистрации исходного положения рычага зеркальное
изображение индекса с помощью измерительной системы все время
приводят в одно и то же положение относительно делений шкалы.
В некоторых автоколлимационных системах на станине упругой
системы установлено второе, неподвижное, зеркало. В окуляр
рассматривают два изображения штрихов: подвижное от зеркала
маятника гравиметра и неподвижное от неподвижного зеркала
станины. Положение неподвижного зеркала регулируют таким
образом, чтобы в исходном (нулевом) положении системы пло-
скости зеркал были параллельными. В этом случае подвижное
и неподвижное изображения штрихов в момент измерения совпа-
дают.
В некоторых гравиметрах вместо автоколлимационной системы
применяется шкальный микроскоп (рис. 6.13, б). Для этого на
подвижной части упругой системы устанавливается тонкий мате-
риальный указатель ~4 (кварцевая или металлическая нить диа-
151
метром 3—10 мкм), и его изображение рассматривается в микро-
скоп. При измерениях изображение индекса совмещают каждый
раз с определенным делением шкалы.
Оптическая регистрация позволяет увеличивать смещение до
1000 раз. В астазированных гравиметрах используется эта система
регистрации как наиболее простая в изготовлении и юстировке
н дающая приемлемую для астазированных систем точность. Для
цеастазированных систем оптический способ в большинстве слу-
чаев неприменим, поскольку его точность недостаточна для ре-
гистрации малых смещений в приборах этого типа.
Электрическая регистрация применяется в некоторых типах
гравиметров, особенно цеастазированных, когда необходимо уве-
личение в 104—10“ раз. Электрические регистрирующие устрой-
ства преобразуют поступательные движения подвижного груза
упругой системы в изменения электрического напряжения или
силы тока. Эти устройства называются ультрамикрометрами.
Конструкции их весьма многообразны. Довольно часто исполь-
зуются емкостные ультрамикрометры (рис. 6.14), в которых пере-
мещение подвижной части упругой системы приводит к изменению
емкости плоскопараллельного конденсатора, одна из обкладок
которого расположена па подвижной части упругой системы,
другая на корпусе гравиметра. Конденсатор 1 переменной емкости,
образованный подвижной и неподвижной обкладками, подстроеч-
ный конденсатор 2 и катушка индуктивности 3 составляют коле-
бательный контур, включенный в базовую цепь триода 5. В кол-
лекторную цепь включен колебательный контур 4. Оба колеба-
тельных контура индуктивно связаны между собой. В исходном
положении подвижной части гравиметра подстроечным конден-
сатором 2 можно добиться резонанса контуров. В этом случае
в коллекторной цепи сила тока резко падает. При смещении по-
движного груза гравиметра емкость конденсатора изменяется
и резонанс нарушается, сила тока в коллекторной цепи увеличи-
вается. Таким образом, изменение силы тока является показателем
перемещения подвижного груза гравиметра.
Фотоэлектрическая регистрация основана на использовании
эффекта фотоэлементов. В гравиметрах для фотоэлектрической
регистрации в основном применяют фотоэлементы с запорным
слоем и внешним фотоэффектом. Создаваемый фототок зависит
от температуры, источников освещения и ряда других внешних
факторов. Чтобы нейтрализовать внешние помехи, применяют
дифференциальные схемы включения фотоэлементов. Для этого
два фотоэлемента включают навстречу друг другу или же исполь-
зуют уже готовые дифференциальные фотоэлементы.
Регистрирующее устройство (рис. 6.15, а) действует следу-
ющим образом. Свет электрической лампочки 1 падает па щель 2.
Равномерно освещенная щель посредством объектива 3 и зеркала 4,
установленного на рычаге маятника, проецируется в масштабе
1:1 на два фотоэлемента 5, включенных дифференциально.
152
Рис. 6.14. Схема емкостного ультра-
микрометра.
Рис. 6.15. Фотоэлектрическая реги
стрирукицая система.
Фототоки, вызванные световыми потоками, текут навстречу друг
другу, и гальванометр 6 фиксирует лишь разностный ток. Если
в исходном (нулевом) положении рычага эта система отрегулиро-
вана так, что световые потоки, падающие на оба фотоэлемента,
равны (рис. 6.15, б), то в цепи гальванометра тока не будет. При
смещении рычага гравиметра вверх или вниз изображение щели
сдвигается, освещая большую площадь у одного фотоэлемента
и соответственно меньшую у другого, в цепи появляется разно-
стный фототок (рис. 6.15, в).
Электрические и,фотоэлектрические способы регистрации яв-
ляются более чувствительными по сравнению с оптическими. Опп
применяются в донных и скважинных гравиметрах, а также в гра-
виметрах, следящих за вариациями силы тяжести во времени,
т. е. в тех случаях, когда необходимо дистанционное управление
упругой системой гравиметра.
Измерительная система гравиметра
Приращение силы тяжести измеряется статическими грави-
метрами в большинстве случаев компенсационным методом —
возвращением подвижной части упругой системы в исходное (нуле-
вое) положение. Компенсирующий момент, возвращающий упру-
гую систему в исходное положение, является мерой приращения
силы тяжести. В разных типах гравиметров компенсирующий
момент создается разными способами: закручиванием подвеса
маятника, растяжением главной пружины, наклоном всей упругой
системы и т. д.
В большинстве современных приборов измерительное (ком-
пенсационное) устройство имеет обычно винтовую пружину с очень
153
Рис. 6.16. Схема метода возвратного
потенциала.
малой жесткостью. Натяжение
этой пружины и создает мо-
мент, являющийся мерой при-
ращения силы тяжести. Дефор-
мация пружины определяется
по делениям на головке мик-
рометрического винта.
Компенсировать изменение
силы тяжести можно также
электростатическим зарядом,
сообщаемым обкладкам конденсатора (рис. 6.16). Одна обклад-
ка 1 конденсатора закреплена неподвижно на раме прибора, дру-
гая 2 на подвижном рычаге упругой системы. Если па плас-
тины подать разность потенциалов V, то между ними возникает
сила притяжения
где s — диэлектрическая постоянная; S — площадь пластины;
d — расстояние между пластинами.
Приращение силы тяжести можно выразить через разности
потенциалов и У2, измеренные вольтметром на исходной и ря-
довой точках при начальном положении подвижной части упругой
системы гравиметра:
Ag = Cv(y?_ yj),
где cv — постоянная гравиметра, 10’5 м/с2 на 1 В2.
Конструктивно схема возвратного потенциала может быть
выполнена по-разному. Такие измерительные устройства исполь-
зуются в гравиметрах, требующих дистанционного управления.
В некоторых гравиметрах измерение и компенсация прираще-
ний силы тяжести осуществляются методом наклона. Идея этого
метода состоит в том, что рычаг упругой системы приводят в исход-
ное положение, наклоняя всю упругую систему вдоль рычага
маятника или вдоль оси вращения рычага. Если исходное поло-
жение рычага горизонтально при некотором значении силы тя-
жести g0, то, чтобы привести рычаг маятника в исходное поло-
жение в точках, где значение силы тяжести g = g0 -f- Ag, надо
наклонить прибор на угол а, определяемый соотношением
go = (£o+ Ag) cos а;
откуда
Ag = g0(seca — 1).
В этом случае мерой приращения силы тяжести является
наклон чувствительной системы гравиметра. Угол а измеряют
или по угломерному кругу, или тангенциальным методом с по-
154
мощью микрометрического винта. Следует заметить, что компен-
сация силы тяжести методом наклона чувствительной системы
вдоль оси вращения подвижного рычага может быть использована
во многих гравиметрах, теория которых допускает такой наклон.
И наконец, в случае непрерывной записи изменения силы тя-
жести применяется фотографическая или любая другая регистра-
ция на движущейся ленте положения подвижной части чувстви-
тельной системы.
Более детально измерительные устройства различных типов
рассмотрены при описании отдельных систем гравиметров.
Необходимо отметить, что при расчете и изготовлении измери-
тельной системы в ней предъявляются менее жесткие требования
в отношении стабильности, чем к чувствительному элементу.
Эти требования в основном определяются точностью и диапазоном
измерений приращения силы тяжести. Например, при диапазоне
100' 10 5 и погрешности измерений 0,01 ИГ5 м/с2 точность измери-
тельного устройства должна быть не хуже 110 !. Естественно, при
увеличении диапазона измерений требования к измерительным
устройствам повышаются.
Эталонирование гравиметров
Результаты измерений силы тяжести гравиметрами выра-
жаются в делениях шкалы измерительного устройства. Для того
чтобы перевести результаты измерений в единицы силы тяжести,
необходимо определить переводной коэффициент, или цену деле-
ния, гравиметра. Процесс определения цены деления отсчетного
устройства гравиметра называется эталонированием.
Эталонирование гравиметров может быть выполнено различ-
ными способами.
1. Наблюдение на пунктах с известным значением силы тя-
жести.
2. Наблюдение изменения показаний гравиметра при наклоне.
3. Навеска грузиков.
Наблюдения на двух или более пунктах с известным значением
силы тяжести позволяют вычислить цену деления гравиметра.
Пусть на пункте с силой тяжести получен отсчет slt на пункте
с силой тяжести g.: — отсчет s2. Тогда, если шкала гравиметра
линейна, имеем
gl = PSll gi =“ «2,
откуда
Ag = g2-^i = c(s2-s1);
с= Ag-/(s2 — Sj). (6.37)
Точность определения цены деления этим методом зависит
от погрешности эталонной разности Ag. Если цену деления надо
155
определить с относительной погрешностью 1 • КГ4, то эталонное
значение Ag должно быть измерено с той же погрешностью 1 • 10“4,
т. е. на приращении Ag = 500-10~® м/с2 ошибка не может превы-
шать 0,05- 1(ГВ м/с2. С уменьшением эталонного приращения про-
порционально увеличивается погрешность эталонирования.
Ошибка в цене деления входит как систематическая во все после-
дующие измерения приращений силы тяжести. Чтобы найти цену
деления для различных участков шкалы отсчетного устройства,
используют несколько пунктов со значениями силы тяжести,
попадающими в интервал измерения.
Способ эталонирования гравиметров на пунктах с известной
силой тяжести позволяет определять цену деления в условиях,
близких к тем, при которых гравиметр работает в поле. В то же
время этот способ является громоздким и сравнительно дорогим,
поскольку он связан со значительными транспортными расхо-
дами. Поэтому он применяется главным образом для независи-
мого контроля результатов эталонирования, выполненного другими
методами, или в тех случаях, когда нет возможности прибегнуть
к иным способам эталонирования.
Для эталонирования гравиметров описываемым методом обычно
используют специально созданные международные, националь-
ные, местные полигоны (базисы). Силу тяжести в пунктах полиго-
нов определяют по специальной программе с помощью высоко-
точных маятников и гравиметров с известной ценой деления
шкалы. Чтобы изменение силы тяжести между пунктами было ма-
ксимальным, их обычно располагают в меридиональном напра-
влении.
Наиболее крупным международным полигоном является Се-
веро-Американский, протягивающийся вдоль западного по-
бережья от Фербенкса (Аляска) до Мехико (Мексика). Этот базис
включает 33 пункта и имеет диапазон изменения силы тяжести
5129 1(Г® м/с2, относительная погрешность составляет 3,5-КГ4.
Западно-Европейский полигон Рим (Италия) — Гаммерфест (Нор-
вегия) имеет диапазон 2500-10”8 м/с2 при относительной погреш-
ности 3- КГ4. Ряд стран создали свои национальные полигоны
с различными приращениями силы тяжести. В нашей стране есть
полигоны с относительной погрешностью (1 <- 2)- КГ4 при раз-
ностях силы тяжести от 80- 1СГ6 до 1000- КГ5 м/с2 и 5- КГ8—1 • КГ4
при разностях (1000 3000)-КГ® м/с2. Большинство современных
гравиметров имеет диапазон измерений не более 100-10"® м/с2,
для их эталонирования пригодны полигоны с приращением силы
тяжести 200-10"® м/с2. Такие полигоны удобно создавать в горных
местностях, где наблюдается значительное изменение силы тя-
жести по высоте на коротких расстояниях.
Пункты наблюдений на эталонировочных полигонах закре-
пляют долговременными знаками (бетонными или каменными стол-
бами, плитами); к этим пунктам должен быть обеспечен хороший
подъезд.
156
Способ наклона более удобен и нашел широкое распростране-
ние в практике эталонирования гравиметров. В этом случае ис-
пользуется зависимость показаний гравиметра от наклона: при
наклоне гравиметра на угол |3 его показания изменяются так,
как будто сила тяжести уменьшилась на величину
Ag = g(₽2/2).
Изменения показаний гравиметра при наклоне выражаются
уравнением
— sj -- g(P72),
где «j и s0 — отсчеты при наклоне гравиметра па угол р и в исход-
ном положении.
Отсюда
В этом случае для достижения точности эталонирования
110"4 значение g в пункте эталонирования необходимо знать
приблизительно до 100- 10'6 м/с2. Действительно, рассматривая Ag
как эталонное значение силы тяжести, логарифмируя и дифферен-
цируя по независимым переменным Ag и g выражение (6.36),
находим
d hg/hg = dg/g.
Полагая d Ag!Ag == 1- IO'4, имеем dg — 100- 10'® м/с2. С такой
приближенностью значение силы тяжести известно всегда.
Найдя логарифмическую производную в формуле (6.36) по
независимым переменным Ag и р, получим
dAg/Ag = 2(dp/P),
т. е. относительная погрешность эталонной разности силы тяжести
прямо пропорциональна погрешности измерения угла р и обратно
пропорциональна значению самого угла. Кроме того, макси-
мально допустимая ошибка измерения угла р должна быть в 2
раза меньше погрешности эталонирования:
1 de ddg
р ~2 с~ Ag '
(6.39)
В табл. 6.2 приведены значения rfp/p, на которые надо ориен-
тироваться при расчете точности эталонирования. Значение g
принято равным 981-10'2 м/с2.
Максимально возможный наклон гравиметра определяется его
конструкцией и диапазоном измерения без перестройки. Боль-
шинство гравиметров имеет диапазон (100 200)-10'5 м/с2. Для
таких гравиметров, как видно из табл. 6.2, наклон возможен
только в пределах 1—1,5°. При этом требуется очень высокая
157
Таблица 6.2
Точность эталонирования методом наклона
р Ag, Ю““ м/с2 4^-, ЮЧ Ag ’ при dp = 0,5" (4p)max яри 4^-. i.io-i Ag
0° 10' 0 30 1 00 2 00 3 00 4 00 4 37 149 598 1345 2391 16,6 5,6 2,8 1,4 0 9 0,7 0,03" 0,09 0,18 0,36 0.54 0.72
точность измерения угла наклона. Чтобы обеспечить такую точ-
ность, наклон гравиметра осуществляется или на экзаменаторе
для исследования уровней, или же на специально изготовленной
наклономерной плите. Эта массивная плита стоит на трех винтах.
Один из винтов (которым задается наклон плиты) изготовляется
с возможно большей точностью. Если b — база плиты (расстояние
от винта до линии, проходящей через упоры двух других винтов),
h — шаг измерительного винта, то при повороте винта на один
оборот плита наклоняется на угол [3 = h/b. Если п — число пол-
ных оборотов микровинта, то
ля=g 4-=4- • -г w. (б-4°)
где
К = fc/2) (W
— постоянный коэффициент для данного пункта наблюдений
и данного микровинта.
Тогда цена деления
с =/c«7(so — s„). (6.41)
Углы наклона плиты можно измерять непосредственно в угло-
вых единицах, используя теодолит. Для этого на плите закре-
пляют зеркало, а теодолит снабжают автоколлиматором. Ось
трубы теодолита каждый раз устанавливают перпендикулярно
к зеркалу, совмещая горизонтальные линии сетки окуляра с их
отражением от зеркала. Углы наклона отсчитывают на вертикаль-
ном круге теодолита. При подготовке этой установки к работе
необходимо добиться, чтобы оси наклона плиты и теодолита были
параллельны. Такое положение будет достигнуто, когда при
наклоне плиты или трубы теодолита вертикальные линии сетки
окуляра все время совпадают с их отражениями от зеркала плиты.
Для эталонирования бестермостатных отечественных грави-
метров методом наклона в ИФЗ АН СССР разработана специаль-
на
пая установка УЭГП, где углы наклона гравиметра измеряют
с помощью теодолитного круга непосредственно в угловых еди-
ницах. Эта установка представляет собой вращающуюся вокруг
горизонтальной осн раму, выполненную в виде цилиндрического
кольца, в которой закрепляется гравиметр. На одной оси с рамой
размещен вертикальный круг теодолита для измерения углов
наклона гравиметра. Другая установка для эталонирования грави-
метров методом наклона (УЭГ-2) состоит из наклономерной плиты
с подставкой для гравиметра, двух накладных уровней для приве-
дения оси вращения плиты и подставки в горизонтальное положе-
ние и оптического теодолита. Углы наклона плиты и соответственно
чувствительной системы гравиметра измеряются автоколлима-
ционным способом по вертикальному кругу теодолита. Эти уста-
новки обеспечивают определение цены деления гравиметров с отно-
сительной погрешностью 11СГ4.
Чувствительность астазированных гравиметров при наклоне
вдоль маятника изменяется. При некотором угле наклона в сто-
рону поднятия рычага система приобретает бесконечно большую
чувствительность, и наоборот, при наклоне в сторону опускания
рычага система теряет чувствительность. В результате пропадает
возможность получить обе ветви параболы, что снижает точность
определения цены деления. Рекомендуется поэтому наклонять
гравиметр в поперечном к рычагу направлении, т. е. вдоль оси
вращения рычага. В этом случае чувствительность прибора ме-
няется незначительно и обе ветви параболы получаются во всем
рабочем диапазоне гравиметра.
Процесс наблюдений на наклономерной плите осуществляется
следующим образом. Гравиметр устанавливают на горизонталь-
ную плиту, ось вращения чувствительной системы совмещают
с направлением наклона плиты. При этом оба уровня гравиметра
должны быть тщательно выверены. После этого, взяв отсчет при
нулевом положении уровней, задают гравиметру наклон микро-
метренным винтом плиты и снова берут отсчет. Затем последова-
тельно увеличивают наклон. Достигнув максимального наклона
в одну сторону, сразу же задают максимальный наклон в противо-
положную сторону и выполняют наблюдения, последовательно
уменьшая наклон и приближаясь к исходному положению. При
такой методике среднее значение из отсчетов при наклоне в про-
тивоположные стороны свободно от влияния изменения нуль-
пункта, а также от ошибок в юстировке уровня, вдоль которого
наклоняют прибор. При эталонировании наклоном получают
систему уравнений, число которых равно числу углов наклона
в одну какую-либо сторону. Решая эту систему, находят цену
деления и ее погрешность.
Метод эталонирования гравиметров с помощью дополнитель-
ных грузиков состоит в том, что на одном и том же пункте к основ-
ному подвижному грузу чувствительной системы добавляют до-
полнительные грузики с известной массой и наблюдают изменение
159
показаний гравиметра. Если массе подвижной системы грави-
метра т соответствует отсчет slt то после добавления грузика с мас-
сой Ат происходит кажущееся изменение силы тяжести и отсчет
гравиметра становится з2. При добавлении грузика вес подвижной
массы увеличивается на g Am = Agm, т. е.
Ag = g (Am/m).
Ho Ag c (s2 — 8Х), следовательно,
с=—--------^L = -S.^L. (6.42)
s2 — st т as т
Этот метод эталонирования может быть использован только
в гравиметрах, имеющих специальные устройства для навешива-
ния дополнительных масс.
В некоторых гравиметрах при их эталонировании обнаружи-
вается нелинейность шкалы измерительной системы, т. е. отсчет s
гравиметра зависит от изменения силы тяжести нелинейно. Такую
зависимость можно представить в виде
gr = cos 4-qs2, (6.43)
где с0 — цена деления гравиметра для начала шкалы (з = 0);
сх — квадратичный член, учитывающий изменение цены деления
в рабочем диапазоне гравиметра.
Приращение силы тяжести, измеренное гравиметром между
двумя точками, в которых сила тяжести соответственно g,: и g0,
Agzii == gt — go = Co (sz — sn) 4- c1 (sj — So). (6.44)
В большинстве, случаев нелинейность отсчетной шкалы не-
велика и при измерении малых приращений ею можно пренебречь.
Для больших приращений и высокоточных наблюдений даже ма-
лую нелинейность следует учитывать.
Уравнение (6.44) можно преобразовать к виду
Agjo — sl (с0 Д- cxsz) s0 (c0 cxs0) = S[Csi s0ci0 (6.45)
или
Ag.-o =- co [ (sz p ~ (s« + ] = co (sfS — so»). (6.46)
Можно построить график зависимости цены деления шкалы csi
от отсчетах; и, используя этот график, вычислять Ag по формуле
(6.45) или же построить график поправок (ci/co) s* как функцию
отсчета sz и вычислять Ag по формуле (6.46) (рис. 6.17).
Выявить нелинейность шкалы измерительного устройства гра-
виметра можно несколькими способами.
При эталонировании гравиметра по наблюдениям па пунктах
с известными значениями силы тяжести или методом наклона,
160
Рис. 6.17. Зависимость цены деления csi и поправки за не-
линейность измерительной шкалы (cj/cg) s? гравиметра от от-
счета Sj.
измерив два приращения силы тяжести между тремя пунктами или
наклонив гравиметр на два угла от исходного положения, можно
составить следующие уравнения:
Agw = gi — go = Co(si - so)+ (si - So); I
, 2 2. (6.47)
Ag20 = g'l — go = Co (S9 — So) + Cl (®2 — So). J
Решив эти уравнения, определим с0, ct и отношение е\/с0, что
позволит составить графики или таблицы для csi- и (Cj/co) s®.
Если есть только два пункта с известной разностью силы тя-
жести между ними или гравиметр можно наклонить только на
один определенный угол, то нелинейность шкалы можно уста-
новить, проэталонировав гравиметр два раза, перестроив при
этом диапазон перед последующим эталонированием. В этом слу-
чае система уравнений (6.47) может быть записана так:
Agio = gi — go = Со (Si — So) + Cl (si — 4) =-
= Co (si — So) Cl (sj2 — So2), (6.48)
где Sj и s0 — отсчеты до перестройки диапазона; si и So — отсчеты
после перестройки диапазона.
Из уравнения (6.48) можно определить с^/с'о, а затем найти с0.
Нелинейность измерительной шкалы гравиметра можно также
выявить, беря отсчеты, соответствующие крайним положениям
индекса регистрирующей системы, каждый раз перестраивая
диапазон измерений.
При эталонировании гравиметров с помощью дополнительных
грузиков линейность шкалы отсчетного устройства проверяют,
несколько раз перестраивая диапазон измерений.
6
В. С. Миронов
161
Естественно, что точность определения нелинейности шкалы
может быть повышена, если проводить наблюдения па большем
числе пунктов или при большем числе наклонов гравиметра, не-
сколько раз перестраивая диапазон измерений, что позволит
составить большее число уравнений типа (6.47) и решить их мето-
дом наименьших квадратов.
Определив цену деления измерительной шкалы гравиметра
с высокой точностью, порядка 1 • 1СГ4, в некоторых гравиметрах
можно обнаружить зависимость цены от температуры. При не-
линейной шкале сначала необходимо ввести поправку за нелиней-
ность, а после этого исследовать температурную характеристику
шкалы.
Глава 7
НЕКОТОРЫЕ ТИПЫ ГРАВИМЕТРОВ
ГРАВИМЕТРЫ
С МЕТАЛЛИЧЕСКИМИ ПРУЖИНАМИ
В Советском Союзе и за рубежом было создано несколько кон-
струкций металлических гравиметров на основе различных прин-
ципов.
Гравиметры с плоской кольцевой пружиной
Идея первого отечественного металлического гравиметра, упру-
гим элементом которого служит кольцевая пружина, предложена
М. С. Молоденским в 1938 г. Им же разработана теория этого
гравиметра, конструкция которого послужила основой для соз-
дания нескольких различных типов гравиметров.
Гравиметр ГКМ, применявшийся при геологоразведочных работах в 40-х го-
дах, имеет следующий принцип устройства. Плоская элинварпая ленточная
пружина / постоянного сечения одним концом жестко крепится к станице 4,
а другим к рычагу 2 (рис. 7.1). Второй конец рычага подвешен к станине на двух
тонких металлических нитях. Под действием веса рычага и реакции нитей пру-
жина принимает форму кольца. При изменении силы тяжести меняется вес ры-
чага и он поднимается или опускается. Мерой изменения силы тяжести является
вертикальное смещение конца рычага, что регистрируется емкостным ультра-
микрометром. Измерения проводят компенсационным способом; при помощи
измерительной пружины <3, связанной одним концом с рычагом, а другим с микро-
метрическим винтом, рычаг приводят в постоянное исходное положение.
Прибор термостатирован. Диапазон измерений без перестройки (700-Г750) X
X 10~6 м/с2; погрешность измерений (0,5 0,7)-10’5 м/с2; масса прибора около
26 кг.
Гравиметр ГКА является улучшенной конструкцией гравиметра ГКМ, он
отличается более простым регистрирующим устройством, меньшими массой и
размерами, повышенной точностью наблюдений. Этот гравиметр использовался
ври гравиметрических съемках в 50-х и начале 60-х годов.
Основным упругим элементом гравиметра ГКА (рис. 7.2), как и ГКМ, яв-
ляется ленточная пружина 1, изогнутая в кольцо под действием изгибающего
162
Рис. 7.1. Схема гравиметра ГКМ.
Рис. 7.2. Схема гравиметра ГКА.
момента рычага 5 с грузом на конце. Осью вращения рычага служит скреплен-
ная с ним тонкая вольфрамовая нить 4. Концы нити заделаны в станине через
упругую связь. Ось вращения рычага находится в центре кольцевой пружины.
При изменении силы тяжести ^изменяется вес подвижного груза, что вызывает
угловое смещение рычага.
Чтобы увеличить это смещение, предусмотрено астазирующсс устройство,
состоящее из дегазирующей плоской пружины 2 и гибкой металлической нити 3.
Астазирующая пружина одним концом закреплена в раме прибора, другим
соединена нитью с отростком рычага. В пулевом, горизонтальном, положении ры-
чага нить проходит через его ось вращения и'момент астазирующей пружины
относительно оси вращения рычага равен нулю. При отклонении рычага от
горизонтального положения возникает добавочный момент астазирующей пру-
жины, приводящий к дополнительному смещению рычага, т. е. чувствительность
упругой системы к изменениям силы тяжести определяется не только деформа-
цией главной кольцевой пружины, но п натяжением астазирующей пружины
нее плечом. При выборе параметров астазирующего устройства исходят из угло-
вой чувствительности гравиметра (около 30" на 1-10~8 м/с2). Сила натяжения
астазирующей пружины должна быть равна весу рычага. В этом случае всю
нагрузку от рычага несет на себе астазирующая пружина, а ось вращения ста-
новится полностью разгруженной.
Измерения с гравиметром проводят компенсационным способом. Изменение
силы тяжести компенсируется натяжением пружины 6, один конец которой при-
креплен к подвижному концу рычага, другой к микрометрическому винту 8.
Для расширения интервала измерения с рычагом связана диапазонная пру-
жина 7. Регистрация пулевого положения рычага осуществляется оптической
автоколлнмационной системой.
Упругая система гравиметра помещена в двухступенчатый термостат. Диа-
пазон измерений около 150-Ю-5 м/с.2; погрешность (0,34-0,5)-10“5 м/с2; масса
прибора 13 кг.
Гравиметры
с горизонтальными винтовыми пружинами
Использовать горизонтальные винтовые пружины в качестве
упругого элемента гравиметра предложил А. Граф, на этом прин-
ципе он сконструировал несколько моделей неастазированных
гравиметров. В СССР на таком принципе разработаны астазиро-
ванные системы гравиметров.
Гравиметр GS-l 1 создан фирмой «Аскання Верке» (ФРГ) и в настоящее
время является единственным пеастазированным прибором, обеспечивающим
&
163
Рис. 7.3. Схема гравиметра GS-1I.
погрешность измерения силы тяжести не больше (0,024-0,05) -10'6 м/с2. Этот при-
бор известен также под названием гравиметра Графа.
Конструкция гравиметра GS-11 основана на принципе крутильных пру-
жинных весов (рис. 7.3). Две винтовые пружины 2, расположенные почти гори-
зонтально, натянуты и закручены так, что рычаг 1 с грузиком (маятник), укреп-
ленный между ними, находится в горизонтальном положении. Изменение силы
тяжести приводит к нарушению горизонтального положения маятника.
Измерения проводят компенсационным методом. При вращении головки 15
измерительного устройства изменяется натяжение измерительной пружины 17,
нижний конец которой соединен с маятником, а верхний — с подвижной карет-
кой 16, несущей стеклянную пластинку с делениями прецизионной шкалы.
Изменение положения прецизионной шкалы наблюдается в окуляр 13 но спе-
циальному индексу масштабной пластинки клинового микрометра. Нулевое по-
164
ложение рычага регистрируется фотоэлектрическим способом. Световой луч
от лампочки 11, пройдя через конденсор 12, щель 9 и объектив 7, падает на зер-
кало 4 рычага маятника и, отразившись от него, попадает на неподвижное
зеркало 6, расположенное напротив. От зеркала 6 луч снова идет на зеркало 4
и от него на два фотоэлемента 8, включенные по дифференциальной схеме. Раз-
ностный фототок подается на зеркальный гальванометр 10, показания кото-
рого могут быть отсчитаны по шкале. Зависимость между удлинением измери-
тельной пружины и показаниями зеркального гальванометра линейная. Поэтому
при измерениях нет необходимости устанавливать гальванометр точно на нуль.
Недалеко от центра тяжести маятника к рычагу прикреплена вторая пру-
жина, диапазонная, 19, предназначенная для изменения диапазона измерений.
Один оборот головки впита 18 диапазонной пружины соответствует изменению
силы тяжести на 200 -10~5 м/с2. Полный диапазон измерений без перестройки
(6004-800) -10“ 5 м/с2.
Для устранения влияний температуры на показания прибора применены
металлическая температурная компенсация и термостатирование. Для темпера-
турной компенсации использованы две слабые спиральные пружины, соосные
с главными и расположенные внутри их. Меняя натяжение этих пружин, под-
бирают необходимый температурный коэффициент. Термостат гравиметра двух-
ступенчатый, с электрическим подогревом. В зависимости от внешней темпера
туры внутри гравиметра может быть установлена температура 25, 35, 40, 45" С.
Постоянство температуры в термостате поддерживается до 0,01'" С.
Упругая система гравиметра герметизирована; на случай нарушения гер-
метизации имеется барокомпенсатор 8 (два полых цилиндра). Против магнит-
ных влияний предусмотрен пермаллоевый экран.
Гравиметр GS-11 имеет устройство, позволяющее контролировать цену деле-
ния и проверять линейность деформации измерительной пружины в полевых
условиях. Для этого на рычаге упругой системы сделаны два углубления, рас-
положенные на определенном расстоянии от оси вращения и одно от другого.
В одном из углублений помещен металлический шарик. Во время перевозок и
при небольших наклонах прибора шарик остается в лунке. Переместить шарик
из лунки можно только наклонив прибор на 90°. Перемещение шарика изменяет
момент массы на постоянную величину, которая соответствует кажущемуся из-
менению силы тяжести примерно на 200'10~5 м/с2.
Гравиметр GS-11 чувствителен к тряске и толчкам. Недопустимы также зна-
чительные наклоны прибора, при этом меняются показания гальванометра.
Поэтому эталонировать гравиметр методом наклона нельзя. При транспорти-
ровке гравиметра его упругую систему арретируют двумя рычагами 5 в поло-
жении, близком к положению равновесия.
Электропитание гравиметра осуществляется от двух аккумуляторов по 6 В.
Один служит для освещения фотоэлементов, другой — для работы термостатов
и подсветки шкалы гальванометра.
При наблюдениях гравиметр устанавливают на специальную треногу и ни-
велируют по уровням 14. Продолжительность наблюдений около 3 мип. Масса
прибора 20,5, треноги 7,3 кг. Смещение нуль-пункта гравиметра при изменении
внешней температуры на 10° С обычно не превышает 0,05-Ю"5 м/с2 за 1 ч.
Дальнейшим развитием конструкции прибора GS-11 являются гравиметры
GS-12, -15 и -16. К отличительным особенностям гравиметра GS-12 относится
принцип измерительной системы: вместо диапазонной пружины использован
комплект металлических шариков, которые с помощью специального устрой-
ства можно помещать на рычаг чувствительной системы. В гравиметре GS-I6
зеркальный гальванометр заменен стрелочным индикатором, фиксирующим го-
ризонтальное положение рычага системы, и расширен до 2000-Ю-5 м/с2 диапазон
измерений без перестройки. Погрешность наблюдений с указанными грави-
метрами составляет 0,02 -10“5 м/с2. При помощи дополнительного устройства (фо-
торегистрирующей приставки) этими гравиметрами можно непрерывно регистри-
ровать суточные вариации силы тяжести. В этом случае резко уменьшается сме-
щение нуль-пункта гравиметров и погрешность снижается до 0,001 • 10 ” м/с3.
Поэтому гравиметры GS находят широкое применение при регистрации вариа-
ций силы тяжести.
165
Гравиметр ГВП-2 представляет собой прибор, позволяющий
одновременно измерять приращение силы тяжести и разность
высот между пунктами наблюдений. Идея такого прибора была
высказана в 1944 г. В. В. Федынским. В гравиметрах, упругая
система которых не герметизирована, необходимо применять баро-
метрическую компенсацию, чтобы исключить влияние атмосфер-
ного давления на показания гравиметра. В. В. Федынский пред-
ложил построить гравиметр с двумя упругими системами: одна
полностью барометрически компенсирована, а другая, наоборот,
имеет очень большой барометрический коэффициент. Поскольку
системы обладают существенно разными эффективными плотно-
стями, то каждая дает свое измеренное значение Ag действитель’
ной разности силы тяжести. Это значение определяется действи"
тельным приращением силы тяжести Ag и ее кажущимся изме-
нением, вызванным изменением атмосферного давления:
Agx=Ag + ^ \р\
Ag2 = Ag 4- Ка Др,
(7.1)
где Ki и — барометрические коэффициенты упругих систем;
Ар — разность атмосферного давления в пунктах наблюдений.
Из уравнений (7.1) имеем
Ар = (Agi - Ags)/(KX - Kt). (7.2)
Одну из систем можно полностью барометрически скомпенси-
ровать, положив, например, К2 = 0. Тогда
Ap = (l/K1)(Ag1-Ai2) = (l/Kl)(Ai1-Ag);
А А ~ ('"’)
Ag = Ag2.
Из этих уравнений следует, что прибором, имеющим две упру-
гие системы с разными барометрическими коэффициентами, можно
измерить изменение атмосферного давления Ар и приращение
силы тяжести Ag.
Из теории барометрического нивелирования известно, что
разность высот ДН двух близко расположенных пунктов может
быть вычислена по формуле
А# = .4Др,
где А — барометрическая ступень, являющаяся функцией сред-
него давления и средней температуры в пунктах наблюдений.
Обозначив А!К\ через /<0 (высотный коэффициент гравиметра),
получим
АЯ = К0(Д£г-Д^. (7.4)
Высотный коэффициент гравиметра зависит не только от пара-
метров упругой системы, но и от давления и температуры воздуха.
186
Численные значения Ко определяют экспериментально на пунктах
с известным значением высот и силы тяжести либо в барокамере
при различном давлении. При этом должны быть известны темпе-
ратура и давление воздуха. Для перевычисления коэффициента /<0
к другим значениям давления и температуры используют формулу
/<о=л-о_рД1±1&., (7.5)
где Ко — высотный коэффициент прибора при р0 = 101 325 Па
«=. 1 • 105 Па и t = 0°С.
При конструировании гравиметра-высотомера, меняя объемный
момент рычага, надо выбрать оптимальные значения /<0, обеспечи-
вающие наилучшую точность определения силы тяжести. При
этом руководствуются следующими соображениями.
Конечным результатом гравиметрической съемки является
система значений силы тяжести g0, приведенных к уровню моря
с помощью поправки ЪН:
g9 = g+bH. (7.6)
Если применяется поправка Буге, то.
д = 0,3086 —0,0419а,
где о — плотность промежуточного слоя.
Разность Ago силы тяжести между любым пунктом наблюде-
ния и исходным пунктом, приведенная к исходному уровню высот,
может быть записана в виде
Ag0 = Ag+bAtf, (7.7)
или, заменяя АД его значением из уравнения (7.4), находим
Ag0 = д£ + (ДЯ1 - Ag) = (1 - WQ Ag + ькп Agv (7.8)
Обозначив средние квадратические погрешности измеренных
величин Ag0, Ag и Agx соответственно через е0, eg, еЛ/, напишем
?-'о’|/Г(1 —/Д\о)'(/?/<<,)’!•'>/. (7.9)
Если обе системы гравиметра имеют одинаковую точность,
т. е. — р.ц, то
е0 = вг V1-1 2НаЖ- 1). (7.10)
Из этого уравнения можно найти оптимальное значение высот-
ного коэффициента Ко, исходя из условия, что при одинаковой
средней квадратической погрешности обеих упругих систем по-
грешность определения разности силы тяжести Ag0, приведенной
к уровню моря, должна быть минимальной, т. е.
е0/Ей = K(l(W<o ~ J)= min. (7-И)
167
Дифференцируя это выражение по К„ и приравнивая произ-
водную нулю, получаем
d (gp/Eg) 2W„ — b _ у
dKQ ' /2&X0(&K0— 1) + 1
t. e.
^=1/(26).
Если при изготовлении гравиметра-высотомера соблюдено это
условие, т. е. выбрано оптимальное значение /<0 1/(2Ь), то
е0 — eg/]/2 = 0,78£. (7.12)
Уравнение (7.12) показывает, что при оптимальном высотном
коэффициенте гравиметра-высотомера погрешность приведенного
к уровню моря значения силы тяжести составляет 0,7 погрешности
измерений с обычным гравиметром, т. е. точность наблюдений
с гравиметром-высотомером равна точности наблюдений одно-
временно с двумя гравиметрами, которые, по существу, и заме-
няет гравиметр-высотомер.
При рассмотрении точности нами не принимались во внимание
погрешности самого барометрического нивелирования, возни-
кающие из-за изменения метеорологических условий. Эти погреш-
ности учитывают, применяя особую методику наблюдений или
данные барометрических станций.
Конструкция первого гравиметра-высотомера была разрабо-
тана В. В. Федынским и А. М. Лозинской в 1951 г. на базе грави-
метра ГК А.
Гравиметр ГВП-2 (рис. 7.4) является более совершенной моделью грави-
метра-высотомера. Он имеет две упругие системы: высотомерную а с большим
барометрическим коэффициентом и гравиметровую б, барометрически компен-
сированную.
Упругим элементом обеих систем являются две цилиндрические винтовые
горизонтально расположенные пружины 3, изготовленные из элинвара. Пру-
168
жины навиты навстречу другу другу и прикреплены одним концом к корпусу
прибора, а другим к рычагу системы. Рычаг 4 гравиметровой системы изготов-
лен из алюминия и имеет латунный грузик, зеркало 5 и барокомпенсатор 7.
Для повышения чувствительности системы к изменениям силы тяжести она аста-
зирована пружиной 2. При горизонтальном положении рычага пружина на-
ходится в плоскости его оси вращения, при отклонении рычага от этого положе-
ния пружина создает момент вращения.
Приращения силы тяжести измеряют компенсационным методом: на каждой
точке рычаг приводят в горизонтальное положение, изменяя натяжение измери-
тельной пружины /, соединенной с микрометром и рычагом упругой системы.
Регистрация положения рычага оптическая, автоколлимационная. Диапазон из-
мерений перестраивают, изменяя натяжение диапазонной пружины 6.
Упругая система гравиметра термокомпенсирована с помощью биметалличе-
ской пластины, соединенной с рычагом через тонкую пружину. При изменении
температуры биметаллическая пластина изгибается и натягивает пружину таким
образом, что компенсирует изменение момента главных пружин из-за изменения
температуры. Измерительная пружина соединена с рычагом через биметалличе-
скую пластину температурного компенсатора.
В высотомерной системе вместо латунного груза на конце рычага 4 укреп-
лен полый цилиндр 8, создающий большой объемный момент.
При транспортировке упругие системы гравиметра арретируют; для защиты
от магнитного поля имеется пермаллоевый экран. Для поддержания постоянной
температуры прибор помещают в электрический термостат и сосуд Дьюара, что
обеспечивает высокий коэффициент термостатирования.
Точность измерений определяется методикой работ, при коротких рейсах
погрешность силы тяжести составляет 0,2-10-5 м/с2, высоты 1,5 м; масса при-
бора 6,5 кг.
Гравиметр ГМТ-1, разработанный во ВНИИГеофизике, предназначен для
измерения больших приращений силы тяжести без перестройки [(10004-1500) X
X 10“5 м/с2]. Они применяются в основном при создании опорных гравиметри-
ческих сетей.
По устройству упругой системы гравиметр ГМТ-1 принципиально не от-
личается от гравиметра ГВП-2. Главные пружины гравиметра не цилиндриче-
ские, а навиты по поверхности параболоида вращения, что позволяет несколько
сократить размеры прибора и получить достаточную чувствительность при мень-
ших напряжениях в пружинах. Гравиметр ГМТ-1 герметизирован при атмо-
сферном давлении; на случай разгерметизации предусмотрена барометрическая
компенсация. Чувствительная система помещена в двухступенчатый термостат,
заключенный в сосуд Дьюара, и температурно компенсирована. Термостат на-
строен на температуру +45° С. Погрешность измерений (0,14-0,2) • 10~ 5 м/с2;
масса прибора 8 кг.
Гравиметр ГМТ-2 предназначен для детальных гравиметрических работ
и принципиально не отличается от гравиметра ГМТ-1. Диапазон измерений без
перестройки составляет около 150 -10‘5 м/с2; погрешность наблюдений 0,06 X
X ЦТ" м/с2.
КВАРЦЕВЫЕ ГРАВИМЕТРЫ
С ГОРИЗОНТАЛЬНОЙ КРУТИЛЬНОЙ НИТЬЮ
И ЖИДКОСТНОЙ ТЕМПЕРАТУРНОЙ
КОМПЕНСАЦИЕЙ
В 1940 г. в Датском геодезическом институте Г. Норгардом
был сконструирован кварцевый неастазированный гравиметр.
Гравиметр Норгарда послужил основой для создания несколь-
ких аналогичных конструкций гравиметров, широко применяв-
шихся при гравиметрических исследованиях в СССР.
Упругая система гравиметра Норгарда (рис. 7.5) представляет
собой тонкую кварцевую нить 6, натянутую на кварцевой раме 1
169
Рис. 7.5. Схема упругой системы гравиметра Норгарда,
и закрученную ла некоторый угол. К середине нити приварен
кварцевый рычаг (маятник) 5 с торцевым зеркалом 3 и металли-
ческим грузиком 4. Маятник удерживается силой закручивания
нити в положении, близком к горизонтальному. При изменении
силы тяжести изменяется момент веса маятника и, следовательно,
угол закручивания инти.
Приращение силы тяжести измеряется нулевым методом:
наклоняя кварцевую систему вдоль рычага маятника, задают
нити постоянный угол закручивания. Чтобы зафиксировать это
положение, к раме кварцевой системы прикреплено неподвижное
зеркало 2, которое параллельно подвижному зеркалу 3 при исход-
ном положении маятника. Угол наклона системы служит мерой
приращения силы тяжести.
Постоянный угол закручивания нити подвеса маятника ре-
гистрирует автоколлимационная система. Диапазон измерений
перестраивают, изменяя угол предварительного закручивания
нити. Для этого один ее конец приварен к штоку 7, вращающемуся
в подшипниках.
Для уменьшения температурного влияния кварцевая система
помещена в жидкость. Принцип жидкостной температурной ком-
пенсации состоит в следующем. При повышении температуры
жесткость кварца, в противоположность жесткости металлов, уве-
личивается приблизительно на 120-10"в 1/°С. Вследствие этого
первоначальный угол закручивания нити уменьшается, и рычаг
стремится подняться вверх. Но с ростом температуры умень-
шается плотность жидкости и, следовательно, ослабевает архи-
медова сила, выталкивающая рычаг. Поэтому момент веса рычага
увеличивается, и рычаг стремится опуститься вниз. Соответ-
ствующим подбором жидкости и размеров*'рычага можно достичь
полной температурной компенсации при определенной темпе-
ратуре.
По аналогичному принципу в СССР в 1945—1953 гг. было
создано несколько конструкций гравиметров. К ним относятся
гравиметры СН-3 (Всесоюзный институт разведочной геофизики).
ГАЭ (ИФЗ АН СССР), ГКОМ НИИГР (Научно-исследовательский
институт геофизических методов разведки), морские гравиметры
для определения силы тяжести с борта корабля (ИФЗ АН СССР,
ВНИИГеофизика).
170
При произвольном расположении рычага относительно гори-
зонтальной плоскости уравнение равновесия упругой системы
гравиметра Норгарда имеет следующий вид;

т (0о I- + g Hi ( 1
- -у-) /2j cos а = О,
(7.13)
где и ;л2 — масса кварцевого рычага и металлического грузика;
и /2 — расстояние от оси вращения до центра тяжести рычага
и грузика; 6, б( и 62 — плотность жидкости, кварца и грузика;
0О — угол предварительного закручивания нити подвеса рычага,
когда он лежит в горизонтальной плоскости; т — крутильная
жесткость нити подвеса; а — угол отклонения рычага от
горизонта.
Положительное направление отсчета углов совпадает с на-
правлением движения рычага от горизонтальной плоскости вверх.
Из уравнения равновесия (7.13), считая в нем все величины,
кроме g и а, постоянными, получаем уравнение чувствительности
системы к изменению силы тяжести
g [ 1 + + «) tg «I
При ос — О
= e0/g,
т. е. чувствительность системы пропорциональна полной дефор-
мации — полному углу закручивания 0О нити подвеса рычага.
Из уравнения (7.14) следует, что чувствительность зависит
от угла наклона рычага к горизонту и его знака. При уменьшении
угла (а < 0) маятник находится ниже горизонта, чувствитель-
ность системы уменьшается и при а = —л/2 имеем daJdg = 0.
При увеличении угла (« >0) маятник располагается выше го-
ризонта, чувствительность системы растет и при tg а —
= —1/(0о -г и) становится бесконечно большой. Таким образом,
система Норгарда относится к дегазированным нелинейным си-
стемам, но поскольку в рабочем диапазоне угла а чувствитель-
ность изменяется мало, эту систему часто называют неастазиро-
ванной, что не совсем верно.
Чтобы получить зависимость показаний гравиметра от темпе-
ратуры и уравнение термокомпенсации, введем следующие обо-
значения:
т = т0(1-|-р/); 6 = 60(14-?/),
где р — термоэластический коэффициент второго рода для кварца;
у — коэффициент объемного расширения жидкости.
171
Полагая остальные параметры системы при изменении тем-
пературы постоянными, находим температурный коэффициент
„ Гн _ .,х_________________________МФ + 6х/л-Л___________1 , ,
Л ТО, (б, _ бо) 6aW]Z] -|-(fi.,-60) /ТД J ' И-10-1
Если упругая система, в том числе и грузик, целиком изготов-
лена из кварца, то ее температурный коэффициент
dg
dt
(7-16)
При р 120-10-6, у «== 800-Ю-6 1/°С, 60 = 0,8, Sx = 2,2 г/см3
температурный коэффициент составит (240-г 250) • 10“6 м/с2 на 1° С.
Из уравнения (7.15) следует, что при заданной плотности
жидкости 60 и коэффициенте ее объемного расширения у с помощью
металлического грузика температурный коэффициент гравиметра
можно сделать равным нулю. Положив в уравнении (7.15) dgidt = 0
и разрешив его относительно т212/(т11)), получим уравнение, из
которого определим это отношение, обеспечивающее полную
температурную компенсацию упругой системы при заданных
значениях (3, у, 60, 61( 53:
т212 _ (Ф — 60) Р — А 62 /7 171
mdi (Ф-Ф1Р-7Ф Ф ' ( '
Отношение тг12/(тимеет следующие значения: для платины
(62 »=; 22 г/см3) 2,4; для серебра (б2 лэ 11 г/см3) 4; для латуни
(8.2 8 г/см3) 7, т. е. чем больше плотность материала грузика,
тем при меньшей его массе может быть достигнута полная темпе-
ратурная компенсация. Поэтому во всех гравиметрах с жидкостной
температурной компенсацией для изготовления грузиков при-
меняется платина. Она позволяет при малой общей массе маят-
ника, малой нагрузке на нить обеспечить достаточную температур-
ную компенсацию системы.
Температурный коэффициент объемного расширения у жид-
кости в свою очередь является функцией температуры, термоэла-
стический коэффициент [I значительно меньше и в меньшей сте-
пени зависит от температуры, поэтому при заданных значениях
всех величин, входящих в равенство (7.15), температурный коэф-
фициент равен нулю только при определенной температуре /,,.
При других температурах гравиметр имеет остаточный темпера-
турный коэффициент, в первом приближении выражающийся
кривой второго порядка. Для ослабления температурных влияний
упругие системы гравиметров помещают в термостат.
При компенсационном способе измерений методом наклона
можно написать уравнение для любой точки
—т0о — mgol — mgxl cosax = mg.,l cos а2 — mgnl cos a.,, (7.18)
гДе go — значение силы тяжести в точке, где рычаг находится
в горизонтальном положении при угле закручивания нити на
172
угол 0О; т — приведенная масса рычага в жидкости; I — при-
веденное расстояние от оси вращения до центра тяжести рычага.
Отсюда найдем
gn " go/cosa„
(7.19)
или
gn -go О I tg2 а,г)’/2.
Имея в виду относительный характер измерений с гравиметром,
из последнего уравнения находим
gr = gn - go = go (seca — 1). (7.20)
Разность значений gr в двух пунктах определяет приращение
силы тяжести между этими пунктами:
Ag = (gr)i - (gr)2=go(seca1 -seca2). (7.21)
Таким образом, для вычисления ,\g необходимо знать а и g0.
Угол а измеряют при наблюдениях с гравиметром, а g0 рассчи-
тывают, проводя измерения на пункте с известной силой тяжести.
Поскольку уравнение (7.21) справедливо при положительных и
отрицательных значениях а, прибор наклоняют в обе стороны,
тем самым уменьшая ошибки, возникающие из-за негоризонталь-
ности рычага в исходном положении.
Рассмотрим схему гравиметра Норгарда (рис. 7.6). Упругая
система (см. рис. 7.5) монтируется в металлической коробке
и заполняется термокомпенсационной жидкостью. На одной из
сторон коробки имеется окно, через
которое луч света попадает на си-
стему и возвращается обратно. Ко-
робка с упругой системой заклю-
чена внутри цилиндрического кор-
пуса гравиметра. Пространство меж-
ду корпусом гравиметра и коробкой
заполнено теплоизолирующим мате-
риалом. В верхней части корпуса
имеется цилиндрическая труба, в
которой смонтированы оптическая
система и опорные пластины микро-
метрического устройства. Цилиндри-
ческий корпус устанавливается в
наружном корпусе гравиметра на
два шарнка-шарнира и опирается
опорными пластинами на микромет-
рические винты.
Угол наклона чувствительной си-
стемы измеряется тангенциальным
способом: по расстоянию между кон-
ца ми ми крометр и ческ и х в и нтов. Св я з ь
Рис. 7.6. Схема гравиметра Нор-
гарда.
173
угла а с линейным переме-
щением микровинтов опре-
деляется формулой
ta(aJ-R) - tg^ + tgP =
']_tgatgp
== k+lm , (7.22)
где k— полоиина расстоя-
ния между спорными по-
верхностями; L— расстоя-
ние между осями враще-
ния цилиндра и микро-
метрических винтов; т -
Рис. 7.7. Схема гравиметра ГАЭ. отсчет ПО МИКрОВИНТу;
0 — угол между осевой
линией корпуса и линией, проходящей через внешнюю поверх-
ность опорной площадки.
Используя уравнения (7.20) и (7.22), получаем связь между gr
и отсчетом т по микрометрическому винту:
gr = Ст2 - Dm' - Em1 - Ftn\
(7.23)
где С, D, Е и F -— некоторые постоянные коэффициенты, выра-
жающиеся через k, L и gn.
Диапазон измерений с гравиметром без перестройки около
1500-10~5 м/с2. Перестраивают диапазон, изменяя предваритель-
ный угол закручивания нитей вращением штока кварцевой си-
стемы или совмещая другие штрихи подвижной и неподвижной
шкал. Погрешность измерений (0,1-4-0,2)-10'8 м/с2; масса прибора
15 кг.
Гравиметр СН-3, разработанный в 1948 г. в ВИРГ и довольно широко ис-
пользовавшийся при гравиметрических исследованиях в СССР, построен по
принципу системы Норгарда. В качестве термокомпенсационной жидкости в гра-
виметре СН-3 используется раствор спирта в воде. Соотношение составных ча-
стей определяет плотность раствора, а тем самым и момент силы тяжести рычага,
что позволяет перестраивать диапазон измерений. Гравиметр имеет двухступен-
чатый термостат, обеспечивающий независимость показаний от температуры.
В измерительной системе использован только один микрометрический винт и
набор калиброванных вкладышей.
Диапазон измерений без перестройки около 2500-10~5 м/с2; погрешность
(0,14-0,4)-10*5 м/с2; масса прибора 22, треноги 11 кг.
Гравиметр ГАЭ разработан в отделе гравиметрии Института физики
Земли АН СССР иод руководством Ю. Д. Буланже и предназначен для созда-
ния сетей опорных гравиметрических пунктов. Несколько серий этих при-
боров было изготовлено в 1953 и 1954 г. Прибор представляет собой усо-
вершенствованную и приспособленную для измерения больших разностей силы
тяжести модель гравиметра СН-3. Основным усовершенствованиям подверг-
лось измерительное устройство прибора. В гравиметре ГАЭ тангенциальный
метод заменен измерением непосредственно угла с помощью угломерного круга,
в качестве которого применен горизонтальный круг оптического теодолита
ОТ-02. В гравиметре этот круг установлен в вертикальной плоскости.
174
Наружный корпус гравиметра (рис. 7.7) представляет собой прямоуголь-
ный ящик, изготовленный из дюралюминия. На внутренних перегородках кор-
пуса соосно укреплены две полуоси / и 6, на которых вращается рама 7, жестко
связанная с подвижным корпусом 2 и угломерным кругом 8. Внутри прибора
установлен осветитель 5 угломерного круга. Через систему линз и призм изо-
бражение делений угломерного круга передается на оптический микрометр 4
и от него в отсчетный микроскоп 3. Поворот рамы относительно наружного кор-
пуса осуществляется специальным винтом (на рисунке не показан).
Процесс наблюдения сводится к установке прибора по уровням и измере-
нию угла раствора кварцевой системы по угломерному кругу. Точность отсчета
по угломерному кругу составляет 0,1". Средняя квадратическая погрешность
измерения угла раствора одним приемом при я = 2,5° равна 0,75". На каждом
пункте угол измеряют пятью приемами, снижая погрешность до 0,33", что соответ-
ствует погрешности приращения силы тяжести 0,07-10’6 м/с2.
Результаты полевых испытаний гравиметров ГАЭ показали, что эти при-
боры, обеспечивая достаточно высокую точность [средняя квадратическая по-
грешность наблюдений (0.2:- 0,3) • 10‘ 5 м/с21, обладают большой устойчивостью
параметров и не нуждаются в частом эталонировании. Для обработки наблю-
дений с гравиметрами ГАЭ разработаны специальные таблицы.
ГРАВИМЕТРЫ, ПОСТРОЕННЫЕ
ПО ПРИНЦИПУ ВЕРТИКАЛЬНОГО
СЕЙСМОГРАФА ГОЛИЦЫНА
В основу большинства конструкций современных гравиметров,
как кварцевых, так и металлических, положена идея вертикаль-
ного сейсмографа Голицына. В СССР на этом принципе созданы
кварцевые бестермостатные гпавиметры ГАК-ЗМ, -4М, -ПТ, -7Т,
-7Ш, ГНУ-KI, -К2, ГНШ-К, «Дельта», ВИРГ-61, ГАГ-2. В США
построены гравиметры «Атлас», «Уорден» (кварцевые), «Северная
Америка», «Вестерн», «Магнолия», Дакоста—Ромберга (металли-
ческие). В Канаде разработан гравиметр «Шарп». Особенно широ-
кое распространение получили кварцевые гравиметры, поскольку
в большинстве они являются бестермостатными приборами, об-
ладающими малыми массой и размерами, что позволяет исполь-
зовать их при работах в сложных и труднодоступных районах.
Идея приспособить вертикальный сейсмограф Голицына для
измерения приращения силы тяжести впервые была высказана
В. В. Нумеровой в 1935 г. Детальная разработка теории верти-
кального маятника была начата Л. Г. Шнирманом и продолжена
К. Е. Веселовым, П. И. Лукавчепко и др.
Идея вертикального сейсмографа Голицына состоит в следу-
ющем. На тонкой горизонтальной нити, являющейся осью враще-
ния, укреплен горизонтально расположенный рычаг с грузом на
конце (маятник). Маятник удерживается в горизонтальном поло-
жении силой натяжения главной пружины, нижний конец которой
прикреплен к маятнику, и силой закручивания осей подвеса
маятника. При изменении силы тяжести маятник с грузиком
на конце отклоняется от горизонтального положения, растягивая
главную пружину и закручивая нить подвеса до тех пор, пока
момент силы тяжести не будет уравновешен моментом главной
.пружины и моментом закручивания осей подвеса.
175
Рис. 7.8. Схема маятника Голицына.
При измерениях маятник
всегда приводится в горизон-
тальное положение введением
в систему дополнительного мо-
мента, компенсирующего изме-
нение момента силы тяжести и
являющегося, таким образом,
мерой приращения силы тяжес-
ти. Компенсирующий момент
может создаваться дополнитель-
ным растяжением или сжатием
главной пружины, закручива-
нием нити подвеса маятника
з
с помощью специальных
устройств либо непосредственным действием на маятник дополни-
тельных пружин. Для фиксации горизонтального (исходного)
положения маятника на нем устанавливается индекс. По пере-
мещению индекса можно судить об отклонении маятника от го-
ризонтальной плоскости. В частности, при оптическом (самом про-
стом) способе регистрации положения маятника изображение индек-
са рассматривают в микроскоп с большим увеличением и совмещают
его с одним из штрихов шкалы или сетки окуляра микроскопа.
Рассмотрим теорию вертикального сейсмографа Голицына как
чувствительной системы для измерения силы тяжести. Для этого
выведем уравнение равновесия системы, ее угловой чувствитель-
ности, оценим поведение системы при изменении температуры
и наклона.
Для вывода уравнения равновесия прямоугольную систему
координат расположим так, как показано на рис. 7.8. Начало
координат находится на оси вращения маятника, ось х проходит
через нижнюю точку крепления главной пружины в исходном
положении, ось у направлена вверх, ось z — вдоль нити подвеса
маятника. Предполагается, что вся система симметрична отно-
сительно плоскости хОу. Введем следующие обозначения: г —
расстояние от оси вращения маятника до нижней точки крепления
главной пружины; I — расстояние от оси вращения маятника до
его центра тяжести, при этом предполагается, что вся масса т
маятника сосредоточена в его центре тяжести; х, у и хг, — коор-
динаты верхней и нижней точек крепления главной пружины;
т и f — жесткость нити подвеса маятника и главной пружины;
d — плечо пружины; L и Lo —- полная и начальная длина пру-
жины; L — L„ --- AL — удлинение пружины; а — угол отклоне-
ния маятника от исходного положения; а0 — угол первоначаль-
ного закручивания нити подвеса маятника; |3 — угол отклонения
исходного положения маятника от горизонтальной плоскости,
т. е. наклон всего прибора.
За положительное направление отсчета углов примем направ-
ление против движения часовой стрелки. Отметим, что ось враще-
176
ния маятника горизонтальна.
Предполагается, что пружина и
нити работают в режиме закона
Гука, весточки крепления пру-
жин являются идеальными шар-
нирами, сами пружины неве-
сомы.
Если система находится в \
положении равновесия, то мо-
мент силы тяжести уравнове-
шивается суммой крутящего мо-
мента нити подвеса маятника и
момента главной пружины, т. е.
Mg = Л4Т -h Mf, (7.24)
где Мй = mgl cos (а + р) •—•
момент силы тяжести; Мх —
= т (а0 + а) — момент круче-
ния нити подвеса маятника;
х
М/ — fd AL — момент главной
пружины.
Полная длина пружины L
Рис. 7.9. Возможные способы располо-
жения главной пружины относительно
неподвижного маятника.
определяется расстоянием меж-
ду точками ее крепления с координатами (х, у) и (хъ у}), а плечо
пружины — расстоянием от оси вращения до линии оси пружины.
Тогда
AL = )Л(х - Л',)2 + (г/ — у,)1 - Lo-
Х1У~ У1Х
У(х~х^ у- (у- йЕ
(7.25)
(7.26)
Учитывая, что хх -= г cos а и yt — г sin а, и подставляя
выражения AL, d, лу и ух в формулу (7.24), получаем
mgl cos (а 4- Р) + г (а0 а) — fr (у cos а — х sin а) (1 — Lo/L) — О,
где.
(7-27)
L = |/ х2 -j- у2 -г г2 — 2г (х cos а у sin а).
Из уравнения (7.27) следует: если координатную систему
вместе с точками крепления главной пружины поворачивать
относительно оси вращения так, чтобы центр тяжести маятника
оставался неподвижным, то упругий момент системы изменяться
не будет. Таким образом, полученное уравнение равновесия
справедливо для любой системы маятника Голицына, независимо
от того, каким образом расположена главная пружина относи-
тельно горизонтальной плоскости (рис. 7.9).
177
Дифференцируя формулу (7.27) по g и а, находим уравнение
угловой чувствительности системы
= —ml cos (а + 0) Г т — mgl sin (а -ф 0) -ф
+ [г (у sin а -ф х cos а) 1--ф fr2 —(у cos а — х sin а)2 ] .
(7.28)
Поскольку за положительное направление отсчета углов при-
нято направление против часовой стрелки, то чувствительность
daldg имеет физический смысл, только когда она отрицательна,
т. е. всегда необходимо иметь знаменатель величиной положи-
тельной.
Рассмотрим влияние наклона гравиметра на его чувствитель-
ность. Поскольку сумма упругих моментов главной пружины
и нити подвеса маятника не зависит от наклона прибора, для крат-
кости обозначим ее в уравнении равновесия через Л1 (<х). Угол
наклона оси вращения маятника относительно горизонтальной
плоскости обозначим у. Уравнение равновесия принимает вид
mgl cos (а -ф 0) cos у -ф М (а) = 0. (7.29)
Введя для производной по а от упругого момента М (а) обо-
значение дМ («)/<?«, получим
— — —ml cos (а Р) cosy (а) ~ sin(“ 4~ Р) cos у j .
(7.30)
Если маятник гравиметра при измерениях приводится в исход-
ное положение, то а = 0. Когда исходное положение маятника
и ось вращения горизонтальны, 0 = у = 0 и чувствительность
(-у).“-4твг««Г-с.- <М‘>
Если гравиметр наклоняется только вдоль оси вращения
маятника, а сам маятник удерживается в исходном положении,
то а = 0 = 0 и чувствительность
_^ = C = C0cosY, (7.32)
т. е. изменение чувствительности системы при наклоне всего при-
бора вдоль оси вращения маятника незначительно.
Иначе меняется чувствительность при наклоне прибора вдоль
маятника (сс — у — 0). В этом случае
—/nZcOsp Г Л4(a) - mgl sin 0 = С. (7.33)
Из уравнений (7.31) и (7.33) найдем
C = Cocos0/(l + gCosin0). (7.34)
178
Дифференцируя уравнение (7.34)
по (3 и полагая (3 = 0, имеем
dC/dfi = — Cig. (7.35)
Из выражения (7.35) следует, что
изменение чувствительности при на-
клоне всего прибора вдоль маятника
пропорционально квадрату началь-
ной чувствительности, т. е. чувстви-
тельности при горизонтальном поло-
жении маятника и его оси вращения.
В зависимости от знака dfi чувстви-
тельность или возрастает (о!(3 >0),
или убывает ((7(3 < 0). Уравнение
зависимости изменения 'чувствитель-
ности от угла наклона прибора вдоль
маятника справедливо, если при на-
Ркс. 7.10. Зависимость чувстви-
тельности гравиметра от его на-
клоне гравиметра изменение его по- клона вдоль маятника,
казаний компенсируется, т. е. а=0.
Из уравнения (7.34) следует: если sin |3 — —\l(Ceg), то
dalcig = оо и система становится неустойчивой. Этот угол (3
можно назвать критическим. При нашем выборе направления
отсчета критический угол всегда положителен. Если прибор на-
клоняется так, что центр тяжести маятника поднимается выше
горизонта, чувствительность системы растет; при опускании
центра тяжести ниже горизонта чувствительность падает
(рис. 7.10).
При изменении силы тяжести или компенсирующей ее силы
маятник отклоняется от исходного положения. Рассмотрим про-
исходящее при этом изменение чувствительности. Положим в урав-
нениях равновесия (7.27) и чувствительности (7.28), что Lo — 0,
т = 0 и |3 = 0, т. е. главная пружина имеет нулевую начальную
длину, оси подвеса бесконечно тонки, исходное положение,
в которое приводится маятник, горизонтально. В этом случае
уравнения принимают вид
tngl cos ос == fr (у cos а — х sin а); (7.36)
da . ml cos а (7.37)
dg fr (у sin а х cos а) — tngl sin а
При а = 0 mgl => fry, 1 (da/dg)0 = —ml/(frx) = Co. | (7.38)
Из уравнений (7.36), (7.37) и (7.38) получим
-4— = — cos3 а — Со cos2 а. (7.39)
“s frx
179
Из этого выражения следует: если в системе с главной пружи-
ной нулевой длины и бесконечно тонкими нитями подвеса маятник
отклоняется от горизонтальной плоскости при изменении силы
тяжести или компенсирующей силы, то его чувствительность
изменяется пропорционально квадрату косинуса угла отклонения
и не зависит от направления наклона. В этом случае максималь-
ную чувствительность система имеет при горизонтальном положе-
нии маятника (а = 0). В любом положении в пределах —л/2 <
< а С +л/2 система имеет конечную чувствительность при усло-
вии, что в горизонтальном положении чувствительность конечна.
Физически это означает, что изменение производной по углу
от момента упругих сил компенсируется обратным по знаку и
почти равным по значению изменением производной от момента
силы тяжести.
Свойство упругих систем с пружинами нулевой длины мало
изменять чувствительность при отклонении маятника от исходного
положения, когда изменяется сила тяжести, является очень
важным и используется в ряде конструкций гравиметров. Физиче-
ский смысл пружины нулевой длины заключается в том, что в та-
кой пружине при отсутствии растягивающей силы концы пружины
совместились бы в одной точке, если бы соседние витки, опира-
ющиеся один на другой, не препятствовали этому.
Изготовление подобных пружин в настоящее время не пред-
ставляет затруднений. Для этого металлические пружины нави-
вают с предварительным натяжением, а затем к ним прикрепляют
нерастяжимые связки такой длины, чтобы при растяжении пру-
жина развивала силу F = fL. При изготовлении пружины нуле-
вой длины из кварца ее сначала навивают обычным образом,
а затем выворачивают, как чулок, и к ней приваривают кварцевые
стержни, равные длине пружины в ненагруженном состоянии.
Значительно большие технические трудности представляет изго-
товление осей подвеса маятника, имеющих малую жесткость.
В металлических гравиметрах применяют специальный способ
подвески маятника на оси вращения. В кварцевых гравиметрах
стараются сделать оси подвеса маятника как можно тоньше.
В случае, если жесткостью осей подвеса маятника пренебречь
нельзя, уравнение чувствительности упругой системы с пружиной
нулевой длины примет вид
da ml cos2 а
frx -p т cos a -J- т (a0 -p a) sin a
При изменении а чувствительность может стать бесконечно
большой, когда
frx + т cos a -j- т (a0 ~р a) sina = 0. (7.41)
При увеличении а слагаемое т cos а всегда повышает значение
чувствительности. Слагаемое т (а0 -р a) sin а характеризует часть
изменения момента силы тяжести, не уравновешенную главной
180
пружиной. Эта часть момента компенсируется силой закручива-
ния нити подвеса маятника. Слагаемое! (а0 + а) sin а может быть
или положительным, или отрицательным в зависимости от знака
угла а0. Если угол а0 положительный, т. е. крутящий момент
совпадает по направлению с моментом силы тяжести, то система
более чувствительна при отклонении маятника вниз. Если угол ап
отрицательный, т. е. крутящий момент совпадает по направлению
с моментом упругой силы главной пружины, то система более
чувствительна при отклонении маятника вверх.
Полагая в уравнении (7.40) углы а малыми, имеем
=------------. (7.42)
тоа 4“ та2 ~г т р frx
Из этого выражения следует, что при а0 = 0 любое отклоне-
ние маятника от горизонтального положения приводит к умень-
шению чувствительности, т. е. если система имеет конечную чув-
ствительность в горизонтальном положении, то она имеет конеч-
ную чувствительность и при отклонении маятника от горизонта.
При этом уменьшение чувствительности происходит тем быстрее,
чем больше жесткость оси подвеса маятника. Таким образом,
в системах с пружиной нулевой длины выгодно, чтобы начальный
угол закручивания нити подвеса был равным нулю.
Исследованием поведения чувствительности при изменении
силы тяжести и компенсирующей силы для пружин с ненулевой
начальной длиной при т = 0 было установлено следующее. Чув-
ствительность систем с пружиной положительной начальной длины
(£0 0) возрастает при уменьшении а, г. е. при наклоне маятника
ниже горизонтальной плоскости, и уменьшается при увеличении ос,
т. е. при наклоне маятника выше горизонта. Для систем с пружи-
ной отрицательной начальной длины (Lo < 0) чувствительность
возрастает при увеличении а (уменьшении силы тяжести). В обоих
случаях чувствительность становится бесконечно большой при
некотором значении угла а. Таким образом, начальная длина
главной пружины оказывает заметное влияние на свойства упру-
гой системы.
Из всех рассмотренных систем наибольшей устойчивостью
при изменении силы тяжести и компенсирующей силы обладает
система, главная пружина которой есть пружина нулевой длины.
Ее чувствительность при отклонениях маятника от исходного
горизонтального положения, связанных с изменением силы тя-
жести, практически не меняется, в то время как системы с положи-
тельной или отрицательной длиной главных пружин меняют свою
чувствительность (рис. 7.11). Начальная длина главной пружины
оказывает на чувствительность влияние, аналогичное влиянию
предварительного закручивания оси подвеса маятника: положи-
тельный угол закручивания действует на чувствительность так же,
как пружина положительной длины, отрицательный угол — как
пружина отрицательной длины.
181
Таким образом, предваритель-
ное закручивание оси подвеса
маятника и ненулевая начальная
длина пружины приводят к изме-
нению чувствительности системы
при изменении силы тяжести и
понижают ее устойчивость. Поэто-
му при использовании маятника
Голицына в качестве упругой си-
стемы гравиметра необходимо для
большей устойчивости брать глав-
ные пружины с нулевой длиной,
а также стремиться к тому, чтобы
угол предварительного закручива-
ния оси подвеса маятника был
близким к нулю. Упругая система
гравиметра, построенная по прин-
ципу маятника Голицына, является
наиболее целесообразной по срав-
нению с другими механическими
Рис 711 Изменение чувствитель-
ности гравиметра при отклонении
маятника горизонтального по-
ложения Для систем с Раз.,личной
начальной Длиной главной пру-
жины.
системами, в которых используются различные дополнительные
астазирую'щие устройства. Этим системам присущи недостатки
систем с начальной длиной главной пружины и начальным углом
закручивания нити подвеса маятника.
Казалось бы, влияние начальной длины пружины можно
скомпенсиРоваТЬ пРеДваРительиым закручиванием осей подвеса
маятника, например, применить пружины с отрицательной на-
чальной длиной, задать нитям подвеса положительный угол за-
кручивания и добиться таким образом хорошей устойчивости
системы при значительной толщине осей подвеса и ненулевой на-
чальной длине пружины. Однако такая взаимная компенсация
может быть осуществлена только в некоторых пределах, и полу-
чить устойчивую систему с высокой чувствительностью не удается.
Кроме того, введение взаимной компенсации вызывает дополни-
тельные деформации в главной пружине и осях подвеса, что ухуд-
шает механические свойства системы.
Из уравнений равновесия и чувствительности следует, что
показания гравиметра наиболее устойчивы, когда маятник го-
ризонтален. т. е. а = 0 и р = 0. Поэтому дальнейший анализ
этих уравнений будем проводить при условии, что маятник гори-
зонтален- Тогда, полагая в уравнениях (7.27) и (7.28) а = р = 0,
имеем
mgl -Гта0 = fry 1
(7.43)
_______Др________
V (х — г)2 + у2
— ml
dg
(7-44)
[K(x-r)2 + !/2P
182
При заданных параметрах системы и чувствительности решение
этих уравнений позволяет найти точку (х, у) крепления верхнего
конца главной пружины. Поскольку уравнения равновесия и
чувствительности есть уравнения соответственно четвертой и ше-
стой степени, то получить аналитическое выражение для х и у
невозможно. Решить эту систему можно только графическим
методом.
Исследуем решения системы для некоторых частных случаев.
Положим, что начальная длина пружины Lo = 0. Тогда уравне-
ния примут вид
mgl + та0 = fry,
da/dg — —tnl/(x + frx).
(7-45)
При горизонтальном положении маятника уравнение равнове-
сия в системе (7.45) есть уравнение прямой, параллельной оси х.
Это значит, что при перемещении верхней точки крепления пру-
жины по этой прямой равновесие системы не нарушается, но изме-
нение абииссы х сказывается на чувствительности. Перемещение
верхнего конца главной пружины в направлении, параллельном
оси у, без изменения х приводит к нарушению равновесия, но не
влияет па чувствительность системы. Таким образом, система
с пружиной нулевой длины обладает замечательным свойством:
ее чувствительность не зависит от координаты у, а положение
равновесия не зависит от координаты х. Это позволяет компенси-
ровать изменение силы тяжести дополнительным сжатием или
растяжением главной пружины. В большинстве систем грави-
метров с пружиной пулевой длины приращение силы тяжести
измеряют именно таким способом.
Точка пересечения кривых, представляющих собой решение
системы (7.45) и выражающих условия равновесия и чувствитель-
ности, дает положение верхнего конца главной пружины. Полагая
da/dg = со, находим х = —xl(fr), что определяет положение
точки крепления верхнего конца главной пружины, соответ-
ствующее бесконечно большой чувствительности. Полагая т = 0,
получаем
da/dg ——ml/(frx). (7.46)
В этом случае бесконечно большая чувствительность системы
наступает при х — 0. Уравнение равновесия в этом случае при-
нимает вид
У = mgUtfr).
(7.47)
Полагая в уравнении (7.46) da/dg — С — const и учитывая
уравнение (7.47), имеем
y=—Cgx, (7.48)
183
Это выражение есть уравнение прямой, проходящей через
начало координат. Когда т =±- 0, но а0 = 0, уравнение принимает
вид
У = -С§[х4-т/(/г)], (7.49)
т. е. в этом случае прямая изочувствительности проходит через
точку х — —x/(fr).
При возрастании чувствительности прямая (7.48) приближается
к оси у, а прямая (7.49) к линии —xl(fr) (рис. 7.12).
Из уравнений (7.48) и (7.49) следует, что ощутимая жесткость
оси подвеса при одном и том же значении х снижает чувстви-
тельность системы и для поддержания чувствительности на том же
уровне необходима дополнительная деформация главной пружины.
В случае, когда начальная длина главной пружины отлична
от нуля, Л. Г. Шнирман предложил для анализа поведения систем
использовать графический метод. Можно представить, что каждая
пружина конечной начальной длины состоит из двух частей:
из пружины нулевой длины, имеющей ту же жесткость, что и пру-
жина конечной длины, и жесткого нерастяжимого стержня с дли-
ной, равной первоначальной длине пружины. Условие равновесия
для фиктивной пружины с нулевой длиной выражается первым
уравнением системы (7.45): при перемещении верхнего конца
пружины вдоль прямой, параллельной оси х, равновесие не на-
рушается. При этом перемещении верхний конец стержня описы-
вает некоторую кривую, симметричную относительно прямой
х — г. Если Lo >0, эта кривая располагается выше прямой
Lo = 0 и выпуклостью вверх, а при Lo < 0 — ниже прямой
Ln = 0 и выпуклостью вниз (рис. 7.13). Для пружин сжатия
(Lo О L) кривые образуют петли под осью х.
Чтобы исследовать зависимость чувствительности от координат
точки крепления верхнего конца пружины, перепишем уравнение
чувствительности (7.44) в ином виде:
£)]J. (7'И)
где L1 — У(х — г)2 Ду3 — длина пружины при горизонтальном
положении маятника.
184
Используя уравнения (7.43) и (7.45), исключаем Lx из урав-
нения чувствительности:
.„/Г, I f..„ Уо I Л2 (У~ У»)3 I’1 /7 КМ
гЛх_+__--------__j , (7.51)
где уп— ордината крепления верхнего конца главной пружины,
если она имеет нулевую длину.
Далее, исключая из уравнения Lo и перенося начало координат
в точку крепления нижнего конца’главной пружины, т. е. полагая
х = X + г, при т = 0 имеем
[ml (da/dg) '+[г2]уя
+ /ЛАД(ХЫ)-0.
(7-52)
Это уравнение дает
связь координат верхней
точки крепления главной
пружины с ее угловой
чувствительностью. Меняя
значение da/dg, получаем
семейство кривых изочув-
ствительности. Нарис.7.14
приведены кривые изочув-
ствительпости для различ-
ных значений da/dg, а так-
же кривые возможного
перемещения верхней точ-
ки крепления главной
пружины без изменения
чувствительности для пру-
жин различной начальной
длины (кривые равнове-
Рис. 7.13. Кривые равновесия
упругой системы гравиметра для
пружин с различной начальной
длиной.
I- Ьу0Хуг ml (da/dg) 1 Х2у
Рис. 7.14. Кривые изочувствительности и рав-
новесия для пружин с различной начальной
длиной.
185
сия). Точки пересечения кривых изочувствительности и кривых
равновесия определяют положение верхней точки крепления глав-
ной пружины для системы с заданными параметрами /, г, ml,
Lo, da/dg. Все кривые изочувствительности пересекают ось х в
точках 0 и х — г.
Из уравнения (7.51) следует, что наличие жесткости т нити
подвеса смещает всю кривую изочувствительности влево на рас-
стояние TZ//(/77/0).
Полагая в уравнении (7.52) X — 0, т. е. х = г, получаем
du/dg^.— mlHfr*). (7.53)
Это уравнение показывает, что чувствительность системы
постоянна и изменение угла а пропорционально изменению силы
тяжести, т. е. система стала неастазированной. Линия изочув-
ствительпости неастазированной системы параллельна оси у
и только вблизи оси х образует петлю, симметричную относительно
оси абсцисс. Эта линия делит остальные кривые изочувствитель-
ности на две группы. Первая группа располагается слева от нее
в верхней полуплоскости и справа в нижней полуплоскости.
Чем дальше кривая этой группы отстоит от линии изочувствитель-
ности неастазированной системы, тем больше чувствительность.
Левая крайняя кривая соответствует бесконечно большой чув-
ствительности и служит границей, разделяющей области устой-
чивого и неустойчивого равновесия. Вторая группа кривых рас-
полагается справа от линии изочувствительности неастазирован-
ной системы в верхней полуплоскости и слева от нее в нижней
полуплоскости. В этой группе по мере удаления от делящей кри-
вой чувствительность уменьшается.
Таким образом, кривая изочувствительности неастазирован-
ной системы делит всю плоскость на две части, в одной из которых
чувствительность системы может быть только больше, чем чув-
ствительность неастазированной системы, в другой — только
меньше. Между линией чувствительности, соответствующей не-
астазированной системе, и линией чувствительности, для которой
da!dg — оо, располагается область чувствительности, большей,
чем чувствительность неастазированной системы, но практически
с той же самой полной деформацией главной пружины. Каждую
кривую изочувствительности делит на две части линия равнове-
сия, для которой Lo = 0. Отрезки кривых изочувствительности,
расположенные выше прямой Lo = 0, соответствуют главным
пружинам с положительной начальной длиной, а отрезки кривых,
лежащие ниже этой прямой, — пружинам с отрицательной на-
чальной длиной. Точки пересечения линий йзочувствительностн
с прямой Lo = 0 соответствуют системам с пружинами нулевой
начальной длины.
Свойство упругой системы изменять свою чувствительность
при перемещении верхней точки подвеса главной пружины ис-
пользуют при регулировке прибора и работе с ним. Действительно,
186
при оптическом способе регистрации горизонтального положения
маятника возможно перемещать начало отсчета, которое фикси-
рует это положение. Если при этом с помощью нивелировочных
винтов гравиметр отрегулировать на минимум чувствительности
к наклону, то изменение начала отсчета эквивалентно перемеще-
нию точки крепления главной пружины по дуге окружности ра-
диусом К х2 + у2. Из рис. 7.13 следует,-что при наклоне грави-
метра по часовой стрелке чувствительность системы уменьшается,
при наклоне против часовой стрелки увеличивается.
Таким образом, рассмотрев чувствительность системы грави-
метра, построенной по принципу вертикального сейсмографа
Голицына, можем сделать следующие основные выводы.
При наклоне гравиметра изменяются его показания и чувстви-
тельность. При этом изменение чувствительности пропорционально
квадрату начальной чувствительности и не зависит от параметров
системы. При наклоне маятника выше горизонта чувствительность
системы возрастает, при наклоне ниже горизонта уменьшается.
Переход маятника упругой системы под действием приращения
силы тяжести или компенсирующей силы в другое положение
приводит к изменению чувствительности. Это изменение мини-
мально в упругой системе с главной пружиной нулевой длины
и малой жесткостью оси подвеса маятника. В случае, когда длина
главной пружины и жесткость оси подвеса маятника равны нулю,
конечная чувствительность системы при горизонтальном положе-
нии маятника остается конечной при любом его положении.
Системы, у которых главные пружины имеют положительную
или отрицательную длину, а ось подвеса маятника — высокую
жесткость и большие предварительные углы закручивания, обла-
дают повышенной реакцией чувствительности на изменения силы
тяжести. В каждой такой системе существует положение маятника,
при котором его чувствительность бесконечно велика. Максималь-
ной устойчивостью обладают системы с главной пружиной нуле-
вой длины и малой жесткостью оси подвеса маятника. Устойчи-
вость систем с пружинами, длина которых отлична от нуля,
можно повысить, закручивая ось подвеса маятника, что компен-
сирует наличие начальной длины пружины. Вместе с тем повыше-
ние устойчивости таким способом вызывает дополнительные де-
формации упругих элементов системы, что нежелательно.
Наклон упругой системы (всего прибора) с одновременным при-
ведением маятника в горизонтальную плоскость при помощи
измерительного или диапазонного устройства изменяет чувстви-
тельность системы. Если верхняя точка крепления главной пру-
жины наклоняется в сторону маятника, чувствительность системы
уменьшается; при наклоне в сторону, противоположную маятнику,
чувствительность системы возрастает. При этом изменение чув-
ствительности тем сильнее, чем больше начальная длина главной
пружины.
187
При горизонтальном положении маятника чувствительность
системы в общем случае тем больше, чем меньше абсцисса точки
крепления верхнего конца главной пружины, и наоборот. Крити-
ческое значение абсциссы, при котором чувствительность системы
становится бесконечно большой, а также характер зависимости
чувствительности от координат верхней точки крепления главной
пружины определяются начальной длиной пружины, жесткостью
и начальным углом закручивания осн подвеса маятника. Наиболее
простая зависимость чувствительности от координат верхней
точки крепления главной пружины существует у систем с пружи-
нами нулевой длины. В этом случае кривые изочувствительности
и равновесия представляют собой прямые линии. Для пружин
с ненулевой начальной длиной кривые изочувствительности и рав-
новесия выражаются соответственно уравнениями шестого и чет-
вертого порядка.
Из всего изложенного следует, что системы с главными пружи-
нами нулевой длины обладают несомненными преимуществами
перед системами с главными пружинами конечной длины, отли-
чаясь большей устойчивостью, малой реакцией чувствительности
на изменения силы тяжести. В большинстве современных грави-
метров, построенных по принципу вертикального сейсмографа
Голицына, упругим элементом чувствительной системы служит
пружина нулевой длины.
Поскольку чувствительность системы к изменениям силы
тяжести меняется нелинейно, измерять приращение силы тяжести
углом отклонения маятника от горизонта, т. е. перемещением
по отсчетной шкале индекса, связанного с маятником, нельзя.
Приходится применять компенсационный метод.
В системах с пружиной нулевой длины приращения силы
тяжести компенсируются дополнительным ее растяжением или
сжатием, что достигается перемещением верхнего конца пружины.
Из уравнения равновесия (7.45) при а = 0 следует
dg/g = dy/y. (7.54)
При перемещении верхнего конца главной пружины по пря-
мой, параллельной оси у, чувствительность системы не изме-
няется, а приращение силы тяжести компенсируется приращением
длины пружины. При этом существует линейная связь между
смещением Аг/ верхнего конца главной пружины и приращением
Ag'. Чтобы осуществлять перемещение верхней точки крепления
главной пружины, применяют различные схемы измерительных
устройств, преобразующих движение микровинта в смещение
этой точки.
В кварцевых гравиметрах («Атлас», «Шарп», ВИРГ-61, «Уор-
ден») используется следующая конструкция измерительного уст-
ройства (рис. 7.15). Ось О' измерительной системы, расположен-
ная на перпендикуляре к оси у, проходящем через верхнюю точку
крепления главной пружины 3, закручивается под действием
188
натяжения измерительной пружи-
ны 1. Верхний конец главной пру-
жины приварен к тяге 2. Если рас-
стояние от верхней точки крепления
главной пружины до оси О' обо-
значить через Ь, то при изменении
угла закручивания измерительной
оси на dB ордината у изменится на
dy = bde. При большой жесткости
измерительной системы можно пре-
небречь весом деталей чувствитель-
Рис. 7.15. Схема измерительной
системы гравиметра.
ной системы и уравнение равновесия измерительной системы
примет вид
ти de — fud„ dLH,
где ти -— жесткость оси измерительной системы; /„ — жесткость,
с/„ — плечо, dL„ — удлинение измерительной пружины.
Тогда
dg = |/л/,/„Л/(т„/н/)| dE„. (7.55)
Эта формула позволяет рассчитать измерительную систему.
При малых углах df) и надлежащем выборе положения нижнего
шарнира измерительной пружины можно считать плечо du по-
стоянным, в этом случае получаем линейную шкалу отсчетного
устройства. Очевидно, что степень линейности шкалы тем выше,
чем меньше dO. При постоянном же значении dO наилучшая ли-
нейность шкалы достигается в случае, когда плечо измеритель-
ной пружины проходит через ее нижний шарнир.
В гравиметрах с металлическими пружинами конструкции
измерительных устройств весьма разнообразны, по принцип
сохраняется тот же.
Измерительные устройства, перемещающие верхнюю точку
крепления главной пружины, применяют только в гравиметрах,
где эта пружина имеет нулевую длину, так как только в этом слу-
чае существует линейная связь между приращением Ag и смеще-
нием А у верхнего конца главной пружины. В гравиметрах, глав-
ная пружина которых имеет ненулевую длину, компенсацию
изменений силы тяжести осуществляют закручиванием нитей
подвеса маятника с помощью измерительного устройства. Такой
способ применен в отечественных кварцевых гравиметрах типа
ГАК; естественно, что его можно использовать и в системах с ну-
левой длиной главной пружины.
Принцип конструкции этого измерительного устройства со-
стоит в следующем. Соосно с осью вращения маятника располо-
жена измерительная рамка, подвешенная на нитях. Изменяя силы
натяжения измерительной и диапазонной пружин, измерительную
рамку можно вращать. Поскольку при измерениях маятник всегда
приводится в горизонтальное положение, то при изменении угла
189
поворота измерительной рамки на dtp начальный угол закручива-
ния нитей подвеса маятника изменится на da(>. При этом значение
da0 должно равняться углу поворота измерительной рамки, взя-
тому с обратным знаком:
da0 == —d(p.
Пренебрегая весом измерительной рамки, а также учитывая,
что жесткость нитей подвеса измерительной рамки тн т, можем
написать условие равновесия измерительной системы:
М'Т— f«dadLa. (7.56)
Из уравнения равновесия системы (7.43) найдем связь между
изменением угла начального закручивания оси маятника и прира-
щением силы тяжести:
da0 — —(ml/т) dg. (7.57)
Тогда из уравнений (7.56) и (7.57) имеем
dg = 1А,4т/(тит/)] dL„. (7.58)
Поскольку измерительные пружины растягивают с помощью
измерительных микровинтов, то удлинение пружин dL.A в форму-
лах (7.55) и (7.58) можно выразить в оборотах микровинта:
dLn = s Ап,
где s — шаг винта; Ага — число оборотов винта.
Тогда формулы (7.55) и (7.58) примут вид
Ag — с Ага,
где с—цена деления гравиметра.
Для формулы (7.55)
с = bd.J ufr/(rnml)‘
для формулы (7.58)
[Ат 1(хит1).
Рассмотрим влияние температуры на показания гравиметра.
В первом приближении положим, что при изменении температуры
параметры упругой системы изменяются по следующему закону:
а = йо (1 Ч-[V 4~ iM2), (7.59)
где а — параметр упругой системы (длина, упругость пружины
и т. д.); рз — температурные коэффициенты параметра; I
температура, отсчитываемая от некоторой температуры 10, приня-
той за исходную.
Введем обозначения: и а2 — коэффициенты линейного
расширения материала пружины и рычага; у2 — термоэласти-
ческие коэффициенты первого рода материала пружины.
190
Имеем
gM = gtnl = gM0 (1 + aj + a./2);
IV == fd A.L = IVO (1 a^t -f- a2^s)s (1 4~ Yi^ + Тз^)>
(7.60)
где gM0 — mgl0 и Wo — f0d0/\L — моменты силы тяжести и упру-
гой силы при температуре t — t0.
Из уравнения (7.60) находим
g = (Г„М40) (1 + ait + a/)2 (1 + V1f + у./),
или с точностью до малых первого порядка
g — ССЖ) [1 + (Vi -I 2«i) t + (уа 4- 2аа) б2].
Температурный коэффициент гравиметра
dg/d/=g[Yi4-2a14-2(y24-2a.,)z'|. (7.61)
Зависимость показаний гравиметра от температуры нели-
нейна; для достижения полной температурной компенсации си-
стемы необходимо, чтобы температурный компенсатор работал
также в нелинейном режиме. Температурную компенсацию упру-
гой системы можно осуществить, создав дополнительный момент,
уравновешивающий кажущееся изменение силы тяжести, вызван-
ное изменением температуры. В системах с главными пружинами
нулевой длины термокомпенсационное устройство должно пере-
мещать верхнюю точку подвеса этой пружины по прямой, парал-
лельной оси у. В системах, использующих пружины конечной
длины, отличной от нуля, термокомпенсацию можно осуществить,
изменив угол а.о начального закручивания осей подвеса маятника.
Определим величины dy и da, соответствующие полной темпе-
ратурной компенсации системы.
Учитывая уравнения (7.54) и (7.61), можно написать
2/ = ["W(A/o)]ll ~(Yi I" aiK - (Y-j + оф2!. (7-62)
тогда
dy = — У [Yi + ai + 2 (Ya 4- “а) 4 (7.63)
так как
da0 = —• (m//x) dg,
то
da0 = — (mgl/т) [ух 4- 2aj 4~ 2 (y2 4- 2aa) /] dt. (7.64)
Температурный компенсатор можно построить таким образом,
чтобы при изменении температуры он смещал верхнюю точку креп-
191
ления главной пружины нулевой длины или закручивал нити
подвеса маятника на
dp = р (ех 4- 2e2l)dt, (7.65)
где р — геометрический параметр компенсатора, определяемый
его конструкцией и размерами; ех и е2 — эффективные температур-
ные коэффициенты параметра р.
Тогда для полной температурной компенсации необходимо,
чтобы
dp = ~-dy и dp —da,„
т. е.
( У (Vi + “1) = Pei>
I //(т2 + аг) =ре2;
j (mgl/r) (71 + 2ах) = pep,
I (mgZ/т) (уа + 2а2) = ре2
или
(Vi + 2®1)/(7з + 2аг) = Б1/Ег- (7-66)
Из уравнения (7.66) следует, что полная температурная ком-
пенсация возможна только при определенном соотношении ej/s2,
т. е. при соответствующем подборе материалов, которые имеют
температурные характеристики, удовлетворяющие этому урав-
нению. Практически не существует материалов, полностью удо-
влетворяющих уравнению (7.66). Например, для кварца
—700, для большинства металлов отношение ех/е3 имеет поло-
жительный знак и колеблется в пределах 1500—10 000. Поэтому,
применяя термокомпенсатор из этих материалов, можно убрагь
только линейную часть изменений показаний гравиметра, завися-
щих от температуры; полная температурная компенсация про-
изойдет только при одной температуре t0. При других температу-
рах гравиметр имеет остаточный температурный коэффициент,
изменяющийся по квадратичной параболе.
Очевидно, что для полной температурной компенсации необ-
ходимо, чтобы параметр р компенсатора был представлен суммой
не менее чем двух членов следующего вида:
р (1 + Ejt 4- М2) = 9(1 4- ~Г и(1 + + м2), (7.67)
где q и п — параметры компенсатора, определяемые его кон-
струкцией; оц, <т2 и A.J, Х2 — эффективные температурные коэф-
фициенты параметров q и п.
В этом случае
dp = [q (oj 4- 2о2/) 4- п (Xj 4- 2А2/)] dl\
I '/(7i + «i) = ^i + пХх;
I ^(7г4-«2) = рта4-пЬг,
192
Рис. 7.16. Схема температурного
компенсатора гравиметра ГАК-ЗМ.
и Va —0.15-10-° i/°C2.
откуда получаем условие полной
температурной компенсации:
(Vi -г + к2) =
= (qa1 + ф- пА2). (7.68)
Приведенные принципы темпе-
ратурной компенсации упругих
систем применяют, как правило,
в кварцевых гравиметрах, посколь-
ку кварц имеет весьма большой
термоэластический коэффициент
модуля упругости, зависящий от
температуры: yt ла +120-10-6 1/°С
В качестве примера температурного компенсатора, снимающего
линейную часть температурной зависимости упругой системы,
рассмотрим компенсатор гравиметра ГАК-ЗМ (рис. 7.16).
При изменении температуры металлическая нить АВ повора-
чивает рычаг СВ, который через тонкую нить CD вращает рамку OD
температурного компенсатора, расположенную соосно с измери-
тельной рамкой. Следствием поворота рамки компенсатора яв-
ляется поворот измерительной рамки и закручивание осей под-
веса маятника. Если жесткость измерительной и диапазонной
пружин мала по сравнению с жесткостью нитей подвеса компен-
сационной рамки, то углы поворота рамки температурного ком-
пенсатора и измерительной рамки практически одинаковы. Так
как маятник всегда приводят в одно и то же положение, то угол
закручивания его оси подвеса равен углу поворота термокомпен-
сационной рамки: da9 = df). Найдем связь между изменением
длины р металлической нити и углом поворота термокомпенса-
ционной рамки.
Из треугольника АВОа, полагая /. OtBA = я/2, находим
dtp — dp! с,
где dp — изменение длины нити АВ в зависимости от температуры.
Но
Р = Ро(1 + + е2^)>
откуда
следовательно,
dp = р0 (ех ф-2е2£) dt,
d<p ~-= (р0/с) (ty -|- 2е./) dt.
(7.69)
Здесь г, и е2 — коэффициенты линейного расширения мате-
риала нити. Полагая в четырехугольнике 0DC0A углы рх и р2
равными л/2, согласно теореме косинусов можно написать
d2 — е2 — ad. cos 6 — bd cos ср = 0,
7 В. С. Миронов
193
откуда
dB/Ар = — (6,’а) (sin ф/sin 0)
или
df) = —(b/a) dtp,
так как ср + 0 = л.
Подставляя значение dtp из формулы (7.69), имеем
rf0 = -^(Ex + 2f^H-
И тогда условие полной температурной компенсации
IVx + 2«i + 2 (у2 -(- 2а2) П (8х + 2е^’
ИЛИ
2а,) =
А7 о
ИЛИ
(Yi + 2а1)/(у8 + 2а3) = е1/е2. (7.70)
Температурная компенсация системы может быть осуществлена
полностью только для какой-то одной температуры; при других
температурах гравиметр имеет температурный коэффициент.
Для кварцевых гравиметров предложено много различных
схем термокомпенсаторов, работающих согласно уравнению
(7.67). Все конструкции термокомпенсирующих устройств могут
быть разделены на две группы. К первой относятся термокомпен-
саторы, в которых составляющие q и п геометрического параметра р
в зависимости от температуры изменяют свои характеристики не-
линейно, в полном соответствии с уравнением (7.67). Ко второй
группе относятся компенсаторы, у которых одна из составляющих
(например, q) геометрического параметра работает в линейном
режиме при изменении температуры, в то время как другая со-
ставляющая (в нашем случае /г) является нелинейной связью
между линейным температурным компенсатором и упругой систе-
мой гравиметра. В результате этого суммарное действие геометри-
ческого параметра р компенсатора также отвечает уравнению
(7.67).
В качестве примера температурного компенсатора первой
группы можно привести компенсатор, используемый в кварцевых
гравиметрах «Уорден», «Атлас», «Шарп», ВИРГ-61 (рис. 7.17).
Гибкий металлический стержень ОВ жестко закреплен в точке О
и шарнирно соединен с кварцевой тягой АВ в точке В, которая
является точкой крепления верхнего конца главной! пружины.
194

Рис. 7.17. Схема нелинейного темпера- Рис. 7.18. Схема нелинейного темпера*
турного компенсатора. турного компенсатора гравиметра
ГАК-7Т.
Тяга АВ может вращаться на нитях, проходящих через точку А.
Вследствие разницы коэффициентов линейного расширения ме-
талла и кварца при изменении температуры изменяется угол <р
и точка В перемещается по дуге. Можно показать, что такой
компенсатор работает в соответствии с формулой (7.66), т. е.
компенсируется только линейная часть температурной харак-
теристики.
Чтобы в этой системе геометрический параметр зависел от
температуры нелинейно, оси подвеса тяги АВ делают достаточно
жесткими и предварительно закручивают. В этом случае металли-
ческий стержень приобретает некоторый прогиб. Теперь при из-
менении температуры изменяются не только линейные размеры
температурного компенсатора, но и упругие силы в стержне ОВ
н в нитях подвеса. Перемещение точки В по дуге определяется
размерами компенсатора и амплитудой предварительного прогиба
металлического стержня, т. е. компенсатор работает согласно
уравнению (7.67).
В кварцевых гравиметрах типа ГАК применяют компенсаторы
второй группы, т. е. имеющие нелинейную связь, преобразу-
ющую линейные изменения длины металлической нити (термо-
компенсатор ГАК.-ЗМ) в нелинейные изменения угла закручива-
ния нитей подвеса маятника. Было предложено и осуществлено
несколько схем таких термокомпенсаторов.
В гравиметрах ГАК-7Т используется принцип нелинейной
связи между подвижной рамкой и рычагом линейного темпера-
турного компенсатора (рис. 7.18). Металлическая нить 1 в зави-
симости от температуры изменяет свою длину, что приводит
к повороту рычага 2, который через прогнутую с помощью пру-
жины 3 нить 4 поворачивает подвижную рамку 5 температурного
компенсатора. Кроме того, с поворотом рычага 2 распрямляется
нить 4, поэтому угол поворота рамки меньше, чем при прямой
нити 4. Чем больше прогнутость нити, тем, очевидно, больше ее
распрямление при повороте рычага и тем больше отношение угла
поворота рычага к углу поворота подвижной рамки. При измене-
нии температуры меняется прогиб нити, а следовательно, и отно-
7* 193
шенне углов, т. е. связь между углами поворота рычага и подвиж-
ной рамки нелинейная. Дальше компенсирующий момент пере-
дается обычным путем: подвижная рамка компенсатора повора-
чивает измерительную рамку, которая и закручивает оси подвеса
маятника.
Из приведенных примеров следует, что температурная компен-
сация систем, построенных по принципу вертикального сейсмо-
графа Голицына, возможна как теоретически, так и практически.
При этом может быть осуществлена компенсация не только линей-
ной, но и нелинейной части температурной характеристики.
Вместе с тем, как уже отмечалось, при резких изменениях тем-
пературы полная температурная компенсация не обеспечивается.
Для результативной работы термокомпенсаторов необходимо,
чтобы все части гравиметра воспринимали изменение температуры
одновременно, что может быть только при хорошей теплоизоля-
ции упругой системы.
Кварцевые астазированные гравиметры, построенные по прин-
ципу вертикального сейсмографа Голицына, в настоящее время
являются наиболее широко распространенными приборами при
гравиметрических исследованиях. Все эти приборы имеют одни
и те же рабочие узлы и различаются в основном только конструк-
цией этих узлов. Упругую систему кварцевых гравиметров изго-
товляют целиком из плавленого кварца, за исключением плати-
нового грузика на конце рычага и металлической нити темпера-
турного компенсатора.
Кварцевая упругая система заключена в металлический кор-
пус, обеспечивающий герметизацию системы. Этот корпус помещен
в сосуд Дьюара, который в свою очередь вставлен в теплоизоли-
рующий контейнер, представляющий собой легкий металлический
цилиндр с нивелировочными винтами, на дне и стенках которого
проложен слой теплоизолирующего материала. В корпусе гра-
виметра монтируются осветитель, микроскоп регистрирующей
системы и измерительное микрометрическое устройство. Наруж-
ный контейнер, в котором прибор транспортируется, обеспечивает
необходимую теплоизоляцию и предохраняет гравиметр от рез-
ких толчков и ударов. Все кварцевые гравиметры имеют довольно
сложные системы температурной компенсации.
Первый отечественный кварцевый астазированный гравиметр
ГАК-ЗМ был создан в 1953 г. К- Е. Веселовым во ВНИИГеофизике.
В дальнейшем на его основе были разработаны гравиметры типа
ГАК: ГАК-ПТ, -ПТМ, -7Н, -7Т, -7Ш, ГНУ-KI, -К2, «Дельта-2».
Эти гравиметры являются малогабаритными бестермостатными
приборами, обеспечивающими достаточно высокую точность на-
блюдений: в зависимости от применяемой методики и типа при-
бора средняя квадратическая погрешность наблюдений составляет
(0,03-0,08) ДО-5 м/с2.
Гравиметр ГАК-7Т (согласно ГОСТ 13017—73 этот прибор называется
ГНУ-К2, т. е. гравиметр наземный узкодиапазонный кварцевый второго класса
196
Рис. 7.19. Схема упругой системы гравиметра ГАК-7Т.
точности) является типичным представителем перечисленной группы приборов.
Рассмотрим принципиальную схему его упругой системы (рис. 7.19).
Горизонтально расположенный маятник 13 с платиновым грузиком на
конце удерживается в равновесии силой упругости главной пружины 18 отри-
цательной длины, диапазонной пружины 2 и силой закручивания нити подвеса 21
маятника. Главная пружина верхним концом прикреплена неподвижно к основ-
ной раме 3 системы, нижним — к отростку 19 маятника. Нижний конец диапазон-
ной пружины 2 также прикреплен к отростку 20 маятника, а верхний — к диа-
пазонному микровинту 1.
Измерительная система гравиметра имеет рамку 17, вращающуюся на нитях.
К этой рамке прикреплены оси подвеса маятника. Измерительная рамка имеет
стержень 16, к которому приварен нижний конец измерительной пружины 4,
верхний ее конец соединен с измерительным микровинтом 5. Силу тяжести из-
меряют компенсационным способом, дополнительно закручивая оси подвеса
маятника. При изменении силы тяжести маятник отклоняется от горизонталь-
ного положения на некоторый угол. Вращением микрометрического винта 5
изменяют натяжение измерительной пружины 4 и тем самым поворачивают из-
мерительную рамку 17, которая в свою очередь изменяет угол закручивания
нитей подвеса 21 маятника, приводя его в исходное положение. Мерой прира-
щения силы тяжести являются обороты счетчика микрометрического устройства.
Диапазон измерительного устройства (604-150)-10“6 м/с2. Перестраивают диа-
пазон измерений, изменяя натяжение диапазонной пружины 2.
Регистрация положения маятника оптическая. На конце маятника установ-
лен тонкий кварцевый стерженек (индекс) 11, расположенный между призмами 10
и 12. Изображение индекса рассматривают в микроскоп 9. В фокальной пло-
скости окуляра 8 микроскопа имеется шкала 7, позволяющая качественно
судить о характере изменения силы тяжести.
197
Рис. 7.20. Общий вид
гравиметра ГАК-7Т.
В устройство для температурной компенсации
входит металлическая нить 6', ее верхний конец при-
креплен к основной раме системы, а нижний к рыча-
гу 15, который может вращаться на нитях 14. Второй
конец этого рычага соединен тонкой кварцевой нитью
22 с подвижной рамкой 23 температурного компенса-
тора. Нить 22 изогнута и оттягивается пружинкой 24.
Нити подвеса измерительной рамки, рамки температур-
ного компенсатора и маятника расположены соосно.
При изменении температуры металлическая нить 6 по-
ворачивает рычаг 15, который, находясь все время
под действием силы закручивания нитей подвеса,
натягивает или отпускает изогнутую кварцевую нить
22, поворачивая рамку 23, и тем самым закручивает
нити подвеса маятника, возвращая его в исходное
положение. Благодаря прогнутости нити связь углов
поворота рычага и рамки нелинейная, что обеспе-
чивает температурную компенсацию линейной и не-
линейной частей температурной характеристики си-
стемы.
Гравиметр ГАК-7Т (рис. 7.20) состоит из собствен-
но гравиметра и внешнего теплоизолирующего контей-
нера. Собственно гравиметр, или средняя часть
(рис. 7.21), включает корпус кварцевой системы, теп-
лозащитный столб и верхнюю панель.
Цилиндрический корпус 11 кварцевой системы имеет на боковой поверх-
ности резьбу. На нее навинчивается стопорное кольцо 7, прижимающее защит-
ный стакан 5 к надетой на корпус резиновой прокладке 8, обеспечивая гермети-
зацию кварцевой системы. Для увеличения теплоемкости корпуса на защитный
стакан сверху надевается еще один стакан 6. Корпус системы имеет четыре от-
верстия: два для оптической системы, по одному для измерительного и диапазон-
ного устройств. На нижней поверхности корпуса вделаны стойка 26 для крепле-
ния кварцевой системы, три стойки 24 для защиты системы при вскрытии и
сборке, держатели объектива 22 микроскопа и призм 23, 25 осветителя. Гермети-
зация осветителя и микроскопа осуществляется при помощи резиновых колец
и плоскопараллельных круглых стекол. В боковую поверхность корпуса ввин-
чен вакуумный кран.
Теплозащитный столб служит пробкой, закрывающей сверху сосуд Дьюара
в теплоизолирующем контейнере, и представляет собой текстолитовый полый
цилиндр 18, нижний конец которого крепится к корпусу кварцевой системы,
а верхний — к панели 1. Внутри цилиндра расположены трубки осветителя,
микроскопа, диапазонного и измерительного устройств. Пространство между
трубками и стенками цилиндра заполнено теплоизолирующим материалом.
Верхняя панель выполнена в виде диска из текстолита. На ней размещены
отсчетное устройство 20 измерительной системы, держатель 21 окуляра микро-
скопа 28, осветитель 27, продольный 19 и поперечный уровни.
Измерительное устройство имеет микрометрическую гайку 16, ввинченную
в корпус кварцевой системы; в эту гайку в свою очередь ввинчен микрометриче-
ский винт 15. При вращении микрометрического винта его поступательное дви-
жение через шарик 14 передается движущемуся во втулке 10 измерительного
устройства штоку 13, к которому прикреплен верхний конец измерительной
пружины. Чтобы исключить люфт, на втулку надета люфтовыбирающая пру-
жина 12, верхний конец которой упирается в головку штока. Для герметизации
подвижного сочленения измерительной системы использован сильфон 9, ниж-
ний конец которого скреплен с подвижным штоком, верхний — с корпусом квар-
цевой системы. Микрометрический винт стержнем 17 соединен с отсчетным уст-
ройством 20, представляющим собой лимб с нониусом.
В диапазонном устройстве подвижный шток 4 перемещается поступательно
при вращении гаек 2 и 3\ одна из них опускает шток при завинчивании, другая
поднимает его. После регулировки диапазона измерений гайки плотно закреп-
198
Рис. 7.21. Разрез средней части гравиметра ГАК-7Т.
ляют шток. Поворачивают гайки специальными диапазонными ключами через
отверстие в верхней панели гравиметра.
Гравиметр ГАК-7Ш (согласно ГОСТ 13017—73 его номенклатура ГНШ-К,
т. е. гравиметр наземный широкодиапазонный кварцевый) является прибором
геодезического типа. В отличие от гравиметра ГАК-7Т он имеет два измери-
тельных микрометрических устройства: обычное, позволяющее измерять прира-
щения силы тяжести в диапазоне (804-100) 10“5 м/с2 с погрешностью до 0,06 X
X 10’6 м/с2, и диапазонное, позволяющее измерять приращения (10004-1500) X
X 10-5 м/с2 с погрешностью (0,24-0,3)• 10"5 м/с2. Для этого к измерительной
рамке приварена вторая измерительная — диапазонная — пружина с большей
жесткостью, верхний конец которой прикреплен к микрометрическому винту.
Внешне гравиметр ГАК-7Ш отличается от гравиметра ГАК-7Т только наличием
второго отсчетного устройства.
Гравиметры ГРК-1, ГРК.-2 не отличаются принципиально от гравиметра
ГАК-7Т.
Гравиметры ГАК-ПТ, ГАК-ПТМ, «Дельта-2» имеют свои особенности в уст-
ройстве упругой системы и корпуса. В упругой системе нет температурного ком-
199
Рис. 7.22. Принципиальная схе-
ма чувствительной системы
гравиметров «Уорден», ВИРГ-61,
«Шарп».
пепсатора нелинейной части температурной
характеристики. Вместо изогнутой кварце-
вой нити, оттягиваемой пружиной, здесь при-
менена прямая нить, поэтому компенсируется
только линейная часть температурного влия-
ния. Диапазонная пружина крепится не к
маятнику, а к измерительной рамке. Погреш-
ность наблюдений составляет (0,054-0,15) X
X10*“ м/с2.
Гравиметры «Уорден» (США), ВИРГ-61
(СССР), «Шарп» (Канада) являются наиболее
совершенными бестермостатными приборами
среди многочисленных конструкций кварце-
вых астазированных гравиметров. Перечи-
сленные гравиметры имеют сходное устрой-
ство, небольшую массу и в зависимости от
применяемой методики позволяют достигнуть
высокой точности: погрешность наблюдений
(0,024-0,06)-КГ5 м/с2.
Основной особенностью этих гравимет-
ров является конструкция чувствительной
кварцевой системы (рис. 7.22).
Горизонтально расположенный маятник
11 с платиновым грузиком на конце подвешен
на двух тонких нитях 7, являющихся осями
вращения маятника. Маятник удерживается
в горизонтальном положении главной квар-
цевой пружиной 6 нулевой длины. При из-
менении силы тяжести маятник отклоняется
от горизонтального положения на некоторый
угол. Приращение силы тяжести измеряют
компенсационным методом. Маятник приво-
дят в горизонтальное положение, дополнительно растягивая или сжимая глав-
ную пружину с помощью измерительного устройства, перемещающего верхний
конец этой пружины.
Измерительное устройство состоит из жесткой кварцевой «фермы» 10, из-
мерительной рамки 15 и диапазонной 12 и измерительной 14 пружин. К верхнему
концу фермы прикреплен верхний конец главной пружины. Нижние концы
диапазонной и измерительной пружин приварены к отросткам измерительной
рамки, а их верхние концы соответственно к диапазонному и измерительному
микровинтам 13. Основание «фермы» вращается относительно горизонтальной
кварцевой оси измерительной системы. Измерительная рамка также может вра-
щаться относительно этой оси, т. е. измерительная рамка и «ферма» соосны.
При вращении микровинтов изменяется натяжение измерительной и диапазонной
пружин, измерительная рамка поворачивается, вызывая закручивание осей
измерительной системы, что в свою очередь приводит к повороту «фермы». Верх-
ний конец «фермы» перемещает верхнюю точку крепления главной пружины,
тем самым удлиняя или укорачивая ее. Перемещение происходит по линии, пер-
пендикулярной к прямой, соединяющей ось вращения маятника и нижнюю
точку крепления пружины при горизонтальном положении маятника. Измери-
тельной пружиной можно скомпенсировать изменение силы тяжести (804-100) X
X КГ--1 м/с2, диапазонной до 5000-10"5 м/с2. Число оборотов микрометрического
винта измеряется счетчиком и является мерой приращения силы тяжести.
Для регистрации горизонтального положения маятника на его оси враще-
ния установлен вертикальный стержень 5, па конце которого приварен тонкий
кварцевый волосок (индекс) 3, параллельный оси вращения. Индекс освещается
лампочкой 8 через призму 4 и рассматривается в микроскоп 2 с 600—800-крат-
ным увеличением. Микроскоп имеет окулярную шкалу 1 для оценки изменения
силы тяжести. В гравиметре «Шарп» отсчетный индекс расположен не па верти-
кальном стержне, а на конце маятника, как у гравиметра типа ГЛК; окуляр
200
Рис. 7.23. Общий вид гравиметра
ГАГ-2.
микроскопа укреплен в эксцентричной втулке. Это позволяет вращением втулки
я окуляра перемещать окулярную шкалу параллельно самой себе, тем самым из-
меняя исходное положение маятника и, следовательно, чувствительность грави-
метра к изменению силы тяжести.
Температурная компенсация чувствительной системы осуществляется с по-
мощью термокомпенсатора. На оси измерительной системы укреплена рамка
температурного компенсатора, жестко скрепленная с измерительной рамкой.
Рамка компенсатора имеет отросток, в который заварен один конец тонкого
вольфрамового стержня 9. Другой конец стержня шарнирно прикреплен к верх-
нему концу измерительной «фермы». Вольфрамовый стержень под действием
упругих сил закручивания измерительных нитей имеет некоторый предвари-
тельный изгиб. Различие в термоупругих свойствах кварца и вольфрама при-
водит к тому, что при изменении температуры «ферма» поворачивается вокруг
оси вращения и таким образом смещает верхний конец главной пружины. Изме-
няя положение точки, в которой закрепляется нижний конец вольфрамового
стержня, и расстояние этой точки до оси вращения «фермы», можно добиться
очень пологой параболической зависимости показаний гравиметра от темпера-
туры — до 0,02 -10'5 м/с2 на 1° С2 и меньше.
Упругая кварцевая система гравиметров находится в герметичном корпусе
при пониженном давлении. Корпус системы для защиты от резких колебаний
внешней температуры помещен в сосуд Дьюара, укрепленный в теплозащитном
контейнере. '
Корпуса гравиметров различаются несущественными деталями. В грави-
метрах «Уорден» и ВИРГ-61 обороты микрометрического винта отсчитываются
на цилиндрическом лимбе, в гравиметре
«Шарп» — на специальном многоразряд-
ном счетчике. Нивелировочные уровни в
гравиметрах «Уорден» и ВИРГ-61 рас-
положены на нижней стороне панели
прибора, в гравиметре «Шарп» — на кор-
пусе кварцевой системы.
Существуют две основные модели гра-
виметра «Уорден»: стандартная с диа-
пазоном около 80-10" ° м/с2 и геодезическая
для измерения больших приращений силы
тяжести. В геодезической модели диапа-
зонное устройство имеет специальный
градуированный лимб, устанавливаемый
на место диапазонного ключа. По этому
лимбу можно отсчитать доли оборота диа-
пазонного винта. Погрешность измерения
приращений силы тяжести с использо-
ванием геодезического лимба составляет
около (0,14-0,2) • 10" 5 м/с2. Отдельные мо-
дели гравиметров «Уорден» имеют элек-
трический термостат.
Геодезический астазированный трави
метр ГАГ-2 (согласно ГОСТ 13017—73
этот прибор относится к типу ГНШ-К1 —
гравиметр наземный широкодиапазонный
кварцевый первого класса точности)
(рис. 7.23) разработан Ю. Д. Буланже
(ИФЗ АН СССР) и С. А. Поддубным
(ВИРГ). Этот гравиметр предназначен для
относительных высокоточных измерений
силы тяжести при развитии опорных гра-
виметрических сетей 1-го и 2-го классов
точности, создании гравиметрических по-
лигонов, мелкомасштабных региональных
исследованиях и работе в горных облас-
201
тях. В приборе использована квар-
цевая система гравиметра ВИРГ-61.
Приращения силы тяжести измеряют-
ся компенсационным способом — на-
клоном оси вращения маятника чув-
ствительной системы, т. е. по принципу
измерений гравиметр ГАГ-2 близок к
гравиметрам Норгарда, СН-3, ГАЭ, в
которых, однако, чувствительная си-
стема наклоняется вдоль маятника, а
не вдоль оси его вращения.
Упругая система гравиметра по-
мещена в герметичный корпус и двух-
ступенчатый термостат. Угол наклона
оси вращения маятника измеряется в
угловой мере специальным угломер-
ным устройством, и поэтому теорети-
чески гравиметр не требует эталони-
рования. Диапазон измерения в сторону увеличения силы тяжести не ограничен,
в сторону уменьшения — зависит от начального угла наклона системы, мини-
мальное предельное значение которого равно нулю.
Полный диапазон измерений без перестройки угла наклона состав-
ляет 4000-Ю-5 м/с2. Погрешность наблюдений при измерении приращений силы
тяжести до 1000- 1(Гй м/с2 не более 0,1-10-6 м/с2, выше 1000-Ю-6 м/с2—до
0,15-10-5 м/с2; масса гравиметра около 25 кг.
Металлические гравиметры, основанные на принципе маятника Голицына,
представлены несколькими зарубежными моделями: «Северная Америка», «Ве-
стерн», «Магнолия», гравиметрами Хейланда и Дакоста — Ромберга. Среди
них наибольшим распространением пользуются гравиметры «Северная Америка»
и Лакоста — Ромберга.
Гравиметр «Северная Америка» применялся в СССР. Рассмотрим схему упру-
гой системы этого гравиметра (рис. 7.24).
Легкий алюминиевый рычаг 6 с грузиком 8 на одном конце и барокомпенса-
тором 3 на другом удерживается в горизонтальном положении наклонно рас-
положенной главной пружиной 10 нулевой длины, изготовленной из специаль-
ного сплава изоэластик. Осью вращения рычага служит шарнир 4, состоящий из
Рис. 7.25. Схема гравиметра Лакоста—Ромберга.
202
двух тонких вольфрамовых проволочек, прикрепленных одним концом к рычагу,
другим к плоским пружинам 5. Ось вращения рычага можно перемещать в вер-
тикальном направлении микрометрическим винтом /, при движении которого на-
тягиваются или ослабляются пружинки 2, благодаря чему смещаются концы
плоских пружин 5. Пружина 9, непосредственно связанная с рычагом, служит для
изменения диапазона измерений. Горизонтальное положение рычага регистри-
руется оптическим способом. Па рычаге укреплена тонкая горизонтальная
нить 7, изображение которой рассматривают в 150-кратный микроскоп.
Отличительной особенностью гравиметра «Северная Америка» является
очень высокая механическая чувствительность и, как следствие, большой период
собственных колебаний системы (до 20—25 с), поэтому гравиметр слабо реагирует
на помехи микросейсмического происхождения.
Упругая система гравиметра не герметизирована. Для защиты ее от влия-
ния температуры служит двухступенчатый термостат. Погрешность наблюдений
(0,014-0,05)-10-5 м/с2.
Гравиметр Лакоста—Ромберга мало отличается от гравиметра «Северная
Америка» за исключением конструкции некоторых узлов: термостатов, микро-
метрических и регистрирующих устройств. В этом гравиметре (рис. 7.25) гсполь-
зована оригинальная система 1 для преобразования движения микрометрического
винта 2 в малые перемещения верхней точки подвеса главной пружины. Реги-
стрирующая система 3 фотоэлектрическая. Гравиметр характеризуется очень
малым смещением нуль-пункта-—не более 1-Ю-5 м/с2 в месяц; погрешность
наблюдений (0,014-0,03)•10'5 м/с2.
СПЕЦИАЛЬНЫЕ
КОНСТРУКЦИИ ГРАВИМЕТРОВ
С ДИСТАНЦИОННЫМ УПРАВЛЕНИЕМ
Рассмотренные выше конструкции гравиметров пригодны
только в таких условиях, когда оператор может находиться рядом
с прибором, в частности при наземных наблюдениях. Кроме
измерений на суше большой интерес представляют определения
силы тяжести в скважинах и на дне морей. В этом случае при-
ходится управлять гравиметром на расстоянии. Для таких на-
блюдений разработаны специальные гравиметры: донные и сква-
жинные.
Донные гравиметры
Так называются приборы, предназначенные для измерения
силы тяжести на дне водных бассейнов. Это потребовало применить
дистанционное управление упругой системой и предусмотреть
устройства для спуска и установки прибора на дне и для подъема
его па борт корабля.
Для наблюдений на дне гравиметр помещают в карданный
подвес, обеспечивающий автоматическую нивелировку прибора.
Карданный подвес закреплен внутри водонепроницаемой камеры
(скафандра), которую на тросе опускают с борта корабля на дно.
Скафандр имеет треногу, которой устанавливается на дно. Все
операции по измерению силы тяжести осуществляются с помощью
телемеханических устройств, управляемых электрическими им-
пульсами. На борту корабля расположен пульт управления,
соединенный специальным кабелем с упругой системой грави-
203
Метра. Все донные гравиметры созданы на базе гравиметров для
наблюдений на суше.
Донными гравиметрами сила тяжести также измеряется ком-
пенсационным методом, т. е. система приводится в одно и то же
положение равновесия. Изменение силы тяжести компенсируют
упругие силы пружин в микрометрических устройствах, приво-
димых в движение электродвигателями, или электростатические
силы (метод возвратного потенциала).
В СССР первые измерения силы тяжести донными гравиме-
трами были проведены в 1949 г. Для этого были приспособлены
гравиметры ГКМ и ГКА, а затем был создан специальный донный
гравиметр ДГПЕ на базе гравиметра ГКА. В дальнейшем кон-
струкции донных гравиметров разрабатывались на основе квар-
цевых астазированных приборов типа ГАК- Создано несколько
моделей донных гравиметров: КДГ-П, -III, ГАК-7ДТ (ГДК),
КДГ-ЭМТ, различающихся в основном способами измерения
и компенсации приращений силы тяжести. В гравиметрах КДГ-П
и -III приращение силы тяжести измеряется методом возвратного
потенциала, в гравиметрах ГАК-7ДТ и КДГ-ЭМТ — с помощью
измерительной пружины, растяжение которой осуществляется
микровинтом, вращаемым электродвигателем. Регистрация изме-
нения силы тяжести во всех моделях фотоэлектрическая.
Гравиметр ГАК-7ДТ (ГДК) имеет следующую принципиальную схему
(рис. 7.26). Фоторегистрирующее устройство состоит из лампочки осветителя 16,
конденсорных линз 15, зеркала 12 на рычаге маятника, разделительной призмы 14,
фотоэлементов 13, индикаторного гальванометра 9, миллиамперметра 8 и рео-
стата 7 накала лампочки. Свет лампочки, отражаясь от зеркала маятника, в виде
узкой полосы попадает на грани призмы. При горизонтальном положении ры-
Гравиметр Пульт управления
Рис. 7.26. Схема донного гравиметра ГАК-7ДТ.
201
чага маятника эта полоса делится призмой на две равные части и разностный ток
в цепи фотоэлементов равен нулю. При отклонении рычага от горизонтальной
плоскости происходит перераспределение светового потока и в цепи фотоэле-
ментов появляется ток, регистрируемый гальванометром 9.
Для компенсации приращений силы тяжести шток микрометрического вин-
та 17 жестко связан с ползунком многосборотного потенциометра 3, преобразую-
щего обороты микрометрического винта в изменение сопротивления. Оно изме-
ряется мостовой схемой, включающей в себя потенциометр 3, такой же измери-
тельный потенциометр 5 со счетчиком оборотов 4 и гальванометр 6 (в гравиметре
КДГ-ЭМТ измерительный потенциометр 5 заменен декадником). Микрометриче-
ский винт вращается через редуктор 1 электродвигателем 2. Скорость враще-
ния регулируется резистором 10, направление — переключателем 11.
Измеряется приращение силы тяжести следующим образом. Изменение силы
тяжести вызывает отклонение рычага маятника от исходного положения. Стрелка
гальванометра 9 также отходит от нуля. Включая электродвигатель 2, возвра-
щают стрелку в нулевое положение. После этого потенциометром 5 измеряют со-
противление потенциометра 3, снимают показания счетчика оборотов 4. Электро-
двигатель и потенциометр 3 размещены на верхней панели собственно грави-
метра. Остальные контрольно-измерительные приборы находятся на пульте
управления.
Упругая система гравиметра герметизирована и помещена в сосуд Дьюара,
укрепленный в теплозащитном корпусе прибора. Гравиметр устанавливают в ска-
фандр и тоже герметизируют. Скафандр имеет форму цилиндра с приваренным
сферическим дном и съемной крышкой. Внутри скафандра укреплен карданный
подвес, в который и помещают гравиметр, для контроля за подвесом в крышке
скафандра имеется отверстие. Для улучшения теплоизоляции внутренняя
полость скафандра выложена слоем войлока или поролона. Все ручки управле-
ния подвижной системой гравиметра и приборы контроля смонтированы на
специальном пульте.
Погрешность измерений (0,104-0,15)-1(Г5 м/с2; масса прибора со скафандром
около 120 кг.
Гравиметр ГМТД разработан во ВНИИГеофизике на базе металлического
гравиметра ГМТ-1. В приборе использована телевизионная установка, с помощью
которой наблюдаются положение отсчетного индекса, шкала микрометрического
винта и положение уровней. Погрешность измерений 0,1 -10 5 м/с2; масса прибора
со скафандром 250 кг.
В США на базе гравиметра с металлическими пружинами
созданы донные гравиметры «Северная Америка», Лакоста—Ром-
берга и др.
Донные гравиметры, как и гравиметры для измерений на
суше, требуют эталонирования отсчетного устройства. Поскольку
с донными гравиметрами можно проводить наблюдения и на
суше, то эталонирование донных гравиметров аналогично этало-
нированию наземных приборов. В донных гравиметрах необ-
ходимо также регулировать карданный подвес.
Скважинные гравиметры
Измеряя силу тяжести в буровых скважинах на различной
глубине, можно определить среднее значение плотности пород,
заключенных между точками наблюдений, в их естественном
залегании, что обеспечивает более достоверную геологическую
интерпретацию наземной гравиметрической съемки. Кроме того,
измерения силы тяжести в скважинах дают материал для вычис-
ления упругих констант пород (волновое сопротивление, модуль
205
Юнга, коэффициент Пуассона и т. д.), позволяют коррелировать
разрезы скважин.
Создание скважинного гравиметра потребовало преодоления
ряда технических трудностей. Прежде всего, точность наблюдений
должна быть достаточно высокой. Например, чтобы определить
плотность пород с погрешностью 0,02 г/см3 в интервале между
точками наблюдений 10 м, необходимо, как следует из формулы
(3.15), добиться погрешности единичного наблюдения силы тя-
жести порядка 0,01 • 10-s м/с2. Скважинный гравиметр должен
иметь большой рабочий диапазон (500-10'8 м/с2 и более) и на-
дежно действовать при многократном повышении давления и тем-
пературы. Значительные трудности возникают в связи с тем, что
размеры гравиметра ограничены диаметром и углом наклона
скважин.
Скважинный гравиметр ГСК-110 создан во ВНИИГеофизике на базе донного
гравиметра ГДК. Корпусу кварцевой системы придана форма снаряда. Корпус
помещен в карданный подвес и вместе с ним в сосуд Дыоара. Этот сосуд заполнен
минеральным маслом, которое одновременно является теплоизолятором и увели-
чивает затухание собственных колебаний корпуса. Сосуд Дыоара в свою очередь
заключен в цилиндрическую стальную трубу, в верхней части которой имеется
специальный разъем для присоединения проводов телеуправления гравиметром
к семижильному каротажному кабелю и пульту управления. Спускают и под-
нимают гравиметр каротажной лебедкой со специальным коллектором.
Рис. 7.27. Схема чувствительной
системы струнного скважинного
гравиметра.
Рис. 7.28. Схема скважин-
ного блока гравиметра.
206
Рис. 7.29. Блок-схема струнного скважинного гравиметра.
Гравиметр работает при температуре до 100° С и глубине скважины до 2500 м.
Диапазон измерения силы тяжести без перестройки (2004-250)-10"6 м/с2, погреш-
ность 0,3-10"“ м/с2. Внешний диаметр скважинного блока ПО мм, масса прибора
60 кг, пульта управления 10 кг.
Струнный скважинный гравиметр высокой точности разработан в США
фирмой ЭССО. Чувствительная система гравиметра (рис. 7.27) состоит из воль-
фрамовой струны / диаметром 25 мкм, длиной 5 см, на которой подвешен плати-
новый груз 3 массой около 1 г. Груз прикреплен к рычагу 4, вращающемуся на
вольфрамовых нитях 5. Такая конструкция ограничивает горизонтальные дви-
жения массы и демпфирует нежелательные гармоники колебаний струны. Около
центральной части струны расположен постоянный магнит 2, создающий поле
0,38 Тл. Металлическая рама 6 чувствительной системы имеет в середине стеклян-
ный изолятор 7. Это позволяет независимо подсоединять каждый конец струны
в электрическую цепь и передавать сигнал, индуцированный вибрацией струны,
в цепь генератора. При заданных размерах струны и массы основная гармоника
колебаний струны 625 Гц.
Струпа, магнит и остальные механические элементы чувствительной си-
стемы помещены в металлический контейнер 3 (рис. 7.28), к которому присоеди-
нен насос, обеспечивающий высокий вакуум. Для самоиивелирования чувстви-
тельной системы контейнер подвешен на металлической нити 2. Верхний конец
нити прикреплен к амортизирующим пружинам / для предохранения чувстви-
тельной системы от вибраций. Подвеска обеспечивает нивелирование при откло-
нении ствола скважины от вертикали до 4,5'. В нижней части контейнера имеется
арретирующий механизм 4, который закрепляет массу чувствительной системы
и контейнер при спуске-подъеме гравиметра и при перевозках. Контейнер вместе
с подвесом и арретиром помещен в термостат 5.
Рассмотрим блок-схему гравиметра (рис. 7.29). Струна и двухкаскадный
усилитель с положительной обратной связью составляют генератор. С выхода
генератора сигнал попадает на второй усилитель, с него по кабелю подается
на поверхность, где фильтруется от посторонних шумов. Фильтр обладает очень
узкой полосой пропускания, 1 Гц. Отфильтрованный сигнал поступает в счет-
ное устройство, где измеряется время, за которое струна совершит 10е колебаний.
Это время составляет около 160 с, точность измерения времени 1 мкс. Панель
управления позволяет контролировать работу всего гравиметра, генерировать
сигналы для арретирования и дезарретирования системы, включать и выключать
питание, фиксировать отклонение ствола скважины более чем на 4,5° и т. д. Наи-
больший наружный диаметр скважинного блока 100 мм. Погрешность измерения
силы тяжести (0,014-0,02)-К) 5 м/с2.
Скважинный гравиметр «Шелл» также основан на колебаниях струны
(рис. 7.30). Струна 2 — инварная проволока диаметром 25 мкм, длиной около
23 см — несет на нижнем конце груз 5 массой около 2 г. Струна помещена в стек-
лянную трубку 1, в которой создан высокий вакуум. В нижней части трубки
имеется арретирующий механизм 6, приводимый в действие электромотором 7.
207
Рис. 7.30. Схема чувствительной системы
скважинного гравиметра «Шелл».
Маятниковые колебания массы
демпфируются постоянными маг-
нитами, расположенными снаружи
трубки. В отличие от гравиметра
фирмы ЭССО в гравиметре «Шелл»
используется не первая, а девятая
гармоника колебания струны. Фор-
мирование этой гармоники обеспе-
чивается четырьмя соленоидами 4,
расположенными около нижней час-
ти струны. Соленоиды разделены
слабыми поляризующими магнита-
ми. Четыре электрода 3 около верх-
ней части струны образуют электро-
статический преобразователь, ко-
торый питает генератор и усили-
тель.
Стеклянная трубка со струной,
электростатическим и магнитными
преобразователями заключена в
латунный контейнер, вокруг кото-
рого навита обмотка термостата.
Контейнер вместе с термостатом
помещен в сосуд Дьюара, который
в свою очередь находится в наруж-
ном металлическом корпусе в кар-
данном подвесе. Диаметр наруж-
ного корпуса 114 мм. Период колебания струны определяют, измеряя время
70 000 колебаний с точностью I мкс по кварцевым часам. Погрешность наблю-
дений с гравиметром 0,05-10~6 м/с2.
Глава 8
МЕТОДИКА ГРАВИМЕТРИЧЕСКОЙ
СЪЕМКИ НА СУШЕ
ОСНОВНЫЕ ВИДЫ СЪЕМКИ
Измерение силы тяжести в отдельных пунк-
тах на площади исследований с целью получить картину распре-
деления аномалий силы тяжести называется гравиметрической
съемкой.
Гравиметрическую съемку проводят для решения разнообраз-
ных геологических задач: от изучения глубинного строения земной
коры до поисков отдельных рудных тел. В зависимости от постав-
ленных задач съемку подразделяют на общую (региональную)
и детальную.
Региональная съемка позволяет получить обзорную картину
гравитационного поля на обширной территории, выявить наи-
более общие закономерности поля и связи его с региональными
геологическими структурами, выделить перспективные участки
для последующего более детального исследования. Региональная
съемка помогает провести тектоническое районирование платфор-
20?
менных и геосинклинальных областей, оконтурить отдельные
структурные элементы, изучить глубинное строение земной коры
и Земли в целом.
Детальная съемка служит для поисков месторождений полез-
ных ископаемых, исследования отдельных структур и рудных тел.
Гравиметрические съемки в СССР проводят в соответствии
с технической инструкцией. Согласно этой инструкции каждая
из съемок должна иметь определенную густоту сети и точность
наблюденных и аномальных значении силы тяжести, чтобы обес-
печить построение карт аномалий силы тяжести соответству-
ющего масштаба (табт. 8.1).
Гравиметрические съемки могут быть площадными и про-
фильными.
Площадной называется такая съемка, при которой пункты
наблюдений распределены по площади более или менее равно-
мерно. В зависимости от геологического строения района до-
пускается отклонение сети от равномерной, что, однако, не должно
снижать достоверности карты аномалий силы тяжести. Поэтому
отношение расстояний между пунктами наблюдений вдоль про-
филя и между профилями не должно быть меньше чем 1 : 5. Пло-
щадная съемка дает наиболее полную и достоверную картину гра-
витационного поля изучаемой территории и является основным
видом гравиметрической съемки.
Профильной называется такая съемка, при которой пункты
наблюдений расположены вдоль отдельных профилей, не связан-
ных или слабо связанных между собой. Такая съемка дает пред-
ставление о характере изменения гравитационного поля лишь
вдоль этих линий наблюдений. Профильную съемку применяют
для предварительного обследования труднодоступных районов
(пустыня, тайга, горы), изучения структур, имеющих сильно
вытянутую форму, уточнения характера поля в районах площад-
ных съемок.
Гравиметрические наблюдения осуществляют отдельными рей-
сами. Каждый рейс представляет собой совокупность последова-
тельных наблюдений, объединенную общим учетом смещения
нуль-пункта гравиметра. При нелинейном смещении нуль-пункта
рейс разделяют на звенья, в каждом из которых смещение нуль-
пункта учитывается как линейное.
На каждом пункте определяют приращение силы тяжести от-
носительно некоторого пункта в районе исследований, который
называется исходным. На исходном пункте обычно известно абсо-
лютное значение силы тяжести. На всех других пунктах съемки
абсолютное значение силы тяжести получают, алгебраически
складывая их приращения и абсолютное значение на исходном
пункте. Иногда при высокоточных детальных съемках небольших
площадей с целью поисков отдельных рудных тел абсолютные
значения силы тяжести не определяют, а вычисляют только ано-
малии силы тяжести относительно условного нуля.
209
Чтобы привести разрозненные съемки разных лет в единую
систему, построить сводные гравиметрические карты на большие
территории, гравиметрические съемки осуществляют по тому же
принципу, который положен в основу создания геодезических сетей.
На всей территории СССР развита сеть высокоточных государ-
ственных опорных пунктов I класса. Эти работы выполняются
Аэрогравиметрической экспедицией АН СССР под руководством
Ю. Д. Буланже. Пункты I класса расположены друг от друга на
расстоянии 200—500 км. Средняя квадратическая погрешность
приращения силы тяжести между двумя пунктами I класса со-
ставляет (0,10-г0,15) КГ® м/с2. За исходный пункт опорной грави-
метрической сети принят пункт «Москва ГАИШ», связанный
с пунктом абсолютных определений силы тяжести в Потсдаме,
и все значения силы тяжести выражены в потсдамской системе.
Между высокоточными пунктами I класса специализирован-
ными организациями создастся сеть опорных пунктов II класса.
Расстояние между пунктами II класса 100—300 км, погрешность
связи их с пунктами I класса не более чем 0,2-10"5 м/с2. Пункты
I и II классов являются основой для дальнейшего сгущения опор-
ной сети, используемой при различных гравиметрических съемках.
По мере совершенствования аппаратуры и методов измерений
значения силы тяжести на опорных пунктах определяют заново
с более высокой точностью.
ОПОРНАЯ СЕТЬ И РЯДОВЫЕ НАБЛЮДЕНИЯ
При проведении съемки с гравиметрами необходимо таким
образом обеспечить увязку всех пунктов наблюдений, чтобы при
передаче абсолютных значений силы тяжести от одного или не-
скольких исходных пунктов не накапливались значительные
ошибки. Кроме того, практически все гравиметры обладают
в той или иной степени смещением нуль-пункта, которое следует
выявлять и тщательно исключать из наблюдений. Для оценки
качества работ необходимы контрольные измерения на отдельных
точках съемки.
Чтобы обеспечить выполнение этих условий, перед началом
съемки создают опорную гравиметрическую сеть III класса, пред-
ставляющую собой жесткую систему пунктов, сила тяжести на
которых определена с более высокой точностью, чем на остальных
пунктах съемки. Повышение точности достигается применением
более совершенных гравиметров, многократными наблюдениями
с одним или с группой приборов, использованием наиболее
быстрых средств передвижения (самолет, вертолет).
Опорная сеть III класса всегда хотя бы одним своим пунктом
привязывается к общегосударственным пунктам I или II класса,
где известно абсолютное значение силы тяжести.
Пункты опорной сети необходимо располагать на площади
исследований равномерно и удобно для подъезда к ним в рядо-
211
Таблица 8.1
Точность и густота сети гравиметрических наблюдений
Масштаб отчетных карт и графиков Сечение изоано- мал, 10~s м/с2 Средняя квадратическая по- грешность *, 10-5 м/с3 Густота сети
Наблюденные значения Аномалии Буге Число пунктов на 1 км2 Расстояние между пунктами, м
Равнины Горы ** Равнины Горы Равнины Горы
1 : 1 000 000 1 : 500 000 1 : 200 000 1 : 100 000 1 : 50 000 I : 25 000 1 : 10 000 1 : 5 000 * Без погре Районы с карты масштаба 1 : «»* Для горю 5 5 2 1 0,5 0,25 0,25 0,2 0,2 0,1 0.1 0,05 шностей и >езкимн фо 5 000. 1х районов 5 5 2 1 1 0,5 0,5 0,25 0,2 0,1 ходпых оп шами рель 0,5 0.5 0,4 0,3 0,15 0,07 0,06 0,06 0,06 0,03 0,03 0,015 орных пуп 1фа при па/ 0,5 0,5 0,4 0,25 0,25 0,12 0,12 0,06 0,06 0,03 ктоп. нчия относ 1,5 1.5 0,8 0,4 0,2 0,1 0,1 0.08 0,08 0.04 0,04 0,02 ительных п 2 2 1 0,5 0,5 0,25 0,25 0,12 0,1 0,05 эевышеннй 0,04—0,1 0,04—0,1 0,1—0,25 0,25—1 2—30 (1—10) *** 4—50 (2—30) 12—60 (4—50) 16—80 (12—60) 20—100 25—200 50—250 100—500 100 м и более в пределах лист 2500—5000 2500—5000 1000—2000 500—1000 100—500 50—250 20—100 10—50 а топографической
вых рейсах. Расстояния между пунктами выбирают исходя из
методики съемки и способа учета смещения нуль-пункта. Пред-
почтительно, чтобы при выполнении рядовых наблюдений каждый
рейс захватывал два-три опорных пункта, причем смещение нуль-
пункта гравиметра в промежутке между наблюдениями на двух
опорных пунктах должно приближаться к линейному. В зависи-
мости от густоты рядовой сети расстояние между опорными пунк-
тами колеблется от 1 до 20 км.
Наблюдения на опорных пунктах следует выполнять замкну-
тыми рейсами, т. е. каждый рейс начинать и заканчивать на одном
и том же опорном пункте. При этом каждый последующий рейс
должен включать несколько пунктов, наблюденных в предыдущих
рейсах. Опорные рейсы планируются таким образом, чтобы они
образовывали систему замкнутых полигонов.
После завершения наблюдений на опорной сети она подвер-
гается уравниванию методом наименьших квадратов.
Пункты опорной сети располагают в легкодоступных и хорошо
опознаваемых местах: у населенных пунктов, перекрестков дорог,
характерных местных ориентиров, пунктов триангуляции и т. д.
На каждый пункт опорной сети составляют кроки с указанием
расстояний до ближайших постоянных ориентиров, а сам пункт
надежно закрепляют на местности столбом или трубой.
Иногда, по условиям местности, не представляется возможным
развить опорную сеть заранее или создание сети перед началом
работ является экономически нецелесообразным. В этом случае
проведение съемки планируют таким образом, чтобы в качестве
опорной сети можно было использовать сеть узловых пунктов или
магистральных профилей. Узловыми называются пункты пересе-
чения трех или более рейсовых маршрутов, которые при оконча-
тельной обработке материалов могут быть использованы как
опорные. Но узловая сеть может быть уравнена только в конце
полевого сезона, после завершения всех наблюдений. Поэтому
во время полевых работ она не может служить основой для по-
строения итоговой карты.
При съемке по системе, магистральных профилей последние
прокладывают по возможности ортогонально к системе остальных
профилей. Наблюдения осуществляют несколькими приборами
по методике с повторением, что обеспечивает несколько большую
точность определения магистральных точек по сравнению с рядо-
выми. Магистральные профили соединяют небольшим числом
связующих профилей, образуя систему замкнутых полигонов,
подлежащую уравниванию. Систему магистральных профилей
привязывают к опорным точкам I и II класса, имеющимся в районе.
После создания опорной сети III класса осуществляют наблю-
дения на рядовых пунктах, для которых опорные являются жест-
кой осноззй. Наблюдения в рядовых рейсах всегда начинают
и заканчивают на опорных пунктах, разных или одном и
том же.
212
Методика наблюдений в рядовых рейсах зависит от характе
ристик гравиметра и особенностей поведения его нуль-пункта,
которое изучается в специальных наблюдениях перед началом
съемки.
Рядовые рейсы с бестермостатными гравиметрами необходимо
строить таким образом, чтобы наблюдения в рейсе или в отдельном
его звене всегда проводились при монотонном изменении тем-
пературы в гравиметре: повышении или понижении, так как коле-
бания температуры приводят к криволинейному смещению нуль-
пункта и снижению точности наблюдений.
Методика построения рейсов может быть двух типов: одно-
кратных наблюдений и наблюдений с повторением.
В первом случае наблюдения на рядовых пунктах проводят
один раз при прямом ходе. Такой рейс должен включать в себя не
менее трех наблюдений на опорных пунктах (в частности, на одном
и том же) в начале, середине и конце рейса. Поправку за смещение
нуль-пункта вводят, сопоставляя разность значений силы тяжести
между опорными пунктами, наблюденную в рейсе, и разность
твердых значений силы тяжести на тех же пунктах. В [слу-
чае нелинейного смещения нуль-пункта его учитывают по
звеньям, в каждом из которых смещение рассматривают как ли-
нейное.
При работе по методике с повторением наблюдения на пунктах
проводят во время прямого и обратного хода. Прямой ход начи-
нают и заканчивают на опорном пункте, а при обратном ходе
повторяют часть рядовых пунктов. Доля повторяемых пунктов
зависит от конкретных условий и составляет от 30 до 100%.
Смещение нуль-пункта определяют по повторным наблюдениям.
Эта методика является менее производительной и более дорого-
стоящей, поэтому она применяется только в исключительных
случаях: при резко нелинейном смещении нуль-пункта, недоста-
точной густоте опорной сети, изолированных, «висячих», маршру-
тах, опирающихся только на один опорный пункт, при многоднев-
ных рейсах. Надо стремиться выбрать такую структуру рейса,
чтобы с достаточной степенью достоверности выявить характер
смещения нуль-пункта. Для этого на некоторых пунктах реко-
мендуется выполнять трехкратные наблюдения или делать двойной
ход в одной и той же последовательности.
Поправку за смещение нуль-пункта вводят пропорционально
времени между наблюдениями на рядовом и опорном пунктах
в предположении, что нуль-пункт меняется линейно. Если в рейсе
есть пункты, на которых проводились повторные измерения, то
их также принимают во внимание при определении поправки за
смещение нуль-пункта. В этом случае вычисляют среднее взвешен-
ное смещение нуль-пункта по всем повторным наблюдениям
в рейсе. За вес принимают время между двумя повторными на-
блюдениями. Тогда за время Л/,-, прошедшее между двумя наблю-
дениями на пункте i, отсчет изменится на Ag, и смещение нуль-
213
пункта будет Среднее взвешенное значение смещения
нуль-пункта
k = 2 (Ч-.-Ч) Ч = 2 (8 п
2 АС 2 АС- ( ’
Иногда рекомендуется формула
Эта формула получена из условия минимума среднего квадра-
тического расхождения исправленных за смещение нуль-пункта
повторных наблюдений, опа более громоздка и преимуществ перед
формулой (8.1) не имеет.
ОЦЕНКА КАЧЕСТВА НАБЛЮДЕНИЙ
При гравиметрической съемке необходимо осуществлять по-
стоянный контроль за работой гравиметра и точностью определе-
ний силы тяжести.
Повторные наблюдения в рейсе в какой-то степени позволяют
судить о поведении гравиметра в этом рейсе, но они не дают пол-
ной характеристики точности и достоверности съемки. Очень
часто сходимость наблюдений внутри рейса очень высокая, но
наблюдения на одних и тех же пунктах в разных рейсах резко
различны и неудовлетворительны. Это обстоятельство связано
со многими причинами, влияющими на работу гравиметра: скач-
кообразное изменение нуль-пункта, колебания теплового режима,
изменение цены деления, нелинейность отсчетной шкалы и т. д.
Поэтому достоверность результатов измерений с гравиметрами
необходимо оценивать не только по внутренней сходимости по-
вторных наблюдений в рейсе, но главным образом по внешней
сходимости — близости повторных наблюдений в разных рейсах
на одних и тех же пунктах.
Согласно действующей инструкции необходимо выполнить от
5 до 10% независимых контрольных наблюдений. Контрольные
измерения следует проводить в разные дни и захватывать пункты
из разных рейсов. Поскольку наибольшие ошибки обычно распо-
лагаются в середине звена, целесообразно эти участки включать
в контрольные рейсы. Контрольные рейсы следует привязывать
к другим опорным пунктам, а не к тем, к которым были привя-
заны рядовые наблюдения. В этом случае контрольные и рядовые
наблюдения являются независимыми.
Основным показателем точности измерений с гравиметром
является средняя квадратическая погрешность единичного на-
блюдения, вычисляемая на основе независимых контрольных
наблюдений по формуле
Е — 2 б2/(/П — »),
(8.3)
214
где б — отклонение от среднего значения; п — число контроль-
ных пунктов; т — число наблюдений на этих пунктах.
В случае двойных наблюдений формула (8.3) примет вид
е = S v2/(2n), (8.4)
где V — разность между первичным и вторичным наблюдениями;
п — число точек с двойными наблюдениями.
При сравнении результатов наблюдений с твердыми значениями
силы тяжести на опорных пунктах погрешность единичного
наблюдения
е = У Е Аа/т, (8.5)
где А — отклонение измеренного значения от твердого; т — ко-
личество наблюдений.
Точность наблюдений на опорной сети оценивают следующим
образом. Предварительно о качестве наблюдений судят по невяз-
кам в замкнутых полигонах. Допустимая невязка полигона
идоп = 2ц. т/р, (8.6)
где ц — средняя квадратическая погрешность единичного при-
ращения Ag; mi «’ число приращений между последовательными
опорными пунктами (число сторон полигона); р — среднее для
данного полигона число независимых определений каждого при-
ращения силы тяжести.
Средняя квадратическая погрешность единичного измерения,
вычисленная по невязке в замкнутом полигоне,
е==в/]/2/п, (8.7)
где и — невязка полигона; т — число сторон в полигоне.
Средняя квадратическая погрешность приращения силы тя-
жести, вес которого при уравнивании опорной сети принят за
единицу,
И = У Е — П), (8.8)
где б — суммарные поправки звеньев полигона или отклонения
значений силы тяжести, полученных для узловых пунктов по
отдельным звеньям, от соответствующих уравненных значений;
т — число звеньев (число связей между опорными пунктами);
п — число определяемых опорных или узловых пунктов (без
«твердых» и исходных); р — вес каждого приращения Ag.
Средняя квадратическая погрешность приращения силы тя-
жести Ag по всей опорной сети
= р/|'' ' рт, (8-9)
где рт — среднее из весов всех звеньев опорной сети.
215
Среднее значение средней квадратической погрешности силы
тяжести g на опорных пунктах
eu^^,„JV2. (8.10)
Это значение погрешности служит основным критерием ка-
чества опорной сети.
После уравнивания опорной сети оценивают точность опреде-
ления силы тяжести на опорных пунктах III класса относительно
исходных пунктов более высокого класса.
Средняя квадратическая погрешность аномалий силы тяжести
на рядовых пунктах
= + (8.Н)
где е — средние квадратические погрешности силы тяжести:
ей— рядовых пунктов; е„ — опорной сети III класса относи-
тельно исходных опорных пунктов; е/г — зависящая от погреш-
ности определения высот; — зависящая от погрешности опре-
деления координат пунктов наблюдения.
СПОСОБЫ УРАВНИВАНИЯ ОПОРНЫХ СЕТЕЙ
Когда гравиметрические измерения проводят по замкнутому
полигону, то сумма истинных приращений силы тяжести от точки
к точке по всему полигону должна равняться нулю. Однако прак-
тически все наблюдения содержат какую-то ошибку, в результате
измеренные значения приращений отличаются от истинных и
сумма их равна не нулю, а некоторой величине и, называемой
невязкой полигона. Под уравниванием опорной сети понимается
вычисление наивероятнейших поправок к наблюденным прираще-
ниям силы тяжести, после внесения которых сумма исправленных
приращений по полигонам будет равна нулю. Практическое зна-
чение уравнивания состоит в том, что в любом пункте опорной сети
значение силы тяжести определяется однозначно, независимо от
приращений, по которым оно вычислено.
Существуют различные способы уравнивания опорных сетей.
В своем классическом виде они используются в геодезии при урав-
нивании триангуляционных и нивелирных ходов. В гравираз-
ведке применяют упрощенные способы уравнивания, предложен-
ные В. В. Поповым. Наиболее часто используют два способа:
способ полигонов, или коррелят, и способ узловых точек.
Способ полигонов, или коррелят
Пусть имеется гравиметрическая сеть, состоящая из не-
скольких полигонов (рис. 8.1). Стороны полигонов, на которых
измерены приращения силы тяжести, называются звеньями поли-
гонов. На невязку в любом полигоне влияют все его стороны
216
Рис 8.1. Схема поли-
гонов опорной сети.
в одном, то за вес
(звенья), но в разной степени, что зависит
от точности, с которой определено прираще-
ние силы тяжести вдоль этого звена: чем вы-
ше точность приращения, тем меньшую по-
правку оно должно получить при распре-
делении невязки. Точность приращений по
различным звеньям полигонов можно оце-
нить весом звена, значение которого опреде-
ляют по тем или иным признакам. Например,
если приращение по одному из звеньев из-
мерено в трех рейсах, а по другому только
звена можно принять число рейсов, т. е. соответственно 3 и 1.
Если наблюдения по звеньям выполнены в одинаковом числе
рейсов, но сами звенья включают разное число опорных пунктов,
то за вес звена можно принять величины, обратные числу пунк-
тов в звене: звено, содержащее 5 пунктов, имеет вес 0,2, а звено,
содержащее 2 пункта, вес 0,5.
Введем следующие обозначения: и — невязка полигона; р —
вес звена, индекс указывает па принадлежность звена тому или
иному полигону (pi, p.2l р3) или одновременно двум полигонам
(P12> Р13- Pit)-
Полагая 1-й полигон изолированным и считая поправки по
звеньям обратно пропорциональными весу звена, для вычисления
поправок в этом полигоне можно написать следующее уравнение:
’1 + «1 = о,
( Pi Pi2 Ри )
где — поправка на единицу веса.
Решив это уравнение,
6, = ^—;
Pi
Введение поправок в
соседних, 2-го и 4-го, полигонов.
Аналогично для 2-го изолированного полигона
щ = 0.
(8.12)
получим поправки к звеньям полигонов:
61S = ^ —; 6u==fe_L.
2 Р12 Pll
звенья 1-го полигона изменит невязки
(—+ —+ — +
\ Р% Р23 Р12 '
(8.13)
Из этого уравнения поправка для стороны, примыкающей
к первому полигону,
= /г2 -—.
12 2 Pi*
Поскольку kt =f= k.2, то при изолированном рассмотрении по-
лигонов задача определения поправок в смежные звенья не под-
дается решению..'Необходимо принять во внимание условие смеж-
ности сторон: разбрасывая невязку в полигоне, в общие звенья
надо вносить поправки, которые удовлетворяли бы уравнениям
217
смежных полигонов. При разбрасывании невязки в 1-м полигоне
во 2-й переходит и прибавляется к его невязке и2 поправка
При разбрасывании невязки во 2-м полигоне в 1-й переходит
и прибавляется к его невязке а, поправка /г., (1/ргз). Уравнения
для совместного распределения невязок в 1-м и 2-м полигонах
принимают вид
При этом предполагается, что 1-й и 2-й полигоны не. имеют
смежных звеньев с 3-м и 4-м полигонами. Учитывая условия
смежности всех четырех полигонов, для определения поправок
к звеньям получаем четыре уравнения:
( — -4—-—I—— --— k„---— k. 4- и, = 0;
\Р1 Р1Э П Pit ) 1 Р12 2 Р14 1 1
k„ - ——М-«»-0;
\ Ра 1 Ри 1 Раз > * Рп Раз ' i /о ,
/ 1 , I , 1х. 1 . 1 h , п. <8Л5>
G’.-i ' Р2З Рэ* ) Раз Дз|.
( — Ч—— kt---— Al---— k3 + U4 — 0.
\ Pi Ph Psi ) Pit Pat
Введя обозначения
_L + _L+J_ = pi: —+ —= pa И T. д., (8.16)
Pi P12 Pi-i Pa Pia Раз
где P — так называемый «периметр» полигона, получим
PiK
PJ\
Рака
Ри /?4== -Ui!
1
023 «3 — и2;
1 /г4 - - — н3;
Раз
(8.17)
КА - А3 = — и4;
Р14 Г 34
Уравнения (8.17) называются нормальными. Число их равно
числу полигонов. Решение системы нормальных уравнений дает
для каждого полигона одно значение поправки klt называемое
коррелятой.
Каждое уравнение системы (8.17) подчиняется общей законо-
мерности. Первый, главный, член в левой части уравнения пред-
ставляет собой произведение корреляты данного полигона на его
«периметр». Остальные члены левой части являются произведе-
ниями величин, обратных весам смежных сторон, на корреляты
218
соседних полигонов. Правая часть уравнения — это невязка
полигона, взятая с обратным знаком.
Объединив в уравнениях (8.17) члены с одинаковыми коэффи-
циентами 1/р, получим поправки для различных звеньев поли-
гонов:
~ № - ^) + 7- (*i - Ы = -В,;
Pl Р12 Р1А
— ъ J_ (А _ ^) -fa — (k4 - #3) == — и,;
Рг 2 Р12 ' “ ’ Ргз 2 37 2
Т- ~г 7 (-з ^г) + ~ (^з — £») =
Рз Г23 Р34
-I - 7- - *1) + ~ (/?4 - *3) = - «4-
Р4 /714 Р34
(8.18)
Для звеньев, принадлежащих только одному полигону, имеем
ба~-Ъ; 6;i--L/?3; (8.19)
Pl Pi Рз Pi
Если же звенья принадлежат двум смежным полигонам, то
поправка в звено определяется как разность соответствующих
коррелят:
б13 = ^(^-й2); =
Pi 2 Pl4
<53, = —— (ka — kJ; б3, — —— tk« — /?,).
Раз Рз4
(8.20)
Следует заметить, что при определении невязок полигон обхо-
дят в одном направлении, обычно по часовой стрелке. Так же
поступают и при вычислении поправок: если используется раз-
ность (&г — /гг), то поправку вводят в звенья 1-го полигона, а если
(/г2 — kJ, то в звенья 2-го полигона. В формулах (8.20) поправки
верхней строки даны для 1-го полигона, нижней — для 3-го.
Контролем правильности вычисления поправок для каждого
полигона является формула
= (8.21)
Вычисленные поправки удовлетворяют условию минимума
суммы квадратов поправок, всякое другое распределение невязок
дает худшее решение, при котором сумма квадратов поправок
будет больше.
При большом числе полигонов решение системы нормальных
уравнений строгим методом вызывает значительные вычислитель-
ные трудности. Обычно применяют метод последовательных
приближений, сущность которого состоит в следующем. Поскольку
в каждом уравнении системы (8.17) первый член значительно
219
больше остальных, то в качестве первого приближения в правой
части можно взять только эти первые члены. Тогда
Ад -- ^+ /и'; I- /-Т
^ = -77 + ^; ^~7Г 4
(8.22)
где kt — поправки, которые необходимо прибавить к результатам
первого приближения, чтобы получить точное решение.
Подставляя значения (8.22) в исходные уравнения, имеем
Pik{ — k-> — 1 Pll k'i - - - ui;
Pin
P.ki - Pi 2 1 P23 /4- — US
PSk'3 - -^k2- Pa 1 P.H k't = - «a;
PM - _L t. _ 1 Psi k'3 = - wi,
(8.23)
где
»г I Ц|
РцРа 1 РцР4
_L —ц«
РгЛ 1 РзЛ ’
PiiPi Р23Р3
, _ 01 1 __из
РцР1 Р31Р 3
Уравнения (8.23) по структуре в точности совпадают с исход-
ными уравнениями, но они определяют уже не сами корреляты kit
а поправки k't к коррелятам. В уравнениях (8.23) первые члены
также значительно больше остальных, кроме того, его свободные
члены (—и)) по абсолютному значению меньше исходных сво-
бодных членов (—и(). Приняв во внимание только первые и свобод-
ные члены уравнэний (8.23), найдем приближенные решения для
поправок коррелят:
(8-24)
кч =--------------угр -Т к-2', ki = — -pi- -j- А’.].
220
Подставив эти решения в уравнения (8.23), получим систему
уравнений третьего приближения:
- 1 К 1 k't = 4'1;
Р12 2 Pit
1 k'z-= - иг;
Pl 2 Р23 (8.25)
Л^з — Ргз Рз4 k'i = - из;
' k'i 1 Z’o «4,
/ <1'4 Pit Рз1 /l3 —
где »2 , «4 . 1>2 u'l »3 .
1)( — Р12^2 * Р14Р 4 P12P1 P2.3P 3
V - 01 . 04 Ui 1— аз
ид — Р23Р г 1 Рз4? 4 РцР1 r P&J* 3
Продолжая процесс приближений, мы получаем все умень-
шающиеся значения поправок k't и свободных членов о), на
каком-то приближении этими поправками можно будет пренебречь.
На основе уравнений (8.23)—(8.25) и последующих прибли-
жений для коррелят окончательно имеем
^== — ^-(«14- о) + Щ -I—);
^’2 = — ^-(U2 + U2 + U2+ ‘ /23 = — J- (U3 -j- 1)3 -j- Oa -j- • r 3 (8.26)
P-4 = — - Поправки в звенья я. 1 1- (О4 01 4- o'i 4- s
— Р1Р1 1и1 ~Г и1 1 Pi и ’
s2=- 1 )- s
РгР а 142 | U2 | Pip2 ’
1 • )== .. \ — •J
из — б4==- РзР 3 1 - (04 4- о) 4- •Sj sa \. P3P 3 S4 .
Р4Р4 1 / / Р4Р1 ’ (8.27)
и12 — Р12 V Pi p-J'
62з = - ^14 -Ч Ргз \ Pl Р3Г Si S4 \ . Pl Pt)'
5.31 где 5,- — о, + or 4- 4-( 5з \ Рз Pt / ’
221
f
Рис, 8.2. Уравнивание опорной сети способом полигонов.
В. В. Попов предложил графический способ последовательных
приближений, исключающий составление нормальных уравнений
и определение коррелят, так как сразу вычисляются суммарные
поправки к звеньям полигонов. Все вычисления проводят на схеме
опорной сети, составленной в достаточно крупном масштабе
(рис. 8.2). На схеме римскими цифрами указывают номера поли-
гонов, арабскими — номера опорных пунктов. После суммирова-
ния приращений по звеньям в середине каждого полигона записы-
вают невязку. Около каждого звена с наружной стороны состав-
ляют табличку для записи поправок, для смежных сторон делают
по две таблички. После этого вычисляют отношение обратного
веса каждого звена к «периметру» полигона Эти отно-
шения записывают над табличками красными чернилами и назы-
вают «красными числами». Сумма этих чисел для каждого поли-
гона всегда должна быть равна единице.
После подготовительных операций начинается разбрасывание
невязок. Безразлично, с какого полигона начинать, хотя удобнее
с полигона, в котором невязка наибольшая. Невязку разбрасы-
вают следующим образом. Невязку полигона умножают на «крас-
ное число» и результат записывают в табличку под этим числом за
границами полигона. Сумма этих произведений должна равняться
невязке. После этого переходят к следующему полигону. В этом
222
полигоне к имеющейся невязке прибавляют невязки звеньев, вы-
брошенные из предыдущего полигона и записанные в табличках
внутри данного полигона. Эту новую невязку умножают на «крас-
ные числа», относящиеся к данному полигону, и записывают
в соответствующие таблички. Так поступают со всеми поли-
гонами опорной сети. На этом заканчивается первое прибли-
жение.
Второе приближение можно начинать с первого полигона или
с последнего, двигаясь тогда в обратном порядке. Вычисляют но-
вые невязки в полигоне, которые получают как сумму невязок,
переданных из смежных полигонов, т. е. как сумму чисел, запи-
санных в табличках и не учтенных при первом приближении.
После этого невязку разбрасывают согласно «красным числам»,
как это делалось в первом приближении. Процесс разбрасывания
невязок продолжают до тех пор, пока все невязки не будут выне-
сены за полигоны; обычно это наступает после второго или третьего
приближения. Затем вычисляют поправки звеньев, для чего под-
считывают сумму чисел в табличках. Суммарная поправка звена
по ходу полигона равна сумме поправок, написанных с внутрен-
ней стороны полигона, минус сумма поправок, написанных с на-
ружной стороны полигона. Эти окончательные суммарные по-
правки записывают в кружках около звеньев. Сумма всех попра-
вок в полигоне должна равняться невязке, взятой с обратным зна-
ком. Чтобы при разбрасывании невязок исключить ошибки, сле-
дует зачеркивать поправки в табличках, как только они учтены и
распределены по звеньям.
Способ узлов
Уравнивать опорную сеть способом коррелят удобно только
в том случае, когда она состоит из небольшого числа простых по-
лигонов. Если же опорные рейсы образуют сложные пересечения
и сеть включает несколько исходных
пнями силы тяжести, которые не под-
лежат изменению при уравнивании,
то метод полигонов становится весь-
ма громоздким. При этих условиях
уравнять опорную сеть проще и бы-
стрее способом узлов, сущность ко-
торого состоит в следующем.
Пусть в опорной сети (рис. 8.3)
есть пункты А и В высшего класса,
значение силы тяжести в которых не
подлежит изменению при уравнива-
нии. Введем обозначения: Agls, Ag23,
Ag34 и т. д. —• измеренные прираще-
ния силы тяжести между опорными
пунктами, при этом Ag\2 = — Ag21;
пунктов с твердыми значе-
223
Pi2> Рчз и т. д* — веса звеньев (например, число наблюдений, вы-
полненных в этом звене).
Принимая твердую точку за исходную и используя наблюден-
ные значения приращений силы тяжести, вычисляем во всех пунк-
тах опорной сети приближенное значение силы тяжести. Если
твердые пункты отсутствуют, то за исходный примем один из пунк-
тов сети, положив в нем силу тяжести равной нулю. В пунктах
опорной сети приближенные значения силы тяжести
g2 =gB-t^gBP, gi—g^ + ^ga, g3 = g-2+ ^g-23 и т. д. (8.28)
Значения силы тяжести на каждый опорный пункт можно
передать от исходного через любой соседний опорный пункт, с ко-
торым данный пункт имеет связь. Например, для пункта 1 можно
получить три разных приближенных значения силы тяжести.
Очевидно, что вероятнейшее значение силы тяжести gt в этом
пункте равно весовому среднему из всех значений git переданных
из соседних пунктов:
т _ Р-н 4- Ag21) 4- р31 (g3 ~р Ag31) 4~ Р.ц (g.i + Agai) /о 29)
1 021 + 031 + 041
При этом предполагается, что в смежных пунктах 2, 3, 4 из-
вестны уравненные значения силы тяжести. Для каждого опор-
ного пункта можно написать аналогичное уравнение, число урав-
нений будет равно числу пунктов.
Уравнению (8.29) можно придать несколько другой вид. Сгруп-
пируем члены, содержащие g-L и Ag,A, и введем обозначения
Е Рi = Р214" Psi + А1
— сумма весов звеньев, сходящихся к данному узлу (вес узла);
«1 = Р-21 ^gn + Pai Agai 4- Рп Д&1-
Тогда уравнение (8.29) примет вид Е Plgl - P-ilg-i — Psiga - (8.30)
Для остальных пунктов сети имеем Е P2g2 — Pitgi — Рз£з — р-^'з = и>;
Е Р& — Р1& ~ Рз&з - Ры&з == . (8.31)
где
\gl2 -{- р3, \g32 рм pBi (\gB.2 4- РвУ,
-= Рзз 4" Раз АЯз» 4- Ра, 4- Раз (Agas 4 ~ £л)-
224
Легко видеть, что уравнения (8.30) и (8.31) подчиняются общей
закономерности. Коэффициент при главном неизвестном, являю-
щемся значением силы тяжести на опорном пункте, равен сумме
весов связей данного узла, взятой со знаком плюс. Коэффициенты
остальных неизвестных, соответствующих пунктам, с которыми
связан данный пункт (не считая твердых), равны весам соответ-
ствующих связей со знаком минус. Свободный член уравнений
равен сумме приращений связей, умноженных на их вес, плюс
сумма отметок твердых пунктов, непосредственно связанных с дан-
ным узлом. Уравнения (8.30) и (8.31) составляют систему нормаль-
ных уравнений.
Решая эту систему, сразу определяют уравненные значения
силы тяжести в узлах опорной сети. При большом числе узлов
систему решают методом последовательных приближений. Первое
приближение получают непосредственно по схеме опорной сети.
Второе приближение находят, подставляя в уравнения первые
приближения для gs. Третье приближение получают, подставляя
в уравнения вторые приближения, и т. д. Процесс заканчивают,
когда два приближения совпадают в пределах точности.
Значительно проще и быстрее можно решить нормальные урав-
нения, если вместо уравненных взять приближенные значения
силы тяжести, имея в виду следующее соотношение:
gi^gi + Xi,
(8.32)
где^, — вероятнейшее значение силы тяжести на опорном пункте;
gt — приближенное значение силы тяжести на этом пункте; х( —
поправка к приближенному значению силы тяжести.
Тогда для пунктов опорной сети, показанной на рис. 8.3, полу-
чаем
Подставим эти значения в уравнения (8.30) и (8.31):
S Р1Х, - р21х3 - pslx8 - pilXi = р.г1 (g2 - S1 + Agal) 4-
+ Psi (gs — gi + Agsi) + Pit (t,'i — gi 4- Ag41);
S P2X2 - P12X1 - Рз2*з - РьгХъ = p12 (g, - + Ag12) 4-
- - p32 (gs - gt + Ag32) + pB2 (gB - g.2 4- \gBJ 4-
+ P52 (go - g-2 + AgB2);
(8.34)
E РьХй — р^г - РззХз — P4t,xt = p№ (g2 — g5 4- Ag.,,) 4-
+ Рз5 (g3 — gi + ^gss) + P15 (gi — gi + Ag«) +
+ Раз (gA ~ g& + Ag/is)-
8 В. С- Миронов
225
Разности g2 — g“i + Л^21 представляют собой невязки звеньев.
Введем для них следующие обозначения:
— gi + ^ёп = »31;
ёз- gi + Л,?з1 =
St — 81 4“ = U41!
ё1~ 82 + ^ёп =
Si — ёз + — uJ3i
Й4 — Sa + ^gta — Ujs,
(8.35)
t. e. в общем случае
Si ~ Sk+ &gik = »ik-
Очевидно, что
= — uw.
Теперь уравнения (8.34) принимают вид
X Л*1 - рв1х2 - АдХз - р4ж = р21О21 + p3iusl +
2 Р2Х2 — Р12Х1 Р32Х3 РзгХЬ =
= Р12Щ2 + /932,,32 ~Ь Рвгиаа “Ь Ро2уб2>
2 РаХа — р№Х2 — р83Ха — р45Х4 =
= РкР& - Г Р35«35 + /W>45 + Ра&АЬ-
Свободный член этих уравнений представляет собой сумму
произведений невязок звеньев, сходящихся к данному узлу, на
их вес. Назовем свободный член невязкой узла и обозначим его щ,
тогда уравнения (8.36) примут вид
2 Рл — раА — Рзрс-з — PtjXt = щ;
2 Р2Х2 — Р12Х1 — Р32Х3 — Pi2X3
2 РзХ3 — Р13Х1 — РчаХ2 ------Р13Х1 — Ръзхз = °3>
2 Р1Х1 — Рих1 — Р31Х3 - PMxt =
S РЪХЬ — Рзьх2 — p3iX3 PtaXl “ U5-
(8.37)
Поскольку поправки в твердые пункты равны нулю, уравне-
ния (8.37) поправок хА и хв не содержат. Система нормальных
уравнений (8.37) по структуре аналогична системе (8.31). Но вме-
сто значений силы тяжести g(- в уравнениях (8.37) неизвестными
являются поправки xt к приближенным значениям силы тяжести
на опорных пунктах. Кроме того, свободный член представляет
собой сумму невязок звеньев, сходящихся к данному узлу, умно-
женных на их вес, а не сумму приращений по этим звеньям, умно-
женных на их вес, как это имело место в уравнениях (8.31). Си-
стему (8.37) решают также методом последовательных приближе-
ний.
226
Как и в способе полигонов, при определении поправок можно
пользоваться схемой опорной сети, что исключает составление нор-
мальных уравнений (8.37). На схеме (рис. 8.4) у опорных пунктов
заготавливают табличку. Предварительно для каждого узла под-
считывают невязки и веса pik звеньев и находят произведения
Ptk^ik- Сумма этих произведений, относящихся к узлу, определяет
его невязку щ которую и записывают в табличку.
Суммируя веса всех звеньев, сходящихся в узле, получают вес
узла 2Д-. Затем вычисляют «красные числа» как отношение веса
р1к каждого звена к весу узла «Красные числа» PuJ^Pi впи-
сывают у каждого узла над звеньями.
Процесс разбрасывания невязок узлов состоит в следующем.
Невязку узла умножают на «красные числа», надписанные
8* 227
у звеньев, сходящихся к узлу. Полученные результаты относят
к пунктам, с которыми связан данный узел, и записывают в таб-
лички этих пунктов под имеющейся там невязкой. Если узел свя-
зан с твердым пунктом (например, Л), то часть невязки, приходя-
щуюся на этот пункт, пишут около него над чертой. Разбросанную
невязку подчеркивают. Затем переходят к следующему узлу. Его
невязку суммируют с невязками, поступившими из смежных
узлов, и эту суммарную невязку разбрасывают таким же образом.
Такие вычисления проводят по всем узлам. После этого начинают
второе приближение: разбрасывают неучтенные невязки, посту-
пившие в узел после того, как его невязка в первом приближении
была разбросана, и т. д. Суммируя невязки в табличках каждого
узла, получают jjP.Xp Поправки в приближенные значения gt на-
ходят как отношение к весУ узла JJP,, тогда
+ (8-38)
ГУСТОТА СЕТИ И ТОЧНОСТЬ СЪЕМКИ
Выбор оптимальной густоты сети — это один из наиболее важ-
ных и сложных вопросов методики гравиметрических работ, ко-
торый до настоящего времени является предметом дискуссии.
Инструкция устанавливает масштаб отчетных гравиметрических
карт и сечение изоаномал, а также основные положения для опре-
деления необходимой густоты сети (см. табл. 8.1). Густота сети
должна быть достаточной для того, чтобы обеспечить выявление
наименьших по площади и интенсивности аномалий силы тяжести,
представляющих интерес для решения конкретной геологораз-
ведочной задачи. При площадных съемках аномалия считается
достоверней, если она отмечается не менее чем тремя точками из
разных рейсов и имеет амплитуду, превышающую утроенную
среднюю квадратическую погрешность аномальных значений силы
тяжести. В случае хорошей коррелируемости аномалии на трех
и более профилях (или по площади) она может считаться досто-
верной и при меньшей интенсивности. Когда гравиразведка при-
меняется в поисково-разведочных целях, расстояние между пунк-
тами наблюдений по профилям, расположенным вкрест прости-
рания изучаемых геологических структур, устанавливается в 2—
3 раза меньше глубины залегания этих структур. На профилях,
используемых для количественных расчетов, густота сети должна
быть такой, чтобы приращение силы тяжести между двумя сосед-
ними точками не превышало утроенной средней квадратической
погрешности аномалий.
Таким образом, если при расчете густоты сети и точности опре-
деления аномалий исходить из геологических параметров искомых
объектов, то необходимо приблизительно оценить интенсивность и
размеры аномалий, которые будут вызваны минимальными инте-
ресующими нас телами или структурами. По результатам оценки
228
можно вычислить густоту сети и необходимую точность аномаль-
ных значений. Для этого поступают следующим образом. Искомый
геологический объект уподобляют некоторой правильной геоме-
трической фигуре, для которой рассчитывают аномальный эффект,
используя аналитические выражения гравитационного эффекта
от тел соответствующей формы. Если искомый объект представляет
собой тело, близкое по форме к изометрическому, то оно может
быть аппроксимировано шаром; если тело имеет явно выраженное
простирание, — горизонтальным цилиндром или пластом.
Пусть, например, искомый объект аппроксимируется шаром
с центром на глубине Л. Максимальное значение аномалии
/\g = kMlh2. (8.39)
Пусть 6g — уровень помех, выше которого аномалия может
быть обнаружена. Тогда для шара равная уровню помех аномалия
6g = AA4/i(x2+/i2r3/2, (8.40)
где х — расстояние от максимума аномалии.
Исключая kM и решая уравнение относительно х, имеем
x^/ijA(Ag/6g)2/3- 1. (8.41)
Эта формула определяет расстояние между точками наблюде-
ний в зависимости от уровня помех, интенсивности ожидаемой
аномалии и глубины залегания тела, создающего аномалию.
Можно получить подобные формулы и для других тел правильной
формы. Естественно, что при определении размеров сети необхо-
димо принимать во внимание плановое расположение искомых
геологических объектов. Если они имеют явно выраженное про-
стирание, то сеть съемки вдоль этого направления разрежается.
Густота гравиметрической сети, определенная подобным обра-
зом, позволяет решить конкретные геологические задачи. Но по-
строить гравиметрическую карту, достоверно отражающую пове-
дение гравитационного поля на исследуемой территории, по такой
сети не всегда возможно. Последнее обстоятельство связано с тем,
что ошибки интерполяции при проведении изолиний могут зна-
чительно превышать погрешность силы тяжести в пунктах наблю-
дения. Поэтому при определении рациональной густоты сети сле-
дует исходить из точности, с которой можно получить аномальные
значения силы тяжести по данной карте, и из степени аномаль-
ности гравитационного поля.
Точность аномальных значений силы тяжести, снятых с карты,
зависит от погрешности наблюденных аномальных значений силы
тяжести, а также от эффективности сети гравиметрической съемки.
Эффективность сети определяется густотой и расположением пунк-
тов наблюдения и характером аномального поля. Точность ано-
мальных значений силы тяжести, полученных интерполяцией по
карте, можно охарактеризовать погрешностью интерполяции —
229
средней квадратической погрешностью интерполированного зна-
чения силы тяжести в любой точке карты. Введение этого понятия
позволяет по-другому подойти к вопросу о густоте сети. Погреш-
ность интерполяции можно получить, найдя разности линейно
интерполированных и наблюденных аномальных значений. Для
этого строят карту с разреженной сетью пунктов, для отброшенных
пунктов интерполяцией получают значения аномалий. При равно-
мерной сети наблюдений можно не строить новой карты, а объеди-
нить пункты наблюдений в группы по три и определить для цен-
трального пункта отклонение наблюденного значения от интерпо-
лированного по двум крайним. Чтобы избавиться от системати-
ческих ошибок, следует объединять пункты из разных рейсов.
Тогда погрешность интерполяции
(8.42)
где
б = (gm+x + gwl_i)/2 - gm (8.43)
- отклонение интерполированного значения от наблюденного;
g — измеренное значение силы тяжести; п — число пунктов, в ко-
торых определены отклонения.
Полагая наблюдения равноточными, из выражения (8.43)
находим е8 = (3/2) el или е( — 1,22еа.
Если еа — средняя квадратическая погрешность аномалии на
пунктах наблюдения, а е; — средняя квадратическая погрешность,
характеризующая эффективность сети съемки (так называемая
чистая погрешность интерполяции), то
в,-= + ё?. (8.44)
Более правильно в этой формуле перед е,- следовало бы написать
коэффициент р 2/3.
Естественно, что при разрежении сети погрешность интерпо-
ляции при прочих равных условиях возрастает, она изменяется
по следующему закону:
В; = k (Ух 4- Уу), (8.45)
где х и у — проекции среднего расстояния между пунктами на оси
координат; k — коэффициент пропорциональности, зависящей от
аномальности поля.
Установлено, что значение k для равнинных территорий и ано-
малий средней интенсивности практически постоянно и равно
(0,32 ± 0,02) ЧО'8 м/с8 на 1 км, При х — у формула (8.45) прини-
мает вид
ez = 2k Ух. (8.46)
Формулы (8.45) и (8.46) позволяют рассчитать густоту сети
гравиметрической съемки,
230
Поскольку Погрешность интерполяции включает в себя по-
грешность определения аномалии силы тяжести, то точность ин-
терполированного значения всегда несколько ниже, чем точность
аномалии. Поэтому рациональная густота сети может быть най-
дена из условия, что чистая погрешность интерполяции е; равна
погрешности еа аномалии, т. е.
е» = У el е? = 2еа.
При х — у
nt = 2А1<х==И2^
или
еа = 2; х = [еда)1а = е!/(4й2). (8.47)
Таким образом, если задана погрешность интерполяции et-,
определяющая точность съемки, то формулы (8.47) указывают не-
обходимую точность аномалий силы тяжести и густоту сети.
Точность интерполированного значения силы тяжести является
решающей и при определении сечения изоаномал. Очевидно, что
сечение изоаномал должно быть выбрано таким, чтобы отклонения
интерполированных значений от истинных лежали в пределах
сечения. Согласно теории ошибок вероятность р попадания изме-
ренного со средней квадратической погрешностью еа значения g3
в интервалы, указанные относительно истинного значения g,
следующая:
p(ga=g± еа) = 0,68;
p(gs = g± 2еа) = 0,95;
p(ga = g ± 2,5еа) = 0,987;
р (ga = g ± Зеа) = 0,997.
(8.48)
Если выбрать сечение изоаномал в 2,5 раза больше погрешно-
сти интерполяции, то в среднем только два пункта из 200 выйдут
из указанных пределов, а вероятность того, что они расположатся
рядом и дадут аномалию, ничтожно мала.
ГЕОДЕЗИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ
Геодезические работы при наземной гравиметрической съемке
включают следующие операции.
1. Разбивка сети (в частности, профилей и магистралей) для
опорных и рядовых наблюдений.
2. Определение координат и высот пунктов наблюдений, что
необходимо для вычисления нормальных значений гравитацион-
ного поля и поправок Буге.
231
3. Нивелировка местности вокруг пункта наблюдений, если
необходимо введение поправок за влияние рельефа.
4. Закрепление пунктов наблюдений на местности.
Следует иметь в виду, что в большинстве случаев стоимость
геодезических работ значительно превосходит (иногда в 2—4 раза)
стоимость собственно гравиметрической съемки. Поэтому из видов
геодезической съемки, которые могут обеспечить проектную точ-
ность определения аномалий силы тяжести, надо использовать наи-
более дешевые.
При задании допустимой погрешности координат пунктов гра-
виметрических наблюдений необходимо исходить из требований
к точности учета нормального поля и из масштаба отчетной грави-
метрической карты. Гравиметрический пункт па карте изобра-
жается кружком диаметром около 1 мм. Центр этого кружка на-
калывают на карту с разбросом 0,2—0,4 мм. Предельная ошибка
определения координат может быть принята равной 1,2 мм отчет-
ной карты. При масштабе карты 1 : 100 000 этому отрезку на мест-
ности соответствует 120 м. В средних широтах нормальное грави-
тационное поле меняется при перемещении по меридиану примерно
на 0,8 1СГ5 м/с2 на 1 км. На основании этого можно оценить необ-
ходимую точность определения координат точек наблюдений.
Легко убедиться, что эти требования сравнительно легко выпол-
нимы.
Более жесткие требования предъявляются к точности опреде-
ления высот пунктов наблюдений. При вычислении аномалий Буге
ошибка в высоте, равная 1 м, приводит к ошибке аномалии 0,2 X
X 10~6 м/с2, т. е. при средней квадратической погрешности съемки
0,02 -10’6 м/с2 высоты точек необходимо найти с погрешностью
не ниже чем 0,1 м.
Инструкцией устанавливаются допустимые погрешности опре-
деления координат и высот пунктов наблюдений в зависимости от
сечения изоаномал отчетной карты и точности аномалий в редук-
ции Буге (табл. 8.2).
В зависимости от требуемой точности координаты пунктов на-
блюдений могут быть определены по топографическим картам соот-
ветствующих масштабов, аэрофотоснимкам, инструментальными
геодезическими методами, автоматическими топопривязчиками
и т. п.
Наиболее дешевым видом работ является опознавание пунктов
по топографическим картам и фотопланам и снятие с них коорди-
нат опознанных пунктов. Для этого сопоставляют окружающую
местность с картой и, пользуясь характерными ориентирами,
наносят на карту положение пункта наблюдений. Желательно
пункты наблюдений по возможности совмещать с ориентирами и
характерными местными объектами. Если пункт расположен
в стороне от ориентиров, то следует измерить азимуты и расстоя-
ния от него до нескольких ориентиров. Определить координаты
по картам и фотопланам с требуемой точностью можно только
232
Таблица 8.2
Точность геодезической привязки гравиметрических
пунктов
Масштаб отчет- ной карты Сечение изо- аномал, 10'6м/с2 Средняя квадратическая погрешность
аномалий Буге, IO’5 м/с3 координат, м высот, м
1: 1 000 000 8 1,5 200 5
1: 500 000 5 1,5 200 5
1 : 200 000 2 0,8 100 2,5
1 : 100 000 1 0,4 80 1,2
1 : 50 000 0,5 0,2 80 0,7
0,25 0,1 40 0,35
1 : 25 000 0,25 0,1 20 0,35
0,2 0,08 20 0,25
1 : 10 000 0,2 0,08 4 0,2
0,1 0,04 4 0,1
1 : 5 000 0.1 0,04 2 0,1
0,05 0,02 2 0,05
в том случае, если масштаб используемых карт не мельче масштаба
отчетной карты, а по возможности крупнее его. Как правило, при
гравиметрических съемках масштаба 1 : 100 000 и мельче снятие
координат пунктов наблюдений с карты дает хорошие результаты.
При более детальных съемках применяют разбивку профилей ве-
шением и промером расстояний между пунктами наблюдений мер-
ной лентой. Концы профилей привязывают инструментально тео-
долитными и мензульными ходами. Координаты остальных пунк-
тов профиля получают интерполированием.
Для определения высот пунктов наблюдений используют топо-
графические карты соответствующего масштаба и сечения, баро-
метрическое, геодезическое и геометрическое (техническое) ниве-
лирование. Снимать высоты с топографических карт можно только
в том случае, если предельная ошибка положения горизонталей
меньше 2/3 предельной допустимой погрешности высот пунктов
наблюдений. При оценке пригодности топографической карты для
снятия высот надо иметь в виду, что согласно инструкции по топо-
графическим съемкам предельная ошибка положения горизон-
талей по высоте составляет при углах наклона местности до 2°
одну треть, а от 2 до 6° две трети сечения горизонталей; за предель-
ную ошибку принята утроенная средняя квадратическая. При
определении высот по топографическим картам эти же карты ис-
пользуют и для снятия координат пунктов.
Наиболее точным методом измерения высот является геометри-
ческое нивелирование. При детальных гравиметрических съемках
с погрешностью не выше 0,1 1СГ5 м/с2 оно является единственным
способом получения высотных отметок. При съемках более низкой
233
точности [(0,2-4—0,4) • 1СГ5 м/с21 используют геодезическое нивели-
рование. Сравнительно быстрым и дешевым методом высотной при-
вязки является барометрическое нивелирование. Современные
микробаронивелиры позволяют получать высотные отметки с по-
грешностью около 0,5 м, что вполне допустимо для построения гра-
виметрических карт сечением 1-10 5 м/с2 и более грубых.
Все пункты наблюдений подлежат закреплению на местности.
Способ закрепления зависит от класса пункта. Опорные пункты
закрепляют столбом или трубой с окопкой и надписью, содержа-
щей помер пункта, год работ и название организации, определив-
шей пункт. Следует иметь в виду, что знак пункта III класса, дол-
жен сохраняться в течение 5—10 лет. Рядовые гравиметрические
пункты отмечают на местности деревянным колышком с надписью
и окопкой, пункт должен сохраниться в течение всего полевого
сезона для возможных контрольных измерений.
Геодезические работы по разбивке, привязке и нивелировке
пунктов измерений должны по времени опережать собственно
гравиметрические наблюдения или, по крайней мере, проводиться
одновременно с ними.
Глава 9
ИЗМЕРЕНИЕ
СИЛЫ ТЯЖЕСТИ В ДВИЖЕНИИ
ОСНОВНЫЕ ТРУДНОСТИ
ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ
НА ПОДВИЖНОМ ОСНОВАНИИ
Проблема определения силы тяжести в дви-
жении с борта корабля или самолета имеет огромное значение.
Поскольку вода покрывает более 70% поверхности земного шара,
то совершенно естественно, что без знания гравитационного поля
на морях и океанах нельзя изучить распределение силы тяжести
на Земле. Знать силу тяжести на акваториях важно для решения
многих задач, и прежде всего для изучения фигуры нашей планеты.
Только при равномерной сети гравиметрических пунктов по всей
Земле можно достаточно точно определить ее сжатие и превышения
геоида над сфероидом. Большое значение приобретает исследова-
ние земной коры вне континентов. В последние годы интенсивно
осваиваются месторождения полезных ископаемых, в первую оче-
редь нефти, в пределах континентального шельфа. Эти работы
продвигаются все дальше и дальше в океан.
Применение на море обычных способов измерения силы тяже-
сти встречает ряд трудностей. Как динамические (маятниковые),
так и статические способы разработаны применительно к непо-
234
движному основанию, на которое устанавливают прибор во время
наблюдений. На корабле вследствие движения и качки прибор
испытывает различные возмущающие ускорения, которые могут
во много раз превосходить измеряемые приращения силы тяжести.
Возмущающие ускорения, складываясь с действительной силой
тяжести, в каждый данный момент образуют так называемую мгно-
венную силу тяжести
I Г ( . d2z \2 . / d2x \2 . / d2y \2
~ \ (л + ~йА ) + ( ДД) + ’
где d?x/dtz, dzy!diz, d-zldt? — компоненты возмущающего ускоре-
ния по осям координат.
Направление мгновенной силы тяжести называется мгновен-
ной вертикалью в отличие от истинной вертикали, направление
которой определяется невозмущенным значением силы тяжести.
Каждый гравиметрический прибор измеряет приращение силы
тяжести вдоль определенного направления — оси чувствитель-
ности прибора. Для гравиметров ось чувствительности жестко
связана с рамой прибора, для маятников ось чувствительности
совпадает с мгновенной вертикалью.
Возмущающие ускорения весьма сложным образом влияют на
поведение чувствительной системы измерительного прибора и мо-
гут исказить или полностью затушевать эффект изменения силы
тяжести. Поэтому прибор, предназначенный для измерения силы
тяжести в движении, должен быть сконструирован таким образом,
чтобы искажающие ускорения или совершенно не действовали на
чувствительную систему, или могли быть уменьшены до малых
значений, которыми можно пренебречь, или позволяли вводить
поправки за их влияние в наблюденные значения силы тяжести.
Чтобы вывести формулы поправок за возмущающие ускорения
и наклоны основания, надо найти проекцию мгновенного значе-
ния силы тяжести на ось чувствительнос-
ти прибора. При выводе формул полагаем,
что углы между осью чувствительности
прибора и истинной и мгновенной верти-
калями малы. Для простоты считаем, что
основание совершает плоское движение,
т. е, перемещается в горизонтальном на-
правлении в плоскости xOz (рис. 9.1).
Пусть ось чувствительности О А составляет
с истинной вертикалью гугол а, а с мгно-
венной вертикалью ОВ — угол Да. Тогда
мгновенное значение силы тяжести, если
пренебречь малыми выше (1/g)2 (d2x!dtz)z,
Рис. 9.1. Мгновенная вер-
тикаль и мгновенная сила
тяжести.
235
Измеренное значение
е, = &ео5Д«-[г+^($У] (--) =
Из этой формулы следует, что горизонтальное ускорение увели-
чивает измеренное значение силы тяжести, а наклон оси чувстви-
тельности относительно мгновенной вертикали уменьшает его.
Надо заметить, что величины d2xldt2 и Да входят в эту формулу
в квадрате, т. е. независимо от знака возмущений в измеренное
значение вносится систематическая ошибка, несмотря на то, что
в среднем значения d2x/dt2 и Да за большой промежуток времени
близки к нулю. Чтобы получить истинное значение силы тяжести
g, в осредненное измеренное значение gr надо ввести поправку
Л _ 1 / d2x \2 . Да2 ,о о.
^Sx, a 2g \ dt2 / "* & 2 ’ ^-3)
где d2xldt2 и Да2 — осредненные за время наблюдений значения
d-xldl2 и Да2.
Аналогично получим поправку для движения в плоскости
уОг:
W)’+*T- <м
Полная поправка за влияние горизонтальных ускорений и на-
клона основания равна сумме составляющих по осям координат:
4«—^-!(Ж+(5У]+4-г<^+эд- и
Первый член формулы — поправка за влияние горизонталь-
ных ускорений — называется поправкой Броуна. Б. Броун
впервые указал на необходимость учитывать систематическую
ошибку, вызванную влиянием горизонтальных ускорений.
Чтобы уменьшить эффект возмущающих ускорений при грави-
метрических измерениях на море, приборы устанавливают в кар-
данный подвес. Карданный подвес, по сути, представляет собой
маятник, который может колебаться относительно двух взаимно
перпендикулярных горизонтальных осей. Подобно любому маят-
нику, он стремится установиться в направлении мгновенной силы
тяжести. Соответствующей регулировкой добиваются совмещения
оси чувствительности прибора с мгновенной вертикалью. В этом
случае углы Да и Др являются ошибками в ориентировке кардан-
ного подвеса относительно мгновенной вертикали. Точность
ориентировки тем выше, чем меньше период собственных колеба-
ний карданного подвеса по сравнению с периодом качки корабля
и чем меньше трение в осях подвеса.
230
Установка оси чувствительности прибора вдоль мгновенной
вертикали требует весьма тщательного учета поправки Броуна,
что при больших значениях d2x/dt2 и d^y/d.t'1 осуществить чрезвы-
чайно трудно. Поэтому, чтобы поддерживать ориентировку оси
чувствительности прибора постоянной, применяют гироскопически
стабилизированные платформы, сохраняющие свою ориентировку
в пространстве. В этом случае регулировкой прибора добиваются
совмещения его оси чувствительности с истинной вертикалью.
Тогда угол а имеет смысл погрешности, с которой установлена
платформа относительно истинной вертикали, и измеренное зна-
чение gr при действии только горизонтального возмущающего
ускорения dPxIdt? равно сумме проекций горизонтального ускоре-
ния d2x/d/2 и ускорения силы тяжести g на ось чувствительности:
gr = gcosa-J--^-sina + —сс-----ya2. (9.6)
Соответственно поправка в измеренное значение силы тяжести
<9-7)
Полная поправка за возмущающие ускорения и наклоны гиро-
платформы
Следует заметить, что легко перейти от формулы (9.7) к фор-
муле (9.3). Действительно, имея в виду, что
1 Л
а = ТТ“Да
(см. рис. 9.1), получаем
Л d^x / 1 d^x л \ , 1 /1 Лгх . \ 2
&gx,a — — -~^г ~ Аа ) + £ (у ~ ) =
--Ж+t* w
Рассмотрим влияние вертикальных ускорений. В случае сов-
местного влияния горизонтальных и вертикальных ускорений
мгновенное значение силы тяжести
- У («+$)’+(£)'+{>)• <9-1 °>
или с точностью до малых второго порядка
। diz . 1 / d2x V , 1 / Д2у \2 min
gn = g + трг У у (у / + ‘2g (у / • (9-11)
237
Вертикальное ускорение не дает систематической компоненты
н мгновенное значение силы тяжести, но вызывает знакоперемен-
ные возмущения. Поскольку направления d2zldt‘i и g совпадают,
измерительная система не может отделить ускорение силы тяже-
сти от возмущающего ускорения d^z/dt? и прибор регистрирует
О
В измеряемую величину необходимо ввести поправку
= (4т I --vl ) (9.13)
dt2 \ dt |f dt |о/ 4 '
где (dzldt) | f — (dz/dt) | n — разность скоростей вертикальных дви-
жений.
При возрастании Т поправка убывает и при продолжительных
наблюдениях (на практике 20 мин) ею можно пренебречь. Следует
заметить, что подобное положение справедливо только для линей-
ной измерительной системы. Если чувствительная система при-
бора нелинейна, то вертикальное возмущающее ускорение вносит
систематическую погрешность в измеренное значение силы тя-
жести. Более детально влияние вертикальных ускорений рассмо-
трим при описании конкретных методов измерения силы тяжести
в движении.
При конструировании приборов для морских измерений кроме
инструментальных существуют и другие трудности. Так, ошибка
координат точки наблюдения в открытом море может существенно
сказаться на точности аномальных значений силы тяжести. Все
наблюдения на море выполняют при движении корабля, поэтому
необходимо вводить поправку за эффект Этвеша, возникающий
вследствие изменения центробежной силы, вызванной суточным
вращением Земли. Для введения этой поправки надо очень точно
знать курс и скорость корабля.
Первые определения силы тяжести на море были выполнены
барометрическим методом в начале XX в. О. Геккером, который
совершил несколько кругосветных путешествий. Ошибка измере-
ний составила (ЗОн-60)-10“5 м/с2. Несколько позднее созданием
приборов для статического способа определения силы тяжести на
море занимались Л. Бриггс и У. Даффилд, однако испытания
приборов не дали положительных результатов. Первые гравиметри-
ческие наблюдения на море с точностью, приемлемой для решения
геодезических и некоторых геологических задач, были осущест-
влены с маятниками голландским геофизиком Ф. Венингом Мейне-
сом в 1923 г. Им же было дано принципиальное решение проблемы
измерения силы тяжести на море маятниковым методом.
Определения силы тяжести на море с гравиметрами были ус-
пешно начаты Г. Норгардом в 1932 г. и Г. Хаальком в 1933 г. Для
этой цели были сконструированы газовые гравиметры. Однакэ
238
широкого распространения они не получили из-за большого тем-
пературного коэффициента, хотя по точности не уступали маятни-
ковым приборам. Практическое применение гравиметра для мор-
ских измерений начинается с 50-х годов, когда были использо-
ваны механические гравиметры с сильным демпфированием чув-
ствительной системы. В СССР были созданы кварцевые морские
гравиметры, за рубежом — металлические.
В настоящее время для морских измерений применяют маят-
никовые и статические приборы. И если при наземных съемках
маятниковые приборы используют только для создания сетей
опорных пунктов высокого класса, то при морских съемках они
играют весьма существенную роль, поскольку при работах на
море приходится совершать длительные рейсы, которые иногда
могут продолжаться несколько недель и больше. В этих условиях
сложно учитывать смещение нуль-пункта гравиметров, иногда
даже невозможно провести повторные наблюдения в одних и тех же
портах. Это затрудняет применение гравиметра при длительных
рейсах и требует создания морского гравиметра с малым смеще-
нием нуль-пункта. Полезным оказывается совместное применение
маятниковых приборов и гравиметров: маятниковые определения
являются опорными для гравиметрических.
МЕТОД ВЕНИНГА МЕЙНЕСА ОПРЕДЕЛЕНИЯ
СИЛЫ ТЯЖЕСТИ НА МОРЕ МАЯТНИКОМ
На штатив маятника, установленный на плывущем корабле,
действуют переменные ускорения d2xldt2, d2y/dt2, d2zldt2, направ-
ленные вдоль осей прибора, а также переменные наклоны относи-
тельно этих осей, т. е. колебания маятника происходят на под-
ставке, имеющей шесть степеней свободы. Колебания маятника на
такой подставке являются негармоническими, а сам маятник в от-
личие от идеального, совершающего гармонические колебания,
называется возмущенным. При небольших, непрерывно меняю-
щихся возмущающих ускорениях и наклонах разница между не-
гармоническими и гармоническими колебаниями невелика, что
позволяет оценить влияние каждого фактора отдельно с достаточ-
ной для практики степенью точности.
Пусть ускорение d2x/dt2 действует в плоскости колебаний маят-
ника, d2y/dt2 — в плоскости, перпендикулярной к колебаниям
(вдоль лезвия призмы маятника), d2z/dt2 — направлено вертикаль-
но вниз. Наклон прибора Да относительно оси х отклоняет пло-
скость качания маятника от вертикали, наклон Д|3 около оси у не
вызывает наклона плоскости качания маятника, но приводит
к отклонению маятника относительно самого прибора.
Идея метода Венинга Мейнеса состоит в том, что наблюдают
колебания двух маятников с близкими периодами, качающихся
в одной плоскости и на одной и той же подставке.
239
Ihi.uiran, что вес возмущающие ускорения, кроме d2x/dt2, от-
сутствуют п подставка настолько жесткая, что подвесы маятников
имеют одно и то же горизонтальное ускорение, получаем уравне-
ния движения маятников:
4- п2 sin ср 4- — • 4дг cos ср = 0;
dtz ' I 11 । g ща 11
d2<p, , , , , n? d2x „
+ >г2, sin <Р2 4- - j- • jjr cos <p2 = 0,
(9-14)
где
«1 = V g/l i^n/T^, л2 = Vё!1ъ = л/Т2
— частоты колебаний соответственно первого и второго маятни-
ков.
Полагая, что маятники изохронны, т. е. nt — п., — п, и совер-
шают малые колебания, т. е. sin ср ср и cos ср 1, получаем
42<Р1 12 d2X
#+«V7-^-=o.
(9.15)
п®Фг +
Я® d2x ___„
У •-dF = u-
Обозначая срх—срг через ср и вычитая из первого уравнения вто-
рое, находим
d2<f/dt2 м2<р = 0. (9.16)
Эта формула есть уравнение движения маятника, не возмущен-
ного горизонтальными ускорениями, с приведенной длиной I =
= g/n2, периодом колебаний Т = л]/ Ug — п/п и углом отклоне-
ния ср от вертикали.
Таким образом, разность углов элонгации двух изохронных
маятников можно рассматривать как угол элонгации некоторого
фиктивного, или разностного, маятника, совершенно не подвер-
женного влиянию горизонтального ускорения d2x/dt2 и имеющего
ту же длину и период, что и действительные маятники при отсут-
ствии горизонтального ускорения. В этом и состоит основная идея
Ф. Венинга Мейнеса об исключении влияния горизонтальных уско-
рений на маятники: два возмущенных маятника дают один фик-
тивный невозмущенный маятник.
Естественно, что амплитуды и фазы колебаний двух действи-
тельных маятников могут быть различны. Но самый выгодный слу-
чай, когда амплитуды колебаний маятников равны, а фазы про-
тивоположны (epi = —<р„), тогда разность <рт — ср2 = 2<р макси-
мальна. Если фазы одинаковы, то при равных амплитудах раз-
ность cpt — срг = 0, т. е. фиктивный маятник остается в покое.
Ф. Венинг Мейнес сконструировал маятниковый прибор, даю-
щий запись непосредственно угла элонгации ср, т. е. запись ко-
240

лебаний фиктивного маятника. Луч
света (рис. 9.2) падает на зеркало
маятника 1 и, отражаясь от него, идет
на зеркало маятника 2, качающегося
в той же плоскости. Затем луч падает
на движущуюся фотоленту. Передви-
жение отраженного луча на ленте
пропорционально разности углов эло-
нгации маятников; запись представ-
ляет собой правильную синусоиду,
по которой можно определить период
фиктивного маятника.
Таким образом, имея два строго изохронных маятника, можно
исключить влияние горизонтальных ускорений. Обеспечить иде-
альную изохронность маятников практически невозможно, всегда
есть некоторая неизохронность, которую необходимо учитывать.
В этом случае угол элонгации фиктивного маятника
2
Рис. 9.2. Схема регистрации
разности углов элонгации.
Ф—Ф1 ("1/»2)ф2-
На такой фиктивный маятник горизонтальные ускорения также
не влияют, и период определяется из следующих уравнений:
Т = АТ;
ДГ = (7\ - 7’2) (п2/я) cos (02 - 0),
(9.17)
где Т1 — Т2 — разность периодов фактических маятников; а2 и а —
амплитуды, О, и 0 — фазы фактического и фиктивного маят-
ников.
Величина ДГ называется поправкой за изохронизм. Для полу-
чения этой поправки необходимо кроме колебаний фиктивного
маятника регистрировать и колебания одного из фактиче-
ских.
Метод Венинга Мейнеса позволяет освободиться от возмущаю-
щего действия горизонтальных ускорений только в первом при-
ближении. Вообще же влиянием горизонтальных ускорений пре-
небрегать нельзя, поскольку они создают кажущееся увеличение
силы тяжести, и карданный подвес, в котором помещается маятни-
ковый прибор, устанавливается по равнодействующей силы тяже-
сти g и возмущающих ускорений, т. е. по направлению мгновен-
ной силы тяжести g„. Так как маятник качается около мгно-
венной вертикали, то на него действует мгновенная сила тяжести
g„; для получения действительной силы тяжести необходимо
к измеренному значению добавить поправки Броуна за дей-
ствие возмущающих горизонтальных ускорений:
241
Если есть вертикальные ускорения, то они складываются с си-
лой тяжести g, и период колебаний маятника
7’ = n]/7(^+-g-)-'/2 (9.19)
или
г- +4->гл-
I d2z
Полагая---малой величиной, имеем
g dt1
При определении Т из большого числа колебаний за длительный
интервал наблюдений можно принять
ЖМ
тогда
Поправка к периоду
АТ = Т_7’0 = ^г(^-)? (9.23)
или поправка к силе тяжести
'9-24)
Это поправка Броуна за вертикальное ускорение. Полная по-
правка Броуна за возмущающее действие ускорений на маятнико-
вый прибор
Кроме горизонтальных и вертикальных возмущающих уско-
рений на период колебаний маятника оказывает влияние наклон
подставки, на которой колеблется маятник. Это влияние учитывают
поправкой за наклон. Наклон подставки в плоскости качания маят-
ника не сказывается на периоде его колебаний, так как ось чув-
ствительности маятника в этой плоскости совпадает с мгновенным
положением его равновесия, которое в свою очередь с очень боль-
шой степенью точности совпадает с направлением соответствующей
компоненты мгновенной силы тяжести. И только при очень боль-
шом наклоне возможно соскальзывание призмы маятника с под-
ставки. Поэтому при медленно меняющихся наклонах опоры, когда
их период значительно больше собственного периода колебаний
242
маятника (более чем в 5 раз), поправка за влияние наклона опре-
деляется только одной компонентой — наклоном подставки в пло-
скости, перпендикулярной к плоскости качания маятника:
Ag₽ = (l/2)gA02. (9.26)
При измерениях на море необходимо в течение всего времени,
пока наблюдают колебания маятников, регистрировать наклон
плоскости этих колебаний.
МАЯТНИКОВЫЕ ПРИБОРЫ ДЛЯ
ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ ПА МОРЕ
Со времени работ Ф. Венинга Мейнеса маятниковые приборы
для определения силы тяжести на море постоянно совершенство-
вались: улучшена общая конструкция прибора, вместо хроно-
метра применяются, как правило, кварцевые часы, привлечена
вспомогательная аппаратура (акселерометры, наклономерные
маятники и т. д.).
Маятниковый прибор Венинга Мейнеса имеет три маятника с близкими
периодами, расположенных в одной плоскости. Регистрирующее устройство
сконструировано так, что на движущейся фотоленте записываются колебания
луча света, последовательно отраженного от двух маятников: среднего и одного
из крайних, что дает один фиктивный маятник. Таким образом из трех действи-
тельных маятников получаются два фиктивных. Кроме того, записываются ко-
лебания среднего маятника для вычисления поправки за изохронизм.
Для того чтобы угол отклонения среднего маятника записать относительно
истинной вертикали, а не относительно какой-то оси, связанной с прибором
и качающейся вместе с ним, в приборе установлен четвертый маятник. Этот маят-
ник качается в той же плоскости, что и три основных маятника, но имеет очень
сильное затухание: практически он не колеблется, сохраняя положение, близ-
кое к вертикали. Другой такой же быстро затухающий маятник расположен
в плоскости, перпендикулярной к плоскости качания основных маятников, и
служит для регистрации наклона плоскости их качания.
Кроме указанных в приборе имеются еще два маятника, период колебаний-
которых очень велик: 30—40с. Это наклономерные маятники, оси их качаний рас-
положены в горизонтальной плоскости взаимно перпендикулярно. Коле-
бания этих маятников также регистрируются, по ним определяют влияние
горизонтальных ускорений, учитываемых поправкой Броуна. Прибор помещен
в карданный подвес.
Для первых морских наблюдений были переделаны обычные маятниковые
приборы. Приспособление четырехмаятникового прибора было осуществлено
Л. В. Сорокиным в 1930 г. Впоследствии приборы были модернизированы в ГАИШ
и ЦНИИГАиК.
Трехмаятниковый прибор для морских измерений (ММП) был построен и
испытан в ЦНИИГАиК в 1963 г. под руководством М. Е. Хейфеца. Прибор имеет
штатив, разделенный на три отсека, и шесть кварцево-металлических маятни-
ков в комплекте. В верхней части штатива расположены подушки для подвески
маятников и блок акселерометров для записи возмущающих ускорений. Для
регистрации отметок времени сконструированы специальные кварцевые часы.
В процессе наблюдений два крайних маятника качаются в противофазе,
средний остается в покое. Для поддержания постоянной температуры прибор
помещен в термостат. При наблюдениях прибор устанавливается в карданный
подвес. Поскольку подвес и система акселерометров рассчитаны на небольшие
ускорения и углы наклона, то измерения с прибором проводят на подводных лод-
ках; на надводных же судах наблюдать можно только в особо благоприятных
243
\ < .'KiiuiMX. При измерениях на подводной лодке средняя квадратическая погреш-
ность составляет (14-2)- 10-G м/с2.
Четырехмаятниковый прибор, построенный М. Е. Хейфецем для измерений
на надводном судне, имеет не полусекундпые, как обычно, а четвертьсекундные
маятники. Это позволяет существенно увеличить устойчивость такого маятника,
поскольку при колебаниях маятник мало отклоняется от осп качания, что весьма
существенно при морских измерениях. Короткий маятник позволил построить
легкий штатив, который можно установить па гироплатформе.
В приборе имеется четыре вольфрамовых маятника, дающих запись двух
фиктивных. В процессе наблюдений на фотограмме регистрируются колебания
всех четырех действительных маятников. Фоторегистратор горизонта, запись
которого осуществляется на той же фотограмме, позволяет определить для лю-
бого момента времени угол наклона прибора. Для регистрации вертикальных уско-
рений служит вертикальный акселерометр.
При наблюдениях прибор устанавливают на гироскопически стабилизиро-
ванную платформу. Испытания показали, что прибор работает устойчиво при
волнении моря до 4 баллов.
Автоматизированный маятниковый прибор АМП для морских наблюдений
создан в 1969 г. в ЦНИИГАиК. Прибор имеет два маятника, обеспечивает фото-
электрическую регистрацию с выводом результатов на печать; погрешность из-
мерений (14-2)-10"® м/с2.
СТАТИЧЕСКИЙ СПОСОБ
ИЗМЕРЕНИЯ СИЛЫ ТЯЖЕСТИ НА МОРЕ
Наиболее существенными помехами при статическом способе,
так же как и при динамическом, являются периодические верти-
кальные и горизонтальные ускорения движения корабля. Другие
мешающие ускорения, например кажущееся увеличение силы
тяжести, вызванное тем, что карданный подвес устанавливается
по равнодействующей ускорения силы тяжести и ускорения дви-
жения судна, подавляются или учитываются так же, как и при
маятниковом методе измерений.
Если подвижную часть упругой системы гравиметра очень
сильно задемпфировать (в сотни раз больше критического значе-
ния), то такая система на ускорения высокой частоты — ускоре-
ния движения корабля — не реагирует и фиксирует изменения
ускорения только низких частот — изменения ускорения силы
тяжести. В этом состоит сущность статического способа измерения
силы тяжести на море.
Для морских измерений можно приспособить систему любого
гравиметра, но предпочтительнее использовать гравиметры вра-
щательного типа, у которых маятник находится в горизонтальном
положении. В этом случае горизонтальная составляющая уско-
рения судна на показания гравиметра влияет слабо. Моменты сил
горизонтальной Мх и вертикальной Mz составляющих ускорения
судна
z/2 у
АД. = т Z sin а; М? = т I cos а,
х dt2 ’ Z >
где cPx/dl2 и dtzldt* — горизонтальное и вертикальное ускорения
корабля; т — масса маятника; I — расстояние от оси вращения
244
до центра тяжести маятника; а — угол отклонения маятника от
горизонта.
Из этих формул следует, что при малом угле а момент сил гори-
зонтального ускорения ничтожно мал по сравнению с влиянием
вертикальной составляющей ускорения. Поэтому вертикальная
составляющая является основной помехой при статическом спо-
собе измерения силы тяжести на море и в движении вообще.
Рассмотрим возможности подавления этой помехи.
Обратимся к уравнению движения упругой системы грави-
метра вращательного типа
/(Фа/с//2) = ЕЛ1,
(9.27)
где 1 — момент инерции системы; — сумма моментов сил,
действующих на систему.
Положим для конкретности, что система представляет собой
горизонтальный маятник, удерживаемый силой закручивания
горизонтальной упругой нити; на конечных выводах это ограни-
чение не скажется. Тогда момент инерции равен m22; момент силы
тяжести (—mgl cos а); момент крутильной нити [—т (0О 4- а) ],
где 90 -— угол предварительного закручивания нити; т — жест-
кость нити.
На рычаг системы при ее движении действует момент, связан-
ный с демпфированием системы и пропорциональный угловой ско-
рости, он равен [—Н (da/dt)], где Н — коэффициент демпфиро-
вания. Надо учесть и момент вертикальной составляющей уско-
рения корабля [m/azcos a cos (со/) 1, где а, — амплитуда верти-
кальной составляющей ускорения корабля; со — угловая частота
колебаний; t — время.
С учетом всех перечисленных моментов сил уравнение движе-
ния системы принимает вид
тР (d2a/dP) -ф Н (da/dt) -ф mgl cos а -ф
-ф т (60 -ф а) = т1аг cos a cos (со/).
Если система находится в положении равновесия, то
mgl cos a = — т (90 -ф a);
da ___ ml cos a
dg ' т — mgl sin a ,
Учитывая эти формулы и полагая, что угол а мал, т. е.
da/dg = — tnl/x = 0o/g,
вводим обозначения
т/(т/2) = /i2; Н/(тР) = 2е.
Тогда уравнение движения принимает вид
(d2a/dP) [- 2е (da/dt) -ф «2а = (a2//) cos (со/).
(9.28)
(9.29)
(9.30)
245
Полученное выражение является линейным неоднородным
уравнением второго порядка. Решение его состоит из решения
однородного уравнения и частного решения линейного неодно-
родного уравнения:
а — j а2.
Поскольку система имеет сильное демпфирование, то е п0, и
решение однородного уравнения
“1 = 9 1Л?----2 ~ а^' (9'31)
где
flj = — е -j- У е2 — /?=; а2 = — е — У е2 — п2
— корни характеристического уравнения; сс0 — начальная ам-
плитуда отклонения маятника от положения равновесия.
Собственные движения системы являются апериодическими.
Частное решение а2 будем искать в виде
а2 = A sin (со/) В cos (со/).
Определив коэффициенты А и В, получим
2е<оаг А I аг(л§ —®2) „„„ , А
а., = ,,, „-----sin (со/) 4- ,,, . > a cos (“Ч
2 Z [(«$ — со2)2 4 4e.-o)-j ' ' 1 I |рг2—ы2)2-j-4g-co2] v 7
или
аа = . |Л о COS (со/ 4- 6), (9.32)
/ И — io2)2 4 4s2<o2 4 1
где
б = — arctg [2ей)/(Пд — ог)| (9.33)
— сдвиг фаз, или фазовая частотная характеристика системы.
Отсюда следует, что маятник совершает вынужденные синусо-
идальные колебания с амплитудой
Z У («ц — со2)2 -р 4е2со2
(9.34)
и сдвигом фаз б.
Общее решение уравнения движения системы может быть за-
писано в виде
а = И1 4- а2 = ------ (а^ - а2еа‘‘) --|-
2 V е2 — пд
4--------
Z У (и? — со2)2 -|- 4е'2ш2
COS (со/ ф- 6).
(9.35)
246
Первое слагаемое этой формулы характеризует апериодические
собственные колебания системы, второе — вынужденные колеба-
ния под действием вертикальной составляющей ускорения ко-
рабля. При непрерывном действии возмущающего ускорения
в случае установившегося процесса первое слагаемое можно не
принимать во внимание, поскольку описываемые им движения
быстро затухают, и рассматривать только второе слагаемое.
Если же системе сообщаются кратковременные импульсы и наблю-
дается ее поведение во времени, то можно ограничиться рассмо-
трением только первого члена уравнения.
Полагая в формуле (9.34) частоту ю = 0, т. е. считая верти-
кальную составляющую ускорения постоянной по амплитуде,
получаем так называемую статическую амплитуду отклонения
системы:
аст = аг/(//12). (9.36)
Поделив уравнение (9.34) на (9.36), получим коэффициент ди-
намичности, или амплитудную частотную характеристику системы
X = . (9.37)
“ст У — со2)2 -|- 4е3ю2
Коэффициент динамичности показывает степень уменьшения
амплитуды колебаний маятника гравиметра под действием сину-
соидального ускорения частотой w по сравнению с амплитудой,
обусловленной постоянным ускорением такого же значения.
Величина, обратная коэффициенту динамичности, называется
коэффициентом подавления помех
К = 1/Х. (9.38)
Из формулы (9.37) следует, что начиная с некоторого, так на-
зываемого оптимального затухания, которое определяется усло-
вием
е > ча!]/'2,
подавляются все колебания, частоты которых не равны нулю, и
при этом тем интенсивнее, чем выше их частота.
Чтобы оценить степень подавления возмущающих ускорений
в перезатушенной системе гравиметра, упростим формулы (9.31),
(9.33), (9.37), имея в виду, что для такого гравиметра 8 п0 и
п0 > и. В этом случае, разлагая |' е2 — rag в ряд по степеням
п0/&, получаем
а1?«аоехр{[ -н§/(2е)]/) ^аоехр(— t/T),
где
Т = 2е/л? (9.39)
— коэффициент, называемый постоянной времени и имеющий раз-
мерность времени.
247
р
Рис. 9.3. Амплитудная л, и фазовая 6 частотные характеристики
перезатушенной системы гравиметра.
Для Z и tp 6 получим
А = (1 +TW)-V2; (9 40)
tg 6 == — Ты. (9.41)
Поскольку Т2ы2 1, то для приближенных оценок в случае
высоких частот можно использовать выражение
X=l/(7w). (9.42)
Графики зависимости коэффициента динамичности А, и сдвига
фаз 6 от частоты ы возмущающего ускорения для различных
постоянных времени Т показывают (рис. 9.3), что амплитуда коле-
баний системы резко уменьшается с увеличением частоты. Таким
образом, перезатушенная система гравиметра является своеоб-
разным механическим фильтром низких частот, который пропу-
скает полезную постоянную компоненту и подавляет переменную
компоненту вертикальной составляющей ускорения. Сдвиг фаз
показаний прибора относительно вертикальных ускорений в та-
кой системе близок к л/2.
Аномалии силы тяжести при измерениях можно рассматривать
как гармонические колебания очень низкой частоты. Поэтому,
чтобы увеличить относительное подавление высокочастотных по-
мех по сравнению с подавлением низкочастотного сигнала, необ-
ходимо резко повысить затухание упругой системы.
Рассмотрим следующий пример. Пусть чувствительность гра-
виметра к изменениям силы тяжести daJdg = —tnllr = 0,01 рад
на Г 10'2 м/с2, тогда при I = 1 см получаем па = 10. Если затуха-
ние упругой системы в = 20’ 103, то Т — 400 с. Частота периоди-
ческих вертикальных колебаний судна «ц — 0,75, вибрации ®2 =
= 100 рад/с, скорость судна 15 км/ч. Положительная аномалия
силы тяжести имеет ширину (расстояние между ее правым и левым
минимумами) 10 км. Тогда частота аномалии силы тяжести
ыа = 2л 15 : (3600-10) = 262,10~° рад/с.
248
Подставляя поочередно значения Wj, ш2, <ла в формулу (9.42),
получаем X (wx) 1/300, т. е. амплитуда возмущений системы,
зависящая от вертикальных колебаний судна, при затухании
е = 20- 103 уменьшается в 300 раз. Так, если вертикальные уско-
рения корабля составляют 1 - 10-а м/с2, то гравиметр их зареги-
стрирует как 3-10“5 м/с2. Коэффициент X (о>2) = 1/(40-103), т. е.
амплитуда возмущений системы, вызываемая вибрацией судна,
уменьшается в 40-103 раз. Для аномалии силы тяжести X (coj =
= 0,94, т. е. вместо аномалии 10' 10“в м/с3 будет зарегистриро-
вана аномалия 9,4- 10" м/с2, амплитуда аномалии снижается
всего на 6%.
Подставив значение соа в формулу (9.41), найдем сдвиг фаз ано-
малии 6 45°, что соответствует линейному смещению максимума
аномалии на 1,2 км (так как полный период 2л соответствует 10 км).
Таким образом, применяя сильно затушенную систему, можно
в достаточной мере подавлять возмущающие ускорения, связанные
с движением корабля. В морских статических гравиметрах одно-
временно используются воздушное, жидкостное, электромагнит-
ное и другие виды демпфирования, действующие па отдельные
узлы прибора (рычаг гравиметра, усилительные и регистрирую-
щие устройства и т. д.). При этом суммарный коэффициент дина-
мичности системы приобретает вид
X = ХгХ2.. .Х„ = \/{ТхТг.. - Тпып),
а сдвиг фаз
п
s = — S arctg (ыТ;),
i=i
где Xz — коэффициенты динамичности отдельных узлов грави-
метра; Tt — соответствующие постоянные времени.
Следует помнить, что приведенные выше формулы справед-
ливы только для случая, когда Т<а> 1 и п0 '> ®.
Оценивая возможность подавления возмущающих ускорений,
мы полагали, что чувствительная система гравиметра находится
идеально точно в горизонтальной плоскости и ее рычаг также все
время удерживается в горизонтальном положении. На практике
при морских измерениях гравиметр или помещают в карданный
подвес, или устанавливают на гироскопически стабилизирован-
ную платформу. При использовании карданного подвеса ось чув-
ствительности гравиметра совпадает с мгновенной вертикалью и из-
меренное значение силы тяжести будет больше, чем ее действитель-
ное значение. В этом случае в наблюденное значение силы тяжести
необходимо ввести поправки Броуна, как и при измерениях с маят-
никовыми приборами.
Измеренное ускорение
249
I Iimi.ii .ти, что по сравнению с силой тяжести g возмущающие
ускорения малы, и разлагая выражение grl в ряд, получаем
„ । d2z , 1 Г / d2x\2 . / d24 \S1 ,n ...
gn — + + ~2g~ ]• (9.44)
При наблюдении в течение времени, превышающего период
вертикальных ускорений, значение d2z'dt2 обращается в нуль и
поправка за действие возмущающих ускорений принимает вид
= = (9.45)
Амплитуду горизонтальных ускорений определяют косвенно,
измеряя углы между истинной вертикалью и направлением резуль-
тирующего ускорения. Поскольку эти углы малы, то
a = v^’ Р = (9'46)
Тогда поправка
Ag — — (g/2) (a2 + ₽2).
(9.47)
Практически создать идеальный карданный подвес, следующий
точно за мгновенной вертикалью, исключительно трудно. Кроме
того, карданный подвес совершает собственные колебания с пе-
риодом То, отклоняясь от положения равновесия на малый угол у.
Гравиметр при этом наклоняется, что приводит к уменьшению
измеренного значения силы тяжести на Agtl = gyil‘2.. Полагая, что
у — у,) sin (сооО, имеем
Agn = (gVo/2)sin2 («</)•
Из-за сильного демпфирования гравиметра его рычаг занимает
положение, соответствующее среднему значению \gn за один пе-
риод колебаний:
т0
А^ = (1/Го) J Ag„^ = g?6/4. (9.48)
о
При раскачивании гравиметра возникает центробежное уско-
рение, приводящее к увеличению измеренного значения силы
тяжести. Эффект центробежного ускорения
Agf = ^Vo“ocos2(°°0’
где R — расстояние между чувствительной системой гравиметра
и точкой подвеса его в кардане.
Среднее значение эффекта в течение одного периода
г»
*gf = (1/Л.) J Ag, dt = ед/2. (9.49)
250
Следовательно, эффекты собст-
венных колебаний карданного под-
веса и центробежного ускорения
гравиметра зависят от частоты w0
и действуют в противоположные
стороны. Зная расстояние 7? и ис-
пользуя регулировочные грузы
карданного подвеса, можно добить-
ся взаимной компенсации этих эф-
фектов. Приравнивая выражения
(9.48) и (9.49), получаем условие
компенсации
£?о/4 =
откуда
То = 2л/о>о = 2л V^ZR/g, т. е. 2R = L, (9.50)
где L — приведенная длина маятника, поскольку карданный под-
вес с находящимся в нем гравиметром можно рассматривать как
маятник; таким образом, поместив чувствительную систему грави-
метра в центр качаний этого маятника, можно избавиться от влия-
ния собственных колебаний карданного подвеса на измеряемое
значение силы тяжести.
При установке на гироплатформе гравиметр стабилизируется
относительно истинной вертикали. В этом случае гравиметр изме-
ряет сумму силы тяжести и вертикальных возмущающих ускоре-
ний. Осредняя наблюдения в течение времени, более длительного,
чем период вертикальных возмущающих ускорений, можно полу-
чить истинное значение силы тяжести. Если бы гиростабилиза-
ция работала безупречно, а маятник гравиметра находился все
время в горизонтальном положении, то отпала бы необходимость
вводить поправки за возмущающие ускорения. Однако даже самые
совершенные гироплатформы обладают некоторой погрешностью
стабилизации, а маятник гравиметра отклоняется от горизон-
тального положения под действием силы тяжести и возмущающих
вертикальных ускорений и, как следствие этого, испытывает дей-
ствие возмущающих ускорений, не только вертикальных, но и го-
ризонтальных. Оценим порядок этих влияний.
Пусть при отсутствии возмущающих ускорений рычаг грави-
метра и гироплатформа горизонтальны (рис. 9.4). Под действием
возмущающих ускорений гироплатформа наклонилась на угол а.
вдоль рычага маятника и на угол р вдоль оси вращения маятника,
а сам маятник наклонился относительно гироплатформы и состав-
ляет с ней угол ср. Тогда на основе формулы (9.8) поправка в изме-
ренное значение силы тяжести за влияние наклонов
= -[>(£+?) + $ ₽] +^[(МГФ)8+Г1 (9.51)
251
НЛП
d2x — , — ,1 —s
— Т^ф + ^ф + т^Ф-
(9.52)
Рассмотрим каждый член формулы. Первый дает поправку за
переменный наклон гироплатформы, второй — за совместное влия-
ние переменного наклона платформы и горизонтальных ускорений
(поправка Гаррисона). Если положить, что d2x/dt2 и а — функции
одной и той же круговой частоты:
d?x/dt2 = йд-соз (cot 6,);
а = aacos (at -j- 5а),
(9.53)
d2x 1
^2 а ~ “2“ ^Х1а COS (бд. ба).
(9.54)
Аналогично можно записать
$ р=4- cos (6v - 6р)-
(9.55)
Для уменьшения поправок (9.54) и (9.55) надо стремиться
уменьшить cos (б,.— би) и cos (б^— 6.,), т- е сделать углы
(бА. — ба) и (бу — бр) близкими к л/2.
Третий член формулы (9.52) — произведение (d2xtdt2) <р —
учитывает совместное влияние горизонтальных и вертикальных
ускорений. Возникновению этого эффекта можно дать следующее
физическое объяснение. Под действием вертикального ускорения,
направленного вверх (рис. 9.5), маятник гравиметра отклоняется
вниз (точка А). Если при этом одновременно действует горизон-
тальное ускорение, направленное вправо (точка В), то на маятник
гравиметра влияет горизонтальная сила, пропорциональная
этому ускорению, но направленная влево. Под действием этой
силы маятник поворачивается по часовой стрелке, увеличивая тем
самым измеренное значение силы тяжести. При изменении знака
горизонтальное ускорение будет направлено влево (точка О),
а сила, приложенная к маятнику, — вправо, но поскольку пе-
риоды вертикального и горизонтального ускорений приблизи-
тельно равны, то маятник уже будет находиться выше горизонта
и; горизонтальная компонента будет опять поворачивать маятник
по часовой стрелке — в сторону увеличения силы тяжести, т. е.
возникает систематический эффект, который следует учитывать.
Это явление в зарубежной литературе называется кросс-каплинг-
эффектом (эффектом взаимных связей) или эффектом орбитального
252
Рис. 9.5. Возникновение
эффекта взаимных свя-
зей.
движения опоры. Происхождение последнего термина ясно из
следующих соображений. Пусть горизонтальное и вертикальное
ускорения суть функции одной и той же частоты:
d2x/d/2 = ах cos (ш/ ф- 6J; 1
d2z/dt2 = аг cos (at 4- б2). ( (9-56)
Отклонение маятника, вызванное вертикальным ускорением,
можно записать в виде
(₽^-й?СО5И + 6г-^-)’ <9’57>
где с — цена деления гравиметра.
Тогда
Ф = cos (6,t - 6, + . (9.58)
Эта величина максимальна при бд. — 6г = + л/2. Положим
= 0, = л/2, тогда
d2x/dt2 = a, cos (at); 1
d2z/dt2 = — atsin(at). ( (9'59)
После интегрирования находим
х = — («х/®2) cos (со/);
z = (a2/w2)sin (at).
(9.60)
Исключив t, получим уравнение траектории движения опоры
Л)2/а| + г2а2/я? = 1. (9.61)
253
Эю есть уравнение эллипса с полуосями ajw й аг/со. Если
опора движется по эллиптической траектории в направлении
часовой стрелки, то соотношение фаз (бЛ. — <5г) = —л/2. Вследст-
вие взаимодействия горизонтального и вертикального ускорений
маятник гравиметра поворачивается на некоторый постоянный угол
также по часовой стрелке, увеличивая измеренное значение силы
тяжести. Если опора движется против часовой стрелки, то раз-
ность фаз (6Л. — 6г) = л/2 и маятник также поворачивается против
часовой стрелки, уменьшая измеренное значение силы тяжести.
Если на гироплатформу поставить два одинаковых гравиметра,
повернув их на 180° относительно друг друга, то вследствие орби-
тального движения опоры маятники гравиметров повернутся на
один и тот же угол. Но один из них покажет заниженное значение
силы тяжести, а другой — завышенное, среднее же показание бу-
дет свободно от ошибки (Л7Л2) <р.
Четвертый член формулы (9.52) gwp определяет совместное
влияние наклонов гироплатформы и маятника относительно этой
платформы под действием возмущающих ускорений. Эта поправка
достигает заметного значения, когда колебания платформы и маят-
ника имеют один и тот же период. Если периоды колебаний не
равны, то поправка близка к нулю.
Последний член формулы (9.52) grp2/2 по своей структуре анало-
гичен поправке за наклон гироплатформы, но в данном случае
поправка возникает из-за наклона самого маятника относительно
гироплатформы. Даже для идеальной гироплатформы этой по-
правки избежать нельзя. Имея в виду соотношения (9.56) и (9.57),
поправку можно выразить через вертикальное ускорение:
§Фа/2 = п^/(4Гсо2с?). (9.62)
Из этой формулы следует, что с увеличением постоянной вре-
мени Т поправка уменьшается.
Оценим порядок рассмотренных поправок. Положим
d2x!dt2 = d2yldt2 = d~z/dt2 = 50-10-2 м/с2; a — p — <p — 10' —
= 0,003 рад. Тогда получим поправки, IO-6 м/с2: ga2!2 = 4,5;
(d2x/dt2) a = 150; (/Px/dl~) <p = 150; gasp = 9,0; g<p2/2 = 4,5.
Таким образом, максимальные ошибки при измерениях на
гироплатформе вносятся вторым и третьим членами. Чтобы при
d2xldt2 = 50-10- м/с2 иметь (d3x/dt2) а с 1 10-5 м/с2, наклоны
платформы не должны превышать 7- -8". Создание гироскопиче-
ской стабилизации с такой точностью — чрезвычайно сложная
задача. Поэтому при использовании реальных стабилизирующих
установок приходится вводить рассмотренные выше поправки.
Для регистрации горизонтальных ускорений используют гори-
зонтальные акселерометры, а для регистрации наклонов — длин-
нопериодные наклономерные маятники с периодом 100 с и более.
Чтобы уменьшить поправки, связанные с углом отклонения мачт-
254
ника гравиметра от исходного горизонтального положения, при-
меняют устройства обратной связи, с помощью которых маятник
все время удерживается в горизонтальном положении.
НЕКОТОРЫЕ ТИПЫ
МОРСКИХ ГРАВИМЕТРОВ
Рис. 9.6. Схема морского
гравиметра ГАЛ.
В Советском Союзе первые образцы морских гравиметров были
разработаны и испытаны в 1956 г. под руководством К. Е. Весе-
лова во ВНИИГеофизике.
Гравиметр СЗ-ВНИИГеофизика построен на базе кварцевого гравиметра
с горизонтальной крутильной нитыо и жидкостной температурной компенсацией.
Отличительной особенностью системы является сильное демпфирование, которое
достигается укреплением плоской пластинки на маятнике, колеблющейся вместе
с ним между двумя неподвижными пластинами. Регулируя зазор между непо-
движными пластинами, можно изменять степень демпфирования системы. На
маятнике имеется зеркало, на раме прибора рядом с маятником установлено не-
подвижное зеркало. Мерой приращения силы тяжести служит изменение угла
закручивания нити маятника. От осветителя луч света падает на оба зеркала
и, отражаясь, попадает в поле микроскопа в виде двух систем штрихов: подвиж-
ной, отраженной от подвижного зеркала системы, и неподвижной, отражен-
ной от постоянного зеркала. Отклонение подвижной системы штрихов от не-
подвижной характеризует изменение угла закручивания нити при изменении
силы тяжести. Для непрерывной регистрации изменения угла закручивания слу-
жит фоторегистратор. Изображения световых штрихов с помощью цилиндриче-
ских линз собираются в точку и через объектив фокусируются па движущуюся
фотоленту — получается кривая изменения силы тяжести по мере движения
корабля. Чтобы уменьшить влияние наклонов, прибор при наблюдениях по-
мещают в карданный подвес или на гироплатформу.
Гравиметр ГАЛ (морской гравиметр Аэро-
гравиметрической лаборатории) разработан и
построен в Институте физики Земли АН СССР
под руководством Е. И. Попова. Этот грави-
метр (рис. 9.6) также создан по принципу гра-
виметра с горизонтальной крутильной нитыо и
жидкостной температурной компенсацией. Упру-
гая система гравиметра состоит из двух квар-
цевых систем; некоторые модели имеют одну
систему. На кварцевых рамках 6 натянуты ни-
ти, к которым приварены маятники 8 с зерка-
лами 7. Нити закручены таким образом, что по-
ложение маятников близко к горизонтальному,
а сами маятники направлены в противоположные
стороны. Мерой приращения силы тяжести
является изменение угла раствора между маят-
никами. Для регистрации этого угла использует-
ся оптическая система.
Луч осветителя 5 освещает сетку, прорезан-
ную на алюминированной грани призмы 4 и
представляющую собой пять параллельных
штрихов. Изображения светящихся штрихов от-
ражаются от зеркал маятников упругой системы
и фокусируются линзами 3 на фотобумагу,
укрепленную на барабане 1. Предварительно
цилиндрической линзой 2 изображения штрихов
стягиваются в точки. Барабан вращается с по-
мощью часового механизма и перемещает фото-
255
Рис. 9.7. Принципиальная схема мор-
ского гравиметра АНГ.
Рассмотренные модели гравиметров
среднюю квадратическую погрешность :
бумагу, па которой получаются две
линии. Расстояние между линиями
определяется углом раствора маят-
ников.
Для устранения температурных
влияний система помещена в жидкость;
кроме того, коробка упругой системы
заключена в двойной термостат. Жид-
кость осуществляет и демпфирование
системы. Прибор устанавливается в
карданный подвес или на гироплат-
форму. Наличие двух идентичных си-
стем, развернутых на 180°, при работе
гравиметра по гироплатформе позво-
ляет избавиться от совместного влия-
ния горизонтальных и вертикальных
ускорений.
В ИФЗ АН СССР были разрабо-
таны гравиметры с фотоэлектрической
регистрацией ГАЛ-М (малогабаритный)
и ТТГ-1 (совместно с Тульским по-
литехническим институтом), а также
автоматизированный морской грави-
метр АМГ. В этих приборах исполь-
зованы две идентичные кварцевые си-
стемы, ориентированные в противопо-
ложных направлениях.
в зависимости от волнения моря дают
аблюдений (5-=-10)• 10"5 м/с2.
В морских перезатушснных гравиметрах мерой изменения
силы тяжести является угол отклонения маятника от горизон-
тальной плоскости, а поскольку в них не применяется компенса-
ционный метод измерений, то отсчетная шкала нелинейна. Эта-
лонирование таких гравиметров представляет известные трудно-
сти, и при больших приращениях силы тяжести в результатах на-
блюдений могут быть значительные систематические ошибки. По-
этому удобнее применять системы с компенсационным способом
измерений.
Гравиметр АНГ (автоматизированный набортный), разработанный во
ВНИЙГеофизике, имеет перезатушенную систему и автоматическую компенса-
цию приращения силы тяжести (рис. 9.7), причем компенсирующая сила реги-
стрируется самописцем. Изменение компенсирующей силы линейно связано
с приращением силы тяжести.
Основным узлом гравиметра АНГ является кварцевая чувствительная си-
стема 1 с горизонтальной крутильной нитью и жидкостной температурной ком-
пенсацией. Жидкость, в которой помещена кварцевая система, одновременно
служит и для демпфирования системы.
Луч от осветителя падает на зеркало 2 маятника чувствительной системы;
отраженный луч направляется делительной призмой 3 на два фоторезистора 4,
включенных в мостовую схему. При горизонтальном положении маятника фото-
ток в цепи моста равен нулю. При отклонении маятника равновесие моста нару-
шается и возникает фототок, который поступает в усилитель 5. После преобра-
зования и усиления ток подается на реверсивный мотор 6. Преобразователь транс-
формирует вращательное движение мотора в поступательное, в результате растя-
гивается или сжимается кварцевая пружина 9, нижний конец которой прикреп-
лен к маятнику системы. Пружина опускает или поднимает маятник до возвра-
256
щеиия его в горизонтальное положение, при котором прекращается фототок и
останавливается вращение мотора. Таким образом, система маятник — фотопре-
образователь — микровинт — измерительная пружина составляют замкнутую
систему с обратной связью, что обеспечивает непрерывную компенсацию измене-
ний силы тяжести.
Ось мотора через редуктор 7 одновременно связана с осью измерительного
потенциометра 8. При вращении оси потенциометра перемещается ползунок,
изменяющий сопротивление резистора, подключенного на вход самописца 10.
Изменение сопротивления является мерой приращения силы тяжести.
Полный ход компенсационной пружины рассчитан на весь диапазон измере-
ний— около 5000-10'° м/с2. Для укрупнения масштаба записи на каждые два
витка измерительного потенциометра сделаны отпайки, соединенные коммутато-
ром. Ручным переключателем самописец подсоединяют к той паре отпаек, между
которыми находится подвижный контакт. Потенциометр имеет 50 витков, и по-
этому шкала самописца может зарегистрировать 1/25 диапазона измерений, т. е.
около 200-10'6 м/с2. На ленте отмечается номер секции потенциометра, с которой
соединен самописец.
Прибор помещен в одноступенчатый термостат. При наблюдениях грави-
метр устанавливают в карданный подвес с масляным демпфированием. При уме-
ренном волнении моря гравиметр АНГ позволяет проводить измерения с погреш-
ностью (3-?5)-10“6 м/с2.
Как показывает опыт работ, в системах, построенных по принципу автома-
тической компенсации, возникают длиннопериодные автоколебания. Для эф-
фективного устранения этих помех вводится дополнительная обратная связь
по производной от сигнала рассогласования. В гравиметре АНГ эта связь кон-
структивно осуществлена в виде поршня, расположенного в одном из сообщаю-
щихся сосудов. Поршень связан с микрометрическим винтом. При вращении
винта поршень перегоняет жидкость в коробке упругой системы так, что ее по-
ток воздействует на маятник системы. Это воздействие пропорционально ско-
рости сигнала рассогласования.
Гравиметр ГМН (морской надводный) является автоматизированным при-
бором; разработан во ВНИИГеофизике. В основу этого прибора положен ранее
созданный гравиметр ГМК.П (морской кварцевый пружинный), в котором исполь-
зована упругая система по принципу вертикального сейсмографа Голицына
с главной пружиной нулевой длины. Демпфирование и температурная компен-
сация системы осуществляется погружением ее в кремнийорганическую жид-
кость. В гравиметре ГМКП предусмотрены фотоэлектрическая система регистра-
ции положения маятника и ручное компенсационное устройство для приведения
маятника в исходное положение.
В гравиметре ГМН (рис. 9.8) ручное компенсационное устройство заменено
автоматическим. Маятник 1 упругой системы удерживается в исходном поло-
жении главной 2 и измерительной 3 пружинами. Луч осветителя 16, отражаясь
от зеркала 15 маятника, падает на середину дифференциального фотопреобра-
зователя 14. Исходному положению маятника соответствует нулевой электриче-
ский сигнал. При отклонении маятника в фотопреобразователе возникает элек-
трический сигнал, поступающий в фильтр низких частот 13, где осуществляется
предварительная фильтрация короткопериодной составляющей ускорений. За-
тем сигнал попадает в усилитель 12, откуда поступает на вход релейного пре-
образователя 11, который обеспечивает подачу на двигатель 9 управляющего на-
пряжения соответствующей полярности. Двигатель через редуктор 7 связан
с микрометрическим винтом 6, вращение которого приводит к поступательному
перемещению верхнего конца измерительной пружины 3. Под действием управ-
ляющего сигнала вращение двигателя продолжается до тех пор, пока рычаг не
вернется в исходное положение. Угол поворота микровинта пропорционален
приращению силы тяжести. Непрерывная запись поворотов микровинта осу-
ществляется с помощью потенциометра 8 на регистраторе 10.
Для подавления автоколебаний в гравиметре имеется форсирующее устрой-
ство, состоящее из вертикальной пластины 4, закрепленной на маятнике, и па-
раллельной ей пластины 5, соединенной со штоком микрометрического винта.
Расстояние между пластинами мало и равняется d. При вертикальном переме-
9 В. С. Миронов
257
10
Рис. 9.8. Принципиальная схема морского'^гравиметра ГМН.
щении штока микровинта на пластину 4 действует сила F, обусловленная вяз-
костью г) жидкости:
F — т| (S/d) v,
где S — площадь пластины; v — относительная скорость перемещения пластин.
Таким образом форсирующее устройство обеспечивает дополнительную
обратную связь по производной от сигнала.
Морской гравиметр «Аскания» GSS-3 является автоматизированным прибо-
ром (рис. 9.9). В качестве чувствительной системы использована цилиндриче-
ская металлическая пружина 4, которая растягивается под действием груза 3,
выполненного в виде трубки. Для того чтобы обеспечить движение груза только
по вертикали, он удерживается пятью растяжками 5 (на схеме показаны только
три). Компенсация силы тяжести осуществляется электромагнитным способом.
В нижней части груза укреплена катушка 2 с компенсационными обмотками, рас-
положенными в поле магнита 7. В верхней части груза находится подвижная
пластина 6 конденсатора, заключенная между двумя неподвижными пластинами,
которые закреплены на станине прибора. При изменении силы тяжести посту-
пательное движение груза преобразуется емкостным способом в переменный
электрический сигнал, который усиливается и выпрямляется фазочувствительным
выпрямителем. Сигнал управляет электромагнитным компенсационным устрой-
ством. В системе обратной связи предусмотрены электромагнитное демпфирова-
ние и фильтрация возмущающих ускорений. Специальным устройством можно
изменять степень фильтрации.
С выхода компенсационного устройства сигнал поступает па два фильтра,
режим работы которых задается в зависимости от способа последующей обра-
ботки данных. С выхода фильтров сигнал идет на цифровой вольтметр, показы-
вающий приращения силы тяжести с точностью до 0,1 -10"5 м/с2. Три последние
цифры преобразуются в аналоговую запись и могут быть зарегистрированы
самописцем. Цифровая регистрация позволяет также проводить запись на маг-
нитную пленку или перфоленту.
Гравиметр помещен в электрический термостат в; кроме того, имеется элек-
тромагнитный термокомпенсатор 1, состоящий из термочувствительного рези-
258
Рис. 9.9. Схема морского гравиметра «Аскания» GSS-3.
стора, усилителя и компенсационной обмотки. Чувствительная система грави-
метра герметизирована. При наблюдениях гравиметр устанавливают на гиро-
платформу.
Морской гравиметр Лакоста является автоматизированным прибором; в про-
цессе наблюдений вычисляются и вносятся в измеренные значения силы тяжести
поправки за влияние возмущающих ускорений.
Упругая система гравиметра Лакоста построена по принципу маятника
Голицына и аналогична системе наземного гравиметра Лакоста—Ромберга (см.
рис. 7.25); отличается она только усиленной подвеской, ограничивающей степени
свободы движения маятника до одной, и увеличенным воздушным затуханием.
Приращение силы тяжести компенсируется перемещением верхней точки креп-
ления пружины с помощью микрометрического устройства. Отклонения маят-
ника от горизонтального положения регистрируются фотоэлектрическим устрой-
ством. Упругая система помещена в термостат.
При наблюдениях гравиметр 3 (рис. 9.10) устанавливают на специальную
платформу 2, стабилизированную гироскопом 4. Для введения поправок за
эффект взаимных связей на гироплатформе стоят горизонтальные акселеро-
метры 1. В процессе наблюдений автоматической следящей системой, действую-
щей на измерительную пружину, маятник гравиметра удерживается в положе-
нии, близком к горизонтальному. При этом непрерывно регистрируются поло-
жение маятника относительно исходного, отсчет по микрометрическому устрой-
ству и показания акселерометров. Все эти данные поступают в специальные вы-
числительные устройства, где они преобразуются в соответствующие поправки,
интегрируются на некотором интервале времени наблюдений (20—30 мин) и осред-
пяются.
Наблюдения можно проводить при значительном волнении моря, при уме-
ренном волнении погрешность определений силы тяжести равна (0,74-1,5) X
.< 10"’ м/с2. В последних моделях гравиметра Лакоста предусмотрено введение
н вычислительный блок данных о скорости и курсе корабля, что позволяет вно-
сить поправки за эффект Этвеша.
9*
259
Рис. 9.10. Блок-схема морского гравиметра Лакоста.
ГРАВИМЕТРИЧЕСКАЯ СЪЕМКА НА МОРЕ
Измерения силы тяжести на море с маятниками и гравиме-
трами проводятся на подводных лодках и, в основном, на кораб-
лях. При наблюдениях на подводной лодке очень трудно с необ-
ходимой точностью определить ее скорость и координаты. В дви-
жении подводная лодка совершает длиннопериодные (несколько
минут) вертикальные и горизонтальные колебания. Чтобы исклю-
чить их влияние, приходится проводить наблюдения в течение не-
скольких десятков минут, что нежелательно. Большинство грави-
метрических измерений на море осуществляется в комплексе
с другими геофизическими, геологическими и гидрографическими
наблюдениями, выполняемыми со специально оборудованных
исследовательских кораблей.
При установке гравиметрической аппаратуры на корабле
очень важным является вопрос о месте ее размещения, поскольку
действие возмущающих ускорений в различных частях корабля
неодинаково. Качка корабля происходит около точки, называемой
метацентром. Метацентр расположен вблизи центра тяжести ко-
рабля. Когда корабль качается на волне, то кроме поступательных
он совершает еще и вращательные движения, поэтому части ко-
рабля, более удаленные от метацентра, колеблются с большим раз-
махом. В направлении от метацентра к носу и корме наблюдается
260
увеличение амплитуды вертикальных ускорений, а выше и ниже
метацентра — увеличение амплитуды горизонтальных ускорений.
Расположить гравиметрическую аппаратуру точно в метацентре
нельзя,' так как здесь находятся судовые двигательные установки
и навигационное оборудование, но все-таки следует разместить
аппаратуру как можно ближе к этой точке. При этом надо иметь
в виду влияние вибраций, возникающих при работе силовых уста-
новок корабля.
Существенное значение имеет тоннаж корабля. Для крупно-
тоннажных судов характерна меньшая амплитуда длиннопериод-
ных ускорений, чем для судов с малым тоннажем, у последних
амплитуда ускорений больше, но период меньше. Амплитуда и
частота возмущающих ускорений зависят от скорости корабля и
направления его движения относительно волн. Очевидно, что с уве-
личением скорости корабля амплитуда и период ускорений умень-
шаются, то же самое происходит и при движении корабля против
волн.
Поскольку все морские определения силы тяжести проводятся
при движении корабля, то в наблюденное значение силы тяжести
необходимо вводить поправку за эффект Этвеша. Этот эффект
связан с тем, что при измерении силы тяжести прибором, который
перемещается относительно земной поверхности, меняется центро-
бежная сила, действующая на прибор, и, следовательно, наблю-
денное значение силы тяжести. Проекция центробежной силы на
вертикаль для точки, неподвижной относительно Земли,
Fc = ^//?,
где Ух — линейная скорость вращения Земли; R — радиус Земли.
Если корабль движется равномерно со скоростью v по азимуту
А, то проекция центробежной силы на вертикаль
„ V2 v2-|-у? + 2wj sin Л v2 2irvr sin А . /о
= ~R =----------R--------- = -R 4----R---+ ТГ’ (9’63)
где
V — v -ф Vi.
Тогда поправка Этвеша в измеренное значение силы тяжести
определяется как
&gE = Fa — Fc = v2/R -ф (2u>i sin A)JR.
Поскольку щ = <j>R cos <p (где co = 2л/86164 — угловая ско-
рость вращения Земли; ср — широта), то
/\gE = 2оэгл sin A cos ср v2/R. (9.64)
При малых скоростях судна (до 30 км/ч) вторым членом по-
правки Этвеша обычно пренебрегают, так как в этом случае он
меньше 1 • 10~5 м/с2. Естественно, что при больших скоростях
второй член необходимо учитывать. Подставив численные значе-
261
ния о, получим приближенную формулу для вычисления поправки
Этвеша (10~5 м/с3), если скорость измеряется в километрах в час:
'= 4,049vsin A cos гр. (9.65)
Из этой формулы следует, что поправка Этвеша достигает мак-
симальных значений при движении по параллели, причем с увели-
чением широты поправка уменьшается. При движении по мери-
диану поправка Этвеша равна нулю.
Для вычисления поправки Этвеша необходимо точно знать ско-
рость и направление движения корабля. Обычно в открытом море
скорость корабля измеряют лагом, а курс — магнитным или гиро-
скопическим компасом. Погрешность определения координат ко-
рабля с помощью этих средств не превышает Г по широте и 1,5'
по долготе. Лагом измеряется скорость корабля относительно
воды, из-за влияния течений и ветра в определении истинной ско-
рости возможны очень большие ошибки. Более точно положение
корабля можно найти с помощью различных радионавигационных
систем, позволяющих определять координаты в каждый данный
момент с точностью от нескольких единиц до сотен метров. Радиус
действия таких систем достигает нескольких сотен километров.
При работах вблизи берегов положение судна можно установить
с помощью наземных радиолокационных станций или береговых
радиомаяков.
Для вычисления аномалий силы тяжести при морских грави-
метрических наблюдениях необходимо знать глубину дна и, если
измерения проводятся на подводной лодке, глубину ее погруже-
ния. Глубину дна обычно определяют эхолотами. Скорость звука
в воде зависит от ее температуры и солености, поэтому точность из-
мерения глубин эхолотом обычно составляет около 1 %, что прием-
лемо только для сравнительно небольших глубин. Для глубин
порядка нескольких километров требуется более высокая точность.
Морские гравиметрические работы в настоящее время в боль-
шинстве своем обеспечивают погрешность определения силы тя-
жести около (2-~5)10~8 м/с2. Повышение точности требует более
совершенной гравиметрической аппаратуры, надежных способов
стабилизации приборов, измерения и подавления возмущающих
ускорений, а также улучшения систем для определения положе-
ния, скорости и курса корабля. Для координатной привязки судов
большие перспективы открывает использование навигационных
систем искусственных спутников Земли. Без существенного же
роста точности навигационных систем повышать точность измере-
ния силы тяжести на море не имеет практического смысла.
ГРАВИЛ1ЕТРИЧЕСКИЕ
ИЗМЕРЕНИЯ В ВОЗДУХЕ
Измерение силы тяжести на борту самолета является значи-
тельно более сложной задачей, чем определение силы тяжести на
корабле, хотя трудности этих измерений принципиально не раз-
262
личаются: в обоих случаях приходится иметь дело с возмущаю-
щими ускорениями, амплитуда которых в тысячи раз превосходит
наблюдаемое значение силы тяжести. Существенное отличие аэро-
гравиметрических измерений от морских состоит в наличии длинно-
периодных вертикальных ускорений, частота которых может быть
близка к частоте изменения силы тяжести. Эти ускорения нельзя
отфильтровать"способами, используемыми при морских измере-
ниях, для их исключения необходимо знать вертикальную ско-
рость самолета. Поскольку горизонтальная скорость самолета
составляет сотни километров в час, то возможность подавлять
возмущающие ускорения, осредняя измерения в течение некото-
рого времени, также ограничена. Время осреднения не должно
быть больше 3—4 мин, в противном случае получим сильно сгла-
женные значения силы тяжести. Высокие скорости самолетов
предъявляют жесткие требования к точности определения по-
правки Этвеша. При вычислении этой поправки уже нельзя пре-
небрегать вторым членом формулы (9.64). Кроме того, необходимо
учитывать колебания скорости и курса самолета, поэтому прихо-
дится непрерывно регистрировать скорость и направление его
движения.
Первые определения силы тяжести на самолете были проведены
в СССР и США в 1959—1960 гг. В СССР были использованы квар-
цевые перезатушенные морские гравиметры и струнные перезату-
шенные гравиметры с масляным демпфированием. Гравиметры
устанавливались в карданные подвесы, одновременно с силой тя-
жести регистрировалась вертикальная скорость самолета. Траек-
тория самолета определялась с помощью фазовой радиогеодезиче-
ской системы «Координатор».
В дальнейшем на базе струнных гравиметров во ВНИИГео-
физике был разработан комплект аппаратуры, включающий струн-
ные аэрогравиметры с жидкостным демпфированием груза, струн-
ные измерители вертикальной скорости, работающие на бароме-
трическом принципе, горизонтальные струнные акселерометры;
была создана также специальная счетно-регистрирующая аппа-
ратура. Экспериментальные полеты с этим комплектом аппара-
туры, выполненные в 1969—1972 гг. на самолетах ИЛ-14 и АН-24,
подтвердили ее работоспособность и показали реальную возмож-
ность проведения аэрогравиметрической съемки с погрешностью
(10ч-15) • 10"® м/с2 при времени осреднения 3—4 мин.
Опыт первых аэрогравиметрических исследований был поло-
жен в основу создания аэрогравиметрического цифрового измери-
тельно-регистрирующего комплекса «Гравитон». Это устройство
позволяет производить предварительную обработку и одновре-
менную регистрацию в цифровой форме на перфоленту сигналов
струнных гравиметров, измерителей вертикальной скорости, гори-
зонтальных акселерометров, барометрического высотомера, тер-
мометра, радиогеодезического приемоиндикатора, измерителей
крена самолета. Испытания всего аэрогравиметрического комп-
263
лекса вместе с устройством «Гравитон» проводились в 1974 г. па
самолете ИЛ-14. На борту самолета было установлено три струн-
ных гравиметра, помещенных в карданные подвесы. Эти испытания
показали возможность измерения силы тяжести с погрешностью
(6н-8)10~5 м/с2 при времени осреднения 4—5 мин. Созданный
комплекс аэрогравиметрической аппаратуры позволил полностью
автоматизировать процесс измерений и получать в полете запись,
пригодную для непосредственного ввода в ЭВМ.
В США подобные работы проводились с морским гравиметром
Лакоста, помещенным в карданный подвес. Траектория самолета
прослеживалась доплеровской навигационной системой, верти-
кальная скорость и высота измерялись радиовысотомером и гипсо-
термометром. Сравнение измеренных значений силы тяжести
с пересчитанными на высоту полета наземными определениями
показало, что средняя квадратическая погрешность составляет
(6-4-8)-10 6 м/с2.
При современном состоянии гравиметрической изученности
Земли аэрогравиметрические измерения такой точности могут
представлять интерес только для изучения труднодоступных райо-
нов и для региональных исследований Мирового океана. Прове-
дение аэрогравиметрической съемки более крупных масштабов
для решения задач разведочной гравиметрии требует существен-
ного повышения точности съемки, что связано с совершенствова-
нием способов определения траектории, вертикальной и горизон-
тальной скорости, высоты и курса самолета, а также с более на-
дежной стабилизацией положения гравиметра.
Раздел III
МЕТОДЫ ИЗМЕРЕНИЯ
ВТОРЫХ ПРОИЗВОДНЫХ
ПОТЕНЦИАЛА СИЛЫ ТЯЖЕСТИ
Глава 10
ТЕОРИЯ И УСТРОЙСТВО
ГРАВИТАЦИОННЫХ ВАРИОМЕТРОВ
ОСНОВНОЕ УРАВНЕНИЕ ВАРИОМЕТРА
Приборы, предназначенные для измерения
вторых производных потенциала силы тяжести, называются гра-
витационными вариометрами и градиентометрами. Гравитацион-
ным вариометром измеряют горизонтальные составляющие Wxz
и №Уг градиента силы тяжести и кривизны WxlJ и W&, гравита-
ционным градиентометром — только горизонтальные составляю-
щие градиента силы тяжести.
Все модели гравитационных вариометров и градиентометров
построены по единому принципу — принципу крутильных весов,
предложенных французским физиком Ш. Кулоном.
Простейшие крутильные весы представляют собой легкое гори-
зонтальное коромысло с двумя равными грузиками на концах
(рис. 10.1, а). Коромысло подвешено в середине на очень тонкой
нити, вокруг которой оно может вращаться. Английский ученый
Г. Кавендиш использовал эти весы для определения гравитацион-
ной постоянной. Венгерский физик Р. Этвеш создал теорию и раз-
работал первый прибор для измерения вторых производных гра-
витационного потенциала. Р. Этвеш показал, что для этой цели
лучше подходят весы, у которых грузики находятся не на одной,
а на разных высотах. Крутильные весы, применявшиеся Ш. Ку-
лоном, Р. Этвеш назвал весами первого рода, а весы с грузиками
на разных высотах -— весами второго рода. В настоящее время
практическое применение имеют весы только второго рода. Форма
коромысла весов может быть самой разной.
Крутильные весы, будучи предоставленными самим себе, в те-
чение некоторого времени совершают затухающие колебания.
После успокоения коромысло занимает положение равновесия,
характеризующееся определенным азимутом. В однородном грави-
тационном поле на грузики действуют одинаковые силы, следова-
265
тельно, положение равновесия наступает при раскрученном со-
стоянии нити. Если гравитационное ноле неоднородно, то сила
тяжести, действующая на отдельные точки весов, различна, и по-
ложение равновесия коромысла определяется соотношением гра-
витационных сил и параметров коромысла.
Зависимость между гравитационными силами и параметрами
коромысла в положении равновесия называется основным уравне-
нием гравитационного вариометра. Для его вывода начало коор-
динат поместим в центре тяжести О всей подвесной системы, ось z
Рис. 10.2. К выводу
основного уравнения
гравитационного вариометра.
направим вертикально
вниз, ось х — на север,
ось//—на восток (рис. 10.2).
Рассмотрим произвольную
точку коромысла с элемен-
тарной массой dm ^и коор-
динатами х, у, г. На эле-
мент dm в гравитационном
поле действует сила gdm,
где g — ускорение свобод-
ного падения (силы тяжес-
ти) в этой точке. Сила тя-
жести g может быть раз-
ложена по осям координат
на три составляющие gx,
gy, g,. Последняя состав-
ляющая поворота коромыс-
ла вокруг вертикальной
оси не вызывает, так как
она параллельна нити под-
266
веса. Две другие составляющие, gx и gv, создают элементарный
крутильный момент
dMz = (xg„ — ygx) dm. (10.1)
Крутильный момент, действующий на систему в целом, равен
интегралу по всему объему коромысла:
Мг = | (xgv — ygx) dm. (10.2)
V
Под действием момента Мг коромысло поворачивается вокруг
оси z на некоторый угол. При этом в крутильной нити возникают
упругие силы, противодействующие повороту коромысла. Пусть
крутильный момент нити равен Л4Т. Так как угол поворота коро-
мысла мал (обычно не более Г), то можно полагать, что момент
кручения Мг пропорционален углу поворота -& коромысла. Угол й
следует отсчитывать от положения коромысла, которое оно зани-
мает при раскрученном состоянии нити, т. е. от положения равно-
весия коромысла в однородном гравитационном поле. Однако
непосредственно это положение определить нельзя, так как все
наблюдения проводятся в неоднородном гравитационном поле.
Пусть это положение временно неизвестно, будем характеризо-
вать его углом ©о, составленным коромыслом с некоторым фикси-
рованным направлением в приборе, например со стороной коробки,
в которой помещается коромысло. Положение равновесия коро-
мысла при закрученной нити будем характеризовать углом й,
составленным коромыслом с тем же направлением. Тогда для
положения равновесия системы
т (<* — ^’о) = ] (xgy — ygJ dm, (10.3)
V
где т — постоянная кручения нити.
Положим, что составляющие силы тяжести в объеме весов
меняются линейно, т. е. вторые производные гравитационного
потенциала постоянны и влиянием производных более высокого
порядка можно пренебречь.
Поскольку g>: и gy являются непрерывными функциями коор-
динат х, у, г, мы можем эти функции разложить в ряд Тэйлора .
С индексом нуль даны значения величин в начале координат,
т. е. в центре тяжести коромысла. Поскольку ось г вертикальна, то
(&)о = (&)« = °.
267
. Заменяя первые производные силы тяжести вторыми производ-
ными гравитационного потенциала
dgx/dx = WxX; dgx/dy — Wxy и т. д„
ограничиваемся в разложении (10.4) только членами первого по-
рядка малости. Подставляем выражение (10.4) в формулу (10.3)
и после несложных преобразований получаем
т (Т — й0) = (Wm - W „) J ху dm — Wxy [ (№ - у'ф dm -ф-
V V
Wyz j xzdtn — \VX2 j yzdm. (10.5)
V V
Интегралы в правой части этого уравнения зависят от формы
и размеров коромысла и его положения в пространстве. Чтобы
упростить вычисление интегралов, введем новую систему коорди-
нат г], £, неподвижно связанную с коромыслом (см. рис. 10.2).
Начало новой системы совпадает с центром тяжести коромысла,
ось £ направлена вдоль коромысла, ось ц — перпендикулярно
к нему, ось £ совпадает с г. Обозначим угол между осями х и |
через а. Заметим, что угол а есть азимут коромысла, отсчитыва-
емый от севера к востоку.
Тогда
х = Е cos а — г) sin а;
у = I sin аф- т] cos а;
и уравнение равновесия гравитационного вариометра принимает
вид
т (Й — fl0) = (1/2) IV'А [sin 2а j (|s — г]2) dm ф- 2 cos 2а [ dm | ф
ф Wx!l [cos 2а [ (£2 — т]2) dm — 2 sin 2а j ф] dtn\ ф-
ф WlJ2 [cosa | dm — sin a j т)£ dm | —
— W„ |sin a j gg dm ф cos a j i|£dm] . (10.6)
Полученное выражение справедливо для крутильных весов
любой формы и размеров. Зная форму и размеры весов, можно
вычислить интегралы, входящие в это уравнение.
Коромысла вариометров обычно имеют простую геометри-
ческую форму, относительная точность измерений с вариометром
не превышает 1%. Поэтому интегралы в выражении (10.6) можно
вычислять приближенно, с точностью порядка 0,1%. Тогда выра-
жение (10.6) можно привести к более простому виду.
У всех вариометров и градиентометров крутильные системы
симметричны относительно одной из вертикальных плоскостей.
268
При нашем выборе координатных осей вертикальной плоскостью
симметрии является плоскость В этом случае всякому элементу
массы dm с координатой г] найдется элемент равной массы с коор-
динатой —1] и, следовательно, интегралы | Eq dm и | т]£dm будут
равны нулю. Выражение (10.6) примет вид
т (fl — fl0) = [(1/2) sin 2а 4~ cos 2а] f (с2 - т]а) dm -ф-
-f (W'..2cosa — IF^sina) ) tfcdm.
(Ю.7)
Крутильная система первого рода симметрична еще и относи-
тельно горизонтальной плоскости Ёщ Следовательно, в этом
случае
I" dm = 0
и уравнение равновесия принимает вид
т (fl — fl0) = [(1/2) Sin 2a -]- WXy cos 2a] J (|a — ц2) dm. (10.8)
Интегралы в уравнениях (10.7) и (10.8) обозначим следующим
образом:
j (Е2 — T)2) dm = К;
j &dm = М.
(10.9)
Введем в рассмотрение момент инерции коромысла относи-
тельно вертикальной оси
4 = j (I® + Л2) dm
и момент инерции относительно плоскости ££
L = J г)2 dm.
Тогда для каждого элемента массы dm будем иметь
(£2 _ ^2) dm = (Е2 г]2) dm — 2rfdtn, (10.10)
т. е.
К = 4 - 2L.
Обычно поперечные размеры коромысла малы по сравнению
с его длиной и можно с достаточным приближением считать L - 0;
К 4- Ошибка при этом для современных вариометров не пре-
вышает 0,1%. Что касается интеграла М, то он легко вычисляется
для различных форм коромысел. Для весов второго рода, где один
грузик расположен на конце коромысла, а другой подвешен на
нити (см. рис. 10.1, б), можно считать, что вся масса грузиков
269
сосредоточена в их центрах, а масса стержня равномерно распре-
делена по его оси. Тогда получим
(10.11)
где h — разность высот грузиков; I — половина расстояния между
грузиками по горизонтали; т — масса грузика.
Для крутильной системы, где оба грузика разнесены по
вертикали и соединены с коромыслом жесткими стержнями
(см. рис. 10.1, в), при вычислении М необходимо принять во вни-
мание массу вертикальных стержней. Так, для Z-образного
коромысла
М =- (т -(- mK) hl, (10.12)
где тА — масса вертикального стержня, примыкающего к гру-
зику.
И наконец, рассмотрим широко применяющееся коромысло
в виде наклонного стержня длиной ‘21 (см. рис. 10.1, г). Обозначим
угол коромысла с горизонтом через (3, массу коромысла tn', тогда
М = [ ££ dm = (т 4~- m'/6) I2 sin 2(5.
Заметим, что для такой формы коромысла
/, — 2 (т -ф т'/6) /2 cos8 [3,
откуда имеем
Это соотношение позволяет определять центробежный момент
инерции М. через момент инерции 12 относительно вертикальной
оси.
С учетом равенств (10.9) уравнение равновесия крутильных
весов (10.7) примет вид
т (0 — 0о) = К cos 2а sin 2а^ 4-
4~ /VI (IT^cos а — WX2 sin а). (10.13)
В уравнение равновесия входят коэффициенты т, /<, /И, .за-
висящие от формы и размеров коромысла. Эти параметры должны
быть определены перед проведением наблюдений с. вариометром.
Установив прибор по какому-то азимуту а, можно определить угол
поворота коромысла г')1. Остальные пять величин, входящие в урав-
нение, неизвестны. Чтобы их найти, необходимо иметь пять урав-
нений; для этого достаточно провести наблюдения с прибором на
одной точке в пяти азимутах.
Задавая подвесной системе различную форму, можно получать
уравнения, в которые входят не все вторые производные. В ча-
стности, если взять весы первого рода (h = 0; М ----- 0), то
т (& — г%) = (1/2) /(1Гда1п 2а 4* cos2a. (10.14)
270
В это уравнение входят лишь три неизвестных, и для их опре-
деления достаточно провести наблюдения только в трех азимутах.
Можно придать коромыслу и такую форму, что в уравнении
останутся только Фо, IFrz и т. е. сделать 1\ = 0. Такая си-
стема (см. рис. 10.1, д) была предложена Г. Шоу и Е. Ланкасте-
ром-Джонсом в их градиометре. Подвесная система градиометра
представляет собой легкий круг радиусом I, подвешенный в центре.
На окружности через 120° расположены три равных грузика т,
причем два из них находятся в плоскости круга, а третий припод-
нят на высоту h. В этом случае
J (I2 - С2) dm = 0; М = mhl
и уравнение равновесия принимает вид
т (& — fl0) = mhl (1F’„2 cosa — 1ГД2sina). (10.15)
Если коромысло вариометра выведено из положения равно-
весия, то оно возвращается в это положение не сразу, а только
через некоторый промежуток времени, в течение которого совер-
шает в основном вращательное движение вокруг вертикальной
оси. Уравнение этого движения имеет вид
= (юле)
где /2 — момент инерции коромысла относительно оси вращения;
Ф —'угол отклонения коромысла от положения равновесия; —
сумма моментов действующих сил.
Решение уравнения (10.16) определяет связь периода соб-
ственных колебаний коромысла с его параметрами и значениями
вторых производных:
= у- |- (2^„ sin 2а — cos 2а) -|-
ф (IE„Z cos а -f- sin а) (10.17)
где II — постоянная затухания.
Поскольку в правой части этой формулы все члены, кроме
первого, малы, то
Т = 2 л У 1г/1.
Соотношение (10.17) верно, если затухание не больше крити-
ческого, т. е.
Д2<4тД.
ОБЩИЕ СВЕДЕНИЯ О ВАРИОМЕТРАХ
При конструировании вариометров необходимо учитывать тре-
бования, предъявляемые теорией прибора, а также условия их
практического применения. Из теории прибора следует, что его
271
конструкция должна обеспечить возможность устанавливать кру-
тильную систему в различных азимутах, а также достаточно точно
отсчитывать угол поворота коромысла вокруг вертикальной оси.
Гравитационные вариометры и градиентометры имеют вертикаль-
ную ось, около которой весь прибор может вращаться. Эта ось
крепится к подставке, на которой есть нивелирные винты и уровни
для установки оси в вертикальное положение.
Для измерения угла закручивания нити на коромысле уста-
новлено зеркало. Второе зеркало укреплено неподвижно внутри
корпуса вариометра. Перед зеркалами находятся линза и источник
света, помещенный от линзы на удалении, равном ее главному
фокусному расстоянию F. На таком же расстоянии от линзы на-
ходится шкала или фотопластинка, на которой регистрируется
положение лучей, отраженных от зеркал. Пучок света, пройдя
через линзу, становится параллельным и попадает на зеркала.
Отраженный от зеркал параллельный пучок, опять пройдя через
линзу, падает на шкалу или фотопластинку в виде светящихся
точек. Очевидно, что при повороте зеркала коромысла светящаяся
точка перемещается по шкале или фотопластинке. Обозначая
отсчеты по шкале, отвечающие положению коромысла до и после
его поворота на угол (0 —й0), соответственно через п0 и п имеем
Л-п0 = 2Е(й-й0) = О^-й0).
Величина D называется оптическим рычагом. В некоторых
вариометрах падающий на зеркало коромысла луч после отраже-
ния попадает сначала на промежуточное (дополнительное) зеркало,
а затем снова на зеркало коромысла и только после вторичного
отражения направляется через линзу на шкалу. В этом случае
очевидно, что оптический рычаг D = 2F-2 = 4 Л.
Кроме указанных условий прибор должен обладать необходи-
мой чувствительностью. Значение чувствительности гравитацион-
ных вариометров диктуется практическими целями. Погрешность
определения вторых производных гравитационного потенциала
должна быть порядка 2—5 Э (этвеш), т. е. (2 ч- 5)-10“9 1/с2. Чув-
ствительность гравитационных вариометров для производных
и ИГ„2 характеризуется величиной (mhl/x) 10"8, а для
и WXI/— величиной (Д/т) 10'9 рад/с2.
Для оценки чувствительности гравитационного вариометра
найдем силу, которую надо приложить, чтобы коромысло повер-
нулось па измеримый угол. Пусть к концу коромысла приложена
сила F, перпендикулярная к коромыслу. Момент FI этой силы
должен равняться т Ай, где Ай — минимально измеримый угол.
Если принять /20 см, т = 0,5-10“’ Н-(м/рад), Ай = 0,1' =
= 3-10“5 рад, то F - 0,75-10"11 Н (или 0,76-10"12 кгс), т. е. сила,
меньшая, чем одна миллионная веса массы 1 мг, уже смещает
коромысло на измеримый угол.
Для обеспечения достаточной точности определения вторых
производных потенциала силы тяжести необходимо также по-
272
стоянство показаний прибора. При установке прибора в один
и тот же азимут коромысло должно в пределах погрешности наблю-
дений занимать одно и то же положение, т. е. смещение нуль-
пункта должно быть невелико и пропорционально времени. Это
условие достигается надлежащей обработкой крутильной инти
и предохранением коромысла вариометра от каких-либо возмуща-
ющих сил, кроме гравитационных. Чтобы исключить влияние
магнитного поля, всю крутильную систему изготовляют из не-
магнитного материала. Для предохранения от электростатических
сил систему делают хорошо проводящей и заключают в металли-
ческий корпус. Чтобы избежать неравномерного нагревания
коромысла и возникновения тепловых конвекционных потоков
воздуха, систему вариометра помещают в многослойный футляр.
Продолжительность наблюдений с вариометром зависит от
периода колебаний коромысла, который в свою очередь опреде-
ляется чувствительностью прибора. Поэтому для уменьшения
времени наблюдений необходимо снизить чувствительность, что
допустимо только в некоторых пределах. Можно сократить про-
должительность измерений, значительно понизив чувствитель-
ность и одновременно резко повысив точность отсчета положения
коромысла, т. е. применив более совершенные методы регистрации.
Кроме того, еще Р. Эгвеш предложил использовать в вариометрах
не одну, а несколько (две) крутильных систем с различным взаим-
ным расположением. Это позволяет сократить общую продолжи-
тельность наблюдений, так как добавление каждого коромысла
приводит к увеличению числа неизвестных на одно, но измерения
в каждом азимуте дают два независимых уравнения. Таким обра-
зом, если при одном коромысле необходимо провести наблюдения
а пяти азимутах, то, имея два коромысла, можно ограничиться
наблюдениями в трех азимутах.
Введение добавочных крутильных систем дает принципиальную
возможность дальнейшего сокращения времени наблюдений. Дей-
ствительно, пусть п — число крутильных систем; N — количество
азимутов. Тогда число неизвестных равно п Т 4 и необходимое
число азимутов N = (/г + 4)/п. При п = 4 необходимо всего два
азимута (N — 2). Очевидно, что дальнейшее увеличение числа
систем уже не уменьшает числа азимутов, т. е. четыре крутильные
системы являются предельным случаем. Однако большинство
вариометров имеет две крутильные системы, так как приборы
с тремя и четырьмя коромыслами весьма громоздки и процесс
наблюдения с ними -гораздо сложнее.
НЕКОТОРЫЕ ТИПЫ ВАРИОМЕТРОВ
К настоящему времени сконструировано около 30 моделей
гравитационных вариометров. Наибольшее распространение на
практике, однако, получили вариометры S-20, Z-40, Е-60, гра-
диентометр ГРБМ-2,
273
Гравитационный вариометр S-20
(рис. 10.3), впоследствии выпускавшийся под
маркой ВГ-1, является одним из совершен-
ных приборов, отличается простотой и
удобством в эксплуатации. Вариометр обла-
дает фотографической регистрацией измере-
ний и устройством для автоматического пе-
ревода из азимута в азимут. Прибор имеет
две крутильные системы, повернутые на 180°
относительно друг друга. Время успокоения
коромысла для вариометра S-20 составляет
20 мин, для ВГ-1 — 15 мин. Погрешность
измерений (2-4-3) -10“9 1/с2.
Вариометр S-20 состоит из трех частей:
верхней (собственно вариометр) 3, средней 2
и колонки 1. В верхнюю часть (вариометр)
входят вертикальная коробка 4 и два агре-
гата 5 крутильных систем. В вертикальной
коробке расположены оптическая система и
некоторые вспомогательные механизмы, в
верху коробки имеются пазы для установки
фотокассеты, на внешней стороне укреплены
два уровня.
Каждый агрегат крутильных весов
(рис. 10.4) состоит из коромысла 3, крутиль-
ной головки 6 и арретира /. Коромысло весов
представляет собой тонкостенную металли-
ческую трубку, в концы которой заделаны
грузики. Коромысло крепится к специаль-
ному бифиляриому подвесу 8, служащему
для уменьшения короткопериодных паразит-
ных колебаний. Бифилярный подвес укреплен
на нижнем конце крутильной нити 5. Верх-
ним концом нить закреплена в крутильной
головке. Крутильные системы вместе с го-
ловками размещены в корпусе агрегата кру-
тильных весов, представляющем собой две
защитные оболочки 7 и 4, изолированные
друг от друга воздушными прослойками и
термоизоляционными прокладками. В нижней части корпуса расположено ар-
ретирное устройство. При вращении арретирных головок арретирный желоб 2,
находящийся во внутренней трубе, подхватывает коромысло по всей его длине и
прижимает к верхней стенке трубы.
Оптическая система вариометра S-20 (рис. 10.5) состоит из осветителя 1 с кон-
денсором и точечной диафрагмой, системы преломляющих призм 2, 6 и зеркал 3,
4, направляющих луч света через объектив 7 на призму 9 коромысла, выполняю-
щую роль зеркала, и на постоянное 10 и температурное 8 зеркала системы. До-
полнительное зеркало 11 обеспечивает удвоение оптического рычага. Отражаясь
от зеркал 8, 10 и от призмы 9, свет попадает на фотопластинку 12 в виде трех то-
чек, фиксирующих положение коромысла, температурного и постоянного зеркал.
Таким образом, при каждой экспозиции на фотопластинке записывается шесть
точек. В приборе имеется подвижное зеркало 5, наклон которого изменяется при
повороте прибора из азимута в азимут, чем предотвращается наложение изобра-
жений бликов на фотопластинке.
Средняя часть вариометра служит для автоматического перевода прибора из
азимута в азимут. В ней смонтированы ведущий механизм и контактные часы.
Сбоку ведущего механизма расположена большая шестерня, приводимая в дви-
жение пружиной ведущего механизма. При работе механизма шестерня катится
по зубчатой нарезке азимутального круга и вращает всю подвижную часть варио-
метра. Снизу в азимутальный диск ввинчено десять стопорных винтов — соот-
274
Рис. 10.4. Агрегат крутильных'весов вариометра S-20.
ветственно возможному числу азимутов при различных системах наблюдений.
Винты, соответствующие азимутам, в которых проводятся наблюдения, должны
быть ввинчены, остальные вывинчены.
Контактные часы через промежутки, равные времени успокоения коро-
мысла (20 мин), замыкают электрическую цепь, включая лампочки, чтобы за-
фиксировать положение равновесия коромысла на фотопластинке, и включают
ведущий механизм.
В нижнем кольце средней части прибора укреплены три нивелировочных
винта.
275
Крутильная система
Рис. 10.6. Вариометр Z-40.
276
Средняя часть прибора устанавливается нижним своим кольцом на колонку,
представляющую^собой алюминиевую трубу, расширяющуюся книзу. Колонка
состоит из нескольких звеньев, что позволяет устанавливать прибор на разной
высоте.
Гравитационный вариометр Z-40 (рис. 10.6) также имеет фотографическую
регистрацию и автоматический перевод из азимута в азимут. Прибор состоит из
тех же частей, что и вариометр S-20: верхней (собственно вариометр) 5, средней 1
и колонки 6. Основное различие этих приборов заключается в устройстве верхней
части, в которой смонтированы две крутильные и оптическая системы, фоторегн-
стрирующее устройство 4, арретирное приспособление и уровни.
представляет собой подвешенное на тонкой вольфра-
мовой нити коромысло, изогнутое в виде лежачей
буквы Z, с грузиками иа концах. Для защиты от
температурных и других влияний коромысло поме-
щено в металлический корпус стройными стенками,
состоящий из алюминиевых коробок и труб, встав-
ленных одна в другую. Между коробками и трубами
имеются воздушные прослойки. В верхней части
прибора расположены осветители 3 с лампочками
и реостатами для регулировки накала. Арретирное
приспособление состоит из главных арретиров и
ирисового арретира, расположенного внутри защит-
ных труб. На боковой стороне корпуса находятся
головки 2 главных арретиров. При арретировании
коромысло прижимается двумя дисками к верхней
части внутреннего корпуса, ирисовые арретиры за-
крепляют концы коромысла с грузиками,
Контактный и ведущий механизмы, колонка и
диск в вариометре Z-40 устроены так же, как и в
вариометре S-20.
Время успокоения вариометра 2-40 в азимуте
40 мин, погрешность измерений (14-2)-10's 1/с2.
Гравитационный вариометр Е-60 разработан
в Венгерском геофизическом институте. Этот ва-
риометр, как и Z-40 и S-20, имеет фоторегистра-
цию и автоматический перевод из азимута в азимут.
Верхняя часть (собственно вариометр) пред-
ставляет собой корпус, состоящий из четырех ко-
робок, последовательно вложенных одна в другую.
Во внутренней коробке расположены две крутильные системы. Коромысло кру-
тильных весов— это горизонтальная дюралюминиевая трубка длиной около
20 см, на конце которой закреплен верхний грузик; нижний грузик подвешен к
другому концу коромысла на металлической нити длиной около 30 см, т. е
коромысло имеет Г-образную форму.
В верхней части вариометра размещено фоторегистрирующее устройство,
состоящее из кассеты с фотопластинкой и часового механизма. При фотореги-
страции на пластинке получают изображения подвижной шкалы, отраженной
от зеркал коромысла, и неподвижного «волоскаа-индекса, по которому можно
взять отсчет показаний прибора в каждом азимуте без каких-либо специальных
приспособлений, пользуясь только лупой. Кроме того, на фотопластинке отпе-
чатывается номер прибора и номер точки наблюдения, благодаря чему исклю-
чаются ошибки в маркировке пластинок. В вариометре Е-бО предусмотрена воз-
можность и визуальных наблюдений.
В средней части прибора размещены ведущий механизм для перевода при-
бора из одного азимута в другой и контактные часы, которые через каждые 20 мин
включают освещение для экспозиции, а затем — ведущий механизм. Время экс-
позиции регулируется от 5 до 30 с. Время успокоения коромысла в азимуте 20 мин,
погрешность измерений (1Ч-2)-10"° 1/с2.
Гравитационный градиентометр ГРБМ-2 предназначен для измерения только
горизонтальных составляющих WX2 и Wyz градиента силы тяжести. Градиенто-
метр состоит из трех частей (рис. 10.7): верхней (собственно градиентометр) /,
колонки // и сферического диска ///. Колонка предназначена для установки
градиентометра и ориентировки его ио азимуту. При полевых измерениях ко-
лонку размещают на сферическом диске. Внешняя оболочка 5 прибора является
жестким каркасом, к которому крепятся детали верхней части. Снизу оболочка
жестко соединена с основанием 7 верхней части, сверху — с корпусом 4 крутиль-
ных систем через опорно-регулировочное кольцо 3. На оболочку помещается
крышка 1 оптической головки градиентометра. Полости корпуса 4 крутильной
системы повторяют конфигурацию коромысла таким образом, что в любом сече-
нии зазоры между стенками и коромыслом одинаковы и равны 1,5 мм. Малый
просвет зазоров и демпферные крылышки создают необходимое затухание кру-
тильной системы. Арретир 6 коромысел представляет собой крестовину с укреп-
ленными на ней четырьмя стойками. Стойки имеют заплечики, а на концах фи-
гурные вилки. Крестовина шарнирно соединена с ручкой арретира, при ее вра-
щении коромысла подхватываются вилками и прижимаются к конусному выступу
крутильной головки. Плата 2 оптической головки является основанием для
размещения деталей оптической системы. В плате и опорно-регулировочном
кольце имеется по четыре окна для светового потока от осветителей к зеркалам
коромысел и обратно.
Чувствительным элементом градиентометра является крутильная система
(рис. 10.8), включающая в себя коромысло 4 с крутильной нитью и крутильную
головку /. Градиентометр имеет четыре крутильные системы, повернутые на 90°
одна относительно другой. Такое расположение позволяет при наименьшем
числе азимутов (два) получить по два независимых значения WX2 и \Ууг, что дает
возможность вести непрерывный контроль за качеством работы прибора.
Коромысло градиентометра представляет собой вертикальную дюралюми-
ниевую трубку, на концах которой укреплены вольфрамовые грузики 3 и 5,
а также демпферные крылышки 2 и 6. Грузики расположены с разных сторон
трубки так, что их центры тяжести и ось трубки лежат в одной вертикальной
плоскости. Внутри коромысла имеется патрубок для крепления крутильной нити
и регулировки вертикальности коромысла. В нижней части коромысла укреплено
зеркало 7. Крутильная нить изготовляется из вольфрамовой проволоки диаметром
18-19 мкм, длина ее 22,1 см. Концы нити зажимаются в сережки. Верхняя
сережка закреплена в крутильной головке, нижняя—в патрубке коромысла.
Крутильной головкой устанавливают коромысло по высоте и азимуту.
Оптическая система (рис. 10.9) служит для регистрации положения равно-
весия коромысла, а также для контроля нивелировки прибора. Она состоит из
четырех самостоятельных оптических каналов (по числу крутильных систем),
попарно одинаковых. Пара 1,11 имеет по одной дополнительной призме по сравне-
277
Рис. 10.7. Градиентометр ГРБМ-2.
278
Рис. 10.8. Крутильные Рис. 10.9. Схема оптической системы градиенто-
ГРБАПр гРаДнентометра метра ГРБ.М-2. j
нию с парой III, IV; эта призма поворачивает плоскость колебаний блика зеркал
крутильных систем па 90“, благодаря чему движение всех четырех бликов ста-
новится параллельным. Все блики направляются в зрительную трубу, четыре
шкалы которой также одинаковы и параллельны.
Время успокоения систем в азимуте 3 мин; погрешность измерений (5-^7) X
X 10-э 1/с2.
Вариометр БГ-63 (Венгрия) являемся комбинированным прибором, который
может работать в режиме или вариометра, или градиентометра. Четыре кру-
279
•сильные системы расположены попарно в двух взаимно перпендикулярных
плоскостях, благодаря чему при наблюдениях в трех азимутах (режим варио-
метра) каждая пара дает независимый результат по градиентам и кривизнам.
При наблюдениях в двух азимутах (режим градиентометра) получаются также
два независимых результата, но только по градиентам. Показания прибора за-
писываются на фотобумагу, протяжка которой осуществляется автоматическим
лентопротяжным механизмом; повороты прибора из азимута в азимут выпол-
няются специальным часовым механизмом.
Время успокоения системы в азимуте от 4 до 12 мин в зависимости от ре-
жима работы прибора; погрешность измерений градиентов около 3-10-® 1/с®,
кривизн 6-Ю-'1 1/с2.
Г лава 11
НАБЛЮДЕНИЯ
С ГРАВИТАЦИОННЫМИ ВАРИОМЕТРАМИ
техника наблюдений
С ВАРИОМЕТРАМИ И ГРАДИЕНТОМЕТРАМИ
Гравитационные вариометры и градиенто-
метры являются чрезвычайно чувствительными приборами ко
всякого рода посторонним влияниям: температуре, ветру, тряске
ит. п. Поэтому все наблюдения с вариометрами в полевых усло-
виях проводят в специальной защитной будке из фанеры или бре-
зента, иногда будку специально утепляют. Будку ставят дверью
в сторону, противоположную прямым солнечным лучам и ветру.
Чтобы обеспечить устойчивость прибора, на пункте наблюде-
ния в землю забивают три кола, на которые устанавливают алю-
миниевый диск так, чтобы канавки на диске приходились над
кольями. Высоту кольев выбирают такой, чтобы центр тяжести
коромысла находился па одном и том же уровне, равном при-
мерно 1 м.
Вариометр вносят в будку, устанавливают и укрепляют по
частям: колонку, среднюю часть и собственно вариометр. После
этого нивелируют прибор по уровням. Ориентируют вариометр
с помощью буссоли или визированием по краю верхней крышки
на веху, выставленную по направлению профиля. Для этого, от-
винтив стопорный винт, освобождают большое зубчатое колесо
средней части и, вращая его, устанавливают необходимые азиму-
тальные винты. Например, при трехазимутальном цикле наблюде-
ний ввинчивают винты с оцифровкой 0, 120 и 240, остальные винты
вывинчивают. Затем, повернув вращающуюся часть прибора та-
ким образом, чтобы ведущий механизм немного не дошел до нуле-
вого азимутального винта, рычагом переводят ведущий механизм
в рабочее положение. Когда прибор остановится в нулевом ази-
муте, начинают вращать его вместе с зубчатым колесом по часовой
стрелке до тех пор, пока буссоль не покажет отсчет, соответству-
280
ющий ориентировке прибора. При этом нижний грузик первого
коромысла должен быть направлен на север или, при ориенти-
ровке прибора по профилю, в положительную сторону профиля.
По окончании ориентировки зубчатое колесо закрепляют зажим-
ным винтом, а ведущий механизм выключают.
Затем, сняв верхнюю крышку вертикальной коробки варио-
метра, укладывают кассету с фотопластинкой и вынимают заслонку
кассеты. Чтобы на фотопластинке отметить начало записи, про-
водят запись бликов от постоянных зеркал при арретированных
пли неуспокоившихся коромыслах. Для этого прибор устанавли-
вают в азимут, предшествующий нулевому, дезарретируют коро-
мысла медленным и одновременным вращением арретирпых голо-
вок. Замыкают осветительную цепь, пока не загорятся лампочки.
За время световой экспозиции, продолжающейся 1,5—2 мин,
на пластинке зафиксируются только блики от постоянных зеркал,
отметив начало записи. По окончании экспозиции ведущий меха-
низм переводит верхнюю часть вариометра в нулевой азимут.
После установки прибора в нулевом азимуте наблюдатель поки-
дает будку и закрывает дверь.
В полевой журнал записывают время пуска прибора, номер
пункта, номер пластинки, ориентировку прибора, количество
азимутов в цикле.
По истечении определенного промежутка времени в зависи-
мости от скорости успокоения коромысла в азимуте и числа ази-
мутов наблюдатель входит в будку, арретирует коромысла и обра-
щает внимание на то, в каком азимуте он застал прибор, что и за-
носит в журнал наблюдений, а также записывает время конца
наблюдений. Из прибора вынимают кассету с фотопластинкой,
предварительно вставив заслонку. Изъятую из прибора фотопла-
стинку, как правило, проявляют тут же, чтобы убедиться в ка-
честве записи. Если запись приемлемая, то прибор разбирают
и переносят или перевозят на следующий пункт. Если же запись
неудовлетворительная, то выясняют причину неполадок и, устра-
нив их, вновь запускают прибор для повторной записи.
При работах с градиентометром ГРБМ-2 все наблюдения также
проводят в защитной будке. Поскольку прибор не автоматизиро-
ван, то из азимута в азимут его переводит оператор, который весь
период наблюдений находится в будке. Укажем последователь-
ность операций при работе с градиентометром ГРБМ-2.
Колонку прибора на точке наблюдений устанавливают на сфе-
рический диск, а на неустойчивых грунтах, когда диском поль-
зоваться нельзя, на заранее забитые по шаблону колья. Перемещая
по диску, колонку грубо нивелируют по круглому уровню на ее
столике. На колонку устанавливают верхнюю часть градиенто-
метра в соответствии с направляющими на столике, столик сце-
пляют с азимутальным кругом в любом фиксируемом положении
и отпускают стопор круга. Вращая азимутальный круг вместе
с верхней частью градиентометра, ориентируют его по буссоли
281
или визированием на веху профиля, после чего азимутальный круг
зажимают стопорным винтом. В этом положении прибор оказы-
вается ориентированным в азимуте 0°.
После включения освещения прибор нивелируют по уровню,
затем поворачивают в любой азимут и осторожно дезарретируют,
после чего переводят в азимут 0°, свет выключают. Спустя при-
близительно 50 с необходимо включить свет и проверить, от всех
ли четырех систем есть в окуляре блики. Если хотя бы один блик
отсутствует, надо слегка щелкнуть пальцем по верхней части
прибора, чтобы ликвидировать залипание системы, и вновь засечь
время. Приблизительно через 40 с вновь проверяют наличие бли-
ков и выключают свет на 1,5—1,8 мин.
Через 2,5—-3 мин после дезарретирования коромысел включают
свет и при условии, что все индексы на шкалах стоят неподвижно,
отсчитывают показания всех систем сверху вниз с точностью
до 0,5 деления шкалы. Затем верхнюю часть прибора поворачивают
в противоположный азимут, засекают время установки и повто-
ряют операции по наблюдению за поведением систем. По оконча-
нии измерений, не арретируя коромысла, оценивают результаты.
При удовлетворительных результатах крутильные системы арре-
тируют и прибор переносят на следующий пункт.
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ
ВТОРЫХ ПРОИЗВОДНЫХ
ПОТЕНЦИАЛА СИЛЫ ТЯЖЕСТИ
Наблюдения с вариометром проводят в трех или, если жела-
тельно сравнить между собой результаты наблюдений по каждому
коромыслу, в пяти азимутах.
Выведем формулы для обработки наблюдений с вариометром
и градиентометром.
Положение равновесия коромысла регистрируется оптическим
способом, описанным выше. Используя соотношение
п — п0 = D (О — й0)
и обозначая
КО/т = a; MD/t, = b,
уравнение равновесия (10.13) можно записать в виде
и — пи =_ а [ Wxu cos 2а -ф (1 /2) sin 2а] -|-
•ф b (№,.2cosa — WX2sina). (П-1)
Для второй крутильной системы, повернутой относительно
первой на 180°, заменяя в уравнении (11.1) а на a + л, можно
написать
п — п'о = a' [U^ycos2a -ф- (1/2) sin 2a] -ф
-ф Ь' (— cos а -ф Wxz sin a), (11.2)
282
где п', п'о, а’, Ь' — соответствующие значения отсчетов и постоян-
ных второго коромысла.
В двух уравнениях мы имеем шесть неизвестных: п„, По, Wxu,
Гд, ^хг> ^уг- Для их определения достаточно провести наблю-
дения в трех азимутах:
= 0°; а., = 120°; а3 = 240°.
Подставляя эти значения азимутов в уравнения (11.1), (11.2)
и обозначая отсчеты положений коромысел в этих азимутах соот-
ветственно через лг, п2, п3 для первого коромысла, nJ, П2, «з Для
второго, получаем шесть уравнений. Решив их, найдем
IV7,, = (аб' — «.'6)/[]/3 (ab' -f- а'6)];
Wy! = (а<з' — а'а)/[3 (ab' -J- а'&)Г,
= — 2 (b'8 -j- М')/[/3 ab’ 4- а'&)]; (1 L3)
2Wxy = — 2 (Ь'ст ]- Ь<т')/[3 (ab' ф- а'£>)1.
где
а = п2 4~ п3 — 2лх;
о' = п(> 4~ «з — 2п{;
6 = п3 — п3,
6' = По — «з-
Складывая для трех азимутов уравнения (11.1), относящиеся
к первому коромыслу, имеем
п0 — (их 4- 4- п3)/3. (11-4)
Точно так же для второго коромысла
Яо = (rtl + П2 4* Пз)/3. (11.5)
Из этих формул следует, что неизвестные п0 и «о, т. е. отсчеты,
соответствующие положению коромысла в однородном поле
(обычно называемые нуль-пунктом коромысла), вычисляются как
средние из трех азимутов. Нуль-пункт не зависит от гравита-
ционного поля, он определяется исключительно крутильными
характеристиками нити. Это свойство нуль-пункта используют
для контроля работы прибора.
Трехазимутальный цикл наблюдений наиболее распространен,
так как позволяет в минимальное время найти все четыре произ-
водные. Как следует из формул (11.3), при трехазимутальном
цикле значения производных получают по показаниям обеих
систем.
Для контроля за работой прибора следует по каждому коро-
мыслу иметь все четыре производные, т. е. необходимо провести
283
наблюдения в пяти азимутах: 0, 72, 144, 216 и 288°. В этом слу
чае
«о = («1 4- «2 4- «з + «4 4 «з)/5; 1
По = (/11 + /?2 | /7-3 -f- «4 4- Пб)/5. I
Вводя обозначения
о = /12 4- пъ — 2л0; = п3 4- п4 — 2л0;
6 = и,, — пъ Sx = п3 — /г4;
р = 1,447/а; цх = 0,553/а;
г ==. 0,276/6; гх = 0,723/6;
q = 0,470/а; qt = 0,761/а;
s = 0,380/7; sx = 0,235/7,
получаем рабочие формулы для первого коромысла
2WX,,^ — (//<т4-m);
гд = — <?А;
^г = — (то -н^);
wx. = — (зб — sxSx).
(И.6)
(11.7)
Формулы для второго коромысла имеют аналогичный вид,
только в выражениях Wxt и №уг знак меняется на противопо-
ложный.
Четырехазимутальный цикл (а = 0,90, 180, 270°) применяют,
когда надо получить независимые значения и W,,z по каждому
коромыслу. В этом случае можно также определить 2Wxy, но по-
скольку найти ИД нельзя, то нельзя вычислить и значение век-
тора кривизны. Для четырехазимутального цикла
= (щ — п2)/(27) = («2 — п.;)/(2/»'); ]
^,,г = (ти — п3)/(27) = (п'з — /г()/(27'). I
(И.8)
Остаются справедливыми формулы для нуль-пунктов
м0= (И14" 4"" ^3 Ч- /ч)41;
/го = (/г( 4- «2 4- пз 4- П4>/4.
Из уравнений (11.8) следует, что наиболее просто и быстро
составляющие 117хг и 117„г могут быть определены, если крутиль-
ные системы расположены в приборе взаимно перпендикулярно.
В этом случае WXx и находят по наблюдениям только в двух
азимутах: 0 и 180° для первого коромысла, 90 и 270° для второго.
Первое коромысло дает величину Wy2, второе WXz. Взаимно пер-
пендикулярное расположение систем впервые было предложено
Г. Хаальком; в настоящее время оно осуществлено в гравитацион-
ном градиентометре ГРБМ-2.
284
В результате полевых наблюдений с вариометром для каждого
пункта получают фотопластинку, на которой зафиксированы поло-
жение равновесия коромысел в нескольких азимутах и изменение
температуры внутри прибора. Положение равновесия измеряют
при помощи специальной стеклянной палетки с полумиллиметро-
выми делениями.
Нуль-пункт крутильных весов не зависит от гравитационного
поля и является постоянной величиной, характеризующей поло-
жение весов при раскрученном состоянии нити. Поэтому измене-
ние нуль-пункта указывает на действие конвекционных потоков
или на неудовлетворительное состояние крутильной нити. Кон-
тролируя поведение нуль-пункта, для каждого коромысла строят
график его смещения. При нормальной работе прибора изменение
нуль-пункта не превышает 0,5—1,0 деления палетки в сутки.
Резкие скачкообразные изменения нуль-пункта в течение суток
указывают, как правило, на необходимость установки коромысел
в оптимальное положение, а значительные непрерывные смеще-
ния — на необходимость замены нити. Следует учитывать, что
отдельные резкие скачки нуль-пункта могут быть связаны с изме-
нением положения зеркал, со сменой лампочек и т. д.
Полученные с пластинок значения п подставляют в одну из
формул (11.3), (11.7), (11.8) и вычисляют наблюденные значения
вторых производных.
ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ВАРИОМЕТРА
Выражения для вычисления вторых производных по наблюде-
ниям с вариометрами содержат постоянные приборов, которые
должны быть определены заранее: D, т, h, I, т, К, М. Поскольку
относительная точность измерения производных не превышает
1%, значения постоянных вариометра достаточно вычислить с точ-
ностью 0,25%.
Оптический рычаг D рассчитывается по формуле
D == 2kF,
где F — фокусное расстояние объектива; k — число отражений
светового луча от зеркала коромысла.
Для определения D необходимо знать фокусное расстояние
объектива F.
Массу грузиков т находят взвешиванием на весах с точностью
до 0,01 г. Следует помнить, что в выражение для т в зависимости
от формы коромысла входит не только масса грузиков, но и масса
жестких частей коромысла, которую определяют при изготовле-
нии прибора на заводе.
Постоянные I и h измеряют линейкой.
Коэффициент кручения нити т определяют с погрешностью
до 0,001-Ю"5 П-м/рад весьма простым способом, предложенным
П. М. Никифоровым. Этот способ заключается в измерении пе-
285
риода Т колебаний груза, подвешенного на испытуемой нити.
Если цилиндрический грузик подвесить на нити за центр его верх-
него основания, то период колебаний такой системы
Т — 2л VЛ/т,
откуда
т -= 4л2/1/72,
где — момент инерции грузика относительно оси вращения.
Для цилиндра
Л = 0,5/нг2,
где пг — масса грузика, г — радиус его основания.
Чтобы наблюдать период колебаний грузика, необходимо
установить на нем зеркало. Найти момент инерции грузика
с зеркалом с достаточной точностью довольно трудно. Поэтому
удобнее проводить наблюдения с двумя грузиками: одним в виде
цилиндра со стержнем для подвешивания к нити и с зеркалом для
наблюдения за периодом колебаний, другим в виде цилиндриче-
ского кольца, надеваемого на первый грузик. Следует иметь
в виду, что общий вес грузиков не должен превышать общей на-
грузки крутильной системы. Момент инерции цилиндрического
кольца
4 0,5/пк (Л2 — г2),
где тк -— масса, Миг — внешний и внутренний радиусы кольца.
Из наблюдений определяют период колебаний 7\, когда под-
вешен только один цилиндрический грузик, а затем период Т2,
когда подвешены оба грузика:
71 = 2n ]/71/т; 7’3 = 2п ]/"(/.2-|- Л)/т,
откуда
4л2/, 2л2«к (/?2— г2)
Т — или г— та — га •
Таким образом, коэффициент т вычисляют без предваритель-
ного определения /х, только через наблюдаемые периоды и момент
инерции /2 цилиндрического кольца. Периоды Т, и Т2 находят
с помощью установки (рис. 11.1), состоящей из деревянного
ящика / с застекленной стенкой и зрительной трубы 4. В ящик
через трубку опускают прикрепленную к установочной головке
испытуемую нить с эталонным грузиком 3 на конце. За периодом
колебаний нити наблюдают через зрительную трубу, которая укре-
плена на штативе вместе со шкалой 5. Шкалу устанавливают так,
чтобы ее изображение в зеркальце 2 было видно в зрительную трубу.
Отмечают момент прохождения какой-либо отметки шкалы через
вертикальную линию креста нитей трубы. Обычно по секундомеру
наблюдают от трех до пяти серий по десять периодов. Среднее
286
арифметическое значение пе-
риода имеет'достаточную точ-
ность.
Значение постоянной Л’
можно принять равным мо-
менту инерции /гкрутильной
системы относительно верти-
кальной осн вращения. Зная
распределение масс грузика
и коромысла, можно вычис-
лить 1г. Однако этот прием
неточен. Чтобы найти доста-
точно точное значение I., на-
блюдают периоды колебаний
Рис. 11.1. К определению коэффициента
кручения нити.
коромысла около вертикаль-
ной оси или в самом вариометре, если затухание не очень велико,
или в специальном ящике с большим объемом. Коромысло может
быть подвешено на своей крутильной нити или на любой другой,
но с известным коэффициентом т.
Для одного пункта наблюдения значения вторых производных
постоянны, также постоянны т, К и М; таким образом, период Т
является функцией а, т. е. азимута системы. Принимая азимут
системы последовательно равным а, а + л/2, а + л, а + (3/2) л
и подставляя эти значения в формулу (10.17), получаем четыре
уравнения, определяющие периоды Т\, Т2, Т3, 7\. Суммируя эти
уравнения, имеем
т _ 2 / 1 , _1 , I 1 \
,, л I р _2 -р —2 р I .
Периоды 1\ определяют по наблюденным периодам Т\ затуха-
ющих колебаний:
Т = I -р 0,5372 [lg ’
Т'
где — отношение амплитуд двух последовательных
колебаний коромысла.
Коромысла удобнее подвешивать на нитях с большим коэффи-
циентом кручения т, чтобы уменьшить период их колебаний.
Время Т' определяют визуально, наблюдая через зрительную
трубу перемещения блика на шкале. Амплитуду колебаний «о
крутильной системы находят по записи этих колебаний на фото-
пластинку. Для этого вариометр устанавливают в одном азимуте,
дезарретируют и настраивают на непрерывную запись.
Центробежный момент инерции М вычисляют по формулам
(10.11), (10.12); для вариометра S-20 он может быть найден через
момент инерции относительно вертикальной оси:
M/K = tg₽,
где 0 — угол наклона коромысла к горизонту.
287
Постоянные К и Л1 можно определить и другими способами,
например наблюдениями с вариометром на эталонных пунктах,
где с высокой точностью известны значения вторых производных.
ВЛИЯНИЕ РЕЛЬЕФА МЕСТНОСТИ
Из наблюдений с гравитационным вариометром и градиенто-
метром получают значения вторых производных гравитационного
потенциала, зависящие от распределения всех масс, слагающих
земной шар. Для геологического использования в измеренные
значения вторых производных необходимо внести поправки, иск-
лючающие действие неровностей дневной поверхности и нормаль-
ное действие земного сфероида.
Поправка за нормальное действие
Эту поправку вводят по формулам (2.59). Если вариометр при
наблюдениях ориентируется не по астрономическому меридиану,
то поправку за нормальное действие вычисляют по формулам
Г¥г = (^г)0сО8Д; 2^ = (Гд)0зЩ2А;
^==-(U7Josin.4; W\ = (lF,),,cos2.4,
где А — азимут ориентировки прибора.
Поправки за влияние рельефа
Вследствие большой чувствительности гравитационных варио-
метров избыток масс, возвышающихся над прибором, а также их
недостаток ниже прибора оказывают существенное влияние на
показания вариометров. Это влияние всегда необходимо учитывать
и вносить соответствующие поправки в наблюденные значения
вторых производных.
Существует много способов, которыми можно рассчитать вли-
яние рельефа окружающей местности на показания вариометра
и вычислить соответствующие поправки. Существо этих поправок
заключается в том, что местность вокруг пункта наблюдений как бы
выравнивается: все возвышения над уровнем стояния прибора
срезаются, а все углубления засыпаются породой, имеющей плот-
ность, равную плотности поверхностных образований.
Все способы учета влияния рельефа можно разделить на три
группы: аналитические, графические и механические. В аналити-
ческих способах определяют превышения рельефа в некоторых
специально выбранных точках вокруг пункта наблюдений, затем
эти превышения подставляют в формулы, которые и дают значение
поправки. В графических способах для вычисления поправок
используют карты рельефа с горизонталями или отдельные про-
фили по ряду направлений и специальные палетки. В механиче-
ских способах применяют специальные приспособления или
счетные механизмы, которые дают поправки непосредственно
на местности или по карте рельефа.
288
Поправка за влияние рельефа довольно быстро (пропорцио-
нально третьей степени расстояния) убывает с удалением от
пункта наблюдений. Поэтому учитывать влияние рельефа особо
точно надо только в непосредственной близости от пункта на-
блюдений. Для удобства вычислений поправку за влияние
рельефа обычно делят на две части: поправку за влияние ближ-
него рельефа (до 50—100 м) и поправку за влияние дальнего
рельефа. Первую поправку необходимо определять всегда и особо
тщательно, вторую же вычисляют упрощенными приемами и не
во всех случаях. Поправку за влияние ближнего рельефа быстрее
и точнее можно найти аналитическим или механическим спосо-
бом, тогда как влияние дальнего рельефа чаще всего определяют
графическим способом.
Исходные формулы для учета влияния рельефа получим из
общих интегральных выражений производных гравитационного
потенциала (1.35). Начало координат поместим в центре тяжести
коромысла, оси х и у в горизонтальной плоскости, ось z направим
вертикально вниз. При вычислениях удобнее пользоваться вер-
тикальной цилиндрической системой координат.
Если при интегрировании отсчитывать высоты точек рельефа
от горизонта основания инструмента и полагать повышения поло-
жительными, а понижения — отрицательными, то пределы ин-
тегрирования по z будут соответственно I — h и /, где 1 — высота
центра тяжести коромысла над основанием инструмента; h —
высота точек рельефа относительно горизонта основания прибора
(рис. 11.2).
Интегрирование выражений (1.35) по г дает
= —/га I cos a da | — I-----------—Г ;
J J г [ z“)3/2 J ’
2л г
W U7 = —ka ( sin a da f — I----------—1 ;
уг J , r L (r“ + za)s/2 ] |/_A
2л r
2WKl/ = 3ko [ sin 2a da I Г----------------—
xy J J r (r*4-za)1/2
о о L ' 1 '
1 г3 1 P
3 ' (г2 + г2)3/2 J |/_Л’
2л г
1Гд = — 3ko f cos 2а da f — I--------------—
Л J J Г L (Г2_рг2)1/2
о о
J___________г3 1 И
3 ’ (г2 + г2)3/2 J 1^-

10 В. С. Миронов
(11-9)
289
Рис. 11.2. К учету влияния рельефа на
показания вариометра.
должна быть выражена через г
Точно вычислить полу-
ченные интегралы нельзя,
так как при интегрировании
можно считать независимыми
переменными две координаты,
третья же должна быть функ-
цией первых двух. Можно
положить независимыми пе-
ременными координаты г и а,
а координата г или превыше-
ние /г, сумма которых рав-
на постоянной величине /,
и а, т. е.
z = F(r, a); h = f(r, а).
Поскольку физическая поверхность Земли очень сложна,
функции F (г, а) и f (г, а) не могут быть выражены аналитически.
Для вычисления интегралов (11.9) необходимо сделать упроще-
ния, заменив реальную поверхность рельефа или часть ее другой
поверхностью, имеющей более или менее простое аналитическое
выражение. При этом поправка за влияние рельефа вычисляется
с некоторой степенью приближения.
Аналитические способы
вычисления поправки за влияние рельефа
В основе всех аналитических способов лежит отыскание при-
ближенной зависимости превышения рельефа h от радиуса г
и угла а. Зависимость /г = / (г, а) находят измерением h в ряде
точек окружающей местности, а промежуточные значения опре-
деляют интерполяцией. Полученную таким образом зависимость
подставляют в общие формулы (11.9), подынтегральные выражения
которых упрощаются, и вычисляют приближенное значение ин-
тегралов.
Способ аналитического учета влияния рельефа был предложен
Р. Этвешем, позже более точные и удобные формулы были вы-
ведены Б. В. Нумеровым, П. М. Никифоровым, В. Швейдаром,
С. В. Евсеевым, Н. Н. Самсоновым, Д. Г. Успенским. Эти формулы
различаются только способами упрощения подынтегрального вы-
ражения и приближенного интегрирования. Поэтому остановимся
только на тех формулах, которые нашли применение на практике.
Способ Нумерова в качестве исходных использует формулы
(11.9). Результат интегрирования по z обозначим
W = т[ (Г2 + г2)1/2 Г’ (Г2 + Z2)3/-j ] |;_А’
(11-Ю)
290
Далее введем следующие обозначения:
А = Зл/гст | f (/-) dr;
о
Г
В = Зл/гст | tp (г) dr.
о
Тогда формулы (11.9) примут вид
W., = — | В cos a da;
хг л .1
о
2л
W = — f В sin а da;
л J
о
2Л
— == J- | Л cos 2аda;
о
2л
2Й7>в = — I 4sin2at!a.
о J
(11.11)
(И-12)
Вычисление топопоправок по формулам (11.12) проводится
в два этапа. Сначала определяют значения функций А и В вдоль
некоторых заданных направлений, а затем вычисляют искомые
поправки интегрированием по а в пределах от 0 до 2л.
Чтобы найти функции А и В, представим интегралы (11.11)
в виде суммы интегралов в пределах от г(- до гм, где i = О,
1, 2, ..., п. Соответственно функции 4 и В примут вид сумм
Л = До Лх 4* Л2 • • • -|- Ап\
в^ва+в^+в2 + ••• + дг.
Чтобы получить наиболее плавный ход функций <р (г) и f (г),
Б. В. Нумеровым были выбраны следующие радиусы интегриро-
вания гг: 0; 1,2; 2; 3; 4,5; 6; 10; 18; 50; 100 при I = 1 м и о =
2 г/см3.
Полагая, что внутри интервала интегрирования превышение h
является линейной функцией г, после интегрирования имеем
/1 = -^1,2 -L А, — 43 -у 44 5 4- А(. -ф- Л1о 4~ Д1а 4" -4И 4~ Дйю>
в — В14- в, 4~ ва 4- Bii3 4" В6 -4 в1п 4- в1а 4- в5п 4- в1т,
где А1Л, А2, ... и В1Л, В2, ... — некоторые постоянные коэффи-
циенты, зависящие соответственно от превышений й12, /г2, ...
Эти коэффициенты можно вычислить заранее и свести в таб-
лицу (табл. 11.1). Получив нивелированием на указанных рас-
10*
291
Таблица 11.1
Значения функций А и В для вычисления топопоправок
по способу Нумерова
М -41,2 ^1,2 Л2, м д2 в2 /г3, м 4з в3 'h.i, м ^4,5
— 10 — 17 — 17 —20 —28 — 16 —30 -36 —14 —50 —39
—9 — 16 -16 — 18 —26 — 14 —27 -32 — 12 —45 —36
—8 — 14 — 14 —16 —23 — 13 —24 —27 — 11 —40 —33
—7 — 12 — 12 — 14 —20 — 11 —21 —23 —9 —35 —29
—6 — И — 11 — 12 — 18 — 10 —18 -22 —8 -30 —25
—5 —9 —9 — 10 — 15 —8 — 15 — 19 —7 —25 —21
—4 —7 —7 -8 — 12 —6 —12 — 15 —5 —20 — 17
—3 -6 —5 (5 —9 -5 —9 —12 —4 -15 — 13
—2 —4 —4 —4 —6 -3 —6 —7 —2 — 10 —8
— 1 —2 —2 —2 —3 —2 —3 —4 — 1 -5 —4
0 0 0 0 0 0 0 0 0 0 0
1 2 2 2 3 2 3 4 1 5 4
2 4 4 4 6 3 6 8 2 10 9
3 6 6 6 10 5 9 12 4 15 13
4 8 7 8 13 7 12 16 5 20 18
5 10 9 10 17 8 15 20 6 25 22
6 .2 11 12 20 10 18 24 7 30 27
7 14 13 14 24 И 21 28 8 35 32
8 :б 15 16 27 13 24 33 10 40 36
9 19 17 18 31 15 27 37 И 45 41
10 21 19 20 35 16 30 42 12 50 46
П р и и е ч а и и е. I = I м, 0 = 2 г/см3. При Iт — ml значения радиусов и превы
стояниях вокруг пункта наблюдений превышения Лг, по этой таб-
лице находим коэффициенты. Суммируя их, получаем значения
функций А и В вдоль заданного направления а = const.
Расположим п радиусов нивелирования через одинаковые
интервалы угла а, равные 2л/я. При п = 8 получим следующие
формулы для вычисления топопоправки:
= 0,25 (Л45 — Л135 -ф- Л225 — Ла15);
— 0,25 (Ло— Л9Г| ф- .4jS(| — Л270);
W кг = 0,25 (60 — Biso) 4-0,177 (В43 — В1зв — В225 -(- ^згв)!
№уг = 0,25 (Вт - В270) (-0,177 (В46 4- В136 - B22S - В31д).
Индексы при А и В указывают азимут радиуса, для которого
вычислена функция.
Для п — 4 получим
№'.„= 0,5 (В0-В1&0); |
U7уг --- 0,5 (Д,<> — Д70). I
(11.14)
Следует отметить, что при п — 4 нельзя определить 2IFXS.
292
84,5 Лв, м Л в, Л1о, м ''Чо 810 Я18, м ^18 818
— 13 —50 —37 —7 — 100 —65 — 10 —200 —102 — 11
— 11 —45 —33 —7 —90 —58 —9 — 180 —92 —9
—9 —40 —29 —б —80 -52 —7 — 160 —82 —8
—8 —35 —26 —5 —70 -46 —6 — 140 —72 —7
—7 —30 —22 —4 —60 -39 —5 — 120 —62 —5
—6 —25 — 19 —4 -50 —33 — 100 —51 —4
—4 —20 — 15 —3 —40 —26 —3 —80 —41 —3
—3 — 15 — 11 —2 —30 —20 —2 —60 —31 —2
—2 — 10 —8 — 1 —20 — 13 — 1 —40 —21 — 1
— 1 -5 —4 —1 — 10 —7 —1 -20 — 10 — 1
0 0 0 0 0 0 0 0 0 0
1 5 4 1 10 7 1 20 10 0
2 10 8 1 20 13 1 40 21 1
3 15 11 2 30 20 2 60 31 I
4 20 15 2 40 27 2 80 42 1
5 25 19 3 50 34 3 100 52 1
5 30 23 3 60 40 3 120 63 1
6 | 35 27 4 70 47 3 140 73 1
7 40 31 4 80 54 3 160 84 1
8 45 35 4 90 61 3 180 95 1
9 ] 50 33 5 100 68 4 200 105 0
шений необходимо умножить „а т.
Способ Самсонова разработай для определения поправки за
влияние рельефа только к горизонтальным составляющим гра-
диента силы тяжести. В этом случае учет влияния рельефа может
быть существенно упрощен, так как при выборе интервалов ин-
тегрирования принимается во внимание поведение только функ-
ции <р (г).
В формуле (11.11) для функции В разобьем промежуток ин-
тегрирования по г на следующие интервалы, м: 0—1,5; 1,5—3,5;
3,5—9,5; 9,5—ос. В первом интервале положим, что h — е.г,
где е = hlt5/r1>5. Интеграл в этом интервале может быть вычислен
точно, без какого-либо упрощения подынтегрального выражения.
Во втором и третьем интервалах интегрирования применим фор-
мулу Симпсона, тогда
3,5
J ф(г) dr = -^-ф(1,5)4--у ф(2,5) + -уф (3,5);
1.5
9.5
| Ф (г) dr = ф (3,5) + 4ф (6,5) -ф ф(9,5).
3,5
(11.15)
293
Интегрирование в пределах 9,5—со выполним в предположе-
нии, что h = /г9,5 = const, получим
B(9,5-oo) = ntohn(r + /rq^)-7=^T]|/ , (11.16)
L V г2 + /г2 J |/_н
где г = 9,5, /г = /г915.
Суммируя формулы (11.15) и (11.16), получаем окончательно
В = В(0- 1,5)4-В(1,5-3,5) +
+ В (3,5-9,5) 4-В (9,5-со). (11.17)
Собирая вместе члены, содержащие Л115, /га>5, ..., /г915, можно
составить таблицу функции В по аргументу Л. Можно вычислить
и другую таблицу, в которой аргументом служат значения В,
а функцией превышения /1. На основании такой таблицы может
быть построена специальная нивелирная рейка с несколькими
шкалами, каждая из которых отвечает определенному радиусу
и дает непосредственно значение функции В. В способе Самсонова
окончательное значение топопоправок получают, подставляя функ-
ции В в формулы Нумерова.
Способ Успенского отличается от способа Самсонова другим
набором точек нивелирования на лучах, а также более точным
учетом влияния рельефа за пределами области интегрирования.
С этой целью для последней точки радиуса нивелировки построены
три шкалы, соответственно для случаев: высота по лучу увеличи-
вается, высота по лучу уменьшается и высота по лучу остается
постоянной. Значения функции В также наносят на специальную
рейку.
Графические и механические способы
учета влияния рельефа местности
При графическом способе часть вычислений, рассмотренных
выше, проводится с помощью вспомогательных графиков или пале-
ток. Существуют два основных приема учета влияния рельефа
графическим способом. При одном из них с помощью палеток
выполняют интегрирование вдоль луча для получения функций А
и В. Для этого необходимо иметь профиль рельефа местности по
избранному направлению. Результат интегрирования подставляют
в формулы (11.13), (11.14). Обычно этот прием применяют для
учета влияния ближнего рельефа.
При другом приеме окружающую местность делят на так назы-
ваемые участки равного действия, т. е. на участки, влияние масс
которых на вторые производные в точке наблюдения одинаково,
если средние превышения этих участков равны. Вычисление вли-
яния рельефа сводится к снятию с карт средних высот этих уча-
стков, суммированию их и умножению на некоторый постоянный
294
коэффициент. Этот прием чаще всего применяют при определении
влияния рельефа, удаленного от точки наблюдения.
Рассмотрим первый прием на примере способа Самсонова.
В выражения (11.9) для производных и 1УД вместо г и г
введем полярные координаты риф:
r = psin<p; z = pcos<p; dzdr — pdp dtp.
Тогда для функций А и В имеем
А = Зл£о | j (sin3 ср/р) dp dtp;
В = Зл/?о | [ (sin2 ф cos (р/р) dp dtp.
(11.18)
Интегрирование в этих формулах распространяется на часть
вертикальной плоскости а = const, заключенную между профилем
рельефа и горизонтом центра тяжести весов.
Интегрируя выражения (11.18) по р в пределах ри— рт+1,
по ф в пределах tpn — ф„+1, получаем действие масс площадки
abed (рис. 11.3):
Aal,cd = лАст [3 (COS ф„ — COS фп+1) —
- (COS3 фп - cos3 ф„+1)] In
р 1
Babcd = nto (sin3 cp„+1 — sin3 ф„) In .
j
Полагая левые части этих выражений равными 1-Ю"9 1/с2
при о — 2 г/см3, можно найти соответствующие лучи (ф„, срге+1)
и окружности (р„„ рт+1), которые всю плоскость интегрирования
разделяют на площадки равного действия. На палетках для
вычисления функций А и В (рис. 11.4) эти площадки заменены
точками в их центрах.
Палетки используют следующим образом. Как и при аналити-
ческом способе, местность вокруг точки наблюдения разбивают
лучами на 4, 8 (и т. д.) равных секторов. Вдоль каждого луча
выполняют нивелирование по характерным точкам рельефа на
произвольных расстояниях и строят соответствующие профили
рельефа; при этом вертикальный
и горизонтальный масштабы долж-
ны быть одинаковы. Накладывают
на профиль палетку для А или В
так, чтобы центр палетки совпал с
центром тяжести коромысла, и под-
считывают число точек, заключен-
ных между кривой рельефа и го-
ризонтальной прямой, проходящей
через подножие инструмента. Точ-
кам на площади, ограниченной
Рис. 11.3. К способу Самсонова.
295
Рис. 11.4. Палетки Самсонова для вычисления функций А и В.
профилем рельефа сверху, приписывают знак плюс, а на площади,
ограниченной профилем рельефа снизу, знак минус. Если профиль
пересекает горизонт центра прибора, то точкам над горизонтом
дают знак плюс для функции А и минус для функции В. Таким
образом получают значения функций Л и В в каждом азимуте
нивелировки. Подставляя их в формулы (11.13), (11.14), находят
поправки WXi, и Wyt.
Рассмотренные палетки можно применять для вычисления
влияния не только рельефа, но и любой границы раздела плот-
ности, например подземного рельефа. Поскольку в формулы для
расчета палеток входит лишь отношение радиусов, то масштаб
профиля рельефа безразличен, что позволяет использовать па-
летки для любых расстояний от точки наблюдения.
Второй прием учета влияния дальнего рельефа местности рас-
смотрим на примере способа Нумерова. Для дальнего рельефа
(более 50—100 м) отношения h/r и Иг малы. Подынтегральные
выражения формул (11.9) могут быть представлены в упрощенном
виде:
(П.2О)
Тогда, выполняя интегрирование по г от гт до rm+x и по а
от ап до а„+1, получаем
=----kah [ (sin 2ая+1 - sin 2а„) М-----!—) ]
£ L \ ' tn rni+i / J
Глг = у Ла (/й — - J) [ (sin ап+1 - sin ая) ]
При этом предполагается, что значение 1г постоянно в пределах
области интегрирования и равно ее средней высоте.
Формулы для 21^Л? и отличаются от формул для W&
и Wxz только тем, что вместо разностей синусов двойного и оди-
нарного углов в них стоят разности косинусов соответственно
двойного и одинарного углов.
(И.21)
296
Полагая в формуле для W&
sin 2ал+1 — sin 2ал = 1/n; l/rm — l/rm+l = \/т,
имеем
Гд = —Лог/i —. (11.22)
а 2 пт ' '
Если подобрать числа п и т так, чтобы произведение пт для
всех секторов было одно и то же, производную 1Гд для первого
квадранта можно вычислить по формуле
Гд = —У/г. (11.23)
2 тп '
Влияние масс в других квадрантах определяется этой же фор-
мулой, только необходимо соответственным образом учесть знаки
(рис. 11.5, а).
Аналогичным образом может быть рассчитана палетка для WXz
(рис. 11.5, б). Чтобы вычислить влияние рельефа на производные
2Wxy и Wyz, строить специальные палетки нет необходимости,
так как для 2Wxl/ используется палетка Wд, повернутая на 45°,
а для Wg. — палетка повернутая на 90°.
Из формул (11.21) следует, что вычисление влияния рельефа
на 1КА2 и W дг более сложно, чем на й 2IFtv. Но вместе с тем
влияние дальнего рельефа убывает быстрее для 1Кхг и Wиг, чем
для К'д и 2 Wxg, и во многих случаях его даже не приходится
вычислять.
При механических способах учета влияния рельефа применяют
различные приспособления, облегчающие вычислительную ра-
боту: специальные счетные линейки, нивелирные рейки, особые
счетные механизмы.
При измерении только горизонтальных составляющих гра-
диента силы тяжести с вариометрами и при наблюдениях с гра-
диентометрами влияние рельефа учитывают способом Самсонова.
При этом значения функции В наносят на специальную рейку так,
чтобы при нивелировке сразу их отсчитывать. Было предложено
несколько конструкций приборов, которые дают значения функ-
ций, подобных А и В, по всему избранному направлению.
Все рассмотренные способы учета влияния рельефа обеспечи-
вают достаточную точность аппроксимации геометрической формы
рельефа. Однако при вычислении поправки необходимо принимать
во внимание и точность определения плотности поверхностных
образований и точность нивелирования. Плотность входит в фор-
мулы постоянным множителем. Поэтому ошибка в значении плот-
ности равноценна (в процентах) такой же ошибке в топопоправке.
Как правило, плотность определяется с погрешностью около 10%.
Очевидно, что влияние рельефа учитывается с точностью такого
же порядка. Если в районе работ плотность пород резко ме-
няется, то при введении поправки надо знать значение плотности
в каждой точке.
297
ПРЕДСТАВЛЕНИЕ
РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
Результаты наблюдений с вариометрами и градиентометрами
после внесения поправок представляются графически (рис, 11.6)
в виде карт векторов горизонтальной составляющей градиента
и кривизны, кривых этих величин по профилям, карт изоаномал
силы тяжести.
Векторы горизонтальной составляющей градиента силы тя-
жести и кривизны определяют по аномальным значениям вторых
производных:
G^dg.ds^]/ + j
tg а =
иг______ (11.24)
/? = /(2Га._у)2 + («7д)2;
tg2^ = -2W-;,/rA.
Fla картографической основе в каждом пункте наблюдений
строят в определенном масштабе вектор горизонтальной составля-
ющей градиента G = dglds как геометрическую сумму векторов
Wxz и Wyz с соблюдением ориентировки и знаков. Обычно масштаб
векторов выбирают равным (10; 20; 50)-10“9 1/с2 в 1 см. Начало
вектора совмещают с пунктом наблюдения.
Карту векторов кривизн R строят аналогичным образом,
только пункт наблюдений в этом случае располагается посредине
вектора R. Иногда обе карты совмещают на одной картографи-
ческой основе.
Кривые вектора составляющей градиента dgldr строят или
вдоль профиля наблюдений, или вдоль избранного направления г
вкрест простирания аномалий, что совпадает со средним напра-
влением векторов в зоне их наибольших значений. На выбранное
направление г проецируют все векторы dglds ближайшей окре-
стности профиля. Проекция
dgldr = (dglds) cos (г, s),
где (г, s) — угол между направлениями г профиля и s вектора.
Значение dgldr откладывают вверх, если проекция вектора
совпадает с положительным направлением оси х профиля, и вниз,
если проекция имеет противоположное направление.
Интегрирование составляющих градиента силы тяжести между
двумя точками Л и В, в которых известны значения GA и GB, вы-
полняется по формуле
kg АВ = Рер А'' = 1(Рл + Рв№\ (11.25)
где рА и рв — проекции векторов GA и GB на направление г; Аг —
расстояние между точками А и В.
299
Рис. 11.5. Палетки Нумерова для вычисления поправок за влияние рельефа местности.
Рис. 11.6. Изображение результатов вариометрической съемки.
Сечение нзоаномал 0,1-10-» м/с2.
Эта формула применима и при интегрировании по полигону
с п сторонами, где для каждой стороны вычисляют прираще-
ние &gn.
Горизонтальные составляющие градиента можно интегриро-
вать вдоль профиля или по карте векторов. В первом случае кри-
вую горизонтальной составляющей градиента делят на участки
Дг, характеризующиеся плавным изменением составляющей. Для
каждого участка Дг снимают ординаты кривой (dgidr)t и (dg/dr)M
и по формуле (11.25) вычисляют приращения Д§ . При интегри-
ровании по карте векторов величины и Arz снимают с карты.
300
Если интегрирование выполняют между точками с координатами
лд, у1 и л'2, z/2, то можно пользоваться формулой
Ag.2-1 = 4 0^1 + ^2) (л-2 - Х1) 4-1 (Г,г1 + 17,,г2) (уг-У1). (11.26)
При площадных съемках, когда пункты наблюдений располо-
жены по площади равномерно, рекомендуется интегрировать гори-
зонтальные составляющие градиента по замкнутым контурам, что
позволяет увязывать полигоны и контролировать точность опре-
деления Ag. В этом случае допустимая невязка полигона
6g = (е/|/ 2/г) L,
где в — средняя квадратическая погрешность аномального гра-
диента; п— число точек в полигоне; L — периметр полигона.
Невязку полигона равномерно разбрасывают на все его сто-
роны.
Интегрирование лучше проводить сначала по большим конту-
рам и по направлениям с плавным изменением горизонтальной
составляющей градиента, создавая таким образом сеть опорных
значений силы тяжести на основных контурах. После этого пере-
ходят к интегрированию меньших контуров, пока не увяжут все
пункты. При интегрировании важное значение имеет линейность
изменения составляющих. Для соблюдения этого условия необ-
ходимо уменьшать расстояния между пунктами наблюдений.
После определения приращений силы тяжести между соседними
пунктами один из пунктов, обычно в области минимальных зна-
чений силы тяжести, принимают за исходный (g = 0). Относи-
тельно этого пункта алгебраическим суммированием значений Ag£
определяют приращения силы тяжести в других пунктах наблю-
дений. Затем строят карту изоаномал силы тяжести. При проведе-
нии изоаномал необходимо помнить, что они должны быть пер-
пендикулярны к направлению векторов. Точность съемки и досто-
верность полученной карты изоаномал оценивают по формулам,
приведенным в главе 8.
Глаза 12
ВОЗМОЖНОСТИ ИЗМЕРЕНИЯ
ВЕРТИКАЛЬНОЙ СОСТАВЛЯЮЩЕЙ
ГРАДИЕНТА СИЛЫ ТЯЖЕСТИ
ОСНОВНЫЕ СПОСОБЫ
До настоящего времени, несмотря на много-
численные попытки, не удалось построить прибор для измерения
вертикальной составляющей градиента силы тяжести. Глав-
301
ная трудность заключается в том, что, как показывают теорети-
ческие исследования, стабильность параметров вертикального
градиентометра должна быть очень высокой. Кроме того, большое
числовое значение этой производной (около 3000 10'® 1/с2) требует
более высокой относительной точности измерений.
По ряду причин вопросу измерения вертикальной составля-
ющей градиента силы тяжести придается весьма важное значение.
Прежде всего, аномалии вертикальной составляющей более четко
локализуют возмущающие массы, чем аномалии силы тяжести.
Вертикальная составляющая градиента практически не зависит
от широты места и высоты пункта наблюдений, что сокращает
число поправок. Зная распределение 1Р2г на земной поверхности,
можно более точно редуцировать наблюденные значения силы тя-
жести, находить кривизну главных нормальных сечений уровен-
ной поверхности и решать другие важные задачи разведочной
и геодезической гравиметрии.
Особое значение приобретает измерение вертикальной соста-
вляющей градиента при гравиметрической съемке в движении —-
аэрогравиразведке. Как было показано, измерение силы тяжести
в движении встречает большие трудности из-за высокого уровня
помех в виде различных ускорений, действующих на гравиметр
кроме силы тяжести. Погрешность современных измерений силы
тяжести на самолете составляет 10-10 5 м/с2; такая точность со-
вершенно недостаточна для разведочных целей. Теоретические
исследования показывают, что наиболее перспективным направле-
нием в разработке аэрогравиметрнческих методов разведки яв-
ляется измерение вертикальной составляющей градиента силы
тяжести, так как в этом случае поступательные возмущающие уско-
рения не оказывают влияния на результаты измерений. Было
предложено много способов как непосредственного, так и косвен-
ного определения Жг2. Рассмотрим кратко основные из них.
В конце прошлого столетия Р. Этвеш предложил определять
вертикальную составляющую градиента силы тяжести по произ-
водным Wy4, Wxu, Wизмеренным гравитационным варио-
метром, и по составляющим уклонения отвеса § и ц, которые
получают из астрономо-геодезических наблюдений. Этот метод
не может быть точным, так как при больших расстояниях между
пунктами наблюдений становится недопустимым предположение
о линейном характере изменения уклонений отвеса, а при малых
расстояниях относительная разность уклонений отвеса опре-
деляется недостаточно точно. В СССР такие исследования произ-
водили Л. В. Сорокин в районе КМА и В. А. Казинский около
Москвы.
Первую попытку непосредственно измерить W# предпринял
в 1881 г. Ф. Жолли, использовав точные призменные весы с тремя
чашками (рис. 12.1). На одном конце коромысла находится одна
чашка, на другом — две, причем они разнесены по высоте на рас-
стояние Л. Ф. Жолли взвешивал одну и ту же массу т на разных
302
Рис. 12.1. Весы Жолли. Рис. 12.2. Вертикальные крутильные
весы.
уровнях. Если массу т положить на верхнюю чашку весов и урав-
новесить, а затем переложить ее на нижнюю чашку, то равновесие
нарушится, так как вес массы т стал больше. Нарушение равно-
весия восстанавливается добавлением дополнительного гру-
зика Д/п.
Обозначив через Ag увеличение силы тяжести g при опуска-
нии массы вниз на расстояние h, получим
g Am = т bg,
отсюда
W^Ag/fc (g.7/) (Am.'m). (12.1)
Позднее измерения W2. по способу Жолли, но с аппаратурой,
совершенно непригодной для полевых условий, были проведены
многими исследователями. Точность этих измерений оставалась
низкой, и значения №гг получались меньше теоретически пред-
полагаемых на 5—7%. В 1930 г. немецкий геофизик Г. Шмервиц
предпринял попытку создать портативный полевой прибор на
принципе весов Жолли, повысив точность взвешивания в 200 раз,
но построить прибор ему не удалось.
Следует отметить, что формула (12.1) не учитывает влияния
горизонтальной составляющей градиента силы тяжести, что до-
пустимо только при измерениях нормального значения «=:
г^ЗОООИО’8 1/с2. Для аномальных, гораздо меньших значений
№-г такое упрощение недопустимо.
В 1920 г. А. Беррот в связи с успехами в конструировании
гравитационных вариометров предложил использовать для изме-
рения №гг жесткое коромысло с грузиками на концах, у которого
ось вращения горизонтальна (рис. 12.2). Такую систему А. Бер-
рот назвал вертикальными крутильными весами и дал их общую
теорию, показав принципиальную возможность измерения этой
системой вертикальной составляющей градиента силы тяжести.
Теория вертикальных крутильных весов была развита М. А. Са-
довским, который установил, что вертикальные крутильные весы
303
являются универсальными: они реагируют и на составляющие
ПЛ,.., 1ГД, WX!/.
В 1923 г. в Германии был предложен прибор для измерения
приращения А1Г,, между двумя точками. Чувствительным эле-
ментом этого прибора являются равноплечие крутильные весы.
Идея измерений состоит в следующем. От пункта к пункту изме-
няется как сила тяжести, так и вертикальная составляющая ее
градиента. При этом изменение у пе вызывает поворота системы,
если плечи и грузики коромысел равны. К повороту весов при-
водит только изменение угол поворота является мерой при-
ращения Следует отметить, что предложенная система была
первой из предназначенных для относительных измерений 1Ггг,
все другие системы разрабатывались применительно к абсолют-
ному определению W2Z. Однако на практике и эта система не была
осуществлена.
ЭЛЕМЕНТЫ ТЕОРИИ
РАВНОПЛЕЧИХ КРУТИЛЬНЫХ ВЕСОВ
Теория равноплечих крутильных весов была впервые дана
В. В. Федынским в 1959 г.
Пусть имеются равноплечие весы (рис. 12.3) с постоянными гру-
зиками т, один из которых прикреплен к коромыслу жестко,
а другой подвешен на невесомой идеально гибкой нити длиной h.
Осью вращения коромысла является горизонтальная упругая
нить. Выберем неподвижную систему координат х, у, г. Начало
координат поместим в точке О пересечения вертикальной плоскости
симметрии весов с осью вращения, ось z направим вертикально
вниз, ось у — вдоль оси враще-
ния коромысла, ось х — гори-
зонтально.
Уравнение равновесия весов
имеет вид
(12.2)
где £44, — сумма моментов,
действующих на коромысло в
положении равновесия.
Будем считать, что на си-
стему действуют только грави-
тационные силы и упругий мо-
мент закручивания нити подве-
са. Момент гравитационных сил
Мг = Мк + Mi + Mit (12.3)
где Мк — момент коромысла;
Му и М2 — моменты грузиков,
304
Момент коромысла
/Ик = j (xgz - - zgx) dm.
Поскольку координаты грузиков
Л1 == I cos а; х2 = — I cos а;
?!== — /sinа; z2 == h -}- /sinа,
где / — плечо коромысла, то
Mj = х2гщ1г; ]
Мг = x2mg.,.. I
(12.4)
Полагая гравитационное поле в объеме, занятом весами, ли-
нейным, выражаем gz и gx через значения этих величин в начале
координат:
& = + * (44 +* (¥), 'лС',. _
е. - (е.\. - х(»о + г (». - + 2и>„ + (6,)„. 2,6
Тогда для момента коромысла имеем
Мк = feJo j xdm U7 2 [ (х2 — z2) dm -|- (W2l — WX.) j xzdm. (12.6)
Если предположить, что ось вращения проходит через центр
тяжести коромысла, то интегралы | xdm и j xzdm обратятся
в нуль и формула (12.6) примет вид
Л4К == j (x2 — z2) dm = (12.7)
Поскольку
§1г (gjo + 1
ёзг = Ш0+^^4-г.Д/гг, / (1ЛЙ)
то сумма моментов грузиков
Ml 4- Л12 = т [IFV. (xf 4-xl) 4- u?4 (л-^1 4- Х2г2)1 =
— mlW„-'2l2 cos2 а — W72z(^ + 2/sina) / cosa]. (12.9)
Тогда выражение момента гравитационных сил примет вид
где
А —К 2т!2 cos2 а; 1
D > О, , М (12.10)
В — т(1г 2/sin a) /cos а. I
305
Момент упругих сил оси вращения, если пренебречь эффектом
стрелы прогиба нити,
Мт = т(а Оо), (12.11)
где т — постоянная кручения нити; 0(, угол предварительного
закручивания нити.
Тогда уравнение равновесия весов (12.2) можно записать в виде
т(а-0о)^Жг-В№„. (12.12)
Наиболее простой вид уравнение равновесия имеет при гори-
зонтальном положении рычага, т. е. при а = 0:
т9о4-Д^.г_ВГгг = 0;1
Д = М0 + 2т/2;
Во = mhl.
(12.13)
Дифференцируя уравнение (12.12) по 11722 май пренебрегая
членами, содержащими вторые производные гравитационного по-
тенциала, получаем формулу чувствительности весов к W2Z.
da/dW„ = В/т, (12.14)
при а = 0
da/dWzz = В0/т = mhl/x.
(12.15)
Повышать чувствительность весов можно, не только изменяя
их параметры, ио и делая систему астазированной с помощью
дополнительных устройств.
В уравнение равновесия весов (12.12) кроме №гг входит и WX2.
При измерении Wz2 влияние 1ГЛ.г на показания прибора необхо-
димо исключить. Для этого надо, чтобы
ствителыше к составляю-
щей Wxz.
К — — 2m/2 cos'2 а,
тогда величина Wxz в уравнение не войдет.
Рассмотрим весы, у которых коромысло
выполнено в виде квадрата с жесткими
диагоналями (рис. 12.4). В точках С и D
находятся грузики такой же массы т, как
и рабочие грузики в точках А и В. Для
такого коромысла соблюдается указанное
выше условие К = —2m/2 cos2 а и весы
не реагируют на составляющую 1Рлг.
Следует отметить, что вертикальные
крутильные весы являются частным слу-
чаем равноплечих весов. Действительно,
положив h = 0, получим вертикальные
крутильные весы; для них
В = тР sin 2а
306
и чувствительность
da/dW2Z = В/х — (т/а/т)з1п2а,
т. е. наибольшей чувствительностью к Wz2 вертикальные весы
обладают при а = 45°.
Теория крутильных весов рассмотрена в предположении, что
ось вращения коромысла проходит через центр тяжести системы
коромысло — грузики. Практически оказывается очень трудно
добиться этого с высокой точностью. При невыполнении же такого
условия уравнение равновесия системы существенно ослож-
няется, так как интегралы J xdm и | xzdm не обращаются в нуль.
Первый интеграл (12.6) дает в уравнение равновесия (12.12)
добавочный член
тс (&)о do cos а — g0 sin a),
где me — масса системы; gn, £0 — координаты центра тяжести
системы коромысло — грузики.
Вторым интегралом | xzdm можно пренебречь, поскольку коро-
мысло находится или в горизонтальном положении (а = 0), или
отклоняется па малые углы.
Следовательно, когда центр тяжести системы не совпадает
с осью вращения, то весы реагируют не только на вертикальную
составляющую градиента силы тяжести, но и на саму силу
тяжести g, т. е. являются одновременно и градиентометром и гра-
виметром. Очевидно, что никакой методикой измерений и кон-
струкцией весов разделить влияния g и W22 не удастся. Един-
ственный путь исключения g из уравнения равновесия состоит
в том, чтобы сделать момент /пеЯоВо пренебрежимо малым, т. е.
поместить центр тяжести весов на ось вращения.
Оцепим погрешность, с которой необходимо выполнить это
условие при разумных параметрах весов. Пусть расстояние Ео
таково, что момент т^оВо отклоняет коромысло не больше, чем
момент, обусловленный dW22 = 10- 1O 'J 1/с2, т. е. mcg0%0 «
< mhldW22. Полагая /ц. = 2 г, пг = 1 г, h. = 50 см, I = 5 см,
получаем с 1,25- 10~я см. Эта величина настолько мала, что
соизмерима с атомными расстояниями. Естественно, совместить
ось вращения системы и ее центр тяжести с такой точностью
невозможно. Даже если бы удалось сделать это, то через некоторое
время центр тяжести весов самопроизвольно сместился бы на зна-
чительно большее расстояние из-за колебаний температуры и
влияния других внешних условий. Отсюда следует важный вывод,
что весы (равноплечие и вертикальные) не могут быть практи-
чески использованы для абсолютных измерений вертикальной
составляющей градиента силы тяжести.
Исследуем возможность измерения с помощью весов прираще-
ния вертикальной составляющей градиентов между двумя
точками. Для простоты рассуждений положим, что показания
307
вёсов’не зависят от горизонтальной составляющей IE,Z. Выше
было показано, как исключить влияние этой величины. Пред-
положим, что наблюдения с весами проведены в двух пунктах,
где значения g одинаковы. Для таких пунктов можно написать
следующие уравнения равновесия:
т0оН-///с£о^-Я17гг1 + Д(1 = О; I
т% + ^о-БГг22 + ^2 = 0. |
Вычитая из второго равенства первое, получаем
Д^гг = «Ж 2 - ^1 = (Л,2 - ЖгЖ (12.17)
Таким образом, равноплечими весами можно определять при-
ращения вертикальной составляющей градиента силы тяжести.
При выводе формулы (12.17) сделано предположение, что сила
тяжести на пунктах измерения постоянна. На самом же деле сила
тяжести от точки к точке меняется и, следовательно, искажает
показания весов. Это искажение тем больше, чем больше коорди-
ната £о, т. е. чем больше момент tncg^0. Найдем, каким должно
быть расстояние £0, чтобы приращение силы тяжести dg0 = ICO х
X 10“8 м/с2 изменяло показания весов не более чем на dW2, =
— 10-10'9 1/с2. Очевидно, что в этом случае должно выполняться
неравенство tn^dg^ < mhldW22. Полагая тс = 2 г, т — 1 г,
h = 50 см, I = 5 см, получаем t0 С 0,125 мкм. Таким образом,
даже при относительном способе измерения W2Z требования
к юстировке системы очень высоки.
Вернемся к рассмотрению возможностей определять абсолют-
ные значения вертикальной составляющей градиента силы тя-
жести способом Жолли. Положим, что коромысло весов Жолли
приводится в горизонтальное положение дополнительным ком-
пенсирующим моментом FK. Уравнение равновесия для верхнего
и нижнего положения взвешиваемого груза с учетом действия
горизонтальной составляющей градиента силы тяжести можно
получить из уравнения равновесия равноплечих весов (12.13),
положив h — 0 и Л — h:
тби I /1Л | №cgo$o Ж AaWxz = 0;
тД) Ж EК2 Ж Ж — 0.
Если за время измерений все величины, входящие в эти урав-
нения, остаются постоянными, то
= (12.19)
Таким образом, при абсолютном измерении по способу
Жолли члены с g9 и WAZ в уравнениях исключаются. Следова-
тельно, при юстировке весов Жолли не требуется высокой точ-
ности совмещения центра тяжести системы с осью вращения;
достаточно, чтобы во время измерения момент mcgo?o оставался
(12.18)
308
постоянным. В этом состоит одно из важных преимуществ весов
Жолли перед вертикальными равноплечими весами. Как след-
ствие этого свойства, стабильность параметров весов Жолли
должна сохраняться только в течение времени измерения па
пункте, изменение же параметров весов в промежутках между
измерениями не влияет на точность WZ2. В равноплечих весах,
наблюдения с которыми проводят без перемещения грузиков,
параметры весов должны быть постоянными и в интервалах между
измерениями. Сложность создания прибора на принципе весов
Жолли заключается в необходимости перемещать грузик по вер-
тикали во время измерений, не нарушая параметров системы.
Оценим требования к постоянству параметров рассмотренных
систем, предназначенных для измерения вертикальной составля-
ющей градиента силы тяжести. Выясним требования к постоян-
ству массы т грузика и плеча I коромысла равноплечих весов.
Момент нижнего грузика системы М = tngl, где g — сила тяжести
в точке расположения грузика. Момент минимального измеря-
емого значения dW22 вертикальной составляющей градиента
равен mhldW^. Очевидно, приращения момента dM, вызванные
изменением массы т и плеча /, не должны превышать указанного
минимального момента, т. е. dM < mhldW„.
Так как
dM — g I7'1г dm? -|- m2dl2,
то
1 / dm2 . d/2
V ~т2' ' ~
Применяя принцип равных влияний, т. е. считая, что члены
под радикалом равны, получаем
— = -^< —* dW (12.20)
т I g /2 гг v '
Эта формула верна и для весов Жолли.
Вертикальные крутильные весы имеют максимальную чув-
ствительность к вертикальной составляющей градиента силы тя-
жести при а = 45°. Следовательно, их можно рассматривать как
весы Жолли, у которых h —I | 2. Тогда формула (12.20) для вер-
тикальных весов приобретает вид
dtn/m = dl/l < (l/g) d\V22.
Пусть требуется измерить вертикальную составляющую гра-
диента с погрешностью 10- 1СГЭ 1/с2. Из формулы (12.20) найдем
dtnhn = dll I = 7 • 1012А (см).
Требования к постоянству параметров систем для измерения
1Гг2 весьма высоки, снижаются они только при увеличении h.
В полевом приборе разность высот грузиков может быть не более
309
50—75 см. Полагая h — 75 см, получаем dtnlm = dill = 5,2 X
X КГ10. Это значит, что при массе грузика 1 г и плече 5 см до-
пустимое отклонение относительно массы другого грузика и плеча
не должно превышать соответственно 5,2-10"10 г и 0,26-10"4 мкм.
Естественно, что поддерживать такое постоянство параметров
системы весьма сложно. Основная трудность измерения вертикаль-
ной составляющей градиента силы тяжести именно в том и состоит,
что к постоянству параметров прибора предъявляются чрезвы-
чайно высокие требования. В этом заключается причина неудач
многих исследований по измерению Wzz.
Для сравнения определим, каким постоянством параметров
обладают горизонтальные крутильные весы, являющиеся в на-
стоящее время единственной системой, измеряющей горизонталь-
ные составляющие градиента силы тяжести. Главной особен-
ностью горизонтальных весов по сравнению с весами для измере-
ния вертикальной составляющей градиента является то, что в них
сила тяжести уравновешивается реакцией нити подвеса и не соз-
дает момента относительно оси вращения системы. Коромысло
весов закручивается только под действием малых моментов,
обусловленных вторыми производными гравитационного потен-
циала. Поскольку максимальные значения этих производных
не превосходят 500-КГ9 1/са и погрешность их составляет 1 X
X 10~9 1/с2, то параметры весов (масса грузика, плечо коромысла,
жесткость нити) за время измерения могут изменяться даже на
1/500 своего значения. При конструировании вариометров основ-
ное внимание обращают не на сохранение параметров системы
постоянными, а на снижение уровня помех, нарушающих поло-
жение равновесия весов (вибрации, конвекционные потоки, элек-
тростатические силы и т. п.).
ИЗМЕРЕНИЕ ВЕРТИКАЛЬНОЙ
СОСТАВЛЯЮЩЕЙ ГРАДИЕНТА
СИЛЫ ТЯЖЕСТИ ГРАВИМЕТРОМ
Кроме работ по созданию прибора для измерения вертикальной
составляющей градиента силы тяжести па базе весов различного
рода предпринимаются попытки абсолютных измерений путем
наблюдения силы тяжести в двух пунктах, разнесенных по вер-
тикали, что стало возможным в связи с успехами в конструиро-
вании чувствительных гравиметров.
В 1938 г. 3. Хаммер проводил опыты по измерению 1Угг на
высотных зданиях Вашингтона, Нью-Йорка и Питтсбурга с раз-
ностью высот точек наблюдения от 138 до 291 м. Эти измерения
подтвердили, что нормальное значение вертикальной составля-
ющей градиента, вычисленное теоретически (3086-10~9 1/с2), соот-
ветствует действительности. Аналогичные наблюдения были вы-
полнены в СССР Б. К. Балавадзе с гравиметром Норгарда на 19
геодезических пунктах Грузии с разностью высот от 14 до 45 м.
ЗЮ
Погрешность измерений составила от 5-10“9 до 45- 10’9 1/с2. В на-
стоящее время подобные измерения продолжаются во многих стра-
нах: Польше, США, ФРГ, Японии, СССР. Для большинства наблю-
дений используют высотные здания, наблюдательные вышки или
триангуляционные пункты. Разница высот пунктов наблюдений
составляет 3—300 м, погрешность измерений (10 ч- 40)-10’8 1/с2.
Эти работы представляют большой интерес для гравиметрии,
но они не могут служить основой для разработки вертикального
градиентометра, поскольку в полевых условиях очень трудно
обеспечить разницу высот в несколько десятков метров. С. Тиссен
предложил измерять вертикальную составляющую градиента гра-
виметром при разности высот 1 м. Столь малый перепад высот
позволяет сократить время наблюдения на пункте и тем самым
повысить точность измерения приращения силы тяжести по вер-
тикали. В связи с крупными достижениями в конструировании
высокочувствительных и портативных гравиметров это предло-
жение открывает большие возможности. Так, в Канаде был ис-
пользован гравиметр «Уорден» со специальной треногой, позволя-
ющей устанавливать прибор на разных уровнях с разностью
высот 3,7 м. Разность силы тяжести Ag & 1,2-10'5 м/с® измерялась
с погрешностью порядка 0,004-10-5 м/с2,. что дало возможность
вычислить вертикальный градиент с погрешностью около 10 X
X 10-9 1/с2. В ФРГ сконструирована специальная вышка высотой
5 м с пятью площадками, на которые можно устанавливать грави-
метр «Аскания»; погрешность определения Wzz составила 12 X
X 10~9 1/с2. Аналогичные исследования проводились в США
с гравиметром Лакоста — Ромберга и также дали обнадежива-
ющие результаты.
При современных технических возможностях вполне реально
создание гравиметра, который при измерениях на малой базе
(1—2 м) даст погрешность единичного наблюдения (0,001 ч-
-т- 0,002)-10’5 м/с2. В этом случае будет решена проблема^абсо-
лютных определений вертикальной составляющей градиента силы
тяжести в полевых условиях.
Раздел IV
ГЕОЛОГИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
ГРАВИТАЦИОННЫХ АНОМАЛИЙ
И ПРИМЕНЕНИЕ ГРАВИРАЗВЕДКИ
Глава 13
ФИЗИЧЕСКИЕ ОСНОВЫ
ГЕОЛОГИЧЕСКОЙ ИНТЕРПРЕТАЦИИ
ГРАВИТАЦИОННЫХ АНОМАЛИЙ
ПЛОТНОСТЬ ГОРНЫХ ПОРОД
Гравитационные аномалии существуют только в том случае,
если горные породы, слагающие район исследований, различаются
по плотности и границы пород с различной плотностью пе яв-
ляются горизонтальными. Разница в плотности горных пород
служит основной предпосылкой успешного применения гравита-
ционного метода для геологических исследований, поисков и раз-
ведки полезных ископаемых. Чем больше различие в плотности
вмещающих пород и исследуемого объекта, тем с большим успехом
может быть применена гравиразведка.
Разность плотности вмещающих пород и плотности тела, соз-
дающего гравитационную аномалию, называется избыточной или
эффективной плотностью.
Сведения о плотности горных пород исследуемого района необ-
ходимы для правильного обоснования и проведения гравиразве-
дочных работ, так как они позволяют оценить порядок ожида-
емых аномалий, выбрать рациональную сеть наблюдений и т. д.
Особо важно знать плотность горных пород при геологическом
истолковании гравитационных аномалий.
Плотностью о любого однородного вещества называется отно-
шение массы т вещества к ее объему V:
(13.1)
Горные породы в общем случае являются телами неоднород-
ными и состоят из вещества в трех фазах: твердой, жидкой и газо-
образной. Плотностью горной породы называется отношение
массы вещества всех фаз, которые свойственны породе в условиях
312
естественного залегания, к объему, занимаемому веществом этих
фаз, т. е.
о = (r?il -|- т3)/(Уг j- У2 | - У3) = tn!V, (13.2)
где тг, т2, та и Уь У2, У3 — соответственно массы и объемы ве-
щества твердой, жидкой и газообразной фаз; т и V — суммарные
масса и объем всех фаз горной породы.
Отношение массы вещества твердой фазы /zi2 к объему V ве-
щества всех фаз называется объемной плотностью
оу = т1/У. (13.3)
Отношение массы вещества твердой фазы к ее объему назы-
вается минералогической плотностью
ом»я = '”1/У1- (13.4)
Объемное содержание в породе вещества, находящегося
в жидкой и газообразной фазах, характеризует пористость гор-
ной породы. Коэффициентом пористости (пористостью) горной
породы называется отношение объема пор ко всему объему породы
/г„ = (У2 -j- Va)/(V1 -г Уа + У3) = (Иа + У3)/У. (13.5)
Обычно пористость kit выражают в процентах или долях еди-
ницы.
Если известна минералогическая плотность и пористость, то
можно определить объемную плотность породы. Из формулы (13.3)
имеем
<Tv = lzi + Иа + Y3 = Тд О ~ h +Г2 + И3 ) ;
откуда, учитывая выражения (13.4) и (13.5), получаем
— пмик (1 Ап)* (13-7)
Влажность горной породы характеризуется объемом или мас-
сой воды, заключенной в порах породы. Отношение массы (веса)
воды в породе к массе (весу) вещества твердой фазы называется
массовым (весовым) коэффициентом влажности
azm = m2/m1. (13.8)
Объемным коэффициентом влажности называется отношение
объема воды к объему вещества твердой фазы:
^/ = y2/yi. (13.9)
Для гравиразведочных целей необходимо знать плотность
пород в их естественном залегании, в условиях естественной влаж-
ности. Если пористость пород мала, что характерно, напри-
мер, для изверженных и метаморфических пород, то можно без
большой погрешности полагать
о —ov, так как т.2 т3 mt.
313
Высокой пористостью пород пренебрегать нельзя. В этом
случае
О = «Ту 4- (rn2 + Wis)/(V1 4- V2 4- V3)
и, так как т3 < /»2> то, учитывая выражение (13.8), получаем
О — (Ту (1 |Wm) = <ТМИ1, ( 1 । £0нг)(1 /?п),
полагая, что все поры заполнены водой, т. е. т2 4- т3 численно
равно V2 + V3, имеем
а = оу+А:п = <тМИ1,(1-/^п)4-йп. (13.10)
Формула (13.10) дает максимально возможное значение плот-
ности, поскольку в реальных условиях не все поры заполнены
водой или другой жидкостью, часть из них заполнена газом.
Однако, поскольку для гравиметрии важны не абсолютные зна-
чения плотности, а избыточные, то при вычислении плотности
пород с близкими значениями пористости в результат вносится
незначительная ошибка. Заметную погрешность можно внести,
вычисляя избыточную плотность пород, сильно различающихся
по пористости.
Плотность горных пород зависит от их химико-минералоги-
ческого состава, пористости и влажности, что определяется усло-
виями как первичного образования горных пород, так и последу-
ющего их существования. Поэтому плотность можно рассматри-
Таблица 13.1
Плотность минералов
Минерал Плотность, г/см3 Минер ал Плотность, г/см3
Авгит 3,3—3,4 Кордиерит 2,5—2,6
Альбит 2,6 Лабрадор 2,7
Анальцим 2,2—2,3 Лимонит 3,6—4,0
Ангидрит 2,9 Магнетит 4,9—5,2
Анортит 2,7—2,8 Микроклин 2,5—2,6
Апатит 3,2 Мусковит 2,8—3,1
Барит 4,5 Нефелин 2,6
Биотит 2,8—3,2 Оливин 3,0—4,4
Гематит 5,1—5,2 Ортоклаз 2,5—2,6
Гипс 2,3 Пирит 4,9—5,2
Гранат 3,2 4,3 Пироксен 2,8—3,7
Доломит 2,6—2,9 Серпентин 2,5—2,6
Ильменит 4,5—5,0 Силлиманит 3,2
Кальцит 2,6—2,8 Ставролит 3,6—3,7
Каменная соль 2.1—2,3 Хлорит 2,6—3.0
Кварц Кианит 2,6—2,7 3,6 -3,8 Эпидот 3,1—3,5
Примечание. В системе СИ единица плотности — кубический метр (кг/м3). килограмм на
314
Таблица 13.2
Плотность магматических и метаморфических пород
Породы Плотность, г/см*
Средняя Пределы изменения
Граниты 2,6 2,4—2,7
Граниты и гранито-гнейсы (типичные для древних ши- 2,7 2,4—3,0
тов)
Гранодиориты, кварцевые диориты 2,7 2,7—2,8
Анортозиты 2,7 2,6—2,8
Диориты 2,8 2,7—2,9
Сиениты 2,8 2,6—2,9
Диабазы, габбро, габбро-диабазы 2,9 2,7—3,3
Базальты 3,0 2,6—3,3
Дуниты, перидотиты, пироксениты 3.2 2,8-3,6
Кварциты 2,7 2,7- 2,8
Мраморы, кристаллические известняки 2,7 2,3—3,0
Кварциты железистые 3,5 3,2—4,3
Г пейсы 2,7 2,6—3,2
Порфириты 2,8 2,7—2,9
Альбитофиры 3,2 2,8—3,6
Серпентиниты 2,6 2,4—3,0
Амфиболиты 2,9 2,7—3,2
Сланцы глинистые 2,3 2,0—2,8
слюдистые 2,6 2,5—2,8
роговообманковые 3,0 2,8—3,4
вать как объективный показатель истории геологических процес-
сов, которым подвергались горные породы. Большинство геоло-
гических процессов в той или иной степени влияют на состав
и структуру минерального скелета породы, на ее пористость
и влажность. Поэтому изучение плотности пород представляет
интерес не только для разведочной гравиметрии, но и для гео-
логии.
Влияние одних процессов на плотность пород изучено до-
вольно детально, для других намечаются только самые общие за-
кономерности. В зависимости от типа пород те или иные факторы
воздействуют на плотность не в одинаковой степени. Для магма-
тических и метаморфических пород характерна малая пористость
(порядка 1—2%) и, как следствие, малая влажность. Поэтому
плотность этих пород определяется их химико-минералогическим
составом.
Плотность главнейших породообразующих минералов при-
ведена в табл. 13.1, плотность наиболее распространенных магма-
тических и метаморфических пород — в табл. 13.2.
Плотность магматических пород в основном определяется соот-
ношением в них относительно легких (кварц, полевые шпаты,
315
нефелин) и тяжелых железо-магнезиальных минералов (амфи-
болы, пироксены, оливин, слюда). Поэтому плотность магмати-
ческих пород увеличивается с повышением их основности. Кроме
состава на плотность оказывают существенное влияние структура
породы, степень ее кристалличности. Плотность у пород с массив-
ной кристаллической структурой больше, чем у пород того же
состава, но неполнокристаллических, аморфных.
У метаморфических пород, являющихся продуктами преобра-
зования магматических и осадочных пород, плотность опреде-
ляется исходным материалом, а также воздействием процессов
метаморфизма. При метаморфизме может происходить как увели-
чение плотности, так и ее уменьшение. Например, при повышении
давления и связанной с ним перекристаллизации в породе проте-
кают реакции, приводящие к уменьшению объема, т. е. к увели-
чению плотности. Алмаз, являющийся полиморфной модифика-
цией углерода и образующийся при высоких давлениях и тем-
пературах, имеет плотность 3,5 г/см3, в то время как более низко-
температурная модификация — графит — имеет плотность
2,1 г/см3.
Примером процесса, вызывающего уменьшение плотности по-
род при метаморфизме, может служить серпентинизация ультра-
основных пород, сопровождающаяся прпвносом относительно
легких компонентов (вода, кремнекислота). В этом случае оливин
(о = 4,1 4- 4,4 г/см3) переходит в серпентин (ст = 2,5 -г- 2,6 г/см8).
Гипергенные изменения пород в коре выветривания также сопро-
вождаются уменьшением плотности, при этих процессах возни-
кают новые минералы с относительно низкой плотностью.
В отличие от магматических и метаморфических пород осадоч-
ные отложения имеют большую пористость (табл. 13.3), исключе-
ние составляют гидрохимические осадки. Поэтому плотность
осадочных пород существенно зависит от их пористости.
Таблица 13.3
Пористость осадочных пород
Породы Пористость, %
Почвы Пески, алевролиты Песчаники Галечники Аргиллиты Мергели Известняки, доломиты Мел Гидрохимические осадки (гипс, ангид- рит, галит) 23—69 2—42 2-55 25—38 4—34 2—31 2—40 17—43 0-5
316
Таблица 13.4
Плотность осадочных пород
Породы Плотность, г/см8
Средняя Пределы изменения
Почвы 2,0 1,5—2,4
Глины, аргиллиты 2,3 1,6—2,8
Пески, алевролиты 2,1 2,0—2,4
Песчаники 2,3 2.1—2,8
Мергели 2,2 2.0—2,6
Из вес и । я Ki ।, дол омиты 2,5 2.1—2,9
Мел 2,2 2,1-2,3
Как следует из табл. 13.3, пористость одной и той же породы
меняется в широких пределах. Пористость породы, а также ее
плотность зависит прежде всего от условий образования породы
и от воздействия геологических факторов, которому порода под-
вергается за весь период своего существования. Отметим некото-
рые из этих факторов.
В условиях естественного залегания на породы давят выше-
лежащие слои, что приводит к уменьшению пористости с глуби-
ной. Этот процесс может сопровождаться частичной перекристал-
лизацией породы и увеличением ее плотности. Как правило,
с глубиной скорость изменения пористости и плотности сни-
жается.
Уменьшению пористости, а следовательно, увеличению плот-
ности способствует метаморфизм пород в процессе складкообразо-
вания. Классическим примером, показывающим зависимость плот-
ности пород от степени метаморфизма, может служить изменение
плотности продуктивной угленосной толщи каменноугольного
возраста в Донбассе, изученное А. Т. Донабедовым и Н. Н. Сам-
соновым по керну скважин. В этом районе плотность пород умень-
шается от центра к периферии. В центральной части Донбасса
пористость пород близка к нулю, и в них не наблюдается увеличе-
ния плотности с глубиной.
Влияние отмеченных факторов приводит к тому, что плотность
одних и тех же осадочных пород в различных геологических
условиях неодинакова (табл. 13.4). Диапазон изменения плот-
ности осадочных пород очень широк, поэтому средние значения
можно принимать только как ориентировочные.
В табл. 13.5 приведена плотность полезных ископаемых, при
поисках и разведке которых применяется или может применяться
гравиразведка.
Сопоставление плотности пород с другими их физическими
свойствами выявляет определенные статистические связи, хотя
317
Таблица 13.5
Плотность полезных ископаемых
Полезные ископаемые Плотность, г/см®
Средняя Пределы изменения
Рудные Железные руды 4,0 3,7—4,3
Хромиты 4,0 3,3—4,4
Колчеданные руды: сплошные 4,5 3,5—5,5
вкрапленные — 3,0—4,6
Полиметаллические руды 4.0 3,2—5,5
Зона окисления колчеданных и полиметаллических —- 0,8—3,1
РУД Нерудные Газ 0,001—0,002
Нефть 0,9 0,7—1,1
Уголь: антрацит — 1,4—1,5
каменный • 1,3—1.4
бурый — 0,8—1,2
Торф 0,7 —•
Каменная соль 2,1 2,1—2,2
Корунд 3,6 3,0-4,0
Барит 4,0 —~
и ограниченные многими условиями. При постоянстве модулей
упругости скорость распространения сейсмических волн в боль-
шинстве случаев пропорциональна плотности: более плотные
породы характеризуются повышенной скоростью упругих волн.
Общей закономерной связи плотности пород с магнитной воспри-
имчивостью не наблюдается. Породы, имеющие одинаковую плот-
ность, могут в зависимости от условий их образования обладать
резко различной магнитной восприимчивостью. У магматических
пород магнитная восприимчивость растет с повышением их плот-
ности и основности. Для осадочных пород корреляционной связи
между магнитными и плотностными характеристиками не обна-
ружено.
При ионной проводимости и постоянной минерализации по-
ровых вод для изверженных и осадочных пород наблюдается пря-
мая зависимость удельного электрического сопротивления от
плотности. Присутствие электроннопроводящих минералов при-
водит к повышению плотности и к уменьшению удельного элек-
трического сопротивления. С увеличением минерализации пла-
стовых вод электрическое сопротивление снижается, плотность
при этом может остаться неизменной.
318
МЕТОДИКА
ИЗУЧЕНИЯ ПЛОТНОСТИ ПОРОД
Достоверные сведения о плотности пород можно получить
только на основе большого числа определений, чтобы исключить
случайные неоднородности образцов. Всегда необходимо стре-
миться к тому, чтобы все типичные разновидности пород и руд
исследуемого района были по возможности охарактеризованы не-
сколькими десятками измерений плотности. Только массовые
определения позволяют составить реальное представление о сред-
ней плотности отдельных разновидностей пород и выявить законо-
мерности ее изменения.
Образцы для определения плотности отбирают из обнажений,
горных выработок или буровых скважин. При отборе образцов
из обнажений надо тщательно следить за тем, чтобы образцы были
свежими, без следов выветривания. Керн буровых скважин ха-
рактеризует породы в их естественном залегании и позволяет
судить об изменении плотности с глубиной.
Измерять плотность образцов можно различными способами.
Наиболее распространенным является гидростатическое взвеши-
вание, сущность которого состоит в следующем.
Образец подвешивают на нити к крючку или чашке техниче-
ских весов любой конструкции и взвешивают. После этого обра-
зец погружают в сосуд с водой и снова взвешивают. Тогда
(13.11)
где Рг и Р2 — вес образца соответственно в воздухе и в воде.
Если образцы сильнопористые, то их парафинируют: погру-
жают на мгновение в расплавленный парафин, который, застывая,
преграждает воде доступ в поры породы. После парафинирования
образец снова взвешивают в воздухе. Значение плотности вычис-
ляют в этом случае по формуле
Р>
(13.12)
где Р{ — вес парафинированного образца в воздухе; <тп — плот-
ность парафина.
Процесс взвешивания образцов значительно ускоряется, если
пользоваться пружинными или безгиревыми весами. На способе
гидростатического взвешивания основан специальный прибор для
измерения плотности — денситометр Н. Н. Самсонова. При по-
гружении образца в воду на шкале денситометра фиксируется
значение плотности.
Плотность пород может быть определена также по поглощению
гамма-излучения в них. Этот метод основан на законе, описыва-
ющем, как ослабляется интенсивность гамма-излучения в зави-
319
Рис. 13.1. Установка для опре-
деления плотности пород гамма-
методом.
Рис. 13.2. Вариационная кривая
плотности пород.
симости от плотности вещества. Для жесткого гамма-излучения
(энергия выше 0,5 МэВ) этот закон имеет вид
1 = 10е~ах^, (13.13)
где 1 и /0 — интенсивность излучения соответственно с образцом
и без образца; о — плотность образца; р — массовый коэффициент
поглощения излучения (для кобальта-60 коэффициент п. = 0,0556);
х — толщина образца на участке измерения плотности.
Установка для определения плотности пород гамма-методом
(рис. 13.1) имеет источник излучения 1, приемник 3 и свинцовый
экран 4. Излучение от источника, проходя через образец 2, ослаб-
ляется, после чего измеряется приемником. Такая установка мо-
жет быть использована для определения плотности пород не
только по образцам, но и в шурфах и горных выработках. Для
измерения в скважинах сконструирован специальный вариант
прибора: между источником и приемником излучения установлен
экран. Прямое излучение в приемник не попадает, и он регистри-
рует только рассеянное породами излучение, которое является
мерой их плотности. По точности определения плотности пород
гамма-метод не уступает гидростатическому взвешиванию.
Для каждой группы образцов, выделенной по литологическому
составу, возрасту или каким-либо другим признакам, вычисляют
среднее арифметическое значение плотности, которое принимают
за наиболее вероятное; кроме того, находят пределы изменения
плотности образцов данной группы. Если группа включает доста-
точное количество образцов (несколько десятков), то для такой
группы строят вариационные кривые плотности (рис. 13.2).
Диапазон изменения плотности делят на некоторое число малых
интервалов (0,05—0,1 г/см3). По оси абсцисс откладывают значе-
ния плотности, по оси ординат — количество образцов (в про-
центах от общего количества в группе), имеющих плотность
в пределах выбранного интервала.
Для однородной группы образцов, в которой колебания плот-
ности около ее среднего значения зависят случайным образом
от многих факторов (точность измерения плотности, случайные
включения, изменения в минералогическом составе и т. д.), ва-
320
риационная кривая плотности представляет собой кривую нор-
мального распределения:
п “ PWfi СХР Н" 262~J’ (!ЗЛ4)
где п — ордината вариационной кривой плотности; б — некото-
рая постоянная, называемая средним квадратическим отклоне-
нием; аср — среднее значение плотности.
В большинстве случаев вариационные кривые плотности не-
симметричны относительно максимальной ординаты, что свиде-
тельствует о неоднородном составе группы образцов. При резко
выраженной неоднородности вариационные кривые могут иметь
по два максимума. Такую группу образцов следует разделить на
две по тем или иным дополнительным признакам и построить
вариационные кривые для каждой подгруппы.
По результатам измерений вычисляют статистические харак-
теристики плотности породы — среднее арифметическое значе-
ние оср и дисперсию D:
1 I ч
<дР - Е ntai L «б
4=1 / £=1
(13.15)
(13.16)
где о; — значение плотности в середине i-ro интервала; пг —
количество определений в t-м интервале; q — число интервалов;
<?
л = 2j ni — общее число определений плотности.
1=1
Дисперсия D характеризует отклонение плотности от ее сред-
него значения. По дисперсии могут быть оценены средние ква-
дратические погрешности определения средней плотности по
одному образцу (е) и определения среднего арифметического
значения плотности (ео)
е = + |/D; го= ± |.'Djn. (13.17)
Погрешности в и &а не следует смешивать с инструментальной
погрешностью измерения плотности визм на приборе: отклоне-
ния е и еа возникают из-за рассеяния значений плотности.
Если плотность пород определена по керну скважин, то можно
построить графики поведения плотности по вертикали. В зависи-
мости от интервала отбора образцов и глубины скважины вычер-
чивают в соответствующем масштабе ее разрез, по оси абсцисс
откладывают значение плотности пород, по оси ординат — глу-
бину, с которой взяты образцы. Такие графики наглядно харак-
теризуют плотность отдельных стратиграфических горизонтов
и изменение плотности с глубиной.
В. С. Миронов
321
Если плотность пород или литологических горизонтов изучена
во многих точках площади исследования, то для каждого такого
горизонта или отдельной литологической разновидности пород
можно построить карту плотности. Для этого необходимо вычис-
лить среднюю плотность породы или горизонта по всем опреде-
лениям в данном пункте или на данном участке. Среднюю плот-
ность пород стратиграфического горизонта или свиты рассчиты-
вают по формуле
(J = Ucfi/lj/U/l;,
где о,- — плотность породы; h; — ее мощность; суммирование
распространяется на все породы, слагающие свиту или горизонт.
На карту наносят значения средней плотности во всех пунктах
и проводят линии равной плотности. Сечение изолиний выбирают
в зависимости от диапазона изменения плотности и от густоты
точек наблюдений. Карты изоплотностей пород дают наглядное
представление о поведении плотности в горизонтальном (лате-
ральном) направлении.
Плотность горных пород может быть определена также по
наблюдениям с гравиметрами в точках, расположенных на земной
поверхности, в шурфах, шахтах и скважинах, а также по изме-
рениям с вариометрами около искусственных или естественных
выемок.
При измерении силы тяжести в скважинах получают плот-
ностной разрез пород, пройденных скважиной. Если принять, что
породы, заключенные между двумя пунктами измерений вдоль
вертикальной скважины, залегают в виде плоского однородного
слоя, то, пренебрегая аномальным вертикальным градиентом
силы тяжести, разность измеренных значений силы тяжести в этих
пунктах можно выразить следующим образом:
gi — g2 = 0,3086 (fti — h2) — 4л/г<т (йх — h2) ф- (Sg^ — 6g2), (13.18)
где /ir — h2 — разность высот пунктов наблюдений; 4л/го (йЛ — /г2) —
удвоенное притяжение плоского слоя с плотностью о; — bg,, —
разность поправок за влияние рельефа в точках наблюдений.
Из этой формулы получаем плотность
0,3086 (ftj — h2) — (#! —g2) 4- — в#2)
0,0838 (hi— h2)
- 3-683 - (13Л9>
UyUOuO (yrj — /12/
Аналогичным образом можно определить плотность пород по
наблюдениям в шахтах.
Плотность промежуточного слоя рассчитывается по грави-
метрическим измерениям на основании зависимости наблюденных
значений силы тяжести от рельефа дневной поверхности. Этот
способ был предложен Л. Неттльтоном и состоит в следующем.
322
По ' профилю, пересекающему
возвышенность или впадину,
выполняют наблюдения силы
тяжести. Построив ряд графи-
ков аномалий силы тяжести в
редукции Буге при различных
значениях плотности а, выби-
рают график Ag, который слабее
других коррелируется с релье-
фом (рис. 13.3); его расчетная
плотность будет соответствовать
плотности промежуточного
слоя. Этому чрезвычайно про-
стому способу присуща некото-
рая неопределенность при выбо-
ре значений плотности.
К. В. Гладкий предложил
Рис. 13.3. Определение платности по-
род промежуточного слоя способом
Неттльтона.
аналитический способ определения плотности промежуточного
слоя по гравиметрическим наблюдениям, который сводится к
решению системы линейных уравнений методом наименьших квад-
ратов. Систему уравнений составляют путем аппроксимации ано-
малий силы тяжести в редукции Буге полиномами различных
порядков. В дальнейшем этот подход использовался рядом
авторов для получения конкретных вычислительных формул
(Л. Д. Немцов, В. М. Березкин).
Пусть в пунктах по профилю наблюдений аномалия силы
тяжести в редукции Буге представляется степенным многочленом
п
AgBZ = L
т=0
(13.20)
где х — расстояние между пунктами по профилю.
Для каждой точки профиля можно написать
AgBZ = g (*/) - Ye (д) + 0,3086/t (х,) — 0,0419ст/г (х£) Д- o<3gp (х,) =
= AgCB. „ (х£) — 0,0419ct/i(xz) 4-o6g-p(xz), (13.21)
где g (xt) и уо — соответственно наблюденное и нормальное зна-
чение силы тяжести; dgp (х;) — поправка за влияние рельефа
при плотности промежуточного слоя ст — 1 г/см3; AgCB. в — ано-
малия в свободном воздухе.
На основе выражений (13.20) и (13.21) получаем
S атх'" = hgCB. в (х£) — [0,0419/г (х£) — 6gp (х£)] <т. (13.22)
т=0
Неизвестными в этом уравнении являются а0, alt а2, ..., ап
и о. Число таких уравнений может быть равно числу неизвестных
И* 323
или превышать его (по числу точек наблюдений на профиле).
Подобная система уравнений позволяет получить различные вы-
числительные формулы, удобные как для ручного счета, так и
для ЭВМ. Наиболее простые формулы соответствуют аномалиям
силы тяжести, меняющимся линейно или по параболическому
закону.
При линейном изменении аномалии Буге
д£б< = «о + ад-
В этом случае есть три неизвестных а0, а± и ст, для определения
которых требуется три уравнения, т. е. три точки наблюдения.
На основе формулы (13.22) получаем следующую систему урав-
нений:
' а-о + адг = А^св. в г - (0,0419^ — 6gpl) or;
а0 + atx2 = Ag,.,. „ 2 - (0,0419/i2 — 6gp2) ст;
й0 + адэ = AgCB. вз - (0,0419/ia — 6gp3) ст.
Полагая, что расстояние между точками наблюдений одинако-
вое, и решая эту систему, получаем
2AgCB. в у - AgcB. al AgcB. В 3
0,0419 (2/i2 — hi — h3) — (26gp2 — 6gpi б£рз)
______0,3086 (2ft3 — hi — h3) -|- 2g2 g, g3_ /13 93)
’ 0,0419 (2/l2-fti-/!.3)-(26gp2-6gp1-6gp3) • 2 >
Если поправки за влияние рельефа невелики, ими можно пре-
небречь; тогда формула (13.23) принимает более простой вид:
ст = 7,365 + „ gl ~2g2 + • (13.24)
В случае параболического закона изменения аномалии Буге
д^ = ао + °л + V?
необходимо иметь четыре точки наблюдений. Составляя и решая
систему из четырех уравнений, получаем
_ _______Ages. в г — 3AgeB, в з Н~3Agcs. is — AgCB, в 3дет
0,0419 (ft4 — 3h3 + 3/i2 — hi) — (Sgpi — 36gpS -p 36gp2 — 6gpl)
Пренебрегая поправками за влияние рельефа, имеем
о _ 7,365 + nn4^73g3ot3f3oTgl h } (13.26)
0,0419 (п^ — oh2 — hy)
Формулы (13.24) и (13.26) проще для вычислений, чем (13.23)
и (13.25). Поэтому при наличии существенных топопоправок, их
324
можно ввести в наблюденные значения силы тяжести, принимая
плотность близкой к действительной, а при вычислении плотности
промежуточного слоя пользоваться формулами (13,24) и (13.26).
Если число точек наблюдений значительно больше, чем число
неизвестных, при решении системы уравнений пользуются мето-
дом наименьших квадратов.
Выделяя в уравнении (13.22) член с неизвестным а0, помещая
начало координат х = 0 в один из пунктов наблюдений, и прене-
брегая топопоправками, получаем
Оо4 Ё = (13.27)
/72=1
«о = AgCB>B(0) - №(0),
(13.28)
где b = 0,0419о.
Из этих выражений следует
Ё атхТ - AgCB. 0 (Л-,-) - AgCB. н (0) - b [h (х,) - h (0)]. (13.29)
771=1
Вводя для сокращения записи приращение силы тяжести отно-
сительно начала координат Agf = AgCB, в (х;) - AgCB, в (0) и
приращение высоты АЛ; = h (у) — h (0), получаем
У атх™ = Ag; — b (13.30)
772=1
Согласно методу наименьших квадратов значение b должно
быть таким, чтобы соблюдалось условие
Г S атхТ — (bgi — b Mh)
i=l m=l
2
== min,
(13.31)
где N — число точек наблюдений на профиле.
Дифференцируя выражение (13.31) по ат и Ь, получаем систему
уравнений. Решая ее, находим значение Ь, а следовательно, и о.
Полагая, что аномалия AgEZ меняется линейно, т. е. AgB,: =
= агх, из условия (13.31) имеем
«1S 4 - S ^gtXi 4b Е =* °;
I 1=1 1=1 2=1
| «1 S А'Мг - 2 АД- А4 4 b Tf = 0-
;=i i=i i=i
325
Если аномалия Ag,.,- меняется по параболическому закону
AgB(- = сцх 4- а2х2, то, дифференцируя выражение (13.31) по п,,
а2 и Ь, получаем
N М N N
nt X 4 я? X •*? — X ^Sixi + ь X AMz = 0;
i=l Z=1 r = l i=l
! «i X А -I- «г X x< — X 4-b X ДМ? = °;
I 6=1 f=1 fc=1 (=1
IN N N N
01 S Д/1.-Х,- -I a2 x Aftz-V? - X Ag, Aft; + b У A/i® = 0.
( Z=1 1=1 1=1 1=1
Решение этой системы также дает значение произведения
& = 0,0419сг, а следовательно, и плотности промежуточного слоя о.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
ГЕОЛОГИЧЕСКОЙ ИНТЕРПРЕТАЦИИ
ГРАВИТАЦИОННЫХ АНОМАЛИЙ
Геологическая интерпретация гравитационных аномалий со-
стоит в выявлении закономерностей их распределения на земной
поверхности, установлении связей этих закономерностей с гео-
логическими объектами и процессами, использовании выявленных
связей для решения различных геологических задач.
Результаты интерпретации зависят от сложности геологиче-
ского строения района исследований, его геологической и геофи-
зической изученности. При ограниченности сведений удается
только установить связь гравитационных аномалии с тем или иным
комплексом пород, слагающих данную территорию, указать
вероятное расположение структурно-тектонических элементов
(зоны разломов, антиклинальные и синклинальные складки,
отдельные рудные тела и т. д.), которым аномалии силы тяжести
и обязаны своим происхождением. Такую геологическую интер-
претацию принято называть качественной. При особо благоприят-
ных условиях кроме качественных связей гравитационного поля
с геологическими особенностями территории появляется возмож-
ность специальными математическими приемами определить те
или иные параметры геологических объектов создающих грави-
тационные аномалии: глубину залегания, размеры, форму и т. д.
Такую геологическую интерпретацию аномалий называют коли-
чественной.
Условность подразделения интерпретации на качественную и
количественную очевидна, так как в обоих случаях определяются
геологические объекты, вызывающие гравитационные аномалии.
Различие заключается в том, что при качественной интерпрета-
ции выясняют природу аномалий, при количественной уточняют
параметры объектов, геологическая природа которых установлена.
326
Качественное истолкование Гравитационных аномалий яв-
ляется первым и основным этапом интерпретации. Эти исследова-
ния выполняют всегда, для чего привлекают все имеющиеся по
изучаемой территории сведения. Прослеживая поведение грави-
тационного поля, сопоставляя это поле с результатами других
геофизических и геологических исследований, устанавливают ве-
роятные геологические факторы, создающие гравитационные ано-
малии, определяют положение отдельных структурных элементов,
намечают участки, перспективные для постановки более детальных
геолого-геофизических съемок, выделяют аномалии для количе-
ственной интерпретации, задают места заложения буровых сква-
жин или горных выработок для проверки и уточнения получен-
ных выводов.
Количественную интерпретацию гравитационных аномалий вы-
полняют не всегда, а только при определенных условиях и допу-
щениях относительно характера гравитационного поля и анома-
лиеобразующих геологических факторов. При количественной
геологической интерпретации принято различать ее прямую и
обратную задачи. Прямая задача состоит в вычислении грави-
тационных аномалий по заданному распределению аномальных
масс. В этом случае предполагается, что известны плотность, форма
и размеры тела; требуется найти значение гравитационных ано-
малий на дневной поверхности, обусловленных этим телом. Обрат-
ная задача, как показывает само название, заключается в вычис-
лении по заданному распределению аномального гравитационного
поля параметров тела: формы, размеров, плотности.
Прямая задача является вспомогательной, поскольку позво-
ляет найти способы решения обратной задачи, например в случае,
когда аномалия создана телом правильной геометрической формы.
Кроме того, сравнением результатов прямой задачи с интерпрети-
руемой аномалией подбирают такое решение, которое совпадает
с этой аномалией, и принимают его за решение обратной задачи.
Исходными формулами для решения прямой задачи являются
выражения (1.31)—(1.36), определяющие производные потен-
циала притяжения как функции распределения гравитирующих
масс. Решение прямой задачи для любого тела заданной формы,
размеров и плотности практически сводится к подстановке соот-
ветствующих пределов интегрирования и вычислению интегралов.
Полученное таким образом решение прямой задачи всегда опре-
деленно и однозначно в том смысле, что при известных параметрах
возмущающего тела всегда можно найти любые составляющие гра-
витационного потенциала в любой точке пространства и это будет
единственное решение. Точность решения прямой задачи может
быть сколь угодно высокой, она определяется лишь точностью
вычисления исходных интегралов.
Совершенно иначе обстоит дело с решением обратной задачи.
Теоретически в общем случае решение обратной задачи неодно-
значно, т. е. по заданному распределению гравитационного потен-
327
циала или его производных нельзя найти однозначное распреде-
ление избыточной плотности, создающей гравитационную анома-
лию. Одному и тому же распределению гравитационного потен-
циала или его производных может отвечать множество распре-
делений избыточной плотности внутри некоторого объема. Неодно-
значность решения обратной задачи следует из того факта, что
возможны такие распределения плотности о0 (£, г], £) внутри
объема v, которые во внешнем пространстве не создают гравита-
ционного поля, т. е. потенциал этих масс во внешнем простран-
стве тождественно равен нулю. II. С. Новиков показал, что не-
обходимым и достаточным условием того, чтобы распределение
плотности о() (£, т], £) в объеме и не создавало внешнего грави-
тационного поля, служит равенство
J F(g, р, £)o0(L 1], £)<b = 0,
где F (|, ip £) — произвольная функция, гармоническая в объеме v
и непрерывная на его границе.
Таким образом, распределение плотности о0 (£> П, С) внутри
объема v создает нулевой внешний потенциал, если это распределе-
ние ортогонально к любой гармонической функции внутри этого
объема.
Примером неоднозначности решения обратной задачи может
быть потенциал притяжения сферического слоя и шара, имеющих
постоянную или изменяющуюся вдоль радиуса плотность, при
условии равенства их массы. Как было показано в главе 1, поле
притяжения этих тел во внешнем пространстве зависит лишь от
их массы и расстояния притягиваемой точки до центра сферы.
В частности, в задаче для однородного шара при условии сохране-
ния его массы, т. е. произведения плотности па объем, можно
найти бесчисленное множество шаров различного радиуса и плот-
ности, создающих одинаковое гравитационное поле во внешнем
пространстве. Отсюда следует, что по внешнему гравитационному
полю определить раздельно радиус и плотность шара нельзя,
т. е. нельзя получить однозначное решение обратной задачи.
Уменьшить степень неоднозначности обратной задачи можно
только привлечением дополнительной информации относительно
гравитирующего тела или, что то же самое, наложением дополни-
тельных условий на формул или избыточную плотность тела.
Эти ограничения устанавливают исходя из реальной геолого-
геофизической обстановки района исследований. Большое значе-
ние при решении обратной задачи имеют сведения о плотности
пород исследуемого региона. Зная возможные пределы изменения
плотности, можно резко повысить степень однозначности решения
обратной задачи.
Для случая известной плотности П. С. Новиков доказал сле-
дующую теорему о единственности решения обратной задачи.
Пусть плотность о (Е, т), ?) — положительная функция, опре-
328
деленная во всех точках пространства; пусть полная вариация
этой функции по любой прямой не превосходит ее минимума.
Предположим, что имеются два объема, выпуклые относительно
некоторой внутренней общей точки и заполненные массами плот-
ностью о (Е, т], £). Тогда, если внешние гравитационные потен-
циалы масс одинаковы, то объемы этих масс совпадают. Однако
вопрос об определении формы этих объемов остается открытым.
В общем случае при решении обратной задачи не существует
методов, позволяющих определить все параметры возмущающего
тела без наложения дополнительных условий на его форму.
Можно найти только некоторые характеристики гравитирующего
тела, по которым нельзя установить однозначное распределение
аномальных масс. Такими характеристиками, вычисляемыми без
наложения дополнительных ограничений на форму и плотность
тела, являются гармонические моменты масс, которые описы-
ваются интегралами вида
Н?, Л, П, Qdv (fe-= 1, 2...2n-H),
V
где Fn<k — гармонический полином степени п.
При п = 0 имеем гармонический момент нулевого порядка,
равный массе тела М\
mOi j = М.
При п — I получаем гармонические моменты первого порядка,
равные произведению соответствующей координаты центра тя-
жести тела на массу тела:
™ы = £оМ; = т113 = Г„Л1.
В практике количественной интерпретации гравитационных
аномалий наложение дополнительных условий на форму возму-
щающего тела должно опираться на полный и всесторонний
анализ всех имеющихся геологических данных по району иссле-
дований. Такой анализ позволяет составить наиболее вероятную
упрощенную схему геологического строения, по которой будет
проводиться количественная интерпретация. Упрощать геологиче-
ское строение при количественной интерпретации приходится
неизбежно, поскольку применять математический аппарат можно
только при некоторой идеализации реальных структур. Эти упро-
щения иногда не соответствуют реальным условиям, но, как будет
показано ниже, не вносят существенных ошибок в окончательный
результат интерпретации.
Наиболее часто делают следующие допущения относительно
строения тел, создающих гравитационные аномалии.
Предполагают, что изучаемые геологические образования имеют
постоянную избыточную плотность относительно вмещающих
пород. В большинстве случаев это соответствует действительно-
329
сти, однако бывают ситуации, когда такое допущение может
быть сделано только с очень грубым приближением. Предполо-
жение о постоянной избыточной плотности существенно облегчает
решение задач количественной интерпретации.
Часто допускают, что геологические образования являются
телами двумерными, т. е. бесконечными по простиранию и име-
ющими постоянное поперечное сечение. Подобных тел в природе
не существует, однако это допущение не вносит больших ошибок
в интерпретацию и существенно упрощает вычисления.
При интерпретации аномалий вторых производных потенциала
силы тяжести в случае двумерной задачи нередко делают пред-
положение о бесконечной протяженности аномалиеобразующего
тела на глубину. Это допущение, также несоответствующее реаль-
ным условиям, приводит к упрощению вычислений, не создавая
в то же время больших погрешностей. Следует отметить, что для
аномалий силы тяжести такого допущения сделать нельзя, по-
скольку в этом случае аномалия силы тяжести обращается в беско-
нечность.
И наконец, предполагают, что тела, создающие гравитацион-
ные аномалии, имеют правильную геометрическую форму. Для
таких тел можно найти аналитическое выражение гравитационной
аномалии, связывающее параметры тела со значением аномалии
в некоторых характерных точках.
В общем случае при решении обратной задачи практически
находят не систему параметров, характеризующих распределение
аномальных масс, а некоторую совокупность параметров, которые
зависят от аналитических свойств функций, описывающих грави-
тационное поле этих масс. Такая совокупность определяет коорди-
наты особых точек поля, которые связаны с параметрами тела.
В принципе особые точки устанавливаются по полю однозначно,
однако полностью поля они не определяют.
Следует отметить еще одно важное обстоятельство. При реше-
нии обратной задачи очень часто делают допущение о правильной
форме тела, создающего гравитационную аномалию. В этом слу-
чае на основе решения обратной задачи определяют особые точки
геометрических особенностей тела, которые являются в то же время
особыми точками производных гравитационного потенциала. Для
тел, ограниченных поверхностями второго порядка, особые точки
располагаются внутри тела (для шара — в его центре, для эллип-
соида— в его фокусах). Для вычисления размеров тела, когда
его особые точки найдены, необходимо знать избыточную плот-
ность этого тела. Поэтому для таких тел обратная задача одно-
значна только при условии, что избыточная плотность тела из-
вестна.
Иначе обстоит дело, когда возмущающее тело ограничено си-
стемой плоскостей и его контур в разрезе представляет собой ло-
маную линию, состоящую из некоторого числа отрезков. В этом
случае точки излома, лежащие на контуре, являются теми геоме-
330
трическими особенностями тела, которые и определяют полностью
его форму. В то же время эти точки являются и особыми точками
производных гравитационного потенциала. Положение особых
точек находится однозначно и сразу же определяется и поверх-
ность гравитирующего тела. Для таких тел обратную задачу
принципиально можно решить однозначно, не задаваясь его из-
быточной плотностью.
Рассмотренная неоднозначность решения обратной задачи
связана со свойствами гравитационного поля и может быть умень-
шена только привлечением дополнительной информации относи-
тельно формы и плотности тела. В практике интерпретации грави-
тационных аномалий приходится иметь дело еще и с неоднознач-
ностью другого происхождения, которая возникает из-за того, что
интерпретируемая аномалия задана не в теоретически чистом
виде, непрерывно и абсолютно точно, а только на ограниченном
интервале, в дискретных точках с некоторой погрешностью наблю-
дений. Кроме того, аномалия мо?кет быть еще осложнена влиянием
посторонних факторов, например соседних тел, рельефа местности
и т. д. Однако эта неоднозначность может быть разрешена без
привлечения дополнительной информации относительно гравити-
рующего тела, а именно: повышением точности наблюдений, изме-
нением густоты сети, применением специальных методов для раз-
деления гравитационного эффекта разных тел и т. д.
При решении обратной задачи важно не только получить све-
дения о геологическом объекте, создающем гравитационные ано-
малии, но и оценить достоверность результатов интерпретации.
Достоверность решения обратной задачи может быть подтверж-
дена его устойчивостью. Решение обратной задачи считается устой-
чивым, когда бесконечно малому изменению размеров и формы
гравитирующего тела соответствуют бесконечно малые изменения
его гравитационного поля. Если гравитирующее тело характе-
ризуется несколькими геометрическими параметрами (глубина,
мощность, протяженность па глубину и т. д.), то понятие устой-
чивости целесообразно относить отдельно к каждому из параме-
тров. В большинстве случаев каждый из параметров при прочих
равных условиях определяется с разной степенью надежности,
а точность одних параметров влияет на точность других. Напри-
мер, глубину вертикального пласта можно установить значительно
точнее, чем его мощность и избыточную плотность, а положение
верхней кромки точнее, чем нижней. К этому следует добавить,
что форма тела определяется надежно, обратная задача устой-
чива только в том случае, если размеры тела достаточно велики по
сравнению с глубиной его залегания. В частности, возвращаясь
к примеру пласта, надо отметить, что его горизонтальную мощ-
ность можно найти достоверно только в том случае, когда глубина
верхней кромки пласта меньше его горизонтальной мощности.
Интерпретация наиболее надежна при благоприятном сочета-
нии геолого-геофизических условий и при наличии достоверной
331
дополнительной информации, что позволяет дать однозначное
решение обратной задачи. На основе геологической интерпрета-
ции гравитационных аномалий делают определенные выводы о гео-
логическом строении территории гравиметрических исследований,
строят тектонические карты, устанавливают положение отдельных
рудных тел и т. д. Но всегда надо иметь в виду, что полученные
из гравиметрических исследований выводы являются только
одним из возможных вариантов интерпретации, т. е. что они
носят условно-вероятностный характер, поскольку сделаны при
соблюдении некоторых условий, достоверность которых предпола-
гается. Эти ограничения накладываются на основе анализа всего
геолого-геофизического материала по району исследований.
Глава 14
ГРАВИТАЦИОННОЕ ПОЛЕ
ТЕЛ ПРАВИЛЬНОЙ ФОРМЫ
СПОСОБЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ТЕЛ
При определении параметров геологических объектов, созда-
ющих гравитационные аномалии, эти объекты часто уподобляют
телам, имеющим правильную форму. Поскольку тело правильной
формы описывается меньшим числом параметров, чем тело слож-
ной формы, то такая замена упрощает количественную интерпре-
тацию и в то же время позволяет довольно надежно оценить коли-
чественно некоторые характеристики реального геологического
тела. Естественно, что достоверность полученных результатов за-
висит от степени соответствия геологического объекта заменя-
ющему его телу правильной формы.
Параметры тела правильной формы можно найти аналитиче-
ским или графическим способом. Независимо от способа прежде
всего необходимо решить прямую задачу: получить аналитические
выражения для различных производных гравитационного потен-
циала, определяющие гравитационное действие тела.
Если любая производная гравитационного потенциала Un
выражена через параметры тела, то можно составить сколько
угодно уравнений общего вида для определения этих параметров:
'Ji, ?1, R, &>, 'lo. So. «. ₽> 7),
где Uni — значения производной гравитационного потенциала
в точках наблюдений с координатами xh yit zy, \R — параметр,
определяющий размеры тела; £(), т]0, to — координаты центра
тяжести тела; а, р, у — углы наклона тела относительно принятой
системы координат; i = 1, 2, 3, ..., т.
332
Решение этой системы уравнений практически определяется
тем, насколько уравнения независимы друг от друга. Очевидно,
что для вычисления всех параметров тела число уравнений должно
быть равно числу параметров. При прочих равных условиях
устойчивость определения параметров тела зависит от числа
параметров: чем оно меньше, тем устойчивее решение.
При аналитическом способе решения задачи исследуют выра-
жения различных производных гравитационного потенциала и
устанавливают связь некоторых характерных точек этих произ-
водных (точки максимума, минимума, перехода через нуль,
перегиба и т. д.) с параметрами тела.
При графическом способе на основе аналитических формул
строят атласы теоретических кривых, палеток производных грави-
тационного потенциала для данной формы тела при различных
его параметрах (глубина, размеры и т. д.). Сравнивая наблюден-
ную кривую с теоретической, подбирают такую теоретическую
кривую, которая наиболее близко совпадает с наблюденной, и тем
самым находят параметры тела.
Следует отметить, что для некоторых тел правильной формы
найти решение прямой задачи в элементарных функциях нельзя,
но его можно получить приближенно с любой степенью точности
и также построить палетки для интерпретации. Ниже рассмотрим
решение прямой и обратной задач для тел правильной простейшей
формы, для которых гравитационный эффект может быть выражен
в элементарных функциях.
МАТЕРИАЛЬНАЯ ТОЧКА, СФЕРА
Многие геологические объекты более или менее изометриче-
ской формы могут быть приближенно уподоблены сферической
массе. К таким объектам относятся рудные залежи гнездообразной
и штокообразной формы, солянокупольные структуры и т. д.
Степень соответствия тем выше, чем больше расстояние от тела
до притягиваемой точки.
Пусть имеется однородная сфе-
рическая масса с центром С, ле-
жащим в плоскости xOz (рис. 14.1).
Начало координат поместим в при-
тягиваемой точке, тогда коорди-
наты центра сферы
1=1, П = 0, S-й.
Массу сферы обозначим М.
Известно, что сферическое тело
однородной плотности притягивает
внешнюю точечную массу так же,
как притягивает ее материальная
Рис. 14.1. Кривые Uz, UX2, U2! и
1/д сферы.
333
точка, которая расположена в центре сферы и имеет массу, рав-
ную массе сферического тела. Поэтому формулы, выражающие
гравитационное действие сферы, могут быть получены непосред-
ственно из подынтегральных выражений (1.33), (1.34), если
вместо т], t, записать координаты центра сферы, а вместо dm
массу сферы. При этих условиях имеем
U2 (0, 0, 0) = Ag (0, 0, 0) = kM (h/i*); j
UK2 (0, 0, 0) = ЗШ (?й/гв);
U,z (0, 0, 0) = kM [(2/г2 - V)/r5l; ( (14.1)
2UX!/ (0, 0, 0) = (0, 0, 0) = 0;
Пд (0, 0, 0) = — 3kM (£2/r5), j
где r~ У с2-(-й2-
Для удобства дальнейшего анализа выведенных формул пере-
несем начало координат в точку проекции центра сферы на пло-
скость хОу, т. е. в точку с координатами (|, 0, 0). Так как х + Ё =
= 0, где х — координата точки наблюдения, то получаем
U, (х, 0, 0) — &.g (х, 0, 0) = kM (й/г3);
УХг (х, 0, 0) = — 3k М (хй/г5);
(х, 0, 0) = Uyz (х, 0, 0) = 0; ’ (14.2)
U(х, 0, 0) = kM [(2й2 - х2)/г6];
1/д(х, 0, 0) = — ЗйЛ4(х2/гБ),
где
Г — У X2 4- й2.
Исследуем вид кривых производных гравитационного потен-
циала. Рассмотрим сначала аномалию силы тяжести
Uz (х, 0, 0) = Ag (х, 0, 0) = kM (h/r3).
Кривая U2 всюду положительна, и JJг (—х) — Uz (х); при
№ ±ос функция U, — 0.
Из условия dUJdx == 0 получаем хшах — 0, т. е. максимум кри-
вой Uz располагается над центром сферы; максимальное значение
ПгП1ах = Ш/й2. (14.3)
Для определения неизвестных й и М поступим следующим
образом.
Обозначим через х„ абсциссу кривой U2, где U 2П —
Тогда
-7^- = п-----------------(14.4)
Рг max (Хда'й2 4 1 )Я‘ “
334
Таблица I4.t
Относительные значения U, сферы
п xnh Xnh п Xnh п Xnh
0,01 4,53 0,30 1,11 0,55 0,70 0,80 0,40
0,05 2,52 0,35 1,01 0,60 0,64 0,85 0,34
0,10 1 91 0,40 0,92 0,65 0,58 0,90 0,27
0,15 1,59 0,45 0,84 0,70 0,52 0,95 0,19
0,20 0,25 1,39 1,23 0,50 0,77 0,75 0,46 0,99 0,08
Примем xn/h = xnh, тогда, решив уравнение (14.4) относи-
тельно x„tl, получим
|/V(4)” -1 • (14-5’
В табл. 14.1 приведены значения х„,( для различных значе-
ний //.
В частности, при и 1/2 имеем хп/1 0,77, тогда х,/2 — 0,77/t
или h = 1,31х1/2.
Масса сферы
M~Uzm^lk. (14.6)
Значения 1/гтах и х1,2 находят по наблюденной кривой U г.
Если известна избыточная плотность о, можно определить
объем V и радиус сферы J?:
М = 1/о = (4/3) л/?3о.
Табл. 14.1 весьма удобна для вычисления Uz. В этом случае
находят Пгтах по формуле (14.3), определяют U2n=nUzmm и
вычисляют абсциссы хп, соответствующие каждому значению п,
по формуле
xn==xnhh. (14.7)
Для горизонтальной составляющей градиента силы тяжести UXi
имеем
UX2 (х, 0, 0) = - 3/?/И (д'/г/г6). (14.8)
Кривая ихг (х, 0, 0) положительна при х < 0 и отрицательна
при % > 0; 1/хг (—х) — — UX2 (+х); при х == О и х — ±оо функ-
ция UX2 — 0. Из условия dUxzldx = 0 получаем
= — Л/2; хш1п = 4- h/2. (14.9)
Расстояние между экстремумами
L ~ -'-’mln ' -'max = Й,
т. е. равно глубине центра сферы.
335
Рис. 14.2. Векторы б по линии наблюдений, не проходящей над центром
сферы.
Полагая в формуле (14.8) х ——h/2, находим
UXi max = 0,858 (kM/h3), (14.10)
откуда можно определить массу сферы М.
Формулы (14.9) верны для профиля, проходящего над центром
сферы, в этом случае
Uxz~G^l +
Если линия наблюдений не проходит над центром сферы, то
в общем случае Uуг (х, у, 0) 4 0 и векторы горизонтальной со-
ставляющей градиента силы тяжести пересекаются в начале
координат — в точке проекции центра сферы на плоскость хОу
(рис. 14.2). Это обстоятельство дает возможность определить ха-
рактер кривой вдоль профиля, проходящего над центром сферы,
если известны значения вдоль бокового профиля. В этом случае
для центрального профиля в качестве х необходимо брать расстоя-
ния от проекции центра до соответствующей точки наблюдения,
а для кривой 17хг использовать соответствующие значения полной
горизонтальной составляющей градиента.
Для вертикальной составляющей градиента силы тяжести
имеем
U„ (х, 0, 0) = кМ [(2/г3 - х2)/Д],
336
откуда следует, что кривая U„ (х, 0, 0) положительна при х2 < 2/i2
и отрицательна при х2 > 2/г2, а при х = хи~±/г[/'2 и при
х = ±оо функция Ua = 0.
Из условия dU2Jdx = 0 получаем
= 0; ™х = ZkM/h?,
хт]п = ± 2h; игг mln = - 0,036Ш7Р.
(14.Н)
По этим формулам определяют неизвестные /г и М.
Рассмотрим величину
1/д (х, о, 0) = — 3kMx2/rb. (14.12)
Функция //д всюду отрицательна, за исключением точки х —
— 0, где (7д = 0. При этом (—х) = [7Д (+ х). Исследование
уравнения на экстремум дает
^min — — I7 2/3; Uniin —
0.558АЛ1//Р,
что позволяет определить h и М.
Таким образом, решением обратной задачи для сферы можно
получить h (положение центра) и М (массу). Радиус сферы можно
найти только при известной избыточной плотности о.
вертикальный
МАТЕРИАЛЬНЫЙ СТЕРЖЕНЬ,
ВЕРТИКАЛЬНЫЙ КРУГОВОЙ ЦИЛИНДР
Геологические объекты, вертикальные размеры которых зна-
чительно больше горизонтальных, а последние малы по сравнению
с глубиной залегания, могут быть уподоблены вертикальному
круговому цилиндру или эквивалентному ему вертикальному
материальному стержню, расположенному на оси цилиндра и
имеющему такое же распределение массы на единицу длины, как
и цилиндр. Примером таких геологических объектов могут слу-
жить столбообразные рудные и интрузивные тела, соляные ку-
пола, кимберлитовые трубки и т. д.
Для вывода аналитических выражений гравитационного
эффекта материального стержня поместим начало координат
в точку проекции стержня на плоскость хОу, примем глубину
верхнего конца стержня равной hL, нижнего /г2, массу единицы
длины стержня dm = Л d£, где Л. — линейная плотность единицы
длины стержня. Рассмотрим поведение элементов гравитационного
поля вдоль профиля, проходящего над центром стержня (| =
337
= 1] = у = z 0). При этих условиях выражения (1.33), (1.34)
принимают вид
(7г(л-, 0, 0) = Ag(x, 0, 0)—
/?% [ = kk ( 1 — 1
hs
Uxz(x, О, 0) = —ЗЛА J
Ai
__ L Л I % % 1 .
[ (х2 4- й2)3/а (X2 4- А2)3/2 I ’
А 2
С 97-2 _ г2
Нгг(х, 0, 0) = а J А_2_ =
hi
= kk I--------------------““L
[(x3 + hl)3№ (x^+hl)3'2 J
(14.13)
где
При /г» -- оо, т. е. когда глубина нижнего конца стержня
значительно больше глубины верхнего, получим (приняв hx = h)
Uz(x, 0, 0) = Ag(x, 0, 0) = /А(х2 /г2)"1'2; '
UXi (х, 0,0)-= — klx (х2 — /г2)’3'2;
UZ2 (х, 0, 0) == kkh (х2 Ц- /гг)-3/2.
(14.14)
Обратная задача для материального вертикального стержня
по Uг (х, 0, 0) решается так же просто, как и для точечной массы.
Исследование кривой Uz показывает, что она всюду положительна
и имеет максимум при х = 0:
пих = kkjh.
Обозначив хп абсциссу, где значение Uzn составляет п-ю долю
от максимального (Uzn!Uz max = п), найдем
Введя обозначение х,г11г == xnh и решив уравнение (14.15)
относительно xnh, получим
xnh = V 1 — гР/п. (14.16)
В табл. 14.2 даны значения xnh для различных п при Л2 = оо.
Пользуясь табл. 14.2, определяем h = x,Jxnh, в частности
/г = X1/2/R 3.
338
'Таблица. 14.?
Относительные значения Uz вертикального стержня
п xnh п xnh п xnh п xnh
0,01 99,98 0,30 3,18 0,55 1,52 0,80 0,75
0,05 19,98 0,35 2,68 0,60 1,33 0,85 0,62
0,10 9,95 0,40 2,29 0,65 1,17 0,90 0,48
0,15 6,59 0,45 1,98 0,70 1,02 0,95 0,33
0,20 0,25 4,90 3,87 0,50 1,73 0,75 0,88 0,99 0,14
Кривая UX2 (х, 0, 0) положительна при х < 0 и отрицательна
при х > 0; при х = 0 и ±оо функция ихг (х, 0, 0) = 0. Исследова-
ние кривой на экстремум дает следующие значения:
А'п.ах = — (.h V 2)/2; Л'га1п = + (й V 2)/2; U хг тах = 0,38л//Г.
Приняв хш1п — хгоах = Л, получим L = /г|/2, что позволяет
вычислить h.
Если значения UХ2 известны по линии, не проходящей над
центром стержня, то они могут быть приведены к центральному
профилю с помощью преобразования, рассмотренного для сферы.
Сравнение выражений U2Z (х, 0, 0) для вертикального беско-
нечного материального стержня и Uz (х, 0, 0) для материальной
точки показывает, что эти формулы совпадают. Следовательно,
глубину h стержня можно определять по табл. 14.1.
ГОРИЗОНТАЛЬНЫЙ МАТЕРИАЛЬНЫЙ СТЕРЖЕНЬ,
ГОРИЗОНТАЛЬНЫЙ КРУГОВОЙ ЦИЛИНДР
Горизонтальному круговому цилиндру Можно уподобить гео-
логические структуры и тела, размеры которых по простиранию
значительно больше, чем вкрест простирания- антиклинальные и
синклинальные складки, линзообразные рудные залежи и др.
Гравитационное действие горизонтального цилиндра бесконеч-
ного простирания эквивалентно действию материального стержня,
расположенного на оси цилиндра и имеющего то же распределе-
ние массы на единицу длины. Формулы для горизонтального бес-
конечного материального стержня могут быть получены непо-
средственно из подынтегральных выражений (1.41) без интегри-
рования:
УДО, 0) = Ag’(0, 0) = 2/еХ-р-^-;
U,ДО, 0) — 4feX ;
ггЛ аа + й2)а (14.17)
1.2_£2 4 7
Уд (0.0) - У„(0, 0) = 2Н ;
Уед (0, 0) и,1г (0, 0) = о,
339
Где к — линейная плотность единицы длины материального
стержня; h — глубина стержня.
Эти формулы выражают также и действие бесконечного гори-
зонтального кругового цилиндра. В этом случае под X необходимо
понимать произведение объемной избыточной плотности цилиндра
на площадь его поперечного сечения:
X = nR2a,
где R — радиус цилиндра.
В природе все реальные геологические тела имеют конечные
размеры по простиранию. В практике интерпретации делают до-
пущение о бесконечном протирании тел. Поэтому, прежде чем
заниматься анализом формул (14.17) для бесконечного горизон-
тального стержня, необходимо оцепить, при каких параметрах
тела можно принимать его простирание бесконечным. Для этого
надо сравнить гравитационное действие конечного и бесконечного
по простиранию материальных стержней.
Найдем формулы для горизонтального стержня конечного про-
стирания. Пусть имеется материальный стержень длиной 2Ь
с линейной плотностью л, симметрично расположенный относи-
тельно плоскости хОг. Тогда из формул (1.33), (1.34) получим для
точки в начале координат
идо, о, 0) = щ = W11X
-ь
иХ2 (О, О, 0) = j 4г =
-ь
+ь
(0, 0, 0) = А-Z J dri =
иЛ(0, о, 0) = 3U j ^£=1*^ =
= 3U(/1$-(2^4-n
где
+ь
/ |+*__ f Дф_____________2&__________.
1 л3 ~ (?2 + е2) (12+ь2-н2)1/а ’
. 1+ь >" д>) _ 2 2^фЗ(^ + ^)&
H-b -J гъ + •
(14.18)
(14.19)
340
Учитывая значения (14.19) л принимая £ = 1г, получаем окон-
чательные выражения для стержня конечной длины:
иг((), о, 0) = 2^>А_А^);
ихг (0, 0, 0) = 2^ (ЗА (b) - f2 (6)];
игг (0, 0, 0) = 2^ + [(2Л2 - I2) А (Ь) - Й2А (£»)];
4/д (0, 0, 0) = 2/А -^-1— [- 3£2А (/>) + (2g2 + Л2) А (6)],
где
fl (6) = (£2 -|-й2 -|-А2)1/« ’ /з (b) = (|2+ft8 + fta)3/2 •
(14.20)
При Ь — ±оо значение A (b) ~f2 (b) = 1 и формулы (14.20)
переходят в (14.17).
Для оценки расхождений' в значениях U2, Uxz, Uzz, Uд при
замене стержня конечной длины бесконечным по простиранию
введем следующие величины:
Ez — 1 — £7гь/й/г „; I
^XZ — 1 ^AtZb/^AzoiJ |
Bzz = 1 UZZb/Uzzo°\
Вд — 1 й/дь/£/доо.
(14.21)
Индексом b показаны величины, относящиеся к конечному
стержню, индексом оо — к бесконечному.
Обозначив
(|/^ + /г2)/^ = р/& = Рь,
получим
А(й) = (1+р2)-’/2; А(&) = (1+р2ь)-3/2- (14-22)
В области наибольшей интенсивности аномалий можно поло-
жить рь < 1, тогда правые части равенств (14.22) можно пред-
ставить разложенными в ряд:
/.(&)= 1-4-рЯ-4^-;
А(й) = 1-4-ри4рь —
341
Ограничиваясь в разложении членами с pj и учитывая фор-
мулы (14.17), (14.20), получаем
Ег = 4-р2ь-4'^;
е«=4-^;
i (14.23)
= 1 - FT7VT 1(2Л2 - I2) /1 (Ь) - 11?Гг (&)];
ед = 1 —3^2Л (b) + (2F + ft2) Ш1-
Из этих формул следует, что погрешности, обусловленные
небесконечностью простирания стержня, для функций U2 и Uхг
имеют постоянные значения, а для Uгг и (7Д зависят от В и ft.
Этот вывод относится к отрезку профиля, для которого р* < 1.
Максимальные погрешности для U и 7/д имеем при 2 = 0 и
h/b = рь:
1 2 I 9 4
— — PHvPft1
3 2 15 4
ЬА — 2 Рь 8 Р*‘
(14.24)
Из формул (14.23) и (14.24) следует, что влияние конечного
простирания на различные производные неодинаково при задан-
ном значении рй, но с уменьшением рь это влияние резко убывает
(табл. 14.3).
Из табл. 14.3 видно, что наибольшее влияние конечное прости-
рание оказывает на Uд, наименьшее — на UXz. Поэтому при интер-
претации гравитационных аномалий двумерные модели геологи-
ческих объектов наиболее пригодны в случае, когда используются
горизонтальная Uxz и вертикальная U,, составляющие, а также
сила тяжести U2.
Проанализируем формулы, выражающие гравитационное дей-
ствие горизонтального бесконечного по простиранию материаль-
ного стержня (рис. 14.3). Перепишем формулы (14.17) для случая,
Таблица 14.3
Влияние конечного простирания тела на производные
гравитационного потенциала
РЬ еХ2 еА
0,5 0,15 0,02 0,05 0,20
0,3 0,04 0 0,04 0,12
0.2 0,02 0 0,02 0,06
0,1 0,01 0 0 0,01
342
когда начало координат располагается над его осью. Так как
х Ч~ | — 0, где х — координата точки наблюдения на оси х,
направленной вкрест простирания стержня, то
0) = Ag(x, о) = 2^^А_;
(X, 0) = - 4Н (гЛ\а)г ; (14.25)
игг (х, 0) = (х, 0) = 277 •
Рассмотрение формул начнем с LL. Кривая Uz всюду положи-
тельна, U2 (-f-x) — U (—х), при х = ± оо функция Uz = 0. При
х — 0 кривая Уг имеет максимальное значение
(/гВВ-Ш (14.26)
Обозначая хп абсциссы, где Uzll = имеем
й2 1
" “ х?( -|- й2 “ 4/й2 + 1 ’
(14.27)
Обозначив x„/h xnh и решив уравнение (14.27) относительно
xnh, получим
xnh = Р(1 — ч)/п. (14.28)
В табл. 14.4 приведены значения xnh для различных п. В част-
ности, отметим, что при п = 0,5 абсцисса х]/2 = 1г.
Формулы (14.26) и (14.28) определяют Л. и Л. Если известна
избыточная плотность о, то можно найти радиус цилиндра
R = Х/(по).
Горизонтальная составляю-
щая градиента U хг (х, 0) по-
ложительна при х < 0_н отри-
цательна при х^> 0, причем
(7Л.г (-х) =-7/хг (+х). При
х — 0 и ±оо функция Uхг = 0.
Исследование функции U хг
на экстремум дает следующие
соотношения:
Хщах = Р 5; xmin = /г.// 3.
Если L — расстояние между
точками максимума и мини-
мума Uxz, то /г = 0,87L.
Значение
^«тах.пип = ± 1,299/А (1//Г2),
(14.29)
Рис. 14.3. Кривые U?, Ux~ и U72 гори-
зонтального цилиндра.
343
Таблица 14.4
Относительные значения Иг горизонтального
стержня
п xnh 11 xnh п xnh п Xnh
0,01 9,35 0,25 1,73 0,50 1,00 0,75 0,58
0,05 4,36 0,30 1,53 0,55 0,90 0,80 0,50
0.10 3,00 0,35 1,36 0,60 0,82 0,85 0,42
0,15 2,38 0,40 1,22 0,65 0,74 0,90 0,33
0,20 2,00 0,45 1,11 0,70 0,66 0,95 0,99 0,23 0,10
откуда
X = 0,011/г2.
Поскольку кривые игг (х, 0) и (х, 0) для любого двумерного
тела совпадают, то в дальнейшем будем рассматривать только игг.
Вертикальная составляющая градиента
игг (х, 0) = 2/Д [(/д2 - х2)/(х2 + h2y\ (14.30)
положительна при |х| < h и отрицательна при |х| > h. При
|х| = h и ±<х> функция U22 = 0. Тогда
= h,
где х0 — абсцисса нулевого значения.
Исследование функции па экстремум показывает,
'''max = 0, Xmin = i II /З,
что
откуда
й = 0,58|хш1п|.
Экстремальные значения
^гтах = 2feW; U22 mln = - 0.25П//12. (14.31)
Составляя отношение UzvJUKmax — /г и решая полученное
уравнение относительно xtlh, находим
xnh = ]/’[|/8п+ Г-(2«+ l)]/(2'i). (14.32)
Значения xnh сведены в табл. 14.5 по аргументу п.
Таким образом, решение прямой задачи по U22, как и no U2,
сводится к вычислению максимального значения U22IUax. и абсцисс
долей максимального значения хп = hxnh.
344
Таблица 14.5
Относительные значения СД горизонтального
стержня
п Xnh п Xnh п xnh п xnh
—0,01 9,85 0,00 1,00 0,30 0,64 0,65 0,39
—0,05 4,09 0,01 0,98 0,35 0,60 0,70 0,35
—0,10 2,43 0,05 0,91 0,40 0,56 0,75 0,31
- 0,125 1,73 0,10 0,84 0,45 0,52 0,80 0,27
—0,10 1,33 0,15 0,78 0,50 0,49 0,85 0,23
—0,05 1,12 0,20 0,73 0,55 0,45 0,90 0,19
—0,01 1,02 0,25 0,68 0,60 0,42 0,95 0,99 0,13 0,06
ВЕРТИКАЛЬНАЯ
МАТЕРИАЛЬНАЯ ПОЛОСА,
вертикальный тонкий пласт
Геологическим аналогом вертикальной материальной полосы
могут служить различные крутопадающие линзообразные и жило-
образные тела при условии, что их горизонтальная мощность
значительно меньше вертикальной и глубины залегания (рис. 14.4).
Для вычисления элементов гравитационного поля вертикаль-
ной полосы в общих формулах (1.39), (1.40) надо положить erdg =
= р (р — поверхностная плотность полосы) и интегрирование
проводить только по переменной в пределах от до (Д и
й2 — глубина верхнего и нижнего конца полосы). Полагая, что
начало координат находится над вертикальной полосой, имеем
hz
U2(x, 0) = Ag (х, 0) = 2/гр j
ftt
^(А', 0) = — 4&р J (Д^3)а
= W ( х>- + Д2 — х2-рЛ2 )
0) -=2/;р J
= W ( Х2 -р Л2 Х2-РЛ1 )
(14.33)
345
Рис. 14.4. Кривые Uz, Uxz и Uzz вер-
тикальной материальной полосы.
При li2~* оо, т. е. когда вер-
тикальная полоса имеет беско-
нечное простирание на глубину,
обозначив /ц = h, получим
£7Ux,0) = -2^[x/(x*+ /?)]; 1
Uzz(x, 0)-2/гр[/г/(ха + /12)]. )
(14.34)
Функция Uz при Л2 -> оо то-
же стремится к бесконечности,
что указывает на сильную за-
висимость ее от глубины h2.
Обратимся к формуле для
аномалии силы тяжести:
Uz(x, 0) = 4g(x, 0)-
Аи1п[(хЧЖЛк1)1-
(14.35)
Функция Uг (х, 0) всюду
положительна и достигает мак-
симума в точке х — 0 (см.
рис. 14.4, а):
^,nax=2Apln(/i.A). (14.36)
Кривая Uz убывает с уве-
личением |х| и при X — ± ОО
обращается в нуль.
Для определения /гх и /г2
найдем абсциссы xi/г и х1/4,
гида'2 и ^гтах/4. Для ука-
где Uz соответственно составляет U
занных точек можно написать
In = k[i In или -у2-
*1/2 + ^2 .
*?/г+Л1 ’
4-/гр In Ф- = /гр In
2 г /ц f
*1/4 + ^2
*1/4 + М
/in
ИЛИ -р- -
hi
^/4+fej V
*1/4+Л1 '
(14.37)
Из этих равенств получаем
hihi =
Д/4 = /ц/г? Д (/ii -j— /12) Г hihi.
Вводя обозначение
/ll -|-Л2 = (-Ч/4 -|- Х1/2)'Х1/2 = 2т,
34G
используя свойства корней квадратного уравнения, находим
hi == т — У т' — x‘i/2;
/г2 = т Vт1 — х{/2.
(14.38)
Определив /гг и Л2, вычислим
Oz шах
1 ~ 2k In (h2/hi) '
Рассмотрим горизонтальную составляющую 1]хг (х, 0). Эта
кривая положительна при к < 0, отрицательна при х > 0 и имеет
экстремальные значения при
Xmax, min = + (1/|/б) +/^ + 12^2 - hl - hl
Найти аналитически по кривой Ux2 параметры вертикальной
полосы, ограниченной по падению на глубину, очень сложно.
Задача решается проще, если положить, что вертикальная полоса
бесконечна на глубину (см. рис. 14.4, б). Тогда
УЛг (х, 0) == — 2Ащ [х/(х2 4- /г2)]. (14.39)
Кривая Uxl (х, 0) в этом случае также положительна при х < 0
и отрицательна при х > 0; при х — 0 и ±оо функция Uxz = 0.
Исследование Uxz на экстремум дает
'•max, mln = — хг max “ k\k,/h.
По этим формулам находят /г и pi.
Кривая вертикальной составляющей градиента силы тяжести
(/„(«, 0) = 24,, (-4^ - -^) (14.40)
положительна при |х| <|х0| — Vhrh2 и отрицательна при
| х | > Vhih2. При х = ±х0 и ± оо функция игг = 0. Макси-
мальное значение функция U22 имеет при хгаах = 0, минимальные
ПРИ Mnin = ± Мг + (Лг + Л2)/М2:
игг max = 2^ ( 4- - -г) ; ™ = - W и, •
\ «г «2 / (Zix + й3) (J/ ht 4- V h2)
Параметры вертикальной полосы по кривой 11гг находят,
используя формулы, которые аналогичны уравнениям кривой U2.
Имея в виду, что х2 — hjh^, обозначаем
2щ = (xmin — Хо)Мо- (14.41)
347
Тогда
hi = /п — ]/"/н2 — Хо,
ha = т 4-V"tn1 — Хо!
Ц = max^O ! Ш Х(|^ .
(14.42)
Формула U2l (х, 0) для вертикальной полосы, бесконечной
на глубину, аналогична выражению U2 (14.25) для горизонталь-
ного цилиндра. Следовательно, для вычисления U22 вертикальной
полосы и определения ее параметров можно использовать выве-
денные ранее соотношения (14.26), (14.28) и табл, 14.4.
ГОРИЗОНТАЛЬНАЯ
МАТЕРИАЛЬНАЯ ПОЛОСА,
ГОРИЗОНТАЛЬНЫЙ ТОНКИЙ ПЛАСТ
Тонкие горизонтально залегающие пласты можно уподобить
материальной горизонтальной полосе с поверхностной плотностью
(.1 = ffd?.
Пусть на глубине h имеется горизонтальная материальная
полоса шириной 2d с поверхностной плотностью ц (рис. 14.5).
Начало координат расположим над серединой полосы и обозна-
чим через 0 угол, под которым видна полоса из точки наблюдения.
Тогда на основании формул (1.39), (1.40) можно записать
+л
U. (*, 0) = 4g (х, 0) = 2^г f =
-d
= 2/гр (arctg-Ц^ - arctg^=^-) =
= 2/гц (cp2 — <pi) — 2/ф6;
+d
UX2(x, 0) = 4M J [(g(i~yh2|a =
r L (x + d)2 + Л2 (x — d)a4-/i2
U (x о) — 2Ащ f ~ IS — *)21 rfs _
-d
(14.43)
~ 2^‘[ (X + с/)2 H-/Г2 (X —d)a+/sa ] •
Из формулы для U2 следует, что кривая силы тяжести всюду
положительна и при х = 0 имеет максимум. Обозначив через Ф
348
Рис. 14.5. Кривые Uz, Uхг и Vzz горизонтальной мате-
риальной полосы.
угол, под которым видна полоса из начала
лучим
координат, no-
^zmax = 2£рФ = 4кц arctg (d/h);
di = 2 arctg (d/h).
(14.44)
Найдем абсциссы jci/2 и Xi/4, где значение Uz соответственно
равно Utmm/2 и Uzmj4:
। *1/2 , xl/2~~d , d
arctg—--------- - arctg—у----= arctg — ;
, *1/4 —d . *1/4 —d 1 x d .
arctg ----------arctg = — arctg ;
отсюда
*1/2 = ± V№ d2‘,
*i/4 = (/i2 + d2) H- 2h У h2 + d2;
и тогда
h = (*i/4 — *i/2)/(2*i/2);
2d = 2 ]/" *1/2 -
U z шах
1 ~ 4k arctg (d//l) •
(14.45)
Величины 2d и h можно найти графически, без вычислений по
формулам (14.45). Физический смысл формулы (14.44) состоит
в том, что из точек xi/г и *i/4 полоса видна под углами соответ-
ственно Ф/2 и Ф/4 (рис. 14.6). Если из начала координат, как
из центра, провести окружность радиусом, равным *1/2, то концы
горизонтальной полосы будут лежать на этой окружности согласно
формуле (14.44), а сама окружность будет геометрическим местом
точек, из которых горизонтальная полоса видна под углом Ф/2.
Далее, если принять самую верхнюю точку Р окружности за центр
349
Рис. 14.6. Графический способ опреде-
ления параметров горизонтальной ма-
териальной полосы по кривой Uz.
При х = 0 и ±оо функция Uxz —
ные значения при
и из него провести новую
окружность с радиусом, равным
расстоянию от точки Р до точ-
ки xi/4, то эта окружность будет
геометрическим местом точек,
из которых полоса видна под
углом Ф/4. Точки пересечения
двух построенных окружнос-
тей определяют положение по-
лосы.
Анализ формулы (14.43),
определяющей значение Йдг, по-
казывает, что Uxz > 0 при
х < 0 и Uxz < 0 при х > 0.
0. Кривая ихг имеет экстремаль-
*пк.х, пип •= ± (1//3) /d2 - /Р + 2 l/ d* + d%3 + h*. (14.46)
Параметры тонкой горизонтальной полосы определяются в об-
щем случае громоздкими формулами. Решение задачи существенно
упрощается, если положить, что глубина залегания полосы зна-
чительно меньше ее ширины, т. е. d h. Тогда, разлагая выра-
жение (14.46) по степеням отношения h/d, получаем хтаХ1ГП1п ^±d.
Функция Uzz положительна при | х | < j/d2 + /г, а при
х | > J/d3 + h2 отрицательна и имеет минимум: в точках
хш1п = ± + h' I 2/i Kd3 + h2.
При х =.0
Uzz(0, 0) = 4/грт d/(d2 | h2).
При условии d > /г|/ 3 функция U2Z достигает максимума
в точках
xmax = ± da — 2h Уd2 -|- h2,
расположенных почти над краями горизонтальной полосы. При
х = х0 — ± У d2 + h2 и при х— ± оо значение Uzz — 0.
Параметры горизонтальной полосы по кривой LL. можно
найти, используя точки лу, хт1п и х = 0, которые дают необ-
ходимые уравнения:
h = (4m - 4)/(2х0); d = У^-h2; р = Uzz (0) x20/^k d). (14.47)
350
ГОРИЗОНТАЛЬНАЯ
МАТЕРИАЛЬНАЯ ПОЛУПЛОСКОСТЬ
Горизонтальная материальная полуплоскость может служить
аналогом сбросов небольшой амплитуды в горизонтально залега-
ющих слоях. Полагая поверхностную плотность р, материальной
полуплоскости равной о dg, глубину залегания равной h и по-
мещая начало координат над левой границей полуплоскости
(рис. 14.7), интегрируем выражение (1.39) по g в пределах от нуля
до бесконечности, получаем
оо
г (х. 0) = 2/фЙ j
о
= 2/гц + arctg-^) = 2Ащ0;
~ , (14.48)
(7лг(х, 0) — 4k[xh f г™—,а , L,a = 2/qi „ ;
» / Г J [(£ — x)2 г х24-Л2
0
U (А- _ 24ц( I — 2ku х
J [(£_х)а_рД2]2 Х2_|_Д2 ’
” 1
где 9 — угол между положительным направлением оси х и на-
правлением на левый край полуплоскости.
Для кривой U. имеем: при х = —оо Uz = 0; при х = 0 Uг =
-= л&и; при х = | оо Uzmax — 2лАц; U. (—х) | Vг (+х) = 2лЛр.
Составив, как и в предыдущих случаях, отношения
С/2П/(2лйр.)=п для различных п, получим xnll (табл. 14.6) по формуле
x„i, = tg[(n/2)(2« - 1)].
Пользуясь табл. 14.6, можно вычислить кривые U (х, 0) для
материальной полуплоскости, а также определить /г; в частности,
для п = 1/4 и п = 3/4 имеем
|х1/4| =х3/4=й. (14.49)
Функция 1/хг (х, 0) для горизонтальной полуплоскости ана-
логична функции Uz (х, 0) для
горизонтального цилиндра, по-
этому для определения h
можно пользоваться формулой
(14.27) и табл. 14.4.
Функция С1гг (х, 0) для го-
ризонтальной полуплоскости
аналогична функции Uгг (х, 0)
для вертикальной полосы, и по-
этому имеем
-^шах. mln = — И ~ ^гг шах^/^ •
Рис. 14.7. Кривая Uz горизонтальной
материальной полуплоскости.
351
Таблица 14.6
Относительные значения U2 горизонтальной
полуплоскости
n xnh n fyih n xnh n xnh
0,01 —31,67 0,30 —0,73 0,55 0,16 0,80 1,38
0,05 —6,31 0,35 —0,51 0,60 0,32 0,85 1,96
0,10 —3,08 0,40 —0,32 0,65 0,51 0,90 3,08
0,15 — 1,96 0,45 —0,16 0,70 0,73 0,95 6,31
0,20 0,25 — 1,38 — 1,00 0,50 0 0,75 1,00 0,99 31,67
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Многие геологические объекты могут быть аппроксимированы
телами, ограниченными плоскими гранями: горсто-грабеновые
структуры, отдельные рудные образования, тела горизонтального
или вертикального залегания и т. п. Наиболее общая форма
для такого рода тел — это прямоугольный параллелепипед. Гра-
витационное действие прямоугольного параллелепипеда представ-
ляет интерес и по другим причинам: из общей формулы можно
получить частные случаи, имеющие широкое применение на прак-
тике (вертикальный уступ, вертикальный пласт). Формулы для
прямоугольного параллелепипеда используются также для по-
строения разного рода палеток и диаграмм, по которым вычисляют
гравитационный эффект трехмерных и двумерных тел произволь-
ной формы.
Пусть имеется прямоугольный параллелепипед, ограниченный
плоскостями х — и §2, у = гц и Т)2, z = и (рис. 14.8),
Полагая начало координат в точке вычисления, из формул
(1.33), (1.34) получаем
t/ДО, 0, 0) = Ag(0, 0, 0)= — kc fg 1п(тЦ-2?) +
I zf* I ГИ I 5* X 1 I*2*
+ n(| + /?) + CarctgKJ|5i
идг(0, 0, 0) = ^[1п(11 + /?)]||::^:|;;
игг (О, О, 0) == - kaarctg-g- |j“’ ;
(0, 0, 0) = to (arctg > - arctg JL)
(14.50)
где
352
Для параллелепипеда с бесконеч-
ным простиранием по оси у из фор-
мул (1.41) получаем следующие вы-
ражения:
^г(0, 0) = Ag(0, 0) =
= ko [^1п(^ + Сг) +
+ 2£ arctg (Ш|^;
б/д.2(0, 0) =
= ka 1п(|2 + ^2) |^;
t/2Z(0, 0) =
= 2ka arctg (g/S) |^'£.
(14.51)
Рис. 14.8. Прямоугольный па-
раллелепипед.
После подстановки пределов имеем
-4- 2£г (arctg -|1- — arctg -Ь-) +
+ 2^ (arctg - arctg ;
и (0 0)-far In <^ + й)(^ + й)
' ми ’
U22 (0> 0) = 2^а (arctg --arctg у- Д
+ arctg у- — arctg .
(14.52)
Эти формулы являются исходными для построения палеток,
используемых при вычислении гравитационного действия двумер-
ных тел произвольного поперечного сечения.
ВЕРТИКАЛЬНЫЙ УСТУП
Вертикальным уступом называется тело бесконечного прости-
рания, ограниченное двумя горизонтальными и одной вертикаль-
ной плоскостью. Поперечное сечение вертикального уступа пред-
ставляет собой полубесконечную полосу со сторонами, парал-
лельными координатным осям х и г (рис. 14.9). Геологическими
аналогами вертикального уступа являются сбросы с крутым
падением плоскости сбрасывателя, вертикальные контакты интру-
зий и соляных куполов, некоторые формы подземного и подвод-
ного рельефа и т. д. Для вывода формул гравитационного дей-
ствия вертикального уступа воспользуемся уравнениями (14.51)
для прямоугольного параллелепипеда бесконечного простирания.
Обозначим через | горизонтальную координату края уступа,
12 В. С. Миронов 353
/ij и /г2 глубину верхней и нижней горизонтальных поверхностей,
ограничивающих уступ. Положив в уравнениях (14.51)
Е2 = оо, получим формулы для вычисления гравитационного
эффекта вертикального уступа:
Д2(0, 0) —Ag(0, 0) = йо[п£ — 2garctg(g/C) —
-BW+oib
нА.г(0,0)^toin(^ + ^)|;,;; (14-53)
Дг2(0, 0) = 2toarctg(^)|£°.
Перенеся начало координат в точку, расположенную над
краем уступа, т. е. в точку (|, 0), и подставив пределы, найдем
(х, 0) — Ag = ko Г л (й2 — hx) ф- 2ft2arctg -Д-
-2ft1arctg-^ + xln-$±|J;
^(Х, 0) —fea In :
Л -f- rii
игг (х, 0) = 2/го (arctg - arctg .
(14.54)
Анализ формулы Uz (х, 0) для вертикального уступа пока-
зывает, что
— оо Uz = 0;
0 — лкп (й2 — hj) — nkaH',
~г оо Uг = 2nka (й2 — hj) — 2nkoII.
(14.55)
при х =
Рис. 14.9. Кривые U2,
Uxz и Uzz вертикального
уступа.
Для симметричных точек
Uг (— х) ф- (+ х) = 2nkaH.
Сравнивая выражения (14.55) с (14.48),
видим, что кривые Uг (х, 0) для верти-
кального уступа и горизонтальной мате-
риальной полуплоскости однотипны, если
принять р = оН. Таким образом, ано-
малия силы тяжести вертикального уступа
может быть уподоблена с некоторым при-
ближением аномалии силы тяжести мате-
риальной полуплоскости при условии,
что глубина полуплоскости h = (Л2 --
-| hi)/2 и вся масса вертикального уступа
сконцентрирована на этой полуплоскости.
Оценим погрешность, вызванную такой
заменой. Для этого составим отношение
В := 1 гор. полупл/^z верт.уст* (14.56)
354
Очевидно, что относительная
погрешность зависит от соотноше-
ний x/h и H/h, причем чем боль-
ше H/h, тем больше и погрешность
при прочих равных условиях. Ам-
плитуда уступа Я может изменять-
ся от нуля до 2/i; при H=2hпогреш-
ность е максимальна (рис. 14.10).
Однако и в самом неблагоприят-
Рис. 14.10. Относительная погреш-
ность е аномалии силы тяжести
при замене вертикального уступа
горизонтальной материальной полу-
плоскостью.
ном случае, когда верхняя грань
вертикального уступа выходит на
поверхность (Я -= 2/i), при x/h =
— 0,25 погрешность от замены фор-
мулы (14.54) формулой (14.48) не
превышает 0,072; при Н = h максимальная погрешность не пре-
восходит 0,02. Следовательно, для определения глубины зале-
гания плоскости, расположенной посредине между верхней и
нижней гранями вертикального уступа, можно пользоваться фор-
мулой, выведенной для горизонтальной материальной полуплос-
кости. При решении прямой задачи для вертикального уступа во
многих случаях можно обращаться к табл. 14.6.
Полученные выводы справедливы только для кривой Uz,
а для кривых U Х2 и Vгг используются совершенно другие приемы
интерпретации.
Формула Uxz для вертикального уступа аналогична формуле LL
для вертикальной материальной полосы, если в последней заме-
нить р, на о. Таким образом, имея кривую t/w параметры верти-
кального уступа можно вычислить по формулам
/ii = tn — т2 — хуг;
Ь т -|- ]/Гт2 — Х]/2;
__ Crz max
2 k In (hi/h1') ’
(14.57)
где
m = (Xl/4 — xi/z)/(2xi/2);
xi/2 и Xi/4 — абсциссы точек наблюдений, в которых функция Uх
достигает значений соответственно 7/ДгП1ах/2 и t/X2raax/4.
Если избыточная плотность о известна, то глубины hr и /г2
можно найти, не прибегая к определению абсциссы Хщ. Поскольку
Uxz max — 2ka In (Mb) И hfa == X1/2,
то, обозначив exp max /(2Ao) 1 — В, получим
hi = Xi/j// B; hi. = a'i/2 V B,
12
355
Рис. 14.11. Номограмма Храмова для вычисления функции И хг
вертикального уступа.
Для вычисления аномалий вертикального уступа Д. Н. Хра-
мов предложил номограмму (рис, 14.11). Для построения номо-
граммы в исходную формулу введены обозначения £ = /г2//гх
и £ = xlht, тогда
Ujo = k In [(g2 + £2)/(g2 + 1)|. (14.58)
Для вычисления UXi по заданным значениям hlt h2 и х опре-
деляем t, и § и находим их на соответствующих крайних шкалах
номограммы. Проводим через эти две точки прямую и в пересе-
чении ее со средней шкалой G снимаем отношение Uхг/о. Умножив
его на заданную плотность о, получим значение U хг.
Рассмотрим функцию Uгг (х, 0), определяемую уравнением
1)2г (х, 0) = 24ю [arctg (й2/х) — arctg (/ix/x)] =
— 24о (<р2 — ср,) = 2/шО,
(14.59)
356
где 0 — угол под которым из точки наблюдения видна вертикаль-
ная грань уступа.
При х = 0 и ± оо функция U22 = 0, при х > 0 значения U22
положительны, при х < 0 — отрицательны (см. рис. 14.9). Абс-
циссы экстремальных значений
-''max = + /Ma! *rain = — (14.60)
и функция
^aamax = [arctg hjhx — arctg /MlJ =
= 2A'O arctg [(/i2 — Л1)/(2хши)]. (14.61)
Если плотность о известна, то, введя обозначение
tg[C/„n,ax/(2^)] = A (14.62)
из уравнений (14.60), (14:61) получим
/lj " хта\ (|/ Л2 — 1 — А); I
1 , _______ (14.63)
Й2 = хгаах(|/Л2- 1 + Л). j
При неизвестном значении о, чтобы определить hlt h2 и о,
необходимо иметь еще одно уравнение. Для этого найдем абсциссу
%!/2, При которой U22 = U22 тах/2 (используем точку I Xi/21 < | Хгаах I).
Решая систему (14.63), получаем
Й2 — Л1 = (l/Xl/г) "|/"(Д/2 — •’max) (-*Г/2 "ф 'Тпах — ^х\ /2хтзг.) •
Введем обозначение
Л, + (-й1) = 2/п;
поскольку h2 (—Й1) = —х?пах,
ней квадратного уравнения,
Г. 2 , 3
Ш -|-Хтах,
hi = — т-\-У т + Хтах
В этом случае и й2 можно
найти также путем простых
геометрических построений
(рис. 14.12). Введем обозначе-
ния: 6гаах — угол 0 в точке zmax;
01/2 и 0[/2 —угол соответственно
в точках Xj/2 и х'\/2, Х1/2 — точ-
ка, лежащая вправо от хтах, в
которой U22 — U22 max/2. Оче-
видно, ЧТО 0[/2 = 01/2 = Ощах/2.
Построим окружность Оь яв-
ляющуюся геометрическим мес-
то, используя свойства кор-
получаем
Рис. 14.12. Графический способ опре-
деления параметров вертикального
уступа по кривой U22.
357
том точек, из которых вертикальная грань уступа видна под углом
0111ах, и окружность О2 геометрическое место точек, из которых
эта грань видна под углом 0|/2- Очевидно, что при к > 0 имеется
только одна точка, которой соответствует угол 0тах, это точка лП1ах.
Поэтому окружность Ох касается оси х в этой точке, а следова-
тельно, центр окружности лежит на перпендикуляре к оси х
в точке хгаах. Ясно, что точки х1/2 и х[/г находятся на концах
хорды окружности 02. Центр этой окружности лежит на перпен-
дикуляре к оси х в точке х0 = (.vj/2 + х[/2)/2. Окружность (?i
касается этого перпендикуляра в центре окружности (Э2, по-
скольку из точки 0.2 вертикальная грань уступа видна под углом
0гаах. Итак, прямая х — Л'п,ах проходит через центр окружности О,,
а параллельная ей прямая х = х0 = (-V1/2 + а[/2)/2 касается окруж-
ности Oj. Отсюда следует, что радиус (ц окружности равен
Таким образом, чтобы построить окружность Ох, надо восста-
новить перпендикуляр к оси х в точке xmax, отложить на нем отре-
зок, равный (xi/2 + х'\/2)/2 — хтах, и из полученной точки
как из центра провести окружность радиусом рх. Точки пересе-
чения этой окружности с перпендикуляром к оси х в начале коорди-
нат определяют положение вертикальной грани уступа. Когда
глубины hx и /г3 найдены, вычисляем плотность и по формуле
(14.61).
НАКЛОННЫЙ УСТУП
Наклонным уступом называется тело бесконечного простира-
ния, ограниченное двумя горизонтальными и одной наклонной
плоскостью (рис. 14.13). Геологическими аналогами наклонного
уступа являются наклонные сбросы, контакты интрузий и т. п.
Аналитические выражения гравитационного действия наклон-
ного уступа можно получить из формул (14.48) для горизонтальной
материальной полуплоскости. Расположим начало координат
в точке наблюдения, обозначим £ — точку пересечения боковой
грани уступа с осью х; а — угол наклона боковой грани. Дей-
ствие наклонного уступа можно рассматривать как сумму дей-
ствий материальных полуплоскостей, расположенных на глубине £,
имеющих поверхностную плотность и = ст dt, и координаты край-
ней точки g — С ctg а. Тогда, используя формулы (14.48), можно
написать
t/ДО, 0) = Д§(0, 0)=2£п j —arctg
ht
h,
(0, 0) = 2ka f ;
г v J (5 — £ Ctg a)2 + £2
ht
(14.64)
h2
u (0, 0) - — 2ko [ 31 z.? у “> ,
" ' 1 1 J (g —^ctgaP-H2
358
После интегрирования находим
и2 (0, 0) = 2ka - arctg g~|ctga) -
__ g sin a ]n _ 2^ sin a cos a — ga sin2 _
T- „„„ , t—gcosa sm al p2 .
— g sin a cos a arctg -—° . „-- ;
ь b g sm2 a J |л,
Uxz (0, 0) — ko | sin2 a In (Д — 2g£ cos asina-j-
, 1-9 9 x । o x 5—E cos a sin al pa .
+ g sin2 a) 4- sin 2 a arctg ----J ;
U2Z (0, 0) = ka | -i- sin 2a In (g2 — 2gg cos asina-|-
,5-9,9\ 0,9 j E — Ё cos a sin al P'1
+ g2sin2a) - 2 sin2 a arctg | sjn-2--j .
(14.65)
Формулы (14.65) довольно сложны, что затрудняет разработку
аналитических методов интерпретации. Для решения прямой
задачи эти формулы можно преобразовать следующим образом.
Введем полярные координаты р и ф, связанные с прямоугольными
координатами соотношениями
g — gctga = pcos <р;
g = psin ф;
p2 = (g —£ctga)2 + £2 =
E2—2grCosa sin a-j-g8 sin2a
sin2 a
(14.66)
Обозначив pj, q>j и p2, ф2 полярные координаты верхнего и
нижнего углов уступа, из выражения (14.65) получим
(/ДО, 0) = ka [2 (/г,ф2 — Я^ф) —
— g [2 sin2 a In (p2/pj) + sin 2a • (ф2 — <Pj)] I;
Uxz(0, 0) = ko [2 sin2 a In (p2/pi) Д- sin 2a-(ф2 — q^)]; (
(/„ (0, 0) = ko [sin 2a In (p2/pi) - 2 sin2a-(tp2 — cpj], |
(14.67)
Формулы (14.67) достаточно прос-
ты и удобны для вычислений грави-
тационного эффекта наклонного усту-
па. Расстояния р и углы ф можно
измерить непосредственно по чертежу
уступа или построить специальную
палетку для вычисления величин
г = In (p2/pj) и 0 = ф2 — фр Сущ-
ность этой палетки сводится к опре-
делению геометрического места точек,
Рис. 14.13. Наклонный уступ.
359
лежит в середине отрезка, а точка Р
ния (рис. 14.14). Так как
Рис. 14.14. К построению
палетки для определения
г и 0.
у которых одна из вели*
чин (г или 0) для некото-
рого отрезка прямой по-
стоянна.
Пусть имеется отрезок
прямой длиной 2d на оси х,
причем начало координат
является точкой наблюде-
<р2 = arcctg [(х + d)/z];
<Pi = arcctg [(х — d)/z],
ТО
0 = (Ра _ (₽i = arcctg (х2 LTrff — (14-68)
Для г = In (p2/pj) имеем
r = _l_ |П (*+ <*>» +<
2 (x-dp-рг2 ’
откуда
l/~(x + <0* + г»
К (х —d)3 + z2‘
Поскольку
cth г = (е' -ф- е-Г)/(еГ — е~г),
то
ethr = ^±^. (14.69)
Уравнения (14.68) и (14.69) можно записать в следующем виде:
х2-|- г2 ф- 2dzctg0 — d2 = 0; 1
x2-\-z2-2dzcihd-pd2 = 0. ) (14.70)
Эти формулы являются уравнениями окружностей. Коорди-
наты их центров и радиусы:
Е0 = О; lr = dcthr;
£0 = - dctgO; Сг = О;
p9 = d/l+ctg20 = ±-^; Pr = d/cth2r-l = ±-^-.
(14.71)
360
Таблица 14.7
Координаты центров и радиусы окружностей палетки г, 0
r, e Pr So P0
0,1 10,033 9,983 9,966 10,016
0.2 5,066 4,967 4,933 5,033
0,3 3,432 3,284 3,232 3,384
0.4 2,632 2,434 2,365 2,568
0,5 2,164 1,919 1,831 2,086
0,6 1,862 1,571 1,431 1,771
0,7 1,654 1,318 1,187 1,552
0,8 1,506 1,126 0,971 1,394
09 1,396 0,974 0,793 1,276
1,0 1,313 0,851 0,642 1,188
1,1 1,249 0,748 0,509 1,122
1.2 1,199 0,662 0,389 1,073
1,3 1,161 0,589 0,277 1,038
1,4 1,129 0,525 0,172 1,015
1,5 1,105 0,469 0,071 1,002
1,6 1,085 0,421 —0.029 1,001
1,7 1,069 0,378 —0,130 1,008
1,8 1,056 0,340 —0,233 1,027
1,9 1,046 0,306 —0,341 1,056
2,0 1,037 0,275 —0,457 1,100
2,1 1,030 0,248 —0,585 1,158
2,2 1,025 0,224 —0,728 1,237
2,3 1,020 0,202 —0,893 1,341
2,4 1,016 0,183 — 1,096 1,480
2,5 1,013 0,165 — 1,338 1,671
2,6 1,011 0,149 — 1,662 1,940
2.7 1,009 0,135 —2,115 2,340
2,8 1,007 0,122 —2,812 2,985
29 1,006 0,110 —4,058 4,179
В табл. 14.7 приведены значения рг, £е и ре при d = 1. На
основе этой таблицы строят палетку г и 0 (рис. 14.15). Вычисления
по палетке осуществляют следующим образом. На кальке строят
разрез тела в таком масштабе, чтобы конечная сторона уступа
была равна длине линии 2d палетки. На профиле наблюдений
отмечают точки, в которых необходимо вычислить значения г
и 0. Совмещая конечную сторону уступа с линией 2d палетки,
в точках на профиле снимают с палетки отсчеты г и 0.
Эта палетка может быть использована для вычисления грави-
тационного эффекта тел, в аналитических выражениях для кото-
рых содержатся In (Ра/Р1) и (<р2 — фц).
Для случая вертикального уступа (при а = л/2) формулы
(14.67) приобретают вид
Uz (0, 0) = Ag (0, 0) = 2ko [02<р2 - /ijcpj) - g In (Pa/pJJ; 1
U.k (°. 0) = 2^or In (p2/P1); (14.72)
(0. 0) = — (ф? - CP1). I
361
Как уже отмечалось, простые и удобные аналитические спо-
собы определения параметров наклонного уступа по аномалиям
U. ие разработаны. Поэтому ограничимся рассмотрением только
общего характера кривых U2 наклонного уступа и их сопоставле-
нием с кривыми вертикального уступа. Если перенести начало
координат в точку пересечения наклонной грани с осью х, то
в формулах (14.65) и (14.72) следует —£ заменять на х.
Для наклонного уступа так же, как и для вертикального, при
х = —g = — оо функция иг — 0, при х — —g = ф-оо значе-
ние Uz — 2^ko (h2 — hj). Но при х = 0, т. е. в точке пересе-
чения боковой грани с осью х, имеем
иг (0) = 2/гст (л — a) (/t2 — Л,).
Таким образом,
при а < л/2 (0) '_> л/ю (/г2 — /ij;
при а > л/2 1)г (0) < л/?а (h, — hj.
362
Угол наклона а заметно влияет на форму кривой только тогда,
когда амплитуда уступа h2 — велика по сравнению с глубиной
hA. Во многих случаях аномалии, обусловленные наклонным усту-
пом, можно рассматривать как созданные действием вертикаль-
ного уступа.
Следует отметить, что по кривой U2 для уступа с углом а
можно легко получить ту же кривую для уступа с углом л—а.
Действительно, два этих уступа образуют бесконечный плоский
слой, аномалия силы тяжести которого равна 2itko (h2 — АД
Поскольку изменение направления простирания уступа равно-
сильно перемене знака координаты х или t в формулах (14.65),
то можно написать следующее соотношение:
U. (х, л — а) == 2лАа (А2 — /гх) — U2 ( х, а),
которое и позволяет построить кривую Uz уступа с углом л—а,
если известна кривая Uz уступа с углом а < л/2.
Простого и удобного решения задачи, которое давало бы
возможность определить параметры наклонного уступа по
каждой из кривых Uxz или U 22, не получено. Предложен метод,
основанный на одновременном использовании кривых U х,
и U„.
Прежде всего проанализируем поведение кривых U Х2 и U 21
над наклонным уступом (рис. 14.16). Для этого формулы (14.67)
перепишем в декартовой системе координат, поместив ее начало
в точке проекции середины наклонной стороны уступа на ось у;
Рис. 14.16. Кривые Uxz и Чгг наклонного уступа.
363
глубину середины наклонной грани обозначим h, а ее длину 2d.
Тогда координаты верхнего и нижнего углов уступа
Г =d cos a; I = —d cos a;
[ = h — d sin a; [ = h -f- d sin a;
p2 = x2 4- ft2 d2 — 2d (x cos a 4- ft sin a);
pl = x2 -|- ft2 + d2 2d (x cos a 4- h sin a);
cp2 — Ф1 = arctg [(ft — d sin a)/(x — d cos a)] —
— arctg [(ft 4- d sin a)/(x 4- d cos a)].
При этом формулы (14.67) принимают вид
(х, 0) = 2/га sin a sin а х
। х2 4 Л2 + d2 + 2d (хcos а Т /1 sin g.)
П х2 4- ft2 + <i2 — 2d (х cos а 4- Л sin а)
. / , h— d sin а , ft 4-d sin а \ 4
4- cos a ( arctg---з----------------------arctg —---
1 \ bx — d cos a b x -j- d cos a I J
Г 1 (14.73)
(x, 0) = 2fto sin а — cos a x
. x2 4- Л2 + d2 4- 2d (x cos a -ph sin a)
П x2 + ft2 4- d2 — 2d (x cos а 4- ft sin a)
/ , ft —d sin a , ft 4- d sin a \ 4
— sin a ( arctg------3---------arctg —.
\ a x — a cos a b x 4- d cos a / J
Кривая U„ при заданной на рис. 14.16 ориентировке оси х
относительно простирания уступа всюду положительна. Более
пологая ветвь этой кривой располагается в направлении падения
боковой грани.
Из условия dUxJdx = 0 получаем экстремум t/vzmax при
xm0X = (d? sin 2a)/(2ft). (14.74)
Кривая игг также асимметрична, ее более пологий экстремум
расположен в направлении падения уступа. Экстремальные зна-
чения кривой отмечаются при
*П№, П11П = ± /ft2+ d2COS 2а. (14.75)
Из этой формулы следует, что экстремальные точки кривой 1)гг
расположены симметрично относительно начала координат. Это
позволяет определять положение проекции середины наклонной
грани уступа (начало координат) как середину отрезка хтах—xmln.
Подставим значения хяих и xmln в уравнение и сложим эти
364
два результата, подставим также хтах для кривой UX2 в выраже-
ние игг, в итоге получим
^22 max + ^аг mln = ^гг Уихг max)'
Таким образом, имея кривую UZ2, можно получить абсциссу,
при которой значение UX2 максимально, как координату точки,
где значение U22 равно сумме U22mxx и У2гга1п.
Уравнения (14.74) и (14.75) связывают три неизвестных пара-
метра. Составить еще одно простое уравнение, выражающее пара-
метры наклонного уступа через характерные точки кривых U Х2
и U22, не удается. Для решения обратной задачи можно исполь-
зовать следующий прием. Кривые UХ2 и U22 могут быть представ-
лены в виде
Uxz (х, 0) = 2/«> sin a [sin а • L (х) + cos а • А (х)[;
IJ22 (х, 0) = 2Л<т sin а [cos а • L (х) — sin а • А (х)],
(14.76)
где
L (х) = 1п (р^/р{); А (х) = tp2 - <рг
Введем полный градиент
С (х, 0) = |/иХг (х, 0) 4- 1Ргг (х, 0) = 2/го sin а • УL1 (х) Д- А2 (х),
тогда
2k<3 sin а • А (х) = G (х, 0) sin б (х);
2ko sin а -L (х) = G (х, 0) cos б (х);
6 (х) = arctg [4 (x)/L (х)[.
Из системы (14.76) получаем
(-5 0) = G (х, 0) sin [а + 6 (х)]; 1
U„ (х, 0) = G (х, 0) cos [а + 6 (x)J. J
(14.77)
(14.78)
Если теперь функции UX2 (х, 0) и U22 (х, 0) рассматривать
соответственно как ординату и абсциссу прямоугольной системы
координат U22, О, IJX2, то выражения (14.78) явятся параметриче-
скими уравнениями, которые определяют некоторую кривую,
симметричную относительно прямой, образующей угол а с осью
абсцисс U22. Таким образом, построив кривые L/22 (х, 0) и UX2 (х, 0)
в координатной системе U22 — абсцисса, UX2 — ордината, по
наклону оси симметрии полученной кривой к оси U22 определим
угол падения а наклонного уступа (рис. 14.17). Зная угол а
и используя уравнения (14.74), (14.75), находим параметры 2d
и h. Для определения 2d и h можно обратиться к графическому
способу.
365
Рис. 14.17. Определение угла падения наклонного уступа.
Умножая первое из уравнений (14.76) на sin и и второе на
cos а и складывая их, получаем
Uхг (х, 0) sin a J- U22 (х, 0) cos а
— 2/го sina«L(x) = G(x, 0)cos6(x). (14.79)
Затем, умножая первое из уравнений на cos а и второе на
sin а и вычитая, имеем
UX2 (М 0) cos а — U(х, 0) sin а =
== 2to sin а • Л (х) == G (х, 0)sin6(x). (14.80)
Сравнивая формулы (14.78) с уравнениями (14.79) и (14.80),
убеждаемся, что последние выражения определяют ту же кривую,
что и формулы (14.78), но в системе координат <72г1, О, Uxzl,
повернутой относительно исходной системы U22, О, ИХ2 на угол а:
U22 j = U22 cos а -ф- UX2 sin а;
U,2 i — —U2, sin а 4- U,2cos а.
Пересечение оси U221 с кривой определяет на профиле
точку хд0, где А (х) = 0. Пересечение оси Пхг1 с кривой определяет
точку Xl„, где L (х) = 0. Максимальная ордината UX21 указы-
вает точку Х/гаах, в которой функция А (х) имеет максимальное
значение, а ордината UX2l!2 указывает точки хЛ1/2 и Хд1/2, где
А (х) = АтЯ1С/2.
366
Рис. 14.18. Графический
способ определения пара-
метров наклонного уступа.
Используя перечисленные точки, можно определить положе-
ние наклонной стороны уступа графически. Построим окружность,
являющуюся геометрическим местом точек, из которых наклонная
сторона уступа видна под максимальным углом Л1Пах (рис. 14.18).
Поскольку на оси х есть только одна точка, принадлежащая этой
окружности, — точка Хдтах, то центр этой окружности должен
лежать па перпендикуляре к оси х, проходящем через точку
Хдшах. Далее> прямая, проведенная через точку Xl, под углом
л/2 — а к оси х, является перпендикуляром к наклонной стороне
уступа в ее середине [это следует из физического смысла функции
L (х) ]. Следовательно, центр С искомой окружности лежит па пе-
ресечении перпендикуляра к оси х в точке Хд и прямой, про-
ходящей через точку Х£о; радиус этой окружности равен хАтя*С.
Прямая, проведенная через точку л'д, под углом л — а к оси х,
определит положение наклонной стороны уступа как хорду MN
окружности.
Для большей достоверности графического решения можно
использовать ТОЧКИ Хд)/2 и Хд, Построим окружность, являю-
щуюся геометрическим местом точек, из которых наклонная
сторона уступа видна под углом Хщах/2. Поскольку на профиле этих
точек две, то центр окружности лежит па пересечении перпен-
дикуляра к оси х в точке х0, являющейся серединой отрезка
ха\12^'аХ1^ и прямой, проходящей через точку xl„, или, что то
же самое, на пересечении указанной прямой и окружности с цен-
тром С. Принимая точку С, за центр и расстояние хЛ1/2Сх за ра-
диус, строим вторую окружность, которая тоже определит
хорду MN.
При интерпретации кривых UX2 и Игг в случае наклонного
уступа используют разного рода палеточные методы, поскольку
эти функции удобны для расчета теоретических кривых. Дело
в том, что кривые (7лг и Uгг при заданных значениях а, а и /г3//г|
можно представить в виде функции одного параметра x/hi — от-
ношения расстояния от точки наблюдения до точки пересечения
наклонного ребра уступа с осью х к глубине верхней плоскости
уступа. Обычно кривые (Д2 и Uгг рассчитывают для углов а <
< л/2. Используя эти кривые, можно построить функции 17хг
367
и U22 для углов л — а. Подставляя в формулы (14.73) значение
л — а, получаем
U„(±x, a) = UXz(+x, п-а)‘, 1
Угг(±х,а) = -П2г(+х, л-а). J U4'bIJ
Таким образом, чтобы от угла а перейти к углу л — а, для
кривой L/Xz достаточно построить ее зеркальное отображение
относительно вертикальной прямой, проходящей через начало
координат; для кривой Uzz кроме зеркального отображения от-
носительно вертикальной прямой необходимо еще и поменять
знак или, что то же самое, построить ее зеркальное отображение
и относительно оси х. Если же одновременно меняется простира-
ние уступа относительно оси х, то для кривой Uxz необходимо еще
поменять и знак (построить ее зеркальное отображение и от-
носительно оси х); для кривой Uzz в этом случае следует только
изменить знак, т. е. построить ее зеркальное отображение отно-
сительно оси X.
Сравнение кривых при различных углах а показывает, что
они заметно различаются только при достаточно больших отно-
шениях Wft], характеризующих вертикальную мощность уступа.
При < 3 кривые остаются практически одинаковыми даже
при значительных изменениях угла а. Отсюда следует, что
при малой мощности уступа (/i2//i1 < 3) определить угол
наклона боковой грани невозможно. С другой стороны, в этом
случае можно пользоваться формулами для вертикального усту-
па и находить по ним глубины й2 и hx раздельно. При уг-
лах а, близких к 90° (а > 50°), кривые Uxz и Uzz наклонного
уступа мало отличаются от соответствующих кривых вертикаль-
ного уступа даже при большой вертикальной мощности [hjhx >
>(5-И0)]. При повышении значений h2/hi и уменьшении
угла а наклон боковой грани начинает заметно сказываться
на форме кривых Uxz и UZ2, вызывая их асимметрию отно-
сительно начала координат, снижая абсолютное значение мак-
симума UXz и увеличивая максимум Uzz.
о Л Пользуясь атласом теоре-
' "" тических кривых UX2 и Uzz
-— наклонного уступа, можно
построить соответствующие
/________________________кривые для любых призм
/ / (рис. 14.19). Такими призма-
/ / ми с достаточной степенью
/ / точности аппроксимируются
Z—\ -----тела произвольной формы,
, а также геологические струк-
Рис. 14.19. Призма, полученная ком- туры типа антиклинален и
бинацией наклонных уступов. синклиналей.
368
НАКЛОННЫЙ СЛОЙ
Наклонным слоем называется тело бесконечного простирания,
ограниченное двумя параллельными наклонными полуплоско-
стями и соединяющей их наклонной гранью (рис. 14.20). Таким
образом, рассмотренные выше вертикальный и наклонный уступы
являются частными случаями наклонного слоя, когда его верхняя
и нижняя грани параллельны оси х.
Пусть начало координат находится в точке наблюдений, а па-
раллельные (боковые) грани слоя составляют с осью х угол Ф.
Введем вспомогательную систему координат х1у1г1 с началом в
точке наблюдений, повернутую на угол Ф относительно исходной
системы хуг. Очевидно, что ось хг параллельна боковым сторонам
слоя, который в этой системе представляется как наклонный
уступ.
Таким образом, в новой системе координат элементы гравита-
ционного поля вычисляются по формулам (14.67) для наклонного
уступа:
(0, 0) = ku (2 [(й2)1 (гр,), - (й1)1 (tri)J -
— [2 sin2 a-In (p2/pi) + sin 2а -9]};
Uxtl (0. 0) = kc [2 sin2 а • In (p2/pi) 4~ Ein 2а • 0];
игг1 (0, 0) = ka [sin 2а- In (p2/pi) — 2sin2 a-0],
(14.82)
где
0 = ((P2)i - (rfi
Puc. 14.20. Наклонный слой.
369
Исходная и вспомогательная системы координат связаны сле-
дующим соотношением:
хх = хсозФ 4 z sin Ф; 1
гх = —х sin Ф -j- z cos Ф. | (14.83)
Теперь надо выразить производные LL, UXi и игг через (7г1,
UX2l и игЛ. Очевидно, что
= + = _^51пФ;
дх дхг дх 1 azj дх сЬд дгх
аналогично
dU dU . .ъ . dU
-т— = -Ч— Sin Ф 4- "3— COS Ф,
дг дхг ' dzY
следовательно,
дЧ)
д2и
. = 4-^- Sin Ф cos Ф 4 — COS2 Ф —
дх дг dxj 1 дхг dzt
д^1/ дЧ)
—— sin2 Ф--------------VT- sin Ф cos Ф;
дх^ дг £
_^_ = ^_81паф+ sin ф Cos Ф -
дг* дх[ 1 дх1 dzY
4 ~^д и— sin Ф cos Ф 4 4^- cos2 Ф.
' дхх дгг 1 ozf
Имея в виду, что для двумерной задачи
дЧЛдх{ = -d-U/dz\,
после простых преобразований получаем
<W дЧУ д'-и . о,,,
, д = -з—5—cos 2Ф v-г- sin 2Ф;
дх дг дхг дг± дг{
дЮ дЮ . „,Т1 . дЧ)
-5-5- = ~Г д sin 2Ф 4-
дг2 дхг ttej 1
Очевидно, что в рассматриваемом
-т-— cos 2Ф.
dzi
случае
(14.84)
ди Г
—— = ©о, так как
дхг ’ J
&
1<11
+ °°-
Тогда
иг = оо sin Ф 4 Ua cos Ф,
(14.85)
откуда следует, что вертикальная составляющая притяжения на-
клонного пласта, бесконечного по простиранию и падению, равна
бесконечности, за исключением случая, когда Ф = 0 или п 1см.
370
формулы (14.65)1. Таким образом, для наклонного Слоя имеет
смысл рассматривать только производные Uхг и С/гг.
Подставляя значения UX2l и U .л из формулы (14.82) в (14.84),
получаем
U xz (0,0) = 2/ео sin a [(sin а cos 2Ф — cos а sin 2Ф) In (p2/pi) 4-
(sin а sin 2Ф ф- cos а cos 2Ф) • 0];
(0, 0) = 2/гсг sin а [(sin а sin 2Ф Ц- cos а cos 2Ф) In (p2/pi) +
— (cos а sin 2Ф — sin а cos 2Ф) 0]
или окончательно
Uxz (0> 0) = 2ko sin а [sin (а — 2Ф) In (p2/Pi) + cos (а — 2Ф)-0]; 1
Uzz (0, 0) = 2ko sin a [cos (а — 2Ф) In (p2/p,) — sin (a — 2Ф)-0]. I
(14.86)
Удобные аналитические способы определения параметров на-
клонного слоя в общем случае не разработаны. Существуют
только решения для некоторых частных форм, например для вер-
тикального и наклонного уступов.
Формулы (14.86) удобны для вычисления и исследования кри-
вых UXz и Uгг. Комбинируя произвольно расположенные наклон-
ные слои, можно получить решение прямой задачи для различных
тел, сечение которых представляется многоугольником.
Параметры слоя определяют в основном по формулам в декар-
товых координатах. Пусть М (х, 0) — точка наблюдения, в кото-
рой находят Uxz и Uzz; N2 (Ё2, £2) и Лф (£1Э £х) - вершины наклонного
слоя (см. рис. 14.2(5). Тогда расстояние от точки М до точек Nr
и N.2
pi = ]/(li - х)2 + d ;
р2 = (?2 — х)“ + Ц ,
а углы
Фг - arctg ; ф2 = arctg 5
Фа - Ф1 = 0 == arctg — arctg '
Обозначим х0 абсциссу точки пересечения конечной стороны
слоя с осью х. Тогда, подставляя значения ръ р2 и 0 в формулы
(14.65), (14.86), получаем:
371
для силы тяжести U2(x, 0) при Ф = 0
U, (х, 0) = Ag = 2ko к arctg - Ci arctg -Д^
-ф (х — х0) sin Г sin а In Д2
/(5i—х)2 + й
+ cos а (arctg
-----arctg
Ь-х & 51-х
(14,87)
для вторых производных потенциала при Ф О
К (g2 — х)2 +
ихг (X, 0) = 2kn sin а sin (а — 2Ф) In _х)2^Г
+ cos (а — 2Ф) (arctg -^-Д— - arctg -|Ду ) J 1
Г /(Е, — х)2 + Й
U2i{x, 0) = 2AffSlna cos (а-2Ф) In
(14.88)
— sin (а — 2Ф) (arctg ----------arctg
Перейдем к рассмотрению других частных случаев наклонного
слоя.
ВЕРТИКАЛЬНЫЙ ПЛАСТ
Вертикальным пластом называется тело, ограниченное двумя
параллельными вертикальными полуплоскостями и соединяющей
их горизонтальной гранью (рис. 14.21). Очевидно, что вертикаль-
ный пласт представляет собой частный случай наклонного слоя,
для которого а = л/2 и Ф = л/2. Чтобы получить формулы 1/хг и 1/гг
вертикального пласта (формулы Uz не рассматриваем, так как U2 —
= оо), положим, что горизонтальная мощность пласта равна 2d,
глубина залегания верхней кромки h. Начало координат поместим
над серединой верхней кромки пласта, тогда |2 = —d, = d,
£2 — £1 — h. Из выражения (14.88)
Ux2 (х, 0) = ka 1л = 2^° In ~ ’
лг' ’ ' (X-pd)^-- fta р
/ 1 ч (14.89)
U2г (х, 0) = 2ka (arctg — arctg х^-) = 2йо0.
Рассмотрим кривую Uz2. Сравнивая формулы (14.89) для U22
вертикального пласта и (14.43) для Uz материальной горизонталь-
ной полосы, видим, что они идентичны, если положить р. = <т.
Таким образом, поведение игг вертикального пласта аналогично по-
372
ведению Uг материальной полосы. Сле-
довательно, находить элементы вер-
тикального пласта по кривой Uгг мож-
но с помощью приемов, рассмотрен-
ных выше для материальной полосы.
Обратимся к анализу кривой (7хг.
Из формулы (14.89) следует, что
при х = 0 и ± оо функция Uxz = О,
при х < 0 [7хг)>0, при х> О U хг < О,
причем ил2 (—х) = —UX2 (+х).
Из условия dU„/dx = 0 имеем
*тах, min = ± И /Р + d'2', (1 4.90)
U xz max
= ka In
И/i3 + d2 + d
K/i2 | d2 —d
Puc. 14.21. Кривые Uxz и Uzz
вертикального пласта.
= kc In
I Хщах I ~b d
I ^max I — d
(14.91)
Пусть Xi/2 абсцисса, где Пд.г i/2 = max/2, тогда
~(*l/2~d)2+^ ' 2 = Ixmax-l-l-d
(Xl/S “I" dy2 + IP | Xmax I — d
(14.92)
Решая это уравнение совместно с выражением (14.90), получаем
d = Ка (2 | хтах | — а), (14.93)
а = (4ах + ^/2)/(2 | х1/21). (14.94)
Следует отметить, что существуют две абсциссы х)/2; одна из
них по абсолютному значению меньше, а другая больше | хтах|.
В формуле (14.94) используется | х[/2 | < j хгаах | . Из формулы
(14.90) определяем глубину верхней кромки пласта
h = У4ах - d2 .
Используя выражения (14.93) и (14.94), получаем
h = (A’max — Х1/а)2/(2 | Х1/2 |). (14 .95)
Определив d, вычислим избыточную плотность пласта
о =___________и_хгты__________ (14 96)
Л1п [(| Хщах | + d)/(| хтах | — d)j • щч.эо;
Следует отметить, что параметры пласта находят без каких-
либо предположений о каждом из них, так как контур пласта це-
ликом определяется положением его угловых точек, являющихся
особыми точками U Х2. Однако при этом следует иметь в виду,
что различные параметры пласта вычисляются с разной степенью
надежности. Наиболее точно определяется /г, менее точно d и о.
373
Особенно ненадежны определения d при 2d < h, так как в этом
случае изменения горизонтальной мощности 2d можно компен-
сировать одновременным изменением плотности о и внешнее ано-
мальное поле останется практически тем же. При 2d <<( h поле
вертикального пласта идентично полю вертикальной матери-
альной полосы и определить d невозможно без знания о. Изменения
же глубины h скомпенсировать изменением плотности о нельзя.
НАКЛОННЫЙ ПЛАСТ
Наклонным пластом называется тело бесконечного простира-
ния, ограниченное сверху горизонтальной гранью, а с боков
двумя параллельными наклонными полуплоскостями (рис. 14.22).
Таким образом, наклонный пласт представляет собой частный
случай наклонного слоя, когда
а — Ф.
Полагая горизонтальную мощность пласта равной 2d, глубину
залегания его верхней кромки h и перенося начало координат
в точку, расположенную над серединой горизонтальной стороны
(?2 — —d, = d, ьг = ?i = d), из формул (14.88) получаем
ихг (Л-, 0) = ko [ a In +
+ sin 2а (arctg - arctg;
г 1 / Lw (14.97)
(,х> °) 8Ш 2и 1п (х - Д)2 + h2
- 2 sin2 a (arctg ^А-- arctg ^А-)].
Эти формулы можно представить в виде
Uxz(x, 0)=L(x) |-Х(х); |
иг^х, 0) = L1(x) + 41(x-),i U ’
Рис. 14.22. Кривые Uхг
и Uzz наклонного пласта.
374
где
г , , , . 3 . (х— d)2h2
L(x) = tosin“alnJrF^^;
, , , ka . „ , (х—d)24-h2
(*) - 9 S П 2a ln (jc+’d)3 Ц-Л2 ’
Л (%) = kaSin 2a (arctg -- arctg
A± (x) = 2ka sin2 a (arctg^-j — arctg —
(14.99)
Сравнение функций L (x), Lt (x) и A (x), Лх (x) с выражениями
для Uхг и U-г вертикального пласта показывает, что функции
L (х) и Lj (х) пропорциональны Uxz, а функции А (х) и Л± (х)
пропорциональны U„. Однако в случае, когда а значительно
отличается от л/2, кривые Uхг и Uzz для наклонного пласта от-
личаются от соответствующих кривых для вертикального пласта:
нарушается их симметрия, сдвигаются точки экстремумов.
Из формул (14.99) следует
L(ArX) — ~1Л~-ху,
А (-фх) = Л(—х);
Отсюда находим следующие
Li (+*) = —й (—*);
А(+х) = Л1(—х).
(14.100)
выражения:
L (±х) = (1/2) \UX2 (±х) - Uxz ( + х)];
Л(±х) = (1/2)[Уд.г(±х) + ^(+х)];
L1(±x) = (l/2) [(7гг (±х) - f^(+x)];
Лх (±х) = (1/2) [U22 (±х) + U,2 (+х)].
(14.101)
Таким образом, кривые L (х), А (х), (х), Аг (х) могут быть
построены из исходных кривых U Х2 и U 22 при условии, что из-
вестно начало координат над серединой пласта. Чтобы определить
положение начала координат, найдем абсциссы точек максимума
и минимума кривых (7д.г, Ua и подставим значения t/xzniax,
^гг max в общие формулы (14.97). Алгебраическая сумма ординат
Uxz шах + ихг mln = ko sin 2а arctg [2hd/(h2 — d2)]; 1
u2z max + U22 mln = 2ko sin3 a arctg [2hd/(h2 - d2)]. J
(14.102)
Но при x = 0
Ил-Д0, 0) = ka sin 2а arctg [2hd/(h2 — d2)]; 1
Нгг(0, 0) — 2ka sin2 a arctg [2/i.d/(/r2 — d2)]. J
Таким образом,
Uxz max 4 Uхг min = Uхг (0, 0); 1
игг max + Uzz roln = Uгг (0, 0). j
(14.103)
(14.104)
375
Рис. 14.23. Определение параметров наклонного пласта
по кривой Uxz.
Эти выражения позволяют весьма просто находить положе-
ние начала координат — середину пласта. Покажем это на при-
мере кривой ихг (рис. 14.23). Строим ординаты максимума и
минимума этой кривой и находим ординату Uxz (0, 0), равную их
алгебраической сумме; таким образом определяем точку О, ле-
жащую между вершинами кривой.
Найдя эту точку, можно по формулам (14.101) построить кри-
вые L (х), А (х). По ним определяют горизонтальную мощность
2с! пласта и глубину h его верхней кромки. Для этого используют
приемы, рассмотренные для вертикального пласта. Из кривых
L (х) и А (х) можно вычислить
Од = 2о sin2 а; 0^=0 sin 2а.
Тогда
а = arctg (ctl/cta); ст = CTL/(2sin2 а) = Стд/siri 2а.
Если параметры пласта определяют по функции Ui£, то ис-
пользуя кривые Li (х) и А1 (х), находят
CTL, = osin2a; стЛ1 = 2стз1п2а;
а = arctg (стЛ1/ст£(); ст = 07.,/sin 2а _ стл,/(2 sin2 а).
376
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ТЕЛ
ПО СООТНОШЕНИЮ РАЗНЫХ ПРОИЗВОДНЫХ
ГРАВИТАЦИОННОГО ПОТЕНЦИАЛА
Выше были рассмотрены способы определения параметров тел
правильной формы по одной из кривых: Uz = Ag, IJxz или Uiz.
В случае, когда имеется не одна наблюденная или вычисленная
производная гравитационного потенциала, можно найти пара-
метры тела по соотношению между экстремальными значениями
разных производных или по абсциссам точек, где значения разных
производных равны.
Приведем примеры подобных соотношений.
Для сферы из формул (14.3), (14.10) получаем
h = 0,86 (Дг дах/Д» гаах).
Из формул (14.3) и (14.11) имеем
U г тах/6^гг шах = /1/2.
Для вертикального материального стержня получаем анало-
гичные формулы:
== 0,38 (U г max/6^'xz гпах)> U2 тах/^' гг max*
Из формул (14.14)
Uxz == Uzz при —х = /г.
Для горизонтального кругового цилиндра, используя формулы
(14.26), (14.29), (14.31), находим
Л 0,65 (Дг гпах/^Дх шах), == г max/^гг шах-
Для вертикальной материальной полосы из формул (14.25)
и (14.39) имеем
UX2 — Uzz при —х = 1г.
Для горизонтальной материальной полуплоскости
Й = 0,32 (7/г пих/ихг гаах), xz =х zz При X = il.
Если имеется только кривая 1/г (х, 0), то производные Urz
и игг можно получить одним из существующих приемов. В част-
ности, производная Uгг max может быть определена графически
(рис. 14.24):
Uxz max — Uг шах/(-*6.
Этот прием является одной из разновидностей использования
касательных к аномальной кривой в некоторых ее характерных
точках. Наиболее удобны для этого точки перегиба, максимума
и минимума кривой. Особенно часто используется точка пере-
гиба, так как ее положение не зависит от ошибок в выборе нор-
мального поля.
377
Рис. 14.24. Определение производной
Uxz max по кривой Uz.
Рис. 14.25. Определение параметров
цилиндра способом касательных.
Идею способа касательных можно показать на примере опре-
деления параметров горизонтального цилиндра по кривой U2
(14.25). Уравнение касательной к кривой U, (рис. 14.25) имеет
вид
- 2»Ур? = £ (2И (*. - А), (14.105)
где и хк — текущие координаты касательной.
Точка перегиба определяется из условия
дЧ7г(х, 0)/<Эх2 = 0,
что дает
х0 = ± /г/ (/ 3.
Подставляя в выражение (14.105), получаем уравнение
касательной в точке перегиба
L/2K = [W(4/i)][1 +ХЛКЗ-Ml-
Положив UZK = 0, найдем абсциссы точек пересечения каса-
тельной с осью х;
хкП = ± |/3 h.
Полагая UZK = Uz niax = Ik'klh, получаем абсциссы точек,
где касательная, проведенная к кривой в точке перегиба, пересе-
кается с касательной к ней в точке ее максимума:
A-Kraax=±(/3-/9)/l-
Таким образом, используя точки хк0 и хктах, можно определить
глубину h центра цилиндра.
Аналогичные формулы можно составить и для других тел. В ча-
стности, для шара по аномалии Uz имеем
х0 = ±/i/2; хк0 == ± (4/3) h; хк гаах = ±0,17h.
Способ касательных нашел широкое применение при интер-
претации магнитных аномалий.
378
ГРАФИЧЕСКИЕ СПОСОБЫ
ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ТЕЛ
Сущность графического способа состоит в том, что к наблюден-
ной кривой подбирают теоретическую кривую, рассчитанную
на основе решения прямой задачи. Совпадение наблюденной кри-
вой с теоретически рассчитанной служит основанием для отожде-
ствления реального геологического объекта, создающего наблю-
денную аномалию, с телом, для которого рассчитана теоретическая
кривая. Преимущество этого способа интерпретации перед
методом характерных точек заключается в использовании всей
наблюденной аномальной кривой.
Основой графического способа интерпретации являются ат-
ласы или палетки теоретических кривых производных гравита-
ционного потенциала, вычисленные и построенные для тел разной
формы и разных параметров. Для изображения кривых обычно
используют относительный масштаб. По горизонтальной оси от-
кладывают не абсолютное значение абсциссы, а ее отношение
к какому-либо параметру тела, например глубине; по верти-
кальной оси откладывают отношение соответствующей производ-
ной к ее максимальному или какому-либо другому значению,
принятому за единицу. Теоретические кривые строят в линейном,
полулогарифмическом или логарифмическом масштабе.
Атлас теоретических кривых [Д, U xz, Uzz в линейном мас-
штабе составлен Д. С. Миковым для различных тел: эллиптических
цилиндров, параллелепипедов, наклонных и вертикальных ступе-
ней, наклонных пластов и др. Атлас кривых U2, Uxz, U zz в лога-
рифмическом масштабе для тел, ограниченных плоскими наклон-
ными гранями, принадлежит А. А. Непомнящих. А. А. Юньков
является автором атласа кривых в логарифмическом и полулога-
рифмическом масштабе для тел в виде параболических цилиндров,
наклонных уступов и др. Для практического использования наи-
более удобны теоретические кривые в логарифмическом или полу-
логарифмическом масштабе.
Сущность построения теоретических кривых и применения
их для интерпретации гравитационных аномалий состоит в сле-
дующем.
Для тела постоянной плотности ст аномалия любой производной
Un (х, у, 0) гравитационного потенциала U может быть представ-
лена в виде
Un(x, у, 0) = kaFs(x, у, |0, g0, По- Я, ₽- Т). (14.106)
где Fs — функция, которая зависит от вида производной гравита-
ционного потенциала, от формы, размеров Д и положения тела,
определяемого координатами центра тяжести ?0, ц0, Д и углами
наклона а, р, у тела относительно принятой системы координат,
а также от переменных координат х, у точки наблюдения. В зави-
симости от формы тела вместо координат ?0, ц0, может стоять
379
глубина верхней и нижней кромок, горизонтальная мощность,
глубина характерных точек тела и т. д.
Если профиль наблюдения совпадает с осью х, начало коорди-
нат совмещено с проекцией центра тяжести тела на плоскость
хОу и все линейные параметры функции Fs выражены в единицах
глубины £0, то выражение (14.106) принимает вид
П„(х, 0, 0) = k<y&nFs (х/С0, /?/С0, а, 0, у). (14.107)
Если геометрические параметры тела и его форма постоянны,
то функция Fs зависит только от х/£0, т. е.
Un(x, 0, 0) = k^nFs (х/Со).
Логарифмируя это равенство, получаем
In Un (х, 0, 0) = In (/?<") --J- 1 п F; (х/ЗД.
Таким образом, форма кривой In U„ (х, 0, 0) определяется
только характером изменения In Fs (x/t0) и не зависит от .
При изменении кривая 1п4/„ (х, 0, 0) перемещается парал-
лельно самой себе вдоль оси ординат.
Если же рассматривать кривую In U п (х, 0, 0) как функцию
аргумента не х/С0, а 1п (x/Со) = 1п х — In £0, то форма кривой
In Un (х, 0, 0) == In + In (1л х ~ 1л Со)
не будет зависеть и от величины £0; при изменении ф, кривая
Uп (х, 0, 0) сдвигается параллельно самой себе вдоль оси абсцисс.
Следовательно, если кривые производных гравитационного
потенциала построены в логарифмическом масштабе, т. е. по оси
ординат отложены величины In П7„(х, 0, О)/(й<т£о~л) ], а по оси
абсцисс 1п (х/to), то форма кривых не зависит ни от ни
от Со- При составлении атласа вычисляют теоретические кривые
In Un (х, 0, 0) как функции In (х/£0) при фиксированных пара-
метрах «•
Чтобы найти параметры тела графическим методом, наблю-
денную кривую ([7Л)Н (х, 0, 0) строят в логарифмическом мас-
штабе: по оси ординат откладывают In (С7„)н (х, 0, 0), а по оси
абсцисс 1пх. В этом случае наблюденная кривая описывается
уравнением
In ((/„)„ (х, 0, 0) = 1п(/есфо"'!) + lnFs(lnx).
Наблюденную кривую сравнивают с теоретическими, вычислен-
ными при /го'С2'1 = 1. Аналитическое выражение теоретической
кривой имеет вид
ln(t/ra)T(x, 0, 0) = lnFs(lnx — In Со).
Наблюденная кривая при совмещении сдвигается относительно
координат теоретической кривой по оси ординат на In (ЛоСо-”)>
а по оси абсцисс на In Со- По этим смещениям определяют о
380
и t0. Остальные параметры тела (R, а) находят по индексам тео-
ретической кривой, с которой совпала наблюденная.
Вид палеток зависит от формы тел и от выбранных функций;
в каждом атласе даны объяснения, как им пользоваться.
Глава 15
ГРАВИТАЦИОННОЕ ПОЛЕ
ТЕЛ ПРОИЗВОЛЬНОЙ ФОРМЫ
ГРАФИЧЕСКИЕ СПОСОБЫ ВЫЧИСЛЕНИЯ
ГРАВИТАЦИОННОГО ЭФФЕКТА ТЕЛ
Реальные геологические объекты, создаю-
щие гравитационные аномалии, могут быть уподоблены телам
правильной формы только приближенно, и поэтому вычисленные
параметры геологических объектов дают в большинстве случаев
лишь самое общее представление об их действительных размерах.
Уточнить параметры объекта можно, если подобрать тело, ано-
малия от которого совпадает с наблюденной. Последовательно
изменяя форму тела, можно добиться близкого соответствия на-
блюденной и вычисленной кривых. Совпадение этих кривых
позволяет утверждать, что полученная конфигурация тела отве-
чает форме реального геологического объекта.
Таким образом, чтобы определить параметры тела произволь-
ной формы, необходимо уметь вычислить гравитационный эффект
тела любой конфигурации. Все способы основаны на замене
гравитационного действия такого тела действием суммы тел про-
стейшей формы, эффект которых может быть точно или прибли-
женно вычислен. В большинстве случаев для этого используют
различные вспомогательные графики-палетки. С их помощью
тело произвольной формы легко может быть разбито на элементы,
которые оказывают одинаковое гравитационное действие на точ-
ку, в которой надо вычислить аномалию. Очевидно, что гравитаци-
онный эффект тела произвольной формы равен эффекту одного
элемента равного действия, умноженному на сумму элементов,
заключенных в объеме тела.
Рассмотрим сначала способы, которыми определяют гравита-
ционное действие двумерных тел произвольной формы.
В полярных координатах производные гравитационного по-
тенциала принимают вид
U г (0, 0) = Ag (О, 0) = 2Ао | | sin tp dp dtp;
s
Uхг (0, 0) = 2ko | j [(sin 2cp)/p] dp dtp;
s
(0, 0) = 2k<j j | [(cos 2<p)/p] dp dtp.
(15.1)
381
Проинтегрировав эти выражения по р в пределах от р,, до
рл+1 и по ф в пределах от ipm до фот+1, получим гравитационное дей-
ствие тела бесконечного простирания, имеющего сечение в виде
кольцевого сектора:
тП (0. 0) = (cos ф,(1 - cos фт+1) (р„+1 — р„);
Ухг тп (0, °) = ka (cos 2фт — cos 2фт+1) In (рл+х/р„);
Пггтл(0, 0) = ko (sin 2<pm — sin 2<pm+1) In (p„+x/p„).
(15.2)
Если построить окружности такими радиусами, чтобы р„+1 —
— р,г = Др, и провести радиусы так, чтобы cos ср,п — cos cpm+1 =
= 1/tn (где т — число секторов, на которое разбивается квад-
рант), то гравитационное действие полученной элементарной
площадки
Н,гПЛ(0, 0) == 2йа (Др//п).
На радиусы и углы палеток /7,г и (7гг накладываем следующие
условия:
In (р«+1/Рл) =•«;
cos 2ф,п — cos 2фт+1 = 2/т;
^mre(0, 0) = Ь(2а//и).
(15.3)
Сравнивая
получаем
второе и третье выражения из формулы (15.2),
sin 2ср = cos [2 (ф — 45°)],
откуда следует, что для вычисления Uzz можно использовать ту
же самую палетку, что и для Uxz, повернув ее на 45°.
Положив в формулах (15.2) Uzmn = 1-10-° м/с2 и Uxzmn —
= 1-10"® 1/с2, получим уравнения для определения Др, ф и
1п (рл+1/рл), ф. Каждое такое уравнение содержит два неизвест-
ных: Др и ф или рл+1/рл и ф. Поэтому для одних и тех же значений
Uxzmn и Uzmn можно построить площадки разной формы. Чтобы
погрешность при подсчете площадок, попадающих в контур тела,
сделать минимальной, надо придать площадкам форму, близкую
к квадратной. Это может быть выполнено наложением дополни-
тельного условия, связывающего р и ф: разность двух соседних
радиусов должна быть равна дуге среднего радиуса
P/I+1 ~ Рп = (фт+1 ~ 1(Р«+1 + Р«)/2],
-куда следует
рп+1/р« -= (2 + Афт)/(2 — Дфт),
Зь
Афт = (фт+1 — фт).
Логарифмируя это равенство и разлагая его правую часть в ряд
по степеням Асрт, получаем
ln-^- = AcPm.[l +1L(A(p,^+...]
или
In (pn+i/pn) = Дф,„ = фт+1 — фт.
Используя это уравнение, находим единственную систему
радиусов и лучей, определяющих границы площадок равного
действия (рис. 15.1).
Следует иметь в виду, что при изменении <р от нуля до л/2
cos 2<pm - cos 2<р„1+т > О,
а в интервале от л/2 до л
cos 2q>m — cos 2<pm+1 < 0.
Таким образом, при изменении ср от нуля до л/2 функция (7лг
имеет положительные значения, а от л/2 до л — отрицательные.
Для палетки Д,. положительные значения Д2г соответствуют
интервалу ф от л/4 до (3/4) л, отрицательные — от нуля до л/4
и от (3/4) л до л. Чтобы проще было считать, на палетках вместо
площадок указаны точками их центры.
Палетки обычно рассчитывают для плотности о0 = 1 г/см3.
Для конкретного объекта результат вычислений по палетке необ-
ходимо умножить на отношение о/а0, где о0 — плотность, для
которой рассчитана палетка; о — плотность геологического объ-
екта.
При использовании палеток для вычисления Ухг и U.z масштаб
разреза не влияет на окончательный результат, так как в формулы
входит отношение рга+1/рл, а не сами эти величины. Необходимо
только, чтобы вертикальный и горизонтальный масштабы разреза
были одинаковыми. С укрупнением масштаба контур тела ло-
жится на более далекие точки, но количество точек, попадающих
в границы тела, остается одним и тем же. Если контур тела рас-
полагается близко к центру палетки, то для повышения точности
вычислений Uxz и Угг масштаб разреза следует укрупнить.
Иначе обстоит дело с палетками для вычислений (]г. В формулу
(15.2) множителем входит разность радиусов р„+1 — ря. Палетку
U2 строят в определенном линейном масштабе. Если масштаб раз-
реза не соответствует масштабу палетки, то окончательный ре-
зультат вычислений по палетке необходимо умножить на Л4/Л1о,
где Мо — масштаб палетки; М — масштаб разреза тела.
Полярные палетки для двумерных тел (см. рис. 15.1) впервые
были предложены К- Юнгом. Весьма простая для построения па-
летка Uz двумерных тел рассчитана Г. А. Гамбурцевым. Принцип
ее состоит в следующем.
383
Рас. 15.1. Палетка Юнга для вычисления Uz, UХ2 и Uzz дву-
мерного тела.
384
Рис. 15.2. Палетка Гам-
бурцева для вычисле-
ния иг.
В формуле (15.1) положим
р sin <р = £,
тогда
sin ср dp = d£;
Uz (0, 0) = 2Ао j sin ip dp dtp = 2ku j dtp de
s s
— 2A(J (£/t+i £n) (фт+1 фт)-
Полагая
&»+! — = А? И Фт+1 - Фт = Дф = Л/ОТ,
имеем
t/zm„(0, 0) = 2л/го (Л£/т).
При построении палетки через равные интервалы Ас проводят
горизонтальные линии и через равные углы л/т из центра палетки
О проводят лучи. Таким образом, вся плоскость оказывается
разбитой на площадки равного действия (рис. 15.2). Некоторый
недостаток этой палетки по сравнению с полярными состоит
в том, что сильно вытянутая форма площадок по краям палетки
приводит к большим погрешностям при подсчете гравитационного
эффекта.
Д. Бартон предложил и разработал методику построения па-
леток для вычисления UХ2 и U2Z, представив пространство в виде
прямоугольных призм равного действия. Исходными служат
формулы (14.52) для прямоугольного параллелепипеда. Положим,
что одна из граней параллелепипеда совпадает с координатной
плоскостью уОг, тогда |х = 0. Помещая начало координат в точку
наблюдения, получаем
U (0 О') = k<3 In •
гг( ’ } Й(Й + Й) ’
(0, 0) = 2/го [arctg О2) - arctg (£х/£а)[.
13 В С. Миронов
(15.4)
385

Введем обозначения
Тогда формулы (15.4) принимают вид
7 7 /Л ОЧ 7, I Л2(«2+1)
Uх, (0, 0) = /го In —' ;
хг v ’ ' и2 4- А2
. А 1 \ <15'5>
У„(0, 0) = 2Ь (arctg—- arctg—).
Задаваясь А, можно выбрать и таким образом, чтобы U Х2
и U„ принимали определенные значения /V. Полагая в равен-
ствах (15.5) UX2 — NX1 и U22 = N22 и вводя соответственно обоз-
начения
р„ = ехр-^; = (15.6)
для постоянного значения А находим и.
Для аномалий UХ2
« = ±4/(1 -/7„)/(Лг - Л2). (15.7)
Для аномалий U2i
и — (А — \ )/(2ргг) ± УЦА - 1)/(2ргг)]2 - А. (15.8)
Используя соотношения (15.6)—(15.8), можно для любых
заданных значений А и W определить и. При этом полагают а =
= 1 г/см3. Выбирая произвольно А и принимая N равным после-
довательно (1, 2, 3, ...)-10’э 1/с2, находим соответствующие зна-
чения ult и2, и3, ..., которые определяют на плоскости xOz си-
стему прямоугольников, действие каждого из них на начало коор-
динат равно 1-I0'8 1/с2.
Построение палеток Бартона сводится к следующему (рис. 15.3).
Рис. 15.3. К расчету палетки
Бартона.
В прямоугольной системе координат
xOz параллельно оси х проводим ряд
прямых:
z0 = z0; ?! = Az,; z2 = A2z,;
zs= 4%; . . .; zn = Anz0.
Значения А и z, выбирают про-
извольно. Однако для палетки UX2
целесообразно взять А таким, чтобы
действие каждого из бесконечных
слоев было равно целому числу
Л/-10'“ 1/с2. Для этого, полагая в
формуле (15.7) и = со, находим
А = exp [N„/(2ko) ]. При построе-
нии палетки U12 следует А выбрать
386
так, чтобы максимальное значение U 2г, определяемое
(15.5), выразилось также целым числом 2V-10~9 1/с2,
нений (15.6) и (15.8) получаем
4-(|+=1" -&)/(1-*1"-Йг).
формулой
Из урав-
(15.9)
Пользуясь формулами (15.7) и (15.8), при N = 1, 2, 3,...
находим иг, и2, ... Из начала координат проводим прямую, со-
ставляющую с осью z угол <р, определяемый условием
tgcp = u.
Поскольку Е2 = то, опуская перпендикуляры из точки
пересечения этой прямой с параллельными прямыми, заданными
уравнениями г„ = Л"г0, получаем ряд прямоугольников, каждый
из которых оказывает на начало координат гравитационное дей-
ствие Uxz или Uzz, равное Ы0“° 1/с2 (рис. 15.4).
Для вычисления гравитационного эффекта трехмерных тел
можно построить палетки, аналогичные рассмотренным. В част-
ности, для тел, уподобляемых цилиндрам, т. е. нормальное се-
чение которых не меняется по простиранию, рассчитывают по-
лярные палетки. В этом случае, полагая, что размеры тела по
простиранию равны 26, а профиль проходит над серединой тела,
из выражения (14.20) имеем
рл+1 '•’гп+1
£/г(0, 0, 0) = 2to j Д г J Sincpdtp. (15.10)
Р;» Р «>,п
После интегрирования по р и получаем
(7г(0, 0, 0) = 2ka In
Pn+l +]/" Pn+1 + &2
Prt + Pn + b~
-(coscp,n+1 —COStpJ.
Задав b различные значения, построим полярные палетки для
вычисления Uz (0, 0, 0).
Следует заметить, что вторые производные для трехмерных
тел в практике интерпретации вычисляют сравнительно редко,
поскольку влияние конечных размеров тела на характер вторых
производных, особенно на Uxz, сказывается значительно слабее,
чем на Uz. Однако для цилиндрических тел с конечным простира-
нием существуют палетки Бартона. Кроме того, для вычисления
эффекта трехмерных тел можно использовать графический способ
Самсонова, рассмотренный при учете влияния рельефа на пока-
зания гравитационного вариометра.
Приведем еще один способ вычисления гравитационного эф-
фекта Uz трехмерных тел. Разобьем тело горизонтальными пло-
13* 387
е Z 9 ? i 8 3 / I 3 £ t s 9 Z 9
s 8 Z 9 S / г 3 / 3 £ t s 91 3 9 S
е 9 L 9 Г V c 3 / / I 3 £ t S 9 i 8 S
0 ? 9 1 9 S' i 8 3 / / 3 £ t\ S . 1 vU r~ * C !
// to « 8 г 9 9 t £ г / / 3 1 I ri /-| Q 9 Z ₽ 6 1 fl 1 и
а и 01 £ S 3 9 9 0 £ 3 / l\ 3 £ d sj 9 Z g| L // 3)
я И Iй 6 1 е |z 9 s t £ 1* d г d t £ sj Z 8 R 0! и 3/\
ei 31 И 1 i f 8 Z 9 9 t Г 3 / / з г t\ £98 P| R 01 li\ 31 j £1
к/ 31 к 6 1 в z b к 1 И? \з |/ d d 6*1 g| °>\ u\ 3i\ £4
|£7 3! 1" 1/7/ |S 1 s к |s |s к нЛ /1 з\ si tl p| s>| z| g| s| o/| // 3l\ £1 | M
|#-х 1» la \Н V> 1/ \9 |Z Is |С|/-|Г|? |/ /1 ?l?l /kkl /ГОГ®1 //I 3Jl c/l «L
1 1 1 1 1 1 1 II I I I I I 1 l L
1 1 11 L_LJL 1 1 1 1 1 ii i11 11 i I ii l 1 I
1 1 1 II 1 1 1 1 i 111 i 111 i 1, 1, I , I I
ГТ^ 1 I 1 III 1 i iiii и г id I l l _J L
। Illi 1 111 Bmp-- 1 111' ’' nr Ц—*—।—1—।—1— 1
+ £31'1 =tf iiumimAA i i- —

3
1 1 1 1 11111 Г—Г J_ELl_LT'T-r T т t — —
1 1 1 1 1 1 1 1 1 1 /“ V'l ‘1 'l Г 1 ’i'll ' I""' —" - 1 I”“
i 1 I 11111111 111,111111 1 I
_J , 1_ „ . L 11,1,111 ,1 J 1, 1,1 ,1 ! ,1 1 , 1 I 1 [_
, jz:. . , i, i _ 1, 1; 1.1,11 , 1 , 1 I
i , i ' i,i, i ,i ,i ,i ,1 ,i 1,. 1, 1,1,11 ,11 I 1
1 1 L 1 L 11 1 J J L 1 L I 111 1 1 I
-6 j -5 | -#| -3 | -2| -/| 0 | /| //]/ 1\ 1,4 \ 1 | 0 | y| -2\ -3| -4 \ -J | -6
-S | -5 | -4\ -3| -2\ -Z| 0 | /| 1,4\1 1\ 1,4\ Z| 0 | -/| -2\ -3 | -4 [ -5 j
-5 I -T|-«3 I ~2I I 0 I Й r /| <,4\ 1 | 0 | -1 | -2\ -3 j -4 | -J ]
-J — 4 -3-2-10 1 1,4 1 l\ 1,4 1 0 ~f -2 -3 -4 -5
-4 -3 -2 -10 1 . 1,4 1 1 1,4 1 0 -1-2 -3 -4
-3 -2-10 1 1,4 1 1 1.4 10-1-2 -3 j
-3 -z\ -1 0 1 1,4 1 1 1,4 1 0 -1 -2 -J
-2 -1 0 1 1,4 1 1 1,4 10 -1 -2
-2—10 1 1,4 1 1 1,4 1 0 -1-1
-1 0 1 1,4 1 1 1,4 1 0 -1
—10 1 1,4 1 1 1,4 1 O S
Рис. 15.4. Палетка Бартона для вычисления Ux, и £4г-
К вычислению гравитацион-
Рис. 15.5.
кого эффекта трехмерного тела.
скостями на слои толщиной А?
(рис. 15.5). Действие каж-
дого реального слоя можно
заменить действием мате-
риального слоя, расположен-
ного на средней глубине z—h0
и имеющего поверхностную
плотность j-t = о Az. На этом
принципе основано несколько
типов палеток, различающих-
ся формой площадок равного
действия. Е. А. Мудрецовой
построены палетки в цилинд-
рической системе координат,
площадками равного действия
являются секторы. В палет-
ках, предложенных А. К. Маловичко и О. Л. Таруниной, пло-
щадки представляют собой квадраты.
В качестве примера рассмотрим способ построения палетки
Мудрецовой для вычисления U2. Располагая начало координат
в точке наблюдения, для одного материального слоя имеем
t/jo, о, o)=q
Js V + «о) '
(15.11)
Интегрируя по г в пределах от до гп+1 и по а в пределах
от а,„ до а„,+1, получаем Uz от элементарной площадки слоя:
<Лжл(0. °- 0) = /?р/7и / J— - / „ \ «,„). (15.12)
\]Лч. + '’о pn+i+fto/
Проведем радиусы г через равные углы
«т+1 — «т = 2л//?г
и положим
И ^0 — Ло/ 4~ ^0 — Стл,
тогда
Угшп(0, 0, 0) =(2л/гаАг/т)стП.
Чтобы получить притяжение всего материального слоя, надо
определить число N элементарных площадок, умещающихся на
площади слоя:
U. (0, 0, 0) = (2л£<г Az, /т) cmnN. (15.13)
Палетки рассчитывают для ha = 1; 2, ... единиц масштаба,
в котором построено тело. Горизонтальные сечения тела изобра-
жают в виде карты изоглубин через интервалы Аг — 1; 2, ...
.390
единиц масштаба чертежа. По палетке, соответствующей данной
глубине /г0, подсчитывают гравитационный эффект каждого мате-
риального слоя и результаты суммируют. Можно использовать
и одну палетку, но при этом следует каждый контур материального
слоя строить в своем масштабе глубины ha.
Трехмерное тело можно разделить не только на горизонтальные
пласты постоянной мощности, но и на вертикальные столбики.
Сечение столбиков в горизонтальной плоскости представляет
собой кольцевые секторы с радиусами гп и гп+1 и углами ат и
ат+1, а высота столбиков равна разности глубин верхней
и нижней h2 граней тела. Помещая начало координат в точку
наблюдений, для элементарного столбика имеем
am+i гп+1 Л2
(/,„„(0. О, 0) = /«, f J J .
ат rn hi
После интегрирования в указанных пределах получаем
Uz тп (0, 0, 0) = Ли (у гп+1 й? — у"4 •-[- й| -
— "Угп+1 ~|~ ^2 ф- |/ гп "ф ^4) (аш+1 — Я(п). (15.14)
Вводя обозначения
У 4+1 + — У г\ + /г? =
У 4+1 + ^2 - У = с'тг1
(13.15)
и разбивая окружность радиуса г на равные углы
— а„, = 2л/;и, (15.16)
получаем
Uz тп (0» 0, 0) :== (2л/?О7Ш) (Сщп Стп)‘
Для всего тела
т п
и г (0, о, 0) - уу 2 s(Стп ~CmiY
т—1 п=1
(15.17)
Выбрав радиусы г„ и г„+1, для различных /г составляем таб-
лицу стп. Накладываем палетку на план изоглубип верхней и
нижней поверхностей тела. По значениям й, определенным в се-
редине площадки, из таблицы находим стп для верхней границы
тела и СтП для нижней. Суммируя стп и с'тп по формуле (15.17),
определяем окончательное значение 0г (0, 0, 0).
391
ОПРЕДЕЛЕНИЕ массы и координат
ЦЕНТРА ТЯЖЕСТИ ТЕЛА
Способы определения массы и координат центра тяжести тела
по гравитационным аномалиям относятся к так называемым
прямым методам интерпретации, т. е. методам, которые позволяют
находить параметры тела без каких-либо предположений о его
форме. Уравнения, связывающие указанные параметры тела с ано-
малиями, могут быть наиболее просто получены из формул Грина
(1.77), (1.78).
Положим, что в формуле (1.78) Р = U есть гравитационный
потенциал. Тогда, учитывая уравнение Пуассона (1.72), получим
формулу Гаусса
J (dU/dri)dS=~ink [ о dv = —4л/гЛ4. (15.18)
S v
Интегрирование проводится по поверхности S, охватывающей
аномальные массы М. В нашем случае производная dU/dn за-
дана на горизонтальной плоскости. Чтобы получить соответству-
ющую формулу, положим, что поверхность S представляет собой
вертикальный круговой цилиндр, верхнее основание которого
совпадает с земной поверхностью, а нижнее расположено глубже
аномальной массы. Радиус цилиндра таков, что вся аномальная
масса находится внутри цилиндра. Тогда интеграл по поверхности
можно представить в виде суммы трех интегралов: двух по осно-
ваниям цилиндра и третьего по его боковой поверхности. При
увеличении радиуса цилиндра до бесконечности третий интеграл
обратится в нуль, а первые два будут равны между собой. В этом
случае
+ <ю -1-00
j j Uz^ т], 0) d^dx} = 2nkM
или
•f-oo +oo
M J J 4, 0)d^/n.
(15.19)
Интегрируя это выражение по частям, получаем формулы для
определения массы через другие производные гравитационного
потенциала:
+ оо
и, 0)d| dt],
и поскольку при £ —* оо величина tUг —> 0, то
4-оо 4-со
-кг[
(15.20)
392
Аналогично
4ое Доо
Й-J J
— 0Q —ОО
Для двумерных тел, когда простирание тела параллельно
оси у, справедливы равенства
Доо
[ Uz(l, 0)сЦ = 2лН;
—• оо
Доо
f Шдг(£, 0)dg = -2^A.
— оо
Полагая в формуле (1.77) Р = U, Q = | и Q = р, получаем
соответственно
Доо Део 1
[ j" 7/, (Е, р, 0)Ed£dp = 2n& | £ dm = 2л/?.Ш'о;
v (15.22)
| j I/г (£, р, о) Р dt dp = ink | p dm — 2nkMy0,
-oo -oo v
где
x° = ~M J -dm’ y° = ЛГ f n dni
V V
— координаты центра тяжести тела.
Вертикальную координату г0 центра тяжести найти сложнее.
Формулы, определяющие г0, впервые были получены Г. А. Гамбур-
цевым. Вывод этих формул опускаем; укажем только, что, полагая
в формуле (1.77) Q = 2, можно получить следующее выражение:
Дсо Део
[ [ I и & Р, 0) - dt dp = —2nkMzH.
J J [ J/ g2 » -^2 ।
— co —oo
Применяя к этой формуле интегрирование по частям, вслед-
ствие чего под интегралом появятся производные различного
порядка, получим формулы Гамбурцева:
Доо Доо
j j (В, Р, о) + 2g2(7„ (Ё, р, O)]dgdp = 6лАЛ4?0;
Доо Д оо
[ j 1^А.(Ё, р, 0) — Р, 0)] dBdp = — 2nkMzn\
(15.23)
Доо Доо
[ J [Д(£, Р, 0) + 2^x(i> Р, O)ld|dp = 2n^Mz0.
— ро -оо
393
Из формул (15.23) следует, что для вычисления коорди-
наты z0 необходимо предварительно определить Ux, Uy, Uгг, U.
Эти величины современной гравиметрической аппаратурой не-
посредственно измерить нельзя, но их можно вычислить по задан-
ному на земной поверхности распределению аномальной силы
тяжести (см. главу 16).
Для определения координат х0 и у0 по 1/хг и Uin имеем формулы
| j Z?UXi{Z, т), 0) dZ dp = — 4л.К'Их0;
—2л/?Л1л'о;
(15.24)
'2пкМуп\
0) а'Е dp -= —4ji/</Wi/(I.
Координаты центра тяжести двумерного тела определяются
формулами
J ZU, (£, 0) dZ = 2лШ0;
- 00
J Z*Uxz (|, 0) dl - - -4л/Ах0;
— 00 +со (15.25)
J Ж(Е, O)-F£/«(l, 0)1 dg =
= — j [2fek + ZUX (Е, 0)] dZ —2лН?0.
j
Если известна избыточная плотность о, то, пользуясь фор-
мулами (15.19), (15.20), можно сначала найти массу тела, а затем
его объем V = М/о и вероятные размеры. В двумерной задаче
по формулам (15.21) вычисляем Л. и, если известна плотность о,
узнаем площадь поперечного сечения тела S = Х/о.
Таким образом, применяя прямые методы интерпретации, мо-
жно определять только аномальную массу и объем тела, но не
его форму. Чтобы установить форму тела, необходимы дополни-
тельные сведения. Имея такие сведения, форму тела обычно на-
ходят способом подбора.
Полученные выше формулы для определения массы и координат
центра тяжести тела применимы только для тел ограниченного
простирания на глубину, т.е. замкнутого поперечного сечения,
поскольку эти формулы выведены из выражений (1.77) и (1.78) при
394
интегрировании по поверхности,
охватывающей аномальные массы.
В практике интерпретации гра-
витационных аномалий часто рас-
сматриваются тела с бесконечным
простиранием на глубину. В этом
случае приведенные выше фор-
мулы непосредственно применить
нельзя; следует найти соотноше-
ния, позволяющие установить
связь между конечным на глубину
телом и бесконечным и затем
оценить их массы и положение
центра тяжести.
Пусть имеется полубесконеч-
Рис. 15.6. К определению парамет-
ров трехмерного тела с бесконеч-
ным простиранием на глубину.
ный цилиндр, верхнее основание
которого ограничено произвольной поверхностью (рис. 15.6). Смес-
тим этот цилиндр в направлении его оси р на отрезок Ар и рас-
смотрим разность гравитационных полей двух цилиндров. По-
скольку нижнее основание цилиндра находится на бесконечности,
то гравитационное поле обусловливается только ограниченной
массой М, образовавшейся при смещении цилиндра. Если грави-
тационный потенциал всего цилиндра равен U, а его ограниченной
массы М соответственно U, то при малом Ар
dU/dp = (7/Ар.
Полагая
lim (о Ар) = р.,
Др->0
где р — поверхностная плотность массы М; о — объемная плот-
ность цилиндра, получаем
dU/др = U.
Пусть сс есть угол, составленный направлением р с горизон-
тальной плоскостью хОу (угол падения цилиндра); А — угол
между проекцией направления р на плоскость хОу и осью х (ази-
мут направления р); тогда
U = UX cos a cos А -- Uy cos а sin 4 | Uг sin а.
Если система координат выбрана так, что ось х совпадает с про-
екцией р, а ось у перпендикулярна к ней, т. е. А = 0, то
или
Поскольку
1) = Uх cos а -ф- Uг sin а
Ux = Uxx cos а ф Usz sin а; |
= Uxz cos а -ф- sin а. \
+ оо +оо
j j их& л, o)d?rfr] = o,
— оо — со
(15.26)
(15.27)
395
то из системы (15.27) следует, что
tga =
, 11, O)dgdr] .
Если теперь в формулы для расчета массы и координат центра
тяжести тела, ограниченного на глубину, вместо производных от
U подставить соответствующие производные от U, то вместо
массы М будем определять М = р.8 — crApS, где 8 — площадь
поперечного сечения с координатами центра тяжести х0, у0, z0.
Действительно, разбивая цилиндр на элементарные цилиндры,
площадь сечения которых dS, имеем
4-оо +оо
М = о- J j (dpcosф)-^,
- 00 — 00
где <р — угол между направлением р и нормалью к площадке,
образованной пересечением элементарного цилиндра с поверх-
ностью верхнего основания заданного цилиндра.
Из уравнений (15.20)—(15.23), (15.26), (15.27) получаем
4-оэ 4-оо 4-оо 4-со
cosa] | U Kz (g,r) , O)dgdr] -|- sin a | | Uzz (g, ц, O)dgdr] =2n£<rS;
-о» —ое -оо —оо
4-оо 4-эо
COS а j j Л, O)dgdi] -ф
— оо — оо
4-ое 4"Оо
4- sin a j j Wгг (?• 0) dg dq = 2n£aSx0;
— oo —oo
4-oo 4-oo
cosa j j '!> O)dgdp +
-00 —00
4-oo 4-oo
sin a j | i|t/2z(g, t|, O)dgdi] = 2л/го8у0;
cosa | j [C7A. (S, г), 0) 4~ 2g£7A..i (g, Ц, O)]dgdi] 4*
— co — oo
4-oo 4-oo
-ф sin a j j [(d2(g, n, 0)4-2g(/re(g, 1], O)]dgdi] =
-00—00
4-oo 4-oo
= cosa | j [t/.v(g, i], 0) -j- 21]7/ед (g, r), 0)]dgdp4-
— 00 —00
4- oo 4-oo
4-sin a j j [(/г(|, 11, 0) 4- %r\Uy2 (g, 1], 0)1 dg di] — 2nfo-Sz0.
— 00 —00
(15.28)
396
В случае двумерной задачи полу-
чим выражение, аналогичное урав-
нению (15.26). Однако поскольку
логарифмический потенциал опреде-
ляется с точностью до постоянной,
то удобнее пользоваться системой
(15.27):
Uг = —U,, cos ос 4-L/,., sin а; I
1 22 (15.29)
U ,г = Uz, sin а ф- Uxzcosa. |
Эти выражения можно записать
иначе:
LL., = U, cos а т LO sin а; 1
2 _J J (15.30)
игг — 1/г sin а — Их cos а. |
Уравнения (15.29) и (15.30) связывают поле U пласта, имею-
щего бесконечное простирание па глубину, угол падения ос и
произвольное расположение верхней кромки, с полем ограничен-
ной массы в виде бесконечно тонкой полосы, совпадающей с верх-
ней кромкой пласта (рис. 15.7).
Угол падения пласта находится из условия
[ (7v(g, O)dg = O,
Рис. 15.7. К определению пара-
метров двумерного тела с беско-
нечным простиранием на глу-
бину.
что дает
tga —
На основе формул (15.21), (15.25) и (15.29) получаем
+ос +оо )
since J (g, €)) cos се. | Uxz(Z, 0)d^ — 2nkM = 4nkod;
— OC — 00
+ oc -f-co
since | 0) cos a j tUxz (£, 0) = 2л£Л4х0 = 4nko dxa;
— 00 — oo
4~oo
J {B (£> 0)sin « — (5, 0) cos a] 4kad] d£ =
— oo
— 2nkMz0 = 4nko dz0.
(15.31)
Аналогично трехмерному случаю можно показать, что М =
— О'Ар-2d, где 2d — истинная мощность пласта.
397
Из уравнений (15.30) получаем
4оо -Too
J Li2г (£, O)dg = sin« [ (72(Е, 0)d£ = 2n£A4sina;
— сю — oo
+ oo 4-oo
j t/A.2(S, O)dg = cosa J ДДЕ, 0) — 2nkM cos a.
— oo -co
(15.32)
Таким образом, для тел с бесконечным простиранием на глу-
бину возможно определить положение центра тяжести их верхней
кромки и угол падения тела.
Формулы для расчета массы и координат центра тяжести ано-
мального тела предполагают интегрирование в бесконечных пре-
делах по всей плоскости наблюдений. Практически аномалии
силы тяжести и вторых производных гравитационного потенциала
бывают известны только на ограниченных по профилю или по
площади участках. Для вычисления интегралов в бесконечных
пределах приходится вводить поправку за конечные пределы
интегрирования, т. е. учитывать остаточный интеграл в интервале
от г до +оо, где г — радиус окружности, в границах которой
проведено интегрирование. Поскольку с удалением от тела его
аномалия все меньше и меньше зависит от формы тела, то можно
положить, что начиная с некоторого радиуса г„ аномалия Uz
в первом приближении соответствует эффекту сферического тела
массой М, т. е.

/г2,Л2чЗ/2 f3
(г) = (г„) j - (о) ,
так как /г -С г. Тогда
2л гп з 2п <»
0 0 о г„
Значение первого интеграла находят методами численного
интегрирования; второй можно вычислить точно. Окончательно
имеем

1
2л/г
"2л гп
j j Uz(r, a) г dr da 4
-о о
2nUz (г п) Г п
398
Рис. 15.8. Графики для учета остаточных интегралов при
определении массы тела по гравитационным аномалиям.
1 — цилиндр; 2 — сфера.
В случае двумерной задачи также полагаем, что начиная с не-
которого расстояния аномалия совпадает с эффектом кругового
цилиндра. Тогда
= (UO* 2);
1
2лй
оо
J Дг®^ + 2(/г(Еп)Й J
~^п Чг
1
2лй
j г/г(ё)^ + 2(/г (?„)?„
L-5
Остаточный интеграл может быть значительным (рис. 15.8).
Даже для сферы, наиболее локализованного тела, вычисленный
интеграл Uz составляет только 55% от полного значения при убы-
вании поля до 0,1 максимума. По графикам можно ввести поправку
в вычисленное значение М.
Другим фактором, затрудняющим использование формул
(15.19)—(15.25), является их сильная зависимость от выбора
«нормального» поля. Присутствие в аномалии постоянной составля-
ющей искажает результат интегрирования.
При вычислении координат центра тяжести масс возникают
принципиально те же трудности, что и при определении массы тела.
Но поскольку координаты центра тяжести выражаются через от-
ношение интегралов, то при вычислении этих интегралов в одних
и тех же пределах остаточный интеграл можно не учитывать.
Естественно, что при интерпретации гравитационных аномалий
наибольший интерес вызывает определение вертикальной коорди-
наты центра тяжести тела. Однако приемы вычисления ее по
формулам разработаны недостаточно. Е. Г. Булахом предложены
простые приемы приближенной оценки вертикальной коор-
399
возмущающих масс по гравитационным ано-
малиям.
динаты центра тяжести г0
на основе вычисления ин-
тегралов (15.19)—(15.21)
в конечных пределах. Рас-
смотрим идею этого спо-
соба применительно к дву-
мерной задаче.
Пусть имеется цилинд-
рическое тело с поперечным
сечением S (рис. 15.9). Вы-
делим внутри этого тела
элементарный горизонталь-
ный цилиндр с линейной
плотностью Z = odS и коор-
динатами центра тяжести
хв, z0. Вертикальная состав-
ляющая притяжения эле-
ментарного цилиндра
0) = 2Н(л-о, гв) %
(5—хо> Т го
Умножим обе части этого равенства на di и проинтегрируем
в пределах от а до Ь:
ь ь
j dUz (Ё, 0) di = 2k/. (хв, 2С) J г» di
а а
= 2kk (х0, z0) (arctg b — arctg г^° ) = 2kK (х0, zfl) <р (х0, гв),
где <р (х0, z0) — угол видимости отрезка ab из точки (х0, г0).
Для цилиндрического тела имеем
ь
| C/2(g, O)dg = 2Л J J zB)<p(xB, z0)dS. (15.33)
a S
Во всем пространстве z > 0 угол ср положителен, поэтому,
если плотность X (хв, z0) не меняет знака по всей области интегри-
рования, то, применяя к правой части выражения (15.33) теорему
о среднем, получаем
ь
J B'z (L 0) di — 2k(f (Ло, z0) J j л (x0, zB) dS = 2/e<p (xB, zB) X. (15.34)
a S
Положим, что аномальное тело квазисимметрично. В этом
случае центр аномалии [точка % = |гаах, где U2(i) = Uzm!X]
и проекция центра тяжести тела на ось х или совпадают, или на-
ходятся достаточно близко друг от друга. Расположим начало
400
координат в этой точке. Из всей совокупности точек (х0, z0) тела
выберем точку (0, г0), где ср (0, z0) = ср, и назовем ее центром
возмущающих масс. Если при этом отрезок ab расположить сим-
метрично относительно начала координат, т. е. положить b — а —
= 2а, то
<p = 2arctg(a/z0).
Тогда для выражения (15.34) получаем
ь
Ia = O)dg — 4/<Aarctg(a'z0). (15.35)
а
Эта формула позволяет при известном X определить z0:
z0 = actg[/a/(4A!2i)].
Используя выражения (15.21), имеем
z0 = a ctg [л/0/(2Л»)],
где
/„ = j Uz^, 0)dg = 2n/A.
— оо
Положим, что при изменении отрезка интегрирования 2а
координаты точки (0, z0) не изменяются. При таких допущениях
Е. Г. Булахом получены простые формулы для приближенной
оценки глубины залегания центра масс z0 и избыточной плотности А,
на единицу длины аномального тела.
Поместив начало координат в точке максимального значения
аномалии, вычислим интеграл (15.35) при двух интервалах ин-
тегрирования: (—и (—a2-:a2); получим
/(11 = 4Н arctg (aj/Zo); 1
4ЛА arctg(a2/z0). f
Для простоты вычислений интервал интегрирования выберем
так, чтобы
Аза — 2/а1.
Тогда
arctg (a2/z0) = 2arctg (a^),
откуда имеем
Zq — afa2/(a2 — 2ai). (15.37)
Определив из этого выражения z0, легко найдем избыточную
плотность единицы длины аномального тела по формуле (15.35).
Заметим, что соотношение (15.37) справедливо только для тел,
аномалии которых симметричны или квазисимметричны, Точное
значение zu эта формула дает только для кругового цилиндра.
401
ПРЕОБРАЗОВАНИЕ
ТРЕХМЕРНЫХ АНОМАЛИЙ В ДВУМЕРНЫЕ
В тех случаях, когда формулы для двумерных тел нельзя при-
менить к трехмерным, специальным приемом сводят трехмерную
аномалию к двумерной. Рассмотрим этот прием на примере ано-
малии U2, поскольку для Uxz и Uzz требования к двумерности
значительно слабее. В точке с координатами (0, у, 0) имеем
Вг Ла
с, d~ di] dt,
.1 П [?3 -Hn — + S2]3/2 -
Умножаем обе части этого выражения на dy и интегрируем
их по у в пределах ±оо;
(15.38)
Учитывая выражение (14.19) и полагая
Ж
ст j di] =
Hi
получаем
+<»
J t72(0, у, Q)dy~2kea f
(15.39)
Правая часть этого выражения представляет собой формулу Uz
двумерного тела. Отсюда следует, что трехмерную задачу можно
свести к двумерной, если вдоль профиля, расположенного вкрест
+<»
простирания тела, рассматривать не кривую Uz, а кривую | U2dy.
— со
По такой кривой получаем истинные геометрические параметры
тела, но не плотность п.
При использовании этого приема на практике приходится
ограничиваться интегрированием в конечных пределах, поскольку
аномалия известна в ограниченной области и на периферии может
быть искажена влиянием соседних аномалий. Оценим относи-
тельную погрешность е, возникающую из-за ограничения пре-
делов интегрирования.
Положим, что тело, создающее гравитационную аномалию,
представляет собой шар. Помещая начало координат над центром
шара, имеем
+у
f dy
J (ла ф- у"- + ha)3/2
dy
(х2 + г/2+Л2)3/2
= 1 -
У
402
где
р2 = х2 + Л2.
Принимая hly < 1, в центов аномалии (х = 0; р = /г) получаем
—-[• +(1)’Г,Я“4(1),-4(1Г-
Для различных отношений hly рассчитана погрешность е:
hly ......................... 0,5 0,3 0,2 0,1
е............................ 0,15 0,04 0,02 0,01
Отсюда видим, что уже при hly = 0,2 конечность пределов ин-
тегрирования мало сказывается на окончательном результате.
Уменьшить погрешность интерпретации, связанную с заменой
трехмерной задачи двумерной, можно также трансформацией
аномалий силы тяжести в такие производные, для которых тре-
бования к двумерности невелики. Такого же результата можно
добиться и соответствующим расположением интерпретационных
профилей относительно аномального тела.
ОПРЕДЕЛЕНИЕ
РЕЛЬЕФА КОНТАКТНОЙ ПОВЕРХНОСТИ
Контактной поверхностью называется поверхность раздела
двух сред с разными плотностями. Определение рельефа контакт-
ной поверхности по наблюдениям силы тяжести имеет большое
значение в практике гравиметрических работ. Контактной по-
верхности могут быть уподоблены рельеф кристаллического фун-
дамента, отдельные складчатые структуры и т. д.
Пусть MN — горизонтальная поверхность, на которой про-
ведены наблюдения силы тяжести (рис. 15.10). Ниже ее распола-
гается поверхность S произвольной формы, разделяющая две тол-
щи пород с разной плотностью. Пусть сг^ — плотность пород
верхней толщи, ст2 — плотность пород нижней толщи; избыточная
плотность ст = ст2 — стт. Очевидно, что при о > 0 положительным
формам рельефа границы S соответствуют положительные прира-
щения аномалии Uи наоборот, отрицательным формам границы S
соответствуют отрицательные приращения аномалии.
Рис. 15.10.
поверхность.
Контактная
Полагая начало координат в точке наблюдения О, из формулы;
(1.35) имеем выражение аномалии U2 от контактной поверхности
2л м г
Пг(0, 0, 0) = Ла J JJ <15'41)
где г и а — полярные координаты точки наблюдения; г — глу-
бина контактной поверхности в этой точке; h — средняя глубина
контактной поверхности.
Поскольку глубина z является функцией координат г и а,
определение ее связано с решением уравнения, в котором эта
функция находится под знаком интеграла. Относительно функ-
ции z (г, а) выражение (15.41) является нелинейным интегральным
уравнением, алгоритмов для решения которого не разработано.
Поэтому точное решение задачи о контактной поверхности невоз-
можно. Необходимо упростить математическую постановку задачи,
чтобы получить приближенное решение.
Проинтегрировав выражение (15.41) по г, получим
2 Jt СО
°- Ч-Н 1 (W-W - тй? <15-42)
Будем полагать, что отклонения Ай = z (г, а) — h действи-
тельной поверхности от плоскости на глубине h малы по сравне-
нию с h. При этом допущении подынтегральное выражение (15.42)
может быть разложено в ряд Тэйлора по степеням отношения
Д/г/г:
г___________г _ г/г Д/г . 1 . г (г2 — 2/г2) (Д/г)2 _
1<г2 + /г2 Кг2 + z2 “ (г2 + /г2)3/а *” 2 (г2 +/г2)5/2 + ’ ’ ’
Ограничиваясь в разложении членами с Д/г в первой степени
и подставляя их в формулу (15.41), получаем
2Л со
Уг(0, 0, 0) = /ea J J frda. (15.43)
и о 'г ' '
Положим
о А/г = р (г, a, h),
где р (г, а, /г) — поверхностная плотность плоского слоя, рас-
положенного на глубине h.
Так как значение силы тяжести на поверхности плоского слоя
(7г(г, а, /г) = 2лАр = 2лйа Д/г, (15.44)
то формула (15.43) принимает вид
2л ос
иг (О, О, 0) •= -Д- ( [ иАг' • (15.45)
г v ’ 2л J J (Г2 1 /,2)3/2 К >
404
Ё случае двумерной задачи
Ч-оо £ + бЛ
t/ДО, 0)^2to J f In (15.46)
— oo fl — oo
Подынтегральное выражение (15.46) разлагаем в ряд, считая,
что отклонения контактной поверхности от плоскости A/z (£) =
= г] (Е) — h малы по сравнению с h. Получаем
Uz (0, 0) = /го J In (1 + =
- а>
, 7 Г 2/г Д/i ч- Д/г2 /2/г Д/г + Д/г2)2 , 1 ,е л-г\
= j [ x2 + h2 - + • • • ] ft. (15.47)
— во
Ограничиваясь первым членом разложения и вводя поверх-
ностную плотность н (?, /г) = о Ah (£), находим
i/ДО, 0) = А J , (15.48)
— оо
где
U2 (Е, /г) = 2л/та Ah (g) = 2л£р (Е, /г)
— значение IL в точках плоскости £ = /г.
Полученные выражения (15.45), (15.48) являются не чем иным,
как интегралом Пуассона 1см. формулу (1.115)].
Таким образом, упрощение задачи об определении контактной
поверхности свелось к трансформированию наблюденных значе-
ний силы тяжести на некоторую вспомогательную поверхность
на глубине/г (см. главу 16). Такое упрощение позволяет применять
для решения задачи различные методы аналитического продол-
жения аномалий силы тяжести в нижнее полупространство на
некоторую глубину h. Затем, используя формулу Ah =
= U2 (г, a, h)/(2nka), находят превышения рельефа относительно
выбранной вспомогательной поверхности. Полученное таким об-
разом решение можно уточнить методом последовательных при-
ближений.
Следует заметить, что метод последовательных приближений
можно использовать для нахождения рельефа контактной поверх-
ности и без предварительного определения Uz(r, а, К) на вспомо-
гательной плоскости h. В этом случае за первое приближение
U\ (h) принимают наблюденное значение Uz и, используя формулу
(15.44), строят рельеф контактной поверхности. При этом, естест-
венно, должны быть известны избыточная плотность и глубина
границы хотя бы в одной точке. Используя методы решения пря-
мой задачи, вычисляют гравитационный эффект U} полученной
405
в первом приближении контактной поверхности. Находя раз-
ность наблюденного и вычисленного значений аномалий силы
тяжести А = иг — UI, в качестве второго приближения анали-
тически продолженного значения берут Ulz (h) = Uг -ф А =
= 2UZ — Uz и строят новую поверхность, гравитационный
эффект U" которой можно также подсчитать. Для последующих
приближений
Z/Г1 (й) = 3UZ - U\ - U"\
U'?(h) = 4Uz-U\-U" -t/’11; (15.49)
ипг (h) = nUz-U'z-Ulzl------ и'Г1-
Легко доказать, что процесс является сходящимся.
Число приближений зависит от сложности рельефа контакт-
ной поверхности, ее средней глубины и относительных превыше-
ний. При сравнительно спокойном рельефе для приблизительной
оценки часто применяют самую простую формулу U2 — 2nkc \h,
т. е. предполагают прямую пропорциональность между изменением
аномалий силы тяжести и глубиной. Следует отметить, что эта
формула дает результат тем точнее, чем меньше средняя глубина
контактной поверхности.
Рассмотрим для примера контактную поверхность в виде
вертикального уступа.
Пусть и — координаты точек, расположенных по обе
стороны от вертикальной границы уступа; h2 и й2 — глубина уступа
в этих точках. Можно написать
Uz (-|—оо) — U. (—оо) == 2л/ю (Л2 — /у);
при больших значениях х2 и х2
Uz(x1)-Uz(xi)^2nka(hi-h1). (15.50)
Заменяя вертикальный уступ материальной плоскостью на
глубине 1г = (h2 + hJ/2 и фиксируя точки х2 и х2, получаем, что
наиболее точно соотношение (15.50) выполняется при минималь-
ной глубине материальной полуплоскости, поскольку в этом слу-
чае аномалия Uz меняется наиболее резко и быстро приближается
к своим предельным значениям. Если глубину залегания мате-
риальной полуплоскости увеличивать, то изменение кривой Uг
над уступом (материальной полуплоскостью) становится все бо-
лее плавным, предельные значения достигаются при больших
абсциссах х2 и х.2, разность U2 (х.2) — Uz (ху) отличается от предель-
ного значения все больше, причем всегда
Uг (ху) - U2 (х2) < 2nks (йа - h2).
Из приведенного рассуждения следует, что гравитационный
эффект контактной поверхности зависит также от ее средней
406
глубины и применение формулы (15.44) для построения первого
приближения контактной поверхности будет давать удовлетвори-
тельные результаты только при неглубоком ее залегании.
Если известна средняя глубина контактной поверхности h,
то можно получить более точную формулу для вычисления пре-
вышений Д/i. Рассмотрим такой случай на примере двумерной за-
дачи.
Положил!, что относительно средней глубины h превышение
контактной поверхности h — £ вдоль профиля, совпадающего
с осью х, характеризуется следующей функцией:
h — Z = А/г cos (<og).
Тогда гравитационное действие контактной поверхности мо-
жно рассматривать как действие материальной плоскости, распо-
ложенной на глубине 1г и имеющей переменную поверхностную
плотность
и. = и Д/г cos (cog) — р0 cos (cog).
В этом случае гравитационное действие этой плоскости на самой
плоскости
/72 (g, /г) = 2л/гр — 2n/?ii(l cos (cog),
а на поверхности наблюдений на основании интеграла Пуассона
+оо
U, (0, 0) = A J cos (соЕ) = иг (/г)
- оо
или
f/z(0, 0) == 2л/го (/г — £) ехр (fe-2jt/i/Z), (15.51)
где
2 л// = со.
Полагая в точках хх и х2 глубину контактной поверхности соот-
ветственно /гх и /г2, получаем
(Xj) — U2 (х2) 2л£о (/г2 — /гх) ехр (—2л/г//). (15.52)
Это выражение является обобщением формулы (15.50), которая
получается из пего при условии
ехр (—2л/г//) —* 1,
т. е. при h—>0 или /—* оо.
При выполнении этих условий, т. е. при уменьшении средней
глубины контактной поверхности (/г —> 0) или при увеличении
поперечных размеров элементов рельефа этой поверхности
(I - ► со), повышается точность формулы (15.50). В пределе полу-
чается вертикальный уступ (горизонтальный слой), которому
соответствует формула (15.50).
407
По упрощенной формуле (15.50)
значения превышений контактной
поверхности относительно ее сред-
ней глубины получаются зани-
женными и это занижение тем
больше, чем глубже контактная
поверхность. При оценке гра-
витационного действия контакт-
Рис. 15.11. К оценке гравитацион- НОЙ поверхности ПО ЭТОЙ фор-
ного действия контактной поверх- муле без учета средней глубины
ности' всегда получаются завышенные
значения гравитационного эффек-
та. Таким образом, реальная оценка гравитационного влияния
контактной поверхности должна базироваться на учете не только
избыточной плотности этой поверхности, но и ее средней глу-
бины. Если под эффективной плотностью контактной поверхности
понимать
оа = о ехр (—2n/i//),
то можно отметить, что при прочих равных условиях эффективная
плотность уменьшается с глубиной контактной поверхности
(табл. 15.1).
Зависимость эффективной плотности от глубины границы раз-
дела особенно важно иметь в виду при оценке гравитационного
действия структур, у которых эти границы подобны друг другу
(рис. 15.11). Неучет средних глубин залегания отдельных границ
в этом случае может привести к существенным ошибкам. Дейст-
вительно, обозначая средние глубины залегания границ Л1( /га, ...,
hn, избыточные плотности Oj, <т.2, .... ст„, «период» контактной
поверхности /, для такой структуры на основании формулы
(15.22) можно написать
U2 (xt) - U2 (х2) = 2л/г<тц (й/г - /1П),
где
п
са = ехр(—2лй,/7);
i=i
/г,1 и й,2 — глубины залегания любой из поверхностей соответст-
венно в точках X] и х2.
Пусть
о1 = о2 == ц3 = о; = й2/2 = /i3/3 = 1г, 1г/1 — 0,1.
Тогда по формуле (15.52) получим
£7г (хх) — L/j (х2) = 2nko [ехр (—2л/г//) ф- ехр (—4лЛ//) ф-
+ ехр (—6л/г//)| (/iia - Йц) = 0,97 [2л/ш (hn — /in)J.
408
Таблица 15.1
Зависимость эффективной плотности от глубины
контактной поверхности
h!l Стд/а hll СГд/сТ h!l ntt/a
0,00 1,000 0,20 0,284 0,50 0,043
0,05 0,730 0,25 0,208 0,75 0,009
0,10 0,534 0,30 0,150 1,00 0,002
0,15 0,381 0,40 0,081
Формула же (15.50) дает
Uг (xj — Uг (л-3) = 3 • 2nka (hi2 — hn).
Таким образом, действительный гравитационный эффект струк-
туры в 3 раза меньше, чем вычисленный по формуле (15.50).
При этом влияние верхней контактной поверхности оказывается
наибольшим по сравнению с влиянием двух других поверхностей.
Отсюда следует, что при определении рельефа контактной поверх-
ности всегда надо стремиться найти реальную зависимость ано-
малий Uz от глубины этой поверхности, используя известные
значения ее глубины в некоторых точках исследуемого района.
Коэффициент пропорциональности между Uz и Д/г в действитель-
ности всегда меньше 2 л/га.
Вертикальный уступ является предельным случаем структур
флексурообразного типа, что позволяет использовать формулы,
выражающие гравитационное действие уступа, в качестве оценоч-
ных для вычисления предельно возможной глубины этих структур.
Из формулы
Uxz max = 2ka In (h^hj
для произвольной флексурообразной структуры, имея в виду, что
Н — кг — hlt получаем
'' exp [UA2 max/(2*o)] — 1
и, так как Н U2 тах/(2лАп),
тп max
1 2лЛст {exp [UX2 max/(2fea)] — 1}
Разлагая exp [Uxz max/(2Aa) I в ряд по степеням Uxz maJ(2ko) и
ограничиваясь в разложении тремя первыми членами, имеем
_____________Uz max_____________
п [1 +!/« max/(4£<Z)) Uxz max
(15.53)
409
Рис. 15.12. Определение tAzniax
графическим способом по кри-
вой иг.
Значение UX2WX можно опре-
делить по кривой Uz графически
(рис. 15.12):
U xz max = U г max Д
Тогда формула (15.53) примет
вид
, __________L___________
л [1 + УХг шах/(4*а)] ~
~ Я[1 +(/гтах/(4*а/.)] <15-54)
По этой формуле можно оценивать предельную глубину масс
любой формы, но чем больше отличается структура от вертикаль-
ного уступа, тем приближеннее такая оценка.
ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ
ПОЛЯ И ЕГО ИСПОЛЬЗОВАНИЕ
ПРИ ИНТЕРПРЕТАЦИИ АНОМАЛИЙ
В результате съемки получают распределение гравитационного
поля на поверхности наблюдений. Используя аппарат аналити-
ческого продолжения, можно находить распределение наблюден-
ного поля выше и ниже этой поверхности. Полученная таким об-
разом картина аномального поля в пространстве может существен-
но повысить результативность интерпретации, помогает составить
более полное представление о телах и структурах, позволяет ис-
пользовать методы интерпретации, для которых требуется знать
распределение поля на нескольких уровнях, дает возможность
строить вертикальные карты изолиний аномального поля.
Сравнение этих карт с вертикальными картами, рассчитанными
для тел правильной формы, позволяет найти некоторые элементы
залегания возмущающего объекта или же оценить достоверность
замены реального объекта телом правильной формы. Аналитиче-
ские выражения изолиний для тел простейших геометрических
форм можно получить, разрешив уравнения гравитационных эф-
фектов этих тел относительно координат точки наблюдения.
Обозначим отношение гравитационного эффекта тела к соот-
ветствующему постоянному коэффициенту (kM, 2Н, 2£р), входя-
щему в аналитические выражения этого эффекта, через р. Для
разных тел получим следующие выражения.
Для 1)г шара и игг вертикального материального стержня,
нижний конец которого уходит в бесконечность, из формул (14.1)
и (14.14) имеем
р = U2/(kM) = £/„/(П) = h (х2 + /г2)3'2
или
(х2 4- й2)а/2 = h!р,
410
откуда
ха -|- h2 = У(h/p)2',
х ^y^ih/p^-h2. (15.55)
По этой формуле рассчитывают вертикальную карту изолиний
U2 шара и Uzz вертикального материального стержня (рис. 15.13).
Аналогично можно рассчитать и построить вертикальные карты
изолиний и для других тел.
Для аномалии U., создаваемой вертикальным материальным
стержнем, имеем
р = Uz/(kk) = l/|/x2 + /i2;
х24-й2 = 1/р2. (15.56)
Это выражение представляет собой уравнение окружности
с центром в точке (0, h) и радиусом \!р (рис. 15.14).
Для Uz горизонтального материального стержня (кругового
цилиндра), Uzz вертикальной материальной полосы и UXi гори-
зонтальной полуплоскости имеем
п _ ДД_ — _____< I к 571
' ~ 2W. 2Лр ~ 2kp ~ x2+h2 ’ 1 ;
Для Uхг вертикальной материальной полосы и Uzz горизон-
тальной полуплоскости •
Р =-^ = = • (15.58)
' 2ft.ii 2/гц х2 4- Л2 ' '
Из формул (15.57) и (15.58) соответственно получаем
х2 + h2 - hip = 0; (15.59)
x24-/i2 + x/p = 0. (15.60)
Выражение (15.59) представляет собой уравнение окружности
с центром в точке [0, 1/(2/?) 1 и радиусом 1/(2/?) (рис. 15.15, а).
Формула (15.60) также является уравнением окружностей с цен-
трами в точках [± 1/(2/?), Л] и радиусом 1/(2/?) (рис. 15.15, б).
Для и Uzz горизонтального материального стержня (кру-
гового цилиндра) имеем
Uхг 2хД . игг h2 — х2 /15 611
Р ~ 2П (ха4-Л2)а’ Р ~ W “ (х2 + h2)2 ЦО-о!)
или, вводя полярные координаты
получаем
р — — (sin 2<р)/р2; р -= (cos 2ср)/р2. (15.63)
411
Рис. 15.13. Вертикальная карта изолиний Uz шарр и игг вертикального мате-
риального стержня.
Рис. 15.14. Вертикальная карта изолиний Uz вертикального материального
стержня.
412
Рис. 15.15. Вертикальная карта изолиний иг горизонтального стержня, 11хг
горизонтальной полуплоскости, t/zz вертикальной полосы (о) и Uxz верти-
кальной полосы, Uzz горизонтальной полуплоскости (б).
Задаваясь р для различных ср, определяют р и строят верти-
кальную карту изолиний (рис. 15.16).
Если гравитационный эффект тел (U. вертикальной мате-
риальной полосы, ихг вертикального контакта и вертикального
пласта) выражается формулой вида
р = 1П (pss/pr).
где р2 и р, — расстояние точки наблюдения до двух заданных то-
чек, то на основе выражения (14.71) заключаем, что изолинии
элементов гравитационного поля таких тел представляют собой
окружности с координатами центров
хц = 0, йц = (Л2 — ftj) cth р
413
Рис. 15.16. Вертикальная карта изолиний UX2 и Uzz горизонтального материаль-
ного стержня (кругового цилиндра).
и радиусами
Г = ± (/г2 — Л1)/(2 sh р)
— для U2 материальной вертикальной полосы и UХ2 вертикаль-
ного контакта;
хц = dethp, йц —/1
и радиусами
г = ± d/sh р
—для U >2 вертикального пласта (см. рис. 14.15).
Если же гравитационный эффект тела горизонтальной ма-
териальной полосы, U вертикального пласта и вертикального
контакта) определяется формулой вида
р = е,
где 0 — угол, под которым из точки наблюдения виден отрезок,
соединяющий две точки тела, определяющие его форму, то изо-
линии в этом случае согласно формулам (14.71) представляют
собой окружности с центрами в точках
Хц = 0, йц — h — d etg р
414
и радиусами
. г — ±d/sin/j
— для Uz горизонтальной материальной полосы и Uzz вертикаль-
ного пласта;
Хц = [(^2 — /*1)/2] ctg р, ha = h
и радиусами
г = ± (й.2 — йх)/(2 sm р)
— для игг вертикального контакта (см. рис. 14.15).
И наконец, для аномалии силы тяжести Uz материальной гори-
зонтальной полуплоскости из формулы (14.48) имеем
х = 1г 1g (р — л/2),
т. е. в этом случае изолинии представляют собой лучи, исходящие
из точки с координатами (0, /г).
Вертикальные карты изолиний элементов гравитационного
поля для различных простейших тел показывают, что особые
точки этих тел являются своего рода фокусами, к которым схо-
дятся изолинии, причем характер изолиний в окрестностях особых
точек зависит от формы тела. Изолинии аномалий силы тяжести Uz
шара, горизонтального цилиндра и аномалий {/гг-и Uxz вертикаль-
ной материальной полосы и горизонтальной полуплоскости ка-
саются друг друга в особой точке. Изолинии аномалий силы тя-
жести Uz горизонтальной материальной полосы, аномалий U zz
вертикального контакта и вертикального пласта пересекаются
в особых точках. Изолинии аномалий U2 вертикальной материаль-
ной полосы и аномалий Uxz вертикального контакта и пласта стя-
гиваются к особой точке.
Рассмотренные соотношения особых точек простейших тел
с поведением изолиний позволяют использовать вертикальные
карты для определения элементов залегания объектов. Например,
если аномалия силы тяжести может быть уподоблена аномалии
вертикального материального стержня, то, используя несколько
пар точек х,- и хк, в которых Uz (xz) = Uz (хк), строим направление
радиуса окружности. Точка пересечения радиусов укажет по-
ложение верхнего конца вертикального стержня.
Рассмотрим некоторые из этих способов применительно к дву-
мерным телам.
Если практические кривые Uz, и Uxz Uzz могут быть уподоб-
лены аналогичным теоретическим кривым соответственно гори-
зонтального цилиндра, горизонтальной полуплоскости и верти-
кальной материальной полосы, бесконечной на глубину, то,
выбрав также несколько пар точек хг и хк, в которых Uz (х;) =
— построим радиусы, точки пересечения которых дают
положение центров окружностей. Проведем из этих точек окруж-
ности радиусом Ох/. Линия касания семейства окружностей оп-
415
Рис, 15.17. Палетка
для определения глу-
бины залегания гори-
зонтального мате-
риального стержня.
ределит глубину центра цилиндра, глубину полуплоскости и
материальной вертикальной полосы. Если же практические кри-
вые V г и U гг можно уподобить теоретическим кривым соответствен-
но 11г материальной горизонтальной полосы и Uгг вертикального
контакта или вертикального пласта, то таким же образом найдем
центры окружностей и, проведя окружности, получим две точки
их пересечения; хорда, соединяющая эти точки, отметит поло-
жение тела.
Определение параметров тела способом характерных точек,
в котором используется отношение некоторой доли максимального
значения аномалии к полному максимуму, можно распространить
и на случай вертикального распределения поля. Для тел, имеющих
одну особую точку (сфера, горизонтальный цилиндр, горизонталь-
ная материальная полуплоскость, вертикальный материальный
стержень, нижний конец которого уходит в бесконечность), были
получены следующие соотношения между абсциссой хп части
максимума и глубиной h в этой точке
= xnhh.
Это уравнение определяет семейство прямых, пересекающихся
в особой точке. Таким образом, если поведение аномалии тела,
имеющего одну особую точку, известно на двух или более уровнях,
то найти положение особой точки можно следующим образом.
Через точки, в которых значения аномалии, выраженные в долях
ее максимума, на заданной высоте одинаковы, проводим прямые
линии, пересечение этих прямых и укажет положение особой точки.
Для различных простых тел с одной особой точкой можно заранее
построить лучевые палетки, которые позволяют быстро находит
параметры аналогичных реальных тел (рис. 15.17).
Использовать эти палетки на практике весьма просто. Палетку
накладывают на профиль таким образом, чтобы вертикальная
линия палетки (/2Шах совпадала с максимальной ординатой ано-
малии. Затем палетку перемещают вдоль этой ординаты, доби-
ваясь, чтобы лучи палетки пересекли линию профиля в точках
с соответствующими значениями аномалии: луч max — в то-
чке Uz = игт.а/2, луч Уг0|26П1ах в точке Uz = б/гГ|1ах/4. При таком
совмещении центр палетки совпадает с особой точкой па раз-
резе.
416
Рис. 15.18. К определе-
нию глубины возмущаю-
щего тела по наблюде-
ниям на разных уровнях.
Глубину особой точки можно определить и аналитически
по абсциссам любых точек, в которых аномалия составляет п-ю
долю от максимальной на этой высоте:
/i = [хл1/(хя2 — хя1)] A/i, (15.64)
где ДА — разница уровней, па которых известны аномальные зна-
чения; хп1 и хп2 — абсциссы точек, в которых значения поля со-
ставляют п-ю долю от максимума на данной высоте (рис. 15.18).
Для тел, имеющих две и более особые точки, аналогичные
зависимости носят более сложный характер и получить их в об-
щем виде трудно.
В частности, по аномалии 1)гг вертикального пласта и Uг
горизонтальной материальной полосы было установлено
4/2 == /I2 + rf2,
по аномалии UХ2 вертикального пласта
''•max — № “Ь
где h — глубина полосы или верхней кромки пласта; d — поло-
вина горизонтальной мощности полосы или пласта.
Эти выражения представляют собой уравнения равнобочной
гиперболы, действительная ось которой совпадает с верхней
кромкой пласта (с материальной полосой), а длина этой оси равна
горизонтальной мощности пласта (материальной полосы). Асимп-
тотами гиперболы являются прямые х — ±h, пересекающиеся
в центре верхней кромки пласта (в центре полосы).
Таким образом, если известны значения Uz< Uzz и Uxz на не-
скольких уровнях, то определить положение особых точек пласта
можно графическим или аналитическим путем. При графическом
способе по значениям 0,5//z?max, Uxz тах или 0,5(7ггаах и по удален-
ным точкам гиперболы проводим ее асимптоты, которые пересе-
каются в центре верхней кромки пласта или полосы и таким об-
разом указывают на глубину. Построив по асимптоте и одной из
точек, принадлежащих гиперболе, ветвь гиперболы, найдем
длину ее действительной оси, которая будет равна горизонталь-
ной мощности пласта (полосы) 2d.
Чтобы получить h и d аналитическим путем, необходимо иметь
распределение Uz, Uzz и U хг на двух уровнях.
14 В. С. Мироио,
417
Тогда по /Д и Uu
(•Vi/2)o = h2 + d2;
(*1/2)! = (Л ± A/1)2 + d2,
no UX2
(^max)o = /t2 + d2\
Mi=(ll±\h)2+d2.
Решая эти уравнения, находим
;,„± . d_ (15.65)
Н = ± faax)l-_(xn.ax)l ~^а .; d = ± |/(ХпихГо - (15.66)
Для Uхг и U2Z вертикального контакта соответственно
/11/12 = Х1/2'> ЙДг = Хтах •
Для IL вертикальной материальной полосы
йДз = Xf/2.
Положив /гх = h — d и h2 = h Д d, где h — глубина се-
редины уступа или материальной полосы; 2d — амплитуда сброса
или вертикальные размеры полосы, получим
h2 — (xi/2)2 = d2 и h2 — (xmax)3 = d2. (15.67)
Эти выражения представляют собой уравнения равнобочных
гипербол, действительная ось которых совпадает с линией верти-
кального сброса (материальной полосы), размеры этой оси равны
2d. Асимптотами гиперболы являются прямые х = +h. Следо-
вательно, определение положения особых точек для сброса по /Д2
и СДи вертикальной материальной полосы по Uг можно проводить
так же, как для вертикального пласта.
В случае наклонного контакта для Дгг справедливы соотно-
шения
хтах = У № d2 cos 2а ;
xs = (J2 sin 2a)/(2/i),
где xs— точка, в которой
^гг ОС) = ^гг шах “1“ гг ш1п'
Имея кривую Дг2 на уровне ±А/г, получаем
h = ± [(Xniax)i - (tfmax)o - A/i2]/(2 A/i); d2 cos 2a == (хшах)§ - /i2;
/t = +(Xs)q A/i/[(.vs)x — (^s)oji tg 2a == 2h(A's)(i/[(rn;aK)o h J.
418
Рассмотренные способы определения особых точек тела (по-
ложения самого тела), которые используют пространственное
распределение аномалий, можно применять только в исключи-
тельно благоприятных условиях, когда реальное тело достаточно
точно аппроксимируется простейшими геометрическими формами.
В этом случае достаточно знать распределение функций на двух
уровнях. При более сложной конфигурации тела нахождение
особых точек тела связано с экстраполяцией аномального поля
до каждой из этих точек. Поэтому чтобы составить более полное
представление о поведении поля в пространстве и более опреде-
ленно выявить закон экстраполяции, приходится рассчитывать
распределение аномалин на нескольких уровнях.
Глава 16
МЕТОДЫ ТРАНСФОРМАЦИИ
ГРАВИТАЦИОННЫХ АНОМАЛИЙ
ОБЩИЕ ПРИНЦИПЫ
ТРАНСФОРМАЦИИ АНОМАЛИЙ
Гравитационные аномалии, которые полу-
чают в результате гравиметрической съемки, отражают многие
геологические факторы, каждый из которых вносит свой вклад
в наблюдаемое поле. Поэтому в гравитационном поле геологиче-
ские образование проявляются в виде наложенных, сложных
аномалий. При решении конкретных геологических задач из этого
суммарного поля необходимо выделить аномалии, отвечающие
отдельным, интересующим нас объектам. Для этого исходные
гравитационные аномалии преобразуют так, чтобы подчеркнуть,
усилить одни особенности гравитационного поля и исключить или
подавить другие. Преобразование, или трансформация, гравита-
ционных аномалий имеет много общего с разделением сигналов
в теории связи, хотя обладает и своими, только ей присущими
специфическими особенностями.
Основная цель трансформации гравитационных аномалий
заключается в наиболее полном разделении исходного наблюден-
ного поля на составляющие, каждая из которых отвечает источни-
кам разной геологической природы, залегающим на разных глуби-
нах и т. и. Поэтому трансформация аномалий — это составная
часть геологической интерпретации, ее первый этап, которым в зна-
чительной степени определяется конечный результат. Трансформа-
ция направлена на упрощение, разложение гравитационного поля,
что приводит в предельном случае к выявлению эффекта каж-
дого тела.
14'
419
Задача трансформации наиболее проста, когда отдельные ано-
малии независимы друг от друга и резко различаются характером
своего проявления в общем поле. Однако практически такое поло-
жение наблюдается чрезвычайно редко, поскольку реальные
гравитационные аномалии оказываются частично взаимозависи-
мыми, что обусловлено густотой сети, точностью съемки, взаимо-
связью геологических структур и т. п. Поэтому в общем случае
не удается полностью изолировать аномальные эффекты разных
источников. Чтобы обеспечить наиболее падежное разделение
аномалий, необходимо привлекать всю имеющуюся геологическую
информацию. Это позволяет наложить дополнительные ограничи-
тельные условия на разделяемые аномалии, выбрать наиболее
рациональную методику трансформации. Любые трансформации
гравитационных аномалий всегда опираются на некоторые априор-
ные геологические предпосылки. Ими могут быть интервал глубин
ожидаемых объектов, размеры аномалий, их градиенты и т. д.
Очевидно, что все эти величины взаимосвязаны. В некоторых слу-
чаях может быть непосредственно учтен гравитационный эффект
известных геологических разрезов на отдельных участках исследо-
вания.
Надо всегда иметь в виду, что ни одним из методов трансформа-
ции нельзя выделить из суммарного наблюденного поля каких-
либо особенностей, не содержащихся в исходном поле. Иными
словами, трансформация не приводит к получению новой инфор-
мации, она только подчеркивает одни особенности исходного
поля, подавляя и исключая другие. Сточки зрения теории инфор-
мации любая трансформация исходных данных ведет к частичной
потере содержащейся в них информации. Это относится и к транс-
формации гравитационных аномалий.
К настоящему времени разработаны многочисленные методы
трансформации гравитационных аномалий. Однако большинство
из них основано на известном соответствии порядка геологических
структур и отвечающих им аномалий: чем крупнее гравитирующий
объект и чем глубже он залегает, тем более обширные по площади
и малые по градиенту аномалии он создает, и наоборот, чем меньше
размеры объекта и глубина его залегания, тем ограниченнее
аномалия по площади и резче ее градиенты. Первые аномалии
обычно называют региональными, а вторые — локальными. Есте-
ственно, что понятие региональных и локальных аномалий явля-
ется относительным и определяется масштабом съемки. Аномалия,
локальная для одного масштаба съемки, станет региональной для
другого, более крупного. Существование прямого соответствия
порядка аномалий порядку вызывающих их геологических струк-
тур позволяет в ясных случаях, не прибегая к сложным вычисле-
ниям, разделять региональные и локальные аномалии простым
графическим методом на основе самых общих представлений
о геологическом строении исследуемой территории. Этот метод
основан на сглаживании изоаномал или графиков. Разность
420
наблюденных и сглаженных аномалий относят к локальным, или
остаточным, аномалиям.
Метод сглаживания применяют, когда изолинии гравитацион-
ного поля имеют преимущественное простирание в каком-либо
одном направлении и располагаются примерно на одинаковых
расстояниях друг от друга, т. е. когда региональное поле может
быть уподоблено наклонной плоскости. При относительно простом
характере поля этим методом можно воспользоваться и тогда, когда
региональное поле описывается поверхностью выше первого
порядка. Исключение регионального фона графическим методом
проводится на практике следующим образом. На гравиметрической
карте выбирают ряд параллельных профилей, совпадающих
с направлением максимального изменения гравитационного поля,
и строят графики поля вдоль этих профилей. На каждом из них
проводят линию регионального фона. Эти линии переносят на
карту и строят уже изолинии регионального поля. Разность
наблюденного исходного поля и регионального фона определяет
локальные аномалии.
Как уже отмечалось, указанный метод можно применять только
при сравнительно простом характере поля. Кроме того, в этом
случае невозможно оценить степень разделения аномалий. Полу-
ченный региональный фон существенно зависит от опыта интерпре-
татора.
Многочисленные методы трансформации гравитационных ано-
малий можно разделить на два класса в зависимости от характера
априорных сведений, использованных при выборе и обосновании
метода. К первому, наиболее многочисленному, классу относятся
трансформации, основанные на подобии геологических структур и
гравитационных аномалий, т. е. на статистическом различии между
аномалиями разной геологической природы. Второй класс состав-
ляют трансформации, которые непосредственно учитывают уже
известную геологическую информацию. В этом случае аномалии
разной природы могут иметь одинаковое внешнее проявление.
Методы трансформации гравитационных аномалий, основанные
на подобии геологических структур и аномалий, можно разделить
условно на три большие группы.
1. Осреднение.
2. Аналитическое продолжение гравитационных аномалий как
гармонических функций.
3. Вычисление высших производных гравитационного потен-
циала.
Рассмотрим каждую группу методов разделения аномалий.
ОСРЕДНЕНИЕ АНОМАЛИЙ
Разделение гравитационных аномалий на региональную и
локальную составляющие с помощью осреднения широко распро-
странено на практике. Сущность метода осреднения сводится
421
к следующему. Наблюдаемое аномальное поле можно рассматри-
вать как сумму двух составляющих: региональной Uг и локаль-
ной U h
U = Ur-\-Ut.
(16.1)
Наблюдаемое гравитационное поле осредняют в пределах круга
радиусом /?; среднее значение можно выразить интегралом
R
(7(0, 0, 0)=^4 \U(r, a, 0)rdrda. (16.2)
о о
Радиус выбирают таким, чтобы он значительно превосходил
размеры локальных аномалий, подлежащих выделению, и был
намного меньше размеров региональных аномалий. При соблюде-
нии этого условия локальные аномалии (положительные и отри-
цательные) в значительной мере компенсируют друг друга, в то
время как региональная составляющая изменяется в меньшей
степени, т. е. U ^=> Uг. В частности, если региональное поле меня-
ется по линейному закону, то осреднение на него совершенно не
влияет. Значение региональной составляющей совпадает со значе-
нием осредненного поля, отнесенным к центру круга:
U (0, 0, 0) = t/r(0, 0, 0).
Таким образом, операция осреднения подчеркивает плавно
меняющиеся аномалии и исключает или подавляет аномалии
с резкими градиентами, т. е. аномалии, связанные с плотностными
неоднородностями на небольших глубинах. Локальные аномалии
получаются как разность наблюденного и осредненного полей:
Ut = U-U.
Для выяснения физического смысла осредненных аномалий
введем понятие меры осреднения — отношение осредненного зна-
чения поля к его исходному значению:
s = UIU. (16.3)
Мера осреднения одновременно характеризует степень точности
выделения локальных аномалий.
Пусть аномальное поле U-, создается шаром с массой М,
залегающим на глубине h:
U Дп а, 0) = /гЖ р _Д5)з/2- (16-4)
422
Найдем среднее значение Uг в пределах круга радиусом /?,
положив, что центр круга совпадает с проекцией центра шара.
Подставив выражение (16.4) в формулу (16.2), получим
йдо, 0, 0)=^-( [ Л- Y (16.5)
* v ' nR2 J J (f2 _p /,2)ЗД R- \ [/^2 ’
Положим /И/(л7?2) = p. Тогда уравнение (16.5) становится
аналогичным формуле притяжения однородного кругового мате-
риального диска с поверхностной плотностью п, который располо-
жен на глубине h, имеет массу, равную массе шара Л4, и радиус R,
равный радиусу осреднения. Таким образом, операция осреднения
в круге радиусом R аномалии U2 точечной массы на глубине h
равносильна раскатыванию этой массы в материальный диск,
расположенный на той же глубине и имеющий радиус, равный
радиусу осреднения.
Меру осреднения для шара получим, разделив выражение
(16.5) на значение U2 (0, 0, 0) над центром шара:
2hM /. Л X / kM\-i _ 2Л2 /. 1 \
6 — Л2 \ ' К/?2 + Л8 / \ Л2 ) № \ |/ J J- /?2/Л2 / ‘
Обозначив Rih = приведем равенство (16.6) к виду
в=тт(’-7тг)-
Это выражение позволяет выбрать радиус осреднения, зада-
ваясь точностью определения локальных аномалий при заданной
глубине Л. На практике радиус осреднения следует выбирать эмпи-
рически, исходя из заданного гравитационного поля. Для этого
в нескольких точках, расположенных на участках карты с разным
характером гравитационного поля, вычисляют осредненные значе-
ния поля при разных радиусах осреднения. Строят график зависи-
мости осредненного поля от радиуса осреднения. По графику
находят оптимальный радиус: незначительные изменения этого
радиуса мало сказываются на осредненных значениях поля.
Для регионального фона, имеющего вид наклонной плоскости,
графики осредненного значения U2 выходят на асимптоту: при
дальнейшем увеличении радиуса осредненное значение аномалии
практически не меняется. Если в суммарном гравитационном поле
присутствуют аномалии нескольких порядков, графики осреднен-
ного значения поля имеют несколько точек перегиба. В этом слу-
чае оптимальный радиус осреднения выбирают не по асимптоти-
ческому значению осредненного поля, а по точке перегиба. Опре-
делив оптимальный радиус, по формуле (16.7) можно оценить меру
точности выделения локальных аномалий, задаваясь глубиной их
источников.
423
Кроме осреднения внутри круга можно проводить эту операцию
и по площадям другой формы. В частности, на практике удобнее
пользоваться квадратной палеткой. Ее преимущество заключается
в несколько меньшем объеме вычислений. Карту разбивают гори-
зонтальными и вертикальными линиями на квадраты определенного
размера и в вершинах квадратов выписывают значения поля,
подлежащие осреднению. При квадрате со стороной 2а аномалия
Uг точечной массы трансформируется в аномалию материального
квадрата со стороной 2а, который расположен на той же глубине
и имеет массу, равную точечной. Осредненное значение аномалии
в этом случае выражается равенством
+а +а
й2(о, о, о) = f f -- =
' 4°2 Ja Ja (g2 + •]- + h2y3/-
hM , a2
-^arc'eTF₽W (,M>
а мера осреднения
1 аи
‘’?“t87w' (,М)
где ah — alh.
Осреднение внутри круга или квадрата применяют, когда
форма аномалий близка к изометричной. В случае же ясно выра-
женного простирания аномалий осреднение выполняют по эллипсу
или прямоугольнику.
При осреднении двумерных аномалий вместо поля бесконечной
горизонтальной материальной линии получим поле горизонтальной
полосы. Над горизонтальной линией
t/z(0, 0) = 2/гА/К
Заменяя массу к массой полосы длиной 2а, находим вертикаль-
ную составляющую притяжения полосы над ее серединой
U г (0, 0) =± 4&р arctg (c//i),
где ц = V(2a).
Тогда степень осреднения
Л , а 1
8 = — arctg -г- = — arctg щ.
а 6 ft ал & "
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ АНОМАЛИЙ
КАК ГАРМОНИЧЕСКИХ ФУНКЦИЙ
Если гравитационный потенциал или его производные заданы
в некоторой области, не занятой притягивающими массами, то
они могут быть определены во всем пространстве, в том числе и
424
внутри притягивающих масс, за исключением особых точек, т. е.
тех точек, где потенциал и его производные теряют свои гармони-
ческие свойства (см. главу 1). Определение гармонической функ-
ции U (х, у, г) в области ее существования по значениям, заданным
в некоторой более узкой области, называется аналитическим про-
должением этой функции. В рассматриваемом случае под гармо-
нической функцией U (х, у, z) понимаются гравитационный
потенциал и его любые производные.
Аналитическое продолжение гравитационных аномалий широко
применяется в практике интерпретации не только для разделения
аномалий разных порядков, но и для количественной оценки пара-
метров возмущающих объектов (см. главу 15).
Обратимся к использованию аналитического продолжения как
средства разделения гравитационных аномалий.
Сущность метода состоит в том, что с увеличением расстояния от
своих источников аномалии убывают по-разному в зависимости от
глубины и размеров источника: аномалии мелких, неглубоко
залегающих объектов убывают быстрее, чем аномалии объектов
более крупных и более глубоких. Американский геофизик С. Пир-
сон назвал аналитическое продолжение гравитационных аномалий
«гравиметрическим фокусированием», поскольку с приближением
к возмущающему объекту в аномальном поле начинают подчерки-
ваться детали, которые на большом расстоянии от объекта были
незаметны, и наоборот, при удалении от объекта сохраняется
только общая картина поля, детали же исчезают. Такое поведение
гравитационного поля является как бы результатом действия опти-
ческой линзы: изображение исследуемого объекта фокусируется,
а изображение объектов, более удаленных, размазывается, стано-
вится нечетким.
Пусть имеются два шара: один на глубине h с массой М, другой
на глубине nh с массой п3М. Аномалии силы тяжести над центрами
этих шаров
i/д (0, 0, 0) = 1гМ1№-,
(72г(0, 0, 0) =/?и:1М/(/г/г2) = (ЛМ//г2)«,
т. е. аномалия первого шара в п раз меньше, чем второго.
Если аномалии этих шаров аналитически продолжить на высоту
Н — h, то
г/д(0, О, =
и тогда
при п > 1.
U!2 (0, О, —Я) 4я3
Яг1(0, 0, -Я) - + 1)2>'г
(16.10)
425
Из неравенства (16.10) следует, что при аналитическом продол-
жении гравитационных аномалий в верхнее полупространство
аномалии неглубоко залегающих сконцентрированных масс убы-
вают сильнее, чем аномалии более глубоко расположенных источ-
ников; тем самым подчеркивается влияние региональных аномалий
и ослабляется влияние локальных.
При аналитическом продолжении аномалий этих шаров в ниж-
нее полупространство на глубину Н — 0,5/г соответственно полу-
чим
в этом случае
С/г2 (0. О, Я) /;3
(0, 0, //) (2п — I)2
(16.11)
при п > 1 .
Таким образом, при продолжении аномалий в нижнее полупро-
странство региональная аномалия U№ возрастает медленнее, чем
локальная 1)л, т. е. локальная аномалия выделяется в общем
гравитационном поле рельефнее.
Рассмотрим способы аналитического продолжения гравита-
ционных аномалий в верхнее и нижнее полупространство.
Если гармоническая функция задана па сфере или плоскости,
то задача ее определения во внешнем пространстве решается инте-
гралом Пуассона (1.112), (1.115). Способы аналитического продол-
жения гармонических функций различаются только приемами
вычисления этого интеграла. Приведем некоторые схемы числен-
ного определения интеграла Пуассона, когда исходная функция
задана на плоскости.
В прямоугольной системе координат, когда ось г направлена
вниз, интеграл Пуассона имеет вид
[/(Л-, у, ] J
f7(g, Т), 0) dgrfq_
[(|-^)3+(Л-^)2 + 2213/2 ’
(16.12)
где U (х, у, —г) и U (£, ц, 0) — значение гармонической функции
соответственно в точке (х, у, —г) и в точках плоскости хОу.
В вертикальной цилиндрической системе координат г, а, г
с началом в точке, являющейся проекцией точки вычислений на
плоскость хОу, интеграл Пуассона принимает вид
2л оо
,,,,, n , 2 С С и (г, а, (У) г dr da .,с .
У(0, О, -z) = -2^-J J --(г2 + г2)3/2 • (16.13)
426
Интегрируя выражение (16.12) по р, получаем интеграл Пуас-
сона для двумерной задачи
У(*-, - 4-AJ
U(t 0)^
а-ч2 + ?3
Для точки с координатами (0, —А) на высоте h
и (0, -А) =
h Г и (g, 0) rfg
nJ g2 + Л2 •
(16.14)
Чтобы вычислить интеграл (16.14), введем новую переменную
Ф = arctg ; г/ф =
Тогда выражение (16.14) принимает вид
+я/5
г/(о, -л)=4: J (1615)
' -л/2
т. е. значение U (0, —А) определяется как интегральное среднее
функции U (ф, 0) по углу видимости ф.
По формуле (16.15) рассчитаны палетки для вычисления U (0,
—А), описанные Б. А. Андреевым. Из точки (0, —А), для которой
надо найти аналитически продолженное значение функции
(рис. 16.1), проводят систему лучей через равные углы Аф == п/п,
где п — достаточно большое число; тогда
п
U(0,
1=1
где U[ — среднее значение функции на t-м интервале, который
виден из точки (0, —А) под углом Аф и ограничен точками пересе-
чения лучей с осью х.
Полученная таким образом палетка может быть использована
для пересчета поля на любой уровень без предварительной пере-
Рис. 16.1. Палетка Андреева для пересчета потенциального поля на высоту.
427
стройки кривой U (S, 0). Высота пересчета определяется расстоя-
нием точки (0, —/г) до оси х и выражается в единицах горизонталь-
ного масштаба кривой. Находить средние значения функции внутри
интервалов становится значительно проще, если при некоторой
фиксированной высоте пересчета через точки пересечения лучей
с осью х провести вертикальные линии, а сами лучи, исходящие из
точки (0, —Л), убрать. Однако в этом случае палетка пригодна для
пересчета поля только на один фиксированный уровень, обычно
5 см в масштабе чертежа. Для пересчета того же графика на другой
уровень необходимо изменить горизонтальный масштаб исходной
кривой так, чтобы в его 5 см укладывалась высота пересчета.
Более удобна для массовых расчетов палетка, предложенная
В. Н. Страховым, идея построения которой состоит в следующем.
Интеграл (16.14) можно записать в виде
-|-оо
(7(0, -h) =4- J
-оо
где
h -- g/Л; к. 0) = 1/(1 + Ц).
Интеграл (16.16) выразим как ряд частных интегралов в конеч-
ных пределах и остаточные члены, которыми можно пренебречь.
Каждый из частных интегралов вычислим при помощи квадратур-
ных формул Гаусса, которые при заданном числе ординат являются
наиболее точными. Тогда вычислительная формула примет вид
+п +п
t/(0, У 0)^„г = 4 У 0),
i=~n
' (16.17)
где A, — коэффициенты гауссовых квадратурных формул; —
узлы этих формул; Ас,,, — длины соответствующих интервалов
интегрирования.
В табл. 16.1 приведены значения величин, необходимых для
построения палетки по формуле (16.17).
Палетка В. Н. Страхова (рис. 16.2) представляет собой систему
вертикальных линий, проведенных через точки гауссовых абсцисс
Таблица 16.1
Коэффициенты палетки Страхова (пересчет вверх)
i В/if Ci ггц — 1/C(- i mill Q mi =
0 0 1,136 0,88 4 4,366 0,075 13,3
1 1,077 0,424 2,36 5 6,057 0,065 15,4
2 1,812 0,110 9,09 6 8,943 0.030 33.3
3 2,634 0,189 5,29 7 12,5 O’, 032 31,4
428
5-
5-
4-
3-
2-
2-
1-
200-
-5-J
-200
-64
12-
11
10-
9-
8-
3-
1-
14
13
11 -
10-
в-
7-
6-
5-
о-
2-
35
25
80-
20-
-200-
70-
во-
15-
20-
15-
10-
150-
50-
10-
40-
100-
30-
5-
20
10-
50-

3 -
6
' 4-

2
0
9 -
4
511
О
Рис. 16.2. Палетка Страхова для пересчета потенциального
поля на высоту.
Приведена левая верхняя четверть палетки.
и имеющих равномерные шкалы, масштабные множители которых
определяются из соотношения mL — 1/Сг. Если за единицу измере-
ния ординат кривой U 0) принят 1 мм, то на i-й шкале этой
единице соответствует отрезок длиной /пг. Расстояние h (т. е.
— 1) удобно выбрать равным 1 см.
Используют палетку следующим образом. Кривую U (?, 0)
вычерчивают в соответствующем горизонтальном масштабе (1г =
= 1 см). Вертикальный масштаб кривой не играет особой роли,
но желательно, чтобы кривая U (|, 0) имела максимальную
429
амплитуду 10—15 см в масштабе графика. Проекцию точки, для
которой вычисляют U (0, —ft), совмещают с началом О палетки.
По каждой шкале снимают отсчет и эти отсчеты суммируют. Сумма
отсчетов, деленная на л, равна значению U (0, —ft) в миллиметрах
ординат кривой. Палетка Страхова при том же числе ординат имеет
более высокую точность, чем палетка Андреева. Кроме того, про-
цесс вычислений несколько быстрее и не так утомителен, как
снятие средних значений внутри интервалов.
В случае трехмерной задачи интеграл Пуассона (16.13) удобно
вычислять в вертикальной цилиндрической системе координат
(г, а, г):
у<°. °.<1618’
Формулы для подсчета U (0, 0, —ft) получают, разбивая интег-
рал (16.18) на ряд частных интегралов в конечных пределах
и остаточный член, которым обычно пренебрегают. В этом случае
выражение (16.18) принимает вид
п т “(+1 rk+l
П(0, 0, -ft) = ~ У V Uik f da Г . 2hrdriw2 , (16.19)
i=0 &=-o rk v 1
где Uik — среднее значение U (г, a, 0) в пределах площадки
интегрирования.
Существующие способы аналитического продолжения трехмер-
ных полей в верхнее полупространство различаются приемами
вычисления частных интегралов и выбором пределов интегрирова-
ния. Если при вычислении выражения (16.19) всю область интегри-
рования разбить на площадки равного действия, то пределы интег-
рирования будут меняться нелинейно и их придется выбирать по
определенному закону. Если же установить пределы интегрирова-
ния, подчинив их наперед заданному закону, то область интегри-
рования разобьется па площадки, вклад которых в суммарный
интеграл будет неодинаковым.
По первому принципу построена палетка, рассчитанная
Н. Р. Малкиным. Выполняя интегрирование в формуле (16.19),
получаем
п т
и (0, о, -ft) =- А. у у uik (a.+1 _ a.) [ . -Л—\ •
Полагая
2 л . h h ____________[
430
имеем
п tn
Z=o k=o
Чтобы построить палетку, из начала координат проводят лучи
через угол 2я/п = 2л/10 и концентрические окружности, радиусы
которых г.'г находят из соотношения
h
h h _________ 1 _____
У “ V r|+l + ЛЗ 1 '
(16.20)
Положив в этой формуле h - 1, получим радиусы окружностей:
0,48; 0,75; 1,02; 1,33; 1,73; 2,28; 3,17; 4,91; 9,8. Таким образом,
лучами и окружностями вся площадь разбивается на 100 площадок.
По каждой из площадок определяют среднее значение Uik и вычис-
ляют сумму 0,0122 Иц,, соответствующую значению U (0, 0, —/г)
на высоте, равной 1 см в масштабе карты. При вычислении функции
U (0, 0, —/г) на ином уровне необходимо изменить радиусы окруж-
ностей пропорционально высоте пересчета.
Рассмотрим вывод формулы для построения палетки на основе
второго принципа, когда радиусы окружностей подчиняются
наперед заданному распределению. Введем среднее на окружности
радиусом г значение U (г) величины U (г, а, 0):
2 л
Щг) j U^r' “> °')da-
о
Тогда интеграл Пуассона можно представить в виде равенства
со
77(0, 0, -й)^р(г) ^ ^^/2 • (16.21)
Разбивая, как и прежде, общин интервал интегрирования на
отдельные частные интервалы и применяя на каждом из них
теорему о среднем, получаем
о, -h) - j +
После интегрирования имеем
U (0, 0, -й) - - + (1 - ) 4.
4 2 \ |/rs /j2 / 1 2 \ и г| 4- ft- / 1
4 Tier / ----------. A 4 .., (16.23)
431
или
т
и (О, О, -/I) = KaU (0) 4- (г,) 4 • • • = X Л,[/ (г,),
<-о
где
к(=j- ( --- —=^=
(16.24)
(16.25)
Задавая различные радиусы, по соотношению (16.25) можно
вычислить коэффициенты Ki- В палетке, предложенной А. К. Ма-
ловичко, принято Г1 = г2 — г, = га — г.2 = /г. Коэффициенты этой
палетки приведены в табл. 16.2, а вычислительная формула имеет
вид
5
и (0, 0, ^й) - и (г,) + S Ki [U (г,) - и (/<,)].
1=0
Для вывода среднего на окружности значения U (г) обычно
используют восемь равномерно расположенных на ней точек. На
основе выражения (16.25) можно построить палетки и с другим
законом изменения радиусов окружностей.
Аналитическое продолжение гармонических функций в нижнее
полупространство представляет значительно более сложную проб-
лему, чем аналитическое продолжение вверх. Принципиальная
сложность состоит в неустойчивости этой задачи: малому измене-
нию заданной на плоскости функции могут соответствовать боль-
шие изменения ее значений, рассчитанных на глубине.
Существует довольно много способов аналитического продол-
жения вниз, основанных на различных принципах и неодинаковых
по сложности вычислений. Остановимся на некоторых из них,
наиболее простых.
Несложные вычислительные формулы можно получить, исходя
из теоремы Гаусса о среднем значении гармонической функции.
Применительно к условиям двумерной задачи значение гармони-
ческой функции в центре окружности равно интегральному сред-
нему ее значений, взятых по окружности:
(7(0, 0) = U(r, a)ds. (16.26)
s
Таблица 16.2
Коэффициенты палетки
Малевич ко
Г[ к П К
0 0,1464 3 0,1024
1 0,2764 4 0,0600
2 0,1954 5 0,0390
432
Заменяя интегрирование сум-
мированием и ограничиваясь че-
тырьмя точками на окружности
(рис. 16.3), получаем
U (0, й) = 4U (0, 0) - [У (О, —й) +
| U ( —h, О) + У(й, 0)]. (16.27)
Очевидно, что для использова-
ния этой формулы предварительно
надо любым из рассмотренных
способов определить У (0, —й).
В случае трехмерной задачи
Рис. 16.3. К выводу формулы
(16.27).
интегральное среднее по поверх-
ности сферы заменяют средним
арифметическим по шести точкам
на этой поверхности: четырем на
экваторе, плоскость которого совпадает с плоскостью хОу [У (—h,
0, 0), У (0, —й, 0), У(0, h, 0), У (h, 0, 0)], и двум на полюсах
[У (0, 0, й), У (0, 0, —й)).
Тогда
U °- °) = f U (г, ср, й) dS = 4- [U (-1г, 0, 0) +
s
+ У (1г, 0, 0) -f- У (0, -й, 0) + У (0, й, 0) -ф У (0, 0, —й) ф
-фУ(0, 0, й)]. (16.28)
Обозначим
У(г) = ^[У(—й, 0, 0)-фУ(й, 0, 0) + У(0, —й, 0)ф-У(0, й, 0)
— среднее значение функции на окружности радиусом г = й.
На глубине й искомое значение функции
У(0, 0, й) = 6У(0, 0, 0) — 4У (г) — У (0, 0, —й). (16.29)
Формулы (16.27) и (16.29) составляют основу так называемого
метода сеток.
При вычислении по методу сеток в случае двумерной задачи
вертикальную плоскость разбивают горизонтальными и вертикаль-
ными линиями на квадраты со стороной, равной наименьшей
глубине пересчета. В вершинах квадратов, расположенных на
уровне й = 0, выписывают наблюденные значения функции
У (Е, 0), а в вершинах, расположенных выше уровня наблюде-
ний, —значения У (0, —й), определенные одним из рассмотрен-
ных выше способов. По формуле (16.27) вычисляют значение У (0,
й). Подобным образом можно определить значение У на глубинах
2й, Зй и т. д.
433
Вычислительные формулы для аналитического продолжения
гармонических функций в нижнее полупространство можно
получить и другим путем. Выразим интеграл Пуассона для значе-
ний U (0, 0), заданных на поверхности, через искомую функцию
U (£, h) на глубине h:
н(°, °)=4 f (16-з°)
— со
Не известная нам функция U (£, h) находится под знаком интег-
рала, поэтому задача сводится к решению интегрального уравне-
ния. Это решение можно получить методом последовательных
приближений. Если под интегралом (16.30) вместо U (£, h) рас-
смотреть U (|, 0), то найдем значение функции U (0, —ft) на высоте
/г. Тогда, вычислив разность
= U (0, 0) - U (0, —ft)
и положив, что она остается постоянной с изменением ft, можно
в первом приближении написать
и (0, ft) = и (0, 0) - ьги
или
£7(0, ft) = 2/7 (0, 0) — £7(0, —ft).
Вычислив значение функции на высоте —2ft, найдем вторую
разность Д2/7 как приращение между первыми разностями в интер-
валах (Оч—ft) и (—h-.—2h), а также второе приближение
U (0, ft) = U (0, 0) 4- Ах£7 + Д2/7
или
U (0, ft) == 3U (0, 0) - 3U (0, ft) +/7(0, -2ft).
Продолжая этот процесс и ограничиваясь разностями п-го
порядка, получаем приближенную формулу
£7(0, ft) = S (—1)^1£/(0, —ftft), (16.31)
ft=0
где биномиальные коэффициенты
/п/г+1 __ (Я 1) I
0,1+1 (А + 1) 1 (п — й)Т '
Заменив в уравнении (16.31) функции U (0, —/г/i) их выраже-
ниями через интеграл Пуассона и выделив первый член суммы,
получим
П +оо
/7(0, /г) = («+!) /7(0, 0) + 2(-l/d^f (16.32)
/г—1 —оо
434
Каждый интеграл этого уравнения можно представить в виде
суммы интегралов, у которых в интервале интегрирования функ-
цию U (|, 0) можно считать постоянной и равной ее среднему
значению в этом интервале. Тогда уравнение (16.32) можно запи-
сать в виде
где
и (О, h) = (n + l)U (0, 0) + s UiK,,
f==»-co
4 ^1+1
j.- / j kh f dz
Ki ~ L( 1 >c,,+l ~ J 14^ =
jb(-i)fcc*:}-i-
( arctg— arctg-^-').
\ b kh b kh /
(16.33)
(16.34)
На основе формул (16.33) и (16.34) можно построить палетку для
определения функции U (0, (i). В. Н. Страховым предложена удоб-
ная палетка для вычисления поля в нижнем полупространстве
в случае двумерной задачи. С учетом третьего приближения (п = 3)
формула (16.33) примет вид
(7(0, /г) = 4(7(0, 0)-66/(0, — h) + 4(7 (0, — 2h) - (7 (0, —3(t)
(16.35)
или
(7(0, Л) = 4(7(0, 0) -IX (16.36)
где
Е и = 6(7(0, —/г)-4(7(0, — 2/t) + (7(0, —3/0. (16.37)
Используя интеграл Пуассона (16.14), имеем
= ~ j ( X п1 S2 Т 47г2 + -- 97г2 ) =
-00
(16.38)
где
м zt \_______________§_________8 ! 3 . е ___
Л (ъЛ) ! +ё2 4 + ц Т 9 + ц . =й Л •
Интеграл (16.38) разбивается на ряд частных интегралов,
каждый из которых вычисляется при помощи квадратурных фор-
435
Таблица 16.3
Коэффициенты палетки Страхова (пересчет вниз)
1 Вл/ Ct щ — 1/С,- I Ы Ci mi = 1/C,
0 0 1,5680 0,637 4 4,366 0,0279 35,8
1 1,077 0,4030 2,48 5 6,057 0,0209 47,8
2 1,812 0,0824 12,8 6 8,943 0,0102 98,4
3 2,634 0,1020 9,84 7 12,113 0,0115 87,2
8 17,887 0,0044 225,0
мул Гаусса. Пренебрегая влиянием удаленных зон, окончательную
вычислительную формулу можно представить в виде
+п
У ЛД(ЕЛ/) (/(£,„•, 0)Д£ы
i—-n
+п
V 0), (16.39)
где At — коэффициенты гауссовых квадратурных формул; |Аг —
узлы этих формул; Д|Лг — длины соответствующих интервалов
интегрирования.
Значения i.hi и С;, необходимые для построения палетки, при-
ведены в табл. 16.3.
Палетка представляет собой систему вертикальных липни, вос-
становленных в узлах гауссовых формул и имеющих равномерные
шкалы, масштабные множители которых определяются из соотно-
шения zn; = 1/Сг. Палетку вычерчивают в масштабе h — 1 см и
накладывают на график U (t, 0), совмещая проекцию точки, в кото-
рой вычисляют U (0, ft), с центром палетки. Сумма отсчетов ординат
по шкалам определяет значение 2 U в миллиметрах чертежа кри-
вой. Функцию U (0, Л) вычисляют по формуле (16.36).
Подобные формулы можно вывести и для расчетов поля в ниж-
нем полупространстве в случае трехмерной задачи, если в выраже-
нии (16.31) использовать значения функции U (0, —kh), вычислен-
ные при помощи интеграла Пуассона для трехмерной области.
Повторив все вышеприведенные рассуждения, получим формулу
для вычисления функции U (0, 0, Л) в нижнем полупространстве
по ее значениям, заданным на поверхности наблюдений:
и (0, 0, ft) = (п +1) и (0, о, 0) + У (-1)'^} j
или
U (0, 0, ft) = (п ф- 1) (У (0, 0, 0) + £ U
i=l
где
kh____________kh______'
0+*2*2)1'8 (г?+1 + ^2)1/2 ’
436
На основе этих формул можно построить палетки.
Формулы для аналитического продолжения в нижнее полу-
пространство можно получить разложением функции U в ряд
Тэйлора. Для точек (0, —й) и (0, +й), находящихся соответственно
в верхнем и нижнем полупространстве, разложения принимают вид
/7(0, -й) ^(0)------2г.^-(0)+^-.^(0)------------;
/7(0, Л) = ^(О) ! А.^{0) , (0)1 ... (16-40)
Складывая эти выражения, получаем ряд из четных производ-
ных:
и (0, -й) + и (0, й) = 2 [.U (0) + • -g- (0) + g- (0) + • • j .
(16.41)
Разность выражений (16.40) дает ряд из нечетных производных:
t/(0, й)-17(0, -й) -_2|А-^(0) г уг (0) + • • • ] •
(16.42)
Четные производные на поверхности наблюдений определяют
методом конечных разностей, а нечетные — с помощью интеграль-
ных формул. В частности, для двумерной задачи, имея в виду, что
игг = —Охх и U2ггг — Uxxxx, из формулы (16.41) получаем
и (0, й) + и (0, -й) = 2 [ и (0) - Uxx + -g /7ЛЛ,,.] (16.43)
и, выражая U хх и Uхххх через конечные разности, находим
t/(0, й) + /7(0, -й) = 5,5/7 (0, 0) - 2,034 [U (й, 0)-J-С/(—й, 0)] +
+ 0,316[/7(2й, 0) + /7(—2й, 0)j - 0,025 [/7 (Зй, 0) -|- U (—Зй, 0)].
(16.44)
Сходная по структуре формула получена С. В. Шалаевым:
U (0, й) + И (0, — й) = 6,665/7 (0, 0) — 3,015 [/7 (й, 0) + U (—h, 0)] +
+ 0,8935 [//(2й, 0)4-/7(—2й, 0)1 - 0,2710[1/(Зй, 0) + /7(—Зй, 0)1 +
+ 0,07918 [U (4h, 0) + U (—4Й, 0)] — 0,02104 [U (5й, 0) + U (—5h, 0)] +
+ 0,04921 [U (6й, 0) + /7(—6й, 0)1—0,0009929 [U (7h, 0) + V ( -7h, 0)].
(16.45)
437
И наконец, не останавливаясь па выводе, дадим формулу
В. Н. Страхова, в которой используются значения функции 0
только на поверхности наблюдений:
U (0, /0 = 7,30296/(0, 0)-2,3258 [/7 (0,5/i, 0) ф- U (—0,5ft, 0)] -
- 0,5683 \U (h, 0)ф-6/(—ft, 0)] - 0,1931 [У (2ft, 0) ф-
'(/(—2ft, 0)] ф-0,0178 [У (3ft, 0) + 6/(-3ft, 0)| -
- 0,0411 [U (6ft, 0) 4- U (~6ft, 0)] -
- 0,0030 [(/(9ft, 0)4-6/(—9ft, 0)]. (16.46)
ВЫЧИСЛЕНИЕ
ВЫСШИХ ПРОИЗВОДНЫХ ПОТЕНЦИАЛА
Выражение одних производных гравитационного потенциала
через другие имеет весьма существенное значение при интерпрета-
ции гравитационных аномалий, поскольку в ряде случаев позво-
ляет существенно упростить задачу определения параметров тела.
Вычисление производных более высокого порядка, чем измеряемые,
широко применяется для разделения локальных и региональных
аномалий. Сущность разделения таким способом состоит в сле-
дующем.
Выражение потенциала на поверхности наблюдений для начала
координат имеет вид
6/(0, 0, 0) = йо [ , • (16.47)
V aJ (s'+ n2-H2),/2
Если размеры возмущающего тела увеличить в я раз и отодви-
нуть его от начала координат (точки наблюдения) в п раз дальше,
чем располагалось исходное тело, то = nt,, ци = яц, 'Qn = nt, и
Un (0, 0, 0) = /го [ , - = n4J, (16.48)
"' ’ ’ ' J п (Ф + т|2 + £“)1/2 v '
V
т. е. при таких условиях потенциал притяжения увеличился в я2
раз.
Найдем первую производную по г потенциала притяжения этих
тел. Для первого тела имеем
Uг (0, 0, 0) = fen [
J (е* + 4 +1)1
для второго
6/гД0, 0, 0, 0),
“ я (I + Ч + £ )'
438
т. е. аномалия притяжения второго тела в п раз больше, чем
первого.
Вычислив вторую вертикальную производную потенциала пер-
вого и второго тел, получим
^„(0. 0, 0) = Ао [ 0, 0),
j w г'1 । ь '
т. е. вторая производная потенциала первого и второго тел оди-
накова.
Третья вертикальная производная первого тела в п раз больше,
чем второго:
Уг:г „ (0, 0, 0) = Зто j di dt = 1 (o, o, 0).
В общем случае можно написать для m-й производной
U(nm> (16.49)
Полученное соотношение верно не только для вертикальных,
но и для любых горизонтальных и смешанных производных.
Таким образом, чем выше порядок производной, тем сильнее
она отражает влияние небольших и неглубоко залегающих масс;
влияние же крупных, но глубоко залегающих объектов мало ска-
зывается па высоких производных, т. е. при вычислении высших
производных подчеркиваются локальные аномалии и исключается
или подавляется региональная составляющая аномального поля.
Формулы, устанавливающие связь между различными произ-
водными гравитационного потенциала на плоскости наблюдений
и в верхнем полупространстве, могут быть получены на основе
дифференцирования интеграла Пуассона (1.115), (16.12), дающего
решение внешней задачи Дирихле для плоскости, или же интеграла
(1.124), определяющего решение задачи Неймана.
Запишем интеграл (1.124) в декартовых координатах:
+оо +оо
Д(х, у, — z) = ^- Г f —------, (16.50)
2л J J [(g_x)2 + (n_^4. Др/- v
— ОО —со
Чтобы получить общую формулу производных т, п, р-га по-
рядка гармонической функции по координатам х, у, z, необходимо
продифференцировать обе части уравнения (16.50). В подынтег-
ральном выражении от х, у, z зависит только [(§ — х)2 + (ц -
— г/)2 + г2]"1/2 — величина, обратная расстоянию между точкой,
где определяется значение функции, и текущей точкой плоскости,
на которой задана нормальная производная 1)г (§, т], 0). Послед-
439
няя от .V, у и z не зависит, а является функцией только | и 1].
Получаем
dm+n+pU (х,у,-г) = 1 7 7 и 0) О™
дхтдупдгр 2п J J гкь> I, ) дхт п дгР
— ОО —оо
X
Xl[(g-x)2 + (1|1-.V)2 + r]1/2}dUl1-
(16.51)
Это выражение является общим решением задачи определения
гармонической функции в пространстве по значениям ее нормальной
производной, заданной на плоскости. Дифференцируя ядро подын-
тегральных функций (16.51) по соответствующим координатам,
получаем конкретные формулы, связывающие различные производ-
ные гравитационного потенциала.
На практике удобнее пользоваться вертикальной цилиндри-
ческой системой координат г, а, г. Приведем некоторые из формул
для вычисления различных производных гармонической функции:
1 ’7 7 U, (г, а, 0) г dr da
П(0, 0, -Z) = —j ] (,2 4-22)1/2 ’
о о
2л оо
r, п \ 1 f f Uz ir, “• 0) г2 cos a dr da . ,1С со,
ИДО, 0, -2) = j ) М + ?)з/2------------------------’ <16-52)
0 0 \ I /
2л оо
иу (0, 0, -г) = J f UAr’ (16.53)
оо I + г 1
, ,n п ч Iff U г (г, а, 0) (2г2 cos2 а—г2 sin2 а— г2) г dr da.
,Л.(О, О, -г)-^ J ) -----------------i----(777)^---------------------’
0 0 1
(16.54)
2л оо
, /Л А х Iff Uz\r, а, 0) (2r2 sin2 а — г2 cos2 а — z2) г dr da .
7(0, 0, -г) = ЪГ] | ~----ТТда-----------------------'
0 0 \ I /
(16.55)
Нд(о, 0, -Z) = _JLJ ]пг(г, а, 0) f37^r5^-; (16.56)
t/„(0, 0, —2)= J- f ][/г(г, а, 0) ~2z2)r drda 6 5?)
22 v ’ ’ 7 2л J J 24 ’ ’ ' (г2 4- z2)5/2
0 0 1
2л оо
С„(0, О, Jl/Дг, а, 0) ' (16.58)
0 0 v ' 7
440
2jt OO
0. -*)-Ц.(г. «, 0) <16-5»)
0 0 1 ~r 7
2л oo
26^(0, 0, —z) = -^- U2(r, a, 0) r3 Sin 2(XX--; (16.60)
0 0 \ 1 /
2л oo
</w(0, 0, -Z) = —2-J a, 0) +
0 0
, , n4. r2 (cos a -|- sin a) dr da /1R
+ UyA^ a. 0)]---- ---------------• (16.61)
v c f
В случае двумерного поля интеграл, дающий решение задачи
Неймана, получим, проинтегрировав выражение (16.50) по г]
в пределах ±оо:
У(х. -г)--Н<Л(Е, 0)1п Д.+- ft (16.62)
— ОО
тогда
Л«+Р 1 Г дт+Р 1
е' „ U (х. —z)= — иг(£„ 0) \ In r - -dl
дх”1 дгр л J ' дхт дгр К(§—х)2 -[-г2
(16.63)
Отсюда дифференцированием находим
+ »
t/A(0, -г) = 4 J 0)-^^-^; (16.64)
— 00
+ <ю
1 С t
^(0, -z) = -4 f t/ДВ, 0)^^В; (16.65)
J U, ] <0
-00
(У?г(0, -2) = -^ (0, -г) = t/д (0, -2) =
+сю
If ?2 _?2
=4! °)(Ft^^; (16-66)
— ОО
+оо
^(0, -г) = 4 j t/2(g, 0) т^-+г-г2)2 di. (16.67)
—90
Прежде чем рассматривать способы вычисления полученных
интегралов, необходимо отметить следующее. Целый ряд интегра-
лов 1(16.58), (16.59), (16.67)] не позволяют вычислить производные
на плоскости наблюдений, так как при г — 0 подынтегральное
выражение обращается в нуль. Значения этих производных могут
441
быть вычислены на основе интегральных формул только на некото-
рой высоте над плоскостью наблюдений.
Интегралы (16.52)—(16.57), (16.60), (16.61), (16.64)—(16.66) при
2 = 0 являются несобственными и сходятся только при определен-
ном характере изменения функции U, так как при г —> 0 (или £ —> 0)
подынтегральная функция стремится к бесконечности. Чтобы
избежать этого, в указанных интегралах будем рассматривать
вместо U (г, а, 0) разность U (г, а, 0) — U (0, 0, 0), где U (0,
0, 0) — значение исходной производной в начале координат. Можно
показать, что такая замена не влияет на значение исходного ин-
теграла. Например, для интеграла (16.52) при z •= 0 имеем
[ |(/Д0, 0, 0)-^^-drda = 0,
о о
тогда
2Л оо
Hv(0, 0, 0)-4Ч j [^(ч «, 0)-(/Д0, 0, 0)]^-drda.
о о
Можно показать справедливость такой замены и для других
интегралов. Подобная замена в подынтегральных выражениях
приводит к тому, что теперь при г или £, стремящихся к нулю,
подынтегральное выражение обращается в неопределенность,
которая может быть раскрыта. В общем случае порядок стремления
к нулю для разности Uz (г, а, 0) — Uz (0, 0, 0) должен быть не
ниже, чем для г или g. Например, если в формуле (16.57) для
вычисления Uzz положить
t/Дг, а, 0)-(/Д0, 0, О) = сг2,
где с — некоторая постоянная, то
,. иг(г, а, 0)—иг(0, 0, 0)
1ип ? -—-——j——---------- — с
г->о г
и интеграл имеет конечное значение.
Для приближенного вычисления рассмотренных интегралов
в случае трехмерной задачи всю площадь интегрирования разби-
вают концентрическими окружностями и лучами на площадки.
Можно считать, что внутри каждой площадки функция U {г, а, 0)
или ее производные, входящие в подынтегральные выражения,
остаются постоянными, т. е. интеграл представляется в виде
суммы
п т
£ L (ч. «ь 0) к1к,
1=0 й=0
где Кik — некоторые постоянные коэффициенты.
Естественно, что для интегралов, которые при г = 0 расхо-
дятся, разбивку на площадки можно начинать только с некоторого
442
радиуса г0. Влияние центральной зоны О-э/у учитывают поправ-
ками, вычисленными при определенных предположениях о харак-
тере изменения функции в окрестностях точки (0, 0, 0). Вкладом
интеграла за пределами радиуса г,„ как правило, пренебрегают
или также вносят соответствующие поправки.
Не останавливаясь на выводе вычислительных формул, при-
ведем в качестве примера палетки и формулы для определения
вертикальной составляющей градиента потенциала притяжения
U. (0, 0, 0) на плоскости наблюдений по значениям функции
U (г, а, 0). Исходной служит формула (16.57), из нее получаем
2Л оо
(/2(0, 0, а, 0) — <7(0, 0, 0)]-^- =
О о
где
= [ ((/(г)-(У(О, 0, 0)]-^-, (16.68)
6
2л
= U а^,а
6
— среднее значение U (г, а, 0) на окружности радиусом г.
В палетке, составленной К. Ф. Тяпкиным, вся область интегри-
рования разбита на площадки равного действия (рис. 16.4, а).
Вычислительная формула имеет вид
5 1П 14 ю
иг (0, 0, 0) -V £ Wlk + 6Uik, (16.69)
0 1=1 /{=1 0 1=6 ft=l
где
8t/(ft = Ulk-U (0, 0, 0).
Постоянных коэффициентов в формуле два: во внутреннем
круге 0,5; во внешнем 0,05. Величина г0 играет роль единицы
измерения, принятой при построении палетки и выраженной
в масштабе карты, с которой снимаются отсчеты, и может быть
любой. Приведем радиусы центров площадок равного действия
в единицах г0:
Г1 = 0,31 г,= 1,37 /п = 3,63
'2 “ 0,36 г7 = 2,11 г12 = 4,45
0,45 г8 = 2,35 г13 - 5,70
г'1 ~ 0,57 га = 2,68 г и = 8,00
0,80 г10 — 3,08
В палетке, предложенной А. К. Маловичко (рис. 16.4, б),
концентрические окружности проведены через равные интервалы
443
Рис. 16.4. Палетки Тяпкина (а), Маловичко (б) и Веселова (в) для вычисле
ния иг по распределению U.
так, что г2 — Г] = г, — г2 — ... = г, = 1. Вычислительная фор-
мула, реализуемая с помощью этой палетки, имеет вид
5 _ _ _ _
(0, 0, 0) = S /(,. [(7 (/-.) - U (re)J + и (га) + U (r6) - 2U (0),
i=i
(16.70)
где U (г,-) — среднее значение U на окружности радиусом г;.
Коэффициенты Ki равны: Кл — 0,250; Кг = 0,333; К3 — 0,125;
- 0,067; К8 - 0,042.
Радиусы и соответствующие им коэффициенты палетки, рассчи-
танной К. Е. Веселовым (рис. 16.4, е), представлены в табл. 16.4.
444
Таблица 16.4
Коэффициенты палетки Веселова
ri/r0 ri/r0 К Со К(г0
0,1 2,5 2,735 0,160 10,190 0,029
0,2 7,5 4,123 0,094 13,564 0,021
0,566 1,25 5,831 0,053 18,559 0,017
1,058 1,755 0,536 0,260 7,736 0,033 21,8 0,046
Здесь г0 также равно единице измерения, принятой при построении
палетки. Если первые два радиуса (0,1 и 0,2) заменить одним, то
вместо первых двух строк будет: гг/г(| = 0,4; /фт0 = 10,0.
Вычислительная формула, реализуемая палеткой, имеет вид
13
iA(0, 0, 0)=S U ($*<• (16.71)
i=i
В двумерной задаче формула (16.66) вертикальной составля-
ющей градиента потенциала притяжения при г - 0 примет вид
+ОО
£/Д0, 0) = -^ J [(/(ё, 0) — (7 (0, 0)]f-.
Из сравнения этого выражения с формулой (16.68) следует, что
в двумерном случае коэффициенты линейной палетки в л раз
меньше соответствующих коэффициентов палеток для трехмерной
задачи; расстояния же узлов линейной палетки от центральной
точки равны радиусам трехмерной палетки. Поэтому соотношения,
выведенные для трехмерной задачи, можно использовать для
построения линейных палеток.
В практике интерпретации часто возникает необходимость
вычислить горизонтальные производные по заданному распределе-
нию вертикальной или, наоборот, по распределению горизонталь-
ной производной требуется найти распределение вертикальной.
Построим палетку для такого пересчета в случае двумерной задачи.
Исходными служат интегралы (16.64) и (16.65), но будем рассмат-
ривать только формулу (16.64), так как выражение (16.65) имеет
то же ядро и отличается только знаком. Поскольку эти интегралы
при § = 0 становятся несобственными, вычисление их проведем
следующим образом:
^(0, о)=-А- J о)^ =
— оо
445
г
где (—Д£-4-Д£) — малый интервал, в пределах которого можно
положить
UAl, 0) = [7,(0, O) + |((/Jo;
Uz (0, 0) — значение U 2 (|, 0) в точке (0, 0).
Тогда
Л? Д5 Д6
[ U2& 0)f = J ^2(0. 0)f-+ J (Д2Д)^ = ДД,
-Д£ -Д£ -д?
т. е. первый интеграл выражения (16.71) равен приращению Д6Л,
в интервале (—ДЕ-ьД^).
Остальные два интеграла разобьем на ряд частных интегралов,
в пределах интегрирования которых будем считать значение
Uz (|, 0) постоянным и равным среднему внутри интервала интег-
рирования, так что
i+i
J иг& o)A = ^i(g, 0)1п^ = ад.(|, о).
i
Вычислительная формула принимает вид
Ux (0, 0) = ± [ Е Uit (£, 0) - I [7,. (-Е, 0)]. (16.72)
Для построения палетки примем Д| = 1 и /(, = 0,1л, тогда
Ui^ = e°-314= 1,368,
т. е. расстояния Ef от начала координат составляют геометрическую
прогрессию, знаменатель которой равен 1,368 (1; 1,37; 1,87; 2,56;
3,51; 4,80; 6,57; 8,93; 12,3; 16,8; 23,0). Палетку (рис. 16.5) строят на
прозрачном материале, интервал ДВ выбирают в зависимости от
градиента кривой, обычно ДЕ = 0,5 или 1 см; чем меньше интервал,
тем выше точность палетки.
0
о
Рис. 16.5. Палетка для вычисления Ux по распределению Uz.
446
Как уже отмечалось, некоторые производные, широко при-
меняемые при интерпретации гравитационных аномалий, не могут
быть вычислены на поверхности наблюдений с помощью интег-
ральных формул', в частности UX2 и U2t2 по U2. В этом случае для
вычисления производных могут быть использованы формулы, кото-
рые получаются как результат дифференцирования различных
интерполяционных формул. В зависимости от способа численного
дифференцирования и от исходных выражений можно составить
различные вычислительный формулы. Рассмотрим метод получения
таких формул.
Пусть функция U (х) задана на некотором отрезке через равные
интервалы г так, что значения ее аргумента х располагаются
посредине интервалов
.... х — Зг, х — 2г, х — г, х, х + г, х 4- 2r, х -f- Зг, ...
Разности предыдущего и последующего значений функции
U (х) называются первыми разностями (х), разности после-
дующих и предыдущих первых разностей называются вторыми
разностями Д26/ (х) и т. д. (табл. 16.5). Порядок разности обозна-
чается индексом при Д, аргументом разности является полусумма
аргументов функций, из которых составлена разность.
Конечные разности можно выразить через значения функции:
Д// (х — 0,5г) = U (х — г) — U (х);
\хи (х 4- 0,5г) = и (х) - и (х 4- г);
Д26/ (х) = U (х — г) — 2U (х) 4~ U (х -ф- г);
Ла/7 (х — 0,5г) = U (х — 2r) — 3U (х — г) -ф-
+ 3U (х) - U (х 4- г);
Дя6/ (х 4- 0,5г) = U (х - г) - 3U (х) 4-
4- зи (х 4- г) - и (х 4- 2г)-
(х) = и (х - 2г) - 46/ (х - г) 4-
+ 667 (х) - 4/7 (X + г) 4- U (х -Ь 2г);
Д,67 (х) = 6/ (х - Зг) - 667 (х - 2г) 4- 156/ (х - г) -
— 20Е/ (х) 4- 156/ (х 4- г) - 5U (х 4- 2г) +
4-(/(х + Зг).
(16.73)
Будем считать, что среднее арифметическое разностей нечетного
порядка, расположенных симметрично относительно середины
447
интервала, равно их значению, приведенному к середине интервала,
т. е.
Art/ (х) = [(х - 0,5r) -h Ait/ (x + 0,5r)]/2 =
= [t/(x-r)-t/(x4-r)]/2;
A3t/(x) — [A3t/(x — 0,5r)-|-A3t7 (x + 0,5r)]/2 _ i <16'74>
== [U (x - 2r) - 2t/ (x - r) -J- 2t/ (x -1- /) — t/ (x + 2r)]/2.
Функция U (xA) может быть представлена через конечные
разности A/.t/ (х) интерполяционной формулой Стирлинга:
U (х/г) == U (х h kr) --= U (х) + ± A.U (х) + A2t7 (х) +
+ + A3t/ (х) + A4t/ (х) +
(fe+2)(, + l),(//l)(fe 2) (х) + _ (1б
Собирая в этой формуле члены с одинаковыми степенями k
и сравнивая полученное выражение с разложением функции
U (хЛ.) в ряд Тейлора по степеням kr, получаем
t/ (х/() = U (х -ф- kr) — U (х) 4- — -2j-4-
^згз дзц г г , \ I ЙГ.,,,, 1 , ,,, , ,
Н з"] Ч* ’ ‘ (-') + "ТУ I W 6~ ^,lt/ (х) 4~
4- з^- Ast/ (х) - \-.U (х) 4- • • • ] 4- [ A2t/ (х) - ± A4t/ (х) 4-
4- i Act/ (г) - АЯС/ (х) 4-...]4-^-[Ast/(x)-
--LA6t/(x) + -^rA7t/(x) +••.] +
+ ^-[Ait/(x)--l-Aet/(x)-b..._] +
4-Al[A5t/(x)-4- A,t/(x)+ (16.76)
откуда следует
^-4f4.y(«)~44>(/w+wA-uw--4
/4 = 4[А^<-')-4Л*(/«+4-Л»и« — ] ,l6'77)
15 в, с. Миронов 449
Таблица 16.5
Конечные разности
Аргумент Функция Разности
Д2£/ Д4£/ Л5У
х —- Зг и (х — Зг)
х — 2г U (х — 2г) . ,,/ 3 X Д2(/ (х — 2г) 3 \
Д>{/(х—j-r) \3и /-Тг)
X — г U (х — г) М'(х-4-г) (X - г) х Д4С/ (х — г)
х и W Л1У (*+44 (*) txju чх + -г0 AtU (х)
л -- г и (х +И Д2(/ (х 4- г) л'40 Ай(/ (х -j- г)
X 2г U(x \ 2г) Н*+4г) Д8(/ (х 4- 2г)
х -р Зг U (х -|- Зг)
С учетом разностей третьего порядка, положив х = 0, получим
-g- = 2 [6/(-г) - U (г)]/(3г) - [6/ (-2г) - U (2r)]/( 12г). (16.78)
Если разности третьего порядка не учитывать, то
dU/dx = [U (—/) - U (г)]/(2г). (16.79)
Для второй производной с учетом разностей второго и четвер-
того порядка имеем
^ = ^-^(-r)-2i7(0)-bi/(r)];
(16.80)
Уравнения (16.78)—(16.80) служат исходными для вывода'
целого ряда формул, позволяющих определять вторую вертикаль-
ную производную гармонической функции но распределению этой
функции на плоскости.
Действительно, из уравнения Лапласа получаем
W_ (дЮ дЮ\ ‘
~dF------(16-81)
Для второй производной по у можно написать формулы,
аналогичные уравнениям (16.80). Тогда в простейшем случае
дЧ1 / д2и , д2и \ 1 Г.,,/п. Г1/ ,
5г2 “ (, дх2 + ду2 ) г2 [4t;(0) f)x
[6/(0)- U(r)], (16.82)
где U (r) — среднее значение функции U на окружности радиусом
г, определенное по четырем точкам (рис. 16.6).
Располагая точки в углах квадрата, описанного около
Рис. 16.6. Схема расположения точек
при вычислении Ргг по распределе-
нию U.
окружности, получаем формулу
Сагитова
(16.83)
Используя второе уравнение
(16.80), из формулы (16.81)
находим
^-±{5Д(0) + 4-[Щ/-).( +
+ t/(r)!/ + 6/(-r)A.-h^(-'%]-
--±[(/(2r)x + 6/(2r),+
+ (/(-2гК-фД( 2r),,]j.( 16.84)
450
Таблица 16.6
Формулы для вычисления d2Uldz2
Авторы Формула
Л. В. Канторович, В. Милн, В. И. Кры- лов [201/ (0) - 16(7 (г) - Ш (г/2“)]
Д. Ю. Панов nS" = ~з/~[W (0) + 4Z? (г) ~ 8U (г^)]
Р. Гендсрсон, И. Зитц -^-=_L-[3i/(0)~4t7(r) +U(rlA2)]
Л. П. Жоголев = ^-[34/ (0) — 247 (г) -U (л/2)1
Введя средние значения функции на окружностях радиусами г
и 2г, получим формулу Маловнчко
= -L [ 5U (0) - и (г) - 4 V (2г) ]. (16.85)
Поскольку уравнения (16.82)—(16.85) определяют вторую вер-
тикальную производную, то очевидно, что любая их линейная
комбинация также определяет эту производную; общий вид таких
формул
А2Ц 1 — _ ________________
= -рт (0) + ArU (/у) + А.ги (га) + • • • + AnJ (г„)], (16.86)
где
S А = о.
1=1
В табл. 16.6 приведены некоторые из формул,
на практике.
В случае двумерной задачи, имея в виду, что
из формул (16.83), (16.85) получаем
32/ / 1 — _
[15t/ (0) - 1647 (г) + U (2г)];
применяемые
игг =
(16.87)
d2U 2 —
[47(0) -и (г)],
где U (г) и U (2г) — среднее значение U на концах интервалов
г и 2г соответственно.
Точность определения второй производной по формулам,
приведенным в табл. 16.6, и по другим, им подобным, зависит от
приближенности самой формулы и от погрешности исходных
данных.
15*
451
Влияние этой погрешности ориентировочно можно оценить по
формуле
где еиг и ер (г) — средние квадратические погрешности опреде-
ления Uz2 и U (г); А/ — коэффициенты формулы (16.86).
Оценить погрешность, возникающую из-за приближенности
формул, трудно, поскольку она зависит от того, насколько шаг г
соответствует характеру исходного поля. В общем случае точность
вычислений возрастает при уменьшении г. Однако с уменьшением г
растет влияние погрешностей исходных данных, поэтому при
вычислении второй вертикальной производной надо стремиться
подобрать оптимальный размер шага г, при котором формула будет
достаточно точной, а влияние погрешности исходных данных не
очень сильным. При этих условиях суммарная погрешность
вычисленных значений будет минимальной. Следует отметить, что
при соответствующем подборе г вычисления по любой из выше-
приведенных формул дают близкие результаты.
Чрезмерное увеличение шага г резко уменьшает влияние
погрешностей исходных данных, но одновременно приводит
к снижению точности из-за приближенности формул, и в конечном
итоге вычисленное значение [)гг будет не реальной второй производ-
ной, а некоторой величиной, похожей на нее.
ТРАНСФОРМАЦИЯ АНОМАЛИЙ
КАК ПРОЦЕСС ЧАСТОТНОЙ ФИЛЬТРАЦИИ
Цель всех способов трансформации гравитационных аномалий
заключается в том, чтобы из суммарного гравитационного поля
выделить аномалии интересующих нас при решении конкретной
геологической задачи объектов. Другие составляющие гравита-
ционного поля считаются помехами. Поэтому задачу трансформа-
ции гравитационных аномалий можно рассматривать как задачу
выделения полезного сигнала на уровне помех.
Все приведенные конкретные трансформации гравитационных
аномалий могут быть представлены в виде общих интегральных
выражений:
для трехмерной задачи
Ulr(x, у, z) = [J 1], O)jp(g— х, У} —у, z)d£dp; (16.88)
s
для двумерной задачи
Utr(x, 0)P(s-x, z)< (16.89)
где Utr (х, у, z) и U/r (х, г) — трансформированные, U (|, ц, 0)
и U (|, 0) — исходные гравитационные аномалии; Р (| — X,
452
г] - у, z) и Р (I — х, z) — ядра интегральных преобразований
соответственно для трехмерной и двумерной задач, определяющие
четкость выделения интересующих нас особенностей гравитацион-
ного поля.
Выражения (16.88) и (16.89), представляющие собой интегралы
от произведения двух функций, называются интегралами свертки.
В теории связи интегралами свертки описывается процесс частот-
ной фильтрации сигналов. По аналогии трансформации гравита-
ционных аномалий можно рассматривать как процесс частотной
фильтрации, а различные способы трансформаций уподоблять
частотным фильтрам с соответствующими характеристиками.
Можно поставить задачу нахождения оптимальной трансформации,
при которой сохраняются все особенности полезного сигнала и
существенно подавляются сигналы-помехи. Перед описанием ча-
стотной фильтрации гравитационных аномалии необходимо кратко
остановиться на основных положениях частотного анализа.
Из курса математической физики известно, что
j cos |о> (Е - л-)] d<o = _ xz)2 + а-. (16.90)
и
Тогда интеграл Пуассона для двумерной задачи можно пред-
ставить в виде
U (х, —z) - -J- j е-“г du [ U (g, 0) cos [ш (| - х)| dE. (16.91)
О — оо
Эта формула называется обобщенным интегралом Фурье.
Полагая в ней г — 0, получаем интеграл Фурье
U(x, 0)=J-p<o J U(l, 0) cos [<о (g — х)] dg, (16.92)
О —со
который представляет непериодическую функцию U (х, 0) в виде
бесконечного числа элементарных периодических функций, беско-
нечно близких по частоте <в.
Выражения (16.91) и (16.92) могут быть записаны в комплексной
форме:
U (х, —z)_j du | U (5, 0)e~traM|;
— оо — ев
+ оо +оо
£/(х, 0) = -^- J [ (7(|, (16.93)
— оо —оо
Полагая
+оо
j t/(g, 0)e-‘“4| = S(<o), (16.94)
— 00
453
получаем
4 со
U (х, 0)=-^- J S(co) еСахс1ы.
— по
(16.95)
Функция S (со) называется комплексным спектром преобразо-
вания Фурье функции U (х, 0):
S (со) = А (со) 4- 'В (со) = | S (со) | e'v (а>,
где
+ «Э
Л(со) = j U (g, 0) cos(cog) dg — ReS (со);
-to
4-оо
В (со) = J и (g, 0) sin (cog) dg = Im S (co)
— действительная и мнимая части спектра S (со).
Тогда
| S (со) | = И А2 (со) 4- В2 (со)
— модуль, или частотная характеристика, спектра;
ср (со) = arctg |В (со)/Л (со)]
аргумент, или фазовая характеристика, спектра.
В случае трехмерной задачи также можно получить интеграл
Фурье. Воспользовавшись известным из курса математической
физики соотношением
—= J e-™J„ (cor) со dco, (16.96)
' Т ' Q
для интеграла Пуассона (16.13) в цилиндрических координатах
найдем
(7(0, 0, —z) = _J_j | j" U (г, a, O)e-“V0 (cor)rcodrdcoda, (16.97)
ООО
где Ja (cor) — функция Бесселя первого_рода нулевого порядка.
Вводя среднее значение функции U (г) на окружности ра-
диусом г
2л
О
454
из формулы (16.97) получаем интеграл Фурье для трехмерной
задачи:
И (0, 0, —z)= j ше~аг dco j U (г) Jo (cor) r dr', (16.98)
о о
при z = О
U (0, 0, 0) — [ со dco J U (г) Jo (ar) г dr. (16.99)
о о
Аналогично формуле (16.98) можно написать выражение интег-
рала Фурье для среднего значения функции U (г,) па окружности
радиусом г(-:
00 00
U (r.) = J coJo (corjdco [ U (г) Jo (cor) г dr.
о о
Если обозначить
03
J U (г) Jo (cor) г dr — S (со),
о
то формулы (16.98) и (16.100) примут вид
U (О, 0, —z) = J е_“г5 (ш) со dco;
о
(16.100)
(16.101)
(16.102)
б/ (г,) = j S (со) Jo (cor) со da,
о 1
Функция S (со), выраженная формулой (16.101), называется
спектром преобразования Ханкеля функции U (г). Для исследова-
ния трансформаций гравитационного поля спектральное представ-
ление исходной и трансформированной функций оказывается
весьма удобным. Приведем основные свойства спектров.
1. Спектр S (со) суммы функций 2 U, (х) равен сумме спектров
S, (со) слагаемых:
S (со) = 2 (щ). (16.103)
2. Спектр S- (со) функции U (х — |), смещенной относительно
исходной функции U (х) на величину £, равен спектру S (со)
исходной функции, умноженному на е',и£:
ЗДсо) = е_£ш^5(со). (16.104)
3. Спектр S„ (со) для п-й производной функции U (х) равен
спектру S (со) этой функции, умноженному на (tco)":
Sn (со) = (ico)nS (со). (16.105)
455
4. Спектр 5г (со) производной функции U (х) по параметру г
равен производной спектра 5 (со) исходной функции по тому же
параметру Z:
S,(co) = <5S(co)/dz. (16.106)
5. Равенство Парсеваля
( U2,(х)dx = -J— [ S(co)S(—co)dco = —f |S(<o)|2d<o (16.107)
J 2Л J JT J
— oo — oo (I
показывает, что энергию функции можно вычислить, интегрируя
либо квадрат самой функции, либо квадрат модуля спектра.
6. Спектр Slr (со) функции Utr (х), являющейся сверткой двух
функций U (х — g) и Р (g), равен произведению спектров S (со)
и Ф (со) этих функций:
Sir (со) = S (со) Ф (со) (16.108)
или
Ф(со)=5„ (co)/S(co).
Отношение Ф (со) спектров трансформированной и исходной
функции называется частотной характеристикой трансформации,
а функция Р (g) — переходной характеристикой. Функция Ф (со)
является спектром функции Р (g), характеризующей преобразова-
ние, производимое над исходной функцией U (g — х).
Имея в виду, что выражение (16.88) может быть представлено
в цилиндрических координатах формулой
£/„(0, 0, г)= J U (г) Р (г) г dr,
О
где
2л
t7(r) = 277 J С(г, а, 0)Р(а)с1а
О
— средневзвешенное по углу а значение функции U на окруж-
ности радиусом г, получаем:
для трехмерной задачи
Ф (со)j P(r)Jn(for)rdr\ (16.109)
о
для двумерной задачи
CD (со) = f Р (g, г) е-‘^ dg = 2 j Р (g, z) cos (cog) dg. (16.110)
— oo О
Подставляя в формулы (16.109) и (16.110) аналитические выра-
жения Р (г) и Р (g, г) для различных трансформаций, получаем
456
соответствующие частотные
характеристики этих транс-
формаций, показывающие,
какой частоты составляющие
гравитационного поля выде-
ляются, а какой подавляются.
На рис. 16.7 и в табл. 16.7
приведены частотные характе-
ристики наиболее распро-
страненных трансформаций
гравитационных аномалий.
Осреднением и аналитиче-
ским продолжением аномалий
в верхнее полупространство
подавляются высокочастот-
ные составляющие гравита-
ционного поля; аналитиче-
ским продолжением в нижнее
Рис. 16.7. Частотные характеристики
различных трансформаций (по К. В. Глад-
кому).
/ — осреднение; аналитическое продолжение:
2 —в верхнее полупространство, 3 — в нижнее
полупространство; вычисление производной:
4 — первой, 5 — второй, 6 — на высоте.
полупространство и вычислением высших производных эти состав-
ляющие усиливаются. Расчет высших производных на высоте явля-
ется своеобразным полосовым фильтром, который подавляет как вы-
сокие, так и низкие частоты, пропуская только частоты в опре-
деленном интервале, зависящем от порядка производной и от
высоты h.
Практическое использование частотных характеристик ослож-
няется двумя обстоятельствами: гравитационные аномалии всегда
заданы в конечной области (на площади или по профилю) и не
непрерывно, а только в отдельных точках. При этих условиях
Таблица 16.7
Частотные характеристики трансформаций
Трансформация Частотная характери- стика трансформации
Осреднение: трехмерная задача двумерная задача Аналитическое продолжение: в верхнее полупространство в нижнее полупространство Вычисление n-й вертикальной производной: на плоскости наблюдений на высоте Л Вычисление п-й горизонтальной производной: на плоскости наблюдений на высоте h 271 (cor)/sin (шт) sin (шт)/(шг) е-"’" еш!‘ wn ып^а‘‘ (<ш)п
457
интегральные выражения (16.109) и (16.110) частотных характе-
ристик трансформаций соответственно принимают вид
ф(0))2= ^Р(г) J0(ior)rdr= J0(wr,) j P(r)rdr =
0 i=0 т,-
= У KjJ0 (tort)>
i=0
Ф(со)2 = 2 [° P(g, z) cos (<og) dg =
0
= 2 cos (cog,) j P (g, z) d£ = 2 У, К, cos (cog,),
£=0 1; 1=0
(16.111)
где
P (r) rdr
£«+i
Ki = f P(?, 2)dg
— коэффициенты, зависящие от вида трансформаций.
Частотные характеристики, полученные по дискретным точкам
(рис. 16.8), обладают свойством периодичности, исчезающей толь-
ко при Дг —> 0 и Дс 0. Поэтому при построении вычислитель-
ных схем различных трансформаций следует так выбирать ин-
тервалы Дг и Ag и коэффициенты К,, чтобы не подчеркивались
нежелательные составляющие спектра трансформируемой функции.
Практические формулы трансформаций выполняют роль по-
лосовых фильтров, ширина пропускания которых определяется
коэффициентами /<, и радиусами г,- и g,.
Выражения (16.111) можно использовать для определения коэф-
фициентов Ki в различных вычислительных формулах трансфор-
маций, исходя из условия
Рис. 16.8. Сопоставление интегральных (7)
и дискретных (2) частотных характе-
ристик (по К. В. Гладкому).
| [Ф (ы) — Ф (со)2|2 dco = min.
о
(16.112)
Поскольку аналитическое
выражение Ф (со) для кон-
кретного вида трансформации
известно, то коэффициенты /<,•
вычисляют при некоторых
фиксированных значениях rz
или Е,- и при ограниченном
458
диапазоне w = ®„, полагая, что частоты за пределами суще-
ственно не искажают результаты трансформации.
Важной задачей является оценка связи между выделенными
при трансформациях аномалиями и глубиной источников, вызы-
вающих эти аномалии. Эту связь наиболее просто установить,
изучив поведение аномалии единичной точечной массы, располо-
женной на глубине z, при различного рода трансформациях. По
определению И. Г. Клушина, амплитуду Л4 (г) этой аномалии
можно рассматривать как глубинную характеристику трансфор-
мации:
оо
М (z) = | Ф (<о) е*“ги doj. (16.113)
п
Для нетрансформированной аномалии точечной массы Ф (<о) —
= 1 и амплитуда
00
М0(г)= j е~юг(ис1ш = 1 /г2. (16.114)
и
Если в формулу (16.113) подставить аналитические выражения
частотной характеристики Ф (ы) из табл. 16.7, то получим глубин-
ные характеристики конкретных видов трансформации. Поскольку
в действительности используются не интегральные частотные
характеристики Ф (©), а дискретные Ф (<л)2, определяемые выра-
жениями (16.111), то, заменяя в формуле (16.113) величину Ф (со)
ее приближенным значением Ф (w)E, получаем глубинную харак-
теристику различных формул трансформации:
п оо н
м (Z) = У Ki I Jo (аг,) с-“гсо dco = У & щ'лм/э •
I 4 I ' i I
1=0 0 z=0 4
Составив отношение
N (г) = = У . К'г* , (16.115)
‘—°
найдем так называемую относительную глубинную характеристику
трансформации, позволяющую приближенно оценить интервал
глубин, в котором располагаются источники выделенных аномалий,
а также сравнить разные вычислительные формулы.
Осреднение поля и аналитическое продолжение на высоту имеют
качественно одинаковые относительные глубинные характери-
стики: в трансформированном поле основное отражение находят
глубоко залегающие массы (рис. 16.9). Однако пересчет на высоту
более существенно влияет на аномалии глубоко залегающих
объектов: даже при глубине, в 8—10 раз превышающей высоту
пересчета, Af (z) 0,8, в то время как при осреднении аномалий
начиная с глубины всего в 3—4 радиуса осреднения АГ (z) «=> 1.
459
Рис. 16.9. Относительные глубинные характеристики трансформаций:
осреднения (а), пересчета вверх (б), вычисления второй вертикальной про-
изводной (в) (по И. Г. Клушину).
Качественное совпадение глубинных характеристик методов осред-
нения и пересчета на высоту позволяет найти приближенное соот-
ношение радиуса осреднения R и высоты пересчета h, при котором
получаются одинаковые результаты: по И. Г. Клушину, R
(3,5—5) h. Иначе выглядят относительные глубинные характе-
ристики при вычислении производных исходной функции: здесь
основное влияние на трансформированные аномалии оказывают
неглубоко залегающие массы.
Можно найти такие формулы трансформации, которые позво-
ляют выделять аномалии, связанные с источниками, расположен-
ными в некотором интервале глубин, т. е. относительная глубинная
характеристика таких трансформаций имеет максимум на заданной
глубине. В качестве примера приведем трансформацию Саксова —
Пигарда
ЩО, о, o),r = iZ/Crj — б7(г3)]/(г2 — rt), (16.116)
где U (г^ и U (г2) — средние значения функции U на окружностях
радиусами г1 и га.
Эта трансформация, в сущности, представляет собой разность
двух трансформаций, осуществляемых методом вариаций с раз-
ными радиусами (этот метод был предложен Б. А. Андреевым и
У. Гриффином):
(0, 0, 0) = 1/(0, 0, O)-U(r).
Относительная глубинная характеристика трансформации
(16.116) имеет вид (рис. 16.10):
I Г ч>3 1
A(z) =—-— -----------—--------------—.. (16.117
4-г?) 7 (4 + г9) .1
4G0
Введя обозначение rv —
= пг2, найдем N (2) —
= ^"(z)nMX при
г/га=/(/г4/6—ns)/(l — п*/5).
(16.118)
Эта формула исполь-
зуется для выбора рацио-
нального соотношения
трансформаций с радиу-
сами г\ и г2.
Оценки глубин, полу-
ченные по относительной
Рис. 16.10. Относительная глубинная харак-
теристика трансформации Саксова—Нигарда.
глубинной характеристике, являются предельными, поскольку
они предполагают резкое изменение плотности. В реальных
условиях источникп аномалий располагаются на несколько мень-
шей глубине.
ИСПОЛЬЗОВАНИЕ
ЭЛЕМЕНТОВ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНЫХ
ТРАНСФОРМАЦИЙ АНОМАЛЬНОГО ПОЛЯ
Основной проблемой трансформации гравитационных аномалий
является определение оптимальных параметров трансформации,
при которых обеспечивается наиболее полное выделение аномалий
объектов, представляющих интерес при решении данной геологи-
ческой задачи. Выбор оптимальных параметров опирается на
комплекс сведений об аномальных объектах: форма, размеры,
глубина залегания и т. и. Количественная и качественная информа-
ция может быть получена из общегеологических соображений,
результатов других методов, анализа самого гравитационного
поля. Естественно, чем больше имеется сведений об аномальных
массах, тем более обоснованно можно выбрать оптимальные
параметры трансформации.
Однако большинство существующих методов трансформации не
учитывает всего многообразия факторов, влияющих на результаты
трансформации, а также не принимает во внимание случайный
характер этих факторов. Поэтому выбор оптимальной трансформа-
ции должен основываться на знании статистических закономер-
ностей явлений, отраженных в суммарном гравитационном поле.
При таком подходе можно использовать статистические характе-
ристики отдельных составляющих суммарного гравитационного
поля, т. е. наиболее общие сведения об исследуемых объектах.
Следует учитывать, что как сами предпосылки, так и полученные
на их основе выводы относятся не к отдельным аномалиям и ано-
мальным телам, а к статистическим совокупностям аномалий и
461
Рис. 16.11. Семейство реализаций случайной функции.
аномальных тел. Поэтому для решения задачи привлекается
аппарат математической статистики, в частности теория случайных
функций. Такой подход к трансформации рассматривается в рабо-
тах И. Г. Клушина, К. В. Гладкого, Ф. М. Гольцмана, С. А. Сер-
керова, М. Г. Сербуленко, О. А. Соловьева и др.
Случайной называется функция, которая в результате опыта
может принять тот или иной конкретный вид, заранее не известный.
Этот конкретный вид именуется реализацией случайной функции.
Проведя над случайной функцией серию опытов, получим группу,
или семейство, реализаций этой функции. Рассмотрим пример.
Поле силы притяжения U, какого-либо тела можно полагать
случайной функцией координат точки наблюдения. Если измерить
поле вдоль профиля несколько раз, то каждая кривая U г (х)
будет представлять собой реализацию случайной функции и сово-
купность этих кривых образует семейство реализаций (рис. 16.11).
Любая реализация есть обычная, неслучайная, функция; таким
образом, в результате каждого опыта случайная функция превра-
щается в неслучайную. Если зафиксировать значение аргумента
х = A'j, то случайная функция превратится в случайную величину.
Эта случайная величина называется сечением случайной функции
U2 при данном х. Если сделать сечение семейства реализаций, то
найдем п значений случайной величины U2, полученных в п опытах.
Для характеристики случайных величин пользуются число-
выми характеристиками этих величин: математическим ожиданием
М и дисперсией D. Математическое ожидание М случайной вели-
чины X определяется равенством
М(Х) — х — р,х„ (16.119)
£=1
где р,—вероятности возможных значений xz случайной величины X,
п
L pi =1 •
1=1
462
Математическое ожидание иногда называют средним значением
случайной величины.
Формула (16.119) относится к прерывной случайной величине.
Для непрерывной величины X математическое ожидание опреде-
ляется интегралом
+ оо
М(Х)= j xf(x)dx, (16.120)
— оо
где f (х) — плотность распределения величины X,
+по
/ /(x)dx=l.
— со
Дисперсия D случайной величины X для дискретного и непре-
рывного ее распределения выражается соответственно формулами
/9 (А) н L (*, - х)2Рь 4- по (16.121)
£)(Х) [ (х - х)2 /(х) dx. -00
Дисперсия случайной величины характеризует рассеивание,
разброс, ее значений около математического ожидания.
Средним квадратическим отклонением (стандартом) называют
о (А)
Аналогичными характеристиками описывают и случайные
функции. Характеристики случайных величин представляют собой
числа, а характеристиками случайных функций в общем случае
являются не числа, а функции.
Математическим ожиданием случайной функции X (х) называ-
ется неслучайная функция тх (х), которая при каждом значении
аргумента х равна математическому ожиданию соответствующего
сечения случайной функции:
тх (х) - [Х(х)].
Математическое ожидание случайной функции есть некоторая
средняя функция, около которой варьируют ее конкретные реали-
зации (см. рис. 16.11).
Дисперсией случайной функции X (х) называется неслучайная
функция Dx (х), значение которой для каждого аргумента х
равно дисперсии соответствующего сечения случайной функции:
Dx(x) = D[X(x)].
Дисперсия случайной функции характеризует разброс возмож-
ных реализаций функции относительно ее математического ожида-
ния, т. е. степень случайности случайной функции.
463
Рис. 16.12. Реализация двух разных случайных функций, имеющих одинаковое
математическое ожидание и одинаковую дисперсию.
Средним квадратическим отклонением случайной функции
называют функцию
стх W = VDx(x).
Математическое ожидание и дисперсия являются важными
характеристиками случайной функции, по для описания особен-
ностей случайных функций этих характеристик недостаточно. При
одинаковом математическом ожидании и одинаковой дисперсии
(рис. 16.12) две случайные функции Хх (х) и Х2 (х) имеют совер-
шенно разный вид, определяемый их конкретными реализациями:
для функции X, (х) характерно плавное изменение, для функции
Х2 (х) — неправильные колебания. Различие в плавности измене-
ния функций X, (х) и Х2 (х) ни дисперсия, ни математическое ожи-
дание описать не могут. Для этого вводится специальная харак-
теристика, называемая корреляционной (автокорреляционной)
функцией. Корреляционная функция характеризует степень зави-
симости между сечениями случайной функции, относящимися
к разным аргументам х.
Рассмотрим два сечения функции X (х) с абсциссами хх и х2
(рис. 16.13). Очевидно, что чем ближе значения хй и х2, тем ближе
и значения функции X (х,) и X (х2). Очевидно также, что с увеличе-
нием интервала т между сечениями связь X (хх) и X (х2) вообще
должна убывать.
Функция автокорреляции определяется выражением
Kx(xlt х2) = Л1 {[Х(х1)-тх(х1)][Х(хг)-тЛ(х2)]|. (16.122)
Полагая х, = х2 = х, имеем
Кх (х, х) = М [ [ X (х) - тх (х)!2} = Dx (х),
т. е. при хг — х2 корреляционная функция обращается в диспер-
сию случайной функции.
Вместо корреляционной функции Кх (хъ х2) часто используют
нормированную корреляционную функцию
Rx (*1, л-2) = Кх (Хр х2)/[пх (Х1) пх (хг)|, (16.123)
464

Рис. 16.13. К определению корреля-
ционной функции.
Рис. 16.14. Корреляционная функция
стационарной случайной функции.
которая представляет собой коэффициент корреляции величин
X (jCj) и X (х2); при хх = хг = х
Rx (х, х) = Кх (X, х)/[сгх (х)]2 = Dx (х)/[сгх (х)]2 = 1.
Случайная функция называется стационарной, если ее матема-
тическое ожидание и дисперсия постоянны, а корреляционная
функция зависит только от разности аргументов х, — х2 = т:
тх (х) const; Dx (х) — const;
Кх (xi> А'а) — Кх (х2 ~~ xi) = Кх (г)-
Нормированная корреляционная функция стационарной слу-
чайной функции (коэффициент корреляции) определяется выра-
жением
^х (т) = кх (т)/Кх (0) = (T)/Dx.
Коэффициент корреляции изменяется от нуля до единицы:
Rx (т) = 0 показывает, что никакой корреляции между X (х)
и X (х 4* т) нет; Rx (т) = 1 соответствует полной корреляции
(рис. 16.14). Так как при больших интервалах т корреляционная
функция обращается в пуль, обычно в практических случаях счи-
тают, что корреляция исчезает при Rx (т) = 0,3. Значение т,
при котором Rx (т) — 0,3, называют радиусом автокорреляции R.
Иногда за радиус корреляции принимают площадь, ограничен-
ную кривой Rx (т) и осью х:
оо
я = j (т) th.
о
Форма кривой Rx (т) и радиус автокорреляции R позволяют
судить о степени изменчивости функции X (х) при изменении х.
При слабой коррелируемости кривая Rx (т) убывает быстро; при
плавной функции X (х) кривая Rx (т) изменяется медленно. При
наличии периодичности в функции X (х) кривая Rx (т) становится
465
знакопеременной. Для большинства практических случаев коэффи-
циент корреляции может быть аппроксимирован выражениями
/?х(т) = ехр(— т2//?); 1
/?х(т) = №/(^ + т2), j
(16.124)
где X — некоторое постоянное число.
Гравитационные аномалии можно рассматривать как стацио-
нарные случайные функции, поскольку их конкретные реализации
непрерывно колеблются около средней функции, амплитуда и
резкость этих колебаний постоянны на протяжении всего отрезка
задания аномалии.
Стационарная случайная функция называется эргодической,
если одна-единственная конкретная реализация достаточной
продолжительности дает хорошее представление о свойствах слу-
чайной функции в целом. Эргодическое свойство состоит в том, что
каждая отдельная реализация случайной функции является пред-
ставительной для всей совокупности реализаций и может заменить
эту совокупность. Стремление корреляционной функции (г)
к нулю при т —> оо указывает на эргодичность функции. Для эрго-
дических стационарных функций существенно упрощается опре-
деление их характеристик, в частности математическое ожидание
, и автокорреляционную функцию можно приближенно найти по
одной представительной реализации:
L
М [X (х)] = тх = 2_ J X (х) dx; (16.125)
О
L-T
Хх(т) = 72_ J |Х(л-)-тД[Х(х + т)-тД^л-. (16.126)
о
Разбивая интервал интегрирования L на п равных частей дли-
ной Дх = L/n, для математического ожидания вместо формулы
(16.125) имеем
(16.127)
“ i=l
Аналогично можно вычислить корреляционную функцию для
значений т = </Дх:
п-ч
хх(т = цДл-) = —Ц-L хда, (16.128)
п я 1=1
где
X/ = X,- — т х.
При q — О
Dx =Kx(0) = 2-i да. (16.129)
п i=i
466
Вычисление корреляционной функции проводят для q —
— О, 1, 2, ... до таких значений q, при которых корреляционная
функция становится практически равной пулю или начинает со-
вершать колебания около нуля. Для определения пгх и с удов-
летворительной точностью надо, чтобы число точек п было доста-
точно большим (100 или более).
При исследовании случайных функций широко используют их
спектральное представление. Различие спектрального представле-
ния случайной стационарной и неслучайной функции состоит
в том, что для случайной функции амплитуды колебаний являются
случайными величинами. Спектром случайной стационарной функ-
ции описывается распределение дисперсий ио различным частотам:
П,\ — Хх(0) = I G(w)dw;
б
(16.130)
функция G (со) называется спектральной плотностью стационарной
случайной функции.
Формула (16.130) представляет собой разложение дисперсии
Dx на сумму элементарных слагаемых G (со) с/со, каждое из которых
является дисперсией, относящейся к элементарному участку
частот da. Функцию G (со) называют еще энергетическим спектром
случайной функции. Энергетическим спектром описывается частот-
ный состав стационарного процесса. Эта характеристика случайной
функции не является самостоятельной, а полностью определяется
корреляционной функцией. Согласно теореме Винера — Хинчина
корреляционная функция и спектральная плотность связаны
следующими соотношениями:
+оо
Кх (т) = [С (<в) е‘0)Т сйо;
— со
G(co) = -^~ | Кх (т) с~“оТ/!т.
— оо
(16.131)
Так как Кх (т) и G (со) являются четными функциями своих
аргументов, то эти соотношения можно записать в виде
ос
Кх (т) — J G (со) cos (сот) Фо;
о
G (со) = j Кх (т) cos (сот) ch.
о
(16.132)
467
Для изотропной (обладающей круговой симметрией) стационар-
ной случайной функции, зависящей от двух координат, формулы
(16.130) и (16.132) принимают вид
Dx = Кх (0) = | G (со) Аы = 2п [ G (со) со Фо;
о о
00
Кх СО 2л j G (<о) /0 (on) о) day;
о
00
G = 27 J Кх Т dT'
О
(16.133)
Формулы (16.131)—(16.133) имеют большое значение и широко
используются при исследовании линейных преобразований, совер-
шаемых над случайными стационарными функциями. Линейными
называются такие преобразования, при которых оператор преобра-
зования обладает свойством аддитивности. Примерами линейного
преобразования служат операторы дифференцирования, умноже-
ния на определенную функцию, интегрирования с заданным «весом»
и т. д. Все используемые трансформации и преобразования грави-
тационных аномалий являются линейными операторами.
При линейном преобразовании стационарной случайной функ-
ции ее спектральная плотность умножается на квадрат модуля
частотной характеристики преобразования:
Gtr (со) =С(И)|Ф (со) |2, (16.134)
где Ctr (со) — спектральная плотность трансформированной функ-
ции.
На основе преобразования (16.134) составляющие дисперсии,
соответствующие колебаниям разной частоты, трансформируются
(усиливаются или ослабляются) в зависимости от конкретного
вида формулы (16.134) и значений со.
Применим полученные формулы для построения оптимальной
трансформации, в результате которой из суммы двух стационар-
ных случайных функций должна быть выделена одна из них. Эта
задача рассмотрена И. Г. Клушиным.
Пусть суммарной случайной функцией является наблюденная
вдоль профиля гравитационная аномалия U, состоящая из анома-
лии U г, которая подлежит выделению, и осложняющей ее анома-
лии Un:
U -Ur -\-Un.
Конкретно функция Un может проявляться в виде региональной
или локальной аномалии более высокого, чем Ur, порядка, в виде
погрешности наблюдений и т. д.
468
В качестве критерия оптимальности трансформации возьмем
минимум средней квадратической погрешности приближеннятранс-
формированной аномалии Utr к значениям аномалии U,., которые
наблюдались бы при отсутствии помехи U п. При этом предполага-
ется, что аномалии U, и Un не коррелируются друг с другом
(коэффициент взаимной корреляции равен нулю):
К„,Дг) = А'л, г СО = 0.
Если Gr (со) и Gn (со) — спектральные плотности аномалий
Uг и U,v то после преобразования
Gr ,г (со) = Gr (со) | Ф (со) |2; Gn ir (со) = G„ (со) | Ф (со) |2.
Величина Gr (со) | 1 — Ф (со) |2 определяет искажения, вносимые
трансформацией в выделяемую аномалию Uг. Среднее значение
квадрата суммарной ошибки, возникающей в результате трансфор-
мации, получаем из выражения
е2 = J [Gr (со) | 1 - Ф (со) |2 Gn (со) | Ф (со) |2]2 dco. (16.135)
о
Характеристику преобразования Ф(со) необходимо подобрать
таким образом, чтобы интеграл (16.135) имел наименьшее значение.
Поскольку в подынтегральное выражение входят только спектраль-
ные плотности аномалии и помехи, учитывающие амплитуды состав-
ляющих, а не их фазы, то характеристика трансформации является
вещественной функцией. Минимальное значение интеграл имеет
при
Ф (со) = Gr (co)/[Gr (со) 4- Gn (со) ]. (16.136)
В этом случае выражение для суммарной средней квадратиче-
ской ошибки принимает вид
оо
е® = J {Gr (“) Gn (®) + Сп (“)11
о
Из этой формулы следует, что ошибка (или точность) выделения
интересующей нас аномалии Uг зависит от произведения Gr(co)Gn(co),
которое характеризует перекрытие энергетических спектров по-
лезной аномалии Uг и помехи Uп. Таким образом, когда аномалии
Uг и U п не коррелируются между собой, а их спектры Gr (со) и
G,, (со) не перекрываются, то произведение спектров равно нулю и
трансформация с характеристикой (16.136) разделяет аномалии
точно. Однако такая ситуация на практике встречается редко;
обычно эффективность разделения аномалий зависит от соотноше-
ния их энергетических спектров. В частности, при
СлН »</;(<•>)
469
ошибка
е2 | Gr (со) dco = Кг (0) = Dr =
б
где Ur — среднее значение квадрата выделяемой аномалии.
Таким образом, в этом предельном случае никакого выделения
аномалии не будет.
Для перехода от характеристики трансформации (16.136)
к аналитическому выражению и численной формуле воспользуемся
преобразованием Фурье.
Имея в виду равенство (16.93), получаем выражение для функ-
ции U, подвергнутой трансформации:
+ оо +ос
Ulr(x, 0) = [" (со) dco | U (Е, 0)e_‘“^d^. (16.137)
СО
Если функция Ф (со) такова, что интеграл | Ф (со) dco равпо-
о
мерно сходится, то, поменяв порядок интегрирования в правой
части выражения (16.137), получим
+ ос
^(х,0) = -^/ U&0)K$-x)dl,
— оо
(16.138)
где
+ оо
к(Е — х) = [ с(га <£-*> __Gr ------dco =
’ J Gr (со) + й„ (со) “°
— оо
oTiTOM1'"1 ’ (16.139)
О
— весовая функция оптимальной трансформации.
На основе формулы (16.138) можно построить палетку. Пусть
точки наблюдений расположены через равные интервалы Кх
так, что х — п Кх. Тогда выражение (16.138) преобразуется в сумму
U (п) К (0) 4- £' + «О + U (п — гп) | К (т)
/71=1
Av I
,(16.140)
где
со
К (т) = 2 [ cos (com Дх) „ . , dco,
v ' J ’ Gr (co) Gn (co)
I)
Значениями К (.tri) определяются числовые коэффициенты па-
летки. На основе формулы (16.140) можно рассчитать палетку
и с равными весовыми коэффициентами.
470
Таким образом, для построения оптимальной трансформации
необходимо знать спектральную плотность G (со) разделяемых
аномалий, которую определяют по функции автокорреляции
(л). При вычислении G (со) по графику Кх (т) используют раз-
личные приемы численного интегрирования или аппроксимируют
КА- (т) формулой
Кх(т)= S ягехр(—&?т2), (16.141)
с=1
тогда
т
= <16142>
1=1
Для приближенной оценки G (со) и Кх (?) можно пользоваться
средним значением квадрата амплитуды выделяемых аномалий и
радиусом их корреляции R. На основе формулы (16.140) можно
построить оптимальные трансформации для различных конкрет-
ных случаев распределения аномалий. Аналогичным приемом
получают формулы оптимальной трансформации и для трех-
мерной задачи.
Для некоторых частных случаев распределения источников гра-
витационного поля возможно построение не оптимальных, а точ-
ных трансформаций для разделения аномалий. Ряд таких задач
исследовал М. Г. Сербуленко. Рассмотрим некоторые ситуации,
представляющие практический интерес. Пусть имеются две об-
ласти и v.2, которые разделены расстоянием А; пусть они со-
здают двумерные гравитационные аномалии, причем такие, что
при параллельном переносе вдоль направления А одной из обла-
стей их аномалии совпадают; пусть спектры гравитационного
поля этих областей соответственно будут (со) и S2 (ы). Тогда
на основе перечисленных условий соотношение между спектрами
имеет вид
S2(to)^S1(co)e-^\
где А = Ах — t'Az.
Спектр суммарного поля
S (со) = S, (со) + S2 (со) = S, (со) (1 + е-‘^)
или
Si (со) — S (со), (1 е-‘®л) = S (со) Ф (со),
где
Ф(ш) = 1/(1 4 е‘“д) (16.143)
— частотная характеристика трансформации для точного выде-
ления аномалии, создаваемой областью из суммарного гра-
витационного поля.
471
Разлагая выражение (16.143) в биномиальный ряд (имеем
в виду, что со > 0), получаем
Ф (oj) = 1 _Дг^-ico Лх £-6)2 Дг£-/<о2 Дх_^-оЗ Дг^-АаЗ Д.г _|_ ... Qg I44)
Эта частотная характеристика представляет собой последова-
тельность, состоящую из преобразований, которые определяют
суммарное поле на высотах Дг, 2Дг, ЗДг, ..., nAz с одновремен-
ным сдвигом его по горизонтали на расстояние Дх, 2Дх, ...,
пДх. В частных случаях или Дх, или Да может быть равно нулю,
тогда в первом случае будем иметь последовательность только
пересчетов исходной функции в верхнее полупространство, во
втором — только сдвигов в горизонтальном направлении.
К трансформации, определяемой выражением (16.144), могут
быть сведены многие практические задачи. В частности, если име-
ются две контактные поверхности, согласно залегающие и от-
стоящие по высоте на расстояние Д/г друг от друга, то задача вы-
деления поля (х, 0) верхней контактной поверхности из сум-
марного поля U (х, 0) = Ut (х, 0) 4- U2 (х, 0) решается при по-
мощи следующей трансформации:
4-00
(X, 0) = U (х, 0) — — Г U 1-
' v 7 л J (§—х)2(ДА)2
— со
2Дй7 U (I, 0)di ЗДЛ 7 (7(g, O)dg
+ л J (1—х)2 + (2ДД)2 л J (g - х)2 + (3 Д/1)2 'г
или
(х, 0) = U (х, 0) - U (х, - Д/г) -|
+ (7(х, — 2Д/г)— t/(x, — 3 Д/г)-|--- (16.145)
Этот метод можно легко распространить на случай большего
числа одинаковых тел или контактных поверхностей.
На основе общего выражения (16.136) можно построить опти-
мальные трансформации для разделения аномалий, если заданы
некоторые дополнительные ограничения. В качестве примера,
обратимся опять к двум контактным поверхностям. Пусть они
характеризуются статистически однородным и независимым рас-
пределением превышений Д/гг (|, /гх) и Д/г2 (£, /г2) относительно
средних глубин hx и /г2. М. Г. Сербуленко показал, что в этом слу-
чае возможно оптимальное разделение аномалий этих поверхностей
при очень широких допущениях: неизвестном виде функций
ДЛ2 (Е, hj) и Д/г2 (£, /г2), а также неизвестном выражении их авто-
корреляционных функций, которые полагаются одинаковыми.
Пусть Gni (со) — энергетический спектр поля на уровне контакт-
ной поверхности hx. Тогда энергетический спектр поля, создава-
472
емого первой контактной поверхностью на уровне наблюде-
ний, будет
Gi (со) = GOi (w) e-2<oAi,
поскольку при преобразовании энергетического спектра его не-
обходимо умножить на квадрат модуля частотной характеристики
преобразования.
Соответственно для второй контактной поверхности получаем
G2 (со) = Go, (со) <г2“'‘=;
применяя формулу (16.136), имеем
ф (ш) = G01 (со) e-a2ftV[Goi (со) е~«2А> GOi (со) е~и2Л=]
или
ф(ш)= 1/[1 -I- IV'(с») е-“2Л''], (16.146)
где
IF (со) == GOi (co)/G01 (со); Л/i = h2 — ht.
При со > 0 выражение (16.146) можно записать биномиальным
рядом
- ф (со) = 1 — W (со) е-“2 м + W2 (со) е-<°4 v' — IV3 (со) е-“6 Л -|-(16.147)
Если энергетические спектры G01 (со) и 6’02 (ю) совпадают, то
ф(со)== 1 — ги!А'' 4-е-м‘,А'‘ — е-га6Д,,+ • • , (16.148)
т. е. получаем трансформацию, сходную с (16.144), но пересчеты
в верхнее полупространство проводятся только через четные
интервалы Д/г, а именно: 2Д/г, 4Д/г и т. д.
Следует отметить, что соотношения (16.144)—(16.148) спра-
ведливы при ст3 — о2 — стг — ст1 = ст, где ст — избыточная плот-
ность, а ст1; ст2 и ст3 — плотность слоев. Если это условие не вы-
полняется, т. е.
ст3 — Ст1 = ст'; ст3 — о2 = ст",
то перечисленные выражения принимают вид
Ф(Ш)= 1 - (-^)е-“АЛ i- -)
ср (со) -= 1 _ W (со) е-<->2 да 4.
+ (тгУ w'2 (<о) <г“4 л" ~ (5“У w' И е“а6 л" Н_;
Ф(<в) = 1 — й~®2Дй
473
Рассмотренный прием можно распространить и на большее
число контактных поверхностей. Например, для трех границ
при о' = о" = а = 1 будем иметь
Ф(ш) = 1/(1 _р-а2дл. (16.149)
где
/Х/ц -— /ig — /1^, — /Гз — hi-
Разложение формулы (16.149) в биномиальный ряд решает
задачу выделения поля Uг (х, 0) из суммы полей 1/г (х, 0) ф-
4-6^2 (х, 0) ф- U3 (х, 0).
Когда полезные аномалии соизмеримы с уровнем случайных
помех, задача выделения аномалии может быть решена на основе
корреляции ожидаемого и наблюденного распределения полей.
Н. Винером было показано, что оптимальным оператором для вы-
деления слабых сигналов на фоне сильных помех является такой,
который осуществляет взаимную корреляцию входной функции
и полезного сигнала. В этом случае участки записи, которые по
частотной характеристике совпадают с ожидаемым сигналом,
выделяются наиболее рельефно, т. е. оптимально выявляется по-
лезный сигнал.
Задача разделения аномалий может быть сформулирована
следующим образом.
Имеется дискретное распределение значений аномалии U (х);
известно также, что в некоторых точках этого распределения при-
сутствует искомая аномалия Ur (х), которая осложнена помехами
Un (х). Требуется оценить наблюденные значения с точки зрения
наличия или отсутствия аномалии Uг (х). Эта задача получила
исчерпывающее решение в теории информации. Как практическое
приложение, она нашла широкое применение в радиолокации.
Привлечение этого метода для выделения слабых геофизических
аномалий рассмотрено в работах А. Г. Тархова, А. А. Сидорова,
В. Н. Никитина, О. А. Демидовича и др. Решение задачи в такой
постановке сводится к статистической оценке наблюденного поля
на отсутствие или наличие аномалии Ur (х). Решению придается
вероятностный смысл с указанием надежности. Задача может
быть решена на основе теоремы гипотез Байеса, которая позволяет
определить вероятность причин, если заданы вероятности след-
ствий.
Относительно полезной аномалии Uг (х) имеются две гипотезы:
гипотеза Нг — аномалия Uг (х) есть, и гипотеза Н 0 — аномалии
Ur (х) нет. Вероятности реализации каждой из гипотез неизвестны.
Можно предполагать, что обе гипотезы равновероятны. Это пред-
положение отвечает максимальной неопределенности, т. е.
Р(Яф = Р(Яо) = О,5.
Если известны условные вероятности (функции правдоподо-
бия) наблюденной аномалии: Р [U при наличии полезной
474
аномалии и Р [1/ [х^1Н„] при отсутствии ее, то формула Байеса
позволяет по распределению U (х/) (i — 1, 2, т) вычислить
условную вероятность наличия полезной аномалии
Р [Hr/U (X,)] =
Р(НГ)Р [U(Xi)/Hr] _ L
- P(Hr)P\U(Xi)/Hr]+P(H„)P[U(Xi)/H0] ~ 1 + L
и условную вероятность отсутствия полезной аномалии
P[Hofl/(Xi)] =
Р (Hr) Р [U М/Нг] + Р (Но) Р [Lf (Xi)!H0]
тфг. <16151>
где
Р [U (x^/Hri/P [U (Xi)/H0\ = L (16.152)
— отношение правдоподобия.
Очевидно, что аномалия будет выделена, если L > 1. Таким об-
разом, для суждения о наличии полезной аномалии Uг необходимо
вычислить отношение правдоподобия L, т. е. определить численные
значения условных вероятностей Р [U (х,-)/Яг] и Р [U (х,)/Я01.
Найти их сравнительно просто, если наблюденные значения U (х,)
представляются стационарной случайной функцией, а помехи яв-
ляются некоррелированными, имеют нулевое среднее и распре-
делены но нормальному закону Гаусса. Ожидаемые аномалии
Ur(Xi) должны быть заданы. В этом случае условная вероятность
Р [U(xi)/H0] полностью определяется численными значениями
наблюденных аномалий U (х,) и подчиняется нормальному распре-
делению:

P[Z7(xf)///0] =

(16.153)
где i = 1, 2, ..., т — порядковый номер точки наблюдения;
q — порядковый номер аномального значения на интервале п; о2 —
дисперсия аномалии U (х,) или помехи Un (х£).
Если из наблюденной аномалии U (х;) вычесть поточечно зна-
чения Ur (xq), то условная вероятность Р [У (х4)/Яг1 определится
разностями £7(х;) — U г (х^):
Р \U (х,)/Нг] = exp (- 2g S [U (xi+7.,) - Ur (x?)M
V 2л о I. 2(7 J
(t = 1, 2,..
(16.154)
Используя выражения (16.153) и (16.154), записываем отно-
шение правдоподобия L (16.152) и, подставляя его в формулу
475
(16.50), получаем уравнение для определения искомой вероят-
ности
P{HJU (л;)] =
= ехр
I Г 1 г\
X р + ехр — 2-0- Е U'r (т?) ехр
ехр
0=1
<7=1
(16.155)
-1
Все величины, входящие в это выражение, известны. На его
основе и выполняют практические вычисления по выделению ано-
малий, соизмеримых с помехами. Вероятности, превышающие 0,5,
указывают на местоположение искомых аномалий.
При практическом применении формулы (16.155) следует при-
держиваться определенной последовательности. Предварительно
находят постоянные величины, входящие в формулу: /г — число
точек, по которым определена аномалия; U (xt) — среднее значе-
ние наблюденного поля, которое сводится к нулю и поэтому в фор-
муле (16.155) отсутствует; о2—дисперсию помех и ожидаемой
аномалии Ur (х,) и, наконец, значение экспоненты
ехр —-^гХ^гС^) •
(16.156)
Последняя формула может быть существенно упрощена, если
учесть, что наилучшие результаты получаются, когда дисперсия
ожидаемой аномалии и дисперсия помех равны между собой:
о2 = оу, где Оу — дисперсия ожидаемой аномалии Ur (х/). Тогда
Ou = ~ Е Щ (хч) = а2
" в=1
и
ехр
= егпР
Для удовлетворения равенства Оу = о2 все значения U r (xq)
необходимо умножить на <з!ои, тогда
п п
4 У (xi+<M) Ur (х„) = -А- V и (х^) иг (х,) = рК (Л-,.),
а <уи <уПи
где
р = 1/(ооц); К (х() = % U (xi+q^) Uг (xq).
«=i
Величина К (х{) представляет собой функцию взаимной кор-
реляции между аномалиями U (х() и Ur (хг), вычисление которой
476
и является основной операцией при определении условных ве-
роятностей.
Окончательно формула (16.155) принимает вид
р [нг/и (х,)] = 1 4- ] =
= е»к (xi)-',/2/[ j ерК (*<) -«/2],
Следует еще раз подчеркнуть, что рассмотренный способ выделе-
ния аномалий целесообразно применять далеко не во всех случаях.
Положительные результаты этот способ дает только при выполне-
нии ряда специфических условий, оговоренных при выводе фор-
мулы (16.155): помехи не коррелпрованы и распределены по нор-
мальному закону, а полезная аномалия полностью определена.
Поэтому предварительно наблюденную кривую необходимо лю-
бым подходящим способом преобразовать в знакопеременную,
привести ее к нулевому среднему и вычислить дисперсию. Ожида-
емая аномалия выбирается таким образом, чтобы она оптимально
соответствовала полезной аномалии и была подобна ей по форме.
Дисперсия ожидаемой аномалии должна быть равна дисперсии
помех-, а сумма ординат этой аномалии должна быть равна пулю.
Эти требования определяют оптимальные условия выделения
полезных аномалий.
ТРАНСФОРМАЦИИ ГРАВИТАЦИОННЫХ
АНОМАЛИЙ НА ОСНОВЕ КОНКРЕТНОЙ
ГЕОЛОГИЧЕСКОЙ ИНФОРМАЦИИ
Все рассмотренные выше способы трансформации исходят из
морфологического различия аномалии (по размерам, форме и т. п.),
и выбор параметров трансформации основывается на некоторых
осредненных геологических характеристиках изучаемых объектов.
Накопление сведений об исследуемом объекте позволяет ис-
пользовать конкретную геологическую информацию для разделе-
ния гравитационных аномалий путем последовательного учета
гравитационных эффектов, вызванных уже известными геологи-
ческими факторами. Этот метод требует весьма значительного объ-
ема сведений о геологическом строении исследуемой территории.
Так, распределение плотности в той части геологического разреза,
гравитационный эффект которой исключается из наблюденного
поля, должно быть известно с такой же детальностью, как и рас-
пределение аномалий на поверхности наблюдений. К сожалению,
на практике это достигается чрезвычайно резко. Обычно грави-
тационные аномалии, выделенные таким методом, бывают отя-
гощены большими ошибками, связанными со сложностью гео-
логического строения, что не позволяет использовать их для коли-
чественной интерпретации. Для получения достоверных результа-
тов надо иметь достаточную уверенность в реальности и точности
477
геологического разреза, по которому рассчитывается гравитаци-
онный эффект, чтобы ошибки в представлении разреза и в вычисли-
тельных операциях не сказывались существенно на остаточных
аномалиях.
Идея разделения гравитационных аномалий на основе конкрет-
ной априорной геологической информации, не зависящего в то же
время от неточностей в знании физической характеристики раз-
реза, реализована в корреляционном методе трансформации ано-
малий. Вопросы корреляционных зависимостей между грави-
тационными аномалиями и различными геологическими структу-
рами рассматривались Р. М. Деменицкой, Л. С. Вольвовским,
Б. А. Андреевым и др. Наиболее полное решение этой проблемы
применительно к разделению гравитационных полей отражено
в работах Г. II. Каратаева, В. И. Шрайбмана, М. С. Жданова
и др.
Сущность корреляционного метода трансформации аномалий
заключается в том, что наблюденное гравитационное поле U
разделяется на локальную (остаточную) Ut и региональную (фо-
новую) U г составляющие:
U = Ur +U
под региональной составляющей Uг гравитационного поля пони-
мается та его часть, после вычитания которой из наблюденного
поля оставшаяся локальная составляющая Ut лучше всего корре-
лируется с исследуемой геологической границей. Региональная
составляющая отыскивается в виде некоторого многочлена
UrN (х, y)=PN(x, у) = У аптхпут,
п, т
где апт — коэффициенты полинома; х, у — координаты точек
площади исследования; N — степень аппроксимирующего много-
члена.
Коэффициенты а„т находят из условия минимума средней
квадратической остаточной дисперсии (или ошибки приближения)
составляющей Ut по исследуемой границе:
е2 (^лг, Л) = D (UlN) [!-/?> (t/!Ar, h)] = min,
где h — глубина залегания исследуемой границы; Rx (U[N, h) —
коэффициент корреляции.
Этим самым достигается выделение компоненты гравитацион-
ного поля, наилучшим образом коррелирующей с изучаемым гео-
логическим объектом. Операции по вычислению коэффициентов
многочлена довольно трудоемки. В настоящее время корреляцион-
ный метод разделения аномалий запрограммирован для счета
на электронных вычислительных машинах.
478
ПРИМЕНЕНИЕ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
ПРИ ОБРАБОТКЕ И ИНТЕРПРЕТАЦИИ
ГРАВИМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ
Внедрение в практику интерпретации геофизических, и в том
числе гравиразведочных, исследований электронных вычислитель-
ных машин (ЭВМ) открывает большие возможности для автомати-
ческой обработки измерений и создает условия для поиска новых
эффективных решений без опасения, что сложность вычислитель-
ных схем не позволит их реализовать. На основе технических воз-
можностей ЭВМ можно создать качественно новые методы интер-
претации. Применение ЭВМ позволяет проводить переинтерпре-
тацию гравиметрических материалов прошлых лет для больших
территорий с учетом новых геолого-геофизических сведений.
Существующие ЭВМ по способу представления величин разде-
ляются на машины непрерывного действия, или аналоговые, и
машины дискретного действия, или цифровые. При интерпретации
гравиметрических данных применяются в основном цифровые
вычислительные машины.
ЭВМ предназначены для решения различных математических
задач, связанных с большим объемом вычислений. Они могут осу-
ществлять длинные последовательности арифметических и логи-
ческих действий, хранить промежуточные результаты и исполь-
зовать их для продолжения вычислений. .Любая современная
ЭВМ состоит из следующих основных устройств: ввода информа-
ции, запоминающего, арифметического, вывода результатов, уп-
равления.
Все исходные данные для счета на ЭВМ должны быть представ-
лены в виде цифр. ЭВМ оперирует с числами не в десятичной,
а в двоичной системе счисления, в которой применяются только
две цифры: 0 и 1. Использование двоичной системы позволяет
упростить схем}' электронной машины, поскольку числам в этой
системе отвечают всего два устойчивых состояния электронных
элементов: одно состояние изображает цифру 0, другое 1. Переход
счетного устройства из одного состояния в другое происходит
по сигналу извне.
Исходные числовые данные и программу записывают на спе-
циальных бланках в десятичной системе счисления и пробивают
на перфокартах или перфолентах, где каждой цифре соответствует
определенная комбинация отверстий. Устройство ввода воспри-
нимает информацию и переносит ее в запоминающее устройство,
храпящее исходные числа и команды машине для проведения тех
или иных операций. Арифметическое устройство выполняет ариф-
метические и логические операции над числами по командам
запоминающего устройства. Устройство управления передает
команды в ту схему ЭВМ, которая производит соответствующие
операции. Устройство вывода направляет результаты счета на
печать, которая в зависимости от типа машины выполняется на
479
бумаге в виде таблицы цифр или на перфокартах с последующим
перенесением на бумагу.
Для решения на ЭВМ любую задачу необходимо соответству-
ющим образом подготовить. Подготовка сводится к трем этапам.
Первый этап состоит в сведении математической задачи,
выраженной разного рода функциями, к последовательности
арифметических действий и логических правил. Второй этап
заключается в нахождении оптимального алгоритма (система
правил, четко и однозначно определяющих процесс выполнения
заданной работы), обеспечивающего наиболее эффективный спо-
соб использования машины. Третьим этапом является перевод
алгоритма на язык машины — программирование.
Машина выполняет ограниченный вид действий (сложение,
вычитание, умножение, перенос числа из одной ячейки в другую
и т. п.). Каждая такая операция совершается по команде специ-
ального управляющего сигнала. Команда включает в себя код
операции, т. е. указание, что должна сделать машина с числами
(сложить, умножить), и адрес, показывающий, из каких ячеек
надо взять эти числа и в какую ячейку направить после выполне-
ния операции.
При составлении программы каждую задачу представляют в виде
определенной последовательности большого числа элементарных
команд. Эта последовательность команд и является програм-
мой — точным и полным описанием алгоритма решения задачи
в терминах элементарных операций машины. Программу проби-
вают на перфокарте и вводят в машину вместе с исходными дан-
ными задачи. После этого вычисления осуществляются автомати-
чески.
Совершенство программы, удобство ее использования на прак-
тике являются важнейшими условиями успешного применения
ЭВМ для массовой обработки и интерпретации гравиразведочных
данных. Программа должна обеспечивать простоту подготовки
исходных данных, контроль правильности перфорации и ввода
в машину. Эффективность ЭВМ резко возрастает, если над одним
и тем же материалом проводятся многократные действия и весь
процесс обработки разбивается на такие этапы, что конечные ре-
зультаты одного этапа служат исходным материалом для вычисле-
ний на следующем этапе. К настоящему времени такой единой
универсальной программы для обработки гравиметрических дан-
ных не создано; вся обработка разбивается на отдельные этапы,
для каждого из которых существует своя программа.
Наиболее часто применяют ЭВМ при решении следующих
задач.
1. Первичная обработка результатов наблюдений (вычисление
различных поправок, в первую очередь топографических; постро-
ение карты изоаномал).
2. Различные трансформации гравитационного поля (расчет
пространственного распределения поля, вычисление производ-
480
ных гравитационного потенциала, корреляционных функций,
условных вероятностей и т. д.).
3. Расчет гравитационного поля тел с заданными формой,
положением и плотностью для построения палеток и номограмм.
4. Определение параметров тела (форма, положение) методом
автоматического подбора.
Первичная обработка гравиметрических данных состоит в учете
разного рода поправок, получении аномальных значений и постро-
ении карты изоаиомал. На этом этапе ЭВМ находят наибольшее
применение при вычислении поправок за влияние рельефа местно-
сти. Рельеф задают сразу для всей площади, в пределах которой
надо найти поправки. Многие методы предполагают задание рель-
ефа в виде так называемой цифровой модели местности. Модель
представляет собой прямоугольник, разбитый на квадраты. Для
каждого квадрата указывают среднюю высоту над уровнем моря
или высоту в центре этого квадрата. Таким образом, реальный
рельеф аппроксимируют системой отдельных параллелепипедов
с квадратным сечением. При вычислении поправки притяжение
каждого параллелепипеда заменяется притяжением вертикальной
материальной линии, проходящей через его центр. Таблица
исходной информации состоит из средних высот материальных
вертикальных линий и координат точек, в которых вычисляются
поправки.
Топопоправки рассчитывают или для точек квадратной сетки,
или непосредственно для пунктов наблюдений, расположенных
в общем случае произвольно. Первый способ удобен тем, что
позволяет вычислить поправки еще до полевых работ. Поправки
в пунктах наблюдений получают затем по карте поправок путем
интерполяции. Однако интерполированные значения поправок
пригодны только для сравнительно пологого рельефа. Наиболее
целесообразно находить поправку непосредственно для пункта
наблюдений, но это может быть осуществлено только после по-
лучения координат и высот этих пунктов. Использование ЭВМ
для вычисления топопоправок за среднюю и ближнюю зоны умень-
шает затраты ручного труда в 5—10 раз; особенно велик выигрыш,
когда топопоправки требуется вводить на большой площади.
Для автоматического построения гравиметрических карт надо
найти интерполированные значения наблюденной функции, за-
данной по неравномерной сети, в узлах равномерной квадратной
сети; определить значения изолиний и их координаты уже для
принятого сечения и шага равномерной сети. Значения функции
в узлах равномерной сети рассчитываются машиной на основе
параболической интерполяции. Исходной информацией служат
значения функции в пунктах наблюдений и прямоугольные ко-
ординаты этих пунктов. В программе предусмотрен автоматиче-
ский выбор оптимальных параметров интерполяции при заданной
средней квадратической погрешности исходных данных. Полу-
ченные в узлах равномерной сети значения функции могут слу-
Ю В. С. Мироно:
481
жить исходными данными для решения различных задач. Чтобы
найти значения изолиний и их координат, задают сечение резуль-
тативной карты, шаг между точками, значение функции в узлах
квадратной сети. Эти данные получаются как результат любого
этапа обработки (вычисление поправок, различные трансформации
и т. п.).
Основной объем использования ЭВМ в гравиразведке связан
с трансформацией гравитационного поля. Наиболее распростра-
ненными трансформациями являются пересчет поля в верхнее
и нижнее полупространства, осреднение, вычисления высших
производных, условных вероятностей, функций автокорреляции
и взаимной корреляции. Применение ЭВМ дает возможность, один
раз подготовив исходные данные, выполнить анализ поля многими
методами. Однако следует иметь в виду, что практическая эффек-
тивность такого анализа зависит не от числа выполненных транс-
формаций, а прежде всего от правильности геологического об-
основания параметров преобразования: уровней пересчета, раз-
мера площадок при вычислении статистических характеристик,
формы ожидаемой аномалии в способе условных вероятностей
и т. п.
Для трансформации гравитационных аномалий создано мно-
жество программ, которые различаются не только вычислитель-
ными схемами, но и способами подготовки исходных данных.
Большинство программ требует задания исходных данных в узлах
квадратной сетки, в этих же узлах получают трансформированные
значения исходной функции. Такие условия обеспечивают простоту
программ. Если исходные материалы представлены в виде карты,
то приходится искать интерполированные значения поля в узлах
квадратной сетки либо с помощью специальных считывающих
устройств, либо вручную. Если исходными данными служат ка-
талоги пунктов наблюдений, то для интерполяции можно исполь-
зовать блоки программы автоматического построения карт. По-
скольку при гравиметрической съемке сеть наблюдений на участ-
ках сложного поля сгущают, то желательно и трансформирован-
ное поле вычислить в этих местах по более густой сетке. Разра-
ботаны программы, где таблицей исходной информации является
каталог наблюденных значений гравитационного поля и трансфор-
мированные значения вычисляются непосредственно для пунктов
измерений. Чтобы уменьшить влияние случайных ошибок, перед
трансформациями исходное поле сглаживается по способу наимень-
ших квадратов.
Применение ЭВМ привело к интенсивному росту трансформаций
исходного поля. Иногда строят до десяти карт различных транс-
формаций. При этом зачастую забывают, что цель трансформа-
ции — представить результаты наблюдений в виде, наиболее под-
ходящем для решения конкретной геологической задачи. Примене-
ние трансформаций целесообразно только тогда, когда густота
сети и точность съемки позволяют выделить особенности гра-
482
витационного поля, которые хотят подчеркнуть более рель-
ефно.
Использование ЭВМ для вычисления гравитационного эффекта
тел правильной геометрической формы, для которых существуют
аналитические выражения этого эффекта, не вызывает принци-
пиальных трудностей, и задача сводится только к программирова-
нию. Если же гравитационный эффект тела правильной формы
аналитически не выражается, то для его вычисления привлекают
программы, разработанные для определения действия тел, огра-
ниченных произвольной поверхностью. В этих программах при-
менены различные аппроксимационные методы численного реше-
ния задачи: реальное тело заменено суммой элементарных тел,
гравитационный эффект которых сравнительно просто вычисля-
ется на ЭВМ (вертикальные материальные линии, параллелепи-
педы, тонкие горизонтальные пластины, в каждую из которых впи-
сывается многоугольник).
Значительные трудности возникают при использовании ЭВМ
для решения обратной задачи: определения параметров геологи-
ческих объектов по гравитационным аномалиям. Эту задачу ре-
шают методом подбора. При ручном способе интерпретации сте-
пень совпадения наблюденной и подобранной кривой оценивают
на глаз. При работе с ЭВМ необходимо устанавливать строгие
критерии выбора такой теоретической кривой Ф (х), которая наи-
меньшим образом отклоняется от наблюденной функции Д(х).
Для этого параметры модели, аппроксимирующей геологический
объект, и наблюденные значения поля связывают линейными урав-
нениями. При выборе модели учитывают все имеющиеся в распо-
ряжении интерпретатора геологические сведения. Находят при-
ближенное решение системы уравнений, поскольку искать точное
решение не имеет смысла из-за погрешностей измерений и модели-
рования.
В качестве критерия близости наблюденной U (xf) и подоб-
ранной Ф (xz) кривых можно использовать величину
Е = £ [(/(х/)-Ф(х,-)]а = П1Ш,
1=1
где Xi — координаты точки наблюдения; п — число точек, исполь-
зуемых при аппроксимации.
В том случае, когда случайные погрешности независимы и
распределены по нормальному закону, этот критерий оценки
является наилучшим. Е. Г. Булах для отыскания минимума
функции F использовал метод наискорейшего спуска: параметры
модели многократно изменяются, пока функция F не достиг-
нет минимума. Для выполнения этих вычислений составлена соот-
ветствующая программа. Можно показать, что функция F имеет
не один минимум и окончательное решение зависит от принятых
исходных величин. Таким образом, при недостаточной геологи-
16’ 483
ческой информации об искомом объекте целесообразно искать
несколько решений, меняя начальные значения искомых вели-
чин. Это позволит или убедиться в практической тождественности
результатов, или получить несколько вариантов интерпрета-
ции.
Е. Г. Булах и А. А. Юньков линеаризовали задачу определе-
ния параметров геологического объекта, заменив его системой
параллелепипедов или материальных линий, координаты которых
известны. В этом случае гравитационное поле аппроксимирующей
модели линейно зависит от плотности элементарных тел. Однако
при большом числе этих тел задача отыскания их плотности ста-
новится неустойчивой.
С. В. Шалаев для решения обратной задачи предложил вместо
системы линейных уравнений рассматривать систему линейных
неравенств типа
|6/(хг)-Ф(х;)|<в,.,
где б,- — малое положительное число, зависящее от точности на-
блюдений и погрешности моделирования.
При таком подходе решение задачи становится устойчивее;
кроме того, в виде неравенств легко записать любую приближен-
ную информацию, которой располагает интерпретатор (например,
пределы изменения плотности тела, глубины залегания и т. п.).
Глава 17
ПРИМЕНЕНИЕ ГРАВИРАЗВЕДКИ
ИЗУЧЕНИЕ ФИГУРЫ ЗЕМЛИ
Гравиразведка начала развиваться истори-
чески значительно раньше других геофизических методов. Пер-
вое практическое применение результаты гравиметрических из-
мерений нашли при изучении формы Земли уже в XVIII в. Было
установлено, что относительные изменения силы тяжести неве-
лики по сравнению с ее полным значением. Это обстоятельство
подтвердило факт приблизительной шарообразности Земли и
одновременно указало, что плотность масс внутри земного шара
меняется только в радиальном направлении, т. е. в первом при-
ближении можно принять, что Земля состоит из концентрических
слоев постоянной плотности. Более точно поверхность Земли пред-
ставляется эллипсоидом вращения с малым сжатием
а = (а — с)/а.
484
Распределение силы тяжести на поверхности такого эллипсоида
с точностью до малых второго порядка определяется формулой
(2.43):
gv = ge [1 + (-j*q ~ ~ тгг/а) sin'2'(' +
+ ---Гqa) sin *2<р] ’
где q = co2a/gs — отношение центробежной силы к силе тяжести
на экваторе.
При известных из астрономо-геодезических наблюдений зна-
чениях а и ю и измеренных значениях g,(, могут быть определены
ge, q и а. В СССР с 1946 г. в качестве основы всех геодезических
работ принят эллипсоид Красовского со сжатием а — 1/298,3.
Для этого эллипсоида
& = 978,0490-10'2 м/с2;
4 = 1/288,4; « = 6378245 м; с = 6356863 м.
Изучение орбит искусственных спутников Земли существенно
расширило наши познания о глобальном характере гравитацион-
ного поля и позволило резко повысить точность определения сжатия
планеты. Экваториальное вздутие Земли оказывает заметное вли-
яние на орбиты искусственных спутников. Если спутник движется
к северо-востоку, пересекая экватор в направлении с юга на
север, то точка пересечения его орбиты с плоскостью экватора по-
степенно смещается к западу. Скорость этого перемещения поз-
воляет вычислить сжатие: а = 1/298,25 с точностью до 1/30 000.
Это значение хорошо согласуется со сжатием эллипсоида Кра-
совского.
Приведенные данные разрешают найти массу Земли и ее сред-
нюю плотность.
На основе уравнения (2.38) получаем, что масса
Среднюю плотность находим из соотношения
Л4 = оср (4/3) ла2с.
В этих формулах с наибольшей погрешностью (0,03%) известна
величина k. Таким образом, масса Земли М может быть вычислена
с той же точностью, что и гравитационная постоянная. Подстав-
ляя численные значения, получаем
М = 5,977 • 1027 г; оср = 5,517 г/см3.
Средняя плотность Земли более чем вдвое превышает среднюю
плотность горных пород, обнажающихся на ее поверхности
485
(2,67 г/см3). Отсюда следует вполне естественный вывод, что плот-
ность вещества внутренних зон Земли должна быть значительно
больше средней плотности пород, расположенных вблизи днев-
ной поверхности.
Полагая, что по форме Земля близка к эллипсоиду вращения,
имеем для нее два главных момента инерции: А — относительно
экваториальной оси, С — относительно полярной. Главные мо-
менты инерции можно определить по результатам астрономических
наблюдений и известному значению сжатия.
Астрономические наблюдения показывают, что направление
оси вращения Земли не остается неизменным в пространстве.
Ось вращения прецессирует с периодом 25 735 лет, описывая
коническую поверхность с углом 23°27'. Теория вращения сим-
метричного тела позволяет по периоду прецессии определить
так называемую постоянную прецессии:
т] = (С — Л)/С.
Для однородного вращающегося тела должно соблюдаться
равенство ц = а; для Земли имеем ц — 1/305, т. е. т] <а. Это
еще раз свидетельствует о том, что плотность вещества Земли
увеличивается к центру планеты. Величина С—А связана со сжа-
тием, угловой скоростью вращения, массой и размерами Земли
соотношением (2.31), из которого получаем
(С - А)/(Маа) = (2/3) (а - <?/2) -= 0,0018265.
Тогда
С/(Ма2) = (2/3) (а - <?/2)/i] = 0,3306. (17.1)
Если бы Земля была однородной сферой, то соблюдалось бы
отношение С/(Ма)2 = 0,4.
Таким образом, и моменты инерции Земли, так же как и ее
средняя плотность, указывают, что с глубиной плотность веще-
ства планеты должна сильно увеличиваться.
Среднюю плотность и моменты инерции необходимо знать
при изучении распределения плотности внутри Земли, поскольку
любая модель этого распределения должна удовлетворять реаль-
ным значениям средней плотности и моментов инерции.
До запуска искусственных спутников, когда сжатие было
известно с невысокой точностью, предполагали, что фигура пла-
неты с ее экваториальным вздутием соответствуют форме жидкого
вращающегося тела в состоянии гидростатического равновесия.
Теоретическое значение сжатия а0 гидростатически уравновешен-
ной Земли можно найти по формуле (17.1), зная полярный момент
инерции С.
В теории фигур равновесия жидкого тела доказывается соот-
ношение
4-=(».-1) 4-=1 -1
486
Расчеты показывают, что для гидростатически уравновешенной
Земли сжатие должно быть равно 1/299,8. По спутниковым на-
блюдениям сжатие составляет 1/298,25, что превышает теоретиче-
ское значение па 0,5%. Эта разница свидетельствует о том, что
состояние Земли отличается от гидростатического равновесия.
Современное экваториальное вздутие приблизительно на 200 м
больше, чем оно должно было бы быть при гидростатическом
равновесии. Отступление формы Земли от гидростатически урав-
новешенной фигуры, по всей вероятности, связано с вращением
земного шара и свойствами вещества внутри его.
Гравиметрические данные позволяют определить уклонение
геоида от эллипсоида вращения, используя формулу Стокса:
S
где R — средний радиус эллипсоида; S — элемент его поверх-
ности; у — нормальное значение силы тяжести;
S (ф) = cosec + 1 — 5 cos ф — 6 sin -L
— 3 cos ф • In (sin— 4* sin2 -i-)
— функция Стокса; ф — широта относительно точки, для которой
рассчитывается Л/, принимаемой за полюс (ф = 0).
До последнего времени использование теоремы Стокса было
затруднено из-за недостаточной и неравномерной гравиметриче-
ской изученности земной поверхности (теорема Стокса предпо-
лагает интегрирование по всей поверхности Земли). Однако раз-
ными авторами было опубликовано несколько карт геоида. На-
блюдение орбит искусственных спутников Земли позволяет зна-
чительно усовершенствовать эти определения. Спутниковые на-
блюдения доставляют более точные данные о поведении грави-
тационного поля на обширных территориях, чем измерения,
выполненные на поверхности Земли. Но так как спутниковый
метод дает осредненную характеристику гравитационного поля
на отрезках 700—1500 км, то при изучении локальных вариаций
геоида (на расстояниях до 2000 км) гравиметрические наблюдения
на поверхности Земли являются наилучшим методом решения этой
задачи.
Карта отклонений геоида от сфероида со сжатием 1/298,25,
построенная по результатам спутниковых измерений и наблюде-
ний силы тяжести на поверхности Земли (рис. 17.1), показывает,
что расстояние между этими фигурами в общем невелико и меня-
ется в пределах ± 70 м, причем наибольшие отклонения отмеча-
ются в экваториальной области. Поднятия и прогибы геоида
прослеживаются на многие тысячи километров и не обнаруживают
прямой связи с основными морфологическими структурами
487
Рис. 17.2. Средние превышения гео
ида (7) над сфероидом (2) в произволь-
ном меридиональном сечении (по
Д. Кинг-Хеле).
Земли — континентами и океа-
нами. По-видимому, рельеф'по-
верхности геоида обусловлен
плотностными неоднородностя-
ми вещества в глубинных слоях
Земли.
Одним из интересных выво-
дов спутниковой геодезии яв-
ляется «грушевидность» Земли
(рис. 17.2). Отклонения геоида
сфероида в произвольном ме-
ридиональном сечении составляют около 20 м, в то время как
экваториальное вздутие Земли достигает 20 км.
ИЗУЧЕНИЕ СТРОЕНИЯ ЗЕМНОЙ КОРЫ
Изучение глубинного строения Земли имеет не только большое
теоретическое, но и огромное практическое значение: в настоящее
время все более отчетливо вырисовываются связи между строе-
нием глубинных зон Земли и распределением месторождений
полезных ископаемых.
Ведущую роль в изучении внутреннего строения планеты
играют методы сейсмологии. По их данным в первом приближении
Землю разделяют на три основные геосферы, различающиеся
по своим физическим свойствам: земную кору, оболочку (мантию)
и ядро. Земная кора, самая верхняя из геосфер, отделяется от ман-
тии границей Мохоровичича (поверхность М), на которой на-
блюдается резкий скачок скорости распространения продольных
и поперечных волн. Эта граница, возможно, связана с изменением
либо химического, либо агрегатного состояния вещества.
По сейсмологическим данным земная кора также имеет сло-
истое строение: в ней выделяются три слоя, которые характери-
зуются увеличивающимися с глубиной скоростью распростране-
ния упругих волн и плотностью: слой осадочных пород и два
слоя кристаллических пород, условно называемые гранитным
и базальтовым. Граница раздела базальтового и гранитного слоев
не всегда выражена достаточно отчетливо, а соотношение их
мощностей различно в разных местах.
Сейсмологическими исследованиями установлено, что мощ-
ность земной коры изменяется от 4—8 км на океанах до 30—
80 км на материках, при этом на океанах, как показывают сейсми-
ческие данные, отсутствует гранитный слой. В соответствии с та-
ким строением земную кору обычно разделяют на три типа: кон-
тинентальный, океанический и переходный. Такое деление коры
489
Рис. 17.1. Карта превышений геоида над сфероидом (а = 1/298,25), построенная по результатам спут-
никовых наблюдений и измерений силы тяжести на поверхности Земли (по Д. Кинг-Хеле).
Превышения, м: 1 — положительные. 2 — нулевые. 3 — отрицательные.
соответствует ее классифи-
кации по тектоническим
признакам (океанические
впадины, платформы, гео-
синклинали), что опреде-
ляет связь типа коры с
тектоническими особеннос-
тями развития поверхност-
ных геологических струк-
тур.
Распределение силы
тяжести на земной поверх-
ности непосредственно обу-
словлено строением Земли,
особенно ее верхних час-
тей: земной коры и сла-
гающих кору структур.
Использование гравимет-
рических данных для изу-
чения земной коры тесно
связано с так называемой
теорией изостазии — тео-
рией, предполагающей
равновесное в гидростати-
ческом смысле состояние
земной коры относительно
подстилающего ее субстра-
та, который рассматрива-
ется как жидкость. Хотя
субстрат и не является
жидкостью, по реакции на длительно действующие силы его
можно считать жидкостью и оперировать понятиями гидроста-
тики.
Возникновение теории изостазии связано с попыткой Ф. Пратта
и Г. Эри объяснить расхождения между наблюденными и вычи-
сленными значениями отклонения отвеса, обнаруженные во
время триангуляций в Индии в 1855 г. Наблюденные отклонения
были значительно меньше вычисленных с учетом массы Гималаев.
Поэтому Ф. Пратт полагал, что земная кора под Гималаями должна
иметь меньшую плотность, чем в низменных районах Ганга.
Г. Эри предложил иную гипотезу. Он считал, что земная кора
имеет постоянную плотность, но разную мощность, и ее блоки
плавают в субстрате, подобно льду в воде (рис. 17.3).
Согласно гипотезе Пратта земная кора простирается до не-
которой глубины Т (считая от уровня моря), на которой находится
поверхность равного давления, называемая поверхностью компен-
сации или изостатической поверхностью. На этой границе наблю-
дается одинаковое давление вышележащих слоев. Для выпол-
490
нения этого условия необходимо, чтобы плотность отдельных бло-
ков земной коры, расположенных выше поверхности изостати-
ческой компенсации, была разной и удовлетворяла равенству
(Нк + Т) ок = (Т - Н„) ом + 1,03Ям = Та0, (17.2)
где Нк — высота континента над уровнем моря; Ям — глубина
моря; <т0 — плотность земной коры на уровне моря; <тк и ои -
плотность континентальной и морской коры.
Из этого равенства следует, что стк < о0 < <тм, т. е. чем выше
расположена дневная поверхность относительно уровня моря,
тем меньше плотность земной коры.
В гипотезе Эри земная кора имеет постоянную плотность сг0
и плавает на более тяжелом субстрате с плотностью о. По закону
Архимеда имеем:
h = h0 + [<г/(ст — ст0)] Н; (17.3)
для моря
Л==йо + К<т- 1,03)/(о-о0)]Я, (17.4)
где h — мощность земной коры; й0 — мощность земной коры на
уровне моря; Н — превышение точки над уровнем моря (положи-
тельное на суше, отрицательное на море).
Таким образом, нижняя граница земной коры является как бы
зеркальным отображением рельефа физической поверхности
Земли: чем больше высота дневной поверхности, тем на большей
глубине находится подошва коры, и наоборот; при этом превыше-
ния рельефа подошвы коры больше превышении рельефа дневной
поверхности. Положив пп = 2,7 и о = 3,2 г/см3, получим, что
отношение этих перепадов составляет для суши около 5,4, для
моря 3,4.
Гипотеза Эри также предполагает наличие, поверхности ком-
пенсации, за нее можно принять границу, проходящую через
наиболее глубоко погруженные корни гор. Хотя гипотезы Пратта
и Эри по-разному задают распределение масс в земной коре,
но обе они удовлетворяют условию равенства давления на неко-
торой определенной глубине. Если же оценивать эти гипотезы
с геологической точки зрения, то гипотеза Эри гораздо правдопо-
добнее, хотя и вносит много элементов схематизма. Но обе ги-
потезы совершенно не учитывают механических свойств пород,
слагающих земную кору, например, силы сцепления.
Ф. Венингом Мейнесом была предложена схема региональной
изостатической компенсации, принимающая во внимание механи-
ческие свойства земной коры, например ее прочность, препятст-
вующую прогибу при небольших нагрузках. По этой гипотезе
земная кора рассматривается как упругая плоская пластина,
прогибающаяся под действием топографических масс, возвы-
шающихся над уровнем моря. По своему физическому смыслу ги-
потеза Бенинга Мейнеса аналогична гипотезе Эри: земная кора
491
постоянной плотности и переменной мощности находится в со-
стоянии гидростатического равновесия по отношению к субстрату.
Каждая из названных изостатических гипотез выводит закон
распределения масс в земной коре в зависимости от рельефа днев-
ной поверхности. Поэтому, приняв одну из этих гипотез, можно
вычислить действие масс, компенсирующих действие рельефа
дневной поверхности, — изостатическую поправку 8gz. Эту по-
правку обычно вводят в наблюденное значение силы тяжести сов-
местно с топографической поправкой bgt, удаляющей влияние
внешних масс. Аномалии силы тяжести, учитывающие эти по-
правки, называются изостатическими:
&g> =g«- Yo + 6g,- 4- 8g, 4- 6gft,
где bgh — поправка за высоту.
Изостатические редукции вычисляют с помощью специальных
палеток и таблиц. Существует много способов определения этих
поправок, даже для каждой из гипотез в зависимости от принятых
исходных данных (глубина компенсации, плотность коры и под-
стилающего субстрата) имеется несколько вариантов. При помощи
поправочных коэффициентов можно перейти не только от одного
варианта к другому в пределах одной гипотезы, но и от одной
гипотезы к другой.
Следует отметить, что аномалии в свободном воздухе (Фая)
и Буге являются предельными случаями изостатических аномалий:^
первая соответствует глубине компенсации нуль, вторая — беско-
нечности. В первом случае массы, расположенные над уровнем
моря, опускаются на уровень моря и конденсируются в беско-
нечно тонкий слой, во втором эти массы целиком исключаются,
что равносильно их размазыванию на бесконечно большую глу-
бину. Отсюда следует, что по своей амплитуде изостатические ано-
малии находятся между аномалиями Буге и в свободном воздухе.
В случае идеальной изостатической компенсации изостатиче-
ские аномалии должны быть равны нулю. Наличие аномалий озна-
чает, что изостатического равновесия в виде принятой схемы в дан-
ной области не существует.
По своему физическому смыслу изостатические аномалии от-
носятся к категории геологических редукций: на основе определен-
ных гипотез вносится поправка за геологическое строение района.
Изостатические редукции базируются на весьма общих предполо-
жениях о строении земной коры в целом, и в этом их существенный
недостаток по сравнению с редукциями, которые не зависят от
гипотез о геологическом строении исследуемой территории (в сво-
бодном воздухе, Буге, топографическая).
Эти замечания не означают, что принцип изостазии вообще
ставится под сомнение. Вычисление изостатических аномалий,
а также их сравнение с аномалиями Буге и в свободном воздухе
показывает, что земная кора в целом находится в состоянии гидро-
статического равновесия, но это равновесие соблюдается только
492
для весьма обширных территорий крупных структур планетар-
ного масштаба. Но во многих районах земного шара изостати-
ческого равновесия не наблюдается. Весьма интенсивные изо-
статические аномалии отмечены в районах островных дуг, на Кав-
казе, в Крыму, на о. Кипр. Принцип изостазии объясняет гло-
бальное распределение аномалий силы тяжести, но оказывается
малопригодным при истолковании аномалий более высоких по-
рядков. Эти аномалии находят простое и естественное объясне-
ние в свойствах и мощностях пород поверхностной части земной
коры и в ее тектонике.
Сопоставление аномалий силы тяжести с высотой точек наблю-
дения позволяет сделать некоторые заключения о строении зем-
ной коры. Для небольших территорий наблюдается зависимость
аномалий в свободном воздухе от высоты: аномалии повторяют
дневной рельеф с тем или иным коэффициентом корреляции. Для
аномалии Буге при соответствующем выборе плотности аналогич-
ной зависимости не наблюдается.
Таких выводов сделать нельзя, если рассматривать подобные
корреляции для обширных областей. В этом случае оказывается,
что аномалии в свободном воздухе колеблются в пределах ± 100 X
X Ю"5 м/с2 и в среднем близки к нулю; корреляции с высотой не
существует, среднее значение аномалий составляет па суше
4-9-10'6, на море 4-3 -10'5 м/с2. Диапазон изменения аномалий
Буге значительно больше: в горных областях аномалии Буге
достигают — 500-10'®, на океанах 4-450-10-5 м/с2. Средние зна-
чения аномалий Буге на суше составляют —87-10"5, на море
4-230-10"5 м/с2.
Сопоставление аномалий Буге с высотой выявляет их линейную
корреляцию. Подобное поведение аномалий подтверждает прин-
цип изостатической компенсации, так как избытки масс, высту-
пающие над уровнем моря, компенсируются недостатком масс
на глубине. Корреляция аномалий Буге с высотой позволяет
искать эмпирические зависимости между тремя величинами: глу-
биной границы Мохоровичича, аномалией силы тяжести и вы-
сотой. Естественно, при этом используют осредненные значения
аномалий и рельефа. Эти статистические связи определялись мно-
гими авторами на основе сопоставления мощности коры по сей-
смическим данным с аномалиями силы тяжести и рельефом. Ре-
зультаты, полученные Р. М. Деменицкой (рис. 17.4, 17.5), выра-
жаются следующими уравнениями:
й = 35(1 — th 0,0037 kg);
h = 33 th (0,387/ - 0,18) 4- 38,
где h — мощность коры, км; kg — аномалия силы тяжести в ре-
дукции Буге, 105 м/с2; Н — высота над уровнем моря, км.
Эти зависимости позволяют определить наиболее вероятное
значение мощности земной коры в любом пункте земного шара.
493
(17.5)
Рис. 17.4. Связь между мощностью земной коры и ано-
малиями силы тяжести в редукции Буге (по Р. М. Де-
меницкой).
/ — складчатые области; II — платформы; III — щиты;
/V— шельф, острова, океанические хребты; V — океаничес-
кие плиты.
Довольно большой разброс точек на кривых (± 100-10~5 м/с2)
связан с влиянием внутреннего строения земной коры и припо-
верхностных геологических структур, а также с «аномальной»
мощностью коры, не соответствующей ее изостатическому состо-
янию. Относительная ошибка определения мощности коры колеб-
Рис. 17.5. Связь между мощностью земной коры и высотой земной
поверхности над уровнем моря (по Р. М. Деменицкой).
/—горы; //—равнины; ///—материковые отмели; IV—моря; И—океаны.
494
лется в пределах от 15 до 40%, составляя в среднем около 20%.
Для разных областей эта ошибка неодинакова: на океанах 1,3—
4 км, на континентах 5—8 км. Зависимости, подобные соотноше-
ниям (17.5), могут быть получены и для отдельных регионов. Ана-
лиз корреляционных графиков совместно сданными ГСЗ позволяет
определить рельеф границы М с точностью 3 км.
Гравитационное поле и мощность земной коры обусловлены
геологическим развитием данной области (см. рис. 17.4). Наиболь-
шие мощности (до 70 км) наблюдаются в складчатых областях;
в районах шельфов и платформ мощность коры составляет обычно
20—40 км, в океанических впадинах 10 км и меньше.
По найденным эмпирическим зависимостям можно изучать
характер изменения плотности земной коры и подстилающего ее
субстрата. Центральную часть кривой (от 20 до 50 км) аппрокси-
мирует прямая
h = /г0 + Ag/(2n ko), (17.6)
где h0 — мощность земной коры при Ag = 0 (в рассматриваемом
случае Ло = 35 км); о — избыточная плотность коры относительно
субстрата.
Эта зависимость относится к областям платформ, невысоких
горных сооружений древней складчатости, шельфов. Из уравне-
ния (17.6) находим ст = —0,2 г/см3. Аппроксимируя прямой те
участки графика, которые относятся к океаническим и высоко-
горным областям, получаем ст = —(0,4-ь 0,5) г/см3. Такие ре-
зультаты можно объяснить или повышением плотности субстрата
под океанами и высокогорными областями, или уменьшением
плотности коры. Последнее предположение, в частности, согла-
суется с сейсмическими данными и является наиболее вероятным
объяснением изменения избыточной плотности коры.
В общем случае совместное решение уравнений (17.5) и (17.6)
позволяет определить избыточную плотность земной коры при ее
меняющейся мощности:
_ arcth (1 — /t/Ар) , - 7 7,
“ 0,0232Хг(Л —/г0) ' k ’
Вторая формула (17.5), выражающая связь между мощностью
коры и дневным рельефом, в сущности, представляет собой эм-
пирическое уравнение изостазии, единое для материков и океанов.
Вид этого уравнения показывает, что в действительности изоста-
зию надо рассматривать как явление более сложное, чем это описы-
вается гипотезами Эри и Пратта. Указанное уравнение можно
выразить через значения плотности ст, тогда оно примет
вид
/г = hn + (2,94 - 12,54/7)/(184,4ст).
Так как избыточная плотность коры является величиной пере-
менной (наименьшая в платформенных областях, наибольшая на
495
океанических и высокогорных территориях), то характер изо-
стазии имеет весьма сложный вид.
Рассмотренные закономерности, описывающие связь аномалий
силы тяжести с мощностью земной коры, представляют интерес
для познания коры в планетарном масштабе; использование этих
закономерностей для изучения отдельных, даже очень крупных,
геотектонических структур может иметь только ограниченное зна-
чение.
ГЕОЛОГИЧЕСКОЕ КАРТИРОВАНИЕ
Обосновать постановку геологических работ на поиски различ-
ных полезных ископаемых возможно только на базе знания наи-
более общих закономерностей строения территории, выяснения
взаимосвязей крупных, доминирующих структур, от которых
зависят структурные особенности более высокого порядка и зако-
номерности размещения полезных ископаемых. Изучение указан-
ных связей является основной задачей региональной геологии
и составляет предмет важнейшей части геологического картирова-
ния— тектонического районирования, определяемого В. В. Бе-
лоусовым как «классификация участков земной коры по призна-
кам их строения и истории структурного развития».
При решении этих задач гравиразведка имеет весьма важное
значение, поскольку крупные региональные структуры четко
отражаются на гравиметрических картах обширными и интенсив-
ными гравитационными аномалиями.
При исследовании геосинклинальных областей в региональном
плане гравиразведка решает следующие основные задачи: выясне-
ние общего структурного плана исследуемого района, определе-
ние положения и взаимосвязи отдельных тектонических структур,
изучение отдельных крупных структур, представляющих интерес
для поставки более детальных гравиметрических или других
геофизических съемок.
В гравитационном, отношении геосинклинальные области ха-
рактеризуются интенсивными (порядка 100-10 5 м/с2) региональ-
ными аномалиями, как положительными, так и отрицательными.
Для большинства крупных структур наблюдается «обратная»
зависимость: положительным геологическим структурам типа
антиклинориев отвечают региональные отрицательные аномалии
и, наоборот, отрицательным, синклинорным, структурам отве-
чают положительные аномалии. Такое соотношение связано
с рельефом глубинных зон земной коры: мощность коры увеличи-
вается в антиклинорных зонах и уменьшается в синклинорных.
«Обратную» связь между региональными структурами и грави-
тационными аномалиями некоторые исследователи трактуют с по-
зиций историко-геологических, а именно: аномалии отражают ре-
ликты древнего, доинверсионного, структурного рельефа гео-
синклинальных областей, который в процессе инверсии геотекто-
496
пических условий не был полностью преобразовал в наиболее
глубоких своих частях. Отмеченная эмпирическая закономер-
ность наблюдается только в геосипклинальпых областях, где
процессы складчатости завершены, причем только в структурах,
образовавшихся при инверсии геотектонического режима. В тех
случаях, когда поднятия сохранялись в течение всего периода раз-
вития геосинклинали, над положительными структурами наблюда-
ются и положительные гравитационные аномалии. «Прямое» со-
ответствие гравитационных аномалий геологическим структурам
отмечено и в современных геосинклиналях, в районах островных
дуг, где над прогибами наблюдаются отрицательные, а над под-
нятиями положительные аномалии силы тяжести.
По характеру распределения гравитационных аномалий внутри
геосинклинальнон области, их взаимному расположению можно
судить о поведении глубинных геологических структур, общем
структурном плане территории, положении отдельных геологи-
ческих структур относительно друг друга. Детальные работы поз-
воляют выделить структуры более высокого порядка, представ-
ляющие непосредственный интерес для поисково-разведочных
работ. В этом случае гравиметрические исследования решают за-
дачи и геологического картирования. Выявлена также связь
гравитационного поля с особенностями металлогении отдельных
регионов, что позволяет использовать региональные гравиметри-
ческие исследования при металлогеническом прогнозировании.
Гравитационная характеристика платформенных областей
резко отлична от характеристики геосинклиналей. Наблюдаются
слабоинтенсивные аномалии, как положительные, так и отрица-
тельные, амплитуда которых, за редким исключением, не пре-
восходит (20-т-ЗО) • 1СГ5 м/с2. Основной задачей региональных ис-
следований на платформах является изучение внутренней струк-
туры и рельефа поверхности кристаллического фундамента, по-
скольку развитие фундамента определяет формирование струк-
тур в осадочной толще. Эти структуры представляют непосред-
ственный интерес при выборе площадей для поисково-разведочных
работ.
Основными факторами, определяющими гравитационные ано-
малии в пределах платформ, являются внутренняя структура и
рельеф фундамента, строение и состав толщи осадочных пород.
Влияние этих факторов в различных платформенных областях
неодинаково. Наиболее отчетливо внутренняя структура фунда-
мента проявляется в гравитационных аномалиях на кристалли-
ческих щитах, где фундамент расположен на относительно не-
большой глубине. В этом случае отдельные блоки фундамента,
различающиеся по плотности, создают довольно интенсивные
гравитационные аномалии. Увеличение мощности осадочного по-
крова несколько ослабляет эти аномалии, но если глубина фун-
дамента не превышает 2—3 км, определяющим аномалиеобразую-
щим фактором остается структура фундамента.
497
По морфологическим особенностям и геологической природе
аномалии силы тяжести, связанные со структурой фундамента,
можно разделить на три группы. Более или менее изометричные
в плане аномалии обычно отвечают массивам интрузивных пород
или метаморфическим комплексам. Линейно-вытянутые полосо-
видные аномалии связаны со складчатыми комплексами фунда-
мента, осадочными образованиями, выполняющими впадины фун-
дамента, и с пластовыми интрузиями. Аномалии типа гравитаци-
онной ступени, характеризующиеся возрастанием поля в одном
направлении, прослеживают контакты крупных блоков фунда-
мента и глубинные разломы.
Определение рельефа кристаллического фундамента по грави-
тационным аномалиям является непростой задачей, поскольку
в большинстве случаев гравитационный эффект рельефа фунда-
мента осложняется влиянием его плотностной неоднородности.
Степень этого влияния зависит от глубины фундамента, состава
и возраста слагающих его пород. Наиболее четко оно обнаружи-
вается в районах развития докембрийского, как правило, более
неоднородного по плотности фундамента, менее отчетливо — в рай-
онах развития палеозойского фундамента при большой глубине
его залегания.
Если фундамент перекрывается мощной толщей осадочных
образований, то для некоторых районов можно установить линей-
ную корреляцию между глубиной фундамента и аномалиями
силы тяжести, что позволяет не только определить форму и раз-
меры впадин фундамента, но и получить количественную харак-
теристику его рельефа. Подобные соотношения в чистом виде
являются скорее исключением, чем правилом. Но даже и при силь-
ном влиянии структуры фундамента на гравитационные аномалии
можно составить качественную характеристику его рельефа по
характеру локальных аномалий: в районах поднятий фундамента
эти аномалии проявляются резче, чем в районах погружения.
Структуры, развитые в осадочном покрове, иногда можно вы-
делить по сопровождающим их гравитационным аномалиям. При-
рода этих аномалий различна. Если структуры имеют большую
амплитуду и сложены резко отличными по плотности породами, то
аномалии создаются самими структурами. Когда структуры оса-
дочного чехла пологие, с малой амплитудой, то сопровождающие
их аномалии непосредственно с этими структурами не связаны.
В этом случае аномалии отражают строение и рельеф фундамента,
дислокациями которого и создаются структуры осадочного чехла.
Такое косвенное соответствие гравитационных аномалий струк-
турам осадочного чехла имеет большое практическое значение для
выделения областей, перспективных на поиски месторождений,
контролируемых такого рода структурами. В первую очередь
это относится к нефтяным и газовым месторождениям. Кроме
того, изучение структуры фундамента имеет большое значение
для постановки поисковых работ на ряд других полезных иско-
498
паемых: железо, никель, хром, алмазы, редкие и цветные металлы
и т. д.
Гравиметрические съемки решают разнообразные задачи гео-
логического картирования, которые определяются масшта-
бом исследований. Гравиметрические наблюдения масштаба
1 : 200 000 — 1 : 50 000 позволяют картировать контролирующие
размещение рудных месторождений геологические структуры и их
отдельные элементы: литологически благоприятные для кон-
центрации полезного ископаемого породы, зоны тектонических
нарушений, пликативные структуры и т. д. Весьма эффективна
гравиразведка при изучении интрузивных массивов, что имеет
большое значение для металлогенического прогнозирования, по-
скольку связь с интрузиями целого ряда полезных ископаемых
не вызывает сомнения. По аномалиям силы тяжести отчетливо
определяются контуры массивов, к которым могут быть приуро-
чены месторождения железа скарнового типа, меди и других ме-
таллов. Не менее информативна гравиразведка при картировании
пликативных структур и разрывных нарушений.
Гравиметрические исследования, проводимые для геологиче-
ского картирования, при укрупнении масштаба одновременно
решают и задачи поисков месторождений.
поиски и разведка месторождений
Нефть и газ
Гравиразведочные работы при поисках нефтяных и газовых
месторождений проводятся уже давно; фактически история раз-
вития и применения гравиразведки тесно связана с поисками
нефтяных месторождений. В СССР гравиразведочные работы были
начаты в 1925 г. в Урало-Эмбинской области, и с этого времени гра-
виразведка является одним из основных методов при исследовании
нефтегазоносных провинций. Естественно, что в большинстве слу-
чаев месторождения нефти и газа не могут служить непосредствен-
ным объектом гравиметрических исследований из-за незначи-
тельности гравитационного эффекта, создаваемого ими. Съемки
проводят для поисков структурных форм, с которыми могут быть
связаны скопления нефти и газа. Эти структуры весьма разно-
образны, и не на каждой из них можно получить положительные
результаты.
Рассмотрим основные типы структур, на которых применение
гравиразведки эффективно: соляные купола, антиклинальные
складки, куполовидные платформенные поднятия, рифовые мас-
сивы.
Соляные купола представляют собой штоки каменной соли,
которая в результате тектонических движений была выжата
вверх и частично прорвала или приподняла перекрывающие
ее породы. Нефть бывает приурочена к песчано-глинистым породам,
499
Рис. 17.6. Аномалия силы
тяжести (10'6 м/с2) над
соляным куполом (по
Э. Э. Фотиадн).
расположенным в бортовой части купола или над его сводом. Со-
ляной шток, составляющий ядро купола, имеет значительные
размеры: его площадь может достигать нескольких сотен квадрат-
ных километров, вертикальная мощность — нескольких километ-
ров. Плотность соли практически постоянна (2,1 г/см3) и обычно
она меньше плотности вмещающих пород (2,2—2,4 г/см3). Поэтому
над соляным куполом наблюдается интенсивный минимум силы
тяжести: от п-10’8 до п-10-10’в м/с2 (здесь и дальше п — 1ч-10)
(рис. 17.6). Такие аномалии отмечены в ряде районов развития
солянокупольной тектоники: на Урало-Эмбинской площади СССР,
в Румынии, ФРГ, Иране.
Штоки каменной соли бывают покрыты толщей гипсо-ангид-
ритовых пород значительной мощности, образующих кепрок.
Поскольку плотность гипса 2,3, а ангидрита 2,8—2,9 г/см3,
то кепрок имеет положительную избыточную плотность и создает
положительную гравитационную аномалию, которая, накладываясь
на минимум силы тяжести купола, осложняет его. В этом случае
непосредственно над куполом наблюдается довольно интенсивный
максимум силы тяжести на фоне слабого минимума, который более
отчетливо проявляется по периферии купольной структуры
(рис. 17.7). Подобного рода структуры развиты в Нордвнк-Хатанг-
ском районе СССР и На побережье Мексиканского залива в США.
В районе Днепровско-Донецкой впадины соляные купола
окаймлены плотными брекчированными изверженными породами,
вынесенными к поверхности в процессе образования купола.
Эта брекчия, окружая купол со всех сторон, создает дополнитель-
ный кольцевой максимум силы тяжести на фоне общего минимума.
Af
Рис. 17.7. Аномалия силы тяжести над соляным куполом
с кепроком.
500
Рис. 17.8. Определение формы соляного купола по грави-
тационным данным (по Э. Э. Фотиади).
Во всех районах солянокупольной тектоники гравиразведка
является ведущим методом как при определении границ этих
районов, так и при поисках куполов, поскольку аномалии над
ними имеют весьма характерный вид и геологическая природа
аномалий не вызывает сомнения. По данным гравиразведки на-
ходят положение купола в плане, т. е. общую конфигурацию. При
детальном исследовании важно определить форму вертикального
сечения купола, особенно его бортовых частей (рис. 17.8). Реше-
ние подобной задачи представляет значительные трудности. Трех-
мерность купола ограничивает применение простых вычислитель-
ных способов и палеток и резко усложняет вычисления. Хроме
того, надо еще учесть гравитационное влияние перекрывающих
пород, соседних куполов, региональный фон и т. д.
Рельеф соляных куполов изучают комплексом из высокоточной
детальной гравиметрической съемки и сейсморазведки (рис. 17.9).
Конфигурация верхней части купола прослежена по сейсмическим
данным, характер погружения крыльев установлен по результатам
гравиразведки. Одно из крыльев имеет очень крутое падение,
другое пологое. Мощность купола оценена в 3—4 км.
гравиметрическим (2) на-
блюдениям (по Л. Э. Ли).
501
Рис. 17.10. Положительная аномалия силы тяжести над антиклинальной склад-
кой.
1 — изоаномалы Ag, 10“Б м/с2; 2 — тектонические нарушения; 3 — маркирующий гори-
зонт.
Антиклинальные структуры, развитые в геосинклинальных
областях и краевых прогибах платформ, часто являются благо-
приятными объектами для обнаружения их гравиразведкой.
В этих условиях плотность мощной толщи осадочных образований
возрастает с глубиной, поэтому над антиклинальными складками
наблюдаются максимумы силы тяжести (рис. 17.10). Наряду
с положительными аномалиями над антиклинальными структурами
часто можно наблюдать и отрицательные. Это объясняется по-
слойным изменением плотности пород, что связано с изменением
их фациально-литологического состава от периферии складки
к ее своду, с выклиниванием пачек более плотных отложений,
с увеличением раздробленности и трещиноватости пород в сводо-
вых частях складки. Примером таких структур (рис. 17.11) могут
служить антиклинали Апшеронского полуострова, Западного
Предкавказья, Прикарпатского прогиба.
Минимумы силы тяжести над антиклиналями наблюдаются
и при обратной последовательности распределения плотности,
когда более плотные породы залегают выше легких. Такие струк-
туры известны в Ферганской долине и в Калифорнии. Имеются
области, где одни антиклинальные структуры отмечаются миниму-
мами, другие — максимумами. Таким образом, установить соответ-
ствие антиклинальных структур наблюденной картине гравитаци-
онного поля довольно сложно из-за разного знака аномалий. Поэ-
тому требуется тщательно учитывать все геологические факторы
и привлекать данные других геофизических методов.
Месторождения нефти и газа часто связаны с рифовыми мас-
сивами, которые представляют собой отдельные гребни или гряды
известняков, возникших как фациальные образования в результате
трансгрессий и регрессий моря и изменения условий осадко-
502
накопления. В гравитационном поле
рифы отражаются вместе с другими
геологическими факторами, которые по
своему действию иногда значительно
превосходят эффект от рифов. Чтобы
выявить рифовые массивы по грави-
метрической карте, надо выделить сла-
бые по интенсивности локальные ано-
малии на фоне сложного поля.
Значительный опыт накоплен по
применению гравиразведки для поисков
рифов в Предуральском прогибе. Здесь
рифовые образования перекрыты тол-
щей гидрохимических осадков (ангид-
рит, гипс, соль) кунгурского яруса.
Из-за резкого изменения мощности и
высокой пластичности соль местами об-
разует поднятия, подобные по форме
рифовым массивам. Геологоразведоч-
ными работами было установлено, что
и рифовые образования, и соляные под-
нятия сопровождаются поднятиями ан-
гидритовых отложений кунгурского
яруса, являющегося опорным электри-
ческим горизонтом с высоким удель-
ным сопротивлением. Комплексирова-
ние гравиразведки с электроразведкой
позволило выделять поднятия кунгур-
ских отложений, связанные с рифами,
и отличать их от поднятий, связанных
с солью. Электроразведка отмечает
Рис. 17.11. Минимумы силы
тяжести (10”5 м/с2) над анти-
клинальными структурами.
структуры кунгурского яруса, связанные как с куполами соли,
так и с рифовыми массивами. Но если поднятию соответствует гра-
витационный максимум, то оно несолевого происхождения и
может быть отнесено к рифовому массиву; если же поднятию от-
вечает минимум силы тяжести, то оно солевого происхождения.
Дальнейшее исследование перспективных площадей проводится
сейсмическими и буровыми работами.
Значительное число месторождений нефти и газа, обнаружен-
ных на платформах, приурочено к куполовидным поднятиям
в осадочной толще. Такие поднятия характеризуются малой ам-
плитудой (несколько десятков метров), очень пологими углами
падения крыльев (несколько градусов) и достаточно большой
глубиной залегания (1—2 км и более). Выявление подобного рода
структур гравиразведкой представляется исключительно трудной
задачей, поскольку полезные аномалии имеют очень малую ам-
плитуду (не превышают /г-0,1-10-5 м/с2), а выделять их необхо-
димо из общего поля, иногда резко дифференцированного. Поэтому
503
до последнего времени полагали, что гравиразведка даже при вы-
сокой точности наблюдений для поисков подобного рода структур
неприменима.
Детальное исследование физических свойств пород осадочного
чехла показало, что в пределах малых куполовидных поднятий
существует послойное изменение плотности пород: от периферии
к своду структуры плотность пород уменьшается, что зависит от
литолого-фациальных или тектонических факторов. Эти изме-
нения плотности незначительны, но, проявляясь в мощной толще
осадочных пород на большой площади, они создают дополнитель-
ный гравитационный эффект, который может быть даже больше
«прямого» гравитационного эффекта структуры. Так, изменение
плотности, равное 0,1 г/см3, может вызвать аномалию п-10*8 м/с2,
что достаточно надежно регистрируется высокоточными грави-
метрическими измерениями. В этом случае куполовидным подня-
тиям соответствуют минимумы силы тяжести.
Подобные изменения плотности карбонатных пород установлены
на структурах Волго-Уральской провинции. Недостаток плотности
составляет для пород пермского возраста 0,3 г/см3, каменноуголь-
ного возраста 0,1—0,2 г/см3. Разуплотнение пород создает над
структурами слабые [(2ч-4) 10*5 м/с2] минимумы силы тяжести.
Однако это положение не распространяется на всю Волго-Ураль-
скую провинцию, поскольку в разных ее частях геологическая
обстановка различна. В частности, на юге провинции, где развиты
куполовидные поднятия с крутыми склонами и большими ампли-
тудами, «прямой» гравитационный эффект превалирует над эф-
фектом изменения плотности. В этом районе крупные и резкие
куполовидные поднятия отмечаются не минимумами, а максиму-
мами силы тяжести (2-ь4) • 10*5 м/с2. Изменение плотности на купо-
ловидных структурах установлено и в южной части Западно-
Сибирской низменности. В частности, для пород эоцена разуп-
лотнение равно 0,2—0,5, мела 0,28, юры 0,14 г/см3. Полученные
данные указывают на возможность успешного применения грави-
разведки при поисках локальных структур в пределах платфор-
менных областей.
Имеются попытки использовать гравиразведку в комплексе
с другими геофизическими и геохимическими методами для пря-
мых поисков нефти и газа. Геологической предпосылкой применения
гравиразведки для этой цели является наличие разности между
плотностью пефте- и газонасыщенных коллекторов и плотностью
коллекторов, насыщенных водой. Эта разница составляет для кол-
лекторов нефти 0,05—0,07 г/см3, для коллекторов газа 0,16—
0,22 г/см3. Элементарные расчеты показывают, что над нефте-
и газоносными структурами на фоне общей гравитационной ано-
малии можно ожидать локальные минимумы (порядка п-0,1 х
X 10*® м/с2). Высокоточные гравиметрические съемки, проведен-
ные на известных нефтяных месторождениях Мангышлака, За-
падной Сибири, Азербайджана, подтвердили наличие локальных
504
минимумов (0,15-г-0,3) -10-5 м/с2. Однако выделить этот полезный
эффект из общего гравитационного поля чрезвычайно трудно:
необходимо с высокой точностью учитывать факторы, которые
могут создавать такие же аномалии (уменьшение плотности пород
в сводовой части структуры, фациальные изменения и т. и ). Кроме
того, сама структура, содержащая нефтегазовую залежьц может
создавать гравитационную аномалию. В этом случае гравитацион-
ные эффекты залежи и структуры практически неразделимы.
Поэтому наблюдаемые локальные минимумы можно связывать
с залежами нефти и газа только тогда, когда учтены и исключены
все другие факторы.
Уголь
Применение гравиразведки в угленосных бассейнах имеет
50-летнюю историю. В СССР гравиразведочные работы на уголь
впервые были проведены в 1929 г. в Донбассе для решения струк-
турно-картировочных задач. В дальнейшем эти исследования
выполнялись в бассейнах Урала, Казахстана, Средней Азии.
Угли по плотности резко отличаются от вмещающих пород:
плотность каменного угля составляет 1,5—1,7 г/см3, бурого 0,8—
1,2 г/см3. Однако в большинстве случаев поиски непосредственно
угольных пластов оказываются невозможными из-за малой мощ-
ности пластов и условий их залегания. Основной же целью гра-
виметрических работ является решение задач общегеологического
порядка: прослеживание границ угленосного бассейна, опреде-
ление мощности угленосных отложений, оценка глубины и рельефа
подстилающих образований и т. д. Только в особо благоприятных
условиях можно зафиксировать отдельные угольные пласты;
это относится к бурым углям, мощность пластов которых иногда
составляет многие десятки и даже сотни метров.
Гравиразведочные работы в Донбассе стали классическим при-
мером подобного рода исследований в угленосных бассейнах.
Донбасс принадлежит к числу бассейнов полуоткрытого типа:
в его центральной части угленосные отложения каменноугольного
возраста обнажены и доступны для непосредственной разработки,
на периферии же бассейна эти отложения перекрыты более моло-
дыми образованиями мезо-кайнозоя.
Основная проблема Большого Донбасса заключалась в выяс-
нении истинных контуров бассейна, в пределах которого угленос-
ные отложения находятся на глубине, доступной для эксплуата-
ции. Эта задача решалась комплексом геофизических методов,
в числе которых была и гравиразведка. Применение гравиразведки
основывалось на значительном перепаде между плотностью отло-
жений каменноугольного возраста (2,3—2,7 г/см3) и перекрыва-
ющих их образований мезо-кайнозоя (1,5—2,2 г/см3). Колебания
плотности пород одного возраста в основном связаны с разной
степенью метаморфизма. Породы карбона в центре Донбасса
505
Рис. 17.12. Аномалия си-
лы тяжести в юго-восточ-
ной части Донбасса (по
Н. Н. Самсонову).
интенсивно дислоцированы и имеют максимальную плотность,
к периферии бассейна плотность этих пород уменьшается. Подоб-
ная же закономерность, хотя и менее отчетливо, наблюдается
и в поведении плотности перекрывающих образований.
Отложения каменноугольного возраста имеют структурно-
эрозионную поверхность, на периферии бассейна наблюдаются
резкие уступообразные погружения, связанные с тектоническими
нарушениями и размывом. Этими погружениями ограничивается
центральная область неглубокого залегания угленосных отложе-
ний, за пределами которой эти отложения находятся на большой
глубине, недоступной для эксплуатации. Выявить положение
уступообразных погружений и являлось основной задачей грави-
разведки. Наиболее успешно эта задача решалась в юго-восточной
части Донбасса, где избыточная плотность отложений карбона
относительно перекрывающей толщи мезо-кайнозоя максимальна
и составляет 0,7—1,0 г/см3 (рис. 17.12). По кривой аномалии
силы тяжести выделяются два уступообразных погружения и под-
нятие угленосных отложений в южной части профиля.
На северной окраине бассейна плотность образований каменно-
угольного возраста резко меняется. Поэтому при количественной
интерпретации гравиразведочных данных следует учитывать это
изменение, а также влияние рельефа кристаллического фунда-
мента (рис. 17.13), для чего привлекаются данные других методов,
в частности сейсморазведки и мелкого бурения.
Перед гравиразведкой в Донбассе стояла еще задача определе-
ния глубины и рельефа докембрийского кристаллического фунда-
мента, на котором залегают девонские известняки, подстилающие
каменноугольные образования. Однако решить эту задачу грави-
метрической съемкой не удалось из-за малой разницы плотности
пород докембрия и палеозоя, а также непостоянной плотности
докембрийских и каменноугольных образований.
506
В случаях, когда угле-
носная и подстилающая ее
толщи резко различаются
по плотности и при этом
каждая из них характери-
зуется относительно по-
стоянной плотностью, гра-
виразведочными работами
можно оконтурить области
развития угленосных отло-
жений, определить глуби-
ну и рельеф кровли под-
стилающих их пород, а в
отдельных случаях и най-
Рис. 17.13. Аномалии силы тяжести в север-
ной части Донбасса (по С. И. Субботину).
ти мощность собственно угленосной толщи.
Подобные соотношения наблюдаются в ряде угленосных бас-
сейнов Урала, Казахстана и Средней Азии, где угленосные пес-
чано-глинистые образования юры или пермо-карбона подсти-
лаются более плотными породами палеозоя (рис. 17.14). Перед
гравиразведочными исследованиями в этом случае стоит задача -—
оконтурить площади развития угленосных образований, пере-
крытых отложениями мезо-кайнозоя. Плотность пород мезо-кайно-
зоя 1,9 г/см8, угленосных образований пермо-карбона 2,3 г/см8,
пород, подстилающих угленосные, около 2,7 г/см®. Таким образом,
есть две гравитационноактивные границы: подошва угленосной
толщи и подошва породмезо-кайнозоя; перепад плотности на каждой
границе равен 0,4 г/см3. Следовательно, мульды, выполненные от-
ложениями мезо-кайнозоя и пермо-карбона, должны отмечаться ми-
нимумами гравитационного поля. Поданным бурения известно, что
мощность мезо-кайнозойских образований меняется незначитель-
но, поэтому основной гравитационный эффект наблюдается вслед-
Рис. 17.14. Аномалия силы тяжести и геологический разрез мульды,
выполненной угленосными образованиями.
507
Рис. 17.15. Карта аномалий силы тяжести в редукции Буге угле-
носного бассейна Колли (по Р. Ф. Тьеру).
1 — изоаномалы Ag, 10-6 м/с2; 2 — контуры угленосного бассейна по гра-
виметрическим данным; 3 — обнажения пород фундамента.
508
ствие изменения рельефа подстилающих угленосную толщу
пород.
Рассмотрим результаты гравиметрических исследований в угле-
носном бассейне Колли в Австралии. Этот бассейн представляет
собой впадину в докембрийском фундаменте, выполненною перм-
скими угленосными отложениями, которые перекрыты кайнозой-
скими аллювиально-озерными образованиями. Отдельные, редкие
обнажения пород фундамента, представленных гранитоидами,
известны за пределами бассейна. На гравиметрической карте в ре-
дукции Буге (рис. 17.15) двумя интенсивными минимумами силы
тяжести отмечаются области развития угленосных отложений.
Границы этих образований, т. е. контуры бассейна, четко фикси-
руются зонами высоких градиентов силы тяжести при переходе
от пермских отложений на граниты.
На гравиметрической карте отчетливо видно, что две впадины
бассейна Колли разделены поднятием фундамента, протягива-
ющимся с юго-востока к обнажениям гранитоидов на северной
окраине бассейна. Это поднятие отмечается узкой положительной
аномалией. Последующее бурение подтвердило результаты интер-
претации гравиметрического материала. В восточной впадине па
площади около 20 км2 бурением были открыты угольные пласты
мощностью до 10 м.
В благоприятных условиях гравиразведка применяется для
выделения в угленосной толще отдельных угольных свит и даже
угольных пластов. Наибольшие возможности в этом отношении
представляют буроугольные месторождения, где мощность
пластов может достигать 100 м и больше. Такие работы проводи-
лись на буроугольных месторождениях восточного склона Урала
и в других районах.
Примером гравиметрических работ, решающих задачу оконту-
ривания угленосного бассейна и выделения угольных пластов, мо-
гут служить исследования, выполненные в небольшом угольном
бассейне Блэр-Атол в Австралии. Основной угольный пласт
имеет здесь мощность до 35 м и залегает на глубине 7—50 м.
Угленосные отложения пермо-карбонового возраста заполняют
мелкую впадину в глинистых сланцах палеозоя. Вся площадь
бассейна перекрыта более молодыми образованиями (песчаники,
сланцы, местами базальты). Гравиметрические исследования
должны были определить, продолжается ли бассейн на север.
В районе бассейна плотность углей равна 1,33, угленосных отло-
жений 2,4, пород фундамента 2,65 (сланцы) и 2,8—3,0 г/см3
(базальты).
На карте локальных аномалий (рис. 17.16), отчетливо выде-
ляется минимум треугольной формы, ограниченный изолинией
11-10*6м/с2. Площадь, занятая этим минимумом, совпадает с об-
ластью развития основного угольного пласта. За исключением
слабого минимума к северу от этой площади, перспективных
аномалий не обнаружено. На основе гравиметрических исследо-
509
Рис. 17.16. Карга локаль-
ных аномалий силы тя-
жести (10*6 м/с2) угленос-
ного бассейна Блэр-Атол
(по Р. Ф. Тьеру).
Рис. 17.17. Аномалия
силы тяжести и геологи-
ческий разрез угленосного
бассейна Блэр-Атол (по
Р. Ф. Тьеру).
1 — уголь; 2 — угленосная
толща; 3 — породы фунда-
мента. Гравитационный эф-
фект: I —осадочной толщи,
II — угольного пласта.
Положение профиля см. на
рис. 17.16.
510
г
ваний сделано заключение, что бассейн не имеет продолжения
на север. Тщательный анализ позволяет установить связь между
аномалиями силы тяжести и распространением угля (рис. 17.17).
В гравитационный эффект вносят приблизительно одинаковый
вклад собственно угольные пласты и пермские отложения. Яв-
ная корреляция мощности угольных пластов и аномалий силы
тяжести дала возможность оценить по гравиметрическим дан-
ным запасы углей. Эта оценка хорошо согласуется с данными
бурения.
Рудные месторождения
Гравиразведочные работы уже давно нашли широкое при-
менение при поисках и разведке месторождений железа, меди,
никеля, хромитов, полиметаллов. При этом до последнего времени
основное внимание уделялось выявлению непосредственно самих
рудных тел, что существенно сужало возможности метода,
поскольку гравиразведка исключалась из работ по изучению
структурных особенностей рудных регионов и по их геологиче-
скому картированию. В какой-то мере это положение оправдыва-
лось тем, что до появления гравиметров основные работы выпол-
нялись вариометрами — приборами с низкой производитель-
ностью; это не позволяло применять их для исследований в сред-
них и мелких масштабах. Создание портативных высокоточных
гравиметров качественно изменило возможности гравиметриче-
ского метода при изучении рудных районов, при поисках и раз-
ведке рудных месторождений. Гравиразведка привлекается для
решения задач региональной и структурной геологии таких
сложно построенных территорий, как районы рудной минерали-
зации. В настоящее время гравиметрическая съемка выполняется
на всех стадиях изучения рудных областей: от региональных
исследований и тектонического районирования до детальной и экс-
плуатационной разведки месторождений. Поиски рудных тел
ведут и из подземных выработок.
Региональные гравиметрические исследования широко
используются для изучения глубинного строения рудных районов
и составления металлогенических карт. Крупные глубинные
структуры, отражающиеся в гравитационном поле, позволяют
в некоторых районах установить пространственную связь между
распределением аномалий и рудной минерализацией, а в некото-
рых случаях помогают выявить связь между структурно-металло-
геническими зонами и аномалиями. В частности, установлено, что
полиметаллический пояс Рудного Алтая, ограниченный Иртыш-
ской и Северо-Восточной зонами смятия, приурочен к полосе
положительных аномалий силы тяжести. Калбинский редко-
металльный пояс связан с узкой отрицательной аномалией, про-
тягивающейся вдоль левобережья Иртыша и Иртышской зоны
смятия. Золоторудный пояс, располагающийся западнее парал-
511
дельно Калбинскому поясу, характеризуется повышением грави-
тационного поля.
Подобного типа закономерности выявлены и в других рудных
районах Советского Союза. Например, зеленокаменный пояс
Урала, вмещающий медноколчеданные месторождения, отмечается
повышенным гравитационным полем. Положительными анома-
лиями прослеживаются структуры, к которым приурочены медно-
колчеданные и полиметаллические месторождения Армении. Ред-
кометалльным месторождениям Центрального Казахстана отве-
чают локальные минимумы силы тяжести.
Весьма велико значение гравиразведки при геологическом
картировании и металлогеническом прогнозировании в среднем
и крупном масштабах (1 : 200 000, 1 : 100 000, 1 : 50 000,
1 : 25 000): для изучения структурных особенностей района, его
тектоники, картирования элементов геологического строения
(толщи пород определенного литологического состава, антикли-
нальные складки, зоны тектонических нарушений, массивы ин-
трузивных пород и т. д.), контролирующих размещение рудных
месторождений. Внедрение в практику гравиразведочных работ
высокоточных гравиметров способствовало дальнейшему расшире-
нию детальных исследований, направленных на непосредственные
поиски рудных тел и месторождений. Детальные гравиметрические
съемки решают также задачи геологического картирования, вы-
деляют и прослеживают геологические факторы, контролирующие
распределение рудных залежей: литологпчески благоприятные
для локализации рудных тел породы, тектонические нарушения
и зоны, контакты и т. п. В отдельных, случаях гравиметри-
ческие наблюдения из горных выработок могут быть использо-
ваны для разведки уже известных рудных тел на стадии экс-
плуатации.
Постановка гравиразведочных работ в рудных районах имеет
целый ряд специфических особенностей, вытекающих из харак-
тера изучаемого объекта и геологии рудных месторождений.
Горные породы, слагающие рудные районы, как правило, сильно
дислоцированы и метаморфизованы, разбиты многочисленными
системами сбросов, прорваны интрузиями различного состава.
Отдельные комплексы пород характеризуются изменчивостью ли-
тологического состава, резкими колебаниями мощности на срав-
нительно коротких расстояниях. Эти факторы обусловливают чрез-
вычайно сложную картину гравитационного поля, создают высо-
кий уровень помех геологического происхождения, учесть которые
в ряде случаев очень трудно. Существенные трудности возникают
и при учете влияния рельефа дневной поверхности, который во
многих рудных районах сильно расчленен.
Большинство рудных объектов, при поисках которых при-
меняется гравиразведка, обладает большой избыточной плот-
ностью, но размеры рудных тел, представляющих промышленный
интерес, зачастую незначительны, и аномальный эффект от них
512
соизмерим с аномалиями нерудного характера. Все эти обсто-
ятельства обусловливают и специфику гравиразведочных работ
на рудных месторождениях: при поисках и затем при разведке
обнаруженных объектов применяются высокоточные гравиметры,
а в некоторых случаях оказывается более целесообразным исполь-
зовать градиентометры и вариометры. Чтобы выделить аномалии
рудных объектов на фоне больших цомех, применяют специаль-
ную методику полевых наблюдений и обработки полученного
материала, а также комплексирование гравиразведки с другими
геофизическими методами (в частности, с магниторазведкой и
электроразведкой) н бурением. При съемках на рудных месторож-
дениях количественная интерпретация часто дает ценные резуль-
таты, вплоть до оценки запасов полезных ископаемых.
Наиболее широко и эффективно гравиметрическая съемка при-
меняется при поисках и разведке железных руд, хромитов, медно-
колчеданных и полиметаллических месторождений.
Железорудные месторождения типа КМА и Кривого Рога уже
давно изучаются гравиразведкой. Первые гравиразведочные ра-
боты в СССР были поставлены именно на железорудном место-
рождении в Щигровском районе Курской магнитной аномалии
в 1921 г. Изучение КМА было начато в 1919 г. по инициативе
В. И. Ленина. С 1925 г. гравиразведочные работы проводятся
на месторождениях Кривого Рога.
Железорудные месторождения КМА и Кривого Рога связаны
с железистыми кварцитами докембрийского возраста. Железо-
рудная толща сложена разного рода сланцами (глинистыми, сери-
цитовыми, роговообманковыми), гранито-гнейсами, песчаниками,
известняками, аркозовыми и железистыми кварцитами. Тектоника
железорудной толщи очень сложна, метаморфизованные породы
собраны в изоклинальные складки, разбиты..многочисленными
сбросами и надвигами, прорваны более поздними докембрийскими
и, возможно, палеозойскими интрузиями. Докембрийские обра-
зования глубоко эродированы и представляют собой серии круто-
падающих пластов. Кристаллические породы докембрия обычно
перекрыты более молодыми образованиями, мощность которых
в разных районах различна.
Содержание железа в железистых кварцитах составляет 25—
45%, основным рудным минералом является магнетит. Богатые
руды с содержанием железа до 50—65% образовались в результате
либо гидротермального метаморфизма, либо выветривания желе-
зистых кварцитов. Основными рудными минералами богатых руд
являются мартит, гематит, сидерит и в редких случаях магнетит.
Залежи богатых руд представляют собой оруденелые зоны в голо-
вах пластов железистых кварцитов или штоки и отдельные линзы
внутри толщи железистых кварцитов.
Плотность пород железорудной формации довольно хорошо
изучена. Плотность железистых кварцитов, богатых железных
руд и различных сланцев существенно зависит от содержания
17 В. С. Миронов
513
в них железа. Железистые кварциты характеризуются весьма
широким диапазоном изменения средней плотности: от 2,84 до
3,50 г/см3. Переслаивание кварцитов со сланцами приводит
к уменьшению средневзвешенного значения плотности. Иногда
наблюдается повышение общей плотности горизонтов железистых
кварцитов в связи с процессами их оруденения. Для богатых
железных руд также характерны широкие пределы изменения
плотности: от 3,25 до 5,0 г/см3. Амфиболиты и амфиболитовые
сланцы имеют плотность 2,88—3,0 г/см3. Наименьшей плотностью
обладают различные сланцы (за исключением амфиболитовых),
гнейсы, граниты: 2,54—2,82 г/см3.
Приведенные значения показывают, что наибольшую плот-
ность имеют железистые кварциты и богатые железные руды.
В зависимости от того, с какими породами контактируют желе-
зистые кварциты, их избыточная плотность может меняться в пре-
делах от 0,1 до 1,0 г/см3. Наиболее характерная избыточная
плотность кварцитов составляет 0,3—0,6 г/см3.
Достаточно резкая дифференциация метаморфических пород
по плотности позволяет не только расчленять их методами грави-
разведки на сланцевые и железистые горизонты, но и прослежи-
вать внутри этих горизонтов отдельные слои: оруденелые желе-
зистые кварциты, магнетитсодержащие сланцы и т. и.
Среди железных руд наибольшую избыточную плотность отно-
сительно кварцитов имеют амфибол-магнетитовые руды (0,3—
0,5 г/см3), которые при благоприятном соотношении мощностей
могут быть обнаружены гравиразведкой. Руды окисленные, мар-
титовые и гематитовые мало отличаются по плотности от желези-
стых кварцитов. Но если они залегают среди песчаников и слан-
цев на малой глубине и имеют значительную мощность, то также
могут быть прослежены гравиразведкой.
Изучение месторождений железистых кварцитов может быть
разделено на три этапа.
1. Выделение площадей распространения пород железорудной
формации, изучение общей структуры железорудного бассейна.
2. Поиски в пределах этих площадей месторождений железных
руд, что сводится к геологическому картированию железорудной
толщи.
3. Поиски богатых руд.
Роль гравиразведки в общем комплексе геофизических методов
на различных этапах неодинакова.
Задачи первого этапа — обнаружить зоны развития пород
железорудной формации в закрытых районах, определить про-
тяженность этих зон и приближенно оценить их мощность для
последующей постановки геолого-геофизических исследований —
решаются в основном методами магниторазведки, поскольку
железистые кварциты обладают большой магнитной восприимчи-
востью. Гравиразведкой железистые кварциты выделяются доста-
точно четкими локальными аномалиями только в том случае, если
514
Рис. 17.18. Результаты гравиметрических и магпи-
торазведочпых работ в железорудном бассейне (по
3. А. Крутпховской и Г. К. Кужелову).
1 — изоаномалы Ag; 2 — расчетные кривые Ag; 3 — кон-
тур магнитной аномалии; 4 — интерпретационные про-
фили: 5 — железистые кварциты: 6 — тектонические
нарушения.
они залегают в виде мощных толщ среди однородных по плот-
мости пород. В большинстве случаев мощность железистых квар-
цитов невелика (несколько десятков — сотен метров) и их грави-
тационный эффект мал: от /? -0,1 • 10“6 до п 10'8 м/с2 в исключитель-
ных случаях. Поэтому гравиметрическая съемка для непосред-
ственных поисков железистых кварцитов не применяется. На пер-
вом этапе гравиразведку используют для изучения общей струк-
туры выделенных магниторазведкой железистых пород, поскольку
довольно сложное складчатое строение железорудной формации
не всегда находит достаточно четкое отражение в магнитном поле.
17* 515
КЗ/ EZ?
Рис. 17.19. Картирование пластов
железистых кварцитов вариомет-
рической съемкой (по 3. А. Кру-
тиховской и Г. К. Кужелову).
/ — амфиболиты; 2— железистые квар-
циты; 3 — сланцы; 4 — граниты.
В решении этой задачи грави-
разведочные данные имеют перво-
степенное значение, позволяя по-
лучить не только плановое рас-
положение структурных элементов
железорудной формации, но и оце-
нить ее распространение на глу-
бину, В качестве примера приведем
результаты гравиразведочных и
магниторазведочных работ на од-
ном из железорудных месторож-
дений (рис. 17.18). В данном случае
магниторазведкой определены об-
щие контуры распространения по-
род железорудной формации, а на
основе гравиметрических иссле-
дований построены разрезы, ха-
рактеризующие строение железо-
рудной формации по простиранию
и на глубину.
На втором этапе исследований
проводят детальное картирование
площадей распространения желе-
лезистых кварцитов, изучают
структурные особенности их зале-
гания, определяют мощность, вы-
являют тектонические нарушения и т. д. При решении этих
задач основное значение приобретает гравиразведка. Ведущим
методом является вариометрическая (градиентометрическая)
съемка, масштаб и детальность которой определяются глубиной
железорудной формации. Как правило, работы проводят в масш-
табе 1 : 5000—1 : 25 000, расстояние между профилями задают
примерно равным средней глубине залегания железорудной фор-
мации, а шаг по профилю •— в два-три раза меньше мощности
толщи. При необходимости на участках интенсивного изменения
гравитационного поля проводят детализационные наблюдения.
Рассмотрим пример картирования двух пластов железистых
кварцитов, которые четко выделяются по кривым Uxz
(рис. 17.19). К востоку от железорудной формации по аномалиям
0хг прослеживаются породы повышенной плотности, представлен-
ные амфиболитами, которые отделены от железистых кварцитов
довольно мощной толщей сланцев. Картирование амфиболитов
имеет определенное значение при исследовании общей структуры
осадочно-метаморфической толщи.
Районы развития железорудных формаций характеризуются
кроме сложной складчатой структуры еще и большим количеством
разрывных нарушений. Очень важно обнаружить и проследить
разломы, поскольку с ними очень часто связаны рудопроявления;
516
Рис. 17.20. Картирование зоны разлома варио-
метрической съемкой (по К. В. Климовой).
1 - железистые кварциты; 2 — сланцы; 3 — мета*
базиты; 4 -- гнейсы; 5 — разлом; кривые: 6 — AZ,
' ихг-
Рис, 17.21. Картирова-
ние тектонического на-
рушения варкометриче-
ской съемкой (по
3. А. Крутиховской).
Условные обозначения см.
на рис. 17.20.
таким образом, наличие нарушений является одним из поисковых
признаков богатых железных руд. Зоны разломов могут быть
прослежены вариометрической съемкой по смещению отдельных
горизонтов (рис. 17.20) или по их исчезновению (рис. 17.21).
Отличительной особенностью гравиразведочных работ на же-
лезорудных месторождениях типа КМА и Кривого Рога является
возможность интерпретировать полученные данные не только
качественно, но и количественно — рассчитывать элементы за-
легания тел железистых кварцитов. Пластовая форма железистых
кварцитов и практически бесконечная их протяженность по про-
стиранию и на глубину позволяют использовать способы расчета
для двумерных тел: подбор пластов и суммирование теоретических
кривых U хг.
Поиски богатых железных руд (третий этап исследований)
являются наиболее сложной задачей и осуществляются комплек-
517
Рис. 17.22. Гравитационная и магнитная аномалии на Соколовском (а) и Южно-
Алешинском (б) железорудных месторождениях контактово-метасоматического
типа (по Н. П. Клепчипу и А. П. Куба).
Кривые Ag: 1 — наблюденная, 2 — вычисленная: кривые AZ: 3 — наблюденная, 4
вычисленная; 5 — контур рудного тела по результатам интерпретации.
сом геофизических съемок, хотя до настоящего времени методика
этих работ еще далека от совершенства. Назовем геофизические
поисковые признаки, которые в некоторой степени облегчают
поиски богатых руд.
1. Общее увеличение избыточной плотности железистых квар-
цитов, обнаруживаемое на основе интерпретации гравитационных
аномалий. Поскольку избыточная плотность кварцитов суще-
ственно зависит от содержания железа, то присутствие в толще
железистых кварцитов прослоев богатых руд повышает средне-
взвешенное значение их плотности.
2. Понижение напряженности магнитного поля при сохране-
нии интенсивности гравитационной аномалии. Такое соотноше-
ние может указывать на зоны развития процессов мартитизации,
т. е. на возможное присутствие богатых руд.
Необходимым условием применения указанных критериев
является наличие данных о глубине залегания и характере рель-
ефа верхней кромки железистых пород, так как отсутствие этих
сведении приводит к большим погрешностям в интерпретации,
в частности к преувеличенным значениям избыточной плотности.
Железорудные месторождения контактово-метасоматического
типа также являются объектом гравиметрических исследований.
Железные руды таких месторождений представлены магнетитом,
рудными скарнами и отличаются от вмещающих пород высокой
плотностью и магнитной восприимчивостью (избыточная плот-
ность руд достигает 1 г/см3). Благодаря этому руды четко вы-
деляются грави- и магниторазведкой (рис. 17.22).
I
518
При поисках месторождений-железа коптактово-мстасомати-
ческого типа ведущим геофизическим методом является аэро-
магнитная съемка в масштабе 1 : 50 000. Последующую детали-
зацию выявленных аномалий осуществляют с помощью грави-
метрической и магнитной съемок'В масштабе 1:10 000. При маг-
нитной съемке выделяется множество слабых магнитных аномалий,
которые могут быть связаны как с зонами мартитовых руд, так и
с окисленными в верхних частях магнетитовыми телами. Резуль-
таты высокоточных гравиметрических работ позволяют классифи-
цировать магнитные аномалии на рудные и безрудные. Для опре-
деления параметров рудных тел и предварительной оценки за-
пасов па перспективных участках проводят детальные гравиметри-
ческие и магнитные исследования в масштабе 1 : 5000.
Месторождения хромитов в СССР изучаются гравиразведкой
с 1929 г. К настоящему времени накоплен значительный мето-
дический опыт подобного рода работ. Основными объектами грави-
метрических съемок служат месторождения хромитов Урала и
Казахстана. Известны также положительные примеры гравп-
разведочных работ на хромиты за рубежом: в Турции, на Кубе
и др.
Как объект гравиразведки месторождения хромитов имеют
ряд специфических особенностей, что обусловливает своеобразие
методики гравиметрической съемки. Месторождения хромитов
генетически связаны с массивами ультраосповпых пород (дуниты,
перидотиты, ппроксенпты, нориты). Под действием процессов
авто- и гидротермального метаморфизма ультраосновные породы
сильйо изменены, серпентпнизнрованы, местами полностью пре-
вращены в серпентиниты. Рудные тела имеют обычно форму линз
и жил, иногда штоков и гнезд.
Размеры рудных тел, как правило, невелики, но на некоторых
месторождениях их объем может достигать нескольких сотен
и даже тысяч кубических метров. Иногда встречаются тела, име-
ющие объем сотни тысяч и миллионы кубических метров. Рудные
тела залегают в серпентинизнровапных дунитах или перидотитах,
вблизи контактов их с вмещающими эффузивно-осадочными или
интрузивными породами кислого состава. Очень часто рудные
тела имеют простирание, параллельное контакту ультраосновного
массива с вмещающими породами, и крутое падение. Нередко
они бывают разбиты тектоническими нарушениями.
Плотностная характеристика хромитов и вмещающих их пород
достаточно хорошо изучена (табл. 17.1). Избыточная плотность
хромитов варьирует от 1,0 до 1,5 г/см3, что является благоприят-
ным фактором для постановки jравиразведочных работ. Однако
необходимо иметь в виду значительный диапазон изменения плот-
ности серпептипизированпых пород, что может создавать анома-
лии, подобные аномалиям пал хромитовыми телами, в случаях,
когда среди этих образований залегают останцы неизмененных
ультраосповпых пород.
519
Таблица 17.1
Плотность хромитов и ультраосиовных пород
Порода Плотность, г/см8
Максимальная Минимальная Средняя
Серпентиниты Серпецтнцитированные ду- ниты 1! перидотиты Пироксеннты 1 lopirn.i Габбро Хромиты 2,78 2,87 3,15 3,10 3,10 4,40 2,10 2,25 2,90 2,86 2,82 3,35 2,50 2,55 3,00 2,05 2,95 4,00
На хромитовых месторождениях гравиразведочные работы
проводят для решения следующих основных задач: оконтурива-
ние и картирование массивов ультраосиовных пород, поиски руд-
ных тел, разведка хромитовых тел.
Применение гравиразведки для оконтуривания и картирования
массивов ультраосиовных пород основывается на том, что в боль-
шинстве случаев эти породы обладают значительной положитель-
ной избыточной плотностью относительно вмещающих их эффу-
зивно-осадочных и изверженных пород кислого и среднего состава.
Поэтому в большинстве случаев ультраосновные массивы вы-
деляются довольно интенсивными положительными аномалиями.
Вместе с тем широкий диапазон изменения плотности серпенти-
низированных ультраосиовных пород в некоторых случаях не
позволяет установить четких контактов их с вмещающими поро-
дами. Поэтому гравиметрические наблюдения по картированию
ультраосиовных массивов всегда сопровождаются магнитными
исследованиями, поскольку ультраосновные породы даже при
интенсивной серпентинизации нередко имеют весьма высокую
магнитную восприимчивость и четко выделяются в магнитном
поле. Комплексное применение гравиразведки и магнитораз-
ведки позволяет не только определять контуры ультраосиовных
массивов, но и изучать их строение, выделять разности ультра-
основных пород, прослеживать тектонические нарушения и т. д.
Гравиразведка является практически единственным геофизи-
ческим методом, использующимся для поисков рудных тел, сло-
женных хромитами. Иногда гравиметрическая съемка сопрово-
ждается магниторазведкой, хотя непосредственное выделение хро-
митовых тел по магнитным данным не всегда оказывается возмож-
ным из-за резких колебаний намагниченности вмещающих пород.
В некоторых случаях магниторазведка позволяет обоснованно
отличить положительные гравитационные аномалии, связанные
с телами хромитов, от аномалий, обязанных своим происхожде-
520
нием изменению плотности вмещающих пород. Другие геофизи-
ческие методы (ВЭЗ, мнкросейсморазведка) используются к.чк
вспомогательные для определения подземного рельефа.
Поскольку размеры тел хромитов, даже представляющих
промышленный интерес, обычно невелики, их гравитационный
эффект имеет резко локализованный характер, аномалии быстро
убывают с удалением от тела. Так же резко сказывается на ин-
тенсивности аномалий и глубина залегания рудного тела: с уве-
личением глубины гравитационный эффект быстро уменьшается.
Как правило, аномалии горизонтальной составляющей градиента
силы тяжести равны /г-10-109 и zz-100-10 9 1/с2 при расстоянии
между экстремумами 10—20 м (рис. 17.23). Аномалии силы тя-
жести составляют от /г-0,01 • 10“® до /г-0,1 10"® м/с2 (рис. 17.24),
в исключительных случаях они достигают и-10“5 м/с2. Подобные
аномалии можно обнаружить только при детальной варио.метрн-
ческой (градиентометрической) или высокоточной гравиметри-
ческой съемке. При этом наблюдения проводят по очень густой
сети (20 ' 20 м) с последующей детализацией обнаруженных
аномалий.
Аномалии хромитовых тел часто бывают сильно осложнены
региональным фоном, и для их выделения приходится использо-
вать различные трансформации поля (рис. 17.25). После снятия
регионального фона выделилась широтная зона, состоящая из
двух положительных локальных аномалий силы тяжести. После-
дующее бурение подтвердило, что эти аномалии связаны с телом
521 .

Рис. 17.24. Карта аномалий силы тяжести
над хромитовой залежью (по У. Е, Дэвису
и др.).
I — изоаномалы Ag. 10“s м/с2; 2 — выходы руд-
кого тела на поверхность; скважины: 3 — вскрыв-
шие РУДУ, 4 — пустые.
хромитов, имеющим форму
неправильной линзы с
пережимом в центре. Руд-
ное тело залегает на глуби-
не от 43 до 92 м (западная
аномалия) и от 58 до 170 м
(восточная). В плане длина
рудного тела превышает
200 м при мощности от 30
до 70 м. Такая конфигура-
ция тела хорошо согла-
суется с гравиметрически-
ми данными.
Опыт показывает, что
гравиразведка может быть
использована не. только
для поисков новых рудных
тел, но и для разведки уже
известных рудныхзалежей.
Если для района исследо-
ваний достаточно надежно
известна средняя плот-
ность хромитовых залежей
и вмещающих пород, то
гравитационные аномалии
можно интерпретировать
количественно: определять
форму, размеры или, что
более достоверно, массу
(запасы) рудной залежи.
Обычно форму и площадь
сечения рудного тела на-
ходят методом подбора, в
случаях же четкой лока-
лизации аномалий можно
использовать формулы
(15.33), (15.35). Но при
этом необходимо иметь в
виду, что нижняя граница рудного тела определяется неуверенно
и полученная площадь относится к разрезу тела до глубины,
примерно равной утроенной горизонтальной мощности тела.
Рассмотрим пример использования гравиметрической
съемки для разведки рудных тел на одном из хромитовых место-
рождений (рис. 17.26, 17.27). Перед постановкой гравиметри-
ческих работ известное рудное тело хромитов было практически
выработано, оставшаяся его часть представляла собой горизон-
тальный слой мощностью около 4 м (профиль СС). На основе
интерпретации гравитационной аномалии и магниторазведочных
522
Рис. 17.26. Карта аномалий силы тяжести (10-5 м/с2) над хромитовой
залежью (по С. Джюнгулу),
1 — контур хромитовой залежи; 2 — интерпретационные профили.
Рис. 17.27. Гравитационные н магнитные аномалии над хромитовым рудным
телом и результаты их интерпретации (по С. Джюнгулу).
Контур хромитовой залежи: 1 по гравиметрическим данным. 2 - разведанный перед
эксплуатацией месторождения; 3 рельеф дневной поверхности до разработки место-
рождения.

данных были определены контуры поперечного сечения Новых
тел, а также подсчитаны запасы хромитовых руд (330 тыс. т).
Последующая разведка бурением подтвердила результаты интер-
претации. Запасы вновь открытых рудных тел составили ио дан-
ным бурения 250 тыс. т. Такое согласие гравиметрических и буро-
вых данных (в запасы, определенные по гравиметрическим данным,
входят 80 тыс. т известной части рудного тела) указывает на пра-
вильность выбора избыточной плотности при расчетах п на тща-
тельность учета всех мешающих факторов, в частности рельефа
дневной поверхности.
Обычно подобные расчеты по гравиметрическим данным имеют
ошибку порядка 25—40%, что вполне допустимо при подсчете
запасов по низшим категориям.
Сульфидные месторождения изучаются гравиразведкой с 30-х
годов, но до последнего времени эти работы имели в известной мере
опытный характер в силу специфических особенностей физических
свойств сульфидных руд и разнообразия геологических условий
сульфидных месторождений. С сульфидными месторождениями
связан целый комплекс и слезных ископаемых: медь (медноколче-
данные месторождения), свинец, цинк (полиметаллические место-
рождения), никель, кобальт и др.
В геологическом отношении районы сульфидных месторожде-
ний характеризуются сложной структурой и тектоникой, много-
образием литологических разностей пород. В большинстве своем
эти месторождения приурочены к толщам эффузивно-осадочных
образований различного возраста. Вмещающие породы часто
сильно дислоцированы и метаморфизованы. Для некоторых
месторождений устанавливается тяготение их к антиклинальным
и брахиантпклинальным структурам, зонам пересечения текто-
нических нарушений, определенным литологическим разностям
пород. Форма рудных тел весьма разнообразна: это линзы, пласты,
жилы, гнезда, штоки. Размеры тел по простиранию и падению
варьируют в широких пределах даже в границах одного и того
же месторождения. Мощность тел колеблется от единиц до не-
скольких десятков, а иногда и сотен метров.
Состав рудных тел для различных месторождений также весьма
разнообразен. В состав руд входят пирит, халькопирит, галенит,
сфалерит, пирротин и другие сульфиды. Кроме массивных руд
на отдельных месторождениях широко представлены вкраплен-
ные руды; часто рудные тела сопровождаются сильно развитой
зоной пиритизации. На сульфидных месторождениях нередко
присутствуют окисленные руды.
Сплошные сульфидные руды имеют довольно выдержанную
плотность (4,2—4,7 г/см3) в зависимости от минералогического
состава сульфидов. Вкрапленные руды характеризуются до-
статочно большим диапазоном изменения плотности: 2,9—4,2 г/см8,
что определяется содержанием в них сульфидов. Плотность оки-
сленных руд также меняется в широких пределах: от 2,0 до
525
3,0 г'см®. Средние плотности разнообразных по составу рудо-
вмещающих пород различаются между собой на 0,1—0,3 г/см3
и в среднем составляют 2,6—2,8 г/см3. Из-за разной степени мета-
морфизма и внутри одной литологической разности пород могут
наблюдаться колебания плотности такого же порядка.
Таким образом, сплошные сульфидные руды имеют значитель-
ную (до 1,6 —2,0 г/см3) избыточную плотность относительно вме-
щающих пород. Избыточная плотность вкрапленных руд значи-
тельно меньше и меняется в широких пределах. Окисленные руды
могут иметь не только избыточную, но л недостаточную плотность
до —0,6 г/см3.
Большая избыточная плотность сульфидных руд является
благоприятным фактором для постановки гравиразведочных ра-
бот. При определенных условиях залегания рудных тел и доста-
точных их размерах можно получить заметные аномалии силы тя-
жести и ее градиентов. Но необходимо учитывать целый ряд гео-
логических факторов, создающих аномалии силы тяжести, кото-
рые могут быть соизмеримы с аномалиями рудных тел. Сюда
относятся сильно изменяющаяся мощность рыхлых образований,
невыдержанность плотностных характеристик отдельных литоло-
гических разностей пород, резко пересеченный рельеф дневной
поверхности. Указанные факторы существенно снижают эффектив-
Рис. 17.28. Аномалия силы тяжести над крупным сульфидным рудным телом.
Сульфидные руды: 1 — сплошные, 2 — вкрапленные, 3 — окисленные; 4 — кварцевые
порфиры; 5 — туфы кварцевых порфиров; 6 — глинисто-кремнистые сланцы; 7 — текто-
нические нарушения.
526
иость гравиразведки на некоторых типах сульфидных место-
рождений. В настоящее время накоплен большой методический
опыт гравиметрических исследований на сульфидных месторожде-
ниях Урала, Казахстана, Рудного Алтая.
Установлено, что гравиразведкой отчетливо фиксируются
лишь крупные месторождения, рудные тела которых имеют пре-
имущественно линзовидную или пластообразную форму с крутыми
углами падения, размеры тел по падению и простиранию соста-
вляют первые сотни метров, горизонтальная мощность изменяется
от нескольких десятков до сотни метров. Аномалии тел подобного
рода равны не менее 1-Ю*5, иногда (3 ч- 5)-10'й м/с2, а горизон-
тальная составляющая градиента силы тяжести достигает п
X 100-10"8 1/с2. Такие аномалии легко могут быть обнаружены
и выделены на фоне аномалий, обусловленных факторами не-
рудного происхождения (рис. 17.28). Если же крупные рудные
тела имеют изометричную форму в плане и резко ограниченное
распространение на глубину (штоки и гнезда), то гравитационные
аномалии составляют от
0,4-IO"8 до (1 ч- 2) АО"5 м/с2
и от (40 -г 50) 10'8 до
п -100 -10-9 1/с2.
Месторождения мелкие и
средние, рудные тела которых
имеют линзо- или пластооб-
разную форму с крутыми
углами падения и горизон-
тальной мощностью от еди-
ниц до первых десятков мет-
ров, создают слабые анома-
лии: (0,2 ч- 0,4)-10'5, иногда
до LIO-5 м/с2. Значения вто-
рых производных изменяются
от п 10-10-9до п-100-10-91/с2
в зависимости от размеров и
глубины залегания рудных
тел. Таким образом, эти ме-
сторождения могут фиксиро-
ваться гравиразведкой толь-
ко при благоприятных усло-
виях залегания, поскольку
по амплитуде их эффект срав-
ним с аномалиями, обуслов-
ленными другими факторами:
изменяющейс я мощностью
наносов, неоднородностью
вмещающих пород по плот-
ности и др. Поэтому поста-
новка гравиразведочных ра-
О 100 200м |°%%| 3
Рис. 17.29. Гравитационная аномалия над
сульфидным телом (по С. Вернеру).
/ — изоаномалы Ад, 10“й м/с2; сульфидные
руды: 2 — сплошные, вкрапленные.
527
Рис. 17.30. Результаты вариометрических работ на сульфидном место-
рождении.
1 -- рыхлые образования; 2 — глинистые сланцы; туфы: 3 — основных пород;
4 — кислых пород; 5 — кварцевые порфиры; руды: б — сплошные, 7 — окислен-
ные; 8 — тектонические нарушения; 9 — контур рудного тела, соответствующий
аномалии Uxz выч-
бот на сульфидных месторождениях требует всестороннего и по
возможности полного учета всех мешающих факторов, создающих
аномалии нерудного происхождения.
При поисках сульфидных месторождений используют ком-
плекс исследований, включающий магнито-, грани- и электро
разведку, а также геохимические методы. Благодаря высокой
электропроводимости сульфидных руд электрорззведочные методы
играют при этом основную роль. Однако электроразведка обнару-
живает большое число аномалий проводимости, среди них только
некоторые связаны с рудными телами. Гравиметрическая съемка
на выделенных электроразведкой аномалиях помогает решить
вопрос о их природе (рис. 17,29). Аномалия силы тяжести
528
2,3X10"5 м/с® имеет близкую к изометричной форму, несколько
вытянутую в северо-западном направлении. Наличие интенсивной
положительной гравитационной аномалии, совпадающей с ано-
малией проводимости, позволило рекомендовать эту площадь
для бурения на сульфидное тело. Бурение установило наличие
вкрапленных и сплошных сульфидных руд. Запасы руд, оце-
ненные по аномалии силы тяжести, составляют 2,5 млн. т.
Гравиметрические исследования в пределах уже известных
сульфидных месторождений могут оказать существенную помощь
при определении направления разведочных работ (рис. 17.30).
Рудное тело, представленное пиритом, халькопиритом и другими
сульфидами со средней плотностью 3,8 г/см3, залегает средн
эффузивных образований с плотностью 2,65 г/см3; верхняя часть
тела сложена окисленными рудами с плотностью 2,35 г/см3. Для
известного по данным бурения контура рудного тела была рас-
считана теоретическая кривая (/хгвЬ1Ч. Чтобы добиться удовлет-
ворительного совпадения наблюденной и теоретической кривых,
пришлось предположить присутствие небольшого рудного тела
слева от основного. Разведочными работами существование этого
тела было подтверждено.
Месторождения других полезных
ископаемых
С повышением точности гравиметрических измерений и раз-
работкой способов учета влияния различных мешающих факторов
применение гравпразведкй значительно возросло; появились но-
вые области ее приложения, в частности россыпные, остаточные
и другие типы экзогенных месторождений, нерудное сырье (ал-
мазы, пегматиты, корунд), изучение карста и т. д. Объектами
исследования при поисках месторождений экзогенного проис-
хождения являются кора выветривания, рыхлые образования,
рельеф коренных пород, поскольку погребенные долины, лога,
депрессии служат местами аккумуляции полезного ископаемого.
Рыхлые образования, заполняющие отрицательные формы
рельефа, характеризуются недостатком плотности 0,5—1,0 г/см3,
что при большой и достаточно резко изменяющейся мощности
этих отложений позволяет достаточно уверенно прослеживать
рельеф коренных пород.
Приведем пример прослеживания иод наносами погребенной
долины (рис. 17.31), с которой связаны россыпные месторождения
золота. На кривой аномалии силы тяжести она отмечается мини-
мумом. Для детального исследования погребенных долин, веро-
ятно, более предпочтительно использовать градиентометрические
наблюдения, которые позволят изучить мелкие формы рельефа.
Зная в некоторых точках глубину до коренных пород, по анома-
лиям силы тяжести можно найти мощность рыхлых образований.
539
Рис. 17.31. Картирование погребенной
долины по аномалии силы тяжести (по
К. Н. Анисимову).
Рис. 17.32. Картирование депрессии
в коренных породах по аномалии силы
тяжести (по Д. С. Вашгалю).
1 — рыхлые образования; 2 мраморы;
3 — серпентиниты; 4 — сланцы.
По результатам высокоточной гравиметрической съемки можно
картировать депрессии в коренных породах, выполненные рых-
лыми отложениями, к которым приурочены месторождения сили-
катного никеля (рис. 17.32). Пониженные значения силы тяжести
достаточно четко выделяют места увеличенной мощности наносов,
что подтвердили ВЭЗ и бурение. В данном случае решение задачи
гравпразведкой оказалось экономически более выгодным, чем
постановка ВЭЗ по той же сети. Кроме того, при малой ширине
депрессий и крутых углах наклона их бортов количественная
оценка этих структур может быть проведена более точно по дан-
ным гравиразведки.
Высокоточные гравиметрические и градиентометрические
съемки находят применение при поисках месторождений бокситов
платформенного типа. Горизонты бокситов залегают в депрессиях
фундамента, который перекрыт мощным чехлом рыхлых образо-
ваний. Мощность бокситовых горизонтов составляет несколько
десятков метров, достигая в глубоко врезанных депрессиях и
карстах первых сотен метров. Для поисков бокситов довольно
успешно применяется и магниторазведка, которая легко обнару-
живает магнитные бокситы на немагнитном фундаменте. Однако
присутствие изверженных породи изменяющаяся намагниченность
фундамента осложняют применение магниторазведки, создавая
аномалии, не связанные с бокситами. Гравиразведка исполь-
зуется для разделения магнитных аномалий на рудные и без-
рудные. Магнитные аномалии 50—100 нТл могут быть вызваны
линзами бокситов или порфиритами. Но над линзами бокситов
аномалии силы тяжести слабые отрицательные (рис. 17.33), а над
порфиритами — слабые положительные. Интенсивность аномалий,
как правило, не превосходит (0,1 -ь 0,5) 10 5 м/с2.
Гравиразведка может быть использована при поисках корен-
ных месторождений алмазов, связанных с кимберлитовыми труб-
530
HZ, нТл; Мд, 10 ^м/с1
Рис. 17.33. Аномалия вариаций силы тяжести 6Ag и магнитная аномалия AZ
над бокситами.
I бокситы: 2 — бокситоиосные глины: 3 — пестроцветиые глины; 4 — туфолесчаиики,
алевролиты; 5 — известняки; 6 - диориты, диорит-порфиры.
ками; она также служит для разделения аномалий на рудные
и безрудные. Основным методом для поисков кимберлитовых тру-
бок является магниторазведка. Поскольку кимберлиты обладают
высокой магнитной восприимчивостью, то они легко обнаружи-
ваются аэромагнитной съемкой масштаба I : 25 000 с последующей
детализацией наземными магнитными наблюдениями.^Это отно-
сится к тем случаям, когда кимберлиты расположены вне зоны
развития пород трапповой формации. В зонах траппов, также
создающих сильные магнитные аномалии, кимберлитовые трубки
выделяются магниторазведкой неоднозначно. В этих условиях
гравиразведка привлекается как вспомогательный метод. Плот-
ность кимберлита (2,33—2,60 г/см3) меньше плотности пород
трапповой формации (2,7—3,1 г/см3) примерно на 0,2—-0,5 г/см3
и меньше плотности карбонатных пород (2,40—2,65 г/см3) на 0,1 —
0,2 г/см3. Поэтому над кимберлитовыми трубками наблюдаются
отрицательные аномалии силы тяжести; магнитные же аномалии,
связанные с траппами, сопровождаются положительными анома-
лиями силы тяжести (рис. 17.34).
Известен положительный опыт применения гравиразведки при
поисках пегматитовых жил; их мощность составляет 0,5 10 м,
протяженность — несколько сотен метров. Пегматитовые жилы
по отношению к вмещающим их породам — гнейсам различного
состава — обладают отрицательной избыточной плотностью 0,1 —
0,3 г/см3. Результаты опытных исследований показали, что гра-
531
Рис. 17.34. Гравитационные и магнитные аномалии над кимберлитовой
трубкой (а) и трапповым силлом (б) (по В. М. Бондаренко).
I — карбонатные породы; 2 — кимберлит; 3 — породы трапповой формации.
532
Рис. 17.35. Кривая Uxz над пе- Рис. 17.36. Аномалия силы тяжести над ко-
большим телом корунда (по рундовой залежью (по К. Зундбергу).
Б. А. Андрееву).
диснтомстрнчсской съемкой можно непосредственно обнаружи-
вать пегматитовые жилы при благоприятных условиях: доста-
точно крутом падении жил и сравнительно постоянной мощности
рыхлых отложений. В этом случае можно даже рассчитать пара-
метры пегматитовых жил.
Высокоточные гравиметрические и градиентометрические изме-
рения успешно используются при поисках и разведке корунда.
В большинстве случаев гравиразведка является практически един-
ственным геофизическим методом, который эффективен при по-
исках корунда. Наиболее крупные промышленные месторождения
корунда связаны с вторичными кварцитами, образовавшимися
в результате контактового метасоматоза эффузивных порфиров
с гранитными интрузиями. Плотность вторичных кварцитов
близка к 2,3—2,5 г/см8, плотность корунда колеблется от 3,5
до 4,0 г/см3, т. с. избыточная плотность корунда составляет 1,0 —
1,5 г/см8. Над залежами корунда должны наблюдаться положи-
тельные гравитационные аномалии. Корундовые тела небольших
размеров достаточно четко могут быть выявлены вариометри-
ческой съемкой {рис. 17.35). Более крупные залежи уверенно вы-
деляются и высокоточной гравиметрической съемкой (рис. 17.36).
Основным мешающим фактором при поисках корунда является
резко пересеченный рельеф, характерный для районов развития
вторичных кварцитов. Учитывать влияние рельефа сложно, осо-
бенно при градиентометрических наблюдениях.
ПОДЗЕМНАЯ (ШАХТНАЯ) ГРАВИРАЗВЕДКА
При поисках и разведке рудных месторождений все шире
применяется подземная, или шахтная, гравиразведка. В отдель-
ных случаях она используется при решении и некоторых других
задач: поисках месторождений угля, соли и т. д. Гравиметрические
наблюдения в шахтах проводят для поисков пропущенных и глу-
боко залегающих рудных тел, аномальный эффект которых на
533
Рис. 17.37. Аномалии силы тяжести сульфидного руд-
ного тела, наблюденные па дневной поверхности и в гор-
ных выработках (по И. Н. Капцовой).
дневной поверхности незначителен. Кроме того, измерения в гор-
ных выработках дают дополнительный материал для интерпрета-
ции, позволяя более точно определять параметры тела. Так,
наблюдения с гравиметром на одном из медноколчеданных место-
рождений, проведенные на дневной поверхности и в горных вы-
работках на глубинах 190 и 250 м, позволили проследить контур
рудного тела (рис. 17.37).
Рассмотрим результаты измерений силы тяжести вдоль ствола
шахты, пересекающего сульфидное рудное тело неправильной
формы (рис. 17.38). Избыточная плотность сульфидных руд отно-
сительно вмещающих рудное тело известняков колеблется в пре-
делах 0,9—1,5 г/см3. С приближением к сульфидному телу анома-
лия силы тяжести возрастает, достигая +1,4- 10~й м/с2, а при пере-
сечении тела — резко убывает и, перейдя через нуль, образует
минимум —1,8 - 10~в м/с3. Асимметрия кривой Ag' хорошо подчер-
кивает неправильную форму тела.
Особенно большое значение подземная гравиразведка при-
обретает на железорудных месторождениях (Криворожский бас-
сейн, Горная Шорня, Урал). На действующих рудниках увели-
чивается глубина отработки рудных тел, на дневной поверхности
образуются огромные карьеры и отвалы, возникают зоны обру-
шения. Это существенно затрудняет проведение наземных гео-
физических работ и снижает их эффективность. Рассмотрим ре-
зультаты гравиметрических и градиентометрических измерений
на шахте Центральная (горизонт 490 м) Криворожского бассейна
(рис. 17.39). Гравиметрическая съемка выявила здесь два уча-
стка положительных аномалий силы тяжести. Градиентометри-
ческая съемка подтвердила существование положительных ано-
малий, а бурение установило наличие рудных тел. Одно из тел,
выделенных по гравиметрической съемке, предполагалось и по
534
Рис. 17.38. Кривая Ag вдоль ствола шахты, пересекающего
сульфидное рудное тело (по Д. Р. Роджерсу).
геологическим данным, по гравиразведка позволила существенно
уточнить его положение.
Приведем результаты гравиметрических исследований на од-
ном из медно-цинковых месторождений (рис. 17.40). Сульфидные
тела, представленные сплошными и вкрапленными рудами, за-
легают в известняках, имеющих выдержанную плотность 2,7 г/см3.
Зоны минерализации резко отличаются по плотности от вмеща-
ющих пород, при этом наблюдается практически линейная зави-
симость плотности руд от содержания сульфидов: при изменении
концентрации сульфидов от 10 до 50% плотность руд меняется
от 3,0 до 5,0 г/см3. В результате гравиметрической съемки, вы-
полненной на разных горизонтах, составлены вертикальные карты
аномалий силы тяжести. Зоны оруденения фиксируются резким
увеличением вертикального градиента силы тяжести. По этому
признаку выделены контуры рудных тел: на верхнем разрезе за-
лежь представлена пологопадающей линзой, на нижнем — объек-
тами неправильной формы, приуроченными к зоне брекчирования.
Гравиразведочные работы в горных выработках имеют свои
особенности. Наблюденные здесь аномалии силы тяжести зависят
от положения тела относительно выработки, что сильно ослож-
535
S'"! -^15 ^6
Рас. 17.39. Результаты гравиметрических и градиентометрических работ в под-
земных выработках железорудного бассейна (по А. И. Канюка и др.).
1 — геологические границы; контур залежи: 2 — предполагаемый по геологическим
данным, 3 — предполагаемый по гравиметрическим данным, 4 — установленный геолого-
гравиметрическими работами; 5 — горные выработки и точки наблюдений; 6 — горные
выработки, пройденные после гравиметрических работ.

^50— / p ;---------J
Pile. 17.40. Результаты подземных гравиметрических исследований на медно-
цинковом месторождении (по Д. С. Самнеру).
1 — изоаномалы Ag, 10“R м/с2; 2 — контур рудного тела но гравиметрическим данным,*
3 — горные выработки.
<537
няет интерпретацию полученного материала. Если, например,
сферическое тело с положительной избыточной плотностью рас-
положено под выработкой, то оно создает гравитационный макси-
мум; если же оно находится над выработкой, то отмечается мини-
мумом; если центр тяжести тела совпадает с горизонтом выработки,
то тело вообще не вызывает аномального эффекта. Поэтому под-
земные наблюдения целесообразно проводить одновременно грави-
метром и градиентометром, поскольку по направлению полного
вектора горизонтальной составляющей градиента можно судить
о положении рудного тела.
При гравиметрических измерениях необходимо тщательно учи-
тывать влияние горных выработок, которое может быть соизме-
римым со слабыми аномалиями рудных тел. При градиентометри-
ческих наблюдениях имеют значение неровности стенок горных
выработок и отклонение их от некоторой стандартной формы.
Учет этого влияния при вариометрических и градиентометриче-
ских съемках весьма трудоемок, поэтому основные исследования
выполняют с гравиметрами, а детализационные — с градиенто-
метрами или вариометрами.
Опытно-методические работы подтвердили целесообразность
проведения подземных гравиметрических наблюдений в комплексе
с другими геофизическими методами при поисках слепых рудных
тел и при детальной разведке уже известных вскрытых горными
выработками залежей. В настоящее время подземную гравираз-
ведку широко внедряют в практику геологоразведочных работ.
СПИСОК ЛИТЕРАТУРЫ
Андреев Б. А., Клушин. И. Г. Геологическое истолко-
вание гравитационных аномалий. Л., Недра, 1965. 496 с.
Березкин В. М. Применение гравиразведки для поисков нефти и газа. М.,
Недра, 1973. 264 с.
Веселов К. Е. Кварцевые астазированные гравиметры. М., Гостопгехнздат,
1961. 176 с.
Веселов К. Е., Сагитов М. У. Гравиметрическая разведка. М., Недра, 1968.
512 с.
Гладкий К- В- Гравиразведка и магниторазведка. М., Недра, 1967. 320 с.
Грушинский Н. П. Теория фигуры Земли. М., Наука, 1976. 512 с.
Грушинский. И. П., Сажина Н. Б. Гравитационная разведка. М., Недра,
1972. 390 с.
Деменицкая Р. М. Кора и мантия Земли. М., Недра, 1975. 254 с.
Идельсон Н. И. Теория потенциала. Л.—М., Гостеортехиздат, 1936. 424 с.
Инструкция по гравиметрической разведке. М., Недра, 1975. 87 с.
Макаров Н. И. Геодезическая гравиметрия. М., Недра, 1968. 408 с.
Маловичко А. К. Основной курс гравиразведки. Пермь, Изд-во Перм. ун-та.
Ч. 1. 1960. 322 с. Ч. 2. 1962. 278 с.
Немцов Л. Д. Высокоточная гравиразведка. М., Недра, 1967. 240 с.
Определение силы тяжести на море/Под ред. Н. П. Грушинского. М., Недра,
1970. 247 с.
Подземная гравиразведка (методическое руководство)/Н. Р. Бурьян,
А. А. Юньков, Н. М. Анищенко и др. Л., Недра, 1979. 159 с.
Сорокин Л. В. Гравиметрия и гравиметрическая разведка. М.—Л., Гостоп-
техиздат, 1953. 484 с.
Справочник геофизика. Т. 5. Гравиразведка/Под ред. Е. А. Мудрецовой. М.,
Недра, 1968. 512 с.
Успенский Д. Г. Гравиразведка. Л., Недра, 1968. 330 с.
Устройство, наладка, ремонт и эксплуатация гравиметрической аппара-
туры/Под ред. К. Е. Веселова. М., Недра, 1964. 224 с.
Федынский В. В. Разведочная геофизика. М., Недра, 1967. 672 с.
Шванк О. А., Люстих Е. И. Интерпретация гравитационных наблюдений.
М.—Л., Гостоптехиздат, 1947. 400 с.
Шокан, П. Ф. Гравиметрия. М., Геодезиздат, 1960. 316 с.
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию ................................... 3
Предисловие к первому изданию .................................... 4
Введение........................................................... 5
Раздел I
ОСНОВЫ ТЕОРИИ
ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ
Глава 1. Сила притяжения и ее потенциал .......................... 10
Сила притяжения ............................. —
Потенциал притяжения и его физический смысл 14
Вторые производные потенциала притяжения и
их физический смысл ........................ 17
Общие интегральные выражения производных
потенциала притяжения ...................... 21
Потенциал притяжения сферического слоя и
шара ....................................... 27
Уравнения Лапласа и Пуассона................ 33
Формулы Грина .............................. 35
Формулы Грина для гармонических функций 40
Задачи Дирихле и Неймана ................... 43
Глава 2. Гравитационное поле Земли ............................... 49
Сила тяжести и ее потенциал................. —
Разложение потенциала силы тяжести в ряд 52
Геоид....................................... 56
Сила тяжести на поверхности уроненного сферо-
ида (геоида) ............................... 58
Нормальное распределение силы тяжести . . . 59
Нормальные значения вторых производных
потенциала силы тяжести ................... 66
Изменения силы тяжести во времени........ 67
Глава 3. Редукции силы тяжести.................................... 72
Понятие редукций и их виды................... —
Поправка за высоту точки наблюдения и редук-
ция в свободном воздухе .................... 77
Поправка за промежуточный слой и редукция
Буге........................................ 78
Редукция Прея............................... 79
Аномалии силы тяжести на море............... 80
Поправка за влияние рельефа местности ... 81
Методы вычисления поправки за влияние рель-
ефа ........................................ 86
540
Раздел 11
МЕТОДЫ ИЗМЕРЕНИЯ
СИЛЫ ТЯЖЕСТИ
Глава 4. Задачи и способы измерения силы тяжести................... 04
Значение определений силы тяжести для раз-
личных областей науки ........................ —
Классификация методов измерения силы тя-
жести ...................................... 95
Глава 5. Динамические методы измерения силы тяжести ............... 96
Основы маятникового метода определения силы
тяжести ..............................
Физический маятник ......................... 99
Абсолютные определения силы тяжести . . . 101
Относительные определения силы тяжести маят-
ником ...................................... 111
Маятниковые приборы для относительных опре-
делений силы тяжести........................ 112
Поправки в наблюденный период колебаний
маятника для учета внешних влияний . . . 116
Упругий маятник .......................... 118
Струнные гравиметры . ..................... 119
Глава 6. Статические методы измерения силы тяжести................ 121
Общие сведения о статических гравиметрах
Физические свойства упругих материалов, при-
меняемых в гравиметрах ..................... 123
Элементы теории механических гравиметров 128
Глава 7. Некоторые типы гравиметров............................... 162
Гравиметры с металлическими пружинами
Кварцевые гравиметры с горизонтальной кру-
тильной нитью и жидкостной температурной
компенсацией ............................... 169
Гравиметры, построенные по принципу верти-
кального сейсмографа Голицына .............. 174
Специальные конструкции гравиметров с ди-
станционным управлением .................... 203
Глава 8. Методика гравиметрической съемки на суше ................ 208
Основные виды съемки ........................ —
Опорная сеть и рядовые наблюдения........ 211
Оценка качества наблюдений................. 214
Способы уравнивания опорных сетей .... 216
Густота сети и точность съемки............. 228
Геодезическое обеспечение гравиметрической
съемки...................................... 231
Глава 9. Измерение силы тяжести в движении ....................... 234
Основные трудности измерения силы тяжести
на подвижном основании ..................
Метод Бенинга Мейнеса определения силы тя-
жести на море маятником .................... 239
Маятниковые приборы для измерения силы
тяжести на море............................. 243
Статический способ измерения силы тяжести
на море..................................... 244
Некоторые типы морских гравиметров . . . 255
Гравиметрическая съемка на море ........... 260
Гравиметрические измерения в воздухе .... 262
541
Раздел III
МЕТОДЫ ИЗМЕРЕНИЯ
ВТОРЫХ ПРОИЗВОДНЫХ
ПОТЕНЦИАЛА СИЛЫ ТЯЖЕСТИ
Глава 10. Теория и устройство гравитационных вариометров .... 265
Основное уравнение вариометра .............. —
Общие сведения о вариометрах ............. 271
Некоторые типы вариометров ........ 273
Глава 11. Наблюдения с гравитационными вариометрами............ 280
Техника наблюдений с вариометрами и гради-
ентометрами .............................. —
Формулы для вычисления вторых производ-
ных потенциала силы тяжести .............. 282
Определение постоянных вариометра .... 285
Влияние рельефа местности................. 288
Представление результатов наблюдений . . . 299
Глава 12. Возможности измерения вертикальной составляющей градиента
силы тяжести . ................................................ 301
Основные способы............................ —
Элементы теории равноплечих крутильных
весов .................................... 304
Измерение вертикальной составляющей гради-
ента силы тяжести гравиметром............. 310
Раздел IV
ГЕОЛОГИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
ГРАБИТАЦИОННЫX АНОМАЛИЙ
И ПРИМЕНЕНИЕ ГРАВИРАЗВЕДКИ
Глава 13. Физические основы геологической интерпретации гравита-
ционных аномалий............................................... 312
Плотность горных пород...................... —
Методика изучения плотности пород ........ 319
Основные положения геологической интерпре-
тации гравитационных аномалий ............ 326
Глава 14. Гравитационное поле тел правильной формы............. 332
Способы определения параметров тел....... —
Материальная точка, сфера .................. 333
Вертикальный материальный стержень, верти-
кальный круговой цилиндр ................. 337
Горизонтальный материальный стержень, гори-
зонтальный круговой цилиндр .............. 339
Вертикальная ’ материальная полоса, верти-
кальный тонкий пласт ..................... 345
Горизонтальная материальная полоса, гори-
зонтальный тонкий пласт .................. 348
Горизонтальная материальная полуплоскость 351
Прямоугольный параллелепипед ............. 352
Вертикальный уступ ...................... 353
Наклонный уступ ......................... 358
Наклонный хло'й.......................... 369
Вертикальный пласт....................... 372
Наклонный пласт ......................... 374
542
Определение параметрон тел по соотношению
разных производных гравитационного потен-
z цнала ...................................... 377
Графические способы определения параметров
тел ......................................... 379
Глава 15. Гравитационное поле тел произвольной формы................ 381
Графические способы вычисления гравитацион-
ного эффекта тел .............................. —
Определение массы и координат центра тя-
жести тела................................... 392
Преобразование трехмерных аномалий в дву-
мерные ...................................... 402
Определение рельефа контактной поверхности 403
Пространственное распределение поля и его
использование при интерпретации аномалий 410
Глава 16. Методы трансформации гравитационных аномалий........ 419
Общие принципы трансформации аномалии
Осреднение аномалий ......................... 421
Аналитическое продолжение аномалий как
гармонических функций ....................... 424
Вычисление высших производных потенциала 438
Трансформация аномалий как процесс частот-
ной фильтрации............................... 452
Использование элементов теории вероятностей
и математической статистики для определения
оптимальных трансформаций аномального ноля 461
Трансформации гравитационных аномалий па
основе конкретной геологической информации 477
Применение вычислительных машин при обра-
ботке и интерпретации гравиметрических на-
блюдений .................................... 479
Г лава 17. Применение гравпразведки................................. 484
Изучение фигуры Земли ......................
Изучение строения земной коры ............... 489
Геологическое картирование................... 496
Поиски и разведка месторождений ............. 499
Подземная (шахтная) гравиразведка ..... 533
Список литературы................................................. 539
- (Ijt) ,yti| to + [ _. , , . [g/м — (>x) d-XQ К Л /?/ IJ* d M fl-4-*) n s’ - f'r> У "*W«KS = hp2p5(o 'к ‘5)'/?} J )V?BS = Up5p(o •!» 4)'/if J
sl(»>)a.lWo“r<m)"o Л Ip (ira) SOS (1) \y J = (<n) 0 0 op(»)SO3{<»)£) j'’=(l)*'.V Ч“/з вйгМр ‘i')’n
S’ 5«/-a(0 ‘3)/l J “(™)S mp™,s(ra)sf ^- — (0'*)/? «’-“•eV ч?г = (о '*)'/; u
• IP -'H(u 41'/)*f '*)/? ,„U I'» + .<« - И *f *f л .,л ,, . , нилтнг;/ И.» ’’ "i ,-2J-„, )V7~'(O ‘0 '*)“/? гЛ sVS -“H"/£~"=(0 ‘0 '*)"/) •у И'«“ (0 ‘0 ‘*)'Л
к Г | С
Г

U (-', ’/. ’> - to (-“ '! ,
(/(.г, г).= tojjln|a -.r)> I к-гИЖ
г/, Ct, s, г)=fa j 4г14 <гч <?
Uu (х, II, г) - 3to J -<l=4fc£L
О’,Т'. I/.г) =,la j [-3^;~-'*' - 4]
г " [1 + тяг(1 “ 3 sin’ - ^cos>f ]
g=g.O +Psin*<p)
r (ie 4
— 2n.kah
C/I(xjZ)=2to JjiTidEd?
s
£/„(.r, Z) = 4to jj <Е-л) В-г) dl^
s
U„ (X, г) = 2to j j g-Я’т;<?-*)• 4 .Jf.
Age . — g — ?• + 0,3086(1
= ё — To + (0,3086 — 0,0419o) h
^gnm - (Г"+' ~ Г» + - 1Т‘„+, + Л‘)
В.С. Миронов

КУРС
ГРАВИРАЗВЕДКИ
НЕДРА