Text
С. РОУ
ГЕОМЕТРИЧЕСКІЯ
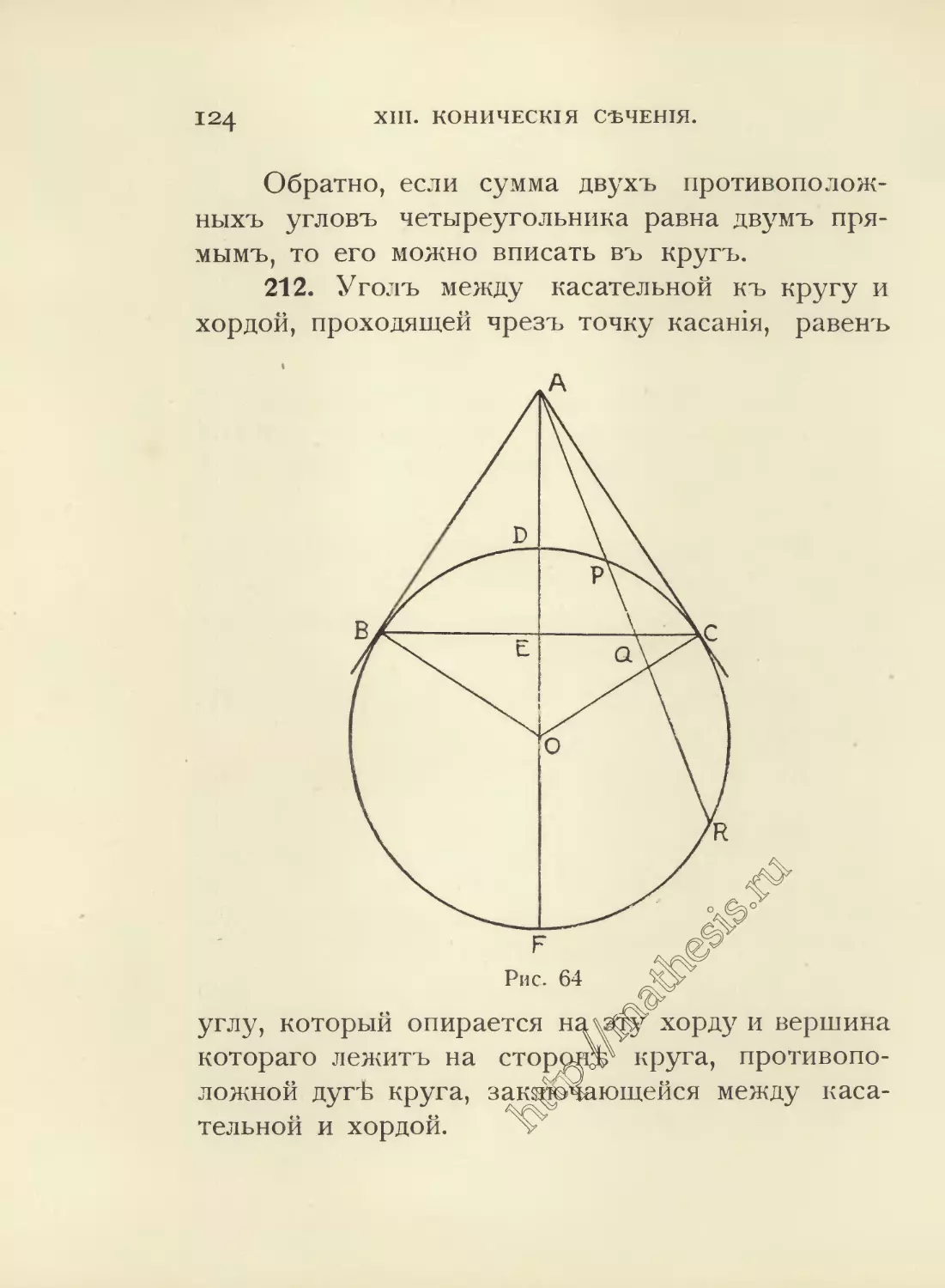
УПРАЖНЕНІЯ
съ кускомъ бумаги
Зипсіага Роѵ?
ГЕОМЕТРИЧЕСКІЯ УПРАЖНЕНІЯ
съ кускомъ бумаги
СУНДНРЛ РОУ
(/7^----------
ѵ/
ГЕОМЕТРИЧЕСКІЯ =
= УПРАЖНЕНІЯ
съ кускомъ бумаги
ІТер. съ англійскаго
Съ 87 рисунками и чертежами
Одесса 1910
Тип. Ю.-Р. О-ва
Печатнаго Дѣла.
Одесса, Пушкин-
ская 18, 1910
Содержаніе
Введеніе........ .................
I. Квадратъ ................
II. Равносторонній треугольникъ .
Квадраты и прямоугольники
Пятиугольникъ .................
Шестиугольникъ . ...........
Восьмиугольникъ.............
Девятиугольникъ.............
іоугольникъ и ізугольникъ
Пятнадцатиугольникъ . ...
Ряды .......................
Многоугольники..............
Общія начала................
Коническія сѣченія..........
Отдѣленіе I. Кругъ . .
Отдѣленіе II. Парабола .
Отдѣленіе III. Эллипсъ .
Отдѣленіе IV. Гипербол^
Различныя кривыя . . . •
III.
IV.
V.
VI.
VII.
VIII.
IX.
XI.
XII.
XIII.
XIV.
Стр.
I
і
ю
іб
34
4°
45
5і
53
56
58
75
93
139
146
!52
Введеніе
і. Идея этой книги была внушена мнѣ упраж-
неніемъ Ко. VIII. Фребелевскаго дѣтскаго сада
—складываніемъ бумаги. Для этого упражненія
дѣтямъ даютъ сотни двѣ различно окрашенныхъ
бумажныхъ квадратовъ, ножъ для разглаживанія
бумаги и наставленія для складыванія. Бумага съ
одной стороны окрашена и глазирована. Но она,
конечно, можетъ быть прокрашена насквозь и
одинакова съ обѣихъ сторонъ. Да и всякая бу-
мага умѣренной толщины будетъ годиться для
нашей цѣли. На цвѣтной бумагѣ, однако, сгибы
будутъ виднѣе и она пріятнѣй для глазъ. Упраж-
ненія для дѣтскихъ садовъ продаются во всѣх^
складахъ учебныхъ пособій, а цвѣтную бум^у
обоихъ указанныхъ сортовъ можно имѣз^^ въ
каждомъ писчебумажномъ магазинѣ. Из^всякаго
листа бумаги можно получить квадратьСкакъ ука-
зано въ первыхъ параграфахъ эт©|р книги, но
полезно и удобно имѣть квадратв$ш$е заготовлен-
ными заранѣе, въ нарѣзанномъ^§йдѣ.
Роу. Геометрическія упражненія
1
II
ВВЕДЕНІЕ.
2. Для этихъ упражненій не требуется чер-
тежныхъ инструментовъ и единственными необхо-
димыми вещами являются перочинный ножъ и
полоски бумаги—послѣднія для откладыванія рав-
ныхъ длинъ. Сами квадраты замѣняютъ обыкно-
венную прямую и Т-образную линейку.
3. При складываніи бумаги нѣкоторые важ-
ные геометрическіе пріемы можно выполнять го-
раздо легче, чѣмъ при помощи циркуля и линейки,
единственныхъ инструментовъ, примѣненіе кото-
рыхъ освящено Евклидовой геометріей. Примѣрами
могутъ с ужить дѣленіе отрѣзковъ и угловъ на двѣ
или на большее число равныхъ частей, проведеніе
перпендикуляровъ къ прямымъ или линій, парал-
лельныхъ даннымъ. Зато при помощи складыванія
бумаги нельзя описать окружность, хотя извѣстное
число точекъ круга, а также и другихъ кривыхъ,
можно получить различными способами. Настоящія
упражненія состоятъ не просто въ черченіи геомет-
рическихъ фигуръ, обыкновенно съ прямыми ли-
ніями, и въ сгибаніи по нимъ, но требуютъфсмыс-
леннаго приложенія простыхъ пріемовъ^дѣ скла-
дываніе бумаги особенно удобно. ЭтстЖудетъ ясно
съ самаго начала книги.
4, Эти упражненія дѣтск^х^^адовъ не толь-
ко даютъ интересное занятіе ^дьчикамъ и дѣвоч-
камъ, но подготовляютъ і^^умъ къ надлежащей
оцѣнкѣ науки и искусёфа. Съ другой стороны,
ВВЕДЕНІЕ.
III
связавъ дальнѣйшее обученіе наукѣ и искусству
съ занятіями въ дѣтскомъ саду, можно сдѣлать
ихъ болѣе интересными и заложить для нихъ болѣе
прочное основаніе. Это особенно примѣнимо къ
геометріи, лежащей въ основѣ всякой науки и
искусства. Широко пользуясь упражненіями дѣт-
скихъ садовъ, можно сдѣлать школьное изуче-
ніе геометріи на плоскости очень интереснымъ.
Было бы совершенно правильно требовать отъ
учениковъ складыванія этихъ чертежей на бумагѣ.
Это давало бы имъ отчетливыя и точныя фигуры
и невольно запечатлѣвало бы въ ихъ умахъ истины
предложеній. Ни одного утвержденія не приходилось
бы принимать на вѣру. Что теперь должны созда-
вать воображеніе и идеализація плохихъ чертежей,
то можно видѣть конкретно. Тогда была бы не-
возможна ошибка вродѣ нижеслѣдующей.
/. Доказать, что всякій треугольникъ есть
равнобедренный. Пусть АВС, рис. і, будетъ какой-
нибудь треугольникъ. Раздѣлите А В въ 2 попо-
ламъ и чрезъ 2 проведите 2 О перпендикулярнф
къ А В. Раздѣлите уголъ А СВ линіей С О пой-
ламъ.
і) Если СО и 2 О не встрѣчайся, онѣ
параллельны. Значитъ, С О перпендцк^ярно къ
А В. Поэтому А С= В С.
2) Пусть С О и 2 О встрѣчя^^я въ какой-
нибудь точкѣ О. Проведите О ^Перпендикулярно
тѵ
ВВЕДЕНІЕ.
къ В С и О У перпендикулярно къ А С. Соедините
О А, О В. Согласно I, 26 Евклида треугольники
У О С и X О С при наложеніи совпадаютъ; со-
гласно I, 47 и I, 8 Евклида треугольники АОУ
и ВОХ также при наложеніи совпадаютъ. Слѣ-
довательно,
А У+ УС^-ВХ+ХС,
т. е. АС=ВС.
Рис. 2 при помощи склаЛ^Йнія бумаги пока-
зываетъ, что, каковъ бы ни &ылъ взятый треуголь-
никъ, СО и АО не мои/встрѣчаться внутри
него.
ВВЕДЕНІЕ.
V
О есть средина дуги АОВ круга, описаннаго
около треугольника АВС.
6. Складываніе бумаги не совсѣмъ чуждо
намъ. Складываніе бумажныхъ квадратовъ въ
видѣ различныхъ предметовъ—лодочки, двойной
Рис. 2
лодочки, чернильницы, пѣтушка и т. ц^^орошо
извѣстно, какъ и вырѣзываніе бумшж^ѣъ симме-
тричныхъ формахъ для украшеній°}ф1ри письмѣ
на санскритскомъ или маратскоцѣЭфыкахъ бумага
складывается вертикально илиі^изонтально, что-
VI
ВВЕДЕН 1Е.
бы строки и столбцы выходили прямыми. При
перепискѣ бумагъ въ канцеляріяхъ дѣлаютъ пра-
вильныя поля, сгибая бумагу по вертикали. Вдвое
сложенные прямоугольные куски бумаги всегда
были въ употребленіи для письма и до введенія
обрѣзанной на машинѣ почтовой бумаги и конвер-
товъ разныхъ величинъ листы желаемаго размѣра
получались при помощи складыванія и разрыванія
большихъ листовъ; одна половина бумаги склады-
валась въ конвертъ для другой половины. По-
слѣдній пріемъ сберегалъ бумагу и обладалъ оче-
виднымъ преимуществомъ прикрѣпленія почтовыхъ
знаковъ непосредственно къ самой писанной бу-
магѣ. Къ складыванію бумаги прибѣгали и при
изученіи XI книги Евклида, трактующей о фигу-
рахъ трехъ измѣреній. Но имъ рѣдко пользова-
лись для плоскихъ фигуръ.
7. Я не пытался написать полный трактатъ
или руководство геометріи а старался лишь пока-
зать, какимъ образомъ можно сложить или опре-
дѣлить точками на бумагѣ правнльные^много-
угольники, круги и другія кривыя. Я ^^ьзовался
случаемъ представить читателю нѣкрт||щія хорошо
извѣстныя задачи древней и совр^ейной геомет-
ріи и показать, какъ къ ге©4р?ріи можно съ
выгодой прилагать алгебру и дтаггоиометрію; а это
освѣщаетъ каждый изъ этцхѣ> предметовъ, обык-
новенно предлагаемыхъ сдѣльно.
В ВЕДЕНІЕ.
VII
8. Первыя девять главъ говорятъ о склады-
ваніи правильныхъ многоугольниковъ, разсматри-
ваемыхъ въ первыхъ четырехъ книгахъ Евклида,
и девятиугольника. Въ основу былъ положенъ
бумажный квадратъ дѣтскаго сада и при его
помощи разрабатывались другіе правильные мно-
гоугольники. Глава I показываетъ, какъ нужно
дѣлить основной квадратъ и какъ можно скла-
дывать его въ равные прямоугольные равнобед-
ренные треугольники и въ квадраты. 'Глава II
занимается равносторонними треугольниками, по-
строенными на одной изъ сторонъ квадрата. Гла-
ва III посвящена Пиѳагоровой теоремѣ, предложе-
ніямъ второй книги Евклида и нѣкоторымъ инте-
реснымъ задачамъ, связаннымъ съ ними. Здѣсь
также показывается, какимъ образомъ на данномъ
основаніи можно построить прямоугольный тре-
угольникъ съ заданной высотой. Это сводится къ
нахожденію точекъ на нѣкоторомъ кругѣ даннаго
діаметра.
р. Глава X трактуетъ объ ариѳметической/
геометрической и гармонической пропорціи°^° о
ісуммованіи нѣкоторыхъ ариѳметическихъ прогрес-
сій. Говоря о пропорціяхъ, мы беремъштрѣзки,
длины которыхъ представляютъ дорастающую
прогрессію. Прямоугольный кусокъуЗумаги, рас-
черченный на квадратики, даетт^^имѣръ ариѳме-
тической прогрессіи. Для геоі^фрической пропор-
VIII
ВВЕДЕНІЕ.
ціи мы пользуемся тѣми свойствами прямоуголь-
наго треугольника, что перпендикуляръ изъ вер-
шины прямого угла на гипотенузу есть среднее
геометрическое между отрѣзками гипотенузы и
что каждый изъ катетовъ есть среднее геометри-
ческое между проекціей катета на гипотенузу и
всей гипотенузой. Въ связи съ этимъ излагается
и Делосская задача объ удвоеніи куба. Въ вопросѣ
о гармонической пропорціи прилагается свойство
биссекторовъ внутренняго и соотвѣтственнаго
внѣшняго угловъ треугольника дѣлить противопо-
ложную сторону въ отношеніи двухъ другихъ сто-
ронъ треугольника. Это даетъ интересный способъ
графическаго поясненія инволюціонныхъ системъ.
Суммы натуральныхъ чиселъ и ихъ кубовъ полу-
чаются графически и отсюда выводятся суммы
нѣкоторыхъ другихъ рядовъ.
іо. Въ главѣ XI трактуется общая теорія
правильныхъ многоугольниковъ и опредѣленіе чис-
ловой величины лг. Предложенія этой главы очень
интересны.
іі. Глава XII излагаетъ нѣкото|лря общія
начала, прилагавшіяся въ предшестш|Іэпіихъ гла-
вахъ,—она касается равенства, сишОріии подобія
фигуръ, пересѣченія прямыхъ лирѣ! и коллинеар-
ности точекъ.
12. Главы XIII и ХІ\^ѵяаняты коническими
сѣченіями и другими интересными кривыми. Меж-
ВВЕДЕНІЕ.
IX
ду другими свойствами круга излагаются его гар-
моническія свойства. Объясняются также теоріи
инверсіи и соосныхъ круговъ. Въ отношеніи дру-
гихъ кривыхъ показывается, какимъ образомъ при
помощи складыванія можно намѣчать на бумагѣ
ихъ точки. Дается исторія нѣкоторыхъ изъ кри-
выхъ и показывается ихъ приложеніе къ рѣшенію
классическихъ задачъ нахожденія двухъ геометри-
ческихъ среднихъ для двухъ данныхъ отрѣзковъ
и дѣленія даннаго плоскаго угла на три равныя
части. Хотя изслѣдованіе свойствъ этихъ кривыхъ
требуетъ болѣе глубокаго знанія математики, но
ихъ полученіе легко понятно и интересно.
13. Я старался не только помочь изученію
геометріи въ школахъ, но и доставить математи-
ческое развлеченіе старому и малому въ привлека-
тельной и доступной формѣ. „Старые" вродѣ меня
найдутъ, можетъ быть, эту книгу полезной для
того, чтобы воскресить въ памяти старые уроки
и взглянуть на современное развитіе того, и очень
интереснаго и поучительнаго, чѣмъ пренебреги
университетскіе преподаватели.
Мадрасъ, Индія, 1893.
I. Квадратъ
1. Верхняя сторона куска бумаги, лежащей
на ровномъ столѣ, есть плоская поверхность;
плоскую поверхность представляетъ и нижняя
сторона ея, касающаяся стола.
2. Эти двѣ поверхности раздѣлены веществомъ
бумаги. Такъ какъ вещество это очень тонко, то
другія стороны бумаги не представляютъ замѣт-
ной поверхности и практически являются линіями.
Эти двѣ поверхности, хотя и различны, неотдѣ-
лимы другъ отъ друга.
3. Взгляните на кусокъ бумаги неправильной
формы, показанный на рис. 3, и на эту страницу
въ формѣ прямоугольника. Попробуемъ дать пт§
вому форму послѣдней. °^°
4. Положите кусокъ бумаги неправ<^>ной
формы на столъ и сложите его вдвое. Пдаь полу-
ченный такимъ образомъ сгибъ буде^^Ѵ' X. Это
прямая линія. Теперь проведите полномъ по сгибу
и отдѣлите меньшую часть кусь^^Мы получимъ
такимъ образомъ прямолинейной край.
2
I. КВАДРАТЪ.
Рис^’
I. КВАДРАТЪ.
3
5. Снова, какъ раньше, сложите бумагу по
линіи ВУ такъ, чтобы край X'X накладывался
на себя. Развернувъ бумагу, мы видимъ, что сгибъ
В У идетъ подъ прямымъ угломъ къ краю XX.
Изъ наложенія очевидно, что уголъ УВХ' равенъ
углу ХВ У и что каждый изъ этихъ угловъ равенъ
углу страницы. Теперь, какъ раньше, проведите
ножомъ по второй складкѣ и удалите меньшую
часть.
6. Повторите указанный пріемъ и образуйте
края СВ и В А. Изъ наложенія очевидно, что
углы при А, В, С, В суть прямые, равные другъ
другу, и что стороны ВС, СВ соотвѣтственно
равны сторонамъ ВА, АВ. Этотъ кусокъ бумаги
(рис. з) по формѣ подобенъ этой страницѣ.
7. Его можно сдѣлать равнымъ страницѣ по
величинѣ, взявъ большій кусокъ бумаги и отмѣ-
ривъ АВ и В С равными сторонамъ послѣдней.
8. Такая фигура называется прямоугольни-
комъ. Наложеніе показываетъ, что і) ея четыре
, угла суть прямые и равные, 2) четыре стороны
всѣ равны, но з) двѣ длинныя стороны
между собой, а двѣ короткія между собо|||^
9. Теперь возьмите прямоугол^^^^ кусокъ
бумаги А'В1 СВ и сложите его цДиркось такъ,
чтобы одна изъ короткихъ сторон^°СД легла на
одну изъ длинныхъ, В А', какѣ^та рис. 4. Теперь
4
I. КВАДРАТЪ.
сложите и удалите часть А' В' ВА, которая выда-
ется. Развернувъ листъ, вы найдете, что АВСВ
теперь есть квадратъ, т. е. четыре угла получен-
ной фигуры суть прямые и всѣ ея стороны равны
Рис. 4
10, Ребро сгиба, проходяще^ черезъ два про-
тивоположныхъ угла В, В*^|^ь діагональ этого
квадрата. Другая діагонай^получится, если сло-
I. КВАДРАТЪ.
5
жить квадратъ черезъ другую пару угловъ, какъ
на рис. 5.
11. Мьт видимъ, что діагонали пересѣкаются
другъ съ другомъ подъ прямыми углами и что
онѣ взаимно дѣлятся пополамъ.
Рнс 5
12. Точка пересѣченія діагоналей назі^штся
центромъ квадрата.
13. Каждая діагональ дѣлитъ ква^фЭТъ на два
совпадающихъ при наложеніи пга^Гоу гольныхъ
равнобедренныхъ треугольника, в^Оііины которыхъ
лежатъ въ противоположныхѣ^глахъ квадрата.
6
I. КВАДРАТЪ.
14. Двѣ діагонали вмѣстѣ раздѣляютъ квад-
ратъ на четыре совпадающихъ при наложеніи
прямоугольныхъ равнобедренныхъ треугольника
съ вершинами въ центрѣ квадрата.
15. Теперь снова сложите бумагу, какъ на
рис. 6, наложивъ одну сторону квадрата на про-
тивоположную ей. Мы получимъ сфоъ, проходя-
щій чрезъ центръ квадрата. ОнъЛсфпендикуляренъ
къ другимъ сторонамъ и і) дѣлитъ ихъ пополамъ,
2) параллеленъ также перш^ы двумъ сторонамъ,
I. КВАДРАТЪ.
7
3) самъ дѣлится центромъ пополамъ, 4) дѣлитъ
квадратъ на два совпадающихъ при наложеніи
прямоугольника, изъ которыхъ каждый есть, слѣ-
довательно, половина перваго; 5) каждый изъ этихъ
прямоугольниковъ равновеликъ одному изъ тре-
угольниковъ, на которые квадратъ дѣлится каждой
діагональю.
Рис. 7
16. Еще разъ сложимъ квадратъ^ налагая
другъ на друга двѣ другія стороны.оЙ^лучающійся
теперь иупомянутый въ § 15 сгиб^^^лятъ квадратъ
на четыре совпадающихъ при ѣфМэженіи квадрата.
Роу. Геометрическія упражненія
8
I. КВАДРАТЪ.
17. Снова сложивъ чрезъ тѣ углы меньшихъ
квадратовъ, которые лежатъ на срединахъ сторонъ
большаго квадрата, мы получаемъ квадратъ, впи-
санный въ предыдущій (рис. 7).
18. Этоть квадратъ равенъ половинѣ боль-
шого и имѣетъ тотъ же центръ.
19. Соединивъ средины с ъ внутренняго
квадрата, мы получимъ квадратъ, равный четверти
первоначальнаго (рис. 8). П^торяя этотъ пріемъ,
мы можемъ получить скЗ^ко угодно квадратовъ,
относящихся другъ къ другу, какъ
I. КВАДРАТЪ.
9
і
і і і і ііі
, - , р , И т. д., или — , -2 , —
2 4 О іб 2 22 2
Каждый такой квадратъ равенъ половинѣ
ближайшаго большаго, т. е. четыре треугольника,
остающіеся отъ этого большаго, вмѣстѣ равны
половинѣ его. Сумма всѣхъ этихъ треугольниковъ»
какъ бы мы ни увеличивали число ихъ, не можетъ
быть больше первоначальнаго квадрата и въ концѣ
концовъ составитъ его весь.
Слѣдовательно,
1 + и т. д. до безконечности = і.
2 22 1 23
20. Центръ квадрата есть центръ его опи-
саннаго и вписаннаго круговъ. Послѣдній кругъ
касается сторонъ въ ихъ срединахъ, такъ какъ
онѣ ближе къ центру, чѣмъ всякія другія точки
на сторонахъ.
21. Всякій сгибъ чрезъ центръ квадрата дѣ-
литъ его на двѣ совпадающія при наложеніи тра-
пеціи. Второй сгибъ чрезъ центръ, подъ прямыіѵи^
углами къ первому, раздѣляетъ его на чеъыре
совпадающихъ при наложеніи четереугольнб^а, у
которыхъ два противоположныхъ угла бута пря-
мые. Эти четыреугольники концикличны)?т. е. вер-
шины каждаго лежатъ на одной окАжности.
II. Равносторонній треугольникъ
22. Теперь возьмите квадратный кусокъ бумаги
(рис. 9) и сложите его вдвое, налагая два проти-
II. РАВНОСТОРОННІЙ ТРЕУГОЛЬНИКЪ.
II
сторонъ и перпендикулярный къ этимъ сторонамъ.
Взявъ какую-нибудь точку на этой линіи, сложите
чрезъ нее и два сосѣднихъ, по обѣ стороны отъ
нея, угла квадрата. Мы получимъ такимъ обра-
зомъ равнобедренный треугольникъ, въ основаніи
котораго лежитъ сторона квадрата.
Рис. ю
23. Средняя линія раздѣляет
ный треугольникъ на два совпадай
женіи прямоугольныхъ треугол^^
24. Уголъ при вершинѣ "дйлится пополамъ.
12
II. РАВНОСТОРОННІЙ треугольникъ.
25. Если мы возьмемъ на средней линіи та-
кую точку, разстоянія которой отъ двухъ угловъ
квадрата равны его сторонѣ, мы получимъ равно-
сторонній треугольникъ (рис. іо). Эту точку легко*
опредѣлить, повертывая надъ А А' основаніе А В
около одного изъ его концовъ, пока другой ко-
нецъ, В, не упадетъ на среднюю линію, въ С.
26. Сложите равносторонш^треугольникъ,
накладывая каждую изъ сторопчріа основаніе. Мы
получимъ такимъ образомъ высоты этого тре-
угольника, именно А А', СО (рис. и).
II. равносторонній треугольникъ.
13
27. Каждая изъ высотъ раздѣляетъ треуголь-
никъ на два совпадающихъ при наложеніи прямо-
угольныхъ треугольника.
28. Онѣ дѣлятъ стороны пополамъ и перпен-
дикулярны къ нимъ.
29. Онѣ проходятъ чрезъ одну общую точку.
30. Пусть высоты А А9 и С С9 встрѣчаются
въ О. Проведемъ В О и продолжимъ ее до встрѣчи
съ АС въ В'. Теперь докажемъ, что ВВ' есть
третья высота. Изъ треугольниковъ С О А и СО А,
0 0 = 0 А9. Изъ треугольниковъ О О В и А' О В,
/ О В С = /_А9 В О. Затѣмъ изъ треугольниковъ
А ВВ' и СВ* В слѣдуетъ, что /_АВ' В = /_ВВ'С,
т. е. каждый изъ нихъ есть прямой уголъ. Зна-
читъ, ВОВ' есть высота равносторонняго тре-
угольника А В С. Она также дѣлитъ А С попо-
ламъ въ В'.
31. Можно, сходно съ предыдущимъ, пока-
зать, что О Ау ОВ и ОС равны и что также рав-
ны О А9, ОВ' и ОС.
32. Поэтому изъ Оу какъ центра, можно ощф
сать окружности, которыя пройдутъ соотвѣтственно
чрезъ Ау В и С и чрезъ А9у В' и О. По^рдній
кругъ касается сторонъ треугольника. <^5^
33. Равносторонній треугольникъ^^ В С дѣ-
лится на шесть совпадающихъ отц наложеніи
прямоугольныхъ треугольников’^^глы которыхъ
при точкѣ О всѣ равны, и на^ри совпадающихъ
і4
II. РАВНОСТОРОННІЙ ТРЕУГОЛЬНИКЪ.
при наложеніи, симметричныхъ, конциклическиха»
четыреугольника.
34. Треугольникъ А О С равенъ удвоенному
треугольнику А' О С\ отсюда А 0~-2 О А'. Анало-
гично, В0 = 20В' и СО ~-=^2 ОС. Значитъ, ра-
діусъ круга, описаннаго около треугольника 4ВС,
вдвое больше радіуса вписаннаго круга.
35. Прямой уголъ А квадрата дѣлится линія-
ми А О, Я С на три равныя части. Уголъ В А С= %
прямого угла. Углы С'А О и ОАВ' равный пря-
мого угла каждый. То же относится къ угламъ
при В и С.
36. Шесть угловъ при О равны | прямого
каждый.
37. Перегните бумагу по линіямъ А' В\ В' С
и С'А' (рис. 12). Въ такомъ случаѣ А' В' С есть
равносторонній треугольника». Онъ равень чет-
верти треугольника А В С.
38. А’ В', В' С\ С А1 параллельны соотвѣт-
ственно АВ, ВС, СА и равны половинамъ ихъ.
39. АС', А'В' есть ромба». С'В и
С В' С' А' также.
40. А’В’, В'С, С'А' дѣлятъ сооті^рственныя
высоты пополамъ».
41. СС2-СА С'2=СС* + У^2 = АС2,
сл йдовательно, С С'2 = | . 1 С 2оѵѴ
и потому С С = і- V з . А С 3 • - =
^о‘866 ... X А Ву.
II. РАВНОСТОРОННІЙ ТРЕУГОЛЬНИКЪ.
і5
42. /\АВС= прямоугольнику со сторонами,
равными X О и СО, т. е. А В X іУ 3 • А В =
--=ІУ/з-АВ^ = о-433... ААВ\
Рпс 12
43. Углы треугольника Я С' С относятся°^5к -
ду собою, какъ 1:2:3, а ихъ стороны^Я<акъ
ю:Ѵз<ѵ;. Ж
III. Квадраты и прямоугольники
44. Сложите данный квадратъ, какъ указано-
на рис. 13. Это дастъ хорошо извѣстное доказа-
есть прямоугольный треугольникъ, то квадратъ,.
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
»7
построенный на Е Н^ равенъ суммѣ квадратовъ
на ЕС и СІЕ
Легко видѣть, что Е С есть квадратъ и что
треугольники ЕСН, НВ С, КВС и ЕЕК при
наложеніи совпадаютъ.
Если треугольники ЕСН и НВС отрѣзать
отъ квадратовъ ЕА и ВВ и помѣстить на другіе
два треугольника, то составится квадратъ ЕН СК.
Если АВ = а, СА = 1) и ЕН= с, то а2 В =с\
45. Сложите данный квадратъ согласно рис. 14.
Здѣсь прямоугольники А Е, ВС, СН и В Е при
наложеніи совпадаютъ, какъ и треугольники, изъ
которыхъ они составлены. Е Е С Н есть квадратъ,
какъ и К Е М IV.
Пусть АК=а, КВ = Ъ и IV К= с,
въ такомъ случаѣ а2 -|- В = А, т. е. []КІМЕ
Е^АВСВ = (а-\-Ь)2.
Но квадратъ АВСВ превышаетъ кваДЙй'ъ
КЕМЕ четырьмя треугольниками АК
СМЕ и ВИМ.
А эти четыре треугольника равны
двумъ прямоугольникамъ, т. е.
Значитъ, (а + 6)2 = а1 2 а
і8 III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
46. ЕЕ-^а — Ь и Г\ЕЕСН=(а—Ьу.
Квадратъ Е Е С Н меньше квадрата К Л М 1Ѵ
четырьмя треугольниками Е Ет К, С К Д НЬМ и
ЕММ.
Но эти четыре треугольника составляють два
прямоугольника, т. е. 2 а Ъ.
Слѣдовательно, (а — I))2 = а2 ДА2 — 2 а Ь.
Рис. 14 ДД
47. Квадратъ А В СI) прев^маегь квадратъ
Е ЕСН четырьмя прямоугольниками А Е. В О,
СН и I) Е.
Слѣдовательно, (а — (а — Ь)2= 4 <7 Ь.
Ш. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
19
48. На рис. 15 квадратъ А В С Р = (а-\-Ъ)*
и квадратъ Е Е С ЕІ — (а — А)2. Также квадратъ
АКСК= квадрату ЕЕ СМ=а2. Квадратъ КВЕЕ=
квадрату іѴНМВ=Ь\
Рис. 15
Квадраты АВСО и Е Е С // вмѣстѣ равны
четыремъ послѣднимъ квадратамъ, сложенным^
вмѣстѣ, или дважды взятому квадрату АКС]^
дважды взятому квадрату КВ ЕЕ, т. е.
(<7 — I))2 = 2 а1 , 2 Ь\ ^#4^
49. На рис. іб прямоугольникъ /^рравенъ.
(а 4-^) (а — Ь).
Такъ какъ прямоугольникъ Ш=ГМ, то
прямоугольникъ Р Е = квадрату^^А"— квадратъ
А Е, т. е. (а Ь) (<? —Ь) = а2 —
20
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
50. Если внутри даннаго квадрата построить»
квадраты, у которыхъ былъ бы общимъ одинъ изъ
прямыхъ угловъ даннаго квадрата, то линіи, со-
единяющія вершину этого прямого угла со среди-
нами противолежащихъ сторонъ даннаго квадрата,
раздѣлятъ соотвѣтственныя стороны всѣхъ^внут-
реннихъ квадратовъ пополамъ (рис 17). ^°самомъ
дѣлѣ, углы, которые эти линіи образук^ь съ діаго-
налью, равны и ихъ величина одвдРи та же для
всѣхъ квадратовъ, въ чемъ мрдафг убѣдиться на-
ложеніемъ. Слѣдовательно, срадины сторонъ внут-
реннихъ квадратовъ должнШфежать на этихъ ли-
ніяхъ.
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
21
51. Данъ квадратный кусокъ бумаги АВСВ
(рис. і8); путемъ складыванія найти на А В такую
точку X, чтобы прямоугольникъ АВ'ХВ былъ
равновеликъ квадрату, построенному на А X.
Сложите В С пополамъ и возьмите средину.
Наложите Е В на ЕI) и найдите Е С
такія, чтобы Е С = Е В.
Возьмите А X— АС.
Дополните прямоугольник
ратъ АХКІ.
НХ и квад-
22
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ
Пусть ХИ пересѣкаетъ Е А въ М Возьмите
Е У = ЕВ.
Въ такомъ случаѣ ЕВ — Е В = Е У = А” М и
ХМ^АХ.
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
23
Но АХ* = ^ХМ2 = ВУ\
Слѣдовательно А X = В У и А У = X В.
Отсюда ЛВ'ХВ=А Х\
Въ этомъ случаѣ говорятъ, что точка X дѣ-
литъ отрѣзокъ А В въ среднемъ и крайнемъ от-
ношеніи*)-
Такимъ же образомъ
АВ'АУ=ВУ\
т. е. точка У также дѣлитъ отрѣзокъ АВ въ
среднемъ и крайнемъ отношеніи.
52. Изъ В, какъ центра, можно описать окруж-
ность, которая пройдетъ чрезъ В, С и У. Она
коснется ЕА въ С, такъ какъ ЕС есть кратчай-
шее разстояніе Е отъ линіи ЕС А.
53. Такъ какъ
ВП = ВХ,
то, отнимая ВК, мы получаемъ:
прямоугольникъ XК X У = квадрату СНКР
или АХ' УХ=АУ*,
т. е. АХ дѣлится точкой У въ среднемъ и край-
немъ отношеніи. <
Подобнымъ же образомъ В У дѣлитсяо
среднемъ и крайнемъ отношеніи въ точкѣ Х^у
54. Т акъ какъ А В' X В = А X2,
то 3АВ' ХВ = АХ2^-ВХ' ВС-Ѣ&- СВ
=АВ^ВХ\
*) Это дѣленіе называютъ также пз<^Жмъ дѣленіемъ
аигеа 8 ее Но.
Роу. Геометрическія упражненія
3
24
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
55. Такъ какъ каждый изъ прямоугольниковъ
ВН и УР равенъ АВ' ХВ, то прямоугольникъ
/7УЦ-квадратъ СК = АХ2 = А В' ХВ.
56. Отсюда прямоугольникъ НТ= прямо-
угольнику ВК, т. е. А X* XВ — А В* X У.
57. Отсюда прямоугольникъ Н Х =
= АХ’ ХВ—ВХ2.
58. Пусть А В = а, X В = .ѵ.
Въ такомъ случаѣ (а— а)2=ла, по § 51.
<72Н-.ѵ‘г = Зг7Л', по § 54;
отсюда а2 — з а а — °
И А’ = ?(з — у 5).
Значитъ, л2 = 2 (7 —3 V5)
и а—л =^ (У5 — і) = « X °‘6і8о ...
и
(я —л-)2 = ^(з — У5) = й'2 X 0/3819...
Прямоуг. ВРКХ = (а — х)х °^°
=«2(У 5-2)^x0-2360...
Е X2 = 5 ЕВ’ В\
ЕА =
III. КВАДРАТЫ II ПРЯМОУГОЛЬНИКИ.
25
59. На языкѣ пропорцій
АВ:АХ=АХ:ХВ.
60. Пусть X дѣлитъ А В въ среднемъ и край-
немъ отношеніи. Постройте прямоугольникъ СВХН
(рис. 19). Раздѣлите прямоугольникъ пополамъ
рИС. 19
линіей МXО. Найдите точку X, повер^йѣ ХА
около X такъ, чтобы А упала на М Ш^сдѣлайте
сгибы ХХУ ХВ и ХА. Тогда ВЛЛДУсть равно-
бедренный треугольникъ, у кото^йСЬр углы А В X
и ВХА вдвое больше угла
26
ПІ. КВАДРАТЫ II ПРЯМОУГОЛЬНИКИ.
АХ=ХХ=ХВ
/_АВХ= ^ХХВ
/_ХАХ=/_ХХА
^ХХВ=2^ХАХ
/_АВХ=2^ХАВ.
АХг=М№+4ЛГ
= В X2 — В ЛВ-\-А ХР
= АХ* + АВ.АХ
=АВ-ХВ + АВ-АХ
= АВ'г
Отсюда А Х=А В
и ^ХАВ=2- прямого угла.
61. Прямой уголъ въ А можно раздѣлить на
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
27
пять равныхъ частей, какъ на рис. 20. Здѣсь Аг'
находится согласно § 6о. Затѣмъ сдѣлайте сгибъ
А И' С), раздѣлите перегибомъ А В пополамъ,
сложите по діагонали А С и такимъ образомъ
получите точки 0', Р.
Рис. 21
62. Построить прямоугольный треугольникъ
по данной гипотенузѣ АВ и высотѣ^/
Сдѣлайте сгибъ Е Е (рис. $9° параллельно
АВ на разстояніи заданной ві
'ы.
28
III. КВАДРАТЫ II ПРЯМОУГОЛЬНИКИ.
Возьмите С, средину А В, Найдите II, пере-
гнувъ СВ около С такъ, чтобы В упало на ЕЕ.
Сдѣлайте сгибы чрезъ Н и А, С и В.
А Н В есть искомый треугольникъ.
63. АВ СВ (рис. 22) есть прямоугольникъ.
Требуется найти равновеликій ему квадратъ.
Отмѣрьте В М=В С.
Посредствомъ перегиба найдите О, средину
АМ.
Перегните ОМ около точки О такъ, чтобы
М упала на линію В С; это дастъ вершину Р
прямоугольнаго треугольника А МР.
\ моуголь-
Этотъ квадратъ равенъ данному
нику. (
Такъ какъ ВР=РО и угльИдавны, то тре-
угольникъ В М Р при наложеш^очевидно, совпа-
даетъ съ треугольникомъ
Слѣдовательно, О 8
Значитъ, треугольнтфн I) А Т и 08 Р при
III. КВАДРАТЫ II ПРЯМОУГОЛЬНИКИ.
29
наложеніи совпадаютъ. Поэтому РС=5Р и тре-
угольники и СРТ при наложеніи совпа-
даютъ.
Такимъ образомъ, | | АВСВ можно раз-
дѣлить на три части, которыя можно сложить
вмѣстѣ въ квадратъ РВРО.
Рис. 23
64. Возьмите четыре равныхъ квадрата иіж|>
рѣжьте каждый изъ нихъ на двѣ части линіей|отъ
средины одной изъ сторонъ къ вершиы^^дного
изъ противолежащихъ угловъ. Возьмите^рЙе одинъ
такой же квадратъ. Полученныя йо|еміз частей
квадратовъ можно расположить оо^5 цѣлаго такъ,
чтобы все вмѣстѣ составило"Ш^лный квадратъ,
3°
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
какъ на рис. 23. Это складываніе представляетъ ин-
тересную задачу.
Пятый квадратъ также можно, конечно, раз-
рѣзать на двѣ части, что еще усложнитъ склады-
ваніе.
65. Можно предложить сходныя задачи, раз-
рѣзая квадраты чрезъ одинъ изъ угловъ и одну
изъ точекъ, дѣлящихъ противоположную сторону
на три части, какъ на рис. 24.
III. КВАДРАТЫ II ПРЯМОУГОЛЬНИКИ.
З1
і2 + 22=5
і2 + 3’ = І°
22 + з2 = іЗ-
Этотъ пріемъ можно продолжить дальше, но
число квадратовъ становится слишкомъ неудоб-
нымъ по своей значительности.
68. Снова разсмотрите рис. 13 въ § 44. Ес^щѢ
удалить четыре треугольника по угламъ дав^Го
тамъ квадрата, то останется квадратъ. Есл^руда-
лить два прямоугольника Г К и К С, то І^анется
два соприкасающихся квадрата.
69. Данный квадратъ можно ддарѣзать на
части, которыя можно сложить в^два квадрата.
Есть нѣсколько способовъ для^отбго. Рис. 23, въ
32 III. КВАДРАТЫ II ГірЯМОУГОЛЬНИКИ.
§ 65, наводитъ на слѣдующій изящный методъ:
требуемые куски суть (і) квадратъ въ центрѣ и
(2) четыре симметричныхъ, при наложеніи совпада-
ющихъ четыреугольника по угламъ, вмѣстѣ съ
четырьмя треугольниками. На этомъ рисункѣ линіи
Рие. 26
проходятъ отъ срединъ сторонъ вершинамъ,
угловъ даннаго квадрата и средиЖ квадратъ ра-
венъ одной пятой его. Величий^рредняго квадрата
можно измѣнять, если вм^^^о угловъ на сторо-
нахъ даннаго квадрата братѣ другія точки.
III. КВАДРАТЫ И ПРЯМОУГОЛЬНИКИ.
33
70. Данный квадратъ молено раздѣлить на три
равные квадрата слѣдующимъ образомъ (рис. 26):
Возьмите В С = половинѣ діагонали квадрата.
Сдѣлайте сгибъ чрезъ С и С
Сдѣлайте сгибъ В М перпендикулярно къ С С.
Возьмите МР, С V и IV Р каждый = В М.
Сдѣлайте сгибы РН, 1Ѵ К, ЬР подъ прямы-
ми углами къ С какъ на рис. 26.
Возьмите РК=В М и перегните по КЕ подъ
прямымъ угломъ къ IV К.
Въ такомъ случаѣ куски 1,4 и 6, зсъ5, и 2
съ 7 образуютъ три равныхъ квадрата.
Теперь СС2==зВбД
а изъ треугольниковъ С В С и С М В
ВМ ВС
ВС ~СС’
Полагая ВС—а} мы имѣемъ
IV. Пятиугольникъ
71. Изъ квадрата АВСВ вырѣзать правиль-
ный пятиугольникъ.
Раздѣлите ВА въ крайнемъ и среднемъ от-
ношеніи точкой X и возьмите М по срединѣ А X.
Рис. 27
Тогда АВ-АХ=ХВ* и^М=МХ.
Возьмите ВХ=А
Тогда М 7Ѵ= X В.
IV. ПЯТИУГОЛЬНИКЪ.
35
Отложите X Р и МX равными М такъ,
чтобы РиТ? лежали соотвѣтственно на ВС
Отложите КО и Р<О=МХ и ХР.
МХРО.Х есть искомый пятиугольникъ.
На рис. 19, стр. 25, отрѣзокъ А А, равный А Ву
имѣетъ точку X на перпендикулярѣ МО. Если
передвинуть А по АВ на разстояніе МВ, то,
очевидно, А передвинется на В С и X въ М.
Поэтому, на рис. 27, ХХ=АВ. Аналогично
МР=А В. Слѣдовательно, РР равно А В и па-
раллельно ему.
прямого /
и потому А КМК=1 прямого X-
Аналогично /_РХМ=^ прямого
Изъ треугольниковъ МРК и ОРХ полу-
чается, что /_Х М Х= /_ХОР = прямого
Такъ какъ каждый изъ трехъ угловъ Л/, А
и 0_ пятиугольника равенъ | прямого угла, то ос-
тальные два угла вмѣстѣ равны 12/5 прямого угла,
и кромѣ того они равны. Слѣдовательно, каждый
изъ нихъ равенъ прямого угла.
Значитъ, всѣ углы этого пятиугольника ра^іы.
Стороны этого пятиугольника также ^^йны,
по построенію.
72. Основаніе МЫ пятнугольник^^вно ХВ,
т. е. равно (У5 — і)=А В X с^бгоо. • • , § 5&
Наибольшая ширина пяти^юльника есть А В.
зб
IV. ПЯТИУГОЛЬНИКЪ.
73. Если р будетъ высота, то
А В* = р* +
/ТЧ-1’
2
= />2 + ^В2.3-Е5.
Отсюда р2=АВ-\і
3 — ^5^
8 )
И /=Л5.Уіо+2У5
4
= А В X о’95іо- • В соз і8°.
74. Если К будетъ радіусъ описаннаго круга,
о АВ гАВ
то К =---- = - - -
2 СОЗ і8° ]/ю-|-2У5
=АВл/5~ 7/5
Г ІО
А 5X0-5257...
75. Если чрезъ г означимъ радіхХй, вписан-
наго круга, то изъ рис. 28 очевш^^^что
-лв.Ѵ^(|/Х|/ХЙ
IV. ПЯТИУГОЛЬНИКЪ.
37
Ѵб —(Ѵ5— і)'
Ѵ40
=АВ.
^5 + ^5
= АВХ 0’4253....
38
IV. ПЯТИУГОЛЬНИКЪ.
77. Пусть точки пересѣченія РК съ МО и
будутъ, на рис. 27, Е и Р.
Тогда, такъ какъ —і)..,§72>
УВ
„ г г г> МА і
то 1<г.~г Р=------• - -
2 СО8 360
=АВ.^-- -
/5 + *
=АВ.*—Ѣ5
ЕЕ=АВ— 2НЕ=АВ- АВ(3- /5)
= АВ(]А5 — 2).. .(2)
ХГ=М1Ѵ.
ІіЕ:1іЕ=НЕ:ЕГ (по § 51) .......(3)
К5 —1 :3— /5 = 3— /5:2(/5 — 2) • • • -(4)
такъ какъ А В=МIV.
По § 76 площадь пятиугольника
= АВ*.
IV. ПЯТИУГОЛЬНИКЪ.
39
Значитъ, площадь внутренняго пятиугольника
= ЕГг. — . {,/25+10/ 5
4
=лв+(ГЗ-2)2.Л-р25+іоу5.
Большій пятиугольникъ относится къ мень-
шему, какъ
МЫРЕГ*
=2:(7 — 3/5)
= і: 0*145898 ...
78. Если на рис. 27 взять углы ЕК и ЕЕ
равными угламъ ЕКО или ЕОР, причемъ точки
К, Е лежатъ на сторонахъ О Р и ОР соотвѣт-
ственно, то ЕЕЕОК будетъ правильный пяти-
угольникъ, при наложеніи совпадающій съ внут-
реннимъ пятиугольникомъ. Такимъ же образомъ
можно построить пятиугольники и на остальныхъ
сторонахъ внутренняго пятиугольника. Получаю-
щаяся фигура изъ шести пятиугольниковъ очень
интересна.
Р о у. Геометрическія упражненія
4
V. Шестиугольникъ
79. Вырѣзать изъ даннаго квадрата правиль-
ный шестиугольникъ.
>
Рис. 29Іор
Сложите квадратъ средины противопо-
ложныхъ сторонъ и полуЩ^е линіи АОВ и С О В.
V. ШЕСТИУГОЛЬНИКЪ.
41
На двухъ отрѣзкахъ А О и О В постройте
равносторонніе треугольники (§ 25) АОЕ, АНО]
ВВС и вос.
Проведите ЕЕ и НС.
АНСВРЕ будетъ правильный шестиуголь-
никъ.
Нѣтъ необходимости приводить доказатель-
ство этого.
Наибольшая ширина шестиугольника будетъ
АВ.
80. Высота шестиугольника будетъ
. А 5=0’866 ....\АВ.
2
81. Если 7? есть радіусъ описаннаго круга, то
В=-АВ.
2
82. Если г есть радіусъ вписаннаго круга, то
. Л 5=0’433 • • • • X а В.
4
83. Площадь шестиугольника равна 6 площа-
дямъ треугольника НС О,
\6,^ѴзАВ Г
4 4
= 3'8 3 . А 52=о-6495 ....
Слѣдовательно, шестиугольни^°=|-.АВ.СВ
или въ раза больше равносторонняго треуголь-
ника, построеннаго на А В.
42
V. ШЕСТИУГОЛЬНИКЪ.
84. Рис. 30 представляетъ примѣръ орнамента
изъ равностороннихъ треугольниковъ и шести-
угольниковъ.
85. Образуйте шестиугольникъ изъ равносто-
ронняго треугольника, перегнувъ его такъ, чтобы
вершины сошлись въ центрѣ.
Рис. 30
Сторона этого шестиуго^^^іка равна 4 сто-
роны взятаго равносторонняго треугольника.
Площадь этого шес^у^ольника=^ площади
взятаго треугольника.
V. ШЕСТИУГОЛЬНИКЪ.
43
86. Шестиугольникъ можно раздѣлить на рав-
ные правильные шестиугольники и равносторон-
ніе треугольники, какъ показываетъ рис. 31, дѣлая
Рис. 31
перегибы чрезъ точки, дѣлящія стороны на три
равныя части.
VI. Восьмиугольникъ
87. Въ данномъ квадратѣ построить правиль-
ный восьмиугольникъ.
Рис. 32
Въ данный квадратъ впишите другой квад-
ратъ, соединивъ срединцХд, Д С, Ь сторонъ
даннаго.
VI. ВОСЬМИУГОЛЬНИКЪ.
45
Раздѣлите пополамъ углы между сторонами
даннаго и вписаннаго квадратовъ. Пусть эти бис-
сектрисы пересѣкаются въ Р, С и II.
АЕВЕССВН будетъ правильный восьми-
угольникъ.
Треугольники АЕВ, ВЕС, С С Г) и ОНА
равнобедренные и при наложеніи совпадаютъ.
Слѣдовательно, стороны полученнаго восьмиуголь-
ника равны.
Каждый изъ угловъ при вершинахъ Е, Е,
С, Н тѣхъ же треугольниковъ равенъ полутора
прямому углу, такъ какъ ихъ углы при основаніи
равны четверти прямого угла каждый.
Слѣдовательно, каждый изъ угловъ восьми-
угольника при точкахъ Л, В, С, В равенъ полу-
тора прямому углу.
Значитъ, всѣ углы нашего восьмиугольника
равны между собою.
Наибольшую ширину восьмиугольника пред-
ставляетъ сторона даннаго квадрата а.
88. Если К есть радіусъ описаннаго кр^ѣа,
а а сторона взятаго квадрата, то
73_
89. Каждая сторона стягива^
центрѣ, равный половинѣ прябфо.
уголъ при
46
VI. ВОСЬМИУГОЛЬНИКЪ.
90. Проведите радіусъ О Е} пусть онъ пере-
сѣкаетъ А В въ точкѣ К (рис. зз). Тогда
АК=ОК=СА =-^= .
К 2 2І/ 2
VI. ВОСЬМИУГОЛЬНИКЪ.
47
= — . (2- 1^2).
4
Слѣдовательно, А Е=^. |/2 — /2.
91. Высота восьмиугольника есть С Е (рис. 33).
Но СЕ*=АС* — АЕ*
2 2
=а2 — — . (2--- V 2) = — . (2-НК2)-
4 4
Слѣдовательно, С Е= • |/2 + V 2
92. Площадь восьмиугольника равна восьми
площадямъ треугольника А О Е и
=4[ОЕ.АК=4г =
93. Можно также получить правильный вось-
миугольникъ, дѣля углы даннаго квадрата на че-
тыре равныя части.
Легко видѣть, что ЕЕ=АѴсторон^
даннаго квадрата.
ХЕ=а(Ѵ2— і);
ХЕ= IV Н= IV К;
= а
48
VI. ВОСЬМИУГОЛЬНИКЪ.
Но КТ^а^а? (У 2—і)2 = г72(4 — 2/2)
Слѣдовательно, {/4 — 2У 2.
Такимъ образомъ СЕ=ХХ—2ХЕ
=аѴ я— 2б/(У2— і)
=а (2 — V2).
VI. ВОСЬМИУГОЛЬНИКЪ.
49
и
Я22=Я02 + 0^2
^(6-4у2 + 2)
4
= а2(2 — V 2).
Слѣдовательно, Я2Г=л|/2—И 2.
НК=К2.—Н2.
=«1/4 — 2 У 2—а |/2— У 2
= а . (|/г—У2). (У2 — і)
=а ]/ іо — 7 1/2.
А ѣ = — НК = — і/то — 7 У 2.
2 2 ѵ
/I А=^^2О 14 V 2.
Дѣля стороны восьмиугольника пополамъ и
соединяя полученныя такимъ образомъ точки съ
центромъ, мы раздѣлимъ перигонъ (=4 прямымъ)
на шестнадцать равныхъ частей. Такимъ образомъ
можно легко построить іб-угольникъ, затѣмъ
32-угольникъ и вообще правильный 2и-угффЙйкъ.
94. Площадь восьмиугольника радм& восьми
площадямъ треугольника НО А и
=8.|Яо4ЙЙ
5о
VI. ВОСЬМИУГОЛЬНИКЪ.
=НО^2
\а ( /—а]2 /~
= — (2 - у 2) . 2 |/2
4
. (6 — 41/2)
= ^•(3 V 2 — 4)
*=а2.Ѵ2 . (/2 — і)2.
95. Отношеніе этого восьмиугольника къ вось-
миугольнику § 92
— (2—К2)2 : і или 2 : (К2 4- і)2;
ихъ основанія относятся между собою, какъ
VII. Девятиугольникъ
96. При помощи складыванія бумаги можно
довольно точно раздѣлить уголъ на три равныя
Рис. 35
части и такимъ путемъ построит;
правильный девятиугольникъ.
г&йблизительно
52
VII. ДЕВЯТИУГОЛЬНИКЪ.
Получите три равныхъ угла при центрѣ рав-
носторонняго треугольника (§ 25).
Для удобства складыванія вырѣжьте эти три
угла А О С, Г О С и СО А.
Раздѣлите каждый изъ нихъ на три части,
какъ на рис. 35, и отложите на ихъ сторонахъ
отрѣзки = О А.
97. Каждый изъ угловъ девятиугольника ра-
венъ 14/9 прямого угла или 140°.
Каждая сторона девятиугольника стягиваетъ
уголъ при центрѣ въ | прямого угла или 40°.
Половина этого угла есть угла девяти-
угольника.
98. 0^4 = 67 2, гдѣ а есть сторона квадрата;
она есть также радіусъ описаннаго круга 7?.
Радіусъ вписаннаго круга
= 7? . СО8 20°
= ^а СО8 20°
= |~ X 0-9396926
= а X 0-4698463.
Площадь девятиугольника равна лерйти пло-
щадямъ треугольника А О Ь и
=9.7?. ^Т?5Іп 4<-Хх
= |7?2.5ІП4О^^>
9а2., зХ о г
= у X сф27876
- -Х ХоХХ'З6-
VIII. Десятиугольникъ и двѣнадцати-
угольникъ
99. Рис. 36, З7 показываютъ, какъ можно
получить правильные десятиугольникъ и двѣна-
дцатиугольникъ изъ пятиугольника и шестиуголь-
ника соотвѣтственно.
Рис. 36
Главную часть работы состшѣггѣ полученіе
угловъ при центрѣ.
54
VIII. ІО УГОЛЬНИКЪ И 12 УГОЛЬНИКЪ.
На рис. 36 радіусъ вписаннаго въ пятиуголь-
никъ круга принятъ за радіусъ круга, описаннаго
около десятиугольника, чтобы послѣдній не вышелъ
за предѣлы взятаго квадрата.
100. Правильный десятиугольникъ можно по-
лучить также слѣдующимъ образомъ:
Рис. 37
Найдите точки X, У (рис. 38), въ § 51,
раздѣливъ А В въ среднемъ и щЖЙйемъ отно-
шеніи.
Возьмите М посрединѣ^^^;
Сдѣлайте перегибы ХОтИ О, УВ подъ пря-
мыми углами къ А В.
VIII. ІО УГОЛЬНИКЪ И 12 УГОЛЬНИКЪ.
55
Возьмите точку О на М О такъ, чтобы
У О =А У или УО=ХВ.
Продолжите УОи ХО до пересѣченія съ
X С и У В въ точкахъ С и И.
Рис. 38 %
Раздѣлите углы ХО С и И ОУ на чеж|)е
равныя части линіями НО Е, КОЕ и Ь
Отложите О//, ОК, ОЕ, ОЕ, О 0 0
равными ОУ или ОX.
Соедините послѣдовательно точда А", /У, К,
Ц С, Д Е. Е, С и У Какъ въ
/ У0Х=1 прямого }Оа=з60.
Роу. Геометрическія упражненія
5
IX. Пятнадцатиугольникъ
101. Рис. 39 показываетъ полученіе пятна-
дцатиугольника изъ пятиугольника.
• Пусть А В С О Е будетъ пятиугольникъ и О
его центръ.
Рис. 39
должите В О до пересѣченной А В въ точкѣ К.
IX. ПЯТНАДЦАТИУГОЛЬНИКЪ.
57
Сдѣлайте перегибъ С Е Е1 подъ прямымъ
угломъ къ О Г. Отложите О С = О Н=О П.
Въ такомъ случаѣ ССН есть равносторонній
треугольникъ и углы ООО и НОИ равны 1200
каждый.
Но уголъ ВО А равенъ 1440; слѣдовательно,
уголъ ООА равенъ 240.
Значитъ, отъ угла ЕОА, равнаго 720, линія
О С отдѣляетъ третью часть.
Раздѣлите уголъ ЕОС пополамъ линіей О Е,
пересѣкающей ЕА въ точкѣ Д и пусть ОС пе-
ресѣкаетъ ЕА въ точкѣ М\ тогда
ое=ом.
На О А и О Е отложите ОР м равными
ОЕ или ОМ.
Въ такомъ случаѣ РМ, МЕ и ЕО будутъ
«сторонами пятнадцатиугольника.
Поступая подобнымъ же образомъ съ углами
А ОВ, ВО С, С О В и В О Е, мы получимъ и всѣ
остальныя стороны пятнадцатиугольника.
X. Ряды
4риѳмстичсская прогрессія
102. Рис. 40 иллюстрируетъ ариѳметическую
прогрессію. Горизонтальныя линіи влѣво отъ діа-
гонали, включая верхній и нижній края, образу-
X. Р я д ы.
59
103. Части горизонтальныхъ линій вправо
отъ діагонали также образуютъ ариѳметическую
прогрессію, но онѣ идутъ въ обратномъ порядкѣ,
постепенно уменьшаясь отъ одного члена къ дру-
гому на ту же самую величину.
104. Вообще, если I есть послѣдній членъ
прогрессіи, 5 ея сумма, то предыдущій чертежъ
графически доказываетъ формулу
5 = ^ («+/).
105. Если между а и с въ прогрессіи есть
еще одинъ членъ, то этотъ средній членъ равенъ
а -|-г
2
106. Для того чтобы между а и I вставить п
•среднихъ членовъ, вертикальную линію нужно
перегибами раздѣлить на п -ф-1 равныхъ частей.
Разность между двумя сосѣдними членами будетъ
I — а
107. Обращаясь къ обратному ряду и педю-
ставляя а и I одно на мѣсто другого, мы^юлу-
чимъ прогрессію
а, а —(I, а — ъсі,..., /.
Ея члены положительны, пок^ѴОф/— і)б/,
послѣ чего они будутъ нулемъотрицатель-
нымъ числомъ. ДД
6о
X. Р я д ы.
Геометри ческая прогрессія
108. Въ прямоугольномъ треугольникѣ пер-
пендикуляръ, опущенный изъ вершины прямого
угла на гипотенузу, есть среднее геометрическое
между отрѣзками гипотенузы. Отсюда, если длины
двухъ отрѣзковъ представляютъ собою два сосѣд-
нихъ или сосѣднихъ черезъ одинъ члена геоме-
трической прогрессіи, то эту прогрессію можно
Рис. 41
опредѣлить согласно рис. 41. Здѣсь О Р^О Р2>
О Р3, О Р4 и О Рь составляютъ геомед^іческую
прогрессію, знаменатель отношенія іюШртй равенъ
ОЛ:ОР2.
Если ОРХ есть единица ѵж&ны, то данная
прогрессія состоитъ изъ степежЙ отношенія, пока-
затели которыхъ представ^Мтъ рядъ натураль-
ныхъ чиселъ.
X. Р я д ы.
бі
109. Если представить данную прогрессію въ
видѣ а, а г, а г\..., то
Рх Р^=а Vі + г2.
Рг Р3 = а г Кт + г2..
Р3 Р, = а Р V і + Р.
Значитъ, эти отрѣзки также образуютъ гео-
метрическую прогрессію съ знаменателемъ отно-
шенія г,
110. Члены указанной прогрессіи можно взять
въ обратномъ порядкѣ, причемъ отношеніе будетъ
правильной дробью. Сумма такой прогрессіи, про-
долженной до безконечности, будетъ
ор,-ор;
111. Поступая согласно указанію § ю8, можно
найти геометрическое среднее между двумя дан-
ными отрѣзками; продолжая этотъ пріемъ, можно
найти з, 7, 15 и т. д. среднихъ членовъ. Вообще?
можно найти 2м—і среднихъ, гдѣ п есть
положительное число.
112. Простымъ перегибаніемъ бума^ь^ чрезъ
извѣстныя точки нельзя найти дв^д^Ьметриче-
скихъ среднихъ между двумя дашпдмй отрѣзками..
Это можно выполнить, однако, а^ъ^ующимъ обра-
зомъ: на рис. 41 даны ОРХ ^^ОР^ требуется
6з
X. РЯДЫ.
найти Р2 и Р3. Возьмите два прямыхъ угла изъ
бумаги и положите ихъ такъ, чтобы одинъ изъ
нихъ вершиной лежалъ на прямой О Р2 и одна
сторона его проходила чрезъ Рр а другой ле-
жалъ вершиной на прямой О Р3 и одна сторона
его проходила чрезъ Р4; затѣмъ перемѣщайте ихъ,
сохраняя указанное условіе, такъ, чтобы напра-
вленія двухъ другихъ сторонъ ихъ совпали. Вер-
шины угловъ тогда опредѣлятъ положеніе Р2 и Р3.
113. Этотъ пріемъ дастъ кубическій корень
изъ даннаго числа, такъ какъ, если О Рх есть еди-
ница, то нашъ рядъ есть і, г, г2, г3.
114. Съ этой задачей связана любопытная
легенда. „Аѳиняне, страдая въ 430 г. до Р. X. отъ
сильной эпидеміи сыпного тифа, обратились къ
Делосскому оракулу съ просьбой указать, какъ
имъ избавиться отъ бѣды. Аполлонъ отвѣтилъ,
что они должны удвоишь величину его алтаря, имѣв-
шаго форму куба. Ничего не могло быть легче,
казалось, и былъ сооруженъ новый алтарь, каждая
сторона котораго была вдвое больше, чѣ^ь^у ста-
раго. Справедливо разгнѣванный богѣрсусилилъ
эпидемію еще больше. На Делосъ ота^^или новую
депутацію, которой онъ отвѣтил^Слто съ нимъ
шутить нельзя и что его алта^ долженъ быть
ровно вдвое больше. Подозр^йя тайну, аѳиняне
обратились къ геометрамт^Зямый знаменитый изъ
нихъ, Платонъ, уклонил^ отъ этой задачи и по-
X. РЯДЫ.
63
слалъ пхъ къ Евклиду, который и изучилъ спе-
ціально весь этотъ вопросъ". (Имя Евклида было
поставлено вмѣсто имени Гиппократа). Гиппократъ
свелъ вопросъ къ нахожденію двухъ геометриче-
скихъ среднихъ между двумя данными отрѣзками,
изъ которыхъ одинъ вдвое длиннѣе другого. Если
члены этого ряда обозначимъ чрезъ я, х, у и 2<т,
то х3=2я3. Ему однако не удалось найти этихъ
среднихъ. Ученикъ Платона Менэхмъ, жившій
между 375 и 325 г. до Р. X., далъ три слѣдую-
щихъ уравненія:
а: х=х :у =у: 2а.
Это соотношеніе даетъ три слѣдующихъ ура-
вненія:
х2—ау .............(і)
у2— ъах.............(2)
ху=2а2 .............(3)
(і) и (2) представляютъ уравненія параболъ,
а (3) уравненіе равносторонней гиперболы. Урав-
ненія (і) и (2) или уравненія (і) и (3) даютъ
х3 = 2<?3. Для рѣшенія задачи надо было взят^
пересѣченіе (а) двухъ параболъ (і) и (2) и іШЫ-
сѣченіе (/?) параболы (і) съ равностороннжЯги-
перболой (3). ЛС?
115. Перегните бумагу по^^кимъ-нпбудь
линіямъ АК, РВ, какъ на рис^р, гдѣ Р есть
точка на АВ, а В на краю бумаги. Перегните
64
X. Р я д ы.
еще разъ такъ, чтобы А Р и РК обѣ совпали съ
линіей РВ. Пусть полученные сгибы будутъ РХ,
РУ, а точки X, У лежатъ на АВ.
Въ такомъ случаѣ точки А, X, В, У соста-
вятъ гармоническій рядъ. Это означаетъ, что от-
рѣзокъ АВ дѣлится внутренне въ точкѣ X и
внѣшне въ точкѣ У такъ, что
АХ:ХВ=А У:ВУ
Очевидно, что всякая линія, пересѣкающая
РА, РX, РВ и РУ, дѣлится ими гармонически.
Рис. 42
116. Найдите У по даннымъ А, X. Для
этого перегните бумагу по процзвШьной линіи
ХР и отмѣтьте на ней точку /^Соотвѣтствую-
щую точкѣ В, Сложите по лингвѣ АКРК и В Р.
Раздѣлите уголъ В Р Р попрЖргь линіей Р У, сдѣ-
лавъ сгибъ чрезъ точку чтобы Р В и Р К
совпали.
X. РЯДЫ.
Такъ какъ X Р дѣлитъ уголъ А РВ попо-
ламъ, то
АХ\ХВ=АР\ВР
^АУ:В У.
117. АХ:ХВ=А У:ВУ
или А У— X У: X У— В У=А У: В У
Такимъ образомъ, А У, X У и ВУ образу-
ютъ гармоническій рядъ, а X У есть гармониче-
ское среднее между А У и В У.
Подобнымъ же образомъ А В есть гармони-
ческое среднее между А X и А У,
118. Если даны ВУ и ХУ, то для того, чтобы
найти третій членъ А У, намъ нужно только по-
строить какой-нибудь прямоугольный треугольникъ,
на ХУ, какъ гипотенузѣ, и взять уголъ АРХ=
углу ХР В.
119. Пусть АХ=а, АВ=Ь и А У=с.
Тогда
или
или
Когда
Когда
•66
X. РЯДЫ.
Поэтому, когда X есть средина АВ, У лежитъ
на безконечномъ разстояніи справа отъ В. У при-
ближается къ В по мѣрѣ приближенія X къ этой
точкѣ и наконецъ всѣ эти точки совпадаютъ
При перемѣщеніи X отъ средины А В влѣво,
У перемѣщается съ безконечнаго разстоянія слѣва
къ точкѣ А и наконецъ Ху А и У совпадаютъ.
120. Если Е есть средина АВ, то
ЕХ.Е }Т=ЕА^ЕВ*
для всѣхъ положеній X и У относительно А и В.
Каждая изъ двухъ системъ паръ точекъ X
и У называется системой въ инволюціи; точка Е
носитъ названіе центра, а А или В фокуса систе-
мы. Эти двѣ системы вмѣстѣ можно разсматри-
вать, какъ одну.
с - - - « -
Рис. 43
121. По даннымъ А X и А ^ріъжно найти В
слѣдующимъ образомъ:
Продолжите ХА и возьмите АС = ХА.
Найдите средину /)<^^ѣзка А У.
Возьмите СЕ = /9^ф^илиАЕ = ВС.
X. РЯД ы.
Перегните бумагу чрезъ А такъ, чтобы пря-
мая АЕ была перпендикулярна къ САУ.
Найдите Е такъ, чтобы Б Е = Б С.
Сложите по ЕЕ и проведите ЕВ такъ, что-
бы ЕВ была перпендикулярна къ ЕЕ.
СБ есть среднее ариѳметическое между АХ
и АУ
А Е есть среднее геометрическое между А X
и А У.
А Е есть также среднее геометрическое между
С Б или А Е и А В.
Значитъ, А В есть среднее гармоническое
между А X и л 1 У.
122. Вотъ очень простой способъ найти сред-
нее гармоническое между двумя данными отрѣз-
ками.
сторонахъ квадрата отрѣзки
даннымъ. Получите діагонали
Возьмите на
АВ, СБ) равные
А Б, В С и стороны А С) В Б трапеціи А С
Проведите сгибъ чрезъ Л, точку пересѣчен^уЬді-
агоналей, такъ, чтобы прямая ЕЕ С біЖг пер-
пендикулярна къ другимъ сторонамъ кшйфата или
параллельна АВ и СБ. Пусть /^Лбцгересѣкаетъ
А С и В Б въ Е и С. Въ такомъ^ф^чаѣ Е С есть
среднее гармоническое между АС^и. СБ.
68
X. Р я д ы.
Такъ какъ
и
ВЕ__ СЕ
АВ~ СВ
ЕС _ЕЕ _ ЕВ
СЁ~ СВ СВ ’
ЕЕ ЕЕ _СЕ ЕВ
АВ'СВ~ СВ+ СВ~
X. Р я д ы.
69
124. Для того чтобы найти геометрическое
среднее, возьмите на НК отрѣзокъ НЕ — ЕС.
Проведите сгибъ Е М подъ прямымъ угломъ къ
НК. Возьмите О, средину НК, и найдите наЬМ
такую точку М, чтобы ОМ=ОН. Отрѣзокъ
НМ есть геометрическое среднее между А В и
СВ, а равно и между ГС и НК. Такимъ обра-
зомъ, мы видимъ, что геометрическое среднее
двухъ количествъ есть геометрическое среднее
ихъ ариѳметическаго и гармоническаго среднихъ.
Рис. 45
Суммованге нѣкоторыхъ рядоі^
125. Найти сумму ряда
X. РЯДЫ.
Раздѣлите данный квадратъ на нѣкоторое
число равныхъ квадратовъ, какъ на рис. 45. На
немъ взято 49 квадратовъ, но ихъ число можно
увеличить по произволу.
Число квадратовъ будетъ очевидно квадра-
томъ нѣкотораго числа, а именно, квадратомъ
числа дѣленій стараго даннаго квадрата.
О 1 А 2. В 3 С 4 О 5 Е Ь Г 7
а 2 4 Ь Я 1 О 12 14
ъ 3 Ь 9 12 >5 (8 21
4 8 12 Но 20 24 2»
а 5 ІО I 5 20 25 30 35
е Іо 12 ІЯ 24 30 З/о 42
г 7 14 21 2» 35 42 4<Ь
Рис- 46
Каждый изъ малыхъ квадр^овъ будемъ
считать единицей; фигуру, образованную едини-
цами А 0-\-а, будемъ называть гномономъ.
Числа квадратовъ едірЦіщъ въ каждомъ изъ
гномоновъ А О а, В О Ь д. будутъ соотвѣт-
X. РЯДЫ.
Слѣдовательно, сумма ряда і, 3, 5, 7, 9, и,
13 есть у2.
Вообще і + 3 + 5 + •. • • + (27/ — і) = п2.
126. Найти сумму кубовъ и первыхъ нату-
ральныхъ чиселъ.
Разбейте квадратъ перегибами на 49 равныхъ
квадратовъ, какъ въ предыдущемъ параграфѣ, и
отмѣтьте буквами гномоны. Заполните эти ква-
драты числами таблицы умноженія.
Число въ начальномъ квадратѣ есть і = і3.
Суммы чиселъ въ гномонахъ А а, В Ь и т. д.
суть 2 -(- 4 2 = 23, З3> 43> 53’ 63 и 73.
Сумма чиселъ въ первомъ горизонтальномъ
ряду есть сумма семи первыхъ чиселъ натураль-
наго ряда. Назовемъ ее 5.
Тогда суммы чиселъ въ рядахъ />, с, сі и
т. д. суть
25, 35, 45, 55, 6з II 75.
Поэтому сумма всѣхъ этихъ чиселъ есть
Значитъ, сумма кубовъ первыхъ семи чиселъ
натуральнаго ряда равна квадрату суммы эр^₽
чиселъ.
Вообще,
Слѣдовательно, 2
Р о у. Геометрическія упражненія
6
72
X. РЯДЫ.
А также [«. (я+і)2] — [(и — і). п\- = (и24-я)2 —
— (п~ — п)-=4 ? А
Полагая п = і, 2, 3... по порядку, имѣемъ
4.і3 = (і.2)’2 — (о.і)2
4.23 = (2.3)-’ — (І.2)2
4-33 = (3-4У2 —(2-ЗУ2
4. и® = [и. (и -|-1) ]2; — [ (« — і).«|2.
Складывая, мы получаемъ
4^тг = \п(п 1) ]2?
откуда
2іг =
'//(/г—(— і)'
127. Если 8п есть сумма первыхъ п натураль-
ныхъ чиселъ, то
8ц^ 8п~—і — 11
128. Найти сумму ряда
і . 2+2.3+ з. 4+ ... +(п — і).
На рис. 46 числа, расположена®? по діаго-
нали, начиная съ і, представляю’
туральныхъ чиселъ по порядку^
ъадраты на-
Числа одного гномона О\^ожно вычесть изъ
соотвѣтственныхъ чисед^^лѣдующаго гномона.
Этотъ пріемъ даетъ
X. РЯДЫ.
73
п* — {и — і)3 = п1 —{и — і)2
+ 2 [п(п — і) + (;г— 2)—(у/ — з).... + т]
— и2-]- (п — і)2 —[—2 [і —2.... —[— (уу— і)]
= п~ -\-(п — і)2 -|- п(п — і)
— [и — (п — I /]2 —[— 3 (/г — т) п
= і+з(^ —
Но ііл — {и — і)3 = і -}- з {п — і) п
и (уу -- і)3 — (у/ — 2)3 = г 3 --2) (УУ — П
23 — I3 = I -[-3.2.1
I3 — О3 = I -)-о.
Сложеніе этихъ равенствъ даетъ
7/з = п 3 [т <2 2 3 _ _р _ г)
Значитъ,
І.2 + 2.3.... + (уу— І).У2
У/3 —11__{и — і) у/(уу 4- I).
~Т- з
129. Найти сумму квадратовъ первыхъ п на-
туральныхъ чиселъ
__ 2_
I Іоэтому
2
74
X. РЯДЫ.
= " (>1 +1)
6
[
2
130. Найти сумму ряда
і’2 + з2+52----+(2« — і)2-
Такъ какъ /г5— (п—і)3 = п~(;/ — і)2-}-//(п—і),
по § 128, =(2/г—і)2— (и— і).п,
то, полагая н = т, 2, 3...,
мы найдемъ і3 — о3 = і2 — о. і
23 — і3 = з2 — 1.2
3:і —23 = 52 —2-3
11? — (11 — і)3 — (2/7 — і)2 — (;г — 1). п.
Складывая, мы имѣемъ
Отсюда
и ’ — и
— и
XI. Многоугольники
131. Найдите центръ О квадрата, перегиба*?
его по діагоналямъ. Раздѣлите пополамъ прямые
углы при центрѣ, затѣмъ эти половины прямыхъ
угловъ и т. д. Такимъ образомъ вы получите
при центрѣ 2й равныхъ угловъ; каждый изъ нихъ
будетъ равенъ прямого угла (и — цѣлое поло-
жительное число). На каждой изъ линій, идущихъ
изъ центра, отложите по равному отрѣзку. Со-
единяя затѣмъ концы этихъ радіусовъ въ послѣ-
довательномъ порядкѣ, вы получите правильный
многоугольникъ о 2м сторонахъ.
132. Найдемъ величины периметровъ и пло-
щадей такихъ многоугольниковъ. На рис. 47 пусть
О А и ОАХ будутъ два взаимно перпендикуляру
пыхъ радіуса. Пусть радіусы СС/2, ОА3, О А± иот<^к
дѣлятъ прямой уголъ Ах О А на 2, 4, 8.... ч^р^й.
Проведите прямыя А Аѵ А А21 АА3...., і^рѣча-
ющія радіусы ОА21 0А31 ОА4.... подт^рямыми
углами въ точкахъ В2, В3.... В^^комъ слу-
чаѣ /д, В2, В3.... суть средины соотвѣтствующихъ
хордъ; ААѴ Л/12, А А3, А А4. /^будутъ стороны
76
XI. МНОГОУГОЛЬНИКИ.
вписанныхъ многоугольниковъ О 22, 23, 24. ... сто-
ронахъ, а 0Вѵ ОВ^,... будутъ» соотвѣтствующія
Рис. 47
Пусть О А = В.
Пусть а (2м) обозначаетъ сторону вписаннаго
многоугольника о 2м сторонахъ, Ь (2”) соотвѣт-
ственную аиоѳему, р(2п) его периметръ и ^\2М) его
площадь.
Для квадрата
2*,
&(2*)=^<2;
А (22) =^7?2. 2.
XI. МНОГОУГОЛЬНИКИ.
77
Для восьмиугольника:
въ треугольникахъ А В2 О и АВ1А2
ЛВ2^ОА_
В\А2 А А2
Поэтому ^А А22=В. ВхА2=В [7? — Ь (22)]
= 7? ( 7? - - V 2І = 47?'2 . (2 - /2),
V 2 7
или А Аг=К |/ 2 — V 2=а (г3)..........(і)
р (23) = 7?. 23 |/г—]/2 • • • • (2)
6(2:і) = ОВг = VОА^АВ?•—'|/7?^і — ? 2)
= Ѵ^Д^-) = |7?|/^+Т1 .... (з)
А (23) — і периметра X апоѳему
= 7? .22. 2— V2 .^-7? |/2 —V2
= К1.2 V2.
Подобнымъ образомъ для многоугольника о
78
XI. МНОГОУГОЛЬНИКИ.
а для многоугольника о 32 сторонахъ:
а (23) = 7? і/^2 - 2 -|- |/ 2 2 ;
р (25) = 7? . 2® . |/^2 — }2 —|— Р 2 —|— Г 2І
^(23) = ^|/^2 + ]/о.4-|/'24- Ѵ2;
Л(25) = К1.23 . 2 -- |/ 2 -ф- V 2 .
Такимъ образомъ общій законъ здѣсь ясенъ,
ур
Итакъ, А (2й) = —• р (2й-1).
При неопредѣленномъ возрастаніи числа
сторонъ апоѳема, очевидно, приближается къ сво-
ему предѣлу, радіусу. Такимъ образомъ предѣлъ
выраженія
і/г + і/г + Ѵг....
есть 2; въ самомъ дѣлѣ, если обозначить этотл,
предѣлъ чрезъ х, то х=У*2-|-х, это квадратное
уравненіе даетъ: л==2 или—і; но второе Значеніе,
конечно, недопустимо. °^°
133. Ес ли чрезъ концы раді^с^рѣ провести
перпендикулярныя къ нимъ прямѣй^ то мы полу-
чимъ правильные многоугольніжгфописанные около
круга, а также около получ^адьіхъ въ предыду-
щемъ параграфѣ многоуго^фиковъ, съ тѣмъ же
числомъ сторонъ.
XI. МНОГОУГОЛЬНИКИ.
79
На рис. 48 пусть А Е будетъ сторона впи-
саннаго, а ЕС сторона описаннаго многоуголь-
ника. .
Тогда, изъ треугольниковъ ЕІЕ и ЕЮ
ОЕ _ЕЕ _ЕС .
01 ~ ЕІ ~АЁ ’
А Е
слѣдовательно, ЕС = К-д-^‘
Рис. 48
Величины АЕ и 01 извѣстны изъ предыду-
щаго § и ЕС находится помощью простой под-^
становки. о
Площади этихъ двухъ многоугольниковъ^^о-
сятся другъ къ другу, какъ Е С2: А Е2, т.<^>какъ
ІѴ-.ОІ2.
134. Въ предыдущихъ параграфсжв было по-
казано, какъ можно получить пра^^Гьные много-
угольники о 22, 23. .. 2м сторонсЩъ. Если же данъ
8о
XI. МНОГОУГОЛЬНИКИ.
многоугольникъ о т сторонахъ, то легко получить
многоугольникъ о 2й. т сторонахъ.
135. На рис. 48 отрѣзки АВ и СБ суть
стороны вписаннаго и описаннаго многоугольника
о п сторонахъ. Чрезъ середину Е стороны СБ
проведите прямыя А Е и В Е. Отрѣзки А Е и ВЕ
представляютъ стороны вписаннаго многоуголь-
ника 02;/ сторонахъ.
Перегните бумагу по А Е и В С, подъ пря-
мыми углами къ А С и ВБ] эти перпендикуляры
встрѣтятъ С Б въ точкахъ Е и С.
Тогда ЕС представитъ сторону описаннаго-
многоугольника о 27/ сторонахъ.
Проведите ОЕ. ОС и ОЕ.
Пусть />, Р будутъ периметры вписаннаго и
описаннаго многоугольника о п сторонахъ, А. В
ихъ площади; чрезъ р', Р' обозначимъ периметры
вписаннаго и описаннаго многоугольника о 2/;
сторонахъ, а чрезъ А\ В' ихъ площади.
Тогда
р = п. А В, Р = п. С Б, р' = 2;/. А Е, Р' =? а// • Р С.
Такъ какъ ОЕ дѣлитъ пополам^^ С ОЕ, а
А В параллельна С Г), то
СЕ _С0 —СО
ЕЕ~0Е АІ^АВ;
СЕ СБ-Щв
значитъ,
XI. МНОГОУГОЛЬНИКИ.
81
ИЛИ 4/7 .С Е _ //. и .АІЗ . ЕЕ п. АВ
откуда 2Р Р' ~ Р
и р, _ ^Р±_ Р^Р'
Далѣе, изъ подобія треугольниковъ ЕІЕ и
АНЕ
Е± ЕЕ
АІГ АЕ
или А Е1-2АН .ЕЕ]
значитъ, . А Е2 — ^п2 .АВ.ЕЕ
или р' =УР' р‘
Съ другой стороны,
А = 2п Д АОН, В = 2п /\СОЕ,
А’= 2н/\А0 Е, В'= 2іі р\Е О Е.
Такъ какъ треугольники А О Н и А ОЕ имѣ(
ютъ одну и ту же высоту А ІЦ то °^°
/\АОН ОН
/\АОЕ~ ОЕ'
Подобнымъ же образомъ
Д Л .
82
XI. МНОГОУГОЛЬНИКИ.
Затѣмъ, такъ какъ АВ\\СИ,
то
ДЛ ОН_{\ А ОЕ
&АОЕ ^СОЕ'
Поэтому’
Л А’
,,, = . или А = V А В-
л п
Теперь найдемъ В'. Такъ какъ у треуголь-
никовъ СОЕ и ЕОЕ высота общая, а ОЕ
дѣлитъ уголъ Е О С пополамъ, то
&СОЕ СЕ ОС-\-ОЕ. ^ЕОЕ~ЕЕ~ ОЕ
затѣмъ ОЕ=ОА
ОС _ОЕ_^АОЕ.
ОА~ОН~ &АОН'
поэтому ДСОЕ /\АОЕ+ АОН &ГОЕ ^АОН
Изъ этого уравненія легко получаемъ, что
2В
В'
. 2 А В
слѣдовательно, В —т
136. По даннымъ радіу^^/? и апоѳемѣ г
правильнаго многоугольнйка^найти радіусъ 7?' и
апоѳему г' правильнаго ^^оугольника того же
периметра^ но съ двоіінЕ^іъ числомъ сторонъ.
XI. МНОГОУГОЛЬНИКИ.
83
Пусть А В будетъ сторона перваго много-
угольника, О его центръ, О А радіусъ описаннаго
круга, О В его апоѳема. На продолженіи апоѳемы
ОВ отложите ОС=ОА или ОВ. Проведите А С,
В С. Перегните по О А' и О В' перпендикулярно
къ А С и ВС, опредѣляя такимъ образомъ точки
А', В.
Проведите прямую А' В’, пересѣкающую О С
В'. Хорда А' В' будетъ равна половинѣ А В, а
въ
уголъ В О А' равенъ половинѣ угла В О А. О А'
и О В' представляютъ радіусъ В' и апоѳему г
второго многоугольника.
Но О В’ есть среднее ариѳметическое ме^°
ОС и ОВ, а О А' есть среднее геометрцч^кое
между О С и ОВ. Поэтому
г' = і(7?+г), =
137. Теперь на ОС отложит^ЭОВ=О^Г и
проведите А' Е.
84
XI. МНОГОУГОЛЬНИКИ.
Тогда, такъ какъ А'ІУ меньше А'С, а
/_Е'А'С дѣлится пополамъ прямою А* Е, то
Е И’ меньше, чѣмъ |С7)', т. е. меньше |С79;
слѣдовательно,
7?, — гх меньше, чѣмъ (7? — г).
Съ увеличеніемъ числа сторонъ многоуголь-
никъ будетъ приближаться къ кругу того же
периметра, а 7? и г будутъ приближаться къ
радіусу круга.
Другими словами,
7? г 7?! — /'і + Т?2 — г2 .
Р
=діаметру круга =- .
ЗЪ
Далѣе,
и
= или 7?. 44=7?.
7?і
^2 2
~е2=ё~ и Т- х
Перемножая эти два ряда равенствъ, находимъ:
= радіусу круга
7? • 7 Ь 2 з
7?;’7?2‘7?3
138. Радіусъ круга заключается ^ркду 7?„ и г„,
а число сторонъ многоугольника рОѣо 4. 2"; вели-
2
чина зи заключается межд^^и . Поэтому,бе-
ря достаточно большое щйсло сторонъ, можно
вычислить зі съ любоіТ^тепенью точности.
XI. МНОГОУГОЛЬНИКИ.
85
Радіусы и апоѳемы правильныхъ многоуголь-
никовъ о 4, 8, іб.... 2048 сторонахъ имѣютъ слѣ-
дующія величины:
4-угольникъ: г=0'500000, 7? = гр2=0'707107
8-угольникъ: 75 =0’603553, = 0'653281
2048-угольникъ: = 0’636620, Т?9 = 0’636620.
Отсюда л = —5т— = 3’141 59 • •••
0’636620 °
139. Если /?" есть радіусъ правильнаго мно-
гоугольника того же периметра о 477 сторонахъ,
то
т?'2(т?+т?')
27?
или вообще
7?/, д. і _
140. Радіусы 7?р Т?2,.... послѣдователь^
• ^2
уменьшаются, поэтому отношеніе менып^ди-
ницы и можетъ быть приравнено косинку нѣко-
тораго угла а.
2
а
- — со
86
XI. МНОГОУГОЛЬНИКИ.
Вообще = СО8 ~г~ 1 •
№ 2а-]
Перемножая почленно такія равенства, полу-
чаемъ:
по а а а
. СО8 « . СО8 - . СО8^ч . . . . СО8 7 ,
2 2- 2/,~1
тг । • (X (X
Предѣлъ произведенія со8 а . со8 —.... со8 -2
, 81П 2 а
при к = оо равенъ - ;
этотъ результатъ из-
вѣстенъ подъ именемъ формулы Эйлера.
141. Карлъ Фридрихъ Гауссъ (Саи88, 1777—
1855) доказалъ, что кромѣ правильныхъ много-
угольниковъ о 2м, 3.2м, 5.2й, 15.2м сторонахъ съ
помощью элементарной геометріи могутъ быть
построены только такіе правильные многоуголь-
ники, у которыхъ число сторонъ представляетъ
произведеніе 2м и одного или нѣсколькихъ раз-
личныхъ чиселъ вида 2т і. Мы здѣсь укажемъ,
какъ могутъ быть построены многоугольники о 5
и 17 сторонахъ. °^°
Намъ понадобятся слѣду ющіяжэремы
(і) Если Си/) суть двѣ тс^Ш полуокруж-
ности АСЭВ. если О симметрично съ С по
-_________
*) Доказательство этиі^Игеоремъ можно найти у
Саіаіап, Тйёогётез еі РгоЫ%ф^8 сіе Сёотёігіе Еіётепіаіге.
XI. МНОГОУГОЛЬНИКИ.
87
отношенію къ діаметру АВ, а /? обозначаетъ
радіусъ круга, то
АС.ВВ=ВАС'В- СВ)..I.
АВ.ВС=К.(СВ+СВ)..II.
А С.ВС=В.СС......ІИ.
(2) Пусть окружность нѣкотораго круга раз-
дѣлена на нечетное число равныхъ частей, пусть
А О будетъ діаметръ, проходящій чрезъ одну
изъ точекъ дѣленія А и чрезъ средину О про-
тивоположной дуги. Обозначимъ буквами Аѵ А2....
Ап и ^4/, А2 .... Ап' точки дѣленія по обѣ стороны
этого діаметра, начиная съ ближайшихъ къ А.
Въ такомъ случаѣ
О А.. ОА2 . О А..... О А„. = Вѣ.IV.
и ОАі.ОА2.ОАі....ОАп=Я*.
142. Очевидно, что если хорда О Ап опредѣ-
лена, то уголъ Ап О А найденъ и остается раздѣ-
лить его на п равныхъ частей, чтобы получить
прочія хорды. о
143. Возьмемъ сначала пятиугольникъ.
По IV теоремѣ
оаа.оа2=р2.
По I теоремѣ о\ѵ
7? (О Л — О Аг) = О Ах. О А, =
Слѣдовательно, О Аг — О А2
Роу. Геометрическія упражненія
88
XI. МНОГОУГОЛЬНИКИ.
Отсюда вытекаетъ слѣдующее построеніе.
Проведите діаметръ А СО и картельную
А Е. Найдите средину Е радіуса А 6хй° отложите
АЕ= АС.
На А С, какъ на діаметрѣХѳпишите кругъ
АЕСЕ.
Проведите ЕЕ, встрѣрющую внутренній
кругъ въ А и Е.
Тогда Е Е = 0 А^Е Е=О Ат
XI. МНОГОУГОЛЬНИКИ.
89
144. Разсмотримъ теперь 17 угольникъ.
Въ данномъ случаѣ *)
ОАХ.ОА2. ОА^ОА,. ОА6. ОА6. О А,. О Аѣ=№.
ОАХ. О А, .ОАі. ОА3=К\
О А3. О А3. О Ае. О Ах = Рі.
По I и II теоремамъ
ОАх.ОАі = Р(ОА3-]-ОАъ)
ОА3.ОА3 = Р(ОАв — ОА7)
ОА3.ОА3 = Р(ОА2-\-ОА3)
ОА6.ОА2 = Р(ОАх — ОАі').
Пусть
ОА+ОА=Х ОАе — ОА7=ЛГ,
ОА2 + ОАя=Р, ОАх — ОАі—0_.
Тогда ММ=КІ и Р^=Кг.
Подставляя значенія М, Ы, Р и 0 въ формулы
мы=р\ рд=кг А
У
и пользуясь теоремами I и II, находимъ:
{М—У) — \Р—О)^=К.
*) Здѣсь указаны лишь главные шаги. вопросъ
изложенъ у Саіаіап, Тігёогётея еі РгоЫё^гёя' сІе Оёотеігіе
Еііпгепіаіге, и у Кіеіп, Знаменитыя и элементар-
ной геометріи.
90
XI. МНОГОУГОЛЬНИКИ.
Подобнымъ же образомъ, подставляя значенія М,
.V, Р и 0 въ написанную выше формулу и при-
нимая во вниманіе I и II теоремы, мы найдемъ,
что
(Л/-7Ѵ)(Р—б?) = 4Р2.
Отсюда опредѣляются М—7Ѵ, Р—О, М, 7Ѵ,
Р и О.
Съ другой стороны,
ОА^ОА^Р,
ОА2.ОА8=РЛт.
Отсюда опредѣляется 0А3.
145. Разрѣшая эти уравненія, найдемъ
^/-7Ѵ=17?(і+ТІ7)-
Р-О=^Р(-і+Ѵ^).
Р = Т+/17+І/34 — 2 Ѵ17).
7Ѵ=|Т?(— Т — /17+ І/34+Ѵ217).
О Д = 17?[—I + V17+1/ 34 — 2'
— 2І/ 17+3/17+1/170—26К17—^'34+2ѴІ7 1
=і 7?[ —і + К17+1 /34
— 2 ^ѵ+з^Г^-1/і7°+з8 Г'1?!-
XI. МНОГОУГОЛЬНИКИ.
91
146. Геометрическое построеніе будетъ слѣ-
дующее:
Пусть В А будетъ діаметръ даннаго круга;
О его центръ; С средина О А. Проведите АВ
перпендикулярно къ О А и отложите А В=А В.
Проведите СВ. По обѣ стороны отъ С найдите
на СВ такія точки Е и Л', чтобы СЕ=СЕ' =СА.
(3
Рис.
Раздѣлите ЕВ пополамъ въ тотеѣ С и Е'В
въ С'. Проведите ВГ перпендикуМярно къ СВ и
отложите В Е= О А. у
92
XI. МНОГОУГОЛЬНИКИ.
Проведите ГС и ГС'.
Найдите на Г С такую точку Н и на продол-
женіи ЕС такую точку /А, чтобы СН=ЕС и
СН’ = СЕ.
Очевидно, что
ЕЕ = М— тѴ,
ЕЕ' = Р—О,
а также, что
РН=^ откуда (ЕЕ+ГН)ГН=ЕЕ~К2\
ЕН'=Р, откуда (ЕН'-РЕ')ЕН=[)Е2=Е.
На ЕЕ найдите К такъ, чтобы РК=ГН.
Проведите Кѣ перпендикулярно къ 1) Е и
отмѣтьте на КЬ такую точку А, чтобы Е А было
перпендикулярно къ Е А.
Въ такомъ случаѣ
ЕІР=ЕГ.ГК=КЕ\
Наконецъ, проведите ААуѴ перпендикулярно
къ РН' и отложите /А ЛГ=ЕА. Проведите РМ
перпендикулярно къ РН'. На /V М найдите такую
точку Л/, чтобы Н' М была перпендикулярна къ
къ ЕМ. Проведите М Е' перпендикулярномъРН\
Въ такомъ случаѣ о&°
ГН’.ЕГ=ГМі=ЕЬ^
Но ГГ'+Г'Я'
Слѣдовательно,
XII. Общія начала
147. На предыдущихъ страницахъ мы при-
мѣняли разнообразные пріемы, каковы, напр.,
дѣленіе конечныхъ линій на двѣ и на три равныя
части, дѣленіе прямыхъ угловъ на двѣ или на
другое число равныхъ частей, проведеніе перпен-
дикуляровъ къ данной линіи и т. д. Займемся
теперь теоріей этихъ пріемовъ.
148. Всеобщимъ началомъ является принципъ
конгруэнтности или совмѣщенія при наложеніи.
Фигуры и отрѣзки прямыхъ линій называются
конгруэнтными, если они тождественно равны или
равны во всѣхъ отношеніяхъ.
Складывая вдвое листъ бумаги, мы получаемъ
прямолинейные края двухъ плоскостей, совпадаю-
щіе другъ съ другомъ. Эта линія можетъ быть /
также разсматриваема, какъ пересѣченіе дву^|>
плоскостей, если обращать вниманіе на ихъ ^с-
положеніе во время процесса перегибанія,^^
Раздѣляя отрѣзокъ или уголъ на н^юторое
число равныхъ частей, мы получаемтЛ^ѣкоторое
число конгруэнтныхъ частей. Равшдв отрѣзки или
равные углы конгруэнтны.
94
XII. ОБЩІЯ НАЧАЛА.
А'
149. Данъ отрѣзокъ X' X, раздѣляемый точ-
кой А9 на двѣ части. Найдемъ средину О этого
отрѣзка, перегнувъ его вдвое. Въ такомъ случаѣ
---1 1 1
д-----------а-х
Рис. 52
О А’ равно половинѣ разности между А9 X и
X А". Перегните X X въ точкѣ О и возьмите на
О X точку А, соотвѣтствующую точкѣ А'. Тогда
отрѣзокъ А А' равенъ разности между А' X и
X А' и дѣлится точкой О пополамъ. Если брать
А9 ближе къ О, то А* О уменьшается, а въ то
же время А' А уменьшается вдвое скорѣе. Этимъ
свойствомъ пользуются при нахожденіи средины
какого-нибудь отрѣзка при помощи циркуля.
150. Предыдущія разсужденія можно прило-
жить и къ углу. Биссектрису легко найти помощью
циркуля, находя точку пересѣченія двухъ круговъ.
151. На линіи Х9Х отрѣзки вправо отъ О
можно разсматривать, какъ положительные, а
отрѣзки влѣво отъ О, какъ отрицательное^ Дру-
гими словами, точка, перемѣщающаяся^^ О къ
А, движется въ положительную сторой^; а точка,
движущаяся въ шротивоположно^^направленіи
О А' въ отрицательную.
лх-ох~^
ОА'=ОХ'^'Х',
гдѣ обѣ части уравненіяЛкрицателі.ньі.
XII. ОБЩІЯ НАЧАЛА.
95
152. Если О Ау одна сторона угла А О Ру
неподвижна и если линія ОР вращается вокругъ
Оу то углы, образуемые ею съ О Ау имѣютъ раз-
личную величину. Всѣ такіе углы, образуемые
ОР при ея вращеніи въ сторону, противополож-
ную направленію вращенія стрѣлки часовъ, счи-
таются положительными. Углы же, образуемые
ОР при ея вращеніи въ противоположную сто-
рону, считаются отрицательными.
153. Послѣ полнаго оборота ОР совпадаетъ
съ О А. Описанный при этомъ уголъ называется
угломъ при точкѣ (перигономъ); онъ равенъ, оче-
видно, четыремъ прямымъ угламъ. Если ОР со-
вершитъ половину оборота, она окажется на одной
прямой съ О А. Описанный уголъ называется
угломъ при прямой; онъ равенъ двумъ прямымъ
угламъ. Когда ОР совершитъ четверть оборота,
она будетъ перпендикулярна къ О А. Всѣ прямые
углы равны. Равны между собой также всѣ углы
при прямой и всѣ углы при точкѣ.
154. Двѣ прямыя, пересѣкающія другъ друг^л,
подъ прямымъ угломъ, образуютъ четыре конгр^у
энтныхъ квадранта. Двѣ прямыя съ инымъ в^фім-
, нымъ наклономъ другъ къ другу образу^ѣ^ че-
тыре угла, изъ которыхъ вертикально-противопо-
ложные попарно конгруэнтны.
155. Положеніе точки на плосдЭсти опредѣ-
ляется ея разстояніями отъ дву^» такихъ пря-
96
XII. ОБЩІЯ НАЧАЛА.
мыхъ. При этомъ разстояніе отъ каждой изъ пря-
мыхъ берется по линіи, параллельной другой
изъ нихъ. Аналитическая геометрія изслѣдуетъ
свойства плоскихъ фигуръ при помощи такого
именно метода. Эти двѣ прямыя называются осями
координатъ; разстоянія точки отъ осей называютъ
координатами, а пересѣченіе осей началомъ ко-
ординатъ. Этотъ методъ былъ найденъ Декартомъ
въ 1637 году. Онъ оказалъ громадную услугу
современнымъ изслѣдованіямъ.
156. Если двѣ оси X’ X, У У' пересѣкаются
въ О, то разстоянія, измѣряемыя въ направленіи
О X, т. е. вправо отъ О, положительны, а раз-
стоянія, измѣряемыя влѣво отъ О, отрицательны.
Подобнымъ же образомъ отсчитываемыя въ на-
правленіи О У разстоянія положительны, а взятыя
въ направленіи ОУ отрицательны.
157. Осевая симметрія опредѣляется слѣду-
ющимъ образомъ: если двѣ фигуры, лежащія въ
одной и той же плоскости, могутъ быть приве-
дены въ совпаденіе вращеніемъ *одной и^> нихъ
около нѣкоторой опредѣленной прямоі^ѣ той же
плоскости на величину угла при пря^ри, то эти
двѣ фигуры называются симметриййыіми по отно-
шенію къ этой прямой, какъ оси^имметріи.
158. Центральная симмет^^опредѣляется слѣ-
дующимъ образомъ: если <^®Ѣ фигуры, лежащія
въ одной и той же плось&ти, могутъ быть при-
XII. ОБЩІЯ НАЧАЛА.
97
ведены въ совпаденіе вращеніемъ, на величину
угла при прямой, одной изъ нихъ около нѣкото-
рой неподвижной точки той же плоскости, то эти
двѣ фигуры называются симметричными по отно-
шенію къ этой точкѣ, какъ центру симметріи.
Въ первомъ случаѣ вращеніе происходитъ
внѣ данной плоскости, а во второмъ въ ней.
Если въ двухъ разсмотрѣнныхъ случаяхъ
каждая изъ двухъ фигуръ представляетъ половину
нѣкоторой фигуры, то эта цѣлая фигура называ-
ется симметричной но отношенію къ этой оси или
къ этому центру,—послѣдніе носятъ названіе оси
и центра симметріи или просто оси и центра.
159. Возьмемъ въ квадрантѣ ХОУ какой-
нибудь треугольникъ Р О К. Найдемъ его изобра-
женіе въ квадрантѣ УОХ\ складывая бумагу по
оси У У и прокалывая ее въ вершинахъ тре-
угольника.
Найдемъ такимъ образомъ изображенія этихъ
двухъ треугольниковъ въ четвертомъ и третьемъ
квадрантахъ. Нетрудно видѣть, что треугольники
въ сосѣднихъ квадрантахъ обладаютъ осевой
метріей, а треугольники въ противоположі^^ь
квадрантахъ обладаютъ центральной симм^^ей.
160. Правильные многоугольники сѣ^нечет-
нымъ числомъ сторонъ обладаютъ оІ^еЬой сим-
метріей, а правильные многоугольшщи°съ четнымъ
числомъ сторонъ обладаютъ йфйральноіі сим-
метріей.
98
XII. ОБЩІЯ НАЧАЛА.
161. Если фигура имѣетъ двѣ взаимно-пер-
пендикулярныя оси симметріи, то точка ихъ пере-
сѣченія является центромъ симметріи. Это имѣетъ
мѣсто для правильныхъ многоугольниковъ съ чет-
нымъ числомъ сторонъ, а также для нѣкоторыхъ
Рис. 53
кривыхъ, какъ, напримѣръ, для кр^а, эллипса, ги-
перболы и лемнискаты; правильные многоугольники
съ нечетнымъ числомъ сторб^ь могутъ имѣть нѣ-
сколько осей симметріи, ъ^Эсреди нихъ не будетъ
ни одной пары взаимнѳжрпендикулярныхъ. Если
XII. ОБЩІЯ НАЧАЛА.
99>
сложить листъ бумаги вдвое и обрѣзать, то полу-
ченный кусокъ бумаги будетъ имѣть ось симмет-
ріи; если же обрѣзать сложенный вчетверо листъ,,
то получится кусокъ, обладающій центральной
симметріей (рис. 54).
Рис. 54
162. Параллелограммы имѣютъ центръ
метріи. Четыреугольникъ, имѣющій форму (Жчаж-
наго змѣя, или трапеція съ двумя равныта°ѣторо-
нами, противоположными и равно надарненными
къ двумъ другимъ сторонамъ, имѣ^^° ось сим-
метріи.
ІОО
XII. ОБЩІЯ НАЧАЛА.
163. По лощеніе точки на плоскости можетъ
опредѣляться также ея разстояніемъ отъ нѣкото-
рой неподвижной точки и наклономъ прямой,
соединяющей обѣ точки, къ нѣкоторой неподвиж-
ной прямой, проведенной чрезъ неподвижную
точку.
Если О А есть неподвижная прямая, а Р дан-
ная точка, то длина О Р и /_АО Р вполнѣ опре<-
дѣляютъ положеніе точки Р.
О называется полюсомъ, О А полярной осью,
ОР радіусомъ-векторомъ, /_А О Р векторіальнымъ
угломъ. Отрѣзокъ ОР и /_АОР называются
полярными координатами точки Р.
164. Симметричное по отношенію къ^си О А
изображеніе какой-нибудь фигуры мол^^тюлучить
перегибаніемъ по О А. Радіусы-век^^ьі соотвѣт-
ственныхъ точекъ равно наклонеШ^ къ этой оси.
165. Данъ треугольникъ С. Продолжите
его стороны СА, АВ, Дъѵ соотвѣтственно до
точекъ /), Е, Г. Предпц^^имъ, что въ А стоитъ
человѣкъ, обращенный0іицомъ къ Р' если онъ
XII. ОБЩІЯ НАЧАЛА.
ІО1
пойдетъ отъ А къ Д отъ В къ С и отъ С къ
А, то онъ послѣдовательно опишетъ углы ВАВ,
ЕВ Су ГСО. Но придя къ своему начальному
положенію въ А, онъ пройдетъ всѣ углы при
точкѣ, т. е. четыре прямыхъ угла. Изъ этого мы
заключаемъ, что сумма трехъ внѣшнихъ угловъ
равна четыремъ прямымъ угламъ.
Рис. 56
То же самое заключеніе приложимо къ лю-
бому выпуклому многоугольнику.
166. Пусть этотъ человѣкъ стоитъ въ А
лицомъ къ Су затѣмъ поворачивается по напра-
вленію А В и идетъ вдоль А Ву В С и С А. Въ этомъ^
случаѣ онъ сдѣлаетъ поворотъ, равный углу
прямой, т. е. двумъ прямымъ угламъ. Онъ ц^іѣ-
довательно поворачивается на углы С А В^Е В С
и ЕС А. Поэтому /_ЕВ Е/_Е СА В
(отрицательный уголъ)=углу при прогой.
Этимъ свойствомъ пользуютс^при повора-
чиваніи паровозовъ на желѣзныэ^^орогахъ. Локо-
102
XII. ОБЩІЯ НАЧАЛА.
мотивъ, стоящій на Е) А, передней частью къ А,
переводятъ на С Е, передней частью къ Е. Затѣмъ
его пускаютъ заднимъ ходомъ и ведутъ на ЕВ.
Наконецъ, переднимъ ходомъ его переводятъ по
В А на А В. Паровозъ описалъ одинъ за другимъ
углы А С В, СВ А и В АС. Поэтому, три вну-
треннихъ угла треугольника вмѣстѣ равны двумъ
прямымъ угламъ.
167. То свойство треугольника, его три
внутренніе угла вмѣстѣ равны прямымъ
угламъ, можно иллюстрировать с^юмощью куска
бумаги слѣдующимъ образомъ,^
Перегните треугольникъуіо СС, перпенди-
кулярно къ АВ. Раздѣли^^'В пополамъ въ 7Ѵ
и А С' пополамъ въ
XII. ОБЩІЯ НАЧАЛА.
103
Перегните по Лт А' и М В\ перпендикулярно
къ АВ\ эти перпендикуляры пересѣкутъ В С \\
А С въ А' и В’. Проведите А' С и В' С'.
Перегибая углы по Е А', МВ' и А' В\ мы
найдемъ, что углы А, В, С треугольника соотвѣт-
ственно равны угламъ ВСА, В С А9 и А'СВ',
которые вмѣстѣ составляютъ два прямыхъ угла.
168. Возьмите какую-нибудь прямую АВС.
Проведите перпендикуляры къ АВС въ точкахъ
И, В и С. На этихъ перпендикулярахъ возьмите
точки /9, Е, Е, равно отстоящія отъ основаній
РЕ Е
А В с
Рис. 58
перпендикуляровъ. При помощи наложенія легкое
видѣть и доказать, на основаніи равенства
угольниковъ, что отрѣзокъ В Е равенъ А В ^Пер-
пендикуляренъ къ А В и къ В Е и что Е /^рГвенъ
В С и перпендикуляренъ к ь В Е и къ С7%|Йо А В
(=В Е) есть кратчайшее разстояніе мей^у прямыми
А I) и ВЕ; это разстояніе сохраня^^постоянную
величину. Поэтому АВ и ВЕ иногда не могутъ
Ро у. Геометрическія упражненія
8
104
XII. ОБЩІЯ НАЧАЛА.
встрѣтиться, т. е. онѣ параллельны. Отсюда заклю-
чаемъ, что прямыя, перпендикулярныя къ одной и
той же прямой, параллельны между собой.
Два угла ВАВ и ЕВА вмѣстѣ равны
двумъ прямымъ угламъ. Если вращать прямыя
АВ и ВЕ около А и В на встрѣчу другъ другу,
то онѣ встрѣтятся и сумма внутреннихъ угловъ бу-
детъ меньше двухъ прямыхъ. При продолженіи же
въ другую сторону эти прямыя не будутъ встрѣ-
чаться. Въ этомъ и заключается столь извѣстный
двѣнадцатый постулатъ Евклидовыхъ Началъ.
а в с о е г
Рис. 59
нѣкоторая прямая А С Н ^трѣча-
и С У7 въ /У, то о
4 СВ,
дополненіе
169. Если
етъ ВЕ въ С
/_С А В — накрестъ лежащему
такъ какъ каждый изъ нихъ
а
/_НС Е= соотвѣтствевдрм}' /_С А В.
Поэтому каждый изъц^хъ равенъ
Слѣдовательно, два^ѣла С А В и ЕС>
стѣ равны двумъ прямымъ.
XII. ОБЩІЯ НАЧАЛА.
ІО5
170. Возьмите прямую А X и отмѣтьте на
ней, начиная отъ А, равные отрѣзки АВ, ВС,
СВ, ВЕ.... Возставьте въ точкахъ В, С, В, Е....
перпендикуляры къ АЕ. Пусть нѣкоторая прямая
А Е' пересѣкаетъ эти перпендикуляры въ точкахъ
В\ С', В’, Е’.... Получившіеся отрѣзки А В\ В' С\
С В', В' Е'.... всѣ равны между собой.
Если АВ, ВС, СВ, ВЕ не равны, то
АВ:ВС=АВ\В С,
ВС:С[)=В'С: С'77 и т. д.
171. Если А В СВ Е.... представляетъ нѣко-
торый многоугольникъ, то подобные ему много-
угольники могутъ быть получены слѣдующимъ
образомъ.
Возьмите внутри многоугольника какую-ни-
будь точку О и проведите линіи О А, О В, ОС....
На О А возьмите какую-нибудь точку А и прове-
дите линіи А' В, В' С, СВ’.... параллельно АВ, ВС,^
СВ.... Полученный многоугольникъ А' В' СВ'. в
будетъ подобенъ многоугольнику АВСВ.^Х.
Многоугольники, построенные такимъ обрЖЪмъ
вокругъ общей точки, находятся въ персрсѣтив-
номъ отношеніи между собой. ТочкауСу можетъ
лежать и внѣ многоугольника. ОнаЭпазьівается
центромъ перспективы.
іоб
XII. ОБЩІЯ НАЧАЛА.
172. Раздѣлить данный отрѣзокъ на 2, 3, _р
5 .... равныхъ частей. Пусть А В есть данный
отрѣзокъ. Проведите перпендикулярно къ А В,
въ разныя отъ нея стороны, прямыя А С и ВО
и отложите АС=ВР. Соедините С и Р прямой,
пересѣкающей А В въ Р2. Въ такомъ случаѣ
АР^В.
Рис. 60
Теперь продолжите АС и отеките С Е=
= Е Е=Е С = ....= А С или В /ЖЭДроведите ли-
ніи Р Е, РЕ. Р С....; пустьЛ^нѣ пересѣкаютъ
А В въ точкахъ Р3, Р4, Р5 . А.
Изъ подобія треугольниковъ получится
Р,В:А^ВІ):АЕ.
XII. ОБЩІЯ НАЧАЛА.
ІО7
Отсюда Р.В\АВ=ВО\АР
= *:3-
Подобнымъ же образомъ
Р^В-.А в=і:4
и т. д. Если А В=і,
то АРг = Т ; 1.2’ ЛЛ= 1 ; 2.3 ЛА= 1 ; 3-4’
оконча
Поэтому
Пли еще
3-4
і----------------------
Но
тельной суммѣ равняется А В.
іо8
XII. ОБЩІЯ НАЧАЛА.
Складывая, находимъ:
_і_ . ..-_[_ — - — і —
1.2 2.3 1 //-ф-1
ГА Т і Г і 1 1
Отсюда + —.... + 7-----------------. = і — .
1.2 2.3 (//- 1)7/ 11
Предѣлъ і—1 при //—сю равенъ т.
173. Слѣдующій простой пріемъ можетъ быть
употребленъ для дѣленія отрѣзка на произволь-
ное число равныхъ частей.
Возьмите прямоугольный кусокъ бумаги и
отмѣтьте // равныхъ отрѣзковъ на каждой или на
одной изъ двухъ смежныхъ сторонъ. Перегните
бумагу чрезъ точки дѣленія такъ, чтобы полу-
чить перпендикуляры къ сторонамъ. Отмѣтьте
точки дѣленія и углы цифрами о, і, 2,... . и. Пусть
требуется раздѣлить сторону другого куска бу-
маги А В на и равныхъ частей. Для этого помѣ-
стите А В такъ, чтобы точка А или В наф^іилась
въ о, а В или А лежала на перпендпі^мрѣ, про-
ходящемъ чрезъ и.
Въ этомъ случаѣ отрѣзок^уИ В долженъ
быть больше О іѴ. Но для ме^^іихъ отрѣзковъ
можно взять меныную сторош^ прямоугольника.
Тѣ точки, въ которьі&ѵі В пересѣкаетъ пер-
пендикуляры, и суть искомыя точки дѣленія.
XII. ОБЩІЯ НАЧАЛА.
109
174. Центръ средняго положенія. Если пря-
мая АВ содержитъ (///+/г) равныхъ частей и дѣ-
лится въ точкѣ С такъ, что А С содержитъ ж,
а С В содержитъ п этихъ частей, то, опустивъ
изъ точекъ Л, С, В на нѣкоторую прямую пер-
пендикуляры А В, СВ и В Е, получимъ
т . В Е +11. А И = (/// 4- и). СЕ.
Въ самомъ дѣлѣ, проведите параллельно Е В
прямую ВСН, которая пересѣчетъ СЕ въ 0 и
А В въ Н. Предположите, что чрезъ точки дѣ-
ленія А В проведены прямыя параллельно В И.
Эти прямыя раздѣлятъ А Н на (ш + //), а С С
на 11 равныхъ частей.
Поэтому
и . А Н= (иі іі) .С С]
и такъ какъ В Н и В Е равны С Е каждый, то
и . Н В іи . В Е{т Ц- и) С Е.
Отсюда, складывая, получаемъ
и . (А Н+НВ)+т . ВЕ=(иі+п) .(СС^СЕ)
пли и. А В -4- іи . ВЕ = (ш -Си). СЕ. Л
С называется центромъ средняго положенія
или среднимъ центромъ точекъ А и В дл^^исте-
мы кратныхъ т и и.
Этотъ принципъ можно распространить и на
случай любого числа точекъ, те^ежащихъ на
одной прямой. Въ этомъ случаѣ^ёсли Р будутъ
ПО
XII. ОБЩІЯ НАЧАЛА.
обозначать основанія перпендикуляровъ, опущен-
ныхъ на какую-нибудь прямую изъ точекъ Л, В.
С и т. д., если сі, Ь, с.... суть соотвѣтствующіе
множители кратности, а М есть средній центръ, то
а.АР+Ь.ВР+с.СР+ ...
= (<7+/;+с+ ...). МР.
Если всѣ множители равны то
а (А Р+ВР+СР+ ,..)=па. М Р.
гдѣ н есть число точекъ.
175. Центръ средняго положенія нѣсколькихъ
точекъ съ равными множителями получается слѣ-
дующимъ образомъ. Найдите средину С прямой,
соединяющей двѣ какія-нибудь точки А и В, соеди-
ните С съ какой-нибудь третьей точкой Си раздѣли-
те С Свъ Н такъ, чтобы СН—'І2 С С; соедините И
съ четвертой точкой В и раздѣлите Н В въ К
такъ, чтобы НК=ЧВ. и т. д.: послѣдняя най-
денная такимъ образомъ точка и будетъ центромъ
средняго положенія данной системы точекъ.
176. Понятіе о среднемъ центрѣ ижг центрѣ
средняго положенія заимствовано ц|йь статики,
ибо система матеріальныхъ точект^^омѣщенныхъ
въ Л, В, С .... и обладающихъ лжами с....,
была бы въ равновѣсіи окрлу средняго центра
7И, еслибы могла свободно вращаться около М
подъ дѣйствіемъ силы ’й^кёсти.
XII. ОБЩІЯ НАЧАЛА.
III
Поэтому средній центръ находится въ тѣс-
ной связи съ центромъ тяжести статики.
177. Средній центръ трехъ точекъ, не лежа-
щихъ на одной прямой, совпадаетъ съ пересѣче-
ніемъ медіанъ треугольника, имѣющаго вершины
въ этихъ трехъ точкахъ. Онъ является также цен-
тромъ тяжести или центромъ массы тонкой тре-
угольной пластинки равномѣрной плотности.
178. Если М есть средній центръ точекъ А.
В, С.... для множителей а, Ь, с...., а Р какая-
нибудь другая точка, то
а . А /)2 + I). ВР~ + с . СР1 4- ....
=а . А М2 + Ъ.ВМ2^с. СМ2^....
+ Р>/2О + Л4-с + ....).
Поэтому въ правильномъ многоугольникѣ,
если О есть центръ вписаннаго или описаннаго
круга, а Р какая-нибудь точка, то
лр2+вр2 + ....=ол2+оя2+....+^. 0Р-
= ;/.(/?-+О Р-).
Отсюда
АВ? + А С2-\-А Л- +.. ..=2п. К2.^
Подобнымъ 'же образомъ
/?А-’ + ВС2+7?Л>-2 + .
с а1+св2 + св2+... :/?2.
112
XII. ОБЩІЯ НАЧАЛА.
Складывая, находимъ:
2 (А В'14~ А С~ + А1)'- ....) = и . 2.П . /?2.
Отсюда
А В2 + А С2 + А I)2 +.... =п2. Я2.
179. Сумма квадратовъ отрѣзковъ, соединя-
ющихъ средній центръ съ точками системы, пред-
ставляетъ минимумъ.
Если М есть средній центръ, а Р какая-
нибудь другая точка, не принадлежащая къ этой
системѣ, то
^РА2=^МА2-^^РМ2 (гдѣ 2 стоитъ вмѣ-
сто словъ: „сумма всѣхъ выраженій типа44).
Отсюда слѣдуетъ, что 2 РА2 представляетъ
минимумъ, когда РМ=о, т. е. когда Р есть сред-
ній центръ.
180. Свойства пересѣченій прямыхъ и кол-
линеарности точекъ могутъ быть повѣрены при
помощи складыванія бумаги. Приведемъ нѣсколько
примѣровъ:
і) Медіаны треугольника встр^йются въ
одной точкѣ. Эта точка называется Центроидомъ.
2) Высоты треугольника пресѣкаются въ
одной точкѣ, называемой ортоЫргромъ.
3) Перпендикуляры къ^Ьрединамъ сторонъ
треугольника встрѣчаются^^ одной точкѣ, назы-
ваемой центромъ описаннаго круга.
XII. ОБЩІЯ НАЧАЛА.
4) Биссектрисы угловъ треугольника про-
ходятъ чрезъ одну точку Эта точка называется
центромъ вписаннаго круга.
5) Пусть АВСО будетъ нѣкоторый парал-
лелограммъ, а Р какая-нибудь точка. Проведите
чрезъ Р параллельно В С и А В прямыя 6’77 п
ЕЕ. Тогда діагонали ЕС, НЕ и прямая 1) В
пересѣкутся въ одной точкѣ.
6) Если двѣ подобныя, но неравныя прямо-
линейныя фигуры расположены такимъ образомъ,
что ихъ соотвѣтственныя стороны параллельны,
то прямыя, соединяющія соотвѣтственныя вер-
шины, пересѣкаются въ одной точкѣ. Эта точка
называется центромъ подобія.
7) Если два треугольника расположены та-
кимъ образомъ, что ихъ вершины лежатъ по-
парно на пересѣкающихся прямыхъ, то точки
пересѣченія соотвѣтственныхъ сторона, лежатъ
на одной прямой. Это положеніе извѣстно подъ
именемъ теоремы Дезарга. О такихъ двухъ треу^
гольникахъ говорятъ, что они находятся въ
спективномъ отношеніи. Точка пересѣченія^Яря-
мыхъ, проходящихъ чрезъ вершины, иД^рямая,
соединяющая точки пересѣченія сторо^С назы-
ваются центромъ и осью перспективц^Ѵ
8) Средины діагоналей полн^^четыреуголь-
ника лежатъ на одной прямой.
ІІ4
XII. ОБЩІЯ НАЧАЛА.
9) Если изъ какой-нибудь точки окружности,
описанной около треугольника, опустить (п про-
должить, если надо) на его стороны перпендику-
ляры, то основанія ихъ будутъ лежать на одной
прямой. Эта прямая называется прямой Симсона.
Симсонова прямая дѣлитъ пополамъ прямую,
соединяющую ортоцентръ съ той точкой, изъ
которой опущены перпендикуляры.
іо) Ортоцентръ, центръ описаннаго круга
п центроидъ всякаго треугольника лежатъ на од-
ной прямой.
Средина прямой, соединяющей ортоцентръ
и центръ описаннаго круга, есть центръ т. наз.
„круга девяти точекъэто названіе объясняется
тѣмъ, что онъ проходитъ чрезъ основанія вы-
сотъ и медіанъ треугольника и чрезъ средины
частей высотъ, заключенныхъ между ортоцентромъ
и вершинами.
Центръ круга девяти точекъ вдвое дальше
отъ ортоцентра, чѣмъ отъ центроида. Въ этомъ
состоитъ теорема Понселе.
и) Если какія-нибудь шесть точ^ъ окруж-
ности А, В. С, /9, Е. Е соединить пос^довательно
въ произвольномъ порядкѣ, то тощій пересѣченія
первой соединительной прямоносъ четвертой,
второй съ пятой и третьей Л шестой (продол-
женныхъ, если надо) леж^Ог на одной прямой.
Эта терема принадлежии^Паскалю.
XII. ОБЩІЯ НАЧАЛА.
и5
12) I Ірямыя, соединяющія вершины треу-
гольника съ точками касанія его со вписанной
окружностью, пересѣкаются въ одной точкѣ. Тѣмъ
же свойствомъ обладаютъ внѣвписанныя окруж-
ности.
13) Внутреннія биссектрисы двухъ угловъ
треугольника и внѣшняя биссектриса третьяго
угла пересѣкаютъ противоположныя стороны въ
точкахъ, лежащихъ на одной прямой.
14) Внѣшнія биссектрисы угловъ треуголь-
ника пересѣкаютъ противоположныя стороны въ
точкахъ, лежащихъ на одной прямой.
15) Прямыя, проведенныя чрезъ какую-
нибудь точку перпендикулярно къ прямымъ, сое-
диняющимъ эту же точку съ вершинами какого-
нибудь треугольника, встрѣчаютъ противополож-
ныя стороны треугольника въ точкахъ, лежащихъ
на одной прямой.
іб) Если взять какую-нибудь точку О на
оси симметріи двухъ равныхъ треугольниковъ
А В С, А В' С', то прямыя А' О, В О и СО Пересѣ^
каютъ стороны ВС, СА и АВ въ точкахъ?^|^-
жащихъ на одной прямой.
17) Точки пересѣченія паръ касат^^ныхъ
къ какому-нибудь кругу въ концахъ хдрдъ, про-
ходящихъ чрезъ данную точку, леж&^р на одной
прямой. Эта прямая называется таОярой данной
точки относительно даннаго круді.”
Ііб
XII. ОБЩІЯ НАЧАЛА.
і8) Изогонально сопряженныя прямые трехъ
пересѣкающихся прямыхъ АХ, ВХ, СХ по от-
ношенію къ угламъ треугольника АВС пересѣ-
каются въ одной точкѣ. (Двѣ прямыя А А У
называются изогонально сопряженными по отно-
шенію къ углу В А С, если онѣ составляютъ
равные углы съ его биссектрисой).
19) Если въ треугольникѣ АВС прямыя
А А’, ВВ, СС\ проведенныя изъ каждаго угла
къ противоположной сторонѣ, сходятся въ одной
точкѣ, то ихъ изотомическія сопряженныя отно-
сительно соотвѣтственныхъ сторонъ также схо-
дятся въ одной точкѣ. (Прямыя А А, А А" назы-
ваются изотомическпмп сопряженными относи-
тельно стороны В С треугольника АВС, если
отрѣзки ВА' и СА" равны между собой).
20) Три симмедіаны треугольника пересѣ-
каются въ одной точкѣ. (Изогонально сопряжен-
ная медіаны А М треугольника называется ея
симмедіаной).
XIII. Коническія сѣченія
Отдѣлъ I.—Кругъ
181. Листъ бумаги можно согнуть но мно-
гимъ направленіямъ, проходящимъ чрезъ одну и
ту же точку. Точки, взятыя на каждой такой пря-
мой въ одномъ и томъ же разстояніи отъ общей
точки, будутъ лежать на окружности нѣкотораго
круга, а общая точка будетъ его центромъ. Кругъ
есть геометрическое мѣсто точекъ, равноотстоя-
щихъ отъ неподвижной точки, его центра.
182. Можно провести любое число концентри-
ческихъ круговъ. Они не могутъ пересѣкаться.
183. Центръ можно разсматривать, какъ пре-
дѣлъ концентрическихъ круговъ, описанныхъ око-
ло него, какъ около центра, если величина радіуса
безпредѣльно уменьшается.
184. Круги съ равными радіусами могутъ,
быть совмѣщены и равны. о
185. Кривизна круга одинакова по всей оі^Яу/к-
ности. Поэтому, если вращать кругъ ^рдэугъ
центра, то онъ будетъ скользить вдопй^самого
себя. Отношеніе къ кругу какой-нибтак фигуры,
неизмѣнно связанной съ центромъ^^ измѣнится,
если фигуру вращать около цещгда.
ті8
ХШ. КОНИЧЕСКІЯ СТЕЧЕНІЯ.
186. Прямая можетъ пересѣкать кругъ только
въ двухъ точкахъ.
187. Всякій діаметръ дѣлится въ центрѣ круга
пополамъ. По длинѣ онъ равенъ двумъ радіусамъ.
Всѣ діаметры, какъ и радіусы, равны между
собой.
188. Центръ круга есть въ то же время его
центръ симметріи; концы любого діаметра суть,
соотвѣтственныя точки.
189. Каждый діаметра» является осью симмет-
ріи круга и наоборотъ.
190. Предложенія §§ і88, 189 вѣрны и для
системъ концентрическихъ круговъ.
191. Каждый діаметръ дѣлитъ кругъ на двѣ
равныя части, называемыя полукругами.
192. Два взаимно-перпендикулярныхъ діаметра
дѣлятъ кругъ на четыре равныя части, называемыя
квадрантами.
193. Дѣля пополамъ прямые углы, люразу-
емые діаметрами, затѣмъ раздѣляя предамъ эти
половины прямыхъ угловъ и т. д., ^рктчаемъ 2'4
равныхъ круговыхъ секторовъ. Уг^&, образуемый
радіусами каждаго сектора, р^фъ прямого угла
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
іі9
194. Какъ было показано въ предыдущихъ
главахъ, прямой уголъ можно раздѣлить на 3, 5,
9, іо, 12, 15 и 17 равныхъ частей. И каждая часть
прямого угла, полученная такимъ образомъ, мо-
жетъ быть подраздѣлена на 2м равныхъ частей.
195. Можно вписать кругъ въ правильный
многоугольникъ и описать около него. Первый
кругъ будетъ касаться сторонъ многоугольника
въ ихъ срединахъ.
196. Равныя дуги стягиваютъ равные углы
при центрѣ и наоборотъ. Доказать это можно
помощью наложенія. Если перегнуть кругъ по
діаметру, то обѣ полуокружности совпадаютъ.
Каждая точка одной полуокружности имѣетъ на
другой соотвѣтственную точку, лежащую подъ нею.
197. Каждые два радіуса образуютъ равно-
бедренный треугольникъ, основаніемъ котораго
служитъ хорда, соединяющая концы радіусовъ.
198. Радіусъ, дѣлящій пополамъ уголъ между
двумя другими радіусами, перпендикуляренъ
хордѣ—основанію и дѣлитъ ее пополамъ.
199. Если взять опредѣленный діаме^^^ь^ то
можно провести сколько угодно такихъ^л&ръ ра-
діусовъ, чтобы радіусы каждой пары щЬіи равно
наклонены къ діаметру по разныя^^^эроны отъ
него. Хорды, соединяющія конщ^каждой такой
Роу. Геометрическія упражненія
9
120
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
пары радіусовъ, будутъ перпендикулярны къ взя-
тому діаметру; всѣ такія хорды будутъ парал-
лельны между собой.
200. Тотъ же діаметръ дѣлитъ пополамъ всѣ
упомянутыя хорды и всѣ дуги, стягиваемыя этими
хордами, т. е. геометрическое мѣсто срединъ си-
стемы параллельныхъ хордъ является діаметромъ.
201. Перпендикуляры къ срединамъ всѣхъ
хордъ круга проходятъ чрезъ центръ.
202. Равныя хорды равно отстоятъ отъ центра.
203. Концы двухъ радіусовъ, равно накло-
ненныхъ къ діаметру по разныя его стороны,
находятся на одинаковомъ разстояніи отъ каждой
точки этого діаметра. Слѣдовательно, можно опи-
сать любое число круговъ, проходящихъ чрезъ
эти двѣ точки, съ центрами на этомъ діаметрѣ.
Другими словами, геометрическимъ мѣстомъ цент-
ровъ круговъ, проходящихъ чрезъ двѣ данныя
точки, является прямая, перпендикулярномъ пря-
мой, соединяющей обѣ точки, въ еясдй>единѣ.
204. Пусть С С1 будетъ нѣкоторая хорда,
перпендикулярная къ радіусу О^сВъ такомъ слу-
чаѣ углы А О С и А О С' Лзфшы между собой.
Предположите, что обѣ тожи С, С' движутся съ
равной скоростью къ ,Д|угбгда хорда С С будетъ
все время оставаться параллельной самой себѣ и
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
121
перпендикулярной къ О А. Наконецъ, точки С,
А и С совпадутъ въ А, а САС остается пер-
пендикулярной къ О А. Точка А есть послѣдняя
точка, общая хордѣ и окружности. С А С', будучи
продолжена, въ концѣ концовъ обращается въ
касательную къ кругу.
205. Касательная перпендикулярна къ діаметру,
проходящему чрезъ точку касанія, и обратно.
206. Если двѣ хорды круга параллельны, то
дуги, соединяющія ихъ концы сходнымъ образомъ,
равны. Такъ, напримѣръ, равны дуги, соединяю-
щія концы каждой хорды съ діагонально проти-
воположными концами второй хорды и проходя-
щія чрезъ другіе концы. Это легко видѣть, пере-
гнувъ кругъ по діаметру, перпендикулярному къ
параллельнымъ хордамъ.
207. Двѣ хорды (§ 206) и прямыя, соединя-
ющія ихъ концы сходнымъ образомъ, образуютъ
трапецію, у которой имѣется ось симметріи,
именно діаметръ, перпендикулярный къ паралле^-0
нымъ хордамъ. Діагонали такой трапеціи пе^жсѣ-
каются на діаметрѣ. Складываніемъ легкф<убѣ-
диться въ томъ, что углы между каждрй^зъ па-
раллельныхъ хордъ и каждой діагонаѣ^р трапеціи
равны между собой. Точно такъ ж<НЖавны между
собой углы, стягиваемые другимшрМвными дугами
122
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
208. Уголъ при центрѣ круга, стягиваемый
какой-нибудь дугой, вдвое больше угла съ вер-
шиной на окружности, стягиваемаго тою же дугой
Вписанный уголъ равенъ половинѣ централь-
наго угла, опирающагося на ту же дугу.
Даны
вписанный уголъ А V В и центральный уголъ
А О В, опирающіеся на одну и ту же дугу А В.
Доказать, что лА VВ=^лА ОВ.
Доказательство:
і. Предположите, что чрезъ центръД? про-
веденъ діаметръ КО, продолженный пересѣ-
ченія съ окружностью въ точкѣ Х.А^
Тогда лХ ѴВ= л УВ^
2. Но ЛОВ=л$$В+аѴВО
ѵв.
3- Отсюда слѣдуетт^у^о
аХН^ХОВ.
XIII. КОНИЧЕСКІЯ СЬЧЕНІЯ.
І23
4. Подобнымъ же образомъ
лА ѴХЦлАОХ
(каждый изъ нихъ = нулю на рис. 62),
и, слѣдовательно,
/Л ѴВ=І^АОВ.
Доказательство относится одновременно ко
всѣмъ тремъ чертежамъ, на которыхъ точка А
переходитъ въ X (рис. 62) и затѣмъ далѣе за X
(рис. 63).
209. Углы, стягиваемые одинаковой дугой,
во всѣхъ частяхъ окружности имѣютъ одну и
ту же величину, такъ какъ центральный уголъ
остается однимъ тѣмъ же.
210. Уголъ, вписанный въ полукругъ, равенъ
прямому углу.
211. Если хорда ВС перпендикулярна къ
діаметру круга А В, то для четыреугольника
АС ВВ діаметръ А В является осью симметріи.
Такъ какъ каждый изъ угловъ В С А и А В В(
есть прямой, то сумма двухъ другихъ угло^Й
ВВС и САВ, равна двумъ прямымъ угЖмъ.
Если А9 и В9 суть какія-нибудь другія тодХи на
дугахъ ВАС и СВВ, то лСАВ^^СА'В,
л В ВС = /ОВ'С. Слѣдовательно?^: С А9 В -\-
/I) В9 двумъ прямымъ углам^^Поэтому и
л В9 С А' л А’ В В9=двумъ пр^іымъ угламъ.
124
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
Обратно, если сумма двухъ противополож-
ныхъ угловъ четыреугольника равна двумъ пря-
мымъ, то его можно вписать въ кругъ.
212. Уголъ между касательной къ кругу и
хордой, проходящей чрезъ точку касанія, равенъ
углу, который опирается на зфу хорду и вершина
котораго лежитъ на сторону круга, противопо-
ложной дугѣ круга, заключающейся между каса-
тельной и хордой.
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
І25
Пусть А С будетъ касательная къ кругу въ
А, а АВ какая-нибудь хорда. Возьмите центръ О
круга и проведите О А и О В. Изъ О опустите
на АВ перпендикуляръ ОВ.
Тогда аВАС^/АОІ)=^лВОА.
213. Перпендикуляры къ концамъ радіусовъ
касаются круга въ этихъ концахъ (рис. 64). Пря-
мая, соединяющая центръ съ точкой пересѣченія
двухъ касательныхъ, дѣлитъ пополамъ углы между
этими касательными и между радіусами къ точкамъ
касанія. Та же прямая дѣлитъ пополамъ прямую,
соединяющую точки касанія. Обѣ касательныя
равны.
Въ этомъ нетрудно убѣдиться, перегибая
чертежъ чрезъ центръ и точку пересѣченія каса-
тельныхъ.
Пусть А С, АВ будутъ двѣ касательныя, а
АВЕОР прямая, проходящая чрезъ точку пере-
сѣченія касательныхъ А и чрезъ центръ О и
пересѣкающая кругъ въ точкахъ В и В. а прямую^
ВС въ точкѣ Е.
Въ такомъ случаѣ А С или А В является
среднимъ геометрическимъ между А В и А Е
есть среднее гармоническое, А О средн^ ариѳ-
метическое.
АВ2=АВ.АЕ
АВ*=ОА.АЕ*^§^
126
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
г АВ.АР ъАБ.АГ
Поэтому А Е - —т -
Подобнымъ же образомъ, если чрезъ А
провести какую-нибудь другую хорду, встрѣчаю-
щую кругъ въ Р и 7?, а В С въ С}, то отрѣзокъ
Л будетъ гармоническимъ, а А С геометриче-
скимъ среднимъ между АР и АР.
Рис. 65
214. Перегните прямоугол треугольникъ
О С\В по СА перпендикуляренъ его гипотенузѣ.
Найдите на А;В такую ттп^у чтобы ОБ = ОС
(рис. 65). V
ХПТ. КОНИЧЕСКІЯ СѢЧЕНІЯ.
127
Тогда О А . О В = О С2 - О В2,
откуда О А: О С=О С: О В,
ОА:ОВ=О В:ОВ.
Опишемъ кругъ съ центромъ въ О и радіу-
сомъ, равнымъ О С или О В.
Точки А и В являются взаимно-обратными
по отношенію къ центру обращенія О и къ кругу
обращенія СВЕ.
Поэтому, если взять центръ этого круга за
начало координатъ, то для основанія ординаты
какой-нибудь точки круга обратной точкой будетъ
точка пересѣченія касательной и оси абсциссъ.
215. Согните по ВВС перпендикулярно къ
ОВ. Прямая ЕВО носитъ названіе поляры точки
А по отношенію къ полярному кругу СВЕ и
полярному центру О, а точка А называется полю-
сомъ прямой ЕВО. Обратно, В есть полюсъ С А,
а С А есть поляра В относительно того же круга.
216. Продолжите ОС до встрѣчи съ ЕВО
въ Е и перегните по А Н перпендикулярно къ О С. *
Точки Е и Н являются взаимно-обратнымш§х
А Н есть поляра Е, а перпендикуляръ^къ
О Е въ Е является полярой точки Н.
217. Точки Ау В, Еу Н лежатъ лйг одной
окружности; другими словами, двѣ Тючки и ихъ
взаимно-обратныя точки лежатъ ц^^дной окруж-
ности и наоборотъ.
128
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
Теперь возьмите на Т7ВС какую-нибудь
другую точку С. Проведите О С и перегните по
АК перпендикулярно къ ОС. Точки К и С
будутъ взаимно-обратны относительно круга СВЕ.
218. Точки Е,В,С лежатъ на одной прямой,
а ихъ поляры проходятъ чрезъ одну точку А.
Итакъ, поляры коллинеарныхъ точекъ схо-
дятся въ одной точкѣ.
219. Точки, расположенныя такъ, что каждая
изъ нихъ лежитъ на полярѣ другой, называются
сопряженными точками; прямыя, расположенныя
такимъ образомъ, что каждая проходитъ чрезъ
полюсъ другой, называются сопряженными пря-
мыми.
А и Е суть сопряженныя точки, какъ и А и
В, А и С.
Точка пересѣченія поляръ двухъ точекъ
служитъ полюсомъ прямой, соединяющей эти двѣ
точки. XV
220. Если А перемѣщается то и В
движется къ В. Въ концѣ конщ^І/ А и Е со-
впадаютъ, а ЕВС становится картельной въ В.
Поэтому поляра какоц^иГбудь точки круга
есть въ то же время ка^О^ельная къ кругу въ
этой же точкѣ.
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
129
221. Если А движется обратно къ О, то В
удаляется въ безконечность. Поляра центра об-
ращенія или полярнаго центра есть безконечно-
удаленная прямая.
222. Уголъ между полярами двухъ точекъ
равенъ углу при полярномъ центрѣ, опирающе-
муся на эти двѣ точки.
223. Кругъ, описанный изъ Д какъ центра,
радіусомъ В Су пересѣкаетъ кругъ С В Е орто-
гонально.
224. Раздѣлите А В пополамъ точкой Е и пере-
гните по Е 7Ѵ перпендикулярно къ А В. Центры
всѣхъ круговъ, проходящихъ чрезъ А и Д будутъ
лежать на этой прямой. Эти круги пересѣкаютъ
кругъ СВЕ ортогонально. Такими кругами явля-
ются, между прочимъ, круги, описанные около
четыреугольниковъ АВЕН и АВСК. АЕ и
А С являются діаметрами этихъ круговъ соотвѣт-
ственно. Изъ этого слѣдуетъ, что, если два круга
пересѣкаютъ другъ друга ортогонально, то концы/
какого-нибудь діаметра одного изъ нихъ являются
сопряженными точками по отношенію къ друір^У
кругу.
225. Точки Оу Ау Н и К лежатъ^^Ш одной
окружности. Такъ какъ Д А и К вз^^йо-обратны
съ точками, лежащими на прямой^О^ С, то линіей,
обратною нѣкоторой прямой, яѣйжтся кругъ, про-
13°
ХШ. КОНИЧЕСКІЯ СЪЧЕНІЯ.
ходящій чрезъ центръ круга обращенія и чрезъ
полюсъ этой прямой, причемъ эти точки будутъ
концами его діаметра; и обратно.
226. Если продолженіе В О встрѣчаетъ кругъ
С В Е въ В', то В и В' гармонически сопряжены
съ А и В. Подобнымъ же образомъ, если какая-
нибудь прямая, проходящая чрезъ В, пересѣкаетъ
А С въ А', а кругъ СВЕ въ и то (1 и б7'
представляютъ гармоническія сопряженныя точекъ
А' и В.
227. Отложите въ какомъ-нибудь направленіи
ЬМ=ЬВ=ЬА и согните по М О' перепендику-
лярно къ ЕМ\ пусть этотъ перпендикуляръ пере-
сѣчетъ продолженіе АВ въ точкѣ О'.
Кругъ, описанный около О', какъ центра,
радіусомъ О' М, пересѣчетъ кругъ съ центромъ
въ Е и съ радіусомъ Е М ортогонально.
Но ОЕ2=ОЕ2^-ЕЕ2
и О'В=О'МЦкМ^
поэтому О Е2 — О' Е2= О Е2 — О' М2
и, слѣдовательно, является радикальнфі осью
круговъ 0(0 С) и О1 (О’М).
Беря другія точки на полуокруддажти А МВ
и повторяя то же самое построен^жы получимъ
двѣ системы безконечнаго числалеутовъ, соосныхъ
съ 0(0 С) и О' (О' М), а именно^по одной системѣ
съ каждой стороны радика^НЙрй оси Е 7Ѵ”. Точеч-
нымъ кругомъ каждой си^емы является точка А
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
іЗ1
или Д которую можно разсматривать, какъ кругъ
безконечно-малаго радіуса.
Эти двѣ безконечныя системы круговъ можно
разсматривать, какъ одну соосную систему, круги
которой составляютъ непрерывный рядъ отъ без-
конечно-большого до безконечно-малаго круга,
причемъ радикальная ось является безконечно-
большимъ, а предѣльныя точки безконечно-малыми
кругами. Эта система соосныхъ круговъ называ-
ется предѣльно-точечнымъ образомъ.
Въ двухъ пересѣкающихся кругахъ общая
хорда является ихъ радикальной осью. Поэтому
всѣ круги, проходящіе чрезъ А и Д оказываются
соосными. Эта система соосныхъ круговъ назы-
вается образомъ общей точки.
228. Возьмите двѣ прямыя ОАВ и ОРО
Изъ точекъ А и В прямой ОАВ опустите пер-
пендикуляры і4Ри на прямую ОРС). Круги,
описанные около А и В радіусами АР и В^
касаются прямой въ Р и С). Поэтому
ОА-.ОВ=АР-.В0.. Л
Это соотношеніе имѣетъ мѣсто какъ втертомъ
случаѣ, когда перпендикуляры направлены^ъ одну
сторону, такъ и тогда, когда они леж^ь по раз-
ныя стороны отъ ОАВ. Касательная^въ первомъ
случаѣ является внѣшней, а вр^^оромъ внут-
ренней.
132
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
Въ первомъ случаѣ О лежитъ внѣ АВ} а
во второмъ между А и В. Въ первомъ случаѣ О
называется внѣшнимъ, а во второмъ внутреннимъ
центромъ подобія обоихъ круговъ.
229. Прямая, соединяющая концы двухъ па-
раллельныхъ между собой радіусовъ двухъ кру-
говъ, проходитъ чрезъ центръ подобія круговъ:
внѣшній, если радіусы направлены въ одну сто-
рону, внутренній, если они имѣютъ противопо-
ложныя направленія.
230. Два радіуса какого-нибудь круга, про-
веденные въ точки пересѣченія этого круга съ
какой-нибудь прямой, проходящей чрезъ тотъ или
другой центръ подобія, соотвѣтственно парал-
лельны двумъ радіусамъ другого круга, проходя-
щимъ чрезъ точки его пересѣченія съ той же
самой прямою.
231. Всѣ сѣкущія, проходящія чрезъ центръ
подобія двухъ круговъ, разсѣкаются этими кру-
гами на пропорціональныя части.
232. Если Вх и В2, суть точі^гі^пере-
сѣченія, причемъ Вѵ В2 и Ви являйся соот-
вѣтственными точками, то
овх.овг=овх.
Отсюда видно, что обращеніе круга, не про-
ходящаго чрезъ центръ р^^щенія, даетъ снова
кругъ.
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
133
Центръ обращенія есть центръ подобія пер-
воначальнаго круга и обратнаго ему.
Первоначальный кругъ, кругъ ему обратный
и кругъ обращенія оказываются соосными.
Рис. 66
233. Методъ обращенія является однимъ изъ
наиболѣе важныхъ въ геометріи. Онъ былъ от-
крытъ докторами Стёббсомъ и Инграмомъ (ЗіиЬЬз,
Іп^гат), членами Тгіпйу Соііе^е, въ Дублинѣ,
около 1842 г. Этотъ методъ былъ употребленъ
сэромъ Вилліамомъ Томсономъ для геометриче-
скаго доказательства нѣкоторыхъ изъ наиболѣе
трудныхъ теоремъ математической теоріи элек-
тричества.
Отдтьлъ II.—Парабола
234. Параболой называется кривая, описыва-
емая точкой, которая движется по плоркр^ти та-
кимъ образомъ, что ея разстояніео^ѣь данной
точки постоянно равно ея разстоущСю отъ данной
прямой. Ху
134
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
235. Рис. 67 показываетъ, какъ можно полу-
чить параболу на бумагѣ. Сторона квадрата ММ
служитъ директрисой, О вершиной, Г фокусомъ.
Перегибая по ОХ, вы получите ось. Верхнюю
половину квадрата раздѣлите на нѣсколько частей
Рис. 67
прямыми, параллельными оси. Эти пряШй встрѣ-
чаютъ директрису въ нѣсколькихъ^®5чкахъ. Пе-
регибайте бумагу, совмѣщая кажМиб изъ этихъ
точекъ съ фокусомъ, и отмѣчай^ каждый разъ
ту точку на соотвѣтствующщгррризонтальной пря-
мой, въ которой послѣдн^рфіерегибается. Полу-
ченныя такимъ образомт^очки будутъ лежать на
XIII. КОНИЧЕСКІЯ СЪЧЕНІЯ.
і35
параболѣ. Перегибаніе даетъ въ то же время и
касательную къ кривой въ мѣстѣ перегиба.
236. Отрѣзокъ ЕЕ, перпендикулярный къ
О X, называется полупараметромъ параболы.
237. Получивъ точки верхней половины кри-
вой. можно получить и соотвѣтствующія точки
нижней половины, складывая бумагу вдвое по оси
и прокалывая ее въ уже найденныхъ точкахъ.
Рис. 68
238. Если ось параболы и ея касатед|Іиую
въ вершинѣ принять за оси координатъ, зйрурав-
неніе параболы получитъ такой видъ;
Параболу можно опредѣлит къ кривую,
описываемую точкой, которая %йжется по пло-
Роу. Геометрическія упражненія
10
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
136
скости такимъ образомъ, что квадратъ ея разсто-
янія отъ данной прямой измѣняется такъ же, какъ
ея разстояніе отъ нѣкоторой другой прямой; или
такъ, что ордината является средней пропорціо-
нальной между абсциссой и параметромъ (Іаіиз
гесіит), который равенъ 4. О Р. Отсюда слѣдующее
построеніе.
Возьмите на продолженіи Е О отрѣзокъ
ОТ=^.ОЕ.
Раздѣлите ТЛт пополамъ въ М.
На О У возьмите О такъ, чтобы М 2 =
= МЕ=МТ.
Перегните чрезъ по ()Р, перпендикулярно
къ О У.
Пусть Р будетъ точка пересѣченія ^Р съ
ординатой точки 7Ѵ.
Р будетъ точкой кривой.
239. Субнормаль = 2. ОЕ, а ЕР=ЕС=ЕТ.
Эти свойства наводятъ на слѣдующее по-
строеніе.
Возьмите на оси какую-нибудь точк^ТѴ.
Отъ 7Ѵ со стороны, противопол&рйой вер-
шинѣ, отложите ЕС=2.0Г.
Перегните по Е Р перпендцМсіярно къ ОС
и найдите наТѴР точку Р, длящрѣорой ЕР=ЕС,
Точка. Р принадлежиттэо^ривой.
Изъ центра Е можно^дщсать кругъ, прохо-
дящій чрезъ О, Р и
XIII. КОНИЧЕСКІЯ СЪЧЕНІЯ.
137
Удвоенная ордината этого круга есть въ то
же время удвоенная ордината параболы, т. е. въ
то время какъ Р движется вдоль оси, Р описы-
ваетъ параболу.
240. Возьмите между О и Р (рис. 69) какую-
нибудь точку 7Ѵ'. Согните по Р Р'Р' перпенди-
кулярно къ ОР.
Рис. 69
Найдите такую точку 7?, чтобы О Р=$ШР.
Сложите по РР перпендикулярное?» ОР,
гдѣ 7Ѵ лежитъ на оси. Перегните по ДІѵ перпен-
дикулярно къ оси.
На О X отложите ОТ^О Р^
138
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
На 7?тѴ' найдите Р', для которой ЕР=ЕТ.
Перегните по Р' Р и этимъ перегибомъ опре-
дѣлите точку Р на 7ѴР.
Точки Р и Р' принадлежатъ кривой.
241. 7Ѵ и 7Ѵ' совпадаютъ, если РРР' равно
параметру.
Если Р' перемѣщается отъ Р къ О, то 7Ѵ
движется отъ Р въ безконечность.
Въ то же время Т движется къ О, а Т (О Т' =
О Р) удаляется въ противоположномъ направленіи
въ безконечность.
242. Найти площадь, ограниченную парабо-
лой, осью и какой-нибудь ординатой.
Дополните прямоугольникъ О РР К. Пусть
отрѣзокъ ОК будетъ раздѣленъ на л равныхъ
частей; предположимъ, что въ О лі такихъ частей
заключается г и что іл л представляетъ (г-}-і)-ую
часть. Проведите перпендикулярно къ О К прямыя
тр и л д, которыя пересѣкутъ параболу въ р и
(р проведите рл' перпендикулярно къ пср.Криво-
линейная площадь О Р К есть предѣлъ сумы ряда
прямоугольниковъ, построенныхъ по^^іо т п на
частяхъ, соотвѣтствующихъ тп.
Но | |/>п • І~II НК=р т .ті^РК. ОК, а по
свойству параболы
рлг.РК^^^ОК2
и т л : О К : л.
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
139
Отсюда
р т . т п: Р К. ОК=г^ : пл
и □^«=^ХП^л:
Поэтому сумма ряда такихъ прямоугольни-
ковъ
х= + х п Л, к
(п— 1)77(27;— і)
I . 2.3.
2//:і —3«2 + » ч/|-
1.2.3.77'* 4
=Р—-+Д1хп^
^3 277 1 6;;-у 1-
=іІ_2і въ предѣлѣ, т. е. для п = оо.
Криволинейная площадь ОРК=^ площади
тѴЛГ, а слѣдовательно, параболическая площадь
ОРЫ^ГЭЫК.
243. Такой же способъ доказательства при-
мѣняется и для нахожденія параболической пло-
щади, ограниченной какими нибудь діаметромъ
ординатой.
Отдѣленіе Ш.—Эллипсъ
244. Эллипсомъ называется криваз^^оторую
описываетъ точка, движущаяся по плоскости такъ,
что ея разстояніе отъ данной то^^находится въ
постоянномъ, меньшемъ единиі^^ отношеніи къ
ея разстоянію отъ данной прямой.
140
XIII. КОНИЧЕСКІЯ СЪЧЕНІЯ.
Пусть Е будетъ фокусъ, О У директриса,
XX' перпендикуляръ къ ОУ въ точкѣ Е. Пусть
ЕА:АО и есть указанное постоянное отношеніе,
причемъ Е А меньше А О. Здѣсь А есть точка
эллипса, называемая вершиной.
Какъ въ § ііб, найдите на. XX' такую точку
А', чтобы
ЕА!\АО=ЕА :А0.
Такая точка А' тоже принадлежитъфллипсу
и представляетъ его вторую вершину^ф^
Перегните отрѣзокъ А А' вдво^%ы получите
его средину С, называемую центамъ; отмѣтьте
Е' и О', соотвѣтствующія Е Въ О' перегните
по О'У' перпендикулярно къ^м X. Точка /"'пред-
ставляетъ второй фокусл^^О'У' вторую дирек-
трису.
ХПІ. КОНИЧЕСКІЯ СЪЧЕНІЯ.
І4І
Перегнувъ, проведите чрезъ С перпендику-
ляръ къ А А'.
ЕА:АО=ЕА’:А'О
= (ЕА+ЕА'): (А О+А'О)
=АА':ОО'
= С А: С О.
На перпендикулярѣ чрезъ С возьмите точки В1
В' по разныя стороны отъ С и на такомъ раз-
стояніи, чтобы ВВ и В В' равнялись каждый С А.
Эти точки В, В’ принадлежатъ кривой.
А А9 называется большой, а В В’ малой осью.
245. Чтобы найти другія точки кривой, возь-
мите на директрисѣ какую-нибудь точку Е и
перегните бумагу по Е А и по Е А’. Перегните
еще по Е Е и отмѣтьте точку Р, въ которой ЕА’
послѣ перегибанія пересѣчетъ продолженіе ЕА.
Сгибаніемъ по РЕ опредѣлите точку Р' на ЕА',
Точки Р и Р9 принадлежатъ кривой.
Согните бумагу чрезъ Р и Р' такъ, чтобы
КРЕ и К'Р Р были перпендикулярны къ дирек-«
трисѣ, гдѣ К и К' суть точки директрисы.
Е и Р лежатъ на ЕЕ.
ЕЕ дѣлитъ уголъ А9РР пополамъ,
слѣдовательно, лЕ ЕР^= лРЕВ и РР^РЕ.
Далѣе,
= ВА\АО.
142
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
Подобнымъ же образомъ
ЕР'-.Р' К^РР'.РК'
=ГА'\А' О
=ГА:АО.
Если ЕО—РО, то Е Р перпендикулярно къ
ГО и Р Р=Р Р'. Отрѣзокъ Р Р' есть параметръ.
246. Когда найдено нѣсколько точекъ лѣвой
половины кривой, то соотвѣтствующія точки дру-
гой половины можно найти, складывая бумагу
вдвое вдоль малой оси и прокалывая ее въ уже
найденныхъ точкахъ.
247. Эллипсъ можетъ быть опредѣленъ еще
и такимъ образомъ:
Если точка Р движется такъ, что отношеніе
РЕ2 :АР. РА' сохраняетъ постоянное значеніе,
гдѣ РР представляетъ разстояніе точки Р отъ пря-
мой, соединяющей двѣ неподвижныя точки А и А',
а Р лежитъ между А и А', то геометрическое
мѣсто Р есть эллипсъ, для котораго А А* есть ось.
248. Для круга РР~=А Р. РА'.
Для эллипса РРРАР.РА' представляетъ
постоянное отношеніе. о ^5^
Это отношеніе можетъ быть ^^ѣьше или
больше единицы. Въ первомъ с^^аѣ лАРА'
тупой, а кривая лежитъ внутр^Ліомогательнаго
круга, описаннаго около А у-Ддюікъ діаметра. Во
второмъ случаѣ лАРА' обЙЗьйі и кривая лежитъ
внѣ указаннаго круга. Е^ртіервомъ случаѣ А А'
служитъ большой, а во второмъ малой осью.
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
143
249. Данное выше опредѣленіе отвѣчаетъ
Ь2
уравненію у2=~2 (2<7Л — Л?2)>
причемъ начало координатъ находится въ вер-
шинѣ эллипса.
250. А7Ѵ. ІЯ А' равняется квадрату, построен-
ному на ординатѣ 0_И вспомогательнаго круга, и
РЯ-.дЯ=ВС:А С.
Рис. 71
251. Рис.
дѣлить точки,
шеніе меньше
большой полуоси. Чрезъ какую-ні^Зф, ________
на А С проведите прямую Е Е -і^іродолжите ее
71 показываетъ, какъ можн^Упре-
когда указанное постоянное отно-
единицы. Отложите С Е^А С, т. е.
тт--- --------точку Е
і44
XIII. КОНИЧЕСКІЯ СЪЧЕНІЯ.
до встрѣчи со вспомогательнымъ кругомъ въ О.
Проведите прямую В' Е и продолжите ее до
встрѣчи съ ординатой О Л7 въ Р. Тогда
=В'С'.В С=ВС\АС. Такой же точно способъ
примѣнимъ и въ случаѣ отношенія, большаго
единицы. Если точки одного квадранта найдены,
то по нимъ легко найдутся соотвѣтственныя точки
другихъ квадрантовъ.
Рис- 72
252. Если Р и Р' суть ижы двухъ сопря-
женныхъ діаметровъ эллипса уи ординаты МР и
М' Р' встрѣчаютъ вспоуМ^ельпый кругъ въ 2
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
45
Возьмите теперь прямоугольный кусокъ кар-
тона или бумаги и отложите на двухъ смежныхъ
краяхъ его, начиная отъ вершины ихъ угла,
отрѣзки, равные малой и большой оси. Вращая
картонъ вокругъ С, нанесите соотвѣтствующія
точки внѣшняго и внутренняго вспомогательныхъ
круговъ. Пусть О, Р и О9, Р9 будутъ точки, лежа-
щія на одной прямой. Согните по ординатамъ
(9Л7и О'М' и перпендикулярно къ этимъ орди-
натамъ, по КР и 7?'Р'. Точки Р и Р' принадле-
жатъ кривой.
253. Точки этой кривой можно также легко
найти, пользуясь слѣдующимъ свойствомъ кониче-
скихъ сѣченій.
Фокальное разстояніе какой-нибудь точки
коническаго сѣченія равно длинѣ ординаты, про-
долженной до встрѣчи съ касательной къ кривой
на концѣ параметра.
254. Даны двѣ точки А и А'. Проведите
прямую А А9 и продолжите ее въ обѣ стороны.
Въ какой-нибудь точкѣ Р на продолженіи А9 А
возставьте къ А Р перпендикуляръ Р Р. Чр^ъ
какую-нибудь точку Р на РК проведите ід^гыя
Р А и Р А’. Въ А согните по А Р, пер^ѣіику-
лярно къ А Р; пусть Р будетъ точка пересѣченія
АР съ РА'. Геометрическое мѣс^ѵ^точекъ Р,
соотвѣтствующихъ различнымъ подо^ейіямъ точки
Р на Р Р, есть эллипсъ; А А' есть^о оольшая ось.
146
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
Въ самомъ дѣлѣ, согните по РіѴ перпен-
дикулярно къ А А1.
Такъ какъ РК параллельно КО, то
РР:А’ Р=КО:А'О.
Съ другой стороны, изъ треугольниковъ АРі\
и РАК
РЫ\АіЧ=АР\КР.
Слѣдовательно, : А 7Ѵ. А1 И=А Р: А1 Р,
т. е. равняется нѣкоторой постоянной величинѣ,
меньшей единицы; а изъ построенія очевидно,
что і\т должно лежать между А и А'.
Рис. 73
Отдѣлъ /Г.—Гипербола °
255. Гиперболой называется к^^ая, описы-
ваемая точкой, которая движетс^рѣо плоскости
такимъ образомъ, что ея разстояніе отъ данной
точки находится въ постоянн^гь, большемъ еди-
ницы, отношеніи къ ея гаОётоянію отъ данной
прямой. стст
XIII. КОНИЧЕСКІЯ СЪЧЕНІЯ.
47
256. Построеніе здѣсь такое же, какъ и для
эллипса, но расположеніе частей иное. Какъ объ-
яснено въ § 119, гл. X, А9 лежитъ слѣва отъ дирек-
трисы. Каждая директриса проходитъ между А
и А\ а фокусы лежатъ внѣ этихъ точекъ. Кривая
состоитъ изъ двухъ вѣтвей, открытыхъ каждая
съ одной стороны. Эти вѣтви лежать цѣликомъ
внутри двухъ вертикальныхъ угловъ, образуемыхъ
двумя прямыми, проходящими чрезъ центръ и на-
зываемыми асимптотами. Эти послѣднія касаются
кривой въ безконечности.
257. Гиперболу можно опредѣлить такъ: Если
точка Р движется такимъ образомъ, что отноше-
ніе Р А М. А’ сохраняетъ постоянную вели-
чину,—гдѣ РтѴ есть разстояніе Р отъ прямой,
соединяющей двѣ неподвижныя точки А и А', а
7Ѵ не лежитъ между А и А'—то геометрическое
мѣсто Р есть гипербола, а А А' ея поперечная
ось.
Такое опредѣленіе соотвѣтствуетъ уравненію
гдѣ за начало координатъ принята лежащая сндава
вершина гиперболы.
Рис. 74 показываетъ, какъ можно йайти точ-
о о • , ѵлЖ.
ки этой кривой на основаніи послѣдней формулы.
Пусть С есть центръ и А вей^ина кривой.
СВ'=СВ^?
С А'= С А= С" А = а.
148
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
Чрезъ С проведите, перегнувъ бумагу, ка-
кую-нибудь прямую СВ и отложите на ней
СВ= С А. Согните по В ѵѴперпендикулярно къ СВ.
Согните по 1Ѵ перпендикулярно къ СА и отло-
жите 1УО=ОМ. Согните по прямой С>А", пере-
сѣкающей СА въ точкѣ 5. Согните по В' 5, пе-
ресѣкающей ОЫ въ точкѣ Р.
Рис. 74
Эта точка Р принадлежи^^нашей кривой.
Въ самомъ дѣлѣ, такъ#|сакъ ВЫ касается
круга на діаметрѣ А А', 2
В №=А Ы. А+А Ы);
XIII. КОНИЧЕСКІЯ СѢЧЕНІЯ.
149
но такъ какъ
то
Затѣмъ
О /V2=.ѵ (2а+т).
длт_А"С
РГГВ'С'
Возводя въ квадратъ, находимъ:
х (2а-\-х) _ а~
т2 Ь~
или
О ^2 , о
У~= -2(2<ъѵ + .т-).
СІ
Если д Ы=Ъ, то 7Ѵ есть фокусъ, а СІЭ одна
изъ асимптотъ. Если дополнить прямоугольникъ
со сторонами А С и В С, то эта асимптота будетъ
его діагональю.
258. Гиперболу можно построить также, поль-
зуясь свойствомъ, указаннымъ въ § 253.
259. Гипербола называется равнобочной, если
ея поперечная и сопряженная оси равны. Тогда
а = Ь и послѣднее уравненіе обращается въ /
у- = (2а+х\х.
Въ этомъ случаѣ построеніе пронг^^ѣакъ
какъ ордината гиперболы представляетаф^еомет-
рическое среднее между АМ п Л'ЛГМ, слѣдова-
тельно, равняется касательной из'^^’ къ кругу,
описанному около А А', какъ дйЦ^тра.
!5°
XIИ. КОНИЧЕСКІЯ СЪЧЕНІЯ.
260. Полярное уравненіе прямоугольной
гиперболы, центръ которой принятъ за начало
(полюсъ), а одна изъ осей за полярную ось, имѣ-
етъ видъ
Г~ СО8 2 () =
о
или г-=- ’ а.
СО8 2 0
Пусть О X, О У будутъ оси; раздѣлите пря-
мой уголъ У О X на нѣкоторое число равныхъ
частей. Пусть ХО А, А ОВ будутъ два изъ этихъ
равныхъ угловъ. Согните по ХВ перпендикулярно
Рис. 75
къ О X. На продолженіи В О оо^5ките ОЕ^ОХ.
Согните по ОС перпендикулярно къ ВЕ и най-
дите на ОС такую точку ^^чтобы уголъ ГОВ
былъ прямымъ. Отлож&йръМ = О О. Полученная
точка А будетъ лежать ъа нашей кривой.
XIII. КОНИЧЕСКІЯ сученія.
І5І
Въ самомъ дѣлѣ, такъ какъ каждый изъ
угловъ ХОА и АОВ равенъ 0, то
ОВ=--~
СО8 20
Поэтому ОА'- = О(Р=ОВ.ОВ'=——-а,
СО8 2Ѳ
слѣдовательно, г1 соз 2 0=а\
261. Точки трисекціи ряда сопредѣльныхъ
круговыхъ дугъ лежатъ на вѣтвяхъ двухъ гипер-
болъ, эксцентрицитетъ которыхъ равенъ 2. Эта
теорема даетъ способъ трисекціи угла.
Роу. Геометрическія упражненія.
11
XIV. Различныя кривыя
262. Въ этой послѣдней главѣ я намѣренъ
дать указанія относительно построенія нѣкоторыхъ
общеизвѣстныхъ кривыхъ.
Циссоида
263. Это названіе означаетъ плющевидную
кривую. Опредѣляется она такъ: Пусть 00 А
(рис. 76) будетъ полукругъ на неподвижномъ діа-
метрѣ О А и пусть ОМ и КК означаютъ двѣ
ординаты этого полукруга, равноудаленныя отъ
центра. Проведите прямую ОР, встрѣчающую
въ точкѣ Р. Геометрическимъ мѣстомъ та-
кихъ точекъ Р и будетъ циссоида.
Если 0А=2а, то уравненіе кцивоі0есть
у1 (2 а — х) = т-. °^>°
Пусть Р Р встрѣчаетъ въ точі^ Р перпен-
дикуляръ, возставленный въ С. /Проведите линію
АР, пересѣкающую СР въ^Й^у
РЦ\СР=ОР\ ос-лу: А С=РМ:ЕС}
откуда слѣдуетъ, что
ПЫ-.Р^СБ-.СЕ.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
х53
Съ другой стороны
Л /V: Р М= О АС О М= О /V: А Лт= О №: ЛТР-
= О СССР2.
Слѣдовательно,
СР:СЕ=ООС СР2.
Рис. 76
геометрическое срё'дйее между
Если СЕ есть
С Р и СЕ, то
СР: СЕ=ОС: СР
и ОС-.СР = СР:СЕ
і54
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
Значитъ, С Р и СЕ представляютъ два геометри-
ческихъ среднихъ между ОС и СЕ.
264. Циссоида была придумана Діоклесомъ
(II ст. до Р. Хр.) для нахожденія двухъ среднихъ
геометрическихъ между двумя отрѣзками выше-
описаннымъ образомъ. Если даны ОС и СЕ, то
точка Р опредѣляется помощью этой кривой, а по
ней опредѣляется и ,точка Р.
265. Если отрѣзки РР и ОК равны каждый
О О, то уголъ А О О дѣлится прямой О Р на три
равныя части.
Проведите ОЕ. Легко видѣть, что ОЕ па-
раллельно О А и
РО=РР=РЕ = ОО.
Отсюда лЕОО=^ОР О=ълОЕ О=ълА ОЕ.
Іуонхоида
266. Эта кривая принадлежитъ Никомеду
(около 150 г. до Р. Хр.). Пусть О будетъ неподвиж-
ная точка, а ея разстояніе отъ нѣкоторой непо-
движной прямой /9т1/. Проведите чрезъ С^учокъ
лучей, встрѣчающихъ Р М. На каждомг^гаъ этихъ
лучей отложите, по обѣ стороны от^^ересѣченія
его съ РМ, по отрѣзку Ь. Геоме'^Тческое мѣсто
опредѣленныхъ такимъ образомъ^точекъ и есть
конхоида. Смотря по томуД^рудетъ ли 6>, =
или <?, начало представлявъ узелъ, остріе или
сопряженную точку. Пашѣ'рисунокъ изображаетъ
тотъ случай, когда Ь>а.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
155
267. Этоіі кривой также пользовались для
нахожденія двухъ геометрическихъ среднихъ и
для трисекціи угла.
Пусть О А бу-
детъ большій изъ тѣхъ
двухъ отрѣзковъ, для
которыхъ требуется
найти два геометриче-
скихъ среднихъ.
Раздѣлите О А по-
поламъ въ В\ изъ О,
какъ изъ центра, опи-
шите, окружность ра-
діусомъ О В. Чрезъ В
проведите хорду В С,
равную меньшему изъ
двухъ данныхъ отрѣз-
ковъ. Проведите А С
и продолжите А С и
В С до точекъ В и /Г,
лежащихъ на одной
прямой съ О и отсто-
ящихъ другъ отъ дру-
га на разстояніе/)Е—
= 0В или В А.
Отрѣзки Е В и СЕ и
нихъ пропорціональныхъ.
Пусть Е и С будутъ точід^й’ерес Ьченія О Е
съ кругомъ.
мыхъ сред-
т5б
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
На основаніи теоремы Менелая
ВС.ЕБ. б А = С Е .0 Б. В А,
поэтому
или
ВС.ОА = СЕ.ОБ
ВС О_Ѵ.
СЕ~ОА'
слѣдо вате л ьно,
ВЕ ОБ+ОА_СЕ
СЕ~ О А О А'
Рис. 78
Но СЕ.ЕЕ -ВБ.ЕС. • о
Поэтому СЕ.ОБ=ВЕ.ЕС,
ОА.ОБ=ЕС-
и наконецъ О А: С Е= СЕ О І)\ ВС.
Положеніе Е найдено пржномощи конхоиды,
для которой А В служиттіХМимптотой, О фоку-
сомъ, а В Е постоянным^Ътрѣзкомъ.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
т57
268. Трисекція угла выполняется такимъ обра-
зомъ. На рис. 77 пусть (р=лМОѴ, который
требуется раздѣлить на три части. На ОМ от-
ложите произвольный отрѣзокъ ОМ=Ь. Изъ цен-
тра М радіусомъ Ъ опишите кругъ и проведите
чрезъ М перпендикулярно къ оси X, имѣющей
начало вчэ О, вертикальную прямую, представляю-
щую асимптоту конхоиды, которую надо построить.
Постройте конхоиду. Соедините О съ Л, т. е. съ
пересѣченіемъ круга и конхоиды. Полученный
у. А О У равенъ одной трети ср.
Всрсъера *)
269. Если О() А (рис. 79) представляетъ полу-
кругъ, №() одну изъ его ординатъ и отрѣзокъ
АгР равенъ четвертой пропорціональной къ О7Ѵ,
О А и (2IV, то геометрическое мѣсто точекъ Р
есть версьера.
Согните по АМ перпендикулярно къ О А.
Согните чрезъ О, О и М.
Дополните прямоугольникъ ЫА МР.
РІР0^=ОМ\О0
= ОА'.СШ.
Точка Р есть одна изъ точекъ нашейй^йвой.
Ея уравненіе есть
ху-=п~ (а—х).
*) По имени нашедшей ее эту^Дшнію называютъ
также анъезъерой. Прим. пер.
158
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
Эта кривая была предложена Маріей Гаэта-
ной Аньези, профессоромъ математики въ Болоньѣ
въ XVIII столѣтіи.
Рис. 79
Кубическая парабола
270. Уравненіе этой кривой ецзъ а2у=х3.
Пусть ОХ, О У будутъ ш
0А=а и 0Х=х. ./СГ
гмоугольныя оси,
На оси О У возьми'
В=х.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
159
Проведите ВА и затѣмъ, перпендикулярно
къ А В, прямую А С, которая встрѣтитъ ось О У
въ точкѣ С.
Проведите СХ и, перпендикулярно къ СХ,
прямую X У.
ХО У дополните до прямоугольника.
Точка Р принадлежитъ разсматриваемой^фивой.
у=ХР = О
или
ібо
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
Гармоническая кривая или синусоида
271. Это та кривая, форму которой прини-
маетъ звучащая струна. Въ ней ординаты пропор-
ціональны синусамъ угловъ, которые во столько
же разъ меньше четырехъ прямыхъ угловъ, во
сколько разъ соотвѣтствующія абсциссы меньше
нѣкотораго даннаго отрѣзка.
Рис. 81
Пусть АВ есть данный отрѣзо^°*(рис. 8і).
Продолжите В А до Си согните п^рЙ Б перпен-
дикулярно къ А В. Прямой угол^р^О А С раздѣ-
лите на нѣсколько равныхъ „ пастей, напримѣръ,
на четыре. На каждомъ ратаук отложите отрѣ-
зокъ, равный амплитудѣ^олебанія, АС=АР=
=Ад=АК = АВ.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
ібі
Изъ точекъ Р, О, У? опустите на А С пер-
пендикуляры; отрѣзки РР\ О О', Р Рг и БА бу-
дутъ пропорціональны синусамъ угловъ РА С,
О_АС РАС, Р АС.
Раздѣлите А В пополамъ въ Р; отрѣзки А Е
и ЕВ раздѣлите каждый на вдвое большее число
частей, чѣмъ было взято частей прямого угла.
Проведите ординаты 55', ТТ, ѴІѴ, V V’ и т. д.,
соотвѣтственно равныя РР’, 00Е РР’, В Аит.д.
Тогда точки 5, Г, У7, V и будутъ точками иско-
мой кривой, причемъ V будетъ ея верхней точ-
кой. Складывая но V V и дѣлая проколы въ 5,
Т, Е, Ѵу мы получимъ соотвѣтственныя точки
части ѴЕ кривой. Часть кривой, соотвѣтствую-
щая отрѣзку. Е В, равна части И 17Е, но лежитъ
по другую сторону А В. Разстояніе А Е равно
длинѣ полуволны, которая повторяется отъ Е до
В по другую сторону АВ. Точка Е есть точка
перегиба кривой; въ ней радіусъ кривизны стано-
вится безконечно большимъ.
Овалы рассини
272. Если точка движется по
кимъ образомъ, что произведеніе ея ра^юяніи
отъ двухъ неподвижныхъ точекъ плоскшфі сохра-
няетъ постоянную величину, то эта ОПИСЬІ-
ваетъ одинъ изъ оваловъ КассиншОіеподвижныя
точки называются фокусами, уравненіе кривой
іб2
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
есть гг' = /?’2, гдѣ г и г означаютъ разстоянія ка-
кой-нибудь точки кривой отъ ея фокусовъ, а к
есть нѣкоторая постоянная.
Пусть Е и Е' будутъ фокусы. Проведите
прямую ЕЕ'. Раздѣлите ЕЕ' пополамъ въ С и
чрезъ С проведите В СВ перпендикулярно къ ЕЕ'.
Найдите такія точки Ви В\ чтобы ЕВ=ЕВ = к.
Ясно, что такія точки В, В’ принадлежатъ нашей
кривой.
В'
Рис 82
Согните по ЕК перпендику^^шо къ ЕЕ' и
отложите Е /г; на ЕЕ' отлож^Вё СА = СА' = СК.
Полученныя точки А, А' летавъ на нашей кривой.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
Слѣдовательно,
СА2 — СЕ2==к2 = (СА+СЕ)(СА — СЕ)=Е'А . ЕА.
Продолжите ЕА и отложите А Т=ЕК. На
А Т возьмите какую-нибудь точку 71/ и проведите
71/7/. Перегните по КМ’ перпендикулярно къ М К\
КМ' пересѣчетт> ЕА1 въ 71/'.
Въ такомъ случаѣ Е М. / М' = к2.
Изъ Е и Е', какъ изъ центровъ, опишите
дуги радіусами ЕМ и Е М‘\ эти дуги пересѣкутся
въ нѣкоторой точкѣ Р. Эта точка принадлежитъ
нашей кривой.
Когда найдено нѣсколько точекъ между А
п Д соотвѣтственныя точки въ другихъ квадран-
тахъ можно намѣтить, перегнувъ бумагу.
Если ЕЕ1 = Ѵ ър а гг' = |^2, то кривая при-
нимаетъ форму лемнискаты (§ 279).
Если ЕЕ’ больше, чѣмъ К2Д то кривая со-
стоитъ изъ двухъ отдѣльныхъ оваловъ, по одному
вокругъ каждаго фокуса.
Логариѳмическая кривая
273. Уравненіе этой кривой есть
Ордината въ началѣ равна единицѣ^
Когда абсцисса возрастаетъ вѣЛ^риѳметиче-
ской прогрессіи, ордината увеличивается въ геоме-
трической.
164
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
Значенія у, отвѣчающія цѣлымъ значеніям и
а, можно получить помощью построенія, даннаго
въ § 108.
Эта кривая уходитъ въ безконечность, не
выходя изъ угла X О У.
Если .т отрицательно, то У = ~х и, слѣдова-
тельно, приближается къ нулю при возрастаніи
аосолютной величины .ѵ. Поэтому отрицательная
сторона оси ОХ является асимптотой этой кривой-
Обыкновенная цгыіная линія
274. Цѣнной линіей называется форма, при-
нимаемая тяжелой (вѣсомой) нерастяжимой нитью,
свободно висящей на двухъ точкахъ и находя-
щейся подъ дѣйствіемъ только силы тяжести.
Уравненіе этой кривой имѣетъ видъ
с( — - —А
у=~Іес+е г|
если за ось у принять вертикальную прямую,
проходящую чрезъ самую низкую точк^З^ривой,
а за ось .ѵ горизонтальную прямую, ц^?ащую въ
плоскости нити на разстояніи с кн^^т отъ са^ой
низкой точки кривой; с называется параметромъ
кривой, а с есть основаніе ~ уральныхъ лога-
риѳмовъ.
Если
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
і65
если X —2Г, то — (с-+г—) и т. д.
275. Изъ уравненія
можно графически опредѣлить е.
се — 2 у + с = о
V е=~ (у+ Ѵу-е^
с]/~е =у+Уу1 — с~ •
Уу1 — с2 можно найти, какъ геометрическое среднее
между у+е и у — с.
Кардіоида или сердцевидная кривая
276. Чрезъ какую-нибудь неподвижную точку
О, лежащую на окружности радіуса а, проведите
пучокъ прямыхъ; на каждой изъ нихъ отложите,
считая отъ точки ея пересѣченія съ окружностью,
по отрѣзку, равному 2<7, въ ту и въ другую ст^
рону. Концы этихъ отрѣзковъ лежатъ на к^рВіК
оидѣ. '
Уравненіе этой кривой есть г=2л(^|^О5 Ѳ).
Въ началѣ координатъ будетъ острое кривой.
Кардіоида есть обращеніе па^^лы относи-
тельно ея фокуса, какъ центра б^ращенія.
ібб
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
Улитка
277. Чрезъ какую-нибудь постоянную точку
на кругѣ проведите пучокъ хордъ; на каждой изъ
нихъ отложите въ обѣ стороны отъ точки встрѣчи
съ окружностью по отрѣзку опредѣленной длины.
Рис. 83
Если эти отрѣзки постоянной длины равны
діаметру взятаго круга, то кривая будетъ карді-
оидой.
Если же эти отрѣзки больше діам^ра, то
кривая лежитъ цѣликомъ внѣ круга. о
Если отрѣзки короче діаметра, ^р^часть кри-
вой лежитъ внутри круга въ вид^йетли.
Если наконецъ длина отрѣгфЬвъ равна поло-
винѣ діаметра, то кривая поДда&етъ названіе три-
сектрисы вслѣдствіе того^Эчто при ея помощи
можно раздѣлить люббтуголъ на .три части.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
167
Уравненіе этой кривой есть г=а соз Ѳ+&.
Улитка перваго рода представляетъ обраще-
ніе эллипса, улитка второго рода представляетъ
обращеніе гиперболы, причемъ въ томъ и дру-
гомъ случаѣ за центръ обращенія надо брать
одинъ изъ фокусовъ. Петля есть обращеніе той
же вѣтви гиперболы около другого фокуса.
278. Трисектрису примѣняютъ слѣдующимъ
образомъ: <
Данъ уголъ АОВ, Отложите отрѣзки
О В, равные радіусу круга. Опишите кругъ р<||буса
О А (или О В) съ центромъ въ О. Продолл^ё А О
неопредѣленно далеко за кругъ. ѢІалолште трисек-
трису такъ, чтобы точка О совпала с^йентромъ ея
круга, а О В съ осью петли. Пуст^Энѣшняя часть
кривой пересѣчетъ продолженій^ О въ точкѣ С.
Роу. Геометрическія упражненія
12
т68
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
Проведите прямую В С, встрѣчающую кругъ въ
2?, и прямую ОВ.
Покажемъ, что
лА СВ=^лА ОВ.
Въ самомъ дѣлѣ,
СВ=ВО=ОВ.
Отсюда лА ОВ= лА СВ-{- лСВ О
=лАСВ+лОВВ
= лАСВ+ълАС В
=З^АСВ.
Лемниската Бернулли
279. Полярное уравненіе этой и
етъ видъ:
Г2 = «2СО8 2б.
Пусть О будетъ начало І^пусть ОА=а.
Продолжите А О и пш^дите О В перпен-
дикулярно къ О А.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
169
Возьмите лАОР=§ и лА0В=2§.
Изъ А опустите на ОВ перпендикуляръ АВ.
На продолженіи АО отложите ОС=ОВ.
На О В найдите такую точку В, для которой
.а/іПС есть прямой.
Отложите ОР=ОБ.
Тогда Р будетъ одной изъ точекъ нашей
кривой.
г‘2 = ОВ* = ОС. О А
= ОВ.ОА
=а СО82О. а
= (Р СО8 2 0.
Какъ было упомянуто выше, эта кривая пред-
ставляетъ частный случай оваловъ Кассини.
о
Рис. 86
Она есть обращеніе прямоугольной гипер-
болы, если центръ послѣдней цМіж» за центръ
обращенія, а также представляе^ подарную кри-
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
170
вую той же гиперболы по отношенію къ ея центру
Площадь этой кривой равняется а2.
Циклоида
280. Циклоидой называется путь, описывае-
мый точкой окружности круга, катящагося по
неподвижной прямой.
Пусть А и А’ суть положенія точки, описы-
вающей циклоиду, когда она касается неподвиж-
ной прямой въ началѣ и въ концѣ одного полнаго
оборота круга. А А' равняется длинѣ окружности
взятаго круга.
Рис. 87
Длину окружности круга можно /^лучить
слѣдующимъ образомъ. Оберните поляку бумаги
вокругъ какого-нибудь цилиндрич^щ^Яо предмета
и отмѣтьте двѣ совпадающія тоіщй. Разверните
затѣмъ бумагу и перегните ее^резъ эти точки.
Тогда отрѣзокъ прямой, заключенный между
этими точками, по длинѣ (^^^етъ равенъ окруж-
ности, соотвѣтствующей^аметру цилиндра.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
І7І
Пользуясь пропорціональностью, можно найти
окружность для любого діаметра и наоборотъ.
Раздѣлите А А9 пополамъ въ /9; возставьте
въ Р перпендикуляръ къ А А9 и отложите на
немъ РВ =діаметру производящаго круга.
Точки А, А9 и В принадлежатъ кривой.
Найдите средину О отрѣзка ВО.
Чрезъ О проведите нѣсколько радіусовъ, дѣ-
лящихъ правую полуокружность на нѣсколько
равныхъ дугъ, напримѣръ, на четыре.
Отрѣзокъ АР раздѣлите на такое же число
равныхъ частей.
Чрезъ концы этихъ радіусовъ при помощи
перегиба проведите прямыя, перпендикулярныя
къ ВР.
Пусть ЕЕ Р будетъ одна изъ такихъ пря-
мыхъ, Е конецъ соотвѣтствующаго радіуса и пусть
С будетъ точка соотвѣтственнаго дѣленія отрѣзка
АВ} начиная отъ Р. Отложите РР=ЕА или
длинѣ дуги В Е.
Точка Р есть точка кривой. /ф
Другія точки, соотвѣтствующія другимт^йЯ-
камъ дѣленія А Р, можно получить таюр&г же
образомъ.
Кривая симметрична по отношцнй^ къ оси
В Р\ поэтому соотвѣтствующія точкА лѣвой поло-
вины кривой можно получить, сй^^ывая бумагу
по ВР.
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
і72
Длина кривой въ 4 раза больше ВВ, а ея
площадь въ з раза больше площади производя-
щаго круга.
Трохоида
281. Если кругъ катится по прямой такъ же,
какъ въ случаѣ циклоиды, то каждая точка, лежа-
щая въ плоскости круга, но не на его окружно-
сти, описываетъ кривую, называемую трохоидой.
Эпициклоида
282. Эпициклоидой называется путь, описы-
ваемый точкой окружности круга, который катится
по окружности другого, неподвижнаго круга, ка-
саясь его съ наружной стороны.
Гипоциклоида
Если катящійся кругъ касается непо-
круга съ его внутренней стороны, то
283.
движнаго
кривая, которую описываетъ точка окружности
перваго круга, называется гипоциклоидой^'
Если радіусъ неподвижнаго круг&^Йъ цѣлое
число разъ больше радіуса катящар^Ж круга, то
окружность перваго слѣдуетъ раздѣ.п_ить на такое
же число равныхъ частей.
Эти части въ свою очередь надо раздѣлить
на нѣкоторое число равні^^частей каждую; тогда
положеніе центра катяш^Ьэся круга и производя-
XIV. РАЗЛИЧНЫЯ КРИВЫЯ.
173
щей точки, соотвѣтствующія каждой точкѣ части
неподвижнаго круга, можно найти, дѣля окруж-
ность катящагося круга на такое же число рав-
ныхъ частей.
Рвадратриса
284. Пусть О А СВ представляетъ квадратъ.
Если радіусъ О А круга равномѣрно поворачива-
ется около центра О на прямой уголъ отъ поло-
женія О А до положенія ОВ и если въ то же
время прямая, перпендикулярная къ ОВ, равно-
мѣрно перемѣщается параллельно самой себѣ отъ
положенія О А до ВС, то геометрическое мйсто
точекъ пересѣченія радіуса и прямой называется
квадратрисой.
Эта кривая была придумана Гиппіадомъ изъ
Элиды (420 до Р. Хр.) для раздѣленія угла на
нѣсколько равныхъ частей.
Если Р и Р’ суть точки кривой, то углы
А ОР и АОР' относятся другъ къ другу, какъ
ординаты точекъ Р и Р.
Спиралъ Архимеда
285. Если прямая О А равномѣрно ^^щается
вокругъ О, какъ центра, то точка которая
равномѣрно движется отъ О вдолѣ^^^4, описы-
ваетъ спираль Архимеда.
КЛіЧѴААііАЧ Книгоиздательство научныхъ и популярно-науч-
ШІЯ I Р I* ныхъ сочиненій изъ области физико-математиче-
1(1 00 И V О скихъ наукъ.
Одесса, уп. Новосельскаго, 66.
А. В. КЛОССОВСКІИ
заслуженный профессоръ.
ОСНОВЫ МЕТЕОРОЛОГІИ
ХѴІ-|-527 стр. большого 8°. Съ 199 рис., 2 цвѣти, и 3 черн. табл. Ц. 4 р
СОДЕРЖАНІЕ.
Ч. I. Статическая метеорологія.
Введеніе.—Распространеніе и составъ атмосферы.—Физиче-
скія свойства атмосферы.—Вода въ атмосферѣ.—Непрерывная вод-
ная оболочка (океаны), ея распространеніе и свойства.—Солнечное
лучеиспусканіе.—Расходъ тепла.—Тепловое состояніе земной коры
въ самыхъ верхнихъ ея слояхъ.—Тепловое состояніе земного ядра.
—Тепловыя условія океановъ.—Тепловое состояніе нижнихъ сло-
евъ земной атмосферы.—Давленіе воздуха.—Образованіе гидро-
метеоровъ.—Температура и давленіе въ болѣе высокихъ слояхъ
атмосферы.—Нномальныя отклоненія.
Ч. II. Динамическая метеорологія и метеорологическая оптика.
Основныя начала динамики атмосферы. — Распредѣленіе
воздушныхъ теченій на земной поверхности.—Циклоны и анти-
циклоны. —Теоретическія соображенія о происхожденіи циклоновъ
и антициклоновъ.—Состояніе вопроса о предсказаніи погоды.—
Динамика океановъ.—Метеорологическая оптика.
Ч. III. Земной магнетизмъ. Электрометеорологія. Методь^^ср-
временной метеорологіи. "
Земной магнетизмъ.—Электрометеорологія.—Методы^ж зада-
чи современной метеорологіи.—Серія метеорологическихъЙ^лектро-
метрическихъ и магнитныхъ наблюденій.—ЛитературѣѣЙг указанія.
Описаніе таблицъ. у,'
Среднее годовое распредѣленіе осадковш@>земной поверх-
ности по Зупану.—Среднее распредѣленіе воздЛдныхъ теченій на
земной поверхности.—Морскія теченія по ШрТГу.—Карты равныхъ
склоненій (изогоны) и равныхъ наклоненіиШзоклины), приведен-
ныя къ эпохѣ 1 января 1905 г.—Карта ^^ныхъ горизонтальныхъ
напряженій (изодинамы), приведенная къ эпохѣ 1 января 1905 г.
Магнитная буря 30 января—1 февраля 1881 года. Магнитная буря
28 февраля 1896 года.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ".
Проф. Г. А. ЛОРЕНЦЪ
КУРСЪ ФИЗИКИ
Разрѣшенный авторомъ переводъ съ нѣмецкаго
подъ редакціей проф. Н. П. Кастерина.
Т. I. VIII—|—348 стр. большого 8°. Съ 236 рис. Ц. 2 р. 75 к.
Содержаніе перваго тома. Главы 1 — ѴН1: Движеніе и силы.
—Работа и энергія.—Твердыя тѣла неизмѣнной формы.—Равно*
вѣсіе и движеніе жидкостей и газовъ.—Свойства газовъ.—Прин-
ципы термодинамики.—Свойства твердыхъ тѣлъ.—Свойства жид-
костей и паровъ.—Именной и предметный указатели.
ИЗЪ ОТЗЫВОВЪ О НЪМЕЦКОМЪ ИЗДАНІИ: „Несмотря на чрезвычайную
конкурренцію переводъ отнюдь не представляется излишнимъ—и не только потому,
что книга составлена такимъ выдающимся физикомъ, какъ проф. Лоренцъ, но прежде
всего потому, что эта книга существенно отличается отъ другихъ и по своей цѣли
и по выполненію. Изложеніе отличается необычайной легкостью и простотой и дѣ-
лаетъ книгу въ высшей степени интересной для всѣхъ, кто отъ опытной физики
требуетъ больше, нежели только описанія опытовъ41.
ВеіЫйіівт =и (Іеп Апппіеп йет Гіѵуяііс.
Готовится къ печати II томъ съ добавленіями автора къ рус^ду изданію.
Содержаніе второго тома. Главы IX - ХѴіИг/^блебательное
движеніе тѣлъ.—Распространеніе колебаній.—Отраженіе и пре-
ломленіе свѣта.—Природа свѣта.— Поляризоѣдндіій свѣтъ.—Элек-
тростатика. — Электрическіе токи.—Дѣйствія^магнитнаго поля. —
Электрическія колебанія. Распространеніедэ$=ктромагнитныхъ на-
рушеній равновѣсія.—Явленія, объясняемая при помощи теоріи
электроновъ.—Задачи. Таблицы. Предметный и именной указатели.
ТОМЪ II (около 30 печатныхъ листовъ) выйдетъ въ
• свѣтъ въ началѣ 1910 г.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ".
Вышли въ свѣтъ слѣдующій изданій:
1. С. Арреніусъ, проф. ФИЗИКА НЕБА. Пер. съ нѣм. подъ ред-
прив.-доц. А. Р. Орбинскаго. VIII—|—250 стр. 8°. Съ 68 рис. и 1 черн-
и 1 цвѣти, табл. Ц. 2 р. *)
~2 и 3. Абрагамъ, проф. СБОРНИКЪ ЭЛЕМЕНТАРНЫХЪ ОПЫ
ТОВЪ ПО ФИЗИКѢ, составл. при участ. мног. проф. и преподав. физики.
Пер. съ фр. подъ ред. грив.-доц. Б. П. Вейнберга.
Часть I: ХѴІ-|-272 стр. Со мног. (свыше 300) рис. Ц. 1 р. 50 к.
Часть II: 434-|-ЬХХѴ стр. со мног. (свыше 4<Ю) рис. Ц. 2 р. 75 к.
4. УСПѢХИ ФИЗИКИ. Сборы, статей о важн открытіяхъ послѣды,
лѣтъ въ общедост. изложеніи, подъ ред. „Вѣсти. Оп. Физ. и Элемент.
Матем.“. ІѴ-НН8 стр. 8°. Съ 41 рис. и 2 табл. Изд. 2-е. Ц. 75 к. *)
(Распродано).
5. Ф. Ауэрбахъ, проф. ЦАРИЦА МІРА И ЕЯ ТѢНЬ. Общедоступн.
изложеніе основаній ученія объ энергіи и энтропіи. Пер. съ нѣм. Съ
предисл. Ш. Э. Гилъома. ѴІІІ-|-5б стр. 8°. Изд. 4-е. Ц. 40 к. *)
6. С. Ньюкомъ, проф. АСТРОНОМІЯ ДЛЯ ВСѢХЪ. Пер. съ
англ. Съ предисл. прив.-доц. А. Р. Орбинскаго. ХХІѴ--|-286 стр. 8°.
Съ портр. автора, 64 рис. и 1 табл. Ц. 1 р. 5<> к. *)
7. Г. Веберъ ИІ. Вельштейнъ. ЭНЦИКЛОПЕДІЯ ЭЛЕМЕНТАР-
НОЙ МАТЕМАТИКИ. Томъ I ЭНЦИКЛОПЕДІЯ ЭЛЕМЕНТАРНОЙ
АЛГЕБРЫ, обработ. проф. Веберомъ. Пер. съ нѣм. подъ ред. прив.-
доц. В. Ф. Кагана. Книга I. ОСНОВАНІЯ АРИѲМЕТИКИ. Книга II.
АЛГЕБРА Книга III. АНАЛИЗЪ. Х1Ѵ-}-623 стр. 8°. Съ 38 чертеж.
Ц. 3 р. 50 к. *)
8. Дж. Перри, проф. ВРАЩАЮЩІЙСЯ ВОЛЧОКЪ. Публ. ]^ія.
Пер. съ англ. VII—|—95 стр. 8°. Съ 63 рис. Изд. 2-е Ц. 60 к. =4^)°
9. Р. Дедекиндъ, проф. НЕПРЕРЫВНОСТЬ И И^В^ОНАЛЬ-
НЫЯ ЧИСЛА Пер. прив -доц. С. I ІІатуновскаго, съ прШ> его статьи:
ДОКАЗАТЕЛЬСТВО СУЩЕСТВОВАНІЯ ТРАНСЦЕНДЕНТНЫХЪ ЧИ-
СЕЛЪ. Изд. 2-е. 40 стр. 8°. Ц. 40 к.*). ѴѴѵ"
----------------------------------------"Дп----
*) Изданія, отмѣченныя звѣздочкой, Учен. Ком. М. Н. П.
признаны заслуживающими вниманія при пополн. учен. библ.
среди, учебн. заведеній.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ".
10. К.' Шейдъ, проф. ПРОСТЫЕ ХИМИЧЕСКІЕ ОПЫТЫ ДЛЯ
ЮНОШЕСТВА. Пер. съ нѣм. подъ ред лаб. Новорос. унив. Е. С. Елъ-
чанинова. II—|—192 стр. 6°. Съ 79 рис. Ц. 1 р. 20 к.
11. Э. Вихертъ, проф. ВВЕДЕНІЕ ВЪ ГЕОДЕЗІЮ. Лекціи для
преподав. среди, учебн заведеній. Пер, съ нѣм. 80 стр. 16°. Съ 41 рис.
Ц. 35 к.*).
12. Б. Шмидъ. ФИЛОСОФСКАЯ ХРИСТОМАТІЯ. Пособіе для
среди, учебн. зав. и для самообраз. Пер. съ нѣм. подъ ред. проф. Н. Н.
Ланге. ѴІ-|-17І стр. 8°. Ц. 1 р.*).
13. С. Тромгольтъ. ИГРЫ СО СПИЧКАМИ. Задачи и развле-
ченія. Пер. съ нѣм. 146 стр. 16°. Со мн. рис. Ц. 50 к.
1<А . Риги, проф. СОВРЕМЕННАЯ ТЕОРІЯ ФИЗИЧЕСКИХЪ
ЯВЛЕНІЙ. (Радіоактивность, іоны, электроны). Пер. съ 3-го (1907) итал.
изд. ХІІ-|-156 стр. 8°. Съ 21 рис. Ц. 1 р.*).
15. В. Ветгэмъ. проф. СОВРЕМЕННОЕ РАЗВИТІЕ ФИЗИКИ.
Пер. съ англ, подъ ред. прив.-доц Б. И. Вейнберга и А. Р. Орбинскаго.
Съ прилож. рѣчи перваго министра Англіи А. Ваіроиг'. НѢСКОЛЬКО
МЫСЛЕЙ О НОВОЙ ТЕОРІИ ВЕЩЕСТВА. ѴШ+319 стр. 8°. Съ 5
портр., 6 отд. табл. и 33 рис. Ц. 2 р.*).
16. П. Лакуръ и Я. Аппель. ИСТОРИЧЕСКАЯ ФИЗИКА. Пер-
съ нѣм. подъ ред. „Вѣсти. Оп. Физ. и Элем. Матем.“. Въ двухъ томахъ-
875 стр. 8°. Съ 799 рис. и 6 отд. табл. Ц. 7 р. 50 к.*).
17. А. В. Клоссовскій, проф. ФИЗИЧЕСКАЯ ЖИЗНЬ НАШЕЙ
ПЛАНЕТЫ. Изд. 2-е, испр. и доп. 45 стр. 8°. Ц. 40 к.
18. С. А. Арреніусъ. ОБРАЗОВАНІЕ МІРОВЪ. Перев. съ нѣм.
подъ ред. проф. Имп. Юрьев. Унив. 7(. Д. Покровскаго. ѴІЦ4т200 стр. 8°.
Съ 60 рис. Ц 1 р. 75 к.*).
19. Н. Г. Ушинскій, проф ЛЕКЦІИ ПО
ѴІ1І-|-136 стр. 8°. Съ 34 рис. на 15 отд. табл. Ц.
20. В. Ф. Каганъ- прив.-доц. ЗАДАЧА ОБОСНОВАНІЯ ГЕОМЕТ-
РІИ. 35 стр. 8°. Съ 11 рис. Ц. 35 к._
21. В. Циммерманъ, проф. ОБЪеЛ^ ШАРА, ШАРОВОГО СЕГ-
МЕНТА и ШАРОВОГО СЛОЯ. 34 ($Щ60. У-25 к.
*) Изданія, помѣченныя звѣздочкой, Учен. Цом. М. Н. П
признаны заслуживающими вниманія при пополн. учен. библ.
средн. учебн. заведеній.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ".
22. 0. Леманъ, проф. ЖИДКІЕ КРИСТАЛЛЫ и ТЕОРІИ ЖИЗНИ.
Пер. съ нѣм. 48 стр. 8°. Съ 30 рис. Ц. 40 к.
23. Г. Гейбергъ, проф. НОВОЕ СОЧИНЕНІЕ АРХИМЕДА. Пер.
съ нѣм. ХѴ-|-’27 стр. 8°. Ц. 40 к *).
24. А. Риги, проф. ЭЛЕКТРИЧЕСКАЯ ПРИРОДА МАТЕРІИ.
Пер. съ итал. 28 стр. 8°. 1Д. 30 к.*).
25. г. Ковалевскій,проф. ВВЕДЕНІЕ ВЪ ИСЧИСЛЕНІЕ БЕЗКО-
НЕЧНО МАЛЫХЪ. Пер. съ нѣм. подъ ред. пр.-доц. С. ІПатуновскаго.
VIII -|- 140 стр. 8°. Съ 18 черт. И. 1 р.:=:)
26. Б. Вейнбергъ, прив.-доц. СНѢГЪ, ИНЕИ, ГРАДЪ, ЛЕДЪ и
ЛЕДНИКИ. IV—127 сір. 8°. Съ 138 рис. и 2 фототип. табл. Ц. 1 р.*).
27. ТОМПСОНЪ, Сильванусъ. ДОБЫВАНІЕ СВѢТА. Общедоступ-
ная лекція. Ѵ1ІІ-(-88 стр. 16°. Съ 28 рис. Ц. 50 к.*)
28. А. Слаби, проф. РЕЗОНАНСЪ и ЗАТУХАНІЕ ЭЛЕКТРИЧЕ-
СКИХЪ ВОЛНЪ. 42 стр. 8°. Съ 36 рис. Ц. 40 к.
29. К. Снайдеръ, КАРТИНА МІРА ВЪ СВѢТѢ СОВРЕМЕННАГО
ЕСТЕСТВОЗНАНІЯ. Перев. съ нѣм. подъ ред. проф. В. В. Завьялова.
ѴІІІ-|-193 стр. 8°. Съ 16 отд. портрет. Ц. 1р. 50 к.
~0. В. Рамзай, проф. БЛАГОРОДНЫЕ и РАДІОАКТИВНЫЕ
ГАЗЫ. Пер подъ ред. Вѣсти. Опытн. Физ. и Эл. Мат. 37 стр. 16°.
Съ 16 рис. Ц. 25 к.
31. К. Бруни, проф. ТВЕРДЫЕ РАСТВОРЫ. Пер. съ итал. подъ
ред. Вѣсти. Опытн. Физ. и Эл. Матем. 37 стр. 16°. Ц. 25 к.
32. Р. С БОЛЛЪ, проф. ВѢКА и ПРИЛИВЫ, Пер. съ англ, подъ
ред. прив.-доц, А. Р. Орбинскаго. 104 стр. 8°. Съ 4 рис. и 1 табл.
Ц. 75 к._______________________________________
33. А. Слаби, проф БЕЗПРОВОЛОЧНЫЙ ТЕЛЕФОНЪ, <Ш^р. съ
нѣм. подъ ред. Вѣсти. Оп. Физ. и Эл. ЪІатем. 28 стр. Съ 23
рис. Ц 30 к.
34. Л. Кутюра, АЛГЕБРА ЛОГИКИ. Пер. съ фр. ^Прибавленіями
проф. И. Слешинскаго. 128 стр. 8°. Ц. 90 к.
^35, Веберъ и Велыптейнъ, проф. ЭНЦИКЛОтеМіЯ ЭЛЕМЕНТАР-
НОЙ ГЕОМЕТРІИ. Т. II, кн. I. Основанія геоц^ші. Пер. съ нѣм. подъ
ред. и съ прим. прив.-доц. В. Ф. Кагана. ШІЬф 362 стр. 8°. Съ 142
черт. и 5 рис. Ц. 3 р._________________________________
36. Ф. Линдеманъ. СПЕКТРЪ и ФОРМА АТОМОВЪ. Рѣчь ректора
Мюнхенск. унив. Перев. съ нѣм. 25 стр. 16°. Изд. 2-е. Ц. 15 коп.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЬ".
37. Г Лоренцъ, проф. КУРСЪ ФИЗИКИ. Пер. съ нѣм. подъ ред.
проф, Н. П. Цастерина. Т. I. VIII —|—348 стр. Съ 236 рис. Ц. 2 р.
75 к. (Т. II печатается).
38. В. А. Гернетъ. ОБЪ ЕДИНСТВЪ ВЕЩЕСТВА. 46 стр. 16”.
1909. Ц. 25 к._________________________________________
39. П. Зееманъ, проф. ПРОИСХОЖДЕНІЕ ЦВѢТОВЪ СПЕКТРА.
Съ приложеніемъ статьи В. Ритиа „ЛИНЕЙНЫЕ СПЕКТРЫ И
СТРОЕНІЕ АТОМОВЪ". 50 стр. 16°. 1910. Ц. 30 к._________
40. С. Вьюкомъ, проф. ТЕОРІЯ ДВИЖЕНІЯ ЛУНЫ (Исторія и
современное состояніе этого вопроса). 26 стр. 16°. 1910. Ц. 20 к.
41. А- Клоссовскій, проф. ОСНОВЫ МЕТЕОРОЛОГІИ. ХѴІ-|-525
стр. большого 8°. Съ 199 рис., 2 цвѣтн. и 3 черн. табл. 1910. Ц. Р. 4
42. Ф Кэджори, проф. ИСТОРІЯ ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ
(съ нѣкоторыми указаніями для препод). Перев. съ англ, подъ ред. и
съ примѣч. прив.-доц. И. Ю. Тимченко. ХІІ-ф-368 стр. 8°. Съ рис.
1910. Ц- 2 р. 50 к.____________________________________
43. В. Рамзай, проф. ВВЕДЕНІЕ ВЪ ИЗУЧЕНІЕ ФИЗИЧЕСКОЙ
ХИМІИ. Перев. съ англ, подъ ред. проф. 77. Г. Меликова. IV—75
стр. 16°. 1910. Ц. 40 к.
Имѣются на складѣ:
Д. Ефремовъ. НОВАЯ ГЕОМЕТРІЯ ТРЕУГОЛЬНИКА. 334-|-ХІІІ
стр. 8°. Ц. 2 руб.
Ф. Мультонъ, проф. ЭВОЛЮЦІЯ СОЛНЕЧНОЙ СИСТЕМЫ.
90 стр. 16°. Съ 12 рис. Ц. 50 коп.
Печатаются и готовятся къ п|^аТи:
Дж Дж Томсонъ, проф. КОРИУСКУЛЯРНАЯ'ТЕОРІЯ ВЕЩЕ-
СТВА. Пер. съ англ, подъ ред. В. О. Ф. и Эл.
[ерев. съ франц. пгдъ
Г. Пуанкаре, проф. НАУКА и МЕТ<
ред. прив.-доц. В. Ф. Іуагана
Г Ковалевскій, проф. КУРСЪ ДИФФЕРЕНЦІАЛЬНАГО и ИНТЕ-
ГРАЛЬНАГО ИСЧИСЛЕНІИ. Съ нѢ^СЫіодъ ред. С. Шатуновскаго.
Оствальдъ, В. проф. НАТУРФИЛОСОФІЯ. Съ нѣм. подъ ред.
прив.-доц. Л. Мандельштама.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ“.
Веберъ и Велыптейнъ, проф. ЭНЦИКЛОПЕДІЯ ЭЛЕМЕНТАР-
НОЙ МАТЕМАТИКИ. Томъ II. кн. 2 и 3. ТРИГОНОМЕТРІЯ, АНАЛИ-
ТИЧЕСКАЯ ГЕОМЕТРІЯ и СТЕРЕОМЕТРІЯ.
Г. Лоренцъ, проф. КУРСЪ ФИЗИКИ. Пер. съ нѣм. подъ ред. проф.
Н, П. Кастерина. Т. II.
АДЛЕРЪ, А. Теорія геометрическихъ построеній. Перев. съ нѣмец-
А каго подъ ред. прив.-доц. С. О. Шатуновскаго.
НИМФЮРЪ, Р. д-ръ. Воздухоплаваніе. Его научныя основы и тех-
ническое развитіе. Переводъ съ нѣм. Съ 42 рис.
КЛЕЙНЪ, Ф. проф. Лекціи по элементарной математикѣ для учи-
телей. Пер. съ нѣм. подъ ред. прив.-доц. В. Кагана.
ТРЕЛЬСЪ-ЛУНДЪ. Небо и міровоззрѣніе въ круговоротѣ временъ.
Пер. съ нѣмецкаго.
ДОВЕЛЛЬ, П. Обитаемость Марса. Пер. съ англ. Со мног. рис.
ШУБЕРТЪ, Г. проф. Математическія развлеченія. Пер. съ нѣм.
подъ ред. „В. Оп. Ф. и Эл. Мат.“.
ПОРЕЛЬ, Е. проф. Курсъ математики для среднихъ учебныхъ заве-
** деній. Въ обработкѣ проф. П. Штэккеля.
рОДДИ, Ф. проф. Что такое радій? Переводъ съ англійскаго.
МАРКОВЪ, А. акад. Исчисленіе конечныхъ разностей. Въ двухъ
частяхъ. Изд. 2-ое. /Ч
ЛЕБЪ. Динамика живого вещества. Переводъ
проф. В. В. Завьялова.
ГАМПСОНЪ Б. и ШЕФЕРЪ К. Парадоксы природы. Книга юно-
шества, объясняющая явленія, которыя находятся в^дротиво-
рѣчіи съ повседневнымъ опытомъ Пер. съ нѣм.
---------------------------------------------------------------------------------------------------------
с;кСѣѣм. подъ ред.
--------------------------------------------------------------
> французскаго.
ФУРВЬЕ ДАЛЬБЪ. Два новыхъ міра (Инфра-міръ. Супра-міръ).
Перев. съ англійскаго.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ".
УСПѢХИ ФИЗИКИ. Сборникъ статей подъ ред. „Вѣсти. Оп. Физ.
и Эл, Мат“ Выпускъ второй.
Подробный каталогъ изданій высылается по требованію безплатно.
Выписывающіе изъ главнаго склада изданій „МАТЕЗИСЪ ‘ (Одесса, Новосельск., 66)
на сумму 5 р. и болѣе за пересылку не платятъ.
Отдѣленіе склада для Москвы: Книжный магазинъ „Образованіе44,
Москва, Кузнецкій мостъ, 11. Отдѣленіе склада для С--Петербурга.
Книжный магазинъ Г. С. Цукермана, С.-Петербургъ, Александр.
пл., 5.
ОЕЪЯВЛІЕМІЕ
ВѢСТНИКЪ
Опытной Физики и Элементарной Математики
Выходитъ 24 раза въ годъ отд. вып., не менѣеМрІ стр. каждый.
_ (хр
подъ ред. пр.-доц. 7}.
Подп. цѣна съ пер. за годъ 6 р., за *А^ода 3 р. Учащіе въ
низшихъ училищахъ и всѣ учащіесяѴцйатятъ за годъ 4 р., за
7/года 2 А/
Пробный номе^рбезплатно.
Адр.: Одесса. Въ редакцію „Вѣстника Опытной Физики и Элемен-
тарн. Математики".
(7
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ
П. ЛНКУРЪ и Я. АППЕЛЬ.
ИСТОРИЧЕСКІЯ ФИЗИКП
пер. съ нѣмецкаго подъ ред. „Вѣстника Опытной Физики и Элементарной Математики”.
Въ 2-хъ томахъ большого формата 875 стран. Съ 799 рисун-
ками и б отдѣльными таблицами.
Содержаніе I тома. МІРОЗДАНІЕ. Свѣдѣнія и открытія
до 1630 г. СВЪТЪ. Отъ древнѣйшихъ временъ до Ньютона. СИЛА.
МІРОЗДАНІЕ. Свѣдѣнія и открытія послѣ 1630 года. ЗВУКЪ.
ПРИРОДА СВЪТА. СПЕКТРАЛЬНЫЙ АНАЛИЗЪ.
Содержаніе II тома. ТЕПЛОТА. МАГНИТИЗМЪ. ЭЛЕКТРИ-
ЧЕСТВО до 1790 года. ЭЛЕКТРИЧЕСКІЙ ТОКЪ. ПОГОДА.
Цѣна 7 р. 50 к.
Учен. 1{ом. Мгін. Нар. ГІр. признана заслуживъ вниманія
при пополненіи ученич. библіотекъ среди, учебн. зав.
Изъ отзывовъ объ „Исторической Физикѣ".
„Нельзя не привѣтствовать этого интереснаго изданія... Книга читается легко;
она содержитъ весьма удачно подобранный матеріалъ и обильно снабжена хорошо
выполненными рисунками. Переводъ никакихъ замѣчаній не вызываетъ... представ-
ляется весьма желательнымъ, чтобы наши среднія учебныя заведенія подписались
на эту интересную книгу44. Проф. О. Хвольсонъ. Журн. Ш. Н. Пр.
„Такія книги, какъ „Историческая Физика44, представляютъ собо^рѣдкое
явленіе въ міровой учебной литературѣ какъ по широтѣ замысла, тарт^иню мастер-
ству выполненія. Авторы обнаружили много вкуса и критическаго чѵ^ьЗРвъ выборѣ
изъ необозримой грунты историческихъ фактовъ наиболѣе подходяийфо матеріала и
много искусства въ его распланировати.
Замѣтимъ еще, что съ внѣшней стороны книга издана прЖгсасно, и что вполнѣ
литературный переводъ близокъ къ оргпналу44. Н. Томили ійь.
Русская мартъ 1909.
„Своеобразная прелесть историческаго изложет^Хдумается мнѣ, можетъ
способствовать возбужденію интереса къ физикѣ вкМхъ учащихся, у которыхъ
преобладаетъ склонность ко всему „псторпческому^О которымъ нерѣдко физика
представляется предметомъ чуждымъ и труднцмр^^Кромѣ того, „Историческая
Физика44 можетъ доставить очень пригодное ч^ей^ взрослымъ, которые полагали
бы возобновить и освѣтить забытыя или плохоѵусвоенныя свѣдѣнія по физикѣ.
Нечего и говорить, что для преподаванія физики она доставляетъ превосходный
матеріалъ, и что опа можетъ быть даваема для чтенія, при содѣйствіи преподавателя
въ руки учащихся44. Н. Дрентельнъ. Педагогическій Сборникъ.
Цѣна 90 коп
Тип. Ю.-Р. О-ва
Печатнаго Дѣла.
Одесса, Пушкин
ская 18, 1910