Author: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И.
Tags: учебные пособия и учебники по математике математика
ISBN: 5-90131-08-12
Year: 1994
Text
МАТЕМАТИКА 6
ВБК 22.1*72
М24
Авторы:
Н. Я. ВИЛЕНКИН, А. С. ЧЕСНОКОВ. С. И. ШВАРЦБУРД, В. И. ЖОХОВ
Учебник получил премию на Всесоюзном конкурсе учебников по математике для средней общеобразовательной школы
Сведения о пользовании учебником
№ Фамилия и имя ученика Учебный год Состояние учебника
В начале года В конце года
1
2
3
4
б
Математика: Учеб, для 6 кл. сред. шк./Н. Я. Виленкин, М34 А. С. Чесноков, С. И. Шварцбурд, В. И. Жохов — 2-е изд.— М.: Просвещение, 1994 — 256 с.: ил.— ISBN 5-90131-08-12.
Дорогие ребята!
В учебнике для 6 класса, как и в учебнике для 5 класса, применяются различные условные обозначения. Напомним, что они означают:
— вопросы к объяснительному тексту учебника.
— упражнения для работы в классе по теме данного пункта.
— упражнения для повторения ранее пройденного материала. Некоторые из этих упражнений имеют дополнительные номера: 1), 2), 3), 4) и т. д. Они предназначены для самостоятельной работы. При этом нечетные номера — это задания для 1-го варианта, а четные — для 2-го варианта.
— упражнения для домашней работы.
|Я В этой рубрике вы найдете рассказы об истории возникно-“ вения и развития математики. Не зная прошлого развития науки, трудно понять ее настоящее.
В По тому, как человек говорит, можно судить о его куль-туре и развитии, об умении думать. Поэтому учитесь говорить правильно — в этом вам помогут примеры и пояснения данной рубрики.
м
Чтобы изучение математики было успешным, чтобы учиться было интересно, нужно быть внимательным, уметь хорошо и быстро запоминать, быть сообразительным, обладать сильной волей. Развить эти качества вам помогут специальные игры и упражнения этой рубрики.
Г л aka I.
ОБЫКНОВЕННЫЕ ДРОБИ
9 1. ДЕЛИМОСТЬ ЧИСЕЛ
1. Делители и кратные
20 яблок можно разделить поровну между 4 ребятами. Каждый получит по б яблок. А если надо разделить (не разрезая) 20 яблок между 6 ребятами, то каждый получит по 3 яблока, а еще 2 яблока останутся. Говорят, что число 4 является делителем числа 20, а число 6 не является делителем числа 20.
Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.
Число 1 является делителем любого натурального числа.
Пусть на столе лежат пачки, в каждой из которых по 8 печений. Не раскрывая пачек, можно взять 8 печений, 16 печений, 24 печенья, а 18 печений так взять нельзя. Числа 8, 16, 24 делятся на 8, а 18 на 8 не делится. Говорят, что числа 8, 16, 24 кратны числу 8, а число 18 не кратно числу 8.
Кратным натуральному числу а называют натуральное число, которое делится без остатка на а.
Любое натуральное число имеет бесконечно много кратных. Например, первые пять чисел, кратных 8, такие: 8, 16, 24, 32, 40. Наименьшим из кратных натурального числа является само это число.
©Какое число называют делителем данного натурального
числа? Какое число называют кратным натуральному числу а? Какое число является делителем любого натурального числа? Какое число и кратно п, и является делителем п?
1. На сколько равных кучек можно разложить 36 орехов?
2. В каждой коробке лежат 6 чайных ложек. Можно ли, не вскрывая коробок, взять: а) 42 ложки; б) 49 ложек?
4
IB Следите aa верным употреблением слов кратно и кратное (в значении существительного):
кратно (какому числу?):
— число пятнадцать кратно числу три (или пятнадцать д. li-кратно трем)
д. п.
кратное (какого числа?):
— число пятнадцать — кратное числа три (или пятнадцать — кратное трех) р. п.
р.п.
— числа девять, двенадцать, пятнадцать — кратные трех р.п.
Слово делитель употребляется с родительным падежом зависимого слова: — число шесть — делитель числа тридцать (шесть — р. п.
делитель тридцати)
р.П. — делители одиннадцати — числа один и одиннадцать р. п.
Слова делится (без остатка) и кратно заменяют друг друга. — сорок пять делится на девять — сорок пять кратно девяти
3. Верно ли, что: а) б — делитель 46;
б) 16 — делитель 8; в) 17 — делитель 162;
г) 27 — кратное 3;
д) 6 — кратное 12;
е) 166 — кратное 13?
4. Является ли число 16 делителем 105? Является ли делителем числа 106 частное 106:16?
6. Выберите из чисел 15, 4, 6, 8, 10, 12, 14, 16 те, которые являются:
а) делителями 20; в) делителями 16 и кратными 4;
б) кратными 4; г) кратными 3 и делителями 18.
в. Напишите все делители числа: а) 6; б) 18; в) 25; г) 19.
7. Напишите все двузначные числа, кратные числу: а) 8; б) 11; в) 48; г) 99.
5
8. Мальчику дали 90 к. и попросили купить на все деньги конфет одного сорта. В буфете продавали конфеты по 2 к., по 5 к. и по 11 к. за штуку. Какие конфеты мог купить мальчик?
9. Докажите, что число 70 625 кратно 217, а число 729 является делителем числа 225 261.
10. На координатном луче отмечено число а (рис. 1). Отметьте на этом луче четыре числа, кратных числу а.
0 а
Рве. 1
11. Проверьте, что каждое из чисел 6, 28, 496 равно сумме
всех его делителей, не считая самого числа.
Рже. 2
12. Проверьте, что каждое из чисел 220 и 284 равно сумме делителей другого числа, не считая его самого.
13. Докажите, что произведение двух натуральных чисел кратно каждому из множителей.
14. На рисунке 2 изображен в натуральную величину один кадр фотопленки. Каких размеров получится фотография при пятикратном увеличении? Уместится ли изображение этого кадра при десятикратном увеличении на листе
бумаги, размер которого 24 X 30 см?
15. Вычислите устно:
а) 5+0,8; б) 0,76 — 0,3; в) 0,2-4; г) 6:10;
0,23+7; 2,54-2; 2,1*3; 0,8:2;
0,48+0,2; 0,82-0,02; 0,7*10; 2,1:7;
0,6+0,34; 0,63-0,6; 0,5-2; 0,5:10
2,7 +1,12; 0,8 -0,25; 0,25*4; 4,1:2.
16. Найдите пропущенные числа:
6
17. На координатном луче отмечены числа 1 и т (рис. 3). С помощью циркуля отметьте на луче числа: m + 1; т — 1; т + т.
О 1 т
I I-------------1----------
Рже. s
18. Даны три числовых выражения и три программы вычисления нх значений на микрокалькуляторе. Укажите, какая программа соответствует каждому из данных выражений.
а) 16,2 0,8+1,4;
6) 16,2+0,8-1,4;
в) 16,2-(0,8+ 1,4).
19. Найдите неполное частное и остаток при делении: а) 243 на 16; б) 3629 на 12; в) 1075 на 29; г) 1632 на 51.
20. Найдите остаток от деления:
а) 273 на 10; в) 3843 на 5;
б) 3785 на 2; г) 4236 на 5;
21. При делении числа а на число Ь получили неполное частное с и остаток г. С помощью формулы a=bc-f-r заполните пустые клетки таблицы.
22. Выполните действие: а) 3,4+ 2,5; б) 5,7-1,3;
17,2 + 2,8; 8-3,4;
5,9+ 3,7; 12,3-1,8;
4,587 + 7,64; 10,273-5,49;
д) 100 на 3;
е) 1000 на 9.
а 458 278
ь 15 10
с 8 10
г 4 8
в) 2,4-3; г) 3,5:7;
3,02-7; 8,4:4;
2,6-3,7; 60,8:1,9;
4,5-2,06; 20,52:3,8.
23. Решите задачу:
1) В первом мешке было 54,4 кг крупы, во втором — в 1,7 раза меньше, чем в первом, а в третьем — на 2,6 кг больше, чем во втором. Сколько килограммов крупы было в трех мешках вместе?
2) На первую машину погрузили 4,6 т картофеля, на вторую — в 1,4 раза больше, чем на первую, а на третью — на
7
1,6 т меньше, чем на вторую. Сколько тонн картофеля погрузили на все три машины вместе?
24. Найдите все делители числа 30 и запишите их в по-рядке возрастания.
25. Выберите из чисел 14, 21, 31, 42, 51, 63, 68, 75 те, которые:
а) кратны 7; б) кратны 17; в) не кратны 8; г) не кратны 2. 26. Выполните деление с остатком: 385:13; 548:12; 3710:30. 27. Площадь первого поля 27,3 га. Площадь второго поля на 4,8 га меньше площади, первого, а площадь третьего поля в 1,6 раза больше площади второго. Чему равна площадь всех трех полей вместе?
28. Выполните действия:
а) 18,36+0,64:0,8; в) 3,44:0,4 + 24,56;
б) 80 11-42558:519; г) 684-245-675-246.
2. Признаки делимости на 10, на 5 и на 2
Всякое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10. Чтобы получить частное, достаточно отбросить эту цифру 0.
Например, 280 делится без остатка на 10, так как 280:10 = = 28.
При делении же числа 283 на 10 получаем неполное частное 28 и остаток 3 (т. е. последнюю цифру записи этого числа). Поэтому если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0, то по число делится- без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре.
Число 10 = 2-5. Поэтому число 10 делится без остатка и на 2, и на 5. Отсюда и любое число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.
Например, 60=6-10 = 6-(2-5) = (6*2)-5 = 12-5, значит, 60:5=12. А из того, что 60=6-(5-2)=(6-5)-2 = 30-2, получаем, что 60:2 = 30.
Каждое число можно представить в виде суммы полных десятков и единиц, например: 246 = 240+6, 1435=1430 + 5. Так как полные десятки делятся на 5, то и все число делится
на б лишь в том случае, когда на б делится число единиц. Это возможно только тогда, когда в разряде единиц стоит цифра О или б.
Если запись натурального числа оканчивается цифрами О или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится.
Например, числа 870 и 875 делятся без остатка на б, а числа 872 и 873 иа б без остатка не делятся.
Числа, делящиеся без остатка на 2, называют четными, а числа, которые при делении на 2 дают остаток 1, называют исчишыми. Из однозначных чисел числа 0, 2, 4, 6 и 8 четны, а числа 1, 3, б, 7 и 9 нечетны. Поэтому и цифры 0, 2, 4, в, 8 называют четными, а цифры 1, 3, б, 7, 9 — нечетными.
Все полные десятки делятся на 2 без остатка (т. е. они четны). Значит, любое натуральное число четно лишь в случае, когда в разряде единиц стоит четная цифра, и нечетно, когда в разряде единиц стоит нечетная цифра.
Если запись натурального числа оканчивается четной цифрой, то зто число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то зто число нечетно.
Например, числа 2, 60, 84,96, 308 четные, а числа 3, 61, 86, 97, 609 нечетные.
Как по записи натурального числа определить, делится оио без остатка на 10 или не делится на 10? Как по записи натурального числа узнать, делится оно без остатка на б или не делится на б? Как по записи натурального числа узнать, делится оио без остатка на 2 или не делится на 2?
0 29. Запишите натуральные числа от 1 до 30 в порядке возрастания и подчеркните красным карандашом каждое второе число, а синим — каждое пятое. Какие числа окажутся подчеркнуты красным карандашом, какие — синим? Какие числа подчеркнуты обоими цветами? Назовите числа, не делящиеся ни на 2, ни на б.
30. Назовите три числа, которые:
а) делятся на 2; в) делятся на 2 и на б;
б) делятся на б; г) не делятся ни на 2 и ни на б.
31. Назовите:
а) два четных числа, кратных б;
9
б) два нечетных числа, кратных б;
в) два четных числа, которые не делятся на б;
г) два нечетных числа, которые не делятся на б.
32. Какие из чисел 200, 320, 3000, 60 000, 861, 76 640 делятся на 100? Какие из них делятся на 1000? Сформулируйте признаки делимости на 100, на 1000.
33. Напишите все трехзначные числа, в запись которых могут входить лишь цифры 0, 2, 5 и которые:
а) делятся на 2; б) делятся на 5.
84. Коля принес несколько коробок с яйцами, по 10 яиц в каждой коробке. Может ли быть, что он принес 32 яйца? 43 яйца? 50 яиц?
35. Толя купил 2 кг крупы. Может ли его покупка стоить 92 к.? 68 к.? 87 к.?
36. Купили 5 кг хлеба. Может ли покупка стоить 92 к.? 90 к.? 75 к.?
37. Можно ли, используя только цифры 3 н 4, записать: а) число, которое делится на 10; в) число, кратное 5; б) четное число; г) нечетное число?
38. Какие числа, кратные 5, удовлетворяют неравенству: а) 64<х<78; б) 405<х<460; в) 24<р<49; г) 1<р<30?
Ф39. Вычислите устно:
а) 17+0,3; б) 0,728—0,7; в) 0,2-5; г) 2,6:2;
0,05+25; 0,8-0,25; 4-2,5; 1,8:9;
0,37 + 2,03; 1 — 0,6; 0,5-20; 3,7:10;
3,84+0,2; 0,7-0,07; 0,24-1000; 5,3:0,1;
1,27 + 2,3; -3 — 0,85; 2,7-100; 6:0,3.
40. Какие различные натуральные числа надо вписать в кружки (рис. 4), чтобы произведение каждых двух чисел, по-
мещенных в кружках, соединенных отрезком, равнялось 70? Подумайте, как можно назвать набор чисел, оказавшихся в кружках.
41. Если к числу прибавить 4, то полученное число разделится без остатка на 6. Чему равен остаток от деления первого числа на 6?
42. На микрокалькуляторе по программе 12 + = получен результат 24.
10
Попробуйте объяснить, почему получилось такое число. Подумайте, какие числа будут появляться на индикаторе после каждого нажатия клавиши -»= при выполнении программы:
8 +
43. Подтвердите примерами следующее свойство суммы: а) если каждое слагаемое кратно числу а, то и сумма кратна числу а; б) если только одно слагаемое суммы не кратно чис-. лу а, то сумма не кратна числу а.
44. Назовите наименьший и наибольший делители числа 24. Назовите наименьшее кратное числу 24. Есть ли у этого числа наибольшее кратное? Назовите какое-нибудь число, кратное и 5 и 12.
45. Запишите все двузначные числа, являющиеся:
а) делителями 100; в) делителями 100 и кратными 25. б) кратными 25;
46. Число Ь является делителем числа а. Докажите, что частное от деления а на Ь также является делителем числа а. Проверьте это утверждение, если а =18, а 5 = 3.
47. Докажите, что:
а) если а кратно b, а b кратно с, то а кратно с;
б) если а и Ь делятся на 6, то и а-^-Ь делится на 6.
48. Какие из дробей , 7-, т, 77-, -%- являются пра-О О У 4 11 d
аильными и какие неправильными?
49. При каких натуральных значениях а дробь будет
В
правильной я при каких натуральных значениях b дробь 7-^—
D-f-2
будет неправильной?
60. Решите уравнение:
а) (х+2,3)-0,2=0,7; в) 4,2x4-8,4 = 14,7;
б) (2,8-х):0,3 = 5; г) 0,39:х-0,1 =0,16.
51. Решите задачу:
1) Я задумал число. Если его увеличить в 11 раз и результат уменьшить на 2,75, то получится 85,25. Какое число я задумал?
2) Я задумал число. Если его увеличить на 9,2 и результат увеличить в 11 раз, то получится 110. Какое число я задумал?
11
®52. Найдите среди чисел 154,161, 174, 178, 191, 315, 320, 346, 425, 475 числа:
а) кратные 2; б) кратные 5; в) кратные 10; г) нечетные.
53. Напишите:
а) все четные числа, большие 10 и меньшие 21;
б) все нечетные числа, большие 12, но меньшие 23.
54. Напишите три четырехзначных числа, кратные 5.
55. Выберите из дробей -J-, 41 » т; . 4-» Ф. Щ и г 7 9 19 18 4 5 128 888
сначала все правильные дроби, а затем неправильные.
56. Решите уравнение:
а) (4,9-х): 1,2 = 3; б) 3,8 «(х-0,2)=2,28.
57. Найдите значение выражения:
а) (93-7 4-141):72; в) 7091 + 9663 — (243 916+76 446):527:3; б) (357-348:6)-4; г) 8607+7605+(376012-83314):414:7.
3. Признаки делимости на 9 и на 3
Узнаем, не выполняя деления, можно ли 846 яиц разложить в 9 корзин поровну.
В числе 846 содержится 8 сотен, 4 десятка н 6 единиц. Если раскладывать поровну в 9 корзин одну сотню яиц, то в каждую корзину можно положить 11 яиц, а одно яйцо останется. От восьми сотен останется 8 яиц.
Если раскладывать поровну в 9 корзин один десяток яиц, то в каждую корзину надо положить одно яйцо и одно яйцо останется. От четырех десятков останется 4 яйца.
Не разложенными в корзины останутся 8 яиц от сотен, 4 яйца от десятков и еще 6 яиц: 8 + 4 + 6 = 18. Число 18 является суммой цифр числа 846. Так как 18 яиц можно разложить поровну в 9 корзин (по 2 яйца в каждую), то н все 846 яиц можно разложить поровну в 9 корзин. Это значит, что число 846 делится без остатка на 9.
•• Если сумма цифр числа делится на 9, то и число делится на 9; если сумма цифр числа не делится на 9, то и число не делится на 9.
Пример 1. Число 76 455 делится на 9, так как сумма его цифр: 7+6 + 4 + 5 + 5 = 27 — делится на 9.
Пример 2. Число 51 634 не делится на 9, так как сумма его цифр: .5 + 1 + 6 + 3 + 4 = 19 — не делится на 9.
12
Так же обосновывается признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр чиелр не делится на 3, то и число не делится на 3.
Как по записи натурального числа узнать, делится оно на 9 или не делится на 9? Как по записи натурального числа узнать, делится оно на 3 или не делится на 3?
58. Какие из чисел 75 432, 2 772 825, 5 402 070 делятся на 3? Какие из иих делятся на 9?
59. Запишите какие-нибудь три четырехзначных числа, которые делятся на 9.
80. Какие цифры следует поставить вместо звездочек в записи 2*5, 46», *14, чтобы получившиеся числа делились на 3?
61. Напишите три числа, записанные только с помощью: а) цифры 1, которые делятся на 3;
б) цифры 6, которые делятся на 9.
62. Любое ли число, которое оканчивается цифрой 3, делится на 3?
63. Мама принесла детям три одинаковых подарка. Может ли быть, что во всех этих подарках было 25 конфет? 75 конфет? 63 конфеты?
64. В каждом стойле коровника 9 коров. Может ли быть, что всего в коровнике 542 коровы? 288 коров?
65. Оля купила 9 пакетов молока. Может ли сдача, полученная с двух рублей, равняться 60 к.? 56 к.?
0 66. Вычислите устно:
а) 6+0,1-1-0,04; б) 0,7-0,15; в) 0,3-5; г) 5:100;
7+0,05+0,8; 4-0,5; 4-0,5; 26:10;
3,4+0,007+0,06; 0,6—0,02; 50-0,02; 0,8:4;
19 + 1,02+0,18; 3 — 1,3; 2,9-10; 2:0,1;
2,01 + 1,3+0,09; 5—0,08; 31-0,01; 8:0,4.
67. Найдите пропущенные числа:
о)
13
68. Подумайте, каким числом (четным или нечетшлм) является:
а) квадрат четного числа; б) квадрат нечетного числа; в) куб четного числа.
69. Длина прямоугольника 20 м, ширина — натуральное число метров. Верно ли, что значение площади (в квадратных метрах):
а) кратно 2; б) кратно 5; в) кратно 4; г) кратно 8?
70. Значение какого числового выражения можно вычислить на микрокалькуляторе по программе:
а) 15,3 X 0,05 + 1,4 =
б) 8,6 + 2,2 X 0,3 =
71. Верно ли утверждение:
а) если каждое слагаемое не кратно числу а, то и сумма не кратна числу а;
б) если уменьшаемое и вычитаемое кратны числу а, то и разность кратна числу а?
72. Как быстро узнать, делятся ли на 2:
а) суммы: 37 843 + 54321; 48345+75634; 37244+52486;
б) разности: 87 338—56 893; 153 847—112353;
84 537-26 237?
73. Любое ли число, делящееся на 5, делится и на 10?
74. Всегда ли запись числа, делящегося на 5, оканчивается цифрой 5? Может ли число, не делящееся на 5, оканчиваться цифрой 5?
75. Какой цифрой оканчивается запись числа, делящегося на 5, если оно: а) четно; б) нечетно?
76. Какие цифры можно поставить вместо звездочки, чтобы полученное число делилось на 5: а) 378*; б) 25*5; в) 4*13?
77. Запишите 1-|-, 3—, 2-^-, 8^ и 9^-в виде неправиль-5 9 11 15 20
ных дробей.
78. Исключите целую часть из чисел:
18 25 17 12 18 15
7 ’ 3’ 2 ’ 2 ’ 9*4*
79. Решите уравнение:
1) 17л— 11л— 2л = 511; 3) 4х+6х-х=21,6;
2) 23а — 8а— 13а=33; 4) Чу — у + 3у = 61,2.
80. Вычислите: 0,5632:5,12 + 42,56:3,8—(11—3,9:1,5). Вычисления проверьте с помощью микрокалькулятора.
14
4JK 81. Какие из чисел 240,242, 244, 246, 248,250, 252 кратны 8? Какие из них делятся на 9?
82. В записи *723, 5*36, 111* вместо звездочки поставьте такие цифры, чтобы получившиеся числа делились на 9.
83. Представьте числа 1-|-, 3-^ , 18-|-, 14-|^ в ®иде неправильных дробей.
о. „ ____ 62 79 1356 238
84. Исключите целую часть из чисел: — , — , ——, •
11 IB 226 14
85. Найдите значение выражения 4,7 k 4-5,3k — 0,83, если k=0,83; 8,3; 0,083.
86. Решите уравнение:
а) х4-Зх-|-5 = 17; в) 3,2у — 2,7^ = 0,6;
б) 3,5x4-2,2х=4,56; г) 3,7z-z = 0,54.
87. Найдите значение выражения
(5,98 4- 5,36): 2,8: (5 • 0,003 4-15 • 0,029).
4. Простые и составные числа
Число 7 делится только на 1 и само на себя. Другими словами, число 7 имеет только два делителя: 1 и 7. У числа 9 три делителя: 1, 3 и 9. Число 18 имеет шесть делителей: 1, 2, 3, 6, 9 и 18.
Такие числа, как 9 и 18, называют составными числами, а такие, как 7, — простыми числами.
Натуральное число называют простым, если оно имеет только два делителя: единицу и само ото число. Натуральное число называют составным, если оно имеет более двух делителей.
Число 1 имеет только один делитель: само это число. Поэтому его не относят ни к составным, ни к простым числам.
Первыми десятью простыми числами являются 2, 3, 5, 7, 11, 13, 17,19, 23, 29. На форзаце учебника приведена таблица простых чисел от 2 до 997.
Число 78 составное, потому что, кроме 1 и 78, оно делится, например, еще на 2. Так как 78:2 = 39, то 78=2*39. Говорят, что число 78 разложено на множители 2 и 39. Любое составное число можно разложить на два множителя, каждый из которых больше 1. Простое число так разложить на множители нельзя.
15
©Какие натуральные числа называют простыми? Какие натуральные числа называют составными? Почему число 1 не является ни простым, ни составным?
88. Сколько делителей имеет каждое из чисел: 31,25,100?
89. С помощью таблицы простых чисел, помещенной на форзаце учебника, определите, какие из чисел 101, 121, 253, 409, 561, 563, 863, 997 являются простыми, а какие составными.
90. Докажите, что числа 2968, 3600, 888 888, 676 767 являются составными.
91. Может ли произведение двух простых чисел быть: а) простым числом; б) составным числом?
92. Может ли площадь квадрата выражаться простым числом, если длина его стороны выражается натуральным числом?
93. Известно, что число т делится на 9. Простым или составным является число т?
94. Разложите на два множителя числа: 38; 77; 145; 159.
95. Сколькими способами можно разложить на два множителя числа 18; 42; 55? Способы, при которых произведения отличаются только порядком множителей, считайте за один способ.
96. Верно ли, что все четные числа являются составными?
97. Может ли выражаться простым числом объем куба, длина ребра которого выражается натуральным числом?
А 98. Вычислите устно:
а) 0,014-1,14-0,09; б) 15 — 2,3; в) 2,5-2,7-4; г) 1:10;
8,1 4-2,994-1.01; 0,3 — 0,29; 3,90,5-2; 8,08:8;
1,884-3,7 4-0,12; 7—0,2; 1,25-1,9-8; 9:100;
2,8 4-1.854-2,15; 6 — 2,75; 4-5,6-0,25; 6,73:10;
1,074-0,884-1,93; 16,4 — 4; 0,5-30-0,1; 0,7:0,01.
99. Найдите пропущенные числа, если а = 33; 42; 75:
Четное число
100. Выразите в процентах числа: 0,01; 0,29; 0,8; 1.
16
101. Выразите в виде десятичных дробей : 2%, 5%, 10%. 20%. 50%. 68%, 100%, 130%.
102. Длина и ширина прямоугольного параллелепипеда выражаются натуральным числом сантиметров, а высота равна 15 см. Можно ли утверждать, что объем (в кубических сантиметрах) этого параллелепипеда выражается числом: а) кратным 2; б) кратным 3; в) кратным 5?
103. Какую цифру нужно приписать к числу 10 слева и справа, чтобы получилось четырехзначное число, делящееся: а) на 9; б) на 3; в) на 6?
104. Выпишите из чисел 215 783, 3 289 775, 21 112 221, 44 856, 555 444, 757 575, 835 743 те, которые:
а) кратны 3; в) делятся без остатка на 3 и на 5;
б) кратны 9; г) кратны 9 и 2.
105. Верно ли, что если число оканчивается цифрой 6, то оно делится на 6? Верно ли, что если число делится на 6, то его запись оканчивается цифрой 6?
100. Какие цифры можно поставить вместо звездочки, чтобы число делилось без остатка на 3 и на 5: а) 241»; б) 1734»; в) 43*5?
107. Стакан вмещает 210 г крупы. Крупой наполнили у-стакана. Сколько граммов крупы насыпали в стакан?
108. Дочь пообещала: «Я схожу в булочную и вымою посуду». Можно ли обещание считать выполненным, если
дочь: а) вымыла посуду, но не сходила в булочную; б) сходила в булочную и не вымыла посуду; в) и вымыла посуду, н сходила в булочную; в) не вымыла посуду и не была в булочной? Подумайте, в чем сходство этой задачи с задачей нахождения решений неравенства 2<х<6 среди чисел 1; 3; 5; 7. 4JK 109. Докажите, что числа 575, 10 053, 3627, 565 656 яв-ляются составными.
110. С помощью таблицы простых чисел, помещенной на форзаце учебника, выберете из чисел 122, 132, 153, 157, 187, 499, 550, 621, 881, 865 и 909 простые числа.
111. Запишите все делители числа 90. Выпишите из них те, которые являются простыми числами.
112. Разложите на два множителя всеми возможными способами числа 30, 33, 42, 99. Способы, при которых произведения отличаются только порядком множителей, считайте за один способ.
А\
17
113. Периметр прямоугольника 66 дм. Длина его одной стороны составляет уу периметра. Найдите площадь прямоугольника. I
114. Найдите значение выражения (15,964:5,2 —1,2)-0,1.
5. Разложение на простые множители
Число 210 является произведением чисел 21 и 10. Значит, 210=21-10. Числа 21 и 10 составные. Их тоже можно представить в виде произведения: 21 = 3-7, 10 = 2-5. Получаем: 210=3-7-2*5. Теперь в произведении 3-7-2-5 все множители — простые числа. Таким образом, число 210 разложено
Число 210 можно разложить на простые множители иным способом: 210 = 30-7 = 10-3-7 = 5-2-3-7. Получились те же самые простые множители, только записанные в другом порядке. Обычно записывают множители в порядке их возрастания: 210 = 2-3-5-7.
Всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.
При разложении чисел на простые множители используют признаки делимости.
Разложим, например, на простые множители число 756. Оно делится на 2, так как оканчивается четной цифрой 756:2 = 378. Проведем вертикальную черту и запишем слева от нее делимое 756, а справа делитель 2. Частное запишем под числом 756.
Число 378 тоже делится на 2. При делении получаем в частном 189.
189 не делится на 2, так как оканчивается нечетной цифрой. Но 189 делится на 3, так как сумма его цифр (1 + 8+9 = 18) делится на 3. Имеем 189:3 = 63.
6. Имеем
756 378
189
63
21
7 1
2 2
3 3
3 7
18
Число 63 также делится на 3. При делении получим число 21.
Число 21 также делим на 3, причем получаем в частном простое число 7.
При делении числа 7 на 7 получаем 1.
Разложение на множители закончено.
Значит, 756 = 2- 2- 3- 3- 3-7.
о Существуют ли составные числа, которые нельзя разло-жить иа простые множители? Чем могут отличаться два разложения одного и того же числа на простые множители?
0115. Разложите на простые множители числа:
а) 216; 162; 144; 512; 675; 1024;
6) 60; 180; 220; 350; 400; 1200; 8000;
в) 11; 1001; 1225; 21780; 45 630.
116. Напишите все двузначные числа, разложение которых иа простые множители состоит:
а) из двух одинаковых множителей;
б) из трех одинаковых множителей.
117. Запишите все двузначные числа, которые раскладываются на два различных простых множителя, один из которых равен:
а) 11; б) 13; в) 23; г) 47.
118. Выясните, делится ли число а на число Ь без остатка, если:
а) а = 2-2-2-3-5-7 и Ь = 2 3-7;
б) а = 3-3-5-511 и Ь = 3-3-5;
в) а = 3-3-5-713 и Ь = 3-5-513;
г) а = 2-3-37-7 и fe = 21;
д) а = 2-2-3-3-3-5-7 и Ь = 135;
е) а = 2-2-2-3-3-5 5-5 и Ь = 1000.
В случае, когда а делится на Ь, найдите частное.
119. Вычислите устно:
а) 3,99+2,01; б) 0,7 — 0,06; в) 1,6:100; г) 0,4 0,31-25;
2,3+0,007; 1-0,48; 5:10; 3,8-1,7-2,8-1,7;
3,62 + 1,08; 2 — 1,02; 12:1000; 4,7 12,5-0,8;
3,06 + 1,94;. 0,65-0,5; 2,3:0,1; 3,1 3,7+ 3,1 6,3;
12,77 + 0,13; 0,8-0,25; 4:0,01; 49,3 + 0 49,3.
120. При каких натуральных значениях а произведение 23а является простым числом?
19
121. Существует ли прямоугольник, стороны которого выражаются натуральными числами, а периметр — простым числом?
122. Найдите по два простых делителя каждого из чисел: 54; 62; 143; 182; 3333; 5005.
128. Какие простые числа являются решениями неравенства 17<р<44?
124. Могут ли быть простыми числами координаты то* чек А, В, С я D (рис. 5), если р — простое число?
Рас. б
125. Представьте а) число 3 в виде дроби со знаменателем 5; б) число 1 со знаменателем 12.
126. Выполните действие:
в> 2т+3т;
e)4A-2-L.
127. Из 35 учащихся пятого класса 22 выписывают журнал «Юный натуралист», 27 — газету «Пионерская правда», а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают газету я журнал?
128. а) Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги?
б) Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше массы гуся?
129. Для какого числового выражения составлена программа вычислений на микрокалькуляторе: б)
а) 7,46
б) 10,2
180. Стороны треугольника 12 см, 17 см и х см. а) Составьте
выражение для вычисления периметра этого треугольника, б) Подумайте, каким может быть значение х и каким быть не
может.
20
13L Решите задачу:
1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При этом первая бригада собрала на 1,52 ц больше второй. Сколько центнеров хлопка собрала каждая бригада?
2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй?
182. Найдите значение выражения:
1) (13—9,5:8,8) 0,8; 8) (1,3-2,8+1):0,8;
2) (16,1:4,6 —3,07)-0,2; 4) (3,7-2,3-5):0,3.
Ш188. На поверхности куба (рис. 6) найдите кратчайший путь:
а) из точки А в точку С через точку В;
б) из точки А в точку С, который пересекал бы все боковые ребра куба, кроме ребра АС.
®184. Разложите на простые множители числа:
а> 54; 65; 99; 162; 10 000; б) 1500; 7000; 3240; 4608.
135. Выполните действия:
а) т+т—г; б> в) г)
136. Два тракториста вспахали 12,32 га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист?
187. У покупателя было 22,3 р. В гастрономе он израсходовал в 6 раз меньше денег, чем в универмаге. Сколько денег
израсходовал покупатель в универмаге, если у него осталось 1,3 р.?
188. Выполните действия:
а) (424,2 —98,4): 3,6-0,9+ 9,1; б) (96,6+ 98,6): 6,4-1,2—0,2.
в. Наибольший общий делитель. Взаимно простые числа
Задача. Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка» и 36 конфет «Чебурашка», если надо использовать все конфеты?
21
Решение. Каждое из чисел 48 и 36 должно делиться на число подарков. Поэтому сначала выпишем все делители числа 48.
Получим: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
Затем выпишем все делители числа 36.
Получим: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Общими делителями чисел 48 и 36 будут: 1, 2, 3, 4, 6, 12.
Видим, что наибольшим из этих чисел является 12. Его называет наибольшим общим делителем чисел 48 и 36.
Значит, можно составить 12 подарков. В каждом подарке будет 4 конфеты «Ласточка» (48:12=4) и 3 конфеты «Чебурашка» (36:12=3).
Наибольшее натуральное число, на которое делятся без остатка числа а и Ь, называют наибольшим общим делителем зтих чисел.
Найдем наибольший общий делитель чисел 24 и 36.
Делителями 24 будут 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми.
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Наибольший общий делитель можно найти, не выписывая всех делителей данных чисел.
Разложим на миожители числа 48 и 36, получим: 48=2-2-2-2-3, 36 = 2-2-3-3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа (т. е. две двойки).
Остаются множители 2-2-3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36.
Так же находят наибольший общий делитель трех и более чисел.
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо: 1) разложить их на простые множители; 2) из мнохсителей, входящих в разложение одного из зтих чисел, вычеркнуть те, которые не входят в разложение других чисел; 3) найти произведение оставшихся множителей.
Если все данные числа делятся на одно из них, то зто число и является наибольшим общим делителем данных чисел.
22
Например, наибольшим общим делителем чисел 15, 45, 75 н 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
©Какое число называют наибольшим общим делителем двух натуральных чисел? Какие два числа называют взаимно простыми? Как найти наибольший общий делитель нескольких натуральных чисел? Число а кратно числу Ь. Какое число является наибольшим общим делителем чисел а и Ь?
0139. Найдите все общие делители чисел:
а) 18 и 60; б) 72, 96 и 120; в) 35 и 88.
140. Найдите разложение на простые множители наибольшего общего делителя чисел а и Ь, если:
а) а = 2-2-33 и Ь = 2-3-3-5; б) а = 5-5-7-7-7 и Ь = 3-5-7-7.
DB предложениях с сочетаниями общий делитель, наибольший общий делитель числительные читают в родительном падеже, если перед ними нет слова чисел, и в винительном падеже в противном случае:
— пять — общий делитель двадцати н тридцати р. п. р. п.
— число пять — наибольший общий делитель чисел дмдцять и двадцать пять
в. п. в. п.
141. Найдите наибольший общий делитель чисел:
а) 12 и 18; в) 675 и 825; д) 324, 111 и 432;
б) 50 и 175; г) 7920 и 594; е) 320, 640 и 960.
142. Являются ли взаимно простыми числа:
а) 35 и 40; б) 77 и 20; в) 10, 30, 41; г) 231 и 280?
143. Найдите среди чисел 9, 14, 15 и 27 три пары взаимно
простых чисел.
144. Запишите все правильные дроби со знаменателем 12, у которых числитель и знаменатель — взаимно простые числа.
145. Ребята получили на новогодней елке одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке? Сколько апельсинов и сколько яблок было в каждом подарке?
23
146. Для поездки за город работникам завода было выделено несколько автобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек — на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?
147. Вычислите устно:
а) 0,7 - 10 б) 5 : 10 в) 4-0,8 г) 0,9 + 0,06 Д) 1-0,7
: 2 • 0,2 : 0,8 : 0,3 • 5
-0,3 + 2 : 10 -0,2 : 15
: 0,4 : 0,7 • 0,5 • 0,01 • 100
? ? ? ? ?
148. С помощью рисунка 7 определите, являются ли числа а, Ь и с простыми.
0 5 13
I------1 I I----1--------------1--------
ас b
Рве. 7
149. Существует ли куб, ребро которого выражается натуральным числом и у которого:
а) сумма длин всех'ребер выражается простым числом;
б) площадь поверхности выражается простым числом?
150. Разложите на простые множители числа: а) 875; 2376; 5625; б) 2025; 3969; 13125.
151. Почему, если одно число можно разложить на два простых множителя, а второе — на три простых множителя, то эти числа не равны?
152. Можно ли найти четыре различных простых числа, чтобы произведение двух из них равнялось произведению двух других?
153. Найдите значение выражения:
а) (3-3-511):(311); в) (2-3-7-18):(8-7);
б) (2-2-8.5-7):(2-3-7); г) (3.5-1117-28):(3-11-17).
154. Сравните:
а>тит; 6>НИ£: »>1тит; г>2Ти8Т-
155. С помощью транспортира постройте Z-AOB=35° и z2DEF=140°.
24
156. Решите задачу:
1) Луч ОМ разделил развернутый- угол АОВ иа два угла АОМ и МОВ. Угол АОМ в 3 раза больше угла МОВ. Чему равны углы АОМ и ВОМ1 Постройте эти углы.
2) Луч ОК разделил развернутый угол COD на два угла СОК и KOD. Угол СОК в 4 раза меньше угла KOD. Чему равны углы СОК и KOD1 Постройте эти углы.
157. Решите задачу:
.1) Рабочие отремонтировали дорогу длиной 820 м за три
дня. Во вторник они отремонтировали этой дороги, а в сре-
О
ду оставшейся части. Сколько метров дороги отремонтиро-и
вали рабочие в четверг?
2) На ферме содержатся коровы, овцы и козы, всего 3400 жи-Q
нотных. Овцы и козы вместе составляют — всех животных, а козы составляют — общего числа овец и коз. Сколько на ферме коров, сколько овец и сколько коз?
158. Представьте в виде обыкновенной дроби числа 0,3;
3 17
0,13; 0,2 и в виде десятичной дроби числа —; 4—; 3— .
159. Выполните действие, записав каждое число в виде десятичной дроби: а) б) 1-^-+2^.
160. Вы умеете представлять числа в виде произведения простых чисел. Попробуйте представить в виде суммы простых слагаемых числа 10, 36; 54, 15, 27 и 49 так, чтобы слагаемых было возможно меньше. Какие предложения о представлении чисел в виде суммы простых слагаемых вы можете высказать?
®161. Найдите наибольший общий делитель чисел а и Ь, если:
а) а=3-3-5-5-5-7, Ь = 3-5-511;
б) а=2-2-2-3-5-7, 6 = 31113.
162. Найдите наибольший общий делитель чисел:
а) 585 и 360; б) 680 и 612; в) 60, 80 и 48; г) 195, 156 и 260.
163. Докажите, что числа 864 и 875 взаимно простые.
164. Сравните: а) и б) 1-|- и в) и 2-|-.
У У О О 0 0
25
165. Постройте угол АОС, равный 130°. Проведите внутри угла АОС луч ОВ так, чтобы Z.BOC—40°. Измерьте угол АОВ.
166. В городе построен завод, на котором будут работать 840 рабочих следующих профессий: токари, слесари и фрезеровщики. При этом токарей будет втрое, а слесарей вдвое больше, чем фрезеровщиков. Сколько токарей нужно для завода?
167. В инкубатор заложили 1200 яиц. Из всех яиц вылу-24
пились цыплята. При этом оказалось, что петушки составляют 2
— всех вылупившихся цыплят. Сколько петушков и сколько О
курочек вылупилось из яиц?
168. Представьте в виде обыкновенной дроби: 0,5; 0,16; 0,25.
169. Представьте в виде десятичной дроби: _4_. в . 7 . 4J_ б ’ 125 ' 20 ’ *2 '
170. Найдите значение выражения:
а) 1,53-54—0,42-(512-491,2)4-1,116;
б) ((27,12 4- 43,08) • 0,007— 0,0314) • 100.
7. Наименьшее общее кратное
Задача. Шаг Володи 75 см, а шаг Кати 60 см. На каком наименьшем расстоянии они оба сделают по целому числу шагов?
Решение. Число сантиметров пути должно делиться без остатка и на 75, и на 60, т. е. оно должно быть кратным и 75, и 60.
Выпишем числа, кратные 75. Получим:
75, 150, 225, 300, 375, 450, 525, 600, 675, 750.
Затем выпишем числа, кратные 60. Получим:
60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660.
Общими кратными чисел 75 и 60 будут числа 300, 600,... .
Наименьшим из них является 300. Это число называют наименьшим общим кратным чисел 75 и 60.
Значит, наименьшим расстоянием, на котором Володя и Катя сделают целое число шагов, будет 300 см. Прй этом Володя сделает 4 шага (300:75=4), а Катя — 5 шагов (300:60 = 5).
26
Наименьшим общим кратным натуральных чисел а и Ь называют наименьшее натуральное число, которое кратно ua,ub.
Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители: 75=3-5-5, а 60=2-2-3*5.
Выпишем миожители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения второго числа.
Получаем пять множителей 2-2-3-5-5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трех и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо: 1) разложить их на простые множители; 2) выписать множители, входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложений остальных чисел; 4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим "кратным данных чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа, е Какое число называют наименьшим общим кратным натуральных чисел а и Ь? Как найти наименьшее общее кратное нескольких чисел? Какое число является наименьшим общим кратным чисел тип, если число m кратно числу л?
4VX 171. Найдите разложение на простые множители наи-меньшего общего кратного чисел а и Ь, есля:
а) а=3-5, 5 = 7-5; б) а = 2-2-3-3-5, 5 = 2-2-3-7.
172. Найдите наименьшее общее кратное чисел а и 5, если: а) а=2-2-3*5-5 и 5 = 2-З-З-Э-5;
б) а=3-3-7-7 и 5 = 2-3-3-5-7-7;
в) а=2-2-5-5-11 и 5 = 2-2-3-5-11;
г) а = 2-5-5-7 и 5 = 2-2-5-5-7.
173. Найдите наименьшее общее кратное чисел:
а) 6 и 8; в) 72 и 99; д) 34, 51 и 68;
б) 12 и 16; г) 396 и 180; е) 168, 231 и 60.
27
174. Являются ли числа 54 и 65 взаимно простыми? Найдите наименьшее общее кратное.чисел 54 и 65. Равно ли оно произведению 54 и 65? Запишите какие-нибудь два взаимно простык числа. Найдите наименьшее общее кратное этих чисел. Сделайте вывод.
175. Найдите наименьшее общее кратное чисел: а) 45 и 135; б) 34 и 170. Равно ли оно одному из данных чисел?
176. Вдоль дороги от пункта А поставлены столбы через каждые 45 м. Эти столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять иа месте старого.
177. В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй 20 суток и третий 12'суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они
впервые снова вместе уйдут в плавание?
178. Вычислите устно:
а) 0,75-0,7 б) 1-0,25 в) 0,9 — 0,09 г) 23,9-3,9
• 20 • 2 : 9 - 0,15
-0,2 : 0,3 + 0,6 -0,8
: 0,4 -0,05 • 10 :0,1
? ? t ? ?
179. Каждую из дробей а о — и —, где а и 0 о b — натураль-
ные числа, можно представить в виде десятичной. Могут ли а и 5, b и 6 быть взаимно простыми? Могут ли два одинаковых числа быть взаимно простыми?
180. Найдите наибольший общий делитель для числителя - ' . 3 14 .22 .39
и знаменателя дроби: а) —; б) — ; в) — ; г) — .
О 21 DO 00
181. Какие из следующих утверждений верны: а) два четных числа не могут быть взаимно простыми; б) четное и нечетное числа всегда взаимно простые; в) два различных простых числа всегда взаимно простые; г) простое и составное числа могут быть взаимно простыми; д) любое натуральное число и натуральное число, не являющееся ни простым, ни составным, обязательно взаимно простые; е) последовательные натуральные числа всегда взаимно простые.
28
182. Найдите наибольший общий делитель чисел:
а) 12 и 24; б) 6 и 9; в) 75 и 45; г) 81 и 243; д) 4725 и 7875.
183. Лист картона имеет форму прямоугольника, длина которого 48 см, а ширина 40 см. Этот лист надо разрезать без отходов на равные квадраты. Какие наибольшие квадраты можно получить из этого листа?
184. Число т кратно 12. Докажите, что число т делится на 4.
185. Назовите все двузначные числа, записанные одинаковыми цифрами. Найдите наибольший общий делитель всех этих чисел.
186. Запишите в виде дроби частные: 3:7; 5:11; 23:34.
187. Запишите в виде частного дроби: ; 0,6; 0,13.
188. Запишите в виде обыкновенной дроби частные 18:7; 23:8; 16:5; 343:14 и выделите целые части.
189. Найдите среднее арифметическое чисел: 3,8; 4,2; 3,5; 4,1.
190. Среднее арифметическое двух чисел равно 54. Одно число в 2 раза больше другого. Найдите эти числа.
191. Решите задачу:
1) В цистерне было 38 т керосина. В первый день израсходовали в 2,4 раза больше керосина, чем во второй день. После этого в цистерне осталось 9,1 т керосина. Сколько тонн керосина израсходовано в первый день?
2) Утром на базе было 19 т муки. До обеда с базы выдали в 3,2 раза больше муки, чем после обеда. К вечеру на базе осталось 4,3 т муки. Сколько тонн муки выдали с базы до обеда?
192. По таблице простых чисел (см. форзац) подсчитайте, сколько простых чисел в каждой из первых десяти сотен
(т. е. среди чисел от 1 до 100, от 101 до 200 и т. д.). Заметили ли вы какие-либо закономерности в расположении простых чисел? Два простых числа, разность которых равна 2, называют близнецами. Найдите в таблице все пары чисел-близнецов. Какие иэ них самые большие? Сколько таких пар среди первых 500 натуральных чисел? среди чисел от 500 до 1000? Ученые др сих пор не знают, есть ли самая большая пара чисел-близнецов.
А\
29
®193. Найдите наименьшее общее кратное чисел:
а) 18 и 45; б) 30 и 40; в) 210 и 350; г) 20, 70 и 15.
194. Найдите наименьшее общее кратное чисел а и Ь, если: а) а=55-713, Ь = 5-7-713; б) а = 504, Ь = 540.
195. Саша, Коля и Сережа собрали 51 стакан малины. Сережа собрал в 2 раза больше малины, чем Саша, а Коля — на 3 стакана больше, чем Саша. Сколько стаканов малины собрал каждый из мальчиков?
196. Масса первых трех искусственных спутников Земли, запущенных в 1957—1958 гг., была равна 1918,9 кг. Найдите массу каждого из этих спутников, если масса второго была больше массы первого на 424,7 кг, а масса третьего — больше массы второго на 818,7 кг.
197. Решите уравнение:
а) (х+36,1)-5,1 = 245,82; в) (*+ 24,3): 18,3 = 3,1;
б) (т-0,67) 0,02 = 0,0152; г) (у-15,7): 19,2 = 4,7.
198. Запишите в виде дроби частные 27:8; 72:8; 483:18; 1225:12 и выделите из них целые части.
199. Найдите среднее арифметическое чисел 5,24; 6,97; 8,56; 7,32 и 6,23.
200. Поезд шел 3 ч со скоростью 65,2 км/ч и 2 ч со скоростью 83,3 км/ч. Найдите среднюю скорость поезда за эти 5 часов.
201. Найдите значение выражения:
а) 51 -(3,75:3 + 86,45:24,7)• 2,4; б) (650 000:3125-196,5)-3,14.
НП и ф а г 6 р (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, числа 6 (6 = 1+2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные числа 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвертое — 8128 — стало известно в I в. н. э. Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор ученые не знают, есть ли - нечетные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представ
30
лено в виде произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.
Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются иеравиомерно — в одних частях ряда их больше, в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже .встречаются простые числа. Возникает вопрос: существует ли последнее самое большое простое число? Древнегреческий математик Евклид (III в. до в. э.) в своей книге «Начала», бывшей иа протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом есть еще большее простое число.
Для отыскания простых чисел другой греческий математик того же времени — Эратосфен придумал такой способ. Ои записывал все числа от 1 до какого-то числа, а потом
вычеркивал единицу, которая ие является ии простым, ни составным числом, затем вычеркивал через одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее вычеркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). В конце концов оставались иевычеркнутыми только простые числа:
ff 2 3 Jr 5
11 it 13 iff iff
if it a if »
31 ЗГ 33
4/ ft H if
if it 53 iff iff
i 7 ff iff
4ff 17 iff 19 iff
iff iT iff 29 &
iff 37 iff if iff
iff 47 iff Ji iff
iff iff iff 59
Так как греки делали записи на покрытых воском табличках или иа натянутом папирусе, а числа ие вычеркивали, а выкалывали иглой, то таблица в конце вычислений напоминала решето. Поэтому метод Эратосфена называют решетом Эратосфена". в этом решете «отсеиваются» простые числа от составных.
31
Итак, простыми числами от 2 до 60 являются 17 чисел: 2, 3, б, 7, 11, 13, 17, 19, 23, 29, 31. 37, 41, 43, 47, 63, 69.
Таким способом и в настоящее время составляют таблицы простых чисел, но уже с помощью вычислительных машин.
§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ
8. Основное свойство дроби
Разделим круг на 4 равные части и 3 из них закрасим, а потом каждую четверть круга разделим еще на б равных частей (рис. 8). Тогда весь круг окажется разделенным на 4-5 = 20 частей, а в трех закрашенных четвертях круга будет 3 • б таких
частей. Поэтому , т. е. •
4 4*0 ZU 4 ZU
Рис. 8
Это равенство можно записать и так:
16 _ 15:5 8
20 20:5 4 '
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
32
Это свойство называют основным свойством дроби.
„ „ 2 4 9 3 16 2
Например, -=- ; - =
Дее равные дроби являются различными записями одного и того же числа.
©Сформулируйте основное свойство дроби. Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3?
0 202. Используя рисунок 9, дроби:
объясните, почему равны
D Равенство двух дробей можно читать разными способа-Q Q
ми. Например, равенство -^-=— можно прочитать так: — дробь трн седьмых равна дроби девять двадцать первых и. п. д. п.
— дроби три седьмых и девять двадцать первых равны — три седьмых равны девяти двадцать первым
и. п. д. п.
203. По рисунку 10 объясните, почему равны дроби:
• б) 1 =А = зо . в) 3 =—= 45 . г) 2__А = 4 12 60 ’ ' 2 12 60 ’ ' 4 12 60 ’ ' 3 12 60 ’
Рис. 10
2 Зак. 607
33
204. Поясните с помощью часов, почему:
_2___8__ 40 . бч 2_=_2_=2£ • »^—=—=—
' 3 “ 12 “ 60 ’ ' 6 12 60 ’ 1 6 12 60 ’
205. Начертите два отрезка АВ и CD длиной по 8 см. Отметьте цветным карандашом отрезка АВ и отрезка CD. Сравните с помощью циркуля цветные части отрезков АВ и CD.
206. Начертите координатный луч, приняв за единичный отрезок 18 клеток тетради. Отметьте на координатном луче точки ____________ 12345678 1 23 с координатами —, —, —, —, —, —, —, —, —-, ——, 9 9 9 9 9 9 9 9 6 6 6
4"» 4"» 4"» Какие из этих чисел изображаются на коор-О О о о
динатном луче одной и той же точкой? Запишите соответствующие равенства.
207. Умножьте числитель и знаменатель каждой дроби на 5. Напишите соответствующие равенства.
208. Разделите числитель и знаменатель каждой дроби —, —, —, — на 3. Запишите соответствующие равенства. 3 6 9 33
209. Сколько двенадцатых долей содержится в ,
5 6’3
210. Объясните, почему верно равенство:
„1 4 8 . 44 _ 11
а) 5 10 ’ 100 25 ’
211. Запишите в виде обыкновенных дробей частные: 3:8;
12:32; 20:48; 5:12. Какие из полученных дробей равны?
212. Какое натуральное число надо записать вместо буквы,
чтобы было верным равенство:
а)21=Т: б)Т8=Т’ в) *51 ’ Г)Т“Т-
Ф213. Вычислите устно:
а) 50
• 10 б) 300:60 в) 124-0,6 г) 1 — 0,4 д) 0,7-0,06
: 125 40 : 3 • 5 : 8
• 75 :50 -0,2 -0,5 • 10
-160 •19 • 2,5. : 5 : 0,4
? ? ? ? ?
34
214. Какое число надо умножить ма 3, чтобы получить: 3,3; 33,3; 6,6; 6,66; 0,99; 0,999?
215. Найдите значение выражения:
а) 23 + 2,6; б) 0,324-1,1; в) (1,6-0,7)2; г) (0,6-0,5 4-0,7 )3.
216. На координатном луче (рис. 11) отмечены числа а и 3. Кратно ли число а трем? Отметьте на луче два общих кратных чисел а и 3.
0 За
> I -------------------------------------------------
Рис. 11
217. Найдите, использовав рисунок 12, координаты точек А, В, С и D. Есть ли среди этих точек такие, координаты которых — общие кратные чисел тип?
О/''' "'''х
I---- I I------+------1 III-------------1---
Ч____S с D
Рис. 12
218. На сколько процентов увеличится площадь прямоугольника, если его длину увеличить на 30%, а ширину — на 20 %?
219. Составьте программу вычисления на микрокалькуляторе значения выражения: а) 2,85-(3,27 —1,45); б) 3,6
1 т о,оУ Ш 220. Найдите методом «решета Эратосфена* все простые числа среди первых ста натуральных чисел.
22L Разложите на простые множители числа:
1) 375; 8505; 41472; 2) 425; 4225; 8775.
222. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 1) 2450 и 3500; 2) 792 и 2178.
223. Решите задачу:
1) Школьники во время каникул совершили велосипедный поход. Весь путь составил 79,2 км. Первые 48,6 км они двих’а-лись со скоростью 12,15 км/ч и сделали привал на 2,5 ч, а потом ехали со скоростью 15,3 км/ч. Сколько времени они были в походе?
2) Отряд партизан, выполняя боевое задание, прошел 32,4 км. Первые 4,5 ч они шли по дороге со скоростью 5,2 км/ч и сделали привал на 1,6 ч, а остальное время они шли по болотистой местности со скоростью 2,5 км/ч. Сколько времени партизаны затратили на весь переход?
2*
35
224. Составьте задачу по выражению Ta+'fe-
225. Выполните действия: 8,12-0,254- 3,24*0,25.
226. Выполните действия с помощью микрокалькулятора и округлите ответ до сотых:
а) 2,835:0,225*4,537 — 32,929;
б) (4,9764-15,2473)*2,14— 5,0784.
лук 227. Разделите числитель и знаменатель каждой из дро-
бей -7= , , 4т; на 9. Напишите соответствующие
27 36 63 72
равенства.
228. Начертите координатный луч, приняв за единичный отрезок длину 12 клеток тетради. Отметьте на луче точки с коорди-3 1 6 2 9 4 ,.
натами: -r»-s"*rs->-s-»77-»-3-* Какие из этих чисел являются 4 и 12 о 12 и
координатами одной и той же точки?
229. Сколько: а) шестых долей содержится в ;
2 3 3 2
б) пятнадцатых долей содержится в -|-i 4~?
б 3 б 3
280. Найдите наибольший общий делитель и наименьшее общее кратное чисел:
а) 18 и 36; б) 33 и 44; в) 378 и 441; г) 11 340 и 37 800.
281. Решите уравнение:
а) 2,45*(т—8,8)=4,41; б) 7.54Л—3,6Л = 5,91.
9. Сокращение дробей
Если числитель и знаменатель дроби разделить на 5, то _ - з 15 з
получится равная ей дробь —, т. е. —=—.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
Q
Дробь — сократить нельзя, так как числа 3 н 4 — взаимно
простые числа. Такую дробь называют несократимой.
Наибольшее число, на которое можно сократить дробь,— это наибольший общий делитель ее числителя и знаменателя. Например, наибольшим общим делителем чисел 150 и 225
36
является 75. Значит, дробь можно сократить на 75, полу-225
Тот же ответ можно получить, сокращая дробь последо-225
вательно на общие делители чисел 160 и 225, используя для их
160 60 ю 2
нахождения признаки делимости:
225 75 15 3
Иногда удобно при сокращении дроби разложить числитель и знаменатель на несколько множителей, а потом уже сократить.
Например, .6'2/0 = - Сократим на 3-3-5 и
леи ле-ли z,o,u,z,o
136 3 3 тт < 3
получим Дробь — несократимая.
1OU z • z 4 4
®Что называют сокращением дроби? Какую дробь называют несократимой?
Q 232.CoKp.™TO«po«bf.l|,^.iSj.
283. Сократите дроби:
. 22 126 76 24 126 100 108 .
66 ’ 75 ’ 100 ’ 360 ’ 1000 ’ 250 * 126 ’
61 42 61 * * * * * * * * * * * * * * 76 40 3 18 45 120
' 720 ’ 300 ’ 64 ’ 243 ’ 300 ’ 900 ’ 180 *
284. Сократите:
. 2-3 2-8 5-4 7-5 . 4-5 15-3 14-9 2-3
4-5 ’ 7-2 ’ 4-9 ’ 2-7 ’ °* 3-6 ’ 11-10 ’ 15-7 ’ 9-8 ’
285. Представьте в виде обыкновенной несократимой дроби:
0,2; 0,8; 0,5; 0,15; 0,24; 0,35; 0,75; 0,05; 0,125; 0,025; 0,008;
0,375.
286. Какую часть часа составляют 45 мин, 12 мин, 15 мин,
40 мин, 35 мин?
237. Какую часть развернутого угла составляют 30°, 45°, 60°, 90°, 120°, 135°, 150°?
288. Какую часть килограмма составляют 125 г, 250 г,
750 г?
289. Выполните действие:
а)— 4-—; б)——— ; в) 4——3—; г) 9— — 9 — .
’ 15 ~ 15 ’ ' 20 20 ’ ’ 8 8 ’ '12 12
37
. 240. Один рабочий изготовил 16 одинаковых деталей за 6 ч, а другой 24 такие же детали за 15 ч. Какой из них тратил на изготовление одной детали больше времени и на сколько?
241. Из 20 м ткани сшили 8 одинаковых платьев для взрослых, а из 12 м сшили 8 детских платьев. Сколько метров ткани
пошло на одно детское платье и сколько на одно платье для взрослых?
242. Применив распределительный закон, представьте числитель дроби в виде произведения, а затем сократите:
12-5-Ь 12-9 . gx 8-8-87 .
12-21 ’ 8-5
14-5 — 14-2 . . 19-8 — 19-6
28 ’ f 38
243. Вычислите устно:
а) 460 • 2 б) 3644-116 в) 20 • 0,5 г) 4,8 : 2 д) 3-0,4 — 250 : 6 —2,5 4-0,8 : 0,13
: 13 4-70 : 1,6 : 0,4 - 0,1
• 7 -8 • 0,12 - 0,2 : 0,2
? ? ? ? ?
244. Найдите пропущенные числа:
°)
245. Найдите среди чисел 1, 3, 10, 12, 13, 16, 16, 39 пары взаимно простых чисел.
246. Найдите равные среди чисел:
J_; А; 1; J_; 10 ; А; ; 0,б; J 0,4.
247. При каких натуральных значениях буквы равны дроби: a)f и£; б) f и ±; в) f и -J-; г) f и f ?
248. В бригаде 5 рабочих. Зарплата первого рабочего увеличилась на 10%, второго — на 20%, третьего — на 30%, а у
38
четвертого и пятого осталась прежней. На сколько процентов в среднем выросла зарплата рабочего этой бригады, если раньше все они имели одинаковую зарплату?
Н 249. Древнегреческих, а также древнеиндийских математиков интересовали числа, которые соответствовали количеству точек, расположенных в виде некоторой геометрической фигуры — треугольника, квадрата
н др. Такие числа называли фи- • • • • •
гурными. Например, число 10 на- е е • • • • зывали треугольным, число 16 — ••• • • • •
квадратным (рис. 13). Такое пред- •••« ставление помогало древним уче- 13
ным изучать свойства чисел. Ис-
пользуя рисунок 13, попробуйте найти еще несколько треугольных и квадратных чисел. Какими свойствами обладают эти числа? Подумайте, как можно находить треугольные и квадратные числа, используя ряд натуральных чисел.
250. Разделите числитель и знаменатель дроби:
*» 35 “ S: б> Hi “ »> V “ 3: г> ЗГ, “ 7'
251. Умножьте числитель и знаменатель дроби:
a) f на 7; б) на 4; в) на 8; г) g на 2.
252. Собственная скорость катера 12,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите скорость катера по течению и против течения.
253. Скорость движения теплохода по течению реки 22,7 км/ч. Скорость течения 1,9 км/ч. Найдите собственную скорость теплохода и его скорость против течения.
254. Бригада изготовила за 3 дня 6000 деталей при плане 5100 деталей. Причем в первый день была изготовлена треть всех выпущенных деталей, а во второй день плана. Сколько Б
деталей изготовила бригада в третий день?
255. Найдите значение выражения:
3) 2f-1-L+3-|-;
4) 7f + lf-2f.
39
256. Решите задачу:
1) Путешественник проплыл протйв течения реки на моторной лодке 3 ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч?
2) Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28 км/ч. Сколько времени затратил путешественник на обратный путь?
257. Сократите дроби:
. 4 8 JL JL • «I — 3 — 6 • в1— 88 2 50
а* 10 ’ 12 ’ 9 ’ 12 ’ ’ 8 ’ 12 ’ 2 ’ 30 ’ ' 60 ’ 33 * 100 * 100 *
258. Сократите: J4, 5-8 6-9 9-10-16
259. Представьте в виде обыкновенной несократимой дроби следующие десятичные дроби: 0,875; 0,75; 0,035.
260. Выполните действие и сократите результат:
Л j I Q 7 4 1 л ® । о 4
12 12 ’ 14 + 14 ’ 318 — 1 18 ’ Г) 415+315 ‘
261. Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.
262. За 4 кг конфет и 3 кг печенья заплатили 12 р. 20 к. За 2 кг таких же конфет и 3 кг такого же печенья заплатили 8 р. 20 к. Сколько стоит 1 кг печенья?
263. Выполните действия:
а) (867 000:2125 —396,4)-2,15; б) (26,16:6 + 2,6-1,4):0,4-0,4.
10. Приведение дробей к общему знаменателю
Умножим числитель и знаменатель дроби — на одно и то же 4
в 3 6
число 2. Получим равную ей дробь , т. е. —= —. Говорят, что
о 4 о
мы привели дробь -5- к новому знаменателю 8. Дробь можно при-4
вести к любому знаменателю, кратному знаменателю данной дроби.
40
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем. При приведении дроби к новому знаменателю ее числитель и знаменатель умножают на дополнительный множитель.
Пример 1. Приведем дробь у- к знаменателю 35.
Решение. Число 35 кратно 7, так как 35:7 = 5. Дополнительным множителем является число 5. Умножим числитель
„ - _ 2 2-5 10
и знаменатель данной дроби на 5, получим —=—=— .
Любые две дроби можно привести к одному и тому же знаменателю, или иначе к общему знаменателю.
„ 2 10 4 12
Например, Т= ТК и .
Общим знаменателем дробей может быть любое общее кратное их знаменателей (например, произведение знаменателей).
Обычно дроби приводят к наименьшему общему знаменатели». Он равен наименьшему общему кратному знаменателей данных дробей.
Пример 2. Приведем к наименьшему общему знамена-, з 5 телю дроби — и —.
4 6
Решение. Наименьшим общим кратным чисел 4 и 6 является 12.
Чтобы привести дробь 4- к знаменателю 12, надо умно-4
жить числитель и знаменатель этой дроби на дополнительный множитель 3 (12:4 = 3). Получим = .
4 4 *3 12
Чтобы привести дробь к знаменателю 12, надо числитель О
и знаменатель этой дроби умножить на дополнительный мно-
житель 2 (12:6 = 2). Получим .
о 6*2 12
Итак, 9 , а . 4 12 в 12
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
41
2) разделить яашжмшй общий змаиекателъ на яшимгыи данных дробей, т. е. мейл* для каждой дроби дополнительный множитель; 8) умножить чиелитель и ммииематель каждой дроби на et дополнительный множитель.
В более сложных случаях наименьший общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Пример 3. Приведем дроби и 44-к наименьшему обще-00 100
му знаменателю.
Решение. Разложим знаменатели данных дробей на простые множители: 60=2-2*3*5; 168 = 2*2*2*3*7. Найдем наименьший общий знаменатель: 2-2-2-3-5-7 = 840.
Дополнительным множителем для дроби является произведение 2.* 7, т. е. тех множителей, которые надо добавить к разложению числа 60, чтобы получить разложение общего о.п тт - 11 11-2-7 154
знаменателя 840. Поэтому — =6О.2.7=й^о •
Q1
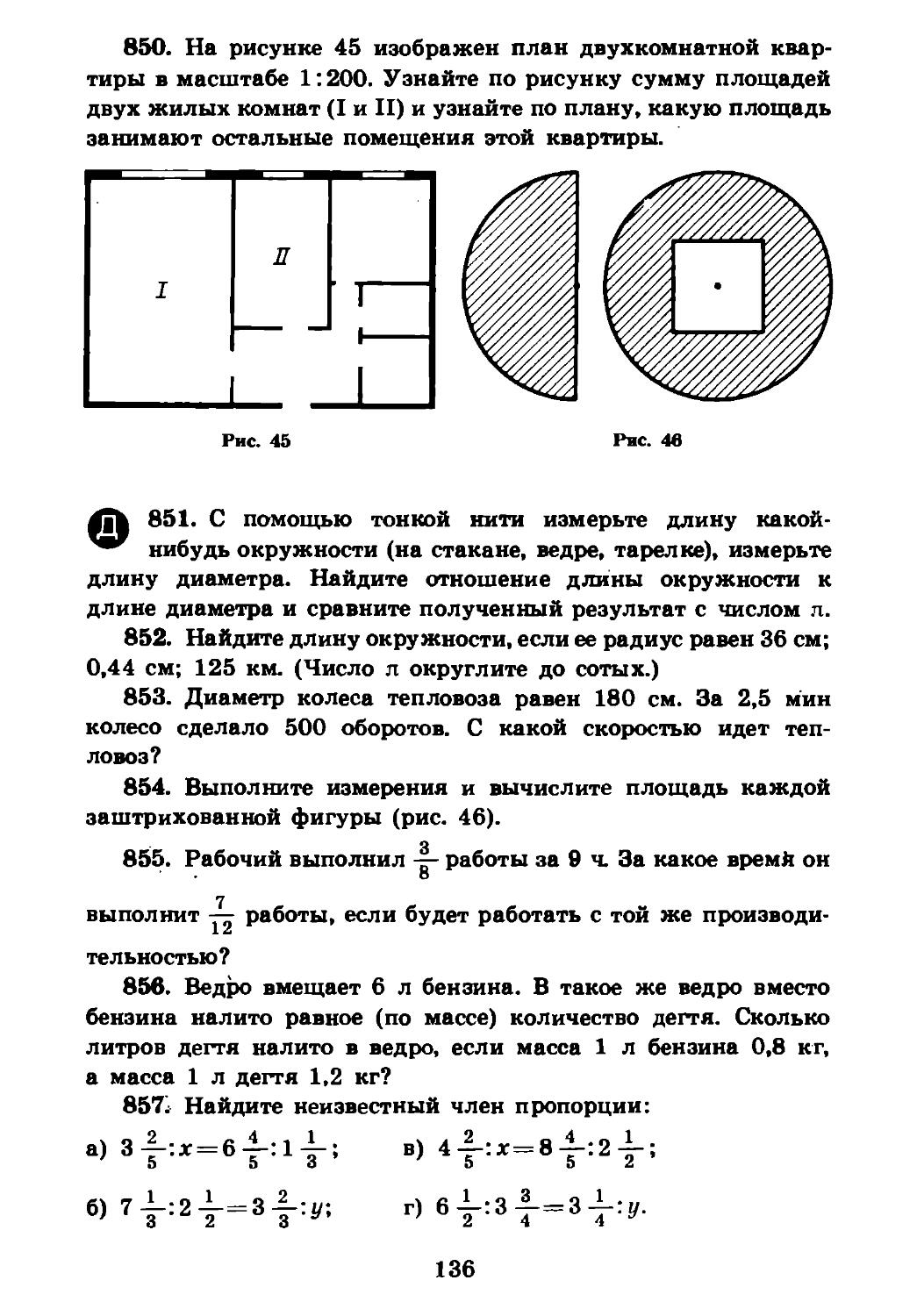
Для дроби — таким же способом находим дополнительный 100
Е 31 31-5 155
множитель 5. Значит, —=-------=— .
о. 108 1в8 5 840 *
Итак,—=^^ — = —
60 840 ’ 168 840
К какому новому знаменателю можно привести данную дробь? Можно ли привести дробь у- к знаменателю 35? к знаменателю 25? Какое число называют дополнительным множителем? Как найти дополнительный множитель? Какое число может служить общим знаменателем двух дробей? Как привести дроби к наименьшему общему знаменателю?
264. Приведите дробь:
а) к знаменателю 18; в) к знаменателю 78;
0 13
б) к знаменателю 60; г) к знаменателю 51.
265. Выразите в минутах, а потом в шестидесятых долях часа:
. 3 7 2 11 .5 3 .5 7
а) — ч и — ч; б) — ч и — ч; в) — ч и — ч; г) — ч и — ч.
'4 15 3 20 ' 12 5'6 20
42
266. Сколько содержится:
а) восьмых в 4~; в) пятнадцатых в д) двадцатых в 4 5 5
б) десятых в ; г) сотых в ; е) сотых в ?
267. Сократите дроби , 44 , 44 , 44 , а потом приведите
15 26 40 32
их к знаменателю 24. 268. Можно ли привести к знаменателю 36 дроби:
3 ’ 9 ’ 12 ’ 5 ’ 7 ’ 45 Г
269. Можно ли представить в виде десятичной дроби:
_2_.J_.-2_.-l_. 12. -9-? 5 ’ 25 ’ 3 ’ 7 ’ 15 ’ 18
270. Запишите в виде десятичной дроби, приведя:
а) -х-t 4- и 4- к знаменателю 10; '25 5
б) 4"» 44 • 44 » 44 к знаменателю 100;
в) —. Дг . 444. 444 к знаменателю 1000. ' 8 125 125 500
271. Запишите в виде десятичной дроби: з 2 з 5 13 7
5 ’ 25 ’ 4 ’ 8 ’ 125 * 200 '
272. Приведите к наименьшему общему знаменателю дроби:
•>т , 8 Г> 15 И 11 . 12 ’ «> То к)
б>т н П 4 д) 9 10 и 5 12 ’ и . 13 Л) 750
и т ’ ♦ е) И И 12 “ 18 . 18 ’ И) Л и 77 . 10 М) 297 и — 363 '
ф 273. Вычислите устно:
а) 16 . 4 б) 95 : 5 в) 38 . 0,01 г) 0,6 : 3 Д) 2-1,2
+ 11 + 56 : 1,9 • 1.5 • 0,5
: 15 : 25 . 50 + 2,9 : 0,1
• 17 • 27 . 0,3 : 0,8 + 0,9
+ 18 + 29 -0,2 — 1.3 : 0,7
? ? ? ? ?
43
274. Найдите пропущенные числа, если х=0,8; 0,16;
0,06; 1:
275. На какое число надо умножить 24; 8; 16; 6; 12, чтобы
получить 48?
276. С помощью транспортира разделите одну окружность
на 6, а другую на 3 равные дуги. Постройте многоугольники,
Рис. 14
изображенные на рисунке 14. У каждого из этих многоугольников равны стороны и равны углы. Такие многоугольники называют правильными. Подумайте, является ли правильным
многоугольником прямоугольник; квадрат.
277 Сократите- ™ 150 140 ззо сократите. в0 , 120, мо , 4в5 .
278. Найдите наибольший общий делитель числителя н знаменателя и сократите дробь:
al 168 . Xi 880 - в\ 3240 - 2838
’ 100 ’ °' 1008 ’ 972 ’ Г' 7425 '
279. При каком значении х верно равенство:
а) —= —; в)^=А;
' 35 7 ’ ' 05 х ’
6)— = — ; г) — = —? ' 0 48 ' * 35
280. Жук ползет вверх по стволу дерева (рис. 16) со скоростью 6 см/с. По тому же дереву ползет вниз гусеница. Сейчас она находится на 60 см ниже жука. С какой скоростью ползет гусеница, если через 5 с расстояние между ней и жуком будет 100 см?
44
281. Космический корабль «Вега-1» двигался к комете Галлея со скоростью 34 км/с, а сама комета двигалась ему навстречу со скоростью 46 км/с. Какое расстояние было между ними за 15 мин до встречи?”
282. Сократите: 1) ; 2)
283. Найдите значение выражения: л । q 7 к 13 q 7 23 13 ( 5 лч 7 । 14 1
П 4Й + З33 ;2) 518-218 ’ 3) 48“ 48 +48 ’ 4) 45 + 45 -« *
284. Выполните действия и проверьте ваши вычисления с помощью микрокалькулятора:
1) 111 - ((0,9744:0,24 +1,02) • 2,5 - 2,75);
2) 200 - ((9,08 - 2,8828:0,38) • 8,5+0,84).
285. Приведите дробь:
а) к знаменателю 24; в) к знаменателю 57;
О 1Н
б) к знаменателю 65; г) -Ц к знаменателю 78.
13 13
288. Представьте в виде десятичной дроби:
4 8 1 3 17
5 ’ 25 ’ 4 ’ 50 ’ 20 ‘
287. Сократите дроби 4г • 41 • тУк • • а потом приведите
оО 4Э 1UU oU
их к знаменателю 60.
288. Приведите дроби к наименьшему общему знаменателю: .5 1 у 3 5 у 7 2 . 7 13 9.
а) 7 И 2 ; ) 28 И 39 ’ Д 13 И 11 ’ Ж) 80 ’ 540 И 20 ’
7 „ 1 . у 8 . 5 . _у 3 .2 . у 52 7 61
б) 20 “ 15 ’ Г) 11 И 8 ’ 22 И 33 ’ 3) 105 ’ 95 И 63 '
289. Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.
290. Из двух пунктов, расстояние между которыми 210 км, вышли одновременно навстречу друг другу два алектропоевда. Скорость одного из них на 5 км/ч больше скорости другого. Найдите скорость каждого электропоезда, если они встретились через 2 ч после своего выхода.
291. Выполните действия:
а) 62,3+(50,1 - 3,3 • (96,96:9,6)) • 1,8;
б) 51,8 + (70,2 - 4,4 • (73,73:7,3))-1,6.
45
11. Сравнение, сложение и вычитание дробей с разными знаменателями
з
И 5 ‘
общему знаменателю 15. о
Мы умеем сравнивать, складывать и вычитать дроби с одинаковыми знаменателями.
¥гобы сравнить (сложить или вычесть) дроби с разными знаменателями, надо: 1) привести данные дроби к наименьшему общему знаменателю; 2) сравнить (сложить или вычесть) полученные дроби.
2
Пример 1. Сравним дроби —
3
Решение. Приведем дроби к
ГГ _ _ . 2 2 6 10 .3 3-3
Получим 3— 3.5 — 15 » 5—5.3 —15' Так как ™ >^, то
2 з
Пример 2. Найдем значение суммы ——|- —.
3 5
„ 2 . ,3 10 . В 1В , 4
Решение. —=-----------------—=1—.
8 ~ 5 15 ' 15 15 15
2 3
Пример 3. Найдем значение разности —----—.
3 5
„ _ 2 3 10 В 1
Решение.------—=------=—.
решение. 3 5 15 15 15-
Для сложения и вычитания дробей верны изученные ранее свойства этих действий. Они иногда помогают упрощать вычисления.
Пример 4. Найдем значение выражения
10 .J5._l_._7_
51 + В + В +5Г
Решение. Сгруппируем дроби, имеющие одинаковые знаменатели:
10 - /10 ,2_\ , -17 . 6 1 I 2 ,
51 + 9 + В + 51 \51-’51/_’\В_’В/ 51 В 3^3
31
Пример 5. Найдем значение выражения —
Решение. Используя свойство вычитания суммы из чис
ла, получим:
31__ /17 , 1 \ 31 _ 17__1_=м_____1_=_?_____L=_L
35 \ 35 “г 5 / 35 35 5 35 5 5 5 5 ’
46
©Как сравнить две дроби с разными знаменателями? Расскажите, как сложить дроби с разными знаменателями. Расскажите, как выполнить вычитание дробей с разными знаменателями.
0 292. Сравните дроби: i 2 . 8 . л 4 . 2 . ,7 3 ,19 .4
а) 3 И 21 ’ 16 “ б ’ 30 И 10 ’ Г) 60 И 16 '
ОПри сравнении дробей первую из них читают в именительном падеже, а вторую — в дательном либо добавляют слово дробь и не изменяют названия дробей.
Например, запись — <— читают: 90 46
— четыре девяностых меньше шести сорок пятых
— дробь четыре девяностых меньше дроби шесть сорок пятых
293. Что меньше: а) или ; б) тгг или ?
10 30 14 21
294. Что больше: а) или ; б) -Ц или -Ц ? 12 48 18 10
295. Расположите в порядке возрастания дроби: . 4 7 8 11 . д. 11 5 5 3
а' 5 ’ 10 ’ 15 ’ 30 ’ ' 12 ’ 24 ’ 6 ’ 8 '
296. Докажите неравенство:
я\ 123 _ J_. д. 361 1 . . 43 17
1 800 ^8 ‘ * 1 * * 6000^15 ’ f 1575'^*630’
297. Объясните, не приводя дроби к общему знаменателю,
1 12244 w
почему —>— Сформулируйте правило
о 7 О 7 О 7
сравнения двух дробей с одинаковыми числителями и разными знаменателями. Используя это правило, сравните:
. 5 „ 5 . XV 7 „ 7 . , 14 14
а) 9 “ 11 ’ б) 13 и 8 . 27 И 25 '
298. Запишите все дроби с числителем 2, большие, чем .
299. Сравните промежутки времени двумя способами: 1) выразив их в минутах и 2) приведя дроби к наименьшему общему знаменателю: ,4 3 7 11 ,3 2 ,6 8
а> 15 4 * * * “ W Ч! б> 20 4 “ 30 Ч; В> ТЧИ-3-Ч; Г> 12 ЧИ1б Ч-
47
300. Запишите все дроби со знаменателем б, большие, чем , и меныпие, чем . Отметьте эти дроби на координатном д 6
луче.
301. Рисунки занимают книги, а таблицы книги. Что X X itit
занимает больше места в книге: рисунки или таблицы?
302. 20 шагов папы составляют 16 м, а 10 моих шагов 7 м. Чей шаг короче?
303. Через узкую трубу бассейн наполняется за 10 ч, а через широкую — за 4 ч. Какая труба дает меньше воды: широкая за 3 ч или узкая за 7 ч?
304. Трехметровое бревно распилили на 7 равных частей, а четырехметровое — на 10. Части какого бревна длиннее?
305. Миша, Юра и Нина решали в классе одну и ту же зада-1 2
чу. Один из них затратил на решение — урока, другой — урока,
а третий урока. Какую часть урока затратил на эту задачу 16
каждый из них, если известно, что Нина решила задачу быстрее Миши, а Юра быстрее Нины?
300. Начертите координатный луч, приняв за единичный отрезок отрезок, длиной в 18 клеток тетради. Отметьте на этом луче точку А (). Отложите вправо от точки А отрезок АС, равный единичного отрезка. Найдите координату точки С.
Отложите от точки С влево отрезок CD, равный единичного отрезка. Найдите координату точки D. Как можно найти координаты точек С и D, не выполняя построений?
D Суммы и разности дробей можно читать разными способами.
Например: 2 9
—+—-----сумма двух третьих и трех пятых
— к двум третьим прибавить три пятых
— сумма дробей две третьих и три пятых
-----1--из двух третьих вычесть три пятых — разность дробей две третьих и три пятых
48
307. Выполните действие:
а)т+т; г)т+т; Ж)Т“Т; к)т-0;
6)f+f; д)-|-+0; 3>T-f; л)т+т;
в\ 3 , з . el —_—• и) —__— • —__и 2
В) 5 3 5 ’ 7 6 ’ М) Т+Т-
308. На координатном луче отмечены точки А (-А-) и
В ) (рис. 16). Отметьте на луче точку с координатами:
а) —+—; б) -1—L.
т п п т
/ 2
0 т п
В А
Рве. 16
309. Найдите значение выражения:
а) т+т; 1 5 г) -- 3 . 14 ’ ж> т+т; к) ^+^ ;
б) 1 4 2 ’ д)т- 5 . 12 ’ з) А» -11; 1 21 15 ’ „1 11 _ 2 . 21 35 ’
а SH 1 сл|со « • е>Т2- 7 . 20 ’ и) А1_А 22 55 ’
310. Замените десятичную дробь обыкновенной дробью
выполните действие:
а) 0,5+4“; б) -|- + 0,75; в)Ц-0,4; г) 0,95-^. о О 10 12
311. Замените обыкновенную дробь десятичной и выполните действие: а) 2,15+4?; б) 4—0,35.
20 4
312. Выполните действие —+ 4г • 4г + 44 • 4-4“ > -Ц — 44
4 60 25 1 20 5 2 40 200
сначала в обыкновенных дробях, а потом в десятичных.
313 Выполните действия:
•>£-G-+1+ «£+(4-т)-
314. Выполните действие: . 7 .11 . <.19 8 . . 5 . 17 .
а) 20 + 30 ’ 60 45 ’ В) 48 + 36 ’
. 11
г) 30
16
45 '
49
315. Найдите значение выражения:
--L-Lu-Z- • 1 3 .11 2 . . 13 1 /29 . 5 \, 8 4 ' 12 ’ в) 7 + 14 21 ’ Д) 18 24 \72 + 38 ) ’
« •> (f-T)+ й+т)+т-
316. Решите уравнение:
•>*+£-т+т: •>»-5>=Т-£’
«>(т-)+3=15= Г>1-(Ь")=1-
317. Найдите значение выражения:
а) -|_ + о,7—в) А_+ 0,6;
б) 0,8-0,3 —г) Z-4-0,4 —0,6.
318. Найдите значение выражения:
_v 1 । 1 । 3 । 5 б .2.1. 6
а) т+п+т+12 ’ б) й+т+т+тт •
319. Использовав свойство вычитания числа из суммы, найдите значение выражения:
*>(п+т)-п> «> (!+£)-£
320. Использовав свойство вычитания суммы из числа, найдите значение выражения:
•> (£+т)=«> £-(!-+£)•
321. Найдите значение выражения 777+-^, если а=1;
1 и 10 2; 5; 7.
322. Найдите значение выражения ——, если х=4;
1Z X
5; 6.
323. Петя играл в футбол ч, а в волейбол ч. Что больше заняло времени: игра в футбол или игра в волейбол — и на сколько? Сколько времени затратил Петя на обе игры?
324. Тракторист вспахал в первый час поля, во второй О
час Z- поля и в третий час Z- поля. Какую часть поля вспахал 5 4
тракторист за эти 3 ч?
50
325. В первый день асфальтом покрыли км дороги, а
во второй день — на км больше, чем в первый день. Сколько э
километров дороги покрыли асфальтом за эти два дня?
326. Длина прямоугольника -у- м, а ширина на м меньше длины. Найдите ширину прямоугольника и его периметр.
327. В палатку привезли т моркови и т свеклы. К ве-
черу продали т привезенных овощей. Сколько тонн овощей осталось?
328. За первый месяц завод выполнил годового плана, а за второй — на 4- годового плана меньше. Какую часть годо-24 вого плана выполнил завод за два месяца?
329. При покупке книги Ваня получил сдачу р. Сколько он получил бы сдачи, если бы купил книгу, которая дороже купленной на р.?
330. Два поезда вышли одновременно из двух городов навстречу друг другу. Каждый час они приближаются друг к другу на всего расстояния между городами. Какую часть расстояния между городами проходил за час один из них, если другой проходил за час -у- этого расстояния?
331. Из села в город одновременно вышли две автомашины: грузовая и легковая. Каждый час грузовая автомашина отставала от легковой на £- всего расстояния от села до города. Ка-кую часть этого расстояния проходила грузовая автомашина за 1 ч, если легковая за 1 ч проходила этого расстояния?
о
332. Один комбайн может убрать все поле за 6 дней, а другой — за 4 дня. Какую часть поля уберут оба комбайна за один день?
333. Один мотор израсходует полный бак бензина за 18 ч, а другой — за 12 ч. Какую часть полного бака израсходуют оба мотора, если первый будет работать 5 ч, а второй 7 ч?
51
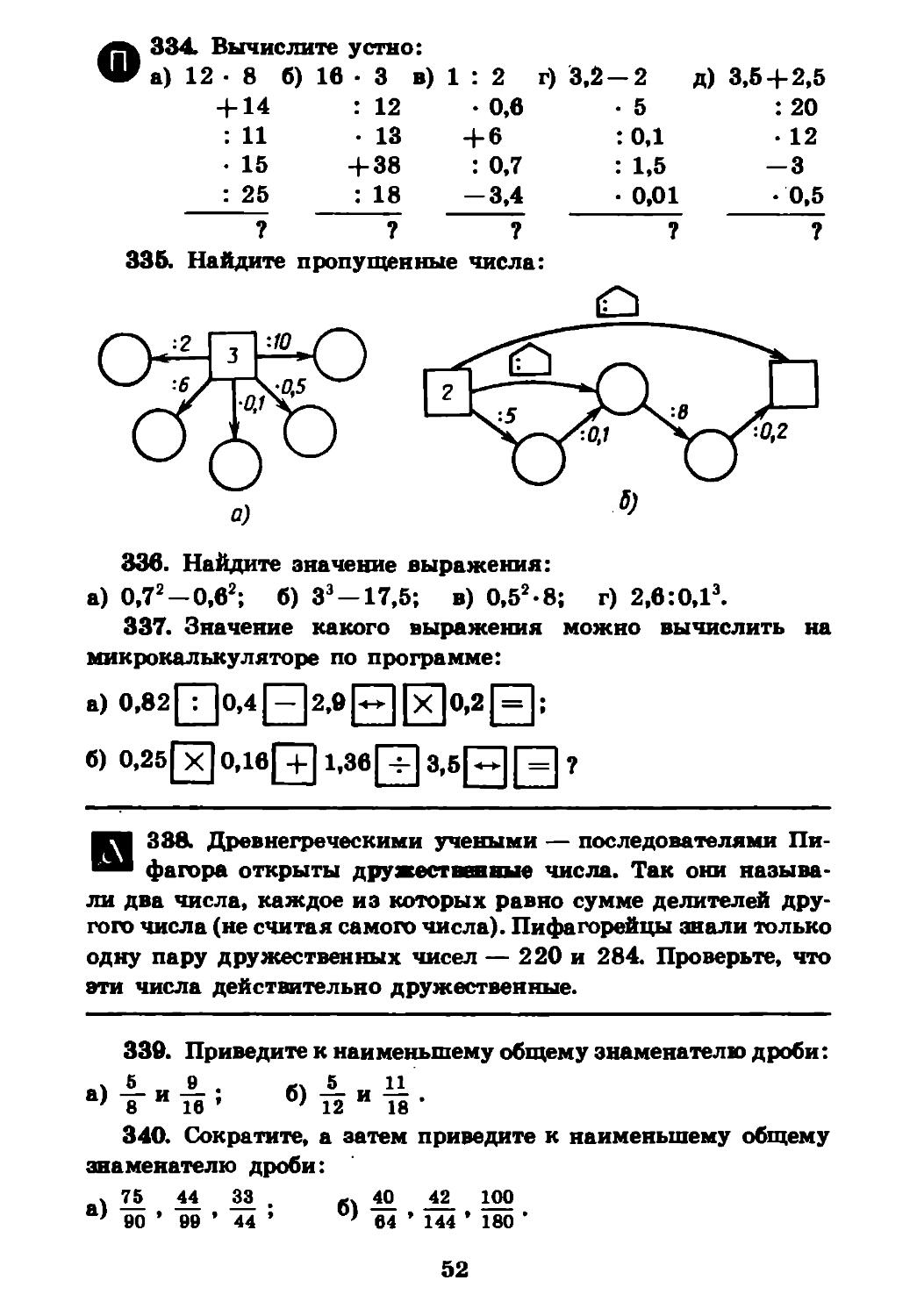
ХДй 334. Вычислите устно:
™ а) 12 • 8 б) 16 - 3 в) 1 : 2 г) 3,2 — 2 д) 3,5+ 2,5
+ 14 : 12 - 0,6 • 5 : 20
: 11 • 13 + 6 : 0,1 • 12
• 15 + 38 : 0,7 : 1,5 -3
: 25 : 18 -3,4 • 0,01 • 0,5
? ? ? ? ?
335. Найдите пропущенные числа:
О
336. Найдите значение выражения:
а) 0,72 — 0,в2; б) 33-17,5; в) 0,52-8; г) 2,6:0,13.
337. Значение какого выражения можно вычислить на микрокалькуляторе по программе:
Я 338. Древнегреческими учеными — последователями Пи-“ фагора открыты дружественные числа. Так они называли два числа, каждое из которых равно сумме делителей другого числа (не считая самого числа). Пифагорейцы знали только одну пару дружественных чисел — 220 и 284. Проверьте, что эти числа действительно дружественные.
339. Приведите к наименьшему общему знаменателю дроби:
340. Сократите, а затем приведите к наименьшему общему знаменателю дроби:
. 75 44 33 . g. 40 42 100
' 00 ’ 00 ’ 44 ’ ' 04 ’ 144 ’ 180 ’
52
841. Запишите числа:
а) 3-|-, 17-^-, 9-у так, чтобы их дробная часть была правильной дробью;
б) 3-—, 6-^ , 11уу в виде натуральных чисел.
842. Запишите в виде неправильной дроби дробную часть чисел 3-|-, 5-|-, 2-^т, уменьшив* целую часть на 1.
4 в 17
848. Решите задачу:
1) Из аэропорта вылетел самолет со скоростью 600 км/ч. Через 0,6 ч вслед за ним вылетел другой самолет со скоростью 760 км/ч. Через сколько часов второй самолет после своего вылета будет впереди на 226 км?
2) С автовокзала вышел автобус со скоростью 60 км/ч. Через 0,6 ч вслед за ним вышла легковая автомашина со скоростью 76 км/ч. Через сколько часов после своего выезда легковая автомашина будет впереди автобуса на 46 км?
844 Решите задачу:
1) Пес бросился догонять своего хозяина, когда тот отошел от него на 1,8 км, н догнал его через 3 мин. С какой скоростью шел хозяин, если пес бежал со скоростью 0,7 км/мин?
2) Служебная собака бросилась догонять нарушителя границы, когда между ними было 1,8 км. С какой скоростью бежал нарушитель, если скорость собаки 19 км/ч и она догнала его через 0,2 ч?
846. Выполните действия,и проверьте ваши вычисления с помощью микрокалькулятора:
1) (28,376+ 36,99:6,9-3,46 • 2,8): 3,52;
2) (6,4 • 8,26- 32,896+36,61:6,3): 4,48.
846. Сравните дроби:
V -L и ± ± и -5- •
а‘ 7 И 21 ’ В Я 20 * Ю в И 1В ’ Ж' 115 “ 175 ’
3 8 .4 1в к В 7 . _< 9 16
Б Н 16 ’ Г 7 И 28 ’ е) 12 Н 18 ’ 3 85 И 117 '
847. Выполните действие:
*) т+f; в> т+т; д>т-Ь Ж)т+Ь
б> т+т; г> т+Ь е)т-Ь
53
„Ч 1 , 7 . v 3 1 . . б . 3 . . 23 3 . . 9 3
) 8 +12 ’ М) 4 в ’ Н) 9 + 4 ’ °) 40 8 ’ ЗБ 28 *
348. Один трактор может вспахать поле за 14 ч, а другой тот же участок за 8 ч. Какой трактор больше вспашет: первый за 7 ч или второй за 5 ч?
349. Автобус проходит расстояние от города до деревни за 8 ч, а легковая автомашина — за 6 ч. Кто из них пройдет большее расстояние: автобус за 5 ч или легковая автомашина за 4 ч?
350. Слесарь может выполнить задание за 6 ч, а его ученик это же задание за 8 ч. Какую часть задания они могут выполнить вместе за 1 ч?
351. Из пунктов А и В одновременно навстречу друг другу вышли два пешехода. Один из них за 1 ч проходит -^-расстояния О
АВ, а другой расстояния АВ. На какую часть расстояния АВ О
они сближаются каждый час?
352. Периметр треугольника АВС равен м. Сторона АВ
17 9
равна — м, сторона ВС на — м короче АВ. Найдите длину стороны АС.
353. В книге три рассказа. Наташа прочла первый рассказ за -5- ч, на чтение второго рассказа она потратила на ч боль-о О
7
ше, а чтение третьего рассказа заняло на — ч меньше» чем
1 £
чтение первого и второго рассказов вместе. Сколько времени ушло у Наташи на чтение всей книги?
354. На решение задачи и уравнения Митя затратил ч.
О
Сколько времени выполняла эту работу Оля, если на решение задачи она затратила на ч меньше, а на решение уравне-
ния — на ч больше, чем Митя?
355. Выполните действия:
54
356. Найдите значение выражения:
а) Х + 0.34-А ; б) 1—0,4--^ .
357. Дорога иэ села в город проходит через рабочий поселок. Из села в город вышла легковая автомашина со скоростью 1,5 км/мин. В то же самое время из рабочего поселка в город вышла грузовая автомашина со скоростью 1 км/мин. Через 20 мин легковая автомашина догнала грузовую. Найдите расстояние от деревни до рабочего поселка.
358. Теплоход «Ракета» идет по реке со скоростью 55 км/ч. Впереди теплохода идет баржа со скоростью 25 км/ч. Какое расстояние будет между ними через 3 ч, если сейчас баржа впереди теплохода на 50 км?
359. С железнодорожной станции в 12 ч вышел скорый поезд со скоростью 70 км/ч. На 8 ч раньше с этой же станции был отправлен в том же направлении товарный поезд. В 16 ч скорый поезд догнал товарный. Найдите скорость товарного поезда.
360. Найдите значение выражения:
а) 18,305:0,7 - 0,0368:0,4 + 0,492:1,2;
б) (0,0288:1,8 + 0,7 + 0,7 • 0,12) • 35,24;
в) (15,964:5,2-1,2).0,1;
г) (21,62-3,5-52,08:8,4).0,5.
361. Запишите числа:
а) 7^, 8-Ц в виде натурального числа; б о7
8 12 25
б) 4—, 15— , 8— так, чтобы их дробная часть была правнль-d 7 4
ной дробью.
362. Запишите дробную часть чисел 2-|~, 7-^, 1-|- в виде 9 15 9
неправильной дроби, уменьшив целую часть этих чисел на 1.
12. Сложение и вычитание смешанных чисел
Переместительное и сочетательное свойства сложения позволяют свести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Пример 1. Найдем значение суммы 16-|-4-194-.
8 4
55
Решение. Приведем дробные части чисел к наименьшему общему знаменателю 8, затем представим смешанные числа в виде суммы их цеЛой и дробной части:
16-|-=ie4--|i; 19-|-=19-|г=194-|-.
0 0 4 0 0
Значит, 1в^-+19^-=1в4-|-4-194-|- = 0 4 0 О
=(1'6-|-19)4- (f+f) =36 +т_=3б'в’* \ 0 0 / в в
Пишут короче: 16-l-4-19^-=16-f-4-19-|-=35-|-. 8 4 0 0 0
Пример 2. Найдем значение суммы 5-|—|-34-. о 4
Решение. Сначала приводим дробные части данных чисел к наименьшему общему знаменателю 12, после отдельно складываем целые и дробные части:
к 5 । о 3 р 10 । q 9 _о 19 _Q 7
5т+3т=бТ2+312-8п -9IS-
Чтобы сложить смешанные числа, надо: 1) привести дробные части этих чисел к наименьшему общему знаменателю; 2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из згой дроби и прибавить ее к полученной целой части.
При вычитании смешанных чисел пользуются свойствами вычитания суммы из числа и вычитания числа из суммы.
7 1
Пример 3. Найдем значение разности 5—— 2 —.
Решение. Приведем дробные части к наименьшему обще* му знаменателю 18 и представим данные числа в виде суммы целой и дробной части:
5 —= 5 — =54-—; 2—=2 —= 24-—.
9 18 ~ 18 ’ в 18 '18
По свойству вычитания суммы из числа имеем:
в-5-2-5-=(в+^)-(2+^) =
=B+li_2_i=(B-2)+(i4-A)=3+ll=3il.
56
Пишут короче: 5-1—2-1-= 5- 2 ~ = 311 . *7 О 1" 1" ю
Если дробная часть уменьшаемого окажется меньше дробной части вычитаемого, то надо превратить в дробь с тем же знаменателем одну единицу целой части уменьшаемого.
Пример 4. Найдем значение разности 3 — 1 .
Решение. Приведем дробные части данных чисел к наименьшему общему знаменателю 18:
34-=3Л;
9 18 6 18
Так как дробная часть уменьшаемого меньше дробной части вычитаемого, то уменьшаемое записываем так;
3т=3й-3+й-2+1+£-2+т1+-й“2+1|-211-
Значит,
Обычно пишут короче:
3-—1—=3-8 1 1*1 =2 — — 1 И =111
9 6 18 18 18 18 18
Чтобы выполнить вычитание смешанных чисел, надо: 1) привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробней части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть; 2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
Расскажите, как сложить смешанные числа и на каких свойствах сложения основано сложение смешанных чисел. Расскажите, как выполнить вычитание смешанных чисел и на каких свойствах основано правило вычитания смешанных чисел.
363. Выполните сложение:
*’3Т+5Л! Л> Т-1-4-4; ж) 7 + 3f;
б”в-+2А: г) 1¥'+2f; е>81+й; 3>Т+4Т-
57
364. Выполните вычитание:
а) 1 —-j-; Д) б 2 6 ; и) б) 2--J-; е)6 —Б-|-; к) . _5 9_ . 1 12 10 ’ й 3 11 . 6 10 16 ’ И) 10f-4^; o)7f-5-L;
В) 9-Ц ; ж) 8 ^--4; л) к2 JL. 6 8 10 ’
г)7-1^; з)б£-А; м) • * ез|а со 1 Р)б|--3-|-.
365. Найдите значение выражения:
’Н1-й): >»£-' (2т+3 * *п);
в>2~(^~й)! г>8 * * *н-;
«> (в«-|-+Э-|-)- (lS-10-g-) *
»> (16т-2т)- (6 *т+»т)+
,)(20-l»X)+(17|~17)+(2i-^).
366. Выполните действие:
а) 2,4-Ь1-|-; б)3,7-2-|-; в)7-±—6,2; г) 9^-1,8. о 5 о J.D
367. Решите уравнение:
.|x+21=S; ,)„-e|-=^! ,)3^-x=12-+lf;
в) 23f+a=30; г) ц2-_х=3^; .) ,+f-i=|--X.
368. Найдите по формуле А = т—6 -5- : в
3 7
а) значение А, если m = 6 —; 8 ; 11;
б) значение т, если А = 6 ; 3 ; 0.
369. Школьный бассейн наполняется через первую трубу
за 4 ч, а через вторую за 6 ч. Какую часть бассейна останется
наполнить после совместной работы обеих труб в течение часа?
370. Новая машина может выкопать канаву за 8 ч, а ста-
рая — за 12 ч. Новая машина работала 3 ч, а старая 5 ч.
Какую часть канавы осталось выкопать?
58
371. От ленты длиной 8 м отрезали кусок длиной 3 м.
2о
Найдите длину оставшейся части.
372. Одна шахматная партия длилась ч, а другая ч.
12- 6
Сколько времени длилась третья партия, если на все три партии было затрачено 3 ч?
373. Когда от веревки отрезали кусок, то оставшаяся часть имела длину 2 м. Какой длины была бы оставшаяся часть, если
2 3
бы от веревки отрезали на — м меньше? на — м больше? о 4
374. Запишите все числа, знаменатель дробной части которых равен 12, большие 2 -5- и меньшие 3-^- .
О 12
375. На координатном луче отмечена точка А (рис. 17).
Отметьте на луче точки, координаты которых равны:
а) 1-+-—; б) 2——; в) 2 + —; г) 1 + 1 —. Л Л Л л
7л
О л / 2
- < I ।-------------
А
Рис. 17
376. Найдите периметр треугольника АВС, если АВ = 3 м,
5
ВС = 2-^~ м и АС = 2^Г м. 4 10
377. На одной машине 4 т ipysa, а на другой на 1 т 10 о
меньше. Сколько тонн груза на двух машинах?
378. В одном ящике 5 кг винограда, что на 2 кг мень-
10 о
ше, чем в другом ящике. Сколько килограммов винограда в двух ящиках?
379. На окраску окон израсходовали 2 кг краски. На
з
окраску дверей пошло на 4 — кг меньше, чем на окраску пола.
5
Сколько всего израсходовали краски, если на окраску пола
19
пошло 10 — кг?
59
380. Три колхозных звена вырастили горох на площади 72 -Ц га. Первое и второе звенья вырастили горох на площади 44 -7- га, а второе и третье — на площади 62 4- га. Найдите 4 20
площадь каждого участка.
381. На сахарный завод в понедельник привезли 212-4- т свеклы, во вторник — на 297 4~ т больше, чем в понедельник, а О
в среду — на 114 — т меньше, чем во вторник и понедельник б
вместе. Из 7 т свеклы получается 1 т сахара. Сколько сахара получится из привезенной свеклы?
382. В трех бидонах 10 л молока. В первом и втором бидоне было 6 4~ л, а во втором и третьем Б 4- л молока. Сколько 4 3
литров молока было в каждом бидоне?
383. Теплоход по течению реки проходит 33 км за 1 ч. Скорость течения 2 4~ км/ч. Найдите скорость теплохода против течения.
384. Скорость катера по течению реки 17 4” км/ч, а против течения 12 4” км/ч. Какова скорость течения?
386. Федя и Вася шли навстречу друг другу. Каждый час расстояние между ними уменьшалось на 8 4~ км. Найдите ско-рость Феди, если скорость Васи 3 4" км/ч.
386. Первый велосипедист догонял второго, причем расстояние между ними уменьшалось каждый час на 2 4~ км. С ка-кой скоростью ехал первый велосипедист, если второй ехал со скоростью 12 км/ч?
387. Найдите значение выражения:
.) 12.+2e+2i+6f+i+4i; .)8f-(4f+2f);
6) r>(l»i+»X)_7X.
60
388. Вычислите устно:
а)
70 : 5 б) 15 • 6 в) 1,4 + 5,6 г) 1 : 4 д) 4-3,4
• 7 -18 : 2 + 0,05 1,4
-18 : 12 -1,7 • 7 + 0,06
: 5 + 90 : 0,3 + 3,4 : 1,8
+ 64 : 16 • 0,1 : 5 3
? ? ? ? ?
389. Найдите пропущенные чис-
ла:
390. Найдите натуральные значения т, при которых верно неравенство:
т 2
85 < 17 ’
391. На сколько процентов увеличится объем куба, если длину каждого его ребра увеличить на 20%?
392. Почтовый самолет поднялся с аэродрома в 10 ч 40 мин
утра, пробыл в полете 5 ч 15 мин, а на земле во время поса
док 1 ч 37 мин. Когда самолет вернулся на аэродром?
м
393. Четырехугольник с равными сторонами называют ромбом (рис. 18). Подумайте, является ли ромб правиль-
ным многоугольником. В чем сходство решения этой задачи
с нахождением решений двойного неравенства 0<.у< 10 среди чисел 0,12; 15; 2,7; 10,5?
6)
61
394- Докажите переместительное и сочетательное свойства сложения для дробей с одинаковыми знаменателями на основе таких же свойств для натуральных чисел.
395. Выполните действие:
6>f+-b r>W-’
396. В киоск для продажи поступили марки по 3 к., по 5 к. и по 10 к. Число марок каждого вида было одинаково. Какова стоимость всех марок по 5 к., если: а) общая стоимость всех марок 21 р. 60 к., б) стоимость всех марок по 10 к. больше стоимости всех марок по 3 к. иа 6 р. 30 к?
,„397. Выполните вычисления с помощью микрокалькулятора и результат округлите до тысячных:
3,281 - 0,57 + 4,356 • 0,278 -13,758:6,83.
398. Решите задачу:
1) Для борьбы с вредителями садов приготовляется из-вестково-серный отвар, состоящий из 6 частей серы, 3 частей негашеной извести и 50 частей воды (по массе). Сколько получится килограммов отвара, если воды взять на 8,8 кг больше, чем серы?
2) Для приготовления фарфора на 1 часть гипса берут 2 части песку и 25 частей глины (по массе). Сколько получится килограммов фарфора, если взять глины на 6,9 кг больше, чем песку?
399. Выполните действия:
1) 7225:85 + 64-2345 - 248 838:619;
2) 54-3465—9025:95 + 360 272:712.
400. Выполните действие:
»>91т+3та; r>39f+12f; ж) 4+af;
6>1К+2Й! Д)Зв-|-+12^; з)3-|-+3.
В) 5 4-+41 ; е) 5—+—;
401. Найдите значение разности:
6>3-П’ a)4-3f;
62
Г) 7-|~5; е) 6^-3а) 161— 4;
д) 45-44|-; ж)10А_7^; и)19А_8Я.
402. Решите уравнение:
в> 1~*=т+^’ б> ‘+1=т+т; в> «+2Ь5Т-1Т-
408. Найдите значение выражения:
ft)3£+f-2A: в)в^-3Т-1Т =
б)т+2-г+2т; г) з|-ф31
404. Один тракторист вспахал -%- поля, а другой того же 9 о
поля. Какую часть поля осталось вспахать?
406. Бочки горючего хватает для работы одного двигателя иа 7 ч, а другого иа 5 ч. Какая часть горючего останется от полной бочки после 2 ч работы первого двигателя и 3 ч работы второго двигателя?
400. Для экспедиции, работающей в тайге, сбросили с вертолета упаковку с продуктами, которая упала на землю через 3 с. С какой высоты была сброшена эта упаковка, если в первую секунду оиа пролетела 4^ м, а в каждую следующую секунду она пролетела на 9 м больше, чем в предыдущую?
О
407. Сколько времени пошло на изготовление детали, если ее обрабатывали на токарном станке 2 4* ч, на фрезерном 4
стайке 3 у ч и на сверлильном станке 1 ч?
408. Найдите значение выражения:
a)5.7 + 3f-7f; в) 3 £+4.8-1 f.
409. Из двух сел одновременно навстречу друг другу вышли два пешехода и встретились через 1,5 ч. Расстояние между селами 12,3 км. Скорость одного пешехода 4,4 км/ч. Найдите скорость другого пешехода.
410. Для приготовления варенья из вишни на 3 части сахара берут 2 части ягод (по массе). Сколько килограммов сахара и сколько килограммов ягод надо взять, чтобы получить 10 кг варенья, если при варке его масса уменьшится в 1,5 раза?
63
411. Найдите значение выражения:
а) (44,96+ 28,84:(13,7-10,9)): 1,8; б) 102,816:(3,2-6,3) + 3,84.
412. Решите уравнение:
а) (х— 4,7).7,3 = 38,69; в) 23,5 - (2,3а + 1,2а) = 19,3;
б) (3,6 —а)-5,8 = 14,5; г) 12,98 - (3,8х - 1,3х) = 11,23.
Н Раздел математики, в котором изучаются свойства чисел и действий над ними, называют теорией чисел.
Начало созданию теории чисел положили древнегреческие ученые Пифагор, Евклид, Эратосфен и другие.
Некоторые проблемы теории чисел формулируются очень просто — их может понять любой шестиклассник. Но решение итих проблем иногда настолько сложно, что на него уходят столетия, а на некоторые вопросы ответов нет до сих пор. Например, древнегреческим математикам была известна всего одна пара дружественных чисел — 220 и 284. И лишь в XVIII в. знаменитый математик, член Петербургской академии наук Леонард Эйлер нашел еще 65 пар дружественных чисел (одна из них 17 296 и 18 416). Однако до сих пор не известен общий способ нахождения пар дружественных чисел.
Почти 250 лет назад член Петербургской академии наук Христиан Гольдбах высказал предположение, что любое нечетное число, большее 5, можно представить в виде суммы трех простых чисел. Например: 21 = 3 + 7 +11, 23 = 5+ 7 +11 и т. п.
Л. Эйлер
И. М. Виноградов
64
Доказать это предположение сумел лишь 200 лет спустя замечательный советский математик, академик Иван Матвеевич Виноградов (1891—1983). Но утверждение «Любое четное число, большее 2, можно представить в виде суммы двух простых чисел» (например: 28 = 11 + 17, 58 = 19 + 37, 924 = 311 + 813 и т. д.) до сих пор не доказано.
9 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
13. Умножение дробей
Задача 1. Метр ткани стоит -у- р. Сколько рублей стоят 4
5 м ткани?
Решение. Для решения задачи надо найти произведение ~ 5. Но умножить на натуральное число 5 — значит найти 4 4
3 сумму пяти слагаемых, каждое из которых равно —:
3 е __ з ,3.3.3. 3 _34-34-34-34-3_3-5_ 15 __3 3 4’° 4'4'4'4'4 4 4 4 ° 4 '
о
Значит, 5 м ткани стоят 3 — р. 4
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения.
Задача 2. Длина прямоугольника -f- дм, а ширина дм о 3
(рис. 19). Чему равна площадь прямоугольника?
Р е ш е н и е. Из рисунка видно, что данный прямоугольник можно получить так: разделить одну сторону квадрата со стороной 1 дм на 5 одинаковых частей и взять 4 такие части, а другую сторону разделить на 3 одинаковые части и взять 2 такие части. При таком делении квадрат будет состоять из 15 равных частей, а прямоугольник будет состоять из 8 таких частей. Зна-чит, площадь прямоугольника равна — дм. Но мы знаем, что 10
площадь прямоугольника равна произведению длины и
3 Зшс 607
85
ширины. Поэтому считают, что 8
число — получено от умноже-15
НИИ f на f.
Итак, 8
5 3 5-3 15
Чтобы умножить дробь на дробь, надо: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем, а второе — знаменателем.
Обычно вначале обозначают произведение числителей и произведение знаменателей, затем производят сокращение и только потом выполняют умножение. В ответе, если это возможно, из дроби исключают целую часть.
Например:
4 14_4-14_4-2_8___.3. 3 4 _ 3-4 1_ 1
7 ' .5 — 7-5 ~ 5 — 5 — 1 5 ’ 815 815~2-5~ 10'
Задача 3. Сколько километров проедет велосипедист за l-^-ч, если будет двигаться со скоростью 9 км/ч?
12 б
Решение. Так как пройденный путь равен произведению скорости и времени, то для решения задачи надо найти произ-3 5
ведение чисел 9 -г- и 1 — . б 12
Представим каждое из этих чисел в виде неправильной дроби:
о_з___ 48. 1 _5__17 у 5 5 ’ 12 12
Теперь воспользуемся правилом умножения дробей. Получим:
„3 л 5 48 17 _ 48-17 _ 4 • 17 _ 68 _ jq 3
У 5 ’ 12 ~ 5 ’ 12 5 12 5 5 10 5 ‘
5 3
Таким образом, за 1 —г ч велосипедист проедет 13 — км. 12 » б
Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
66
С помощью умножения дробей решают такие же задачи, как и с помощью умножения натуральных чисел.
Задача 4. 1кг муки стоит р. Сколько стоят -2- кг муки?
25 4
Решение. Такие задачи с натуральными числами или с десятичными дробями мы решали с помощью умножения. Ре-
11 3 33
шим и эту задачу умножением: — *—• 25 4 100
3 33
Итак, — кг муки стоят — р., т. е. 33 к.
4 100 г
Тот же ответ можно получить, если выразить данные числа в десятичных дробях: ii = 0,44 и -|-=0,75.
0,44 0,75 = 0,33, но 0,33 р. = 33 к.
Умножение дробей обладает переместительным и сочетательным свойствами. Кроме того, для любого значения а:
а-0=0-а = 0; а-1 = 1-а = а.
Например,0 = 0, 1-|—1 = 1-|-. У 5 5
©Расскажите, как умножить дробь на натуральное число.
Расскажите, как выполнить умножение двух дробей и как выполнить умножение смешанных чисел. Какими свойствами обладает действие умножения дробей? Запишите свойства нуля и единицы при умножении.
413. Выполните умножение:
а) 4-2; в) -~40; д) -^--ЗО; ж)-|-1;
О lu Z о
б) ^12; -) -F-24; е)£.11; з)И.О.
у
414. Сторона квадрата — м. Найдите периметр квадрата.
О
g
415. 1 кг крупы стоит — р. Сколько стоят 2 кг, 5 кг, 10 кг такой же крупы?
416. Найдите периметр треугольника АВС, если АВ=£- м,
15
ВС больше АВ в 4 раза, а АС меньше ВС на м.
15
417. Выполните умножение:
«)Т"2: б>нч-6: »т-в= •’тг4-5-
3* 67
О Произведение дробей, квадраты и кубы дробей читают так:
з 16
—— три восьмых умножить на шестнадцать двадцать первых
— произведение чисел три восьмых и шестнадцать двадцать первых
— произведение трех восьмых и шестнадцати двадцать первых.
— квадрат пяти седьмых
— пять седьмых в квадрате
—куб двух пятых — две пятых в кубе
5
418. Станок-автомат изготовляет одну деталь за — мин.
За сколько минут станок изготовит 3 детали, 4 детали, 60 деталей?
419. Выполните действие:
.35 .27 .23. . 129. /4 V,
а) Т* 7 ’ Г) 5 ' 11 ’ Ж) 5 * 2 ’ ) 25 ’ 16 ’ Ц 5 ) ’
1 3 . . 1 4 . И 3 . . 14 34 . . /2\3.
б) 8 ‘ 4 ’ д) 2 ’ 9 ’ 3) 15 ‘ 5 ’ ) 17 ‘ 63 ’ \ 3 ) ’
. 4 5 . . 11 8 . . 15 5 . „ч 17 13 . . / 1 \2
В) 7 ‘ 6 ’ 12 ‘ 9 ’ И) 16 ‘ 9 ’ М) 26 ' 18 ’ П) к 7 )
420. Сторона квадрата м. Чему равна площадь квадрата?
421. Найдите объем куба, ребро которого м.
4 3 1
422. 1 кг пряников стоит — р. Сколько стоят — кг, — кг,
2 ' Л
— кг пряников?
5
423. Автомашина движется со скоростью км/мин. Какое
расстояние пройдет автомашина за мин, за мин?
3 б
424. Найдите значение выражения двумя спосо
бе
бами: по правилу умножения обыкновенных дробей и по правилу умножения десятичных дробей. Сравните результаты.
1 3
425. Найдите произведение — и —. Проверьте результат, 2 4
представив эти числа в виде десятичных дробей.
426. Представьте первый множитель в виде обыкновенной дроби и выполните умножение: а) 0,75 «4-; б) 0,8--f-.
У в
427. Представьте первый множитель в виде десятичной
1 3
дроби и выполните умножение: а) —•0,3; б) —-6,4.
5 ZU
428. Выполните действия: а) б)
'576*' ю 49 з
429. Измерения прямоугольного параллелепипеда равны
-2- дм, дм и v дм. Найдите его объем. 5 5 4
430. Представьте в виде произведения двух дробей число:
а> Т’ б) Т’ в) т; г) 1тг-
431. Найдите значение выражения:
«> тМ-Ь-Ь
432. Выполните умножение:
a)l-|-lf; Д)2^-А; и)3-|-1£; H)0-lf;
б)4т-т-; к>1|-2т’ о)1т-1:
ж)31.4; л)7А..2^; ") з£-0.
3)16.5f;
433. Найдите по формуле пути 8 = vt значение в, если:
а) и = 9-|- км/ч, t = 4 ч; б) и=3 -|- м/мин, t=-|- мин.
434. Найдите по формуле объема прямоугольного параллелепипеда V = abc значение V, если а = 4~ дм, Ь = 2-|- дм, 5 2
4 3 С = 1 — дм.
4
69
435. Найдите массу металлической детали, объем которой равен 3 дм3, если масса 1 дм3 этого металла равна 7 кг. о б
436. Два велосипедиста выехали одновременно из одного и того же пункта и двигались в одном и том же направлении.
Скорость первого велосипедиста 12 -7- км/ч, а скорость второго 4
в 1 раза больше. Какое расстояние будет между ними через б
437. Маша и Вера вышли из двух сел навстречу друг другу. Маша шла со скоростью 3 км/ч, и ее скорость была в 1 раза меньше скорости Веры. Через 1 4- ч девочки встретились. Най-дите расстояние между селами.
438. Для турпохода было куплено 1 4~ кг сыра и в 1 раза
2 о
больше Колбасы. Стоимость 1 кг сыра 2 р., а колбасы 2 р.
б 5
Сколько стоит вся покупка?
439. С первого поля, площадь которого 57 -у- га, собирали
с 1 га по 32 ц пшеницы, а со второго поля, площадь которого
в 1 раза больше площади первого поля, собирали по 36 -j- ц б 4
пшеницы с 1 га. Сколько всего центнеров пшеницы собрали с этих двух полей?
440. Найдите значение выражения:
о
б> (>т) -2+*т:
441. Вычислите устно:
а) 14 + 49 б) 125 2 в) 0,5 • 8 г) 6 0,9 д) 0,6 • 5
: 3 : 50 + 1,2 + 2,7 + 2,4
+ 59 - 140 -2,5 -0,9 -3
: 20 -196 : 3 : 8 : 0,8
? ? ? ? ?
70
442. Найдите пропущенные числа:
443. Сумму данных дробей сложите с их разностью. Попробуйте догадаться, как быстрее и проще получить ответ:
а) — и — ; б) — и 4-. ' 5 10 4 в
444. Представьте дробь :
а) в виде разности двух дробей со знаменателем 3; 18; 21;
б) в виде суммы двух дробей со знаменателем 3; 9; 12.
445. На координатном луче (рис. 20) отмечены дробь
и число а. Покажите, где расположены на луче точки А 2 Рис. 20
0 7 а
।----------1-----------------------------1-----------
[kA] 446. Кто быстрее? Найдите в таблице последовательно все
числа от 1 до 25:
29 6 18 2 /5 11 19 3 16 7
20 15 9 22 5 23 6 13 9 22
3 25 12 19 11 25 20 18 2 15
10 23 7 1 16 8 17 9 12 21
17 9 21 19 в /4 1 29 10 5
447. Найдите значение выражения:
•> *f+5f •-» 20т-2т; »> (т+3т)- (Й+Н)-
в)
71
448. На складе было 8 -7- т зерна. Сколько зерна стало на 4
1 7
складе после того, как привезли 2 — т, а затем увезли 3 — т?
о D
449. Сколько килограммов составляют:
а) 1% центнера; б) 7% центнера; в) 2,5% центнера?
450. Сколько квадратных метров составляют:
а) 1% гектара; в) 15% ара;
б) 3,6% гектара; г) 0,07% квадратного километра?
451. Запишите, какую часть числа составляют: 1%, 3%, 15%, 25%, 10%, 20%, 50%.
452. Запишите в виде десятичной и в виде обыкновенной дроби: 35%, 48%, 75%, 110%, 125%.
Образец записи: 5% = 0,05 = ^ = ^ .
453. Запишите в виде процентов: 0,7; 0,12; .
Образец записи: — 0,06 = 6%.
454. Решите задачу:
1) Задание рабочие выполнили за три дня. В первый день
они сделали всей работы, во второй день всей работы. Ка-5 о
кую часть всей работы они выполнили в третий день?
2) Поле было засеяно за три дня. В первый день была
засеяна 4- всего поля, во второй день 4- всего поля. Какая О о
часть всего поля была засеяна в третий день?
455. Решите уравнение:
1) х— 6-|-=l-i-; 2) 14—i/=104-.
' 9 в ’ ' 8 ” 6
456. Упростите выражение:
1) 3,7x4-2,51/ +l,6* + 4,8i/; 2) 4,5m + l,9n + 3,2m+4,3n.
457. Выполните умножение:
JL.JL- г) • Ж) А.4-а) 10 6 ’ Г’ 7 5 ’ ж) 16 4’
б) Л. 2° ; д) .И ; з) 23 — ;
' 25 21 ’ 37 85 ’ ' 46 ’
1 н) 2 — • 6 — •
к) 5-2 4-; } 2 15 ° 11 ’
и
в) ; е) ТГб’Й ’ и) Й’39
М) 4-|—2;
13 q 7
П) 43 8 28
72
458. Найдите значение выражения:
а) — те, если т=—; —; 2 —; 1 —; — ; ' 5 "*•’ "*• 2 5 2 816
-.4 14.1
б)-х, если х = —; — ; 4 —.
459. Скорость улитки м/мин. Какое расстояние проползет улитка за -7- ч; за ч; за 4- ч?
4 о о
480. Найдите объем прямоугольного параллелепипеда, измерения которого равны м, м, м.
461. Масса 1 дм3 стали равна 7 кг. Найдите массу стального куба, ребро которого 2 дм.
462. Колесо делает 27 оборота в минуту. Сколько оборо-
6
тов оно совершит за 3 мин; за 1 мин; за мин? 4 о
463. Выполните действия:
464. Выразите обыкновенной дробью: 26%, 45%, 80%, 90%.
465. Запишите в виде процентов:
0,23; 0,4; 0,07; -L; ; А .
О ZU OU
466. Моторная лодка догоняет плот. Сейчас расстояние между ними 35 км. Скорость плота 2,5 км/ч, а скорость моторной лодки 9,5 км/ч. Какое расстояние будет между ними через t часов, если 1 = 0,5; 3; 5?
467. Решите уравнение:
а) 9,5х—(3,2x4-1,8х)-|-3,75 = 6,9;
б) ll,3i/ — (9,70—0,8у)4-7,4 = 17.
468. Выполните действия:
7,72-2,25 —4,06:(0,8244-1,176) —12,423
73
14. Нахождение дроби от числа
Задача 1. Путешественник прошел за два дня 20 км. В первый день он прошел -у- этого расстояния. Сколько километ-ров прошел путешественник в первый день?
Решение. Длина пути равна 20:4=6, т. е. 5 км, а длина
Q
— пути равна 5*3 = 15, т. е. 15 км. Тот же ответ получится, 4
если 20 умножить на -2-, т. е. 20*4-=20,'3 =5*3 = 15. 4 4 4
Ответ: 15 км.
Задача 2. Огород занимает всего земельного участка. О
Картофель занимает огорода. Какую часть всего земельного о
участка занимает картофель?
Решение. Изобразим весь земельный участок в виде прямоугольника ABCD (рис. 21). Из рисунка видно, что участок, занятый картофелем, занимает земельного участка. Тот же 15
4 2
ответ можно получить, если умножить — на —:
В первой задаче мы находили -у- от 20, а во второй -уу- от -у-.
4 do
Такие задачи называют задачами на нахождение дроби от числа и решают их с помощью умножения.
Чтобы найти дробь от числа, нужно умножить число на оту дробь.
74
Решим еще две задачи на нахождение дроби от числа.
Задача 3. Путешественник прошел за два дня 20 км. В первый день он прошел 0,6 всего пути. Сколько километров прошел путешественник в первый день?
Решение. Так как 0,6=> то для решения задачи надо умножить 20 на у-. Получим 20 • -^ = 2°р6 =12. Значит, в первый день путешественник прошел 12 км.
Тот же ответ получится, если умножить 20 на 0,6.
Имеем: 20-0,6 = 12.
Задача 4. Огород занимает 8 га. 46% площади этого огорода занято картофелем. Сколько гектаров занято картофелем?
Решение. Так как 45%=0,45, то для решения задачи надо умножить 8 на 0,45. Получим 8*0,45 = 3,6. Значит, картофелем занято 3,6 га.
©Сформулируйте правило нахождения дроби от числа. Расскажите, как найти несколько процентов от числа.
©469. На рисунке 22 изображен отрезок АВ, разделенный на 12 равных частей. Определите по рисунку, какую часть составляет:
а) отрезок AM от отрезка АВ; г) отрезок AN от отрезка АВ; б) отрезок AM от отрезка АС; д) отрезок AN от отрезка АС; в) отрезок AM от отрезка AN; е) отрезок АС от отрезка АВ.
I------1---1---1------1---1---1-----1-------1
AM N С В
Рис. 22
470. На рисунке 23 изображен квадрат ABCD, разделенный на 16 равных частей. Определите по рисунку, какую часть составляет: а) квадрат AEFP от квадрата ABCD;
б) квадрат AEFP от квадрата AMNK;
в) квадрат AMNK от квадрата ABCD.
N
F
Рис. 23
75
471. Найдите:
а) -2- от 12; г) от ; ж) 0,2 от 0,8; к) 35% от 12,6; 4 8 25
б) 4-от в4*» д) о»4 от зо? з) о»7 от 4»2; л> 4^% от
в) от тг ; е) 0,55 от 40; и) 30% от 50; м) 65% от 5 .
о ю и
472. В книге 140 страниц. Алеша прочитал 0,8 этой книги. Сколько страниц прочитал Алеша?
473. В книге 140 страниц. Володя прочитал 4* этой книги.
5
Сколько страниц прочитал Володя?
. 474. В книге 140 страниц. Максим прочитал 80% этой кни-гй. Сколько страниц прочитал Максим?
475. Площадь одной комнаты 21 м, а площадь второй комнаты составляет площади первой комнаты. Найдите площадь двух комнат.
476. Брат и сестра купили книгу за 90 к. Брат заплатил 0,3 стоимости книги, а сестра — остальную сумму. Сколько копеек Заплатила сестра за книгу?
477. Стол стоит 86,5 р. Стоимость стула составляет 0,2 стоимости стола. Сколько стоят стол и 6 стульев?
478. У мальчика было 72 к. На этих денег он купил
6
альбом, а на 0,25 оставшихся денег — карандаш. Сколько стоит карандаш?
479. Рабочий получил премию 102,8 р. и положил в Сбербанк 75% премии. Сколько денег у него осталось?
480. Длина комнаты 6 м. Ширина составляет длины,
о
высота составляет 0,6 ширины. Найдите площадь и объем этой комнаты.
481. Площадь огорода 0,04 га. Капустой засажено 0,8 огорода, а остальная часть — другими овощами. Сколько гектаров было засажено другими овощами?
482. Вклад в сберегательном банке каждый год увеличивается на 2%. В какую сумму превратится вклад в 7 50 р. через год? через два года?
483. По норме рабочий должен изготовить 45 деталей. Он выполнил норму на 120%. Сколько деталей изготовил рабочий?
76
484. Фотоаппарат стоил 60 р. Эта цена была снижена на 15%, а через некоторое время новая цена была снижена на 12%. Сколько стал стоить фотоаппарат после второго снижения?
485. В первый день Ира прочитала всей книги, во вто-о
рой 4- оставшейся части. Какую часть всей книги Ира про-4
читала во второй день? Какую часть книги Ира прочитала за два дня?
486. ( В овощную палатку привезли 8 т картофеля. В первый день продали 0,6 всего привезенного картофеля, а во второй день продали того количества, которое было продано в первый день. Какая часть всего привезенного картофеля была продана во второй день? Сколько тонн картофеля было продано во второй день?
487. На автобазе были грузовые и легковые автомашины. Грузовые автомашины составляли — всех машин. — легковых автомашин были «Волги», а остальные автомашины — «Москвичи». Какую часть всех машин автобазы составляли «Москвичи»?
488. До обеда путник прошел 0,75 намеченного пути, а после обеда он прошел пути, пройденного до обеда. Прошел о
ли путник за день весь намеченный путь?
489. На ремонт тракторов в зимнее время было затрачено 39 дней, а на ремонт комбайнов — на 7 дней меньше. Время
7
ремонта прицепного инвентаря составило — того времени, кото-рое ушло на ремонт комбайнов. На сколько дней больше длился ремонт тракторов, чем ремонт прицепного инвентаря?
490. В первую неделю бригадой было выполнено 30% месячной нормы, во вторую неделю 0,8 того, что было выполнено
2 в первую неделю, а в третью неделю — того, что выполнили
о
во вторую неделю. Сколько процентов месячной нормы осталось выполнить бригаде в четвертую неделю?
77
491. Найти несколько процентов от числа можно с помощью микрокалькулятора. Например, найти 32,5% от числа
6,24 можно по программе 6,24 рк 32,5 %
. Выполните
действия по этой программе.
Найдите с помощью микрокалькулятора:
а) 0,5% от 18,24; б) 97% от 16,8.
492. Вычислите устно:
а) 100-89 б) 80 • 4 в) 0,7 • 0,7 г) 2,8 : 7 д) 0,72 : 0,9
• 6 4-180 4-0,08 • 8 4-3,2
— 12 : 25 -0,23 4-2,4 : 5
: 6 • 14 : 2 : 0,7 • 0,7
? ? ? ? ?
493. Найдите значение выражения:
494. К какому числу надо прибавить 4~, чтобы получить
3
1;
2_. 1 . . X 3 ’ 2 ’ 1 в
495. Найдите пропущенные числа:
496. Папа начинает работу в 7 ч 15 мин, а мама — в 9 ч. Когда заканчивает работу каждый из них, если рабочий день папы 8 ч 15 мин и перерыв на обед 1 ч, а рабочий день мамы
О 7 ч и перерыв на обед — ч?
4
м
497. Нужно срочно доставить 9 пакетов в пункты, указанные на плане звездочкой (рис. 24). Посыльный, посмот-
рев на план, быстро сообразил, как ему ехать. Он вручил паке-
78
ты, объехав пункты, ни разу не проезжая дважды одним и тем же путем. Какой маршрут выбрал посыльный?
498. Выполните действие:
а)-Н"Г; r>2V-1!-; ж>1"5;
do 2 d о 4 d
499. Найдите значение выражения:
6>(l+-8-)-(23f-16f)'£-f-
500. Между какими последовательными натуральными числами расположены числа 1 4-, 3 ?
2 в 7 25
501. Найдите какие-нибудь три решения неравенства: а) х<1; б) 3<х<5; в) 4<х<5.
502. Скорость полета вороны 40 км/ч. Скорость полета скворца в 1 раза больше скорости вороны, а скорость голу-6
бя в 1 раза больше скорости скворца. Найдите скорость полета голубя.
503. Основанием прямоугольного параллелепипеда служит квадрат со стороной 1,1 дм. Найдите высоту параллелепипеда, если его объем 2,42 дм3.
504. Решите задачу:
1) На 65 к. купили 19 марок по 3 к. и по 5 к. Сколько купили трехкопеечных и сколько пятикопеечных марок?
79
2) Колхоз купил для детского сада 36 трехколесных и двухколесных велосипедов. У этих велосипедов 93 колеса. Сколько трехколесных и сколько двухколесных велосипедов было куплено?
505. Выполните действия и вычисления проверьте с помощью микрокалькулятора:
1) (0,67394-1,4261)" 557,55:(16,7-2,9—42,13);
2) (1,3892 4- 0,8108) • 537,84:(15,8 • 3,6 — 52,48);
3) 801,4 -(74- 525,35:7,9) • (64,4 - 6,88:8,6);
4) 702,3 - (59- 389,64:6,8)• (59,3 - 5,64:9,4).
506. Решите уравнение:
1) 165,64 —(а —12,5)= 160,54; 2) 278,74-(6,5-Ь) = 276,84.
® 507. Штангист тяжелого веса поднял штангу в 156 кг, а штангист легчайшего веса поднял штангу, масса которой составляет — массы первой. На сколько килограммов масса 1 о
первой штанги больше массы второй штанги?
508. Сплав состоит из олова и сурьмы. Масса сурьмы з тт -
в этом сплаве составляет — массы олова. Найдите массу сплава, если олова в нем 27,2 кг.
509. Бригада лесорубов получила задание заготовить 540 м3 дров. Это задание было выполнено на 120%. Сколько кубометров дров заготовила бригада лесорубов?
510. Учащиеся одной школы вырастили 4300 кррликов. 0,4 этих кроликов сдали государству. Сколько кроликов сдали учащиеся государству?
511. Сберегательный банк платит вкладчикам по срочным вкладам 3% годовых (т. е. вклад за один год увеличивается на 3%). Сколько денег будет у вкладчика через год, если он положил на срочный вклад 550 р.?
512. С бахчи собрали 27 т арбузов. В столовую направили этих арбузов, а -у- остатка отвезли на рынок. Сколько тонн арбузов отвезли на рынок?
513. Лес, луг и пашня занимают 650 га. Из них лес за-
О
нимает 20% всей земли, — оставшейся земли — пашня. Сколько гектаров занимает луг?
80
514. Колхоз за три дня продал государству 651 т зерна.
В первый день было продано всего зерна, во второй 0,9 то-о 1
го, что было продано в первый день. Сколько тонн зерна было продано в третий день?
3
515. Школьники решили -у всех заработанных денег пере-7
числить в детский сад, -уу оставшихся денег израсходовать на покупку материалов для технического кружка, а остальные деньги отложить для турпохода. Какую часть всех денег решено отложить на турпоход? Сколько денег было отложено на турпоход, если всего было заработано 588 р.?
516. Первая бригада прополола 30% всей площади, занятой свеклой, вторая бригада прополола 80% того, что прополола первая бригада. Остальную площадь прополола третья бригада. Сколько процентов всей площади прополола третья бригада?
517. В трех ящиках было 76 кг вишни. Во втором ящике было в 2 раза больше, чем в первом, а в третьем — на 8 кг больше вишни, чем в первом. Сколько килограммов вишни было в каждом ящике?
518. Выполните действия:
а) 27,36 0,1 — 0,09; б) (54,23-3,2 —54,13-3,2+ 0,68): 0,2;
в) (23,82 + 54,58) • (1,202 + 0,698) — 2,1 • (3,53— 1,89);
г) 316 219—(27 090:43+16 422:119).
519. Вырежьте из плотной бумаги фигуру, показанную на рисунке 25, и склейте фигуру, изображенную на рисунке 26.
81
Эти фигуры называют пирамидами. У пирамид боковые грани — треугольники, а основание — многоугольник. Название пирамиды зависит от того, какой многоугольник является ее основанием. На рисунке 26, а изображена треугольная пирамида, а на рисунке 26, б — четырехугольная.
15. Применение распределительного свойства умножения
Распределительное свойство умножения относительно сло
жения и относительно вычитания позволяет упрощать вычисления.
Пример
1. Найдем значение выражения
Решение. /4—-М .15 = 4-15-4-15 = 12-5 = 7.
\ 5 3 / 5 3
Пример 2. Найдем значение произведения 2 4- -7.
14
Решение. Представим вначале число 2 4т в виде суммы
14
его целой и дробной частей: 2 4т = 2+4? , а затем применим 14 14
распределительное свойство. Получим:
2гг7=(2+тг)-?=2-7+тг7=14+-Н14-Ь
Чтобы умножить смешанное число на натуральное число, можно: 1) умножить целую часть на натуральное число; 2) умножить дробную часть на ото натуральное число; 3) сложить полученные результаты.
Пример 3. Найдем значение выражения
5-8-Т+1Т’Т-
82
Решение. На основе распределительного свойства умножения представим эту сумму в виде произведения суммы _ з . , 5 2
5 -^-+1 т и числа — : ВО •
5—•—|-1 —=(б—+1 -^-—=7-—=2. 8 7'87 \ 8 8 ) 7 7
Используя распределительное свойство умножения, можно уп-
3.1 3.1,.
рощать выражения вида -а-}- —а и — Ь——о: о 4 4 О
В простых случаях можно писать сразу:
-^-х-{--|-х = х — две третьих и одна третья х — это х;
3 3
7 5 2
— х—д-х = —х — разность семи девятых х и пяти девятых х — это две девятых х.
Расскажите, как можно умножить* смешанное число на натуральное число.
520. Найдите значение выражения:
‘>(т-+т.)-21= » (т+А)-2*
*>(п_т)'12: Г>(тг-А)-14-
521. Выполните умножение:
a) 6-~4; в) 3 7-L; д) 4-1-4; ж) 10-5-|-; и) 27-J-9;
б) 9-1-2; г) е) 2-1-8; з) 11|.8; к) 12^13.
7 < О о ю
522. Найдите значение выражения:
•> (4т+6т) в:
б>(3т+т)7; е> вт-7т-2Т вТ=
r)(4-li.2).J-; 3)зА.зА+зА.А.
83
523. Упростите выражение:
а) ^-х+4~х‘’ Д) 34-z+^-z; и) -f-c+1-c—1-с; '99'63 3 9 9
б)та-па; *) 2-J-t-ift; *) k~Tk'
в) п ж) £ х+ (А х~тх); л) п у+к v> r)fb-fb; з) Н Л-(^Л + ТЛ); M>Tb + ft-
524. Решите уравнение:
а) (f х~г)-15 = 8: в>тх+тх = 18;
б> Г^)‘21 = 1; г> + Гт = 7-
\ < о / 12 d 4
525. Шаг дяди Степы 1 м. Какое расстояние он пройдет, О
если сделает 5 шагов; 12 шагов; 20 шагов; 24 шага?
526. Продолжительность жизни березы 150 лет. Сосна живет в 2 раза больше березы. Мамонтово дерево живет в 5 раз d
дольше сосны. Какова продолжительность жизни Мамонтова дерева?
527. Квартира состоит из двух комнат. Длина большей комнаты 5 — м, а ширина 4 м. Длина меньшей комнаты 4 м, а ширина 3 — м. На сколько площадь одной комнаты меньше площади другой?
528. Площадь поля а га. В первый день вспахали поля.
3
Какая площадь осталась невспаханной? Найдите значение 'получившегося выражения при а = 57; 234; 142-|~.
2
529. В первый день туристы прошли — всего пути, во второй день всего пути. Сколько километров пройдено за два дня, если весь путь п км? Составьте выражение для решения задачи, упростите его и найдите значение при п=27; 36; 33 —.
530. Семья рабочего получила двухкомнатную квартиру общей площадью с м2. Одна комната составляла 0,36 общей
84
площади, а вторая составляла площади первой комнаты. Че-и
му равна площадь двух комнат вместе? Найдите значение получившегося выражения при с = 50; 75.
531. У Вити было а р. За книгу он заплатил имевшихся у него денег, а за альбом 0,6 стоимости книги. Сколько денег осталось у Вити после покупки книги и альбома? Найдите значение получившегося выражения при а =1,2; 4-^-.
О
532. На складе было т кг гвоздей. Кладовщик в первый раз выдал 40% имевшихся гвоздей, во второй раз — 75% остатка. Сколько килограммов гвоздей осталось на складе? Найдите значение получившегося выражения при т = 1200; 300; 50.
533. Выполните действия:
б>(4-2£)(10-8£): ’1‘н+11ГГ
534. Сравните выражения
(e_62.).(6_3f)„e.6f_6.3f.
535. Найдите значение выражения:
а) 2^-а + Ь, если а=2^~ , Ь = 3^- ; & 12 40
б) 8-|-(а+Ь), если а = 2-|-, Ь = 1
О 536. Вычислите устно:
а) 70—56 б) 900 : 150 в) 8 • 0,9 г) 4,2 : 0,6 д) 0,63 : 0,7
• 3 • 80 -5,4 • 0,8 + 3,1
+ 14 + 240 + 3 + 0,4 : 8
: 4 : 18 : 16 : 10 : 0,1
? ? ? ? ?
537. Выполните умножение устно: , 2 .5 8 11 . . 3 5 7 9. о 1 л 1 с 1 a 1
a)TVn"u5 6)Т7ТТ; в) 3—.4.т.5.-.6--.
538. Вычислите: а) ) ; б) +-|-; в) (1—) .
85
539. От какого числа надо отнять —, чтобы получить 1; —; 4 8
5 . 11 . j 7_?
8 ’ 12 ’ 1 8 1
540. Подумайте, как из числа, записанного в центре (рис. 27), можно получить числа, записанные в кружках.
°)
Рис. 27
м
541. Москва основана в 1147 г., а С.-Петербург - в 1703 г. Сколько лет Москве и сколько лет С.-Петербургу? На сколько лет Москва старше С.-Петербурга?
542. Подсчитайте по модели, сколько 1раней, вершин, ребер у треугольной пирамиды; у четырехугольной пира-
миды. Попробуйте догадаться, сколько граней, вершин, ребер у шестиугольной пирамиды.
543. Куплено 15 кг яблок. На приготовление варенья из-
2
расходовали — купленных яблок. Сколько килограммов яблок было израсходовано на варенье? Сколько килограммов яблок осталось?
544. У мальчика было 60 к. На мороженое он истратил 25% этих денег. Сколько стоит мороженое? Сколько денег у него осталось?
545. В саду 30 плодовых деревьев. 0,6 всех деревьев — яблони. Сколько яблонь в саду? Сколько в саду других плодовых деревьев?
546. Турист прошел в первый день всего намеченного пу-
8
2
ти. Причем до обеда он прошел —- пути, пройденного за этот О
день. Какую часть всего намеченного пути прошел турист в первый день до обеда?
86
547. В первый день со склада вывезли 40% имевшегося там угля. Во второй день было вывезено 75% остатка. Сколько процентов всего имевшегося на складе угля вывезли во второй день? Сколько процентов всего имевшегося там угля осталось?
548. В магазин привезли 658 кг персиков. В первый день
2
продали — всех персиков, а во второй день 0,3 оставшихся
персиков. Сколько килограммов персиков продали во второй день?
549. Найдите значение выражения:
_ \ 21 5 3 4 \ . е 2 . 5 । д 10 п 3 . / 3 \
а> 25‘У “Те’15 ’ В) 15'5"1Т + 6 27*3Т: ДЦТР
б) 5п-А-2т ТГ г) 15Т~4Т'(1Т~И);е) (т)2-
550. Выполните действия:
1) (3,52:1,1 4- 6,2) • (7,2 - 4,62:2,2);
2) (2,86:2,6 - 0,8) • (3,4 4- 7,04:3,2).
ЯЛ 551. Выполните умножение:
а) 7^-2; в) 8^-5; д) 6-|-2; Л о 40 О
б) 5^-8; г) 5-3е) 9-|-9.
552. Найдите значение выражения:
•>(31--2А)'5: г>3п15п-3^-2А-
“’Oi?-1^)-341 «>(2т+4т)-1п!
,)eA.5X+3ll.5J_; е>
553. Упростите и найдите значение выражения:
а) та+иа при а=4Т; п ;
б) ^-у + у-^-у при У = 2Т; Т’’
в) т—^-т + -1- т при т = 2±; 6-J-; Ю 4 14 4 4
\ 1 | 3 4 __ __ 1 13 , 9
г I — хч--х—-~х при х=1 — ; — .
* 3 1 4 9 н 23 46
554. Турист шел 3 ч со скоростью 4 — км/ч и 3 ч со ско-
4
ростью 4 — км/ч. Сколько километров прошел турист за 4
эти 6 ч?
87
555. В первом ящике 12 кг сахара, а во втором в 2 раза больше. Сколько сахара будет во втором ящике, если в него
2 положить еще 2 — кг?
О
556. Олег решал уравнение в течение ч. Задачу он
решал на ч дольше, чем уравнение. Сколько времени решал О
он уравнение и сколько задачу?
557. На покупку бумаги Катя истратила у- имевшихся у нее денег, а на покупку красок 80% оставшихся денег. Сколько денег истратила Катя на покупку красок, если у нее было 1 р. 40 к.?
558. В первый день маслобойня переработала поступившего количества семян подсолнечника, во второй день 0,6 остатка. Сколько тонн семян подсолнечника переработала маслобойня за эти два дня, если было привезено с т семян? Найдите значение получившегося выражения при с = 90; 63.
559. Фабрика выпустила т м ткани трех цветов: голубого, зеленого и черного. Ткань голубого цвета составляла 30% всей выпущенной ткани. Ткань зеленого цвета составляла 0,8 количества ткани голубого цвета. Сколько метров ткани черного цвета выпустила фабрика? Найдите значение получившегося выражения при т — 5520; 22 000.
560. Найдите значение выражения:
а) (3,75:1,25 —0,75): 1,5 + 0,75;
б) (14—12,725) • 12,4 - 2,6: (11,2 — 7,95).
16. Взаимно обратные числа
Если умножить на , то получится 1: 15 8
8 15 8-15 .
15 ' 8 — 15-8- '
Точно так же 1 получится при умножении 7 на
75 на — ит. д.
88
Два числа, произведение которых равно 1, называют взаимно обратными.
г. «г * 8 15 „ 1
Значит, взаимно обратными будут числа — и — , 7 и —, 10 0 I
— и . Числу , где а =#= 0 и Ь =#= О, обратно число —.
75 23 b а
n a b ab «I
В самом деле, —---- = 1.
о а оа
§ Пример 1. Найдем число, обратное числу 3 — .
5 -
Решение. Запишем число 3 — в виде неправильной 6
дроби:
„ 5 _3-6 + 5 _ 23
3 6 — 6 6 ’
.Значит, обратным З-f- будет число . 6 ао
5 3 7
Пример 2. Найдем значение произведения
11 7 3
„ 537 5/8745,5
11 7 3 11 \ 7 3 ) 11 11
Значит, если число х сначала умножить на некоторое число а, а потом умножить на число, обратное а, то получим опять х.
Какие числа называют взаимно обратными? Как записать число, обратное дроби -£-? Как записать число, обратное ь
натуральному числу? Как записать число, обратное смешанному числу?
561. Будут ли взаимно обратными числа:
а) 7 и ; в) 0,2 и 5; Д) З-J- и 2|;
б) 48 и ; г) 2,5 и 0,4; е) 0 и 1?
562. Найдите число, обратное числу:
а) ; б) 5; в) г) д) f; е) 7 Н ; ж) 0,8; з) 1,25.
568. Найдите значение выражения:
\ 1 77 ® 6 Q Л *1 3 V 1 1 Е 12
а) 1 вГТ Т; б) 3’4 Т Т’ в) ТГ5’6 и •
89
564. Решите уравнение:
а) 4-х=1; в) 0,8а = 1; гП 8 8 . Д) 19 Х 19 ’
б)Ц«/=1; г) 0,76 = 1; 565. Вычислите устно: е) ™У=*. о 5
а) 200 — 101 б) 200 • 5 в) 3 • 0,3 г) 0,45 : 9 д) 5,6 : 0,7
: 3 -130 4-4,1 • 6 : 20
4-37 : 29 : 100 4-2,7 + 4,8
:5 4-270 • 20 : 0,01 : 26
? ? ? ? ?
566. Представьте в виде неправильной дроби:
Ч-иэ -1® сч
м
на какой чтобы
567. Найдите наименьшее и наибольшее значение выра-3 ,1,22
женин — х, если х = 1; —; 1 —; —. 5 7 3 9
568. Верно ли выполнены вычисления:
а) 16-2-^-=16-24-16:2 = 324-8 = 40;
б) 424 4-=42-44-42:3 = 1684-14= 182; О
в) 72.-|-= 72-72:4 = 72-18 = 54;
г) 84--|-=84 —84:6 = 84—14 = 70? и
Ответ объясните.
569. На озере находятся 7 островов, которые соединены между собой мостами так, как показано на рисунке 28. н доставить катер путешественников, по каждому мосту и только один раз? С какого острова катер должен снять этих людей? Почему нельзя доставить путешественников на остров At
570. Выполните умножение:
a) 3-|~5; в) 2-|-4; д) 2~6.
б) 74; r)lf.3;
остров долже могли пройти
они
90
571. Найдите значение выражения:
а)—.— ; в) 2— —; д) —И.6.
б) _L.2 —; г) р_+
’ 7 3 Цй Т15 / 4 ’
572. За три дня турист прошел 40 км. В первый день он прошел 40%, а во второй день 30% всего пути. Сколько километров прошел турист за третий день?
573. Среднее арифметическое трех чисел равно 3,1. Найдите эти числа, если второе число больше первого на 0,9, а третье число больше первого в 2 раза.
574. Выполните действия:
1) (7,061:2,3 —2,2)-(4,2 +17,391:5,27);
2) (3,7 14,058:6,39) • (23,641:4,7 - 4,6).
575. Найдите числа, обратные числам:
а) 10 • 12 . 23. Л. 43 . 10. 41. ' 27 ’ 59 ’ 98 ’ 122 ’ 315 ’ 3 ’ 8 ’
б) 11 ; 80; 100; 1; 0,5; 1,2.
14 4U
576. Выполните действия:
а) ТГ8Т; в) °’21f; д) (°>2+°>4)-т-
г> °.8~; 1.0 4 О
577. Положили сушить 150 кг вишни. После сушки их масса уменьшилась на 80%. Сколько килограммов вишни получилось после сушки?
578. Среднее арифметическое четырех чисел 2,75. Найдите эти числа, если второе больше первого в 1,5 раза, третье больше первого в 1,2 раза и, наконец, четвертое больше первого в 1,8 раза.
579. Найдите значение выражения:
а) 208,57 -108,57: ((60,4 - 57,6) • (3,6 + 3,45));
б) 565,3- 465,3:((1,25 + 5,8)• (55,8-49,2)).
17. Деление
Задача. Площадь прямоугольника -|-м2. Длина одной сто-роны — м. Найдем длину другой стороны.
91
Решение. Обозначим длину другой стороны через х м. По формуле площади прямоугольника должно выполняться равенство -|-х=у-. Умножим обе части равенства на число обратное числу —. Так как произведение —• 4- равно 1, то полу-чим, что х=-~-|-, или ж —• Таким образом, длина другой 20 стороны прямоугольника равна — м.
В этой задаче мы нашли неизвестный множитель в произ-ведении —*х=—. По смыслу деления это число равно част-4 7
5 3 „
ному от деления числа — на число —. Видим, что это частное 7 4
равно произведению делимого и числа, обратного делителю, т. е. _5_._3_ = _5_._£=2°
7 ’ 4 — 7 " 3 21’
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
2 1
Пример 1. Разделим 2 — на 1 — .
5 15
Решение. Представим сначала числа 2 4- и 1 4~ в виде не-5 15
правильных дробей: 2 ; 1 тг •
5 5 15 15
„ о 2 - 1 12.16 12 15 12-15 3-3 9 о 1
5 15 5 15 5 16 5-16 4 4 4
Пример 2. Разделим на 6.
О
Решение. Числом, обратным делителю, является 4~, так
О
как 6 -^=1. Значит, 4-:6 = 4-*4-=-^ . 6 8 8 6 48
©Сформулируйте правило деления дробей. Как выполняется деление смешанных чисел?
580. Выполните деление:
в)т:т; д)т:^; ж>т:3;
1.3. \ 3,5 . 7 .л. _\ к, 2
б)Т-Т’ r)Ii-TT- е) Т-2; 3) 5 Т;
02
H)8:f; и) А:3Х ; т)0:5^;
К)Т:Т: И’1Г1^ р) 4-|~:3; У)3^:1;
л) з 4-°) Ю-J-: 2 4-; с) 1JL; ф)3 —
' 2 3 3 3 ’ ’ 11 39 81
D Частное двух дробей можно читать разными способами:
2 .11
—— две седьмых разделить на
и. п.
одиннадцать четырнадцатых;
в. п.
— частное чисел две седьмых и
в. п.
одиннадцать четырнадцатых;
в. п. — частное двух седьмых и
р. п.
одиннадцати четырнадцатых.
р.п.
581. Представьте в виде дроби частное:
а) »)т:а; г)
л к b a k п I
582. Найдите по формуле площади прямоугольника S—ab значение:
a) S, если а=4-|- и Ь=4~‘, б) а, если S=15 и Ь=7 6 7 2
583. С какой скоростью должен передвигаться трактор, чтобы пройти 15 км за ч; за — ч?
6 3
584. За кг сухарей заплатили р. Сколько стоит 1 кг
сухарей? Сколько сухарей можно купить на 1 р.?
585. Сумма двух чисел равна 12 Одно из них в 1 ра-
за больше другого. Найдите эти числа.
93
586. Если задуманное число умножить на 2 и к произведению прибавить 1 уу , то получится 8 уу. Найдите задуманное число.
587. Площадь прямоугольника м2. Найдите периметр 64
прямоугольника, если его ширина м.
о
588. Длина и ширина прямоугольника соответственно рав-
ны 5 м и 2 — 5 8
м. Найдите ширину другого прямоугольника.
длина которого 3 — м, а площадь равна площади первого 5
прямоу го л ьни ка.
589. Представьте делимое в виде обыкновенной дроби о О
и выполните действие: а) 0,25: — ; б) 0,6: — .
4 О
590. Представьте делимое в виде десятичной дроби и выполните действие: а) —:0,2; б) —:0,375.
25 8
591. Выполните действия:
a) J-. ' 3 7 7 ’ Ж) (6Т“4Т ):2f;
б) И;2_.21 ’ 12 24 22 3) ( Hi;
В) И:А.А; ' 16 8 4 ’ И)( ^т+Ч) :1—; 2
. 13 -7_. 13 , ' 14'25'25 ’ к) ( 00 о>|- 1 го
la СО CTl | w л) 1 '1т+2ъ-;
”(2т+1т)-1-г-> м) 1 (3M).
592, Найдите значение выражения:
а) (т±0,254-|-):1^;
б) 8:0,16 —36,4;
в) 6,25-8^3-^-:5,5 + 2,4-4; 3 12
94
593. Решите уравнение:
а) -уХ = 2-|-; ж) m +
б> т^=2^-т; 3)
B)fa+f=l; и)^г+^г_^_г = 2±;
Г) 3-b* = lf:2; К) 3f.(f x+f) = 2-|-;
д) л) (тж-т) т=т;
е) f x+f х=2^; м) f г+-|-г-3= <
v О О
594. Коля и Митя нашли 64 гриба. Коля нашел в 1 у- раза больше грибов, чем Митя. Сколько грибов нашел каждый?
595. Луч ОМ разделил угол СОК, равный 90°, на два угла СОМ и МОК. Угол СОМ больше угла МОК в 2 раза. Чему рав-ны углы СОМ и МОК1 Постройте эти углы с помощью тран
спортира.
596. Отец старше сына в 3 раза, а сын моложе отца на о
28 лет. Сколько лет отцу и сколько лет сыну?
597. За два дня турист прошел 26 км. Путь, пройденный в первый день, составлял у- пути, пройденного во второй день. Сколько километров прошел турист в каждый из этих дней?
598. Месячный заработок сына составил 75% заработка отца. Сколько заработал каждый из них, если вместе они заработали 350 р.?
599. Первый плотник сделал на 9 оконных рам меньше, чем второй. Сколько рам сделал каждый плотник, если число рам,
5 сделанных первым плотником, составляет числа рам, сделай-
о ных вторым?
600. Два пешехода вышли одновременно навстречу друг Другу из двух пунктов, расстояние между которыми 5 км. Скорость первого пешехода составляла скорости второго. Най-и
дите скорости каждого пешехода, если они встретились через полчаса.
95
601. Мотоциклист стал догонять велосипедиста, когда между ними было 33 км, и догнал его через — ч. Известно, что 4
скорость велосипедиста составляла скорости мотоциклиста. 1.4
Найдите скорости мотоциклиста и велосипедиста.
3 1
602. За 8 — м сукна и 7 — м сатина заплатили 225 р. Сколько стоит 1 м сатина и сколько стоит 1 м сукна, если за сукно заплатили в 14 раз больше, чем за сатин?
603. За 32 м ткани и 20 м клеенки заплатили 80 р. Стон-
2
мость ткани составила — стоимости клеенки. Что дороже: 1 м о
ткани или 1 м клеенки? На' сколько рублей?
604. Турист 3 ч шел пешком со скоростью 5 км/ч, а далее 4 ч он ехал на поезде, скорость которого в 12 раз больше. Оставшийся путь турист проехал на автобусе за 8 ч. С какой средней скоростью двигался турист за время путешествия, если скорость автобуса составляла —- скорости поезда?
5
605. Вычислите устно:
а) 184 — 112 б) 700 : 14 в) 0,64 : 0,8 г) 3,6 • 0,1 Д) 1—0,44
: 8 • 9 • 9 : 0,6 : 0,7
+ 45 + 90 + 2,8 + 3,6 • 0,5
: 3 : 18 : 100 : 1,4 -0,12
? ? ? ? ?
606. Найдите число, обратное дроби: -i~; 1-i-; 0,7.
Z О о
Сравните данное число и ему обратное.
607. Существует ли число:
а) обратное самому себе; б) не имеющее обратного?
608. Не выполняя умножения, сравните:
а) 3—иЗ; 6)1—-—и—; в)— ?и?; г)-.1-и1.
Ш 609. Кроме неравенств со знаками > и <, которые называют строгими, используют нестрогие неравенства, для которых введены знаки (больше или равно) и (меньше или равно). Неравенства 3^4 и 5^5 верные, так как одно из условий выполнено: 3 меньше, чем 4; 5 равно 5.
96
Подумайте, какие натуральные числа являются решениями неравенства:
а) х^4; б) 5^хгС9; в) 3<х^5.
610. Найдите число, обратное числу:
а) 4-; 6)4; в)з|-; г) 0,8; д) 1,4.
611. Докажите, что числа а и b взаимно обратны, если: а) а=0,5, 5 = 2; б) а=1,25, 5=4-; в) а = 0,15, Ь = 6^-.
О 3
612. Выполните деление и результат округлите до сотых: а) 3,2:0,7; б) 14,28:3,6; в) 175:23; г) 0,00677:1,3.
613. Округлите числа:
а) 0,479; 1,071; 2,750; 4,4981 до десятых;
б) 0,0825; 0,8537; 1,3576; 4,57003 до тысячных.
614. Баян стоил 106 р. Сколько стал стоить баян после снижения его цены на 15%?
615. Решите задачу:
1) Из 250 лошадей-было 30 вороиых, а 0,7 всех лошадей были серыми. Кроме вороных и серых, были лишь лошади рыжей масти. Сколько было лошадей рыжей масти?
2) Купили 120 тюбиков клея. Из иих в 30 тюбиках был резиновый клей, а в 0,4 остальных тюбиков был казеиновый клей. Кроме резинового и казеинового клея, был куплен и силикатный клей. Сколько тюбиков силикатного клея было куплено?
616. Решите уравнение:
1) (0,2х+0,4х)-3,5 = 6,3; 3) (х—0,2х):0,4 = 1,6;
2) (0,7х—0,2х)-6,4 = 9,6; 4) (0,4х+х):0,7 = 1,6.
4|й 617. Выполните деление:
*) Т:Т: в> П5:1Ьа) «Ф »>
6> • г) Ц:9; е) 7:3; з) 3f:l Я; к) 2 £:13-|-.
618. Найдите значение выражения:
a) 7f:4f.8;6) И f:£:4 f; в) lf-2f:lf; г) f.^lf.
619. Выполните действия:
a) f :T+2T-f-1:1T;
б) 2-J-: (1 4—-|")+(т+т):3Т;
4 Зак. 607
97
620. Решите уравнение:
а) (х —8)~=2; б) 2 f х-2 -|-=2 О ООО
621. Сколько оборотов сделает колесо на расстоянии 48 м, в з 4 „
если длина окружности колеса равна — м; — м; — м?
Zo 4 о
622. За 4- ч мотоциклист проехал 20 — км. С какой ско-о 5
ростью ехал мотоциклист?
623. На изготовлейие 16 одинаковых деталей требуется
6 ч. Сколько времени занимает изготовление одной детали? о
624. В двух сосудах 35 л жидкости. Известно, что в одном сосуде жидкости в 1 раза меньше, чем в другом. Сколько О жидкости в каждом сосуде?
625. В двух пачках 156 тетрадей. Число тетрадей в одной пачке составляет -у- числа тетрадей другой пачки. Сколько тетрадей в каждой пачке?
626. Стоимость зимнего пальто на 84 р. больше стоимости летнего пальто. Сколько стоит каждое пальто, если стоимость летнего пальто составляет 60% стоимости зимнего?
627. Два катера движутся навстречу друг другу. Сейчас между ними 25 км. Скорость одного из них составляет ско-рости другого. Найдите скорость каждого катера, если известно, 5 что они встретятся через — ч.
12
628. Турист ехал на автобусе 1 ч и на поезде 4 ч.
3 15
Всего этими видами транспорта турист проехал 456 км. При этом на автобусе он проехал того пути, который он проехал на поезде. С какой скоростью турист ехал на автобусе и с какой — на поезде?
629. Выполните деление и округлите ответ до тысячных: а) 1,765:1,3; б) 5,394:23; в) 2,6:11,2.
98
630. Вычислите:
а) 74:100-0,4:104-17,8:1000;
б) 0,35 • 10 4- 0,0237 • 100 - 0,00087 • 1000;
в) 37 0,01 — 0,2 0,14-8,9 0,001;
г) 0,7:0,14- 0,0474:0,01 — 0,00174:0,001.
18. Нахождение числа по его дроби
Задача 1. Расчистили от снега катка, что составляет 5
800 м2. Найдите площадь всего катка.
Решение. Обозначим площадь катка через х м2. По условию этой площади равны 800 м2, т. е. — х=800.
5 5
Значит, х=800 :-|-=800--|-= 2000. Площадь катка равна 2000 м2.
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
Задача 2. Пшеницей засеяно 2400 га, что составляет 0,8 всего поля. Найдите площадь всего поля.
Решение. Так как 2400:0,8 = 24 000:8 = 3000, то площадь всего поля равна 3000 га.
Задача 3. Увеличив производительность труда на 7%, рабочий сделал за этот же срок на 98 деталей больше, чем намечалось по плану. Сколько деталей рабочий должен был сделать по плану?
Решение. Так как 7% = 0,07, а 98:0,07 = 1400, то рабочий по плану должен был сделать 1400 деталей.
©Сформулируйте правило нахождения числа по данному значению его дроби. Расскажите, как найти число по данному значению его процентов.
631. Девочка прошла на лыжах 300 м, что составляло
— всей дистанции. Какова длина дистанции? о
632. Свая возвышается над водой на 1,5 м, что состав-
ляет — длины всей сваи. Какова длина всей сваи?
16
4
99
633. На элеватор отправили 211,2 т зерна, что составляет 0,88 зерна, намолоченного за день. Сколько зерна намолотили за день?
634. За рационализаторское предложение инженер получил сверх месячного оклада 68,4 р., что составляет 18% этого оклада. Чему равен месячный оклад инженера?
635. Масса вяленой рыбы составляет 55% массы свежей рыбы. Сколько нужно взять свежей рыбы, чтобы получить 231 кг вяленой?
fj
636. Масса винограда в первом ящике составляет — массы винограда во втором ящике. Сколько килограммов винограда было в двух ящиках, если в первом ящике был 21 кг винограда?
637. Продано полученных магазином лыж, после чего о
осталось 120 пар лыж. Сколько пар лыж было получено магазином?
638. При сушке картофель теряет 85,7% своей массы. Сколько надо взять сырого картофеля, чтобы получить 71,5 т сушеного?
639. Вкладчик Сбербанка внес некоторую сумму на срочный вклад, и через год у него на сберкнижке было 576 р. 80 к. Какова была сумма вклада, если по срочным вкладам Сбербанк платит 3% годовых?
К
640. В первый день туристы прошли — намеченного пути,
24
а во второй день 0,8 того, что прошли в первый день. Как велик намеченный путь, если во второй день туристы прошли 24 км?
641. Ученик сначала прочитал 75 страниц, а потом еще несколько страниц. Их количество составило 40% от прочитанного в первый раз. Сколько страниц в книге, если всего
3 О
прочитано — книги?
4
642. Велосипедист сначала проехал 12-^- км, а потом еще 4
3 несколько километров, что составило — от первого отрезка
пути. После этого ему осталось проехать всего пути. Какова о
длина всего пути?
100
3 1
643. — от числа 12 составляет — неизвестного числа. Най-
5 4
дате это число.
644. 36% от 128,1 составляет 49% неизвестного числа. Найдите это число.
645. В киоске в первый день продано 40% всех тетрадей, во второй день 53% всех тетрадей, а в третий день — остальные 847 тетрадей. Сколько тетрадей продал киоск за три дня?
646. Овощная база в первый день отпустила 40% всего имевшегося картофеля, во второй день 60% остатка, а в третий день — остальные 72 т. Сколько тонн картофеля было на базе?
647. Трое рабочих изготовили некоторое число деталей. Первый рабочий изготовил 0,3 всех деталей, второй 0,6 остатка, а третий — остальные 84 детали. Сколько всего деталей изготовили рабочие?
648. В первый день тракторная бригада вспахала участ-ка, во второй день остатка, а в третий день — остальные 216 га. Определите площадь участка.
649. Автомобиль прошел в первый час -g- всего пути, во
второй час -7- оставшегося пути, а в третий час остальной путь. 5
Известно, что в третий час он прошел на 40 км меньше, чем во второй час. Сколько километров прошел автомобиль за эти 3 ч?
650. Находить число по заданному значению его процентов
можно с помощью микрокалькулятора. Например, найти число,
2,4% которого составляют 7,68, можно по следующей програм-
ме: 7,68 4- 2,4 %
. Выполните вычисления.
Найдите с помощью микрокалькулятора: а) число, 12,7% которого равны 4,5212; б) число, 8,52% которого равны 3,0246.
<9 651. Вычислите устно:
а) 162 — 127 б) 900 : 150 в) 1,5 • 6 г) 7 — 2,1 д) 3,64-3,2
: 7 -70 : 1,8 : 7 : 0,2
• 19 -312 - 0,12 • 1.4 -33,5
4-15 : 18 4-0,44 4-0,02 • 9
? ? ? ? ?
101
062. Не выполняя деления, сравните:
a)9:f И9; Ив; В)
663. Во сколько раз меньше своего обратного число:
—; —; —; 0,3? Б 3 в
064. Придумайте число, которое меньше своего обратного в 4 раза; в 9 раз.
666. Разделите устно центральное число на число в кружочках:
a) S)
050. Сколько квадратных плиток со стороной 20 см понадобится для настилки пола в комнате, длина которой 5,6 м, а ширина 4,4 м. Решите задачу двумя способами.
м
657. Найдите правило размещения чисел в полукругах и вставьте недостающие числа (рис. 29).
058. Выполните деление: О ЛО JJ
6>Т;-Ь з) 1-|-:2;
в) fи) 6:f;
г) f:y-;
«)f:5; л) 2т:1т;
е) тт;4; M)3g:6-L
11 20 О
102
3 1
659. За — ч велосипедист проехал 7 — км. Сколько кило-о 2
метров проедет велосипедист за 2 ч, если будет ехать с такой же скоростью?
660. За ч пешеход прошел 1 км. Сколько километров и i
пройдет пешеход за 2 ч, если будет идти с такой же скоростью?
661. Сократите дробь: 1) —; 2) ^22.; 3) 212. 4) 1122.. х/ 4g() , 3500 , о/ gl() , -*/ 2б50
662. Найдите значение выражения:
1) 2 -|-:2 f-1 f; 3) 1 -J-.2 j-:7 j-;
2)2— • —:3—; 4)3—:7-- — .
’ 4 13 8 ’ ' 3 3 5
663. Выполните действия:
1) 10,1+ 9,9-107,1:3,5:6,8 -4,8;
2) 12,3 + 7,7 187,2:4,5:6,4-3,4.
664. Из бочки вылили находившегося там керосина.
Сколько литров керосина было в бочке, если из нее вылили 84 л?
665. При покупке в кредит цветного телевизора было уплачено наличными 234 р., что составляет 36% стоимости телевизора. Сколько стоит телевизор?
666. Рабочий получил путевку в санаторий со скидкой 70% и уплатил за нее 42 р. Сколько стоит путевка в санаторий?
о
667. Столб, врытый в землю на — своей длины, возвыша-1*5
ется над землей на 5 м. Найдите всю длину столба.
668. Токарь, выточив на станке 145 деталей, перевыполнил план на 16%. Сколько деталей надо было выточить по плану?
669. Точка С делит отрезок АВ на два отрезка АС и СВ. Длина отрезка АС составляет 0,65 длины отрезка СВ. Найдите длины отрезков СВ и АВ, если АС = 3,9 см.
670. Лыжная дистанция разбита на три участка. Длина первого участка составляет 0,48 длины всей дистанции, длина
второго участка составляет длины Первого участка. Какова
103
длина всей дистанции, если длина второго участка 5 км? Какова длина третьего участка?
671. Из полной бочки взяли 14,4 кг квашеной капусты и затем еще этого количества. После этого в бочке осталось
находившейся там ранее квашеной капусты. Сколько кило-о
граммов квашеной капусты было в полной бочке?
672. Когда Костя прошел 0,3 всего пути от дома до школы, ему еще осталось пройти до середины пути 150 м. Какой длины путь от дома Кости до школы?
673. Три группы школьников посадили деревья вдоль дороги. Первая группа посадила 35% всех имевшихся деревьев, вторая - 60% оставшихся деревьев, а третья группа — остальные 104 дерева. Сколько всего деревьев посадили?
674. В цеху имелись токарные, фрезерные и шлифовальные станки. Токарные станки составляли уу всех этих станков. Чис-. 2
ло шлифовальных станков составляло — числа токарных стан-
5
ков. Сколько всего станков этих видов было в цеху, если фрезерных станков было на 8 меньше, чем токарных?
675. Выполните действия:
а) (1,704:0,8 — 1,73)7,16 2,64;
б) 227,36:(865,6 — 20,8 • 40,5)• 8,38 + 1,12;
в) (0,9464: (3,5 • 0,13) + 3,92) • 0,18;
г) 275,4:(22,74 + 9,66) • (937,7 - 30,6 • 30,5).
19. Дробные выражения
Так как дробь -у- равна частному 2:3, то и частное от деления одного выражения на другое можно записать с помощью черты. Например, выражение (41,3 — 4,4):( 15,3 + 33,9| 41 3 4 4 т->
можно записать так: —-—. Выполнив указанные действия, 10,3 । 33,У
найдем значение этого выражения: 0,75, или -у-.
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
104
тт 3,7 4 8 а — Ь 9,6 <
Например, ’ , , —-, — дробные выра-
1,0— U»0 G “г и Ли жения.
Выражение, стоящее над чертой, называют числителем, а выражение, стоящее под чертой,— знаменателем дробного выражения. Числителем и знаменателем дробного выражения могут быть любые числа, а также числовые или буквенные выражения.
С дробными выражениями можно выполнять действия по тем же правилам, что и с обыкновенными дробями.
Пример 1. Найдем значение выражения ——.
4
Решение. Умножив числитель и знаменатель этого дробного выражения на 6, получим:
34 _34e_2i_,.
“То-2’1-,|.в
4
Пример 2. Найдем
16,4 . 3
произведение —— и 1 —.
1,4 4
_ 16,4 . 3
Решение, -г2— 1,4
_ 16,4
4 — 1,4
— = 16,4-7 ==4Л=41=2 5
4 1,4-4 0.2 2
Пример 3. Найдем сумму
е ©
2__. 3
0,7 1,4 ‘
„ 2.3 4 + 3 7 70 е
Решение. -= -„ = т—= —= 5.
0,7 1,4 1,4 1,4 14
При сложении дробных выражений удобнее сначала представить их в виде обыкновенных дробей, а потом уже выполнять сложение:
2 ,3 20 , 30 _ 20 . 15 _ 35 _ к
0,7 '1,4— 7 '14 7 7 7
Какое выражение называют дробным? Как называют выражение, находящееся над чертой? под чертой?
676. Назовите числитель и знаменатель выражения:
d
5,1 —2-j-В) 7,45-3,2 ’
а) Ы ’ 3,6
. М-зь
7 4аЬ
б)
105
677. Напишите дробное выражение, числитель которого За — 25, а знаменатель 6,7х + у.
678. Запишите в виде дробного выражения частное: (3,8 • 4,5 - 0,7): (6,3:2,1 - 2,6).
Найдите значение этого выражения.
679. Найдите значение выражения:
. 2,4-12,6-3,5 .
' 6,3-4,8-31,5 ’ . 1,7-4,92-7,2 . 4,8-0,82-5,1 ’
а)
б)
В)
3,2 .
12,8 ’
1,2 .
0,15 ’
8.4 .
2,4 ’
г)
Д)
3
2Т
А»
•4
080. Выполните
действие:
и)
К)
а)
0,68-4-;
4
г) 0,121 ;
ж) 5,6:3-i-;
б)
3,212:4-; о
д) 43,75 • А.; оо
з)
10 4--6,3; о
8,4 -2-Ь 12,1
1,25-4-1,1
2А.jA.il 3 7 5
3 3 2 5
3У 4 3"?Т
к)
Л)
в) -|“-24,6; О
е) Ц-8,4;
И)
2i-4’2-
м)
2,3 . 6,7 .
1,5 '4,5 ’
1,5 1,9 ,
3,2 ' 9,6 ’
7,4 9,1
5,7 11,4 ’
681. Выполните действия:
О 1
4-1,8-14:0,07 а) -Ч—Ч— -5:О’49-21Г
12’75Г5Л’8
1 4-2,04:20
0,2-6,2:0,31 -4--0.9
б> -------4-----—
2+1—0,22:0,01
Г)
5
£
7
•0,4
682. Найдите значение
а । а
выражения <7—у+ 2.8 + 4.4 ,
если:
а) а=2А-+1 < о
б) а= 1,8 (1 — 0,6).
2 jc х
683. Найдите значение выражения ——— , если:
а) х = 18,1 — 10,7 и у = 35 — 23,8;
б) х = 10-|— 1^-и у=ц А+9-|— ± О Z О «5 10
106
684. Найти с помощью микрокалькулятора значение вы-
ражения
5,4 — 3,275 3,4-12,5
можно по программе:
5,4 — 3,275 4- 3,4 4- 12,5 = , а значение выражения
3,995
„„„„ „ . „„„„ по такой программе: 0.675-2.4—0.022 *
0,675 X 2,4 — 0,022 4-. 3,995 **
ней вычисления:
. 2,185:43,7 + 1,05 .
0,44-12,5 ’
. (4,2-2,7): 0,003
J 2,125:1,7
Выполните вычисления по этим программам. Постройте программу нахождения и выполните по . 3,2-1,05 . 0,6-11,2 ’ б) _____;
’ 0,85:3,4 + 1,92 '
значения выражения
685. Вычислите устно:
а) 270-214 б) 100:25 в) 6 — 1,2 г) 1-0,79 Д) 9-4,5
: 28 •15 : 8 : 0,3 : 1,5
• 37 :120 • 10 + 5,3 • 1,7
+ 26 •180 : 5 : 1,5 + 4,9
? ? ? ? ?
686. На координатном луче отмечены числа а и b (рис. 30).
Можно ли указать на луче точку с координатой b:4-; Z и
Рже. 30
Ь
687. Вычислите:
688. Найдите произведение дробей и и произведение 3 7
дробей, обратных данным. Каким свойством обладают эти два произведения? Проверьте ваше предположение еще на одном примере. Докажите это свойство в общем виде (с помощью буквенных выражений).
689. Найдите наибольшее и наименьшее значения выражения 1 4-:х, если х= 1; 4-; 2 4~; 4-.
3 9 5*3
107
690. Составьте задачу по уравнению:
a)x.3^f ; б) в)2^:а=^.
М
091. Ваня и Таня должны были встретиться на станции, чтобы вместе поехать на поезде, который отправляется
в 8 ч утра. Ваня думает, что его часы спешат на 35 мин, хотя в действительности они отстают на 15 мин. А Таня думает, что ее
часы отстают на 15 мин, хотя они на самом деле спешат на 10 мин. Что произойдет, если каждый из них, полагаясь на свои часы, будет стремиться прийти за 5 мин до отхода поезда?
. 2
692. Возраст Сережи составляет — возраста отца. Сереже
12 лет. Сколько лет отцу?
693. Комбайнер за 1 ч скосил пшеницу с площади 3 га, что составляет 15% того, что он скосил за день. Какую площадь скосил комбайнер за день?
094. 25% всех деревьев сада составляют груши, остальные 150 деревьев — яблони. Сколько грушевых деревьев в саду?
695. Площадь 60 га составляет 0,75 площади поля. Чему равна площадь поля?
690. Найдите число, если:
а) 0,9 его равны 1 б) -|-его равны 3,5; в) 35% его равны 49.
7 о
697. Участок земли, площадь которого 6 а, составляет сада, а площадь сада составляет всего приусадебного 3 7
участка. Чему равна площадь всего приусадебного участка?
698. За фрукты заплатили 2 р. 10 к., что составляет 30% стоимости всей покупки. Стоимость покупки составляет 25% денег, имевшихся у покупателя. Сколько денег было у покупателя?
699. Решите задачу:
1) В книге 240 страниц. В субботу мальчик прочитал 7,5% всей книги, а в воскресенье — на 12 страниц больше. Сколько страниц ему осталось прочитать?
2) Для птицефермы заготовили 2600 т корма. В первый месяц было израсходовано 8,5% корма, а во второй месяц — на 30 т больше. Сколько тонн корма осталось?
108
700. Найдите значение выражения: а)
2,56 • 0,44 • 2,26 3,2 0,12-0,6
б)
5.72. А
12 4з 4- 44-4 4 ж) —5—-п2:1
3 18
В)
8,4:2
О
е)
г)
1A.2l.2l 1 7 2 5 2 4
5-I.1 ® .±
6 7 4
28,8:13 4-+6,6: —
7 3
>П=*“
; д) 11,7:1-|-;
; 3)
6,3-!f
701. Никита
з
истратил — своих денег на покупку книги и
своих денег на покупку альбома. Сколько денег было у Ни-14
киты, если альбом дешевле книги на 7 к.?
702. Поезд проходит расстояние между городами за в ч со скоростью 68 км/ч. Какое время потребуется велосипедисту, чтобы проехать этого расстояния со скоростью 17 км/ч?
О
703. Получили сплав из куска меди объемом 15 см3 и куска цинка объемом 10 см3. Какова масса 1 см3 сплава, если масса 1 см3 меди 8,9 г, а масса 1 см3 цинка 7,1 г? Полученный результат округлите до десятых долей грамма.
704. Кухня в 10 м2 составляет 0,4 всех нежилых помещений квартиры. Площадь нежилых помещений составляет
— площади всей квартиры. Найдите площадь всей квартиры.
Л\
705. Вырежьте из плотной бумаги фигуры, изображенные на рисунке 31, и склейте фигуры, изображенные на рисун-
109
Рис. 32
ке 32. Эти фигуры называют призмами. У прямой призмы боковые грани — прямоугольники, а верхнее и нижнее основания — равные многоугольники. На рисунке 32, а изображена треугольная призма, а на рисунке 32, б — четырехугольная. Каждый прямоугольный параллелепипед — это четырехугольная призма.
НВ самых древних дошедших до нас письменных источниках — вавилонских глиняных табличках и египетских папирусах встречаются не только натуральные числа, но и дроби.
Дроби были нужны, чтобы выразить результат измерения длины, массы, площади в случаях, когда единица измерения не укладывалась в измеряемой величине целое число раз.
Тогда вводили новую, меньшую единицу измерения. Названия этих новых единиц измерения и стали первыми названиями дробей. Например, дробь до сих пор называют «половина»; у римлян слово «унция* сначала было названием двенадцатой доли единицы массы, но потом унция стала обозначать одну двенадцатую долю любой величины (говорили: «Семь унций пути», т. е. семь двенадцатых пути).
В Древнем Вавилоне, как вы знаете, дроби были шестидесятеричными, т. е. записывались, например, в виде 4; 52; 03. Это означало: 4Ч- —+ —,. И сейчас, когда мы пишем 3 ч 21 мин во во2
47 с, то, по сути дела, записываем доли часа в шестидесятеричной системе счисления: 21 мин=^- ч, 47 с — ч=-^- ч.
60 6U" oOUU
1 2
У египтян были особые знаки для дробей — и — и общий Л «5
способ записи для долей (т. е. дробей с числителем 1). Все остальные дроби они записывали в виде суммы долей.
тт „ . 7 _ 1 I * 1 5 _ 1 , 1 7 _ 14 _ 1 . 1
Например. 12 3 + 4 ’ 24 8 12 ’ 13 26 2 ~^26 ’
(Подумайте, как можно быстро находить такую сумму.)
110
Запись дробей с помощью числителя и знаменателя появилась в Древней Греции, только греки знаменатель записывали сверху, а числитель — снизу. Дроби в привычном для нас виде впервые стали записывать индусы около 1500 лет назад, но они не использовали черту между числителем и знаменателем. Черта дроби стала общеупотребительной лишь с XVI в.
В старину применяли в основном обыкновенные дроби. Это объяснялось различными соотношениями между единицами измерения: они делились и на 12, и на 16, и на 40 частей. Но потом было замечено, что самыми удобными для вычислений являются десятичные дроби. С XVII—XVIII в. они получили всеобщее распространение, особенно после создания и введения в большинстве стран метрической системы мер.
$ 4. ОТНОШЕНИЯ И ПРОПОРЦИИ
20. Отношения
Задача 1. От куска материи длиной 5 м отрезали 2 м. Какую часть куска материи отрезали?
Решение. Сначала узнаем, какую часть всего куска материи составляет 1 м. Так как в куске 5 м, то он составляет 1 2
— куска. Значит, 2 м составляют — всего куска материи. Тот D О
же ответ можно получить, разделив 2 на 5. Действительно, 2 2:5=—. Ответ можно также записать в виде десятичной О
2 дроби или в процентах: —=0,4 = 40%.
О
Частное двух чисел называют отношением этих чисел. Отношение показывает, во сколько раз первое число больше второго или какую часть первое число составляет от второго.
Если две величины измерены одной и той же единицей измерения, то отношение их значений называют также отношением этих величин (отношением длин, отношением масс, отношением площадей и т. д.).
Задача 2. Длина железной дороги 360 км. Электрифицировано 240 км этой дороги. Какая часть дороги электрифицирована? Во сколько раз вся дорога длиннее ее электрифицированной части?
111
Решение. Чтобы найти, какая часть дороги электрифицирована, берем отношение 240:360. Записываем это отношение в виде дроби и сокращаем ее на 120. Получим 240:360=|^ = 360
2 2
=—. Значит, электрифицировано — всей дороги. 3 3
Чтобы узнать, во сколько раз вся дорога длиннее своей электрифицированной части, берем отношение 360:240. Записываем его в виде дроби и сокращаем эту дробь на 120. Получим 360:240=^=-|-= 1-^-= 1,5. Значит, вся дорога в 1,5 240 2 2
раза длиннее ее электрифицированной части.
2 3
Числа — и — взаимно обратны, поэтому и отношения 2 к 3 о 2
и 3 к 2 также называют взаимно обратными.
Если величины измерены разными единицами измерения, то для нахождения их отношения надо предварительно перейти к одной единице измерения.
Задача 3. Масса станка 9,6 ц, а масса электромотора 36 кг. Найдите отношение массы электромотора к массе станка.
Решение. Выразим массу станка в килограммах. Получим 9,6 ц = 960 кг. Значит, отношение массы электромотора к массе станка равно ^-=4; = 0,0375. о60 oU
Итак, масса электромотора составляет 0,0375 массы станка.
Этот ответ можно выразить в процентах: 0,0375 = 3,75%. Значит, масса электромотора составляет 3,75% массы станка.
©Что называют отношением двух чисел? Что показывает отношение двух чисел? Как узнать, какую часть число а составляет от числа 5? Как узнать, сколько процентов одно число составляет от другого?
706. Найдите отношение:
а) 124 к 3; в) 12,3 к 3; д) 0,25 к 0,55; ж) б 4- к 8,2; 6
б) 6 к 20; г) 9,1 к 0,07; е) 8 Л к ; з) 1,35 к 5-f--1о 1о О
707. Проволока разрезана на два куска. Первый кусок имеет длину 9 м, а второй 14,4 м. Найдите, какую часть всей проволоки составляет первый кусок; второй кусок. Какую часть первый кусок составляет от длины второго куска?
112
g Возможны разные способы использования термина от-" ношение в речи.
Читая выражение 35:27, можно сказать:
— отношение числа тридцать пять к числу двадцать семь р. п. в. п. д. п. в. п.
— отношение чисел тридцать пять и двадцать семь р. п. в. п. в. п.
— отношение тридцати пяти к двадцати семи
р. п. д. п.
708. Внутри угла АОС проведен луч ОВ так, что Z.AOB = = 56° и Z. ВОС = 40°. Какую часть угла АОС составляет угол АОВ\ угол ВОС? Выполните построение этих углов с помощью транспортира.
709. Площадь прямоугольника 22,05 дм2. Длина этого прямоугольника 10,5 дм. Найдите отношение длины прямоугольника к его ширине. Что показывает это отношение? Запишите отношение, обратное полученному отношению. Что будет показывать это отношение?
710. Отношение а к b равно . Найдите обратное отношение. Чему будет равно отношение m к п, если отношение п к m равно 1,25?
711. Сплав из свинца и олова содержит 1,52 кг свинца и 0,7 6 кг олова. В каком отношении взяты свинец и олово? Какую часть сплава (по массе) составляет олово и какую часть свинец?
712. Какую часть урока заняла самостоятельная работа, которая длилась 20 мин, если продолжительность урока 45 мин?
713. В классе 36 учащихся. Из них 15 мальчиков, а остальные девочки. Какую часть учащихся составляют мальчики, а какую девочки? Чему равно отношение числа девочек к числу мальчиков и что оно показывает?
714. Два колхоза построили дорогу. Первый колхоз построил у- дороги, второй — остальную часть. Во сколько раз часть дороги, построенная первым колхозом, больше, чем часть дороги, построенная вторым?
113
715. Расстояние от села до города автомашина прошла за 3 ч. В первый час она прошла четверть всего расстояния, во второй час треть всего расстояния. Во сколько раз расстояние, пройденное в третий час, больше расстояния, пройденного во второй час? Какую часть расстояние, пройденное в первый час, составляет от расстояния, пройденного в третий час?
710. Молоко разлили в три бидона. В первый налили 0,1 всего молока, во второй 0,3 всего молока, а в третий 0,6 всего молока. Что показывает отношение:
а) 0,1 к 0,3; б) 0,1 к 0,6; в) 0,3 к 0,6; г) (0,34-0,1) к 0,6?
717. В классе 40 учащихся. 8 учащихся учатся на «5». Сколько процентов учащихся класса составляют отличники?
718. Из 250 семян погибли 10. Найдите процент всхожести семян.
719. В связи с повышением разряда рабочий стал вместо 240 р. получать 300 р. На сколько процентов повысилась зарплата рабочего?
720. По коэффициенту трудового участия (КТУ) заработок между тремя рабочими распределили следующим образом: первому — 40% всех денег, второму — 35% всех денег, а третьему — остальные 25%. Определите, округлив результаты до десятых, сколько процентов составляли деньги, полученные: а) первым рабочим, от денег, полученных двумя другими;, б) вторым рабочим, от денег, полученных двумя другими; в) первым рабочим, от денег, полученных вторым; г) вторым рабочим, от денег, полученных первым;
д) третьим рабочим, от денег, полученных первым.
721. Имеющиеся деньги брат и сестра распределили так, что сестра получила в 3 раза больше, чем брат. Определите: а) какую часть денег получила сестра и какую брат; б) сколько процентов всех денег получила сестра и сколько брат; в) какую часть деньги брата составляют от денег сестры.
722. Известно, что сумма углов любого треугольника равна 180°. В треугольнике АВС найдите Z-A, если:
а) ЛВ=75°; ЛС=80°;
б) Z.A больше Z.B на 20° и меньше Z.C на 40°;
2 1
в) Z.B составляет —, a Z.C составляет — суммы всех углов о О
треугольника;
г) Z.A составляет и Z.C = 70°.
б
114
723. Что показывает отношение: а) пути, пройденного автомашиной, ко времени ее движения; б) числа деталей, изготовленных станком-автоматом, ко времени его работы; в) стоимости купленных яблок к их массе; г) объема прямоугольного параллелепипеда к площади его основания?
724. Найти, сколько процентов число 9,729 составляет от числа 84,6, можно с помощью микрокалькулятора по программе 9.7291 4-184.61 % I — . Выполните по этой програм
ме вычисления.
С помощью микрокалькулятора: а) найдите, сколько процентов составляет 0,0912 от 36,48 и 13,524 от 16,8; б) решите задачу: «Из 327 га вспахано 225 га. Сколько процентов земли вспахано? Сколько процентов земли осталось вспахать?» Ответ округлите до десятых долей процента.
725. Вычислите устно:
а) 16 * 10 б) 800 : 25 в) 7 : 5 г) 0,5 : 20 Д) 4-2,8
4-190 • 30 -0,2 -1,8 • 7
-200 -510 * 6 : 4,1 : 0,42
: 5 : 10 4-3,8 4-5,2 • 0,01
• 7 • 2 : 5 : 1,2 4-3,3
? ? ? ? ?
726. Найдите пропущенные числа:
а)
727. На сколько надо увеличить знаменатель дроби ,
• Л . 4" • чтобы получить дробь 4- ? 1( о 4
728. Выразите в процентах числа:
0,2; 0,15; 4-; ; 1; 3.
2 о 4 ZU
115
729. Половина от половины числа равна половине. Найдите
это число.
Л\
730. Кто быстрее? Найдите в таблице последовательно все числа от 26 до 50:
42 47 54 29 43
50 28 39 48 35
40 33 36 26 30
49 44 31 38 46
32 37 45 41 27
37 30 47 46 44
42 33 27 36 39
34 48 50 31 43
28 41 38 49 26
45 32 29 40 35
731. Найдите значение выражения:
. б ' о . 1 T+ 1 Т . 1,26,6
а> -• °’4; в) -^5----; д) -оТоТ;
б ,п - . 7,6 . . 1,8
’ “ , : г)тт—г1
Т 4
2
732. На покупку овощей и фруктов истрачено — из имев-
3 о
шихся 18 р. Стоимость фруктов составляла — стоимости всей
покупки. Сколько денег истрачено на покупку фруктов?
733. На окраску окон и дверей было истрачено 3,2 кг белил, что составляет всех белил, истраченных на ремонт. А на ре-О
монт было истрачено — всех купленных белил. Сколько кило-5
граммов белил было куплено?
734. Найдите объем прямоугольного параллелепипеда, если:
1) его ширина 2,5 см и составляет высоты, а длина в 3,4 раза О
больше высоты;
2) его высота 3,5 см и составляет 0,7 ширины, а длина в 2,4 раза больше ширины.
® 735. Двое мальчиков бросали баскетбольный мяч в корзину. Один мальчик из 20 бросков имел 13 попаданий, а другой из 26 бросков имел 15 попаданий. Найдите для каждого
116
мальчика, какую часть составляли попадания от числа бросков. Чей результат лучше?
786. Крутизной лестницы называют отношение высоты ступеньки к ее глубине. Чему равна крутизна лестницы, если высота ступеньки 18 см, а глубина 30 см?
737. Автобус в первый час прошел 30 км, во второй 24 км, а в третий 42 км. Какую часть всего пути прошел автобус в каждый час? Какую часть пути, оставшуюся после первого часа движения, прошел автобус во второй час и какую в третий час?
788. Для варенья на 3,6 кг ягод было взято 4,2 кг сахарного песку. В каком отношении по массе были взяты ягоды и сахарный песок?
789. В сосуд налили 240 г воды и положили 10 г соли. Найдите процентное содержание соли в растворе. Через некоторое время 50 г воды испарилось. Какое теперь стало процентное содержание соли в растворе?
740. Комбайнер намолотил 76 т зерна, превысив задание на 12 т. На сколько процентов комбайнер перевыполнил задание?
741. На складе были пшеница, овес и кукуруза, причем пшеница составляла 64%, овес 16% всего количества зерна. В товарный состав загрузили всю пшеницу и всю кукурузу. Какой процент погруженного зерна составляла пшеница? Какой процент погруженного зерна составляла бы пшеница, если вместо кукурузы погрузили бы овес?
742. Длина прямоугольника а см, а ширина Ь см. Длина другого прямоугольника т см, а ширина п см. Найдите отношение площади первого прямоугольника к площади второго. Найдите значение получившегося выражения, если:
а) а=9, Ь—2, т = 8, п=3;
б) а = 6,4, 5=0,2, т=3,2, п = 0,5.
743. Найдите значение выражения:
а)
(2,3 4-5,8)-3 у
(4,9—2,3):у V
. 0,21 1,25 .
13,6—11,1 ’
б)
4: А+2.26.0,8 О Ю
2,781 7,825 2,06 3,13 '
117
21. Пропорции
отношению с к de или
Средние
а : b = с id
I______________I
Крайние
Отношения 3,6:1,2 и 6,3:2,1 равны, так как значения частных равны 3. Поэтому можно записать равенство 3,6:1,2 = „ „. „ . 3,6 6,3
= 6,3:2,1, или
Равенство двух отношений называют пропорцией.
С помощью букв пропорцию записывают так: a:b = c:d или -7-=—г - Эти записи читают так: «Отношение а к Ь равно о а
«а так относится к Ь, как с относится к а».
В пропорции -7-=-^-, или a:b = c:d, b d
числа а и d называют крайними членами, а числа b и с — средними члеиами пропорции. В дальнейшем будем считать, что все члены пропорции отличны от нуля: а=#=0, b=#=0, с#=0, d#=0.
D 3,6 6,3 „
В пропорции —=— найдем произведение ее крайних и произведение ее средних членов. Получим 3,6-2,1 = 7,56; 1,2-6,3 = 7,56. Значит, 3,6-2,1 = 1,2-6,3.
В верной пропорции произведение крайних членов равно произведению средних. Верно и обратное утверждение: если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.
Это свойство называют основным свойством пропорции.
Пропорция 20:16 = 5:4 верна, так как 20-4 = 16-5 = 80. Поменяем местами в этой пропорции средние члены. Получим новую пропорцию: 20:5 = 16:4. Она тоже верна, так как при такой перестановке произведение крайних и произведение средних членов не изменилось. Эти произведения не изменятся, если в пропорции 20:5=16:4 поменять местами крайние члены.
Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.
Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны.
Пример 1. Найдем в пропорции 0,5:а = 2:13 неизвестный средний член а.
118
Решение. Используя основное свойство пропорции, получим а • 2 = 0,5 • 13. Отсюда а =0,5'73 ; а = 3,25.
Пример 2. Решим уравнение 8,735 = 0*5 •
3Т
Решение. Используя основное свойство пропорции, получим 8,75-0,75 = 3 -7— х. .Отсюда х==8-75'0’75 , Представим 3 4“ 4 3 . 4
Зт
в виде десятичной дроби 3,75 и сократим выражение на 0,75, имеем х=1,75.
О
©Что такое пропорция? Как называются числа х и у в пропорции х: а = b: у? Как называются числа т и п в пропорции а:т = п:Ь? Сформулируйте основное свойство пропорции. Какие перестановки членов пропорции снова приводят к верным пропорциям? Останется ли пропорция верной, если поменять местами какой-нибудь средний ее член с одним из крайних? Приведите пример. Останется ли пропорция верной, если оба средних члена поменять местами с крайними членами? Проверьте ваш ответ на пропорции 3:4 = 9:12.
0744. Запишите пропорцию:
а) 5 так относится к 3, как 2 относится к 1,2;
1 2
б) 0,9 так относится к —, как 45 относится к 16 —; 3 о
в) отношение к 0,1 равно отношению 14 к 4,9.
Проверьте полученные пропорции, определяя отношения чисел.
745. Из каких отношений 0,6:5; 4,2:7; 4~:6,25 можно сос-4
та вить верную пропорцию?
746. Прочитайте пропорции и проверьте, верные ли они, используя основное свойство пропорции:
а) 4-|-:3 4~=36:26; г) °-Эб— °-105 .
2 4 0,6 0,18 ’
б)3:7,5 = 2-|-:б2-; Д)^=?;
в)2-^:9 = 1:39; е) £=-^.
119
747. Решите уравнение:
а) у.51,6 = 11,2:34,4; е) у:3 -|-=4 -j-:2 -1-;
б) 67,8 _ а 7,62 . 6,35 ’ ж) -1-х:5 = 16:0,8;
в) , .25 ЬТ = ,_4_.2О . 7 ’ 21 ’ з) 0,2:(х —2)=-|-:2
г) 5-|-:3
5 2 4 и) 2 0,24 = 1 4-:(х + 0,06).
д) 12,3 6 7х . 4,2 ’
748. Переставив средние или крайние члены пропорции, сос-
тавьте три новые верные пропорции из пропорции:
а) 5:15 = 4:12; б) в) f=f *
749. Используя верное равенство 4*9=0,2>180, составьте четыре верные пропорции.
750. Вычислите устно:
а) 15 10 б) 900 : 15 в) 1 : 4 г) 1,4 + 3,6 д) 3 • 1,6
+ 350 -9 —0,1 : 0,25 —1,2
: 25 + 260 • 6 • 0,14 : 1,8
• 20 : 16 : 4,5 —2,7 —0,2
-150 20 +0,38 • 7,3 • 0,4
? ? ? ? ?
751. Какой знак действия надо подставить вместо ♦, чтобы
получилось верное равенство:
а) -g-*l-|-=l; б) 2 * 1-^-=-|-; в) г) 0,3*-|-=А?
752. Найдите отношение величин:
а) 1,5 м и 30 см;
б) 1 кг и 250 г;
в) 1 ч и 15 мин;
г) 50 см2 и 1 дм2. 5 3
753. — числа равны — этого числа. Какое это число?
754. Какое число надо прибавить к числителю и знамена-
7 3
телю дроби — , чтобы получить дробь — ? Z < <
755. Какие из фигур (рис. 33) являются развертками: а) четырехугольной призмы; б) треугольной призмы; в) треугольной пирамиды?
м
120
Рже. 33
756. Из ружья сделано 50 выстрелов, при этом 5 пуль пролетели мимо цели. Определите процент попаданий.
757. Угол А равен 30°, а угол В равен 50°. Какую часть угол А составляет от угла В? Во сколько раз угол В больше угла А?
758. Бригаде было дано задание собрать 280 ц винограда. Она собрала 350 ц. На сколько процентов бригада перевыполнила задание? На сколько процентов бригада выполнила задание?
759. В парке посадили клены и дубы, причем на каждые 4 клена приходится один дуб. Сколько процентов от всех посаженных деревьев составляют клены? Сколько всего посадили деревьев в парке, если кленов посадили 480?
®760. Верна ли пропорция:
а) 2,04:0,6 = 2,72:0,8; б) 0,0112:0,28 = 0,204:0,51?
781. Решите уравнение:
а) 2 4-А = 4-^-1 4-; в) у:4-=34-:1 —;
' 3 2 9 ' * 5 8 4
б)8^т = 3-|-1А-; r)z:^=3-|-:f.
782. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?
763. Через 2 ч после выхода со станции А тепловоз увеличил скорость на 12 км/ч и через 5 ч после начала движения прибыл в пункт назначения В. Какова была скорость тепловоза в начале пути, если расстояние от А до В равно 261 км?
121
2
764. Если к — неизвестного числа прибавить 0,8, то полу-
чится 1,2. Найдите неизвестное число.
765. Выполните действия: а) (3,2:44-4 -|-:3,2 )-4,8;
б) (385,7:0,19 - 30)• 0,2 -(35,7 • 3,29 4- 2,547).
22. Прямая и обратная пропорциональные зависимости
Если станок с числовым программным управлением за 2 ч изготовляет 28 деталей, то за вдвое большее время, т. е. за 4 ч он изготовит вдвое больше таких деталей, т. е. 28 • 2 = 56 деталей. Во сколько раз больше времени будет работать станок, во столько раз больше деталей он изготовит. Значит, равны отношения 4:2 и 56:28. Следовательно, верна пропорция 4:2 = 56:28. Такие величины, как время работы станка и число изготовленных деталей, называют прямо пропорциональными величинами.
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Пусть путь из города А в город В поезд со скоростью 40 км/ч проходит за 12 ч. Если скорость движения увеличить вдвое, •т. е. сделать ее равной 80 км/ч, то на этот же путь поезд затратит вдвое меньше времени, т. е. 6 ч. Во сколько раз увеличится скорость движения, во столько же раз уменьшится время движения. В этом случае отношение 80:40 будет равно не отношению 6:12, а обратному отношению 12:6. Следовательно, верна пропорция 80:40=12:6. Такие величины, как скорость и время, называют обратно пропорциональными величинами.
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины.
122
Не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, рост ребенка увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, так как при удвоении возраста рост ребенка не удваивается.
Задачи на пропорциональные величины можно решить с помощью пропорции.
Задача 1. За 3,2 кг товара заплатили 11,52 р. Сколько следует заплатить за 1,5 кг этого товара?
Решение. Запишем кратко условие задачи в виде таблицы, обозначив буквой, х стоимость (в рублях) 1,5 кг этого товара. Запись будет иметь следующий вид:
Количество Стоимость
товара товара
I покупка I 3,2 кг I 11,52 р.
II покупка | 1,5 кг | х р.
Зависимость между количеством товара и стоимостью покупки прямо пропорциональная, так как если купить товара в несколько раз больше, то и стоимость покупки увеличится во столько же раз. Условно обозначим такую зависимость одинаково направленными стрелками.
Запишем пропорцию: y|-= 11^-2 .
Теперь найдем неизвестный член пропорции:
х= 1,5-11,52 =5Д_
Ответ: 5,4 р.
Задача 2. Два прямоугольника имеют одинаковую площадь. Длина первого прямоугольника 3,6 м, а ширина 2,4 м. Длина второго прямоугольника 4,8 м. Найдите ширину второго прямоугольника.
Решение. Обозначив буквой х ширину (в метрах) второго прямоугольника, запишем кратко условие задачи:
Длина Ширина
I прямоугольник | 3,6 м 2,4 м
II прямоугольник | 4,8 м х м
Зависимость между шириной и длиной при одном и том же значении площади прямоугольника обратно пропорциональ
123
ная, так как если увеличить длину прямоугольника в несколько раз, то надо ширину во столько же раз уменьшить. Условно обозначим такую зависимость противоположно направленными стрелками.
Запишем пропорцию:
Теперь найдем неизвестный член пропорции:
х=^=1.в.
Ответ: 1,8 м.
©Какие величины называют прямо пропорциональными?
Что можно сказать об отношениях соответствующих значений таких величин? Приведите примеры прямо пропорциональных величин. Какие величины называют обратно пропорциональными? Что можно сказать об отношениях соответствующих значений таких величин? Приведите примеры обратно пропорциональных величин. Приведите примеры величин, у которых зависимость не является ни прямо, ни обратно пропорциональной.
41Х 766. Определите, является ли прямой пропорциональной, обратной пропорциональной, или не является пропорциональной зависимость между величинами: а) путем, пройденным автомашиной с постоянной скоростью, и временем ее движения; б) стоимостью товара, купленного по одной цене, и его количеством; в) площадью квадрата и длиной его стороны; г) массой стального бруска и его объемом; д) числом рабочих, выполняющих с одинаковой производительностью труда некоторую работу, и временем выполнения этой работы; е) стоимостью товара и его количеством, купленным на определенную сумму денег; ж) возрастом человека и размером его обуви; з) объемом куба и длиной его ребра; и) периметром квадрата и длиной его стороны; к) дробью и ее знаменателем, если числитель не изменяется; л) дробью и ее числителем, если знаменатель не изменяется.
Задачи 767—778 решите, составив пропорцию.
767. Стальной шарик объемом 6 см3 имеет массу 46,8 г. Какова масса шарика из той же стали, если его объем 2,5 см3?
768. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
124
769. Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистят эту площадку?
770. Для перевозки груза потребовалось 24 машины грузоподъемностью 7,5 т. Сколько нужно машин грузоподъемностью 4,5 т, чтобы перевезти тот же груз?
771. Для определения всхожести семян посеяли горох. Из 200 посеянных горошин взошло 170. Какой процент горошин дали всходы (процент всхожести)?
772. Во время воскресника по озеленению города на улице посадили липы. Принялось 95% всех посаженных лип. Сколько посадили лип, если принялось 57 лип?
773. В лыжной секции занимаются 80 учащихся. Среди них 32 девочки. Какой процент участников секции составляют девочки и какой мальчики?
774. Колхоз по плану должен засеять 980 га кукурузой. Но план выполнили на 115%. Сколько гектаров кукурузы посеял колхоз?
775. За 8 месяцев рабочий выполнил 96% годового плана. Сколько процентов годового плана выполнит рабочий за 12 месяцев, если будет работать с той же производительностью?
776. За три дня было убрано 16,5% всей свеклы. Сколько потребуется дней, чтобы убрать 60,5% всей свеклы, если работать с той же производительностью?
777. В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5 т железа?
778. Для приготовления борща на каждые 100 г мяса надо взять 60 г свеклы. Сколько свеклы надо взять на 650 г мяса?
779. Вычислите устно:
а) 800 : 16 б) 309 + 541 в) 5 — 3,4 г) 2,5+ 3,5 Д) 7,5 : 25
• 7 -360 • 4 : 1,5 • 1.6
-80 : 70 + 2,7 • 0,125 +0,2
: 30 • 30 : 13 : 0,17
• 15 : 21 • 0,03. : 0,03 -0,1
? ? ? ? ?
780. Представьте в виде суммы двух дробей с числителем 1
- - 5 8 0 4 18
каждую из следующих дробей: —, —, — , —, — .
125
781. Из чисел 3, 7, 9 и 21 составьте две верные пропорции.
782. Средние члены пропорции 6 и 10. Какими могут быть крайние члены? Приведите примеры.
783. При каком значении х верна пропорция:
а)—=—; 6)—= — ; в) —=—; г) —=—; д) A=_L ?
7 4 х ’ 7 4 9’ ' 6 18 ' ’ х 5,Д'х хС
784. Найдите отношение:
а) 2 мин к 10 с; в) 0,1 кг к 0,1 г; д) 3 дм3 к 0,6 м3.
б) 0,3 м2 к 0,1 дм2; г) 4 ч к 1 сут;
785. Где на координатном луче должно быть расположено число с, чтобы была верна пропорция -т-=4- (рис. 34)?
Ь а
0 a b d
I------1 ।------1 ।------1 ।--
Рис. 34
786. Развивайте свою память! Закройте таблицу листом бумаги. На несколько секунд откройте первую строку и затем, вновь закрыв ее, постарайтесь повторить или записать три числа этой строки. Если вы верно воспроизвели все числа, переходите ко второй строке таблицы. Если в какой-либо строке допущена ошибка, сами напишите несколько наборов из такого же, как в строке, количества двузначных чисел и тренируйтесь в их запоминании. Если вы можете без ошибок воспроизвести не менее пяти двузначных чисел, у вас хорошая память.
787. Решите уравнение: а) 4,5:(3х) = 4:28;
б) (2х).'9 = 2-|-:5-i-;
в) 1,25:0,4 = 1,35:(0,Зх);
г) l-i-:l=(2x):-|-. О о
788. Можно ли составить верную пропорцию из следующих чисел:
а) 15; 14; 8 и 75; б) -i-; 11 А? Z Z 4 АО
789. Из равенства произведений 3-24 = 8-9 составьте три верные пропорции.
126
790. Длина отрезка АВ равна 8 дм, а длина отрезка CD равна 2 см. Найдите отношение длин отрезков АВ и CD. Какую часть длины отрезка АВ составляет длина отрезка CD?
791. Путевка в санаторий стоит 460 р. Профсоюз оплачивает 70% стоимости путевки. Сколько за путевку заплатит отдыхающий?
792. Найдите значение выражения:
б)
12-0,8-1,8
Г2 + 2Й
¥
793. Решите задачу:
1) При обработке детали из отливки массой 40 кг в отходы ушло 3,2 кг. Какой процент составляет масса детали от массы отливки?
2) При сортировке зерна из 1750 кг в отходы ушло 105 кг. Какой процент зерна остался?
794. Найдите значение выражения:
1) 6,0008:2,64-4,23 0,4; 2) 2,91 1,2 + 12,6288:3,6.
795. Из 20 кг яблок получается 16 кг яблочного пюре. Сколько яблочного пюре получится из 45 кг яблок?
796. Трое маляров могут закончить работу за 5 дней. Для ускорения работы добавили еще двух маляров. За какое время они закончат работу, считая, что все маляры будут работать с одинаковой производительностью?
-797 . За 2,5 кг баранины заплатили 4,75 р. Сколько баранины можно купить по той же цене на 6,65 р.?
798. В сахарной свекле содержится 18,5% сахара. Сколько сахара содержится в 38,5 т сахарной свеклы? Ответ округлите до десятых долей тонны.
799. В семенах подсолнечника нового сорта содержится 49,5% масла. Сколько килограммов таких семян надо взять, чтобы в них содержалось 29,7 кг масла?
800. В 80 кг картофеля содержится 14 кг крахмала. Найдите процентное содержание крахмала в таком картофеле.
801. В семенах льна содержится 47% масла. Сколько масла содержится в 80 кг семян льна?
802. Рис содержит 75% крахмала, а ячмень 60%. Сколько надо взять ячменя, чтобы в нем содержалось столько же крахмала, сколько его содержится в 5 кг риса?
127
803. Найдите значение выражения: а) 203,81: (141 -136,42) + 38,4:0,7 5;
б) 96:7,54-288,51:(80 —76,74).
23. Масштаб
Участки земной поверхности изображают на бумаге в уменьшенном виде. Например, отрезок 1000 м изображают на карте (рис. 35) отрезком в 1 см. Так как 1000 м = 100 000 см, то каж-
М 1: 100000
Ряс. 35
дый отрезок на карте в 100 000 раз меньше соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
В рассмотренном нами примере масштаб карты равен 1:100 000 = =— . Говорят, что карта сде-юоооо
лана в масштабе одна стотысячная.
Задача 1. Длина отрезка на карте 3 см. Найдем длину соответствующего отрезка на местности, если масштаб карты 1:1 000 000.
Решение. Обозначим длину отрезка на местности (в сантиметрах) буквой х и найдем отношение длины отрезка на карте к длине отрезка на местности: 3 :х, которое и будет равно масштабу карты.
Значит, 3: х = 1:1 000 000.
Решив уравнение, получим х = 3 • 1 000 000 = 3 000 000. Но 3 000 000 см = 30 000 м = 30 км.
Ответ: длина отрезка иа местности 30 км.
Задача 2. Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1:100 000?
Решение. Обозначим длину (в километрах) отрезка на карте буквой х и составим пропорцию: х:4,5= 1:100 000.
Решив уравнение, получим х= 4,5 ЛОО 000 = 0,000045.
Но 0,000045 км=0,045 м = 4,5 см.
Ответ: длина отрезка на карте 4,5 см.
128
®Что называют масштабом карты? Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? уменьшены в 50 раз?
©804. Определите по карте (рис. 36) расстояние от опушки леса (точка А) до точки пересечения дороги с рекой. Масштаб карты 1:100 000.
805. Расстояние между городами А и В на карте равно 8,5 см. Найдите расстояние между городами на местности, если масштаб карты . * .
н 1 000 000
806. Длина железной дороги Москва - Петербург приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб 1:10 000 000.
807. Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной странице тетради это расстояние в масштабе одна десятимиллионная?
808. На рисунке 37 дан план квартиры в масштабе 1:100. Определите по плану, какие размеры имеют кухня, ванная и комнаты и какова их площадь в действительности.
809. Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на этой карте расстояние между ними 12,6 см?
810. Длина железнодорожной магистрали 3140 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе: а) 1:10 000 000; б) 1:2 000 000?
5 Зак. 607
129
811. Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на карте длина отрезка, изображающего отрезок 10 км? Какой Отрезок на местности изображает отрезок на карте длиной 1,8 см?
812. Длина детали на чертеже, сделанном в масштабе 1:5, равна 7,2 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 1:3? в масштабе 2:1?
<D 813. Вычислите устно:
а) 370+ 230 б) 720 : 18 в) 7,2 : 2,4 г) 6 — 4,5 д) 8 • 1,2
: 50 + 280 - 0,6 - 0,4 + 0,4
• 30 : 16 : 0,12 : 1,2 • 0,01
+ 340 -50 0,125 -7 : 0,5
: 14 : 125 +7,5 +0,8 : 0,1
? ? ? ? ?
814. Какое число надо отнять от числителя и знаменателя
дроби , чтобы получить дробь ?
815. Составьте три пропорции, используя верное равенство: а) 18:2=54:6; в) 2,8-45=6,3-20;
б) 4,5:1,5 = 1,26:0,42; г) 3,9 0,14 = 0,6 0,91.
816. Две трети от двух третьих числа равны двум третьим. Какое это число?
817. Сколько гектаров в 1 м2? Сколько часов в 1 с? Сколько литров в 1 см3?
IWI 818. Известно, что объем пирамиды в 3 раза меньше объема призмы такой же высоты и с таким же основанием (рис. 38). Вычислите объем четырехугольной пирамиды, „ 2
в основании которой прямоугольник со сторонами — дм и о
9 Е
— дм, а высота равна 5 дм.
130
819. За 4 одинаковые коробки цветных карандашей заплатили 4,4 р. Сколько стоят 12 таких коробок карандашей?
820. Некоторое расстояние ласточка пролетела за 0,5 ч со скоростью 50 км/ч. За сколько минут пролетит то же расстояние стриж, если будет лететь со скоростью 100 км/ч?
821. Начертите окружность и постройте два ее радиуса, угол между которыми 120°. Закрасьте часть круга между этими радиусами. Какая часть круга окажется закрашенной и какая часть круга останется незакрашенной?
822. Решите задачу:
1) Сумма двух чисел 7,2, причем большего числа равна
3 меньшему числу. Найдите эти числа.
2) Разность двух чисел 1,5, причем большего числа равна меньшему числу. Найдите эти числа.
823. Решите уравнение:
32 2 —
1)-1±=^; 2)-^-=К
' 21 1.5 ’ ' 3± г
7 5
4|к 824. Найдите с помощью карты расстояние от Москвы до Киева.
825. Измерьте длину и ширину своей комнаты. Начертите в тетради план этой комнаты в масштабе 1:100.
826. Расстояние на местности в 20 м изображено на плане отрезком 1 см. Определите масштаб плана.
827. Длина дома на плане 25 см. Чему равна длина дома на местности, если план сделан в масштабе 1:300?
828. Расстояние между городами на местности равно 1300 км. Каким отрезком будет изображено это расстояние на карте, масштаб которой 1:10 000 000?
829. Длина детали на чертеже,? сделанном в масштабе 1:3, равна 2,4 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 2:1?
830. Найдите значение выражения:
. 10^;12 6 *
2 22
8:2-?- 2^4
б)-----—7 7-
5^:7 4:А
4 9
5
131
24. Длина окружности и площадь круга
Возьмем круглый стакан, поставим на лист бумаги и обведем его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить ее, то длина нитки будет приближенно равна длине нарисованной окружности (рис. 39).
2яг
Рве. 89
Длина окружности прямо пропорциональна длине ее диаметра. Поэтому для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом. Его обозначают греческой буквой л (читается: «пи»). Если обозначить длину окружности буквой С, а длину диаметра буквой d, то C:d=n. Поэтому C=nd.
Так как диаметр окружности вдвое больше ее радиуса, то длина окружности с радиусом г равна 2лг.
Получили другую формулу длины окружности:
С = 2лг.
Подсчеты показали, что с точностью до десятитысячных л» 3,1416. Если значение л округлить до сотых, то получим значение 3,14. Примерно такую же точность дает значение
22
л« —. В старших классах будет рассказано, как проводились такие подсчеты.
На рисунке 40 изображены круг и два квадрата ABCD и EFKM. Радиус круга равен г, поэтому длина стороны квадрата' ABCD равна 2г, а его площадь 4г2. Площадь треугольника EOF вдвое меньше площади квадрата AEOF, поэтому площадь
132
EFKM вдвое меньше площади квадрата ABCD, т. е. равна 2г2. Площадь круга S больше площади квадрата EFKM, но меньше площади квадрата ABCD:
2r2<S<4r2.
Примерно площадь круга равна Зг2. Можно доказать, что
S=nr2.
©Напишите формулы для нахождения длины окружности по длине ее диаметра и по длине ее радиуса. Пропорциональна ли длина окружности длине ее радиуса? Напишите формулу площади круга. Пропорциональна ли площадь круга длине его радиуса?
0831. Найдите длину окружности, радиус которой равен 24 см; 4,7 дм; 18,5 м. Число л округлите до сотых.
О Формулы длины окружности и площади круга читаются так:
С = nd — цэ равно пи дэ;
С = 2лг — цэ равно двум пи эр;
S = лг2 — эс равно пи эр квадрат.
Выражение л «3,14 читают:
пи приближенно равно трем целым четырнадцати сотым
832. Чему равна длина окружности, если ее радиус равен
22
1,54 м; 5,67 дм? Значение числа л возьмите равным —.
833. Диаметр долгоиграющей пластинки равен 50 см. Найдите длину окружности этой пластинки. Число л округлите до десятых.
834. Выполните необходимые измерения х^*~***^. и найдите длину половины окружности, f изображенной на рисунке 41. / \
835. Определите диаметр окружности, ес- * *
ли ее длина равна 56,52 дм; 37,68 см Рас* 41 (л «3,14).
836. Колесо на расстоянии 380 м сделало 150 оборотов. Найдите диаметр колеса. Результат округлите до сотых метра (л «3,14).
133
837. Измерьте радиус и вычислите площадь каждого круга на рисунке 42.
838. Окружность арены цирка имеет длину 40,8 м. Найдите диаметр и площадь арены (л«3).
839. Диаметр циферблата Кремлевских курантов 6,12 м, длина минутной стрелки 3,27 м. Найдите площадь циферблата. Какой путь проходит конец минутной стрелки курантов за час? Ответы округлите до сотых долей метра.
840. Выполните измерения и вычислите п лощадь каждой заштрихованной фигуры на рисунке 43.
841. По рисунку 44 найдите площадь пятиугольника
OABCD. Сравните ее с площадью четверти круга, радиус OD которого равен 5 см.
134
842. Вычислите устно:
а) 5004-310 б) 910 : 13 в) 1,5 • 0,6 г) 6,84-2,2 Д) 5-3,6
: 90 • 8 4-2,5 : 6 4
• 60 -80 : 1,7 4-3 : 14
— 120 : 160 -0,6 • 0,2 : 0,02
: 14 • 350 : 0,2 : 1,8 4-0,7
? ? ? ? ?
843. Какой знак действия надо поставить вместо *, чтобы получилось верное равенство:
. 1 2 11 . 6 . 1 п -.а.
а> Т*Т=15 ; В> 35*1й = 0Д6;
б> тг> *2т=3т?
844. Некоторое число вычли из числителя дроби и приба-39
вили к ее знаменателю. Получили дробь Найдите это число.
845. Масштаб карты 1:100 000. Заполните таблицу:
Расстояние между пунктами на карте / 4 см 16 мм
Расстояние между пунктами на местности 1 км 5,5 км 800 м
846. Запишите масштаб карты, если отрезок на местности в 1 км изображается на карте отрезком 10 см.
847. Запишите масштаб рисунка, если он изображает фигуру, увеличивая ее в 50 раз.
848. Решите задачу, составив пропорцию:
1) В 2,5 кг баранины содержится 0,4 кг белков. Сколько килограммов белков содержится в 3,2 кг баранины?
2) В 6,5 кг свинины содержится 2,6 кг жиров. Сколько жиров содержится в 10,5 кг такой свинины?
849. Вычислите:
1) 321-|-; 3) (3,1)3 + 2,75; 5) (1-|-)2-23;
2) 2-|-:23; 4) 26-(2,1)2; 6) (2 -j-)': )\
135
850. На рисунке 45 изображен план двухкомнатной квартиры в масштабе 1:200. Узнайте по рисунку сумму площадей двух жилых комнат (I и II) и узнайте по плану, какую площадь занимают остальные помещения этой квартиры.
4|Ъ 851. С помощью тонкой нити измерьте длину какой-нибудь окружности (на стакане, ведре, тарелке), измерьте длину диаметра. Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом л.
852. Найдите длину окружности, если ее радиус равен 36 см;
0,44 см; 125 км. (Число л округлите до сотых.)
853. Диаметр колеса тепловоза равен 180 см. За 2,5 мин колесо сделало 500 оборотов. С какой скоростью идет тепловоз?
854. Выполните измерения и вычислите площадь каждой заштрихованной фигуры (рис. 46).
О
855. Рабочий выполнил -т- работы за 9 ч. За какое времй он О
7 , , ,
выполнит — работы, если будет работать с той же производительностью?
858. Ведро вмещает 6 л бензина. В такое же ведро вместо бензина налито равное (по массе) количество дегтя. Сколько литров дегтя налито в ведро, если масса 1 л бензина 0,8 кг, а масса 1 л дегтя 1,2 кг?
857; Найдите неизвестный член пропорции:
а) 3-|-:х = 61; в) 4-|-:х=8-^:2 -L;
») 7т:2т=31-:!'; г> 6т:3т”3т:’-
136
25. Шар
Футбольный мяч, глобус, арбуз дают нам представление о шаре. Все точки поверхности шара одинаково удалены от центра шара. Отрезок, соединяющий точку поверхности шара с центром, называют радиусом шара. Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара. Диаметр шара равен двум радиусам. Поверхность шара называют сферой.
©Что называется радиусом шара? диаметром шара? Что такое сфера?
0 858. Диаметр земного шара приближенно равен 12,7 тыс. км. Скольким тысячам километров равен радиус и длина экватора Земли? (Число тысяч округлите до десятых.)
859. Один из самых больших глобусов Земли был изготовлен в 1889 г. для Парижской всемирной выставки. Его диаметр был 12,7 м. В каком масштабе этот глобус изображал Землю? Какова длина экватора и меридианов на этом глобусе?
860. Площадь поверхности Луны приближенно равна 38 млн. км2, что составляет 0,075 площади поверхности Земли. Найдите площадь поверхности Земли. (Результат округлите до миллионов квадратных километров.)
861. Диаметр планеты Меркурий приближенно равен 5 тыс. км. Диаметр планеты Венера в 2,48 раз больше, а диаметр планеты Марс составляет диаметра планеты Венера. Най-о!
дите диаметр планеты Венера и планеты Марс.
862. Вычислите устно:
а) 320 4-180 б) 630 : 90 в) 3,5 4-4,5 г) 0,5 • 1,8
: 20 • 60 : 10 -0,15
• 6 4-180 -0,3 : 0,3
-80 : 15 • 17 4-5,5
• 13 • 25 4-2,5 : 1,6
? ? ? ?
863. Масштаб плана 1:1000. На плане изображен круглый бассейн. Определите диаметр бассейна и его площадь, если на плане радиус бассейна 1 см.
137
864. Заполните таблицу:
Г 1 ч0,5
d 3
С Л 5 л 1
S л 16л 1
м
865. Цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 расставьте в клетки так, чтобы равенства были верными:
866. Длина окружности 1,2 м. Чему равна длина другой окружности, у которой диаметр в 2 раза больше диаметра первой окружности?
867. Найдите площадь — круга, у которого радиус 8 см.
4
Найдите площадь второго круга, у которого радиус составля-
3 ет радиуса первого круга.
4
868. Решите задачу:
1) В 'двух строительных бригадах 88 человек. В первой 2
бригаде в 2 — раза меньше людей, чем во второй. Сколько чело-3
век в каждой бригаде?
2) На двух животноводческих фермах работают 26 человек.
На первой ферме работают в 1 раза больше людей, чем на ь
второй. Сколько человек работают на каждой ферме?
869. Найдите значение выражения: »ЪХ+£>ХЧ^ еслих = 5^;
2) ±у+±у-±у, У=ХТ1-
® 870. Длина экватора Луны примерно равна 10,9 тыс. км. Чему равен диаметр Луны? (Результат округлите до сотен километров.)
871. Длина окружности 3,5 дм. Чему равна длина второй
138
окружности, у которой диаметр составляет диаметра первой окружности?
872. Найдите площадь круга, у которого диаметр равен 12 см. Найдите площадь круга, у которого диаметр в 2 раза меньше диаметра первого круга.
873. Для перевозки картофеля выделили две автомашины. На первую машину погрузили в 1,2 раза больше картофеля, чем на вторую. Сколько тонн картофеля погрузили на каждую автомашину, если на вторую погрузили на 0,9 т меньше, чем на первую?
874. Найдите значение выражения:
а) 150,88: (3,2 • 2,3) - 60,27 :(4,1 • 1,4);
б) 592,92:(2,7 • 7,2) -102,48:(6,1 • 1,6).
Н Слово «пропорция» (от латинского proportio) означает «соразмерность», «определенное соотношение частей между собой».
Учение об отношениях и пропорциях особенно успешно развивалось в IV в. до н. э. в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III в. до н. э.), там, в частности, приводится и доказательство основного свойства пропорции.
С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т. д.— примеры рычагов. Выигрыш, который дает рычаг в прилагаемом
139
усилии, определяется пропорцией —=4-, где М и т — массы т I
грузов, a L и I — «плечи» рычага.
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
Золотым сечением и даже «божест-венной пропорцией» называли мате-14 матики древности и средневековья де-
ление отрезка, при котором длина ® С А всего отрезка так относится к длине
Рве- 47 его большей части, как длина боль-
шей части к меньшей. На рисунке 47 точка С делит отрезок АВ в отношении золотого сечения. Это отношение приближенно равно 0,618«-|-. Золотое сечение чаще всёго применяется в произведениях искусства, архитектуре, встречается в природе.
На рисунке изображена знаменитая скульптура Аполлона Бельведерского, разделенная в таком отношении (точка С делит отрезок AD, точка В делит отрезок АС).
Красивейшее произведение древнегреческой архитектуры — Парфенон — построено в V в. до н. э. Отношение высоты здания
к его длине равно 0,618.
140
Окружающие нас предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длины, близкое к- числу 0,618.
Рассматривая расположение листьев на общем стебле растений, можно заметить, чтр между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).
Глава II.
РАЦИОНАЛЬНЫЕ ЧИСЛА
§ 5. ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА
26. Координаты на прямой
Точка О на прямой АВ (рис. 48) разбивает эту прямую на два дополнительных луча ОА и ОВ. Выберем единичный отрезок и примем точку О за начало отсчета. Тогда положение точки на каждом из лучей задается ее координатой. Чтобы отличить друг от друга координаты на этих лучах, условились ставить перед координатами на одном луче знак « + », а перед координатами на другом луче знак «—».
-4 -3 -2 -1 0 +7 + 2 + 3 + 4
А~~* 1 ' 0 ' ' ' 5
Рис. 48
Числа со знаком «+» перед ними называют положительными. Пишут: -|-1, -|-5, +-?-» -|-3,6 — и читают:
о 4
«Плюс один», «Плюс пять», «Плюс две третьих», «Плюс две целых одна четвертая», «Плюс три целых шесть десятых» (рис. 49).
-5 -3,6 -2± 0 + | + / + 2^ +3,6 +5
Рис. 49
Числа со знаком «—» перед ними называют отрицатель-2 1
иыми. Пишут: —1, —5, ——, —2 — , —3,6 — и читают: «Минус один», «Минус пять», «Минус две третьих», «Минус две целых одна четвертая», «Минус три целых шесть десятых» (рис. 49). Для краткости записи обычно опускают знак « -|- » перед
142
положительными числами и вместо -|-7 пишут 7. Поэтому + 7 = 7, +2-|-=2-^-, +6,3 = 6,3, т. е. +7 и 7 —это одно
0 О
и то же число, только по-разному обозначенное.
Начало отсчета (или начало координат) — точка О изображает 0 (нуль). Само число 0 не является ни положительным, ни отрицательным. Оно отделяет положительные числа от от
рицательных.
Прямые могут находиться в различных положениях. Поэтому дополнительные лучи могут идти не только влево и вправо, но, например, вверх и вниз. Если прямая расположена горизонтально, то обычно положительными считают координаты точек, расположенных справа от точки О, а отрицательными — координаты точек, расположенных слева от точки О (см. рис. 49). Если прямая расположена вертикально, то положительными считают координаты точек, находящихся выше точки О, а отрицательными — точек, находящихся ниже точки О (рис. 50). Положительное направление отмечают стрелкой.
Прямую с выбранными на ней началом отсчета, единичным отрезком и направлением называют координатной прямой.
Число, показывающее положение точки на прямой, называют координатой этой точки.
Точка А на рисунках 49 и 50 имеет координату — 2 —, точ-4
ка В — координату — 3,6, а точка С — координату 3,6.
Пишут: А^ — 2 В ( — 3,6), С (3,6).
С координатной прямой мы встречаемся на уроках истории («линия времени»). Шкалу с положительными и отрицательными числами и нулем имеют термометры. Начало отсчета соответствует температуре таяния льда 0 °C. При 100 °C закипает вода.
©Что такое координатная прямая? Что называют координатой точки на прямой? Какими числами являются координаты точек на горизонтальной прямой, расположенных: а) справа от начала координат; б) слева от начала координат? Какую координату имеет начало координат? Какими числами
143
Рис. 51
обозначают координаты точек на вертикальной прямой, расположенных: а) выше начала координат; б) ниже начала координат?
© 875. Белка вылезла из дупла и бегает по стволу дерева вверх и вниз (рис. 51). Покажите, где будет находиться белка, если она удалится от дупла на 3 м. Сколько ответов можно дать на этот вопрос? Покажите на рисунке, где окажется белка, если она будет находиться: а) выше дупла на 2 м; б) ниже дупла на 3 м; в) ниже дупла на 1,5 м; г) выше дупла на 2,5 м.
876. Поезд вышел со станции Петропавловск (рис. 52) и идет со скоростью 90 км/ч. В какой город придет поезд через 3 ч? Где будет находиться поезд: а) через 10 ч,
если он идет в Новосибирск; б) через 5 ч, если он идет в Челябинск?
877. Из пионерского лагеря (рис. 53) выходит отряд пионеров и движется по шоссе. Покажите, где будет находиться отряд: а) через 3 ч, если он идет со скоростью 3 км/ч; б) через 2 ч, если он идет со скоростью 4 км/ч. Что еще надо знать, чтобы на каждый вопрос был только один ответ?
878. Находясь в походе, туристы оставили пакеты в пунктах К, М и Р (см. рис. 53). Где по отношению к лагерю находятся эти пункты?
144
879. Проведите горизонтальную прямую и отметьте на ней точку О. Отметьте на этой прямой точки А, В, С и К, если известно, что:
а) А правее О на 6 клеток; б) В левее О на 5,5 клетки;
в) С правее О на 7 у- клетки; г) К левее О на 2 клетки.
880. Измерьте в сантиметрах расстояние от точки О (рис. 54) до точек С и Р. Где на прямой находится каждая из этих точек по отношению к точке О?
С ' О Г
Рис. 54
881. Запишите координаты точек О, А, В, С, D, Р, К, М и Е (рис. 55). Начало отсчета — точка О.
-1012
Е МКР АО В CD
Рис. 55
882. Изобразите на координатной прямой точки А (1), В (8,3), С (— 6), D (6), М ( - 2,4), К (2,4).
883. Треугольный флажок находится в точке с координатой — 2, а прямоугольный — в точке с координатой + 2 (рис. 56). Отметьте и обозначьте начало отсчета и единичный отрезок. Запишите координаты точек В, С и D.
Рис. 56
VB Названия знаков -|- и — при числе во всех случаях по падежам не склоняют.
Например: а= -10 — а равно минус десяти х= +1,3 — икс равен плюс одной целой трем десятым — 15 левее — 7 — минус пятнадцать левее минус семи
145
884. Отметьте на координатной прямой точку, имеющую координату х, если х =— 7; 3,3; —5,2; — 1; 2; —1,8;-|-; —
3 л
885. Изобразите точкой на координатной прямой число а, если:
а) а=— 6; +3; —5; —8; +10; +9; +7; —7;
б) а = 2; -1; 3; -5; 4; О о
888. Найдите по шкале (рис. 57) высоты гор и глубины морей и океанов.
Метры
9000 8000 7000 6000 5000 4000 3000 2000 1000
О -1000 -2000 -3000 -4000 -5000 -6000 -7000 -8000 -9000 -10000 -11000 -12000
Рис. 57
887. На координатной прямой изображены точки А (— 2) и В (7). Найдите расстояние между точками А и В в единичных отрезках.
888. Назовите какие-нибудь три числа, расположенные на координатной прямой: а) правее числа 11; б) левее числа —8; в) левее числа —820; г) правее числа —78.
889. Установите на демонстрационном термометре столбик так, чтобы термометр показывал температуру: —12 °C, —11 °C, — 7 °C, +3°С, -8,5 °C, +7,3 °C.
146
890. На здании Московского университета установлен термометр со стрелкой (рис. 58). Какую температуру показывает этот термометр?
891. Из чисел —1,2; 0;
5 4
6; —3 —; 7,2; —10 и 8 выпишите 8
сначала все отрицательные, а потом все положительные числа.
892. Вычислите устно:
40
Рис. 58
а) 5 • 1,4 б) 10 : 4 в) 9-3,2 г) 2,3 + 5,7 Д) 6 : 12
-3,2 -1,2 + 0,5 : 5 • 1,6
: 0,2 • 6 : 9 -0,7 -0,35
• 0,4 + 1,2 • 0,3 1,1 + 0,15
+ 2,4 : 18 : 0,01 + 0,01 :4
? ? ? ? ?
893. Сколько натуральных чисел расположено на координатном луче между числами:
а) 0 и 8; б) 17,5 и 26; в) 2 и 9-^-; г) 116 и 117?
6 2
894. Какое из чисел — правильная дробь или дробь, ей обратная,— на координатном луче расположено ближе к единице?
895. Древнегреческий ученый Аристотель родился в 384 г., а умер в 322 г. Пифагор родился в 570 г. и умер в 500 г. Историк Плутарх родился в 46 г., умер в 127 г. Кто из этих ученых родился раньше? Сколько лет прожил каждый из них?
896. Площадь поверхности планеты Меркурий равна л 15
75 млн. км^ и составляет — площади поверхности планеты
Венера. Найдите площадь поверхности планеты Венера.
897. Вычислите устно:
.) 0.5-1-; в) з,15 (4-|—3f);
б) 3 А.(О,6 + 0,4); г) (?,8 —7-|-)«2-|-.
898. Найдите значение выражения:
а) 0,3 + (0,3)2 + (0,3)3; j__ zjx2. /j_\2 /м3
б) 0,5 —(0,5)2 —(0,5)3; ’ з I 3 ? ’ Цг M U Г
147
.899. Из цифр 7, 8, 3 и 5 составьте четыре различных числа, оканчивающиеся цифрой 7 и кратные 3.
900. На рисунке 59, а изображен цилиндр. Сверху и снизу цилиндр ограничен кругами, которые называются основаниями цилиндра. Развертка боковой поверхности цилиндра — прямоугольник. На рисунке 59, б изображена развертка поверхности цилиндра. Попробуйте вычислить площадь поверхности цилиндра, если его высота 5 см, а радиус оснований 2 см.
901. Решите задачу:
1) Бабушка купила 6 бубликов, 4 булочки по той же цене, что и бублики, и батон за 0,13 р. За все она заплатила 0,73 р. Сколько стоит одна булочка или одни бублик?
2) Дедушка купил внуку 7 тетрадей в клетку и по той же цене 6 тетрадей в линейку. Дедушка купил еще ручку за 0,35 р. За все он заплатил 0,61 р. Сколько стоит одна тетрадь?
3) Для работников завода построен дом на 240 квартир.
Трехкомнатные квартиры составляют 15% всех квартир и
3 числа однокомнатных квартир. Остальные квартиры двухкомнатные.. Сколько в доме двухкомнатных квартир?
4) На лодочной станции было 150 лодок. Трехместные лодки составляли 14% всех лодок и числа пятиместных лодок.
о
148
Остальные лодки были четырех местные. Сколько четырех местных лодок было на станции?
® 902. Где по отношению к узлу веревки находится каждая птица (рис. 60)? (Сторона клетки 1 дм.)
Рис. во
903. Начертите в тетради горизонтальную прямую и отметьте на ней точку О. Отметьте на этой прямой точки M,N,P и. К, если: а) М правее О на 14 клеток; б) N левее О на 15 клеток; в) Р левее О на 9 клеток; г) К правее О на 2 клетки. Напишите координаты точек М, N, Р и К, если единичный отрезок равен: а) одной клетке тетради; б) двум клеткам тетради.
904. Отметьте на координатной прямой точки М (— 4), N (3), Р( —8,5), К (7,5), С (-6), Г (6).
905. Приняв за единичный отрезок длину 6 клеток тетради, начертите координатную прямую и отметьте на ней точки К(Х). С(-ОЛ). D(-l.f). E(-l-). p(l-l-). Л(-А).
906. Начертите шкалу температур от — 60 °C до 60 °C, приняв отрезок длиной 1 см за 10 °C. Отметьте на этой шкале точку замерзания ртути ( — 39 °C), нормальную температуру человеческого тела (37 °C), точку замерзания бензина (— 60 °C), точку кипения ацетона (56 °C), точку замерзания глицерина (-20 °C).
907. Через реку построен мост длиной 234 м. Он имеет пять пролетов, четыре из которых имеют одинаковую длину, а пятый на 14 м длиннее каждого из остальных. Какова длина каждого пролета моста?
908. Экскурсантов можно посадить в лодки или по 4 человека, или по 6 человек. В том недругом случае свободных мест
149
не останется. Сколько было экскурсантов, если их больше 40, но меньше 50?
909. Пионеры за три дня собрали 560 кг семян различных деревьев. В первый день они собрали 35% всех собранных 7
семян, что составляло — количества семян, собранных во вто-о
рой день. Сколько килограммов семян было собрано в третий день?
27. Противоположные числа
Точки с координатами 5 и —5 (рис. 61) одинаково удалены от точки О и находятся по разные стороны от нее. Чтобы попасть из точки О в эти точки, надо пройти одинаковые расстояния, но в противоположных направлениях. Числа 5 н —5 называются противоположными числами: 5 противоположно — 5, а —5 противоположно 5.
Два числа, отличающиеся друг от друга только знаками.
называют противоположными числами. Например, противоположными
числами будут 8 и —8, так как число 8=-|-8, значит, числа 8 и —8 отличаются только знаками. Противоположными числами также будут
2,6 и —2,6; —1- и
8 8
Рис. 61
Для каждого числа есть только одно противоположное ему число.
Число 0 противоположно самому себе.
Число, противоположное числу а, обозначают —а. Если а = —7,8, то — а = 7,8; если а = 8,3, то — а— —8,3; если а = 0, то —а=0. Запись « — (—15)» означает число, противоположное числу —15. Так как число, противоположное числу —15, равно 15, то —( — 15) = 15.
Вообще — ( — а)=а.
Натуральные числа, противоположные им числа и нуль называют целыми числами.
150
©Какие числа называют противоположными? Число Ь противоположно числу а. Какое число противоположно числу Ь? Какое число противоположно нулю? Существует ли число, имеющее два противоположных ему числа? Какие числа называют целыми?
910. Найдите числа, противоположные числам:
-276; 124; -321; 62; 9; —1; 1; —7,8; —9; 0,5;
4-|-; 34“ 8 9
1
4 *
911. Поставьте вместо * такое число, чтобы получилось верное равенство:
а) -(-80)=*; в) -(-247)=*; д) -(--£)=*;
6)3,5=-*; г) 3,2= — *; е)7^= — *.
О Выражение —( — а) можно читать разными способами: — число, противоположное числу минус а — минус минус а
Например, предложение «Если k= — 7, то —k= —( — 7)» можно прочитать так:
— если ка равно минус семи, то минус ка равно числу, противоположному минус семи
— минус ка равно минус минус семи
912. Найдите значение выражения:
а) — т, если т= — 8; —16; —13;
б) k, если- Л = 27; -35; 7,1; -6,9; 80; -90; 7 10 о
в) —(—с), если с = 41; —3,6; 0; —2^-; 30 9
913. Найдите координаты точек А, В и С (рис. 62).
-3 3
В С А
Рис. 62
151
914. Каким числом является — х, если х: а) отрицательное; б) нуль; в) положительное?
915. Заполните пустые места в таблице и отметьте на координатной прямой точки, имеющие своими координатами числа полученной таблицы.
X 3 5 0 -6
X 4 -2 -1
916. Решите уравнение:
а) — х = 607; б) — а = 30,4; в) -у=— 3^.
16
917. Какие целые числа расположены на координатной прямой между числами:
а) — 8 и — 5; г) — 3,6 и 4,2; ж) 7 и — 4 ;
о 5
б) -3 и 0; Д) ~Т и 3; 3) —11 и — 3-|-?
в) -2 и 2; е)2|и5|;
918. Вычислите устно:
а) — б) 6 • — в) — : —
7 3 4 ' 3 ' 7 7
:5. +т :9 ? ? ? 919. Между какими целыми числами на координатной пря-
мой расположено число: 2,6; —3: 0; —6-^-; —0,8? О
920. Найдите числа, которые на координатной прямой находятся на расстоянии: а) 6 единиц от числа —9; б) 10 единиц от числа 4; в) 10 единиц от числа —4; г) 100 единиц от числа 0.
921. Начертите координатную прямую, приняв за единичный отрезок длину 4 клеток тетради, и отметьте на этой прямой точки а(—|-), В(0,5), С (-1,75), d(-2-1-), e(1-J-), F (2,25).
152
Н 922. Отметьте иа «линии времени» следующие события из истории математики: а) Книга «Начала» была написана Евклидом в III в. до н. э. б) Теория чисел зародилась в Древней Греции в VI в. до н. э. в) Десятичные дроби появились в Китае в III в. г) Теория отношений и пропорций была разработана в Древней Греции в IV в. до и. э. д) Позиционная десятичная система счисления распространилась в странах Востока в IX в. Сколько веков назад произошли эти события? Сравните «линию времени» и координатную прямую.
923. Укажите пары взаимно обратных чисел:
4 ; 1,1; 5; 24; 0,2; .
< о 11
924. Витя купил 2,4 кг моркови. Сколько моркови купил
Коля, если известно, что он купил:
а) на 0,7 кг больше Вити;
б) на 0,9 кг меньше Вити;
в) в 3 раза больше Вити;
г) в 1,2 раза меньше Вити;
Q
Д) у того, что купил Витя;
О
е) — того, что купил Витя; 4
ж) 0,5 того, что купил Витя;
з) 20% того, что купил Витя;
и) 120% того, что купил Витя;
к) на 20% больше того, что купил Витя?
925. Решите задачу:
1) Кирпичный завод должен был изготовить для строи-
тельства Дворца культуры 270 тыс. штук кирпича. В первую 4
неделю он изготовил — задания, во вторую неделю он изготовил
на 10% больше, чем в первую неделю. Сколько тысяч штук кирпича осталось изготовить заводу?
2) Колхоз продал государству за три дня 434 т зерна. В пер-
10 я
выи день он продал — этого количества, во второй день — 31
на 10% меньше, чем в первый день, а в третий день — остальное зерно. Сколько тонн зерна продал колхоз в третий день?
926. Ноты отличаются по длительности их звучания. Зна-
ком о обозначают целую, ноту вдвое короче — половин-
ную — J , четвертую —
восьмую —
шестнадца-
тую — J4 . Проверьте равенство длительностей:
а) ° — d J J ; б) J = J4 .
Найдите недостающую ноту:
927. Какие числа противоположны числам:
V 124; —124; 3 — ; —; 0,6; —2,85; —1; 0? 7 7
928. Запишите все натуральные числа, меньшие 5, и числа, им противоположные.
929. Найдите значение:
2
а) т, если — т = —; в) k, если —k =—0,2;
о . X Е 2
-х „ „ о 1 . г) —л, если п=—5 —.
б) — с, если с = 2 —; 7 7
5
930. Во второй день со склада выдали в 2 раза больше проволоки, чем в первый день, а в третий день в 3 раза больше, чем в первый. Сколько килограммов проволоки выдали в эти три дня, если в первый день выдали на 30 кг меньше, чем в третий?
931. В колхозе на поливных землях собирали с гектара 60,8 ц пшеницы. Замена старого сорта пшеницы новым дает прибавку урожая на 25%. Сколько теперь пшеницы собирает колхоз с 23 га поливного поля?
932. Составьте по каждой схеме уравнение и решите его:
933. Найдите значение выражения:
9:11,25
- «Г?-------8,45; б) ±П,81_+8Л9)А02_ 335
2 J \ 2. опок ~ ’
3 11 9 /71
28. Модуль числа
Расстояние точки М (— 6) от начала отсчета О равно 6 единичным отрезкам (рис. 63). Число 6 называют модулем числа -6.
Пишут: |— 61=6.
М(-6) О В(5)
........................—। । । 1—•—*—»—*—'—
6 единиц 5 единиц
Рис. 63
Модулем, числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а).
Модуль числа 5 равен 5, так как точка В (5) удалена от начала отсчета на 5 единичных отрезков.
Пишут: |5|=5.
Модуль числа-Q равен 0, так как точка с координатой 0 совпадает с началом отсчета О, т. е. удалена от нее на 0 единичных отрезков (см. рис. 63).
Пишут: |0| =0.
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного — противоположному числу. Противоположные числа имеют равные модули: | —а| = |а|.
Например, |7| =7; |-|-| =-|-; |1,5| =1,5; |0| =0; | -7| =7;
©Что называют модулем числа? Как обозначают модуль числа? Как найти модуль положительного числа или нуля? Как найти модуль отрицательного числа? Может ли модуль какого-нибудь числа быть отрицательным числом?
0934. Найдите модуль каждого из чисел: 81, 1,3; —5,2;
8 5 9
—; ——2—; —52; 0. Напишите соответствующие 9 < 4о
равенства.
935. Найдите значение выражения |х|, если х= —12,3;
12,3; -66; 83; 3^-; -6^| .
8’7’ 12
155
936. Найдите расстояние (в единичных отрезках) от начала отсчета до каждой из точек: А (3,7), В ( — 7,8), С ( — 200), D (315,6), Е(0), В(—1-), tf(4-|-).
937. Найдите значение выражения:
а) 1 —81 — 1 —5|; ж) 128,511: 1-2,3|;
б) | —10| -1 —151; э) 10,11-1- Ю|;
в) 12401: | —80|; и) 1-11- -1-11;
г) 1-7101-Ы-2901; к) 1-211 •111;
д) 1-2,31 + 13,71; л) 1*11- l-'ll;
е) 1-4,71-1-1,91; м) |-*1 1 = 1+1-
Q Выражения, содержащие модули, читают так:
| — 9 -|-| = 9-1-модуль минус девяти целых одной треть-
ей равен девяти целым одной третьей
938. Точка А лежит от начала отсчета влево на 5,8 единицы, а точка В — вправо на 9,8 единицы. Чему равна координата каждой точки? Чему равен модуль каждой координаты?
939. Найдите:
а) отрицательное число, модуль которого равен 25; —; 7,4;
б) положительное число, модуль которого равен 12; 1; — ; 3,2.
18
940. Напишите все числа, имеющие модуль: а) 26; б)-|-; в)3-^; г) 0; д) 5,7.
941. Известно, что |а| =7. Чему равен | —а|?
942. Из двух чисел выберите то, у которого модуль больше:
а) -5,87 и -7,82; в) -700,1 и 0,24; д) —^-и-|-; о W
б) -2,75 и 0; г) -2-|- и 3-|-; е)—и —L.
943. Среди чисел —( — 7); —3; -1-; —7; 3; —-у-укажите пары: а) противоположных чисел; б) обратных чисел.
944. Вычислите устно:
•> i-f б) 2-f в)||:8
• 2 : 13 • 17
. 3 • 9 -12.
7 8
: 13 : 2
? ? ?
м
945. Какое иэ чисел на координатной прямой расположено правее: —2 или —1; —6 или —7; 0 или —4,2; —11 или —15?
946. На рисунке 64, а изображен конус. Основание конуса — круг, а развертка боковой поверхности — сектор
(см. рис. 64, б). Вычислите площадь поверхности конуса, если радиус еГо основания 3 см, а развертка боковой поверхности — сектор с прямым углом, радиус этого сектора 12 см. Есть ли в
947. Найдите значение k, если — k равно —3,5; 6,8; Ч-;»;
о
948. Решите уравнение: а) — у=— 8,75; б) — р=—. о
949. Нина истратила в магазине 4,8 р. Сколько денег истратила Оля, если известно, что Нина истратила:
а) на 0,3 р. больше Оли;
б) на 0,5 р. меньше Оли;
в) в 2 раза больше Оли;
г) в 1,5 раза меньше Оли;
. 3 „
д) — того, что истратила Оля:
4
е) — того, что истратила Оля;
О
157
ж) 0,2 того, что истратила Оля; и) на 25% больше того, что истратила Оля;
з) 25% того, что истратила к) 125% того, что истратила Оля; Оля?
950. Найдите значение выражения:
1) £7+^. если m = 0,6-|-0,35:-^- и а = 3,4-2,3 —5,32; ха ой о 1о
2) если п = 1,8 -у+0,4:^- и х= 12,68-2,7-3,4.
951. Отметьте на координатной прямой числа, модули которых равны 3; 8; 1; 3,5; 5-|-.
952. Из двух чисел выберите то, у которого больше модуль: а) —45,1 и 8,31; г) -13,8 и —13,7; ж) —
б) —45,3 и 57,8; д)— 2уиЗу; з)уи-у.
в) 76,9 и -57,1; е) 2и — 5 у-;
953. Площадь первого поля составляет у- площади второго поля. Чему равна площадь второго поля, если площадь первого 12,6 га?
954. Премия Иванова составляет 75% премии Сергеева. Чему равна премия Сергеева, если премия Иванова 73,2 р.?
955. Скорость грузовика составила у- скорости легковой автомашины. Найдите скорость легковой автомашины, если скорость грузовика на 22 км/ч меньше скорости легковой автомашины.
956. Урожайность хлопка на первом поле на 12,5% меньше урожайности хлопка на втором поле. Какова урожайность хлопка на первом поле, если на втором поле она равня 28 ц с гектара?
псп гт - 36-1,5 + 3,6-85 , 11,88
957. Найдите значение выражения ------ 1 g----г q11 -
29. Сравнение чисел
Вчера в комнате термометр показывал 18 °C, а сегодня показывает 21 °C. Вчера в комнате было холоднее, чем сегодня. Число 18 меньше числа 21. Можно записать: 18 <21.
158
Вчера на улице термометр показывал —15 °C, а сегодня он показывает — 9 °C. Вчера было холоднее, чем сегодня. Поэтому считают, что —15 меньше —9. Пишут: —15<— 9.
Вчера на улице термометр показывал —10 °C, а сегодня он показывает 5 °C. Вчера было холоднее, чем сегодня. Число —10 меньше числа 5. Пишут: —10<5.
Любое отрицательное число меньше любого положительного числа. Из двух отрицательных чисел меньше то, модуль которого больше. Нуль больше любого отрицательного числа, но меньше любого положительного числа.
Например, — 7,5 <3, так как число —7,5 отрицательное, а число 3 положительное; —15 < — 9, так как числа —15 и — 9 отрицательные и модуль —15 больше модуля —9, т. е. | —151 > | —9|.
На горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой. На рисунке. 65 видим, что точка В (6) лежит правее точки А ( — 10), а точка А ( — 10) лежит правее точки С ( — 15).
-15 -10 0 б
--1 I I I 1-1 I I I'.». 4-4 ....... > -4 .............
С А 0 В
Рис. 65
©Какое число больше: положительное или отрицательное?
Какое из двух отрицательных чисел считают большим, чем другое? А какое из них меньшим? Какое из чисел больше: отрицательное или 0? Какое из чисел меньше: положительное или 0? Как расположены на координатной прямой точки А (а) и В(Ь), если а меньше Ь? если 0 больше Ь?
0958. Отметьте на прямой числа 0; 1; —3; —5; 8; —7; —2;
—10 и 3. Сравните: а) 0 и 3; б) 0 и —5; в) 8 и 0; г) —7 и 0; д) — 2 и 3; е) —7 и 1; ж) 1 и —10; з) 3 и —3; и) 1 и 8; к) —5 и —3; л) —5 и —10; м) — 2 и — 5.
D Неравенства, составленные из положительных и отрицательных чисел, читают так:
6 > — 4 — шесть больше минус четырех
— 8 < — 1 — минус восемь меньше минус единицы
159
959. В Ростове и Воронеже измеряли температуру 1, 6, 11, 16, 21 и 26 декабря в 12 ч дня. Результаты (в градусах Цельсия) указаны в таблице. Сравните температуру в Ростове и Воронеже в одно и то же время.
Число декабря
1 6 11 16 21 26
Температура в Ростове. °C 9,2 3.5 — 2,6 -3.1 - 7.8 -19
Температура в Воронеже, °C 6,4 0 0 - 1.5 -3,6 -21
960. Поставьте вместо * знак < или знак > так, чтобы
получилось верное неравенство:
а) 8,9 * 9,2; г) —5,5*—7,2;
б) —240*3,2; д) —96,9*—90,3;
в) 4,5 *—800; е) —1000*0;
44=
з) -2-I-* -4 4-О Z
961. Пользуясь таблицей, назовите города сначала в порядке возрастания их высоты над уровнем Мирового океана, а затем в порядке убывания.
Название города Высота над уровнем Мирового океана, м Название города Высота над урошем Мирового океана, м
Москва 150 Ереван 1100
С.-Петербург 5 Мехико 2240
Астрахань — 25 Париж 130
962. Сравните венсгва: числа и результат запишите в виде нера-
, 2 3 а) ‘ Т?ИТ = г) —2-|- и 3-|-; ж) -2f и -3-f-;
б) з и —4; о 7 „ 3 . . _ 5 _ 8 Д) ~10 —в"’ 3) ~5йИ -5 2Г •
<в 1 *1“ S 1 . 5 И е) —— и —— ; О Z4
160
963. Между какими соседними целыми числами заключено число:
а) -2,73; б) -9,5; в) —0,63; г) 0,87; д) -1 -|-; е) — 6 ?
Ответ запишите в виде двойного неравенства.
964. Известно, что х и у — положительные числа, а т и п — отрицательные. Сравните:
а) 0 и п; г) 0 и — т; ж) —т и п; к) — |тп| и т\
б) у и 0; д) х и т; з) — х и у, л) х и |х|;
в) —х и 0; е) п и х; и)' |т| и т; м) х и | — х|.
965. Запишите в виде неравенства предложение:
а) — 4,3 — отрицательное число;
б) 27,1 — положительное число;
в) а — отрицательное число;
г) Ь — положительное число.
0966. Белка сидит на дереве в точке М (4), а дятел — в точке N (— 3). Какое расстояние от дятла до белки? Кто из них дальше от дупла, если дупло принято за начало отсчета?
967. На улице температура а °C, а в квартире b °C. На сколько градусов температура в квартире выше, чем на улице? Решите задачу при: а) а = 12, 6 = 20; б) а= —11, 6 = 19.
968. Какие числа имеют модуль, равный 2; 1,7; 5 —; 0; 1; -(-4)?
969. Определите координаты точек В, С и D, если А (тп) (рис. 66).
_________________________________о_______т______________ Рис. ee D С О А В
970. Б старинной задаче имеются такие сведения: «Один купец имел 730 рублей и был должен другому 380 рублей. Второй купец имел 970 рублей и был должен первому 460 рублей». Сколько денег останется у каждого купца после взаимных расчетов? Попробуйте сформулировать задачу, используя понятие отрицательного числа.
971. При каких значениях а верно равенство а+ |а| =0 и при каких неверно?
972. Возраст Москвы около 850 лет, Новгорода 1100 лет, Рима 2700 лет, Александрии 2300 лет, Киева более 1400 лет. В каком веке возник каждый из городов?
6 Зак. 607
161
973. Найдите значение:
а) |х| —|у|, если х=— 64,1, «/=—7,6;
б) |х| + |j/|, если х=—54,5, «/ = 52,8.
974. Определите, у какого из двух чисел модуль больше:
а) —3,815 и —3,823; в) и 0,28;
1 о
6>-2Ти1Т: г>-ти-Й'
м
975. Из рисунка 67 видно, что куб можно составить из
шести одинаковых четырехугольных пирамид, у которых вершина О, а основаниями служат грани куба. Найдите объем пирамиды, если ребро куба 1,2 см. Найдите ребро куба, если объем одной пира-
Рже. 67
миды
— см3 6
976. Найдите неизвестный член пропорции:
1) 3,5:х = 0,8:2,4; 2) 6,8:2,5 = х:1,5.
977. Решите задачу:
1) Для приготовления компота смешали 2,5 кг яблок, 2 кг груш и 0,5 кг вишен. Найдите процентное содержание каждого вида фруктов, взятых для приготовления компота.
2) Смешали 0,16 кг грузинского, 0,52 кг азербайджанского и 0,12 кг индийского чая. Найдите процентное содержание каждого вида чая в полученной смеси.
978. Вычислите:
1) 61,71 :((14,42-13,74)-1,5) + 63,163:7,61;
2) 73,32:((15,41-14,76)-1,6)+ 55,186:6,73.
Проверьте результат вычислений с помощью микрокальку
лятора.
® 979. Поставьте вместо * знак > или < так, чтобы получилось верное неравенство:
а) —3542»—2763; г) —1,16*—1-^-;
О
б) -65,43*-65,39; д) -4~*—4-;
О 4
В) -4-* -0,7; е) -0,8 *-|-.
о о
162
980. Какие цифры можно написать вместо ♦, чтобы получилось верное неравенство:
а) — 384К—384*; г) —999,* >-999,1;
б) '—5 ♦ 83> —5183; Д)—^-<—у!
в) -♦ 5,44 >-25,44; е)
в 4
981. Расположите числа 2,8; 0,5; 0; —1; —1,1; 0,1 и —1,6: а) в порядке возрастания; б) в порядке убывания.
982. За контрольную работу 12 человек получили «5», 20 человек — «4», а остальные 8 человек — «3». Сколько процентов всех учащихся получили «5», сколько — «4» и сколько — «3»?
983. Найдите неизвестный член пропорции -^-:3,1 = х:9,3.
(4.4-4,15 + 1 + ):3-^
984. Вычислите: ___________15 60/ 3
(з 1 - 2,75 ) :0,2 — 2 А
30. Изменение величин
Температура может как повышаться, так1 и понижаться. Пусть, например, утром температура воздуха была 3 °C, в середине дня 9 °C, а вечером 7 °C. За первую половину дня температура повысилась на 6 °C, а за вторую половину дня понизилась на 2 °C. Повышение температуры выражают положительными числами, а понижение,— отрицательными. Так, если температура повысилась на 6 °C, то говорят, что ее изменение равно 6 °C или + 6 °C, если понизилась на 2 °C, то говорят, что ее изменение равно — 2 °C.
Длина пружины может как увеличиваться, так и уменьшаться. Увеличение длины пружины будем выражать положительными числами, а уменьшение — отрицательными.
Точка на координатной прямой может перемещаться влево или вправо по этой прямой. Перемещение точки вправо обозначают положительными числами, а перемещение влево — отрицательными (рис. 68).
Рис. 68 ______-5_____|_____+4___
-2 0 3 ... 7
СОА В
6*
163
Таким образом, увеличение любой величины можно выразить положительными числами, а уменьшение — отрицательными.
©В каком случае изменение температуры положительно, а в каком случае отрицательно? Что значит отрицательное изменение длины пружины? Что означает положительное перемещение точки по координатной прямой и что означает отрицательное перемещение точки по этой прямой? Каким числом выражается перемещение точки на координатной прямой влево и каким вправо?
0985. Объясните смысл предложения:
а) изменение температуры равно t °C, если t = 28; —30; — 8; 4,5; -1,7;
б) изменение длины пружины равно х миллиметрам, если х = = —10; 12; —9; — 4.
986. Изменение температуры равно m градусам. Чему равно т, если температура:
а) понизилась на 6 °C; б) повысилась на 3,6 °C; в) повысилась на 60 °C; г) понизилась на 3,4 °C?
987. Изменение длины пружины равно с мм. Чему равно с, если длина пружины:
а) увеличилась на 6 мм; б) уменьшилась на 5 мм; в) уменьшилась на 23 мм; г) увеличилась на 18 мм?
988. Прочитайте показания термометров, изображенных на рисунке 69.
Какую температуру будет показывать каждый из этих термометров, если температура изменится:
а) на —1 °C; б) на 1 °C; в) на 2 °C; г) на —2 °C?
989. Отметьте на координатной прямой точку А (2). Укажите:
а) точку В, в которую перейдет точка А при перемещении на —6;
б) точку С, в которую перейдет точка А при перемещении на 6;
в) точку D, в которую перейдет точка А при перемещении на —7;
г) точку Е, в которую перейдет точка А при перемещении на 3.
Назовите координаты точек В, С, О и Е.
164
Рис. 69
990. На сколько единиц переместилась точка Р (4) по координатной прямой, если она попала в точку К ( — 2)? А если она попала в точку Т (6)?
991. Среди чисел 1,6; — 2 -g-; 0; — ( —|- ); 12; —19 укажите числа: а) положительные; б) отрицательные; в) неположительные; г) неотрицательные; д) не являющиеся ни положительными, ни отрицательными.
992. Верно ли неравенство: a>b; d<a; b>c\ а>с\ d>b (рис. 70)?
с b
4- I
о
а
Рис. 70
165
м
993. На рисунке 71 под цифрой 1 показан вид фигуры спереди, а под цифрой 2 — вид сверху. Какая это фигура?
/
994. Сравните числа:
а) 0 и 800; г) — %- и —ж) -3,11 и —3,1; 9 9 5 J1
б) -45 и -20; Д) 4-5 и 2«4: з) —и И “Те •
в) -68 и 0; е) -А- и —; и 1и
995. Какие целые числа заключены между числами:
а) —4,8 и 2,85; в) —5,3 и —1,2; д) —84-й —З-^-;
7 5
б) -3,11 и 3,1; г)-2|иЗу; е)-3^и--|-?
996. Назовите какое-нибудь число, которое:
а) меньше 4-, но больше 5 5
5 6
б) меньше---—, но больше--;
7 7 ’
в) меньше 0,17, но больше 0,16.
997. Из всего собранного зерна пшеница составляла 80%, причем 70% этой пшеницы была пшеница твердых сортов. Сколько тонн зерна было собрано, если твердой пшеницы было собрано 560 т?
998. Площадь прямоугольника 11,7 дм2, ширина этого прямоугольника 2,6 дм. Все его стороны увеличили на 0,2 дм. Найдите площадь нового прямоугольника.
999. В воскресенье утром температура воздуха была — 2 °C. Какой стала температура воздуха в понедельник, если за сутки она изменилась: а) на —5 °C; б) на 3 °C; в) на 2 °C?
166
1000. Отметьте на координатной прямой точку С (— 4). Укажите точку В, в которую перейдет точка С при перемещении по координатной прямой на — 3, и точку D, в которую перейдет точка С при перемещении на -|-9.
1001. Отметьте на координатной прямой точку М (— 4). После перемещения по координатной прямой она попала в точку С (3). Чему равно перемещение?
1002. Имелась пачка бумаги. На перепечатывание одной ру-з
копией израсходовали — пачки. На перепечатывание другой О
рукописи ушло 0,8 остатка. Сколько листов бумаги было в пачке, если после перепечатывания этих двух рукописей в ней осталось 40 листов?
1003. Найдите значение выражения:
а) (8,74+ 0,66:13,2-3,79)-0,31; б) (9,68-0,77:15,4+0,87) 4,2.
Н Отрицательные числа появились значительно позже натуральных чисел и обыкновенных дробей. Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. Положительные числа тогда толковались как имущество, а отрицательные — как долг, недостача.
Но ни египтяне, ни вавилоняне, ни древние греки отрицательных чисел не знали. Лишь в VII в. индийские математики начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием.
В Европе отрицательными числами начали пользоваться с XII— XIII вв., но до XVI в., как и в древности, они понимались как долги, большинство ученых считали их «ложными» в отличие от положительных чисел — «истинных».
Признанию отрицательных чисел способствовали работы французского математика, физика и философа Рене Декарта (1596—1650). Он предложил геометрическое истолкование положительных и отрицательных чисел — ввел координатную прямую (1637 г.).
Р. Декарт
167
Окончательное и всеобщее признание как действительно существующие отрицательные числа получили лишь в первой половине XVIII в. Тогда же утвердилось и современное обозначение для отрицательных чисел.
§ в. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
31. Сложение чисел с помощью координатной прямой
Пусть температура воздуха равна 8 °C. Если она изменится на 3 °C (т. е. повысится на 3 °C), то она станет равной 11 °C (рис. 72): 8 + 3 = 11. Таким образом, температура стала равной сумме первоначального значения и изменения.
168
Пусть температура воздуха равна 8 °C. Если она изменится на — 3 °C (т. е. понизится на 3 °C), то она станет равной 5 °C (рис. 73). Будем и в этом случае записывать результат в виде суммы первоначального значения и изменения: 8-|-( — 3) = 5.
На рисунке 74 показано сложение числа 8 с числами 3 и — 3 на координатной прямой.
Рис. 74 г -з t +3
О 5 8 11
I I I I I I I I I I I Н I *-> <-»
О ВАС
Прибавить к числу а число b — значит изменить число а на b единиц.
Любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.
Пример 1. НАйдем сумму —7 и 4.
Решение. На рисунке 75 видно, что при перемещении точки А (— 7) на 4 единицы, т. е. на 4 единицы вправо, она переходит в точку В ( — 3). Значит, ( — 7)+ 4 = 3.
Рис. 75 ! +4 д
-7 -3 О
I । । I I I । । । ।--1 -» ।->— »
А ВО
Пример 2. Найдем сумму чисел —2 и —4.
Решение. На рисунке 76 видно, что при перемещении точки А (— 2) на — 4 единицы, т. е. на 4 единицы влево, она переходит в точку С ( — 6). Значит, ( — 2) +( — 4)=—6.
Рис. 76 [ -4|
~б -2
1 1 ‘ 1 1 ‘ I I t t । । । j
С АО
Пример 3. Найдем сумму чисел 4 и — 4.
Решение. На рисунке 77 видно, что при перемещении точки А (4) на 4 единицы влево она переходит в начало координат 0(0). Значит, 4 + ( —4) = 0.
Рис. 77
169
Сумма двух противоположных чисел равна нулю: о + (— а) = 0.
Пример 4. Найдем сумму чисел — 5 и 0.
Решение. Прибавить к числу — 5 число 0 — значит изменить число — 5 на 0. Другими словами, оставить число — 5 без изменения. Поэтому (— 5) + 0 = — 5.
От прибавления нуля число не изменяется: а + 0=а.
©Что значит прибавить к числу а число Ь? К числу а прибавили число Ь; как изменится число а, если Ь положительное, если Ь отрицательное, если Ь = 0? Чему равна сумма противоположных чисел? Запишите вывод в виде равенства, содержащего букву.
© 1004. Найдите с помощью координатной прямой сумму чисел:
а) —1 и 2; в) —3 и 6; д) — 5 и 6; ж) —и
О о
б) 3 и —4; г) 1 и —5; е) — 3 и — 2; з) — 1-^-и —
О о
О Сумму, в которую входят отрицательные числа, читают так: ( — 4) +( — 6) — сумма минус четырех и минус шести
— к минус четырем прибавить минус шесть
1005. Выполните сложение чисел:
4 и 0; 0 и —3; —5 и 0; —3 и 3; 7 и —7.
1006. Найдите значение выражения:
а) (-3,9+ 3,9)+(-9,1); б) 0+ (4,8+ (-4,8)).
1007. На координатной прямой отмечены числа а и а + 1 (рис. 78). Изобразите на этой же прямой числа а+ 2; а + ( —3); а + ( — 4,5); а+ ( —
а а+1 I ।---Illi-------1--1.................. ►
Рис. 78
170
1008. На координатной прямой точке А соответствует число а + 4, а точке В — число а-|-( — 4). Какое число соответствует середине отрезка АВ?
1000. Температура воздуха была — 2 °C. Какой стала температура воздуха, когда она изменилась на 3 °C; на 1 °C; на 2 °C; на —3 °C; на 5 °C; на —4 °C? Сложение чисел выполняйте с
помощью координатной прямой.
1010. Вычислите устно:
а) 3 : 6 б) 0,4 • 4 в) 2 : о г) 1-i
• 8 4-5,2 1 12 •4
-1.8 — 2 1_ . 3
4 4
-0,18 : 6
? ? ? ?
1011. Назовите координаты точек A, K,C,D,M и В (рис. 79).
А КС
О /
D М 'В
Рис. 79
1012. Какие числа на координатной прямой удалены:
а) от числа 4 на 5 единиц; б) от числа —1 на 3 единицы;
в) от числа —6 на 4 единицы?
1013. Сколько целых чисел расположено между числами — 50,5 и 50,5?
1014. Может ли быть положительным, отрицательным, нулем выражение: а) —а; б) — (—а)?
1015. Найдите сумму: I —7Ц-|—3|; | — 2,31 4~ I — 0,81;
I -1-1 + 141 = 141 + 1 -fl-
1016. Сравните числа:
а) —5,2 и —3,7; в) — 3и —1;
5 6 . 3 7
б)——и——; Г>-Ти—г-
1017. 78% всех выстрелов попало в цель. Сколько было сделано выстрелов, если в цель попало 156 пуль?
1018. От провода длиной 13 м отрезали 30% его длины.
Сколько метров провода осталось?
171
1019. Из 15 срезанных цветов 9 завяло. Сколько процентов срезанных цветов завяло?
1020. Стенной шкаф имеет высоту 1,8 м. Его глубина составляет 30% высоты, а ширина 250% глубины. Найдите объем шкафа.
1021. Выполните действия:
1) б 1,7 • 52,1 — 43,6 •(( 119,62 + 218,48); 13,8);
2) 73,2-48,3-37,4-((166,02+ 219,38): 16,4).
Ш 1022. На рисунке показаны две башни Московского Кремля — Арсенальная и Тайницкая. Рассмотрите форму отдельных их частей: использованы ли архитекторами известные вам фигуры — призма, цилиндр, пирамида, конус? Проверьте, нет ли элементов, размеры которых находятся в отношении золотого сечения.
172
® 1023. Найдите с помощью координатной прямой сумму чисел:
а) —4 и 5; в) —6 и Q; д) 8 и —8; ж) 0 и —3;
б) 3 и —2; г) —7 и 0; е) —би —5; з) —1 и —8.
1024. В пятых классах школы 80 человек. Из них отличники
составляют 21,25%. В шестых классах 90 человек. Отличники
составляют 20%. В сколько человек?
Рас. 80
каких классах больше отличников и на
1025. Найдите объем прямоугольного параллелепипеда, длина которого 21 см, а ширина составляет -|- длины и 30% высоты.
1026. Найдите значение выражения: а) (203 — 20,809 — 1504-83,079): :(1,3472 4-1,1528);
б) 30,3 • (124,9 - (48,96:6,8 4- 36,04): 9,2).
32. Сложение отрицательных чисел
Пусть температура воздуха была равна — 6 °C, а потом она изменилась на — 3 °C (т. е. понизилась на 3 °C). Тогда она станет равной —6-|-( — 3) градусам (рис. 80). Чтобы сложить числа —би — 3 с помощью координатной прямой, надо точку А(— 6) переместить влево на 3 единичных отрезка (рис. 81). Получим точку В (— 9). Значит, — 6 -|--|-( — 3)= — 9. Но 9 = 64-3, причем 6=|-6|, а 3=|—3|.
Рис. 81
। * ।
В А
0
о
173
Чтобы сложить два отрицательных числа, надо: 1) сложить их модули; 2) поставить перед полученным числом знак « — ».
Например,
- 8,7-Н-3,5)= -(8,7 4-3,5)= -12,2;
Сформулируйте правило сложения отрицательных чисел. Может ли при сложении отрицательных чисел получиться нуль? отрицательное число?
© 1027. Число —2 изменили на —5. С какой стороны от начала отсчета расположено полученное число? Чему равно его расстояние от начала отсчета? Чему равна сумма чисел — 2 и —5?
1028. В первую половину ночи температура изменилась на — 5 °C, во вторую — на — 4 °C. На сколько градусов изменилась температура за ночь?
1029. Выполните сложение:
а) -35-Н-9); д) -1,6+(-4,7); и)
б) -7+(-14); е) -5,6+(-2,4); к) —1-+(—£-);
в) —17+( —8); ж) -8,8+ (-4,2); л) — 1-|-+( — 2-f-);
г) -5+(-238); з) -1,75+ (-8,25); м) -5-^+(-3^-).
1030. Поставьте вместо * знак < или > так, чтобы получилось верное неравенство:
а) —17+( — 31)* —17; б) —22 + ( —35) * —35.
1031. Найдите значение выражения х + у+( —16), если:
а) х=—17, {/=-29; б) х=-9,1, {/=-7,4;
в)х=-з£, У=~2^.
1032. Найдите значение выражения:
а) (-0,251 +(-0,37))+(-0,2 + (-0,152));
6>(-3т+(-4т))+(-1т+(-2п))-
174
1033. Вычислите устно:
а) 2 : 4 . • 3 б) 6 • 0,6 4-1,2 в) . 1 г> т+т . 1 1
-1,2 : 0,4 2 1 3
: 0,1 0,3 3 5_
? ?
?
?
1034. Расположите числа —15; —8,8; 3; — —; —5,5;
5 7
-10-^-; 0; —10-|-; —8,2; 1 в порядке убывания, о 7 7
1035. Известно, что х и у — положительные числа. Сравните:
а) 0 и х; в) — х и у, д) |х| и —х; ж) —хи |«/|;
б) —у и 0; г) у и —х; е) |«/| и у; з) |— х| и — у.
1036. При каких значениях т верно неравенство: а) т> — т\ 6) —т>т; в) т>т-{-т?
1037. На координатной прямой отмечены точки А (х)иВ({/). Найдите координату середины С отрезка АВ, если: а) х = 4, у = 8; б) х= — 2, у — — 4; в) х= — 3, у = 5.
1038. Объем цилиндра равен произведению площади одного его основания и высоты. Объем конуса в 3 раза меньше
объема цилиндра с такими же основанием и высотой (рис. 82). Вычислите объем цилиндра и объем конуса, у которых высоты по 12 см и радиусы оснований по 2 см.
м
1039. Выполните действия:
1) ((169,68:5-|—22-|-)-9-|- + 9,7)-22,5;
2) ((253,26:6,3- 31,7) .8 -I-+ 7 -I-Y 32 -J-.
\ О 5 / и
175
1040. Выполните сложение:
а) -464-(-18); д) -5,8+(-1.8); и) -^-+(—
б) -8+(-12); е) -3.74+(-1.74); к) — 3-£-+( —1;
в) _ 144 + (-56); ж) —|-+(__1_); л) _1|_+(_2>8);
г) -6.4+(-3.6); з) —1-+(~|-): м) — 11_(_2,25).
1041. Найдите значение выражения:
»(-3.25+ (-+))+ (-*т+ (-+));
1042. Сплавили кусок меди, объем которого 15 см3, и кусок цинка, объем которого 10 см3. Какова масса 1 см3 сплава, если масса 1 см3 меди 8,9 г, а масса 1 см3 цинка 7,1 г? Результат округлите до десятых долей грамма.
1043. В бассейн налили 1400 м3 воды, что составляет 35% объема всего бассейна. Чему равен объем всего бассейна?
1044. Решите уравнение:
a)
о У
б>£*-лг*=0’51;
в) х — 0,2х=— .
’ 15
' 33. Сложение чисел с разными знаками
Если температура воздуха была равна 9 °C, а потом она изменилась на — 6 °C (т. е. понизилась на 6 °C), то она стала равной 9+(— 6) градусам (рис. 83).
176
Чтобы сложить числа 9 и — 6 с помощью координатной прямой, надо точку А (9) переместить влево на 6 единичных отрезков (рис. 84). Получим точку В(3).
Рис. 84 -6।
0 3 9
---1 I ।-----►—I----1--1—।----1 I I I I I----------* »
О В А
Значит, 9+( — 6)=3. Число 3 имеет тот же знак, что и слагаемое 9, а его модуль равен разности модулей слагаемых 9 и —6.
Действительно, 131 = 3 и 191 — | —61 = = 9 6 = 3.
Если та же температура воздуха 9 °C изменилась на —12 °C (т. е. понизилась на 12 °C), то она стала равной 9+( —12) градусам (рис. 85). Сложив числа 9 и —12 с помощью координатной прямой (рис. 86), получим 9 + +(—12)= —3. Число —3 имеет тот же знак, что и слагаемое —12, а его модуль равен разности модулей слагаемых —12 и 9.
Действительно, |—3|=3 и | —121 — — 1—91=12 — 9 = 3.
Чтобы, сложить два числа с разными знаками, надо: 1) из большего модуля слагаемых вычесть меньший; 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
Обычно сначала определяют и записывают знак суммы, а потом находят разность модулей.
В О
Рис. 8в
177
Например:
1) 6,14-(-4,2) =4-(6,1-4,2) = 1,9, или короче 6,14-( — 4,2) = 6,1 — 4,2 = 1,9;
2) — 3—4-4 —=4——3—=1—;
1 7 7 7 7 7 ’
3) 2,7 4-(-3,4)=-(3,4-2,7)=-0,7;
4) -8^--|-2-|-=-(8-|—2-|-)=-(8^-2A)=_6_L.
При сложении положительных и отрицательных чисел можно использовать микрокалькулятор. Чтобы ввести отрицательное число в микрокалькулятор, надо ввести модуль этого числа, потом нажать клавишу «изменение знака» /—/ . На
нажимать клавиши:
пример, чтобы ввести число —56,81, надо последовательно
5 , 6 , * , 8 , 1 , /—/ . Опера
ции над числами любого знака выполняются на микрокалькуляторе так же, как над положительными числами.
Например, сумму —6,14-3,8 вычисляют по программе
6 1 /—/ 4-3 • 8 = . Короче эту програм
1
8
му пишут так: —6,1 4- 3,8 = .
© Числа а и Ь имеют разные знаки. Какой знак будет иметь сумма этих чисел, если больший модуль имеет отрицательное число? если меньший модуль имеет отрицательное число? если больший модуль имеет положительное число? если меньший модуль имеет положительное число? Сформулируйте правило сложения чисел с разными знаками. Как ввести в микрокалькулятор отрицательное число?
01045. Число 6 изменили на —10. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 6 и —10?
1046. Число 10 изменили на —6. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 10 и -6?
178
1047. Число —10 изменили на 3. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма — 10 и 3?
1048. Число —10 изменили на 15. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма —10 и 15?
1049. В первую половину дня температура изменилась на — 4 °C, а во вторую — на 4-12 °C. На сколько градусов изме-
нилась температура в течение дня?
1050. Выполните сложение:
а) 26-Н-6); ">т+ -т • н) — 3-|“4-2-+;
б) —704-50; О 1
в) -174-30; ->т+(-т)' о) -—4-5— ; 8 16
г) 80 4-( — 120); S я
д) -6,34-7,8; л) -—+4; о 4 п) 2т+(-3п)’
е) -94-10,2; 4 2
ж) 14-(-0,39); м) ——+—; * 5 ' 3 р) 5т+(-5т)-
з) 0,3 4-(-1,2);
1051. Прибавьте:
а) к сумме —би —12 число 20;
б) к числу 2,6 сумму —1,8 и 5,2;
в) к сумме —10 и —1,3 сумму 5 и 8,7;
г) к сумме 11 и —6,5 сумму —3,2 и —6.
1052. Какое из чисел 8; 7,1; —7,1; —7; —0,5 является корнем уравнения —64* =—13,1?
1053. Угадайте корень уравнения и выполните проверку: а) х4-(-3)=-11; в) т + (-12) = 2;
б) — 54-г/=15; г) 3 + п= —10.
1054. Найдите значение выражения:
«) (4+(-о.5))+(-14); •> -3’7+(-5зг+3^);
»)(о.в+т)+(-2Т5); r>f+(-W+f)-
1055. Выполните действия с помощью микрокалькулятора: а) —3,2579-Н —12,308); г) -3,85644-(-0,8397)4-7,84;
б) 7,8547-|-(-9,239); д) -0,083 4-(-6,378) 4-3,9834; в) —0,001544-0,0837; е) —0,0085 4-0,003544-( — 0,00921).
179
1056. Найдите
а) -1б+(-38);
б) -2,3 4-(-3,9);
'>-!-+(Ч);
д) -0.25+ (_!-);
значение суммы:
е> -1+(~г)!
ж) -0.2+ (-i)
Э)2-+1+(-Л);
и) -124- (-юЦ
1057. Найдите значение выражения:
а) — 1,2 4-(—1.3 4-( — 1,4)); б) (-3-|-+(-2^ ))4-(-3-|-).
1058. Сколько целых чисел расположено между числами: а) 0 и 24; б) —12 и —3; в) —20 и 7?
1059. Представьте число —10 в виде суммы двух отрицательных слагаемых так, чтобы:
а) оба слагаемых были целыми числами;
б) оба слагаемых были десятичными дробями;
в) одно из слагаемых было правильной обыкновенной дробью.
1060. Каково расстояние (в единичных отрезках) между точками координатной прямой с координатами:
а) 0 и а; б) —а и а; в) —а и 0; г) а и —За?
м
1061. Радиусы географических параллелей земной поверхности, на которых расположены города Афины и Москва, соответственно равны 5040 км и 3580 км (рис. 87). На сколько параллель Москвы короче параллели Афин?
1062. Составьте уравнение для решения задачи: «Поле площадью 2,4 га разделили на два участка. Найдите площадь каждого участка, если известно, что один из участков:
а) на 0,8 га больше другого;
б) на 0,2 га меньше другого;
в) в 3 раза больше другого;
г) в 1,5 раза меньше другого;
V 2
д) составляет — другого; О
е) составляет 0,2 другого;
ж) составляет 60% другого;
з) составляет 140% другого»
180
1063. Решите задачу:
1) В первый день путешественники проехали 240 км, во второй день 140 км, в третий день они проехали в 3 раза больше, чем во второй, а в четвертый день они отдыхали. Сколько километров они проехали в пятый день, если за 5 дней они проезжали в среднем по 230 км в день?
2) Заработок отца в месяц равен 280 р. Стипендия дочери в 4 раза меньше. Сколько зарабатывает в месяц мать, если в семье 4 человека, младший сын — школьник и на каждого приходится в среднем 185 р.?
1064. Выполните действия:
1) (2,35 + 4,65)-5,3:(40— 2,9); 2) (7,63^-5,13)0,4:(3,17 + 6,83).
1065. Выполните сложение:
а) 17 + (-5); з) — 3,84 + 4,16; м) - i+f;
б) -21 + 19; и) 2_ . 5 . н) — 2 + 1-|-;
в) —8+( — 43); 9'9*
г) -15+ (-18); к) о) з+
д) -0,5 + 6; 7 7 \ 7 )
е) -2,4+ (-3,2); л) т+(-п)= п) 2f+(-1T
ж) 6,1+(-8,3); р)
-5 4-+4,5. о
1066. Представьте в виде суммы двух равных слагаемых каждое из чисел: 10; —8; —6,8; ——3 — ; 1—.
7 9 5
1067. Найдите значение а + Ь, если:
а) а= —1,6, 5 = 3,2; б) а= —2,6, 5 = 1,9; в) а=-^-,5 = -?-. о 4
1068. На одном этаже жилого дома было 8 квартир. 2 квартиры имели жилую площадь по 22,8 м2, 8 квартиры — по 16,2 м2, 2 квартиры — по 34 м2. Какую жилую площадь имела восьмая квартира, если на этом этаже в среднем па каждую квартиру приходилось по 24,7 м2 жилой площади?
1069. В составе товарного поезда было 42 вагона. Крытых вагонов было в 1,2 раза больше, чем платформ, а число
цистерн составляло числа платформ. Сколько вагонов каж-дого вида было в составе поезда?
3 15. 5
1070. Найдите значение выражения 3JL1 .
181
34. Вычитание
Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому.
Например, 8 + 3 = 11, и потому 11 — 8 = 3. Но 11-|-( — 8) тоже равно 3.
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: а — Ь=а + ( — Ь).
Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.
Например, —18 —14=—18 + (—14); —8Ц-6 — k=—8-|-+ 6+(-Л).
Разность двух чисел положительна, если уменьшаемое больше вычитаемого, и отрицательна, если уменьшаемое меньше вычитаемого. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.
Задача. Чему равна длина отрезка АВ, если А (— 5) и В (9)?
Решение. Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т. е. сколько надо прибавить к числу — 5, чтобы получилось число 9. Поэтому если обозначить длину отрезка АВ буквой х, то —5-|-х = 9.
Отсюда х = 9 —( —5); х = 14. .
Значит, длина отрезка равна 14 ^единичным отрезкам.
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
©Что означает вычитание отрицательных чисел? Каким действием можно заменить вычитание числа а из числа Ь?
Ответ запишите в виде соответствующего буквенного равенства. Как найти длину отрезка на координатной прямой?
01071. За день температура воздуха изменилась на —12 °C и к вечеру стала равна — 8 °C. Какой была температура утром?
182
1072. Температура воздуха утром была 5 °C, а к вечеру она стала равной — 2 °C. На сколько градусов изменилась температура воздуха за день?
1073. Вчера термометр показывал х °C, сегодня температура понизилась на 12 °C. Какую температуру показывает термометр сегодня, если х=25; 12; 6; 0? Решите задачу двумя способами: сложением и вычитанием.
1074. Проверьте равенство а — ( — Ь)=о + Ь, если:
а) а =18, 5 = 16; г) а= — 4,8, 5 = 3,9;
б) а =—2,3, Ь= —0,5; д) а=--|-, 5=-|-;
в) а = 44, 5=-7; е) а= -3 , Ь = -2 .
О Разность, в которую входят отрицательные числа, читают так:
( — 7)—(—12) — разность минус семи и минус двенадцати — из минус семи вычесть минус двенадцать — от минус семи отнять минус двенадцать
1075. Выполните вычитание:
а) io—( — 3); ж) 2,5-8,5; н) (~);
б) 12—( — 14); з) 0—( —40,6); о)—1;
в) -21-(-19); и) 0-64,8; п) —L-(—2А
г) 9-(-9); к) — 7,62—( — 7,62);
д) -1,4-1,4; л) -0,21-0; с) -1-|—
е) —5,6—( — 3,1); м) -3-^-0,75; т) 1±-_2А.
1076. Решите уравнение и выполните проверку:
а) -2 + х = 4,3; в) 5-х=1,7; 10 о
б) 8,l + i/= -6; г) 4-i/=-2-|-; е) z + 0,4= -1 о о
183
1077. Представьте в виде суммы разность: а) —28 —( — 32); в) 50-(-24); д) -30-р;
б) —46—30; г) х —80; е) 6—(—а).
1078. Назовите каждое слагаемое в сумме:
а) — 8 + х; в) — т — 25; д) — п + 9 — Л;
б) z —6; г) 10 — а-\-у; е) —а — Ь — с.
1079. Составьте сумму из следующих слагаемых:
а) —х; — у; —4,8; в) р; —20; 6; —Л; 10,3;
б) 1,5; —а; Ь; —с; г) —7,6; т; —п; — Г, —I.
1080. Найдите значение выражения:
а) (62-28)-40; ж) (14,5 -85) + 55,5;
б) —50 + (37 + 30); з) ( — 2,1 + 3,7)+ 4,4;
в) —6 —( — 8 —20); и) ( —1-|—2-|-) + 2,5;
г) —7—( — 12+13); к) (-4f+3-^)-l-|-;
д) 4,1-(-1,8 +2,5); л) -2(-32-±-);
е) (-3,2+ 60)-0,8; м) -3,15-(-4 -|~ + 3
1081. Найдите расстояние между точками А (а) и В (5), если: а) а = 2, 5 = 8; в) а——1, 5 = 6; д) а = 3,2, 5=—4,7;
б) а=—3, 5=—5; г) а = 5, 5=—4; е) а = 8,1, 5=—2,5.
1082. Выполните сложение:
W a) 3,8 + (-8,9); в)—Д)_1А+А;
«5 0 О О
б) -3,4+ 2,5; г) 1-|-+ ( —|-); е) 4+(-3-|-).
1083. Найдите значение выражения:
а) 3,75 + ( —2,11)+1,36; б) — 4,27 + (-3,11) + ( — 0,62).
3 1
1084. Найдите число, противоположное —7,2; —; —2 — ; О 7
3,85.
1085. Решите уравнение:
а) —х = 3,5; г) -т = -6 -|-+5 ;
б) -р=—д) —Л = 11 + ( —12,3);
в) —х=— 7,2 + 9; е) -у = -13+ (-8 £ ).
1086. Между какими соседними целыми числами расположено число: —21; 2-^-; —-Д- ; —7,2; —V'?
о У 11 о
184
1087. Запишите все целые числа, модули которых: а) меньше 4; б) больше 4 и меньше 10.
1088. Может ли сумма двух чисел быть меньше: а) одного из слагаемых; б) каждого из слагаемых? Приведите примеры.
1089. Высота конуса 24 см, а площадь основания 15 см2.
Какой высоты должен быть цилиндр с такой же площадью
основания, чтобы его объем был равен объему конуса (рис. 88)? Нет ли в задаче лишних данных?
м
1090. На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свеклы, а капусты — на 80 кг больше, чем свеклы. Сколько килограммов каждой культуры было собрано?
1091. Решите задачу:
1) В трех ящиках 21 кг гвоздей. В первом ящике в 1 — раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика 2 г,
составляет — массы гвоздей второго ящика. Сколько килограммов гвоздей было в каждом ящике?
2) В овощеводческом совхозе помидоры, огурцы и морковь занимали 560 га. Посевы моркови составляли у- площади, „ 7
занятой под огурцами, а под огурцами занято — площади, О отведенной под помидоры. Как велика площадь, занятая в отдельности помидорами, огурцами и морковью?
1092. Выполните действия:
1) 40,1 - 4,06 (29,58:3,48) + 8,112:0,78;
2) 50,2 —3,04 (45,22:4,76)+ 9,202:0,86.
185
1093. Выполните действие:
а) 26 —( — 5); и) н) f-0,7;
б) -4+(-18); 12 \ 12/ 5
в) 14 —( — 18); K)_3J__/ ill °) ———( — 0,4);
г) 10 — 7; 2 V 4 "
д) 4,7-8,1; Л) 2^—3-5-; п) “3,2-2 -L;
е) -3,34-9,6; 3 9
ж) 7-(-4,9); м) -1-5-1-р) 7,8-8-i-.
з) —5 —( — 2,9); 8 4
1094. Найдите значение выражения (а 4- Ь) — с, если: а) а = 2,6, Ь= —1,4, с = 2,1; б) а=Ь=— 2,4, с =—3,9.
1095. Отметьте на координатной прямой точки А (— 4) и В (9). Найдите расстояние между точками А и В в единичных отрезках.
1096. Найдите расстояние в единичных отрезках между точками:
а) А (-7) и В (-3); в) и ЙГ(-£-);
б) Af (2,3) и АГ (-4,2); г) с(-2-|-) и ©(if).
1097. Найдите значение выражения:
а) 24 —( —13) —(—12); г) 4,7-(-2)-(-1,5);
б) _33 —16 —(—11); д)
7 о 10
в) -4,3-5,4-2,6; е) — 7^-4-4-|—1,2.
15 о
1098. Заполните пустые места таблицы:
Команды «Звезда» «Орел» «Трактор» «Сокол» «Чайка»
Число забитых мячей 49 37 21 в
Число пропущенных мячей 28 23 35
Разность забитых и пропущенных мячей 33 — в — 22
1099. Для учащихся было куплено 70 билетов в кукольный театр. В партер было куплено билетов в 1,5 раза больше, чем на
186
балкон и бельэтаж вместе. Число билетов на балкон составило 0,4 от числа билетов на бельэтаж. Сколько билетов каждого вида было куплено?
1100. В альбоме 1105 марок, число иностранных марок составило 30% от числа советских марок. Сколько иностранных и сколько советских марок было в альбоме?
1101. В доме 300 квартир. Однокомнатные квартиры составляют 28% всех квартир дома, а остальные квартиры — двухкомнатные и трехкомнатные, причем двухкомнатных квартир в 1,7 раза больше, чем трехкомнатных. Сколько квартир каждого вида в доме?
Н Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры.
Индийские математики представляли себе положительные числа как «имущества», а отрицательные числа — как «долги». Вот как индийский математик Брахмагупта (VII в.) излагал правила сложения и вычитания: «Сумма двух имуществ есть имущество», «Сумма двух долгов есть долг», «Сумма имущества и долга равна их разности» и т. д. Попробуйте перевести эти древнеиндийские правила на современный язык.
§ 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
35. Умножение
Задача 1. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход ткани на один костюм изменился на 0,4 м2. На сколько изменился расход ткани на костюмы за день?
Решение. Расход ткани на каждый костюм увеличился на 0,4 м2. Поэтому, чтобы решить задачу, надо умножить 0,4 на 200. Получим 0,4-200 = 80. Значит, расход ткани на костюмы за день увеличился на 80 м2, иными словами, изменился на 80 м2.
Задача 2. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход
187
ткдни на один костюм изменился на —0,4 м2. На сколько изменился расход ткани на костюмы за день?
Решение. Расход ткани на каждый костюм уменьшился на 0,4 м2. Поэтому расход ткани на костюмы за день уменьшился на 80 м2 (0,4-200=80). Это значит, что расход ткани на костюмы за день изменился на —80 м2.
Таким образом, произведение —0,4 и 200 равно —80, т. е. — 0,4 • 200= — (0,4 • 200) = — 80.
Считают, что и 200 •( — 0,4)=-(200-0,4)=—80.
Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак * — ».
Например, (— 1,2) • 0,3 = — (1,2 - 0,3) = — 0,36;
1,2 ( — 0,3)= — (1,2-0,3)= —0,36.
Сравнивая эти два произведения с произведением 1,2-0,3 = = 0,36, можно заметить, что при изменении знака любого множителя знак произведения меняется, а его модуль остается тем же.
Если же меняются знаки обоих множителей, то произведение меняет знак дважды и в результате знак произведения не меняется: 8-1,1 = 8,8; ( — 8)-1,1= — 8,8; ( —8)-( —1,1)=—(—8,8) = = 8,8. Видим, что произведение отрицательных чисел есть число положительное.
Чтобы перемножить два отрицательных числа, надо перемножить их модули.
Например, (— 3,2) • (— 9) = | — 3,21 • | — 91 = 3,2 • 9 = 28,8. Обычно пишут короче: (— 3,2)•( — 9) = 3,2-9 = 28,8.
Так как (— 3) • 2 = — (3 • 2), то можно первый множитель писать без скобок, т. е. (— 3) • 2 = — 3 • 2.
©Сформулируйте правило умножения двух чисел с разными знаками. Как перемножаются два отрицательных числа?
©1102. Уровень воды в реке изменяется каждые сутки на а дм. Как изменится уровень воды в реке за 3 суток, если а = 4; -3?
1103. При увеличении температуры воздуха на 1 °C столбик ртути в термометре поднимается на 3 мм. На сколько изменится высота столбика ртути, если температура воздуха изменится: а) на 15 °C; б) на —12 °C?
188
1104. Турист движется по шоссе со скоростью v км/ч. Сейчас он находится в точке 0 (рис. 89). Если он движется в положительном направлении, то его скорость считают положительной, а в отрицательном направлении — отрицательной. Значение t= —4 означает «4 ч тому назад».
Где будет находиться турист через t ч? Решите задачу при следующих значениях букв:
a) v = 5, t = 4; б) v= — 5, t = 4; в) v = 5, t—— 4; г) v=— 5, t = — 4.
-20 -15 -10 -5 0 5 10 15 20
Рис. 89
1105. Выполните умножение:
а) -5-6; ж) 0,7-(-8); н) 1,2-(-14);
б) 9-(-3); з) -0,5-6; о) —20,5-( — 46);
в) - 8-(-7); и) 12 ( — 0,2); п) -8,8-302;
г) -1011; к) —0,6-( — 0,9); р) -9,8 ( — 50,6);
д) - И(-12); л) —2,5-0,4; с) —17,5-( — 17,4);
е) -1,45 0; м) 0-( —1,1); т) 3,08 -(-4,05).
1106. Найдите значение выражения —42г/, если </ = 0; 1; -1; 3; 5; -30.
D Произведение, в которое входят отрицательные числа, читают так:
2,4 • (— 0,5) — произведение двух целых четырех десятых и минус нуля целых пяти десятых
— две целых четыре десятых умножить на минус нуль целых пять десятых
— 20у — минус двадцать игрек — произведение минус двадцати и игрек
189
1107. Найдите значение произведения:
•>4* r)-3f.(-i); ж)—3-j--l,2;
*1т(-8т)’
*»~Н41)! e>-3f-eT; и> -2^-(-e,23).
1108. Поставьте вместо * знак < или > так, чтобы получилось верное равенство:
а) —68-9*0: в) 7,3-( —8) * 7,3; д) — 8~*0;
б) — 4,5-( —45) * 0; г) 7,3-(-8) * -8;
1109. Выполните умножение и сделайте вывод:
а) 1-( —3,9); б) ( —1)-7,4; в) — 65-( — 1); г) -1-7,4.
1110. Запишите в виде произведения сумму:
а) х + г+х + х + г + х; в) — 2у — 2у — 2у;
б) —а — а — а — а; г) 5х 4- 5х-|-5х-|-5х 4- 5х.
1111. Найдите значение выражения:
а) х + 4 + х-|-4 + х 4- 4, если х=9,1;
б) а — 1 + а— 1-|-а — 1-|-а— 1, если а= — 2,1.
1112. Догадайтесь, чему равен корень уравнения, и выполните проверку:
а) — 8-х=72; б) — 4-х=—40; в) 6 у=— 54; г) -6ч/ = 66.
1113. Найдите значение выражения:
а) 3-( —2)4-( —3)-( —4) —( —5)-7;
б) (-18 + 23-16 + 9Н-18);
в) (-4,54-3,8)-(2,01-3,81);
г) (2,8 —3,9)-( — 4,3 — 2,6);
д) - 4,5 - 0,14-(- 3,7) - (- 2,1)- (- 5,4) • (- 0,2);
е) (2,3 • (-1,8) - 1,4 • (- 0,8)) • (- 1,5);
ж) -3,8 (-1,5)-(-1,2)-0,5-6,5;
з) — 2,3 21 •( — 3,2 4- 2,3 - 4,8 4" 6,7) - 1,57 9.
1114. Выполните действия:
‘>(2Т5-4) (8Й-1О); г>(-т-п-£) п+т’
6> итт-44 д) (4т-2’2)(-тг)-3-05;
в) 22,5-24-(-|— А); е) (—0,25 —-|-4--i-)-( —0,2)4-3,9.
190
1115. Найдите значение:
а) х2, если х=-6; 0,3; -0,7;
7 3 4
б) у3, если у=-3; 0,1; -0,1; -1-i-; 1-г-
о Z о
1116. Выполните действие:
а) 3,7-4,8; г) £ ;
< 14
б) -5,2-4,7; д) -1-L-1-£;
о О
в) -5,6-(-3,8);
1117. Сравните:
а) 1-3,5 + 2,91 и 1-3,51 + 12,91;
б) |-8,7-0,7| и 1-8,71 + 1-0,71.
1118. Вычислите устно:
1119. Представьте число —12 в виде разности: а) двух положительных чисел; б) двух отрицательных чисел; в) отрицательного и положительного чисел.
1120. Может ли быть верным равенство a—b = b — a? Приведите примеры. Найдите условие, при котором данное равенство верно.
1121. Может ли разность двух чисел быть больше их суммы?
1122. Подберите такие отрицательные значения хи у, чтобы значение выражения х — у было равно:
а) —10; б) 2,5; в) 0; г) —1-; д) 1; е) 0,1.
1123. Выполните действия:
а) 3,78—(2,56 —2,97); б) -6,19+(-1,5 + 5,19).
191
1124. Решите уравнение:
а) х+3,2 = 1,8; в) 3,7 — х= -2,3;
б) 4,8 — х = 5,6; г) х —3,9 =—2,7.
1125. Альбом дороже книги на 1,2 р. Сколько стоит книга и сколько стоит альбом, если известно, что: а) альбом дороже книги в 1,5 раза;
б) книга в 1,6 раза дешевле альбома;
в) цена книги составляет — цены альбома;
г) цена книги составляет 0,4 цены альбома;
д) цена книги составляет 80% цены альбома?
1126. Найдите значение выражения:-
3,5. 7 +.4 1 2.1 2 2,6 3 7
п 4,8'8 '3,9 ° 4 . 5,1 ° 3 ~ 4,5 15
* 26 0,8 - 20,44:2,8 ’ ’ 10,26:3,8 4- 1.4• 12
1127. Найдите значение произведения:
а) -24-36; д) -4,3-5,1; и) -1-(-1);
б) —48-( —15); е) -2,7-(-6,4); к) (-3)2;
в) 33-( —11); ж) —1-( —3,84); л) (-2,5)2;
г) 1,6 (-2,5); з) -7,2-0; м) (-0,2)3.
1128. Выполните умножение:
*>т (-’т)! ’>3’в'(~т)’ д>-«•(-!f);
6) г) -4-4,2; е) -2 4-0,125.
1129. Найдите значение выражения:
а) 38.(-3)-(-24).(-4)+(-16).(-30);
б) (-2,84-6,1 —3,4+ 6,2)-( — 3,4);
в) (4,3-7,8)-(-5,6+ 8,3);
г>(-3-Н2т)-(-8-г+7т);
«> 1т(-т)-(-2т)1Т: е)+(-15.3-24.3+).
ИЗО. В среду привезли на 4,8 т больше сена, чем во вторник. Сколько тонн сена привезли за эти два дня, если во вторник привезли в 1,4 раза меньше, чем в среду?
1131. Первое число 60. Второе число составляет 80% первого, а третье число составляет 50% суммы первого и второго. Найдите среднее арифметическое этих чисел.
1132. Среднее арифметическое двух чисел равно 12,32. Одно из них составляет треть от другого. Найдите каждое число.
192
36. Деление
Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель.
Например, разделить —12 на — 4 — это значит найти такое число х, что — 4-х = —12. Сначала найдем знак числа х. Так как при умножении — 4 на х получилось отрицательное число — 12, то множители — 4 и х должны иметь разные знаки. Поэтому х — положительное число. Теперь найдем модуль числа х. Так как модуль произведения равен произведению модулей множителей, то | —12| = | —4| *|х|. Отсюда |х| = = | —12|:|—4|. Но так как х — положительное число, то х=|х|. Значит, х = 3.
Пишут: ( —12):( —4)= | —12|: | — 4| =3, или короче:
( —12):( —4)=12:4 = 3.
Угобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
Например, — 4,5:( —1,5)=4,5:1,5 = 3;
___2_. / ._4___2_ JL = JL 3 ‘ \ 5 / 3 ' 5 — 3 ’ 4 “ 6 ’
Разделить — 24 на 4 — это значит найти такое число х, что 4 • х = — 24. При умножении 4 на х получилось отрицательное число —24, значит, множители 4 и х должны иметь разные знаки. Поэтому х — отрицательное число. При этом должно выполняться равенство |4| • |х| = | — 241. Отсюда |х| = | — 24|: |4| =24:4 = 6. Значит, х — отрицательное число с модулем 6, т. е. х = — 6.
Итак, — 24:4 = — 6.
Рассуждая таким же образом, получим, что 24: (— 4) = — 6.
При делении чисел с разными знаками, надо: 1) разделить люду ль делимого на люду ль делителя; 2) поставить перед полученным числом знак *—».
Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.
Например, 3,6:( — 3)=—(3,6:3)= —1,2;
/ _ /JL-2L\ = _ Z.L _4_\_ L
\ 8/4 \ 8 ' 4 / \ 8 ' 3 / 2 '
При делении нуля на любое число, не равное нулю, получается нуль. Делить на нуль нельзя!
7 Зак. 607
193
©Сформулируйте правило деления отрицательного числа на отрицательное. Сформулируйте правило, деления чисел, имеющих разные знаки. Чему равно частное 0: а, где а =#= О?
1133. Верно ли выполнено деление:
а) — 36:2=—18; в) 2,7:(-1) = 2,7;
б) 60:( —1,5)= —4; г) —7,5:(-5)= 1,5?
1134. Найдите частное:
а) -38:19; д) — 5,1: ( — 17); и) 48,1:(-48,1);
б) 45:( —15); е) 650:( —1,3); к) -950:9,5;
в) — 36:( —6); ж) —4,4:4; л) —5,42: ( — 27,1);
г) 270:( —9); з) -8,6: ( — 4,3); м) 10,01:(-1,3).
О Частное, в которое входят отрицательные числа, читают так:
— 54: ( — 2,7) — частное минус пятидесяти четырех и минус двух целых семи десятых
— минус пятьдесят четыре разделить на минус две целых семь десятых
(— 6m): (— 3) — частное минус шести эм и минус трех — минус шесть эм разделить на минус три
Равенство, содержащее отрицательные числа, читают так: 2 4
—— х = — — — минус две седьмых икс равны минус четы-
рем одиннадцатым
1135. Выполните деление:
а) — 5:( —3); *>£:(-£); м) -4-?-:1^; * 7 21 ’
б) -7:5; о / • 1 \
в) 4:( —18); 3) f :(-8); н)
г) —8:(—3); . 5.3. и) — 5:-|-; °) —1-:( —0,8);
д) 8’4’ п) -5,2:1-|-; О
е* 11 \ 22 /’ 2 / _ 1 \ Л Л / 1 \
я) Р) 3,2: (--L).
194
1136. Выполните действия:
а) — 4-( —5)—( —30):6; д) (-8 + 32):(-6)-7;
б) 15:( —15) —( —24):8; е) -21+(-<3-4 + 5):(-2);
в) -8 (-3 + 12):36 + 2; ж) -6-4 — 64:(-3,3 + 1,7);
г) 2,3(-6-4):5; з) (-6 + 6,4-10):(-8)-(-3).
1137. Найдите значение выражения:
a) (3m + 6m): 9, если т= —12; —5,96;
б) (5,2а— 5,25):5,2, если а=—27, Ь= — 3,64.
1138. Чему равно частное:
а) 87х и 8Т; г) —41с и с;
б) — 3,7А и 3,7; д) — 1,9х и х?
в) 9m и т;
1139. Решите уравнение и выполните проверку:
а) —х-4=!= —100; б) 3 ( —х)=—27; в) —0,1у = 33; г) ^-х= 3
= -1.
1140. Решите уравнение:
а)т*=Ч>; б>
_Ху=Л_; в) —LX=-113
7 у 21 ’ ' 9 27
Г) -f !/ + 5 = 2-|-. о V
1141. Я задумал число, умножил его на 5, а затем из произведения вычел 2,7. В результате получил —21,7. Какое число я задумал?
1142. Найдите значение выражения:
6»тт-- •) °-72:(-I)1 ’
-11
-13 2 К -------•
Г)~б¥-; -2’8:4Т: 2±
1143. Найдите неизвестный член пропорции:
-2,8 — 4,2 .
35 х ’
7
195
1144. Вычислите устно:
1145. При каких значениях множителей произведение ху равно нулю? не равно нулю?
1146. В каких случаях может быть верно равенство: а) х = х2; б) х=х3; в) х2 = х3?
1147. Проверьте на примерах справедливость равенства |аЬ| = |а|-|Ь|. Попробуйте доказать, что это равенство верно при любых значениях а и Ь.
1148. Вычислите:
а) —17-5; г) — 0,20,3; ж) —1,3-( —5);
*>~г (-т); 3) (i-A).(_5):
в)2Т‘(“т): е) (-3)3; и) (-0,3-0,2).(-6).
1149. Представьте числа 9; 16 и 25 в виде произведения двух равных множителей. Сколькими способами можно это сделать?
1150. Найдите значение выражения:
а) - 2,3 • 0,1 + 35 • (-0,01)-(- 2,1)• (-0,2);
б) (4,8 —7,3 + 2,1— 2,7 + 3,1)-( —183).
1151. На рисунке 90 показана карта мира с часовыми поясами. Определите с ее помощью: а) поясное время в Свердловске и во Владивостоке, если в Москве полночь; б) поясное время в Лондоне, Токио, Ныо-Иорке и Дели, если в Москве 11ч утра. Составьте сами и решите несколько задач на опреде
ление поясного времени.
1152. Костя и Вера вышли одновременно из одного и того же пункта в одном и том же направлении. Костя идет со скоростью а км/ч, а Вера — со скоростью b км/ч. Какое расстояние
196
Рис. 90
будет между ними через t ч? Составьте формулу для решения задачи, обозначив искомое расстояние (в километрах) буквой а и зная, что a>b. Найдите по формуле:
а) в, если а = 4,2, 5 = 3,6, t=4-;
0
б) а, если 8 = 2,2, 5 = 3,2,
в) Ь, если 8=0,3, а = 5,4, f=-^-;
г) t, если 8=1,2, а = 5,1, 5 = 3,3.
1153. Решите предыдущую задачу, заменив в ней слова «в одном и том же направлении» на слова «в противоположных направлениях». Найдите по полученной формуле:
а) з, если а = 4,2, 5 = 3,6, t=4-;
О
б) а, если 8 = 2,2, 5 = 3,2, t=-i-;
в) Ъ, если 8 = 1,5, а = 5,4,
О
г) t, если 8 = 5,6, а = 5,1, 5 = 3,3.
1154. При каких целых значениях х верно неравенство:
а) —3,2<х<1,8; б) -5-|-<х<^-; в) -0,3<х<4? о 4
197
1155. Вычислите с помощью микрокалькулятора: а) —3,82•0,375 — 3,8275; б) 4,15 (-1,236)4-3,0994.
1156. Выполните деление:
Va)57:(-19); д) -86,2:(-0,1); и) -1 2_; (-1-L);
б) -123:41; е) -51,34:(-1,7); к) -0,12: (-1
в) -147:(-7); «)-lf:±; л)0,1:(—L);
г) 14,31:( —2,7); з) -f-:(-l^-); м) —£:1,6.
1157. Решите уравнение:
а) — 6,32х = 60,04; г) — -|-х=-|-;
б) у:( —3,08)= —4,5; д) -2,4-(-т)=-0,24;
в) 8,37-( — у) = 20,088; е) -|-х=-0,24.
1158. Найдите значение выражения:
а) (48-57): 0,9; д) 3,2:(- 0,4 • 0,2);
б) ( — 84,2 —15,8):( —0,01); е) -4,9:(-0,2 0,3-0,1);
в) (-24,64-13,8):2,7; ж) 1£: ( » +
г) 643,2: ( — 87,34-85,7); з) ( -0,2 4-|-): 3,2.
1159. Из города одновременно в одном и том же направлении выехали два мотоциклиста. Скорость первого из них была больше скорости второго и составляла 72 км/ч. Через 25 мин расстояние между мотоциклистами было равно 5 км. Найдите скорость второго мотоциклиста.
1160. Найдите значение выражения -^г~:-^-4--т^”1 4~-5,1 3 8,5 4
9 —
1161. Решите уравнением) ™ ; б) ---—=—7—.
— 7,2 0,0 X 1
37. Рациональные числа
Число, которое можно записать в виде отношения где а — целое число, ап — натуральное число, называют рациональным числом.
198
Любое целое число а является рациональным числом, так как его можно записать в виде -у-.
Например, —3=^-; 2=-у-; 0=-у-.
Рациональным числом будет и любая отрицательная дробь, 2 _2
тнк как» инпример» —— можно записать так: . и о
2 п
Числа 0,23; 2 — ; —3,513; —4 — тоже рациональные чис-7 5
л ло 23 п 2 16 «сю 3613 . 2 —22
ла. так как 0.23=--: 2—=—: 3.513=--------: —4—=------.
’ 1ПЛ МЛ u,iu 100 ’ 7 7 ’ ’ 1000 ’ 5 5
Сумма, разность и произведение рациональных чисел тоже рациональные числа.
Например:
__2 3 -14Н-9 -5 .
3 ** 7 21 21 ’
J5 3 5-6 -1 .
8 4 8 8 ’
__3 о 1 -33 8 5 40 ’
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
Например: — 0,5:—=—5^-=-^-=—. F F 7 ю-з зо 6
Вы уже умеете выражать некоторые обыкновенные дроби в виде десятичных дробей.
Например, — =0,28, так как 7:25=0,28. 25
Не все обыкновенные дроби можно представить в виде десятичной дроби.
Например, если будем делить 1 на 3, то получим сначала нуль целых, потом три десятых, а далее при делении все время будут повторяться остаток 1 и в частном цифра 3.
Деление никогда не кончится. Значит, дробь нельзя предста-и
вить в виде десятичной дроби. Но если разрешить писать беско-
7 |25
70 0Ж
50
200 ~200
0
1 13
10 так.
9 ТО
9
нечные десятичные дроби, то -|-= 0,333... о
199
Деля 5 на 11, получим, что -^-= [11
11 50 0,4545...
= 0,454545... 44
J50
55
“50
44
J50
55
В записях 0,333... и 0,4545... одна или несколько цифр начинают повторяться бесконечно много раз. Такие записи называют периодическими дробями.
Вместо 0,333... пишут 0,(3), а вместо 0,4545... пишут 0,(45).
Любое рациональное число можно записать либо в виде десятичной дроби (в частности, целого числа), либо в виде периодической дроби.
Для дроби 0,333... число 0,3 является приближенным
О
значением до десятых с недостатком: 0,3 < Число 0,4 яв-ляется приближенным значением этой дроби до десятых с избытком: <0,4. Таким образом, 0,3 <-^-<0,4.
0 U
К
Если число у1= 0,4545... округлить до десятых, то по-
К
лучим “~0,5, если это число округлить до сотых, то по-
лучим ~~0,45, а если округлить до тысячных, то 0,455.
Какие числа называют рациональными? Покажите, что любое целое число является рациональным числом. Покажите, что любая десятичная дробь является рациональным числом. Какими числами являются сумма, .разность, произведение рациональных чисел? Всегда ли частное двух рациональных чисел является рациональным числом? Какая запись числа называется периодической дробью?
1162. Представьте в виде (где а — целое число, а п — натуральное число) следующие числа:
2 — ; 4; 0,35; 1,23; 1; 0; -1; -4-; —3,18; —Л-; —3 —.
7 з 12 9
200
1163. Представьте в виде — (где а — целое число, а п — п
натуральное число):
»> -7-+п: ’ О-5-3-1’
6) произведения f.( —J-); — 3-1—O,fl; -2-1-11;
в) частные (—I-); 0,27:0,9; —0,26:(— 0,13); —1-:0,6..
8 \ 9 / «
В выражение у-'можно прочитать разными способами: — частное икс и игрек:
— дробь с числителем икс и знаменателем игрек
— дробь; икс, деленный на игрек
Бесконечные десятичные дроби читают так:
0,666... — ноль целых шестьсот шестьдесят шесть тысячных и так далее
0,(6) — ноль целых и шесть в периоде
2,5333... — две целых пять тысяч триста тридцать три десятитысячных и так далее
2,5(3) — две целых пять десятых и три в периоде
1164. Выразите в виде десятичной или периодической дро-
lies. Какие и, дробей А, 11, , f. £ .
— , можно представить в виде десятичной дроби? 24 64
1166. Проверьте, что:
а) 0,222... = -|-; в) 0,818181...=^-; д) 0,4666... = ^ ;
б) 5,(6)=5-|-; г) 0,(06)=^; е) 2,8(12)=2 .
1167. Для дробей — и найдите десятичные прибли-11 9
жения с недостатком и с избытком: а) до десятых; б) до сотых.
Запишите ответ в виде двойного неравенства.
1168. Выразите дроби , 1 , у- в виде прибли-
женного значения десятичной дроби до сотых.
201
1169. Вычислите устно:
1170. Одинаковы ли знаки чисел х и у, если верно неравенство:
a) xj/CO; б) xj/>0; в) ху<— 3; г) xj/>5?
1171. При каких значениях т верно равенство:
a) |m|=m; г) т = \ — т|; ж) m-|-|m|=2m;
б) |т| = — т; д) т= — т; з) т— |т|=2т?
в) —т=|— т|; е) т-|-|т|=0;
1172. Может ли быть верным равенство а:Ъ = Ъ:а? Как доказать, что утверждение «Равенство а: Ь = Ь:а верно при любых значениях а и б» несправедливо?
1173. Отметьте на координатной прямой точки с целыми координатами:
а) модуль которых больше 3 и меньше 7,1;
б) кратными двум, модуль которых больше 5 и меньше Ю-|~.
1174. Выполните деление:
а) —50:( —5); д) -3,б:1,8; ж) —
б) 4:( —5); , ,
в) —3:7; “> ~F:1T; э» -1Т:(-Зт)-
г) 2,4: ( — 6);
1175. Можно ли привести дробь к знаменателю 20; 24;
45; 75; 80; 100; 1000?
1176. Можно ли привести к знаменателю 60 дроби:
4 ’ 7 * 12 ’ 22 1
1177. Можно ли представить в виде десятичной дроби числа
1 2 3 1 3
3*5*7*8*25*7^
202
1178. Можно ли привести к знаменателю 100 дробь , если ш = 2; 25; 3; 4?
1179. Найдите значение выражения:
1) -2,79:3,14-24,24:2,4; 4) (1-1,3 1,6)-(-3,2);
2) 2,07:(-2,3)4-13,13:1,3; 5) 1~):3-|-;
3) (1 — 1,5-1,4)-( — 2,8); 6) (-2-4-2-): (-1-L).
л-ь 1180. Представьте в виде (где а — целое, ап — нату-w ральное число):
а) сумму —5-4-75- и сумму 3,9 —4,7; У 1о
б) произведение — и произведение — 5,б'.( —1,2);
в) частное — 7,5:(—0,25) и частное —0,8: ( — 0,6).
1181. Проверьте, что а) 0,444...=2_; б) 0,3(5)=||-.
1182. Выразите дроби 4? , в виде приближенного 1л 15
значения десятичной дроби, округлив результат до тысячных. 1183. Два мальчика идут навстречу друг другу. Сейчас меж-
ду ними 12 км. Скорость одного из них составляет скорости о
другого. Найдите скорость движения каждого мальчика, если известно, что они встретятся через 1,5 ч.
1184. Найдите значение выражения:
а) ( —0,8-1,2-|-1.0б):( —0,5); б) (-30,15:154-0,91) (-2,4).
38. Свойства действий с рациональными числами
Сложение рациональных чисел обладает переместительным и сочетательным смойствами. Иными словами, если а, Ь и с — любые рациональные числа, то
а4-Ь = Ь-1-о> О4-(Ь4-С)=(°4-Ь)4-С.
Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю. Значит, для любого рационального числа имеем:
а-|-0=а, а4-(—а)=0.
203
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами. Другими словами, если а, b и с — любые рациональные^числа, то
ab=ba, a(bc)—(ab)c.
Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1. Значит, для любого рационального числа а имеем:
а-1 = а. а-—=1, если а=+0.
а
Умножение числа на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:
а-0 = 0.
Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если а • Ь = О, то либо а = 0, либо Ь = 0 (может случиться, что и а=0, и Ь = 0).
Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел а, Ь и с имеем:
(а+ Ь)-с = ас+ Ьс.
Перечислите свойства сложения рациональных чисел.
Перечислите свойства умножения рациональных чисел. В каком случае произведение двух чисел равно нулю?
49Ж 1185. Сформулируйте словами переместительное свойство сложения a-j-Ь = b-j-a и проверьте его при:
а) а = 0,7, Ь = 1,2; б) а = - 3 b = -1-1-.
1186. Сформулируйте словами сочетательное свойство сложения а+(Ь+с) = (а + Ь)+с и проверьте его при:
а) а— — 0,7, Ь= — 0,3 и с = 1,2;
6)O=-1-J-, b=-lf, с=- 1-J-.
1187. Сложив отдельно положительные и отдельно отрицательные числа, найдите значение выражения:
а) —17 + 83 + 49 — 27 — 36 + 28;
б) 2,15 — 3,81 — 5,76+3,27 + 5,48 — 4,33;
в) 4f+2-|— 5f-3-|—2-|-;
г) 0,8—5-+О.З—1-+0,4.
о О Z
204
1188. Сложив сначала противоположные числа, найдите значение выражения:
а) 387-243 — 753 — 387-1-243;
б) —6,37 + 2,4 — 3,2 + 6,37 — 2,4;
B)3f+2f-5i-3f-2f;
г) 0,5 + 2-^—3,3 —2,8 —4~+3,3. 5 2
1189. Упростите выражение:
а) х + 8 —х —22; в) а — т + 7 — 8 + т;
б) — х—а + 12 + а —12; г) 6,1 — * + 2,8 + р—8,8 + * — р.
1190. Выбрав удобный порядок вычислений, найдите значение выражения:
а) 7,8 + 32,8 —3; в) 4 £-А_3 £-3 + 1 -L;
6) 4-1—3-1—9,5 + 54-; г) 3 -|— 0,8-2 -|-+2,5 + 0,3 +1 2- .
1191. Сформулируйте словами переместительное свойство умножения ab — ba и проверьте его при:
а) а= —0,3, 5 = 0,4; б) а = — 24~. Ь= — 44~-
о О
1192. Сформулируйте словами сочетательное свойство умножения a(bc)=(ab) с и проверьте его при:
а) а = 0,2, Ь= — 0,5, с = 3,2; б) а= — Ь = — 1-^-, с= —
1193. Выбирая удобный порядок вычислений, найдите значение выражения:
а) -2-( —50)6-12; д) — 3-1-. ( — 1— 3)•( — 7);
б) 11-(-4)-(-7)-25;
в) — 0,2-0,8-( — 5)-( —1,25); е) -0,2-2 -|-(-0,5). ( —).
о \ 13 /
1194. Какое получится число (положительное или отрицательное), если перемножить:
а) одно отрицательное число и два положительных числа;
б) два отрицательных и одно положительное число;
в) 7 отрицательных и несколько положительных чисел;
г) 20 отрицательных и несколько положительных?
Сделайте вывод.
205
1196. Определите знак произведения:
а) — 2-( —3)>( —9)-( —1,3)-14-( —2,7)-( —2,9);
б) 4 (-11).(-12).(-13) (-15) (-17) 80-90.
1196. Решите уравнение, использовав свойство произведения, равного нулю:
а) 4(х-5)=0; в) 1,5(41-х)=0; д) (х-1) (х-2) = 0;
б) — 8«(2,6-J-х) = 0; г) (Зх-6)-2,4=0; е) (х4-3)• (х4-4) = 0.
1197. Сформулируйте словами распределительное свойство умножения (а4- Ь)*с=ас-|- Ьс и проверьте его при:
а) а=0,2, Ь=-0,3, с =0,5; б) а= Ь= --|-,с = -1
1198. Выбирая удобный порядок вычислений, найдите зна
чение выражения:
а) 0,3.(-0,6)-(-0,7).(-0,6); в) -^-.0,84-0,3. (-£);
W8.(-i)+7.(_i); r)(-f-i).(-28).
1200. Найдите сумму всех целых чисел:
а) от —6 до 7; б) от —18 до 17; в) от —22 до 20.
1201. Решите уравнение:
а) |х|=5,2; б) |a| = -3-J-; в) |j/|=0.
1202. Придумайте такие значения х и у, при которых верно соотношение:
а) —=1; б) —=0; в) — =-1; г) —>0; д) —>1; е) —<1. У У У У У У
1203. Найдите наибольшее значение выражения:
а) —|х|; б) 2— |х|; в) - |х-1|; г) -(х-1)2.
206
1204. Решать некоторые математические задачи помогают специальные схемы, состоящие из точек и соединяющих их дуг или стрелок .(рис. 91)г. Такие схемы называют грАфами, точки называют вершйнами грАфа, а дуги — ребрами грАфа. Решите с помощью графов задачу:
а) В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим (рис. 91, а). Оказалось, что каждый из мальчиков знаком только с двумя другими. Кто с кем знаком? (Ребро графа означает «мы знакомы».)
б) Во дворе гуляют братья и сестры одной семьи. Кто из этих детей мальчики, а кто девочки (рис. 91, б)? (Пунктирные ребра графа означают «я — сестра», а сплошные — «я брат».)
Рис. 91 а) &)
1205. Вычислите:
а) 2-^-4; в) 0,5-(-4); д) 1 -1 ; ж) ^-5^-;
б) г) 8:(-0,4); е) -1Л;’ з) 0,25—
1206. Сравните:
а) 23 и З2; б) (-2)3 и (-3)2; в) I3 и I2; г) (-1)3 и (-1)2.
1207. Округлите 5,2853 до тысячных; до сотых; до десятых; до единиц.
1208. Решите задачу:
1) Мотоциклист догоняет велосипедиста. Сейчас между ними 23,4 км. Скорость мотоциклиста в 3,6 раза больше скорости велосипедиста. Найдите скорости велосипедиста и мотоциклиста, если известно, что мотоциклист догонит велосипедиста че-2 рез — ч.
О
207
2) Легковая автомашина догоняет автобус. Сейчас между ними 18 км. Скорость автобуса составляет скорости легковой автомашины. Найдите скорости автобуса и легковой автомашины, если известно, что легковая автомашина догонит автобус через ч.
1209. Найдите значение выражения:
1) (0,7245:0,23 - 2,45) • 0,18+0,074;
2) (0,8925:0,17 — 4,65) • 0,17 4- 0,098;
3) (-2,84-3,7—4,8) 1,5:0,9;
4) (5,7-6,6-1,9)-2,1:(-0,49).
Проверьте ваши вычисления с помощью микрокалькулятора.
®1210. Выбрав удобный порядок вычислений, найдите значение выражения:
а) -244-(-16)4-(-Ю)4-234-17;
б) 364-724-24 — 36 — 72 — 24;
в) -3,4-7,74-4,2-8,94-3,5;
г) -3,94-8,64-4,7 4-3,9-4,7;
д) 4т-3т-5т+1т-5т+2т:
е) 6-|—5-|—44-4-5 |-4-4 3 9 7'9'7 3
1211. Упростите выражение:
а) —36-|-т-|-24; в) 5,7 — 7,7 + а; д) —0,375-|-fc;
б) п-1-42 — 13; г) —0,444-х—0,22; е) m-f-S—
9 3
1212. Найдите значение выражения:
.) — 5-(—1,2)-( —7); .) -f.fl f. (-i);
в) —12,5-2,4-( —3)-( —5); г) -0,7-(-f).4.5-10.
1213. Выполните действия:
а) 0,8-(-0,3)-0,6 (-0,3); г) 23,7-2-|-(-5,3);
6) -f-0,4-0,4.(-f ); „.(-l-L-lf).^
•> »(f-f)-»-
208
1214. Ученикам дали задание собрать 2,5 т металлолома. Они собрали 3,2 т металлолома. На сколько процентов учащиеся выполнили задание и на сколько процентов они перевыполнили задание?
1215. Автомашина прошла 240 км. Из них 180 км она шла по проселочной дороге, а остальной путь — по шоссе. Расход бензина на каждые 10 км проселочной дороги составил 1,6 л, а по шоссе — на 25% меньше. Сколько литров бензина в среднем расходовалось на каждые 10 км пути?
1216. Выезжая из села, велосипедист заметил на мосту пешехода, идущего в том же направлении, и догнал его через 12 мин. Найдите скорость пешехода, если скорость велосипедиста 15 км/ч, а расстояние от села до моста 1 км 800 м?
1217. Выполните действия:
а) — 4,8 • 3,7 — 2,9 • 8,7 — 2,6 • 5,3 + 6,2 • 1,9;
б) -14,31:5,3 — 27,81:2,7 + 2,565:3,42 + 4,1 • 0,8;
в) 3,5 • 0,23 - 3,5 •( - 0,64)+0,87 • (- 2,5).
НС рациональными числами люди, как вы знаете, знакомились постепенно. Вначале при счете предметов возникли натуральные числа. На первых порах их было немного. Так, еще недавно у туземцев островов в Торресовом проливе (отделяющем Новую Гвинею от Австралии) были в языке названия только двух чисел: «урапун» (один) и «оказа» (два). Островитяне считали так: «оказа-урапун» (три), «оказа-оказа» (четыре) и т. д. Все числа, начиная с семи, туземцы называли словом, обозначавшим «много».
Ученые полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи — 6000 лет назад, а 5000 лет тому назад в Древнем Египте и в Древнем Вавилоне появляются названия для громадных чисел — до миллиона. Но долгое время натуральный ряд чисел считался конечным: люди думали, что существует самое большое число.
Величайший древнегреческий математик и физик Архимед (287—212 гг. до и. э.) придумал способ описания громадных чисел. Самое большое число, которое умел называть Архимед, было настолько велико, что для его цифровой записи понадобилась бы лента в две тысячи раз длиннее, чем расстояние от Земли до Солнца.
209
Но записывать такие громадные числа еще не умели. Это стало возможным только после того, как индийскими математиками в VI в. была придумана цифра нуль и ею стали обозначать отсутствие единиц в разрядах десятичной записи числа.
При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Действия над дробями еще в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввел в 1585 г. голландский математик и инженер Симон Стевйн.
Отрицательные числа появились позднее, чем дроби. Долгое время 'такие числа считали «несуществующими», «ложными» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»?
Однако несмотря на такие сомнения и недоумения, правила умножения и деления положительных и отрицательных чисел были предложены в III в. греческим математиком Д и о-фбнтом (в виде: «Вычитаемое, умноженное на прибавляемое, дает вычитаемое; вычитаемое на вычитаемое дает прибавляемое» и т. д.), а позже индийский математик Б х й с к а-р а (XII в.) выразил те же правила в понятиях «имущество», «долг» («Произведение двух имуществ или двух долгов есть имущество; произведение имущества и долга есть долг». То же правило и при делении).
Было установлено, что свойства действий над отрицательными числами те же, что и над положительными (например, сложение и умножение обладают переместительным свойством). И наконец с начала прошлого века отрицательные числа стали равоправными с положительными.
В дальнейшем в математике появились новые числа — иррациональные, комплексные и другие. О них вы узнаете в старших классах.
210
§ а РЕД1ЕНИЕ УРАВНЕНИИ
39. Раскрытие скобок
Выражение a + {b + c) можно записать без скобок: a-|-(b-j-c)=a-j-b-j-c. Эту операцию называют раскрытием скобок.
Пример 1. Раскроем скобки в выражении а + ( — Ь + с).
Решение.
а+( —ft-f-c)=a-f-((—ft)-f-c)=a-f-(—Ь)4-с=а —Ы-с.
Если перед скобками стоит знак « + », то можно опустить скобки и этот знак « + », сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком * + ».
Пример 2. Найдем значение выражения
-2,87-+-(2,87-7,639).
Решение. Раскрывая скобки, получим - 2,87 + (2,87 - 7,639) = = — 2,87 + 2,87 — 7,639 = 0 — 7,639 = — 7,639.
Чтобы найти значение выражения — (— 9 + 5), надо сложить числа —9 и 5 и найти число, противоположное полученной сумме: —( —9 + 5)= —( —4) = 4.
То же значение можно получить по-другому: вначале записать числа, противоположные данным слагаемым (т. е. изменить их знаки), а потом сложить: 9+( — 5) = 4. Таким образом, —( — 9 + 5) = 9 — 5 = 4.
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
Значит, — (а + Ь) = — а — Ь.
Пример 3. Найдем значение выражения
16 —(10 —18 + 12).
Решение.
16-(10-18 + 12) = 16+(- (10-18 + 12)) = = 16+(-10 +18 -12)= 16-10 + 18 -12 = 12.
Чтобы раскрыть скобки, перед которыми стоит знак «—», надо заменить этот знак на * + », поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
211
Пример 4. Найдем значение выражения 9,36—(9,36—5,48).
Решение.
9,36 - (9,36 - 5,48)= 9,36 + (- 9,36 + 5,48) = = 9,36 — 9,36 + 5,48=0 + 5,48 = 5,48.
Раскрытие скобок и применение переместительного и сочетательного свойств сложения позволяют упрощать вычисления.
Пример 5. Найдем значение выражения (_4-20)+(6 + 13)-(7-8)-5.
Решение. Сначала раскроем скобки, а потом найдем отдельно сумму всех положительных и отдельно сумму всех отрицательных чисел и, наконец, сложим полученные результаты: (_4-20)+(6 + 13)-(7-8)-5 = = -4-20+6 + 13-7 + 8-5 =
=(6 + 13 + 8)+(-4-20-7-5)= 27 —36=-9.
Пример 6. Найдем значение выражения — 3-|-+2-|“— if.
Решение. Сначала представим каждое слагаемое в виде суммы их целой и дробной частей, затем раскроем скобки, потом сложим отдельно целые и отдельно дробные части и, наконец, сложим полученные результаты:
-3f+2f-lf_-(3+f)+(2+l)-(1+i)_ --3-F+2+f-1-T=<-3+2-1)+(-5-+-J—т)“ --2+^±^--2+^=-2-i=-2i.
©Как раскрывают скобки, перед которыми стоит знак « + » ?
Как можно найти значение выражения, противоположное сумме нескольких чисел? Как раскрыть скобки, перед которыми стоит знак « — » ?
1218. Раскройте скобки:
® а) 3,4+(2,6+ 8,3); в) т+(п-Л);
б) 4,57+(2,6-4,57); г) с + (-а + Ь).
1219. Найдите значение выражения:
а) -(-5,75 + 3,24); б) -(6,38-2,47); в) -(—|—f).
212
1220. Раскройте скобки:
а) 8б+(7,8 + 98); г) -(80-16)4-84; ж) a — (b-k — п);
б) (4,7-17)4-7,5; д) — а4~(т —2,6); з) — (а —Ь4~с);
в) 64—(904-100); е) с4~(— а-by, и) (т-п)-(р-Л).
1221. Раскройте скобки и найдите значение выражения:
а) 5,4 4-(3,7 —5,4); . /8 7 Ш (ч \.
б) —8,794-(—1,764-8,79); \ 4 7»)+Г 2 0 )’
в) 3,44-(2,9-3,44-4,1); . Я 154-f-2—2 16V
г) (4,67 —3,94) 4-(3.94 — 3,67); М) ЗД5+ к 3 2’16?
д) 7,2-(3,2-5,9); , _5__
е) (4,84-2,75)-(4,8-3,25); 12 \12 з /’
ж) —6,9—(4,21 —10,9); о)-4- ('2-^-4-1^-V
э) (3,72 —5,43)—(4,574-3,22); ’ » \ 8 "г± 4 /’
к> 4т+(-1-т)! ₽> (’Н-3-2)-(2^+1-8)-
1222. Упростите выражение:
а) 0,44-(т-22);
б) (б-х)4-^-;
в) — 0,16 4- (4,06 — т);
г) (16-а)-20^;
д) р4-(1,4—р);
е) _в4-(в-1,1);
ж> f- (т~ “)!
з) — 8,3 —( — х—8,3);
и) т—(п-Ут);
к) —(п —х)—х;
л) р4-( — m-yk — р);
м) — а — (т — а~Ур);
н) — (т — а) — (Л4-°);
о) m-y(k — а — т);
п) т—(а 4- т)—( — а — т)‘, р) а—(а— Ь).
1223. Напишите сумму двух выражений и упростите ее:
а) — 4 — т и т 4-6,4;
б) 1,1-|-аи —26—а;
в) а4-13 и —134-Ь;
г) а+b и р—Ь;
д) —т + п н —k — n е) т — п и п — т.
1224. Напишите разность двух выражений и упростите ее:
а) —3-|-а и а-|-60,1;
б) 3,2 — пи —n-|-l-j-;
в) т-У п и k~yrrr.
г) — а+b и Ь — а;
д) —р — а и k — а;
е) т — а и —а-ут — Ь.
213
1225. Решите уравнение:
а) 7,2—(6,2 —х) = 2,2; г) (х+3)-17= -20;
б) —5 + (а —25)=—4; д)-(10-5)4-23,5=—40,4;
1226. Решите с помощью уравнения задачу:
а) На одной полке 42 книги, а на другой 34. Со второй полки сняли несколько книг, а с первой — столько, сколько осталось на второй. После этого на первой полке осталось 12 книг. Сколько книг сняли со второй полки?
б) В первом классе 42 ученика, во втором на 3 ученика меньше, чем в третьем. Сколько учеников в третьем классе, если всего в этих трех классах 125 учеников?
1227. Найдите значение выражения:
-5то+3й; г> -5т+£; ’
б)3£-<£; Д) 2 f+3 6 А ; 3)5f-2^-4f.
1229. Найдите наибольшее значение выражения: а) 157 —х, если х=68; —19; 0,17; — 5-|-;
б) — ЗОх, если х=0,2; —0,7; 8; —2 — ;
з
в) х:(—0,5), если х = 12,5; —3,5; —1-|-; 6.
214
м
1230. Укажите 4 последовательных целых числа, если: а) меньшее иа них равно —12; в) меньшее из них равно в; б) большее из них равно —18; г) большее из них равно k.
1231. Найдите координаты середины отрезка, если координаты его концов равны:
а) —3 и 5; б) —в и 1; в) —2,6 и 1,5; г) —8 и —1-|-.
1232. Каким числом будет значение выражения x-j-y, если: а) х>0, у>0; в) х>0, у<0; д) х>0, у=0;
б) х<0, у<0; г) х=0, у<0; е) х=0, у=0?
1233. Решите с помощью графа задачу: «Вера, Нина, Оля и Люба надели платья разных цветов (красное, синее, бе-
лое, голубое). На вопрос, кто из них в каком платье, три девочки ответили: 1) Оля — в синем, Люба — в белом; 2) Оля — в красном, Нина — в синем; 3) Вера — в синем, Люба в голубом. В каждом ответе только одна часть верна, а остальные нет. Какого цвета платье надела каждая девочка?»
1234. Найдите значение выражения:
а) 35-8-1-14-35-1-8-14; г) —1-(-3,2)-1-|-.(-10);
б) |-о,4—|—|-0,б; з в . з / 1 \
2 4.1.
* 3-7*2’ е)
1235. Представьте:
JL ® 1 о 1 а в 1®,
а) в виде десятичных дробей: —; —; 3 — ; 4—; 1-г»
D 4 Z ли 4
б) в виде обыкновенных дробей: 1,2; 3,25; 0,75; 1,125.
1236. Найдите неизвестный член пропорции:
1) 4-т-:7-*-=х:12; 2) 6-1-:х=6-|-:4,1.
'48 '2 в
1237. Решите уравнение:
1) -2 (3,1х—1)4-3 (1,2х4-1) = -14,5;
2) -5(4,2у4-1)4-4(1,4у —2)= -20,7.
1238. Раскройте скобки и найдите значение выражения: а) 8,757-(7,8-1,043); г) (2 -|-|-1 f)- (1 -^4-|-);
б) 3,964-(2,375-3,96); Д) - (2,77-7-|-)-(о,23-4-|-);
•> т+ (т-т)! •> - (т+1-37)- (-2.8’-т)•
215
124U. гешите уравнение: а) 8,4-(х-7,2) = 8,6;
б) -1,8+(х-4,8)=-7,1;
в) 3,3-(х-6,7) = 100;
1239. Упростите выражение:
а) 0,2—(х —3,3); в) 2,9-(х-6,7); д) с-(а+с);
б) m-(3,5 + m); г)0-(8-|—х); е) (m + n)-(n-m).
«>1т-0'+т)=1-г-
1241. Найдите значение выражения:
в>4£-2п-
б)2^-4^1^ г>1 f+2 т-5 -Ь
1242. Решите задачу, составив пропорцию:
а) Затрачивая на изготовление каждой детали ч, бригада
3
выпускала за смену 540 деталей. Сколько деталей будет выпускать за смену бригада, если на изготовление каждой детали будут затрачивать ч? На сколько процентов повысится D
при этом производительность труда?
б) Масса 15 л керосина 12,3 кг. Какова масса 35 л керосина?
в) Из 0,3 т свежих яблок получается 57 кг сушеных. Сколько сушеных яблок получится из 5,5 т свежих?
1243. Решите уравнение:
а) 4,8:1,5 = 13: (-g-x); б) 4 -|-:(2х) = 1,3:3.
40. Коэффициент
Переместительное и сочетательное свойства умножения позволяют упрощать выражения.
Пример 1. Упростим выражение 0,3а • (— 0,7 Ь).
Решение. Это выражение является произведением четырех множителей: 0,3-а-( — 0,7)-Ь. Сгруппировав отдельно числовые и отдельно буквенные множители, получим:
0,За(-0,7Ь)=0,За(-0,7)Ь = =(0,3 • (- 0,7)) • (а • Ь) = - 0,21а Ь.
216
Число —0,21 называют коэффициентом в полученном выражении.
Если выражение является произведением числа и одной или нескольких букв, то зто число называют числовым коэффициентом (или просто коэффициентом).
Коэффициент обычно пишут перед буквенными множителями.
Коэффициентом такого выражения, как а или ab, считают 1, так как а = 1*а; ab — 1-ab.
При умножении —1 на любое число а получается число — а:
— 1 -а = — а.
Поэтому числовым коэффициентом выражения —а считают число —1.
Пример 2. Найдем коэффициент выражения — а-( —Ь).
Решение. Так как —а •(—&)=аЬ, то, значит, коэффициентом выражения — а-( — Ь) является 1.
©Что называют числовым коэффициентом выражения? Чему равен коэффициент выражения ах? А выражения —ах?
1244. Упростите выражение:
а) -8,3 Юж;
б) 4-(—6,5)-т;
в) ж-(-1,5). 2,2;
г) -3,2а(-3);
ж) Л-;
э) О,в.г.(А).
-!-«•( —3);
1245. Найдите коэффициент произведения:
а) 8пг.7; ж) —с •( — &);
б) — 4-( —12ж); 2 /-3 \
в) -2р.(-1,4); } 15 т' ( 4
2 (~т ъ\ /~з\. и) —2,бт-( —3);
г) з 8 8 /’ к) -0,11ж-(-2т);
д) 6с-(-7); л) -2,7аЬ(-1);
е) —т-п‘, м) — 1—( —m)-( —1-у).
1246. Определите знак коэффициента:
а) -а-(-Ь).(—в) -5а.6Ь(-0,Зс);
б) -За.(-2Ь).Зс.(-4); г) m-0,3n•(-5р)-(-1
217
1247. Упростите выражение и подчеркните коэффициент:
a) -3m-(-8fc); ж) -|-а.(-6Ь)- ( __L\
б) 5а-( —6Ь); 3 * * б) \ 8 /
в) — 2с-( —0,4Ь); 3) (-1-|-ь)-(-0,5).(-4с);
г) 4-( —2х)-(3у); 7
д) -0,5-(-3n)-(0,2m); и) Тт'
е) -0,6 5с ( — 20);
1248. Вычислите устно:
1249. На координатной прямой (рис. 92) отмечены числа а и Ь. Определите знак произведения ab.
b 0 а
II ।
а 1 2 b
I ч- ч------1-
b -2 -1а
Il II
Ф S) Ряс. 02
1250. Найдите произведение всех целых чисел:
а) от —6 до —1; в) модуль которых меньше 10;
б) от —12 до 1; г) моду ль которых больше 3 и меньше 5,6.
1251. Каким числом будет произведение ху, если:
а) х>0, у>0; в) х>0, у<0; д) х<0, у = 0;
б) х<0, у<0; г) х = 0, р<0; е) х=0, р=0?
1252. Найдите наименьшее целое положительное и наибольшее целое отрицательное решение неравенства:
а) |х| >4; б) |х—3|>5; в) |х|>3-|-.
1253. Найдите значение выражения:
а) (3,2-5)-(3,24-7); б) (-|—1,2)- (-1,8+|-).
218
1254. Вычислите:
-1+4-; -2+^-; 3—1-^-; -2--^-; -5-2-f-. 1 7 4 7 3 7 7
1255. Найдите значение выражения:
а) — (m + n)+(k + m)—(k — 0,13), если п=—2,13;
б) (c + d + fc) —(с+fc—15,3), если d= —14,7.
1256. Напишите сумму двух выражений и упростите ее:
а) а + Ь и р — Ь; б)— m + n и — k — п.
1257. Напишите разность двух выражений и упростите ее: а) — о + ЬиЬ — а; б) —4—т и 6,4—т.
1258. Найдите значение выражения:
1) -2,6 (3-3,8)+ 4,2 (4-2,7); 2) -1,212:0,4 + 2,9-(2-4,3).
1259. Упростите выражение и подчеркните его числовой коэффициент: /
а) -а-(-7);
б) Ь-( —4m);
в) ЗаЬ-2;
г) — тп • (— 5);
д) 2а-( — 35);
ж) к) -|-m--^-n-6fc.
о О I У
а'ткТ1'
1260. Выполните действия:
а) -13,6(-7,2 + 313,2:8,7); в) -9,396:2,7-0,2-1,7;
б) -16,3 (-8,3+ 212,8:7,6); г) -0,8-1,6-14,911:3,7.
1261. Решите уравнение:
а) 1-|-:3,75 = 4х: 15; б) ^-:13=4-х:44-.
1262. Из 3,2 кг ржаной муки получается 4,48 кг хлеба. Сколько муки расходует хлебозавод на выпечку 28 т хлеба?
1263. 8 каменщиков сложили стены дома за 42 дня. Сколько нужно каменщиков, чтобы сложить стены такого же дома за 28 дней?
1264. Выполнив план на 25%, трактористы вспахали 144 га. Сколько земли нужно вспахать, чтобы выполнить 65% плана?
41. Подобные слагаемые
Распределительное свойство умножения (а+Ь)-с = ас + Ьс справедливо для любых чисел а, Ь и с.
Замену выражения (а+ 5)-с выражением ас + bc или выражения с-(а+5) выражением са + сЬ также называют раскрытием скобок.
219
Пример 1. Раскроем скобки в выражении — 3*(а — 2Ь).
Решение. Умножим —3 на каждое из слагаемых а и — 2Ь. Получим — 3*(а —2Ь)= —3*а-|-( —3)*( —2Ь)= —За-|-6Ь.
Пример 2. Упростим выражение 2m — 7m4~3m.
Решение. В данном выражении все слагаемые имеют общий множитель т. Значит, по распределительному свойству умножения 2m —7m-|-3m = m*(2 —7 4-3). В скобках записана сумма коэффициентов всех слагаемых. Она равна — 2. Поэтому 2m — 7 m 4- 3m = — 2m.
В выражении 2m — 7m 4-3m все слагаемые имеют общую буквенную часть и отличаются друг от друга только коэффициентами. Такие слагаемые называют подобными.
Слагаемые, имеющие одинаковую буквенную часть, повывают подобными слагаемыми.
Подобные слагаемые могут отличаться только коэффициентами.
Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Пример 3. Приведем подобные слагаемые в выражении 5а-\-а — 2а.
Решение. В данной сумме все слагаемые подобны, так как у них одинаковая буквенная часть а. Сложим коэффициенты: 54-1 — 2=4. Значит, 5а4~а — 2а = 4а.
©Какие слагаемые называют подобными? Чем могут отличаться друг от друга подобные слагаемые? На основании какого свойства умножения выполняют приведение (сложение) подобных слагаемых?
О
1265. Раскройте скобки:
а) (а—b4-е)'8;
б) — 5'(т — n—fc);
в) а-(Ь~ m-|-n);
г) —а*(6Ь —Зс-|-4);
д) (Зт-2*4-1)«(-3);
е) — 2а*(Ь-|-2с —Зт);
ж) ( —2а-|-ЗЬ4-5с)"4т;
з) — а*(Зт-|-Л— п).
1266. Выполните действия, применив распределительное
свойство умножения:
а) 9*134-9*7; д) 1,5*134-1.5*7;
б) 2719—1719; е) 0,9*0,8 —0,8 0,8;
в) 8.114-16*11;
г) 9*17 — 3*17; Ж) з ’ 7 + з ' 7 ;
220
1267. Сложите подобные слагаемые:
а) — 9х4-7х —5х4-2х;
б) 5а — 6а 4- 2а — 10а;
в) 11р4-2р4-20р—7р;
г) — 3,8fc — fe + 3,8fc + fc;
д) а 4-6,2а—6,5а — а;
е) — 18n — 12n4-7,3n4-6,5nj
Ж) Am+Am_Am_Am;
з) ‘Га_Та+та-Т£о:
и) Ь4-0,4Ь—1-Ь-— Ь.
5 2
О Выражения вида 7х — Зх4-6х—4х читают так:
— сумма семи икс, минус трех икс, шести икс и минус четырех икс
— семь икс минус три икс плюс шесть икс минус четыре икс
1268. Выполните приведение подобных слагаемых:
а) 10а4-Ь — 10Ь —а; е) — 6а 4-5а — х4-4;
б) — 8у4-7х4-6у4-7х; ж) 23х —234-404-4х;
в) -8x4-5,2а 4-3x4-5а; з) — а4-х4-1.1а —1.3х;
г) 5а 4-7а —9,2m 4-15m; и) — 12p4-3fc4-3,2p—2,3fc;
Д) Тж-Ту“-Пж4’Ту; “) 0,5a-f Ь—|-а—|-Ь.
1269. Раскройте скобки и приведите подобные слагаемые: а) 7-(2х-3)4-4-(Зх — 2);
б) -2-(4fc4-8)-3-(5fe-l);
в) —8.(2 —2у)4-4-(3 —4у);
г) (Зх—11)-2 —5-(4 —Зх);
д) (8a-l)-(-6)4-(3a-7).(-2);
е) -0,5-( —2x4-4)—(10—х);
1270. Найдите значение выражения:
а) 4х —2a4-6x —3a4-4a, если х= — 0,15, а=0,03;
б) — 6,3m4-8 — 3,2m — 5, если m=—2; —i-; —0,4.
0
1271. Решите уравнение:
а) 3-(2х4-8)-(5х4-2)=0; в) 8«(3-2х)4-5-(8х4-5)=9.
б) -3-(Зу4-4)-|-4.(2у-1)=0;
221
1272. Килограмм картофеля стоит 20 к., а килограмм капусты 14 к. Картофеля купили на 3 кг больше, чем капусты. За все заплатили 1 р. 62 к. Сколько купили килограммов картофеля и сколько капусты?
1273. Турист шел 3 ч пешком и 4 ч ехал на велосипеде. Всего он проделал путь в 62 км. С какой скоростью он шел пешком, если пешком он шел медленнее на 5 км/ч, чем ехал на велосипеде?
1274. Вычислите устно:
а) 34 — 90 б) —23 — 29 в) -14- ( — 7) г) 45 — 90
: (-14) : (-13) : (-2) : (-15)
•(-15) • (-17) — 2 • (-17)
+ 39 -32 : 17 -49
? ? ? ?
1275. Чему равна сумма тысячи слагаемых, каждое из которых равно —1? Чему равно произведение тысячи Множителей, каждый из которых равен —1?
1276. Найдите значение выражения
1-3 + 5-7+ 9-11+... + 97-99.
1277. Решите устно уравнение:
а) х + 4=0; в) m + m + m = 3m;
б) а + 3=а-1; г) (у-3)(у + 1)=0.
1278. Выполните умножение:
.)0,2+-5 + ; .) ав1+«+;
«) 3.5 18 ++ -1+».
1279. Чему равен коэффициент в каждом из выражений: — 3m; -%-cd; mk; —am; — p-( — к); —|-a~b; 0,2b-4c;
5 3 4
-За (-0,25)?
1280. Расстояние от Москвы до Нижнего Новгорода 440 км. Каким должен быть масштаб карты, чтобы на ней это расстояние имело длину 8,8 см?
1281. Какой длины отрезком изображается на карте расстояние 35 км, если масштаб карты 1 : 100 000?
1282. Расстояние от Киева до Одессы изображается на карте, масштаб которой 1 : 10 000 000, отрезком 6,5 см. Определите это расстояние на местности.
222
1283. Прямоугольник иа плане, масштаб которого 2 : 5, имеет длину 38 мм, а ширину 26 мм. Найдите площадь этого прямоугольника й натуре.
1284. Отрезок на плане, масштаб которого 2 : 7, изображается отрезком 4,2 см. Какой длины будет этот отрезок на плане, сделанном в масштабе 5 : 3?
1285. Решите задачу:
1) Комбайнер перевыполнил план на 15% и убрал зерновые на площади 230 га. Сколько гектаров по плану должен убрать комбайнер?
2) Бригада плотников израсходовала на ремонт здания 4,2 м3 досок. При этом она сэкономила 16% выделенных для ремонта досок. Сколько кубических метров досок было выделено на ремонт здания?
1286. Найдите значение выражения:
1) — 3,4-7,1 — 3,6-6,8+ 9,7-8,6; 2) — 4,1-8,3+ 2,5-7,9 —3,9-4,2.
м
1287. Решите с помощью графа задачу: «Марина, Лариса, Жанна и Катя умеют играть на разных инструментах (пианино, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий, испанский), но каждая только один. Известно: 1) девушка, которая играет на гитаре, говорит по-испански; 2) Лариса не играет ни на скрипке, ни на виолончели и не знает английского языка; 3) Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского языка; 4) девушка, которая говорит по-немецки, не играет на виолончели; 5) Жанна знает французский язык, но не играет на скрипке. Кто на каком инструменте играет и какой иностранный язык знает?»
® 1288. Раскройте скобки:
а) (х+у —г)-3; г) (2х —у + 3)-(—2);
б) 4-(т — п — р\, д) (3m —2п+р)-( —1);
в) — 8-(а — Ь — с); е) (а + 5— Ь—с)-т.
1289. Найдите значение выражения, применив распределительное свойство умножения:
а) 915Т + 9143; г) ±.Л.+Л..Л.. е) 12,9-Л— 11.3.Л-.
о о о о В в
б) 3,5-2,4 — 3,5-1,4; t 5 : а
в) 4,75-3,2 + 3,2-3,25; д) 1 Т14-1 Т'Т;
223
1290. Приведите подобные слагаемые:
a) 3m 4-2m 4-4m;
б) Та+та~та;
в) 0,96-1,364-0,76;
г) х — 0,2х — 0,7х;
д)
е) с —0,8с—|-с—|-с;
ж) 0,3а —0,26 —0,7а 4-0,26;
э) 4а —6а —2а4-12—11;
и) -|-а4—1-6 —£-а-4-6;
3 8 в 4
К)2.А_2 3 1
’ 7 3 14 3 ’
л) 0,2m—I— 4т+^-: “ <7
\ 1 .1 1 । 2
м) Va+Vc—va+vc>
Z о Z о
1291. Раскройте скобки и приведите подобные слагаемые: а) 5m —(3m 4-5) 4-(2m —4);
б) —5 (х4-3)4-4 (х —2)—6 (2x4-1);
в) 0,2 (6х — 5)—4(0,2х — 2);
г) 0,4 (1,5у 4-3) —2,5 (3 — 0,бу);
д) Т'-(т'~Г');
ж) -у (1,8m — 5,4)--у-(2,1m — 4,2);
з) -|-(0,3y- 0,6)- ^-(0,4у- 0,8).
1292. Решите уравнение:
а) 3 (у —5) —2 (у —4)=8; в) -L(3x-6)—|-(7х-21) = 9;
б) — 5 (5 —х)—4х= 18; г) 5,4 (Зу-2)-7,2 (2у-3)= 1,2.
1293. Купили один стол и 6 стульев за 67 р. Стул дешевле стола на 18 р. Сколько стоит стул и сколько стоит стол?
1294. В трех классах 119 учащихся. В первом классе учащихся на 4 человека больше, чем во втором, и на 3 человека меньше, чем в третьем классе. Сколько учащихся в каждом классе?
1295. Определите масштаб карты, если расстояние между двумя пунктами на местности 750 м, а на карте 25 мм.
1296. Какой длины отрезком изображается на карте расстояние 6,5 км, если масштаб карты 1 : 25 000?
1297. На карте отрезок имеет длину 12,6 см. Какова длина этого отрезка на местности, если масштаб карты 1 : 150 000?
224
42. Решение уравнений
Пример 1. Решим уравнение 4-(х + 5) = 12.
Решение. По правилу отыскания неизвестного множителя имеем х + 5 = 12:4, т. е. х + 5 = 3. Это же уравнение можно получить, разделив обе части данного уравнения на 4 или умножив обе части на 4~. Теперь легко найти значение х. Имеем 4
х = 3 —5, или х = — 2.
Число — 2 является корнем уравнения х + 5 = 3 и уравнения 4.(х+ 5)= 12, так как —2+5=3 и 4-( —2 + 5)=12.
Корни уравнения не изменяются, если его обе части умножить или разделить на одно и то же число, не равное нулю.
Пример 2. Решим уравнение 2х + 5 = 17.
Р е ш е н и е. По правилу отыскания неизвестного слагаемого имеем 2х=17 —5, т. е. 2х=12. Уравнения 2х + 5 = 17 и 2х = 17 — 5 имеют один и тот же корень 6, так как 2-6 + 5 = 17 и 2-6 = 17 — 5.
Уравнение 2х = 17 —5 можно записать так: 2х=17+( —5). Видим, что корень уравнения 2х + 5 = 17 не изменяется, если перенести слагаемое 5 из левой части уравнения в правую, изменив его знак на противоположный.
Пример 3. Решим уравнение 5х = 2х+6 (рис. 93).
Ряс. 93
Решение. Вычтем из обеих частей уравнения по 2х (снимем с обеих чашек весов по две буханки хлеба). Получим 5х —2х = 2х —2х + 6. Но 2х — 2х = 0, значит, 5х —2х = 6. Это уравнение можно получить из данного, если слагаемое 2х перенести из правой части в левую, изменив его знак на противоположный. Решая дальше уравнение 5х — 2х = 6, получим Зх = 6 и х = 2.
Число 2 есть корень уравнения 5х — 2х=6 и уравнения 5х = 2х+6, так как 5-2 —2-2 = 6 и 5-2 = 2-2 + 6.
8 Зак. 607
225
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
Пример 4. Решим уравнение х 4-12 = х.
Решение. Умножим левую и правую части уравнения на 3 для того, чтобы освободиться от дробного коэффициента. Получим х4-36 = 3х. Перенесем с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое Зх из правой части в левую: х — Зх= — 36. Упростим левую часть уравнения: — 2х= —36. Теперь разделим обе части уравнения на —2, получим х=18.
Число 18 является корнем данного уравнения -^-х-|-12 = х,
3
так как верно равенство — 18 4-12 = 18.
Во всех рассмотренных примерах мы приводили данные уравнения к виду ах=Ь, где а=#=0.
Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным.
©Обе части уравнения умножили на число, не равное О.
Изменились ли корни данного уравнения? Обе части уравнения разделили на одно и то же число, отличное от нуля. Изменились ли корни данного уравнения? Сформулируйте правило переноса слагаемых из одной части уравнения в другую. Какие уравнения называют линейными?
1298. Перенесите из левой части уравнения в правую то слагаемое, которое не содержит неизвестного:
а) 8x4-5,9 = 7x4-20; б) 6х—8= — 5х—1,6.
1299. Соберите в левой части уравнения все слагаемые, содержащие неизвестное, а в правой — не содержащие неизвестное:
а) 15у —8 =—6у4-4,6; б) — 16г 4-1,7 = 2г —1.
1300. Решите уравнение:
а) 6х—12 = 5x4-4; д) 4 4-25у = б4-24у;
б) — 9а 4-8= — 10а — 2; е) 11 — 5г = 12—6г;
в) 1m4-1 =8m4-9; ж) 4fe-|-7= — 3-|-5fe;
г) — 12n —3 = lln —3; з) 6 — 2c = 8 — Зе.
226
О Уравнения вида —7у4-9= —8у—3 читают так:
— сумма минус семи игрек и девяти равна сумме минус восьми игрек и минус трех. Корень этого уравнения — число минус двенадцать.
1301. С помощью умножения обеих частей уравнения на одно и то же число освободитесь от дробных чисел и решите уравнение:
а) 2-х + 3=^-х+’5; в) -±-х+-А-х + 5 = х;
б) ГУ + 2=ТУ~3; г) 0,2х + 2,3 = 0,7х-3,2.
1302. Решите уравнение и выполните проверку:
а) -40(-7x4-5)= -1600; в) 2,1 (4—6у)=-42;
б) ( —20х—50)-2 = 100; г) -3 (2-15х)=-6.
1303. Найдите корень уравнения:
а) 0,5х-|-3=0,2х; д) А*-12,5=-|-Л—
б) —0,4а —14 = 0,За; е) 4,7 —8г = 4,9—Юг;
в) 2х —6 -L=-Lx4-7 ж) 7,3а = 1,6а;
г) 6,9 —9п= —5п —33,1; з) —19t = llt.
1304. Решите уравнение, используя основное свойство пропорции:
„Ч Ж-З 7 . 5 2.5 . х х + 7 2х-3 . 0,2 _ 0.7
а) -б~=Т; 6)^T3=IJ’ в>—г) 7+з-7-7-
1305. В первом бидоне в 3 раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько молока было в каждом бидоне?
1306. Длина отрезка АВ на 2 см больше, чем длина отрезка CD. Если длину отрезка АВ увеличить на 10 см, а длину отрезка CD увеличить в 3 раза, то получатся равные результаты. Найдите длину отрезка АВ.
1307. Автобус проходит расстояние от города до села за 1,8 ч, а легковая автомашина — за 0,8 ч. Найдите скорость автобуса, если известно, что она меньше скорости легковой автомашины на 50 км/ч.
1308. На первую автомашину погрузили на 0,6 т зерна больше, чем на вторую. Если бы на первую автомашину погрузили в 1,2 раза больше, а на вторую в 1,4 раза больше, то груза на обеих автомашинах было бы поровну. Сколько тонн груза погрузили на каждую автомашину?
1309. Мама получила премию. На покупку пальто было израсходовано всей премии, а на покупку туфель премии и еще осталось 75 р. Какую премию получила мама?
1310. Мебельный гарнитур состоял из стенки, дивана и стола со стульями. Стоимость стенки составляла ~~ стоимости 4
3 всего гарнитура, а стоимость дивана — стоимости стенки.
Стол со стульями стоил 160 р. Сколько стоил весь гарнитур?
1311. Три завода получили заказ на изготовление моторов.
Первый завод выполнил 0,56 всего заказа, второй того, что 14
выполнил первый завод, а третий завод изготовил остальные 240 моторов. Сколько всего моторов изготовили все три завода?
1312. Веревку длиной 63 м разрезали на два куска так, что 0,4 длины первого куска были равны 0,3 длины второго куска. Найдите длину каждого куска веревки.
1813. За 2,5 кг конфет было заплачено 5,5 р. Сколько денег надо доплатить, чтобы купить 2,9 кг таких конфет?
1314. В растворе содержится 40% соли. Если добавить 120 г соли, то в растворе будет содержаться 70% соли. Сколько граммов соли было в растворе первоначально?
1315. Вычислите устно:
а) 8 — 70 б) -194-100 в) -18-46 г) -15 • 6
-19 : (-3) : 16 : 9
: 3 -13 -77 • (-13)
• (-2) 4-6 : (-3) -260
? ? ? ?
1316. При каких значениях а верно неравенство:
а) ас— а; б) — аса; в) — а>а?
1317. Приведите подобные слагаемые:
a) 9,5m-f-3m; г) -^~т — т; ж) —4х —x-f-3;
б) 6Ь — Ь; д) 1,2у4-3,6у — 0,7у; з) 7х — бу— 2х4-8у.
в) а — 2-а; е) -н~а+'5~а~'ч~а; <3 V V о
1318. Упростите выражение:
а) 2х—(x-f-1); б) n-f-2(3n —1).
1319. Расфасовочная машина может всю привезенную продукцию обработать за 20 ч. Определите: а) какую часть всей
продукции она обработает за 1 ч; б) сколько процентов всей продукции она обработает за 1 ч; в) какую часть всей продукции она обработает за 8 ч; г) сколько процентов всей продукции она обработает за 9 ч.
1820. За какое время все свекловичное поле уберет уборочная машина, если известно, что она за 1 ч убирает:
а) 5% всего поля; б) у- всего поля; в) 0,4 всего поля?
1821. За какое время израсходует двигатель весь бензин из бака, если он: а) за 3 ч расходует 12% всего бензина; б) за 3 ч
расходует всего бензина; в) за 6 ч расходует 0,24 всего 15
бензина?
1322. Докажите, что при любом значении буквы значение
выражения:
1) 5-(Ту-2)-7-(бу+ 2) равно -24;
2) 4«(8а-|-3)—8-(4а — 3) равно 36.
1323. Найдите значение выражения:
1) (503,44:12,4 — 225,36:7.2) *(1,6905:0,49);
2) (971,1:23,4 - 211,14:6,9)• (6,5704:0,86).
1324. Древнегреческая задача.
— Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы.
— Вот сколько,— ответил Пифагор,— половина изучает математику, четверть — природу, седьмая часть проводит время в размышлении, и, кроме того, есть еще три женщины. ® 1325. Решите уравнение и выполните проверку:
а) — 20(х —13) = — 220; г) (2,8 —0,1х).3,7 = 7,4;
б) (30 —7х).8 = 352; д) (Зх—1,2).7 = 10,5;
‘o-h+T*-1-1-!-
1326. Решите уравнение:
а) — 27x4-220 =—5х; ж) -4-(—z4-7)=z-|-17;
б) 7а= -310 4-За; з) с-32=(с-|-8).(-7);
в) -2х4-16=5х —19; и) 12 —2-(Л-|-3)=26;
г) 25 —ЗЬ = 9 —5Ь; к) — 5(За-|-1)—11 = —16;
д) 34-11!/= 2034-у; Л) — 3,2п-|-4,8=—2.(1,2п-|-2,4);
е) 3 (4х —8) = 3х—6; м) -5-(0,8г-1,2)=-г-|-7,2.
1327. Одно число больше другого в 4,5 раза. Если от большего числа отнять 54, а к меньшему прибавить 72, то получатся равные результаты. Чему равны эти числа?
229
1328. Бутылка с кефиром в 2 раза тяжелее пустой бутылки (рис. 94). Галя выпила половину бутылки кефира. Сколько граммов кефира выпила Галя?
1329. У Миши и Коли было поровну денег. Когда Миша купил себе книгу, а Коля альбом, который в 1,4 раза дешевле книги, то у Миши осталось 20 к., а у Коли 40 к. Сколько стоит альбом, сколько стоит книга и сколько денег было у каждого мальчика?
1330. На одной полке было в 3 раза больше книг, чем на другой. Когда с одной полки сняли 8 книг, а на другую положили 32 книги, то иа полках стало книг поровну. Сколько книг было на каждой полке первоначально?
1331. В двух бочках 725 л бензина. Когда из первой боч-1 2
ки взяли —, а из второй бочки — бензина, то в обеих бочках бензина стало поровну. Сколько литров бензина было в каждой бочке первоначально?
1332. Решите уравнение, используя основное свойство про-2-* 1А . 4,6 8,4 3 2
п°рщ<и; a) в) —=—-J-.
х+ 3 Х 1 8
1333. Смешали индийский и грузинский чай. Индийский чай составил 30% всей смеси. Если в эту смесь добавить еще 120 г индийского чая, то он будет составлять 45% смеси. Сколько граммов индийского чая было в смеси первоначально?
1334. Поезд шел 3,5 ч со скоростью 64,4 км/ч. На сколько надо увеличить скорость поезда, чтобы пройти это расстояние за 2,8 ч?
1335. Одна поливочная машина может полить всю улицу за 15 мин, а другая — за 12 мин. Какую часть улицы польют обе машины за 1 мин? за 3 мин?
230
HI Среди задач, которые с давних времен приходилось решать людям, много было похожих, однотипных: вычисление площадей участков, нахождение объемов фигур определенной формы, деление доходов, вычисление стоимости товара, измерение массы с помощью различных единиц и другие.
Для однотипных задач в разное время, в разных странах пытались отыскать общие способы, правила решения. В этих правилах раскрывалось, как найти неизвестную величину через данные числа для группы похожих задач. Так возникла Алгебра — один из разделов математики, в котором вначале в основном рассматривалось решение различных уравнений.
Некоторые алгебраические понятия и общие приемы решения задач знали уже в Древнем Вавилоне и Египте более 4000 лет назад. Большой вклад в создание алгебры внес выдающийся древнегреческий математик Диофант (III в.), которого по праву называют «отцом алгебры». Диофант умел решать очень сложные уравнения, применял для неизвестных буквенные обозначения, ввел специальный символ для вычитания, использовал сокращения слов.
В начале нашей эры греческая наука и культура пришли в упадок. Но к тому времени больших успехов в развитии математики достигли индийские ученые. С V по XII в. ими было сделано много открытий, значительно обогатились начала алгебры. Культуру древних индийцев усвоили их соседи — ара-
2.41
бы, узбеки, персы, таджики и другие народы. И в IX—XV в. мировым центром наук становится Средняя Азия, подарившая миру много ученых-математиков. Их труды в дальнейшем оказали большое влияние на развитие науки в Европе.
В 826 г. арабский ученый а л ь-Х о р е з м й иаписал книгу «Китаб аль-джебр валь-мукабала», что означает «Книга о восстановлении и противопоставлении». Это был первый в мире учебник алгебры. С этого времени алгебра становится самостоятельной наукой. Само слово «алгебра» произошло от слова «аль-джебр» — восполнение: так аль-Хорезми называл перенос отрицательных слагаемых из одной части уравнения в другую с переменой знака. В дальнейшем большой вклад в развитие алгебры внесли европейские ученые Франсуа Виёт (1540—1603) и Рене Декарт, которые ввели в алгебру буквы и разработали правила действий с буквенными выражениями.
§ 9. КООРДИНАТЫ НА ПЛОСКОСТИ
43. Перпендикулярные прямые
Две прямые, образующие при пересечении прямые углы, называют перпендикулярными (рис. 95). Пишут: AB.LMN. Эту запись читают: «Прямая АВ перпендикулярна прямой MN*.
Если AB.LMN, то MN.LAB.
Ряс. 95
Для построения перпендикулярных прямых используют чертежный треугольник (рис. 96) или транспортир (рис. 97).
Ряс. 96
Ряс. 97
Отрезки (или лучи), лежащие на перпендикулярных прямых, называют перпендикулярными отрезками (или лучами) (рис. 98).
©Какие прямые называют перпендикулярными? Какие отрезки и какие лучи называют перпендикулярными? С помощью каких чертежных инструментов строят перпендикулярные прямые?
01336. Постройте с помощью транспортира две перпендикулярные прямые.
1337. Определите сначала на глаз, а потом проверьте с помощью чертежного треугольника, какие пары прямых на рисунке 99 перпендикулярны.
Ряс. 100
1338. Начертите прямую МР и отметьте точку А, не лежащую на этой прямой. Проведите с помощью чертежного треугольника через точку А прямую, перпендикулярную прямой МР. Сколько прямых, перпендикулярных МР, можно провести через точку А?
1339. Начертите в тетради прямую АВ и отметьте точку М так, как показано на рисунке 100. Проведите через точку М перпендикуляр к прямой АВ.
233
Ряс. 101
1340. Какие иа отрезков, изображенных на рисунке 101, перпендикулярны?
1341. Начертите прямой угол. Отметьте на сторонах угла по одной точке и проведите через них прямые, перпендикулярные сторонам угла. Отметьте точку пересечения этих прямых. Что за четырехугольник получился на чертеже?
01342. Найдите корень уравнения:
а) 2х-5 = х+2; в) 0,5у-0,6=^0,1у4-0,2;
б) тх+т=тх; г) tz=tz—г-
1343. Сумма трех последовательных целых чисел равна нулю. Какие это числа?
Л\
1344. Расставьте числа 1, —2, 3, —4, 5, —6, 7, —8, 9 в клетках квадрата (рис. 102) так, чтобы их произведения по всем горизонталям, вертикалям и диагоналям были положительны.
1345. Трое ребят нашли в лесу 200 грибов. Никита нашел 40% всех грибов, Олег числа грибов, которые нашел Ники-4
та, Дима нашел остальные грибы. Сколько грибов нашел Дима?
1346. От куска провода отрезали 50%, а потом еще 20%
остатка. После этого осталось 60 м провода. Сколько метров провода было в куске первоначально?
1347. Старинная задача. В клетке сидят фазаны и кролики. У них 19 голов и 62 ноги. Сколько фазанов н сколько кроликов в клетке?
1348. Найдите значение выражения:
2т4т-14:(-2)
’ (9-1,5): 25
2)
(8,5-4,7): 38
®1349. Перечертите рисунок 103 в тетрадь. Проведите через точки М и Р прямые, перпендикулярные прямой I.
234
а) б) б)
Рас. 103
1350. Начертите два перпендикулярных отрезка АВ и MN так, чтобы они: а) не пересекались; б) пересекались.
1351. Начертите два перпендикулярных луча так, чтобы они: а) не пересекались; б) пересекались; в) имели общее начало.
1352. Цена на яблоки была такой же, как и цена на груши. Через некоторое время цену на яблоки снизили на 20 к., а цену на груши — на 10 к. При этом в кг яблок стали стоить столько, сколько 5 кг груш. Какой была цена на яблоки первоначально?
1353. Выполните действия:
а) 12 4-7,8-(8,1-8,4);
б) -в-4,5-(5,2 — 10,6);
в) 18,2:( — 9,1)0,7- 3,4(-2,3): 17;
г) -16,4:(- 8,2) • (- 0,6) 4- 5,2 • 3,8:(-19).
44. Параллельные прямые л Две различные прямые могут либо пересекаться в одной точке, либо не пе-ресекаться. Две непересекающиеся пря-яме на плоскости называют парал- х. лелънылш. Пишут: АВЦЛ/N. Эту запись в
читают: «Прямая АВ параллельна пря- 'Ч N
мой MN». Если АВЦМЛГ, то МУЦАВ (рис. 104). Рже. 104
235
Рже. 107
Отрезки (лучи), лежащие на параллельных прямых, называют параллельными отрезками (лучами) (рис. 105, 106).
Прямые m и п на рисунке 107 перпендикулярны прямой I. Они параллельны друг другу.
Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.
Поэтому противоположные стороны любого прямоугольника параллельны (рис. 108). Они образуют прямые углы с двумя другими сторонами этого прямоугольника.
На рисунке 109 показано, как с помощью треугольника и линейки можно построить прямую п, параллельную прямой т.
Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
©Какие прямые называют параллельными? Какие отрезки называют параллельными? На плоскости проведена прямая и отмечена точка, не лежащая на этой прямой. Сколько прямых, параллельных данной, можно провести через эту точку? Могут ли пересечься две прямые, перпендикулярные одной и той же прямой?
236
1364. Начертите пять параллельных друг другу прямых.
1355. Начертите прямую I и отметьте точки М и К вне этой прямой. Проведите через точки М и К прямые, параллельные прямой I.
1866. Начертите треугольник и проведите через вершину прямую, параллельную противоположной
1357. Найдите с помощью линейки и треугольника все пары параллельных прямых, изображенных иа рисунке 110.
1358. Начертите прямую т и отметьте на ней три точки А, В и С. Через эти точки проведите прямые, перпендикулярные прямой т. Отметьте на этих прямых параллельные отрезки.
1359. Постройте угол АОВ, равный 35°. Отметьте точку М на стороне ОА и точку N на стороне ОВ. Проведите через точку М прямую, перпендикулярную стороне ОВ, а через точку N прямую, перпендикулярную стороне О А.
1360. Решите уравнение:
каждую стороне.
1861
1862.
1863.
1364.
число?
1366.
=х + 7; б) 2-x=f х-Ы; в) I г) f. Приведите подобные слагаемые: х—7 + 2х —5х + 1. Вычислите: 1^..
0,4 3 3 12
Что больше: а или 2а? а или —-?
5 7
— некоторого числа равны этого числа. Какое это • и
До конца суток осталось -д- того времени, которое прошло от начала суток. Который сейчас час?
Ш 1866. Из пятидесяти звеньев составлена цепь. Найдите длину этой цепи, если просвет каждого звена 16 мм, а тол-16
щина 4 мм (рис. 111).
Рис. ill
237
1867. Выполните действия:
1) 46,09:1,6-(2 -r-4-s—2,5.2 -М :4 ;
2) ( 6,05: JL _ 2,8 •-£-)• 0,8 +1,6 • 0,1875.
1368. Перечертите рисунок 112 в тетрадь. Проведите
через точку К прямую: а) параллельную прямой а; б) перпендикулярную прямой а.
1869. Начертите угол АВС, равный 75°. На стороне ВА отметьте точку М и проведите через нее две прямые, одна из которых параллельна, а другая перпендикулярна стороне ВС.
1370. В лаборатории стояли 25 столов с ящиками. В одних столах было по 3-ящика, а в других — по 4 ящика. Сколько было столов с тремя ящиками и сколько было столов с четырьмя ящиками, если общее число всех ящиков равно 91?
1371. По норме рабочий должен изготовить 72 детали, а он изготовил 90 деталей. На сколько процентов рабочий выполнил норму и на сколько процентов он перевыполнил норму?
1372. На — земельного участка разбит сад. сада зани-7 4
мают яблони. Какую площадь занимают яблони, если площадь земельного участка 1 га?
4
1373. Найдите значение выражения:
6>(7-8т)-2т-16;(т-т);
в) (204,42:40,5 - 3,2 • 1,2) • 6 7:2 —.
2 3
238
45. Координатная плоскость
Места в зрительном зале кинотеатра задают двумя числами: первым числом обозначают номер ряда, а вторым — номер кресла в этом ряду (см. рис. на форзаце). При этом места (3; 8) и (8; 3) различны: первое является креслом № 8в третьем ряду, а второе — креслом № 3 в восьмом ряду.
Подобным образом можно обозначить и положение точки на плоскости. Для этой цели на плоскости проводят две перпендикулярные координатные прямые х и у, которые пересекаются в начале отсчета — точке О (рис. 113). Эти прямые называют системой координат на плоскости, а точку О — началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Пусть М — некоторая точка плоскости. Проведем через нее прямую МА, перпендикулярную координатной прямой х, и прямую МВ, перпендикулярную координатной прямой у. Так как точка А имеет координату в, а точка В — координату — 5, то положение точки М определяется парой чисел (в; — б). Эту пару чисел называют координатами точки М. Число в называют абсциссой точки М, а число —б называют ординатой точки М. Координатную прямую х называют осью абсцисс, а координатную прямую у — осью ординат.
Точку М с абсциссой в и ординатой —б обозначают так: М(6; —б). При этом всегда на первом месте пишут абсциссу точки, а на втором — ее ординату. Если переставить коорди-
239
Каждой точке М на координатной плоскости соответствует пара чисел: ее абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами. На рисунке 114 показано, как попасть в точку С с координатами (— 4; —3): сначала надо пройти по оси х от начала отсчета влево на 4 единицы, а потом на 3 единицы вниз.
В географии положение точек на земной поверхности тоже определяют двумя числами — географическими координатами: широтой и долготой.
©Под каким углом пересекаются координатные прямые х и у, образующие систему координат на плоскости? Как называют каждую из этих прямых? Как называют точку пересечения зтих прямых? Как называют пару чисел, определяющих положение точки на плоскости? Как называют первое число? второе число? Расскажите, как найти абсциссу и ординату точки на координатной плоскости. Расскажите, как построить точку по ее координатам.
©1374. По рисунку 115 определите, сколько клеток надо пройти слева направо и сколько снизу вверх, чтобы попасть из точки О в точки М, К, Р и N.
1375. Шестиклассники участвовали в спортивной игре. Сначала звено было в точке О (рис. 116). Командир эвена получил приказ: «Идите на восток 5 км, а затем на север 4 км».
240
Назовите координаты точки В, в которую должно попасть это звено. Сформулируйте приказы для других звеньев, которые должны попасть из точки О в точки С, D, Е, К, М, N. Назовите координаты этих точек.
1376. Возьмите географическую карту и назовите широту и долготу городов: Москвы. Киева, Алма-Аты.
1377. Постройте координатные прямые х и у и отметьте точки А (2; 8), В(3; -4), С( — 4; 5), D(-3; -7), Е(0;5), М(0; -4), ЛГ(6; 0), Р(-7; 0).
1378. Найдите координаты точек А, В, С и D (рис. 117).
D Запись М (— 2; 7) читают так:
— точка эм с абсциссой минус два и ординатой семь — точка эм с координатами минус два и семь
— координаты точки эм — пара чисел минус два и семь
1379. У каких точек на координатной плоскости абсцисса равна нулю? У каких точек равна нулю ордината? Какая точка имеет координаты (0; 0)?
1380. Где расположены на координатной плоскости точки, абсцисса которых равна 4? А где расположены точки, ордината которых равна —1?
1381. Изобразите на координатной плоскости точки А (-2; -2), В(-1; -1), С(0; 0), D(l; 1), Е(2; 2). Проверьте с помощью линейки, лежат ли эти точки на одной прямой и лежит ли на этой прямой точка М ( — 5; 5).
241
1382. Постройте на координатной плоскости четырехугольник ABCD, если А(-10;-2), В(-2; -2), С(-2; -6), D(—10; —в). Является ли он прямоугольником? квадратом? Найдите периметр и площадь этого четырехугольника, если единичный отрезок равен 1 см. Проведите отрезки АС и BD и найдите координаты точки Е пересечения этих отрезков.
1383. Постройте треугольник ОВС, где О (0; 0), В (4; 6), С(1;5).
1384. На миллиметровой бумаге (рис. 118) отмечены точки А, В, С, D, Е, F, К и М. Найдите их координаты.
1385. В координатной плоскости проведена линия (рис. 119). Найдите на этой линии точку:
а) абсцисса которой равна 2; 1,7; —1,2;
б) ордината которой равна 1,8; 2,1; —1,6; —2,5; —3,2.
1888. Даны точки А (1; 3), В (-1; 4), С (7; -5), D (0; 6). Какие из этих точек расположены: а) выше оси абсцисс; б) левее оси ординат?
У; г
0 1||1|||1||1|1х
Рве. 119
242
1387. Вычислите устно:
а) —2,8 —3,2 б) 1,4 —8,2 в) 0,8-7 г) -10 + 1,8
: 1,2 : 3,4 -1,9 : 0,41
• 1,6 • 0,5 : 3 + 5,4
+ 8,5 +0,8 • 0,2 • 0,5
? ? ? ?
1388. Что больше: х или х2? х2 или х3?
Л\
м
1389. Найдите все дроби со знаменателем 15, которые больше 4- и меньше 1.
9
1390. Числа 90 и 100 разделили на одно и то же число.
В первом случае получили остаток 18, а во втором слу
чае — остаток 4. Найдите делитель.
1391. Из корзины взяли 6 яблок, затем треть остатка и еще 6 яблок. После этого в корзине осталась половина первоначального числа яблок. Сколько яблок было в корзине?
1392. Попробуйте найти простой способ для вычисления
значения выражения
1 । 1 । 1 I 1 I 1 I I 1 I 1 I 1 1-2 '2-3 ' 3-4 Г4-5 Т5-6 “ 6-7 ' 7-8 ' «-9 ' 910 ‘
1393. Начертите какой-нибудь треугольник АВС. Через вершину С проведите прямую I, параллельную стороне АВ, и прямую т, перпендикулярную стороне АВ.
1394. Найдите длину окружности, радиус которой 7 см, 0,7 см, 0,14 см, приняв л аг-у-.
1395. Найдите радиус окружности, длина которой 6,28 мм, 3,14 см, 0,0628 м, приняв л«3,14.
1396. Вычислите:
( —0,4)2; ( —0,1)3; (0,6)2; (0,2)3; 4-+4,2; 2^-+3,75. 5 4
1397. Найдите объем и площадь поверхности куба, ребро которого равно: а) 4 см; б) 0,2 м.
1398. Решите уравнение:
1) 0,8(9 + 2х)=0,5(2 — Зх); 2) 0,5-(х + 3) = 0,8-(10 — х).
1399. Решите задачу:
1) На заводе производится смена оборудования. После того как 51 станок заменили новыми, осталось заменить еще 83% станков. Сколько всего станков на заводе надо заменить новыми?
243
2) Купили пачку бумаги. После того как израсходовали 30 листов, осталось 85% пачки. Сколько листов бумаги было в пачке?
1400. Решите уравнение:
1) (13,4 - у) • 4,3 - 20,05 = 78,05 + 6,7у;
2) (16,2 - х)- 3,2 - 50,08 = — 8,12 - 5,1х.
®1401. Постройте ломаные линии ABCDE и MNK по координатам точек А (—6; 2), В ( — 4; 6), С (1; 1), D (2; — 5), В (8; -1) и М(-5; -5), N(-l; 7), *(8; 4). Найдите координаты точек пересечения ломаных ABCDE и MNK.
1402. Постройте четырехугольник ABCDE по координатам его вершин А( — 8; 6), В (6; 5), С(1; —3), D ( — 7; 1). Найдите координаты точки пересечения отрезков АС и BD.
1403. Отметьте на координатной плоскости точки М (0; 5), N (8; 1), С (2; 2), D ( —6; —2). Найдите координаты точки пересечения прямых MN и CD. На какой из этих прямых лежит точка К (0; 1)?
1404. Постройте треугольник АВК по координатам его вершин А ( — 2; —2), В(1; 5), К (6; —2). Найдите координаты точки пересечения стороны АК с осью ординат.
1406. Решите уравнение:
а) - 8,7*(2,5х — 7,6)= - 3,66 +2,1х;
б) 0,4(0 — 0,6)=0,5-(у-0,8)+0,08.
1406. Отметьте точку М и проведите через нее две прямые т и I так, чтобы они образовали угол, равный 62s.
1407. Постройте угол COD, равный 50s. Через точку М, лежащую на стороне OD, проведите прямую т, параллельную стороне ОС, а через точку К, лежащую на стороне ОС, проведите прямую п, параллельную стороне OD. Измерьте транспортиром углы, образовавшиеся при пересечении прямых тип.
1408. Найдите значение выражения:
а) -3,8-(4-4,9)+13,4 (3-2,8);
б) —3,636:0,6 + 2,6-(5 —1,1).
46. Столбчатые диаграммы
В селе 90 домов. Из них 15 под железной крышей, а 45 под шиферной и 30 под черепичной. Число домов каждого вида изображено на круговой диаграмме (рис. 120). По-другому
244
Рк. 130
эти числа можно изобразить с помощью столбчатой диаграммы (рис. 121). Для этого надо нарисовать три столбика, высота которых соответствует количеству домов каждого вида. Пусть высота первого столбика 15 мм, второго 45 мм, третьего 30 мм. Если бы каждый дом изображался столбиком в 2 мм, то высоты всех трех столбиков на рисунке увеличились бы в 2 раза.
© 1409. В селе 22 двухэтажных дома, а остальные 68 — одноэтажные. Постройте круговую и столбчатую диаграммы (один дом — 2 мм).
1410. Постройте столбчатую диаграмму, показывающую массы первых десяти космических кораблей серии «Венера».
Назвал не и год запуска Венера-1 1931 Венера-2 1966 Венера-8 1966 Венера-4 1967 Венера-б 1969
Масса, кг 648.6 968 960 1106 1180
Название и год запуска Венера-6 1969 Веиера-7 1970 Венера-8 1972 Венера-9 1976 Веавра-10 1976
Масса, кг 1180 1180 1184 4986 6033
1411. Постройте столбчатую диаграмму по следующим данным:
а) наибольшая глубина озера Байкал 1620 м, Онежского озера 127 м, озера Иссык-Куль 668 м, Ладожского озера 225 м;
б) расстояние до Солнца от планеты Меркурий « 58 млн. км, от
245
планеты Венера «108 млн. км, от планеты Земля ж 150 млн. км, от планеты Марс «228 млн. км.
1412. Отметьте на координатной плоскости точки А ( — 2; 4), В (— 4; —5), С (8; 0),D (—4; 4). Найдите координаты точки пересечения прямых АВ и CD.
1413. На координатной плоскости отмечены точки А (2; 3),
В( —3;4), С( —5;6), D (3; -4), Е(0; -5), К(0;3), N(-2;0), М (5; 0). Какие из этих точек расположены:
а) выше оси абсцисс;
б) ниже оси абсцисс;
в) правее оси ординат;
1414. Вычислите:
г) левее оси ординат: д) на оси абсцисс;
е) на оси ординат?
(—+—Y16; 2:— 1—; 12— :2-—6; —• —+—.
\ 8 ' 4 / ’ 3 2’ 2 2 *47'47
1415. Раскройте скобки: —(4-|-12х); (4—
1416. Из делителя вычли — его. Как изменится частное?
5
1417. Какой цифрой оканчивается разность
1.2.3- 4-.... 26-27 —1-3-5-7 ..... 25-27?
па 1418. Запишите в виде двойного неравенства условия, которым подчиняются:
а) абсциссы любой точки фигуры;
б) ординаты любой точки фигуры (рис. 122).
1419. -|- см3 вещества имеют массу г. Найдите массу 1 см3 этого вещества. Найдите объем этого вещества, если его масса равна 1 г.
1420. Найдите значение выражения:
1) (1,75--|—1,75:1У4,5 —4,5;
2) (2,75-2,75:4-М-2,7-2,7.
X 11 о /
®1421. Постройте столбчатую диаграмму по следующим данным:
а) площадь КНР равна 9,6 млн. км2, площадь Индии - 3,3 млн. км2 и площадь США - 9,4 млн. км2;
б) длина Днепра 2,2 тыс. км, Дона 1,9 тыс. км, Днестра 1,4 тыс. км, Печоры 1,8 тыс. км, Волги 3,5 тыс. км.
246
Рис. 122
а)
6)
1422. В одной пачке было в 2,5 раза больше тетрадей, чем в другой. Когда из второй пачки переложили в первую 5 тетрадей, то во второй стало в 3 раза меньше тетрадей, чем в первой. Сколько тетрадей было в каждой пачке первоначально?
1423. Для оклейки стен обоями на 1 м2 требуется: обоев 0,25 рулона, крахмала 0,09 кг, клея 0,01 кг, газетной бумаги 0,07 кг. Сколько материалов потребуется для оклейки обоями комнаты, если площадь всех ее стен вместе с окнами и дверями 35,3 м2, а площадь окон и дверей равна 10,2 м2? Ответ округлите с избытком до десятых долей килограммов и до целых рулонов.
1424. Найдите значение выражения:
а) (1,6-1-154,66:70,3): 1,9-0,3; в) (о,3-^)-2-5—1-:1,4;
б) (89,54:2,2 + 3,3):1,1 + 0,9; г) (1,08-^)- 0,25:4-.
\ 26 /7 3
Заключение
Математика — самая древняя из наук, она была и остается необходимой людям. Слово «математика» греческого происхождения. Оно означает «наука», «размышление». В древности часто полученные знания, открытия старались сохранить в тайне. Например, в школе Пифагора запрещено было делиться своими знаниями с непифагорейцами. За нарушение этого правила один из учеников, требовавший свободного обмена знаниями,— Гиппас был изгнан из школы. Сторонников Гип-паса стали называть математиками, т. е. приверженцами науки.
Все без исключения начинают изучать основы математики уже с первых классов школы, потому что эта наука нужна всем, особенно сейчас, когда математика проникла во все отрасли знаний — физику и химию, науки о языке и медицину, астрономию и биологию и т. д. Математики учат вычислительные машины сочинять стихи и музыку, измерять размеры атомов и проектировать плотины электростанций.
Математика необходима в любой профессии, какую бы вы ни выбрали для себя. Но кроме того, вы могли заметить: это и очень интересная и увлекательная наука. Любите ее. Если вы и не станете математиками, знания пригодятся вам и на Земле, и в космосе.
С седьмого класса вы начинаете более глубоко изучать два раздела — два предмета: алгебру и геометрию. Желаем вам успехов и радости открытий в необозримом море — математике!
ОТВЕТЫ
Глава I
23. 1) 121 кг; 2) 15,5 т. 27. 85,8 га. 28. а) 19,16; 6) 798; в) 33,16; г) 1530. 50. а) 1,2; 6) 1,3; в) 1,5; г) 1,5. 51. 1) 8; 2) 0,8. 57. а) 11; 6) 1196; в) 16 552; г) 16 313. 70. 1) 127,75; 2) 16,5; 3) 2,4; 4) 6,8. 80. 2,91. 86. а) 3; 6) 0,8; в) 1,2; г) 0,2. 87. 9. 113. 270 дм2. 114. 0,187. 131. 1) 10,96 ц; 9,44 ц; 2) 30,7 га; 33,5 га. 132. 1) 3,15; 2) 0,086; 3) 5,8; 4) 11,7. 136. 5,6 га; 6,72 га. 137. 18 р. 138. а) 90,55; 6) 36,4. 156. 1) 45°; 135°; 2) 36°; 144°. 157. 1) 164 м; 2) 1600; 1400; 400. 166. 420. 170. а) 75; 6) 46. 101. 1) 20,4 т; 2) 3 т. 105. 12; 15; 24. 106. 83,6 кг; 508,3 кг; 1327 кг. 107. а) 12,1; 6) 1,43; в) 32,43; г) 105,94. 201. а) 39,6; 6) 36,11. 223. 1) 8,5 ч; 2) 9,7 ч. 225. 2,84. 226. а) 24,24; 6) 38,20. 231. а) 10,6; 6) 1,5. 248. На 12%. 254. 1960. 256. 1) 21 ч; 2) 3 ч. 261. 101,4 км. 262.1,4 р. 263. а) 24,94; 6) 19,6. 280. 2 м/с. 281. 72 000 км. 282. 1) А; 2) А. 284.1) 101,05; 2) 181,99. 289. 3,2 км/ч; 12,8 км/ч. 290. 55 км/ч, 50 км. 291. а) 92,486; 6) 92,816. 343. 1) Через 3,5 ч; 2) через 5 ч. 344. 1) 0,1 км/мин; 2) 10 км/ч. 345. 1) 7,05; 2) 6,05. 352. А м. 353.. 1А ч.
354. 43 мин. 355. а) А; 6) А ; в) А ; г) А. 356. а) 0,3; 6) А. 357. 10 км.
358. 40 км. 350. 40 км/ч. 360. а) 26,468; 6) 3,524; в) 0,187; г) 34,735. 301. На 72,8%. 307.1,067. 398. 1) 11,8 кг, 2) 8,4 кг. 399. 1) 149 763; 2) 187 521.
403. а) 1 у; 6) 5; в) 2±; г) 6. 404. А. 405. А. 406. 44 А м.
407. 6 ч 29 мин. 408. а) 1,6; 6) 6,4. 409. 3,8 км/ч. 410. 9 кг; 6 кг. 411. а) 30,7; 6) 8,94. 412. а) 10; 6) 1,1; в) 1,2; г) 0,7. 448. 7 т. 454. 1) А : 2) А .
ч 10 24
463. а) 4 ; 6) ; в) 2 А; г) 6; д) 0,5; е) А ; ж) А . з) А. 466. 35-7Г;
31,5 м; 14 м; 0. 467. а) 0,7; 6) 4. 468. 2,917. 499. а) бА; б) 5 А 502. 56 км/ч. 503. 2 дм. 504. 1) 15 и 4; 2) 21 и 15. 505. 1) 185,85; 2) 268,92; 3) 824,4; 4) 602,51. 506. 1) 17,6; 2) 4,6. 507. На 48 кг. 508. 32 кг. 509. 648 мэ. 511. 566,5 р. 512. 18 т. 513 200 га. 514. 252 т. 515. А ; 140 р. 516. 46%. 517. 17 кг; 34 кг; 25 кг. 518. а) 2,646; 6) 5; в) 145,516; г) 315 451. 547. 45%; 15%. 548. 141 кг. 549. а) А; 6) 1 А ; в) 47 А . г) 18|; д) g; е) g.
249
2 1
550. 1) 47,94; 2) 1,68. 552. a) 7 4 ; б) 27; в) 63; г) 43; д) 10; е) 4 • 554. 27 км. о 2
666. 27 у кг. 666. у ч. 667. 80 к. 668. у с; 70 т; 49 т. 669. 0,46m; 2639,2 м; 10120 м. 560. а) 2,25; 6) 15,01. 672. 12 кы. 676. 2,1; 3; 4,2. 674. 1) 6,626; 2) 2,637. 677. 30 кг. 678. 2; 3;'2,4; 3,6. 676. а) 203,07; 6) 666,3.
2 7
616. 1) 46; 2) 64. 616. 1) 3; 2) 3: 3) 0.8; 4) 0.8. 618. а) 12; 6) 14; а) 2 ; г) .
3 10
3 3 1
610. а) 1 — ; 6) 3; а) у ; г) 10; д) 1 — ; е) 3. 620. а) 13; 6) 2. 624. 15 л, 20 л. 625. 72; 84. 626. 126 р., 210 р. 627. 28 км/ч; 32 км/ч. 628. 54 км/ч; 90 км/ч. 630. а) 0,7178; 6) 5; в) 0,3589; г) 10. 662. 1) 1-f-; 2) Д ; 3) 4-; 4) 4-. о 13 о б
668. 1) 49,8; 2) 56,96. 670. 26 км; 8 кы. 671. 64,4 кг. 672. 760 ы. 673. 400. 674. 88. 676. а) 0,224; 6) 83,244; в) 1,08; г) 37,4. 697. 21 а. 608. 28 р. 699. 1) 192; 2) 2128 т. 700. а) 11; 6) 1,66; в) 3,6; г) 7,7; д) 6,3; е) 8; ж) 1; з) 16. 701. 96 к. 702. 3 ч. 703. 8,2 г. 704. 90 м9. 782. 9 р. 788. 6,4 кг. 734. 1) 136 сы3; 2) 210 сы3. 739. 4%; 6%. 740. 18,76%. 741. 76^-%; 80%. 743. а) 9; 6) 30;
1ft 1
в) 0,106; г) 3,86. 761. а) 2 у ; 6) •£ ; в) 2; г) 1 у. 768. 45 км/ч. 764. 1,4. 7 17 4
765. а) 11,04; 6) 280. 787. а) 10,6; 6) 2; а) 1,44; г) 0,4. 792. а) 1 у ; 6) 2. 798. 1) 92%; 2) 94%. 794. 1) 4; 2) 7. 795. 36 кг. 796. 3 дня. 797. 8,6 кг. 798. 7,1 т. 799. 60 кг. 800. 17,6%. 801. 37,6 кг. 802. 6,25 кг. 808. а) 95,7; 6) 101,3. 820. 16 мни. 822. 1) 6,4 и 1,8; 2) 2 и 0,5. 828. 1) 2,66;
2
2) 2,25. 829. 14,4 см. 980. а) 2; б) 6 . 848. 1) 0,512 кг; 2) 4,2 кг. 849. 1) 10,5;
3
2) 4-; 3) 32,541; 4) 21,59; б) 18; 6) 128. 853. -67,8 кы/ч. 856. 14 ч. 866. 4 л. О
867. а)|; 6) 1в) 1|; г) 11.868. 1) 24; 64; 2) 14; 12. 869. 1) у; 2) у. 871. 2,6 дм. 872. «118 см9; =»28,3 см9. 878. 6,4 т; 4,6 т. 874. а) 10; 6) 20.
Глава II
901.1) 6 к; 2) 2 к; 3) 160; 4) 106.907. Четыре по 44 м и 68 ы. 908. 48.909.140 кг. 925. 1) 18 тыс.; 2) 168 т. 980. 90 кг. 981. 1748 ц. 982. а) 3; 6) 2. 983. а) 0,05; 6) 3,86. 956. 77 км/ч. 966. 24,6 ц. 957. 308. 976. 1) 10,6; 2) 4,08. 977. 1) 50%, 40%, 10%; 2) 20%, 65%, 16%. 978. 1) 68,8; 2) 78,7. 982. 30%, 50%, 20%. 983. 2 у . 984. 0,4. 997. 1000 т. 998. 13,16 дм9.1002. 500.1003. а) 1,66; 6) 44,1. 1020. 1,3122 м3. 1021. 1) 2146,37; 2) 2656,66. 1024. В шестых классах на 1 человека. 1026. 5670 см3. 1026. а) 46,108; 6) 3642,06. 1039. 1) 1804,5; 2) 2624,3.
О
1042. 8,2 г. 1044. а) 2,88; б) 3,4; а) 1068. 1) 350 км; 2) 190 р. 1064. 1) 1; 3
о
2) 0,1. 1068. 35,4 ма. 1060. 15; 18; 9. 1070. 14 -у. 1090. 40 кг. 200 кг, 120 кг.
250
1091. 1) 12 кг. 7 кг. 2 кг; 2) 280 га, 246 га. 36 га. 1092. 1) 16,99; 2) 32,02. 1099. 42; 20; 8. 1100. 266; 860. 1101. 80; 84; 138. 1126. 1) 4-; 2) -i-.
о 0 2
1129. а) 270; б) -20,74; в) —9,46; д) у ; е) 2; а) —24. 1180. 28,8 т. 1181. 64. 1182. 18,48; 8,18. 1160. а) —1; 6) 0. 1155. а) -6,26; 6) —2,03. 1158. а) —10; 6) 10 000; а) -4; г) -402; д) —40; е) 30,626; ж) -8,6; а) . 1159. 60 км/ч. 1160. 2. 1161. а) -10,6; 6) -2,6. 1179. 1) 9,2; 2) 9,2; 3) 3,08; 4) 3,466; 6) —у ; 6) —. 1183. 3,2 км/ч; 4,8 км/ч. 1184. а) —0,2; 6) 2,64. 1206. 1) 13,6 км/ч; 48,6 км/ч; 2) 46 км/ч; 72 км/ч. 1209. 1) 0,2; 2) 0,2; 3) —6,6; 4) 12. 1259. а) -0,06; 6) ; в) -у ; г) 20; д) -37; е) —7.
1214. На 128%, на 28%. 1215. 1,6 л. 1216. 6 км/ч. 1217. а) -44,99; 6) —8,97; а) 0,87. 1286. 1) 8; 2) 3,9. 1237. 1) 7,6; 2) 0,6. 1240. а) 7; 6) — 1;
11 1 б 2 13
а) -90; г) --; д) -у. 1241. а) -2 у; 6) Г) -1^.
Z о о О О
1242. а) 600; на 11 у%; 6) 28,7 кг; в) 1046 кг. 1243. а) 4,6; 6) 6. 1258. 1) 7,64; 2) -9,7. 1260. а) -391,68; 6) -321,11; в) -3,82; г) -6,31. 1261. аХ1,75; 6) 0,6.1262. 20 т. 1263.12.1264. 374,4 га. 1285. 1) 200 га; 2) 6 м3.1286.1) 34,8; 2) -30,66.1292. а) 16; 6) 43; в) - 6; г) -6 у . 1293. 7 р; 26 р. 1294. 40; 36; 43. 1295. 1:30 000. 1296. 26 см. 1297. 18,9 км. 1323. 1) 32,086; 2) 83,276. 1824. 28. 1327. 162; 36. 1328. 260 г. 1829. 60 к.; 70 к.; 90 к. 1830. 60; 20.
3
1331. 376 л; 360 л. 1332. а) 2,5; 6) 3.1333. 132 г. 1334. На 16,1 км/ч. 1335. — ;
20 о
1345. 100. 1346. 160 м. 1347. 7; 12. 1348. 1) 10; 2) 10. 1352. 70 к.
1353. а) 9,66; 6) 18,3; в) -0,94; г) -2,24. 1367. 1) 29,06; 2) 60,3. 1370. 9; о 1
16. 1371. На 126%, на 26%. 1372. га. 1373. а) 1 ; 6) 19; а) 10,8.
1891. 60. 1398. 1) -2; 2) 6. 1399. 1) 300; 2) 200. 1400. 1) -3,68; 2) -6,2. 1405. а) 2,8; 6) 0,8.1408. а) 6,1; 6) 4,08. 1422. 100; 40. 14ЙЗ. 7 рулонов; 2,3 кг; 0,3 кг; 1,8 кг. 1424. а) 1,7; 6) 40,9; а) у ; г) 1.
Приложения
L ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсцисса точки 239 Алгебра 231 Конус 167 Координата точки на плоскости 239 прямой 143
В Координатная плоскость 239 — прямая 143
Вычгашм дробей 46 — отрицательных и положительных Коэффициент 217 Кратное 4
чисел 182 — сметанный чисел 67 Л
Г Линейное уравнение 226
Граф 207 М
Д Масштаб 128 Модуль числа 166
Деление дробей 92 — отрицательных и положительных чисел 193 — смешанных чисел 92 Делитель 4 Диаграмма круговая 244 — столбчатая 246 Длина окружности 132 Дополнительный множитель 41 Дробное жсраженпе 104 Дробь несократимая 36 — периодическая 200 Н Наибольший общий делитель 22 Наименьшее общее кратное 26 Нахождение дроби числа 74 — нескольких процентов числа 76, 77 —отношения 112, 116 — числа по его дроби 99 процентам 99, 101 Неравенство нестрогое 96
3 — строгое 96 О
Знаменатель общий 41 п»мчтьтий 41 Золотое сечение 140 Ордината точки 239 Основное свойство дроби 32
252
---- пропорция 118
Ось абсцисс 239 — ординат 239 Отношение 111 Отношения взаимно обратные 112
П
Параллельные лучи 236 — отрезки 236 — прямые 235
Перпендикулярные лучи 233
— отрезки 233 — прямые 232 Пирамида 82 Площадь круга 133 Подобные слагаемые 220 Приведение дроби к новому знаменателю 40
Призма ПО
Прививки делимости на 2,6 и 10 в -------3,9 12
Пропорциональная зависимость прямая 122 ----обратная 122 Пропорция 118
—, крайние члены 118
—, средние члены 118
Р
Разложение на множители 15 ----простые множители 18 Раскрытие скобок 211, 220
Решение уравнений 225
С
Свойства действий с рациональными числами 203, 204
Система координат на плоскости 239
Сложение дробей 46 — отрицательных и положительных чисел 169, 173, 177
— подобных слагаемых 220 — смешанных чисел 56 Сокращение дроби 36 Сравнение дробей 46 — отрицательных и положительных чисел 159
Сфера 137
У
Умножение дробей 66
— отрицательных и положительных чисел 188
— смешанных чисел 66, 82
ц
Цилиндр 148
Цифры нечетные 9 — четные 9
Ч
Числа близнецы 29 — взаимно-обратные 89 — взаимно-простые 22 — дружественные 52 — нечетные 9 — отрицательные 142 — положительные 142 — простые 15 — противоположные 150 — рациональные 198 — совершенные 30 — составные 15 — фигурные 39 — целые 150 — четные 9
Ш
Шар 137
Шара диаметр 137
— радиус 137
II. СКЛОНЕНИЕ ЧИСЛИТЕЛЬНЫХ
Количественные числительные по типу
склонения можно разделить на пять групп:
1-4 5—20, 30 50—80 40, 90, 100
И. четыре шестнадцать восемьдесят сорок сто
Р. четырех шестнадцати восьмидесяти сорока ста
Д. четырем шестнадцати восьмидесяти сорока ста
В. как И. или Р. шестнадцать восемьдесят сорок сто
Т. четырьмя шестнадцатью восьмьюдесятью сорока ста
П. о четырех о шестнадцати о восьмидесяти о сорока о ста
В составных количественных 200—900 числительных склоняются
все части:
И. триста девятьсот пятьсот семьдесят три
Р. трехсот девятисот пятисот семидесяти трех
Д. тремстам девятистам пятистам семидесяти трем /
В. триста девятьсот пятьсот семьдесят три
Т. тремястами девятьюстами пятьюстами семьюдесятью тремя
П. о трехстах о девятистах о пятистах семидесяти трех
Порядковые числительные
В составных порядковых числительных склоняется только последнее слово:
И. двадцать пятый Р. двадцать пятого Д. двадцать пятому В. как И. или Р. Т. двадцать пятым П. о двадцать пятом
четыреста тридцать шестой четыреста тридцать шестого четыреста тридцать - шестому как И. или Р. четыреста тридцать шестым о четыреста тридцать шестом
Дробные числительные
В состав дробных числительных аходят количественные и порядковые числительные. При склонении дробных
числительных изменяются все их части:
И. две целых тридцать семь сто семьдесят девятых Р. двух целых тридцати семи сто семьдесят девятых Д. двум целым тридцати семи сто семьдесят девятым В. как И.
Т. двумя целыми тридцатью семью сто семьдесят девятыми П. о двух целых тридцати семи сто семьдесят девятых
2Л
179
И. ноль (нуль) целых двести девяносто семь тысячных 0,297
Р. нуля целых двухсот девяноста семи тысячных
Д. нулю целых двумстам девяноста семи тысячным В. как И.
Т. нулем целых двумястами девяноста семью тысячными
П. о нуле целых двухстах девяноста семи тысячных
ОГЛАВЛЕНИЕ
Дорогие ребята! ................. 3
Глава I. Обыкновенные дроби.
§ 1. Делимость чисел. 1. Делители и кратные..................................... 4
2. Признаки делимости на 10, на 5 и на 2.................. 8
3. Признаки делимости на 9 н на 3....................... 12
4. Простые н составные числа..............................16
5. Разложение на простые множители .......................18
в. Наибольший общий делитель. Взаимно простые числа .... 21
7. Наименьшее общее кратное...............................26
S 2. Сложение и вычитание дробей с разными знаменателями. 8. Основное свойство дроби................................32
9. Сокращение дробей..................................... Зв
10. Приведение дробей к общему знаменателю................40
11. Сравнение, сложение и вычитание дробей с разными знаменателями 46
12. Сложение и вычитание смешанных чисел..................55
§ 3. Умножение и деление обыкновенных дробей. 13. Умножение дробей......................................65
14. Нахождение дроби от числа.............................74
15. Применение распределительного свойства умножения......82
16. Взаимно обратные числа................................88
17. Деление...............................................91
18. Нахождение числа по его дроби.........................99
19. Дробные выражения....................................104
! 4. Отношения и пропорции. 20. Отношения............................................111
21. Пропорция........................................ . 118
22. Прямая и обратная пропорциональные зависимости.......122
23. Масштаб..............................................128
24. Длина окружности и площадь круга.....................132
25. Шар..................................................137
Глава II. Рациоыальиые числа.
S 5. Положительные и отрицательные числа.
26. Координаты на прямой......................................142
27. Противоположные числа.....................................150
28. Модуль числа..............................................155
29. Сравнение чисел...........................................158
30. Изменение величин.........................................163
S в. Сложение и вычитание положительных и отрицательных чисел. 31. Сложение чисел с помощью координатной прямой..............168
25fi
82. Сложение отрицательных чисел..............................178
33. Сложение чисел с разными знаками..........................176
84. Вычитание.................................................182
S 7. Умножение и деление положительных и отрицательных чисел. 86. Умножение ................................................187
36. Деление...................................................103
37. Рациональные числа ...................................... 108
38. Свойства действий с рациональными числами.................208
§ 8. Решение уравнений.
89. Раскрытие скобок........................................ 211
40. Коэффициент............................................. 216
41. Подобные слагаемые........................................210
42. Решение уравнений.........................................226
9 9. Координаты на плоскости.
48. Перпендикулярные прямые...................................282
44. Параллельные прямые..................................... 236
46. Координатная плоскость.................................. 280
46. Столбчатые диаграммы......................................244
Заключение................................................... 248
Ответы........................................................240
Приложения....................................................262
I. Предметный указатель........................................ —
II. Склонение числительных....................................264
Учебное издание
п-т—Наум Яковлевич Чгамимв * пгт! пи Семенович Шварцбурд Семен Исаакович Жохов Владимир Иванович
МАТЕМАТИКА
Учебник для 6 класса средней школы
Зав. редакцией Т. А. Бурмистрова Редактор Н. И. Никитина Младшие редакторы О. В. Агапова, Е. В. Казакова Художники В. В. Костин, О. Л. Корнилова Художественный редактор Ю. В. Пахомов Технический редактор Н. А. Киселёва Редактор карт М. Г. Дзидзигури Корректоры И. А. Корогодина, Г. И. Мосякина
Подписано к печати 29.07.94. Формат 60 х 88 Х/1б. Гарнитура школьная. Печать офсетная. Усл. псч. л. 16. Тираж 5000 экз. Заказ № 607.
Ордена Трудового Красного Знамени издательство «Просвещение» Комитета Российской Федерации по печати. 127521, Москва, 3-й проезд Марьиной рощи, 41.
Саратовский ордена Трудового Красного Знамени полиграфический комбинат Комитета Российской Федерации по печати. 410004, Саратов, ул. Чернышевского, 59.
ТАБЛИЦА ПРОСТЫХ ЧИСЕЛ (до 997)
юлка к
СССР
у
Библиотека бесплатных учебников на сайте:
ussrvopros.ru
(перейти
каталогу